├── .gitignore
├── LICENSE
├── README.md
├── SUMMARY.md
├── Source_Code
├── haqqinda
│ └── conferences_attended.png
├── python_kodlar
│ ├── __init__.py
│ ├── fesil11
│ │ └── fesil11_binary_search_tree.py
│ ├── fesil12
│ │ └── fesil12_bubble_sort.py
│ ├── fesil2
│ │ ├── fesil2_2.12_bit_strings_itertools.py
│ │ ├── fesil2_2.12_bit_strings_recursion.py
│ │ ├── fesil2_2.5_factorial_pdb.py
│ │ ├── fesil2_2.5_pdb.py
│ │ ├── fesil2_2.5_pycallgraph.py
│ │ ├── fesil2_2.9_hanoi_qulleleri.py
│ │ └── fesil2_2.9_is_array_sorted.py
│ ├── fesil3
│ │ └── fesil3_3_6_linked_lists.py
│ ├── fesil4
│ │ └── fesil4_doubly_linked_lists.py
│ ├── fesil5
│ │ └── fesil5_circular_linked_lists.py
│ ├── fesil6
│ │ ├── __init__.py
│ │ ├── fesil6_dynamic_array_stack.py
│ │ ├── fesil6_linked_list_stack.py
│ │ └── fesil6_list_stack.py
│ ├── fesil7
│ │ ├── fesil7_circular_array_queue.py
│ │ ├── fesil7_dynamic_circular_queue.py
│ │ └── fesil7_linked_list_queue.py
│ ├── fesil8
│ │ ├── __init__.py
│ │ └── fesil8_binary_tree_node.py
│ └── fesil9
│ │ ├── __init__.py
│ │ └── fesil9_problems_solutions.py
└── resources
│ ├── Misc_files
│ └── AzePUG_Algo_Data_Structures_book.png
│ ├── fesil11
│ ├── fesil11_delete_node_with_2_childs_resized.png
│ ├── fesil11_deleting_leaf_node_bst_resized.png
│ ├── fesil11_deleting_node_with_one_child_resized.png
│ └── fesil11_inserting_bst.png
│ ├── fesil12
│ ├── fesil12_sum_of_n_1.png
│ └── fesil12_sum_of_n_numbers.png
│ ├── fesil2
│ └── fesil2_2.5.png
│ ├── fesil3
│ ├── delete_first_node_singly_linked_list.png
│ ├── delete_from_end_singly_list_1.png
│ ├── delete_from_end_singly_list_2.png
│ ├── delete_from_end_singly_list_3.png
│ ├── delete_intermediate_node_singly_linked_list_1.png
│ ├── delete_intermediate_node_singly_linked_list_2.png
│ ├── delete_last_node_singly_list_result.png
│ ├── deleting_first_node_singly_linked_list_1.png
│ ├── deleting_first_node_singly_linked_list_2.png
│ ├── diff_python_c++.png
│ ├── insert_at_beginning_linked_list_1.png
│ ├── insert_at_beginning_linked_list_2.png
│ ├── insert_at_position_singly_linked_list_visualize.png
│ ├── insert_at_the_end_singly_linked_list_1.png
│ ├── insert_at_the_end_singly_linked_list_2.png
│ ├── insert_into_middle_singly_linked_list_1.png
│ ├── insert_into_middle_singly_linked_list_2.png
│ ├── linked_list_basic_show.png
│ ├── linked_list_insert_visual.png
│ └── singly_linked_list_insert_at_end.png
│ ├── fesil4
│ ├── doubly_linked_list_delete_first_node_1.png
│ ├── doubly_linked_list_delete_first_node_2.png
│ ├── doubly_linked_list_insert_at_beginning_1.png
│ ├── doubly_linked_list_insert_at_beginning_2.png
│ ├── doubly_linked_list_insert_at_end_1.png
│ ├── doubly_linked_list_insert_at_end_2.png
│ ├── doubly_linked_list_insert_at_end_3.png
│ ├── doubly_linked_list_insert_at_middle_1.png
│ ├── doubly_linked_list_insert_at_middle_2.png
│ └── doubly_linked_list_visualization_1.png
│ ├── fesil5
│ ├── circular_linked_list_1.png
│ ├── circular_linked_list_2.png
│ ├── circular_linked_list_3.png
│ ├── circular_linked_list_4.png
│ ├── circular_linked_list_5.png
│ └── circular_linked_list_6.png
│ ├── fesil7
│ ├── fesil7_array_queue.jpg
│ ├── fesil7_array_queue_2.jpg
│ ├── fesil7_circular-increment.jpg
│ └── fesil7_circular_queue_program.jpg
│ └── fesil8
│ ├── fesil8_binary_tree_graphic.png
│ ├── fesil8_data_binary_tree.png
│ ├── fesil8_skew_tree.png
│ └── fesil8_tree_data_structure.png
└── book
├── 0.1.Terminlər.md
├── 0.Haqqında.md
├── 1.Giriş.md
├── 10.Düzülü_İkili_Ağaclar_Threaded_Binary_Tree_Traversals.md
├── 11.İkili_Axtarış_Ağacları_Binary_Search_Trees.md
├── 12.Sıralama_Sorting.md
├── 2.Recursion_and_Backtracking.md
├── 3.Birtərəfli_Əlaqəli_listlər_singly_linked_lists.md
├── 4.İkitərəfli_Əlaqəli_listlər_doubly_linked_lists.md
├── 5.Dövri_Əlaqəli_listlər_circular_linked_lists.md
├── 6.Stack_Yığın.md
├── 7.Növbələr_Queues.md
├── 8.Ağaclar_Trees.md
└── 9.İkili_Ağaclar_Tapşırıqlar_və_Həllər.md
/.gitignore:
--------------------------------------------------------------------------------
1 | # Byte-compiled / optimized / DLL files
2 | __pycache__/
3 | *.py[cod]
4 | *$py.class
5 |
6 | # C extensions
7 | *.so
8 |
9 | # Distribution / packaging
10 | .vscode
11 | .Python
12 | env/
13 | build/
14 | develop-eggs/
15 | dist/
16 | downloads/
17 | eggs/
18 | .eggs/
19 | lib/
20 | lib64/
21 | parts/
22 | sdist/
23 | var/
24 | wheels/
25 | *.egg-info/
26 | .installed.cfg
27 | *.egg
28 |
29 | # PyInstaller
30 | # Usually these files are written by a python script from a template
31 | # before PyInstaller builds the exe, so as to inject date/other infos into it.
32 | *.manifest
33 | *.spec
34 |
35 | # Installer logs
36 | pip-log.txt
37 | pip-delete-this-directory.txt
38 |
39 | # Unit test / coverage reports
40 | htmlcov/
41 | .tox/
42 | .coverage
43 | .coverage.*
44 | .cache
45 | nosetests.xml
46 | coverage.xml
47 | *,cover
48 | .hypothesis/
49 |
50 | # Translations
51 | *.mo
52 | *.pot
53 |
54 | # PyCharm stuff
55 | .idea
56 | .vagrant
57 |
58 | # Django stuff:
59 | *.log
60 | local_settings.py
61 |
62 | # Flask stuff:
63 | instance/
64 | .webassets-cache
65 |
66 | # Scrapy stuff:
67 | .scrapy
68 |
69 | # Sphinx documentation
70 | docs/_build/
71 |
72 | # PyBuilder
73 | target/
74 |
75 | # Jupyter Notebook
76 | .ipynb_checkpoints
77 |
78 | # pyenv
79 | .python-version
80 |
81 | # celery beat schedule file
82 | celerybeat-schedule
83 |
84 | # dotenv
85 | .env
86 |
87 | # virtualenv
88 | .venv
89 | venv/
90 | ENV/
91 |
92 | # Spyder project settings
93 | .spyderproject
94 |
95 | # Rope project settings
96 | .ropeproject
97 |
98 |
--------------------------------------------------------------------------------
/LICENSE:
--------------------------------------------------------------------------------
1 | MIT License
2 |
3 | Copyright (c) 2017 Azerbaijan Python User Group
4 |
5 | Permission is hereby granted, free of charge, to any person obtaining a copy
6 | of this software and associated documentation files (the "Software"), to deal
7 | in the Software without restriction, including without limitation the rights
8 | to use, copy, modify, merge, publish, distribute, sublicense, and/or sell
9 | copies of the Software, and to permit persons to whom the Software is
10 | furnished to do so, subject to the following conditions:
11 |
12 | The above copyright notice and this permission notice shall be included in all
13 | copies or substantial portions of the Software.
14 |
15 | THE SOFTWARE IS PROVIDED "AS IS", WITHOUT WARRANTY OF ANY KIND, EXPRESS OR
16 | IMPLIED, INCLUDING BUT NOT LIMITED TO THE WARRANTIES OF MERCHANTABILITY,
17 | FITNESS FOR A PARTICULAR PURPOSE AND NONINFRINGEMENT. IN NO EVENT SHALL THE
18 | AUTHORS OR COPYRIGHT HOLDERS BE LIABLE FOR ANY CLAIM, DAMAGES OR OTHER
19 | LIABILITY, WHETHER IN AN ACTION OF CONTRACT, TORT OR OTHERWISE, ARISING FROM,
20 | OUT OF OR IN CONNECTION WITH THE SOFTWARE OR THE USE OR OTHER DEALINGS IN THE
21 | SOFTWARE.
22 |
--------------------------------------------------------------------------------
/README.md:
--------------------------------------------------------------------------------
1 | 
2 |
3 | [BrandCream](https://www.facebook.com/brandingcream/) tərəfindən hazırlanıb.
--------------------------------------------------------------------------------
/SUMMARY.md:
--------------------------------------------------------------------------------
1 | İçindəkilər:
2 |
3 | * [Haqqında](./book/0.Haqqında.md)
4 |
5 | * [Giriş](./book/1.Giriş.md)
6 |
7 | * [Rekursiya və Backtracking](./book/2.Recursion_and_Backtracking.md)
8 |
9 | * [Birtərəfli Əlaqəli listlər-singly linked lists](./book/3.Birtərəfli_Əlaqəli_listlər_singly_linked_lists.md)
10 |
11 | * [İkitərəfli Əlaqəli listlər-doubly linked lists](./book/4.İkitərəfli_Əlaqəli_listlər_doubly_linked_lists.md)
12 |
13 | * [Dövri Əlaqəli listlər-circular linked lists](./book/5.Dövri_Əlaqəli_listlər_circular_linked_lists.md)
14 |
15 | * [Yığın-stack](./book/6.Stack_Yığın.md)
16 |
17 | * [Növbələr-queues](./book/7.Növbələr_Queues.md)
18 |
19 | * [Ağaclar-trees](./book/8.Ağaclar_Trees.md)
20 |
21 | * [İkili ağaclar-tapşırıqlar](./book/9.İkili_Ağaclar_Tapşırıqlar_və_Həllər.md)
22 |
23 | * [Düzülü İkili Ağaclar](./book/10.Düzülü_İkili_Ağaclar_Threaded_Binary_Tree_Traversals.md)
24 |
25 | * [İkili Axtarış Ağacları - BST](./book/11.İkili_Axtarış_Ağacları_Binary_Search_Trees.md)
26 |
27 | * [Sıralama - Sorting](./book/12.Sıralama_Sorting.md)
28 |
--------------------------------------------------------------------------------
/Source_Code/haqqinda/conferences_attended.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/AzePUG/Data_Structures_Algo_Python/3e3892c32699f8b398339558bc1a3a22a8aa85be/Source_Code/haqqinda/conferences_attended.png
--------------------------------------------------------------------------------
/Source_Code/python_kodlar/__init__.py:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/AzePUG/Data_Structures_Algo_Python/3e3892c32699f8b398339558bc1a3a22a8aa85be/Source_Code/python_kodlar/__init__.py
--------------------------------------------------------------------------------
/Source_Code/python_kodlar/fesil11/fesil11_binary_search_tree.py:
--------------------------------------------------------------------------------
1 | class BSTNode:
2 | def __init__(self, data):
3 | # root node
4 | self.data = data
5 | # Sol övlad(left child)
6 | self.left = None
7 | # Sağ övlad(right child)
8 | self.right = None
9 |
10 | def get_data(self):
11 | return self.data
12 |
13 | def get_left_child(self):
14 | return self.left
15 |
16 | def get_right_child(self):
17 | return self.right
18 |
19 | class BSTree:
20 |
21 | def __init__(self):
22 | self.root = None
23 |
24 | def create_tree(self, val):
25 | # Ağacın özünü burda yaradırıq.
26 | if self.root is None:
27 | # Birinci elementi root element edirik
28 | self.root = BSTNode(data=val)
29 |
30 | else:
31 | # Root-u hazırkı node edirik
32 | current = self.root
33 |
34 | while True:
35 | # Əgər verilmiş qiymət hal-hazırkı qiymətdən kiçikdirsə,
36 | # Onu sol node edirik
37 | if val < current.data:
38 | if current.left:
39 | current = current.left
40 | else:
41 | current.left = BSTNode(data=val)
42 | break;
43 | # Əgər verilmiş qiymət hal-hazırkı qiymətdən böyükdürsə,
44 | # Onu sağ node edirik
45 | elif val > current.data:
46 | if current.right:
47 | current = current.right
48 | else:
49 | current.right = BSTNode(data=val)
50 | else:
51 | break
52 |
53 | def find_element(self, root, data):
54 | # Axtarışa root-dan başlayırıq.
55 | current_node = root
56 | while current_node is not None and data != current_node.get_data():
57 | # Yoxlayırıq ki, axtardığımız element hal-hazırkı node data-sından böyükdür ya yox.
58 | # Əgər böyükdürsə, o zaman sağ altağaca keçirik.
59 | if data > current_node.get_data():
60 | current_node = current_node.get_right_child()
61 | # Əgər kiçikdirsə, o zaman sol altağaca keçirik.
62 | else:
63 | current_node = current_node.get_left_child()
64 | return current_node
65 |
66 | # Rekursiv üsul
67 | def find_min_element(self, root):
68 | current_node = root
69 | if current_node.get_left_child() == None:
70 | return current_node
71 | else:
72 | return self.find_min_element(current_node.get_left_child())
73 |
74 | # Rekursiv olmayan üsul
75 | def find_min_element_non_recursive(self, root):
76 | current_node = root
77 | if current_node is None:
78 | return None
79 | while current_node.get_left_child() is not None:
80 | current_node = current_node.get_left_child()
81 | return current_node
82 |
83 | # Rekursiv üsul
84 | def find_max_element(self, root):
85 | current_node = root
86 | if current_node.get_right_child() == None:
87 | return current_node
88 | else:
89 | return self.find_max_element(current_node.get_right_child())
90 |
91 | # Rekursiv olmayan üsul
92 | def find_max_element_non_recursive(self, root):
93 | current_node = root
94 | if current_node is None:
95 | return None
96 | while current_node.get_right_child() is not None:
97 | current_node = current_node.get_right_child()
98 | return current_node
99 |
100 |
101 | def predecessor_bst(self, root):
102 | # Inorder Predecessor
103 | temp = None
104 | if root.get_left_child():
105 | temp = root.get_left_child()
106 | while temp.get_right_child():
107 | temp = temp.get_right_child()
108 | return temp
109 |
110 |
111 | def successor_bst(self, root):
112 | # Inorder Successor
113 | temp = None
114 | if root.get_right_child():
115 | temp = root.get_right_child()
116 | while temp.get_left_child():
117 | temp = temp.get_left_child()
118 | return temp
119 |
120 | def insert_node(self, root, node_data):
121 | if root is None:
122 | root = BSTNode(data=node_data)
123 | else:
124 | if node_data < root.get_data():
125 | if root.get_left_child() is None:
126 | root.left = BSTNode(data=node_data)
127 | else:
128 | self.insert_node(root.get_left_child(), node_data)
129 | else:
130 | if root.get_right_child() is None:
131 | root.right = BSTNode(data=node_data)
132 | else:
133 | self.insert_node(root.get_right_child(), node_data)
134 | return node_data
135 |
136 |
137 | def delete_node(self, root, node_data):
138 | # Düz işləmir!
139 | # Base Case
140 | if root is None:
141 | return root
142 | # Əgər silinməli olan dəyər root dəyərdən kiçikdirsə,
143 | # deməli sol altağacda axatarmaq lazımdır.
144 | if node_data < root.get_data():
145 | root.left = self.delete_node(root.get_left_child(), node_data)
146 | # Əgər silinməli olan dəyər root dəyərdən böyükdürsə,
147 | # deməli sağ altağacda axatarmaq lazımdır.
148 | elif node_data > root.get_data():
149 | root.right = self.delete_node(root.get_right_child(), node_data)
150 | # Bu halda deməli silinməli node-u tapmışıq
151 | else:
152 | # Bir child-ı olan və yaxud ümumiyyətlə child-ı olmayan Node üçün
153 | if root.get_left_child() is None :
154 | temp = root.get_right_child()
155 | root = None
156 | return temp
157 |
158 | elif root.get_right_child() is None :
159 | temp = root.get_left_child()
160 | root = None
161 | return temp
162 |
163 | # İki child-ı olan Node üçün: inorder successor-u tapırıq
164 | # (sağ altağacda ən kiçik)
165 | temp = self.successor_bst(root.get_right_child())
166 | # inorder successor-un dəyərini bu node-a mənimsədirik.
167 | root.data = temp.get_data()
168 |
169 | # inorder successor-u silirik.
170 | root.right = self.delete_node(root.get_right_child() , temp.get_data())
171 |
172 |
173 |
174 |
175 |
176 |
177 |
178 | if __name__ == "__main__":
179 | tree = BSTree()
180 | arr = [8, 3, 1, 6, 4, 7, 10, 14, 13]
181 | for i in arr:
182 | tree.create_tree(i)
183 | print("Mövcud elementi axtarmaq -> ", tree.find_element(tree.root, 13))
184 | print("Mövcud olmayan elementi axtarmaq -> ", tree.find_element(tree.root, 85))
185 |
186 | print("Minimal elementi axtarmaq rekursiya -> ", tree.find_min_element(tree.root).data)
187 | print("Minimal elementi axtarmaq rekursiv olmayan -> ", tree.find_min_element_non_recursive(tree.root).data)
188 |
189 | print("Maximal elementi axtarmaq rekursiv -> ", tree.find_max_element(tree.root).data)
190 |
191 | print("Maximal elementi axtarmaq rekursiv olmayan -> ", tree.find_max_element_non_recursive(tree.root).data)
192 |
193 | print("Inorder Predecessor -> ", tree.predecessor_bst(tree.root).data)
194 | print("Inorder Successor -> ", tree.successor_bst(tree.root).data)
195 | print("BST-yə element daxil edirik -> ", tree.insert_node(tree.root, 25))
196 | print("Maximal elementi axtarmaq rekursiv -> ", tree.find_max_element(tree.root).data)
197 | print("BST-dən element silirik -> ", tree.delete_node(tree.root, 25))
198 | print("Maximal elementi axtarmaq rekursiv -> ", tree.find_max_element(tree.root).data)
199 |
--------------------------------------------------------------------------------
/Source_Code/python_kodlar/fesil12/fesil12_bubble_sort.py:
--------------------------------------------------------------------------------
1 | def bubbleSort(alist):
2 | for passnum in range(len(alist)-1,0,-1):
3 | for i in range(passnum):
4 | if alist[i]>alist[i+1]:
5 | temp = alist[i]
6 | alist[i] = alist[i+1]
7 | alist[i+1] = temp
8 |
9 | alist = [54,26,93,17,77,31,44,55,20]
10 | bubbleSort(alist)
11 | print(alist)
12 |
13 |
--------------------------------------------------------------------------------
/Source_Code/python_kodlar/fesil2/fesil2_2.12_bit_strings_itertools.py:
--------------------------------------------------------------------------------
1 | from itertools import product
2 | n = 4
3 | bin_str_list = [''.join(p) for p in product('01', repeat=n)]
4 |
5 | print(bin_str_list)
6 |
--------------------------------------------------------------------------------
/Source_Code/python_kodlar/fesil2/fesil2_2.12_bit_strings_recursion.py:
--------------------------------------------------------------------------------
1 | def bin_str_list(n):
2 | if n == 0:
3 | #base case
4 | return ['']
5 | else:
6 | # Rekursiya
7 | return [i + '0' for i in bin_str_list(n-1)] + [i + '1' for i in bin_str_list(n-1)]
8 |
9 | print(bin_str_list(4))
10 |
--------------------------------------------------------------------------------
/Source_Code/python_kodlar/fesil2/fesil2_2.5_factorial_pdb.py:
--------------------------------------------------------------------------------
1 | import pdb
2 |
3 | def factorial(n):
4 | if n == 0 or n == 1:
5 | pdb.set_trace()
6 | return 1
7 |
8 | return n * factorial(n - 1)
9 |
10 | if __name__ == "__main__":
11 | pdb.set_trace()
12 | factorial(5)
13 |
--------------------------------------------------------------------------------
/Source_Code/python_kodlar/fesil2/fesil2_2.5_pdb.py:
--------------------------------------------------------------------------------
1 | import pdb
2 |
3 | def print_func(n):
4 | if n == 0: # funksiyanı bitirən əsas hal.
5 | pdb.set_trace()
6 | return 0
7 | elif n > 0:
8 | print(n)
9 | return print_func(n - 1) # rekursiv çağırış
10 |
11 |
12 | if __name__ == "__main__":
13 | pdb.set_trace()
14 | print_func(4)
15 |
--------------------------------------------------------------------------------
/Source_Code/python_kodlar/fesil2/fesil2_2.5_pycallgraph.py:
--------------------------------------------------------------------------------
1 | from pycallgraph import PyCallGraph
2 | from pycallgraph.output import GraphvizOutput
3 |
4 | def print_func(n):
5 | if n == 0: # funksiyanı bitirən əsas hal.
6 | return 0
7 | elif n > 0:
8 | print(n)
9 | return print_func(n - 1) # rekursiv çağırış
10 |
11 |
12 | if __name__ == "__main__":
13 | graphviz = GraphvizOutput()
14 | graphviz.output_file = 'fesil2_2.5.png'
15 |
16 | with PyCallGraph(output=graphviz):
17 | print_func(4)
18 |
--------------------------------------------------------------------------------
/Source_Code/python_kodlar/fesil2/fesil2_2.9_hanoi_qulleleri.py:
--------------------------------------------------------------------------------
1 | def hanoi_qulleleri(disk_sayi, menbe_sutun, komekci_sutun, hedef_sutun):
2 | print("hanoi_qulleleri( ", disk_sayi, menbe_sutun, komekci_sutun, hedef_sutun, " cagrildi...)")
3 | if disk_sayi:
4 | # (n - 1) sutununu menbeden komekciye yerleshdirmek
5 | hanoi_qulleleri(disk_sayi-1, menbe_sutun, hedef_sutun, komekci_sutun)
6 | # deyildiyi kimi, n-ci diski menbeden hedefe yerleshdiririk
7 | if menbe_sutun:
8 | disk = menbe_sutun.pop()
9 | print("Disk {}-in menbe_sutun-dan hedef_sutun-a yerleshdirilmesi".format(disk))
10 | hedef_sutun.append(disk)
11 | # (n - 1) sutununu komekciden hedefe yerleshdiririk
12 | hanoi_qulleleri(disk_sayi-1, komekci_sutun, menbe_sutun, hedef_sutun)
13 |
14 |
15 | menbe_sutun = [3, 2, 1]
16 | hedef_sutun = []
17 | komekci_sutun = []
18 | hanoi_qulleleri(len(menbe_sutun), menbe_sutun, komekci_sutun, hedef_sutun)
19 |
20 | print("son netice")
21 | print(menbe_sutun, komekci_sutun, hedef_sutun)
22 |
--------------------------------------------------------------------------------
/Source_Code/python_kodlar/fesil2/fesil2_2.9_is_array_sorted.py:
--------------------------------------------------------------------------------
1 | def massiv_siralidirmi(massiv):
2 | print("Yeni massiv : {}".format(massiv))
3 | # Esas hal
4 | if len(massiv) == 1:
5 | return True
6 | # Rekursiya
7 | if massiv[0] <= massiv[1] and massiv_siralidirmi(massiv[1:]):
8 | return True
9 | else:
10 | return False
11 |
12 | massiv1 = [23, 34, 45, 56, 88, 97, 101, 125]
13 | # True qayitmalidir
14 | print(massiv_siralidirmi(massiv=massiv1))
15 |
16 | massiv2 = [23, 34, 45, 56, 88, 97, 101, 125, 5]
17 | # False qayitmalidir
18 | print(massiv_siralidirmi(massiv2))
19 |
--------------------------------------------------------------------------------
/Source_Code/python_kodlar/fesil3/fesil3_3_6_linked_lists.py:
--------------------------------------------------------------------------------
1 | class Node:
2 | # konstruktor
3 | def __init__(self, data=None, next_node=None):
4 | self.data = data
5 | self.next_node = next_node
6 |
7 | # node-un data field-ini mənimsətmək üçün metod
8 | def set_data(self, data):
9 | self.data = data
10 |
11 | # node-un data field-ini almaq üçün metod
12 | def get_data(self):
13 | return self.data
14 |
15 | # node-un növbəti field-ini mənimsətmək üçün metod
16 | def set_next_node(self, next_node):
17 | self.next_node = next_node
18 |
19 | # node-un növbəti field-ini almaq üçün metod
20 | def get_next_node(self):
21 | return self.next_node
22 |
23 | # əgər bir node sonrakına point edirsə, true qaytar
24 | def has_next(self):
25 | return self.next_node is not None
26 |
27 |
28 | class SinglyLinkedList:
29 | # Birtərəfli bağlı list
30 | def __init__(self, head=None):
31 | self.head = head
32 |
33 | def list_size(self):
34 | current = self.head
35 | count = 0
36 | while current:
37 | count += 1
38 | current = current.get_next_node()
39 | return count
40 |
41 | def insert_at_beginning(self, data):
42 | new_node = Node()
43 | new_node.set_data(data)
44 |
45 | if self.list_size() == 0:
46 | self.head = new_node
47 | else:
48 | new_node.set_next_node(self.head)
49 | self.head = new_node
50 |
51 | def insert_at_end(self, data):
52 | new_node = Node()
53 | new_node.set_data(data)
54 |
55 | current = self.head
56 | while current.get_next_node() is not None:
57 | current = current.get_next_node()
58 |
59 | current.set_next_node(new_node)
60 |
61 | def insert_at_pos(self, pos, data):
62 | # Əgər düzgün pozisiya verilmirsə, None qaytar
63 | if pos > self.list_size() or pos < 0:
64 | print("Pozisiya səhvdir, None qaytarıram..")
65 | return None
66 | else:
67 | # Əgər pozisiya 0-dırsa, bu o deməkdir ki, biz listin əvvəlinə daxil etmək istəyirik
68 | if pos == 0:
69 | print("Əvvələ daxil etmə...")
70 | self.insert_at_beginning(data)
71 | # Əgər pozisiya list-in node sayına bərabərdirsə, bu o deməkdir ki, node-u listin sonuna daxil etmək lazımdır
72 | elif pos == self.list_size():
73 | print("Ən sona daxil etmə...")
74 | self.insert_at_end(data)
75 | else:
76 | print("Verilmiş pozisiyaya daxil etmə...")
77 | new_node = Node()
78 | new_node.set_data(data)
79 | count = 1
80 | current = self.head
81 | # Verilmiş pozisiyadan bir əvvəlki node-u tapırıq
82 | while count < (pos - 1):
83 | count += 1
84 | current = current.get_next_node()
85 | # Yeni node-un next pointerini, verilmiş pozisiyadan bir əvvəlki node-un point etdiyi node-a yönləndiririk.
86 | new_node.set_next_node(current.get_next_node())
87 | # Verilmiş pozisiyadan bir əvvəlki node-un next pointer-ini isə bizim daxil etmək istədiyimiz node-a yönləndiririk.
88 | current.set_next_node(new_node)
89 |
90 | def delete_first_node(self):
91 | if self.list_size() == 0:
92 | print("List boşdur...")
93 | else:
94 | # Müvəqqəti node
95 | temp = self.head
96 | # Head node-u əvvəlki head-dən sonrakı node-a mənimsədirik.
97 | # Bununla da faktiki olaraq, əvvəlki head-i arxada qoyuruq.
98 | self.head = self.head.get_next_node()
99 | # Müvəqqəti node-u silirik.
100 | del(temp)
101 |
102 | def delete_last_node(self):
103 | if self.list_size() == 0:
104 | print("List boşdur...")
105 | else:
106 | # Yuxarıda dediyimiz kimi 2 node haqqında məlumatı saxlamalıyıq
107 | current_node = self.head
108 | previous_node = None
109 |
110 | while current_node.get_next_node() is not None:
111 | previous_node = current_node
112 | current_node = current_node.get_next_node()
113 |
114 | previous_node.set_next_node(None)
115 |
116 | del(current_node)
117 |
118 | def delete_from_list_by_data(self, data):
119 | # Burada, current, tapılan node-u, data-ya əsasən silirik.
120 | current_node = self.head
121 | previous_node = None
122 | found = False
123 |
124 | # current_node None olsa dayan, found True olsa dayan
125 | while current_node and found is False:
126 | if current_node.get_data() == data:
127 | found = True
128 | else:
129 | previous_node = current_node
130 | current_node = current_node.get_next_node()
131 |
132 | if current_node is None:
133 | # Fərqlilik məqsədilə Exception-dan istifadə edirik
134 | raise ValueError("Data listdə tapılmadı...")
135 | if previous_node is None:
136 | # Bu o deməkdir ki, axtarılan data elə 1ci(head) node-da tapılıb.
137 | # Bu zaman head-i sadəcə növbəti node-a işarəliyirik.
138 | # Əslində bu hal, list-in əvvəlindən node silməyə bərabərdir.
139 | self.head = current_node.get_next_node()
140 | else:
141 | # Əvvəlki node-un next pointerini, hal-hazırkı(current) node-un next pointer-inə yönləndiririk.
142 | # Beləcə current node-un özünü sanki itiririk, silirik.
143 | previous_node.set_next_node(current_node.get_next_node())
144 |
145 | def delete_at_position(self, pos):
146 | count = 0
147 | current_node = self.head
148 | previous_node = self.head
149 |
150 | if pos > self.list_size() or pos < 0:
151 | print("Pozisiya səhvdir, None qaytarıram..")
152 | return None
153 | elif pos == 0:
154 | # Bu o deməkdir ki, listin əvvəlindən node silirik.
155 | self.delete_first_node()
156 | elif pos == self.list_size():
157 | # Bu o deməkdir ki, listin sonundan node silirik.
158 | self.delete_last_node()
159 | else:
160 | # Əgər listin axırına çatmamışıqsa və count verilmiş pozisiyadan kiçikdirsə, davam elə
161 | while (current_node.get_next_node() is not None) or count < pos:
162 | count = count + 1
163 | if count == pos:
164 | # Əgər verilmiş pozisiyaya çatdıqsa, əvvəlki node-un next pointer-ini, indiki node-un next pointerinə yönləndiririk.
165 | previous_node.set_next_node(current_node.get_next_node())
166 | return
167 | else:
168 | # Əgər hələ pozisiyaya çatmamışıqsa, o zaman davam edirik.
169 | previous_node = current_node
170 | current_node = current_node.get_next_node()
171 |
172 |
173 | def clear(self):
174 | # Head-i NULL edirik
175 | self.head = None
176 |
--------------------------------------------------------------------------------
/Source_Code/python_kodlar/fesil4/fesil4_doubly_linked_lists.py:
--------------------------------------------------------------------------------
1 | class Node:
2 | # Konstruktor
3 | # Əgər istifadəçi tərəfindən heçnə verilmirsə, bu zaman None(NULL) olaraq inisializasiya edirik
4 | def __init__(self, data=None, next_node=None, prev_node=None):
5 | self.data = data
6 | self.next_node = next_node
7 | self.prev_node = prev_node
8 |
9 | # node-un data field-ini mənimsətmək üçün metod
10 | def set_data(self, data):
11 | self.data = data
12 |
13 | # node-un data field-ini almaq üçün metod
14 | def get_data(self):
15 | return self.data
16 |
17 | # node-un növbəti(next) field-ini mənimsətmək üçün metod
18 | def set_next_node(self, next_node):
19 | self.next_node = next_node
20 |
21 | # node-un növbəti(next) field-ini almaq üçün metod
22 | def get_next_node(self):
23 | return self.next_node
24 |
25 | # əgər bir node sonrakına point edirsə, True qaytar
26 | def has_next(self):
27 | return self.next_node is not None
28 |
29 | # node-un əvvəlki(previous) field-ini mənimsətmək üçün metod
30 | def set_prev_node(self, prev_node):
31 | self.prev_node = prev_node
32 |
33 | # node-un əvvəlki(previous) field-ini almaq üçün metod
34 | def get_prev_node(self):
35 | return self.prev_node
36 |
37 | # node-dan əvvəlki varsa, True
38 | def has_prev(self):
39 | return self.prev_node is not None
40 |
41 | class DoublyLinkedList:
42 |
43 | def __init__(self, head=None, tail=None):
44 | self.head = head
45 | self.tail = tail
46 |
47 | def insert_at_beginning(self, data):
48 | new_node = Node(data)
49 |
50 | if self.head is None:
51 | self.head = new_node
52 | self.tail = new_node
53 | else:
54 | new_node.set_prev_node(None)
55 | new_node.set_next_node(self.head)
56 | self.head.set_prev_node(new_node)
57 | self.head = new_node
58 |
59 | def insert_at_end(self, data):
60 | new_node = Node(data, next_node=None, prev_node=None)
61 |
62 | if self.head is None:
63 | self.head = new_node
64 | self.tail = self.head
65 | else:
66 | current = self.head
67 | # Sonuncu node-u tapırıq
68 | while current.get_next_node() is not None:
69 | current = current.get_next_node()
70 | # Hal-hazırkı sonuncu node üçün next pointeri yeni node edirik.
71 | current.set_next_node(new_node)
72 | # Yeni node-un əvvəlki pointerini hal-hazırkı(while-da tapılan) node edirik.
73 | new_node.set_prev_node(current)
74 | # Yeni node-un next pointerini NULL-a yönləndiririk.
75 | new_node.set_next_node(None)
76 | self.tail = new_node
77 |
78 | def list_size(self):
79 | current = self.head
80 | count = 0
81 | while current:
82 | count += 1
83 | current = current.get_next_node()
84 | return count
85 |
86 | def insert_at_pos(self, pos, data):
87 | if pos > self.list_size() or pos < 0:
88 | print("Pozisiya səhvdir, None qaytarıram..")
89 | return None
90 | else:
91 | # Əgər pozisiya 0 verilibsə və yaxud head node None-dırsa, əvvələ daxil et.
92 | if pos == 0 or self.head is None:
93 | print("Əvvələ daxil etmə...")
94 | self.insert_at_beginning(data)
95 | elif pos == self.list_size():
96 | print("Ən sona daxil etmə...")
97 | self.insert_at_end(data)
98 | elif pos > 0:
99 | print("Verilmiş pozisiyaya daxil etmə...")
100 | new_node = Node()
101 | new_node.set_data(data)
102 |
103 | count = 0
104 | current = self.head
105 | # Verilmiş pozisiyadan bir əvvəlki node-u tapırıq, yəni pozisional node-u
106 | while count < (pos - 1):
107 | current = current.get_next_node()
108 | count += 1
109 | # Yeni node-un next pointerini, pozisional node-dan növbəti node-a yönləndiririk.
110 | new_node.set_next_node(current.get_next_node())
111 | # Yeni node-un əvvəlki pointerini, hal-hazırkı node-a yönləndiririk.
112 | new_node.set_prev_node(current)
113 | # Pozisional node-dan(hal-hazırkı node) sonrakı node-un previous pointerini new_node-a yönləndiririk.
114 | current.get_next_node().set_prev_node(new_node)
115 | # Pozisional node-un next pointerini new_node-a yönləndiririk.
116 | current.set_next_node(new_node)
117 |
118 |
119 | def delete_first_node(self):
120 | if self.list_size() == 0:
121 | print("List boşdur...")
122 | else:
123 | # Müvəqqəti node
124 | temp = self.head
125 | # Head node-u əvvəlki head-dən sonrakı node-a mənimsədirik.
126 | # Bununla da faktiki olaraq, əvvəlki head-i arxada qoyuruq.
127 | self.head = self.head.get_next_node()
128 | # Yeni head və yaxud yeni node-umuzun sol(previous) node-a pointeri None edirik.
129 | self.head.set_prev_node(None)
130 | # Müvəqqəti node-u silirik.
131 | del(temp)
132 |
133 | def delete_last_node(self):
134 | if self.list_size() == 0:
135 | print("List boşdur...")
136 | else:
137 | # Head node-dan başlayırıq
138 | current_node = self.head
139 | # Sonuncu node-u aşkarlayırıq
140 | while current_node.get_next_node() is not None:
141 | current_node = current_node.get_next_node()
142 | # Sonuncu node-dan bir əvvəlki node-u tapırıq
143 | previous_node = current_node.get_prev_node()
144 | # Bir əvvəlki node-un növbəti
145 | previous_node.set_next_node(None)
146 | # current node-u silirik
147 | del(current_node)
148 |
149 | def traverse_and_print(self):
150 | if self.list_size() == 0:
151 | print("List boşdur...")
152 | elif self.list_size() == 1:
153 | print(self.head.data)
154 | else:
155 | # Head node-dan başlayırıq
156 | current_node = self.head
157 | print(current_node.get_data())
158 | while True:
159 | current_node = current_node.get_next_node()
160 | if current_node is None:
161 | break
162 | print(current_node.get_data())
163 |
164 | def delete_from_list_by_data(self, data):
165 | # Burada, current, tapılan node-u, data-ya əsasən silirik.
166 | current_node = self.head
167 | found = False
168 |
169 | # current_node None olsa dayan, found True olsa dayan
170 | while current_node and found is False:
171 | if current_node.get_data() == data:
172 | found = True
173 | else:
174 | current_node = current_node.get_next_node()
175 |
176 | if current_node is None:
177 | # Fərqlilik məqsədilə Exception-dan istifadə edirik
178 | raise ValueError("Data listdə tapılmadı...")
179 | if current_node.get_prev_node() is None:
180 | # Bu o deməkdir ki, axtarılan data elə 1ci(head) node-da tapılıb.
181 | # Bu zaman head-i sadəcə növbəti node-a işarəliyirik.
182 | # Əslində bu hal, list-in əvvəlindən node silməyə bərabərdir.
183 | self.head = current_node.get_next_node()
184 | else:
185 | # Əvvəlki node-un next pointerini, hal-hazırkı(current) node-un next node-una yönləndiririk.
186 | current_previous_node = current_node.get_prev_node()
187 | current_previous_node.set_next_node(current_node.get_next_node())
188 | # Sonrakı node-un əvvəlki pointerini isə hal-hazırkı(current) node-un əvvəlki node-una yönləndiririk.
189 | current_next_node = current_node.get_next_node()
190 | current_next_node.set_prev_node(current_node.get_prev_node())
191 |
192 | def delete_at_position(self, pos):
193 | count = 0
194 | current_node = self.head
195 |
196 | if pos > self.list_size() or pos < 0:
197 | print("Pozisiya səhvdir, None qaytarıram..")
198 | return None
199 | elif pos == 0:
200 | # Bu o deməkdir ki, listin əvvəlindən node silirik.
201 | self.delete_first_node()
202 | elif pos == self.list_size():
203 | # Bu o deməkdir ki, listin sonundan node silirik.
204 | self.delete_last_node()
205 | else:
206 | # Əgər listin axırına çatmamışıqsa və count verilmiş pozisiyadan kiçikdirsə, davam elə
207 | while (current_node.get_next_node() is not None) or count < pos:
208 | count = count + 1
209 | if count == pos:
210 | # Əgər verilmiş pozisiyaya çatdıqsa, əvvəlki node-un next pointer-ini, indiki node-un next pointerinə yönləndiririk.
211 | current_previous_node = current_node.get_prev_node()
212 | current_previous_node.set_next_node(current_node.get_next_node())
213 |
214 | # Sonrakı node-un əvvəlki pointerini isə hal-hazırkı(current) node-un əvvəlki node-una yönləndiririk.
215 | current_next_node = current_node.get_next_node()
216 | current_next_node.set_prev_node(current_node.get_prev_node())
217 | return
218 | else:
219 | # Əgər hələ pozisiyaya çatmamışıqsa, o zaman davam edirik.
220 | current_node = current_node.get_next_node()
221 |
--------------------------------------------------------------------------------
/Source_Code/python_kodlar/fesil5/fesil5_circular_linked_lists.py:
--------------------------------------------------------------------------------
1 | class Node:
2 | # konstruktor
3 | def __init__(self, data=None, next_node=None):
4 | self.data = data
5 | self.next_node = next_node
6 |
7 | # node-un data field-ini mənimsətmək üçün metod
8 | def set_data(self, data):
9 | self.data = data
10 |
11 | # node-un data field-ini almaq üçün metod
12 | def get_data(self):
13 | return self.data
14 |
15 | # node-un növbəti field-ini mənimsətmək üçün metod
16 | def set_next_node(self, next_node):
17 | self.next_node = next_node
18 |
19 | # node-un növbəti field-ini almaq üçün metod
20 | def get_next_node(self):
21 | return self.next_node
22 |
23 | # əgər bir node sonrakına point edirsə, true qaytar
24 | def has_next(self):
25 | return self.next_node is not None
26 |
27 |
28 | class CircularLinkedList:
29 | def __init__(self, head=None):
30 | self.head = head
31 |
32 | def circular_list_length(self):
33 | current_node = self.head
34 | if current_node is None:
35 | return 0
36 |
37 | count = 1
38 | current_node = current_node.get_next_node()
39 | # Dövri əlaqəli listdə yenidən head node-a gedib çıxmışıq ya yox, onu yoxlayırıq.
40 | while current_node != self.head:
41 | current_node = current_node.get_next_node()
42 | count = count + 1
43 |
44 | return count
45 |
46 | def print_data_circular_list(self):
47 | current_node = self.head
48 | if current_node is None:
49 | return 0
50 |
51 | print(current_node.get_data())
52 | current_node = current_node.get_next_node()
53 | while current_node != self.head:
54 | print(current_node.get_data())
55 | current_node = current_node.get_next_node()
56 |
57 |
58 | def insert_at_end(self, data):
59 | current_node = self.head
60 | new_node = Node()
61 | new_node.set_data(data)
62 |
63 | if self.head is None:
64 | self.head = new_node
65 | new_node.set_next_node(self.head)
66 | else:
67 | current_node = current_node.get_next_node()
68 | while current_node.get_next_node() != self.head:
69 | current_node.get_next_node()
70 | # Yeni node-u öz-özünə point edirik.
71 | new_node.set_next_node(new_node)
72 | # Yeni node-u head node-a yönləndiririk.
73 | new_node.set_next_node(self.head)
74 | # Hal-hazırkı(faktiki olaraq əvvəlki) node-u isə yeni node-a yönləndiririk.
75 | current_node.set_next_node(new_node)
76 |
77 | def insert_at_beginning(self, data):
78 | current_node = self.head
79 | new_node = Node()
80 | new_node.set_data(data)
81 | # Yeni node-u öz-özünə point edirik.
82 | new_node.set_next_node(new_node)
83 |
84 | if self.head is None:
85 | self.head = new_node
86 | new_node.set_next_node(self.head)
87 | else:
88 | current_node.get_next_node()
89 | while current_node.get_next_node() != self.head:
90 | current_node = current_node.get_next_node()
91 | # Yeni node-u head node-a yönləndiririk.
92 | new_node.set_next_node(self.head)
93 | # Yeni node-u yeni head edirik
94 | self.head = new_node
95 | # Hal-hazırkı tapılan node-u isə yeni head-ə yönləndiririk və yaxud yeni head-ə
96 | # current_node.set_next_node(new_node)
97 | current_node.set_next_node(self.head)
98 |
99 | def delete_from_end(self):
100 | # Müvəqqəti dəyişən
101 | temp = self.head
102 | current_node = self.head
103 |
104 | if self.head is None:
105 | print("List boşdur...")
106 | else:
107 | if current_node.get_next_node() == self.head:
108 | self.head = None
109 | return
110 | while current_node.get_next_node() != self.head:
111 | temp = current_node
112 | current_node = current_node.get_next_node()
113 | # Müvəqqəti node, əslində sondan bir əvvəli node-dur.
114 | # Burda bu node-un növbəti pointer-ini faktiki olaraq head-ə yönləndiririk.
115 | temp.set_next_node(self.head)
116 | return
117 |
118 | def delete_from_beginning(self):
119 | current_node = self.head
120 |
121 | if self.head is None:
122 | print("List boşdur...")
123 | else:
124 | if current_node.get_next_node() == self.head:
125 | self.head = None
126 | return
127 | # Sonuncu node-un tapılması
128 | while current_node.get_next_node() != self.head:
129 | current_node = current_node.get_next_node()
130 | # Sonuncu node-un pointerini hal-hazırkı head-den sonrakı node-a yönləndiririk.
131 | current_node.set_next_node(self.head.get_next_node())
132 | # Head node-u sürüşdürürük
133 | self.head = self.head.get_next_node()
134 |
--------------------------------------------------------------------------------
/Source_Code/python_kodlar/fesil6/__init__.py:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/AzePUG/Data_Structures_Algo_Python/3e3892c32699f8b398339558bc1a3a22a8aa85be/Source_Code/python_kodlar/fesil6/__init__.py
--------------------------------------------------------------------------------
/Source_Code/python_kodlar/fesil6/fesil6_dynamic_array_stack.py:
--------------------------------------------------------------------------------
1 | # Digər moduldan class-larımızı import edirik
2 | from fesil6_list_stack import StackUnderFlow
3 |
4 |
5 | class DynamicStack:
6 | def __init__(self, limit=10):
7 | self.stk = []
8 | self.limit = limit
9 |
10 | def is_empty(self):
11 | # Əgər python listin boşdursa, deməli stack boşdur bu zaman True qaytarırıq.
12 | return self.stk == []
13 |
14 | def push(self, item):
15 | if len(self.stk) >= self.limit:
16 | self.resize()
17 | self.stk.append(item)
18 | print("Stack after push -> {}".format(self.stk))
19 |
20 | def pop(self):
21 | if len(self.stk) == 0:
22 | raise StackUnderFlow("Stack underflow aşkarlandı!")
23 | else:
24 | # Python list-də built-in olan pop() metodunu çağırırıq.
25 | return self.stk.pop()
26 |
27 | def peek(self):
28 | if len(self.stk) == 0:
29 | raise StackUnderFlow("Stack underflow aşkarlandı!")
30 | else:
31 | # List slicing
32 | return self.stk[-1]
33 |
34 | def size(self):
35 | return len(self.stk)
36 |
37 | def delete_stack(self):
38 | # Stack-i silmək, faktiki olaraq python listi sıfırlamaqla əldə oluna bilər.
39 | self.stk = []
40 |
41 | def resize(self):
42 | # Python üçün resize əməliyyatı əslində, sadəcə limit-i 2-qat artırmaq deməkdir.
43 | # Belə ki, yeni array(list) yaradıb köhnəni ora kopyalamağa ehtiyac yoxdur, çünki onsuz da listin hər hansı limiti yoxdur.
44 | print("Resizing array...")
45 | self.limit = 2 * self.limit
--------------------------------------------------------------------------------
/Source_Code/python_kodlar/fesil6/fesil6_linked_list_stack.py:
--------------------------------------------------------------------------------
1 | class Node:
2 | # konstruktor
3 | def __init__(self, data=None, next_node=None):
4 | self.data = data
5 | self.next_node = next_node
6 |
7 | # node-un data field-ini mənimsətmək üçün metod
8 | def set_data(self, data):
9 | self.data = data
10 |
11 | # node-un data field-ini almaq üçün metod
12 | def get_data(self):
13 | return self.data
14 |
15 | # node-un növbəti field-ini mənimsətmək üçün metod
16 | def set_next_node(self, next_node):
17 | self.next_node = next_node
18 |
19 | # node-un növbəti field-ini almaq üçün metod
20 | def get_next_node(self):
21 | return self.next_node
22 |
23 | # əgər bir node sonrakına point edirsə, true qaytar
24 | def has_next(self):
25 | return self.next_node is not None
26 |
27 |
28 | class LinkedListStack:
29 | def __init__(self):
30 | self.head = None
31 |
32 | def is_empty(self):
33 | return self.head is None
34 |
35 | def push(self, data):
36 | temp = Node()
37 | temp.set_data(data=data)
38 | temp.set_next_node(self.head)
39 | self.head = temp
40 |
41 | def pop(self):
42 | if self.head is None:
43 | raise IndexError("Yığın boşdur...")
44 | temp = self.head.get_data()
45 | self.head = self.head.get_next_node()
46 | return temp
47 |
48 | def peek(self):
49 | if self.head is None:
50 | raise IndexError("Yığın boşdur...")
51 | return self.head.get_data()
52 |
53 | def size(self):
54 | current = self.head
55 | count = 0
56 | while current:
57 | count += 1
58 | current = current.get_next_node()
59 | return count
60 |
61 | def delete_stack(self):
62 | self.head = None
63 |
64 |
--------------------------------------------------------------------------------
/Source_Code/python_kodlar/fesil6/fesil6_list_stack.py:
--------------------------------------------------------------------------------
1 | # Öz məxsusi exception-larımızı hazırlayırıq
2 | class Error(Exception):
3 | pass
4 |
5 |
6 | class StackOverFlow(Error):
7 | def __init__(self, message):
8 | self.message = message
9 |
10 |
11 | class StackUnderFlow(Error):
12 | def __init__(self, message):
13 | self.message = message
14 |
15 |
16 | class ArrayStack:
17 |
18 | def __init__(self, limit=10):
19 | self.stk = []
20 | self.limit = limit
21 |
22 | def is_empty(self):
23 | # Əgər python listin boşdursa, deməli stack boşdur bu zaman True qaytarırıq.
24 | return self.stk == []
25 |
26 | def is_full(self):
27 | # Əgər python listin uzunluğu verilmiş limitə bərabərdirsə bu zaman deyə bilərik ki, stack doludur.
28 | # Əgər stack doludursa, True qaytarırıq.
29 | return len(self.stk) == self.limit
30 |
31 | def push(self, item):
32 | if len(self.stk) >= self.limit:
33 | raise StackOverFlow("Stack overflow aşkarlandı!")
34 | else:
35 | self.stk.append(item)
36 | print("Stack after push -> {}".format(self.stk))
37 |
38 | def pop(self):
39 | if len(self.stk) == 0:
40 | raise StackUnderFlow("Stack underflow aşkarlandı!")
41 | else:
42 | # Python list-də built-in olan pop() metodunu çağırırıq.
43 | return self.stk.pop()
44 |
45 | def peek(self):
46 | if len(self.stk) == 0:
47 | raise StackUnderFlow("Stack underflow aşkarlandı!")
48 | else:
49 | # List slicing
50 | return self.stk[-1]
51 |
52 | def size(self):
53 | return len(self.stk)
54 |
55 | def delete_stack(self):
56 | # Stack-i silmək, faktiki olaraq python listi sıfırlamaqla əldə oluna bilər.
57 | self.stk = []
58 |
59 |
60 | # if __name__ == "__main__":
61 | # try:
62 | # our_stack = ArrayStack(limit=5)
63 | # our_stack.pop()
64 | #
65 | # except (StackUnderFlow, StackOverFlow) as err:
66 | # print("{}: {}".format(err.__class__.__name__, err))
67 | # else:
68 | # print("Stack əməliyyatları uğurla yerinə yetirildi...")
--------------------------------------------------------------------------------
/Source_Code/python_kodlar/fesil7/fesil7_circular_array_queue.py:
--------------------------------------------------------------------------------
1 | class CircularQueue:
2 |
3 | def __init__(self, limit=5):
4 | self.que = []
5 | self.limit = limit
6 | self.front = -1 # Ön
7 | self.rear = -1 # Arxa, son
8 |
9 | def is_full(self):
10 | if self.front == 0 and self.rear == (self.limit - 1):
11 | return True
12 | elif self.front == self.rear + 1:
13 | return True
14 | return False
15 |
16 | def is_empty(self):
17 | return self.front == -1
18 |
19 | def en_queue(self, data):
20 | if self.is_full():
21 | print("Növbə doludur...")
22 | else:
23 | if self.front == -1:
24 | self.front = 0
25 | # REAR-i artırırıq, irəli çəkirik.
26 | self.rear = (self.rear + 1) % self.limit
27 | self.que.append(data)
28 | print("EnQueue-dən sonra, növbə, ", self.que)
29 | print("FRONT -> ", self.front)
30 | print("REAR -> ", self.rear)
31 |
32 | def de_queue(self):
33 | if self.is_empty():
34 | print("Növbə boşdur...")
35 | else:
36 | # Python list element silindikdən sonra, listi özü yenidən indexlədiyi üçün.
37 | # Həmişə pop(0) olaraq çağırmaq lazımdır. pop(self.front) düzgün nəticə vermir.
38 | data = self.que.pop(0)
39 | # Əgər bərabərdilərsə o zaman cəmi 1 elementi var, bu səbəbdən sildikdən sonra resetləyirik.
40 | if self.front == self.rear:
41 | self.front = -1
42 | self.rear = -1
43 | else:
44 | # FRONT-u artırırıq, irəli çəkirik.
45 | self.front = (self.front + 1) % self.limit
46 |
47 | print("Silinən element - ", data)
48 | print("FRONT -> ", self.front)
49 | print("REAR -> ", self.rear)
50 |
51 | def size(self):
52 | return len(self.que)
53 |
54 |
55 | if __name__ == "__main__":
56 | obj = CircularQueue(limit=5)
57 | obj.en_queue(56)
58 | obj.en_queue(44)
59 | obj.en_queue(85)
60 | obj.en_queue(66)
61 | obj.en_queue(99)
62 | obj.en_queue(111)
63 | obj.de_queue()
64 | obj.de_queue()
65 | obj.en_queue(111)
66 | obj.de_queue()
67 | obj.de_queue()
68 | obj.de_queue()
69 |
--------------------------------------------------------------------------------
/Source_Code/python_kodlar/fesil7/fesil7_dynamic_circular_queue.py:
--------------------------------------------------------------------------------
1 | class DynamicCircularQueue:
2 |
3 | def __init__(self, limit=5):
4 | self.que = []
5 | self.limit = limit
6 | self.front = -1 # Ön
7 | self.rear = -1 # Arxa, son
8 |
9 | def is_full(self):
10 | if self.front == 0 and self.rear == (self.limit - 1):
11 | return True
12 | elif self.front == self.rear + 1:
13 | return True
14 | return False
15 |
16 | def is_empty(self):
17 | return self.front == -1
18 |
19 | def en_queue(self, data):
20 | if self.is_full():
21 | print("Növbə doludur, ikiqat artırıram...")
22 | self.limit = self.limit * 2
23 | else:
24 | if self.front == -1:
25 | self.front = 0
26 | # REAR-i artırırıq, irəli çəkirik.
27 | self.rear = (self.rear + 1) % self.limit
28 | self.que.append(data)
29 | print("EnQueue-dən sonra, növbə, ", self.que)
30 | print("FRONT -> ", self.front)
31 | print("REAR -> ", self.rear)
32 |
33 | def de_queue(self):
34 | if self.is_empty():
35 | print("Növbə boşdur...")
36 | else:
37 | # Python list element silindikdən sonra, listi özü yenidən indexlədiyi üçün.
38 | # Həmişə pop(0) olaraq çağırmaq lazımdır. pop(self.front) düzgün nəticə vermir.
39 | data = self.que.pop(0)
40 | # Əgər bərabərdilərsə o zaman cəmi 1 elementi var, bu səbəbdən sildikdən sonra resetləyirik.
41 | if self.front == self.rear:
42 | self.front = -1
43 | self.rear = -1
44 | else:
45 | # FRONT-u artırırıq, irəli çəkirik.
46 | self.front = (self.front + 1) % self.limit
47 |
48 | print("Silinən element - ", data)
49 | print("FRONT -> ", self.front)
50 | print("REAR -> ", self.rear)
51 |
52 | def size(self):
53 | return len(self.que)
54 |
55 |
56 | if __name__ == "__main__":
57 | obj = DynamicCircularQueue(limit=5)
58 | obj.en_queue(56)
59 | obj.en_queue(44)
60 | obj.en_queue(85)
61 | obj.en_queue(66)
62 | obj.en_queue(99)
63 | obj.en_queue(111)
64 | obj.en_queue(222)
65 |
66 |
--------------------------------------------------------------------------------
/Source_Code/python_kodlar/fesil7/fesil7_linked_list_queue.py:
--------------------------------------------------------------------------------
1 | class Node:
2 | # konstruktor
3 | def __init__(self, data=None, next_node=None):
4 | self.data = data
5 | self.next_node = next_node
6 |
7 | # node-un data field-ini mənimsətmək üçün metod
8 | def set_data(self, data):
9 | self.data = data
10 |
11 | # node-un data field-ini almaq üçün metod
12 | def get_data(self):
13 | return self.data
14 |
15 | # node-un növbəti field-ini mənimsətmək üçün metod
16 | def set_next_node(self, next_node):
17 | self.next_node = next_node
18 |
19 | # node-un növbəti field-ini almaq üçün metod
20 | def get_next_node(self):
21 | return self.next_node
22 |
23 | # əgər bir node sonrakına point edirsə, true qaytar
24 | def has_next(self):
25 | return self.next_node is not None
26 |
27 |
28 | class LinkedListQueue:
29 | def __init__(self, head=None):
30 | self.front = None
31 | self.rear = None
32 | self.head = head
33 |
34 | def size(self):
35 | current = self.head
36 | count = 0
37 | while current:
38 | count += 1
39 | current = current.get_next_node()
40 | return count
41 |
42 | def en_queue(self, data):
43 | # Listin sonuna node daxil edirik
44 | print("Növbəyə daxil edirik...")
45 | new_node = Node()
46 | new_node.set_data(data)
47 | if self.size() == 0:
48 | self.head = new_node
49 | # List-də heç bir element olmadığı üçün front və rear eyni yerdədirlər.
50 | self.front = self.head
51 | self.rear = self.front
52 | else:
53 | current = self.head
54 | while current.get_next_node() is not None:
55 | current = current.get_next_node()
56 |
57 | current.set_next_node(new_node)
58 | # Rear-i burda sonuncu node edirik
59 | self.rear = current.get_next_node()
60 |
61 | def de_queue(self):
62 | # Listin əvvəlindən node silirik
63 | if self.size() == 0:
64 | print("Növbə boşdur...")
65 | else:
66 | print("Növbədən çıxardırıq...")
67 | # Müvəqqəti node
68 | temp = self.head
69 | # Head node-u əvvəlki head-dən sonrakı node-a mənimsədirik.
70 | # Bununla da faktiki olaraq, əvvəlki head-i arxada qoyuruq.
71 | self.head = self.head.get_next_node()
72 | # Həmçinin front-u da yeni head-ə bərabər edirik, faktiki olaraq irəli sürüşdürürük.
73 | self.front = self.head
74 | # Müvəqqəti node-u silirik.
75 | del(temp)
76 |
77 | def queue_rear(self):
78 | if self.rear is None:
79 | print("Növbə boşdur...")
80 | else:
81 | return self.rear.get_data()
82 |
83 | def queue_front(self):
84 | if self.front is None:
85 | print("Növbə boşdur...")
86 | else:
87 | return self.front.get_data()
88 |
89 |
90 | if __name__ == "__main__":
91 | obj = LinkedListQueue()
92 | obj.en_queue(56)
93 | obj.en_queue(44)
94 | obj.en_queue(85)
95 | obj.en_queue(66)
96 | print("Növbənin uzunluğu: ", obj.size())
97 | obj.en_queue(99)
98 | obj.en_queue(111)
99 | obj.de_queue()
100 | obj.de_queue()
101 | obj.en_queue(222)
102 | print("Növbənin uzunluğu: ", obj.size())
103 | print("Növbənin ilk elementi: ", obj.queue_front())
104 | print("Növbənin son elementi: ", obj.queue_rear())
--------------------------------------------------------------------------------
/Source_Code/python_kodlar/fesil8/__init__.py:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/AzePUG/Data_Structures_Algo_Python/3e3892c32699f8b398339558bc1a3a22a8aa85be/Source_Code/python_kodlar/fesil8/__init__.py
--------------------------------------------------------------------------------
/Source_Code/python_kodlar/fesil8/fesil8_binary_tree_node.py:
--------------------------------------------------------------------------------
1 | # Kod mənbəsi: https://gist.github.com/thinkphp/1450738
2 | # Lakin, iterativ üsullar və bəzi dəyişikliklər edildi.
3 |
4 | from queue import Queue
5 |
6 | class Node:
7 | def __init__(self, data):
8 | # root node
9 | self.data = data
10 | # Sol övlad(left child)
11 | self.left = None
12 | # Sağ övlad(right child)
13 | self.right = None
14 |
15 | def get_data(self):
16 | return self.data
17 |
18 | def get_left_child(self):
19 | return self.left
20 |
21 | def get_right_child(self):
22 | return self.right
23 |
24 |
25 |
26 | class BinaryTree:
27 |
28 | def __init__(self):
29 | self.root = None
30 |
31 | def create_tree(self, val):
32 | # Ağacın özünü burda yaradırıq.
33 | if self.root is None:
34 | # Birinci elementi root element edirik
35 | self.root = Node(data=val)
36 |
37 | else:
38 | # Root-u hazırkı node edirik
39 | current = self.root
40 |
41 | while True:
42 | # Əgər verilmiş qiymət hal-hazırkı qiymətdən kiçikdirsə,
43 | # Onu sol node edirik
44 | if val < current.data:
45 | if current.left:
46 | current = current.left
47 | else:
48 | current.left = Node(data=val)
49 | break;
50 | # Əgər verilmiş qiymət hal-hazırkı qiymətdən böyükdürsə,
51 | # Onu sağ node edirik
52 | elif val > current.data:
53 | if current.right:
54 | current = current.right
55 | else:
56 | current.right = Node(data=val)
57 | else:
58 | break
59 |
60 |
61 | def preorder_traversal_recursive(self, node):
62 | if node is not None:
63 | # Birinci root node print olunur(ziyarət olunur)
64 | print(node.data, end=" ")
65 | self.preorder_traversal_recursive(node.left)
66 | self.preorder_traversal_recursive(node.right)
67 |
68 |
69 | def preorder_traversal_iterative(self, node):
70 | if node is not None:
71 | stack = []
72 | # root node-u listə daxil edirik.
73 | stack.append(node)
74 | while stack:
75 | node = stack.pop()
76 | print(node.data, end=" ")
77 | if node.right:
78 | stack.append(node.right)
79 | # Ən sonda node.left-i append edirik çünki bizə lazımdı sol node-u pop() etsin.
80 | if node.left:
81 | stack.append(node.left)
82 |
83 | def inorder_traversal_recursive(self, node):
84 | if node is not None:
85 | # Birinci sol altağac emal olunur(ziyarət olunur)
86 | self.inorder_traversal_recursive(node.left)
87 | print(node.data, end=" ")
88 | self.inorder_traversal_recursive(node.right)
89 |
90 | def inorder_traversal_iterative(self, node):
91 | if node is not None:
92 | stack = []
93 | while stack or node:
94 | if node:
95 | stack.append(node)
96 | node = node.left
97 | else:
98 | node = stack.pop()
99 | print(node.data, end=" ")
100 | node = node.right
101 |
102 | def postorder_traversal_recursive(self, node):
103 | if node is not None:
104 | self.postorder_traversal_recursive(node.left)
105 | self.postorder_traversal_recursive(node.right)
106 | print(node.data, end=" ")
107 |
108 | def postorder_traversal_iterative(self, root):
109 | solution = []
110 | used = set()
111 | stack = []
112 |
113 | if root != None:
114 | stack.append(root)
115 |
116 | while len(stack) > 0:
117 | node = stack.pop()
118 |
119 | if node in used:
120 | solution.append(node.data)
121 | else:
122 | used.add(node)
123 | stack.append(node)
124 | if node.right != None:
125 | stack.append(node.right)
126 | if node.left != None:
127 | stack.append(node.left)
128 | return solution
129 |
130 | def level_order_traversal(self, node):
131 | if node is not None:
132 | result = []
133 | q = Queue()
134 | q.put(node) # root node-u daxil edirik.
135 |
136 | while not q.empty():
137 | node = q.get() # Dequeue FIFO
138 | result.append(node.get_data())
139 |
140 | if node.left is not None:
141 | q.put(node.left)
142 |
143 | if node.right is not None:
144 | q.put(node.right)
145 |
146 | return result
147 |
148 |
149 |
150 | if __name__ == "__main__":
151 | tree = BinaryTree()
152 | arr = [8, 3, 1, 6, 4, 7, 10, 14, 13]
153 | for i in arr:
154 | tree.create_tree(i)
155 |
156 | print("PreOrder Recursive Traversal - ", end="")
157 | tree.preorder_traversal_recursive(tree.root)
158 | print("")
159 | print("PreOrder Iterative Traversal - ", end="")
160 | tree.preorder_traversal_iterative(tree.root)
161 | print("")
162 | print("InOrder Recursive Traversal - ", end="")
163 | tree.inorder_traversal_recursive(tree.root)
164 | print("")
165 | print("InOrder Iterative Traversal - ", end="")
166 | tree.inorder_traversal_iterative(tree.root)
167 | print("")
168 | print("PostOrder Recursive Traversal - ", end="")
169 | tree.postorder_traversal_recursive(tree.root)
170 | print("")
171 | print("PostOrder Iterative Traversal - ", end="")
172 | print(tree.postorder_traversal_iterative(tree.root))
173 | print("LevelOrder Traversal - ", end="")
174 | print(tree.level_order_traversal(tree.root))
--------------------------------------------------------------------------------
/Source_Code/python_kodlar/fesil9/__init__.py:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/AzePUG/Data_Structures_Algo_Python/3e3892c32699f8b398339558bc1a3a22a8aa85be/Source_Code/python_kodlar/fesil9/__init__.py
--------------------------------------------------------------------------------
/Source_Code/python_kodlar/fesil9/fesil9_problems_solutions.py:
--------------------------------------------------------------------------------
1 | from queue import Queue
2 |
3 | class Node:
4 | def __init__(self, data):
5 | # root node
6 | self.data = data
7 | # Sol övlad(left child)
8 | self.left = None
9 | # Sağ övlad(right child)
10 | self.right = None
11 |
12 | def get_data(self):
13 | return self.data
14 |
15 | def get_left_child(self):
16 | return self.left
17 |
18 | def get_right_child(self):
19 | return self.right
20 |
21 |
22 | class BinaryTreeExercises:
23 |
24 | def __init__(self):
25 | self.root = None
26 | self.max_data = 0.0
27 |
28 | def create_tree(self, val):
29 | # Ağacın özünü burda yaradırıq.
30 | if self.root is None:
31 | # Birinci elementi root element edirik
32 | self.root = Node(data=val)
33 |
34 | else:
35 | # Root-u hazırkı node edirik
36 | current = self.root
37 |
38 | while True:
39 | # Əgər verilmiş qiymət hal-hazırkı qiymətdən kiçikdirsə,
40 | # Onu sol node edirik
41 | if val < current.data:
42 | if current.left:
43 | current = current.left
44 | else:
45 | current.left = Node(data=val)
46 | break;
47 | # Əgər verilmiş qiymət hal-hazırkı qiymətdən böyükdürsə,
48 | # Onu sağ node edirik
49 | elif val > current.data:
50 | if current.right:
51 | current = current.right
52 | else:
53 | current.right = Node(data=val)
54 | else:
55 | break
56 |
57 | def find_max_recursive(self, node):
58 | if not node:
59 | return self.max_data
60 |
61 | if node.get_data() > self.max_data:
62 | self.max_data = node.get_data()
63 |
64 | self.find_max_recursive(node.left)
65 | self.find_max_recursive(node.right)
66 |
67 | return self.max_data
68 |
69 | def find_max_level_order_traversal(self, node):
70 | if node is not None:
71 | q = Queue()
72 | q.put(node) # root node-u daxil edirik.
73 |
74 | while not q.empty():
75 | node = q.get() # Dequeue FIFO
76 | # növbədən çıxartdıqdan sonra müqayisə edirik.
77 | if node.get_data() > self.max_data:
78 | self.max_data = node.get_data()
79 |
80 | if node.left is not None:
81 | q.put(node.left)
82 |
83 | if node.right is not None:
84 | q.put(node.right)
85 |
86 | return self.max_data
87 |
88 | def find_data_recursive(self, node, data):
89 | if node is None:
90 | return 0
91 |
92 | if node.get_data() == data:
93 | return 1
94 | elif data < node.get_data():
95 | return self.find_data_recursive(node.left, data)
96 | else:
97 | return self.find_data_recursive(node.right, data)
98 |
99 | def find_data_level_order_traversal(self, node, data):
100 | if node is not None:
101 | q = Queue()
102 | q.put(node) # root node-u daxil edirik.
103 |
104 | while not q.empty():
105 | node = q.get() # Dequeue FIFO
106 | # növbədən çıxartdıqdan sonra yoxlayırıq.
107 | if node.get_data() == data:
108 | return 1
109 | if node.left is not None:
110 | q.put(node.left)
111 |
112 | if node.right is not None:
113 | q.put(node.right)
114 | # 0 qayıdırsa, deməli data Ağacda yoxdur.
115 | return 0
116 |
117 | def insert_in_binary_using_tree_level_order(self, node, data):
118 | new_node = Node(data)
119 | if node is None:
120 | node = new_node # Ağac boşdursa, yeni node-u root node edirik.
121 | return node
122 |
123 | q = Queue()
124 | q.put(node) # Root node-u növbəyə daxil edirik.
125 |
126 | while not q.empty():
127 | node = q.get() # Dequeue FIFO
128 | # növbədən çıxartdıqdan sonra yoxlayırıq.
129 | if node.get_data() == data:
130 | return "Already in tree"
131 | if node.left is not None:
132 | q.put(node.left)
133 | else:
134 | # Əgər hal-hazırkı node-un datasından kiçikdirsə
135 | if new_node.get_data() < node.get_data():
136 | node.left = new_node
137 | return "Inserted as left node"
138 |
139 | if node.right is not None:
140 | q.put(node.right)
141 | else:
142 | # Əgər hal-hazırkı node-un datasından böyükdürsə
143 | if new_node.get_data() > node.get_data():
144 | node.right = new_node
145 | return "Inserted as right node"
146 |
147 | def find_tree_size_recursive(self, node):
148 | if node is None:
149 | return 0
150 |
151 | return self.find_tree_size_recursive(node.left) + self.find_tree_size_recursive(node.right) + 1
152 |
153 | def find_tree_size_iterative(self, node):
154 | if node is None:
155 | return 0
156 |
157 | q = Queue()
158 | q.put(node) # Root node-u növbəyə daxil edirik.
159 | count = 0
160 |
161 | while not q.empty():
162 | node = q.get()
163 | count = count + 1
164 | if node.left is not None:
165 | q.put(node.left)
166 | if node.right is not None:
167 | q.put(node.right)
168 |
169 | return count
170 |
171 | def level_order_traversal_in_reverse(self, node):
172 | if node is None:
173 | return 0
174 |
175 | q = Queue()
176 | s = [] # LIFO üçün istifadə edəcəyimiz list
177 | q.put(node) # root node-u daxil edirik.
178 |
179 | while not q.empty():
180 | node = q.get() # Dequeue FIFO
181 | s.append(node.get_data()) # LIFO
182 |
183 | if node.left is not None:
184 | q.put(node.left)
185 |
186 | if node.right is not None:
187 | q.put(node.right)
188 |
189 | while(s):
190 | print(s.pop(), end=' ')
191 |
192 | def delete_binary_tree(self, node):
193 | if node is None:
194 | return
195 |
196 | self.delete_binary_tree(node.left)
197 | self.delete_binary_tree(node.right)
198 | node.data = None
199 | node.left = None
200 | node.right = None
201 | self.root = None
202 |
203 | def max_depth_recursive(self, node):
204 | if node is None:
205 | return 0
206 | return max(self.max_depth_recursive(node.left), self.max_depth_recursive(node.right)) + 1
207 |
208 | def max_depth_iterative(self, node):
209 | if node is None:
210 | return 0
211 | q_list = []
212 | q_list.append([node, 1])
213 | while q_list:
214 | node, depth = q_list.pop() # Buna Python-da unpacking deyilir.
215 | if node.left is not None:
216 | q_list.append([node.left, depth + 1]) # Əgər sol node varsa, onu listə əlavə et və depth-i artır.
217 | if node.right is not None:
218 | q_list.append([node.right, depth + 1]) # Əgər sağ node varsa, onu listə əlavə et və depth-i artır.
219 |
220 | return depth
221 |
222 | def deepest_node(self, node):
223 | if node is None:
224 | return 0
225 |
226 | q = Queue()
227 | q.put(node)
228 |
229 | while not q.empty():
230 | node = q.get()
231 | if node.left is not None:
232 | q.put(node.left)
233 | if node.right is not None:
234 | q.put(node.right)
235 |
236 | return node.get_data()
237 |
238 | def number_of_leafs_iterative(self, node):
239 |
240 | if node is None:
241 | return 0
242 |
243 | q = Queue()
244 | q.put(node)
245 | count = 0 # sayğac
246 |
247 | while not q.empty():
248 | node = q.get()
249 | if (node.left is None) and (node.right is None):
250 | count = count + 1
251 | else:
252 | if node.left is not None:
253 | q.put(node.left)
254 | if node.right is not None:
255 | q.put(node.right)
256 |
257 | return count
258 |
259 | def number_of_full_nodes_iterative(self, node):
260 |
261 | if node is None:
262 | return 0
263 |
264 | q = Queue()
265 | q.put(node)
266 | count = 0 # sayğac
267 |
268 | while not q.empty():
269 | node = q.get()
270 | if (node.left is not None) and (node.right is not None):
271 | count = count + 1
272 | else:
273 | if node.left is not None:
274 | q.put(node.left)
275 | if node.right is not None:
276 | q.put(node.right)
277 |
278 | return count
279 |
280 | def number_of_half_nodes_iterative(self, node):
281 | if node is None:
282 | return 0
283 |
284 | q = Queue()
285 | q.put(node)
286 | count = 0 # sayğac
287 |
288 | while not q.empty():
289 | node = q.get()
290 | if (node.left is None and node.right is not None) or \
291 | (node.right is None and node.left is not None):
292 | count = count + 1
293 | else:
294 | if node.left is not None:
295 | q.put(node.left)
296 | if node.right is not None:
297 | q.put(node.right)
298 |
299 | return count
300 |
301 | def check_tree_structures_to_be_same(self, node1, node2):
302 | # Əgər ağacların nə sol nə də sağ altağacları qalıbsa və data-lar da bərabərdirsə o zaman True qaytarırır.
303 | if (not node1.left) and \
304 | (not node1.right) and \
305 | (not node2.left) and \
306 | (not node2.right) and node1.data == node2.data:
307 | return True
308 | # Aşağıda isə görürük ki, iki ağac bir-biri ilə fərqlənir
309 | if (node1.data != node2.data) or (node1.left and not node2.left) or \
310 | (not node1.left and node2.left) or (node1.right and not node2.right) or \
311 | (not node1.right and node2.right):
312 | return False
313 |
314 | left = self.check_tree_structures_to_be_same(node1.left, node2.left) if node1.left and node2.left else True
315 | right = self.check_tree_structures_to_be_same(node1.right, node2.right) if node1.right and node2.right else True
316 |
317 | return left and right
318 |
319 | def diameter_of_tree(self, node):
320 | if node is None:
321 | return 0
322 |
323 | # sol və sağ altağacların hündürlüyünü tapırıq.
324 | lheight = self.max_depth_recursive(node.left)
325 | rheight = self.max_depth_recursive(node.right)
326 |
327 | # sol və sağ altağacların diametrlərini tapırıq.
328 | ldiameter = self.diameter_of_tree(node.left)
329 | rdiameter = self.diameter_of_tree(node.right)
330 |
331 | # Ağac üçün max dəyəri qaytarmalıyı.
332 | # sol və sağ altağacın diametrləri arasından maksimumu tapırıq.
333 | # sol və sağ altağacın hündürlüklərini cəmləyib üzərinə 1 gəlirik.
334 | # Yuxarıdakı ikisində maksimumu tapırıq.
335 | return max(lheight + rheight + 1, max(ldiameter, rdiameter))
336 |
337 |
338 |
339 | if __name__ == "__main__":
340 | tree = BinaryTreeExercises()
341 | arr = [8, 3, 1, 6, 4, 7, 10, 14, 13]
342 | for i in arr:
343 | tree.create_tree(i)
344 | print("find_max_recursive() -> ", end='')
345 | print(tree.find_max_recursive(tree.root))
346 | print("find_max_level_order_traversal() -> ", end='')
347 | print(tree.find_max_level_order_traversal(tree.root))
348 | print("find_data_recursive() search 88 -> ", end='')
349 | print(tree.find_data_recursive(tree.root, 88))
350 | print("find_data_recursive() search 14 -> ", end='')
351 | print(tree.find_data_recursive(tree.root, 14))
352 | print("find_data_level_order_traversal() search 88 -> ", end='')
353 | print(tree.find_data_level_order_traversal(tree.root, 88))
354 | print("find_data_level_order_traversal() search 14 -> ", end='')
355 | print(tree.find_data_level_order_traversal(tree.root, 14))
356 | print("insert_in_binary_using_tree_level_order(tree.root, 21) -> ", end='')
357 | print(tree.insert_in_binary_using_tree_level_order(tree.root, 21))
358 | print("find_tree_size_recursive() -> ", end='')
359 | print(tree.find_tree_size_recursive(tree.root))
360 | print("find_tree_size_iterative() -> ", end='')
361 | print(tree.find_tree_size_iterative(tree.root))
362 | print("level_order_traversal_in_reverse() -> ", end='')
363 | tree.level_order_traversal_in_reverse(tree.root)
364 | # print("")
365 | # print("delete_binary_tree() -> ")
366 | # tree.delete_binary_tree(tree.root)
367 | # print("find_tree_size_recursive() -> ", end='')
368 | # print(tree.find_tree_size_recursive(tree.root))
369 | # print("find_tree_size_iterative() -> ", end='')
370 | # print(tree.find_tree_size_iterative(tree.root))
371 | print("")
372 | print("max_depth_recursive() -> ", end='')
373 | print(tree.max_depth_recursive(tree.root))
374 | print("max_depth_iterative() -> ", end='')
375 | print(tree.max_depth_iterative(tree.root))
376 | print("deepest_node() -> ", end='')
377 | print(tree.deepest_node(tree.root))
378 | print("number_of_leafs_iterative() -> ", end = '')
379 | print(tree.number_of_leafs_iterative(tree.root))
380 | print("number_of_full_nodes_iterative() -> ", end='')
381 | print(tree.number_of_full_nodes_iterative(tree.root))
382 | print("number_of_half_nodes_iterative() -> ", end='')
383 | print(tree.number_of_half_nodes_iterative(tree.root))
384 | tree2 = BinaryTreeExercises()
385 | arr2 = [8, 3, 1, 6, 4, 7, 10, 14, 13]
386 | for i in arr2:
387 | tree2.create_tree(i)
388 | print("insert_in_binary_using_tree_level_order(tree2.root, 21) -> ", end='')
389 | print(tree.insert_in_binary_using_tree_level_order(tree2.root, 21))
390 | print("check_tree_structures_to_be_same(tree.root, tree2.root) -> ", end='')
391 | print(tree.check_tree_structures_to_be_same(tree.root, tree2.root))
392 | print("insert_in_binary_using_tree_level_order(tree2.root, 88) -> ", end='')
393 | print(tree.insert_in_binary_using_tree_level_order(tree2.root, 88))
394 | print("check_tree_structures_to_be_same(tree.root, tree2.root) -> ", end='')
395 | print(tree.check_tree_structures_to_be_same(tree.root, tree2.root))
396 | print("diameter_of_tree() -> ", end='')
397 | print(tree.diameter_of_tree(tree.root))
398 |
399 |
400 |
--------------------------------------------------------------------------------
/Source_Code/resources/Misc_files/AzePUG_Algo_Data_Structures_book.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/AzePUG/Data_Structures_Algo_Python/3e3892c32699f8b398339558bc1a3a22a8aa85be/Source_Code/resources/Misc_files/AzePUG_Algo_Data_Structures_book.png
--------------------------------------------------------------------------------
/Source_Code/resources/fesil11/fesil11_delete_node_with_2_childs_resized.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/AzePUG/Data_Structures_Algo_Python/3e3892c32699f8b398339558bc1a3a22a8aa85be/Source_Code/resources/fesil11/fesil11_delete_node_with_2_childs_resized.png
--------------------------------------------------------------------------------
/Source_Code/resources/fesil11/fesil11_deleting_leaf_node_bst_resized.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/AzePUG/Data_Structures_Algo_Python/3e3892c32699f8b398339558bc1a3a22a8aa85be/Source_Code/resources/fesil11/fesil11_deleting_leaf_node_bst_resized.png
--------------------------------------------------------------------------------
/Source_Code/resources/fesil11/fesil11_deleting_node_with_one_child_resized.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/AzePUG/Data_Structures_Algo_Python/3e3892c32699f8b398339558bc1a3a22a8aa85be/Source_Code/resources/fesil11/fesil11_deleting_node_with_one_child_resized.png
--------------------------------------------------------------------------------
/Source_Code/resources/fesil11/fesil11_inserting_bst.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/AzePUG/Data_Structures_Algo_Python/3e3892c32699f8b398339558bc1a3a22a8aa85be/Source_Code/resources/fesil11/fesil11_inserting_bst.png
--------------------------------------------------------------------------------
/Source_Code/resources/fesil12/fesil12_sum_of_n_1.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/AzePUG/Data_Structures_Algo_Python/3e3892c32699f8b398339558bc1a3a22a8aa85be/Source_Code/resources/fesil12/fesil12_sum_of_n_1.png
--------------------------------------------------------------------------------
/Source_Code/resources/fesil12/fesil12_sum_of_n_numbers.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/AzePUG/Data_Structures_Algo_Python/3e3892c32699f8b398339558bc1a3a22a8aa85be/Source_Code/resources/fesil12/fesil12_sum_of_n_numbers.png
--------------------------------------------------------------------------------
/Source_Code/resources/fesil2/fesil2_2.5.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/AzePUG/Data_Structures_Algo_Python/3e3892c32699f8b398339558bc1a3a22a8aa85be/Source_Code/resources/fesil2/fesil2_2.5.png
--------------------------------------------------------------------------------
/Source_Code/resources/fesil3/delete_first_node_singly_linked_list.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/AzePUG/Data_Structures_Algo_Python/3e3892c32699f8b398339558bc1a3a22a8aa85be/Source_Code/resources/fesil3/delete_first_node_singly_linked_list.png
--------------------------------------------------------------------------------
/Source_Code/resources/fesil3/delete_from_end_singly_list_1.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/AzePUG/Data_Structures_Algo_Python/3e3892c32699f8b398339558bc1a3a22a8aa85be/Source_Code/resources/fesil3/delete_from_end_singly_list_1.png
--------------------------------------------------------------------------------
/Source_Code/resources/fesil3/delete_from_end_singly_list_2.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/AzePUG/Data_Structures_Algo_Python/3e3892c32699f8b398339558bc1a3a22a8aa85be/Source_Code/resources/fesil3/delete_from_end_singly_list_2.png
--------------------------------------------------------------------------------
/Source_Code/resources/fesil3/delete_from_end_singly_list_3.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/AzePUG/Data_Structures_Algo_Python/3e3892c32699f8b398339558bc1a3a22a8aa85be/Source_Code/resources/fesil3/delete_from_end_singly_list_3.png
--------------------------------------------------------------------------------
/Source_Code/resources/fesil3/delete_intermediate_node_singly_linked_list_1.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/AzePUG/Data_Structures_Algo_Python/3e3892c32699f8b398339558bc1a3a22a8aa85be/Source_Code/resources/fesil3/delete_intermediate_node_singly_linked_list_1.png
--------------------------------------------------------------------------------
/Source_Code/resources/fesil3/delete_intermediate_node_singly_linked_list_2.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/AzePUG/Data_Structures_Algo_Python/3e3892c32699f8b398339558bc1a3a22a8aa85be/Source_Code/resources/fesil3/delete_intermediate_node_singly_linked_list_2.png
--------------------------------------------------------------------------------
/Source_Code/resources/fesil3/delete_last_node_singly_list_result.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/AzePUG/Data_Structures_Algo_Python/3e3892c32699f8b398339558bc1a3a22a8aa85be/Source_Code/resources/fesil3/delete_last_node_singly_list_result.png
--------------------------------------------------------------------------------
/Source_Code/resources/fesil3/deleting_first_node_singly_linked_list_1.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/AzePUG/Data_Structures_Algo_Python/3e3892c32699f8b398339558bc1a3a22a8aa85be/Source_Code/resources/fesil3/deleting_first_node_singly_linked_list_1.png
--------------------------------------------------------------------------------
/Source_Code/resources/fesil3/deleting_first_node_singly_linked_list_2.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/AzePUG/Data_Structures_Algo_Python/3e3892c32699f8b398339558bc1a3a22a8aa85be/Source_Code/resources/fesil3/deleting_first_node_singly_linked_list_2.png
--------------------------------------------------------------------------------
/Source_Code/resources/fesil3/diff_python_c++.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/AzePUG/Data_Structures_Algo_Python/3e3892c32699f8b398339558bc1a3a22a8aa85be/Source_Code/resources/fesil3/diff_python_c++.png
--------------------------------------------------------------------------------
/Source_Code/resources/fesil3/insert_at_beginning_linked_list_1.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/AzePUG/Data_Structures_Algo_Python/3e3892c32699f8b398339558bc1a3a22a8aa85be/Source_Code/resources/fesil3/insert_at_beginning_linked_list_1.png
--------------------------------------------------------------------------------
/Source_Code/resources/fesil3/insert_at_beginning_linked_list_2.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/AzePUG/Data_Structures_Algo_Python/3e3892c32699f8b398339558bc1a3a22a8aa85be/Source_Code/resources/fesil3/insert_at_beginning_linked_list_2.png
--------------------------------------------------------------------------------
/Source_Code/resources/fesil3/insert_at_position_singly_linked_list_visualize.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/AzePUG/Data_Structures_Algo_Python/3e3892c32699f8b398339558bc1a3a22a8aa85be/Source_Code/resources/fesil3/insert_at_position_singly_linked_list_visualize.png
--------------------------------------------------------------------------------
/Source_Code/resources/fesil3/insert_at_the_end_singly_linked_list_1.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/AzePUG/Data_Structures_Algo_Python/3e3892c32699f8b398339558bc1a3a22a8aa85be/Source_Code/resources/fesil3/insert_at_the_end_singly_linked_list_1.png
--------------------------------------------------------------------------------
/Source_Code/resources/fesil3/insert_at_the_end_singly_linked_list_2.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/AzePUG/Data_Structures_Algo_Python/3e3892c32699f8b398339558bc1a3a22a8aa85be/Source_Code/resources/fesil3/insert_at_the_end_singly_linked_list_2.png
--------------------------------------------------------------------------------
/Source_Code/resources/fesil3/insert_into_middle_singly_linked_list_1.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/AzePUG/Data_Structures_Algo_Python/3e3892c32699f8b398339558bc1a3a22a8aa85be/Source_Code/resources/fesil3/insert_into_middle_singly_linked_list_1.png
--------------------------------------------------------------------------------
/Source_Code/resources/fesil3/insert_into_middle_singly_linked_list_2.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/AzePUG/Data_Structures_Algo_Python/3e3892c32699f8b398339558bc1a3a22a8aa85be/Source_Code/resources/fesil3/insert_into_middle_singly_linked_list_2.png
--------------------------------------------------------------------------------
/Source_Code/resources/fesil3/linked_list_basic_show.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/AzePUG/Data_Structures_Algo_Python/3e3892c32699f8b398339558bc1a3a22a8aa85be/Source_Code/resources/fesil3/linked_list_basic_show.png
--------------------------------------------------------------------------------
/Source_Code/resources/fesil3/linked_list_insert_visual.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/AzePUG/Data_Structures_Algo_Python/3e3892c32699f8b398339558bc1a3a22a8aa85be/Source_Code/resources/fesil3/linked_list_insert_visual.png
--------------------------------------------------------------------------------
/Source_Code/resources/fesil3/singly_linked_list_insert_at_end.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/AzePUG/Data_Structures_Algo_Python/3e3892c32699f8b398339558bc1a3a22a8aa85be/Source_Code/resources/fesil3/singly_linked_list_insert_at_end.png
--------------------------------------------------------------------------------
/Source_Code/resources/fesil4/doubly_linked_list_delete_first_node_1.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/AzePUG/Data_Structures_Algo_Python/3e3892c32699f8b398339558bc1a3a22a8aa85be/Source_Code/resources/fesil4/doubly_linked_list_delete_first_node_1.png
--------------------------------------------------------------------------------
/Source_Code/resources/fesil4/doubly_linked_list_delete_first_node_2.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/AzePUG/Data_Structures_Algo_Python/3e3892c32699f8b398339558bc1a3a22a8aa85be/Source_Code/resources/fesil4/doubly_linked_list_delete_first_node_2.png
--------------------------------------------------------------------------------
/Source_Code/resources/fesil4/doubly_linked_list_insert_at_beginning_1.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/AzePUG/Data_Structures_Algo_Python/3e3892c32699f8b398339558bc1a3a22a8aa85be/Source_Code/resources/fesil4/doubly_linked_list_insert_at_beginning_1.png
--------------------------------------------------------------------------------
/Source_Code/resources/fesil4/doubly_linked_list_insert_at_beginning_2.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/AzePUG/Data_Structures_Algo_Python/3e3892c32699f8b398339558bc1a3a22a8aa85be/Source_Code/resources/fesil4/doubly_linked_list_insert_at_beginning_2.png
--------------------------------------------------------------------------------
/Source_Code/resources/fesil4/doubly_linked_list_insert_at_end_1.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/AzePUG/Data_Structures_Algo_Python/3e3892c32699f8b398339558bc1a3a22a8aa85be/Source_Code/resources/fesil4/doubly_linked_list_insert_at_end_1.png
--------------------------------------------------------------------------------
/Source_Code/resources/fesil4/doubly_linked_list_insert_at_end_2.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/AzePUG/Data_Structures_Algo_Python/3e3892c32699f8b398339558bc1a3a22a8aa85be/Source_Code/resources/fesil4/doubly_linked_list_insert_at_end_2.png
--------------------------------------------------------------------------------
/Source_Code/resources/fesil4/doubly_linked_list_insert_at_end_3.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/AzePUG/Data_Structures_Algo_Python/3e3892c32699f8b398339558bc1a3a22a8aa85be/Source_Code/resources/fesil4/doubly_linked_list_insert_at_end_3.png
--------------------------------------------------------------------------------
/Source_Code/resources/fesil4/doubly_linked_list_insert_at_middle_1.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/AzePUG/Data_Structures_Algo_Python/3e3892c32699f8b398339558bc1a3a22a8aa85be/Source_Code/resources/fesil4/doubly_linked_list_insert_at_middle_1.png
--------------------------------------------------------------------------------
/Source_Code/resources/fesil4/doubly_linked_list_insert_at_middle_2.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/AzePUG/Data_Structures_Algo_Python/3e3892c32699f8b398339558bc1a3a22a8aa85be/Source_Code/resources/fesil4/doubly_linked_list_insert_at_middle_2.png
--------------------------------------------------------------------------------
/Source_Code/resources/fesil4/doubly_linked_list_visualization_1.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/AzePUG/Data_Structures_Algo_Python/3e3892c32699f8b398339558bc1a3a22a8aa85be/Source_Code/resources/fesil4/doubly_linked_list_visualization_1.png
--------------------------------------------------------------------------------
/Source_Code/resources/fesil5/circular_linked_list_1.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/AzePUG/Data_Structures_Algo_Python/3e3892c32699f8b398339558bc1a3a22a8aa85be/Source_Code/resources/fesil5/circular_linked_list_1.png
--------------------------------------------------------------------------------
/Source_Code/resources/fesil5/circular_linked_list_2.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/AzePUG/Data_Structures_Algo_Python/3e3892c32699f8b398339558bc1a3a22a8aa85be/Source_Code/resources/fesil5/circular_linked_list_2.png
--------------------------------------------------------------------------------
/Source_Code/resources/fesil5/circular_linked_list_3.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/AzePUG/Data_Structures_Algo_Python/3e3892c32699f8b398339558bc1a3a22a8aa85be/Source_Code/resources/fesil5/circular_linked_list_3.png
--------------------------------------------------------------------------------
/Source_Code/resources/fesil5/circular_linked_list_4.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/AzePUG/Data_Structures_Algo_Python/3e3892c32699f8b398339558bc1a3a22a8aa85be/Source_Code/resources/fesil5/circular_linked_list_4.png
--------------------------------------------------------------------------------
/Source_Code/resources/fesil5/circular_linked_list_5.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/AzePUG/Data_Structures_Algo_Python/3e3892c32699f8b398339558bc1a3a22a8aa85be/Source_Code/resources/fesil5/circular_linked_list_5.png
--------------------------------------------------------------------------------
/Source_Code/resources/fesil5/circular_linked_list_6.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/AzePUG/Data_Structures_Algo_Python/3e3892c32699f8b398339558bc1a3a22a8aa85be/Source_Code/resources/fesil5/circular_linked_list_6.png
--------------------------------------------------------------------------------
/Source_Code/resources/fesil7/fesil7_array_queue.jpg:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/AzePUG/Data_Structures_Algo_Python/3e3892c32699f8b398339558bc1a3a22a8aa85be/Source_Code/resources/fesil7/fesil7_array_queue.jpg
--------------------------------------------------------------------------------
/Source_Code/resources/fesil7/fesil7_array_queue_2.jpg:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/AzePUG/Data_Structures_Algo_Python/3e3892c32699f8b398339558bc1a3a22a8aa85be/Source_Code/resources/fesil7/fesil7_array_queue_2.jpg
--------------------------------------------------------------------------------
/Source_Code/resources/fesil7/fesil7_circular-increment.jpg:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/AzePUG/Data_Structures_Algo_Python/3e3892c32699f8b398339558bc1a3a22a8aa85be/Source_Code/resources/fesil7/fesil7_circular-increment.jpg
--------------------------------------------------------------------------------
/Source_Code/resources/fesil7/fesil7_circular_queue_program.jpg:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/AzePUG/Data_Structures_Algo_Python/3e3892c32699f8b398339558bc1a3a22a8aa85be/Source_Code/resources/fesil7/fesil7_circular_queue_program.jpg
--------------------------------------------------------------------------------
/Source_Code/resources/fesil8/fesil8_binary_tree_graphic.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/AzePUG/Data_Structures_Algo_Python/3e3892c32699f8b398339558bc1a3a22a8aa85be/Source_Code/resources/fesil8/fesil8_binary_tree_graphic.png
--------------------------------------------------------------------------------
/Source_Code/resources/fesil8/fesil8_data_binary_tree.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/AzePUG/Data_Structures_Algo_Python/3e3892c32699f8b398339558bc1a3a22a8aa85be/Source_Code/resources/fesil8/fesil8_data_binary_tree.png
--------------------------------------------------------------------------------
/Source_Code/resources/fesil8/fesil8_skew_tree.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/AzePUG/Data_Structures_Algo_Python/3e3892c32699f8b398339558bc1a3a22a8aa85be/Source_Code/resources/fesil8/fesil8_skew_tree.png
--------------------------------------------------------------------------------
/Source_Code/resources/fesil8/fesil8_tree_data_structure.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/AzePUG/Data_Structures_Algo_Python/3e3892c32699f8b398339558bc1a3a22a8aa85be/Source_Code/resources/fesil8/fesil8_tree_data_structure.png
--------------------------------------------------------------------------------
/book/0.1.Terminlər.md:
--------------------------------------------------------------------------------
1 | # Kitabda istifadə olunan terminlər və qısaltmalar
2 |
3 | ## Input
4 | - Məlumatların kompüterə daxil edilməsi
5 | - İnformasiya girişi
6 | - Proqramın giriş məlumatları
7 | - Giriş
8 | - Daxiletmə
9 |
10 | ## ADT (Abstract Data Types)
11 | - Mücərrəd məlumat tipləri
12 |
13 | ## Backtrack
14 | - Eyni yolla geri dönüş
15 | - Əks trayektoriya
16 |
17 | ## Debug (Debugging)
18 | - Dibaq. Sazlama, Qaydayaqoyma. Xətanı tapmaq üçün proqramın başlanğıc kodunun yoxlanılması. Xətaların aradan götürülməsi
19 |
20 | ## Thread
21 | - "Zəncir", axın, silsilə. Əmrlərin (və ya başqa yazıların) ardıcıllığı
22 |
23 | ## Node
24 | - Qovşaq. Düyün.
25 |
26 | ## String
27 | - Sətir. Simvollar ardıcıllığı
28 |
--------------------------------------------------------------------------------
/book/0.Haqqında.md:
--------------------------------------------------------------------------------
1 | # Kitaba tələbat haqqında
2 | Əziz oxucu, `Data strukturları və Alqoritmlər` mövzusu, hər bir proqramçının hər şeydən öncə qavramalı, üzərində ciddi düşünməli olduğu mövzudur. Bu mövzuda, öz dilimizdə mənbə azlığı qənaətinə gəldim və bu işi görməyə qərara verdim.
3 |
4 | # Nəyə görə Python?
5 | Son illərdə bu dilin reytinqlərdə birinci yerdə durması, çox geniş istifadəçi kütləsinin olması, Open Source, öyrənilməsi asan, çox geniş kitabxanalara sahib olması və s. kitabdakı nümunələrin Python-da olması fikrimi qətiləşdirdi.
6 |
7 | Bundan əlavə Python müxtəlif sahələrdə istifadə edilir. Veb proqramlaşdırma üçün zəngin imkanlara malik kitabxanalarının olması onu veb proqramçılar arasında sevilən dil edir, statistika, riyazi hesablamalar üçün kitabxanalar və sürətli işləməsi onu Data Science və Maşın öyrənməsi sahəsində istifadə edilən ən populyar dil etmişdir.
8 |
9 | Təsadüfi deyil ki, Python bir çox ölkələrdə eləcə də Azərbaycanda məktəb proqramına salınmışdır. Dünyanın bir çox universitetlərində də ilk dil olaraq Python öyrədilir.
10 |
11 | Python-a vaxt və sərmayə ayırmaq faydalıdır. Belə ki, bu dil, günümüzün yeni peşələrinə daha tez uyğunlaşmanıza yardımçı olacaq.
12 |
13 | # Müəllif haqqında
14 | Kitabı Github-da Azerbaijan Python User Group adı altında yazmağıma səbəb budur ki, bu kitab, Open Source, hər tənqidə açıq, havayı və yayıla bilən olmalıdır. Dolayısı ilə, ilkin məqsəd kitaba Azərbaycandan hər kəsin əlavə və dəyişikliklər göndərməsi yönündədir.
15 | Lakin, əsas təşəbbüs, [AzePUG](https://www.facebook.com/groups/python.az/) və [AzeMUG](https://www.facebook.com/groups/mysql.azerbaijan/) qrup lideri [Şəhriyar Rzayevə](https://www.linkedin.com/in/shahriyar-rzayev/) məxsusdur.
16 |
17 | Müəllifin bəzi nailiyyətləri haqqında:
18 |
19 | **Hazırkı vəzifəsi:**
20 | Galera Cluster(Finland) - QA Engineer
21 |
22 | **Sertifikat və nailiyyətlər:**
23 |
24 | Red Hat Certified System Administrator - [RHCSA](https://www.redhat.com/rhtapps/certification/badge/verify/RS4ZT3YPLAFRBTBNKH2BOJAXJAAEQU3CUPSQX2KSDXT6RW46LQ37ULE25V3KCXMMFRIX6PMBNQZGA4U5NQYTCNA62RUWOCM34WWBUYQ%3D/)
25 |
26 | OCP MySQL 5.0 Database Administrator - [OCP](http://rzayevsehriyar.files.wordpress.com/2012/02/20130306_235027.jpg)
27 |
28 | Oracle ACE Associate award - [MySQL ACE](https://apex.oracle.com/pls/apex/f?p=19297:4:::NO:4:P4_ID:15420)
29 |
30 | MySQL 5.7 Community Contributor Award Program 2015(see my name first) -> [MySQL CCAP](https://blogs.oracle.com/mysql/mysql-57-community-contributor-award-program-2015)
31 |
32 | **Community fəaliyyətlərindən:**
33 |
34 | Texniki rəsmi bloq -
35 | [mysql.az](https://mysql.az/)
36 | [azepug.az](https://azepug.az/)
37 |
38 |
39 | Azərbaycanın ekspertlər topluluğunun aktiv üzvü - [technet.az](http://www.technet.az/user/shahriyar/)
40 |
41 | Qatıldığı konfranslar-
42 | 
43 |
44 | **Open Source fəaliyyətlərindən:**
45 |
46 | MySQL-AutoXtrabackup commandline tool - [autoxtrabackup](https://github.com/ShahriyarR/MySQL-AutoXtraBackup)
47 |
48 | MySQL-ə report etdiyi BUG-lar - [MySQL bugs](https://bugs.mysql.com/search.php?cmd=display&status=all&mine=0&reporter=6786791&begin=120)
49 |
50 |
51 | # Kitab kimlər üçün nəzərdə tutulub?
52 | İlk öncə, onu vurğulamaq lazımdır ki, bu kitab Python dilinin özünü öyrətmir. Yəni, proqramlaşdırma dili kitabı deyildir. Kitabdakı alqoritmik məsələləri həll etmək üçün yazılan kod nümunələri Python-dadır. Dolayısı ilə, bu kitab üçün sizin Python dili biliyiniz olmalıdır.
53 |
54 | # Hansı Python?
55 | Kitabdakı kod nümunələri Ubuntu 17.04 əməliyyat sistemində Python-un 3.5 versiyasında test edilib, yerləşdirilib. Lakin, verilmiş nümunələr Python 3.5 olan istənilən əməliyyat sistemində işləməlidir.
56 |
57 | # Kitab necə yazılır?
58 | Kitabın strukturu və əsas ideyaları üçün mənbə kitab:
59 |
60 | [Data Structure and Algorithmic Thinking with Python: Data Structure and Algorithmic](https://www.amazon.com/Data-Structure-Algorithmic-Thinking-Python/dp/8192107590/)
61 |
62 | Nəzərə alsaq ki, verilmiş kitabda kod, açıqlamalar və digər izahlarda səhvlər var, mən bunların hamısını düzəltməyə çalışıram.
63 | Bizim kitabdakı, şəkillərin hamısını özüm hazırlayıram, kod parçalarını Pythonic və sadə yazmağa çalışıram.
64 | Java kod parçalarını isə community üzvləri PR(pull request) şəklində göndərirlər və mən də təsdiq edirəm.
65 | Java kod parçalarını müəllif özü şəxsən test etmir.
66 | Əlavə köməkçi mənbələr:
67 |
68 | [Essential Algorithms](https://www.amazon.com/Essential-Algorithms-Rod-Stephens-dp-1118612108/dp/1118612108/)
69 |
70 | # Kitaba kömək və səhvlərin aşkarlanması
71 | Qeyd edək ki, müəllif Azərbaycan dili qrammatikasına bacardığı qədər riayət etməyə çalışır, lakin sözsüz ki, qrammatik səhvlər olur və olmalıdır.
72 | # Kitabda aşkarlanmış qrammatik və məntiqi səhvləri necə bildirmək olar?
73 | Yuxarıda da qeyd etdiyimiz kimi, kitab Open Source layihə kimi Github-da yerləşdirilmişdir -
74 | [Kitab üçün repo](https://github.com/AzePUG/Data_Structures_Algo_Python)
75 |
76 | Aşkarlanan səhvləri, githubda issue kimi bildirə bilərsiniz. Digər bir faydalı iş o olardı ki, aşkarladığınız səhvləri düzəldib layihəmizə Pull Request göndərəsiniz. Bu minvalla kitab öz mükəmməlliyinə çatar.
77 |
--------------------------------------------------------------------------------
/book/10.Düzülü_İkili_Ağaclar_Threaded_Binary_Tree_Traversals.md:
--------------------------------------------------------------------------------
1 | Bundan əvvəlki Ağaclar bəhsində biz, ağacı qət etməyin *preorder*, *inorder* və *postorder* metodlarını araşdırdıq, bəzi tapşırıqlar da yerinə yetirdik. Mövzunun izahını verdiyimiz kod nümunələrində, gördük ki, bu üsullarda köməkçi *stack* və *queue* data strukturlarından istifadə etdik. Bu fəsildə yeni qət etmə alqoritmlərindən danışacıq. Bu alqoritmlərdə *stack* və *queue* istifadə olunmur. Bu növ qət etmə alqoritmlərinə *threaded binary tree traversals* və yaxud *stack\queue less traversals* deyilir.
2 |
3 | **Adi qət etmə üsullarındakı bəzi çətinliklər**
4 |
5 | * İstifadə olunan əlavə data strukturlarına əlavə yer tələb olunur(yığın və növbə üçün).
6 | * İkili ağacda pointerlərin çox hissəsi NULL-dur. n node-lu ikili ağacın n+1 qədər NULL pointerləri var və bunlar istifadə olunmur.
7 | * Ardıcıl, davamçı node-u tapmaq daha çətindir.
8 |
9 | **Threaded Binary Trees**
10 | Yuxarıda sadalanan bu və ya digər problemləri həll etmək məqsədilə bəzi lazımı məlumatları NULL pointer-lərdə(göstərici, işarətçi) saxlaya bilərik. Əvvəlki qət etmə üsullarını xatırlasaq, görərik ki, biz stack və queue-dən hazırkı pozisiyanı saxlamaq məqsədilə istifadə edirik ki, sol altağacdan sonra sağ altağaca keçə bilək.
11 | Əgər bu kimi faydalı məlumatları NULL pointer-lərdə saxlasaq, bu zaman əlavə stack və queue-dən istifadəyə ehtiyac qalmayacaq.
12 |
13 | Bu məlumatı NULL pointer-lərdə saxlayan İkili ağac növünə isə Düzülü İkili Ağac(Threaded Binary Tree) deyilir.
14 | Bu o deməkdir ki, məsələn, preorder traversal üçün, NULL sol pointer, preorder sələfi(predecessor), NULL sağ pointer isə xələfi(successor) özündə saxlayır. Bu xüsusi pointer-lərə isə thread-lər deyilir.
15 |
16 | **Düzülü İkili Ağacların təsnifatı**
17 | Məlumatın, sol, sağ və ya hər iki NULL pointerlərdə saxlanmasından asılı olaraq:
18 | * Sol Düzülü İkili Ağac(left threaded binary tree)
19 | * Sağ Düzülü İkili Ağac(right threaded binary tree)
20 | * Tam Düzülü İkili Ağac(fully threaded binary tree or threaded binary tree)
21 |
22 | **Düzülü İkili Ağacların növləri**
23 | Yuxarıdalı müzakirəmizə əsasən, Threaded Binary Tree üçün aşağıdakı təsvir növlərimiz var:
24 | * PreOrder Threaded Binary Tree: NULL sol pointer PreOrder sələf, NULL sağ pointer isə PreOrder xələf məlumatı saxlayır.
25 | * İnOrder Threaded Binary Tree: NULL sol pointer İnOrder sələf, NULL sağ pointer isə İnOrder xələf məlumatı saxlayır.
26 | * PostOrder Threaded Binary Tree: NULL sol pointer PostOrder sələf, NULL sağ pointer isə PostOrder xələf məlumatı saxlayır.
27 |
--------------------------------------------------------------------------------
/book/11.İkili_Axtarış_Ağacları_Binary_Search_Trees.md:
--------------------------------------------------------------------------------
1 | # Binary Search Trees (İkili Axtarış Ağacları)
2 |
3 | ## Nəyə görə BST-lər?
4 |
5 | Əvvəlki fəsillərdə bir neçə ağac növündən bəhs etdik və onların heç birində node-da saxlanılan məlumatlar üçün məhdudiyyət yox idi. Nəticə etibari ilə, ağacda element axtaranda həm sol altağacı, həm də sağ altağacı yoxlayırdıq ki, bu da ən pis halda `O(n)` vaxt mürəkkəbliyi verirdi.
6 |
7 | Bu fəsildə ikili ağacın digər variantına baxacıq: İkili Axtarış Ağacları(BSTs). Adından da göründüyü kimi, bu ağac məhz axtarış üçündür. Artıq BST-də biz node-larda saxlanılan data(məlumat)-ya müəyyən tələblər qoyuruq ki, nə saxlanıla bilər nə yox. Bunun nəticəsində biz ən pis halda `O(logn)` mürəkkəblik əldə etmiş oluruq.
8 |
9 | ## İkili Axtarış Ağacının xüsüsiyyəti
10 |
11 | BST-lər üçün bir şeyi yadda saxlamaq lazımdır ki, bütün sol altağacın elementləri root-dan kiçik, bütün sağ altağacın elementləri isə root-dan böyük olmalıdır. Onu da qeyd edim ki, bu tələb bütün node-lar tərəfindən ödənilir. Yəni həm sol, həmdə sağ altağacların özləri də BST olmalıdırlar.
12 |
13 | ## BST declaration - BST elan olunması, təyin edilməsi.
14 |
15 | Adi ikili ağacın və ikili axtarış ağacının elan olunması(deklarasiyası) arasında heç bir fərq yoxdur. Fərqlilik, yalnız saxlanılan məlumatdadır(data), struktur eynidir. Lakin, hər ehtimala qarşı, biz tipin(class) adını BSTNode olaraq qeyd edək:
16 | > Bütün kodlara buradan baxa bilərsiniz: [fesil11_binary_search_tree.py](../Source_Code/python_kodlar/fesil11/fesil11_binary_search_tree.py)
17 |
18 | ```python
19 | class BSTNode:
20 | def __init__(self, data):
21 | # root node
22 | self.data = data
23 | # Sol övlad(left child)
24 | self.left = None
25 | # Sağ övlad(right child)
26 | self.right = None
27 |
28 | def get_data(self):
29 | return self.data
30 |
31 | def get_left_child(self):
32 | return self.left
33 |
34 | def get_right_child(self):
35 | return self.right
36 | ```
37 |
38 | ## BST-lər üzərində əməliyyatlar
39 |
40 | **Əsas əməliyyatlar**
41 |
42 | * İkili axtarış ağacında minimum, maximum və axtarılan elementin tapılması.
43 | * BST-yə element daxil etmək.
44 | * BST-dən element silmək.
45 |
46 | **Əlavə əməliyyatlar**
47 |
48 | * Verilmiş ağacın BST olub olmamasını yoxlamaq.
49 | * BST-nin elementlərini sıralamaq və s.
50 |
51 |
52 | ## BST-lər üçün vacib qeydlərə nəzər salaq
53 |
54 | * Root node, hər zaman sol altağac data-sı və sağ altağac data-sı arasında yerləşdiyi üçün, BST üzərində inorder traversal sıralanmış list qaytarır.
55 | * Təsəvvür edin ki, biz hər hansı elementi BST-də axtarırıq və sol altağac root node, bizim axtardığımız elementdən kiçikdirsə, o zaman sol tərəfə getməyin bir mənası qalmır. Burdan belə bir nəticə çıxır ki, biz ikili axtarış ağacında, ya sol, ya da sağ altağacda axtarış aparırıq. Heç vaxt hər iki tərəfdə axtarmırıq. Məhz bu səbəbdən BST-də axtarış sürətlidir.
56 |
57 | ## BST-də element axtarmaq
58 |
59 | BST-də axtarış, kifayət qədər sadə və aydın əməliyyatdır. Root node-la başlayırıq, sola və ya sağa doğru gedirik.
60 | Əgər axtardığımız element, node-un datasından kiçikdirsə sol altağacda axtarırıq, əksinə böyükdürs, sağ tərəfdə axtarırıq.
61 | Əgər axtarılan məlumat tapılmadısa, o zaman NULL(None) qaytarırıq. Bu məqsədlə yazmış olduğumuz sadə koda baxaq:
62 |
63 | ```python
64 | def find_element(self, root, data):
65 | # Axtarışa root-dan başlayırıq.
66 | current_node = root
67 | while current_node is not None and data != current_node.get_data():
68 | # Yoxlayırıq ki, axtardığımız element hal-hazırkı node data-sından böyükdür ya yox.
69 | # Əgər böyükdürsə, o zaman sağ altağaca keçirik.
70 | if data > current_node.get_data():
71 | current_node = current_node.get_right_child()
72 | # Əgər kiçikdirsə, o zaman sol altağaca keçirik.
73 | else:
74 | current_node = current_node.get_left_child()
75 | return current_node
76 | ```
77 |
78 | İnteraktiv Python mode-dan istifadə edərək, kodumuzu test edək. İlk öncə, kod olan qovluğa keçirik `Data_Structures_Algo_Python/Source_Code/python_kodlar/fesil11`. Daha sonra:
79 |
80 | ```python
81 | $ python3
82 | Python 3.6.6 (default, Sep 12 2018, 18:26:19)
83 | [GCC 8.0.1 20180414 (experimental) [trunk revision 259383]] on linux
84 | Type "help", "copyright", "credits" or "license" for more information.
85 |
86 | >>> import fesil11_binary_search_tree
87 | >>> tree = fesil11_binary_search_tree.BSTree()
88 | >>> arr = [8, 3, 1, 6, 4, 7, 10, 14, 13]
89 | >>> for i in arr:
90 | ... tree.create_tree(i)
91 | ...
92 |
93 | >>> print(tree.find_element(tree.root, 11))
94 | None
95 |
96 | >>> print(tree.find_element(tree.root, 10))
97 |
98 | ```
99 |
100 | 11 bizim ağacda yoxdur, bu səbəbdən None qaytardıq, 10 isə var və müvafiq obyekti return etmişik.
101 |
102 | ## BST-də minimum elementi tapmaq:
103 |
104 | Sol child-ı olmayan ən sol node özündə ağacın ən kiçik, minimum elementini saxlayır.
105 | Yəni ikili axtarış ağacında, minimal data-lı node, sol altağacda yerləşir və həmin node-un sol node-u yoxdur.
106 |
107 | 
108 |
109 | Aşağıdakı kod, rekursiv üsulla yazılıb:
110 |
111 | ```python
112 | # Rekursiv üsul
113 | def find_min_element(self, root):
114 | current_node = root
115 | if current_node.get_left_child() == None:
116 | return current_node
117 | else:
118 | return find_min_element(current_node.get_left_child())
119 | ```
120 | Vaxt mürəkkəbliyi: Ən pis halda `O(n)`
121 | Yer mürəkkəbliyi: `O(n)` rekursiv stack yarandığı üçün.
122 |
123 | Bu kodu bir də rekursiv olmayan üsulla yazmağa çalışaq:
124 |
125 | ```python
126 | # Rekursiv olmayan üsul
127 | def find_min_element_non_recursive(self, root):
128 | current_node = root
129 | if current_node is None:
130 | return None
131 | while current_node.get_left_child() is not None:
132 | current_node = current_node.get_left_child()
133 | return current_node
134 | ```
135 |
136 | Vaxt mürəkkəbliyi: `O(n)`
137 | Yer mürəkkəbliyi: `O(1)`
138 |
139 | Kodumuzu bu dəfə python faylı run edərək test edək:
140 |
141 | ```python
142 | $ python3 fesil11_binary_search_tree.py
143 | Mövcud elementi axtarmaq -> <__main__.BSTNode object at 0x7f8a50f7df28>
144 | Mövcud olmayan elementi axtarmaq -> None
145 | Minimal elementi axtarmaq rekursiya -> 1
146 | Minimal elementi axtarmaq rekursiv olmayan -> 1
147 | ```
148 |
149 | ## BST-də maximum elementi tapmaq
150 |
151 | Minimum elementi biz sol altağacda axtarırdıqsa, maximum elementi biz təbii ki, sağ altağacda axtaracıq.
152 | Maximum element sağ node-u olmayan, ən sağdakı node-da saxlanılır.
153 |
154 |
155 | Rekursiv üsulla biz kodu belə yaza bilərik:
156 |
157 | ```python
158 | # Rekursiv üsul
159 | def find_max_element(self, root):
160 | current_node = root
161 | if current_node.get_right_child() == None:
162 | return current_node
163 | else:
164 | return self.find_max_element(current_node.get_right_child())
165 | ```
166 | Vaxt mürəkkəbliyi: Ən pis halda `O(n)`
167 | Yer mürəkkəbliyi: `O(n)` rekursiv stack yarandığı üçün.
168 |
169 | Başqa cür də belə yaza bilərik:
170 |
171 | ```python
172 | # Rekursiv olmayan üsul
173 | def find_max_element_non_recursive(self, root):
174 | current_node = root
175 | if current_node is None:
176 | return None
177 | while current_node.get_right_child() is not None:
178 | current_node = current_node.get_right_child()
179 | return current_node
180 | ```
181 |
182 | Vaxt mürəkkəbliyi: `O(n)`
183 | Yer mürəkkəbliyi: `O(1)`
184 |
185 | Kodumuzu test edirik:
186 |
187 | ```python
188 | $ python3 fesil11_binary_search_tree.py
189 | Mövcud elementi axtarmaq -> <__main__.BSTNode object at 0x7f831e8a5fd0>
190 | Mövcud olmayan elementi axtarmaq -> None
191 | Minimal elementi axtarmaq rekursiya -> 1
192 | Minimal elementi axtarmaq rekursiv olmayan -> 1
193 | Maximal elementi axtarmaq rekursiv -> 14
194 | Maximal elementi axtarmaq rekursiv olmayan -> 14
195 | ```
196 |
197 | ## Inorder Predecessor and Successor
198 |
199 | Bunu birbaşa tərcümə etdikdə, simmetrik xələf və sələfin tapılması kimi edə bilərik. Lakin, ondansa elə inorder predcessor və successor deyək.
200 | İkili axtarış ağacındakı X node-un 2 child-ı varsa, onun inorder predecessor-u sol altağacdakı maximum elementdir(yəni ən sağ node-da qalan), inorder successor isə sağ altağacdakı minimum elementdir(yəni ən sol node-da qalan):
201 |
202 | 
203 |
204 | Kod nümunələrinə baxaq:
205 |
206 | ```python
207 | def predecessor_bst(self, root):
208 | # Inorder Predecessor
209 | temp = None
210 | if root.get_left_child():
211 | temp = root.get_left_child()
212 | while temp.get_right_child():
213 | temp = temp.get_right_child()
214 | return temp
215 |
216 |
217 | def successor_bst(self, root):
218 | # Inorder Successor
219 | temp = None
220 | if root.get_right_child():
221 | temp = root.get_right_child()
222 | while temp.get_left_child():
223 | temp = temp.get_left_child()
224 | return temp
225 | ```
226 |
227 | Nəticələrə baxaq:
228 |
229 | ```python
230 | $ python3 fesil11_binary_search_tree.py
231 | Mövcud elementi axtarmaq -> <__main__.BSTNode object at 0x7fb58514e160>
232 | Mövcud olmayan elementi axtarmaq -> None
233 | Minimal elementi axtarmaq rekursiya -> 1
234 | Minimal elementi axtarmaq rekursiv olmayan -> 1
235 | Maximal elementi axtarmaq rekursiv -> 14
236 | Maximal elementi axtarmaq rekursiv olmayan -> 14
237 | Inorder Predecessor -> 7
238 | Inorder Successor -> 10
239 | ```
240 |
241 | ## İkili ağaca element daxil etmək
242 |
243 | BST-yə data əlavə etmək üçün, ilk öncə onu hara daxil edəcəyimizi tapmalıyıq. Biz daxil edəcəyimiz yeri, `find_element` funksiyasını yazarkən istifadə etdiyimiz məntiqlə tapırıq. Daxil edəcəyimiz yeri axtararkən, əgər data artıq ağacda varsa, sadəcə onu görməzdən gəlirik(ignore) və ağacı olduğu kimi geri qaytarırıq(return).
244 |
245 | Məsələn aşağıdakı BST-yə 5 elementini daxil etmək istədikdə, ilk öncə yoxlamalıyıq ki, bu element root node-dan(6) böyükdür, ya kiçik.
246 | Kiçik olduğu üçün sol altağaca düşürük. Sol altağacda 2 node-u üçün də eyni şeyi yoxlayırıq, 5 2-dən böyük olduğu üçün bu dəfə sağ altağaca düşürük. Burada görürük ki, 5 4-dən böyükdür və 4-un sağ altağacı yoxdur dolayısı ilə 5 üçün ən ideal yer elə buradır:
247 |
248 | 
249 |
250 | Bu məqsədlə kodumuzu yazaq:
251 |
252 | ```python
253 | def insert_node(self, root, node_data):
254 | if root is None:
255 | root = BSTNode(data=node_data)
256 | else:
257 | if node_data < root.get_data():
258 | if root.get_left_child() is None:
259 | root.left = BSTNode(data=node_data)
260 | else:
261 | self.insert_node(root.get_left_child(), node_data)
262 | else:
263 | if root.get_right_child() is None:
264 | root.right = BSTNode(data=node_data)
265 | else:
266 | self.insert_node(root.get_right_child(), node_data)
267 | return node_data
268 | ```
269 |
270 | ```python
271 | $ python3 fesil11_binary_search_tree.py
272 | Mövcud elementi axtarmaq -> <__main__.BSTNode object at 0x7fcb2f6cb1d0>
273 | Mövcud olmayan elementi axtarmaq -> None
274 | Minimal elementi axtarmaq rekursiya -> 1
275 | Minimal elementi axtarmaq rekursiv olmayan -> 1
276 | Maximal elementi axtarmaq rekursiv -> 14
277 | Maximal elementi axtarmaq rekursiv olmayan -> 14
278 | Inorder Predecessor -> 7
279 | Inorder Successor -> 10
280 | BST-yə element daxil edirik -> 25
281 | Maximal elementi axtarmaq rekursiv -> 25
282 | ```
283 |
284 | ## BST-dən element silmək
285 |
286 | İkili axtarış ağacından element silmək, digər əməliyyatlara nəzərən mürəkkəbdir. Məsələnin, çətin tərəfi ondan ibarətdir ki, sildiyimiz node leaf node olmaya bilər. Yəni ondan sonra da node-lar ola bilər. Elementi silmək üçün, təbii ki, yuxarıda olduğu kimi həmin elementi axtarıb tapmaq lazımdır. Silinəcək elementi tapdıqdan sonra, aşağıdakı işlərdən birini görüb həmin elementi silə bilərik.
287 |
288 | * Əgər tapılan node leaf node-dursa, yəni onun child-ı yoxdursa, bu zaman məsələ sadədir. Sadəcə həmin node-un parent-inin point etdiyi yeri(silinməli olan node-a baxır hal-hazırda) NULL(None)-a yönləndiririk:
289 |
290 | 
291 |
292 | * Əgər tapılan(silinməli olan) node-in bir child-ı varsa, bu zaman onun silinməli olan node-un parent-ini onun child-ına yönləndirmək lazımdır:
293 |
294 | 
295 |
296 | * Əgər silinməli olan node-un 2 child-ı varsa, o zaman ümumi qəbul olunmuş qayda budur ki, silinən elementi onun özünün sol altağacındakı maximum elementlə əvəzləmək lazımdır. Qeyd etməliyik ki, sol alt ağacdakı ən böyük elementin sağ node-u yoxdur.
297 | Daha aydın başa düşmək üçün aşağıdakı şəklə diqqət edək:
298 |
299 | 
300 |
301 | Gördüyümüz kimi, silinməli olan element 8-dir. Bu zaman 8-ə nəzərən sol altağacdakı maximum element 7 tapılır və 8-lə əvəzlənir.
302 |
303 | Kod nümunəmizə nəzər yetirək:
304 |
--------------------------------------------------------------------------------
/book/12.Sıralama_Sorting.md:
--------------------------------------------------------------------------------
1 | # Sıralama(sorting)
2 |
3 | ## Sıralama nədir?
4 | Sıralama verilmiş elementləri müəyyən qanunauyğunluğa əsasən(azalan və ya çoxalan) düzən(sahmana salan) alqoritmdir.
5 |
6 | ## Sıralama nəyə görə vacibdir?
7 | Sıralama, kompüter elmlərində vacib bölmələrdən birini təşkil edir. Bu sahədə bir çox araşdırmalar aparılıb.
8 | Sıralama, bir çox hallarda, verilmiş problemin mürəkkəbliyini azalda bilir. Məlumat bazası(database) alqoritmləri və axtarışlar üçün geniş istifadə olunur.
9 |
10 | # Sıralama alqoritmlərinin sinifləndirilməsi
11 | Aşağıdakı parametrlərə əsasən biz, sıralama alqoritmlərini sinifləndirə bilirik.
12 |
13 | ## Müqayisə sayına görə
14 | Bu üsul zamanı, sıralama alqoritmləri müqayisələrin sayına əsasən sinifləndirilir. Müqayisə əsaslı sıralama alqoritmləri üçün ən yaxşı hal - `O(nlogn)` ən pis hal isə `O(n^2)` hesab olunur. Müqayisə əsaslı(comparison-based) sıralama alqoritmləri listin elementlərini müqayisə etməklə emal edirlər.
15 |
16 | Bu mövzumuzda müqayisəli olmayan(non-comparison və ya linear) sıralama alqoritmlərindən də bəhs edəcəyik. Misal olaraq, Counting sort, Bucket sort və Redix sort göstərə bilərik.
17 |
18 | ## Yerdəyişmə sayına görə
19 | Bu zaman, sıralama alqoritmləri edilən yerdəyişmələrin sayına əsasən kateqoriyalaşdırılır. Buna bəzən inversiyalar da deyilir(swaps, inversions).
20 |
21 | ## Yaddaş istifadəsinə görə
22 | Bəzi sıralama alqoritmləri "yerində" (in-place) sayılır və müvəqqəti sıralama üçün `O(1)` və ya `O(logn)` yaddaş tələb edirlər.
23 |
24 | ## Rekursiyaya görə
25 | Sıralama alqoritmləri ya rekursiv(quick sort) ya da rekursiv olmayan(non-recursive) üsuldan istifadə edə bilərlər və ya hər ikisindən(merge sort).
26 |
27 | # Bubble sort
28 | Ən sadə sıralama alqoritmi Bubble sort-dur. Elementləri birincidən axırıncıya qədər gəzir, hər bir cütü müqayisə edir və lazım olduqda, yerdəyişmə edir. Bubble sort, yerdəyişməyə ehtiyac qalmayana qədər öz iterasiyasına(irəliləyişinə) davam edir.
29 |
30 | Gəlin bu sıralama alqoritminin koduna baxaq:
31 | Mənbə: [InteractivePython](http://interactivepython.org/runestone/static/pythonds/SortSearch/TheBubbleSort.html)
32 |
33 | ```python
34 | def bubbleSort(alist):
35 | for passnum in range(len(alist)-1,0,-1):
36 | for i in range(passnum):
37 | if alist[i]>alist[i+1]:
38 | temp = alist[i]
39 | alist[i] = alist[i+1]
40 | alist[i+1] = temp
41 | ```
42 |
43 | Elə təsəvvür edək ki, `n` elementli bir listimiz var, bu zaman üzərindən keçib müqayisə aparmalı olduğumuz `n - 1` qədər cütümüz var. Birinci iterasiyadan(qarşılıqlı müqayisələrdən) sonra ən böyük ədəd ən sona yerləşir. Bundan sonra bizdə `n - 1` elementli list qalır ki, bu zaman da `n - 2` qədər cütləri müqayisə etmək lazımdır. Bu proses son iki element müqayisə olunduqdan sonra(müqayisə olunmalı listdə 2 element qalır, 1 cüt) bitir. Birinci addımda(əvvəldən axıra kimi, cütlərin müqayisəsi nəzərdə tutulur) müqayisə olunası cütlərin sayı `n - 1`-dir, ikinci addımda `n - 2`-dir, üçüncü addımda `n - 3`-dür və ən axırıncı addımda, müqayisə olunan cütlərin sayı 1-dir. Bu da bizə `1 .. n - 1` sayda elementdə ibarət olan ədədi silsiləni verir.
44 | Yadımızdadır ki, ilk n elementin cəmi düsturu:
45 | 
46 |
47 | Bizə isə ilk `n - 1` elementin cəmi lazım olduğu üçün, düsturda n-i, n - 1-lə əvəzləmək lazımdır:
48 | 
49 |
50 | Bu düstura əsasən alqoritmin mürəkkəbliyinin, `O(n^2)` olduğu aşkarlanır.
51 |
--------------------------------------------------------------------------------
/book/2.Recursion_and_Backtracking.md:
--------------------------------------------------------------------------------
1 | # Rekursiya və Backtracking
2 |
3 | > Hal-hazırda backtracking sözünə öz dilimizdə tam uyğun tərcümə tapa bilmədim.
4 | > Aşağıdakılar rus və türk dillərindən götürülüb:
5 | > sarfınazar etmək, vazgeçmek, sözünden dönmek, aynı yoldan geri dönmek.
6 | > отход, отступление, отступать
7 |
8 | ## 2.1 Giriş
9 | Bu fəsildə, ən vacib məsələlərdən olan, *rekursiya* və onunla əlaqəli *backtracking* mövzularına toxunacağıq.
10 |
11 | ## 2.2 Rekursiya nədir?
12 | Öz-özünü çağıran istənilən funksiya *rekursiv* funksiya adlanır. Problemin rekursiv həlli dedikdə, o başa düşülür ki, problem hər dəfə daha kiçik problemlə işləmək üçün özünün surətini(kopyasını) çağırır. Bu kimi, rekursiv addımlar, digər rekursiv çağırışlarla nəticələnə bilər.
13 |
14 | Yəni, hər funksiya müəyyən problem üçün özü özünü bir neçə və yaxud sonsuz sayda çağıra bilər. Bu isə bizi vadar edir ki, rekursiv əməliyyatları(rekursiya) müəyyən şərtlər altında mütləq sonlandıraq, tamamlandıraq. Digər sözlə, rekursiya sonlu olmalıdır.
15 |
16 | Daha sadə, izah etməli olsaq, rekursiya, bir problemin, daha kiçik, xırda hissələrlə, öz-özünü çağırması ardıcıllığıdır. Bir şeyi yadda saxlamaq lazımdır ki, bu ardıcıllıqlar, son nəticədə əsas problemə əsaslanmalıdırlar.
17 |
18 | ## 2.3 Nəyə görə rekursiya?
19 | Rekursiya riyaziyyatdan götürülmüş faydalı bir üsuldur(metoddur). Rekursiv üsulla yazılmış kod, ümumən iterativ üsulla yazılan koddan daha qısa, kodu yazmaq daha sadə olur.
20 |
21 | Rekursiya, bir-birinin oxşarı olan alt tapşırıqlar kimi göstərilə bilən daha böyük tapşırıqların həllində daha faydalı olur. Məsələn, sıralama, axtarış, kəsişmə problemlərinin, adətən, sadə rekursiv həlləri mövcuddur.
22 |
23 | ## 2.4 Rekursiv funksiyanın formatı haqqında
24 | Rekursiv funksiya, bir tapşırığı icra etmək üçün, öz-özünü çağırmaqla alt tapşırıqları(subtasks) həll edir. Bir neçə icradan sonra, elə vəziyyət gəlir ki, alt tapşırıq daha öz-özünü çağırmadan icra olunur. Bu hala, əsas hal(base case) deyilir, harda ki, funksiya artıq rekursiv olmur(does not recur). Bundan öncəki, alt tapşırığı həll etmək üçün, funksiyanın öz-özünü çağırması hallarına isə kursiv hal deyilir(cursive case).
25 |
26 | Rekursiv funksiyaya misal olaraq, faktorialın hesablanmasını göstərə bilərik. n! faktorial 1-dən n-ə qədər olan bütün ədədlərin hasilidir. Faktorialın açıqlaması:
27 |
28 | ```
29 | n! = 1, əgər n = 0
30 | n! = n * (n - 1)!, əgər n > 0
31 | ```
32 | Bu tərif(açıqlama) çox asanlıqla, rekursiv üsulla göstərilə də bilər. Daha sadə desək, tapşırığın özü n!-dir, lakin bir də bunun alt tapşırığı var (n - 1)!.
33 | Rekursiv hal üçün, n-nin 1-dən böyük hallarında, (n - 1)!-in dəyərini aşkarlamaq üçün funksiya öz-özünü çağırır və həmin qiyməti n-ə vurur.
34 |
35 | Bu funksiyanın əsas halı(base case) n 0 və ya 1 olanda qeydə alınır. Bu zaman heç bir rekursiv çağrışa ehtiyac olmadan 1 qaytarılır.
36 |
37 | Rekursiv üsulla faktorial hesablayan kod:
38 |
39 | ```python
40 | # Python kod
41 | def factorial(n):
42 | if n == 0 or n == 1:
43 | return 1
44 |
45 | return n * factorial(n - 1)
46 |
47 | print(factorial(10))
48 | ```
49 |
50 | ```java
51 | // Java code
52 | public static int factorial(int n) {
53 | if(n == 0 || n == 1)
54 | return 1;
55 | return n * factorial(n - 1);
56 | }
57 | ```
58 |
59 | ## 2.5 Rekursiya və yaddaş vizualizasiyası haqqında.
60 | Bir şeyi qeyd etməliyik ki, hər rekursiv çağırış, yaddaşda həmin funksiyanın kopyasını saxlayır. Funksiya bitdikdən sonra(hər hansı məlumatı return etdikdə), məlumatı geri qaytaran həmin funksiya yaddaşdan silinir. Rekursiv kod çox sadə görsənir, əslində isə, vizualizasiya və kodu icrasını izləmək(tracing) çətinləşir.
61 |
62 |
63 | ```python
64 | # Python kod
65 | def print_func(n):
66 | if n == 0: # funksiyanı bitirən əsas hal.
67 | return 0
68 | else:
69 | print(n)
70 | return print_func(n - 1) # rekursiv çağırış
71 |
72 | print(print_func(4))
73 | ```
74 |
75 | ```java
76 | // Java code
77 | public static int printFunc(int n) {
78 | if (n == 0) // funksiyanı bitirən əsas hal.
79 | return 0;
80 | System.out.println(n);
81 | return printFunc(n - 1); // rekursiv çağırış
82 | }
83 | ```
84 |
85 | **Sual:** Yuxarıdakı `print_func()` funksiyası toplam neçə dəfə çağrılacaq.
86 | **Cavab:** Toplamda 5 dəfə. 1 dəfə `print()` daxilində, 4 dəfə də rekursiv şəkildə
87 |
88 | Aşağıdakı şəkilə diqqət yetirsək bunu aydın görərik. Sağ tərəfdəki ox öz-özünü 4 dəfə çağırmağa işarədir:
89 |
90 | 
91 |
92 | > Bu şəkli hazırlayan kod: [fesil2_2.5_pycallgraph.py](../Source_Code/python_kodlar/fesil2/fesil2_2.5_pycallgraph.py)
93 |
94 | Digər tərəfdən, biz yuxarıda dedik ki, hər bir rekursiv çağırış yaddaşda saxlanılır. Yəni biz bu çağırışları istədiyimiz anda `stack frame`-də görə bilərik.
95 | Bunu göstərmək üçün mən interaktiv debugger olan pdb-dən istifadə etmək istəyirəm. Pdb haqqında daha ətraflı oxuya bilərsiniz: [pdb doc](https://docs.python.org/3.5/library/pdb.html)
96 |
97 |
98 | > pdb ilə kod nümunəsi: [fesil2_2.5_pdb.py](../Source_Code/python_kodlar/fesil2/fesil2_2.5_pdb.py)
99 |
100 | ```python
101 | $ python3 fesil2_2.5_pdb.py
102 | > /home/shako/REPOS/Data_Structures_Algo_Python/Source_Code/fesil2_2.5_pdb.py(14)()
103 | -> print_func(4)
104 | (Pdb) c
105 | 4
106 | 3
107 | 2
108 | 1
109 | > /home/shako/REPOS/Data_Structures_Algo_Python/Source_Code/fesil2_2.5_pdb.py(6)print_func()
110 | -> return 0
111 | ```
112 |
113 | Bundan sonra, biz interaktiv debuggerin daxilində `where` əmrini yazsaq o bizə, ən yeni frame ən aşağıda olmaqla, `stack trace` çıxardacaq:
114 |
115 | ```python
116 | (Pdb) where
117 | /home/shako/REPOS/Data_Structures_Algo_Python/Source_Code/fesil2_2.5_pdb.py(14)()
118 | -> print_func(4)
119 | /home/shako/REPOS/Data_Structures_Algo_Python/Source_Code/fesil2_2.5_pdb.py(9)print_func()
120 | -> return print_func(n - 1) # rekursiv çağırış
121 | /home/shako/REPOS/Data_Structures_Algo_Python/Source_Code/fesil2_2.5_pdb.py(9)print_func()
122 | -> return print_func(n - 1) # rekursiv çağırış
123 | /home/shako/REPOS/Data_Structures_Algo_Python/Source_Code/fesil2_2.5_pdb.py(9)print_func()
124 | -> return print_func(n - 1) # rekursiv çağırış
125 | /home/shako/REPOS/Data_Structures_Algo_Python/Source_Code/fesil2_2.5_pdb.py(9)print_func()
126 | -> return print_func(n - 1) # rekursiv çağırış
127 | > /home/shako/REPOS/Data_Structures_Algo_Python/Source_Code/fesil2_2.5_pdb.py(6)print_func()
128 | -> return 0
129 | ```
130 |
131 | Diqqət etsəniz, yuxarıda dediyimizin sübutu olaraq 4 rekursiv çağırışın hər birinin kopyasının var olduğunu görürük.
132 |
133 | Bəs bizim faktorial kodumuz? Onu da debugger ilə çalışdırıb, icra edib, rekursiv çağırışlara və həmçinin `frame`-də yuxarı doğru(up komandası ilə) getməklə verilmiş `n` rəqəminin həmin an üçün dəyərinə baxa bilərik.
134 |
135 | > Factorial + debugger kodumuz: [fesil2_2.5_factorial_pdb.py](../Source_Code/python_kodlar/fesil2/fesil2_2.5_factorial_pdb.py)
136 |
137 | Debugger ilə istifadə nəticəsi:
138 |
139 | ```python
140 | $ python3 fesil2_2.5_factorial.py
141 | > /home/shako/REPOS/Data_Structures_Algo_Python/Source_Code/fesil2/fesil2_2.5_factorial.py(12)()
142 | -> factorial(5)
143 | (Pdb) c
144 | > /home/shako/REPOS/Data_Structures_Algo_Python/Source_Code/fesil2/fesil2_2.5_factorial.py(6)factorial()
145 | -> return 1
146 | (Pdb) where
147 | /home/shako/REPOS/Data_Structures_Algo_Python/Source_Code/fesil2/fesil2_2.5_factorial.py(12)()
148 | -> factorial(5)
149 | /home/shako/REPOS/Data_Structures_Algo_Python/Source_Code/fesil2/fesil2_2.5_factorial.py(8)factorial()
150 | -> return n * factorial(n - 1)
151 | /home/shako/REPOS/Data_Structures_Algo_Python/Source_Code/fesil2/fesil2_2.5_factorial.py(8)factorial()
152 | -> return n * factorial(n - 1)
153 | /home/shako/REPOS/Data_Structures_Algo_Python/Source_Code/fesil2/fesil2_2.5_factorial.py(8)factorial()
154 | -> return n * factorial(n - 1)
155 | /home/shako/REPOS/Data_Structures_Algo_Python/Source_Code/fesil2/fesil2_2.5_factorial.py(8)factorial()
156 | -> return n * factorial(n - 1)
157 | > /home/shako/REPOS/Data_Structures_Algo_Python/Source_Code/fesil2/fesil2_2.5_factorial.py(6)factorial()
158 | -> return 1
159 | (Pdb) p n
160 | 1
161 | (Pdb) up
162 | > /home/shako/REPOS/Data_Structures_Algo_Python/Source_Code/fesil2/fesil2_2.5_factorial.py(8)factorial()
163 | -> return n * factorial(n - 1)
164 | (Pdb) p n
165 | 2
166 | (Pdb) up
167 | > /home/shako/REPOS/Data_Structures_Algo_Python/Source_Code/fesil2/fesil2_2.5_factorial.py(8)factorial()
168 | -> return n * factorial(n - 1)
169 | (Pdb) p n
170 | 3
171 | (Pdb) up
172 | > /home/shako/REPOS/Data_Structures_Algo_Python/Source_Code/fesil2/fesil2_2.5_factorial.py(8)factorial()
173 | -> return n * factorial(n - 1)
174 | (Pdb) p n
175 | 4
176 | (Pdb) up
177 | > /home/shako/REPOS/Data_Structures_Algo_Python/Source_Code/fesil2/fesil2_2.5_factorial.py(8)factorial()
178 | -> return n * factorial(n - 1)
179 | (Pdb) p n
180 | 5
181 | (Pdb) up
182 | > /home/shako/REPOS/Data_Structures_Algo_Python/Source_Code/fesil2/fesil2_2.5_factorial.py(12)()
183 | -> factorial(5)
184 | ```
185 |
186 | ## 2.6 Rekursiya İterasiyaya qarşı
187 | Rekursiya haqqında danışanda, ağla gələn ilk suallardan biri budur ki, hansı daha yaxşıdır? İterasiya ya Rekursiya?
188 | Bu suala cavab, bizim nə etmək istədiyimizə bağlıdır. Rekursiv üsul problemi həll etməyi asanlaşdırır. Lakin, bu zaman da əlavə tələblər qoyur. Belə ki, hər bir rekursiv çağırış üçün bizə əlavə yaddaş lazım olur.
189 |
190 | ### Rekursiya
191 | * Əsas hala(base case) çatdıqda, proqram dayanır.
192 | * Hər öz-çağırış(recursive call) əlavə `stack frame`(yaddaş) işğal edir.
193 | * Sonsuz, bitməyən(əsas hala çatmayan) rekursiv çağırışlar, yaddaşın bitməsinə və `stack overflow` ilə nəticələnə bilər.
194 | * Bəzi problemlərə, bu üsulla həllər yazmaq, daha sadə, daha anlaşıqlı və daha qısa olur.
195 |
196 | ### İterasiya
197 | * Şərt doğru olmayanda proqram dayanır.
198 | * Hər iterasiya əlavə kopyanın yaddaşda saxlanmasına ehtiyac duymur.
199 | * Məsələyə, problemə, iterativ üsulla həll yazmaq, ilk baxışdan tam aydın olmaya bilir.
200 |
201 | ## 2.7 Rekursiya haqqında qeydlər
202 | * Rekursiv alqoritmlərin, 2 halı var, rekursiv hal və əsas hal.
203 | * Hər bir rekursiv funksiya, əsas hala çatdıqda sonlanmalıdır.
204 | * Ümumən götürdükdə, iterativ həllər, rekursiv həllərdən daha üstün hesab olunur(öz çağırışların çoxluğu səbəbi ilə).
205 | * Rekursiv üsulla həll oluna bilən, problemin həm də iterativ üsulla həlli var.
206 | * Bəzi problemlər üçün, aydın iterativ üsul mövcud olmur.
207 | * Bəzi problemlər, məhz elə rekursiv üsulun malıdır, ona tam uyğundur, bəziləri isə yox.
208 |
209 | ## 2.8 Rekursiv alqoritmlərə misal:
210 | * Fibonaççi ardıcıllığı, Faktorialın tapılması
211 | * Birləşdirməklə sıralama(Merge Sort), Cəld sıralama(Quick Sort)
212 | * İkili axtarış(binary search)
213 | * Hanoy qüllələri problemi
214 |
215 | ## 2.9 Rekursiya məsələləri və həlləri:
216 | Bir sıra rekursiv problemləri burada müzakirə edək.
217 |
218 | **Məsələ 1** Hanoy qüllələri tapmacasının(puzzle) müzakirəsi
219 |
220 | **Həlli** Hanoy qüllələri riyazi tapmacadır. 3 çubuq(qüllə) və verilmiş qədər disklərdən ibarətdir. Burdakı disklərin hər biri istənilən çubuğa sürüşdürülə bilən şəkildədir. Tapmaca, bir sütun(çubuq) üzərində olan disklərlə başlayır, disklər formaca kiçikdən böyüyə düzülür. Ən kiçik ölçüsü olan disk ən üstdə, ən böyüyü isə altda olmaqla yerləşdirilir. Məsələnin məğzi bundan ibarətdir ki, bir qüllədə olan bütün diskləri digərinə keçirdək(ötürək, sürüşdürək). Lakin, bunu edərkən, müəyyən şərtlərə diqqət yetirməliyik:
221 | * Hər dəfə yalnız bir disk sürüşdürülə bilər.
222 | * Hər sürüşmə, əvvəlki sütundan ən üst diski götürüb, digər sütuna(çubuğa) ötürməkdən ibarətdir.
223 | * Bu zaman, bu disk, digər çubuqda, artıq mövcud olan disklərin üzərinə qoyulmalıdır.
224 | * Ölçücə böyük olan disklər, özündən kiçiklərin üzərinə qoyula bilməz.
225 |
226 | **Alqoritm**
227 | * Ən üst (n - 1) qədər diskləri "Mənbə" sütundan, "Köməkçi" sütuna yerləşdir(sürüşdür). Faktiki olaraq, n - 1 sütununu "Köməkçi" sütuna yerləşdiririk.
228 | * n-ci diski "Mənbə" sütundan, "Hədəf" sütuna yerləşdir,
229 | * (n - 1) diskləri "Köməkçi" sütundan, "Hədəf" sütuna yerləşdir,
230 | * Bu alqoritmdə, hər dəfə (n - 1) diskləri "Mənbə" sütundan, "Köməkçi" sütuna daşımaq, öz-özlüyündə yeni əməliyyat kimi görsənir və dolayısı ilə rekursiya üçün ideal istifadə yeridir.
231 | 3 diskli qüllə üçün bu problemi həll etsək belə çıxır ki, istənilən sayda qüllə üçün bunu həll etmiş olarıq.
232 | Məsələni vizual olaraq göstərmək üçün aşağıdakı gif faylı burda yerləşdirirəm:
233 |
234 | 
235 |
236 | İndi isə kodumuzu yazaq:
237 | > Hanoy qüllələri kodumuz: [fesil2_2.9_hanoi_qulleleri.py](../Source_Code/python_kodlar/fesil2/fesil2_2.9_hanoi_qulleleri.py)
238 |
239 | ```python
240 | def hanoi_qulleleri(disk_sayi, menbe_sutun, komekci_sutun, hedef_sutun):
241 | print "hanoi_qulleleri( ", disk_sayi, menbe_sutun, komekci_sutun, hedef_sutun, " çağrıldı...)"
242 | if disk_sayi:
243 | # (n - 1) sütununu mənbədən köməkçiyə yerləşdirmək
244 | hanoi_qulleleri(disk_sayi-1, menbe_sutun, hedef_sutun, komekci_sutun)
245 | # deyildiyi kimi, n-ci diski mənbədən hədəfə yerləşdiririk
246 | if menbe_sutun:
247 | disk = menbe_sutun.pop()
248 | print("Disk {}-in menbe_sutun-dan hedef_sutun-a yerləşdirilməsi".format(disk))
249 | hedef_sutun.append(disk)
250 | # (n - 1) sütununu köməkçidən hədəfə yerləşdiririk
251 | hanoi_qulleleri(disk_sayi-1, komekci_sutun, menbe_sutun, hedef_sutun)
252 |
253 |
254 | menbe_sutun = [3, 2, 1]
255 | hedef_sutun = []
256 | komekci_sutun = []
257 | hanoi_qulleleri(len(menbe_sutun), menbe_sutun, komekci_sutun, hedef_sutun)
258 |
259 | print("son nəticə")
260 | print(menbe_sutun, komekci_sutun, hedef_sutun)
261 | ```
262 |
263 | Kodu icra etdikdə belə bir mənzərə ilə qarşılaşırıq:
264 |
265 | ```python
266 | $ python3 fesil2_2.9_hanoi_qulleleri.py
267 | hanoi_qulleleri( 3 [3, 2, 1] [] [] çağrıldı...)
268 | hanoi_qulleleri( 2 [3, 2, 1] [] [] çağrıldı...)
269 | hanoi_qulleleri( 1 [3, 2, 1] [] [] çağrıldı...)
270 | hanoi_qulleleri( 0 [3, 2, 1] [] [] çağrıldı...)
271 | Disk 1-in menbe_sutun-dan hedef_sutun-a yerləşdirilməsi
272 | hanoi_qulleleri( 0 [] [3, 2] [1] çağrıldı...)
273 | Disk 2-in menbe_sutun-dan hedef_sutun-a yerləşdirilməsi
274 | hanoi_qulleleri( 1 [1] [3] [2] çağrıldı...)
275 | hanoi_qulleleri( 0 [1] [2] [3] çağrıldı...)
276 | Disk 1-in menbe_sutun-dan hedef_sutun-a yerləşdirilməsi
277 | hanoi_qulleleri( 0 [3] [] [2, 1] çağrıldı...)
278 | Disk 3-in menbe_sutun-dan hedef_sutun-a yerləşdirilməsi
279 | hanoi_qulleleri( 2 [2, 1] [] [3] çağrıldı...)
280 | hanoi_qulleleri( 1 [2, 1] [3] [] çağrıldı...)
281 | hanoi_qulleleri( 0 [2, 1] [] [3] çağrıldı...)
282 | Disk 1-in menbe_sutun-dan hedef_sutun-a yerləşdirilməsi
283 | hanoi_qulleleri( 0 [3] [2] [1] çağrıldı...)
284 | Disk 2-in menbe_sutun-dan hedef_sutun-a yerləşdirilməsi
285 | hanoi_qulleleri( 1 [1] [] [3, 2] çağrıldı...)
286 | hanoi_qulleleri( 0 [1] [3, 2] [] çağrıldı...)
287 | Disk 1-in menbe_sutun-dan hedef_sutun-a yerləşdirilməsi
288 | hanoi_qulleleri( 0 [] [] [3, 2, 1] çağrıldı...)
289 | son nəticə
290 | [] [] [3, 2, 1]
291 | ```
292 |
293 |
294 | **Məsələ 2** Verilmiş massivin sıralanmış olduğunu aşkarlayın.
295 |
296 | **Həlli**
297 | > Kod faylı: [fesil2_2.9_is_array_sorted.py](../Source_Code/python_kodlar/fesil2/fesil2_2.9_is_array_sorted.py)
298 |
299 | ```python
300 | def massiv_siralidirmi(massiv):
301 | print("Yeni massiv : {}".format(massiv))
302 | # Əsas hal
303 | if len(massiv) == 1:
304 | return True
305 | # Rekursiya
306 | if massiv[0] <= massiv[1] and massiv_siralidirmi(massiv[1:]):
307 | return True
308 | else:
309 | return False
310 |
311 | massiv1 = [23, 34, 45, 56, 88, 97, 101, 125]
312 | # True qayıtmalıdır
313 | print(massiv_siralidirmi(massiv=massiv1))
314 |
315 | massiv2 = [23, 34, 45, 56, 88, 97, 101, 125, 5]
316 | # False qayıtmalıdır
317 | print(massiv_siralidirmi(massiv2))
318 | ```
319 |
320 | ```python
321 | $ python3 fesil2_2.9_is_array_sorted.py
322 | Yeni massiv : [23, 34, 45, 56, 88, 97, 101, 125]
323 | Yeni massiv : [34, 45, 56, 88, 97, 101, 125]
324 | Yeni massiv : [45, 56, 88, 97, 101, 125]
325 | Yeni massiv : [56, 88, 97, 101, 125]
326 | Yeni massiv : [88, 97, 101, 125]
327 | Yeni massiv : [97, 101, 125]
328 | Yeni massiv : [101, 125]
329 | Yeni massiv : [125]
330 | True
331 | Yeni massiv : [23, 34, 45, 56, 88, 97, 101, 125, 5]
332 | Yeni massiv : [34, 45, 56, 88, 97, 101, 125, 5]
333 | Yeni massiv : [45, 56, 88, 97, 101, 125, 5]
334 | Yeni massiv : [56, 88, 97, 101, 125, 5]
335 | Yeni massiv : [88, 97, 101, 125, 5]
336 | Yeni massiv : [97, 101, 125, 5]
337 | Yeni massiv : [101, 125, 5]
338 | Yeni massiv : [125, 5]
339 | False
340 | ```
341 |
342 | # 2.10 Backtracking nədir?
343 | Backtracking özlüyündə `brute force` üsulun inkişaf etmiş formasıdır. Backtracking zamanı, problemin həllinin sistematik olaraq mümkün bütün həllərin arasından axtarışı həyata keçirilir. Bütün mümkün həll variantlarından, hər hansı birini seçirik, əgər seçdiyimiz variant bizim problemi həll edirsə, o zaman biz həlli print edirik. Yox əgər seçdiyimiz variant problemi həll etmədisə, o zaman geri dönüb, mümkün həllər arasından digər birini seçirik və beləcə problemi həll edənə qədər davam edirik. Əgər, mümkün variantlar arasında problemin həlli tapılmırsa, o zaman belə nəticəyə gəlirik ki, problemin həlli yoxdur.
344 |
345 | Backtracking rekursiyanın bir formasıdır. Adətkar ssenari belə olur ki, biz hər hansı həll variantları ilə qarşılaşırıq və onlardan birini seçməli oluruq. Seçim etdikdən sonra isə yeni variantlar gəlir. Bu prosedur, son nəticəyə gəlib çıxana qədər, təkrarlanmaqda davam edir. Əgər siz, düzgün ardıcıllıqları seçmisinizsə, sizin üçün son hal hədəf halıdır, əks təqdirdə isə yox.
346 | Backtracking, seçməli tree/graph traversal metodu kimi düşünülə bilər. Ağac(tree) hər hansı başlanğıc nöqtəsini(root node) və final(son) hədəf halını(goal state) - yarpaqlardan birini göstərmək üsuludur. Adi `brute force` üsul, müəyyən hallarda sonsuz sayda həll variantlarına gətirib çıxara bilir. Backtracking bizə bundan yayınmaqda kömək edir. Backtracking sanki, saflaşdırılmış `brute force`-dur.
347 | Hər node-da, biz açıq-aşkar mümkün olmayan həll variantlarını aradan çıxardırıq və beləcə rekursiv şəkildə potensial lazımlı variantları seçirik.
348 |
349 | # 2.11 Backtracking alqoritmlərinə misal olaraq
350 | * İkili stringlər(binary strings) - bütün binary string-ləri generasiya etmək.
351 | * N-Queens problemi
352 | * Knapsack problemi
353 | * Hamiltonian Cycles
354 | * Qraf rəngləmə problemi
355 |
356 | # 2.12 Backtracking: məsələlər və həllər
357 |
358 | **Məsələ 3** Bütün ikili stringləri n bitlərlə generasiya edin. Qəbul edirik ki, A[0..n-1] n ölçülü massivdir.
359 | Məsələ adından dəhşətli görsənə bilər, lakin, qısa olaraq bizə elə bir funksiya lazımdır ki, məsələn, n = 3 ötürdükdə, 3 bitli bütün mümkün variantları bizə sıralasın.
360 | Yəni belə bir şey:
361 |
362 | ```python
363 | n = 3
364 | bin_str = [000, 100, 010, 001, 110 101, 011, 111]
365 | ```
366 |
367 | Aşağıdakı kod parçası bu məsələni rekursiv üsulla həll edir:
368 | > Nümunə kod: [fesil2_2.12_bit_strings_recursion.py](../Source_Code/python_kodlar/fesil2/fesil2_2.12_bit_strings_recursion.py)
369 |
370 | ```python
371 | def bin_str_list(n):
372 | if n == 0:
373 | #əsas hal
374 | return ['']
375 | else:
376 | # Rekursiya
377 | return [i + '0' for i in bin_str_list(n-1)] + [i + '1' for i in bin_str_list(n-1)]
378 |
379 | print(bin_str_list(4))
380 | ```
381 |
382 | Kodun icrasından alınan nəticə:
383 |
384 | ```python
385 | $ python3 fesil2_2.12_bit_strings_recursion.py
386 | ['0000', '1000', '0100', '1100', '0010', '1010', '0110', '1110', '0001', '1001', '0101', '1101', '0011', '1011', '0111', '1111']
387 | ```
388 |
389 | Maraq üçün qeyd edək ki, Python-da `itertools` adlı çox gözəl kitabxana var ki, biz onun köməyi ilə də bu problemi həll edə bilərik:
390 | Aşağıdakı kod parçasının icrası da eyni nəticəni bizə verir:
391 |
392 | > Nümunə kod: [fesil2_2.12_bit_strings_itertools.py](../Source_Code/python_kodlar/fesil2/fesil2_2.12_bit_strings_itertools.py)
393 |
394 | ```python
395 | from itertools import product
396 | n = 4
397 | bin_str_list = [''.join(p) for p in product('01', repeat=n)]
398 |
399 | print(bin_str_list)
400 | ```
401 |
--------------------------------------------------------------------------------
/book/5.Dövri_Əlaqəli_listlər_circular_linked_lists.md:
--------------------------------------------------------------------------------
1 | # Dövri Əlaqəli listlər(circular linked lists)
2 |
3 | Birtərəfli və İkitərəfli əlaqəli listlərdə, listin sonu NULL(None)-la bitirdi. Dövri əlaqəli listin isə sonu yoxdur.
4 | Dolayısı ilə, dövri əlaqəli listi başdan ayağa qət edərkən ehtiyatlı olmalıyıq. Əks təqdirdə, bu qət etmə əməliyyatı heç vaxt sonlanmayacaq. Dövri əlaqəli listdə hər node-un özündən sonra bir node var. Yuxarıda da deyildiyi kimi, burda, NULL pointer-li node yoxdur. Bəzi hallarda, dövri əlaqəli listlər faydalı ola bilər. Əslində, tip deklarasiyasında, dövri və birtərəfli listlər arasında fərq yoxdur.
5 |
6 | Aşağıdakı kod, Dövri Əlaqəli list üçün tip elanıdır(declaration):
7 | > Bütün kodlara baxmaq üçün keçid: [fesil5_circular_linked_lists.py](../Source_Code/python_kodlar/fesil5/fesil5_circular_linked_lists.py)
8 |
9 | ```python
10 | class Node:
11 | # konstruktor
12 | def __init__(self, data=None, next_node=None):
13 | self.data = data
14 | self.next_node = next_node
15 |
16 | # node-un data field-ini mənimsətmək üçün metod
17 | def set_data(self, data):
18 | self.data = data
19 |
20 | # node-un data field-ini almaq üçün metod
21 | def get_data(self):
22 | return self.data
23 |
24 | # node-un növbəti field-ini mənimsətmək üçün metod
25 | def set_next_node(self, next_node):
26 | self.next_node = next_node
27 |
28 | # node-un növbəti field-ini almaq üçün metod
29 | def get_next_node(self):
30 | return self.next_node
31 |
32 | # əgər bir node sonrakına point edirsə, true qaytar
33 | def has_next(self):
34 | return self.next_node is not None
35 | ```
36 | ```
37 | // Java kod
38 | public class Node {
39 |
40 | private int data;
41 | private Node next_node;
42 |
43 | // konstruktor
44 |
45 | public Node(int data, Node next_node) {
46 | this.data = data;
47 | this.next_node = next_node;
48 | }
49 |
50 | public Node() {
51 | }
52 |
53 | // node-un data field-ini mənimsətmək üçün metod
54 | public void set_data(int data){
55 | this.data = data;
56 | }
57 |
58 | // node-un data field-ini almaq üçün metod
59 | public int get_data(){
60 | return data;
61 | }
62 |
63 | // node-un növbəti field-ini mənimsətmək üçün metod
64 | public void set_next_node(Node next_node){
65 | this.next_node = next_node;
66 | }
67 |
68 | // node-un növbəti field-ini almaq üçün metod
69 | public Node get_next_node(){
70 | return next_node;
71 | }
72 |
73 | // əgər bir node sonrakına point edirsə, true qaytar
74 | public boolean has_next(){
75 | return next_node != null;
76 | }
77 | }
78 | ```
79 | > QEYD: Dövri əlaqəli listdə də biz elementlərə head node vasitəsilə çatırıq.
80 |
81 | **Dövri əlaqəli listdə node sayının hesablanması**
82 |
83 | Dövri əlaqəli list-in elementlərinə head node vasitəsilə çatırıq. Burda incə məqam odur ki, biz dövri əlaqəli listi əvvəldən axıra kimi qət etmək istəyiriksə, head node-dan başlayıb elə head node-da da dayanmalıyıq. Çünki, bizdə listin sonunu göstərən, NULL-a yönəldilən node yoxdur.
84 | Təbii ki, əgər list boşdursa, o zaman head node NULL olacaq və bu zaman count-u 0-a bərabər edirik.
85 | Yox əgər list boş deyilsə, bu pointeri birinci node-a qoyuruq və list boyu irəliləyirik, yenidən head node-u gördükdə isə dayanırıq. Çünki, artıq başladığımız nöqtəyə çatdıq.
86 |
87 | 
88 |
89 | Aşağıdakı kod nümunəmizə baxaq:
90 |
91 | ```python
92 | class CircularLinkedList:
93 | def __init__(self, head=None):
94 | self.head = head
95 |
96 | def circular_list_length(self):
97 | current_node = self.head
98 | if current_node is None:
99 | return 0
100 |
101 | count = 1
102 | current_node = current_node.get_next_node()
103 | # Dövri əlaqəli listdə yenidən head node-a çatmağımızı yoxlayaq.
104 | while current_node != self.head:
105 | current_node = current_node.get_next_node()
106 | count = count + 1
107 |
108 | return count
109 | ```
110 | ```
111 | // Java kod
112 | public class CircularLinkedList {
113 |
114 | private Node head;
115 |
116 | public CircularLinkedList() {
117 | }
118 |
119 | public CircularLinkedList(Node head) {
120 | this.head = head;
121 | }
122 |
123 | public int circular_list_length(){
124 | Node current_node = head;
125 | if(current_node == null) return 0;
126 |
127 | int count = 1;
128 | current_node = current_node.get_next_node();
129 | // Dövri əlaqəli listdə yenidən head node-a çatmağımızı yoxlayaq.
130 | while(current_node != head){
131 | current_node = current_node.get_next_node();
132 | count++;
133 | }
134 |
135 | return count;
136 | }
137 | }
138 | ```
139 | **Dövri listin elementlərini göstərmək**
140 |
141 | Eyni əməliyyatı burada da icra edirik. Sadəcə burada node-un data-sını print edirik.
142 |
143 | ```python
144 |
145 | def print_data_circular_list(self):
146 | current_node = self.head
147 | if current_node is None:
148 | return 0
149 |
150 | current_node = current_node.get_next_node()
151 | print(current_node.get_data())
152 | while current_node != self.head:
153 | current_node = current_node.get_next_node()
154 | print(current_node.get_data())
155 | ```
156 | ```
157 | // Java kod
158 | public void print_data_circular_list(){
159 | Node current_node = head;
160 |
161 | if(current_node != null){
162 | current_node = current_node.get_next_node();
163 | System.out.println(current_node.get_data());
164 | while(current_node != head){
165 | current_node = current_node.get_next_node();
166 | System.out.println(current_node.get_data());
167 | }
168 | }
169 | }
170 | ```
171 | *Vaxt mürəkkəbliyi: O(n), n ölçülü listi qət etdiyi üçün*
172 |
173 | *Yer(space) mürəkkəbliyi: O(1), əlavə dəyişən səbəbilə*
174 |
175 | **Dövri əlaqəli listin sonuna node əlavə etmək**
176 |
177 | Nəzərə alsaq ki, dövri əlaqəli listdə, listin sonunu göstərə biləcək NULL pointer yoxdur, bu zaman deyə bilərik ki, listin sonuna node əlavə etmək, onun hal-hazırda head-inə baxan node-la head-in arasına node daxil etmək deməkdir.
178 | Bu məqsədlə aşağıdakı addımları etməliyik:
179 |
180 | * Yeni node yaradırıq və müvəqqəti olaraq, həmin node-un növbəti pointerini özünə yönəldirik.
181 |
182 | 
183 |
184 | * Daha sonra, listi əvvəldən axıra qədər qət edərək, növbəti node-u head node olan, hal-hazırkı node-u tapırıq(faktiki olaraq, sonuncu node-u). Bundan sonra, biz yeni node-umuzu head node-a yönləndiririk.
185 |
186 | 
187 |
188 | * Ən sonda isə, keçmiş(əvvəlki) node-un növbəti(next) pointerini bizim indiki yeni node-umuza yönləndiririk.
189 |
190 | 
191 |
192 | Kod nümunəmiz aşağıdakı kimi olacaq:
193 |
194 | ```python
195 | def insert_at_end(self, data):
196 | current_node = self.head
197 | new_node = Node()
198 | new_node.set_data(data)
199 |
200 | if self.head is None:
201 | self.head = new_node
202 | new_node.set_next_node(self.head)
203 | else:
204 | current_node = current_node.get_next_node()
205 | while current_node.get_next_node() != self.head:
206 | current_node.get_next_node()
207 | # Yeni node-u özü-özünə point edirik.
208 | new_node.set_next_node(new_node)
209 | # Yeni node-u head node-a yönləndiririk.
210 | new_node.set_next_node(self.head)
211 | # Hal-hazırkı(faktiki olaraq əvvəlki) node-u isə yeni node-a yönləndiririk.
212 | current_node.set_next_node(new_node)
213 | ```
214 | ```
215 | // Java kod
216 | public void insert_at_end(int data){
217 | Node current_node = head;
218 | Node new_node = new Node();
219 | new_node.set_data(data);
220 | if(head == null){
221 | head = new_node;
222 | new_node.set_next_node(head);
223 | }else{
224 | current_node = current_node.get_next_node();
225 |
226 | while(current_node.get_next_node() != head){
227 | current_node = current_node.get_next_node();
228 | }
229 | // Yeni node-u özü-özünə point edirik.
230 | new_node.set_next_node(new_node);
231 | // Yeni node-u head node-a yönləndiririk.
232 | new_node.set_next_node(head);
233 | // Hal-hazırkı(faktiki olaraq əvvəlki) node-u isə yeni node-a yönləndiririk.
234 | current_node.set_next_node(new_node);
235 | }
236 | }
237 | ```
238 | *Vaxt mürəkkəbliyi: O(n), n ölçülü listi qət etdiyi üçün*
239 |
240 | *Yer(space) mürəkkəbliyi: O(1), əlavə dəyişən olması səbəbilə*
241 |
242 | İndi isə kodumuzu test edək:
243 |
244 | ```python
245 | obj = CircularLinkedList()
246 | obj.insert_at_end(44)
247 | obj.insert_at_end(3)
248 | obj.insert_at_end(99)
249 | print("Printing list length -> {}".format(obj.circular_list_length()))
250 | obj.print_data_circular_list()
251 | ```
252 |
253 | Bu dəfə faylımızı modul kimi icra edək, yəni PDB-dən istifadə etmədən:
254 |
255 | ```python
256 | $ python3 fesil5_circular_linked_lists.py
257 | Printing list length -> 3
258 | 44
259 | 3
260 | 99
261 | ```
262 | ```
263 | // Java kod
264 | public static void main(String[] args) {
265 | CircularLinkedList cll = new CircularLinkedList();
266 | cll.insert_at_end(44);
267 | cll.insert_at_end(3);
268 | cll.insert_at_end(99);
269 | System.out.println(cll.circular_list_length());
270 | cll.print_data_circular_list();
271 | }
272 | ```
273 | Bizim dövri əlaqəli listimizin vizual görüntüsü:
274 |
275 |
276 | 
277 |
278 | **Dövri əlaqəli listin əvvəlinə node əlavə etmək**
279 |
280 | Dövri əlaqəli listin əvvəlinə node əlavə etmək, onun sonuna node əlavə etməklə
281 | oxşardır. Fərq bundadır ki, biz yeni node-u head node edirik.
282 |
283 | Nümunə kodumuza baxaq:
284 |
285 | ```python
286 | def insert_at_beginning(self, data):
287 | current_node = self.head
288 | new_node = Node()
289 | new_node.set_data(data)
290 | # Yeni node-u özü-özünə point edirik.
291 | new_node.set_next_node(new_node)
292 |
293 | if self.head is None:
294 | self.head = new_node
295 | new_node.set_next_node(self.head)
296 | else:
297 | current_node.get_next_node()
298 | while current_node.get_next_node() != self.head:
299 | current_node = current_node.get_next_node()
300 | # Yeni node-u head node-a yönləndiririk.
301 | new_node.set_next_node(self.head)
302 | # Yeni node-u yeni head edirik
303 | self.head = new_node
304 | # Hal-hazırkı tapılan node-u isə yeni head-ə yönləndiririk və yaxud yeni node-a yönləndiririk.
305 | # current_node.set_next_node(new_node)
306 | current_node.set_next_node(self.head)
307 | ```
308 | ```
309 | // Java kod
310 | public void insert_at_beginning(int data) {
311 | Node current_node = head;
312 | Node new_node = new Node();
313 |
314 | new_node.set_data(data);
315 | // Yeni node-u özü-özünə point edirik.
316 | new_node.set_next_node(new_node);
317 |
318 | if(head == null){
319 | head = new_node;
320 | new_node.set_next_node(head);
321 | }else{
322 | current_node.get_next_node();
323 | while(current_node.get_next_node() != head){
324 | current_node = current_node.get_next_node();
325 | }
326 | // Yeni node-u head node-a yönləndiririk.
327 | new_node.set_next_node(head);
328 | head = new_node;
329 | // Hal-hazırkı tapılan node-u isə yeni head-ə yönləndiririk və yaxud yeni node-a yönləndiririk.
330 | // current_node.set_next_node(new_node)
331 | current_node.set_next_node(head);
332 | }
333 | }
334 | ```
335 | *Vaxt mürəkkəbliyi: O(n), n ölçülü listi qət etdiyi üçün*
336 |
337 | *Yer(space) mürəkkəbliyi: O(1), əlavə dəyişən olması səbəbilə*
338 |
339 | Kodumuzun nəticəsi:
340 |
341 | ```python
342 | obj = CircularLinkedList()
343 | obj.insert_at_end(44)
344 | obj.insert_at_end(3)
345 | obj.insert_at_end(99)
346 | obj.insert_at_beginning(101)
347 | obj.insert_at_beginning(6)
348 | print("Printing list length -> {}".format(obj.circular_list_length()))
349 | obj.print_data_circular_list()
350 | ```
351 |
352 | ```python
353 | Printing list length -> 5
354 | 6
355 | 101
356 | 44
357 | 3
358 | 99
359 | ```
360 | ```
361 | // Java kod
362 | public static void main(String[] args) {
363 | CircularLinkedList cll = new CircularLinkedList();
364 | cll.insert_at_end(44);
365 | cll.insert_at_end(3);
366 | cll.insert_at_end(99);
367 | cll.insert_at_beginning(101)
368 | cll.insert_at_beginning(6)
369 | System.out.println(cll.circular_list_length());
370 | cll.print_data_circular_list();
371 | }
372 | ```
373 | Yuxarıdakı əməliyyatlardan sonra bizim dövri əlaqəli listimizin vizual görüntüsü aşağıdakı kimidir:
374 |
375 | 
376 |
377 | **Dövri əlaqəli listdən sonuncu node-u silmək**
378 |
379 | Xatırlayırıqsa, dövri əlaqəli listdə listin sonundakı elementdən sonrakı element listin başlanğıcı, head node-udur.
380 | Dolayısı ilə sonuncu node-u silmək demək, əslində ondan əvvəlki node-u head node-a yönləndirmək deməkdir.
381 | Bu zaman listi qət edərkən həm də əlavə bir dəyişəndən istifadə edib, hal-hazırkı node-dan əvvəlki node-u orda saxlamaq lazımdır.
382 |
383 | Kod nümunəmizə diqqət etsək bu daha da aydın olacaq:
384 |
385 | ```python
386 | def delete_from_end(self):
387 | # Müvəqqəti dəyişən
388 | temp = self.head
389 | current_node = self.head
390 |
391 | if self.head is None:
392 | print("List boşdur...")
393 | else:
394 | if current_node.get_next_node() == self.head:
395 | self.head = None
396 | return
397 | while current_node.get_next_node() != self.head:
398 | temp = current_node
399 | current_node = current_node.get_next_node()
400 | # Müvəqqəti node, əslində sondan bir əvvəlki node-dur.
401 | # Burada bu node-un növbəti pointer-ini faktiki olaraq head-ə yönləndiririk.
402 | temp.set_next_node(self.head)
403 | return
404 | ```
405 | ```
406 | // Java kod
407 | public void delete_from_end(){
408 | // Müvəqqəti dəyişən
409 | Node temp = head;
410 | Node current_node = head;
411 |
412 | if(head == null){
413 | System.out.println("List boşdur...");
414 | }else{
415 | while(current_node.get_next_node() != head){
416 | temp = current_node;
417 | current_node = current_node.get_next_node();
418 | }
419 | // Müvəqqəti node, əslində sondan bir əvvəlki node-dur.
420 | // Burada bu node-un növbəti pointer-ini faktiki olaraq head-ə yönləndiririk.
421 | temp.set_next_node(head);
422 | }
423 | }
424 | ```
425 | *Vaxt mürəkkəbliyi: O(n), n ölçülü listi qət etdiyi üçün*
426 |
427 | *Yer(space) mürəkkəbliyi: O(1)*
428 |
429 | Kodumuzu test edirik:
430 |
431 | ```python
432 | obj = CircularLinkedList()
433 | obj.insert_at_end(44)
434 | obj.insert_at_end(3)
435 | obj.insert_at_end(99)
436 | obj.insert_at_beginning(101)
437 | obj.insert_at_beginning(6)
438 | print("Printing list length -> {}".format(obj.circular_list_length()))
439 | obj.print_data_circular_list()
440 | obj.delete_from_end()
441 | print("Printing list length -> {}".format(obj.circular_list_length()))
442 | obj.print_data_circular_list()
443 | ```
444 |
445 | Burada gördüyümüz kimi, sonuncu node, data-sı 99 olandır və o da silindi.
446 |
447 | ```python
448 | Printing list length -> 5
449 | 6
450 | 101
451 | 44
452 | 3
453 | 99
454 | Printing list length -> 4
455 | 6
456 | 101
457 | 44
458 | 3
459 | ```
460 | ```
461 | // Java kod
462 | public static void main(String[] args) {
463 | CircularLinkedList cll = new CircularLinkedList();
464 | cll.insert_at_end(44);
465 | cll.insert_at_end(3);
466 | cll.insert_at_end(99);
467 | cll.insert_at_beginning(101)
468 | cll.insert_at_beginning(6)
469 | System.out.println(cll.circular_list_length());
470 | cll.print_data_circular_list();
471 | cll.delete_from_end();
472 | System.out.println(cll.circular_list_length());
473 | cll.print_data_circular_list();
474 | }
475 | ```
476 |
477 | **Dövri əlaqəli listdən birinci node-un silinməsi**
478 |
479 | Bu əməliyyat özü-özlüyündə, head node-un sürüşdürülməsidir.
480 | Lakin, bu zaman sonuncu node-un növbəti pointerini dəyişib, sürüşdürülmüş(yeni) head node-a yönləndirmək lazımdır.
481 |
482 | Aşağıdakı sadə kodla bu aydın olacaq:
483 |
484 | ```python
485 | def delete_from_beginning(self):
486 | current_node = self.head
487 |
488 | if self.head is None:
489 | print("List boşdur...")
490 | else:
491 | if current_node.get_next_node() == self.head:
492 | self.head = None
493 | return
494 | # Sonuncu node-un tapılması
495 | while current_node.get_next_node() != self.head:
496 | current_node = current_node.get_next_node()
497 | # Sonuncu node-un pointerini hal-hazırkı head-dən sonrakı node-a yönləndiririk.
498 | current_node.set_next_node(self.head.get_next_node())
499 | # Head node-u sürüşdürürük
500 | self.head = self.head.get_next_node()
501 | ```
502 | ```
503 | // Java kod
504 | public void delete_from_beginning(){
505 | Node current_node = head;
506 |
507 | if(head == null){
508 | System.out.println("List boşdur...");
509 | }else{
510 | // Sonuncu node-un tapılması
511 | while(current_node.get_next_node() != head){
512 | current_node = current_node.get_next_node();
513 | }
514 |
515 | // Sonuncu node-un pointerini hal-hazırkı head-dən sonrakı node-a yönləndiririk.
516 | current_node.set_next_node(head.get_next_node());
517 | // Head node-u sürüşdürürük
518 | head = head.get_next_node();
519 | }
520 | }
521 | ```
522 | Kodumuzu test edək:
523 |
524 | ```python
525 | obj = CircularLinkedList()
526 | obj.insert_at_end(44)
527 | obj.insert_at_end(3)
528 | obj.insert_at_end(99)
529 | obj.insert_at_beginning(101)
530 | obj.insert_at_beginning(6)
531 | print("Printing list length -> {}".format(obj.circular_list_length()))
532 | obj.print_data_circular_list()
533 | obj.delete_from_end()
534 | print("Printing list length -> {}".format(obj.circular_list_length()))
535 | obj.print_data_circular_list()
536 | obj.delete_from_beginning()
537 | print("Printing list length -> {}".format(obj.circular_list_length()))
538 | obj.print_data_circular_list()
539 | ```
540 |
541 | Nəticəyə nəzər yetirsək görərik ki, ilk öncə listdən sonuncu olan 99 silinir, daha sonra isə birinci olan 6:
542 |
543 | ```python
544 | Printing list length -> 5
545 | 6
546 | 101
547 | 44
548 | 3
549 | 99
550 | Printing list length -> 4
551 | 6
552 | 101
553 | 44
554 | 3
555 | Printing list length -> 3
556 | 101
557 | 44
558 | 3
559 | ```
560 | ```
561 | // Java kod
562 | public static void main(String[] args) {
563 | CircularLinkedList cll = new CircularLinkedList();
564 | cll.insert_at_end(44);
565 | cll.insert_at_end(3);
566 | cll.insert_at_end(99);
567 | cll.insert_at_beginning(101)
568 | cll.insert_at_beginning(6)
569 | System.out.println(cll.circular_list_length());
570 | cll.print_data_circular_list();
571 | cll.delete_from_end();
572 | System.out.println(cll.circular_list_length());
573 | cll.print_data_circular_list();
574 | cll.delete_from_beginning();
575 | System.out.println(cll.circular_list_length());
576 | cll.print_data_circular_list();
577 | }
578 |
579 | ```
580 | Nəticə doğrudur.
581 |
582 | **Dövri əlaqəli listlərin istifadə yeri haqqında**
583 |
584 | Dövri əlaqəli listi, kompüterin hesablama resurslarının idarəsində istifadə edə bilərik.
585 | Həmçinin Stack və Queue yaratmaq üçün dövri əlaqəli listdən istifadə oluna bilər.
586 |
587 | Hörmətli oxucu, bununla da biz dövri əlaqəli listlər mövzusunu başa vurmuş oluruq.
588 |
--------------------------------------------------------------------------------
/book/7.Növbələr_Queues.md:
--------------------------------------------------------------------------------
1 | # Növbə(queue)
2 |
3 | ## 7.1 Növbə nədir?
4 |
5 | Növbə də yığın kimi məlumatı saxlamaq üçün sadə data strukturudur.
6 | Növbədə, datanın daxil olma ardıcıllığı önəmlidir.
7 | Əslində, əsl həyatda növbədə gözləmək necədirsə, burda da elədir. Növbəyə ilk daxil olan, yəni növbədə birinci olan, xidmətdən də ilk istifadə edir.
8 | Avtobusa birinci minir, bankda kassada manatını dollara birinci çevirir, dükanda dolu səbətini kassada ilk boşaldaraq, digər növbədəkilərin həsrət dolu baxışlarına tuş gəlir.
9 |
10 | **Tərif**
11 |
12 | Növbə elementlərin daxil olma ardıcıllığını saxlayan bir listdir. Bu listə element onun sonuna(rear) daxil edilir və onun əvvəlindən(front) silinir.
13 | Dolayısı ilə, növbəyə ilk daxil edilən element, ilk də silinəcək(növbədən çıxacaq).
14 | Buna həm də FİFO(First İn First Out) deyilir.
15 |
16 | **Xüsusi terminlər**
17 |
18 | Yığında olduğu kimi, bəzi xüsusi terminləri də burda qeyd etməliyik.
19 | Elementin növbəyə daxil edilməsinə *EnQueue*, elementin növbədən silinməsinə isə *DeQueue* deyilir.
20 | Boş növbədə *DeQueue* əməliyyatı *underflow*, dolu növbədə *EnQueue* isə *overflow* adlanır.
21 | Biz bu halları *exception* kimi qəbul edirik.
22 |
23 | ## 7.2 Növbə gündəlik həyatda?
24 |
25 | Məntiq olaraq, biz növbə prinsipini o zaman yaradırıq və o zaman tələb edirik ki, gələnlərin ardıcıllıq haqqları qorunsun.
26 | Yəni sadə olaraq, yuxudan daha tez duran, daha isti çörəyi ala bilir və yaxud, bankda növbədə ilk nömrəsini alan ilk olaraq, müştəri xidmətlərinin rahat qoltuğuna otura bilir.
27 | Növbə mədəniyyəti də bu mənada, ilk gələn üstün olur anlayışını qorumaq üçün yaratdığımız məfhumdur.
28 | Bu prinsipi pozmağa cəhd edən şəxsə, haqlı etirazlar səslənir.
29 | Dolayısı ilə, bizə növbə o zaman lazım olur ki, orada daxil olma ardıcıllığı əhəmiyyətlidir.
30 | Gündəlik həyatımızı növbəsiz və növbəni müxtəlif üsullarla pozmağa çalışan insanlarsız təsəvvür etmək mümkün deyil.
31 |
32 |
33 | ## 7.3 Queue ADT(abstract data type)
34 |
35 | Aşağıdakı əməliyyatlar, növbəni ADT edir.
36 | Növbə üçün daxil etmə və silmə əməliyyatları FİFO sxemini izləməlidir.
37 | Sadəlik üçün, biz elementlərin integer olduğunu qəbul edirik.
38 |
39 | **Əsas növbə əməliyyatları**
40 | * EnQueue(): Növbənin sonuna element daxil edir.
41 | * DeQueue(): Növbənin əvvəlindən elementi silir və qaytarır.
42 |
43 | **Köməkçi növbə əməliyyatları**
44 | * QueueSize(): Növbədə olan elementlərin sayını qaytarır.
45 | * IsEmptyQueue(): Növbə boşdursa True, növbədə elementlər varsa False qaytarır.
46 |
47 |
48 | ## 7.4 Exceptions
49 |
50 | Boş növbə üçün DeQueue əməliyyatı *Empty Queue Exception* verməlidir.
51 | Eyni zamanda, dolu bir növbə üçün EnQueue əməliyyatı *Full Queue Exception* verməlidir.
52 |
53 |
54 | ## 7.5 Növbələr harda istifadə oluna bilər?
55 |
56 | **Birbaşa istifadə edən:**
57 | * Əməliyyat sisteminin, bərabər prioritetli job scheduler-ini xatırlamaq mühüm məqamdır.
58 | Bunu printer üzərində izah etmək daha uyğun olacaq. Belə ki, mən 5 fərqli sənədi çap etmək üçün əmr icra edirəm. Bu zaman printer ona daxil olan sənədlərin ardıcıllığını(bərabər prioritet) qoruyur.
59 | Yəni ilk daxil olan sənəd, ilk də çap olunur.
60 | * Multiprogramming.
61 | * Asinxron məlumat transferi(file İO, pipe, socket).
62 | * Müştəri xidmətlərinin gözləmə prinsipini icra edən call center.
63 |
64 | **Dolayı yolla istifadə edən:**
65 | * Alqoritmlər üçün köməkçi data stukturu ola bilər.
66 | * Digər data strukturlarının komponenti kimi iştirak edə bilər.
67 |
68 |
69 | ## 7.6 Növbələri necə yaradaq?
70 |
71 | Biz növbəni bir çox üsuldan istifadə edərək yarada bilərik və onlardan bəziləri aşağıdakılardır:
72 |
73 | * Dövri massivdən istifadə etməklə.(Dövri Növbə)
74 | * Dinamik dövri massivdən istifadə etməklə.
75 | * Əlaqəli listlərdən istifadə etməklə.
76 |
77 | Lakin, ilk öncə yaxşı olardı ki, dövri olmayan massivlə növbə yaratmağın çatışmazlığına nəzər yetirək.
78 | Bizim üçün növbə əməliyyatları aşağıdakı qaydada icra olunacaq:
79 |
80 | * `FRONT` və `REAR` adlı 2 göstəricimiz(pointer) var. Müvafiq olaraq, massivin ilk və son elementlərini özlərində saxlayırlar.
81 | * Növbəni yaradanda `FRONT` və `REAR`-ə -1 dəyər veririk.
82 | * EnQueue əməliyyatı zamanı, `REAR`-ın dəyərini artırırıq.
83 | * DeQueue əməliyyatı zaman, `FRONT`-un dəyərini artırırıq.
84 | * EnQueue-dən qabaq, növbənin dolu olub-olmamağını yoxlayırıq.
85 | * DeQueue-dən qabaq, növbənin boş olub-olmamağını yoxlayırıq.
86 | * Birinci elementi enqueue edəndə, `FRONT`-u 0-a bərabər edirik.
87 | * Ən sonuncu elementi dequeue etdikdən sonra isə `FRONT` və `REAR`-i yenidən -1 edirik.
88 |
89 | Aşağıdakı şəkilə diqqət yetiririk(Mənbə: [Queue](https://www.programiz.com/dsa/queue))
90 |
91 | 
92 |
93 | Gördüyünüz kimi, yuxarıda sadaladığımız addımların hamısını icra etmiş oluruq.
94 |
95 | Bu metodun ciddi çatışmazlığı var, aşağıdakı növbəti şəkildən də göründüyü kimi, bir neçə dequeu və enqueue əməliyyatlarından sonra,
96 | massivin uzunluğu(həcmi) qısalır. 0 və 1-ci indexləri biz yalnız massivi yenidən inisializasiya etsək istifadə edə bilərik.
97 |
98 | 
99 |
100 | Məhz bu səbəbdəndir ki, dövri növbələr daha səmərəli hesab olunur.
101 |
102 | **Dövri massivlə növbə yaratmaq**
103 | *Bu necə işləyir?*
104 | Dövri növbənin iş prinsipi, növbənin sonuna çatanda, yenidən başlamaqdır.
105 | Növbəyə element daxil etdikdə, `REAR`-i artırdığımızı bilirik.
106 | Növbənin sonuna çatdıqda yenidən başlamaq məqsədilə də modul bölmədən istifadə edirik.
107 | Deyək ki, bizim növbəmizin(massivin) uzunluğu 5-dir.
108 | Bu zaman `REAR`-i aşağıdakı qaydada artırırıq(unutmuruq ki, ilkin qiymət -1-dir).
109 |
110 | ```python
111 | >>> (-1+1)%5
112 | 0
113 | >>> (0+1)%5
114 | 1
115 | >>> (1+1)%5
116 | 2
117 | >>> (2+1)%5
118 | 3
119 | >>> (3+1)%5
120 | 4
121 | >>> (4+1)%5
122 | 0
123 | ```
124 |
125 | Gördüyünüz kimi, massivin sonuna çatanda `REAR` 0-landı, yəni yenidən başlandı.
126 | Bu da əslində dövri sözünün burdakı yerinin isbatıdır.
127 | Element daxil etməyə davam edə bilərik, sözsüz əgər boş yer varsa.
128 | Mənbə: [Circular Queue](https://www.programiz.com/dsa/circular-queue)
129 |
130 | `if REAR + 1 == 5 (overflow!), REAR = (REAR + 1)%5 = 0 (start of queue)`
131 |
132 | 
133 |
134 |
135 | Yuxarıda dediyimiz, Növbə əməliyyatları eyni şəkildə burda da təkrarlanır lakin bəzi əlavələrimiz var.
136 | Belə ki, Növbənin dolu olmasını yoxlamağın 2 yeni halını qeyd etməliyik:
137 | * Hal 1: `FRONT=0` and `REAR=SIZE-1` -> adi hal, heç dequeue etmədən, yalnız element daxil etdikdə, limitə(size-a) çatırıq.
138 | * Hal 2: `FRONT=REAR+1` -> Bu zaman növbə əvvəldən yenidən başlayır(circular increment), lakin yeni element daxil edilsə `REAR` necə deyərlər, `FRONT`-a bərabərləşir.
139 | Bu da o deməkdir ki, növbə doludur.
140 |
141 | Aşağıdakı şəkildə bu məsələ daha aydın görsənir:
142 |
143 | 
144 |
145 | İndi isə yuxarıdakı addımları izləməklə kodumuzu yazaq:
146 | > Bütün koda baxmaq üçün: [fesil7_circular_array_queue.py](../Source_Code/python_kodlar/fesil7/fesil7_circular_array_queue.py)
147 |
148 | ```python
149 | class CircularQueue:
150 |
151 | def __init__(self, limit=5):
152 | self.que = []
153 | self.limit = limit
154 | self.front = -1 # Ön
155 | self.rear = -1 # Arxa, son
156 |
157 | def is_full(self):
158 | if self.front == 0 and self.rear == (self.limit - 1):
159 | return True
160 | elif self.front == self.rear + 1:
161 | return True
162 | return False
163 |
164 | def is_empty(self):
165 | return self.front == -1
166 |
167 | def en_queue(self, data):
168 | if self.is_full():
169 | print("Növbə doludur...")
170 | else:
171 | if self.front == -1:
172 | self.front = 0
173 | # REAR-i artırırıq, irəli çəkirik.
174 | self.rear = (self.rear + 1) % self.limit
175 | self.que.append(data)
176 | print("EnQueue-dən sonra, növbə, ", self.que)
177 | print("FRONT -> ", self.front)
178 | print("REAR -> ", self.rear)
179 |
180 | def de_queue(self):
181 | if self.is_empty():
182 | print("Növbə boşdur...")
183 | else:
184 | # Python list element silindikdən sonra, listi özü yenidən indexlədiyi üçün.
185 | # Həmişə pop(0) olaraq çağırmaq lazımdır. pop(self.front) düzgün nəticə vermir.
186 | data = self.que.pop(0)
187 | # Əgər bərabərdilərsə o zaman cəmi 1 elementi var, bu səbəbdən sildikdən sonra resetləyirik.
188 | if self.front == self.rear:
189 | self.front = -1
190 | self.rear = -1
191 | else:
192 | # FRONT-u artırırıq, irəli çəkirik.
193 | self.front = (self.front + 1) % self.limit
194 |
195 | print("Silinən element - ", data)
196 | print("FRONT -> ", self.front)
197 | print("REAR -> ", self.rear)
198 |
199 | def size(self):
200 | return len(self.que)
201 | ```
202 |
203 | Kod kommentlərindən, fikrimcə məsələ daha da aydın olacaq.
204 | İndi isə kodumuzu test edək:
205 |
206 | ```python
207 | obj = CircularQueue(limit=5)
208 | obj.en_queue(56)
209 | obj.en_queue(44)
210 | obj.en_queue(85)
211 | obj.en_queue(66)
212 | obj.en_queue(99)
213 | obj.en_queue(111)
214 | obj.de_queue()
215 | obj.de_queue()
216 | obj.en_queue(111)
217 | obj.de_queue()
218 | obj.de_queue()
219 | obj.de_queue()
220 | ```
221 |
222 | Nəticə:
223 |
224 | ```python
225 | EnQueue-dən sonra, növbə, [56]
226 | FRONT -> 0
227 | REAR -> 0
228 | EnQueue-dən sonra, növbə, [56, 44]
229 | FRONT -> 0
230 | REAR -> 1
231 | EnQueue-dən sonra, növbə, [56, 44, 85]
232 | FRONT -> 0
233 | REAR -> 2
234 | EnQueue-dən sonra, növbə, [56, 44, 85, 66]
235 | FRONT -> 0
236 | REAR -> 3
237 | EnQueue-dən sonra, növbə, [56, 44, 85, 66, 99]
238 | FRONT -> 0
239 | REAR -> 4
240 | Növbə doludur...
241 | FRONT -> 0
242 | REAR -> 4
243 | Silinən element - 56
244 | FRONT -> 1
245 | REAR -> 4
246 | Silinən element - 44
247 | FRONT -> 2
248 | REAR -> 4
249 | EnQueue-dən sonra, növbə, [85, 66, 99, 111]
250 | FRONT -> 2
251 | REAR -> 0
252 | Silinən element - 85
253 | FRONT -> 3
254 | REAR -> 0
255 | Silinən element - 66
256 | FRONT -> 4
257 | REAR -> 0
258 | Silinən element - 99
259 | FRONT -> 0
260 | REAR -> 0
261 | ```
262 |
263 | *Performans*
264 |
265 | | | |
266 | | -------------|:-------------:
267 | | n sayda en_queue() əməliyyatı üçün yer mürəkkəbliyi | O(n) |
268 | | en_queue() üçün vaxt mürəkkəbliyi | O(1)(ortalama) |
269 | | de_queue() üçün vaxt mürəkkəbliyi | O(1) |
270 | | size() üçün vaxt mürəkkəbliyi | O(n) |
271 | | is_empty() üçün vaxt mürəkkəbliyi | O(1) |
272 | | is_full() üçün vaxt mürəkkəbliyi | O(1) |
273 |
274 | **Dinamik dövri massivlə növbə yaratmaq**
275 |
276 | Python üçün, bu üsulun adi dövri massivdəki kodumuzdan yeganə fərqi, növbə doludur mesajı əvəzinə onun limitini 2 qat artırmaqla davam edirik.
277 |
278 | > Bütün koda baxmaq üçün [fesil7_dynamic_circular_queue.py](../Source_Code/python_kodlar/fesil7/fesil7_dynamic_circular_queue.py)
279 |
280 | Yəni dəyişiklik məhz en_queue() metodunda olacaq:
281 |
282 | ```python
283 | def en_queue(self, data):
284 | if self.is_full():
285 | print("Növbə doludur, ikiqat artırıram...")
286 | self.limit = self.limit * 2
287 | else:
288 | if self.front == -1:
289 | self.front = 0
290 | # REAR-i artırırıq, irəli çəkirik.
291 | self.rear = (self.rear + 1) % self.limit
292 | self.que.append(data)
293 | print("EnQueue-dən sonra, növbə, ", self.que)
294 | print("FRONT -> ", self.front)
295 | print("REAR -> ", self.rear)
296 | ```
297 |
298 | Kodumuzu test edirik:
299 |
300 | ```python
301 | obj = DynamicCircularQueue(limit=5)
302 | obj.en_queue(56)
303 | obj.en_queue(44)
304 | obj.en_queue(85)
305 | obj.en_queue(66)
306 | obj.en_queue(99)
307 | obj.en_queue(111)
308 | obj.en_queue(222)
309 | ```
310 |
311 | Nəticə:
312 |
313 | ```python
314 | EnQueue-dən sonra, növbə, [56]
315 | FRONT -> 0
316 | REAR -> 0
317 | EnQueue-dən sonra, növbə, [56, 44]
318 | FRONT -> 0
319 | REAR -> 1
320 | EnQueue-dən sonra, növbə, [56, 44, 85]
321 | FRONT -> 0
322 | REAR -> 2
323 | EnQueue-dən sonra, növbə, [56, 44, 85, 66]
324 | FRONT -> 0
325 | REAR -> 3
326 | EnQueue-dən sonra, növbə, [56, 44, 85, 66, 99]
327 | FRONT -> 0
328 | REAR -> 4
329 | Növbə doludur, ikiqat artırıram...
330 | FRONT -> 0
331 | REAR -> 4
332 | EnQueue-dən sonra, növbə, [56, 44, 85, 66, 99, 222]
333 | FRONT -> 0
334 | REAR -> 5
335 | ```
336 |
337 | **Birtərəfli Əlaqəli listlərlə növbə yaratmaq**
338 |
339 | Növbə yaratmaq üçün digər bir üsul isə, əlaqəli listlərdən istifadə etməkdir.
340 | Bu zaman EnQueue əməliyyatı listin sonuna element daxil edir.
341 | DeQueue isə listin əvvəlindən element silir.
342 |
343 | İlk öncə tipimizi elan edək:
344 |
345 | > Bütün koda baxmaq üçün [fesil7_linked_list_queue.py](../Source_Code/python_kodlar/fesil7/fesil7_linked_list_queue.py)
346 |
347 | ```python
348 | class Node:
349 | # konstruktor
350 | def __init__(self, data=None, next_node=None):
351 | self.data = data
352 | self.next_node = next_node
353 |
354 | # node-un data field-ini mənimsətmək üçün metod
355 | def set_data(self, data):
356 | self.data = data
357 |
358 | # node-un data field-ini almaq üçün metod
359 | def get_data(self):
360 | return self.data
361 |
362 | # node-un növbəti field-ini mənimsətmək üçün metod
363 | def set_next_node(self, next_node):
364 | self.next_node = next_node
365 |
366 | # node-un növbəti field-ini almaq üçün metod
367 | def get_next_node(self):
368 | return self.next_node
369 |
370 | # əgər bir node sonrakına point edirsə, true qaytar
371 | def has_next(self):
372 | return self.next_node is not None
373 | ```
374 |
375 | Aşağıda isə Əlaqəli listlə EnQueue və DeQueue məntiqini icra edirik.
376 |
377 | Bu zaman əlaqəli listin ilk və son elementini, növbə üçün saxlayırıq:
378 |
379 | ```python
380 | class LinkedListQueue:
381 | def __init__(self, head=None):
382 | self.front = None
383 | self.rear = None
384 | self.head = head
385 |
386 | def size(self):
387 | current = self.head
388 | count = 0
389 | while current:
390 | count += 1
391 | current = current.get_next_node()
392 | return count
393 |
394 | def en_queue(self, data):
395 | # Listin sonuna node daxil edirik
396 | print("Növbəyə daxil edirik...")
397 | new_node = Node()
398 | new_node.set_data(data)
399 | if self.size() == 0:
400 | self.head = new_node
401 | # List-də heç bir element olmadığı üçün front və rear eyni yerdədirlər.
402 | self.front = self.head
403 | self.rear = self.front
404 | else:
405 | current = self.head
406 | while current.get_next_node() is not None:
407 | current = current.get_next_node()
408 |
409 | current.set_next_node(new_node)
410 | # Rear-i burda sonuncu node edirik
411 | self.rear = current.get_next_node()
412 |
413 | def de_queue(self):
414 | # Listin əvvəlindən node silirik
415 | if self.size() == 0:
416 | print("Növbə boşdur...")
417 | else:
418 | print("Növbədən çıxardırıq...")
419 | # Müvəqqəti node
420 | temp = self.head
421 | # Head node-u əvvəlki head-dən sonrakı node-a mənimsədirik.
422 | # Bununla da faktiki olaraq, əvvəlki head-i arxada qoyuruq.
423 | self.head = self.head.get_next_node()
424 | # Həmçinin front-u da yeni head-ə bərabər edirik, faktiki olaraq irəli sürüşdürürük.
425 | self.front = self.head
426 | # Müvəqqəti node-u silirik.
427 | del(temp)
428 |
429 | def queue_rear(self):
430 | if self.rear is None:
431 | print("Növbə boşdur...")
432 | else:
433 | return self.rear.get_data()
434 |
435 | def queue_front(self):
436 | if self.front is None:
437 | print("Növbə boşdur...")
438 | else:
439 | return self.front.get_data()
440 | ```
441 |
442 | Kodumuzu test edirik:
443 |
444 | ```python
445 | obj = LinkedListQueue()
446 | obj.en_queue(56)
447 | obj.en_queue(44)
448 | obj.en_queue(85)
449 | obj.en_queue(66)
450 | print("Növbənin uzunluğu: ", obj.size())
451 | obj.en_queue(99)
452 | obj.en_queue(111)
453 | obj.de_queue()
454 | obj.de_queue()
455 | obj.en_queue(222)
456 | print("Növbənin uzunluğu: ", obj.size())
457 | print("Növbənin ilk elementi: ", obj.queue_front())
458 | print("Növbənin son elementi: ", obj.queue_rear())
459 | ```
460 |
461 | Nəticə:
462 |
463 | ```
464 | Növbəyə daxil edirik...
465 | Növbəyə daxil edirik...
466 | Növbəyə daxil edirik...
467 | Növbəyə daxil edirik...
468 | Növbənin uzunluğu: 4
469 | Növbəyə daxil edirik...
470 | Növbəyə daxil edirik...
471 | Növbədən çıxardırıq...
472 | Növbədən çıxardırıq...
473 | Növbəyə daxil edirik...
474 | Növbənin uzunluğu: 5
475 | Növbənin ilk elementi: 85
476 | Növbənin son elementi: 222
477 | ```
478 |
479 | Bununla da massivlər və əlaqəli listlərdən istifadə etməklə Növbə(Queue) yaratmağı izahlı surətdə göstərmiş olduq.
480 |
--------------------------------------------------------------------------------
/book/8.Ağaclar_Trees.md:
--------------------------------------------------------------------------------
1 | # Ağaclar(trees)
2 |
3 | ## 8.1 Ağac nədir?
4 |
5 | Ağac da əlaqəli listlər kimi bir data strukturudur. Bildiyimiz kimi, əlaqəli listlərdə hər node özündən sonrakı node-a yönəlir(işarə edir).
6 | Yəni əlaqəli list xətti data strukturudur, düz xətt boyunca hər node digərinə işarə edir.
7 | Ağaclar isə qeyri-xəttidir və hər node bir neçə node-a işarə edə bilər.
8 | Ağac strukturu əslində iyerarxik bir düzülüşün qrafik olaraq göstərilməsidir.
9 | Ağacların ADT(Abstract Data Type)-də, elementlərin sırası(daxil edilmə ardıcıllığı) önəmli deyil. Əgər bu bizə önəmlidirsə, o zaman xətti data stukturlarından istifadə etməliyik.
10 |
11 | ## 8.2 Xüsusi məlumatlar
12 |
13 | Ağaclarla bağlı bəzi məxsusi məlumatları burda sadalamaqda fayda var.
14 | Qeyd edək ki, bəzi sözləri dilimizə bir-başa tərcümə edərkən, bəzən məna itirilir.
15 | Lakin, sözlərin əslini ingiliscə qeyd etməyə çalışıram.
16 | Məsələn, valideyn(parent) və övlad(child) sözləri burada sələf(predecessor) və xələf(successor) mənasında işlənilir.
17 |
18 | 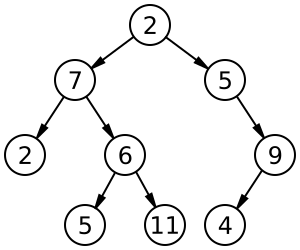
19 |
20 | * Ağaclarda *root* elə bir node-a deyilir ki, onun valideyni(parents) olmasın. Daha başqa cür desək, ondan əvvəl node olmasın.
21 | Bir Ağac stukturunda yalnız bir root ola bilər(elə həqiqi həyatda da, ağacın bir kökü olur).
22 | Bizim nümunəmizdə `(2)` root node-dur.
23 | * Valideyndən övlada gedən əlaqəyə *edge* deyilir(a link from parent to child).
24 | * Xələfi(övladı, uşağı) olmayan node leaf(yarpaq) adlanır(leaf node). Bizim nümunəmizdə, `(2)`, `(5)`, `(11)` və `(4)` leaf node-lardır.
25 | * Eyni valideyn node-un övladları, qardaş(siblings) node-lar adlanırlar(təbii olaraq). Bizim halda, `(7)` və `(5)` `(2)`-yə nəzərən, `(5)` və `11` `(6)`-ya nəzərən sibling node-durlar.
26 | * Verilmiş dərinlikdə olan bütün node-lar eyni səviyyədə(level) hesab olunurlar. Məsələn, `(7)` və `(5)` eyni səviyyədə - level 1-dədirlər. root node-un səviyyəsi 0-dır.
27 | * Node-un dərinliyi(depth) root node-dan ona qədər olan məsafə ilə ölçülür. Məsələn, node `(9)`-un dərinliyi 2-dir(`2 - 5 - 9`).
28 | * Node-un hündürlüyü, həmin node-dan ən dərin node-a qədər olan məsafəsinə bərabərdir. Məsələn, `(7)`-nin hündürlüyü 2-dir(`7 - 6 - 11`).
29 | * Ağacın hündürlüyü isə, root node-dan sonuncu ən altdakı node-a qədər məsafəyə bərabərdir. Məsələn, bizim nümunə ağacın hündürlüyü 3-dür.
30 | * Node-un ölçüsü(size), özü də daxil olmaqla ardıcıllarının sayına bərabərdir. Məsələn, `(7)`-nin ölçüsü 3-dür(`7 - 6 - 11`).
31 | * Əgər ağacın hər bir node-unun yalnız bir övladı(uşağı, xələfi) varsa, belə ağaca meyilli, əyri ağac(skew tree) deyilir.
32 | Əgər hər node-un yalnız sol xələfi varsa buna sola meyilli ağac(left skew tree), yalnız sağ xələfi varsa, sağa meyilli ağac(right skew tree) deyilir.
33 | Aşağıdakı şəkilə diqqət edək:
34 |
35 | 
36 |
37 | ## 8.3 İkili ağaclar(binary tree)
38 |
39 | Ağac nə zaman ikili ağac adlandırıla bilər?
40 | Əgər ağacdakı hər node-un 0 və ya 1 və ya 2 ardıcılı(child) varsa bu zaman həmin ağaca ikili ağac deyə bilərik.
41 |
42 | ## 8.4 İkili ağac növləri
43 |
44 | **Dəqiq ikili ağac(strict binary tree)**
45 |
46 | Əgər hər bir node-un yalniz 2 ardıcılı və ya 0 ardıcılı varsa, bu zaman belə ağaca dəqiq ikili ağac deyilir.
47 |
48 | 
49 |
50 | **Dolu ikili ağac(full binary tree)**
51 |
52 | Əgər hər bir node-un yalnız və yalnız 2 ardıcılı(child) varsa və hər bir node eyni səviyyədədirsə(level), belə ağaca dolu ikili ağac deyilir.
53 |
54 | 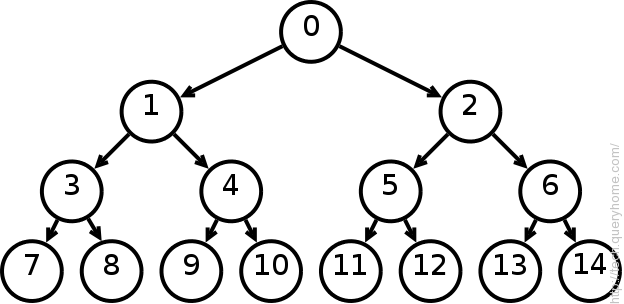
55 |
56 |
57 | **Tam ikili ağac(complete binary tree)**
58 |
59 | Bu elə bir ikili ağac növüdür ki, orada bütün səviyyələr tam doludur, yalnız sonuncudan başqa, hansı ki, bütün məlumatlar solda yerləşir.
60 |
61 | 
62 |
63 |
64 | ## 8.5 İkili ağacların xüsusiyyətləri
65 |
66 | Aşağıdakı xüsusiyyətlər üçün, ağacın hündürlüyünü `h` kimi götürək.
67 | Həmçinin, `root` node-un hündürlüyünü `0` qəbul edək.
68 |
69 | Bu zaman hündürlüyü 0(`h=0`) olan ağacın h level-ində(səviyyəsində) node sayı `2^0(2 üstü 0) = 1`, hündürlüyü 1(`h=1`) olan ağacın h level-ində isə `2^1=2` qədər node var.
70 |
71 | Yuxarıdakılara əsasən:
72 |
73 | * Dolu ikili ağac üçün node-ların sayı `n`, 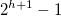-ə bərabərdir.
74 | Dolu(full) ikili ağacda `h` level olduğunu bilirik. Bu səbəbdən biz, hər səviyyədə olan node sayını toplamalıyıq:
75 |
76 | 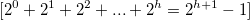
77 |
78 | * Tam ikili ağacda isə node-ların sayı `n`, minimum 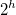-a, maksimum 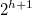-ə bərabərdir.
79 | * Dolu ikili ağacda, leaf node-larin sayı 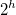-dır.
80 | * Tam ikili ağacda, n node üçün, NULL link-lərin(wasted pointers) sayı `n+1`-dir.
81 |
82 | **İkili ağacların strukturu**
83 |
84 | İndi isə ikili ağacın strukturunu təyin edək.
85 | Node-u(data-nı özündə saxlayan) ifadə etməyin bir üsulu budur ki, data ilə bərabər onun sağ və sol ardıcıllarına işarə edən linkləri saxlamaqdır.
86 |
87 | 
88 |
89 | ```python
90 | class Node:
91 | def __init__(self, data):
92 | # root node
93 | self.data = data
94 | # Sol övlad(left child)
95 | self.left = None
96 | # Sağ övlad(right child)
97 | self.right = None
98 |
99 | def get_data(self):
100 | return self.data
101 |
102 | def get_left_child(self):
103 | return self.left
104 |
105 | def get_right_child(self):
106 | return self.right
107 | ```
108 |
109 | **İkili ağaclar üzərində əməliyyatlar**
110 |
111 | *Əsas əməliyyatlar*
112 |
113 | * Ağaca element daxil etmək.
114 | * Ağacdan element silmək.
115 | * Ağacda element axtarmaq.
116 | * Ağacı əvvəldən axıra qət etmək.
117 |
118 | *Əlavə əməliyyatlar*
119 |
120 | * Ağacın ölçüsünü(size) tapmaq.
121 | * Ağacın hündürlüyünü tapmaq.
122 | * Cəmin ən çox olduğu səviyyəni(level-i) tapmaq.
123 | * Least common ancestor(ən az ümumi sələf) LCA-nın tapılması və s.
124 |
125 | ## 8.6 İkili ağacı qət etmək haqqında(tree traversal)
126 |
127 | Ağacları emal etmək üçün, onları qət etməyin mexanimzini bilməliyik və bu bölmədə bu haqda danışacağıq.
128 | Ağacın hər bir node-unu ziyarət etmək, ağacı qət etmək adlanır(tree traversal).
129 | Hər node yalnız bir dəfə emal olunur, lakin bir neçə dəfə ziyarət oluna bilər.
130 | Xətti data strukturlarında(əlaqəli listlər, yığın, növbələr) elementlər, ardıcıl olaraq ziyarət olunur. Lakin ağaclarda bunu bir neçə üsulu var.
131 | Ağacı(data stukturu olan ağac) qət etmək, ağacda nəyisə axtarmağa bənzəyir, bir fərqlə ki, qət edərkən, müəyyən bir ardıcıllığa dayanırıq.
132 | Digər tərəfdən, ağacı qət etmək onun bütün node-larını ziyarət etmək deməkdirsə, ağacda axtarış lazımlı(axtarılan) node tapılanda dayanır.
133 |
134 | **Ağacı qət etməyin mümkün növləri**
135 |
136 | İkili ağacın root node-undan başlayaraq, 3 əsas addım var ki, onların icra olunma ardıcıllığı qət etməyin növünü müəyyənləşdirir.
137 | Bu addımlar aşağıdakılardır:
138 | * Hal-hazırkı node-da əməliyyat aparmaq(bu elə node-u ziyarət etmək deməkdir və `D` hərfi ilə işarələnir).
139 | * Sol ardıcıl node-u qət etmək(`L` hərfi ilə işarələnir).
140 | * Sağ ardıcıl node-u qət etmək(`R` hərfi ilə işarələnir).
141 | Yuxarıdakı anlayışlara əsasən, bizim 6 mümkün variantımız olacaq:
142 |
143 | 1. LDR: Sol altağacı(subtree) emal et, hazırkı node-u emal et və daha sonra sağ altağacı emal et.
144 | 2. LRD: Sol altağacı emal et, sağ altağacı emal et və hazırkı node-u emal et.
145 | 3. DLR: Hazırkı node-u emal et, sol altağacı emal et və daha sonra sağ altağacı emal et.
146 | 4. DRL: Hazırkı node-u emal et, sağ altağacı emal et və sol altağacı emal et.
147 | 5. RDL: Sağ altağacı emal et, hazırkı node-u emal et və sol altağacı emal et.
148 | 6. RLD: Sağ altağacı emal et, sol altağacı emal et və hazırkı node-u emal et.
149 |
150 | **Qət etməni təsnifləşdirmək**
151 |
152 | Node-ların hansı ardıcıllıqla emal olunması, qət etmənin də növünü müəyyən edir.
153 | Təsnifləşdirmə, hal-hazırkı node-un hansı ardıcıllıqla emal olunması əsasında baş verir.
154 | Bu o deməkdir ki, əgər biz hal-hazırkı node(`D`)-a əsasən təsnifat aparırıqsa və bu node ortada gəlirsə, bu zaman bizim üçün elə də fərq etmir ki, `L` `D`-dən solda ya `R` `D`-dən sağda yerləşir.
155 | Eynilə bizim üçün `L`-in `D`-dən sağda, `R`-in `D`-dən solda olmasının da əhəmiyyəti yoxdur.
156 | Bu səbəbdən, biz yuxarıdakı 6 mümkün variantı 3-ə endirə bilərik:
157 | > Qeyd: Aşağıdakıları öz dilimizdə və rus dilində verirəm ki, daha aydın olsun. Bəzilərini isə tərcümə edə bilmədim.
158 |
159 | * Preorder (DLR) Traversal - предварительный обход - ilkin, ön qət etmə.
160 | * İnorder (LDR) Traversal - ...
161 | * Postorder (LRD) Traversal - постобработка - ...
162 |
163 | Geri qalan müzakirəmiz üçün aşağıdakı diaqramı əsas götürək:
164 |
165 | 
166 |
167 | **PreOrder Traversal**
168 |
169 | Bu qət etmə zamanı hər node, onun istənilən altağacından əvvəl emal olunur.
170 | Bu başa düşülən ən sadə qət etmə üsuludur. Lakin, bu zaman da ağacda aşağı irəlilədikcə bəzi məlumatları yadda saxlamalıyıq.
171 |
172 | Yuxarıdakı şəklimizə baxsaq, bu qət etmə zamanı ilk öncə `1` daha sonra sol altağac daha sonra da sağ altağac emal olunacaq.
173 |
174 | Burdan belə nəticə çıxır ki, sol altağacın emalından sonra proses sağ altağaca keçməlidir. Soldan sağa keçmək üçün isə biz `root`-u yadda saxlamalıyıq.
175 | PreOrder Traversal aşağıdakı kimi təyin olunur:
176 | * root-u ziyarət et.
177 | * Sol altağacı PreOrder şəkildə qət et.
178 | * Sağ altağacı PreOrder şəkildə qət et.
179 |
180 | Göründüyü kimi, bu Rekursiya üçün əla nümunədir.
181 | Yuxarıda verilmiş kod şəklə əsasən, bizim PreOrder qət etməmizin nəticəsi `8 3 1 6 4 7 10 14 13` olmalıdır.
182 |
183 | Gəlin Ağacı yaradan kodla PreOrder traversal edən koda baxaq:
184 |
185 | > QEYD: aşağıdakı linkdən ağac yaradan kodu vizuallaşdıraraq daha rahat anlaya bilərsiniz.
186 |
187 | [Kodun Vizuallaşdırılması](http://www.pythontutor.com/visualize.html#code=%23%20D%C4%B0QQ%C6%8FT!%20%C4%B0%C5%9Fl%C9%99k%20olmayan%20kod%20n%C3%BCmun%C9%99si!%0A%0Aclass%20Node%3A%0A%20%20%20%20def%20__init__%28self,%20data%29%3A%0A%20%20%20%20%20%20%20%20%23%20root%20node%0A%20%20%20%20%20%20%20%20self.data%20%3D%20data%0A%20%20%20%20%20%20%20%20%23%20Sol%20%C3%B6vlad%28left%20child%29%0A%20%20%20%20%20%20%20%20self.left%20%3D%20None%0A%20%20%20%20%20%20%20%20%23%20Sa%C4%9F%20%C3%B6vlad%28right%20child%29%0A%20%20%20%20%20%20%20%20self.right%20%3D%20None%0A%0A%20%20%20%20def%20get_data%28self%29%3A%0A%20%20%20%20%20%20%20%20return%20self.data%0A%0A%20%20%20%20def%20get_left_child%28self%29%3A%0A%20%20%20%20%20%20%20%20return%20self.left%0A%0A%20%20%20%20def%20get_right_child%28self%29%3A%0A%20%20%20%20%20%20%20%20return%20self.right%0A%0A%0A%0Aclass%20BinaryTree%3A%0A%20%20%20%20%0A%20%20%20%20def%20__init__%28self%29%3A%0A%20%20%20%20%20%20%20%20self.root%20%3D%20None%0A%20%20%20%20%0A%20%20%20%20def%20create_tree%28self,%20val%29%3A%0A%20%20%20%20%20%20%20%20%23%20A%C4%9Fac%C4%B1n%20%C3%B6z%C3%BCn%C3%BC%20burda%20yarad%C4%B1r%C4%B1q.%0A%20%20%20%20%20%20%20%20if%20self.root%20is%20None%3A%0A%20%20%20%20%20%20%20%20%20%20%20%20%23%20Birinci%20elementi%20root%20element%20edirik%0A%20%20%20%20%20%20%20%20%20%20%20%20self.root%20%3D%20Node%28data%3Dval%29%0A%20%20%20%20%20%20%20%20%0A%20%20%20%20%20%20%20%20else%3A%0A%20%20%20%20%20%20%20%20%20%20%20%20%23%20Root-u%20haz%C4%B1rk%C4%B1%20node%20edirik%0A%20%20%20%20%20%20%20%20%20%20%20%20current%20%3D%20self.root%0A%0A%20%20%20%20%20%20%20%20%20%20%20%20while%20True%3A%0A%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%23%20%C6%8Fg%C9%99r%20verilmi%C5%9F%20qiym%C9%99t%20hal-haz%C4%B1rk%C4%B1%20qiym%C9%99td%C9%99n%20ki%C3%A7ikdirs%C9%99,%0A%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%23%20Onu%20sol%20node%20edirik%20%20%0A%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20if%20val%20%3C%20current.data%3A%0A%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20if%20current.left%3A%0A%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20current%20%3D%20current.left%0A%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20else%3A%0A%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20current.left%20%3D%20Node%28data%3Dval%29%0A%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20break%3B%0A%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%23%20%C6%8Fg%C9%99r%20verilmi%C5%9F%20qiym%C9%99t%20hal-haz%C4%B1rk%C4%B1%20qiym%C9%99td%C9%99n%20b%C3%B6y%C3%BCkd%C3%BCrs%C9%99,%0A%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%23%20Onu%20sa%C4%9F%20node%20edirik%20%20%0A%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20elif%20val%20%3E%20current.data%3A%0A%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20if%20current.right%3A%0A%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20current%20%3D%20current.right%0A%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20else%3A%0A%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20current.right%20%3D%20Node%28data%3Dval%29%0A%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20else%3A%0A%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20break%0A%20%20%20%20%0A%0A%20%20%20%20def%20print_tree%28self,%20node%29%3A%0A%20%20%20%20%20%20%20%20%20%20%20%20if%20node%20is%20not%20None%3A%0A%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20self.print_tree%28node.get_left_child%28%29%29%0A%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20print%28node.data%29%0A%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20self.print_tree%28node.get_right_child%28%29%29%0A%20%20%20%20%0A%20%20%20%20def%20preorder_traversal_recursive%28self,%20node%29%3A%0A%20%20%20%20%20%20%20%20if%20node%20is%20not%20None%3A%0A%20%20%20%20%20%20%20%20%20%20%20%20print%28node.data%29%0A%20%20%20%20%20%20%20%20%20%20%20%20self.preorder_traversal_recursive%28node.left%29%0A%20%20%20%20%20%20%20%20%20%20%20%20self.preorder_traversal_recursive%28node.right%29%0A%20%20%20%20%0A%20%20%20%20def%20preorder_traversal_iterative%28self,%20node%29%3A%0A%20%20%20%20%20%20%20%20if%20node%20is%20not%20None%3A%0A%20%20%20%20%20%20%20%20%20%20%20%20stack%20%3D%20%5B%5D%0A%20%20%20%20%20%20%20%20%20%20%20%20stack.append%28node%29%0A%20%20%20%20%20%20%20%20%20%20%20%20while%20stack%3A%0A%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20node%20%3D%20stack.pop%28%29%0A%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20print%28node.data%29%0A%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20if%20node.right%3A%0A%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20stack.append%28node.right%29%0A%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20if%20node.left%3A%0A%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20%20stack.append%28node.left%29%0A%0A%0A%0Aif%20__name__%20%3D%3D%20%22__main__%22%3A%0A%20%20%20%20tree%20%3D%20BinaryTree%28%29%0A%20%20%20%20arr%20%3D%20%5B8,%203,%201,%206,%204,%207,%2010,%2014,%2013%5D%0A%20%20%20%20for%20i%20in%20arr%3A%0A%20%20%20%20%20%20%20%20tree.create_tree%28i%29&cumulative=false&curInstr=208&heapPrimitives=false&mode=display&origin=opt-frontend.js&py=3&rawInputLstJSON=%5B%5D&textReferences=false)
188 |
189 | > Bütün kodlara buradan baxa bilərsiniz: [fesil8_binary_tree_node.py](../Source_Code/python_kodlar/fesil8/fesil8_binary_tree_node.py)
190 |
191 | ```python
192 | class BinaryTree:
193 |
194 | def __init__(self):
195 | self.root = None
196 |
197 | def create_tree(self, val):
198 | # Ağacın özünü burda yaradırıq.
199 | if self.root is None:
200 | # Birinci elementi root element edirik
201 | self.root = Node(data=val)
202 |
203 | else:
204 | # Root-u hazırkı node edirik
205 | current = self.root
206 |
207 | while True:
208 | # Əgər verilmiş qiymət hal-hazırkı qiymətdən kiçikdirsə,
209 | # Onu sol node edirik
210 | if val < current.data:
211 | if current.left:
212 | current = current.left
213 | else:
214 | current.left = Node(data=val)
215 | break;
216 | # Əgər verilmiş qiymət hal-hazırkı qiymətdən böyükdürsə,
217 | # Onu sağ node edirik
218 | elif val > current.data:
219 | if current.right:
220 | current = current.right
221 | else:
222 | current.right = Node(data=val)
223 | else:
224 | break
225 |
226 |
227 | def preorder_traversal_recursive(self, node):
228 | if node is not None:
229 | print(node.data)
230 | self.preorder_traversal_recursive(node.left)
231 | self.preorder_traversal_recursive(node.right)
232 |
233 | def preorder_traversal_iterative(self, node):
234 | if node is not None:
235 | stack = []
236 | # root node-u listə daxil edirik.
237 | stack.append(node)
238 | while stack:
239 | node = stack.pop()
240 | print(node.data, end=" ")
241 | if node.right:
242 | stack.append(node.right)
243 | # Ən son node.left-i append edirik çünki bizə lazımdı sol node-u pop() etsin.
244 | if node.left:
245 | stack.append(node.left)
246 | ```
247 |
248 | Yuxarıdakı kod nümunəsində biz rekursiv və iterativ 2 metod yazmışıq, kommentlərlə kodları izah etməyə çalışmışam. Hər 2 metod üçün:
249 |
250 | *Vaxt mürəkkəbliyi O(n), Yer mürəkkəbliyi O(n)*
251 |
252 | Kodumuzu test etdikdə, görürük ki, istədiyimiz nəticəni ala bilirik:
253 | ```python
254 | $ python3 fesil8_binary_tree_node.py
255 | PreOrder Recursive Traversal - 8 3 1 6 4 7 10 14 13
256 | PreOrder Iterative Traversal - 8 3 1 6 4 7 10 14 13
257 | ```
258 |
259 | **InOrder Traversal**
260 |
261 | InOrder qət etmə zamanı, root node altağacların arasında(ortasında) ziyarət edilir.
262 | Bu növ qət etmə aşağıdakı qaydada təyin olunur:
263 |
264 | * Sol altağacı InOrder şəkildə qət et.
265 | * root-u ziyarət et.
266 | * Sağ altağacı InOrder şəkildə qət et.
267 |
268 | InOrder qət etmə bizə `1 3 4 6 7 8 10 13 14` nəticəsini verməlidir.
269 | Əgər yuxarıdakı şəkilə fikir versəniz görərsiniz ki, hər bir altağac sol tərəfli olaraq qət olunur.
270 | Aşağıdakı kod parçaları, InOrder qət etmənin rekursiv və iterativ üsulunu göstərir:
271 |
272 | ```python
273 | def inorder_traversal_recursive(self, node):
274 | if node is not None:
275 | # Birinci sol altağac emal olunur(ziyarət olunur)
276 | self.inorder_traversal_recursive(node.left)
277 | print(node.data, end=" ")
278 | self.inorder_traversal_recursive(node.right)
279 |
280 | def inorder_traversal_iterative(self, node):
281 | if node is not None:
282 | stack = []
283 | while stack or node:
284 | if node:
285 | stack.append(node)
286 | node = node.left
287 | else:
288 | node = stack.pop()
289 | print(node.data, end=" ")
290 | node = node.right
291 | ```
292 |
293 | *Vaxt mürəkkəbliyi O(n), Yer mürəkkəbliyi O(n)*
294 |
295 | Kodumuzu test edək:
296 |
297 | ```python
298 | $ python3 fesil8_binary_tree_node.py
299 | PreOrder Recursive Traversal - 8 3 1 6 4 7 10 14 13
300 | PreOrder Iterative Traversal - 8 3 1 6 4 7 10 14 13
301 | InOrder Recursive Traversal - 1 3 4 6 7 8 10 13 14
302 | InOrder Iterative Traversal - 1 3 4 6 7 8 10 13 14
303 | ```
304 |
305 | **PostOrder Traversal**
306 |
307 | Postorder qət etmə zamanı, root node bütün altağaclardan sonra ziyarət edilir, yəni ən sonda.
308 | Postorder qət etmə aşağıdakı qaydada təyin olunur:
309 |
310 | * Sol altağacı PostOrder şəkildə qət et.
311 | * Sağ altağacı PostOrder şəkildə qət et.
312 | * root-u ziyarət et.
313 |
314 | Yuxarıdakı şəklimizə baxsaq bu zaman deyə bilərik ki, bizdə 8 ən sonda görsənəcək və hər bir altağacın özünün root node-u da ən sonda ziyarət olunmalıdır. Dolayısı ilə, nəticəmiz `1 4 7 6 3 13 14 10 8` şəklində olmalıdır.
315 |
316 | Rekursiv kodumuza baxaq:
317 |
318 | ```python
319 | def postorder_traversal_recursive(self, node):
320 | if node is not None:
321 | self.postorder_traversal_recursive(node.left)
322 | self.postorder_traversal_recursive(node.right)
323 | print(node.data, end=" ")
324 | ```
325 |
326 | *Vaxt mürəkkəbliyi O(n), Yer mürəkkəbliyi O(n)*
327 |
328 | PostOrder qət etmənin rekursiv üsulu kifayət qədər aydın görünür. Lakin, iterativ üsulu biraz daha izah etmək lazımdır. Əgər xatırlayırsınızsa, preorder və inorder qət etmə zamanı, stack-dən pop etdikdən sonra biz eyni təpəciyə qayıtmırdıq(vertex). PostOrder qət etmədə isə sanki aşağıdan yuxarı irəlilədiyimiz üçün eyni node-u 2 dəfə keçirik və məcburuq ki, hər hansı üsulla qeydiyyat aparaq ki, bu node-u istifadə etmişik ya yox.
329 | Aşağıdakı kod parçasında biz əlavə olaraq 1 list və istifadə olunmuşları qeyd etmək üçün de 1 set istifadə edirik:
330 |
331 | >Mənbə: [leetcode-python-binary-tree-postorder](http://jelices.blogspot.com/2014/05/leetcode-python-binary-tree-postorder.html)
332 |
333 | ```python
334 | def postorder_traversal_iterative(self, root):
335 | solution = []
336 | used = set()
337 | stack = []
338 |
339 | if root != None:
340 | stack.append(root)
341 |
342 | while len(stack) > 0:
343 | node = stack.pop()
344 |
345 | if node in used:
346 | solution.append(node.data)
347 | else:
348 | used.add(node)
349 | stack.append(node)
350 | if node.right != None:
351 | stack.append(node.right)
352 | if node.left != None:
353 | stack.append(node.left)
354 | return solution
355 | ```
356 | *Vaxt mürəkkəbliyi O(n), Yer mürəkkəbliyi O(n)*
357 |
358 | Kodumuzu test edək:
359 |
360 | ```python
361 | $ python3 fesil8_binary_tree_node.py
362 | PreOrder Recursive Traversal - 8 3 1 6 4 7 10 14 13
363 | PreOrder Iterative Traversal - 8 3 1 6 4 7 10 14 13
364 | InOrder Recursive Traversal - 1 3 4 6 7 8 10 13 14
365 | InOrder Iterative Traversal - 1 3 4 6 7 8 10 13 14
366 | PostOrder Recursive Traversal - 1 4 7 6 3 13 14 10 8
367 | PostOrder Iterative Traversal - [1, 4, 7, 6, 3, 13, 14, 10, 8]
368 | ```
369 |
370 | >Qeyd: Kod parçalarındakı loop-ları başa düşməyin ən yaxşı üsulu kağız üzərində qələmlə çəkmək, vizual olaraq prosesi görməkdir.
371 |
372 | **Level Order Traversal**
373 |
374 | Bu fəsildə son toxunduğumuz mövzu səviyyəyə uyğun qət etmədir.
375 | Bu zaman bizim nəticə `8, 3, 10, 1, 6, 14, 4, 7, 13` olacaq.
376 | Yəni eyni səviyyədə olan node-lar soldan sağa qət ediləcək.
377 |
378 | Aşağıdakı ardıcıllığa diqqət yetiririk:
379 |
380 | * root node-u ziyarət et.
381 | * Hər level-də ilk öncə sol daha sonra sağ node-u ziyarət et.
382 | * Bütün səviyyələr ziyarət edilənə qədər, eyni addımı təkrar et.
383 |
384 | Bu məqsədlə biz Python-da olan queue modulundan istifadə edərək, ziyarət etdiyimiz node-ları növbəyə düzəcəyik(FİFO).
385 |
386 | ```python
387 | def level_order_traversal(self, node):
388 | if node is not None:
389 | result = []
390 | q = Queue()
391 | q.put(node) # root node-u daxil edirik.
392 |
393 | while not q.empty():
394 | node = q.get() # Dequeue FIFO
395 | result.append(node.get_data())
396 |
397 | if node.left is not None:
398 | q.put(node.left)
399 |
400 | if node.right is not None:
401 | q.put(node.right)
402 |
403 | return result
404 | ```
405 |
406 | Ümumi kod nəticəmiz aşağıdakı kimi olacaq:
407 |
408 | ```python
409 | $ python3 fesil8_binary_tree_node.py
410 | PreOrder Recursive Traversal - 8 3 1 6 4 7 10 14 13
411 | PreOrder Iterative Traversal - 8 3 1 6 4 7 10 14 13
412 | InOrder Recursive Traversal - 1 3 4 6 7 8 10 13 14
413 | InOrder Iterative Traversal - 1 3 4 6 7 8 10 13 14
414 | PostOrder Recursive Traversal - 1 4 7 6 3 13 14 10 8
415 | PostOrder Iterative Traversal - [1, 4, 7, 6, 3, 13, 14, 10, 8]
416 | LevelOrder Traversal - [8, 3, 10, 1, 6, 14, 4, 7, 13]
417 | ```
418 |
419 | Hörmətli oxucu, bununla da bizim Ağac və xüsusən də ikili ağaclar haqqında söhbətimizə burda fasilə veririk.
420 | Növbəti fəsildə, bəzi tapşırıqları yerinə yetirməyə çalışacıq.
421 |
--------------------------------------------------------------------------------
/book/9.İkili_Ağaclar_Tapşırıqlar_və_Həllər.md:
--------------------------------------------------------------------------------
1 | # İkili ağaclar - tapşırıqlar və həllər
2 |
3 | Bu fəsildə ikili ağaclarla bağlı tapşırıq və onların həllərinə nəzər yetirəcik.
4 | İlk öncə tapşırığın izahını daha sonra da kod parçasını göstərəcəyik.
5 |
6 | ## Tapşırıq - 1
7 |
8 | *Şərt:*
9 |
10 | İkili ağacda maximum elementi tapın.
11 |
12 | *Həlli:*
13 |
14 | Bir üsulumuz bu ola bilər ki, ilk öncə sol altağacda maximum elementi tapaq, daha sonra sol altağacda maximum elementi tapaq və onu root elementlə müqayisə edək. Gördüyünüz kimi, bu işi rekursiv üsulla həll edə bilərik.
15 | > Qeyd: bütün kodlara baxmaq üçün [fesil9_problems_solutions.py](../Source_Code/python_kodlar/fesil9/fesil9_problems_solutions.py)
16 |
17 | Kod nümunəmiz:
18 |
19 | ```python
20 | def find_max_recursive(self, node):
21 | if not node:
22 | return self.max_data
23 |
24 | if node.get_data() > self.max_data:
25 | self.max_data = node.get_data()
26 |
27 | self.find_max_recursive(node.left)
28 | self.find_max_recursive(node.right)
29 |
30 | return self.max_data
31 | ```
32 |
33 | Bizim nümunə ağacımız üçün yuxarıdakı kod 14 qaytaracaq:
34 |
35 | ```python
36 | tree = BinaryTree()
37 | arr = [8, 3, 1, 6, 4, 7, 10, 14, 13]
38 | for i in arr:
39 | tree.create_tree(i)
40 |
41 | print(tree.find_max_recursive(tree.root))
42 | ```
43 |
44 | ## Tapşırıq - 2
45 |
46 | *Şərt:*
47 |
48 | Rekursiyadan istifadə etmədən ağacdakı maximum elementi tapın.
49 |
50 | *Həlli:*
51 |
52 | `Level Order Traversal` metodundan(bax 8-ci fəsilə) istifadə etməklə, hər səviyyədə(level) elementləri Növbədən silərkən müqayisə apararaq, maximum elementi aşkarlaya bilərik.
53 |
54 | Kod nümunəmiz:
55 |
56 | ```python
57 | def find_max_level_order_traversal(self, node):
58 | if node is not None:
59 | q = Queue()
60 | q.put(node) # root node-u daxil edirik.
61 |
62 | while not q.empty():
63 | node = q.get() # Dequeue FIFO
64 | # növbədən çıxartdıqdan sonra müqayisə edirik.
65 | if node.get_data() > self.max_data:
66 | self.max_data = node.get_data()
67 |
68 | if node.left is not None:
69 | q.put(node.left)
70 |
71 | if node.right is not None:
72 | q.put(node.right)
73 |
74 | return self.max_data
75 | ```
76 |
77 | ## Tapşırıq - 3
78 |
79 | *Şərt:*
80 |
81 | Ikili ağacda verilmiş data-lı node-un olub-olmamasını yoxlamaq və yaxud ağacda element axtarmaq.
82 |
83 | *Həlli:*
84 |
85 | İlk ağıla gələn təbii üsul, root-dan başlamaq, öncə sol altağacda, daha sonra da sağ altağacda verilmiş elementi axtarmaqdır.
86 |
87 | Rekursiv kod nümunəmiz:
88 |
89 | ```python
90 | def find_data_recursive(self, node, data):
91 | if node is None:
92 | return 0
93 |
94 | if node.get_data() == data:
95 | return 1
96 | elif data < node.get_data():
97 | return self.find_data_recursive(node.left, data)
98 | else:
99 | return self.find_data_recursive(node.right, data)
100 | ```
101 |
102 | Kodumuzu sınayaq:
103 |
104 | ```python
105 | tree = BinaryTree()
106 | arr = [8, 3, 1, 6, 4, 7, 10, 14, 13]
107 | for i in arr:
108 | tree.create_tree(i)
109 | print("find_max_recursive() -> ", end='')
110 | print(tree.find_max_recursive(tree.root))
111 | print("find_max_level_order_traversal() -> ", end='')
112 | print(tree.find_max_level_order_traversal(tree.root))
113 | print("find_data_recursive() search 88 -> ", end='')
114 | print(tree.find_data_recursive(tree.root, 88))
115 | print("find_data_recursive() search 14 -> ", end='')
116 | print(tree.find_data_recursive(tree.root, 14))
117 | ```
118 |
119 | Nəticə:
120 |
121 | ```python
122 | $ python3 fesil9_problems_solutions.py
123 | find_max_recursive() -> 14
124 | find_max_level_order_traversal() -> 14
125 | find_data_recursive() search 88 -> 0
126 | find_data_recursive() search 14 -> 1
127 | ```
128 |
129 | ## Tapşırıq - 4
130 |
131 | *Şərt:*
132 |
133 | Yuxarıdakı axtarışı iterativ üsulla edin.
134 |
135 | *Həlli:*
136 |
137 | Bu zaman ağıla gələn üsul budur ki, Level Order Traversal-dan istifadə edərək, hər level-də axtarış edək, yoxlayaq ki, verilmiş(axtarılan) data hansı node-dadır.
138 |
139 | Kod nümunəmiz:
140 |
141 | ```python
142 | def find_data_level_order_traversal(self, node, data):
143 | if node is not None:
144 | q = Queue()
145 | q.put(node) # root node-u daxil edirik.
146 |
147 | while not q.empty():
148 | node = q.get() # Dequeue FIFO
149 | # növbədən çıxartdıqdan sonra yoxlayırıq.
150 | if node.get_data() == data:
151 | return 1
152 | if node.left is not None:
153 | q.put(node.left)
154 |
155 | if node.right is not None:
156 | q.put(node.right)
157 | # 0 qayıdırsa, deməli data Ağacda yoxdur.
158 | return 0
159 | ```
160 |
161 | Nəticə:
162 |
163 | ```python
164 | $ python3 fesil9_problems_solutions.py
165 | find_max_recursive() -> 14
166 | find_max_level_order_traversal() -> 14
167 | find_data_recursive() search 88 -> 0
168 | find_data_recursive() search 14 -> 1
169 | find_data_level_order_traversal() search 88 -> 0
170 | find_data_level_order_traversal() search 14 -> 1
171 | ```
172 |
173 | ## Tapşırıq - 5
174 |
175 | *Şərt:*
176 |
177 | İkili ağaca element daxil etməyin üsulunu yazın.
178 |
179 | *Həll:*
180 |
181 | Bu məqsədlə yenidən, Level Order Traversal üsulundan istifadə edə bilərik.
182 | Belə ki, hər level(səviyyə)-də sağ və ya sol node-u olmayan node-u aşkarlayaraq, ora daxil edə bilərik.
183 |
184 | Kod nümunəmiz:
185 |
186 | ```python
187 | def insert_in_binary_using_tree_level_order(self, node, data):
188 | new_node = Node(data)
189 | if node is None:
190 | node = new_node # Ağac boşdursa, yeni node-u root node edirik.
191 | return node
192 |
193 | q = Queue()
194 | q.put(node) # Root node-u növbəyə daxil edirik.
195 |
196 | while not q.empty():
197 | node = q.get() # Dequeue FIFO
198 | # növbədən çıxartdıqdan sonra yoxlayırıq.
199 | if node.get_data() == data:
200 | return "Already in tree"
201 | if node.left is not None:
202 | q.put(node.left)
203 | else:
204 | # Əgər hal-hazırkı node-un datasından kiçikdirsə
205 | if new_node.get_data() < node.get_data():
206 | node.left = new_node
207 | return "Inserted as left node"
208 |
209 | if node.right is not None:
210 | q.put(node.right)
211 | else:
212 | # Əgər hal-hazırkı node-un datasından böyükdürsə
213 | if new_node.get_data() > node.get_data():
214 | node.right = new_node
215 | return "Inserted as right node"
216 | ```
217 |
218 | ## Tapşırıq - 6
219 |
220 | *Şərt:*
221 |
222 | Ağacın ölçüsünü(elementlərinin sayını, node-ların sayını) tapın.
223 |
224 | *Həlli:*
225 |
226 | Rekursiv olaraq sağ və sol altağacları ziyarət etmək lazımdır. Son nəticənin də üstünə 1 gəlmək lazımdır(root node-u).
227 |
228 | ```python
229 | def find_tree_size_recursive(self, node):
230 | if node is None:
231 | return 0
232 |
233 | return self.find_tree_size_recursive(node.left) + self.find_tree_size_recursive(node.right) + 1
234 | ```
235 |
236 | ## Tapşırıq - 7
237 |
238 | *Şərt:*
239 |
240 | Ağacın ölçüsünü iterativ üsulla tapın(yuxarıdakı məsələni).
241 |
242 | *Həlli:*
243 |
244 | Yenə də Level Order Traversal edərək hər səviyyədəki node sayını hesablayırıq.
245 |
246 | ```python
247 | def find_tree_size_iterative(self, node):
248 | if node is None:
249 | return 0
250 |
251 | q = Queue()
252 | q.put(node) # Root node-u növbəyə daxil edirik.
253 | count = 0
254 |
255 | while not q.empty():
256 | node = q.get()
257 | count = count + 1
258 | if node.left is not None:
259 | q.put(node.left)
260 | if node.right is not None:
261 | q.put(node.right)
262 |
263 | return count
264 | ```
265 |
266 | Nəticə:
267 |
268 | ```python
269 | $ python3 fesil9_problems_solutions.py
270 | find_max_recursive() -> 14
271 | find_max_level_order_traversal() -> 14
272 | find_data_recursive() search 88 -> 0
273 | find_data_recursive() search 14 -> 1
274 | find_data_level_order_traversal() search 88 -> 0
275 | find_data_level_order_traversal() search 14 -> 1
276 | insert_in_binary_using_tree_level_order(tree.root, 21) -> Inserted as right node
277 | find_tree_size_recursive() -> 10
278 | find_tree_size_iterative() -> 10
279 | ```
280 |
281 | ## Tapşırıq - 8
282 |
283 | *Şərt:*
284 |
285 | Level Order Traversal-ın elementləri əks(reverse) ardıcıllıqla çap edən növünü yazın.
286 |
287 | *Həlli:*
288 |
289 | Adi qaydada etdiyimiz Level Order Traversal zamanı, bir də köməkçi list-dən istifadə etsək, hər dəfə Queue-dən çıxartdığımız node-u həmin listə yığsaq son nəticədə bizdə Stack əmələ gələcək. Yəni faktiki olaraq, ən son gələni ən birinci çıxarda biləcəyik(LİFO). Bunu list-dən pop() edərək əldə edirik. Aşağıdakı kod parçasına diqqət yetirək:
290 |
291 | ```python
292 | def level_order_traversal_in_reverse(self, node):
293 | if node is None:
294 | return 0
295 |
296 | q = Queue()
297 | s = [] # LIFO üçün istifadə edəcəyimiz list
298 | q.put(node) # root node-u daxil edirik.
299 |
300 | while not q.empty():
301 | node = q.get() # Dequeue FIFO
302 | s.append(node.get_data()) # LIFO
303 |
304 | if node.left is not None:
305 | q.put(node.left)
306 |
307 | if node.right is not None:
308 | q.put(node.right)
309 |
310 | while(s):
311 | print(s.pop(), end=' ')
312 | ```
313 |
314 | Nəticəmizdən də göründüyü kimi ağacın elementlərini tərsinə olaraq çıxara bildik:
315 |
316 | ```python
317 | $ python3 fesil9_problems_solutions.py
318 | find_max_recursive() -> 14
319 | find_max_level_order_traversal() -> 14
320 | find_data_recursive() search 88 -> 0
321 | find_data_recursive() search 14 -> 1
322 | find_data_level_order_traversal() search 88 -> 0
323 | find_data_level_order_traversal() search 14 -> 1
324 | insert_in_binary_using_tree_level_order(tree.root, 21) -> Inserted as right node
325 | find_tree_size_recursive() -> 10
326 | find_tree_size_iterative() -> 10
327 | level_order_traversal_in_reverse() -> 13 7 4 21 14 6 1 10 3 8
328 | ```
329 |
330 | ## Tapşırıq - 9
331 |
332 | *Şərt:*
333 |
334 | Ağacı silmək üçün alqoritm düşünün.
335 |
336 | *Həlli:*
337 |
338 | Ağacı silmək üçün, bütün node-ları ziyarət etməli və bir-bir silməliyik.
339 | Təbii ki, parent node-u silməzdən əvvəl onun child node-larını silməliyik. Belə olan halda hansı metod bizə uyğundur? İnOrder, PreOrder, PostOrder yoxsa Level Order Traversal?
340 | Keçmiş fəsildən xatırladığımız kimi, PostOrder qət etmə zamanı root node-lar ən sonda ziyarət olunur, dolayısı ilə biz bu üsuldan istifadə etməklə ilk öncə child node-ları daha sonra da parent node-ları silə bilərik.
341 |
342 | Aşağıdakı kod nümunəsi bu işi görəcək:
343 |
344 | ```python
345 | def delete_binary_tree(self, node):
346 | if node is None:
347 | return
348 |
349 | self.delete_binary_tree(node.left)
350 | self.delete_binary_tree(node.right)
351 | node.data = None
352 | node.left = None
353 | node.right = None
354 | self.root = None
355 | ```
356 |
357 | Nəticə:
358 |
359 | ```python
360 | $ python3 fesil9_problems_solutions.py
361 | find_max_recursive() -> 14
362 | find_max_level_order_traversal() -> 14
363 | find_data_recursive() search 88 -> 0
364 | find_data_recursive() search 14 -> 1
365 | find_data_level_order_traversal() search 88 -> 0
366 | find_data_level_order_traversal() search 14 -> 1
367 | insert_in_binary_using_tree_level_order(tree.root, 21) -> Inserted as right node
368 | find_tree_size_recursive() -> 10
369 | find_tree_size_iterative() -> 10
370 | level_order_traversal_in_reverse() -> 13 7 4 21 14 6 1 10 3 8
371 | delete_binary_tree() ->
372 | find_tree_size_recursive() -> 0
373 | find_tree_size_iterative() -> 0
374 | ```
375 |
376 | ## Tapşırıq - 10
377 |
378 | *Şərt:*
379 |
380 | Ağacın hündürlüyünü(height or depth) tapan alqoritmi qurun.
381 |
382 | *Həlli:*
383 |
384 | Bu məqsədlə, rekursiv olaraq sol altağacın, daha sonra sağ altağacın hündürlüyünü hesablaya bilərik. Daha sonra bu hündürlüklərdən ən böyüyünü(maksimum) götürüb üzərinə 1 gəlmək lazımdır.
385 | Aşağıdakı kod parçası rekursiv olaraq, bu işi görür:
386 |
387 | ```python
388 | def max_depth_recursive(self, node):
389 | if node is None:
390 | return 0
391 | return max(self.max_depth_recursive(node.left), self.max_depth_recursive(node.right)) + 1
392 | ```
393 |
394 | ## Tapşırıq - 11
395 |
396 | *Şərt:*
397 |
398 | Yuxarıdakı tapşırığı iterativ üsulla həll edin.
399 |
400 | *Həlli:*
401 |
402 | Level Order Traversal üsulundan istifadə etməklə, hər səviyyədə depth dəyişənini artırmaqla ən sonda ağacın ümumi hündürlüyünü tapmış oluruq:
403 |
404 | ```python
405 | def max_depth_iterative(self, node):
406 | if node is None:
407 | return 0
408 | q_list = []
409 | q_list.append([node, 1])
410 | while q_list:
411 | node, depth = q_list.pop() # Buna Python-da unpacking deyilir.
412 | if node.left is not None:
413 | q_list.append([node.left, depth + 1]) # Əgər sol node varsa, onu listə əlavə et və depth-i artır.
414 | if node.right is not None:
415 | q_list.append([node.right, depth + 1]) # Əgər sağ node varsa, onu listə əlavə et və depth-i artır.
416 |
417 | return depth
418 | ```
419 |
420 | Kod nəticəmiz:
421 |
422 | ```python
423 | $ python3 fesil9_problems_solutions.py
424 | find_max_recursive() -> 14
425 | find_max_level_order_traversal() -> 14
426 | find_data_recursive() search 88 -> 0
427 | find_data_recursive() search 14 -> 1
428 | find_data_level_order_traversal() search 88 -> 0
429 | find_data_level_order_traversal() search 14 -> 1
430 | insert_in_binary_using_tree_level_order(tree.root, 21) -> Inserted as right node
431 | find_tree_size_recursive() -> 10
432 | find_tree_size_iterative() -> 10
433 | level_order_traversal_in_reverse() -> 13 7 4 21 14 6 1 10 3 8
434 | max_depth_recursive() -> 4
435 | max_depth_iterative() -> 4
436 | ```
437 |
438 | ## Tapşırıq - 12
439 |
440 | *Şərt:*
441 |
442 | Ağacın ən dərin node-unu tapmaq üçün alqoritm qurun.
443 |
444 | *Həlli:*
445 |
446 | Yenidən Level Order Traversal etməklə ən sonda Növbədən(Queue) çıxarılan node-un data-sını geri qaytara bilərik.
447 |
448 | ```python
449 | def deepest_node(self, node):
450 | if node is None:
451 | return 0
452 |
453 | q = Queue()
454 | q.put(node)
455 |
456 | while not q.empty():
457 | node = q.get()
458 | if node.left is not None:
459 | q.put(node.left)
460 | if node.right is not None:
461 | q.put(node.right)
462 |
463 | return node.get_data()
464 | ```
465 |
466 | ## Tapşırıq - 13
467 |
468 | *Şərt:*
469 |
470 | Ağacda leaf node-ların sayını tapın.
471 |
472 | *Həlli:*
473 |
474 | Xatırlayaq ki, lead node elə bir node-a deyilir ki, onun xələfi(ardıcılı, övladı) olmasın.
475 | Yəni, onun sağ və sol node-ları None(NULL) olsun.
476 | Level Order Traversal üsulundan istifadə etməklə, Növbədən çıxarılan hər node-un sağ və solunun None olub olmadığını yoxlaya bilərik. Əgər bu şərt doğru olsa deməli elə bu node leaf node-dur.
477 |
478 | ```python
479 | def number_of_leafs_iterative(self, node):
480 |
481 | if node is None:
482 | return 0
483 |
484 | q = Queue()
485 | q.put(node)
486 | count = 0 # sayğac
487 |
488 | while not q.empty():
489 | node = q.get()
490 | if (node.left is None) and (node.right is None):
491 | count = count + 1
492 | else:
493 | if node.left is not None:
494 | q.put(node.left)
495 | if node.right is not None:
496 | q.put(node.right)
497 |
498 | return count
499 | ```
500 |
501 | Nəticə:
502 |
503 | ```python
504 | $ python3 fesil9_problems_solutions.py
505 | find_max_recursive() -> 14
506 | find_max_level_order_traversal() -> 14
507 | find_data_recursive() search 88 -> 0
508 | find_data_recursive() search 14 -> 1
509 | find_data_level_order_traversal() search 88 -> 0
510 | find_data_level_order_traversal() search 14 -> 1
511 | insert_in_binary_using_tree_level_order(tree.root, 21) -> Inserted as right node
512 | find_tree_size_recursive() -> 10
513 | find_tree_size_iterative() -> 10
514 | level_order_traversal_in_reverse() -> 13 7 4 21 14 6 1 10 3 8
515 | max_depth_recursive() -> 4
516 | max_depth_iterative() -> 4
517 | deepest_node() -> 13
518 | number_of_leafs_iterative() -> 4
519 | ```
520 |
521 | ## Tapşırıq - 14
522 |
523 | *Şərt:*
524 |
525 | Ağacda full node-ların sayını tapın.
526 | Qeyd edək ki, full node həm sol, həm də sağ node-ları var olan node-a deyilir. Yəni, sağ və sol node-ları None(NULL) olmayan node-ların sayını tapmaq lazımdır.
527 |
528 | *Həlli:*
529 |
530 | Yuxarıdakı tapşırıqda leaf node tapdığımız kodda sayğacın şərtini dəyişməklə nəticə əldə edə bilərik.
531 |
532 | ```python
533 | def number_of_full_nodes_iterative(self, node):
534 |
535 | if node is None:
536 | return 0
537 |
538 | q = Queue()
539 | q.put(node)
540 | count = 0 # sayğac
541 |
542 | while not q.empty():
543 | node = q.get()
544 | if (node.left is not None) and (node.right is not None):
545 | count = count + 1
546 | else:
547 | if node.left is not None:
548 | q.put(node.left)
549 | if node.right is not None:
550 | q.put(node.right)
551 |
552 | return count
553 | ```
554 |
555 | ## Tapşırıq - 15
556 |
557 | *Şərt:*
558 |
559 | Ağacda olan yarım node-ların(half nodes) sayını tapın.
560 | Qeyd edək ki, yarım node elə bir node-a deyilir ki, onun ya sağ ya da sol node-u olsun. Yəni sağ ya sol node-lardan biri None(NULL) olsun.
561 |
562 | *Həlli:*
563 |
564 | Yenidən yuxarıdakı kodumuzda sayğac şərtini dəyişirik:
565 |
566 | ```python
567 | def number_of_half_nodes_iterative(self, node):
568 | if node is None:
569 | return 0
570 |
571 | q = Queue()
572 | q.put(node)
573 | count = 0 # sayğac
574 |
575 | while not q.empty():
576 | node = q.get()
577 | if (node.left is None and node.right is not None) or \
578 | (node.right is None and node.left is not None):
579 | count = count + 1
580 | else:
581 | if node.left is not None:
582 | q.put(node.left)
583 | if node.right is not None:
584 | q.put(node.right)
585 |
586 | return count
587 | ```
588 |
589 | Nəticələrimiz:
590 |
591 | ```python
592 | $ python3 fesil9_problems_solutions.py
593 | find_max_recursive() -> 14
594 | find_max_level_order_traversal() -> 14
595 | find_data_recursive() search 88 -> 0
596 | find_data_recursive() search 14 -> 1
597 | find_data_level_order_traversal() search 88 -> 0
598 | find_data_level_order_traversal() search 14 -> 1
599 | insert_in_binary_using_tree_level_order(tree.root, 21) -> Inserted as right node
600 | find_tree_size_recursive() -> 10
601 | find_tree_size_iterative() -> 10
602 | level_order_traversal_in_reverse() -> 13 7 4 21 14 6 1 10 3 8
603 | max_depth_recursive() -> 4
604 | max_depth_iterative() -> 4
605 | deepest_node() -> 13
606 | number_of_leafs_iterative() -> 4
607 | number_of_full_nodes_iterative() -> 1
608 | number_of_half_nodes_iterative() -> 2
609 | ```
610 |
611 | ## Tapşırıq - 16
612 |
613 | *Şərt:*
614 |
615 | Verilmiş iki Ağacın bir-birinə struktur olaraq bərabərliyini yoxlayın.
616 |
617 | *Həlli:*
618 |
619 | * Əgər hər iki ağac boşdursa(yəni None-dursa), o zaman True qaytarın.
620 | * Əgər hər iki ağac doludursa, o zaman sağ və sol altağacların strukturlarını rekursiv olaraq yoxlamaq lazımdır.
621 |
622 | Kodumuz:
623 |
624 | ```python
625 | def check_tree_structures_to_be_same(self, node1, node2):
626 | # Əgər ağacların nə sol nə də sağ altağacları qalıbsa və data-lar da bərabərdirsə o zaman True qaytarırır.
627 | if (not node1.left) and \
628 | (not node1.right) and \
629 | (not node2.left) and \
630 | (not node2.right) and node1.data == node2.data:
631 | return True
632 | # Aşağıda isə görürük ki, iki ağac bir-biri ilə fərqlənir
633 | if (node1.data != node2.data) or (node1.left and not node2.left) or \
634 | (not node1.left and node2.left) or (node1.right and not node2.right) or \
635 | (not node1.right and node2.right):
636 | return False
637 |
638 | left = self.check_tree_structures_to_be_same(node1.left, node2.left) if node1.left and node2.left else True
639 | right = self.check_tree_structures_to_be_same(node1.right, node2.right) if node1.right and node2.right else True
640 |
641 | return left and right
642 | ```
643 |
644 | Test etmək üçün eyni strukturda ikinci ağacı yaradırıq daha sonra əvvəlki ağacda olduğu kimi, 21 daxil edirik:
645 |
646 | ```python
647 | tree2 = BinaryTreeExercises()
648 | arr2 = [8, 3, 1, 6, 4, 7, 10, 14, 13]
649 | for i in arr2:
650 | tree2.create_tree(i)
651 | print("insert_in_binary_using_tree_level_order(tree2.root, 21) -> ", end='')
652 | print(tree.insert_in_binary_using_tree_level_order(tree2.root, 21))
653 | print("check_tree_structures_to_be_same(tree.root, tree2.root) -> ", end='')
654 | print(tree.check_tree_structures_to_be_same(tree.root, tree2.root))
655 | ```
656 |
657 | Bu zaman True qayıdacaq. Lakin əlavə olaraq ikinci ağaca 88 daxil etsək bu zaman artıq struktur fərqlənəcək və False qayıdacaq:
658 |
659 | ```python
660 | print("insert_in_binary_using_tree_level_order(tree2.root, 88) -> ", end='')
661 | print(tree.insert_in_binary_using_tree_level_order(tree2.root, 88))
662 | print("check_tree_structures_to_be_same(tree.root, tree2.root) -> ", end='')
663 | print(tree.check_tree_structures_to_be_same(tree.root, tree2.root))
664 | ```
665 |
666 | Nəticə:
667 |
668 | ```python
669 | $ python3 fesil9_problems_solutions.py
670 | find_max_recursive() -> 14
671 | find_max_level_order_traversal() -> 14
672 | find_data_recursive() search 88 -> 0
673 | find_data_recursive() search 14 -> 1
674 | find_data_level_order_traversal() search 88 -> 0
675 | find_data_level_order_traversal() search 14 -> 1
676 | insert_in_binary_using_tree_level_order(tree.root, 21) -> Inserted as right node
677 | find_tree_size_recursive() -> 10
678 | find_tree_size_iterative() -> 10
679 | level_order_traversal_in_reverse() -> 13 7 4 21 14 6 1 10 3 8
680 | max_depth_recursive() -> 4
681 | max_depth_iterative() -> 4
682 | deepest_node() -> 13
683 | number_of_leafs_iterative() -> 4
684 | number_of_full_nodes_iterative() -> 1
685 | number_of_half_nodes_iterative() -> 2
686 | insert_in_binary_using_tree_level_order(tree2.root, 21) -> Inserted as right node
687 | check_tree_structures_to_be_same(tree.root, tree2.root) -> True
688 | insert_in_binary_using_tree_level_order(tree2.root, 21) -> Inserted as right node
689 | check_tree_structures_to_be_same(tree.root, tree2.root) -> False
690 | ```
691 |
692 | ## Tapşırıq - 17
693 |
694 | *Şərt:*
695 |
696 | Ağacın diametrini tapan kodu yazın. Qeyd edək ki,ağacın diametri iki node arasında ən uzun məsafəyə bərabərdir.
697 |
698 | *Həlli:*
699 |
700 | İlk öncə sol daha sonra sağ altağacın hündürlüyünü(maximum dərinliyini) tapmaq lazımdır. Bunu biz artıq 10-cu tapşırıqda etmişik. Daha sonra sol altağacın diametrini daha sonra da sağ altağacın diametrini tapmaq lazımdır.
701 | Son nəticədə isə bunların arasından maksimumu qaytarmaq lazımdır.
702 | Aşağıdakı kod bunu edir:
703 |
704 | > Mənbə: [diameter-of-a-binary-tree](https://www.geeksforgeeks.org/diameter-of-a-binary-tree/)
705 |
706 | ```python
707 | def diameter_of_tree(self, node):
708 | if node is None:
709 | return 0
710 |
711 | # sol və sağ altağacların hündürlüyünü tapırıq.
712 | lheight = self.max_depth_recursive(node.left)
713 | rheight = self.max_depth_recursive(node.right)
714 |
715 | # sol və sağ altağacların diametrlərini tapırıq.
716 | ldiameter = self.diameter_of_tree(node.left)
717 | rdiameter = self.diameter_of_tree(node.right)
718 |
719 | # Ağac üçün max dəyəri qaytarmalıyı.
720 | # sol və sağ altağacın diametrləri arasından maksimumu tapırıq.
721 | # sol və sağ altağacın hündürlüklərini cəmləyib üzərinə 1 gəlirik.
722 | # Yuxarıdakı ikisində maksimumu tapırıq.
723 | return max(lheight + rheight + 1, max(ldiameter, rdiameter))
724 | ```
725 |
--------------------------------------------------------------------------------