├── .DS_Store ├── main.py ├── README.md ├── bee.py ├── tools.py └── main.ipynb /.DS_Store: -------------------------------------------------------------------------------- https://raw.githubusercontent.com/BetterBench/2D-Binnnig-BottomLeft-Python/HEAD/.DS_Store -------------------------------------------------------------------------------- /main.py: -------------------------------------------------------------------------------- 1 | from tools import * 2 | import random 3 | 4 | # BL（bottom-up left-justified）法求解二位装箱问题 5 | # @BetterBench 6 | # 思想：首先将选中的物体放在箱子的右上角，然后尽量向下向左作连续移动，直到不能移动为止 7 | # 输入参数 8 | itemNum=10 #物品数目 9 | AllItem=np.array([[random.randint(1, 5) for j in range(1, 3)] for i in range(1,itemNum+1)]) #随机生成30个物品 10 | Bin=[5,5] #箱子宽度与高度 11 | ran=list(range(itemNum)) 12 | random.shuffle(ran) #随机生成装箱序列 13 | 14 | ansBXY=np.zeros((itemNum,3)) #[箱子编号，X坐标，Y坐标] 15 | RPNXY=[]; 16 | BinNum=1; 17 | flagItem=np.zeros(itemNum) #标记物品是否被装入箱子，0没有装入，1装入 18 | # 开始装箱 19 | 20 | for i in range(itemNum): 21 | if flagItem[ran[i]]==0: 22 | item=AllItem[ran[i],:] 23 | itemRP=Bin #起点全部在箱子右上角顶点 24 | flagOL=overlap(item,AllItem,itemRP,RPNXY) #如果重合flagOL=1；反之flagOL=0 25 | if flagOL==0: 26 | itemRP=finalPos(item,AllItem,itemRP,RPNXY) #更新物品从当前位置向下向左移动后到最终位置后右上角顶点坐标 27 | print(itemRP) 28 | if len(itemRP)>0: 29 | RPNXY.append([ran[i],itemRP[0],itemRP[1]]) 30 | flagItem[ran[i]]=1 31 | print() -------------------------------------------------------------------------------- /README.md: -------------------------------------------------------------------------------- 1 | # 【Python】实现二维装箱Bottom-Left算法及可视化 2 | 3 | # 1 题目 4 | 5 | 将若干个矩形物品装进矩形箱子中，并且在装箱的过程中不允许将矩形物品斜着放，即平行于横坐标。一般来说求解的目标是最小化箱子的箱子数目或者是箱子空间占用率。 6 | 7 | 当该算法适用于矩阵存储时，求解的最优目标是箱子的最大化空间占用率。以下即是求解的过程 8 | 9 | # 2 装箱算法 10 | 11 | ## 2.1 所有装箱算法 12 | 13 | 参考【[A Thousand Ways to Pack the Bin - A Practical Approach to Two-Dimensional Rectangle Bin Packing](http://pds25.egloos.com/pds/201504/21/98/RectangleBinPack.pdf)】 14 | 15 | ![1](https://img-blog.csdnimg.cn/c93482726ec6406db7f96a7bfdc55809.png?x-oss-process=image/watermark,type_d3F5LXplbmhlaQ,shadow_50,text_Q1NETiBAQmV0dGVyIEJlbmNo,size_20,color_FFFFFF,t_70,g_se,x_16#pic_center) 16 | 17 | 以下我将会介绍其中一种叫Bottom-Left装箱算法。算法过程就是，矩形从箱子的右上角开始进入，先尽可能向下移动，再向左移动，一直循环，直至不再移动。在以下算法过程中，以0-1背包问题的思路去实现，即某个矩形装进箱子，则flag相应为1，未装进的flag为0。输出单个箱子占用率。 18 | 19 | ## 2.2 Bottom-Left具体算法过程 20 | 21 | 初始化是，输入箱子大小[W,H] 22 | 23 | 再输入每一个矩形的长和宽 24 | 25 | > 4 5 26 | > 27 | > 4 7 28 | > 29 | > 4 2 30 | > 31 | > 4 4 32 | > 33 | > 7 4 34 | 35 | 36 | 37 | 初始装箱顺序为：12345 38 | 39 | 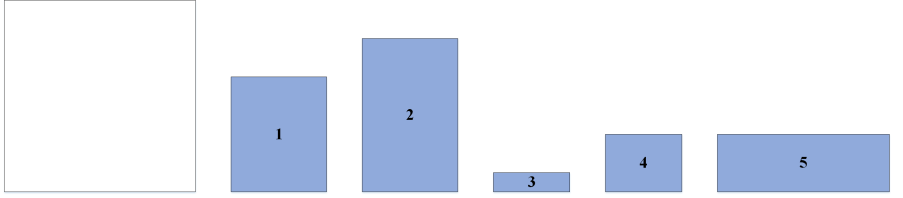![5](https://img-blog.csdnimg.cn/93c275d9f352482d99c729f544673fa1.png#pic_center) 40 | 41 | 第一步：装第一个矩形，从右上角进入，一直向下移动，然后移动一直向左移动，直到左下角。用一个列表记录装进箱子的矩阵。表示为【x,y,width,height】x和y使右上角坐标。该矩形的flag标记为1。 42 | 43 | 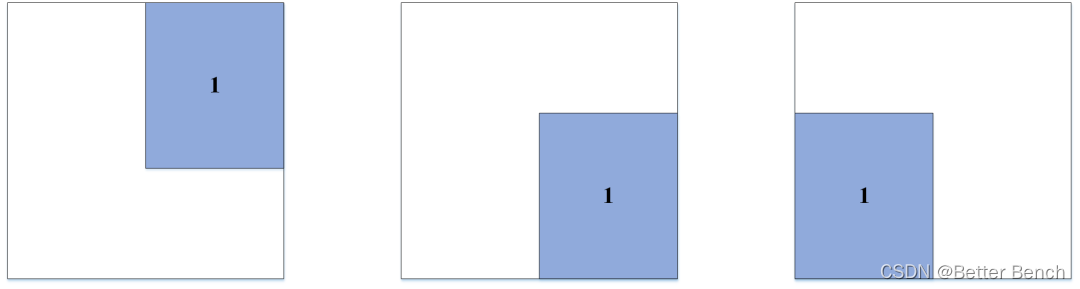![6](https://img-blog.csdnimg.cn/8f89b8fcb0b84cd8bec6682abb85621d.png?x-oss-process=image/watermark,type_d3F5LXplbmhlaQ,shadow_50,text_Q1NETiBAQmV0dGVyIEJlbmNo,size_20,color_FFFFFF,t_70,g_se,x_16#pic_center) 44 | 45 | 第二步：装第二个矩形，先将矩形放入右上角，再判断第二个矩形是否与箱子中的矩形是否相交（**overlap函数**）。如果相交，就不放进箱子，换下一个矩形，如果不相交，计算可向下移动的距离（**downHAtPoint函数**），向下移动，并更新矩形位置（**Update_itemRP函数**），最后计算可向左移动的距离（**leftWAtPoint函数**），向左移动，并更新位置，直至可移动距离为0。将第二个矩形最终位置信息【x,y,width,height】添加进列表。该矩形的flag标记未1。 46 | 47 | 7 48 | 49 | 第三步：剩下的矩形，和第二步一样。如果该矩形装不进箱子，就换下一个矩阵，继续装，直至遍历完所有箱子。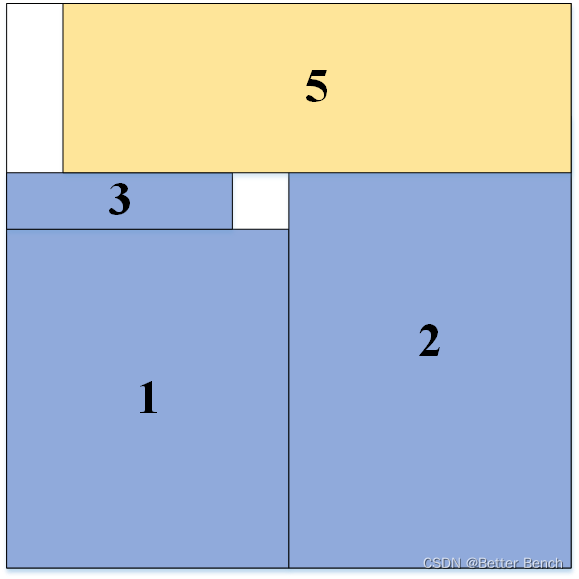 50 | 51 | 10 52 | 53 | 54 | 55 | # 3 Python 实现 56 | 57 | 本算法实现中，只用了一个箱子。如果想要多个箱子来装，可以修改本人去掉注释的地方，启用下一个箱子。 58 | 59 | ## 3.1 main.py主函数 60 | 61 | ```python 62 | from tools import * 63 | import random 64 | 65 | # BL（bottom-up left-justified）法求解二位装箱问题 66 | # @BetterBench 67 | # 思想：首先将选中的物体放在箱子的右上角，然后尽量向下向左作连续移动，直到不能移动为止 68 | # 输入参数 69 | itemNum=30 #物品数目 70 | AllItem=np.array([[random.randint(1, 5) for j in range(1, 3)] for i in range(1,itemNum+1)]) #随机生成30个物品，[width,height] 71 | Bin=[10,10] #箱子宽度与高度 72 | ran=list(range(itemNum)) 73 | random.shuffle(ran) #随机生成装箱序列 74 | 75 | ansBXY=np.zeros((itemNum,3)) #[箱子编号，X坐标，Y坐标] 76 | RPNXY=[]; 77 | BinNum=1; 78 | flagItem=np.zeros(itemNum) #标记物品是否被装入箱子，0没有装入，1装入 79 | # 开始装箱 80 | 81 | for i in range(itemNum): 82 | if flagItem[ran[i]]==0: 83 | item=AllItem[ran[i],:] 84 | itemRP=Bin #起点全部在箱子右上角顶点 85 | flagOL=overlap(item,AllItem,itemRP,RPNXY) #如果重合flagOL=1；反之flagOL=0 86 | if flagOL==0: 87 | itemRP=finalPos(item,AllItem,itemRP,RPNXY) #更新物品从当前位置向下向左移动后到最终位置后右上角顶点坐标 88 | RPNXY.append([ran[i],itemRP[0],itemRP[1]]) # 记录装进箱子的矩形【ID,width,height】 89 | flagItem[ran[i]]=1 90 | # 启用第下一个箱子 91 | # if list(flagItem).count(0)>0: 92 | # BinNum=BinNum+1 93 | # RPNXY=[] 94 | ``` 95 | 96 | 输出哪些矩形被装进箱子 97 | 98 | ```python 99 | print(flagItem) 100 | ``` 101 | 102 | > array([0., 0., 1., 1., 1., 0., 1., 0., 1., 1., 0., 0., 1., 1., 1., 1., 0., 0., 0., 1., 0., 0., 0., 0., 0., 0., 0., 0., 1., 0.]) 103 | 104 | 计算箱子占用率 105 | 106 | ```python 107 | rect_area = 0 108 | bin_area = Bin[0]*Bin[1] 109 | for id in RPNXY: 110 | width,height = AllItem[id[0]] 111 | rect_area += width*height 112 | print('占用率:{}'.format(rect_area/bin_area)) 113 | ``` 114 | 115 | > 占用率:0.81 116 | 117 | 可视化装箱后的结果 118 | 119 | ```python 120 | import matplotlib.pyplot as plt 121 | import matplotlib.patches as patches 122 | import random 123 | fig, ax = plt.subplots(1, 1) 124 | ax1 = fig.gca() 125 | for i in RPNXY: 126 | width,height = AllItem[i[0]] 127 | rx,ry = i[1],i[2] 128 | lx,ly = rx-width,ry-height 129 | plt.xlim((0, Bin[0])) 130 | plt.ylim((0, Bin[1])) 131 | color = "#"+''.join([random.choice('0123456789ABCDEF') for j in range(6)]) 132 | rect = patches.Rectangle((lx, ly), width,height,linewidth=1, facecolor = color) 133 | ax1.add_patch(rect) 134 | plt.show() 135 | ``` 136 | 137 | ![result](https://img-blog.csdnimg.cn/43d7ff75a7b04326ab226edc1829b3eb.png?x-oss-process=image/watermark,type_d3F5LXplbmhlaQ,shadow_50,text_Q1NETiBAQmV0dGVyIEJlbmNo,size_11,color_FFFFFF,t_70,g_se,x_16#pic_center) 138 | 139 | -------------------------------------------------------------------------------- /bee.py: -------------------------------------------------------------------------------- 1 | import numpy as np 2 | import random, math, copy 3 | import matplotlib.pyplot as plt 4 | from tools import * 5 | import random 6 | 7 | 8 | def fitness(Bin,AllItem,ran): 9 | # ran 是装箱顺序 10 | itemNum=AllItem.shape[0] #物品数目 11 | RPNXY=[]; 12 | flagItem=np.zeros(itemNum) #标记物品是否被装入箱子，0没有装入，1装入 13 | # 开始装箱 14 | 15 | for i in range(itemNum): 16 | if flagItem[ran[i]]==0: 17 | item=AllItem[ran[i],:] 18 | itemRP=Bin #起点全部在箱子右上角顶点 19 | flagOL=overlap(item,AllItem,itemRP,RPNXY) #如果重合flagOL=1；反之flagOL=0 20 | if flagOL==0: 21 | itemRP=finalPos(item,AllItem,itemRP,RPNXY) #更新物品从当前位置向下向左移动后到最终位置后右上角顶点坐标 22 | if len(itemRP)>0: 23 | RPNXY.append([ran[i],itemRP[0],itemRP[1]]) 24 | flagItem[ran[i]]=1 25 | rect_area = 0 26 | bin_area = Bin[0]*Bin[1] 27 | for id in RPNXY: 28 | width,height = AllItem[id[0]] 29 | rect_area += width*height 30 | score = rect_area/bin_area 31 | print('利用率:{}'.format(score)) 32 | return score 33 | 34 | class ABSIndividual: 35 | def __init__(self,bin,item): 36 | self.score = 0. 37 | self.invalidCount = 0 #无效次数（成绩没有更新的累积次数） 38 | self.bin = bin #箱子宽度与高度 39 | self.allitem = item 40 | self.ran = list(range(self.allitem.shape[0]))# 装箱顺序 41 | self.calculateFitness() 42 | 43 | def calculateFitness(self): 44 | self.score = fitness(self.bin,self.allitem,self.ran) #计算当前成绩 45 | 46 | class ArtificialBeeSwarm: 47 | def __init__(self, foodCount, onlookerCount,Bin, item, maxIterCount=1000, maxInvalidCount=200): 48 | self.foodCount = foodCount #蜜源个数，等同于雇佣蜂数目 49 | self.onlookerCount = onlookerCount #观察蜂个数 50 | self.item = item #各参数上下界 51 | self.maxIterCount = maxIterCount #迭代次数 52 | self.maxInvalidCount = maxInvalidCount #最大无效次数 53 | self.Bin = Bin 54 | self.foodList = [ABSIndividual(self.Bin,self.item) for k in range(self.foodCount)] #初始化各蜜源 55 | self.foodScore = [d.score for d in self.foodList] #各蜜源最佳成绩 56 | self.bestFood = self.foodList[np.argmax(self.foodScore)] #全局最佳蜜源 57 | 58 | def updateFood(self, i): #更新第i个蜜源 59 | vi = copy.deepcopy(self.foodList[i]) 60 | order =list(range(vi.allitem.shape[0])) 61 | random.shuffle(order) #随机生成装箱序列 62 | vi.ran = order 63 | vi.calculateFitness() 64 | if vi.score > self.foodList[i].score: #如果成绩比当前蜜源好 65 | self.foodList[i] = vi 66 | if vi.score > self.foodScore[i]: #如果成绩比历史成绩好（如重新初始化，当前成绩可能低于历史成绩） 67 | self.foodScore[i] = vi.score 68 | if vi.score > self.bestFood.score: #如果成绩全局最优 69 | self.bestFood = vi 70 | self.foodList[i].invalidCount = 0 71 | else: 72 | self.foodList[i].invalidCount += 1 73 | 74 | def employedBeePhase(self): 75 | for i in range(0, self.foodCount): #各蜜源依次更新 76 | self.updateFood(i) 77 | 78 | def onlookerBeePhase(self): 79 | foodScore = [d.score for d in self.foodList] 80 | maxScore = np.max(foodScore) 81 | accuFitness = [(0.9*d/maxScore+0.1, k) for k,d in enumerate(foodScore)] #得到各蜜源的 相对分数和索引号 82 | for k in range(0, self.onlookerCount): 83 | i = random.choice([d[1] for d in accuFitness if d[0] >= random.random()]) #随机从相对分数大于随机门限的蜜源中选择跟随 84 | self.updateFood(i) 85 | 86 | def scoutBeePhase(self): 87 | for i in range(0, self.foodCount): 88 | if self.foodList[i].invalidCount > self.maxInvalidCount: #如果该蜜源没有更新的次数超过指定门限，则重新初始化 89 | self.foodList[i] = ABSIndividual(self.bound) 90 | self.foodScore[i] = max(self.foodScore[i], self.foodList[i].score) 91 | 92 | def solve(self): 93 | trace = [] 94 | trace.append((self.bestFood.score, np.mean(self.foodScore))) 95 | for k in range(self.maxIterCount): 96 | self.employedBeePhase() 97 | self.onlookerBeePhase() 98 | self.scoutBeePhase() 99 | trace.append((self.bestFood.score, np.mean(self.foodScore))) 100 | print(self.bestFood.score) 101 | self.printResult(np.array(trace)) 102 | 103 | def printResult(self, trace): 104 | x = np.arange(0, trace.shape[0]) 105 | plt.plot(x, [(1-d)/d for d in trace[:, 0]], 'r', label='optimal value') 106 | plt.plot(x, [(1-d)/d for d in trace[:, 1]], 'g', label='average value') 107 | plt.xlabel("Iteration") 108 | plt.ylabel("function value") 109 | plt.title("Artificial Bee Swarm algorithm for function optimization") 110 | plt.legend() 111 | plt.show() 112 | 113 | if __name__ == "__main__": 114 | random.seed() 115 | itemNum = 1000 116 | AllItem=np.array([[random.randint(1, 5) for j in range(1, 3)] for i in range(1,itemNum+1)]) #随机生成30个物品，[width,height] 117 | Bin=[100,100] #箱子宽度与高度 118 | iternum = 100 # 迭代次数 119 | maxInvalidCount = 50 120 | abs = ArtificialBeeSwarm(30, 30, Bin,AllItem, iternum, maxInvalidCount) 121 | abs.solve() 122 | print() -------------------------------------------------------------------------------- /tools.py: -------------------------------------------------------------------------------- 1 | 2 | from matplotlib.pyplot import axis 3 | import numpy as np 4 | 5 | def Horizontal_Lines_Intersect(line1,line2): 6 | # 判断两条水平线段经过竖直移动后是否会相交，如果相交，计算两条水平线段竖直距离是多少 7 | # 思路：分5种情况：1）左方不相交；2）左方相交；3）右方相交；4）右方不相交；5）line1完全包含line2 8 | # 输入line1： 第一条线段[x1,y1,x2,y2] 9 | # 输入line2： 第二条线段[x1,y1,x2,y2] 10 | # 输出flag： 判断两条水平线段经过竖直移动后是否会相交，flag=1相交，flag=0不相交 11 | # 输出HD： 两条竖直线段距离是多少，如果平移动后相交，HD为正数，反之为负数 12 | #第一种情况，line1完全在line2左方，即line1右端顶点x坐标小于等于line2左端顶点x坐标，且两条线段经过竖直移动后不会相交 13 | if line1[2]<=line2[0]: 14 | flag=0 15 | HD=line1[1]-line2[1] 16 | #第二种情况，line1在line2左方，即line1右端顶点x坐标大于line2左端顶点x坐标且小于等于且line2右端顶点x坐标，但两条线段经过竖直移动后会相交 17 | elif (line1[2]>line2[0]) and (line1[2]<=line2[0]): 18 | flag=1 19 | HD=line1[1]-line2[1] 20 | #第三种情况，line1在line2右方，即line1左端顶点x坐标大于等于line2左端顶点x坐标且小于且line2右端顶点x坐标，但两条线段经过竖直移动后会相交 21 | elif (line1[0]>=line2[0]) and (line1[0]=line2[2]: 26 | flag=0 27 | HD=line1[1]-line2[1] 28 | #第五种情况，line1完全包含line2，即line1左端顶点x坐标小于等于line2左端顶点x坐标， 29 | #line1右端顶点x坐标大于等于line2右端顶点x坐标，且两条线段经过竖直移动后会相交 30 | else: 31 | flag=1 32 | HD=line1[1]-line2[1] 33 | return flag,HD 34 | 35 | ###################################### 36 | # 根据物品右上角顶点坐标和物品宽度和高度，求出物品下端水平线段左右两端坐标[leftx,lefty,rightx,righty] 37 | # 输入item： 物品[宽度，高度] 38 | # 输入RPXY：物品右上角顶点坐标[x,y] 39 | # 输出leftLine： 物品下端水平线段左右两端坐标[leftx,lefty,rightx,righty] 40 | def Point_Horizontal_Line(item,RPXY): 41 | RBPXY=[RPXY[0],RPXY[1]-item[1]]# 物品右下角顶点坐标 42 | LBPXY=[RPXY[0]-item[0],RPXY[1]-item[1]] #物品左下角顶点坐标 43 | bottomLine=[] 44 | bottomLine.extend(LBPXY) 45 | bottomLine.extend(RBPXY) 46 | return bottomLine 47 | 48 | # 计算在当前箱子中，物品item在箱子内任意位置可以下降的最大高度 49 | # 输入item： 物品[宽度，高度] 50 | # 输入AllItem： 各个物品[宽度，高度] 51 | # 输入itemRP： 此时物品右上角顶点坐标[x,y] 52 | # 输入RPNXY： 当前箱子中所有物品右上角顶点坐标数组 53 | # 输出downH： 物品item在箱子内任意位置可以下降的最大高度（如果能装入当前箱子，则downH为正数；如果不能装入当前箱子，则为负数） 54 | def downHAtPoint(item,AllItem,itemRP,RPNXY): 55 | bottomLine=Point_Horizontal_Line(item,itemRP) #物品下端水平线段左右两端坐标[leftx,lefty,rightx,righty] 56 | RP_NUM=len(RPNXY) #箱子内物品数目 57 | if RP_NUM!=0: 58 | sRPNXY=np.array(sorted(list(RPNXY), key=lambda x:x[2],reverse=True))#将RPNXY按照Y坐标降序排列 59 | sRBPNXY=sRPNXY.copy() 60 | sRBPNXY[:,1]=sRPNXY[:,1]-AllItem[sRPNXY[:,0],0] #将RPNXY按照Y坐标降序排列后的左上角顶点坐标 61 | 62 | topLine=np.concatenate((sRBPNXY[:,1:3],sRPNXY[:,1:3]),axis=1) #物品按照Y坐标降序排列后，物品上端水平线段左右两端坐标[leftx,lefty,rightx,righty] 63 | # 逐个遍历sRPNXY中的物品 64 | alldownH=[] # 储存所有满足相交条件的下降距离 65 | for i in range(RP_NUM): 66 | #判断两条水平线段经过竖直移动后是否会相交，flag=1相交，flag=0不相交 67 | #两条水平线段距离是多少，如果竖直移动后相交，HD为正数，反之为负数 68 | flag,HD=Horizontal_Lines_Intersect(bottomLine,topLine[i,:]) 69 | if (flag==1) and (HD>=0): 70 | alldownH.append(HD) 71 | # 如果不存在满足相交条件的物品，则直接下降到箱子最底端 72 | if len(alldownH)==0: 73 | downH=itemRP[1]-item[1] 74 | else: # 如果存在满足相交条件的物品，则下降距离为alldownH中的最小值 75 | downH=min(alldownH) 76 | else: 77 | downH=itemRP[1]-item[1] #此时箱子没有物品，物品直接下降到箱子底端 78 | return downH 79 | 80 | # 判断两条竖直线段经过水平移动后是否会相交，如果相交，计算两条竖直线段水平距离是多少 81 | # 思路：分5种情况：1）上方不相交；2）上方相交；3）下方相交；4）下方不相交；5）line1完全包含line2 82 | # 输入line1： 第一条线段[topx,topy,bottomx,bottomy] 83 | # 输入line2： 第二条线段[topx,topy,bottomx,bottomy] 84 | # 输出flag： 判断两条竖直线经过水平移动后是否会相交，flag=1相交，flag=0不相交 85 | # 输出HD： 两条竖直线段距离是多少，如果平移动后相交，HD为正数，反之为负数 86 | def Vertical_Lines_Intersect(line1,line2): 87 | # 第一种情况，line1完全在line2上方，且两条线段经过平移后不会相交 88 | if line1[3]>=line2[1]: 89 | flag=0 90 | HD=line1[0]-line2[0] 91 | # 第二种情况，line1在line2上方，但两条线段经过平移后会相交 92 | elif (line1[3]=line2[3]): 93 | flag=1 94 | HD=line1[0]-line2[0] 95 | # 第三种情况，line1在line2下方，但两条线段经过平移后会相交 96 | elif (line1[1]<=line2[1]) and (line1[1]>line2[3]): 97 | flag=1 98 | HD=line1[0]-line2[0] 99 | # 第四种情况，line1完全在line2下方，且两条线段经过平移后不会相交 100 | elif line1[1]<=line2[3]: 101 | flag=0 102 | HD=line1[0]-line2[0] 103 | else: 104 | flag=1 105 | HD=line1[0]-line2[0] 106 | return flag,HD 107 | 108 | # 根据物品右上角顶点坐标和物品宽度和高度，求出物品左端竖直线段上下两端坐标[topx,topy,bottomx,bottomy] 109 | # 输入item： 物品[宽度，高度] 110 | # 输入RPXY：物品右上角顶点坐标[x,y] 111 | # 输出leftLine： 物品左端竖直线段上下两端坐标[topx,topy,bottomx,bottomy] 112 | def Point_Vertical_Line(item,RPXY): 113 | LUPXY=[RPXY[0]-item[0],RPXY[1]] #物品左上角顶点坐标 114 | LBPXY=[RPXY[0]-item[0],RPXY[1]-item[1]] #物品左下角顶点坐标 115 | leftLine=[] 116 | leftLine.extend(LUPXY) 117 | leftLine.extend(LBPXY) 118 | return leftLine 119 | 120 | # 计算在当前箱子中，物品item在箱子内任意位置可以向左移动的最大距离 121 | # 输入item： 物品[宽度，高度] 122 | # 输入Item： 各个物品[宽度，高度] 123 | # 输入itemRP： 此时物品右上角顶点坐标[x,y] 124 | # 输入RPNXY： 当前箱子中所有物品右上角顶点坐标数组 125 | # 输出leftW： 物品item在箱子内任意位置可以向左移动的最大距离 126 | def leftWAtPoint(item,Item,itemRP,RPNXY): 127 | leftLine=Point_Vertical_Line(item,itemRP) #物品左端竖直线段上下两端坐标[topx,topy,bottomx,bottomy] 128 | RP_NUM=len(RPNXY)#箱子内物品数目 129 | if RP_NUM!=0: 130 | sRPNXY=np.array(sorted(list(RPNXY), key=lambda x:x[0])) #将RPNXY按照X坐标降序排列 131 | sRBPNXY=sRPNXY.copy() 132 | sRBPNXY[:,2]=sRPNXY[:,2]-Item[sRPNXY[:,0],1] #将RPNXY按照X坐标降序排列后的右下角顶点坐标 133 | rightLine=np.concatenate((sRPNXY[:,1:3],sRBPNXY[:,1:3]),axis=1)#物品按照X坐标降序排列后，右端线段上下两端坐标[topx,topy,bottomx,bottomy] 134 | #逐个遍历sRPNXY中的物品 135 | allLeftW=[] #储存所有满足相交条件的左移距离 136 | for i in range(RP_NUM): 137 | #判断两条竖直线经过水平移动后是否会相交，flag=1相交，flag=0不相交 138 | #两条竖直线段距离是多少，如果平移动后相交，HD为正数，反之为负数 139 | flag,HD=Vertical_Lines_Intersect(leftLine,rightLine[i,:]) 140 | if (flag==1) and (HD>=0): 141 | allLeftW.append(HD) 142 | # 如果不存在满足相交条件的物品，则直接移动箱子最左端 143 | if len(allLeftW)==0: 144 | leftW=itemRP[0]-item[0] 145 | else: #如果存在满足相交条件的物品，则左移距离为allLeftW中的最小值 146 | leftW=min(allLeftW) 147 | else: 148 | leftW=itemRP[0]-item[0] 149 | return leftW 150 | 151 | # 计算物品在箱子中从右上角下降downH又向左移动leftW后，右上角顶点的坐标 152 | # 输入itemRP： 此时物品右上角顶点坐标[x,y] 153 | # 输入downH： 物品item从右上角可以下降的最大高度 154 | # 输入leftW： 物品item从右上角下降最大高度以后，可以向左移动的最大距离 155 | # 输出itRPXY： 物品item在箱子中下降downH又向左移动leftW后，右上角顶点的坐标 156 | def Update_itemRP(itemRP,downH,leftW): 157 | h=itemRP[1]-downH #y坐标 158 | w=itemRP[0]-leftW #x坐标 159 | return [w,h] 160 | # 矩形类，[x,y,width,height]左下角坐标、长和宽 161 | class Rectangle: 162 | def __init__(self, x, y,w,h): 163 | self.x = x 164 | self.y = y 165 | self.width = w 166 | self.height = h 167 | # 计算物品从当前位置向下向左移动后到最终位置后右上角顶点坐标 168 | # 输入item： 物品[宽度，高度] 169 | # 输入Item： 各个物品[宽度，高度] 170 | # 输入itemRP： 此时物品右上角顶点坐标[x,y] 171 | # 输入RPNXY： 当前箱子中所有物品右上角顶点坐标数组 172 | # 输出finalRP：物品item在箱子内任意位置向下向左移动后到最终位置后右上角顶点坐标 173 | def finalPos(item,Item,itemRP,RPNXY): 174 | # 当物品item不能再继续下降或不能继续左移的时候，跳出循环 175 | while 1: 176 | downH=downHAtPoint(item,Item,itemRP,RPNXY) #计算物品item在箱子内itemRP位置处可以下降的最大高度 177 | leftW=0 178 | itemRP=Update_itemRP(itemRP,downH,leftW) #更新物品item当前位置右上角顶点坐标 179 | downH=0 180 | leftW=leftWAtPoint(item,Item,itemRP,RPNXY) #计算物品item在箱子内itemRP位置处可以向左移动的最大距离 181 | itemRP=Update_itemRP(itemRP,downH,leftW) #更新物品item当前位置右上角顶点坐标 182 | if (downH==0)and (leftW==0): 183 | finalRP=itemRP 184 | break 185 | return finalRP 186 | 187 | # 判断物品item在当前位置itemRP与箱子中其他物品是否有重合 188 | # 输入item： 物品[宽度，高度] 189 | # 输入Item： 各个物品[宽度，高度] 190 | # 输入itemRP： 此时物品右上角顶点坐标[x,y] 191 | # 输入RPNXY： 当前箱子中所有物品右上角顶点坐标数组 192 | # 输出flagOL： 如果重合flagOL=1；反之flagOL=0 193 | def overlap(item,Item,itemRP,RPNXY): 194 | flagOL=0 # 初始化不存在重合情况 195 | itemLBP=[itemRP[0]-item[0],itemRP[1]-item[1]] #左下角顶点坐标 196 | A = Rectangle(itemLBP[0],itemLBP[1],item[0],item[1]) 197 | num=len(RPNXY) # 箱子中物品数目 198 | if num>0: 199 | for i in range(num): 200 | width=Item[RPNXY[i][0],0] #Item(RPNXY(i,1),:)宽度 201 | height=Item[RPNXY[i][0],1] #Item(RPNXY(i,1),:)高度 202 | LBPXY=[RPNXY[i][1]-width,RPNXY[i][2]-height] #在箱子中的当前矩形Item(RPNXY(i,1),:)的左下角顶点坐标 203 | B = Rectangle(LBPXY[0],LBPXY[1],width,height) 204 | area=rectint(A,B)#计算物品A与B相交的面积 205 | #如果AB相交，则满足下列关系 206 | if area>0: 207 | flagOL=1 208 | break 209 | return flagOL 210 | # 计算两个矩形相交的面积，和MATLAB中rectint函数作用一样 211 | def rectint(rect1, rect2): 212 | xl1, yb1, xr1, yt1 = rect1.x,rect1.y,rect1.x+rect1.width,rect1.y+rect1.height # （xl1, yb1）为矩形左下角坐标， （xr1, yt1）为右上角坐标 213 | xl2, yb2, xr2, yt2 = rect2.x,rect2.y,rect2.x+rect2.width,rect2.y+rect2.height # （xl2, yb2）为矩形左下角坐标， （xr2, yt2）为右上角坐标 214 | xmin = max(xl1, xl2) 215 | ymin = max(yb1, yb2) 216 | xmax = min(xr1, xr2) 217 | ymax = min(yt1, yt2) 218 | width = xmax - xmin 219 | height = ymax - ymin 220 | if width <= 0 or height <= 0: 221 | return 0 222 | cross_square = width * height 223 | return cross_square -------------------------------------------------------------------------------- /main.ipynb: -------------------------------------------------------------------------------- 1 | { 2 | "cells": [ 3 | { 4 | "cell_type": "code", 5 | "execution_count": 2, 6 | "metadata": {}, 7 | "outputs": [], 8 | "source": [ 9 | "from tools import *\n", 10 | "import random\n", 11 | "\n", 12 | "# BL（bottom-up left-justified）法求解二位装箱问题\n", 13 | "# @BetterBench\n", 14 | "# 思想：首先将选中的物体放在箱子的右上角，然后尽量向下向左作连续移动，直到不能移动为止\n", 15 | "# 输入参数\n", 16 | "itemNum=30 #物品数目\n", 17 | "AllItem=np.array([[random.randint(1, 5) for j in range(1, 3)] for i in range(1,itemNum+1)]) #随机生成30个物品，[width,height]\n", 18 | "Bin=[10,10] #箱子宽度与高度\n", 19 | "ran=list(range(itemNum))\n", 20 | "random.shuffle(ran) #随机生成装箱序列\n", 21 | "\n", 22 | "ansBXY=np.zeros((itemNum,3)) #[箱子编号，X坐标，Y坐标]\n", 23 | "RPNXY=[];\n", 24 | "BinNum=1;\n", 25 | "flagItem=np.zeros(itemNum) #标记物品是否被装入箱子，0没有装入，1装入\n", 26 | "# 开始装箱\n", 27 | "\n", 28 | "for i in range(itemNum):\n", 29 | " if flagItem[ran[i]]==0:\n", 30 | " item=AllItem[ran[i],:]\n", 31 | " itemRP=Bin #起点全部在箱子右上角顶点\n", 32 | " flagOL=overlap(item,AllItem,itemRP,RPNXY) #如果重合flagOL=1；反之flagOL=0\n", 33 | " if flagOL==0:\n", 34 | " itemRP=finalPos(item,AllItem,itemRP,RPNXY) #更新物品从当前位置向下向左移动后到最终位置后右上角顶点坐标\n", 35 | " RPNXY.append([ran[i],itemRP[0],itemRP[1]]) # 记录装进箱子的矩形【ID,width,height】\n", 36 | " flagItem[ran[i]]=1\n", 37 | "# 启用第下一个箱子\n", 38 | "# if list(flagItem).count(0)>0:\n", 39 | "# BinNum=BinNum+1\n", 40 | "# RPNXY=[]" 41 | ] 42 | }, 43 | { 44 | "cell_type": "code", 45 | "execution_count": 3, 46 | "metadata": {}, 47 | "outputs": [ 48 | { 49 | "data": { 50 | "text/plain": [ 51 | "array([[2, 4],\n", 52 | " [2, 5],\n", 53 | " [5, 4],\n", 54 | " [1, 1],\n", 55 | " [1, 3],\n", 56 | " [5, 1],\n", 57 | " [4, 3],\n", 58 | " [5, 4],\n", 59 | " [3, 2],\n", 60 | " [2, 1],\n", 61 | " [4, 1],\n", 62 | " [5, 5],\n", 63 | " [1, 3],\n", 64 | " [5, 1],\n", 65 | " [1, 1],\n", 66 | " [5, 1],\n", 67 | " [5, 5],\n", 68 | " [3, 1],\n", 69 | " [4, 4],\n", 70 | " [5, 4],\n", 71 | " [3, 3],\n", 72 | " [4, 2],\n", 73 | " [3, 1],\n", 74 | " [3, 4],\n", 75 | " [5, 1],\n", 76 | " [5, 4],\n", 77 | " [2, 5],\n", 78 | " [5, 1],\n", 79 | " [1, 3],\n", 80 | " [2, 5]])" 81 | ] 82 | }, 83 | "execution_count": 3, 84 | "metadata": {}, 85 | "output_type": "execute_result" 86 | } 87 | ], 88 | "source": [ 89 | "AllItem" 90 | ] 91 | }, 92 | { 93 | "cell_type": "code", 94 | "execution_count": 4, 95 | "metadata": {}, 96 | "outputs": [ 97 | { 98 | "data": { 99 | "text/plain": [ 100 | "array([0., 0., 1., 1., 1., 0., 1., 0., 1., 1., 0., 0., 1., 1., 1., 1., 0.,\n", 101 | " 0., 0., 1., 0., 0., 0., 0., 0., 0., 0., 0., 1., 0.])" 102 | ] 103 | }, 104 | "execution_count": 4, 105 | "metadata": {}, 106 | "output_type": "execute_result" 107 | } 108 | ], 109 | "source": [ 110 | "flagItem" 111 | ] 112 | }, 113 | { 114 | "cell_type": "code", 115 | "execution_count": 20, 116 | "metadata": {}, 117 | "outputs": [ 118 | { 119 | "data": { 120 | "text/plain": [ 121 | "[[3, 2, 3], [2, 5, 3], [8, 3, 4], [5, 4, 5]]" 122 | ] 123 | }, 124 | "execution_count": 20, 125 | "metadata": {}, 126 | "output_type": "execute_result" 127 | } 128 | ], 129 | "source": [ 130 | "# 右上角定点坐标\n", 131 | "RPNXY" 132 | ] 133 | }, 134 | { 135 | "cell_type": "code", 136 | "execution_count": 4, 137 | "metadata": {}, 138 | "outputs": [ 139 | { 140 | "data": { 141 | "text/plain": [ 142 | "array([[1, 3],\n", 143 | " [5, 5],\n", 144 | " [1, 3],\n", 145 | " [3, 5],\n", 146 | " [2, 3],\n", 147 | " [2, 1],\n", 148 | " [3, 3],\n", 149 | " [5, 3],\n", 150 | " [3, 1],\n", 151 | " [4, 3]])" 152 | ] 153 | }, 154 | "execution_count": 4, 155 | "metadata": {}, 156 | "output_type": "execute_result" 157 | } 158 | ], 159 | "source": [ 160 | "AllItem" 161 | ] 162 | }, 163 | { 164 | "cell_type": "markdown", 165 | "metadata": {}, 166 | "source": [ 167 | "# 2 计算利用率" 168 | ] 169 | }, 170 | { 171 | "cell_type": "code", 172 | "execution_count": 5, 173 | "metadata": {}, 174 | "outputs": [ 175 | { 176 | "name": "stdout", 177 | "output_type": "stream", 178 | "text": [ 179 | "利用率:0.81\n" 180 | ] 181 | } 182 | ], 183 | "source": [ 184 | "rect_area = 0\n", 185 | "bin_area = Bin[0]*Bin[1]\n", 186 | "for id in RPNXY:\n", 187 | " width,height = AllItem[id[0]]\n", 188 | " rect_area += width*height\n", 189 | "print('利用率:{}'.format(rect_area/bin_area))" 190 | ] 191 | }, 192 | { 193 | "cell_type": "markdown", 194 | "metadata": {}, 195 | "source": [ 196 | "# 3 可视化" 197 | ] 198 | }, 199 | { 200 | "cell_type": "code", 201 | "execution_count": 7, 202 | "metadata": {}, 203 | "outputs": [ 204 | { 205 | "name": "stderr", 206 | "output_type": "stream", 207 | "text": [ 208 | ":16: MatplotlibDeprecationWarning: savefig() got unexpected keyword argument \"kpi\" which is no longer supported as of 3.3 and will become an error two minor releases later\n", 209 | " plt.savefig('result.png',kpi=300)\n" 210 | ] 211 | }, 212 | { 213 | "data": { 214 | "image/png": "iVBORw0KGgoAAAANSUhEUgAAAXIAAAD8CAYAAABq6S8VAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjMuMiwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy8vihELAAAACXBIWXMAAAsTAAALEwEAmpwYAAAKj0lEQVR4nO3db4hl9X3H8c/XNdiNdf0Xl0olFYOrVhOJGSwkGH3YkNjaCNI8aEuFLoWSPLCpBJJQaCtIhbRQKHSlUHxU6INFik1SamOR0oSuFKEYG0JQUkNTTWJToiTafPtgRnbZZNe5d+/k7FdfLxi4c+ecOV8Ow3t/c+aevdXdAWCuc5YeAIAzI+QAwwk5wHBCDjCckAMMJ+QAwwk5wHC7CnlV3VRVn9t5fGlV3VFVt1XVe/d2PABez+uGvKr2J/nuCU99PMkj3f1Ykjuq6tw9mg2AXXjdCHf3y0m+WlWvPXVNd7+y8/iHSd6R5D9O3KeqDic5nCTnn3/+e6699tqNDQyb0k++uPQInOR/9r+49Ai56NCVS4+QJHniiSde6O7LdrPtOqvpk1fxP3KPf3cfSXIkSba2tvrYsWNrHAb21qsHjy49Aif5u3c9vPQI+aV/+KulR0iSVNWzu912nT92Pr1zuSVJKsnX1vgeAGzIrlbkVXVdkrdX1VVJHkjyoar6RpKj3f3qXg4IwOntKuTd/eUkP3/CU3+zN+MAsCqvIwcYTsgBhhNygOGEHGA4IQcYTsgBhhNygOGEHGA4IQcYTsgBhhNygOGEHGA4IQcYTsgBhhNygOGEHGA4IQcYbp03X17JC//2XB688JN7fRhY2W+et7X0CLARVuQAwwk5wHBCDjCckAMMJ+QAwwk5wHBCDjCckAMMJ+QAwwk5wHBCDjCckAMMJ+QAwwk5wHBCDjCckAMMJ+QAwwk5wHBCDjDcWiGvqnOr6p6quqWqPlZVtenBANiddVfkNyb5QXc/nqSTXLy5kQBYxblr7vdkkl+vqtuTPNXd3z7xi1V1OMnhJLmkDpzZhLBHLv7meUuPcNbYd/TZpUdIkjz050tPkBy4+ztLj7CydVfkB5I8uvNxZ1VdfuIXu/tId29199YF9dYznRGA01g35Lcm+b/ufinJI0lu3txIAKxi3ZB/IclNVXVLkquSfH5zIwGwirWukXf3i0n+cOfTxzc2DQAr8zpygOGEHGA4IQcYTsgBhhNygOGEHGA4IQcYTsgBhhNygOGEHGA4IQcYTsgBhhNygOGEHGA4IQcYTsgBhhNygOGqu/f0AFfuu7w/+dN37+kxYB3/+t+/sfQIcEoP/tQ1T3T31m62tSIHGE7IAYYTcoDhhBxgOCEHGE7IAYYTcoDhhBxgOCEHGE7IAYYTcoDhhBxgOCEHGE7IAYYTcoDhhBxgOCEHGG7tkFfV/qp6/yaHAWB1a4W8qg4luTfJFzc7DgCrOnfVHarqLUnuT3JXd7+6+ZEAWMXKIU/ywSSPJrmxqn61u3/v5A2q6nCSw0lySR04swlhjxw579DSIyRJnr75d5cegbPQgytsu86llUNJnuruJ5J8v6puPHmD7j7S3VvdvXVBvXWNQwCwW+uE/JkkB3ce70vy8samAWBl64T8aJJrquqWJM9191c2PBMAK1j5Gnl3v5LkD3Y+fXyz4wCwKjcEAQwn5ADDCTnAcEIOMJyQAwwn5ADDCTnAcEIOMJyQAwwn5ADDCTnAcEIOMJyQAwwn5ADDCTnAcEIOMJyQAwy38jsErept7/7Z/Nax+/b6MKf10T+7bdHjc3Y6W34ufifvWXoEhrMiBxhOyAGGE3KA4YQcYDghBxhOyAGGE3KA4YQcYDghBxhOyAGGE3KA4YQcYDghBxhOyAGGE3KA4YQcYDghBxhOyAGGE3KA4dYOeVXdUFX3b3IYAFa3Vsir6ook1ye5aKPTALCylUNeVRdlO+JfOs02h6vqWFUde/75589gPABezzor8ruSXJfk7iTvrKoPnLxBdx/p7q3u3rrsssvOdEYATuPcVXfo7iNJUlVXJjnY3Z/d9FAA7J5XrQAMt/KK/DXd/UyS397cKACsw4ocYDghBxhOyAGGE3KA4YQcYDghBxhOyAGGE3KA4YQcYDghBxhOyAGGE3KA4YQcYDghBxhOyAGGE3KA4YQcYLi13yFot7715H/moYP37vVhTu/Tyx4eTuflv3966RHy7oseWXoETlaf2fWmVuQAwwk5wHBCDjCckAMMJ+QAwwk5wHBCDjCckAMMJ+QAwwk5wHBCDjCckAMMJ+QAwwk5wHBCDjCckAMMJ+QAwwk5wHArv9VbVV2Y5KNJLknyUnd/auNTAbBr67xn59VJ7uvurqqjVXV+d39v04MBsDsrh7y7jyVJVe1L8sKPi3hVHU5yOEkuPefAmc4IwGmcyTXyjyT5xI/7Qncf6e6t7t664Jz9Z3AIAF7PWiGvqtuTPNzd36qqizc8EwArWOePnfcmuTbJrVV1MMlfJvmnTQ8GwO6sc438j/diEADW43XkAMMJOcBwQg4wnJADDCfkAMMJOcBwQg4wnJADDCfkAMMJOcBwQg4wnJADDCfkAMMJOcBwQg4wnJADDCfkAMOt/A5BE/3Lp29fegQ4pbt/7R+XHoHhrMgBhhNygOGEHGA4IQcYTsgBhhNygOGEHGA4IQcYTsgBhhNygOGEHGA4IQcYTsgBhhNygOGEHGA4IQcYTsgBhhNygOGEHGC4ld+zs6oqyYeT/FeSS7r7bzc+FQC7ts6K/JeTfLO7/znJz1TVdRueCYAVVHevtkPVnyT50+5+tqp+McnPdfdfnLTN4SSHdz69Icm/b2LYN4C3JXlh6SHOEs7Fcc7Fcc7Fcdd09wW72XDlSytJaufjNT/yL0F3H0lyJEmq6lh3b61xnDcc5+I45+I45+I45+K4qjq2223XubTyWJKrdh5fkeTxNb4HABuyTsgfTnKwqn4hyTe6+8sbngmAFax8aaW3L6r/9Qq7HFn1GG9gzsVxzsVxzsVxzsVxuz4XK/+xE4CzixuCAIYTclhYVe2vqvcvPQdz7VnIa9udVfW+qrp9r45ztquqC6vqU1X1mar6o6XnOVtU1Q1Vdf/Scyytqg4luTfJF5eeZUlVdW5V3VNVt1TVx3buIH/TqaqbqupzO48vrao7quq2qnrv6fbbyxW5O0C3XZ3kvu6+J8n1VXX+0gMtraquSHJ9kosWHmVRVfWWJPdn++fjB0vPs7Abk/ygux/P9r0pFy88z09cVe1P8t0Tnvp4kke6+7Ekd1TVKV+cspchvzXJ13cefz3Jm/JXx+4+1t1dVfuSvNDd31t6piVV1UXZjviXFh7lbPDBJI8mubGqHlh6mIU9meTqnd/en+ruby890E9ad7/c3V894alruvuVncc/TPKOU+27lyF/3TtA32Q+kuQTSw9xFrgryXVJ7k7yzqr6wMLzLOlQtqP1RJLvV9WNSw+0oAPZ/kft0SR3VtXlC89zNji5z6ds6Dq36O/WY9m+A/SZvMnvAN1ZZTzc3f9bVRd393eWnmkpO/99Q6rqyiQHu/uzy060qGeSHNx5vC/Jy8uNsrhbs31p5aWqeiTJzdm++fDN7Omq2t/dL2d7Ufy1U224lytyd4Amqap7k/xKkt+vqoeSvGvhkTh7HE1yTVXdkuS57v7K0gMt6AtJbto5F1cl+fzC8yxi52+Jb6+qq5I8kORDVfW+JEe7+9VT7ueGIIDZvI4cYDghBxhOyAGGE3KA4YQcYDghBxhOyAGGE3KA4YQcYLj/B7UJ4jcsQwKLAAAAAElFTkSuQmCC", 215 | "text/plain": [ 216 | "
" 217 | ] 218 | }, 219 | "metadata": { 220 | "needs_background": "light" 221 | }, 222 | "output_type": "display_data" 223 | } 224 | ], 225 | "source": [ 226 | "\n", 227 | "\n", 228 | "import matplotlib.pyplot as plt\n", 229 | "import matplotlib.patches as patches\n", 230 | "import random\n", 231 | "fig, ax = plt.subplots(1, 1)\n", 232 | "ax1 = fig.gca()\n", 233 | "for i in RPNXY:\n", 234 | " width,height = AllItem[i[0]]\n", 235 | " rx,ry = i[1],i[2]\n", 236 | " lx,ly = rx-width,ry-height\n", 237 | " plt.xlim((0, Bin[0]))\n", 238 | " plt.ylim((0, Bin[1]))\n", 239 | " color = \"#\"+''.join([random.choice('0123456789ABCDEF') for j in range(6)])\n", 240 | " rect = patches.Rectangle((lx, ly), width,height,linewidth=1, facecolor = color)\n", 241 | " ax1.add_patch(rect)\n", 242 | "# plt.show()\n", 243 | "plt.savefig('result.png',kpi=300)" 244 | ] 245 | } 246 | ], 247 | "metadata": { 248 | "interpreter": { 249 | "hash": "cd78fef2128015050713e82ca51c6520b11aee7c9ee8df750520bbbc7384cbaa" 250 | }, 251 | "kernelspec": { 252 | "display_name": "Python 3.8.5 ('base')", 253 | "language": "python", 254 | "name": "python3" 255 | }, 256 | "language_info": { 257 | "codemirror_mode": { 258 | "name": "ipython", 259 | "version": 3 260 | }, 261 | "file_extension": ".py", 262 | "mimetype": "text/x-python", 263 | "name": "python", 264 | "nbconvert_exporter": "python", 265 | "pygments_lexer": "ipython3", 266 | "version": "3.8.5" 267 | }, 268 | "orig_nbformat": 4 269 | }, 270 | "nbformat": 4, 271 | "nbformat_minor": 2 272 | } 273 | --------------------------------------------------------------------------------