├── README.md
├── Tencent_RE BERT model.ipynb
└── Confusion_Matrix.ipynb
/README.md:
--------------------------------------------------------------------------------
1 | # Financial-Fraud-Detection-Using-Text-Mining
2 | Groupmate: Vickie Chang, Chris Yeung
3 |
4 | Applied BERT based model to extract relations from 29 annual reports of listed companies and news; Used spaCy library and BERT model for name-entity recognition and relations extraction, and generated a network graph that summarises the key relation
5 |
6 | ## Methodology
7 | 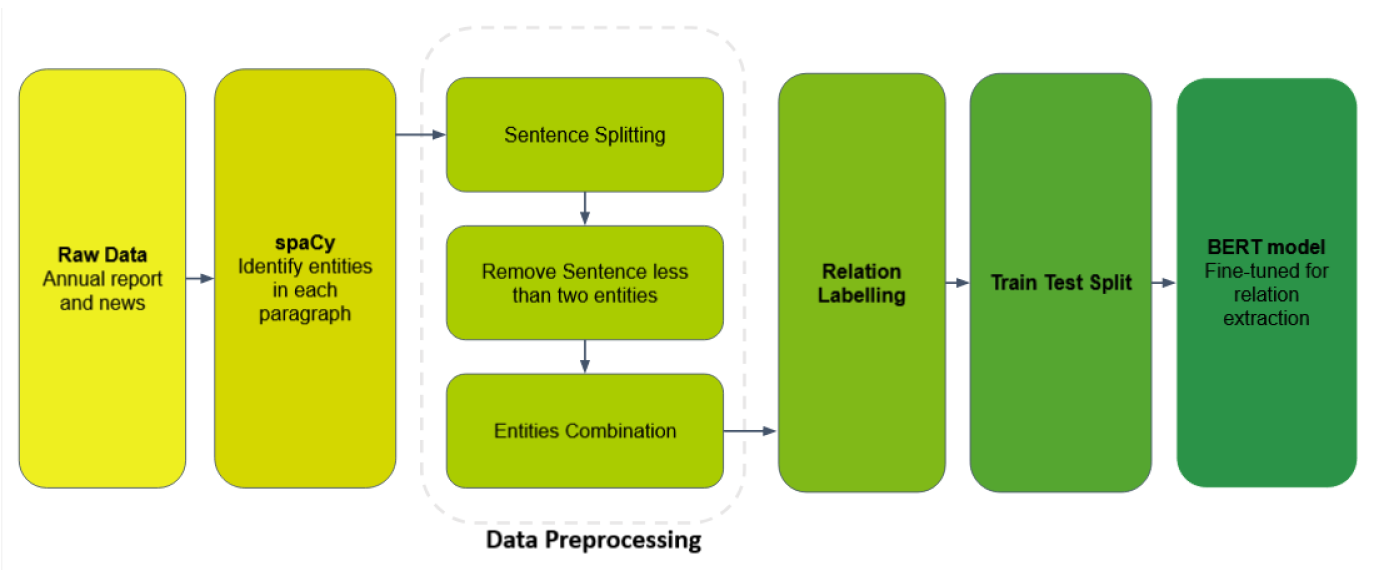
8 |
9 | 29 sets of annual report and news from Reuter are inputted to the trained SpaCy pipeline to identify entities. The entity comes along with a label to classify the entity's nature. The paragraph is then split into sentences. Sentences containing less than two entities are removed as they contain no valid relations. For sentences containing three or more entities, combinations of two are generated from the multiple entities in a sentence by using itertools from the combinations package and hence each sentence contains exactly two entities. Then the relations between the entities in each sentence are manually labelled. The data are then splited into train and test set for training the BERT model from [plkmo/BERT-Relation-Extraction](https://github.com/plkmo/BERT-Relation-Extraction). We have then apply our model on data related to Tencent as a case study target.
10 |
11 | - [Data_preprocessing.ipynb](https://github.com/Christy-Lo/Financial-Fraud-Detection-Using-Text-Mining/blob/main/data_preprocessing.ipynb) contains code of data collection and data preprocessing.
12 | - [Tencent_RE BERT model.ipynb](https://github.com/Christy-Lo/Financial-Fraud-Detection-Using-Text-Mining/blob/main/Tencent_RE%20BERT%20model.ipynb) contains code to implement the github repo of [plkmo/BERT-Relation-Extraction](https://github.com/plkmo/BERT-Relation-Extraction)
13 | - The confusion matrix and network graph are generated in [Confusion_Matrix.ipynb](https://github.com/Christy-Lo/Financial-Fraud-Detection-Using-Text-Mining/blob/main/Confusion_Matrix.ipynb) and [RelationGenerator.ipynb](https://github.com/Christy-Lo/Financial-Fraud-Detection-Using-Text-Mining/blob/main/RelationGenerator.ipynb)
14 |
15 | ## Training Data
16 | We have labelled a total of 2973 sentences with the following labels
17 | Labels | Number | Percentage
18 | --- | --- | ---
19 | Colleague | 475 | 15.98%
20 | Relative | 61 | 2.05%
21 | Employee-Company | 407 | 13.69%
22 | Educated-Institute | 83 | 2.79%
23 | Founder-Company | 51 | 1.72%
24 | Shareholder-Company | 143 | 4.81%
25 | Within-Same-Company-Group | 78 | 2.62%
26 | Cooperate-Partner | 76 | 2.56%
27 | Subsidary-ParentCompany | 98 | 3.30%
28 | Same-Entity | 97 | 3.26%
29 | Other | 1404 | 47.23%
30 |
31 | ## Example of data
32 | Input:
33 | ```
34 | Subsidary-ParentCompany(e1,e2)
35 | Sentence: As [E1]Advance Data Services Limited[/E1] is wholly-owned by [E2]Ma[/E2] Huateng, Mr Ma has an interest in these shares as disclosed under the section of “Directors’ Interests in Securities”.
36 | ```
37 |
38 | Output:
39 | ```
40 | Predicted: Subsidary-ParentCompany(e1,e2)
41 | ```
42 |
43 | ## Model Preformance and Visualization
44 | We have choosen to train the model with 11 epoch based on the training accuracy, losses and f1 score
45 | Parameter at Epoch 11|Value
46 | --- | ---
47 | Train accuracy | 0.8767857
48 | Losses | 0.3696946
49 | Test F1 score | 0.2857143
50 |
51 | Losses|F1 score
52 | ---|---
53 | |
54 | Training Accuracy|
55 | |
56 |
57 | #### Confusion Matrix
58 |
59 |
60 | #### Network Graph
61 | 
62 |
63 |
64 | ## Acknowledgement
65 | We would like to thanks Dr. K. P. Chow's research team for sharing their research data. We do not own any of the data. We have also refer to different tutorial throughout the project and we do not own the code. The links are stated when their code are adopted.
66 |
--------------------------------------------------------------------------------
/Tencent_RE BERT model.ipynb:
--------------------------------------------------------------------------------
1 | {"cells":[{"cell_type":"markdown","metadata":{"id":"8jEeZ9vU227n"},"source":["This notebook is implementing the github repositary \"BERT-Relation-Extraction\" from plkmo (link:https://github.com/plkmo/BERT-Relation-Extraction)"]},{"cell_type":"markdown","metadata":{"id":"exG7jPDgPpoq"},"source":["This notebook will guide you how to run the trained model.
\n","[IMPORTANT]: Before going into the code below, add the shortcut of the Project folder to your drive: \n","1. Right-click our project folder \n","2. Click \"Add shortcut to Drive\"\n","3. Select \"My Drive\" and click \"ADD SHORTCUT\""]},{"cell_type":"code","execution_count":null,"metadata":{"colab":{"base_uri":"https://localhost:8080/"},"executionInfo":{"elapsed":21500,"status":"ok","timestamp":1640166514513,"user":{"displayName":"Tsz Chung Yeung","photoUrl":"https://lh3.googleusercontent.com/a/default-user=s64","userId":"17478010975126361284"},"user_tz":-480},"id":"HKqwBS-G2pv7","outputId":"cf38e41d-19e8-4d61-d9e0-4954da6b6a35"},"outputs":[{"name":"stdout","output_type":"stream","text":["Mounted at /content/drive\n"]}],"source":["# Connect to Google drive\n","from google.colab import drive\n","drive.mount('/content/drive')"]},{"cell_type":"code","execution_count":null,"metadata":{"colab":{"base_uri":"https://localhost:8080/"},"executionInfo":{"elapsed":1140705,"status":"ok","timestamp":1640167675974,"user":{"displayName":"Tsz Chung Yeung","photoUrl":"https://lh3.googleusercontent.com/a/default-user=s64","userId":"17478010975126361284"},"user_tz":-480},"id":"QhsK49jo3pAK","outputId":"28b1df3b-f85e-419d-8b8e-c5652add1194"},"outputs":[{"name":"stdout","output_type":"stream","text":["Collecting seqeval\n"," Downloading seqeval-1.2.2.tar.gz (43 kB)\n","\u001b[?25l\r\u001b[K |███████▌ | 10 kB 15.4 MB/s eta 0:00:01\r\u001b[K |███████████████ | 20 kB 21.3 MB/s eta 0:00:01\r\u001b[K |██████████████████████▌ | 30 kB 23.1 MB/s eta 0:00:01\r\u001b[K |██████████████████████████████ | 40 kB 18.4 MB/s eta 0:00:01\r\u001b[K |████████████████████████████████| 43 kB 1.6 MB/s \n","\u001b[?25hRequirement already satisfied: numpy>=1.14.0 in /usr/local/lib/python3.7/dist-packages (from seqeval) (1.19.5)\n","Requirement already satisfied: scikit-learn>=0.21.3 in /usr/local/lib/python3.7/dist-packages (from seqeval) (1.0.1)\n","Requirement already satisfied: scipy>=1.1.0 in /usr/local/lib/python3.7/dist-packages (from scikit-learn>=0.21.3->seqeval) (1.4.1)\n","Requirement already satisfied: threadpoolctl>=2.0.0 in /usr/local/lib/python3.7/dist-packages (from scikit-learn>=0.21.3->seqeval) (3.0.0)\n","Requirement already satisfied: joblib>=0.11 in /usr/local/lib/python3.7/dist-packages (from scikit-learn>=0.21.3->seqeval) (1.1.0)\n","Building wheels for collected packages: seqeval\n"," Building wheel for seqeval (setup.py) ... \u001b[?25l\u001b[?25hdone\n"," Created wheel for seqeval: filename=seqeval-1.2.2-py3-none-any.whl size=16181 sha256=cfd19263ce99ae7501a95906f50047f672b86a4d57cb38a94333f8405059ef4c\n"," Stored in directory: /root/.cache/pip/wheels/05/96/ee/7cac4e74f3b19e3158dce26a20a1c86b3533c43ec72a549fd7\n","Successfully built seqeval\n","Installing collected packages: seqeval\n","Successfully installed seqeval-1.2.2\n","Collecting boto3\n"," Downloading boto3-1.20.26-py3-none-any.whl (131 kB)\n","\u001b[K |████████████████████████████████| 131 kB 13.0 MB/s \n","\u001b[?25hCollecting jmespath<1.0.0,>=0.7.1\n"," Downloading jmespath-0.10.0-py2.py3-none-any.whl (24 kB)\n","Collecting botocore<1.24.0,>=1.23.26\n"," Downloading botocore-1.23.26-py3-none-any.whl (8.5 MB)\n","\u001b[K |████████████████████████████████| 8.5 MB 46.2 MB/s \n","\u001b[?25hCollecting s3transfer<0.6.0,>=0.5.0\n"," Downloading s3transfer-0.5.0-py3-none-any.whl (79 kB)\n","\u001b[K |████████████████████████████████| 79 kB 8.0 MB/s \n","\u001b[?25hRequirement already satisfied: python-dateutil<3.0.0,>=2.1 in /usr/local/lib/python3.7/dist-packages (from botocore<1.24.0,>=1.23.26->boto3) (2.8.2)\n","Collecting urllib3<1.27,>=1.25.4\n"," Downloading urllib3-1.26.7-py2.py3-none-any.whl (138 kB)\n","\u001b[K |████████████████████████████████| 138 kB 50.9 MB/s \n","\u001b[?25hRequirement already satisfied: six>=1.5 in /usr/local/lib/python3.7/dist-packages (from python-dateutil<3.0.0,>=2.1->botocore<1.24.0,>=1.23.26->boto3) (1.15.0)\n","Installing collected packages: urllib3, jmespath, botocore, s3transfer, boto3\n"," Attempting uninstall: urllib3\n"," Found existing installation: urllib3 1.24.3\n"," Uninstalling urllib3-1.24.3:\n"," Successfully uninstalled urllib3-1.24.3\n","\u001b[31mERROR: pip's dependency resolver does not currently take into account all the packages that are installed. This behaviour is the source of the following dependency conflicts.\n","requests 2.23.0 requires urllib3!=1.25.0,!=1.25.1,<1.26,>=1.21.1, but you have urllib3 1.26.7 which is incompatible.\n","datascience 0.10.6 requires folium==0.2.1, but you have folium 0.8.3 which is incompatible.\u001b[0m\n","Successfully installed boto3-1.20.26 botocore-1.23.26 jmespath-0.10.0 s3transfer-0.5.0 urllib3-1.26.7\n","Requirement already satisfied: spacy in /usr/local/lib/python3.7/dist-packages (2.2.4)\n","Requirement already satisfied: catalogue<1.1.0,>=0.0.7 in /usr/local/lib/python3.7/dist-packages (from spacy) (1.0.0)\n","Requirement already satisfied: plac<1.2.0,>=0.9.6 in /usr/local/lib/python3.7/dist-packages (from spacy) (1.1.3)\n","Requirement already satisfied: srsly<1.1.0,>=1.0.2 in /usr/local/lib/python3.7/dist-packages (from spacy) (1.0.5)\n","Requirement already satisfied: wasabi<1.1.0,>=0.4.0 in /usr/local/lib/python3.7/dist-packages (from spacy) (0.8.2)\n","Requirement already satisfied: thinc==7.4.0 in /usr/local/lib/python3.7/dist-packages (from spacy) (7.4.0)\n","Requirement already satisfied: cymem<2.1.0,>=2.0.2 in /usr/local/lib/python3.7/dist-packages (from spacy) (2.0.6)\n","Requirement already satisfied: tqdm<5.0.0,>=4.38.0 in /usr/local/lib/python3.7/dist-packages (from spacy) (4.62.3)\n","Requirement already satisfied: murmurhash<1.1.0,>=0.28.0 in /usr/local/lib/python3.7/dist-packages (from spacy) (1.0.6)\n","Requirement already satisfied: blis<0.5.0,>=0.4.0 in /usr/local/lib/python3.7/dist-packages (from spacy) (0.4.1)\n","Requirement already satisfied: setuptools in /usr/local/lib/python3.7/dist-packages (from spacy) (57.4.0)\n","Requirement already satisfied: numpy>=1.15.0 in /usr/local/lib/python3.7/dist-packages (from spacy) (1.19.5)\n","Requirement already satisfied: requests<3.0.0,>=2.13.0 in /usr/local/lib/python3.7/dist-packages (from spacy) (2.23.0)\n","Requirement already satisfied: preshed<3.1.0,>=3.0.2 in /usr/local/lib/python3.7/dist-packages (from spacy) (3.0.6)\n","Requirement already satisfied: importlib-metadata>=0.20 in /usr/local/lib/python3.7/dist-packages (from catalogue<1.1.0,>=0.0.7->spacy) (4.8.2)\n","Requirement already satisfied: typing-extensions>=3.6.4 in /usr/local/lib/python3.7/dist-packages (from importlib-metadata>=0.20->catalogue<1.1.0,>=0.0.7->spacy) (3.10.0.2)\n","Requirement already satisfied: zipp>=0.5 in /usr/local/lib/python3.7/dist-packages (from importlib-metadata>=0.20->catalogue<1.1.0,>=0.0.7->spacy) (3.6.0)\n","Requirement already satisfied: chardet<4,>=3.0.2 in /usr/local/lib/python3.7/dist-packages (from requests<3.0.0,>=2.13.0->spacy) (3.0.4)\n","Requirement already satisfied: certifi>=2017.4.17 in /usr/local/lib/python3.7/dist-packages (from requests<3.0.0,>=2.13.0->spacy) (2021.10.8)\n","Collecting urllib3!=1.25.0,!=1.25.1,<1.26,>=1.21.1\n"," Downloading urllib3-1.25.11-py2.py3-none-any.whl (127 kB)\n","\u001b[K |████████████████████████████████| 127 kB 12.2 MB/s \n","\u001b[?25hRequirement already satisfied: idna<3,>=2.5 in /usr/local/lib/python3.7/dist-packages (from requests<3.0.0,>=2.13.0->spacy) (2.10)\n","Installing collected packages: urllib3\n"," Attempting uninstall: urllib3\n"," Found existing installation: urllib3 1.26.7\n"," Uninstalling urllib3-1.26.7:\n"," Successfully uninstalled urllib3-1.26.7\n","\u001b[31mERROR: pip's dependency resolver does not currently take into account all the packages that are installed. This behaviour is the source of the following dependency conflicts.\n","datascience 0.10.6 requires folium==0.2.1, but you have folium 0.8.3 which is incompatible.\u001b[0m\n","Successfully installed urllib3-1.25.11\n","Collecting en_core_web_lg==2.2.5\n"," Downloading https://github.com/explosion/spacy-models/releases/download/en_core_web_lg-2.2.5/en_core_web_lg-2.2.5.tar.gz (827.9 MB)\n","\u001b[K |████████████████████████████████| 827.9 MB 658 kB/s \n","\u001b[?25hRequirement already satisfied: spacy>=2.2.2 in /usr/local/lib/python3.7/dist-packages (from en_core_web_lg==2.2.5) (2.2.4)\n","Requirement already satisfied: wasabi<1.1.0,>=0.4.0 in /usr/local/lib/python3.7/dist-packages (from spacy>=2.2.2->en_core_web_lg==2.2.5) (0.8.2)\n","Requirement already satisfied: requests<3.0.0,>=2.13.0 in /usr/local/lib/python3.7/dist-packages (from spacy>=2.2.2->en_core_web_lg==2.2.5) (2.23.0)\n","Requirement already satisfied: numpy>=1.15.0 in /usr/local/lib/python3.7/dist-packages (from spacy>=2.2.2->en_core_web_lg==2.2.5) (1.19.5)\n","Requirement already satisfied: tqdm<5.0.0,>=4.38.0 in /usr/local/lib/python3.7/dist-packages (from spacy>=2.2.2->en_core_web_lg==2.2.5) (4.62.3)\n","Requirement already satisfied: srsly<1.1.0,>=1.0.2 in /usr/local/lib/python3.7/dist-packages (from spacy>=2.2.2->en_core_web_lg==2.2.5) (1.0.5)\n","Requirement already satisfied: cymem<2.1.0,>=2.0.2 in /usr/local/lib/python3.7/dist-packages (from spacy>=2.2.2->en_core_web_lg==2.2.5) (2.0.6)\n","Requirement already satisfied: plac<1.2.0,>=0.9.6 in /usr/local/lib/python3.7/dist-packages (from spacy>=2.2.2->en_core_web_lg==2.2.5) (1.1.3)\n","Requirement already satisfied: setuptools in /usr/local/lib/python3.7/dist-packages (from spacy>=2.2.2->en_core_web_lg==2.2.5) (57.4.0)\n","Requirement already satisfied: thinc==7.4.0 in /usr/local/lib/python3.7/dist-packages (from spacy>=2.2.2->en_core_web_lg==2.2.5) (7.4.0)\n","Requirement already satisfied: preshed<3.1.0,>=3.0.2 in /usr/local/lib/python3.7/dist-packages (from spacy>=2.2.2->en_core_web_lg==2.2.5) (3.0.6)\n","Requirement already satisfied: murmurhash<1.1.0,>=0.28.0 in /usr/local/lib/python3.7/dist-packages (from spacy>=2.2.2->en_core_web_lg==2.2.5) (1.0.6)\n","Requirement already satisfied: catalogue<1.1.0,>=0.0.7 in /usr/local/lib/python3.7/dist-packages (from spacy>=2.2.2->en_core_web_lg==2.2.5) (1.0.0)\n","Requirement already satisfied: blis<0.5.0,>=0.4.0 in /usr/local/lib/python3.7/dist-packages (from spacy>=2.2.2->en_core_web_lg==2.2.5) (0.4.1)\n","Requirement already satisfied: importlib-metadata>=0.20 in /usr/local/lib/python3.7/dist-packages (from catalogue<1.1.0,>=0.0.7->spacy>=2.2.2->en_core_web_lg==2.2.5) (4.8.2)\n","Requirement already satisfied: typing-extensions>=3.6.4 in /usr/local/lib/python3.7/dist-packages (from importlib-metadata>=0.20->catalogue<1.1.0,>=0.0.7->spacy>=2.2.2->en_core_web_lg==2.2.5) (3.10.0.2)\n","Requirement already satisfied: zipp>=0.5 in /usr/local/lib/python3.7/dist-packages (from importlib-metadata>=0.20->catalogue<1.1.0,>=0.0.7->spacy>=2.2.2->en_core_web_lg==2.2.5) (3.6.0)\n","Requirement already satisfied: chardet<4,>=3.0.2 in /usr/local/lib/python3.7/dist-packages (from requests<3.0.0,>=2.13.0->spacy>=2.2.2->en_core_web_lg==2.2.5) (3.0.4)\n","Requirement already satisfied: certifi>=2017.4.17 in /usr/local/lib/python3.7/dist-packages (from requests<3.0.0,>=2.13.0->spacy>=2.2.2->en_core_web_lg==2.2.5) (2021.10.8)\n","Requirement already satisfied: idna<3,>=2.5 in /usr/local/lib/python3.7/dist-packages (from requests<3.0.0,>=2.13.0->spacy>=2.2.2->en_core_web_lg==2.2.5) (2.10)\n","Requirement already satisfied: urllib3!=1.25.0,!=1.25.1,<1.26,>=1.21.1 in /usr/local/lib/python3.7/dist-packages (from requests<3.0.0,>=2.13.0->spacy>=2.2.2->en_core_web_lg==2.2.5) (1.25.11)\n","Building wheels for collected packages: en-core-web-lg\n"," Building wheel for en-core-web-lg (setup.py) ... \u001b[?25l\u001b[?25hdone\n"," Created wheel for en-core-web-lg: filename=en_core_web_lg-2.2.5-py3-none-any.whl size=829180942 sha256=a75086f01ac3cd4374754144b0c52726ff47f3f000043724139fe3941ed79a94\n"," Stored in directory: /tmp/pip-ephem-wheel-cache-ldg6f_mp/wheels/11/95/ba/2c36cc368c0bd339b44a791c2c1881a1fb714b78c29a4cb8f5\n","Successfully built en-core-web-lg\n","Installing collected packages: en-core-web-lg\n","Successfully installed en-core-web-lg-2.2.5\n","\u001b[38;5;2m✔ Download and installation successful\u001b[0m\n","You can now load the model via spacy.load('en_core_web_lg')\n"]}],"source":["# Install the required libs\n","!pip install seqeval\n","!pip install boto3\n","!pip install spacy\n","#!pip3 install torch==1.10.0+cu102 torchvision==0.11.1+cu102 torchaudio===0.10.0+cu102 -f https://download.pytorch.org/whl/cu102/torch_stable.html\n","!python -m spacy download en_core_web_lg"]},{"cell_type":"code","execution_count":null,"metadata":{"colab":{"base_uri":"https://localhost:8080/"},"executionInfo":{"elapsed":1528911,"status":"ok","timestamp":1640169204878,"user":{"displayName":"Tsz Chung Yeung","photoUrl":"https://lh3.googleusercontent.com/a/default-user=s64","userId":"17478010975126361284"},"user_tz":-480},"id":"XaZkTdYyWTtJ","outputId":"3110dbe5-d64e-4373-92fb-a82469c8a996"},"outputs":[{"name":"stdout","output_type":"stream","text":["/content/drive/.shortcut-targets-by-id/1jqlh-dTe4b6_AZhAYDBHkKjWweeOh9HE/COMP4805 Project/Go to Street/__Tencent/BERT-Relation-Extraction\n","12/22/2021 10:08:15 AM [INFO]: TensorFlow version 2.7.0 available.\n","12/22/2021 10:08:15 AM [INFO]: PyTorch version 1.10.0+cu111 available.\n","12/22/2021 10:08:15 AM [INFO]: Pre-trained blanks tokenizer not found, initializing new tokenizer...\n","12/22/2021 10:08:16 AM [INFO]: https://s3.amazonaws.com/models.huggingface.co/bert/bert-base-uncased-vocab.txt not found in cache or force_download set to True, downloading to /tmp/tmpjzc21nbv\n","100% 231508/231508 [00:00<00:00, 917110.82B/s]\n","12/22/2021 10:08:16 AM [INFO]: copying /tmp/tmpjzc21nbv to cache at /root/.cache/torch/transformers/26bc1ad6c0ac742e9b52263248f6d0f00068293b33709fae12320c0e35ccfbbb.542ce4285a40d23a559526243235df47c5f75c197f04f37d1a0c124c32c9a084\n","12/22/2021 10:08:16 AM [INFO]: creating metadata file for /root/.cache/torch/transformers/26bc1ad6c0ac742e9b52263248f6d0f00068293b33709fae12320c0e35ccfbbb.542ce4285a40d23a559526243235df47c5f75c197f04f37d1a0c124c32c9a084\n","12/22/2021 10:08:16 AM [INFO]: removing temp file /tmp/tmpjzc21nbv\n","12/22/2021 10:08:16 AM [INFO]: loading file https://s3.amazonaws.com/models.huggingface.co/bert/bert-base-uncased-vocab.txt from cache at /root/.cache/torch/transformers/26bc1ad6c0ac742e9b52263248f6d0f00068293b33709fae12320c0e35ccfbbb.542ce4285a40d23a559526243235df47c5f75c197f04f37d1a0c124c32c9a084\n","12/22/2021 10:08:16 AM [INFO]: Adding [E1] to the vocabulary\n","12/22/2021 10:08:16 AM [INFO]: Adding [/E1] to the vocabulary\n","12/22/2021 10:08:16 AM [INFO]: Adding [E2] to the vocabulary\n","12/22/2021 10:08:16 AM [INFO]: Adding [/E2] to the vocabulary\n","12/22/2021 10:08:16 AM [INFO]: Adding [BLANK] to the vocabulary\n","12/22/2021 10:08:16 AM [INFO]: Saved BERT tokenizer at ./data/BERT_tokenizer.pkl\n","12/22/2021 10:08:16 AM [INFO]: Reading training file /content/drive/MyDrive/COMP4805 Project/Go to Street/__Tencent/train_data_dm1.txt...\n","12/22/2021 10:08:18 AM [INFO]: Reading test file /content/drive/MyDrive/COMP4805 Project/Go to Street/__Tencent/test_data_dm1.txt...\n","12/22/2021 10:08:18 AM [INFO]: Mapping relations to IDs...\n","100% 2400/2400 [00:00<00:00, 1755857.25it/s]\n","prog-bar: 100% 266/266 [00:00<00:00, 32935.35it/s]\n","prog-bar: 100% 2400/2400 [00:00<00:00, 98614.10it/s]\n","12/22/2021 10:08:18 AM [INFO]: Finished and saved!\n","12/22/2021 10:08:18 AM [INFO]: Tokenizing data...\n","prog-bar: 100% 2400/2400 [00:03<00:00, 660.69it/s]\n","prog-bar: 100% 2400/2400 [00:00<00:00, 46084.92it/s]\n","\n","Invalid rows/total: 0/2400\n","12/22/2021 10:08:22 AM [INFO]: NumExpr defaulting to 2 threads.\n","12/22/2021 10:08:22 AM [INFO]: Tokenizing data...\n","prog-bar: 100% 266/266 [00:00<00:00, 635.77it/s]\n","prog-bar: 100% 266/266 [00:00<00:00, 44502.79it/s]\n","\n","Invalid rows/total: 0/266\n","12/22/2021 10:08:22 AM [INFO]: Loaded 2400 Training samples.\n","12/22/2021 10:08:25 AM [INFO]: https://s3.amazonaws.com/models.huggingface.co/bert/bert-base-uncased-config.json not found in cache or force_download set to True, downloading to /tmp/tmp08u7j8mp\n","100% 433/433 [00:00<00:00, 429447.54B/s]\n","12/22/2021 10:08:25 AM [INFO]: copying /tmp/tmp08u7j8mp to cache at /root/.cache/torch/transformers/4dad0251492946e18ac39290fcfe91b89d370fee250efe9521476438fe8ca185.7156163d5fdc189c3016baca0775ffce230789d7fa2a42ef516483e4ca884517\n","12/22/2021 10:08:25 AM [INFO]: creating metadata file for /root/.cache/torch/transformers/4dad0251492946e18ac39290fcfe91b89d370fee250efe9521476438fe8ca185.7156163d5fdc189c3016baca0775ffce230789d7fa2a42ef516483e4ca884517\n","12/22/2021 10:08:25 AM [INFO]: removing temp file /tmp/tmp08u7j8mp\n","12/22/2021 10:08:25 AM [INFO]: loading configuration file https://s3.amazonaws.com/models.huggingface.co/bert/bert-base-uncased-config.json from cache at /root/.cache/torch/transformers/4dad0251492946e18ac39290fcfe91b89d370fee250efe9521476438fe8ca185.7156163d5fdc189c3016baca0775ffce230789d7fa2a42ef516483e4ca884517\n","12/22/2021 10:08:25 AM [INFO]: Model config {\n"," \"architectures\": [\n"," \"BertForMaskedLM\"\n"," ],\n"," \"attention_probs_dropout_prob\": 0.1,\n"," \"finetuning_task\": null,\n"," \"hidden_act\": \"gelu\",\n"," \"hidden_dropout_prob\": 0.1,\n"," \"hidden_size\": 768,\n"," \"initializer_range\": 0.02,\n"," \"intermediate_size\": 3072,\n"," \"is_decoder\": false,\n"," \"layer_norm_eps\": 1e-12,\n"," \"max_position_embeddings\": 512,\n"," \"model_type\": \"bert\",\n"," \"num_attention_heads\": 12,\n"," \"num_hidden_layers\": 12,\n"," \"num_labels\": 2,\n"," \"output_attentions\": false,\n"," \"output_hidden_states\": false,\n"," \"output_past\": true,\n"," \"pad_token_id\": 0,\n"," \"pruned_heads\": {},\n"," \"torchscript\": false,\n"," \"type_vocab_size\": 2,\n"," \"use_bfloat16\": false,\n"," \"vocab_size\": 30522\n","}\n","\n","12/22/2021 10:08:26 AM [INFO]: https://s3.amazonaws.com/models.huggingface.co/bert/bert-base-uncased-pytorch_model.bin not found in cache or force_download set to True, downloading to /tmp/tmpq4br_7yv\n","100% 440473133/440473133 [00:19<00:00, 22301674.14B/s]\n","12/22/2021 10:08:46 AM [INFO]: copying /tmp/tmpq4br_7yv to cache at /root/.cache/torch/transformers/aa1ef1aede4482d0dbcd4d52baad8ae300e60902e88fcb0bebdec09afd232066.36ca03ab34a1a5d5fa7bc3d03d55c4fa650fed07220e2eeebc06ce58d0e9a157\n","12/22/2021 10:08:47 AM [INFO]: creating metadata file for /root/.cache/torch/transformers/aa1ef1aede4482d0dbcd4d52baad8ae300e60902e88fcb0bebdec09afd232066.36ca03ab34a1a5d5fa7bc3d03d55c4fa650fed07220e2eeebc06ce58d0e9a157\n","12/22/2021 10:08:47 AM [INFO]: removing temp file /tmp/tmpq4br_7yv\n","12/22/2021 10:08:47 AM [INFO]: loading weights file https://s3.amazonaws.com/models.huggingface.co/bert/bert-base-uncased-pytorch_model.bin from cache at /root/.cache/torch/transformers/aa1ef1aede4482d0dbcd4d52baad8ae300e60902e88fcb0bebdec09afd232066.36ca03ab34a1a5d5fa7bc3d03d55c4fa650fed07220e2eeebc06ce58d0e9a157\n","Model config: {\n"," \"architectures\": [\n"," \"BertForMaskedLM\"\n"," ],\n"," \"attention_probs_dropout_prob\": 0.1,\n"," \"finetuning_task\": null,\n"," \"hidden_act\": \"gelu\",\n"," \"hidden_dropout_prob\": 0.1,\n"," \"hidden_size\": 768,\n"," \"initializer_range\": 0.02,\n"," \"intermediate_size\": 3072,\n"," \"is_decoder\": false,\n"," \"layer_norm_eps\": 1e-12,\n"," \"max_position_embeddings\": 512,\n"," \"model_type\": \"bert\",\n"," \"num_attention_heads\": 12,\n"," \"num_hidden_layers\": 12,\n"," \"num_labels\": 2,\n"," \"output_attentions\": false,\n"," \"output_hidden_states\": false,\n"," \"output_past\": true,\n"," \"pad_token_id\": 0,\n"," \"pruned_heads\": {},\n"," \"torchscript\": false,\n"," \"type_vocab_size\": 2,\n"," \"use_bfloat16\": false,\n"," \"vocab_size\": 30522\n","}\n","\n","12/22/2021 10:08:50 AM [INFO]: Weights of BertModel not initialized from pretrained model: ['bert.classification_layer.weight', 'bert.classification_layer.bias']\n","12/22/2021 10:10:03 AM [INFO]: FREEZING MOST HIDDEN LAYERS...\n","[FROZE]: embeddings.word_embeddings.weight\n","[FROZE]: embeddings.position_embeddings.weight\n","[FROZE]: embeddings.token_type_embeddings.weight\n","[FROZE]: embeddings.LayerNorm.weight\n","[FROZE]: embeddings.LayerNorm.bias\n","[FROZE]: encoder.layer.0.attention.self.query.weight\n","[FROZE]: encoder.layer.0.attention.self.query.bias\n","[FROZE]: encoder.layer.0.attention.self.key.weight\n","[FROZE]: encoder.layer.0.attention.self.key.bias\n","[FROZE]: encoder.layer.0.attention.self.value.weight\n","[FROZE]: encoder.layer.0.attention.self.value.bias\n","[FROZE]: encoder.layer.0.attention.output.dense.weight\n","[FROZE]: encoder.layer.0.attention.output.dense.bias\n","[FROZE]: encoder.layer.0.attention.output.LayerNorm.weight\n","[FROZE]: encoder.layer.0.attention.output.LayerNorm.bias\n","[FROZE]: encoder.layer.0.intermediate.dense.weight\n","[FROZE]: encoder.layer.0.intermediate.dense.bias\n","[FROZE]: encoder.layer.0.output.dense.weight\n","[FROZE]: encoder.layer.0.output.dense.bias\n","[FROZE]: encoder.layer.0.output.LayerNorm.weight\n","[FROZE]: encoder.layer.0.output.LayerNorm.bias\n","[FROZE]: encoder.layer.1.attention.self.query.weight\n","[FROZE]: encoder.layer.1.attention.self.query.bias\n","[FROZE]: encoder.layer.1.attention.self.key.weight\n","[FROZE]: encoder.layer.1.attention.self.key.bias\n","[FROZE]: encoder.layer.1.attention.self.value.weight\n","[FROZE]: encoder.layer.1.attention.self.value.bias\n","[FROZE]: encoder.layer.1.attention.output.dense.weight\n","[FROZE]: encoder.layer.1.attention.output.dense.bias\n","[FROZE]: encoder.layer.1.attention.output.LayerNorm.weight\n","[FROZE]: encoder.layer.1.attention.output.LayerNorm.bias\n","[FROZE]: encoder.layer.1.intermediate.dense.weight\n","[FROZE]: encoder.layer.1.intermediate.dense.bias\n","[FROZE]: encoder.layer.1.output.dense.weight\n","[FROZE]: encoder.layer.1.output.dense.bias\n","[FROZE]: encoder.layer.1.output.LayerNorm.weight\n","[FROZE]: encoder.layer.1.output.LayerNorm.bias\n","[FROZE]: encoder.layer.2.attention.self.query.weight\n","[FROZE]: encoder.layer.2.attention.self.query.bias\n","[FROZE]: encoder.layer.2.attention.self.key.weight\n","[FROZE]: encoder.layer.2.attention.self.key.bias\n","[FROZE]: encoder.layer.2.attention.self.value.weight\n","[FROZE]: encoder.layer.2.attention.self.value.bias\n","[FROZE]: encoder.layer.2.attention.output.dense.weight\n","[FROZE]: encoder.layer.2.attention.output.dense.bias\n","[FROZE]: encoder.layer.2.attention.output.LayerNorm.weight\n","[FROZE]: encoder.layer.2.attention.output.LayerNorm.bias\n","[FROZE]: encoder.layer.2.intermediate.dense.weight\n","[FROZE]: encoder.layer.2.intermediate.dense.bias\n","[FROZE]: encoder.layer.2.output.dense.weight\n","[FROZE]: encoder.layer.2.output.dense.bias\n","[FROZE]: encoder.layer.2.output.LayerNorm.weight\n","[FROZE]: encoder.layer.2.output.LayerNorm.bias\n","[FROZE]: encoder.layer.3.attention.self.query.weight\n","[FROZE]: encoder.layer.3.attention.self.query.bias\n","[FROZE]: encoder.layer.3.attention.self.key.weight\n","[FROZE]: encoder.layer.3.attention.self.key.bias\n","[FROZE]: encoder.layer.3.attention.self.value.weight\n","[FROZE]: encoder.layer.3.attention.self.value.bias\n","[FROZE]: encoder.layer.3.attention.output.dense.weight\n","[FROZE]: encoder.layer.3.attention.output.dense.bias\n","[FROZE]: encoder.layer.3.attention.output.LayerNorm.weight\n","[FROZE]: encoder.layer.3.attention.output.LayerNorm.bias\n","[FROZE]: encoder.layer.3.intermediate.dense.weight\n","[FROZE]: encoder.layer.3.intermediate.dense.bias\n","[FROZE]: encoder.layer.3.output.dense.weight\n","[FROZE]: encoder.layer.3.output.dense.bias\n","[FROZE]: encoder.layer.3.output.LayerNorm.weight\n","[FROZE]: encoder.layer.3.output.LayerNorm.bias\n","[FROZE]: encoder.layer.4.attention.self.query.weight\n","[FROZE]: encoder.layer.4.attention.self.query.bias\n","[FROZE]: encoder.layer.4.attention.self.key.weight\n","[FROZE]: encoder.layer.4.attention.self.key.bias\n","[FROZE]: encoder.layer.4.attention.self.value.weight\n","[FROZE]: encoder.layer.4.attention.self.value.bias\n","[FROZE]: encoder.layer.4.attention.output.dense.weight\n","[FROZE]: encoder.layer.4.attention.output.dense.bias\n","[FROZE]: encoder.layer.4.attention.output.LayerNorm.weight\n","[FROZE]: encoder.layer.4.attention.output.LayerNorm.bias\n","[FROZE]: encoder.layer.4.intermediate.dense.weight\n","[FROZE]: encoder.layer.4.intermediate.dense.bias\n","[FROZE]: encoder.layer.4.output.dense.weight\n","[FROZE]: encoder.layer.4.output.dense.bias\n","[FROZE]: encoder.layer.4.output.LayerNorm.weight\n","[FROZE]: encoder.layer.4.output.LayerNorm.bias\n","[FROZE]: encoder.layer.5.attention.self.query.weight\n","[FROZE]: encoder.layer.5.attention.self.query.bias\n","[FROZE]: encoder.layer.5.attention.self.key.weight\n","[FROZE]: encoder.layer.5.attention.self.key.bias\n","[FROZE]: encoder.layer.5.attention.self.value.weight\n","[FROZE]: encoder.layer.5.attention.self.value.bias\n","[FROZE]: encoder.layer.5.attention.output.dense.weight\n","[FROZE]: encoder.layer.5.attention.output.dense.bias\n","[FROZE]: encoder.layer.5.attention.output.LayerNorm.weight\n","[FROZE]: encoder.layer.5.attention.output.LayerNorm.bias\n","[FROZE]: encoder.layer.5.intermediate.dense.weight\n","[FROZE]: encoder.layer.5.intermediate.dense.bias\n","[FROZE]: encoder.layer.5.output.dense.weight\n","[FROZE]: encoder.layer.5.output.dense.bias\n","[FROZE]: encoder.layer.5.output.LayerNorm.weight\n","[FROZE]: encoder.layer.5.output.LayerNorm.bias\n","[FROZE]: encoder.layer.6.attention.self.query.weight\n","[FROZE]: encoder.layer.6.attention.self.query.bias\n","[FROZE]: encoder.layer.6.attention.self.key.weight\n","[FROZE]: encoder.layer.6.attention.self.key.bias\n","[FROZE]: encoder.layer.6.attention.self.value.weight\n","[FROZE]: encoder.layer.6.attention.self.value.bias\n","[FROZE]: encoder.layer.6.attention.output.dense.weight\n","[FROZE]: encoder.layer.6.attention.output.dense.bias\n","[FROZE]: encoder.layer.6.attention.output.LayerNorm.weight\n","[FROZE]: encoder.layer.6.attention.output.LayerNorm.bias\n","[FROZE]: encoder.layer.6.intermediate.dense.weight\n","[FROZE]: encoder.layer.6.intermediate.dense.bias\n","[FROZE]: encoder.layer.6.output.dense.weight\n","[FROZE]: encoder.layer.6.output.dense.bias\n","[FROZE]: encoder.layer.6.output.LayerNorm.weight\n","[FROZE]: encoder.layer.6.output.LayerNorm.bias\n","[FROZE]: encoder.layer.7.attention.self.query.weight\n","[FROZE]: encoder.layer.7.attention.self.query.bias\n","[FROZE]: encoder.layer.7.attention.self.key.weight\n","[FROZE]: encoder.layer.7.attention.self.key.bias\n","[FROZE]: encoder.layer.7.attention.self.value.weight\n","[FROZE]: encoder.layer.7.attention.self.value.bias\n","[FROZE]: encoder.layer.7.attention.output.dense.weight\n","[FROZE]: encoder.layer.7.attention.output.dense.bias\n","[FROZE]: encoder.layer.7.attention.output.LayerNorm.weight\n","[FROZE]: encoder.layer.7.attention.output.LayerNorm.bias\n","[FROZE]: encoder.layer.7.intermediate.dense.weight\n","[FROZE]: encoder.layer.7.intermediate.dense.bias\n","[FROZE]: encoder.layer.7.output.dense.weight\n","[FROZE]: encoder.layer.7.output.dense.bias\n","[FROZE]: encoder.layer.7.output.LayerNorm.weight\n","[FROZE]: encoder.layer.7.output.LayerNorm.bias\n","[FROZE]: encoder.layer.8.attention.self.query.weight\n","[FROZE]: encoder.layer.8.attention.self.query.bias\n","[FROZE]: encoder.layer.8.attention.self.key.weight\n","[FROZE]: encoder.layer.8.attention.self.key.bias\n","[FROZE]: encoder.layer.8.attention.self.value.weight\n","[FROZE]: encoder.layer.8.attention.self.value.bias\n","[FROZE]: encoder.layer.8.attention.output.dense.weight\n","[FROZE]: encoder.layer.8.attention.output.dense.bias\n","[FROZE]: encoder.layer.8.attention.output.LayerNorm.weight\n","[FROZE]: encoder.layer.8.attention.output.LayerNorm.bias\n","[FROZE]: encoder.layer.8.intermediate.dense.weight\n","[FROZE]: encoder.layer.8.intermediate.dense.bias\n","[FROZE]: encoder.layer.8.output.dense.weight\n","[FROZE]: encoder.layer.8.output.dense.bias\n","[FROZE]: encoder.layer.8.output.LayerNorm.weight\n","[FROZE]: encoder.layer.8.output.LayerNorm.bias\n","[FROZE]: encoder.layer.9.attention.self.query.weight\n","[FROZE]: encoder.layer.9.attention.self.query.bias\n","[FROZE]: encoder.layer.9.attention.self.key.weight\n","[FROZE]: encoder.layer.9.attention.self.key.bias\n","[FROZE]: encoder.layer.9.attention.self.value.weight\n","[FROZE]: encoder.layer.9.attention.self.value.bias\n","[FROZE]: encoder.layer.9.attention.output.dense.weight\n","[FROZE]: encoder.layer.9.attention.output.dense.bias\n","[FROZE]: encoder.layer.9.attention.output.LayerNorm.weight\n","[FROZE]: encoder.layer.9.attention.output.LayerNorm.bias\n","[FROZE]: encoder.layer.9.intermediate.dense.weight\n","[FROZE]: encoder.layer.9.intermediate.dense.bias\n","[FROZE]: encoder.layer.9.output.dense.weight\n","[FROZE]: encoder.layer.9.output.dense.bias\n","[FROZE]: encoder.layer.9.output.LayerNorm.weight\n","[FROZE]: encoder.layer.9.output.LayerNorm.bias\n","[FROZE]: encoder.layer.10.attention.self.query.weight\n","[FROZE]: encoder.layer.10.attention.self.query.bias\n","[FROZE]: encoder.layer.10.attention.self.key.weight\n","[FROZE]: encoder.layer.10.attention.self.key.bias\n","[FROZE]: encoder.layer.10.attention.self.value.weight\n","[FROZE]: encoder.layer.10.attention.self.value.bias\n","[FROZE]: encoder.layer.10.attention.output.dense.weight\n","[FROZE]: encoder.layer.10.attention.output.dense.bias\n","[FROZE]: encoder.layer.10.attention.output.LayerNorm.weight\n","[FROZE]: encoder.layer.10.attention.output.LayerNorm.bias\n","[FROZE]: encoder.layer.10.intermediate.dense.weight\n","[FROZE]: encoder.layer.10.intermediate.dense.bias\n","[FROZE]: encoder.layer.10.output.dense.weight\n","[FROZE]: encoder.layer.10.output.dense.bias\n","[FROZE]: encoder.layer.10.output.LayerNorm.weight\n","[FROZE]: encoder.layer.10.output.LayerNorm.bias\n","[FREE]: encoder.layer.11.attention.self.query.weight\n","[FREE]: encoder.layer.11.attention.self.query.bias\n","[FREE]: encoder.layer.11.attention.self.key.weight\n","[FREE]: encoder.layer.11.attention.self.key.bias\n","[FREE]: encoder.layer.11.attention.self.value.weight\n","[FREE]: encoder.layer.11.attention.self.value.bias\n","[FREE]: encoder.layer.11.attention.output.dense.weight\n","[FREE]: encoder.layer.11.attention.output.dense.bias\n","[FREE]: encoder.layer.11.attention.output.LayerNorm.weight\n","[FREE]: encoder.layer.11.attention.output.LayerNorm.bias\n","[FREE]: encoder.layer.11.intermediate.dense.weight\n","[FREE]: encoder.layer.11.intermediate.dense.bias\n","[FREE]: encoder.layer.11.output.dense.weight\n","[FREE]: encoder.layer.11.output.dense.bias\n","[FREE]: encoder.layer.11.output.LayerNorm.weight\n","[FREE]: encoder.layer.11.output.LayerNorm.bias\n","[FREE]: pooler.dense.weight\n","[FREE]: pooler.dense.bias\n","[FREE]: classification_layer.weight\n","[FREE]: classification_layer.bias\n","12/22/2021 10:10:03 AM [INFO]: Starting training process...\n","[Epoch: 1, 224/ 2400 points] total loss, accuracy per batch: 2.827, 0.214\n","[Epoch: 1, 448/ 2400 points] total loss, accuracy per batch: 2.208, 0.585\n","[Epoch: 1, 672/ 2400 points] total loss, accuracy per batch: 1.977, 0.451\n","[Epoch: 1, 896/ 2400 points] total loss, accuracy per batch: 1.777, 0.504\n","[Epoch: 1, 1120/ 2400 points] total loss, accuracy per batch: 1.522, 0.522\n","[Epoch: 1, 1344/ 2400 points] total loss, accuracy per batch: 1.540, 0.571\n","[Epoch: 1, 1568/ 2400 points] total loss, accuracy per batch: 1.389, 0.598\n","[Epoch: 1, 1792/ 2400 points] total loss, accuracy per batch: 1.416, 0.621\n","[Epoch: 1, 2016/ 2400 points] total loss, accuracy per batch: 1.314, 0.661\n","[Epoch: 1, 2240/ 2400 points] total loss, accuracy per batch: 1.124, 0.670\n","12/22/2021 10:11:02 AM [INFO]: Evaluating test samples...\n","100% 9/9 [00:05<00:00, 1.51it/s]\n","/usr/local/lib/python3.7/dist-packages/seqeval/metrics/sequence_labeling.py:171: UserWarning: 1 seems not to be NE tag.\n"," warnings.warn('{} seems not to be NE tag.'.format(chunk))\n","/usr/local/lib/python3.7/dist-packages/seqeval/metrics/sequence_labeling.py:171: UserWarning: 0 seems not to be NE tag.\n"," warnings.warn('{} seems not to be NE tag.'.format(chunk))\n","/usr/local/lib/python3.7/dist-packages/seqeval/metrics/sequence_labeling.py:171: UserWarning: 5 seems not to be NE tag.\n"," warnings.warn('{} seems not to be NE tag.'.format(chunk))\n","/usr/local/lib/python3.7/dist-packages/seqeval/metrics/sequence_labeling.py:171: UserWarning: 3 seems not to be NE tag.\n"," warnings.warn('{} seems not to be NE tag.'.format(chunk))\n","/usr/local/lib/python3.7/dist-packages/seqeval/metrics/sequence_labeling.py:171: UserWarning: 2 seems not to be NE tag.\n"," warnings.warn('{} seems not to be NE tag.'.format(chunk))\n","/usr/local/lib/python3.7/dist-packages/seqeval/metrics/sequence_labeling.py:171: UserWarning: 10 seems not to be NE tag.\n"," warnings.warn('{} seems not to be NE tag.'.format(chunk))\n","/usr/local/lib/python3.7/dist-packages/seqeval/metrics/sequence_labeling.py:171: UserWarning: 11 seems not to be NE tag.\n"," warnings.warn('{} seems not to be NE tag.'.format(chunk))\n","/usr/local/lib/python3.7/dist-packages/seqeval/metrics/sequence_labeling.py:171: UserWarning: 13 seems not to be NE tag.\n"," warnings.warn('{} seems not to be NE tag.'.format(chunk))\n","/usr/local/lib/python3.7/dist-packages/seqeval/metrics/sequence_labeling.py:171: UserWarning: 4 seems not to be NE tag.\n"," warnings.warn('{} seems not to be NE tag.'.format(chunk))\n","/usr/local/lib/python3.7/dist-packages/seqeval/metrics/sequence_labeling.py:171: UserWarning: 6 seems not to be NE tag.\n"," warnings.warn('{} seems not to be NE tag.'.format(chunk))\n","/usr/local/lib/python3.7/dist-packages/seqeval/metrics/sequence_labeling.py:171: UserWarning: 9 seems not to be NE tag.\n"," warnings.warn('{} seems not to be NE tag.'.format(chunk))\n","/usr/local/lib/python3.7/dist-packages/seqeval/metrics/sequence_labeling.py:171: UserWarning: 8 seems not to be NE tag.\n"," warnings.warn('{} seems not to be NE tag.'.format(chunk))\n","/usr/local/lib/python3.7/dist-packages/seqeval/metrics/v1.py:57: UndefinedMetricWarning: Precision is ill-defined and being set to 0.0 due to no predicted samples. Use `zero_division` parameter to control this behavior.\n"," _warn_prf(average, modifier, msg_start, len(result))\n","12/22/2021 10:11:08 AM [INFO]: ***** Eval results *****\n","12/22/2021 10:11:08 AM [INFO]: accuracy = 0.6652777777777777\n","12/22/2021 10:11:08 AM [INFO]: f1 = 0.0\n","12/22/2021 10:11:08 AM [INFO]: precision = 0.0\n","12/22/2021 10:11:08 AM [INFO]: recall = 0.0\n","Epoch finished, took 64.60 seconds.\n","Losses at Epoch 1: 1.7093487\n","Train accuracy at Epoch 1: 0.5397321\n","Test f1 at Epoch 1: 0.0000000\n","[Epoch: 2, 224/ 2400 points] total loss, accuracy per batch: 1.065, 0.701\n","[Epoch: 2, 448/ 2400 points] total loss, accuracy per batch: 1.026, 0.728\n","[Epoch: 2, 672/ 2400 points] total loss, accuracy per batch: 1.043, 0.692\n","[Epoch: 2, 896/ 2400 points] total loss, accuracy per batch: 1.162, 0.661\n","[Epoch: 2, 1120/ 2400 points] total loss, accuracy per batch: 1.023, 0.665\n","[Epoch: 2, 1344/ 2400 points] total loss, accuracy per batch: 0.922, 0.759\n","[Epoch: 2, 1568/ 2400 points] total loss, accuracy per batch: 0.889, 0.714\n","[Epoch: 2, 1792/ 2400 points] total loss, accuracy per batch: 0.823, 0.781\n","[Epoch: 2, 2016/ 2400 points] total loss, accuracy per batch: 0.880, 0.741\n","[Epoch: 2, 2240/ 2400 points] total loss, accuracy per batch: 0.897, 0.732\n","12/22/2021 10:12:12 AM [INFO]: Evaluating test samples...\n","100% 9/9 [00:05<00:00, 1.54it/s]\n","12/22/2021 10:12:18 AM [INFO]: ***** Eval results *****\n","12/22/2021 10:12:18 AM [INFO]: accuracy = 0.7284722222222223\n","12/22/2021 10:12:18 AM [INFO]: f1 = 0.06896551724137931\n","12/22/2021 10:12:18 AM [INFO]: precision = 0.16666666666666666\n","12/22/2021 10:12:18 AM [INFO]: recall = 0.043478260869565216\n","Epoch finished, took 65.68 seconds.\n","Losses at Epoch 2: 0.9729615\n","Train accuracy at Epoch 2: 0.7174107\n","Test f1 at Epoch 2: 0.0689655\n","[Epoch: 3, 224/ 2400 points] total loss, accuracy per batch: 0.815, 0.746\n","[Epoch: 3, 448/ 2400 points] total loss, accuracy per batch: 0.892, 0.741\n","[Epoch: 3, 672/ 2400 points] total loss, accuracy per batch: 0.763, 0.795\n","[Epoch: 3, 896/ 2400 points] total loss, accuracy per batch: 0.807, 0.763\n","[Epoch: 3, 1120/ 2400 points] total loss, accuracy per batch: 0.669, 0.790\n","[Epoch: 3, 1344/ 2400 points] total loss, accuracy per batch: 0.578, 0.830\n","[Epoch: 3, 1568/ 2400 points] total loss, accuracy per batch: 0.668, 0.812\n","[Epoch: 3, 1792/ 2400 points] total loss, accuracy per batch: 0.656, 0.804\n","[Epoch: 3, 2016/ 2400 points] total loss, accuracy per batch: 0.792, 0.759\n","[Epoch: 3, 2240/ 2400 points] total loss, accuracy per batch: 0.913, 0.750\n","12/22/2021 10:13:20 AM [INFO]: Evaluating test samples...\n","100% 9/9 [00:06<00:00, 1.49it/s]\n","12/22/2021 10:13:26 AM [INFO]: ***** Eval results *****\n","12/22/2021 10:13:26 AM [INFO]: accuracy = 0.7909722222222223\n","12/22/2021 10:13:26 AM [INFO]: f1 = 0.15\n","12/22/2021 10:13:26 AM [INFO]: precision = 0.1875\n","12/22/2021 10:13:26 AM [INFO]: recall = 0.125\n","Epoch finished, took 63.58 seconds.\n","Losses at Epoch 3: 0.7551882\n","Train accuracy at Epoch 3: 0.7790179\n","Test f1 at Epoch 3: 0.1500000\n","[Epoch: 4, 224/ 2400 points] total loss, accuracy per batch: 0.796, 0.746\n","[Epoch: 4, 448/ 2400 points] total loss, accuracy per batch: 0.663, 0.804\n","[Epoch: 4, 672/ 2400 points] total loss, accuracy per batch: 0.713, 0.777\n","[Epoch: 4, 896/ 2400 points] total loss, accuracy per batch: 0.621, 0.817\n","[Epoch: 4, 1120/ 2400 points] total loss, accuracy per batch: 0.598, 0.830\n","[Epoch: 4, 1344/ 2400 points] total loss, accuracy per batch: 0.595, 0.844\n","[Epoch: 4, 1568/ 2400 points] total loss, accuracy per batch: 0.602, 0.812\n","[Epoch: 4, 1792/ 2400 points] total loss, accuracy per batch: 0.539, 0.839\n","[Epoch: 4, 2016/ 2400 points] total loss, accuracy per batch: 0.623, 0.817\n","[Epoch: 4, 2240/ 2400 points] total loss, accuracy per batch: 0.587, 0.821\n","12/22/2021 10:14:30 AM [INFO]: Evaluating test samples...\n","100% 9/9 [00:06<00:00, 1.50it/s]\n","12/22/2021 10:14:36 AM [INFO]: ***** Eval results *****\n","12/22/2021 10:14:36 AM [INFO]: accuracy = 0.8076388888888889\n","12/22/2021 10:14:36 AM [INFO]: f1 = 0.19354838709677416\n","12/22/2021 10:14:36 AM [INFO]: precision = 0.375\n","12/22/2021 10:14:36 AM [INFO]: recall = 0.13043478260869565\n","Epoch finished, took 65.80 seconds.\n","Losses at Epoch 4: 0.6336020\n","Train accuracy at Epoch 4: 0.8107143\n","Test f1 at Epoch 4: 0.1935484\n","[Epoch: 5, 224/ 2400 points] total loss, accuracy per batch: 0.671, 0.804\n","[Epoch: 5, 448/ 2400 points] total loss, accuracy per batch: 0.570, 0.817\n","[Epoch: 5, 672/ 2400 points] total loss, accuracy per batch: 0.567, 0.799\n","[Epoch: 5, 896/ 2400 points] total loss, accuracy per batch: 0.578, 0.817\n","[Epoch: 5, 1120/ 2400 points] total loss, accuracy per batch: 0.562, 0.808\n","[Epoch: 5, 1344/ 2400 points] total loss, accuracy per batch: 0.737, 0.790\n","[Epoch: 5, 1568/ 2400 points] total loss, accuracy per batch: 0.503, 0.866\n","[Epoch: 5, 1792/ 2400 points] total loss, accuracy per batch: 0.476, 0.866\n","[Epoch: 5, 2016/ 2400 points] total loss, accuracy per batch: 0.526, 0.844\n","[Epoch: 5, 2240/ 2400 points] total loss, accuracy per batch: 0.537, 0.848\n","12/22/2021 10:15:39 AM [INFO]: Evaluating test samples...\n","100% 9/9 [00:05<00:00, 1.57it/s]\n","/usr/local/lib/python3.7/dist-packages/seqeval/metrics/sequence_labeling.py:171: UserWarning: 12 seems not to be NE tag.\n"," warnings.warn('{} seems not to be NE tag.'.format(chunk))\n","12/22/2021 10:15:45 AM [INFO]: ***** Eval results *****\n","12/22/2021 10:15:45 AM [INFO]: accuracy = 0.8215277777777777\n","12/22/2021 10:15:45 AM [INFO]: f1 = 0.25\n","12/22/2021 10:15:45 AM [INFO]: precision = 0.5\n","12/22/2021 10:15:45 AM [INFO]: recall = 0.16666666666666666\n","Epoch finished, took 64.10 seconds.\n","Losses at Epoch 5: 0.5728274\n","Train accuracy at Epoch 5: 0.8258929\n","Test f1 at Epoch 5: 0.2500000\n","[Epoch: 6, 224/ 2400 points] total loss, accuracy per batch: 0.475, 0.839\n","[Epoch: 6, 448/ 2400 points] total loss, accuracy per batch: 0.563, 0.839\n","[Epoch: 6, 672/ 2400 points] total loss, accuracy per batch: 0.559, 0.817\n","[Epoch: 6, 896/ 2400 points] total loss, accuracy per batch: 0.528, 0.830\n","[Epoch: 6, 1120/ 2400 points] total loss, accuracy per batch: 0.368, 0.902\n","[Epoch: 6, 1344/ 2400 points] total loss, accuracy per batch: 0.503, 0.826\n","[Epoch: 6, 1568/ 2400 points] total loss, accuracy per batch: 0.539, 0.830\n","[Epoch: 6, 1792/ 2400 points] total loss, accuracy per batch: 0.579, 0.830\n","[Epoch: 6, 2016/ 2400 points] total loss, accuracy per batch: 0.533, 0.821\n","[Epoch: 6, 2240/ 2400 points] total loss, accuracy per batch: 0.478, 0.853\n","12/22/2021 10:16:48 AM [INFO]: Evaluating test samples...\n","100% 9/9 [00:05<00:00, 1.72it/s]\n","12/22/2021 10:16:53 AM [INFO]: ***** Eval results *****\n","12/22/2021 10:16:53 AM [INFO]: accuracy = 0.8291666666666667\n","12/22/2021 10:16:53 AM [INFO]: f1 = 0.12500000000000003\n","12/22/2021 10:16:53 AM [INFO]: precision = 0.2\n","12/22/2021 10:16:53 AM [INFO]: recall = 0.09090909090909091\n","Epoch finished, took 63.52 seconds.\n","Losses at Epoch 6: 0.5125597\n","Train accuracy at Epoch 6: 0.8388393\n","Test f1 at Epoch 6: 0.1250000\n","[Epoch: 7, 224/ 2400 points] total loss, accuracy per batch: 0.478, 0.848\n","[Epoch: 7, 448/ 2400 points] total loss, accuracy per batch: 0.540, 0.844\n","[Epoch: 7, 672/ 2400 points] total loss, accuracy per batch: 0.506, 0.844\n","[Epoch: 7, 896/ 2400 points] total loss, accuracy per batch: 0.417, 0.853\n","[Epoch: 7, 1120/ 2400 points] total loss, accuracy per batch: 0.406, 0.888\n","[Epoch: 7, 1344/ 2400 points] total loss, accuracy per batch: 0.422, 0.875\n","[Epoch: 7, 1568/ 2400 points] total loss, accuracy per batch: 0.495, 0.853\n","[Epoch: 7, 1792/ 2400 points] total loss, accuracy per batch: 0.428, 0.879\n","[Epoch: 7, 2016/ 2400 points] total loss, accuracy per batch: 0.504, 0.812\n","[Epoch: 7, 2240/ 2400 points] total loss, accuracy per batch: 0.459, 0.830\n","12/22/2021 10:17:56 AM [INFO]: Evaluating test samples...\n","100% 9/9 [00:05<00:00, 1.59it/s]\n","12/22/2021 10:18:01 AM [INFO]: ***** Eval results *****\n","12/22/2021 10:18:01 AM [INFO]: accuracy = 0.8527777777777777\n","12/22/2021 10:18:01 AM [INFO]: f1 = 0.25\n","12/22/2021 10:18:01 AM [INFO]: precision = 0.5\n","12/22/2021 10:18:01 AM [INFO]: recall = 0.16666666666666666\n","Epoch finished, took 62.60 seconds.\n","Losses at Epoch 7: 0.4655859\n","Train accuracy at Epoch 7: 0.8526786\n","Test f1 at Epoch 7: 0.2500000\n","[Epoch: 8, 224/ 2400 points] total loss, accuracy per batch: 0.414, 0.875\n","[Epoch: 8, 448/ 2400 points] total loss, accuracy per batch: 0.449, 0.853\n","[Epoch: 8, 672/ 2400 points] total loss, accuracy per batch: 0.411, 0.875\n","[Epoch: 8, 896/ 2400 points] total loss, accuracy per batch: 0.440, 0.875\n","[Epoch: 8, 1120/ 2400 points] total loss, accuracy per batch: 0.397, 0.879\n","[Epoch: 8, 1344/ 2400 points] total loss, accuracy per batch: 0.471, 0.862\n","[Epoch: 8, 1568/ 2400 points] total loss, accuracy per batch: 0.490, 0.857\n","[Epoch: 8, 1792/ 2400 points] total loss, accuracy per batch: 0.448, 0.848\n","[Epoch: 8, 2016/ 2400 points] total loss, accuracy per batch: 0.447, 0.848\n","[Epoch: 8, 2240/ 2400 points] total loss, accuracy per batch: 0.475, 0.871\n","12/22/2021 10:19:04 AM [INFO]: Evaluating test samples...\n","100% 9/9 [00:05<00:00, 1.56it/s]\n","12/22/2021 10:19:09 AM [INFO]: ***** Eval results *****\n","12/22/2021 10:19:09 AM [INFO]: accuracy = 0.8451388888888889\n","12/22/2021 10:19:09 AM [INFO]: f1 = 0.3870967741935483\n","12/22/2021 10:19:09 AM [INFO]: precision = 0.75\n","12/22/2021 10:19:09 AM [INFO]: recall = 0.2608695652173913\n","Epoch finished, took 63.69 seconds.\n","Losses at Epoch 8: 0.4440956\n","Train accuracy at Epoch 8: 0.8642857\n","Test f1 at Epoch 8: 0.3870968\n","[Epoch: 9, 224/ 2400 points] total loss, accuracy per batch: 0.384, 0.857\n","[Epoch: 9, 448/ 2400 points] total loss, accuracy per batch: 0.412, 0.884\n","[Epoch: 9, 672/ 2400 points] total loss, accuracy per batch: 0.394, 0.879\n","[Epoch: 9, 896/ 2400 points] total loss, accuracy per batch: 0.405, 0.866\n","[Epoch: 9, 1120/ 2400 points] total loss, accuracy per batch: 0.416, 0.862\n","[Epoch: 9, 1344/ 2400 points] total loss, accuracy per batch: 0.398, 0.866\n","[Epoch: 9, 1568/ 2400 points] total loss, accuracy per batch: 0.443, 0.857\n","[Epoch: 9, 1792/ 2400 points] total loss, accuracy per batch: 0.437, 0.875\n","[Epoch: 9, 2016/ 2400 points] total loss, accuracy per batch: 0.334, 0.911\n","[Epoch: 9, 2240/ 2400 points] total loss, accuracy per batch: 0.418, 0.875\n","12/22/2021 10:20:14 AM [INFO]: Evaluating test samples...\n","100% 9/9 [00:05<00:00, 1.62it/s]\n","12/22/2021 10:20:19 AM [INFO]: ***** Eval results *****\n","12/22/2021 10:20:19 AM [INFO]: accuracy = 0.8458333333333333\n","12/22/2021 10:20:19 AM [INFO]: f1 = 0.29411764705882354\n","12/22/2021 10:20:19 AM [INFO]: precision = 0.5\n","12/22/2021 10:20:19 AM [INFO]: recall = 0.20833333333333334\n","Epoch finished, took 65.18 seconds.\n","Losses at Epoch 9: 0.4042539\n","Train accuracy at Epoch 9: 0.8732143\n","Test f1 at Epoch 9: 0.2941176\n","[Epoch: 10, 224/ 2400 points] total loss, accuracy per batch: 0.432, 0.888\n","[Epoch: 10, 448/ 2400 points] total loss, accuracy per batch: 0.394, 0.871\n","[Epoch: 10, 672/ 2400 points] total loss, accuracy per batch: 0.418, 0.871\n","[Epoch: 10, 896/ 2400 points] total loss, accuracy per batch: 0.397, 0.879\n","[Epoch: 10, 1120/ 2400 points] total loss, accuracy per batch: 0.404, 0.884\n","[Epoch: 10, 1344/ 2400 points] total loss, accuracy per batch: 0.409, 0.871\n","[Epoch: 10, 1568/ 2400 points] total loss, accuracy per batch: 0.302, 0.915\n","[Epoch: 10, 1792/ 2400 points] total loss, accuracy per batch: 0.446, 0.871\n","[Epoch: 10, 2016/ 2400 points] total loss, accuracy per batch: 0.314, 0.897\n","[Epoch: 10, 2240/ 2400 points] total loss, accuracy per batch: 0.287, 0.915\n","12/22/2021 10:21:24 AM [INFO]: Evaluating test samples...\n","100% 9/9 [00:05<00:00, 1.59it/s]\n","12/22/2021 10:21:29 AM [INFO]: ***** Eval results *****\n","12/22/2021 10:21:29 AM [INFO]: accuracy = 0.8715277777777778\n","12/22/2021 10:21:29 AM [INFO]: f1 = 0.2\n","12/22/2021 10:21:29 AM [INFO]: precision = 0.5\n","12/22/2021 10:21:29 AM [INFO]: recall = 0.125\n","Epoch finished, took 65.42 seconds.\n","Losses at Epoch 10: 0.3803434\n","Train accuracy at Epoch 10: 0.8861607\n","Test f1 at Epoch 10: 0.2000000\n","[Epoch: 11, 224/ 2400 points] total loss, accuracy per batch: 0.333, 0.888\n","[Epoch: 11, 448/ 2400 points] total loss, accuracy per batch: 0.407, 0.888\n","[Epoch: 11, 672/ 2400 points] total loss, accuracy per batch: 0.298, 0.920\n","[Epoch: 11, 896/ 2400 points] total loss, accuracy per batch: 0.368, 0.862\n","[Epoch: 11, 1120/ 2400 points] total loss, accuracy per batch: 0.356, 0.888\n","[Epoch: 11, 1344/ 2400 points] total loss, accuracy per batch: 0.370, 0.866\n","[Epoch: 11, 1568/ 2400 points] total loss, accuracy per batch: 0.368, 0.893\n","[Epoch: 11, 1792/ 2400 points] total loss, accuracy per batch: 0.370, 0.888\n","[Epoch: 11, 2016/ 2400 points] total loss, accuracy per batch: 0.340, 0.888\n","[Epoch: 11, 2240/ 2400 points] total loss, accuracy per batch: 0.403, 0.857\n","12/22/2021 10:22:35 AM [INFO]: Evaluating test samples...\n","100% 9/9 [00:06<00:00, 1.45it/s]\n","12/22/2021 10:22:41 AM [INFO]: ***** Eval results *****\n","12/22/2021 10:22:41 AM [INFO]: accuracy = 0.8451388888888889\n","12/22/2021 10:22:41 AM [INFO]: f1 = 0.25000000000000006\n","12/22/2021 10:22:41 AM [INFO]: precision = 0.4\n","12/22/2021 10:22:41 AM [INFO]: recall = 0.18181818181818182\n","Epoch finished, took 66.58 seconds.\n","Losses at Epoch 11: 0.3612770\n","Train accuracy at Epoch 11: 0.8839286\n","Test f1 at Epoch 11: 0.2500000\n","[Epoch: 12, 224/ 2400 points] total loss, accuracy per batch: 0.281, 0.915\n","[Epoch: 12, 448/ 2400 points] total loss, accuracy per batch: 0.304, 0.906\n","[Epoch: 12, 672/ 2400 points] total loss, accuracy per batch: 0.323, 0.906\n","[Epoch: 12, 896/ 2400 points] total loss, accuracy per batch: 0.427, 0.871\n","[Epoch: 12, 1120/ 2400 points] total loss, accuracy per batch: 0.374, 0.871\n","[Epoch: 12, 1344/ 2400 points] total loss, accuracy per batch: 0.409, 0.871\n","[Epoch: 12, 1568/ 2400 points] total loss, accuracy per batch: 0.337, 0.893\n","[Epoch: 12, 1792/ 2400 points] total loss, accuracy per batch: 0.325, 0.871\n","[Epoch: 12, 2016/ 2400 points] total loss, accuracy per batch: 0.404, 0.862\n","[Epoch: 12, 2240/ 2400 points] total loss, accuracy per batch: 0.344, 0.875\n","12/22/2021 10:23:41 AM [INFO]: Evaluating test samples...\n","100% 9/9 [00:06<00:00, 1.49it/s]\n","12/22/2021 10:23:47 AM [INFO]: ***** Eval results *****\n","12/22/2021 10:23:47 AM [INFO]: accuracy = 0.8458333333333333\n","12/22/2021 10:23:47 AM [INFO]: f1 = 0.2777777777777778\n","12/22/2021 10:23:47 AM [INFO]: precision = 0.4166666666666667\n","12/22/2021 10:23:47 AM [INFO]: recall = 0.20833333333333334\n","Epoch finished, took 64.50 seconds.\n","Losses at Epoch 12: 0.3527097\n","Train accuracy at Epoch 12: 0.8839286\n","Test f1 at Epoch 12: 0.2777778\n","[Epoch: 13, 224/ 2400 points] total loss, accuracy per batch: 0.265, 0.942\n","[Epoch: 13, 448/ 2400 points] total loss, accuracy per batch: 0.317, 0.906\n","[Epoch: 13, 672/ 2400 points] total loss, accuracy per batch: 0.306, 0.897\n","[Epoch: 13, 896/ 2400 points] total loss, accuracy per batch: 0.288, 0.920\n","[Epoch: 13, 1120/ 2400 points] total loss, accuracy per batch: 0.281, 0.915\n","[Epoch: 13, 1344/ 2400 points] total loss, accuracy per batch: 0.319, 0.902\n","[Epoch: 13, 1568/ 2400 points] total loss, accuracy per batch: 0.327, 0.875\n","[Epoch: 13, 1792/ 2400 points] total loss, accuracy per batch: 0.389, 0.875\n","[Epoch: 13, 2016/ 2400 points] total loss, accuracy per batch: 0.347, 0.915\n","[Epoch: 13, 2240/ 2400 points] total loss, accuracy per batch: 0.313, 0.902\n","12/22/2021 10:24:48 AM [INFO]: Evaluating test samples...\n","100% 9/9 [00:06<00:00, 1.44it/s]\n","12/22/2021 10:24:54 AM [INFO]: ***** Eval results *****\n","12/22/2021 10:24:54 AM [INFO]: accuracy = 0.8527777777777777\n","12/22/2021 10:24:54 AM [INFO]: f1 = 0.35294117647058826\n","12/22/2021 10:24:54 AM [INFO]: precision = 0.6\n","12/22/2021 10:24:54 AM [INFO]: recall = 0.25\n","Epoch finished, took 64.61 seconds.\n","Losses at Epoch 13: 0.3150250\n","Train accuracy at Epoch 13: 0.9049107\n","Test f1 at Epoch 13: 0.3529412\n","[Epoch: 14, 224/ 2400 points] total loss, accuracy per batch: 0.341, 0.902\n","[Epoch: 14, 448/ 2400 points] total loss, accuracy per batch: 0.248, 0.933\n","[Epoch: 14, 672/ 2400 points] total loss, accuracy per batch: 0.310, 0.906\n","[Epoch: 14, 896/ 2400 points] total loss, accuracy per batch: 0.363, 0.888\n","[Epoch: 14, 1120/ 2400 points] total loss, accuracy per batch: 0.361, 0.888\n","[Epoch: 14, 1344/ 2400 points] total loss, accuracy per batch: 0.317, 0.888\n","[Epoch: 14, 1568/ 2400 points] total loss, accuracy per batch: 0.302, 0.911\n","[Epoch: 14, 1792/ 2400 points] total loss, accuracy per batch: 0.297, 0.897\n","[Epoch: 14, 2016/ 2400 points] total loss, accuracy per batch: 0.281, 0.911\n","[Epoch: 14, 2240/ 2400 points] total loss, accuracy per batch: 0.389, 0.866\n","12/22/2021 10:25:58 AM [INFO]: Evaluating test samples...\n","100% 9/9 [00:06<00:00, 1.46it/s]\n","12/22/2021 10:26:04 AM [INFO]: ***** Eval results *****\n","12/22/2021 10:26:04 AM [INFO]: accuracy = 0.875\n","12/22/2021 10:26:04 AM [INFO]: f1 = 0.14285714285714288\n","12/22/2021 10:26:04 AM [INFO]: precision = 0.3333333333333333\n","12/22/2021 10:26:04 AM [INFO]: recall = 0.09090909090909091\n","Epoch finished, took 64.89 seconds.\n","Losses at Epoch 14: 0.3208379\n","Train accuracy at Epoch 14: 0.8991071\n","Test f1 at Epoch 14: 0.1428571\n","[Epoch: 15, 224/ 2400 points] total loss, accuracy per batch: 0.248, 0.924\n","[Epoch: 15, 448/ 2400 points] total loss, accuracy per batch: 0.291, 0.906\n","[Epoch: 15, 672/ 2400 points] total loss, accuracy per batch: 0.284, 0.929\n","[Epoch: 15, 896/ 2400 points] total loss, accuracy per batch: 0.322, 0.906\n","[Epoch: 15, 1120/ 2400 points] total loss, accuracy per batch: 0.329, 0.893\n","[Epoch: 15, 1344/ 2400 points] total loss, accuracy per batch: 0.312, 0.915\n","[Epoch: 15, 1568/ 2400 points] total loss, accuracy per batch: 0.306, 0.897\n","[Epoch: 15, 1792/ 2400 points] total loss, accuracy per batch: 0.254, 0.938\n","[Epoch: 15, 2016/ 2400 points] total loss, accuracy per batch: 0.292, 0.915\n","[Epoch: 15, 2240/ 2400 points] total loss, accuracy per batch: 0.296, 0.915\n","12/22/2021 10:27:04 AM [INFO]: Evaluating test samples...\n","100% 9/9 [00:05<00:00, 1.59it/s]\n","12/22/2021 10:27:10 AM [INFO]: ***** Eval results *****\n","12/22/2021 10:27:10 AM [INFO]: accuracy = 0.8638888888888889\n","12/22/2021 10:27:10 AM [INFO]: f1 = 0.21428571428571427\n","12/22/2021 10:27:10 AM [INFO]: precision = 0.42857142857142855\n","12/22/2021 10:27:10 AM [INFO]: recall = 0.14285714285714285\n","Epoch finished, took 63.15 seconds.\n","Losses at Epoch 15: 0.2933859\n","Train accuracy at Epoch 15: 0.9138393\n","Test f1 at Epoch 15: 0.2142857\n","[Epoch: 16, 224/ 2400 points] total loss, accuracy per batch: 0.359, 0.893\n","[Epoch: 16, 448/ 2400 points] total loss, accuracy per batch: 0.199, 0.929\n","[Epoch: 16, 672/ 2400 points] total loss, accuracy per batch: 0.285, 0.920\n","[Epoch: 16, 896/ 2400 points] total loss, accuracy per batch: 0.292, 0.902\n","[Epoch: 16, 1120/ 2400 points] total loss, accuracy per batch: 0.310, 0.915\n","[Epoch: 16, 1344/ 2400 points] total loss, accuracy per batch: 0.259, 0.924\n","[Epoch: 16, 1568/ 2400 points] total loss, accuracy per batch: 0.276, 0.920\n","[Epoch: 16, 1792/ 2400 points] total loss, accuracy per batch: 0.278, 0.915\n","[Epoch: 16, 2016/ 2400 points] total loss, accuracy per batch: 0.337, 0.897\n","[Epoch: 16, 2240/ 2400 points] total loss, accuracy per batch: 0.335, 0.902\n","12/22/2021 10:28:15 AM [INFO]: Evaluating test samples...\n","100% 9/9 [00:05<00:00, 1.55it/s]\n","12/22/2021 10:28:21 AM [INFO]: ***** Eval results *****\n","12/22/2021 10:28:21 AM [INFO]: accuracy = 0.8527777777777777\n","12/22/2021 10:28:21 AM [INFO]: f1 = 0.3243243243243243\n","12/22/2021 10:28:21 AM [INFO]: precision = 0.4\n","12/22/2021 10:28:21 AM [INFO]: recall = 0.2727272727272727\n","Epoch finished, took 66.07 seconds.\n","Losses at Epoch 16: 0.2928523\n","Train accuracy at Epoch 16: 0.9116071\n","Test f1 at Epoch 16: 0.3243243\n","[Epoch: 17, 224/ 2400 points] total loss, accuracy per batch: 0.234, 0.933\n","[Epoch: 17, 448/ 2400 points] total loss, accuracy per batch: 0.307, 0.888\n","[Epoch: 17, 672/ 2400 points] total loss, accuracy per batch: 0.261, 0.893\n","[Epoch: 17, 896/ 2400 points] total loss, accuracy per batch: 0.342, 0.888\n","[Epoch: 17, 1120/ 2400 points] total loss, accuracy per batch: 0.280, 0.933\n","[Epoch: 17, 1344/ 2400 points] total loss, accuracy per batch: 0.208, 0.929\n","[Epoch: 17, 1568/ 2400 points] total loss, accuracy per batch: 0.302, 0.911\n","[Epoch: 17, 1792/ 2400 points] total loss, accuracy per batch: 0.331, 0.888\n","[Epoch: 17, 2016/ 2400 points] total loss, accuracy per batch: 0.224, 0.929\n","[Epoch: 17, 2240/ 2400 points] total loss, accuracy per batch: 0.330, 0.902\n","12/22/2021 10:29:22 AM [INFO]: Evaluating test samples...\n","100% 9/9 [00:06<00:00, 1.47it/s]\n","12/22/2021 10:29:29 AM [INFO]: ***** Eval results *****\n","12/22/2021 10:29:29 AM [INFO]: accuracy = 0.875\n","12/22/2021 10:29:29 AM [INFO]: f1 = 0.23529411764705882\n","12/22/2021 10:29:29 AM [INFO]: precision = 0.4\n","12/22/2021 10:29:29 AM [INFO]: recall = 0.16666666666666666\n","Epoch finished, took 64.96 seconds.\n","Losses at Epoch 17: 0.2818146\n","Train accuracy at Epoch 17: 0.9093750\n","Test f1 at Epoch 17: 0.2352941\n","[Epoch: 18, 224/ 2400 points] total loss, accuracy per batch: 0.294, 0.902\n","[Epoch: 18, 448/ 2400 points] total loss, accuracy per batch: 0.256, 0.924\n","[Epoch: 18, 672/ 2400 points] total loss, accuracy per batch: 0.267, 0.924\n","[Epoch: 18, 896/ 2400 points] total loss, accuracy per batch: 0.300, 0.911\n","[Epoch: 18, 1120/ 2400 points] total loss, accuracy per batch: 0.373, 0.879\n","[Epoch: 18, 1344/ 2400 points] total loss, accuracy per batch: 0.243, 0.920\n","[Epoch: 18, 1568/ 2400 points] total loss, accuracy per batch: 0.241, 0.933\n","[Epoch: 18, 1792/ 2400 points] total loss, accuracy per batch: 0.304, 0.911\n","[Epoch: 18, 2016/ 2400 points] total loss, accuracy per batch: 0.285, 0.924\n","[Epoch: 18, 2240/ 2400 points] total loss, accuracy per batch: 0.221, 0.938\n","12/22/2021 10:30:30 AM [INFO]: Evaluating test samples...\n","100% 9/9 [00:06<00:00, 1.47it/s]\n","12/22/2021 10:30:36 AM [INFO]: ***** Eval results *****\n","12/22/2021 10:30:36 AM [INFO]: accuracy = 0.8486111111111111\n","12/22/2021 10:30:36 AM [INFO]: f1 = 0.31249999999999994\n","12/22/2021 10:30:36 AM [INFO]: precision = 0.45454545454545453\n","12/22/2021 10:30:36 AM [INFO]: recall = 0.23809523809523808\n","Epoch finished, took 65.29 seconds.\n","Losses at Epoch 18: 0.2783521\n","Train accuracy at Epoch 18: 0.9165179\n","Test f1 at Epoch 18: 0.3125000\n","[Epoch: 19, 224/ 2400 points] total loss, accuracy per batch: 0.251, 0.924\n","[Epoch: 19, 448/ 2400 points] total loss, accuracy per batch: 0.306, 0.893\n","[Epoch: 19, 672/ 2400 points] total loss, accuracy per batch: 0.240, 0.924\n","[Epoch: 19, 896/ 2400 points] total loss, accuracy per batch: 0.253, 0.906\n","[Epoch: 19, 1120/ 2400 points] total loss, accuracy per batch: 0.314, 0.902\n","[Epoch: 19, 1344/ 2400 points] total loss, accuracy per batch: 0.267, 0.924\n","[Epoch: 19, 1568/ 2400 points] total loss, accuracy per batch: 0.263, 0.902\n","[Epoch: 19, 1792/ 2400 points] total loss, accuracy per batch: 0.313, 0.888\n","[Epoch: 19, 2016/ 2400 points] total loss, accuracy per batch: 0.308, 0.920\n","[Epoch: 19, 2240/ 2400 points] total loss, accuracy per batch: 0.228, 0.933\n","12/22/2021 10:31:39 AM [INFO]: Evaluating test samples...\n","100% 9/9 [00:05<00:00, 1.51it/s]\n","12/22/2021 10:31:45 AM [INFO]: ***** Eval results *****\n","12/22/2021 10:31:45 AM [INFO]: accuracy = 0.8597222222222222\n","12/22/2021 10:31:45 AM [INFO]: f1 = 0.35294117647058826\n","12/22/2021 10:31:45 AM [INFO]: precision = 0.6\n","12/22/2021 10:31:45 AM [INFO]: recall = 0.25\n","Epoch finished, took 64.45 seconds.\n","Losses at Epoch 19: 0.2742667\n","Train accuracy at Epoch 19: 0.9116071\n","Test f1 at Epoch 19: 0.3529412\n","[Epoch: 20, 224/ 2400 points] total loss, accuracy per batch: 0.251, 0.924\n","[Epoch: 20, 448/ 2400 points] total loss, accuracy per batch: 0.228, 0.924\n","[Epoch: 20, 672/ 2400 points] total loss, accuracy per batch: 0.297, 0.915\n","[Epoch: 20, 896/ 2400 points] total loss, accuracy per batch: 0.226, 0.933\n","[Epoch: 20, 1120/ 2400 points] total loss, accuracy per batch: 0.229, 0.933\n","[Epoch: 20, 1344/ 2400 points] total loss, accuracy per batch: 0.338, 0.884\n","[Epoch: 20, 1568/ 2400 points] total loss, accuracy per batch: 0.275, 0.920\n","[Epoch: 20, 1792/ 2400 points] total loss, accuracy per batch: 0.302, 0.911\n","[Epoch: 20, 2016/ 2400 points] total loss, accuracy per batch: 0.298, 0.893\n","[Epoch: 20, 2240/ 2400 points] total loss, accuracy per batch: 0.306, 0.911\n","12/22/2021 10:32:47 AM [INFO]: Evaluating test samples...\n","100% 9/9 [00:05<00:00, 1.61it/s]\n","12/22/2021 10:32:52 AM [INFO]: ***** Eval results *****\n","12/22/2021 10:32:52 AM [INFO]: accuracy = 0.8673611111111111\n","12/22/2021 10:32:52 AM [INFO]: f1 = 0.30303030303030304\n","12/22/2021 10:32:52 AM [INFO]: precision = 0.4166666666666667\n","12/22/2021 10:32:52 AM [INFO]: recall = 0.23809523809523808\n","Epoch finished, took 65.04 seconds.\n","Losses at Epoch 20: 0.2749758\n","Train accuracy at Epoch 20: 0.9147321\n","Test f1 at Epoch 20: 0.3030303\n","12/22/2021 10:32:55 AM [INFO]: Finished Training!\n","12/22/2021 10:33:12 AM [INFO]: Loading tokenizer and model...\n","12/22/2021 10:33:13 AM [INFO]: loading configuration file https://s3.amazonaws.com/models.huggingface.co/bert/bert-base-uncased-config.json from cache at /root/.cache/torch/transformers/4dad0251492946e18ac39290fcfe91b89d370fee250efe9521476438fe8ca185.7156163d5fdc189c3016baca0775ffce230789d7fa2a42ef516483e4ca884517\n","12/22/2021 10:33:13 AM [INFO]: Model config {\n"," \"architectures\": [\n"," \"BertForMaskedLM\"\n"," ],\n"," \"attention_probs_dropout_prob\": 0.1,\n"," \"finetuning_task\": null,\n"," \"hidden_act\": \"gelu\",\n"," \"hidden_dropout_prob\": 0.1,\n"," \"hidden_size\": 768,\n"," \"initializer_range\": 0.02,\n"," \"intermediate_size\": 3072,\n"," \"is_decoder\": false,\n"," \"layer_norm_eps\": 1e-12,\n"," \"max_position_embeddings\": 512,\n"," \"model_type\": \"bert\",\n"," \"num_attention_heads\": 12,\n"," \"num_hidden_layers\": 12,\n"," \"num_labels\": 2,\n"," \"output_attentions\": false,\n"," \"output_hidden_states\": false,\n"," \"output_past\": true,\n"," \"pad_token_id\": 0,\n"," \"pruned_heads\": {},\n"," \"torchscript\": false,\n"," \"type_vocab_size\": 2,\n"," \"use_bfloat16\": false,\n"," \"vocab_size\": 30522\n","}\n","\n","12/22/2021 10:33:13 AM [INFO]: loading weights file https://s3.amazonaws.com/models.huggingface.co/bert/bert-base-uncased-pytorch_model.bin from cache at /root/.cache/torch/transformers/aa1ef1aede4482d0dbcd4d52baad8ae300e60902e88fcb0bebdec09afd232066.36ca03ab34a1a5d5fa7bc3d03d55c4fa650fed07220e2eeebc06ce58d0e9a157\n","Model config: {\n"," \"architectures\": [\n"," \"BertForMaskedLM\"\n"," ],\n"," \"attention_probs_dropout_prob\": 0.1,\n"," \"finetuning_task\": null,\n"," \"hidden_act\": \"gelu\",\n"," \"hidden_dropout_prob\": 0.1,\n"," \"hidden_size\": 768,\n"," \"initializer_range\": 0.02,\n"," \"intermediate_size\": 3072,\n"," \"is_decoder\": false,\n"," \"layer_norm_eps\": 1e-12,\n"," \"max_position_embeddings\": 512,\n"," \"model_type\": \"bert\",\n"," \"num_attention_heads\": 12,\n"," \"num_hidden_layers\": 12,\n"," \"num_labels\": 2,\n"," \"output_attentions\": false,\n"," \"output_hidden_states\": false,\n"," \"output_past\": true,\n"," \"pad_token_id\": 0,\n"," \"pruned_heads\": {},\n"," \"torchscript\": false,\n"," \"type_vocab_size\": 2,\n"," \"use_bfloat16\": false,\n"," \"vocab_size\": 30522\n","}\n","\n","12/22/2021 10:33:17 AM [INFO]: Weights of BertModel not initialized from pretrained model: ['bert.classification_layer.weight', 'bert.classification_layer.bias']\n","12/22/2021 10:33:19 AM [INFO]: Loaded checkpoint model.\n","12/22/2021 10:33:19 AM [INFO]: Loaded model and optimizer.\n","12/22/2021 10:33:19 AM [INFO]: Done!\n"]}],"source":["# Train the model\n","# --train_data: Full path of the trainning dataset\n","# --test_data: Full path of the testing dataset\n","\n","%cd '/content/drive/MyDrive/GitHub/BERT-Relation-Extraction'\n","!CUDA_LAUNCH_BLOCKING=1 python main_task.py --train_data=\"/content/drive/MyDrive/GitHub/train_data_dm1.txt\" --test_data=\"/content/drive/MyDrive/GitHub/test_data_dm1.txt\" --num_epochs=20"]},{"cell_type":"code","execution_count":null,"metadata":{"colab":{"base_uri":"https://localhost:8080/"},"executionInfo":{"elapsed":83077,"status":"ok","timestamp":1640169461501,"user":{"displayName":"Tsz Chung Yeung","photoUrl":"https://lh3.googleusercontent.com/a/default-user=s64","userId":"17478010975126361284"},"user_tz":-480},"id":"mhK3SG57ZCiP","outputId":"71eeefe2-8e9b-4eb6-bbeb-79868d632599"},"outputs":[{"name":"stdout","output_type":"stream","text":["/content/drive/.shortcut-targets-by-id/1jqlh-dTe4b6_AZhAYDBHkKjWweeOh9HE/COMP4805 Project/Go to Street/__Evergrande/BERT-Relation-Extraction\n","12/22/2021 10:36:38 AM [INFO]: Loading tokenizer and model...\n","12/22/2021 10:36:46 AM [INFO]: TensorFlow version 2.7.0 available.\n","12/22/2021 10:36:46 AM [INFO]: PyTorch version 1.10.0+cu111 available.\n","12/22/2021 10:36:47 AM [INFO]: loading configuration file https://s3.amazonaws.com/models.huggingface.co/bert/bert-base-uncased-config.json from cache at /root/.cache/torch/transformers/4dad0251492946e18ac39290fcfe91b89d370fee250efe9521476438fe8ca185.7156163d5fdc189c3016baca0775ffce230789d7fa2a42ef516483e4ca884517\n","12/22/2021 10:36:47 AM [INFO]: Model config {\n"," \"architectures\": [\n"," \"BertForMaskedLM\"\n"," ],\n"," \"attention_probs_dropout_prob\": 0.1,\n"," \"finetuning_task\": null,\n"," \"hidden_act\": \"gelu\",\n"," \"hidden_dropout_prob\": 0.1,\n"," \"hidden_size\": 768,\n"," \"initializer_range\": 0.02,\n"," \"intermediate_size\": 3072,\n"," \"is_decoder\": false,\n"," \"layer_norm_eps\": 1e-12,\n"," \"max_position_embeddings\": 512,\n"," \"model_type\": \"bert\",\n"," \"num_attention_heads\": 12,\n"," \"num_hidden_layers\": 12,\n"," \"num_labels\": 2,\n"," \"output_attentions\": false,\n"," \"output_hidden_states\": false,\n"," \"output_past\": true,\n"," \"pad_token_id\": 0,\n"," \"pruned_heads\": {},\n"," \"torchscript\": false,\n"," \"type_vocab_size\": 2,\n"," \"use_bfloat16\": false,\n"," \"vocab_size\": 30522\n","}\n","\n","12/22/2021 10:36:47 AM [INFO]: loading weights file https://s3.amazonaws.com/models.huggingface.co/bert/bert-base-uncased-pytorch_model.bin from cache at /root/.cache/torch/transformers/aa1ef1aede4482d0dbcd4d52baad8ae300e60902e88fcb0bebdec09afd232066.36ca03ab34a1a5d5fa7bc3d03d55c4fa650fed07220e2eeebc06ce58d0e9a157\n","Model config: {\n"," \"architectures\": [\n"," \"BertForMaskedLM\"\n"," ],\n"," \"attention_probs_dropout_prob\": 0.1,\n"," \"finetuning_task\": null,\n"," \"hidden_act\": \"gelu\",\n"," \"hidden_dropout_prob\": 0.1,\n"," \"hidden_size\": 768,\n"," \"initializer_range\": 0.02,\n"," \"intermediate_size\": 3072,\n"," \"is_decoder\": false,\n"," \"layer_norm_eps\": 1e-12,\n"," \"max_position_embeddings\": 512,\n"," \"model_type\": \"bert\",\n"," \"num_attention_heads\": 12,\n"," \"num_hidden_layers\": 12,\n"," \"num_labels\": 2,\n"," \"output_attentions\": false,\n"," \"output_hidden_states\": false,\n"," \"output_past\": true,\n"," \"pad_token_id\": 0,\n"," \"pruned_heads\": {},\n"," \"torchscript\": false,\n"," \"type_vocab_size\": 2,\n"," \"use_bfloat16\": false,\n"," \"vocab_size\": 30522\n","}\n","\n","12/22/2021 10:36:50 AM [INFO]: Weights of BertModel not initialized from pretrained model: ['bert.classification_layer.weight', 'bert.classification_layer.bias']\n","12/22/2021 10:37:09 AM [INFO]: Loaded checkpoint model.\n","12/22/2021 10:37:09 AM [INFO]: Loaded model and optimizer.\n","12/22/2021 10:37:09 AM [INFO]: Done!\n","Input a xlsx file, the model will generate a new excel folder with relations.\n","Please input the path of data: /content/drive/MyDrive/COMP4805 Project/Go to Street/__Tencent/TestingData_Tencent.xlsx\n","Sentence: SHANGHAI, Dec 17 ([E1]Reuters[/E1]) - Chinese regulators have given [E2]Tencent Holdings[/E2] (0700.HK) approval to publish updates to nine of its mobile apps including QQ Music and WeCom, media reported on Friday.\n","Predicted: Other \n","\n","Other\n","Sentence: SHANGHAI, Dec 17 ([E1]Reuters[/E1]) - Chinese regulators have given Tencent Holdings (0700.HK) approval to publish updates to nine of its mobile apps including [E2]QQ Music and WeCom[/E2], media reported on Friday.\n","Predicted: Other \n","\n","Other\n","Sentence: SHANGHAI, Dec 17 (Reuters) - Chinese regulators have given [E1]Tencent Holdings[/E1] (0700.HK) approval to publish updates to nine of its mobile apps including [E2]QQ Music and WeCom[/E2], media reported on Friday.\n","Predicted: Other \n","\n","█ Part of the output data are hidden for copyright protection █\n","\n","Subsidary-ParentCompany(e1,e2)\n","Sentence: As [E1]Advance Data Services Limited[/E1] is wholly-owned by [E2]Ma[/E2] Huateng, Mr Ma has an interest in these shares as disclosed under the section of “Directors’ Interests in Securities”.\n","Predicted: Subsidary-ParentCompany(e1,e2) \n","\n","Subsidary-ParentCompany(e1,e2)\n","Sentence: As Advance Data Services Limited is wholly-owned by [E2]Ma[/E2][E1]Ma Huateng[/E1], Mr Ma has an interest in these shares as disclosed under the section of “Directors’ Interests in Securities”.\n","Predicted: Other \n","\n","Other\n","Sentence: [E1]The Audit Committee[/E1], together with the Auditor, has reviewed the [E2]Group[/E2]’s audited consolidated financial statements for the year ended 31 December 2020. The Audit Committee has also reviewed the accounting principles and practices adopted by the Group and discussed auditing, risk management, internal control and financial reporting matters.\n","Predicted: Other \n","\n","Other\n","Sentence: As far as the [E2]Board[/E2] is aware, the [E1]Group[/E1] has complied with the relevant laws and regulations that have a significant impact on the Group in all material respects.\n","Predicted: Other \n","\n","Other\n","Generating output to result.xlsx...\n","Done!\n"]}],"source":["# Run the pretrained model\n","# Return the predicted result with mapping\n","# Input: Path of the dataset, in .xlsx format\n","\n","%cd \"/content/drive/MyDrive/GitHub/BERT-Relation-Extraction\""]}],"metadata":{"accelerator":"GPU","colab":{"collapsed_sections":[],"name":"Tencent_RE BERT model.ipynb","provenance":[],"toc_visible":true},"kernelspec":{"display_name":"Python 3","name":"python3"},"language_info":{"name":"python"}},"nbformat":4,"nbformat_minor":0}
2 |
--------------------------------------------------------------------------------
/Confusion_Matrix.ipynb:
--------------------------------------------------------------------------------
1 | {
2 | "nbformat": 4,
3 | "nbformat_minor": 0,
4 | "metadata": {
5 | "colab": {
6 | "name": "Confusion Matrix.ipynb",
7 | "provenance": [],
8 | "collapsed_sections": []
9 | },
10 | "kernelspec": {
11 | "name": "python3",
12 | "display_name": "Python 3"
13 | },
14 | "language_info": {
15 | "name": "python"
16 | }
17 | },
18 | "cells": [
19 | {
20 | "cell_type": "code",
21 | "source": [
22 | "#pip install --upgrade matplotlib"
23 | ],
24 | "metadata": {
25 | "id": "hw_XNoDVBJ_F"
26 | },
27 | "execution_count": null,
28 | "outputs": []
29 | },
30 | {
31 | "cell_type": "markdown",
32 | "source": [
33 | "This file generates the confusion matrix and heat map of the model output result\n",
34 | "\n",
35 | "Tutorial link: https://matplotlib.org/stable/gallery/images_contours_and_fields/image_annotated_heatmap.html"
36 | ],
37 | "metadata": {
38 | "id": "HvgjoLRSTxPk"
39 | }
40 | },
41 | {
42 | "cell_type": "code",
43 | "execution_count": 1,
44 | "metadata": {
45 | "colab": {
46 | "base_uri": "https://localhost:8080/"
47 | },
48 | "id": "Jyk7wd4DRRLj",
49 | "outputId": "f750ca1c-71e3-4e63-fd1e-8fa414b3e799"
50 | },
51 | "outputs": [
52 | {
53 | "output_type": "stream",
54 | "name": "stdout",
55 | "text": [
56 | "Mounted at /content/drive\n"
57 | ]
58 | }
59 | ],
60 | "source": [
61 | "# Connect to Google drive\n",
62 | "from google.colab import drive\n",
63 | "drive.mount('/content/drive')"
64 | ]
65 | },
66 | {
67 | "cell_type": "code",
68 | "source": [
69 | "import numpy as np\n",
70 | "import matplotlib\n",
71 | "import matplotlib.pyplot as plt\n",
72 | "import pandas as pd"
73 | ],
74 | "metadata": {
75 | "id": "dSRUyn-qWjdl"
76 | },
77 | "execution_count": 2,
78 | "outputs": []
79 | },
80 | {
81 | "cell_type": "code",
82 | "source": [
83 | "from sklearn.metrics import confusion_matrix\n",
84 | "from sklearn import preprocessing\n",
85 | "le = preprocessing.LabelEncoder()"
86 | ],
87 | "metadata": {
88 | "id": "-s6_j-yccMLx"
89 | },
90 | "execution_count": 3,
91 | "outputs": []
92 | },
93 | {
94 | "cell_type": "code",
95 | "source": [
96 | "input_data = pd.read_excel(\"/content/drive/MyDrive/GitHub/result_tencent_with_Prediction_v3.xlsx\", sheet_name=\"Sheet1\")\n",
97 | "\n",
98 | "le.fit([\"Colleague\", \"Relative\",\"Employee-Company\",\"Educated-Institute\",\"Founder-Company\",\"Shareholder-Company\",\"Within-Same-Company-Group\",\"Cooperate-Partner\",\"Subsidary-ParentCompany\",\"Same-Entity\",\"Other\"])\n",
99 | "\n",
100 | "input_data['Label-short'] = input_data['Label-short'].astype(str)\n",
101 | "input_data['Prediction-short'] = input_data['Prediction-short'].astype(str)\n",
102 | "\n",
103 | "labell=le.classes_\n",
104 | "label2=labell\n",
105 | "print(labell)\n",
106 | "\n",
107 | "Tencent = confusion_matrix(input_data['Label-short'], input_data['Prediction-short'])\n",
108 | "print(Tencent)"
109 | ],
110 | "metadata": {
111 | "colab": {
112 | "base_uri": "https://localhost:8080/"
113 | },
114 | "id": "SjnyX0sxba3G",
115 | "outputId": "40fd06b5-2c5a-4f68-f801-b4776bfb5f70"
116 | },
117 | "execution_count": 22,
118 | "outputs": [
119 | {
120 | "output_type": "stream",
121 | "name": "stdout",
122 | "text": [
123 | "['Colleague' 'Cooperate-Partner' 'Educated-Institute' 'Employee-Company'\n",
124 | " 'Founder-Company' 'Other' 'Relative' 'Same-Entity' 'Shareholder-Company'\n",
125 | " 'Subsidary-ParentCompany' 'Within-Same-Company-Group']\n",
126 | "[[ 1 0 0 0 0 20 0 1 0 0 0]\n",
127 | " [ 0 14 0 1 0 16 0 1 2 1 0]\n",
128 | " [ 0 0 33 0 0 3 0 0 0 0 0]\n",
129 | " [ 0 2 1 113 0 26 0 1 0 0 0]\n",
130 | " [ 0 0 0 2 0 1 0 0 0 0 0]\n",
131 | " [ 2 6 5 52 0 465 6 9 0 3 0]\n",
132 | " [ 0 0 0 0 0 6 0 0 0 0 0]\n",
133 | " [ 0 0 0 0 0 15 0 2 0 0 0]\n",
134 | " [ 0 4 0 0 0 15 0 8 1 5 0]\n",
135 | " [ 0 4 0 0 0 16 0 0 0 8 0]\n",
136 | " [ 0 0 1 0 0 0 0 0 0 0 0]]\n"
137 | ]
138 | }
139 | ]
140 | },
141 | {
142 | "cell_type": "code",
143 | "source": [
144 | "from numpy.lib.twodim_base import triu_indices\n",
145 | "#Reference: https://matplotlib.org/stable/gallery/images_contours_and_fields/image_annotated_heatmap.html\n",
146 | "\n",
147 | "def heatmap(data, row_labels, col_labels, ax=None,\n",
148 | " cbar_kw={}, cbarlabel=\"\", **kwargs):\n",
149 | " \"\"\"\n",
150 | " Create a heatmap from a numpy array and two lists of labels.\n",
151 | "\n",
152 | " Parameters\n",
153 | " ----------\n",
154 | " data\n",
155 | " A 2D numpy array of shape (M, N).\n",
156 | " row_labels\n",
157 | " A list or array of length M with the labels for the rows.\n",
158 | " col_labels\n",
159 | " A list or array of length N with the labels for the columns.\n",
160 | " ax\n",
161 | " A `matplotlib.axes.Axes` instance to which the heatmap is plotted. If\n",
162 | " not provided, use current axes or create a new one. Optional.\n",
163 | " cbar_kw\n",
164 | " A dictionary with arguments to `matplotlib.Figure.colorbar`. Optional.\n",
165 | " cbarlabel\n",
166 | " The label for the colorbar. Optional.\n",
167 | " **kwargs\n",
168 | " All other arguments are forwarded to `imshow`.\n",
169 | " \"\"\"\n",
170 | "\n",
171 | " if not ax:\n",
172 | " ax = plt.gca()\n",
173 | "\n",
174 | " # Plot the heatmap\n",
175 | " im = ax.imshow(data, **kwargs)\n",
176 | "\n",
177 | " # Create colorbar\n",
178 | " cbar = ax.figure.colorbar(im, ax=ax, **cbar_kw)\n",
179 | " cbar.ax.set_ylabel(cbarlabel, rotation=-90, va=\"bottom\")\n",
180 | "\n",
181 | " # Show all ticks and label them with the respective list entries.\n",
182 | " ax.set_xticks(np.arange(len(col_labels)))\n",
183 | " ax.set_xticklabels(col_labels)\n",
184 | " ax.set_yticks(np.arange(len(row_labels)))\n",
185 | " ax.set_yticklabels(row_labels)\n",
186 | "\n",
187 | " # Let the horizontal axes labeling appear on top.\n",
188 | " ax.tick_params(top=False, bottom=triu_indices,\n",
189 | " labeltop=False, labelbottom=True)\n",
190 | "\n",
191 | " # Rotate the tick labels and set their alignment.\n",
192 | " plt.setp(ax.get_xticklabels(), rotation=45, ha=\"right\",rotation_mode=\"anchor\")\n",
193 | "\n",
194 | " # Turn spines off and create white grid.\n",
195 | " #ax.spines[:].set_visible(False)\n",
196 | "\n",
197 | " ax.set_xticks(np.arange(data.shape[1]+1)-.5, minor=True)\n",
198 | " ax.set_yticks(np.arange(data.shape[0]+1)-.5, minor=True)\n",
199 | " ax.grid(which=\"minor\", color=\"w\", linestyle='-', linewidth=3)\n",
200 | " ax.tick_params(which=\"minor\", bottom=False, left=False)\n",
201 | "\n",
202 | " return im, cbar\n",
203 | "\n",
204 | "\n",
205 | "def annotate_heatmap(im, data=None, valfmt=\"{x:.2f}\",\n",
206 | " textcolors=(\"black\",\"white\"),\n",
207 | " threshold=125, **textkw):\n",
208 | " \"\"\"\n",
209 | " A function to annotate a heatmap.\n",
210 | "\n",
211 | " Parameters\n",
212 | " ----------\n",
213 | " im\n",
214 | " The AxesImage to be labeled.\n",
215 | " data\n",
216 | " Data used to annotate. If None, the image's data is used. Optional.\n",
217 | " valfmt\n",
218 | " The format of the annotations inside the heatmap. This should either\n",
219 | " use the string format method, e.g. \"$ {x:.2f}\", or be a\n",
220 | " `matplotlib.ticker.Formatter`. Optional.\n",
221 | " textcolors\n",
222 | " A pair of colors. The first is used for values below a threshold,\n",
223 | " the second for those above. Optional.\n",
224 | " threshold\n",
225 | " Value in data units according to which the colors from textcolors are\n",
226 | " applied. If None (the default) uses the middle of the colormap as\n",
227 | " separation. Optional.\n",
228 | " **kwargs\n",
229 | " All other arguments are forwarded to each call to `text` used to create\n",
230 | " the text labels.\n",
231 | " \"\"\"\n",
232 | "\n",
233 | " if not isinstance(data, (list, np.ndarray)):\n",
234 | " data = im.get_array()\n",
235 | "\n",
236 | " # Normalize the threshold to the images color range.\n",
237 | " if threshold is not None:\n",
238 | " threshold = im.norm(threshold)\n",
239 | " else:\n",
240 | " threshold = im.norm(data.max())/2.\n",
241 | "\n",
242 | " # Set default alignment to center, but allow it to be\n",
243 | " # overwritten by textkw.\n",
244 | " kw = dict(horizontalalignment=\"center\",\n",
245 | " verticalalignment=\"center\")\n",
246 | " kw.update(textkw)\n",
247 | "\n",
248 | " # Get the formatter in case a string is supplied\n",
249 | " if isinstance(valfmt, str):\n",
250 | " valfmt = matplotlib.ticker.StrMethodFormatter(valfmt)\n",
251 | "\n",
252 | " # Loop over the data and create a `Text` for each \"pixel\".\n",
253 | " # Change the text's color depending on the data.\n",
254 | " texts = []\n",
255 | " for i in range(data.shape[0]):\n",
256 | " for j in range(data.shape[1]):\n",
257 | " kw.update(color=textcolors[int(im.norm(data[i, j]) > threshold)])\n",
258 | " text = im.axes.text(j, i, valfmt(data[i, j], None), **kw)\n",
259 | " texts.append(text)\n",
260 | "\n",
261 | " return texts"
262 | ],
263 | "metadata": {
264 | "id": "eHpj3r2ighug"
265 | },
266 | "execution_count": 26,
267 | "outputs": []
268 | },
269 | {
270 | "cell_type": "code",
271 | "source": [
272 | "fig, ax = plt.subplots(figsize = (10,8))\n",
273 | "im = ax.imshow(Tencent)\n",
274 | "\n",
275 | "im, cbar = heatmap(Tencent, labell, label2, ax=ax,cmap=\"YlGn\", cbarlabel=\"Number of occurances\")\n",
276 | "\n",
277 | "texts = annotate_heatmap(im, valfmt=\"{x:}\")\n",
278 | "\n",
279 | "ax.set_title(\"Tencent Confusion Matrix\")\n",
280 | "ax.set_xlabel(\"Prediction\")\n",
281 | "ax.set_ylabel(\"Actual Label\")\n",
282 | "fig.tight_layout()\n",
283 | "plt.show()"
284 | ],
285 | "metadata": {
286 | "colab": {
287 | "base_uri": "https://localhost:8080/",
288 | "height": 585
289 | },
290 | "id": "lvMUzetoX7Iu",
291 | "outputId": "3159a37c-9bfa-42d3-f894-8d587e7cc76c"
292 | },
293 | "execution_count": 27,
294 | "outputs": [
295 | {
296 | "output_type": "display_data",
297 | "data": {
298 | "image/png": "iVBORw0KGgoAAAANSUhEUgAAAqQAAAI4CAYAAAC84vuRAAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADh0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uMy4yLjIsIGh0dHA6Ly9tYXRwbG90bGliLm9yZy+WH4yJAAAgAElEQVR4nOzdeZxWdf3+8dc1IJgimoKAoJKi7PsA7hGY5IZKCIpliEaW9S3JrfyW+/eHZZpJpqbmGpq5YC5oKuQSyiK4YYoKOoCmqKgoCgzv3x/nDNyMswEzcw7D9Xw87gf32T7nOp+5gfd8znIrIjAzMzMzy0pR1gHMzMzMbPPmgtTMzMzMMuWC1MzMzMwy5YLUzMzMzDLlgtTMzMzMMuWC1MzMzMwy5YLUzKyBk3SUpBJJyyT13oh2XpI0sBaj1TtJ+0t6JescZrYuF6RmtklKi6uy12pJywumj8s6XyFJIalDNeu0kXSdpLclfSLpP5LOk7R1LUS4BPhxRDSLiNkb2khEdI2IqbWQZx2SpqZ91LPc/LvT+QNr2E61/RwRT0REx42Ia2Z1wAWpmW2S0uKqWUQ0A94CDi+Yd2vW+daHpO2BacBXgL0jYhvgm8B2wO61sItdgZdqoZ269CpwfNmEpB2AvYH3amsHkhrXVltmVrtckJpZgyKpSNJZkl6X9L6kv6UFH5Lap6No35P0lqQlks4u2LaRpF+m234iaZakndNlnST9U9IHkl6RNKJguxsk/VHS/el2z0jaPV32eLrac+no7cgKYo8DPgG+ExELACKiJCJ+GhHPp+3sI2mGpI/SP/cp2P9USRdIeird/8OSWkhqKmkZ0Cjd/+vp+uuMJKb5L0zft5B0n6Sl6bE+IakoXbZA0oHp+6aSfi9pcfr6vaSm6bKBkhZK+rmkd9NR3xOq+dHdCoyU1CidPha4G1hRkLO/pGlptrclTZDUpLJ+LshxpqR3gL+UzUu32T09xj7p9E6S3tvUL0sw2xS5IDWzhuYnwJHA14GdgA+BP5ZbZz+gIzAY+LWkzun8cSSF0CFAc2AM8Fl62vyfwF+BHYFjgCsldSlo8xjgPOCrwGvARQARcUC6vGc6ent7BZkPBO6KiNUVHVBaUN8P/AHYAbgUuD8dRSwzCjghzdcEOC0ivkhHkMv2X5PR1p8DC4GWQCvgl0BF3zF9NrAX0AvoCfQH/rdgeWtgW6AtcCLwR0lfrWK/i4G5wEHp9PHATeXWKQVOBVqQjJ4OBn4EVfZza2B7klHisYWNRcTrwJnALZK2Av4C3FgXlyWYWdVckJpZQ3MycHZELIyIL4BzgeHlTteeFxHLI+I54DmSggrgJOB/I+KVSDwXEe8DhwELIuIvEbEqvQ7zTuDogjbvjojpEbGKZLSv13pk3gF4u4rlhwLzIuLmdP8Tgf8Ahxes85eIeDUilgN/W8/9F1oJtAF2jYiV6TWXFRWkxwHnR8S7EfEeSTH+3XLtnJ+28QCwjOSXgKrcBBwvqROwXURMK1wYEbMi4um0DxYAV5P84lGV1cA5aXG+vPzCiPgzyS8Qz6THfXb5dcys7vl6GjNraHYF7pZUONpYSjLaV+adgvefAWWjiDsDr1fS5gBJSwvmNQZurkGbNfE+STFUmZ2AN8vNe5Nk9LE29l/otyRF/MOSAK6JiPE1yPRmOq/M+2lxvj6Z7gJ+R9IfN5dfKGlPktHhYmArkp/BrGrafC8iPq9mnT8D9wJj019izKyeeYTUzBqaEuDgiNiu4LVlRCyq4bYVndYuAf5Vrs1mEfHDWsr8CHBU2bWaFVhMUhQX2gWoyTFV5DOSgq5M67I3EfFJRPw8InYDhgLjJA2uQaZd0nkbLCI+Ax4EfkgFBSnwJ5KR4T0iojnJ5QSqrtmqFkpqBvweuA44t+x6YzOrXy5IzayhuQq4SNKuAJJaSjqihtteC1wgaQ8leqTXad4H7Cnpu5K2SF/9Cq49rc5/gd2qWH4pyTWrNxbkbivpUkk9gAfS/Y+S1Di9MapLmmtDzAFGpTdxfYuC096SDpPUQcnw6Ecko8sVXds6EfjftH9bAL8GbtnAPIV+CXy97OaucrYBPgaWpaf1y/9CUF0/V+RyYGZEnERyne5V67m9mdUCF6Rm1tBcTnL69WFJnwBPAwNquO2lJNdfPkxS+FwHfCUiPiG52eYYklHAd4CLgaY1bPdckmJzaeHd+WUi4gNgH5LrLp9Jcz9KUhC+VnAd689JTmefARwWEUtquP/yfkpy/elSkmtB7ylYtgfJiO0ykkdRXRkRUypo40JgJvA88ALwbDpvo0TE4oh4spLFp5HcvPUJyWn28jeInUsV/Vxe+ovKt1hb2I4D+ihnz7E12xyo4mvVzczMzMzqh0dIzczMzCxTLkjNzMzMLFMuSM3MzMwsUy5IzczMzCxTfjC+bfJatGgR7du3zzqGmZk1AAsWvMGSJR9U93zbWqEWzYIVpbXX4CefPxQR36q9BuuPC1Lb5LVv356ZM2dmHcPMzBqA4uKe1a9UW1aUwl5fq732/vlyi9prrH65ILUGZKO+JKYWFX57ojNVLG95IO+ZSlfPzTDHWo2KuhRM5a+fnKkyecsD+c9UD0T13zW2mfA1pGZmZmaWKY+QmpmZmWVFHiIFj5CamZmZWcY8QmpmZmaWFQ+QAi5IzczMzLLjU/aAT9mbmZmZWcY8QmpmZmaWFQ+QAi5IzczMzLIhoMgVKfiUvZmZmZllzCOkZmZmZlnxACngEVIzMzMzy5hHSM3MzMwyIT/2KeURUtvsjRkzjh137EG3boOyjrKOyZOn0LHj/nTosC/jx0/IOk7u8oAzVaak5G0GDx5N926H06P7UP7wh5sB+OCDpQw56CQ6dTyYIQedxIcffpRJPshHPxXK478DeesjcKY6oVp8bcJckG4mJLWWdJuk1yXNkvSApD0rWbe9pBfT9wMl3Ve/aevX6NEjmDz51qxjrKO0tJRTTjmbBx+8hblzpzBx4j3Mnfuq8zhTjTRu3Jjf/vYMXnjxHzz174n86cqJzJ37GhdffC2DBg/gP688yKDBA7j44mvrPRvkp58K5e3fgTz2kTNZXXJBuhmQJOBuYGpE7B4RfYFfAK2yTZYPBxywF9tvv13WMdYxffpsOnRoz2677UqTJk045pgjmDTpIedxphpp06Ylffp0AWCbbbamU6fdWLToXf5x7xSOP/5IAI4//kjunfRYvWeD/PRTobz9O5DHPnKmOlCbo6MeIbVNwDeAlRFxVdmMiHgOeFLSbyW9KOkFSSOrakTS1pKulzRd0mxJR6Tz20t6QtKz6WufdH6RpCsl/UfSP9NR2eHpsgWSWqTviyVNrWofm5tFi95h5513WjPdrl0bFi16x3kKOFPNLFiwiDlzXmbAgB7897/v06ZNSwBat27Bf//7fiaZ8thPeZPHPnKmOiLV3msT5puaNg/dgFkVzB8G9AJ6Ai2AGZIer6Kds4HHImKMpO2A6ZIeAd4FvhkRn0vaA5gIFKfttwe6ADsCLwPXV5O1wn1ExKeFK0kaC4wF2GWXXapp0mzztGzZp4w4+mdceulZNG/ebJ1lktAm/h+YmTUcHiHdvO0HTIyI0oj4L/AvoF8V6x8EnCVpDjAV2BLYBdgC+LOkF4A7SArQsvbviIjVEfEOMKUGmSrbxzoi4pqIKI6I4pYtW9ag2U1L27atKSlZvGZ64cK3adu2tfMUcKaqrVy5kqOH/4xjRx3KUcO+CUCrVjvw9tvvAfD22++x447bZ5ItT/2UV3nsI2eqIz5lD7gg3Vy8BPSthXYEfDsieqWvXSLiZeBU4L8kI63FQJMatLWKtZ+/LWuwj81Kv369mDdvPvPnv8WKFSu47bZJDB16kPM4U41EBN8/6dd07rwbp546es38ww7/BjfddA8AN910D4cP/Ua9Z4P89FOe5bGPnKmO+JQ94IJ0c/EY0DQ9zQ2ApB7AUmCkpEaSWgIHANOraOch4CfpTVJI6p3O3xZ4OyJWA98FGqXznwK+nV5L2goYWNDWAtYWyd+uwT7qzLHH/oi99x7KK6+8Trt2fbnuuol1vctqNW7cmAkTLmTIkFF07jyQESMOp2vXjs7jTDXy1FPPcsst9zJlynT69hlG3z7DeOCBxznzzJN45JFpdOp4MI8++jRnnnlSvWeD/PRTobz9O5DHPnImq0uKiKwzWD2QtBPwe5Ii8HOSgvBnJNdhHgwEcGFE3C6pPXBfRHSTNBA4LSIOk/SVtI19SH6ZmZ/O3wO4M21jMnBKRDSTVARcSVKIlpCMfl4cEf+UtD9wHfAxyan54ogYWNk+qjq24uLimDlzJrC4qtXq0U4F752pYnnLA3nPVLp6boY51mpU1KVgKn/95EyVyVseyGum4uKezJz5XL0MN2r7rYLBFT6BccP8/blZEVFcew3WH9/UtJmIiMXAiAoWnZ6+CtddQHIjFBExlaRgJCKWAz+ooO15QI+CWWem81dLOi0ilknagWT09YV02RPAl/4WVrYPMzMza7hckFpduy+9W74JcEF6c5OZmZnBJn/tZ21xQWp1KiIGZp3BzMwst3w3D+BuMDMzM7OMeYTUzMzMLCs+Yw+4IDUzMzPLhvA1pCmfsjczMzOzTHmE1MzMzCwrHiAFPEJqZmZmZhnzCKmZmZlZJjb976CvLS5IzczMzLLiehTwKXszMzMzy5hHSK0B2SnrABVwpurlLQ/kMVOjoi5ZR6hA/vrJmWoib3kgn5nqiU/ZAy5IzczMzLIhfMo+5VP2ZmZmZpYpj5BaA7I46wCptaeeVsdrGeZYq0gdCqby0E+Fp+fykAfynqk0Xs0wx1qNtGfBVP76KY+ZIhZmmCMhtSuYyl8f5TNTPfEpe8AFqZmZmVl2XI8CPmVvZmZmZhnzCKmZmZlZVjw0CLgbzMzMzCxjHiE1MzMzy4LwTU0pF6RmZmZmWXE9CviUvZmZmZllzCOkZmZmZlnxKXvABamZmZlZdlyPAj5lb2ZmZmYZ8wipmZmZWSbkU/Ypj5CaAZMnT6Fjx/3p0GFfxo+fkEmGE8ecRetWA+jR/ZAvLbv0d9fRqGgPliz5IINkiTz0UXljxoxjxx170K3boKyjrJGHfjppzC9o02pvenY/bJ35E664ma6dv0WPbody5hm/ySRbmTz0U6E8fpZKShYzaNAIunYdRLdug7n88uuyjpTLfsrbZ8k2jAvSjSSptaTbJL0uaZakByTtmXWuMpKOlNRlA7ZbIOkFSc9LelhS6/XYtr2kUeu7z6yUlpZyyiln8+CDtzB37hQmTryHuXNfrfcc3xs9jAcevP5L80tK3ubhfz7JLrvsVO+ZyuSlj8obPXoEkyffmnWMNfLST8ePHsb9D167zrwpU57m3nsf5dk59/L8i/fz89NOrPdcZfLST4Xy9lkCaNy4EZdc8iteeukxpk2bxJVX3uh+KiePn6X1olp+bcJckG4ESQLuBqZGxO4R0Rf4BdCqnnM0qmLxkcB6F6Spb0RED2Am8MsaZmkMtAdqrSCt5vg22vTps+nQoT277bYrTZo04ZhjjmDSpIfqcpcVOuCA/my//bZfmj9u3EVcfPEZKMPTOnnpo/IOOGAvtt9+u6xjrJGXfjrggH5f+ixdfdVEzjhzLE2bNgFgxx13qPdcZfLST4Xy9lkCaNOmFX36dAdgm22a0blzBxYteifTTHnrpzx+ltaXVHuvTZkL0o3zDWBlRFxVNiMingOelPRbSS+mo4wjISlgK5k/UNLjku6X9IqkqyQVpcsOkjRN0rOS7pDULJ2/QNLFkp4Fjpb0fUkzJD0n6U5JW0naBxgK/FbSHEm7p6/J6WjuE5I61eA4Hwc6SOqfZpkt6d+SOqZZRku6V9JjwKPAeGD/dJ+npsvvSvc7T9Kac4U1Pb6N/DlVadGid9h557Wjj+3atcn8H/0ykyY9QtudWtGzZ+dMc+S5j/Ikz/0079UFPPnETPbe62i+MfA7zJjxfGZZ8txPebVgQQmzZ7/EgAG9s46SK/4sbRhJjdL/y+9Lp78m6RlJr0m6XVKTdH7TdPq1dHn7usrkm5o2TjdgVgXzhwG9gJ5AC2CGpMeBfSqZD9CfZCTzTWAyMEzSVOB/gQMj4lNJZwLjgPPTbd6PiD4AknaIiD+n7y8EToyIKyTdC9wXEX9Plz0KnBwR8yQNAK4EqrsY6DDgBeA/wP4RsUrSgcD/Ad9O1+kD9IiIDyQNBE6LiMPSfY5Oj7s38AXwiqQrgOU1Pb7N0WefLWf8//sTkx+6Ieso1gCsWlXKhx98xL+n/Y0ZM17g2JE/Y97rj2Y68m41s2zZpwwf/gMuu+xcmjffJus4Vstq8+9g1HzVnwIvA83T6YuByyLiNklXAScCf0r//DAiOkg6Jl1vZK0FLuCCtG7sB0yMiFLgv5L+BfSrYv7HwPSIeANA0sR03c9JitSn0g9sE2BawX5uL3jfLS1EtwOaAV86Z5GOPu4D3FHwF6BpFccxRVIp8DxJ4bgtcKOkPUg+91sUrPvPiKjqjptHI+KjNMdcYNc0a02Pr/yxjAXGAuyyyy5V7LZ6bdu2pqRk8ZrphQvfpm3bGl8yW2def/0t5s9fSO9ehwOwcOE7FPc9kqefuZPWrVvWa5a89lHe5Lmf2rZrxZHDvokk+vfvQVFREUuWfEjLltvXf5Yc91PerFy5kuHDxzJq1JEMG3Zw1nFypyF8lur7d0JJ7YBDgYuAcenlh4NYe6ndjcC5JAXpEel7gL8DEyQpItaj9q0Zn7LfOC8BfWuprfI/3CC5RPmfEdErfXWJiMI7ET4teH8D8OOI6A6cB2xZwT6KgKUF7fWKiM7p0P2c9HV+wfrfSNc5PiKWAhcAUyKiG3B4uX0UZqnIFwXvS0l+GVqf41tHRFwTEcURUdyy5cYVZ/369WLevPnMn/8WK1as4LbbJjF06EEb1WZt6N69I+/89xnemD+VN+ZPpV271sycdU+9F6OQ3z7Kmzz30xFHHMjUKc8A8Oqr81mxYiUtWnw1kyx57qc8iQhOOul0OnXag3HjxmYdJ5f8WfqSFpJmFrwq+uD8HjgDWJ1O70BSG6xKpxcCbdP3bYESgHT5R+n6tc4F6cZ5DGha+AOX1ANYCoxMC72WwAHAdOCJSuYD9E+v4SgiGQ5/Enga2FdSh7TtrVX5HfzbAG9L2gI4rmD+J+kyIuJjYL6ko9P2JKlnRJQWFIW/ruJ4twUWpe9HV7Hemn1WY32Or840btyYCRMuZMiQUXTuPJARIw6na9eO9R2DUaN+xr77jOCVV+azy877cd11d9R7hsrkpY/KO/bYH7H33kN55ZXXadeuL9ddNzHTPHnpp+NGjWO/fY7hlVfms+vOB3D9dXdwwphvM39+CT27H8Zxx47j+hvGZ3a6Pi/9VChvnyWAp56awc0338mUKU/Ru/cQevcewgMPPJZpprz1Ux4/S+tDQJFUay9gSdlgTfq6Zp39SYcB70ZERZcbZkp1MOq6WZG0E8lvG31JTrEvAH5Gcjr5YJKRzgsj4vZ0WPw3FcwfSHLd5CdAB2AK8KOIWC1pEMk1G2Wn1v83Iu6VtAAojoglaY4fkvzG8x7wDLBNRIyWtC/wZ5IRyuEkvxH9CWhDcsr9togoHBUtO6512k/n7U0ylP8pcD/wnYhon14jWhwRP07X24LkkoEdSEZuPyy3/D7gkoiYWtPjq0pxcXHMnDkTWFzdqvVk7QX2q+O1DHOsVZTU/Kk89FPhI6zykAfynqk08vEom0br/M6Yv37KY6aIhRnmSCRnacvkr4/ylKm4uCczZz5XL7+tFbVqFluM7FFr7a24YtqsiCiubLmk/wd8F1hFcpazOcnTgoYArdN7RPYGzo2IIZIeSt9PU/IUnXeAlnVxyt4FaQ6UvwnI1o8L0uq5IK2JfGdyQVqVfP/sXJBWJp8/t4ZckBYqrD0k3QHcWXBT0/MRcaWkU4DuEXFyelPTsIgYUWuBC/iUvZmZmVlGcvJc/DNJbnB6jeTsZtnXgl0H7JDOHwectXG7qZzvss+BiJgKTM04hpmZmW0mCmuP9Ck//StY53Pq+FngZVyQmpmZmWXEzwJOuCA1MzMzy4jr0YSvITUzMzOzTHmE1MzMzCwDwiOkZVyQmpmZmWXE15AmfMrezMzMzDLlEVIzMzOzLMin7Mt4hNTMzMzMMuURUjMzM7NMyNeQplyQmpmZmWXE9WjCBak1IDtlHeBLitQh6wgVyFs/5S0P5DFTI+2ZdYQK5K+f8phJapd1hHLy10f5zGT1yQWpmZmZWQaEb+Yp44LUzMzMLCO+hjThgtQakMVZB0gVnnrKX6aVq2dlmCOxRVHfgqn89VEeM0UszDDHWuuefs5fPzlTZfKWB/KfyeqTC1IzMzOzjHiANOGC1MzMzCwLfjD+Gr6W1szMzMwy5RFSMzMzswwI39RUxiOkZmZmZpYpj5CamZmZZcQDpAkXpGZmZmYZ8Sn7hE/Zm5mZmVmmPEJqZmZmlhEPkCZckJqZmZllxPVowqfszczMzCxTLkjNgMmTp9Cx4/506LAv48dPyDoOkH2mzz//gn32Op6+vY+lZ/cRnHfu1QCMPel8+vY+lj69jmHk0WewbNln9Z6tTNZ9VJG8Zfr8888ZMOAwevU6iG7dBnPOOb/LOhKQv36C/GXKWx5wptomJTc11dZrU+aCdCNIKpU0p+B1VgXrDJR0Xy3vd6CkfTZguwWSWlQwf7SkDfpbLOmX5ab/nf7ZXtKoDWmjvpWWlnLKKWfz4IO3MHfuFCZOvIe5c1/NMlIuMjVt2oSHH7mKWbMnMvPZv/LwQ//mmadf4JJLxzFr9kSenXMbu+zSmiv/+Ld6zVUmD320KWRq2rQpjz56O3PmPMzs2ZN56KGpPP30s5lmymM/5S1T3vI4k9U1F6QbZ3lE9Cp4ja+n/Q4E1rsgrSPrFJMRUZarPVCjgrR8G/Vt+vTZdOjQnt1225UmTZpwzDFHMGnSQ1lGykUmSTRrthUAK1euYuXKVUiiefNmAEQEy5d/kdkF+Xnoo00hU/Jz3BpY9+eYpTz2U94y5S2PM9UdqfZemzIXpHVA0rck/UfSs8CwgvnnSjqtYPpFSe3T98dLel7Sc5JuTucdLukZSbMlPSKpVbr+ycCp6ajs/pJaSrpT0oz0tW+6/Q6SHpb0kqRrqcG105JukPQHSf+W9Iak4en8NpIeT/f5Yrrf8cBX0nm3pustS5saD+yfLju1/CispPvSkd6K2viOpOnpvKslNdqwn0TNLFr0DjvvvNOa6Xbt2rBo0Tt1uctq5SVTaWkpxX1G0bb1Nxl84AD6D+gGwEljzmPnnYbwyisLOOXHx9R7LshPHxXKYyZIfo69ew+hVateHHjg/gwY0DvTPHnsp7xlylsecKa6UqTae23KXJBunLJCquw1UtKWwJ+Bw4G+QOvqGpHUFfhfYFBE9AR+mi56EtgrInoDtwFnRMQC4CrgsnRU9gng8nS6H/Bt4Np0+3OAJyOiK3A3sEsNj6sNsB9wGElhCclo50MR0QvoCcyJiLNYO0p8XLk2zgKeSJddVtmOyrchqTMwEtg33VcpUL5tJI2VNFPSzPfee6+Gh2Xrq1GjRsx89q/Mf+sBZs54iRdffA2Aa68/hzcXPkinTl/jjtsfzjilVadRo0bMnv0QJSXTmTFjDi+++J+sI5mZrcMF6cYpf8r+dqATMD8i5kVEALfUoJ1BwB0RsQQgIj5I57cDHpL0AnA60LWS7Q8EJkiaA9wLNJfUDDigbP8RcT/wYQ2P656IWB0Rc4FW6bwZwAmSzgW6R8QnNWxrfQ0mKeRnpMczGNit/EoRcU1EFEdEccuWLTdqh23btqakZPGa6YUL36Zt22p/j6hTecu03Xbb8PWBxTz80LQ18xo1asSIkQdx912PZZIpb30E+cxUaLvttmXgwH2YPHlqpjny2E95y5S3POBMdaP2bmjK+lKcjeWCtH6tYt0+37Ka9a8AJkREd+AHVaxfRDKSWlYYt42IZZWsi6RTCkZ1d6pglS8KVweIiMdJCtxFwA2Sjq8me3k1PXYBNxYcS8eIOHc997Ve+vXrxbx585k//y1WrFjBbbdNYujQg+pyl5tEpvfe+5ClS5PfO5Yv/5xHH3mGPffclddeKwGSa0jv+8fjdOzUvl5zlclDH20Kmd57732WLv0IgOXLl/PII4/TqVOHTDPlsZ/ylilveZypbghfQ1rGD8avff8B2kvaPSJeB44tWLaA5DQ4kvoAX0vnPwbcLenSiHhf0vbpKOm2JAUgwPcK2vkEaF4w/TDwE+C3adu9ImIO8DjJqfYLJR0MfBUgIv4I/LFs45r8ViVpV2BhRPxZUlOgD3ATsFLSFhGxstwmnwDblDv2H0kqAtoC/QuWFbbxKDBJ0mUR8a6k7YFtIuLNakNuoMaNGzNhwoUMGTKK0tLVjBkzkq5dO9bV7jaZTG+/vYQTTziH0tLVrF69muFHf5NDDt2Pb3z9JD7++FMigh499mTClV96uES9yEMfbQqZ3n77XUaPPpXS0lJWr17N0UcfzmGHHZhppjz2U94y5S2PM1ldU3JW2TaEpFLghYJZkyPiLEnfAn4PfAY8AeweEYdJ+gowiaQgewbYGzg4IhZI+h7JaflSYHZEjJZ0BHAZyan2x4B+ETFQ0p7A34HVJIXoyyQFZmeSXzIej4iTJe0ATEz392/gIKBv2aUBBccxGiiOiB9LugG4LyL+ni5bFhHNCvKtBJYBx0fEfEkXA0OBZ9NrQMvW3wJ4CNgBuCHtj1tITse/TFIcnxsRUytoYyTwC5IR1ZXAKRHxdGU/h+Li4pg5cyawuLJV6lnhoHP+Mq1cPSvDHIktivoWTOWvj/KYKWJhhjnWktoVTOWvn5ypMnnLA3nNVFzck5kzn6uX8cambZtHmx/0q7X23jznsVkRUVxrDdYjF6S2yXNBWhMuSKuX75+bC9Kq5Ptnl49MecsDec1U3wXpTifXXkG64NebbkHqa0jNzMzMLFO+htTMzMwsI5v4vUi1xiOkZmZmZpYpj5CamZmZZWRTf35obXFBamZmZpaBsueQmk/Zm5mZmVnGPEJqZmZmlgWBijxECi5IzczMzDLja0gTPmVvZmkQWgsAACAASURBVGZmZpnyCKmZmZlZJuQR0pRHSM3MzMwsUx4hNTMzM8uIB0gTLkitAdkp6wAVyF+mLYr6Zh2hnPz1UR4zSe2yjlCB/PWTM9VE3vJAPjPVveQ5pK5IwafszczMzCxjHiE1MzMzy4KfQ7qGC1JrQBZnHSC19tRTxMIMc6y17unePPTT2j6a99GtGeZYa49tjyuYykMfQWE/rVr9fIY51mpc1KNgKn/95EyVyVseyH+m+uFT9gmfsjczMzOzTHmE1MzMzCwjHiFNuCA1MzMzy4QfjF/Gp+zNzMzMLFMeITUzMzPLgATy0CDgEVIzMzMzy5hHSM3MzMwy4mtIEy5IzczMzDLigjThU/ZmZmZmlimPkJqZmZllxSOkgAtSMzMzs2zIp+zL+JS9GTB58hQ6dtyfDh32Zfz4CVnHoaRkMYMGjaBr10F06zaYyy+/LutIjBkzjh137EG3boPqdb+/OOUa9urwIw7d+6w18x685xkO2etMOn71u7ww+40185+b9TpD9/slQ/f7JYfv+0se/seMes0K+fgslZS8w4GDT6RHt6Po2f0o/vCHW9csmzDhr3TrcgQ9ux/FWWdelkk+yEc/Fcrq812VvPUROJPVHRekVZBUKmlOweus6reqUbsLJLWojbY2YN/9JT0u6RVJsyVdK2mrLLLkRWlpKaeccjYPPngLc+dOYeLEe5g799VMMzVu3IhLLvkVL730GNOmTeLKK2/MPNPo0SOYPPnW6lesZcNGHcB1fz99nXl7dG7HhJt/Sr99Oq4zf8/O7bhr6gXc++T/cd2dp/PrU//CqlWl9ZY1L5+lxo0b8ZvfnsbzL97Nk/++hauuvI25c19n6pTp/OPeqcyafQfPvXA3435+fL1ng/z0U6GsPt+VyWMfOVPdUFHtvTZlm3j8Orc8InoVvMZnHWhjSGoF3AGcGREdI6I3MBnYJttk2Zo+fTYdOrRnt912pUmTJhxzzBFMmvRQppnatGlFnz7dAdhmm2Z07tyBRYveyTTTAQfsxfbbb1fv++23bye2/WqzdeZ16NiW3fbY6UvrfmWrpjRu3AiALz5fWe+XZuXls9SmTUv69OkMwDbbbE2nTruxeNG7XH3VHZxxxhiaNm0CwI477lDv2SA//VQoq893ZfLYR85kdckF6QZIRzj/XzpqOlNSH0kPSXpd0snpOgPTkcj709HIq6Qv//4iaZykF9PXz9J555e9T6cvkvTT9P3pkmZIel7SeQXrfEfS9DTT1ZIaVRD9FODGiJhWNiMi/h4R/5W0vaR70nafltQjbfdcSTdKekLSm5KGSfqNpBckTZa0RUGflM2fLqlDOv9wSc+ko7GPpEVxWbvXS5oq6Q1J/1PdsdeVRYveYeed1xY37dq1ybz4K7RgQQmzZ7/EgAG9s46ySXhu5mscsteZHL7vLzjv0hPWFKj1IY+fpQULFjFnzn/oP6A7r857kyeffJZ99j6OQd8Yw4wZL2aSKY/9lDd57CNnqn1Kv8u+tl6bMhekVftKuVP2IwuWvRURvYAngBuA4cBewHkF6/QHfgJ0AXYHhhU2LqkvcAIwIN32+5J6A9cDx6frFAHHALdIOgjYI223F9BX0gGSOgMjgX3TTKXAcRUcTzdgViXHeh4wOyJ6AL8EbipYtjswCBgK3AJMiYjuwHLg0IL1PkrnTwB+n857EtgrHY29DTijYP1OwJD0eM5Ji9sKj718WElj018GZr733nuVHNKmb9myTxk+/Adcdtm5NG++WQ9k11jP4g488PTF/P2x87n6sn/wxecrso6UmWXLPmPE0T/nd5eeTvPmzShdtYoPPviIp/59C+MvPpVRx5xORGQd02yz5oI04bvsq7Y8LfAqcm/65wtAs4j4BPhE0heSys77TI+INwAkTQT2A/5e0MZ+wN0R8Wm6zl3A/hHxB0nvp8VpK5JC8f20ID0ImJ1u34ykQO0B9AVmpB/IrwDvruex7gd8GyAiHpO0g6Tm6bIHI2KlpBeARiSn+cuOvX1BGxML/iy7W6IdcLukNkATYH7B+vdHxBfAF5LeBVpFxIKKjr182Ii4BrgGoLi4eKP+R23btjUlJYvXTC9c+DZt27bemCZrxcqVKxk+fCyjRh3JsGEHZx1nk9OhY1u23npLXn15Id1771Yv+8zTZ2nlypWMGD6OY0cdwlHDDkzzteKoowYjif79u1NUVMSSJR/SsuX29ZotT/2UV3nsI2eyuuQR0g33Rfrn6oL3ZdNlhX75Qml9CqdrgdEkI6jXp/ME/L+Ca1o7RMR16fwbC+Z3jIhzJR1VMLpbDLxEUriury8AImI1sDLWDqkUHmv54yt7fwUwIR05/QGwZfl2U6UFbVV07HWmX79ezJs3n/nz32LFihXcdtskhg49qK53W6WI4KSTTqdTpz0YN25splk2JSUL3l1zE9Oit5bwxrzFtN2lZb3tPy+fpYjg+yedS6fOu3HqqWtvXBp6xDeYOjV58sCrry5gxYqVtGjx1XrPl5d+yrM89pEz1QF5hLSMR0jrVn9JXwPeJDmlfk255U8AN0gaT1JUHgV8N112N3A+sAUwKp33EHCBpFsjYpmktsBK4FFgkqTLIuJdSdsD20TE3Wk7AEgqAaZLuj8inknnDQOeSrMcl7Y/EFgSER+v5wd8JDA+/bPsOtVtgUXp++/VsJ2Kjr3ONG7cmAkTLmTIkFGUlq5mzJiRdO3asfoN69BTT83g5pvvpHv3TvTuPQSAiy46k0MOye6RNMce+yOmTp3GkiUf0K5dX8477zROPPHYOt/vqSdOYPqTL/Ph+8vYv8tP+J+zvs22X92aC868iQ+WfMLYEZfQufuuXH/Xmcx6+lWu+f0/aNy4EUVF4pxLRrP9DvV3qUNePktPPTWbW2+5j27d96BvnxEAXHjhTzhhzFGcdOKv6dVjGFs02YLr/3JBJv+J5aWfCmX1+a5MHvvImeqGijbtQrK2yNcPVU5SKclp6TKTI+IsSQuA4ohYIml0+v7H6TYLgGKS6zXPBz4BOgBTgB9FxOpy248DxqTtXxsRZddeIukqYGlEnFUw76fASenkMuA7EfF6en3rL0hGvVcCp0TE0xUc097Ab4AdSUY4HwdOJRm5vB7YDfgMGBsRz0s6F1gWEZek2y+LiGbp+zXL0mO6HTiYZOTz2Ih4TdIRJKfvPwQeA/pFxMAK2n0ROCwiFlR27JUpLi6OmTNnAourW7WerL3APmJhhjnWktoVTOWhn9b20byP8vGonT22LbzsOg99BIX9tGr18xnmWKtxUY+Cqfz1kzNVJm95IK+Ziot7MnPmc/VSJW7d/qvR9VeDa629GSfdOSsiimutwXrkEdIqRESFt+dGRPuC9zeQ3NS0zrJ01OHjiDismu0vBS4tv056Q89ewNHltr0cuLyCNm8nKQirlN5hv38Fiz4Djqxg/XPLTTerbBnw24g4s9z6k4BJNWi3W9n7yo7dzMysYdn0T7XXFl9DmkOSugCvAY9GxLys89SnzfnYzcxs8yKSr7KvrdemzCOkdSQipgJTN3DbuSSnzjcZhaO+G9nOJnfsZmZmtnFckJqZmZllQfiUfcqn7M3MzMwsUx4hNTMzM8uIR0gTLkjNzMzMMuLnkCZ8yt7MzMxsMyBpS0nTJT0n6SVJ56XzvybpGUmvSbpdUpN0ftN0+rV0efu6yuaC1MzMzCwL9f/VoV8AgyKiJ9AL+JakvYCLgcsiogPJF9mcmK5/IvBhOv+ydL064YLUzMzMLAP1/RzSSCxLJ7dIXwEMAv6ezr+RtV+Uc0Q6Tbp8sOroolcXpGZmZmYNQwtJMwteY8uvIKmRpDnAu8A/gddJvqp7VbrKQqBt+r4tUAKQLv8I2KEugvumJjMzM7NM1PpXhy6p7rvsI6IU6CVpO+BuoFNtBthQHiE1MzMz28xExFJgCrA3sJ2kskHKdsCi9P0iYGeAdPm2wPt1kccjpNaA7JR1gC+R2mUdoQL56qc9tj0u6wgVyFcfATQu6pF1hArkr5+cqSbylgfymal+1OdjnyS1BFZGxFJJXwG+SXKj0hRgOHAb8D1gUrrJven0tHT5YxERdZHNBamZmZlZFur/q0PbADdKakRylvxvEXGfpLnAbZIuBGYD16XrXwfcLOk14APgmLoK5oLUzMzMbDMQEc8DvSuY/wbQv4L5nwNHr88+JH1M8gCBwpFUkdScTSOiwstFXZBaA7I46wCpwlNPzlSxtXkiFmaYY611L6/IQx9B/n5u4Ew1lbdMecsD+c9UTxrYV4dGRPPCaUnNgFOAscBdlW3ngtTMzMwsIw2sHl1D0leBn5Jcg3or0C8iPqhsfRekZmZmZlYrJO0I/BwYQXINao+I+KS67VyQmpmZmWVAQFHDGyJ9g+TRUNcBy4GxhTduRcTvKtrIBamZmZlZJmr9wfh5cDFJrQ2wdU03ckFqZmZmZrUiIi7YkO1ckJqZmZllQQ3vlH16Den3gfYU1JkRcUJV27kgNTMzM7PaMgn4F/AQsLqmG7kgNTMzM8tAA72pacuIOGt9N6rwaflmZmZmVveKpFp75cRDko7Uet6t5YLUzMzMzGrLj4A7geWSPk5ffg6pmZmZWV41tMc+lf/q0JryCKkZMHnyFDp23J8OHfZl/PgJWccB8pcpb3lKShYzaNAIunYdRLdug7n88uuyjgTkr5/GjBnHjjv2oFu3QVlHWUfe+gnylylvecCZapsQRbX4ygNJX6/oVd12Lkg3kqRSSXMKXu3rcF+jJW3U3zZJ/SU9LukVSbMlXStpq9rKuCkqLS3llFPO5sEHb2Hu3ClMnHgPc+e+6kw5zgPQuHEjLrnkV7z00mNMmzaJK6+8MfNMeeyn0aNHMHnyrZlmKC+P/ZS3THnL40y2Hn5e8PolcDdwXnUbuSDdeMsjolfBa0HWgcpIalxuuhVwB3BmRHSMiN7AZGCbLPLlxfTps+nQoT277bYrTZo04ZhjjmDSpIecKcd5ANq0aUWfPt0B2GabZnTu3IFFi97JNFMe++mAA/Zi++23yzRDeXnsp7xlylseZ6o7Raq9Vx5ExNCC1xCgE7C0uu1ckNYBSb0kPS3peUl3S/pqOn+qpOL0fQtJC9L3oyXdJWmypHmSflPQ1gmSXpU0Hdi3YH5LSXdKmpG+9k3nnyvpZklPATeXi3YKcGNETCubERF/j4j/Stpe0j1p5qcl9Sho70ZJT0h6U9IwSb+R9EKad4t0vQUF86dL6pDOP1zSM+lo7CNpUVzW7vVpn7wh6X/S+edL+lnBcV4k6ae19KOp0KJF77DzzjutmW7Xrk3mhU3eMuUtT3kLFpQwe/ZLDBjQO9Mcee+nvMhjP+UtU97ygDPZBlsKdKtuJRekG+8rBafr707n3UQyCtkDeAE4pwbt9AJGAt2BkZJ2ltSGZJh7X2A/oEvB+pcDl0VEP+DbwLUFy7oAB0bEseX20Q2YVcn+zwNmp5l/mR5Dmd2BQcBQ4BZgSkR0B5YDhxas91E6fwLw+3Tek8Be6WjsbcAZBet3AoYA/YFz0uL2euB4AElFwDHpPtchaaykmZJmvvfee5Uckm0Oli37lOHDf8Bll51L8+ab9WC/mW1qlNzUVFuvPJD0mKQp6etfwBskZ2er5LvsN97yiOhVNiFpW2C7iPhXOutGavCDAB6NiI/SNuYCuwItgKkR8V46/3Zgz3T9A4EuBR/A5pKape/vjYjl63kc+5EUtkTEY5J2kFR2p9yDEbFS0gtAI5LT/JAU2+0L2phY8Odl6ft2wO1pcd0EmF+w/v0R8QXwhaR3gVYRsUDS+5J6A61IiuT3y4eNiGuAawCKi4tjPY91HW3btqakZPGa6YUL36Zt29Yb0+RGy1umvOUps3LlSoYPH8uoUUcybNjBWcfJbT/lTR77KW+Z8pYHnKkuNNAH459W8L4pcBAwr7qNPEJav1axts+3LLfsi4L3pVT/y0IRychj2bWrbSNiWbrsUwBJRxWM3hYDLwF9NyD3FwARsRpYGRFlBeDqcjmjgvdXABPSkdMfsO5xV3bM1wKjgRNIRkzrVL9+vZg3bz7z57/FihUruO22SQwdelBd73aTypS3PAARwUknnU6nTnswbtzYTLOUyWM/5VEe+ylvmfKWx5mspiLi2YLXtIg4D6j20juPkNayiPhI0oeS9o+IJ4DvknynK8ACkoJwOjC8Bs09A1wuaQfgY+Bo4Ll02cPAT4DfQnLdakTMKZflbpK720jXKQGmS7o/Ip5J5w0DngKeAI4DLpA0EFgSER+v5ymAkcD49M+y61S3BRal779Xw3buBs4HtgBGrU+ADdG4cWMmTLiQIUNGUVq6mjFjRtK1a8e63u0mlSlveQCeemoGN998J927d6J37yEAXHTRmRxySHaPN8pjPx177I+YOnUaS5Z8QLt2fTnvvNM48cTyV/PUrzz2U94y5S2PM9WdhjZCqnUf8VREcili+UG4L2+3drDLNoSkZRHRrNy8XsBVwFYk106cEBEfSuoE/I1kNPB+4DsR0V7SaKA4In6cbn8fcElETJV0AvALkouC5wArIuLHkloAfwQ6k/xi8XhEnCzpXGBZRFxSSd69gd8AO5KMcD4OnEryYbke2A34DBgbEc+Xb6/weAuXpTdo3Q4cTDLyeWxEvCbpCJLT9x8CjwH9ImJgBe2+CBxW9pQCSVcBS2vyfbjFxcUxc+ZMYHF1q9aTnQreO1PF1uaJWJhhjrWkdgVTeegjyN/PDZyppvKWKW95IK+Ziot7MnPmc/VSJW6/R8s48PJv11p7dxx69ayIKK61BjeApHsLJleRDMZdERHzK94i3c4FqdWGtCAtjogltdBWEfAscHREVHvdiQvSmshbJhekNZO3nxs4U03lLVPe8kBeM7kgzYZP2VuuSOoC3AfcXZNi1MzMbNMllJNvWKotkv5S1fKIOKGi+S5IrVZERPtaamcuyWUDZmZmDV5Du4aU5JGQu5A8YUjACOBN4J9VbeSC1MzMzMxqSz+gf8ETeW6QNCMifljVRpUWpJKuYN3H+KwjIv5ng2KamZmZGVKDHCHdhuRM5+sA6Tc3VvutJVWNkM6snVxmZmZmtpk4FZgiaT7JwObuwMnVbVRpQRoRNxZOS9oqIj7b2JRmZmZmlmhoI6QR8WA6KtqR5BrS/0TEiuq2q/abmiTtnX6V5X/S6Z6SrtzYwGZmZmabO6n2Xnmg5Bt1vgecA/wK+F76OMcq1eSrQ38PDAHeB4iI54ADNjyqmZmZmTVQFwKHAFeTfEtTS5JvcaxSje6yj4iScl8hWboBAc3MzMwsJRreKXvgcKBPRKyStDwi/k/SM9VtVJOCtETSPkBI2gL4KfDyRoY1MzMz28ypIRakiohVayakJkDT6jaqySn7k4FTgLYk3+3VK502MzMzMyv0rqQ90vfNgaeAP1a3UbUjpOl3kx+3cdnMzMzMrLyG9tWhwJGsvbTzB8C8iHizuo2qLUgl7QZcDuxF8jypacCpEfHGhmc1qws7ZR2gAs5UHald1hEqkK8+SjhTzThT9fKWB/KZyTZQH4D03qOVQHtJ7SPiX1VtVJNrSP9KMtR6VDp9DDARGLDBUc3MzMw2cw30m5p+XvB+a6A/MJtqntBUk4J0q4i4uWD6Fkmnr38+MzMzMyvU0ArSiBhaOC1pF+CK6rar6rvst0/fPijpLOA2klP2I4EHNjyqWd2IWJh1BGDdU9A1uGymXki7rnkfUZJhkoS085r3n5dOyTDJWls2+kbB1OLMcqxr7WlMHdQlwxxrxcNz177P4ed7dSzILkiBIrUvmMrD52ntZymP/1bmo4/Alw7Uvoh4S1JHSY0iotLHhlY1QjqLpAAtK91/UNg+8IuNj2lmZma2eWqgzyH9kojoVN06VX2X/ddqN46ZmZmZrSW0GRSkNVGjb2qS1A3oAmxZNi8ibqqrUGZmZma2+ajJY5/OAQaSFKQPAAcDTwIuSM3MzMw2QlEDHCCV1Jrk7nqAGRHxdnXb1OSbmoYDg4F3IuIEoCew7QanNDMzM7PkGlJUa688kDSS5Jn13waGAU9LOra67Wpyyn55RKyWtEpSc+BdYOfqNjIzMzOzzc7ZQN+I+ADWPLVpKskz7CtVk4J0pqTtgD+T3Hm/jKTyNTMzM7MN1TAfjA/wUcH7pTXZoCbfZf+j9O1VkiYDzYEl65/NzMzMzBq4+4DJkspGRI8D7q9uoxrdZV8mInnisKS3gF3WM6CZmZmZFWhoj32KiF9KOozkhniAyyPi3uq2W6+CtEDD6j0zMzOzetZQH4wfEfeRjJQCIOlXEXFBVdtsaEEaG7idmZmZmTVQkh7jywOXxZL2Aa6LiL9XtF2lj32SdIWkP1TwugLYrvaim2WrpGQxgwaNoGvXQXTrNpjLL78u60gALF36EUcf/UM6dx5Ely6DmTZtVtaR+NrX9qFHj2/Su/e36Nfv0EwydNz9WIp7nciAvt9n3wEnA/CLM66iZ9fv0a/3SYz49q9YunRZJtkAJk+eQseO+9Ohw76MHz+hXvddVFTEs1feyT/Ov3LNvAtH/5RXrn+Audf+g58c+R0Avt6jH0vvfobZf7qL2X+6i18d98N6zQn5/Hz/4fK/0KP7ELp3O4jLf3991nEy/SxV5PPPP2fAgMPo1esgunUbzDnn/C7rSED++mn9iCLV3isnTgN+XvAaBywELgDOr2yjqkZIZ27gMttMSGoH/JHkSxOKSIbnT0+nd4qIB9L1zgWWRcQlGUWtUuPGjbjkkl/Rp093PvlkGcXFh/DNb+5Ply57ZprrZz87jyFDvs4dd/yJFStW8NlnyzPNU+axx26nRYvtM80w+ZFLadFi7eOQBx/Ylwv+7/s0btyIs8+6ht+O/ysXjR9b77lKS0s55ZSz+ec/J9KuXRv69TuEoUMPqrfP0k+P+i4vv/U6zbdqBsDog45i55at6XTioUQELbdb+3N74oVZHP7rH1XWVJ3L2+f7xRdf4dprb+PpZ+6hSZMtOOTg0Rx62CA6dGifSZ6sP0sVadq0KY8+ejvNmm3NypUr2X//YRx88DfYa68+mWXKYz+trwZ4Demz5edJujci/i2p0gfkVzpCGhE3VvWqreC2aVLyN+gu4J6I2APYE2gGXAT0Ag6pxX01qq22KtKmTSv69OkOwDbbNKNz5w4sWvROXe6yWh999DGPPz6dE08cCUCTJk3Ybjt/H0VlDjyoH40bJx+T/nt1ZtGi9zLJMX36bDp0aM9uu+1KkyZNOOaYI5g06aF62XfbFq04tP/XuXbynWvm/fCwkZx/65+ISK6yem/pB/WSpTp5/Hy//PJr9O/fi622+gqNGzfmgAP6c/ddkzPLk+VnqTKSaNZsawBWrlzFypWrMi+m8thP9mURcWb65+DK1qnJNzWZVWQQ8HlE/AUgIkqBU4GTgN8AIyXNSb+xAaCLpKmS3pD0P2WNSPqOpOnpuleXFZ+Slkn6naTngL3r66AWLChh9uyXGDCgd33tskLz55fQsuUOjBlzGn36HMJJJ53Jp59+lmkmSP5DGjLkOxQXH8I119yaWYbDDz6dffr/gOv+fN+Xlt/0lwcZ8q3+FWxZ9xYteoedd95pzXS7dm3q7Zeb3//wLM649hJWr169Zt7uO+3CyK8fzIwJf+OBi66mw067rlm2d5dezPnTXTxw0dV02bVDvWQsk8fPd7duHXnyyem8//6HfPbZch58cColJdV+22GdyfKzVJXS0lJ69x5Cq1a9OPDA/TP/tzKv/VRTSp9D2sBO2W8QF6S2obqSfFHCGhHxMbAAuBC4PSJ6RcTt6eJOwBCS77Y9R9IWkjoDI4F9I6IXUEryvDKArYFnIqJnRDxZfueSxkqaKWnme+/VzmjYsmWfMnz4D7jssnNp3nybWmlzQ61aVcqzz77IySd/h2effYCtt/4K48f/KdNMAE88cSezZj3AAw/cxJVX3sTjjz9T7xke/dflTJtxDffcN56r/3QPTz7+3JplF//fLTRq3IhjRh1Y77mydOiAr/Pu0g94dt7cdeY33aIJn6/4gn4/HsGfH7iD639+IQDPvjaXXb9zIL1+OIwr7rmVe869ol7z5vHz3blzB04/42S+NeR4Djn4e/Ts2YVGjer05MwmqVGjRsye/RAlJdOZMWMOL774n6wjWQPhgtTqy/0R8UVELCH5+tlWwGCgLzBD0px0erd0/VLgzgpbAiLimogojojili1bbnS4lStXMnz4WEaNOpJhww7e6PY2Vrt2rWnXrvWa0Yfhww9h9uwXM04Fbdu2BmDHHVtw5JFDmD59TgYZWqYZvsrQI/ZjxozkP8Sbb5zMA/c/zQ03n53ZacS2bVtTUrJ4zfTChW+v6bP/z96dx2lV1+8ff13DkhtugcomqCgiOw6iloZLYuSSK6JmiEua+s3UUrNfaVlhWWailqlZamDmgisuCO4Jg6go5pKYgBuUG6Igw/v3xzk3HMYZZgZm5pwZrqeP+8F9zn2W63y8Gd7z+ZylMX2p9yAO2HkPZv/1Acb/8DfsOWAI1599EXMXvM2tjz8AwG2PP0i/rZPz6j5a9DEff5r0SN477RHatGrNFzdsumtVi/r9Pu64EUyruJMpD/+dTTbZiO222yq3LHl9l+pq4403YujQXZk4cUquOYreTnVR1oCvopB0kKTfpq+D67LO6lxl/3tJv2+42NZMzSIpJpeTtCHJAxOWVrP84sz7SpIL6gT8Je1JHRARPSPi/HSZT9PTABpdRHD88d9n++235Ywzmv5CmOpsscVmdO3aiZde+jcAkyY9Tq9e2+aa6eOPF/HRRwuXv3/ggUfp06dnE2f4hI8+WrT8/YMPVNC791bcP3Eqv734Jv5x+4Wst946TZopa/DgAbzyymxmz36DJUuWMH78BA44YJ9G3+8Pr72ErkftyVbHfJUjfnEmDz3zFN+86Gxuf3wSe/QfAiRX1r88CYQbzAAAIABJREFU93UANt+k/YrMPftSVlbGfz+s09P9GkQRv98A776bPITwjTfmcdttExl55IG5Zcnru7Qq8+f/l/ffT54I+cknn/Dgg4+w/fZNe7pHVUVsp/qS1GCvIpB0EXAi8Fz6+rakX9e23upeZW82CRgj6ZiI+Gt67udvgOuAd4AhddzGBEmXRMS7kjYF2kXEfxotdTUef3wa119/C337bs/AgcMA+PnPz2b48D2bMsbn/P7353P00aezZMlnbL11V669Nt+bFLzzznwOPjgp2JcuXcrIkd9g332HNmmGd995jxGH/jjNUMmII/Zin313onfPo1m8+DP22/f7AOw0ZAcuu+J7TZoNoHXr1owdeyHDhh1JZeUyRo8eQe/eTVu0Z4256WpuPOdXfO/gY1j4ySKOvyRpu0N324eT9zuCpZVL+WTJYo74xZlNnq1o32+Aww49mf/+933atGnNZWN/ysYbb5hblqJ9lwDeeutdRo36HpWVlSxbtozDDtuf/fbL9/SYIraTMRzoHxGlE9qvkzST5C48NVLp6kuz+pLUFbiC5PzQMuAekvuPrQ/cB7QBfgn0InPbJ0nPA/tFxOvpRU/nput/BpwSEf+UtDAiNqhLjvLy8qioqCBibsMe4GpK7oaVaOLaukbSiotZIubkmCSRfHUSn1ZOzjHJCuu02iMz9WaNyzWtFRdraJ8dcsyxQty/4jzVIn6/lyVPuM5dmbpnporwfVrxXSriz8pitBFAJ8rL+1NR8WyTdDd26tUxjrvuuAbb3oU7/3x6RJQ32AZXQ3ox8t4RMT+d3gx4ICL6r2q9Wp/UJKkDcDbJvSWXj4VFRL7dR5a7SCqb/av5aDEweBXr9cm8vwm4qZpl6lSMmpmZNWdlxRhpb0g/A6ZKepTkyZ5DqaV3FOr26NAbSQqGrwMnAd8C8rnJn5mZmZkVVkT8Q9IjJHfVEfCDiHintvXqUpB+MSKukfTdiHgYeFjStDXMa2ZmZraWE/rcY99bhIEkPaOQnI5X61Mm6lKQfpb++Zakr5Oc6JHvcwPNzMzMmjlBs7+hfVWSfgAcAPw5nfUjSf0j4qJVrVeXgvRCSRsBZwKXARuSPJHHzMzMzCzrW0B5RHwCIOkGYBqwZgVpRJSezfcBsMeqljUzMzOzOlKLvKhpcakYBYiIxZJqva94Xa6y/zPJVVIriYjR9Y5oZmZmZi3ZPZI2iYj3ACRtDNxb20p1GbK/K/N+HeAginPDMDMzM7Nmq6Vd1BQRPwKQtEE6/T7ww9rWq8uQ/UrPE5c0Dnhs9WKamZmZGbTYi5p6AH8FuqTTbwJHRcS/V7Vejc+yX4Vtgc1WYz0zMzMza9n+CFwUEVtGxJbAL4A/1LZSXc4h/YiVzyF9m+TJTWZmZma2BlrgRU3tI2JCaSIi7pD009pWqsuQfbs1TWZmZmZmn6cWNmQPLJHUNiKWAEhqCyytbaW69JBOioi9aptnljepS94RPkfqlneEz5G65h1hJeu0KuLd5DrlHeBz4v5ZeUf4nCJ+v8vUPe8I1SjW96mIPyuL1ka2Rg4DWmWmy9J5q1RjQSppHWA9oL2kTWD5ZWAbAp1XP6eZmZmZCVHW8q6yf11SFyW/sWbrzNmrWm9VPaTfBk4n+bVlOisK0g+BsWuQ1czMzMxaIEljgMOBWcCy0mzg4VWtV2NBGhGXApdKOi0iLmuooGaNpyi3x80OPTlT9YqWB4qeKeI/OeZYYeVh+uK1kzPVpGh5oPiZmkYLvKjpIKBnRHxWn5XqctunZeld9gGQtImk79Q3nZmZmZllKLmoqaFeBTEbWL++K9XlSU0nRMTlpYmIeE/SCcAV9d2ZmZmZmbVoC4GnJU0CPi3NjIjTVrVSXQrSVpIUEQEgqRXQdk2SmpmZma3tBC3uoibgjvRVL3UpSCcCN0n6Yzr97XSemZmZma2BlnYOaUT8dXXWq0tBejZwInByOv0A8KfV2ZmZmZmZ5UPJjaj/CmxO8hTOqyLiUkmbAjcB3YHXgcPTUzQFXAoMBxYBoyLi6Vr28Rp8vts3IrZa1Xp1eVLTMpJnkP4h3dFuwGXAKbWta2ZmZmY1a+KLkZYCZ0bE05LaAdMlPQCMAiZFxBhJ5wDnkHRIfg3YNn0NAa5M/1yV8sz79YERQPvagtWlhxRJA4GRJPeVmg3cWpf1zMzMzKx6AsqasCCNiLeAt9L3H0l6keRhRwcCQ9PF/gJMISlIDwT+ml5H9E9JG0vqmG6npn38LzP5P+BiSRW1ZVvVk5q2IylCRwILSLpyFRFFfM6fmZmZ2dqufZXi76qIuKq6BSV1BwYCTwGbZ4rMt0mG9CEpVudkVpubzquxIK3BrySVpaPu1VpVD+m/gEeB/SLi1TT89+oZwMzMzMxqUJcbwtfDgogor20hSRsAtwCnR8SH2dMGIiIkxeoGkPRt4Gckt38aBcwENlxVMQqrboeDSSrgyZL+JGkvqjlJ1czMzMyaB0ltSIrRGyOidArmO5I6pp93BN5N588DumZW75LOW5WzgR2AA4ALI+I9kovjV6nGgjQibo+II4Dtgckkz7XfTNKVkvapbcNmZmZmtioN95SmulwclV41fw3wYkT8NvPRHcC30vffAiZk5h+jxM7AB6s6fzT1brrc80DpSZ9tastWl6vsPwb+BvxN0ibAYSTV7/21rWtmZmZm1ZOa9qIm4EvAN4GZkp5J5/0QGAP8XdJxwH9ILmIHuIfklk+vktz26dg67OMp4G5JNwLrS/pZuv4q1evUhYh4LyKuioi96rOeWdFNnDiZnj13o0ePLzFmzNi84wDFy1S0POBMdfX++x9w2GEn06vXnuyww148+eT0vCMVsp2KlqloecCZmruIeCwiFBH9ImJA+ronIv4bEXtFxLYRsXfpSvlInBIR20RE34io9Wp5oB3JxU9fAe4juUjqm7Wt1MDn0lpzJqlS0jOSnpd0p6SNa1n+fEln1bLMNyTtkJn+qaS9GypzQ6isrOSUU87j3ntvYNasyYwbdzuzZr3sTAXO40z1c/rpFzBs2Fd48cWHeOaZe+nVq0eueYrYTkXLVLQ8ztR4ytRwryKIiNGZ13ci4vKI+LS29VyQWtYn6W9LfUjuHdYQDz/4BsnJzQBExI8j4sEG2G6DmTp1Bj16dGfrrbvRtm1bjjjiQCZMuM+ZCpzHmerugw8+5JFHpnLccSMAaNu2LRtvvFGumYrYTkXLVLQ8ztR41ID/FYGkayX9ueqrtvVckFpNniS51xiStpE0UdJ0SY9K2r7qwpJOkDRN0rOSbpG0nqRdSa6y+3Xa87qNpOskHSppX0k3Z9YfKumu9P0+kp6U9LSkm9PbUzSaefPepmvXTsunu3TpyLx5bzfmLmtVtExFywPOVFezZ8+hQ4cvMnr0WQwaNJzjjz+bjz9elGumIrZT0TIVLQ84k9XZXcCd6et+YD3gw9pWckFqnyOpFbAXydV1AFcBp0XEjsBZwBXVrHZrRAyOiP7Ai8BxEfFEuo3vpz2v/84s/yAwRNL66fQIYLyk9sCPgL0jYhBQAZxRTcYTJVVIqpg/f/4aH7NZS7V0aSVPP/08J510NE8/fQ/rr78uY8ZcmXcsM6P0pKYWN2R/a+Y1LiJGsPLjRKvlgtSy1k2vuis9peGBtHdyV+Dm9LM/Ah2rWbdP2ns6EzgK6L2qHUXEUmAisL+k1sDXSW4zsTPJEP/j6f6+BXSrZv2rIqI8Iso7dOiwmoeb6Nx5C+bMeXP59Ny5b9G58xZrtM01VbRMRcsDzlRXXbpsQZcuWzBkyEAADj10ODNmPJ9rpiK2U9EyFS0POJOtHkm9WPHkpxq5ILWsTyJiAEkBKJJzSMuA9zNX4w2IiF7VrHsdcGpE9AUuANapw/7Gk9xaYk+gIiI+Svf7QGZfO0TEcWt+aDUbPHgAr7wym9mz32DJkiWMHz+BAw7I91a7RctUtDzOVHdbbLEZXbt24qWXkgGKSZMep1evbXPNVMR2KlqmouVxpsZTJjXYqwgkfSjpo/TPD0hGSn9Q23q13ofU1j4RsUjS/wG3kwzPz5Z0WETcnN5Ut19EPFtltXbAW+kTII5ixZMcPko/q87DwLXACSTFKcA/gcsl9YiIV9Mh/c4R0WiXTbZu3ZqxYy9k2LAjqaxcxujRI+jdu2dj7a5ZZipaHmeqn9///nyOPvp0liz5jK237sq1116ca54itlPRMhUtjzM1nqJcjNRQImLD1VlPEav9uFJrYSQtjIgNMtN3An8HHgOuJBmqbwOMj4ifSjofWBgRF0s6meQ3oPkkN8VtFxGjJH0J+BOwGDgU+H/AXRHxj3QfY0medbtZRCxK5+0JXAR8IY3yo4gonc/6OeXl5VFRUQG8WdMiTaxT5r0zVa9oeaDomSL+k2OOFaTsGTTFaydnqknR8kBRM5WX96ei4tkmqRK36tMlfnrLdxtse8ds/4PpdXmWfWOTNAz4ajo5KSLurW0d95DactliNJ3ePzO5bzXLn595fyVJ0Vp1mcfJ3PaJpPjMfn4qcGqVeQ8Bg+ue3MzMrPkpXdTUkkj6Ackddkq3ejpPUr+IuGhV67kgNTMzM8tDgc79bEDfAsoj4hMASTcA00hGPmvki5rMzMzMrKEsLhWjABGxGKisbSX3kJqZmZnlRC2vh/QeSZtExHsA6WPIfQ6pmZmZWRGJljdUHRE/ApDUDlgWEe8DP6xtvZbWDmZmZmaWE0ndJT0G/AuYL+lBSVvXtp4LUjMzM7OctLQb45Pcced3EdGZpCj9NnB5bSu5IDUzMzOzhtKxdK9xkvvd/xtoX9tKPofUzMzMLCct8KKmlWpLSTsBi2pbyT2kZmZmZjkoXdTUUK+CGC+pX/q+DfBLkkeEr5J7SM3MzMysQUTEhZn3feq6XoEKajMzM7O1i6QGexWBpFtKV9VLulLSc5IOq20995BaC9Ip7wDVcKbaFS0PFDGT1C3vCNUoXjs5U10ULQ8UM1MTKNbV8Q1l24h4TdJgYBtgGHA/cPOqVnIPqZmZmZk1tP2Av0fEW8DS2hZ2D6mZmZlZDpS+WpgHJT0FbAbsKGlD4IPaVnJBai3Im3kHSGWHnpypekXLA0XPVBkv55hjhVbaLjNVvHaKmJtjjhWkLpmpIrRTsb/fxcxkqyMizkivsp9Tep49MLS29VyQmpmZmeWkKBcjNaSIeK6+67ggNTMzM8tJWUsctF8NvqjJzMzMzHLlHlIzMzOznLTAEfvV4oLUzMzMLAeClngf0tXiIXszMzMzy5V7SM3MzMxyIl/UBLggNTMzM8uNR+wTHrI3MzMzs1y5h9TMzMwsB0K+D2nKPaRmZmZmlisXpGbAxImT6dlzN3r0+BJjxozNOw5QvExFywPOVJPjR59Lx813oX/f/ZbPu+D8y9iyy27sOPBAdhx4IPfc83Au2UqK0E5Zc+a8yZ57Hk7v3nvSp89eXHrpNXlHKlwbgTM1OCWPDm2oV3PmgrQZk3SepBckPSfpGUlDmmi/QyV9kO6z9Nq7lnVGSeqUmb5a0g7p+x82duZVqays5JRTzuPee29g1qzJjBt3O7NmvZxnpMJlKloeZ1q1Y0YdzN33Xv25+d89fRTTZ0xg+owJDB/+lSbPVVKUdspq3boVF1/8/3jhhYd48skJXHHFX/x3zpmahNRwr+bMBWkzJWkXYD9gUET0A/YG5jRhhEcjYkDm9WAty48ClhekEXF8RMxKJ3MtSKdOnUGPHt3ZeututG3bliOOOJAJE+7LM1LhMhUtjzOt2u67D2bTTTdq8v3WVVHaKatjx80ZNKgvAO3abUCvXj2YN+/t3PIUsY2cyRqTC9LmqyOwICIWA0TEgoh4U9KPJU2T9Lykq5T24UuaIukSSRWSXpQ0WNKtkl6RdGFpo5KOljQ17fX8o6RWdQ0kqXu67T+lPbf3S1pX0qFAOXBjut110zzlksYA66bzb5T0U0mnZ7b5c0nfbahGq868eW/TtevyWpkuXTrm+g8RFC9T0fKAM62OKy6/kYH99+f40efy3nsf5Jaj6O30+utzmDHjBYYMGZhbhiK2kTM1jrL0wqaGeDVnLkibr/uBrpJelnSFpNL429iIGBwRfYB1SXpRS5ZERDnwB2ACcArQBxgl6YuSegEjgC9FxACgEjiqhv3vVmXIfpt0/rbA5RHRG3gfOCQi/gFUAEelvamflDYSEecAn6TzjwKuBY4BkFQGHAHcsCYNZWZw0skjefnVB5g+YwJbdNyM7585Ju9IhbRw4ccceui3ueSS89lww3Z5x7EWTvgc0hLf9qmZioiFknYEdgP2AG6SdA7wkaQfAOsBmwIvAHemq92R/jkTeCEi3gKQ9BrQFfgysCMwLf1irwu8W0OERyMiW+wiqTswOyKeSWdNB7rX87hel/RfSQOBzYEZEfHfqstJOhE4EWDLLbeszy4+p3PnLZgz583l03PnvkXnzlus0TbXVNEyFS0POFN9bb55++Xvjz/hMA7c/6TcshS1nT777DMOPfREjjzyGxx88NdyzVLENnIma0zuIW3GIqIyIqZExE+AU0l6M68ADo2IvsCfgHUyqyxO/1yWeV+abk3yy9pfMueF9oyI8yUdlOkJLa8lVna7lazeLz1Xk5xzeixJj+nnRMRVEVEeEeUdOnRYjV2sMHjwAF55ZTazZ7/BkiVLGD9+AgccsM8abXNNFS1T0fI4U/299daK3y1vv+1BevfZNrcsRWyniOD447/P9ttvyxlnnJhrFihmGzlT4yhrwFdz5h7SZkpST2BZRLySzhoAvAT0AxZI2gA4FPhHPTY7CZgg6ZKIeFfSpkC7iLgNuC2z76GrEfkjoKbxr88ktYmIz9Lp24CfAm2AI1djX/XSunVrxo69kGHDjqSychmjR4+gd++ejb3bZpWpaHmcadWOOvIMHp4ylQUL3qNb1935yfmn8fDDU3n2mX8hQbfunbnyDz9t8lwlRWmnrMcfn8b1199C377bM3DgMAB+/vOzGT58z1zyFLGNnKlxNPeh9oaiiMg7g62GdLj+MmBjYCnwKskQ9unASOBt4GXgP2kv5xTgrIioSAvKs0pD7lU+GwGcS/LL1mfAKRHxzyr7HkpyDurszOwLSc4TvSs9fxVJZwEbpPs/BPgF8AmwC3BvZp8XAQcAT6fnkSLpD8D76Tmmq1ReXh4VFRXAm7Ut2kQ6Zd47U/WKlgeKnqkyinErm1baLjNVvHaKmJtjjhWkLpmpIrRTsb/fRcpUXt6fiopnm6RK3L5/t7jmvvMabHtf7vjt6em1Is2Oe0ibqYiYDuxazUc/Sl9Vlx+aeT8FmFLDZzcBN9Wy7ylATfeU6ZNZ7uLM+1uAWzLLZfd5NnB2aTq9mGln4LBV5TAzM2vemv/FSA2luZ9yYC1MerP8V4FJmdMRzMzMrAVzD6kVSnqz/K3zzmFmZtbYhHsGS1yQmpmZmeVBvqipxIW5mZmZmeXKPaRmZmZmOVEzf+RnQ3FBamZmZpYDAWWuRwEP2ZuZmZlZztxDamZmZpYTD9kn3ENqZmZmZrlyD6mZmZlZTsp82yfABamZmZlZblyPJjxkb2ZmZma5cg+ptSCd8g5QDWeqXdHyQBEztdJ2eUeoRvHaSeqSd4RqFK2dipYHipmp8Sn9z1yQmpmZmeXG55AmPGRvZmZmZrlyD6m1IG/mHSC1YugpYk6OOVaQumamitBO2eG5IuSBomeqjJdzzLHCyqcOFK+dlsXr+cXIKFP3zFQR2sk/l+qm6U8dcP9owgWpmZmZWQ4kD9mXeMjezMzMzHLlHlIzMzOznMg9pIB7SM3MzMwsZ+4hNTMzM8uJ+0cTLkjNzMzMciFf1JTykL2ZmZmZ5co9pGZmZmY5EPjRoSkXpGZmZmY58Yh9wkP2ZmZmZpYr95CamZmZ5cRD9gn3kJoBEydOpmfP3ejR40uMGTM27zgAVFZWMmjQ19h//1F5RwGK2UbOVL3jR59Lx813oX/f/ZbPu+D8y9iyy27sOPBAdhx4IPfc83Au2UqK0E5V/e6Sa+jbZx/69R3GkUf+H59+ujjXPKNHn8Fmm/WjT589c82RtdVWu9Kv31cZOHBfBg/+et5xgGJ+l6z+1sqCVNJ5kl6Q9JykZyQNkfS6pPaNsK9Rkur1N6SmLJLOl3TWGub5mqQKSbMkzZD0mzXZXktQWVnJKaecx7333sCsWZMZN+52Zs16Oe9YXHrptfTq1SPvGEAx28iZanbMqIO5+96rPzf/u6ePYvqMCUyfMYHhw7/S5LlKitJOWfPmvc1ll13H1Gl38NzM+6isrGT8+DtzzTRq1OFMnHhjrhmq89BDNzFjxkSmTbs77yiF/C7Vlxrwv+ZsrStIJe0C7AcMioh+wN7AnDXcZiFPfaiaS1IfYCxwdETsAJQDr+aRrUimTp1Bjx7d2XrrbrRt25YjjjiQCRPuyzXT3Llvcc89kzjuuCNyzVFSxDZypprtvvtgNt10oybfb10VpZ2qWrq0kk8++ZSlS5eyaNGndOq0Wa55dt99ZzbddONcMxRdUb9LdaYGfjVja11BCnQEFkTEYoCIWBARb6afnSbpaUkzJW0PIGknSU+mvYlPSOqZzh8l6Q5JDwGTJK0v6VpJU9NlD8zss5OkiZJekfSr0kxJI9N9PS/pourCpr25L0t6DOiZmb9Nus3pkh7N5L1O0h8kPQX8qsrmfgD8PCL+lR57ZURcma7XXdJDaa/xJElbZrZ3paR/SnpN0tD0OF+UdF0mz0JJl6Q9z5MkdUjnnyBpmqRnJd0iab3Mdn+ftulrkg5N5/9V0jcy272xSls2uHnz3qZr107Lp7t06ci8eW835i5r9b3vnc9FF/2QsrJi/BUtYhs5U/1dcfmNDOy/P8ePPpf33vsgtxxFbKfOnbfgzDNPoHu3L9G50xA22qgd++yze66ZikgSw4YdTXn5cK66Kv/e2yJ+l2z1FONfu6Z1P9A1LfKukJQdt1oQEYOAK4HS0Pi/gN0iYiDwY+AXmeUHAYdGxFeA84CHImInYA/g15LWT5cbAIwA+gIjJHWV1Am4CNgz/XxwthADkLQjcET6+XBgcObjq4DTImLHNOsVmc+6ALtGxBlVjr0PML2GdrkM+Evaa3wj8PvMZ5sAuwDfA+4ALgF6A30lDUiXWR+oiIjewMPAT9L5t0bE4IjoD7wIHJfZbkfgyyQ91mPSedcAo9Lj3wjYFch/XKgJ3XXXg3To0J4dd+yXdxRrQU46eSQvv/oA02dMYIuOm/H9M8fUvtJa5L33PuCOOx7g3689wtx5/+Tjjxdxww235R2rcB599BamT7+He+75K1dc8VceeeSpvCM1ex6yT6x1BWlELAR2BE4E5gM3SRqVfnxr+ud0oHv6fiPgZknPs6IQK3kgIv6Xvt8HOEfSM8AUYB1gy/SzSRHxQUR8CswCupEUl1MiYn5ELCUpAqv+Or4bcFtELIqID0mKQSRtQFKo3Zzu748kxV3JzRFRWa+GSQrOv6XvrycpFEvujIgAZgLvRMTMiFgGvMCKdloG3JS+vyGzfp+0B3cmcBQrt9/tEbEsImYBmwNExMPAtmkP60jglrR9ViLpxPRc2Ir58+fX81BX1rnzFsyZ8+by6blz36Jz5y3WaJtr4vHHK7jzzgfYaqtdGTnyVB566Am++c3v5pYHitdG4Ez1tfnm7WnVqhVlZWUcf8JhTJs2M7csRWynBx98jO7du9Khwxdp06YNBx00jCefeDrXTEVU+v+02Wbt+cY3hjF16jO55ynad6k+hJAa7tWcrXUFKSwfqp4SET8BTgUOST8qXVJZyYpbYv0MmBwRfYD9SQrNko8z7wUcEhED0teWEfFile1W3fbqKgPez+xrQET0qppL0inpRVvPpD2yL5AU4/VVyr+MlY9lGTUfS6R/XgecGhF9gQtYuf2y28r+TforcDRwLHBttRuPuCoiyiOivEOHDnU5hhoNHjyAV16ZzezZb7BkyRLGj5/AAQfss0bbXBO//OU5zJkzldmzn2DcuLHsueeuXH/9pbnlgeK1kTPV31tvvbv8/e23PUjvPtvmlqWI7bTllp146qkZLFr0CRHBQw89Qa9e2+SaqWg+/ngRH320cPn7Bx54lD59etayVuMq4nepyNJT7t5NO9lK8zaV9EB6WuEDkjZJ5ys9te7V9HS+QY2Zba0rSCX1lJT9STwA+M8qVtkImJe+H7WK5e4jOQdV6X4G1hJlKvAVSe0ltSLpDax6H5ZHgG9IWldSO5KCmLS3dLakw9J9SVL/qjuIiMszBeubwK+BH0raLl2vTNJJ6eJPkJweAElP5qO15K+qDDg0fX8k8Fj6vh3wlqQ26Xbr4jrg9PQYZtUzR721bt2asWMvZNiwI+nVayiHH74/vXvn+0O2aIrYRs5Us6OOPIMv73oEL700m25dd+faa27mnLN/zYB++zOw//5MmfJPfvPbc5s8V0lR2ilryJCBHHLI1yjfcT/699uXZcuWccKJI3PNNHLkd9hllwN46aV/06XLjlxzzbhc87zzznx22+0QBgwYxpAh+zN8+J7su+/QXDMV8btUX018TdN1wL5V5p1DMpK7LTApnQb4GrBt+jqR5HTGRqNkJHbtkZ6XeRmwMbCU5CrzE4EKoDwiFkgqBy6OiKFKrsr/C0mv490kV6h3T4f5yyPi1HS76wK/IxlKLwNmR8R+1Sx3V7rtKZJGAj8k+R7dHRFnp8u8nslyHvAt4F3gDeDpiLhY0lYkX46OQBtgfET8NL3Q6K6I+EcNx78fSU/leiS9mHdFxA8kdQP+DLQnOZXh2Ih4I7s9Sd3T933SbWU/W0hyXus+adYRETFf0skkF1PNB54C2kXEqKo5JS2MiA0yOSeSDOn/obb/p+Xl5VFRUQG8WduiTWTFCfYRa3QDhwYjdc1MFaGdOmXeFyEPFD1TZRTjVjatkt9nU8Vrp2Xxen4xMsrUPTNVhHZvco8HAAAgAElEQVTyz6W66UR5eX8qKp5tkvHvfoO2ibse+WWDba9buxHTI6J8VctU82/5S8DQiHhLUkeS0wl7Svpj+n5c1eUaLHA219pWkFrjqFpQruG21iM5X3VQRNR6KbAL0toV7wd/sYu/ImZyQboqLkhr559LddPsC9L/AAsys66KiKuyy1RTkL4fERun7wW8FxEbpx1oYyLisfSzScDZEVHRYIEzCnn/TFt7Sdqb5Er7S+pSjJqZmTVnDXwx0oLaekhXJSJCUi49lS5IrUE0VO9oRDxIchcCMzMza3zvSOqYGbIvXQE5D8h2Y3dhxTU1DW6tu6jJzMzMrCgK8KCmO0iuVSH9c0Jm/jHphdM7Ax801vmj4B5SMzMzs1wkhWTT3T9U0jhgKNBe0lySh9iMAf4u6TiSuw4dni5+D8lDeV4FFpHcirHRuCA1MzMzWwtERE33MturmmUDOKVxE63ggtTMzMwsJ839CUsNxQWpmZmZWU5cjiZ8UZOZmZmZ5co9pGZmZma5kIfsU+4hNTMzM7NcuYfUzMzMLCdNedunInNBamZmZpaDpr4PaZG5ILUWpFPeAT5H6lr7Qk2uaO1UtDxQxEyttF3eEapRvHYqU/e8I1SjWO3kn0tWRC5IzczMzPIg8DVNCRekZmZmZjnxkH3CBam1IG/mHSC1YugpYk6OOVZYeYiuCO2UHZ4rQh4oeqbKeDnHHCusfOpA8drJmWqyIs+yeD2/GBkrn15RhDYCnzqQHxekZmZmZjlxD2nCBamZmZlZTnwOacI3xjczMzOzXLmH1MzMzCwXSl/mHlIzMzMzy5V7SM3MzMxyIEA+iRRwQWpmZmaWG5ejCQ/Zm5mZmVmu3ENqZmZmlhPfhzThgtTMzMwsJz6HNOEhezMzMzPLlQtSM2DixMn07LkbPXp8iTFjxuYdB4DKykoGDfoa++8/Ku8oQDHbyJmqd/zoc+m4+S7077vfSvPHXnY9vXvtS78+X+fsH/wql2wlRWinqoqWqWh5AH53yTX07bMP/foO48gj/49PP12cd6RCtlNdqYFfzVmhC1JJ50l6QdJzkp6RNGQVy54v6ax6bPseSRuv6XbqQ1JlehzPS7pZ0nqNsZ90XxtL+k6Vedulx/2KpKcl/V3S5o2VobmorKzklFPO4957b2DWrMmMG3c7s2a9nHcsLr30Wnr16pF3DKCYbeRMNTtm1MHcfe/VK82bPPmf3HHHJJ5+5g6ee/5uzjzruCbPVVKUdipypqLlAZg3720uu+w6pk67g+dm3kdlZSXjx9+Za6YitpOtnsIWpJJ2AfYDBkVEP2BvYE5DbT8ihkfE+2u6HUn1OQ/3k4gYEBF9gCXASY2wj5KNgeUFqaR1gLuBKyNi24gYBFwBdFiNbbcoU6fOoEeP7my9dTfatm3LEUccyIQJ9+Waae7ct7jnnkkcd9wRueYoKWIbOVPNdt99MJtuutFK8/74h3H84OwT+cIX2gKw2WZfbPJcJUVppyJnKlqekqVLK/nkk09ZunQpixZ9SqdOm+Wap6jtVB9qwP+as8IWpEBHYEFELAaIiAUR8aak1yW1B5BULmlKZp3+kp5MewBPSJfpKOmRTM/kbun87HbOk/SypMeAnqWNSTpB0jRJz0q6pdSjKek6SX+Q9BTwq3R/HdLPyiS9WppehUeBHpL2l/SUpBmSHiz1WKY9tddLehy4XlKHNMO09PWlzHLXSpoi6TVJ/5dufwywTXrcvwaOBJ6MiOW/zkbElIh4XtI6kv4saWaaY49026Mk3S7pgbS9TpV0RrrMPyVtmi43RdKlmTbeKZ2/U/r/Y4akJyT1zGz3VkkT07b7VTp/tKTfVWn/S2r7oqypefPepmvXTsunu3TpyLx5bzf2blfpe987n4su+iFlZcX4K1rENnKm+nnl5dd57NEKdtn5MPYYejTTpj2XW5YitlPRMhUtD0Dnzltw5pkn0L3bl+jcaQgbbdSOffbZPddMRWyn+hFSw72as2L8a1e9+4GuaaF4haSv1GGdfsCewC7AjyV1IinE7ouIAUB/4JnsCpJ2BI4ABgDDgcGZj2+NiMER0R94EciOcXUBdo2IM4AbgKPS+XsDz0bE/JpCpj2eXwNmAo8BO0fEQGA88IPMojsAe0fESOBS4JKIGAwcAmTH47YHhgE7AT+R1AY4B/h32iP7faAPML2GSKcAERF9gZHAX9IeVdL1Dk7b5efAojTrk8AxmW2sl7bxd4Br03n/AnZLl/8x8IvM8gOAEUBfYISkrsDfgf3T/ADHZrZVtQ1PlFQhqWL+/Bqbulm6664H6dChPTvu2C/vKNaCLF1ayXv/+4Annvw7F/3qB4wccToRkXcsa0bee+8D7rjjAf792iPMnfdPPv54ETfccFvesayFKOxtnyJiYVos7gbsAdwk6ZxaVpsQEZ8An0iaTFKgTQOuTYuc2yPimSrr7AbcFhGLACTdkfmsj6QLSYa/NwCy4wA3R0Rl+v5aYALwO2A08Oca8q0rqbT/R4FrSHpkb5LUEWgLzM4sf0d6PJAUujtkfgPaUNIG6fu7057kxZLeBep7XuiXgcsAIuJfkv4DbJd+NjkiPgI+kvQBUOphnUnyC0DJuHT9RyRtqOT83HYkxe22QABtMstPiogPACTNArpFxBxJDwH7SXoRaBMRM6sLHBFXAVcBlJeXr9G/qp07b8GcOW8un5479y06d95iTTa5Rh5/vII773yAe++dzKefLubDDz/im9/8Ltdff2lumYrWRuBM9dW5y+Z84+CvIomddupHWVkZCxa8R4cOmzZ9lgK2U9EyFS0PwIMPPkb37l3p0CE53eOgg4bx5BNPc/TRB+WWqYjtVF/Nfai9oRS5h5SIqEyHlX8CnErSM7iUFbnXqbrK5zcRjwC7A/OA6yQdQ91dB5ya9hxeUGV/H2d2Mgd4R9KeJEXwvZK6pkPYz0gqnStaOod0QEScFhFLSArBsek+vl3TPtJj3jmzfueIWJh+lr3MsZLqf9F4AdixHsdekt32ssz0sir7+VzbAz8jKWj7APuz8rHVlPlqYBRJ72hNhX2DGjx4AK+8MpvZs99gyZIljB8/gQMO2Kcpdl2tX/7yHObMmcrs2U8wbtxY9txz11yLUSheGzlT/R144N5MmfwUAC+/PJslSz6jfftNcslSxHYqWqai5QHYcstOPPXUDBYt+oSI4KGHnqBXr21yzVTEdqoXgRrw1ZwVtoc0Pd9wWUS8ks4aAPwHWJeksLqXpEDNOlDSL4H1gaHAOZK6AXMj4k+SvgAMAv6aWecRkkL1lyTtsT/wx/SzdsBbae/qUSRFbU2uJhm6vz7tOZ2TZq7NRpntfmsVy90PnAb8GkDSgGp6e7M+SvOX/A04V9LXI+LudBu7A/8j6a09CnhI0nbAlsBLJG1VVyOAyZK+DHwQER9Iyh7bqLpsJCKeSofvB7FyD2yjad26NWPHXsiwYUdSWbmM0aNH0Lt3z9pXXIsUsY2cqWZHHXkGD0+ZyoIF79Gt6+785PzTOHb0IRx/3A/p33c/2rZtw7XXjcntnLOitFORMxUtD8CQIQM55JCvUb7jfrRu3ZoBA3fghBNH5pqpiO1kq0dFPYcoHa6/jGS4fCnwKnAi0ItkqPtDYApQHhFDJZ0PbA1sC7QHfpUWod8Cvg98BiwEjomI2ZJeT9ddIOk8kmLwXeAN4OmIuFjSySTndM4HngLaRcQoSdcBd0XEPzJ52wD/BXaKiH/VcEwLI2KDKvMOBC4B3gMeAgZnjmdhRFycLtceuDw9/tbAIxFxUjXLPQ/sFxGvS/obSVF3b0R8X9L2JKcVbJO2x3PAd4EPgCuB8rStz4iIyZJGpW10arrtbJst/0zJhWXPAF8hGZYfHRFTldwp4S8kPb13A0dHRPdqtnsXcHFETEmnzwEGRESdLjEvLy+PiooK4M1al20aK06wTzrP85fU+CVFaKdOmfdFyANFz1QZxbiVTSttl5kqXjs5U01W5FkWr+cXI6NM3TNTRWgjgE6Ul/enouLZJvltbcfy7eLxpxru3qnrth42PSLKG2yDTaiwBWlzI6mc5KKj3fLO0tTSgvSsiKhooO3dRdKWk+qyvAvS2rkgrYtiZ3JBuirF/n9XjEwuSOsmj4L08gbb3rqt92m2BWmhzyFtLtIevVuAc/PO0pwpuZn/yyTn2tapGDUzM7Pmr7DnkDYnETGG5L6fa6WIGNpA23mfFVf3m5mZtXDCfYMJt4KZmZmZ5co9pGZmZmY58X1IEy5IzczMzHLjghQ8ZG9mZmZmOXMPqZmZmVlu3DcILkjNzMzMctICnvnZQFyWm5mZmVmu3ENqZmZmlhNfZZ9wD6mZmZmZ5co9pGZmZma5cd8guCC1FqVT3gE+R+qad4RqFK2dipYHipiplYr4VN3itZMz1a5M3fOOUI1itVHT8pA9uCw3MzMzs5y5h9TMzMwsF8J9gwkXpNaCvJl3gFR26MmZqle0POBMdeVMdVO0TEXLA8XP1DR8lX3CZbmZmZmZ5co9pGZmZma5cQ8puCA1MzMzy4nPIS1xK5iZmZlZrtxDamZmZpYbD9mDe0jNzMzMLGfuITUzMzPLidw3CLggNTMzM8uRh+zBQ/ZmZmZmljP3kJqZmZnlQiD3kIILUjMzM7McebAa3ApmAEycOJmePXejR48vMWbM2LzjAMXLNHr0GWy2WT/69Nkz7yjLFa2NwJnqypmaXx5wJms8jVaQSrpE0umZ6fskXZ2Z/o2kH0s6J53+hqQdMp9PkVRezXbLJf2+nlk2l3SXpGclzZJ0z+od1eqTdJakf0l6RtI0Scc0dYaGIumM9Fhmpm36W0lt8s61uiorKznllPO4994bmDVrMuPG3c6sWS87UxWjRh3OxIk35pohq4ht5EzO1FLzOFPjEKAG/K85a8we0seBXQEklQHtgd6Zz3cF7o+IMen0N4AdqEVEVETE/9Uzy0+BByKif0TsAJxTz/XXiKSTgK8CO0XEAGAvmulldemx7APsHBF9gcHAu8C61SzbqonjrZapU2fQo0d3tt66G23btuWIIw5kwoT7nKmK3XffmU033TjXDFlFbCNncqaWmseZrLE1ZkH6BLBL+r438DzwkaRNJH0B6AX0kzRW0q7AAcCv0x7EbdL1DpM0VdLLknYDkDRU0l3p+/MlXZv2pr4mqaZCtSMwtzQREc+l628gaZKkp9PevgPT+d3THsDr0n3fKGlvSY9LekXSTuly66f7nyppRmn9avwQODkiPkz3/2FE/CXdxl7pujPTbX0hnf+6pF+m7VEhaVDay/zvtCgstcUjku6W9JKkP6TFP5KuTNd7QdIFpSDpdi/IHPP2ksrS4+qQLlMm6dXSdBXnpcfyfnosSyJiTOnYJC1Me7+fBXZJe1OfT1+nZ9r3+UymsySdn76fIunS9LifL7V1Y5o37226du20fLpLl47Mm/d2Y+92lYqYqWiK2EbOVDfO1PzygDM1HjXgq/lqtII0It4ElkrakqQ39EngKZIitRyYCSxJl30CuAP4fkQMiIh/p5tpHRE7AacDP6lhV9sDw4CdgJ/UMHR8OXCNpMmSzpNU+vZ+ChwUEYOAPYDfSMsvd+sB/Cbd/vbAkcCXgbNICkxIirOH0ox7kBTU62d3LGlDoF1EvFY1lKR1gOuAEWlvY2vg5Mwib6Q9qo+myx0K7AxckFlmJ+A0kt7lbYCDS9kiohzoB3xFUr/MOgvSY74SOCsilgE3AEeln+8NPBsR86s5lg0iYnbVY8lYH3gqIvoDnwDHAkPS3CdIGriKdUvWS4/7O8C11S0g6cS04K6YP39+dYuYmZkVnEhKsYZ6NV+Nnf4JkmK0VJA+mZl+vA7r35r+OR3oXsMyd0fE4ohYQDJ0vHnVBSLiPmBr4E8kxeWMtPdPwC8kPQc8CHTOrD87ImamxdoLwKSICJJCupRlH+AcSc8AU4B1gC3rcFwlPdP9lE54+Quwe+bzO9I/Z5IUeR+lReJiSaWx06kR8VpEVALjSIpmgMMlPQ3MIOmhzp4OUV27XguUzmsdDfy5tvCShqU9ma+nvdwAlcAt6fsvA7dFxMcRsTDd7261bTc9DiLiEWDDzLEuFxFXRUR5RJR36FBdR27dde68BXPmvLl8eu7ct+jceYs12uaaKmKmoiliGzlT3ThT88sDzmSNq7EL0tJ5pH1Jhuz/SdJDuitJsVqbxemfldR8i6rFmfeVQGtJp6SF0jOl3tCI+F9E/C0ivglMIyn8jgI6ADumPXLvkBSVVbe7LDO9LJNFwCFpr+6AiNgyIl6U9Od03/ekQ9kLJW1dh+Ot6diy+6+aIaqsE5K2IunJ3Ssi+gF3Z44ru93l7RoRc4B3JO1J0ut6r6SumXY8KXMsW6Xr3Je22/NA23Sbn6bF8aosZeXv3jpVPv/cMdWyvTUyePAAXnllNrNnv8GSJUsYP34CBxywT2PusllmKpoitpEzOVNLzeNMjclD9tD49yF9gqQwKvXg/S/t7eoNnADsl1n2I6BdQ+w0Ii4nGaYHIC2y/hkRiyS1IxnafoOkMH43Ij6TtAfQrZ67ug84TdJpERGSBkbEjIg4tspyvwQulzQiIj6UtAHJ0Prfge6SekTEq8A3gYfrmWGntED8DzACuArYEPgY+EDS5sDXSHpwa3M1ydD99en/rznAgGqO5UpJR0TE++kpDlULypJHgeskjSH5m3IQyTG+A2wm6YvAQpLvwcTMeiOAyZK+DHwQER/UIftqa926NWPHXsiwYUdSWbmM0aNH0Lt3z8bcZbPMNHLkd5gy5UkWLPgfXbrsyAUXnMVxx43MLU8R28iZnKml5nGmxuNn2ScauyCdSXJ1/d+qzNsgIhZo5acTjAf+pOTCpEMbOMeOwFhJpZ65qyNimqTZwJ2SZgIVwL/qud2fAb8DnksvJprNykV2yZXABsA0SZ8BnwG/iYhPJR0L3CypNUnP7R/qmWEaMJbknNfJJEPkyyTNSI9nDnU7PQKSUwT+zKqH668kPU9U0mKSgvJxklMDVhIRT0u6Dpiazro6ImYASPppOn8en2/3T9P8bUhOH2h0w4fvxfDhezXFruqsaJnGjbsi7wifU7Q2AmeqK2eqXdHygDNZ41FyWqQ1R5KGklyUVF0RvDrbKwcuiYi6nOfZKCRNITmmirquU15eHhUVFcCbtS7bNDpl3jtT9YqWB5yprpypboqWqWh5oKiZysv7U1HxbJOMf5eX942p026tfcE6alW23fT0guZmx48ONQCUPKDgZFZcaW9mZmaNrnmf+9lQXJA2YxExhbqdG1qXbY0BxtS6YCOLiKF5ZzAzM7Om5YLUzMzMLDe+qAncCmZmZmaWM/eQmpmZmeWkyh2H1louSM3MzMxy0fxvaN9QPGRvZmZmZrlyD6mZmZlZbtw3CC5IzczMzHLkIXtwWW5mZma21pC0r6SXJL2aPhSnENxDamZmZpYLoSbsG5TUCrgc+CowF5gm6Y6ImNVkIWrgHlIzMzOztcNOwKsR8VpELAHGAwfmnAlwD6m1KJ3yDlANZ6pd0fKAM9WVM9VN0TIVLQ8UM1NTadJzSDsDczLTc4EhTRmgJi5IrdmbPn36Akn/aYBNtQcWNMB2GpIz1Y0z1a5oecCZ6sqZ6qahMnVrgG3UyfTpz90ndW7fgJtcR1JFZvqqiLiqAbffaFyQWrMXER0aYjuSKiKivCG21VCcqW6cqXZFywPOVFfOVDdFzFSbiNi3iXc5D+iame6SzsudzyE1MzMzWztMA7aVtJWktsARwB05ZwLcQ2pmZma2VoiIpZJOBe4DWgHXRsQLOccCXJCaZRXxPBtnqhtnql3R8oAz1ZUz1U0RMxVORNwD3JN3jqoUEXlnMDMzM7O1mM8hNTMzM7NcuSA1MzMzs1y5IDUza+EkNemdt83M6ssFqVmBSeomqV0BchS6oJG0Sd4ZiizSiwUkdZLkn/vNjP+f2drAX3Jb6xWt2CrlkbQr8Cdg/bzzZAqa7SWtK2mDPDNlSeoOnC6pVVH+4U7baXjeObIkfQv4JdAm5xyF+vtWlaTtJPXIO0eJpF7AV9L3hWg7Sb0lnZh3DihOm9ia822fbK1WKrYkDQW6A4si4u95Zkrz7A4cDFwZEW/nnQdA0neB4cBLwIeSLomI/+aZLbUpcBDw97zvp5f+49gKOBRYl4LcWkXSaGAQ8IuIWJxjjuwvNwcAC4GlEfFIXpmy0tGIU4HbgVcllUXEspxjjQD6AZMj59vipN9vAQOAbfPMUpL+vNwV2CidnJh3Jls9hehNMMtL+sPsq8DlJM9AHifp5Lx+687sdwhwPEmxlfuQnaR9gIMiYhjJc547Af+T1CrHTBunBc7TwJ+BUyXl2psMlEXEUmA8sL+kPfIIkellL32fvgx8J/N5Lp0RmWL0DOAMoBz4haS988hTVUR8BMwBzpe0fp7FaOnvVkScD3yhID3ubdI2eRzYR9LBeQXJfMd3B24Gdgf+JOncvDLZmnFBamutdIh3feCbwFHA/4BngNubuiciUzhsKalVRPwaOA04U9L2EbGsKYvkGgrg2yR9G/gCcHLaRn3zKEolbQv8FLhG0qbAEyS9ba3Sz5v8FwpJOwAnSeodEa8CVwJbpZ81WRtleyGBLQEiYjRwBXCnpLbp01qarCjNFsiStgR2j4ihwIYkvwg+JGndpsqTyVWW/tlN0tcB0r97TwE7Z5dp4lyDgFGZQn0K6fPHc/xluSfwc0kDIuJ14Eckf//b5NFGaWdCOXAI8O2IOJekKP2mpDObOo+tORektjaLiPgYmAmMAi4GDo+ItyQd35S9NukP1+HAjcCFkv4YEX8GbiDpte3TVEWypI1Jhi2RdHh67uHrwHHAsRGxb0QsVvL4ue/RROckZoqaMuA/wGXAB8BYYF+SHuWzYEVPXBPbFuhI8v9rJLA9cJikDSKisqlCZHohTwUul3SJpO9ExKkkPVtTJX0h7clt0kzAF4G3gc8k/YZkKPqItNft65K6NUUeSe0kfTH9RW9nku/2KEnjJA0mKZSHpNnz6CVtD2xO0nv83XTeGZJ2aMrvdpXidz3gPZJfAs8Evgr0BTZu6l+YM/YBDgS6S1ovImYDxwJ7SVonhzy2BlyQ2lpJyYUC4yR9AfgvcDjwnYj4t6R+wOlAkxURknoDvyDpqS0DtkuHDH8B3Ar8o6mGoyPifWAzSQuBM4GbSArAv5MUMydLOg4YDfw6Ij5tolylov0PwAUR8UpEfA/4HfAk8DywraTNmiJPpkAeJGlf4P6I+BHJd2dTkuLrK8CJTf2PtZLzMw8HRpIUfQMAIuJY4EXg4ewxNFGmfsBfSHrY3wIOAE6MiE+VnON6LtAk3yWgB0lv8ckkPX03R8RhwCvAniS9o2dK2rMpwmS+S7tIOhB4Lf27fxiwMUmB3DHN1mS9tunfuZ0lHQu8nWY6luQ88s4kBeF5klo3caHcS9IxaZ6xwF5Az/TjL5AUz65vmhlf1GRrq4XAxyS9bCcB25GcN/YpyT9W50XE5CbMsw5wPbA1MBQYGREfSxoUET+TdGPam9tU/kZyAVOHUsEp6SaSdjqUpGfymIh4vqkCpT1XP09fZ0q6nmSobmr6+cvAH0mKiTsaO0/6j/XewNUkveyXSdo/Ih4iGYK+hqRI7p1Dj207kiH6Q0l+sSr1eHePiJGSOpaOoQkzLSQ5P3NT4PfAUuAOSQ8A+wNHRsQ7jRlAUhdgg4iYIekZknPHR0XETICI+P/tnWW4HeXVhu+VAIEEDe5O8OBW3AIETXD3BitOcXd3hwLFirsV11BcS3EvxT1Y8nw/nneT+Q6BtpSZc06y7uva19l79pzsldlzZta75Fn7RsTIwCPA+vhacGebMojfnHIuLYEzItcA50fEWpJujYjDJH0XER8Ba0XEaU1F3ItNpwHPAdtExO64uerp8r31x4uubvj7rNueLoBw9HqRiBgs6eiyWD8tIp7DjvIJkr6u257kN0ZSPvIxwjyASSrPJ8MX27Nw5+gMwILAbOX9qNGOKD+7lp8TA8/jSOQ4ZdvSODo6XsPHaDFg4fL8OBw1GqO8nrGdvrcZgHOBPcrrLvjGfS4wVmW/I7HD2qUhmy4B5i6vDwbub3uMcD3ivA0dpy7l5yLAy8ADlfe2wwuwkRqwo0fl+bSV58cD15bnAawNLF/dp2a7fo/VBkbF0eMjgX8Bsw7jGM4H3IdT0nXbNTN2jpcor9cFPgeWbLPfLcBCDR2rXsANlfN7+3I9Who79a39HgCWacim8crP0XDt/8nA+mXbLuX76tOELfn47R8Z0k5GGCJiLODBiNiibHoH6zJOBpwHvC3pIQ2NltQdEVkKOCIiVsc3xSNw6nmNiOiDa1rPl/RhXXbAMDuy1we2ioheckr8NuDRkt48LyLGrdOen2E8nNFZICJml+v6VsPf3SkRMVKJknQHLlGNdX8R0SXcgLMOdiRa6fC9gTtwKcjMZd9pcer+nzXZMnEMbcxZB9g9IubDTV5XAwMjYoVSB7wxcIZqrh2NiNmAdctxmgF/P8eGtWv/CLwREavIXCrpZkmv1GxTAEg6Ay/6LgFekbQbdkrviogJImJGYM/ya93wd1dbWUMM1c7dAEf2Zyz1vRdj5/n2EoUnrI06KfB2XfaUz4mIGAUvzqfHCwYknQDciR2/30XEKBExKa51rfX7K3ZNDNwTEStLGgRcATwKrB0R60k6Gjd/bd/6+0s6F1HjPTdJOgwRMamkd8ISIWdhPcbzy3sHYfmZPSQ92ZA9v8MRkcuxY3Myjq6Nh+Vw3gBulXRD3enCik2TSXq7PD+62HKEpL9HxB9xOcGJakDrs/V/Lg7Nv4BvgYmAP2A1hGskPVscjbkkPVZ+r6tqSmdWbBpJ7lIfG9gGGAe4RdLtZb9DgeslPVRu7GNLer8GeyYHdsXnTXdc73s1sCV2cN7CTsVquJP9uMVVLaUAACAASURBVNZiq07CXfSDsC7k+MCbeHH1IXbyPsf1iEfXbUuxpzswlaTny9/d07hedRZci/x4Ob+3xGU8e0m6PiKmxhmMl2uwqXUu9ZBLc0bG3+Uk2Fl+uJxj6wMfyKn7HsCoqkn7t2JTN7lpMfDidHGcpr+w7LcDcK8st0ZE9JT0cR02DcPGDXGN9j6SbizbbgPeBXaR9GFEHACc1bqWJZ2HdEiT4ZbKBXY+HPV4UNKREbEgcAFwLHZ2tgcGSPp7Q3ZNhZ3R8yVdFu7y3QP4K3BOWf3/v/9DTXZURcpnAXYD/lxxrE4GeuNmr2ciYmRJ39dhy8/YtwJu9LoBR0J3w80dA7CDemnLwarbaa+cS8sBG2Kn5m5cI7oTMDq+ad9clw3DsGk0fCwmwvJS+xenaw3cqLOnpBujyDs1EBkdFfhe0uCwFNepOHJ2HPApjratif/ehgDTAp/XvdgqDvK+uIa1P7CcpOciYn+8EN1HrimdDfhO0j9qtqd6Lm2FFxSP4/NpX9zEdDVwf+s7a/D87gtsgVU17iiO+UbA77CTfE7b32nApnmAmYAXcUPeYrg8Zi9cTnQKsGMTi62kXjJlnwy3lIvZCjgl9wWwWURsJekh3M0+N+4UP6FOZzQiukeRswnrZ86Pb8jrRMQ4kgbiC+yqwNYlWvLj/6Emm3oytGN3UWBW3JjTP0pnsSwTNCnW9evWsDM6Ny6nWA34GtfzXVCen40dwB8d97qdmooDcRgu75gV10MuDBwFfI+FwmsvZwgPBJigLFzuxDJKEwKrl+/pcqzRekZErCjphwac0TFwbeGMEbEL7r4+AEfZtwWmkfR3SQcAfYDekj5rIvIv6U1gIHa0/tyK8MuC848Cx0TE3JKeqdsZLZ/baoY7CkeO58fO1dr4mH2DHfcxqr/TgE3L4evQIVjK7fSIWL9kkv6Gm4gmbdim5bG6x7zA4Tg6+iI+Xofjv8VT0xkdPsgu+2S4pKSbxsE6mftIui8sp7J+uWkfz1A9xm/rWu0XO6bGgukfYwmenXA6dXU8g/04SY9ExJ7AkIYcv5GAPhGxNxaTXxwLb/fDNVldyvZHgFPU0LjJyvcwEk4XToOjWmviCOlFOB29hxrsog3XP86FxzhOy9Amq72xM3oIbphrYpTqnMBCETEOToHvj1PNM+IFxeWSroyI73GjXO1I+iLcwX4gbjhZTdILEXEsTkWvERE3SXpC0iNN2NTmb/omXCqwWVhi6ipJn0raPyJ2paHgTLkedMd1x2viyP80WMpsXdypvgdu8vqkCZuKXaPg69R6xZ7e+Np5WET8IOnsiLhZ0jsN2jQ6Q6XBbi+ZrhWBxSWdEREPA0j6oO5obdIMGSFNhktkPsbRo+nLtmtxRGnHiFir7Ppda/8a7XgORz22AwbK4s1/wzfJHljHbxxJf5P0aB12tIiIJSJiB7mm8RMcJX5W0hBJbwDX46jRPjgaeGDZXivlRg2uO0TSwyXqsRxORT+L07/vAxM34YxWbELSlzgiOgjYHdgIOBNLKh0KdFcNtYZt7JksXLc6BKea1wFuKk7wJcCrZfuG4TrX6yS9WrNN1Yafm3Am4kmgR0SMWSKOR2AB9aWL49MIJcLWp5SezIvrtffHJRd9ImLtiLgUOL5uJ7l1nMr14Csse/UhrvtdTdKZ+FqwNj6/X6rTnqpNxa7vJJ2GNZm3xynwy3BJynERMXHDzuiSuP65G462I8u7PQ6sF669/UDSB+W9dEaHA9IhTYYbWhfYiOhZokdgAfBpI2L+8vo+4DVgj7AmY601UOXnUtjxOxmYPyJWKGnU24t9P+DmjyZ4ArgmIqbBpQz98JzsIwCKU3UNTqsuqwYamMrnKiJWAv4aEecXJwLc4bxSRKyI0/cHNxVhKzYtGxF7hBs5uuLmic9w1/zcuPlsQ9WvhLAK7io+FztVKwPnAEuUdPMXuJbufTwutHud9hSbqjXIE+Gofx8sA7Q1ZdIRjkweAlwo6bu67arYNxeuyfwGnzsH4nTvHjjSNgC4uomMRMU5PjYi/oBlpj4AJgBGCQ/qGAT8sSnHr9jUNyIOD0/zGlfWgX0X6BLWIP0XlqKqRSWiSgxVi5gNNwt+hBd9EVYiAX9/nwKNLWyS5simpmS4ojg1f8SdvU/hGq2DgKnKLnPim9EOwBWS7qnZnnlxpHEXSU+WdGG/YtPb+EZ5Zd0X/IjooiKFVC78HwJ/krRzqdfcGUcgn8XyM39s2HnoBeyHhwO8BvwJ17Ruh6NJo+M065UN2NJqppgd16+dj9Ph8+Hz53AcdZ8FR5KurtmeJbDg/zq42WQMLKD+OD5W0+BzbAJ8nt+rhrqei33b4PGNDwNPSLoqInbExyzwFJ356i5nCMsCdZenrc2Ga47/KOm2iFgEyxcNxtrD72G934/qTPdWzqVZ8Dl9LdZAbU3SWhI774EzAVfUYcfP2NYbD8A4EjcKzQ70xdH/OXCEcqcGzu8xgW9k8f+J8Tl+kaRNI2JCXLKzJC4FmRLYV9JVddqUtBPqAGKo+cjHb/HAN74n8Q16N5zaPLi8NwseedcLWBSvtKeo2Z6JsTNzW2XbeMWOgdhpXrJOG8pnjgNsU56vhVNg42EH9MjK8bmwHL+ZG/zOuuCbzNs4glZ9byBulOkCjFK21TasoM1nL4IjkutVtp2I5ZzADuk0TdiEGzi2Lc9HLT+nwA7g5bhp6G58I5+qgWMzauX5JjjrMAVwK3AXsF15r0/5O5ylAZtmxMoHi5bXk+HpQjdU9lkIK2schh3Xps7xBXF3+LqVbRvicgvK9WqyJs6lyufPi53RXSrbjqQMUijXh8nrtql8b9fgxeiYZduWuJRqgfK6e7FnMWCmJo9TPpp9tLsB+cjHb/UojlZvvMq/F9etfQwcW9ln7nLjmrUBe8bG0YaBwOaV7V2KQzNXg8fmWJzqeogy2ahc5F8HDqvs17Mhe6LN6+1wDeTclW2HAWu107m0MI6inVrZNgpuqhqzyWOEI3r7t7YxdLrXrHhowUzF2ZqmAZt6YQm16cvrrXC5yXbA7Tj6fweOHDf1Xc2ES1+2bHPcJsFSatXvcGGgV8Pn0ui4tOOOyrZxikM4fpO2VD5/7nItuAiYoLL9SmpeqFc+a2Zcr75+2+txcUo/azml+RgxHu1uQD7y8WsflRvPKMDI5flowF+AlcvrY3BtVq/K701Usz0L4SjsfOX1uliMf6OGj0+XyvPZcQr8hTb7jIebm45qh+9vSSxzM1d5vTXwQvnZp9zEa48gt/nuZmFotKo3jiJvXhyIhcvrKRs+TksVx6o1wrELluWZDEdxx2j4OzsVRz4nKdvGx1Gu1jG8Ddf+jduAPT1x7eph5fXIuHFxxfJ6Uqxje16Dx6h6Ls1bnnfHC65zcMp+Xlxu0bRzPBeOSnbFXfV34PKlOXBJyhvAdA3YMUY5pzdss30NyhhSHEUeTDqlI8wjZZ+STosklWaPfrir92QcKXkNmCYi+uO0+dyS/hFlio+k935rWyq1YivhyN4pePzmQZIujoghuDmnq6Rzf+vP/xl7WjWjywMfSpotIs6JiGewE/g9IOzYTFS3TW3smxvX9z4B7BQRD0o6NSK+xV3rl+NFxVNN2FO+u6VxreZrEXEHluJZA9eRroPTrjuqAdWBNgzEjUJrle/1UWBIRCyER1vWfh1vnd+S7owI4RrIjSLiL7geeVasUzkebtLbW81IYIEbvaaMiDlx/fgzkm4AkKezbQWcGRGzymoNtVLOpT54IMA3EXEzzlDMiuvan8PC91uoAd3TFhGxGI7KPozHJp+MG7ta5/nfcWnPyw3IKHXBafnbK/ZtXGy6LyJGkXRBeMrWmDXakXQgsss+6bRExMK4Y3Z3HHXYrVxEH8d1iXsBl0tqaTH+5vPNI2LCiJgEmCgixsLpzFWw/M1grOO3saRLgZuxrmfttG4mEbEtdvw+Lts3wzekxyNiCyzVM5JqniVebGmpDoyLdTz3K/ZcC8wUEVvLk2D+iHVRv6n+Xs02dccSU6tj3cyxsV7s6/j7nAJ4VdJ1rW7gppBlgs7CWqPHlK7oA3G3/Q6qWa+yrXMi6S4sSD4xlin6FsuEHY7nnO+pGkalDgu5eetU3Ix3izdp+4rtM+LvctW6ndHKuTQSzpCsgc+p1jjg7jhT8RGOLt9e/b2abRoTR2VXwxmIV/F53hXYGP+tvVRx5Jvodh5E8UHCmqNf4MXxOVgvdjxJp8tNabUdo6TjkF32SaehOH59JP2pvN4cX9yHYCdmPUmvRRlxGdb2/KSu1X652V2Im5PAUY8bcZ3d6TjF2x/fMLdp2d0UYSHpM4Cl5W7iJYAf5CEBe2CB9+PUkLRTsWkl3DzxFfBPSSuV7f1xF/TTkk4sDtcyWAS7VlH+YtOCeDziOpLeLdHHlfEN8yh8rG7BY1QvrtOeX7BzNKwz2gdHJW9uOMK2LW7AGRM3oUyI06rv4TrXb/Hi5sumbKrYNh6uO5wLd2E/Xzrrz8Bp4Vr1fSt2rIJVPGbBDUMPRsQM2CH9Cp9LX+BrxvmSdmrAppWAlXDd6B8kPRAR0xU758UZia5YBeB0PL74N1+8D8Ouc3AD5YLl9WiSBkXEHFiia4Ckd+u2I+lAtHfNQD7y8Z8+cC3d3fhCBXb2bsYNTK2O53Vw9KYblRrKGmzphcXtV8UTjrbA6bBxcCf7PmW/VXF39hINHJ+2jUIT4bThueXnfTj9vGZ5v1vD39+MWHh/bhwJeQs7xK331wRmq7yuvcGq2PI4nv50Lx5c0HpvYVyDPGN5vSAN1Nd1hMcwzqWtcHp1GlxmcULZviiOaO2IndF2s7Wc7zuVv8NN8Yz4FRu0Y1bgQdykcxrwGEObv3qV4zRzed0DT2Oq26Z5y3FYDtcb3wb0KO9NjyPavcvrOWmgPpr/X9t+DaXREkeyFyh/j8u3x7mUj/Z9ZIQ06fBExFTYKbil1GZtjaORl+J075O4ZnPq8vOPkm6s2aZjgH6Spi6vZ8YNOpvhCNam2MEZAKwujwatXe+wPJ8RZ93+ERGr4vT3ubipaW/gO0lH1GHHL9g3Hk4xL4g751+OiPHxDfxOSb+v7NtV0uC669hKlGhvHKndo2y7Hhhb0iLl9diSPm3ZVJctHY0oI3Urr/fHC6tNcGPTarj++AcclXxbFlVvFyJiAmA6XGKxGS7jWVvS9Q3UQ7b+5vYF/iVpx7JtLxyF3EQeo9pd0tetDE6d9pTPnwyX63wpafOy7SJcd7yGPO61FZX8Uae4CarHICLOxeUfI2NH/QhJ1zRlS9JxyKampDMwE3BWRAyQdEOp4dsGp8DWYai24LjA7pJurPsmJAvKTxER18tp57lwKvM7SZdHxKg4WrqVymShGp3Rquj9jjha+2VE3CdpZxyFICLWwWnoDeuwYxh2/fgdSPowIs7GEjj9IuJKWcD8d7iedWasADCk5fjV7UTgdPznQO+IWFTSvZJWiojbI+JRSfOU9xnBnNFlcUPek3is7JVYQukW4GVgFUk/lBT+d/LYyybsajUOzlY2fS7pjbLYGYhrkh+MiNOAS9RMc06LD4EP8FS4eSQ9KumQch24pJzn3wI04YwWvsdR2tUior+kKyWtFxFXA9dFxNKSBhWbmkjRT1m+r5HkkqqJcMR404iYtLWf3IiWs+lHQDJCmnQKImJlPH5wL7mxZHksCP4nlekmETG+pA8aiKz9GC2LiKtwg84XeCb1Tzr4a46MjiTph/J8ATxxaXMcvXoM+KukrSNiHtxwtZ88I75WKs7DcljcflQ803winNJ8C7hW0ksNRoxaNs2FF+NfYpmbPcsuN0l6oOw7jxqqO+xIlO/rADzlaAIsm7Qblna6HThR0lHhjujdcLPQiw3atwpuZPwbPpdOxwvRHpLOG8b+ddWPt86l+XG6+XNJAyPiKKwVe7Gkx8u+08kjeWulYtN8eDH8Oe7q3xDLOt0s6dqy7xySnqzbpvJZXbAc3xO44e2KEr29BThE0iVN2JF0fLLLPumwRAztrJR0HW6kOCQiVpF0M04hblUiNeAoRe2RtZJO7lqe98M1WoNazmi06cKu0RmdAR+PCUvK8gCc8hpV0ue4PnKJiDi7OFcbNeGMwo/SN4tiJ/RR3FF7CxbnPxc78f3CjTq1Rx8rN+s+uNRjHazB2Bc4CTfG9Q83wjCCOqM9serCwZJOwZ39I+Mo1j9wHeKaEXEejsKv3rAzOgkW4F8KT1qbHKtW3NJyRpv422uz2DoHH5dTIuIoSbvi83mTsgikCWe0fI5KdPtSPNWoJVd2N3YG14yIfmXfRpzR8llDZKWI/YA5S9R4IeCsdEaTKpmyTzoklYv+nDhd+JY8I3sQcEREDJHrw7oC/4LGpEp+NLH1RNKAiLg4rF3ZV9I3DdkwEY48bIOjx0fj5pPFIuJuSe9HxILAXRExoWqu8YuIKXBjxx1y/eF8wDWy5NWlEfEucB0ub7gCf6eDarZpHOBrSd+GpW92xZ3Gt0TEJXiIwvZY/3AHyrk0IiLp4ygqCBFxj6S3Szr88Ih4HEcl18bKFkj6tGETR8YlAxtjR2sDuQ5y4Yj4u6SP6kw9h+XKhsjKHd2xc7xHuQ6NjEtP3gcOwgux2tUGyvczGPgaX5MGANsXmy7Dihbf4w76kYCX6rapjX298bALYbm59fAgh8sq+zRav5p0XDJCmnQoImKUNhGIq4AVgIvDAteP4RTriSVSepOkx2q26ScaeKWGboqIuCwippW0Lk7bz1qnLW1suBdHQXrg5px78Y1nFWDJiJioOA1zNeCMzoSdu4VxcwlY+3Ts8n4XScdhp2Y8SbdJ+nvNNrVkuTYPNyd9DvwD+KrY8zfclb1xOT6HNBnx64jIzYC7AI9FxEn4HnEMFnPfAafLBzfhjLb+7iJi7GLbGziSvTOuzX45IpbCEe6xa7ZlJjxmc+ew3vAgLC7/SbHte9zwNaMse7WjpBdqtqkX/ptbB0+f+wbri44fbkp7EmvDbomd0rObypBUrpkH4Sjysdhp/gdwQDWSnc5o0iIjpEmHoaSgdwWuiogXcKf6ZvJ0mCXx6vqDUoPUjSL2XrNNLee4L5Zw+hbXPv6VoSMJXwGQtGrd9rS1S9L95eK/KnZKD8Y37d8D30fENdQwEKCNLVPhyUpt68HuxCUVOwDXRMTEOGo6Wp32FJtaDvLhwO0VB+o7fF49hm+QnwODw2LmX9VtV2dA0s1l8XcbMHFrMRMRZ2Epri8asqM1+Wyr8ASv7fHf3DfAXhFxF/AHPBCjtsEO5Vy6BJ9Lt0j6rGx/EzdbzleOyXjAZBHRAzustVGc0SuxhuhVlazM21jq6SE8eemT8ujWROamdV2iyLpJWrmUWqwP/BnXbM+Oa8q/ruyfJNnUlHQMwl3WF+AI32Vyc9LpwPPAKaVucz3saC3burg2cUGLiGXwhX8Ajh5NIGmpiJhZZQpUE2mn8OSSDyuvq931C+MRqp9jxYHF8QjF2oWlS13mopL2KpEPYU3K7yNiepy+/BSLhR+o+iW5AguiPy3p5GG8fwVOc/4LWAQ3el1Xp02dkXDj4DF4OEEjk5fK57YWgT2xvNvueDE6LhaWH4SlpwJ4TtJddV4HIuJo4LVSV9v2vRNwveZf8WCH2iXnKja9J+noYbx3HG5q6ob1Tw+SdHXdNlU+vy8ugbkH1/XvWr7PuXCZ0UnABZIOaMqmpHOQEdKk3Sm1fScDp0o6t5LueRRriy6AZ3k/g6fCVOs3a2taqGyaFneuT1Ee65ftH5X9a3VGy/GYEHg4Iv4g6dpqGUGJLL+M6zI3BHaWdGhd9gyDyYCF2xyHVtf8P7Fu7KfA+JLeaigqMgFOX1Z1TVv2bYId0dGAS2WpoIzUtKFESkcBbgmrDjSSWi3Oy6JYRu0xSQ8BD0XEoXgi21FtncOav7tJ8d9X1VnuIjfrbB/utO8BXCl32jdxLk2IG5V+VNqonN9HAVMVmz6W9FhT53eJJi+Dr5cf4Aj2ORGxmYaqDjwP7BsNqWsknYesIU06AoOwDNCV5XXX8vMqHMnaJSIuxvWAl6rGRphw1/eM5fkcYX28cXHEbQc85ei1iFgB+H2p1ar7Rh1yB/8fgEPD+oGSNCQs9XQ/MJmkB4HzgbNrtqctt+LasHlatWHhJg9wN/YCkr6R9BY0ooIg3H3dOyJGLc5o2KwYG49RvEvWZXywCZs6K7JM0KJNOKOVmtEFcb1mP6x8sF2xZU98ndi/LGKb4i6ge1nYtM6TLhHRPSJ2xzPg75Q0sNjZxLn0IG5eHKfljOJDOBJebL0k6a8q9fUNZJG6hAdd3AZMLukOnN06BA9PuKiyiJ4fK4CMPMx/LBlhSYc06Qj0wJ3XC8OPDUMjSfoYj+C7HjfvbCR32v+kyeg3ZHJgrYg4FneEgwvyuwJvyKLNS5VtA1XznHX4f0X/n+E08/XhCUxgyZkfZ3VLeqjJ9GrhYxwRXRePH6Sk6+fBU3Pao3P9BVwisGBxSiVrx/bCTR4TtYNNnRI1NJu+RB7nxU06AyRtikt0loiIrcs+uwA7yQ1qTfEWsDpuFOxS7PgBL1xXAnrWbUBE9Cgpb8Kz3r/B9dArF6e0NVBiHrxwHrdum6qUz/8Aq3z0jojVyjF6HXf6fwe0Bhp8giXDvm7SxqTjkyn7pN2RRzOehKMh78jdoa0V/ZzA74CtW85fnat9SS9GxFe4bu0oSe/Aj8L8V4elgqbEN8Xb6rKjLWEh8j/gWroVgTMi4mtJ+5f3o9jfaKSvpAK/LpGio4DNImJfXFO3La6pe6hJmwAkXVnqkjcHZomIp3CK/oRi02tN25T8PJWU8oJ49O4r5Zy+C18Ldi6L1BPVsBJCKV2YAneMTx0Rn+FF2PFY6L0JndHRgV0j4ju8aN4Sly4thB3AO/H9/Ahcs1lrhz/8v/KFBbGz+aA8SW8wcGpYmu/aiHgFqyK0pkI1dt1MOhfZ1JR0CEq6p7WyvwzfiBbC4ty7SLqp5s+vzoKfDDcozIvT4bdLejfcPdsFT4X5yUSmmu3bDegq6bDyej3gTGA9tdPc5+IwdCkp8S64e3Ywlul6F3hT0j11169Vbozz44jMBxra7LUZXkAsgzt8L1JD882Tf0/luxu/RNhai691cQPc/aWOdSngfdUs8VaxawGswvBs5VxaCY8xXhafS9c0eS5FxBY4M3ORpAFl2zI4Kro0PvevUgOjkys2rYAb3y7EGrWnSjotLNB/EfB7SVfVbUcyfJAOadJhiIgJgTVxE8zjuJnosLLKrrOLtnVTXBynef8h6fZysV0f17J2w9GbXYFvmnCw2mzbAFiipDFb227HYwsXayL9VTlO0+CGri6ySPikuKN2O3mCVuOEZ4Ufg2+ATxUb98ejZt8K1wb/UEoJ0hntQETEilhk/hngAUlXF+erH3Ckau6iH4Y98+Amy80lPRuWNTsfL/7eLnWardKiRhZb5XlvoDdOi18j6Yh/9zt1Uv7GTsbX6+lw7fpA/B2eFFZp+EbSXXXbkgwfZMo+6TDIeocnhSeMDMHaeW/XfYEtTtZKwIFYK2+XUid6ME4XroDrWw9W/ZOFqjegAbjTeBQ8hWmT8Kzsy3CK7A3ggKZqscpxWhlLXz0FDImIM3DE6Ph2dEZnwDfpi4szOhZOzQ/U0EaqH7+3dEbbl7AuZTe5OXAR3PjSH6ebF4iIySWdGNYa3icinpT0SUO2zYbPpZuKMzo6llG7WdLb8GP9KOV57Q16ZaE8J1YcuCAi/oEHg3wJ3I4dwn2BL+RazkbOb0mvhhvOxsUarbMDq+FJX1KRXMsFYPKfkg5p0uFQm6lCdV/MImJyfENcGTdXTYYlg/bHDt/NETGBPIqzdue42DQAp8C2wB3sr+LGikNxo1BvYAtJb9ZlS1uK47c3rvHbHacKW2nwVrq1PcYATo4d9yUi4losDbavpJYsTt4QOwjh6VlXAgdGxOfYidkIR9imxFN9Vi3f2QkRcW1TzmhhNGB8YIwSAXwbOFzSU8X+Rs+l4rCfjRehV0fEjsUpHYBLdrbCNdGfNWBLK0MyO3ZCX5D0Slm8vyPp84h4FngSD8UAcgGY/Odkyj4ZoYmIhXCX7Ms4Lf8n7JzOhiM2d+ExgLV201cu9oE7+k/EEdt+uImpnyqTViJiTDXUaVyxbW58bB7C41s3kMc3zgU8rwYmwbSxZ2Zcs/o2XkRsi+voLpb0z+q+TdiV/DIl9X0DcJykcyrbewCn4AEFb0TELViZYT9Jr9dsU/XcHoyVLL7G5R+P4iEd71b3rdOeNrb1AvYCLpdrVZcEjgOOlXR+id5OIOnVBmxpHaelsbD9O+XxJJ5i9Rcsgj8zsL2ycSn5FaTsUzLCUiJ+h+Ga0Rfwqv9vcgf2p1jr7+QGnNGxgOnLy97YQf4e33wWB/pL+iYidouINcp+tY9vLM4xeMwfwCvFvhOwHuvL4SlNh+EIZe2UCKxKfdrlwAY4evwplgebBNi0RL0zOtOxWAK4Q9I5Yd3KOSJic1w3viiOcM+CO8qPbcAZrZ5L52E1j8fwlKOT8Lm+QXGk2+NcWhCYBli6LEDvxONT94uILSR92YQzCj+WDswJ7AasJmlp4GIc1V4QD+S4C9gyndHk15Ip+2SEpNz4rgKukPRS2fwPYP2wqHsfnBJ/vmY7ApgV62XOCPSStEhYpuhUYE5JgyJiLSz51A+auTmWm9ByOIX6Cr5Z34CjkBtHxOO4dmwv1ax9GhE9JH0lDwOYFpcMrIS1INcCvpV0W1hyph95beuIvApsXhYxa+H0+OzATXhBsRPwFZZbe6ouI9qcS5Pg6U8rYbH214FPJb1QzqWdcPSvdipRyMmBLyWdFxEfYq3hfhFxhaS7ixPf6ISjsNLBIniBPCXW+X0AT9GbXx5N+pMxvUny35Ap+2SEoW3KLSJOw9JSS8gi/C3Jp4WB11UmrzRg1+jABTiCBdLSkAAAIABJREFUtJuks8r2fYC+ODI5Fe4gf7YJm8rnLwqcjqOQ52Bt0eOAGbBz/Alwt6Sb6kxnlgjy/sD9sr5oD1xb+yXWY1y3RGv74kkxPSR9Woctya8nIrrj72tjXCJzAvAsHg+8JpY0Ckn/qut8iohxgJ2BZyT9pSw+9wdeatkmaxH3ww1DQ9TQYIBiX1+sd/okLkNZBdeSzwa8CFzYsqfuEoKKg9wDGFQc+IPwpKW9JD0SHtCxEb5GfN0O9ePJcEQ6pMkIQeXiujBOg70m6b6IOB3LS/Vvqiazak/l9eLAkrh+9HFJV5btc+J6usFq0+zVgI074UjI+9gx7V9q/MYsDQxdyk2q7hvjJLh2dWaclr8LjyudDo8pHBwR8+EIzUaS/l6XLcn/TkT0bC0Ay+vFcdnHqnWf4+HRsb/HZTEPypJyV+MI6ViSvqqcS5tIeq5Oe9rYNgtwLm5eXASrfMyIo6GbYF3kQ1S6/RuyaVVgU6z0sTm+FmxfHufjxfvRkq5vyqZk+CUd0mSEISxZtA8WbO4PnFfq2c7FF/7lmnBKqw5cicR8Anwm6fGI2AV3jV8HjAd0l/Snum1qY18vPJpwdpwaHw1YUR4OsDqOaB3TRDSkspDoC6wKTIC/w4/wvPqz8Kzs1XFn/bV125T8NpTo5DLYGd1T0o01f17XsnhZHjt4Y+Bo5NP47+1DXJayNrB/E+dS5fyeEvgWC9wLT2VbR5ZWmrdEIydWadZryKYx8XHZEzdW9sWR7JeB/XBG5yy567+rPLo0SX412dSUjBCEhdFXx5qZ7+AV/60Astj8S3gKS+1UnNHtsaZnb+C4Eo04BngNNwkcBTzchE0tSvnA1jga+Qh2/C4Avgp30+8LPNdUaq5Sx3os8HfcCb0TluaZD9cefgP8oUS74mf/saTDUJzR+fB3uXcDzmgUZ3RpfC7dgOerr4frIPvgmsgPsapGI+dSOb+XxPrHCwB74MahRYozujDW9Zy8CWe0YtNieFrdI5IelLQncDVuZOqFa8cvxQ2EvdMZTX4LMkKajBCU+rVTcd3h7Dgd90p4SsyrdTcvDcOeBbFz1xen5hYsb50i6YpS69ZNDY8oLbZtg2/US2EHfmFca/stcIJqnpzVxpauOIr1VKn5mwYfs0WxfNCDdduQ1ENxSseV9F6NNaNTYh/rzfCEpf2AD2WN0/FwGnoBfF43PlGoZCMOBU6Tp8NtgOu0twQmwjqjezaREq9ERufBChYP4UX6mZJOK/schvWa5wHGxlmLG1QGUCTJ/0JGSJPhklZ0IyKmjIjx5GlGN+KpS8cUZ3RRHC3p0ZQ95fkowPP4Zrg2dviWwxGaoyNiY0mfNOmMRsT04WlVSDoFuB9YqKQt98cTWNZp0hkttgwGgqJ+IMvc3IXrRwdExIQZFe2cSPq+dY7XeD5tANwdEVPJE5bexDJKk0n6EDgDS66tHhET1WTDTwjLXnXFf/dTY8mrrpL+jNP18+LmwR1lDdKmorWL4cEbm0paF2sxzx4RW5Z99sCyT4NKxPaMdEaT34qURkmGOyor/eVx9OHTiHgI1z4dCuxfnNEVgJ0kPVK3TZU0/RbYmdpD0mclSnOKpG8j4mPcKNBopKbcGFcD5g5LyrR0RVu6kV9hOZ7/93+pyZbqNJjJJN2EhwTsgutZD8Kp1reBQ5tu9Eo6F5IOLuU6V0VEf9wU1wtYMzyieGQ82ev0JhaAlcVcd0lfRsTJWFN4bqB/RFwu6eJh/D+aSmVOC6wPPMPQ5kEBK0TESJJOBV5u/T+aKt1JRgwyZZ8Ml0TEvDg9txsWdp8bp+rPwfWjPRjaSNRU+nkAlitaTxbiJyJ2wPWiN+E0+RKqWRC8fG7L8ZumbHq/3CB3wsdndew4r6OGZ9RHxDK4y/lTPJr0CNwVvQGOZo2FZWeubtKupPMSEYfgaOQqOCK5Ela16AIcKOmaBmyoLpS3BwbiCWeXRcRW2FH+G3BJUw5oxaZJgY/kARyr4MzRhpIeKOVDywNPq0HZuWTEIyOkyXBHRIyB0+GztWpDI+IzXKc5g6TLqvvXdfGvOrolTT87sJksut1N0reSjo+Id4AJgb5NOKPwY3puVVzH+jXwekRcLenYYu89uBN5uibsaREeB7o97up/KSJOLHacIWnDUnP3raTXmywdSDoPFSerN474PSVpr4j4Cjfm9Je0W3jAwg+ylFmdOrqtaGKrgekovDDdCAvejy/plHCT48J4DnwT0dqWbFtfvHD/MCLexQ1LuwLnRMQAWYz/slLykCS1kQ5pMlxQvaFI+iIiTgKmi4hTJG1TakbfBOYCLmvCmak4o10kfRcWmF43Ip5SGUcaEcsCt6oZualulc+dAM9+X0/S3yNiU+B3EfGGpEclPRQRnwNnR8Qlpd6uLrtaDkQXHLnqDcyClQ+2x00ee0bEoZKeaf1eOqPJsCjn0srAIVhHd52IeAEvvgK4PSKWk/RK9XfqsCUipge2i4hngbdwdL8f1kKeG2dxdo6IH+RGqynqLh2IiFEkfaehU8+OwWn6rsWmU3G2ZjzgT2F1jRw0kdRONjUlnZ6KQ7N0ROwZEXtjuaLdgVEj4q/hhp1VcPShMWemfO75JULa0hPdoLy3Fr5JjtGAHWMD94S7+1uMXh4Al+Cu2dXavD8OUGudWPnuFsEjVI/G2qJ9I2LREljaAX+fSfJviYhRcbPgxpLWwOnnrsAGkg7B2pqTNGDHjMCFWJ1iFvy39TnwT2A7PJr4aiw1tUlxRt+s2aZewL7lugSuoX2+LEIfxt317wLLSDoTWFxusMzFX1I76ZAmnZ7i0CwKnIlnUS+C9Q1HB47HNaR7Yq3K28LyL785UWiz+U4sdH84jtY8hzt6b8UztLeS9E4d9lSRR2leCZwVEfPLs+evB5aJiF6SBuEb9agRMXL5f7wDrKDKVJ0a6Y3Hfs6MU5ov4cjWksX+bavR0SRpMYy/OYCJcTYEXKv5FhadR9Iuku6v2abx8PjPcyXtisekdsOLvm+wnm6XiJgfNw1t0IAzOjPWO329PMCax1NFxM4Akj7A0dBe5f3GpkIlSTqkSaemcjNaFmv5XYx18r7GF/lncDTiMWANgBproUappOnnioiZ5A71vngW9R7AX3DKbmschajdySqpcCQdhaOPfw6PJL0eR2dPjIg9cWr8r7IcjyS9Lcss1WnbKMW2k4EDgKtw3erJOFKzXkT0bP0fkqRKmzrtKcJyTt/gc3n+iOhT3n8a6B4RY/2MA/ubUkpcLgN+HxHdy9/RZ8Ckkr4HHsWKH+cAF0l6qU57SobkTOB4SWe3rjulhGdrYLGIODXcULgylqBrya4lSSNkl30yXBARG+PI6H4qs54j4kFgXdypPTduIjhYNUgFRcR0OAq6C25IOBFHZf4i6cWwMP+zwBPAuq1azrqplDP8OHaw1IvuhscAvoG7jacEHpN0X1PNQhExB/5Ojm5FicOi/FtVbJuwbqc46ZxExPjARpKOLpH0Y7BCxDF4yti8eDH6MF6w/kHSDQ3Y9eMYzYg4G5gfO579cef6a+W9iXGCp7bBABWbJgLOA/pJ+rrt50XEFLie9WPgXuVs+qQdSIc06XRUnKw5cS3YG1jGaT18IxqImxcuAVaR9HaJsI1chyNYIi6TYUdqCmAbhur5/Qu4Vu6s3xlHaVcqqbFaqRynFYC9cB3m3ThSshouGdhS7TTtKCJ6Yt3Vl3Ca/l9AdzzAYFKgd4kwJ8lPiIgl8N/Y+1jBYnt8PdgFuAZnAMbGEfd/qVmJt6pTegq+NsxcrgM9mj6vSwnB2biu9tOwpugP5do1Ndb8vbeyfypYJI2TDmnSaSjp3e+Lk7UccBrW71wYOBIYF9drzoUjJcdLurLOi2sU6ZTyvB+wMY4y7ICd042xk/UZvmluqQYnm5Qatf1x9GMKYEZgfEnbh2VmtsfH67O6b0AVB3kuLLz/Lq5hOxc3dhyPHftVcRrzyTrtSTo3pRZ8SVwSsyCeLPZDeNrQjsA9wNmSvmgn+0aR9F15fiK+Ti2uBhQ1fsae67HM1WrldcspXQKn6feR9GV72JYkkA5p0kmIiBmwNt5VuDnoCDxd5c6IWBpHHq+TdGNY5HlkNahVWaKf/XAT06y4cWFb3Fi1FL5xHibpubptqdg0Lk4VjiNpsbJtDhwZPUHSwPBIxdcbtKkvcDAuXZgER7MPAk4BRsPHakATqdWkczKMdPMCuD77CeAoSV+VFP6u+Fx6o0HbppUl5rpKGhwRkwBzSbohIi4C5sMNQ2oqAhlD9UZHAu7FmYjVcTPVXFj9Y3dJNzZhT5L8HOmQJh2e0h16Ab5wXibpg4g4Hc+DP6Vc+DfAYtPLyXPr67Zpbuz0DoyIbljeZWdJb0bE1Dht3xNPFPpnNYVXs13VJo/AkY+jgZMlnVC2n43Fwk+q266ykJha0q3hEY5XY8f8nlLXdj7u/j8HR7jHlPRyW6cjSeAnZSjzYafqRFwvujwuSzmuOKXjSPqkKbtwVuZx4BhJ55aF8e14xO2fy36zqR3UIqJoEJdr1WXF1i5Ya/QgSdfk31zS3mTnatKhiYgxccf1qZJOwaldcJfqhMAC5fVTuJmoiWjo8rgOs+X4Ctc8rgpQmhYexTfMg0pkopGZz+VmvUSJ2PaRdC1u7OgTEceWFP6CuOu41i7a4oxegyV4wMdgMJ7djSwAfjIwo6TBkt6X9HLr/1GXXUnnpZzfS+EO9SuBAVhv+F5cezwFsGupGf+sSbtKffruQK/SxDgnXjD/OYaqRDQ+erOk5r+NiKmArSWtgrM32+KpVemMJh2CdEiTjs4g3K1+ZXndtfy8Cjs3u0TExThCeamsp1kbpXZ1b2APSU+XtHg33LW+fESs19oV62ruLemHBtNzc2KtwVGAiyNiM0m3YMdvNRwt3aREKLv+wj/1v9oxM5a42kPSea2mMhwx+lNETFh27QpMHxHdS5QpSX5Cm3NjMVyjPS5uaDxV0jeSbgcuBi6XNKRV292AbbNHxJglA/AYrhWfUNINspzZjzRRp11+zh8RK0XEvKVOdAJ8XWhJwL0i6aVWuU46o0lHIFP2SYcmrJ93H5Uap0ox/sQ4Tfcx8IakJ2puYOqJI7T9SlRhWiylsg9wP9AH10I+CPwOWF7S83XY0sauVhpzCmACYApJV5XauguBwyWdHRF9sMzSPZLOqNmmhbF8TJfy+jbgZknHRcRBWBHhXDy1agdJN9dpT9L5CU8XmgwvRBcBpsJd469ExOa4hOa0hm2aB3evP40nMh2OO/+nxpOYvm/SnmJTH9wgeDweA7oq8AkwpaSLyj4ZEU06HDnLPunQyBIlJwH9I+IdufO6dSGdEzt+W5d0Wa0rfUkfl5viQRHxKtY7vEbS3WWXGyPiYRy5+VINTGCqNCz0wQ7eG8DXEfFwqW9dF7i+REPPxZHTtSLisjrr6yTdHxF9y3F6BXhA0nHlvX0i4jF8A79L0gN12ZEMH4SVGXbAqhDj4IalPxZndM6yfdeGbZofN+j1w+UoS2Hn9GWse9wD+LTBxsrAdesDsBM6Hp4M97A8me3+st+PyiBJ0pHICGnS4QkLYLdSdJcBdwEL4alDu0i6qWF7lsNyU3tKOrwSse2LHdF7GrChe6t5q9yQ18a6iz/g1PwQ4MTSULUAMJqku0pTw0hqSAex1PvdQpliVbU7Sf4TSnnHwcDskuYv27YAVsFqFhMDR0i6rkGbZsNO8JuSDqxsn6HYczKeerZTUzZVbNgNGAs7yOsVp31jYKCkF5q2J0n+U7KGNOnwyCLyJ+LV/ik4DX0Mrk+8qenaw1KT2QfYOCLGLs7oxljrs9Z51AAR0Qs4PCImK3Vr52FZqWckDQRakkm7R8QkkgYWZzQkfduUMwog6Q7sOLwYEePJU2IyM5P8Im3+pj/H5/SgiNgFQNJZwB9wY84Gkq5r+DrQE8uWzViahSh2vVgWpEsA45YFYG1UakYnKfXs4HHAGzLUGe2No8fj/sw/kyQdgoyQJp2KEi0ZAnSTJzC1Wy1U6bY/EtdprYs1D2vVGS0RmL8AJ0k6t2ybDMsp3SDpgLJtCSwYfnZHiIqUkoILcEd9I1I8SeekUhO9KB6g8K2kv5ZymRWB5ySd2E42TQe8J+nL0ri3F64Zv1ZlZHHZvx/W111ANQvzl+NyIp4//4akvSLictwQ+gPWGt23yQhykvwa0iFNkv+BiFgRd/zP2YAzOjNwEXBAaarqiutnT4qIaXDK/hJJB5f9G9Nh/E8oJQ1fVWpuk2SYlL+rw4Bj8dSlMyWdHNYfXQd4TNLxDdnSqtNeEdgX12L+gBejkwA746amy1SmsBVn+h1Jr9RkU8tB7o6Pz/146tlp2GHfLSIWwk2Ob0t6NBuZko5OOqRJ8j/SVF3kMDrX/wo8KWnX8noa4A7gQkn71G3PryVvjMkvERGT42j6ZsD82OHqjsfJHhYRKwOvqWaB+ajMnC8NTKcDK+EygeXxZKjdsVO6G26yanIq1NJAf2BsHAF9KSzvdA7woaRNmrIlSX4LsoY0Sf5HmmrSkXQ/0DciXo2I24H7Ws5oef9V3Ox1WxP2/FrSGU2qDKP28xNgc1zzuDuwdPm5T0TsKem6BpzRnrgGu3/ZNAqwKTAzsAxushwVp8rfxxJPTTqjcwMH4jGgUwFLR8SkpZt+C2CiiJi9KXuS5LcgmwuSpBMh6ebSYXwrsGxre0nPbQdsJem+jEImnYXWeRoRM+IpXl+UZpyZcF305xExBHeuP9iQWV1wB/98EfGFpNuKjccC2xRJtRVxc1PPav1o3ZSmxouAfSRdXqTm1gEUETdKeisiVpH0XVM2JclvQUZIk6STUTrXVwZeBIiI6XE68c+SPi37pDOadGgiYqqI2Kk8Xxa4G48EPSs85OE9YOGIOADre14t6e66u+kjoqukD4EncfRx65IeBzugu0XEIjhye6Kkp+u0Zxi8Vx67ghep2EFdGlglPLc+ndGk05E1pEnSSSl6qFfhZoZdlNOOkk5CqXWcBStGnI2nL92KF1kDgHnxNK9ZcJr8rVaUsma7Ws1CywAnYHm5fni4w2XAQ1h2bmTcQHjlz/5jv71Nk2AN4TcjYhRcZ9tN0mplv+WBdyU9VbdNSVIH6ZAmSSemCM+PKenq9rYlSf4TSmr+WlyT+SXW0f0KO34f4CjktsCiwCaS3iy/V+dY4KnwUIsPi3rFIVj0/tSImAg3WM0FHCnp4YgYVdI3dZfGVJzRlYD9gXew7NSWETE61mWeSFKfumxIkqbIlH2SdGIk3SHp6oZFwZPkV1EcvyuwY/dAieYtg8XcN5b5CDtaDwATtn635jKU/sBU4alrg4G3gWUjYiJJ7+HO9VmADSNifEnf1GlTcYqp6LEehDv8rwc2jYhzsc7oNsDHpckpSTo1GSFNkiRJGiEiNgHmkLR9RHTBUcdJsLO3PXCgpFPLviNL+r5B2yYCbsSTxcByU28CFwOj41HFO0h6tmY7ZsQyUjtL+iQiZgW6YU3RvYGNgGtwecO6wPfFiU6STk1GSJMkSZKmeBWYp0zuOhuLyh+BHb6XgANKExNNOKOtzEJEjF4ioY/gBqHvsXM6FXATnoR2cgPOaC/sAP8dEED5zCexo3y2pJdxxLY3MEU6o8nwQso+JUmSJE3xCHA5dkJfxo1Dz2LHD9zQNE4ThlTqM1cGVo2InSUNiIgTcVnBGpLuLE7it5Jer7mOdSyslnGKpHMqzvJ4pbb1GWCBiBgJS76tKenFOmxJkvYgU/ZJkiRJo0RET0kfV14vjp3U5UqauhEd3dJNfwQewTuwsv0AYA1gGUnv1G1H+cwuWGj/eBxJ3haYA9fYHgj8E5gJWAE4TjmbPhnOyAhpkiRJ0igtZzQiRsYO12HAnpI+Ke83FSlZFPgz8GZErAusCDwhab+IGBtHbhtxSPE0qLFwLW0f4Dk8o/4u3Lz0R0lHRcQpkr7O4RfJ8EZGSJMkSZLGKc7ofMABwAmSrm/gM1tp+pEk/RAR/XCH/ay4dnMIMAWwl6TP67ZnGPZNACyMG73Oxw1L30TEkcCrkk6PiC6ShjRtW5LUTTqkSZIkSbtQnNJxJb1Xc31mT2AsSa+VgRKLA5/jWtEAPis2zIEjpv2brs/8OUczIhbGHf6bS3qgSZuSpEkyZZ8kSZK0C6WT/r3yvC5ndDQs4TQ4Ip7CovcHAxsA42KR/ldLPenJwE7t4IwGdoyJiHGAr4HxgYWwBulO6Ywmwzsp+5QkSZIMt0gaBDwI9ABWA86TdHF5/jmeGPUDMBqOQt5Yt01VualSPiBJgyNiUmAgsADwEZbD2kLSjTn8IhneyZR9kiRJMlxSTYNHxMzAXjjyuIOk58v2R4B1ir5nk7atDGwJjIqdztci4gjgHUkntrU/SYZ3MkKaJEmSDJdIGhIR00fETcAnwH7AC0D/iJgrIqbHUchGxeUjojewKy4deAS4qExkOjad0WREJR3SJEmSZLijkuL+BHgaOA2n6M8ApgYuwbqfu0t6rWZbJo+IZcvzaYAdgJckDZS0B54GdSowWcv2dEaTEY10SJMkSZLhgoiYOCKmLi+nApD0IXAU8AQeufkecDhwB54Xf22d9Znl354BeC8iegBvA68Dk0TECsXGg4G7gdMjYozUF01GRLKGNEmSJOn0RMSMwFV4qtHdWFD+akl7lvfHB07C4vMb4HGgXzRkWxdcGnAZcCbu7N8Nd/nfLumWst+0kl5pwqYk6WhkhDRJkiTp1ETEVFhT9BhJl0p6D1gKWCEidgWQ9AHwKDAImLIJZ7Q4opT0+3fAhcAmwHLAscAHwMqtSCkeGZokIySpQ5okSZJ0dpYA7pB0TnEC58LTjv4C7BARQ4APgbWATSQ9W6cxETESMLg0Vc0LdAP+KenCiPgejwIdgufW7wq8Bo2OTE2SDkc6pEmSJEln51Vg84jog53O0YA5cAr/FVzDOTtwaAPO6ETATsARETE7bp66FlgoIraR9JeIGAzsju/Bh6QjmiTpkCZJkiSdn0eAy4EjgJeBE4BncWNTd2BvYFCJWNY2orTwKTATngj1ObCmpHsjYn3gvIjYWNIVJYr6XjqjSWLSIU2SJEk6NZK+Bo6PiAskfdzaXvQ+5wfGxOM46xxROjIwqqQvImIj3Nm/OHB3RHQt6fohwJURsYakS+uwI0k6K+mQJkmSJMMFLWe0OIfLAIcBe0r6Z52fW+pWlwa+iIhpcYR0J1wjuiLWQX1b0sUlMppjQJOkDSn7lCRJkgw3FGd0PuAA4ARJ19f8eePj6Ou8WN90ImCXkpYfDTgb+Bg4WtIbld+ru3QgSToVKfuUJEmSDDdI+h74G7C+pOtrFr0fH9gK6Ak8ADyEG6wGRcQkkgYBGwOTAntGxKgVO9MZTZIKmbJPkiRJhiuKU/peeV5XzehIwAAc2BGOjh4F9AK2AMbBuqM9sAh+D0nf1GFLkgwPZMo+SZIkSf4LWun2iJgPOA+PIX0Xd/QfinVR1yvbtgCWkPREO5mbJJ2CdEiTJEmS5D8kIiYH1gXOlvRRRPTFzVPn4LGko+L61ZmwQP8bku5oL3uTpLOQDmmSJEmS/IdExMG4g/4mYA/gI+ygjgs8CSwIjAwcJunDyu9lE1OS/AJZQ5okSZIk/4aIGEnSD8B+2PmcDafjX8JNSyOX528BG5V9fnRI0xlNkl8mI6RJkiRJ8guUcaCrA49LejAi5gQWw87n98DaQF/gPkkrRsTokr5sP4uTpPORsk9JkiRJ8st0B6YDDi4jQF8Axga+kHQdnkt/N7BARMyWzmiS/PdkhDRJkiRJ/g0RMQqwJHAmcCxO0a8KDJD0TET0BHpKerkdzUySTktGSJMkSZLk3yDpO0m3AMsC0+Nu+nGAfSNiQkkfpzOaJL+ejJAmSZIkyX9BRIwLzArsAPQBZpb0ersalSSdnHRIkyRJkuRXEhFzSHqyve1Iks5OOqRJkiRJ8l8SEV0kDam8Tp3RJPkfSIc0SZIkSZIkaVeyqSlJkiRJkiRpV9IhTZIkSZIkSdqVdEiTJEmSJEmSdiUd0iRJkiRJkqRdSYc0SZKkgxARgyPiyYh4NiIuj4ju/8O/dV5ErF6enx0RM//CvotHxEKV1wMiYsNf+9lJkiT/LemQJkmSdBwGSZpD0qzAd8CA6psRMdKv+UclbS7p+V/YZXHgR4dU0umSLvg1n5UkSfJrSIc0SZKkY3IfMF2JXt4XEdcBz0dE14g4KiIeiYinI+L3YB3MiDg5Iv4REbcDE7T+oYi4OyLmKc+Xi4jHI+KpiLgjIqbCju+OJTq7SETsHxG7lP3niIiB5bOujohxKv/mERHxt4h4MSIWafToJEkyXPGrVttJkiRJfZRI6PLALWXTXMCskl6LiC2BzyTNGxHdgAci4jZgTqAXMDMwIfA8cG6bf3d84Cxg0fJv9ZT0cUScDnwp6eiy31KVX7sA2E7SPRFxILAfHpkJMJKk+SJihbJ96d/6WCRJMmKQDmmSJEnHYbSIaI2hvA84B6fS/ybptbJ9WWD2Vn0oMBYwPbAocImkwcC7EXHnMP79BYB7W/+WpI9/yZiIGAsYW9I9ZdP5wOWVXa4qPx8DpvrP/otJkiQ/JR3SJEmSjsMgSXNUN0QEwFfVTThieWub/Vao37yf8G35OZi8nyRJ8j+QNaRJkiSdi1uBrSJiZICImCEiegD3AmuVGtOJgSWG8bsDgUUjYuryuz3L9i+AMdruLOkz4JNKfegGwD1t90uSJPlfyRVtkiRJ5+JsnB5/PBw+/QBYFbgaWBLXjr4JPNT2FyV9UGpQr4qILsD7wDLA9cAVEbEKsF2bX9sIOL1IUL0KbFLHfypJkhGbkNTeNiRJkiRJkiQjMJmyT5IkSZIkSdqVdEiTJEmSJEmSdiUd0iRJkiRJkqRdSYc0SZIkSZIkaVfSIU2SJEmSJEnalXRIkyRJkiRJknYOucezAAAAEUlEQVQlHdIkSZIkSZKkXfk/rqguqsjDNE0AAAAASUVORK5CYII=\n",
299 | "text/plain": [
300 | ""
301 | ]
302 | },
303 | "metadata": {
304 | "needs_background": "light"
305 | }
306 | }
307 | ]
308 | },
309 | {
310 | "cell_type": "code",
311 | "source": [
312 | "fig, ax = plt.subplots(figsize = (8,6))\n",
313 | "im = ax.imshow(Tencent)\n",
314 | "\n",
315 | "# Show all ticks and label them with the respective list entries\n",
316 | "ax.set_xticks(np.arange(len(labell)))\n",
317 | "ax.set_xticklabels(labell)\n",
318 | "ax.set_yticks(np.arange(len(label2)))\n",
319 | "ax.set_yticklabels(label2)\n",
320 | "\n",
321 | "# Rotate the tick labels and set their alignment.\n",
322 | "plt.setp(ax.get_xticklabels(), rotation=45, ha=\"right\",rotation_mode=\"anchor\")\n",
323 | "\n",
324 | "# Loop over data dimensions and create text annotations.\n",
325 | "for i in range(len(labell)):\n",
326 | " for j in range(len(labell)):\n",
327 | " text = ax.text(j, i, Tencent[i, j], ha=\"center\", va=\"center\", color=\"w\")\n",
328 | "\n",
329 | "ax.set_title(\"Tencent Heatmap\")\n",
330 | "fig.tight_layout()\n",
331 | "plt.show()"
332 | ],
333 | "metadata": {
334 | "colab": {
335 | "base_uri": "https://localhost:8080/",
336 | "height": 441
337 | },
338 | "id": "u0aihRTLAHKv",
339 | "outputId": "9a92477c-0f68-4e28-d48a-047014ba0992"
340 | },
341 | "execution_count": 28,
342 | "outputs": [
343 | {
344 | "output_type": "display_data",
345 | "data": {
346 | "image/png": "iVBORw0KGgoAAAANSUhEUgAAAb0AAAGoCAYAAADSNTtsAAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADh0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uMy4yLjIsIGh0dHA6Ly9tYXRwbG90bGliLm9yZy+WH4yJAAAgAElEQVR4nOzdeXgUVdbH8e+vk7DIaggiE1QcUUQUoyAo6IiKC467zuCMG24MoriAK7igDu7riAoKiLuIivrqAAqIIiqbIKiAouwOQgj7Zpbz/tEVaGMIgVR3SPp8nicP3beqzrm3KuT0rerukpnhnHPOJYNIeXfAOeecSxQves4555KGFz3nnHNJw4uec865pOFFzznnXNLwoueccy5peNFzzjmXNLzoOVdJSVoX81MgaWPM8wvKu3+xJJmkJiUs7yzp82La50vqEEL+PpJeKWsct+tLLe8OOOfiw8xqFj6WNB+4wsxGl1+PnCt/PtNzLslIiki6VdJPklZIelNSerCscTDrukTSQknZknrHbJsiqVew7VpJUyXtFSw7UNLHknIkzZH095jthkh6WtKHwXYTJe0XLPssWO2bYBbaqQxju0zSLEkrJY2StE/MsiclLZK0Juj3MUH7KUAvoFOQ/5ugfZykf0v6Imj/P0n1JL0axJgsqfH24gfL+kh6S9LQYPxfSzp0Z8fpdp4XPeeST3fgLOBY4E/ASuDpIuscDTQFTgDulNQsaO8B/AM4FagNXAZskFQD+Bh4DdgDOB94RtJBMTHPB+4GdgfmAn0BzOwvwfJDzaymmQ3dmUFJOpNo8ToHqA+MB16PWWUykAWkB/0cJqmamY0E7gOGBvlji9H5wEVAJrAf8CXwQhBjFnDX9uLHLD8TGBaz/F1JaTszVrfzvOg5l3y6Ar3NbLGZbQb6AOdJir3ccbeZbTSzb4BvgMJCcAVwu5nNsahvzGwFcBow38xeMLM8M5sGvA38LSbmcDObZGZ5wKtEC8SOOFLSqtgfYO8i47rfzGYFOe4Dsgpne2b2ipmtCPr3KFCVaGEvyQtm9pOZrQZGAD+Z2egg/jDgsMIVSxF/qpm9ZWa5wGNANeDIHdwHroy86DmXfPYBhscUjllAPtAgZp2lMY83AIXXB/cCftpGzDZFCtIFwJ6liFlaX5lZ3dgfYGGRPjwZkz8HENFZGpJuDE59rg6W1wEytpPz15jHG4t5HnvddHvxFxU+MLMCYDHRmbZLIH8ji3PJZxFwmZlNKLog9hpVCdvuB3xbTPunZnZiGB3cSYuAvmb2atEFwfW1m4merv3OzAokrSRaFAHKdLuZUsSH6AuGwvUjQCPgl7LkdTvOZ3rOJZ/+QN/C036S6gfXw0pjIHCvpP0V1UJSPeAD4ABJF0lKC36OiLkWuD2/An/e4ZH8Xn/gNknNASTVkVR4erUWkAcsB1Il3Un0mmRs/sZBMdoZ24sP0FLSOcFp5OuBzcBXO5nP7SQves4lnyeB94GPJK0l+oe3TSm3fQx4E/gIWAMMAqqb2VrgJKJv/PiF6KnMB4le1yqNPsCLwanJv29v5eKY2fAg5xuS1hCdjXYMFo8CRgI/AAuATcScbiR6fQ5ghaSvdyL99uIDvAd0IvrGoYuAc4Lrey6B5DeRdc65+JLUB2hiZheWd1+Snc/0nHPOJQ0ves4555KGn950zjmXNHym55xzLmn45/TcLqOKqlo1apR3N1wCKSUlIXksPz8hedyuYRPr+c02q7hlXvTcLqMaNWijE8q7Gy6BUmrXSUie/FWrE5LH7Rom2phtLvPTm84555KGFz3nnHNJw4uec865pOFFzznnXNLwoueccy5peNFzzjmXNLzoOeecSxpe9FyF03PQVby5dCDPzXg0rnlanZzF4FlPMuSHp+h0y1meI8E5MjJ358H3bmTAl/cw4Iu7OfNf0c9w1qxbg/ve6cGgyX25750e1KyzWyj5IP77yn93yz+HF70KRtKekt6Q9JOkqZL+K+mAbazbWNK3weP2kj5IbG/j46Mh4+jVsW9cc0QiEbr3u5xep/bliuY3cNz57di7WSPPkcAcBXkFPH/Hm/zrqDu5/qT7OP3y49i7aUM6Xd+R6Z/O4vIjejP901n8/fqO2w9WConYV/67W/45vOhVIJIEDAfGmdl+ZtYSuA1oUL49S6yZ42exNmddXHM0bd2EX+YuZem8ZeTl5jFu6ATantnKcyQwR86vq5k7YyEAG9dtZtEP/6New905qmMWo9/4AoDRb3xB21MPK3MuSMy+8t/d8s/hRa9iOQ7INbP+hQ1m9g3wuaSHJX0raaakTiUFkVRD0mBJkyRNk3Rm0N5Y0nhJXwc/bYP2iKRnJM2W9HEwuzwvWDZfUkbwuJWkcSXlqCgyMtNZvnjFlufZi3PIyKznOcopR4O96rFfi72ZM/Vn6u5Rm5xfo18rlvPrauruUTuUHIkYRyJUlmMerxz+3ZsVy8HA1GLazwGygEOBDGCypM9KiNMbGGtml0mqC0ySNBpYBpxoZpsk7Q+8DrQK4jcGDgL2AGYBg7fT12JzmNn62JUkdQG6AFQjvGszrvKoVqMqt7/YjQG9hrJh7aY/LPfbo7kd4TO9yuFo4HUzyzezX4FPgSNKWP8k4FZJ04FxQDVgbyANeF7STGAY0SJXGH+YmRWY2VLgk1L0aVs5fsfMnjOzVmbWKo2qpQibGNlLcqjfaOuryoxG6WQvWVHCFp4jHjlSUlO448Wr+OStr5jwwdcArFq2hvQG0S+qTm9Qh9XL14aSKxH7KhEq+jGPdw4vehXLd0DLEOIIONfMsoKfvc1sFnAD8CvRGWMroEopYuWx9feoWilyVAhzJs8lc/+G7Nl4D1LTUmnfqR1fvj/FcyQ4xw3/uYSFP/yPd575eEvbVyOn0+H8tgB0OL8tX46YHkquROyrRKjoxzzeOfz0ZsUyFrhPUhczew5AUgtgFdBJ0otAOvAX4CZ+X4RijQK6S+puZibpMDObBtQBFptZgaRLgMKbnU0ALgni1wfaA68Fy+YTLcQjgHNLkaPMer16HS3aN6dORi1eW9ifl/q8ycjBY8MIvUVBfgH9ug/i/pG9iaREGPXCJyz4frHnSGCO5m2a0OH8tsz7bjFPf3onAEPuHc7QJ0bQa3BXTr7waJYtWkHfywaUORckZl/5727555CfD69YJP0JeIJoodlEtOhcT/S6WEfAgH+b2VBJjYEPzOxgSe2BG83sNEnVgxhtic7S5gXt+wNvBzFGAlebWU1JEeAZosVuEdFZ3INm9rGkY4BBwBqipzFbmVn7beUoaWy1lW5+P73kklLX76fnwjfRxrDGcoq9iawXPVcqkmqa2TpJ9YBJQLvg+l5ovOglHy96Lh5KKnp+etOV1gfBuzCrAPeGXfCccy4RvOi5UjGz9uXdB+ecKyt/96Zzzrmk4UXPOedc0vCi55xzLml40XPOOZc0/I0sLqlEdov/93sWbNgQ9xyVheXmlXcXKhYV+y78cFXyj7H5TM8551zS8KLnnHMuaXjRc845lzS86DnnnEsaXvScc84lDS96zjnnkoYXPeecc0nDi55zzrmk4UXPVUitTs5i8KwnGfLDU3S65axQYvZ45nKGznuKAZP6/mHZud1PYdS6F6ldr2YouQrFYxyxeg66ijeXDuS5GY+GHjtWfI7HZQz9+T8MmPjv37Wf8a8ODJx6P89N6svl9/49lFyFKsPxqN+oHg+PvpOBMx/j+RmPcnb3jqHnqMi/V170ApL2lPSGpJ8kTZX0X0kHlHe/Ckk6S9JBO7HdfEkzJc2Q9JGkPXdg28aS/rmjOeMtEonQvd/l9Dq1L1c0v4Hjzm/H3s0alTnuR69+Tu+zHvlDe/3MdA4/4WB+XZhd5hyx4jWOWB8NGUevjn8s4mGK6/E4+/d/VA895kDa/vUwrjrqDrq07s1bT44oc55CleV45OflM+Cml7nikB5c27Y3Z3Q7mb2bZYaaoyL/XnnRAyQJGA6MM7P9zKwlcBvQIMH9SClh8VnADhe9wHFm1gKYAvQqZV9SgcZAaEVvO+Mrtaatm/DL3KUsnbeMvNw8xg2dQNszW5U57rcT5rB25fo/tP/rwX8y6PahWMhfzxSvccSaOX4Wa3PWhRqzqPgdjx/+cDxOu+J4hj72Ibm/Rb++bHX22jLnKVRZjkfO0lXMnTYPgI3rNrFw9hIyMtNDzVGRf6+86EUdB+SaWf/CBjP7Bvhc0sOSvg1mS50gWiS30d5e0meSPpQ0R1J/SZFg2UmSvpT0taRhkmoG7fMlPSjpa+Bvkq6UNFnSN5LelrSbpLbAGcDDkqZL2i/4GRnMSsdLOrAU4/wMaCKpddCXaZK+kNQ06EtnSe9LGguMAR4Ajgly3hAsfyfI+6OkhwoDl3Z8ZTxOAGRkprN88Yotz7MX55CRWS+M0H9w1F8PI/uXlfz87aLQYydyHPGUyHFkNtmTg9sewJNj7+DhEbdywOH7hha7shyPWA32qU+TrH2ZPXFueXdlh8XrePgXTkcdDEwtpv0cIAs4FMgAJkv6DGi7jXaA1kRnZAuAkcA5ksYBtwMdzGy9pFuAHsA9wTYrzOxwAEn1zOz54PG/gcvN7ClJ7wMfmNlbwbIxQFcz+1FSG+AZ4PjtjPM0YCYwGzjGzPIkdQDuA84N1jkcaGFmOZLaAzea2WlBzs7BuA8DNgNzJD0FbCzt+IqS1AXoAlCN+H8Z9I6oWr0K5994Ored+XB5d8UFUlIj1Nq9Jtcdfy9NW+5L7xe7cckhN5V3t3ZJ1WpU5c5hPXm2xxA2rN1Y3t3ZZXjRK9nRwOtmlg/8KulT4IgS2tcAk8zsZwBJrwfrbiJaCCdEz6RSBfgyJs/QmMcHB8WuLlATGFW0U8Esqi0wTFu/db1qCeP4RFI+MINocaoDvChpf8CAtJh1PzaznBJijTGz1UE/vgf2Cfpa2vH9jpk9BzwHUFvppTp/mL0kh/qNtr7iy2iUTvaSFSVssXMa/nkP9mxcn2e/vBeIXtt7+vN7uPbYu1m5bHWZ4ydqHPGWyHFkL1nJhPenADBn6jwKCow6GbVCOc1ZWY4HQEpqCne91ZOxr43n8+GTyrs7OyVex8NPb0Z9B7QMKVbRP9wGiGgxyQp+DjKzy2PWib1wMQS4xswOAe4GqhWTIwKsiomXZWbNJKUEpyKnS7onZv3jgnUuNrNVwL3AJ2Z2MHB6kRx/vKj1e5tjHucTfeG0I+MrszmT55K5f0P2bLwHqWmptO/Uji+DP4Rhmv/dYjrt251Lmt/IJc1vZPmSHK4++s5QCh4kbhzxlshxfPHB1xz6l2YAZDZpQFqVlNCu61WW4wHQc2BXFs5awttPfFjeXdlp8ToePtOLGgvcJ6lLMPNAUgtgFdBJ0otAOvAX4Cai++1fxbQfCLSWtC/R05udiM5ivgKeltTEzOZKqgFkmtkPxfSlFvA/SWnABcCSoH1tsAwzWyNpnqS/mdmw4I04LYLrkFmlGG+dmLidS1hvS87t2JHxlVlBfgH9ug/i/pG9iaREGPXCJyz4fnGZ4976wlW0OOZA6tSryStzHuflvsMZ9dJn299wJ8VrHLF6vXodLdo3p05GLV5b2J+X+rzJyMFjQ80Rt+MxuOvW4zH7MV6+711GvfwZPZ65nAET/03ub3k8/K+BIYwgqrIcj+btmnLiRcfy84wF9J8avew++PbXmTRiWmg5KvLvlcJ+R1pFJelPwBNEZ3ybgPnA9USvN3UkOmP7t5kNDYrMQ8W0tyd6HWst0AT4BOhmZgWSjgceZOtpyNvN7H1J84FWZpYd9OMq4GZgOTARqGVmnSW1A54nOtM6DygAngUaEj09+YaZxc7uCsf1u/hB21HAi0RnYB8CF5pZ4+CaXSszuyZYL43o6dV6RGegK4ss/wB4xMzGlXZ8JamtdGujE7a3Wpn4TWR3LZEaNRKSp2B9qCcbyo/fRLZUJtoY1lhOsTvLi16Iir7xw+0YL3rJx4veDvKiVyolFT2/pueccy5p+DW9EJnZOGBcOXfDOefcNvhMzznnXNLwoueccy5peNFzzjmXNLzoOeecSxr+RhaXVBLxcYLUhqW+e9NOy/vf0rjnSAT/eMcOqgQfJyhvPtNzzjmXNLzoOeecSxpe9JxzziUNL3rOOeeShhc955xzScOLnnPOuaThRc8551zS8KLnnHMuafiH012F1OrkLLo9cSmRlAgjBo1h6IPvVogcaVVTefjt60mrmkpKSoTPP5zOK4/+l+sf+Sf7H7o3ApbMW8aj17/Cpg2/lX0QVNx9FSutahqPjbs7ut9SUxj/9le8dPewUHNA5dhXnqNkPtMDJOVLmh7zc2sx67QP7hQeZt72ktruxHbzJWUU095ZUr+d7EuvIs+/CP5tLOmfOxMjXiKRCN37XU6vU/tyRfMbOO78duzdrFGFyJG7OY9b//4frj7xAa4+6QFatm/GgYc35rk+73D1iQ/Q7cQHWLZkJadfemwIo6jY+ypW7uZcbupwN10Pv5muh99Mq5OzaNZm/1BzVJZ95Tm2EzeEvlUGG80sK+bngQTlbQ/scNGLk98VLDMr7FdjoFRFr2iMeGnaugm/zF3K0nnLyMvNY9zQCbQ9s1WFyVE4g0tNTSE1LQUzY8O6TVuWV62WFtrXTVX0fRVr0/rNAKSmbd1vYaos+8pzlMyLXgkknSJptqSvgXNi2vtIujHm+beSGgePL5Y0Q9I3kl4O2k6XNFHSNEmjJTUI1u8K3BDMLo+RVF/S25ImBz/tgu3rSfpI0neSBgIqRd+HSPqPpC8k/SzpvKC9oaTPgpzfBnkfAKoHba8G660LQj0AHBMsu6HobFLSB8GMtbgYF0qaFLQNkJSyc0fi9zIy01m+eMWW59mLc8jIrBdG6ITkiEREv49u4fUZ9zPts9nMmbYAgBseu4DXpvelUZMGvD/401ByVfR9FSsSEf2nPsSwpQP5evRMZk+aG2r8yrKvPEfJvOhFFf6xLvzpJKka8DxwOtAS2O63CEtqDtwOHG9mhwLXBYs+B440s8OAN4CbzWw+0B94PJhdjgeeDJ4fAZwLDAy2vwv43MyaA8OBvUs5robA0cBpRIsXRGdto8wsCzgUmG5mt7J1tntBkRi3AuODZY9vK1HRGJKaAZ2AdkGufKBobCR1kTRF0pRcNpdyWBVbQYFxzUkPclGrOzjgsH3Yp2lDAB7v8SoXHn47i378lb+ccXg593LXU1BgdG15M//YuytNj9iPxs33Ku8uuQrI38gStTH4w7yFpCxgnpn9GDx/BeiynTjHA8PMLBvAzHKC9kbAUEkNgSrAvG1s3wE4SNoykastqSbwF4KZppl9KGllKcf1rpkVAN9LahC0TQYGS0oLlk8vZawddQLRFwuTg/FUB5YVXcnMngOeA6it9FKdr8pekkP9Rltf8WU0Sid7yYoStthxicixfs1GZkz4kVbtm7Fgzv+A6B/2T9+bynndOvDxmxPLnKOy7KtY61dv4Jtx39Hq5Czmf7cotLiVZV95jpL5TG/n5PH7fVdtO+s/BfQzs0OAf5WwfoTojLDw2mKmma3bxrpIujpmdvqnYlaJnToJwMw+I1pElwBDJF28nb4XVdqxC3gxZixNzazPDuYq1pzJc8ncvyF7Nt6D1LRU2ndqx5fvTwkjdNxz1EmvSY3a1QGoUi2Nw/5yIIt/XkbDxlvfl3TkSYeweO6vZc4FFXtfxaqTUYsadXYDovvt8A4tWDRnSag5Ksu+8hwl85nets0GGkvaz8x+Av4Rs2w+0VOGSDoc2DdoHwsMl/SYma2QlB7M9uoQLTIAl8TEWQvUjnn+EdAdeDiInRXMxD4jelry35I6ArsDmNnTwNOFG8fMELdJ0j7AYjN7XlJV4HDgJSBXUpqZ5RbZZC1Qq8jYu0mKAJlA65hlsTHGAO9JetzMlklKB2qZ2YLtdnI7CvIL6Nd9EPeP7E0kJcKoFz5hwfeLyxo2ITl2b1CbG5+4kEgkgiJi/P9NY9Lo73h4+PXsVrMaEsz7fgn9bnszhFFU7H0VK73h7tz8wtVEUqL77bNhXzLxw69DzVFZ9pXnKJnCfgdURSQpH5gZ0zTSzG6VdArwBLABGA/sZ2anSaoOvEf0j/5E4Cigo5nNl3QJcBPRa1jTzKyzpDOBx4GVRAvjEWbWXtIBwFtAAdFiN4toEWtG9AXJZ2bWVVI94PUg3xfASUDLwtOoMePoDLQys2skDQE+MLO3gmXrzKxmTP9ygXXAxWY2T9KDwBnA18E1ucL104BRQD1gSLA/XiF66nIW0QLcx8zGFROjE3Ab0ZlhLnC1mX21reNQW+nWRids52jt+vwmsjugFC/UQuF/55LKRBvDGssp9pfLi57bZXjRKz0vejvI/84llZKKnl/Tc845lzS86DnnnEsaXvScc84lDS96zjnnkoYXPeecc0nDi55zzrmk4R9Od8klAW+RT8THCTae2Xr7K5VR9fcmxT1HSr30uOcAyM+O39eiuYrFZ3rOOeeShhc955xzScOLnnPOuaThRc8551zS8KLnnHMuaXjRc845lzS86DnnnEsaXvScc84lDf9wuquQWp2cRbcnLiWSEmHEoDEMffDdUOPXb1SPm4dcze4N6mJm/Pf50Qx/akSoOXoOuoo2f23JqmWr6dKiZ5li3XbNKbRt9WdWrt7AxdcNAeC4tgdwWad27NOoHlfe/DJzfvoVgGb778nNV50MgIDBQ7/gs4k/lil/PI5Hxp9256Z+nalbvzaY8d+XP+e958cCcMbl7Tn9svYU5BcwafS3DLrnnTLng/j/XoV5zEsS73FU5BxJUfSKuTP6G2b2QAhx5xO9U3n29tYNm6TWwCNAA6J3dp8KXGtmGxLdl0SLRCJ073c5t5x0L9mLc+g36X6+fH8KC2ctDi1Hfl4+A256mbnT5lG9ZjWemfwAU0fPYOGsJaHl+GjION7rN5KbX7ymzLH+O/Zb3v7v19x+3alb2n5emE2vB9/l5qtO+t26Py/I5oobXyK/wKi3ew2GPH4JEybPJb9g5260Gq/jUZCXz/N3vcXcmYuoXqMqT43uxbRPZ1G3fi2O6ngo3Y77N7m/5VEno1aZ8sR7HLHCPObbkohxVOQcyXJ6c6OZZcX8lLnglSdJDYBhwC1m1tTMDgNGAuH879/FNW3dhF/mLmXpvGXk5eYxbugE2p7ZKtQcOUtXMXfaPAA2rtvEwtlLyMgM9yuzZo6fxdqcdaHE+ub7xaxZu+l3bQsW57Dol5V/WHfzb3lbClyVtNQy31Q8XscjZ9ka5s5cBMDG9ZtZ9MNS6jWsy2mdj+XN/4wi97c8AFZnry1zLkjM71WYx3xbEjGOipwjWYpesSTNl3S/pOmSpkg6XNIoST9J6hqs017SZ5I+lDRHUn9Jf9hvknpI+jb4uT5ou6fwcfC8r6Trgsc3SZosaYaku2PWuVDSpKBPAySlFNP1q4EXzezLwgYze8vMfpWULundIO5XkloEcftIelHSeEkLJJ0j6SFJMyWNlJQWs08K2ydJahK0ny5poqRpkkYHhbcw7mBJ4yT9LOna7Y29rDIy01m+eOt3KWYvziEjs14YoYvVYJ/6NMnal9kT58YtR6IdtH9DXn7yUl58ojOP9P94p2d5kJjj0WCveux3yF7MmTqPzP32oPmRTXhixC089G4PDsjaJ5Qcif69ipdEjKMi50iWolc9KCKFP51ili00syxgPDAEOA84Erg7Zp3WQHfgIGA/4JzY4JJaApcCbYJtr5R0GDAYuDhYJwKcD7wi6SRg/yBuFtBS0l8kNQM6Ae2CPuUDFxQznoOJns4szt3ANDNrAfQCXopZth9wPHAG8ArwiZkdAmwE/hqz3uqgvR/wRND2OXBkMKt8A7g5Zv0DgZOD8dwVFNBix160s5K6BC84puSyeRtDKj/ValTlzmE9ebbHEDas3Vje3QnN9z/+j4uue4Erb36ZC89tQ5W04l5b7Rqq1ajK7YO7MOCON9mwbhMpKRFq1a3B9R0fZODd79Dr+SvLu4uuAkmKa3oEpze3sez94N+ZQE0zWwuslbRZUt1g2SQz+xlA0uvA0cBbMTGOBoab2fpgnXeAY8zsP5JWBAWwAdFitCIoeicB04LtaxItgi2AlsBkRe8GUB1YtoNjPRo4F8DMxkqqJ6l2sGyEmeVKmgmkED0lWjj2xjExXo/59/HgcSNgqKSGQBVgXsz6H5rZZmCzpGVAAzObX9zYi3bWzJ4DngOorfRSTTeyl+RQv9HWV3wZjdLJXhL+t+inpKZw11s9GfvaeD4fHv87DpSHBYtz2LjpN/bdO2PLG112VDyPR0pqhDsGd+GTtycx4cPp0Xz/W8WED6P/dX6YNp8CM+rUq8nqFWU7bZio36t4S8Q4KnKOZJnplaRwelEQ87jweeGLgqJ/jHfkXNBAoDPRmeDgoE3A/THXGJuY2aCg/cWY9qZm1kfS2TGz1FbAd0SL447aDGBmBUCu2ZarObFjLTq+wsdPAf2CGeC/gGpF4wbyY2IVN/YymzN5Lpn7N2TPxnuQmpZK+07t+PL9KWGF36LnwK4snLWEt5/4MPTY5anhHnVIiURvsdSgfm32yazH0mVrdjpePI/HDU9czMIflvJO/zFb2r4YMZ1Dj24KQOaf9yAtLaXMBQ8S93sVb4kYR0XOkSwzvbJqLWlfYAHR04/PFVk+Hhgi6QGihets4KJg2XDgHiAN+GfQNgq4V9KrZrZOUiaQC4wB3pP0uJktk5QO1DKz4UEcACQtAiZJ+tDMJgZt5wATgr5cEMRvD2Sb2Rrt2H3kOgEPBP8WXjesAxS+dfGSUsYpbuxlVpBfQL/ug7h/ZG8iKRFGvfAJC74P711jAM3bNeXEi47l5xkL6D/1IQAG3/46k0ZM286Wpdfr1eto0b45dTJq8drC/rzU501GDh67U7H69DiNrOZ7Ubd2dd55viuD3pjA2nWbuP6KE6hbpzoP334uP85bRs973qJFs0wuPOcc8vILKCgwHh3wMavLcOo2XsejeZv96PD3I5n3/WKeHtsbgCF93+Oj176gx5MX0//TO8jLzeeR7i+WORck5vcqzGO+LYkYR0XOISvrW7cqgGI+sjDSzG6N/ciBpFkpRGMAACAASURBVM7B42uCbeYDrYheP7sHWAs0AT4BuplZQZHtewCXBfEHmlnhtTAk9QdWmdmtMW3XAVcET9cBF5rZT8H1xtuIzsJzgavN7KtixnQU8BCwB9GZ2mfADURnYIOBPxP9KEMXM5shqQ+wzsweCbZfZ2Y1g8dblgVjGgp0JDqD+4eZzZV0JtFTnSuBscARZta+mLjfAqeZ2fxtjX1baivd2uiE7a1WNgm4iWyZ3w5ZCpXmJrIZiXmjiN9ENrlMtDGssZxi/7MnRdEri2C2dKOZnbaT20eAr4G/mVnZPgGcAArxs4c7OnYveqXnRW/HeNFLLiUVPb+mF0eSDgLmAmMqQsELUzKP3Tm36/JretthZuOAcTu57fdETzNWGGbWOKQ4FW7szrnKz2d6zjnnkoYXPeecc0nDi55zzrmk4UXPOedc0vA3srjkUkk+olP9/cnl3YVQ+EcJXKL5TM8551zS8KLnnHMuaXjRc845lzS86DnnnEsaXvScc84lDS96zjnnkoYXPeecc0nDi55zzrmk4UXPVUitTs5i8KwnGfLDU3S65SzPsQ31G9Xj4dF3MnDmYzw/41HO7t4x9BwQ/3H0HHQVby4dyHMzHg09dqzKcMw9R8m86AUk5UuaHvPTOI65OkvqV8YYrSV9JmmOpGmSBkraLaw+7soikQjd+11Or1P7ckXzGzju/Hbs3ayR5yhGfl4+A256mSsO6cG1bXtzRreT2btZZqg5EjGOj4aMo1fHvqHGLKqyHHPPsZ24IfStsthoZlkxP/PLu0OFJKUWed4AGAbcYmZNzewwYCRQqzz6l2hNWzfhl7lLWTpvGXm5eYwbOoG2Z7byHMXIWbqKudPmAbBx3SYWzl5CRmZ6qDkSMY6Z42exNmddqDGLqizH3HOUzIteCSRlSfpK0gxJwyXtHrSPk9QqeJwhaX7wuLOkdySNlPSjpIdiYl0q6QdJk4B2Me31Jb0taXLw0y5o7yPpZUkTgJeLdO1q4EUz+7KwwczeMrNfJaVLejfo81eSWsTEe1HSeEkLJJ0j6SFJM4P+pgXrzY9pnySpSdB+uqSJwaxydFB4C+MODvbJz5KuDdrvkXR9zDj7SroujOOSkZnO8sVbv7Mxe3EOGZn1wghd6XLEarBPfZpk7cvsiXNDjZvoccRLZTnmnqNkXvS2qh5zanN40PYS0dlUC2AmcFcp4mQBnYBDgE6S9pLUELibaLE7GjgoZv0ngcfN7AjgXGBgzLKDgA5m9o8iOQ4Gpm4j/93AtKDPvYIxFNoPOB44A3gF+MTMDgE2An+NWW910N4PeCJo+xw4MphVvgHcHLP+gcDJQGvgrqCADgYuBpAUAc4Pcv6OpC6SpkiaksvmbQzJlVW1GlW5c1hPnu0xhA1rN5Z3d5wrN36Xha02mllW4RNJdYC6ZvZp0PQi0VOK2zPGzFYHMb4H9gEygHFmtjxoHwocEKzfAThIUuH2tSXVDB6/b2Y7+hfqaKLFEzMbK6mepNrBshFmlitpJpBC9JQoRAt645gYr8f8+3jwuBEwNCjgVYB5Met/aGabgc2SlgENzGy+pBWSDgMaEC3Ef/hKfTN7DnguOvD0Ut0CIXtJDvUbbX3Fl9Eonewl4X5bf2XJAZCSmsJdb/Vk7Gvj+Xz4pNDjJ2oc8VZZjrnnKJnP9HZOHlv3XbUiy2KnK/ls/4VFhOgMqvBaYqaZFV68WA8g6eyYWWgr4Dug5U70ezOAmRUAuWZb7rNTUKSfVszjp4B+wQzwX/x+3Nsa80CgM3Ap0ZlfKOZMnkvm/g3Zs/EepKal0r5TO758f0pY4StVDoCeA7uycNYS3n7iw9BjQ+LGEW+V5Zh7jpL5TG8bzGy1pJWSjjGz8cBFQOGsbz7RojMJOK8U4SYCT0qqB6wB/gZ8Eyz7COgOPAzR64hmNr1IX4YDhadckbQImCTpQzObGLSdA0wAxgMXAPdKag9km9mamJlkaXQCHgj+LbxuWAdYEjy+pJRxhgP3AGnAP3ekAyUpyC+gX/dB3D+yN5GUCKNe+IQF3y8OK3ylytG8XVNOvOhYfp6xgP5To5eYB9/+OpNGTAstRyLG0evV62jRvjl1Mmrx2sL+vNTnTUYOHhtqjspyzD1HyWSV5KaaZSVpnZnVLNKWBfQHdgN+Bi41s5WSDgTeJDqr+RC40MwaS+oMtDKza4LtPwAeMbNxki4FbgNWAdOB38zsGkkZwNNAM6IvQj4zs66S+gDrzOyRbfT3KOAhYA+iM7XPgBuIzsAGA38GNgBdzGxG0Xix441dFrwpZyjQkegM7h9mNlfSmURPda4ExgJHmFn7YuJ+C5xW+O5XSf2BVWZ26/aOQW2lWxudsL3VHMCOvYjZOf63wVVQE20Mayyn2P8kXvTc7wRFr5WZZYcQKwJ8DfzNzH7c3vpe9HaAFz3ntqmkoufX9FxcSDoImEv0jT3bLXjOOZcIfk3P/Y6ZNQ4pzvdET7E659wuw2d6zjnnkoYXPeecc0nDi55zzrmk4UXPOedc0vA3srhdS5zfiq+UlLjGB7CC+L/VP6VJ47jnyP/hp7jnGPXL9O2vFIJT9g73DgDFUvznEJb7W9xzVPaPw/hMzznnXNLwoueccy5peNFzzjmXNLzoOeecSxpe9JxzziUNL3rOOeeShhc955xzScOLnnPOuaThH053FU79RvW4ecjV7N6gLmbGf58fzfCnRoSep0ad3egxoAuNmzfCDB69cgCzJoZ7l6SX5z7FxrUbKcgvID8vn6uP7B1K3BfH3MKG9ZujcfMLuPa8flxxU0faHNeMvNx8flmYw2O9hrF+7aZQ8rU6OYtuT1xKJCXCiEFjGPrgu2WIFkH1hkP+r9iqLgCo5g1QrSNQgG14DTa8BFVao7r9IT96N23b9BGs71emcSTimJ91zcmcetlxIDFi8CcMf2pkqPEh7OPxR2lV03hs3N2kVU0lJTWF8W9/xUt3Dws1B8RnHF70HJIaEb17+0FEZ/8fADcFz/9kZv8N1utDCXdzT5T8vHwG3PQyc6fNo3rNajwz+QGmjp7BwllLQs3T7bFLmDzqG+49/wlS01KoulvVUOMXurHDvaxZsTb0uLdc/BxrVm3Y8vzrL+Yy+LFRFOQXcFnPU+jUpT2DHy37H9xIJEL3fpdzy0n3kr04h36T7ufL96ewcNbinQu42yWQ9xOoZvR59XMhpSGWfTJgEEnfuu5vU7YUxjDE+5g3PqgRp152HN3b3Unub3nc98EtTPzvNH756dfQcoR+PIqRuzmXmzrczab1m0lJTeHxz+5h8sjpob5AiNc4/PRmkpMk4B3gXTPbHzgAqAn0BbKAU0PMFcp3gOUsXcXcafMA2LhuEwtnLyEjM307W+2Y3WpX55CjD2TkC58AkJebz/rVG7az1a7t6wk/UpBfAMDsbxaRsWedUOI2bd2EX+YuZem8ZeTl5jFu6ATanrmTX/sV2RNVbY9tfHNLk6r/A1vXDwi+uqogp+ydLkYijvleB/6J2ZN+YvPG3yjIL2DmZ7Nod9YRoeYI9XiUYNP6zQCkpqWQmpaChfzVYvEahxc9dzywycxeADCzfOAG4ArgIaCTpOmSOgXrHyRpnKSfJV1bGETShZImBesOKCxwktZJelTSN8BRYXe+wT71aZK1L7Mnzg017p777sGq7DXcOLArz0y6nxv6X0m1OMz0zIwHRvTi6Yn3ceoVJ4Qa975Bl/PU29fQ8e+t/7D8pHNbMeWzOaHkyshMZ/niFVueZy/OISOz3k7FUu3e2NqHgIKtjal7Q7W/onrvoN0HQso+W5dVyUL13o+2pzbZyRFEJeKYz/9+MQcf3ZRa6TWpWr0KR5ySRf1G4b5gC/N4lCQSEf2nPsSwpQP5evRMZk8K9/9gvMbhRc81B6bGNpjZGmA+8G9gqJllmdnQYPGBwMlAa+AuSWmSmgGdgHZmlgXkAxcE69cAJprZoWb2edHkkrpImiJpSi6bd6jj1WpU5c5hPXm2xxA2rN24Q9tuT0pKCvsfti8fDPiYbq1vY9P6zXS6+YxQcwDccOxddGt9G71Pe4AzrjqJQ445MJS4Pf/Zn2vOfYrbr3yB0/95FAe32nfLsvP/dRz5eQWM/b/EfNlzqVU9DgpWQN53RRZUAduMrTgH2/AmqnN/tDn3e2x5e2zFGdj6l1HdZ8uUPhHHfNHsX3jzkf/jgQ9v5b7/u4WfZizYMvuuaAoKjK4tb+Yfe3el6RH70bj5XuXdpVLxoud21IdmttnMsoFlQAPgBKAlMFnS9OD5n4P184G3txXMzJ4zs1Zm1iqN0r+qTklN4a63ejL2tfF8PnzSzo5lm7KXrGD54hxmT47eaWD8OxNpkrXvdrbacSt+WQnAquVrmPDeZJoeUbbZypa4y9YAsDpnPV+M/o6mLRoBcOLZLWlz3IE8dNMboeQByF6SQ/1GW1+BZzRKJ3vJihK2KJ7SDoeqJ6D6n6A6T0DVI1GdR6BgKWz+KLrS5o8gNXhhYOvAgtOPv30KSgXtXoZxJOaYjxzyKVcfdTs9O9zLupXrWfLj0lDjh3U8Smv96g18M+47Wp2cFWrceI3Di577nmjB2kJSbWBvIK+Y9WOnY/lE3wwl4MVgRphlZk3NrE+wzqbglGmoeg7sysJZS3j7iQ/DDg3Ayl9Xs3zxChod0BCAw44/ONQ3AgBU260q1WtW2/K45YktmP/dojLHrVo9jeo1qmx5fHi7/Zn/w6+0PPoAzrv8L/S56iU2b8otc55CcybPJXP/huzZeA9S01Jp36kdX74/ZYfj2LpHseXHYMuPw1ZfD5u/wlbfCJtGQ5UjoytVaQ350eu5RDK2bpzWAoiArdzpcSTimAPUrV8bgPp71ePos45g7BtfhBo/rONRkjoZtahRZzcAqlRL4/AOLVg0J9w3ksVrHP7uTTcGeEDSxWb2UnAt7lFgCPAr0KaUMd6T9LiZLZOUDtQyswXx6HDzdk058aJj+XnGAvpPfQiAwbe/zqQR00LN8/QNQ7j1xWtIrZLK0nm/8sgVA0KNX7dBHfq81ROAlNQIn7wxgSmjvilz3N3r1eLOfhdF46ZE+OSD6Uz9/AcGj7qRtCqp3Df4cgBmf7OQp/qU/S3gBfkF9Os+iPtH9iaSEmHUC5+w4PvwioWtH4DqPAa7dQbbgK0OPtZR7RRU/Z9AXvT056rry5wr3scc4I43rqN2vVrk5ebx1HVDQn+zTLyPB0B6w925+YWriaREUER8NuxLJn74dag54jUOhf2OG1fxSNoLeIbo9boI8F/gRqLX40YBacD9QDNiPrIg6VvgNDObH7zR5bZg+1zgajP7StI6M6tZmn7UVrq1iXQId3BF+E1kS89vIruD/CaypRfnujPRxrDGcoodiM/0HGa2CDi9mEWbgW2+n9rMDo55PBQYWsw6pSp4zjmXCH5NzznnXNLwoueccy5peNFzzjmXNLzoOeecSxpe9JxzziUNL3rOOeeShn9kwe1a4vz5Hcsr7ktmKp5EfIYuERLy+Tkqz3FPiEr+2W2f6TnnnEsaXvScc84lDS96zjnnkoYXPeecc0nDi55zzrmk4UXPOedc0vCi55xzLml40XPOOZc0vOi5CqnVyVkMnvUkQ354ik63nOU5kiBHjTq7cccb1zNo5iMMnPEIzdrsH3qOyrKvPMe2edGrhCTlS5ou6VtJ/yep7nbW7yPpxu2sc5akg2Ke3yMpvrc534ZIJEL3fpfT69S+XNH8Bo47vx17N2vkOSpxDoBuj13C5FHfcPkhN9K15S0snL0k1PiVZV95ju3EDaFvbtez0cyygjub5wBXhxDzLGBL0TOzO81sdAhxd1jT1k34Ze5Sls5bRl5uHuOGTqDtmeF+nZXn2LVy7Fa7OoccfSAjX/gEgLzcfNav3hBqjsqyrzxHybzoVX5fApkAkvaTNFLSVEnjJR1YdGVJV0qaLOkbSW9L2k1SW+AM4OFgBrmfpCGSzpN0iqRhMdu3l/RB8PgkSV9K+lrSMEk1wxhQRmY6yxev2PI8e3EOGZn1wgjtOXbRHHvuuwerstdw48CuPDPpfm7ofyXVdqsaao7Ksq88R8m86FViklKAE4D3g6bngO5m1hK4EXimmM3eMbMjzOxQYBZwuZl9EcS4KZhBxn7b8WigjaQawfNOwBuSMoDbgQ5mdjgwBehRTB+7SJoiaUoum8s8Zlc5paSksP9h+/LBgI/p1vo2Nq3fTKebzyjvbrkKyIte5VRd0nRgKdAA+DiYZbUFhgXLBgANi9n24GAWOBO4AGheUiIzywNGAqdLSgX+CrwHHEn0dOiEIN8lwD7FbP+cmbUys1ZplO6Ve/aSHOo32vqKL6NROtlLVpSwxY7zHLtajhUsX5zD7MnR11vj35lIk6x9Q85RWfaV5yiJF73KaaOZZREtMiJ6TS8CrApmaoU/zYrZdghwjZkdAtwNVCtFvjeAvwPHA1PMbG2Q9+OYXAeZ2eVlHxrMmTyXzP0bsmfjPUhNS6V9p3Z8+f6UMEJ7jl00x8pfV7N88QoaHRB9nXbY8QezcNbiUHNUln3lOUrm99OrxMxsg6RrgXeJnsqcJ+lvZjZMkoAWZvZNkc1qAf+TlEZ0plf4Frm1wbLifAoMBq4kWgABvgKeltTEzOYGpz8zzeyHso6rIL+Aft0Hcf/I3kRSIox64RMWfB/uH0DPsWvlAHj6hiHc+uI1pFZJZem8X3nkigGhxq8s+8pzlExWyW8YmIwkrTOzmjHP/w94E/gceJboac004A0zu0dSH2CdmT0i6SrgZmA5MBGoZWadJbUDngc2A+cBdwAfmNlbQY5+QGdgDzPbELQdDzwIW85b3m5mhdcX/6C20q2NTghpL7iKQKmJed3tN5FNLhNtDGssR8Ut86Lndhle9JKPFz0XDyUVPb+m55xzLml40XPOOZc0vOg555xLGl70nHPOJQ0ves4555KGFz3nnHNJw4uec865pOHfyOKcKzeqGu6dErYlIZ/TU7EfCwuXf666zHym55xzLml40XPOOZc0vOg555xLGl70nHPOJQ0ves4555KGFz3nnHNJw4uec865pOFFz1VIrU7OYvCsJxnyw1N0uuUsz1EJc/R45jKG/vwfBkz895a2C287i1fnPM4zE+7hmQn3cMRJLULJVSje+6p+o3o8PPpOBs58jOdnPMrZ3TuGngMq7jFPRA4versASb0lfSdphqTpktokKG97SauDnIU/HbazTWdJf4p5PlDSQcHjXvHuM0AkEqF7v8vpdWpfrmh+A8ed3469mzXyHJUsx0evfk7vsx/9Q/vwp0fRrd2ddGt3J5M/mlHmPIUSsa/y8/IZcNPLXHFID65t25szup3M3s0yQ81RkY95InJ40Stnko4CTgMON7MWQAdgUQK7MN7MsmJ+Rm9n/c7AlqJnZleY2ffB04QUvaatm/DL3KUsnbeMvNw8xg2dQNszW3mOSpbj2wk/sHbl+hB6WDqJ2Fc5S1cxd9o8ADau28TC2UvIyEwPNUdFPuaJyOFFr/w1BLLNbDOAmWWb2S+S7pQ0WdK3kp6Tot9xJGmcpMclTZE0S9IRkt6R9KOkLeeBJF0oaVIwexsgKaW0HZLUOIj9fDAD/UhSdUnnAa2AV4O41YP+tJL0AFA9aH9V0j2Sro+J2VfSdWHssIzMdJYvXrHlefbiHDIy64UR2nPsojlind6lA89+eS89nrmMmnV3Cy1uosfRYJ/6NMnal9kT54Yat7Ic83jl8KJX/j4C9pL0g6RnJB0btPczsyPM7GCgOtHZYKHfzKwV0B94D7gaOBjoLKmepGZAJ6CdmWUB+cAF28h/TJHTm/sF7fsDT5tZc2AVcK6ZvQVMAS4IZoUbC4OY2a3AxqD9AmAwcDGApAhwPvBK0eSSugQFfEoum3dsz7mk88HAsVza4ia6tb2TnKWr6XLf+eXdpZ1SrUZV7hzWk2d7DGHD2o3b38CFxr9wupyZ2TpJLYFjgOOAoZJuBdZKuhnYDUgHvgP+L9js/eDfmcB3ZvY/AEk/A3sBRwMtgcnBBLE6sGwbXRhvZrEFFUmNgXlmNj1omgo03sFxzZe0QtJhQANgmpmtKGa954DnAGorvVTfppu9JIf6jba+4stolE72kj+ELhPPsWvlKLRq+Zotj0cM+ZR7hl1fwto7JlHjSElN4a63ejL2tfF8PnxS6PEryzGPVw6f6e0CzCzfzMaZ2V3ANURnZc8A55nZIcDzQLWYTQqnRAUxjwufpwICXoy5TtfUzPpIOjtmRre9k+OxcfPZuRdIA4leA7yU6MwvFHMmzyVz/4bs2XgPUtNSad+pHV++PyWs8J5jF8xRKL1BnS2P255+OPO/XxJa7ESNo+fAriyctYS3n/gw9NhQeY55vHL4TK+cSWoKFJjZj0FTFjAHaAFkS6oJnAe8tQNhxwDvSXrczJZJSgdqmdlwYHhM7vY70eW1QK1tLMuVlGZmucHz4cA9QBrwz53IVayC/AL6dR/E/SN7E0mJMOqFT1jw/eKwwnuOXSTHrYO70uKYA6lTryavzH6Ml+97lxZHH8h+LfbCDH5dmM1/rh1S9gEEErGvmrdryokXHcvPMxbQf+pDAAy+/XUmjZgWWo6KfMwTkUPm92cqV8GpzaeAukAeMBfoAlwP/ANYCvwALAhma+OAG81sSlC0biw8PVlkWSfgNqKz+VzgajP7qkju9kSvCc6Laf430et2HwTXE5F0I1AzyH8ucB+wETgKGBGT80HgDODr4LoekvoDq4JrfiWqrXRroxNKve9cxRepUSMheQrWJ+BdoH4/vV3GRBvDGssp9oB40XNxE7yB5WvgbzEz2W3yopd8vOjtIP97XSolFT2/pufiIvjA+lxgTGkKnnPOJYJf03NxEXxg/c/l3Q/nnIvlMz3nnHNJw4uec865pOFFzznnXNLwoueccy5peNFzzjmXNPzdmy65REp9s4mdV5Af/xxul6PUtLjnsNzf4p6jsv8f8Zmec865pOFFzznnXNLwoueccy5peNFzzjmXNLzoOeecSxpe9JxzziUNL3rOOeeShn9Oz1VIrU7OotsTlxJJiTBi0BiGPvhuXPJEIuLpifeR/ctK7jjzodDjJ2IcFTVHj2cuo80pWaxavoZ/tbkdgAtvO4uOnY9ldfZaAF64+y0mfzSjzLkKJWJfnXPtKZxy6XFgxrxvF/HIlc+Ruzk3tPg9B11Fm7+2ZNWy1XRp0TO0uEW9PPcpNq7dSEF+Afl5+Vx9ZO/Qc8TjeFTomZ6k3pK+kzRD0nRJbSTNl5QRh1ydJfXbwW2K7YukPsHdyMvSn46Spkj6XtI0SY+WJV5FEolE6N7vcnqd2pcrmt/Acee3Y+9mjeKS6+xrO7Jw9i9xiZ2IcVTkHB+9+jm9z/7jr/Xwp0fRrd2ddGt3Z6gFLxH7qt6fduesq0/mmqNup8vhtxJJidD+70eFmuOjIePo1bFvqDG35cYO99K11a1xKXjxOh4VtuhJOgo4DTjczFoAHYBFZYy5S858i/ZL0sFAP+BCMzsIaEX0hq1JoWnrJvwydylL5y0jLzePcUMn0PbMVqHnychMp82phzNi8NjQY0NixlGRc3w74QfWrkzAHc8Difq9SklJoWr1KkRSIlTdrSo5/1sZavyZ42exNmddqDHLQ7yOR4UtekBDINvMNgOYWbaZFb4k7y7pa0kzJR0IIKm1pC+DWdEXkpoG7Z0lvS9pLDBGUg1JgyVNCtY9MybnnySNlPSjpC3nuiT9I8j1raQHi+tsMCv9QdLnQNOY9v2CmFMljY/p7xBJ/SVNBIqeV7sZ6Gtms4Ox55vZs8F2jSWNDWa/YyTtHRPvWUlfSfpZUvtgnLMkDYnpzzpJjwcz6DGS6gftV0qaLOkbSW9L2i0m7n+CffqzpPOC9pcknRUT99Ui+3KnZfw/e+cdZlV1tfHfO/SiImIFARUEQQEBUVAsiA17xRJ7idg1mqgkamJN7L0hYuzd2DV2o6hYg733qCCK7bMA6/tjreMcR5C5594ZGGa/z7Ofe0/ba+9T9tqr7o7tmfTh5z9vT/5wCh06LlSJqn+BUaftzMWHX8mMGVbxuqF++jGv0Mhj472Gc/74YznkvN1o2651xeqtj358/vEXXH/GHVzx5llc8965fDf1O565b2JFadQXzIyT7jqSc588gRF7rF3x+uvqeTRkpncvsGQwkvMkrZE7NtnM+gPnA5ka8VVgqJmtCBwFnJA7vz+wlZmtAYwGHjCzQcBawMmS2sR5/YCRwArASElLSloC+DswLI6vlB/sASQNALaN4yOAlXKHLwL2N7MB0dbzcsc6AUPM7JAafV8eeGYW9+Vs4LKQfq8EzsodWxAYDBwM3AqcDvQGVpDUL85pAzxtZr2Bh4GjY/9NZraSmfUFXgF2z9W7OLAaLnmfFPsuAXaJ/i8ADAHuqNlYSXuFmvbpn/hhFl2qf6y8YX++/Gwqbzz7zpxuSkIOt495gF37HMY+Q45iyidT2euEbed0k0pC23atGbLRAHbqcRDbdd2Plm1asPZ2q87pZhXCwWsczT6DjmD0Riexyah1WWFozzndpFqhwTI9M/sGGADsBUwCrpW0Sxy+KX6fAbrG/wWA6yW9SPVgn+HfZjYl/q8LHC7peeAhoCXQOY7db2ZTzex74GWgC87AHjKzSWY2DWc0q9do7lDgZjP7zsy+whkOktrizOD6oHchzkAyXG9mpWZmHQxcFf8vx5lRhtvMzICJwKdmNtHMZgAvUX2fZgDXxv8rctcvH5LoRGAHfnn/bjGzGWb2MrAogJk9DHQPSXE74Ma4P7+AmV1kZgPNbGAzWtSqg5M/msLCnapnfB06tWfyR5//xhWlo/eQZRm88QAuf/NsRl95AP3W6s2fLtu3ojTqox/zCo0MX076ihkzDDPjrnEP02PA0hWruz76seKw5fnk3UlMnfw106dN5z+3TKDX4O4VncM/JQAAIABJREFUpVFf+PxjV8t+OekrHvvXBHqs1K2i9dfV82iwTA9+Vus9ZGZHA/sBW8ahTGSYTrWH6rHAg2a2PLAxzswy5A0HArY0s35ROpvZKzXqrVl3UVQBX+Zo9TOz5Wq2S9K+4ajzfEiWL+EMv1Rk7Z/BL/syg1n3JdPtjQP2M7MVgL/yy/uXr0u5//8EfgfsCowt0N6Z4rUJb9Kx++Is1nURmjZrypojV2X8rU9XqnoAxo6+hu277suO3fbn+B3O4vkHX+LvO59bURr10Y95hUaG9osu8PP/IRv3592XP6pY3fXRj0kffE7PlbvRolVzAFZcq3edOUrVJVq2bkGrti1//j9gnT68+1JZLhW/Ql09j7nScaM2CJvcDDN7I3b1A97DVY8zwwJA9oXs8htV34PbBPc3M5O0opk99xvnPwWcFV6aX+BSzdk1znkEGCfpRPyebwxcaGZfSXpH0tZmdr0kAX3M7IX8xWZ2LvDziCvpZOAmSf8xs9clVQF7mdkFwOO4KvVyXCJ79DfaPjNUAVsB1wDbA/+J/fMB/5PULOqtzWgzDr8/n4QUWBHMmD6Dc/a/hBPvHk1VkyruufRB3nv5w0pVX2+oj340ZBqHj92bPkN7ssBCbbni1dO4/IRb6LNaT5bpsyRm8On7kznrgHHldyBQH/fq1Qlv8ehNT3Hek8czfdp03nz+Pe4cU1lHqSOvPJA+a/ZmgQ7zcdX7F/DPY67j7go7Y7VbdAGOucHDIZo0reLBax7j6XtemM1VpaGunodc29XwEHays4F2wDTce3Ev4GlgoJlNljQQOMXM1gxvz8tw6ekO3POxa6hEB5rZflFvK+AMXO1YBbxjZhvN5Lzbo+6HJG0HHIlLOXeY2Z/inHdzbRkN7Ax8BrwPPGtmp0haCrc9Lg40A64xs7+Fc8ntZnbDLPq/ES5xtcalsdvN7I+SugCXAh1wte+uZvZ+vj5JXeP/8lFX/tg3uJ1x3WjrSDObJGkU7kAzCXgSmM/MdqnZTknfmFnbXDvvxtWfF8zumc6v9rayKm8Q/wXm8bXCGhqq2rSZ/UkVwIxv694LVM2a1zmNtJ5e7fCk3c9XNkUzO9ZgmV5C3aAm0yqzrta4/bC/mU2d3fmJ6TU+JKZXGhLTqx1+i+k1aJtewtwLScNxL8+za8PwEhISEuoDDdaml1A3qJSUZ2b34d6tCQkJCXMNkqSXkJCQkNBokJheQkJCQkKjQWJ6CQkJCQmNBonpJSQkJCQ0GiSml5CQkJDQaJC8NxMSEhIqgHqJoasHqEndx+nZHIxlTZJeQkJCQkKjQWJ6CQkJCQmNBonpJSQkJCQ0GiSml5CQkJDQaJCYXkJCQkJCo0FiegkJCQkJjQaJ6SUkJCQkNBokppfQIDFwvX6MfeVMxr1+NiP/tFmd0amqEudPOJFj//XHOqm/PvrRUGkcct5uXPv2WVz45HG/2L/J74cz5pkTueip49n92G0qQitDQ71Xc4LGFgesz0XP/Z2Lnj2JI/65L81aNKs4jbroR70wPUmjJb0k6b+Snpe08m+ce4ykQ0uo+05J7cqtpxRImh79eFHS9bFYap1AUjtJ+9TYt2z0+w1Jz0q6TtKiddWGuQ1VVVXsf87uHDniePbofTBrbbsqnZfrVCe0Nj9gA95/9eM6qbs++tGQadx75X8Yvfmpv9jXd2hPhmy4IqMG/4W9Bo3mhjPvKptOhoZ8r+qbxkJLLMhm+67HfoP/zF79D6eqSRVrbjO4ojTqqh91zvQkDQY2wlfP7gMMBz6oVP1mNsLMviy3HkmlZKf5PzPrZ2bLAz8Ce9cBjQztgJ+ZnqSWwB3A+WbW3cz6A+cBCxeou0Gix6BufPzmJ3zyzmdM+2kaD137GEM2HVhxOh06tmflEf25a+wDFa8b6qcfDZnGi4+9ztdf/HLF8432GMa1p93BTz9OA2Dq5K/LppOhId+r+qYB0KRJE1q0ak5VkypatG7BlP99UdH666of9SHpLQ5MNrMfAMxsspl9LOldSR0AJA2U9FDumr6Sxocks2ecs7ikR3IS1tDYn69ntKTXJf0H6JFVJmlPSRMkvSDpxkwykzRO0gWSngT+EfQWjmNVkt7Mtn8DjwLdJG0s6UlJz0m6L5O8QuK8XNJjwOWSFo42TIiyau68sZIekvS2pAOi/pOAZaLfJwPbA+PN7LasAWb2kJm9KKmlpEslTYx2rBV17yLpFkn/jvu1n6RD4pwnJLWP8x6SdGbuHg+K/YPieTwn6XFJPXL13iTp7rh3/4j9u0k6o8b9P312L0pt0aFjeyZ9+PnP25M/nEKHjgtVqvqfMeq0nbn48CuZMcMqXjfUTz/mFRoZOnZbjOWHLMuZD/yFk+86nGX7L1WxuueVe1UfND7/+AuuP+MOrnjzLK5571y+m/odz9w3saI06qof9cH07gWWDGZ0nqQ1anFNH2AYMBg4StIS+GB/j5n1A/oCz+cvkDQA2BboB4wAVsodvsnMVjKzvsArwO65Y52AIWZ2CHAFsEPsHw68YGaTZtXIkNw2ACYC/wFWMbMVgWuAvBGoFzDczLYDzgRON7OVgC2BMbnzegLrAYOAoyU1Aw4H3grJ8jBgeeCZWTRpX8DMbAVgO+CykAyJ67aI+3I88F20dTywU66O1nGP9wHGxr5XgaFx/lHACbnz+wEjgRWAkZKWBK4DNo72A+yaq6vmPdxL0tOSnv6JH2bRrfrHyhv258vPpvLGs+/M6aYk5NCkaRXzLdiWA4cdy5g/X8voy/aZ/UUJFUfbdq0ZstEAdupxENt13Y+WbVqw9narzulm1Qp1nnDazL4JhjQUWAu4VtLhs7nsX2b2f8D/SXoQZwITgLExkN5iZs/XuGYocLOZfQcg6dbcseUlHYerCtsC9+SOXW9mWfbTscC/gDOA3YBLZ9G+VpIy+o8Cl+CS5bWSFgeaA/nR8tboDzgz7SUpOza/pLbx/46QiH+Q9BlQqp1uNeBsADN7VdJ7wLJx7EEz+xr4WtJUIJMUJ+KTjAxXx/WPSJpfbi+dD2eg3QED8hbr+81sKoCkl4EuZvaBpAeAjSS9AjQzs5lOA83sIuAivxHtayVSTf5oCgt3qp7xdejUnskfff4bV5SO3kOWZfDGAxi0wYo0b9mM1vO34k+X7cvfdz63YjTqox/zCo1qWl/w2K1PA/DaM+8wY4axQIf5KqLmnFfuVX3QWHHY8nzy7qSf7/t/bplAr8Hduf/qxypGo676US+OLGY2PVRwRwP74RLOtBz9ljUv+XUV9giwOvARME7STtQe44D9QgL6aw16PxsNzOwD4FNJw3BGe5ekJUPd97ykzHaX2fT6mdn+ZvYjzmzOCRq/nxWN6PMques7mtk3cSwv6kxn5pOSl4ABJfQ9Q77uGbntGTXo/OreA8fiTHN5YGN+2bdZtXkMsAsu5c1q8lAIr014k47dF2exrovQtFlT1hy5KuNjIKwUxo6+hu277suO3fbn+B3O4vkHX6oow4P66ce8QiPD47c/S9/VlwOgY7dFada8ScXsevPKvaoPGpM++JyeK3ejRavmAKy4Vu+KO3zVVT/qXNIL+88MM3sjdvUD3gNa4YP3XTgTzGNTSScCbYA1gcMldQE+NLOLJbUA+gP/zF3zCM4MT8T7tTFwYRybD/hfSIk74IxzVhiDqzkvDwnwg2jz7LBArt6df+O8e4H9gZMBJPWbidSax9fR/gxXAUdI2tDM7og6Vgem4FLnDsADkpYFOgOv4feqthgJPChpNWCqmU2VlO/bLrWpxMyeDFVnf34pSZaNGdNncM7+l3Di3aOpalLFPZc+yHsvf1hJEvWC+uhHQ6Zx+Ni96TO0Jwss1JYrXj2Ny0+4hXsuf4RDztudC588jp9+nMbJvx8z+4pqiYZ8r+qbxqsT3uLRm57ivCePZ/q06bz5/HvcOaayDl911Q+Z1Y2R/mcCrto8G1ctTgPeBPYClsPVgl8BDwEDzWxNSccASwPdgQ7AP4LR7QwcBvwEfAPsZGbvSHo3rp0saTTOcD4D3geeNbNTJI3CbWyTgCeB+cxsF0njgNvN7IZce5sBnwODzOzVWfTpGzNrW2PfpsDpwBfAA8BKuf58Y2anxHkdgHOj/02BR8xs75mc9yKwkZm9K+kqnHHcZWaHSeqJq2CXifvxX+BAYCpwPjAw7vUhZvagpF3iHu0Xdefv2c/H5M5EzwNr4CrM3czsKbkH7mW4xHoH8Dsz6zqTem8HTjGzh2L7cKCfmW07s/tYE/Orva2stWtzanFU1f1aYczBtcIaGqratKkXOjO+/Xb2JyUAoGbN65xGXa89+KTdz1c2RTM7VudMr6FB0kDc0WTonG5LfSOY3qFmVhFdSDDB083s/tqcn5he40NienMf5nWmlzKy5BCSyY3AEXO6LQ0Z8oD613HbZ60YXkJCQkJ9oM5teg0JZnYSHhfXKGFma1aoni+p9hpNSEhImGuQJL2EhISEhEaDxPQSEhISEhoNEtNLSEhISGg0SEwvISEhIaHRIDG9hISEhIRGg+S9mdC4kGLo5iqk+Lm5D3UdQzenkSS9hISEhIRGg8T0EhISEhIaDRLTS0hISEhoNEhMLyEhISGh0SAxvYSEhISERoPE9BISEhISGg0S00tISEhIaDRITC+hQWLgev0Y+8qZjHv9bEb+abMGSeMPl4ziuk/GcNF/T6143XnMC/cq0Ug0KkVjtkxP0umSDspt3yNpTG77VElHxVp0SNpMUq/c8YdiYdaa9Q6UdFYpjZW0qKTbJb0g6WVJd5ZyfSUg6VBJr0p6XtIESTvVdxsqBUmHRF8mxj09LVaOn6tRVVXF/ufszpEjjmeP3gez1rar0nm5Tg2Oxr3jHuLIDY6vaJ01Ma/cq0Qj0agUjdpIeo8BQwAkVQEdgN6540OAe2MtOoDNgF7MBmb2tJkdUFpz+RvwbzPra2a9gMNLvL4sSNobWAcYZGb9gLWBma7OO7cj+rIusIqZrQCsBHwGtJrJufWw3Hjt0WNQNz5+8xM+eeczpv00jYeufYwhm/5qXjXX05j46Ct8PeWbitZZE/PKvUo0Eo1K0agN03scGBz/ewMvAl9LWlBSC2A5oI+kcyQNATYBTg5JaJm4bmtJT0l6XdJQAElrSro9/h8jaWxIhW9LmhUzXBz4MNsws//G9W0l3S/p2ZBaNo39XUOSGRe0r5Q0XNJjkt6QNCjOaxP0n5L0XHb9THAkMMrMvgr6X5nZZVHH2nHtxKirRex/V9KJcT+eltQ/pOW3gvFk9+IRSXdIek3SBTHBQNL5cd1Lkv6aNSTq/Wuuzz0lVUW/Fo5zqiS9mW3XwOjoy5fRlx/N7KSsb5K+CSn+BWBwSIUvRjkod39fzLXpUEnHxP+HJJ0Z/X4xu9eVQIeO7Zn04ec/b0/+cAodOi5UqerrjUZ9YF65V4lGolEpGrNlemb2MTBNUmdcqhsPPIkzwoHARODHOPdx4FbgMDPrZ2ZvRTVNzWwQcBBw9CxI9QTWAwYBR89CzXYucImkByWNlrRE7P8e2NzM+gNrAadKyiSwbsCpUX9PYHtgNeBQnImBM4AHoo1r4Uy7TZ6wpPmB+czs7ZqNktQSGAeMDKmpKTAqd8r7IRk+GudtBawC/DV3ziBgf1xKXgbYImubmQ0E+gBrSOqTu2Zy9Pl84FAzmwFcAewQx4cDL5jZpJn0pa2ZvVOzLzm0AZ40s77A/wG7AitHu/eUtOJvXJuhdfR7H2DszE6QtFcw9ad/4odaVJmQkJBQHLV1ZHkcZ3gZ0xuf236sFtffFL/PAF1ncc4dZvaDmU3G1WyL1jzBzO4BlgYuxhnYcyHFCDhB0n+B+4COuevfMbOJwRBeAu43M8OZddaWdYHDJT0PPAS0BDrXol8ZegSd12P7MmD13PFb43cizki+Dkb0g6R2cewpM3vbzKYDV+OMGWAbSc8Cz+GSdl51PLP7OhbI7Iy7AZfOrvGS1guJ7N2Q1gGmAzfG/9WAm83sWzP7JugOnV290Q/M7BFg/lxff4aZXWRmA81sYDNa1KJKmPzRFBbuVD3j69CpPZM/+vw3rigd9UGjPjCv3KtEI9GoFI3aMr3MrrcCrt58Apf0huAMcXbIpvDTmfXKDvlp/nSgqaR9YzB+PpPqzGyKmV1lZjsCE3DmsgOwMDAgJItPccZVs94Zue0ZubYI2DKk035m1tnMXpF0adC+M9R+30hauhb9nVXf8vRrtsFqXGOSlsIl0rXNrA9wR65f+Xp/vq9m9gHwqaRhuPR4l6Qlc/dx71xflopr7on79iLQPOr8Phjwb2Eav3yHWtY4/qs+zaa+WuG1CW/SsfviLNZ1EZo2a8qaI1dl/K1PV6LqeqVRH5hX7lWikWhUikZtlxZ6HB98M0lkSszaewN7Ahvlzv0amK/slgFmdi6u0gQgBvInzOw7SfPhasD3ceb7mZn9JGktoEuJpO4B9pe0v5mZpBXN7Dkz27XGeScC50oaaWZfSWqLqyGvA7pK6mZmbwI7Ag+X2IZBwYTeA0YCFwHzA98CUyUtCmyAS6KzwxhczXl5PK8PgH4z6cv5krY1sy9DHVyTaWV4FBgn6SR8grA53sdPgUUkLQR8g78Hd+euGwk8KGk1YKqZTa1F22eLGdNncM7+l3Di3aOpalLFPZc+yHsvfzj7C+cyGkdeeSB91uzNAh3m46r3L+Cfx1zH3WMfqCiNeeVeJRqJRqVo1JbpTcS9Nq+qsa+tmU2uNp8BcA1wsdwZZauyW/hLDADOkZRJGGPMbIKkd4DbJE0EngZeLbHeY4EzgP+GA8k7/JKRZzgfaAtMkPQT8BNwqpl9L2lX4HpJTXEJ9IIS2zABOAe3QT6IqxNnSHou+vMBtVMlg6tTL+W3VZvnE3Y7ST/gTOsxXI36C5jZs5LGAU/FrjFm9hyApL/F/o/49X3/PtrfDFe1VgxP3fUcT931q6ZWFHVN44QdzqyzuvOYF+5VopFoVApy81bCnISkNXFHlJkx2iL1DQRON7Pa2N3qBJIewvtUa33E/GpvK2vtumtUQkJCo8CTdj9f2ZSZhpOlldPnMciTBIyi2oMzISEhISGQJL2EuQZJ0ktISKgEfkvSS7k3ExISEhIaDRLTS0hISEhoNEhMLyEhISGh0SAxvYSEhISERoPE9BISEhISGg2S92bCXANJk/CMNLVFB2ByHTUn0Ug0GjqN+qIzN9LoYmYzW10mMb2EhgtJT8cKFIlGopFozCE6DY1GUm8mJCQkJDQaJKaXkJCQkNBokJheQkPGRYlGopFozHE6DYpGsuklJCQkJDQaJEkvISEhIaHRIDG9hISEhIRGg8T0EhISGgRUY7XqhIQiSEwvIeE3IKmLpPnqqO56HcQlLVif9CoNCwcESUtISmNXLZDu06+RbkhCg0NdM4usfklDgIuBNnVBIzeI95TUSlLbStPJ0esKHCSpSV0NhNGPEXVRd47GzsCJQLM6qLveJiGSlpXUrY5pLAesEf/rpG+Sekvaq47qrpM2p5XTExoUMmYhaU2gK/CdmV1XSRpR/+rAFsD5ZvZJJevPaABIOhAYAbwGfCXpdDP7vNL0gPbA5sB1ZvZSJSuOwakJsBXQCrizkvXn6OwG9AdOMLMfKlx3fhKyCfANMM3MHqkknah/PmA/4BbgTUlVZjaj0nSAkUAf4EGrsJt+PHMB/YDulaw7Q3yHQ4AFYvPuStSbJL2EBoX4ENYBzsVz8V0taVSlZoW5elYG9sCZRZ2oiSStC2xuZusBXYAlgCmSmlSQRrsY0J8FLgX2k1RpybXKzKYB1wAbS1qrEpXmJO7smawG7JM7XrFJe47hHQIcAgwETpA0vFI0crS+Bj4AjpHUptIML3t/zOwYoEUdSd/Not2PAetK2qJSFeee++rA9cDqwMWSjqhE/YnpJTQYhGquDbAjsAMwBXgeuKXcmWxuYO0sqYmZnQzsD/xBUk8zm1EuY50F47xZ0u+BFsCo6McKlWB8kroDfwMukdQeeByXYJrE8bInCpJ6AXtL6m1mbwLnA0vFscJ9yEteQGcAM9sNOA+4TVJzM5tWLuPLM1ZJnYHVzWxNYH58UvWApFZl0qiK3y6SNgSI9+tJYJX8OeVCUn9glxyzfghYMo5VamLYAzheUj8zexf4M/7ONqtEP2JiOxDYEvi9mR2BM74dJf2h3PoT00toSDAz+xaYCOwCnAJsY2b/k7RHObPy+NBGAFcCx0m60MwuBa7Apcnly2GsktrhKi0kbRO2qXeB3YFdzWx9M/tB0n7AwRS0WeUG8Sp8xYqzganAOcD6uPR6aNbnov3JoTuwOH6PtgN6AltLamtm04tWmpO89gPOlXS6pH3MbD9cunhKUouQMAsjdw8WAj4BfpJ0Kq4W3DakmQ0ldSm1bknzSVooJkyr4M96F0lXS1oJZ6wrRzsqJe11ABbFpdQDY98hknqV+f7mGWZr4At8MvUHYB1gBaBdJSaHgXWBTYGuklqb2TvArsDaklqWVbOZpZLKXF+A5YBrcYloN+BjoF8c6wO8CKxVRv29camxC/B34EGgTRz7C/Bqtl0GjeNwSetJoGX05c/AWcAofFB8Fli+TDoj8LRNJ+b2DYqB5FHgamCRgnVnWZz640y0VWwPA/bFJwnf4SpCldmPTYBHgPmA+4GLcseuBp7It6kMOn2AO4LOWcAbwGJxbDfgGWDRAvWuiEvXo4DbgRVi/9+APwEvAJ8Dw8poe/Y8BuNMoltsdwGOBo4FvgL2i/1VZdBaBWc8i+fu20bAjUHjDKBpmc9iOWCn+H8ocDOwYmyvjkuurcuiUc7FqaRSXwVX0YyNwbwKOAl3BLgGeBrYtMz6BwB/ANYKprR07O8fv0tXoA+9gqm9ndvXHdgQt7edUQGGtxLwHO5UMh64PD9I4M4/9wCblEFjOC6l3hYMomfuWEvgcOCSCtyvHYBtY6C9F2ie9SF+F6/Qu7U0cEEwim7AacBTwPHAf0t9JkCn7J7g6tgZ2UCeO6cZPlEYC+wV+wox73hnP8Lt3F8C68X+7H4dhE92mpRxj9bCJ343xvc2PKsPn7xtD1xIwYlhfNPCNTiXADvE/qOBJ2Lf3bgNvLznXYmXJpVU6qoAS+T+d8JtRhfHB7IsPsPNZtC1HjSoniFnH+7iwMu4SnDB2DccuAnoUIF+rAGsFv9PD2YxX2z3LLf+qGfZGESPiO0qfGIwFlggd94/YkAvedYfNK4GBsT2ccB/avYBnzisVLAfVfE7FHgTeCx3bH9cZVtIosgPysAyuf9nAP/K3g2c2W6QP6cEGr/HJeGWwHZxvz8lxzxzfRwUDKldwf70wpndWrG9PS51Datx3t3AkII0euCSavbMD4zvYjjQNnfeY8A6BWl0iN9WuM3+HOB3se/QuEfrFan7V7QqUUkqqdRFwV2V3wX2jG3hTg13AZdRrpoD1sbtglsFg9gZlxz3AtbD1Z2FJEiqmWr2ezFuL+wR2+fiYQqj8JnsQhW4X0OAfwL/Avrk7tm9uNqxKR5zeA6lSy9VMSAdjavlds8d+ysuXfaK7WWCWXWqZd2L55jAdsCRwQyaACcDp+Iq251xVWMhaRi3O+0ZfVk2GMFpQFtcWjmr6PPOP+v4vxCumhsU238AJgGL4HbPP8f+ofhka8ESaTWJfpwY92QU0CJ3D2cAw2O7G24H71xqf4DmuPT1WtbmOLZf3L/14pyO8cxL1ojE83+J0D7Ee7YLzmgzie9YPBSmV9nfSbkVpJJKXRSgY/yuHh/czrljx+KMr18Z9a+KM7XRuD1wb2B5YE3gVlya2CjOLWwzyg/8OIMdBywX23/CVUK9C9adMdRl8QlCS1x9eRpuK1w+O4+Ypcd2rdVcORpN47dd3LNTskE19p8ADI7/zamlzRBXW58FbBMD3UTc5vUJ7iDRE1dv3opLrCuU8Sw6AwsHExgcA/XV8awvij4dWrDu1lQz/VVx++AJ+AQkU5H/CXgLV5luHPuWIuxwJT6PzN7cDJ8knBN0s+f0O6rVnG0oYVKVo5ExUeHS1yWE9BX7D8r6Ftvty3g2O+Gq/w1z++6N7yWTAv9KLSdSv0mr3ApSSaVSJfexDcLVcn+M7cG4OnAUHjD+MME4CtLpijsubBPbq8TgtB/hmFGzTaX2If73xiXSPHM4B1fVZCrZZmXesxE48z4uBohFYlA/BVdhrjCztpX4PNYHrsJtdavgktFRuNpugzLb3wr3Vv07cF2OcWyNS5QbxnZTiqs0W1Ktxm6PS/PH456OTXHniaPxEJjJ+ASi1HvVGRiDq0k/ICYywDG4xJI5Y6xASPtlfB/rx/t6GK6taBIM4Ux80ta05jUFaGwY3+AZVDPonfHJwe4zu6YAjYE4M10Z92TdOJ75RrhK9T7KmOTMkn6lK0wllXJKDOIP4Q4Yr+Gxa+CMcEwMIFuUWGdroEv8745nqrgNVz9l9ruV4iP7AwUZUQyoa8f/1YPOobgdcljuvLeDYbQo814NiEFiKXy2/zKucloCl5DOpAQpYhY01sdVl+viKtInYl+rYBynU0A1i0uMi8T/vjjjexhnppmEsSXwISFxF2z/fDGI9o5nsS3O5C7EGdKyuXNXIjQMBWntAXyLZ4zJ7z8GeICctF0GjeG4NDwUuCHq3QFXdf4dd5wpSVX6G898JVwN/xHV9rU98MlV4fsU9WwQ38FZuKf0UTij2wjXvIwv9TuvbUlpyBLmCkRsz4L44PcXM3tU0qbA7yIe6wyqY7N+qBG8PLt6l8IDqKfgbtaH4LPxrfB8lKeb2QRJRwIzzOyngt1oCqwn6c/47HtNXH23BbBtxM41ASYA51rBVFq5vjfF1VhL4wxiG+CPuO1wR9yh5buCfUGeC7Q/zryXodpR5s/ATzjTW8KKpU1bERgiT4LdAmcM3+LMektJ15vZjZJ+wpl5IZjZ15I64SrTVrj336uSTsPLuYQIAAAgAElEQVQlpa0l3Wlmz5nZhFLrr/Ee3ok7kewuT5l2k5l9aWbHSDqMMuKi4z1ujaf92gZ36sq8TrcHpgFH4I43X5RBpzn+vewQ9WcTkhMlTTOzMZLuMrOPyqDRFg9H2cvM7pM0CGd2a5rZhZKeBDCzSbX9zktCXXDSVFIpWnAJb7fc9ijco3JkbBd16z4ZV1/9Kbab4rPmU+JY4dkx7s59UPw/Ah/4zssd74Y7xzyM2y3KteG1q7H/ZKpVUEfj8YxFPSdVY7s1zrgfxiWkqvj/JAW8WvHBuh3uzXozLkVsEMeynJSn4TGLhWO++KWauXO0+WpcOp4/9nfHVZ2HEe79BWmth6utN8XtX4NxbcVIXLK8huLag5rPozlul7ybau3FQ3EvC0lfM/um8AD3f2fvEa5O/R9lhongYRrr4JOnf+T2b4bHZJYVC1ubkjKyJMwx5LKHtFf1sjcPA8tIWjm2HwXeAY6Q1NXiCymx/rXxwe4cYGVJI8xsmpndF/Sm4QNJUTwH3CJpaVxtuQWe8/DvAObpuW7BB8d1rWDCZzMzSRsD/5Z0maRz4pDwnJcb4Umlj7MCUkuOxrqSjpB0EC6Zfoxndfkffh/fw+POJpdSd0juN+AD3jH4bP8SYC1JA8xzUp4LfIYzqtZF+pCXDiQthkv16+Eu9fsQWVDwycnxwBVm9mNBWv1x1dz3+L3/G/A6PvnZCHeQutkKag/ieawn6TRJB+DOSZkXaHP5Sgr/h0/mCklfQWNDSSdF5puFzOxT/LlXyXOpfoqHRfyv1PpzadhWwBMYfI7bBiVpqzjtdTzGsHmRPpSEuuaqqaTyWwU3Xv8Hd5T4Ez7InhDbVwGv4Kq1s4E1CtSf2eqy7C274XbBlXHvvf0oOHslF+eGS0BTgFNje0C0/1h8xn86ZUgTUWePqHMDXA04Hh88WuA2qiuBLQvWnUmRffAg5CNwJ5xXcEeQM3Dnn3cpECCMS8Ovx31ZCHcm+g9u0zk4nu8SuPpuM8rwBMzR3Bf3ADyWsA8FrQvjvr1FifZI3L1+mfi/AmHvjO2h8e4eG32pyuqnuLNHbzxQfnTU+0K8B6Nw296LwFZl3qe+eMjAzviE5Glc0vtjvG/vFHzm81MdIL848AMwNrYXxScgN8R79SJ1ZMP7Vbvqg0gqqcys4J5nz+O2gz/isUXHxbHeuKt6D9wp5HVKjzNaPAbue3P7OkS9TwDvUzAFFG5/3Df+j8QdPTrEQPqPXB+uiD4Wji+KwbML7tRxRY1jT+Bq2qrcAFNUBZw5R+yQ23cWcFv87051pppSB/HRVKfCahm/nXE16fX45OMhnKl2Ldj+lrn/u+Jags54BpoHgf3j2HrxvpWkZsYnGv/Fk1KDq2pfAm7PnTMEV8+eSPlxpIPxScf2uX07AXfG/6UJF/4ynvlKOGM7NLfvH0RCgHinlyyVRtyrW3B1e6ZO3gv4EVgltltH/WtQHcZTVkq5WrWtrgmkksqsSjCKvrh79CP4zHkKcFrunAEUSAUV17bDZ69PAHvk9lfFAN6/zPafhqtkxhMZT+Ijfpdf5r0sJLXUHADwbCRv88uYuxMJe2cFnsdqeHxc3h7ZHJcg5y+nD7gH6zHZPqpDCJbHpbHlgmEUSveGT46OBLrH9ihcZb0/LulvgefvPLhg/cvhqvC9avRrCdz2lb9nq1EwLKEGzba4Kvn+3L4Fg0ktXKFnPiDe3yvJxVbi6cZKmmTmru2FS4u/q/ndBuObmjG+OVHmCNFUGmfJDRTNCcM+7lF3LdXZGE7FbRQ9ctctVmL9Q3DpMMuGsT2eEWXnCvQhr9Lsg6uYXq1xTgc8C/3JFaA3DI/BygKc98HVj/vgEst7FJdW8yq0TGLoi0ure8QAu1psdymzH2sHc8hSWVXhgdWdcOlyvgrcp/NwCW6J2LcwLm1k/bwXV2uWqtJsj9sFT4ztZnioQJa8oCOuMh9XZh/yzyNzIGmNT3QuwdXMK+HqxrKYKu6V2xM3JyyFTwgOwtXLg+K9KjncBXdG+je/zjW6NZGiDJdWpzOHGF8KWUioN5iZhTPDFkCbcMR4GP+Il5a0Ja6SHGBmr8nXtZtutVi5PHNeCEePE3GHiFGSjjWzqyTNwJ09mpjZ2CLtDxoz4v8GwGQzW0HSJZIm4ozpJ8DwwXyxInRy9Abg3qXP4cvDPG5m50n6AbcdXY9PFl4oUn/cr+G4jesdSffjLvBb44Hi2+HqtYPN7L1y+oJL248BI+M+Pg3MkK+MvRAUG4uy525mD0gy3DlmZ0nX4oHmywNDJXXAHZb+bMVCLMYCXSStiNueJ5rZ7QBm9pGkUcBF8iWoXizSl3ge6+H23+8l3YVrE5bHbXkv4V6ae5rZa0VoAEhaA5cWn8S9Z8/BHW6yZ/8Krrp/s0DIQBWuwrwvR2+XoPGofB3Ef0pqjdv86h9zgtOm0jgLLjU8gTO226m2TWyDf+jPkjOYUwv9Pm4QXyLqXABX1SyDq1aew/MB7hLn/o4KZHjA7U8v8cuExWNwqW9PfDBZoGDd2Wx/IZzpZKEIW+POHvvE9i648b9H/roSabTGmeqKUf6OO0u0x6WNN4BD4tzCS9Lk6HbEbTwP46tk/A2Pwetbzr2qsa8vboc8Enfw2Q5f3udxyktbtyge3P4pcHWNYz1x1XyhZAO559EU9ybtjXtnXkh15phWuEPLVaV8HzOhMX/0YxA+KTs43t2eeGjK/URYT8G+LIBL7pnmoC0eQ9oOj4v9RQL3UvpQqVKvxFJpXCWY0a657T1wt+5NYxBaKvZnqs4sO0qtPoT4UJ+OD+kmPCC7Pe4A8AKuatkFX99t1wr1aRDOTDOvvLWAofH/iBhACsXh5WhsjM+2nyacSGL/llH/AbH9N5zJlzzYBo0TggFl6sAhwYz+gasGV8FtltuX058adFvhDjPH4eq0Sti+sti+MThj7Y97mx5OdU7SthWg0wFnpjdQnS4tSxg9sMy6N8VV8I8TqyHgyQAuwFX+i+E5ND8nZ/Mu8MwvwhNUrxr7usVzuBJntn3i+J4UnOjgqtjx+Wcev/3wHKpLFKm3Yu/gnCSeyrxdcDvOQ8Desb0lnij6Eaq9ALfD0xq1KOUjwx0XnsLd25eMj/Qq3A41Es/qQhw/i4ILzPJrZ5LFcKl0bPw+iqsCszye5aYW64mnSBuAq0g/AE7PHd+GX+bTLNlJJup+Fp8kPEIsxhrHVotBNlsPbjBlpjKr8DtV83mMwlVpS+OTkTNj/+ox+B5MmQub5unG8z8k3rXd8LCLwmnSos7lg9n9Dnf4eYZqh5we0Y+Mybah2HJHK0Vb18eZ9r1UJ63ujkt/fWN7RQrYcPmlvfsWwsELl/JWiXeurFytFXmH5nQDUpn3Ch6DtX78Xw/P5rALPuO+B1ejdcZdlV8kl1m9BBqnAu/ktnvhNq75cVXgXbjk9R7VTgHlJI/uSbUqcTNckuiDeyL+hTJUQjkaHXDbxzNUr4C9MK5mvLDGuU1qtrGWNLrhk4y8d+ltwKO57XZ5GnNTocakAg9yb4/nTL2DcJKK5zKAAiue/wbtRXBpeIl45t9SrX4uGjLQE2eg+YnN6GAY2cSjdfwWzerSCc8KMya370o8q0u2pmMmjZWlxs63EZ8Y3oVPSsYDm83p98csMb1U6qDgwdM/JwqO7duDGbWPQTf76Aov3xNMLosh+x3OULMYsB2BA4ARBfuQn7UejKuwniKCz3PHtsNzaRZa9aFmv3EV0DjcCzELgl4k7mevCgxKy+KS751EvFnsvw94umbf56aCh7jcjNsFt4x9F8VzuYrqZXX2I0ILij4P3Ea3AtWpvjrgXpQ75ra75a8pSK8Dnhj8VnIqUty2+hxudy1r8oHbIw/Dpcktc/tvxuMXy60/u0fZ/V+M8CjG1c0dqV4qrN5teL9q75xuQCrzZsG96CZSHYqwAT4T3yp3zsLxW6q00iT3/yaqs7LPNLShQP35pVlWwZnrArgU+QYRk4UvjXITBZ1jcgPs+rhDyTm4qnalGAgPpVrNVVbuRtzONSgYZxvcQeJ4wraT9WdOvze/0Y/1cQehffEQjjH4BKoHrgI+LM7bBZ+gLFsGrU1xh6uzcNX1MHzCtku571fueayMM/EsUPvkeAfy69MVUivnaAzCNS2Dg3lmHpqb5s4tx7mnKt6l17PvGpcqXwS2m9PvzCzbPacbkMq8U2p+/HhowsTsI4sP8H6qM3OUM0POM74LgAdy24UlFVwS+js+O14Elx7vJNRkwfheIVRFlB9ftjrudLNtDHwv4TaWvrgU8yfc+aPkPuUGv/ViYDodz5+5DT4bPxZ3ABk6p9+d2fSjPZ6tJ1MldsIz7awW271xaXscHhZRTvabJXCptw0uMY7HHaLmy51T1MEjP8l5Me79M0Q8Z7x3Z1OByUcw1LdxZ6UP8ATePYHf41qWiqX8wrUdx+Pmi22AA+f0O/Ob7Z3TDUhl3ii5D3pFPMNKn9jegF+uFD2Cyqwr1rTG9lXBUFuWWe/q+Az/b7hzzTq4NLcN1eu/tcNVTyXbi3Bb5giq14w7FPhr7vjBwVRbxcBVstoUd+bJ6p8/BvHMxjoIj4vcBGfsJ1KGVFSP79eG+IQgS2l1B9W5O3+Hh6m0o8YKFAXodMEnUfsGA81UmKtRYN3AuHYhqj2TW0fbs++hGT4xPAx37z+XsOWVSKND9tyD+dyUo9EPd1zZCbd57kuZoTv4pKxF1Lc0br5YuMY5c6eafE43IJWGXeKlz89g34kP90Xcs24RPNv8O+TUKiXSmKlEGAzkOqptX7dQmVly5sF4bHzYG+Oz420JFeqs2jSbepfDJYcTqF5ZezeqPQ6r4vcyIt9hARo9Y1Ddl2qHlHNx1/qs/s3xtd6gAq789fiubYCrl8/GHSQ2xyWXp3F1Z8lSd+7dbZfbdx4uJWUTt7XxSU4Rr8nlcNv1ccSK7LgEv1runIHAJfG/5KTkuIr3fjxLT5fYd0q8W9nkZxg+SRBleBjn7teteF7Zc3Ctwalx3+ZKRpcvKSNLQmFIWhafod4k6VX8I9vdPDvGMHwhyklmdoOkFnhezVJpZJlWNsS9Jn8A/mVm/6Y69dNbAGa2WZn9ybJ7/CeWJdoMXzD1OFy99nvgJ0m3xHYpdXfFbYPHm9nVuUMP4JljDsKXJ1ocl8ZaFWj/cnhKt5OA+8zsyzj0I/5snsFjFr8CpktqinsgNgiY2V2R+eRefGWMTwEkXYyHbnxdoM4si8+oyHRzIP5efQ+MlvQg7hD1x+w9qy3ieVyNP4+7zWxq7H8fuFjSoGhzB6CTpDZ4Cr5SaPTA82SegE9kvo9DH+K24fG45uCLKC1y55RCJ8vM0gn4wMw2kbQELmVfjntJ98GlzO/qZPHXSmFOc91UGmahOqnsvlQ7pFyADxCZO/0OeBxYPvt9EQlpHdxmMwAfRO7P2pA7p6idpUON7bzX5mq43eUYXOJbj4KBtXHt8RkNfMadBeV3x9VRY3FnjSIhHJkEsd8sjt+AM8SzcKllkzn9DpXx7m2AO6ssUkYdmcTSHg/QH4xLLVfjTj/Lxbu9HxHjWeq7i0tb+87i2Jn46hsnUzBsJ0fj0FkcOx23c15NjWxHBWltiGtsxgXdvJPUCDxH69Fz+v2YXUmSXkLJkDQ/PkCcZ2Zjs8VacSa4FO7x+Bhuq/gEH5ABn1nXov6as8Rl8GwunaP8LvZ/HudXWeTELKEPwm1aT0o6wMz+letHJsW+iTOLnYA/mNkJpdCogU7AajXami0s+j9cNfUlPoH4oOBMeRFcLUeWtzRHb1dcxdkKuMbMHp+rZ+O/AXOJrzlwt6SBpT77qMMkrY7bPJ8xs/HAeEkn4M5DJ5vZuTWvKZFMR/wdymssqsxshpkdKF8ouQ1wo5k9UfB5LIpPYpDU1Mym5Z75yXjMbBtgipk9U/SZh9S6Dv4dTsInt5dI2t3Mno1zXgaOktTMCi6aWx9IK6cnFMH/4R5hN8Z2k/i9Cc+efqikq3Cd/zVmVmuVjaRWuF0KSf0kdcQdAS7E0yVtY2bvSBoB/F5SiyKDHj5L/QT/eE+QNNwcMyStgts/OpnZ47iNbUwBGnncA7wGDMytJN0sju2Ju65/b2YfQOkDbJw/AegrqWUwPDkZtcPtkg+a2Y3RpyKD+FwDM/sXHmdYZLKDpMGEFyOwpaT9o94j8Xf7mJjclYMHgdYxAcnudZWk1pIOB94wswfM7ImgXeR5PA6sIWnBjOF599QUn+S8YWb/NrNnitCQVCVpYVylvKSZ3Y9L2cfjCbyvzE0WV8a1Mc1mWtlcgsT0EoqgDa7SWA0gPramZjYFT6N0G+5gsrOZ3ZSXoGqBJfFM/KfhxnJwFWMT4D3zjPZrx74nzOyHIh3IDZZT8STCt0nKbILr40ujPB3njjezz4rQyWEKLtltj3u4YmY/SRqIu5N/Wmb94EsO9QYGB+MzM5uOOzrsRZmrPsxtMLNvClxjklbC3ez3NrPdcFvtWpL2iXMOxRNtf1VmEz/AkywPyyY6ZjYNn9RtjKtWS4KkNpL6x/9+uO3xR2CTYHwz4pkPxCeJC5XTgahvEu6U1lfS5tGHd/EcrT/iQfzgNsOtzOy7cmjWNZJ6M6FkmNmXks7GZ8gfmdnz+HI64AP6qvhqAD/E+bWeXZrZ65K+xZMFn2xmHwFI2gS4WdLVuFv5IWZ2bzn9iCVPDsBtjxsBF0r6zsyOieMqtf2zoCMz+y5m9ycDu0s6Cl93bD88hdn4cmhEO2+U1AtXQfWW9AKuzjwzaLxTLo2GjJxqbzBuY30rnvGD+Pv7h5i8nWVmr5dLL9SwnXEv4KUkTcUnP2cAR5rZmwWqbQscJulHfIK4F24+GIIzpQfwcf3veMD+q6USyKliB+MM7XEzu13SdOA8STPCHPAWMCrT5JT7PdYXVOb3nNBIESqPbCZ5HT5wDMEzxR9qZneWWN/PtgZJnXBnhSxJ7n1m9nF4t1XhiXJnu8ZeLWj+EXe6OTG2d8CdQXYws1vKrT/qFO4cMz1m+31wFfAI4GPgfTN7uFRbS25gWhmfdU+y6rX+dscnBuvgXnVXmtltDdWGVy5y92rhkFqyCc/2wN/MvXWb46EJn2WqwIK0VsE9ZF/MPY+NcceYdfHncUs5z0PSnrim40oz2zv2rYNLd8Px9+EmM7ujDBoj8DCEK/BQnfPM7HxJ6+Jq4d+b2U2l1jtXwOYCb5pUGmbBjej74y7RV+Kpm7LsK0VSM62Je8wNj+0ReND5Vrg0dg4uuRTxAJ3Z2ms7AmNr7LsPt421LnhPsr4sjcdlZUHJmVNDxbLM4xL1E1Rnx18a+CcR4xf3qlm+XY214JL8PbjX4eaxb0883q+Qd+ZMaAyM57F8bHfFPUOzteWaUp2fspzk531x56rx/Eai86L9iffozmh/xkSvAfaP4xtQcNWSuaEk9WZCYZjHSZ0t6To8bq2FmX1Y6uzS7OdYqb/hMT+Hht3uOFztNAK3Hx5nJTjFZKghRe6Ne+w1xwfAXSWdjEurK+Az8b9aQbtE9GUTPNPKC/jq4Bfis/wzzOyuIvXWhNy7dBS+qOgLkhbA1ZhPWLUzzM/3qpTnMS9AHkPWwtzpaSjueLElrvZbRdKSZnaWPH70L5KeN7MvyqC3Av487jSzFyW1xbPd3GVmH8LP9jzif8mOSpLWxM0Hz5ivPv4acJakb/DJ2j7AUcDX5ra4Qs/czN4Ox56F8BjDPngigH/Ep3RO9Llhag7mNNdNJRXcNjEufjfF45bOw+1fbeOcLAVYOfk698bX9+uOM+ntcWeCC6KMJ2bpZdBYFs/6vyA+wN6PO/4snDunEquQr407+tyMqzJbACvmjjdayQ53FHkJX1dxIVx70A93UHoaZ073EDkiKZj9pgbNQfE8rsMlpebkVoQv93ngnphv4kHon+OOVuBMcALlxfpl2ok++KLIi+fesX/F/wFxzwrnNZ1byhxvQCqNu+B2wI1ioOqLB9EuheeGfCWYX6G0SbmPWbhq6Tzcg3EfXH3Tssb585fRj4zWgBiYNg4mmuVu7F+TXsH6e+HemG3i92x8LbnFa57bGAuuknsRzwyU398Gn1h1ie278VCUrhV43v3inV0Ut4EdRC6JQQUYXg9cbZ3l0hyGaxF2ju22xKLMZfRjeHxv98V9OTi+lYfx0KRXgHXn9POtREkhCwlzDKGiOxF4zdzLbCHgKXMvwy/xGKRzrEBYQqj7usdmX1yi+wnPUrEmvq7Y95L+KGnrOK/kNFa5cIyW8ftW0DsTjyl8U9J6eD8LxX3Jg41N0gZ4KrMd8SD0L/HwkCWA3SQtCY1PlVkDa+EZey6JGLN+kvbAE4avjocm9MYZxWlm9m6pBGo8j3G4bfUZXLo/G3/+O8pTz1XieQzGpcfhkuY3swfwdGlHS9rTzL4xs7eLVBz9WBFfv3FzMxuO29G7BN2dcCe1vayBeGfODsmmlzBHEAPPTcANZvZG7H4N+J08aHs9YE8ze7lA3QKWx+PVshXPh4YL/3m4GvD/JI3EHWS2gGKDUwwa6wObhQv3M3juxneBXSQ9i9tFRluJsX6S2pjZt+YB88vgYRwb41LxSOAHM7s3XMm3IH3P4JOBPWKiMRJ35umDS/ZfAofg+UZPNrMXSqm4xvNYAs/csjEu7b0LfGlmr8bzOARP+1Yyct6mSwLfmNk4SZNx9ewWkm4ws4eCmZeV+SS8VofiE8EueKznY3hWpZXN7GbcgWzewZwWNVNpPIVfr7d3Pq6maZ/b1wl3kV6lTFptcab6Bc48s/1/wT3srsQ/7nJteKvjGSoGUJ1LcQl8ELkYD+AdMbP+z6beBXCpNFshvA2uNtsDtxlmatMN8QwYZS2pM68UfOmeg+JZ3IAP6Avi6uWT8FRt2dqIpTyPBXHHqpGx3Qx3jtkF10gsG/u3wCX6slaviOf6LJ6P9V6cee+Khyrsna+/lH7kz493Klt549igs1Jsb4bbi9vSAFZOKKWkOL2EekFu9roarqp5x8welXQBnltzSyszA0ZNb7LwdhuGZ3N51sxujP0r4hlQpltk6i+D5iH47Pgz3BlmSzN7L9RQX4UqbEaBOLwlcG/DXrgK80HckaAb7ngxXdIgfBa+s5m9Uk4/5jVIam+eISjbXhNXMW9W5JnLU7n9HleTP24enH0zLuktYGbf5p7Hrmb2Uhlt740zu61wpn0cLt3/hDO+lfDk5R+WQWMzfOWN5vhE6jNcZXogsUAvcIqZ3VaUxtyKxPQS6g3hyv8XXMraEl8W6BJJY/GPev2ijK9GWMIWuIQ31cyelXQo7hl6K76MS2szu7TMvvTAU0D1wdWOrYCNzIPot8IdG061AnlBcxOEbDmlRfD79jnuqXcxnvdwK+Ao8zyUCTNBqMrXwRnekWZ2R4E6suTdG+BMZz5cMvov/k5NxtXa2wLHFHkeuWfeBV8+azgernMAsJ15GMFKZjZB0uJm9r8yaMwf7T4SdyLbELd5vgkcjdtFLzYPi2hintZsnkFyZEmoF8gTSW+Fx6t9hM8w7wEwz3/4Bp61ohByDO9APEauL3B6zGhPxZdE2QlXPz5ZuCNOoy3uAdoLZ0Kf495138rzIh4FvFSE4WV9CTvhabjXXGYjWhh3jf8SZ7i/Wh0ioRrB8Abh9+7PBRmeguENx5/H7Xi+yR1wu9d6uJp8MnBw0ecRz3wYHqe6CnAE7lwyNBjeanic3JJFGF6Oxhp4cPkEM3vcPMH2zbjzSg9cBXwN7hjVd15jeECy6aVSPwW3tYzD1T+PUL3a+UZUKPYH9za7C5/MnYCrBB/Ek+CC22UWqxCtfXFbTis8tvBkfPB7gAJZaWrU3STan9mPlsYz31wPDJnTz7IhFdz2VvJq97hTR+f43xSX7LK4vg64dH8LFcpMgjOcG6nORrQjzki3wCdYE4mQhQJ1Zxq9gfjk7yp8OaJRuXNOxGMbWwGL47GMZccvzo1ljjcglXmz5D60LsRCrcDWuHddxhRWB14njOdFacT/5rjzR0c86PwRPGD7OMKTsgJ96p4feHAnlbXjfxsKOknMgtaJuC0vSyO2fAxU/8TjwRptLF59FODP8a52je0943lkKcUWDCZxbjkTKXyC1gS3pT2LO8dkizBvH+/BGTlmWHQitQbuOJalXNs2tvfKnbNsvl1z+hnUVUkuzgkVR852sAEusXwpaTzVGSWOkS/gOQJfLWFCETqWjQKegLcbcISZTZXUATjXzH6QNAU3zD9YZp+a4KmYBoSreBZ3l8WFfYu7wv+ibbWsO7tfffBB9U58hfNDcYniWFyl9iFwgpXpfJMwe5jZcaGSv0nSljjD6wFsI0+71wxfIPkCK5D8PGeDbm1m30g6B48THYCvXnK9mV01k3YVdcJYBl98eSLVTlEGjJCvLHEe8GbWLiuomm8ISI4sCXUC+ZplR+N2iZb4x9wHuASXytpQ7WhSOIefPJfmnvjKCK/GvoNw+92duO1lLSsWhJwxo6Vj12cxQB0SfdgKZ7bbWZk5NeVZ8s/B7XXv4SnM2uNqru64FDvaPG4qoZ4g6Xg8Pm5T3DlpY9wjuApfoaHk1ThqTAoPxENoXjaz6ySNwpnrU8DVZXwXGY2OwOfmiRg2xe2SO5nZY5IWxO17/zWzF4vQaZCY06JmKvNewb3bLsQXfc32LYO7YW9TZt01VZrnAf1iu0Xu2Nb4WnVl2Qtx78ln8SWOriDi5uLYYHwpov3LpNELd5DoHttn4QxwhdjuQbWaLak166hQLQT0xW1pmd35SNxhKbPxLUN1OrOSVxOJ/8PwdGmD8VCX/wL7xrED470upDalOvZuQ6rTiJ2Nq/63wENs1oxzms7p+17fJak3EyqCvLRmZl/LF5ntJulcM9vXzN6S9D4eJHxdUekuuybi336Ur7G3vaQXLNKVydf8uscKhD9IapGrZxGcce5gZq9I2g1YVdJ7ZhNq664AABVzSURBVPa0mY2X9BUwRtLVZja5BDrZTLwKlx764quev4EPeqcDR0o6wcwm1ux/QuURz2MT3K72KrCdpFdxb1wB90la38zeyl9Tm7oldQf2l/QivqL6AjgDWhrXghyNL2I7zczOlNTZSlSbSmpuZj9adQafU3GVZpOgcR6u+egAXBqexl+WQmNeQApZSCgbuQF8uKQjJf0Zd+M/HGgp6d/ypYM2xb0byxq8o67L5CmUsni7HePYSHyQmq9Ave2Ah+UrRmdoGwXgaqAdbtvLH18QX7Wh1oj7NRR3UDkFj73bUNLq5jgIv4cJ9QRJLXEHj13MbGtcFdgE2NHMjsdj25YoUG9PXEvwAz6x2Rz4Cvgf7pW7p7naejK+1FVnM3u/RBo9gKPi2wC3Ob4ck7Mncc/fj4F1zOwiXNL7ojFOohLTSygbMYCvjqv63sWzSByCM4QzcJvekXhc2b2Saq1hUKDG7gfwYPOT8Bn5S8BWku7B8yGOMrOPCvTjS1wVdLGklc1zZd4GrCOph/n6dLfijLxZtOsjPM3YlFnXPEv0xVM/9cJDHt7ApYth0Z798lJeQmUxi3i6xXFtBLit7QM8UBwzO9TM/lMijQ54SrSxZnYYnoi8BT55+h6PwayStDLuWLJjAYbXC4/vezcKeGhCV0l/iLZPwqW6HnG8cDaXho7E9BLKQm7gWBc439zjbBPgO/wDnojPZp/B7WxYbjHNWqB5TqXZX9Jy5p6SG+KLvh6BJ/bN4pnWKcIoQs2ImZ2MS12Xy9OV3YZLjWdJOhJXO/7bzH4KiexDKzHDfUiomC/G+Vc8R2g33I73MbCDpPZZmxIqj7x6XVJnSZ3M7Hv8+a4sab04/l+gtaQFZsEkfxOh8r4O+L2k1vGuTAU6mtlP+Pp+J+AOXldadfL12vajHT7ZPMPMxmTvfqjo9wHWkHReOEptgseSYvNi0HltMaeNiqnMGwVPvHsJEccU+x7H1zcTHhh7NhHHVss6u+FJg7vi0uJFeDquLLlvazyW6kYKrrkX9WQODPk16XbDpcg+uP1lczyR8dD8NQVo9cMH1o65ffviTg29cK/WQmujpVLrZ7AwcGj8H4bHP74Uz3yF+H0OdzB5G08vV4ROk9z/MXi4wEHAo8BSuWOLUyCAPs5fDF8bsPXMrgc6x3d5MgWD2+e1kkIWEkpGzoa3Im7jeA8frHfAvdyewBnd1Xgg+ochtTSzWq6NF7PqTnhmiM44Y8hijT7FV3R+NdQ3W+Mf9KQy+jICGI3b0R7CGezmuLp0LzN7vNS6Z0GvPR43+AY+EH2KM+87cO+6vuaSbEIdQdJa+Hv0GT6pORB/jw/Fs6zchqsfuwGfWhlhNcrlrpR0Lv4+94p3t025zzrUp2NwO+SX8pi7afH9LIVPQh/JnV84PGheQWJ6CbVGqOV+CiaxPp7R4U48I/s/8EVgl8RtIs1xlcuNpX5o4Zk5I/5vgUuRU/BZcufYbo2rifrgTOmDMvq1MnAM7kHXGU9+vbCZHSjP5Xlg9GlqqQNGjqn2x4PZP8btLWNxx4UzcOa+Ga7eer5oPxJqh7ApD8NV5IPx1G7T5HkpD8bd/MeYWcmLCs+CXnMz+zH+n4V/L2tamauK5Oq/DZhmZpvHdsb41sJVmn8xs28qQWuewJwWNVNpGAVYFrd1bYDPIK8DhsWx4Xhc3oax3ZEKxJUBf8BtEMfiSXGvxhlrF1wFdQXQu8x+LYTP7h/O7esXtFaJ7a5l0tgQV5eNxVVRx+BegRfgUt+HFFShpVLSc6ip+lsF+Fc8jzaxbxiev7VLmbSyGL8spdgS2TP+//bOPdzO8UzjvyekCEUSIU3UBEUFIVqRquMIIQ5RqXZKjWNIi2sIMqGtNgQN01SD1LSJK5dUqpQMKVWVmbQO1cE4jZmOEOfKNXWYigZNsu/5435Xs5qq7HWIvffaz++6vmvv9a21v/dbex2e733e57lv7DKyENdUNPL5qPTjrY2XEuaW91UPvJzwROUzmVvV/62jTyC3zr/htaaHcIqxX9l3DbY9qXyoj8V6l70aGOcTVYFmHVxmXWkI3hKX9l9LWXujas2kxnGqm4QDt1IspAgKl/0zKE3ntY5TLhBGlt/XK4Fun3K7P5aAOqV8QW3KSkPYbDxfQxsrs1qjWDmr740LsL6NtTYrga93I+OU9+6TwIll30DslnFs1eN2atLzWqfyswTwn5b318PYOzDfV6tsWR2WvC9h762rgOmSrsYpOXAQ3AxfLYMd0Bfjsut6xjkYr6MtLbuEvyyOAJD0bBlzGHBRSVE1Yt2zX1kPHCn7n50BjIyIqSXd+SlcuYdqqHSLiG3xzPEjZVcbLktfUo61GP8/Py5phaT/lfR05bzqeT7J6imv+f64UvJm7D4+EV+o3Y7T2ueWteffNzKOvG49EdguInoBQ7EW7OyqityGZb9KGvPdiBgEfFnSaCymcDpWDvqXXMP7SzLoJavjbdyrdHO5vVb5eQv+Mj8nIubgVOMNci9bTZT1wa9iwejHI6IvvnKdABwcEcdUHor72r4qaXm9H+ZSgDMbrzvOiYiTJN2Jg9Fn8IzyBEm/CAtNt/e4g3H7xHmSZlWKd4C7sQLGZuWhawHbRESvesrgk/azyv93H7wu3BcXX02X9I6ku7Hdzk2S2lSn2HJEDImIDcNC1Q/j9ebNJP1Ebk/5E7W+dyvPIyJ2j4jDwoayy8OqQbMp3+WSnpG0UEVrNgPee9DRU83cOveGq9j+bG2AoteHZzMn4tnY0LKv1pLrPng2VEnFbI1LuvfFaxWH4IbbOfiLqi4tTVamt7bA6x1HltvDsfvDyeX2yDLWqXWMsSfQVnX7LmwsCl6XXISD+/8AB3f0a9tdNizz9iWcUp5d3l+VNbeTqfKVa2CMT+Im9Ovw2vfWOIU6i2IP1YQxRuI06an4gvOw8p47puoxmcpc3f+xo08gt86/lS+La1kp7FxZxxuFe4Dq7pErxzkEizoPAX4OnL3K/ZtgJYmBdR6/suA/Eiuo3I9nXwPL/mG4deBUPDM7DM9ca17bwYU+i8rz+MYq9x1R7v90R7+m3WXDVbfzsdzbXnjttnLBMxRf0B3U4Bi7l9d7K9xTehK27/l+Of7G5XH19nYGnp3OLZ+DT+PU+6arPK5lPfCauWXLQrJaIqIfK9NCN+IP9B74Q32O7P/W6BgH4faH8yV9s6rs+hDgLUm/qOOYvSQtLb8PxbqK84DlOI3ZBkyT9EpEDAfWk/RvEbEOns3W1UNV1o7upKjJVJ9H8sFR0smTgSGSdi/7xuLCpXdwpmKKpNsaGGMn3NLygqQLq/ZvW45/FVbwGV/3E1l5zAlYKGF/PLt7JiKOBx5QsdVK2kFHR93cusaGi1bOwOmV63EDesUBvSkpFeAArIJSuTI+HvuKbVnHsbbDFj2b4wrKx3Dj/Ebl/r2wEex3gAFVf9es5zIKzyoqrvHdzsKlI7bq16+87qOx2MA5Vfu3wlW0WzX6muN1wjtwSnzQe9y/CW5LqSkbwsp0/ACgb/n9Iry+XknN7oyrRDNzUMOWM72kJsrVcxv+EL/U7OqwUsV5GbZBORoYJ+nJGo+xLS4ouVLStWXf5jg99BNJk8q+/XBqdYbWwJVyRIzEazwfl/RGs4+f/DlVQgB7YyGAdyVVHD4OBZ6UNK1JY3wMWCybCg/Gaj73Y6Wgl6oefyQOVsNVY7N7Oe9puFf1eUlfiYibcHHZcpy6vUANzFS7Ixn0kk5HRByKq0OH1hHwBuOZ6CS5ZHstXM59ZdgBfR52pJ5cHt97TQakkp79g6QFa2qMZCXlvXMptgU6C/iepKuKzNwXgIclXVHnsXvIXnWHYvuqe3HwuQzPyM7Ga203qigElQD8sqo8+FYzRiWo9irnfy9W8PkuDtoTImIP3N/5kqSHsi2hNjLoJZ2SetfBImJP4JeSepTbPwcelW1dKIFvPvADSV9r5jmv5rzyi2kNExEfxTPrk3BxyVlYru56SZeGDWKfVY0uHNUamaWH8xpc7HQ6Lkx6BPflDcBtNv8o6fkGnscIYAyunL5A0sLSmjATeFXSCfUeO8k+vaSTUk/AK393LzZjXRQRdwP3VAJeuX8RLsK5qzln2u7zyoDXZN6jx/EN3ILQFwehEeXn1yLifEm31RHw+gATI2JM2fUh3KYzGK9Bn4kdQKZhAeuxDQa8TwAX4mriQcCIiBgoezuOBfpHxJB6j5+4DypJWgpJPy1Vej/DMlMAlLTQGbgv656cfXVtKq9d2Jl8CbBErmjcHq/dvhkRbbiCsl6XjB640nNYRCyRdFcZcypwmqQHSrqzD9Cnej2vVsLu59djgeibIuLXOCWriLhd0osRMVpFvDqpj5zpJS2JpPlYYf4pgIjYBqelZssO6Tn76qJExKCIGF9+PxBXZ16CHe+3wHJ4e0bEJKyhOlfSglrVb8K2QK/ipvNBwJdL6hEc5CZExF54RjlN0uMNPrXFZTsXfPGGg+AIYHRErJMBr3FyTS9paUr/3y24GOCc8kWSdFHK2tYOuDp3BlYm+Rm+uBkH7IZ9HXfAKcgXK7OzGsepFJQcgNtavgUcCTyDe1V/hQUMeuLCqJv/6sFWP8YA3NLyQti+6zpcHV2xCjoY+K2kx2odI/lLMuglLU9pFt9Q0tyOPpekfkoa81a8pvYWlvj6Aw5Gv8Ozr9OBvbF26gvl79qdxg6LN78l6dVS+XsxbjyfHhH9cZHMrsBlkn4dEetKeqfWVHlVwDsMuz68jFsgTomIDYCrsZv6yPYeM2kfmd5MWh5J8yXNrTW9lXQeSjD6MQ4295VZzwHAh7FruCS9hoPFfVhMAag5jT0GGFQUgVZgr8MDI6K/7JAxE88i/z4i+kl6p5YxSiClqp/wIlwJOg84MSKuxX14pwGvl8KWpInkTC9Jkk5PRJyAtV//IexesStuEdgBy4BdKGl6eWxPScsaGKs/thsaXXadBbyAVVc2wPJ7Z0qqyR6ozFQnYG3ZNyJiR+wmsikWIj8O21I9hYUZlqkGW6ukfeRML0mSrsAi4JNF5WYGbgSfgoPQQmBSKVyhnoBXyQJExAZlRvcgLiJZhgPgICw3Nhe4qo6Atx0Omv9N8Zwsx3gUB9cZsq/iTCwvtkUGvDVDtiwkSdIVeBC4CQe6p3FxyX/iYAQuYuldz4Gr1tcOB46IiLMljYuIaTilepSkfy2B611Jz9W4TrgRrhy+WtLMqgC7SVk7fAIYHjZGPhD4nKSn6nkuyerJ9GaSJF2GiOgj6fWq2/viQHhQSRnW1XtZqjSnYMm6B6r2TwKOAg6Q9HKd59wDN69fgWespwO74DXJC4FXgO2xSPm3lVqaa5Sc6SVJ0mWoBLyI6ImDxqXYjuqNcn+9V/F7Y4PZFyLiaCxQ/Yikr0fExnhGWVfQwyouG+G1x5HYGeFebNF1GpYtuzwirpa0NEUT1iw500uSpEtRAt4wYBLwHUnz6jhGJaVZ8W08Eldu7ojX3tqALYCvSHqzCee8KXY5H4CthpaVVofLgEWSrokiaN3oWMn7k0EvSZIuRwl8fSUtrnF9rQ/2VHy2CBfsC7yJ1+4C+H055i545jem0fW1vxbMwuLo3wdOlnRfI2Mk7SfTm0mSdDlKhebi8nt7A956uP1gRUQ8hhvPJwPHYpHqW4FFZX3vKmB8EwJe4GBKRPQGlgL9sOj5RWWMDHgfINmykCRJt0DS21h4en3gM8AsSXPK729ipZfl2HH9ZEm31zpGdetDSZ1K0oqIGAg8AAwHXsOtFmMl3Z6iCR8smd5MkqTlqU4xxkqn8364yfy/yv4HgS+UfrlGxjocOAVbDo0tqdQp2Ex22qrnk3yw5EwvSZKWR3Y83yYi7sC+e18HfgOMiYhdiwvHBljAum4iYmfskjCZ0uBelFemZsDrHGTQS5KkpalKH74BPA58F6cz/xnYEvgh7qObKOnZGo/90WJvRERshU1lF0p6QNJ5WMVlOrB55Vwy4HUsGfSSJGk5IuIjEbFluTkIQPbGuxx4BMt9LQa+CczHepi31rK+Vh67LbA4ItbH4tTPAQMiYlQZczL2+7smIj6c/XcdT67pJUnSUhRh51uw2skC3AQ+V9L55f5+wJW4YfxYLC22pM6xeuC06I3A93AF6ARcDXq3pDvL47aW9EwDTytpEjnTS5KkZaiyIPqWpBuKePT+wKiIqDiS/w54CFv4/E09Aa8EO0qq8o/YUPYE4CBgKvb3O7wy48PyY0knIPv0kiRpJfYD5hdh52oLoh8BZ0ZEG/Aq8HlsNFurW8LawIpSGLMbtgZ6RdIPImIZlhVrwzqb5wLPQkPyaEmTyaCXJEkrsQg4uVgQfR733O2C053P4DW4IcAldQS8/sB4YEpEDMEFMLcCe0TEaZJ+FBErgIn4u/XiDHadjwx6SZK0Eu9nQdQLm7W+XWZqtQo7/x92Q7gYV39+TtIvI+KLwKyIOF7Sj8tscHEGvM5JBr0kSVoGSUuBKyLiulUsiHYGdgc2xFJgtciX9QTWlbQkIo7DFaD7AgsiYq2S2mwDbo6IoyTd0NxnlTSTDHpJkrQc72NB9EotxynrgiOAJRGxNZ7pjcdrdofivr+XJM0pM7yUFOvkZMtCkiQtSaMWRKW1YSmwG+7n6w+cU1KY6wEzgNeBf5L0fNXfpR9eJyZbFpIkaUmKE8O/A1+UNK/GxvN+wJeAPsB9wK9wkczbETGgiFcfDwwEzo+IdavGzYDXicn0ZpIkLUudFkRrA+PwpEB4lnc5sB0wFuiN+/LWx43o60t6p+knn6wRMr2ZJElSqHJUHwbMwhJlv8WVn5fgPsBjyr6xwH6SHumg003qIINekiQJFo8GjgZmSHotIg7BBTAzsWTZunh9cHvc9P68pPkddb5JfWTQS5IkASJiMq7MvAM4D5u9Ho11NB8FPgX0BC4t4tWVv8vClS5EruklSdKtKQ7ny7HHXl9gJ5y6XIgLVXqW318EjiuP+VPQy4DXtciZXpIk3ZYiLfZZ4D8k3R8RQ4F9cIBbBvwdcAhwj6RDI2IDSW913BknjZItC0mSdGd6AR8DJhc5sd8AGwNLJN2GdTQXAMMjYqcMeF2fnOklSdKtiYgPAX+L/fCm4nTmEcA4SU9ERB+gj6SnO/A0kyaRM70kSbo1kv5YzF4PBLbBVZq9gQsiYjNJr2fAax1yppckSVKIiL7AjsCZwEhgsKTnOvSkkqaSQS9JkuQ9iIhdJD3a0eeRNJcMekmSJFVERA9JbVW3sw+vhciglyRJknQbspAlSZIk6TZk0EuSJEm6DRn0kiRJkm5DBr0kSZKk25BBL0mSJOk2ZNBLkiRJug3/D6pC7WZdRZziAAAAAElFTkSuQmCC\n",
347 | "text/plain": [
348 | ""
349 | ]
350 | },
351 | "metadata": {
352 | "needs_background": "light"
353 | }
354 | }
355 | ]
356 | }
357 | ]
358 | }
--------------------------------------------------------------------------------