├── README.md
├── LICENSE
├── 005_轻松手撕10大排序算法.md
├── 004_简单易懂的快速幂取模算法.md
├── 002_为什么Swift和Python要抛弃++--?.md
├── 003_程序员必学:快速幂算法.md
└── 001_如何直观形象地树状打印一棵二叉树?.md
/README.md:
--------------------------------------------------------------------------------
1 | > 自己闲时写的一些技术文章
2 | ## 博客原地址
3 | - [M了个J](https://www.cnblogs.com/mjios/)
4 | - 因为博客的CSS样式是自己写的,所以阅读体验会比github更好
5 |
6 |
7 |
8 |
9 | ## 微信公众号(xmg_mj)
10 | - 可以第一时间阅读最新的技术文章
11 | - 欢迎关注(。◕ˇ∀ˇ◕)
12 | 
--------------------------------------------------------------------------------
/LICENSE:
--------------------------------------------------------------------------------
1 | MIT License
2 |
3 | Copyright (c) 2020 M了个J
4 |
5 | Permission is hereby granted, free of charge, to any person obtaining a copy
6 | of this software and associated documentation files (the "Software"), to deal
7 | in the Software without restriction, including without limitation the rights
8 | to use, copy, modify, merge, publish, distribute, sublicense, and/or sell
9 | copies of the Software, and to permit persons to whom the Software is
10 | furnished to do so, subject to the following conditions:
11 |
12 | The above copyright notice and this permission notice shall be included in all
13 | copies or substantial portions of the Software.
14 |
15 | THE SOFTWARE IS PROVIDED "AS IS", WITHOUT WARRANTY OF ANY KIND, EXPRESS OR
16 | IMPLIED, INCLUDING BUT NOT LIMITED TO THE WARRANTIES OF MERCHANTABILITY,
17 | FITNESS FOR A PARTICULAR PURPOSE AND NONINFRINGEMENT. IN NO EVENT SHALL THE
18 | AUTHORS OR COPYRIGHT HOLDERS BE LIABLE FOR ANY CLAIM, DAMAGES OR OTHER
19 | LIABILITY, WHETHER IN AN ACTION OF CONTRACT, TORT OR OTHERWISE, ARISING FROM,
20 | OUT OF OR IN CONNECTION WITH THE SOFTWARE OR THE USE OR OTHER DEALINGS IN THE
21 | SOFTWARE.
22 |
--------------------------------------------------------------------------------
/005_轻松手撕10大排序算法.md:
--------------------------------------------------------------------------------
1 | > 昨天我在B站上传了一套视频[《轻松手撕10大排序算法》](https://www.bilibili.com/video/BV1PT4y13767),里面详细讲解了10大排序算法的编码实现、优化思路。只要你认真听了,绝对可以轻松拿下排序算法。建议选择1.5~2倍语速服用,效果会更佳哦。
2 |
3 | 个人觉得,一些复杂、难懂的算法,通过视频来学习,效果会更好。原因如下:
4 | - 通过视频可以清晰看到每一个算法的每一行代码是如何写出来的(应该先写哪一句,然后再写哪一句);而文章(博客)呢,基本都是直接将整段代码贴出来,容易让新手打退堂鼓
5 | - 在视频里可以增加很多生动形象的动画、描述,有助于快速理解算法思路;而文章呢,就算是有GIF动态图,效果还是欠佳,因为不能像视频那样很方便地自由暂停、重放
6 | - ......视频还有很多的好处,就不一一列举了
7 |
8 | 下面列出几张视频中用到的课件图片
9 | 
10 | 
11 | 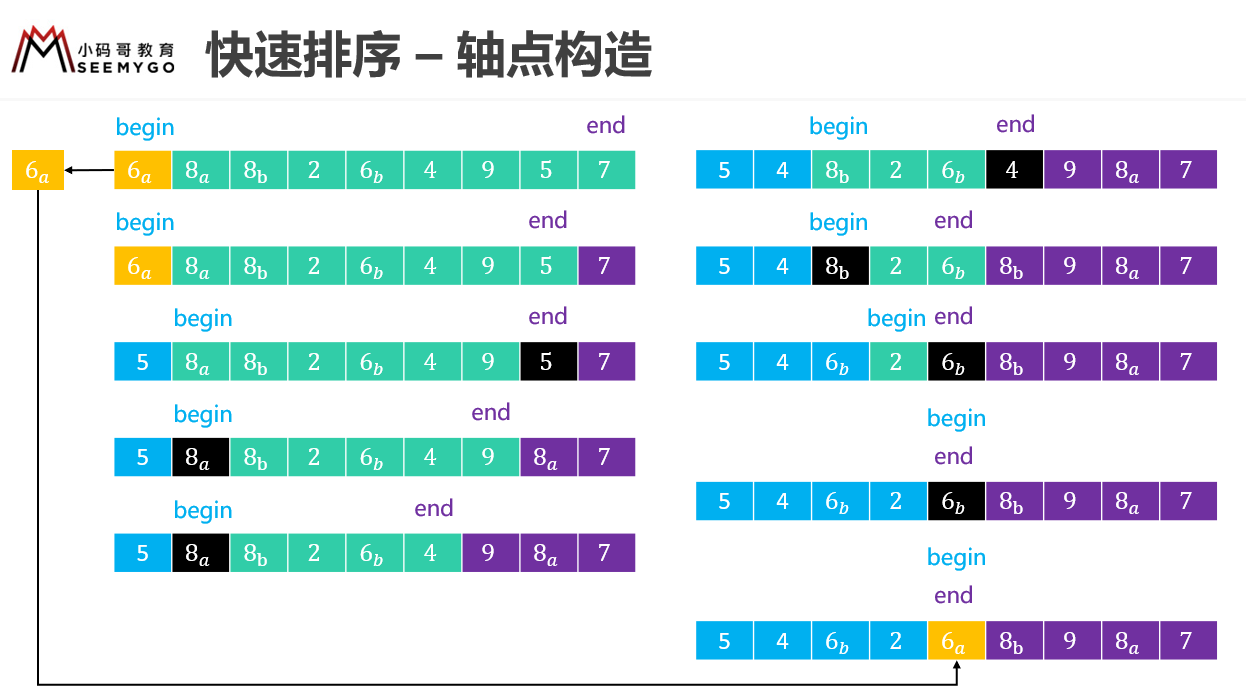
12 | 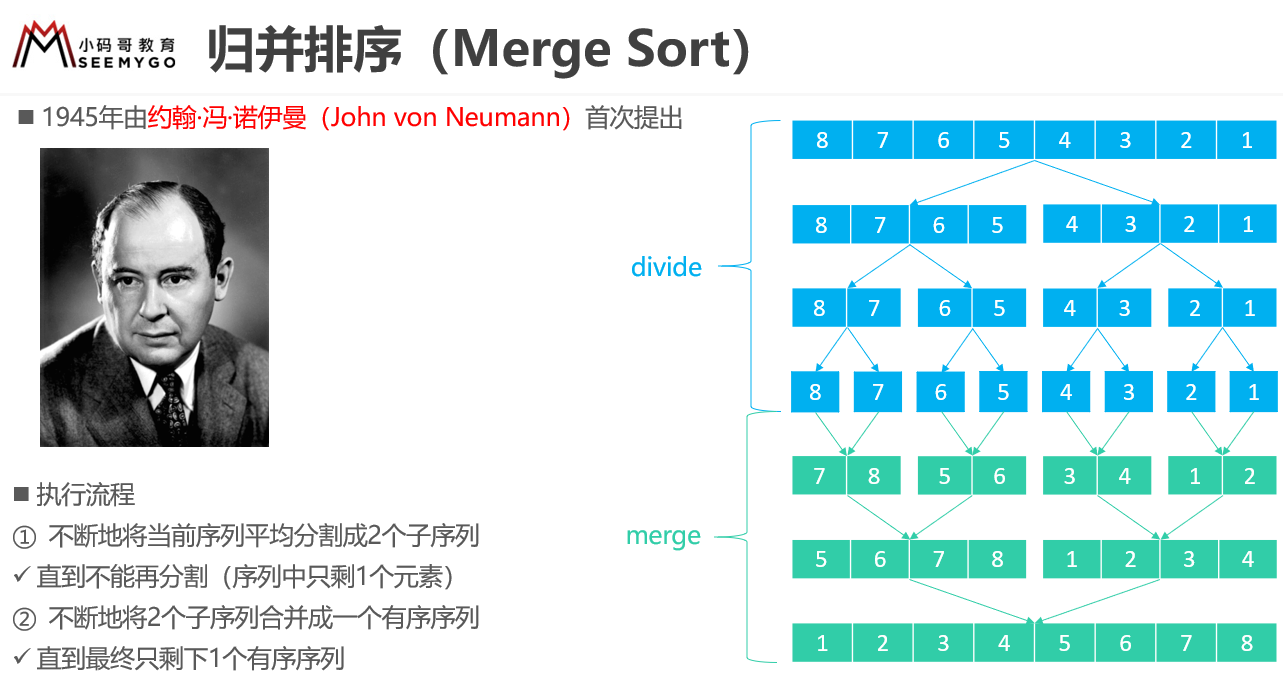
13 | 
14 | 
15 | 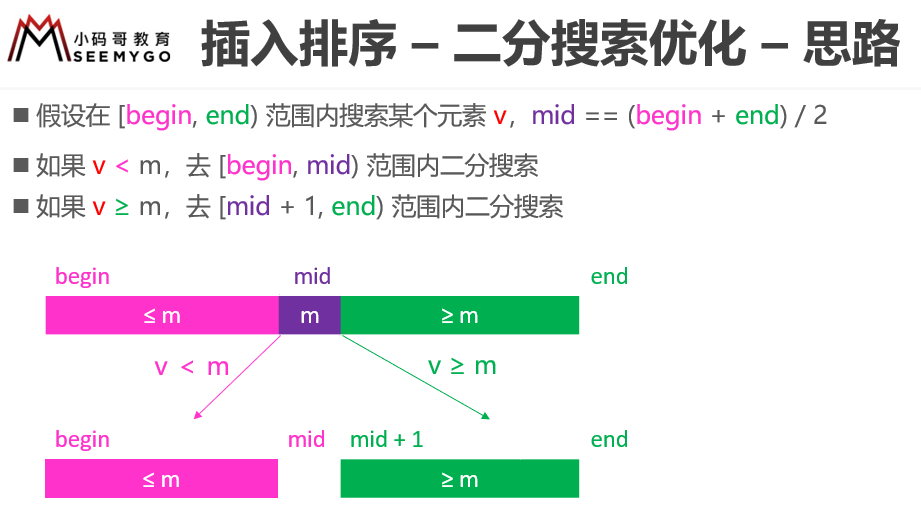
16 | 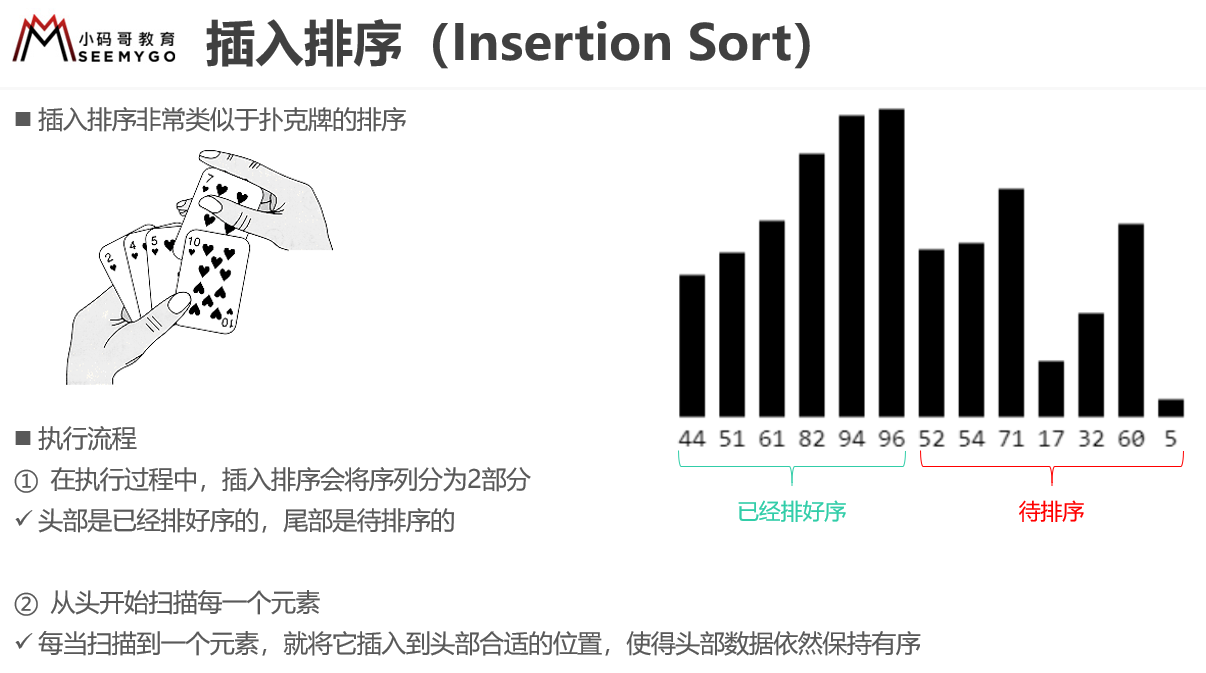
17 |
18 | 如果你特别希望我写点什么方面的内容,也可以留言建议,谢谢。欢迎关注
19 | 
--------------------------------------------------------------------------------
/004_简单易懂的快速幂取模算法.md:
--------------------------------------------------------------------------------
1 | > 本文是上一篇文章《[程序员必学:快速幂算法](https://www.cnblogs.com/mjios/p/12690097.html)》的续集,上一篇文章详细地介绍了快速幂算法,提供了递归、非递归的2种实现方案
2 |
3 | ## 抛出问题
4 | 请设计一个算法求x的y次幂模z的结果:**(x ^ y) % z**
5 | - x、y、z都是整数
6 | - z ≠ 0, y ≥ 0
7 | - x、y的绝对值可能很大,比如(1234 ^ 4567) % 30
8 |
9 | ## 思考
10 | 由于x、y的绝对值可能很大,x ^ y的结果可能会溢出。所以先求x ^ y,再对z取模,显然是不现实的。
11 |
12 | 这里要借助模运算的一条运算规则
13 | > (a * b) % p = *(*(a % p) * (b % p)*)* % p
14 |
15 | 
16 |
17 | 
18 |
19 | 根据上面的推导,就可以很容易写出代码实现
20 |
21 | ## 递归实现
22 | ```java
23 | int powMod(int x, int y, int z) {
24 | if (y == 0) return 1 % z;
25 | int half = powMod(x, y >> 1, z);
26 | half = (half * half) % z;
27 | if ((y & 1) == 0) { // y是偶数
28 | return half;
29 | } else { // y是奇数
30 | return (half * (x % z)) % z;
31 | }
32 | }
33 | ```
34 |
35 | ## 非递归实现
36 | ```java
37 | int powMod(int x, int y, int z) {
38 | int result = 1 % z;
39 | x %= z;
40 | while (y != 0) {
41 | if ((y & 1) == 1) {
42 | result = (result * x) % z;
43 | }
44 | x = (x * x) % z;
45 | y >>= 1;
46 | }
47 | return result;
48 | }
49 | ```
50 |
51 | ## 测试用例
52 | ```java
53 | // 4
54 | powMod(1234, 4567, 30);
55 | // 699
56 | powMod(123, 456, 789);
57 | ```
58 |
59 | 如果你特别希望我写点什么方面的内容,也可以留言建议,谢谢。欢迎关注
60 | 
--------------------------------------------------------------------------------
/002_为什么Swift和Python要抛弃++--?.md:
--------------------------------------------------------------------------------
1 | ## 简单好用的++、--
2 | 说到自增(++)\自减(--)运算符,小伙伴们应该都不会陌生,在很多编程语言的代码中,都经常出现它们的身影。
3 | - 比如常用的**for**语句
4 |
5 | ```c
6 | for (int i = 0; i < n; i++) {
7 | // TODO
8 | }
9 | ```
10 |
11 | - 比如经典的一行代码实现字符串拷贝
12 |
13 | ```c
14 | // 将src的内容拷贝至dest
15 | void strcpy(char *dest, char *src) {
16 | while (*dest++ = *src++);
17 | }
18 |
19 | int main() {
20 | char s1[10], *s2 = "xmg_mj";
21 | strcpy(s1, s2);
22 | printf("%s", s1); // xmg_mj
23 | return 0;
24 | }
25 | ```
26 |
27 | 使用得当的话,自增(++)\自减(--)运算符的确可以让代码简洁又优雅。
28 |
29 |
30 | ## 但是
31 | 2大热门编程语言**Swift**、**Python**并不支持自增(++)、自减(--)运算符,这是为什么呢?
32 |
33 | 这里先给出几个参考链接,有兴趣的小伙伴可以自行去阅读一下:
34 |
35 | - **Swift之父Chris Lattner的说明**
36 | - 从Swift3开始不支持++、--
37 | - https://github.com/apple/swift-evolution/blob/master/proposals/0004-remove-pre-post-inc-decrement.md
38 |
39 | - **来自Stack Overflow的一个问答**
40 | - Why are there no ++ and -- operators in Python?
41 | - https://stackoverflow.com/questions/3654830
42 |
43 | - **来自Google研发总监(Director of Research)Peter Norvig的观点**
44 | - The Python IAQ: Infrequently Answered Questions
45 | - http://norvig.com/python-iaq.html
46 |
47 | 这里只列出几个显而易见的理由
48 | - 有了强大又简洁的**for-in**,**for**语句中可以完全不需要++、--
49 |
50 | ```Swift
51 | // C++
52 | for (int i = 0; i < 5; i++) {
53 | cout << i << endl;
54 | }
55 |
56 | // Swift
57 | for i in 0..<5 {
58 | println(i)
59 | }
60 |
61 | // Python
62 | for i in range(5):
63 | print(i)
64 | ```
65 |
66 | - 尽管**while (\*d++ = \*s++);**看起来似乎简单而优雅,但对于初学者来说绝非简单,会增加学习成本。而**Swift**、**Python**更倾向于希望任何人都能快速上手这门编程语言。
67 |
68 | - 当混合使用前缀和后缀的++、--时
69 | - 会降低代码的可读性,比如**while (n++ > --k)**,经验丰富的程序员也必须停下来思考一下代码的具体含义是什么
70 | - 运行结果可能会有不确定性
71 |
72 | ## 运行结果的不确定性
73 | 下面列出2段代码,变量b的结果是什么呢?(值得一提的是:实际开发中我们并不会这么写,这里把它列出来仅仅是为了讨论一些技术细节)
74 |
75 | ```c
76 | int a, b;
77 |
78 | // 第1段代码
79 | a = 1;
80 | b = a++ + ++a + a++ + ++a;
81 |
82 | // 第2段代码
83 | a = 1;
84 | b = a++ + a++ + a++ + a++;
85 | ```
86 |
87 | 实际上,上面的C语言代码在MSVC、MinGW编译器下得出的结果是不完全一致的
88 | - MSVC:微软出品
89 | - MinGW:GNU出品(可以理解为Windows版本的GCC)
90 |
91 | ### 第1段代码
92 | 结果一致,符合绝大部分人的预期,所以就不展开讨论了
93 |
94 | ```c
95 | a = 1;
96 | b = a++ + ++a + a++ + ++a;
97 | // MSVC:b = 1 + 3 + 3 + 5 = 12
98 | // MinGW:b = 1 + 3 + 3 + 5 = 12
99 | ```
100 |
101 | ### 第2段代码
102 | 结果不一致
103 | - MSVC的结果是1 + 1 + 1 + 1 = 4
104 | - MinGW的结果是1 + 2 + 3 + 4 = 10
105 |
106 | ```c
107 | a = 1;
108 | b = a++ + a++ + a++ + a++;
109 | // MSVC:b = 1 + 1 + 1 + 1 = 4
110 | // MinGW:b = 1 + 2 + 3 + 4 = 10
111 | ```
112 |
113 | 你可能好奇:你怎么知道MinGW的计算过程是1 + 2 + 3 + 4呢?根据最终结果10反推回去猜出来的么?NO!如果是这样做的话,那就有点侮辱了程序员这个职业了。
114 |
115 | 像这种不太容易从表面去理解的代码,你若想知道它的真正本质,那就要搬出强有力且精准的武器了,它就是**汇编语言(Assembly Language)**。
116 |
117 | 简单说明一下使用**汇编语言**的理由:
118 | - 众所周知,**C语言**代码最终都会被编译为**机器语言**代码(也叫做**机器指令**,只由0和1组成)
119 | - 那通过研究最终的**机器指令**来探索**C语言**代码的本质?由于**机器指令**极其晦涩难懂,因此,对一般人来说,这并不是一种高效的办法
120 | - 最佳的办法是:研究一下介于**C语言**、**机器语言**之间的**汇编语言**代码
121 | - **C语言** → **汇编语言** ↔ **机器语言**
122 | - **汇编语言**代码比**机器指令**可读性高很多
123 | - 每一条**机器指令**都有与之对应的**汇编语言**代码
124 | - 因此,你研究**汇编语言**代码,基本就等同于研究**机器指令**,可读性+精准性兼具
125 |
126 |
127 | 看看MSVC环境下的汇编代码
128 |
129 | 
130 |
131 | - 红框代码:将4个a相加的结果赋值给b,由于a的初始值是1,所以b = 1 + 1 + 1 + 1 = 4
132 | - 绿框代码:让a执行4次自增1的操作,相当于执行4次a += 1
133 |
134 |
135 | 看看MinGW环境下的汇编代码
136 |
137 | 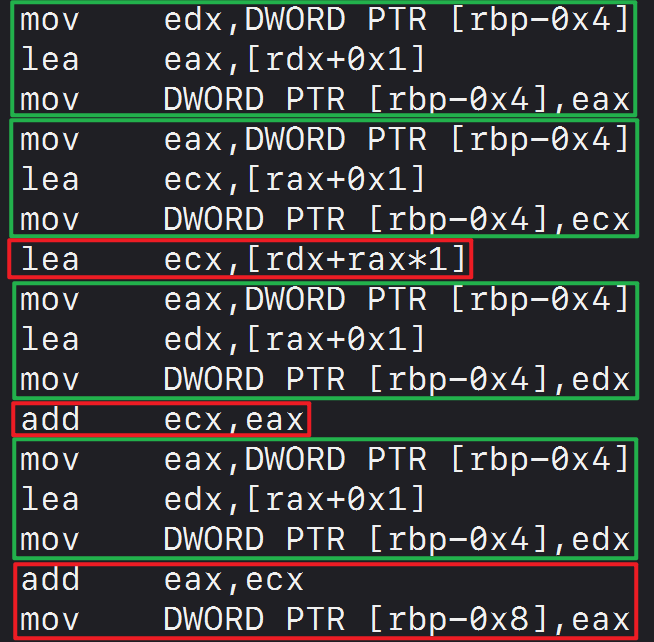
138 |
139 |
140 | - 为了保证能基本看懂这段汇编代码,建议你可以理解为[rbp-0x4]代表变量a,[rbp-0x8]代表变量b
141 | - 绿框代码:让a执行自增1的操作,相当于执行a += 1
142 | - 红框代码:将a每次自增1之前的值累加起来,最后赋值给b
143 | - 可以看到,绿框、红框代码是交替执行的,所以最终b = 1 + 2 + 3 + 4 = 10
144 |
145 |
146 |
147 |
148 | ### 最后2段代码
149 | 最后再放2段代码出来,在MSVC和MinGW下的结果也是不一致的
150 |
151 | ```c
152 | a = 1;
153 | b = ++a + ++a + ++a + ++a;
154 | // MSVC:b = 5 + 5 + 5 + 5 = 20
155 | // MinGW: b = 3 + 3 + 4 + 5 = 15
156 |
157 | a = 1;
158 | b = ++a + ++a + a++ + a++;
159 | // MSVC:b = 2 + 3 + 3 + 4 = 12
160 | // MinGW:b = 3 + 3 + 3 + 4 = 13
161 | ```
162 |
163 | 根据前面的一些讲解,相信你现在可以推断出MSVC的结果了。
164 |
165 | 但MinGW的结果可能还是会让人感觉到奇怪:它其实是先让最前面的2个**++a**执行a自增1的操作,后面的2个**++a\a++**就照常处理,所以最终b = 3 + 3 + ...
166 |
167 | 好了,就此打住,建议不要去纠结这些细节了,因为本来就不推荐这种写法。你只需要知道:多个前缀、后缀的自增自减一起使用时,结果具有不确定性。
168 |
169 | 总的来说,++、--是把双刃剑,再者,它并非是编码过程中必不可缺的,所以被**Swift**、**Python**抛弃也是正常的事。
170 |
171 | ## 关于汇编
172 | 经常看到有人说:**汇编语言**都是上古时期的编程语言了,没啥用,甚至还有人说C\C++这么古老的语言,没有任何学习价值。我个人并不赞同这些观点。掌握好汇编,可以更好地了解代码的本质,扫除一些基本的知识误区。
173 |
174 | 因为时间和篇幅的关系,这篇文章并没有详细解释每一句汇编代码的作用。如果你对汇编感兴趣,可以参考以下图片
175 |
176 | 
177 |
178 | 之前有在B站上传一些汇编教程,有需要的小伙伴可以向公众号发送汇编两字,获取教程地址
179 |
180 | ## 最后的思考题
181 | 最后留一道思考题,可以将思考的结果直接留言评论
182 |
183 | 不是说**Python**不支持自增(++)\自减(--)运算符么,为什么下面的**Python**代码能运行成功呢?
184 |
185 | ```Python
186 | a = 10
187 | b = ++a
188 |
189 | c = a++ + ++a
190 | ```
191 |
192 | 如果你特别希望我写点什么方面的内容,也可以留言建议,谢谢
193 |
194 | 欢迎关注
195 | 
--------------------------------------------------------------------------------
/003_程序员必学:快速幂算法.md:
--------------------------------------------------------------------------------
1 | 前阵子,有小伙伴在我B站的算法教程底下留言
2 | 
3 | 小伙伴们有任何疑问或者希望我讲解任何内容,都可以在我的[个人B站](https://space.bilibili.com/325538782)或公众号(xmg_mj)留言哦,我会尽我最大能力、尽量抽时间去写文章或录视频来回应大家。
4 |
5 | ## 关于快速幂
6 | 其实快速幂相关的问题,是参加算法竞赛(NOI、ACM等)的小伙伴必须要掌握的一小块基础内容。当然,就算你不打算参加算法竞赛,个人觉得只要你是一名程序员,就必须要掌握快速幂算法。
7 |
8 | 在《计算机程序设计艺术》一书中就有提到快速幂算法,此书的英文名是The Art of Computer Programming,简称TAOCP。
9 | 
10 |
11 | TAOCP出自**Donald Ervin Knuth**前辈之手。Knuth前辈是在计算机领域成就颇丰的知名科学家,是著名的KMP算法的发明人之一,在1974年获得“计算机领域的诺贝尔奖”:图灵奖(当年他才36岁)。目前TAOCP已经出版了第1、2、3、4A卷,按照计划,还有第4B、5、6、7卷未出版。第一卷首发于1968年,Knuth前辈今年是82岁高寿,据说他计划在105岁之前完成这部巨著。
12 |
13 | 
14 |
15 | 关于TAOCP,微软创始人Bill Gates曾说过
16 | > If you think you're a really good programmer… read (Knuth's) Art of Computer Programming… You should definitely send me a resume if you can read the whole thing.
17 |
18 | 大概意思是:如果你认为自己是一位非常优秀的程序员,那就应该阅读Knuth的TAOCP;如果你能读懂全部内容,可以直接给我发送一份简历。据说Knuth前辈的言辞更加犀利:看不懂就别当程序员了!不过TAOCP对于新手来说,阅读难度的确比较大,书中的所有示例都使用了Knuth前辈自创的**MIX汇编语言**。
19 |
20 | ## 阅读本文之前的提醒
21 | 今天就抽空写一篇文章来讲解一下经典的快速幂算法哈。不过要想彻底看懂本文,有几个前提条件
22 | - 熟悉算法中的2个基础概念:时间复杂度、空间复杂度
23 | - 如果你压根没听过这2个概念,说明你的算法基础**完全**为0,真的没有在开玩笑!
24 | - 可以向公众号发送**复杂度**获取相关教程
25 | - 熟悉二进制和十进制的转换
26 | - 如果连这个都不熟悉的话,那你的编程底子就真的需要好好补补啦
27 | - 可以向公众号发送**进制**获取相关教程
28 | - 熟悉常见的位运算操作
29 | - n & 1的结果是n最低二进制位的值,也可以用于判断n的奇偶性
30 | - 求正整数n / 2,可以用位运算取代:n >> 1
31 | - 如果不明白上述操作的原理,可以向公众号发送**位运算**获取相关教程
32 |
33 | ## 什么是幂(Power)?
34 | 众所周知,x的n次幂,是指x的n次方,也就是n个x相乘,比如2的4次幂就是2 \* 2 \* 2 \* 2。
35 |
36 | 为了简化描述,后面x的n次幂,我就简化为x ^ n(本文中的 ^ 并不是按位异或的意思)
37 |
38 | 那如何通过编程求幂?假设**只考虑x、n是整数且n大于等于0**的情况,最容易想到的方法如下所示(这里采用的编程语言是Java,但没有涉及Java特殊的语法。所以就算你没用过Java,也可以看懂)
39 | ```java
40 | int power(int x, int n) {
41 | int result = 1;
42 | while (n-- > 0) {
43 | result *= x;
44 | }
45 | return result;
46 | }
47 | ```
48 | 很显然,这种方法的时间复杂度是**O(n)**、空间复杂度是**O(1)**
49 |
50 | ## 什么是快速幂?
51 | 所谓快速幂,就是用效率更高(时间复杂度更低)的方法求幂,可以将时间复杂度优化至**O(logn)**。这里介绍2种求解方法:递归、非递归
52 | ### 递归
53 |
54 | 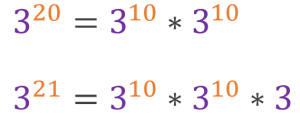
55 |
56 | 根据上图中的等式,不难写出以下代码
57 | ```java
58 | int fastPower(int x, int n) {
59 | if (n == 0) return 1;
60 | int result = fastPower(x, n >> 1);
61 | result *= result;
62 | return (n & 1) == 0 ? result : result * x;
63 | }
64 | ```
65 | 这个方法的时间、空间复杂度都是**O(logn)**。
66 |
67 | 那如何分析出这个方法的复杂度呢?
68 |
69 | 如果你的算法功底比较薄弱,可以代入特定值作一个大概的分析,比如当n为16时,方法的递归调用过程如下图所示
70 | 
71 |
72 |
73 | 不难看出,每次调用时,n的规模都减半,所以时间和空间复杂度都是**O(logn)**
74 |
75 | 如果你的算法功底还行,那就可以用更专业的方法去分析它的复杂度(没有一定的算法基础,可能会看不懂)
76 | - 这其实是典型的应用分治策略的算法
77 | - 假设T(n)是数据规模为n时的时间复杂度,不难得出递推式:**T(n) = T(n / 2) + O(1)**
78 | - 最后通过**主定理**(Master Theorem)可以直接得出结论:**T(n) = O(logn)**
79 |
80 | ### 非递归
81 | 我们以求3 ^ 21为例子,来分析一下非递归的代码应该怎么写。
82 |
83 | 首先21的二进制形式是10101
84 | 
85 |
86 | 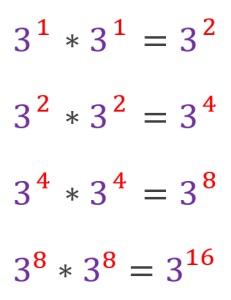
87 |
88 | 不难得出以下结论
89 | - 3 ^ n(n为2、4、8、16)都可以由3 ^ 1累乘出来
90 | - 每一个3 ^ n都有对应的二进制位
91 | - 3 ^ 1对应二进制位的值是1,其实是二进制**10101**的最后1位
92 | - 3 ^ 2对应二进制位的值是0,其实是二进制**1010**的最后1位
93 | - 3 ^ 4对应二进制位的值是1,其实是二进制**101**的最后1位
94 | - 3 ^ 8对应二进制位的值是0,其实是二进制**10**的最后1位
95 | - 3 ^ 16对应二进制位的值是1,其实是二进制**1**的最后1位
96 | - 如果3 ^ n对应二进制位的值是**0**,就不用乘进最终结果
97 | - 比如3 ^ (8 * **0**)、3 ^ (2 * **0**)
98 | - 因为它们最终的值都是3 ^ 0,也就是1
99 | - 如果3 ^ n对应二进制位的值是**1**,就需要乘进最终结果
100 | - 比如3 ^ (16 * **1**)、3 ^ (4 * **1**)、3 ^ (1 * **1**)
101 |
102 | 所以,综合以上种种结论,可以总结出以下解题步骤
103 | - 利用3 ^ 1,不断累乘出3 ^ n(n为2、4、8、16)
104 | - 每当累乘出一个3 ^ n,就查看其对应二进制位的值是1还是0,来决定是否要将它乘进最终结果
105 | ```java
106 | int fastPower(int x, int n) {
107 | int result = 1;
108 | while (n != 0) {
109 | if ((n & 1) == 1) {
110 | result *= x;
111 | }
112 | x *= x;
113 | n >>= 1;
114 | }
115 | return result;
116 | }
117 | ```
118 | 代入3和21,fastPower(3, 21)的执行流程如下
119 | #### 第1轮while循环
120 | - 第4行代码
121 | - n的二进制是10101(十进制是21)
122 | - x = 3 ^ 1, 其对应二进制位的值是1(n的最后一个二进制位)
123 | - 所以**需要**执行第5行代码:将x乘进最终结果
124 | - result = 3 ^ 1
125 | - 第7行代码
126 | - x = (3 ^ 1) * (3 ^ 1) = 3 ^ 2
127 | - 第8行代码
128 | - n右移1位,其二进制变成了1010(对应的十进制是啥?不重要!!!)
129 |
130 | #### 第2轮while循环
131 | - 第4行代码
132 | - n的二进制是1010
133 | - x = 3 ^ 2, 其对应二进制位的值是0(n的最后一个二进制位)
134 | - 所以**不需要**执行第5行代码:不需要将x乘进最终结果
135 | - result = 3 ^ 1
136 | - 第7行代码
137 | - x = (3 ^ 2) * (3 ^ 2) = 3 ^ 4
138 | - 第8行代码
139 | - n右移1位,其二进制变成了101(对应的十进制是啥?不重要!!!)
140 |
141 | #### 第3轮while循环
142 | - 第4行代码
143 | - n的二进制是101
144 | - x = 3 ^ 4, 其对应二进制位的值是1(n的最后一个二进制位)
145 | - 所以**需要**执行第5行代码:将x乘进最终结果
146 | - result = (3 ^ 1) * (3 ^ 4)
147 | - 第7行代码
148 | - x = (3 ^ 4) * (3 ^ 4) = (3 ^ 8)
149 | - 第8行代码
150 | - n右移1位,其二进制变成了10(对应的十进制是啥?不重要!!!)
151 |
152 | #### 第4轮while循环
153 | - 第4行代码
154 | - n的二进制是10
155 | - x = 3 ^ 8, 其对应二进制位的值是0(n的最后一个二进制位)
156 | - 所以**不需要**执行第5行代码:不需要将x乘进最终结果
157 | - result = (3 ^ 1) * (3 ^ 4)
158 | - 第7行代码
159 | - x = (3 ^ 8) * (3 ^ 8) = 3 ^ 16
160 | - 第8行代码
161 | - n右移1位,其二进制变成了1(对应的十进制是啥?不重要!!!)
162 |
163 | #### 第5轮while循环
164 | - 第4行代码
165 | - n的二进制是1
166 | - x = 3 ^ 16, 其对应二进制位的值是1(n的最后一个二进制位)
167 | - 所以**需要**执行第5行代码:将x乘进最终结果
168 | - result = (3 ^ 1) * (3 ^ 4) * (3 ^ 16)
169 | - 第7行代码
170 | - x = (3 ^ 16) * (3 ^ 16) = 3 ^ 32
171 | - 第8行代码
172 | - n右移1位,其二进制变成了0
173 |
174 | #### 最后
175 | - 由于n = 0,所以退出while循环
176 | - 最终result = (3 ^ 1) * (3 ^ 4) * (3 ^ 16)
177 | - 复杂度分析
178 | - 每执行一次while的循环体,n >>= 1, 会导致n的值减半
179 | - 所以时间复杂度:**O(logn)**、空间复杂度:**O(1)**
180 |
181 | ## Leetcode
182 | Leetcode上的第50号题[50. Pow(x, n)](https://leetcode-cn.com/problems/powx-n/),刚好就可以用今天讲解的快速幂算法。以下是我的代码实现
183 | ```java
184 | // 递归
185 | double myPow(double x, int n) {
186 | if (n == 0) return 1;
187 | if (n == -1) return 1 / x;
188 | double half = myPow(x, n >> 1);
189 | half *= half;
190 | return ((n & 1) == 1) ? half * x : half;
191 | }
192 |
193 | // 非递归
194 | double myPow(double x, int n) {
195 | long y = (n < 0) ? -((long) n) : n;
196 | double result = 1.0;
197 | while (y > 0) {
198 | if ((y & 1) == 1) {
199 | result *= x;
200 | }
201 | x *= x;
202 | y >>= 1;
203 | }
204 | return (n < 0) ? (1 / result) : result;
205 | }
206 | ```
207 | 需要提醒的是
208 | - 这里我用的编程语言是Java,大家可以根据自己熟悉的编程语言,对一些语法细节作出相应的调整
209 | - Leetcode上的n可能是个负数,所以上面的代码针对负数的情况作了一些处理
210 |
211 | ## 更多快速幂相关的问题
212 | 时间有限,这篇文章就先说到这了哈。给小伙伴们留2个快速幂相关的问题,有空的话,可以去研究一下
213 | - 使用矩阵快速幂求斐波那契数列
214 | - 请设计一个算法求x的y次幂模z的结果:(x ^ y) % z
215 | - 假设x、y都可能是很大的整数(y大于等于0,z不等于0)
216 |
217 | 如果你特别希望我写点什么方面的内容,也可以留言建议,谢谢。欢迎关注
218 | 
--------------------------------------------------------------------------------
/001_如何直观形象地树状打印一棵二叉树?.md:
--------------------------------------------------------------------------------
1 | > 网上绝大部分的二叉树打印效果都十分潦草,也不够直观形象,最近自己用JS写了个图形化小工具`BinaryTreeGraph`,也用Java写了个打印器`BinaryTreePrinter`,还有个Objective-C版本`BinaryTreePrinterOC`
2 | > 具体代码实现请看[github](https://github.com/CoderMJLee/BinaryTrees)
3 | ## BinaryTreeGraph(JS版)
4 | - 在线演示:[BinaryTreeGraph](http://520it.com/binarytrees/)
5 |
6 | 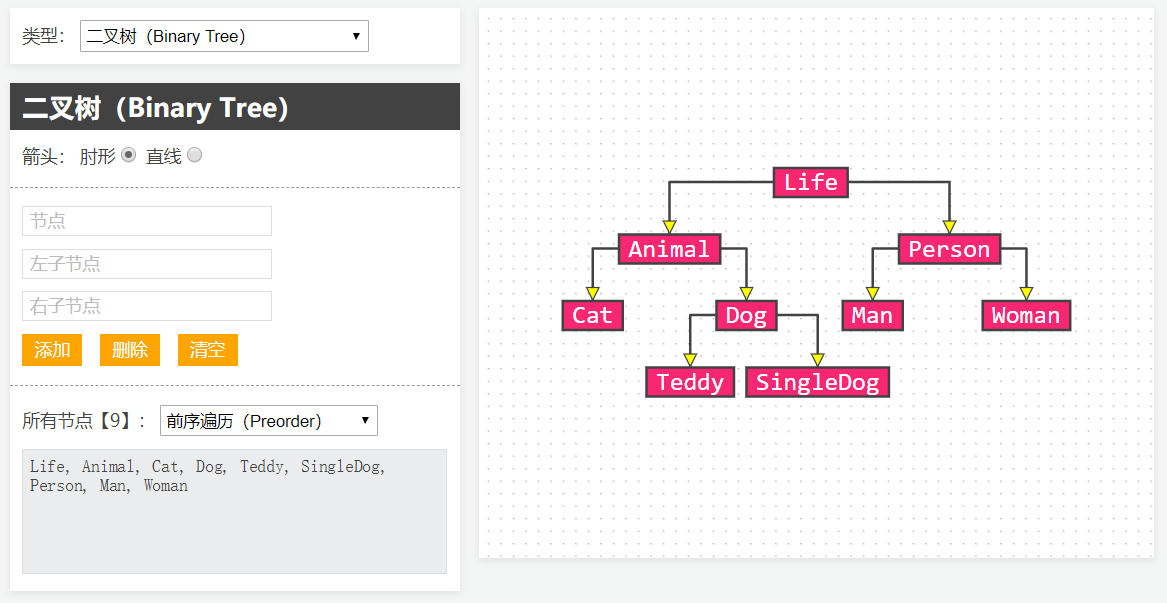
7 |
8 | 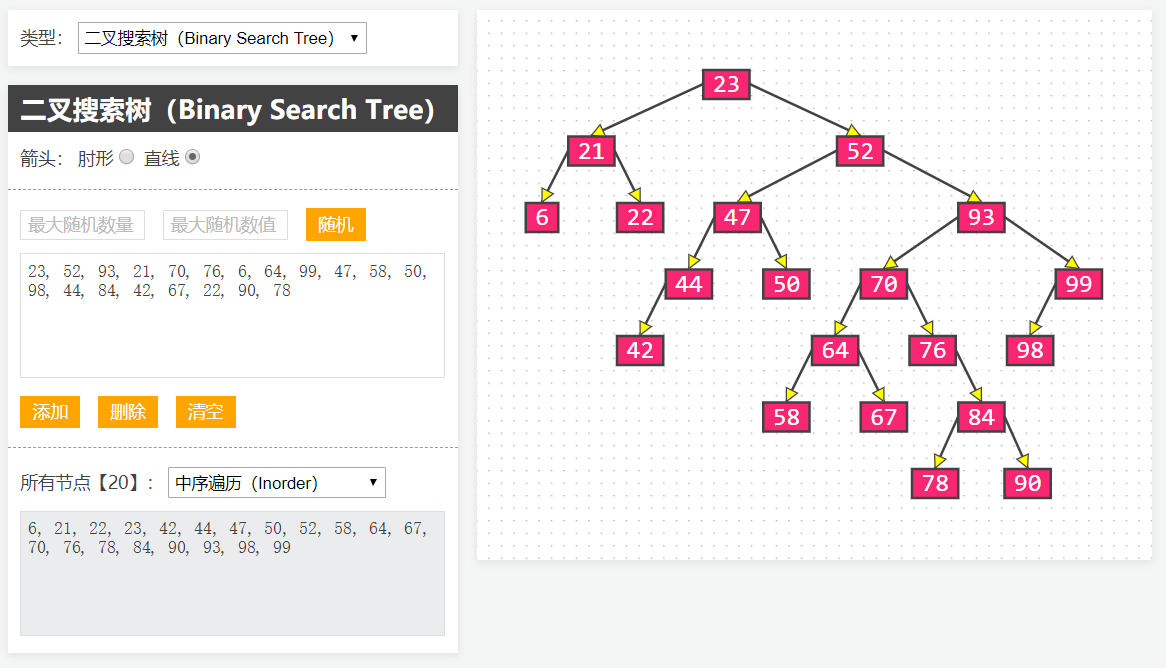
9 |
10 | 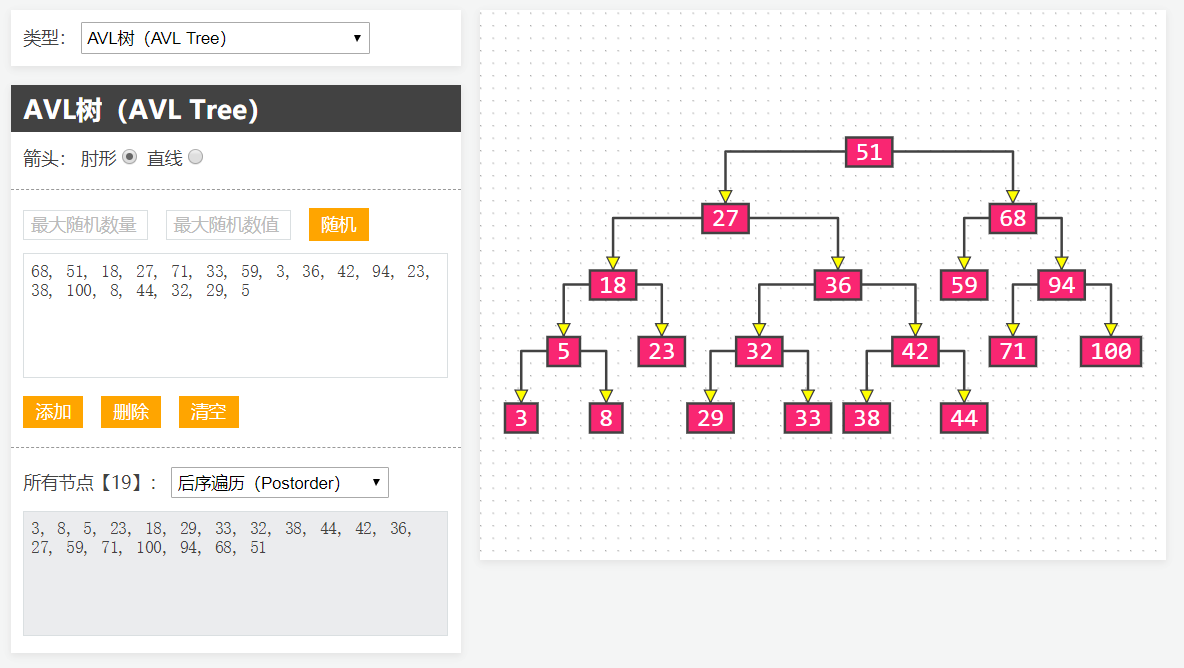
11 |
12 | 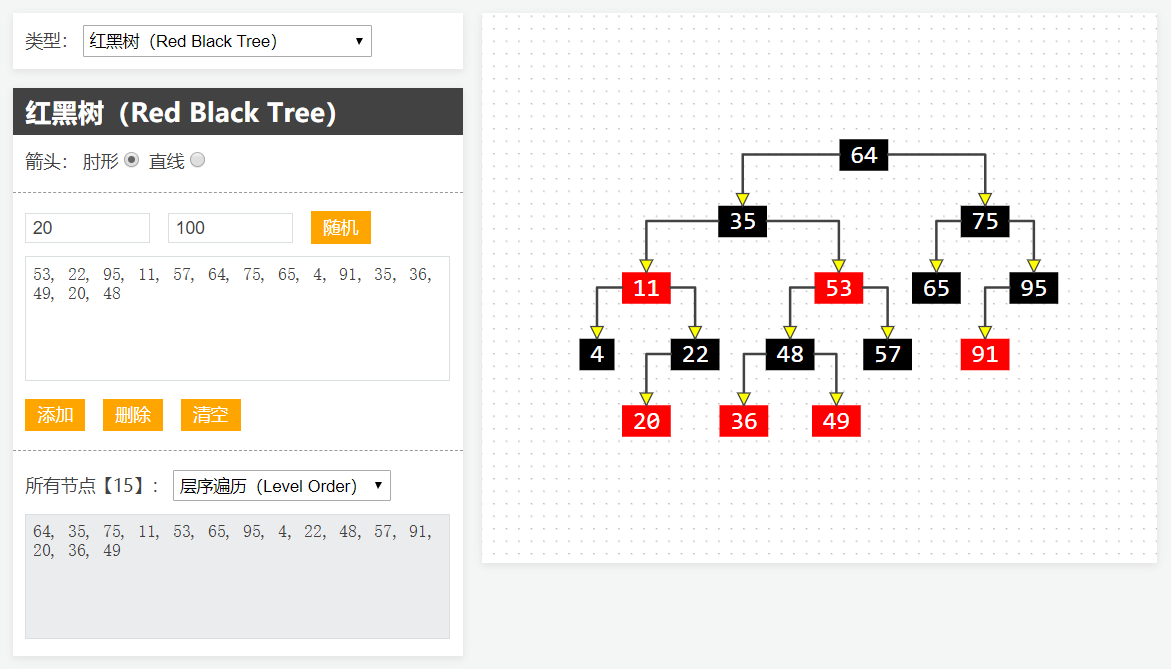
13 |
14 | 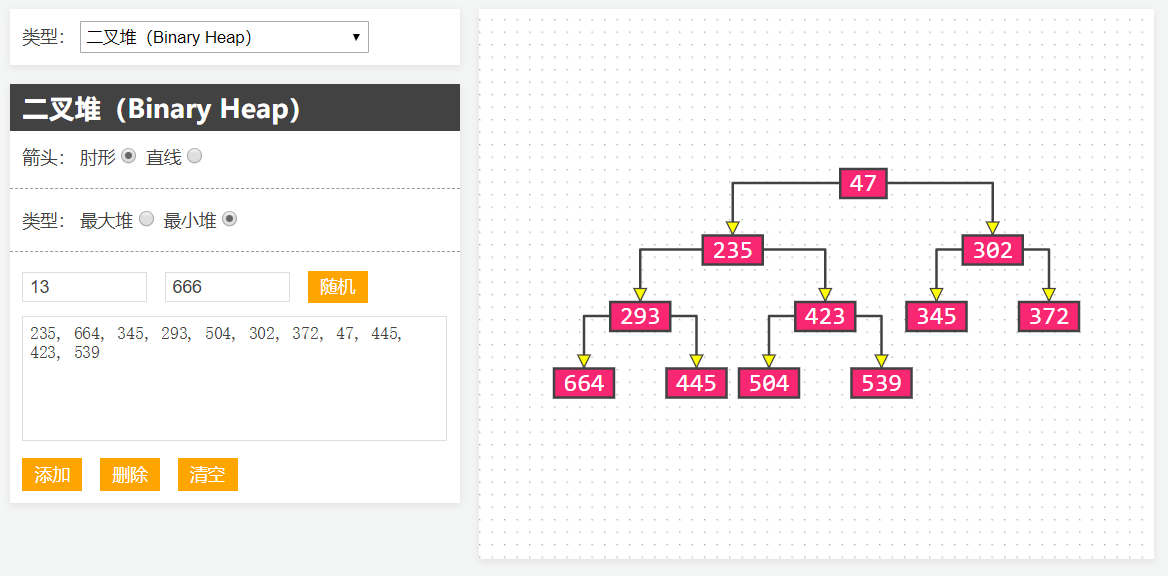
15 |
16 | ## BinaryTreePrinter(Java版)
17 | ### 简介
18 | - 树状打印一棵二叉树
19 | - 比如输入一棵二叉搜索树
20 | - [381, 12, 410, 9, 40, 394, 540, 35, 190, 476, 760, 146, 445, 600, 800]
21 | - 就会输出
22 |
23 | 
24 |
25 | - 或者输出
26 |
27 | 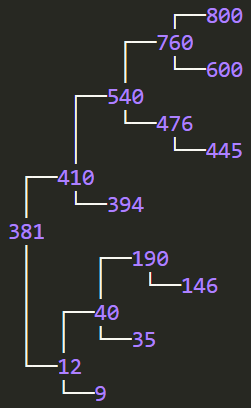
28 |
29 | ### 核心API
30 | ```java
31 | public final class BinaryTrees {
32 | // 打印一棵二叉树
33 | public static void print(BinaryTreeInfo tree);
34 | public static void print(BinaryTreeInfo tree, PrintStyle style);
35 |
36 | // 打印一棵二叉树(打印完自动换行)
37 | public static void println(BinaryTreeInfo tree);
38 | public static void println(BinaryTreeInfo tree, PrintStyle style);
39 |
40 | // 获得一棵二叉树的打印字符串
41 | public static String printString(BinaryTreeInfo tree);
42 | public static String printString(BinaryTreeInfo tree, PrintStyle style);
43 |
44 | // 可选的打印样式
45 | public enum PrintStyle {
46 | LEVEL_ORDER,
47 | INORDER
48 | }
49 | }
50 | ```
51 |
52 | ### 示例
53 | #### 实现BinaryTreeInfo
54 | - 根节点是谁?
55 | - 如何查找左节点?
56 | - 如何查找右节点?
57 | - 如何打印单个节点?
58 |
59 | ```java
60 | /**
61 | * BinarySearchTree是你自己编写的二叉树类
62 | */
63 | public class BinarySearchTree implements BinaryTreeInfo {
64 | /**这里省略了大量代码,只贴出了脉络代码**/
65 |
66 | private Node root;
67 | private static class Node {
68 | E element;
69 | Node left;
70 | Node right;
71 | }
72 |
73 | /********** BinaryTreeInfo **********/
74 | @Override
75 | public Object root() {
76 | // 根节点是谁?
77 | return root;
78 | }
79 |
80 | @Override
81 | public Object left(Object node) {
82 | // 如何查找左节点?
83 | return ((Node)node).left;
84 | }
85 |
86 | @Override
87 | public Object right(Object node) {
88 | // 如何查找右节点?
89 | return ((Node)node).right;
90 | }
91 |
92 | @Override
93 | public Object string(Object node) {
94 | // 如何打印单个节点?
95 | return ((Node)node).element;
96 | }
97 | /********** BinaryTreeInfo **********/
98 | }
99 | ```
100 |
101 | #### 打印
102 | ```java
103 | // 随机生成的一棵二叉搜索树(random generation)
104 | BinarySearchTree bst = ...;
105 |
106 | // PrintStyle.LEVEL_ORDER(层序打印)
107 | BinaryTrees.println(bst);
108 |
109 | // PrintStyle.INORDER(中序打印)
110 | BinaryTrees.println(bst, PrintStyle.INORDER);
111 | ```
112 |
113 | 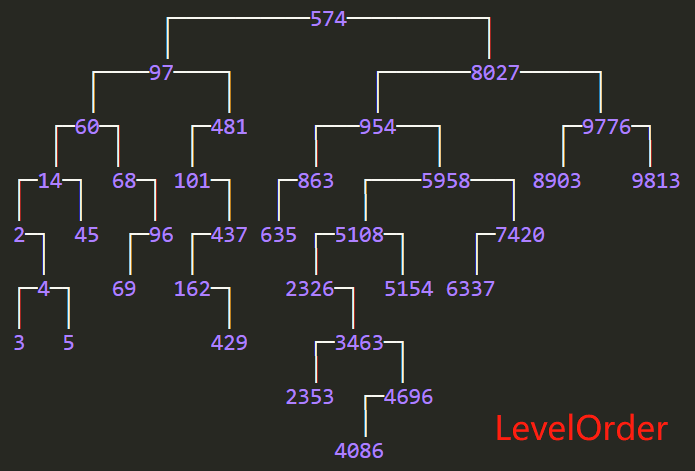
114 |
115 | 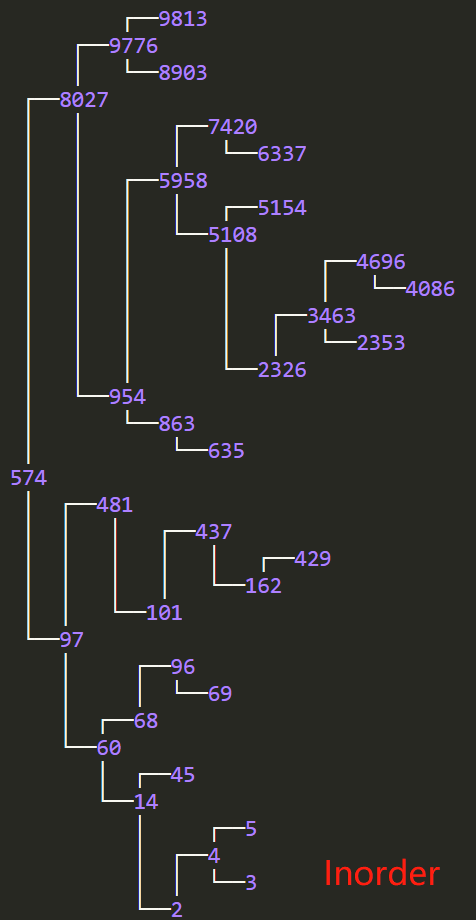
116 |
117 | #### 生成字符串写入文件
118 | ```java
119 | Files.writeToFile("F:/test/bst.txt", BinaryTrees.printString(bst));
120 | ```
121 |
122 | #### 不需要定义二叉树类
123 | ```java
124 | BinaryTrees.println(new BinaryTreeInfo() {
125 | @Override
126 | public Object root() {
127 | return 8;
128 | }
129 |
130 | @Override
131 | public Object left(Object node) {
132 | if (node.equals(8)) return 3;
133 | if (node.equals(3)) return 1;
134 | if (node.equals(6)) return 4;
135 | if (node.equals(14)) return 13;
136 | return null;
137 | }
138 |
139 | @Override
140 | public Object right(Object node) {
141 | if (node.equals(8)) return 10;
142 | if (node.equals(10)) return 14;
143 | if (node.equals(3)) return 6;
144 | if (node.equals(6)) return 7;
145 | return null;
146 | }
147 |
148 | @Override
149 | public Object string(Object node) {
150 | return node;
151 | }
152 | });
153 |
154 | BinaryTrees.println(new BinaryTreeInfo() {
155 | @Override
156 | public Object root() {
157 | return "Life";
158 | }
159 |
160 | @Override
161 | public Object left(Object node) {
162 | if (node.equals("Life")) return "Animal";
163 | if (node.equals("Person")) return "Man";
164 | if (node.equals("Animal")) return "Cat";
165 | if (node.equals("Dog")) return "Teddy";
166 | return null;
167 | }
168 |
169 | @Override
170 | public Object right(Object node) {
171 | if (node.equals("Life")) return "Person";
172 | if (node.equals("Person")) return "Woman";
173 | if (node.equals("Animal")) return "Dog";
174 | if (node.equals("Dog")) return "SingleDog";
175 | return null;
176 | }
177 |
178 | @Override
179 | public Object string(Object node) {
180 | return node;
181 | }
182 | });
183 | ```
184 |
185 | 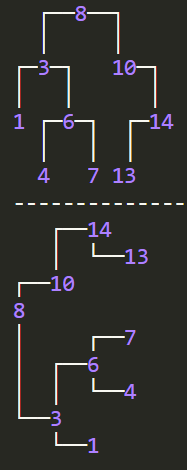
186 |
187 | 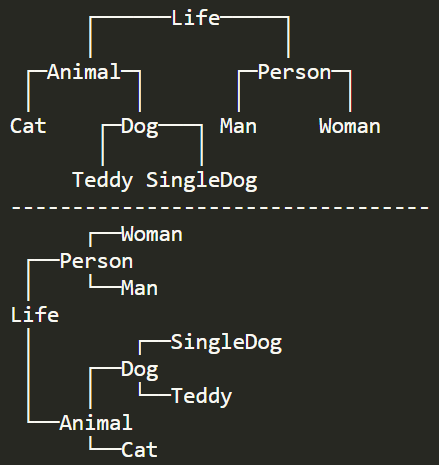
188 |
189 | #### 二叉堆
190 | ```java
191 | public class BinaryHeap implements BinaryTreeInfo {
192 | private int size;
193 | private E[] elements;
194 |
195 | @Override
196 | public Object root() {
197 | return 0;
198 | }
199 |
200 | @Override
201 | public Object left(Object node) {
202 | int index = ((int)node << 1) + 1;
203 | return index >= size ? null : index;
204 | }
205 |
206 | @Override
207 | public Object right(Object node) {
208 | int index = ((int)node << 1) + 2;
209 | return index >= size ? null : index;
210 | }
211 |
212 | @Override
213 | public Object string(Object node) {
214 | return elements[(int)node];
215 | }
216 | }
217 |
218 | BinaryHeap heap = new BinaryHeap<>();
219 | for (int i = 0; i < 10; i++) {
220 | heap.add((int)(Math.random() * 100));
221 | }
222 | BinaryTrees.println(heap);
223 | ```
224 | 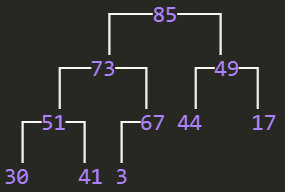
225 | ## BinaryTreePrinterOC
226 | - 实现`MJBinaryTreeInfo`协议
227 |
228 | ```objc
229 | @interface MJBSTNode : NSObject {
230 | @public
231 | id _element;
232 | MJBSTNode *_left;
233 | MJBSTNode *_right;
234 | }
235 | @end
236 |
237 | @interface MJBinarySearchTree : NSObject
238 | @end
239 |
240 | @interface MJBinarySearchTree() {
241 | MJBSTNode *_root;
242 | }
243 | @end
244 |
245 | @implementation MJBinarySearchTree
246 | #pragma mark - MJBinaryTreeInfo
247 | - (id)left:(MJBSTNode *)node {
248 | return node->_left;
249 | }
250 |
251 | - (id)right:(MJBSTNode *)node {
252 | return node->_right;
253 | }
254 |
255 | - (id)string:(MJBSTNode *)node {
256 | return node->_element;
257 | }
258 |
259 | - (id)root {
260 | return _root;
261 | }
262 | @end
263 | ```
264 |
265 | - 打印
266 |
267 | ```objc
268 | [MJBinaryTrees println:bst];
269 |
270 | [MJBinaryTrees println:bst style:MJPrintStyleLevelOrder];
271 |
272 | [MJBinaryTrees println:bst style:MJPrintStyleInorder];
273 |
274 | NSString *str = [MJBinaryTrees printString:bst];
275 | NSString *file = @"/Users/mj/Desktop/1.txt";
276 | [str writeToFile:file atomically:YES encoding:NSUTF8StringEncoding error:nil];
277 | ```
--------------------------------------------------------------------------------