52 |
53 | **测试阶段:测试阶段可能不是分batch测试的,并且在模型推断时常常只输入一个样本,那么就不能再计算测试阶段的batch的均值和方差,这就需要用到训练集的数据。训练时计算的均值和方差会不断累积下来,通过移动平均的方法来近似得到整个样本集的均值和方差。**
54 |
55 |
56 |

58 |
59 |
60 |
61 |
62 |
63 | ## 4.求导:
64 |
65 |
66 |

67 |
68 |
69 |
--------------------------------------------------------------------------------
/优化篇/优化器-scr.md:
--------------------------------------------------------------------------------
1 | # 优化器
2 |
3 | ## 概述:
4 |
5 | **优化器在DL中起着灯塔的作用,指引参数往正确的方向更新,一个好的优化器能够使模型收敛速度加快,跳出局部最优,训练过程平稳等**
6 |
7 |
8 |
9 | ## 定义:
10 |
11 | $$
12 | \Large 1.待优化参数:w\\
13 | \Large 2.迭代次数: t\\
14 | \Large 3.一阶动量:m _ { t } = \phi ( g _ { 1 } , g _ { 2 } , \cdots , g _ { t } )\\
15 | \Large 4.二阶动量:V _ { t } = \psi ( g _ { 1 } , g _ { 2 } , \cdots , g _ { t } )\\
16 | \Large 5.当前时刻下降梯度: \Delta w_{t}= -\alpha \cdot m_{t}/ \sqrt{V_{t}} \\
17 | \Large 6.根据下降梯度参数进行更新: w_{t+1}=w_{t} + \Delta w_{t}
18 | $$
19 |
20 |
21 |
22 | ## SGD
23 |
24 | $$
25 | \Large SGD算法没有动量的概率,一阶动量m_{t} = g_{t};二阶动量V_{t} = I^2;\\
26 | \Large \Delta w_{t} = -\alpha * g_{t}\\
27 | \Large w_{t+1} = w_{t} + \Delta w_{t}
28 | $$
29 |
30 |
31 |
32 | #### 优点:
33 |
34 | - **SGD法由于每次仅仅采用mini-batch来迭代,计算速度很快。**
35 |
36 | #### 缺点:
37 |
38 | - **下降速度慢,训练容易震荡**
39 | - **可能陷入局部最优点**
40 |
41 |
42 |
43 | # SGDM:SGD with Nesterov Moment
44 |
45 | **为了抑制SGD的震荡,SGDM认为梯度下降过程可以加入惯性即历史时刻的梯度信息。**
46 | $$
47 | \Large m_{t} = \beta_{1} * m_{t-1} + (1-\beta_{1}) * g_{t}\\
48 | \Large \Delta w_{t} = -\alpha*m_{t}\\
49 | \Large w_{t+1} = w_{t} + \Delta w_{t}\\
50 | \Large 例如:\\
51 | \Large m_{1} = \beta_{0}*m_{0}+(1-\beta_{1})*g_{1},m_{0}=0\\
52 | \Large m_{1} = (1-\beta_{1})*g_{1}\\
53 | \Large m_2 = \beta_{1}*m_{1}+(1-\beta_{1})*g_{1}=\beta_{1}*((1-\beta_{1})*g_{1}) + (1-\beta_{1})*g_{2}\\
54 | \Large m_3 = \beta_{1}*m_{2}+(1-\beta_{1})*g_{3} = \beta_{1}*(\beta_{1}*((1-\beta_{1})*g_{1}) + (1-\beta_{1})*g_{2})+(1-\beta_{1})*g_{3}\\
55 | \Large 从上式可以看出离当前时刻越远的惯性,它对当前时刻的m_{t}影响呈指数衰减。只有越近时刻的惯性对当前时刻的m_{t}影响越大。
56 | $$
57 |
58 | #### 优点:
59 |
60 | - **动量的存在使得 SGD 算法在训练的过程中更加的稳定。**
61 |
62 | #### 缺点:
63 |
64 | - **没有解决SGD容易陷入局部最优的问题**
65 |
66 |
67 |
68 | # NAG:SGD with Nesterov Acceleration
69 |
70 | **SGD 还有一个问题是困在局部最优的沟壑里面震荡。想象一下你走到一个盆地,四周都是略高的小山,你觉得没有下坡的方向,那就只能待在这里了。可是如果你爬上高地,就会发现外面的世界还很广阔。因此,我们不能停留在当前位置去观察未来的方向,而要向前一步、多看一步、看远一些。 NAG全称Nesterov Accelerated Gradient,是在SGD、SGD-M的基础上的进一步改进,改进点在于定义1。我们知道在时刻t的主要下降方向是由累积动量决定的,自己的梯度方向说了也不算,那与其看当前梯度方向,不如先看看如果跟着累积动量走了一步,那个时候再怎么走。因此,NAG在步骤1,不计算当前位置的梯度方向,而是计算如果按照累积动量走了一步,那个时候的下降方向:**
71 | $$
72 | \Large g_{t}= \nabla f( \omega _{t}- \alpha \cdot m_{t-1}) \\
73 | \Large m_{t} = \beta_{1} * m_{t-1} + (1-\beta_{1}) * g_{t}\\
74 | \Large \Delta w_{t} = -\alpha*m_{t}\\
75 | \Large w_{t+1} = w_{t} + \Delta w_{t}
76 | $$
77 |
78 | #### 优点:
79 |
80 | - **收敛快**
81 | - **在一定程度上解决了陷入局部最优的问题**
82 |
83 | #### 缺点:
84 |
85 | - **学习率未自适应**
86 |
87 |
88 |
89 | # AdaGrad
90 |
91 | **此前我们都没有用到二阶动量。二阶动量的出现,才意味着“自适应学习率”优化算法时代的到来。SGD及其变种以同样的学习率更新每个参数,但深度神经网络往往包含大量的参数,这些参数并不是总会用得到。对于经常更新的参数,我们已经积累了大量关于它的知识,不希望被单个样本影响太大,希望学习速率慢一些;对于偶尔更新的参数,我们了解的信息太少,希望能从每个偶然出现的样本身上多学一些,即学习速率大一些。**
92 | $$
93 | \Large 二阶动量就是迄今为止该维度上所有梯度的和 \\
94 | \Large V_{t}= \sum _{ \tau =1}^{t}g_{ \tau }^{2} \\
95 | \Large m_{t} = g_{t} (这时还没用到一阶动量)\\
96 | \Large \Delta w_{t} = -\alpha*m_{t} / \sqrt{V_{t}} \\
97 | \Large w_{t+1} = w_{t} + \Delta w_{t}\\
98 | \Large 从上式可以看出实际上学习率\alpha变成了\alpha / \sqrt{V_{t}},\\
99 | \Large 一般为了避免分母为0,会在分母上加一个小的平滑项。
100 | \Large 所以参数更新的越频繁\Large \sqrt{V_{t}}就越大,\Delta w_{t}就变化越小。
101 | $$
102 |
103 | #### 优点:
104 |
105 | - **引入二阶动量可以对不同参数进行不同速度的改变,达到自适应学习率的目的**
106 |
107 | #### 缺点:
108 |
109 | - **由于二阶动量是单调递增的,所以会使得学习率单调递减至0,可能会使得训练过程提前结束,即便后续还有数据也无法学到必要的知识。**
110 |
111 |
112 |
113 | # AdaDelta / RMSProp
114 |
115 | **由于AdaGrad单调递减的学习率变化过于激进,我们考虑一个改变二阶动量计算方法的策略:不累积全部历史梯度,而只关注过去一段时间窗口的下降梯度。这也就是AdaDelta名称中Delta的来历。修改的思路很简单。前面我们讲到,指数移动平均值大约就是过去一段时间的平均值,因此我们用这一方法来计算二阶累积动量:**
116 | $$
117 | \Large V_{t}= \beta _{2}*V_{t-1}+(1- \beta _{2})g_{t}^{2} \\
118 | \Large m_{t} = g_{t} (这时还没用到一阶动量)\\
119 | \Large \Delta w_{t} = -\alpha*m_{t} / \sqrt{V_{t}} \\
120 | \Large w_{t+1} = w_{t} + \Delta w_{t}\\
121 | $$
122 |
123 | #### 优点:
124 |
125 | - **使用加权平均使得学习率不会单调递减至0,可以加快收敛速度。**
126 |
127 |
128 |
129 | # Adam
130 |
131 | **Adam和Nadam的出现就很自然而然了——它们是前述方法的集大成者。我们看到,SGD-M在SGD基础上增加了一阶动量,AdaGrad和AdaDelta在SGD基础上增加了二阶动量。把一阶动量和二阶动量都用起来,就是Adam了——Adaptive + Momentum。**
132 | $$
133 | \Large m_{t}= \beta _{1} \cdot m_{t-1}+(1- \beta _{1}) \cdot g_{t} \\
134 |
135 | \Large V _ { t } = \beta _ { 2 } * V _ { t - 1 } + ( 1 - \beta _ { 2 } ) g _ { t } ^ { 2 } \\
136 |
137 | \Large \Delta w_{t} = -\alpha*m_{t} / \sqrt{V_{t}} \\
138 |
139 | \Large w_{t+1} = w_{t} + \Delta w_{t}\\
140 |
141 | \Large \beta_{1}一般取0.9,\beta_{2}一般取0.999初始化的时候m_{0} = 0,V_{0}=0,所以在训练初期m_{t},V_{t}都会接近0,因此我们常常\\
142 | \Large 根据下式进行误差修正:\tilde { m } _ { t } = m _ { t } / ( 1 - \beta _ { 1 } ^ { t } )tilde{V}_{t}=V_{t}/(1- \beta _{2}^{t})
143 | $$
144 |
145 |
146 | # Nadam
147 |
148 | **Adam是集大成者,但它居然遗漏了Nesterov, Nadam就是加上了Nesterov按照NAG的步骤1:**
149 | $$
150 | \Large g _ { t } = \nabla f ( w _ { t } - \alpha \cdot m _ { t - 1 } / \sqrt { V _ { t } } )\\
151 | \Large m_{t}= \beta _{1} \cdot m_{t-1}+(1- \beta _{1}) \cdot g_{t} \\
152 |
153 | \Large V _ { t } = \beta _ { 2 } * V _ { t - 1 } + ( 1 - \beta _ { 2 } ) g _ { t } ^ { 2 } \\
154 |
155 | \Large \Delta w_{t} = -\alpha*m_{t} / \sqrt{V_{t}} \\
156 |
157 | \Large w_{t+1} = w_{t} + \Delta w_{t}\\
158 | $$
--------------------------------------------------------------------------------
/优化篇/优化器.md:
--------------------------------------------------------------------------------
1 | # 优化器
2 |
3 | ## 概述:
4 |
5 | **优化器在DL中起着灯塔的作用,指引参数往正确的方向更新,一个好的优化器能够使模型收敛速度加快,跳出局部最优,训练过程平稳等**
6 |
7 |
8 |
9 | ## 定义:
10 |
11 |
12 |

13 |
14 |
15 |
16 |
17 | ## SGD
18 |
19 |
20 |

21 |
22 |
23 |
24 |
25 | #### 优点:
26 |
27 | - **SGD法由于每次仅仅采用mini-batch来迭代,计算速度很快。**
28 |
29 | #### 缺点:
30 |
31 | - **下降速度慢,训练容易震荡**
32 | - **可能陷入局部最优点**
33 |
34 |
35 |
36 | # SGDM:SGD with Nesterov Moment
37 |
38 | **为了抑制SGD的震荡,SGDM认为梯度下降过程可以加入惯性即历史时刻的梯度信息。**
39 |
40 |
41 |

42 |
43 |
44 | #### 优点:
45 |
46 | - **动量的存在使得 SGD 算法在训练的过程中更加的稳定。**
47 |
48 | #### 缺点:
49 |
50 | - **没有解决SGD容易陷入局部最优的问题**
51 |
52 |
53 |
54 | # NAG:SGD with Nesterov Acceleration
55 |
56 | **SGD 还有一个问题是困在局部最优的沟壑里面震荡。想象一下你走到一个盆地,四周都是略高的小山,你觉得没有下坡的方向,那就只能待在这里了。可是如果你爬上高地,就会发现外面的世界还很广阔。因此,我们不能停留在当前位置去观察未来的方向,而要向前一步、多看一步、看远一些。 NAG全称Nesterov Accelerated Gradient,是在SGD、SGD-M的基础上的进一步改进,改进点在于定义1。我们知道在时刻t的主要下降方向是由累积动量决定的,自己的梯度方向说了也不算,那与其看当前梯度方向,不如先看看如果跟着累积动量走了一步,那个时候再怎么走。因此,NAG在步骤1,不计算当前位置的梯度方向,而是计算如果按照累积动量走了一步,那个时候的下降方向:**
57 |
58 |
59 |

60 |
61 |
62 | #### 优点:
63 |
64 | - **收敛快**
65 | - **在一定程度上解决了陷入局部最优的问题**
66 |
67 | #### 缺点:
68 |
69 | - **学习率未自适应**
70 |
71 |
72 |
73 | # AdaGrad
74 |
75 | **此前我们都没有用到二阶动量。二阶动量的出现,才意味着“自适应学习率”优化算法时代的到来。SGD及其变种以同样的学习率更新每个参数,但深度神经网络往往包含大量的参数,这些参数并不是总会用得到。对于经常更新的参数,我们已经积累了大量关于它的知识,不希望被单个样本影响太大,希望学习速率慢一些;对于偶尔更新的参数,我们了解的信息太少,希望能从每个偶然出现的样本身上多学一些,即学习速率大一些。**
76 |
77 |
78 |

79 |
80 |
81 | #### 优点:
82 |
83 | - **引入二阶动量可以对不同参数进行不同速度的改变,达到自适应学习率的目的**
84 |
85 | #### 缺点:
86 |
87 | - **由于二阶动量是单调递增的,所以会使得学习率单调递减至0,可能会使得训练过程提前结束,即便后续还有数据也无法学到必要的知识。**
88 |
89 |
90 |
91 | # AdaDelta / RMSProp
92 |
93 | **由于AdaGrad单调递减的学习率变化过于激进,我们考虑一个改变二阶动量计算方法的策略:不累积全部历史梯度,而只关注过去一段时间窗口的下降梯度。这也就是AdaDelta名称中Delta的来历。修改的思路很简单。前面我们讲到,指数移动平均值大约就是过去一段时间的平均值,因此我们用这一方法来计算二阶累积动量:**
94 |
95 |
96 |

97 |
98 |
99 | #### 优点:
100 |
101 | - **使用加权平均使得学习率不会单调递减至0,可以加快收敛速度。**
102 |
103 |
104 |
105 | # Adam
106 |
107 | **Adam和Nadam的出现就很自然而然了——它们是前述方法的集大成者。我们看到,SGD-M在SGD基础上增加了一阶动量,AdaGrad和AdaDelta在SGD基础上增加了二阶动量。把一阶动量和二阶动量都用起来,就是Adam了——Adaptive + Momentum。**
108 |
109 |
110 |

111 |
112 |
113 |
114 | # Nadam
115 |
116 | **Adam是集大成者,但它居然遗漏了Nesterov, Nadam就是加上了Nesterov按照NAG的步骤1:**
117 |
118 |
119 |

120 |
--------------------------------------------------------------------------------
/优化篇/正则项-SRC.md:
--------------------------------------------------------------------------------
1 | # 机器学习中的正则项
2 |
3 | ## 概述:
4 |
5 | **在机器学习或深度学习过程中,我们的目的是学习一个模型或则函数*f*,使得代价函数*L*在训练集中最小。这就涉及到一个问题,由于损失函数只考虑在训练集上的最小值,称之为经验风险最小化,由于训练集当中噪声的存在,冗余的特征可能成为过拟合的一种来源。这是因为,对于噪声,模型无法从有效特征当中提取信息进行拟合,故而会转向冗余特征。**
6 |
7 |
8 |
9 |
10 |
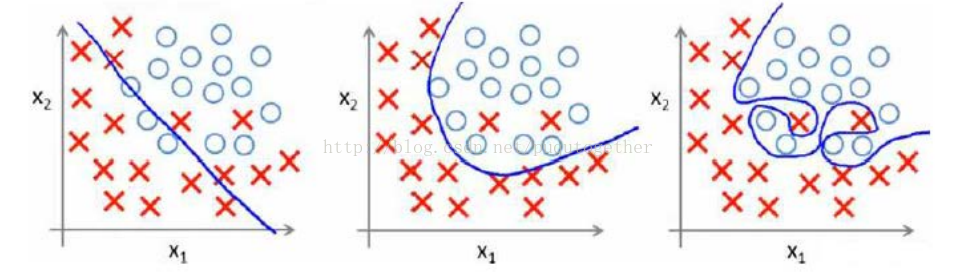
11 | **如上图最右边所示,函数为了拟合噪声产生的冗余特征,引入了额外的参数使模型出现了过拟合现象。为了对抗过拟合,我们需要向损失函数中加入描述模型复杂程度的正则项将经验风险最小化问题转化为结构风险最小化。正则化是结构风险最小化策略的实 现,是在经验风险上加一个正则化项或罚项。正则化项一般是模型复杂度的单调递增函数,模型越复杂,正则化值就越大。比如,正则化项可以是模型参数向量的范数。**
12 |
13 | ## 正则项:
14 |
15 | 模型选择如下式子所示:
16 | $$
17 | f^* = \min _ { f \in F } \frac { 1 } { N } \sum _ { i = 1 } ^ { N } L ( y _ { i } , f ( x _ { i } ) ) + \lambda J ( f )\\
18 | x_{i},y_{i}分别是训练样本的特征的标签,特征可以是D维的即x_{i} = [{x_{i}^{1},x_{i}^{2},...,x_{i}^{D}}],N为训练样本的个数,深度学习中一般为mini-batch的大小,\\L是损失函数,f是模型由D个参数构成:W=[{w^{1},w^{2},...,w^{D}}],J是正则项,\lambda是常数。
19 | $$
20 |
21 | #### L0正则项:
22 |
23 | $$
24 | f^* = \min _ { f \in F } \frac { 1 } { N } \sum _ { i = 1 } ^ { N } L ( y _ { i } , f ( x _ { i } ) ) + \lambda ||W||_{0}\\
25 | 通过引入L0正则,实际上是向优化过程引入了一种惩罚机制:当优化算法希望增加模型复杂度(此处特指将原来为零的参数更新为非零的情形)\\以降低模型的经验风险(即降低全局损失)时,在结构风险上进行大小为\lambda||W||_{0}的的惩罚,当增加模型复杂度在经验风险上的收益不足时整个结\\构风险实际上会增大而非减小。因此优化算法会拒绝此类更新。
26 | $$
27 |
28 |
29 |
30 | **引入L0正则项会使模型更加稀疏,以及使得模型易于解释,但L0正则项也有无法避免的问题:非连续、非凸、不可微。因此,在引入L0正则项的目标函数无法在方向传播中进行优化。**
31 |
32 |
33 |
34 | #### L1正则项目:
35 |
36 | $$
37 | f^* = \min _ { f \in F } \frac { 1 } { N } \sum _ { i = 1 } ^ { N } L ( y _ { i } , f ( x _ { i } ) ) + \lambda ||W||_{1}\\
38 | 通过引入L0正则项类似,引入L1正则项是在结构风险上进行大小为\lambda|W|的惩罚,以达到稀疏化的目的。
39 | $$
40 |
41 | #### L2正则项目:
42 |
43 | **L1正则项能够到达抗过拟合并使参数空间更稀疏,但是L1正则项是不连续的,所以在参数空间内不可求导,所以引入L2正则项:**
44 | $$
45 | f^* = \min _ { f \in F } \frac { 1 } { N } \sum _ { i = 1 } ^ { N } L ( y _ { i } , f ( x _ { i } ) ) + \lambda ||W||_{2}\\
46 | $$
47 |
48 | #### L1正则与L2正则对比:
49 |
50 | - **L1正则鲁棒性更强,对异常值更不敏感**。
51 |
52 | - **L2正则较L1正则运算更方变**
53 |
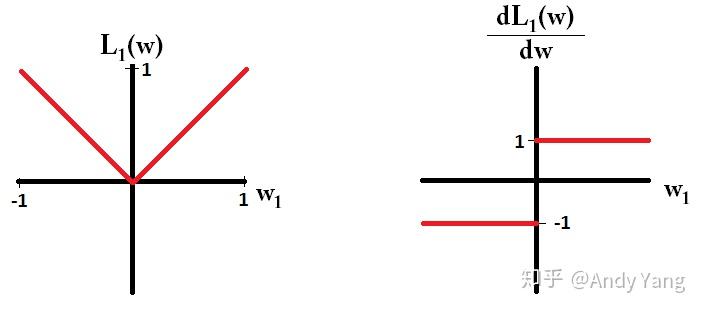
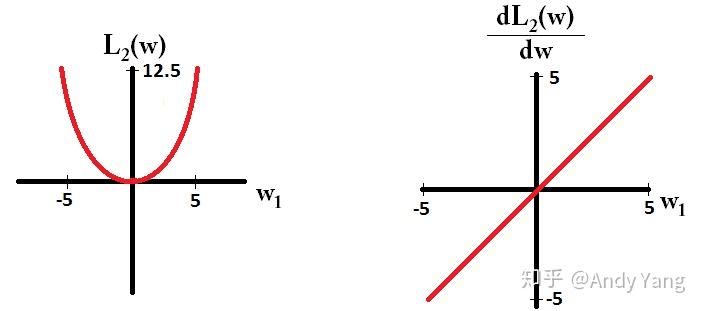
54 | - **L1正则比L2正则更容易稀疏:**
55 | $$
56 | \frac{dL_{1}}{dw}=sign(w)\\
57 | \frac{dL_{2}}{dw}=w
58 | $$
59 |
60 |
61 |
62 |
63 |
64 |
65 |
66 |
67 |
68 |
69 | **于是会发现,在梯度更新时,不管 L1 的大小是多少(只要不是0)梯度都是1或者-1,所以每次更新时,它都是稳步向0前进。**
70 |
71 | **而看 L2 的话,就会发现它的梯度会越靠近0,就变得越小。也就是说加了 L1 正则的话基本上经过一定步数后很可能变为0,**
72 |
73 | **而 L2 几乎不可能,因为在值小的时候其梯度也会变小。于是也就造成了 L1 输出稀疏的特性。**
--------------------------------------------------------------------------------
/优化篇/正则项.md:
--------------------------------------------------------------------------------
1 | # 机器学习中的正则项
2 |
3 | ## 概述:
4 |
5 | **在机器学习或深度学习过程中,我们的目的是学习一个模型或则函数*f*,使得代价函数*L*在训练集中最小。这就涉及到一个问题,由于损失函数只考虑在训练集上的最小值,称之为经验风险最小化,由于训练集当中噪声的存在,冗余的特征可能成为过拟合的一种来源。这是因为,对于噪声,模型无法从有效特征当中提取信息进行拟合,故而会转向冗余特征。**
6 |
7 |
8 |

9 |
10 |
11 | **如上图最右边所示,函数为了拟合噪声产生的冗余特征,引入了额外的参数使模型出现了过拟合现象。为了对抗过拟合,我们需要向损失函数中加入描述模型复杂程度的正则项将经验风险最小化问题转化为结构风险最小化。正则化是结构风险最小化策略的实 现,是在经验风险上加一个正则化项或罚项。正则化项一般是模型复杂度的单调递增函数,模型越复杂,正则化值就越大。比如,正则化项可以是模型参数向量的范数。**
12 |
13 | ## 正则项:
14 |
15 | 模型选择如下式子所示:
16 |
17 |
18 |

19 |
20 |
21 | #### L0正则项:
22 |
23 |
24 |

25 |
26 |
27 |
28 |
29 | **引入L0正则项会使模型更加稀疏,以及使得模型易于解释,但L0正则项也有无法避免的问题:非连续、非凸、不可微。因此,在引入L0正则项的目标函数无法在方向传播中进行优化。**
30 |
31 |
32 |
33 | #### L1正则项目:
34 |
35 |
36 |

37 |
38 |
39 | #### L2正则项目:
40 |
41 | **L1正则项能够到达抗过拟合并使参数空间更稀疏,但是L1正则项是不连续的,所以在参数空间内不可求导,所以引入L2正则项:**
42 |
43 |
44 |

45 |
46 |
47 | #### L1正则与L2正则对比:
48 |
49 | - **L1正则鲁棒性更强,对异常值更不敏感**。
50 |
51 | - **L2正则较L1正则运算更方变**
52 |
53 | - **L1正则比L2正则更容易稀疏:**
54 |
55 |
56 |

57 |
58 |
59 |
60 |

61 |
62 |
63 |
64 |

65 |
66 |
67 | **于是会发现,在梯度更新时,不管 L1 的大小是多少(只要不是0)梯度都是1或者-1,所以每次更新时,它都是稳步向0前进。**
68 |
69 | **而看 L2 的话,就会发现它的梯度会越靠近0,就变得越小。也就是说加了 L1 正则的话基本上经过一定步数后很可能变为0,**
70 |
71 | **而 L2 几乎不可能,因为在值小的时候其梯度也会变小。于是也就造成了 L1 输出稀疏的特性。**
--------------------------------------------------------------------------------
/优化篇/激活函数-SRC.md:
--------------------------------------------------------------------------------
1 | # 激活函数
2 |
3 | ## 概述
4 |
5 | **激活函数对于人工神经网络模型去学习、理解非常复杂和非线性的函数来说具有十分重要的作用。它们将非线性特性引入到我们的网络中。如果不用激活函数,每一层输出都是上层输入的线性函数,无论神经网络有多少层,输出都是输入的线性组合,这种情况就是最原始的感知机(Perceptron)。没有激活函数的每层都相当于矩阵相乘。就算你叠加了若干层之后,无非还是个矩阵相乘罢了。如果使用的话,激活函数给神经元引入了非线性因素,使得神经网络可以任意逼近任何非线性函数,这样神经网络就可以应用到众多的非线性模型中。**
6 |
7 |
8 |
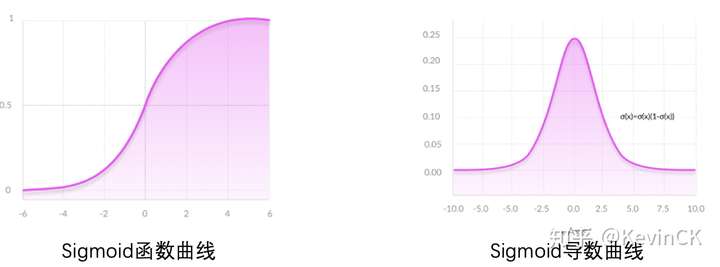
9 | ## 1.Sigmoid激活函数
10 |
11 | $$
12 | \large \sigma (x)= \frac{1}{1+e^{-x}} \\
13 | \large \sigma^, (x) = \sigma (x)*(1 - \sigma (x))
14 | $$
15 |
16 |
17 |
18 |
19 |
20 | #### 优点:
21 |
22 | - **平滑,处处可导数**
23 | - **求导容易**
24 | - **能够把输入的连续实值变换为0和1之间的输出**
25 |
26 | #### 缺点:
27 |
28 | - **非0均值,会导致后一层的神经元将得到上一层输出的非0均值的信号作为输入, 改变了数据的分布,收敛速度变慢。**
29 | - **容易梯度爆炸或消失**
30 | - **存在梯度饱和区**
31 |
32 | $$
33 | \large \left\{\begin{array}{l}
34 | \large y_{1} = w_{1} * x_{1} \\
35 | \large z_{1} = \sigma(y_{1}) \\
36 | \large y_{2} = z_{1}*w_{2} \\
37 | \large z_{2} = \sigma(y_{2}) \\
38 | \large y_{out} = z_{2}*w_{3}
39 | \large \end{array}\right. \\
40 | \large 损失函数L_{loss}=||y_{out} - y_{truth}||^2 \\
41 | \large \frac{dL_{loss}}{dw_{1}}=\frac{dL_{loss}}{dy_{out}}*\frac{dy_{out}}{dz_{2}}
42 | \large *\frac{dz_{2}}{dy_{2}}*\frac{dy_{2}}{dz_{1}}*\frac{dz_{1}}{dy_{1}}*\frac{dy_{1}}{dw_{1}}\\
43 | \large \frac{dL_{loss}}{dw_{1}}=||y_{out} - y_{truth}||*w_{3}*\sigma^,(y_{2})*
44 | \large w_{2}*\sigma^,(y_{1})*x_{1}\\
45 | \large 由于\sigma^,(x)在[0.0.25]之间,所以当初始化参数在[0,4]之间的时候,\\
46 | \large 会发生梯度消失,参数初始化在[4,~]的时候会发生梯度爆炸。
47 | $$
48 |
49 | - **指数操作比较耗时。**
50 |
51 |
52 |
53 | ## 2.tanh函数
54 |
55 | **tanh为双曲正切函数。tanh和 sigmoid 相似,都属于饱和激活函数,区别在于输出值范围由 (0,1) 变为了 (-1,1),可以把 tanh 函数看做是 sigmoid 向下平移和拉伸后的结果。**
56 | $$
57 | \large \tanh(x)= \frac{e^{x}-e^{-x}}{e^{x}+e^{-x}} \\
58 | \large \tanh(x)= \frac{2}{1+e^{-2x}}-1
59 | $$
60 | **从公式中,可以更加清晰看出tanh与sigmoid函数的关系(平移+拉伸)。**
61 |
62 |
63 |
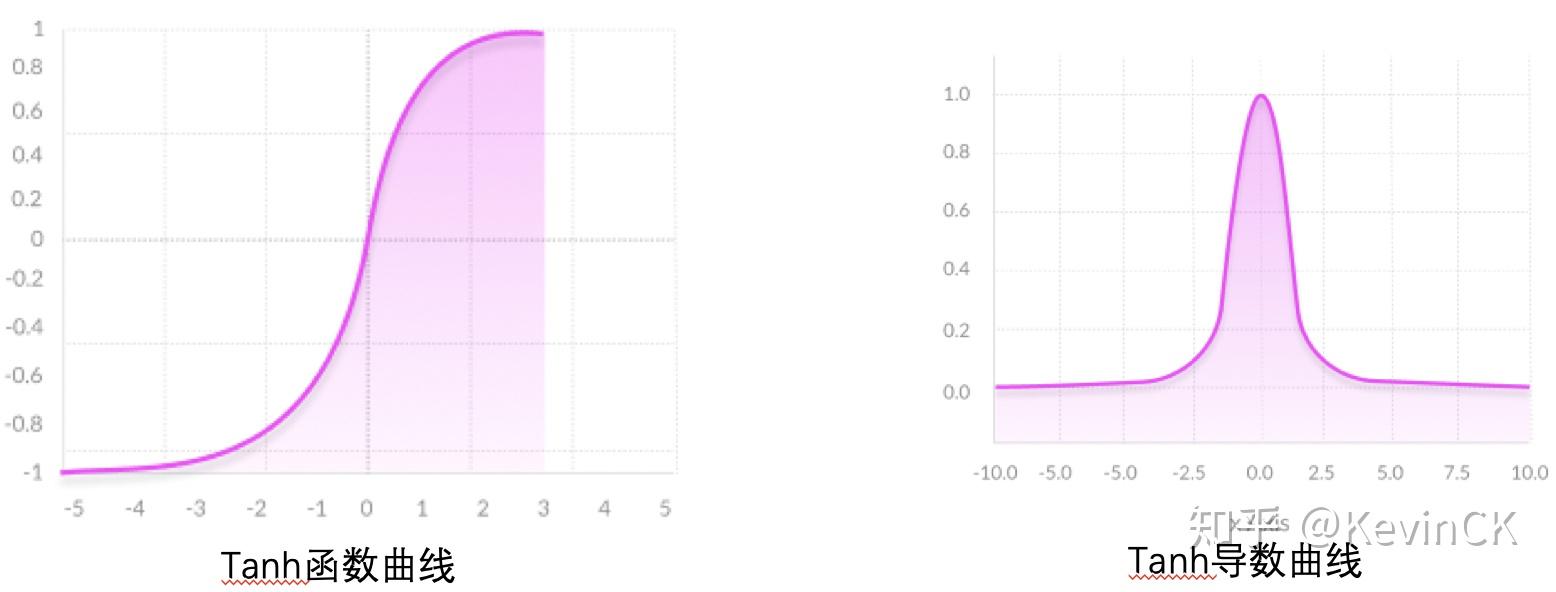
64 |
65 |
66 | #### 优点:
67 |
68 | - **平滑,处处可导数**
69 | - **求导容易**
70 | - **能够把输入的连续实值变换为0和1之间的输出**
71 | - **是0均值的,不会改变数据分布**
72 |
73 | #### 缺点:
74 |
75 | - **幂运算的问题仍然存在;**
76 | - **tanh导数范围在(0, 1)之间,相比sigmoid的(0, 0.25),梯度消失(gradient vanishing)问题会得到缓解,但仍然还会存在。**
77 | - **同样存在梯度饱和区**
78 |
79 |
80 |
81 | ## 3.ReLU函数
82 |
83 | **relu(Rectified Linear Unit)——修正线性单元函数:该函数形式比较简单**
84 | $$
85 | \large relu(x) = max(0,x)
86 | $$
87 |
88 |
89 |
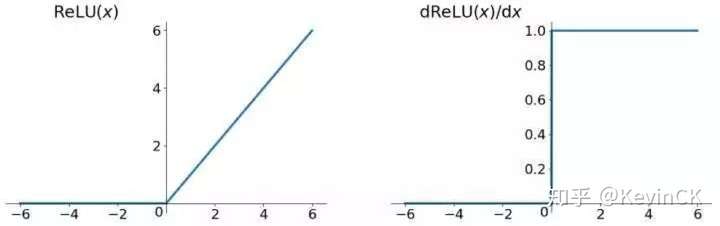
90 |
91 |
92 | #### 优点:
93 |
94 | - **ReLU将x<0的输出置为0,就是一个去噪音,稀疏矩阵的过程。而且在训练过程中,这种稀疏性是动态调节的,网络会自动调整稀疏比例,保证矩阵有最优的有效特征**。
95 | - **解决了梯度消失问题,收敛速度快于Sigmoid和tanh函数**
96 | - **计算速度快**
97 | - **使网络变得更加稀疏**
98 |
99 |
100 |
101 | #### 缺点:
102 |
103 | - **ReLU函数在0出不可导**
104 |
105 | - **还是存在梯度爆炸的问题**
106 |
107 | - **ReLU 强制将x<0部分的输出置为0(置为0就是屏蔽该特征),可能会导致模型无法学习到有效特征,所以如果学习率设置的太大,就可能会导致网络的大部分神经元处于‘dead’状态,所以使用ReLU的网络,学习率不能设置太大。**
108 |
109 | - **非0均值**
110 |
111 |
112 |
113 | ## 4.Leaky ReLU, PReLU(Parametric Relu), RReLU(Random ReLU)函数
114 |
115 | ### 1.Leaky ReLU
116 |
117 | $$
118 | \large Leaky Relu(x) = \left\{\begin{array}{l} x,x>0 \\
119 | \large \alpha * x, x < 0
120 | \large \end{array}\right.
121 | $$
122 |
123 |
124 |
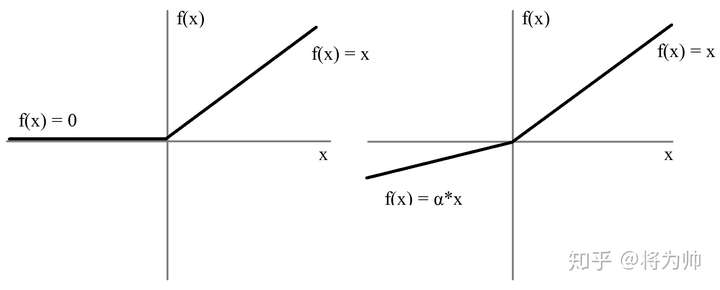
125 |
126 |
127 | #### 优点:
128 |
129 | - **LeakyReLU的提出就是为了解决神经元”死亡“问题,LeakyReLU与ReLU很相似,仅在输入小于0的部分有差别,ReLU输入小于0的部分值都为0,而LeakyReLU输入小于0的部分,值为负,且有微小的梯度。**
130 |
131 | #### 缺点:
132 |
133 | - **少了Relu的稀疏性**
134 |
135 | #### 2.ReLU
136 |
137 | ***PRelu*(参数化修正线性单元)中的作为一个可学习的参数,会在训练的过程中进行更新。**
138 |
139 | #### 3.RReLU
140 |
141 | ***RReLU*,负值的斜率在训练中是随机的,在之后的测试中就变成了固定的了。**
142 |
143 |
144 |
145 | ## 5.ELU 函数
146 |
147 | $$
148 | \LARGE ELU(x) = \left\{\begin{array}{l} x,x>0 \\
149 | \alpha * (e^x-1), x < 0
150 | \end{array}\right.
151 | $$
152 |
153 |
154 |

155 |
156 |
157 | #### 优点:
158 |
159 | - **解决RELU非0均值,输出的分布是零均值的,可以加快训练速度。**
160 |
161 | - **解决LeakyReLU单侧不饱和,ELU是单侧饱和的,可以更好的收敛。**
162 |
163 | #### 缺点
164 |
165 | - **计算复杂**
166 | - **在0处不可导**
--------------------------------------------------------------------------------
/优化篇/激活函数.md:
--------------------------------------------------------------------------------
1 | # 激活函数
2 |
3 | ## 概述
4 |
5 | **激活函数对于人工神经网络模型去学习、理解非常复杂和非线性的函数来说具有十分重要的作用。它们将非线性特性引入到我们的网络中。如果不用激活函数,每一层输出都是上层输入的线性函数,无论神经网络有多少层,输出都是输入的线性组合,这种情况就是最原始的感知机(Perceptron)。没有激活函数的每层都相当于矩阵相乘。就算你叠加了若干层之后,无非还是个矩阵相乘罢了。如果使用的话,激活函数给神经元引入了非线性因素,使得神经网络可以任意逼近任何非线性函数,这样神经网络就可以应用到众多的非线性模型中。**
6 |
7 |
8 |
9 | ## 1.Sigmoid激活函数
10 |
11 |
12 |

13 |
14 |
15 |
16 |

17 |
18 |
19 | #### 优点:
20 |
21 | - **平滑,处处可导数**
22 | - **求导容易**
23 | - **能够把输入的连续实值变换为0和1之间的输出**
24 |
25 | #### 缺点:
26 |
27 | - **非0均值,会导致后一层的神经元将得到上一层输出的非0均值的信号作为输入, 改变了数据的分布,收敛速度变慢。**
28 |
29 | - **容易梯度爆炸或消失**
30 |
31 | - **存在梯度饱和区**
32 |
33 |
34 |

35 |
36 |
37 | - **指数操作比较耗时。**
38 |
39 |
40 |
41 | ## 2.tanh函数
42 |
43 | **tanh为双曲正切函数。tanh和 sigmoid 相似,都属于饱和激活函数,区别在于输出值范围由 (0,1) 变为了 (-1,1),可以把 tanh 函数看做是 sigmoid 向下平移和拉伸后的结果。**
44 |
45 |
46 |

47 |
48 |
49 | **从公式中,可以更加清晰看出tanh与sigmoid函数的关系(平移+拉伸)。**
50 |
51 |
52 |

53 |
54 |
55 | #### 优点:
56 |
57 | - **平滑,处处可导数**
58 | - **求导容易**
59 | - **能够把输入的连续实值变换为0和1之间的输出**
60 | - **是0均值的,不会改变数据分布**
61 |
62 | #### 缺点:
63 |
64 | - **幂运算的问题仍然存在;**
65 | - **tanh导数范围在(0, 1)之间,相比sigmoid的(0, 0.25),梯度消失(gradient vanishing)问题会得到缓解,但仍然还会存在。**
66 | - **同样存在梯度饱和区**
67 |
68 |
69 |
70 | ## 3.ReLU函数
71 |
72 | **relu(Rectified Linear Unit)——修正线性单元函数:该函数形式比较简单**
73 |
74 |
75 |

76 |
77 |
78 |
79 |

80 |
81 |
82 | #### 优点:
83 |
84 | - **ReLU将x<0的输出置为0,就是一个去噪音,稀疏矩阵的过程。而且在训练过程中,这种稀疏性是动态调节的,网络会自动调整稀疏比例,保证矩阵有最优的有效特征**。
85 | - **解决了梯度消失问题,收敛速度快于Sigmoid和tanh函数**
86 | - **计算速度快**
87 | - **使网络变得更加稀疏**
88 |
89 |
90 |
91 | #### 缺点:
92 |
93 | - **ReLU函数在0出不可导**
94 |
95 | - **还是存在梯度爆炸的问题**
96 |
97 | - **ReLU 强制将x<0部分的输出置为0(置为0就是屏蔽该特征),可能会导致模型无法学习到有效特征,所以如果学习率设置的太大,就可能会导致网络的大部分神经元处于‘dead’状态,所以使用ReLU的网络,学习率不能设置太大。**
98 |
99 | - **非0均值**
100 |
101 |
102 |
103 | ## 4.Leaky ReLU, PReLU(Parametric Relu), RReLU(Random ReLU)函数
104 |
105 | ### 1.Leaky ReLU
106 |
107 |
108 |

109 |
110 |
111 |
112 |

113 |
114 |
115 | #### 优点:
116 |
117 | - **LeakyReLU的提出就是为了解决神经元”死亡“问题,LeakyReLU与ReLU很相似,仅在输入小于0的部分有差别,ReLU输入小于0的部分值都为0,而LeakyReLU输入小于0的部分,值为负,且有微小的梯度。**
118 |
119 | #### 缺点:
120 |
121 | - **少了Relu的稀疏性**
122 |
123 | #### 2.ReLU
124 |
125 | ***PRelu*(参数化修正线性单元)中的作为一个可学习的参数,会在训练的过程中进行更新。**
126 |
127 | #### 3.RReLU
128 |
129 | ***RReLU*,负值的斜率在训练中是随机的,在之后的测试中就变成了固定的了。**
130 |
131 |
132 |
133 | ## 5.ELU 函数
134 |
135 |
136 |

137 |
138 |
139 |
140 |

141 |
142 |
143 | #### 优点:
144 |
145 | - **解决RELU非0均值,输出的分布是零均值的,可以加快训练速度。**
146 |
147 | - **解决LeakyReLU单侧不饱和,ELU是单侧饱和的,可以更好的收敛。**
148 |
149 | #### 缺点
150 |
151 | - **计算复杂**
152 | - **在0处不可导**
--------------------------------------------------------------------------------
/分割篇/readme.md:
--------------------------------------------------------------------------------
1 |
2 |
--------------------------------------------------------------------------------
/分割篇/实例分割/Hybrid Task Cascade for Instance Segmentation.md:
--------------------------------------------------------------------------------
1 | # **Hybrid Task Cascade for Instance Segmentation**
2 |
3 | ## 1.概述
4 |
5 | **Hybrid Task Cascade for Instance Segmentation在cascade mask rcnn基础上进行改进,充分利用detection与segmentation的联系,使得detection与segmentation由之前的并行学习改为串行学习,让segmentation能够学习到detection信息,同时也添加语义分割模块辅助训练进一步提升网路性能。**
6 |
7 | **paper link:https://arxiv.org/pdf/1901.07518.pdf**
8 |
9 | **code link: https://github.com/open-mmlab/mmdetection**
10 |
11 |
12 |

.
13 |
14 |
15 | **图1**
16 |
17 | ## 2.具体实现
18 |
19 | ### 2.1 提出背景
20 |
21 | **cascade rcnn证明通过级联的方式确实能够提升网络的性能,参看[cascade rcnn](https://github.com/Hanson0910/DL-Algorithm-Summary/blob/main/%E7%9B%AE%E6%A0%87%E6%A3%80%E6%B5%8B%E7%AF%87/Anchor-Base/two-stage/Cascade-RCNN.md),所以提出了cascade mask rcnn,但是cascade mask-rcnn存在如下问题:**
22 |
23 | - **图1(a)所示,cascade Mask R-CNN的每一级的mask分支与bbox分支是并行训练的,也就是说两个分支没有进行相互作用,mask分支没有从bbox学到任何信息。**
24 | - **各级mask分支之间没有进行相互作用,互相独立,这不利于网络性能提升。**
25 |
26 | **Cascade Mask R-CNN公式如下式所示:**
27 | $$
28 | \large \begin{aligned}
29 | \mathbf{x}_{t}^{b o x} &=\mathcal{P}\left(\mathbf{x}, \mathbf{r}_{t-1}\right), & \mathbf{r}_{t}=B_{t}\left(\mathbf{x}_{t}^{b o x}\right) \\
30 | \mathbf{x}_{t}^{\text {mask }} &=\mathcal{P}\left(\mathbf{x}, \mathbf{r}_{t-1}\right), & \mathbf{m}_{t}=M_{t}\left(\mathbf{x}_{t}^{\text {mask }}\right)
31 | \end{aligned} \\
32 | \large x为backbone输出的特征,x_t^{box},x_t^{mask}分别表示roi经过x后通过roi pooling得到的box和mask特征。\\
33 | \large r_t和m_t分别代表预测的box和mask,B_t,M_t代表box和mask的head。
34 | $$
35 |
36 | ### **2.2解决方案**
37 |
38 | - **针对2.1的第一个问题,提出了图1(b)的结构,每一级的mask特征都由这一级的box提供,而不是上一级。**
39 | $$
40 | \large \begin{array}{ll}
41 | \mathbf{x}_{t}^{b o x}=\mathcal{P}\left(\mathbf{x}, \mathbf{r}_{t-1}\right), & \mathbf{r}_{t}=B_{t}\left(\mathbf{x}_{t}^{b o x}\right) \\
42 | \mathbf{x}_{t}^{\text {mask }}=\mathcal{P}\left(\mathbf{x}, \mathbf{r}_{t}\right), & \mathbf{m}_{t}=M_{t}\left(\mathbf{x}_{t}^{m a s k}\right)
43 | \end{array}
44 | $$
45 |
46 | - **针对2.1中问题2,提出了图1(c)的结构,不同级的mask特征进行融合**
47 | $$
48 | \large \begin{array}{ll}
49 | \mathbf{x}_{t}^{b o x}=\mathcal{P}\left(\mathbf{x}, \mathbf{r}_{t-1}\right), & \mathbf{r}_{t}=B_{t}\left(\mathbf{x}_{t}^{b o x}\right) \\
50 | \mathbf{x}_{t}^{\text {mask }}=\mathcal{P}\left(\mathbf{x}, \mathbf{r}_{t}\right), & \mathbf{m}_{t}=M_{t}\left(\mathcal{F}\left(\mathbf{x}_{t}^{\text {mask }}, \mathbf{m}_{t-1}^{-}\right)\right)
51 | \end{array}\\
52 | \large \mathcal{F}\left(\mathbf{x}_{t}^{\text {mask }}, \mathbf{m}_{t-1}\right)=\mathbf{x}_{t}^{m a s k}+\mathcal{G}_{t}\left(\mathbf{m}_{t-1}^{-}\right)\\
53 | \large \mathcal{G}_{t}是1*1的卷积层
54 | $$
55 |
56 |
57 | **其中**:
58 | $$
59 | \large \begin{aligned}
60 | \mathbf{m}_{1}^{-} &=M_{1}^{-}\left(\mathbf{x}_{t}^{\text {mask }}\right) \\
61 | \mathbf{m}_{2}^{-} &=M_{2}^{-}\left(\mathcal{F}\left(\mathbf{x}_{t}^{\text {mask }}, \mathbf{m}_{1}^{-}\right)\right) \\
62 | & \vdots \\
63 | \mathbf{m}_{t-1}^{-} &=M_{t}^{-}\left(\mathcal{F}\left(\mathbf{x}_{t}^{\text {mask }}, \mathbf{m}_{t-2}^{-}\right)\right)
64 | \end{aligned}\\
65 | \large M_t^{-}代表mask-head,M_{t}的特征转换单元,由4个连续的3*3卷积组成,转换特征m_{t-1}^{-}\\
66 | \large 再接一个1*1的卷积为了维度对齐。
67 | $$
68 |
69 |
70 |

.
71 |
72 |
73 | 图2
74 |
75 | - **在上面基础上添加一个语义分割部分辅助训练,语义分割部分能够提供一个全局的空间上下文信息,帮助区分正负样本,如图1(d)所示。**
76 |
77 | $$
78 | \large \begin{aligned}
79 | \mathbf{x}_{t}^{b o x} &=\mathcal{P}\left(\mathbf{x}, \mathbf{r}_{t-1}\right)+\mathcal{P}\left(S(\mathbf{x}), \mathbf{r}_{t-1}\right) \\
80 | \mathbf{r}_{t} &=B_{t}\left(\mathbf{x}_{t}^{b o x}\right) \\
81 | \mathbf{x}_{t}^{\text {mask }} &=\mathcal{P}\left(\mathbf{x}, \mathbf{r}_{t}\right)+\mathcal{P}\left(S(\mathbf{x}), \mathbf{r}_{t}\right) \\
82 | \mathbf{m}_{t} &=M_{t}\left(\mathcal{F}\left(\mathbf{x}_{t}^{\text {mask }}, \mathbf{m}_{t-1}^{-}\right)\right)
83 | \end{aligned}
84 | $$
85 |
86 | **语义分割S由特征由FPN组成,如下图所示:**
87 |
88 |
89 |

.
90 |
91 |
92 | 图3
93 |
94 | ## 3.总结
95 |
96 | **Hybrid Task Cascade for Instance Segmentation最指的学习的地方应该是其对网路设计的思路,通过分析baseline(cascade mask-rcnn)再结合其它论文(cascade rcnn)的有点来改进网路,再在其基础上进行改进,这种网络设计的思路可以指导我们以后自己设计网络。Segmentation和detection本来就是一个相辅相成的东西,让它们相互作用是一个非常棒的idea,可以互相学习。**
97 |
98 |
--------------------------------------------------------------------------------
/分割篇/实例分割/InstaBoost-SRC.md:
--------------------------------------------------------------------------------
1 | # ****InstaBoost****
2 |
3 | ## 1.概述
4 |
5 | **InstaBoost是一种数据增广方式,用在示例分割和目标检测上。通过把实例crop出来再随机放置在图像背景区域来达到数据增广提升检测精度的目的。**
6 |
7 | ## 2.具体实现
8 |
9 | ### 2.1 随机InstaBoost
10 |
11 | **随机InstaBoost主要是通过随机仿射变化把crop出的实例随机安放在目标周围,仿射变换的公式如下:**
12 | $$
13 | \large \mathbf{H}=\left[\begin{array}{ccc}
14 | s \cos r & s \sin r & t_{x} \\
15 | -s \sin r & s \cos r & t_{y} \\
16 | 0 & 0 & 1
17 | \end{array}\right]\\
18 | \large 其中t_{x},t_{y}表示平移量,s表示缩放量,r表示旋转量。通过\left\{t_{x},t_{y},s,r\right\}4维空间可以定义一个目标自然出现频率的模型\\
19 | \large 定义一个概率密度函数f(.)测量把目标O放置在图像I中的合理性:
20 | \large P(x,y,s,r|I,O) = f(t_{x},t_{y},s,r|I,O),x = x_{0} + t_{x},y = y_{0}+t_{y}\\
21 | \large 在\left\{x_{0},y_{0},1,0\right\}的概率应该为最大值(这个比较好理解,目标不动当然概率密度函数在这个点的值最大),\\
22 | \large argmaxP(x,y,s,r)=(x_{0},y_{0},1,0)\\
23 | \large 按常理分析,在\left\{x_{0},y_{0},1,0\right\}处的一个小的区域,概率图P(x,y,s,r|I,O)应该有一个较大响应,\\
24 | \large 那么InstaBoost则通过在目标\left\{x_{0},y_{0},1,0\right\}处的一个小的区域范围内随机采样,最后通过仿射矩阵\mathbf{H}把目标移动到相应区域。
25 | $$
26 | **随机InstaBoost这样做比较直观好理解,但是也有一个明显的短板就是实例只能在原周围区域进行变换。为了补充这个短板作者又提出了** **Appearance consistency heatmap guided InstaBoost来接触只能在目标周围区域变换的限制。**
27 |
28 |
29 |
30 | ### 2.2 Appearance consistency heatmap guided InstaBoost
31 |
32 | **appearance consistency heatmap是用来评估在任意位置(x0,y0)转换到(x,y)的RGB空间相似性。**
33 | $$
34 | \large 通过把上式的概率密度函数f(.)分成3个独立的条件概率分布f_{x,y}(,),f_{s}(.),f_{r}(.),则\\
35 | P(x,y,s,r)=f_{xy}(t_{x},t_{y}|s,r)f_{s}(s|r)f_{r}(r)\\
36 | \quad \large =f_{xy}(t_{x},t_{y})f_{s}(s)f_{r}(r)\\
37 | \large Appearance\quad consistency\quad heatmap \quad M(x, y)=E[P(x, y)] \propto f_{x y}\left(t_{x}, t_{y}\right)
38 | $$
39 |
40 |
41 | **上式定义了appearance consistency heatmap,接下来详细讲解一下appearance consistency heatmap,它主要由三部分组成:**
42 |
43 | - **Appearance descriptor**
44 |
45 | **为了测量目标在原来位置与pasted位置的相似度,首先需要定义一个目标邻近区域背景编码后的描述子,它基于如下直觉:随着距离的增加,实例在appearance consistency中对周围环境的影响越小。定义一个appearance描述算子:**
46 | $$
47 | \large \mathcal D(c_{x},c_{y}) = \left\{(C_{i}(c_{x},c_{y}),w_{i})|i\in\left\{1,2,3\right\}\right\}\\
48 | \large C_{i}表示轮廓区域i带权重w_{i},给定一个实例中心(c_{x},x_{y}),i=1表示最里面的轮廓区域\\
49 | \large w_{1}>w_{2}>w_{3}
50 | $$
51 |
52 |
53 | - **Appearance distance**
54 |
55 | **Appearance distance是用来测量一对appearance描述算子之间的距离:**
56 | $$
57 | \large d\left(\mathcal{D}_{1}, \mathcal{D}_{2}\right)=\sum_{i=1}^{3} \sum_{\left(x_{1}, y_{1}\right) \in \mathcal{C}_{1 i} \atop\left(x_{2}, y_{2}\right) \in \mathcal{C}_{2 i}} w_{i} \Delta\left(I_{1}\left(x_{1}, y_{1}\right), I_{2}\left(x_{2}, y_{2}\right)\right)\\
58 | \large I_{k}(x,y)表示在图像k位置(x,y)处的RGB值,\Delta表示距离,一般用欧式距离。
59 | $$
60 |
61 |
62 |
63 | - **Heatmap generation**
64 | $$
65 | \large 目标原位置的appearance描述子\mathcal D_{0},图像中所有其它位置的\mathcal {D},Appearance distances通过如下方式进行归一化:\\
66 | \large h(x) = -log(\frac{x-m}{M-m})\\
67 | \large M = max(d(\mathcal D,\mathcal D_{0})),m = min(d(\mathcal D,\mathcal D_{0}))\\
68 | \large HeatmapH通过在背景区域的所有位置像素和原实例点(x_{0},y_{0})处的归一化距离h(.)求得,x是(x_{0},y_{0})处RGB的值,\\它上面公式感觉少了一个\large RGB的求和项,如果按照公式来那么这个值肯定是单通道的。
69 | $$
70 |
71 | ## 补充
72 |
73 | - 图像matting
74 |
75 | 在将图片前景和背景按照标注进行分离的过程中,如果完全按照标注去切割前景,前景的边界处会呈不自然的多边形锯齿状,这与 COCO 数据标注方式有关。为了解决这一问题,研究者使用《A global sampling method for alpha matting》一文中提出的方法对前景轮廓做 matting 处理,以得到与物体轮廓契合的边界。
76 |
77 | - 图像inpainting
78 |
79 | 在前景背景分离后,背景上会存在若干个空白区域,这些区域可以使用 inpainting 算法进行填补。论文中使用了《Navier-stokes, fluid dynamics, and image and videoinpainting》文章中提出的 inpainting 算法。
80 |
81 |
82 |

.
83 |
84 |
85 | ## 感想
86 |
87 | **InstaBoost这种增广思路在之前就有,目标检测用的比较多。作者通过建模找出合适的pasted位置,总体精度能提升2个点左右,还是蛮有效的。但是从它公式来看要遍历所以背景区域像素点,还有做log运算计算量可想而知,当然作者最后通过resize图像到一个小的分辨率做运算再resize回来,确实能减少不少时间,但是感觉计算量还是不老少。**
--------------------------------------------------------------------------------
/分割篇/实例分割/InstaBoost.md:
--------------------------------------------------------------------------------
1 | # ****InstaBoost****
2 |
3 | ## 1.概述
4 |
5 | **InstaBoost是一种数据增广方式,用在示例分割和目标检测上。通过把实例crop出来再随机放置在图像背景区域来达到数据增广提升检测精度的目的。**
6 |
7 | ## 2.具体实现
8 |
9 | ### 2.1 随机InstaBoost
10 |
11 | **随机InstaBoost主要是通过随机仿射变化把crop出的实例随机安放在目标周围,仿射变换的公式如下:**
12 |
13 |

.
14 |
15 |
16 | **随机InstaBoost这样做比较直观好理解,但是也有一个明显的短板就是实例只能在原周围区域进行变换。为了补充这个短板作者又提出了** **Appearance consistency heatmap guided InstaBoost来接触只能在目标周围区域变换的限制。**
17 |
18 |
19 |
20 | ### 2.2 Appearance consistency heatmap guided InstaBoost
21 |
22 | **appearance consistency heatmap是用来评估在任意位置(x0,y0)转换到(x,y)的RGB空间相似性。**
23 |
24 |
25 |

.
26 |
27 |
28 |
29 | **上式定义了appearance consistency heatmap,接下来详细讲解一下appearance consistency heatmap,它主要由三部分组成:**
30 |
31 | - **Appearance descriptor**
32 |
33 | **为了测量目标在原来位置与pasted位置的相似度,首先需要定义一个目标邻近区域背景编码后的描述子,它基于如下直觉:随着距离的增加,实例在appearance consistency中对周围环境的影响越小。定义一个appearance描述算子:**
34 |
35 |
36 |

.
37 |
38 |
39 |
40 |
41 | - **Appearance distance**
42 |
43 | **Appearance distance是用来测量一对appearance描述算子之间的距离:**
44 |
45 |
46 |

.
47 |
48 |
49 | - **Heatmap generation**
50 |
51 |
52 |

.
53 |
54 |
55 | ## 补充
56 |
57 | - 图像matting
58 |
59 | 在将图片前景和背景按照标注进行分离的过程中,如果完全按照标注去切割前景,前景的边界处会呈不自然的多边形锯齿状,这与 COCO 数据标注方式有关。为了解决这一问题,研究者使用《A global sampling method for alpha matting》一文中提出的方法对前景轮廓做 matting 处理,以得到与物体轮廓契合的边界。
60 |
61 | - 图像inpainting
62 |
63 | 在前景背景分离后,背景上会存在若干个空白区域,这些区域可以使用 inpainting 算法进行填补。论文中使用了《Navier-stokes, fluid dynamics, and image and videoinpainting》文章中提出的 inpainting 算法。
64 |
65 |
66 |

.
67 |
68 |
69 | ## 感想
70 |
71 | **InstaBoost这种增广思路在之前就有,目标检测用的比较多。作者通过建模找出合适的pasted位置,总体精度能提升2个点左右,还是蛮有效的。但是从它公式来看要遍历所以背景区域像素点,还有做log运算计算量可想而知,当然作者最后通过resize图像到一个小的分辨率做运算再resize回来,确实能减少不少时间,但是感觉计算量还是不老少。**
--------------------------------------------------------------------------------
/分割篇/实例分割/Mask-Scoring-R-CNN.md:
--------------------------------------------------------------------------------
1 | # **Mask Scoring R-CNN**
2 |
3 | ## 1.概述
4 |
5 | **Mask Scoring R-CNN是在Mask R-CNN基础上添加MaskIOU分支增加分类准确性。**
6 |
7 | **paper link:https://arxiv.org/abs/1903.00241**
8 |
9 | **code link:https://github.com/zjhuang22/maskscoring_rcnn**
10 |
11 | ## 2.具体实现
12 |
13 | ### 2.1 网络结构
14 |
15 |
16 |

.
17 |
18 |
19 | **可以看出mask scoring rcnn是在mask rcnn的基础上添加了一个MaskIOU分支**
20 |
21 | ### 2.2 训练阶段
22 |
23 | - **RPN阶段产生proposal**
24 | - **RCNN分支训练过程**
25 | - **mask rcnn训练过程**
26 | - **获取目标的预测mask,然后二值化**
27 | - **计算二值化mask与gt mask的l2 loss**
28 |
29 | ### 2.3 前向阶段
30 |
31 | - **maskiou head的输出直接与rcnn分支的类别输出相乘作为最终的分类得分**
32 |
33 |
34 |
35 | ## 3.总结
36 |
37 | **Mask Scoring R-CNN这篇文章总体来说中规中矩,没有什么特别的地方,添加一个额外的分支辅助训练,最终效果有一定的提升,但是我认为maskiou部分用二值化mask去做回归可能会导致网络训练过程不易收敛。**
--------------------------------------------------------------------------------
/分割篇/实例分割/mask-rcnn.md:
--------------------------------------------------------------------------------
1 | # **Mask R-CNN**
2 |
3 | ## 1.概述
4 |
5 | **Mask R-CNN是在faster RCNN基础上添加mask分支,同时提出ROI-Align来消除ROI-Pooling的量化误差,并添加FPN结构大大提升效果。**
6 |
7 | **paper link:https://arxiv.org/pdf/1703.06870.pdf**
8 |
9 | **code link:https://github.com/facebookresearch/Detectron**
10 |
11 | ## 2.具体实现
12 |
13 | ### 2.1 网络结构
14 |
15 | - **backbone采用resnet系列**
16 | - **neck部分采用FPN+RPN**
17 | - **head为faster-rcnn的分类和回归head+rpn后面接mask head**
18 |
19 |
20 |

.
21 |
22 |
23 | ### 2.2 mask branch细节
24 |
25 | **mask分支通过对RPN阶段生成的ROI通过ROI-Align操作生成m*m大小的proposal,再把这些prorosal通过卷积成K(类别数)个维度**
26 |
27 |
28 |
29 | ### 2.3 ROI Align
30 |
31 | **roi-align是争对roi-pooling提出,roi-pooling会产生两次量化误差:**
32 |
33 | - **第一次是bbox在特征图位置的量化误差,例如图片大小为(225,225),特征图16倍下采样,那么坐标(x,y)在特征图为位置为(x * 16 / 255, y * 16 / 255),坐标会向下取整。**
34 |
35 | - **第二次是roi-pooling的时候会把bbox划分为n*n个bin,如下图所示,一个宽高为(7,5)大小的bbox,分成2 * 2大小的bin,由于不能整除,会按下图向上取整和向下取整的方式去划分:**
36 |
37 |
38 |
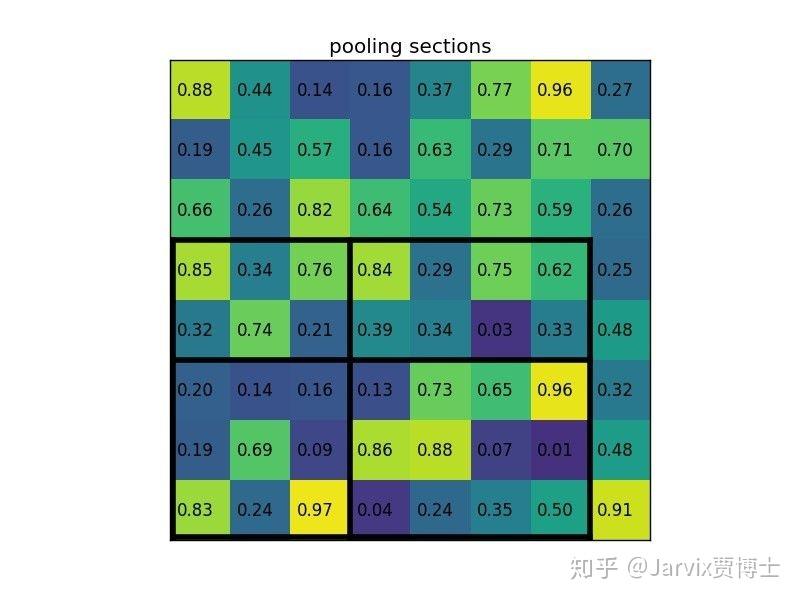
.
39 |
40 |
41 | **由于两次量化误差的存在随着下采样倍数的提升,误差偏差会变得非常大,如果是分类这类问题对位置信息不是很敏感可能体现的不是很明显,但是检测和分割这类问题对位置信息很敏感就会严重影响效果。因此提出了roi-align**
42 |
43 | **roi align就是也是利用roi pooling的思想,但是不进行量化取整,如下图所示:**
44 |
45 |
46 |

.
47 |
48 |
49 | - **在每个bin里面选取n个点(对应上图右边每个bin 4个蓝色的点)**
50 | - **然后再通过双线性插值求得这4个点的值**
51 | - **通过对n个bin里面的数值进行max pooling or avg pooling**
52 |
53 |
54 |
55 | ### 2.4 mask traget选取
56 |
57 | **在训练过程中mask target为roi与groud truth的交集,即只选取roi里面的mask的ground truth作为训练target。**
58 |
59 |
60 |
61 | ### 2.5 Inference
62 |
63 | **inference的时候不同于训练时仅用rpn部分产生的proposal经过mask分支,而是通过faster-rcnn最终输出的检测框作为mask分支的输入。最后仅选取类别分支输出的指定类别那一维度的mask。**
64 |
65 |
66 |
67 |
68 |
69 | ## 3.感想
70 |
71 | **看mask rcnn这篇论文的时间比较晚,虽然现在有各种花式网络各种新的技巧出现也丝毫不能影响mask rcnn在实例分割中的地位,添加mask分支、采用fpn、提出roi align,该文章的工作非常扎实实用,这种端对端的多任务学习也会在一定程度上对检测效果带来提升。**
--------------------------------------------------------------------------------
/分割篇/实例分割/readme.md:
--------------------------------------------------------------------------------
1 |
2 |
--------------------------------------------------------------------------------
/分割篇/语义分割/readme.md:
--------------------------------------------------------------------------------
1 |
2 |
--------------------------------------------------------------------------------
/分类篇/长尾效应/Bilateral-Branch Network with Cumulative Learning.md:
--------------------------------------------------------------------------------
1 |
2 |
3 | # Bilateral-Branch Network with Cumulative Learning-1
4 |
5 | ## 1.概述
6 |
7 | **这篇文章针对分类问题中的长尾效应设计了一个双分支网络,两份分支共享权重,但是输入的数据的分布相反。**
8 |
9 |
10 |

.
11 |
12 |
13 |
14 | ## 2.具体实现
15 |
16 | **如上图所示两个分支的结构是一样的权重共享,输入不一样,上面一个分支的输入是原始数据分布,下面一个分支的输入是原始分布的reverse版。其中通过一个变量a来控制两个分支的权重。**
17 |
18 |
19 |

.
20 |
21 |
22 | **a是根据训练阶段来动态改变的,具体公式如下:**
23 |
24 |
25 |

.
26 |
27 |
28 |
--------------------------------------------------------------------------------
/分类篇/长尾效应/DECOUPLING REPRESENTATION AND CLASSIFIER SRC - 副本.md:
--------------------------------------------------------------------------------
1 |
2 |
3 | # DECOUPLING REPRESENTATION AND CLASSIFIER
4 |
5 | ## 1.概述
6 |
7 | **目标分类过程中的长尾效应是一个很常见的问题,这篇文章通过试验发现类别较多的类特征权重值要大一些,类别较少的特征权重值要小一些。基于以上发现作责提出了一种特征归一化的方式来解决长尾效应问题。**
8 |
9 |
10 |

.
11 |
12 |
13 | ## 2.具体实现
14 |
15 | **常见的长尾效应解决方案有:**
16 |
17 | - **class-balancing strategies**
18 | - **loss re-weighting**
19 | - **data re-sampling**
20 | - **transfer learning**
21 |
22 | **Decoupling在上面基础上分为两步来解决长尾效应:**
23 |
24 | 1. **在长尾数据上训练一个分类模型,然后再fix住backbone,再利用Class-balanced sampling finetune 分类head,也可以利用渐近训练的方式,类别j的采样概率如下式所示:**
25 | $$
26 | \large p_{j}^{\mathrm{PB}}(t)=\left(1-\frac{t}{T}\right) \large p_{j}^{\mathrm{IB}}+\frac{t}{T} p_{j}^{\mathrm{CB}}, \\
27 | \large t为当前epoch,T为总epoch,p_{j}^{IB}为instance-balance采样概率,p_{j}^{CB}\\
28 | \large 为class-balance采样策略
29 | $$
30 |
31 |
32 | **采样公式为:**
33 | $$
34 | \large p_{j}=\frac{n_{j}^{q}}{\sum_{i=1}^{C} n_{i}^{q}}\\
35 | \large n_{j}^{q}为类别j的个数,C为类别数,q为参数,
36 | instance-sample时,q取1,class-sample时,q取0
37 | $$
38 |
39 | 2. 权重归一化
40 |
41 | 根据上图左半部分可以看到,样本数越多的类别权重会大一些,这样会使样本多的内别响应更大一些,样本数越小的类别权重会小一些。通过如下式进行权重归一化:
42 | $$
43 | \large \widetilde{w_{i}}=\frac{w_{i}}{\left\|w_{i}\right\|^{\tau}}
44 | $$
45 |
46 |
47 |
--------------------------------------------------------------------------------
/分类篇/长尾效应/DECOUPLING REPRESENTATION AND CLASSIFIER.md:
--------------------------------------------------------------------------------
1 |
2 |
3 | # DECOUPLING REPRESENTATION AND CLASSIFIER
4 |
5 | ## 1.概述
6 |
7 | **目标分类过程中的长尾效应是一个很常见的问题,这篇文章通过试验发现类别较多的类特征权重值要大一些,类别较少的特征权重值要小一些。基于以上发现作责提出了一种特征归一化的方式来解决长尾效应问题。**
8 |
9 |
10 |

.
11 |
12 |
13 | ## 2.具体实现
14 |
15 | **常见的长尾效应解决方案有:**
16 |
17 | - **class-balancing strategies**
18 | - **loss re-weighting**
19 | - **data re-sampling**
20 | - **transfer learning**
21 |
22 |
23 |

.
24 |
--------------------------------------------------------------------------------
/分类篇/长尾效应/readme.md:
--------------------------------------------------------------------------------
1 |
2 |
--------------------------------------------------------------------------------
/多任务篇/readme.md:
--------------------------------------------------------------------------------
1 |
2 |
--------------------------------------------------------------------------------
/多任务篇/yolop.md:
--------------------------------------------------------------------------------
1 |
2 |
3 | # You Only Look Once for Panoptic Driving Perception
4 |
5 | ## 1.概述
6 |
7 | **yolop是一个多任务学习框架,包含目标检测和车道线道路分割。**
8 |
9 |
10 |

.
11 |
12 |
13 |
14 |
15 | **图1**
16 |
17 | ## 2.具体实现
18 |
19 | ### 2.1. Bckbone:
20 |
21 | **Yolop的backbone为CSPDarknet**
22 |
23 |
24 |
25 | ### 2.2. Neck:
26 |
27 | **yolop的neck部分为FPN+SPP**
28 |
29 |
30 |
31 | ### 2.3. Head:
32 |
33 | #### 2.3.1 Detection Head
34 |
35 | **Detection Head与yolo4一样,添加了PANet module**
36 |
37 | #### 2.3.2 Segment Head
38 |
39 | **Segment Head是在FPN8倍下采样层基础上上采样至输入分辨率,输出两通道**
40 |
41 |
42 |
43 | ### 2.4 Loss
44 |
45 | #### 2.4.1 Det Loss
46 |
47 | **detection loss分为如下几部分**
48 |
49 | - **class loss 采用focal loss**
50 | - **obj loss采用focal loss**
51 | - **box loss采用CIOU loss**
52 |
53 | #### 2.4.2 Segment loss
54 |
55 | **segment loss采用ce loss + iou loss**
56 |
57 |
58 |
59 | ## 3.总结
60 |
61 | **yolop属于一个组合式的论文整体没有什么创新,一个典型的多任务学习范式,应该很多人都尝试过这种方法,可能别人是在retinanet、efficientdet等基础上进行多任务学习。工程属性还是很强的,看试验结果在Jetson TX2上运行时间可以达到24ms/fps(没找到输入是多大)**
62 |
63 |
64 |
65 |
--------------------------------------------------------------------------------
/目标检测篇/Anchor-Base/one-stage/EfficientDet-SRC.md:
--------------------------------------------------------------------------------
1 |
2 |
3 | # EfficientDet
4 |
5 | ## 1.概述
6 |
7 | **EfficientDet主要从FPN的结构出发,分析了不同种类的FPN网络结构,提出BIFPN的网络结构在提高检测精度的同时也能提升检测速度。作者观察到 PANet 的效果比 FPN ,NAS-FPN 要好,就是计算量更大;作者从 PANet 出发:**
8 |
9 | - **移除掉了只有一个输入的节点。这样做是假设只有一个输入的节点相对不太重要。这样把 PANet 简化。**
10 | - **在相同 level 的输入和输出节点之间连了一条边,假设是能融合更多特征,有点 skip-connection 的意味**。
11 | - **PANet 只有从底向上连,自顶向下两条路径,作者认为这种连法可以作为一个基础层,重复多次。**
12 |
13 |
14 |
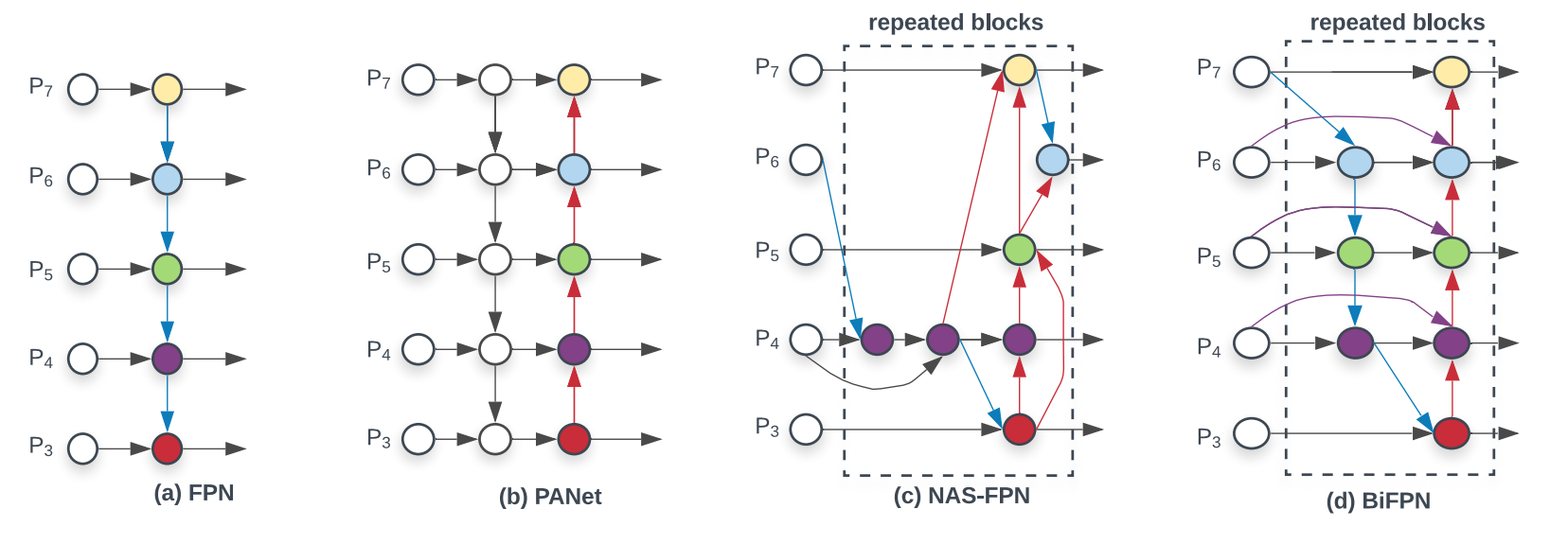
.
15 |
16 |
17 |
18 | **图1**
19 |
20 | ## 2.具体实现
21 |
22 | ### 2.1. Bckbone:
23 |
24 | **EfficientDet的主干网络为EfficientNet,EfficientNet的网络性能如下图所示:**
25 |
26 |
27 |
28 |
29 |

.
30 |
31 |
32 |
33 | **图2**
34 |
35 | ### 2.2. Neck:
36 |
37 | **EfficientDet的Neck部分为BIFPN,BIFPN的机构如图1(d)所示,多层BIFPN的网路结构如下图所示:**
38 |
39 |
40 |
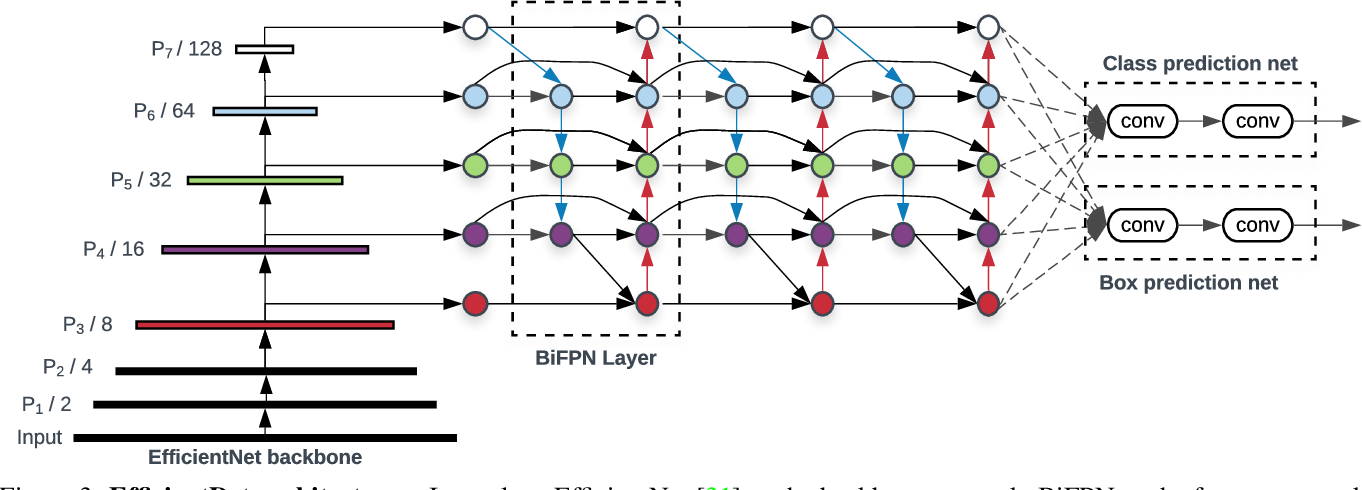
.
41 |
42 |
43 | 图3
44 | $$
45 | \large BIFPN名称双向特征金字塔,主要思想是学习一个可学的标量 w_{i} 来加权每一个FPN层,作者认为不同输入对应的FPN层重要程度不一样。\\
46 | \large 如果对每一个FPN分支仅学习一个权重,那么这个权重是不可控的(比如极大或则极小),\\
47 | \large 导致学习过程不可控。一个自然的想法是用softmax归一化,但是softmax函数很耗时,\\
48 | \large 所以用了如下结构替换:\\
49 | \large O=\sum_{i} \frac{w_{i}}{\epsilon+\sum_{j} w_{j}} \cdot I_{i}
50 | \large I_{i}为特征图
51 | $$
52 | **以P6特征为例。BIFPN的表达式如下**:
53 | $$
54 | \begin{aligned}
55 | \large P_{6}^{t d} &=\operatorname{Con} v\left(\frac{w_{1} \cdot P_{6}^{i n}+w_{2} \cdot \operatorname{Resize}\left(P_{7}^{i n}\right)}{w_{1}+w_{2}+\epsilon}\right) \\
56 | \large P_{6}^{\text {out }} &=\operatorname{Conv}\left(\frac{w_{1}^{\prime} \cdot P_{6}^{i n}+w_{2}^{\prime} \cdot P_{6}^{t d}+w_{3}^{\prime} \cdot \text { Resize }\left(P_{5}^{\text {out }}\right)}{w_{1}^{\prime}+w_{2}^{\prime}+w_{3}^{\prime}+\epsilon}\right)
57 | \end{aligned}\\
58 | \large P_{6}^{t d}是P_{6}的中间特征。
59 | $$
60 |
61 | $$
62 | \large BIFPN宽度: W_{bifpn}=64*(1.35^φ),φ表示Efficient的深度(D0,D1,D2...D7).\\
63 | \large BIFPN深度: D_{bifpn}=3+φ \\
64 | \large Box/class prediction network宽度:W_{pred} = W_{bifpn}.\\
65 | \large Box/class prediction network深度:D_{\text {box }}=D_{\text {class }}=3+\lfloor\phi / 3\rfloor
66 | $$
67 |
68 | ```
69 | # Weight
70 | self.p6_w1 = nn.Parameter(torch.ones(2, dtype=torch.float32), requires_grad=True)
71 | self.p6_w1_relu = nn.ReLU()
72 | self.p5_w1 = nn.Parameter(torch.ones(2, dtype=torch.float32), requires_grad=True)
73 | self.p5_w1_relu = nn.ReLU()
74 | self.p4_w1 = nn.Parameter(torch.ones(2, dtype=torch.float32), requires_grad=True)
75 | self.p4_w1_relu = nn.ReLU()
76 | self.p3_w1 = nn.Parameter(torch.ones(2, dtype=torch.float32), requires_grad=True)
77 | self.p3_w1_relu = nn.ReLU()
78 |
79 | self.p4_w2 = nn.Parameter(torch.ones(3, dtype=torch.float32), requires_grad=True)
80 | self.p4_w2_relu = nn.ReLU()
81 | self.p5_w2 = nn.Parameter(torch.ones(3, dtype=torch.float32), requires_grad=True)
82 | self.p5_w2_relu = nn.ReLU()
83 | self.p6_w2 = nn.Parameter(torch.ones(3, dtype=torch.float32), requires_grad=True)
84 | self.p6_w2_relu = nn.ReLU()
85 | self.p7_w2 = nn.Parameter(torch.ones(2, dtype=torch.float32), requires_grad=True)
86 | self.p7_w2_relu = nn.ReLU()
87 |
88 | self.attention = attention
89 |
90 |
91 | P7_0 -------------------------> P7_2 -------->
92 | |-------------| ↑
93 | ↓ |
94 | P6_0 ---------> P6_1 ---------> P6_2 -------->
95 | |-------------|--------------↑ ↑
96 | ↓ |
97 | P5_0 ---------> P5_1 ---------> P5_2 -------->
98 | |-------------|--------------↑ ↑
99 | ↓ |
100 | P4_0 ---------> P4_1 ---------> P4_2 -------->
101 | |-------------|--------------↑ ↑
102 | |--------------↓ |
103 | P3_0 -------------------------> P3_2 -------->
104 | """
105 | ```
106 |
107 |
108 |
109 | ### 2.3. Head:
110 |
111 | **EfficientDet的Head部分跟RetinaNet一样分为cls和reg两部分,如图3所示**
112 |
113 |
114 |
115 | ### 2.4. Sample Assignment:
116 |
117 | **EfficientDet的Sample Assignment跟RetinaNet方式一样,t把iou < 0.4作为负样本, > 0.5作为正样本,其余为难例忽略。**
118 |
119 |
120 |
121 | ### 2.5. Anchor生成
122 |
123 | **EfficientDet的anchor生成跟RetinaNet一样:**
124 |
125 | - **ratios:[0.5,1,2]**
126 | - **scales:[[2^0, 2^(1.0 / 3.0), 2^(2.0 / 3.0)]]**
127 |
128 |
129 |
130 | ### 2.6. Decode部分:
131 |
132 | **EfficientDet decode部分跟[ssd decode部分一样](https://github.com/Hanson0910/DL-Algorithm-Summary/blob/main/%E7%9B%AE%E6%A0%87%E6%A3%80%E6%B5%8B%E7%AF%87/Anchor-Base/one-stage/SSD.md)**
133 |
134 |
135 |
136 | ### 2.7. LOSS部分:
137 |
138 | **retinanet把iou < 0.4作为负样本, > 0.5作为正样本,其余为难例忽略,分类loss用focal loss,回归loss用smooth-L1 loss。分类loss计算代码。**
139 |
140 | **focal loss部分会在分类loss部分单独总结。**
141 |
142 |
143 |
144 |
145 |
146 |
--------------------------------------------------------------------------------
/目标检测篇/Anchor-Base/one-stage/EfficientDet.md:
--------------------------------------------------------------------------------
1 |
2 |
3 | # EfficientDet
4 |
5 | ## 1.概述
6 |
7 | **EfficientDet主要从FPN的结构出发,分析了不同种类的FPN网络结构,提出BIFPN的网络结构在提高检测精度的同时也能提升检测速度。作者观察到 PANet 的效果比 FPN ,NAS-FPN 要好,就是计算量更大;作者从 PANet 出发:**
8 |
9 | - **移除掉了只有一个输入的节点。这样做是假设只有一个输入的节点相对不太重要。这样把 PANet 简化。**
10 | - **在相同 level 的输入和输出节点之间连了一条边,假设是能融合更多特征,有点 skip-connection 的意味**。
11 | - **PANet 只有从底向上连,自顶向下两条路径,作者认为这种连法可以作为一个基础层,重复多次。**
12 |
13 |
14 |

.
15 |
16 |
17 |
18 | **图1**
19 |
20 | ## 2.具体实现
21 |
22 | ### 2.1. Bckbone:
23 |
24 | **EfficientDet的主干网络为EfficientNet,EfficientNet的网络性能如下图所示:**
25 |
26 |
27 |
28 |
29 |

.
30 |
31 |
32 |
33 | **图2**
34 |
35 | ### 2.2. Neck:
36 |
37 | **EfficientDet的Neck部分为BIFPN,BIFPN的机构如图1(d)所示,多层BIFPN的网路结构如下图所示:**
38 |
39 |
40 |

.
41 |
42 |
43 | 图3
44 |
45 |
46 |
47 | **以P6特征为例。BIFPN的表达式如下**:
48 |
49 |
50 |

.
51 |
52 |
53 |
54 |

.
55 |
56 |
57 | ```
58 | # Weight
59 | self.p6_w1 = nn.Parameter(torch.ones(2, dtype=torch.float32), requires_grad=True)
60 | self.p6_w1_relu = nn.ReLU()
61 | self.p5_w1 = nn.Parameter(torch.ones(2, dtype=torch.float32), requires_grad=True)
62 | self.p5_w1_relu = nn.ReLU()
63 | self.p4_w1 = nn.Parameter(torch.ones(2, dtype=torch.float32), requires_grad=True)
64 | self.p4_w1_relu = nn.ReLU()
65 | self.p3_w1 = nn.Parameter(torch.ones(2, dtype=torch.float32), requires_grad=True)
66 | self.p3_w1_relu = nn.ReLU()
67 |
68 | self.p4_w2 = nn.Parameter(torch.ones(3, dtype=torch.float32), requires_grad=True)
69 | self.p4_w2_relu = nn.ReLU()
70 | self.p5_w2 = nn.Parameter(torch.ones(3, dtype=torch.float32), requires_grad=True)
71 | self.p5_w2_relu = nn.ReLU()
72 | self.p6_w2 = nn.Parameter(torch.ones(3, dtype=torch.float32), requires_grad=True)
73 | self.p6_w2_relu = nn.ReLU()
74 | self.p7_w2 = nn.Parameter(torch.ones(2, dtype=torch.float32), requires_grad=True)
75 | self.p7_w2_relu = nn.ReLU()
76 |
77 | self.attention = attention
78 |
79 |
80 | P7_0 -------------------------> P7_2 -------->
81 | |-------------| ↑
82 | ↓ |
83 | P6_0 ---------> P6_1 ---------> P6_2 -------->
84 | |-------------|--------------↑ ↑
85 | ↓ |
86 | P5_0 ---------> P5_1 ---------> P5_2 -------->
87 | |-------------|--------------↑ ↑
88 | ↓ |
89 | P4_0 ---------> P4_1 ---------> P4_2 -------->
90 | |-------------|--------------↑ ↑
91 | |--------------↓ |
92 | P3_0 -------------------------> P3_2 -------->
93 | """
94 | ```
95 |
96 |
97 |
98 | ### 2.3. Head:
99 |
100 | **EfficientDet的Head部分跟RetinaNet一样分为cls和reg两部分,如图3所示**
101 |
102 |
103 |
104 | ### 2.4. Sample Assignment:
105 |
106 | **EfficientDet的Sample Assignment跟RetinaNet方式一样,把iou < 0.4作为负样本, > 0.5作为正样本,其余为难例忽略。**
107 |
108 |
109 |
110 | ### 2.5. Anchor生成
111 |
112 | **EfficientDet的anchor生成跟RetinaNet一样:**
113 |
114 | - **ratios:[0.5,1,2]**
115 | - **scales:[[2^0, 2^(1.0 / 3.0), 2^(2.0 / 3.0)]]**
116 |
117 |
118 |
119 | ### 2.6. Decode部分:
120 |
121 | **EfficientDet decode部分跟[ssd decode部分一样](https://github.com/Hanson0910/DL-Algorithm-Summary/blob/main/%E7%9B%AE%E6%A0%87%E6%A3%80%E6%B5%8B%E7%AF%87/Anchor-Base/one-stage/SSD.md)**
122 |
123 |
124 |
125 | ### 2.7. LOSS部分:
126 |
127 | **retinanet把iou < 0.4作为负样本, > 0.5作为正样本,其余为难例忽略,分类loss用focal loss,回归loss用smooth-L1 loss。分类loss计算代码。**
128 |
129 | **focal loss部分会在分类loss部分单独总结。**
130 |
131 |
132 |
133 |
134 |
135 |
--------------------------------------------------------------------------------
/目标检测篇/Anchor-Base/one-stage/GHM-SRC.md:
--------------------------------------------------------------------------------
1 |
2 |
3 | # **Gradient Harmonized Single-stage Detector**
4 |
5 | ## 1.概述
6 |
7 | **Gradient Harmonized Single-stage Detector分析了一阶段目标检测器样本不均问题,认为大量简单的背景占领了整了训练过程,同时对比了OHEM和Focal Loss,认为OHEM直接放弃那些简单样本,这样效率是很低的;同时Focal Loss需要tune两个参数,并且Focal Loss是一个静态loss,不能适应数据的动态分布。作者提出l gradient harmonizing mechanism(GHM)--梯度协调机制,动态改变个样本梯度,降低简单样本和极难例的样本梯度,增加medium样本的梯度。**
8 |
9 |
10 |

.
11 |
12 |
13 |
14 | **图1**
15 |
16 | ## 2.具体实现
17 |
18 | ### 2.1 问题描述
19 |
20 | **ce loss为:**
21 | $$
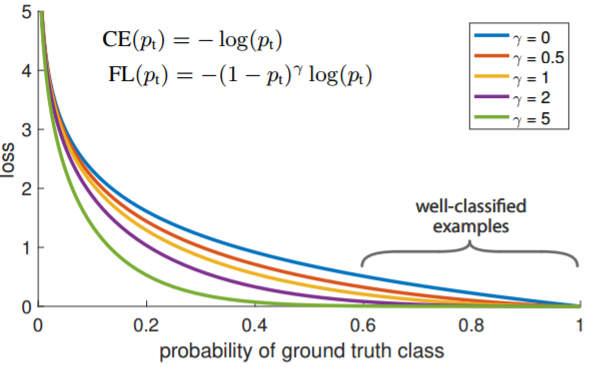
22 | \large L_{CE}(p,p^{*})= \begin{cases} - \log (p)ifp^{*}=1 \\\\ - \log (1-p)ifp^{*}=0 \end{cases}\\
23 | \large p \in \left[ 0,1 \right] 为预测概率,这里p = sigmoid(x),p ^ { * } \in \{ 0,1 \} 为ground-truth,
24 | $$
25 |
26 |
27 | **求导为:**
28 | $$
29 | \large L_{C E}\left(p, p^{*}\right)= \begin{cases}-\log (p) & \text { if } p^{*}=1 \\ -\log (1-p) & \text { if } p^{*}=0\end{cases}
30 | $$
31 |
32 |
33 | $$
34 | \large g=\left|p-p^{*}\right|= \begin{cases}1-p & \text { if } p^{*}=1 \\ p & \text { if } p^{*}=0\end{cases}
35 | $$
36 | ***g* 为梯度的L1 范数,代表该样本该样本的贡献大小。**
37 |
38 |
39 |

.
40 |
41 |
42 | **如上图所示,为了更加清楚显示坐标轴经过log函数,可以看出大量easy-sample贡献了绝大部分梯度,还有一部分very-hard-sample贡献比较多的梯度,这些very-hard-sample可能是一些异常值,如果收敛模型被迫学习那些异常值可能对其它例子的分类不那么准确。为此提出了Gradient Density的概念**
43 |
44 |
45 |
46 | ### 2.2 Gradient Density
47 |
48 | $$
49 | \large G D ( g ) = \frac { 1 } { l _ { \epsilon } ( g ) } \sum _ { k = 1 } ^ { N } \delta _ { \epsilon } ( g _ { k } , g )\\
50 | \large g_k表示第k个样本的梯度,N表示样本的个数
51 | $$
52 |
53 | $$
54 | \begin{aligned}
55 | &\delta_{\epsilon}(x, y)= \begin{cases}1 & \text { if } y-\frac{\epsilon}{2}<=x
77 |  .
78 |
.
78 |
79 |
80 | **从上图可以看出GHM-C能够把easy-sample和very-hard-sample的梯度个将下来,其实focal-loss也可以,但是focal-loss对very-hard-sample好像没辙。**
81 |
82 |
83 |
84 | ### 2.4 Unit Region Approximation
85 |
86 | $$
87 | \large 2.3中的计算量太大,为log(N^2),所以采用近似计算的方式。\\
88 | \large 把区间\epsilon分成M份,每一份的长度为\epsilon,此时的\epsilon不是原先的\epsilon。
89 | \large \\M=\frac {1}{\epsilon} \\
90 | \large r_{j}是索引为j的uint \quad reign \quad r_{j}=[(j-1) \epsilon, j \epsilon)\\
91 | \large R_{j}表示在r_{j}区间内的样本数,\operatorname{ind}(g)=t \text { s.t. }(t-1) \epsilon<=g
 72 |
72 |  99 |
99 |  62 |
62 |  84 |
84 |  147 |
147 |  162 |
162 |  92 |
92 |  105 |
105 |  9 |
9 |  63 |
63 |  67 |
67 |  9 |
9 |  61 |
61 |  65 |
65 |  18 |
18 |  64 |
64 |  90 |
90 |  125 |
125 |  155 |
155 |  17 |
17 |  53 |
53 |  80 |
80 |  113 |
113 |  141 |
141 |  .
39 |
.
39 |  .
47 |
.
47 |  .
15 |
.
15 |  .
30 |
.
30 |  .
41 |
.
41 |  .
15 |
.
15 |  .
30 |
.
30 |  .
41 |
.
41 |  13 |
13 | 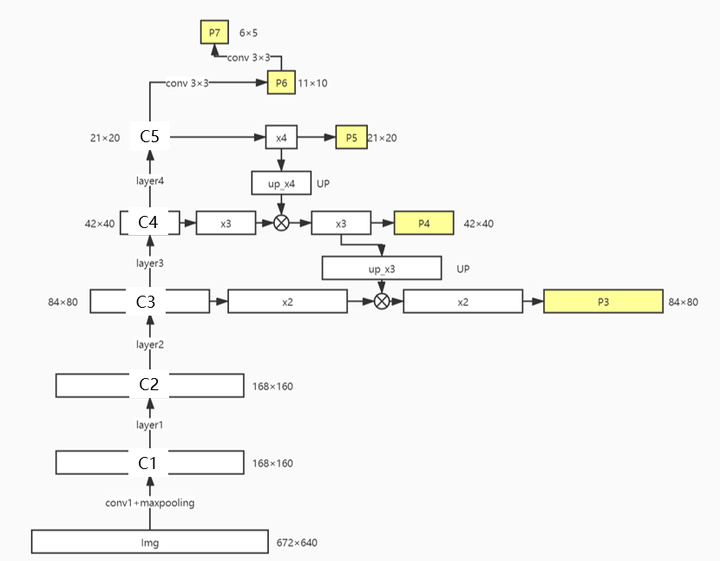 25 |
25 | 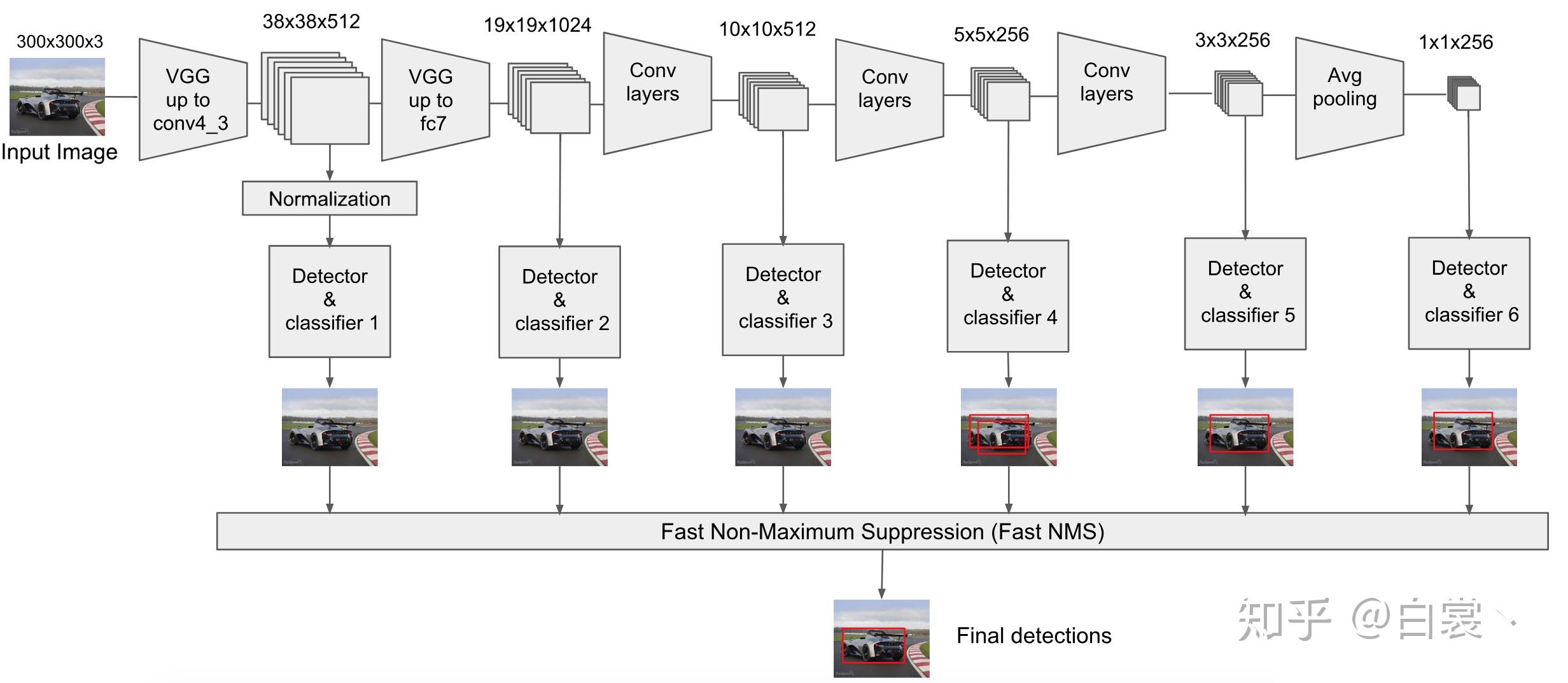 13 |
13 | 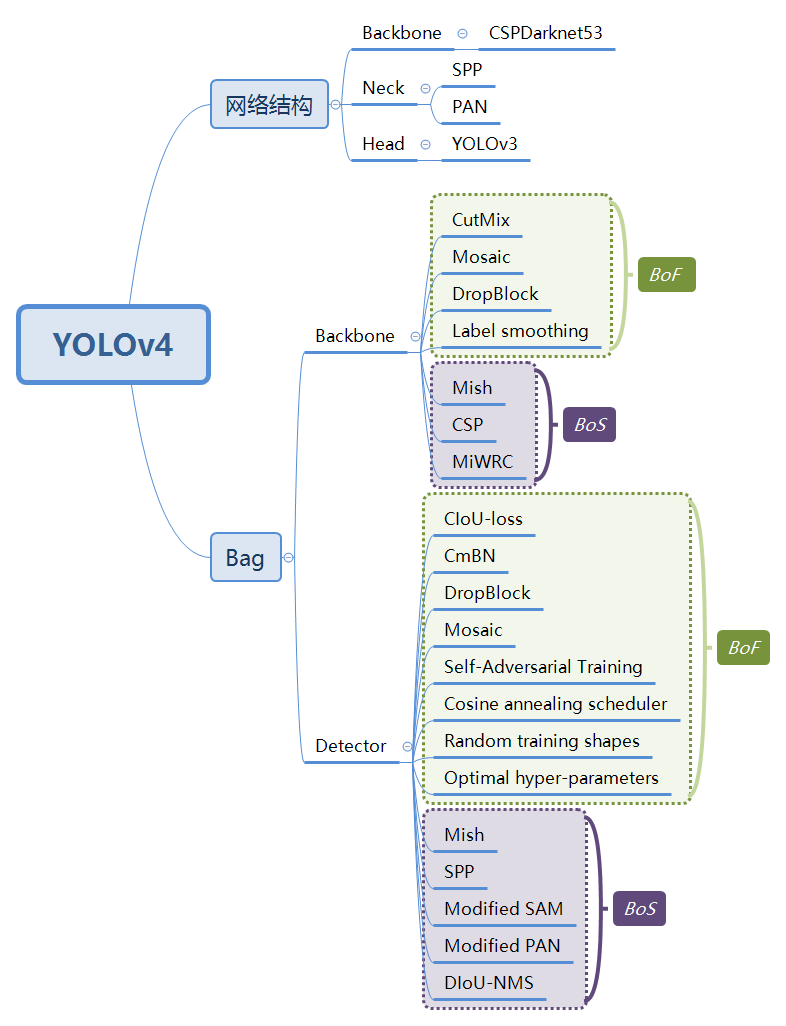 14 |
14 | 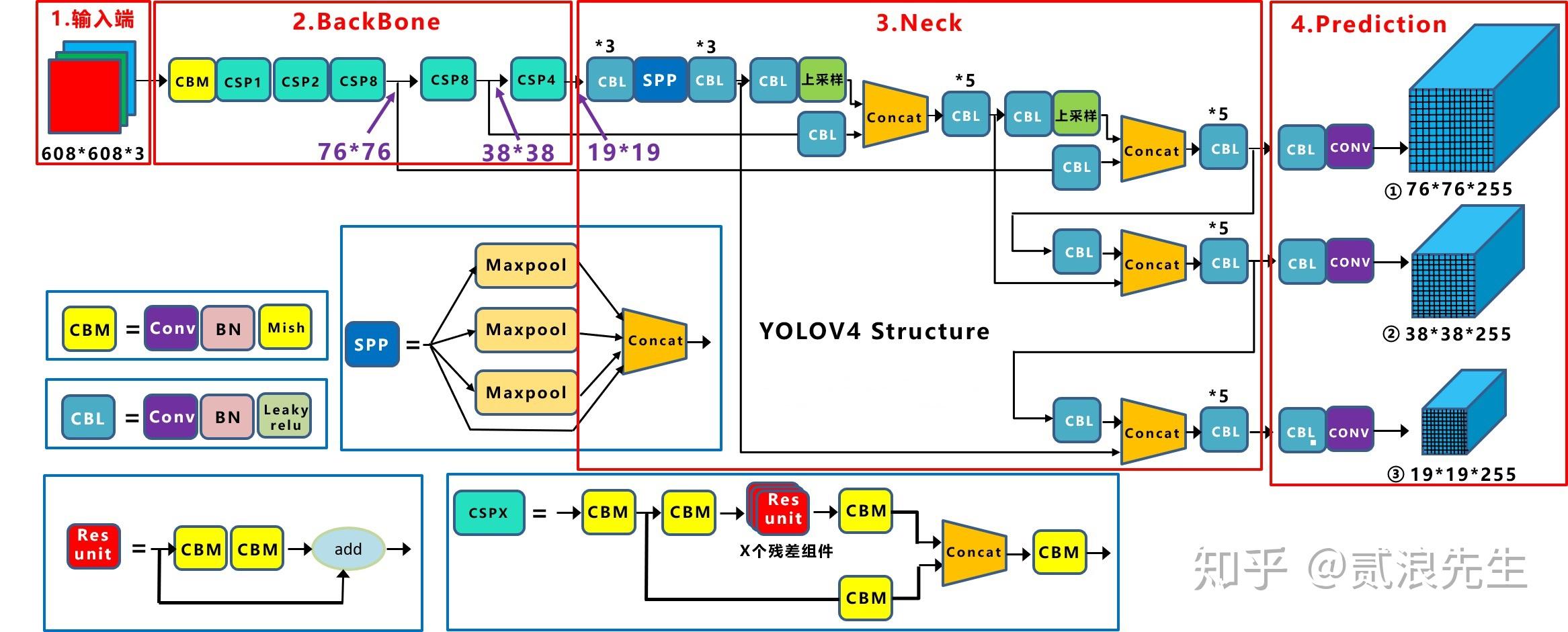 22 |
22 | 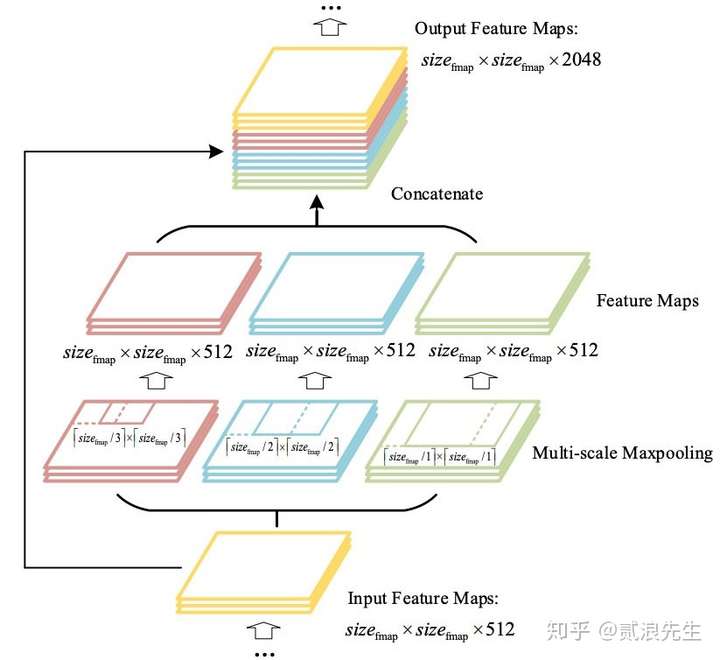 56 |
56 | 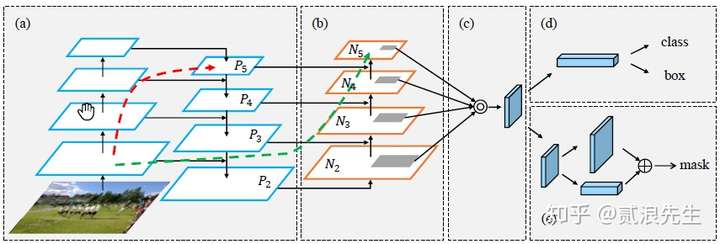 64 |
64 | 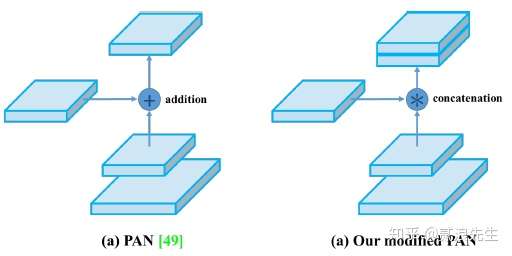 70 |
70 |  82 |
82 |  88 |
88 | 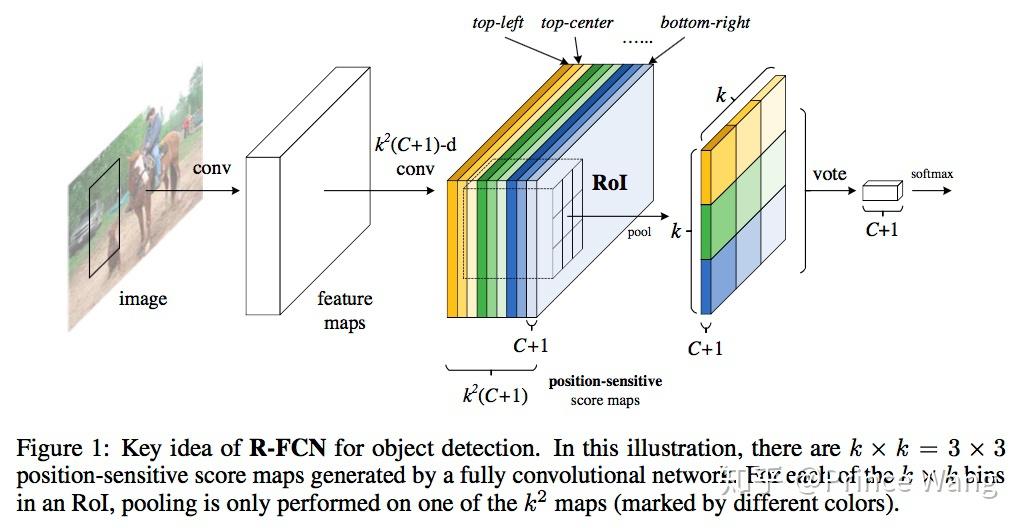 9 |
9 | 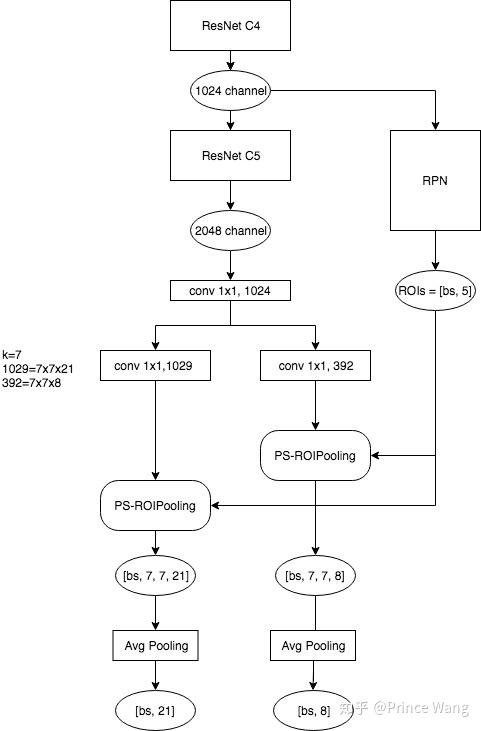 34 |
34 | 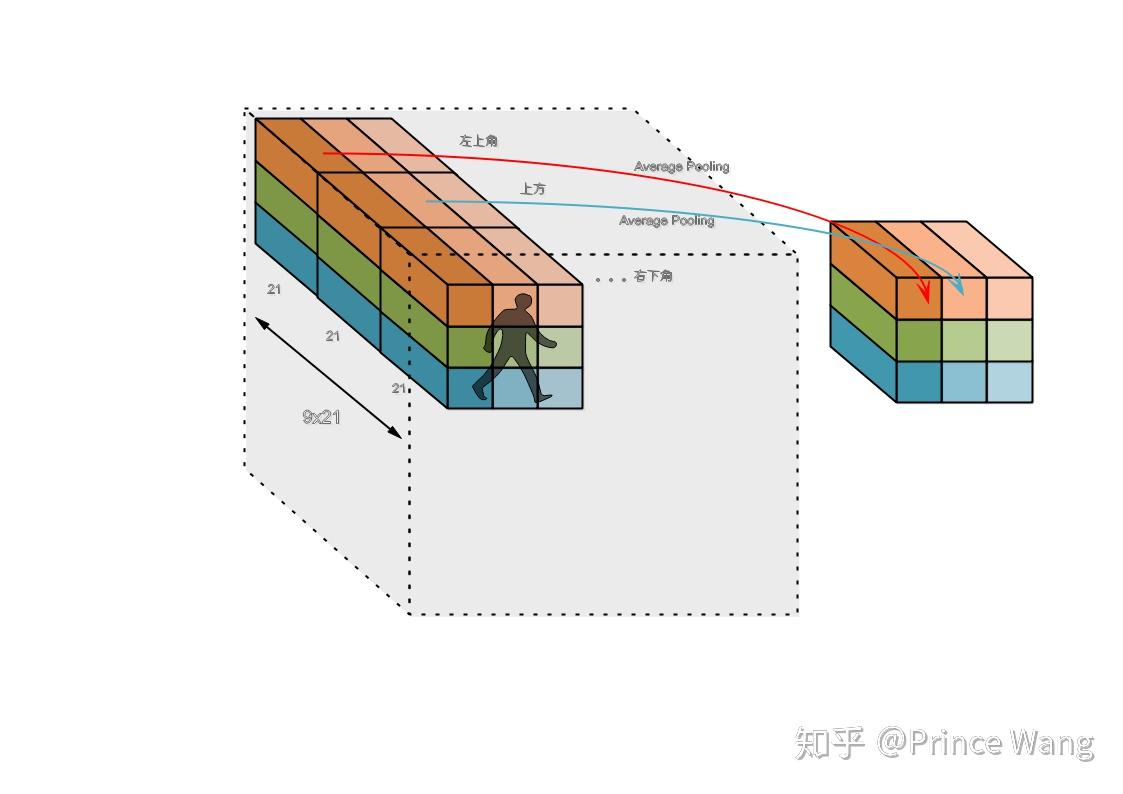 44 |
44 | 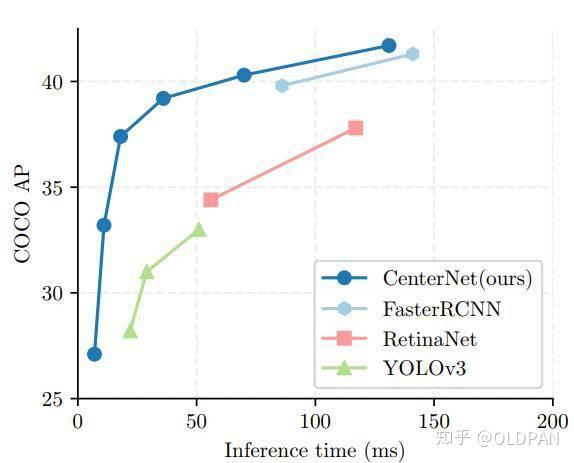 9 |
9 |  9 |
9 |  9 |
9 |  9 |
9 | 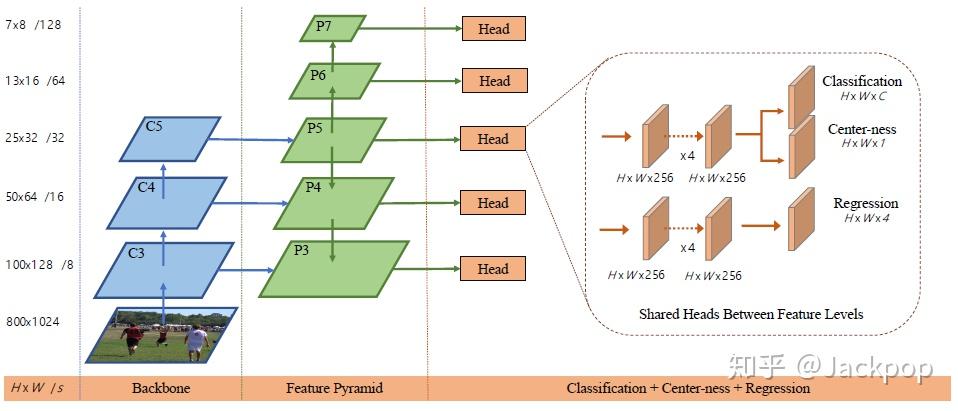 9 |
9 |  9 |
9 |  9 |
9 | 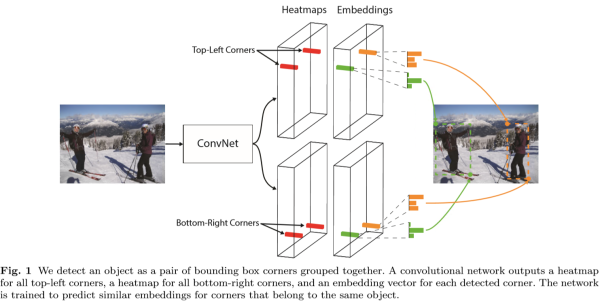 9 |
9 | 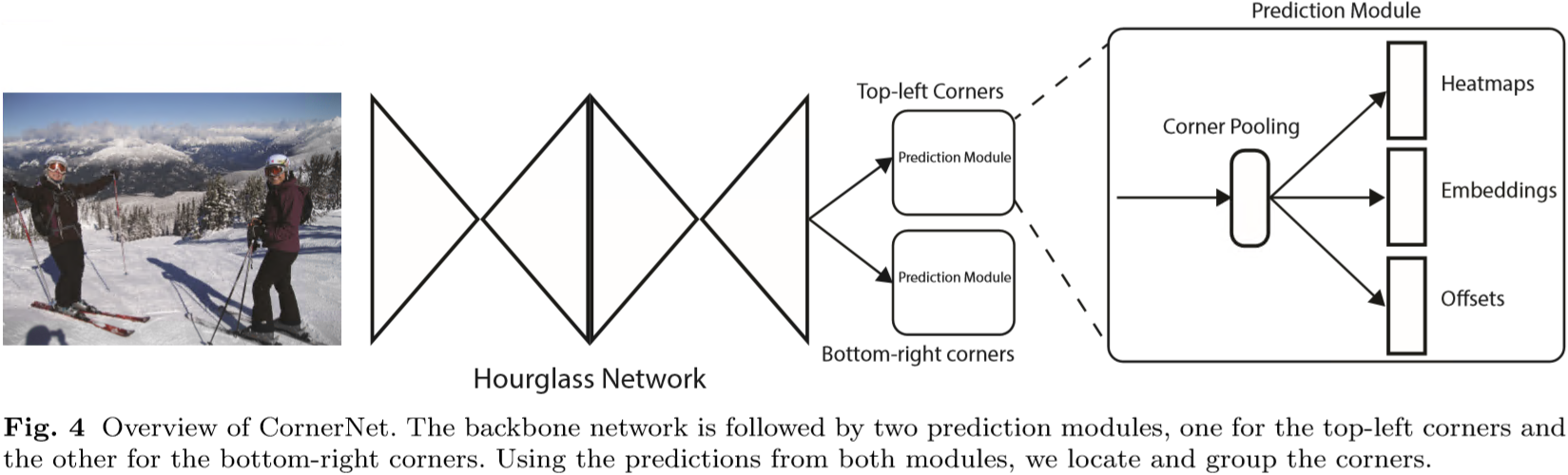 21 |
21 | 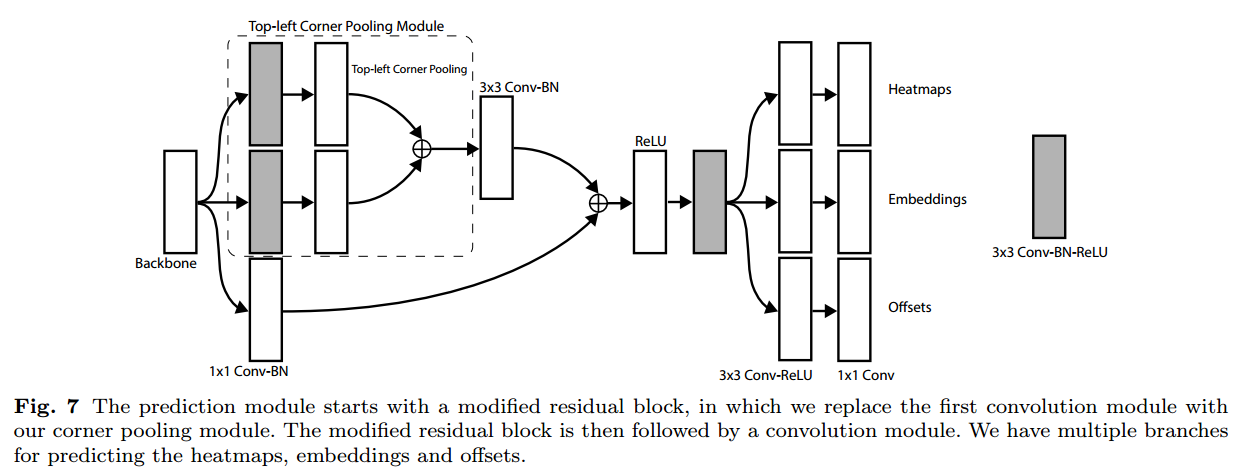 45 |
45 |  53 |
53 | 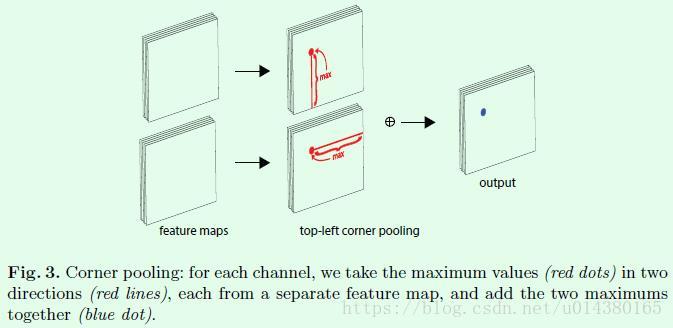 63 |
63 |  73 |
73 | 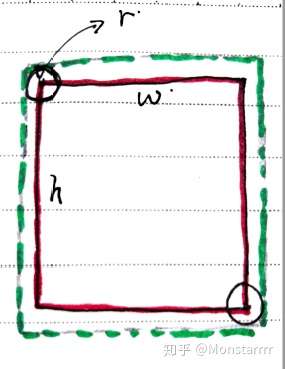 81 |
81 | 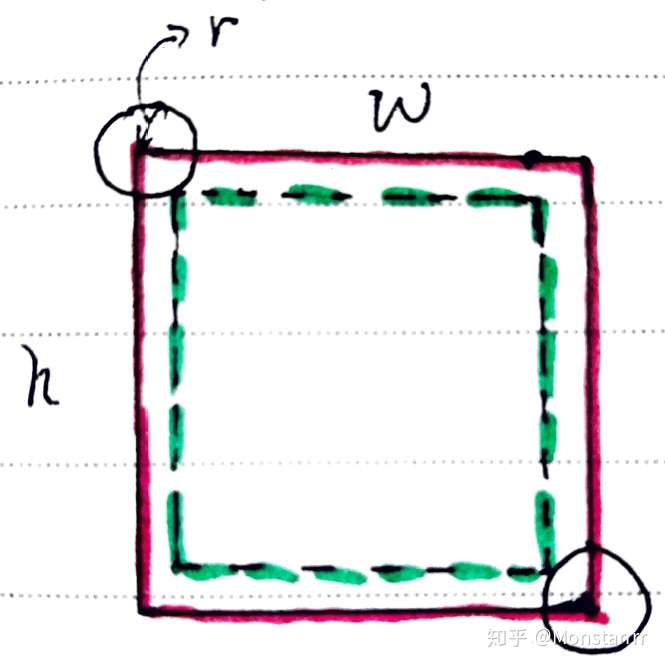 93 |
93 | 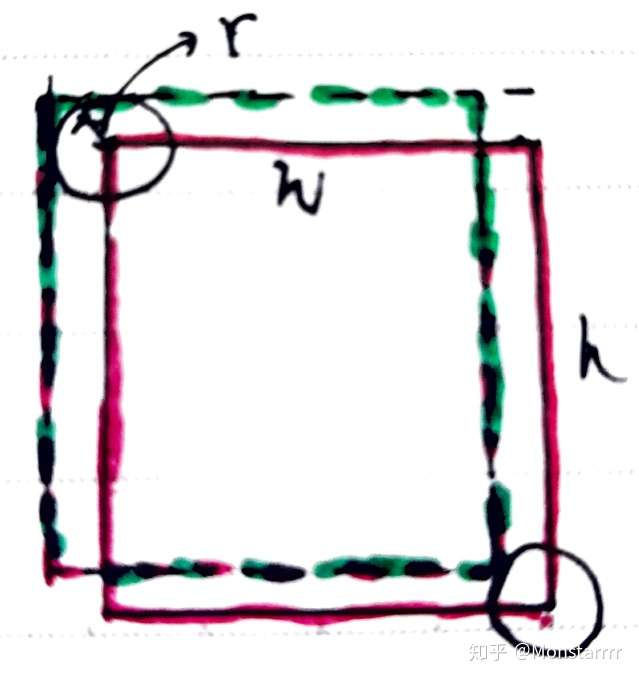 104 |
104 |  9 |
9 |  21 |
21 |  45 |
45 |  53 |
53 |  63 |
63 |  73 |
73 |  81 |
81 |  91 |
91 |  102 |
102 | 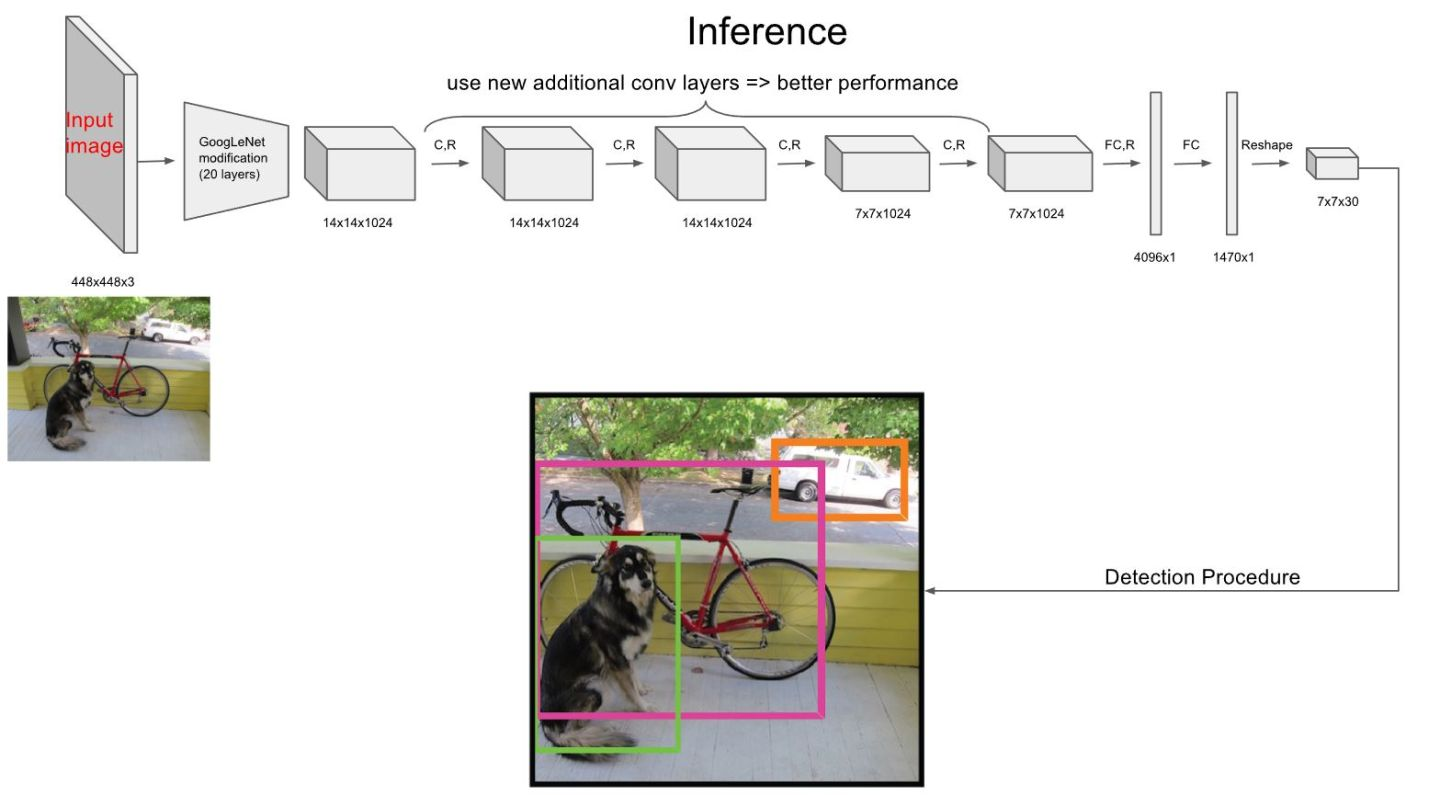 9 |
9 | 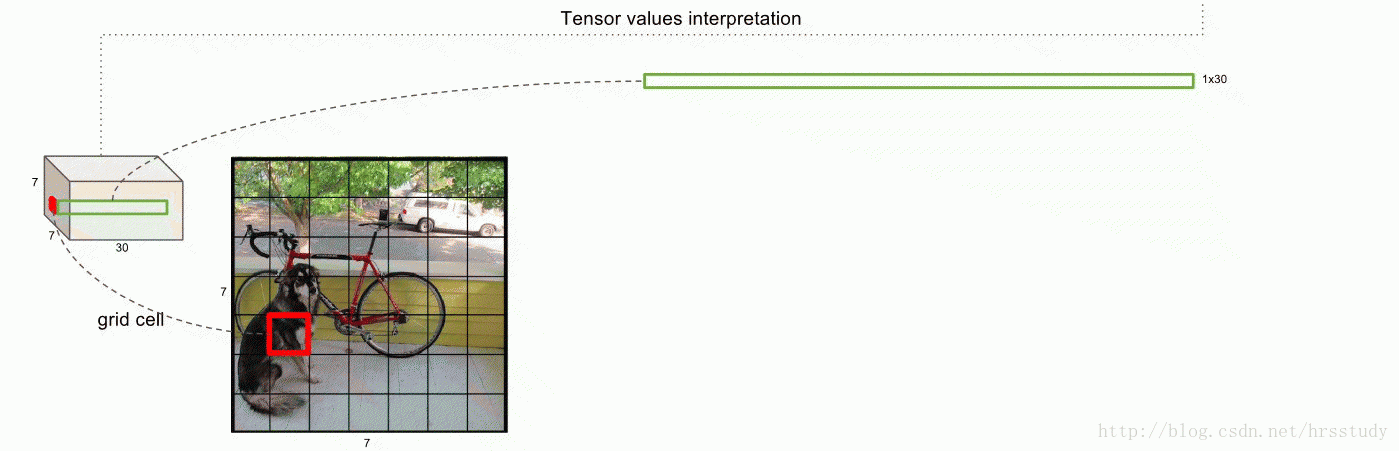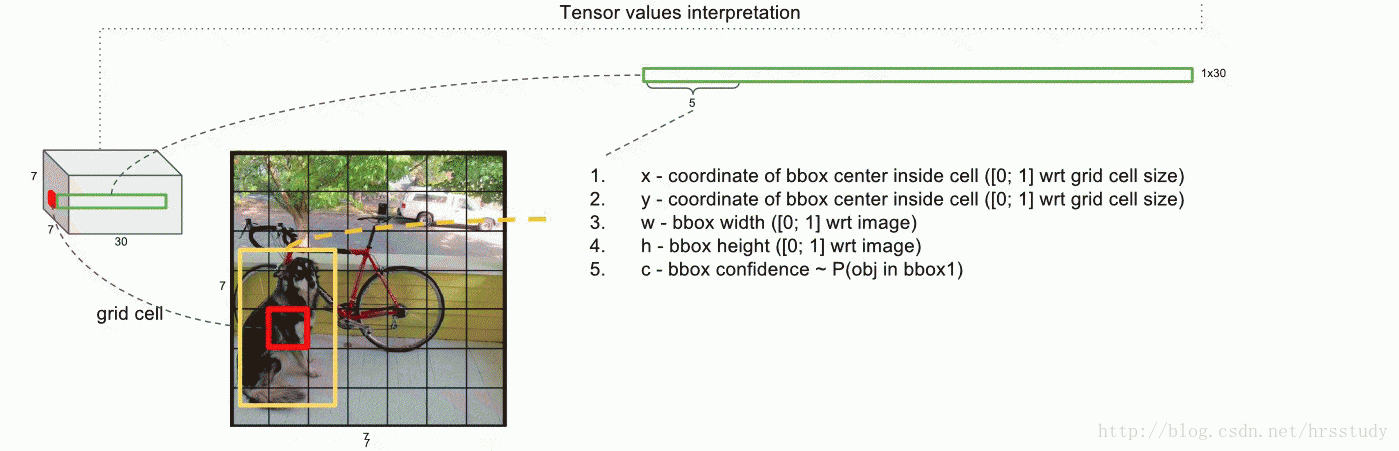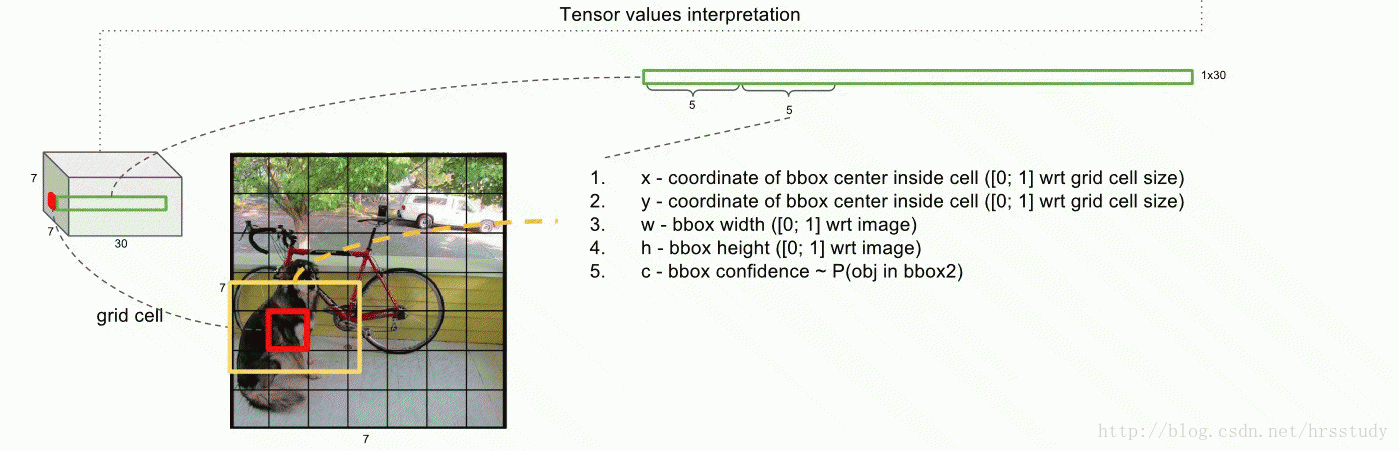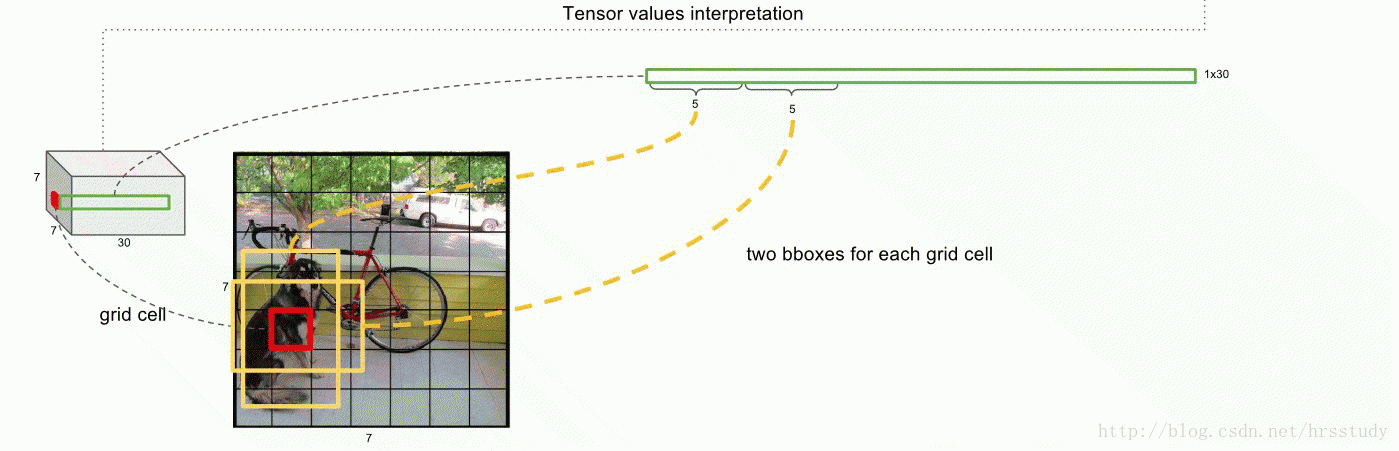 36 |
36 |  48 |
48 |