├── 00_atari_dqn.py
├── 01_dqn.py
├── 02_ddqn.py
├── 03_priority_replay.py
├── 04_dueling.py
├── 05_multistep_td.py
├── 06_distributional_rl.py
├── 07_noisynet.py
├── README.md
├── images
├── ddqn.png
├── distributional_algorithm2.png
├── distributional_learn.png
├── distributional_project.png
├── distributional_projected.png
├── distributional_rl.png
├── dqn.png
├── dqn_algorithm.png
├── dqn_net.png
├── dueling_detail.png
├── dueling_details.png
├── dueling_netarch.png
├── gym_cartpole_v0.gif
├── noisy_net_algorithm.png
├── p2.png
├── rlblog_images
│ ├── IS.jpg
│ ├── LSTM.png
│ ├── PPO.png
│ ├── README.md
│ ├── RNN-unrolled.png
│ ├── ppo.png
│ ├── r1.png
│ └── r2.png
└── sards.png
└── tutorial_blogs
├── Building_Rainbow_Step_by_Step_with_TensorFlow2.0.md
└── gym_tutorial.md
/00_atari_dqn.py:
--------------------------------------------------------------------------------
1 | """
2 | Deep Q-Network(DQN) for Atari Game, which has convolutional layers to handle images input and other preprocessings.
3 |
4 | Using:
5 | TensorFlow 2.0
6 | Numpy 1.16.2
7 | Gym 0.12.1
8 | """
9 |
10 | import tensorflow as tf
11 | print(tf.__version__)
12 |
13 | import gym
14 | import time
15 | import numpy as np
16 | import tensorflow.keras.layers as kl
17 | import tensorflow.keras.optimizers as ko
18 |
19 | np.random.seed(1)
20 | tf.random.set_seed(1)
21 |
22 | # Minor change from cs234:reinforcement learning, assignment 2 -> utils/preprocess.py
23 | def greyscale(state):
24 | """
25 | Preprocess state (210, 160, 3) image into
26 | a (80, 80, 1) image in grey scale
27 | """
28 | state = np.reshape(state, [210, 160, 3]).astype(np.float32)
29 | # grey scale
30 | state = state[:, :, 0] * 0.299 + state[:, :, 1] * 0.587 + state[:, :, 2] * 0.114
31 | # karpathy
32 | state = state[35:195] # crop
33 | state = state[::2,::2] # downsample by factor of 2
34 | state = state[:, :, np.newaxis]
35 | return state.astype(np.float32)
36 |
37 |
38 | class Model(tf.keras.Model):
39 | def __init__(self, num_actions):
40 | super().__init__(name='dqn')
41 | self.conv1 = kl.Conv2D(32, kernel_size=(8, 8), strides=4, activation='relu')
42 | self.conv2 = kl.Conv2D(64, kernel_size=(4, 4), strides=2, activation='relu')
43 | self.conv3 = kl.Conv2D(64, kernel_size=(3, 3), strides=1, activation='relu')
44 | self.flat = kl.Flatten()
45 | self.fc1 = kl.Dense(512, activation='relu')
46 | self.fc2 = kl.Dense(num_actions)
47 |
48 | def call(self, inputs):
49 | # x = tf.convert_to_tensor(inputs, dtype=tf.float32)
50 | x = self.conv1(inputs)
51 | x = self.conv2(x)
52 | x = self.conv3(x)
53 | x = self.flat(x)
54 | x = self.fc1(x)
55 | x = self.fc2(x)
56 | return x
57 |
58 | def action_value(self, obs):
59 | q_values = self.predict(obs)
60 | best_action = np.argmax(q_values, axis=-1)
61 | return best_action[0], q_values[0]
62 |
63 |
64 | class DQNAgent:
65 | def __init__(self, model, target_model, env, buffer_size=1000, learning_rate=.001, epsilon=.1, gamma=.9,
66 | batch_size=4, target_update_iter=20, train_nums=100, start_learning=10):
67 | self.model = model
68 | self.target_model = target_model
69 | self.model.compile(optimizer=ko.Adam(), loss='mse')
70 |
71 | # parameters
72 | self.env = env # gym environment
73 | self.lr = learning_rate # learning step
74 | self.epsilon = epsilon # e-greedy when exploring
75 | self.gamma = gamma # discount rate
76 | self.batch_size = batch_size # batch_size
77 | self.target_update_iter = target_update_iter # target update period
78 | self.train_nums = train_nums # total training steps
79 | self.num_in_buffer = 0 # transitions num in buffer
80 | self.buffer_size = buffer_size # replay buffer size
81 | self.start_learning = start_learning # step to begin learning(save transitions before that step)
82 |
83 | # replay buffer
84 | self.obs = np.empty((self.buffer_size,) + greyscale(self.env.reset()).shape)
85 | self.actions = np.empty((self.buffer_size), dtype=np.int8)
86 | self.rewards = np.empty((self.buffer_size), dtype=np.float32)
87 | self.dones = np.empty((self.buffer_size), dtype=np.bool)
88 | self.next_states = np.empty((self.buffer_size,) + greyscale(self.env.reset()).shape)
89 | self.next_idx = 0
90 |
91 |
92 | # To test whether the model works
93 | def test(self, render=True):
94 | obs, done, ep_reward = self.env.reset(), False, 0
95 | while not done:
96 | obs = greyscale(obs)
97 | # Using [None] to extend its dimension [80, 80, 1] -> [1, 80, 80, 1]
98 | action, _ = self.model.action_value(obs[None])
99 | obs, reward, done, info = self.env.step(action)
100 | ep_reward += reward
101 | if render: # visually
102 | self.env.render()
103 | time.sleep(0.05)
104 | self.env.close()
105 | return ep_reward
106 |
107 | def train(self):
108 | obs = self.env.reset()
109 | obs = greyscale(obs)[None]
110 | for t in range(self.train_nums):
111 | best_action, q_values = self.model.action_value(obs)
112 | action = self.get_action(best_action)
113 | next_obs, reward, done, info = self.env.step(action)
114 | next_obs = greyscale(next_obs)[None]
115 | self.store_transition(obs, action, reward, next_obs, done)
116 | self.num_in_buffer += 1
117 |
118 | if t > self.start_learning: # start learning
119 | losses = self.train_step(t)
120 |
121 | if t % self.target_update_iter == 0:
122 | self.update_target_model()
123 |
124 | obs = next_obs
125 |
126 | def train_step(self, t):
127 | idxes = self.sample(self.batch_size)
128 | self.s_batch = self.obs[idxes]
129 | self.a_batch = self.actions[idxes]
130 | self.r_batch = self.rewards[idxes]
131 | self.ns_batch = self.next_states[idxes]
132 | self.done_batch = self.dones[idxes]
133 |
134 | target_q = self.r_batch + self.gamma * \
135 | np.amax(self.get_target_value(self.ns_batch), axis=1) * (1 - self.done_batch)
136 | target_f = self.model.predict(self.s_batch)
137 | for i, val in enumerate(self.a_batch):
138 | target_f[i][val] = target_q[i]
139 |
140 | losses = self.model.train_on_batch(self.s_batch, target_f)
141 |
142 | return losses
143 |
144 |
145 |
146 | # def loss_function(self, q, target_q):
147 | # n_actions = self.env.action_space.n
148 | # print('action in loss', self.a_batch)
149 | # actions = to_categorical(self.a_batch, n_actions)
150 | # q = np.sum(np.multiply(q, actions), axis=1)
151 | # self.loss = kls.mean_squared_error(q, target_q)
152 |
153 |
154 | def store_transition(self, obs, action, reward, next_state, done):
155 | n_idx = self.next_idx % self.buffer_size
156 | self.obs[n_idx] = obs
157 | self.actions[n_idx] = action
158 | self.rewards[n_idx] = reward
159 | self.next_states[n_idx] = next_state
160 | self.dones[n_idx] = done
161 | self.next_idx = (self.next_idx + 1) % self.buffer_size
162 |
163 | def sample(self, n):
164 | assert n < self.num_in_buffer
165 | res = []
166 | while True:
167 | num = np.random.randint(0, self.num_in_buffer)
168 | if num not in res:
169 | res.append(num)
170 | if len(res) == n:
171 | break
172 | return res
173 |
174 | def get_action(self, best_action):
175 | if np.random.rand() < self.epsilon:
176 | return self.env.action_space.sample()
177 | return best_action
178 |
179 | def update_target_model(self):
180 | print('update_target_mdoel')
181 | self.target_model.set_weights(self.model.get_weights())
182 |
183 | def get_target_value(self, obs):
184 | return self.target_model.predict(obs)
185 |
186 | if __name__ == '__main__':
187 | env = gym.make("Pong-v0")
188 | obs = env.reset()
189 | num_actions = env.action_space.n
190 | model = Model(num_actions)
191 | target_model = Model(num_actions)
192 | agent = DQNAgent(model, target_model, env)
193 | # reward = agent.test()
194 | agent.train()
195 |
--------------------------------------------------------------------------------
/01_dqn.py:
--------------------------------------------------------------------------------
1 | """
2 | A simple version of Deep Q-Network(DQN) including the main tactics mentioned in DeepMind's original paper:
3 | - Experience Replay
4 | - Target Network
5 | To play CartPole-v0.
6 |
7 | > Note: DQN can only handle discrete-env which have a discrete action space, like up, down, left, right.
8 | As for the CartPole-v0 environment, its state(the agent's observation) is a 1-D vector not a 3-D image like
9 | Atari, so in that simple example, there is no need to use the convolutional layer, just fully-connected layer.
10 |
11 | Using:
12 | TensorFlow 2.0
13 | Numpy 1.16.2
14 | Gym 0.12.1
15 | """
16 |
17 | import tensorflow as tf
18 | print(tf.__version__)
19 |
20 | import gym
21 | import time
22 | import numpy as np
23 | import tensorflow.keras.layers as kl
24 | import tensorflow.keras.optimizers as ko
25 |
26 | np.random.seed(1)
27 | tf.random.set_seed(1)
28 |
29 | # Neural Network Model Defined at Here.
30 | class Model(tf.keras.Model):
31 | def __init__(self, num_actions):
32 | super().__init__(name='basic_dqn')
33 | # you can try different kernel initializer
34 | self.fc1 = kl.Dense(32, activation='relu', kernel_initializer='he_uniform')
35 | self.fc2 = kl.Dense(32, activation='relu', kernel_initializer='he_uniform')
36 | self.logits = kl.Dense(num_actions, name='q_values')
37 |
38 | # forward propagation
39 | def call(self, inputs):
40 | x = self.fc1(inputs)
41 | x = self.fc2(x)
42 | x = self.logits(x)
43 | return x
44 |
45 | # a* = argmax_a' Q(s, a')
46 | def action_value(self, obs):
47 | q_values = self.predict(obs)
48 | best_action = np.argmax(q_values, axis=-1)
49 | return best_action[0], q_values[0]
50 |
51 | # To test whether the model works
52 | def test_model():
53 | env = gym.make('CartPole-v0')
54 | print('num_actions: ', env.action_space.n)
55 | model = Model(env.action_space.n)
56 |
57 | obs = env.reset()
58 | print('obs_shape: ', obs.shape)
59 |
60 | # tensorflow 2.0: no feed_dict or tf.Session() needed at all
61 | best_action, q_values = model.action_value(obs[None])
62 | print('res of test model: ', best_action, q_values) # 0 [ 0.00896799 -0.02111824]
63 |
64 |
65 | class DQNAgent: # Deep Q-Network
66 | def __init__(self, model, target_model, env, buffer_size=100, learning_rate=.0015, epsilon=.1, epsilon_dacay=0.995,
67 | min_epsilon=.01, gamma=.95, batch_size=4, target_update_iter=400, train_nums=5000, start_learning=10):
68 | self.model = model
69 | self.target_model = target_model
70 | # print(id(self.model), id(self.target_model)) # to make sure the two models don't update simultaneously
71 | # gradient clip
72 | opt = ko.Adam(learning_rate=learning_rate, clipvalue=10.0) # do gradient clip
73 | self.model.compile(optimizer=opt, loss='mse')
74 |
75 | # parameters
76 | self.env = env # gym environment
77 | self.lr = learning_rate # learning step
78 | self.epsilon = epsilon # e-greedy when exploring
79 | self.epsilon_decay = epsilon_dacay # epsilon decay rate
80 | self.min_epsilon = min_epsilon # minimum epsilon
81 | self.gamma = gamma # discount rate
82 | self.batch_size = batch_size # batch_size
83 | self.target_update_iter = target_update_iter # target network update period
84 | self.train_nums = train_nums # total training steps
85 | self.num_in_buffer = 0 # transition's num in buffer
86 | self.buffer_size = buffer_size # replay buffer size
87 | self.start_learning = start_learning # step to begin learning(no update before that step)
88 |
89 | # replay buffer params [(s, a, r, ns, done), ...]
90 | self.obs = np.empty((self.buffer_size,) + self.env.reset().shape)
91 | self.actions = np.empty((self.buffer_size), dtype=np.int8)
92 | self.rewards = np.empty((self.buffer_size), dtype=np.float32)
93 | self.dones = np.empty((self.buffer_size), dtype=np.bool)
94 | self.next_states = np.empty((self.buffer_size,) + self.env.reset().shape)
95 | self.next_idx = 0
96 |
97 | def train(self):
98 | # initialize the initial observation of the agent
99 | obs = self.env.reset()
100 | for t in range(1, self.train_nums):
101 | best_action, q_values = self.model.action_value(obs[None]) # input the obs to the network model
102 | action = self.get_action(best_action) # get the real action
103 | next_obs, reward, done, info = self.env.step(action) # take the action in the env to return s', r, done
104 | self.store_transition(obs, action, reward, next_obs, done) # store that transition into replay butter
105 | self.num_in_buffer = min(self.num_in_buffer + 1, self.buffer_size)
106 |
107 | if t > self.start_learning: # start learning
108 | losses = self.train_step()
109 | if t % 1000 == 0:
110 | print('losses each 1000 steps: ', losses)
111 |
112 | if t % self.target_update_iter == 0:
113 | self.update_target_model()
114 | if done:
115 | obs = self.env.reset()
116 | else:
117 | obs = next_obs
118 |
119 | def train_step(self):
120 | idxes = self.sample(self.batch_size)
121 | s_batch = self.obs[idxes]
122 | a_batch = self.actions[idxes]
123 | r_batch = self.rewards[idxes]
124 | ns_batch = self.next_states[idxes]
125 | done_batch = self.dones[idxes]
126 |
127 | target_q = r_batch + self.gamma * np.amax(self.get_target_value(ns_batch), axis=1) * (1 - done_batch)
128 | target_f = self.model.predict(s_batch)
129 | for i, val in enumerate(a_batch):
130 | target_f[i][val] = target_q[i]
131 |
132 | losses = self.model.train_on_batch(s_batch, target_f)
133 |
134 | return losses
135 |
136 | def evalation(self, env, render=True):
137 | obs, done, ep_reward = env.reset(), False, 0
138 | # one episode until done
139 | while not done:
140 | action, q_values = self.model.action_value(obs[None]) # Using [None] to extend its dimension (4,) -> (1, 4)
141 | obs, reward, done, info = env.step(action)
142 | ep_reward += reward
143 | if render: # visually show
144 | env.render()
145 | time.sleep(0.05)
146 | env.close()
147 | return ep_reward
148 |
149 | # store transitions into replay butter
150 | def store_transition(self, obs, action, reward, next_state, done):
151 | n_idx = self.next_idx % self.buffer_size
152 | self.obs[n_idx] = obs
153 | self.actions[n_idx] = action
154 | self.rewards[n_idx] = reward
155 | self.next_states[n_idx] = next_state
156 | self.dones[n_idx] = done
157 | self.next_idx = (self.next_idx + 1) % self.buffer_size
158 |
159 | # sample n different indexes
160 | def sample(self, n):
161 | assert n < self.num_in_buffer
162 | res = []
163 | while True:
164 | num = np.random.randint(0, self.num_in_buffer)
165 | if num not in res:
166 | res.append(num)
167 | if len(res) == n:
168 | break
169 | return res
170 |
171 | # e-greedy
172 | def get_action(self, best_action):
173 | if np.random.rand() < self.epsilon:
174 | return self.env.action_space.sample()
175 | return best_action
176 |
177 | # assign the current network parameters to target network
178 | def update_target_model(self):
179 | self.target_model.set_weights(self.model.get_weights())
180 |
181 | def get_target_value(self, obs):
182 | return self.target_model.predict(obs)
183 |
184 | def e_decay(self):
185 | self.epsilon *= self.epsilon_decay
186 |
187 | if __name__ == '__main__':
188 | test_model()
189 |
190 | env = gym.make("CartPole-v0")
191 | num_actions = env.action_space.n
192 | model = Model(num_actions)
193 | target_model = Model(num_actions)
194 | agent = DQNAgent(model, target_model, env)
195 | # test before
196 | rewards_sum = agent.evalation(env)
197 | print("Before Training: %d out of 200" % rewards_sum) # 9 out of 200
198 |
199 | agent.train()
200 | # test after
201 | rewards_sum = agent.evalation(env)
202 | print("After Training: %d out of 200" % rewards_sum) # 200 out of 200
203 |
--------------------------------------------------------------------------------
/02_ddqn.py:
--------------------------------------------------------------------------------
1 | """
2 | A simple version of Double Deep Q-Network(DDQN), minor change to DQN.
3 | To play CartPole-v0.
4 |
5 | Using:
6 | TensorFlow 2.0
7 | Numpy 1.16.2
8 | Gym 0.12.1
9 | """
10 |
11 | import tensorflow as tf
12 | print(tf.__version__)
13 |
14 | import gym
15 | import time
16 | import numpy as np
17 | import tensorflow.keras.layers as kl
18 | import tensorflow.keras.optimizers as ko
19 |
20 | np.random.seed(1)
21 | tf.random.set_seed(1)
22 |
23 | # Neural Network Model Defined at Here.
24 | class Model(tf.keras.Model):
25 | def __init__(self, num_actions):
26 | super().__init__(name='basic_ddqn')
27 | # you can try different kernel initializer
28 | self.fc1 = kl.Dense(32, activation='relu', kernel_initializer='he_uniform')
29 | self.fc2 = kl.Dense(32, activation='relu', kernel_initializer='he_uniform')
30 | self.logits = kl.Dense(num_actions, name='q_values')
31 |
32 | # forward propagation
33 | def call(self, inputs):
34 | x = self.fc1(inputs)
35 | x = self.fc2(x)
36 | x = self.logits(x)
37 | return x
38 |
39 | # a* = argmax_a' Q(s, a')
40 | def action_value(self, obs):
41 | q_values = self.predict(obs)
42 | best_action = np.argmax(q_values, axis=-1)
43 | return best_action if best_action.shape[0] > 1 else best_action[0], q_values[0]
44 |
45 | # To test whether the model works
46 | def test_model():
47 | env = gym.make('CartPole-v0')
48 | print('num_actions: ', env.action_space.n)
49 | model = Model(env.action_space.n)
50 |
51 | obs = env.reset()
52 | print('obs_shape: ', obs.shape)
53 |
54 | # tensorflow 2.0: no feed_dict or tf.Session() needed at all
55 | best_action, q_values = model.action_value(obs[None])
56 | print('res of test model: ', best_action, q_values) # 0 [ 0.00896799 -0.02111824]
57 |
58 |
59 | class DDQNAgent: # Double Deep Q-Network
60 | def __init__(self, model, target_model, env, buffer_size=200, learning_rate=.0015, epsilon=.1, epsilon_dacay=0.995,
61 | min_epsilon=.01, gamma=.9, batch_size=8, target_update_iter=200, train_nums=5000, start_learning=100):
62 | self.model = model
63 | self.target_model = target_model
64 | # gradient clip
65 | opt = ko.Adam(learning_rate=learning_rate, clipvalue=10.0)
66 | self.model.compile(optimizer=opt, loss='mse')
67 |
68 | # parameters
69 | self.env = env # gym environment
70 | self.lr = learning_rate # learning step
71 | self.epsilon = epsilon # e-greedy when exploring
72 | self.epsilon_decay = epsilon_dacay # epsilon decay rate
73 | self.min_epsilon = min_epsilon # minimum epsilon
74 | self.gamma = gamma # discount rate
75 | self.batch_size = batch_size # batch_size
76 | self.target_update_iter = target_update_iter # target network update period
77 | self.train_nums = train_nums # total training steps
78 | self.num_in_buffer = 0 # transition's num in buffer
79 | self.buffer_size = buffer_size # replay buffer size
80 | self.start_learning = start_learning # step to begin learning(no update before that step)
81 |
82 | # replay buffer params [(s, a, r, ns, done), ...]
83 | self.obs = np.empty((self.buffer_size,) + self.env.reset().shape)
84 | self.actions = np.empty((self.buffer_size), dtype=np.int8)
85 | self.rewards = np.empty((self.buffer_size), dtype=np.float32)
86 | self.dones = np.empty((self.buffer_size), dtype=np.bool)
87 | self.next_states = np.empty((self.buffer_size,) + self.env.reset().shape)
88 | self.next_idx = 0
89 |
90 | def train(self):
91 | # initialize the initial observation of the agent
92 | obs = self.env.reset()
93 | for t in range(1, self.train_nums):
94 | best_action, q_values = self.model.action_value(obs[None]) # input the obs to the network model
95 | action = self.get_action(best_action) # get the real action
96 | next_obs, reward, done, info = self.env.step(action) # take the action in the env to return s', r, done
97 | self.store_transition(obs, action, reward, next_obs, done) # store that transition into replay butter
98 | self.num_in_buffer = min(self.num_in_buffer + 1, self.buffer_size)
99 |
100 | if t > self.start_learning: # start learning
101 | losses = self.train_step()
102 | if t % 1000 == 0:
103 | print('losses each 1000 steps: ', losses)
104 |
105 | if t % self.target_update_iter == 0:
106 | self.update_target_model()
107 | if done:
108 | obs = self.env.reset()
109 | else:
110 | obs = next_obs
111 |
112 | def train_step(self):
113 | idxes = self.sample(self.batch_size)
114 | s_batch = self.obs[idxes]
115 | a_batch = self.actions[idxes]
116 | r_batch = self.rewards[idxes]
117 | ns_batch = self.next_states[idxes]
118 | done_batch = self.dones[idxes]
119 | # Double Q-Learning, decoupling selection and evaluation of the bootstrap action
120 | # selection with the current DQN model
121 | best_action_idxes, _ = self.model.action_value(ns_batch)
122 | target_q = self.get_target_value(ns_batch)
123 | # evaluation with the target DQN model
124 | target_q = r_batch + self.gamma * target_q[np.arange(target_q.shape[0]), best_action_idxes] * (1 - done_batch)
125 | target_f = self.model.predict(s_batch)
126 | for i, val in enumerate(a_batch):
127 | target_f[i][val] = target_q[i]
128 |
129 | losses = self.model.train_on_batch(s_batch, target_f)
130 |
131 | return losses
132 |
133 | def evalation(self, env, render=True):
134 | obs, done, ep_reward = env.reset(), False, 0
135 | # one episode until done
136 | while not done:
137 | action, q_values = self.model.action_value(obs[None]) # Using [None] to extend its dimension (4,) -> (1, 4)
138 | obs, reward, done, info = env.step(action)
139 | ep_reward += reward
140 | if render: # visually show
141 | env.render()
142 | time.sleep(0.05)
143 | env.close()
144 | return ep_reward
145 |
146 | # store transitions into replay butter
147 | def store_transition(self, obs, action, reward, next_state, done):
148 | n_idx = self.next_idx % self.buffer_size
149 | self.obs[n_idx] = obs
150 | self.actions[n_idx] = action
151 | self.rewards[n_idx] = reward
152 | self.next_states[n_idx] = next_state
153 | self.dones[n_idx] = done
154 | self.next_idx = (self.next_idx + 1) % self.buffer_size
155 |
156 | # sample n different indexes
157 | def sample(self, n):
158 | assert n < self.num_in_buffer
159 | res = []
160 | while True:
161 | num = np.random.randint(0, self.num_in_buffer)
162 | if num not in res:
163 | res.append(num)
164 | if len(res) == n:
165 | break
166 | return res
167 |
168 | # e-greedy
169 | def get_action(self, best_action):
170 | if np.random.rand() < self.epsilon:
171 | return self.env.action_space.sample()
172 | return best_action
173 |
174 | # assign the current network parameters to target network
175 | def update_target_model(self):
176 | self.target_model.set_weights(self.model.get_weights())
177 |
178 | def get_target_value(self, obs):
179 | return self.target_model.predict(obs)
180 |
181 | def e_decay(self):
182 | self.epsilon *= self.epsilon_decay
183 |
184 | if __name__ == '__main__':
185 | test_model()
186 |
187 | env = gym.make("CartPole-v0")
188 | num_actions = env.action_space.n
189 | model = Model(num_actions)
190 | target_model = Model(num_actions)
191 | agent = DDQNAgent(model, target_model, env)
192 | # test before
193 | rewards_sum = agent.evalation(env)
194 | print("Before Training: %d out of 200" % rewards_sum) # 9 out of 200
195 |
196 | agent.train()
197 | # test after
198 | # env = gym.wrappers.Monitor(env, './recording', force=True) # to record the process
199 | rewards_sum = agent.evalation(env)
200 | print("After Training: %d out of 200" % rewards_sum) # 200 out of 200
201 |
--------------------------------------------------------------------------------
/03_priority_replay.py:
--------------------------------------------------------------------------------
1 | """
2 | A simple version of Prioritized Experience Replay based on Double DQN.
3 | To play CartPole-v0.
4 |
5 | Using:
6 | TensorFlow 2.0
7 | Numpy 1.16.2
8 | Gym 0.12.1
9 | """
10 |
11 | import tensorflow as tf
12 | print(tf.__version__)
13 |
14 | import gym
15 | import time
16 | import numpy as np
17 | import tensorflow.keras.layers as kl
18 | import tensorflow.keras.optimizers as ko
19 |
20 | np.random.seed(1)
21 | tf.random.set_seed(1)
22 |
23 | # Neural Network Model Defined at Here.
24 | class Model(tf.keras.Model):
25 | def __init__(self, num_actions):
26 | super().__init__(name='basic_prddqn')
27 | # you can try different kernel initializer
28 | self.fc1 = kl.Dense(32, activation='relu', kernel_initializer='he_uniform')
29 | self.fc2 = kl.Dense(32, activation='relu', kernel_initializer='he_uniform')
30 | self.logits = kl.Dense(num_actions, name='q_values')
31 |
32 | # forward propagation
33 | def call(self, inputs):
34 | x = self.fc1(inputs)
35 | x = self.fc2(x)
36 | x = self.logits(x)
37 | return x
38 |
39 | # a* = argmax_a' Q(s, a')
40 | def action_value(self, obs):
41 | q_values = self.predict(obs)
42 | best_action = np.argmax(q_values, axis=-1)
43 | return best_action if best_action.shape[0] > 1 else best_action[0], q_values[0]
44 |
45 |
46 | # To test whether the model works
47 | def test_model():
48 | env = gym.make('CartPole-v0')
49 | print('num_actions: ', env.action_space.n)
50 | model = Model(env.action_space.n)
51 |
52 | obs = env.reset()
53 | print('obs_shape: ', obs.shape)
54 |
55 | # tensorflow 2.0 eager mode: no feed_dict or tf.Session() needed at all
56 | best_action, q_values = model.action_value(obs[None])
57 | print('res of test model: ', best_action, q_values) # 0 [ 0.00896799 -0.02111824]
58 |
59 |
60 | # replay buffer
61 | class SumTree:
62 | # little modified from https://github.com/jaromiru/AI-blog/blob/master/SumTree.py
63 | def __init__(self, capacity):
64 | self.capacity = capacity # N, the size of replay buffer, so as to the number of sum tree's leaves
65 | self.tree = np.zeros(2 * capacity - 1) # equation, to calculate the number of nodes in a sum tree
66 | self.transitions = np.empty(capacity, dtype=object)
67 | self.next_idx = 0
68 |
69 | @property
70 | def total_p(self):
71 | return self.tree[0]
72 |
73 | def add(self, priority, transition):
74 | idx = self.next_idx + self.capacity - 1
75 | self.transitions[self.next_idx] = transition
76 | self.update(idx, priority)
77 | self.next_idx = (self.next_idx + 1) % self.capacity
78 |
79 | def update(self, idx, priority):
80 | change = priority - self.tree[idx]
81 | self.tree[idx] = priority
82 | self._propagate(idx, change) # O(logn)
83 |
84 | def _propagate(self, idx, change):
85 | parent = (idx - 1) // 2
86 | self.tree[parent] += change
87 | if parent != 0:
88 | self._propagate(parent, change)
89 |
90 | def get_leaf(self, s):
91 | idx = self._retrieve(0, s) # from root
92 | trans_idx = idx - self.capacity + 1
93 | return idx, self.tree[idx], self.transitions[trans_idx]
94 |
95 | def _retrieve(self, idx, s):
96 | left = 2 * idx + 1
97 | right = left + 1
98 | if left >= len(self.tree):
99 | return idx
100 | if s <= self.tree[left]:
101 | return self._retrieve(left, s)
102 | else:
103 | return self._retrieve(right, s - self.tree[left])
104 |
105 |
106 | class PERAgent: # Double DQN with Proportional Prioritization
107 | def __init__(self, model, target_model, env, learning_rate=.0012, epsilon=.1, epsilon_dacay=0.995, min_epsilon=.01,
108 | gamma=.9, batch_size=8, target_update_iter=400, train_nums=5000, buffer_size=200, replay_period=20,
109 | alpha=0.4, beta=0.4, beta_increment_per_sample=0.001):
110 | self.model = model
111 | self.target_model = target_model
112 | # gradient clip
113 | opt = ko.Adam(learning_rate=learning_rate) # , clipvalue=10.0
114 | self.model.compile(optimizer=opt, loss=self._per_loss) # loss=self._per_loss
115 |
116 | # parameters
117 | self.env = env # gym environment
118 | self.lr = learning_rate # learning step
119 | self.epsilon = epsilon # e-greedy when exploring
120 | self.epsilon_decay = epsilon_dacay # epsilon decay rate
121 | self.min_epsilon = min_epsilon # minimum epsilon
122 | self.gamma = gamma # discount rate
123 | self.batch_size = batch_size # minibatch k
124 | self.target_update_iter = target_update_iter # target network update period
125 | self.train_nums = train_nums # total training steps
126 |
127 | # replay buffer params [(s, a, r, ns, done), ...]
128 | self.b_obs = np.empty((self.batch_size,) + self.env.reset().shape)
129 | self.b_actions = np.empty(self.batch_size, dtype=np.int8)
130 | self.b_rewards = np.empty(self.batch_size, dtype=np.float32)
131 | self.b_next_states = np.empty((self.batch_size,) + self.env.reset().shape)
132 | self.b_dones = np.empty(self.batch_size, dtype=np.bool)
133 |
134 | self.replay_buffer = SumTree(buffer_size) # sum-tree data structure
135 | self.buffer_size = buffer_size # replay buffer size N
136 | self.replay_period = replay_period # replay period K
137 | self.alpha = alpha # priority parameter, alpha=[0, 0.4, 0.5, 0.6, 0.7, 0.8]
138 | self.beta = beta # importance sampling parameter, beta=[0, 0.4, 0.5, 0.6, 1]
139 | self.beta_increment_per_sample = beta_increment_per_sample
140 | self.num_in_buffer = 0 # total number of transitions stored in buffer
141 | self.margin = 0.01 # pi = |td_error| + margin
142 | self.p1 = 1 # initialize priority for the first transition
143 | # self.is_weight = np.empty((None, 1))
144 | self.is_weight = np.power(self.buffer_size, -self.beta) # because p1 == 1
145 | self.abs_error_upper = 1
146 |
147 | def _per_loss(self, y_target, y_pred):
148 | return tf.reduce_mean(self.is_weight * tf.math.squared_difference(y_target, y_pred))
149 |
150 | def train(self):
151 | # initialize the initial observation of the agent
152 | obs = self.env.reset()
153 | for t in range(1, self.train_nums):
154 | best_action, q_values = self.model.action_value(obs[None]) # input the obs to the network model
155 | action = self.get_action(best_action) # get the real action
156 | next_obs, reward, done, info = self.env.step(action) # take the action in the env to return s', r, done
157 | if t == 1:
158 | p = self.p1
159 | else:
160 | p = np.max(self.replay_buffer.tree[-self.replay_buffer.capacity:])
161 | self.store_transition(p, obs, action, reward, next_obs, done) # store that transition into replay butter
162 | self.num_in_buffer = min(self.num_in_buffer + 1, self.buffer_size)
163 |
164 | if t > self.buffer_size:
165 | # if t % self.replay_period == 0: # transition sampling and update
166 | losses = self.train_step()
167 | if t % 1000 == 0:
168 | print('losses each 1000 steps: ', losses)
169 |
170 | if t % self.target_update_iter == 0:
171 | self.update_target_model()
172 | if done:
173 | obs = self.env.reset() # one episode end
174 | else:
175 | obs = next_obs
176 |
177 | def train_step(self):
178 | idxes, self.is_weight = self.sum_tree_sample(self.batch_size)
179 | # Double Q-Learning
180 | best_action_idxes, _ = self.model.action_value(self.b_next_states) # get actions through the current network
181 | target_q = self.get_target_value(self.b_next_states) # get target q-value through the target network
182 | # get td_targets of batch states
183 | td_target = self.b_rewards + \
184 | self.gamma * target_q[np.arange(target_q.shape[0]), best_action_idxes] * (1 - self.b_dones)
185 | predict_q = self.model.predict(self.b_obs)
186 | td_predict = predict_q[np.arange(predict_q.shape[0]), self.b_actions]
187 | abs_td_error = np.abs(td_target - td_predict) + self.margin
188 | clipped_error = np.where(abs_td_error < self.abs_error_upper, abs_td_error, self.abs_error_upper)
189 | ps = np.power(clipped_error, self.alpha)
190 | # priorities update
191 | for idx, p in zip(idxes, ps):
192 | self.replay_buffer.update(idx, p)
193 |
194 | for i, val in enumerate(self.b_actions):
195 | predict_q[i][val] = td_target[i]
196 |
197 | target_q = predict_q # just to change a more explicit name
198 | losses = self.model.train_on_batch(self.b_obs, target_q)
199 |
200 | return losses
201 |
202 | # proportional prioritization sampling
203 | def sum_tree_sample(self, k):
204 | idxes = []
205 | is_weights = np.empty((k, 1))
206 | self.beta = min(1., self.beta + self.beta_increment_per_sample)
207 | # calculate max_weight
208 | min_prob = np.min(self.replay_buffer.tree[-self.replay_buffer.capacity:]) / self.replay_buffer.total_p
209 | max_weight = np.power(self.buffer_size * min_prob, -self.beta)
210 | segment = self.replay_buffer.total_p / k
211 | for i in range(k):
212 | s = np.random.uniform(segment * i, segment * (i + 1))
213 | idx, p, t = self.replay_buffer.get_leaf(s)
214 | idxes.append(idx)
215 | self.b_obs[i], self.b_actions[i], self.b_rewards[i], self.b_next_states[i], self.b_dones[i] = t
216 | # P(j)
217 | sampling_probabilities = p / self.replay_buffer.total_p # where p = p ** self.alpha
218 | is_weights[i, 0] = np.power(self.buffer_size * sampling_probabilities, -self.beta) / max_weight
219 | return idxes, is_weights
220 |
221 | def evaluation(self, env, render=True):
222 | obs, done, ep_reward = env.reset(), False, 0
223 | # one episode until done
224 | while not done:
225 | action, q_values = self.model.action_value(obs[None]) # Using [None] to extend its dimension (4,) -> (1, 4)
226 | obs, reward, done, info = env.step(action)
227 | ep_reward += reward
228 | if render: # visually show
229 | env.render()
230 | time.sleep(0.05)
231 | env.close()
232 | return ep_reward
233 |
234 | # store transitions into replay butter, now sum tree.
235 | def store_transition(self, priority, obs, action, reward, next_state, done):
236 | transition = [obs, action, reward, next_state, done]
237 | self.replay_buffer.add(priority, transition)
238 |
239 | # rank-based prioritization sampling
240 | def rand_based_sample(self, k):
241 | pass
242 |
243 | # e-greedy
244 | def get_action(self, best_action):
245 | if np.random.rand() < self.epsilon:
246 | return self.env.action_space.sample()
247 | return best_action
248 |
249 | # assign the current network parameters to target network
250 | def update_target_model(self):
251 | self.target_model.set_weights(self.model.get_weights())
252 |
253 | def get_target_value(self, obs):
254 | return self.target_model.predict(obs)
255 |
256 | def e_decay(self):
257 | self.epsilon *= self.epsilon_decay
258 |
259 |
260 | if __name__ == '__main__':
261 | test_model()
262 |
263 | env = gym.make("CartPole-v0")
264 | num_actions = env.action_space.n
265 | model = Model(num_actions)
266 | target_model = Model(num_actions)
267 | agent = PERAgent(model, target_model, env)
268 | # test before
269 | rewards_sum = agent.evaluation(env)
270 | print("Before Training: %d out of 200" % rewards_sum) # 9 out of 200
271 |
272 | agent.train()
273 | # test after
274 | # env = gym.wrappers.Monitor(env, './recording', force=True)
275 | rewards_sum = agent.evaluation(env)
276 | print("After Training: %d out of 200" % rewards_sum) # 200 out of 200
277 |
--------------------------------------------------------------------------------
/04_dueling.py:
--------------------------------------------------------------------------------
1 | """
2 | A simple version of Dueling Double DQN with Prioritized Experience Replay. Just slightly modify the network architecture.
3 | To play CartPole-v0.
4 |
5 | Using:
6 | TensorFlow 2.0
7 | Numpy 1.16.2
8 | Gym 0.12.1
9 | """
10 |
11 | import tensorflow as tf
12 | print(tf.__version__)
13 |
14 | import gym
15 | import time
16 | import numpy as np
17 | import tensorflow.keras.layers as kl
18 | import tensorflow.keras.optimizers as ko
19 |
20 | np.random.seed(1)
21 | tf.random.set_seed(1)
22 |
23 | # Neural Network Model Defined at Here.
24 | class Model(tf.keras.Model):
25 | def __init__(self, num_actions):
26 | super().__init__(name='basic_prdddqn')
27 | # you can try different kernel initializer
28 | self.shared_fc1 = kl.Dense(16, activation='relu', kernel_initializer='he_uniform')
29 | self.shared_fc2 = kl.Dense(32, activation='relu', kernel_initializer='he_uniform')
30 | # there is a trick that combining the two streams' fc layer, then
31 | # the output of that layer is a |A| + 1 dimension tensor: |V|A1|A2| ... |An|
32 | # output[:, 0] is state value, output[:, 1:] is action advantage
33 | self.val_adv_fc = kl.Dense(num_actions + 1, activation='relu', kernel_initializer='he_uniform')
34 |
35 | # forward propagation
36 | def call(self, inputs):
37 | x = self.shared_fc1(inputs)
38 | x = self.shared_fc2(x)
39 | val_adv = self.val_adv_fc(x)
40 | # average version, you can also try the max version.
41 | outputs = tf.expand_dims(val_adv[:, 0], -1) + (val_adv[:, 1:] - tf.reduce_mean(val_adv[:, 1:], -1, keepdims=True))
42 | return outputs
43 |
44 | # a* = argmax_a' Q(s, a')
45 | def action_value(self, obs):
46 | q_values = self.predict(obs)
47 | best_action = np.argmax(q_values, axis=-1)
48 | return best_action if best_action.shape[0] > 1 else best_action[0], q_values[0]
49 |
50 |
51 | # To test whether the model works
52 | def test_model():
53 | env = gym.make('CartPole-v0')
54 | print('num_actions: ', env.action_space.n)
55 | model = Model(env.action_space.n)
56 |
57 | obs = env.reset()
58 | print('obs_shape: ', obs.shape)
59 |
60 | # tensorflow 2.0 eager mode: no feed_dict or tf.Session() needed at all
61 | best_action, q_values = model.action_value(obs[None])
62 | print('res of test model: ', best_action, q_values) # 0 [ 0.00896799 -0.02111824]
63 |
64 |
65 | # replay buffer
66 | class SumTree:
67 | # little modified from https://github.com/jaromiru/AI-blog/blob/master/SumTree.py
68 | def __init__(self, capacity):
69 | self.capacity = capacity # N, the size of replay buffer, so as to the number of sum tree's leaves
70 | self.tree = np.zeros(2 * capacity - 1) # equation, to calculate the number of nodes in a sum tree
71 | self.transitions = np.empty(capacity, dtype=object)
72 | self.next_idx = 0
73 |
74 | @property
75 | def total_p(self):
76 | return self.tree[0]
77 |
78 | def add(self, priority, transition):
79 | idx = self.next_idx + self.capacity - 1
80 | self.transitions[self.next_idx] = transition
81 | self.update(idx, priority)
82 | self.next_idx = (self.next_idx + 1) % self.capacity
83 |
84 | def update(self, idx, priority):
85 | change = priority - self.tree[idx]
86 | self.tree[idx] = priority
87 | self._propagate(idx, change) # O(logn)
88 |
89 | def _propagate(self, idx, change):
90 | parent = (idx - 1) // 2
91 | self.tree[parent] += change
92 | if parent != 0:
93 | self._propagate(parent, change)
94 |
95 | def get_leaf(self, s):
96 | idx = self._retrieve(0, s) # from root
97 | trans_idx = idx - self.capacity + 1
98 | return idx, self.tree[idx], self.transitions[trans_idx]
99 |
100 | def _retrieve(self, idx, s):
101 | left = 2 * idx + 1
102 | right = left + 1
103 | if left >= len(self.tree):
104 | return idx
105 | if s <= self.tree[left]:
106 | return self._retrieve(left, s)
107 | else:
108 | return self._retrieve(right, s - self.tree[left])
109 |
110 |
111 | class DDDQNAgent: # Dueling Double DQN with Proportional Prioritization
112 | def __init__(self, model, target_model, env, learning_rate=.001, epsilon=.1, epsilon_dacay=0.995, min_epsilon=.01,
113 | gamma=.9, batch_size=8, target_update_iter=400, train_nums=5000, buffer_size=300, replay_period=20,
114 | alpha=0.4, beta=0.4, beta_increment_per_sample=0.001):
115 | self.model = model
116 | self.target_model = target_model
117 | # gradient clip
118 | opt = ko.Adam(learning_rate=learning_rate, clipvalue=10.0) #, clipvalue=10.0
119 | self.model.compile(optimizer=opt, loss=self._per_loss) #loss=self._per_loss
120 |
121 | # parameters
122 | self.env = env # gym environment
123 | self.lr = learning_rate # learning step
124 | self.epsilon = epsilon # e-greedy when exploring
125 | self.epsilon_decay = epsilon_dacay # epsilon decay rate
126 | self.min_epsilon = min_epsilon # minimum epsilon
127 | self.gamma = gamma # discount rate
128 | self.batch_size = batch_size # minibatch k
129 | self.target_update_iter = target_update_iter # target network update period
130 | self.train_nums = train_nums # total training steps
131 |
132 | # replay buffer params [(s, a, r, ns, done), ...]
133 | self.b_obs = np.empty((self.batch_size,) + self.env.reset().shape)
134 | self.b_actions = np.empty(self.batch_size, dtype=np.int8)
135 | self.b_rewards = np.empty(self.batch_size, dtype=np.float32)
136 | self.b_next_states = np.empty((self.batch_size,) + self.env.reset().shape)
137 | self.b_dones = np.empty(self.batch_size, dtype=np.bool)
138 |
139 | self.replay_buffer = SumTree(buffer_size) # sum-tree data structure
140 | self.buffer_size = buffer_size # replay buffer size N
141 | self.replay_period = replay_period # replay period K
142 | self.alpha = alpha # priority parameter, alpha=[0, 0.4, 0.5, 0.6, 0.7, 0.8]
143 | self.beta = beta # importance sampling parameter, beta=[0, 0.4, 0.5, 0.6, 1]
144 | self.beta_increment_per_sample = beta_increment_per_sample
145 | self.num_in_buffer = 0 # total number of transitions stored in buffer
146 | self.margin = 0.01 # pi = |td_error| + margin
147 | self.p1 = 1 # initialize priority for the first transition
148 | # self.is_weight = np.empty((None, 1))
149 | self.is_weight = np.power(self.buffer_size, -self.beta) # because p1 == 1
150 | self.abs_error_upper = 1
151 |
152 | def _per_loss(self, y_target, y_pred):
153 | return tf.reduce_mean(self.is_weight * tf.math.squared_difference(y_target, y_pred))
154 |
155 | def train(self):
156 | # initialize the initial observation of the agent
157 | obs = self.env.reset()
158 | for t in range(1, self.train_nums):
159 | best_action, q_values = self.model.action_value(obs[None]) # input the obs to the network model
160 | action = self.get_action(best_action) # get the real action
161 | next_obs, reward, done, info = self.env.step(action) # take the action in the env to return s', r, done
162 | if t == 1:
163 | p = self.p1
164 | else:
165 | p = np.max(self.replay_buffer.tree[-self.replay_buffer.capacity:])
166 | self.store_transition(p, obs, action, reward, next_obs, done) # store that transition into replay butter
167 | self.num_in_buffer = min(self.num_in_buffer + 1, self.buffer_size)
168 |
169 | if t > self.buffer_size:
170 | # if t % self.replay_period == 0: # transition sampling and update
171 | losses = self.train_step()
172 | if t % 1000 == 0:
173 | print('losses each 1000 steps: ', losses)
174 |
175 | if t % self.target_update_iter == 0:
176 | self.update_target_model()
177 | if done:
178 | obs = self.env.reset() # one episode end
179 | else:
180 | obs = next_obs
181 |
182 | def train_step(self):
183 | idxes, self.is_weight = self.sum_tree_sample(self.batch_size)
184 | # Double Q-Learning
185 | best_action_idxes, _ = self.model.action_value(self.b_next_states) # get actions through the current network
186 | target_q = self.get_target_value(self.b_next_states) # get target q-value through the target network
187 | # get td_targets of batch states
188 | td_target = self.b_rewards + \
189 | self.gamma * target_q[np.arange(target_q.shape[0]), best_action_idxes] * (1 - self.b_dones)
190 | predict_q = self.model.predict(self.b_obs)
191 | td_predict = predict_q[np.arange(predict_q.shape[0]), self.b_actions]
192 | abs_td_error = np.abs(td_target - td_predict) + self.margin
193 | clipped_error = np.where(abs_td_error < self.abs_error_upper, abs_td_error, self.abs_error_upper)
194 | ps = np.power(clipped_error, self.alpha)
195 | # priorities update
196 | for idx, p in zip(idxes, ps):
197 | self.replay_buffer.update(idx, p)
198 |
199 | for i, val in enumerate(self.b_actions):
200 | predict_q[i][val] = td_target[i]
201 |
202 | target_q = predict_q # just to change a more explicit name
203 | losses = self.model.train_on_batch(self.b_obs, target_q)
204 |
205 | return losses
206 |
207 | # proportional prioritization sampling
208 | def sum_tree_sample(self, k):
209 | idxes = []
210 | is_weights = np.empty((k, 1))
211 | self.beta = min(1., self.beta + self.beta_increment_per_sample)
212 | # calculate max_weight
213 | min_prob = np.min(self.replay_buffer.tree[-self.replay_buffer.capacity:]) / self.replay_buffer.total_p
214 | max_weight = np.power(self.buffer_size * min_prob, -self.beta)
215 | segment = self.replay_buffer.total_p / k
216 | for i in range(k):
217 | s = np.random.uniform(segment * i, segment * (i + 1))
218 | idx, p, t = self.replay_buffer.get_leaf(s)
219 | idxes.append(idx)
220 | self.b_obs[i], self.b_actions[i], self.b_rewards[i], self.b_next_states[i], self.b_dones[i] = t
221 | # P(j)
222 | sampling_probabilities = p / self.replay_buffer.total_p # where p = p ** self.alpha
223 | is_weights[i, 0] = np.power(self.buffer_size * sampling_probabilities, -self.beta) / max_weight
224 | return idxes, is_weights
225 |
226 | def evaluation(self, env, render=True):
227 | obs, done, ep_reward = env.reset(), False, 0
228 | # one episode until done
229 | while not done:
230 | action, q_values = self.model.action_value(obs[None]) # Using [None] to extend its dimension (4,) -> (1, 4)
231 | obs, reward, done, info = env.step(action)
232 | ep_reward += reward
233 | if render: # visually show
234 | env.render()
235 | time.sleep(0.05)
236 | env.close()
237 | return ep_reward
238 |
239 | # store transitions into replay butter, now sum tree.
240 | def store_transition(self, priority, obs, action, reward, next_state, done):
241 | transition = [obs, action, reward, next_state, done]
242 | self.replay_buffer.add(priority, transition)
243 |
244 | # rank-based prioritization sampling
245 | def rand_based_sample(self, k):
246 | pass
247 |
248 | # e-greedy
249 | def get_action(self, best_action):
250 | if np.random.rand() < self.epsilon:
251 | return self.env.action_space.sample()
252 | return best_action
253 |
254 | # assign the current network parameters to target network
255 | def update_target_model(self):
256 | self.target_model.set_weights(self.model.get_weights())
257 |
258 | def get_target_value(self, obs):
259 | return self.target_model.predict(obs)
260 |
261 | def e_decay(self):
262 | self.epsilon *= self.epsilon_decay
263 |
264 |
265 | if __name__ == '__main__':
266 | test_model()
267 |
268 | env = gym.make("CartPole-v0")
269 | num_actions = env.action_space.n
270 | model = Model(num_actions)
271 | target_model = Model(num_actions)
272 | agent = DDDQNAgent(model, target_model, env)
273 | # test before
274 | rewards_sum = agent.evaluation(env)
275 | print("Before Training: %d out of 200" % rewards_sum) # 9 out of 200
276 |
277 | agent.train()
278 | # test after
279 | # env = gym.wrappers.Monitor(env, './recording', force=True)
280 | rewards_sum = agent.evaluation(env)
281 | print("After Training: %d out of 200" % rewards_sum) # 200 out of 200
282 |
--------------------------------------------------------------------------------
/05_multistep_td.py:
--------------------------------------------------------------------------------
1 | """
2 | A simple version of Multi-Step TD Learning Based on Dueling Double DQN with Prioritized Experience Replay.
3 | To play CartPole-v0.
4 |
5 | Using:
6 | TensorFlow 2.0
7 | Numpy 1.16.2
8 | Gym 0.12.1
9 | """
10 |
11 | import tensorflow as tf
12 | print(tf.__version__)
13 |
14 | import gym
15 | import time
16 | import numpy as np
17 | import tensorflow.keras.layers as kl
18 | import tensorflow.keras.optimizers as ko
19 |
20 | from collections import deque
21 |
22 | np.random.seed(1)
23 | tf.random.set_seed(1)
24 |
25 | # Neural Network Model Defined at Here.
26 | class Model(tf.keras.Model):
27 | def __init__(self, num_actions):
28 | super().__init__(name='basic_nstepTD')
29 | # you can try different kernel initializer
30 | self.shared_fc1 = kl.Dense(16, activation='relu', kernel_initializer='he_uniform')
31 | self.shared_fc2 = kl.Dense(32, activation='relu', kernel_initializer='he_uniform')
32 | # there is a trick that combining the two streams' fc layer, then
33 | # the output of that layer is a |A| + 1 dimension tensor: |V|A1|A2| ... |An|
34 | # output[:, 0] is state value, output[:, 1:] is action advantage
35 | self.val_adv_fc = kl.Dense(num_actions + 1, activation='relu', kernel_initializer='he_uniform')
36 |
37 | # forward propagation
38 | def call(self, inputs):
39 | x = self.shared_fc1(inputs)
40 | x = self.shared_fc2(x)
41 | val_adv = self.val_adv_fc(x)
42 | # average version, you can also try the max version.
43 | outputs = tf.expand_dims(val_adv[:, 0], -1) + (val_adv[:, 1:] - tf.reduce_mean(val_adv[:, 1:], -1, keepdims=True))
44 | return outputs
45 |
46 | # a* = argmax_a' Q(s, a')
47 | def action_value(self, obs):
48 | q_values = self.predict(obs)
49 | best_action = np.argmax(q_values, axis=-1)
50 | return best_action if best_action.shape[0] > 1 else best_action[0], q_values[0]
51 |
52 |
53 | # To test whether the model works
54 | def test_model():
55 | env = gym.make('CartPole-v0')
56 | print('num_actions: ', env.action_space.n)
57 | model = Model(env.action_space.n)
58 |
59 | obs = env.reset()
60 | print('obs_shape: ', obs.shape)
61 |
62 | # tensorflow 2.0 eager mode: no feed_dict or tf.Session() needed at all
63 | best_action, q_values = model.action_value(obs[None])
64 | print('res of test model: ', best_action, q_values) # 0 [ 0.00896799 -0.02111824]
65 |
66 |
67 | # replay buffer
68 | class SumTree:
69 | # little modified from https://github.com/jaromiru/AI-blog/blob/master/SumTree.py
70 | def __init__(self, capacity):
71 | self.capacity = capacity # N, the size of replay buffer, so as to the number of sum tree's leaves
72 | self.tree = np.zeros(2 * capacity - 1) # equation, to calculate the number of nodes in a sum tree
73 | self.transitions = np.empty(capacity, dtype=object)
74 | self.next_idx = 0
75 |
76 | @property
77 | def total_p(self):
78 | return self.tree[0]
79 |
80 | def add(self, priority, transition):
81 | idx = self.next_idx + self.capacity - 1
82 | self.transitions[self.next_idx] = transition
83 | self.update(idx, priority)
84 | self.next_idx = (self.next_idx + 1) % self.capacity
85 |
86 | def update(self, idx, priority):
87 | change = priority - self.tree[idx]
88 | self.tree[idx] = priority
89 | self._propagate(idx, change) # O(logn)
90 |
91 | def _propagate(self, idx, change):
92 | parent = (idx - 1) // 2
93 | self.tree[parent] += change
94 | if parent != 0:
95 | self._propagate(parent, change)
96 |
97 | def get_leaf(self, s):
98 | idx = self._retrieve(0, s) # from root
99 | trans_idx = idx - self.capacity + 1
100 | return idx, self.tree[idx], self.transitions[trans_idx]
101 |
102 | def _retrieve(self, idx, s):
103 | left = 2 * idx + 1
104 | right = left + 1
105 | if left >= len(self.tree):
106 | return idx
107 | if s <= self.tree[left]:
108 | return self._retrieve(left, s)
109 | else:
110 | return self._retrieve(right, s - self.tree[left])
111 |
112 |
113 | class MSTDAgent: # Multi-Step TD Learning Based on Dueling Double DQN with Proportional Prioritization
114 | def __init__(self, model, target_model, env, learning_rate=.0008, epsilon=.1, epsilon_dacay=0.995, min_epsilon=.01,
115 | gamma=.9, batch_size=8, target_update_iter=400, train_nums=5000, buffer_size=300, replay_period=20,
116 | alpha=0.4, beta=0.4, beta_increment_per_sample=0.001, n_step=3):
117 | self.model = model
118 | self.target_model = target_model
119 | # gradient clip
120 | opt = ko.Adam(learning_rate=learning_rate, clipvalue=10.0) # , clipvalue=10.0
121 | self.model.compile(optimizer=opt, loss=self._per_loss) # loss=self._per_loss
122 |
123 | # parameters
124 | self.env = env # gym environment
125 | self.lr = learning_rate # learning step
126 | self.epsilon = epsilon # e-greedy when exploring
127 | self.epsilon_decay = epsilon_dacay # epsilon decay rate
128 | self.min_epsilon = min_epsilon # minimum epsilon
129 | self.gamma = gamma # discount rate
130 | self.batch_size = batch_size # minibatch k
131 | self.target_update_iter = target_update_iter # target network update period
132 | self.train_nums = train_nums # total training steps
133 |
134 | # replay buffer params [(s, a, r, ns, done), ...]
135 | self.b_obs = np.empty((self.batch_size,) + self.env.reset().shape)
136 | self.b_actions = np.empty(self.batch_size, dtype=np.int8)
137 | self.b_rewards = np.empty(self.batch_size, dtype=np.float32)
138 | self.b_next_states = np.empty((self.batch_size,) + self.env.reset().shape)
139 | self.b_dones = np.empty(self.batch_size, dtype=np.bool)
140 |
141 | self.replay_buffer = SumTree(buffer_size) # sum-tree data structure
142 | self.buffer_size = buffer_size # replay buffer size N
143 | self.replay_period = replay_period # replay period K
144 | self.alpha = alpha # priority parameter, alpha=[0, 0.4, 0.5, 0.6, 0.7, 0.8]
145 | self.beta = beta # importance sampling parameter, beta=[0, 0.4, 0.5, 0.6, 1]
146 | self.beta_increment_per_sample = beta_increment_per_sample
147 | self.num_in_buffer = 0 # total number of transitions stored in buffer
148 | self.margin = 0.01 # pi = |td_error| + margin
149 | self.p1 = 1 # initialize priority for the first transition
150 | # self.is_weight = np.empty((None, 1))
151 | self.is_weight = np.power(self.buffer_size, -self.beta) # because p1 == 1
152 | self.abs_error_upper = 1
153 |
154 | # multi step TD learning
155 | self.n_step = n_step
156 | self.n_step_buffer = deque(maxlen=n_step)
157 |
158 | def _per_loss(self, y_target, y_pred):
159 | return tf.reduce_mean(self.is_weight * tf.math.squared_difference(y_target, y_pred))
160 |
161 | def train(self):
162 | # initialize the initial observation of the agent
163 | obs = self.env.reset()
164 | for t in range(1, self.train_nums):
165 | best_action, q_values = self.model.action_value(obs[None]) # input the obs to the network model
166 | action = self.get_action(best_action) # get the real action
167 | next_obs, reward, done, info = self.env.step(action) # take the action in the env to return s', r, done
168 |
169 | # n-step replay buffer
170 | # minor modified from github.com/medipixel/rl_algorithms/blob/master/algorithms/common/helper_functions.py
171 | temp_transition = [obs, action, reward, next_obs, done]
172 | self.n_step_buffer.append(temp_transition)
173 | if len(self.n_step_buffer) == self.n_step: # fill the n-step buffer for the first translation
174 | # add a multi step transition
175 | reward, next_obs, done = self.get_n_step_info(self.n_step_buffer, self.gamma)
176 | obs, action = self.n_step_buffer[0][:2]
177 |
178 | if t == 1:
179 | p = self.p1
180 | else:
181 | p = np.max(self.replay_buffer.tree[-self.replay_buffer.capacity:])
182 | self.store_transition(p, obs, action, reward, next_obs, done) # store that transition into replay butter
183 | self.num_in_buffer = min(self.num_in_buffer + 1, self.buffer_size)
184 |
185 | if t > self.buffer_size:
186 | # if t % self.replay_period == 0: # transition sampling and update
187 | losses = self.train_step()
188 | if t % 1000 == 0:
189 | print('losses each 1000 steps: ', losses)
190 |
191 | if t % self.target_update_iter == 0:
192 | self.update_target_model()
193 | if done:
194 | obs = self.env.reset() # one episode end
195 | else:
196 | obs = next_obs
197 |
198 | def train_step(self):
199 | idxes, self.is_weight = self.sum_tree_sample(self.batch_size)
200 | assert len(idxes) == self.b_next_states.shape[0]
201 |
202 | # Double Q-Learning
203 | best_action_idxes, _ = self.model.action_value(self.b_next_states) # get actions through the current network
204 | target_q = self.get_target_value(self.b_next_states) # get target q-value through the target network
205 | # get td_targets of batch states
206 | td_target = self.b_rewards + \
207 | self.gamma * target_q[np.arange(target_q.shape[0]), best_action_idxes] * (1 - self.b_dones)
208 | predict_q = self.model.predict(self.b_obs)
209 | td_predict = predict_q[np.arange(predict_q.shape[0]), self.b_actions]
210 | abs_td_error = np.abs(td_target - td_predict) + self.margin
211 | clipped_error = np.where(abs_td_error < self.abs_error_upper, abs_td_error, self.abs_error_upper)
212 | ps = np.power(clipped_error, self.alpha)
213 | # priorities update
214 | for idx, p in zip(idxes, ps):
215 | self.replay_buffer.update(idx, p)
216 |
217 | for i, val in enumerate(self.b_actions):
218 | predict_q[i][val] = td_target[i]
219 |
220 | target_q = predict_q # just to change a more explicit name
221 | losses = self.model.train_on_batch(self.b_obs, target_q)
222 |
223 | return losses
224 |
225 | # proportional prioritization sampling
226 | def sum_tree_sample(self, k):
227 | idxes = []
228 | is_weights = np.empty((k, 1))
229 | self.beta = min(1., self.beta + self.beta_increment_per_sample)
230 | # calculate max_weight
231 | min_prob = np.min(self.replay_buffer.tree[-self.replay_buffer.capacity:]) / self.replay_buffer.total_p
232 | max_weight = np.power(self.buffer_size * min_prob, -self.beta)
233 | segment = self.replay_buffer.total_p / k
234 | for i in range(k):
235 | s = np.random.uniform(segment * i, segment * (i + 1))
236 | idx, p, t = self.replay_buffer.get_leaf(s)
237 | idxes.append(idx)
238 | self.b_obs[i], self.b_actions[i], self.b_rewards[i], self.b_next_states[i], self.b_dones[i] = t
239 | # P(j)
240 | sampling_probabilities = p / self.replay_buffer.total_p # where p = p ** self.alpha
241 | is_weights[i, 0] = np.power(self.buffer_size * sampling_probabilities, -self.beta) / max_weight
242 | return idxes, is_weights
243 |
244 | def evaluation(self, env, render=True):
245 | obs, done, ep_reward = env.reset(), False, 0
246 | # one episode until done
247 | while not done:
248 | action, q_values = self.model.action_value(obs[None]) # Using [None] to extend its dimension (4,) -> (1, 4)
249 | obs, reward, done, info = env.step(action)
250 | ep_reward += reward
251 | if render: # visually show
252 | env.render()
253 | time.sleep(0.05)
254 | env.close()
255 | return ep_reward
256 |
257 | # store transitions into replay butter, now sum tree.
258 | def store_transition(self, priority, obs, action, reward, next_state, done):
259 | transition = [obs, action, reward, next_state, done]
260 | self.replay_buffer.add(priority, transition)
261 |
262 | # minor modified from https://github.com/medipixel/rl_algorithms/blob/master/algorithms/common/helper_functions.py
263 | def get_n_step_info(self, n_step_buffer, gamma):
264 | """Return n step reward, next state, and done."""
265 | # info of the last transition
266 | reward, next_state, done = n_step_buffer[-1][-3:]
267 |
268 | for transition in reversed(list(n_step_buffer)[:-1]):
269 | r, n_s, d = transition[-3:]
270 |
271 | reward = r + gamma * reward * (1 - d)
272 | next_state, done = (n_s, d) if d else (next_state, done)
273 |
274 | return reward, next_state, done
275 |
276 |
277 | # rank-based prioritization sampling
278 | def rand_based_sample(self, k):
279 | pass
280 |
281 | # e-greedy
282 | def get_action(self, best_action):
283 | if np.random.rand() < self.epsilon:
284 | return self.env.action_space.sample()
285 | return best_action
286 |
287 | # assign the current network parameters to target network
288 | def update_target_model(self):
289 | self.target_model.set_weights(self.model.get_weights())
290 |
291 | def get_target_value(self, obs):
292 | return self.target_model.predict(obs)
293 |
294 | def e_decay(self):
295 | self.epsilon *= self.epsilon_decay
296 |
297 |
298 | if __name__ == '__main__':
299 | test_model()
300 |
301 | env = gym.make("CartPole-v0")
302 | num_actions = env.action_space.n
303 | model = Model(num_actions)
304 | target_model = Model(num_actions)
305 | agent = MSTDAgent(model, target_model, env)
306 | # test before
307 | rewards_sum = agent.evaluation(env)
308 | print("Before Training: %d out of 200" % rewards_sum) # 9 out of 200
309 |
310 | agent.train()
311 | # test after
312 | # env = gym.wrappers.Monitor(env, './recording', force=True)
313 | rewards_sum = agent.evaluation(env)
314 | print("After Training: %d out of 200" % rewards_sum) # 200 out of 200
315 |
--------------------------------------------------------------------------------
/06_distributional_rl.py:
--------------------------------------------------------------------------------
1 | """
2 | A simple version of Distributional RL Based on Multi-Step Dueling Double DQN with Prioritized Experience Replay.
3 | To play CartPole-v0.
4 |
5 | Using:
6 | TensorFlow 2.0
7 | Numpy 1.16.2
8 | Gym 0.12.1
9 | """
10 |
11 | import tensorflow as tf
12 | print(tf.__version__)
13 |
14 | import gym
15 | import time
16 | import numpy as np
17 | import tensorflow.keras.layers as kl
18 | import tensorflow.keras.optimizers as ko
19 |
20 | from collections import deque
21 |
22 | np.random.seed(1)
23 | tf.random.set_seed(1)
24 |
25 | # Neural Network Model Defined at Here.
26 | class Model(tf.keras.Model):
27 | def __init__(self, num_actions, num_atoms):
28 | super().__init__(name='basic_distributional_rl')
29 | self.num_actions = num_actions
30 | self.num_atoms = num_atoms
31 | # you can try different kernel initializer
32 | self.shared_fc1 = kl.Dense(16, activation='relu', kernel_initializer='he_uniform')
33 | self.shared_fc2 = kl.Dense(32, activation='relu', kernel_initializer='he_uniform')
34 | # still use the dueling network architecture, but now:
35 | # V | v_0| v_1| ... | v_N-1|
36 | # A |a1_0|a1_1| ... |a1_N-1|
37 | # |a2_0|a2_1| ... |a2_N-1|
38 | # . . .
39 | # . . .
40 | # |an_0|an_1| ... |an_N-1|
41 | # the output of that layer is a (|A| + 1) * N dimension tensor
42 | # each column is a |A| + 1 dimension tensor for each atom.
43 | self.val_adv_fc = kl.Dense((num_actions + 1) * num_atoms, activation='relu', kernel_initializer='he_uniform')
44 |
45 | # forward propagation
46 | def call(self, inputs):
47 | x = self.shared_fc1(inputs)
48 | x = self.shared_fc2(x)
49 | val_adv = self.val_adv_fc(x)
50 | # average version, you can also try the max version.
51 | val_adv = tf.reshape(val_adv, [-1, self.num_actions + 1, self.num_atoms])
52 | outputs = tf.expand_dims(val_adv[:, 0], 1) + (val_adv[:, 1:] - tf.reduce_mean(val_adv[:, 1:], -1, keepdims=True))
53 | # you may need tf.nn.log_softmax()
54 | outputs = tf.nn.softmax(outputs, axis=-1)
55 |
56 | return outputs
57 |
58 | # a* = argmax_a' Q(s, a')
59 | def action_value(self, obs, support_z):
60 | r_distribute = self.predict(obs)
61 | q_values = np.sum(r_distribute * support_z, axis=-1)
62 | best_action = np.argmax(q_values, axis=-1)
63 | return best_action if best_action.shape[0] > 1 else best_action[0], q_values[0]
64 |
65 |
66 | # To test whether the model works
67 | def test_model():
68 | num_atoms = 11
69 | support_z = np.linspace(-5.0, 5.0, num_atoms)
70 | env = gym.make('CartPole-v0')
71 | print('num_actions: ', env.action_space.n)
72 | model = Model(env.action_space.n, num_atoms)
73 |
74 | obs = env.reset()
75 | print('obs_shape: ', obs.shape)
76 |
77 | # tensorflow 2.0 eager mode: no feed_dict or tf.Session() needed at all
78 | best_action, q_values = model.action_value(obs[None], support_z)
79 | print('res of test model: ', best_action, q_values) # 0 [ 0.00896799 -0.02111824]
80 |
81 |
82 | # replay buffer
83 | class SumTree:
84 | # little modified from https://github.com/jaromiru/AI-blog/blob/master/SumTree.py
85 | def __init__(self, capacity):
86 | self.capacity = capacity # N, the size of replay buffer, so as to the number of sum tree's leaves
87 | self.tree = np.zeros(2 * capacity - 1) # equation, to calculate the number of nodes in a sum tree
88 | self.transitions = np.empty(capacity, dtype=object)
89 | self.next_idx = 0
90 |
91 | @property
92 | def total_p(self):
93 | return self.tree[0]
94 |
95 | def add(self, priority, transition):
96 | idx = self.next_idx + self.capacity - 1
97 | self.transitions[self.next_idx] = transition
98 | self.update(idx, priority)
99 | self.next_idx = (self.next_idx + 1) % self.capacity
100 |
101 | def update(self, idx, priority):
102 | change = priority - self.tree[idx]
103 | self.tree[idx] = priority
104 | self._propagate(idx, change) # O(logn)
105 |
106 | def _propagate(self, idx, change):
107 | parent = (idx - 1) // 2
108 | self.tree[parent] += change
109 | if parent != 0:
110 | self._propagate(parent, change)
111 |
112 | def get_leaf(self, s):
113 | idx = self._retrieve(0, s) # from root
114 | trans_idx = idx - self.capacity + 1
115 | return idx, self.tree[idx], self.transitions[trans_idx]
116 |
117 | def _retrieve(self, idx, s):
118 | left = 2 * idx + 1
119 | right = left + 1
120 | if left >= len(self.tree):
121 | return idx
122 | if s <= self.tree[left]:
123 | return self._retrieve(left, s)
124 | else:
125 | return self._retrieve(right, s - self.tree[left])
126 |
127 |
128 | class DISTAgent: # Distributional RL Based on Multi-Step Dueling Double DQN with Proportional Prioritization
129 | def __init__(self, model, target_model, env, learning_rate=.001, epsilon=.1, epsilon_dacay=0.995, min_epsilon=.01,
130 | gamma=.9, batch_size=8, target_update_iter=400, train_nums=5000, buffer_size=300, replay_period=20,
131 | alpha=0.4, beta=0.4, beta_increment_per_sample=0.001, n_step=3, atom_num=11, vmin=-3.0, vmax=3.0):
132 | self.model = model
133 | self.target_model = target_model
134 | # gradient clip
135 | opt = ko.Adam(learning_rate=learning_rate, clipvalue=10.0) # , clipvalue=10.0
136 | self.model.compile(optimizer=opt, loss=self._per_loss) # loss=self._per_loss
137 |
138 | # parameters
139 | self.env = env # gym environment
140 | self.lr = learning_rate # learning step
141 | self.epsilon = epsilon # e-greedy when exploring
142 | self.epsilon_decay = epsilon_dacay # epsilon decay rate
143 | self.min_epsilon = min_epsilon # minimum epsilon
144 | self.gamma = gamma # discount rate
145 | self.batch_size = batch_size # minibatch k
146 | self.target_update_iter = target_update_iter # target network update period
147 | self.train_nums = train_nums # total training steps
148 |
149 | # replay buffer params [(s, a, r, ns, done), ...]
150 | self.b_obs = np.empty((self.batch_size,) + self.env.reset().shape)
151 | self.b_actions = np.empty(self.batch_size, dtype=np.int8)
152 | self.b_rewards = np.empty(self.batch_size, dtype=np.float32)
153 | self.b_next_states = np.empty((self.batch_size,) + self.env.reset().shape)
154 | self.b_dones = np.empty(self.batch_size, dtype=np.bool)
155 |
156 | self.replay_buffer = SumTree(buffer_size) # sum-tree data structure
157 | self.buffer_size = buffer_size # replay buffer size N
158 | self.replay_period = replay_period # replay period K
159 | self.alpha = alpha # priority parameter, alpha=[0, 0.4, 0.5, 0.6, 0.7, 0.8]
160 | self.beta = beta # importance sampling parameter, beta=[0, 0.4, 0.5, 0.6, 1]
161 | self.beta_increment_per_sample = beta_increment_per_sample
162 | self.num_in_buffer = 0 # total number of transitions stored in buffer
163 | self.margin = 0.01 # pi = |td_error| + margin
164 | self.p1 = 1 # initialize priority for the first transition
165 | # self.is_weight = np.empty((None, 1))
166 | self.is_weight = np.power(self.buffer_size, -self.beta) # because p1 == 1
167 | self.abs_error_upper = 1
168 |
169 | # multi step TD learning
170 | self.n_step = n_step
171 | self.n_step_buffer = deque(maxlen=n_step)
172 |
173 | # distributional rl
174 | self.atom_num = atom_num
175 | self.vmin = vmin
176 | self.vmax = vmax
177 | self.support_z = np.expand_dims(np.linspace(vmin, vmax, atom_num), 0)
178 | self.delta_z = (vmax - vmin) / (atom_num - 1)
179 |
180 | def _per_loss(self, y_target, y_pred):
181 | return tf.reduce_mean(self.is_weight * tf.math.squared_difference(y_target, y_pred))
182 |
183 | def _kl_loss(self, y_target, y_pred): # cross_entropy loss
184 | return tf.reduce_mean(self.is_weight * tf.nn.softmax_cross_entropy_with_logits(labels=y_pred, logits=y_target))
185 |
186 | def train(self):
187 | # initialize the initial observation of the agent
188 | obs = self.env.reset()
189 | for t in range(1, self.train_nums):
190 | best_action, _ = self.model.action_value(obs[None], self.support_z) # input the obs to the network model
191 | action = self.get_action(best_action) # get the real action
192 | next_obs, reward, done, info = self.env.step(action) # take the action in the env to return s', r, done
193 |
194 | # n-step replay buffer
195 | # minor modified from github.com/medipixel/rl_algorithms/blob/master/algorithms/common/helper_functions.py
196 | temp_transition = [obs, action, reward, next_obs, done]
197 | self.n_step_buffer.append(temp_transition)
198 | if len(self.n_step_buffer) == self.n_step: # fill the n-step buffer for the first translation
199 | # add a multi step transition
200 | reward, next_obs, done = self.get_n_step_info(self.n_step_buffer, self.gamma)
201 | obs, action = self.n_step_buffer[0][:2]
202 |
203 | if t == 1:
204 | p = self.p1
205 | else:
206 | p = np.max(self.replay_buffer.tree[-self.replay_buffer.capacity:])
207 | self.store_transition(p, obs, action, reward, next_obs, done) # store that transition into replay butter
208 | self.num_in_buffer = min(self.num_in_buffer + 1, self.buffer_size)
209 |
210 | if t > self.buffer_size:
211 | # if t % self.replay_period == 0: # transition sampling and update
212 | losses = self.train_step()
213 | if t % 1000 == 0:
214 | print('losses each 1000 steps: ', losses)
215 |
216 | if t % self.target_update_iter == 0:
217 | self.update_target_model()
218 | if done:
219 | obs = self.env.reset() # one episode end
220 | else:
221 | obs = next_obs
222 |
223 | def train_step(self):
224 | idxes, self.is_weight = self.sum_tree_sample(self.batch_size)
225 | assert len(idxes) == self.b_next_states.shape[0]
226 |
227 | # Double Q-Learning
228 | best_action_idxes, _ = self.model.action_value(self.b_next_states, self.support_z) # get actions through the current network
229 | target_distrib = self.get_target_value(self.b_next_states) # get target distrib through the target network
230 | target_q = np.sum(target_distrib * self.support_z, axis=-1)
231 |
232 | # get td_targets of batch states
233 | td_target = self.b_rewards + \
234 | self.gamma * target_q[np.arange(target_q.shape[0]), best_action_idxes] * (1 - self.b_dones)
235 |
236 | predict_distrib = self.model.predict(self.b_obs)
237 | predict_q = np.sum(predict_distrib * self.support_z, axis=-1)
238 |
239 | td_predict = predict_q[np.arange(predict_q.shape[0]), self.b_actions]
240 | abs_td_error = np.abs(td_target - td_predict) + self.margin
241 | clipped_error = np.where(abs_td_error < self.abs_error_upper, abs_td_error, self.abs_error_upper)
242 | ps = np.power(clipped_error, self.alpha)
243 | # priorities update
244 | for idx, p in zip(idxes, ps):
245 | self.replay_buffer.update(idx, p)
246 |
247 | Tdistrib = target_distrib[np.arange(target_distrib.shape[0]), best_action_idxes]
248 | perjected_distrib = self.projected_distrib(Tdistrib)
249 |
250 | # perjected_distrib = np.c_[perjected_distrib, self.b_actions]
251 | null_distrib = np.zeros_like(predict_distrib)
252 | for i, val in enumerate(self.b_actions):
253 | null_distrib[i][val] = perjected_distrib[i]
254 |
255 | # print(self.b_actions)
256 | # print(perjected_distrib[:, -1].astype(np.int32))
257 | # print(predict_distrib[np.arange(self.batch_size), perjected_distrib[:, -1].astype(np.int32)])
258 |
259 | losses = self.model.train_on_batch(self.b_obs, null_distrib)
260 |
261 | return losses
262 |
263 | # proportional prioritization sampling
264 | def sum_tree_sample(self, k):
265 | idxes = []
266 | is_weights = np.empty((k, 1))
267 | self.beta = min(1., self.beta + self.beta_increment_per_sample)
268 | # calculate max_weight
269 | min_prob = np.min(self.replay_buffer.tree[-self.replay_buffer.capacity:]) / self.replay_buffer.total_p
270 | max_weight = np.power(self.buffer_size * min_prob, -self.beta)
271 | segment = self.replay_buffer.total_p / k
272 | for i in range(k):
273 | s = np.random.uniform(segment * i, segment * (i + 1))
274 | idx, p, t = self.replay_buffer.get_leaf(s)
275 | idxes.append(idx)
276 | self.b_obs[i], self.b_actions[i], self.b_rewards[i], self.b_next_states[i], self.b_dones[i] = t
277 | # P(j)
278 | sampling_probabilities = p / self.replay_buffer.total_p # where p = p ** self.alpha
279 | is_weights[i, 0] = np.power(self.buffer_size * sampling_probabilities, -self.beta) / max_weight
280 | return idxes, is_weights
281 |
282 | def evaluation(self, env, render=True):
283 | obs, done, ep_reward = env.reset(), False, 0
284 | # one episode until done
285 | while not done:
286 | action, q_values = self.model.action_value(obs[None], self.support_z) # Using [None] to extend its dimension (4,) -> (1, 4)
287 | obs, reward, done, info = env.step(action)
288 | ep_reward += reward
289 | if render: # visually show
290 | env.render()
291 | time.sleep(0.05)
292 | env.close()
293 | return ep_reward
294 |
295 | # store transitions into replay butter, now sum tree.
296 | def store_transition(self, priority, obs, action, reward, next_state, done):
297 | transition = [obs, action, reward, next_state, done]
298 | self.replay_buffer.add(priority, transition)
299 |
300 | # rank-based prioritization sampling
301 | def rand_based_sample(self, k):
302 | pass
303 |
304 | # e-greedy
305 | def get_action(self, best_action):
306 | if np.random.rand() < self.epsilon:
307 | return self.env.action_space.sample()
308 | return best_action
309 |
310 | # assign the current network parameters to target network
311 | def update_target_model(self):
312 | self.target_model.set_weights(self.model.get_weights())
313 |
314 | def get_target_value(self, obs):
315 | return self.target_model.predict(obs)
316 |
317 | def e_decay(self):
318 | self.epsilon *= self.epsilon_decay
319 |
320 | # minor modified from https://github.com/medipixel/rl_algorithms/blob/master/algorithms/common/helper_functions.py
321 | def get_n_step_info(self, n_step_buffer, gamma):
322 | """Return n step reward, next state, and done."""
323 | # info of the last transition
324 | reward, next_state, done = n_step_buffer[-1][-3:]
325 |
326 | for transition in reversed(list(n_step_buffer)[:-1]):
327 | r, n_s, d = transition[-3:]
328 |
329 | reward = r + gamma * reward * (1 - d)
330 | next_state, done = (n_s, d) if d else (next_state, done)
331 |
332 | return reward, next_state, done
333 |
334 | def projected_distrib(self, Tdistrib):
335 | Tz = np.broadcast_to(self.support_z, [self.batch_size, self.support_z.shape[1]])
336 | Tz = (self.gamma ** self.n_step) * Tz
337 | # stupid tensorflow don't know how to broad cast, angry!!!
338 | for i in range(self.batch_size):
339 | Tz[i] += self.b_rewards[i]
340 | Tz = tf.clip_by_value(Tz, self.vmin, self.vmax)
341 | m = np.zeros_like(Tdistrib)
342 | b = (Tz - self.vmin) / self.delta_z
343 | l, u = tf.cast(tf.math.floor(b), tf.int32), tf.cast(tf.math.ceil(b), tf.int32)
344 | assert m.shape == l.shape
345 | Ldistrib = Tdistrib * (tf.cast(u, tf.float64) - b)
346 | Udistrib = Tdistrib * (b - tf.cast(l, tf.float64))
347 | for i in range(self.batch_size):
348 | np.add.at(m[i], np.asarray(l)[i], Ldistrib[i])
349 | np.add.at(m[i], np.asarray(u)[i], Udistrib[i])
350 | return tf.clip_by_value(m, 0.0, 1.0)
351 |
352 |
353 |
354 | if __name__ == '__main__':
355 | test_model()
356 |
357 | num_atoms = 11
358 | env = gym.make("CartPole-v0")
359 | num_actions = env.action_space.n
360 | model = Model(num_actions, num_atoms)
361 | target_model = Model(num_actions, num_atoms)
362 | agent = DISTAgent(model, target_model, env, atom_num=num_atoms)
363 | # test before
364 | rewards_sum = agent.evaluation(env)
365 | print("Before Training: %d out of 200" % rewards_sum) # 9 out of 200
366 |
367 | agent.train()
368 | # test after
369 | # env = gym.wrappers.Monitor(env, './recording', force=True)
370 | rewards_sum = agent.evaluation(env)
371 | print("After Training: %d out of 200" % rewards_sum) # 200 out of 200
372 |
--------------------------------------------------------------------------------
/07_noisynet.py:
--------------------------------------------------------------------------------
1 | """
2 | A simple version of Multi-Step TD Learning Based on Dueling Double DQN with Prioritized Experience Replay.
3 | To play CartPole-v0.
4 |
5 | Using:
6 | TensorFlow 2.0
7 | Numpy 1.16.2
8 | Gym 0.12.1
9 | """
10 |
11 | import tensorflow as tf
12 | print(tf.__version__)
13 |
14 | import gym
15 | import time
16 | import numpy as np
17 | import tensorflow.keras.layers as kl
18 | import tensorflow.keras.optimizers as ko
19 |
20 |
21 | from collections import deque
22 |
23 | np.random.seed(1)
24 | tf.random.set_seed(1)
25 |
26 | # Neural Network Model Defined at Here.
27 | class Model(tf.keras.Model):
28 | def __init__(self, num_actions):
29 | super().__init__(name='basic_nstepTD')
30 | # you can try different kernel initializer
31 | self.shared_fc1 = kl.Dense(16, activation='relu', kernel_initializer='he_uniform')
32 | self.shared_fc2 = kl.Dense(32, activation='relu', kernel_initializer='he_uniform')
33 | # there is a trick that combining the two streams' fc layer, then
34 | # the output of that layer is a |A| + 1 dimension tensor: |V|A1|A2| ... |An|
35 | # output[:, 0] is state value, output[:, 1:] is action advantage
36 | self.val_adv_fc = NoisyDense(num_actions + 1, input_dim=32)
37 |
38 | # forward propagation
39 | def call(self, inputs):
40 | x = self.shared_fc1(inputs)
41 | x = self.shared_fc2(x)
42 | val_adv = self.val_adv_fc(x)
43 | # average version, you can also try the max version.
44 | outputs = tf.expand_dims(val_adv[:, 0], -1) + (val_adv[:, 1:] - tf.reduce_mean(val_adv[:, 1:], -1, keepdims=True))
45 | return outputs
46 |
47 | # a* = argmax_a' Q(s, a')
48 | def action_value(self, obs):
49 | q_values = self.predict(obs)
50 | best_action = np.argmax(q_values, axis=-1)
51 | return best_action if best_action.shape[0] > 1 else best_action[0], q_values[0]
52 |
53 |
54 | # Factorized Gaussian Noise Layer
55 | # Reference from https://github.com/Kaixhin/Rainbow/blob/master/model.py
56 | class NoisyDense(kl.Layer):
57 | def __init__(self, units, input_dim, std_init=0.5):
58 | super().__init__()
59 | self.units = units
60 | self.std_init = std_init
61 | self.reset_noise(input_dim)
62 | mu_range = 1 / np.sqrt(input_dim)
63 | mu_initializer = tf.random_uniform_initializer(-mu_range, mu_range)
64 | sigma_initializer = tf.constant_initializer(self.std_init / np.sqrt(self.units))
65 |
66 | self.weight_mu = tf.Variable(initial_value=mu_initializer(shape=(input_dim, units), dtype='float32'),
67 | trainable=True)
68 |
69 | self.weight_sigma = tf.Variable(initial_value=sigma_initializer(shape=(input_dim, units), dtype='float32'),
70 | trainable=True)
71 |
72 | self.bias_mu = tf.Variable(initial_value=mu_initializer(shape=(units,), dtype='float32'),
73 | trainable=True)
74 |
75 | self.bias_sigma = tf.Variable(initial_value=sigma_initializer(shape=(units,), dtype='float32'),
76 | trainable=True)
77 |
78 | def call(self, inputs):
79 | # output = tf.tensordot(inputs, self.kernel, 1)
80 | # tf.nn.bias_add(output, self.bias)
81 | # return output
82 | self.kernel = self.weight_mu + self.weight_sigma * self.weights_eps
83 | self.bias = self.bias_mu + self.bias_sigma * self.bias_eps
84 | return tf.matmul(inputs, self.kernel) + self.bias
85 |
86 | def _scale_noise(self, dim):
87 | noise = tf.random.normal([dim])
88 | return tf.sign(noise) * tf.sqrt(tf.abs(noise))
89 |
90 | def reset_noise(self, input_shape):
91 | eps_in = self._scale_noise(input_shape)
92 | eps_out = self._scale_noise(self.units)
93 | self.weights_eps = tf.multiply(tf.expand_dims(eps_in, 1), eps_out)
94 | self.bias_eps = eps_out
95 |
96 |
97 | # To test whether the model works
98 | def test_model():
99 | env = gym.make('CartPole-v0')
100 | print('num_actions: ', env.action_space.n)
101 | model = Model(env.action_space.n)
102 |
103 | obs = env.reset()
104 | print('obs_shape: ', obs.shape)
105 |
106 | # tensorflow 2.0 eager mode: no feed_dict or tf.Session() needed at all
107 | best_action, q_values = model.action_value(obs[None])
108 | print('res of test model: ', best_action, q_values) # 0 [ 0.00896799 -0.02111824]
109 |
110 |
111 | # replay buffer
112 | class SumTree:
113 | # little modified from https://github.com/jaromiru/AI-blog/blob/master/SumTree.py
114 | def __init__(self, capacity):
115 | self.capacity = capacity # N, the size of replay buffer, so as to the number of sum tree's leaves
116 | self.tree = np.zeros(2 * capacity - 1) # equation, to calculate the number of nodes in a sum tree
117 | self.transitions = np.empty(capacity, dtype=object)
118 | self.next_idx = 0
119 |
120 | @property
121 | def total_p(self):
122 | return self.tree[0]
123 |
124 | def add(self, priority, transition):
125 | idx = self.next_idx + self.capacity - 1
126 | self.transitions[self.next_idx] = transition
127 | self.update(idx, priority)
128 | self.next_idx = (self.next_idx + 1) % self.capacity
129 |
130 | def update(self, idx, priority):
131 | change = priority - self.tree[idx]
132 | self.tree[idx] = priority
133 | self._propagate(idx, change) # O(logn)
134 |
135 | def _propagate(self, idx, change):
136 | parent = (idx - 1) // 2
137 | self.tree[parent] += change
138 | if parent != 0:
139 | self._propagate(parent, change)
140 |
141 | def get_leaf(self, s):
142 | idx = self._retrieve(0, s) # from root
143 | trans_idx = idx - self.capacity + 1
144 | return idx, self.tree[idx], self.transitions[trans_idx]
145 |
146 | def _retrieve(self, idx, s):
147 | left = 2 * idx + 1
148 | right = left + 1
149 | if left >= len(self.tree):
150 | return idx
151 | if s <= self.tree[left]:
152 | return self._retrieve(left, s)
153 | else:
154 | return self._retrieve(right, s - self.tree[left])
155 |
156 |
157 | class NoisyAgent: # Multi-Step TD Learning Based on Dueling Double DQN with Proportional Prioritization
158 | def __init__(self, model, target_model, env, learning_rate=.005, epsilon=.1, epsilon_dacay=0.995, min_epsilon=.01,
159 | gamma=.9, batch_size=8, target_update_iter=400, train_nums=4000, buffer_size=300, replay_period=20,
160 | alpha=0.4, beta=0.4, beta_increment_per_sample=0.001, n_step=3):
161 | self.model = model
162 | self.target_model = target_model
163 | # gradient clip
164 | opt = ko.Adam(learning_rate=learning_rate, clipvalue=10.0) # , clipvalue=10.0
165 | self.model.compile(optimizer=opt, loss=self._per_loss) # loss=self._per_loss
166 |
167 | # parameters
168 | self.env = env # gym environment
169 | self.lr = learning_rate # learning step
170 | self.epsilon = epsilon # e-greedy when exploring
171 | self.epsilon_decay = epsilon_dacay # epsilon decay rate
172 | self.min_epsilon = min_epsilon # minimum epsilon
173 | self.gamma = gamma # discount rate
174 | self.batch_size = batch_size # minibatch k
175 | self.target_update_iter = target_update_iter # target network update period
176 | self.train_nums = train_nums # total training steps
177 |
178 | # replay buffer params [(s, a, r, ns, done), ...]
179 | self.b_obs = np.empty((self.batch_size,) + self.env.reset().shape)
180 | self.b_actions = np.empty(self.batch_size, dtype=np.int8)
181 | self.b_rewards = np.empty(self.batch_size, dtype=np.float32)
182 | self.b_next_states = np.empty((self.batch_size,) + self.env.reset().shape)
183 | self.b_dones = np.empty(self.batch_size, dtype=np.bool)
184 |
185 | self.replay_buffer = SumTree(buffer_size) # sum-tree data structure
186 | self.buffer_size = buffer_size # replay buffer size N
187 | self.replay_period = replay_period # replay period K
188 | self.alpha = alpha # priority parameter, alpha=[0, 0.4, 0.5, 0.6, 0.7, 0.8]
189 | self.beta = beta # importance sampling parameter, beta=[0, 0.4, 0.5, 0.6, 1]
190 | self.beta_increment_per_sample = beta_increment_per_sample
191 | self.num_in_buffer = 0 # total number of transitions stored in buffer
192 | self.margin = 0.01 # pi = |td_error| + margin
193 | self.p1 = 1 # initialize priority for the first transition
194 | # self.is_weight = np.empty((None, 1))
195 | self.is_weight = np.power(self.buffer_size, -self.beta) # because p1 == 1
196 | self.abs_error_upper = 1
197 |
198 | # multi step TD learning
199 | self.n_step = n_step
200 | self.n_step_buffer = deque(maxlen=n_step)
201 |
202 | def _per_loss(self, y_target, y_pred):
203 | return tf.reduce_mean(self.is_weight * tf.math.squared_difference(y_target, y_pred))
204 |
205 | def train(self):
206 | # initialize the initial observation of the agent
207 | obs = self.env.reset()
208 | for t in range(1, self.train_nums):
209 | action, q_values = self.model.action_value(obs[None]) # input the obs to the network model
210 | # action = self.get_action(best_action) # get the real action -- no need the e-greedy exploration
211 | next_obs, reward, done, info = self.env.step(action) # take the action in the env to return s', r, done
212 |
213 | # n-step replay buffer
214 | ####################################################################################################
215 | # minor modified from github.com/medipixel/rl_algorithms/blob/master/algorithms/common/helper_functions.py
216 | temp_transition = [obs, action, reward, next_obs, done]
217 | self.n_step_buffer.append(temp_transition)
218 | if len(self.n_step_buffer) == self.n_step: # fill the n-step buffer for the first translation
219 | # add a multi step transition
220 | reward, next_obs, done = self.get_n_step_info(self.n_step_buffer, self.gamma)
221 | obs, action = self.n_step_buffer[0][:2]
222 | ####################################################################################################
223 |
224 | if t == 1:
225 | p = self.p1
226 | else:
227 | p = np.max(self.replay_buffer.tree[-self.replay_buffer.capacity:])
228 | self.store_transition(p, obs, action, reward, next_obs, done) # store that transition into replay butter
229 | self.num_in_buffer = min(self.num_in_buffer + 1, self.buffer_size)
230 |
231 | if t > self.buffer_size:
232 | # if t % self.replay_period == 0: # transition sampling and update
233 | losses = self.train_step()
234 | if t % 1000 == 0:
235 | print('losses each 1000 steps: ', losses)
236 |
237 | if t % self.target_update_iter == 0:
238 | self.update_target_model()
239 | if done:
240 | obs = self.env.reset() # one episode end
241 | else:
242 | obs = next_obs
243 |
244 | def train_step(self):
245 | idxes, self.is_weight = self.sum_tree_sample(self.batch_size)
246 | assert len(idxes) == self.b_next_states.shape[0]
247 |
248 | # Double Q-Learning
249 | best_action_idxes, _ = self.model.action_value(self.b_next_states) # get actions through the current network
250 | target_q = self.get_target_value(self.b_next_states) # get target q-value through the target network
251 | # get td_targets of batch states
252 | td_target = self.b_rewards + \
253 | self.gamma * target_q[np.arange(target_q.shape[0]), best_action_idxes] * (1 - self.b_dones)
254 | predict_q = self.model.predict(self.b_obs)
255 | td_predict = predict_q[np.arange(predict_q.shape[0]), self.b_actions]
256 | abs_td_error = np.abs(td_target - td_predict) + self.margin
257 | clipped_error = np.where(abs_td_error < self.abs_error_upper, abs_td_error, self.abs_error_upper)
258 | ps = np.power(clipped_error, self.alpha)
259 | # priorities update
260 | for idx, p in zip(idxes, ps):
261 | self.replay_buffer.update(idx, p)
262 |
263 | for i, val in enumerate(self.b_actions):
264 | predict_q[i][val] = td_target[i]
265 |
266 | target_q = predict_q # just to change a more explicit name
267 | losses = self.model.train_on_batch(self.b_obs, target_q)
268 |
269 | return losses
270 |
271 | # proportional prioritization sampling
272 | def sum_tree_sample(self, k):
273 | idxes = []
274 | is_weights = np.empty((k, 1))
275 | self.beta = min(1., self.beta + self.beta_increment_per_sample)
276 | # calculate max_weight
277 | min_prob = np.min(self.replay_buffer.tree[-self.replay_buffer.capacity:]) / self.replay_buffer.total_p
278 | max_weight = np.power(self.buffer_size * min_prob, -self.beta)
279 | segment = self.replay_buffer.total_p / k
280 | for i in range(k):
281 | s = np.random.uniform(segment * i, segment * (i + 1))
282 | idx, p, t = self.replay_buffer.get_leaf(s)
283 | idxes.append(idx)
284 | self.b_obs[i], self.b_actions[i], self.b_rewards[i], self.b_next_states[i], self.b_dones[i] = t
285 | # P(j)
286 | sampling_probabilities = p / self.replay_buffer.total_p # where p = p ** self.alpha
287 | is_weights[i, 0] = np.power(self.buffer_size * sampling_probabilities, -self.beta) / max_weight
288 | return idxes, is_weights
289 |
290 | def evaluation(self, env, render=True):
291 | obs, done, ep_reward = env.reset(), False, 0
292 | # one episode until done
293 | while not done:
294 | action, q_values = self.model.action_value(obs[None]) # Using [None] to extend its dimension (4,) -> (1, 4)
295 | obs, reward, done, info = env.step(action)
296 | ep_reward += reward
297 | if render: # visually show
298 | env.render()
299 | time.sleep(0.05)
300 | env.close()
301 | return ep_reward
302 |
303 | # store transitions into replay butter, now sum tree.
304 | def store_transition(self, priority, obs, action, reward, next_state, done):
305 | transition = [obs, action, reward, next_state, done]
306 | self.replay_buffer.add(priority, transition)
307 |
308 | # minor modified from https://github.com/medipixel/rl_algorithms/blob/master/algorithms/common/helper_functions.py
309 | def get_n_step_info(self, n_step_buffer, gamma):
310 | """Return n step reward, next state, and done."""
311 | # info of the last transition
312 | reward, next_state, done = n_step_buffer[-1][-3:]
313 |
314 | for transition in reversed(list(n_step_buffer)[:-1]):
315 | r, n_s, d = transition[-3:]
316 |
317 | reward = r + gamma * reward * (1 - d)
318 | next_state, done = (n_s, d) if d else (next_state, done)
319 |
320 | return reward, next_state, done
321 |
322 |
323 | # rank-based prioritization sampling
324 | def rand_based_sample(self, k):
325 | pass
326 |
327 | # e-greedy
328 | def get_action(self, best_action):
329 | if np.random.rand() < self.epsilon:
330 | return self.env.action_space.sample()
331 | return best_action
332 |
333 | # assign the current network parameters to target network
334 | def update_target_model(self):
335 | self.target_model.set_weights(self.model.get_weights())
336 |
337 | def get_target_value(self, obs):
338 | return self.target_model.predict(obs)
339 |
340 | def e_decay(self):
341 | self.epsilon *= self.epsilon_decay
342 |
343 |
344 | if __name__ == '__main__':
345 | test_model()
346 |
347 | env = gym.make("CartPole-v0")
348 | num_actions = env.action_space.n
349 | model = Model(num_actions)
350 | target_model = Model(num_actions)
351 | agent = NoisyAgent(model, target_model, env)
352 | # test before
353 | rewards_sum = agent.evaluation(env)
354 | print("Before Training: %d out of 200" % rewards_sum) # 9 out of 200
355 |
356 | agent.train()
357 | # test after
358 | # env = gym.wrappers.Monitor(env, './recording', force=True)
359 | rewards_sum = agent.evaluation(env)
360 | print("After Training: %d out of 200" % rewards_sum) # 200 out of 200
361 |
362 |
--------------------------------------------------------------------------------
/README.md:
--------------------------------------------------------------------------------
1 | ## TensorFlow 2.0 for Deep Reinforcement Learning
2 | 
3 |
4 | This is a simple tutorial of deep reinforcement learning with tensorflow 2.0, which has simple demos and detailed model implementations to help beginners get start in this research region.
5 |
6 | ### How to install TensorFlow 2.0
7 | ```
8 | $ conda create --name tensorflow_2_0
9 | $ conda activate tensorflow_2_0
10 | $ pip install tensorflow==2.0.0-b1 # pip install tensorflow-gpu==2.0.0-b1 for GPU version
11 | ```
12 | Test:
13 | ```
14 | >>> import tensorflow as tf
15 | >>> tf.__version__
16 | '2.0.0-beta1'
17 | ```
18 |
19 | ### TensorFlow 2.0 Tutorial
20 | * [Official Tutorial](https://www.tensorflow.org/tutorials/)
21 | * [Hands-on ML2](https://github.com/ageron/handson-ml2)
22 | * [Summary of some of the new features in TensorFlow 2.0](https://colab.research.google.com/github/zaidalyafeai/Notebooks/blob/master/TF_2_0.ipynb)
23 | * [Model building with TensorFlow 2.0](https://colab.research.google.com/drive/17u-pRZJnKN0gO5XZmq8n5A2bKGrfKEUg)
24 |
25 |
26 | ### Python Tutorial
27 | * Welcome to visit my [Fast Py3 Repo](https://github.com/Huixxi/Fast-Py3). This is a fast python3 tutorial.
28 |
29 | ### Gym Tutorial
30 | * [Basic Gym](https://github.com/Huixxi/TensorFlow2.0-for-Deep-Reinforcement-Learning/blob/master/tutorial_blogs/gym_tutorial.md)
31 |
32 | ### Reinforcement Learning
33 | Book notes ...
34 |
35 | ### Deep Reinforcement Learning
36 | * Rainbow
37 | ([Building Rainbow Step by Step with TensorFlow2.0](https://github.com/Huixxi/TensorFlow2.0-for-Deep-Reinforcement-Learning/blob/master/tutorial_blogs/Building_Rainbow_Step_by_Step_with_TensorFlow2.0.md))
38 | * [Deep Q-Network](https://github.com/Huixxi/TensorFlow2.0-for-Deep-Reinforcement-Learning/blob/master/01_dqn.py)
39 | * +[Double DQN](https://github.com/Huixxi/TensorFlow2.0-for-Deep-Reinforcement-Learning/blob/master/02_ddqn.py)
40 | * +[Prioritized Experience Replay](https://github.com/Huixxi/TensorFlow2.0-for-Deep-Reinforcement-Learning/blob/master/03_priority_replay.py)
41 | * +[Dueling Network](https://github.com/Huixxi/TensorFlow2.0-for-Deep-Reinforcement-Learning/blob/master/04_dueling.py)
42 | * +[Multi-Step Q-Learning](https://github.com/Huixxi/TensorFlow2.0-for-Deep-Reinforcement-Learning/blob/master/05_multistep_td.py)
43 | * +[Distributional RL](https://github.com/Huixxi/TensorFlow2.0-for-Deep-Reinforcement-Learning/blob/master/06_distributional_rl.py)(Failed Yet, But I Will Try My BestTo Make It Work Soon!)
44 | * +[Noisy Network](https://github.com/Huixxi/TensorFlow2.0-for-Deep-Reinforcement-Learning/blob/master/07_noisynet.py)(Failed Yet, But I Will Try My Best To Make It Work Soon!)
45 |
46 | ### Paper Reading
47 | * Welcome to visit my personal blog website: [HU's Blog](https://huixxi.github.io/). There is a list of **RL Paper Overviews**.
48 |
49 | 
50 |
--------------------------------------------------------------------------------
/images/ddqn.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/Huixxi/TensorFlow2.0-for-Deep-Reinforcement-Learning/d1c191e7bfbb44357a4066ced3b96fa8c847875a/images/ddqn.png
--------------------------------------------------------------------------------
/images/distributional_algorithm2.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/Huixxi/TensorFlow2.0-for-Deep-Reinforcement-Learning/d1c191e7bfbb44357a4066ced3b96fa8c847875a/images/distributional_algorithm2.png
--------------------------------------------------------------------------------
/images/distributional_learn.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/Huixxi/TensorFlow2.0-for-Deep-Reinforcement-Learning/d1c191e7bfbb44357a4066ced3b96fa8c847875a/images/distributional_learn.png
--------------------------------------------------------------------------------
/images/distributional_project.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/Huixxi/TensorFlow2.0-for-Deep-Reinforcement-Learning/d1c191e7bfbb44357a4066ced3b96fa8c847875a/images/distributional_project.png
--------------------------------------------------------------------------------
/images/distributional_projected.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/Huixxi/TensorFlow2.0-for-Deep-Reinforcement-Learning/d1c191e7bfbb44357a4066ced3b96fa8c847875a/images/distributional_projected.png
--------------------------------------------------------------------------------
/images/distributional_rl.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/Huixxi/TensorFlow2.0-for-Deep-Reinforcement-Learning/d1c191e7bfbb44357a4066ced3b96fa8c847875a/images/distributional_rl.png
--------------------------------------------------------------------------------
/images/dqn.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/Huixxi/TensorFlow2.0-for-Deep-Reinforcement-Learning/d1c191e7bfbb44357a4066ced3b96fa8c847875a/images/dqn.png
--------------------------------------------------------------------------------
/images/dqn_algorithm.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/Huixxi/TensorFlow2.0-for-Deep-Reinforcement-Learning/d1c191e7bfbb44357a4066ced3b96fa8c847875a/images/dqn_algorithm.png
--------------------------------------------------------------------------------
/images/dqn_net.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/Huixxi/TensorFlow2.0-for-Deep-Reinforcement-Learning/d1c191e7bfbb44357a4066ced3b96fa8c847875a/images/dqn_net.png
--------------------------------------------------------------------------------
/images/dueling_detail.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/Huixxi/TensorFlow2.0-for-Deep-Reinforcement-Learning/d1c191e7bfbb44357a4066ced3b96fa8c847875a/images/dueling_detail.png
--------------------------------------------------------------------------------
/images/dueling_details.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/Huixxi/TensorFlow2.0-for-Deep-Reinforcement-Learning/d1c191e7bfbb44357a4066ced3b96fa8c847875a/images/dueling_details.png
--------------------------------------------------------------------------------
/images/dueling_netarch.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/Huixxi/TensorFlow2.0-for-Deep-Reinforcement-Learning/d1c191e7bfbb44357a4066ced3b96fa8c847875a/images/dueling_netarch.png
--------------------------------------------------------------------------------
/images/gym_cartpole_v0.gif:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/Huixxi/TensorFlow2.0-for-Deep-Reinforcement-Learning/d1c191e7bfbb44357a4066ced3b96fa8c847875a/images/gym_cartpole_v0.gif
--------------------------------------------------------------------------------
/images/noisy_net_algorithm.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/Huixxi/TensorFlow2.0-for-Deep-Reinforcement-Learning/d1c191e7bfbb44357a4066ced3b96fa8c847875a/images/noisy_net_algorithm.png
--------------------------------------------------------------------------------
/images/p2.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/Huixxi/TensorFlow2.0-for-Deep-Reinforcement-Learning/d1c191e7bfbb44357a4066ced3b96fa8c847875a/images/p2.png
--------------------------------------------------------------------------------
/images/rlblog_images/IS.jpg:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/Huixxi/TensorFlow2.0-for-Deep-Reinforcement-Learning/d1c191e7bfbb44357a4066ced3b96fa8c847875a/images/rlblog_images/IS.jpg
--------------------------------------------------------------------------------
/images/rlblog_images/LSTM.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/Huixxi/TensorFlow2.0-for-Deep-Reinforcement-Learning/d1c191e7bfbb44357a4066ced3b96fa8c847875a/images/rlblog_images/LSTM.png
--------------------------------------------------------------------------------
/images/rlblog_images/PPO.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/Huixxi/TensorFlow2.0-for-Deep-Reinforcement-Learning/d1c191e7bfbb44357a4066ced3b96fa8c847875a/images/rlblog_images/PPO.png
--------------------------------------------------------------------------------
/images/rlblog_images/README.md:
--------------------------------------------------------------------------------
1 | To save some pictures used in my blogs.
2 |
--------------------------------------------------------------------------------
/images/rlblog_images/RNN-unrolled.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/Huixxi/TensorFlow2.0-for-Deep-Reinforcement-Learning/d1c191e7bfbb44357a4066ced3b96fa8c847875a/images/rlblog_images/RNN-unrolled.png
--------------------------------------------------------------------------------
/images/rlblog_images/ppo.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/Huixxi/TensorFlow2.0-for-Deep-Reinforcement-Learning/d1c191e7bfbb44357a4066ced3b96fa8c847875a/images/rlblog_images/ppo.png
--------------------------------------------------------------------------------
/images/rlblog_images/r1.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/Huixxi/TensorFlow2.0-for-Deep-Reinforcement-Learning/d1c191e7bfbb44357a4066ced3b96fa8c847875a/images/rlblog_images/r1.png
--------------------------------------------------------------------------------
/images/rlblog_images/r2.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/Huixxi/TensorFlow2.0-for-Deep-Reinforcement-Learning/d1c191e7bfbb44357a4066ced3b96fa8c847875a/images/rlblog_images/r2.png
--------------------------------------------------------------------------------
/images/sards.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/Huixxi/TensorFlow2.0-for-Deep-Reinforcement-Learning/d1c191e7bfbb44357a4066ced3b96fa8c847875a/images/sards.png
--------------------------------------------------------------------------------
/tutorial_blogs/Building_Rainbow_Step_by_Step_with_TensorFlow2.0.md:
--------------------------------------------------------------------------------
1 | # Building Rainbow Step by Step with TensorFlow 2.0
2 | *[Rainbow: Combining Improvements in Deep Reinforcement Learning](https://arxiv.org/pdf/1710.02298.pdf)*
3 | `Journal: The Thirty-Second AAAI Conference on Artificial Intelligence (AAAI-18)`
4 | `Year: 2017`
5 | `Institute: DeepMind`
6 | `Author: Matteo Hessel, Joseph Modayil, Hado van Hasselt`
7 | `#`*Deep Reinforcement Learning*
8 |
9 | **Abstract
**
10 | This paper examines six main extensions to DQN algorithm and empirically studies their combination. (It is a good paper which gives you a summary of several important technologies to alleviate the problems remaining in DQN and provides you some valuable insights in this research region.)
11 | [Baseline: Deep Q-Network(DQN) Algorithm Implementation in CS234 Assignment 2](https://github.com/Huixxi/CS234-Reinforcement-Learning/tree/master/assignment%202)
12 |
13 | ## INTRODUCTION
14 | Because the traditional tabular methods are not applicable in arbitrarily large state spaces, we turn to those approximate solution methods (`linear approximator & nonlinear approximator` `value-function approximation & policy approximation`), which is to find a good approximate solution using limited computational resources. We can use a `linear function`, or `multi-layer artificial neural networks`, or `decision tree` as a parameterized function to approximate the value-function or policy.(More, read Sutton's book [Reinforcement Learning: An Introduction](http://incompleteideas.net/book/the-book-2nd.html) Chapter 9).
15 |
16 | The following methods are all `value-function approximation` and `gradient-based(using the gradients to update the parameters)`, and they all use **experience replay** and **target network** to eliminate the correlations present in the sequence of observations.
17 |
18 | ## 1>Linear
19 | Using a linear function to approximate the value function(always the action value).
20 | $$
21 | \hat v(s, w) \doteq w^Tx(s) \doteq \sum \limits_{i=1}^d w_i x_i
22 | $$
23 | $w$ is the parameters, $x(s)$ is called a *feature vector* representing state $s$, and the state $s$ is the images(frames) observed by the agent in most time. So a linear approximator implemented with *tensorflow* can be just a fully-connected layer.
24 | ``` python
25 | import tensorflow as tf
26 | # state: a sequence of image(frame)
27 | inputs = tf.layers.flatten(state)
28 | # scope, which is used to distinguish q_params and target_q_params
29 | out = layers.fully_connected(inputs, num_actions, scope=scope, reuse=reuse)
30 | ```
31 |
32 | ## 2>Nonlinear-DQN
33 | ***Deep Q-Network.*** The main difference of *DQN* from *linear approximator* is the architecture of getting the *q_value*, it is nonlinear.
34 |
35 |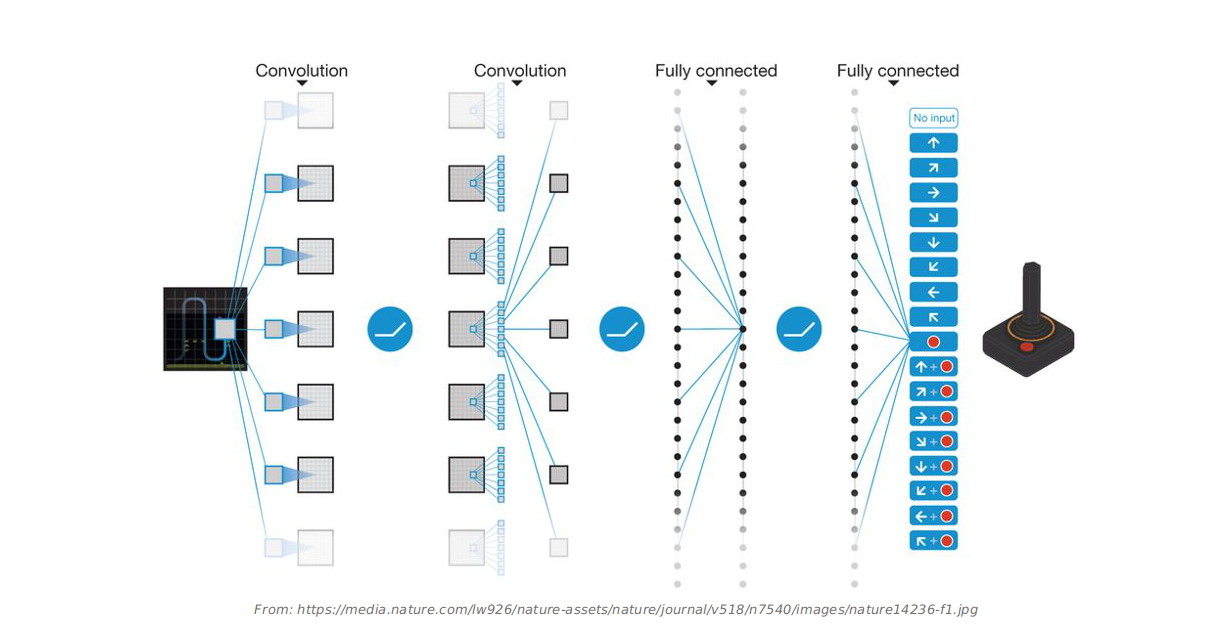 
36 |
37 | And the total algorithm is as follows:
38 |
39 | 
40 |
41 | The approximator of DeepMind DQN implemented with *tensorflow* as described in their [Nature paper](https://www.nature.com/articles/nature14236) can be:
42 | ``` python
43 | import tensorflow as tf
44 | with tf.variable_scope(scope, reuse=reuse) as _:
45 | conv1 = layers.conv2d(state, num_outputs=32, kernel_size=(8, 8), stride=4, activation_fn=tf.nn.relu)
46 | conv2 = layers.conv2d(conv1, num_outputs=64, kernel_size=(4, 4), stride=2, activation_fn=tf.nn.relu)
47 | conv3 = layers.conv2d(conv2, num_outputs=64, kernel_size=(3, 3), stride=1, activation_fn=tf.nn.relu)
48 | full_inputs = layers.flatten(conv3)
49 | full_layer = layers.fully_connected(full_inputs, num_outputs=512, activation_fn=tf.nn.relu)
50 | out = layers.fully_connected(full_layer, num_outputs=num_actions)
51 | ```
52 |
53 | [Do DQN from scratch(basic version)](https://github.com/Huixxi/TensorFlow2.0-for-Deep-Reinforcement-Learning/blob/master/01_dqn.py)
54 |
55 |
56 |
57 | ## 3>Nonlinear-DDQN
58 | ***Double DQN.*** The main difference of *DDQN* from *DQN* is the way of calculating the target q value.
59 | As a reminder,
60 | In Q-Learning:
61 | $$
62 | Q(s,a) \leftarrow Q(s,a) + \alpha[r + \lambda max_{a'}Q(s',a') − Q(s,a)]
63 | $$
64 | $$
65 | Y_t^{Q} = R_{t+1} + \lambda max_{a'}Q(S_{t+1},a') = R_{t+1} + \lambda Q(S_{t+1},argmax_{a'}Q(S_{t+1},a'))
66 | $$
67 | In DQN:
68 |
69 | 
70 |
71 | where $\theta_{i-1}$ is the target network parameters which is always represeted with $\theta_t^-$.
72 | $$
73 | Y_t^{DQN} = R_{t+1} + \lambda max_{a'}Q(S_{t+1},a';\theta_t^-)
74 | $$
75 | There is a problem with deep q-learning that "It is known to sometimes learn unrealistically high action values because it includes a maximization step over estimated action values, which tends to prefer overestimated to underestimated values" as said in [DDQN paper](https://arxiv.org/pdf/1509.06461.pdf).
76 | The idea of Double Q-learning is to reduce overestimations by decomposing the max operation in the target into action selection and action evaluation.
77 | $$
78 | Y_t^{DoubleQ} = R_{t+1} + \lambda Q(S_{t+1}, argmax_{a'}Q(S_{t+1},a';\theta_t);\theta_t^-)
79 | $$
80 | Implement with *tensorflow* (the minimal possible change to DQN in cs234 assignment 2)
81 | ``` python
82 | # DQN
83 | q_samp = tf.where(self.done_mask, self.r, self.r + self.config.gamma * tf.reduce_max(target_q, axis=1))
84 | actions = tf.one_hot(self.a, num_actions)
85 | q = tf.reduce_sum(tf.multiply(q, actions), axis=1)
86 | self.loss = tf.reduce_mean(tf.squared_difference(q_samp, q))
87 |
88 | # DDQN
89 | max_q_idxes = tf.argmax(q, axis=1)
90 | max_actions = tf.one_hot(max_q_idxes, num_actions)
91 | q_samp = tf.where(self.done_mask, self.r, self.r + self.config.gamma * tf.reduce_sum(tf.multiply(target_q, max_actions), axis=1))
92 | actions = tf.one_hot(self.a, num_actions)
93 | q = tf.reduce_sum(tf.multiply(q, actions), axis=1)
94 | self.loss = tf.reduce_mean(tf.squared_difference(q_samp, q))
95 | ```
96 |
97 | [Do Double DQN from scratch(basic version)](https://github.com/Huixxi/TensorFlow2.0-for-Deep-Reinforcement-Learning/blob/master/02_ddqn.py)
98 |
99 |
100 |
101 | ## 4>Prioritized experience replay
102 | ***Prioritized experience replay.*** Improve data efficiency, by replaying more often transitions from which there is more to learn.
103 | ***And the total algorithm is as follows:***
104 |
105 | 
106 |
107 | * Prioritizing with Temporal-Difference(TD) Error
108 | TD-Error: how far the value is from its next-step bootstrap estimate $$ r + \lambda V(s') - V(s) $$
109 | Where the value $r + \lambda V(s') $ is known as the TD target.
110 | Experiences with high magnitude TD error also appear to be replayed more often. TD-errors have also been used as a prioritization mechanism for determining where to focus resources, for example when choosing where to explore or which features to select. However, the TD-error can be a poor estimate in some circumstances as well, e.g. when rewards are noisy.
111 |
112 | * Stochastic Prioritization
113 | Because `greedy prioritization` results in high-error transitions are replayed too frequently causing lack of diversity which could lead to `over-fitting`. So `Stochastic Prioritization` is intruduced in order to add diversity and find a balance between greedy prioritization and random sampling.
114 | We ensure that the probability of being sampled is monotonic in a transition’s priority, while guaranteeing a non-zero probability even for the lowest-priority transition. Concretely, the probability of sampling transition i as
115 | $$
116 | P(i) = \frac{p_i^{\alpha}}{\sum_kp_k^{\alpha}}
117 | $$
118 | (Note: the probability of sampling transition $P(i)$ has nothing to do with the probability to sample a transition(experience) in the replay buffer(sum tree), which is based on the transition's priority $p_i$. So don't be confused by it, the $P(i)$ is used to calculate the `Importance Sampling(IS) Weight`.)
119 | where $p_i > 0$ is the priority of transition $i$. The exponent α determines how much prioritization is used, with $\alpha = 0$ corresponding to the uniform case.
120 | * proportional prioritization: $p_i = |\delta_i| + \epsilon$
121 | * rank-based prioritization: $p_i = \frac{1}{rank(i)}$ , where $rank(i)$ is the rank of transition $i$ sorted according to $\delta_i$.
122 |
123 | * Importance Sampling(IS)
124 | Because prioritized replay introduces a bias that changes this distribution uncontrollably. This can be corrected by using importance-sampling (IS) weights:
125 | $$
126 | w_i = (\frac{1}{N} \frac{1}{P(i)})^\beta
127 | $$
128 | that fully compensate for the non-uniform probabilities $P(i)$ if $\beta = 1$. These weights can be folded into the Q-learning update by using $w_i\delta_i$ instead of $\delta_i$. For stability reasons, we always normalize weights by $1 / max_i w_i$ so that they only scale the update downwards.
129 | `IS` is annealed from $\beta_0$ to $1$, which means its affect is felt more strongly at the end of the stochastic process; this is because the unbiased nature of the updates in RL is most important near convergence.
130 |
131 | [Do Double DQN with prioritized experience replay from scratch(basic version)](https://github.com/Huixxi/TensorFlow2.0-for-Deep-Reinforcement-Learning/blob/master/03_priority_replay.py)
132 |
133 |
134 | ## 5>Dueling network architecture
135 | ***Dueling network architecture.*** Generalize across actions by separately representing state values and action advantages.
136 | The dueling network is a neural network architecture designed for value based RL which has a $|A|$ dimension output that Q-value for each action. It features two streams of computation, the **state value** and **action advantage** streams, sharing a convolutional encoder, and merged by a special aggregator layer.
137 |
138 |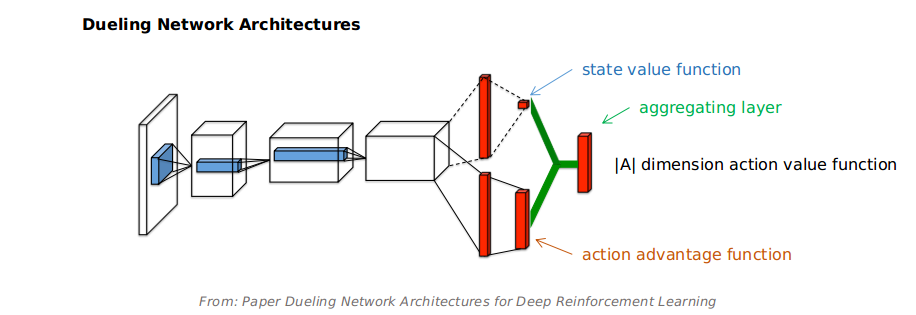 
139 |
140 | The aggregator can be expressed as:
141 | $$
142 | Q(s, a; \theta, \alpha, \beta) = V(s; \theta, \beta) + \big(A(s, a; \theta, \alpha) - \frac{1}{|A|} \sum_{a'}A(s, a'; \theta, \alpha)\big)
143 | $$
144 | where $\theta, \beta, \alpha$, respectively, the parameters of the shared convolutional encoder, value stream, and action advantage stream.
145 | **The details of dueling network architecture for Atari:**
146 |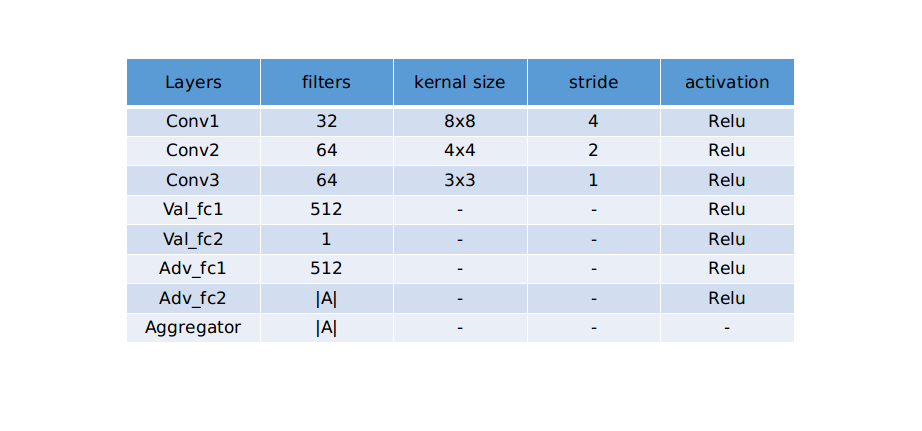 
147 |
148 | Since both the value and the advantage stream propagate gradients to the last convolutional layer in the backward pass, we rescale the combined gradient entering the last convolutional layer by $1/\sqrt{2}$. This simple heuristic mildly increases stability. In addition, we clip the gradients to have their norm less than or equal to $10$.
149 |
150 | **Other tricks:**
151 |
152 | * ***Human Starts:*** Using 100 starting points sampled from a human expert’s trajectory.
153 | * ***Saliency maps:*** To better understand the roles of the value and the advantage streams.
154 |
155 | [Do Dueliing Double DQN with prioritized experience replay from scratch(basic version)](https://github.com/Huixxi/TensorFlow2.0-for-Deep-Reinforcement-Learning/blob/master/04_dueling.py)
156 |
157 |
158 |
159 | ## 6>Multi-step bootstrapping
160 | ***Multi-step bootstrap targets.*** Shift the bias-variance tradeoff and helps to propagate newly observed rewards faster to earlier visited states.
161 | The best methods are often intermediate between the two extremes. *n-step TD learning method* lies between **Monte Carlo** and **one-step TD methods**.
162 |
163 | * Monte Carlo methods perform an update for each state based on the entire sequence of observed rewards from that state until the end of the episode
164 | $$
165 | G_t \doteq R_{t+1} + \gamma R_{t+2} + \gamma^2R_{t+3} + \dots + \gamma^{T−t−1}R_T
166 | $$
167 |
168 | * The update of one-step TD methods(also called TD(0) methods), on the other hand, is based on just the one next reward, bootstrapping from the value of the state one step later as a proxy for the remaining rewards.
169 | $$
170 | G_{t:t+1} \doteq R_{t+1} + \gamma V_t(S_{t+1})
171 | $$
172 |
173 | * Now, n-step TD methods perform a tradeoff that update each state after **n** time steps, based on **n** next rewards, bootstrapping from the value of the state **n** step later as a proxy for the remaining rewards.
174 | $$
175 | G_{t:t+n} \doteq R_{t+1} + \gamma R_{t+2} + \dots + \gamma ^{n−1}R_{t+n} + \gamma^n V_{t+n−1}(S_{t+n})
176 | $$
177 |
178 |
179 | We know that Q-learning is a kind of TD learning. All the implementations before are based on TD(0) learing updating. Now, we are going to implement a n-step deep Q-learning method, the most different part is how to calculate the *target* Q value.
180 | In one-step DQN:
181 | $$
182 | q_{target} = R_{t+1} + \gamma_{t+1} \max q_{\bar{\theta}}(S_{t+1}, a')
183 | $$
184 |
185 | In one-step Double DQN, the loss is :
186 | $$
187 | q_{target} = R_{t+1} + \gamma_{t+1} q_{\bar{\theta}}(S_{t+1}, \arg\max_{a'} q_{\theta}(S_{t+1}, a'))
188 | $$
189 |
190 | In multi-step Double DQN, the loss is :
191 | $$
192 | R^{(n)}\_t = \sum\limits_{k=0}^{n-1} \gamma_t^{(k)}R_{t+k+1}
193 | $$
194 |
195 | $$
196 | q_{target} = R^{(n)}\_t + \gamma_{t}^n q_{\bar{\theta}}(S_{t+n}, \arg\max_{a'} q_{\theta}(S_{t+n}, a'))
197 | $$
198 |
199 | (The algorithm looks easy to implement and stability guaranteed, but it brings much fluctuation and seems learning rate sensitive when used to train the agent to play CartPole-v0. So if you check this model, you maybe should pay a little bit more attention to it.)
200 |
201 | [Do Multi-Step Dueliing Double DQN with prioritized experience replay from scratch(basic version)](https://github.com/Huixxi/TensorFlow2.0-for-Deep-Reinforcement-Learning/blob/master/05_multistep_td.py)
202 |
203 |
204 |
205 | ## 7>Distributional Q-learning
206 | ***Distributional Q-learning.*** Learn a categorical distribution of discounted returns, instead of its expectation.
207 | In Q learning:
208 | $$
209 | Q(s, a) = \sum\limits_{i=0}^{n} p_{r_i}r_i(s, a) + \gamma \sum\limits_{s' \in S} P(s'|s, a)\max_{a' \in A(s')}Q(s', a')
210 | $$
211 | $$
212 | Q(s, a) = E_{s, a}[ r(s, a) ] + \gamma E_{s, a, s'}[ \max_{a' \in A(s')}Q(s', a') ] \\
213 | $$
214 | $$
215 | Q(s, a) = E_{s, a, s'}[ r(s, a) + \gamma \max_{a' \in A(s')}Q(s', a') ]
216 | $$
217 | Where $Q(s, a)$ is the expection of the discounted returns.
218 | Now, in distributional rl, instead of calculating the expection, we work directly with the full distribution of the returns of state $s$, action $a$ and following the current policy $\pi$, denoted by a random variable $Z(s, a)$.
219 |
220 |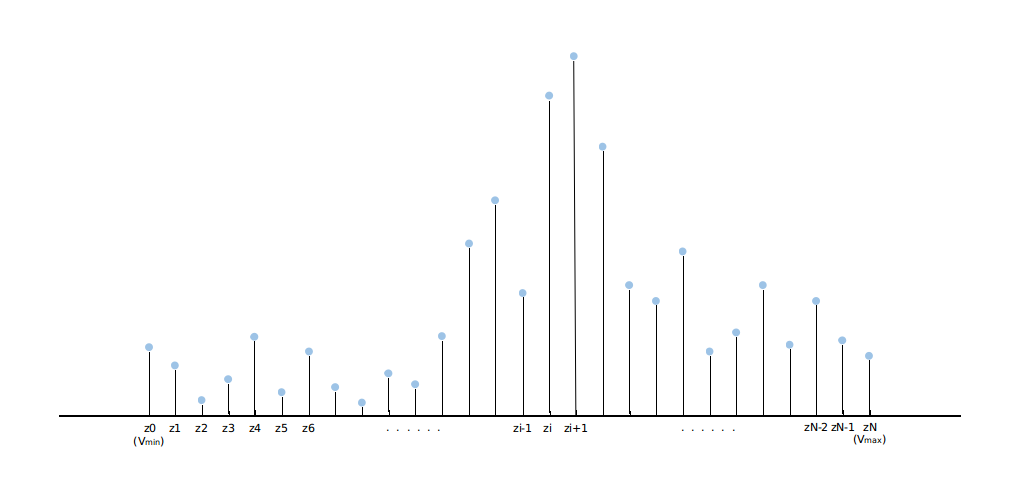 
221 |
222 | Where $z_i - z_{i-1} = \Delta z = (V_{min} - V_{max}) / N$, we assume that the range of the return $z_i$ is from $V_{min}$ to $V_{max}$, $N$ is the number of atoms, $(z_i, p_i(s, a))$. Now, for each state-action pair $(s, a)$, there is a corresponding distribution of its returns, not a expection value. We calculate the action value of $(s, a)$ as $Q(s, a) = E[Z(s, a)]$. Even through we still use the expected value, what we're going to optimize is the distribution:
223 | $$
224 | \sup_{s, a} dist(R(s, a) + \gamma Z_{\bar{\theta}}(s', a^\*), Z_{\theta}(s, a)) \\
225 | a^* = \arg\max_{a′}Q(s′, a′) = \arg\max_{a′}E[Z(s′, a′)]
226 | $$
227 | The difference is obverse that, we still use a deep neural network to do function approximation, in traditional DQN, our output for each input state $s$ is a $|A|$-dim vector, each element corresponds to an action value $q(s, a)$, but now, the output for each input state $s$ is a $|A|N$-dim matrix, that each row is a $N$-dim vector represents the return distribution of $Z(s, a)$, then we calculate the action-value of $(s, a)$ through:
228 | $$
229 | q(s, a) = E[Z(s, a)] = \sum\limits_{i=0}^{N} p_i(s, a) z_i
230 | $$
231 | ***KL Divergence***
232 | Now, we need to minimize the distance between the current distribution and the target distribution.
233 | ***Note:*** the following content are mainly from that great blog: https://mtomassoli.github.io/2017/12/08/distributional_rl/#kl-divergence
234 | If $p$ and $q$ are two distributions with same support (i.e. their $pdfs$ are non-zero at the same points), then their KL divergence is defined as follows:
235 | $$
236 | KL(p||q) = \int p(x) \log \frac{p(x)}{q(x)}dx \\
237 | KL(p||q) = \sum\limits_{i=1}^{N} p(x_i) \log\frac{p(x_i)}{q(x_i)} = \sum\limits_{i=1}^{N} p(x_i)[ \log{p(x_i)} - \log{q(x_i)}]
238 | $$
239 | "Now say we’re using DQN and extract $(s, a, r, s′)$ from the replay buffer. A “sample of the target distribution” is $r + \gamma Z_{\bar{\theta}}(s′, a^\*)$. We want to move $Z_{\theta}(s, a)$ towards this target (by keeping the target fixed)."
240 |
241 |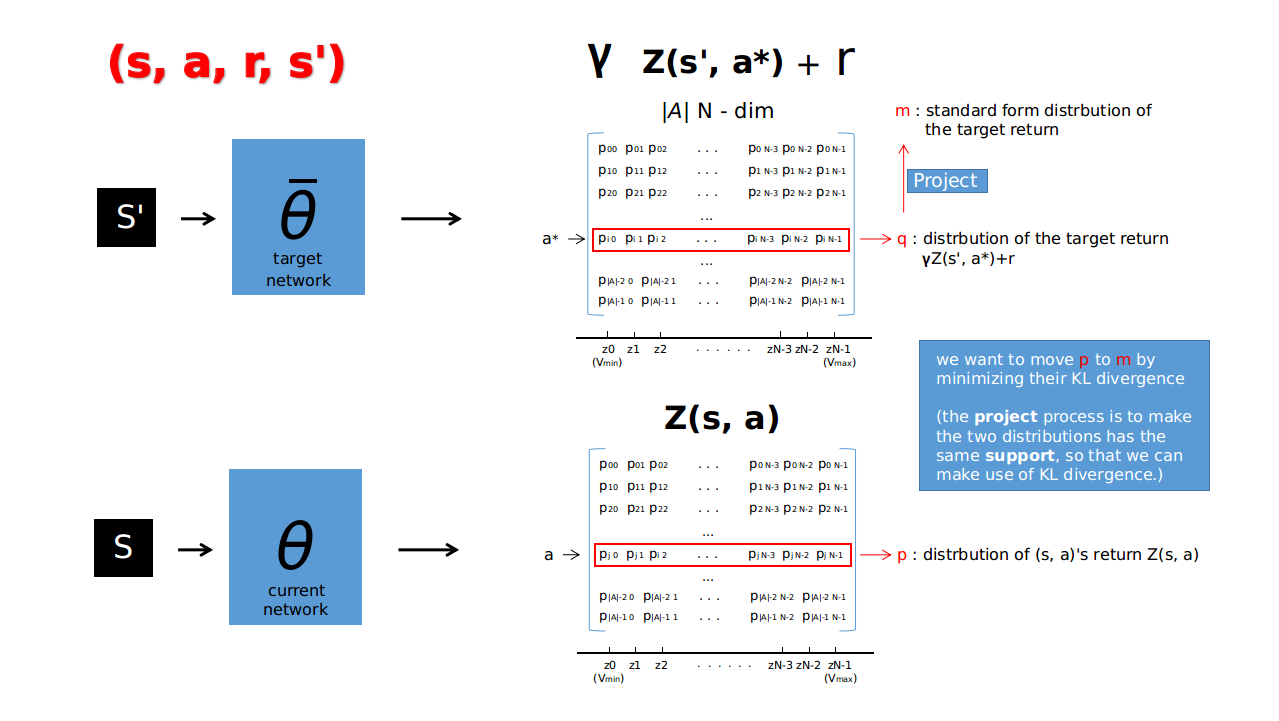 
242 |
243 |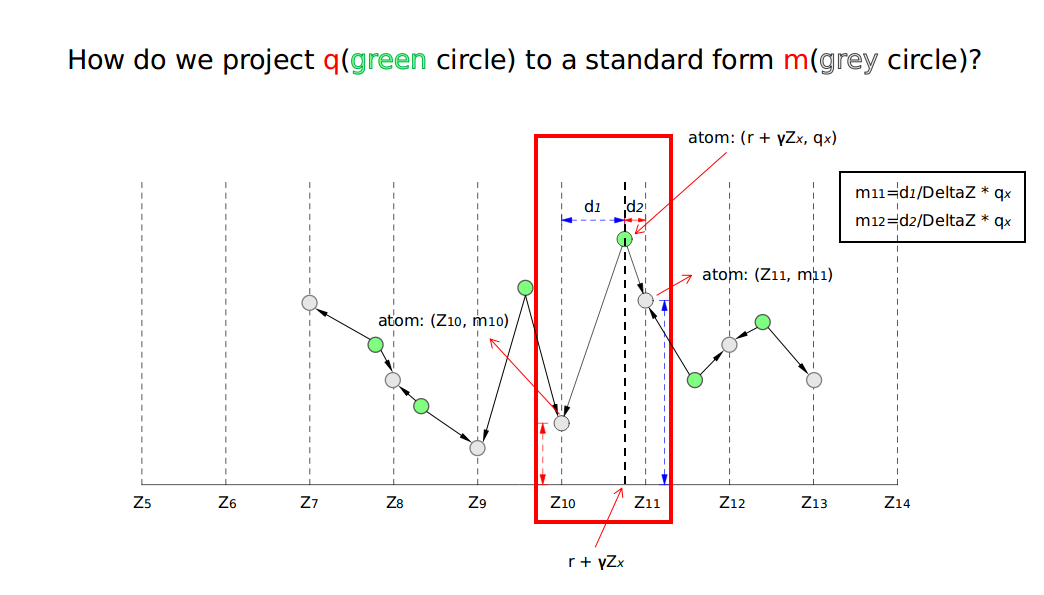 
244 |
245 | Then, their KL loss is:
246 | $$
247 | KL(m||p_{\theta}) = \sum\limits_{i=1}^{N} m_i \log\frac{m_i}{p_{\theta, i}} = \sum\limits_{i=1}^{N} m_i[ \log{m_i} - \log{p_{\theta, i}}] = H(m, p_{\theta}) − H(m)
248 | $$
249 | The gradient of the KL loss is:
250 | $$
251 | \nabla_{\theta} KL(m||p_{\theta}) = \nabla_{\theta} \sum\limits_{i=1}^{N} m_i \log\frac{m_i}{p_{\theta, i}} = \nabla_{\theta}[H(m, p_{\theta}) − H(m)] = \nabla_{\theta}H(m, p_{\theta})
252 | $$
253 | So, we can just use the *cross-entropy*:
254 | $$
255 | H(m, p_{\theta}) = - \sum\limits_{i=1}^{N} m_i \log{p_i(s, a; \theta)}
256 | $$
257 | as the loss function.
258 |
259 | ***The total algorithm is as follows:***
260 |
261 | 
262 |
263 | [Do Distributional RL Based on Multi-Step Dueling Double DQN with Prioritized Experience Replay from scratch(basic version)](https://github.com/Huixxi/TensorFlow2.0-for-Deep-Reinforcement-Learning/blob/master/06_distributional_rl.py)
264 | I feel really sorry to say that actually, this is a failed implementation, just as a reference, but I still hope it to be helpful to someone, and I promise I will try my best to fix it. Further more, I really hope some good guy can check my code, find the wrong place, even as a contributor to make it work together, thanks a lot.
265 |
266 |
267 |
268 | ## 8>Noisy DQN
269 | ***Noisy DQN.*** Use stochastic network layers for exploration.
270 | By now, the exploration method we used are all e-greedy methods, but in some games such as Montezuma’s Revenge, where many actions must be executed to collect the first reward. the limitations of exploring using e-greedy policies are clear. Noisy Nets propose a noisy linear layer that combines a deterministic and noisy stream.
271 | A normal linear layer with $p$ inputs and $q$ outputs, represented by:
272 | $$
273 | y = wx + b
274 | $$
275 | A noisy linear layer now is:
276 | $$
277 | y = (\mu^w + \sigma^w \odot \epsilon^w)x + (\mu^b + \sigma^b \odot \epsilon^b)
278 | $$
279 | Where where $\mu^w + \sigma^w \odot \epsilon^w$ and $\mu^b + \sigma^b \odot \epsilon^b$ replace $w$ and $b$, respectively. The parameters $\mu^w \in R^{q \times p}$, $\mu^b \in R^q$, $\sigma^w \in R^{q\times p}$ and $\sigma^b \in R^q$ are learnable whereas $\epsilon^w \in R^{q\times p}$ and $\epsilon^b \in R^q$ are noise random variables. There are two kinds of Gaussian Noise:
280 |
281 | * **Independent Gaussian Noise:**
282 | The noise applied to each weight and bias is independent, where each entry $\epsilon^w_{i,j}$ (respectively each entry $\epsilon^b_j$) of the random matrix $\epsilon^w$ (respectively of the random vector $\epsilon^b$ ) is drawn from a unit Gaussian distribution. This means that for each noisy linear layer, there are $pq + q$ noise variables (for p inputs to the layer and q outputs).
283 |
284 | * **Factorised Gaussian Noise:**
285 | By factorising $\epsilon^w_{i,j}$, we can use $p$ unit Gaussian variables $\epsilon_i$ for noise of the inputs and and $q$ unit Gaussian variables $\epsilon_j$ for noise of the outputs (thus $p + q$ unit Gaussian variables in total). Each $\epsilon^w_{i,j}$ and $\epsilon^b_j$ can then be written as:
286 | $$
287 | \epsilon^w_{i,j} = f(\epsilon_i)f(\epsilon_j) \\
288 | \epsilon^b_j = f(\epsilon_j)
289 | $$
290 | where $f$ is a real-valued function. In our experiments we used $f(x) = sgn(x) \sqrt{|x|}$. Note that
291 | for the bias $\epsilon^b_j$ we could have set $f(x) = x$, but we decided to keep the same output noise for weights and biases.
292 |
293 | ***The total algorithm is as follows:***
294 | 
295 |
296 | [Do Noisy Network Based on Multi-Step Dueling Double DQN with Prioritized Experience Replay from scratch(basic version)](https://github.com/Huixxi/TensorFlow2.0-for-Deep-Reinforcement-Learning/blob/master/07_noisynet.py)
297 | Run well, but too slow.(I don't know why...)
298 |
299 |
300 | ## 9>Rainbow
301 | Finally, we get the integrated agent: Rainbow. It used a **multi-step** distributional loss:
302 | $$
303 | D_{KL}(\Phi_z d_t^{(n)} || d_t)
304 | $$
305 | Where $\Phi_z$ is the projection onto $z$, and the target distribution $d_t^{(n)}$ is:
306 | $$
307 | d_t^{(n)} =(R_t^{(n)} + \gamma_t^{(n)} z, p_\bar{\theta} (S_{t+n}, a^{\*}\_{t+n}))
308 | $$
309 | Using **double Q-learning** gets the greedy action $a^\*\_{t+n}$ of $S_{t+n}$ through *online network*, and evaluates such action using the *target network*.
310 |
311 | In Rainbow, it uses the KL loss to **prioritize transitions** instead of using the absolute TD error, maybe more robust to noisy stochastic environments because the loss can continue to decrease even when the returns are not deterministic.
312 | $$
313 | p_t \propto (D_{KL}(\Phi_z d_t^{(n)} || d_t))^w
314 | $$
315 |
316 | The network architecture is a **dueling network architecture** adapted for use with return **distributions**. The network has a shared representation $f_{\xi}(s)$, which is then fed into a value stream $v_{\eta}$ with $N_{atoms}$ outputs, and into an advantage stream $a_{\xi}$ with $N_{atoms} \times N_{actions}$ outputs, where $a_{\xi}^i(f_{\xi}(s),a)$ will denote the output corresponding to atom $i$ and action $a$. For each atom $z^i$, the value and advantage streams are aggregated, as in dueling DQN, and then passed through a softmax layer to obtain the normalised parametric distributions used to estimate the returns’ distributions:
317 | $$
318 | p_{\theta}^i(s, a) = \frac{exp(v_{\eta}^i + a_{\Phi}^i(\phi, a) - \bar{a}\_{\Phi}^i(s))}{\sum_j exp(v_{\eta}^j + a_{\Phi}^j(\phi, a) - \bar{a}\_{\Phi}^j(s))}
319 | $$
320 | where $\phi = f_{\xi}(s)$, and $\bar{a}\_{\Phi}^i(s) = \frac{1}{N_{actions}}\sum_{a'}a_{\Phi}^i(\phi, a')$
321 |
322 | Then replace all linear layers with their noisy equivalent(factorised Gaussian noise version).
323 |
324 | Done, and thanks for reading, I hope it could be helpful to someone.
325 | Any suggestion is more than welcome, thanks again.
326 |
327 |
328 | ## REFERENCES
329 | **Blogs:**
330 | [1.Self Learning AI-Agents III:Deep (Double) Q-Learning(Blog)](https://towardsdatascience.com/deep-double-q-learning-7fca410b193a)
331 | [2.【强化学习】Deep Q Network(DQN)算法详解(Bolg)](https://blog.csdn.net/qq_30615903/article/details/80744083)
332 | [3.Improvements in Deep Q Learning: Dueling Double DQN, Prioritized Experience Replay, and fixed…(Blog)](https://www.freecodecamp.org/news/improvements-in-deep-q-learning-dueling-double-dqn-prioritized-experience-replay-and-fixed-58b130cc5682/)
333 | [4.Let’s make a DQN: Double Learning and Prioritized Experience Replay(Blog)](https://jaromiru.com/2016/11/07/lets-make-a-dqn-double-learning-and-prioritized-experience-replay/)
334 | [5.Distributional RL](https://mtomassoli.github.io/2017/12/08/distributional_rl/#ref-2017arXiv171010044D)
335 |
336 |
337 | **Books:**
338 | [1.Reinforcement Learning: An Introduction (Chapter 6, 7, 9)](http://incompleteideas.net/book/the-book-2nd.html)
339 |
340 |
341 | **Papers:**
342 | [1.Rainbow: Combining Improvements in Deep Reinforcement Learning](https://www.aaai.org/ocs/index.php/AAAI/AAAI18/paper/viewFile/17204/16680)
343 | [2.Human-level control through deep reinforcement learning](https://daiwk.github.io/assets/dqn.pdf)
344 | [3.Implementing the Deep Q-Network](https://arxiv.org/pdf/1711.07478.pdf)
345 | [4.Deep Reinforcement Learning with Double Q-learning](https://www.aaai.org/ocs/index.php/AAAI/AAAI16/paper/view/12389/11847)
346 | [5.Prioritized Experience Replay](https://arxiv.org/pdf/1511.05952.pdf)
347 | [6.Dueling Network Architectures for Deep Reinforcement Learning](https://arxiv.org/pdf/1511.06581.pdf)
348 | [7.Understanding Multi-Step Deep Reinforcement Learning: A Systematic Study of the DQN Target](https://arxiv.org/pdf/1901.07510.pdf)
349 | [8.Distributed Prioritized Experience Replay](https://arxiv.org/pdf/1803.00933.pdf)
350 | [9.A Distributional Perspective on Reinforcement Learning](https://arxiv.org/pdf/1707.06887.pdf)
351 | [10.Noisy Networks for Exploration](https://arxiv.org/pdf/1706.10295.pdf)
352 |
353 |
354 | **GitHub Repos:**
355 | [1.inoryy/tensorflow2-deep-reinforcement-learning for the whole TF2 Network Architecture](https://github.com/inoryy/tensorflow2-deep-reinforcement-learning)
356 | [2.keras-rl for Deuling Network](https://github.com/germain-hug/Deep-RL-Keras/blob/master/DDQN/agent.py#L49)
357 | [3.jaromiru/AI-blog for Prioritized Experience Replay](https://github.com/jaromiru/AI-blog/blob/master/SumTree.py)
358 | [4.rl_algorithms for Multi-Step TD Learning](https://github.com/medipixel/rl_algorithms/)
359 | [5.Kaixhin/Rainbow for Distribution RL & Noisy Net](https://github.com/Kaixhin/Rainbow/blob/master/model.py#L10)
360 | [6.keras for Noisy Net](https://github.com/keras-team/keras/blob/master/keras/layers/core.py#L796)
361 | [7.dopamine for Rainbow](https://github.com/google/dopamine/blob/master/dopamine/agents/rainbow/rainbow_agent.py)
362 | [8.tensorflow gudie](https://www.tensorflow.org/guide/keras/custom_layers_and_models)
363 |
364 |
365 |
366 |
367 |
368 |
369 |
370 |
--------------------------------------------------------------------------------
/tutorial_blogs/gym_tutorial.md:
--------------------------------------------------------------------------------
1 | # OpenAI Gym An Introduction
2 | Official Docs: http://gym.openai.com/docs/
3 | Github: https://github.com/openai/gym
4 |
5 | ## Installation
6 | * Simply install `gym` using `pip3`:
7 | `pip3 install gym`
8 |
9 | * Full installation containing all environments
10 | `pip3 install gym[all]`
11 | You can ignore the failed building message of `mujoco-py`, which needs a license.
12 |
13 | ## Environment
14 | Check all environment in gym using:
15 | * `print(gym.envs.registry.all())`
16 | * `print([env.id for env in gym.envs.registry.all()]) # list version`
17 |
18 | `['Copy-v0', 'RepeatCopy-v0', 'ReversedAddition-v0', 'ReversedAddition3-v0', 'DuplicatedInput-v0', 'Reverse-v0', 'CartPole-v0', 'CartPole-v1', 'MountainCar-v0', ...`
19 |
20 | ## Basic Usage
21 | Take "CartPole-v0" environment as an example:
22 | ```python
23 | import gym
24 | import time
25 |
26 | env = gym.make("CartPole-v0") # setup a environment for the agent
27 | initial_observation = env.reset()
28 | done = False
29 |
30 | # one episode, when done is True, break.
31 | while not done:
32 | env.render() # make the environment visiable
33 | action = env.action_space.sample() # randomly select an action from total actions the agent can take
34 | next_observation, reward, done, info = env.step(action)
35 | time.sleep(0.1) # for better display effect
36 |
37 | env.close() # close the environment
38 | ```
39 | Here, the agent is a random agent that just take a random action in each step. You can change it as a **linear agent** or a **neural network agent** which accept the observation and return an action not randomly select from the action space.
40 | Note, `env.step(action)` that takes an action and returns four different things:
41 | * **observation (object):** an environment-specific object representing your observation of the environment.
42 | * **reward (float):** amount of reward achieved by the previous action.
43 | * **done (boolean):** whether it’s time to reset the environment again.
44 | * **info (dict):** diagnostic information useful for debugging.
45 |
46 | 
47 |
48 | ## Spaces
49 | (Just copy from the official docs. Still take "CartPole-v0" as example.)
50 | Every environment(discrete) comes with an `action_space` and an `observation_space`. These attributes are of type `Space`, and they describe the format of valid actions and observations:
51 | ```python
52 | import gym
53 | env = gym.make('CartPole-v0')
54 | print(env.action_space)
55 | #> Discrete(2)
56 | print(env.observation_space)
57 | #> Box(4,)
58 | ```
59 | The `Discrete` space allows a fixed range of non-negative numbers, so in this case valid `actions` are either `0` or `1`. The `Box` space represents an `n`-dimensional box, so valid `observations` will be an array of `4` numbers. We can also check the `Box`’s bounds:
60 | ```python
61 | print(env.observation_space.high)
62 | #> array([ 2.4 , inf, 0.20943951, inf])
63 | print(env.observation_space.low)
64 | #> array([-2.4 , -inf, -0.20943951, -inf])
65 | ```
66 | `Box` and `Discrete` are the most common `Space`s. You can sample from a `Space` or check that something belongs to it:
67 | ```c++
68 | from gym import spaces
69 | space = spaces.Discrete(8) # Set with 8 elements {0, 1, 2, ..., 7}
70 | x = space.sample()
71 | assert space.contains(x)
72 | assert space.n == 8
73 | ```
74 | For `CartPole-v0` one of the actions applies force to the left, and one of them applies force to the right.
75 |
--------------------------------------------------------------------------------