├── Linux
├── Centos-环境配置总结.html
├── Linux硬链接和软连接的区别与总结.html
└── Shell.html
├── README.md
├── algorithm
├── BFS.html
├── BFS算法秒杀数字华容道.html
├── BST.html
├── Kruskal最小生成树算法.html
├── K个一组翻转链表-变题.html
├── Prim最小生成树算法.html
├── nSum.html
├── x的平方根-变题.html
├── 下降路径最小和-回溯-动规.html
├── 不一样的下一个更大元素.html
├── 买卖股票的最佳时机-变题.html
├── 二分图.html
├── 二分搜索-第K小问题.html
├── 二分搜索.html
├── 二分题目模版式题解.html
├── 二叉树--纲领篇.html
├── 二叉树-遍历-分解.html
├── 二叉树.html
├── 二叉树中的最大路径和-变题.html
├── 二叉树关于行的相关操作技巧.html
├── 二叉树序列化&反序列化.html
├── 二叉树的中序遍历-变题.html
├── 二叉树的层序遍历-变题.html
├── 二叉树的最近公共祖先-变题.html
├── 二叉树祖先问题.html
├── 二叉树路径相关技巧.html
├── 二叉树遍历.html
├── 二维数组的花式遍历技巧.html
├── 从前序与中序遍历序列构造二叉树-变题.html
├── 位运算技巧.html
├── 全排列-变题.html
├── 判定完美矩形.html
├── 前缀后缀法.html
├── 前缀和之奇偶篇.html
├── 前缀和之异或篇.html
├── 前缀和之等价条件.html
├── 前缀和数组.html
├── 动态规划之二分查找优化.html
├── 动态规划之最长回文子序列.html
├── 动态规划解题套路框架.html
├── 动态规划设计:最长递增子序列.html
├── 单调栈-拓展应用.html
├── 单调栈.html
├── 单调队列.html
├── 单链表的六大解题套路.html
├── 原地寻找数组中重复-消失的数字.html
├── 双指针之接雨水问题.html
├── 双指针技巧秒杀七道数组-链表题目.html
├── 反转链表.html
├── 可被三整除的最大和-变题.html
├── 合并两个有序数组-变题.html
├── 合并两个有序链表-变题.html
├── 含泪总结周赛中的三道DP问题.html
├── 含泪总结周赛中的两道DP问题.html
├── 含泪总结周赛中的两道图问题.html
├── 周赛:将区间分为最少组数.html
├── 周赛:满足不等式的数对数目.html
├── 回文子串的两种方法-中心扩展-动态规划.html
├── 回溯(DFS).html
├── 回溯之博弈论:我能赢吗.html
├── 回溯算法:删除无效的括号.html
├── 回溯算法:单词拆分.html
├── 回溯算法:括号生成.html
├── 图的遍历.html
├── 多线程顺序打印.html
├── 多路归并技巧总结.html
├── 大数据小内存问题.html
├── 子数组之-与-或.html
├── 子数组之性质篇-或-与-GCD-乘法.html
├── 子数组之滑动窗口篇.html
├── 字符串相加-变题.html
├── 完全二叉树的节点个数.html
├── 岛屿数量-变题.html
├── 差分数组技巧.html
├── 常数时间删除-查找数组中的任意元素.html
├── 并查集-Union-Find.html
├── 手撸LRU.html
├── 抽象类的二分搜索.html
├── 按权重随机选择.html
├── 排列-组合-子集问题.html
├── 排序汇总.html
├── 排序链表-变题.html
├── 接雨水-变题.html
├── 搜索旋转排序数组-变题.html
├── 数位DP.html
├── 数据流中位数.html
├── 数组中的第K个最大元素-变题.html
├── 无重复字符的最长子串-变题.html
├── 最大子数组和-变题.html
├── 最小栈-最大栈.html
├── 最小覆盖子串-变题.html
├── 最短路径-Dijkstra.html
├── 最长公共子序列-变题.html
├── 最长公共子序列-模版-输出.html
├── 最长回文子串-变题.html
├── 最长递增子序列-变题.html
├── 最长递增子序列-系列.html
├── 有效的括号-变题.html
├── 比较版本号-变题.html
├── 求素数的三种方法.html
├── 浅析:搜索旋转排序数组.html
├── 浅析:无权值最短路径算法-BFS.html
├── 浅析:最小基因变化.html
├── 浅析:最小路径和.html
├── 浅析:检查是否有合法括号字符串路径.html
├── 浅浅记录一下周赛-2022-08-07.html
├── 浅浅记录一次华为伪笔试2022-09-14.html
├── 浅浅记录一次字节伪笔试2022-08-21.html
├── 浅浅记录一次用友笔试-2023-08-06.html
├── 浅浅记录一次百度伪笔试2022-09-13.html
├── 深度剖析:地下城游戏.html
├── 滑动窗口.html
├── 滑动窗口专项练习.html
├── 滑动窗口之RABIN-KARP字符匹配算法.html
├── 爬楼梯-变题.html
├── 环形链表-变题.html
├── 环检测-拓扑排序.html
├── 田忌赛马.html
├── 目标和-回溯-动规.html
├── 相交链表-变题.html
├── 秒杀子数组类题目.html
├── 秒杀所有岛屿题目(DFS).html
├── 秒杀所有括号类问题.html
├── 线段树详解.html
├── 经典动态规划:0-1背包问题.html
├── 经典动态规划:子集背包问题.html
├── 经典动态规划:完全背包问题.html
├── 经典动态规划:编辑距离.html
├── 经典回溯算法:集合划分问题.html
├── 表达式计算.html
├── 记录自己傻逼时刻.html
├── 详解前缀树TrieTree.html
├── 详解堆排序-优先队列.html
├── 详解归并排序及其应用.html
├── 详解快排及其应用.html
├── 贪心之加油站.html
├── 队列-栈-互相转换.html
└── 集合划分变题-未给定具体划分大小.html
├── git
└── Git总结.html
├── go
├── Go-基础数据类型.html
└── 点点点语法糖-万能类型.html
├── index.html
├── java
├── AbstractQueuedSynchronizer.html
├── CAS.html
├── CPU密集型-IO密集型.html
├── ConcurrentHashMap.html
├── HashMap源码剖析.html
├── HotSpot的算法细节实现.html
├── IO模型.html
├── Java-8-Stream-sorted.html
├── Java-NIO.html
├── Java-小技巧总结.html
├── Java内存模型.html
├── Java并发中的锁.html
├── Java线程池.html
├── Java集合框架.html
├── Random.html
├── System-gc.html
├── ThreadLocal.html
├── equals-hashCode.html
├── interrupt-LockSupport-park-unpark.html
├── synchronized关键字.html
├── volatile关键字.html
├── 从字节码角度分析i++和++i.html
├── 代理模式-静态-动态.html
├── 伪共享.html
├── 内存泄漏-内存溢出.html
├── 剖析-Bootstrap-Extension-Application-ClassLoader.html
├── 动态语言-动态类型语言.html
├── 单例模式.html
├── 双亲委派模型.html
├── 反射机制.html
├── 各区域OOM汇总.html
├── 垃圾回收相关概念.html
├── 垃圾收集器前言.html
├── 垃圾收集算法.html
├── 字符串常量池.html
├── 实战-静态变量-实例变量-局部变量.html
├── 对象的创建.html
├── 强软弱虚引用.html
├── 方法区.html
├── 方法调用.html
├── 方法调用面试题.html
├── 注解.html
├── 浅记字节字符流乱码问题.html
├── 生存还是死亡.html
├── 破坏双亲委派模型.html
├── 简单工厂-工厂方法-抽象工厂-模式.html
├── 类加载器.html
├── 类加载子系统-导读.html
├── 类加载的时机.html
├── 类加载的过程.html
├── 经典垃圾收集器.html
├── 自定义类加载器.html
├── 虚拟机栈.html
├── 虚拟机栈面试题.html
├── 运行时常量池.html
├── 运行时数据区域-导读.html
├── 运行时数据区域.html
├── 运行时数据区常用参数汇总.html
├── 逃逸分析.html
└── 重载-重写.html
├── markdown
├── Algorithm
│ ├── BFS.md
│ ├── BFS算法秒杀数字华容道.md
│ ├── BST.md
│ ├── Kruskal最小生成树算法.md
│ ├── K个一组翻转链表-变题.md
│ ├── Prim最小生成树算法.md
│ ├── nSum.md
│ ├── x的平方根-变题.md
│ ├── 下降路径最小和-回溯-动规.md
│ ├── 不一样的下一个更大元素.md
│ ├── 买卖股票的最佳时机-变题.md
│ ├── 二分图.md
│ ├── 二分搜索-第K小问题.md
│ ├── 二分搜索.md
│ ├── 二分题目模版式题解.md
│ ├── 二叉树--纲领篇.md
│ ├── 二叉树-遍历-分解.md
│ ├── 二叉树.md
│ ├── 二叉树中的最大路径和-变题.md
│ ├── 二叉树关于行的相关操作技巧.md
│ ├── 二叉树序列化&反序列化.md
│ ├── 二叉树的中序遍历-变题.md
│ ├── 二叉树的层序遍历-变题.md
│ ├── 二叉树的最近公共祖先-变题.md
│ ├── 二叉树祖先问题.md
│ ├── 二叉树路径相关技巧.md
│ ├── 二叉树遍历.md
│ ├── 二维数组的花式遍历技巧.md
│ ├── 从前序与中序遍历序列构造二叉树-变题.md
│ ├── 位运算技巧.md
│ ├── 全排列-变题.md
│ ├── 判定完美矩形.md
│ ├── 前缀后缀法.md
│ ├── 前缀和之奇偶篇.md
│ ├── 前缀和之异或篇.md
│ ├── 前缀和之等价条件.md
│ ├── 前缀和数组.md
│ ├── 动态规划之二分查找优化.md
│ ├── 动态规划之最长回文子序列.md
│ ├── 动态规划解题套路框架.md
│ ├── 动态规划设计:最长递增子序列.md
│ ├── 单调栈-拓展应用.md
│ ├── 单调栈.md
│ ├── 单调队列.md
│ ├── 单链表的六大解题套路.md
│ ├── 原地寻找数组中重复-消失的数字.md
│ ├── 双指针之接雨水问题.md
│ ├── 双指针技巧秒杀七道数组-链表题目.md
│ ├── 反转链表.md
│ ├── 可被三整除的最大和-变题.md
│ ├── 合并两个有序数组-变题.md
│ ├── 合并两个有序链表-变题.md
│ ├── 含泪总结周赛中的三道DP问题.md
│ ├── 含泪总结周赛中的两道DP问题.md
│ ├── 含泪总结周赛中的两道图问题.md
│ ├── 周赛:将区间分为最少组数.md
│ ├── 周赛:满足不等式的数对数目.md
│ ├── 回文子串的两种方法-中心扩展-动态规划.md
│ ├── 回溯(DFS).md
│ ├── 回溯之博弈论:我能赢吗.md
│ ├── 回溯算法:删除无效的括号.md
│ ├── 回溯算法:单词拆分.md
│ ├── 回溯算法:括号生成.md
│ ├── 图的遍历.md
│ ├── 多线程顺序打印.md
│ ├── 多路归并技巧总结.md
│ ├── 大数据小内存问题.md
│ ├── 子数组之-与-或.md
│ ├── 子数组之性质篇-或-与-GCD-乘法.md
│ ├── 子数组之滑动窗口篇.md
│ ├── 字符串相加-变题.md
│ ├── 完全二叉树的节点个数.md
│ ├── 岛屿数量-变题.md
│ ├── 差分数组技巧.md
│ ├── 常数时间删除-查找数组中的任意元素.md
│ ├── 并查集-Union-Find.md
│ ├── 手撸LRU.md
│ ├── 抽象类的二分搜索.md
│ ├── 按权重随机选择.md
│ ├── 排列-组合-子集问题.md
│ ├── 排序汇总.md
│ ├── 排序链表-变题.md
│ ├── 接雨水-变题.md
│ ├── 搜索旋转排序数组-变题.md
│ ├── 数位DP.md
│ ├── 数据流中位数.md
│ ├── 数组中的第K个最大元素-变题.md
│ ├── 无重复字符的最长子串-变题.md
│ ├── 最大子数组和-变题.md
│ ├── 最小栈-最大栈.md
│ ├── 最小覆盖子串-变题.md
│ ├── 最短路径-Dijkstra.md
│ ├── 最长公共子序列-变题.md
│ ├── 最长公共子序列-模版-输出.md
│ ├── 最长回文子串-变题.md
│ ├── 最长递增子序列-变题.md
│ ├── 最长递增子序列-系列.md
│ ├── 有效的括号-变题.md
│ ├── 比较版本号-变题.md
│ ├── 求素数的三种方法.md
│ ├── 浅析:搜索旋转排序数组.md
│ ├── 浅析:无权值最短路径算法-BFS.md
│ ├── 浅析:最小基因变化.md
│ ├── 浅析:最小路径和.md
│ ├── 浅析:检查是否有合法括号字符串路径.md
│ ├── 浅浅记录一下周赛-2022-08-07.md
│ ├── 浅浅记录一次华为伪笔试2022-09-14.md
│ ├── 浅浅记录一次字节伪笔试2022-08-21.md
│ ├── 浅浅记录一次用友笔试-2023-08-06.md
│ ├── 浅浅记录一次百度伪笔试2022-09-13.md
│ ├── 深度剖析:地下城游戏.md
│ ├── 滑动窗口.md
│ ├── 滑动窗口专项练习.md
│ ├── 滑动窗口之RABIN-KARP字符匹配算法.md
│ ├── 爬楼梯-变题.md
│ ├── 环形链表-变题.md
│ ├── 环检测 & 拓扑排序.md
│ ├── 田忌赛马.md
│ ├── 目标和-回溯-动规.md
│ ├── 相交链表-变题.md
│ ├── 秒杀子数组类题目.md
│ ├── 秒杀所有岛屿题目(DFS).md
│ ├── 秒杀所有括号类问题.md
│ ├── 线段树详解.md
│ ├── 经典动态规划:0-1背包问题.md
│ ├── 经典动态规划:子集背包问题.md
│ ├── 经典动态规划:完全背包问题.md
│ ├── 经典动态规划:编辑距离.md
│ ├── 经典回溯算法:集合划分问题.md
│ ├── 表达式计算.md
│ ├── 记录自己傻逼时刻.md
│ ├── 详解前缀树TrieTree.md
│ ├── 详解堆排序-优先队列.md
│ ├── 详解归并排序及其应用.md
│ ├── 详解快排及其应用.md
│ ├── 贪心之加油站.md
│ ├── 队列-栈-互相转换.md
│ └── 集合划分变题-未给定具体划分大小.md
├── Git
│ └── Git总结.md
├── Go
│ ├── Go-基础数据类型.md
│ └── 点点点语法糖-万能类型.md
├── Java
│ ├── AbstractQueuedSynchronizer.md
│ ├── CAS.md
│ ├── CPU密集型-IO密集型.md
│ ├── ConcurrentHashMap.md
│ ├── HashMap源码剖析.md
│ ├── HotSpot的算法细节实现.md
│ ├── IO模型.md
│ ├── Java-8-Stream-sorted.md
│ ├── Java-NIO.md
│ ├── Java内存模型.md
│ ├── Java并发中的锁.md
│ ├── Java线程池.md
│ ├── Java集合框架.md
│ ├── Random.md
│ ├── System-gc.md
│ ├── ThreadLocal.md
│ ├── equals-hashCode.md
│ ├── interrupt-LockSupport-park-unpark.md
│ ├── synchronized关键字.md
│ ├── volatile关键字.md
│ ├── 从字节码角度分析i++和++i.md
│ ├── 代理模式-静态-动态.md
│ ├── 伪共享.md
│ ├── 内存泄漏-内存溢出.md
│ ├── 剖析-Bootstrap-Extension-Application-ClassLoader.md
│ ├── 动态语言-动态类型语言.md
│ ├── 单例模式.md
│ ├── 双亲委派模型.md
│ ├── 反射机制.md
│ ├── 各区域OOM汇总.md
│ ├── 垃圾回收相关概念.md
│ ├── 垃圾收集器前言.md
│ ├── 垃圾收集算法.md
│ ├── 字符串常量池.md
│ ├── 实战-静态变量-实例变量-局部变量.md
│ ├── 对象的创建.md
│ ├── 强软弱虚引用.md
│ ├── 方法区.md
│ ├── 方法调用.md
│ ├── 方法调用面试题.md
│ ├── 注解.md
│ ├── 浅记字节字符流乱码问题.md
│ ├── 生存还是死亡.md
│ ├── 破坏双亲委派模型.md
│ ├── 简单工厂-工厂方法-抽象工厂-模式.md
│ ├── 类加载器.md
│ ├── 类加载子系统-导读.md
│ ├── 类加载的时机.md
│ ├── 类加载的过程.md
│ ├── 经典垃圾收集器.md
│ ├── 自定义类加载器.md
│ ├── 虚拟机栈.md
│ ├── 虚拟机栈面试题.md
│ ├── 运行时常量池.md
│ ├── 运行时数据区域-导读.md
│ ├── 运行时数据区域.md
│ ├── 运行时数据区常用参数汇总.md
│ ├── 逃逸分析.md
│ └── 重载-重写.md
├── Linux
│ ├── Centos-环境配置总结.md
│ ├── Linux硬链接和软连接的区别与总结.md
│ └── Shell.md
├── Mac
│ ├── Mac 快捷键.md
│ └── Mac设置整理.md
├── MySQL
│ ├── B+树索引.md
│ ├── InnoDB中row_id的秘密.md
│ ├── InnoDB数据页的结构.md
│ ├── InnoDB的Buffer-Pool.md
│ ├── InnoDB记录的存储结构.md
│ ├── MVCC.md
│ ├── MySQL-容易被忽略的小知识.md
│ ├── MySQL主键自增一定连续吗.md
│ ├── MySQL事务.md
│ ├── MySQL加锁实战分析.md
│ ├── MySQL基础知识汇总.md
│ ├── MySQL搭建主从复制.md
│ ├── MySQL索引.md
│ ├── RR隔离级别下彻底解决幻读了吗.md
│ ├── binlog.md
│ ├── redo-log.md
│ ├── undo-log.md
│ ├── 两阶段提交.md
│ ├── 分库分表.md
│ ├── 联合索引-最左前缀匹配原则.md
│ ├── 覆盖索引-索引条件下推.md
│ └── 锁.md
├── Network
│ ├── DNS.md
│ ├── GET-POST请求.md
│ ├── HTTP-HTTPS.md
│ ├── HTTP-状态码.md
│ ├── HTTP-缓存策略.md
│ ├── HTTP-队头阻塞问题.md
│ ├── SYN-泛洪攻击.md
│ ├── Solutions-7th-Edition.docx
│ ├── TCP-三次握手-四次挥手.md
│ ├── TCPIP网络模型.md
│ ├── TCP重传-滑动窗口-流量控制-拥塞控制.md
│ ├── 网络层那点事儿.md
│ ├── 计算机网络(top-down)-习题&实验.md
│ └── 计算机网络--自顶向下.md
├── OS
│ ├── CPU缓存一致性.md
│ ├── IO多路复用.md
│ ├── 中断.md
│ └── 零拷贝.md
├── Redis
│ ├── Redis-Cluster.md
│ ├── Redis-Sentinel.md
│ ├── Redis主从复制.md
│ ├── Redis基本数据结构.md
│ ├── Redis持久化机制.md
│ ├── Redis缓存更新策略.md
│ └── Redis阻塞.md
├── RocketMQ
│ └── 浅记RocketMQ消息丢失问题.md
└── Spring
│ ├── JWT.md
│ ├── Spring-AOP.md
│ ├── Spring-IoC.md
│ ├── Spring-MVC.md
│ ├── Spring事务.md
│ └── Spring循环依赖.md
├── mysql
├── B+树索引.html
├── InnoDB中row_id的秘密.html
├── InnoDB数据页的结构.html
├── InnoDB的Buffer-Pool.html
├── InnoDB记录的存储结构.html
├── MVCC.html
├── MySQL-容易被忽略的小知识.html
├── MySQL主键自增一定连续吗.html
├── MySQL事务.html
├── MySQL加锁实战分析.html
├── MySQL基础知识汇总.html
├── MySQL搭建主从复制.html
├── MySQL索引.html
├── RR隔离级别下彻底解决幻读了吗.html
├── binlog.html
├── redo-log.html
├── undo-log.html
├── 两阶段提交.html
├── 分库分表.html
├── 联合索引-最左前缀匹配原则.html
├── 覆盖索引-索引条件下推.html
└── 锁.html
├── network
├── DNS.html
├── GET-POST请求.html
├── HTTP-HTTPS.html
├── HTTP-状态码.html
├── HTTP-缓存策略.html
├── HTTP-队头阻塞问题.html
├── SYN-泛洪攻击.html
├── TCP-三次握手-四次挥手.html
├── TCPIP网络模型.html
├── TCP重传-滑动窗口-流量控制-拥塞控制.html
├── 网络层那点事儿.html
└── 计算机网络--自顶向下.html
├── os
├── CPU缓存一致性.html
├── IO多路复用.html
├── 中断.html
└── 零拷贝.html
├── other
├── Mac设置整理.html
├── Secret.html
├── Secret.md
├── test.txt
├── 图论.html
├── 图论作业-1.html
├── 图论作业-2.html
├── 图论作业-3.html
├── 图论作业-4.html
├── 网络安全最终总结.html
├── 网络安全问答题总结.html
├── 超级无敌精华汇总.html
└── 超详细证明题总结.html
├── redis
├── Redis-Cluster.html
├── Redis-Sentinel.html
├── Redis主从复制.html
├── Redis基本数据结构.html
├── Redis持久化机制.html
├── Redis缓存更新策略.html
└── Redis阻塞.html
├── rocketmq
└── 浅记RocketMQ消息丢失问题.html
└── spring
├── JWT.html
├── Spring-AOP.html
├── Spring-IoC.html
├── Spring-MVC.html
├── Spring事务.html
└── Spring循环依赖.html
/markdown/Algorithm/BFS算法秒杀数字华容道.md:
--------------------------------------------------------------------------------
1 | # BFS 算法秒杀数字华容道
2 |
3 | [773. 滑动谜题](https://leetcode.cn/problems/sliding-puzzle/)
4 |
5 |
6 |
7 | 本篇文章介绍如何用「BFS」解决数字华容道问题,**详情可见 [滑动谜题](https://leetcode.cn/problems/sliding-puzzle/)**
8 |
9 | 这个题目还算友好,规模是固定的 2 x 3
10 |
11 | 对于这种计算最小步数的问题,我们就要敏感地想到 BFS 算法,这里再列举几个题目:**[打开转盘锁](https://leetcode-cn.com/problems/open-the-lock/)**、**[最小基因变化](https://leetcode-cn.com/problems/minimum-genetic-mutation/)** 都可以看作求最小步数的问题,均是使用 BFS
12 |
13 | **关于 BFS 框架的详细总结可见 [BFS 算法框架](./BFS.html)**
14 |
15 | **关于「最小基因变化」的题解可见 [浅析:最小基因变化](./浅析:最小基因变化.html)**
16 |
17 |
18 |
19 | 我们需要搞清楚,每次可以做的选择是什么?如下图所示,对于这种情况,可以有三种选择:
20 |
21 | 
22 |
23 | 我们的的终点是什么:
24 |
25 | 
26 |
27 | 现在的问题是,如何才可以把二维数组转换成更好处理的形式 -> 字符串
28 |
29 | 首先我们肯定需要把二维数组**拉平**,如下图所示:
30 |
31 | 
32 |
33 | 拉平后,如何找到每次可做的选择呢?
34 |
35 | 
36 |
37 | 对于上图,下标为 4 的位置,可做的选择为`[1, 3, 5]`
38 |
39 | 由于规模是固定的,所以可以手动计算出拉平后每个位置的选择
40 |
41 | ```java
42 | // neighbor[i] 表示下标为 i 的位置可做的选择
43 | int[][] neighbor = new int[][]{
44 | {1, 3},
45 | {0, 4, 2},
46 | {1, 5},
47 | {0, 4},
48 | {3, 1, 5},
49 | {4, 2}
50 | };
51 | ```
52 |
53 | **(PS:居然现在才知道二维数组中一维的大小可以不同,一直以为必须相同)**
54 |
55 | 下面给出完整代码:
56 |
57 | ```java
58 | public int slidingPuzzle(int[][] board) {
59 | int m = 2, n = 3;
60 | // 终点
61 | String target = "123450";
62 | // 起点
63 | StringBuffer sb = new StringBuffer();
64 | for (int i = 0; i < m; i++) {
65 | for (int j = 0; j < n; j++) {
66 | sb.append(board[i][j]);
67 | }
68 | }
69 | String start = sb.toString();
70 | int[][] neighbor = new int[][]{
71 | {1, 3},
72 | {0, 4, 2},
73 | {1, 5},
74 | {0, 4},
75 | {3, 1, 5},
76 | {4, 2}
77 | };
78 | int step = 0;
79 | Queue q = new LinkedList<>();
80 | Set vis = new HashSet<>();
81 | q.offer(start);
82 | vis.add(start);
83 | while (!q.isEmpty()) {
84 | int size = q.size();
85 | for (int i = 0; i < size; i++) {
86 | String cur = q.poll();
87 | if (cur.equals(target)) return step;
88 | // 找到 0 的位置
89 | int idx = 0;
90 | for (; cur.charAt(idx) != '0'; idx++);
91 | // 把邻居加入队列
92 | for (int adj : neighbor[idx]) {
93 | String next = swap(cur, idx, adj);
94 | if (!vis.contains(next)) {
95 | q.offer(next);
96 | vis.add(next);
97 | }
98 | }
99 | }
100 | step++;
101 | }
102 | return -1;
103 | }
104 | // 交换
105 | private String swap(String s, int i, int j) {
106 | char[] c = s.toCharArray();
107 | char t = c[i];
108 | c[i] = c[j];
109 | c[j] = t;
110 | return new String(c);
111 | }
112 | ```
113 |
114 |
--------------------------------------------------------------------------------
/markdown/Algorithm/Kruskal最小生成树算法.md:
--------------------------------------------------------------------------------
1 | # Kruskal 最小生成树算法
2 |
3 |
4 |
5 | [1584. 连接所有点的最小费用](https://leetcode-cn.com/problems/min-cost-to-connect-all-points/)
6 |
7 |
8 |
9 | 首先弄清楚**最小生成树**概念之前,请先弄清楚 「**生成子图**」「**树**」「**生成树**」概念
10 |
11 | - 生成子图:一个图的生成子图指**顶点集相同**,边集可不同的子图 -> 详情见 [图论--定义 10](../other/图论.html)
12 |
13 | - 树:不含圈的连通图称为树 -> 详情见 [图论--定义 35](../other/图论.html)
14 |
15 | - 生成树:若图 $G$ 的生成子图 $T$ 是树,则称 $T$ 为 $G$ 的**生成树** -> 详情见 [图论--定义 40](../other/图论.html)
16 | - 最小生成子树:在连通赋权图 $G$ 中,边权之和最小的生成树称为 $G$ 的**最小生成树** -> 详情见 [图论--定义 43](../other/图论.html)
17 |
18 |
19 |
20 | 可利用**图的连通性**来解决最小生成树的问题,很容易想到可以运用**「并查集」**算法来辅助生成最小生成树
21 |
22 | 关于并查集算法的详细总结可点击该处 -> [并查集](./并查集-Union-Find.html)
23 |
24 |
25 |
26 | 针对上述四个概念,我们一一来分析并提出解决方案
27 |
28 | - **问题一:**如何判断一个图是否为原图的生成子图
29 | - **问题二:**如何判断生成子图是一棵树
30 | - **问题三:**如何获得最小生成树
31 |
32 | **问题一:利用并查集的连通分支的数量来判断**
33 |
34 | 设顶点集的数量为 n,并查集中的节点数同为 n,一一对应
35 |
36 | 若最终并查集的连通分支数量为 1,则表明所有节点都在同一连通分支中,即子图为生成子图;反之则在多个分支中
37 |
38 | 总结就是,**对于添加的这条边,如果该边的两个节点本来就在同一连通分量里,那么添加这条边会产生环;反之,如果该边的两个节点不在同一连通分量里,则添加这条边不会产生环**
39 |
40 | **问题二:利用并查集的连通性来判断**
41 |
42 | 显而易见,如果在一个连通分支中,新增一条边,则会出现环/圈
43 |
44 | 故每次进行`union(u,v)`操作时前进行判断,如果`connected(u,v)==true`,则跳过。这样就可以保证生成子图是一棵树
45 |
46 | **问题三:对边进行非递减排序,从权值小的开始得到生成子树**
47 |
48 |
49 |
50 | 对于算法的形象化模拟可以看下面动图
51 |
52 | 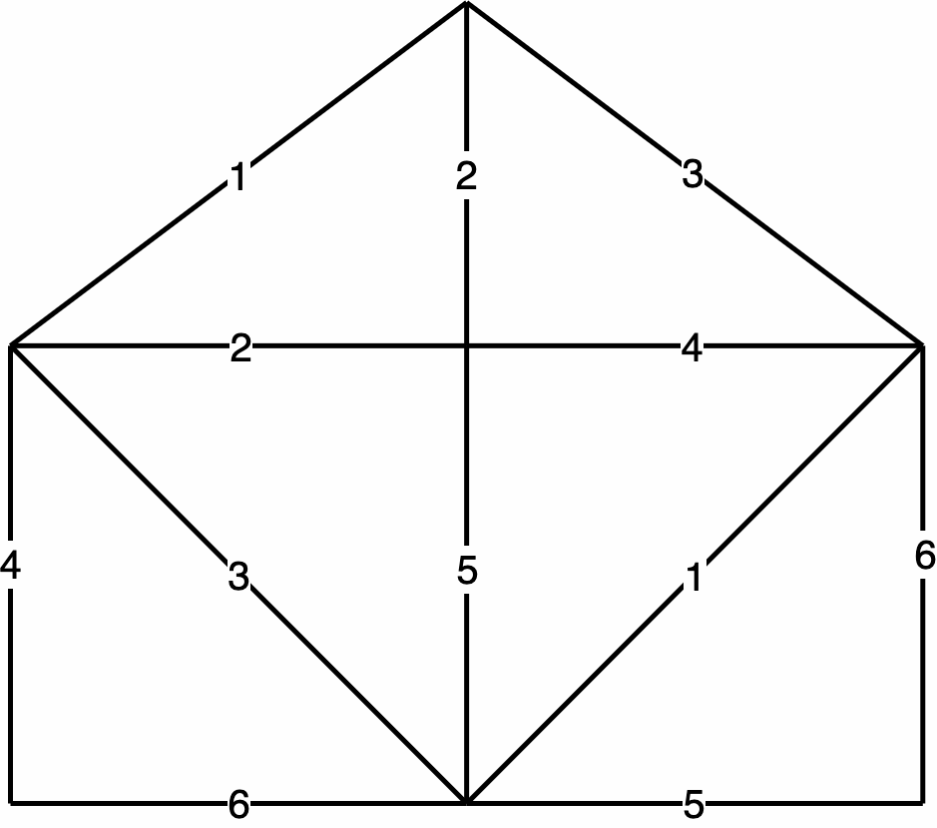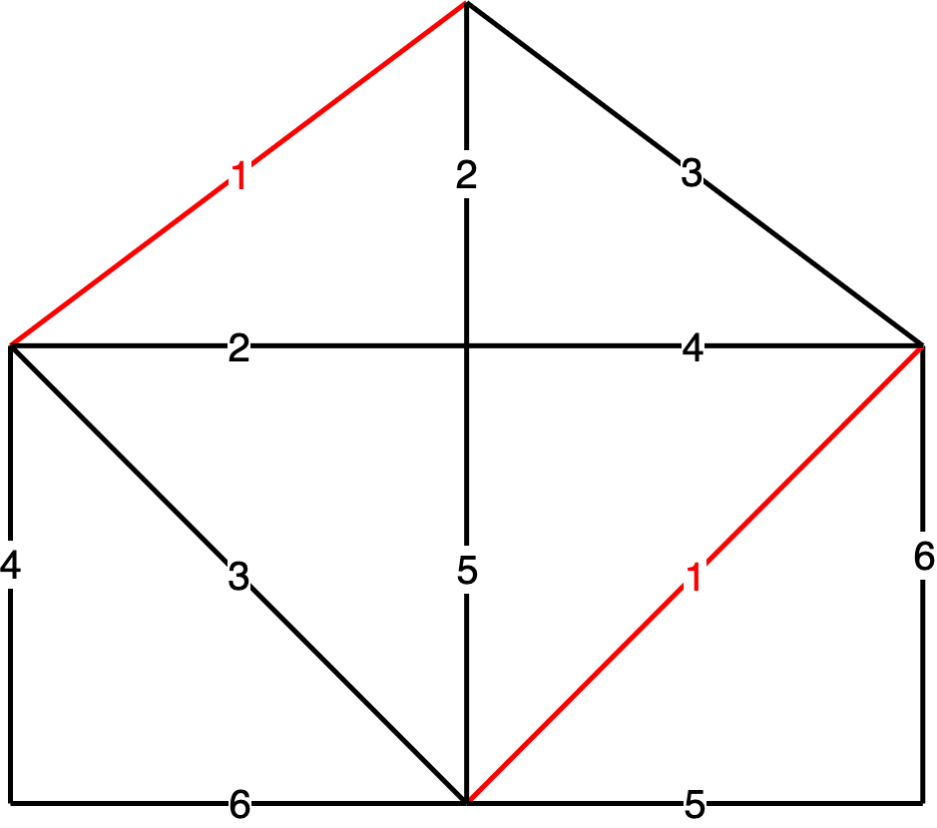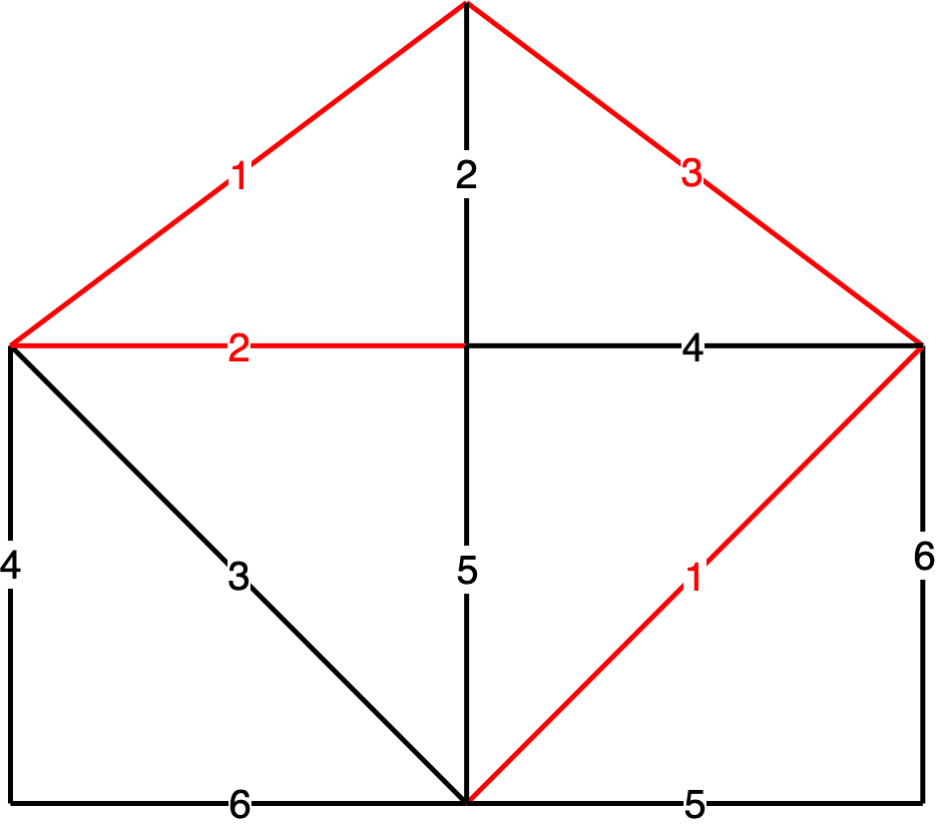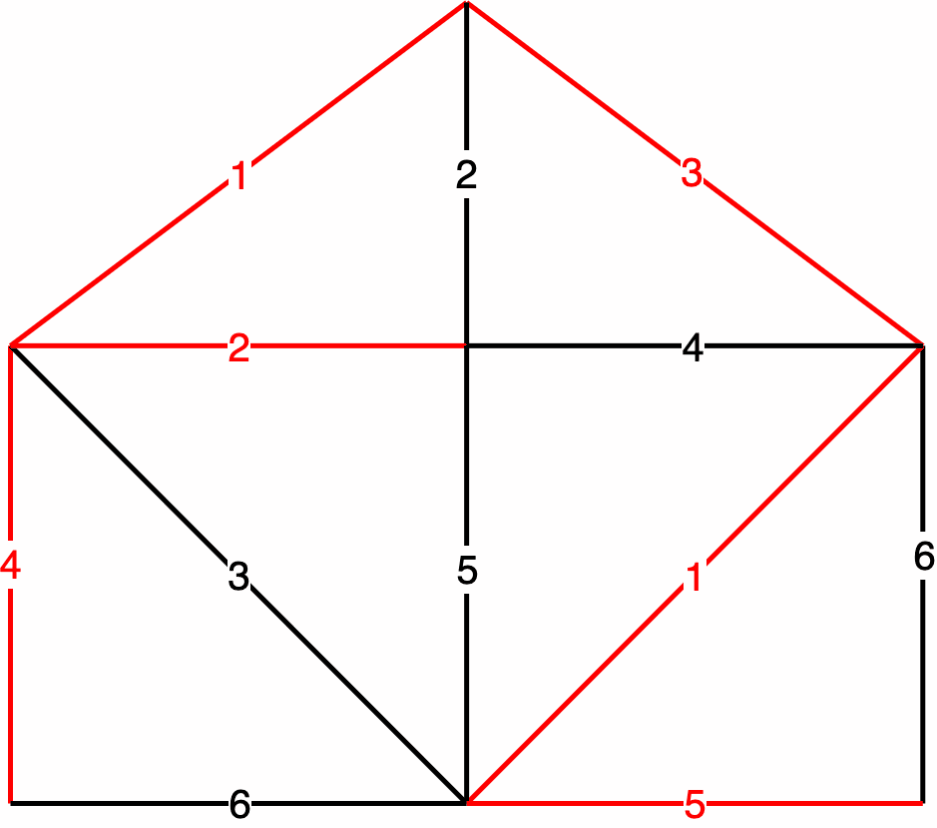 53 |
54 |
55 |
56 | 关于 Kruskal 算法的核心思想 可见 [图论 -- Kruskal 算法部分](../other/图论.html)
57 |
58 |
59 |
60 | **算法模版**
61 |
62 | ```java
63 | int minimumCost(int n, int[][] edges) {
64 | // 编号为 0...n
65 | UF uf = new UF(n + 1);
66 | // 对所有边按照权重从小到大排序
67 | Arrays.sort(edges, (a, b) -> (a[2] - b[2]));
68 | // 记录最小生成树的权重之和
69 | int mst = 0;
70 | for (int[] edge : edges) {
71 | int u = edge[0];
72 | int v = edge[1];
73 | int weight = edge[2];
74 | // 若这条边会产生环,则不能加入 mst
75 | if (uf.connected(u, v)) {
76 | continue;
77 | }
78 | // 若这条边不会产生环,则属于最小生成树
79 | mst += weight;
80 | uf.union(u, v);
81 | }
82 | // 保证所有节点都被连通
83 | // uf.count() == 1 说明所有节点被连通
84 | return uf.count() == 1 ? mst : -1;
85 | }
86 |
87 | class UF {
88 | // 见 并查集总结 的实现
89 | }
90 | ```
91 |
92 |
--------------------------------------------------------------------------------
/markdown/Algorithm/Prim最小生成树算法.md:
--------------------------------------------------------------------------------
1 | # Prim 最小生成树算法
2 |
3 | 关于 Prim 算法的核心思想 可见 [图论 -- Prim 算法部分](../other/图论.html)
4 |
5 | 对于算法的形象化模拟可以看下面动图
6 |
7 |
53 |
54 |
55 |
56 | 关于 Kruskal 算法的核心思想 可见 [图论 -- Kruskal 算法部分](../other/图论.html)
57 |
58 |
59 |
60 | **算法模版**
61 |
62 | ```java
63 | int minimumCost(int n, int[][] edges) {
64 | // 编号为 0...n
65 | UF uf = new UF(n + 1);
66 | // 对所有边按照权重从小到大排序
67 | Arrays.sort(edges, (a, b) -> (a[2] - b[2]));
68 | // 记录最小生成树的权重之和
69 | int mst = 0;
70 | for (int[] edge : edges) {
71 | int u = edge[0];
72 | int v = edge[1];
73 | int weight = edge[2];
74 | // 若这条边会产生环,则不能加入 mst
75 | if (uf.connected(u, v)) {
76 | continue;
77 | }
78 | // 若这条边不会产生环,则属于最小生成树
79 | mst += weight;
80 | uf.union(u, v);
81 | }
82 | // 保证所有节点都被连通
83 | // uf.count() == 1 说明所有节点被连通
84 | return uf.count() == 1 ? mst : -1;
85 | }
86 |
87 | class UF {
88 | // 见 并查集总结 的实现
89 | }
90 | ```
91 |
92 |
--------------------------------------------------------------------------------
/markdown/Algorithm/Prim最小生成树算法.md:
--------------------------------------------------------------------------------
1 | # Prim 最小生成树算法
2 |
3 | 关于 Prim 算法的核心思想 可见 [图论 -- Prim 算法部分](../other/图论.html)
4 |
5 | 对于算法的形象化模拟可以看下面动图
6 |
7 | 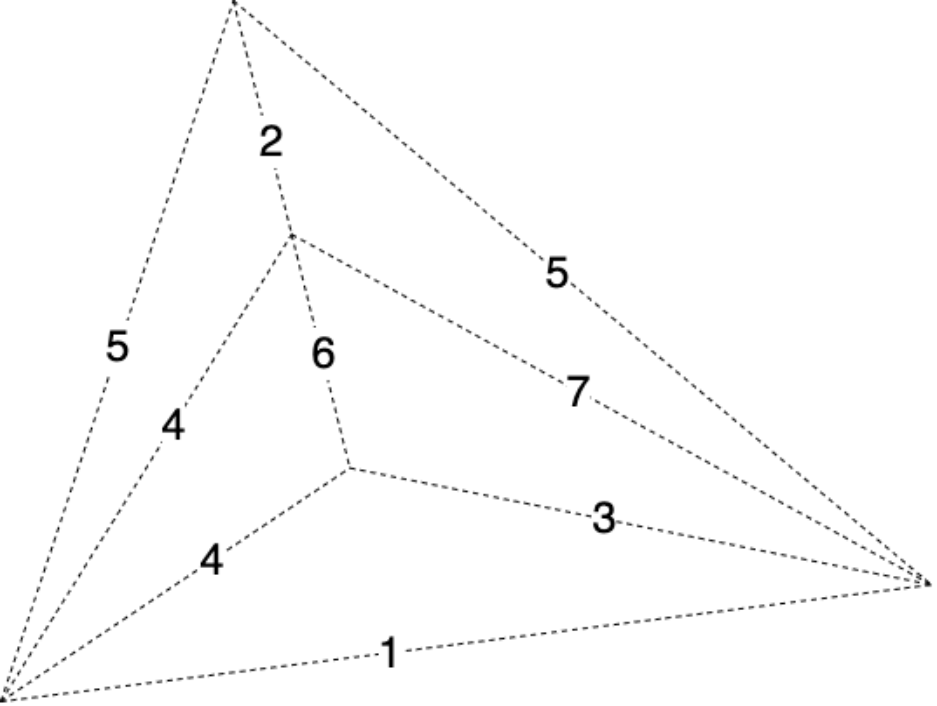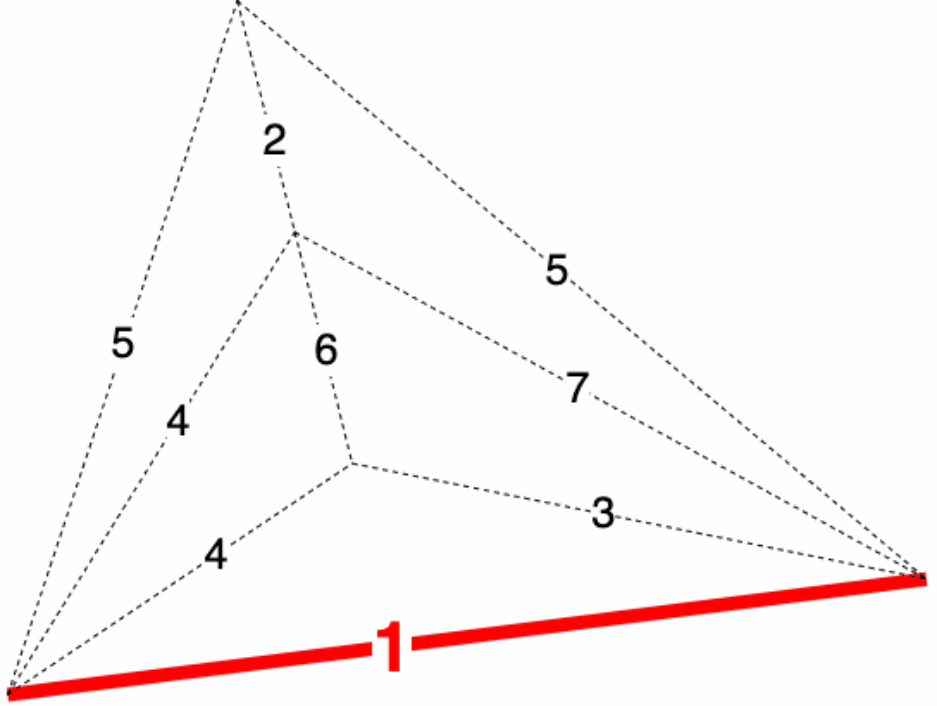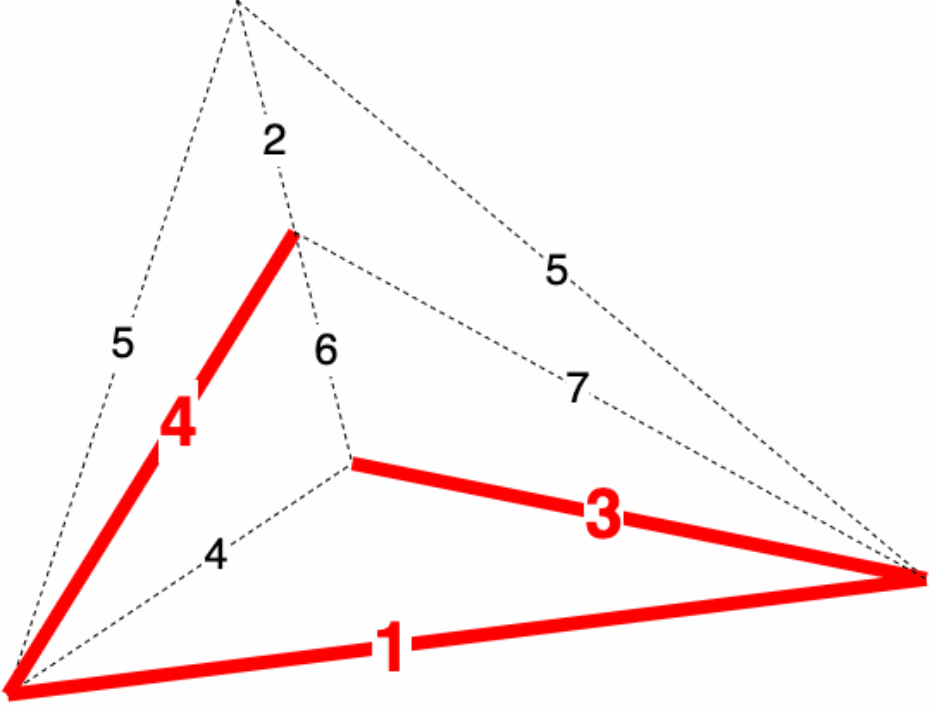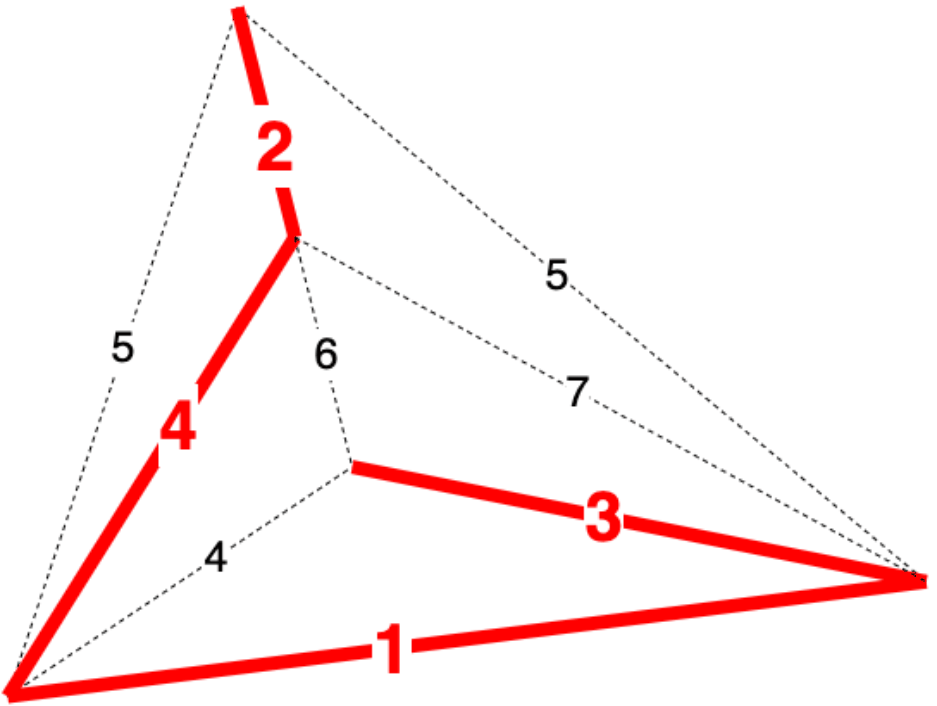 8 |
9 | 下面和 Kruskal 算法一样,解释以下三个问题,可与 Kruskal 算法对比观看
10 |
11 | - **问题一:**如何判断一个图是否为原图的生成子图
12 | - **问题二:**如何判断生成子图是一棵树
13 | - **问题三:**如何获得最小生成树
14 |
15 | **问题一:利用`inMST[]`数组来判断所有节点是否已在生成树中,详细实现可见`allConnected()`方法**
16 |
17 | **问题二:利用`inMST[]`数组来记录已加入生成树中的节点,以保证无环**
18 |
19 | **问题三:利用优先队列按照边的权重从小到大排序,可保证最终的生成子树为最小生成子树**
20 |
21 |
22 |
23 | **算法模版**
24 |
25 | ```java
26 | public class Prim {
27 | // 存在横切边的数据结构
28 | private final Queue pq;
29 | // 记录已经成为最小生成树的节点
30 | private boolean[] inMST;
31 | // 记录最小生成树的权重和
32 | private Integer weightSum = 0;
33 | // graph 是用邻接表表示的一幅图
34 | // graph[s] 记录节点 s 所有相邻的边
35 | // 三元组 int[]{from, to, weight} 表示一条边
36 | private final List[] graph;
37 |
38 | public Prim(List[] graph) {
39 | this.graph = graph;
40 | // 按照边的权重从小到大排序
41 | this.pq = new PriorityQueue<>(Comparator.comparingInt(a -> a[2]));
42 | // 图中有 n 个节点
43 | int n = graph.length;
44 | this.inMST = new boolean[n];
45 | // 随便从一个点开始切分都可以,我们不妨从节点 0 开始
46 | inMST[0] = true;
47 | cut(0);
48 | // 不断进行切分,向最小生成树中添加边
49 | while (!pq.isEmpty()) {
50 | int[] edge = pq.poll();
51 | int to = edge[1];
52 | int weight = edge[2];
53 | if (inMST[to]) {
54 | // 节点 to 已经在最小生成树中,跳过
55 | // 否则这条边会产生环
56 | continue;
57 | }
58 | // 将边 edge 加入最小生成树
59 | weightSum += weight;
60 | inMST[to] = true;
61 | // 节点 to 加入后,进行新一轮切分,会产生更多横切边
62 | cut(to);
63 | }
64 | }
65 | // 将 s 的横切边加入优先队列
66 | private void cut(int x) {
67 | // 遍历 s 的邻边
68 | for (int[] edge : graph[x]) {
69 | int to = edge[1];
70 | if (inMST[to]) {
71 | // 相邻接点 to 已经在最小生成树中,跳过
72 | // 否则这条边会产生环
73 | continue;
74 | }
75 | // 加入横切边队列
76 | pq.offer(edge);
77 | }
78 | }
79 | // 最小生成树的权重和
80 | public int weightSum() {
81 | return this.weightSum;
82 | }
83 | // 判断最小生成树是否包含图中的所有节点
84 | public boolean allConnected() {
85 | for (int i = 0; i < graph.length; i++) {
86 | if (!inMST[i]) {
87 | return false;
88 | }
89 | }
90 | return true;
91 | }
92 | }
93 | ```
94 |
95 |
--------------------------------------------------------------------------------
/markdown/Algorithm/x的平方根-变题.md:
--------------------------------------------------------------------------------
1 | # x 的平方根「变题」
2 |
3 | [69. x 的平方根](https://leetcode.cn/problems/sqrtx/)
4 |
5 |
6 |
7 | ```java
8 | public int mySqrt(int x) {
9 | int l = 0, r = x;
10 | while (l < r) {
11 | int m = l + r + 1 >> 1;
12 | if (x / m >= m) l = m;
13 | else r = m - 1;
14 | }
15 | return l;
16 | }
17 | ```
18 |
19 | ### 变题一:保留小数位
20 |
21 | ```java
22 | // epsilon 保留小数位 -> 1e-7
23 | public double mySqrt(double x, double epsilon){
24 | double l = 0, r = x;
25 | if (x == 0 || x == 1){
26 | return x;
27 | }
28 | while (l < r){
29 | double mid = l - (l - r) / 2;
30 | if (Math.abs(mid * mid - x) < epsilon){
31 | return mid;
32 | } else if (mid * mid < x){
33 | l = mid;
34 | } else {
35 | r = mid;
36 | }
37 | }
38 | return l;
39 | }
40 | ```
41 |
42 |
--------------------------------------------------------------------------------
/markdown/Algorithm/二分图.md:
--------------------------------------------------------------------------------
1 | # 二分图
2 |
3 | 具体定义见[传送门](../other/图论.html)
4 |
5 | 利用染色的思路去解题
6 |
7 | ## [785. 判断二分图](https://leetcode-cn.com/problems/is-graph-bipartite/)
8 |
9 | ```java
10 | // dfs
11 | private boolean ok = true;
12 | public boolean isBipartite(int[][] graph) {
13 | int n = graph.length;
14 | // visited[i] = 0 : 未染色 ; 1 : red ; -1 : blue
15 | int[] visited = new int[n];
16 | for (int i = 0; i < n; i++) {
17 | if (visited[i] == 0) {
18 | dfs(graph, visited, i, 1);
19 | }
20 | }
21 | return ok;
22 | }
23 | private void dfs(int[][] graph, int[] visited, int v, int color) {
24 | if (!ok) return ;
25 | visited[v] = color;
26 | for (int i : graph[v]) {
27 | // 未染色
28 | if (visited[i] == 0) {
29 | dfs(graph, visited, i, (-1) * color);
30 | } else {
31 | if (visited[i] == visited[v]) {
32 | ok = false;
33 | }
34 | }
35 | }
36 | }
37 |
38 | // bfs
39 | private boolean ok = true;
40 | public boolean isBipartite(int[][] graph) {
41 | int n = graph.length;
42 | // visited[i] = 0 : 未染色 ; 1 : red ; -1 : blue
43 | int[] visited = new int[n];
44 | for (int i = 0; i < n; i++) {
45 | if (visited[i] == 0) {
46 | bfs(graph, visited, i);
47 | }
48 | }
49 | return ok;
50 | }
51 | private void bfs(int[][] graph, int[] visited, int start) {
52 | Queue queue = new LinkedList<>();
53 | queue.add(start);
54 | visited[start] = 1;
55 | while (!queue.isEmpty() && ok) {
56 | int v = queue.poll();
57 | for (int i : graph[v]) {
58 | if (visited[i] == 0) {
59 | visited[i] = visited[v] * (-1);
60 | queue.offer(i);
61 | } else {
62 | if (visited[i] == visited[v]) {
63 | ok = false;
64 | }
65 | }
66 | }
67 | }
68 | }
69 | ```
70 |
71 | ## [886. 可能的二分法](https://leetcode-cn.com/problems/possible-bipartition/)
72 |
73 | ```java
74 | private boolean ok = true;
75 | public boolean possibleBipartition(int n, int[][] dislikes) {
76 | List[] graph = buildGraph(n, dislikes);
77 | int[] visited = new int[n + 1];
78 | for (int i = 1; i <= n; i++) {
79 | if (visited[i] == 0) dfs(graph, visited, i, 1);
80 | }
81 | return ok;
82 | }
83 | private List[] buildGraph(int n, int[][] dislikes) {
84 | List[] graph = new ArrayList[n + 1];
85 | for (int i = 1; i <= n; i++) {
86 | graph[i] = new ArrayList();
87 | }
88 | int m = dislikes.length;
89 | for (int i = 0; i < m; i++) {
90 | graph[dislikes[i][0]].add(dislikes[i][1]);
91 | graph[dislikes[i][1]].add(dislikes[i][0]);
92 | }
93 | return graph;
94 | }
95 | private void dfs(List[] graph, int[] visited, int p, int color) {
96 | if (!ok) return ;
97 | visited[p] = color;
98 | for(int i : graph[p]) {
99 | if (visited[i] == 0) {
100 | dfs(graph, visited, i, color * (-1));
101 | } else {
102 | if (visited[i] == visited[p]) ok = false;
103 | }
104 | }
105 | }
106 | ```
107 |
108 |
--------------------------------------------------------------------------------
/markdown/Algorithm/二分搜索.md:
--------------------------------------------------------------------------------
1 | # 二分搜索
2 |
3 |
4 |
5 | [704. 二分查找](https://leetcode-cn.com/problems/binary-search/)
6 |
7 | [34. 在排序数组中查找元素的第一个和最后一个位置](https://leetcode-cn.com/problems/find-first-and-last-position-of-element-in-sorted-array/)
8 |
9 | ### 基础版二分搜索
10 |
11 | 相信大家对「二分搜索」都不陌生,比较高效的一个搜索策略。前提是,搜索的数组必须是有序的!!!
12 |
13 | 但是这个算法的麻烦之处在于「对边界的判断」。先看一个最基础的二分搜索模版
14 |
15 | ```java
16 | public int search(int[] nums, int target) {
17 | int lo = 0;
18 | int hi = nums.length - 1;
19 | while (lo <= hi) {
20 | int mid = lo - (lo - hi) / 2;
21 | if (nums[mid] == target) return mid;
22 | else if (nums[mid] < target) lo = mid + 1;
23 | else if (nums[mid] > target) hi = mid - 1;
24 | }
25 | return -1;
26 | }
27 | ```
28 |
29 | 这里面有几个需要注意的点:
30 |
31 | - 搜索区间:全闭区间`[lo, hi]`
32 | - 结束条件:`lo = hi + 1`
33 | - 当每次收缩区间时,`lo`和`hi`都是不包括`mid`的。**原因:既然区间是全闭,所以收缩时,`num[mid]`不符合条件**
34 |
35 | ### 进阶版:寻找最左相等元素
36 |
37 | 下面有一个进阶版的二分搜索:寻找最左或最右的相等元素,如果不存在,返回 -1。**详情可见题目 [在排序数组中查找元素的第一个和最后一个位置](https://leetcode-cn.com/problems/find-first-and-last-position-of-element-in-sorted-array/)**
38 |
39 | 先给出模版,然后再进一步解释。先介绍寻找最左相等元素
40 |
41 | ```java
42 | private int leftBound(int[] nums, int target) {
43 | int lo = 0, hi = nums.length - 1;
44 | while (lo <= hi) {
45 | int mid = lo - (lo - hi) / 2;
46 | // 向左收缩
47 | if (nums[mid] == target) hi = mid - 1;
48 | else if (nums[mid] < target) lo = mid + 1;
49 | else if (nums[mid] > target) hi = mid - 1;
50 | }
51 | // 结束情况 : lo = hi + 1
52 | // 未找到的情况
53 | if (lo == nums.length || nums[lo] != target) return -1;
54 | return lo;
55 | }
56 | ```
57 |
58 | 和常规版的二分搜索不同之处:
59 |
60 | - 寻找到相等元素,不是立刻返回,而是向左收缩区间
61 |
62 | - 对于未找到元素的情况:(1) 可能比所有元素大;(2) 可能比所有元素小
63 | - 当比所有元素大时,区间会收缩到`[hi + 1, hi]`,例:`[5, 4]`,其中`num.length = 5`
64 | - 当比所有元素小时,区间会收缩到`[lo, lo - 1]`,例:`[0, -1]`
65 |
66 | - 对于第一种情况,我们通过`lo == nums.length`判断;对于第二种情况,我们通过`nums[lo] != target`判断
67 |
68 | - 注意:必须第一种情况的判断写在前面,不然可能会出现越界
69 |
70 | **为什么对于找到元素的情况,最后返回`lo`就是正确下标呢????**
71 |
72 | **原因:**首先,结束循环的条件为`lo = hi + 1`;如果找到了相等元素,此时循环内的`mid`就是正确下标;而由于收缩,`hi = mid - 1`,刚好比正确下标少 1。所以`lo`刚好是正确下标
73 |
74 | ### 进阶版:寻找最右相等元素
75 |
76 | 下面介绍寻找最右相等元素的情况,其实和最左相似度很高
77 |
78 | ```java
79 | private int rightBound(int[] nums, int target) {
80 | int lo = 0, hi = nums.length - 1;
81 | while (lo <= hi) {
82 | int mid = lo - (lo - hi) / 2;
83 | // 向右收缩
84 | if (nums[mid] == target) lo = mid + 1;
85 | else if (nums[mid] < target) lo = mid + 1;
86 | else if (nums[mid] > target) hi = mid - 1;
87 | }
88 | // 结束情况 : hi = lo - 1
89 | // 未找到的情况
90 | if (hi < 0 || nums[hi] != target) return -1;
91 | return hi;
92 | }
93 | ```
94 |
95 | - 对于未找到元素的情况:(1) 可能比所有元素大;(2) 可能比所有元素小
96 | - 当比所有元素大时,区间会收缩到`[hi + 1, hi]`,例:`[5, 4]`,其中`num.length = 5`
97 | - 当比所有元素小时,区间会收缩到`[lo, lo - 1]`,例:`[0, -1]`
98 |
99 | - 对于第二种情况,我们通过`hi < 0`判断;对于第一种情况,我们通过`nums[hi] != target`判断
100 |
101 | - 注意:必须第二种情况的判断写在前面,不然可能会出现越界
102 |
103 | **为什么对于找到元素的情况,最后返回`hi`就是正确下标呢????**
104 |
105 | **原因:**首先,结束循环的条件为`hi = lo - 1`;如果找到了相等元素,此时循环内的`mid`就是正确下标;而由于收缩,`lo = mid + 1`,刚好比正确下标多 1。所以`hi`刚好是正确下标
106 |
107 | ### 一个好问题
108 |
109 | 相信大家会有一个疑问,为什么「寻找最左相等元素」和「寻找最右相等元素」最后对于未找到的情况的判断方式有些区别呢???
110 |
111 | __前者通过`lo`来判断,后者通过`hi`来判断__
112 |
113 | 这就要回到上面每种情况最后提出的那个问题了。对于「寻找最左相等元素」,`lo` 是正确下标,我们需要通过正确下标判断是否找到了目标元素;同理「寻找最右相等元素」也一样
114 |
--------------------------------------------------------------------------------
/markdown/Algorithm/二叉树中的最大路径和-变题.md:
--------------------------------------------------------------------------------
1 | # 二叉树中的最大路径和「变题」
2 |
3 | [124. 二叉树中的最大路径和](https://leetcode.cn/problems/binary-tree-maximum-path-sum/)
4 |
5 |
6 |
7 | 开头先来一个小插曲,关于「二叉树路径」相关的总结可见 **[二叉树路径相关技巧](https://lfool.github.io/LFool-Notes/algorithm/二叉树路径相关技巧.html)**
8 |
9 | ```java
10 | private int ans = -1000;
11 | public int maxPathSum(TreeNode root) {
12 | f(root);
13 | return ans;
14 | }
15 | private int f(TreeNode root) {
16 | if (root == null) return 0;
17 | int l = f(root.left);
18 | int r = f(root.right);
19 | ans = Math.max(ans, Math.max(0, l) + Math.max(0, r) + root.val);
20 | return Math.max(0, Math.max(Math.max(0, l), Math.max(0, r))) + root.val;
21 | }
22 | ```
23 |
24 | ### 变题一:输出最大路径
25 |
26 | ```java
27 | class Solution {
28 | private int ans = -1000;
29 | private List path = new ArrayList<>();
30 | public int maxPathSum(TreeNode root) {
31 | f(root);
32 | System.out.println(path);
33 | return ans;
34 | }
35 | private Pair f(TreeNode root) {
36 | Pair cur = new Pair(0, new ArrayList<>());
37 | if (root == null) return cur;
38 | Pair l = f(root.left);
39 | Pair r = f(root.right);
40 | if (l.sum < 0) l = new Pair(0, new ArrayList<>());
41 | if (r.sum < 0) r = new Pair(0, new ArrayList<>());
42 | int sum = l.sum + r.sum + root.val;
43 | if (ans < sum) {
44 | ans = sum;
45 | path = new ArrayList<>();
46 | path.addAll(l.path);
47 | path.add(root.val);
48 | path.addAll(r.path);
49 | }
50 |
51 | if (l.sum > r.sum) {
52 | cur.sum = l.sum + root.val;
53 | cur.path.addAll(l.path);
54 | cur.path.add(root.val);
55 | } else {
56 | cur.sum = r.sum + root.val;
57 | cur.path.add(root.val);
58 | cur.path.addAll(r.path);
59 | }
60 |
61 | return cur;
62 | }
63 | }
64 | class Pair {
65 | int sum;
66 | List path;
67 | public Pair(int sum, List path) {
68 | this.sum = sum;
69 | this.path = path;
70 | }
71 | }
72 | ```
73 |
74 | ### 变题二:相邻字符不同的最长路径
75 |
76 | **题目详情可见 [相邻字符不同的最长路径](https://leetcode.cn/problems/longest-path-with-different-adjacent-characters/)**
77 |
78 | ```java
79 | private int ans = 1;
80 | private char[] s;
81 | private List[] tree;
82 | public int longestPath(int[] parent, String S) {
83 | s = S.toCharArray();
84 | tree = new ArrayList[parent.length];
85 | Arrays.setAll(tree, e -> new ArrayList<>());
86 | for (int i = 1; i < parent.length; i++) {
87 | tree[parent[i]].add(i);
88 | }
89 | f(0);
90 | return ans;
91 | }
92 | private int[] f(int v) {
93 | int c = s[v] - 'a';
94 | int[] res = new int[]{1, c};
95 | if (tree[v].size() == 0) return res;
96 | Queue q = new PriorityQueue<>((a, b) -> b[0] - a[0]);
97 | for (int next : tree[v]) {
98 | q.offer(f(next));
99 | }
100 | int sum = 1, cnt = 0;
101 | while (!q.isEmpty() && cnt < 2) {
102 | int[] cur = q.poll();
103 | if (cur[1] != c && cnt < 1) {
104 | res[0] += cur[0];
105 | sum += cur[0];
106 | cnt++;
107 | } else if (cur[1] != c && cnt < 2) {
108 | sum += cur[0];
109 | cnt++;
110 | }
111 | }
112 | ans = Math.max(ans, sum);
113 | return res;
114 | }
115 | ```
116 |
--------------------------------------------------------------------------------
/markdown/Algorithm/二叉树的中序遍历-变题.md:
--------------------------------------------------------------------------------
1 | # 二叉树的中序遍历「变题」
2 |
3 | [94. 二叉树的中序遍历](https://leetcode.cn/problems/binary-tree-inorder-traversal/)
4 |
5 |
6 |
7 | 开头先来一个小插曲,关于「二叉树遍历」相关的总结可见 **[二叉树遍历](https://lfool.github.io/LFool-Notes/algorithm/二叉树遍历.html)**
8 |
9 | ```java
10 | // 递归
11 | // 时间复杂度 : O(n)
12 | // 空间复杂度 : O(n) -> 递归栈
13 | private List ans = new ArrayList<>();
14 | public List inorderTraversal(TreeNode root) {
15 | traversal(root);
16 | return ans;
17 | }
18 | private void traversal(TreeNode root) {
19 | if (root == null) return ;
20 | traversal(root.left);
21 | ans.add(root.val);
22 | traversal(root.right);
23 | }
24 |
25 | // 非递归
26 | // 时间复杂度 : O(n)
27 | // 空间复杂度 : O(n) -> 辅助栈
28 | public List inorderTraversal(TreeNode root) {
29 | List ans = new ArrayList<>();
30 | Deque st = new ArrayDeque<>();
31 | while (!st.isEmpty() || root != null) {
32 | while (root != null) {
33 | st.push(root);
34 | root = root.left;
35 | }
36 | TreeNode top = st.poll();
37 | ans.add(top.val);
38 | root = top.right;
39 | }
40 | return ans;
41 | }
42 |
43 | // 莫里斯
44 | // 时间复杂度 : O(n)
45 | // 空间复杂度 : O(1)
46 | public List inorderTraversal(TreeNode root) {
47 | List ans = new ArrayList<>();
48 | while (root != null) {
49 | if (root.left != null) {
50 | TreeNode pre = root.left;
51 | while (pre.right != null) {
52 | pre = pre.right;
53 | }
54 | pre.right = root;
55 | TreeNode tmp = root;
56 | root = root.left;
57 | tmp.left = null;
58 | } else {
59 | ans.add(root.val);
60 | root = root.right;
61 | }
62 | }
63 | return ans;
64 | }
65 | ```
--------------------------------------------------------------------------------
/markdown/Algorithm/二叉树的最近公共祖先-变题.md:
--------------------------------------------------------------------------------
1 | # 二叉树的最近公共祖先「变题」
2 |
3 | [236. 二叉树的最近公共祖先](https://leetcode.cn/problems/lowest-common-ancestor-of-a-binary-tree/)
4 |
5 |
6 |
7 | 开头先来一个小插曲,关于「祖先」问题的总结可见 **[二叉树祖先问题](./二叉树祖先问题.html)**
8 |
9 | ```java
10 | // 方法一:递归
11 | public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
12 | if (root == null) return null;
13 | if (root == p || root == q) return root;
14 | TreeNode left = lowestCommonAncestor(root.left, p, q);
15 | TreeNode right = lowestCommonAncestor(root.right, p, q);
16 | if (left == null || right == null) return left == null ? right : left;
17 | return root;
18 | }
19 |
20 | // 方法二:记录父节点,然后找相交点 (同相交链表找交点的方法)
21 | private Map parent = new HashMap<>();
22 | public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
23 | getParent(root, null);
24 | TreeNode pp = p, qq = q;
25 | // 找交点的过程
26 | while (pp != qq) {
27 | if (pp == null) pp = q;
28 | else pp = parent.get(pp.val);
29 | if (qq == null) qq = p;
30 | else qq = parent.get(qq.val);
31 | }
32 | return pp;
33 | }
34 | // 记录每个节点的父节点
35 | private void getParent(TreeNode root, TreeNode p) {
36 | if (root == null) return ;
37 | parent.put(root.val, p);
38 | getParent(root.left, root);
39 | getParent(root.right, root);
40 | }
41 | ```
42 |
43 | ### 变题一:二叉搜索树的最近公共祖先
44 |
45 | **题目详情可见 [二叉搜索树的最近公共祖先](https://leetcode.cn/problems/lowest-common-ancestor-of-a-binary-search-tree/)**
46 |
47 | 相比于上面的题目来说更简单,因为二叉搜索树有序!!
48 |
49 | ```java
50 | public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
51 | if (p.val > q.val) return lowestCommonAncestor(root, q, p);
52 | if (root == null) return null;
53 | if (p.val <= root.val && root.val <= q.val) return root;
54 | if (q.val < root.val) return lowestCommonAncestor(root.left, p, q);
55 | else return lowestCommonAncestor(root.right, p, q);
56 | }
57 | ```
58 |
59 | ### 变题二:最深叶节点的最近公共祖先
60 |
61 | **题目详情可见 [最深叶节点的最近公共祖先](https://leetcode.cn/problems/lowest-common-ancestor-of-deepest-leaves/)**
62 |
63 | ```java
64 | private int[] height = new int[1010];
65 | public TreeNode lcaDeepestLeaves(TreeNode root) {
66 | getH(root);
67 | return f(root);
68 | }
69 | private TreeNode f(TreeNode root) {
70 | if (root == null) return null;
71 | if (root.left == null && root.right == null) return root;
72 | if (root.left == null) return f(root.right);
73 | if (root.right == null) return f(root.left);
74 | int lh = height[root.left.val];
75 | int rh = height[root.right.val];
76 | if (lh == rh) return root;
77 | else if (lh < rh) return f(root.right);
78 | else return f(root.left);
79 | }
80 | private int getH(TreeNode root) {
81 | if (root == null) return 0;
82 | height[root.val] = Math.max(getH(root.left), getH(root.right)) + 1;
83 | return height[root.val];
84 | }
85 | ```
86 |
87 | ### 变题三:N 叉树的最近公共祖先
88 |
89 | 建议使用开头给出的方法二,记录父节点!!递归分支太多,不好判断,但也是可以用递归滴!!
90 |
--------------------------------------------------------------------------------
/markdown/Algorithm/位运算技巧.md:
--------------------------------------------------------------------------------
1 | [toc]
2 |
3 | # 位运算技巧
4 |
5 | ## 有趣小技巧
6 |
7 | ### 大小写相互转换
8 |
9 | ```java
10 | // 转小写
11 | (char) ('a' | ' ') = 'a'
12 | (char) ('A' | ' ') = 'a'
13 |
14 | // 转大写
15 | (char) ('b' & '_') = 'B'
16 | (char) ('B' & '_') = 'B'
17 |
18 | // 大小写互转
19 | (char) ('d' ^ ' ') = 'D'
20 | (char) ('D' ^ ' ') = 'd'
21 | ```
22 |
23 | ### 判断两个数是否异号
24 |
25 | ```java
26 | int x = -1, y = 2;
27 | boolean f = ((x ^ y) < 0); // true
28 |
29 | int x = 3, y = 2;
30 | boolean f = ((x ^ y) < 0); // false
31 | ```
32 |
33 | ### 不用临时变量交换两个数
34 |
35 | ```java
36 | int a = 1, b = 2;
37 | a ^= b;
38 | b ^= a;
39 | a ^= b;
40 | // 现在 a = 2, b = 1
41 | ```
42 |
43 | ### 加减一
44 |
45 | ```java
46 | // 加一
47 | int n = 1;
48 | n = -~n;
49 | // 现在 n = 2
50 |
51 | // 减一
52 | int n = 2;
53 | n = ~-n;
54 | // 现在 n = 1
55 | ```
56 |
57 | ## 算法常用操作
58 |
59 | ### `n & (n - 1)`
60 |
61 | > 可以消除 n 的二进制中最后一位 1
62 |
63 | 例题:
64 |
65 | - **详情可见 [191. 位1的个数](https://leetcode-cn.com/problems/number-of-1-bits/)**
66 |
67 | - 判断一个数是不是 2 的指数(如果一个数是 2 的指数,那么该数的二进制中只会有一个 1)
68 |
69 | ### `a ^ a = 0` `a ^ 0 = a`
70 |
71 | **详情可见 [136. 只出现一次的数字](https://leetcode-cn.com/problems/single-number/)**
72 |
73 | ### 「任意位置」置 1 or 0
74 |
75 | **详情可见 [698. 划分为k个相等的子集](https://leetcode-cn.com/problems/partition-to-k-equal-sum-subsets/)**
76 |
77 | ```java
78 | // 注意:「<<」优先级大于「|=」「^=」
79 | // 将第 i 位标记为 1
80 | used |= 1 << i;
81 |
82 | // 将第 i 位标记为 0
83 | used ^= 1 << i;
84 | ```
85 |
86 | ### 判断某一位置是否为 1
87 |
88 | ```java
89 | ((used >> i) & 1) == 1
90 | ```
91 |
92 | ### 低位的 0 变成 1
93 |
94 | ```java
95 | n |= n + 1;
96 | ```
97 |
98 | ### 低位的 1 变成 0
99 |
100 | ```java
101 | n &= n - 1;
102 | ```
103 |
104 | ## 实战题目
105 |
106 | ### 二叉树中的伪回文路径
107 |
108 | **题目详情可见 [二叉树中的伪回文路径](https://leetcode-cn.com/problems/pseudo-palindromic-paths-in-a-binary-tree/)**
109 |
110 | 这是一道综合运用位运算的高级题目 哈哈哈哈哈 我感觉很值得总结一波
111 |
112 | 首先这个题目肯定是需要用遍历的方法去写,遍历出所有路径
113 |
114 | 其次是需要搞清楚怎么判断是否为一个伪回文路径
115 |
116 | - 出现次数为奇数的数字要么只有一个 要么没有
117 |
118 | ```java
119 | // 记录每条路径
120 | private int count = 0;
121 | // 记录结果
122 | private int res = 0;
123 | public int pseudoPalindromicPaths (TreeNode root) {
124 | traversal(root);
125 | return res;
126 | }
127 | private void traversal(TreeNode root) {
128 | if (root == null) return ;
129 | // 对于每一个节点的表示:2:10 3:100 4:1000,以此类推
130 | // 刚好可以用左移来表示:1 << root.val
131 | // 当一个数出现两次后,则 10 ^ 10 = 0,利用了异或操作的特性,刚好可以抵消出现偶数次数的情况
132 | count ^= (1 << root.val);
133 | if (root.left == null && root.right == null) {
134 | if ((count & (count - 1)) == 0) res++;
135 | }
136 | traversal(root.left);
137 | traversal(root.right);
138 | // 再进行一次异或,刚好可以抵消上面异或操作
139 | // 正好是后序遍历离开节点时的操作
140 | count ^= (1 << root.val);
141 | }
142 | ```
143 |
144 | ### 最小 XOR
145 |
146 | **题目详情可见 [最小 XOR](https://leetcode.cn/problems/minimize-xor/)**
147 |
148 | ```java
149 | public int minimizeXor(int num1, int num2) {
150 | int c1 = Integer.bitCount(num1);
151 | int c2 = Integer.bitCount(num2);
152 | // num1 低位的 0 变成 1
153 | for (; c1 < c2; c1++) num1 |= num1 + 1;
154 | // num2 低位的 1 变成 0
155 | for (; c2 < c1; c2++) num1 &= num1 - 1;
156 | return num1;
157 | }
158 | ```
--------------------------------------------------------------------------------
/markdown/Algorithm/全排列-变题.md:
--------------------------------------------------------------------------------
1 | # 全排列「变题」
2 |
3 | [46. 全排列](https://leetcode.cn/problems/permutations/)
4 |
5 |
6 |
7 | 开头先来一个小插曲,关于「排列」问题的总结可见 **[排列 / 组合 / 子集 问题](./排列-组合-子集问题.html)**
8 |
9 | ```java
10 | // 回溯
11 | // 时间复杂度 : O(n * n!) -> n! 为叶子结点数量,每到叶子结点时就会 copy 一次 List,时间为 O(n)
12 | // 空间复杂度 : O(n * n!) -> 回溯深度为 n,需要 O(n) 的栈空间;但存储答案的 List 需要 O(n * n!) 空间,两者取最大值
13 | private boolean[] used;
14 | private List track = new ArrayList<>();
15 | private List> ans = new ArrayList<>();
16 | public List> permute(int[] nums) {
17 | used = new boolean[nums.length];
18 | f(nums);
19 | return ans;
20 | }
21 | private void f(int[] nums) {
22 | if (track.size() == nums.length) {
23 | ans.add(new ArrayList<>(track));
24 | return ;
25 | }
26 | for (int i = 0; i < nums.length; i++) {
27 | if (used[i]) continue;
28 | used[i] = true;
29 | track.add(nums[i]);
30 | f(nums);
31 | track.remove(track.size() - 1);
32 | used[i] = false;
33 | }
34 | }
35 |
36 | // 迭代
37 | // 时间复杂度 : O(n * n!) -> n! 为叶子结点数量,每到叶子结点时就会 copy 一次 List,时间为 O(n)
38 | // 空间复杂度 : O(n * n!) -> 临时的 List 和存储答案的 List
39 | public List> permute(int[] nums) {
40 | List> ans = new LinkedList<>();
41 | List> temp = new LinkedList<>();
42 | ans.add(new LinkedList<>());
43 | for (int x : nums) {
44 | for (List list : ans) {
45 | // 分别在 List 的 [0...n] 处插入当前元素
46 | for (int i = 0; i <= list.size(); i++) {
47 | // copy
48 | List t = new LinkedList<>(list);
49 | // LinkedList 插入时不需要移动,但需要遍历查找到第 i 个位置
50 | t.add(i, x);
51 | temp.add(t);
52 | }
53 | }
54 | ans = new LinkedList<>(temp);
55 | temp = new LinkedList<>();
56 | }
57 | return ans;
58 | }
59 | ```
60 |
61 | ### 变题一:全排列 (有重复)
62 |
63 | **题目详情可见 [全排列 II](https://leetcode.cn/problems/permutations-ii/)**
64 |
65 | **字符串版本题目可见 [面试题 08.08. 有重复字符串的排列组合](https://leetcode.cn/problems/permutation-ii-lcci/)**
66 |
67 | ```java
68 | private boolean[] used;
69 | private List track = new ArrayList<>();
70 | private List> ans = new ArrayList<>();
71 | public List> permuteUnique(int[] nums) {
72 | int n = nums.length;
73 | used = new boolean[n];
74 | // 注意要排序
75 | Arrays.sort(nums);
76 | f(nums);
77 | return ans;
78 | }
79 | private void f(int[] nums) {
80 | if (track.size() == nums.length) {
81 | ans.add(new ArrayList<>(track));
82 | return ;
83 | }
84 | for (int i = 0; i < nums.length; i++) {
85 | if (used[i]) continue;
86 | if (i > 0 && nums[i] == nums[i - 1] && !used[i - 1]) continue;
87 | used[i] = true;
88 | track.add(nums[i]);
89 | f(nums);
90 | used[i] = false;
91 | track.remove(track.size() - 1);
92 | }
93 | }
94 | ```
95 |
--------------------------------------------------------------------------------
/markdown/Algorithm/判定完美矩形.md:
--------------------------------------------------------------------------------
1 | # 判定完美矩形
2 |
3 | [391. 完美矩形](https://leetcode.cn/problems/perfect-rectangle/)
4 |
5 | 本篇文章来总结一个比较有意思的题目!
6 |
7 | 我们需要从两个角度去判断
8 |
9 | 其一:求出左下角和右上角的顶点坐标,判断期望面积是否和实际面积相等。如果不相等,一定不是完美矩形;如果相等,也不一定是完美矩形
10 |
11 | 其二:根据最后有效顶点数,如果不等于 4,一定不是完美矩形;如果等于 4,也需要和一中求出的顶点匹配才满足完美矩阵
12 |
13 | ```java
14 | public boolean isRectangleCover(int[][] rectangles) {
15 | // 左下角和右上角的顶点坐标
16 | int minX = 100010, minY = 100010;
17 | int maxX = -100010, maxY = -100010;
18 | int actualArea = 0;
19 | Set set = new HashSet<>();
20 | for (int[] rect : rectangles) {
21 | int x = rect[0], y = rect[1], a = rect[2], b = rect[3];
22 | minX = Math.min(minX, x);
23 | minY = Math.min(minY, y);
24 | maxX = Math.max(maxX, a);
25 | maxY = Math.max(maxY, b);
26 | // 期望面积
27 | actualArea += (a - x) * (b - y);
28 | // 计算有效顶点数
29 | int[][] points = new int[][]{ {x, y}, {x , b}, {a, y}, {a, b} };
30 | for (int[] p : points) {
31 | String s = p[0] + "," + p[1];
32 | if (set.contains(s)) set.remove(s);
33 | else set.add(s);
34 | }
35 | }
36 | // 期望面积和实际面积不相等
37 | if (actualArea != (maxX - minX) * (maxY - minY)) return false;
38 | // 有效顶点数不等于 4
39 | if (set.size() != 4) return false;
40 | int[][] points = new int[][]{ {minX, minY}, {minX , maxY}, {maxX, minY}, {maxX, maxY} };
41 | for (int[] p : points) {
42 | String s = p[0] + "," + p[1];
43 | // 有效顶点和一中求出的顶点不匹配
44 | if (!set.contains(s)) return false;
45 | }
46 | return true;
47 | }
48 | ```
49 |
50 |
--------------------------------------------------------------------------------
/markdown/Algorithm/前缀后缀法.md:
--------------------------------------------------------------------------------
1 | # 前缀后缀法
2 |
3 | [剑指 Offer 66. 构建乘积数组](https://leetcode.cn/problems/gou-jian-cheng-ji-shu-zu-lcof/)
4 |
5 | [238. 除自身以外数组的乘积](https://leetcode.cn/problems/product-of-array-except-self/)
6 |
7 | [768. 最多能完成排序的块 II](https://leetcode.cn/problems/max-chunks-to-make-sorted-ii/)
8 |
9 | [6190. 找到所有好下标](https://leetcode.cn/problems/find-all-good-indices/)
10 |
11 |
12 |
13 | 该类型的题目最大的特点:
14 |
15 | - 判断一个数左右两边是否满足要求
16 | - 求一个数左右两边的乘积
17 |
18 | 整体思路:用两个数组,分别统计「从左到右」和「从右到左」的信息
19 |
20 | 直接看题吧!!
21 |
22 | ### 构建乘积数组
23 |
24 | **题目详情可见 [剑指 Offer 66. 构建乘积数组](https://leetcode.cn/problems/gou-jian-cheng-ji-shu-zu-lcof/)**
25 |
26 | 对于这个题目,用两个数组分别统计「从左到右」和「从右到左」的乘积
27 |
28 | 「从左到右」:`left[i]`表示`[0...i-1]`的乘积
29 |
30 | 「从右到左」:`right[i]`表示`[i+1...n-1]`的乘积
31 |
32 | ```java
33 | public int[] constructArr(int[] a) {
34 | int n = a.length;
35 | int[] left = new int[n];
36 | int[] right = new int[n];
37 | int product = 1;
38 | for (int i = 0; i < n; i++) {
39 | left[i] = product;
40 | product *= a[i];
41 | }
42 | product = 1;
43 | for (int i = n - 1; i >= 0; i--) {
44 | right[i] = product;
45 | product *= a[i];
46 | }
47 | int[] ans = new int[n];
48 | for (int i = 0; i < n; i++) {
49 | ans[i] = left[i] * right[i];
50 | }
51 | return ans;
52 | }
53 | ```
54 |
55 | ### 除自身以外数组的乘积
56 |
57 | **题目详情可见 [除自身以外数组的乘积](https://leetcode.cn/problems/product-of-array-except-self/)**
58 |
59 | 几乎和上一题一模一样!!
60 |
61 | ### 最多能完成排序的块 II
62 |
63 | **题目详情可见 [最多能完成排序的块 II](https://leetcode.cn/problems/max-chunks-to-make-sorted-ii/)**
64 |
65 | 用两个数组分别存前缀最大值和后缀最小值
66 |
67 | 如果`i`和`i + 1`之间可以分块,那么必有`prefMax[i] <= suffMin[i + 1]`
68 |
69 | ```java
70 | public int maxChunksToSorted(int[] arr) {
71 | int n = arr.length;
72 | int[] prefMax = new int[n];
73 | int[] suffMin = new int[n];
74 | prefMax[0] = arr[0];
75 | for (int i = 1; i < n; i++) prefMax[i] = Math.max(prefMax[i - 1], arr[i]);
76 | suffMin[n - 1] = arr[n - 1];
77 | for (int i = n - 2; i >= 0; i--) suffMin[i] = Math.min(suffMin[i + 1], arr[i]);
78 | int ans = 1;
79 | for (int i = 0; i < n - 1; i++) {
80 | if (prefMax[i] <= suffMin[i + 1]) ans++;
81 | }
82 | return ans;
83 | }
84 | ```
85 |
86 | ### 找到所有好下标
87 |
88 | **题目详情可见 [找到所有好下标](https://leetcode.cn/problems/find-all-good-indices/)**
89 |
90 | 对于这个题目,用两个数组分别统计「从左到右」和「从右到左」的最长非递增/非递减的子数组长度
91 |
92 | 「从左到右」:`left[i]`表示`[0...i-1]`中最长非递增的长度
93 |
94 | 「从右到左」:`right[i]`表示`[i+1...n-1]`的最长非递减的长度
95 |
96 | ```java
97 | public List goodIndices(int[] nums, int k) {
98 | int n = nums.length;
99 | int[] left = new int[n];
100 | int[] right = new int[n];
101 | int cnt = 0;
102 | for (int i = 0; i < n; i++) {
103 | left[i] = cnt;
104 | if (i > 0 && nums[i - 1] < nums[i]) cnt = 0;
105 | cnt++;
106 | }
107 | cnt = 0;
108 | for (int i = n - 1; i >= 0; i--) {
109 | right[i] = cnt;
110 | if (i < n - 1 && nums[i] > nums[i + 1]) cnt = 0;
111 | cnt++;
112 | }
113 | List ans = new ArrayList<>();
114 | for (int i = 0; i < n; i++) {
115 | if (left[i] >= k && right[i] >= k) ans.add(i);
116 | }
117 | return ans;
118 | }
119 | ```
--------------------------------------------------------------------------------
/markdown/Algorithm/前缀和之奇偶篇.md:
--------------------------------------------------------------------------------
1 | # 前缀和之奇偶篇
2 |
3 | [1915. 最美子字符串的数目](https://leetcode.cn/problems/number-of-wonderful-substrings/)
4 |
5 | [1542. 找出最长的超赞子字符串](https://leetcode.cn/problems/find-longest-awesome-substring/)
6 |
7 |
8 |
9 | 本篇文章总结两个关于「前缀和」结合「奇偶」,同时又包含「异或」的题目!!
10 |
11 | 关于「前缀和」以及「异或」的总结可见:
12 |
13 | - **[前缀和数组](./前缀和数组.html)**
14 | - **[前缀和之异或篇](./前缀和之异或篇.html)**
15 |
16 | ### 最美子字符串的数目
17 |
18 | **题目详情可见 [最美子字符串的数目](https://leetcode.cn/problems/number-of-wonderful-substrings/)**
19 |
20 | 题目要求计算出字符串中**至多一个**字母出现奇数次的所有子串数量,所以会有两种情况:
21 |
22 | - 子串所有字母出现的次数全都是偶数
23 | - 子串只有一个字母出现的次数是奇数
24 |
25 | 而且题目中还有一个额外的附加条件:字符串中的字符由前十个小写英文字母组成
26 |
27 | 由于只需要知道一个字母出现次数的奇偶性,而不需要知道一个字母到底出现了多少次
28 |
29 | 所以可以用一个长度为 10 位的数字表示某一个子串中各字母出现的奇偶次数,如果出现次数为偶数,则该位为 0,否则为 1
30 |
31 | 正好可以利用「异或」运算的特点,`0 ^ 1 = 1; 1 ^ 1 = 0`
32 |
33 | 上面描述的可能比较抽象,具体看图:
34 |
35 | 
36 |
37 | 最终可以得到二机制为`0000110000`的值为字符串`accaefffdd`的奇偶性表示。显然,这不是一个符合要求的字符串
38 |
39 | **分析第一种情况**
40 |
41 | 但如果可以在`accaefffdd`的所有以`a`开头的子串中找到一个奇偶性为`0000110000`的子串`x`,那么显然字符串`accaefffdd`去除`x`后剩下的子串肯定符合要求
42 |
43 | 从「异或」的角度分析,`0000110000 ^ 0000110000 = 0`,显然剩下的子串中字母出现的次数均为偶数
44 |
45 | 从具体的例子分析,`accaef`的奇偶性表示为`0000110000`,和原字符串相同,所以去除`accaef`后剩下的字符串为`ffdd`,显然符合要求
46 |
47 | 上面分析的都是第一种情况,即:子串所有字母出现的次数全都是偶数。我们的目标统计奇偶性完全相同的数量
48 |
49 | **分析第二种情况**
50 |
51 | 下面分析第二种情况,即:子串只有一个字母出现的次数是奇数,其实也差不多,只需找出只有一位不同的奇偶性数量即可
52 |
53 | 从具体的例子分析,`accae`的奇偶性表示为`0000010000`,和原字符串只有一位不同,所以去除`accae`后剩下的字符串为`fffdd`,显然符合第二种情况
54 |
55 | **处理技巧**
56 |
57 | 最后还有一个处理的技巧,由于 10 位即可表示出所有的情况,所以可以用一个大小为 1024 的数组来统计每种情况的数量
58 |
59 | **具体代码**
60 |
61 | ```java
62 | public long wonderfulSubstrings(String word) {
63 | // 统计每种情况的个数
64 | int[] cnt = new int[1024];
65 | // 全 0 的情况
66 | cnt[0] = 1;
67 | // 记录字符串的奇偶性
68 | int sum = 0;
69 | long ans = 0L;
70 | for (int i = 0; i < word.length(); i++) {
71 | // 更新奇偶性
72 | sum ^= 1 << ((int) word.charAt(i) - 'a');
73 | // 累加第一种情况的数量
74 | ans += cnt[sum];
75 | // 累加第二种情况的数量
76 | for (int j = 1; j < 1024; j <<= 1) {
77 | ans += cnt[sum ^ j];
78 | }
79 | // 更新数量
80 | cnt[sum]++;
81 | }
82 | return ans;
83 | }
84 | ```
85 |
86 | ### 找出最长的超赞子字符串
87 |
88 | **题目详情可见 [找出最长的超赞子字符串](https://leetcode.cn/problems/find-longest-awesome-substring/)**
89 |
90 | 这个题目其实和上一个题目相似度有 90%
91 |
92 | 首先一个字符串需要可以变成回文子串,回文子串有两种情况:
93 |
94 | - 偶数情况:`aabb`
95 | - 奇数情况:`aabcc`
96 |
97 | 所以刚好对应上题的两种情况
98 |
99 | 不同的在于,本题需要统计的不是每种情况出现的数量,而是每种情况最先出现的下标
100 |
101 | 为什么是最先出现的下标呢?因为需要计算**最长**的超赞子字符串的长度
102 |
103 | ```java
104 | public int longestAwesome(String s) {
105 | // 统计每种情况最先出现的下标
106 | int[] cnt = new int[1024];
107 | // 初始位 -2
108 | Arrays.fill(cnt, -2);
109 | // 原因:aa 的奇偶性表示为 0,当前下标为 1,所以长度为 1 - cnt[0] = 1 - (-1) = 2
110 | cnt[0] = -1;
111 | int sum = 0, ans = -1;
112 | for (int i = 0; i < s.length(); i++) {
113 | sum ^= 1 << ((int) s.charAt(i) - '0');
114 | // 已经出现该情况,且为偶数
115 | if (cnt[sum] != -2) ans = Math.max(ans, i - cnt[sum]);
116 | // 已经出现该情况,且为奇数
117 | for (int j = 1; j < 1024; j <<= 1) {
118 | if (cnt[sum ^ j] != -2) ans = Math.max(ans, i - cnt[sum ^ j]);
119 | }
120 | // 记录首次出现下标
121 | if (cnt[sum] == -2) cnt[sum] = i;
122 | }
123 | return ans;
124 | }
125 | ```
--------------------------------------------------------------------------------
/markdown/Algorithm/前缀和之异或篇.md:
--------------------------------------------------------------------------------
1 | # 前缀和之异或篇
2 |
3 | [1310. 子数组异或查询](https://leetcode.cn/problems/xor-queries-of-a-subarray/)
4 |
5 | [1371. 每个元音包含偶数次的最长子字符串](https://leetcode.cn/problems/find-the-longest-substring-containing-vowels-in-even-counts/)
6 |
7 |
8 |
9 | 今天遇到了两个「前缀和」结合「异或」的题目,感觉很有意思,特意来总结一波!**关于前缀和详细介绍可见 [前缀和数组](./前缀和数组.html)**
10 |
11 |
12 |
13 | 对于「+ -」操作来说,是一对逆运算,比如:`n + 3 - 3 = n`
14 |
15 | 而对于「异或」操作来说,自身就是一种逆运算,任何两个相同的数的异或结果为 0,所以有:`n ^ 3 ^ 3 = n`
16 |
17 | 至于为什么有这种特性,可以模拟一下「异或」运算的过程就懂了
18 |
19 | 来看一个样例:`[1,2,3,4,5]`
20 |
21 | - 其中`sum(1,5) = 1 + 2 + 3 + 4 + 5 = 15`,`sum(1,2) = 1 + 2 = 3`,`sum(3,5) = 3 + 4 + 5 = 12`
22 | - 其中`XOR(1,5) = 1 ^ 2 ^ 3 ^ 4 ^ 5 = 1`,`XOR(1,2) = 1 ^ 2 = 3`,`XOR(3,5) = 3 ^ 4 ^ 5 = 2`
23 |
24 | 所以:`sum(1,2) + sum(3,5) = sum(1,5)` -> `sum(3,5) = sum(1,5) - sum(1,2)`
25 |
26 | 同理:`sum(1,2) ^ sum(3,5) = sum(1,5)` -> `sum(3,5) = sum(1,5) ^ sum(1,2)`
27 |
28 | 有了这样一个简单的推导,下面直接上题目
29 |
30 | ### 子数组异或查询
31 |
32 | **题目详情可见 [子数组异或查询](https://leetcode.cn/problems/xor-queries-of-a-subarray/)**
33 |
34 | 这个题目就是个模版题,直接把「和」换成「异或」即可
35 |
36 | ```java
37 | public int[] xorQueries(int[] arr, int[][] queries) {
38 | int[] preSum = new int[arr.length + 1];
39 | for (int i = 1; i < preSum.length; i++) preSum[i] = preSum[i - 1] ^ arr[i - 1];
40 | int[] ans = new int[queries.length];
41 | for (int i = 0; i < queries.length; i++) {
42 | int[] query = queries[i];
43 | ans[i] = preSum[query[1] + 1] ^ preSum[query[0]];
44 | }
45 | return ans;
46 | }
47 | ```
48 |
49 |
50 | ### 每个元音包含偶数次的最长子字符串
51 |
52 | **题目详情可见 [每个元音包含偶数次的最长子字符串](https://leetcode.cn/problems/find-the-longest-substring-containing-vowels-in-even-counts/)**
53 |
54 | 我们把五个元音字母看作是五个特殊标记
55 |
56 | 如果一个子数组里面包含偶数个相同的元音字母,那么这个子数组中所有元音字母的异或结果肯定是 0,因为相同的元素异或为 0。例:`'a' ^ 'a' = 0`
57 |
58 | 所以我们只计算含有元音字母的前缀和,非元音字母的位置直接继承前一个结果,具体实现可见代码
59 |
60 | ```java
61 | public int findTheLongestSubstring(String s) {
62 | List vowel = Arrays.asList('a', 'e', 'i', 'o', 'u');
63 | int[] preSum = new int[s.length() + 1];
64 | for (int i = 1; i < preSum.length; i++) {
65 | if (vowel.contains(s.charAt(i - 1))) {
66 | // 如果是元音,就做「异或」操作
67 | preSum[i] = preSum[i - 1] ^ (int) s.charAt(i - 1);
68 | // 如果不是元音,直接继承前一个结果
69 | } else preSum[i] = preSum[i - 1];
70 | }
71 | int ans = 0;
72 | // 结尾从最后一个元素开始搜索 [......i]
73 | for (int i = s.length() - 1; i >= 0; i--) {
74 | // 开头从第一个元素开始搜索 [j......]
75 | // 注意:一定要 j <= i,因为存在 "d" 这样的情况
76 | for (int j = 0; j <= i; j++) {
77 | // 如果找到含有偶数个元音的子数组,直接开始上一个元素结尾的搜索
78 | // 以 i 为结尾的子数组不可能有更长满足条件的情况
79 | if ((preSum[i + 1] ^ preSum[j]) == 0) {
80 | ans = Math.max(ans, i - j + 1);
81 | break;
82 | }
83 | }
84 | }
85 | return ans;
86 | }
87 | ```
88 |
--------------------------------------------------------------------------------
/markdown/Algorithm/前缀和之等价条件.md:
--------------------------------------------------------------------------------
1 | # 前缀和之等价条件
2 |
3 | [2364. 统计坏数对的数目](https://leetcode.cn/problems/count-number-of-bad-pairs/)
4 |
5 | [4507. 子数组异或和](https://www.acwing.com/problem/content/description/4510/)
6 |
7 |
8 |
9 | 本篇文章来总结一下前缀和的变体,其实就是一丢丢的小技巧!!
10 |
11 | ### 统计坏数对的数目
12 |
13 | **题目详情可见 [统计坏数对的数目](https://leetcode.cn/problems/count-number-of-bad-pairs/)**
14 |
15 | 这是某一次周赛的一道题目,虽然题目不难,但之所以在这里单独拿出来,是为了引出一个小技巧!!
16 |
17 | 这个题目的关键条件:`i < j` 且 `j - i != nums[j] - nums[i]`
18 |
19 | 如果第一眼没反应过来,估计直接就双重循环了
20 |
21 | 但是如果稍微把条件改变一波:`i < j`且`nums[i] - i != nums[j] - j`,然后把`nums[i] - i`看作一个整体,借助`HashMap`,直接一重循环就可以了
22 |
23 | 下面直接给出代码:
24 |
25 | ```java
26 | public long countBadPairs(int[] nums) {
27 | long ans = 0;
28 | Map map = new HashMap<>();
29 | for (int i = 0; i < nums.length; i++) {
30 | int target = nums[i] - i;
31 | int cnt = map.getOrDefault(target, 0);
32 | map.put(target, cnt + 1);
33 | // cnt 是相等的数量,i - cnt 是不等的数量
34 | ans += i - cnt;
35 | }
36 | return ans;
37 | }
38 | ```
39 |
40 | 虽然这个题目没有用到前缀和,但是确为我们揭示了一个小技巧:**利用交换律,使之变成等价条件,利于求解**
41 |
42 | ### 子数组异或和
43 |
44 | **题目详情可见 [子数组异或和](https://www.acwing.com/problem/content/description/4510/)**
45 |
46 | **关于「前缀和数组」的详细介绍可见 [前缀和数组](./前缀和数组.html)**、**关于「前缀和之异或篇」的详细介绍可见 [前缀和之异或篇](./前缀和之异或篇.html)**,建议先看完这两篇文章,否则可能会存在不好理解的地方!!
47 |
48 | 这个题目的关键条件:`sum[i] ^ sum[i - m] = sum[i - m] ^ sum[i - 2m]`
49 |
50 | 同样的,如果第一眼没反应过来,估计直接就双重循环,然后超时!!
51 |
52 | 但是如果两边同时异或一个`sum[i - m]`,那么条件就变成了`sum[i] = sum[i - 2m]`,然后再借助`HashMap`即可!
53 |
54 | 这里还有另外一个条件:连续子数组的长度为偶数。怎么才能保证在`HashMap`中找到的结果满足该条件呢?
55 |
56 | 如果`i`为偶数,那么`i - 2m`为偶数;如果`i`为奇数,那么`i - 2m`为奇数,所以只需要用两个`HashMap`分别存奇偶数即可!
57 |
58 | 下面直接给出代码:
59 |
60 | ```java
61 | public long xorSum(int[] nums, int n) {
62 | long ans = 0;
63 | // map1 存放奇数;map2 存放偶数
64 | Map map1 = new HashMap<>();
65 | Map map2 = new HashMap<>();
66 | int[] preSum = new int[n + 1];
67 | for (int i = 1; i <= n; i++) preSum[i] = preSum[i - 1] ^ nums[i - 1];
68 | map2.put(0, 1);
69 | for (int i = 1; i <= n; i++) {
70 | if (i % 2 == 0) {
71 | int cnt = map2.getOrDefault(preSum[i], 0);
72 | ans += cnt;
73 | map2.put(preSum[i], cnt + 1);
74 | } else {
75 | int cnt = map1.getOrDefault(preSum[i], 0);
76 | ans += cnt;
77 | map1.put(preSum[i], cnt + 1);
78 | }
79 | }
80 | return ans;
81 | }
82 | ```
83 |
--------------------------------------------------------------------------------
/markdown/Algorithm/前缀和数组.md:
--------------------------------------------------------------------------------
1 | # 前缀和数组
2 |
3 | [303. 区域和检索 - 数组不可变](https://leetcode.cn/problems/range-sum-query-immutable/)
4 |
5 | [304. 二维区域和检索 - 矩阵不可变](https://leetcode.cn/problems/range-sum-query-2d-immutable/)
6 |
7 | [560. 和为 K 的子数组](https://leetcode.cn/problems/subarray-sum-equals-k/)
8 |
9 |
10 |
11 | 如果要得到「区间和」,能想到最简单的方法就是遍历所求区间,循环相加即可。如果这种需求有很多,此时,时间复杂度为 $O(n^2)$
12 |
13 | 基于上面描述的场景,我们完全可以使用「前缀和」优化,前缀和数组中每个元素的值为区间`[0..i]`的元素和
14 |
15 | **注意:**前缀和适用于**不变数组**;对于变化的数组,可以使用「线段树」,**关于线段树的详细介绍可见 [线段树详解](./线段树详解.html)**
16 |
17 | ### 区域和检索 - 数组不可变
18 |
19 | **题目详情可见 [区域和检索 - 数组不可变](https://leetcode-cn.com/problems/range-sum-query-immutable/)**
20 |
21 | **建议:**`preSum[]`整体向后偏移一位,简便处理
22 |
23 | 
24 |
25 | 如果求区间`[2,4]`的和,只需计算`preSum[4 + 1] - preSum[2]`即可
26 |
27 | 下面给出详细代码:
28 |
29 | ```java
30 | class NumArray {
31 | // 记录前缀和的数组
32 | private int[] preSum;
33 | public NumArray(int[] nums) {
34 | // preSum 从 1 开始,避免越界问题
35 | preSum = new int[nums.length + 1];
36 | for (int i = 1; i < preSum.length; i++) {
37 | preSum[i] = preSum[i - 1] + nums[i - 1];
38 | }
39 | }
40 | public int sumRange(int left, int right) {
41 | return preSum[right + 1] - preSum[left];
42 | }
43 | }
44 | ```
45 |
46 | ### 二维区域和检索 - 矩阵不可变
47 |
48 | **题目详情可见 [二维区域和检索 - 矩阵不可变](https://leetcode-cn.com/problems/range-sum-query-2d-immutable/)**
49 |
50 | 
51 |
52 | 如果求红色区间的和,只需求`preSum[4,4] - preSum[1,4] - preSum[4,1] + preSum[1,1]`即可
53 |
54 | - `preSum[4,4]`:黄 + 蓝 + 绿 + 红
55 |
56 | - `preSum[1,4]`:黄 + 蓝
57 |
58 | - `preSum[4,1]`:黄 + 绿
59 |
60 | - `preSum[1,1]`:黄
61 |
62 | 下面给出详细代码:
63 |
64 | ```java
65 | class NumMatrix {
66 | private int[][] preSum;
67 | public NumMatrix(int[][] matrix) {
68 | int m = matrix.length;
69 | int n = matrix[0].length;
70 | preSum = new int[m + 1][n + 1];
71 | for (int i = 1; i < m + 1; i++) {
72 | for (int j = 1; j < n + 1; j++) {
73 | preSum[i][j] = preSum[i - 1][j] + preSum[i][j - 1] - preSum[i - 1][j - 1] + matrix[i - 1][j - 1];
74 | }
75 | }
76 | }
77 | public int sumRegion(int row1, int col1, int row2, int col2) {
78 | return preSum[row2 + 1][col2 + 1] - preSum[row1][col2 + 1] - preSum[row2 + 1][col1] + preSum[row1][col1];
79 | }
80 | }
81 | ```
82 |
83 | ### 和为 K 的子数组
84 |
85 | **题目详情可见 [和为 K 的子数组](https://leetcode-cn.com/problems/subarray-sum-equals-k/)**
86 |
87 | 借鉴「两数和」的思路,利用`HashMap`。下面给出详细代码:
88 |
89 | ```java
90 | public int subarraySum(int[] nums, int k) {
91 |
92 | Map preSum = new HashMap<>();
93 | preSum.put(0, 1);
94 |
95 | int sum = 0;
96 | int res = 0;
97 | for (int i = 0; i < nums.length; i++) {
98 | sum += nums[i];
99 | int target = sum - k;
100 | if (preSum.containsKey(target)) res += preSum.get(target);
101 | preSum.put(sum, preSum.getOrDefault(sum, 0) + 1);
102 | }
103 | return res;
104 | }
105 | ```
--------------------------------------------------------------------------------
/markdown/Algorithm/单调队列.md:
--------------------------------------------------------------------------------
1 | # 单调队列
2 |
3 | [239. 滑动窗口最大值](https://leetcode-cn.com/problems/sliding-window-maximum/)
4 |
5 |
6 |
7 | 存在一种这样的场景:快速得到 n 个元素中的最大值,而且这 n 个元素还在不断的变化中!
8 |
9 | **题目详情可见 [滑动窗口最大值](https://leetcode-cn.com/problems/sliding-window-maximum/)**
10 |
11 | ### 数据结构实现
12 |
13 | 基于上述的场景,我们构造出了一种新的数据结构:**单调队列**
14 |
15 | 每次把新元素都从队尾插入,而队头的元素永远的最大的。如果要删除某一个元素时,我们判断是否为队头元素,如果不是,则不删;否则删除队头元素
16 |
17 | 该数据结构的具体方法如下:
18 |
19 | ```java
20 | public class MonotonicQueue {
21 | // 双链表,支持头部和尾部增删元素
22 | private final LinkedList q = new LinkedList<>();
23 | // 在队尾添加元素 n
24 | public void push(int n);
25 | // 队头元素如果是 n,删除它
26 | public void pop(int n);
27 | // 返回当前队列中最大值
28 | public int max();
29 | }
30 | ```
31 |
32 | 如下图所示。每当我们调用`push(n)`时,对于元素 3, 2, 1 将会被删掉,元素 4 接到 元素 5 的后面
33 |
34 |
8 |
9 | 下面和 Kruskal 算法一样,解释以下三个问题,可与 Kruskal 算法对比观看
10 |
11 | - **问题一:**如何判断一个图是否为原图的生成子图
12 | - **问题二:**如何判断生成子图是一棵树
13 | - **问题三:**如何获得最小生成树
14 |
15 | **问题一:利用`inMST[]`数组来判断所有节点是否已在生成树中,详细实现可见`allConnected()`方法**
16 |
17 | **问题二:利用`inMST[]`数组来记录已加入生成树中的节点,以保证无环**
18 |
19 | **问题三:利用优先队列按照边的权重从小到大排序,可保证最终的生成子树为最小生成子树**
20 |
21 |
22 |
23 | **算法模版**
24 |
25 | ```java
26 | public class Prim {
27 | // 存在横切边的数据结构
28 | private final Queue pq;
29 | // 记录已经成为最小生成树的节点
30 | private boolean[] inMST;
31 | // 记录最小生成树的权重和
32 | private Integer weightSum = 0;
33 | // graph 是用邻接表表示的一幅图
34 | // graph[s] 记录节点 s 所有相邻的边
35 | // 三元组 int[]{from, to, weight} 表示一条边
36 | private final List[] graph;
37 |
38 | public Prim(List[] graph) {
39 | this.graph = graph;
40 | // 按照边的权重从小到大排序
41 | this.pq = new PriorityQueue<>(Comparator.comparingInt(a -> a[2]));
42 | // 图中有 n 个节点
43 | int n = graph.length;
44 | this.inMST = new boolean[n];
45 | // 随便从一个点开始切分都可以,我们不妨从节点 0 开始
46 | inMST[0] = true;
47 | cut(0);
48 | // 不断进行切分,向最小生成树中添加边
49 | while (!pq.isEmpty()) {
50 | int[] edge = pq.poll();
51 | int to = edge[1];
52 | int weight = edge[2];
53 | if (inMST[to]) {
54 | // 节点 to 已经在最小生成树中,跳过
55 | // 否则这条边会产生环
56 | continue;
57 | }
58 | // 将边 edge 加入最小生成树
59 | weightSum += weight;
60 | inMST[to] = true;
61 | // 节点 to 加入后,进行新一轮切分,会产生更多横切边
62 | cut(to);
63 | }
64 | }
65 | // 将 s 的横切边加入优先队列
66 | private void cut(int x) {
67 | // 遍历 s 的邻边
68 | for (int[] edge : graph[x]) {
69 | int to = edge[1];
70 | if (inMST[to]) {
71 | // 相邻接点 to 已经在最小生成树中,跳过
72 | // 否则这条边会产生环
73 | continue;
74 | }
75 | // 加入横切边队列
76 | pq.offer(edge);
77 | }
78 | }
79 | // 最小生成树的权重和
80 | public int weightSum() {
81 | return this.weightSum;
82 | }
83 | // 判断最小生成树是否包含图中的所有节点
84 | public boolean allConnected() {
85 | for (int i = 0; i < graph.length; i++) {
86 | if (!inMST[i]) {
87 | return false;
88 | }
89 | }
90 | return true;
91 | }
92 | }
93 | ```
94 |
95 |
--------------------------------------------------------------------------------
/markdown/Algorithm/x的平方根-变题.md:
--------------------------------------------------------------------------------
1 | # x 的平方根「变题」
2 |
3 | [69. x 的平方根](https://leetcode.cn/problems/sqrtx/)
4 |
5 |
6 |
7 | ```java
8 | public int mySqrt(int x) {
9 | int l = 0, r = x;
10 | while (l < r) {
11 | int m = l + r + 1 >> 1;
12 | if (x / m >= m) l = m;
13 | else r = m - 1;
14 | }
15 | return l;
16 | }
17 | ```
18 |
19 | ### 变题一:保留小数位
20 |
21 | ```java
22 | // epsilon 保留小数位 -> 1e-7
23 | public double mySqrt(double x, double epsilon){
24 | double l = 0, r = x;
25 | if (x == 0 || x == 1){
26 | return x;
27 | }
28 | while (l < r){
29 | double mid = l - (l - r) / 2;
30 | if (Math.abs(mid * mid - x) < epsilon){
31 | return mid;
32 | } else if (mid * mid < x){
33 | l = mid;
34 | } else {
35 | r = mid;
36 | }
37 | }
38 | return l;
39 | }
40 | ```
41 |
42 |
--------------------------------------------------------------------------------
/markdown/Algorithm/二分图.md:
--------------------------------------------------------------------------------
1 | # 二分图
2 |
3 | 具体定义见[传送门](../other/图论.html)
4 |
5 | 利用染色的思路去解题
6 |
7 | ## [785. 判断二分图](https://leetcode-cn.com/problems/is-graph-bipartite/)
8 |
9 | ```java
10 | // dfs
11 | private boolean ok = true;
12 | public boolean isBipartite(int[][] graph) {
13 | int n = graph.length;
14 | // visited[i] = 0 : 未染色 ; 1 : red ; -1 : blue
15 | int[] visited = new int[n];
16 | for (int i = 0; i < n; i++) {
17 | if (visited[i] == 0) {
18 | dfs(graph, visited, i, 1);
19 | }
20 | }
21 | return ok;
22 | }
23 | private void dfs(int[][] graph, int[] visited, int v, int color) {
24 | if (!ok) return ;
25 | visited[v] = color;
26 | for (int i : graph[v]) {
27 | // 未染色
28 | if (visited[i] == 0) {
29 | dfs(graph, visited, i, (-1) * color);
30 | } else {
31 | if (visited[i] == visited[v]) {
32 | ok = false;
33 | }
34 | }
35 | }
36 | }
37 |
38 | // bfs
39 | private boolean ok = true;
40 | public boolean isBipartite(int[][] graph) {
41 | int n = graph.length;
42 | // visited[i] = 0 : 未染色 ; 1 : red ; -1 : blue
43 | int[] visited = new int[n];
44 | for (int i = 0; i < n; i++) {
45 | if (visited[i] == 0) {
46 | bfs(graph, visited, i);
47 | }
48 | }
49 | return ok;
50 | }
51 | private void bfs(int[][] graph, int[] visited, int start) {
52 | Queue queue = new LinkedList<>();
53 | queue.add(start);
54 | visited[start] = 1;
55 | while (!queue.isEmpty() && ok) {
56 | int v = queue.poll();
57 | for (int i : graph[v]) {
58 | if (visited[i] == 0) {
59 | visited[i] = visited[v] * (-1);
60 | queue.offer(i);
61 | } else {
62 | if (visited[i] == visited[v]) {
63 | ok = false;
64 | }
65 | }
66 | }
67 | }
68 | }
69 | ```
70 |
71 | ## [886. 可能的二分法](https://leetcode-cn.com/problems/possible-bipartition/)
72 |
73 | ```java
74 | private boolean ok = true;
75 | public boolean possibleBipartition(int n, int[][] dislikes) {
76 | List[] graph = buildGraph(n, dislikes);
77 | int[] visited = new int[n + 1];
78 | for (int i = 1; i <= n; i++) {
79 | if (visited[i] == 0) dfs(graph, visited, i, 1);
80 | }
81 | return ok;
82 | }
83 | private List[] buildGraph(int n, int[][] dislikes) {
84 | List[] graph = new ArrayList[n + 1];
85 | for (int i = 1; i <= n; i++) {
86 | graph[i] = new ArrayList();
87 | }
88 | int m = dislikes.length;
89 | for (int i = 0; i < m; i++) {
90 | graph[dislikes[i][0]].add(dislikes[i][1]);
91 | graph[dislikes[i][1]].add(dislikes[i][0]);
92 | }
93 | return graph;
94 | }
95 | private void dfs(List[] graph, int[] visited, int p, int color) {
96 | if (!ok) return ;
97 | visited[p] = color;
98 | for(int i : graph[p]) {
99 | if (visited[i] == 0) {
100 | dfs(graph, visited, i, color * (-1));
101 | } else {
102 | if (visited[i] == visited[p]) ok = false;
103 | }
104 | }
105 | }
106 | ```
107 |
108 |
--------------------------------------------------------------------------------
/markdown/Algorithm/二分搜索.md:
--------------------------------------------------------------------------------
1 | # 二分搜索
2 |
3 |
4 |
5 | [704. 二分查找](https://leetcode-cn.com/problems/binary-search/)
6 |
7 | [34. 在排序数组中查找元素的第一个和最后一个位置](https://leetcode-cn.com/problems/find-first-and-last-position-of-element-in-sorted-array/)
8 |
9 | ### 基础版二分搜索
10 |
11 | 相信大家对「二分搜索」都不陌生,比较高效的一个搜索策略。前提是,搜索的数组必须是有序的!!!
12 |
13 | 但是这个算法的麻烦之处在于「对边界的判断」。先看一个最基础的二分搜索模版
14 |
15 | ```java
16 | public int search(int[] nums, int target) {
17 | int lo = 0;
18 | int hi = nums.length - 1;
19 | while (lo <= hi) {
20 | int mid = lo - (lo - hi) / 2;
21 | if (nums[mid] == target) return mid;
22 | else if (nums[mid] < target) lo = mid + 1;
23 | else if (nums[mid] > target) hi = mid - 1;
24 | }
25 | return -1;
26 | }
27 | ```
28 |
29 | 这里面有几个需要注意的点:
30 |
31 | - 搜索区间:全闭区间`[lo, hi]`
32 | - 结束条件:`lo = hi + 1`
33 | - 当每次收缩区间时,`lo`和`hi`都是不包括`mid`的。**原因:既然区间是全闭,所以收缩时,`num[mid]`不符合条件**
34 |
35 | ### 进阶版:寻找最左相等元素
36 |
37 | 下面有一个进阶版的二分搜索:寻找最左或最右的相等元素,如果不存在,返回 -1。**详情可见题目 [在排序数组中查找元素的第一个和最后一个位置](https://leetcode-cn.com/problems/find-first-and-last-position-of-element-in-sorted-array/)**
38 |
39 | 先给出模版,然后再进一步解释。先介绍寻找最左相等元素
40 |
41 | ```java
42 | private int leftBound(int[] nums, int target) {
43 | int lo = 0, hi = nums.length - 1;
44 | while (lo <= hi) {
45 | int mid = lo - (lo - hi) / 2;
46 | // 向左收缩
47 | if (nums[mid] == target) hi = mid - 1;
48 | else if (nums[mid] < target) lo = mid + 1;
49 | else if (nums[mid] > target) hi = mid - 1;
50 | }
51 | // 结束情况 : lo = hi + 1
52 | // 未找到的情况
53 | if (lo == nums.length || nums[lo] != target) return -1;
54 | return lo;
55 | }
56 | ```
57 |
58 | 和常规版的二分搜索不同之处:
59 |
60 | - 寻找到相等元素,不是立刻返回,而是向左收缩区间
61 |
62 | - 对于未找到元素的情况:(1) 可能比所有元素大;(2) 可能比所有元素小
63 | - 当比所有元素大时,区间会收缩到`[hi + 1, hi]`,例:`[5, 4]`,其中`num.length = 5`
64 | - 当比所有元素小时,区间会收缩到`[lo, lo - 1]`,例:`[0, -1]`
65 |
66 | - 对于第一种情况,我们通过`lo == nums.length`判断;对于第二种情况,我们通过`nums[lo] != target`判断
67 |
68 | - 注意:必须第一种情况的判断写在前面,不然可能会出现越界
69 |
70 | **为什么对于找到元素的情况,最后返回`lo`就是正确下标呢????**
71 |
72 | **原因:**首先,结束循环的条件为`lo = hi + 1`;如果找到了相等元素,此时循环内的`mid`就是正确下标;而由于收缩,`hi = mid - 1`,刚好比正确下标少 1。所以`lo`刚好是正确下标
73 |
74 | ### 进阶版:寻找最右相等元素
75 |
76 | 下面介绍寻找最右相等元素的情况,其实和最左相似度很高
77 |
78 | ```java
79 | private int rightBound(int[] nums, int target) {
80 | int lo = 0, hi = nums.length - 1;
81 | while (lo <= hi) {
82 | int mid = lo - (lo - hi) / 2;
83 | // 向右收缩
84 | if (nums[mid] == target) lo = mid + 1;
85 | else if (nums[mid] < target) lo = mid + 1;
86 | else if (nums[mid] > target) hi = mid - 1;
87 | }
88 | // 结束情况 : hi = lo - 1
89 | // 未找到的情况
90 | if (hi < 0 || nums[hi] != target) return -1;
91 | return hi;
92 | }
93 | ```
94 |
95 | - 对于未找到元素的情况:(1) 可能比所有元素大;(2) 可能比所有元素小
96 | - 当比所有元素大时,区间会收缩到`[hi + 1, hi]`,例:`[5, 4]`,其中`num.length = 5`
97 | - 当比所有元素小时,区间会收缩到`[lo, lo - 1]`,例:`[0, -1]`
98 |
99 | - 对于第二种情况,我们通过`hi < 0`判断;对于第一种情况,我们通过`nums[hi] != target`判断
100 |
101 | - 注意:必须第二种情况的判断写在前面,不然可能会出现越界
102 |
103 | **为什么对于找到元素的情况,最后返回`hi`就是正确下标呢????**
104 |
105 | **原因:**首先,结束循环的条件为`hi = lo - 1`;如果找到了相等元素,此时循环内的`mid`就是正确下标;而由于收缩,`lo = mid + 1`,刚好比正确下标多 1。所以`hi`刚好是正确下标
106 |
107 | ### 一个好问题
108 |
109 | 相信大家会有一个疑问,为什么「寻找最左相等元素」和「寻找最右相等元素」最后对于未找到的情况的判断方式有些区别呢???
110 |
111 | __前者通过`lo`来判断,后者通过`hi`来判断__
112 |
113 | 这就要回到上面每种情况最后提出的那个问题了。对于「寻找最左相等元素」,`lo` 是正确下标,我们需要通过正确下标判断是否找到了目标元素;同理「寻找最右相等元素」也一样
114 |
--------------------------------------------------------------------------------
/markdown/Algorithm/二叉树中的最大路径和-变题.md:
--------------------------------------------------------------------------------
1 | # 二叉树中的最大路径和「变题」
2 |
3 | [124. 二叉树中的最大路径和](https://leetcode.cn/problems/binary-tree-maximum-path-sum/)
4 |
5 |
6 |
7 | 开头先来一个小插曲,关于「二叉树路径」相关的总结可见 **[二叉树路径相关技巧](https://lfool.github.io/LFool-Notes/algorithm/二叉树路径相关技巧.html)**
8 |
9 | ```java
10 | private int ans = -1000;
11 | public int maxPathSum(TreeNode root) {
12 | f(root);
13 | return ans;
14 | }
15 | private int f(TreeNode root) {
16 | if (root == null) return 0;
17 | int l = f(root.left);
18 | int r = f(root.right);
19 | ans = Math.max(ans, Math.max(0, l) + Math.max(0, r) + root.val);
20 | return Math.max(0, Math.max(Math.max(0, l), Math.max(0, r))) + root.val;
21 | }
22 | ```
23 |
24 | ### 变题一:输出最大路径
25 |
26 | ```java
27 | class Solution {
28 | private int ans = -1000;
29 | private List path = new ArrayList<>();
30 | public int maxPathSum(TreeNode root) {
31 | f(root);
32 | System.out.println(path);
33 | return ans;
34 | }
35 | private Pair f(TreeNode root) {
36 | Pair cur = new Pair(0, new ArrayList<>());
37 | if (root == null) return cur;
38 | Pair l = f(root.left);
39 | Pair r = f(root.right);
40 | if (l.sum < 0) l = new Pair(0, new ArrayList<>());
41 | if (r.sum < 0) r = new Pair(0, new ArrayList<>());
42 | int sum = l.sum + r.sum + root.val;
43 | if (ans < sum) {
44 | ans = sum;
45 | path = new ArrayList<>();
46 | path.addAll(l.path);
47 | path.add(root.val);
48 | path.addAll(r.path);
49 | }
50 |
51 | if (l.sum > r.sum) {
52 | cur.sum = l.sum + root.val;
53 | cur.path.addAll(l.path);
54 | cur.path.add(root.val);
55 | } else {
56 | cur.sum = r.sum + root.val;
57 | cur.path.add(root.val);
58 | cur.path.addAll(r.path);
59 | }
60 |
61 | return cur;
62 | }
63 | }
64 | class Pair {
65 | int sum;
66 | List path;
67 | public Pair(int sum, List path) {
68 | this.sum = sum;
69 | this.path = path;
70 | }
71 | }
72 | ```
73 |
74 | ### 变题二:相邻字符不同的最长路径
75 |
76 | **题目详情可见 [相邻字符不同的最长路径](https://leetcode.cn/problems/longest-path-with-different-adjacent-characters/)**
77 |
78 | ```java
79 | private int ans = 1;
80 | private char[] s;
81 | private List[] tree;
82 | public int longestPath(int[] parent, String S) {
83 | s = S.toCharArray();
84 | tree = new ArrayList[parent.length];
85 | Arrays.setAll(tree, e -> new ArrayList<>());
86 | for (int i = 1; i < parent.length; i++) {
87 | tree[parent[i]].add(i);
88 | }
89 | f(0);
90 | return ans;
91 | }
92 | private int[] f(int v) {
93 | int c = s[v] - 'a';
94 | int[] res = new int[]{1, c};
95 | if (tree[v].size() == 0) return res;
96 | Queue q = new PriorityQueue<>((a, b) -> b[0] - a[0]);
97 | for (int next : tree[v]) {
98 | q.offer(f(next));
99 | }
100 | int sum = 1, cnt = 0;
101 | while (!q.isEmpty() && cnt < 2) {
102 | int[] cur = q.poll();
103 | if (cur[1] != c && cnt < 1) {
104 | res[0] += cur[0];
105 | sum += cur[0];
106 | cnt++;
107 | } else if (cur[1] != c && cnt < 2) {
108 | sum += cur[0];
109 | cnt++;
110 | }
111 | }
112 | ans = Math.max(ans, sum);
113 | return res;
114 | }
115 | ```
116 |
--------------------------------------------------------------------------------
/markdown/Algorithm/二叉树的中序遍历-变题.md:
--------------------------------------------------------------------------------
1 | # 二叉树的中序遍历「变题」
2 |
3 | [94. 二叉树的中序遍历](https://leetcode.cn/problems/binary-tree-inorder-traversal/)
4 |
5 |
6 |
7 | 开头先来一个小插曲,关于「二叉树遍历」相关的总结可见 **[二叉树遍历](https://lfool.github.io/LFool-Notes/algorithm/二叉树遍历.html)**
8 |
9 | ```java
10 | // 递归
11 | // 时间复杂度 : O(n)
12 | // 空间复杂度 : O(n) -> 递归栈
13 | private List ans = new ArrayList<>();
14 | public List inorderTraversal(TreeNode root) {
15 | traversal(root);
16 | return ans;
17 | }
18 | private void traversal(TreeNode root) {
19 | if (root == null) return ;
20 | traversal(root.left);
21 | ans.add(root.val);
22 | traversal(root.right);
23 | }
24 |
25 | // 非递归
26 | // 时间复杂度 : O(n)
27 | // 空间复杂度 : O(n) -> 辅助栈
28 | public List inorderTraversal(TreeNode root) {
29 | List ans = new ArrayList<>();
30 | Deque st = new ArrayDeque<>();
31 | while (!st.isEmpty() || root != null) {
32 | while (root != null) {
33 | st.push(root);
34 | root = root.left;
35 | }
36 | TreeNode top = st.poll();
37 | ans.add(top.val);
38 | root = top.right;
39 | }
40 | return ans;
41 | }
42 |
43 | // 莫里斯
44 | // 时间复杂度 : O(n)
45 | // 空间复杂度 : O(1)
46 | public List inorderTraversal(TreeNode root) {
47 | List ans = new ArrayList<>();
48 | while (root != null) {
49 | if (root.left != null) {
50 | TreeNode pre = root.left;
51 | while (pre.right != null) {
52 | pre = pre.right;
53 | }
54 | pre.right = root;
55 | TreeNode tmp = root;
56 | root = root.left;
57 | tmp.left = null;
58 | } else {
59 | ans.add(root.val);
60 | root = root.right;
61 | }
62 | }
63 | return ans;
64 | }
65 | ```
--------------------------------------------------------------------------------
/markdown/Algorithm/二叉树的最近公共祖先-变题.md:
--------------------------------------------------------------------------------
1 | # 二叉树的最近公共祖先「变题」
2 |
3 | [236. 二叉树的最近公共祖先](https://leetcode.cn/problems/lowest-common-ancestor-of-a-binary-tree/)
4 |
5 |
6 |
7 | 开头先来一个小插曲,关于「祖先」问题的总结可见 **[二叉树祖先问题](./二叉树祖先问题.html)**
8 |
9 | ```java
10 | // 方法一:递归
11 | public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
12 | if (root == null) return null;
13 | if (root == p || root == q) return root;
14 | TreeNode left = lowestCommonAncestor(root.left, p, q);
15 | TreeNode right = lowestCommonAncestor(root.right, p, q);
16 | if (left == null || right == null) return left == null ? right : left;
17 | return root;
18 | }
19 |
20 | // 方法二:记录父节点,然后找相交点 (同相交链表找交点的方法)
21 | private Map parent = new HashMap<>();
22 | public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
23 | getParent(root, null);
24 | TreeNode pp = p, qq = q;
25 | // 找交点的过程
26 | while (pp != qq) {
27 | if (pp == null) pp = q;
28 | else pp = parent.get(pp.val);
29 | if (qq == null) qq = p;
30 | else qq = parent.get(qq.val);
31 | }
32 | return pp;
33 | }
34 | // 记录每个节点的父节点
35 | private void getParent(TreeNode root, TreeNode p) {
36 | if (root == null) return ;
37 | parent.put(root.val, p);
38 | getParent(root.left, root);
39 | getParent(root.right, root);
40 | }
41 | ```
42 |
43 | ### 变题一:二叉搜索树的最近公共祖先
44 |
45 | **题目详情可见 [二叉搜索树的最近公共祖先](https://leetcode.cn/problems/lowest-common-ancestor-of-a-binary-search-tree/)**
46 |
47 | 相比于上面的题目来说更简单,因为二叉搜索树有序!!
48 |
49 | ```java
50 | public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
51 | if (p.val > q.val) return lowestCommonAncestor(root, q, p);
52 | if (root == null) return null;
53 | if (p.val <= root.val && root.val <= q.val) return root;
54 | if (q.val < root.val) return lowestCommonAncestor(root.left, p, q);
55 | else return lowestCommonAncestor(root.right, p, q);
56 | }
57 | ```
58 |
59 | ### 变题二:最深叶节点的最近公共祖先
60 |
61 | **题目详情可见 [最深叶节点的最近公共祖先](https://leetcode.cn/problems/lowest-common-ancestor-of-deepest-leaves/)**
62 |
63 | ```java
64 | private int[] height = new int[1010];
65 | public TreeNode lcaDeepestLeaves(TreeNode root) {
66 | getH(root);
67 | return f(root);
68 | }
69 | private TreeNode f(TreeNode root) {
70 | if (root == null) return null;
71 | if (root.left == null && root.right == null) return root;
72 | if (root.left == null) return f(root.right);
73 | if (root.right == null) return f(root.left);
74 | int lh = height[root.left.val];
75 | int rh = height[root.right.val];
76 | if (lh == rh) return root;
77 | else if (lh < rh) return f(root.right);
78 | else return f(root.left);
79 | }
80 | private int getH(TreeNode root) {
81 | if (root == null) return 0;
82 | height[root.val] = Math.max(getH(root.left), getH(root.right)) + 1;
83 | return height[root.val];
84 | }
85 | ```
86 |
87 | ### 变题三:N 叉树的最近公共祖先
88 |
89 | 建议使用开头给出的方法二,记录父节点!!递归分支太多,不好判断,但也是可以用递归滴!!
90 |
--------------------------------------------------------------------------------
/markdown/Algorithm/位运算技巧.md:
--------------------------------------------------------------------------------
1 | [toc]
2 |
3 | # 位运算技巧
4 |
5 | ## 有趣小技巧
6 |
7 | ### 大小写相互转换
8 |
9 | ```java
10 | // 转小写
11 | (char) ('a' | ' ') = 'a'
12 | (char) ('A' | ' ') = 'a'
13 |
14 | // 转大写
15 | (char) ('b' & '_') = 'B'
16 | (char) ('B' & '_') = 'B'
17 |
18 | // 大小写互转
19 | (char) ('d' ^ ' ') = 'D'
20 | (char) ('D' ^ ' ') = 'd'
21 | ```
22 |
23 | ### 判断两个数是否异号
24 |
25 | ```java
26 | int x = -1, y = 2;
27 | boolean f = ((x ^ y) < 0); // true
28 |
29 | int x = 3, y = 2;
30 | boolean f = ((x ^ y) < 0); // false
31 | ```
32 |
33 | ### 不用临时变量交换两个数
34 |
35 | ```java
36 | int a = 1, b = 2;
37 | a ^= b;
38 | b ^= a;
39 | a ^= b;
40 | // 现在 a = 2, b = 1
41 | ```
42 |
43 | ### 加减一
44 |
45 | ```java
46 | // 加一
47 | int n = 1;
48 | n = -~n;
49 | // 现在 n = 2
50 |
51 | // 减一
52 | int n = 2;
53 | n = ~-n;
54 | // 现在 n = 1
55 | ```
56 |
57 | ## 算法常用操作
58 |
59 | ### `n & (n - 1)`
60 |
61 | > 可以消除 n 的二进制中最后一位 1
62 |
63 | 例题:
64 |
65 | - **详情可见 [191. 位1的个数](https://leetcode-cn.com/problems/number-of-1-bits/)**
66 |
67 | - 判断一个数是不是 2 的指数(如果一个数是 2 的指数,那么该数的二进制中只会有一个 1)
68 |
69 | ### `a ^ a = 0` `a ^ 0 = a`
70 |
71 | **详情可见 [136. 只出现一次的数字](https://leetcode-cn.com/problems/single-number/)**
72 |
73 | ### 「任意位置」置 1 or 0
74 |
75 | **详情可见 [698. 划分为k个相等的子集](https://leetcode-cn.com/problems/partition-to-k-equal-sum-subsets/)**
76 |
77 | ```java
78 | // 注意:「<<」优先级大于「|=」「^=」
79 | // 将第 i 位标记为 1
80 | used |= 1 << i;
81 |
82 | // 将第 i 位标记为 0
83 | used ^= 1 << i;
84 | ```
85 |
86 | ### 判断某一位置是否为 1
87 |
88 | ```java
89 | ((used >> i) & 1) == 1
90 | ```
91 |
92 | ### 低位的 0 变成 1
93 |
94 | ```java
95 | n |= n + 1;
96 | ```
97 |
98 | ### 低位的 1 变成 0
99 |
100 | ```java
101 | n &= n - 1;
102 | ```
103 |
104 | ## 实战题目
105 |
106 | ### 二叉树中的伪回文路径
107 |
108 | **题目详情可见 [二叉树中的伪回文路径](https://leetcode-cn.com/problems/pseudo-palindromic-paths-in-a-binary-tree/)**
109 |
110 | 这是一道综合运用位运算的高级题目 哈哈哈哈哈 我感觉很值得总结一波
111 |
112 | 首先这个题目肯定是需要用遍历的方法去写,遍历出所有路径
113 |
114 | 其次是需要搞清楚怎么判断是否为一个伪回文路径
115 |
116 | - 出现次数为奇数的数字要么只有一个 要么没有
117 |
118 | ```java
119 | // 记录每条路径
120 | private int count = 0;
121 | // 记录结果
122 | private int res = 0;
123 | public int pseudoPalindromicPaths (TreeNode root) {
124 | traversal(root);
125 | return res;
126 | }
127 | private void traversal(TreeNode root) {
128 | if (root == null) return ;
129 | // 对于每一个节点的表示:2:10 3:100 4:1000,以此类推
130 | // 刚好可以用左移来表示:1 << root.val
131 | // 当一个数出现两次后,则 10 ^ 10 = 0,利用了异或操作的特性,刚好可以抵消出现偶数次数的情况
132 | count ^= (1 << root.val);
133 | if (root.left == null && root.right == null) {
134 | if ((count & (count - 1)) == 0) res++;
135 | }
136 | traversal(root.left);
137 | traversal(root.right);
138 | // 再进行一次异或,刚好可以抵消上面异或操作
139 | // 正好是后序遍历离开节点时的操作
140 | count ^= (1 << root.val);
141 | }
142 | ```
143 |
144 | ### 最小 XOR
145 |
146 | **题目详情可见 [最小 XOR](https://leetcode.cn/problems/minimize-xor/)**
147 |
148 | ```java
149 | public int minimizeXor(int num1, int num2) {
150 | int c1 = Integer.bitCount(num1);
151 | int c2 = Integer.bitCount(num2);
152 | // num1 低位的 0 变成 1
153 | for (; c1 < c2; c1++) num1 |= num1 + 1;
154 | // num2 低位的 1 变成 0
155 | for (; c2 < c1; c2++) num1 &= num1 - 1;
156 | return num1;
157 | }
158 | ```
--------------------------------------------------------------------------------
/markdown/Algorithm/全排列-变题.md:
--------------------------------------------------------------------------------
1 | # 全排列「变题」
2 |
3 | [46. 全排列](https://leetcode.cn/problems/permutations/)
4 |
5 |
6 |
7 | 开头先来一个小插曲,关于「排列」问题的总结可见 **[排列 / 组合 / 子集 问题](./排列-组合-子集问题.html)**
8 |
9 | ```java
10 | // 回溯
11 | // 时间复杂度 : O(n * n!) -> n! 为叶子结点数量,每到叶子结点时就会 copy 一次 List,时间为 O(n)
12 | // 空间复杂度 : O(n * n!) -> 回溯深度为 n,需要 O(n) 的栈空间;但存储答案的 List 需要 O(n * n!) 空间,两者取最大值
13 | private boolean[] used;
14 | private List track = new ArrayList<>();
15 | private List> ans = new ArrayList<>();
16 | public List> permute(int[] nums) {
17 | used = new boolean[nums.length];
18 | f(nums);
19 | return ans;
20 | }
21 | private void f(int[] nums) {
22 | if (track.size() == nums.length) {
23 | ans.add(new ArrayList<>(track));
24 | return ;
25 | }
26 | for (int i = 0; i < nums.length; i++) {
27 | if (used[i]) continue;
28 | used[i] = true;
29 | track.add(nums[i]);
30 | f(nums);
31 | track.remove(track.size() - 1);
32 | used[i] = false;
33 | }
34 | }
35 |
36 | // 迭代
37 | // 时间复杂度 : O(n * n!) -> n! 为叶子结点数量,每到叶子结点时就会 copy 一次 List,时间为 O(n)
38 | // 空间复杂度 : O(n * n!) -> 临时的 List 和存储答案的 List
39 | public List> permute(int[] nums) {
40 | List> ans = new LinkedList<>();
41 | List> temp = new LinkedList<>();
42 | ans.add(new LinkedList<>());
43 | for (int x : nums) {
44 | for (List list : ans) {
45 | // 分别在 List 的 [0...n] 处插入当前元素
46 | for (int i = 0; i <= list.size(); i++) {
47 | // copy
48 | List t = new LinkedList<>(list);
49 | // LinkedList 插入时不需要移动,但需要遍历查找到第 i 个位置
50 | t.add(i, x);
51 | temp.add(t);
52 | }
53 | }
54 | ans = new LinkedList<>(temp);
55 | temp = new LinkedList<>();
56 | }
57 | return ans;
58 | }
59 | ```
60 |
61 | ### 变题一:全排列 (有重复)
62 |
63 | **题目详情可见 [全排列 II](https://leetcode.cn/problems/permutations-ii/)**
64 |
65 | **字符串版本题目可见 [面试题 08.08. 有重复字符串的排列组合](https://leetcode.cn/problems/permutation-ii-lcci/)**
66 |
67 | ```java
68 | private boolean[] used;
69 | private List track = new ArrayList<>();
70 | private List> ans = new ArrayList<>();
71 | public List> permuteUnique(int[] nums) {
72 | int n = nums.length;
73 | used = new boolean[n];
74 | // 注意要排序
75 | Arrays.sort(nums);
76 | f(nums);
77 | return ans;
78 | }
79 | private void f(int[] nums) {
80 | if (track.size() == nums.length) {
81 | ans.add(new ArrayList<>(track));
82 | return ;
83 | }
84 | for (int i = 0; i < nums.length; i++) {
85 | if (used[i]) continue;
86 | if (i > 0 && nums[i] == nums[i - 1] && !used[i - 1]) continue;
87 | used[i] = true;
88 | track.add(nums[i]);
89 | f(nums);
90 | used[i] = false;
91 | track.remove(track.size() - 1);
92 | }
93 | }
94 | ```
95 |
--------------------------------------------------------------------------------
/markdown/Algorithm/判定完美矩形.md:
--------------------------------------------------------------------------------
1 | # 判定完美矩形
2 |
3 | [391. 完美矩形](https://leetcode.cn/problems/perfect-rectangle/)
4 |
5 | 本篇文章来总结一个比较有意思的题目!
6 |
7 | 我们需要从两个角度去判断
8 |
9 | 其一:求出左下角和右上角的顶点坐标,判断期望面积是否和实际面积相等。如果不相等,一定不是完美矩形;如果相等,也不一定是完美矩形
10 |
11 | 其二:根据最后有效顶点数,如果不等于 4,一定不是完美矩形;如果等于 4,也需要和一中求出的顶点匹配才满足完美矩阵
12 |
13 | ```java
14 | public boolean isRectangleCover(int[][] rectangles) {
15 | // 左下角和右上角的顶点坐标
16 | int minX = 100010, minY = 100010;
17 | int maxX = -100010, maxY = -100010;
18 | int actualArea = 0;
19 | Set set = new HashSet<>();
20 | for (int[] rect : rectangles) {
21 | int x = rect[0], y = rect[1], a = rect[2], b = rect[3];
22 | minX = Math.min(minX, x);
23 | minY = Math.min(minY, y);
24 | maxX = Math.max(maxX, a);
25 | maxY = Math.max(maxY, b);
26 | // 期望面积
27 | actualArea += (a - x) * (b - y);
28 | // 计算有效顶点数
29 | int[][] points = new int[][]{ {x, y}, {x , b}, {a, y}, {a, b} };
30 | for (int[] p : points) {
31 | String s = p[0] + "," + p[1];
32 | if (set.contains(s)) set.remove(s);
33 | else set.add(s);
34 | }
35 | }
36 | // 期望面积和实际面积不相等
37 | if (actualArea != (maxX - minX) * (maxY - minY)) return false;
38 | // 有效顶点数不等于 4
39 | if (set.size() != 4) return false;
40 | int[][] points = new int[][]{ {minX, minY}, {minX , maxY}, {maxX, minY}, {maxX, maxY} };
41 | for (int[] p : points) {
42 | String s = p[0] + "," + p[1];
43 | // 有效顶点和一中求出的顶点不匹配
44 | if (!set.contains(s)) return false;
45 | }
46 | return true;
47 | }
48 | ```
49 |
50 |
--------------------------------------------------------------------------------
/markdown/Algorithm/前缀后缀法.md:
--------------------------------------------------------------------------------
1 | # 前缀后缀法
2 |
3 | [剑指 Offer 66. 构建乘积数组](https://leetcode.cn/problems/gou-jian-cheng-ji-shu-zu-lcof/)
4 |
5 | [238. 除自身以外数组的乘积](https://leetcode.cn/problems/product-of-array-except-self/)
6 |
7 | [768. 最多能完成排序的块 II](https://leetcode.cn/problems/max-chunks-to-make-sorted-ii/)
8 |
9 | [6190. 找到所有好下标](https://leetcode.cn/problems/find-all-good-indices/)
10 |
11 |
12 |
13 | 该类型的题目最大的特点:
14 |
15 | - 判断一个数左右两边是否满足要求
16 | - 求一个数左右两边的乘积
17 |
18 | 整体思路:用两个数组,分别统计「从左到右」和「从右到左」的信息
19 |
20 | 直接看题吧!!
21 |
22 | ### 构建乘积数组
23 |
24 | **题目详情可见 [剑指 Offer 66. 构建乘积数组](https://leetcode.cn/problems/gou-jian-cheng-ji-shu-zu-lcof/)**
25 |
26 | 对于这个题目,用两个数组分别统计「从左到右」和「从右到左」的乘积
27 |
28 | 「从左到右」:`left[i]`表示`[0...i-1]`的乘积
29 |
30 | 「从右到左」:`right[i]`表示`[i+1...n-1]`的乘积
31 |
32 | ```java
33 | public int[] constructArr(int[] a) {
34 | int n = a.length;
35 | int[] left = new int[n];
36 | int[] right = new int[n];
37 | int product = 1;
38 | for (int i = 0; i < n; i++) {
39 | left[i] = product;
40 | product *= a[i];
41 | }
42 | product = 1;
43 | for (int i = n - 1; i >= 0; i--) {
44 | right[i] = product;
45 | product *= a[i];
46 | }
47 | int[] ans = new int[n];
48 | for (int i = 0; i < n; i++) {
49 | ans[i] = left[i] * right[i];
50 | }
51 | return ans;
52 | }
53 | ```
54 |
55 | ### 除自身以外数组的乘积
56 |
57 | **题目详情可见 [除自身以外数组的乘积](https://leetcode.cn/problems/product-of-array-except-self/)**
58 |
59 | 几乎和上一题一模一样!!
60 |
61 | ### 最多能完成排序的块 II
62 |
63 | **题目详情可见 [最多能完成排序的块 II](https://leetcode.cn/problems/max-chunks-to-make-sorted-ii/)**
64 |
65 | 用两个数组分别存前缀最大值和后缀最小值
66 |
67 | 如果`i`和`i + 1`之间可以分块,那么必有`prefMax[i] <= suffMin[i + 1]`
68 |
69 | ```java
70 | public int maxChunksToSorted(int[] arr) {
71 | int n = arr.length;
72 | int[] prefMax = new int[n];
73 | int[] suffMin = new int[n];
74 | prefMax[0] = arr[0];
75 | for (int i = 1; i < n; i++) prefMax[i] = Math.max(prefMax[i - 1], arr[i]);
76 | suffMin[n - 1] = arr[n - 1];
77 | for (int i = n - 2; i >= 0; i--) suffMin[i] = Math.min(suffMin[i + 1], arr[i]);
78 | int ans = 1;
79 | for (int i = 0; i < n - 1; i++) {
80 | if (prefMax[i] <= suffMin[i + 1]) ans++;
81 | }
82 | return ans;
83 | }
84 | ```
85 |
86 | ### 找到所有好下标
87 |
88 | **题目详情可见 [找到所有好下标](https://leetcode.cn/problems/find-all-good-indices/)**
89 |
90 | 对于这个题目,用两个数组分别统计「从左到右」和「从右到左」的最长非递增/非递减的子数组长度
91 |
92 | 「从左到右」:`left[i]`表示`[0...i-1]`中最长非递增的长度
93 |
94 | 「从右到左」:`right[i]`表示`[i+1...n-1]`的最长非递减的长度
95 |
96 | ```java
97 | public List goodIndices(int[] nums, int k) {
98 | int n = nums.length;
99 | int[] left = new int[n];
100 | int[] right = new int[n];
101 | int cnt = 0;
102 | for (int i = 0; i < n; i++) {
103 | left[i] = cnt;
104 | if (i > 0 && nums[i - 1] < nums[i]) cnt = 0;
105 | cnt++;
106 | }
107 | cnt = 0;
108 | for (int i = n - 1; i >= 0; i--) {
109 | right[i] = cnt;
110 | if (i < n - 1 && nums[i] > nums[i + 1]) cnt = 0;
111 | cnt++;
112 | }
113 | List ans = new ArrayList<>();
114 | for (int i = 0; i < n; i++) {
115 | if (left[i] >= k && right[i] >= k) ans.add(i);
116 | }
117 | return ans;
118 | }
119 | ```
--------------------------------------------------------------------------------
/markdown/Algorithm/前缀和之奇偶篇.md:
--------------------------------------------------------------------------------
1 | # 前缀和之奇偶篇
2 |
3 | [1915. 最美子字符串的数目](https://leetcode.cn/problems/number-of-wonderful-substrings/)
4 |
5 | [1542. 找出最长的超赞子字符串](https://leetcode.cn/problems/find-longest-awesome-substring/)
6 |
7 |
8 |
9 | 本篇文章总结两个关于「前缀和」结合「奇偶」,同时又包含「异或」的题目!!
10 |
11 | 关于「前缀和」以及「异或」的总结可见:
12 |
13 | - **[前缀和数组](./前缀和数组.html)**
14 | - **[前缀和之异或篇](./前缀和之异或篇.html)**
15 |
16 | ### 最美子字符串的数目
17 |
18 | **题目详情可见 [最美子字符串的数目](https://leetcode.cn/problems/number-of-wonderful-substrings/)**
19 |
20 | 题目要求计算出字符串中**至多一个**字母出现奇数次的所有子串数量,所以会有两种情况:
21 |
22 | - 子串所有字母出现的次数全都是偶数
23 | - 子串只有一个字母出现的次数是奇数
24 |
25 | 而且题目中还有一个额外的附加条件:字符串中的字符由前十个小写英文字母组成
26 |
27 | 由于只需要知道一个字母出现次数的奇偶性,而不需要知道一个字母到底出现了多少次
28 |
29 | 所以可以用一个长度为 10 位的数字表示某一个子串中各字母出现的奇偶次数,如果出现次数为偶数,则该位为 0,否则为 1
30 |
31 | 正好可以利用「异或」运算的特点,`0 ^ 1 = 1; 1 ^ 1 = 0`
32 |
33 | 上面描述的可能比较抽象,具体看图:
34 |
35 | 
36 |
37 | 最终可以得到二机制为`0000110000`的值为字符串`accaefffdd`的奇偶性表示。显然,这不是一个符合要求的字符串
38 |
39 | **分析第一种情况**
40 |
41 | 但如果可以在`accaefffdd`的所有以`a`开头的子串中找到一个奇偶性为`0000110000`的子串`x`,那么显然字符串`accaefffdd`去除`x`后剩下的子串肯定符合要求
42 |
43 | 从「异或」的角度分析,`0000110000 ^ 0000110000 = 0`,显然剩下的子串中字母出现的次数均为偶数
44 |
45 | 从具体的例子分析,`accaef`的奇偶性表示为`0000110000`,和原字符串相同,所以去除`accaef`后剩下的字符串为`ffdd`,显然符合要求
46 |
47 | 上面分析的都是第一种情况,即:子串所有字母出现的次数全都是偶数。我们的目标统计奇偶性完全相同的数量
48 |
49 | **分析第二种情况**
50 |
51 | 下面分析第二种情况,即:子串只有一个字母出现的次数是奇数,其实也差不多,只需找出只有一位不同的奇偶性数量即可
52 |
53 | 从具体的例子分析,`accae`的奇偶性表示为`0000010000`,和原字符串只有一位不同,所以去除`accae`后剩下的字符串为`fffdd`,显然符合第二种情况
54 |
55 | **处理技巧**
56 |
57 | 最后还有一个处理的技巧,由于 10 位即可表示出所有的情况,所以可以用一个大小为 1024 的数组来统计每种情况的数量
58 |
59 | **具体代码**
60 |
61 | ```java
62 | public long wonderfulSubstrings(String word) {
63 | // 统计每种情况的个数
64 | int[] cnt = new int[1024];
65 | // 全 0 的情况
66 | cnt[0] = 1;
67 | // 记录字符串的奇偶性
68 | int sum = 0;
69 | long ans = 0L;
70 | for (int i = 0; i < word.length(); i++) {
71 | // 更新奇偶性
72 | sum ^= 1 << ((int) word.charAt(i) - 'a');
73 | // 累加第一种情况的数量
74 | ans += cnt[sum];
75 | // 累加第二种情况的数量
76 | for (int j = 1; j < 1024; j <<= 1) {
77 | ans += cnt[sum ^ j];
78 | }
79 | // 更新数量
80 | cnt[sum]++;
81 | }
82 | return ans;
83 | }
84 | ```
85 |
86 | ### 找出最长的超赞子字符串
87 |
88 | **题目详情可见 [找出最长的超赞子字符串](https://leetcode.cn/problems/find-longest-awesome-substring/)**
89 |
90 | 这个题目其实和上一个题目相似度有 90%
91 |
92 | 首先一个字符串需要可以变成回文子串,回文子串有两种情况:
93 |
94 | - 偶数情况:`aabb`
95 | - 奇数情况:`aabcc`
96 |
97 | 所以刚好对应上题的两种情况
98 |
99 | 不同的在于,本题需要统计的不是每种情况出现的数量,而是每种情况最先出现的下标
100 |
101 | 为什么是最先出现的下标呢?因为需要计算**最长**的超赞子字符串的长度
102 |
103 | ```java
104 | public int longestAwesome(String s) {
105 | // 统计每种情况最先出现的下标
106 | int[] cnt = new int[1024];
107 | // 初始位 -2
108 | Arrays.fill(cnt, -2);
109 | // 原因:aa 的奇偶性表示为 0,当前下标为 1,所以长度为 1 - cnt[0] = 1 - (-1) = 2
110 | cnt[0] = -1;
111 | int sum = 0, ans = -1;
112 | for (int i = 0; i < s.length(); i++) {
113 | sum ^= 1 << ((int) s.charAt(i) - '0');
114 | // 已经出现该情况,且为偶数
115 | if (cnt[sum] != -2) ans = Math.max(ans, i - cnt[sum]);
116 | // 已经出现该情况,且为奇数
117 | for (int j = 1; j < 1024; j <<= 1) {
118 | if (cnt[sum ^ j] != -2) ans = Math.max(ans, i - cnt[sum ^ j]);
119 | }
120 | // 记录首次出现下标
121 | if (cnt[sum] == -2) cnt[sum] = i;
122 | }
123 | return ans;
124 | }
125 | ```
--------------------------------------------------------------------------------
/markdown/Algorithm/前缀和之异或篇.md:
--------------------------------------------------------------------------------
1 | # 前缀和之异或篇
2 |
3 | [1310. 子数组异或查询](https://leetcode.cn/problems/xor-queries-of-a-subarray/)
4 |
5 | [1371. 每个元音包含偶数次的最长子字符串](https://leetcode.cn/problems/find-the-longest-substring-containing-vowels-in-even-counts/)
6 |
7 |
8 |
9 | 今天遇到了两个「前缀和」结合「异或」的题目,感觉很有意思,特意来总结一波!**关于前缀和详细介绍可见 [前缀和数组](./前缀和数组.html)**
10 |
11 |
12 |
13 | 对于「+ -」操作来说,是一对逆运算,比如:`n + 3 - 3 = n`
14 |
15 | 而对于「异或」操作来说,自身就是一种逆运算,任何两个相同的数的异或结果为 0,所以有:`n ^ 3 ^ 3 = n`
16 |
17 | 至于为什么有这种特性,可以模拟一下「异或」运算的过程就懂了
18 |
19 | 来看一个样例:`[1,2,3,4,5]`
20 |
21 | - 其中`sum(1,5) = 1 + 2 + 3 + 4 + 5 = 15`,`sum(1,2) = 1 + 2 = 3`,`sum(3,5) = 3 + 4 + 5 = 12`
22 | - 其中`XOR(1,5) = 1 ^ 2 ^ 3 ^ 4 ^ 5 = 1`,`XOR(1,2) = 1 ^ 2 = 3`,`XOR(3,5) = 3 ^ 4 ^ 5 = 2`
23 |
24 | 所以:`sum(1,2) + sum(3,5) = sum(1,5)` -> `sum(3,5) = sum(1,5) - sum(1,2)`
25 |
26 | 同理:`sum(1,2) ^ sum(3,5) = sum(1,5)` -> `sum(3,5) = sum(1,5) ^ sum(1,2)`
27 |
28 | 有了这样一个简单的推导,下面直接上题目
29 |
30 | ### 子数组异或查询
31 |
32 | **题目详情可见 [子数组异或查询](https://leetcode.cn/problems/xor-queries-of-a-subarray/)**
33 |
34 | 这个题目就是个模版题,直接把「和」换成「异或」即可
35 |
36 | ```java
37 | public int[] xorQueries(int[] arr, int[][] queries) {
38 | int[] preSum = new int[arr.length + 1];
39 | for (int i = 1; i < preSum.length; i++) preSum[i] = preSum[i - 1] ^ arr[i - 1];
40 | int[] ans = new int[queries.length];
41 | for (int i = 0; i < queries.length; i++) {
42 | int[] query = queries[i];
43 | ans[i] = preSum[query[1] + 1] ^ preSum[query[0]];
44 | }
45 | return ans;
46 | }
47 | ```
48 |
49 |
50 | ### 每个元音包含偶数次的最长子字符串
51 |
52 | **题目详情可见 [每个元音包含偶数次的最长子字符串](https://leetcode.cn/problems/find-the-longest-substring-containing-vowels-in-even-counts/)**
53 |
54 | 我们把五个元音字母看作是五个特殊标记
55 |
56 | 如果一个子数组里面包含偶数个相同的元音字母,那么这个子数组中所有元音字母的异或结果肯定是 0,因为相同的元素异或为 0。例:`'a' ^ 'a' = 0`
57 |
58 | 所以我们只计算含有元音字母的前缀和,非元音字母的位置直接继承前一个结果,具体实现可见代码
59 |
60 | ```java
61 | public int findTheLongestSubstring(String s) {
62 | List vowel = Arrays.asList('a', 'e', 'i', 'o', 'u');
63 | int[] preSum = new int[s.length() + 1];
64 | for (int i = 1; i < preSum.length; i++) {
65 | if (vowel.contains(s.charAt(i - 1))) {
66 | // 如果是元音,就做「异或」操作
67 | preSum[i] = preSum[i - 1] ^ (int) s.charAt(i - 1);
68 | // 如果不是元音,直接继承前一个结果
69 | } else preSum[i] = preSum[i - 1];
70 | }
71 | int ans = 0;
72 | // 结尾从最后一个元素开始搜索 [......i]
73 | for (int i = s.length() - 1; i >= 0; i--) {
74 | // 开头从第一个元素开始搜索 [j......]
75 | // 注意:一定要 j <= i,因为存在 "d" 这样的情况
76 | for (int j = 0; j <= i; j++) {
77 | // 如果找到含有偶数个元音的子数组,直接开始上一个元素结尾的搜索
78 | // 以 i 为结尾的子数组不可能有更长满足条件的情况
79 | if ((preSum[i + 1] ^ preSum[j]) == 0) {
80 | ans = Math.max(ans, i - j + 1);
81 | break;
82 | }
83 | }
84 | }
85 | return ans;
86 | }
87 | ```
88 |
--------------------------------------------------------------------------------
/markdown/Algorithm/前缀和之等价条件.md:
--------------------------------------------------------------------------------
1 | # 前缀和之等价条件
2 |
3 | [2364. 统计坏数对的数目](https://leetcode.cn/problems/count-number-of-bad-pairs/)
4 |
5 | [4507. 子数组异或和](https://www.acwing.com/problem/content/description/4510/)
6 |
7 |
8 |
9 | 本篇文章来总结一下前缀和的变体,其实就是一丢丢的小技巧!!
10 |
11 | ### 统计坏数对的数目
12 |
13 | **题目详情可见 [统计坏数对的数目](https://leetcode.cn/problems/count-number-of-bad-pairs/)**
14 |
15 | 这是某一次周赛的一道题目,虽然题目不难,但之所以在这里单独拿出来,是为了引出一个小技巧!!
16 |
17 | 这个题目的关键条件:`i < j` 且 `j - i != nums[j] - nums[i]`
18 |
19 | 如果第一眼没反应过来,估计直接就双重循环了
20 |
21 | 但是如果稍微把条件改变一波:`i < j`且`nums[i] - i != nums[j] - j`,然后把`nums[i] - i`看作一个整体,借助`HashMap`,直接一重循环就可以了
22 |
23 | 下面直接给出代码:
24 |
25 | ```java
26 | public long countBadPairs(int[] nums) {
27 | long ans = 0;
28 | Map map = new HashMap<>();
29 | for (int i = 0; i < nums.length; i++) {
30 | int target = nums[i] - i;
31 | int cnt = map.getOrDefault(target, 0);
32 | map.put(target, cnt + 1);
33 | // cnt 是相等的数量,i - cnt 是不等的数量
34 | ans += i - cnt;
35 | }
36 | return ans;
37 | }
38 | ```
39 |
40 | 虽然这个题目没有用到前缀和,但是确为我们揭示了一个小技巧:**利用交换律,使之变成等价条件,利于求解**
41 |
42 | ### 子数组异或和
43 |
44 | **题目详情可见 [子数组异或和](https://www.acwing.com/problem/content/description/4510/)**
45 |
46 | **关于「前缀和数组」的详细介绍可见 [前缀和数组](./前缀和数组.html)**、**关于「前缀和之异或篇」的详细介绍可见 [前缀和之异或篇](./前缀和之异或篇.html)**,建议先看完这两篇文章,否则可能会存在不好理解的地方!!
47 |
48 | 这个题目的关键条件:`sum[i] ^ sum[i - m] = sum[i - m] ^ sum[i - 2m]`
49 |
50 | 同样的,如果第一眼没反应过来,估计直接就双重循环,然后超时!!
51 |
52 | 但是如果两边同时异或一个`sum[i - m]`,那么条件就变成了`sum[i] = sum[i - 2m]`,然后再借助`HashMap`即可!
53 |
54 | 这里还有另外一个条件:连续子数组的长度为偶数。怎么才能保证在`HashMap`中找到的结果满足该条件呢?
55 |
56 | 如果`i`为偶数,那么`i - 2m`为偶数;如果`i`为奇数,那么`i - 2m`为奇数,所以只需要用两个`HashMap`分别存奇偶数即可!
57 |
58 | 下面直接给出代码:
59 |
60 | ```java
61 | public long xorSum(int[] nums, int n) {
62 | long ans = 0;
63 | // map1 存放奇数;map2 存放偶数
64 | Map map1 = new HashMap<>();
65 | Map map2 = new HashMap<>();
66 | int[] preSum = new int[n + 1];
67 | for (int i = 1; i <= n; i++) preSum[i] = preSum[i - 1] ^ nums[i - 1];
68 | map2.put(0, 1);
69 | for (int i = 1; i <= n; i++) {
70 | if (i % 2 == 0) {
71 | int cnt = map2.getOrDefault(preSum[i], 0);
72 | ans += cnt;
73 | map2.put(preSum[i], cnt + 1);
74 | } else {
75 | int cnt = map1.getOrDefault(preSum[i], 0);
76 | ans += cnt;
77 | map1.put(preSum[i], cnt + 1);
78 | }
79 | }
80 | return ans;
81 | }
82 | ```
83 |
--------------------------------------------------------------------------------
/markdown/Algorithm/前缀和数组.md:
--------------------------------------------------------------------------------
1 | # 前缀和数组
2 |
3 | [303. 区域和检索 - 数组不可变](https://leetcode.cn/problems/range-sum-query-immutable/)
4 |
5 | [304. 二维区域和检索 - 矩阵不可变](https://leetcode.cn/problems/range-sum-query-2d-immutable/)
6 |
7 | [560. 和为 K 的子数组](https://leetcode.cn/problems/subarray-sum-equals-k/)
8 |
9 |
10 |
11 | 如果要得到「区间和」,能想到最简单的方法就是遍历所求区间,循环相加即可。如果这种需求有很多,此时,时间复杂度为 $O(n^2)$
12 |
13 | 基于上面描述的场景,我们完全可以使用「前缀和」优化,前缀和数组中每个元素的值为区间`[0..i]`的元素和
14 |
15 | **注意:**前缀和适用于**不变数组**;对于变化的数组,可以使用「线段树」,**关于线段树的详细介绍可见 [线段树详解](./线段树详解.html)**
16 |
17 | ### 区域和检索 - 数组不可变
18 |
19 | **题目详情可见 [区域和检索 - 数组不可变](https://leetcode-cn.com/problems/range-sum-query-immutable/)**
20 |
21 | **建议:**`preSum[]`整体向后偏移一位,简便处理
22 |
23 | 
24 |
25 | 如果求区间`[2,4]`的和,只需计算`preSum[4 + 1] - preSum[2]`即可
26 |
27 | 下面给出详细代码:
28 |
29 | ```java
30 | class NumArray {
31 | // 记录前缀和的数组
32 | private int[] preSum;
33 | public NumArray(int[] nums) {
34 | // preSum 从 1 开始,避免越界问题
35 | preSum = new int[nums.length + 1];
36 | for (int i = 1; i < preSum.length; i++) {
37 | preSum[i] = preSum[i - 1] + nums[i - 1];
38 | }
39 | }
40 | public int sumRange(int left, int right) {
41 | return preSum[right + 1] - preSum[left];
42 | }
43 | }
44 | ```
45 |
46 | ### 二维区域和检索 - 矩阵不可变
47 |
48 | **题目详情可见 [二维区域和检索 - 矩阵不可变](https://leetcode-cn.com/problems/range-sum-query-2d-immutable/)**
49 |
50 | 
51 |
52 | 如果求红色区间的和,只需求`preSum[4,4] - preSum[1,4] - preSum[4,1] + preSum[1,1]`即可
53 |
54 | - `preSum[4,4]`:黄 + 蓝 + 绿 + 红
55 |
56 | - `preSum[1,4]`:黄 + 蓝
57 |
58 | - `preSum[4,1]`:黄 + 绿
59 |
60 | - `preSum[1,1]`:黄
61 |
62 | 下面给出详细代码:
63 |
64 | ```java
65 | class NumMatrix {
66 | private int[][] preSum;
67 | public NumMatrix(int[][] matrix) {
68 | int m = matrix.length;
69 | int n = matrix[0].length;
70 | preSum = new int[m + 1][n + 1];
71 | for (int i = 1; i < m + 1; i++) {
72 | for (int j = 1; j < n + 1; j++) {
73 | preSum[i][j] = preSum[i - 1][j] + preSum[i][j - 1] - preSum[i - 1][j - 1] + matrix[i - 1][j - 1];
74 | }
75 | }
76 | }
77 | public int sumRegion(int row1, int col1, int row2, int col2) {
78 | return preSum[row2 + 1][col2 + 1] - preSum[row1][col2 + 1] - preSum[row2 + 1][col1] + preSum[row1][col1];
79 | }
80 | }
81 | ```
82 |
83 | ### 和为 K 的子数组
84 |
85 | **题目详情可见 [和为 K 的子数组](https://leetcode-cn.com/problems/subarray-sum-equals-k/)**
86 |
87 | 借鉴「两数和」的思路,利用`HashMap`。下面给出详细代码:
88 |
89 | ```java
90 | public int subarraySum(int[] nums, int k) {
91 |
92 | Map preSum = new HashMap<>();
93 | preSum.put(0, 1);
94 |
95 | int sum = 0;
96 | int res = 0;
97 | for (int i = 0; i < nums.length; i++) {
98 | sum += nums[i];
99 | int target = sum - k;
100 | if (preSum.containsKey(target)) res += preSum.get(target);
101 | preSum.put(sum, preSum.getOrDefault(sum, 0) + 1);
102 | }
103 | return res;
104 | }
105 | ```
--------------------------------------------------------------------------------
/markdown/Algorithm/单调队列.md:
--------------------------------------------------------------------------------
1 | # 单调队列
2 |
3 | [239. 滑动窗口最大值](https://leetcode-cn.com/problems/sliding-window-maximum/)
4 |
5 |
6 |
7 | 存在一种这样的场景:快速得到 n 个元素中的最大值,而且这 n 个元素还在不断的变化中!
8 |
9 | **题目详情可见 [滑动窗口最大值](https://leetcode-cn.com/problems/sliding-window-maximum/)**
10 |
11 | ### 数据结构实现
12 |
13 | 基于上述的场景,我们构造出了一种新的数据结构:**单调队列**
14 |
15 | 每次把新元素都从队尾插入,而队头的元素永远的最大的。如果要删除某一个元素时,我们判断是否为队头元素,如果不是,则不删;否则删除队头元素
16 |
17 | 该数据结构的具体方法如下:
18 |
19 | ```java
20 | public class MonotonicQueue {
21 | // 双链表,支持头部和尾部增删元素
22 | private final LinkedList q = new LinkedList<>();
23 | // 在队尾添加元素 n
24 | public void push(int n);
25 | // 队头元素如果是 n,删除它
26 | public void pop(int n);
27 | // 返回当前队列中最大值
28 | public int max();
29 | }
30 | ```
31 |
32 | 如下图所示。每当我们调用`push(n)`时,对于元素 3, 2, 1 将会被删掉,元素 4 接到 元素 5 的后面
33 |
34 |  35 |
36 | 具体实现如下:
37 |
38 | ```java
39 | // 在队尾添加元素 n
40 | public void push(int n) {
41 | // 将小于 n 的元素全部删除
42 | while (!q.isEmpty() && q.getLast() < n) {
43 | q.pollLast();
44 | }
45 | // 然后将 n 加入尾部
46 | q.addLast(n);
47 | }
48 | ```
49 |
50 | 如果每个元素被加入时都这样操作,最终单调队列中的元素大小就会保持一个**单调递减**的顺序,因此我们的 `max` 方法可以可以这样写:
51 |
52 | ```java
53 | // 返回当前队列中最大值
54 | public int max() {
55 | return q.getFirst();
56 | }
57 | ```
58 |
59 | `pop(n)`方法在队头删除元素`n`,也很好写:
60 |
61 | ```java
62 | // 队头元素如果是 n,删除它
63 | public void pop(int n) {
64 | if (n == q.getFirst()) {
65 | q.pollFirst();
66 | }
67 | }
68 | ```
69 |
70 | 至此,对于数据结构`MonotonicQueue`的全部方法已经实现
71 |
72 | ### 实战题目
73 |
74 | 现在我们回到本文开头提到的题目,直接使用我们自己实现的数据结构就很好解决了。具体代码如下:
75 |
76 | ```java
77 | public int[] maxSlidingWindow(int[] nums, int k) {
78 | MonotonicQueue window = new MonotonicQueue();
79 | List list = new ArrayList<>();
80 | for (int i = 0; i < nums.length; i++) {
81 | // 填满 k - 1 个元素
82 | if (i < k - 1) window.push(nums[i]);
83 | else {
84 | // 窗口向前移动一格
85 | window.push(nums[i]);
86 | list.add(window.max());
87 | window.pop(nums[i - k + 1]);
88 | }
89 | }
90 | int[] res = new int[list.size()];
91 | for (int i = 0; i < list.size(); i++) {
92 | res[i] = list.get(i);
93 | }
94 | return res;
95 | }
96 | ```
--------------------------------------------------------------------------------
/markdown/Algorithm/双指针之接雨水问题.md:
--------------------------------------------------------------------------------
1 |
2 | # 双指针之接雨水问题
3 |
4 | [11. 盛最多水的容器](https://leetcode.cn/problems/container-with-most-water/)
5 |
6 | [42. 接雨水](https://leetcode.cn/problems/trapping-rain-water/)
7 |
8 |
9 |
10 | 本篇文章来总结两个「接雨水」的问题!!
11 |
12 | 我一开始直接暴力,感觉方法很蠢!其实可以用双指针高效的解决这类问题,**关于双指针相关内容可见 [双指针技巧秒杀七道数组/链表题目](./双指针技巧秒杀七道数组-链表题目.html)**
13 |
14 | ### 盛最多水的容器
15 |
16 | **题目详情可见 [盛最多水的容器](https://leetcode.cn/problems/container-with-most-water/)**
17 |
18 | 定义两个指针,一个指向数组的开头,一个指向数组的结尾。如何移动指针才能使我们可以更加逼近最优解??
19 |
20 | **当然是移动两个里面高度更小的指针**
21 |
22 | ```java
23 | public int maxArea(int[] height) {
24 | int l = 0, r = height.length - 1;
25 | int ans = 0;
26 | while (l <= r) {
27 | int area = Math.min(height[l], height[r]) * (r - l);
28 | ans = Math.max(ans, area);
29 | if (height[l] < height[r]) l++;
30 | else r--;
31 | }
32 | return ans;
33 | }
34 | ```
35 |
36 | ### 接雨水
37 |
38 | **题目详情可见 [接雨水](https://leetcode.cn/problems/trapping-rain-water/)**
39 |
40 | 这个题目也差不多,我们需要维护一个高度`h`,表示能使水不流走的最大高度!!
41 |
42 | 在使用双指针收缩区间的时候,不断的更新该高度`h`
43 |
44 | ```java
45 | public int trap(int[] height) {
46 | int h = 0, ans = 0;
47 | int l = 0, r = height.length - 1;
48 | while (l <= r) {
49 | if (height[l] < height[r]) {
50 | h = Math.max(h, height[l]);
51 | ans += h - height[l];
52 | l++;
53 | } else {
54 | h = Math.max(h, height[r]);
55 | ans += h - height[r];
56 | r--;
57 | }
58 | }
59 | return ans;
60 | }
61 | ```
62 |
63 |
--------------------------------------------------------------------------------
/markdown/Algorithm/可被三整除的最大和-变题.md:
--------------------------------------------------------------------------------
1 | # 可被三整除的最大和「变题」
2 |
3 | [1262. 可被三整除的最大和](https://leetcode.cn/problems/greatest-sum-divisible-by-three/)
4 |
5 |
6 |
7 | 其实这是一个 0-1 背包问题,**关于「0-1 背包」可见 [经典动态规划:0-1 背包问题](./经典动态规划:0-1背包问题.html)**
8 |
9 | 对于每个数,都有两种选择:选择它 or 不选它
10 |
11 | 先给出`dp[i][j]`的定义:对于前`i`个数,当前余数为`j`,这种情况下背包最大和就是`dp[i][j]`
12 |
13 | 这里需要强调一下:假设选择某个数,记为`a`,其余数记为`x = n % 3`,那么前一状态就是`dp[i - 1][(j - x + 3) % 3]`
14 |
15 | ```java
16 | public int maxSumDivThree(int[] nums) {
17 | int n = nums.length;
18 | int[][] dp = new int[n + 1][3];
19 | // base case: 0 个数,余数大于 0 时,和赋值为最小值
20 | dp[0][1] = Integer.MIN_VALUE;
21 | dp[0][2] = Integer.MIN_VALUE;
22 | for (int i = 1; i <= n; i++) {
23 | // nums[i - 1] 的余数
24 | int x = nums[i - 1] % 3;
25 | for (int j = 0; j < 3; j++) {
26 | // dp[i - 1][j]: 表示不选
27 | // dp[i - 1][(j - x + 3) % 3] + nums[i - 1]: 表示选择
28 | dp[i][j] = Math.max(dp[i - 1][j], dp[i - 1][(j - x + 3) % 3] + nums[i - 1]);
29 | }
30 | }
31 | return dp[n][0];
32 | }
33 | ```
34 |
35 | ### 变题:可被 k 整除的最大和
36 |
37 | 不说废话,直接给出通解:
38 |
39 | ```java
40 | public int maxSumDivK(int[] nums, int k) {
41 | int n = nums.length;
42 | int[][] dp = new int[n + 1][k];
43 | // base case: 0 个数,余数大于 0 时,和赋值为最小值
44 | for (int i = 1; i < k; i++) dp[0][i] = Integer.MIN_VALUE;
45 | for (int i = 1; i <= n; i++) {
46 | // nums[i - 1] 的余数
47 | int x = nums[i - 1] % k;
48 | for (int j = 0; j < k; j++) {
49 | // dp[i - 1][j]: 表示不选
50 | // dp[i - 1][(j - x + k) % k] + nums[i - 1]: 表示选择
51 | dp[i][j] = Math.max(dp[i - 1][j], dp[i - 1][(j - x + k) % k] + nums[i - 1]);
52 | }
53 | }
54 | return dp[n][0];
55 | }
56 | ```
--------------------------------------------------------------------------------
/markdown/Algorithm/合并两个有序数组-变题.md:
--------------------------------------------------------------------------------
1 | # 合并两个有序数组「变题」
2 |
3 | [88. 合并两个有序数组](https://leetcode.cn/problems/merge-sorted-array/)
4 |
5 |
6 |
7 | ```java
8 | // 技巧:从后向前
9 | public void merge(int[] nums1, int m, int[] nums2, int n) {
10 | int k = m + n - 1;
11 | int i = m - 1, j = n - 1;
12 | while (i >= 0 && j >= 0) {
13 | if (nums1[i] >= nums2[j]) {
14 | nums1[k--] = nums1[i--];
15 | } else {
16 | nums1[k--] = nums2[j--];
17 | }
18 | }
19 | while (i >= 0) nums1[k--] = nums1[i--];
20 | while (j >= 0) nums1[k--] = nums2[j--];
21 | }
22 | ```
23 |
24 | ### 变题一:要求去重
25 |
26 | ```java
27 | public void merge(int[] nums1, int m, int[] nums2, int n) {
28 | int k = m + n - 1, prev = nums1[m - 1] + nums2[n - 1] + 1;
29 | int i = m - 1, j = n - 1;
30 | while (i >= 0 && j >= 0) {
31 | if (nums1[i] >= nums2[j]) {
32 | if (nums1[i] == prev) i--;
33 | else {
34 | nums1[k] = nums1[i--];
35 | prev = nums1[k--];
36 | }
37 | } else {
38 | if (nums2[j] == prev) j--;
39 | else {
40 | nums1[k] = nums2[j--];
41 | prev = nums1[k--];
42 | }
43 | }
44 |
45 | }
46 | while (i >= 0) {
47 | if (nums1[i] == prev) i--;
48 | else {
49 | nums1[k] = nums1[i--];
50 | prev = nums1[k--];
51 | }
52 | }
53 | while (j >= 0) {
54 | if (nums2[j] == prev) i--;
55 | else {
56 | nums1[k] = nums2[j--];
57 | prev = nums1[k--];
58 | }
59 | }
60 | System.out.println(m + n - k - 1);
61 | for (i = k + 1; i < m + n; i++) {
62 | nums1[i - k - 1] = nums1[i];
63 | }
64 | }
65 | ```
66 |
67 | ### 变题二:合并 K 个有序数组
68 |
69 | ```java
70 | // 时间复杂度 : O(nlogk)
71 | // 空间复杂度 : O(n) -> 若不算返回数组 O(k)
72 | public int[] merge(int[][] nums) {
73 | int idx = 0, n = 0;
74 | for (int i = 0; i < nums.length; i++) n += nums[i].length;
75 | int[] ans = new int[n];
76 | Queue q = new PriorityQueue<>((a, b) -> nums[a[0]][a[1]] - nums[b[0]][b[1]]);
77 | for (int i = 0; i < nums.length; i++) {
78 | if (nums[i].length != 0) q.offer(new int[]{i, 0});
79 | }
80 | while (!q.isEmpty()) {
81 | int[] cur = q.poll();
82 | ans[idx++] = nums[cur[0]][cur[1]];
83 | if (cur[1] + 1 < nums[cur[0]].length) q.offer(new int[]{cur[0], cur[1] + 1});
84 | }
85 | return ans;
86 | }
87 | // 调用过程
88 | int[] arr = merge(new int[][]{
89 | {2, 3, 6},
90 | {1, 4, 5, 7, 9},
91 | {2, 8, 10}
92 | });
93 | ```
94 |
95 | ### 变题三:合并 K 个有序数组并去重
96 |
97 | 直接在变题二的基础上修改即可!
98 |
99 | ```java
100 | public int[] merge(int[][] nums) {
101 | int idx = 0, n = 0;
102 | for (int i = 0; i < nums.length; i++) n += nums[i].length;
103 | int[] ans = new int[n];
104 | Queue q = new PriorityQueue<>((a, b) -> nums[a[0]][a[1]] - nums[b[0]][b[1]]);
105 | for (int i = 0; i < nums.length; i++) {
106 | if (nums[i].length != 0) q.offer(new int[]{i, 0});
107 | }
108 | int prev = nums[q.peek()[0]][q.peek()[1]] - 1;
109 | while (!q.isEmpty()) {
110 | int[] cur = q.poll();
111 | // 修改部分
112 | if (prev != nums[cur[0]][cur[1]]) {
113 | ans[idx++] = nums[cur[0]][cur[1]];
114 | prev = nums[cur[0]][cur[1]];
115 | }
116 | if (cur[1] + 1 < nums[cur[0]].length) q.offer(new int[]{cur[0], cur[1] + 1});
117 | }
118 | return ans;
119 | }
120 | ```
--------------------------------------------------------------------------------
/markdown/Algorithm/含泪总结周赛中的两道DP问题.md:
--------------------------------------------------------------------------------
1 | # 🥹含泪总结周赛中的两道「DP」问题
2 |
3 | [6109. 知道秘密的人数](https://leetcode.cn/problems/number-of-people-aware-of-a-secret/)
4 |
5 | [6110. 网格图中递增路径的数目](https://leetcode.cn/problems/number-of-increasing-paths-in-a-grid/)
6 |
7 | ### 知道秘密的人数
8 |
9 | **题目详情可见 [知道秘密的人数](https://leetcode.cn/problems/number-of-people-aware-of-a-secret/)**
10 |
11 | 比赛的时候一直在思考状态转移,自己心中想的`dp[i]`含义是「第`i`天知道秘密的总人数」,一直不知道怎么推出状态转移
12 |
13 | 直到看到别人的定义:`dp[i]`表示第`i`天**新**知道秘密的人数,瞬间就懂了!!!
14 |
15 | 所以第`i`天新增的人数都来自`(i - forget, i - delay]`区间内的人的分享,故有:$dp[i] = \sum\limits^{i - delay}_{j = i - forget + 1}dp[j]$
16 |
17 | 对于每次求`dp[i]`都有一个区间内的累加过程,所以可以利用「前缀和」优化一波!!
18 |
19 | ```java
20 | public int peopleAwareOfSecret(int n, int delay, int forget) {
21 | int mod = (int) 1e9 + 7;
22 | long[] f = new long[n + 1];
23 | long[] preSum = new long[n + 1];
24 | f[1] = 1;
25 | preSum[1] = 1;
26 | for (int i = 2; i <= n; i++) {
27 | int l = Math.max(0, i - forget);
28 | int r = Math.max(0, i - delay);
29 | // 注意:对于相减的求余需要加上一个 mod,转化成正数范围内!!
30 | f[i] = (preSum[r] - preSum[l] + mod) % mod;
31 | preSum[i] = (preSum[i - 1] + f[i]) % mod;
32 | }
33 | return (int) (preSum[n] - preSum[Math.max(0, n - forget)] + mod) % mod;
34 | }
35 | ```
36 |
37 | ### 网格图中递增路径的数目
38 |
39 | **题目详情可见 [网格图中递增路径的数目](https://leetcode.cn/problems/number-of-increasing-paths-in-a-grid/)**
40 |
41 | 这个题目就是一个「记忆化搜索」,为了避免路径重复,可以求出以某一个点为结尾的所有路径,所以把所有点都遍历一遍即可!
42 |
43 | ```java
44 | private int m, n;
45 | private int[][] grid;
46 | private int[][] emeo;
47 | private int mod = (int) 1e9 + 7;
48 | private int[][] dirs = new int[][] { {-1, 0}, {1, 0}, {0, -1}, {0, 1} };
49 | public int countPaths(int[][] grid) {
50 | int ans = 0;
51 | this.grid = grid;
52 | this.m = grid.length;
53 | this.n = grid[0].length;
54 | emeo = new int[m][n];
55 | // 遍历所有点
56 | for (int i = 0; i < m; i++) {
57 | for (int j = 0; j < n; j++) {
58 | ans = (ans + dp(i, j)) % mod;
59 | }
60 | }
61 | return ans;
62 | }
63 | // 以点 (i, j) 结尾的所有路径
64 | private int dp(int i, int j) {
65 | // 已经求过了,直接返回
66 | if (emeo[i][j] != 0) return emeo[i][j];
67 | long ans = 1L;
68 | // 往四个方向递归遍历
69 | for (int[] dir : dirs) {
70 | int ii = i + dir[0], jj = j + dir[1];
71 | if (ii >= 0 && ii < m && jj >= 0 && jj < n && grid[ii][jj] < grid[i][j]) {
72 | ans = (ans + dp(ii, jj)) % mod;
73 | }
74 | }
75 | // 保存结果
76 | emeo[i][j] = (int) ans;
77 | return emeo[i][j];
78 | }
79 | ```
--------------------------------------------------------------------------------
/markdown/Algorithm/回溯之博弈论:我能赢吗.md:
--------------------------------------------------------------------------------
1 | # 回溯之博弈论:我能赢吗
2 |
3 | [464. 我能赢吗](https://leetcode.cn/problems/can-i-win/)
4 |
5 | ### 概念介绍
6 |
7 | 今天学习到了两个新的概念**「状态压缩」**和**「记忆化搜索」**
8 |
9 | - **状态压缩:**利用二进制来表示当前状态。其原理就是把元素的使用情况抽象成一种状态,其实现方式为如果第`i`个元素被使用了,就把状态的第`i`位标记为`1`,反之则为`0`
10 | - **记忆化搜索:**一般记忆化搜索都是结合「状态压缩」来使用,说白了就是暴力搜索存在「重叠子问题」,利用「备忘录 emeo」来记录状态的结果
11 |
12 | 虽然这两个名词是我今天第一次弄明白意思,但是这两个方法的思想在之前经常使用!!在文章**「[经典回溯算法:集合划分问题](./经典回溯算法:集合划分问题.html)」**和**「[回溯算法:单词拆分](./回溯算法:单词拆分.html)」**均有使用这两种方法
13 |
14 | ### 问题分析
15 |
16 | **问题详情可见 [我能赢吗](https://leetcode.cn/problems/can-i-win/)**
17 |
18 | 首先来介绍「博弈论」和「回溯算法」是如何相结合滴!!**关于回溯算法的详细介绍可见 [回溯(DFS)](./回溯(DFS).html)**
19 |
20 | 其实如果回溯的题目做多了之后,就可以对这一类题目的套路有更加深刻的理解。也就是文章 **[回溯(DFS)](./回溯(DFS).html)** 里面说的需要搞清楚「路径」「选择」「结束条件」三个要素!
21 |
22 | 回到这个题目上面来,对于「先手」和「后手」来说,只有次序的不一样,其他部分完全一致
23 |
24 | 每个人每次的「选择」即为从`n`个数中选择一个,但有一个前提:已经被选过的数无法再被选择,所以需要一个标记
25 |
26 | 简简单单的画一下这个问题的「回溯树」吧!!
27 |
28 | 
29 |
30 | ### 代码实现
31 |
32 | 下面给出完整的代码
33 |
34 | ```java
35 | // 记录状态的结果
36 | // 1 表示 true;-1 表示 false
37 | private int[] emeo;
38 | private int maxChoosableInteger;
39 | private int desiredTotal;
40 | public boolean canIWin(int maxChoosableInteger, int desiredTotal) {
41 | // 如果所有数之和小于 desiredTotal
42 | if (maxChoosableInteger * (maxChoosableInteger + 1) / 2 < desiredTotal) return false;
43 | // 初始化,注意数组大小为 1 << maxChoosableInteger
44 | // 原因:n 个数,一共有 2^n 种状态
45 | emeo = new int[1 << maxChoosableInteger];
46 | this.maxChoosableInteger = maxChoosableInteger;
47 | this.desiredTotal = desiredTotal;
48 | return dfs(0, 0) == 1;
49 | }
50 | // state 记录的是 n 个数字的使用情况
51 | // 若第 i 个数字被使用,那么 state 中第 i 为 1
52 | private int dfs(int state, int curTotal) {
53 | // 该状态已经有结果,直接返回
54 | if (emeo[state] != 0) return emeo[state];
55 | // 选择列表
56 | for (int i = 0; i < maxChoosableInteger; i++) {
57 | // 已经被使用,跳过
58 | if (((state >> i) & 1) == 1) continue;
59 | // 胜利
60 | if (curTotal + i + 1 >= desiredTotal) {
61 | emeo[state] = 1;
62 | break;
63 | }
64 | // 后手若为 false,等价于 先手胜利
65 | if (dfs(state | (1 << i), curTotal + i + 1) == -1) {
66 | emeo[state] = 1;
67 | break;
68 | }
69 | }
70 | // n 个数遍历完,如果 emeo[state] = 0,说明先手无法获得胜利
71 | // 所以直接置 emeo[state] = -1
72 | if (emeo[state] == 0) emeo[state] = -1;
73 | return emeo[state];
74 | }
75 | ```
--------------------------------------------------------------------------------
/markdown/Algorithm/子数组之-与-或.md:
--------------------------------------------------------------------------------
1 | # 子数组之「与」「或」
2 |
3 | [6189. 按位与最大的最长子数组](https://leetcode.cn/problems/longest-subarray-with-maximum-bitwise-and/)
4 |
5 | [2411. 按位或最大的最小子数组长度](https://leetcode.cn/problems/smallest-subarrays-with-maximum-bitwise-or/)
6 |
7 |
8 |
9 | 本篇文章总结一下子数组和「与」「或」相结合的两个题目
10 |
11 | ### 按位与最大的最长子数组
12 |
13 | **题目详情可见 [按位与最大的最长子数组](https://leetcode.cn/problems/longest-subarray-with-maximum-bitwise-and/)**
14 |
15 | 比赛的时候浪费了很多时间,没有一眼看出题目中隐藏的细节
16 |
17 | 这里就需要清楚「与」运算的一个特点:`x & x = x`;`x ^ y = y`,其中`y < x`
18 |
19 | 简单来说,相同的两个数相与,还是等于原数;不同的两个数相与,结果的是较小的那个数
20 |
21 | 对于一个数组`[a, b, c, d]`,以`a`开头的所有子数组有:`[a], [a, b], [a, b, c], [a, b, c, d]`
22 |
23 | 那么一定存在:`(a) >= (a & b) >= (a & b & c) >= (a & b & c & d)`
24 |
25 | 所以,「与运算」具有单调非递增的特性
26 |
27 | 既然需要得到「按位与」最大的最长子数组,等价于找最大值连续的最大长度
28 |
29 | 例:`1234452444332`,这个例子中最大最长子数组为`444`
30 |
31 | 下面给出代码:
32 |
33 | ```java
34 | public int longestSubarray(int[] nums) {
35 | // 求出最大值
36 | int max = Arrays.stream(nums).max().getAsInt();
37 | int ans = 0, cnt = 0;
38 | for (int i = 0; i < nums.length; i++) {
39 | if (nums[i] != max) cnt = 0;
40 | else cnt++;
41 | ans = Math.max(ans, cnt);
42 | }
43 | return ans;
44 | }
45 | ```
46 |
47 | ### 按位或最大的最小子数组长度
48 |
49 | **题目详情可见 [按位或最大的最小子数组长度](https://leetcode.cn/problems/smallest-subarrays-with-maximum-bitwise-or/)**
50 |
51 | 和「与运算」相同,「或运算」也有一个特点:`x | x = x`;`x | y = y`,其中`y > x`
52 |
53 | 简单来说,相同的两个数相或,还是等于原数;不同的两个数相或,结果的是较大的那个数
54 |
55 | 同样的,举一个例子,但是为了和本题相互呼应,把例子稍微改改
56 |
57 | 对于一个数组`[a, b, c, d]`,以`d`结尾的所有子数组有:`[a, b, c, d], [b, c, d], [c, d], [d]`
58 |
59 | 那么一定存在:`(a | b | c | d) >= (b | c | d) >= (c | d) >= (d)`
60 |
61 | 所以,「或运算」具有单调非递减的特性
62 |
63 | 先给出代码,结合注释食用更佳:
64 |
65 | ```java
66 | public int[] smallestSubarrays(int[] nums) {
67 | int n = nums.length;
68 | int[] ans = new int[n];
69 | // 从左向右遍历 👉
70 | for (int i = 0; i < n; i++) {
71 | int x = nums[i];
72 | ans[i] = 1;
73 | // 从 i - 1 向左遍历 👈
74 | for (int j = i - 1; j >= 0; j--) {
75 | // 相等表示 x = nums[j],为了最短,选择不相或
76 | // 而且 j - 1 及前面的都不用再判断了,因为 nums[j - 1] >= nums[j],所以不需要判断
77 | if ((nums[j] | x) == nums[j]) break;
78 | // 注意:nums[j] 会累计或运算
79 | nums[j] |= x;
80 | // 更新结果
81 | ans[j] = i - j + 1;
82 | }
83 | }
84 | return ans;
85 | }
86 | ```
87 |
--------------------------------------------------------------------------------
/markdown/Algorithm/完全二叉树的节点个数.md:
--------------------------------------------------------------------------------
1 | # 完全二叉树的节点个数
2 |
3 | [222. 完全二叉树的节点个数](https://leetcode.cn/problems/count-complete-tree-nodes/)
4 |
5 | ### 完全二叉树 & 满二叉树
6 |
7 | 首先介绍一下「完全二叉树」和「满二叉树」的区别!
8 |
9 | - 一个二叉树,如果每一个层的结点数都达到最大值,则这个二叉树就是满二叉树
10 | - 若设二叉树的深度为 h,除第 h 层外,其它各层 (1 ~ h-1) 的结点数都达到最大个数,第 h 层所有的结点都连续集中在最左边,这就是完全二叉树
11 |
12 | 下面给出图,可以更加明显的看出区别:
13 |
14 |
35 |
36 | 具体实现如下:
37 |
38 | ```java
39 | // 在队尾添加元素 n
40 | public void push(int n) {
41 | // 将小于 n 的元素全部删除
42 | while (!q.isEmpty() && q.getLast() < n) {
43 | q.pollLast();
44 | }
45 | // 然后将 n 加入尾部
46 | q.addLast(n);
47 | }
48 | ```
49 |
50 | 如果每个元素被加入时都这样操作,最终单调队列中的元素大小就会保持一个**单调递减**的顺序,因此我们的 `max` 方法可以可以这样写:
51 |
52 | ```java
53 | // 返回当前队列中最大值
54 | public int max() {
55 | return q.getFirst();
56 | }
57 | ```
58 |
59 | `pop(n)`方法在队头删除元素`n`,也很好写:
60 |
61 | ```java
62 | // 队头元素如果是 n,删除它
63 | public void pop(int n) {
64 | if (n == q.getFirst()) {
65 | q.pollFirst();
66 | }
67 | }
68 | ```
69 |
70 | 至此,对于数据结构`MonotonicQueue`的全部方法已经实现
71 |
72 | ### 实战题目
73 |
74 | 现在我们回到本文开头提到的题目,直接使用我们自己实现的数据结构就很好解决了。具体代码如下:
75 |
76 | ```java
77 | public int[] maxSlidingWindow(int[] nums, int k) {
78 | MonotonicQueue window = new MonotonicQueue();
79 | List list = new ArrayList<>();
80 | for (int i = 0; i < nums.length; i++) {
81 | // 填满 k - 1 个元素
82 | if (i < k - 1) window.push(nums[i]);
83 | else {
84 | // 窗口向前移动一格
85 | window.push(nums[i]);
86 | list.add(window.max());
87 | window.pop(nums[i - k + 1]);
88 | }
89 | }
90 | int[] res = new int[list.size()];
91 | for (int i = 0; i < list.size(); i++) {
92 | res[i] = list.get(i);
93 | }
94 | return res;
95 | }
96 | ```
--------------------------------------------------------------------------------
/markdown/Algorithm/双指针之接雨水问题.md:
--------------------------------------------------------------------------------
1 |
2 | # 双指针之接雨水问题
3 |
4 | [11. 盛最多水的容器](https://leetcode.cn/problems/container-with-most-water/)
5 |
6 | [42. 接雨水](https://leetcode.cn/problems/trapping-rain-water/)
7 |
8 |
9 |
10 | 本篇文章来总结两个「接雨水」的问题!!
11 |
12 | 我一开始直接暴力,感觉方法很蠢!其实可以用双指针高效的解决这类问题,**关于双指针相关内容可见 [双指针技巧秒杀七道数组/链表题目](./双指针技巧秒杀七道数组-链表题目.html)**
13 |
14 | ### 盛最多水的容器
15 |
16 | **题目详情可见 [盛最多水的容器](https://leetcode.cn/problems/container-with-most-water/)**
17 |
18 | 定义两个指针,一个指向数组的开头,一个指向数组的结尾。如何移动指针才能使我们可以更加逼近最优解??
19 |
20 | **当然是移动两个里面高度更小的指针**
21 |
22 | ```java
23 | public int maxArea(int[] height) {
24 | int l = 0, r = height.length - 1;
25 | int ans = 0;
26 | while (l <= r) {
27 | int area = Math.min(height[l], height[r]) * (r - l);
28 | ans = Math.max(ans, area);
29 | if (height[l] < height[r]) l++;
30 | else r--;
31 | }
32 | return ans;
33 | }
34 | ```
35 |
36 | ### 接雨水
37 |
38 | **题目详情可见 [接雨水](https://leetcode.cn/problems/trapping-rain-water/)**
39 |
40 | 这个题目也差不多,我们需要维护一个高度`h`,表示能使水不流走的最大高度!!
41 |
42 | 在使用双指针收缩区间的时候,不断的更新该高度`h`
43 |
44 | ```java
45 | public int trap(int[] height) {
46 | int h = 0, ans = 0;
47 | int l = 0, r = height.length - 1;
48 | while (l <= r) {
49 | if (height[l] < height[r]) {
50 | h = Math.max(h, height[l]);
51 | ans += h - height[l];
52 | l++;
53 | } else {
54 | h = Math.max(h, height[r]);
55 | ans += h - height[r];
56 | r--;
57 | }
58 | }
59 | return ans;
60 | }
61 | ```
62 |
63 |
--------------------------------------------------------------------------------
/markdown/Algorithm/可被三整除的最大和-变题.md:
--------------------------------------------------------------------------------
1 | # 可被三整除的最大和「变题」
2 |
3 | [1262. 可被三整除的最大和](https://leetcode.cn/problems/greatest-sum-divisible-by-three/)
4 |
5 |
6 |
7 | 其实这是一个 0-1 背包问题,**关于「0-1 背包」可见 [经典动态规划:0-1 背包问题](./经典动态规划:0-1背包问题.html)**
8 |
9 | 对于每个数,都有两种选择:选择它 or 不选它
10 |
11 | 先给出`dp[i][j]`的定义:对于前`i`个数,当前余数为`j`,这种情况下背包最大和就是`dp[i][j]`
12 |
13 | 这里需要强调一下:假设选择某个数,记为`a`,其余数记为`x = n % 3`,那么前一状态就是`dp[i - 1][(j - x + 3) % 3]`
14 |
15 | ```java
16 | public int maxSumDivThree(int[] nums) {
17 | int n = nums.length;
18 | int[][] dp = new int[n + 1][3];
19 | // base case: 0 个数,余数大于 0 时,和赋值为最小值
20 | dp[0][1] = Integer.MIN_VALUE;
21 | dp[0][2] = Integer.MIN_VALUE;
22 | for (int i = 1; i <= n; i++) {
23 | // nums[i - 1] 的余数
24 | int x = nums[i - 1] % 3;
25 | for (int j = 0; j < 3; j++) {
26 | // dp[i - 1][j]: 表示不选
27 | // dp[i - 1][(j - x + 3) % 3] + nums[i - 1]: 表示选择
28 | dp[i][j] = Math.max(dp[i - 1][j], dp[i - 1][(j - x + 3) % 3] + nums[i - 1]);
29 | }
30 | }
31 | return dp[n][0];
32 | }
33 | ```
34 |
35 | ### 变题:可被 k 整除的最大和
36 |
37 | 不说废话,直接给出通解:
38 |
39 | ```java
40 | public int maxSumDivK(int[] nums, int k) {
41 | int n = nums.length;
42 | int[][] dp = new int[n + 1][k];
43 | // base case: 0 个数,余数大于 0 时,和赋值为最小值
44 | for (int i = 1; i < k; i++) dp[0][i] = Integer.MIN_VALUE;
45 | for (int i = 1; i <= n; i++) {
46 | // nums[i - 1] 的余数
47 | int x = nums[i - 1] % k;
48 | for (int j = 0; j < k; j++) {
49 | // dp[i - 1][j]: 表示不选
50 | // dp[i - 1][(j - x + k) % k] + nums[i - 1]: 表示选择
51 | dp[i][j] = Math.max(dp[i - 1][j], dp[i - 1][(j - x + k) % k] + nums[i - 1]);
52 | }
53 | }
54 | return dp[n][0];
55 | }
56 | ```
--------------------------------------------------------------------------------
/markdown/Algorithm/合并两个有序数组-变题.md:
--------------------------------------------------------------------------------
1 | # 合并两个有序数组「变题」
2 |
3 | [88. 合并两个有序数组](https://leetcode.cn/problems/merge-sorted-array/)
4 |
5 |
6 |
7 | ```java
8 | // 技巧:从后向前
9 | public void merge(int[] nums1, int m, int[] nums2, int n) {
10 | int k = m + n - 1;
11 | int i = m - 1, j = n - 1;
12 | while (i >= 0 && j >= 0) {
13 | if (nums1[i] >= nums2[j]) {
14 | nums1[k--] = nums1[i--];
15 | } else {
16 | nums1[k--] = nums2[j--];
17 | }
18 | }
19 | while (i >= 0) nums1[k--] = nums1[i--];
20 | while (j >= 0) nums1[k--] = nums2[j--];
21 | }
22 | ```
23 |
24 | ### 变题一:要求去重
25 |
26 | ```java
27 | public void merge(int[] nums1, int m, int[] nums2, int n) {
28 | int k = m + n - 1, prev = nums1[m - 1] + nums2[n - 1] + 1;
29 | int i = m - 1, j = n - 1;
30 | while (i >= 0 && j >= 0) {
31 | if (nums1[i] >= nums2[j]) {
32 | if (nums1[i] == prev) i--;
33 | else {
34 | nums1[k] = nums1[i--];
35 | prev = nums1[k--];
36 | }
37 | } else {
38 | if (nums2[j] == prev) j--;
39 | else {
40 | nums1[k] = nums2[j--];
41 | prev = nums1[k--];
42 | }
43 | }
44 |
45 | }
46 | while (i >= 0) {
47 | if (nums1[i] == prev) i--;
48 | else {
49 | nums1[k] = nums1[i--];
50 | prev = nums1[k--];
51 | }
52 | }
53 | while (j >= 0) {
54 | if (nums2[j] == prev) i--;
55 | else {
56 | nums1[k] = nums2[j--];
57 | prev = nums1[k--];
58 | }
59 | }
60 | System.out.println(m + n - k - 1);
61 | for (i = k + 1; i < m + n; i++) {
62 | nums1[i - k - 1] = nums1[i];
63 | }
64 | }
65 | ```
66 |
67 | ### 变题二:合并 K 个有序数组
68 |
69 | ```java
70 | // 时间复杂度 : O(nlogk)
71 | // 空间复杂度 : O(n) -> 若不算返回数组 O(k)
72 | public int[] merge(int[][] nums) {
73 | int idx = 0, n = 0;
74 | for (int i = 0; i < nums.length; i++) n += nums[i].length;
75 | int[] ans = new int[n];
76 | Queue q = new PriorityQueue<>((a, b) -> nums[a[0]][a[1]] - nums[b[0]][b[1]]);
77 | for (int i = 0; i < nums.length; i++) {
78 | if (nums[i].length != 0) q.offer(new int[]{i, 0});
79 | }
80 | while (!q.isEmpty()) {
81 | int[] cur = q.poll();
82 | ans[idx++] = nums[cur[0]][cur[1]];
83 | if (cur[1] + 1 < nums[cur[0]].length) q.offer(new int[]{cur[0], cur[1] + 1});
84 | }
85 | return ans;
86 | }
87 | // 调用过程
88 | int[] arr = merge(new int[][]{
89 | {2, 3, 6},
90 | {1, 4, 5, 7, 9},
91 | {2, 8, 10}
92 | });
93 | ```
94 |
95 | ### 变题三:合并 K 个有序数组并去重
96 |
97 | 直接在变题二的基础上修改即可!
98 |
99 | ```java
100 | public int[] merge(int[][] nums) {
101 | int idx = 0, n = 0;
102 | for (int i = 0; i < nums.length; i++) n += nums[i].length;
103 | int[] ans = new int[n];
104 | Queue q = new PriorityQueue<>((a, b) -> nums[a[0]][a[1]] - nums[b[0]][b[1]]);
105 | for (int i = 0; i < nums.length; i++) {
106 | if (nums[i].length != 0) q.offer(new int[]{i, 0});
107 | }
108 | int prev = nums[q.peek()[0]][q.peek()[1]] - 1;
109 | while (!q.isEmpty()) {
110 | int[] cur = q.poll();
111 | // 修改部分
112 | if (prev != nums[cur[0]][cur[1]]) {
113 | ans[idx++] = nums[cur[0]][cur[1]];
114 | prev = nums[cur[0]][cur[1]];
115 | }
116 | if (cur[1] + 1 < nums[cur[0]].length) q.offer(new int[]{cur[0], cur[1] + 1});
117 | }
118 | return ans;
119 | }
120 | ```
--------------------------------------------------------------------------------
/markdown/Algorithm/含泪总结周赛中的两道DP问题.md:
--------------------------------------------------------------------------------
1 | # 🥹含泪总结周赛中的两道「DP」问题
2 |
3 | [6109. 知道秘密的人数](https://leetcode.cn/problems/number-of-people-aware-of-a-secret/)
4 |
5 | [6110. 网格图中递增路径的数目](https://leetcode.cn/problems/number-of-increasing-paths-in-a-grid/)
6 |
7 | ### 知道秘密的人数
8 |
9 | **题目详情可见 [知道秘密的人数](https://leetcode.cn/problems/number-of-people-aware-of-a-secret/)**
10 |
11 | 比赛的时候一直在思考状态转移,自己心中想的`dp[i]`含义是「第`i`天知道秘密的总人数」,一直不知道怎么推出状态转移
12 |
13 | 直到看到别人的定义:`dp[i]`表示第`i`天**新**知道秘密的人数,瞬间就懂了!!!
14 |
15 | 所以第`i`天新增的人数都来自`(i - forget, i - delay]`区间内的人的分享,故有:$dp[i] = \sum\limits^{i - delay}_{j = i - forget + 1}dp[j]$
16 |
17 | 对于每次求`dp[i]`都有一个区间内的累加过程,所以可以利用「前缀和」优化一波!!
18 |
19 | ```java
20 | public int peopleAwareOfSecret(int n, int delay, int forget) {
21 | int mod = (int) 1e9 + 7;
22 | long[] f = new long[n + 1];
23 | long[] preSum = new long[n + 1];
24 | f[1] = 1;
25 | preSum[1] = 1;
26 | for (int i = 2; i <= n; i++) {
27 | int l = Math.max(0, i - forget);
28 | int r = Math.max(0, i - delay);
29 | // 注意:对于相减的求余需要加上一个 mod,转化成正数范围内!!
30 | f[i] = (preSum[r] - preSum[l] + mod) % mod;
31 | preSum[i] = (preSum[i - 1] + f[i]) % mod;
32 | }
33 | return (int) (preSum[n] - preSum[Math.max(0, n - forget)] + mod) % mod;
34 | }
35 | ```
36 |
37 | ### 网格图中递增路径的数目
38 |
39 | **题目详情可见 [网格图中递增路径的数目](https://leetcode.cn/problems/number-of-increasing-paths-in-a-grid/)**
40 |
41 | 这个题目就是一个「记忆化搜索」,为了避免路径重复,可以求出以某一个点为结尾的所有路径,所以把所有点都遍历一遍即可!
42 |
43 | ```java
44 | private int m, n;
45 | private int[][] grid;
46 | private int[][] emeo;
47 | private int mod = (int) 1e9 + 7;
48 | private int[][] dirs = new int[][] { {-1, 0}, {1, 0}, {0, -1}, {0, 1} };
49 | public int countPaths(int[][] grid) {
50 | int ans = 0;
51 | this.grid = grid;
52 | this.m = grid.length;
53 | this.n = grid[0].length;
54 | emeo = new int[m][n];
55 | // 遍历所有点
56 | for (int i = 0; i < m; i++) {
57 | for (int j = 0; j < n; j++) {
58 | ans = (ans + dp(i, j)) % mod;
59 | }
60 | }
61 | return ans;
62 | }
63 | // 以点 (i, j) 结尾的所有路径
64 | private int dp(int i, int j) {
65 | // 已经求过了,直接返回
66 | if (emeo[i][j] != 0) return emeo[i][j];
67 | long ans = 1L;
68 | // 往四个方向递归遍历
69 | for (int[] dir : dirs) {
70 | int ii = i + dir[0], jj = j + dir[1];
71 | if (ii >= 0 && ii < m && jj >= 0 && jj < n && grid[ii][jj] < grid[i][j]) {
72 | ans = (ans + dp(ii, jj)) % mod;
73 | }
74 | }
75 | // 保存结果
76 | emeo[i][j] = (int) ans;
77 | return emeo[i][j];
78 | }
79 | ```
--------------------------------------------------------------------------------
/markdown/Algorithm/回溯之博弈论:我能赢吗.md:
--------------------------------------------------------------------------------
1 | # 回溯之博弈论:我能赢吗
2 |
3 | [464. 我能赢吗](https://leetcode.cn/problems/can-i-win/)
4 |
5 | ### 概念介绍
6 |
7 | 今天学习到了两个新的概念**「状态压缩」**和**「记忆化搜索」**
8 |
9 | - **状态压缩:**利用二进制来表示当前状态。其原理就是把元素的使用情况抽象成一种状态,其实现方式为如果第`i`个元素被使用了,就把状态的第`i`位标记为`1`,反之则为`0`
10 | - **记忆化搜索:**一般记忆化搜索都是结合「状态压缩」来使用,说白了就是暴力搜索存在「重叠子问题」,利用「备忘录 emeo」来记录状态的结果
11 |
12 | 虽然这两个名词是我今天第一次弄明白意思,但是这两个方法的思想在之前经常使用!!在文章**「[经典回溯算法:集合划分问题](./经典回溯算法:集合划分问题.html)」**和**「[回溯算法:单词拆分](./回溯算法:单词拆分.html)」**均有使用这两种方法
13 |
14 | ### 问题分析
15 |
16 | **问题详情可见 [我能赢吗](https://leetcode.cn/problems/can-i-win/)**
17 |
18 | 首先来介绍「博弈论」和「回溯算法」是如何相结合滴!!**关于回溯算法的详细介绍可见 [回溯(DFS)](./回溯(DFS).html)**
19 |
20 | 其实如果回溯的题目做多了之后,就可以对这一类题目的套路有更加深刻的理解。也就是文章 **[回溯(DFS)](./回溯(DFS).html)** 里面说的需要搞清楚「路径」「选择」「结束条件」三个要素!
21 |
22 | 回到这个题目上面来,对于「先手」和「后手」来说,只有次序的不一样,其他部分完全一致
23 |
24 | 每个人每次的「选择」即为从`n`个数中选择一个,但有一个前提:已经被选过的数无法再被选择,所以需要一个标记
25 |
26 | 简简单单的画一下这个问题的「回溯树」吧!!
27 |
28 | 
29 |
30 | ### 代码实现
31 |
32 | 下面给出完整的代码
33 |
34 | ```java
35 | // 记录状态的结果
36 | // 1 表示 true;-1 表示 false
37 | private int[] emeo;
38 | private int maxChoosableInteger;
39 | private int desiredTotal;
40 | public boolean canIWin(int maxChoosableInteger, int desiredTotal) {
41 | // 如果所有数之和小于 desiredTotal
42 | if (maxChoosableInteger * (maxChoosableInteger + 1) / 2 < desiredTotal) return false;
43 | // 初始化,注意数组大小为 1 << maxChoosableInteger
44 | // 原因:n 个数,一共有 2^n 种状态
45 | emeo = new int[1 << maxChoosableInteger];
46 | this.maxChoosableInteger = maxChoosableInteger;
47 | this.desiredTotal = desiredTotal;
48 | return dfs(0, 0) == 1;
49 | }
50 | // state 记录的是 n 个数字的使用情况
51 | // 若第 i 个数字被使用,那么 state 中第 i 为 1
52 | private int dfs(int state, int curTotal) {
53 | // 该状态已经有结果,直接返回
54 | if (emeo[state] != 0) return emeo[state];
55 | // 选择列表
56 | for (int i = 0; i < maxChoosableInteger; i++) {
57 | // 已经被使用,跳过
58 | if (((state >> i) & 1) == 1) continue;
59 | // 胜利
60 | if (curTotal + i + 1 >= desiredTotal) {
61 | emeo[state] = 1;
62 | break;
63 | }
64 | // 后手若为 false,等价于 先手胜利
65 | if (dfs(state | (1 << i), curTotal + i + 1) == -1) {
66 | emeo[state] = 1;
67 | break;
68 | }
69 | }
70 | // n 个数遍历完,如果 emeo[state] = 0,说明先手无法获得胜利
71 | // 所以直接置 emeo[state] = -1
72 | if (emeo[state] == 0) emeo[state] = -1;
73 | return emeo[state];
74 | }
75 | ```
--------------------------------------------------------------------------------
/markdown/Algorithm/子数组之-与-或.md:
--------------------------------------------------------------------------------
1 | # 子数组之「与」「或」
2 |
3 | [6189. 按位与最大的最长子数组](https://leetcode.cn/problems/longest-subarray-with-maximum-bitwise-and/)
4 |
5 | [2411. 按位或最大的最小子数组长度](https://leetcode.cn/problems/smallest-subarrays-with-maximum-bitwise-or/)
6 |
7 |
8 |
9 | 本篇文章总结一下子数组和「与」「或」相结合的两个题目
10 |
11 | ### 按位与最大的最长子数组
12 |
13 | **题目详情可见 [按位与最大的最长子数组](https://leetcode.cn/problems/longest-subarray-with-maximum-bitwise-and/)**
14 |
15 | 比赛的时候浪费了很多时间,没有一眼看出题目中隐藏的细节
16 |
17 | 这里就需要清楚「与」运算的一个特点:`x & x = x`;`x ^ y = y`,其中`y < x`
18 |
19 | 简单来说,相同的两个数相与,还是等于原数;不同的两个数相与,结果的是较小的那个数
20 |
21 | 对于一个数组`[a, b, c, d]`,以`a`开头的所有子数组有:`[a], [a, b], [a, b, c], [a, b, c, d]`
22 |
23 | 那么一定存在:`(a) >= (a & b) >= (a & b & c) >= (a & b & c & d)`
24 |
25 | 所以,「与运算」具有单调非递增的特性
26 |
27 | 既然需要得到「按位与」最大的最长子数组,等价于找最大值连续的最大长度
28 |
29 | 例:`1234452444332`,这个例子中最大最长子数组为`444`
30 |
31 | 下面给出代码:
32 |
33 | ```java
34 | public int longestSubarray(int[] nums) {
35 | // 求出最大值
36 | int max = Arrays.stream(nums).max().getAsInt();
37 | int ans = 0, cnt = 0;
38 | for (int i = 0; i < nums.length; i++) {
39 | if (nums[i] != max) cnt = 0;
40 | else cnt++;
41 | ans = Math.max(ans, cnt);
42 | }
43 | return ans;
44 | }
45 | ```
46 |
47 | ### 按位或最大的最小子数组长度
48 |
49 | **题目详情可见 [按位或最大的最小子数组长度](https://leetcode.cn/problems/smallest-subarrays-with-maximum-bitwise-or/)**
50 |
51 | 和「与运算」相同,「或运算」也有一个特点:`x | x = x`;`x | y = y`,其中`y > x`
52 |
53 | 简单来说,相同的两个数相或,还是等于原数;不同的两个数相或,结果的是较大的那个数
54 |
55 | 同样的,举一个例子,但是为了和本题相互呼应,把例子稍微改改
56 |
57 | 对于一个数组`[a, b, c, d]`,以`d`结尾的所有子数组有:`[a, b, c, d], [b, c, d], [c, d], [d]`
58 |
59 | 那么一定存在:`(a | b | c | d) >= (b | c | d) >= (c | d) >= (d)`
60 |
61 | 所以,「或运算」具有单调非递减的特性
62 |
63 | 先给出代码,结合注释食用更佳:
64 |
65 | ```java
66 | public int[] smallestSubarrays(int[] nums) {
67 | int n = nums.length;
68 | int[] ans = new int[n];
69 | // 从左向右遍历 👉
70 | for (int i = 0; i < n; i++) {
71 | int x = nums[i];
72 | ans[i] = 1;
73 | // 从 i - 1 向左遍历 👈
74 | for (int j = i - 1; j >= 0; j--) {
75 | // 相等表示 x = nums[j],为了最短,选择不相或
76 | // 而且 j - 1 及前面的都不用再判断了,因为 nums[j - 1] >= nums[j],所以不需要判断
77 | if ((nums[j] | x) == nums[j]) break;
78 | // 注意:nums[j] 会累计或运算
79 | nums[j] |= x;
80 | // 更新结果
81 | ans[j] = i - j + 1;
82 | }
83 | }
84 | return ans;
85 | }
86 | ```
87 |
--------------------------------------------------------------------------------
/markdown/Algorithm/完全二叉树的节点个数.md:
--------------------------------------------------------------------------------
1 | # 完全二叉树的节点个数
2 |
3 | [222. 完全二叉树的节点个数](https://leetcode.cn/problems/count-complete-tree-nodes/)
4 |
5 | ### 完全二叉树 & 满二叉树
6 |
7 | 首先介绍一下「完全二叉树」和「满二叉树」的区别!
8 |
9 | - 一个二叉树,如果每一个层的结点数都达到最大值,则这个二叉树就是满二叉树
10 | - 若设二叉树的深度为 h,除第 h 层外,其它各层 (1 ~ h-1) 的结点数都达到最大个数,第 h 层所有的结点都连续集中在最左边,这就是完全二叉树
11 |
12 | 下面给出图,可以更加明显的看出区别:
13 |
14 |  15 |
16 | 对于求「满二叉树」的节点个数,这里有一个公式:$n=2^{depth}-1$,其中 $depth$ 为树的深度
17 |
18 | 上图中的满二叉树的深度为 4,所以其节点个数为:$n=2^4-1=15$
19 |
20 | 今天要介绍的题目就是基于这个原理!
21 |
22 | ### 问题分析
23 |
24 | 对于「完全二叉树」,一定存在是「满二叉树」的子树
25 |
26 |
15 |
16 | 对于求「满二叉树」的节点个数,这里有一个公式:$n=2^{depth}-1$,其中 $depth$ 为树的深度
17 |
18 | 上图中的满二叉树的深度为 4,所以其节点个数为:$n=2^4-1=15$
19 |
20 | 今天要介绍的题目就是基于这个原理!
21 |
22 | ### 问题分析
23 |
24 | 对于「完全二叉树」,一定存在是「满二叉树」的子树
25 |
26 |  27 |
28 | 如上图所示,三角形框出来的子树就是「满二叉树」
29 |
30 | 对于这些是「满二叉树」的子树,求节点个数不需要遍历,直接利用公式即可!
31 |
32 | **现在存在一个问题:怎么判断子树是「满二叉树」呢?**
33 |
34 | - 只需要求出「左高」和「右高」,相等即为「满二叉树」
35 |
36 | **左高:**顾名思义,一直通过左孩子节点求出来的高度;**右高:**顾名思义,一直通过右孩子节点求出来的高度
37 |
38 | 描述的比较抽象,直接看图:
39 |
40 |
27 |
28 | 如上图所示,三角形框出来的子树就是「满二叉树」
29 |
30 | 对于这些是「满二叉树」的子树,求节点个数不需要遍历,直接利用公式即可!
31 |
32 | **现在存在一个问题:怎么判断子树是「满二叉树」呢?**
33 |
34 | - 只需要求出「左高」和「右高」,相等即为「满二叉树」
35 |
36 | **左高:**顾名思义,一直通过左孩子节点求出来的高度;**右高:**顾名思义,一直通过右孩子节点求出来的高度
37 |
38 | 描述的比较抽象,直接看图:
39 |
40 |  41 |
42 | 其中绿色路径就是「左高」,为 4;橙色路径就是「右高」,为 3
43 |
44 | 所以以 0 为根节点的树不是「满二叉树」,但是以 1 和 5 为根节点的树是「满二叉树」
45 |
46 | ### 代码实现
47 |
48 | 下面给出完整代码:
49 |
50 | ```java
51 | public int countNodes(TreeNode root) {
52 | if (root == null) return 0;
53 | int lh = 0, rh = 0;
54 | TreeNode left = root, right = root;
55 | // 求左高
56 | while (left != null) {
57 | left = left.left;
58 | lh++;
59 | }
60 | // 求右高
61 | while (right != null) {
62 | right = right.right;
63 | rh++;
64 | }
65 | // 以 root 为根节点的树是「满二叉树」
66 | if (lh == rh) return (int) Math.pow(2, lh) - 1;
67 | // 否则,按照正常方式遍历
68 | return countNodes(root.left) + countNodes(root.right) + 1;
69 | }
70 | ```
71 |
72 |
--------------------------------------------------------------------------------
/markdown/Algorithm/差分数组技巧.md:
--------------------------------------------------------------------------------
1 | # 差分数组技巧
2 |
3 | [1109. 航班预订统计](https://leetcode-cn.com/problems/corporate-flight-bookings/)
4 |
5 | [1094. 拼车](https://leetcode-cn.com/problems/car-pooling/)
6 |
7 |
8 |
9 | 在介绍差分数组之前,先回顾了一下「前缀和数组」**详情可见 [前缀和数组](./前缀和数组.html)**
10 |
11 | **前缀和主要适用的场景是原始数组不会被修改的情况下,频繁查询某个区间的累加和**
12 |
13 | **差分数组的主要适用场景是频繁对原始数组的某个区间的元素进行增减**
14 |
15 |
16 |
17 | **使用场景:**对于一个数组`nums[]`
18 |
19 | - 要求一:对`num[2...4]`全部 + 1
20 | - 要求二:对`num[1...3]`全部 - 3
21 | - 要求三:对`num[0...4]`全部 + 9
22 |
23 | 看到上述情景,首先想到的肯定是遍历(bao li)法。直接对数组循环 3 遍,每次在规定的区间上按要求进行操作,此时时间复杂度`O(3n)`
24 |
25 | 但是当这样的操作变得频繁后,时间复杂度也呈线性递增
26 |
27 | 所以针对这种场景,出现了「差分数组」的概念,举个简单的例子
28 |
29 |
41 |
42 | 其中绿色路径就是「左高」,为 4;橙色路径就是「右高」,为 3
43 |
44 | 所以以 0 为根节点的树不是「满二叉树」,但是以 1 和 5 为根节点的树是「满二叉树」
45 |
46 | ### 代码实现
47 |
48 | 下面给出完整代码:
49 |
50 | ```java
51 | public int countNodes(TreeNode root) {
52 | if (root == null) return 0;
53 | int lh = 0, rh = 0;
54 | TreeNode left = root, right = root;
55 | // 求左高
56 | while (left != null) {
57 | left = left.left;
58 | lh++;
59 | }
60 | // 求右高
61 | while (right != null) {
62 | right = right.right;
63 | rh++;
64 | }
65 | // 以 root 为根节点的树是「满二叉树」
66 | if (lh == rh) return (int) Math.pow(2, lh) - 1;
67 | // 否则,按照正常方式遍历
68 | return countNodes(root.left) + countNodes(root.right) + 1;
69 | }
70 | ```
71 |
72 |
--------------------------------------------------------------------------------
/markdown/Algorithm/差分数组技巧.md:
--------------------------------------------------------------------------------
1 | # 差分数组技巧
2 |
3 | [1109. 航班预订统计](https://leetcode-cn.com/problems/corporate-flight-bookings/)
4 |
5 | [1094. 拼车](https://leetcode-cn.com/problems/car-pooling/)
6 |
7 |
8 |
9 | 在介绍差分数组之前,先回顾了一下「前缀和数组」**详情可见 [前缀和数组](./前缀和数组.html)**
10 |
11 | **前缀和主要适用的场景是原始数组不会被修改的情况下,频繁查询某个区间的累加和**
12 |
13 | **差分数组的主要适用场景是频繁对原始数组的某个区间的元素进行增减**
14 |
15 |
16 |
17 | **使用场景:**对于一个数组`nums[]`
18 |
19 | - 要求一:对`num[2...4]`全部 + 1
20 | - 要求二:对`num[1...3]`全部 - 3
21 | - 要求三:对`num[0...4]`全部 + 9
22 |
23 | 看到上述情景,首先想到的肯定是遍历(bao li)法。直接对数组循环 3 遍,每次在规定的区间上按要求进行操作,此时时间复杂度`O(3n)`
24 |
25 | 但是当这样的操作变得频繁后,时间复杂度也呈线性递增
26 |
27 | 所以针对这种场景,出现了「差分数组」的概念,举个简单的例子
28 |
29 |  30 |
31 | `diff[]`和`nums[]`的关系:`diff[i] = nums[i] - nums[i - 1]`,`diff[0]`除外
32 |
33 | **问题一:**这样处理的好处是什么呢?????
34 |
35 | 当我们需要对`nums[]`进行上述三个要求时,不需要一次一次的遍历整个数组了,而只需要对`diff[]`进行一次`O(1)`的操作即可
36 |
37 | - 要求一:`diff[2] += 1;`
38 | - 要求二:`diff[1] += (-3); diff[3 + 1] -= (-3);`
39 | - 要求三:`diff[0] += 9;`
40 |
41 | **总结:**对于改变区间`[i, j]`的值,只需要进行如下操作`diff[i] += val; diff[j + 1] -= val`
42 |
43 |
30 |
31 | `diff[]`和`nums[]`的关系:`diff[i] = nums[i] - nums[i - 1]`,`diff[0]`除外
32 |
33 | **问题一:**这样处理的好处是什么呢?????
34 |
35 | 当我们需要对`nums[]`进行上述三个要求时,不需要一次一次的遍历整个数组了,而只需要对`diff[]`进行一次`O(1)`的操作即可
36 |
37 | - 要求一:`diff[2] += 1;`
38 | - 要求二:`diff[1] += (-3); diff[3 + 1] -= (-3);`
39 | - 要求三:`diff[0] += 9;`
40 |
41 | **总结:**对于改变区间`[i, j]`的值,只需要进行如下操作`diff[i] += val; diff[j + 1] -= val`
42 |
43 |  注:当`j + 1 >= diff.length`时,不需要进行`diff[j + 1] -= val`操作
44 |
45 | **问题二:**怎么通过`diff[]`得到更新后的数组呢?????
46 |
47 | ```java
48 | // 复原操作
49 | int[] res = new int[n];
50 | // 下标为 0 的元素相等
51 | res[0] = diff[0];
52 | for (int i = 1; i < n; i++) {
53 | res[i] = diff[i] + res[i - 1];
54 | }
55 | ```
56 |
57 | **问题三:**`diff[]`原理
58 |
59 | 当我们需要对区间`[i, j]`进行`+ val`操作时,我们对`diff[i] += val; diff[j + 1] -= val;`
60 |
61 | 在复原操作时,当我们求`res[i]`时,`res[i - 1]`没有变,而`diff[i]`增加了 3,所以`res[i]`增加 3
62 |
63 | 当我们求`res[i + 1]`时,`res[i]`增加了 3,而`diff[i + 1]`没有变,故`res[i + 1] = diff[i + 1] + res[i]`增加 3。即:虽然`diff[i + 1]`没有变,但是`res[i]`对后面的`res[i + 1]`有一个累积作用
64 |
65 | 当我们求`res[j + 1]`时,`res[j]`增加了 3,而`diff[j + 1]`减少了 3,故`res[j + 1] = diff[j + 1] + res[j]`增加没有变。即:我们在`j + 1`的时候,把上述的累积作用去除了,所以`j + 1`后面的元素不受影响
66 |
67 |
68 |
69 | **完整模版**
70 |
71 | ```java
72 | public class Difference {
73 |
74 | /**
75 | * 差分数组
76 | */
77 | private final int[] diff;
78 |
79 | /**
80 | * 初始化差分数组
81 | * @param nums nums
82 | */
83 | public Difference(int[] nums) {
84 | assert nums.length > 0;
85 | diff = new int[nums.length];
86 | diff[0] = nums[0];
87 | for (int i = 1; i < nums.length; i++) {
88 | diff[i] = nums[i] - nums[i - 1];
89 | }
90 | }
91 |
92 | /**
93 | * 对区间 [i, j] 增加 val(val 可为负数)
94 | * @param i i
95 | * @param j j
96 | * @param val val
97 | */
98 | public void increment(int i, int j, int val) {
99 | diff[i] += val;
100 | if (j + 1 < diff.length) {
101 | diff[j + 1] -= val;
102 | }
103 | }
104 |
105 | /**
106 | * 复原操作
107 | * @return res
108 | */
109 | public int[] result() {
110 | int[] res = new int[diff.length];
111 | res[0] = diff[0];
112 | for (int i = 1; i < diff.length; i++) {
113 | res[i] = res[i - 1] + diff[i];
114 | }
115 | return res;
116 | }
117 | }
118 | ```
119 |
120 |
121 |
122 |
--------------------------------------------------------------------------------
/markdown/Algorithm/按权重随机选择.md:
--------------------------------------------------------------------------------
1 | # 按权重随机选择
2 |
3 | [528. 按权重随机选择](https://leetcode.cn/problems/random-pick-with-weight/)
4 |
5 |
6 |
7 | 见识过很多等概率随机选择,本片文章介绍一种「按权重随机选择」
8 |
9 | 对于样例:`w = [1, 2, 3, 4]`
10 |
11 | - 返回下标 0 的概率为 $\frac{1}{10}$
12 | - 返回下标 1 的概率为 $\frac{2}{10}$
13 | - 返回下标 2 的概率为 $\frac{3}{10}$
14 | - 返回下标 3 的概率为 $\frac{4}{10}$
15 |
16 | 这里使用**「前缀和」**➕**「二分搜索」**。是不是觉得很莫名其妙,这和前缀和、二分搜索有什么关系,不要急,一步一步的来分析!!
17 |
18 | **关于「前缀和」的详细介绍可见 [前缀和数组](./前缀和数组.html)**
19 |
20 | **关于「二分搜索」的详细介绍可见 [二分搜索](./二分搜索.html)**
21 |
22 | **关于`Random`的详细介绍可见 [Random 类](../java/Random.html)**
23 |
24 |
25 |
26 | 我们需要考虑的无非就是如何才能按权重的选择,`Random()`返回的都是等概率的
27 |
28 | 对于样例:`w = [1, 2, 3, 4]`,其「前缀和数组」可视化如下:
29 |
30 | 
31 |
32 | 随机生成一个区间为`[1, 10]`的数:
33 |
34 | - 如果值为 1 返回下标 0
35 | - 如果值为 2,3 返回下标 1
36 | - 如果值为 4,5,6 返回下标 2
37 | - 如果值为 7,8,9,10 返回下标 3
38 |
39 | 刚好上述权重和最初分析的概率是等价的!!
40 |
41 | 对于`target = 5`,返回一个大于等于 5 的最小下标,即为 2
42 |
43 | **注意:`preSum[]`相对于原数组整体向右偏移了一位**
44 |
45 | 下面给出完整代码:
46 |
47 | ```java
48 | class Solution {
49 | private int[] preSum;
50 | private Random random;
51 | public Solution(int[] w) {
52 | random = new Random();
53 | preSum = new int[w.length + 1];
54 | for (int i = 1; i < preSum.length; i++) {
55 | preSum[i] = preSum[i - 1] + w[i - 1];
56 | }
57 | }
58 |
59 | public int pickIndex() {
60 | int target = random.nextInt(preSum[preSum.length - 1]) + 1;
61 | int l = 1, r = preSum.length - 1;
62 | while (l <= r) {
63 | int mid = l - (l - r) / 2;
64 | if (target <= preSum[mid]) r = mid - 1;
65 | else l = mid + 1;
66 | }
67 | // 由于前缀和数组向右偏移了一位
68 | return l - 1;
69 | }
70 | }
71 | ```
72 |
73 |
--------------------------------------------------------------------------------
/markdown/Algorithm/排序汇总.md:
--------------------------------------------------------------------------------
1 | # 排序汇总
2 |
3 | ### 稳定性
4 |
5 | 如果完成排序后,原本有序的元素不会改变其相对的位置,表示该排序是稳定的;如果完成排序后,原本有序的元素会改变其相对的位置,表示该排序是不稳定的
6 |
7 | 举个简单的例子,如果对`[1, 2, 2, 3, 4]`进行排序,如下图所示:
8 |
9 | 
10 |
11 | ### 冒泡排序
12 |
13 | ```java
14 | public int[] sort(int[] nums) {
15 | int n = nums.length;
16 | for (int i = 0; i < n - 1; i++) { // 进行 n - 1 轮遍历,每次都将值最大元素挪到最右边
17 | boolean isChange = false; // 标记是否有交换操作
18 | for (int j = 0; j < n - i - 1; j++) { // 从头开始两两进行交换
19 | if (nums[j] > nums[j + 1]) {
20 | int t = nums[j];
21 | nums[j] = nums[j + 1];
22 | nums[j + 1] = t;
23 | isChange = true;
24 | }
25 | }
26 | if (!isChange) break; // 如果一轮一次交换都没发送,表示元素均有序,直接退出循环
27 | }
28 | return nums;
29 | }
30 | ```
31 |
32 | 时间复杂度:$O(n^2)$;空间复杂度:$O(1)$;稳定
33 |
34 | **注意:**如果数组已经有序,那么在第一轮遍历时就会退出循环,所以最好时间复杂度为 $O(n)$
35 |
36 | ### 选择排序
37 |
38 | ```java
39 | public int[] sort(int[] nums) {
40 | int n = nums.length;
41 | for (int i = 0; i < n; i++) {
42 | int minId = i;
43 | for (int j = i + 1; j < n; j++) {
44 | if (nums[minId] > nums[j]) minId = j;
45 | }
46 | int t = nums[i];
47 | nums[i] = nums[minId];
48 | nums[minId] = t;
49 | }
50 | return nums;
51 | }
52 | ```
53 |
54 | 时间复杂度:$O(n^2)$;空间复杂度:$O(1)$;不稳定
55 |
56 | 关于不稳定,举个例子`[7, 7, 2]`,那么第一轮交换后为`[2, 7, 7]`,两个 7 的相对位置发生了变化
57 |
58 | **注意:**该排序的时间复杂度与数组的特点无关,均为 $O(n^2)$
59 |
60 | ### 插入排序
61 |
62 | ```java
63 | public int[] sort(int[] nums) {
64 | public int[] sortArray(int[] nums) {
65 | int n = nums.length;
66 | for (int i = 1; i < n; i++) {
67 | int t = nums[i];
68 | for (int j = i - 1; j >= 0; j--) {
69 | if (nums[j] <= t) break;
70 | nums[j + 1] = nums[j];
71 | nums[j] = t;
72 | }
73 | }
74 | return nums;
75 | }
76 | }
77 | ```
78 |
79 | 时间复杂度:$O(n^2)$;空间复杂度:$O(1)$;稳定
80 |
81 | **注意:**如果数组已经有序,那么内层循环会第一时间退出,所以最好时间复杂度为 $O(n)$
82 |
83 | ### 归并排序
84 |
85 | **详情可见 [详解归并排序及其应用](./详解归并排序及其应用.html)**
86 |
87 | 时间复杂度:$O(nlogn)$;空间复杂度:$O(n)$;稳定
88 |
89 |
90 | ### 快速排序
91 |
92 | **详情可见 [详解快排及其应用](./详解快排及其应用.html)**
93 |
94 | 时间复杂度:$O(nlogn)$;空间复杂度:$O(logn)$ -> 递归栈所需空间;不稳定
95 |
96 | **注意:**如果数组已经有序,那么时间复杂度为 $O(n^2)$
97 |
98 | ### 堆排序
99 |
100 | **详情可见 [详解堆排序「优先队列」](./详解堆排序-优先队列.html)**
101 |
102 | 时间复杂度:$O(nlogn)$;空间复杂度:$O(1)$;不稳定
103 |
104 | ### 总结
105 |
106 | | 排序算法 | 平均时间复杂度 | 最好时间复杂度 | 最坏时间复杂度 | 空间复杂度 | 稳定性 |
107 | | :------: | :------------: | :------------: | :------------: | :-----------------: | :----: |
108 | | 冒泡排序 | $O(n^2)$ | $O(n)$ | $O(n^2)$ | $O(1)$ | 稳定 |
109 | | 选择排序 | $O(n^2)$ | $O(n^2)$ | $O(n^2)$ | $O(1)$ | 不稳定 |
110 | | 插入排序 | $O(n^2)$ | $O(n)$ | $O(n^2)$ | $O(1)$ | 稳定 |
111 | | 归并排序 | $O(nlogn)$ | $O(nlogn)$ | $O(nlogn)$ | $O(n)$ | 稳定 |
112 | | 快速排序 | $O(nlogn)$ | $O(nlogn)$ | $O(n^2)$ | $O(logn)$ -> 递归栈 | 不稳定 |
113 | | 堆排序 | $O(nlogn)$ | $O(nlogn)$ | $O(nlogn)$ | $O(1)$ | 不稳定 |
--------------------------------------------------------------------------------
/markdown/Algorithm/接雨水-变题.md:
--------------------------------------------------------------------------------
1 | # 接雨水「变题」
2 |
3 | [42. 接雨水](https://leetcode.cn/problems/trapping-rain-water/)
4 |
5 |
6 |
7 | ```java
8 | // 单调栈
9 | // 时间复杂度 : O(n)
10 | // 空间复杂度 : O(n)
11 | public int trap(int[] height) {
12 | int ans = 0;
13 | Deque s = new ArrayDeque<>();
14 | for (int i = 0; i < height.length; i++) {
15 | while (!s.isEmpty() && height[s.peek()] < height[i]) {
16 | int top = s.poll();
17 | if (s.isEmpty()) break;
18 | int left = s.peek();
19 | int curWidth = i - left - 1;
20 | int curHeight = Math.min(height[i], height[left]) - height[top];
21 | ans += curHeight * curWidth;
22 | }
23 | s.push(i);
24 | }
25 | return ans;
26 | }
27 |
28 | // 双指针
29 | // 时间复杂度 : O(n)
30 | // 空间复杂度 : O(1)
31 | public int trap(int[] height) {
32 | int curH = 0, ans = 0;
33 | int l = 0, r = height.length - 1;
34 | while (l < r) {
35 | if (height[l] <= height[r]) {
36 | ans += Math.max(0, curH - height[l]);
37 | curH = Math.max(curH, height[l]);
38 | l++;
39 | } else {
40 | ans += Math.max(0, curH - height[r]);
41 | curH = Math.max(curH, height[r]);
42 | r--;
43 | }
44 | }
45 | return ans;
46 | }
47 | ```
48 |
49 | ### 变题一:二维接雨水
50 |
51 | **题目详情可见 [接雨水 II](https://leetcode.cn/problems/trapping-rain-water-ii/)**
52 |
53 | 木桶原则,从最外圈开始向内收缩
54 |
55 | ```java
56 | public int trapRainWater(int[][] heightMap) {
57 | int m = heightMap.length, n = heightMap[0].length;
58 | boolean[][] vis = new boolean[m][n];
59 | Queue q = new PriorityQueue<>((a, b) -> a[2] - b[2]);
60 | for (int i = 0; i < m; i++) {
61 | q.offer(new int[]{i, 0, heightMap[i][0]});
62 | q.offer(new int[]{i, n - 1, heightMap[i][n - 1]});
63 | vis[i][0] = true;
64 | vis[i][n - 1] = true;
65 | }
66 | for (int i = 0; i < n; i++) {
67 | q.offer(new int[]{0, i, heightMap[0][i]});
68 | q.offer(new int[]{m - 1, i, heightMap[m - 1][i]});
69 | vis[0][i] = true;
70 | vis[m - 1][i] = true;
71 | }
72 | int[][] dirs = { {1, 0}, {-1, 0}, {0, 1}, {0, -1} };
73 | int ans = 0;
74 | while (!q.isEmpty()) {
75 | int[] cur = q.poll();
76 | for (int[] dir : dirs) {
77 | int nx = cur[0] + dir[0], ny = cur[1] + dir[1];
78 | if (nx < 0 || nx >= m || ny < 0 || ny >= n || vis[nx][ny]) continue;
79 | ans += Math.max(0, cur[2] - heightMap[nx][ny]);
80 | q.offer(new int[]{nx, ny, Math.max(cur[2], heightMap[nx][ny])});
81 | vis[nx][ny] = true;
82 | }
83 | }
84 | return ans;
85 | }
86 | ```
87 |
88 |
--------------------------------------------------------------------------------
/markdown/Algorithm/数据流中位数.md:
--------------------------------------------------------------------------------
1 | # [数据流中位数](https://leetcode-cn.com/problems/find-median-from-data-stream/)
2 |
3 |
4 |
5 | ## 思路
6 |
7 | 维护两个优先队列:小根堆 & 大根堆
8 |
9 | 小根堆:存放右半边最小值元素
10 |
11 | 大根堆:存饭左半边最大值元素
12 |
13 | 保持两个优先队列大小始终相等或相差 1
14 |
15 |
16 |
17 | 添加元素:如果需要加入大根堆中,则需要先插入小根堆,然后弹出小根堆顶元素加入大根堆中,这样才可以保证`maxQ 中所有元素 < minQ 中的所有元素`;反之亦然
18 |
19 | 返回中位数:如果两个优先队列大小相等,则返回堆顶元素和的平均值;如果不相等,则返回元素值更多的堆顶
20 |
21 | ## 实现
22 |
23 | ```java
24 | class MedianFinder {
25 | // 小根堆:存放右半边大值元素
26 | Queue minQ;
27 | // 大根堆:存放左半边小值元素
28 | Queue maxQ;
29 |
30 | public MedianFinder() {
31 | minQ = new PriorityQueue<>();
32 | maxQ = new PriorityQueue<>((o1, o2) -> (o2 - o1));
33 | }
34 |
35 | public void addNum(int num) {
36 | // 始终保持 maxQ 中所有元素 < minQ 中的所有元素
37 | if (maxQ.size() <= minQ.size()) {
38 | minQ.offer(num);
39 | maxQ.offer(minQ.poll());
40 | } else {
41 | maxQ.offer(num);
42 | minQ.offer(maxQ.poll());
43 | }
44 | }
45 |
46 | public double findMedian() {
47 | if (minQ.size() == maxQ.size()) return (minQ.peek() + maxQ.peek()) / 2.0;
48 | return minQ.size() > maxQ.size() ? minQ.peek() : maxQ.peek();
49 | }
50 | }
51 | ```
52 |
53 |
--------------------------------------------------------------------------------
/markdown/Algorithm/最小栈-最大栈.md:
--------------------------------------------------------------------------------
1 | # 最小栈 & 最大栈
2 |
3 | [155. 最小栈](https://leetcode-cn.com/problems/min-stack/)
4 |
5 | [895. 最大频率栈](https://leetcode-cn.com/problems/maximum-frequency-stack/)
6 |
7 | ### 最小栈
8 |
9 | **思路:**维护一个调用`push()`每个元素后的最小值栈
10 |
11 | ```java
12 | class MinStack {
13 |
14 | private Stack stack;
15 | private Stack minStack;
16 |
17 | public MinStack() {
18 | stack = new Stack<>();
19 | minStack = new Stack<>();
20 | }
21 |
22 | public void push(int val) {
23 | stack.push(val);
24 | if (minStack.isEmpty()) minStack.push(val);
25 | else if (getMin() <= val) minStack.push(getMin());
26 | else if (getMin() > val) minStack.push(val);
27 | }
28 |
29 | public void pop() {
30 | stack.pop();
31 | minStack.pop();
32 | }
33 |
34 | public int top() {
35 | return stack.peek();
36 | }
37 |
38 | public int getMin() {
39 | return minStack.peek();
40 | }
41 | }
42 | ```
43 |
44 | ### 最大栈
45 |
46 | ```java
47 | public class FreqStack {
48 | // 记录最大频率
49 | private int maxFreq;
50 | // 记录每个元素的频率
51 | private Map valToFreq;
52 | // 记录某一频率的所有元素
53 | private Map> freqToVal;
54 |
55 | public FreqStack() {
56 | maxFreq = 0;
57 | valToFreq = new HashMap<>();
58 | freqToVal = new HashMap<>();
59 | }
60 |
61 | public void push(int val) {
62 | // 获得 val 的频率
63 | int freq = valToFreq.getOrDefault(val, 0) + 1;
64 | // 更新 val to freq
65 | valToFreq.put(val, freq);
66 | // 更新 freq to val
67 | freqToVal.putIfAbsent(freq, new Stack<>());
68 | freqToVal.get(freq).push(val);
69 | // 更新 maxFreq
70 | maxFreq = Math.max(maxFreq, freq);
71 | }
72 |
73 | public int pop() {
74 | // 弹出一个频率最大的元素
75 | Stack valStack = freqToVal.get(maxFreq);
76 | int v = valStack.pop();
77 | // 更新 val to freq
78 | valToFreq.put(v, valToFreq.get(v) - 1);
79 | // 更新 maxFreq
80 | if (valStack.isEmpty()) {
81 | maxFreq--;
82 | }
83 | return v;
84 | }
85 | }
86 | ```
--------------------------------------------------------------------------------
/markdown/Algorithm/最短路径-Dijkstra.md:
--------------------------------------------------------------------------------
1 | # 最短路径-Dijkstra
2 |
3 | [743. 网络延迟时间](https://leetcode-cn.com/problems/network-delay-time)
4 |
5 | [1514. 概率最大的路径](https://leetcode-cn.com/problems/path-with-maximum-probability)
6 |
7 | [1631. 最小体力消耗路径](https://leetcode-cn.com/problems/path-with-minimum-effort)
8 |
9 | ## Dijkstra
10 |
11 | ### 适用条件
12 |
13 | **加权有向图,没有负权重边**
14 |
15 | ### 模版
16 |
17 | ```java
18 | public class State {
19 | // 节点 id
20 | public int id;
21 | // 当前节点距离起点的距离
22 | public int distFromStart;
23 | public State(int id, int distFromStart) {
24 | this.id = id;
25 | this.distFromStart = distFromStart;
26 | }
27 | }
28 |
29 | public class Dijkstra {
30 | public int[] dijkstra(List[] graph, int start) {
31 | // 节点数量
32 | int n = graph.length;
33 | // 记录每个点到 start 的最短距离
34 | int[] distTo = new int[n];
35 | // 初始化为最大值
36 | Arrays.fill(distTo, Integer.MAX_VALUE);
37 | // start to start = 0
38 | distTo[start] = 0;
39 |
40 | // 优先队列,按照 distFromStart 排序(贪心思想)
41 | Queue pq = new PriorityQueue<>(Comparator.comparingInt(o -> o.distFromStart));
42 | // 添加起点
43 | pq.offer(new State(start, 0));
44 |
45 | while (!pq.isEmpty()) {
46 | State curState = pq.poll();
47 | int curNodeId = curState.id;
48 | int curDistFromStart = curState.distFromStart;
49 | // 非最优,直接跳过
50 | if (curDistFromStart > distTo[curNodeId]) {
51 | continue;
52 | }
53 | for (int nextNodeId : adj(curNodeId)) {
54 | int distToNextNode = distTo[curNodeId] + weight(curNodeId, nextNodeId);
55 | // 更新到下一个节点的距离
56 | if (distToNextNode < distTo[nextNodeId]) {
57 | distTo[nextNodeId] = distToNextNode;
58 | pq.offer(new State(nextNodeId, distToNextNode));
59 | }
60 | }
61 | }
62 | return distTo;
63 | }
64 |
65 | /**
66 | * 权重函数
67 | * @param from from 顶点
68 | * @param to to 顶点
69 | * @return 返回 from -> to 权重
70 | */
71 | private int weight(int from, int to) {
72 | return 0;
73 | }
74 |
75 | /**
76 | * 邻接节点
77 | * @param id 当且节点 Id
78 | * @return 返回当前节点的邻接节点
79 | */
80 | private List adj(int id) {
81 | return new ArrayList<>();
82 | }
83 | }
84 | ```
85 |
86 | ### 扩展
87 |
88 | **如果我只想计算起点 `start` 到某一个终点 `end` 的最短路径,是否可以修改算法,提升一些效率?**
89 |
90 | ```java
91 | // 输入起点 start 和终点 end,计算起点到终点的最短距离
92 | int dijkstra(List[] graph, int start, int end) {
93 |
94 | // ...
95 |
96 | while (!pq.isEmpty()) {
97 | State curState = pq.poll();
98 | int curNodeId = curState.id;
99 | int curDistFromStart = curState.distFromStart;
100 |
101 | // 在这里加一个判断就行了,其他代码不用改
102 | if (curNodeID == end) {
103 | return curDistFromStart;
104 | }
105 |
106 | if (curDistFromStart > distTo[curNodeID]) {
107 | continue;
108 | }
109 |
110 | // ...
111 | }
112 |
113 | // 如果运行到这里,说明从 start 无法走到 end
114 | return Integer.MAX_VALUE;
115 | }
116 | ```
117 |
118 | 因为优先级队列自动排序的性质,**每次**从队列里面拿出来的都是 `distFromStart` 值最小的,所以当你**第一次**从队列中拿出终点 `end` 时,此时的 `distFromStart` 对应的值就是从 `start` 到 `end` 的最短距离
119 |
120 | 这个算法较之前的实现提前 return 了,所以效率有一定的提高
121 |
--------------------------------------------------------------------------------
/markdown/Algorithm/最长公共子序列-变题.md:
--------------------------------------------------------------------------------
1 | # 最长公共子序列「变题」
2 |
3 | [1143. 最长公共子序列](https://leetcode.cn/problems/longest-common-subsequence)
4 |
5 |
6 |
7 | 开头先来一个小插曲,关于「最长公共子序列」详细总结可见 **[最长公共子序列 (LCS):「模版」&「输出」](./最长公共子序列-模版-输出.html)**
8 |
9 | ```java
10 | public int longestCommonSubsequence(String text1, String text2) {
11 | int n1 = text1.length(), n2 = text2.length();
12 | int[][] dp = new int[n1 + 1][n2 + 1];
13 | for (int i = 1; i <= n1; i++) {
14 | for (int j = 1; j <= n2; j++) {
15 | if (text1.charAt(i - 1) == text2.charAt(j - 1)) dp[i][j] = dp[i - 1][j - 1] + 1;
16 | else dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - 1]);
17 | }
18 | }
19 | return dp[n1][n2];
20 | }
21 | ```
22 |
23 | ### 变题一:空间优化
24 |
25 | ```java
26 | public int longestCommonSubsequence(String text1, String text2) {
27 | int n1 = text1.length(), n2 = text2.length();
28 | int[] dp = new int[n2 + 1];
29 | for (int i = 1; i <= n1; i++) {
30 | int prevUp = 0;
31 | for (int j = 1; j <= n2; j++) {
32 | int t = prevUp;
33 | prevUp = dp[j];
34 | if (text1.charAt(i - 1) == text2.charAt(j - 1)) dp[j] = t + 1;
35 | else dp[j] = Math.max(dp[j], dp[j - 1]);
36 | }
37 | }
38 | return dp[n2];
39 | }
40 | ```
41 |
42 | ### 变题二:输出最长公共子序列
43 |
44 | ```java
45 | public int longestCommonSubsequence(String text1, String text2) {
46 | int n1 = text1.length(), n2 = text2.length();
47 | int[][] dp = new int[n1 + 1][n2 + 1];
48 | for (int i = 1; i <= n1; i++) {
49 | for (int j = 1; j <= n2; j++) {
50 | if (text1.charAt(i - 1) == text2.charAt(j - 1)) dp[i][j] = dp[i - 1][j - 1] + 1;
51 | else dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - 1]);
52 | }
53 | }
54 | StringBuffer sb = new StringBuffer();
55 | int i = n1, j = n2;
56 | while (i > 0 && j > 0) {
57 | if (text1.charAt(i - 1) == text2.charAt(j - 1)) {
58 | sb.append(text1.charAt(i - 1));
59 | i--; j--;
60 | } else if (dp[i - 1][j] < dp[i][j - 1]) {
61 | j--;
62 | } else i--;
63 | }
64 | System.out.println(sb.reverse().toString());
65 | return dp[n1][n2];
66 | }
67 | ```
68 |
69 |
--------------------------------------------------------------------------------
/markdown/Algorithm/最长递增子序列-变题.md:
--------------------------------------------------------------------------------
1 | # 最长递增子序列「变题」
2 |
3 | [300. 最长递增子序列](https://leetcode.cn/problems/longest-increasing-subsequence/)
4 |
5 |
6 |
7 | 开头先来一个小插曲,关于「最长递增子序列」问题的总结可见 **[动态规划设计:最长递增子序列](./动态规划设计:最长递增子序列.html)**
8 |
9 | ```java
10 | // 时间复杂度 : O(n^2)
11 | // 空间复杂度 : O(n)
12 | public int lengthOfLIS(int[] nums) {
13 | int n = nums.length, ans = 0;
14 | int[] dp = new int[n];
15 | Arrays.fill(dp, 1);
16 | for (int i = 0; i < n; i++) {
17 | for (int j = 0; j < i; j++) {
18 | if (nums[i] > nums[j]) dp[i] = Math.max(dp[i], dp[j] + 1);
19 | }
20 | ans = Math.max(ans, dp[i]);
21 | }
22 | return ans;
23 | }
24 | ```
25 |
26 | ### 变题一:时间优化成 O(nlogn)
27 |
28 | ```java
29 | // 时间复杂度 : O(nlogn)
30 | // 空间复杂度 : O(n)
31 | public int lengthOfLIS(int[] nums) {
32 | int n = nums.length;
33 | int[] top = new int[n];
34 | int piles = 0;
35 | for (int i = 0; i < n; i++) {
36 | int poker = nums[i];
37 | int l = 0, r = piles;
38 | while (l < r) {
39 | int m = l + r >> 1;
40 | if (top[m] >= poker) r = m;
41 | else l = m + 1;
42 | }
43 | if (l == piles) top[piles++] = poker;
44 | else top[l] = poker;
45 | }
46 | return piles;
47 | }
48 | ```
49 |
50 | ### 变题二:输出最长上升子序列,字典序最小
51 |
52 | **题目详情可见 [最长上升子序列(三)](https://www.nowcoder.com/practice/9cf027bf54714ad889d4f30ff0ae5481)**
53 |
54 | ```java
55 | public int[] LIS (int[] nums) {
56 | int n = nums.length;
57 | // p 记录每个数在哪个堆中
58 | int[] top = new int[n], p = new int[n];
59 | int piles = 0;
60 | for (int i = 0; i < n; i++) {
61 | int poker = nums[i];
62 | int l = 0, r = piles;
63 | while (l < r) {
64 | int m = l + r >> 1;
65 | if (top[m] >= poker) r = m;
66 | else l = m + 1;
67 | }
68 | if (l == piles) {
69 | top[piles++] = poker;
70 | p[i] = piles;
71 | } else {
72 | top[l] = poker;
73 | p[i] = l + 1;
74 | }
75 | }
76 |
77 | int[] ans = new int[piles];
78 | for (int i = n - 1; i >= 0; i--) {
79 | if (p[i] == piles) ans[--piles] = nums[i];
80 | }
81 | return ans;
82 | }
83 | ```
84 |
85 | ### 变题三:最长非上升子序列,输出且字典序最小
86 |
87 | ```java
88 | public int[] LIS (int[] nums) {
89 | int n = nums.length;
90 | // p 记录每个数在哪个堆中
91 | int[] top = new int[n], p = new int[n];
92 | int piles = 0;
93 | for (int i = 0; i < n; i++) {
94 | int poker = nums[i];
95 | int l = 0, r = piles;
96 | while (l < r) {
97 | int m = l + r >> 1;
98 | // 反过来
99 | if (top[m] < poker) r = m;
100 | else l = m + 1;
101 | }
102 | if (l == piles) {
103 | top[piles++] = poker;
104 | p[i] = piles;
105 | } else {
106 | top[l] = poker;
107 | p[i] = l + 1;
108 | }
109 | }
110 | int cp = 0;
111 | int[] ans = new int[piles];
112 | // 正向遍历
113 | for (int i = 0; i < n; i++) {
114 | if (p[i] == cp + 1) ans[cp++] = nums[i];
115 | }
116 | return ans;
117 | }
118 | ```
119 |
120 |
--------------------------------------------------------------------------------
/markdown/Algorithm/有效的括号-变题.md:
--------------------------------------------------------------------------------
1 | # 有效的括号「变题」
2 |
3 | [20. 有效的括号](https://leetcode.cn/problems/valid-parentheses/)
4 |
5 |
6 |
7 | 开头先来一个小插曲,关于「括号」相关的总结可见 **[秒杀所有括号类问题](./秒杀所有括号类问题.html)**
8 |
9 | ```java
10 | public boolean isValid(String s) {
11 | Deque st = new ArrayDeque<>();
12 | for (char c : s.toCharArray()) {
13 | if (c == '(' || c == '[' || c == '{') st.push(c);
14 | else if (!st.isEmpty()) {
15 | if (st.poll() != f(c)) return false;
16 | } else return false;
17 | }
18 | return st.isEmpty();
19 | }
20 | private char f(char c) {
21 | if (c == ')') return '(';
22 | else if (c == '}') return '{';
23 | return '[';
24 | }
25 | ```
26 |
27 | ### 变题一:不要求左括号必须以正确的顺序闭合
28 |
29 | 也就是去掉了 **[有效的括号](https://leetcode.cn/problems/valid-parentheses/)** 中的要求二!!
30 |
31 | 🌰 举个例子:`[(])`这种情况也是满足要求滴!
32 |
33 | ```java
34 | public boolean isValid(String s) {
35 | int[] cnt = new int[3];
36 | for (char c : s.toCharArray()) {
37 | if (c == '(' || c == '[' || c == '{') cnt[f(c)]++;
38 | else if (--cnt[f(c)] < 0) return false;
39 | }
40 | return cnt[0] == 0 && cnt[1] == 0 && cnt[2] == 0;
41 | }
42 | private int f(char c) {
43 | if (c == '(' || c == ')') return 0;
44 | if (c == '[' || c == ']') return 1;
45 | return 2;
46 | }
47 | ```
48 |
49 | ### 变题二:要求必须按 { [ ( 的顺序进行关闭
50 |
51 | 🌰 举个例子:`{[()]}, {}[()]`是符合要求的;`[{()}]`是不符合要求的
52 |
53 | 换句话说,`{`的优先级最高,它可以包含其它两种类型的括号;而其它两种类型的括号不能包含它。其它两种同理!
54 |
55 | **思路:**分别为` { [ (`设置权重`2 1 0`,入栈时判断栈顶优先级是否低于当前左括号优先级,如果低于,则非法
56 |
57 | ```java
58 | public boolean isValid(String s) {
59 | // 技巧:栈中直接存优先级
60 | Deque st = new ArrayDeque<>();
61 | for (char c : s.toCharArray()) {
62 | int w = f(c);
63 | if (c == '(' || c == '[' || c == '{') {
64 | // 栈不为空 且 栈顶优先级低于 c
65 | if (!st.isEmpty() && st.peek() < w) return false;
66 | st.push(w);
67 | } else if (!st.isEmpty()) {
68 | if (st.poll() != w) return false;
69 | } else return false;
70 | }
71 | return st.isEmpty();
72 | }
73 | private char f(char c) {
74 | if (c == '(' || c == ')') return 0; // 低
75 | if (c == '[' || c == ']') return 1; // 中
76 | return 2; // 高
77 | }
78 | ```
--------------------------------------------------------------------------------
/markdown/Algorithm/比较版本号-变题.md:
--------------------------------------------------------------------------------
1 | # 比较版本号「变题」
2 |
3 | [165. 比较版本号](https://leetcode.cn/problems/compare-version-numbers/)
4 |
5 |
6 |
7 | ```java
8 | public int compareVersion(String version1, String version2) {
9 | String[] sp1 = version1.split("\\.");
10 | String[] sp2 = version2.split("\\.");
11 | int n1 = sp1.length, n2 = sp2.length;
12 | int i = 0, j = 0;
13 | while (i < n1 || j < n2) {
14 | int s1 = 0, s2 = 0;
15 | if (i < n1) s1 = Integer.parseInt(sp1[i++]);
16 | if (j < n2) s2 = Integer.parseInt(sp2[j++]);
17 | if (s1 != s2) return s1 < s2 ? -1 : 1;
18 | }
19 | return 0;
20 | }
21 | ```
22 |
23 | ### 变题一:不允许使用`String.split()`方法
24 |
25 | ```java
26 | public int compareVersion(String version1, String version2) {
27 | int n1 = version1.length(), n2 = version2.length();
28 | int i = 0, j = 0;
29 | while (i < n1 || j < n2) {
30 | int s1 = 0, s2 = 0;
31 |
32 | int t1 = i, t2 = j;
33 | while (i < n1 && version1.charAt(i) != '.') i++;
34 | while (j < n2 && version2.charAt(j) != '.') j++;
35 |
36 | if (t1 != i) s1 = Integer.parseInt(version1.substring(t1, i));
37 | if (t2 != j) s2 = Integer.parseInt(version2.substring(t2, j));
38 |
39 | if (s1 != s2) return s1 < s2 ? -1 : 1;
40 |
41 | if (i < n1) i++;
42 | if (j < n2) j++;
43 | }
44 | return 0;
45 | }
46 | ```
--------------------------------------------------------------------------------
/markdown/Algorithm/求素数的三种方法.md:
--------------------------------------------------------------------------------
1 | # 求素数的三种方法
2 |
3 | [1175. 质数排列](https://leetcode.cn/problems/prime-arrangements/)
4 |
5 | [204. 计数质数](https://leetcode.cn/problems/count-primes/)
6 |
7 | ### 暴力
8 |
9 | ```java
10 | private List getPrime(int n) {
11 | List list = new ArrayList<>();
12 | for (int i = 2; i <= n; i++) {
13 | boolean ok = true;
14 | // 注意:j * j <= i 即可
15 | for (int j = 2; j * j <= i && ok; j++) {
16 | if (i % j == 0) ok = false;
17 | }
18 | if (ok) list.add(i);
19 | }
20 | return list;
21 | }
22 | ```
23 |
24 | ### 埃氏筛法 (推荐)
25 |
26 | 整个过程如图所示:
27 |
28 |
注:当`j + 1 >= diff.length`时,不需要进行`diff[j + 1] -= val`操作
44 |
45 | **问题二:**怎么通过`diff[]`得到更新后的数组呢?????
46 |
47 | ```java
48 | // 复原操作
49 | int[] res = new int[n];
50 | // 下标为 0 的元素相等
51 | res[0] = diff[0];
52 | for (int i = 1; i < n; i++) {
53 | res[i] = diff[i] + res[i - 1];
54 | }
55 | ```
56 |
57 | **问题三:**`diff[]`原理
58 |
59 | 当我们需要对区间`[i, j]`进行`+ val`操作时,我们对`diff[i] += val; diff[j + 1] -= val;`
60 |
61 | 在复原操作时,当我们求`res[i]`时,`res[i - 1]`没有变,而`diff[i]`增加了 3,所以`res[i]`增加 3
62 |
63 | 当我们求`res[i + 1]`时,`res[i]`增加了 3,而`diff[i + 1]`没有变,故`res[i + 1] = diff[i + 1] + res[i]`增加 3。即:虽然`diff[i + 1]`没有变,但是`res[i]`对后面的`res[i + 1]`有一个累积作用
64 |
65 | 当我们求`res[j + 1]`时,`res[j]`增加了 3,而`diff[j + 1]`减少了 3,故`res[j + 1] = diff[j + 1] + res[j]`增加没有变。即:我们在`j + 1`的时候,把上述的累积作用去除了,所以`j + 1`后面的元素不受影响
66 |
67 |
68 |
69 | **完整模版**
70 |
71 | ```java
72 | public class Difference {
73 |
74 | /**
75 | * 差分数组
76 | */
77 | private final int[] diff;
78 |
79 | /**
80 | * 初始化差分数组
81 | * @param nums nums
82 | */
83 | public Difference(int[] nums) {
84 | assert nums.length > 0;
85 | diff = new int[nums.length];
86 | diff[0] = nums[0];
87 | for (int i = 1; i < nums.length; i++) {
88 | diff[i] = nums[i] - nums[i - 1];
89 | }
90 | }
91 |
92 | /**
93 | * 对区间 [i, j] 增加 val(val 可为负数)
94 | * @param i i
95 | * @param j j
96 | * @param val val
97 | */
98 | public void increment(int i, int j, int val) {
99 | diff[i] += val;
100 | if (j + 1 < diff.length) {
101 | diff[j + 1] -= val;
102 | }
103 | }
104 |
105 | /**
106 | * 复原操作
107 | * @return res
108 | */
109 | public int[] result() {
110 | int[] res = new int[diff.length];
111 | res[0] = diff[0];
112 | for (int i = 1; i < diff.length; i++) {
113 | res[i] = res[i - 1] + diff[i];
114 | }
115 | return res;
116 | }
117 | }
118 | ```
119 |
120 |
121 |
122 |
--------------------------------------------------------------------------------
/markdown/Algorithm/按权重随机选择.md:
--------------------------------------------------------------------------------
1 | # 按权重随机选择
2 |
3 | [528. 按权重随机选择](https://leetcode.cn/problems/random-pick-with-weight/)
4 |
5 |
6 |
7 | 见识过很多等概率随机选择,本片文章介绍一种「按权重随机选择」
8 |
9 | 对于样例:`w = [1, 2, 3, 4]`
10 |
11 | - 返回下标 0 的概率为 $\frac{1}{10}$
12 | - 返回下标 1 的概率为 $\frac{2}{10}$
13 | - 返回下标 2 的概率为 $\frac{3}{10}$
14 | - 返回下标 3 的概率为 $\frac{4}{10}$
15 |
16 | 这里使用**「前缀和」**➕**「二分搜索」**。是不是觉得很莫名其妙,这和前缀和、二分搜索有什么关系,不要急,一步一步的来分析!!
17 |
18 | **关于「前缀和」的详细介绍可见 [前缀和数组](./前缀和数组.html)**
19 |
20 | **关于「二分搜索」的详细介绍可见 [二分搜索](./二分搜索.html)**
21 |
22 | **关于`Random`的详细介绍可见 [Random 类](../java/Random.html)**
23 |
24 |
25 |
26 | 我们需要考虑的无非就是如何才能按权重的选择,`Random()`返回的都是等概率的
27 |
28 | 对于样例:`w = [1, 2, 3, 4]`,其「前缀和数组」可视化如下:
29 |
30 | 
31 |
32 | 随机生成一个区间为`[1, 10]`的数:
33 |
34 | - 如果值为 1 返回下标 0
35 | - 如果值为 2,3 返回下标 1
36 | - 如果值为 4,5,6 返回下标 2
37 | - 如果值为 7,8,9,10 返回下标 3
38 |
39 | 刚好上述权重和最初分析的概率是等价的!!
40 |
41 | 对于`target = 5`,返回一个大于等于 5 的最小下标,即为 2
42 |
43 | **注意:`preSum[]`相对于原数组整体向右偏移了一位**
44 |
45 | 下面给出完整代码:
46 |
47 | ```java
48 | class Solution {
49 | private int[] preSum;
50 | private Random random;
51 | public Solution(int[] w) {
52 | random = new Random();
53 | preSum = new int[w.length + 1];
54 | for (int i = 1; i < preSum.length; i++) {
55 | preSum[i] = preSum[i - 1] + w[i - 1];
56 | }
57 | }
58 |
59 | public int pickIndex() {
60 | int target = random.nextInt(preSum[preSum.length - 1]) + 1;
61 | int l = 1, r = preSum.length - 1;
62 | while (l <= r) {
63 | int mid = l - (l - r) / 2;
64 | if (target <= preSum[mid]) r = mid - 1;
65 | else l = mid + 1;
66 | }
67 | // 由于前缀和数组向右偏移了一位
68 | return l - 1;
69 | }
70 | }
71 | ```
72 |
73 |
--------------------------------------------------------------------------------
/markdown/Algorithm/排序汇总.md:
--------------------------------------------------------------------------------
1 | # 排序汇总
2 |
3 | ### 稳定性
4 |
5 | 如果完成排序后,原本有序的元素不会改变其相对的位置,表示该排序是稳定的;如果完成排序后,原本有序的元素会改变其相对的位置,表示该排序是不稳定的
6 |
7 | 举个简单的例子,如果对`[1, 2, 2, 3, 4]`进行排序,如下图所示:
8 |
9 | 
10 |
11 | ### 冒泡排序
12 |
13 | ```java
14 | public int[] sort(int[] nums) {
15 | int n = nums.length;
16 | for (int i = 0; i < n - 1; i++) { // 进行 n - 1 轮遍历,每次都将值最大元素挪到最右边
17 | boolean isChange = false; // 标记是否有交换操作
18 | for (int j = 0; j < n - i - 1; j++) { // 从头开始两两进行交换
19 | if (nums[j] > nums[j + 1]) {
20 | int t = nums[j];
21 | nums[j] = nums[j + 1];
22 | nums[j + 1] = t;
23 | isChange = true;
24 | }
25 | }
26 | if (!isChange) break; // 如果一轮一次交换都没发送,表示元素均有序,直接退出循环
27 | }
28 | return nums;
29 | }
30 | ```
31 |
32 | 时间复杂度:$O(n^2)$;空间复杂度:$O(1)$;稳定
33 |
34 | **注意:**如果数组已经有序,那么在第一轮遍历时就会退出循环,所以最好时间复杂度为 $O(n)$
35 |
36 | ### 选择排序
37 |
38 | ```java
39 | public int[] sort(int[] nums) {
40 | int n = nums.length;
41 | for (int i = 0; i < n; i++) {
42 | int minId = i;
43 | for (int j = i + 1; j < n; j++) {
44 | if (nums[minId] > nums[j]) minId = j;
45 | }
46 | int t = nums[i];
47 | nums[i] = nums[minId];
48 | nums[minId] = t;
49 | }
50 | return nums;
51 | }
52 | ```
53 |
54 | 时间复杂度:$O(n^2)$;空间复杂度:$O(1)$;不稳定
55 |
56 | 关于不稳定,举个例子`[7, 7, 2]`,那么第一轮交换后为`[2, 7, 7]`,两个 7 的相对位置发生了变化
57 |
58 | **注意:**该排序的时间复杂度与数组的特点无关,均为 $O(n^2)$
59 |
60 | ### 插入排序
61 |
62 | ```java
63 | public int[] sort(int[] nums) {
64 | public int[] sortArray(int[] nums) {
65 | int n = nums.length;
66 | for (int i = 1; i < n; i++) {
67 | int t = nums[i];
68 | for (int j = i - 1; j >= 0; j--) {
69 | if (nums[j] <= t) break;
70 | nums[j + 1] = nums[j];
71 | nums[j] = t;
72 | }
73 | }
74 | return nums;
75 | }
76 | }
77 | ```
78 |
79 | 时间复杂度:$O(n^2)$;空间复杂度:$O(1)$;稳定
80 |
81 | **注意:**如果数组已经有序,那么内层循环会第一时间退出,所以最好时间复杂度为 $O(n)$
82 |
83 | ### 归并排序
84 |
85 | **详情可见 [详解归并排序及其应用](./详解归并排序及其应用.html)**
86 |
87 | 时间复杂度:$O(nlogn)$;空间复杂度:$O(n)$;稳定
88 |
89 |
90 | ### 快速排序
91 |
92 | **详情可见 [详解快排及其应用](./详解快排及其应用.html)**
93 |
94 | 时间复杂度:$O(nlogn)$;空间复杂度:$O(logn)$ -> 递归栈所需空间;不稳定
95 |
96 | **注意:**如果数组已经有序,那么时间复杂度为 $O(n^2)$
97 |
98 | ### 堆排序
99 |
100 | **详情可见 [详解堆排序「优先队列」](./详解堆排序-优先队列.html)**
101 |
102 | 时间复杂度:$O(nlogn)$;空间复杂度:$O(1)$;不稳定
103 |
104 | ### 总结
105 |
106 | | 排序算法 | 平均时间复杂度 | 最好时间复杂度 | 最坏时间复杂度 | 空间复杂度 | 稳定性 |
107 | | :------: | :------------: | :------------: | :------------: | :-----------------: | :----: |
108 | | 冒泡排序 | $O(n^2)$ | $O(n)$ | $O(n^2)$ | $O(1)$ | 稳定 |
109 | | 选择排序 | $O(n^2)$ | $O(n^2)$ | $O(n^2)$ | $O(1)$ | 不稳定 |
110 | | 插入排序 | $O(n^2)$ | $O(n)$ | $O(n^2)$ | $O(1)$ | 稳定 |
111 | | 归并排序 | $O(nlogn)$ | $O(nlogn)$ | $O(nlogn)$ | $O(n)$ | 稳定 |
112 | | 快速排序 | $O(nlogn)$ | $O(nlogn)$ | $O(n^2)$ | $O(logn)$ -> 递归栈 | 不稳定 |
113 | | 堆排序 | $O(nlogn)$ | $O(nlogn)$ | $O(nlogn)$ | $O(1)$ | 不稳定 |
--------------------------------------------------------------------------------
/markdown/Algorithm/接雨水-变题.md:
--------------------------------------------------------------------------------
1 | # 接雨水「变题」
2 |
3 | [42. 接雨水](https://leetcode.cn/problems/trapping-rain-water/)
4 |
5 |
6 |
7 | ```java
8 | // 单调栈
9 | // 时间复杂度 : O(n)
10 | // 空间复杂度 : O(n)
11 | public int trap(int[] height) {
12 | int ans = 0;
13 | Deque s = new ArrayDeque<>();
14 | for (int i = 0; i < height.length; i++) {
15 | while (!s.isEmpty() && height[s.peek()] < height[i]) {
16 | int top = s.poll();
17 | if (s.isEmpty()) break;
18 | int left = s.peek();
19 | int curWidth = i - left - 1;
20 | int curHeight = Math.min(height[i], height[left]) - height[top];
21 | ans += curHeight * curWidth;
22 | }
23 | s.push(i);
24 | }
25 | return ans;
26 | }
27 |
28 | // 双指针
29 | // 时间复杂度 : O(n)
30 | // 空间复杂度 : O(1)
31 | public int trap(int[] height) {
32 | int curH = 0, ans = 0;
33 | int l = 0, r = height.length - 1;
34 | while (l < r) {
35 | if (height[l] <= height[r]) {
36 | ans += Math.max(0, curH - height[l]);
37 | curH = Math.max(curH, height[l]);
38 | l++;
39 | } else {
40 | ans += Math.max(0, curH - height[r]);
41 | curH = Math.max(curH, height[r]);
42 | r--;
43 | }
44 | }
45 | return ans;
46 | }
47 | ```
48 |
49 | ### 变题一:二维接雨水
50 |
51 | **题目详情可见 [接雨水 II](https://leetcode.cn/problems/trapping-rain-water-ii/)**
52 |
53 | 木桶原则,从最外圈开始向内收缩
54 |
55 | ```java
56 | public int trapRainWater(int[][] heightMap) {
57 | int m = heightMap.length, n = heightMap[0].length;
58 | boolean[][] vis = new boolean[m][n];
59 | Queue q = new PriorityQueue<>((a, b) -> a[2] - b[2]);
60 | for (int i = 0; i < m; i++) {
61 | q.offer(new int[]{i, 0, heightMap[i][0]});
62 | q.offer(new int[]{i, n - 1, heightMap[i][n - 1]});
63 | vis[i][0] = true;
64 | vis[i][n - 1] = true;
65 | }
66 | for (int i = 0; i < n; i++) {
67 | q.offer(new int[]{0, i, heightMap[0][i]});
68 | q.offer(new int[]{m - 1, i, heightMap[m - 1][i]});
69 | vis[0][i] = true;
70 | vis[m - 1][i] = true;
71 | }
72 | int[][] dirs = { {1, 0}, {-1, 0}, {0, 1}, {0, -1} };
73 | int ans = 0;
74 | while (!q.isEmpty()) {
75 | int[] cur = q.poll();
76 | for (int[] dir : dirs) {
77 | int nx = cur[0] + dir[0], ny = cur[1] + dir[1];
78 | if (nx < 0 || nx >= m || ny < 0 || ny >= n || vis[nx][ny]) continue;
79 | ans += Math.max(0, cur[2] - heightMap[nx][ny]);
80 | q.offer(new int[]{nx, ny, Math.max(cur[2], heightMap[nx][ny])});
81 | vis[nx][ny] = true;
82 | }
83 | }
84 | return ans;
85 | }
86 | ```
87 |
88 |
--------------------------------------------------------------------------------
/markdown/Algorithm/数据流中位数.md:
--------------------------------------------------------------------------------
1 | # [数据流中位数](https://leetcode-cn.com/problems/find-median-from-data-stream/)
2 |
3 |
4 |
5 | ## 思路
6 |
7 | 维护两个优先队列:小根堆 & 大根堆
8 |
9 | 小根堆:存放右半边最小值元素
10 |
11 | 大根堆:存饭左半边最大值元素
12 |
13 | 保持两个优先队列大小始终相等或相差 1
14 |
15 |
16 |
17 | 添加元素:如果需要加入大根堆中,则需要先插入小根堆,然后弹出小根堆顶元素加入大根堆中,这样才可以保证`maxQ 中所有元素 < minQ 中的所有元素`;反之亦然
18 |
19 | 返回中位数:如果两个优先队列大小相等,则返回堆顶元素和的平均值;如果不相等,则返回元素值更多的堆顶
20 |
21 | ## 实现
22 |
23 | ```java
24 | class MedianFinder {
25 | // 小根堆:存放右半边大值元素
26 | Queue minQ;
27 | // 大根堆:存放左半边小值元素
28 | Queue maxQ;
29 |
30 | public MedianFinder() {
31 | minQ = new PriorityQueue<>();
32 | maxQ = new PriorityQueue<>((o1, o2) -> (o2 - o1));
33 | }
34 |
35 | public void addNum(int num) {
36 | // 始终保持 maxQ 中所有元素 < minQ 中的所有元素
37 | if (maxQ.size() <= minQ.size()) {
38 | minQ.offer(num);
39 | maxQ.offer(minQ.poll());
40 | } else {
41 | maxQ.offer(num);
42 | minQ.offer(maxQ.poll());
43 | }
44 | }
45 |
46 | public double findMedian() {
47 | if (minQ.size() == maxQ.size()) return (minQ.peek() + maxQ.peek()) / 2.0;
48 | return minQ.size() > maxQ.size() ? minQ.peek() : maxQ.peek();
49 | }
50 | }
51 | ```
52 |
53 |
--------------------------------------------------------------------------------
/markdown/Algorithm/最小栈-最大栈.md:
--------------------------------------------------------------------------------
1 | # 最小栈 & 最大栈
2 |
3 | [155. 最小栈](https://leetcode-cn.com/problems/min-stack/)
4 |
5 | [895. 最大频率栈](https://leetcode-cn.com/problems/maximum-frequency-stack/)
6 |
7 | ### 最小栈
8 |
9 | **思路:**维护一个调用`push()`每个元素后的最小值栈
10 |
11 | ```java
12 | class MinStack {
13 |
14 | private Stack stack;
15 | private Stack minStack;
16 |
17 | public MinStack() {
18 | stack = new Stack<>();
19 | minStack = new Stack<>();
20 | }
21 |
22 | public void push(int val) {
23 | stack.push(val);
24 | if (minStack.isEmpty()) minStack.push(val);
25 | else if (getMin() <= val) minStack.push(getMin());
26 | else if (getMin() > val) minStack.push(val);
27 | }
28 |
29 | public void pop() {
30 | stack.pop();
31 | minStack.pop();
32 | }
33 |
34 | public int top() {
35 | return stack.peek();
36 | }
37 |
38 | public int getMin() {
39 | return minStack.peek();
40 | }
41 | }
42 | ```
43 |
44 | ### 最大栈
45 |
46 | ```java
47 | public class FreqStack {
48 | // 记录最大频率
49 | private int maxFreq;
50 | // 记录每个元素的频率
51 | private Map valToFreq;
52 | // 记录某一频率的所有元素
53 | private Map> freqToVal;
54 |
55 | public FreqStack() {
56 | maxFreq = 0;
57 | valToFreq = new HashMap<>();
58 | freqToVal = new HashMap<>();
59 | }
60 |
61 | public void push(int val) {
62 | // 获得 val 的频率
63 | int freq = valToFreq.getOrDefault(val, 0) + 1;
64 | // 更新 val to freq
65 | valToFreq.put(val, freq);
66 | // 更新 freq to val
67 | freqToVal.putIfAbsent(freq, new Stack<>());
68 | freqToVal.get(freq).push(val);
69 | // 更新 maxFreq
70 | maxFreq = Math.max(maxFreq, freq);
71 | }
72 |
73 | public int pop() {
74 | // 弹出一个频率最大的元素
75 | Stack valStack = freqToVal.get(maxFreq);
76 | int v = valStack.pop();
77 | // 更新 val to freq
78 | valToFreq.put(v, valToFreq.get(v) - 1);
79 | // 更新 maxFreq
80 | if (valStack.isEmpty()) {
81 | maxFreq--;
82 | }
83 | return v;
84 | }
85 | }
86 | ```
--------------------------------------------------------------------------------
/markdown/Algorithm/最短路径-Dijkstra.md:
--------------------------------------------------------------------------------
1 | # 最短路径-Dijkstra
2 |
3 | [743. 网络延迟时间](https://leetcode-cn.com/problems/network-delay-time)
4 |
5 | [1514. 概率最大的路径](https://leetcode-cn.com/problems/path-with-maximum-probability)
6 |
7 | [1631. 最小体力消耗路径](https://leetcode-cn.com/problems/path-with-minimum-effort)
8 |
9 | ## Dijkstra
10 |
11 | ### 适用条件
12 |
13 | **加权有向图,没有负权重边**
14 |
15 | ### 模版
16 |
17 | ```java
18 | public class State {
19 | // 节点 id
20 | public int id;
21 | // 当前节点距离起点的距离
22 | public int distFromStart;
23 | public State(int id, int distFromStart) {
24 | this.id = id;
25 | this.distFromStart = distFromStart;
26 | }
27 | }
28 |
29 | public class Dijkstra {
30 | public int[] dijkstra(List[] graph, int start) {
31 | // 节点数量
32 | int n = graph.length;
33 | // 记录每个点到 start 的最短距离
34 | int[] distTo = new int[n];
35 | // 初始化为最大值
36 | Arrays.fill(distTo, Integer.MAX_VALUE);
37 | // start to start = 0
38 | distTo[start] = 0;
39 |
40 | // 优先队列,按照 distFromStart 排序(贪心思想)
41 | Queue pq = new PriorityQueue<>(Comparator.comparingInt(o -> o.distFromStart));
42 | // 添加起点
43 | pq.offer(new State(start, 0));
44 |
45 | while (!pq.isEmpty()) {
46 | State curState = pq.poll();
47 | int curNodeId = curState.id;
48 | int curDistFromStart = curState.distFromStart;
49 | // 非最优,直接跳过
50 | if (curDistFromStart > distTo[curNodeId]) {
51 | continue;
52 | }
53 | for (int nextNodeId : adj(curNodeId)) {
54 | int distToNextNode = distTo[curNodeId] + weight(curNodeId, nextNodeId);
55 | // 更新到下一个节点的距离
56 | if (distToNextNode < distTo[nextNodeId]) {
57 | distTo[nextNodeId] = distToNextNode;
58 | pq.offer(new State(nextNodeId, distToNextNode));
59 | }
60 | }
61 | }
62 | return distTo;
63 | }
64 |
65 | /**
66 | * 权重函数
67 | * @param from from 顶点
68 | * @param to to 顶点
69 | * @return 返回 from -> to 权重
70 | */
71 | private int weight(int from, int to) {
72 | return 0;
73 | }
74 |
75 | /**
76 | * 邻接节点
77 | * @param id 当且节点 Id
78 | * @return 返回当前节点的邻接节点
79 | */
80 | private List adj(int id) {
81 | return new ArrayList<>();
82 | }
83 | }
84 | ```
85 |
86 | ### 扩展
87 |
88 | **如果我只想计算起点 `start` 到某一个终点 `end` 的最短路径,是否可以修改算法,提升一些效率?**
89 |
90 | ```java
91 | // 输入起点 start 和终点 end,计算起点到终点的最短距离
92 | int dijkstra(List[] graph, int start, int end) {
93 |
94 | // ...
95 |
96 | while (!pq.isEmpty()) {
97 | State curState = pq.poll();
98 | int curNodeId = curState.id;
99 | int curDistFromStart = curState.distFromStart;
100 |
101 | // 在这里加一个判断就行了,其他代码不用改
102 | if (curNodeID == end) {
103 | return curDistFromStart;
104 | }
105 |
106 | if (curDistFromStart > distTo[curNodeID]) {
107 | continue;
108 | }
109 |
110 | // ...
111 | }
112 |
113 | // 如果运行到这里,说明从 start 无法走到 end
114 | return Integer.MAX_VALUE;
115 | }
116 | ```
117 |
118 | 因为优先级队列自动排序的性质,**每次**从队列里面拿出来的都是 `distFromStart` 值最小的,所以当你**第一次**从队列中拿出终点 `end` 时,此时的 `distFromStart` 对应的值就是从 `start` 到 `end` 的最短距离
119 |
120 | 这个算法较之前的实现提前 return 了,所以效率有一定的提高
121 |
--------------------------------------------------------------------------------
/markdown/Algorithm/最长公共子序列-变题.md:
--------------------------------------------------------------------------------
1 | # 最长公共子序列「变题」
2 |
3 | [1143. 最长公共子序列](https://leetcode.cn/problems/longest-common-subsequence)
4 |
5 |
6 |
7 | 开头先来一个小插曲,关于「最长公共子序列」详细总结可见 **[最长公共子序列 (LCS):「模版」&「输出」](./最长公共子序列-模版-输出.html)**
8 |
9 | ```java
10 | public int longestCommonSubsequence(String text1, String text2) {
11 | int n1 = text1.length(), n2 = text2.length();
12 | int[][] dp = new int[n1 + 1][n2 + 1];
13 | for (int i = 1; i <= n1; i++) {
14 | for (int j = 1; j <= n2; j++) {
15 | if (text1.charAt(i - 1) == text2.charAt(j - 1)) dp[i][j] = dp[i - 1][j - 1] + 1;
16 | else dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - 1]);
17 | }
18 | }
19 | return dp[n1][n2];
20 | }
21 | ```
22 |
23 | ### 变题一:空间优化
24 |
25 | ```java
26 | public int longestCommonSubsequence(String text1, String text2) {
27 | int n1 = text1.length(), n2 = text2.length();
28 | int[] dp = new int[n2 + 1];
29 | for (int i = 1; i <= n1; i++) {
30 | int prevUp = 0;
31 | for (int j = 1; j <= n2; j++) {
32 | int t = prevUp;
33 | prevUp = dp[j];
34 | if (text1.charAt(i - 1) == text2.charAt(j - 1)) dp[j] = t + 1;
35 | else dp[j] = Math.max(dp[j], dp[j - 1]);
36 | }
37 | }
38 | return dp[n2];
39 | }
40 | ```
41 |
42 | ### 变题二:输出最长公共子序列
43 |
44 | ```java
45 | public int longestCommonSubsequence(String text1, String text2) {
46 | int n1 = text1.length(), n2 = text2.length();
47 | int[][] dp = new int[n1 + 1][n2 + 1];
48 | for (int i = 1; i <= n1; i++) {
49 | for (int j = 1; j <= n2; j++) {
50 | if (text1.charAt(i - 1) == text2.charAt(j - 1)) dp[i][j] = dp[i - 1][j - 1] + 1;
51 | else dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - 1]);
52 | }
53 | }
54 | StringBuffer sb = new StringBuffer();
55 | int i = n1, j = n2;
56 | while (i > 0 && j > 0) {
57 | if (text1.charAt(i - 1) == text2.charAt(j - 1)) {
58 | sb.append(text1.charAt(i - 1));
59 | i--; j--;
60 | } else if (dp[i - 1][j] < dp[i][j - 1]) {
61 | j--;
62 | } else i--;
63 | }
64 | System.out.println(sb.reverse().toString());
65 | return dp[n1][n2];
66 | }
67 | ```
68 |
69 |
--------------------------------------------------------------------------------
/markdown/Algorithm/最长递增子序列-变题.md:
--------------------------------------------------------------------------------
1 | # 最长递增子序列「变题」
2 |
3 | [300. 最长递增子序列](https://leetcode.cn/problems/longest-increasing-subsequence/)
4 |
5 |
6 |
7 | 开头先来一个小插曲,关于「最长递增子序列」问题的总结可见 **[动态规划设计:最长递增子序列](./动态规划设计:最长递增子序列.html)**
8 |
9 | ```java
10 | // 时间复杂度 : O(n^2)
11 | // 空间复杂度 : O(n)
12 | public int lengthOfLIS(int[] nums) {
13 | int n = nums.length, ans = 0;
14 | int[] dp = new int[n];
15 | Arrays.fill(dp, 1);
16 | for (int i = 0; i < n; i++) {
17 | for (int j = 0; j < i; j++) {
18 | if (nums[i] > nums[j]) dp[i] = Math.max(dp[i], dp[j] + 1);
19 | }
20 | ans = Math.max(ans, dp[i]);
21 | }
22 | return ans;
23 | }
24 | ```
25 |
26 | ### 变题一:时间优化成 O(nlogn)
27 |
28 | ```java
29 | // 时间复杂度 : O(nlogn)
30 | // 空间复杂度 : O(n)
31 | public int lengthOfLIS(int[] nums) {
32 | int n = nums.length;
33 | int[] top = new int[n];
34 | int piles = 0;
35 | for (int i = 0; i < n; i++) {
36 | int poker = nums[i];
37 | int l = 0, r = piles;
38 | while (l < r) {
39 | int m = l + r >> 1;
40 | if (top[m] >= poker) r = m;
41 | else l = m + 1;
42 | }
43 | if (l == piles) top[piles++] = poker;
44 | else top[l] = poker;
45 | }
46 | return piles;
47 | }
48 | ```
49 |
50 | ### 变题二:输出最长上升子序列,字典序最小
51 |
52 | **题目详情可见 [最长上升子序列(三)](https://www.nowcoder.com/practice/9cf027bf54714ad889d4f30ff0ae5481)**
53 |
54 | ```java
55 | public int[] LIS (int[] nums) {
56 | int n = nums.length;
57 | // p 记录每个数在哪个堆中
58 | int[] top = new int[n], p = new int[n];
59 | int piles = 0;
60 | for (int i = 0; i < n; i++) {
61 | int poker = nums[i];
62 | int l = 0, r = piles;
63 | while (l < r) {
64 | int m = l + r >> 1;
65 | if (top[m] >= poker) r = m;
66 | else l = m + 1;
67 | }
68 | if (l == piles) {
69 | top[piles++] = poker;
70 | p[i] = piles;
71 | } else {
72 | top[l] = poker;
73 | p[i] = l + 1;
74 | }
75 | }
76 |
77 | int[] ans = new int[piles];
78 | for (int i = n - 1; i >= 0; i--) {
79 | if (p[i] == piles) ans[--piles] = nums[i];
80 | }
81 | return ans;
82 | }
83 | ```
84 |
85 | ### 变题三:最长非上升子序列,输出且字典序最小
86 |
87 | ```java
88 | public int[] LIS (int[] nums) {
89 | int n = nums.length;
90 | // p 记录每个数在哪个堆中
91 | int[] top = new int[n], p = new int[n];
92 | int piles = 0;
93 | for (int i = 0; i < n; i++) {
94 | int poker = nums[i];
95 | int l = 0, r = piles;
96 | while (l < r) {
97 | int m = l + r >> 1;
98 | // 反过来
99 | if (top[m] < poker) r = m;
100 | else l = m + 1;
101 | }
102 | if (l == piles) {
103 | top[piles++] = poker;
104 | p[i] = piles;
105 | } else {
106 | top[l] = poker;
107 | p[i] = l + 1;
108 | }
109 | }
110 | int cp = 0;
111 | int[] ans = new int[piles];
112 | // 正向遍历
113 | for (int i = 0; i < n; i++) {
114 | if (p[i] == cp + 1) ans[cp++] = nums[i];
115 | }
116 | return ans;
117 | }
118 | ```
119 |
120 |
--------------------------------------------------------------------------------
/markdown/Algorithm/有效的括号-变题.md:
--------------------------------------------------------------------------------
1 | # 有效的括号「变题」
2 |
3 | [20. 有效的括号](https://leetcode.cn/problems/valid-parentheses/)
4 |
5 |
6 |
7 | 开头先来一个小插曲,关于「括号」相关的总结可见 **[秒杀所有括号类问题](./秒杀所有括号类问题.html)**
8 |
9 | ```java
10 | public boolean isValid(String s) {
11 | Deque st = new ArrayDeque<>();
12 | for (char c : s.toCharArray()) {
13 | if (c == '(' || c == '[' || c == '{') st.push(c);
14 | else if (!st.isEmpty()) {
15 | if (st.poll() != f(c)) return false;
16 | } else return false;
17 | }
18 | return st.isEmpty();
19 | }
20 | private char f(char c) {
21 | if (c == ')') return '(';
22 | else if (c == '}') return '{';
23 | return '[';
24 | }
25 | ```
26 |
27 | ### 变题一:不要求左括号必须以正确的顺序闭合
28 |
29 | 也就是去掉了 **[有效的括号](https://leetcode.cn/problems/valid-parentheses/)** 中的要求二!!
30 |
31 | 🌰 举个例子:`[(])`这种情况也是满足要求滴!
32 |
33 | ```java
34 | public boolean isValid(String s) {
35 | int[] cnt = new int[3];
36 | for (char c : s.toCharArray()) {
37 | if (c == '(' || c == '[' || c == '{') cnt[f(c)]++;
38 | else if (--cnt[f(c)] < 0) return false;
39 | }
40 | return cnt[0] == 0 && cnt[1] == 0 && cnt[2] == 0;
41 | }
42 | private int f(char c) {
43 | if (c == '(' || c == ')') return 0;
44 | if (c == '[' || c == ']') return 1;
45 | return 2;
46 | }
47 | ```
48 |
49 | ### 变题二:要求必须按 { [ ( 的顺序进行关闭
50 |
51 | 🌰 举个例子:`{[()]}, {}[()]`是符合要求的;`[{()}]`是不符合要求的
52 |
53 | 换句话说,`{`的优先级最高,它可以包含其它两种类型的括号;而其它两种类型的括号不能包含它。其它两种同理!
54 |
55 | **思路:**分别为` { [ (`设置权重`2 1 0`,入栈时判断栈顶优先级是否低于当前左括号优先级,如果低于,则非法
56 |
57 | ```java
58 | public boolean isValid(String s) {
59 | // 技巧:栈中直接存优先级
60 | Deque st = new ArrayDeque<>();
61 | for (char c : s.toCharArray()) {
62 | int w = f(c);
63 | if (c == '(' || c == '[' || c == '{') {
64 | // 栈不为空 且 栈顶优先级低于 c
65 | if (!st.isEmpty() && st.peek() < w) return false;
66 | st.push(w);
67 | } else if (!st.isEmpty()) {
68 | if (st.poll() != w) return false;
69 | } else return false;
70 | }
71 | return st.isEmpty();
72 | }
73 | private char f(char c) {
74 | if (c == '(' || c == ')') return 0; // 低
75 | if (c == '[' || c == ']') return 1; // 中
76 | return 2; // 高
77 | }
78 | ```
--------------------------------------------------------------------------------
/markdown/Algorithm/比较版本号-变题.md:
--------------------------------------------------------------------------------
1 | # 比较版本号「变题」
2 |
3 | [165. 比较版本号](https://leetcode.cn/problems/compare-version-numbers/)
4 |
5 |
6 |
7 | ```java
8 | public int compareVersion(String version1, String version2) {
9 | String[] sp1 = version1.split("\\.");
10 | String[] sp2 = version2.split("\\.");
11 | int n1 = sp1.length, n2 = sp2.length;
12 | int i = 0, j = 0;
13 | while (i < n1 || j < n2) {
14 | int s1 = 0, s2 = 0;
15 | if (i < n1) s1 = Integer.parseInt(sp1[i++]);
16 | if (j < n2) s2 = Integer.parseInt(sp2[j++]);
17 | if (s1 != s2) return s1 < s2 ? -1 : 1;
18 | }
19 | return 0;
20 | }
21 | ```
22 |
23 | ### 变题一:不允许使用`String.split()`方法
24 |
25 | ```java
26 | public int compareVersion(String version1, String version2) {
27 | int n1 = version1.length(), n2 = version2.length();
28 | int i = 0, j = 0;
29 | while (i < n1 || j < n2) {
30 | int s1 = 0, s2 = 0;
31 |
32 | int t1 = i, t2 = j;
33 | while (i < n1 && version1.charAt(i) != '.') i++;
34 | while (j < n2 && version2.charAt(j) != '.') j++;
35 |
36 | if (t1 != i) s1 = Integer.parseInt(version1.substring(t1, i));
37 | if (t2 != j) s2 = Integer.parseInt(version2.substring(t2, j));
38 |
39 | if (s1 != s2) return s1 < s2 ? -1 : 1;
40 |
41 | if (i < n1) i++;
42 | if (j < n2) j++;
43 | }
44 | return 0;
45 | }
46 | ```
--------------------------------------------------------------------------------
/markdown/Algorithm/求素数的三种方法.md:
--------------------------------------------------------------------------------
1 | # 求素数的三种方法
2 |
3 | [1175. 质数排列](https://leetcode.cn/problems/prime-arrangements/)
4 |
5 | [204. 计数质数](https://leetcode.cn/problems/count-primes/)
6 |
7 | ### 暴力
8 |
9 | ```java
10 | private List getPrime(int n) {
11 | List list = new ArrayList<>();
12 | for (int i = 2; i <= n; i++) {
13 | boolean ok = true;
14 | // 注意:j * j <= i 即可
15 | for (int j = 2; j * j <= i && ok; j++) {
16 | if (i % j == 0) ok = false;
17 | }
18 | if (ok) list.add(i);
19 | }
20 | return list;
21 | }
22 | ```
23 |
24 | ### 埃氏筛法 (推荐)
25 |
26 | 整个过程如图所示:
27 |
28 | 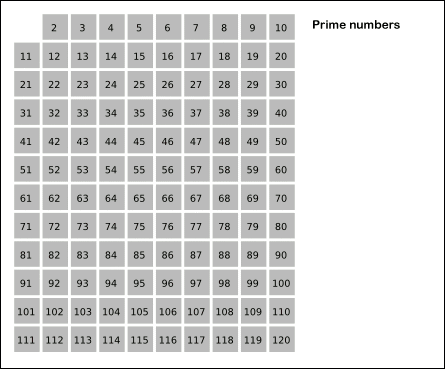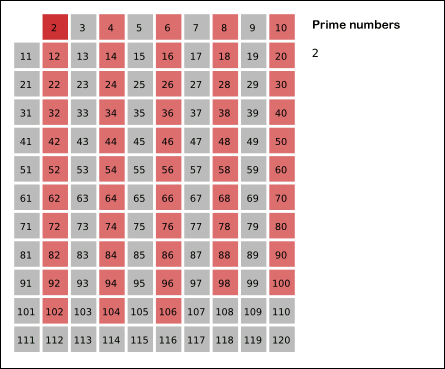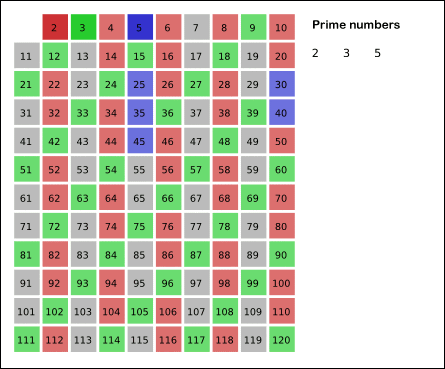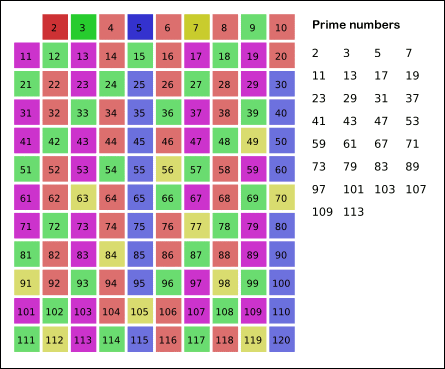 29 |
30 | ```java
31 | private List getPrime(int n) {
32 | List list = new ArrayList<>();
33 | boolean[] isPrime = new boolean[n + 1];
34 | Arrays.fill(isPrime, true);
35 | isPrime[1] = false;
36 | for (int i = 2; i <= n; i++) {
37 | if (!isPrime[i]) continue;
38 | list.add(i);
39 | for (int j = i + i; j <= n; j += i) {
40 | isPrime[j] = false;
41 | }
42 | }
43 | return list;
44 | }
45 | ```
46 |
47 | ### 欧拉筛法
48 |
49 | ```java
50 | private List getPrime(int n) {
51 | List list = new ArrayList<>();
52 | boolean[] vis = new boolean[n + 1];
53 | for (int i = 2; i <= n; i++) {
54 | // 如果没有访问过,一定是素数
55 | if (!vis[i]) {
56 | list.add(i);
57 | vis[i] = true;
58 | }
59 | for (int j = 0; j < list.size(); j++) {
60 | int cur = list.get(j);
61 | if (i * cur > n) break;
62 | vis[i * cur] = true;
63 | if (i % cur == 0) break;
64 | }
65 | }
66 | return list;
67 | }
68 | ```
69 |
70 |
--------------------------------------------------------------------------------
/markdown/Algorithm/浅析:无权值最短路径算法-BFS.md:
--------------------------------------------------------------------------------
1 | # 浅析:无权值最短路径算法(BFS)
2 |
3 | [675. 为高尔夫比赛砍树](https://leetcode.cn/problems/cut-off-trees-for-golf-event/)
4 |
5 |
6 |
7 | 本篇文章介绍一种简单类型的「最短路径」算法
8 |
9 | 提到「最短路径」算法,首先可以想到的肯定是「Dijkstra 算法」,但是「Dijkstra 算法」一般适用于有权值且权值为正的情况。**关于「Dijkstra 算法」详细实现可见 [最短路径-Dijkstra](./最短路径-Dijkstra.html)**
10 |
11 | 而我们今天要介绍的题目是无权值的类型,所以如果使用「Dijkstra 算法」,就略显复杂了!!
12 |
13 | 同时,对于「Dijkstra 算法」,一般计算的是其他所有点到起点的距离;而有些题目仅仅只需要计算两个点的距离而已!
14 |
15 | ### 问题分析
16 |
17 | 对于今天的问题,有两个前提条件「没有两棵树的高度是相同的」且「需要按照树的高度从低向高砍掉所有的树」
18 |
19 | 所以我们只需要对所有树的高度升序排列,然后依次计算两点之间的距离即可!!最后我们的问题就抽象成「计算两点之间的距离」
20 |
21 | 整理一下这个问题的特点
22 |
23 | - 边与边之间无权值
24 | - 只需求两点间的距离
25 |
26 | 我们可以使用 BFS 一层一层的向外扩张,每扩张一层,距离 ➕1。如下图:
27 |
28 |
29 |
30 | ```java
31 | private List getPrime(int n) {
32 | List list = new ArrayList<>();
33 | boolean[] isPrime = new boolean[n + 1];
34 | Arrays.fill(isPrime, true);
35 | isPrime[1] = false;
36 | for (int i = 2; i <= n; i++) {
37 | if (!isPrime[i]) continue;
38 | list.add(i);
39 | for (int j = i + i; j <= n; j += i) {
40 | isPrime[j] = false;
41 | }
42 | }
43 | return list;
44 | }
45 | ```
46 |
47 | ### 欧拉筛法
48 |
49 | ```java
50 | private List getPrime(int n) {
51 | List list = new ArrayList<>();
52 | boolean[] vis = new boolean[n + 1];
53 | for (int i = 2; i <= n; i++) {
54 | // 如果没有访问过,一定是素数
55 | if (!vis[i]) {
56 | list.add(i);
57 | vis[i] = true;
58 | }
59 | for (int j = 0; j < list.size(); j++) {
60 | int cur = list.get(j);
61 | if (i * cur > n) break;
62 | vis[i * cur] = true;
63 | if (i % cur == 0) break;
64 | }
65 | }
66 | return list;
67 | }
68 | ```
69 |
70 |
--------------------------------------------------------------------------------
/markdown/Algorithm/浅析:无权值最短路径算法-BFS.md:
--------------------------------------------------------------------------------
1 | # 浅析:无权值最短路径算法(BFS)
2 |
3 | [675. 为高尔夫比赛砍树](https://leetcode.cn/problems/cut-off-trees-for-golf-event/)
4 |
5 |
6 |
7 | 本篇文章介绍一种简单类型的「最短路径」算法
8 |
9 | 提到「最短路径」算法,首先可以想到的肯定是「Dijkstra 算法」,但是「Dijkstra 算法」一般适用于有权值且权值为正的情况。**关于「Dijkstra 算法」详细实现可见 [最短路径-Dijkstra](./最短路径-Dijkstra.html)**
10 |
11 | 而我们今天要介绍的题目是无权值的类型,所以如果使用「Dijkstra 算法」,就略显复杂了!!
12 |
13 | 同时,对于「Dijkstra 算法」,一般计算的是其他所有点到起点的距离;而有些题目仅仅只需要计算两个点的距离而已!
14 |
15 | ### 问题分析
16 |
17 | 对于今天的问题,有两个前提条件「没有两棵树的高度是相同的」且「需要按照树的高度从低向高砍掉所有的树」
18 |
19 | 所以我们只需要对所有树的高度升序排列,然后依次计算两点之间的距离即可!!最后我们的问题就抽象成「计算两点之间的距离」
20 |
21 | 整理一下这个问题的特点
22 |
23 | - 边与边之间无权值
24 | - 只需求两点间的距离
25 |
26 | 我们可以使用 BFS 一层一层的向外扩张,每扩张一层,距离 ➕1。如下图:
27 |
28 |  29 |
30 | 当我们在向外扩张时,记录一下层数,就可以得到两点之间的距离
31 |
32 | ### 代码实现
33 |
34 | ```java
35 | class Solution {
36 | private int m;
37 | private int n;
38 | private int[][] graph;
39 | // 记录所有的树,其三元组为 [h, i, j]
40 | private List tree = new ArrayList<>();
41 | private int[][] dirs = new int[][]{ {0,1},{0,-1},{1,0},{-1,0} };
42 | public int cutOffTree(List> forest) {
43 | m = forest.size();
44 | n = forest.get(0).size();
45 | graph = new int[m][n];
46 | if (forest.get(0).get(0) == 0) return -1;
47 | for (int i = 0; i < m; i++) {
48 | for (int j = 0; j < n; j++) {
49 | graph[i][j] = forest.get(i).get(j);
50 | // 加入 tree 中
51 | if (graph[i][j] > 1) tree.add(new int[]{graph[i][j], i, j});
52 | }
53 | }
54 | // 根据 h 排序
55 | Collections.sort(tree, Comparator.comparingInt(o -> o[0]));
56 | int ans = 0;
57 | int x = 0, y = 0;
58 | for (int[] t : tree) {
59 | int nx = t[1], ny = t[2];
60 | int dist = bfs(x, y, nx, ny);
61 | if (dist == -1) return -1;
62 | ans += dist;
63 | x = nx;
64 | y = ny;
65 | }
66 | return ans;
67 | }
68 | private int bfs(int X, int Y, int P, int Q) {
69 | if (X == P && Y == Q) return 0;
70 | // 记录节点访问情况
71 | boolean[][] visited = new boolean[m][n];
72 | // 双端队列
73 | Deque deque = new ArrayDeque<>();
74 | deque.addLast(new int[]{X, Y});
75 | visited[X][Y] = true;
76 | int dist = 0;
77 | while (!deque.isEmpty()) {
78 | int size = deque.size();
79 | for (int i = 0; i < size; i++) {
80 | int[] cur = deque.pollFirst();
81 | int x = cur[0], y = cur[1];
82 | for (int[] dir : dirs) {
83 | int nx = x + dir[0], ny = y + dir[1];
84 | // 非法情况
85 | if (nx < 0 || nx >= m || ny < 0 || ny >= n || graph[nx][ny] == 0 || visited[nx][ny]) continue;
86 | // 达到终点
87 | if (nx == P && ny == Q) return dist + 1;
88 | deque.addLast(new int[]{nx, ny});
89 | visited[nx][ny] = true;
90 | }
91 | }
92 | dist++;
93 | }
94 | return -1;
95 | }
96 | }
97 | ```
98 |
99 |
--------------------------------------------------------------------------------
/markdown/Algorithm/浅析:最小基因变化.md:
--------------------------------------------------------------------------------
1 | # 浅析:最小基因变化
2 |
3 | [433. 最小基因变化](https://leetcode-cn.com/problems/minimum-genetic-mutation/)
4 |
5 |
6 |
7 | 本篇文章简单分析一下题目 [最小基因变化](https://leetcode-cn.com/problems/minimum-genetic-mutation/),这个题目是一个 BFS 的模版题,和题目 [打开转盘锁](https://leetcode-cn.com/problems/open-the-lock/) 很相似,**详情可见 [BFS 算法框架](./BFS.html)**
8 |
9 | 下面从两个不同的角度分析本题:「单向 BFS」「双向 BFS」
10 |
11 | ### 单向 BFS
12 |
13 | 我们以`start`作为第 0 层,`bank`中在`start`基础上改变一位基因作为第 1 层,依次类推,直到寻找到目标基因
14 |
15 | 同时,我们需要记录`bank`中基因的访问情况
16 |
17 | 下面给出对应的代码:
18 |
19 | ```java
20 | public int minMutation(String start, String end, String[] bank) {
21 | // 转化成 set 方便查找
22 | Set bankSet = new HashSet<>(Arrays.asList(bank));
23 | // 边界处理:如果 end 不在 bank 中
24 | if (!bankSet.contains(end)) return -1;
25 | // 记录基因访问情况
26 | Set used = new HashSet<>();
27 | Queue q = new LinkedList<>();
28 | q.offer(start);
29 | used.add(start);
30 | int count = 0;
31 | while (!q.isEmpty()) {
32 | int size = q.size();
33 | for (int i = 0; i < size; i++) {
34 | String cur = q.poll();
35 | // 如果找到,返回步数
36 | if (cur.equals(end)) return count;
37 | for (String gene : bankSet) {
38 | // 从 bank 中去找与当前基因只发生一位改变的基因
39 | if (!used.contains(gene) && isChangeOne(cur, gene)) {
40 | q.offer(gene);
41 | // 标记
42 | used.add(gene);
43 | }
44 | }
45 | }
46 | count++;
47 | }
48 | return -1;
49 | }
50 | // 判断两个基因是否只有一位不同
51 | private boolean isChangeOne(String source, String target) {
52 | int changeCount = 0;
53 | for (int i = 0; i < 8; i++) {
54 | if (source.charAt(i) != target.charAt(i)) changeCount++;
55 | if (changeCount > 1) return false;
56 | }
57 | return changeCount == 1;
58 | }
59 | ```
60 |
61 | ### 双向 BFS
62 |
63 | 这个题目也符合「双向 BFS」的适用情况,即终点是明确的
64 |
65 | ```java
66 | public int minMutation(String start, String end, String[] bank) {
67 | Set bankSet = new HashSet<>(Arrays.asList(bank));
68 | if (!bankSet.contains(end)) return -1;
69 | Set used = new HashSet<>();
70 | Set q1 = new HashSet<>();
71 | Set q2 = new HashSet<>();
72 | q1.add(start);
73 | q2.add(end);
74 | int count = 0;
75 | while (!q1.isEmpty() && !q2.isEmpty()) {
76 | Set temp = new HashSet<>();
77 | for (String cur : q1) {
78 | if (q2.contains(cur)) return count;
79 | // 标记
80 | used.add(cur);
81 | for (String gene : bankSet) {
82 | // isChangeOne() 同上
83 | if (!used.contains(gene) && isChangeOne(cur, gene)) {
84 | temp.add(gene);
85 | }
86 | }
87 | }
88 | q1 = q2;
89 | q2 = temp;
90 | count++;
91 | }
92 | return -1;
93 | }
94 | ```
95 |
96 | 这里需要注意的一点,**选择恰当标记的时机**。不可以在加入队列的时候标记,不然这样一个基因只能加入一端的队列中,这样肯定就无法在一端队列中找到相同的基因 🧬,因为双向队列中的基因各不相同
97 |
98 | 下面给出错误的代码,加以警示!!
99 |
100 | ```java
101 | // 标记
102 | // used.add(cur);
103 | for (String gene : bankSet) {
104 | // isChangeOne() 同上
105 | if (!used.contains(gene) && isChangeOne(cur, gene)) {
106 | temp.add(gene);
107 | // 错误标记时机
108 | used.add(gene);
109 | }
110 | }
111 | ```
112 |
--------------------------------------------------------------------------------
/markdown/Algorithm/浅析:最小路径和.md:
--------------------------------------------------------------------------------
1 | # 浅析:最小路径和
2 |
3 | [64. 最小路径和](https://leetcode-cn.com/problems/minimum-path-sum/)
4 |
5 |
6 |
7 | 今天我们来详细分析一波 **[最小路径和](https://leetcode-cn.com/problems/minimum-path-sum/)**,带你从头开始一步一步得到最优化的解决方案!
8 |
9 | ### 暴力 DFS
10 |
11 | 首先第一眼看到这个题目,自然而然想到的就是 DFS,遍历出所有的路径,然后得到和最小的路径
12 |
13 | 关于 DFS 详细的内容可见 **[回溯 (DFS) 算法框架](./回溯(DFS).html)**
14 |
15 | ```java
16 | // 记录最小路径和
17 | private int res = Integer.MAX_VALUE;
18 | public int minPathSum(int[][] grid) {
19 | int m = grid.length;
20 | int n = grid[0].length;
21 | // 从 (0, 0) 开始遍历
22 | dfs(grid, 0, 0, 0, new boolean[m][n]);
23 | return res;
24 | }
25 | private void dfs(int[][] grid, int i, int j, int pathSum, boolean[][] used) {
26 | int m = grid.length;
27 | int n = grid[0].length;
28 | // 先序阶段:首次进入节点 (i, j)
29 | // 越界
30 | if (i < 0 || i >= m || j< 0 || j >= n) return ;
31 | // 判断是否已经被使用
32 | if (used[i][j]) return;
33 | // 标记已被使用
34 | used[i][j] = true;
35 | // 添加到路径中
36 | pathSum += grid[i][j];
37 | // 到达终点
38 | if (i == m - 1 && j == n - 1) res = Math.min(res, pathSum);
39 |
40 | // 每次都往「下」「右」进行搜索
41 | dfs(grid, i + 1, j, pathSum, used);
42 | dfs(grid, i, j + 1, pathSum, used);
43 |
44 | // 后续阶段:即将离开节点 (i, j)
45 | pathSum -= grid[i][j];
46 | used[i][j] = false;
47 | }
48 | ```
49 |
50 | 很显然,这个是超时的!!!
51 |
52 | ### 备忘录 + 递归
53 |
54 | 上面是没有任何优化的暴力 DFS,可以很明显的看到其实是**存在「重叠子问题」**的
55 |
56 | 这里采用自顶向下的解法,所以会有一个递归的`dp`函数,一般来说函数的**参数**就是状态转移中会变化的量,即:「状态」;**函数的返回值**就是`grid[0..i][0..j]`的最小路径和
57 |
58 | ```java
59 | private int res = Integer.MAX_VALUE;
60 | public int minPathSum(int[][] grid) {
61 | int m = grid.length;
62 | int n = grid[0].length;
63 | return dp(grid, m - 1, n - 1, new int[m][n]);
64 | }
65 | private int dp(int[][] grid, int i, int j, int[][] emeo) {
66 | int m = grid.length;
67 | int n = grid[0].length;
68 | // base case
69 | if (i < 0 || i >= m || j< 0 || j >= n) return Integer.MAX_VALUE;
70 | if (emeo[i][j] != 0) return emeo[i][j];
71 |
72 | int minPathSum = Math.min(dp(grid, i - 1, j, emeo), dp(grid, i, j - 1, emeo));
73 |
74 | emeo[i][j] = minPathSum == Integer.MAX_VALUE ? grid[i][j] : minPathSum + grid[i][j];
75 |
76 | return emeo[i][j];
77 | }
78 | ```
79 |
80 | ### DP + 递推
81 |
82 | **明确 base case:**显然是当`i = 0 and j = 0`,最小路径和直接是`grid[0][0]`
83 |
84 | **明确「状态」:原问题和子问题中会发生变化的变量。**`grid[0..i][0..j]`会不断地向 base case 靠近,所以唯一的「状态」就是矩阵`grid[0..i][0..j]`
85 |
86 | **明确「选择」:导致「状态」产生变化的行为。**矩阵`grid[0..i][0..j]`为什么变化呢?因为在选择不同的方向,每选择一种方向,矩阵就会收缩。所以说「上方 or 左方」就是「选择」(每次都可在选择任意一种方向)
87 |
88 | **明确 dp 数组/函数的定义:**这里采用自底向上的解法,所以会有一个递推的`dp`数组,一般来说数组的**下标**就是状态转移中会变化的量,即:「状态」;**数组的值**就是`grid[0..i][0..j]`的最小路径和
89 |
90 | 关于`dp[]`的初始状态,直接看下图:
91 |
92 | 
93 |
94 | ```java
95 | public int minPathSum(int[][] grid) {
96 | int m = grid.length;
97 | int n = grid[0].length;
98 | int[][] dp = new int[m + 1][n + 1];
99 | // 初始化 dp[]
100 | for (int i = 0; i < dp.length; i++) dp[i][0] = Integer.MAX_VALUE;
101 | for (int j = 0; j < dp[0].length; j++) dp[0][j] = Integer.MAX_VALUE;
102 | dp[0][1] = 0;
103 | dp[1][0] = 0;
104 |
105 | for (int i = 1; i < dp.length; i++) {
106 | for (int j = 1; j < dp[0].length; j++) {
107 | dp[i][j] = Math.min(dp[i - 1][j], dp[i][j - 1]) + grid[i - 1][j - 1];
108 | }
109 | }
110 | return dp[m][n];
111 | }
112 | ```
113 |
114 |
--------------------------------------------------------------------------------
/markdown/Algorithm/浅析:检查是否有合法括号字符串路径.md:
--------------------------------------------------------------------------------
1 | # 浅析:检查是否有合法括号字符串路径
2 |
3 | [6059. 检查是否有合法括号字符串路径](https://leetcode-cn.com/problems/check-if-there-is-a-valid-parentheses-string-path/)
4 |
5 |
6 |
7 | 好难好难,这又是一个合法括号问题!!只不过更加的难,太难了,太难了,自闭!!!
8 |
9 | 关于括号相关问题的分析,可见:「**[秒杀所有括号类问题](./秒杀所有括号类问题.html)**」「**[回溯算法:括号生成](./回溯算法:括号生成.html)**」「**[回溯算法:删除无效的括号](./回溯算法:删除无效的括号.html)**」
10 |
11 | 总结分析了这么多,其实关于括号类问题大部分都是使用「DFS」,**关于 DFS 详细分析可见 [回溯 (DFS) 算法框架](./algorithm/回溯(DFS).html)**
12 |
13 | 但是难点就在于「剪枝」,太变态了!!!**[回溯算法:删除无效的括号](./回溯算法:删除无效的括号.html)** 里面详细介绍了一些剪枝的策略!!
14 |
15 | ### 暴力 DFS
16 |
17 | 下面来看今天的问题!第一眼感觉不难,随手就写了一个「DFS」,不就是找到一条从`(0, 0)`到`(m - 1, n - 1)`的满足要求的路径嘛!!和题目 [最小路径和](https://leetcode-cn.com/problems/minimum-path-sum/) 中「暴力 DFS 求解」很类似,**可见 [浅析:最小路径和](./浅析:最小路径和.html)**
18 |
19 | 所以随手就写出了代码:
20 |
21 | ```java
22 | private boolean ok = false;
23 | public boolean hasValidPath(char[][] grid) {
24 | int m = grid.length;
25 | int n = grid[0].length;
26 | dfs(grid, 0, 0, 0, 0, new boolean[m][n]);
27 | return ok;
28 | }
29 | private void dfs(char[][] grid, int i, int j, int left, int right, boolean[][] used) {
30 | int m = grid.length;
31 | int n = grid[0].length;
32 | if (i < 0 || i >= m || j < 0 || j >= n || used[i][j] || left < right || ok) return ;
33 | used[i][j] = true;
34 | if (grid[i][j] == '(') left++;
35 | else right++;
36 | if (i == m - 1 && j == n - 1) {
37 | if (left == right) ok = true;
38 | }
39 | dfs(grid, i + 1, j, left, right, used);
40 | dfs(grid, i, j + 1, left, right, used);
41 | used[i][j] = false;
42 | }
43 | ```
44 |
45 | 无奈,超时了!!!
46 |
47 | ### 剪枝思路分析
48 |
49 | 如何优化呢???剪枝吧!!
50 |
51 | **角度一:**由于只能往下或者往右,且起点为`(0, 0)`,终点为`(m - 1, n -1)`,所以任意一条路径长度均为`m + n - 1`。如果要满足「合法括号」的要求,`m + n - 1` 必为偶数
52 |
53 | **角度二:**起点`(0, 0)`必须为`'('`,而终点`(m - 1, n - 1)`必须为`')'`,才能满足要求
54 |
55 | **角度三:**在「暴力 DFS」中,我们对状态划分比较简单,仅划分为了`m * n`个,即以每个格子为单位,用`used[][]`表示
56 |
57 | 我们现在优化一下代码,不再用`left`和`right`表示左右括号的数量,而是只用一个变量`count`表示,即:遇到左括号就 +1,遇到右括号就 -1。如果`count < 0`,则非法需要被剪枝
58 |
59 | 我们现在分析一下`count`的范围,如果所有的括号均为左括号,那么`count`为最大值,即:`count = m * n - 1`。因为上面分析过了,任意一条路径长度均为`m + n - 1`
60 |
61 | 所以如果我们仅仅以每个格子为状态,我们在回溯的过程中需要撤销标记,可能会导致冗余的计算。如果我们以每个格子的`count`作为状态,那么这个`used[m][n][m + n]`同时还充当了「备忘录 emeo」的角色
62 |
63 | ### 优化后代码实现
64 |
65 | ```java
66 | public boolean hasValidPath(char[][] grid) {
67 | int m = grid.length;
68 | int n = grid[0].length;
69 | // 角度一 + 角度二 的剪枝
70 | if ((m + n) % 2 == 0 || grid[0][0] == ')' || grid[m - 1][n - 1] == '(') return false;
71 | return dfs(grid, 0, 0, 0, new boolean[m][n][m + n]);
72 | }
73 | private boolean dfs(char[][] grid, int i, int j, int count, boolean[][][] used) {
74 | int m = grid.length;
75 | int n = grid[0].length;
76 | // 边界处理
77 | if (i < 0 || i >= m || j < 0 || j >= n) return false;
78 | // count < 0 说明 left < right
79 | // count > m - i + n - j - 1 说明剩下的路径就算都是 ')' 也无法使 count 变为 0
80 | if (count < 0 || count > m - i + n - j - 1) return false;
81 | // 该状态已标记,无法满足合法括号路径
82 | if (used[i][j][count]) return false;
83 | // 到达终点,count = 1 即满足要求
84 | // 可以思考一下为什么 count = 1 就行了
85 | if (i == m - 1 && j == n - 1) return count == 1;
86 | used[i][j][count] = true;
87 | count += (grid[i][j] == '(' ? 1 : -1);
88 | // 处理下方和右方
89 | return dfs(grid, i + 1, j, count, used) || dfs(grid, i, j + 1, count, used);
90 | }
91 | ```
92 |
93 |
--------------------------------------------------------------------------------
/markdown/Algorithm/爬楼梯-变题.md:
--------------------------------------------------------------------------------
1 | # 爬楼梯「变题」
2 |
3 | [70. 爬楼梯](https://leetcode.cn/problems/climbing-stairs/)
4 |
5 |
6 |
7 | ```java
8 | // 时间复杂度 : O(n)
9 | // 空间复杂度 : O(n)
10 | public int climbStairs(int n) {
11 | if (n <= 2) return n;
12 | int[] f = new int[n + 1];
13 | f[1] = 1; f[2] = 2;
14 | for (int i = 3; i <= n; i++) {
15 | f[i] = f[i - 1] + f[i - 2];
16 | }
17 | return f[n];
18 | }
19 | ```
20 |
21 | ### 变题一:空间优化
22 |
23 | ```java
24 | // 时间复杂度 : O(n)
25 | // 空间复杂度 : O(1)
26 | public int climbStairs(int n) {
27 | if (n <= 2) return n;
28 | int f1 = 1, f2 = 2, f = 0;
29 | for (int i = 3; i <= n; i++) {
30 | f = f1 + f2;
31 | f1 = f2;
32 | f2 = f;
33 | }
34 | return f;
35 | }
36 | ```
37 |
38 | ### 变题二:扩展至 m 阶数
39 |
40 | **相似题目可见 [DP3 跳台阶扩展问题](https://www.nowcoder.com/practice/953b74ca5c4d44bb91f39ac4ddea0fee)**
41 |
42 | ```java
43 | public int climbStairs(int n) {
44 | int[] f = new int[n + 1];
45 | f[0] = 1;
46 | for (int i = 1; i <= n; i++) {
47 | for (int j = 1; i - j >= 0 && j <= m; j++) {
48 | f[i] += f[i - j];
49 | }
50 | }
51 | return f[n];
52 | }
53 | ```
54 |
55 | ### 变题三:输出所有跳法
56 |
57 | ```java
58 | private int n;
59 | private List track = new ArrayList<>();
60 | private List> path = new ArrayList<>();
61 | public int climbStairs(int n) {
62 | this.n = n;
63 | int ans = f(0);
64 | System.out.println(path);
65 | return ans;
66 | }
67 | private int f(int i) {
68 | if (i > n) return 0;
69 | if (i == n) {
70 | path.add(new ArrayList<>(track));
71 | return 1;
72 | }
73 | track.add(1);
74 | int t1 = f(i + 1);
75 | track.remove(track.size() - 1);
76 |
77 | track.add(2);
78 | int t2 = f(i + 2);
79 | track.remove(track.size() - 1);
80 | return t1 + t2;
81 | }
82 | ```
83 |
84 | ### 变题四:不能爬到 7 及 7 的倍数
85 |
86 | ```java
87 | public int climbStairs(int n) {
88 | if (n <= 2) return n;
89 | int[] f = new int[n + 1];
90 | f[1] = 1; f[2] = 2;
91 | for (int i = 3; i <= n; i++) {
92 | // 若为 7 的倍数,直接为 0
93 | if (i % 7 == 0) f[i] = 0;
94 | else f[i] = f[i - 1] + f[i - 2];
95 | }
96 | return f[n];
97 | }
98 | ```
99 |
100 |
--------------------------------------------------------------------------------
/markdown/Algorithm/环形链表-变题.md:
--------------------------------------------------------------------------------
1 | # 环形链表「变题」
2 |
3 | [141. 环形链表](https://leetcode.cn/problems/linked-list-cycle/)
4 |
5 |
6 |
7 | 开头先来一个小插曲,关于「单链表」相关的总结可见 **[单链表的六大解题套路](./单链表的六大解题套路.html)**
8 |
9 | ```java
10 | // 快慢指针 (判断是否有环)
11 | public boolean hasCycle(ListNode head) {
12 | ListNode slow = head;
13 | ListNode fast = head;
14 | while (fast != null && fast.next != null) {
15 | slow = slow.next;
16 | fast = fast.next.next;
17 | if (slow == fast) return true;
18 | }
19 | return false;
20 | }
21 | ```
22 |
23 | ### 变题一:找到环入口
24 |
25 | **题目详情可见 [环形链表 II](https://leetcode.cn/problems/linked-list-cycle-ii/)**
26 |
27 | **算法思想一致的题目:[寻找重复数](https://leetcode.cn/problems/find-the-duplicate-number/)**
28 |
29 | ```java
30 | public ListNode detectCycle(ListNode head) {
31 | ListNode slow = head;
32 | ListNode fast = head;
33 | while (fast != null && fast.next != null) {
34 | slow = slow.next;
35 | fast = fast.next.next;
36 | if (slow == fast) {
37 | slow = head;
38 | while (slow != fast) {
39 | slow = slow.next;
40 | fast = fast.next;
41 | }
42 | return slow;
43 | }
44 | }
45 | return null;
46 | }
47 | ```
48 |
49 | ### 变题二:计算环中节点数
50 |
51 | ```java
52 | public int detectCycle(ListNode head) {
53 | ListNode slow = head;
54 | ListNode fast = head;
55 | while (fast != null && fast.next != null) {
56 | slow = slow.next;
57 | fast = fast.next.next;
58 | if (slow == fast) {
59 | int cnt = 0;
60 | // 再走一圈
61 | do {
62 | slow = slow.next;
63 | cnt++;
64 | } while (slow != fast);
65 | return cnt;
66 | }
67 | }
68 | return 0;
69 | }
70 | ```
71 |
72 | ### 其它方法:Set
73 |
74 | ```java
75 | // 判断是否有环 且 找到环入口
76 | public ListNode detectCycle(ListNode head) {
77 | Set set = new HashSet<>();
78 | ListNode p = head;
79 | while (p != null) {
80 | int sz = set.size();
81 | set.add(p.toString());
82 | // 找到环入口
83 | if (sz == set.size()) {
84 | return p;
85 | }
86 | p = p.next;
87 | }
88 | return null;
89 | }
90 | ```
91 |
92 |
--------------------------------------------------------------------------------
/markdown/Algorithm/田忌赛马.md:
--------------------------------------------------------------------------------
1 | # 田忌赛马
2 |
3 | [870. 优势洗牌](https://leetcode.cn/problems/advantage-shuffle/)
4 |
5 |
6 |
7 | 田忌赛马的故事大家都听说过,用自己最弱的去和对方最强的对抗
8 |
9 | 对于题目 [优势洗牌](https://leetcode.cn/problems/advantage-shuffle/) 来说,我们把这个策略更明确一丢丢
10 |
11 | 「如果自己最强的可以战胜对方最强的,那么就直接用最强的去打;否则就用自己最弱的出战,降低损失」
12 |
13 | 按照这个思路,就可以给出完整代码:
14 |
15 | ```java
16 | public int[] advantageCount(int[] nums1, int[] nums2) {
17 | Arrays.sort(nums1);
18 | Queue maxPQ = new PriorityQueue<>((a, b) -> b[1] - a[1]);
19 | for (int i = 0; i < nums2.length; i++) maxPQ.offer(new int[]{i, nums2[i]});
20 | // left 代表最弱的;right 代表最强的
21 | int left = 0, right = nums1.length - 1;
22 | int[] ans = new int[nums1.length];
23 | while (!maxPQ.isEmpty()) {
24 | int[] cur = maxPQ.poll();
25 | int i = cur[0], maxValue = cur[1];
26 | // 打得过
27 | if (maxValue < nums1[right]) {
28 | ans[i] = nums1[right];
29 | right--;
30 | } else {
31 | ans[i] = nums1[left];
32 | left++;
33 | }
34 | }
35 | return ans;
36 | }
37 | ```
--------------------------------------------------------------------------------
/markdown/Algorithm/相交链表-变题.md:
--------------------------------------------------------------------------------
1 | # 相交链表「变题」
2 |
3 | [160. 相交链表](https://leetcode.cn/problems/intersection-of-two-linked-lists/)
4 |
5 |
6 |
7 | 开头先来一个小插曲,关于「单链表」相关的总结可见 **[单链表的六大解题套路](./单链表的六大解题套路.html)**
8 |
9 | ```java
10 | public ListNode getIntersectionNode(ListNode headA, ListNode headB) {
11 | ListNode pa = headA, pb = headB;
12 | while (pa != pb) {
13 | if (pa == null) pa = headB;
14 | else pa = pa.next;
15 | if (pb == null) pb = headA;
16 | else pb = pb.next;
17 | }
18 | return pa;
19 | }
20 | ```
21 |
22 | ### 变题一:存在环的情况
23 |
24 | **思路:**找到环入口,解开环,然后用和上面一样的方法找交点
25 |
26 | ```java
27 | public ListNode getIntersectionNode(ListNode headA, ListNode headB) {
28 | openCycle(headA);
29 | openCycle(headB);
30 |
31 | ListNode pa = headA, pb = headB;
32 | while (pa != pb) {
33 | if (pa == null) pa = headB;
34 | else pa = pa.next;
35 | if (pb == null) pb = headA;
36 | else pb = pb.next;
37 | }
38 | return pa;
39 | }
40 | // 如果存在环的话,解开环
41 | public void openCycle(ListNode head) {
42 | ListNode slow = head;
43 | ListNode fast = head;
44 | while (fast != null && fast.next != null) {
45 | slow = slow.next;
46 | fast = fast.next.next;
47 | if (slow == fast) {
48 | slow = head;
49 | ListNode prev = null;
50 | while (slow != fast) {
51 | slow = slow.next;
52 | prev = fast;
53 | fast = fast.next;
54 | }
55 | prev.next = null;
56 | }
57 | }
58 | }
59 | ```
60 |
61 | ### 无环的其它方法
62 |
63 | 首先将任意一条链表首尾相连,然后从另一条链表开始寻找环入口!!(曲线救国)
64 |
65 | **缺点:**修改了链表的结构
66 |
67 | ```java
68 | public ListNode getIntersectionNode(ListNode headA, ListNode headB) {
69 |
70 | ListNode p = headA;
71 | while (p.next != null) {
72 | p = p.next;
73 | }
74 | p.next = headA;
75 |
76 | return detectCycle(headB);
77 | }
78 | // 找到环入口
79 | public ListNode detectCycle(ListNode head) {
80 | ListNode slow = head;
81 | ListNode fast = head;
82 | while (fast != null && fast.next != null) {
83 | slow = slow.next;
84 | fast = fast.next.next;
85 | if (slow == fast) {
86 | slow = head;
87 | while (slow != fast) {
88 | slow = slow.next;
89 | fast = fast.next;
90 | }
91 | return slow;
92 | }
93 | }
94 | return null;
95 | }
96 | ```
97 |
98 |
--------------------------------------------------------------------------------
/markdown/Algorithm/经典动态规划:完全背包问题.md:
--------------------------------------------------------------------------------
1 | # 经典动态规划:完全背包问题
2 |
3 | [518. 零钱兑换 II](https://leetcode.cn/problems/coin-change-ii/)
4 |
5 |
6 |
7 | 本篇文章介绍「完全背包」问题,但「0-1 背包」「子集背包」和今天介绍的「完全背包」是一个系列的问题!!
8 |
9 | **关于「0-1 背包」的详细介绍可见 [经典动态规划:0-1 背包问题](./经典动态规划:0-1背包问题.html)**
10 |
11 | **关于「子集背包」的详细介绍可见 [经典动态规划:子集背包问题](./经典动态规划:子集背包问题.html)**
12 |
13 | **「完全背包」和其它两种背包唯一的区别就是:物品数量无限**
14 |
15 | ### 问题分析
16 |
17 | 由于只有「物品数量」上的不同,所以其它地方几乎一样,只是`dp`的定义不同,以及状态转移不一样而已!!
18 |
19 | #### 明确「状态」和「选择」
20 |
21 | **状态:**物品数量 & 背包容量
22 |
23 | **选择:**是否装入物品
24 |
25 | #### 明确`dp`数组的定义
26 |
27 | `dp[i][j]`定义如下:对于前`i`个物品,当前背包容量为`j`时,恰好装满的组合数量
28 |
29 | 我们也可以很快确定 base case。即:`dp[...][0] = 1`,因为背包容量为 0,无论物品数量是多少,均只有一种组合,什么也不装!
30 |
31 | #### 根据「选择」,思考状态转移的逻辑
32 |
33 | `dp[i][j]` = 不把物品`i`装进背包的组合数 + 把物品`i`装进背包的组合数
34 |
35 | 如果不把物品`i`装进背包,显然组合数应该等于`dp[i-1][j]`,继承前`i-1`个物品的结果
36 |
37 | 如果把物品`i`装进背包,那么组合数应该等于`dp[i][j - val[i-1]]`
38 |
39 | **注意:**这里是`dp[i][j - val[i-1]]`,而不是`dp[i-1][j - val[i-1]]`,因为物品数量是无限的,所以选择物品`i`装入背包后,还可以继续选择物品`i`装入背包
40 |
41 | 对于题目 [零钱兑换 II](https://leetcode.cn/problems/coin-change-ii/),状态转移方程为:
42 | $$
43 | dp[i][j] = \left\{\begin{matrix}
44 | dp[i-1][j] & , j - coins[i] < 0 \\
45 | dp[i-1][j] + dp[i][j - coins[i]] & , j - coins[i] \ge 0
46 | \end{matrix}\right.
47 | $$
48 |
49 | ### 代码实现
50 |
51 | ```java
52 | public int change(int amount, int[] coins) {
53 | int[][] dp = new int[coins.length + 1][amount + 1];
54 | // base case
55 | for (int i = 0; i <= coins.length; i++) dp[i][0] = 1;
56 | for (int i = 1; i <= coins.length; i++) {
57 | for (int j = 1; j <= amount; j++) {
58 | // 装不下的情况
59 | if (j - coins[i - 1] < 0) dp[i][j] = dp[i - 1][j];
60 | else dp[i][j] = dp[i][j - coins[i - 1]] + dp[i - 1][j];
61 | }
62 | }
63 | return dp[coins.length][amount];
64 | }
65 | ```
66 |
67 | ### 空间优化
68 |
69 | **关于空间优化的技巧可见 [动态规划之最长回文子序列「dp 空间优化」](./动态规划之最长回文子序列.html)**
70 |
71 | ```java
72 | public int change(int amount, int[] coins) {
73 | int[] dp = new int[amount + 1];
74 | // base case
75 | dp[0] = 1;
76 | for (int i = 1; i <= coins.length; i++) {
77 | for (int j = 1; j <= amount; j++) {
78 | // 装不下
79 | // if (j - coins[i - 1] < 0) dp[j] = dp[j];
80 | // else dp[j] = dp[j - coins[i - 1]] + dp[j];
81 |
82 | // 下面是合并写法
83 | if (j - coins[i - 1] >= 0) dp[j] = dp[j - coins[i - 1]] + dp[j];
84 | }
85 | }
86 | return dp[amount];
87 | }
88 | ```
--------------------------------------------------------------------------------
/markdown/Algorithm/贪心之加油站.md:
--------------------------------------------------------------------------------
1 | # 贪心之加油站
2 |
3 | [134. 加油站](https://leetcode.cn/problems/gas-station/)
4 |
5 |
6 |
7 | 为了能够使车可以达到下一站,必须满足:**已有油量 >= 达到下一站所需油量**
8 |
9 | 给出一个样例:`gas = [4, 3, 1, 2, 7, 4]; cost = [1, 2, 7, 3, 2, 5]`
10 |
11 | 当我们经过第`i`个加油站,其油量的变化为:`gas[i] - cost[i]`
12 |
13 | 可以计算出经过每个加油站的变化值:`[3, 1, -6, -1, 5, -1]`
14 |
15 | 假设从第`0`个加油站开始,以变化的累积值绘制图像:
16 |
17 | 
18 |
19 | 当折线全部在 X 轴上方时,才表示可以从起点顺利到达终点!!显然从第`0`个加油站开始,不可以绕环路行驶一周
20 |
21 | 那我们从哪个点开始最可能使折线全部在 X 轴上方呢?
22 |
23 | 根据上图,当`x = 4`时,是最有可能使折线全部在 X 轴上方的,如下图所示:
24 |
25 | 
26 |
27 | 下面给出完整代码:
28 |
29 | ```java
30 | public int canCompleteCircuit(int[] gas, int[] cost) {
31 | int n = gas.length;
32 | int sum = 0, min = 10010, idx = -1;
33 | for (int i = 0; i < n; i++) {
34 | sum += gas[i] - cost[i];
35 | if (sum < min) {
36 | min = sum;
37 | idx = i + 1;
38 | }
39 | }
40 | if (sum < 0) return -1;
41 | return idx % n;
42 | }
43 | ```
44 |
45 |
--------------------------------------------------------------------------------
/markdown/Algorithm/队列-栈-互相转换.md:
--------------------------------------------------------------------------------
1 | # 队列-栈 互相转换
2 |
3 | [232. 用栈实现队列](https://leetcode-cn.com/problems/implement-queue-using-stacks/)
4 |
5 | [225. 用队列实现栈](https://leetcode-cn.com/problems/implement-stack-using-queues/)
6 |
7 |
8 |
9 | ### 用栈实现队列
10 |
11 | **题目详情可见 [用栈实现队列](https://leetcode-cn.com/problems/implement-queue-using-stacks/)**
12 |
13 | 该部分介绍用双栈模拟队列的所有功能!!
14 |
15 | 假如我们现在`push`了两个元素到队列中,效果如下图所示:
16 |
17 | 
18 |
19 | 如果我们现在需要`pop`或者`peek`元素怎么办??
20 |
21 | 可以先把 inStack 中的元素转移到 outStack 中,然后在 outStack 中进行`pop`或者`peek`操作,效果如下图所示:
22 |
23 | 
24 |
25 | 而且此时顺序也是正确的
26 |
27 | 那我们什么时候把 inStack 中的元素转移到 outStack 中呢?
28 |
29 | 很明显在 outStack 为空的时候,一次性把 inStack 所有的元素转移到 outStack 中
30 |
31 | 详细代码如下:
32 |
33 | ```java
34 | class MyQueue {
35 |
36 | private Stack outStack;
37 | private Stack inStack;
38 |
39 | public MyQueue() {
40 | outStack = new Stack<>();
41 | inStack = new Stack<>();
42 | }
43 |
44 | public void push(int x) {
45 | inStack.push(x);
46 | }
47 |
48 | public int pop() {
49 | if (outStack.isEmpty()) inToOut();
50 | return outStack.pop();
51 | }
52 |
53 | public int peek() {
54 | if (outStack.isEmpty()) inToOut();
55 | return outStack.peek();
56 | }
57 |
58 | // 当 outStack 和 inStack 中的元素均为空的时候,模拟队列才为空
59 | public boolean empty() {
60 | return outStack.isEmpty() && inStack.isEmpty();
61 | }
62 |
63 | // 转移元素
64 | private void inToOut() {
65 | while (!inStack.isEmpty()) {
66 | outStack.push(inStack.pop());
67 | }
68 | }
69 | }
70 | ```
71 |
72 | ### 用队列实现栈
73 |
74 | **题目详情可见 [用队列实现栈](https://leetcode-cn.com/problems/implement-stack-using-queues/)**
75 |
76 | 该部分介绍用单个队列来模拟栈的所有功能!!
77 |
78 | 主要分析如何实现下面两个功能
79 |
80 | - `int pop()`移除并返回栈顶元素
81 |
82 | - `int top()`返回栈顶元素
83 |
84 | 如下图所示,对于上面两个功能,首先肯定需要弹出元素 1 和 2,剩下的元素 3 才是我们需要移除或者返回的元素
85 |
86 | 
87 |
88 | 那弹出的元素 1 和 2 怎么处理呢?从队尾放回去就行了!简单粗暴,哈哈哈哈哈。如下图所示:
89 |
90 | 
91 |
92 | 根据上面的思路,我们可以很快实现:
93 |
94 | ```java
95 | class MyStack {
96 |
97 | private Queue queue;
98 |
99 | public MyStack() {
100 | queue = new LinkedList<>();
101 | }
102 |
103 | public void push(int x) {
104 | queue.add(x);
105 | }
106 |
107 | public int pop() {
108 | moveToBack();
109 | return queue.poll();
110 | }
111 |
112 | public int top() {
113 | moveToBack();
114 | int top = queue.poll();
115 | queue.add(top);
116 | return top;
117 | }
118 |
119 | public boolean empty() {
120 | return queue.isEmpty();
121 | }
122 |
123 | private void moveToBack() {
124 | int size = queue.size();
125 | for (int i = 0; i < size - 1; i++) queue.add(queue.poll());
126 | }
127 | }
128 | ```
--------------------------------------------------------------------------------
/markdown/Algorithm/集合划分变题-未给定具体划分大小.md:
--------------------------------------------------------------------------------
1 | # 集合划分变题「未给定具体划分大小」
2 |
3 | [5289. 公平分发饼干](https://leetcode.cn/problems/fair-distribution-of-cookies/)
4 |
5 | [698. 划分为k个相等的子集](https://leetcode-cn.com/problems/partition-to-k-equal-sum-subsets/)
6 |
7 | [473. 火柴拼正方形](https://leetcode.cn/problems/matchsticks-to-square/)
8 |
9 |
10 |
11 | 今天比赛中有一个题目 **[公平分发饼干](https://leetcode.cn/problems/fair-distribution-of-cookies/)**,和「集合划分问题」相似度高达 90%,但是脑子一时没有转过弯,比赛的时候没有写出来,特意总结一波!!
12 |
13 | **关于集合划分问题详细分析,可见 [经典回溯算法:集合划分问题](./经典回溯算法:集合划分问题.html)**
14 |
15 | ### 区别
16 |
17 | 先来说一下本问题和「集合划分问题」的区别!
18 |
19 | 对于「集合划分问题」,题目中给出了每个集合可容纳的大小,可以根据是否溢出来决定是否选择桶
20 |
21 | 但是对于本问题,没有给出每个集合可容纳的大小,只是让我们求所有划分中最大值的最小值 (有点绕!!)
22 |
23 | 所以一时之间不知道如何处理,还是太菜了,不知道如何灵活运用!!😭😭😭
24 |
25 | ### 思路
26 |
27 | 我们使用「球视角」的思路,即:让每个球来选择桶,当最后一个球完成选择,则到达「结束条件」
28 |
29 | **那我们可以从什么角度剪枝呢?**
30 |
31 | **剪枝一:**为了保证每个桶中至少有一个球,所以如果还剩`n`个空桶,但剩余球的数量小于`n`,可直接跳过
32 |
33 | **剪枝二:**对于第一个球,任意放到某个桶中的效果都是一样的,所以我们规定放到第一个桶中
34 |
35 | **剪枝三:**如果桶的大小已经超过了最小值,则肯定不是最优解,可直接跳过
36 |
37 | **剪枝四:**如果当前桶和上一个桶内的元素和相等,则跳过。原因:如果元素和相等,那么当前球选择上一个桶和选择当前桶可以得到的结果是一致的
38 |
39 | **这里还有一个小技巧:**对球排序,优先让值更大的球做选择,这样可以增加回溯的命中率
40 |
41 | #### 代码实现
42 |
43 | ```java
44 | private int ans = Integer.MAX_VALUE;
45 | public int distributeCookies(int[] cookies, int k) {
46 | // 排序
47 | Arrays.sort(cookies);
48 | for (int lo = 0, hi = cookies.length - 1; lo <= hi; lo++, hi--) {
49 | int t = cookies[lo];
50 | cookies[lo] = cookies[hi];
51 | cookies[hi] = t;
52 | }
53 | backtrack(cookies, 0, new int[k]);
54 | return ans;
55 | }
56 | private void backtrack(int[] cookies, int start, int[] bucket) {
57 | if (start == cookies.length) {
58 | // 记录一次划分中的最大值
59 | int max = 0;
60 | for (int b : bucket) {
61 | max = Math.max(max, b);
62 | }
63 | // 记录所有划分中最大值的最小值 (有点绕!!)
64 | ans = Math.min(ans, max);
65 | return ;
66 | }
67 | // 计算空桶数量
68 | int empty = 0;
69 | for (int b : bucket) {
70 | if (b == 0) empty++;
71 | }
72 | // 剪枝一
73 | if (empty > cookies.length - start) return ;
74 | for (int i = 0; i < bucket.length; i++) {
75 | // 剪枝二
76 | if (i > 0 && start == 0) return ;
77 | // 剪枝三
78 | if (i > 0 && bucket[i] == bucket[i - 1]) continue;
79 | // 剪枝四
80 | if (bucket[i] + cookies[start] > ans) continue;
81 | bucket[i] += cookies[start];
82 | // 处理下一个球
83 | backtrack(cookies, start + 1, bucket);
84 | bucket[i] -= cookies[start];
85 | }
86 | }
87 | ```
88 |
89 | 贴一下执行时间:
90 |
91 |
29 |
30 | 当我们在向外扩张时,记录一下层数,就可以得到两点之间的距离
31 |
32 | ### 代码实现
33 |
34 | ```java
35 | class Solution {
36 | private int m;
37 | private int n;
38 | private int[][] graph;
39 | // 记录所有的树,其三元组为 [h, i, j]
40 | private List tree = new ArrayList<>();
41 | private int[][] dirs = new int[][]{ {0,1},{0,-1},{1,0},{-1,0} };
42 | public int cutOffTree(List> forest) {
43 | m = forest.size();
44 | n = forest.get(0).size();
45 | graph = new int[m][n];
46 | if (forest.get(0).get(0) == 0) return -1;
47 | for (int i = 0; i < m; i++) {
48 | for (int j = 0; j < n; j++) {
49 | graph[i][j] = forest.get(i).get(j);
50 | // 加入 tree 中
51 | if (graph[i][j] > 1) tree.add(new int[]{graph[i][j], i, j});
52 | }
53 | }
54 | // 根据 h 排序
55 | Collections.sort(tree, Comparator.comparingInt(o -> o[0]));
56 | int ans = 0;
57 | int x = 0, y = 0;
58 | for (int[] t : tree) {
59 | int nx = t[1], ny = t[2];
60 | int dist = bfs(x, y, nx, ny);
61 | if (dist == -1) return -1;
62 | ans += dist;
63 | x = nx;
64 | y = ny;
65 | }
66 | return ans;
67 | }
68 | private int bfs(int X, int Y, int P, int Q) {
69 | if (X == P && Y == Q) return 0;
70 | // 记录节点访问情况
71 | boolean[][] visited = new boolean[m][n];
72 | // 双端队列
73 | Deque deque = new ArrayDeque<>();
74 | deque.addLast(new int[]{X, Y});
75 | visited[X][Y] = true;
76 | int dist = 0;
77 | while (!deque.isEmpty()) {
78 | int size = deque.size();
79 | for (int i = 0; i < size; i++) {
80 | int[] cur = deque.pollFirst();
81 | int x = cur[0], y = cur[1];
82 | for (int[] dir : dirs) {
83 | int nx = x + dir[0], ny = y + dir[1];
84 | // 非法情况
85 | if (nx < 0 || nx >= m || ny < 0 || ny >= n || graph[nx][ny] == 0 || visited[nx][ny]) continue;
86 | // 达到终点
87 | if (nx == P && ny == Q) return dist + 1;
88 | deque.addLast(new int[]{nx, ny});
89 | visited[nx][ny] = true;
90 | }
91 | }
92 | dist++;
93 | }
94 | return -1;
95 | }
96 | }
97 | ```
98 |
99 |
--------------------------------------------------------------------------------
/markdown/Algorithm/浅析:最小基因变化.md:
--------------------------------------------------------------------------------
1 | # 浅析:最小基因变化
2 |
3 | [433. 最小基因变化](https://leetcode-cn.com/problems/minimum-genetic-mutation/)
4 |
5 |
6 |
7 | 本篇文章简单分析一下题目 [最小基因变化](https://leetcode-cn.com/problems/minimum-genetic-mutation/),这个题目是一个 BFS 的模版题,和题目 [打开转盘锁](https://leetcode-cn.com/problems/open-the-lock/) 很相似,**详情可见 [BFS 算法框架](./BFS.html)**
8 |
9 | 下面从两个不同的角度分析本题:「单向 BFS」「双向 BFS」
10 |
11 | ### 单向 BFS
12 |
13 | 我们以`start`作为第 0 层,`bank`中在`start`基础上改变一位基因作为第 1 层,依次类推,直到寻找到目标基因
14 |
15 | 同时,我们需要记录`bank`中基因的访问情况
16 |
17 | 下面给出对应的代码:
18 |
19 | ```java
20 | public int minMutation(String start, String end, String[] bank) {
21 | // 转化成 set 方便查找
22 | Set bankSet = new HashSet<>(Arrays.asList(bank));
23 | // 边界处理:如果 end 不在 bank 中
24 | if (!bankSet.contains(end)) return -1;
25 | // 记录基因访问情况
26 | Set used = new HashSet<>();
27 | Queue q = new LinkedList<>();
28 | q.offer(start);
29 | used.add(start);
30 | int count = 0;
31 | while (!q.isEmpty()) {
32 | int size = q.size();
33 | for (int i = 0; i < size; i++) {
34 | String cur = q.poll();
35 | // 如果找到,返回步数
36 | if (cur.equals(end)) return count;
37 | for (String gene : bankSet) {
38 | // 从 bank 中去找与当前基因只发生一位改变的基因
39 | if (!used.contains(gene) && isChangeOne(cur, gene)) {
40 | q.offer(gene);
41 | // 标记
42 | used.add(gene);
43 | }
44 | }
45 | }
46 | count++;
47 | }
48 | return -1;
49 | }
50 | // 判断两个基因是否只有一位不同
51 | private boolean isChangeOne(String source, String target) {
52 | int changeCount = 0;
53 | for (int i = 0; i < 8; i++) {
54 | if (source.charAt(i) != target.charAt(i)) changeCount++;
55 | if (changeCount > 1) return false;
56 | }
57 | return changeCount == 1;
58 | }
59 | ```
60 |
61 | ### 双向 BFS
62 |
63 | 这个题目也符合「双向 BFS」的适用情况,即终点是明确的
64 |
65 | ```java
66 | public int minMutation(String start, String end, String[] bank) {
67 | Set bankSet = new HashSet<>(Arrays.asList(bank));
68 | if (!bankSet.contains(end)) return -1;
69 | Set used = new HashSet<>();
70 | Set q1 = new HashSet<>();
71 | Set q2 = new HashSet<>();
72 | q1.add(start);
73 | q2.add(end);
74 | int count = 0;
75 | while (!q1.isEmpty() && !q2.isEmpty()) {
76 | Set temp = new HashSet<>();
77 | for (String cur : q1) {
78 | if (q2.contains(cur)) return count;
79 | // 标记
80 | used.add(cur);
81 | for (String gene : bankSet) {
82 | // isChangeOne() 同上
83 | if (!used.contains(gene) && isChangeOne(cur, gene)) {
84 | temp.add(gene);
85 | }
86 | }
87 | }
88 | q1 = q2;
89 | q2 = temp;
90 | count++;
91 | }
92 | return -1;
93 | }
94 | ```
95 |
96 | 这里需要注意的一点,**选择恰当标记的时机**。不可以在加入队列的时候标记,不然这样一个基因只能加入一端的队列中,这样肯定就无法在一端队列中找到相同的基因 🧬,因为双向队列中的基因各不相同
97 |
98 | 下面给出错误的代码,加以警示!!
99 |
100 | ```java
101 | // 标记
102 | // used.add(cur);
103 | for (String gene : bankSet) {
104 | // isChangeOne() 同上
105 | if (!used.contains(gene) && isChangeOne(cur, gene)) {
106 | temp.add(gene);
107 | // 错误标记时机
108 | used.add(gene);
109 | }
110 | }
111 | ```
112 |
--------------------------------------------------------------------------------
/markdown/Algorithm/浅析:最小路径和.md:
--------------------------------------------------------------------------------
1 | # 浅析:最小路径和
2 |
3 | [64. 最小路径和](https://leetcode-cn.com/problems/minimum-path-sum/)
4 |
5 |
6 |
7 | 今天我们来详细分析一波 **[最小路径和](https://leetcode-cn.com/problems/minimum-path-sum/)**,带你从头开始一步一步得到最优化的解决方案!
8 |
9 | ### 暴力 DFS
10 |
11 | 首先第一眼看到这个题目,自然而然想到的就是 DFS,遍历出所有的路径,然后得到和最小的路径
12 |
13 | 关于 DFS 详细的内容可见 **[回溯 (DFS) 算法框架](./回溯(DFS).html)**
14 |
15 | ```java
16 | // 记录最小路径和
17 | private int res = Integer.MAX_VALUE;
18 | public int minPathSum(int[][] grid) {
19 | int m = grid.length;
20 | int n = grid[0].length;
21 | // 从 (0, 0) 开始遍历
22 | dfs(grid, 0, 0, 0, new boolean[m][n]);
23 | return res;
24 | }
25 | private void dfs(int[][] grid, int i, int j, int pathSum, boolean[][] used) {
26 | int m = grid.length;
27 | int n = grid[0].length;
28 | // 先序阶段:首次进入节点 (i, j)
29 | // 越界
30 | if (i < 0 || i >= m || j< 0 || j >= n) return ;
31 | // 判断是否已经被使用
32 | if (used[i][j]) return;
33 | // 标记已被使用
34 | used[i][j] = true;
35 | // 添加到路径中
36 | pathSum += grid[i][j];
37 | // 到达终点
38 | if (i == m - 1 && j == n - 1) res = Math.min(res, pathSum);
39 |
40 | // 每次都往「下」「右」进行搜索
41 | dfs(grid, i + 1, j, pathSum, used);
42 | dfs(grid, i, j + 1, pathSum, used);
43 |
44 | // 后续阶段:即将离开节点 (i, j)
45 | pathSum -= grid[i][j];
46 | used[i][j] = false;
47 | }
48 | ```
49 |
50 | 很显然,这个是超时的!!!
51 |
52 | ### 备忘录 + 递归
53 |
54 | 上面是没有任何优化的暴力 DFS,可以很明显的看到其实是**存在「重叠子问题」**的
55 |
56 | 这里采用自顶向下的解法,所以会有一个递归的`dp`函数,一般来说函数的**参数**就是状态转移中会变化的量,即:「状态」;**函数的返回值**就是`grid[0..i][0..j]`的最小路径和
57 |
58 | ```java
59 | private int res = Integer.MAX_VALUE;
60 | public int minPathSum(int[][] grid) {
61 | int m = grid.length;
62 | int n = grid[0].length;
63 | return dp(grid, m - 1, n - 1, new int[m][n]);
64 | }
65 | private int dp(int[][] grid, int i, int j, int[][] emeo) {
66 | int m = grid.length;
67 | int n = grid[0].length;
68 | // base case
69 | if (i < 0 || i >= m || j< 0 || j >= n) return Integer.MAX_VALUE;
70 | if (emeo[i][j] != 0) return emeo[i][j];
71 |
72 | int minPathSum = Math.min(dp(grid, i - 1, j, emeo), dp(grid, i, j - 1, emeo));
73 |
74 | emeo[i][j] = minPathSum == Integer.MAX_VALUE ? grid[i][j] : minPathSum + grid[i][j];
75 |
76 | return emeo[i][j];
77 | }
78 | ```
79 |
80 | ### DP + 递推
81 |
82 | **明确 base case:**显然是当`i = 0 and j = 0`,最小路径和直接是`grid[0][0]`
83 |
84 | **明确「状态」:原问题和子问题中会发生变化的变量。**`grid[0..i][0..j]`会不断地向 base case 靠近,所以唯一的「状态」就是矩阵`grid[0..i][0..j]`
85 |
86 | **明确「选择」:导致「状态」产生变化的行为。**矩阵`grid[0..i][0..j]`为什么变化呢?因为在选择不同的方向,每选择一种方向,矩阵就会收缩。所以说「上方 or 左方」就是「选择」(每次都可在选择任意一种方向)
87 |
88 | **明确 dp 数组/函数的定义:**这里采用自底向上的解法,所以会有一个递推的`dp`数组,一般来说数组的**下标**就是状态转移中会变化的量,即:「状态」;**数组的值**就是`grid[0..i][0..j]`的最小路径和
89 |
90 | 关于`dp[]`的初始状态,直接看下图:
91 |
92 | 
93 |
94 | ```java
95 | public int minPathSum(int[][] grid) {
96 | int m = grid.length;
97 | int n = grid[0].length;
98 | int[][] dp = new int[m + 1][n + 1];
99 | // 初始化 dp[]
100 | for (int i = 0; i < dp.length; i++) dp[i][0] = Integer.MAX_VALUE;
101 | for (int j = 0; j < dp[0].length; j++) dp[0][j] = Integer.MAX_VALUE;
102 | dp[0][1] = 0;
103 | dp[1][0] = 0;
104 |
105 | for (int i = 1; i < dp.length; i++) {
106 | for (int j = 1; j < dp[0].length; j++) {
107 | dp[i][j] = Math.min(dp[i - 1][j], dp[i][j - 1]) + grid[i - 1][j - 1];
108 | }
109 | }
110 | return dp[m][n];
111 | }
112 | ```
113 |
114 |
--------------------------------------------------------------------------------
/markdown/Algorithm/浅析:检查是否有合法括号字符串路径.md:
--------------------------------------------------------------------------------
1 | # 浅析:检查是否有合法括号字符串路径
2 |
3 | [6059. 检查是否有合法括号字符串路径](https://leetcode-cn.com/problems/check-if-there-is-a-valid-parentheses-string-path/)
4 |
5 |
6 |
7 | 好难好难,这又是一个合法括号问题!!只不过更加的难,太难了,太难了,自闭!!!
8 |
9 | 关于括号相关问题的分析,可见:「**[秒杀所有括号类问题](./秒杀所有括号类问题.html)**」「**[回溯算法:括号生成](./回溯算法:括号生成.html)**」「**[回溯算法:删除无效的括号](./回溯算法:删除无效的括号.html)**」
10 |
11 | 总结分析了这么多,其实关于括号类问题大部分都是使用「DFS」,**关于 DFS 详细分析可见 [回溯 (DFS) 算法框架](./algorithm/回溯(DFS).html)**
12 |
13 | 但是难点就在于「剪枝」,太变态了!!!**[回溯算法:删除无效的括号](./回溯算法:删除无效的括号.html)** 里面详细介绍了一些剪枝的策略!!
14 |
15 | ### 暴力 DFS
16 |
17 | 下面来看今天的问题!第一眼感觉不难,随手就写了一个「DFS」,不就是找到一条从`(0, 0)`到`(m - 1, n - 1)`的满足要求的路径嘛!!和题目 [最小路径和](https://leetcode-cn.com/problems/minimum-path-sum/) 中「暴力 DFS 求解」很类似,**可见 [浅析:最小路径和](./浅析:最小路径和.html)**
18 |
19 | 所以随手就写出了代码:
20 |
21 | ```java
22 | private boolean ok = false;
23 | public boolean hasValidPath(char[][] grid) {
24 | int m = grid.length;
25 | int n = grid[0].length;
26 | dfs(grid, 0, 0, 0, 0, new boolean[m][n]);
27 | return ok;
28 | }
29 | private void dfs(char[][] grid, int i, int j, int left, int right, boolean[][] used) {
30 | int m = grid.length;
31 | int n = grid[0].length;
32 | if (i < 0 || i >= m || j < 0 || j >= n || used[i][j] || left < right || ok) return ;
33 | used[i][j] = true;
34 | if (grid[i][j] == '(') left++;
35 | else right++;
36 | if (i == m - 1 && j == n - 1) {
37 | if (left == right) ok = true;
38 | }
39 | dfs(grid, i + 1, j, left, right, used);
40 | dfs(grid, i, j + 1, left, right, used);
41 | used[i][j] = false;
42 | }
43 | ```
44 |
45 | 无奈,超时了!!!
46 |
47 | ### 剪枝思路分析
48 |
49 | 如何优化呢???剪枝吧!!
50 |
51 | **角度一:**由于只能往下或者往右,且起点为`(0, 0)`,终点为`(m - 1, n -1)`,所以任意一条路径长度均为`m + n - 1`。如果要满足「合法括号」的要求,`m + n - 1` 必为偶数
52 |
53 | **角度二:**起点`(0, 0)`必须为`'('`,而终点`(m - 1, n - 1)`必须为`')'`,才能满足要求
54 |
55 | **角度三:**在「暴力 DFS」中,我们对状态划分比较简单,仅划分为了`m * n`个,即以每个格子为单位,用`used[][]`表示
56 |
57 | 我们现在优化一下代码,不再用`left`和`right`表示左右括号的数量,而是只用一个变量`count`表示,即:遇到左括号就 +1,遇到右括号就 -1。如果`count < 0`,则非法需要被剪枝
58 |
59 | 我们现在分析一下`count`的范围,如果所有的括号均为左括号,那么`count`为最大值,即:`count = m * n - 1`。因为上面分析过了,任意一条路径长度均为`m + n - 1`
60 |
61 | 所以如果我们仅仅以每个格子为状态,我们在回溯的过程中需要撤销标记,可能会导致冗余的计算。如果我们以每个格子的`count`作为状态,那么这个`used[m][n][m + n]`同时还充当了「备忘录 emeo」的角色
62 |
63 | ### 优化后代码实现
64 |
65 | ```java
66 | public boolean hasValidPath(char[][] grid) {
67 | int m = grid.length;
68 | int n = grid[0].length;
69 | // 角度一 + 角度二 的剪枝
70 | if ((m + n) % 2 == 0 || grid[0][0] == ')' || grid[m - 1][n - 1] == '(') return false;
71 | return dfs(grid, 0, 0, 0, new boolean[m][n][m + n]);
72 | }
73 | private boolean dfs(char[][] grid, int i, int j, int count, boolean[][][] used) {
74 | int m = grid.length;
75 | int n = grid[0].length;
76 | // 边界处理
77 | if (i < 0 || i >= m || j < 0 || j >= n) return false;
78 | // count < 0 说明 left < right
79 | // count > m - i + n - j - 1 说明剩下的路径就算都是 ')' 也无法使 count 变为 0
80 | if (count < 0 || count > m - i + n - j - 1) return false;
81 | // 该状态已标记,无法满足合法括号路径
82 | if (used[i][j][count]) return false;
83 | // 到达终点,count = 1 即满足要求
84 | // 可以思考一下为什么 count = 1 就行了
85 | if (i == m - 1 && j == n - 1) return count == 1;
86 | used[i][j][count] = true;
87 | count += (grid[i][j] == '(' ? 1 : -1);
88 | // 处理下方和右方
89 | return dfs(grid, i + 1, j, count, used) || dfs(grid, i, j + 1, count, used);
90 | }
91 | ```
92 |
93 |
--------------------------------------------------------------------------------
/markdown/Algorithm/爬楼梯-变题.md:
--------------------------------------------------------------------------------
1 | # 爬楼梯「变题」
2 |
3 | [70. 爬楼梯](https://leetcode.cn/problems/climbing-stairs/)
4 |
5 |
6 |
7 | ```java
8 | // 时间复杂度 : O(n)
9 | // 空间复杂度 : O(n)
10 | public int climbStairs(int n) {
11 | if (n <= 2) return n;
12 | int[] f = new int[n + 1];
13 | f[1] = 1; f[2] = 2;
14 | for (int i = 3; i <= n; i++) {
15 | f[i] = f[i - 1] + f[i - 2];
16 | }
17 | return f[n];
18 | }
19 | ```
20 |
21 | ### 变题一:空间优化
22 |
23 | ```java
24 | // 时间复杂度 : O(n)
25 | // 空间复杂度 : O(1)
26 | public int climbStairs(int n) {
27 | if (n <= 2) return n;
28 | int f1 = 1, f2 = 2, f = 0;
29 | for (int i = 3; i <= n; i++) {
30 | f = f1 + f2;
31 | f1 = f2;
32 | f2 = f;
33 | }
34 | return f;
35 | }
36 | ```
37 |
38 | ### 变题二:扩展至 m 阶数
39 |
40 | **相似题目可见 [DP3 跳台阶扩展问题](https://www.nowcoder.com/practice/953b74ca5c4d44bb91f39ac4ddea0fee)**
41 |
42 | ```java
43 | public int climbStairs(int n) {
44 | int[] f = new int[n + 1];
45 | f[0] = 1;
46 | for (int i = 1; i <= n; i++) {
47 | for (int j = 1; i - j >= 0 && j <= m; j++) {
48 | f[i] += f[i - j];
49 | }
50 | }
51 | return f[n];
52 | }
53 | ```
54 |
55 | ### 变题三:输出所有跳法
56 |
57 | ```java
58 | private int n;
59 | private List track = new ArrayList<>();
60 | private List> path = new ArrayList<>();
61 | public int climbStairs(int n) {
62 | this.n = n;
63 | int ans = f(0);
64 | System.out.println(path);
65 | return ans;
66 | }
67 | private int f(int i) {
68 | if (i > n) return 0;
69 | if (i == n) {
70 | path.add(new ArrayList<>(track));
71 | return 1;
72 | }
73 | track.add(1);
74 | int t1 = f(i + 1);
75 | track.remove(track.size() - 1);
76 |
77 | track.add(2);
78 | int t2 = f(i + 2);
79 | track.remove(track.size() - 1);
80 | return t1 + t2;
81 | }
82 | ```
83 |
84 | ### 变题四:不能爬到 7 及 7 的倍数
85 |
86 | ```java
87 | public int climbStairs(int n) {
88 | if (n <= 2) return n;
89 | int[] f = new int[n + 1];
90 | f[1] = 1; f[2] = 2;
91 | for (int i = 3; i <= n; i++) {
92 | // 若为 7 的倍数,直接为 0
93 | if (i % 7 == 0) f[i] = 0;
94 | else f[i] = f[i - 1] + f[i - 2];
95 | }
96 | return f[n];
97 | }
98 | ```
99 |
100 |
--------------------------------------------------------------------------------
/markdown/Algorithm/环形链表-变题.md:
--------------------------------------------------------------------------------
1 | # 环形链表「变题」
2 |
3 | [141. 环形链表](https://leetcode.cn/problems/linked-list-cycle/)
4 |
5 |
6 |
7 | 开头先来一个小插曲,关于「单链表」相关的总结可见 **[单链表的六大解题套路](./单链表的六大解题套路.html)**
8 |
9 | ```java
10 | // 快慢指针 (判断是否有环)
11 | public boolean hasCycle(ListNode head) {
12 | ListNode slow = head;
13 | ListNode fast = head;
14 | while (fast != null && fast.next != null) {
15 | slow = slow.next;
16 | fast = fast.next.next;
17 | if (slow == fast) return true;
18 | }
19 | return false;
20 | }
21 | ```
22 |
23 | ### 变题一:找到环入口
24 |
25 | **题目详情可见 [环形链表 II](https://leetcode.cn/problems/linked-list-cycle-ii/)**
26 |
27 | **算法思想一致的题目:[寻找重复数](https://leetcode.cn/problems/find-the-duplicate-number/)**
28 |
29 | ```java
30 | public ListNode detectCycle(ListNode head) {
31 | ListNode slow = head;
32 | ListNode fast = head;
33 | while (fast != null && fast.next != null) {
34 | slow = slow.next;
35 | fast = fast.next.next;
36 | if (slow == fast) {
37 | slow = head;
38 | while (slow != fast) {
39 | slow = slow.next;
40 | fast = fast.next;
41 | }
42 | return slow;
43 | }
44 | }
45 | return null;
46 | }
47 | ```
48 |
49 | ### 变题二:计算环中节点数
50 |
51 | ```java
52 | public int detectCycle(ListNode head) {
53 | ListNode slow = head;
54 | ListNode fast = head;
55 | while (fast != null && fast.next != null) {
56 | slow = slow.next;
57 | fast = fast.next.next;
58 | if (slow == fast) {
59 | int cnt = 0;
60 | // 再走一圈
61 | do {
62 | slow = slow.next;
63 | cnt++;
64 | } while (slow != fast);
65 | return cnt;
66 | }
67 | }
68 | return 0;
69 | }
70 | ```
71 |
72 | ### 其它方法:Set
73 |
74 | ```java
75 | // 判断是否有环 且 找到环入口
76 | public ListNode detectCycle(ListNode head) {
77 | Set set = new HashSet<>();
78 | ListNode p = head;
79 | while (p != null) {
80 | int sz = set.size();
81 | set.add(p.toString());
82 | // 找到环入口
83 | if (sz == set.size()) {
84 | return p;
85 | }
86 | p = p.next;
87 | }
88 | return null;
89 | }
90 | ```
91 |
92 |
--------------------------------------------------------------------------------
/markdown/Algorithm/田忌赛马.md:
--------------------------------------------------------------------------------
1 | # 田忌赛马
2 |
3 | [870. 优势洗牌](https://leetcode.cn/problems/advantage-shuffle/)
4 |
5 |
6 |
7 | 田忌赛马的故事大家都听说过,用自己最弱的去和对方最强的对抗
8 |
9 | 对于题目 [优势洗牌](https://leetcode.cn/problems/advantage-shuffle/) 来说,我们把这个策略更明确一丢丢
10 |
11 | 「如果自己最强的可以战胜对方最强的,那么就直接用最强的去打;否则就用自己最弱的出战,降低损失」
12 |
13 | 按照这个思路,就可以给出完整代码:
14 |
15 | ```java
16 | public int[] advantageCount(int[] nums1, int[] nums2) {
17 | Arrays.sort(nums1);
18 | Queue maxPQ = new PriorityQueue<>((a, b) -> b[1] - a[1]);
19 | for (int i = 0; i < nums2.length; i++) maxPQ.offer(new int[]{i, nums2[i]});
20 | // left 代表最弱的;right 代表最强的
21 | int left = 0, right = nums1.length - 1;
22 | int[] ans = new int[nums1.length];
23 | while (!maxPQ.isEmpty()) {
24 | int[] cur = maxPQ.poll();
25 | int i = cur[0], maxValue = cur[1];
26 | // 打得过
27 | if (maxValue < nums1[right]) {
28 | ans[i] = nums1[right];
29 | right--;
30 | } else {
31 | ans[i] = nums1[left];
32 | left++;
33 | }
34 | }
35 | return ans;
36 | }
37 | ```
--------------------------------------------------------------------------------
/markdown/Algorithm/相交链表-变题.md:
--------------------------------------------------------------------------------
1 | # 相交链表「变题」
2 |
3 | [160. 相交链表](https://leetcode.cn/problems/intersection-of-two-linked-lists/)
4 |
5 |
6 |
7 | 开头先来一个小插曲,关于「单链表」相关的总结可见 **[单链表的六大解题套路](./单链表的六大解题套路.html)**
8 |
9 | ```java
10 | public ListNode getIntersectionNode(ListNode headA, ListNode headB) {
11 | ListNode pa = headA, pb = headB;
12 | while (pa != pb) {
13 | if (pa == null) pa = headB;
14 | else pa = pa.next;
15 | if (pb == null) pb = headA;
16 | else pb = pb.next;
17 | }
18 | return pa;
19 | }
20 | ```
21 |
22 | ### 变题一:存在环的情况
23 |
24 | **思路:**找到环入口,解开环,然后用和上面一样的方法找交点
25 |
26 | ```java
27 | public ListNode getIntersectionNode(ListNode headA, ListNode headB) {
28 | openCycle(headA);
29 | openCycle(headB);
30 |
31 | ListNode pa = headA, pb = headB;
32 | while (pa != pb) {
33 | if (pa == null) pa = headB;
34 | else pa = pa.next;
35 | if (pb == null) pb = headA;
36 | else pb = pb.next;
37 | }
38 | return pa;
39 | }
40 | // 如果存在环的话,解开环
41 | public void openCycle(ListNode head) {
42 | ListNode slow = head;
43 | ListNode fast = head;
44 | while (fast != null && fast.next != null) {
45 | slow = slow.next;
46 | fast = fast.next.next;
47 | if (slow == fast) {
48 | slow = head;
49 | ListNode prev = null;
50 | while (slow != fast) {
51 | slow = slow.next;
52 | prev = fast;
53 | fast = fast.next;
54 | }
55 | prev.next = null;
56 | }
57 | }
58 | }
59 | ```
60 |
61 | ### 无环的其它方法
62 |
63 | 首先将任意一条链表首尾相连,然后从另一条链表开始寻找环入口!!(曲线救国)
64 |
65 | **缺点:**修改了链表的结构
66 |
67 | ```java
68 | public ListNode getIntersectionNode(ListNode headA, ListNode headB) {
69 |
70 | ListNode p = headA;
71 | while (p.next != null) {
72 | p = p.next;
73 | }
74 | p.next = headA;
75 |
76 | return detectCycle(headB);
77 | }
78 | // 找到环入口
79 | public ListNode detectCycle(ListNode head) {
80 | ListNode slow = head;
81 | ListNode fast = head;
82 | while (fast != null && fast.next != null) {
83 | slow = slow.next;
84 | fast = fast.next.next;
85 | if (slow == fast) {
86 | slow = head;
87 | while (slow != fast) {
88 | slow = slow.next;
89 | fast = fast.next;
90 | }
91 | return slow;
92 | }
93 | }
94 | return null;
95 | }
96 | ```
97 |
98 |
--------------------------------------------------------------------------------
/markdown/Algorithm/经典动态规划:完全背包问题.md:
--------------------------------------------------------------------------------
1 | # 经典动态规划:完全背包问题
2 |
3 | [518. 零钱兑换 II](https://leetcode.cn/problems/coin-change-ii/)
4 |
5 |
6 |
7 | 本篇文章介绍「完全背包」问题,但「0-1 背包」「子集背包」和今天介绍的「完全背包」是一个系列的问题!!
8 |
9 | **关于「0-1 背包」的详细介绍可见 [经典动态规划:0-1 背包问题](./经典动态规划:0-1背包问题.html)**
10 |
11 | **关于「子集背包」的详细介绍可见 [经典动态规划:子集背包问题](./经典动态规划:子集背包问题.html)**
12 |
13 | **「完全背包」和其它两种背包唯一的区别就是:物品数量无限**
14 |
15 | ### 问题分析
16 |
17 | 由于只有「物品数量」上的不同,所以其它地方几乎一样,只是`dp`的定义不同,以及状态转移不一样而已!!
18 |
19 | #### 明确「状态」和「选择」
20 |
21 | **状态:**物品数量 & 背包容量
22 |
23 | **选择:**是否装入物品
24 |
25 | #### 明确`dp`数组的定义
26 |
27 | `dp[i][j]`定义如下:对于前`i`个物品,当前背包容量为`j`时,恰好装满的组合数量
28 |
29 | 我们也可以很快确定 base case。即:`dp[...][0] = 1`,因为背包容量为 0,无论物品数量是多少,均只有一种组合,什么也不装!
30 |
31 | #### 根据「选择」,思考状态转移的逻辑
32 |
33 | `dp[i][j]` = 不把物品`i`装进背包的组合数 + 把物品`i`装进背包的组合数
34 |
35 | 如果不把物品`i`装进背包,显然组合数应该等于`dp[i-1][j]`,继承前`i-1`个物品的结果
36 |
37 | 如果把物品`i`装进背包,那么组合数应该等于`dp[i][j - val[i-1]]`
38 |
39 | **注意:**这里是`dp[i][j - val[i-1]]`,而不是`dp[i-1][j - val[i-1]]`,因为物品数量是无限的,所以选择物品`i`装入背包后,还可以继续选择物品`i`装入背包
40 |
41 | 对于题目 [零钱兑换 II](https://leetcode.cn/problems/coin-change-ii/),状态转移方程为:
42 | $$
43 | dp[i][j] = \left\{\begin{matrix}
44 | dp[i-1][j] & , j - coins[i] < 0 \\
45 | dp[i-1][j] + dp[i][j - coins[i]] & , j - coins[i] \ge 0
46 | \end{matrix}\right.
47 | $$
48 |
49 | ### 代码实现
50 |
51 | ```java
52 | public int change(int amount, int[] coins) {
53 | int[][] dp = new int[coins.length + 1][amount + 1];
54 | // base case
55 | for (int i = 0; i <= coins.length; i++) dp[i][0] = 1;
56 | for (int i = 1; i <= coins.length; i++) {
57 | for (int j = 1; j <= amount; j++) {
58 | // 装不下的情况
59 | if (j - coins[i - 1] < 0) dp[i][j] = dp[i - 1][j];
60 | else dp[i][j] = dp[i][j - coins[i - 1]] + dp[i - 1][j];
61 | }
62 | }
63 | return dp[coins.length][amount];
64 | }
65 | ```
66 |
67 | ### 空间优化
68 |
69 | **关于空间优化的技巧可见 [动态规划之最长回文子序列「dp 空间优化」](./动态规划之最长回文子序列.html)**
70 |
71 | ```java
72 | public int change(int amount, int[] coins) {
73 | int[] dp = new int[amount + 1];
74 | // base case
75 | dp[0] = 1;
76 | for (int i = 1; i <= coins.length; i++) {
77 | for (int j = 1; j <= amount; j++) {
78 | // 装不下
79 | // if (j - coins[i - 1] < 0) dp[j] = dp[j];
80 | // else dp[j] = dp[j - coins[i - 1]] + dp[j];
81 |
82 | // 下面是合并写法
83 | if (j - coins[i - 1] >= 0) dp[j] = dp[j - coins[i - 1]] + dp[j];
84 | }
85 | }
86 | return dp[amount];
87 | }
88 | ```
--------------------------------------------------------------------------------
/markdown/Algorithm/贪心之加油站.md:
--------------------------------------------------------------------------------
1 | # 贪心之加油站
2 |
3 | [134. 加油站](https://leetcode.cn/problems/gas-station/)
4 |
5 |
6 |
7 | 为了能够使车可以达到下一站,必须满足:**已有油量 >= 达到下一站所需油量**
8 |
9 | 给出一个样例:`gas = [4, 3, 1, 2, 7, 4]; cost = [1, 2, 7, 3, 2, 5]`
10 |
11 | 当我们经过第`i`个加油站,其油量的变化为:`gas[i] - cost[i]`
12 |
13 | 可以计算出经过每个加油站的变化值:`[3, 1, -6, -1, 5, -1]`
14 |
15 | 假设从第`0`个加油站开始,以变化的累积值绘制图像:
16 |
17 | 
18 |
19 | 当折线全部在 X 轴上方时,才表示可以从起点顺利到达终点!!显然从第`0`个加油站开始,不可以绕环路行驶一周
20 |
21 | 那我们从哪个点开始最可能使折线全部在 X 轴上方呢?
22 |
23 | 根据上图,当`x = 4`时,是最有可能使折线全部在 X 轴上方的,如下图所示:
24 |
25 | 
26 |
27 | 下面给出完整代码:
28 |
29 | ```java
30 | public int canCompleteCircuit(int[] gas, int[] cost) {
31 | int n = gas.length;
32 | int sum = 0, min = 10010, idx = -1;
33 | for (int i = 0; i < n; i++) {
34 | sum += gas[i] - cost[i];
35 | if (sum < min) {
36 | min = sum;
37 | idx = i + 1;
38 | }
39 | }
40 | if (sum < 0) return -1;
41 | return idx % n;
42 | }
43 | ```
44 |
45 |
--------------------------------------------------------------------------------
/markdown/Algorithm/队列-栈-互相转换.md:
--------------------------------------------------------------------------------
1 | # 队列-栈 互相转换
2 |
3 | [232. 用栈实现队列](https://leetcode-cn.com/problems/implement-queue-using-stacks/)
4 |
5 | [225. 用队列实现栈](https://leetcode-cn.com/problems/implement-stack-using-queues/)
6 |
7 |
8 |
9 | ### 用栈实现队列
10 |
11 | **题目详情可见 [用栈实现队列](https://leetcode-cn.com/problems/implement-queue-using-stacks/)**
12 |
13 | 该部分介绍用双栈模拟队列的所有功能!!
14 |
15 | 假如我们现在`push`了两个元素到队列中,效果如下图所示:
16 |
17 | 
18 |
19 | 如果我们现在需要`pop`或者`peek`元素怎么办??
20 |
21 | 可以先把 inStack 中的元素转移到 outStack 中,然后在 outStack 中进行`pop`或者`peek`操作,效果如下图所示:
22 |
23 | 
24 |
25 | 而且此时顺序也是正确的
26 |
27 | 那我们什么时候把 inStack 中的元素转移到 outStack 中呢?
28 |
29 | 很明显在 outStack 为空的时候,一次性把 inStack 所有的元素转移到 outStack 中
30 |
31 | 详细代码如下:
32 |
33 | ```java
34 | class MyQueue {
35 |
36 | private Stack outStack;
37 | private Stack inStack;
38 |
39 | public MyQueue() {
40 | outStack = new Stack<>();
41 | inStack = new Stack<>();
42 | }
43 |
44 | public void push(int x) {
45 | inStack.push(x);
46 | }
47 |
48 | public int pop() {
49 | if (outStack.isEmpty()) inToOut();
50 | return outStack.pop();
51 | }
52 |
53 | public int peek() {
54 | if (outStack.isEmpty()) inToOut();
55 | return outStack.peek();
56 | }
57 |
58 | // 当 outStack 和 inStack 中的元素均为空的时候,模拟队列才为空
59 | public boolean empty() {
60 | return outStack.isEmpty() && inStack.isEmpty();
61 | }
62 |
63 | // 转移元素
64 | private void inToOut() {
65 | while (!inStack.isEmpty()) {
66 | outStack.push(inStack.pop());
67 | }
68 | }
69 | }
70 | ```
71 |
72 | ### 用队列实现栈
73 |
74 | **题目详情可见 [用队列实现栈](https://leetcode-cn.com/problems/implement-stack-using-queues/)**
75 |
76 | 该部分介绍用单个队列来模拟栈的所有功能!!
77 |
78 | 主要分析如何实现下面两个功能
79 |
80 | - `int pop()`移除并返回栈顶元素
81 |
82 | - `int top()`返回栈顶元素
83 |
84 | 如下图所示,对于上面两个功能,首先肯定需要弹出元素 1 和 2,剩下的元素 3 才是我们需要移除或者返回的元素
85 |
86 | 
87 |
88 | 那弹出的元素 1 和 2 怎么处理呢?从队尾放回去就行了!简单粗暴,哈哈哈哈哈。如下图所示:
89 |
90 | 
91 |
92 | 根据上面的思路,我们可以很快实现:
93 |
94 | ```java
95 | class MyStack {
96 |
97 | private Queue queue;
98 |
99 | public MyStack() {
100 | queue = new LinkedList<>();
101 | }
102 |
103 | public void push(int x) {
104 | queue.add(x);
105 | }
106 |
107 | public int pop() {
108 | moveToBack();
109 | return queue.poll();
110 | }
111 |
112 | public int top() {
113 | moveToBack();
114 | int top = queue.poll();
115 | queue.add(top);
116 | return top;
117 | }
118 |
119 | public boolean empty() {
120 | return queue.isEmpty();
121 | }
122 |
123 | private void moveToBack() {
124 | int size = queue.size();
125 | for (int i = 0; i < size - 1; i++) queue.add(queue.poll());
126 | }
127 | }
128 | ```
--------------------------------------------------------------------------------
/markdown/Algorithm/集合划分变题-未给定具体划分大小.md:
--------------------------------------------------------------------------------
1 | # 集合划分变题「未给定具体划分大小」
2 |
3 | [5289. 公平分发饼干](https://leetcode.cn/problems/fair-distribution-of-cookies/)
4 |
5 | [698. 划分为k个相等的子集](https://leetcode-cn.com/problems/partition-to-k-equal-sum-subsets/)
6 |
7 | [473. 火柴拼正方形](https://leetcode.cn/problems/matchsticks-to-square/)
8 |
9 |
10 |
11 | 今天比赛中有一个题目 **[公平分发饼干](https://leetcode.cn/problems/fair-distribution-of-cookies/)**,和「集合划分问题」相似度高达 90%,但是脑子一时没有转过弯,比赛的时候没有写出来,特意总结一波!!
12 |
13 | **关于集合划分问题详细分析,可见 [经典回溯算法:集合划分问题](./经典回溯算法:集合划分问题.html)**
14 |
15 | ### 区别
16 |
17 | 先来说一下本问题和「集合划分问题」的区别!
18 |
19 | 对于「集合划分问题」,题目中给出了每个集合可容纳的大小,可以根据是否溢出来决定是否选择桶
20 |
21 | 但是对于本问题,没有给出每个集合可容纳的大小,只是让我们求所有划分中最大值的最小值 (有点绕!!)
22 |
23 | 所以一时之间不知道如何处理,还是太菜了,不知道如何灵活运用!!😭😭😭
24 |
25 | ### 思路
26 |
27 | 我们使用「球视角」的思路,即:让每个球来选择桶,当最后一个球完成选择,则到达「结束条件」
28 |
29 | **那我们可以从什么角度剪枝呢?**
30 |
31 | **剪枝一:**为了保证每个桶中至少有一个球,所以如果还剩`n`个空桶,但剩余球的数量小于`n`,可直接跳过
32 |
33 | **剪枝二:**对于第一个球,任意放到某个桶中的效果都是一样的,所以我们规定放到第一个桶中
34 |
35 | **剪枝三:**如果桶的大小已经超过了最小值,则肯定不是最优解,可直接跳过
36 |
37 | **剪枝四:**如果当前桶和上一个桶内的元素和相等,则跳过。原因:如果元素和相等,那么当前球选择上一个桶和选择当前桶可以得到的结果是一致的
38 |
39 | **这里还有一个小技巧:**对球排序,优先让值更大的球做选择,这样可以增加回溯的命中率
40 |
41 | #### 代码实现
42 |
43 | ```java
44 | private int ans = Integer.MAX_VALUE;
45 | public int distributeCookies(int[] cookies, int k) {
46 | // 排序
47 | Arrays.sort(cookies);
48 | for (int lo = 0, hi = cookies.length - 1; lo <= hi; lo++, hi--) {
49 | int t = cookies[lo];
50 | cookies[lo] = cookies[hi];
51 | cookies[hi] = t;
52 | }
53 | backtrack(cookies, 0, new int[k]);
54 | return ans;
55 | }
56 | private void backtrack(int[] cookies, int start, int[] bucket) {
57 | if (start == cookies.length) {
58 | // 记录一次划分中的最大值
59 | int max = 0;
60 | for (int b : bucket) {
61 | max = Math.max(max, b);
62 | }
63 | // 记录所有划分中最大值的最小值 (有点绕!!)
64 | ans = Math.min(ans, max);
65 | return ;
66 | }
67 | // 计算空桶数量
68 | int empty = 0;
69 | for (int b : bucket) {
70 | if (b == 0) empty++;
71 | }
72 | // 剪枝一
73 | if (empty > cookies.length - start) return ;
74 | for (int i = 0; i < bucket.length; i++) {
75 | // 剪枝二
76 | if (i > 0 && start == 0) return ;
77 | // 剪枝三
78 | if (i > 0 && bucket[i] == bucket[i - 1]) continue;
79 | // 剪枝四
80 | if (bucket[i] + cookies[start] > ans) continue;
81 | bucket[i] += cookies[start];
82 | // 处理下一个球
83 | backtrack(cookies, start + 1, bucket);
84 | bucket[i] -= cookies[start];
85 | }
86 | }
87 | ```
88 |
89 | 贴一下执行时间:
90 |
91 |  --------------------------------------------------------------------------------
/markdown/Git/Git总结.md:
--------------------------------------------------------------------------------
1 | # Git 总结
2 |
3 |
4 |
5 | > 主要介绍 Git 的常用操作
6 |
7 | 首先本地 Git 有三个分区:`working directory`,`stage/index area`,`commit history`
8 |
9 | `working directory`:工作目录
10 |
11 | `stage/index area`:暂存区,`git add`命令会把`working directory`中的修改添加到暂存区
12 |
13 | `commit history`:`git commit`命令会把`暂存区`的内容提交到该分区。每个`commit`都有一个唯一的 Hash 值
14 |
15 | 三者的关系如下图所示:
16 |
17 |
--------------------------------------------------------------------------------
/markdown/Git/Git总结.md:
--------------------------------------------------------------------------------
1 | # Git 总结
2 |
3 |
4 |
5 | > 主要介绍 Git 的常用操作
6 |
7 | 首先本地 Git 有三个分区:`working directory`,`stage/index area`,`commit history`
8 |
9 | `working directory`:工作目录
10 |
11 | `stage/index area`:暂存区,`git add`命令会把`working directory`中的修改添加到暂存区
12 |
13 | `commit history`:`git commit`命令会把`暂存区`的内容提交到该分区。每个`commit`都有一个唯一的 Hash 值
14 |
15 | 三者的关系如下图所示:
16 |
17 | 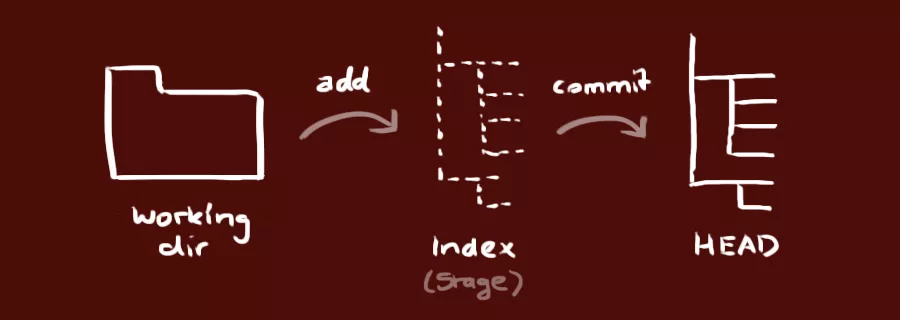 18 |
19 | ## 常用 git 命令
20 |
21 | ```bash
22 | # 初始化 git 项目
23 | git init
24 | # working dir -> stage area
25 | git add .
26 | # stage area -> commit history
27 | git commit -m "xxxx"
28 | # 查看工作区提交情况
29 | git status
30 | # 查看 git commit 提交记录
31 | git log
32 | # 创建新分支
33 | git branch xxx
34 | # 切换新分支
35 | git checkout xxx
36 | # 创建并切换新分支
37 | git checkout -b xxx
38 | # 将 commit history 区的代码恢复到 stage
39 | git reset
40 | ```
41 |
42 | ## 常用 git 操作
43 |
44 |
18 |
19 | ## 常用 git 命令
20 |
21 | ```bash
22 | # 初始化 git 项目
23 | git init
24 | # working dir -> stage area
25 | git add .
26 | # stage area -> commit history
27 | git commit -m "xxxx"
28 | # 查看工作区提交情况
29 | git status
30 | # 查看 git commit 提交记录
31 | git log
32 | # 创建新分支
33 | git branch xxx
34 | # 切换新分支
35 | git checkout xxx
36 | # 创建并切换新分支
37 | git checkout -b xxx
38 | # 将 commit history 区的代码恢复到 stage
39 | git reset
40 | ```
41 |
42 | ## 常用 git 操作
43 |
44 | 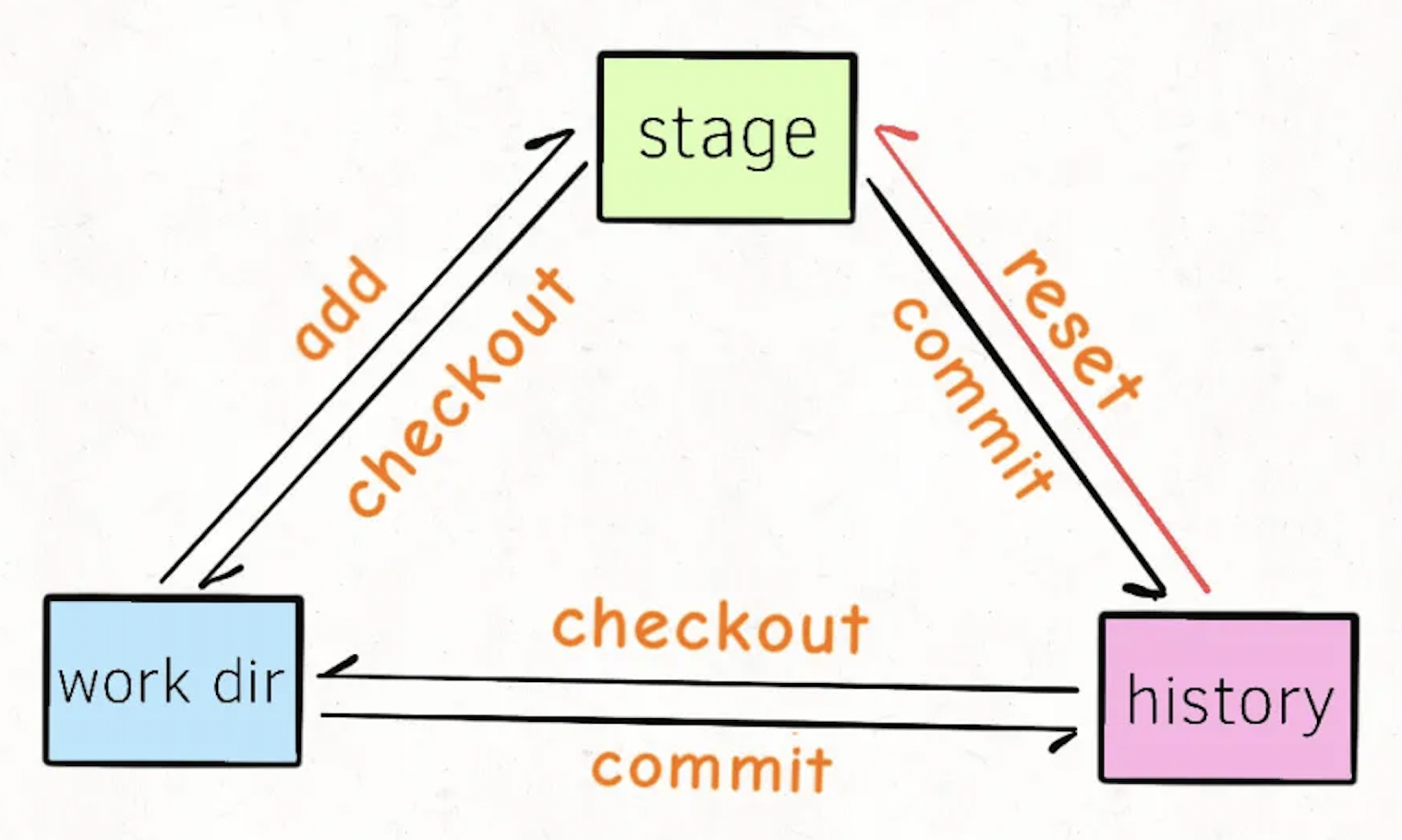 45 |
46 |
47 |
48 | **把`stage`中的修改还原到`working dir`中**
49 |
50 | ```bash
51 | # 恢复某一个文件
52 | git checkout [fileName]
53 | # 恢复所有文件
54 | git checkout .
55 | ```
56 |
57 |
58 |
59 | **把`commit history`区的历史提交还原到`working dir`中**
60 |
61 | ```bash
62 | git checkout HEAD .
63 | ```
64 |
65 |
66 |
67 | **将`commit history`区的文件还原到`stage`区**
68 |
69 | ```bash
70 | git reset [fileName]
71 | git reset .
72 | ```
73 |
74 |
75 |
76 | **撤销`git commit`**
77 |
78 | ```bash
79 | git reset --soft HEAD^
80 | # 等价
81 | git reset --soft HEAD~1
82 | # 撤销两次 git commit
83 | git reset --soft HEAD~2
84 |
85 | # 如果此时我们同时需要撤销远程的提交记录
86 | # -f 表示强制推送到远程
87 | git push -f
88 | ```
89 |
90 | 下面介绍一下几个参数
91 |
92 | `--mixed`:不删除工作空间改动代码,撤销`commit`,并且撤销`git add .`操作
93 |
94 | `--soft `:不删除工作空间改动代码,撤销`commit`,不撤销`git add .`
95 |
96 | `--hard` :删除工作空间改动代码,撤销`commit`,撤销`git add .`
97 |
98 |
99 |
100 | **修改`git commit -m " "`注释**
101 |
102 | ```bash
103 | git commit --amend
104 | ```
105 |
106 |
107 |
108 | **合并相同的`git commit`**
109 |
110 | ```bash
111 | # 选择需要合并 git commit 最早的一个 id 的前一个 (因为不包括本 id 的 git commit)
112 | git rebase -i [git logID]
113 | ```
114 |
115 | 当前我们只要知道`pick`和`squash`这两个命令即可
116 |
117 | - `pick`的意思是要会执行这个 commit
118 | - `squash`的意思是这个 commit 会被合并到前一个commit
119 |
120 |
121 |
122 | **撤销`git rabase`合并**
123 |
124 | ```bash
125 | # 查看本地记录
126 | git reflog
127 |
128 | git reset --hard [id]
129 |
130 | # 同时修改远程的提交
131 | git push -f
132 | ```
133 |
134 |
--------------------------------------------------------------------------------
/markdown/Java/CPU密集型-IO密集型.md:
--------------------------------------------------------------------------------
1 | # CPU 密集型 & I/O 密集型
2 |
3 | 本片文章介绍如何区分 CPU 密集型任务和 I/O 密集型任务~~
4 |
5 | 在设置 **[Java 线程池](../java/Java线程池.html)** 的参数时,需要参考到底是 CPU 密集型任务,还是 I/O 密集型任务,根据任务的不同类型,设置不同线程池大小:
6 |
7 | - **对于 CPU 密集型任务:**设置线程池大小为 CPU 核心数 + 1。比 CPU 核心多 1 是为了防止线程偶发的缺页中断,有多余线程可以补上 CPU 空闲时间
8 | - **对于 I/O 密集型任务:**设置线程池大小为 CPU 核心数 * 2。由于密集的 I/O 处理,增加了 CPU 处于空闲的概率
9 |
10 | 那么到底如何判断是 CPU 密集型任务,还是 I/O 密集型任务呢?
11 |
12 | 从宏观上分析,CPU 密集型任务多为计算型代码,需要始终在 CPU 上运行,而 I/O 密集型任务多为文件读写、DB 读写、网络请求等,总之是一切偏向于 I/O 操作的任务
13 |
14 | 上面的判断方法还是过于主观,比如如何判断是计算型代码呢?如何判断任务中更侧重于 I/O 操作呢?有没有一些硬性指标可以更加客观的去判断呢??
15 |
16 | 在 Linux 中可以使用`top`命令查看进程的 CPU 占用率,如果一个进程大多数时候都是满载使用 CPU,那么可认为是 CPU 密集型;反之为 I/O 密集型
17 |
18 | #### Demo -> CPU 密集型任务
19 |
20 | 下面给出一个 CPU 密集型任务的 Demo:
21 |
22 | ```java
23 | public class Main {
24 | public static void main(String[] args) {
25 | while (true){}
26 | }
27 | }
28 | ```
29 |
30 | 说白了,上面的例子就是一个死循环,肯定会一直占用 CPU 资源,通过`jps`命令获得该任务的 pid:
31 |
32 | ```bash
33 | [root@localhost ~]$ jps
34 | 1953 Jps
35 | 1897 Main
36 | ```
37 |
38 | 然后通过`top -p 1897`查看该任务的执行情况:
39 |
40 | ```bash
41 | [root@localhost ~]$ top -p 1897
42 | top - 15:56:28 up 14 min, 3 users, load average: 1.01, 0.75, 0.38
43 | Tasks: 1 total, 0 running, 1 sleeping, 0 stopped, 0 zombie
44 | %Cpu(s): 12.4 us, 0.0 sy, 0.0 ni, 87.4 id, 0.0 wa, 0.1 hi, 0.0 si, 0.0 st
45 | MiB Mem : 7741.8 total, 6927.3 free, 472.6 used, 341.9 buff/cache
46 | MiB Swap: 2048.0 total, 2048.0 free, 0.0 used. 7025.4 avail Mem
47 |
48 | PID USER PR NI VIRT RES SHR S %CPU %MEM TIME+ COMMAND
49 | 1897 root 20 0 4726724 53576 16584 S 99.3 0.7 6:02.43 java
50 | ```
51 |
52 | 从结果中可以看出该任务的 CPU 占用率为 99.3%,可认为几乎满载了!!
53 |
54 | #### Demo -> I/O 密集型任务
55 |
56 | 下面给出一个 I/O 密集型任务的 Demo:
57 |
58 | ```java
59 | public static void main(String[] args) {
60 | try {
61 | BufferedReader in = new BufferedReader(new FileReader("test.txt"), 1024);
62 | String str;
63 | while ((str = in.readLine()) != null) {
64 | System.out.println(str);
65 | }
66 | System.out.println(str);
67 | } catch (IOException e) {
68 | }
69 | }
70 | ```
71 |
72 | 上面例子中,`test.txt`是一个 6G 的大文件,通过`BufferedReader`读取到内存中,并将读取到的内容输出到终端
73 |
74 | 通过系统自带的性能监控软件可以看到该任务从磁盘读取了大量数据,可认为它是 I/O 密集性,如下图所示:
75 |
76 | 
--------------------------------------------------------------------------------
/markdown/Java/Java-8-Stream-sorted.md:
--------------------------------------------------------------------------------
1 | # Java 8 Stream sorted()
2 |
3 | 介绍`Stream sorted()`三种排序的实现「自然排序」「比较器」「反向排序」
4 |
5 | `sorted()`:它使用自然排序对流的元素进行排序。元素类必须实现`Comparable`接口
6 |
7 | `sorted(Comparator comparator)`:这里我们使用`lambda`表达式创建`Comparator`的实例。我们可以按升序和降序对流元素进行排序
8 |
9 | 以下代码行将按自然顺序对列表进行排序
10 |
11 | ```java
12 | list.stream().sorted()
13 | ```
14 |
15 | 为了反转自然排序`Comparator`提供了`reverseOrder()`方法。我们使用它如下
16 |
17 | ```java
18 | list.stream().sorted(Comparator.reverseOrder())
19 | ```
20 |
21 | 以下代码行使用`Comparator`对列表进行排序
22 |
23 | ```java
24 | list.stream().sorted(Comparator.comparing(Student::getAge))
25 | ```
26 |
27 | 为了反转顺序,`Comparator`提供了`reversed()`方法。我们使用这种方法如下
28 |
29 | ```java
30 | list.stream().sorted(Comparator.comparing(Student::getAge).reversed())
31 | ```
32 |
33 | ### Stream sorted() with List
34 |
35 | ```java
36 | // 升序
37 | // 前提:Person 类必须实现 Comparable 接口
38 | List list = new ArrayList<>();
39 | List sortedList = new ArrayList<>();
40 | list.stream().sorted().forEach(sortedList::add);
41 |
42 | // 降序
43 | // 前提:Person 类必须实现 Comparable 接口
44 | list.stream().sorted(Comparator.reverseOrder()).forEach(sortedList::add);
45 |
46 | // 根据年龄升序
47 | // Person 类不需要实现 Comparable 接口
48 | list.stream().sorted(Comparator.comparing(Person::getAge)).forEach(sortedList::add);
49 | // 根据年龄降序
50 | list.stream().sorted(Comparator.comparing(Person::getAge).reversed()).forEach(sortedList::add);
51 |
52 | // lambda 表达式实现 Comparator 接口
53 | list.stream().sorted((o1, o2) -> {
54 | if (o1.getAge() == o2.getAge()) return o1.getName().compareTo(o2.getName());
55 | return o1.getAge() - o2.getAge();
56 | }).forEach(sortedList::add);
57 | ```
58 |
59 | ### Stream sorted() with Set
60 |
61 | ```java
62 | Set set = new HashSet<>();
63 | List sorted = set.stream().sorted().collect(Collectors.toList());
64 | System.out.println(sorted);
65 | // 和 List 几乎一模一样
66 | ```
67 |
68 | 需要注意的一点是,不能把排序后的结果重新输出到另一个`Set`中,因为`Set`无顺序,会破坏顺序
69 |
70 | ### Stream sorted() with Map
71 |
72 | `Map`同`Set`一样无顺序,如果把排序后的结果重新输出到另一个`Map`中中,可能会导致顺序被破坏
73 |
74 | 我们可以使用`LinkedHashMap`,这样会保证顺序
75 |
76 | ```java
77 | // 前提:key 对应的类必须实现 Comparable 接口
78 | Map map = new LinkedHashMap<>();
79 | Map sortedMap = new LinkedHashMap<>();
80 | map.entrySet().stream().sorted(Map.Entry.comparingByKey()).forEachOrdered(e -> sortedMap.put(e.getKey(), e.getValue()));
81 |
82 | // 前提:value 对应的类必须实现 Comparable 接口
83 | map.entrySet().stream().sorted(Map.Entry.comparingByValue()).forEachOrdered(e -> sortedMap.put(e.getKey(), e.getValue()));
84 |
85 | // lambda 表达式实现 Comparator 接口
86 | // value 对应的类不需要实现 Comparable 接口
87 | map.entrySet().stream().sorted(((o1, o2) -> {
88 | if (o1.getValue().getAge() == o2.getValue().getAge()) return o2.getValue().getName().compareTo(o1.getValue().getName());
89 | return o1.getValue().getAge() - o2.getValue().getAge();
90 | })).forEachOrdered(e -> sortedMap.put(e.getKey(), e.getValue()));
91 | ```
--------------------------------------------------------------------------------
/markdown/Java/synchronized关键字.md:
--------------------------------------------------------------------------------
1 | # synchronized 关键字
2 |
3 | ### 关于锁和同步
4 |
5 | **类锁 vs 对象锁**
6 |
7 | - 类锁:类的所有对象共享一把锁🔒
8 | - 对象锁:每个对象拥有一把锁 🔒
9 |
10 | 同步是对同一把锁而言的,同步这个概念是在多个线程争夺同一把锁的时候才能实现的,如果多个线程争夺不同的锁,那多个线程是不能同步的
11 |
12 | - 两个线程:一个取对象锁,一个取类锁,则不能同步
13 | - 两个线程:一个取对象 A 的锁,一个取对象 B 的锁,则不能同步
14 |
15 | ### 锁和 synchronized 的关系
16 |
17 | 锁是 Java 中用来实现同步的工具
18 |
19 | 而之所以能对方法或者代码块实现同步的原因就是:只有拿到锁的线程才能执行 synchronized 修饰的方法或代码块,且其他线程获得锁的唯一方法是等目前拿到锁的线程执行完方法将锁释放,如果 synchronized 修饰的代码块或方法没执行完是不会释放这把锁的,这就保证了拿到锁的线程一定可以一次性把它调用的方法或代码块执行完
20 |
21 | ### synchronized 修饰的类型
22 |
23 | 若 synchronized 修饰「静态方法」或者修饰「类的代码块」,则为类锁 🔒
24 |
25 | 若 synchronized 修饰「普通方法」或者修饰「当前对象的代码块」,则为对象锁 🔒
26 |
27 | #### 修饰方法
28 |
29 | - 修饰静态方法:静态方法属于类,所有对象调用的都是同一个方法
30 | - 修饰普通方法:普通方法属于对象,每个对象调用的都是自己的方法
31 |
32 | **注意:**
33 |
34 | - 在定义接口方法时不能使用 synchronized 关键字
35 | - 构造方法不能使用 synchronized 关键字,但可以使用 synchronized 代码块来进行同步
36 | - synchronized 关键字不能被继承。如果子类覆盖了父类被 synchronized 关键字修饰的方法,那么子类的该方法只要没有 synchronized 关键字,那么就默认没有同步
37 |
38 | ```java
39 | public class A {
40 | // 修饰静态方法
41 | public static synchronized void f1(int c) {
42 | for (int i = 0; i < 100; i++) {
43 | System.out.println("静态方法 " + c);
44 | }
45 | }
46 | // 修饰普通方法
47 | public synchronized void f2(int c) {
48 | for (int i = 0; i < 100; i++) {
49 | System.out.println("普通方法" + c);
50 | }
51 | }
52 | public static void main(String[] args) throws InterruptedException {
53 | // 测试静态方法
54 | // f1() 属于类 A,所以下方两个线程存在同步,一定是先输出所有「静态方法 1」,然后再输出所有「静态方法 2」
55 | new Thread(() -> A.f1(1)).start();
56 | new Thread(() -> A.f1(2)).start();
57 | Thread.sleep(1000);
58 | System.out.println("------------------");
59 | // 测试普通方法
60 | A a1 = new A();
61 | A a2 = new A();
62 | // f2() 属于类 A 的对象,所以下方两个线程不存在同步,一个取对象 a1 的锁,一个取对象 a2 的锁
63 | // 输出内容「普通方法 1」「普通方法 2」无规则交替出现
64 | new Thread(() -> a1.f2(1)).start();
65 | new Thread(() -> a2.f2(2)).start();
66 | }
67 | }
68 | ```
69 |
70 | #### 修饰代码块
71 |
72 | - 修饰类:表示对类进行同步
73 | - 修饰当前对象:表示对当前对象进行同步
74 |
75 | ```java
76 | public class B {
77 | public void f1(int c) {
78 | // 修饰类
79 | synchronized (B.class) {
80 | for (int i = 0; i < 100; i++) {
81 | System.out.println("修饰类 " + c);
82 | }
83 | }
84 | }
85 | public void f2(int c) {
86 | // 修饰当前对象
87 | synchronized (this) {
88 | for (int i = 0; i < 100; i++) {
89 | System.out.println("修饰当前对象 " + c);
90 | }
91 | }
92 | }
93 | public static void main(String[] args) throws InterruptedException {
94 | B b1 = new B();
95 | B b2 = new B();
96 | // 测试修饰类
97 | // 同步对象为类的所有对象,一定是先输出所有「修饰类 1」,然后再输出所有「修饰类 2」
98 | new Thread(() -> b1.f1(1)).start();
99 | new Thread(() -> b2.f1(2)).start();
100 | Thread.sleep(1000);
101 | System.out.println("------------------");
102 | // 测试修饰当前对象
103 | // 同步对象为当前对象,下方两个线程不存在同步,一个取对象 b1 的锁,一个取对象 b2 的锁
104 | // 输出内容「修饰当前对象 1」「修饰当前对象 2」无规则交替出现
105 | new Thread(() -> b1.f2(1)).start();
106 | new Thread(() -> b2.f2(2)).start();
107 | }
108 | }
109 | ```
110 |
--------------------------------------------------------------------------------
/markdown/Java/从字节码角度分析i++和++i.md:
--------------------------------------------------------------------------------
1 | # 从字节码角度分析 i++ 和 ++i
2 |
3 | **温馨提醒:**本篇文章内容过于底层,不太熟悉的同学可以先学习 **[操作数栈](./虚拟机栈.html#操作数栈)**
4 |
5 | 本篇文章从字节码的角度分析`i++`和`++j`背后的逻辑!!
6 |
7 | 先给出四个可能会让你很晕~的例子,相信如果搞清楚`i++`和`++j`原理的人可以很快知道每个变量最终的结果
8 |
9 | ```java
10 | public void add() {
11 | // problem 1
12 | int i1 = 10;
13 | i1++;
14 | int i2 = 10;
15 | ++i2;
16 |
17 | // problem 2
18 | int i3 = 10;
19 | int i4 = i3++;
20 | int i5 = 10;
21 | int i6 = ++i5;
22 |
23 | // problem 3
24 | int i7 = 10;
25 | i7 = i7++;
26 | int i8 = 10;
27 | i8 = ++i8;
28 |
29 | // problem 4
30 | int i9 = 10;
31 | i9 = i9++ + ++i9;
32 | }
33 | ```
34 |
35 | 下面再给出通过反编译后,该方法对应的字节码,这也是本篇文章分析的重点
36 |
37 | 如果不知道每个字节码指令对应什么意思,可以去查《虚拟机字节码指令表》
38 |
39 | ```java
40 | // ------------------------- problem 1 -------------------------
41 | 0: bipush 10 // 将单字节的常量值 10 推送至栈顶
42 | 2: istore_1 // 将栈顶 int 型数值存入第二个本地变量 (注意:下标从 0 开始,所以第二个对应下标是 1。下面同理!!)
43 | 3: iinc 1, 1 // 将指定 int 型变量增加指定值 (此处为将第二个本地变量增加 1;若为 i += 2,那么对应的字节码就为 iinc 1, 2)
44 | 6: bipush 10 // 将单字节的常量值 10 推送至栈顶
45 | 8: istore_2 // 将栈顶 int 型数值存入第三个本地变量
46 | 9: iinc 2, 1 // 将第三个本地变量增加 1
47 | // ------------------------- problem 2 -------------------------
48 | 12: bipush 10 // 将单字节的常量值 10 推送至栈顶
49 | 14: istore_3 // 将栈顶 int 型数值存入第四个本地变量
50 | 15: iload_3 // 将第四个 int 型本地变量推送至栈顶
51 | 16: iinc 3, 1 // 将第四个本地变量增加 1
52 | 19: istore 4 // 将栈顶 int 型数值存入第五个本地变量 (注意:此时第四个本地变量为 11,栈顶的值仍为 10,所以第五个本地变量为 10,即 i4 = 10)
53 | 21: bipush 10 // 将单字节的常量值 10 推送至栈顶
54 | 23: istore 5 // 将栈顶 int 型数值存入第六个本地变量
55 | 25: iinc 5, 1 // 将第六个本地变量增加 1
56 | 28: iload 5 // 将第六个 int 型本地变量推送至栈顶
57 | 30: istore 6 // 将栈顶 int 型数值存入第七个本地变量 (注意:此时第六个本地变量为 11,栈顶的值为 11,所以第七个本地变量为 11,即 i6 = 11)
58 | // ------------------------- problem 3 -------------------------
59 | 32: bipush 10 // 将单字节的常量值 10 推送至栈顶
60 | 34: istore 7 // 将栈顶 int 型数值存入第八个本地变量
61 | 36: iload 7 // 将第八个 int 型本地变量推送至栈顶
62 | 38: iinc 7, 1 // 将第八个本地变量增加 1
63 | 41: istore 7 // 将栈顶 int 型数值存入第八个本地变量 (注意:此时第八个本地变量为 11,栈顶的值为 10,所以第八个本地变量最终为 10,即 i7 = 10)
64 | 43: bipush 10 // 将单字节的常量值 10 推送至栈顶
65 | 45: istore 8 // 将栈顶 int 型数值存入第九个本地变量
66 | 47: iinc 8, 1 // 将第九个本地变量增加 1
67 | 50: iload 8 // 将第九个 int 型本地变量推送至栈顶
68 | 52: istore 8 // 将栈顶 int 型数值存入第九个本地变量 (注意:此时第九个本地变量为 11,栈顶的值为 11,所以第九个本地变量最终为 11,即 i8 = 10)
69 | // ------------------------- problem 4 -------------------------
70 | 54: bipush 10 // 将单字节的常量值 10 推送至栈顶
71 | 56: istore 9 // 将栈顶 int 型数值存入第十个本地变量
72 | 58: iload 9 // 将第十个 int 型本地变量推送至栈顶
73 | 60: iinc 9, 1 // 将第十个本地变量增加 1
74 | 63: iinc 9, 1 // 将第十个本地变量增加 1
75 | 66: iload 9 // 将第十个 int 型本地变量推送至栈顶
76 | 68: iadd // 将栈顶两 int 型数值相加并将结果压入栈顶 (注意:此时栈顶两个值分别为「+1 前的值」和「+1 两次后的值」;最终栈顶的值为 10 + 12 = 22)
77 | 69: istore 9 // 将栈顶 int 型数值存入第十个本地变量 (注意:此时第十个本地变量为 12,栈顶的值为 22,所以第十个本地变量最终为 22,即 i9 = 22)
78 | 71: return // 从当前方法返回 void
79 | ```
80 |
81 | **总结:**
82 |
83 | 首先`i++`和`++i`对于变量 i 的效果是等价的,都是使 i 增加 1
84 |
85 | 不同的在于这两个表达式的值:
86 |
87 | - `i++`是先将局部变量表中的 i 推送至操作数栈顶,然后将局部变量表中的 i + 1,最后将操作数栈顶的值赋给表达式,所以表达式的值为 i + 1 之前的值
88 | - `++i`是先将局部变量表中的 i + 1,然后将局部变量表中的 i 推送至操作数栈顶,最后将操作数栈顶的值赋给表达式,所以表达式的值为 i + 1 之后的值
--------------------------------------------------------------------------------
/markdown/Java/内存泄漏-内存溢出.md:
--------------------------------------------------------------------------------
1 | # 内存泄漏 & 内存溢出
2 |
3 | 在介绍 Java 堆溢出的时候提到过这两者的区别,**相关内容可见 [Java 堆溢出](./各区域OOM汇总.html#java-堆溢出)**
4 |
5 | 但是当时并没有介绍的很详细,所以本篇文章专门从不同角度来刨析这两个内容!!
6 |
7 | ### 内存泄漏 (Memory Leak)
8 |
9 | 「内存泄漏」有一个很形象的形容:**占着茅坑不拉屎**;放在内存中就是:**占据着内存资源,但是却毫无用处**
10 |
11 | 言归正传,内存泄漏更严谨的定义:**本应该被回收的对象,由于错误的引用链导致未进行回收**
12 |
13 | 
14 |
15 | 如上图所示,根据「可达性分析算法」很明显对象 D、E、F 可以被正确的回收;但由于错误的引用链导致对象 A、B、C 没有被回收,这就造成了**内存泄漏**
16 |
17 | 还有一种宽泛意义上的内存泄漏:由于开发人员的疏忽,使得对象的生命周期被演延长,最终造成了内存溢出
18 |
19 | ```java
20 | public void f() {
21 | Object obj = new Object();
22 | if (1 + 1 > 0) {
23 | // 使用对象 obj ...
24 | }
25 | // 其它地方都不会使用对象 obj
26 | }
27 | ```
28 |
29 | 上面这种就属于宽泛意义上的内存泄漏,可以直接把`obj`定义在`if`判断里面,当`if`代码块执行完,该对象的生命周期就结束了,可以直接被回收
30 |
31 | #### 例子 🌰
32 |
33 | **单例模式:**单例对象的生命周期自被创建开始一直到应用程序结束,所以在单例程序中,如果持有外部对象的引用,那么该外部对象就不能被回收,导致内存泄漏!
34 |
35 | **提供 close 的资源未关闭导致内存泄漏:**数据库连接`dataSourse.getConnection()`,网络连接 (socket) 和 IO 连接必须手动 close,否则就不能被回收,导致内存泄漏!
36 |
37 | ### 内存溢出 (OOM)
38 |
39 | 内存溢出相比于内存泄漏好理解:**为对象分配内存时,发现内存不够,导致无法完成内存分配**
40 |
41 | 由于 GC 的不断发展,一般情况下,除非应用程序占用内存的速度非常快,导致垃圾回收的速度赶不上内存分配的速度,否则不太容易出现 OOM
42 |
43 | 大多情况下,GC 会进行各年龄段的垃圾回收,实在不行就放大招,来一次独占式的 Full GC 操作,这个时候会回收大量内存,以供程序继续使用
44 |
45 | JavaDoc 对内存溢出给出的官方描述:**Thrown when the Java Virtual Machine cannot allocate an object because it is out of memory, and no more memory could be made available by the garbage collector.**
46 |
47 | 这一句话中有两个重点:**没有空闲内存,而且垃圾回收也无法提供更多内存**
48 |
49 | #### 无空闲内存
50 |
51 | 导致没有空闲内存的原因可能有以下三种:
52 |
53 | **Java 虚拟机堆内存一开始分配不够**
54 |
55 | 在虚拟机启动时,可以通过参数`-Xms -Xmx`指定虚拟机初始内存和最大内存,可能一开始分配的内存就不足以支撑系统正常运行,可以适当增加内存!!
56 |
57 | **程序中存在内存泄漏**
58 |
59 | 内存泄漏会导致无用对象依旧占据内存,使得后续无法为新对象分配内存,导致内存溢出!!
60 |
61 | **存在大量大对象,并且长时间不能被回收 (存在引用)**
62 |
63 | 对于老版本的 JDK,因为永久代的大小是有限的,并且 Java 虚拟机对永久代垃圾回收 (如:常量池回收、卸载不再需要的类型) 非常不积极,所以当不断添加新类型的时候,永久代出现 OOM 的概率非常大,尤其是在运行时存在大量动态类型生成的场合
64 |
65 | 类似 intern 字符串缓存占用太多空间,也会导致 OOM 问题,对应的异常信息,会标记出来和永久代相关:`java.lang.OutOfMemoryError: PermGen space`,这也是字符串常量池移入堆中的原因
66 |
67 | 随着元空间的引入,方法区内存已经不再那么窘迫,所以相应的 OOM 有所改观,出现 OOM 异常信息则变成了:`java.lang.OutofMemoryError:Metaspace`
68 |
69 | 直接内存不足,也会导致 OOM
70 |
71 | #### 垃圾回收
72 |
73 | 上面说:**没有空闲内存,而且垃圾回收也无法提供更多内存才会出现 OOM 异常**
74 |
75 | 这里面隐含了一层意思:**并不是没有空闲内存就会抛出 OOM 异常,而是在发现没有空闲内存时,会先执行一次垃圾回收操作,尽最大努力去清理内存空间,如果回收完内存依旧不够,才会抛出 OOM 异常**
76 |
77 | **例外:**并非所有内存不够的时候都会先执行一次垃圾回收操作,如果要分配的对象过大,如:大到空堆都无法存下,这种情况就会直接抛出 OOM 异常
--------------------------------------------------------------------------------
/markdown/Java/动态语言-动态类型语言.md:
--------------------------------------------------------------------------------
1 | # 动态语言 vs 动态类型语言
2 |
3 | ### 动态语言 VS 静态语言
4 |
5 | #### 动态语言
6 |
7 | 动态语言是一类在运行时可以**改变其结构的语言**
8 |
9 | 例如:新的函数、对象、甚至代码都可以被引进,已有的函数可以被删除或是其他结构上的变化
10 |
11 | 通俗点说就是运行时代码可以根据某些条件改变自身结构
12 |
13 | 主要的动态语言:Object-C、C#、JavaScript、PHP、Python 等
14 |
15 | #### 静态语言
16 |
17 | 与动态语言相对应的,运行时结构不可变的语言就是静态语言,如:Java、C、C++
18 |
19 | Java 不是动态语言,但 Java 可以称之为「准动态语言」,即 Java 有一定的动态性
20 |
21 | 我们可以利用 **[反射机制](./反射机制.html)** 获得类似动态语言的特性,Java 的动态性让编程的时候更加灵活!
22 |
23 | #### 举例
24 |
25 | ```js
26 | function Person(name, age, job) {
27 | this.name = name;
28 | this.age = age;
29 | this.job = job
30 | this.hello = function(name){
31 | alert("Hello, " + name);
32 | };
33 |
34 | person = new Person("Eric", 28, 'worker');
35 | alert(person.name + '' + person.age + '');
36 | person.hello("Alice");
37 | //为对象添加方法
38 | person.work = function() {
39 | alert('I am working');
40 | }
41 | person.work();
42 |
43 | //删除方法
44 | delete person.work;
45 | person.work();
46 | ```
47 |
48 | ### 动态类型语言 VS 静态类型语言
49 |
50 | #### 动态类型语言
51 |
52 | 动态类型语言的关键特性是它的类型检查的主体过程是在运行期而不是编译期进行的
53 |
54 | #### 静态类型语言
55 |
56 | 静态类型语言在编译期就进行了类型检查
57 |
58 | #### 举例
59 |
60 | 举几个很直白的例子!对于 Java,定义一个变量:
61 |
62 | ```java
63 | // 在编译期间就必须明确变量 a 的类型
64 | int a = 10;
65 | ```
66 |
67 | 对于 JS,定义一个变量:
68 |
69 | ```js
70 | // 在运行期间才知道变量 name 和 age 的类型
71 | var name = "abc";
72 | var age = 10;
73 | ```
74 |
75 | 对于 Python,定义一个变量:
76 |
77 | ```python
78 | # 在运行期间才知道变量 info 的类型
79 | info = 1234.3
80 | ```
81 |
82 | 所以 Java 是静态类型语言;而 JS 和 Python 是动态类型语言
83 |
84 | **静态类型语言是判断变量自身的类型信息;动态类型语言是判断变量值的类型信息,变量没有类型信息,变量值才有类型信息**
--------------------------------------------------------------------------------
/markdown/Java/垃圾回收相关概念.md:
--------------------------------------------------------------------------------
1 | # 垃圾回收相关概念
2 |
3 | ### Stop The World
4 |
5 | Stop The World,简称 STW,指在 GC 事件发生过程中,会产生应用程序的停顿。停顿产生时整个应用程序线程会被暂停,没有任何响应
6 |
7 | 被 STW 中断的应用线程会在 GC 之后恢复,频繁中断会让用户感觉像是网速不快造成电影卡顿一样,所以需要减少 STW 发生的时间
8 |
9 | 可达性分析算法中枚举 GC Roots 时会导致所有 Java 执行线程停顿,原因如下:
10 |
11 | - 分析工作必须在一个能保证一致性的快照中进行
12 | - 一致性指整个分析期间整个执行系统看起来像被冻结在某个时间点上
13 | - 如果分析过程中对象引用关系还在不断变化,则分析结果的准确性无法保证
14 |
15 | **注意:**STW 和使用哪款 GC 无关,所有的 GC 都会产生 STW,只能说效率越高的 GC,STW 的时间越短,但并不是没有 STW,我们能做的也只是尽可能的缩短 STW 的时间,如:增量收集算法和分区收集算法
16 |
17 | STW 是 Java 虚拟机在后台自动发起和自动完成的,在用户不可见的情况下,把用户的工作线程全部停掉;开发中不要用`System.gc()`,会导致 STW 的发生
18 |
19 | ### 并行与并发
20 |
21 | #### 程序中的并行与并发
22 |
23 | **并行:**一般指多核处理器,每个线程都单独在一个核心上运行,各线程之间不存在资源竞争的关系
24 |
25 | **并发:**一般指单核处理器,多个线程都在同一个核心上运行,但一个核心同一时刻只能执行一个线程,所以各线程之间交替执行,常见的有时间片轮询算法
26 |
27 | 对于并行,宏观上多个线程之间都在同时执行;微观上多个线程之间也都在同时执行,没有 CPU 资源的竞争
28 |
29 | 对于并发,宏观上多个线程之间都在同时执行;微观上多个线程之间交替执行,同一时刻只有一个线程在执行,存在 CPU 资源的竞争
30 |
31 | #### 垃圾回收的并行与并发
32 |
33 | **并行:**描述的是多条垃圾收集器线程之间的关系,说明同一时间有多条这样的线程在协同工作,通常默认此用户线程处于等待状态
34 |
35 | 典型的 ParNew 就是多线程并行的垃圾收集器,与之相对应的是 Serial 单线程串行垃圾收集器,它们俩运行示意图如下所示:
36 |
37 | 
38 |
39 | **并发:**描述的是垃圾收集器线程与用户线程之间的关系,说明同一时间垃圾收集器线程与用户线程都在运行 (不一定并行,可能是交替执行)。由于用户线程并未被冻结,所以程序仍然能响应服务请求,但由于垃圾收集器线程占用了一部分系统资源,此时应用程序处理的吞吐量将受到一定影响
40 |
41 | 典型的 CMS 就是并发的垃圾收集器,其中初始标记、重新标记两个步骤仍然需要 STW,其它步骤可以和用户线程一起并行执行,它的运行示意图如下所示:
42 |
43 | 
44 |
45 | **总结:**为了提高垃圾回收的效率,GC 经历了「串行回收 -> 并行回收 -> 并发回收」
46 |
47 | - 串行的效率最慢,只有一个 GC 线程,而且用户线程还必须 STW 等待一次完整的 GC 过程执行完成,这样用户感受到的停顿感会十分明显
48 | - 并行在串行的基础上将一个 GC 线程增加到多个 GC 线程,虽然回收的效率会提高一些,但是用户线程依旧必须 STW 等待一次完整的 GC 过程执行完成
49 | - 并发在并行的基础上再度升级,不仅拥有多个 GC 线程,而且用户线程和 GC 线程都在运行 (可能交替执行),虽然必要阶段可能还是需要 STW,但用户体验感明显会好很多
50 |
--------------------------------------------------------------------------------
/markdown/Java/垃圾收集器前言.md:
--------------------------------------------------------------------------------
1 | # 垃圾收集器前言
2 |
3 | 在正式介绍垃圾收集器之前,先来唠一唠垃圾收集器一些细枝末节的东西!!!
4 |
5 | 前文介绍过 **[垃圾收集算法](./垃圾收集算法.html)**,如果说它是内存回收的方法论,那么垃圾收集器就是内存回收的实践者。《Java 虚拟机规范》中对垃圾收集器应该如何实现并没有做出任何规定!!
6 |
7 | **注意:**根据上下文 GC 可能表示 Garbage Collection 或者 Garbage Collector,前者为垃圾收集机制,后者为垃圾收集器
8 |
9 | ### 垃圾收集器发展史
10 |
11 | 1999 年随 JDK1.3.1 一起出现的是串行方式的 Serial 收集器和 Serial Old 收集器,它是第一款垃圾收集器。ParNew 收集器是 Serial 收集器的多线程版本
12 |
13 | 2002 年 2 月 26 日,Parallel Scaverge 收集器和 Concurrent Mark Sweep (CMS) 收集器跟随 JDK1.4.2 一起发布
14 |
15 | Parallel Old 收集器直到 JDK6 才开始提供;Parallel Scaverge / Parallel Old 收集器在 JDK6 之后成为 HotSpot 默认垃圾收集器
16 |
17 | 2012 年,在 JDK7 Update 4 版本中正式提供了商用的 G1 收集器,此前 G1 一直处于实验阶段
18 |
19 | 2017 年,JDK9 中 G1 变成默认的垃圾收集器,替代 CMS
20 |
21 | 2018 年 3 月,JDK10 中 G1 垃圾收集器并行完整垃圾回收,实现并行性来改善最坏情况下的延迟
22 |
23 | **------------- 分水岭 -------------**
24 |
25 | 2018 年 9 月,JDK11 发布,引入 Epsilon 垃圾收集器,又被称为 No-Op (无操作) 收集器。同时,引入 ZGC:可伸缩的低延迟垃圾收集器 (Experimental)
26 |
27 | 2019 年 3 月,JDK12 发布,增强 G1,自动返回未用堆内存给操作系统;同时,引入 Shenandoah GC:低停顿时间的GC (Experimental)
28 |
29 | 2019 年 9 月,JDK13 发布,增强 ZGC,自动返回未用堆内存给操作系统。
30 |
31 | 2020 年 3 月,JDK14 发布,删除 CMS 垃圾收集器,扩展 ZGC 在 MacOS 和 Windows 上的应用
32 |
33 |
34 |
35 | **注意:**分水岭上面属于 7 种经典垃圾收集器,分别为:Serial GC、ParNew GC、Parallel Scaverge GC、Serial Old GC、Parallel Old GC、CMS、G1
36 |
37 | ### 垃圾收集器分类
38 |
39 | **关于串行、并行、并发的解释可见 [垃圾回收的并行与并发](./垃圾回收相关概念.html#并行与并发)**
40 |
41 |
45 |
46 |
47 |
48 | **把`stage`中的修改还原到`working dir`中**
49 |
50 | ```bash
51 | # 恢复某一个文件
52 | git checkout [fileName]
53 | # 恢复所有文件
54 | git checkout .
55 | ```
56 |
57 |
58 |
59 | **把`commit history`区的历史提交还原到`working dir`中**
60 |
61 | ```bash
62 | git checkout HEAD .
63 | ```
64 |
65 |
66 |
67 | **将`commit history`区的文件还原到`stage`区**
68 |
69 | ```bash
70 | git reset [fileName]
71 | git reset .
72 | ```
73 |
74 |
75 |
76 | **撤销`git commit`**
77 |
78 | ```bash
79 | git reset --soft HEAD^
80 | # 等价
81 | git reset --soft HEAD~1
82 | # 撤销两次 git commit
83 | git reset --soft HEAD~2
84 |
85 | # 如果此时我们同时需要撤销远程的提交记录
86 | # -f 表示强制推送到远程
87 | git push -f
88 | ```
89 |
90 | 下面介绍一下几个参数
91 |
92 | `--mixed`:不删除工作空间改动代码,撤销`commit`,并且撤销`git add .`操作
93 |
94 | `--soft `:不删除工作空间改动代码,撤销`commit`,不撤销`git add .`
95 |
96 | `--hard` :删除工作空间改动代码,撤销`commit`,撤销`git add .`
97 |
98 |
99 |
100 | **修改`git commit -m " "`注释**
101 |
102 | ```bash
103 | git commit --amend
104 | ```
105 |
106 |
107 |
108 | **合并相同的`git commit`**
109 |
110 | ```bash
111 | # 选择需要合并 git commit 最早的一个 id 的前一个 (因为不包括本 id 的 git commit)
112 | git rebase -i [git logID]
113 | ```
114 |
115 | 当前我们只要知道`pick`和`squash`这两个命令即可
116 |
117 | - `pick`的意思是要会执行这个 commit
118 | - `squash`的意思是这个 commit 会被合并到前一个commit
119 |
120 |
121 |
122 | **撤销`git rabase`合并**
123 |
124 | ```bash
125 | # 查看本地记录
126 | git reflog
127 |
128 | git reset --hard [id]
129 |
130 | # 同时修改远程的提交
131 | git push -f
132 | ```
133 |
134 |
--------------------------------------------------------------------------------
/markdown/Java/CPU密集型-IO密集型.md:
--------------------------------------------------------------------------------
1 | # CPU 密集型 & I/O 密集型
2 |
3 | 本片文章介绍如何区分 CPU 密集型任务和 I/O 密集型任务~~
4 |
5 | 在设置 **[Java 线程池](../java/Java线程池.html)** 的参数时,需要参考到底是 CPU 密集型任务,还是 I/O 密集型任务,根据任务的不同类型,设置不同线程池大小:
6 |
7 | - **对于 CPU 密集型任务:**设置线程池大小为 CPU 核心数 + 1。比 CPU 核心多 1 是为了防止线程偶发的缺页中断,有多余线程可以补上 CPU 空闲时间
8 | - **对于 I/O 密集型任务:**设置线程池大小为 CPU 核心数 * 2。由于密集的 I/O 处理,增加了 CPU 处于空闲的概率
9 |
10 | 那么到底如何判断是 CPU 密集型任务,还是 I/O 密集型任务呢?
11 |
12 | 从宏观上分析,CPU 密集型任务多为计算型代码,需要始终在 CPU 上运行,而 I/O 密集型任务多为文件读写、DB 读写、网络请求等,总之是一切偏向于 I/O 操作的任务
13 |
14 | 上面的判断方法还是过于主观,比如如何判断是计算型代码呢?如何判断任务中更侧重于 I/O 操作呢?有没有一些硬性指标可以更加客观的去判断呢??
15 |
16 | 在 Linux 中可以使用`top`命令查看进程的 CPU 占用率,如果一个进程大多数时候都是满载使用 CPU,那么可认为是 CPU 密集型;反之为 I/O 密集型
17 |
18 | #### Demo -> CPU 密集型任务
19 |
20 | 下面给出一个 CPU 密集型任务的 Demo:
21 |
22 | ```java
23 | public class Main {
24 | public static void main(String[] args) {
25 | while (true){}
26 | }
27 | }
28 | ```
29 |
30 | 说白了,上面的例子就是一个死循环,肯定会一直占用 CPU 资源,通过`jps`命令获得该任务的 pid:
31 |
32 | ```bash
33 | [root@localhost ~]$ jps
34 | 1953 Jps
35 | 1897 Main
36 | ```
37 |
38 | 然后通过`top -p 1897`查看该任务的执行情况:
39 |
40 | ```bash
41 | [root@localhost ~]$ top -p 1897
42 | top - 15:56:28 up 14 min, 3 users, load average: 1.01, 0.75, 0.38
43 | Tasks: 1 total, 0 running, 1 sleeping, 0 stopped, 0 zombie
44 | %Cpu(s): 12.4 us, 0.0 sy, 0.0 ni, 87.4 id, 0.0 wa, 0.1 hi, 0.0 si, 0.0 st
45 | MiB Mem : 7741.8 total, 6927.3 free, 472.6 used, 341.9 buff/cache
46 | MiB Swap: 2048.0 total, 2048.0 free, 0.0 used. 7025.4 avail Mem
47 |
48 | PID USER PR NI VIRT RES SHR S %CPU %MEM TIME+ COMMAND
49 | 1897 root 20 0 4726724 53576 16584 S 99.3 0.7 6:02.43 java
50 | ```
51 |
52 | 从结果中可以看出该任务的 CPU 占用率为 99.3%,可认为几乎满载了!!
53 |
54 | #### Demo -> I/O 密集型任务
55 |
56 | 下面给出一个 I/O 密集型任务的 Demo:
57 |
58 | ```java
59 | public static void main(String[] args) {
60 | try {
61 | BufferedReader in = new BufferedReader(new FileReader("test.txt"), 1024);
62 | String str;
63 | while ((str = in.readLine()) != null) {
64 | System.out.println(str);
65 | }
66 | System.out.println(str);
67 | } catch (IOException e) {
68 | }
69 | }
70 | ```
71 |
72 | 上面例子中,`test.txt`是一个 6G 的大文件,通过`BufferedReader`读取到内存中,并将读取到的内容输出到终端
73 |
74 | 通过系统自带的性能监控软件可以看到该任务从磁盘读取了大量数据,可认为它是 I/O 密集性,如下图所示:
75 |
76 | 
--------------------------------------------------------------------------------
/markdown/Java/Java-8-Stream-sorted.md:
--------------------------------------------------------------------------------
1 | # Java 8 Stream sorted()
2 |
3 | 介绍`Stream sorted()`三种排序的实现「自然排序」「比较器」「反向排序」
4 |
5 | `sorted()`:它使用自然排序对流的元素进行排序。元素类必须实现`Comparable`接口
6 |
7 | `sorted(Comparator comparator)`:这里我们使用`lambda`表达式创建`Comparator`的实例。我们可以按升序和降序对流元素进行排序
8 |
9 | 以下代码行将按自然顺序对列表进行排序
10 |
11 | ```java
12 | list.stream().sorted()
13 | ```
14 |
15 | 为了反转自然排序`Comparator`提供了`reverseOrder()`方法。我们使用它如下
16 |
17 | ```java
18 | list.stream().sorted(Comparator.reverseOrder())
19 | ```
20 |
21 | 以下代码行使用`Comparator`对列表进行排序
22 |
23 | ```java
24 | list.stream().sorted(Comparator.comparing(Student::getAge))
25 | ```
26 |
27 | 为了反转顺序,`Comparator`提供了`reversed()`方法。我们使用这种方法如下
28 |
29 | ```java
30 | list.stream().sorted(Comparator.comparing(Student::getAge).reversed())
31 | ```
32 |
33 | ### Stream sorted() with List
34 |
35 | ```java
36 | // 升序
37 | // 前提:Person 类必须实现 Comparable 接口
38 | List list = new ArrayList<>();
39 | List sortedList = new ArrayList<>();
40 | list.stream().sorted().forEach(sortedList::add);
41 |
42 | // 降序
43 | // 前提:Person 类必须实现 Comparable 接口
44 | list.stream().sorted(Comparator.reverseOrder()).forEach(sortedList::add);
45 |
46 | // 根据年龄升序
47 | // Person 类不需要实现 Comparable 接口
48 | list.stream().sorted(Comparator.comparing(Person::getAge)).forEach(sortedList::add);
49 | // 根据年龄降序
50 | list.stream().sorted(Comparator.comparing(Person::getAge).reversed()).forEach(sortedList::add);
51 |
52 | // lambda 表达式实现 Comparator 接口
53 | list.stream().sorted((o1, o2) -> {
54 | if (o1.getAge() == o2.getAge()) return o1.getName().compareTo(o2.getName());
55 | return o1.getAge() - o2.getAge();
56 | }).forEach(sortedList::add);
57 | ```
58 |
59 | ### Stream sorted() with Set
60 |
61 | ```java
62 | Set set = new HashSet<>();
63 | List sorted = set.stream().sorted().collect(Collectors.toList());
64 | System.out.println(sorted);
65 | // 和 List 几乎一模一样
66 | ```
67 |
68 | 需要注意的一点是,不能把排序后的结果重新输出到另一个`Set`中,因为`Set`无顺序,会破坏顺序
69 |
70 | ### Stream sorted() with Map
71 |
72 | `Map`同`Set`一样无顺序,如果把排序后的结果重新输出到另一个`Map`中中,可能会导致顺序被破坏
73 |
74 | 我们可以使用`LinkedHashMap`,这样会保证顺序
75 |
76 | ```java
77 | // 前提:key 对应的类必须实现 Comparable 接口
78 | Map map = new LinkedHashMap<>();
79 | Map sortedMap = new LinkedHashMap<>();
80 | map.entrySet().stream().sorted(Map.Entry.comparingByKey()).forEachOrdered(e -> sortedMap.put(e.getKey(), e.getValue()));
81 |
82 | // 前提:value 对应的类必须实现 Comparable 接口
83 | map.entrySet().stream().sorted(Map.Entry.comparingByValue()).forEachOrdered(e -> sortedMap.put(e.getKey(), e.getValue()));
84 |
85 | // lambda 表达式实现 Comparator 接口
86 | // value 对应的类不需要实现 Comparable 接口
87 | map.entrySet().stream().sorted(((o1, o2) -> {
88 | if (o1.getValue().getAge() == o2.getValue().getAge()) return o2.getValue().getName().compareTo(o1.getValue().getName());
89 | return o1.getValue().getAge() - o2.getValue().getAge();
90 | })).forEachOrdered(e -> sortedMap.put(e.getKey(), e.getValue()));
91 | ```
--------------------------------------------------------------------------------
/markdown/Java/synchronized关键字.md:
--------------------------------------------------------------------------------
1 | # synchronized 关键字
2 |
3 | ### 关于锁和同步
4 |
5 | **类锁 vs 对象锁**
6 |
7 | - 类锁:类的所有对象共享一把锁🔒
8 | - 对象锁:每个对象拥有一把锁 🔒
9 |
10 | 同步是对同一把锁而言的,同步这个概念是在多个线程争夺同一把锁的时候才能实现的,如果多个线程争夺不同的锁,那多个线程是不能同步的
11 |
12 | - 两个线程:一个取对象锁,一个取类锁,则不能同步
13 | - 两个线程:一个取对象 A 的锁,一个取对象 B 的锁,则不能同步
14 |
15 | ### 锁和 synchronized 的关系
16 |
17 | 锁是 Java 中用来实现同步的工具
18 |
19 | 而之所以能对方法或者代码块实现同步的原因就是:只有拿到锁的线程才能执行 synchronized 修饰的方法或代码块,且其他线程获得锁的唯一方法是等目前拿到锁的线程执行完方法将锁释放,如果 synchronized 修饰的代码块或方法没执行完是不会释放这把锁的,这就保证了拿到锁的线程一定可以一次性把它调用的方法或代码块执行完
20 |
21 | ### synchronized 修饰的类型
22 |
23 | 若 synchronized 修饰「静态方法」或者修饰「类的代码块」,则为类锁 🔒
24 |
25 | 若 synchronized 修饰「普通方法」或者修饰「当前对象的代码块」,则为对象锁 🔒
26 |
27 | #### 修饰方法
28 |
29 | - 修饰静态方法:静态方法属于类,所有对象调用的都是同一个方法
30 | - 修饰普通方法:普通方法属于对象,每个对象调用的都是自己的方法
31 |
32 | **注意:**
33 |
34 | - 在定义接口方法时不能使用 synchronized 关键字
35 | - 构造方法不能使用 synchronized 关键字,但可以使用 synchronized 代码块来进行同步
36 | - synchronized 关键字不能被继承。如果子类覆盖了父类被 synchronized 关键字修饰的方法,那么子类的该方法只要没有 synchronized 关键字,那么就默认没有同步
37 |
38 | ```java
39 | public class A {
40 | // 修饰静态方法
41 | public static synchronized void f1(int c) {
42 | for (int i = 0; i < 100; i++) {
43 | System.out.println("静态方法 " + c);
44 | }
45 | }
46 | // 修饰普通方法
47 | public synchronized void f2(int c) {
48 | for (int i = 0; i < 100; i++) {
49 | System.out.println("普通方法" + c);
50 | }
51 | }
52 | public static void main(String[] args) throws InterruptedException {
53 | // 测试静态方法
54 | // f1() 属于类 A,所以下方两个线程存在同步,一定是先输出所有「静态方法 1」,然后再输出所有「静态方法 2」
55 | new Thread(() -> A.f1(1)).start();
56 | new Thread(() -> A.f1(2)).start();
57 | Thread.sleep(1000);
58 | System.out.println("------------------");
59 | // 测试普通方法
60 | A a1 = new A();
61 | A a2 = new A();
62 | // f2() 属于类 A 的对象,所以下方两个线程不存在同步,一个取对象 a1 的锁,一个取对象 a2 的锁
63 | // 输出内容「普通方法 1」「普通方法 2」无规则交替出现
64 | new Thread(() -> a1.f2(1)).start();
65 | new Thread(() -> a2.f2(2)).start();
66 | }
67 | }
68 | ```
69 |
70 | #### 修饰代码块
71 |
72 | - 修饰类:表示对类进行同步
73 | - 修饰当前对象:表示对当前对象进行同步
74 |
75 | ```java
76 | public class B {
77 | public void f1(int c) {
78 | // 修饰类
79 | synchronized (B.class) {
80 | for (int i = 0; i < 100; i++) {
81 | System.out.println("修饰类 " + c);
82 | }
83 | }
84 | }
85 | public void f2(int c) {
86 | // 修饰当前对象
87 | synchronized (this) {
88 | for (int i = 0; i < 100; i++) {
89 | System.out.println("修饰当前对象 " + c);
90 | }
91 | }
92 | }
93 | public static void main(String[] args) throws InterruptedException {
94 | B b1 = new B();
95 | B b2 = new B();
96 | // 测试修饰类
97 | // 同步对象为类的所有对象,一定是先输出所有「修饰类 1」,然后再输出所有「修饰类 2」
98 | new Thread(() -> b1.f1(1)).start();
99 | new Thread(() -> b2.f1(2)).start();
100 | Thread.sleep(1000);
101 | System.out.println("------------------");
102 | // 测试修饰当前对象
103 | // 同步对象为当前对象,下方两个线程不存在同步,一个取对象 b1 的锁,一个取对象 b2 的锁
104 | // 输出内容「修饰当前对象 1」「修饰当前对象 2」无规则交替出现
105 | new Thread(() -> b1.f2(1)).start();
106 | new Thread(() -> b2.f2(2)).start();
107 | }
108 | }
109 | ```
110 |
--------------------------------------------------------------------------------
/markdown/Java/从字节码角度分析i++和++i.md:
--------------------------------------------------------------------------------
1 | # 从字节码角度分析 i++ 和 ++i
2 |
3 | **温馨提醒:**本篇文章内容过于底层,不太熟悉的同学可以先学习 **[操作数栈](./虚拟机栈.html#操作数栈)**
4 |
5 | 本篇文章从字节码的角度分析`i++`和`++j`背后的逻辑!!
6 |
7 | 先给出四个可能会让你很晕~的例子,相信如果搞清楚`i++`和`++j`原理的人可以很快知道每个变量最终的结果
8 |
9 | ```java
10 | public void add() {
11 | // problem 1
12 | int i1 = 10;
13 | i1++;
14 | int i2 = 10;
15 | ++i2;
16 |
17 | // problem 2
18 | int i3 = 10;
19 | int i4 = i3++;
20 | int i5 = 10;
21 | int i6 = ++i5;
22 |
23 | // problem 3
24 | int i7 = 10;
25 | i7 = i7++;
26 | int i8 = 10;
27 | i8 = ++i8;
28 |
29 | // problem 4
30 | int i9 = 10;
31 | i9 = i9++ + ++i9;
32 | }
33 | ```
34 |
35 | 下面再给出通过反编译后,该方法对应的字节码,这也是本篇文章分析的重点
36 |
37 | 如果不知道每个字节码指令对应什么意思,可以去查《虚拟机字节码指令表》
38 |
39 | ```java
40 | // ------------------------- problem 1 -------------------------
41 | 0: bipush 10 // 将单字节的常量值 10 推送至栈顶
42 | 2: istore_1 // 将栈顶 int 型数值存入第二个本地变量 (注意:下标从 0 开始,所以第二个对应下标是 1。下面同理!!)
43 | 3: iinc 1, 1 // 将指定 int 型变量增加指定值 (此处为将第二个本地变量增加 1;若为 i += 2,那么对应的字节码就为 iinc 1, 2)
44 | 6: bipush 10 // 将单字节的常量值 10 推送至栈顶
45 | 8: istore_2 // 将栈顶 int 型数值存入第三个本地变量
46 | 9: iinc 2, 1 // 将第三个本地变量增加 1
47 | // ------------------------- problem 2 -------------------------
48 | 12: bipush 10 // 将单字节的常量值 10 推送至栈顶
49 | 14: istore_3 // 将栈顶 int 型数值存入第四个本地变量
50 | 15: iload_3 // 将第四个 int 型本地变量推送至栈顶
51 | 16: iinc 3, 1 // 将第四个本地变量增加 1
52 | 19: istore 4 // 将栈顶 int 型数值存入第五个本地变量 (注意:此时第四个本地变量为 11,栈顶的值仍为 10,所以第五个本地变量为 10,即 i4 = 10)
53 | 21: bipush 10 // 将单字节的常量值 10 推送至栈顶
54 | 23: istore 5 // 将栈顶 int 型数值存入第六个本地变量
55 | 25: iinc 5, 1 // 将第六个本地变量增加 1
56 | 28: iload 5 // 将第六个 int 型本地变量推送至栈顶
57 | 30: istore 6 // 将栈顶 int 型数值存入第七个本地变量 (注意:此时第六个本地变量为 11,栈顶的值为 11,所以第七个本地变量为 11,即 i6 = 11)
58 | // ------------------------- problem 3 -------------------------
59 | 32: bipush 10 // 将单字节的常量值 10 推送至栈顶
60 | 34: istore 7 // 将栈顶 int 型数值存入第八个本地变量
61 | 36: iload 7 // 将第八个 int 型本地变量推送至栈顶
62 | 38: iinc 7, 1 // 将第八个本地变量增加 1
63 | 41: istore 7 // 将栈顶 int 型数值存入第八个本地变量 (注意:此时第八个本地变量为 11,栈顶的值为 10,所以第八个本地变量最终为 10,即 i7 = 10)
64 | 43: bipush 10 // 将单字节的常量值 10 推送至栈顶
65 | 45: istore 8 // 将栈顶 int 型数值存入第九个本地变量
66 | 47: iinc 8, 1 // 将第九个本地变量增加 1
67 | 50: iload 8 // 将第九个 int 型本地变量推送至栈顶
68 | 52: istore 8 // 将栈顶 int 型数值存入第九个本地变量 (注意:此时第九个本地变量为 11,栈顶的值为 11,所以第九个本地变量最终为 11,即 i8 = 10)
69 | // ------------------------- problem 4 -------------------------
70 | 54: bipush 10 // 将单字节的常量值 10 推送至栈顶
71 | 56: istore 9 // 将栈顶 int 型数值存入第十个本地变量
72 | 58: iload 9 // 将第十个 int 型本地变量推送至栈顶
73 | 60: iinc 9, 1 // 将第十个本地变量增加 1
74 | 63: iinc 9, 1 // 将第十个本地变量增加 1
75 | 66: iload 9 // 将第十个 int 型本地变量推送至栈顶
76 | 68: iadd // 将栈顶两 int 型数值相加并将结果压入栈顶 (注意:此时栈顶两个值分别为「+1 前的值」和「+1 两次后的值」;最终栈顶的值为 10 + 12 = 22)
77 | 69: istore 9 // 将栈顶 int 型数值存入第十个本地变量 (注意:此时第十个本地变量为 12,栈顶的值为 22,所以第十个本地变量最终为 22,即 i9 = 22)
78 | 71: return // 从当前方法返回 void
79 | ```
80 |
81 | **总结:**
82 |
83 | 首先`i++`和`++i`对于变量 i 的效果是等价的,都是使 i 增加 1
84 |
85 | 不同的在于这两个表达式的值:
86 |
87 | - `i++`是先将局部变量表中的 i 推送至操作数栈顶,然后将局部变量表中的 i + 1,最后将操作数栈顶的值赋给表达式,所以表达式的值为 i + 1 之前的值
88 | - `++i`是先将局部变量表中的 i + 1,然后将局部变量表中的 i 推送至操作数栈顶,最后将操作数栈顶的值赋给表达式,所以表达式的值为 i + 1 之后的值
--------------------------------------------------------------------------------
/markdown/Java/内存泄漏-内存溢出.md:
--------------------------------------------------------------------------------
1 | # 内存泄漏 & 内存溢出
2 |
3 | 在介绍 Java 堆溢出的时候提到过这两者的区别,**相关内容可见 [Java 堆溢出](./各区域OOM汇总.html#java-堆溢出)**
4 |
5 | 但是当时并没有介绍的很详细,所以本篇文章专门从不同角度来刨析这两个内容!!
6 |
7 | ### 内存泄漏 (Memory Leak)
8 |
9 | 「内存泄漏」有一个很形象的形容:**占着茅坑不拉屎**;放在内存中就是:**占据着内存资源,但是却毫无用处**
10 |
11 | 言归正传,内存泄漏更严谨的定义:**本应该被回收的对象,由于错误的引用链导致未进行回收**
12 |
13 | 
14 |
15 | 如上图所示,根据「可达性分析算法」很明显对象 D、E、F 可以被正确的回收;但由于错误的引用链导致对象 A、B、C 没有被回收,这就造成了**内存泄漏**
16 |
17 | 还有一种宽泛意义上的内存泄漏:由于开发人员的疏忽,使得对象的生命周期被演延长,最终造成了内存溢出
18 |
19 | ```java
20 | public void f() {
21 | Object obj = new Object();
22 | if (1 + 1 > 0) {
23 | // 使用对象 obj ...
24 | }
25 | // 其它地方都不会使用对象 obj
26 | }
27 | ```
28 |
29 | 上面这种就属于宽泛意义上的内存泄漏,可以直接把`obj`定义在`if`判断里面,当`if`代码块执行完,该对象的生命周期就结束了,可以直接被回收
30 |
31 | #### 例子 🌰
32 |
33 | **单例模式:**单例对象的生命周期自被创建开始一直到应用程序结束,所以在单例程序中,如果持有外部对象的引用,那么该外部对象就不能被回收,导致内存泄漏!
34 |
35 | **提供 close 的资源未关闭导致内存泄漏:**数据库连接`dataSourse.getConnection()`,网络连接 (socket) 和 IO 连接必须手动 close,否则就不能被回收,导致内存泄漏!
36 |
37 | ### 内存溢出 (OOM)
38 |
39 | 内存溢出相比于内存泄漏好理解:**为对象分配内存时,发现内存不够,导致无法完成内存分配**
40 |
41 | 由于 GC 的不断发展,一般情况下,除非应用程序占用内存的速度非常快,导致垃圾回收的速度赶不上内存分配的速度,否则不太容易出现 OOM
42 |
43 | 大多情况下,GC 会进行各年龄段的垃圾回收,实在不行就放大招,来一次独占式的 Full GC 操作,这个时候会回收大量内存,以供程序继续使用
44 |
45 | JavaDoc 对内存溢出给出的官方描述:**Thrown when the Java Virtual Machine cannot allocate an object because it is out of memory, and no more memory could be made available by the garbage collector.**
46 |
47 | 这一句话中有两个重点:**没有空闲内存,而且垃圾回收也无法提供更多内存**
48 |
49 | #### 无空闲内存
50 |
51 | 导致没有空闲内存的原因可能有以下三种:
52 |
53 | **Java 虚拟机堆内存一开始分配不够**
54 |
55 | 在虚拟机启动时,可以通过参数`-Xms -Xmx`指定虚拟机初始内存和最大内存,可能一开始分配的内存就不足以支撑系统正常运行,可以适当增加内存!!
56 |
57 | **程序中存在内存泄漏**
58 |
59 | 内存泄漏会导致无用对象依旧占据内存,使得后续无法为新对象分配内存,导致内存溢出!!
60 |
61 | **存在大量大对象,并且长时间不能被回收 (存在引用)**
62 |
63 | 对于老版本的 JDK,因为永久代的大小是有限的,并且 Java 虚拟机对永久代垃圾回收 (如:常量池回收、卸载不再需要的类型) 非常不积极,所以当不断添加新类型的时候,永久代出现 OOM 的概率非常大,尤其是在运行时存在大量动态类型生成的场合
64 |
65 | 类似 intern 字符串缓存占用太多空间,也会导致 OOM 问题,对应的异常信息,会标记出来和永久代相关:`java.lang.OutOfMemoryError: PermGen space`,这也是字符串常量池移入堆中的原因
66 |
67 | 随着元空间的引入,方法区内存已经不再那么窘迫,所以相应的 OOM 有所改观,出现 OOM 异常信息则变成了:`java.lang.OutofMemoryError:Metaspace`
68 |
69 | 直接内存不足,也会导致 OOM
70 |
71 | #### 垃圾回收
72 |
73 | 上面说:**没有空闲内存,而且垃圾回收也无法提供更多内存才会出现 OOM 异常**
74 |
75 | 这里面隐含了一层意思:**并不是没有空闲内存就会抛出 OOM 异常,而是在发现没有空闲内存时,会先执行一次垃圾回收操作,尽最大努力去清理内存空间,如果回收完内存依旧不够,才会抛出 OOM 异常**
76 |
77 | **例外:**并非所有内存不够的时候都会先执行一次垃圾回收操作,如果要分配的对象过大,如:大到空堆都无法存下,这种情况就会直接抛出 OOM 异常
--------------------------------------------------------------------------------
/markdown/Java/动态语言-动态类型语言.md:
--------------------------------------------------------------------------------
1 | # 动态语言 vs 动态类型语言
2 |
3 | ### 动态语言 VS 静态语言
4 |
5 | #### 动态语言
6 |
7 | 动态语言是一类在运行时可以**改变其结构的语言**
8 |
9 | 例如:新的函数、对象、甚至代码都可以被引进,已有的函数可以被删除或是其他结构上的变化
10 |
11 | 通俗点说就是运行时代码可以根据某些条件改变自身结构
12 |
13 | 主要的动态语言:Object-C、C#、JavaScript、PHP、Python 等
14 |
15 | #### 静态语言
16 |
17 | 与动态语言相对应的,运行时结构不可变的语言就是静态语言,如:Java、C、C++
18 |
19 | Java 不是动态语言,但 Java 可以称之为「准动态语言」,即 Java 有一定的动态性
20 |
21 | 我们可以利用 **[反射机制](./反射机制.html)** 获得类似动态语言的特性,Java 的动态性让编程的时候更加灵活!
22 |
23 | #### 举例
24 |
25 | ```js
26 | function Person(name, age, job) {
27 | this.name = name;
28 | this.age = age;
29 | this.job = job
30 | this.hello = function(name){
31 | alert("Hello, " + name);
32 | };
33 |
34 | person = new Person("Eric", 28, 'worker');
35 | alert(person.name + '' + person.age + '');
36 | person.hello("Alice");
37 | //为对象添加方法
38 | person.work = function() {
39 | alert('I am working');
40 | }
41 | person.work();
42 |
43 | //删除方法
44 | delete person.work;
45 | person.work();
46 | ```
47 |
48 | ### 动态类型语言 VS 静态类型语言
49 |
50 | #### 动态类型语言
51 |
52 | 动态类型语言的关键特性是它的类型检查的主体过程是在运行期而不是编译期进行的
53 |
54 | #### 静态类型语言
55 |
56 | 静态类型语言在编译期就进行了类型检查
57 |
58 | #### 举例
59 |
60 | 举几个很直白的例子!对于 Java,定义一个变量:
61 |
62 | ```java
63 | // 在编译期间就必须明确变量 a 的类型
64 | int a = 10;
65 | ```
66 |
67 | 对于 JS,定义一个变量:
68 |
69 | ```js
70 | // 在运行期间才知道变量 name 和 age 的类型
71 | var name = "abc";
72 | var age = 10;
73 | ```
74 |
75 | 对于 Python,定义一个变量:
76 |
77 | ```python
78 | # 在运行期间才知道变量 info 的类型
79 | info = 1234.3
80 | ```
81 |
82 | 所以 Java 是静态类型语言;而 JS 和 Python 是动态类型语言
83 |
84 | **静态类型语言是判断变量自身的类型信息;动态类型语言是判断变量值的类型信息,变量没有类型信息,变量值才有类型信息**
--------------------------------------------------------------------------------
/markdown/Java/垃圾回收相关概念.md:
--------------------------------------------------------------------------------
1 | # 垃圾回收相关概念
2 |
3 | ### Stop The World
4 |
5 | Stop The World,简称 STW,指在 GC 事件发生过程中,会产生应用程序的停顿。停顿产生时整个应用程序线程会被暂停,没有任何响应
6 |
7 | 被 STW 中断的应用线程会在 GC 之后恢复,频繁中断会让用户感觉像是网速不快造成电影卡顿一样,所以需要减少 STW 发生的时间
8 |
9 | 可达性分析算法中枚举 GC Roots 时会导致所有 Java 执行线程停顿,原因如下:
10 |
11 | - 分析工作必须在一个能保证一致性的快照中进行
12 | - 一致性指整个分析期间整个执行系统看起来像被冻结在某个时间点上
13 | - 如果分析过程中对象引用关系还在不断变化,则分析结果的准确性无法保证
14 |
15 | **注意:**STW 和使用哪款 GC 无关,所有的 GC 都会产生 STW,只能说效率越高的 GC,STW 的时间越短,但并不是没有 STW,我们能做的也只是尽可能的缩短 STW 的时间,如:增量收集算法和分区收集算法
16 |
17 | STW 是 Java 虚拟机在后台自动发起和自动完成的,在用户不可见的情况下,把用户的工作线程全部停掉;开发中不要用`System.gc()`,会导致 STW 的发生
18 |
19 | ### 并行与并发
20 |
21 | #### 程序中的并行与并发
22 |
23 | **并行:**一般指多核处理器,每个线程都单独在一个核心上运行,各线程之间不存在资源竞争的关系
24 |
25 | **并发:**一般指单核处理器,多个线程都在同一个核心上运行,但一个核心同一时刻只能执行一个线程,所以各线程之间交替执行,常见的有时间片轮询算法
26 |
27 | 对于并行,宏观上多个线程之间都在同时执行;微观上多个线程之间也都在同时执行,没有 CPU 资源的竞争
28 |
29 | 对于并发,宏观上多个线程之间都在同时执行;微观上多个线程之间交替执行,同一时刻只有一个线程在执行,存在 CPU 资源的竞争
30 |
31 | #### 垃圾回收的并行与并发
32 |
33 | **并行:**描述的是多条垃圾收集器线程之间的关系,说明同一时间有多条这样的线程在协同工作,通常默认此用户线程处于等待状态
34 |
35 | 典型的 ParNew 就是多线程并行的垃圾收集器,与之相对应的是 Serial 单线程串行垃圾收集器,它们俩运行示意图如下所示:
36 |
37 | 
38 |
39 | **并发:**描述的是垃圾收集器线程与用户线程之间的关系,说明同一时间垃圾收集器线程与用户线程都在运行 (不一定并行,可能是交替执行)。由于用户线程并未被冻结,所以程序仍然能响应服务请求,但由于垃圾收集器线程占用了一部分系统资源,此时应用程序处理的吞吐量将受到一定影响
40 |
41 | 典型的 CMS 就是并发的垃圾收集器,其中初始标记、重新标记两个步骤仍然需要 STW,其它步骤可以和用户线程一起并行执行,它的运行示意图如下所示:
42 |
43 | 
44 |
45 | **总结:**为了提高垃圾回收的效率,GC 经历了「串行回收 -> 并行回收 -> 并发回收」
46 |
47 | - 串行的效率最慢,只有一个 GC 线程,而且用户线程还必须 STW 等待一次完整的 GC 过程执行完成,这样用户感受到的停顿感会十分明显
48 | - 并行在串行的基础上将一个 GC 线程增加到多个 GC 线程,虽然回收的效率会提高一些,但是用户线程依旧必须 STW 等待一次完整的 GC 过程执行完成
49 | - 并发在并行的基础上再度升级,不仅拥有多个 GC 线程,而且用户线程和 GC 线程都在运行 (可能交替执行),虽然必要阶段可能还是需要 STW,但用户体验感明显会好很多
50 |
--------------------------------------------------------------------------------
/markdown/Java/垃圾收集器前言.md:
--------------------------------------------------------------------------------
1 | # 垃圾收集器前言
2 |
3 | 在正式介绍垃圾收集器之前,先来唠一唠垃圾收集器一些细枝末节的东西!!!
4 |
5 | 前文介绍过 **[垃圾收集算法](./垃圾收集算法.html)**,如果说它是内存回收的方法论,那么垃圾收集器就是内存回收的实践者。《Java 虚拟机规范》中对垃圾收集器应该如何实现并没有做出任何规定!!
6 |
7 | **注意:**根据上下文 GC 可能表示 Garbage Collection 或者 Garbage Collector,前者为垃圾收集机制,后者为垃圾收集器
8 |
9 | ### 垃圾收集器发展史
10 |
11 | 1999 年随 JDK1.3.1 一起出现的是串行方式的 Serial 收集器和 Serial Old 收集器,它是第一款垃圾收集器。ParNew 收集器是 Serial 收集器的多线程版本
12 |
13 | 2002 年 2 月 26 日,Parallel Scaverge 收集器和 Concurrent Mark Sweep (CMS) 收集器跟随 JDK1.4.2 一起发布
14 |
15 | Parallel Old 收集器直到 JDK6 才开始提供;Parallel Scaverge / Parallel Old 收集器在 JDK6 之后成为 HotSpot 默认垃圾收集器
16 |
17 | 2012 年,在 JDK7 Update 4 版本中正式提供了商用的 G1 收集器,此前 G1 一直处于实验阶段
18 |
19 | 2017 年,JDK9 中 G1 变成默认的垃圾收集器,替代 CMS
20 |
21 | 2018 年 3 月,JDK10 中 G1 垃圾收集器并行完整垃圾回收,实现并行性来改善最坏情况下的延迟
22 |
23 | **------------- 分水岭 -------------**
24 |
25 | 2018 年 9 月,JDK11 发布,引入 Epsilon 垃圾收集器,又被称为 No-Op (无操作) 收集器。同时,引入 ZGC:可伸缩的低延迟垃圾收集器 (Experimental)
26 |
27 | 2019 年 3 月,JDK12 发布,增强 G1,自动返回未用堆内存给操作系统;同时,引入 Shenandoah GC:低停顿时间的GC (Experimental)
28 |
29 | 2019 年 9 月,JDK13 发布,增强 ZGC,自动返回未用堆内存给操作系统。
30 |
31 | 2020 年 3 月,JDK14 发布,删除 CMS 垃圾收集器,扩展 ZGC 在 MacOS 和 Windows 上的应用
32 |
33 |
34 |
35 | **注意:**分水岭上面属于 7 种经典垃圾收集器,分别为:Serial GC、ParNew GC、Parallel Scaverge GC、Serial Old GC、Parallel Old GC、CMS、G1
36 |
37 | ### 垃圾收集器分类
38 |
39 | **关于串行、并行、并发的解释可见 [垃圾回收的并行与并发](./垃圾回收相关概念.html#并行与并发)**
40 |
41 |  42 |
43 | ### 垃圾收集器性能指标
44 |
45 | **停顿时间:**执行一次完整的垃圾收集时,用户线程被暂停的总时间
46 |
47 | **吞吐量:**处理器用于运行用户代码的时间与处理器总消耗时间的比值,计算公式如下:
48 | $$
49 | 吞吐量 = \frac{运行用户代码时间}{运行用户代码时间 + 运行垃圾收集时间}
50 | $$
51 | **对比:**
52 |
53 | - 停顿时间越短越适合需要与用户交互或需要保证服务响应质量的程序,良好的响应速度能提升用户体验感
54 | - 高吞吐量则可以最高效率地利用处理器资源,尽快完成程序的运算任务,主要适合在后台运算而不需要太多交互的分析任务
55 |
56 | ### 垃圾收集器的组合关系
57 |
58 | 本部分的关系是在「按照工作内存区间划分」的基础上进行组合滴!!
59 |
60 | 
61 |
62 | **[JEP 173: Retire Some Rarely-Used GC Combinations](https://openjdk.org/jeps/173)**
63 |
64 | **[JEP 214: Remove GC Combinations Deprecated in JDK 8](https://openjdk.org/jeps/214)**
65 |
66 | **[JEP 366: Deprecate the ParallelScavenge + SerialOld GC Combination](https://openjdk.org/jeps/366)**
67 |
68 | **[JEP 363: Remove the Concurrent Mark Sweep (CMS) Garbage Collector](https://openjdk.org/jeps/363)**
69 |
70 | **注意:JDK8 中默认垃圾收集器为 Parallel Scaverge GC + Parallel Old GC;JDK9 中默认垃圾收集器为 G1**
--------------------------------------------------------------------------------
/markdown/Java/实战-静态变量-实例变量-局部变量.md:
--------------------------------------------------------------------------------
1 | # 实战「静态变量」「实例变量」「局部变量」
2 |
3 | 这篇文章就以实战的方式看看「静态变量」「实例变量」「局部变量」存放的位置!
4 |
5 | 首先要搞清楚一个概念,「静态变量」「实例变量」「局部变量」指的是引用本身,而非它们所指向的对象,它们所指向的对象毫无疑问肯定都存放在堆上,**关于这个观点更多分析可见 [逃逸分析](./逃逸分析.html)**
6 |
7 | 还需要强调一个点,这里是基于 JDK8 的 HotSpot 虚拟机!!
8 |
9 | 根据理论知识可以知道:「静态变量」在 JDK7 及以后就存放在 Java 堆中;「实例变量」随着对象实例存放在 Java 堆中;「局部变量」存放在方法栈帧的局部变量表中
10 |
11 | 首先给出一段测试代码:
12 |
13 | ```java
14 | public class Test {
15 | static class Person {
16 | // 静态变量
17 | static ObjectHolder staticObj = new ObjectHolder();
18 | // 实例变量
19 | ObjectHolder instanceObj = new ObjectHolder();
20 | void foo() throws InterruptedException {
21 | // 局部变量
22 | ObjectHolder localObj = new ObjectHolder();
23 | // 休眠,不然方法执行完,方法栈帧就会出栈
24 | Thread.sleep(10000000);
25 | }
26 | }
27 | private static class ObjectHolder {}
28 | public static void main(String[] args) throws InterruptedException {
29 | Person person = new Person();
30 | person.foo();
31 | }
32 | }
33 | ```
34 |
35 | 我们先分析一下,按照理论来说,此时 Java 堆中肯定存在 3 个`ObjectHolder`对象实例,同时`staticObj`和`instanceObj`也都在 Java 堆中
36 |
37 | 下面通过 VisualVM + JProfiler 软件测试一下!!首先用 VisualVM 保存一个 Java 堆的 dump文件,如下所示:
38 |
39 | 
40 |
41 | 用 JProfiler 打开这个 dump 文件,可以发现在 Java 堆中刚好有 3 个`ObjectHolder`对象实例,如下图所示:
42 |
43 | 
44 |
45 | 我们再找找「静态变量」在哪里,在`java.lang.Class`中可以发现我们定义的静态变量`staticObj`,而这个静态变量指向的对象实例是`0xa87`,如下图所示:
46 |
47 | 
48 |
49 | 继续找「实例变量」在哪里,在`com.lfool.myself.Test$Person`中可以发现我们定义的实例变量`instanceObj`,而这个实例变量指向的对象实例是`0xc3b`,如下图所示:
50 |
51 | 
52 |
53 | 到此为止,我们找出来的所有内容都存放在 Java 堆中,至于「局部变量」,可以通过 JHSDB 软件在栈中发现,这里就不演示了!!!
--------------------------------------------------------------------------------
/markdown/Java/方法调用面试题.md:
--------------------------------------------------------------------------------
1 | # 方法调用面试题
2 |
3 | #### 问题一:下面代码输出的结果
4 |
5 | **详细解析可见 [方法调用](./方法调用.html#静态分派)**
6 |
7 | ```java
8 | public class StaticDispatch {
9 | static abstract class Human {}
10 | static class Man extends Human {}
11 | static class Woman extends Human {}
12 | public void sayHello(Human guy) {
13 | System.out.println("hello, guy!");
14 | }
15 | public void sayHello(Man guy) {
16 | System.out.println("hello, gentleman!");
17 | }
18 | public void sayHello(Woman guy) {
19 | System.out.println("hello, lady!");
20 | }
21 | public static void main(String[] args) {
22 | Human man = new Man();
23 | Human woman = new Woman();
24 | StaticDispatch sr = new StaticDispatch();
25 | sr.sayHello(man);
26 | sr.sayHello(woman);
27 | }
28 | }
29 | ```
30 |
31 | #### 问题二:下面代码依次输出的结果
32 |
33 | **详细解析可见 [方法调用](./方法调用.html#静态分派)**
34 |
35 | ```java
36 | public class Overload {
37 | public static void sayHello(Object arg) {
38 | System.out.println("hello Object");
39 | }
40 | public static void sayHello(int arg) {
41 | System.out.println("hello int");
42 | }
43 | public static void sayHello(long arg) {
44 | System.out.println("hello long");
45 | }
46 | public static void sayHello(Character arg) {
47 | System.out.println("hello Character");
48 | }
49 | public static void sayHello(char arg) {
50 | System.out.println("hello char");
51 | }
52 | public static void sayHello(char... arg) {
53 | System.out.println("hello char...");
54 | }
55 | public static void sayHello(Serializable arg) {
56 | System.out.println("hello Serializable");
57 | }
58 | public static void main(String[] args) {
59 | sayHello('a');
60 | }
61 | }
62 | ```
63 |
64 | 依次注释掉方法
65 | - `sayHello(char arg)`
66 | - `sayHello(int arg)`
67 | - `sayHello(long arg)`
68 | - `sayHello(Character arg)`
69 | - `sayHello(Serializable arg)`
70 | - `sayHello(Object arg)`
71 |
72 | 它会输出什么?!
73 |
74 | #### 问题三:下面代码输出的结果
75 |
76 | **详细解析可见 [方法调用](./方法调用.html#动态分派)**
77 |
78 | ```java
79 | public class FieldHasNoPolymorphic {
80 | static class Father {
81 | public int money = 1;
82 | public Father() {
83 | money = 2;
84 | showMeTheMoney();
85 | }
86 | public void showMeTheMoney() {
87 | System.out.println("I am Father, i have $" + money);
88 | }
89 | }
90 | static class Son extends Father {
91 | public int money = 3;
92 | public Son() {
93 | money = 4;
94 | showMeTheMoney();
95 | }
96 | public void showMeTheMoney() {
97 | System.out.println("I am Son, i have $" + money);
98 | }
99 | }
100 | public static void main(String[] args) {
101 | Father guy = new Son();
102 | System.out.println("This guy has $" + guy.money);
103 | }
104 | }
105 | ```
106 |
107 |
--------------------------------------------------------------------------------
/markdown/Java/注解.md:
--------------------------------------------------------------------------------
1 | # 注解
2 |
3 | ### 什么是注解
4 |
5 | Annotation 是从 JDK5.0 开始引入的新技术
6 |
7 | Annotation 的作用
8 |
9 | - 不是程序本身,可以对程序作出解释
10 | - **可以被其他程序 (如:编译器等) 读取**
11 |
12 | Annotation 的格式
13 |
14 | - 注解是以`@name`在代码中存在,还可以添加一些参数值,例如:`@SuppressWarnings(value = "unchecked")`
15 |
16 | Annotation 在哪里使用?
17 |
18 | - 可以附加在 package、class、method、field 等上面,相当于给他们添加了额外的辅助信息,我们可以通过**反射机制**编程实现对这些元数据的访问
19 |
20 | ### 内置注解
21 |
22 | `@Override`:定义在`java.lang.Override`中,此注解只适用于**修辞方法**,表示一个方法声明打算重写超类中的另一个方法声明
23 |
24 | `@Deprecated`:定义在`java.lang.Deprecated`中,此注解可以用于**修饰方法、属性、类**,表示不鼓励程序员使用这些元素,通常是因为它很危险或者存在更好的选择
25 |
26 | `@SuppressWarnings`:定义在`java.lang.SuppressWarnings`中,用来抑制编译时的警告信息,与前两个注解不同的是需要添加一个参数才能正确使用,这些参数都是已经定义好了的,选择性使用即可
27 |
28 | - `@SuppressWarnings("all")`
29 | - `@SuppressWarnings("unchecked")`
30 | - `@SuppressWarnings(value = {"unchecked", "deprecation"})`
31 | - ...
32 |
33 | ### 元注解
34 |
35 | 元注解的作用:负责注解其他注解
36 |
37 | Java 定义了 4 个标准的 meta-annotation 类型,他们被用来提供对其他 annotation 类型作说明
38 |
39 | 这些类型和它们所支持的类在`java.lang.annotation`包中可以找到:`@Target`、`@Retention`、`@Documented`、`@Inherited`
40 |
41 | - `@Target`:用于描述注解的使用范围 (即:被描述的注解可以用在什么地方)
42 | - `@Retention`:表示需要在什么级别保存该注解信息,用于描述注解的生命周期 (SOURCE < CLASS < **RUNTIME**)
43 | - `@Documented`:说明该注解将被包含在 Javadoc 中
44 | - `@Inherited`:说明子类可以继承父类中的该注解
45 |
46 | ```java
47 | // Target 表示该注解可以用在什么地方:类,方法
48 | @Target(value = {ElementType.TYPE, ElementType.METHOD})
49 | // Retention 表示该注解在什么地方还有效:SOURCE < CLASS < RUNTIME
50 | @Retention(value = RetentionPolicy.RUNTIME)
51 | // Documented 表示该注解将生成在 Javadoc 中
52 | @Documented
53 | // Inherited 表示子类可以继承该注解
54 | @Inherited
55 | public @interface MyAnnotation {
56 | }
57 | ```
58 |
59 | ### 自定义注解
60 |
61 | 使用`@interface`自定义注解时,自动继承`java.lang.annotation.Annotation`接口
62 |
63 | - `@interface`用来声明一个注解,格式:`public @interface name {}`
64 | - 其中的每一个方法实际上是声明了一个配置参数
65 | - 方法的名称就是参数的名称
66 | - 返回值类型就是参数的类型 (返回值只能是基本类型、对象、String、enum)
67 | - 可以通过`default`来声明参数的默认值
68 | - 如果只有一个参数成员,一般参数名为`value`
69 | - 注解元素必须要有值,在定义注解元素时,经常使用「空字符串、0」作为默认值
70 |
71 | ```java
72 | @Target(value = {ElementType.TYPE, ElementType.METHOD})
73 | @Retention(value = RetentionPolicy.RUNTIME)
74 | public @interface MyAnnotation {
75 | // 定义注解参数的格式:参数类型 + 名字 + ()
76 | String name();
77 | int age() default 0;
78 | int id() default -1;
79 | String[] schools() default {"school1", "school2"};
80 | }
81 | public class MyAnnotationTest {
82 | @MyAnnotation(name = "张三", age = 18, id = 1, schools = {"school3"})
83 | public void test01() {
84 | }
85 | @MyAnnotation(name = "张三")
86 | public void test02() {
87 | }
88 | }
89 | ```
--------------------------------------------------------------------------------
/markdown/Java/浅记字节字符流乱码问题.md:
--------------------------------------------------------------------------------
1 | # 浅记「字节/字符流」乱码问题
2 |
3 | ### 字符编码
4 |
5 | Unicode 统一了所有字符的编码,包括中文,它算是一个**字符集**,用 2 字节大小对所有字符进行了唯一编码
6 |
7 | 但是 Unicode 没有规定如何存储,UTF-8 刚好规定了 Unicode 字符如何存储的问题。UTF-8 采用可变长编码,英文用 1 个字节,中文用 3 个字节
8 |
9 | 对于 UTF-8 编码中的任意字节 B:
10 |
11 | - 如果 B 的第一位为 0,则 B 独立的表示一个字符 (ASCII 码) -> **0xxxxxxx**
12 |
13 | - 如果 B 的第一位为 1,第二位为 0,则 B 为一个多字节字符中的一个字节 (非 ASCII 字符) -> **10xxxxxx**
14 |
15 | - 如果 B 的前两位为 1,第三位为 0,则 B 为两个字节表示的字符中的第一个字节 -> **110xxxxx**
16 |
17 | - 如果 B 的前三位为 1,第四位为 0,则 B 为三个字节表示的字符中的第一个字节 -> **1110xxxx**
18 |
19 | - 如果 B 的前四位为 1,第五位为 0,则 B 为四个字节表示的字符中的第一个字节 -> **11110xxx**
20 |
21 | 举个简单的例子,中文汉字「**我**」对应的 Unicode 编码:十进制: 25105;十六进制:0x6211;二进制:01100010 00010001
22 |
23 | 它在 UTF-8 编码下的存储结构为:十六进制:0xE68891;二进制:11100110 10001000 10010001
24 |
25 | 为了方便对比,写到一起:
26 |
27 | ```bash
28 | 1110xxxx 10xxxxxx 10xxxxxx
29 | UTF-8: 11100110 10001000 10010001
30 | Unicode: 0110 001000 010001
31 | ```
32 |
33 | ### 乱码分析
34 |
35 | 在学习字节流和字符流的时候,遇到过一个问题:**为什么 I/O 流操作要分为字节流操作和字符流操作呢?**
36 |
37 | - 如果只有字符流操作,由于字符流是由 Java 虚拟机将字节流转换得到,这个过程比较耗时
38 | - 如果只有字节流操作,如果不知道编码类型的话,很容易出现乱码问题
39 |
40 | 本篇文章就上面的第二点展开讨论为什么会出现乱码问题!!!
41 |
42 | 如果我们用字节流去读 UTF-8 编码的文件,那么每次只能一个字节一个字节的读。对于一个中文汉字需要读三次,每次读的结果如下:11100110、10001000、10010001
43 |
44 | 可以看到三次读出来的结果其实就是上面分析过的 UTF-8 编码下的存储结构,此时就会将每一次的结果转化成一个 ACSII 字符:
45 |
46 | - 11100110 -> 230 -> æ
47 | - 10001000 -> 136 ->
48 | - 10010001 -> 145 ->
49 |
50 | 所以乱码就出现了!!另外可以从下面程序中得到验证:
51 |
52 | ```java
53 | public static void main(String[] args) {
54 | // input.txt 中存储的就是一个中文汉字「我」
55 | // FileInputStream 字节输入流,每次读一个字节
56 | try (FileInputStream fis = new FileInputStream("input.txt")) {
57 | System.out.println("Number of remaining bytes: " + fis.available());
58 | int content;
59 | while ((content = fis.read()) != -1) { // 读一个字节
60 | System.out.println(content + " -> " + (char) content);
61 | }
62 | } catch (IOException e) {
63 | throw new RuntimeException(e);
64 | }
65 | }
66 | ```
67 |
68 | 如果我们改用字符输入流,它每次都读一个字符,而且已经自动处理了编码问题,具体可见下面程序:
69 |
70 | ```java
71 | public static void main(String[] args) {
72 | // input.txt 中存储的就是一个中文汉字「我」
73 | // FileReader 字符输入流,每次读一个字符
74 | try (FileReader fileReader = new FileReader("input.txt")) {
75 | int content;
76 | while ((content = fileReader.read()) != -1) {
77 | System.out.println(content + " -> " + (char) content);
78 | System.out.println(Integer.toBinaryString(content));
79 | }
80 | } catch (Exception e) {
81 | e.printStackTrace();
82 | }
83 | }
84 | // 输出
85 | 25105 -> 我
86 | 110001000010001
87 | ```
88 |
89 | `input.txt`文件中存储的结构是:11100110 10001000 10010001,不信的话可以用二进制文件查看器打开它
90 |
91 | 但程序输出的二进制内容不再是 UTF-8 编码下存储的内容,而是对其进行了解码,转换成了 Unicode 下的编码,所以最后才没有乱码
92 |
93 | **注意:**字符输入流并非每次都读三个字节。如果一个字符只用一个字节存储,那么一次就读一个字节,如果一个字符用三个字节存储,那么一次就读三个字节,可以根据 UTF-8 编码判断每次读几个字节
94 |
95 | **总结:**字节输入流每次读一个字节,字符输入流每次读一个字符,而且字符输入流还自动的对 UTF-8 解码成 Unicode
--------------------------------------------------------------------------------
/markdown/Java/类加载子系统-导读.md:
--------------------------------------------------------------------------------
1 |
2 |
3 |
4 |
5 |
6 | ### 本系列按照从上到下的顺序整理,可直接点击 👉 后面链接跳转!!😝
7 |
8 |
9 |
10 |
11 |
--------------------------------------------------------------------------------
/markdown/Java/类加载的时机.md:
--------------------------------------------------------------------------------
1 | **「JVM 类加载子系统」系列文章**
2 |
3 | - **[类加载的过程](./类加载的过程.html)**
4 | - **[❤️🔥 类加载的时机](./类加载的时机.html)**
5 | - **[类加载器](./类加载器.html)**
6 | - **[剖析 [Bootstrap、Extension、Application] ClassLoader](./剖析-Bootstrap-Extension-Application-ClassLoader.html)**
7 | - **[双亲委派模型](./双亲委派模型.html)**
8 | - **[自定义类加载器](./自定义类加载器.html)**
9 | - **[破坏双亲委派模型](./破坏双亲委派模型.html)**
10 |
11 | # 类加载的时机
12 |
13 | 在类生命周期的七个阶段中,加载、验证、准备、初始化和卸载五个阶段的顺序是确定的,类型的加载过程必须按照这种顺序按部就班地开始,而**解析阶段不一定**
14 |
15 | 解析阶段是 Java 虚拟机将常量池内的符号引用替换成直接引用的过程,所以这个过程可能在加载阶段完成,也可能在运行期间完成,这是为了支持 Java 运行时绑定
16 |
17 | 《Java 虚拟机规范》中并没有强制约束什么情况下必须开始类加载过程的第一个阶段「加载」;但是对于初始化阶段,严格规定了**有且只有**六种情况必须立即对类进行「初始化」
18 |
19 | 1. 遇到`new`、`getstatic`、`putstatic`、`invokestatic`四条字节码指令时,如果类型没有进行初始化,则需要先触发其初始化阶段。能够生成这四条指令的典型 Java 代码场景有:
20 |
21 | - 使用`new`关键字实例化对象的时候
22 | - 读取或设置一个类型的静态字段的时候 (被`final`修饰的静态变量,已在编译期把结果放入常量池,读取该字段是不会引起初始化)
23 | - 调用一个类型的静态方法的时候
24 |
25 | 2. 使用`java.lang.reflect`包的方法对类型进行反射调用的时候,如果类型没有进行过初始化,则需要先触发其初始化
26 | 3. 当初始化类的时候,发现其父类还没有进行过初始化,则需要先触发其父类的初始化
27 | 4. 当虚拟机启动时,用户需要指定一个要执行的主类 (main() 所在的类),虚拟机会先初始化这个类
28 | 5. 使用 JDK7 新加入的动态语言支持时,如果一个`java.lang.invoke.MethodHandle`实例最后的解析结果为`REF_getStatic`、`REF_putStatic`、`REF_invokeStatic`、`REF_newInvokeSpecial`四种类型的方法句柄,并且这个方法句柄对应的类没有进行过初始化,则需要先触发其初始化
29 | 6. 当一个接口中定义了 JDK8 新加入的默认方法 (default 修饰) 时,如果有这个接口的实现类发生了初始化,那该接口要在其之前被初始化
30 |
31 | 这六种场景中的行为称为对一个类型进行**主动引用**;除此之外,所有引用类型的方式都不会触发初始化,称为**被动引用**
32 |
33 | 下面是四种被动引用的例子:
34 |
35 | ```java
36 | // ---------------------- 例子 1 ----------------------
37 | // 对于静态字段,只有直接定义字段的类才会被初始化
38 | // 通过子类引用父类中定义的静态字段,只会触发父类的初始化,而不会触发子类的初始化
39 | public class SuperClass {
40 | static {
41 | System.out.println("Super Class init!");
42 | }
43 | public static int value = 123;
44 | }
45 | public class SubClass extends SuperClass {
46 | static {
47 | System.out.println("SubClass init!");
48 | }
49 | }
50 | public class NotInitialization {
51 | public static void main(String[] args) {
52 | System.out.println(SubClass.value);
53 | }
54 | }
55 | // result
56 | // Super Class init!
57 | // 123
58 | // ---------------------- 例子 2 ----------------------
59 | // 通过数组定义来引用类,不会触发此类的初始化
60 | public class NotInitialization {
61 | public static void main(String[] args) {
62 | SuperClass[] arr = new SuperClass[10];
63 | }
64 | }
65 | // ---------------------- 例子 3 ----------------------
66 | // 调用静态常量,不会触发此类的初始化
67 | public class ConstClass {
68 | static {
69 | System.out.println("ConstClass init!");
70 | }
71 | public static final String HELLOWORLD = "hello world";
72 | }
73 | public class NotInitialization {
74 | public static void main(String[] args) {
75 | System.out.println(ConstClass.HELLOWORLD);
76 | }
77 | }
78 | // result
79 | // hello world
80 | // ---------------------- 例子 4 ----------------------
81 | public static void main(String[] args) throws ClassNotFoundException {
82 | // 不会引起类的初始化
83 | Class myObjClass = MyObj.class;
84 | // 会引起类的初始化
85 | Class aClass = Class.forName("com.lfool.myself.MyObj");
86 |
87 | }
88 | ```
89 |
--------------------------------------------------------------------------------
/markdown/Java/虚拟机栈面试题.md:
--------------------------------------------------------------------------------
1 | # 虚拟机栈面试题
2 |
3 | 本篇文章总结虚拟机栈的面试题!!
4 |
5 | #### 问题一:栈溢出的情况?
6 |
7 | 《Java 虚拟机规范》中描述了两种异常:
8 |
9 | - 如果线程请求的栈深度大于虚拟机所允许的最大深度,将抛出 **StackOverflowError (SOF)** 异常
10 | - 如果虚拟机的栈内存允许动态扩展,当扩展栈容量无法申请到足够的内存时,将抛出 **OutOfMemoryError (OOM)** 异常
11 |
12 | **注意:**栈容量只能由 -Xss 参数来设定
13 |
14 | #### 问题二:调整栈容量,就能保证不出现溢出吗?
15 |
16 | 不能!!通过调整栈容量,可能会使原本出现溢出的代码不出现溢出了;但无法保证所有情况都不出现溢出!!
17 |
18 | 假设原本栈容量可以支持 5000 次调用,但代码有 6000 次调用,就会出现溢出;此时调整栈容量保证其可以支持 7000 次调用,那么原来的代码就不会出现溢出了
19 |
20 | 但如果另外一个代码有 8000 次调用,依旧会出现溢出!!
21 |
22 | #### 问题三:分配栈容量越大越好吗?
23 |
24 | 不一定!!分配越大的栈容量,会压缩其他部分的大小,比如:堆,方法区等
25 |
26 | #### 问题四:垃圾回收是否会涉及到虚拟机栈?
27 |
28 | 这里总结一下「运行时数据区域」的各个部分是否会发生 Error 或者 GC!!
29 |
30 | | | Error | GC |
31 | | :-------------: | :---: | :--: |
32 | | 方法区 | ✅ | ✅ |
33 | | 堆 | ✅ | ✅ |
34 | | 虚拟机栈 | ✅ | ❌ |
35 | | 本地方法栈 | ✅ | ❌ |
36 | | 程序计数器 (PC) | ❌ | ❌ |
37 |
38 | #### 问题五:方法中定义的局部变量是否线程安全?
39 |
40 | 需要分情况讨论,有的情况是线程安全,有的情况是线程不安全,会发生对象逃逸
41 |
42 | ```java
43 | // 情况一:线程安全
44 | // 对象 s1 随着方法调用的结束而消亡,不会被多个线程共享
45 | public static void f1() {
46 | // 注意:StringBuilder 不是线程安全;StringBuffer 是线程安全
47 | StringBuilder s1 = new StringBuilder();
48 | s1.append("a");
49 | s1.append("b");
50 | }
51 |
52 | // 情况二:线程不安全
53 | // 对象 s1 不会随着方法调用的结束而消亡,因为随着方法的返回值逃逸出去了,可能会被多个线程共享
54 | public static StringBuilder f2() {
55 | StringBuilder s1 = new StringBuilder();
56 | s1.append("a");
57 | s1.append("b");
58 | return s1;
59 | }
60 |
61 | // 情况三:线程不安全
62 | // 对象 s1 随着方法的参数传入方法中,不是线程私有,可能会被多个线程共享
63 | public static void f3(StringBuilder s1) {
64 | s1.append("a");
65 | s1.append("b");
66 | }
67 |
68 | // 情况四:线程安全
69 | // 对象 s1 随着方法调用的结束而消亡,不会被多个线程共享;而返回值是 String,它是不可变的
70 | public static String f4() {
71 | StringBuilder s1 = new StringBuilder();
72 | s1.append("a");
73 | s1.append("b");
74 | return s1.toString();
75 | }
76 | ```
--------------------------------------------------------------------------------
/markdown/Java/运行时数据区域-导读.md:
--------------------------------------------------------------------------------
1 |
2 |
3 |
4 |
5 |
6 | ### 本系列按照从上到下的顺序整理,可直接点击 👉 后面链接跳转!!😝
7 |
8 |
9 |
10 |
11 |
--------------------------------------------------------------------------------
/markdown/Java/运行时数据区常用参数汇总.md:
--------------------------------------------------------------------------------
1 | # 「运行时数据区」常用参数汇总
2 |
3 | 👉 **[官方参数说明](https://docs.oracle.com/javase/8/docs/technotes/tools/windows/java.html)**
4 |
5 | ### 堆空间
6 |
7 | `jps`:查看当前运行中的进程
8 |
9 | `jinfo -flag SurvivorRatio ` 查看该进程的 SurvivorRatio 参数值
10 |
11 | `-XX:+PrintFlagsInitial`:查看所有参数的默认初始值
12 |
13 | `-XX:+PrintFlagsFinal`:查看所有参数的最终值 (可能会存在修改,不再是初始值)
14 |
15 | `-Xms`:初始堆空间内存 (默认为物理内存的 1/64)
16 |
17 | `-Xmx`:最大堆空间内存 (默认为物理内存的 1/4)
18 |
19 | `-Xmn`:设置新生代的大小 (初始值和最大值)
20 |
21 | `-XX:NewRatio`:配置新生代与老年代在堆结构的占比 (默认为 2;新生代 : 老年代 = 1 : 2)
22 |
23 | `-XX:SurvivorRatio`:设置新生代中 Eden 和 S0/S1 空间的比例 (默认为 8;Eden : S0 : S1 = 8 : 1 : 1)
24 |
25 | - 如果 Eden 区过大,导致 Survivor 区变小,在 YGC 时增大对象放入老年代的可能,进而是 Major GC 变频繁
26 | - 如果 Eden 区过小,导致 YGC 变频繁,进而使 STW (Stop The World) 时间变多,影响性能
27 |
28 | `-XX:MaxTenuringThreshold`:设置新生代垃圾的最大年龄 (默认为 15,最大也为 15 -> MarkWord 中只有 4 位存放对象 GC 年龄)
29 |
30 | `-XX:+PrintGCDetails`:输出详细的 GC 处理日志
31 |
32 | `-XX:+PrintGC`、`-verbose:gc`:打印 GC 简要信息
33 |
34 | `-XX:HandlePromotionFailure`:是否设置空间分配担保 (JDK 7 之后该参数失效,默认为 true)
35 |
36 | - 只要`「老年代连续空间」> 「新生代对象总大小」or「历次晋升的平均大小」`就会进行 Minor GC,否则将进行 Full GC
37 |
38 | `-XX:+DoEscapeAnalysis`:手动开启逃逸分析
39 |
40 | `-XX:+PrintEscapeAnalysis`:查看逃逸分析的结果
41 |
42 | `-XX:+EliminateAllocations`:开启标量替换
43 |
44 | `-XX:+PrintEliminateAllocations`:查看标量替换的情况
45 |
46 | `-XX:+EliminateLocks`:开启同步消除
47 |
48 | ### 方法区
49 |
50 | JDK7 及以前
51 |
52 | `-XX:PermSize=size`:设置永久代初始分配空间。默认值为 20.75M
53 |
54 | `-XX:MaxPermSize=size`:设置永久代最大可分配空间。32 位机器默认值为 64M;64 位机器默认值为 82M
55 |
56 | JDK8 及以后
57 |
58 | `-XX:MetaspaceSize=size`:设置元空间初始分配空间
59 |
60 | `-XX:MaxMetaspaceSize=size`:设置元空间最大可分配空间
61 |
--------------------------------------------------------------------------------
/markdown/Java/重载-重写.md:
--------------------------------------------------------------------------------
1 | # 重载 vs 重写
2 |
3 | ### 重载
4 |
5 | #### 作用
6 |
7 | 方法重载是让类以一种统一的方式处理不同类型的一种手段,调用方法时通过传递不同个数和类型的参数来决定具体使用哪个方法
8 |
9 | #### 特点
10 |
11 | 重载发生在同一个类中,方法名相同,参数列表不同 (包括:参数个数、类型、顺序)
12 |
13 | 下面给出一些重载的例子:✅
14 |
15 | ```java
16 | public class Test {
17 | // 原方法
18 | public void f(int a, double b) {}
19 | // 参数个数不同
20 | public void f(int a) {}
21 | // 参数类型不同
22 | public void f(int a, int b) {}
23 | // 参数顺序不同
24 | public void f(double b, int a) {}
25 | }
26 | ```
27 |
28 | **注意:**方法重载与返回值无关!若只是返回值不同,其他都相同 (方法名相同,参数列表相同),不属于重载,反而会编译不通过
29 |
30 | 因为对于一个有返回值的方法,我们可以选择不要它的返回值,这样就会产生歧义,如下面所示:❌
31 |
32 | ```java
33 | public class Test {
34 | // 原方法
35 | public void f(int a, double b) {}
36 | // 仅仅只有返回值不同,编译不通过
37 | public int f(int a, double b) {return 0;}
38 |
39 | // 测试
40 | public static void main(String[] args) {
41 | Test test = new Test();
42 | // 即可以认为调用的是 public void f(int a, double b)
43 | // 也可以认为调用的是 public int f(int a, double b),只是不保留返回值而已!
44 | test.f(1, 1.0);
45 | }
46 | }
47 | ```
48 |
49 | #### 重点
50 |
51 | - 重载方法必须有不同的参数列表 (包括:参数个数、类型、顺序)
52 | - 不能通过访问权限,返回类型,抛出异常进行重载
53 | - 方法的异常类型和个数不会对重载造成影响
54 | - 可以有不同的返回类型,只要参数列表不同即可
55 | - 可以有不同的访问修饰符
56 | - 可以抛出不同的异常
57 |
58 | ### 重写
59 |
60 | #### 作用
61 |
62 | 方法重写发生在继承关系的基础之上,子类即可以隐藏和访问父类的方法,也可以重写父类的方法,方便了子类对父类方法的扩展
63 |
64 | #### 特点
65 |
66 | 重写发生在继承关系的基础之上,重写后的方法与原方法有完全相同的返回值类型,方法名,参数列表,唯一不同的只有方法的实现
67 |
68 | #### 重点
69 |
70 | - 静态方法、私有方法、构造方法不能被重写
71 | - 返回值类型,方法名,参数列表必须相同
72 | - 子类和父类在同一个包中,那么子类可以重写父类所有方法,除了 private 和 final 方法
73 | - 重写方法的访问权限不能比父类中的低 (访问权限从低到高的顺序:private -> default -> protected -> public)
74 | - 子类重写父类方法所抛出的异常不能超过父类的范畴;子类重写父类方法要抛出与父类一致的异常,或者不抛出异常
75 |
76 |
77 |
78 | ### 总结
79 |
80 | | | 重载 (Overload) | 重写 (Override) |
81 | | :--------: | :-------------: | :----------------: |
82 | | 发生位置 | 同一个类中 | 继承关系中 |
83 | | 方法名称 | 相同 | 相同 |
84 | | 参数列表 | 必须修改 | 相同 |
85 | | 返回类型 | 可以修改 | 相同 |
86 | | 异常 | 可以修改 | 不能超过父类的范畴 |
87 | | 访问修饰符 | 无要求 | 不能比父类的低 |
88 |
89 |
--------------------------------------------------------------------------------
/markdown/Linux/Linux硬链接和软连接的区别与总结.md:
--------------------------------------------------------------------------------
1 | # Linux硬链接和软连接的区别与总结
2 |
3 | ## 图示软硬链接的区别
4 |
5 |
42 |
43 | ### 垃圾收集器性能指标
44 |
45 | **停顿时间:**执行一次完整的垃圾收集时,用户线程被暂停的总时间
46 |
47 | **吞吐量:**处理器用于运行用户代码的时间与处理器总消耗时间的比值,计算公式如下:
48 | $$
49 | 吞吐量 = \frac{运行用户代码时间}{运行用户代码时间 + 运行垃圾收集时间}
50 | $$
51 | **对比:**
52 |
53 | - 停顿时间越短越适合需要与用户交互或需要保证服务响应质量的程序,良好的响应速度能提升用户体验感
54 | - 高吞吐量则可以最高效率地利用处理器资源,尽快完成程序的运算任务,主要适合在后台运算而不需要太多交互的分析任务
55 |
56 | ### 垃圾收集器的组合关系
57 |
58 | 本部分的关系是在「按照工作内存区间划分」的基础上进行组合滴!!
59 |
60 | 
61 |
62 | **[JEP 173: Retire Some Rarely-Used GC Combinations](https://openjdk.org/jeps/173)**
63 |
64 | **[JEP 214: Remove GC Combinations Deprecated in JDK 8](https://openjdk.org/jeps/214)**
65 |
66 | **[JEP 366: Deprecate the ParallelScavenge + SerialOld GC Combination](https://openjdk.org/jeps/366)**
67 |
68 | **[JEP 363: Remove the Concurrent Mark Sweep (CMS) Garbage Collector](https://openjdk.org/jeps/363)**
69 |
70 | **注意:JDK8 中默认垃圾收集器为 Parallel Scaverge GC + Parallel Old GC;JDK9 中默认垃圾收集器为 G1**
--------------------------------------------------------------------------------
/markdown/Java/实战-静态变量-实例变量-局部变量.md:
--------------------------------------------------------------------------------
1 | # 实战「静态变量」「实例变量」「局部变量」
2 |
3 | 这篇文章就以实战的方式看看「静态变量」「实例变量」「局部变量」存放的位置!
4 |
5 | 首先要搞清楚一个概念,「静态变量」「实例变量」「局部变量」指的是引用本身,而非它们所指向的对象,它们所指向的对象毫无疑问肯定都存放在堆上,**关于这个观点更多分析可见 [逃逸分析](./逃逸分析.html)**
6 |
7 | 还需要强调一个点,这里是基于 JDK8 的 HotSpot 虚拟机!!
8 |
9 | 根据理论知识可以知道:「静态变量」在 JDK7 及以后就存放在 Java 堆中;「实例变量」随着对象实例存放在 Java 堆中;「局部变量」存放在方法栈帧的局部变量表中
10 |
11 | 首先给出一段测试代码:
12 |
13 | ```java
14 | public class Test {
15 | static class Person {
16 | // 静态变量
17 | static ObjectHolder staticObj = new ObjectHolder();
18 | // 实例变量
19 | ObjectHolder instanceObj = new ObjectHolder();
20 | void foo() throws InterruptedException {
21 | // 局部变量
22 | ObjectHolder localObj = new ObjectHolder();
23 | // 休眠,不然方法执行完,方法栈帧就会出栈
24 | Thread.sleep(10000000);
25 | }
26 | }
27 | private static class ObjectHolder {}
28 | public static void main(String[] args) throws InterruptedException {
29 | Person person = new Person();
30 | person.foo();
31 | }
32 | }
33 | ```
34 |
35 | 我们先分析一下,按照理论来说,此时 Java 堆中肯定存在 3 个`ObjectHolder`对象实例,同时`staticObj`和`instanceObj`也都在 Java 堆中
36 |
37 | 下面通过 VisualVM + JProfiler 软件测试一下!!首先用 VisualVM 保存一个 Java 堆的 dump文件,如下所示:
38 |
39 | 
40 |
41 | 用 JProfiler 打开这个 dump 文件,可以发现在 Java 堆中刚好有 3 个`ObjectHolder`对象实例,如下图所示:
42 |
43 | 
44 |
45 | 我们再找找「静态变量」在哪里,在`java.lang.Class`中可以发现我们定义的静态变量`staticObj`,而这个静态变量指向的对象实例是`0xa87`,如下图所示:
46 |
47 | 
48 |
49 | 继续找「实例变量」在哪里,在`com.lfool.myself.Test$Person`中可以发现我们定义的实例变量`instanceObj`,而这个实例变量指向的对象实例是`0xc3b`,如下图所示:
50 |
51 | 
52 |
53 | 到此为止,我们找出来的所有内容都存放在 Java 堆中,至于「局部变量」,可以通过 JHSDB 软件在栈中发现,这里就不演示了!!!
--------------------------------------------------------------------------------
/markdown/Java/方法调用面试题.md:
--------------------------------------------------------------------------------
1 | # 方法调用面试题
2 |
3 | #### 问题一:下面代码输出的结果
4 |
5 | **详细解析可见 [方法调用](./方法调用.html#静态分派)**
6 |
7 | ```java
8 | public class StaticDispatch {
9 | static abstract class Human {}
10 | static class Man extends Human {}
11 | static class Woman extends Human {}
12 | public void sayHello(Human guy) {
13 | System.out.println("hello, guy!");
14 | }
15 | public void sayHello(Man guy) {
16 | System.out.println("hello, gentleman!");
17 | }
18 | public void sayHello(Woman guy) {
19 | System.out.println("hello, lady!");
20 | }
21 | public static void main(String[] args) {
22 | Human man = new Man();
23 | Human woman = new Woman();
24 | StaticDispatch sr = new StaticDispatch();
25 | sr.sayHello(man);
26 | sr.sayHello(woman);
27 | }
28 | }
29 | ```
30 |
31 | #### 问题二:下面代码依次输出的结果
32 |
33 | **详细解析可见 [方法调用](./方法调用.html#静态分派)**
34 |
35 | ```java
36 | public class Overload {
37 | public static void sayHello(Object arg) {
38 | System.out.println("hello Object");
39 | }
40 | public static void sayHello(int arg) {
41 | System.out.println("hello int");
42 | }
43 | public static void sayHello(long arg) {
44 | System.out.println("hello long");
45 | }
46 | public static void sayHello(Character arg) {
47 | System.out.println("hello Character");
48 | }
49 | public static void sayHello(char arg) {
50 | System.out.println("hello char");
51 | }
52 | public static void sayHello(char... arg) {
53 | System.out.println("hello char...");
54 | }
55 | public static void sayHello(Serializable arg) {
56 | System.out.println("hello Serializable");
57 | }
58 | public static void main(String[] args) {
59 | sayHello('a');
60 | }
61 | }
62 | ```
63 |
64 | 依次注释掉方法
65 | - `sayHello(char arg)`
66 | - `sayHello(int arg)`
67 | - `sayHello(long arg)`
68 | - `sayHello(Character arg)`
69 | - `sayHello(Serializable arg)`
70 | - `sayHello(Object arg)`
71 |
72 | 它会输出什么?!
73 |
74 | #### 问题三:下面代码输出的结果
75 |
76 | **详细解析可见 [方法调用](./方法调用.html#动态分派)**
77 |
78 | ```java
79 | public class FieldHasNoPolymorphic {
80 | static class Father {
81 | public int money = 1;
82 | public Father() {
83 | money = 2;
84 | showMeTheMoney();
85 | }
86 | public void showMeTheMoney() {
87 | System.out.println("I am Father, i have $" + money);
88 | }
89 | }
90 | static class Son extends Father {
91 | public int money = 3;
92 | public Son() {
93 | money = 4;
94 | showMeTheMoney();
95 | }
96 | public void showMeTheMoney() {
97 | System.out.println("I am Son, i have $" + money);
98 | }
99 | }
100 | public static void main(String[] args) {
101 | Father guy = new Son();
102 | System.out.println("This guy has $" + guy.money);
103 | }
104 | }
105 | ```
106 |
107 |
--------------------------------------------------------------------------------
/markdown/Java/注解.md:
--------------------------------------------------------------------------------
1 | # 注解
2 |
3 | ### 什么是注解
4 |
5 | Annotation 是从 JDK5.0 开始引入的新技术
6 |
7 | Annotation 的作用
8 |
9 | - 不是程序本身,可以对程序作出解释
10 | - **可以被其他程序 (如:编译器等) 读取**
11 |
12 | Annotation 的格式
13 |
14 | - 注解是以`@name`在代码中存在,还可以添加一些参数值,例如:`@SuppressWarnings(value = "unchecked")`
15 |
16 | Annotation 在哪里使用?
17 |
18 | - 可以附加在 package、class、method、field 等上面,相当于给他们添加了额外的辅助信息,我们可以通过**反射机制**编程实现对这些元数据的访问
19 |
20 | ### 内置注解
21 |
22 | `@Override`:定义在`java.lang.Override`中,此注解只适用于**修辞方法**,表示一个方法声明打算重写超类中的另一个方法声明
23 |
24 | `@Deprecated`:定义在`java.lang.Deprecated`中,此注解可以用于**修饰方法、属性、类**,表示不鼓励程序员使用这些元素,通常是因为它很危险或者存在更好的选择
25 |
26 | `@SuppressWarnings`:定义在`java.lang.SuppressWarnings`中,用来抑制编译时的警告信息,与前两个注解不同的是需要添加一个参数才能正确使用,这些参数都是已经定义好了的,选择性使用即可
27 |
28 | - `@SuppressWarnings("all")`
29 | - `@SuppressWarnings("unchecked")`
30 | - `@SuppressWarnings(value = {"unchecked", "deprecation"})`
31 | - ...
32 |
33 | ### 元注解
34 |
35 | 元注解的作用:负责注解其他注解
36 |
37 | Java 定义了 4 个标准的 meta-annotation 类型,他们被用来提供对其他 annotation 类型作说明
38 |
39 | 这些类型和它们所支持的类在`java.lang.annotation`包中可以找到:`@Target`、`@Retention`、`@Documented`、`@Inherited`
40 |
41 | - `@Target`:用于描述注解的使用范围 (即:被描述的注解可以用在什么地方)
42 | - `@Retention`:表示需要在什么级别保存该注解信息,用于描述注解的生命周期 (SOURCE < CLASS < **RUNTIME**)
43 | - `@Documented`:说明该注解将被包含在 Javadoc 中
44 | - `@Inherited`:说明子类可以继承父类中的该注解
45 |
46 | ```java
47 | // Target 表示该注解可以用在什么地方:类,方法
48 | @Target(value = {ElementType.TYPE, ElementType.METHOD})
49 | // Retention 表示该注解在什么地方还有效:SOURCE < CLASS < RUNTIME
50 | @Retention(value = RetentionPolicy.RUNTIME)
51 | // Documented 表示该注解将生成在 Javadoc 中
52 | @Documented
53 | // Inherited 表示子类可以继承该注解
54 | @Inherited
55 | public @interface MyAnnotation {
56 | }
57 | ```
58 |
59 | ### 自定义注解
60 |
61 | 使用`@interface`自定义注解时,自动继承`java.lang.annotation.Annotation`接口
62 |
63 | - `@interface`用来声明一个注解,格式:`public @interface name {}`
64 | - 其中的每一个方法实际上是声明了一个配置参数
65 | - 方法的名称就是参数的名称
66 | - 返回值类型就是参数的类型 (返回值只能是基本类型、对象、String、enum)
67 | - 可以通过`default`来声明参数的默认值
68 | - 如果只有一个参数成员,一般参数名为`value`
69 | - 注解元素必须要有值,在定义注解元素时,经常使用「空字符串、0」作为默认值
70 |
71 | ```java
72 | @Target(value = {ElementType.TYPE, ElementType.METHOD})
73 | @Retention(value = RetentionPolicy.RUNTIME)
74 | public @interface MyAnnotation {
75 | // 定义注解参数的格式:参数类型 + 名字 + ()
76 | String name();
77 | int age() default 0;
78 | int id() default -1;
79 | String[] schools() default {"school1", "school2"};
80 | }
81 | public class MyAnnotationTest {
82 | @MyAnnotation(name = "张三", age = 18, id = 1, schools = {"school3"})
83 | public void test01() {
84 | }
85 | @MyAnnotation(name = "张三")
86 | public void test02() {
87 | }
88 | }
89 | ```
--------------------------------------------------------------------------------
/markdown/Java/浅记字节字符流乱码问题.md:
--------------------------------------------------------------------------------
1 | # 浅记「字节/字符流」乱码问题
2 |
3 | ### 字符编码
4 |
5 | Unicode 统一了所有字符的编码,包括中文,它算是一个**字符集**,用 2 字节大小对所有字符进行了唯一编码
6 |
7 | 但是 Unicode 没有规定如何存储,UTF-8 刚好规定了 Unicode 字符如何存储的问题。UTF-8 采用可变长编码,英文用 1 个字节,中文用 3 个字节
8 |
9 | 对于 UTF-8 编码中的任意字节 B:
10 |
11 | - 如果 B 的第一位为 0,则 B 独立的表示一个字符 (ASCII 码) -> **0xxxxxxx**
12 |
13 | - 如果 B 的第一位为 1,第二位为 0,则 B 为一个多字节字符中的一个字节 (非 ASCII 字符) -> **10xxxxxx**
14 |
15 | - 如果 B 的前两位为 1,第三位为 0,则 B 为两个字节表示的字符中的第一个字节 -> **110xxxxx**
16 |
17 | - 如果 B 的前三位为 1,第四位为 0,则 B 为三个字节表示的字符中的第一个字节 -> **1110xxxx**
18 |
19 | - 如果 B 的前四位为 1,第五位为 0,则 B 为四个字节表示的字符中的第一个字节 -> **11110xxx**
20 |
21 | 举个简单的例子,中文汉字「**我**」对应的 Unicode 编码:十进制: 25105;十六进制:0x6211;二进制:01100010 00010001
22 |
23 | 它在 UTF-8 编码下的存储结构为:十六进制:0xE68891;二进制:11100110 10001000 10010001
24 |
25 | 为了方便对比,写到一起:
26 |
27 | ```bash
28 | 1110xxxx 10xxxxxx 10xxxxxx
29 | UTF-8: 11100110 10001000 10010001
30 | Unicode: 0110 001000 010001
31 | ```
32 |
33 | ### 乱码分析
34 |
35 | 在学习字节流和字符流的时候,遇到过一个问题:**为什么 I/O 流操作要分为字节流操作和字符流操作呢?**
36 |
37 | - 如果只有字符流操作,由于字符流是由 Java 虚拟机将字节流转换得到,这个过程比较耗时
38 | - 如果只有字节流操作,如果不知道编码类型的话,很容易出现乱码问题
39 |
40 | 本篇文章就上面的第二点展开讨论为什么会出现乱码问题!!!
41 |
42 | 如果我们用字节流去读 UTF-8 编码的文件,那么每次只能一个字节一个字节的读。对于一个中文汉字需要读三次,每次读的结果如下:11100110、10001000、10010001
43 |
44 | 可以看到三次读出来的结果其实就是上面分析过的 UTF-8 编码下的存储结构,此时就会将每一次的结果转化成一个 ACSII 字符:
45 |
46 | - 11100110 -> 230 -> æ
47 | - 10001000 -> 136 ->
48 | - 10010001 -> 145 ->
49 |
50 | 所以乱码就出现了!!另外可以从下面程序中得到验证:
51 |
52 | ```java
53 | public static void main(String[] args) {
54 | // input.txt 中存储的就是一个中文汉字「我」
55 | // FileInputStream 字节输入流,每次读一个字节
56 | try (FileInputStream fis = new FileInputStream("input.txt")) {
57 | System.out.println("Number of remaining bytes: " + fis.available());
58 | int content;
59 | while ((content = fis.read()) != -1) { // 读一个字节
60 | System.out.println(content + " -> " + (char) content);
61 | }
62 | } catch (IOException e) {
63 | throw new RuntimeException(e);
64 | }
65 | }
66 | ```
67 |
68 | 如果我们改用字符输入流,它每次都读一个字符,而且已经自动处理了编码问题,具体可见下面程序:
69 |
70 | ```java
71 | public static void main(String[] args) {
72 | // input.txt 中存储的就是一个中文汉字「我」
73 | // FileReader 字符输入流,每次读一个字符
74 | try (FileReader fileReader = new FileReader("input.txt")) {
75 | int content;
76 | while ((content = fileReader.read()) != -1) {
77 | System.out.println(content + " -> " + (char) content);
78 | System.out.println(Integer.toBinaryString(content));
79 | }
80 | } catch (Exception e) {
81 | e.printStackTrace();
82 | }
83 | }
84 | // 输出
85 | 25105 -> 我
86 | 110001000010001
87 | ```
88 |
89 | `input.txt`文件中存储的结构是:11100110 10001000 10010001,不信的话可以用二进制文件查看器打开它
90 |
91 | 但程序输出的二进制内容不再是 UTF-8 编码下存储的内容,而是对其进行了解码,转换成了 Unicode 下的编码,所以最后才没有乱码
92 |
93 | **注意:**字符输入流并非每次都读三个字节。如果一个字符只用一个字节存储,那么一次就读一个字节,如果一个字符用三个字节存储,那么一次就读三个字节,可以根据 UTF-8 编码判断每次读几个字节
94 |
95 | **总结:**字节输入流每次读一个字节,字符输入流每次读一个字符,而且字符输入流还自动的对 UTF-8 解码成 Unicode
--------------------------------------------------------------------------------
/markdown/Java/类加载子系统-导读.md:
--------------------------------------------------------------------------------
1 |
2 |
3 |
4 |
5 |
6 | ### 本系列按照从上到下的顺序整理,可直接点击 👉 后面链接跳转!!😝
7 |
8 |
9 |
10 |
11 |
--------------------------------------------------------------------------------
/markdown/Java/类加载的时机.md:
--------------------------------------------------------------------------------
1 | **「JVM 类加载子系统」系列文章**
2 |
3 | - **[类加载的过程](./类加载的过程.html)**
4 | - **[❤️🔥 类加载的时机](./类加载的时机.html)**
5 | - **[类加载器](./类加载器.html)**
6 | - **[剖析 [Bootstrap、Extension、Application] ClassLoader](./剖析-Bootstrap-Extension-Application-ClassLoader.html)**
7 | - **[双亲委派模型](./双亲委派模型.html)**
8 | - **[自定义类加载器](./自定义类加载器.html)**
9 | - **[破坏双亲委派模型](./破坏双亲委派模型.html)**
10 |
11 | # 类加载的时机
12 |
13 | 在类生命周期的七个阶段中,加载、验证、准备、初始化和卸载五个阶段的顺序是确定的,类型的加载过程必须按照这种顺序按部就班地开始,而**解析阶段不一定**
14 |
15 | 解析阶段是 Java 虚拟机将常量池内的符号引用替换成直接引用的过程,所以这个过程可能在加载阶段完成,也可能在运行期间完成,这是为了支持 Java 运行时绑定
16 |
17 | 《Java 虚拟机规范》中并没有强制约束什么情况下必须开始类加载过程的第一个阶段「加载」;但是对于初始化阶段,严格规定了**有且只有**六种情况必须立即对类进行「初始化」
18 |
19 | 1. 遇到`new`、`getstatic`、`putstatic`、`invokestatic`四条字节码指令时,如果类型没有进行初始化,则需要先触发其初始化阶段。能够生成这四条指令的典型 Java 代码场景有:
20 |
21 | - 使用`new`关键字实例化对象的时候
22 | - 读取或设置一个类型的静态字段的时候 (被`final`修饰的静态变量,已在编译期把结果放入常量池,读取该字段是不会引起初始化)
23 | - 调用一个类型的静态方法的时候
24 |
25 | 2. 使用`java.lang.reflect`包的方法对类型进行反射调用的时候,如果类型没有进行过初始化,则需要先触发其初始化
26 | 3. 当初始化类的时候,发现其父类还没有进行过初始化,则需要先触发其父类的初始化
27 | 4. 当虚拟机启动时,用户需要指定一个要执行的主类 (main() 所在的类),虚拟机会先初始化这个类
28 | 5. 使用 JDK7 新加入的动态语言支持时,如果一个`java.lang.invoke.MethodHandle`实例最后的解析结果为`REF_getStatic`、`REF_putStatic`、`REF_invokeStatic`、`REF_newInvokeSpecial`四种类型的方法句柄,并且这个方法句柄对应的类没有进行过初始化,则需要先触发其初始化
29 | 6. 当一个接口中定义了 JDK8 新加入的默认方法 (default 修饰) 时,如果有这个接口的实现类发生了初始化,那该接口要在其之前被初始化
30 |
31 | 这六种场景中的行为称为对一个类型进行**主动引用**;除此之外,所有引用类型的方式都不会触发初始化,称为**被动引用**
32 |
33 | 下面是四种被动引用的例子:
34 |
35 | ```java
36 | // ---------------------- 例子 1 ----------------------
37 | // 对于静态字段,只有直接定义字段的类才会被初始化
38 | // 通过子类引用父类中定义的静态字段,只会触发父类的初始化,而不会触发子类的初始化
39 | public class SuperClass {
40 | static {
41 | System.out.println("Super Class init!");
42 | }
43 | public static int value = 123;
44 | }
45 | public class SubClass extends SuperClass {
46 | static {
47 | System.out.println("SubClass init!");
48 | }
49 | }
50 | public class NotInitialization {
51 | public static void main(String[] args) {
52 | System.out.println(SubClass.value);
53 | }
54 | }
55 | // result
56 | // Super Class init!
57 | // 123
58 | // ---------------------- 例子 2 ----------------------
59 | // 通过数组定义来引用类,不会触发此类的初始化
60 | public class NotInitialization {
61 | public static void main(String[] args) {
62 | SuperClass[] arr = new SuperClass[10];
63 | }
64 | }
65 | // ---------------------- 例子 3 ----------------------
66 | // 调用静态常量,不会触发此类的初始化
67 | public class ConstClass {
68 | static {
69 | System.out.println("ConstClass init!");
70 | }
71 | public static final String HELLOWORLD = "hello world";
72 | }
73 | public class NotInitialization {
74 | public static void main(String[] args) {
75 | System.out.println(ConstClass.HELLOWORLD);
76 | }
77 | }
78 | // result
79 | // hello world
80 | // ---------------------- 例子 4 ----------------------
81 | public static void main(String[] args) throws ClassNotFoundException {
82 | // 不会引起类的初始化
83 | Class myObjClass = MyObj.class;
84 | // 会引起类的初始化
85 | Class aClass = Class.forName("com.lfool.myself.MyObj");
86 |
87 | }
88 | ```
89 |
--------------------------------------------------------------------------------
/markdown/Java/虚拟机栈面试题.md:
--------------------------------------------------------------------------------
1 | # 虚拟机栈面试题
2 |
3 | 本篇文章总结虚拟机栈的面试题!!
4 |
5 | #### 问题一:栈溢出的情况?
6 |
7 | 《Java 虚拟机规范》中描述了两种异常:
8 |
9 | - 如果线程请求的栈深度大于虚拟机所允许的最大深度,将抛出 **StackOverflowError (SOF)** 异常
10 | - 如果虚拟机的栈内存允许动态扩展,当扩展栈容量无法申请到足够的内存时,将抛出 **OutOfMemoryError (OOM)** 异常
11 |
12 | **注意:**栈容量只能由 -Xss 参数来设定
13 |
14 | #### 问题二:调整栈容量,就能保证不出现溢出吗?
15 |
16 | 不能!!通过调整栈容量,可能会使原本出现溢出的代码不出现溢出了;但无法保证所有情况都不出现溢出!!
17 |
18 | 假设原本栈容量可以支持 5000 次调用,但代码有 6000 次调用,就会出现溢出;此时调整栈容量保证其可以支持 7000 次调用,那么原来的代码就不会出现溢出了
19 |
20 | 但如果另外一个代码有 8000 次调用,依旧会出现溢出!!
21 |
22 | #### 问题三:分配栈容量越大越好吗?
23 |
24 | 不一定!!分配越大的栈容量,会压缩其他部分的大小,比如:堆,方法区等
25 |
26 | #### 问题四:垃圾回收是否会涉及到虚拟机栈?
27 |
28 | 这里总结一下「运行时数据区域」的各个部分是否会发生 Error 或者 GC!!
29 |
30 | | | Error | GC |
31 | | :-------------: | :---: | :--: |
32 | | 方法区 | ✅ | ✅ |
33 | | 堆 | ✅ | ✅ |
34 | | 虚拟机栈 | ✅ | ❌ |
35 | | 本地方法栈 | ✅ | ❌ |
36 | | 程序计数器 (PC) | ❌ | ❌ |
37 |
38 | #### 问题五:方法中定义的局部变量是否线程安全?
39 |
40 | 需要分情况讨论,有的情况是线程安全,有的情况是线程不安全,会发生对象逃逸
41 |
42 | ```java
43 | // 情况一:线程安全
44 | // 对象 s1 随着方法调用的结束而消亡,不会被多个线程共享
45 | public static void f1() {
46 | // 注意:StringBuilder 不是线程安全;StringBuffer 是线程安全
47 | StringBuilder s1 = new StringBuilder();
48 | s1.append("a");
49 | s1.append("b");
50 | }
51 |
52 | // 情况二:线程不安全
53 | // 对象 s1 不会随着方法调用的结束而消亡,因为随着方法的返回值逃逸出去了,可能会被多个线程共享
54 | public static StringBuilder f2() {
55 | StringBuilder s1 = new StringBuilder();
56 | s1.append("a");
57 | s1.append("b");
58 | return s1;
59 | }
60 |
61 | // 情况三:线程不安全
62 | // 对象 s1 随着方法的参数传入方法中,不是线程私有,可能会被多个线程共享
63 | public static void f3(StringBuilder s1) {
64 | s1.append("a");
65 | s1.append("b");
66 | }
67 |
68 | // 情况四:线程安全
69 | // 对象 s1 随着方法调用的结束而消亡,不会被多个线程共享;而返回值是 String,它是不可变的
70 | public static String f4() {
71 | StringBuilder s1 = new StringBuilder();
72 | s1.append("a");
73 | s1.append("b");
74 | return s1.toString();
75 | }
76 | ```
--------------------------------------------------------------------------------
/markdown/Java/运行时数据区域-导读.md:
--------------------------------------------------------------------------------
1 |
2 |
3 |
4 |
5 |
6 | ### 本系列按照从上到下的顺序整理,可直接点击 👉 后面链接跳转!!😝
7 |
8 |
9 |
10 |
11 |
--------------------------------------------------------------------------------
/markdown/Java/运行时数据区常用参数汇总.md:
--------------------------------------------------------------------------------
1 | # 「运行时数据区」常用参数汇总
2 |
3 | 👉 **[官方参数说明](https://docs.oracle.com/javase/8/docs/technotes/tools/windows/java.html)**
4 |
5 | ### 堆空间
6 |
7 | `jps`:查看当前运行中的进程
8 |
9 | `jinfo -flag SurvivorRatio ` 查看该进程的 SurvivorRatio 参数值
10 |
11 | `-XX:+PrintFlagsInitial`:查看所有参数的默认初始值
12 |
13 | `-XX:+PrintFlagsFinal`:查看所有参数的最终值 (可能会存在修改,不再是初始值)
14 |
15 | `-Xms`:初始堆空间内存 (默认为物理内存的 1/64)
16 |
17 | `-Xmx`:最大堆空间内存 (默认为物理内存的 1/4)
18 |
19 | `-Xmn`:设置新生代的大小 (初始值和最大值)
20 |
21 | `-XX:NewRatio`:配置新生代与老年代在堆结构的占比 (默认为 2;新生代 : 老年代 = 1 : 2)
22 |
23 | `-XX:SurvivorRatio`:设置新生代中 Eden 和 S0/S1 空间的比例 (默认为 8;Eden : S0 : S1 = 8 : 1 : 1)
24 |
25 | - 如果 Eden 区过大,导致 Survivor 区变小,在 YGC 时增大对象放入老年代的可能,进而是 Major GC 变频繁
26 | - 如果 Eden 区过小,导致 YGC 变频繁,进而使 STW (Stop The World) 时间变多,影响性能
27 |
28 | `-XX:MaxTenuringThreshold`:设置新生代垃圾的最大年龄 (默认为 15,最大也为 15 -> MarkWord 中只有 4 位存放对象 GC 年龄)
29 |
30 | `-XX:+PrintGCDetails`:输出详细的 GC 处理日志
31 |
32 | `-XX:+PrintGC`、`-verbose:gc`:打印 GC 简要信息
33 |
34 | `-XX:HandlePromotionFailure`:是否设置空间分配担保 (JDK 7 之后该参数失效,默认为 true)
35 |
36 | - 只要`「老年代连续空间」> 「新生代对象总大小」or「历次晋升的平均大小」`就会进行 Minor GC,否则将进行 Full GC
37 |
38 | `-XX:+DoEscapeAnalysis`:手动开启逃逸分析
39 |
40 | `-XX:+PrintEscapeAnalysis`:查看逃逸分析的结果
41 |
42 | `-XX:+EliminateAllocations`:开启标量替换
43 |
44 | `-XX:+PrintEliminateAllocations`:查看标量替换的情况
45 |
46 | `-XX:+EliminateLocks`:开启同步消除
47 |
48 | ### 方法区
49 |
50 | JDK7 及以前
51 |
52 | `-XX:PermSize=size`:设置永久代初始分配空间。默认值为 20.75M
53 |
54 | `-XX:MaxPermSize=size`:设置永久代最大可分配空间。32 位机器默认值为 64M;64 位机器默认值为 82M
55 |
56 | JDK8 及以后
57 |
58 | `-XX:MetaspaceSize=size`:设置元空间初始分配空间
59 |
60 | `-XX:MaxMetaspaceSize=size`:设置元空间最大可分配空间
61 |
--------------------------------------------------------------------------------
/markdown/Java/重载-重写.md:
--------------------------------------------------------------------------------
1 | # 重载 vs 重写
2 |
3 | ### 重载
4 |
5 | #### 作用
6 |
7 | 方法重载是让类以一种统一的方式处理不同类型的一种手段,调用方法时通过传递不同个数和类型的参数来决定具体使用哪个方法
8 |
9 | #### 特点
10 |
11 | 重载发生在同一个类中,方法名相同,参数列表不同 (包括:参数个数、类型、顺序)
12 |
13 | 下面给出一些重载的例子:✅
14 |
15 | ```java
16 | public class Test {
17 | // 原方法
18 | public void f(int a, double b) {}
19 | // 参数个数不同
20 | public void f(int a) {}
21 | // 参数类型不同
22 | public void f(int a, int b) {}
23 | // 参数顺序不同
24 | public void f(double b, int a) {}
25 | }
26 | ```
27 |
28 | **注意:**方法重载与返回值无关!若只是返回值不同,其他都相同 (方法名相同,参数列表相同),不属于重载,反而会编译不通过
29 |
30 | 因为对于一个有返回值的方法,我们可以选择不要它的返回值,这样就会产生歧义,如下面所示:❌
31 |
32 | ```java
33 | public class Test {
34 | // 原方法
35 | public void f(int a, double b) {}
36 | // 仅仅只有返回值不同,编译不通过
37 | public int f(int a, double b) {return 0;}
38 |
39 | // 测试
40 | public static void main(String[] args) {
41 | Test test = new Test();
42 | // 即可以认为调用的是 public void f(int a, double b)
43 | // 也可以认为调用的是 public int f(int a, double b),只是不保留返回值而已!
44 | test.f(1, 1.0);
45 | }
46 | }
47 | ```
48 |
49 | #### 重点
50 |
51 | - 重载方法必须有不同的参数列表 (包括:参数个数、类型、顺序)
52 | - 不能通过访问权限,返回类型,抛出异常进行重载
53 | - 方法的异常类型和个数不会对重载造成影响
54 | - 可以有不同的返回类型,只要参数列表不同即可
55 | - 可以有不同的访问修饰符
56 | - 可以抛出不同的异常
57 |
58 | ### 重写
59 |
60 | #### 作用
61 |
62 | 方法重写发生在继承关系的基础之上,子类即可以隐藏和访问父类的方法,也可以重写父类的方法,方便了子类对父类方法的扩展
63 |
64 | #### 特点
65 |
66 | 重写发生在继承关系的基础之上,重写后的方法与原方法有完全相同的返回值类型,方法名,参数列表,唯一不同的只有方法的实现
67 |
68 | #### 重点
69 |
70 | - 静态方法、私有方法、构造方法不能被重写
71 | - 返回值类型,方法名,参数列表必须相同
72 | - 子类和父类在同一个包中,那么子类可以重写父类所有方法,除了 private 和 final 方法
73 | - 重写方法的访问权限不能比父类中的低 (访问权限从低到高的顺序:private -> default -> protected -> public)
74 | - 子类重写父类方法所抛出的异常不能超过父类的范畴;子类重写父类方法要抛出与父类一致的异常,或者不抛出异常
75 |
76 |
77 |
78 | ### 总结
79 |
80 | | | 重载 (Overload) | 重写 (Override) |
81 | | :--------: | :-------------: | :----------------: |
82 | | 发生位置 | 同一个类中 | 继承关系中 |
83 | | 方法名称 | 相同 | 相同 |
84 | | 参数列表 | 必须修改 | 相同 |
85 | | 返回类型 | 可以修改 | 相同 |
86 | | 异常 | 可以修改 | 不能超过父类的范畴 |
87 | | 访问修饰符 | 无要求 | 不能比父类的低 |
88 |
89 |
--------------------------------------------------------------------------------
/markdown/Linux/Linux硬链接和软连接的区别与总结.md:
--------------------------------------------------------------------------------
1 | # Linux硬链接和软连接的区别与总结
2 |
3 | ## 图示软硬链接的区别
4 |
5 | 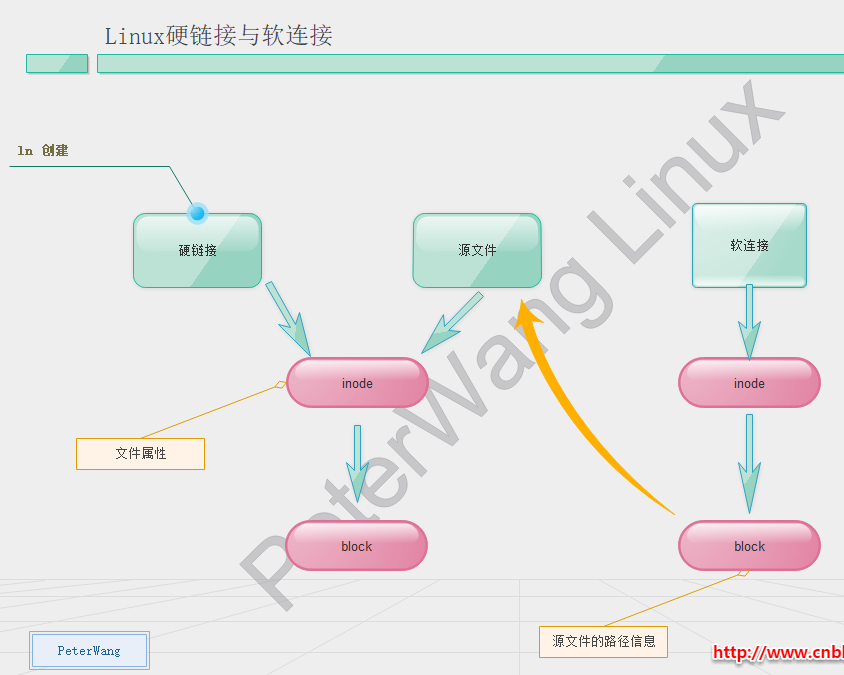 6 |
7 | ## 硬链接
8 |
9 | - 具有相同 inode 节点号的多个文件互为硬链接文件
10 | - 删除硬链接文件或者删除源文件任意之一,文件实体并未被删除
11 | - 只有删除了源文件和所有对应的硬链接文件,文件实体才会被删除
12 | - 硬链接文件是文件的另一个入口
13 | - 可以通过给文件设置硬链接文件来防止重要文件被误删
14 | - 创建硬链接命令 ln 源文件 硬链接文件
15 | - 硬链接文件是普通文件,可以用 rm 删除
16 | - 对于静态文件(没有进程正在调用),当硬链接数为 0 时文件就被删除。注意:如果有进程正在调用,则无法删除或者即使文件名被删除但空间不会释放
17 |
18 | **创建一个硬链接**
19 |
20 | ```shell
21 | ➜ test ln a.txt aHardLink
22 | ➜ test ll
23 | -rw-r--r-- 2 lfool staff 5B 1 29 02:06 a.txt
24 | -rw-r--r-- 2 lfool staff 5B 1 29 02:06 aHardLink
25 | ➜ test ll -i
26 | 8986726 -rw-r--r-- 2 lfool staff 5B 1 29 02:06 a.txt
27 | 8986726 -rw-r--r-- 2 lfool staff 5B 1 29 02:06 aHardLink
28 | ```
29 |
30 | 可以发现两个文件的 inode 编号相同,且大小相同,说明是同一个文件
31 |
32 | ## 软链接
33 |
34 | - 软链接类似 windows 系统的快捷方式
35 | - 软链接里面存放的是源文件的路径,指向源文件
36 | - 删除源文件,软链接依然存在,但无法访问源文件内容
37 | - 软链接失效时一般是白字红底闪烁
38 | - 创建软链接命令 ln -s 源文件 软链接文件
39 | - 软链接和源文件是不同的文件,文件类型也不同,inode 号也不同
40 | - 软链接的文件类型是 「l」,可以用 rm 删除
41 |
42 | **创建一个软连接**
43 |
44 | ```shell
45 | ➜ test ln -s a.txt alink
46 | ➜ test ll
47 | -rw-r--r-- 1 lfool staff 5B 1 29 02:06 a.txt
48 | lrwxr-xr-x 1 lfool staff 5B 1 29 02:06 alink -> a.txt
49 | # 查看文件的 inode 编号
50 | ➜ test ll -i
51 | 8986726 -rw-r--r-- 1 lfool staff 5B 1 29 02:06 a.txt
52 | 8986741 lrwxr-xr-x 1 lfool staff 5B 1 29 02:06 alink -> a.txt
53 | ```
54 |
55 | 可以发现文件和指向文件的软链接的 inode 编号不同,说明是两个文件
56 |
57 | ## 硬链接和软链接的区别
58 |
59 | 原理上,硬链接和源文件的 inode 节点号相同,两者互为硬链接。软连接和源文件的 inode 节点号不同,进而指向的 block 也不同,软连接 block 中存放了源文件的路径名
60 |
61 | 实际上,硬链接和源文件是同一份文件,而软连接是独立的文件,类似于快捷方式,存储着源文件的位置信息便于指向
62 |
63 | 使用限制上,不能对目录创建硬链接,不能对不同文件系统创建硬链接,不能对不存在的文件创建硬链接;可以对目录创建软连接,可以跨文件系统创建软连接,可以对不存在的文件创建软连接
64 |
65 | ## 参考
66 |
67 | 1. [Linux硬链接和软连接的区别与总结](https://xzchsia.github.io/2020/03/05/linux-hard-soft-link/)
68 | 2. [硬链接和软连接(符号链接)的区别](https://www.cnblogs.com/sanjun/p/9971993.html)
69 |
70 |
--------------------------------------------------------------------------------
/markdown/Linux/Shell.md:
--------------------------------------------------------------------------------
1 | # Shell
2 |
3 | ## 常用命令汇总
4 |
5 | `man`:查看每种命令的文档
6 |
7 | `man -k xxx`:查找与 xxx 相关的命令
8 |
9 | `pwd`:显示当前目录
10 |
11 | `ll file*Name`:只能匹配文件,不能匹配目录
12 |
13 | - 使用通配符 「? 任意匹配一个字符 / * 任意匹配任意个字符」
14 | - 基本上可以使用正则表达式
15 |
16 | `ls -i fileName`:查看文件的 inode 编号
17 |
18 | `ln -s [fileName] [linkName]`:创建一个软链接
19 |
20 | ```shell
21 | ➜ test ln -s a.txt alink
22 | ➜ test ll
23 | -rw-r--r-- 1 lfool staff 5B 1 29 02:06 a.txt
24 | lrwxr-xr-x 1 lfool staff 5B 1 29 02:06 alink -> a.txt
25 | ```
26 |
27 | `ln [fileName] [linkName]`:创建一个硬链接
28 |
29 | ```shell
30 | ➜ test ln a.txt aHardLink
31 | ➜ test ll
32 | -rw-r--r-- 2 lfool staff 5B 1 29 02:06 a.txt
33 | -rw-r--r-- 2 lfool staff 5B 1 29 02:06 aHardLink
34 | ➜ test ll -i
35 | 8986726 -rw-r--r-- 2 lfool staff 5B 1 29 02:06 a.txt
36 | 8986726 -rw-r--r-- 2 lfool staff 5B 1 29 02:06 aHardLink
37 | ```
38 |
39 | `rm -rf path`:删除目录或文件
40 |
41 | - -f:强制删除文件或目录
42 | - -r:递归处理,将指定目录下的所有文件与子目录一并处理
43 |
44 | `tree path`:查看目录结构
45 |
46 | `file fileName`:查看文件类型
47 |
48 | `cat / more / less`:显示文件内容(全显示/分批显示)
49 |
50 | `head / tail fileName`:显示文件头部 / 最后几行内容
51 |
52 | - -f:使显示内容保持活动状态,会动态更新显示内容
53 | - -n:规定行数
54 |
55 | `nohup xxx > output.log 2>&1 &`:后台运行,输出到文件中
56 |
57 | `du`:显示文件或目录的大小
58 |
59 | - -h:以 K,M,G 为单位,提高信息的可读性
60 | - -s:仅显示总计
61 | - [fileName] / [dirName] / None:未指定,则显示当前目录下的内容
62 |
63 | `ps -ef | grep python`:查看 python 相关进程
64 |
65 | `lsof -i:8888`:查看端口 8888 的占用情况
66 |
67 | `kill -s 9 PID`:杀死进程 PID
68 |
69 | ## 命令行常用快捷操作
70 |
71 | `Ctrl + a`:跳到本行的行首
72 |
73 | `Ctrl + e`:则跳到页尾
74 |
75 | `Ctrl + u`:删除当前光标前面的文字
76 |
77 | `Ctrl + k`:删除当前光标后面的文字
78 |
79 | `Ctrl + y`:进行恢复
80 |
81 | ## 目录及用途
82 |
83 | | 目录 | 用途 |
84 | | :----: | :----------------------------------------------------------: |
85 | | / | 虚拟目录的根目录,通常不会在这里存储文件 |
86 | | /bin | 二进制目录,存放许多用户级的 GNU 工具 |
87 | | /boot | 启动目录,存放启动文件 |
88 | | /dev | 设备目录,Linux 在这里创建设备节点 |
89 | | /etc | 系统配置文件目录 |
90 | | /home | 主目录,Linux 在这里创建用户目录 |
91 | | /lib | 库目录,存放系统和应用程序的库文件 |
92 | | /media | 媒体文件,可移动媒体设备的常用挂载点 |
93 | | /mnt | 挂载目录,另一个可移动媒体设备的常用挂载点 |
94 | | /opt | 可选目录,常用于存放第三方软件包或数据文件 |
95 | | /proc | 进程目录,存放先用硬件以及当前进程的相关信息 |
96 | | /root | root 用户的主目录 |
97 | | /sbin | 系统二进制目录,存放许多 GNU 管理员级工具 |
98 | | /run | 运行目录,存放系统运作时的运行时数据 |
99 | | /srv | 服务目录,存放本地服务的相关文件 |
100 | | /sys | 系统目录,存放系统硬件信息的相关文件 |
101 | | /tmp | 临时目录,可以在该目录中创建和删除临时工作文件 |
102 | | /usr | 用户二进制目录,大量用户级别的 GUN 工具和数据文件都存储在这里 |
103 | | /var | 可变目录,用以存放经常变化的文件,比如日志文件 |
104 |
105 |
106 |
107 |
108 |
109 | ## 文件或目录信息
110 |
111 |
6 |
7 | ## 硬链接
8 |
9 | - 具有相同 inode 节点号的多个文件互为硬链接文件
10 | - 删除硬链接文件或者删除源文件任意之一,文件实体并未被删除
11 | - 只有删除了源文件和所有对应的硬链接文件,文件实体才会被删除
12 | - 硬链接文件是文件的另一个入口
13 | - 可以通过给文件设置硬链接文件来防止重要文件被误删
14 | - 创建硬链接命令 ln 源文件 硬链接文件
15 | - 硬链接文件是普通文件,可以用 rm 删除
16 | - 对于静态文件(没有进程正在调用),当硬链接数为 0 时文件就被删除。注意:如果有进程正在调用,则无法删除或者即使文件名被删除但空间不会释放
17 |
18 | **创建一个硬链接**
19 |
20 | ```shell
21 | ➜ test ln a.txt aHardLink
22 | ➜ test ll
23 | -rw-r--r-- 2 lfool staff 5B 1 29 02:06 a.txt
24 | -rw-r--r-- 2 lfool staff 5B 1 29 02:06 aHardLink
25 | ➜ test ll -i
26 | 8986726 -rw-r--r-- 2 lfool staff 5B 1 29 02:06 a.txt
27 | 8986726 -rw-r--r-- 2 lfool staff 5B 1 29 02:06 aHardLink
28 | ```
29 |
30 | 可以发现两个文件的 inode 编号相同,且大小相同,说明是同一个文件
31 |
32 | ## 软链接
33 |
34 | - 软链接类似 windows 系统的快捷方式
35 | - 软链接里面存放的是源文件的路径,指向源文件
36 | - 删除源文件,软链接依然存在,但无法访问源文件内容
37 | - 软链接失效时一般是白字红底闪烁
38 | - 创建软链接命令 ln -s 源文件 软链接文件
39 | - 软链接和源文件是不同的文件,文件类型也不同,inode 号也不同
40 | - 软链接的文件类型是 「l」,可以用 rm 删除
41 |
42 | **创建一个软连接**
43 |
44 | ```shell
45 | ➜ test ln -s a.txt alink
46 | ➜ test ll
47 | -rw-r--r-- 1 lfool staff 5B 1 29 02:06 a.txt
48 | lrwxr-xr-x 1 lfool staff 5B 1 29 02:06 alink -> a.txt
49 | # 查看文件的 inode 编号
50 | ➜ test ll -i
51 | 8986726 -rw-r--r-- 1 lfool staff 5B 1 29 02:06 a.txt
52 | 8986741 lrwxr-xr-x 1 lfool staff 5B 1 29 02:06 alink -> a.txt
53 | ```
54 |
55 | 可以发现文件和指向文件的软链接的 inode 编号不同,说明是两个文件
56 |
57 | ## 硬链接和软链接的区别
58 |
59 | 原理上,硬链接和源文件的 inode 节点号相同,两者互为硬链接。软连接和源文件的 inode 节点号不同,进而指向的 block 也不同,软连接 block 中存放了源文件的路径名
60 |
61 | 实际上,硬链接和源文件是同一份文件,而软连接是独立的文件,类似于快捷方式,存储着源文件的位置信息便于指向
62 |
63 | 使用限制上,不能对目录创建硬链接,不能对不同文件系统创建硬链接,不能对不存在的文件创建硬链接;可以对目录创建软连接,可以跨文件系统创建软连接,可以对不存在的文件创建软连接
64 |
65 | ## 参考
66 |
67 | 1. [Linux硬链接和软连接的区别与总结](https://xzchsia.github.io/2020/03/05/linux-hard-soft-link/)
68 | 2. [硬链接和软连接(符号链接)的区别](https://www.cnblogs.com/sanjun/p/9971993.html)
69 |
70 |
--------------------------------------------------------------------------------
/markdown/Linux/Shell.md:
--------------------------------------------------------------------------------
1 | # Shell
2 |
3 | ## 常用命令汇总
4 |
5 | `man`:查看每种命令的文档
6 |
7 | `man -k xxx`:查找与 xxx 相关的命令
8 |
9 | `pwd`:显示当前目录
10 |
11 | `ll file*Name`:只能匹配文件,不能匹配目录
12 |
13 | - 使用通配符 「? 任意匹配一个字符 / * 任意匹配任意个字符」
14 | - 基本上可以使用正则表达式
15 |
16 | `ls -i fileName`:查看文件的 inode 编号
17 |
18 | `ln -s [fileName] [linkName]`:创建一个软链接
19 |
20 | ```shell
21 | ➜ test ln -s a.txt alink
22 | ➜ test ll
23 | -rw-r--r-- 1 lfool staff 5B 1 29 02:06 a.txt
24 | lrwxr-xr-x 1 lfool staff 5B 1 29 02:06 alink -> a.txt
25 | ```
26 |
27 | `ln [fileName] [linkName]`:创建一个硬链接
28 |
29 | ```shell
30 | ➜ test ln a.txt aHardLink
31 | ➜ test ll
32 | -rw-r--r-- 2 lfool staff 5B 1 29 02:06 a.txt
33 | -rw-r--r-- 2 lfool staff 5B 1 29 02:06 aHardLink
34 | ➜ test ll -i
35 | 8986726 -rw-r--r-- 2 lfool staff 5B 1 29 02:06 a.txt
36 | 8986726 -rw-r--r-- 2 lfool staff 5B 1 29 02:06 aHardLink
37 | ```
38 |
39 | `rm -rf path`:删除目录或文件
40 |
41 | - -f:强制删除文件或目录
42 | - -r:递归处理,将指定目录下的所有文件与子目录一并处理
43 |
44 | `tree path`:查看目录结构
45 |
46 | `file fileName`:查看文件类型
47 |
48 | `cat / more / less`:显示文件内容(全显示/分批显示)
49 |
50 | `head / tail fileName`:显示文件头部 / 最后几行内容
51 |
52 | - -f:使显示内容保持活动状态,会动态更新显示内容
53 | - -n:规定行数
54 |
55 | `nohup xxx > output.log 2>&1 &`:后台运行,输出到文件中
56 |
57 | `du`:显示文件或目录的大小
58 |
59 | - -h:以 K,M,G 为单位,提高信息的可读性
60 | - -s:仅显示总计
61 | - [fileName] / [dirName] / None:未指定,则显示当前目录下的内容
62 |
63 | `ps -ef | grep python`:查看 python 相关进程
64 |
65 | `lsof -i:8888`:查看端口 8888 的占用情况
66 |
67 | `kill -s 9 PID`:杀死进程 PID
68 |
69 | ## 命令行常用快捷操作
70 |
71 | `Ctrl + a`:跳到本行的行首
72 |
73 | `Ctrl + e`:则跳到页尾
74 |
75 | `Ctrl + u`:删除当前光标前面的文字
76 |
77 | `Ctrl + k`:删除当前光标后面的文字
78 |
79 | `Ctrl + y`:进行恢复
80 |
81 | ## 目录及用途
82 |
83 | | 目录 | 用途 |
84 | | :----: | :----------------------------------------------------------: |
85 | | / | 虚拟目录的根目录,通常不会在这里存储文件 |
86 | | /bin | 二进制目录,存放许多用户级的 GNU 工具 |
87 | | /boot | 启动目录,存放启动文件 |
88 | | /dev | 设备目录,Linux 在这里创建设备节点 |
89 | | /etc | 系统配置文件目录 |
90 | | /home | 主目录,Linux 在这里创建用户目录 |
91 | | /lib | 库目录,存放系统和应用程序的库文件 |
92 | | /media | 媒体文件,可移动媒体设备的常用挂载点 |
93 | | /mnt | 挂载目录,另一个可移动媒体设备的常用挂载点 |
94 | | /opt | 可选目录,常用于存放第三方软件包或数据文件 |
95 | | /proc | 进程目录,存放先用硬件以及当前进程的相关信息 |
96 | | /root | root 用户的主目录 |
97 | | /sbin | 系统二进制目录,存放许多 GNU 管理员级工具 |
98 | | /run | 运行目录,存放系统运作时的运行时数据 |
99 | | /srv | 服务目录,存放本地服务的相关文件 |
100 | | /sys | 系统目录,存放系统硬件信息的相关文件 |
101 | | /tmp | 临时目录,可以在该目录中创建和删除临时工作文件 |
102 | | /usr | 用户二进制目录,大量用户级别的 GUN 工具和数据文件都存储在这里 |
103 | | /var | 可变目录,用以存放经常变化的文件,比如日志文件 |
104 |
105 |
106 |
107 |
108 |
109 | ## 文件或目录信息
110 |
111 | 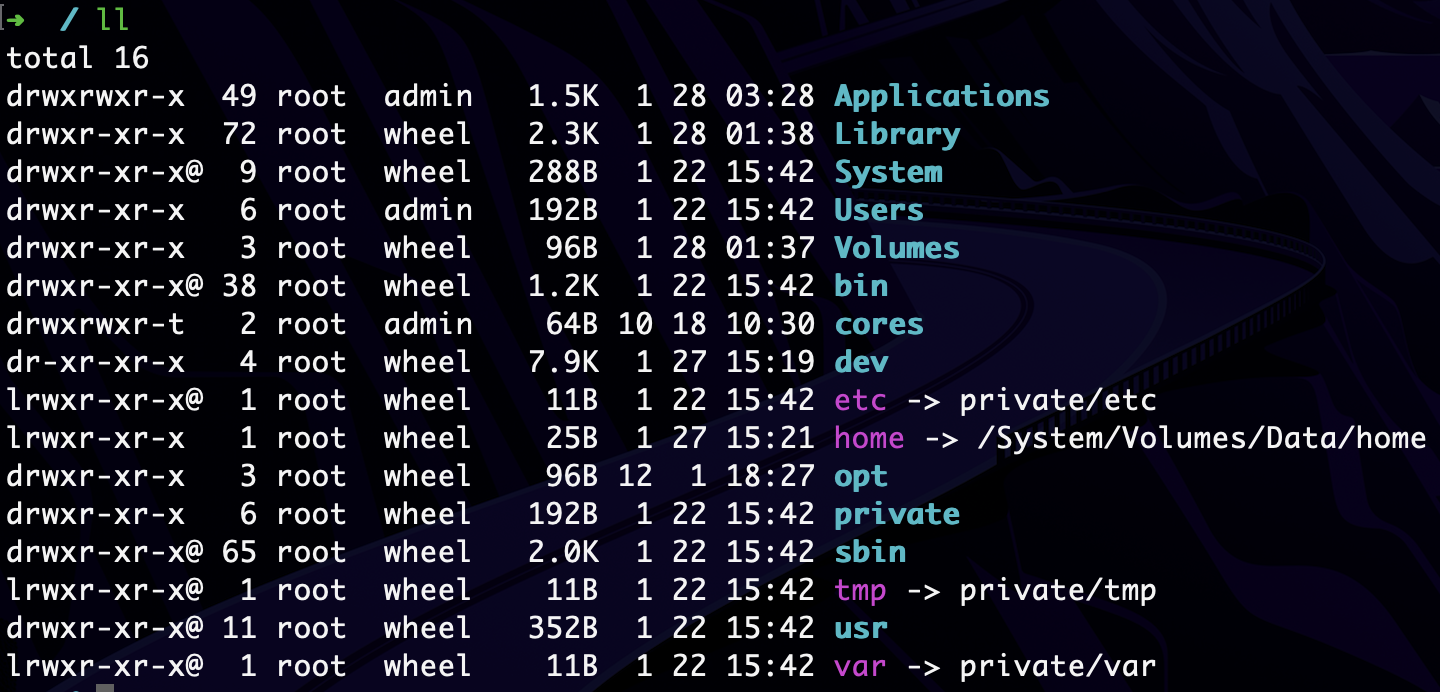 112 |
113 |
112 |
113 | 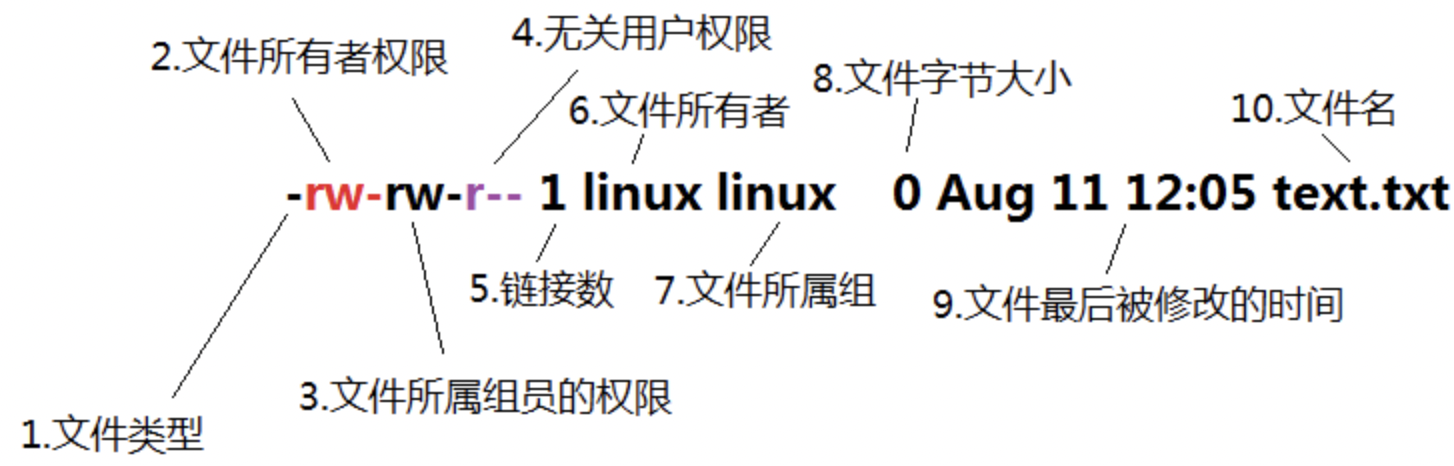 114 |
115 | 文件类型(每行第一个字母):目录(d)、文件(-)、字符型文件(c)、块设备(b)、软链接(l)
116 |
117 | 文件的权限:rwx | rwx | r-x -> 属主权限 | 属组权限 | 其他人权限 (r:读 w:写 x:执行 -:无权限)
118 |
119 | 文件的硬链接总数 [传送门](./Linux硬链接和软连接的区别与总结.html)
120 |
121 | 文件属主的用户名
122 |
123 | 文件属组的组名
124 |
125 | 文件的大小(以字节为单位)
126 |
127 | 文件上次修改时间
128 |
129 | 文件名或目录名
130 |
131 |
--------------------------------------------------------------------------------
/markdown/Mac/Mac 快捷键.md:
--------------------------------------------------------------------------------
1 | # Mac 快捷键
2 |
3 |
4 |
5 | 软件最大化:control + command + F
6 |
7 | 软件最小化:command + M
8 |
9 | 软件关闭:command + Q
10 |
11 |
--------------------------------------------------------------------------------
/markdown/MySQL/MySQL索引.md:
--------------------------------------------------------------------------------
1 | # MySQL 索引
2 |
3 | 由于本篇文章侧重于 MySQL 索引的应用,所以并没有完全详细的介绍 B+ 树索引,但 B+ 树索引又是 MySQL 中默认使用的索引,所以**关于 B+ 树索引细节介绍可见 [B+ 树索引](./B+树索引.html)**
4 |
5 | ### 索引介绍
6 |
7 | **索引是一种用于快速查询和检索数据的数据结构,其本质可以看作是一种排好序的数据结构**
8 |
9 | 索引类似于书的目录,如果一本书没有目录,那么对于读者来说就是一场噩梦,目录可以加快我们查找的速度和效率,索引的作用也一样
10 |
11 | 索引底层数据结构有很多种类型,常见的索引结构:B 树、**[B+ 树](./B+树索引.html)**、Hash 表、红黑树。在 MySQL 中,无论是 InnoDB 存储引擎,还是 MyISAM 存储引擎,使用的都是 **[B+ 树索引](./B+树索引.html)**
12 |
13 | ### 索引优缺点
14 |
15 | 优点:
16 |
17 | - 加快查询检索数据的速度
18 | - 可以通过创建唯一索引保证数据的唯一性
19 |
20 | 缺点:
21 |
22 | - 空间成本:MySQL 中每一个索引都对应一个 B+ 树,需要一定的页来存储索引
23 | - 时间成本:在执行增删改操作时,需要维护索引的正确性,会消耗一定时间
24 |
25 | **注意:**有时候「二级索引 + 回表」的速度并不一定比「全表扫描」快,因为可能回表次数过多,而且页在物理存储上较为分散,需要进行多次磁盘 IO 将对应页加载到内存中,耗时大
26 |
27 | ### 索引底层数据结构
28 |
29 | #### Hash 表
30 |
31 | 将索引列映射到哈希表中,即:key = 索引列的值,value = 记录的位置,通过 key 可以快速获取记录的位置,在没有哈希冲突的情况下时间复杂度 O(1),可以用链地址法或开放定址法解决哈希冲突
32 |
33 | MySQL 之所以没有使用 Hash 表作为索引的底层实现,是因为 Hash 表不支持顺序查询和范围查询,只支持每次查询一个
34 |
35 | #### B 树 & B+ 树
36 |
37 | B 树也称 B- 树,全程为**多路平衡查找树**,B+ 树是 B 树的一个变体。B 树和 B+ 树中的 B 是`Balanced`的意思。目前大部分数据库系统及文件系统都采用 B- 树或其变体 B+ 树作为索引底层实现
38 |
39 | **B 树和 B+ 树的区别:**
40 |
41 | - B 树的所有节点既存放键 (key),也存放数据 (data);而 B+ 树只有叶子节点存放 key 和 data,其它非叶子节点只存放 key
42 | - B 树的叶子节点都是独立的;B+ 树的叶子节点间通过双向链表连接
43 | - B 树的检索过程相当于对范围内的每个节点的关键字做二分查找,可能还没到叶子节点就结束了;而 B+ 树的检索过程很稳定,任何查找都是从根节点到叶子节点
44 |
45 | ### 索引的类型
46 |
47 | **从数据结构维度划分:**
48 |
49 | - **[B+ 树索引](./B+树索引.html#innodb-中的索引方案)**:MySQL 中默认的索引结构,同层节点间双向链表连接,节点内单向链表连接
50 | - Hash 索引:通过键值对的形式,一次即可定位
51 |
52 | **从底层存储方式划分:**
53 |
54 | - **[聚簇索引](./B+树索引.html#聚簇索引)**:InnoDB 中的主键索引就属于聚簇索引,叶子节点存放完成用户记录,非叶子节点存放目录项纪录。数据和索引在一起,索引即数据,数据即索引
55 | - 非聚簇索引:数据和索引分开存储,**[二级索引](./B+树索引.html#二级索引)** 就属于非聚簇索引。MySQL 中的 **[MyISAM](./B+树索引.html#一页面至少存-2-条纪录)** 都是非聚簇索引
56 |
57 | **从应用维度划分:**
58 |
59 | - 主键索引:InnoDB 中的主键索引就属于聚簇索引,表中只会有一个主键索引,主键具有的特性该主键索引都具有,如:值唯一,且不为 NULL
60 | - 普通索引:InnoDB 中的普通索引就属于 **[二级索引](./B+树索引.html#二级索引)**
61 | - 唯一索引:值唯一,可以有 NULL
62 | - **[覆盖索引](./覆盖索引-索引条件下推.html#覆盖索引)**:索引列包含查询列表
63 | - **[联合索引](./B+树索引.html#联合索引)**:索引包含多个列
64 | - 前缀索引:为了降低索引占用的空间,可以只将一个字段的前缀作为索引
65 | - 全文索引:对文本的内容进行分词,然后搜索
66 |
67 | ### 使用索引的建议
68 |
69 | - **选择合适的字段建立索引:**频繁根据该字段查询
70 | - **频繁更新的字段慎重建立索引:**维护成本大
71 | - **限制每张表索引数量 (5 个):**索引会占用一定空间,虽然可以加快查询,但会减慢更新插入
72 | - **尽可能建立联合索引而非单列索引:**索引需要占用空间,联合索引可以减少空间的使用
73 | - **注意避免冗余索引:**比如建立了联合索引 (a, b),又建立了 单列索引 (a),就会出现冗余
74 | - **字符串类型字段尽量使用前缀索引:**可以减少空间的使用
75 | - **避免索引失效:**虽然建立了索引,但是没有使用使用,可以通过`explain`查看执行计划
76 | - **删除长期未使用的索引**
--------------------------------------------------------------------------------
/markdown/MySQL/RR隔离级别下彻底解决幻读了吗.md:
--------------------------------------------------------------------------------
1 | # RR 隔离级别下彻底解决幻读了吗?
2 |
3 | **[幻读](./MySQL事务.html#幻读-phantom)** 指在同一个事务中,同一个查询语句,前后两次执行得到的结果集不同,如:第一次查询得到六条记录,第二次查询得到七条数据
4 |
5 | **结论:**RR 隔离级别下只能最大程度的避免幻读现象的出现,但无法彻底解决幻读现象!!
6 |
7 | MySQL 中有两种读:快照读和锁定读
8 |
9 | - **快照读:**通过 **[MVCC](./MVCC.html)** 可以最大程度避免幻读,每次都只能看到生成 ReadView 之前已经提交事务修改的数据,所以在事务执行过程中多次读的结果是一致的
10 | - **锁定读:**通过加锁可以最大程度避免欢度,在 RR 下会为每个查询时符合条件的记录加 **[Next-Key Lock](./锁.html#next-key-lock)**,既不允许修改记录,也不允许在记录前的间隙插入新记录,所以在事务中多次读的结果是一致的
11 |
12 | ### 快照读 -- 出现幻读的情况
13 |
14 | 
15 |
16 | `update`语句修改的是最新数据。在时刻 4,由于事务 A 修改了`id = 3`的记录,记录中`trx_id`由 200 变成 100,所以该记录对事务 A 可见
17 |
18 | ### 锁定读 -- 出现幻读的情况
19 |
20 | 
21 |
22 | `select * from t`是快照读,不会对记录加锁,通过 MVCC 控制;`select * from t for update`是当前读,读最新的数据,而且会对记录加 **[Next-Key Lock](./锁.html#next-key-lock)**
23 |
24 | **建议:**在开启事务后,立马执行`select ... for update`,对记录加 **[Next-Key Lock](./锁.html#next-key-lock)**,可以最大程度避免幻读
--------------------------------------------------------------------------------
/markdown/MySQL/redo-log.md:
--------------------------------------------------------------------------------
1 | # redo log
2 |
3 | ### redo log 是什么?
4 |
5 | InnoDB 是以页为基本单位来管理内存空间,为了减少磁盘 IO 的开销,增加了 **[Buffer Pool](./InnoDB的Buffer-Pool.html)**,每次访问页面后不着急刷新回磁盘,而是缓存到 Buffer Pool 中,以便下次继续访问
6 |
7 | Buffer Pool 在内存中,所以会导致后续对页面的修改并不能及时刷新回磁盘,如果发生断电或者一些其它的原因会使内存中的数据丢失,重启后啥也没了,必须持久化到磁盘才安全
8 |
9 | 一个很简单的方法就是每次修改后立刻将页面刷新回磁盘,这样做的弊端在于:
10 |
11 | - 如果是少量的修改就刷新一个页面回磁盘,太过于浪费
12 | - 一个修改可能会牵连多个页面的变化,而且这些页面物理上极大可能不在一起,这样刷新回磁盘需要进行很多随机 IO,开销更大
13 |
14 | 基于上面的场景,就有了 redo log (重做日志),它记录了**对哪个表空间哪个页进行了哪些修改**,可以简单理解为就算数据丢失,但只要有对应的 redo log,也可以恢复丢失的数据
15 |
16 | redo log 也需要及时的刷新回磁盘,但它相比于刷新整个页面的优势在于:
17 |
18 | - redo log 占用的空间非常小
19 | - redo log 是顺序写入磁盘,比随机 IO 快很多
20 |
21 | ### redo log 写入过程
22 |
23 | 为了更好的管理 redo log,InnoDB 将 redo log 存储到大小为 512 字节的 block 中 (block 可以理解为页) 的 log blcok body 部分。每个 block 的结构如下所示:
24 |
25 | 
26 |
27 | 和 Buffer Pool 一样,为了缓解磁盘 IO 速度慢的问题,InnoDB 引入了 log buffer,它是内存中一片连续的区域,默认大小为 16MB
28 |
29 | redo log 是顺序写入 log buffer 中,从前往后,有一个 buf_free 指向空闲区域的起始位置,具体结构如下图所示:
30 |
31 | 
32 |
33 | ### redo log 刷盘时机
34 |
35 | log buffer 在内存中,如果不及时的将 log buffer 刷盘,也会导致 redo log 丢失,所以 log buffer 会在出现下面情况时刷盘
36 |
37 | - **log buffer 空间不足时:**如果 redo log 已经占满了 log buffer 一半的空间,就会把 redo log 刷新回磁盘
38 | - **事务提交时:**在事务提交时,将对应的 redo log 刷新回磁盘。由于 redo log 是顺序写入,所以之前的也会一起刷新回磁盘,不可能只刷新回某一个事务的 redo log
39 | - **脏页刷新回磁盘时:**将某个脏页刷新回磁盘时,会保证先将该脏页对应的 redo log 刷新回磁盘
40 | - 后台线程每隔 1s 将 log buffer 中的 redo log 刷新回磁盘
41 | - MySQL 正常关闭时也会将 buffer log 刷新回磁盘
42 |
43 | 对于上面第二点刷盘情况:**事务提交时**,由于这个要求过于严格,会降低数据库新能,所以可以通过参数`innodb_flush_log_at_trx_commit`调整:
44 |
45 | - **0:**每次事务提交时,不主动刷盘,交由后台线程来处理,所以可能丢失上一秒所有事务的数据
46 | - **1:**每次事务提交时,都将 redo log 同步到磁盘,可以保证事务的持久性 (默认值)
47 | - **2:**每次事务提交时,都只把 redo log 写入到 page cache (操作系统的缓存)。如果数据库挂了,但操作系统没挂,依旧可以保证事务的持久性
48 |
49 | 上面三个参数的安全性和性能的关系:
50 |
51 | - 安全:1 > 2 > 0
52 | - 性能:0 > 2 > 1
53 |
54 | **重点:**对于安全性要求高的系统,只能选择 1;对于可以接受 1s 数据丢失的信息,可以选择 0;如果既要求性能也要保证一定的安全性,可以选择 2,折中方案
55 |
56 | ### redo log 文件组
57 |
58 | 当 log buffer 触发刷盘时,会存到 redo log 文件中,它是以日志文件组的形式出现,即:一组中有多个大小相等的日志文件,默认情况下有两个文件:ib_logfile0 和 ib_logfile1
59 |
60 | redo log 是为了记录内存中还没有刷盘的脏页,防止当 MySQL 挂了后脏页丢失,导致修改数据的丢失。所以当脏页已经被刷盘,那么对应的 redo log 就没有用
61 |
62 | 随着系统的运行,redo log 只会越来越多,而日志文件组的数量和大小都是固定的,所以它采用循环写的方式,从头开始写,当写到末尾又回到开头,这样可以在有限的日志文件组中无限的写入 redo log
63 |
64 | 之所以可以覆盖日志文件组开头的数据,是因为开头的数据可能会随着脏页的刷盘而变成无用。用 write pos 表示新 redo log 刷盘时要写入的位置;用 checkpoint 表示当前要擦除的位置
65 |
66 | 
67 |
68 | 图中:
69 |
70 | - write pos 和 checkpoint 都是顺时针移动
71 | - write pos - checkpoint 之间的部分 (红色),用来存新的 redo log
72 | - checkpoint - write pos 之间的部分 (蓝色),表示待刷盘的脏页对应的 redo log
73 |
74 | 当 write pos 追上 checkpoint 时,表示 redo log 文件组满了,不能再将 redo log 刷盘到文件组中
75 |
76 | 此时 MySQL 会阻塞,将 Buffer Pool 中的脏页刷新到磁盘,然后标记 redo log 文件组可以被擦除的部分,最后将可以被擦除的部分擦除,更新 checkpoint (顺时针向前移动)
77 |
78 | 所以,一次 checkpoint 的过程就是将脏页刷新到磁盘中,更新 redo log 日志组中可以被覆盖的位置
--------------------------------------------------------------------------------
/markdown/MySQL/两阶段提交.md:
--------------------------------------------------------------------------------
1 | # 两阶段提交
2 |
3 | ### 分布式事务
4 |
5 | MySQL 分为 server 层和存储引擎层,事务由存储引擎层实现。如果修改服务器 A 中数据库的数据的同时也需要修改服务器 B 中数据库的数据,这两个操作必须同时成功或者失败,也就是必须保证原子性
6 |
7 | 而这两个操作属于两个不同的数据库,存储引擎也不是同一个,无法保证两个操作的原子性。这个时候就需要一个全局事务,由若干个小事务组成,这个全局事务也被称作分布式事务
8 |
9 | ### XA 规范
10 |
11 | 有一个名叫 X/Open 的组织提出了 XA 的规范,用于规范分布式事务,也就是不同的存储引擎只要符合 XA 规范,就可以放到一个分布式事务中管理
12 |
13 | XA 规范提出了两个角色
14 |
15 | - **资源管理器:**全局事务中每一个小事务
16 | - **事务管理器:**管理全局事务中每一个小事务 (后文称之为协调者)
17 |
18 | 要提交一个全局事务,就必须保证所有小事务都要能顺利提交,否则所有事务都应该回滚。XA 规范指出,要提交一个全局事务,必须分两步:(点题)
19 |
20 | - **prepare 阶段:**每个小事务在该阶段会执行各自的事务,并将事务产生的 redo log 刷新到磁盘中,做好提交的准备
21 | - **commit 阶段:**协调者准备提交前,会询问每个小事务是否做好了提交的准备,如果都准备好了就直接提交,否则全部回滚
22 |
23 | ### 外部 XA 事务
24 |
25 | 在外部 XA 事务中,每个小事务在分布在不同的数据库服务器中。在 MySQL 使用 XA 事务的一些操作如下:
26 |
27 | - `XA {start|begin} xid`:开启一个 XA 事务,此时该 XA 事务处于 active 状态。xid 表示每个事务唯一的 id
28 |
29 | - `XA end xid`:告知服务器有 xid 标识的 XA 事务的所有语句全部输入,此时该 XA 事务处于 idle 状态
30 |
31 | - `XA prepare xid`:应用程序让处于 idle 状态的 XA 事务将产生的 redo log 刷新到磁盘中,做好提交的准备,此时该 XA 事务处于 prepare 状态
32 |
33 | - `XA commit xid [one phase]`:对于处于 prepare 状态的 XA 事务,应用程序可以发送`XA commit xid`让服务器提交,此时该 XA 事务处于 commit 状态
34 |
35 | - `XA rollback xid`:应用程序通过该语句让服务器回滚 xid 所标识的 XA 事务,此时该 XA 事务处于 abort 状态
36 |
37 | - `XA recover`:应用程序可以通过该语句查看处于 prepare 状态的 XA 事务
38 |
39 | 下面给出 XA 事务的状态转换图
40 |
41 | 
42 |
43 | ### 内部 XA 事务
44 |
45 | 在内部 XA 事务中,每个小事务可能分布在同一个数据库服务器的不同存储引擎中,或者在存储引擎和插件之间。下面以最典型的 binlog 和 redo log 展开讨论内部 XA 事务
46 |
47 | redo log 以 mtr 为单位添加到 redo log buffer 中,在事务提交时会刷盘,在事务提交前后台线程每隔 1s 刷盘;bilog 以事务为单位先添加到 binlog cache 中,等事务提交后刷新到磁盘中
48 |
49 | 由于 redo log 是存储引擎生成,binlog 是 server 层生成,无法保证这两个刷盘操作的原子性,而这两个操作必须要保证原子性,否则会出现一致性问题
50 |
51 | - 如果 redo log 刷盘成功,binlog 没有刷盘成功,在主从复制的架构中会导致主库和从库数据不一致,因为从库是根据 binlog 来复制数据
52 | - 如果 redo log 没有刷盘成功,binlog 刷盘成功,在主从复制的架构中会导致主库和从库数据不一致,因为主库是根据 redo log 来恢复数据
53 |
54 | 在客户端执行 commit 或者自动提交事务的情况下,MySQL 内部开启一个 XA 事务保证 redo log 和 binlog 刷盘的原子性,binlog 作为协调者,存储引擎作为参与者
55 |
56 | 
57 |
58 | 从上图可以看出,将 redo log 持久化拆分成两个阶段:prepare 和 commit,binlog 在中间穿插写入
59 |
60 | - **prepare 阶段:**先将 XID 写入到 redo log 中,然后将 redo log 刷盘,最后将 redo log 对应的事务设置为 prepare 状态
61 | - **commit 阶段:**先将 XID 写入到 binlog 中,然后将 binlog 刷盘,接着调用存储引擎提交事务接口将 redo log 状态设置为 commit,此状态不需要持久化,可以根据 binlog 中是否存在 XID 判断 redo log 状态
62 |
63 | 假设时刻 1 (redo log 刷盘成功,binlog 刷盘失败) 或者时刻 2 (redo log 和 binlog 都刷盘成功,但还没有写入 commit 标识) 系统挂了,此时的 redo log 都处于 prapare 阶段
64 |
65 | 在 MySQL 重启后会重写扫描 redo log 文件,碰到处于 prepare 状态的 redo log,就会去检查 binlog 中是否存在和 redo log 相同的 XID
66 |
67 | - 如果 binlog 中不存在相同 XID,表示 binlog 没有刷盘成功,直接回滚事务 (对应时刻 1)
68 | - 如果 binlog 中存在相同 XID,表示 binlog 刷盘成功,直接提交事务 (对应时刻 2)
69 |
70 | **总结:**是否回滚事务完全取决于 binlog 是否存在和 redo log 中相同的 XID,如果不存在就需要回滚,否则直接提交即可
71 |
--------------------------------------------------------------------------------
/markdown/MySQL/分库分表.md:
--------------------------------------------------------------------------------
1 | # 分库分表
2 |
3 | 本篇文章主要整理关于 MySQL 分库分表的一些概述,并没有很深入,主要是因为某人多次的拜托 (是谁我不说,自己发现叭)~~
4 |
5 | ### 分库分表判断标准
6 |
7 | 先开门见山,给出写本篇文章的导火索,分库分表的标准是什么?
8 |
9 | 其实分库分表的标准在阿里巴巴 Java 开发手册中提到过:**单表行数超过 500 万行或者单表容量超过 2GB,才推荐进行分库分表**
10 |
11 | **问题一:**是否当单表行数超过 500 万行或者单表容量超过 2GB,才开始分库分表?
12 |
13 | - 不是,如果可以预计 3 年后数据会超过这个量级,就应该在创建表的时候就进行分库分表
14 |
15 | **问题二:**如果 MySQL 服务器配置较好,是否可以超过 500 万这个量级?
16 |
17 | - 虽然服务器配置更好后,数据量过大时,性能也不错,但以发展的眼光看待,考虑分库分表更佳
18 |
19 | 下面主要介绍一下分库分表到底是什么?什么情况下会考虑分库分表?分库分表的方式有哪些?
20 |
21 | ### 什么是分库分表
22 |
23 | **分库**,顾名思义是将一个数据库中的表拆分到多个数据库中,如下图所示:
24 |
25 | 
26 |
27 | 每个数据库连接数都有限制,当并发量过大时,数据库连接数也会增大,这是决定是否分库的直接原因,如果连接数成为数据库的瓶颈时就需要考虑分库
28 |
29 | **分表**,顾名思义是将一个表拆分成多个表,如下图所示:
30 |
31 | 
32 |
33 | 阿里巴巴 Java 开发手册中推荐:单表行数超过 500 万行或者单表容量超过 2GB,才推荐进行分库分表,所以决定是否分表的标准是表中记录数和容量,如果当一个表中数据量过大时就需要考虑分表
34 |
35 | 其实,还可能同时分库分表,这就是既存在并发量过大,又存在单表容量过大的情况~
36 |
37 | **总结:**
38 |
39 | | 切分方案 | 解决问题 |
40 | | :----------: | :------------------------------------: |
41 | | 只分库不分表 | 数据库读/写 QPS 过高;数据库连接数不足 |
42 | | 只分表不分库 | 单表数据量过大,存储性能遇到瓶颈 |
43 | | 既分库又分表 | 连接数不足 + 单表数据量过大 |
44 |
45 |
46 |
47 | ### 如何分库分表
48 |
49 | 上一部分只是介绍了在何种情况下会考虑分库分表,那如果决定了要分库分表,该如何分呢??
50 |
51 | 其实分库分表都有两种不同的分法,垂直和水平,排列组合一下就有四种:垂直分表、水平分表、垂直分库、水平分库
52 |
53 | #### 垂直分表
54 |
55 | 将一张表按照字段切分成多个表,通常是根据字段的关系密集程度进行切分,也可以按照常用字段和不常用字段切分,如下图所示:
56 |
57 | 
58 |
59 | #### 水平分表
60 |
61 | 水平分表又被称为 Sharding,它是将同一个表中的记录拆分到多个结构相同的表中,如下图所示:
62 |
63 | 
64 |
65 | 当一个表中数据不断增多时,水平分表是必然的选择,它可以将数据分布到集群的不同节点上,从而缓解单个数据库的压力
66 |
67 | #### 垂直分库
68 |
69 | 按照业务将表进行分类,分布到不同的数据库中,每个数据库可以放到不同的服务器上,如下图所示:
70 |
71 | 
72 |
73 | #### 水平分库
74 |
75 | 把同一个表的数据按照一定规则拆分到不同的数据库中,每个数据库可以放到不同的服务器上。假设按照表中 id 的奇偶性将数据拆分到不同的数据库中,如下图所示:
76 |
77 | 
78 |
--------------------------------------------------------------------------------
/markdown/Network/DNS.md:
--------------------------------------------------------------------------------
1 | # DNS
2 |
3 | 每一台公网服务器都有一个公网 IP,通过 IP 可以访问它,但世界上服务器那么多,而且 IP 是一串数字,难免不容易记住对应的 IP 地址,所以就有了 DNS (Domain Name System,域名系统)
4 |
5 | DNS 记录了 IP 和域名的对应关系,在通信时需要使用 IP 地址,而域名更便于用户记住,所以用户通过域名访问一个网站时,域名服务器会自动将域名转换成 IP 地址
6 |
7 | 在配置计算机的 IP 相关信息时,往往会配置一个 DNS 服务器的 IP 地址,可以将它称之为本地 DNS 服务器,我们是借助它来获取域名对应的 IP 地址
8 |
9 | ### DNS 结构
10 |
11 | 所有的 DNS 域名服务器是一个树状结构,最上层的是根域,如下图所示:
12 |
13 | 
14 |
15 | ### IP 查询过程
16 |
17 | 下面模拟`www.baidu.com`的查询过程!先给出过程图:
18 |
19 | 
20 |
21 | **第一步:**询问配置的本地 DNS 服务器,`www.baidu.com`的 IP 地址是多少?如果本地 DNS 服务器发现自己本地缓存中没有对应的域名就去根域名服务器询问,如果有缓存中有直接返回给计算机
22 |
23 | **第二步:**本地 DNS 服务器询问根域名服务器,根域名服务器会让本地 DNS 服务器去询问`com`域名服务器
24 |
25 | **第三步:**本地 DNS 服务器询问`com`域名服务器,`com`域名服务器会让本地 DNS 服务器去询问`baidu`域名服务器
26 |
27 | **第四步:**本地 DNS 服务器询问`baidu`域名服务器,`baidu`域名服务器会让本地 DNS 服务器去询问`www`域名服务器
28 |
29 | **第五步:**本地 DNS 服务器询问`www`域名服务器,`www`域名服务直接返回对应的 IP 地址,本地 DNS 服务器会缓存「域名-IP」对应关系,但该缓存有时间期限,一段时间会过期
--------------------------------------------------------------------------------
/markdown/Network/GET-POST请求.md:
--------------------------------------------------------------------------------
1 | # GET && POST 请求
2 |
3 | 在 HTPP/1.1 中,一共有 get、post、put、head、delete、potions、trace、connect 八种不同的请求方法,但本篇文章只介绍最常用的两种 get 和 post
4 |
5 | ### GET
6 |
7 | GET 请求是**从服务器获取指定资源**,指定的资源经服务器返回给客户端,资源可以是静态文本、页面、图片视频等
8 |
9 | GET 请求的参数位置一般写在 URL 中,URL 只能支持 ASCII,所以 GET 请求的参数只允许是 ASCII 字符,而且浏览器会对 URL 长度有限制,HTTP 协议本身没有对 URL 长度做任何规定
10 |
11 | 下面给出一个 GET 请求的示例:`https://www.test.com/get?xxx=111&yyy=222`。该请求中有两个参数:`xxx = 111`和`yyy = 222`
12 |
13 | ### POST
14 |
15 | POST 请求是根据请求负载对指定资源做出处理,一般请求携带的数据会写在消息体中,消息体中的数据可以是任意格式,且浏览器不会限制消息体大小
16 |
17 | GET 请求侧重于获取指定的资源,而 POST 请求侧重于传输实体到服务器进行处理,如登陆时提交表格信息
18 |
19 | 下面给出一个 post 请求的示例:
20 |
21 | ```
22 | https://www.test.com/post
23 |
24 | xxx = 111
25 | yyy = 222
26 | ```
27 |
28 | 该请求体中有两个参数:`xxx = 111`和`yyy = 222`
29 |
30 | ### 安全和幂等
31 |
32 | 首先说一下安全和幂等着两个概念:
33 |
34 | - **安全:**在 HTTP 协议里,安全表示不会修改服务器中的数据,类似于只读操作
35 | - **幂等:**多次请求操作结果相同
36 |
37 | 很显然,GET 请求是安全且幂等的,而 POST 是不安全且不幂等的。所以 GET 请求返回的结果可以被缓存,而 POST 请求返回的结果不可以被缓存
38 |
--------------------------------------------------------------------------------
/markdown/Network/HTTP-状态码.md:
--------------------------------------------------------------------------------
1 | # HTTP 状态码
2 |
3 | 简单来讲,HTTP 状态码的作用是服务器告诉客户端当前请求**响应**的状态,通过状态码就能判断和分析服务器的运行状态
4 |
5 |
114 |
115 | 文件类型(每行第一个字母):目录(d)、文件(-)、字符型文件(c)、块设备(b)、软链接(l)
116 |
117 | 文件的权限:rwx | rwx | r-x -> 属主权限 | 属组权限 | 其他人权限 (r:读 w:写 x:执行 -:无权限)
118 |
119 | 文件的硬链接总数 [传送门](./Linux硬链接和软连接的区别与总结.html)
120 |
121 | 文件属主的用户名
122 |
123 | 文件属组的组名
124 |
125 | 文件的大小(以字节为单位)
126 |
127 | 文件上次修改时间
128 |
129 | 文件名或目录名
130 |
131 |
--------------------------------------------------------------------------------
/markdown/Mac/Mac 快捷键.md:
--------------------------------------------------------------------------------
1 | # Mac 快捷键
2 |
3 |
4 |
5 | 软件最大化:control + command + F
6 |
7 | 软件最小化:command + M
8 |
9 | 软件关闭:command + Q
10 |
11 |
--------------------------------------------------------------------------------
/markdown/MySQL/MySQL索引.md:
--------------------------------------------------------------------------------
1 | # MySQL 索引
2 |
3 | 由于本篇文章侧重于 MySQL 索引的应用,所以并没有完全详细的介绍 B+ 树索引,但 B+ 树索引又是 MySQL 中默认使用的索引,所以**关于 B+ 树索引细节介绍可见 [B+ 树索引](./B+树索引.html)**
4 |
5 | ### 索引介绍
6 |
7 | **索引是一种用于快速查询和检索数据的数据结构,其本质可以看作是一种排好序的数据结构**
8 |
9 | 索引类似于书的目录,如果一本书没有目录,那么对于读者来说就是一场噩梦,目录可以加快我们查找的速度和效率,索引的作用也一样
10 |
11 | 索引底层数据结构有很多种类型,常见的索引结构:B 树、**[B+ 树](./B+树索引.html)**、Hash 表、红黑树。在 MySQL 中,无论是 InnoDB 存储引擎,还是 MyISAM 存储引擎,使用的都是 **[B+ 树索引](./B+树索引.html)**
12 |
13 | ### 索引优缺点
14 |
15 | 优点:
16 |
17 | - 加快查询检索数据的速度
18 | - 可以通过创建唯一索引保证数据的唯一性
19 |
20 | 缺点:
21 |
22 | - 空间成本:MySQL 中每一个索引都对应一个 B+ 树,需要一定的页来存储索引
23 | - 时间成本:在执行增删改操作时,需要维护索引的正确性,会消耗一定时间
24 |
25 | **注意:**有时候「二级索引 + 回表」的速度并不一定比「全表扫描」快,因为可能回表次数过多,而且页在物理存储上较为分散,需要进行多次磁盘 IO 将对应页加载到内存中,耗时大
26 |
27 | ### 索引底层数据结构
28 |
29 | #### Hash 表
30 |
31 | 将索引列映射到哈希表中,即:key = 索引列的值,value = 记录的位置,通过 key 可以快速获取记录的位置,在没有哈希冲突的情况下时间复杂度 O(1),可以用链地址法或开放定址法解决哈希冲突
32 |
33 | MySQL 之所以没有使用 Hash 表作为索引的底层实现,是因为 Hash 表不支持顺序查询和范围查询,只支持每次查询一个
34 |
35 | #### B 树 & B+ 树
36 |
37 | B 树也称 B- 树,全程为**多路平衡查找树**,B+ 树是 B 树的一个变体。B 树和 B+ 树中的 B 是`Balanced`的意思。目前大部分数据库系统及文件系统都采用 B- 树或其变体 B+ 树作为索引底层实现
38 |
39 | **B 树和 B+ 树的区别:**
40 |
41 | - B 树的所有节点既存放键 (key),也存放数据 (data);而 B+ 树只有叶子节点存放 key 和 data,其它非叶子节点只存放 key
42 | - B 树的叶子节点都是独立的;B+ 树的叶子节点间通过双向链表连接
43 | - B 树的检索过程相当于对范围内的每个节点的关键字做二分查找,可能还没到叶子节点就结束了;而 B+ 树的检索过程很稳定,任何查找都是从根节点到叶子节点
44 |
45 | ### 索引的类型
46 |
47 | **从数据结构维度划分:**
48 |
49 | - **[B+ 树索引](./B+树索引.html#innodb-中的索引方案)**:MySQL 中默认的索引结构,同层节点间双向链表连接,节点内单向链表连接
50 | - Hash 索引:通过键值对的形式,一次即可定位
51 |
52 | **从底层存储方式划分:**
53 |
54 | - **[聚簇索引](./B+树索引.html#聚簇索引)**:InnoDB 中的主键索引就属于聚簇索引,叶子节点存放完成用户记录,非叶子节点存放目录项纪录。数据和索引在一起,索引即数据,数据即索引
55 | - 非聚簇索引:数据和索引分开存储,**[二级索引](./B+树索引.html#二级索引)** 就属于非聚簇索引。MySQL 中的 **[MyISAM](./B+树索引.html#一页面至少存-2-条纪录)** 都是非聚簇索引
56 |
57 | **从应用维度划分:**
58 |
59 | - 主键索引:InnoDB 中的主键索引就属于聚簇索引,表中只会有一个主键索引,主键具有的特性该主键索引都具有,如:值唯一,且不为 NULL
60 | - 普通索引:InnoDB 中的普通索引就属于 **[二级索引](./B+树索引.html#二级索引)**
61 | - 唯一索引:值唯一,可以有 NULL
62 | - **[覆盖索引](./覆盖索引-索引条件下推.html#覆盖索引)**:索引列包含查询列表
63 | - **[联合索引](./B+树索引.html#联合索引)**:索引包含多个列
64 | - 前缀索引:为了降低索引占用的空间,可以只将一个字段的前缀作为索引
65 | - 全文索引:对文本的内容进行分词,然后搜索
66 |
67 | ### 使用索引的建议
68 |
69 | - **选择合适的字段建立索引:**频繁根据该字段查询
70 | - **频繁更新的字段慎重建立索引:**维护成本大
71 | - **限制每张表索引数量 (5 个):**索引会占用一定空间,虽然可以加快查询,但会减慢更新插入
72 | - **尽可能建立联合索引而非单列索引:**索引需要占用空间,联合索引可以减少空间的使用
73 | - **注意避免冗余索引:**比如建立了联合索引 (a, b),又建立了 单列索引 (a),就会出现冗余
74 | - **字符串类型字段尽量使用前缀索引:**可以减少空间的使用
75 | - **避免索引失效:**虽然建立了索引,但是没有使用使用,可以通过`explain`查看执行计划
76 | - **删除长期未使用的索引**
--------------------------------------------------------------------------------
/markdown/MySQL/RR隔离级别下彻底解决幻读了吗.md:
--------------------------------------------------------------------------------
1 | # RR 隔离级别下彻底解决幻读了吗?
2 |
3 | **[幻读](./MySQL事务.html#幻读-phantom)** 指在同一个事务中,同一个查询语句,前后两次执行得到的结果集不同,如:第一次查询得到六条记录,第二次查询得到七条数据
4 |
5 | **结论:**RR 隔离级别下只能最大程度的避免幻读现象的出现,但无法彻底解决幻读现象!!
6 |
7 | MySQL 中有两种读:快照读和锁定读
8 |
9 | - **快照读:**通过 **[MVCC](./MVCC.html)** 可以最大程度避免幻读,每次都只能看到生成 ReadView 之前已经提交事务修改的数据,所以在事务执行过程中多次读的结果是一致的
10 | - **锁定读:**通过加锁可以最大程度避免欢度,在 RR 下会为每个查询时符合条件的记录加 **[Next-Key Lock](./锁.html#next-key-lock)**,既不允许修改记录,也不允许在记录前的间隙插入新记录,所以在事务中多次读的结果是一致的
11 |
12 | ### 快照读 -- 出现幻读的情况
13 |
14 | 
15 |
16 | `update`语句修改的是最新数据。在时刻 4,由于事务 A 修改了`id = 3`的记录,记录中`trx_id`由 200 变成 100,所以该记录对事务 A 可见
17 |
18 | ### 锁定读 -- 出现幻读的情况
19 |
20 | 
21 |
22 | `select * from t`是快照读,不会对记录加锁,通过 MVCC 控制;`select * from t for update`是当前读,读最新的数据,而且会对记录加 **[Next-Key Lock](./锁.html#next-key-lock)**
23 |
24 | **建议:**在开启事务后,立马执行`select ... for update`,对记录加 **[Next-Key Lock](./锁.html#next-key-lock)**,可以最大程度避免幻读
--------------------------------------------------------------------------------
/markdown/MySQL/redo-log.md:
--------------------------------------------------------------------------------
1 | # redo log
2 |
3 | ### redo log 是什么?
4 |
5 | InnoDB 是以页为基本单位来管理内存空间,为了减少磁盘 IO 的开销,增加了 **[Buffer Pool](./InnoDB的Buffer-Pool.html)**,每次访问页面后不着急刷新回磁盘,而是缓存到 Buffer Pool 中,以便下次继续访问
6 |
7 | Buffer Pool 在内存中,所以会导致后续对页面的修改并不能及时刷新回磁盘,如果发生断电或者一些其它的原因会使内存中的数据丢失,重启后啥也没了,必须持久化到磁盘才安全
8 |
9 | 一个很简单的方法就是每次修改后立刻将页面刷新回磁盘,这样做的弊端在于:
10 |
11 | - 如果是少量的修改就刷新一个页面回磁盘,太过于浪费
12 | - 一个修改可能会牵连多个页面的变化,而且这些页面物理上极大可能不在一起,这样刷新回磁盘需要进行很多随机 IO,开销更大
13 |
14 | 基于上面的场景,就有了 redo log (重做日志),它记录了**对哪个表空间哪个页进行了哪些修改**,可以简单理解为就算数据丢失,但只要有对应的 redo log,也可以恢复丢失的数据
15 |
16 | redo log 也需要及时的刷新回磁盘,但它相比于刷新整个页面的优势在于:
17 |
18 | - redo log 占用的空间非常小
19 | - redo log 是顺序写入磁盘,比随机 IO 快很多
20 |
21 | ### redo log 写入过程
22 |
23 | 为了更好的管理 redo log,InnoDB 将 redo log 存储到大小为 512 字节的 block 中 (block 可以理解为页) 的 log blcok body 部分。每个 block 的结构如下所示:
24 |
25 | 
26 |
27 | 和 Buffer Pool 一样,为了缓解磁盘 IO 速度慢的问题,InnoDB 引入了 log buffer,它是内存中一片连续的区域,默认大小为 16MB
28 |
29 | redo log 是顺序写入 log buffer 中,从前往后,有一个 buf_free 指向空闲区域的起始位置,具体结构如下图所示:
30 |
31 | 
32 |
33 | ### redo log 刷盘时机
34 |
35 | log buffer 在内存中,如果不及时的将 log buffer 刷盘,也会导致 redo log 丢失,所以 log buffer 会在出现下面情况时刷盘
36 |
37 | - **log buffer 空间不足时:**如果 redo log 已经占满了 log buffer 一半的空间,就会把 redo log 刷新回磁盘
38 | - **事务提交时:**在事务提交时,将对应的 redo log 刷新回磁盘。由于 redo log 是顺序写入,所以之前的也会一起刷新回磁盘,不可能只刷新回某一个事务的 redo log
39 | - **脏页刷新回磁盘时:**将某个脏页刷新回磁盘时,会保证先将该脏页对应的 redo log 刷新回磁盘
40 | - 后台线程每隔 1s 将 log buffer 中的 redo log 刷新回磁盘
41 | - MySQL 正常关闭时也会将 buffer log 刷新回磁盘
42 |
43 | 对于上面第二点刷盘情况:**事务提交时**,由于这个要求过于严格,会降低数据库新能,所以可以通过参数`innodb_flush_log_at_trx_commit`调整:
44 |
45 | - **0:**每次事务提交时,不主动刷盘,交由后台线程来处理,所以可能丢失上一秒所有事务的数据
46 | - **1:**每次事务提交时,都将 redo log 同步到磁盘,可以保证事务的持久性 (默认值)
47 | - **2:**每次事务提交时,都只把 redo log 写入到 page cache (操作系统的缓存)。如果数据库挂了,但操作系统没挂,依旧可以保证事务的持久性
48 |
49 | 上面三个参数的安全性和性能的关系:
50 |
51 | - 安全:1 > 2 > 0
52 | - 性能:0 > 2 > 1
53 |
54 | **重点:**对于安全性要求高的系统,只能选择 1;对于可以接受 1s 数据丢失的信息,可以选择 0;如果既要求性能也要保证一定的安全性,可以选择 2,折中方案
55 |
56 | ### redo log 文件组
57 |
58 | 当 log buffer 触发刷盘时,会存到 redo log 文件中,它是以日志文件组的形式出现,即:一组中有多个大小相等的日志文件,默认情况下有两个文件:ib_logfile0 和 ib_logfile1
59 |
60 | redo log 是为了记录内存中还没有刷盘的脏页,防止当 MySQL 挂了后脏页丢失,导致修改数据的丢失。所以当脏页已经被刷盘,那么对应的 redo log 就没有用
61 |
62 | 随着系统的运行,redo log 只会越来越多,而日志文件组的数量和大小都是固定的,所以它采用循环写的方式,从头开始写,当写到末尾又回到开头,这样可以在有限的日志文件组中无限的写入 redo log
63 |
64 | 之所以可以覆盖日志文件组开头的数据,是因为开头的数据可能会随着脏页的刷盘而变成无用。用 write pos 表示新 redo log 刷盘时要写入的位置;用 checkpoint 表示当前要擦除的位置
65 |
66 | 
67 |
68 | 图中:
69 |
70 | - write pos 和 checkpoint 都是顺时针移动
71 | - write pos - checkpoint 之间的部分 (红色),用来存新的 redo log
72 | - checkpoint - write pos 之间的部分 (蓝色),表示待刷盘的脏页对应的 redo log
73 |
74 | 当 write pos 追上 checkpoint 时,表示 redo log 文件组满了,不能再将 redo log 刷盘到文件组中
75 |
76 | 此时 MySQL 会阻塞,将 Buffer Pool 中的脏页刷新到磁盘,然后标记 redo log 文件组可以被擦除的部分,最后将可以被擦除的部分擦除,更新 checkpoint (顺时针向前移动)
77 |
78 | 所以,一次 checkpoint 的过程就是将脏页刷新到磁盘中,更新 redo log 日志组中可以被覆盖的位置
--------------------------------------------------------------------------------
/markdown/MySQL/两阶段提交.md:
--------------------------------------------------------------------------------
1 | # 两阶段提交
2 |
3 | ### 分布式事务
4 |
5 | MySQL 分为 server 层和存储引擎层,事务由存储引擎层实现。如果修改服务器 A 中数据库的数据的同时也需要修改服务器 B 中数据库的数据,这两个操作必须同时成功或者失败,也就是必须保证原子性
6 |
7 | 而这两个操作属于两个不同的数据库,存储引擎也不是同一个,无法保证两个操作的原子性。这个时候就需要一个全局事务,由若干个小事务组成,这个全局事务也被称作分布式事务
8 |
9 | ### XA 规范
10 |
11 | 有一个名叫 X/Open 的组织提出了 XA 的规范,用于规范分布式事务,也就是不同的存储引擎只要符合 XA 规范,就可以放到一个分布式事务中管理
12 |
13 | XA 规范提出了两个角色
14 |
15 | - **资源管理器:**全局事务中每一个小事务
16 | - **事务管理器:**管理全局事务中每一个小事务 (后文称之为协调者)
17 |
18 | 要提交一个全局事务,就必须保证所有小事务都要能顺利提交,否则所有事务都应该回滚。XA 规范指出,要提交一个全局事务,必须分两步:(点题)
19 |
20 | - **prepare 阶段:**每个小事务在该阶段会执行各自的事务,并将事务产生的 redo log 刷新到磁盘中,做好提交的准备
21 | - **commit 阶段:**协调者准备提交前,会询问每个小事务是否做好了提交的准备,如果都准备好了就直接提交,否则全部回滚
22 |
23 | ### 外部 XA 事务
24 |
25 | 在外部 XA 事务中,每个小事务在分布在不同的数据库服务器中。在 MySQL 使用 XA 事务的一些操作如下:
26 |
27 | - `XA {start|begin} xid`:开启一个 XA 事务,此时该 XA 事务处于 active 状态。xid 表示每个事务唯一的 id
28 |
29 | - `XA end xid`:告知服务器有 xid 标识的 XA 事务的所有语句全部输入,此时该 XA 事务处于 idle 状态
30 |
31 | - `XA prepare xid`:应用程序让处于 idle 状态的 XA 事务将产生的 redo log 刷新到磁盘中,做好提交的准备,此时该 XA 事务处于 prepare 状态
32 |
33 | - `XA commit xid [one phase]`:对于处于 prepare 状态的 XA 事务,应用程序可以发送`XA commit xid`让服务器提交,此时该 XA 事务处于 commit 状态
34 |
35 | - `XA rollback xid`:应用程序通过该语句让服务器回滚 xid 所标识的 XA 事务,此时该 XA 事务处于 abort 状态
36 |
37 | - `XA recover`:应用程序可以通过该语句查看处于 prepare 状态的 XA 事务
38 |
39 | 下面给出 XA 事务的状态转换图
40 |
41 | 
42 |
43 | ### 内部 XA 事务
44 |
45 | 在内部 XA 事务中,每个小事务可能分布在同一个数据库服务器的不同存储引擎中,或者在存储引擎和插件之间。下面以最典型的 binlog 和 redo log 展开讨论内部 XA 事务
46 |
47 | redo log 以 mtr 为单位添加到 redo log buffer 中,在事务提交时会刷盘,在事务提交前后台线程每隔 1s 刷盘;bilog 以事务为单位先添加到 binlog cache 中,等事务提交后刷新到磁盘中
48 |
49 | 由于 redo log 是存储引擎生成,binlog 是 server 层生成,无法保证这两个刷盘操作的原子性,而这两个操作必须要保证原子性,否则会出现一致性问题
50 |
51 | - 如果 redo log 刷盘成功,binlog 没有刷盘成功,在主从复制的架构中会导致主库和从库数据不一致,因为从库是根据 binlog 来复制数据
52 | - 如果 redo log 没有刷盘成功,binlog 刷盘成功,在主从复制的架构中会导致主库和从库数据不一致,因为主库是根据 redo log 来恢复数据
53 |
54 | 在客户端执行 commit 或者自动提交事务的情况下,MySQL 内部开启一个 XA 事务保证 redo log 和 binlog 刷盘的原子性,binlog 作为协调者,存储引擎作为参与者
55 |
56 | 
57 |
58 | 从上图可以看出,将 redo log 持久化拆分成两个阶段:prepare 和 commit,binlog 在中间穿插写入
59 |
60 | - **prepare 阶段:**先将 XID 写入到 redo log 中,然后将 redo log 刷盘,最后将 redo log 对应的事务设置为 prepare 状态
61 | - **commit 阶段:**先将 XID 写入到 binlog 中,然后将 binlog 刷盘,接着调用存储引擎提交事务接口将 redo log 状态设置为 commit,此状态不需要持久化,可以根据 binlog 中是否存在 XID 判断 redo log 状态
62 |
63 | 假设时刻 1 (redo log 刷盘成功,binlog 刷盘失败) 或者时刻 2 (redo log 和 binlog 都刷盘成功,但还没有写入 commit 标识) 系统挂了,此时的 redo log 都处于 prapare 阶段
64 |
65 | 在 MySQL 重启后会重写扫描 redo log 文件,碰到处于 prepare 状态的 redo log,就会去检查 binlog 中是否存在和 redo log 相同的 XID
66 |
67 | - 如果 binlog 中不存在相同 XID,表示 binlog 没有刷盘成功,直接回滚事务 (对应时刻 1)
68 | - 如果 binlog 中存在相同 XID,表示 binlog 刷盘成功,直接提交事务 (对应时刻 2)
69 |
70 | **总结:**是否回滚事务完全取决于 binlog 是否存在和 redo log 中相同的 XID,如果不存在就需要回滚,否则直接提交即可
71 |
--------------------------------------------------------------------------------
/markdown/MySQL/分库分表.md:
--------------------------------------------------------------------------------
1 | # 分库分表
2 |
3 | 本篇文章主要整理关于 MySQL 分库分表的一些概述,并没有很深入,主要是因为某人多次的拜托 (是谁我不说,自己发现叭)~~
4 |
5 | ### 分库分表判断标准
6 |
7 | 先开门见山,给出写本篇文章的导火索,分库分表的标准是什么?
8 |
9 | 其实分库分表的标准在阿里巴巴 Java 开发手册中提到过:**单表行数超过 500 万行或者单表容量超过 2GB,才推荐进行分库分表**
10 |
11 | **问题一:**是否当单表行数超过 500 万行或者单表容量超过 2GB,才开始分库分表?
12 |
13 | - 不是,如果可以预计 3 年后数据会超过这个量级,就应该在创建表的时候就进行分库分表
14 |
15 | **问题二:**如果 MySQL 服务器配置较好,是否可以超过 500 万这个量级?
16 |
17 | - 虽然服务器配置更好后,数据量过大时,性能也不错,但以发展的眼光看待,考虑分库分表更佳
18 |
19 | 下面主要介绍一下分库分表到底是什么?什么情况下会考虑分库分表?分库分表的方式有哪些?
20 |
21 | ### 什么是分库分表
22 |
23 | **分库**,顾名思义是将一个数据库中的表拆分到多个数据库中,如下图所示:
24 |
25 | 
26 |
27 | 每个数据库连接数都有限制,当并发量过大时,数据库连接数也会增大,这是决定是否分库的直接原因,如果连接数成为数据库的瓶颈时就需要考虑分库
28 |
29 | **分表**,顾名思义是将一个表拆分成多个表,如下图所示:
30 |
31 | 
32 |
33 | 阿里巴巴 Java 开发手册中推荐:单表行数超过 500 万行或者单表容量超过 2GB,才推荐进行分库分表,所以决定是否分表的标准是表中记录数和容量,如果当一个表中数据量过大时就需要考虑分表
34 |
35 | 其实,还可能同时分库分表,这就是既存在并发量过大,又存在单表容量过大的情况~
36 |
37 | **总结:**
38 |
39 | | 切分方案 | 解决问题 |
40 | | :----------: | :------------------------------------: |
41 | | 只分库不分表 | 数据库读/写 QPS 过高;数据库连接数不足 |
42 | | 只分表不分库 | 单表数据量过大,存储性能遇到瓶颈 |
43 | | 既分库又分表 | 连接数不足 + 单表数据量过大 |
44 |
45 |
46 |
47 | ### 如何分库分表
48 |
49 | 上一部分只是介绍了在何种情况下会考虑分库分表,那如果决定了要分库分表,该如何分呢??
50 |
51 | 其实分库分表都有两种不同的分法,垂直和水平,排列组合一下就有四种:垂直分表、水平分表、垂直分库、水平分库
52 |
53 | #### 垂直分表
54 |
55 | 将一张表按照字段切分成多个表,通常是根据字段的关系密集程度进行切分,也可以按照常用字段和不常用字段切分,如下图所示:
56 |
57 | 
58 |
59 | #### 水平分表
60 |
61 | 水平分表又被称为 Sharding,它是将同一个表中的记录拆分到多个结构相同的表中,如下图所示:
62 |
63 | 
64 |
65 | 当一个表中数据不断增多时,水平分表是必然的选择,它可以将数据分布到集群的不同节点上,从而缓解单个数据库的压力
66 |
67 | #### 垂直分库
68 |
69 | 按照业务将表进行分类,分布到不同的数据库中,每个数据库可以放到不同的服务器上,如下图所示:
70 |
71 | 
72 |
73 | #### 水平分库
74 |
75 | 把同一个表的数据按照一定规则拆分到不同的数据库中,每个数据库可以放到不同的服务器上。假设按照表中 id 的奇偶性将数据拆分到不同的数据库中,如下图所示:
76 |
77 | 
78 |
--------------------------------------------------------------------------------
/markdown/Network/DNS.md:
--------------------------------------------------------------------------------
1 | # DNS
2 |
3 | 每一台公网服务器都有一个公网 IP,通过 IP 可以访问它,但世界上服务器那么多,而且 IP 是一串数字,难免不容易记住对应的 IP 地址,所以就有了 DNS (Domain Name System,域名系统)
4 |
5 | DNS 记录了 IP 和域名的对应关系,在通信时需要使用 IP 地址,而域名更便于用户记住,所以用户通过域名访问一个网站时,域名服务器会自动将域名转换成 IP 地址
6 |
7 | 在配置计算机的 IP 相关信息时,往往会配置一个 DNS 服务器的 IP 地址,可以将它称之为本地 DNS 服务器,我们是借助它来获取域名对应的 IP 地址
8 |
9 | ### DNS 结构
10 |
11 | 所有的 DNS 域名服务器是一个树状结构,最上层的是根域,如下图所示:
12 |
13 | 
14 |
15 | ### IP 查询过程
16 |
17 | 下面模拟`www.baidu.com`的查询过程!先给出过程图:
18 |
19 | 
20 |
21 | **第一步:**询问配置的本地 DNS 服务器,`www.baidu.com`的 IP 地址是多少?如果本地 DNS 服务器发现自己本地缓存中没有对应的域名就去根域名服务器询问,如果有缓存中有直接返回给计算机
22 |
23 | **第二步:**本地 DNS 服务器询问根域名服务器,根域名服务器会让本地 DNS 服务器去询问`com`域名服务器
24 |
25 | **第三步:**本地 DNS 服务器询问`com`域名服务器,`com`域名服务器会让本地 DNS 服务器去询问`baidu`域名服务器
26 |
27 | **第四步:**本地 DNS 服务器询问`baidu`域名服务器,`baidu`域名服务器会让本地 DNS 服务器去询问`www`域名服务器
28 |
29 | **第五步:**本地 DNS 服务器询问`www`域名服务器,`www`域名服务直接返回对应的 IP 地址,本地 DNS 服务器会缓存「域名-IP」对应关系,但该缓存有时间期限,一段时间会过期
--------------------------------------------------------------------------------
/markdown/Network/GET-POST请求.md:
--------------------------------------------------------------------------------
1 | # GET && POST 请求
2 |
3 | 在 HTPP/1.1 中,一共有 get、post、put、head、delete、potions、trace、connect 八种不同的请求方法,但本篇文章只介绍最常用的两种 get 和 post
4 |
5 | ### GET
6 |
7 | GET 请求是**从服务器获取指定资源**,指定的资源经服务器返回给客户端,资源可以是静态文本、页面、图片视频等
8 |
9 | GET 请求的参数位置一般写在 URL 中,URL 只能支持 ASCII,所以 GET 请求的参数只允许是 ASCII 字符,而且浏览器会对 URL 长度有限制,HTTP 协议本身没有对 URL 长度做任何规定
10 |
11 | 下面给出一个 GET 请求的示例:`https://www.test.com/get?xxx=111&yyy=222`。该请求中有两个参数:`xxx = 111`和`yyy = 222`
12 |
13 | ### POST
14 |
15 | POST 请求是根据请求负载对指定资源做出处理,一般请求携带的数据会写在消息体中,消息体中的数据可以是任意格式,且浏览器不会限制消息体大小
16 |
17 | GET 请求侧重于获取指定的资源,而 POST 请求侧重于传输实体到服务器进行处理,如登陆时提交表格信息
18 |
19 | 下面给出一个 post 请求的示例:
20 |
21 | ```
22 | https://www.test.com/post
23 |
24 | xxx = 111
25 | yyy = 222
26 | ```
27 |
28 | 该请求体中有两个参数:`xxx = 111`和`yyy = 222`
29 |
30 | ### 安全和幂等
31 |
32 | 首先说一下安全和幂等着两个概念:
33 |
34 | - **安全:**在 HTTP 协议里,安全表示不会修改服务器中的数据,类似于只读操作
35 | - **幂等:**多次请求操作结果相同
36 |
37 | 很显然,GET 请求是安全且幂等的,而 POST 是不安全且不幂等的。所以 GET 请求返回的结果可以被缓存,而 POST 请求返回的结果不可以被缓存
38 |
--------------------------------------------------------------------------------
/markdown/Network/HTTP-状态码.md:
--------------------------------------------------------------------------------
1 | # HTTP 状态码
2 |
3 | 简单来讲,HTTP 状态码的作用是服务器告诉客户端当前请求**响应**的状态,通过状态码就能判断和分析服务器的运行状态
4 |
5 | 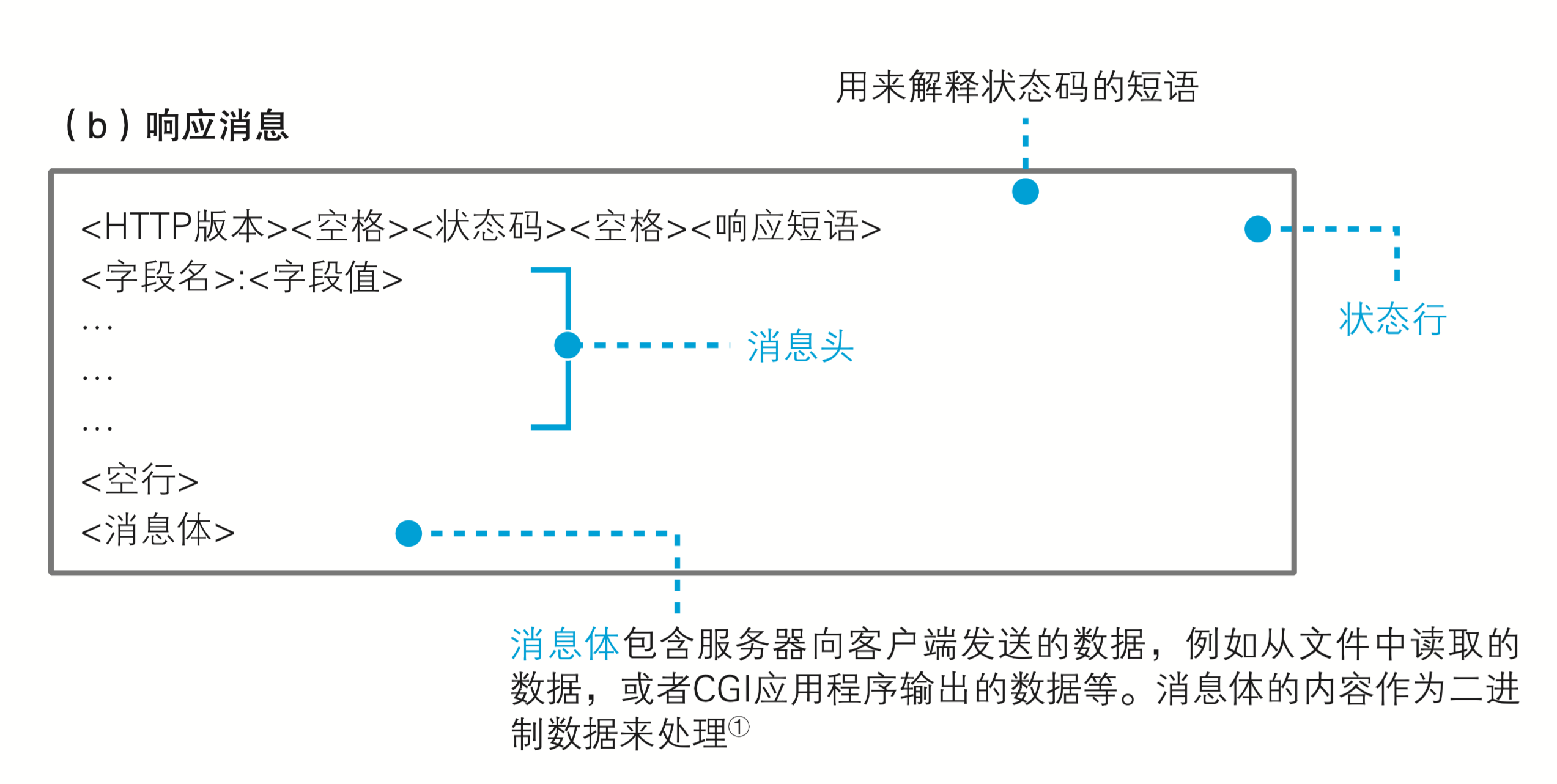 6 |
7 | 状态码的第一位数字表示状态类型,第二、三位数字表示具体的情况
8 |
9 | - **1xx:**表示接收的请求正在处理
10 | - **2xx:**表示请求正常处理完毕 (成功)
11 | - **3xx:**表示重定向
12 | - **4xx:**表示客户端错误
13 | - **5xx:**表示服务端错误
14 |
15 | ### 1xx
16 |
17 | 表示请求已被接受,需要继续处理。这类响应是临时响应,只包含「状态行」和某些可选的响应「头信息」,并以空行结束
18 |
19 | 常见的有:
20 |
21 | - **100 (继续):**这个为临时响应,表示迄今为止的所有内容都是可行的,客户端应该继续发送剩余请求,如果已经完成,则忽略它
22 | - **101 (切换协议):**服务器根据客户端的请求切换协议,主要用于 websocket 或 http2 升级
23 |
24 | ### 2xx
25 |
26 | 表示请求已成功被服务器接收、理解、并接受
27 |
28 | 常见的有:
29 |
30 | - **200 (成功):**请求已成功,请求所希望的响应头或数据体将随此响应返回
31 | - **201 (已创建):**请求成功并且服务器创建了新的资源
32 | - **202 (已创建):**服务器已经接收请求,但尚未处理
33 | - **203 (非授权信息):**服务器已成功处理请求,但返回的信息可能来自另一来源
34 | - **204 (无内容):**服务器成功处理请求,但没有返回任何内容。例如:删除请求或请求是通过表单发送的,响应不应导致刷新表单或加载新页面
35 | - **205 (重置内容):**将文档重置为原始状态。例如,清除表单
36 | - **206 (部分内容):**服务器成功处理了部分请求 (范围请求,服务器成功执行了该范围内的请求)
37 |
38 | ### 3xx
39 |
40 | 表示要完成请求,需要进一步操作。 通常,这些状态代码用来重定向
41 |
42 | 常见的有:
43 |
44 | - **300 (多种选择):**针对请求,服务器可执行多种操作。 服务器可根据请求者 (user agent) 选择一项操作,或提供操作列表供请求者选择
45 | - **301 (永久重定向):**请求的网页已永久移动到新位置。 服务器返回此响应 (对 GET 或 HEAD 请求的响应)时,会自动将请求者转到新位置
46 | - **302 (临时重定向):**服务器目前从不同位置的网页响应请求,但请求者应继续使用原有位置来进行以后的请求
47 | - **303 (查看其它位置):**请求者应当对不同的位置使用单独的 GET 请求来检索响应时,服务器返回此代码
48 | - **304 (缓存重定向):**表示资源没有被修改,可以重定向到缓存文件
49 | - **305 (使用代理):**请求者只能使用代理访问请求的网页。 如果服务器返回此响应,还表示请求者应使用代理
50 | - **307 (临时重定向):**服务器目前从不同位置的网页响应请求,但请求者应继续使用原有位置来进行以后的请求 (和 302 相同)
51 |
52 | ### 4xx
53 |
54 | 表示客户端有错误,妨碍了服务器的处理
55 |
56 | 常见的有:
57 |
58 | - **400 (错误请求):**请求报文中存在语法错误
59 | - **401 (未授权):**请求要求身份验证。对于需要登录的网页,服务器可能返回此响应
60 | - **403 (禁止):**服务器拒绝请求
61 | - **404 (未找到):**服务器找不到请求的网页
62 | - **405 (方法禁用):**禁用请求中指定的方法
63 | - **406 (不接受):**无法使用请求的内容特性响应请求的网页
64 | - **407 (需要代理授权):**此状态代码与 401 (未授权)类似,但指定请求者应当授权使用代理
65 | - **408 (请求超时):**服务器等候请求时发生超时
66 |
67 | ### 5xx
68 |
69 | 表示服务器有错误,在处理请求的过程中有错误或者异常状态发生
70 |
71 | 常见的有:
72 |
73 | - **500 (服务器内部错误):**服务器遇到错误,无法完成请求
74 | - **501 (尚未实施):**服务器不具备完成请求的功能。 例如,服务器无法识别请求方法时可能会返回此代码
75 | - **502 (错误网关):**服务器作为网关或代理,从上游服务器收到无效响应
76 | - **503 (服务不可用):**服务器目前无法使用 (由于超载或停机维护)
77 | - **504 (网关超时):**服务器作为网关或代理,但是没有及时从上游服务器收到请求
78 | - **505 (HTTP 版本不受支持):**服务器不支持请求中所用的 HTTP 协议版本
79 |
80 | ### 适用场景
81 |
82 | **100:**客户端在发送 POST 数据给服务器前,征询服务器情况,看服务器是否处理POST的数据,如果不处理,客户端则不上传 POST 数据,如果处理,则 POST 上传数据。常用于 POST 大数据传输
83 |
84 | **206:**一般用来做断点续传,或者是视频文件等大文件的加载
85 |
86 | **301:**永久重定向会缓存。新域名替换旧域名,旧的域名不再使用时,用户访问旧域名时用 301 就重定向到新的域名
87 |
88 | **302:**临时重定向不会缓存,常用 于未登陆的用户访问用户中心重定向到登录页面
89 |
90 | **304:**协商缓存,告诉客户端有缓存,直接使用缓存中的数据,返回页面的只有头部信息,是没有内容部分
91 |
92 | **400:**参数有误,请求无法被服务器识别
93 |
94 | **403:**告诉客户端进制访问该站点或者资源,如在外网环境下,然后访问只有内网 IP 才能访问的时候则返回
95 |
96 | **404:**服务器找不到资源时,或者服务器拒绝请求又不想说明理由时
97 |
98 | **503:**服务器停机维护时,主动用 503 响应请求或 Nginx 设置限速,超过限速,会返回 503
99 |
100 | **504:**网关超时
--------------------------------------------------------------------------------
/markdown/Network/HTTP-缓存策略.md:
--------------------------------------------------------------------------------
1 | # HTTP 缓存策略
2 |
3 | 当使用浏览器访问一个 Web 资源时,为了提高访问效率,往往会在浏览器和服务器之间增加本地缓存
4 |
5 | 对于首次访问,会将服务器响应的数据缓存到本地;对于后续的访问,会根据缓存策略决定是否直接使用本地缓存。简化的流程如下图所示:
6 |
7 | 
8 |
9 | **注意:**缓存策略完全是根据服务器响应消息的头信息来决定滴!!
10 |
11 | ### 与缓存有关的消息头字段
12 |
13 | 先给出与缓存有关的消息头字段的一些说明:
14 |
15 | 
16 |
17 | ### 强制缓存
18 |
19 | 顾名思义,强制缓存不需要服务器的参与,浏览器可以自己决策是否使用缓存,决策规则如下:
20 |
21 | - 如果本地缓存中不存在要请求的资源,浏览器会直接将请求发送到服务器,完成首次资源请求,根据服务器响应的消息保存相关信息
22 | - 如果本地缓存中存在要请求的资源,先判断缓存是否过期,如果没有过期直接使用本地缓存,如果过期就需要根据下面要介绍的协商缓存进行处理
23 |
24 | 在响应消息中,Expires 是根据 Last-Modified 和 max-age 计算出来的,max-age 表示存活多少秒后过期,而 Last-Modified 表示最后的修改时间
25 |
26 | 如果一个请求直接强制使用缓存,那么该请求会显示`200 OK (from disk cache)`,如下所示:
27 |
28 | ```
29 | Request URL: http://192.168.124.13:8080/index.html
30 | Request Method: GET
31 | Status Code: 200 OK (from disk cache)
32 | Remote Address: 192.168.124.13:8080
33 | Referrer Policy: strict-origin-when-cross-origin
34 | ```
35 |
36 | ### 协商缓存
37 |
38 | 顾名思义,协商缓存是浏览器和服务器共同协商是否使用本地缓存,浏览器负责提供本地缓存的信息,如:最后修改时间和唯一标识,添加在请求消息头中,服务器收到消息后来决策是否允许浏览器使用本地缓存
39 |
40 | If-Modified-Since 和 If-None-Match 是在浏览器第一次发送请求到服务器时,从服务器的响应消息保存。如果浏览器发现本地缓存中不存在要请求的资源,会直接将请求发送到服务器
41 |
42 | 协商缓存基于两种消息头字段实现:
43 |
44 | - **第一种:**请求头中的 If-Modified-Since 和响应头中的 Last-Modified
45 | - **第二种:**请求头中的 If-None-Match 和响应头中的 Etag
46 |
47 | 对于第一种,如果 If-Modified-Since 时间小于 Last-Modified,表示本地缓存中是旧数据,不可以使用本地缓存中的数据,否则可以使用缓存
48 |
49 | 对于第二种,如果 If-None-Match 和 Etag 不相等,表示本地缓存中是旧数据,不可以使用本地缓存中的数据,否则可以使用缓存
50 |
51 | 如果一个请求消息头中同时包含 If-Modified-Since 和 If-None-Match 字段,那么 If-None-Match 优先级更高。先判断 If-None-Match,如果不匹配直接无法使用缓存,如果匹配,再根据 If-Modified-Since 判断
52 |
53 | **问题:**为什么 Etag 的优先级更高??
54 |
55 | Etag 是服务器中资源的唯一标识,它可以解决一些 Last-Modified 难以解决的问题
56 |
57 | - 可能存在文件没有被修改,但修改时间却发生了改变的情况
58 | - Last-Modified 的精度是秒,对于秒以内的变化,Last-Modified 无法感知;但 Etag 却可以保证秒以内多次修改都可以被感知
59 |
60 | **强制缓存和协商缓存区别:**强制缓存不需要将请求发送给服务器,浏览器自己可以决策;协商缓存需要将请求先发送给服务器,由服务器决策,如果可以使用缓存会响应一个 **[304](./HTTP-状态码.html#3xx)** 的消息,表示缓存重定向
61 |
62 | ### 总流程图
63 |
64 | 下面给出缓存策略的总体流程图:
65 |
66 | 
67 |
68 | **注意:**
69 |
70 | - 使用 F5 刷新网页时,跳过强制缓存,但会检查协商缓存
71 | - 使用 ctrl + F5 刷新页面时,直接从服务器加载,跳过强制缓存和协商缓存
72 |
73 | ### 参考文章
74 |
75 | - **[HTTP 缓存技术](https://xiaolincoding.com/network/2_http/http_interview.html#http-缓存技术)**
76 | - **[彻底弄懂浏览器缓存策略](https://mp.weixin.qq.com/s/Ui7Q9k4faiD5mv_LfB4Rrw)**
77 | - **[Cache-Control在请求头和响应头里的区别](https://juejin.cn/post/6960988505816186894)**
78 | - **[为什么我的缓存设置在 chrome 中不生效](https://xie.infoq.cn/article/70b359ab1210efb6f5b253e24)**
79 | - **[Cache-Control和Expires无效的原因](https://www.cnblogs.com/jimaww/p/10234074.html)**
--------------------------------------------------------------------------------
/markdown/Network/SYN-泛洪攻击.md:
--------------------------------------------------------------------------------
1 | # SYN 泛洪攻击
2 |
3 | ### 半连接 & 全连接
4 |
5 | 在 TCP 三次握手的时候,Linux 内核会维护两个队列:
6 |
7 | - 半连接队列,也称 SYN 队列,只进行了一次握手的连接
8 | - 全连接队列,也称 Accept 队列,进行了三次握手的连接
9 |
10 | 
11 |
12 | 关于出队和入队的详细流程如下:
13 |
14 | - 当服务器收到客户端的 SYN 报文时,会创建一个半连接对象,并加入到内核的 SYN 队列中
15 | - 接着服务器发送 SYN-ACK 报文给客户端,等待客户端的 ACK 报文
16 | - 当服务器收到客户端的 ACK 报文时,会取出一个半连接对象,然后创建一个新的连接对象加入 Accept 队列中
17 | - 应用程序通过调用 Socket 提供的`accept()`方法,从 Accept 队列中取出一个连接对象
18 |
19 | **注意:**不管是半连接队列还是全连接队列,都有最大长度限制,超过限制时都会丢弃报文!!
20 |
21 | ### SYN 泛洪攻击是什么
22 |
23 | 客户端和服务器使用 TCP 协议通信前需要进行三次握手建立连接,当服务器收到客户端第一次握手的 SYN 报文后,会发送 SYN-ACK 报文,之后服务器处于 SYN_RECV 状态。**更详细可见 [三次握手](./TCP-三次握手-四次挥手.html#tcp-三次握手过程)**
24 |
25 | **SYN 泛洪攻击:**攻击者会伪造大量不同 IP 的 SYN 报文,服务器收到 SYN 报文后会向客户端发送 SYN-ACK 报文,但攻击者不会回应该报文,这样会逐渐占满半连接队列,使得后续正常连接请求直接被丢弃
26 |
27 | ### 如何避免 SYN 泛洪攻击
28 |
29 | #### 方法一:调大 netdev_max_backlog
30 |
31 | 当网卡接收数据的速度大于内核处理的速度时,会有一个队列保存这些数据包。控制该队列的大小,默认值为 1000,可以通过参数调整为 100000
32 |
33 | ```bash
34 | net.core.netdev_max_backlog = 10000
35 | ```
36 | #### 方法二:增加 TCP 半连接队列大小
37 |
38 | 增大 TCP 半连接队列,要同时增大下面这三个参数:
39 |
40 | - 增大 net.ipv4.tcp_max_syn_backlog
41 | - 增大 listen() 函数中的 backlog
42 | - 增大 net.core.somaxconn
43 |
44 | #### 方法三:开启 net.ipv4.tcp_syncookies
45 |
46 | 开启 net.ipv4.tcp_syncookies 后可以不需要加入到 SYN 半连接队列中,也可以成功建立连接
47 |
48 | #### 方法四:减少 SYN + ACK 重发次数
49 |
50 | 攻击者不会回应服务器的 SYN-ACK 包,服务器会超时重发,在 Linux 默认重发 5 次,可以适当降低重发的次数使处于 SYN_RECV 状态的服务器尽快断开连接
--------------------------------------------------------------------------------
/markdown/Network/Solutions-7th-Edition.docx:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/LFool/LFool-Notes/8d4b7b3aa2f91cd51aa57427d016d86db8712e05/markdown/Network/Solutions-7th-Edition.docx
--------------------------------------------------------------------------------
/markdown/Network/网络层那点事儿.md:
--------------------------------------------------------------------------------
1 | # 网络层那点事儿~
2 |
3 | ### 网络层和链路层
4 |
5 | 传输层提供端到端的可靠传输,也就是不同主机中的进程间通信,通过端口唯一确认主机中的进程,TCP 报文首部也有端口字段,**详情可见 [TCP 报文段格式](./TCP-三次握手-四次挥手.html)**
6 |
7 | 网络层负责将数据从一台主机传输到另一台主机,往往这两台主机在物理上没有直接相连;而链路层也是负责将数据从一台主机传输到另一台主机,往往这两台主机在物理上直接相连
8 |
9 | 下面主要介绍网络层和链路层是如何相互配合将数据从一台主机传输到另一台主机。网络层通过 IP 地址定义一台主机,链路层通过 MAC 地址定位一台主机。下面模拟一种场景,如下图所示:
10 |
11 | 
12 |
13 | **注意:**路由器的每个端口都有一个 IP 地址和 MAC 地址
14 |
15 | 主机 A 向主机 B 发送数据,它们俩在物理上没有直接相连,需要依赖网络层将数据从主机 A 发送到主机 B
16 |
17 | - **第一步:**主机 A 将数据包发送给路由器,此时会通过 ARP 协议获取路由器的 MAC 地址,将报文中的源 MAC 地址设置为主机 A,目标 MAC 地址设置为路由器。链路层根据源/目标 MAC 地址将数据包从主机 A 发送给路由器,因为它俩在物理上直接相连
18 | - **第二步:**路由器将数据包发送给主机 B,将报文中的源 MAC 地址设置为路由器,目标 MAC 地址设置为主机 B。链路层根据源/目标 MAC 地址将数据包从路由器发送给主机 B,因为它俩在物理上直接相连
19 |
20 | 可以看出数据包在传输过程中,报文的源/目标 IP 地址始终保持不变,分别为:`10.0.1.2`和`10.0.5.6`,变化的是 MAC 地址。网络层负责根据 IP 地址寻址➕路由,而链路层负责将数据在两个物理上相邻的节点中传输!!
21 |
22 | **注意:**由于 MAC 地址在网络层封装,所以有些说法认为 ARP 属于网络层,有些说法认为 ARP 属于链路层,但这不重要,只要理解这个过程即可
23 |
24 | ### IP 分类
25 |
26 | IP 主要分为五类:A 类地址、B 类地址、C 类地址、D 类地址、E 类地址,但这里只想简单给出公有 IP 和私有 IP 的分类
27 |
28 | 简单来说,公有 IP 是网络中所有人都可以访问的 IP,而私有 IP 只有在同一个局域网中的人才可以访问。公有 IP 不允许重复;同一个局域网中的私有 IP 不允许重复,但在不同的局域网中可以重复
29 |
30 | 私有 IP 只有三种范围,如下:
31 |
32 | - 10.0.0.0 - 10.255.255.255
33 | - 172.16.0.0 - 172.31.255.255
34 | - 192.168.0.0 - 192.168.255.255
35 |
36 | 在这三个范围之外的所有 IP 都是公有 IP!!
37 |
38 | ### 路由控制
39 |
40 | 上文说:网络层负责将数据从一台主机传输到另一台主机,往往这两台主机在物理上没有直接相连。那么它是如何将数据从一台主机传输到另一台主机呢?
41 |
42 | 网络层有一个重要的设备:路由器,它内部有一张路由转发表,根据目标 IP 地址可以知道该数据包从路由器的哪一个端口转发出去。回到第一部分的例子中,先将例子扩展的更丰富一些,如下图所示:
43 |
44 | 
45 |
46 | 上图中 IP 数据包的源 IP 地址为`10.1.1.30`,目标 IP 地址为`10.1.2.10`
47 |
48 | **第一步:**主机 A 根据目标 IP 地址匹配到`0.0.0.0/0`,那么下一跳就是`10.1.1.1`。这里的`0.0.0.0/0`就是默认路由,在没有匹配到其它路由时就会匹配默认路由,默认路由的下一跳就是默认网关
49 |
50 | **第二步:**路由器根据目标 IP 地址匹配到`10.1.2.0/24`,那么下一跳就是`10.1.0.2`
51 |
52 | **第三步:**路由器根据目标 IP 地址匹配到`10.1.2.0/24`,那么下一跳就是`10.1.2.1`,最终通过交换机将数据发送给目标主机
53 |
54 | ### IP 分片与重组
55 |
56 | 数据链路层的传输单位是帧,不同的数据链路有不同的最大传输单元 (MTU),以太网的 MTU 是 1500 字节。换句话说,MTU = IP 首部 + TCP 首部 + 数据,一旦「IP 首部 + TCP 首部 + 数据」超过了 MTU,那么就会分片
57 |
58 | 在 TCP 中,如果数据长度 > MTU - IP 首部 - TCP 首部,就会进行分片;在网络层中,如果 TCP 首部 + 数据 > MTU - IP 首部,也会进行分片
59 |
60 | 如果 TCP 不分片,仅仅在网络层分片,那么一旦某个分片数据丢失,TCP 需要重传整个数据,因为 TCP 需要保证数据的可靠性,而网络层不需要保证数据的可靠性
61 |
62 | 所以 TCP 也会进行分片,如果某个分片数据在传输过程中丢失,那么只需要重传该分片数据即可,不需要重传所有数据
63 |
64 | 一般来说,TCP 分片已经考虑了 IP 首部的长度,所以在网络层不会超过长度,也就不会再进行分片,但存在一些特殊情况需要在 TCP 分片后,网络层还需要继续分片,如传输链路中存在更小的 MTU
65 |
66 | **详情分析可见 [TCP分段了,IP层就一定不会分片了吗?](https://zhuanlan.zhihu.com/p/372863051)**
--------------------------------------------------------------------------------
/markdown/Network/计算机网络(top-down)-习题&实验.md:
--------------------------------------------------------------------------------
1 | # 计算机网络(top-down) - 习题 & 实验
2 |
3 | ## 第一章
4 |
5 | ### 习题
6 |
7 | 1. “主机”和“端系统”之间有什么不同?列举几种不同类型的端系统。Web 服务器是一种端系统吗?
8 |
9 |
10 |
11 | 2.
12 |
13 | ### 实验
14 |
15 |
--------------------------------------------------------------------------------
/markdown/OS/CPU缓存一致性.md:
--------------------------------------------------------------------------------
1 | # CPU 缓存一致性
2 |
3 | ### 存储器层次结构
4 |
5 | 在计算机系统中,最常见的存储器有内存和磁盘。一个进程运行过程中往往需要将磁盘中的数据加载到内存中才可以访问
6 |
7 | CPU 的运算速度和内存的访问速度相差过大,为了缓解这种差距,在 CPU 和内存之间增加了高速缓存。由于 CPU 是基于寄存器的指令集,所以在 CPU 和高速缓存之间还存在寄存器
8 |
9 | 存储器离 CPU 越近,那么读写速度就越快,但能存储的容量也就越小。一个存储器的层次结构如下图所示:
10 |
11 | 
12 |
13 | 在现在的 CPU 中一般都有多个核心,寄存器、L1 高速缓存、L2 高速缓存都是每个核心独有,而 L3 高速缓存是 CPU 独有,如下图所示:
14 |
15 | 
16 |
17 | ### CPU Cache 结构
18 |
19 | 每个 CPU Cache 都是由缓存行构成,而且 CPU 和 CPU Cache 的交互单位也是缓存行,也就是如果 Cache 中没有数据,CPU 会一次性从内存中读取和缓存行相同大小的数据存入 Cache 中
20 |
21 | CPU Cache 的结构如下图所示:
22 |
23 | 
24 |
25 | 在使用 CPU Cache 的过程中,可能会出现伪共享问题,这也是下面要介绍的 MESI 协议导致的。**关于伪共享的分析可见 [伪共享](../java/伪共享.html)**
26 |
27 | ### CPU Cache 数据写入
28 |
29 | 对于读操作来说很简单,每次先去 Cache 中检查是否有数据,如果有数据就直接返回,如果没有数据就去内存中读,并将读到的数据加到 Cache 中以便下次可以快速读
30 |
31 | 但是对于写操作可能就麻烦一点,这里可以借鉴 **[Redis 缓存更新策略](../redis/Redis缓存更新策略.html)**,下面主要介绍两种写入策略:
32 |
33 | - **写穿透 (Write Through):**如果 Cache 中有数据,先更新 Cache,后更新内存;如果 Cache 中没有数据,直接更新内存
34 | - **写回 (Write Back):**先只更新 Cache,随后异步更新内存
35 |
36 | ### CPU 缓存一致性问题
37 |
38 | 不同线程在不同核心上执行,每个核心存在自己独有的 Cache。由于不可见性,同一个共享变量,可能出现在不同 Cache 中不一致的问题,**原理可见 [处理器重排序](../java/Java内存模型.html#处理器重排序)**
39 |
40 | 要解决缓存不一致的问题,必须保证下面两点:
41 |
42 | - 某个 CPU 核心更新 Cache 中的数据时,其它 CPU 核心必须知道该数据被更新了,这被称为**写传播 (Write Propagation)**
43 | - 所有 CPU 核心看到 Cache 中数据的修改操作顺序必须是一致性的,这被称为**事务的串行化 (Transaction Serialization)**
44 |
45 | 对于第一点使用总线嗅探机制,当某个 CPU 核心更新 Cache 中的数据时,会向总线广播这一事件,所有 CPU 核心都会监听总线上的广播事件,当发现广播事件中包含的数据也存在于自己的 Cache 中时,就会将自己 Cache 中的数据更新成广播中的数据
46 |
47 | 但仅仅做到第一点并不能完全解决缓存不一致的问题,假设存在两个 CPU 核心先后将`i`修改成 100 和 200,但无法保证这两个修改的广播事件的先后顺序,可能出现某个 CPU 核心看到的顺序:先将`i`修改为 200,再将`i`修改为 100,这也是第二点要保证事务串行化执行的原因
48 |
49 | ### MESI 协议
50 |
51 | MESI 协议基于总线嗅探机制实现了事务串行化,该协议保证了缓存一致性。首先,MESI 协议规定了四种状态:
52 |
53 | - **Modified** 已修改:表示 Cache 中的数据已经被修改过,也就是脏数据
54 | - **Exclusive** 独占:表示 Cache 中的数据被自己独占,其它 CPU Cache 中没有该数据,此时数据是干净的
55 | - **Shared** 共享:表示多个 CPU Cache 中都有该数据,此时数据是干净的
56 | - **Invalidated** 已失效:表示 Cache 中的数据无效
57 |
58 | 下面通过表格给出这四种状态之间的转化关系:
59 |
60 | 
61 |
62 | **注意:**如果在独占状态或者已修改状态下写数据,不需要广播该事件。如果是独占状态,表示其它核心的 Cache 中没有该数据,所以不需要广播;如果是已修改状态,表示包含该数据的核心的 Cache 中对应的 Cache Line 已经是已失效状态,所以也不需要广播
63 |
64 | 这里推荐一个可视化网站,可以看到 Cache 四个状态的转换 **[VivioJS MESI animation help](https://www.scss.tcd.ie/Jeremy.Jones/VivioJS/caches/MESIHelp.htm)**
--------------------------------------------------------------------------------
/markdown/OS/中断.md:
--------------------------------------------------------------------------------
1 | # 中断
2 |
3 | ### 用户态 & 内核态
4 |
5 | 用户进程不可以直接操作系统资源,因为如果给予进程的权利过大,可能会出现一些非法的访问,导致系统处于不安全的状态。基于这种原因,将系统所处状态分为用户态和内核态:
6 |
7 | - **用户态:**CPU 只能受限的访问内存,并且不允许访问敏感的系统资源,如:I/O 设备
8 | - **内核态:**CPU 可以访问任意数据,包括系统资源,还可以决定切换进程
9 |
10 | 当一个用户进程需要访问硬件资源时,需要进行系统调用,让操作系统去访问硬件资源,然后将结果返回给用户进程。系统调用相当于内核提供给用户的一套 API,通过 API 可以间接完成对硬件的访问
11 |
12 | 在系统启动时内核会设置好陷阱表,该表中存放了陷阱类型和内核代码位置的对应关系,也就是如果执行到陷阱 A,就会去执行陷阱 A 对应的内核代码
13 |
14 | 当用户线程系统调用时,会执行特殊的陷阱指令,该指令会从用户态转化到内核态,进而去执行该陷阱对应的内核代码。当操作系统执行完对应代码后,会从内核态转化到用户态
15 |
16 | 操作系统也算是一种软件,在单核 CPU 中,如果用户进程在 CPU 上执行,那么操作系统是无法执行滴,只有当用户态转化到内核态,操作系统才可以在 CPU 上执行。所以系统调用不仅从用户态转化到内核态,而且还相当于进行了一次上下文切换,从用户进程切换到操作系统进程
17 |
18 | 下面是通过系统调用完成上下文切换的过程:
19 |
20 | 
21 |
22 | ### 时钟中断
23 |
24 | 对系统资源的访问、上下文切换等操作都需要操作系统来执行。系统调用可以从用户态切换到内核态,让控制权重新回到操作系统手中,但如果一个进程始终都不进行系统调用呢?那就会出现一直不能切换到内核态,从而卡死的情况
25 |
26 | 为了避免这种情况的发生,提出了时钟中断。时钟设备可以每隔几毫秒就生成一次中断,中断产生时,当前正在运行的程序停止,操作系统中预先配置的中断程序会运行,此时操作系统重新获得了 CPU 的控制权
27 |
28 | 下面是通过时钟中断完成上下文切换的过程:
29 |
30 | 
31 |
32 | ### 软中断
33 |
34 | 在处理中断时,中断处理程序会将中断关闭,如果处理时间过长,可能会丢失其它设备的中断信号。为了避免丢失中断信号,将原来的整个中断过程分为两部分:
35 |
36 | - **第一部分:**快速处理中断,该阶段会暂时关闭中断,但一般该阶段耗时较短,只会处理与硬件相关敏感的事情
37 | - **第二部分:**交由操作系统完成中断剩余工作,该阶段会将中断打开,不会丢失中断信号
38 |
39 | 可以将第一部分看作是硬中断,也就是会关闭中断的中断;可以将第二部分看作是软中断,也就是不会关闭中断的中断。软中断可以大大降低中断信号丢失的风险
40 |
41 | ### 参考文章
42 |
43 | - **操作系统导论**
44 | - **[什么是软中断?](https://xiaolincoding.com/os/1_hardware/soft_interrupt.html)**
--------------------------------------------------------------------------------
/markdown/Redis/Redis缓存更新策略.md:
--------------------------------------------------------------------------------
1 | # Redis 缓存更新策略
2 |
3 | 缓存能够有效地加速应用的读写速度,因为它基于内存,减少了磁盘 IO 的开销。但它也存在数据不一致的问题,因为缓存层和存储层的数据存在着一定**时间窗口**的不一致性
4 |
5 | 给出加入缓存层的结构图:
6 |
7 | 
8 |
9 | 下面介绍三种缓存更新策略,没有最优,只有根据业务场景最合适!!
10 |
11 | ### 旁路缓存模式 (Cache Aside Pattern)
12 |
13 | 旁路缓存模式是平时使用较多的一个读写缓存模式,比较**适合于读请求较多的场景**
14 |
15 | 写操作的步骤:
16 |
17 | - 更新 DB
18 | - 直接删除 Cache
19 |
20 | 读操作的步骤:
21 |
22 | - 从 Cache 中读取数据,读取到就直接返回
23 | - 如果 Cache 读取不到,从 DB 中读取数据返回
24 | - 将 DB 中读取到的数据写入 Cache 中
25 |
26 | 
27 |
28 | **问题一:先更新 DB,再删除 Cache,能保证数据一致性吗?**
29 |
30 | 理论上来说还是可能会出现数据不一致的问题,但概率很小,因为删除 Cache 的操作速度快,使 Cache 中和 DB 中数据不一致的时间窗口很短
31 |
32 | 只有在不一致时间窗口内读数据才会出现数据不一致问题,即:读到旧值,如下图
33 |
34 | 
35 |
36 | 下面举一个数据不一致的例子:线程 1 写数据 A,随后线程 2 读数据 A。正确的情况下线程 2 读到的应该是数据 A 的新值,但如果以下面的顺序执行:
37 |
38 | - 线程 1 更新 DB
39 | - 线程 2 读数据 A,直接从缓存中读取并返回,但缓存中是旧值
40 | - 线程 1 删除 Cache
41 |
42 | 此时线程 2 读到的是数据 A 的旧值
43 |
44 | **问题二:为什么删除 Cache,而不是更新 Cache?**
45 |
46 | - 浪费服务端资源:不确定新写入的数据是否会被访问,而且 Cache 存放的数据一般需要经过服务端大量的计算。如果不会被访问又进行了大量的计算,无疑是白白浪费资源
47 | - 增加数据不一致的概率:更新 Cache 比 删除 Cache 更加耗时,所以会增大不一致时间窗口的大小,进而提高数据不一致性的概率
48 |
49 | 
50 |
51 | **问题三:可以先删除 Cache,后更新 DB 吗?**
52 |
53 | 显然不可以,这样会导致数据不一致的时间窗口变大,进而增加了出现数据不一致问题的概率
54 |
55 | 
56 |
57 | 下面举一个数据不一致的例子:线程 1 写数据 A,随后线程 2 读数据 A。正确的情况下线程 2 读到的应该是数据 A 的新值,但如果以下面的顺序执行:
58 |
59 | - 线程 1 删除 Cache
60 | - 线程 2 读数据 A,此时缓存中没有数据,从 DB 中读取并返回,同时存入 Cache 中,Cache 中存入的是旧值
61 | - 线程 1 更新 DB
62 |
63 | 此时线程 2 读到的是数据 A 的旧值,而且 Cache 存入的也是旧值。如果 Cache 没有设置过期时间且未来一段时间没有新的写操作,那么后面读数据 A 时全都是 Cache 中的旧值!!
64 |
65 | **缺陷一:首次请求数据不在 Cache 中**
66 |
67 | - 可以提前将热点数据放入 Cache 中
68 |
69 | **缺陷二:写操作频繁会导致 Cache 中数据频繁被删,会影响命中率?**
70 |
71 | - 对于要求数据强一致性的场景:更新 DB 的同时更新 Cache,但需要用分布式锁保证这两个更新的原子性,否则存在线程安全问题
72 | - 对于可接受短暂数据不一致的场景:更新 DB 的同时更新 Cache,为 Cache 设置一个较短的过期时间
73 |
74 | ### 读写穿透 (Read/Write Through Pattern)
75 |
76 | **核心思想:**更新 DB,缓存存在就更新,不存在就不管
77 |
78 | 读写穿透将 Cache 作为主要的数据存储,从中读取并将数据写入其中,Cache 服务自己负责将此数据读取和写入 DB,从而减轻了程序员的职责
79 |
80 | 这种模式平时使用很少,大概率因为 Redis 分布式缓存并没有提供 Cache 将数据写入 DB 的功能
81 |
82 | 写操作的步骤:
83 |
84 | - 先检查 Cache,如果 Cache 没有,直接更新 DB
85 | - 如果 Cache 中存在,直接更新 Cache,然后 Cache 服务会自己更新 DB
86 |
87 | 读操作的步骤:
88 |
89 | - 从 Cache 中读取数据,读取到就直接返回
90 | - 如果 Cache 读取不到,先从 DB 中加载,写入 Cache 后返回
91 |
92 | 
93 |
94 | ### 异步缓存写入 (Write Back Pattern)
95 |
96 | **核心思想:**只更新缓存,异步更新 DB
97 |
98 | 异步缓存写入和读写穿透很相似,两者都是由 Cache 服务来负责 Cache 和 DB 的读写。它们俩最大的不同在于:读写穿透是同步更新 Cache 和 DB;而异步缓存写入是异步更新 DB
99 |
100 | 消息队列中消息的异步写入磁盘、MySQL 的 InnoDB Buffer Pool 机制都用到了这种策略
101 |
102 | 异步缓存写入下 DB 的写性能非常高,非常适合一些数据经常变化又对数据一致性没有那么高的要求的场景,如:浏览量、点赞量等
--------------------------------------------------------------------------------
/markdown/Redis/Redis阻塞.md:
--------------------------------------------------------------------------------
1 | # Redis 阻塞
2 |
3 | Redis 是典型的单线程架构,所有的读写操作都是在一条主线程中完成,所以如果主线程被阻塞,就会直接影响到应用系统。本篇文章来盘点一下 Redis 中阻塞的常见情况
4 |
5 | ### 命令阻塞
6 |
7 | 虽然 Redis 是基于内存的数据库,但如果执行的命令时间复杂度过高,就会导致主线程阻塞。下面命令的时间复杂度均为`O(n)`,随着数据规模的增加,执行时间也会变长
8 |
9 | - `keys *`:获取所有的 key
10 | - `hgetall`:获取哈希表中所有
11 | - `smembers`:返回集合中的所有成员
12 | - ...
13 |
14 | **所以尽量使用时间复杂度低的命令!!!**
15 |
16 | ### RDB 阻塞
17 |
18 | RDB 是 Redis 持久化的一种机制,**详情可见 [Redis 持久化机制 - RDB](./Redis持久化机制.html#rdb)**
19 |
20 | 生成 RDB 文件有两种命令:
21 |
22 | - `save`:阻塞主线程,直至 RDB 文件创建完毕为止,阻塞期间 Redis 不可以处理任何其它命令
23 | - `bgsave`:执行`fork()`创建子进程,由子进程负责创建 RDB 文件,服务器没有被阻塞,可以正常处理其它命令
24 |
25 | **所以尽量使用`bgsave`命令创建 RDB 文件!!!**
26 |
27 | ### AOF 阻塞
28 |
29 | AOF 是 Rdis 持久化的一种机制,**详情可见 [Redis 持久化机制 - AOF](./Redis持久化机制.html#aof)**
30 |
31 | AOF 持久化一共有四步:命令写入、文件同步、文件重写、重启加载,在文件同步和文件重写时会发生阻塞
32 |
33 | 对于第一步的文件写入,其实只写到了 aof_buf 缓存,还没有写入到文件中;在文件同步时选择写入文件的策略,一共三种:always、everysec、no
34 |
35 | - always:对于每条写入命令,由后台线程立即调用`fsync`阻塞式写入到磁盘中
36 | - everysec:对于每条写入命令,主线程先执行`write`系统调用写入到 aof_buf 缓存,然后由后台线程按每秒一次的频率调用`fsync`阻塞式将缓存写入到磁盘中
37 | - no:对于每条写入命令,执行`write`系统调用写入到 aof_buf 缓存,同步到磁盘由操作系统决定,一般 30s 一次
38 |
39 | 当刷盘频率过高,导致磁盘 IO 开销大,后台刷盘线程需要阻塞到完成后才返回。如果主线程发现距离上一次的`fsync`成功超过 2s,为了数据安全性主线程会阻塞到后台线程执行完为止
40 |
41 | 对于第三步文件重写,会执行`bgrewriteaof`命令触发重写流程,调用`fork()`创建一个子进程完成文件重写,父进程可以正常处理其它命令,但会将其它命令写入 aof_rewrite_buf 缓冲区
42 |
43 | 等到子进程完成文件重写后,由父进程将 aof_rewrite_buf 缓冲中的命令追加到新的 aof 文件中,最后用新 aof 替换旧 aof 文件。父进程追加的步骤需要阻塞完成
44 |
45 | 但是后面的版本通过 pipe (管道) 对最后追加的步骤进行了优化,在子进程文件重写的后期,父进程可以分批将 aof_rewrite_buf 缓冲区中的数据通过管道传递给子进程,由子进程负责追加到 aof 文件
46 |
47 | 这样就可以避免父进程追加时阻塞,但可能存在无法将 aof_rewrite_buf 缓冲区所有内容都传递给子进程处理,所以最后父进程也需要阻塞式追加一部分命令,但相比于优化前少了很多
48 |
49 | ### 大 key 阻塞
50 |
51 | 如果一个 key 对应的 value 占用内存空间很大,就称为大 key。对于大 key 的查询、删除等操作都会消耗更多时间,导致阻塞
52 |
53 | ### 清空数据库时阻塞
54 |
55 | 可以使用`flushdb`或`flushdball`命令清空数据库,该操作和删除大 key 原理一样,消耗时间多,导致阻塞
56 |
57 | ### 集群扩容时阻塞
58 |
59 | Redis 集群的扩容或缩容处于半自动化的状态,需要人工介入,可以利用 redis-trib 实现数据的迁移
60 |
61 | 在扩容或缩容的时候,需要进行数据迁移,Redis 为了保证数据迁移的一致性,迁移的所有操作都是同步的。在执行迁移时,两边的 Redis 均会进入时长不等的阻塞状态
62 |
63 | 对于小 key,该时间可以忽略不计,但如果是大 key,严重的时候可能会触发故障转移,因为长时间得不到回复,会认为 Redis 节点下线
64 |
65 | ### 内存交换引起的阻塞
66 |
67 | Redis 是基于内存的数据库,这是它保证高性能的前提。如果操作系统把 Redis 使用的部分内存换出到磁盘,就会严重影响 Redis 的速度,进而操作阻塞
68 |
69 | ### CPU 竞争引起的阻塞
70 |
71 | Redis 是典型的 CPU 密集型应用,如果 Redis 和其它多核 CPU 密集型应用部署在同一台服务器上,会造成 CPU 竞争,如果 Redis 没有竞争到 CPU 就会引起阻塞
72 |
73 | ### 网络问题引起的阻塞
74 |
75 | 在 Redis 分布式缓存中,为了使缓存具有高可用,都会将不同 Redis 节点部署在不同的服务器上,节点间的通信需要通过网络传输,如果网络不佳就会引起阻塞
--------------------------------------------------------------------------------
/markdown/RocketMQ/浅记RocketMQ消息丢失问题.md:
--------------------------------------------------------------------------------
1 | # 浅记 RocketMQ 消息丢失问题
2 |
3 | 本篇文章主要浅浅介绍一下 RocketMQ 消息丢失问题及解决办法~~
4 |
5 | RocketMQ 核心流程:**「生产者发送消息到 Broker」**->**「Broker 刷盘/同步」**->**「消费者从 Broker 中消费消息」**
6 |
7 | 下面情况可能会出现消息丢失:
8 |
9 | - 生产者往 Broker 中发送消息
10 | - Broker 刷盘
11 | - Broker 主从同步
12 | - 消费者从 Broker 中消费消息
13 | - 整个 RocketMQ 宕机
14 |
15 | ### 生产者往 Broker 中发送消息
16 |
17 | #### 同步发送
18 |
19 | 生产者往 Broker 中同步发送消息时可能会出现以下几种情况:
20 |
21 | - 消息在发往 Broker 的途中丢失
22 | - 消息已经发送到 Broker,但 ACK 丢失
23 | - 消息已经发送到 Broker,同时 Broker 刷盘、主从同步成功 (SEDN_OK)
24 | - 消息已经发送到 Broker,但 Broker 刷盘超时 (FLUSH_DISK_TIMEOUT)
25 | - 消息已经发送到 Broker,但 Broker 主从同步超时 (FlUSH_SLAVE_TIMEOUT)
26 | - 消息已经发送到 Broker,但 Broker 从节点不可用 (SLAVE_NOT_AVAILABLE)
27 |
28 | 对于前两种情况,生产者会在一定时间后重发消息,类似于 TCP 的超时重传机制;对于后四种情况,生产者会收到对应的状态,可根据状态采取不同策略处理消息
29 |
30 | - 如果业务要求不严格,可认为后四种情况均为发送成功
31 |
32 | - 如果业务要求严格,如:只有当消费者成功消费才算不丢失,只有 SEDN_OK 状态才算发送成功,其它三种状态均为失败,可将这些失败的消息存储到数据库,启动定时任务重发
33 |
34 | #### 事务消息
35 |
36 | 除了使用同步发送方式保证消息不丢失外,还可以使用 RocketMQ 分布式事务保证消息不丢失
37 |
38 | 首先会向 Broker 发送一个 half 消息,如果规定时间内 Broker 没有收到本地事务的状态,会间隔规定时间去回查本地事务的状态
39 |
40 | **问题一:**如果 half 消息发送失败怎么处理?
41 |
42 | - 如果 half 消息发送失败可以认为 RocketMQ 服务有问题,可先记录一下,等 RocketMQ 服务可以正常服务后重新执行
43 |
44 | **问题二:**如果本地事务订单入库失败怎么处理?
45 |
46 | - 订单入库失败会抛出异常,如果需要实现自动订单入库可将异常订单缓存一下,等过段时间再次执行
47 |
48 | **问题三:**如何优化的处理下单后等待支付成功?
49 |
50 | - 当订单入库后,设置支付状态为等待支付,并给 Broker 返回一个 UNKNOWN 状态
51 | - Broker 会定期回查本地事务状态,回查过程中检查订单的状态即可,通过设置回查次数和间隔时间可以设置等待支付时间
52 |
53 | ### Broker 刷盘
54 |
55 | Broker 刷盘有两种方式,同步刷盘和异步刷盘
56 |
57 | - **同步刷盘:**当 Broker 收到消息后,并等待刷盘成功后再给生产者返回 ACK,保证了消息的可靠性,但会影响性能
58 | - **异步刷盘:**当 Broker 收到消息后,直接写入 Page Cache 即可给生产者返回 ACK,保证了性能,但存在消息丢失的可能性
59 |
60 | ### Broker 主从同步
61 |
62 | 和 Broker 刷盘一样,Broker 的主从同步也有两种方式,同步主从同步和异步主从同步
63 |
64 | - **同步主从同步:**当 Broker 收到消息后,同步复制到从节点中,然后再给生产者返回 ACK,保证了主节点宕机后,从节点有完整的数据
65 | - **异步主从同步:**当 Broker 收到消息后,异步复制到从节点中,直接给生产者返回 ACK,保证了性能,但主节点宕机后存在消息丢失的可能性
66 |
67 | ### 消费者从 Broker 中消费消息
68 |
69 | 当 Broker 推送消息给消费者,但如果规定时间内没有收到消费者返回的 ACK,表示可能是消息消费失败或者 ACK 丢失,那么 Broker 会重新推送消息给消费者
70 |
71 | 上面机制一定能保证消息成功被消费者消费,但要注意的是必须基于同步消费的前提下,如果是异步消费就可能消费失败的情况
72 |
73 | ### 整个 RocketMQ 宕机
74 |
75 | 当整个 RocketMQ 宕机时,只能设计一个降级方案,比如将消息先缓存到某个地方,当 RocketMQ 恢复后再重新处理
76 |
77 | ### 零丢失方案
78 |
79 | - 站在生产者角度,可以使用同步发送或事务消息
80 | - 站在 Broker 角度,可以使用同步刷盘和同步主从同步
81 | - 站在消费者角度,可是使用同步消费消息
82 |
83 | ### 参考文章
84 |
85 | - **[RocketMQ如何保证消息不丢失? 如何快速处理积压消息?](https://blog.csdn.net/qq_45076180/article/details/113828472)**
86 | - **[面试官再问我如何保证 RocketMQ 不丢失消息,这回我笑了!](https://www.cnblogs.com/goodAndyxublog/p/12563813.html)**
--------------------------------------------------------------------------------
/other/Secret.md:
--------------------------------------------------------------------------------
1 | $\downarrow$ 不同主题表达了本人不同时期的喜好 嘿嘿
2 | $\downarrow$ 好久没更新了,惭愧!!!!!
3 |
4 | $\downarrow$ 呜呜呜!!图论好难,数学好难!!
5 |
6 | $\downarrow$ 整理吐了!!!!!!!!!
7 |
8 | $\downarrow$ 🤮 心累!!!!!!
9 |
10 | $\downarrow$ 😭 终于补了一个坑了,太不容易了!!!!!!
11 |
12 | $\downarrow$ 终于把图论相关的算法过了一遍 耶耶耶耶
13 |
14 | $\downarrow$ 加油 呜呼!!!
15 |
16 | $\downarrow$ 图论简直要死了!!!!!
17 |
18 | $\downarrow$ 调整了一波目录顺序!!
19 |
20 | $\downarrow$ 图论杀了我叭 渡劫归来!!!
21 |
22 | $\downarrow$ 疯狂输出!!!
23 |
24 | $\downarrow$ 终于把 DFS && BFS 的坑补上了!!!
25 |
26 | $\downarrow$ 第一次这么认真写一篇文章,好像花了 5 个小时,写吐了!!!!!
27 |
28 | $\downarrow$ 再一次被图论整崩溃了!!!!!!!!
29 |
30 | $\downarrow$ 终于终于终于终于完结了图论的整理!!!!泪目
--------------------------------------------------------------------------------
/other/test.txt:
--------------------------------------------------------------------------------
1 |
--------------------------------------------------------------------------------
6 |
7 | 状态码的第一位数字表示状态类型,第二、三位数字表示具体的情况
8 |
9 | - **1xx:**表示接收的请求正在处理
10 | - **2xx:**表示请求正常处理完毕 (成功)
11 | - **3xx:**表示重定向
12 | - **4xx:**表示客户端错误
13 | - **5xx:**表示服务端错误
14 |
15 | ### 1xx
16 |
17 | 表示请求已被接受,需要继续处理。这类响应是临时响应,只包含「状态行」和某些可选的响应「头信息」,并以空行结束
18 |
19 | 常见的有:
20 |
21 | - **100 (继续):**这个为临时响应,表示迄今为止的所有内容都是可行的,客户端应该继续发送剩余请求,如果已经完成,则忽略它
22 | - **101 (切换协议):**服务器根据客户端的请求切换协议,主要用于 websocket 或 http2 升级
23 |
24 | ### 2xx
25 |
26 | 表示请求已成功被服务器接收、理解、并接受
27 |
28 | 常见的有:
29 |
30 | - **200 (成功):**请求已成功,请求所希望的响应头或数据体将随此响应返回
31 | - **201 (已创建):**请求成功并且服务器创建了新的资源
32 | - **202 (已创建):**服务器已经接收请求,但尚未处理
33 | - **203 (非授权信息):**服务器已成功处理请求,但返回的信息可能来自另一来源
34 | - **204 (无内容):**服务器成功处理请求,但没有返回任何内容。例如:删除请求或请求是通过表单发送的,响应不应导致刷新表单或加载新页面
35 | - **205 (重置内容):**将文档重置为原始状态。例如,清除表单
36 | - **206 (部分内容):**服务器成功处理了部分请求 (范围请求,服务器成功执行了该范围内的请求)
37 |
38 | ### 3xx
39 |
40 | 表示要完成请求,需要进一步操作。 通常,这些状态代码用来重定向
41 |
42 | 常见的有:
43 |
44 | - **300 (多种选择):**针对请求,服务器可执行多种操作。 服务器可根据请求者 (user agent) 选择一项操作,或提供操作列表供请求者选择
45 | - **301 (永久重定向):**请求的网页已永久移动到新位置。 服务器返回此响应 (对 GET 或 HEAD 请求的响应)时,会自动将请求者转到新位置
46 | - **302 (临时重定向):**服务器目前从不同位置的网页响应请求,但请求者应继续使用原有位置来进行以后的请求
47 | - **303 (查看其它位置):**请求者应当对不同的位置使用单独的 GET 请求来检索响应时,服务器返回此代码
48 | - **304 (缓存重定向):**表示资源没有被修改,可以重定向到缓存文件
49 | - **305 (使用代理):**请求者只能使用代理访问请求的网页。 如果服务器返回此响应,还表示请求者应使用代理
50 | - **307 (临时重定向):**服务器目前从不同位置的网页响应请求,但请求者应继续使用原有位置来进行以后的请求 (和 302 相同)
51 |
52 | ### 4xx
53 |
54 | 表示客户端有错误,妨碍了服务器的处理
55 |
56 | 常见的有:
57 |
58 | - **400 (错误请求):**请求报文中存在语法错误
59 | - **401 (未授权):**请求要求身份验证。对于需要登录的网页,服务器可能返回此响应
60 | - **403 (禁止):**服务器拒绝请求
61 | - **404 (未找到):**服务器找不到请求的网页
62 | - **405 (方法禁用):**禁用请求中指定的方法
63 | - **406 (不接受):**无法使用请求的内容特性响应请求的网页
64 | - **407 (需要代理授权):**此状态代码与 401 (未授权)类似,但指定请求者应当授权使用代理
65 | - **408 (请求超时):**服务器等候请求时发生超时
66 |
67 | ### 5xx
68 |
69 | 表示服务器有错误,在处理请求的过程中有错误或者异常状态发生
70 |
71 | 常见的有:
72 |
73 | - **500 (服务器内部错误):**服务器遇到错误,无法完成请求
74 | - **501 (尚未实施):**服务器不具备完成请求的功能。 例如,服务器无法识别请求方法时可能会返回此代码
75 | - **502 (错误网关):**服务器作为网关或代理,从上游服务器收到无效响应
76 | - **503 (服务不可用):**服务器目前无法使用 (由于超载或停机维护)
77 | - **504 (网关超时):**服务器作为网关或代理,但是没有及时从上游服务器收到请求
78 | - **505 (HTTP 版本不受支持):**服务器不支持请求中所用的 HTTP 协议版本
79 |
80 | ### 适用场景
81 |
82 | **100:**客户端在发送 POST 数据给服务器前,征询服务器情况,看服务器是否处理POST的数据,如果不处理,客户端则不上传 POST 数据,如果处理,则 POST 上传数据。常用于 POST 大数据传输
83 |
84 | **206:**一般用来做断点续传,或者是视频文件等大文件的加载
85 |
86 | **301:**永久重定向会缓存。新域名替换旧域名,旧的域名不再使用时,用户访问旧域名时用 301 就重定向到新的域名
87 |
88 | **302:**临时重定向不会缓存,常用 于未登陆的用户访问用户中心重定向到登录页面
89 |
90 | **304:**协商缓存,告诉客户端有缓存,直接使用缓存中的数据,返回页面的只有头部信息,是没有内容部分
91 |
92 | **400:**参数有误,请求无法被服务器识别
93 |
94 | **403:**告诉客户端进制访问该站点或者资源,如在外网环境下,然后访问只有内网 IP 才能访问的时候则返回
95 |
96 | **404:**服务器找不到资源时,或者服务器拒绝请求又不想说明理由时
97 |
98 | **503:**服务器停机维护时,主动用 503 响应请求或 Nginx 设置限速,超过限速,会返回 503
99 |
100 | **504:**网关超时
--------------------------------------------------------------------------------
/markdown/Network/HTTP-缓存策略.md:
--------------------------------------------------------------------------------
1 | # HTTP 缓存策略
2 |
3 | 当使用浏览器访问一个 Web 资源时,为了提高访问效率,往往会在浏览器和服务器之间增加本地缓存
4 |
5 | 对于首次访问,会将服务器响应的数据缓存到本地;对于后续的访问,会根据缓存策略决定是否直接使用本地缓存。简化的流程如下图所示:
6 |
7 | 
8 |
9 | **注意:**缓存策略完全是根据服务器响应消息的头信息来决定滴!!
10 |
11 | ### 与缓存有关的消息头字段
12 |
13 | 先给出与缓存有关的消息头字段的一些说明:
14 |
15 | 
16 |
17 | ### 强制缓存
18 |
19 | 顾名思义,强制缓存不需要服务器的参与,浏览器可以自己决策是否使用缓存,决策规则如下:
20 |
21 | - 如果本地缓存中不存在要请求的资源,浏览器会直接将请求发送到服务器,完成首次资源请求,根据服务器响应的消息保存相关信息
22 | - 如果本地缓存中存在要请求的资源,先判断缓存是否过期,如果没有过期直接使用本地缓存,如果过期就需要根据下面要介绍的协商缓存进行处理
23 |
24 | 在响应消息中,Expires 是根据 Last-Modified 和 max-age 计算出来的,max-age 表示存活多少秒后过期,而 Last-Modified 表示最后的修改时间
25 |
26 | 如果一个请求直接强制使用缓存,那么该请求会显示`200 OK (from disk cache)`,如下所示:
27 |
28 | ```
29 | Request URL: http://192.168.124.13:8080/index.html
30 | Request Method: GET
31 | Status Code: 200 OK (from disk cache)
32 | Remote Address: 192.168.124.13:8080
33 | Referrer Policy: strict-origin-when-cross-origin
34 | ```
35 |
36 | ### 协商缓存
37 |
38 | 顾名思义,协商缓存是浏览器和服务器共同协商是否使用本地缓存,浏览器负责提供本地缓存的信息,如:最后修改时间和唯一标识,添加在请求消息头中,服务器收到消息后来决策是否允许浏览器使用本地缓存
39 |
40 | If-Modified-Since 和 If-None-Match 是在浏览器第一次发送请求到服务器时,从服务器的响应消息保存。如果浏览器发现本地缓存中不存在要请求的资源,会直接将请求发送到服务器
41 |
42 | 协商缓存基于两种消息头字段实现:
43 |
44 | - **第一种:**请求头中的 If-Modified-Since 和响应头中的 Last-Modified
45 | - **第二种:**请求头中的 If-None-Match 和响应头中的 Etag
46 |
47 | 对于第一种,如果 If-Modified-Since 时间小于 Last-Modified,表示本地缓存中是旧数据,不可以使用本地缓存中的数据,否则可以使用缓存
48 |
49 | 对于第二种,如果 If-None-Match 和 Etag 不相等,表示本地缓存中是旧数据,不可以使用本地缓存中的数据,否则可以使用缓存
50 |
51 | 如果一个请求消息头中同时包含 If-Modified-Since 和 If-None-Match 字段,那么 If-None-Match 优先级更高。先判断 If-None-Match,如果不匹配直接无法使用缓存,如果匹配,再根据 If-Modified-Since 判断
52 |
53 | **问题:**为什么 Etag 的优先级更高??
54 |
55 | Etag 是服务器中资源的唯一标识,它可以解决一些 Last-Modified 难以解决的问题
56 |
57 | - 可能存在文件没有被修改,但修改时间却发生了改变的情况
58 | - Last-Modified 的精度是秒,对于秒以内的变化,Last-Modified 无法感知;但 Etag 却可以保证秒以内多次修改都可以被感知
59 |
60 | **强制缓存和协商缓存区别:**强制缓存不需要将请求发送给服务器,浏览器自己可以决策;协商缓存需要将请求先发送给服务器,由服务器决策,如果可以使用缓存会响应一个 **[304](./HTTP-状态码.html#3xx)** 的消息,表示缓存重定向
61 |
62 | ### 总流程图
63 |
64 | 下面给出缓存策略的总体流程图:
65 |
66 | 
67 |
68 | **注意:**
69 |
70 | - 使用 F5 刷新网页时,跳过强制缓存,但会检查协商缓存
71 | - 使用 ctrl + F5 刷新页面时,直接从服务器加载,跳过强制缓存和协商缓存
72 |
73 | ### 参考文章
74 |
75 | - **[HTTP 缓存技术](https://xiaolincoding.com/network/2_http/http_interview.html#http-缓存技术)**
76 | - **[彻底弄懂浏览器缓存策略](https://mp.weixin.qq.com/s/Ui7Q9k4faiD5mv_LfB4Rrw)**
77 | - **[Cache-Control在请求头和响应头里的区别](https://juejin.cn/post/6960988505816186894)**
78 | - **[为什么我的缓存设置在 chrome 中不生效](https://xie.infoq.cn/article/70b359ab1210efb6f5b253e24)**
79 | - **[Cache-Control和Expires无效的原因](https://www.cnblogs.com/jimaww/p/10234074.html)**
--------------------------------------------------------------------------------
/markdown/Network/SYN-泛洪攻击.md:
--------------------------------------------------------------------------------
1 | # SYN 泛洪攻击
2 |
3 | ### 半连接 & 全连接
4 |
5 | 在 TCP 三次握手的时候,Linux 内核会维护两个队列:
6 |
7 | - 半连接队列,也称 SYN 队列,只进行了一次握手的连接
8 | - 全连接队列,也称 Accept 队列,进行了三次握手的连接
9 |
10 | 
11 |
12 | 关于出队和入队的详细流程如下:
13 |
14 | - 当服务器收到客户端的 SYN 报文时,会创建一个半连接对象,并加入到内核的 SYN 队列中
15 | - 接着服务器发送 SYN-ACK 报文给客户端,等待客户端的 ACK 报文
16 | - 当服务器收到客户端的 ACK 报文时,会取出一个半连接对象,然后创建一个新的连接对象加入 Accept 队列中
17 | - 应用程序通过调用 Socket 提供的`accept()`方法,从 Accept 队列中取出一个连接对象
18 |
19 | **注意:**不管是半连接队列还是全连接队列,都有最大长度限制,超过限制时都会丢弃报文!!
20 |
21 | ### SYN 泛洪攻击是什么
22 |
23 | 客户端和服务器使用 TCP 协议通信前需要进行三次握手建立连接,当服务器收到客户端第一次握手的 SYN 报文后,会发送 SYN-ACK 报文,之后服务器处于 SYN_RECV 状态。**更详细可见 [三次握手](./TCP-三次握手-四次挥手.html#tcp-三次握手过程)**
24 |
25 | **SYN 泛洪攻击:**攻击者会伪造大量不同 IP 的 SYN 报文,服务器收到 SYN 报文后会向客户端发送 SYN-ACK 报文,但攻击者不会回应该报文,这样会逐渐占满半连接队列,使得后续正常连接请求直接被丢弃
26 |
27 | ### 如何避免 SYN 泛洪攻击
28 |
29 | #### 方法一:调大 netdev_max_backlog
30 |
31 | 当网卡接收数据的速度大于内核处理的速度时,会有一个队列保存这些数据包。控制该队列的大小,默认值为 1000,可以通过参数调整为 100000
32 |
33 | ```bash
34 | net.core.netdev_max_backlog = 10000
35 | ```
36 | #### 方法二:增加 TCP 半连接队列大小
37 |
38 | 增大 TCP 半连接队列,要同时增大下面这三个参数:
39 |
40 | - 增大 net.ipv4.tcp_max_syn_backlog
41 | - 增大 listen() 函数中的 backlog
42 | - 增大 net.core.somaxconn
43 |
44 | #### 方法三:开启 net.ipv4.tcp_syncookies
45 |
46 | 开启 net.ipv4.tcp_syncookies 后可以不需要加入到 SYN 半连接队列中,也可以成功建立连接
47 |
48 | #### 方法四:减少 SYN + ACK 重发次数
49 |
50 | 攻击者不会回应服务器的 SYN-ACK 包,服务器会超时重发,在 Linux 默认重发 5 次,可以适当降低重发的次数使处于 SYN_RECV 状态的服务器尽快断开连接
--------------------------------------------------------------------------------
/markdown/Network/Solutions-7th-Edition.docx:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/LFool/LFool-Notes/8d4b7b3aa2f91cd51aa57427d016d86db8712e05/markdown/Network/Solutions-7th-Edition.docx
--------------------------------------------------------------------------------
/markdown/Network/网络层那点事儿.md:
--------------------------------------------------------------------------------
1 | # 网络层那点事儿~
2 |
3 | ### 网络层和链路层
4 |
5 | 传输层提供端到端的可靠传输,也就是不同主机中的进程间通信,通过端口唯一确认主机中的进程,TCP 报文首部也有端口字段,**详情可见 [TCP 报文段格式](./TCP-三次握手-四次挥手.html)**
6 |
7 | 网络层负责将数据从一台主机传输到另一台主机,往往这两台主机在物理上没有直接相连;而链路层也是负责将数据从一台主机传输到另一台主机,往往这两台主机在物理上直接相连
8 |
9 | 下面主要介绍网络层和链路层是如何相互配合将数据从一台主机传输到另一台主机。网络层通过 IP 地址定义一台主机,链路层通过 MAC 地址定位一台主机。下面模拟一种场景,如下图所示:
10 |
11 | 
12 |
13 | **注意:**路由器的每个端口都有一个 IP 地址和 MAC 地址
14 |
15 | 主机 A 向主机 B 发送数据,它们俩在物理上没有直接相连,需要依赖网络层将数据从主机 A 发送到主机 B
16 |
17 | - **第一步:**主机 A 将数据包发送给路由器,此时会通过 ARP 协议获取路由器的 MAC 地址,将报文中的源 MAC 地址设置为主机 A,目标 MAC 地址设置为路由器。链路层根据源/目标 MAC 地址将数据包从主机 A 发送给路由器,因为它俩在物理上直接相连
18 | - **第二步:**路由器将数据包发送给主机 B,将报文中的源 MAC 地址设置为路由器,目标 MAC 地址设置为主机 B。链路层根据源/目标 MAC 地址将数据包从路由器发送给主机 B,因为它俩在物理上直接相连
19 |
20 | 可以看出数据包在传输过程中,报文的源/目标 IP 地址始终保持不变,分别为:`10.0.1.2`和`10.0.5.6`,变化的是 MAC 地址。网络层负责根据 IP 地址寻址➕路由,而链路层负责将数据在两个物理上相邻的节点中传输!!
21 |
22 | **注意:**由于 MAC 地址在网络层封装,所以有些说法认为 ARP 属于网络层,有些说法认为 ARP 属于链路层,但这不重要,只要理解这个过程即可
23 |
24 | ### IP 分类
25 |
26 | IP 主要分为五类:A 类地址、B 类地址、C 类地址、D 类地址、E 类地址,但这里只想简单给出公有 IP 和私有 IP 的分类
27 |
28 | 简单来说,公有 IP 是网络中所有人都可以访问的 IP,而私有 IP 只有在同一个局域网中的人才可以访问。公有 IP 不允许重复;同一个局域网中的私有 IP 不允许重复,但在不同的局域网中可以重复
29 |
30 | 私有 IP 只有三种范围,如下:
31 |
32 | - 10.0.0.0 - 10.255.255.255
33 | - 172.16.0.0 - 172.31.255.255
34 | - 192.168.0.0 - 192.168.255.255
35 |
36 | 在这三个范围之外的所有 IP 都是公有 IP!!
37 |
38 | ### 路由控制
39 |
40 | 上文说:网络层负责将数据从一台主机传输到另一台主机,往往这两台主机在物理上没有直接相连。那么它是如何将数据从一台主机传输到另一台主机呢?
41 |
42 | 网络层有一个重要的设备:路由器,它内部有一张路由转发表,根据目标 IP 地址可以知道该数据包从路由器的哪一个端口转发出去。回到第一部分的例子中,先将例子扩展的更丰富一些,如下图所示:
43 |
44 | 
45 |
46 | 上图中 IP 数据包的源 IP 地址为`10.1.1.30`,目标 IP 地址为`10.1.2.10`
47 |
48 | **第一步:**主机 A 根据目标 IP 地址匹配到`0.0.0.0/0`,那么下一跳就是`10.1.1.1`。这里的`0.0.0.0/0`就是默认路由,在没有匹配到其它路由时就会匹配默认路由,默认路由的下一跳就是默认网关
49 |
50 | **第二步:**路由器根据目标 IP 地址匹配到`10.1.2.0/24`,那么下一跳就是`10.1.0.2`
51 |
52 | **第三步:**路由器根据目标 IP 地址匹配到`10.1.2.0/24`,那么下一跳就是`10.1.2.1`,最终通过交换机将数据发送给目标主机
53 |
54 | ### IP 分片与重组
55 |
56 | 数据链路层的传输单位是帧,不同的数据链路有不同的最大传输单元 (MTU),以太网的 MTU 是 1500 字节。换句话说,MTU = IP 首部 + TCP 首部 + 数据,一旦「IP 首部 + TCP 首部 + 数据」超过了 MTU,那么就会分片
57 |
58 | 在 TCP 中,如果数据长度 > MTU - IP 首部 - TCP 首部,就会进行分片;在网络层中,如果 TCP 首部 + 数据 > MTU - IP 首部,也会进行分片
59 |
60 | 如果 TCP 不分片,仅仅在网络层分片,那么一旦某个分片数据丢失,TCP 需要重传整个数据,因为 TCP 需要保证数据的可靠性,而网络层不需要保证数据的可靠性
61 |
62 | 所以 TCP 也会进行分片,如果某个分片数据在传输过程中丢失,那么只需要重传该分片数据即可,不需要重传所有数据
63 |
64 | 一般来说,TCP 分片已经考虑了 IP 首部的长度,所以在网络层不会超过长度,也就不会再进行分片,但存在一些特殊情况需要在 TCP 分片后,网络层还需要继续分片,如传输链路中存在更小的 MTU
65 |
66 | **详情分析可见 [TCP分段了,IP层就一定不会分片了吗?](https://zhuanlan.zhihu.com/p/372863051)**
--------------------------------------------------------------------------------
/markdown/Network/计算机网络(top-down)-习题&实验.md:
--------------------------------------------------------------------------------
1 | # 计算机网络(top-down) - 习题 & 实验
2 |
3 | ## 第一章
4 |
5 | ### 习题
6 |
7 | 1. “主机”和“端系统”之间有什么不同?列举几种不同类型的端系统。Web 服务器是一种端系统吗?
8 |
9 |
10 |
11 | 2.
12 |
13 | ### 实验
14 |
15 |
--------------------------------------------------------------------------------
/markdown/OS/CPU缓存一致性.md:
--------------------------------------------------------------------------------
1 | # CPU 缓存一致性
2 |
3 | ### 存储器层次结构
4 |
5 | 在计算机系统中,最常见的存储器有内存和磁盘。一个进程运行过程中往往需要将磁盘中的数据加载到内存中才可以访问
6 |
7 | CPU 的运算速度和内存的访问速度相差过大,为了缓解这种差距,在 CPU 和内存之间增加了高速缓存。由于 CPU 是基于寄存器的指令集,所以在 CPU 和高速缓存之间还存在寄存器
8 |
9 | 存储器离 CPU 越近,那么读写速度就越快,但能存储的容量也就越小。一个存储器的层次结构如下图所示:
10 |
11 | 
12 |
13 | 在现在的 CPU 中一般都有多个核心,寄存器、L1 高速缓存、L2 高速缓存都是每个核心独有,而 L3 高速缓存是 CPU 独有,如下图所示:
14 |
15 | 
16 |
17 | ### CPU Cache 结构
18 |
19 | 每个 CPU Cache 都是由缓存行构成,而且 CPU 和 CPU Cache 的交互单位也是缓存行,也就是如果 Cache 中没有数据,CPU 会一次性从内存中读取和缓存行相同大小的数据存入 Cache 中
20 |
21 | CPU Cache 的结构如下图所示:
22 |
23 | 
24 |
25 | 在使用 CPU Cache 的过程中,可能会出现伪共享问题,这也是下面要介绍的 MESI 协议导致的。**关于伪共享的分析可见 [伪共享](../java/伪共享.html)**
26 |
27 | ### CPU Cache 数据写入
28 |
29 | 对于读操作来说很简单,每次先去 Cache 中检查是否有数据,如果有数据就直接返回,如果没有数据就去内存中读,并将读到的数据加到 Cache 中以便下次可以快速读
30 |
31 | 但是对于写操作可能就麻烦一点,这里可以借鉴 **[Redis 缓存更新策略](../redis/Redis缓存更新策略.html)**,下面主要介绍两种写入策略:
32 |
33 | - **写穿透 (Write Through):**如果 Cache 中有数据,先更新 Cache,后更新内存;如果 Cache 中没有数据,直接更新内存
34 | - **写回 (Write Back):**先只更新 Cache,随后异步更新内存
35 |
36 | ### CPU 缓存一致性问题
37 |
38 | 不同线程在不同核心上执行,每个核心存在自己独有的 Cache。由于不可见性,同一个共享变量,可能出现在不同 Cache 中不一致的问题,**原理可见 [处理器重排序](../java/Java内存模型.html#处理器重排序)**
39 |
40 | 要解决缓存不一致的问题,必须保证下面两点:
41 |
42 | - 某个 CPU 核心更新 Cache 中的数据时,其它 CPU 核心必须知道该数据被更新了,这被称为**写传播 (Write Propagation)**
43 | - 所有 CPU 核心看到 Cache 中数据的修改操作顺序必须是一致性的,这被称为**事务的串行化 (Transaction Serialization)**
44 |
45 | 对于第一点使用总线嗅探机制,当某个 CPU 核心更新 Cache 中的数据时,会向总线广播这一事件,所有 CPU 核心都会监听总线上的广播事件,当发现广播事件中包含的数据也存在于自己的 Cache 中时,就会将自己 Cache 中的数据更新成广播中的数据
46 |
47 | 但仅仅做到第一点并不能完全解决缓存不一致的问题,假设存在两个 CPU 核心先后将`i`修改成 100 和 200,但无法保证这两个修改的广播事件的先后顺序,可能出现某个 CPU 核心看到的顺序:先将`i`修改为 200,再将`i`修改为 100,这也是第二点要保证事务串行化执行的原因
48 |
49 | ### MESI 协议
50 |
51 | MESI 协议基于总线嗅探机制实现了事务串行化,该协议保证了缓存一致性。首先,MESI 协议规定了四种状态:
52 |
53 | - **Modified** 已修改:表示 Cache 中的数据已经被修改过,也就是脏数据
54 | - **Exclusive** 独占:表示 Cache 中的数据被自己独占,其它 CPU Cache 中没有该数据,此时数据是干净的
55 | - **Shared** 共享:表示多个 CPU Cache 中都有该数据,此时数据是干净的
56 | - **Invalidated** 已失效:表示 Cache 中的数据无效
57 |
58 | 下面通过表格给出这四种状态之间的转化关系:
59 |
60 | 
61 |
62 | **注意:**如果在独占状态或者已修改状态下写数据,不需要广播该事件。如果是独占状态,表示其它核心的 Cache 中没有该数据,所以不需要广播;如果是已修改状态,表示包含该数据的核心的 Cache 中对应的 Cache Line 已经是已失效状态,所以也不需要广播
63 |
64 | 这里推荐一个可视化网站,可以看到 Cache 四个状态的转换 **[VivioJS MESI animation help](https://www.scss.tcd.ie/Jeremy.Jones/VivioJS/caches/MESIHelp.htm)**
--------------------------------------------------------------------------------
/markdown/OS/中断.md:
--------------------------------------------------------------------------------
1 | # 中断
2 |
3 | ### 用户态 & 内核态
4 |
5 | 用户进程不可以直接操作系统资源,因为如果给予进程的权利过大,可能会出现一些非法的访问,导致系统处于不安全的状态。基于这种原因,将系统所处状态分为用户态和内核态:
6 |
7 | - **用户态:**CPU 只能受限的访问内存,并且不允许访问敏感的系统资源,如:I/O 设备
8 | - **内核态:**CPU 可以访问任意数据,包括系统资源,还可以决定切换进程
9 |
10 | 当一个用户进程需要访问硬件资源时,需要进行系统调用,让操作系统去访问硬件资源,然后将结果返回给用户进程。系统调用相当于内核提供给用户的一套 API,通过 API 可以间接完成对硬件的访问
11 |
12 | 在系统启动时内核会设置好陷阱表,该表中存放了陷阱类型和内核代码位置的对应关系,也就是如果执行到陷阱 A,就会去执行陷阱 A 对应的内核代码
13 |
14 | 当用户线程系统调用时,会执行特殊的陷阱指令,该指令会从用户态转化到内核态,进而去执行该陷阱对应的内核代码。当操作系统执行完对应代码后,会从内核态转化到用户态
15 |
16 | 操作系统也算是一种软件,在单核 CPU 中,如果用户进程在 CPU 上执行,那么操作系统是无法执行滴,只有当用户态转化到内核态,操作系统才可以在 CPU 上执行。所以系统调用不仅从用户态转化到内核态,而且还相当于进行了一次上下文切换,从用户进程切换到操作系统进程
17 |
18 | 下面是通过系统调用完成上下文切换的过程:
19 |
20 | 
21 |
22 | ### 时钟中断
23 |
24 | 对系统资源的访问、上下文切换等操作都需要操作系统来执行。系统调用可以从用户态切换到内核态,让控制权重新回到操作系统手中,但如果一个进程始终都不进行系统调用呢?那就会出现一直不能切换到内核态,从而卡死的情况
25 |
26 | 为了避免这种情况的发生,提出了时钟中断。时钟设备可以每隔几毫秒就生成一次中断,中断产生时,当前正在运行的程序停止,操作系统中预先配置的中断程序会运行,此时操作系统重新获得了 CPU 的控制权
27 |
28 | 下面是通过时钟中断完成上下文切换的过程:
29 |
30 | 
31 |
32 | ### 软中断
33 |
34 | 在处理中断时,中断处理程序会将中断关闭,如果处理时间过长,可能会丢失其它设备的中断信号。为了避免丢失中断信号,将原来的整个中断过程分为两部分:
35 |
36 | - **第一部分:**快速处理中断,该阶段会暂时关闭中断,但一般该阶段耗时较短,只会处理与硬件相关敏感的事情
37 | - **第二部分:**交由操作系统完成中断剩余工作,该阶段会将中断打开,不会丢失中断信号
38 |
39 | 可以将第一部分看作是硬中断,也就是会关闭中断的中断;可以将第二部分看作是软中断,也就是不会关闭中断的中断。软中断可以大大降低中断信号丢失的风险
40 |
41 | ### 参考文章
42 |
43 | - **操作系统导论**
44 | - **[什么是软中断?](https://xiaolincoding.com/os/1_hardware/soft_interrupt.html)**
--------------------------------------------------------------------------------
/markdown/Redis/Redis缓存更新策略.md:
--------------------------------------------------------------------------------
1 | # Redis 缓存更新策略
2 |
3 | 缓存能够有效地加速应用的读写速度,因为它基于内存,减少了磁盘 IO 的开销。但它也存在数据不一致的问题,因为缓存层和存储层的数据存在着一定**时间窗口**的不一致性
4 |
5 | 给出加入缓存层的结构图:
6 |
7 | 
8 |
9 | 下面介绍三种缓存更新策略,没有最优,只有根据业务场景最合适!!
10 |
11 | ### 旁路缓存模式 (Cache Aside Pattern)
12 |
13 | 旁路缓存模式是平时使用较多的一个读写缓存模式,比较**适合于读请求较多的场景**
14 |
15 | 写操作的步骤:
16 |
17 | - 更新 DB
18 | - 直接删除 Cache
19 |
20 | 读操作的步骤:
21 |
22 | - 从 Cache 中读取数据,读取到就直接返回
23 | - 如果 Cache 读取不到,从 DB 中读取数据返回
24 | - 将 DB 中读取到的数据写入 Cache 中
25 |
26 | 
27 |
28 | **问题一:先更新 DB,再删除 Cache,能保证数据一致性吗?**
29 |
30 | 理论上来说还是可能会出现数据不一致的问题,但概率很小,因为删除 Cache 的操作速度快,使 Cache 中和 DB 中数据不一致的时间窗口很短
31 |
32 | 只有在不一致时间窗口内读数据才会出现数据不一致问题,即:读到旧值,如下图
33 |
34 | 
35 |
36 | 下面举一个数据不一致的例子:线程 1 写数据 A,随后线程 2 读数据 A。正确的情况下线程 2 读到的应该是数据 A 的新值,但如果以下面的顺序执行:
37 |
38 | - 线程 1 更新 DB
39 | - 线程 2 读数据 A,直接从缓存中读取并返回,但缓存中是旧值
40 | - 线程 1 删除 Cache
41 |
42 | 此时线程 2 读到的是数据 A 的旧值
43 |
44 | **问题二:为什么删除 Cache,而不是更新 Cache?**
45 |
46 | - 浪费服务端资源:不确定新写入的数据是否会被访问,而且 Cache 存放的数据一般需要经过服务端大量的计算。如果不会被访问又进行了大量的计算,无疑是白白浪费资源
47 | - 增加数据不一致的概率:更新 Cache 比 删除 Cache 更加耗时,所以会增大不一致时间窗口的大小,进而提高数据不一致性的概率
48 |
49 | 
50 |
51 | **问题三:可以先删除 Cache,后更新 DB 吗?**
52 |
53 | 显然不可以,这样会导致数据不一致的时间窗口变大,进而增加了出现数据不一致问题的概率
54 |
55 | 
56 |
57 | 下面举一个数据不一致的例子:线程 1 写数据 A,随后线程 2 读数据 A。正确的情况下线程 2 读到的应该是数据 A 的新值,但如果以下面的顺序执行:
58 |
59 | - 线程 1 删除 Cache
60 | - 线程 2 读数据 A,此时缓存中没有数据,从 DB 中读取并返回,同时存入 Cache 中,Cache 中存入的是旧值
61 | - 线程 1 更新 DB
62 |
63 | 此时线程 2 读到的是数据 A 的旧值,而且 Cache 存入的也是旧值。如果 Cache 没有设置过期时间且未来一段时间没有新的写操作,那么后面读数据 A 时全都是 Cache 中的旧值!!
64 |
65 | **缺陷一:首次请求数据不在 Cache 中**
66 |
67 | - 可以提前将热点数据放入 Cache 中
68 |
69 | **缺陷二:写操作频繁会导致 Cache 中数据频繁被删,会影响命中率?**
70 |
71 | - 对于要求数据强一致性的场景:更新 DB 的同时更新 Cache,但需要用分布式锁保证这两个更新的原子性,否则存在线程安全问题
72 | - 对于可接受短暂数据不一致的场景:更新 DB 的同时更新 Cache,为 Cache 设置一个较短的过期时间
73 |
74 | ### 读写穿透 (Read/Write Through Pattern)
75 |
76 | **核心思想:**更新 DB,缓存存在就更新,不存在就不管
77 |
78 | 读写穿透将 Cache 作为主要的数据存储,从中读取并将数据写入其中,Cache 服务自己负责将此数据读取和写入 DB,从而减轻了程序员的职责
79 |
80 | 这种模式平时使用很少,大概率因为 Redis 分布式缓存并没有提供 Cache 将数据写入 DB 的功能
81 |
82 | 写操作的步骤:
83 |
84 | - 先检查 Cache,如果 Cache 没有,直接更新 DB
85 | - 如果 Cache 中存在,直接更新 Cache,然后 Cache 服务会自己更新 DB
86 |
87 | 读操作的步骤:
88 |
89 | - 从 Cache 中读取数据,读取到就直接返回
90 | - 如果 Cache 读取不到,先从 DB 中加载,写入 Cache 后返回
91 |
92 | 
93 |
94 | ### 异步缓存写入 (Write Back Pattern)
95 |
96 | **核心思想:**只更新缓存,异步更新 DB
97 |
98 | 异步缓存写入和读写穿透很相似,两者都是由 Cache 服务来负责 Cache 和 DB 的读写。它们俩最大的不同在于:读写穿透是同步更新 Cache 和 DB;而异步缓存写入是异步更新 DB
99 |
100 | 消息队列中消息的异步写入磁盘、MySQL 的 InnoDB Buffer Pool 机制都用到了这种策略
101 |
102 | 异步缓存写入下 DB 的写性能非常高,非常适合一些数据经常变化又对数据一致性没有那么高的要求的场景,如:浏览量、点赞量等
--------------------------------------------------------------------------------
/markdown/Redis/Redis阻塞.md:
--------------------------------------------------------------------------------
1 | # Redis 阻塞
2 |
3 | Redis 是典型的单线程架构,所有的读写操作都是在一条主线程中完成,所以如果主线程被阻塞,就会直接影响到应用系统。本篇文章来盘点一下 Redis 中阻塞的常见情况
4 |
5 | ### 命令阻塞
6 |
7 | 虽然 Redis 是基于内存的数据库,但如果执行的命令时间复杂度过高,就会导致主线程阻塞。下面命令的时间复杂度均为`O(n)`,随着数据规模的增加,执行时间也会变长
8 |
9 | - `keys *`:获取所有的 key
10 | - `hgetall`:获取哈希表中所有
11 | - `smembers`:返回集合中的所有成员
12 | - ...
13 |
14 | **所以尽量使用时间复杂度低的命令!!!**
15 |
16 | ### RDB 阻塞
17 |
18 | RDB 是 Redis 持久化的一种机制,**详情可见 [Redis 持久化机制 - RDB](./Redis持久化机制.html#rdb)**
19 |
20 | 生成 RDB 文件有两种命令:
21 |
22 | - `save`:阻塞主线程,直至 RDB 文件创建完毕为止,阻塞期间 Redis 不可以处理任何其它命令
23 | - `bgsave`:执行`fork()`创建子进程,由子进程负责创建 RDB 文件,服务器没有被阻塞,可以正常处理其它命令
24 |
25 | **所以尽量使用`bgsave`命令创建 RDB 文件!!!**
26 |
27 | ### AOF 阻塞
28 |
29 | AOF 是 Rdis 持久化的一种机制,**详情可见 [Redis 持久化机制 - AOF](./Redis持久化机制.html#aof)**
30 |
31 | AOF 持久化一共有四步:命令写入、文件同步、文件重写、重启加载,在文件同步和文件重写时会发生阻塞
32 |
33 | 对于第一步的文件写入,其实只写到了 aof_buf 缓存,还没有写入到文件中;在文件同步时选择写入文件的策略,一共三种:always、everysec、no
34 |
35 | - always:对于每条写入命令,由后台线程立即调用`fsync`阻塞式写入到磁盘中
36 | - everysec:对于每条写入命令,主线程先执行`write`系统调用写入到 aof_buf 缓存,然后由后台线程按每秒一次的频率调用`fsync`阻塞式将缓存写入到磁盘中
37 | - no:对于每条写入命令,执行`write`系统调用写入到 aof_buf 缓存,同步到磁盘由操作系统决定,一般 30s 一次
38 |
39 | 当刷盘频率过高,导致磁盘 IO 开销大,后台刷盘线程需要阻塞到完成后才返回。如果主线程发现距离上一次的`fsync`成功超过 2s,为了数据安全性主线程会阻塞到后台线程执行完为止
40 |
41 | 对于第三步文件重写,会执行`bgrewriteaof`命令触发重写流程,调用`fork()`创建一个子进程完成文件重写,父进程可以正常处理其它命令,但会将其它命令写入 aof_rewrite_buf 缓冲区
42 |
43 | 等到子进程完成文件重写后,由父进程将 aof_rewrite_buf 缓冲中的命令追加到新的 aof 文件中,最后用新 aof 替换旧 aof 文件。父进程追加的步骤需要阻塞完成
44 |
45 | 但是后面的版本通过 pipe (管道) 对最后追加的步骤进行了优化,在子进程文件重写的后期,父进程可以分批将 aof_rewrite_buf 缓冲区中的数据通过管道传递给子进程,由子进程负责追加到 aof 文件
46 |
47 | 这样就可以避免父进程追加时阻塞,但可能存在无法将 aof_rewrite_buf 缓冲区所有内容都传递给子进程处理,所以最后父进程也需要阻塞式追加一部分命令,但相比于优化前少了很多
48 |
49 | ### 大 key 阻塞
50 |
51 | 如果一个 key 对应的 value 占用内存空间很大,就称为大 key。对于大 key 的查询、删除等操作都会消耗更多时间,导致阻塞
52 |
53 | ### 清空数据库时阻塞
54 |
55 | 可以使用`flushdb`或`flushdball`命令清空数据库,该操作和删除大 key 原理一样,消耗时间多,导致阻塞
56 |
57 | ### 集群扩容时阻塞
58 |
59 | Redis 集群的扩容或缩容处于半自动化的状态,需要人工介入,可以利用 redis-trib 实现数据的迁移
60 |
61 | 在扩容或缩容的时候,需要进行数据迁移,Redis 为了保证数据迁移的一致性,迁移的所有操作都是同步的。在执行迁移时,两边的 Redis 均会进入时长不等的阻塞状态
62 |
63 | 对于小 key,该时间可以忽略不计,但如果是大 key,严重的时候可能会触发故障转移,因为长时间得不到回复,会认为 Redis 节点下线
64 |
65 | ### 内存交换引起的阻塞
66 |
67 | Redis 是基于内存的数据库,这是它保证高性能的前提。如果操作系统把 Redis 使用的部分内存换出到磁盘,就会严重影响 Redis 的速度,进而操作阻塞
68 |
69 | ### CPU 竞争引起的阻塞
70 |
71 | Redis 是典型的 CPU 密集型应用,如果 Redis 和其它多核 CPU 密集型应用部署在同一台服务器上,会造成 CPU 竞争,如果 Redis 没有竞争到 CPU 就会引起阻塞
72 |
73 | ### 网络问题引起的阻塞
74 |
75 | 在 Redis 分布式缓存中,为了使缓存具有高可用,都会将不同 Redis 节点部署在不同的服务器上,节点间的通信需要通过网络传输,如果网络不佳就会引起阻塞
--------------------------------------------------------------------------------
/markdown/RocketMQ/浅记RocketMQ消息丢失问题.md:
--------------------------------------------------------------------------------
1 | # 浅记 RocketMQ 消息丢失问题
2 |
3 | 本篇文章主要浅浅介绍一下 RocketMQ 消息丢失问题及解决办法~~
4 |
5 | RocketMQ 核心流程:**「生产者发送消息到 Broker」**->**「Broker 刷盘/同步」**->**「消费者从 Broker 中消费消息」**
6 |
7 | 下面情况可能会出现消息丢失:
8 |
9 | - 生产者往 Broker 中发送消息
10 | - Broker 刷盘
11 | - Broker 主从同步
12 | - 消费者从 Broker 中消费消息
13 | - 整个 RocketMQ 宕机
14 |
15 | ### 生产者往 Broker 中发送消息
16 |
17 | #### 同步发送
18 |
19 | 生产者往 Broker 中同步发送消息时可能会出现以下几种情况:
20 |
21 | - 消息在发往 Broker 的途中丢失
22 | - 消息已经发送到 Broker,但 ACK 丢失
23 | - 消息已经发送到 Broker,同时 Broker 刷盘、主从同步成功 (SEDN_OK)
24 | - 消息已经发送到 Broker,但 Broker 刷盘超时 (FLUSH_DISK_TIMEOUT)
25 | - 消息已经发送到 Broker,但 Broker 主从同步超时 (FlUSH_SLAVE_TIMEOUT)
26 | - 消息已经发送到 Broker,但 Broker 从节点不可用 (SLAVE_NOT_AVAILABLE)
27 |
28 | 对于前两种情况,生产者会在一定时间后重发消息,类似于 TCP 的超时重传机制;对于后四种情况,生产者会收到对应的状态,可根据状态采取不同策略处理消息
29 |
30 | - 如果业务要求不严格,可认为后四种情况均为发送成功
31 |
32 | - 如果业务要求严格,如:只有当消费者成功消费才算不丢失,只有 SEDN_OK 状态才算发送成功,其它三种状态均为失败,可将这些失败的消息存储到数据库,启动定时任务重发
33 |
34 | #### 事务消息
35 |
36 | 除了使用同步发送方式保证消息不丢失外,还可以使用 RocketMQ 分布式事务保证消息不丢失
37 |
38 | 首先会向 Broker 发送一个 half 消息,如果规定时间内 Broker 没有收到本地事务的状态,会间隔规定时间去回查本地事务的状态
39 |
40 | **问题一:**如果 half 消息发送失败怎么处理?
41 |
42 | - 如果 half 消息发送失败可以认为 RocketMQ 服务有问题,可先记录一下,等 RocketMQ 服务可以正常服务后重新执行
43 |
44 | **问题二:**如果本地事务订单入库失败怎么处理?
45 |
46 | - 订单入库失败会抛出异常,如果需要实现自动订单入库可将异常订单缓存一下,等过段时间再次执行
47 |
48 | **问题三:**如何优化的处理下单后等待支付成功?
49 |
50 | - 当订单入库后,设置支付状态为等待支付,并给 Broker 返回一个 UNKNOWN 状态
51 | - Broker 会定期回查本地事务状态,回查过程中检查订单的状态即可,通过设置回查次数和间隔时间可以设置等待支付时间
52 |
53 | ### Broker 刷盘
54 |
55 | Broker 刷盘有两种方式,同步刷盘和异步刷盘
56 |
57 | - **同步刷盘:**当 Broker 收到消息后,并等待刷盘成功后再给生产者返回 ACK,保证了消息的可靠性,但会影响性能
58 | - **异步刷盘:**当 Broker 收到消息后,直接写入 Page Cache 即可给生产者返回 ACK,保证了性能,但存在消息丢失的可能性
59 |
60 | ### Broker 主从同步
61 |
62 | 和 Broker 刷盘一样,Broker 的主从同步也有两种方式,同步主从同步和异步主从同步
63 |
64 | - **同步主从同步:**当 Broker 收到消息后,同步复制到从节点中,然后再给生产者返回 ACK,保证了主节点宕机后,从节点有完整的数据
65 | - **异步主从同步:**当 Broker 收到消息后,异步复制到从节点中,直接给生产者返回 ACK,保证了性能,但主节点宕机后存在消息丢失的可能性
66 |
67 | ### 消费者从 Broker 中消费消息
68 |
69 | 当 Broker 推送消息给消费者,但如果规定时间内没有收到消费者返回的 ACK,表示可能是消息消费失败或者 ACK 丢失,那么 Broker 会重新推送消息给消费者
70 |
71 | 上面机制一定能保证消息成功被消费者消费,但要注意的是必须基于同步消费的前提下,如果是异步消费就可能消费失败的情况
72 |
73 | ### 整个 RocketMQ 宕机
74 |
75 | 当整个 RocketMQ 宕机时,只能设计一个降级方案,比如将消息先缓存到某个地方,当 RocketMQ 恢复后再重新处理
76 |
77 | ### 零丢失方案
78 |
79 | - 站在生产者角度,可以使用同步发送或事务消息
80 | - 站在 Broker 角度,可以使用同步刷盘和同步主从同步
81 | - 站在消费者角度,可是使用同步消费消息
82 |
83 | ### 参考文章
84 |
85 | - **[RocketMQ如何保证消息不丢失? 如何快速处理积压消息?](https://blog.csdn.net/qq_45076180/article/details/113828472)**
86 | - **[面试官再问我如何保证 RocketMQ 不丢失消息,这回我笑了!](https://www.cnblogs.com/goodAndyxublog/p/12563813.html)**
--------------------------------------------------------------------------------
/other/Secret.md:
--------------------------------------------------------------------------------
1 | $\downarrow$ 不同主题表达了本人不同时期的喜好 嘿嘿
2 | $\downarrow$ 好久没更新了,惭愧!!!!!
3 |
4 | $\downarrow$ 呜呜呜!!图论好难,数学好难!!
5 |
6 | $\downarrow$ 整理吐了!!!!!!!!!
7 |
8 | $\downarrow$ 🤮 心累!!!!!!
9 |
10 | $\downarrow$ 😭 终于补了一个坑了,太不容易了!!!!!!
11 |
12 | $\downarrow$ 终于把图论相关的算法过了一遍 耶耶耶耶
13 |
14 | $\downarrow$ 加油 呜呼!!!
15 |
16 | $\downarrow$ 图论简直要死了!!!!!
17 |
18 | $\downarrow$ 调整了一波目录顺序!!
19 |
20 | $\downarrow$ 图论杀了我叭 渡劫归来!!!
21 |
22 | $\downarrow$ 疯狂输出!!!
23 |
24 | $\downarrow$ 终于把 DFS && BFS 的坑补上了!!!
25 |
26 | $\downarrow$ 第一次这么认真写一篇文章,好像花了 5 个小时,写吐了!!!!!
27 |
28 | $\downarrow$ 再一次被图论整崩溃了!!!!!!!!
29 |
30 | $\downarrow$ 终于终于终于终于完结了图论的整理!!!!泪目
--------------------------------------------------------------------------------
/other/test.txt:
--------------------------------------------------------------------------------
1 |
--------------------------------------------------------------------------------
 53 |
54 |
55 |
56 | 关于 Kruskal 算法的核心思想 可见 [图论 -- Kruskal 算法部分](../other/图论.html)
57 |
58 |
59 |
60 | **算法模版**
61 |
62 | ```java
63 | int minimumCost(int n, int[][] edges) {
64 | // 编号为 0...n
65 | UF uf = new UF(n + 1);
66 | // 对所有边按照权重从小到大排序
67 | Arrays.sort(edges, (a, b) -> (a[2] - b[2]));
68 | // 记录最小生成树的权重之和
69 | int mst = 0;
70 | for (int[] edge : edges) {
71 | int u = edge[0];
72 | int v = edge[1];
73 | int weight = edge[2];
74 | // 若这条边会产生环,则不能加入 mst
75 | if (uf.connected(u, v)) {
76 | continue;
77 | }
78 | // 若这条边不会产生环,则属于最小生成树
79 | mst += weight;
80 | uf.union(u, v);
81 | }
82 | // 保证所有节点都被连通
83 | // uf.count() == 1 说明所有节点被连通
84 | return uf.count() == 1 ? mst : -1;
85 | }
86 |
87 | class UF {
88 | // 见 并查集总结 的实现
89 | }
90 | ```
91 |
92 |
--------------------------------------------------------------------------------
/markdown/Algorithm/Prim最小生成树算法.md:
--------------------------------------------------------------------------------
1 | # Prim 最小生成树算法
2 |
3 | 关于 Prim 算法的核心思想 可见 [图论 -- Prim 算法部分](../other/图论.html)
4 |
5 | 对于算法的形象化模拟可以看下面动图
6 |
7 |
53 |
54 |
55 |
56 | 关于 Kruskal 算法的核心思想 可见 [图论 -- Kruskal 算法部分](../other/图论.html)
57 |
58 |
59 |
60 | **算法模版**
61 |
62 | ```java
63 | int minimumCost(int n, int[][] edges) {
64 | // 编号为 0...n
65 | UF uf = new UF(n + 1);
66 | // 对所有边按照权重从小到大排序
67 | Arrays.sort(edges, (a, b) -> (a[2] - b[2]));
68 | // 记录最小生成树的权重之和
69 | int mst = 0;
70 | for (int[] edge : edges) {
71 | int u = edge[0];
72 | int v = edge[1];
73 | int weight = edge[2];
74 | // 若这条边会产生环,则不能加入 mst
75 | if (uf.connected(u, v)) {
76 | continue;
77 | }
78 | // 若这条边不会产生环,则属于最小生成树
79 | mst += weight;
80 | uf.union(u, v);
81 | }
82 | // 保证所有节点都被连通
83 | // uf.count() == 1 说明所有节点被连通
84 | return uf.count() == 1 ? mst : -1;
85 | }
86 |
87 | class UF {
88 | // 见 并查集总结 的实现
89 | }
90 | ```
91 |
92 |
--------------------------------------------------------------------------------
/markdown/Algorithm/Prim最小生成树算法.md:
--------------------------------------------------------------------------------
1 | # Prim 最小生成树算法
2 |
3 | 关于 Prim 算法的核心思想 可见 [图论 -- Prim 算法部分](../other/图论.html)
4 |
5 | 对于算法的形象化模拟可以看下面动图
6 |
7 |  8 |
9 | 下面和 Kruskal 算法一样,解释以下三个问题,可与 Kruskal 算法对比观看
10 |
11 | - **问题一:**如何判断一个图是否为原图的生成子图
12 | - **问题二:**如何判断生成子图是一棵树
13 | - **问题三:**如何获得最小生成树
14 |
15 | **问题一:利用`inMST[]`数组来判断所有节点是否已在生成树中,详细实现可见`allConnected()`方法**
16 |
17 | **问题二:利用`inMST[]`数组来记录已加入生成树中的节点,以保证无环**
18 |
19 | **问题三:利用优先队列按照边的权重从小到大排序,可保证最终的生成子树为最小生成子树**
20 |
21 |
22 |
23 | **算法模版**
24 |
25 | ```java
26 | public class Prim {
27 | // 存在横切边的数据结构
28 | private final Queue
8 |
9 | 下面和 Kruskal 算法一样,解释以下三个问题,可与 Kruskal 算法对比观看
10 |
11 | - **问题一:**如何判断一个图是否为原图的生成子图
12 | - **问题二:**如何判断生成子图是一棵树
13 | - **问题三:**如何获得最小生成树
14 |
15 | **问题一:利用`inMST[]`数组来判断所有节点是否已在生成树中,详细实现可见`allConnected()`方法**
16 |
17 | **问题二:利用`inMST[]`数组来记录已加入生成树中的节点,以保证无环**
18 |
19 | **问题三:利用优先队列按照边的权重从小到大排序,可保证最终的生成子树为最小生成子树**
20 |
21 |
22 |
23 | **算法模版**
24 |
25 | ```java
26 | public class Prim {
27 | // 存在横切边的数据结构
28 | private final Queue 35 |
36 | 具体实现如下:
37 |
38 | ```java
39 | // 在队尾添加元素 n
40 | public void push(int n) {
41 | // 将小于 n 的元素全部删除
42 | while (!q.isEmpty() && q.getLast() < n) {
43 | q.pollLast();
44 | }
45 | // 然后将 n 加入尾部
46 | q.addLast(n);
47 | }
48 | ```
49 |
50 | 如果每个元素被加入时都这样操作,最终单调队列中的元素大小就会保持一个**单调递减**的顺序,因此我们的 `max` 方法可以可以这样写:
51 |
52 | ```java
53 | // 返回当前队列中最大值
54 | public int max() {
55 | return q.getFirst();
56 | }
57 | ```
58 |
59 | `pop(n)`方法在队头删除元素`n`,也很好写:
60 |
61 | ```java
62 | // 队头元素如果是 n,删除它
63 | public void pop(int n) {
64 | if (n == q.getFirst()) {
65 | q.pollFirst();
66 | }
67 | }
68 | ```
69 |
70 | 至此,对于数据结构`MonotonicQueue`的全部方法已经实现
71 |
72 | ### 实战题目
73 |
74 | 现在我们回到本文开头提到的题目,直接使用我们自己实现的数据结构就很好解决了。具体代码如下:
75 |
76 | ```java
77 | public int[] maxSlidingWindow(int[] nums, int k) {
78 | MonotonicQueue window = new MonotonicQueue();
79 | List
35 |
36 | 具体实现如下:
37 |
38 | ```java
39 | // 在队尾添加元素 n
40 | public void push(int n) {
41 | // 将小于 n 的元素全部删除
42 | while (!q.isEmpty() && q.getLast() < n) {
43 | q.pollLast();
44 | }
45 | // 然后将 n 加入尾部
46 | q.addLast(n);
47 | }
48 | ```
49 |
50 | 如果每个元素被加入时都这样操作,最终单调队列中的元素大小就会保持一个**单调递减**的顺序,因此我们的 `max` 方法可以可以这样写:
51 |
52 | ```java
53 | // 返回当前队列中最大值
54 | public int max() {
55 | return q.getFirst();
56 | }
57 | ```
58 |
59 | `pop(n)`方法在队头删除元素`n`,也很好写:
60 |
61 | ```java
62 | // 队头元素如果是 n,删除它
63 | public void pop(int n) {
64 | if (n == q.getFirst()) {
65 | q.pollFirst();
66 | }
67 | }
68 | ```
69 |
70 | 至此,对于数据结构`MonotonicQueue`的全部方法已经实现
71 |
72 | ### 实战题目
73 |
74 | 现在我们回到本文开头提到的题目,直接使用我们自己实现的数据结构就很好解决了。具体代码如下:
75 |
76 | ```java
77 | public int[] maxSlidingWindow(int[] nums, int k) {
78 | MonotonicQueue window = new MonotonicQueue();
79 | List 15 |
16 | 对于求「满二叉树」的节点个数,这里有一个公式:$n=2^{depth}-1$,其中 $depth$ 为树的深度
17 |
18 | 上图中的满二叉树的深度为 4,所以其节点个数为:$n=2^4-1=15$
19 |
20 | 今天要介绍的题目就是基于这个原理!
21 |
22 | ### 问题分析
23 |
24 | 对于「完全二叉树」,一定存在是「满二叉树」的子树
25 |
26 |
15 |
16 | 对于求「满二叉树」的节点个数,这里有一个公式:$n=2^{depth}-1$,其中 $depth$ 为树的深度
17 |
18 | 上图中的满二叉树的深度为 4,所以其节点个数为:$n=2^4-1=15$
19 |
20 | 今天要介绍的题目就是基于这个原理!
21 |
22 | ### 问题分析
23 |
24 | 对于「完全二叉树」,一定存在是「满二叉树」的子树
25 |
26 |  27 |
28 | 如上图所示,三角形框出来的子树就是「满二叉树」
29 |
30 | 对于这些是「满二叉树」的子树,求节点个数不需要遍历,直接利用公式即可!
31 |
32 | **现在存在一个问题:怎么判断子树是「满二叉树」呢?**
33 |
34 | - 只需要求出「左高」和「右高」,相等即为「满二叉树」
35 |
36 | **左高:**顾名思义,一直通过左孩子节点求出来的高度;**右高:**顾名思义,一直通过右孩子节点求出来的高度
37 |
38 | 描述的比较抽象,直接看图:
39 |
40 |
27 |
28 | 如上图所示,三角形框出来的子树就是「满二叉树」
29 |
30 | 对于这些是「满二叉树」的子树,求节点个数不需要遍历,直接利用公式即可!
31 |
32 | **现在存在一个问题:怎么判断子树是「满二叉树」呢?**
33 |
34 | - 只需要求出「左高」和「右高」,相等即为「满二叉树」
35 |
36 | **左高:**顾名思义,一直通过左孩子节点求出来的高度;**右高:**顾名思义,一直通过右孩子节点求出来的高度
37 |
38 | 描述的比较抽象,直接看图:
39 |
40 |  41 |
42 | 其中绿色路径就是「左高」,为 4;橙色路径就是「右高」,为 3
43 |
44 | 所以以 0 为根节点的树不是「满二叉树」,但是以 1 和 5 为根节点的树是「满二叉树」
45 |
46 | ### 代码实现
47 |
48 | 下面给出完整代码:
49 |
50 | ```java
51 | public int countNodes(TreeNode root) {
52 | if (root == null) return 0;
53 | int lh = 0, rh = 0;
54 | TreeNode left = root, right = root;
55 | // 求左高
56 | while (left != null) {
57 | left = left.left;
58 | lh++;
59 | }
60 | // 求右高
61 | while (right != null) {
62 | right = right.right;
63 | rh++;
64 | }
65 | // 以 root 为根节点的树是「满二叉树」
66 | if (lh == rh) return (int) Math.pow(2, lh) - 1;
67 | // 否则,按照正常方式遍历
68 | return countNodes(root.left) + countNodes(root.right) + 1;
69 | }
70 | ```
71 |
72 |
--------------------------------------------------------------------------------
/markdown/Algorithm/差分数组技巧.md:
--------------------------------------------------------------------------------
1 | # 差分数组技巧
2 |
3 | [1109. 航班预订统计](https://leetcode-cn.com/problems/corporate-flight-bookings/)
4 |
5 | [1094. 拼车](https://leetcode-cn.com/problems/car-pooling/)
6 |
7 |
8 |
9 | 在介绍差分数组之前,先回顾了一下「前缀和数组」**详情可见 [前缀和数组](./前缀和数组.html)**
10 |
11 | **前缀和主要适用的场景是原始数组不会被修改的情况下,频繁查询某个区间的累加和**
12 |
13 | **差分数组的主要适用场景是频繁对原始数组的某个区间的元素进行增减**
14 |
15 |
16 |
17 | **使用场景:**对于一个数组`nums[]`
18 |
19 | - 要求一:对`num[2...4]`全部 + 1
20 | - 要求二:对`num[1...3]`全部 - 3
21 | - 要求三:对`num[0...4]`全部 + 9
22 |
23 | 看到上述情景,首先想到的肯定是遍历(bao li)法。直接对数组循环 3 遍,每次在规定的区间上按要求进行操作,此时时间复杂度`O(3n)`
24 |
25 | 但是当这样的操作变得频繁后,时间复杂度也呈线性递增
26 |
27 | 所以针对这种场景,出现了「差分数组」的概念,举个简单的例子
28 |
29 |
41 |
42 | 其中绿色路径就是「左高」,为 4;橙色路径就是「右高」,为 3
43 |
44 | 所以以 0 为根节点的树不是「满二叉树」,但是以 1 和 5 为根节点的树是「满二叉树」
45 |
46 | ### 代码实现
47 |
48 | 下面给出完整代码:
49 |
50 | ```java
51 | public int countNodes(TreeNode root) {
52 | if (root == null) return 0;
53 | int lh = 0, rh = 0;
54 | TreeNode left = root, right = root;
55 | // 求左高
56 | while (left != null) {
57 | left = left.left;
58 | lh++;
59 | }
60 | // 求右高
61 | while (right != null) {
62 | right = right.right;
63 | rh++;
64 | }
65 | // 以 root 为根节点的树是「满二叉树」
66 | if (lh == rh) return (int) Math.pow(2, lh) - 1;
67 | // 否则,按照正常方式遍历
68 | return countNodes(root.left) + countNodes(root.right) + 1;
69 | }
70 | ```
71 |
72 |
--------------------------------------------------------------------------------
/markdown/Algorithm/差分数组技巧.md:
--------------------------------------------------------------------------------
1 | # 差分数组技巧
2 |
3 | [1109. 航班预订统计](https://leetcode-cn.com/problems/corporate-flight-bookings/)
4 |
5 | [1094. 拼车](https://leetcode-cn.com/problems/car-pooling/)
6 |
7 |
8 |
9 | 在介绍差分数组之前,先回顾了一下「前缀和数组」**详情可见 [前缀和数组](./前缀和数组.html)**
10 |
11 | **前缀和主要适用的场景是原始数组不会被修改的情况下,频繁查询某个区间的累加和**
12 |
13 | **差分数组的主要适用场景是频繁对原始数组的某个区间的元素进行增减**
14 |
15 |
16 |
17 | **使用场景:**对于一个数组`nums[]`
18 |
19 | - 要求一:对`num[2...4]`全部 + 1
20 | - 要求二:对`num[1...3]`全部 - 3
21 | - 要求三:对`num[0...4]`全部 + 9
22 |
23 | 看到上述情景,首先想到的肯定是遍历(bao li)法。直接对数组循环 3 遍,每次在规定的区间上按要求进行操作,此时时间复杂度`O(3n)`
24 |
25 | 但是当这样的操作变得频繁后,时间复杂度也呈线性递增
26 |
27 | 所以针对这种场景,出现了「差分数组」的概念,举个简单的例子
28 |
29 |  30 |
31 | `diff[]`和`nums[]`的关系:`diff[i] = nums[i] - nums[i - 1]`,`diff[0]`除外
32 |
33 | **问题一:**这样处理的好处是什么呢?????
34 |
35 | 当我们需要对`nums[]`进行上述三个要求时,不需要一次一次的遍历整个数组了,而只需要对`diff[]`进行一次`O(1)`的操作即可
36 |
37 | - 要求一:`diff[2] += 1;`
38 | - 要求二:`diff[1] += (-3); diff[3 + 1] -= (-3);`
39 | - 要求三:`diff[0] += 9;`
40 |
41 | **总结:**对于改变区间`[i, j]`的值,只需要进行如下操作`diff[i] += val; diff[j + 1] -= val`
42 |
43 |
30 |
31 | `diff[]`和`nums[]`的关系:`diff[i] = nums[i] - nums[i - 1]`,`diff[0]`除外
32 |
33 | **问题一:**这样处理的好处是什么呢?????
34 |
35 | 当我们需要对`nums[]`进行上述三个要求时,不需要一次一次的遍历整个数组了,而只需要对`diff[]`进行一次`O(1)`的操作即可
36 |
37 | - 要求一:`diff[2] += 1;`
38 | - 要求二:`diff[1] += (-3); diff[3 + 1] -= (-3);`
39 | - 要求三:`diff[0] += 9;`
40 |
41 | **总结:**对于改变区间`[i, j]`的值,只需要进行如下操作`diff[i] += val; diff[j + 1] -= val`
42 |
43 |  注:当`j + 1 >= diff.length`时,不需要进行`diff[j + 1] -= val`操作
44 |
45 | **问题二:**怎么通过`diff[]`得到更新后的数组呢?????
46 |
47 | ```java
48 | // 复原操作
49 | int[] res = new int[n];
50 | // 下标为 0 的元素相等
51 | res[0] = diff[0];
52 | for (int i = 1; i < n; i++) {
53 | res[i] = diff[i] + res[i - 1];
54 | }
55 | ```
56 |
57 | **问题三:**`diff[]`原理
58 |
59 | 当我们需要对区间`[i, j]`进行`+ val`操作时,我们对`diff[i] += val; diff[j + 1] -= val;`
60 |
61 | 在复原操作时,当我们求`res[i]`时,`res[i - 1]`没有变,而`diff[i]`增加了 3,所以`res[i]`增加 3
62 |
63 | 当我们求`res[i + 1]`时,`res[i]`增加了 3,而`diff[i + 1]`没有变,故`res[i + 1] = diff[i + 1] + res[i]`增加 3。即:虽然`diff[i + 1]`没有变,但是`res[i]`对后面的`res[i + 1]`有一个累积作用
64 |
65 | 当我们求`res[j + 1]`时,`res[j]`增加了 3,而`diff[j + 1]`减少了 3,故`res[j + 1] = diff[j + 1] + res[j]`增加没有变。即:我们在`j + 1`的时候,把上述的累积作用去除了,所以`j + 1`后面的元素不受影响
66 |
67 |
68 |
69 | **完整模版**
70 |
71 | ```java
72 | public class Difference {
73 |
74 | /**
75 | * 差分数组
76 | */
77 | private final int[] diff;
78 |
79 | /**
80 | * 初始化差分数组
81 | * @param nums nums
82 | */
83 | public Difference(int[] nums) {
84 | assert nums.length > 0;
85 | diff = new int[nums.length];
86 | diff[0] = nums[0];
87 | for (int i = 1; i < nums.length; i++) {
88 | diff[i] = nums[i] - nums[i - 1];
89 | }
90 | }
91 |
92 | /**
93 | * 对区间 [i, j] 增加 val(val 可为负数)
94 | * @param i i
95 | * @param j j
96 | * @param val val
97 | */
98 | public void increment(int i, int j, int val) {
99 | diff[i] += val;
100 | if (j + 1 < diff.length) {
101 | diff[j + 1] -= val;
102 | }
103 | }
104 |
105 | /**
106 | * 复原操作
107 | * @return res
108 | */
109 | public int[] result() {
110 | int[] res = new int[diff.length];
111 | res[0] = diff[0];
112 | for (int i = 1; i < diff.length; i++) {
113 | res[i] = res[i - 1] + diff[i];
114 | }
115 | return res;
116 | }
117 | }
118 | ```
119 |
120 |
121 |
122 |
--------------------------------------------------------------------------------
/markdown/Algorithm/按权重随机选择.md:
--------------------------------------------------------------------------------
1 | # 按权重随机选择
2 |
3 | [528. 按权重随机选择](https://leetcode.cn/problems/random-pick-with-weight/)
4 |
5 |
6 |
7 | 见识过很多等概率随机选择,本片文章介绍一种「按权重随机选择」
8 |
9 | 对于样例:`w = [1, 2, 3, 4]`
10 |
11 | - 返回下标 0 的概率为 $\frac{1}{10}$
12 | - 返回下标 1 的概率为 $\frac{2}{10}$
13 | - 返回下标 2 的概率为 $\frac{3}{10}$
14 | - 返回下标 3 的概率为 $\frac{4}{10}$
15 |
16 | 这里使用**「前缀和」**➕**「二分搜索」**。是不是觉得很莫名其妙,这和前缀和、二分搜索有什么关系,不要急,一步一步的来分析!!
17 |
18 | **关于「前缀和」的详细介绍可见 [前缀和数组](./前缀和数组.html)**
19 |
20 | **关于「二分搜索」的详细介绍可见 [二分搜索](./二分搜索.html)**
21 |
22 | **关于`Random`的详细介绍可见 [Random 类](../java/Random.html)**
23 |
24 |
25 |
26 | 我们需要考虑的无非就是如何才能按权重的选择,`Random()`返回的都是等概率的
27 |
28 | 对于样例:`w = [1, 2, 3, 4]`,其「前缀和数组」可视化如下:
29 |
30 | 
31 |
32 | 随机生成一个区间为`[1, 10]`的数:
33 |
34 | - 如果值为 1 返回下标 0
35 | - 如果值为 2,3 返回下标 1
36 | - 如果值为 4,5,6 返回下标 2
37 | - 如果值为 7,8,9,10 返回下标 3
38 |
39 | 刚好上述权重和最初分析的概率是等价的!!
40 |
41 | 对于`target = 5`,返回一个大于等于 5 的最小下标,即为 2
42 |
43 | **注意:`preSum[]`相对于原数组整体向右偏移了一位**
44 |
45 | 下面给出完整代码:
46 |
47 | ```java
48 | class Solution {
49 | private int[] preSum;
50 | private Random random;
51 | public Solution(int[] w) {
52 | random = new Random();
53 | preSum = new int[w.length + 1];
54 | for (int i = 1; i < preSum.length; i++) {
55 | preSum[i] = preSum[i - 1] + w[i - 1];
56 | }
57 | }
58 |
59 | public int pickIndex() {
60 | int target = random.nextInt(preSum[preSum.length - 1]) + 1;
61 | int l = 1, r = preSum.length - 1;
62 | while (l <= r) {
63 | int mid = l - (l - r) / 2;
64 | if (target <= preSum[mid]) r = mid - 1;
65 | else l = mid + 1;
66 | }
67 | // 由于前缀和数组向右偏移了一位
68 | return l - 1;
69 | }
70 | }
71 | ```
72 |
73 |
--------------------------------------------------------------------------------
/markdown/Algorithm/排序汇总.md:
--------------------------------------------------------------------------------
1 | # 排序汇总
2 |
3 | ### 稳定性
4 |
5 | 如果完成排序后,原本有序的元素不会改变其相对的位置,表示该排序是稳定的;如果完成排序后,原本有序的元素会改变其相对的位置,表示该排序是不稳定的
6 |
7 | 举个简单的例子,如果对`[1, 2, 2, 3, 4]`进行排序,如下图所示:
8 |
9 | 
10 |
11 | ### 冒泡排序
12 |
13 | ```java
14 | public int[] sort(int[] nums) {
15 | int n = nums.length;
16 | for (int i = 0; i < n - 1; i++) { // 进行 n - 1 轮遍历,每次都将值最大元素挪到最右边
17 | boolean isChange = false; // 标记是否有交换操作
18 | for (int j = 0; j < n - i - 1; j++) { // 从头开始两两进行交换
19 | if (nums[j] > nums[j + 1]) {
20 | int t = nums[j];
21 | nums[j] = nums[j + 1];
22 | nums[j + 1] = t;
23 | isChange = true;
24 | }
25 | }
26 | if (!isChange) break; // 如果一轮一次交换都没发送,表示元素均有序,直接退出循环
27 | }
28 | return nums;
29 | }
30 | ```
31 |
32 | 时间复杂度:$O(n^2)$;空间复杂度:$O(1)$;稳定
33 |
34 | **注意:**如果数组已经有序,那么在第一轮遍历时就会退出循环,所以最好时间复杂度为 $O(n)$
35 |
36 | ### 选择排序
37 |
38 | ```java
39 | public int[] sort(int[] nums) {
40 | int n = nums.length;
41 | for (int i = 0; i < n; i++) {
42 | int minId = i;
43 | for (int j = i + 1; j < n; j++) {
44 | if (nums[minId] > nums[j]) minId = j;
45 | }
46 | int t = nums[i];
47 | nums[i] = nums[minId];
48 | nums[minId] = t;
49 | }
50 | return nums;
51 | }
52 | ```
53 |
54 | 时间复杂度:$O(n^2)$;空间复杂度:$O(1)$;不稳定
55 |
56 | 关于不稳定,举个例子`[7, 7, 2]`,那么第一轮交换后为`[2, 7, 7]`,两个 7 的相对位置发生了变化
57 |
58 | **注意:**该排序的时间复杂度与数组的特点无关,均为 $O(n^2)$
59 |
60 | ### 插入排序
61 |
62 | ```java
63 | public int[] sort(int[] nums) {
64 | public int[] sortArray(int[] nums) {
65 | int n = nums.length;
66 | for (int i = 1; i < n; i++) {
67 | int t = nums[i];
68 | for (int j = i - 1; j >= 0; j--) {
69 | if (nums[j] <= t) break;
70 | nums[j + 1] = nums[j];
71 | nums[j] = t;
72 | }
73 | }
74 | return nums;
75 | }
76 | }
77 | ```
78 |
79 | 时间复杂度:$O(n^2)$;空间复杂度:$O(1)$;稳定
80 |
81 | **注意:**如果数组已经有序,那么内层循环会第一时间退出,所以最好时间复杂度为 $O(n)$
82 |
83 | ### 归并排序
84 |
85 | **详情可见 [详解归并排序及其应用](./详解归并排序及其应用.html)**
86 |
87 | 时间复杂度:$O(nlogn)$;空间复杂度:$O(n)$;稳定
88 |
89 |
90 | ### 快速排序
91 |
92 | **详情可见 [详解快排及其应用](./详解快排及其应用.html)**
93 |
94 | 时间复杂度:$O(nlogn)$;空间复杂度:$O(logn)$ -> 递归栈所需空间;不稳定
95 |
96 | **注意:**如果数组已经有序,那么时间复杂度为 $O(n^2)$
97 |
98 | ### 堆排序
99 |
100 | **详情可见 [详解堆排序「优先队列」](./详解堆排序-优先队列.html)**
101 |
102 | 时间复杂度:$O(nlogn)$;空间复杂度:$O(1)$;不稳定
103 |
104 | ### 总结
105 |
106 | | 排序算法 | 平均时间复杂度 | 最好时间复杂度 | 最坏时间复杂度 | 空间复杂度 | 稳定性 |
107 | | :------: | :------------: | :------------: | :------------: | :-----------------: | :----: |
108 | | 冒泡排序 | $O(n^2)$ | $O(n)$ | $O(n^2)$ | $O(1)$ | 稳定 |
109 | | 选择排序 | $O(n^2)$ | $O(n^2)$ | $O(n^2)$ | $O(1)$ | 不稳定 |
110 | | 插入排序 | $O(n^2)$ | $O(n)$ | $O(n^2)$ | $O(1)$ | 稳定 |
111 | | 归并排序 | $O(nlogn)$ | $O(nlogn)$ | $O(nlogn)$ | $O(n)$ | 稳定 |
112 | | 快速排序 | $O(nlogn)$ | $O(nlogn)$ | $O(n^2)$ | $O(logn)$ -> 递归栈 | 不稳定 |
113 | | 堆排序 | $O(nlogn)$ | $O(nlogn)$ | $O(nlogn)$ | $O(1)$ | 不稳定 |
--------------------------------------------------------------------------------
/markdown/Algorithm/接雨水-变题.md:
--------------------------------------------------------------------------------
1 | # 接雨水「变题」
2 |
3 | [42. 接雨水](https://leetcode.cn/problems/trapping-rain-water/)
4 |
5 |
6 |
7 | ```java
8 | // 单调栈
9 | // 时间复杂度 : O(n)
10 | // 空间复杂度 : O(n)
11 | public int trap(int[] height) {
12 | int ans = 0;
13 | Deque
注:当`j + 1 >= diff.length`时,不需要进行`diff[j + 1] -= val`操作
44 |
45 | **问题二:**怎么通过`diff[]`得到更新后的数组呢?????
46 |
47 | ```java
48 | // 复原操作
49 | int[] res = new int[n];
50 | // 下标为 0 的元素相等
51 | res[0] = diff[0];
52 | for (int i = 1; i < n; i++) {
53 | res[i] = diff[i] + res[i - 1];
54 | }
55 | ```
56 |
57 | **问题三:**`diff[]`原理
58 |
59 | 当我们需要对区间`[i, j]`进行`+ val`操作时,我们对`diff[i] += val; diff[j + 1] -= val;`
60 |
61 | 在复原操作时,当我们求`res[i]`时,`res[i - 1]`没有变,而`diff[i]`增加了 3,所以`res[i]`增加 3
62 |
63 | 当我们求`res[i + 1]`时,`res[i]`增加了 3,而`diff[i + 1]`没有变,故`res[i + 1] = diff[i + 1] + res[i]`增加 3。即:虽然`diff[i + 1]`没有变,但是`res[i]`对后面的`res[i + 1]`有一个累积作用
64 |
65 | 当我们求`res[j + 1]`时,`res[j]`增加了 3,而`diff[j + 1]`减少了 3,故`res[j + 1] = diff[j + 1] + res[j]`增加没有变。即:我们在`j + 1`的时候,把上述的累积作用去除了,所以`j + 1`后面的元素不受影响
66 |
67 |
68 |
69 | **完整模版**
70 |
71 | ```java
72 | public class Difference {
73 |
74 | /**
75 | * 差分数组
76 | */
77 | private final int[] diff;
78 |
79 | /**
80 | * 初始化差分数组
81 | * @param nums nums
82 | */
83 | public Difference(int[] nums) {
84 | assert nums.length > 0;
85 | diff = new int[nums.length];
86 | diff[0] = nums[0];
87 | for (int i = 1; i < nums.length; i++) {
88 | diff[i] = nums[i] - nums[i - 1];
89 | }
90 | }
91 |
92 | /**
93 | * 对区间 [i, j] 增加 val(val 可为负数)
94 | * @param i i
95 | * @param j j
96 | * @param val val
97 | */
98 | public void increment(int i, int j, int val) {
99 | diff[i] += val;
100 | if (j + 1 < diff.length) {
101 | diff[j + 1] -= val;
102 | }
103 | }
104 |
105 | /**
106 | * 复原操作
107 | * @return res
108 | */
109 | public int[] result() {
110 | int[] res = new int[diff.length];
111 | res[0] = diff[0];
112 | for (int i = 1; i < diff.length; i++) {
113 | res[i] = res[i - 1] + diff[i];
114 | }
115 | return res;
116 | }
117 | }
118 | ```
119 |
120 |
121 |
122 |
--------------------------------------------------------------------------------
/markdown/Algorithm/按权重随机选择.md:
--------------------------------------------------------------------------------
1 | # 按权重随机选择
2 |
3 | [528. 按权重随机选择](https://leetcode.cn/problems/random-pick-with-weight/)
4 |
5 |
6 |
7 | 见识过很多等概率随机选择,本片文章介绍一种「按权重随机选择」
8 |
9 | 对于样例:`w = [1, 2, 3, 4]`
10 |
11 | - 返回下标 0 的概率为 $\frac{1}{10}$
12 | - 返回下标 1 的概率为 $\frac{2}{10}$
13 | - 返回下标 2 的概率为 $\frac{3}{10}$
14 | - 返回下标 3 的概率为 $\frac{4}{10}$
15 |
16 | 这里使用**「前缀和」**➕**「二分搜索」**。是不是觉得很莫名其妙,这和前缀和、二分搜索有什么关系,不要急,一步一步的来分析!!
17 |
18 | **关于「前缀和」的详细介绍可见 [前缀和数组](./前缀和数组.html)**
19 |
20 | **关于「二分搜索」的详细介绍可见 [二分搜索](./二分搜索.html)**
21 |
22 | **关于`Random`的详细介绍可见 [Random 类](../java/Random.html)**
23 |
24 |
25 |
26 | 我们需要考虑的无非就是如何才能按权重的选择,`Random()`返回的都是等概率的
27 |
28 | 对于样例:`w = [1, 2, 3, 4]`,其「前缀和数组」可视化如下:
29 |
30 | 
31 |
32 | 随机生成一个区间为`[1, 10]`的数:
33 |
34 | - 如果值为 1 返回下标 0
35 | - 如果值为 2,3 返回下标 1
36 | - 如果值为 4,5,6 返回下标 2
37 | - 如果值为 7,8,9,10 返回下标 3
38 |
39 | 刚好上述权重和最初分析的概率是等价的!!
40 |
41 | 对于`target = 5`,返回一个大于等于 5 的最小下标,即为 2
42 |
43 | **注意:`preSum[]`相对于原数组整体向右偏移了一位**
44 |
45 | 下面给出完整代码:
46 |
47 | ```java
48 | class Solution {
49 | private int[] preSum;
50 | private Random random;
51 | public Solution(int[] w) {
52 | random = new Random();
53 | preSum = new int[w.length + 1];
54 | for (int i = 1; i < preSum.length; i++) {
55 | preSum[i] = preSum[i - 1] + w[i - 1];
56 | }
57 | }
58 |
59 | public int pickIndex() {
60 | int target = random.nextInt(preSum[preSum.length - 1]) + 1;
61 | int l = 1, r = preSum.length - 1;
62 | while (l <= r) {
63 | int mid = l - (l - r) / 2;
64 | if (target <= preSum[mid]) r = mid - 1;
65 | else l = mid + 1;
66 | }
67 | // 由于前缀和数组向右偏移了一位
68 | return l - 1;
69 | }
70 | }
71 | ```
72 |
73 |
--------------------------------------------------------------------------------
/markdown/Algorithm/排序汇总.md:
--------------------------------------------------------------------------------
1 | # 排序汇总
2 |
3 | ### 稳定性
4 |
5 | 如果完成排序后,原本有序的元素不会改变其相对的位置,表示该排序是稳定的;如果完成排序后,原本有序的元素会改变其相对的位置,表示该排序是不稳定的
6 |
7 | 举个简单的例子,如果对`[1, 2, 2, 3, 4]`进行排序,如下图所示:
8 |
9 | 
10 |
11 | ### 冒泡排序
12 |
13 | ```java
14 | public int[] sort(int[] nums) {
15 | int n = nums.length;
16 | for (int i = 0; i < n - 1; i++) { // 进行 n - 1 轮遍历,每次都将值最大元素挪到最右边
17 | boolean isChange = false; // 标记是否有交换操作
18 | for (int j = 0; j < n - i - 1; j++) { // 从头开始两两进行交换
19 | if (nums[j] > nums[j + 1]) {
20 | int t = nums[j];
21 | nums[j] = nums[j + 1];
22 | nums[j + 1] = t;
23 | isChange = true;
24 | }
25 | }
26 | if (!isChange) break; // 如果一轮一次交换都没发送,表示元素均有序,直接退出循环
27 | }
28 | return nums;
29 | }
30 | ```
31 |
32 | 时间复杂度:$O(n^2)$;空间复杂度:$O(1)$;稳定
33 |
34 | **注意:**如果数组已经有序,那么在第一轮遍历时就会退出循环,所以最好时间复杂度为 $O(n)$
35 |
36 | ### 选择排序
37 |
38 | ```java
39 | public int[] sort(int[] nums) {
40 | int n = nums.length;
41 | for (int i = 0; i < n; i++) {
42 | int minId = i;
43 | for (int j = i + 1; j < n; j++) {
44 | if (nums[minId] > nums[j]) minId = j;
45 | }
46 | int t = nums[i];
47 | nums[i] = nums[minId];
48 | nums[minId] = t;
49 | }
50 | return nums;
51 | }
52 | ```
53 |
54 | 时间复杂度:$O(n^2)$;空间复杂度:$O(1)$;不稳定
55 |
56 | 关于不稳定,举个例子`[7, 7, 2]`,那么第一轮交换后为`[2, 7, 7]`,两个 7 的相对位置发生了变化
57 |
58 | **注意:**该排序的时间复杂度与数组的特点无关,均为 $O(n^2)$
59 |
60 | ### 插入排序
61 |
62 | ```java
63 | public int[] sort(int[] nums) {
64 | public int[] sortArray(int[] nums) {
65 | int n = nums.length;
66 | for (int i = 1; i < n; i++) {
67 | int t = nums[i];
68 | for (int j = i - 1; j >= 0; j--) {
69 | if (nums[j] <= t) break;
70 | nums[j + 1] = nums[j];
71 | nums[j] = t;
72 | }
73 | }
74 | return nums;
75 | }
76 | }
77 | ```
78 |
79 | 时间复杂度:$O(n^2)$;空间复杂度:$O(1)$;稳定
80 |
81 | **注意:**如果数组已经有序,那么内层循环会第一时间退出,所以最好时间复杂度为 $O(n)$
82 |
83 | ### 归并排序
84 |
85 | **详情可见 [详解归并排序及其应用](./详解归并排序及其应用.html)**
86 |
87 | 时间复杂度:$O(nlogn)$;空间复杂度:$O(n)$;稳定
88 |
89 |
90 | ### 快速排序
91 |
92 | **详情可见 [详解快排及其应用](./详解快排及其应用.html)**
93 |
94 | 时间复杂度:$O(nlogn)$;空间复杂度:$O(logn)$ -> 递归栈所需空间;不稳定
95 |
96 | **注意:**如果数组已经有序,那么时间复杂度为 $O(n^2)$
97 |
98 | ### 堆排序
99 |
100 | **详情可见 [详解堆排序「优先队列」](./详解堆排序-优先队列.html)**
101 |
102 | 时间复杂度:$O(nlogn)$;空间复杂度:$O(1)$;不稳定
103 |
104 | ### 总结
105 |
106 | | 排序算法 | 平均时间复杂度 | 最好时间复杂度 | 最坏时间复杂度 | 空间复杂度 | 稳定性 |
107 | | :------: | :------------: | :------------: | :------------: | :-----------------: | :----: |
108 | | 冒泡排序 | $O(n^2)$ | $O(n)$ | $O(n^2)$ | $O(1)$ | 稳定 |
109 | | 选择排序 | $O(n^2)$ | $O(n^2)$ | $O(n^2)$ | $O(1)$ | 不稳定 |
110 | | 插入排序 | $O(n^2)$ | $O(n)$ | $O(n^2)$ | $O(1)$ | 稳定 |
111 | | 归并排序 | $O(nlogn)$ | $O(nlogn)$ | $O(nlogn)$ | $O(n)$ | 稳定 |
112 | | 快速排序 | $O(nlogn)$ | $O(nlogn)$ | $O(n^2)$ | $O(logn)$ -> 递归栈 | 不稳定 |
113 | | 堆排序 | $O(nlogn)$ | $O(nlogn)$ | $O(nlogn)$ | $O(1)$ | 不稳定 |
--------------------------------------------------------------------------------
/markdown/Algorithm/接雨水-变题.md:
--------------------------------------------------------------------------------
1 | # 接雨水「变题」
2 |
3 | [42. 接雨水](https://leetcode.cn/problems/trapping-rain-water/)
4 |
5 |
6 |
7 | ```java
8 | // 单调栈
9 | // 时间复杂度 : O(n)
10 | // 空间复杂度 : O(n)
11 | public int trap(int[] height) {
12 | int ans = 0;
13 | Deque 29 |
30 | ```java
31 | private List
29 |
30 | ```java
31 | private List 29 |
30 | 当我们在向外扩张时,记录一下层数,就可以得到两点之间的距离
31 |
32 | ### 代码实现
33 |
34 | ```java
35 | class Solution {
36 | private int m;
37 | private int n;
38 | private int[][] graph;
39 | // 记录所有的树,其三元组为 [h, i, j]
40 | private List
29 |
30 | 当我们在向外扩张时,记录一下层数,就可以得到两点之间的距离
31 |
32 | ### 代码实现
33 |
34 | ```java
35 | class Solution {
36 | private int m;
37 | private int n;
38 | private int[][] graph;
39 | // 记录所有的树,其三元组为 [h, i, j]
40 | private List --------------------------------------------------------------------------------
/markdown/Git/Git总结.md:
--------------------------------------------------------------------------------
1 | # Git 总结
2 |
3 |
4 |
5 | > 主要介绍 Git 的常用操作
6 |
7 | 首先本地 Git 有三个分区:`working directory`,`stage/index area`,`commit history`
8 |
9 | `working directory`:工作目录
10 |
11 | `stage/index area`:暂存区,`git add`命令会把`working directory`中的修改添加到暂存区
12 |
13 | `commit history`:`git commit`命令会把`暂存区`的内容提交到该分区。每个`commit`都有一个唯一的 Hash 值
14 |
15 | 三者的关系如下图所示:
16 |
17 |
--------------------------------------------------------------------------------
/markdown/Git/Git总结.md:
--------------------------------------------------------------------------------
1 | # Git 总结
2 |
3 |
4 |
5 | > 主要介绍 Git 的常用操作
6 |
7 | 首先本地 Git 有三个分区:`working directory`,`stage/index area`,`commit history`
8 |
9 | `working directory`:工作目录
10 |
11 | `stage/index area`:暂存区,`git add`命令会把`working directory`中的修改添加到暂存区
12 |
13 | `commit history`:`git commit`命令会把`暂存区`的内容提交到该分区。每个`commit`都有一个唯一的 Hash 值
14 |
15 | 三者的关系如下图所示:
16 |
17 |  18 |
19 | ## 常用 git 命令
20 |
21 | ```bash
22 | # 初始化 git 项目
23 | git init
24 | # working dir -> stage area
25 | git add .
26 | # stage area -> commit history
27 | git commit -m "xxxx"
28 | # 查看工作区提交情况
29 | git status
30 | # 查看 git commit 提交记录
31 | git log
32 | # 创建新分支
33 | git branch xxx
34 | # 切换新分支
35 | git checkout xxx
36 | # 创建并切换新分支
37 | git checkout -b xxx
38 | # 将 commit history 区的代码恢复到 stage
39 | git reset
40 | ```
41 |
42 | ## 常用 git 操作
43 |
44 |
18 |
19 | ## 常用 git 命令
20 |
21 | ```bash
22 | # 初始化 git 项目
23 | git init
24 | # working dir -> stage area
25 | git add .
26 | # stage area -> commit history
27 | git commit -m "xxxx"
28 | # 查看工作区提交情况
29 | git status
30 | # 查看 git commit 提交记录
31 | git log
32 | # 创建新分支
33 | git branch xxx
34 | # 切换新分支
35 | git checkout xxx
36 | # 创建并切换新分支
37 | git checkout -b xxx
38 | # 将 commit history 区的代码恢复到 stage
39 | git reset
40 | ```
41 |
42 | ## 常用 git 操作
43 |
44 |  45 |
46 |
47 |
48 | **把`stage`中的修改还原到`working dir`中**
49 |
50 | ```bash
51 | # 恢复某一个文件
52 | git checkout [fileName]
53 | # 恢复所有文件
54 | git checkout .
55 | ```
56 |
57 |
58 |
59 | **把`commit history`区的历史提交还原到`working dir`中**
60 |
61 | ```bash
62 | git checkout HEAD .
63 | ```
64 |
65 |
66 |
67 | **将`commit history`区的文件还原到`stage`区**
68 |
69 | ```bash
70 | git reset [fileName]
71 | git reset .
72 | ```
73 |
74 |
75 |
76 | **撤销`git commit`**
77 |
78 | ```bash
79 | git reset --soft HEAD^
80 | # 等价
81 | git reset --soft HEAD~1
82 | # 撤销两次 git commit
83 | git reset --soft HEAD~2
84 |
85 | # 如果此时我们同时需要撤销远程的提交记录
86 | # -f 表示强制推送到远程
87 | git push -f
88 | ```
89 |
90 | 下面介绍一下几个参数
91 |
92 | `--mixed`:不删除工作空间改动代码,撤销`commit`,并且撤销`git add .`操作
93 |
94 | `--soft `:不删除工作空间改动代码,撤销`commit`,不撤销`git add .`
95 |
96 | `--hard` :删除工作空间改动代码,撤销`commit`,撤销`git add .`
97 |
98 |
99 |
100 | **修改`git commit -m " "`注释**
101 |
102 | ```bash
103 | git commit --amend
104 | ```
105 |
106 |
107 |
108 | **合并相同的`git commit`**
109 |
110 | ```bash
111 | # 选择需要合并 git commit 最早的一个 id 的前一个 (因为不包括本 id 的 git commit)
112 | git rebase -i [git logID]
113 | ```
114 |
115 | 当前我们只要知道`pick`和`squash`这两个命令即可
116 |
117 | - `pick`的意思是要会执行这个 commit
118 | - `squash`的意思是这个 commit 会被合并到前一个commit
119 |
120 |
121 |
122 | **撤销`git rabase`合并**
123 |
124 | ```bash
125 | # 查看本地记录
126 | git reflog
127 |
128 | git reset --hard [id]
129 |
130 | # 同时修改远程的提交
131 | git push -f
132 | ```
133 |
134 |
--------------------------------------------------------------------------------
/markdown/Java/CPU密集型-IO密集型.md:
--------------------------------------------------------------------------------
1 | # CPU 密集型 & I/O 密集型
2 |
3 | 本片文章介绍如何区分 CPU 密集型任务和 I/O 密集型任务~~
4 |
5 | 在设置 **[Java 线程池](../java/Java线程池.html)** 的参数时,需要参考到底是 CPU 密集型任务,还是 I/O 密集型任务,根据任务的不同类型,设置不同线程池大小:
6 |
7 | - **对于 CPU 密集型任务:**设置线程池大小为 CPU 核心数 + 1。比 CPU 核心多 1 是为了防止线程偶发的缺页中断,有多余线程可以补上 CPU 空闲时间
8 | - **对于 I/O 密集型任务:**设置线程池大小为 CPU 核心数 * 2。由于密集的 I/O 处理,增加了 CPU 处于空闲的概率
9 |
10 | 那么到底如何判断是 CPU 密集型任务,还是 I/O 密集型任务呢?
11 |
12 | 从宏观上分析,CPU 密集型任务多为计算型代码,需要始终在 CPU 上运行,而 I/O 密集型任务多为文件读写、DB 读写、网络请求等,总之是一切偏向于 I/O 操作的任务
13 |
14 | 上面的判断方法还是过于主观,比如如何判断是计算型代码呢?如何判断任务中更侧重于 I/O 操作呢?有没有一些硬性指标可以更加客观的去判断呢??
15 |
16 | 在 Linux 中可以使用`top`命令查看进程的 CPU 占用率,如果一个进程大多数时候都是满载使用 CPU,那么可认为是 CPU 密集型;反之为 I/O 密集型
17 |
18 | #### Demo -> CPU 密集型任务
19 |
20 | 下面给出一个 CPU 密集型任务的 Demo:
21 |
22 | ```java
23 | public class Main {
24 | public static void main(String[] args) {
25 | while (true){}
26 | }
27 | }
28 | ```
29 |
30 | 说白了,上面的例子就是一个死循环,肯定会一直占用 CPU 资源,通过`jps`命令获得该任务的 pid:
31 |
32 | ```bash
33 | [root@localhost ~]$ jps
34 | 1953 Jps
35 | 1897 Main
36 | ```
37 |
38 | 然后通过`top -p 1897`查看该任务的执行情况:
39 |
40 | ```bash
41 | [root@localhost ~]$ top -p 1897
42 | top - 15:56:28 up 14 min, 3 users, load average: 1.01, 0.75, 0.38
43 | Tasks: 1 total, 0 running, 1 sleeping, 0 stopped, 0 zombie
44 | %Cpu(s): 12.4 us, 0.0 sy, 0.0 ni, 87.4 id, 0.0 wa, 0.1 hi, 0.0 si, 0.0 st
45 | MiB Mem : 7741.8 total, 6927.3 free, 472.6 used, 341.9 buff/cache
46 | MiB Swap: 2048.0 total, 2048.0 free, 0.0 used. 7025.4 avail Mem
47 |
48 | PID USER PR NI VIRT RES SHR S %CPU %MEM TIME+ COMMAND
49 | 1897 root 20 0 4726724 53576 16584 S 99.3 0.7 6:02.43 java
50 | ```
51 |
52 | 从结果中可以看出该任务的 CPU 占用率为 99.3%,可认为几乎满载了!!
53 |
54 | #### Demo -> I/O 密集型任务
55 |
56 | 下面给出一个 I/O 密集型任务的 Demo:
57 |
58 | ```java
59 | public static void main(String[] args) {
60 | try {
61 | BufferedReader in = new BufferedReader(new FileReader("test.txt"), 1024);
62 | String str;
63 | while ((str = in.readLine()) != null) {
64 | System.out.println(str);
65 | }
66 | System.out.println(str);
67 | } catch (IOException e) {
68 | }
69 | }
70 | ```
71 |
72 | 上面例子中,`test.txt`是一个 6G 的大文件,通过`BufferedReader`读取到内存中,并将读取到的内容输出到终端
73 |
74 | 通过系统自带的性能监控软件可以看到该任务从磁盘读取了大量数据,可认为它是 I/O 密集性,如下图所示:
75 |
76 | 
--------------------------------------------------------------------------------
/markdown/Java/Java-8-Stream-sorted.md:
--------------------------------------------------------------------------------
1 | # Java 8 Stream sorted()
2 |
3 | 介绍`Stream sorted()`三种排序的实现「自然排序」「比较器」「反向排序」
4 |
5 | `sorted()`:它使用自然排序对流的元素进行排序。元素类必须实现`Comparable`接口
6 |
7 | `sorted(Comparator comparator)`:这里我们使用`lambda`表达式创建`Comparator`的实例。我们可以按升序和降序对流元素进行排序
8 |
9 | 以下代码行将按自然顺序对列表进行排序
10 |
11 | ```java
12 | list.stream().sorted()
13 | ```
14 |
15 | 为了反转自然排序`Comparator`提供了`reverseOrder()`方法。我们使用它如下
16 |
17 | ```java
18 | list.stream().sorted(Comparator.reverseOrder())
19 | ```
20 |
21 | 以下代码行使用`Comparator`对列表进行排序
22 |
23 | ```java
24 | list.stream().sorted(Comparator.comparing(Student::getAge))
25 | ```
26 |
27 | 为了反转顺序,`Comparator`提供了`reversed()`方法。我们使用这种方法如下
28 |
29 | ```java
30 | list.stream().sorted(Comparator.comparing(Student::getAge).reversed())
31 | ```
32 |
33 | ### Stream sorted() with List
34 |
35 | ```java
36 | // 升序
37 | // 前提:Person 类必须实现 Comparable 接口
38 | List
45 |
46 |
47 |
48 | **把`stage`中的修改还原到`working dir`中**
49 |
50 | ```bash
51 | # 恢复某一个文件
52 | git checkout [fileName]
53 | # 恢复所有文件
54 | git checkout .
55 | ```
56 |
57 |
58 |
59 | **把`commit history`区的历史提交还原到`working dir`中**
60 |
61 | ```bash
62 | git checkout HEAD .
63 | ```
64 |
65 |
66 |
67 | **将`commit history`区的文件还原到`stage`区**
68 |
69 | ```bash
70 | git reset [fileName]
71 | git reset .
72 | ```
73 |
74 |
75 |
76 | **撤销`git commit`**
77 |
78 | ```bash
79 | git reset --soft HEAD^
80 | # 等价
81 | git reset --soft HEAD~1
82 | # 撤销两次 git commit
83 | git reset --soft HEAD~2
84 |
85 | # 如果此时我们同时需要撤销远程的提交记录
86 | # -f 表示强制推送到远程
87 | git push -f
88 | ```
89 |
90 | 下面介绍一下几个参数
91 |
92 | `--mixed`:不删除工作空间改动代码,撤销`commit`,并且撤销`git add .`操作
93 |
94 | `--soft `:不删除工作空间改动代码,撤销`commit`,不撤销`git add .`
95 |
96 | `--hard` :删除工作空间改动代码,撤销`commit`,撤销`git add .`
97 |
98 |
99 |
100 | **修改`git commit -m " "`注释**
101 |
102 | ```bash
103 | git commit --amend
104 | ```
105 |
106 |
107 |
108 | **合并相同的`git commit`**
109 |
110 | ```bash
111 | # 选择需要合并 git commit 最早的一个 id 的前一个 (因为不包括本 id 的 git commit)
112 | git rebase -i [git logID]
113 | ```
114 |
115 | 当前我们只要知道`pick`和`squash`这两个命令即可
116 |
117 | - `pick`的意思是要会执行这个 commit
118 | - `squash`的意思是这个 commit 会被合并到前一个commit
119 |
120 |
121 |
122 | **撤销`git rabase`合并**
123 |
124 | ```bash
125 | # 查看本地记录
126 | git reflog
127 |
128 | git reset --hard [id]
129 |
130 | # 同时修改远程的提交
131 | git push -f
132 | ```
133 |
134 |
--------------------------------------------------------------------------------
/markdown/Java/CPU密集型-IO密集型.md:
--------------------------------------------------------------------------------
1 | # CPU 密集型 & I/O 密集型
2 |
3 | 本片文章介绍如何区分 CPU 密集型任务和 I/O 密集型任务~~
4 |
5 | 在设置 **[Java 线程池](../java/Java线程池.html)** 的参数时,需要参考到底是 CPU 密集型任务,还是 I/O 密集型任务,根据任务的不同类型,设置不同线程池大小:
6 |
7 | - **对于 CPU 密集型任务:**设置线程池大小为 CPU 核心数 + 1。比 CPU 核心多 1 是为了防止线程偶发的缺页中断,有多余线程可以补上 CPU 空闲时间
8 | - **对于 I/O 密集型任务:**设置线程池大小为 CPU 核心数 * 2。由于密集的 I/O 处理,增加了 CPU 处于空闲的概率
9 |
10 | 那么到底如何判断是 CPU 密集型任务,还是 I/O 密集型任务呢?
11 |
12 | 从宏观上分析,CPU 密集型任务多为计算型代码,需要始终在 CPU 上运行,而 I/O 密集型任务多为文件读写、DB 读写、网络请求等,总之是一切偏向于 I/O 操作的任务
13 |
14 | 上面的判断方法还是过于主观,比如如何判断是计算型代码呢?如何判断任务中更侧重于 I/O 操作呢?有没有一些硬性指标可以更加客观的去判断呢??
15 |
16 | 在 Linux 中可以使用`top`命令查看进程的 CPU 占用率,如果一个进程大多数时候都是满载使用 CPU,那么可认为是 CPU 密集型;反之为 I/O 密集型
17 |
18 | #### Demo -> CPU 密集型任务
19 |
20 | 下面给出一个 CPU 密集型任务的 Demo:
21 |
22 | ```java
23 | public class Main {
24 | public static void main(String[] args) {
25 | while (true){}
26 | }
27 | }
28 | ```
29 |
30 | 说白了,上面的例子就是一个死循环,肯定会一直占用 CPU 资源,通过`jps`命令获得该任务的 pid:
31 |
32 | ```bash
33 | [root@localhost ~]$ jps
34 | 1953 Jps
35 | 1897 Main
36 | ```
37 |
38 | 然后通过`top -p 1897`查看该任务的执行情况:
39 |
40 | ```bash
41 | [root@localhost ~]$ top -p 1897
42 | top - 15:56:28 up 14 min, 3 users, load average: 1.01, 0.75, 0.38
43 | Tasks: 1 total, 0 running, 1 sleeping, 0 stopped, 0 zombie
44 | %Cpu(s): 12.4 us, 0.0 sy, 0.0 ni, 87.4 id, 0.0 wa, 0.1 hi, 0.0 si, 0.0 st
45 | MiB Mem : 7741.8 total, 6927.3 free, 472.6 used, 341.9 buff/cache
46 | MiB Swap: 2048.0 total, 2048.0 free, 0.0 used. 7025.4 avail Mem
47 |
48 | PID USER PR NI VIRT RES SHR S %CPU %MEM TIME+ COMMAND
49 | 1897 root 20 0 4726724 53576 16584 S 99.3 0.7 6:02.43 java
50 | ```
51 |
52 | 从结果中可以看出该任务的 CPU 占用率为 99.3%,可认为几乎满载了!!
53 |
54 | #### Demo -> I/O 密集型任务
55 |
56 | 下面给出一个 I/O 密集型任务的 Demo:
57 |
58 | ```java
59 | public static void main(String[] args) {
60 | try {
61 | BufferedReader in = new BufferedReader(new FileReader("test.txt"), 1024);
62 | String str;
63 | while ((str = in.readLine()) != null) {
64 | System.out.println(str);
65 | }
66 | System.out.println(str);
67 | } catch (IOException e) {
68 | }
69 | }
70 | ```
71 |
72 | 上面例子中,`test.txt`是一个 6G 的大文件,通过`BufferedReader`读取到内存中,并将读取到的内容输出到终端
73 |
74 | 通过系统自带的性能监控软件可以看到该任务从磁盘读取了大量数据,可认为它是 I/O 密集性,如下图所示:
75 |
76 | 
--------------------------------------------------------------------------------
/markdown/Java/Java-8-Stream-sorted.md:
--------------------------------------------------------------------------------
1 | # Java 8 Stream sorted()
2 |
3 | 介绍`Stream sorted()`三种排序的实现「自然排序」「比较器」「反向排序」
4 |
5 | `sorted()`:它使用自然排序对流的元素进行排序。元素类必须实现`Comparable`接口
6 |
7 | `sorted(Comparator comparator)`:这里我们使用`lambda`表达式创建`Comparator`的实例。我们可以按升序和降序对流元素进行排序
8 |
9 | 以下代码行将按自然顺序对列表进行排序
10 |
11 | ```java
12 | list.stream().sorted()
13 | ```
14 |
15 | 为了反转自然排序`Comparator`提供了`reverseOrder()`方法。我们使用它如下
16 |
17 | ```java
18 | list.stream().sorted(Comparator.reverseOrder())
19 | ```
20 |
21 | 以下代码行使用`Comparator`对列表进行排序
22 |
23 | ```java
24 | list.stream().sorted(Comparator.comparing(Student::getAge))
25 | ```
26 |
27 | 为了反转顺序,`Comparator`提供了`reversed()`方法。我们使用这种方法如下
28 |
29 | ```java
30 | list.stream().sorted(Comparator.comparing(Student::getAge).reversed())
31 | ```
32 |
33 | ### Stream sorted() with List
34 |
35 | ```java
36 | // 升序
37 | // 前提:Person 类必须实现 Comparable 接口
38 | List 42 |
43 | ### 垃圾收集器性能指标
44 |
45 | **停顿时间:**执行一次完整的垃圾收集时,用户线程被暂停的总时间
46 |
47 | **吞吐量:**处理器用于运行用户代码的时间与处理器总消耗时间的比值,计算公式如下:
48 | $$
49 | 吞吐量 = \frac{运行用户代码时间}{运行用户代码时间 + 运行垃圾收集时间}
50 | $$
51 | **对比:**
52 |
53 | - 停顿时间越短越适合需要与用户交互或需要保证服务响应质量的程序,良好的响应速度能提升用户体验感
54 | - 高吞吐量则可以最高效率地利用处理器资源,尽快完成程序的运算任务,主要适合在后台运算而不需要太多交互的分析任务
55 |
56 | ### 垃圾收集器的组合关系
57 |
58 | 本部分的关系是在「按照工作内存区间划分」的基础上进行组合滴!!
59 |
60 | 
61 |
62 | **[JEP 173: Retire Some Rarely-Used GC Combinations](https://openjdk.org/jeps/173)**
63 |
64 | **[JEP 214: Remove GC Combinations Deprecated in JDK 8](https://openjdk.org/jeps/214)**
65 |
66 | **[JEP 366: Deprecate the ParallelScavenge + SerialOld GC Combination](https://openjdk.org/jeps/366)**
67 |
68 | **[JEP 363: Remove the Concurrent Mark Sweep (CMS) Garbage Collector](https://openjdk.org/jeps/363)**
69 |
70 | **注意:JDK8 中默认垃圾收集器为 Parallel Scaverge GC + Parallel Old GC;JDK9 中默认垃圾收集器为 G1**
--------------------------------------------------------------------------------
/markdown/Java/实战-静态变量-实例变量-局部变量.md:
--------------------------------------------------------------------------------
1 | # 实战「静态变量」「实例变量」「局部变量」
2 |
3 | 这篇文章就以实战的方式看看「静态变量」「实例变量」「局部变量」存放的位置!
4 |
5 | 首先要搞清楚一个概念,「静态变量」「实例变量」「局部变量」指的是引用本身,而非它们所指向的对象,它们所指向的对象毫无疑问肯定都存放在堆上,**关于这个观点更多分析可见 [逃逸分析](./逃逸分析.html)**
6 |
7 | 还需要强调一个点,这里是基于 JDK8 的 HotSpot 虚拟机!!
8 |
9 | 根据理论知识可以知道:「静态变量」在 JDK7 及以后就存放在 Java 堆中;「实例变量」随着对象实例存放在 Java 堆中;「局部变量」存放在方法栈帧的局部变量表中
10 |
11 | 首先给出一段测试代码:
12 |
13 | ```java
14 | public class Test {
15 | static class Person {
16 | // 静态变量
17 | static ObjectHolder staticObj = new ObjectHolder();
18 | // 实例变量
19 | ObjectHolder instanceObj = new ObjectHolder();
20 | void foo() throws InterruptedException {
21 | // 局部变量
22 | ObjectHolder localObj = new ObjectHolder();
23 | // 休眠,不然方法执行完,方法栈帧就会出栈
24 | Thread.sleep(10000000);
25 | }
26 | }
27 | private static class ObjectHolder {}
28 | public static void main(String[] args) throws InterruptedException {
29 | Person person = new Person();
30 | person.foo();
31 | }
32 | }
33 | ```
34 |
35 | 我们先分析一下,按照理论来说,此时 Java 堆中肯定存在 3 个`ObjectHolder`对象实例,同时`staticObj`和`instanceObj`也都在 Java 堆中
36 |
37 | 下面通过 VisualVM + JProfiler 软件测试一下!!首先用 VisualVM 保存一个 Java 堆的 dump文件,如下所示:
38 |
39 | 
40 |
41 | 用 JProfiler 打开这个 dump 文件,可以发现在 Java 堆中刚好有 3 个`ObjectHolder`对象实例,如下图所示:
42 |
43 | 
44 |
45 | 我们再找找「静态变量」在哪里,在`java.lang.Class`中可以发现我们定义的静态变量`staticObj`,而这个静态变量指向的对象实例是`0xa87`,如下图所示:
46 |
47 | 
48 |
49 | 继续找「实例变量」在哪里,在`com.lfool.myself.Test$Person`中可以发现我们定义的实例变量`instanceObj`,而这个实例变量指向的对象实例是`0xc3b`,如下图所示:
50 |
51 | 
52 |
53 | 到此为止,我们找出来的所有内容都存放在 Java 堆中,至于「局部变量」,可以通过 JHSDB 软件在栈中发现,这里就不演示了!!!
--------------------------------------------------------------------------------
/markdown/Java/方法调用面试题.md:
--------------------------------------------------------------------------------
1 | # 方法调用面试题
2 |
3 | #### 问题一:下面代码输出的结果
4 |
5 | **详细解析可见 [方法调用](./方法调用.html#静态分派)**
6 |
7 | ```java
8 | public class StaticDispatch {
9 | static abstract class Human {}
10 | static class Man extends Human {}
11 | static class Woman extends Human {}
12 | public void sayHello(Human guy) {
13 | System.out.println("hello, guy!");
14 | }
15 | public void sayHello(Man guy) {
16 | System.out.println("hello, gentleman!");
17 | }
18 | public void sayHello(Woman guy) {
19 | System.out.println("hello, lady!");
20 | }
21 | public static void main(String[] args) {
22 | Human man = new Man();
23 | Human woman = new Woman();
24 | StaticDispatch sr = new StaticDispatch();
25 | sr.sayHello(man);
26 | sr.sayHello(woman);
27 | }
28 | }
29 | ```
30 |
31 | #### 问题二:下面代码依次输出的结果
32 |
33 | **详细解析可见 [方法调用](./方法调用.html#静态分派)**
34 |
35 | ```java
36 | public class Overload {
37 | public static void sayHello(Object arg) {
38 | System.out.println("hello Object");
39 | }
40 | public static void sayHello(int arg) {
41 | System.out.println("hello int");
42 | }
43 | public static void sayHello(long arg) {
44 | System.out.println("hello long");
45 | }
46 | public static void sayHello(Character arg) {
47 | System.out.println("hello Character");
48 | }
49 | public static void sayHello(char arg) {
50 | System.out.println("hello char");
51 | }
52 | public static void sayHello(char... arg) {
53 | System.out.println("hello char...");
54 | }
55 | public static void sayHello(Serializable arg) {
56 | System.out.println("hello Serializable");
57 | }
58 | public static void main(String[] args) {
59 | sayHello('a');
60 | }
61 | }
62 | ```
63 |
64 | 依次注释掉方法
65 | - `sayHello(char arg)`
66 | - `sayHello(int arg)`
67 | - `sayHello(long arg)`
68 | - `sayHello(Character arg)`
69 | - `sayHello(Serializable arg)`
70 | - `sayHello(Object arg)`
71 |
72 | 它会输出什么?!
73 |
74 | #### 问题三:下面代码输出的结果
75 |
76 | **详细解析可见 [方法调用](./方法调用.html#动态分派)**
77 |
78 | ```java
79 | public class FieldHasNoPolymorphic {
80 | static class Father {
81 | public int money = 1;
82 | public Father() {
83 | money = 2;
84 | showMeTheMoney();
85 | }
86 | public void showMeTheMoney() {
87 | System.out.println("I am Father, i have $" + money);
88 | }
89 | }
90 | static class Son extends Father {
91 | public int money = 3;
92 | public Son() {
93 | money = 4;
94 | showMeTheMoney();
95 | }
96 | public void showMeTheMoney() {
97 | System.out.println("I am Son, i have $" + money);
98 | }
99 | }
100 | public static void main(String[] args) {
101 | Father guy = new Son();
102 | System.out.println("This guy has $" + guy.money);
103 | }
104 | }
105 | ```
106 |
107 |
--------------------------------------------------------------------------------
/markdown/Java/注解.md:
--------------------------------------------------------------------------------
1 | # 注解
2 |
3 | ### 什么是注解
4 |
5 | Annotation 是从 JDK5.0 开始引入的新技术
6 |
7 | Annotation 的作用
8 |
9 | - 不是程序本身,可以对程序作出解释
10 | - **可以被其他程序 (如:编译器等) 读取**
11 |
12 | Annotation 的格式
13 |
14 | - 注解是以`@name`在代码中存在,还可以添加一些参数值,例如:`@SuppressWarnings(value = "unchecked")`
15 |
16 | Annotation 在哪里使用?
17 |
18 | - 可以附加在 package、class、method、field 等上面,相当于给他们添加了额外的辅助信息,我们可以通过**反射机制**编程实现对这些元数据的访问
19 |
20 | ### 内置注解
21 |
22 | `@Override`:定义在`java.lang.Override`中,此注解只适用于**修辞方法**,表示一个方法声明打算重写超类中的另一个方法声明
23 |
24 | `@Deprecated`:定义在`java.lang.Deprecated`中,此注解可以用于**修饰方法、属性、类**,表示不鼓励程序员使用这些元素,通常是因为它很危险或者存在更好的选择
25 |
26 | `@SuppressWarnings`:定义在`java.lang.SuppressWarnings`中,用来抑制编译时的警告信息,与前两个注解不同的是需要添加一个参数才能正确使用,这些参数都是已经定义好了的,选择性使用即可
27 |
28 | - `@SuppressWarnings("all")`
29 | - `@SuppressWarnings("unchecked")`
30 | - `@SuppressWarnings(value = {"unchecked", "deprecation"})`
31 | - ...
32 |
33 | ### 元注解
34 |
35 | 元注解的作用:负责注解其他注解
36 |
37 | Java 定义了 4 个标准的 meta-annotation 类型,他们被用来提供对其他 annotation 类型作说明
38 |
39 | 这些类型和它们所支持的类在`java.lang.annotation`包中可以找到:`@Target`、`@Retention`、`@Documented`、`@Inherited`
40 |
41 | - `@Target`:用于描述注解的使用范围 (即:被描述的注解可以用在什么地方)
42 | - `@Retention`:表示需要在什么级别保存该注解信息,用于描述注解的生命周期 (SOURCE < CLASS < **RUNTIME**)
43 | - `@Documented`:说明该注解将被包含在 Javadoc 中
44 | - `@Inherited`:说明子类可以继承父类中的该注解
45 |
46 | ```java
47 | // Target 表示该注解可以用在什么地方:类,方法
48 | @Target(value = {ElementType.TYPE, ElementType.METHOD})
49 | // Retention 表示该注解在什么地方还有效:SOURCE < CLASS < RUNTIME
50 | @Retention(value = RetentionPolicy.RUNTIME)
51 | // Documented 表示该注解将生成在 Javadoc 中
52 | @Documented
53 | // Inherited 表示子类可以继承该注解
54 | @Inherited
55 | public @interface MyAnnotation {
56 | }
57 | ```
58 |
59 | ### 自定义注解
60 |
61 | 使用`@interface`自定义注解时,自动继承`java.lang.annotation.Annotation`接口
62 |
63 | - `@interface`用来声明一个注解,格式:`public @interface name {}`
64 | - 其中的每一个方法实际上是声明了一个配置参数
65 | - 方法的名称就是参数的名称
66 | - 返回值类型就是参数的类型 (返回值只能是基本类型、对象、String、enum)
67 | - 可以通过`default`来声明参数的默认值
68 | - 如果只有一个参数成员,一般参数名为`value`
69 | - 注解元素必须要有值,在定义注解元素时,经常使用「空字符串、0」作为默认值
70 |
71 | ```java
72 | @Target(value = {ElementType.TYPE, ElementType.METHOD})
73 | @Retention(value = RetentionPolicy.RUNTIME)
74 | public @interface MyAnnotation {
75 | // 定义注解参数的格式:参数类型 + 名字 + ()
76 | String name();
77 | int age() default 0;
78 | int id() default -1;
79 | String[] schools() default {"school1", "school2"};
80 | }
81 | public class MyAnnotationTest {
82 | @MyAnnotation(name = "张三", age = 18, id = 1, schools = {"school3"})
83 | public void test01() {
84 | }
85 | @MyAnnotation(name = "张三")
86 | public void test02() {
87 | }
88 | }
89 | ```
--------------------------------------------------------------------------------
/markdown/Java/浅记字节字符流乱码问题.md:
--------------------------------------------------------------------------------
1 | # 浅记「字节/字符流」乱码问题
2 |
3 | ### 字符编码
4 |
5 | Unicode 统一了所有字符的编码,包括中文,它算是一个**字符集**,用 2 字节大小对所有字符进行了唯一编码
6 |
7 | 但是 Unicode 没有规定如何存储,UTF-8 刚好规定了 Unicode 字符如何存储的问题。UTF-8 采用可变长编码,英文用 1 个字节,中文用 3 个字节
8 |
9 | 对于 UTF-8 编码中的任意字节 B:
10 |
11 | - 如果 B 的第一位为 0,则 B 独立的表示一个字符 (ASCII 码) -> **0xxxxxxx**
12 |
13 | - 如果 B 的第一位为 1,第二位为 0,则 B 为一个多字节字符中的一个字节 (非 ASCII 字符) -> **10xxxxxx**
14 |
15 | - 如果 B 的前两位为 1,第三位为 0,则 B 为两个字节表示的字符中的第一个字节 -> **110xxxxx**
16 |
17 | - 如果 B 的前三位为 1,第四位为 0,则 B 为三个字节表示的字符中的第一个字节 -> **1110xxxx**
18 |
19 | - 如果 B 的前四位为 1,第五位为 0,则 B 为四个字节表示的字符中的第一个字节 -> **11110xxx**
20 |
21 | 举个简单的例子,中文汉字「**我**」对应的 Unicode 编码:十进制: 25105;十六进制:0x6211;二进制:01100010 00010001
22 |
23 | 它在 UTF-8 编码下的存储结构为:十六进制:0xE68891;二进制:11100110 10001000 10010001
24 |
25 | 为了方便对比,写到一起:
26 |
27 | ```bash
28 | 1110xxxx 10xxxxxx 10xxxxxx
29 | UTF-8: 11100110 10001000 10010001
30 | Unicode: 0110 001000 010001
31 | ```
32 |
33 | ### 乱码分析
34 |
35 | 在学习字节流和字符流的时候,遇到过一个问题:**为什么 I/O 流操作要分为字节流操作和字符流操作呢?**
36 |
37 | - 如果只有字符流操作,由于字符流是由 Java 虚拟机将字节流转换得到,这个过程比较耗时
38 | - 如果只有字节流操作,如果不知道编码类型的话,很容易出现乱码问题
39 |
40 | 本篇文章就上面的第二点展开讨论为什么会出现乱码问题!!!
41 |
42 | 如果我们用字节流去读 UTF-8 编码的文件,那么每次只能一个字节一个字节的读。对于一个中文汉字需要读三次,每次读的结果如下:11100110、10001000、10010001
43 |
44 | 可以看到三次读出来的结果其实就是上面分析过的 UTF-8 编码下的存储结构,此时就会将每一次的结果转化成一个 ACSII 字符:
45 |
46 | - 11100110 -> 230 -> æ
47 | - 10001000 -> 136 ->
48 | - 10010001 -> 145 ->
49 |
50 | 所以乱码就出现了!!另外可以从下面程序中得到验证:
51 |
52 | ```java
53 | public static void main(String[] args) {
54 | // input.txt 中存储的就是一个中文汉字「我」
55 | // FileInputStream 字节输入流,每次读一个字节
56 | try (FileInputStream fis = new FileInputStream("input.txt")) {
57 | System.out.println("Number of remaining bytes: " + fis.available());
58 | int content;
59 | while ((content = fis.read()) != -1) { // 读一个字节
60 | System.out.println(content + " -> " + (char) content);
61 | }
62 | } catch (IOException e) {
63 | throw new RuntimeException(e);
64 | }
65 | }
66 | ```
67 |
68 | 如果我们改用字符输入流,它每次都读一个字符,而且已经自动处理了编码问题,具体可见下面程序:
69 |
70 | ```java
71 | public static void main(String[] args) {
72 | // input.txt 中存储的就是一个中文汉字「我」
73 | // FileReader 字符输入流,每次读一个字符
74 | try (FileReader fileReader = new FileReader("input.txt")) {
75 | int content;
76 | while ((content = fileReader.read()) != -1) {
77 | System.out.println(content + " -> " + (char) content);
78 | System.out.println(Integer.toBinaryString(content));
79 | }
80 | } catch (Exception e) {
81 | e.printStackTrace();
82 | }
83 | }
84 | // 输出
85 | 25105 -> 我
86 | 110001000010001
87 | ```
88 |
89 | `input.txt`文件中存储的结构是:11100110 10001000 10010001,不信的话可以用二进制文件查看器打开它
90 |
91 | 但程序输出的二进制内容不再是 UTF-8 编码下存储的内容,而是对其进行了解码,转换成了 Unicode 下的编码,所以最后才没有乱码
92 |
93 | **注意:**字符输入流并非每次都读三个字节。如果一个字符只用一个字节存储,那么一次就读一个字节,如果一个字符用三个字节存储,那么一次就读三个字节,可以根据 UTF-8 编码判断每次读几个字节
94 |
95 | **总结:**字节输入流每次读一个字节,字符输入流每次读一个字符,而且字符输入流还自动的对 UTF-8 解码成 Unicode
--------------------------------------------------------------------------------
/markdown/Java/类加载子系统-导读.md:
--------------------------------------------------------------------------------
1 |
2 |
3 |
4 |
5 |
6 | ### 本系列按照从上到下的顺序整理,可直接点击 👉 后面链接跳转!!😝
7 |
8 |
9 |
10 |
11 |
--------------------------------------------------------------------------------
/markdown/Java/类加载的时机.md:
--------------------------------------------------------------------------------
1 | **「JVM 类加载子系统」系列文章**
2 |
3 | - **[类加载的过程](./类加载的过程.html)**
4 | - **[❤️🔥 类加载的时机](./类加载的时机.html)**
5 | - **[类加载器](./类加载器.html)**
6 | - **[剖析 [Bootstrap、Extension、Application] ClassLoader](./剖析-Bootstrap-Extension-Application-ClassLoader.html)**
7 | - **[双亲委派模型](./双亲委派模型.html)**
8 | - **[自定义类加载器](./自定义类加载器.html)**
9 | - **[破坏双亲委派模型](./破坏双亲委派模型.html)**
10 |
11 | # 类加载的时机
12 |
13 | 在类生命周期的七个阶段中,加载、验证、准备、初始化和卸载五个阶段的顺序是确定的,类型的加载过程必须按照这种顺序按部就班地开始,而**解析阶段不一定**
14 |
15 | 解析阶段是 Java 虚拟机将常量池内的符号引用替换成直接引用的过程,所以这个过程可能在加载阶段完成,也可能在运行期间完成,这是为了支持 Java 运行时绑定
16 |
17 | 《Java 虚拟机规范》中并没有强制约束什么情况下必须开始类加载过程的第一个阶段「加载」;但是对于初始化阶段,严格规定了**有且只有**六种情况必须立即对类进行「初始化」
18 |
19 | 1. 遇到`new`、`getstatic`、`putstatic`、`invokestatic`四条字节码指令时,如果类型没有进行初始化,则需要先触发其初始化阶段。能够生成这四条指令的典型 Java 代码场景有:
20 |
21 | - 使用`new`关键字实例化对象的时候
22 | - 读取或设置一个类型的静态字段的时候 (被`final`修饰的静态变量,已在编译期把结果放入常量池,读取该字段是不会引起初始化)
23 | - 调用一个类型的静态方法的时候
24 |
25 | 2. 使用`java.lang.reflect`包的方法对类型进行反射调用的时候,如果类型没有进行过初始化,则需要先触发其初始化
26 | 3. 当初始化类的时候,发现其父类还没有进行过初始化,则需要先触发其父类的初始化
27 | 4. 当虚拟机启动时,用户需要指定一个要执行的主类 (main() 所在的类),虚拟机会先初始化这个类
28 | 5. 使用 JDK7 新加入的动态语言支持时,如果一个`java.lang.invoke.MethodHandle`实例最后的解析结果为`REF_getStatic`、`REF_putStatic`、`REF_invokeStatic`、`REF_newInvokeSpecial`四种类型的方法句柄,并且这个方法句柄对应的类没有进行过初始化,则需要先触发其初始化
29 | 6. 当一个接口中定义了 JDK8 新加入的默认方法 (default 修饰) 时,如果有这个接口的实现类发生了初始化,那该接口要在其之前被初始化
30 |
31 | 这六种场景中的行为称为对一个类型进行**主动引用**;除此之外,所有引用类型的方式都不会触发初始化,称为**被动引用**
32 |
33 | 下面是四种被动引用的例子:
34 |
35 | ```java
36 | // ---------------------- 例子 1 ----------------------
37 | // 对于静态字段,只有直接定义字段的类才会被初始化
38 | // 通过子类引用父类中定义的静态字段,只会触发父类的初始化,而不会触发子类的初始化
39 | public class SuperClass {
40 | static {
41 | System.out.println("Super Class init!");
42 | }
43 | public static int value = 123;
44 | }
45 | public class SubClass extends SuperClass {
46 | static {
47 | System.out.println("SubClass init!");
48 | }
49 | }
50 | public class NotInitialization {
51 | public static void main(String[] args) {
52 | System.out.println(SubClass.value);
53 | }
54 | }
55 | // result
56 | // Super Class init!
57 | // 123
58 | // ---------------------- 例子 2 ----------------------
59 | // 通过数组定义来引用类,不会触发此类的初始化
60 | public class NotInitialization {
61 | public static void main(String[] args) {
62 | SuperClass[] arr = new SuperClass[10];
63 | }
64 | }
65 | // ---------------------- 例子 3 ----------------------
66 | // 调用静态常量,不会触发此类的初始化
67 | public class ConstClass {
68 | static {
69 | System.out.println("ConstClass init!");
70 | }
71 | public static final String HELLOWORLD = "hello world";
72 | }
73 | public class NotInitialization {
74 | public static void main(String[] args) {
75 | System.out.println(ConstClass.HELLOWORLD);
76 | }
77 | }
78 | // result
79 | // hello world
80 | // ---------------------- 例子 4 ----------------------
81 | public static void main(String[] args) throws ClassNotFoundException {
82 | // 不会引起类的初始化
83 | Class
42 |
43 | ### 垃圾收集器性能指标
44 |
45 | **停顿时间:**执行一次完整的垃圾收集时,用户线程被暂停的总时间
46 |
47 | **吞吐量:**处理器用于运行用户代码的时间与处理器总消耗时间的比值,计算公式如下:
48 | $$
49 | 吞吐量 = \frac{运行用户代码时间}{运行用户代码时间 + 运行垃圾收集时间}
50 | $$
51 | **对比:**
52 |
53 | - 停顿时间越短越适合需要与用户交互或需要保证服务响应质量的程序,良好的响应速度能提升用户体验感
54 | - 高吞吐量则可以最高效率地利用处理器资源,尽快完成程序的运算任务,主要适合在后台运算而不需要太多交互的分析任务
55 |
56 | ### 垃圾收集器的组合关系
57 |
58 | 本部分的关系是在「按照工作内存区间划分」的基础上进行组合滴!!
59 |
60 | 
61 |
62 | **[JEP 173: Retire Some Rarely-Used GC Combinations](https://openjdk.org/jeps/173)**
63 |
64 | **[JEP 214: Remove GC Combinations Deprecated in JDK 8](https://openjdk.org/jeps/214)**
65 |
66 | **[JEP 366: Deprecate the ParallelScavenge + SerialOld GC Combination](https://openjdk.org/jeps/366)**
67 |
68 | **[JEP 363: Remove the Concurrent Mark Sweep (CMS) Garbage Collector](https://openjdk.org/jeps/363)**
69 |
70 | **注意:JDK8 中默认垃圾收集器为 Parallel Scaverge GC + Parallel Old GC;JDK9 中默认垃圾收集器为 G1**
--------------------------------------------------------------------------------
/markdown/Java/实战-静态变量-实例变量-局部变量.md:
--------------------------------------------------------------------------------
1 | # 实战「静态变量」「实例变量」「局部变量」
2 |
3 | 这篇文章就以实战的方式看看「静态变量」「实例变量」「局部变量」存放的位置!
4 |
5 | 首先要搞清楚一个概念,「静态变量」「实例变量」「局部变量」指的是引用本身,而非它们所指向的对象,它们所指向的对象毫无疑问肯定都存放在堆上,**关于这个观点更多分析可见 [逃逸分析](./逃逸分析.html)**
6 |
7 | 还需要强调一个点,这里是基于 JDK8 的 HotSpot 虚拟机!!
8 |
9 | 根据理论知识可以知道:「静态变量」在 JDK7 及以后就存放在 Java 堆中;「实例变量」随着对象实例存放在 Java 堆中;「局部变量」存放在方法栈帧的局部变量表中
10 |
11 | 首先给出一段测试代码:
12 |
13 | ```java
14 | public class Test {
15 | static class Person {
16 | // 静态变量
17 | static ObjectHolder staticObj = new ObjectHolder();
18 | // 实例变量
19 | ObjectHolder instanceObj = new ObjectHolder();
20 | void foo() throws InterruptedException {
21 | // 局部变量
22 | ObjectHolder localObj = new ObjectHolder();
23 | // 休眠,不然方法执行完,方法栈帧就会出栈
24 | Thread.sleep(10000000);
25 | }
26 | }
27 | private static class ObjectHolder {}
28 | public static void main(String[] args) throws InterruptedException {
29 | Person person = new Person();
30 | person.foo();
31 | }
32 | }
33 | ```
34 |
35 | 我们先分析一下,按照理论来说,此时 Java 堆中肯定存在 3 个`ObjectHolder`对象实例,同时`staticObj`和`instanceObj`也都在 Java 堆中
36 |
37 | 下面通过 VisualVM + JProfiler 软件测试一下!!首先用 VisualVM 保存一个 Java 堆的 dump文件,如下所示:
38 |
39 | 
40 |
41 | 用 JProfiler 打开这个 dump 文件,可以发现在 Java 堆中刚好有 3 个`ObjectHolder`对象实例,如下图所示:
42 |
43 | 
44 |
45 | 我们再找找「静态变量」在哪里,在`java.lang.Class`中可以发现我们定义的静态变量`staticObj`,而这个静态变量指向的对象实例是`0xa87`,如下图所示:
46 |
47 | 
48 |
49 | 继续找「实例变量」在哪里,在`com.lfool.myself.Test$Person`中可以发现我们定义的实例变量`instanceObj`,而这个实例变量指向的对象实例是`0xc3b`,如下图所示:
50 |
51 | 
52 |
53 | 到此为止,我们找出来的所有内容都存放在 Java 堆中,至于「局部变量」,可以通过 JHSDB 软件在栈中发现,这里就不演示了!!!
--------------------------------------------------------------------------------
/markdown/Java/方法调用面试题.md:
--------------------------------------------------------------------------------
1 | # 方法调用面试题
2 |
3 | #### 问题一:下面代码输出的结果
4 |
5 | **详细解析可见 [方法调用](./方法调用.html#静态分派)**
6 |
7 | ```java
8 | public class StaticDispatch {
9 | static abstract class Human {}
10 | static class Man extends Human {}
11 | static class Woman extends Human {}
12 | public void sayHello(Human guy) {
13 | System.out.println("hello, guy!");
14 | }
15 | public void sayHello(Man guy) {
16 | System.out.println("hello, gentleman!");
17 | }
18 | public void sayHello(Woman guy) {
19 | System.out.println("hello, lady!");
20 | }
21 | public static void main(String[] args) {
22 | Human man = new Man();
23 | Human woman = new Woman();
24 | StaticDispatch sr = new StaticDispatch();
25 | sr.sayHello(man);
26 | sr.sayHello(woman);
27 | }
28 | }
29 | ```
30 |
31 | #### 问题二:下面代码依次输出的结果
32 |
33 | **详细解析可见 [方法调用](./方法调用.html#静态分派)**
34 |
35 | ```java
36 | public class Overload {
37 | public static void sayHello(Object arg) {
38 | System.out.println("hello Object");
39 | }
40 | public static void sayHello(int arg) {
41 | System.out.println("hello int");
42 | }
43 | public static void sayHello(long arg) {
44 | System.out.println("hello long");
45 | }
46 | public static void sayHello(Character arg) {
47 | System.out.println("hello Character");
48 | }
49 | public static void sayHello(char arg) {
50 | System.out.println("hello char");
51 | }
52 | public static void sayHello(char... arg) {
53 | System.out.println("hello char...");
54 | }
55 | public static void sayHello(Serializable arg) {
56 | System.out.println("hello Serializable");
57 | }
58 | public static void main(String[] args) {
59 | sayHello('a');
60 | }
61 | }
62 | ```
63 |
64 | 依次注释掉方法
65 | - `sayHello(char arg)`
66 | - `sayHello(int arg)`
67 | - `sayHello(long arg)`
68 | - `sayHello(Character arg)`
69 | - `sayHello(Serializable arg)`
70 | - `sayHello(Object arg)`
71 |
72 | 它会输出什么?!
73 |
74 | #### 问题三:下面代码输出的结果
75 |
76 | **详细解析可见 [方法调用](./方法调用.html#动态分派)**
77 |
78 | ```java
79 | public class FieldHasNoPolymorphic {
80 | static class Father {
81 | public int money = 1;
82 | public Father() {
83 | money = 2;
84 | showMeTheMoney();
85 | }
86 | public void showMeTheMoney() {
87 | System.out.println("I am Father, i have $" + money);
88 | }
89 | }
90 | static class Son extends Father {
91 | public int money = 3;
92 | public Son() {
93 | money = 4;
94 | showMeTheMoney();
95 | }
96 | public void showMeTheMoney() {
97 | System.out.println("I am Son, i have $" + money);
98 | }
99 | }
100 | public static void main(String[] args) {
101 | Father guy = new Son();
102 | System.out.println("This guy has $" + guy.money);
103 | }
104 | }
105 | ```
106 |
107 |
--------------------------------------------------------------------------------
/markdown/Java/注解.md:
--------------------------------------------------------------------------------
1 | # 注解
2 |
3 | ### 什么是注解
4 |
5 | Annotation 是从 JDK5.0 开始引入的新技术
6 |
7 | Annotation 的作用
8 |
9 | - 不是程序本身,可以对程序作出解释
10 | - **可以被其他程序 (如:编译器等) 读取**
11 |
12 | Annotation 的格式
13 |
14 | - 注解是以`@name`在代码中存在,还可以添加一些参数值,例如:`@SuppressWarnings(value = "unchecked")`
15 |
16 | Annotation 在哪里使用?
17 |
18 | - 可以附加在 package、class、method、field 等上面,相当于给他们添加了额外的辅助信息,我们可以通过**反射机制**编程实现对这些元数据的访问
19 |
20 | ### 内置注解
21 |
22 | `@Override`:定义在`java.lang.Override`中,此注解只适用于**修辞方法**,表示一个方法声明打算重写超类中的另一个方法声明
23 |
24 | `@Deprecated`:定义在`java.lang.Deprecated`中,此注解可以用于**修饰方法、属性、类**,表示不鼓励程序员使用这些元素,通常是因为它很危险或者存在更好的选择
25 |
26 | `@SuppressWarnings`:定义在`java.lang.SuppressWarnings`中,用来抑制编译时的警告信息,与前两个注解不同的是需要添加一个参数才能正确使用,这些参数都是已经定义好了的,选择性使用即可
27 |
28 | - `@SuppressWarnings("all")`
29 | - `@SuppressWarnings("unchecked")`
30 | - `@SuppressWarnings(value = {"unchecked", "deprecation"})`
31 | - ...
32 |
33 | ### 元注解
34 |
35 | 元注解的作用:负责注解其他注解
36 |
37 | Java 定义了 4 个标准的 meta-annotation 类型,他们被用来提供对其他 annotation 类型作说明
38 |
39 | 这些类型和它们所支持的类在`java.lang.annotation`包中可以找到:`@Target`、`@Retention`、`@Documented`、`@Inherited`
40 |
41 | - `@Target`:用于描述注解的使用范围 (即:被描述的注解可以用在什么地方)
42 | - `@Retention`:表示需要在什么级别保存该注解信息,用于描述注解的生命周期 (SOURCE < CLASS < **RUNTIME**)
43 | - `@Documented`:说明该注解将被包含在 Javadoc 中
44 | - `@Inherited`:说明子类可以继承父类中的该注解
45 |
46 | ```java
47 | // Target 表示该注解可以用在什么地方:类,方法
48 | @Target(value = {ElementType.TYPE, ElementType.METHOD})
49 | // Retention 表示该注解在什么地方还有效:SOURCE < CLASS < RUNTIME
50 | @Retention(value = RetentionPolicy.RUNTIME)
51 | // Documented 表示该注解将生成在 Javadoc 中
52 | @Documented
53 | // Inherited 表示子类可以继承该注解
54 | @Inherited
55 | public @interface MyAnnotation {
56 | }
57 | ```
58 |
59 | ### 自定义注解
60 |
61 | 使用`@interface`自定义注解时,自动继承`java.lang.annotation.Annotation`接口
62 |
63 | - `@interface`用来声明一个注解,格式:`public @interface name {}`
64 | - 其中的每一个方法实际上是声明了一个配置参数
65 | - 方法的名称就是参数的名称
66 | - 返回值类型就是参数的类型 (返回值只能是基本类型、对象、String、enum)
67 | - 可以通过`default`来声明参数的默认值
68 | - 如果只有一个参数成员,一般参数名为`value`
69 | - 注解元素必须要有值,在定义注解元素时,经常使用「空字符串、0」作为默认值
70 |
71 | ```java
72 | @Target(value = {ElementType.TYPE, ElementType.METHOD})
73 | @Retention(value = RetentionPolicy.RUNTIME)
74 | public @interface MyAnnotation {
75 | // 定义注解参数的格式:参数类型 + 名字 + ()
76 | String name();
77 | int age() default 0;
78 | int id() default -1;
79 | String[] schools() default {"school1", "school2"};
80 | }
81 | public class MyAnnotationTest {
82 | @MyAnnotation(name = "张三", age = 18, id = 1, schools = {"school3"})
83 | public void test01() {
84 | }
85 | @MyAnnotation(name = "张三")
86 | public void test02() {
87 | }
88 | }
89 | ```
--------------------------------------------------------------------------------
/markdown/Java/浅记字节字符流乱码问题.md:
--------------------------------------------------------------------------------
1 | # 浅记「字节/字符流」乱码问题
2 |
3 | ### 字符编码
4 |
5 | Unicode 统一了所有字符的编码,包括中文,它算是一个**字符集**,用 2 字节大小对所有字符进行了唯一编码
6 |
7 | 但是 Unicode 没有规定如何存储,UTF-8 刚好规定了 Unicode 字符如何存储的问题。UTF-8 采用可变长编码,英文用 1 个字节,中文用 3 个字节
8 |
9 | 对于 UTF-8 编码中的任意字节 B:
10 |
11 | - 如果 B 的第一位为 0,则 B 独立的表示一个字符 (ASCII 码) -> **0xxxxxxx**
12 |
13 | - 如果 B 的第一位为 1,第二位为 0,则 B 为一个多字节字符中的一个字节 (非 ASCII 字符) -> **10xxxxxx**
14 |
15 | - 如果 B 的前两位为 1,第三位为 0,则 B 为两个字节表示的字符中的第一个字节 -> **110xxxxx**
16 |
17 | - 如果 B 的前三位为 1,第四位为 0,则 B 为三个字节表示的字符中的第一个字节 -> **1110xxxx**
18 |
19 | - 如果 B 的前四位为 1,第五位为 0,则 B 为四个字节表示的字符中的第一个字节 -> **11110xxx**
20 |
21 | 举个简单的例子,中文汉字「**我**」对应的 Unicode 编码:十进制: 25105;十六进制:0x6211;二进制:01100010 00010001
22 |
23 | 它在 UTF-8 编码下的存储结构为:十六进制:0xE68891;二进制:11100110 10001000 10010001
24 |
25 | 为了方便对比,写到一起:
26 |
27 | ```bash
28 | 1110xxxx 10xxxxxx 10xxxxxx
29 | UTF-8: 11100110 10001000 10010001
30 | Unicode: 0110 001000 010001
31 | ```
32 |
33 | ### 乱码分析
34 |
35 | 在学习字节流和字符流的时候,遇到过一个问题:**为什么 I/O 流操作要分为字节流操作和字符流操作呢?**
36 |
37 | - 如果只有字符流操作,由于字符流是由 Java 虚拟机将字节流转换得到,这个过程比较耗时
38 | - 如果只有字节流操作,如果不知道编码类型的话,很容易出现乱码问题
39 |
40 | 本篇文章就上面的第二点展开讨论为什么会出现乱码问题!!!
41 |
42 | 如果我们用字节流去读 UTF-8 编码的文件,那么每次只能一个字节一个字节的读。对于一个中文汉字需要读三次,每次读的结果如下:11100110、10001000、10010001
43 |
44 | 可以看到三次读出来的结果其实就是上面分析过的 UTF-8 编码下的存储结构,此时就会将每一次的结果转化成一个 ACSII 字符:
45 |
46 | - 11100110 -> 230 -> æ
47 | - 10001000 -> 136 ->
48 | - 10010001 -> 145 ->
49 |
50 | 所以乱码就出现了!!另外可以从下面程序中得到验证:
51 |
52 | ```java
53 | public static void main(String[] args) {
54 | // input.txt 中存储的就是一个中文汉字「我」
55 | // FileInputStream 字节输入流,每次读一个字节
56 | try (FileInputStream fis = new FileInputStream("input.txt")) {
57 | System.out.println("Number of remaining bytes: " + fis.available());
58 | int content;
59 | while ((content = fis.read()) != -1) { // 读一个字节
60 | System.out.println(content + " -> " + (char) content);
61 | }
62 | } catch (IOException e) {
63 | throw new RuntimeException(e);
64 | }
65 | }
66 | ```
67 |
68 | 如果我们改用字符输入流,它每次都读一个字符,而且已经自动处理了编码问题,具体可见下面程序:
69 |
70 | ```java
71 | public static void main(String[] args) {
72 | // input.txt 中存储的就是一个中文汉字「我」
73 | // FileReader 字符输入流,每次读一个字符
74 | try (FileReader fileReader = new FileReader("input.txt")) {
75 | int content;
76 | while ((content = fileReader.read()) != -1) {
77 | System.out.println(content + " -> " + (char) content);
78 | System.out.println(Integer.toBinaryString(content));
79 | }
80 | } catch (Exception e) {
81 | e.printStackTrace();
82 | }
83 | }
84 | // 输出
85 | 25105 -> 我
86 | 110001000010001
87 | ```
88 |
89 | `input.txt`文件中存储的结构是:11100110 10001000 10010001,不信的话可以用二进制文件查看器打开它
90 |
91 | 但程序输出的二进制内容不再是 UTF-8 编码下存储的内容,而是对其进行了解码,转换成了 Unicode 下的编码,所以最后才没有乱码
92 |
93 | **注意:**字符输入流并非每次都读三个字节。如果一个字符只用一个字节存储,那么一次就读一个字节,如果一个字符用三个字节存储,那么一次就读三个字节,可以根据 UTF-8 编码判断每次读几个字节
94 |
95 | **总结:**字节输入流每次读一个字节,字符输入流每次读一个字符,而且字符输入流还自动的对 UTF-8 解码成 Unicode
--------------------------------------------------------------------------------
/markdown/Java/类加载子系统-导读.md:
--------------------------------------------------------------------------------
1 |
2 |
3 |
4 |
5 |
6 | ### 本系列按照从上到下的顺序整理,可直接点击 👉 后面链接跳转!!😝
7 |
8 |
9 |
10 |
11 |
--------------------------------------------------------------------------------
/markdown/Java/类加载的时机.md:
--------------------------------------------------------------------------------
1 | **「JVM 类加载子系统」系列文章**
2 |
3 | - **[类加载的过程](./类加载的过程.html)**
4 | - **[❤️🔥 类加载的时机](./类加载的时机.html)**
5 | - **[类加载器](./类加载器.html)**
6 | - **[剖析 [Bootstrap、Extension、Application] ClassLoader](./剖析-Bootstrap-Extension-Application-ClassLoader.html)**
7 | - **[双亲委派模型](./双亲委派模型.html)**
8 | - **[自定义类加载器](./自定义类加载器.html)**
9 | - **[破坏双亲委派模型](./破坏双亲委派模型.html)**
10 |
11 | # 类加载的时机
12 |
13 | 在类生命周期的七个阶段中,加载、验证、准备、初始化和卸载五个阶段的顺序是确定的,类型的加载过程必须按照这种顺序按部就班地开始,而**解析阶段不一定**
14 |
15 | 解析阶段是 Java 虚拟机将常量池内的符号引用替换成直接引用的过程,所以这个过程可能在加载阶段完成,也可能在运行期间完成,这是为了支持 Java 运行时绑定
16 |
17 | 《Java 虚拟机规范》中并没有强制约束什么情况下必须开始类加载过程的第一个阶段「加载」;但是对于初始化阶段,严格规定了**有且只有**六种情况必须立即对类进行「初始化」
18 |
19 | 1. 遇到`new`、`getstatic`、`putstatic`、`invokestatic`四条字节码指令时,如果类型没有进行初始化,则需要先触发其初始化阶段。能够生成这四条指令的典型 Java 代码场景有:
20 |
21 | - 使用`new`关键字实例化对象的时候
22 | - 读取或设置一个类型的静态字段的时候 (被`final`修饰的静态变量,已在编译期把结果放入常量池,读取该字段是不会引起初始化)
23 | - 调用一个类型的静态方法的时候
24 |
25 | 2. 使用`java.lang.reflect`包的方法对类型进行反射调用的时候,如果类型没有进行过初始化,则需要先触发其初始化
26 | 3. 当初始化类的时候,发现其父类还没有进行过初始化,则需要先触发其父类的初始化
27 | 4. 当虚拟机启动时,用户需要指定一个要执行的主类 (main() 所在的类),虚拟机会先初始化这个类
28 | 5. 使用 JDK7 新加入的动态语言支持时,如果一个`java.lang.invoke.MethodHandle`实例最后的解析结果为`REF_getStatic`、`REF_putStatic`、`REF_invokeStatic`、`REF_newInvokeSpecial`四种类型的方法句柄,并且这个方法句柄对应的类没有进行过初始化,则需要先触发其初始化
29 | 6. 当一个接口中定义了 JDK8 新加入的默认方法 (default 修饰) 时,如果有这个接口的实现类发生了初始化,那该接口要在其之前被初始化
30 |
31 | 这六种场景中的行为称为对一个类型进行**主动引用**;除此之外,所有引用类型的方式都不会触发初始化,称为**被动引用**
32 |
33 | 下面是四种被动引用的例子:
34 |
35 | ```java
36 | // ---------------------- 例子 1 ----------------------
37 | // 对于静态字段,只有直接定义字段的类才会被初始化
38 | // 通过子类引用父类中定义的静态字段,只会触发父类的初始化,而不会触发子类的初始化
39 | public class SuperClass {
40 | static {
41 | System.out.println("Super Class init!");
42 | }
43 | public static int value = 123;
44 | }
45 | public class SubClass extends SuperClass {
46 | static {
47 | System.out.println("SubClass init!");
48 | }
49 | }
50 | public class NotInitialization {
51 | public static void main(String[] args) {
52 | System.out.println(SubClass.value);
53 | }
54 | }
55 | // result
56 | // Super Class init!
57 | // 123
58 | // ---------------------- 例子 2 ----------------------
59 | // 通过数组定义来引用类,不会触发此类的初始化
60 | public class NotInitialization {
61 | public static void main(String[] args) {
62 | SuperClass[] arr = new SuperClass[10];
63 | }
64 | }
65 | // ---------------------- 例子 3 ----------------------
66 | // 调用静态常量,不会触发此类的初始化
67 | public class ConstClass {
68 | static {
69 | System.out.println("ConstClass init!");
70 | }
71 | public static final String HELLOWORLD = "hello world";
72 | }
73 | public class NotInitialization {
74 | public static void main(String[] args) {
75 | System.out.println(ConstClass.HELLOWORLD);
76 | }
77 | }
78 | // result
79 | // hello world
80 | // ---------------------- 例子 4 ----------------------
81 | public static void main(String[] args) throws ClassNotFoundException {
82 | // 不会引起类的初始化
83 | Class 6 |
7 | ## 硬链接
8 |
9 | - 具有相同 inode 节点号的多个文件互为硬链接文件
10 | - 删除硬链接文件或者删除源文件任意之一,文件实体并未被删除
11 | - 只有删除了源文件和所有对应的硬链接文件,文件实体才会被删除
12 | - 硬链接文件是文件的另一个入口
13 | - 可以通过给文件设置硬链接文件来防止重要文件被误删
14 | - 创建硬链接命令 ln 源文件 硬链接文件
15 | - 硬链接文件是普通文件,可以用 rm 删除
16 | - 对于静态文件(没有进程正在调用),当硬链接数为 0 时文件就被删除。注意:如果有进程正在调用,则无法删除或者即使文件名被删除但空间不会释放
17 |
18 | **创建一个硬链接**
19 |
20 | ```shell
21 | ➜ test ln a.txt aHardLink
22 | ➜ test ll
23 | -rw-r--r-- 2 lfool staff 5B 1 29 02:06 a.txt
24 | -rw-r--r-- 2 lfool staff 5B 1 29 02:06 aHardLink
25 | ➜ test ll -i
26 | 8986726 -rw-r--r-- 2 lfool staff 5B 1 29 02:06 a.txt
27 | 8986726 -rw-r--r-- 2 lfool staff 5B 1 29 02:06 aHardLink
28 | ```
29 |
30 | 可以发现两个文件的 inode 编号相同,且大小相同,说明是同一个文件
31 |
32 | ## 软链接
33 |
34 | - 软链接类似 windows 系统的快捷方式
35 | - 软链接里面存放的是源文件的路径,指向源文件
36 | - 删除源文件,软链接依然存在,但无法访问源文件内容
37 | - 软链接失效时一般是白字红底闪烁
38 | - 创建软链接命令 ln -s 源文件 软链接文件
39 | - 软链接和源文件是不同的文件,文件类型也不同,inode 号也不同
40 | - 软链接的文件类型是 「l」,可以用 rm 删除
41 |
42 | **创建一个软连接**
43 |
44 | ```shell
45 | ➜ test ln -s a.txt alink
46 | ➜ test ll
47 | -rw-r--r-- 1 lfool staff 5B 1 29 02:06 a.txt
48 | lrwxr-xr-x 1 lfool staff 5B 1 29 02:06 alink -> a.txt
49 | # 查看文件的 inode 编号
50 | ➜ test ll -i
51 | 8986726 -rw-r--r-- 1 lfool staff 5B 1 29 02:06 a.txt
52 | 8986741 lrwxr-xr-x 1 lfool staff 5B 1 29 02:06 alink -> a.txt
53 | ```
54 |
55 | 可以发现文件和指向文件的软链接的 inode 编号不同,说明是两个文件
56 |
57 | ## 硬链接和软链接的区别
58 |
59 | 原理上,硬链接和源文件的 inode 节点号相同,两者互为硬链接。软连接和源文件的 inode 节点号不同,进而指向的 block 也不同,软连接 block 中存放了源文件的路径名
60 |
61 | 实际上,硬链接和源文件是同一份文件,而软连接是独立的文件,类似于快捷方式,存储着源文件的位置信息便于指向
62 |
63 | 使用限制上,不能对目录创建硬链接,不能对不同文件系统创建硬链接,不能对不存在的文件创建硬链接;可以对目录创建软连接,可以跨文件系统创建软连接,可以对不存在的文件创建软连接
64 |
65 | ## 参考
66 |
67 | 1. [Linux硬链接和软连接的区别与总结](https://xzchsia.github.io/2020/03/05/linux-hard-soft-link/)
68 | 2. [硬链接和软连接(符号链接)的区别](https://www.cnblogs.com/sanjun/p/9971993.html)
69 |
70 |
--------------------------------------------------------------------------------
/markdown/Linux/Shell.md:
--------------------------------------------------------------------------------
1 | # Shell
2 |
3 | ## 常用命令汇总
4 |
5 | `man`:查看每种命令的文档
6 |
7 | `man -k xxx`:查找与 xxx 相关的命令
8 |
9 | `pwd`:显示当前目录
10 |
11 | `ll file*Name`:只能匹配文件,不能匹配目录
12 |
13 | - 使用通配符 「? 任意匹配一个字符 / * 任意匹配任意个字符」
14 | - 基本上可以使用正则表达式
15 |
16 | `ls -i fileName`:查看文件的 inode 编号
17 |
18 | `ln -s [fileName] [linkName]`:创建一个软链接
19 |
20 | ```shell
21 | ➜ test ln -s a.txt alink
22 | ➜ test ll
23 | -rw-r--r-- 1 lfool staff 5B 1 29 02:06 a.txt
24 | lrwxr-xr-x 1 lfool staff 5B 1 29 02:06 alink -> a.txt
25 | ```
26 |
27 | `ln [fileName] [linkName]`:创建一个硬链接
28 |
29 | ```shell
30 | ➜ test ln a.txt aHardLink
31 | ➜ test ll
32 | -rw-r--r-- 2 lfool staff 5B 1 29 02:06 a.txt
33 | -rw-r--r-- 2 lfool staff 5B 1 29 02:06 aHardLink
34 | ➜ test ll -i
35 | 8986726 -rw-r--r-- 2 lfool staff 5B 1 29 02:06 a.txt
36 | 8986726 -rw-r--r-- 2 lfool staff 5B 1 29 02:06 aHardLink
37 | ```
38 |
39 | `rm -rf path`:删除目录或文件
40 |
41 | - -f:强制删除文件或目录
42 | - -r:递归处理,将指定目录下的所有文件与子目录一并处理
43 |
44 | `tree path`:查看目录结构
45 |
46 | `file fileName`:查看文件类型
47 |
48 | `cat / more / less`:显示文件内容(全显示/分批显示)
49 |
50 | `head / tail fileName`:显示文件头部 / 最后几行内容
51 |
52 | - -f:使显示内容保持活动状态,会动态更新显示内容
53 | - -n:规定行数
54 |
55 | `nohup xxx > output.log 2>&1 &`:后台运行,输出到文件中
56 |
57 | `du`:显示文件或目录的大小
58 |
59 | - -h:以 K,M,G 为单位,提高信息的可读性
60 | - -s:仅显示总计
61 | - [fileName] / [dirName] / None:未指定,则显示当前目录下的内容
62 |
63 | `ps -ef | grep python`:查看 python 相关进程
64 |
65 | `lsof -i:8888`:查看端口 8888 的占用情况
66 |
67 | `kill -s 9 PID`:杀死进程 PID
68 |
69 | ## 命令行常用快捷操作
70 |
71 | `Ctrl + a`:跳到本行的行首
72 |
73 | `Ctrl + e`:则跳到页尾
74 |
75 | `Ctrl + u`:删除当前光标前面的文字
76 |
77 | `Ctrl + k`:删除当前光标后面的文字
78 |
79 | `Ctrl + y`:进行恢复
80 |
81 | ## 目录及用途
82 |
83 | | 目录 | 用途 |
84 | | :----: | :----------------------------------------------------------: |
85 | | / | 虚拟目录的根目录,通常不会在这里存储文件 |
86 | | /bin | 二进制目录,存放许多用户级的 GNU 工具 |
87 | | /boot | 启动目录,存放启动文件 |
88 | | /dev | 设备目录,Linux 在这里创建设备节点 |
89 | | /etc | 系统配置文件目录 |
90 | | /home | 主目录,Linux 在这里创建用户目录 |
91 | | /lib | 库目录,存放系统和应用程序的库文件 |
92 | | /media | 媒体文件,可移动媒体设备的常用挂载点 |
93 | | /mnt | 挂载目录,另一个可移动媒体设备的常用挂载点 |
94 | | /opt | 可选目录,常用于存放第三方软件包或数据文件 |
95 | | /proc | 进程目录,存放先用硬件以及当前进程的相关信息 |
96 | | /root | root 用户的主目录 |
97 | | /sbin | 系统二进制目录,存放许多 GNU 管理员级工具 |
98 | | /run | 运行目录,存放系统运作时的运行时数据 |
99 | | /srv | 服务目录,存放本地服务的相关文件 |
100 | | /sys | 系统目录,存放系统硬件信息的相关文件 |
101 | | /tmp | 临时目录,可以在该目录中创建和删除临时工作文件 |
102 | | /usr | 用户二进制目录,大量用户级别的 GUN 工具和数据文件都存储在这里 |
103 | | /var | 可变目录,用以存放经常变化的文件,比如日志文件 |
104 |
105 |
106 |
107 |
108 |
109 | ## 文件或目录信息
110 |
111 |
6 |
7 | ## 硬链接
8 |
9 | - 具有相同 inode 节点号的多个文件互为硬链接文件
10 | - 删除硬链接文件或者删除源文件任意之一,文件实体并未被删除
11 | - 只有删除了源文件和所有对应的硬链接文件,文件实体才会被删除
12 | - 硬链接文件是文件的另一个入口
13 | - 可以通过给文件设置硬链接文件来防止重要文件被误删
14 | - 创建硬链接命令 ln 源文件 硬链接文件
15 | - 硬链接文件是普通文件,可以用 rm 删除
16 | - 对于静态文件(没有进程正在调用),当硬链接数为 0 时文件就被删除。注意:如果有进程正在调用,则无法删除或者即使文件名被删除但空间不会释放
17 |
18 | **创建一个硬链接**
19 |
20 | ```shell
21 | ➜ test ln a.txt aHardLink
22 | ➜ test ll
23 | -rw-r--r-- 2 lfool staff 5B 1 29 02:06 a.txt
24 | -rw-r--r-- 2 lfool staff 5B 1 29 02:06 aHardLink
25 | ➜ test ll -i
26 | 8986726 -rw-r--r-- 2 lfool staff 5B 1 29 02:06 a.txt
27 | 8986726 -rw-r--r-- 2 lfool staff 5B 1 29 02:06 aHardLink
28 | ```
29 |
30 | 可以发现两个文件的 inode 编号相同,且大小相同,说明是同一个文件
31 |
32 | ## 软链接
33 |
34 | - 软链接类似 windows 系统的快捷方式
35 | - 软链接里面存放的是源文件的路径,指向源文件
36 | - 删除源文件,软链接依然存在,但无法访问源文件内容
37 | - 软链接失效时一般是白字红底闪烁
38 | - 创建软链接命令 ln -s 源文件 软链接文件
39 | - 软链接和源文件是不同的文件,文件类型也不同,inode 号也不同
40 | - 软链接的文件类型是 「l」,可以用 rm 删除
41 |
42 | **创建一个软连接**
43 |
44 | ```shell
45 | ➜ test ln -s a.txt alink
46 | ➜ test ll
47 | -rw-r--r-- 1 lfool staff 5B 1 29 02:06 a.txt
48 | lrwxr-xr-x 1 lfool staff 5B 1 29 02:06 alink -> a.txt
49 | # 查看文件的 inode 编号
50 | ➜ test ll -i
51 | 8986726 -rw-r--r-- 1 lfool staff 5B 1 29 02:06 a.txt
52 | 8986741 lrwxr-xr-x 1 lfool staff 5B 1 29 02:06 alink -> a.txt
53 | ```
54 |
55 | 可以发现文件和指向文件的软链接的 inode 编号不同,说明是两个文件
56 |
57 | ## 硬链接和软链接的区别
58 |
59 | 原理上,硬链接和源文件的 inode 节点号相同,两者互为硬链接。软连接和源文件的 inode 节点号不同,进而指向的 block 也不同,软连接 block 中存放了源文件的路径名
60 |
61 | 实际上,硬链接和源文件是同一份文件,而软连接是独立的文件,类似于快捷方式,存储着源文件的位置信息便于指向
62 |
63 | 使用限制上,不能对目录创建硬链接,不能对不同文件系统创建硬链接,不能对不存在的文件创建硬链接;可以对目录创建软连接,可以跨文件系统创建软连接,可以对不存在的文件创建软连接
64 |
65 | ## 参考
66 |
67 | 1. [Linux硬链接和软连接的区别与总结](https://xzchsia.github.io/2020/03/05/linux-hard-soft-link/)
68 | 2. [硬链接和软连接(符号链接)的区别](https://www.cnblogs.com/sanjun/p/9971993.html)
69 |
70 |
--------------------------------------------------------------------------------
/markdown/Linux/Shell.md:
--------------------------------------------------------------------------------
1 | # Shell
2 |
3 | ## 常用命令汇总
4 |
5 | `man`:查看每种命令的文档
6 |
7 | `man -k xxx`:查找与 xxx 相关的命令
8 |
9 | `pwd`:显示当前目录
10 |
11 | `ll file*Name`:只能匹配文件,不能匹配目录
12 |
13 | - 使用通配符 「? 任意匹配一个字符 / * 任意匹配任意个字符」
14 | - 基本上可以使用正则表达式
15 |
16 | `ls -i fileName`:查看文件的 inode 编号
17 |
18 | `ln -s [fileName] [linkName]`:创建一个软链接
19 |
20 | ```shell
21 | ➜ test ln -s a.txt alink
22 | ➜ test ll
23 | -rw-r--r-- 1 lfool staff 5B 1 29 02:06 a.txt
24 | lrwxr-xr-x 1 lfool staff 5B 1 29 02:06 alink -> a.txt
25 | ```
26 |
27 | `ln [fileName] [linkName]`:创建一个硬链接
28 |
29 | ```shell
30 | ➜ test ln a.txt aHardLink
31 | ➜ test ll
32 | -rw-r--r-- 2 lfool staff 5B 1 29 02:06 a.txt
33 | -rw-r--r-- 2 lfool staff 5B 1 29 02:06 aHardLink
34 | ➜ test ll -i
35 | 8986726 -rw-r--r-- 2 lfool staff 5B 1 29 02:06 a.txt
36 | 8986726 -rw-r--r-- 2 lfool staff 5B 1 29 02:06 aHardLink
37 | ```
38 |
39 | `rm -rf path`:删除目录或文件
40 |
41 | - -f:强制删除文件或目录
42 | - -r:递归处理,将指定目录下的所有文件与子目录一并处理
43 |
44 | `tree path`:查看目录结构
45 |
46 | `file fileName`:查看文件类型
47 |
48 | `cat / more / less`:显示文件内容(全显示/分批显示)
49 |
50 | `head / tail fileName`:显示文件头部 / 最后几行内容
51 |
52 | - -f:使显示内容保持活动状态,会动态更新显示内容
53 | - -n:规定行数
54 |
55 | `nohup xxx > output.log 2>&1 &`:后台运行,输出到文件中
56 |
57 | `du`:显示文件或目录的大小
58 |
59 | - -h:以 K,M,G 为单位,提高信息的可读性
60 | - -s:仅显示总计
61 | - [fileName] / [dirName] / None:未指定,则显示当前目录下的内容
62 |
63 | `ps -ef | grep python`:查看 python 相关进程
64 |
65 | `lsof -i:8888`:查看端口 8888 的占用情况
66 |
67 | `kill -s 9 PID`:杀死进程 PID
68 |
69 | ## 命令行常用快捷操作
70 |
71 | `Ctrl + a`:跳到本行的行首
72 |
73 | `Ctrl + e`:则跳到页尾
74 |
75 | `Ctrl + u`:删除当前光标前面的文字
76 |
77 | `Ctrl + k`:删除当前光标后面的文字
78 |
79 | `Ctrl + y`:进行恢复
80 |
81 | ## 目录及用途
82 |
83 | | 目录 | 用途 |
84 | | :----: | :----------------------------------------------------------: |
85 | | / | 虚拟目录的根目录,通常不会在这里存储文件 |
86 | | /bin | 二进制目录,存放许多用户级的 GNU 工具 |
87 | | /boot | 启动目录,存放启动文件 |
88 | | /dev | 设备目录,Linux 在这里创建设备节点 |
89 | | /etc | 系统配置文件目录 |
90 | | /home | 主目录,Linux 在这里创建用户目录 |
91 | | /lib | 库目录,存放系统和应用程序的库文件 |
92 | | /media | 媒体文件,可移动媒体设备的常用挂载点 |
93 | | /mnt | 挂载目录,另一个可移动媒体设备的常用挂载点 |
94 | | /opt | 可选目录,常用于存放第三方软件包或数据文件 |
95 | | /proc | 进程目录,存放先用硬件以及当前进程的相关信息 |
96 | | /root | root 用户的主目录 |
97 | | /sbin | 系统二进制目录,存放许多 GNU 管理员级工具 |
98 | | /run | 运行目录,存放系统运作时的运行时数据 |
99 | | /srv | 服务目录,存放本地服务的相关文件 |
100 | | /sys | 系统目录,存放系统硬件信息的相关文件 |
101 | | /tmp | 临时目录,可以在该目录中创建和删除临时工作文件 |
102 | | /usr | 用户二进制目录,大量用户级别的 GUN 工具和数据文件都存储在这里 |
103 | | /var | 可变目录,用以存放经常变化的文件,比如日志文件 |
104 |
105 |
106 |
107 |
108 |
109 | ## 文件或目录信息
110 |
111 |  112 |
113 |
112 |
113 |  114 |
115 | 文件类型(每行第一个字母):目录(d)、文件(-)、字符型文件(c)、块设备(b)、软链接(l)
116 |
117 | 文件的权限:rwx | rwx | r-x -> 属主权限 | 属组权限 | 其他人权限 (r:读 w:写 x:执行 -:无权限)
118 |
119 | 文件的硬链接总数 [传送门](./Linux硬链接和软连接的区别与总结.html)
120 |
121 | 文件属主的用户名
122 |
123 | 文件属组的组名
124 |
125 | 文件的大小(以字节为单位)
126 |
127 | 文件上次修改时间
128 |
129 | 文件名或目录名
130 |
131 |
--------------------------------------------------------------------------------
/markdown/Mac/Mac 快捷键.md:
--------------------------------------------------------------------------------
1 | # Mac 快捷键
2 |
3 |
4 |
5 | 软件最大化:control + command + F
6 |
7 | 软件最小化:command + M
8 |
9 | 软件关闭:command + Q
10 |
11 |
--------------------------------------------------------------------------------
/markdown/MySQL/MySQL索引.md:
--------------------------------------------------------------------------------
1 | # MySQL 索引
2 |
3 | 由于本篇文章侧重于 MySQL 索引的应用,所以并没有完全详细的介绍 B+ 树索引,但 B+ 树索引又是 MySQL 中默认使用的索引,所以**关于 B+ 树索引细节介绍可见 [B+ 树索引](./B+树索引.html)**
4 |
5 | ### 索引介绍
6 |
7 | **索引是一种用于快速查询和检索数据的数据结构,其本质可以看作是一种排好序的数据结构**
8 |
9 | 索引类似于书的目录,如果一本书没有目录,那么对于读者来说就是一场噩梦,目录可以加快我们查找的速度和效率,索引的作用也一样
10 |
11 | 索引底层数据结构有很多种类型,常见的索引结构:B 树、**[B+ 树](./B+树索引.html)**、Hash 表、红黑树。在 MySQL 中,无论是 InnoDB 存储引擎,还是 MyISAM 存储引擎,使用的都是 **[B+ 树索引](./B+树索引.html)**
12 |
13 | ### 索引优缺点
14 |
15 | 优点:
16 |
17 | - 加快查询检索数据的速度
18 | - 可以通过创建唯一索引保证数据的唯一性
19 |
20 | 缺点:
21 |
22 | - 空间成本:MySQL 中每一个索引都对应一个 B+ 树,需要一定的页来存储索引
23 | - 时间成本:在执行增删改操作时,需要维护索引的正确性,会消耗一定时间
24 |
25 | **注意:**有时候「二级索引 + 回表」的速度并不一定比「全表扫描」快,因为可能回表次数过多,而且页在物理存储上较为分散,需要进行多次磁盘 IO 将对应页加载到内存中,耗时大
26 |
27 | ### 索引底层数据结构
28 |
29 | #### Hash 表
30 |
31 | 将索引列映射到哈希表中,即:key = 索引列的值,value = 记录的位置,通过 key 可以快速获取记录的位置,在没有哈希冲突的情况下时间复杂度 O(1),可以用链地址法或开放定址法解决哈希冲突
32 |
33 | MySQL 之所以没有使用 Hash 表作为索引的底层实现,是因为 Hash 表不支持顺序查询和范围查询,只支持每次查询一个
34 |
35 | #### B 树 & B+ 树
36 |
37 | B 树也称 B- 树,全程为**多路平衡查找树**,B+ 树是 B 树的一个变体。B 树和 B+ 树中的 B 是`Balanced`的意思。目前大部分数据库系统及文件系统都采用 B- 树或其变体 B+ 树作为索引底层实现
38 |
39 | **B 树和 B+ 树的区别:**
40 |
41 | - B 树的所有节点既存放键 (key),也存放数据 (data);而 B+ 树只有叶子节点存放 key 和 data,其它非叶子节点只存放 key
42 | - B 树的叶子节点都是独立的;B+ 树的叶子节点间通过双向链表连接
43 | - B 树的检索过程相当于对范围内的每个节点的关键字做二分查找,可能还没到叶子节点就结束了;而 B+ 树的检索过程很稳定,任何查找都是从根节点到叶子节点
44 |
45 | ### 索引的类型
46 |
47 | **从数据结构维度划分:**
48 |
49 | - **[B+ 树索引](./B+树索引.html#innodb-中的索引方案)**:MySQL 中默认的索引结构,同层节点间双向链表连接,节点内单向链表连接
50 | - Hash 索引:通过键值对的形式,一次即可定位
51 |
52 | **从底层存储方式划分:**
53 |
54 | - **[聚簇索引](./B+树索引.html#聚簇索引)**:InnoDB 中的主键索引就属于聚簇索引,叶子节点存放完成用户记录,非叶子节点存放目录项纪录。数据和索引在一起,索引即数据,数据即索引
55 | - 非聚簇索引:数据和索引分开存储,**[二级索引](./B+树索引.html#二级索引)** 就属于非聚簇索引。MySQL 中的 **[MyISAM](./B+树索引.html#一页面至少存-2-条纪录)** 都是非聚簇索引
56 |
57 | **从应用维度划分:**
58 |
59 | - 主键索引:InnoDB 中的主键索引就属于聚簇索引,表中只会有一个主键索引,主键具有的特性该主键索引都具有,如:值唯一,且不为 NULL
60 | - 普通索引:InnoDB 中的普通索引就属于 **[二级索引](./B+树索引.html#二级索引)**
61 | - 唯一索引:值唯一,可以有 NULL
62 | - **[覆盖索引](./覆盖索引-索引条件下推.html#覆盖索引)**:索引列包含查询列表
63 | - **[联合索引](./B+树索引.html#联合索引)**:索引包含多个列
64 | - 前缀索引:为了降低索引占用的空间,可以只将一个字段的前缀作为索引
65 | - 全文索引:对文本的内容进行分词,然后搜索
66 |
67 | ### 使用索引的建议
68 |
69 | - **选择合适的字段建立索引:**频繁根据该字段查询
70 | - **频繁更新的字段慎重建立索引:**维护成本大
71 | - **限制每张表索引数量 (5 个):**索引会占用一定空间,虽然可以加快查询,但会减慢更新插入
72 | - **尽可能建立联合索引而非单列索引:**索引需要占用空间,联合索引可以减少空间的使用
73 | - **注意避免冗余索引:**比如建立了联合索引 (a, b),又建立了 单列索引 (a),就会出现冗余
74 | - **字符串类型字段尽量使用前缀索引:**可以减少空间的使用
75 | - **避免索引失效:**虽然建立了索引,但是没有使用使用,可以通过`explain`查看执行计划
76 | - **删除长期未使用的索引**
--------------------------------------------------------------------------------
/markdown/MySQL/RR隔离级别下彻底解决幻读了吗.md:
--------------------------------------------------------------------------------
1 | # RR 隔离级别下彻底解决幻读了吗?
2 |
3 | **[幻读](./MySQL事务.html#幻读-phantom)** 指在同一个事务中,同一个查询语句,前后两次执行得到的结果集不同,如:第一次查询得到六条记录,第二次查询得到七条数据
4 |
5 | **结论:**RR 隔离级别下只能最大程度的避免幻读现象的出现,但无法彻底解决幻读现象!!
6 |
7 | MySQL 中有两种读:快照读和锁定读
8 |
9 | - **快照读:**通过 **[MVCC](./MVCC.html)** 可以最大程度避免幻读,每次都只能看到生成 ReadView 之前已经提交事务修改的数据,所以在事务执行过程中多次读的结果是一致的
10 | - **锁定读:**通过加锁可以最大程度避免欢度,在 RR 下会为每个查询时符合条件的记录加 **[Next-Key Lock](./锁.html#next-key-lock)**,既不允许修改记录,也不允许在记录前的间隙插入新记录,所以在事务中多次读的结果是一致的
11 |
12 | ### 快照读 -- 出现幻读的情况
13 |
14 | 
15 |
16 | `update`语句修改的是最新数据。在时刻 4,由于事务 A 修改了`id = 3`的记录,记录中`trx_id`由 200 变成 100,所以该记录对事务 A 可见
17 |
18 | ### 锁定读 -- 出现幻读的情况
19 |
20 | 
21 |
22 | `select * from t`是快照读,不会对记录加锁,通过 MVCC 控制;`select * from t for update`是当前读,读最新的数据,而且会对记录加 **[Next-Key Lock](./锁.html#next-key-lock)**
23 |
24 | **建议:**在开启事务后,立马执行`select ... for update`,对记录加 **[Next-Key Lock](./锁.html#next-key-lock)**,可以最大程度避免幻读
--------------------------------------------------------------------------------
/markdown/MySQL/redo-log.md:
--------------------------------------------------------------------------------
1 | # redo log
2 |
3 | ### redo log 是什么?
4 |
5 | InnoDB 是以页为基本单位来管理内存空间,为了减少磁盘 IO 的开销,增加了 **[Buffer Pool](./InnoDB的Buffer-Pool.html)**,每次访问页面后不着急刷新回磁盘,而是缓存到 Buffer Pool 中,以便下次继续访问
6 |
7 | Buffer Pool 在内存中,所以会导致后续对页面的修改并不能及时刷新回磁盘,如果发生断电或者一些其它的原因会使内存中的数据丢失,重启后啥也没了,必须持久化到磁盘才安全
8 |
9 | 一个很简单的方法就是每次修改后立刻将页面刷新回磁盘,这样做的弊端在于:
10 |
11 | - 如果是少量的修改就刷新一个页面回磁盘,太过于浪费
12 | - 一个修改可能会牵连多个页面的变化,而且这些页面物理上极大可能不在一起,这样刷新回磁盘需要进行很多随机 IO,开销更大
13 |
14 | 基于上面的场景,就有了 redo log (重做日志),它记录了**对哪个表空间哪个页进行了哪些修改**,可以简单理解为就算数据丢失,但只要有对应的 redo log,也可以恢复丢失的数据
15 |
16 | redo log 也需要及时的刷新回磁盘,但它相比于刷新整个页面的优势在于:
17 |
18 | - redo log 占用的空间非常小
19 | - redo log 是顺序写入磁盘,比随机 IO 快很多
20 |
21 | ### redo log 写入过程
22 |
23 | 为了更好的管理 redo log,InnoDB 将 redo log 存储到大小为 512 字节的 block 中 (block 可以理解为页) 的 log blcok body 部分。每个 block 的结构如下所示:
24 |
25 | 
26 |
27 | 和 Buffer Pool 一样,为了缓解磁盘 IO 速度慢的问题,InnoDB 引入了 log buffer,它是内存中一片连续的区域,默认大小为 16MB
28 |
29 | redo log 是顺序写入 log buffer 中,从前往后,有一个 buf_free 指向空闲区域的起始位置,具体结构如下图所示:
30 |
31 | 
32 |
33 | ### redo log 刷盘时机
34 |
35 | log buffer 在内存中,如果不及时的将 log buffer 刷盘,也会导致 redo log 丢失,所以 log buffer 会在出现下面情况时刷盘
36 |
37 | - **log buffer 空间不足时:**如果 redo log 已经占满了 log buffer 一半的空间,就会把 redo log 刷新回磁盘
38 | - **事务提交时:**在事务提交时,将对应的 redo log 刷新回磁盘。由于 redo log 是顺序写入,所以之前的也会一起刷新回磁盘,不可能只刷新回某一个事务的 redo log
39 | - **脏页刷新回磁盘时:**将某个脏页刷新回磁盘时,会保证先将该脏页对应的 redo log 刷新回磁盘
40 | - 后台线程每隔 1s 将 log buffer 中的 redo log 刷新回磁盘
41 | - MySQL 正常关闭时也会将 buffer log 刷新回磁盘
42 |
43 | 对于上面第二点刷盘情况:**事务提交时**,由于这个要求过于严格,会降低数据库新能,所以可以通过参数`innodb_flush_log_at_trx_commit`调整:
44 |
45 | - **0:**每次事务提交时,不主动刷盘,交由后台线程来处理,所以可能丢失上一秒所有事务的数据
46 | - **1:**每次事务提交时,都将 redo log 同步到磁盘,可以保证事务的持久性 (默认值)
47 | - **2:**每次事务提交时,都只把 redo log 写入到 page cache (操作系统的缓存)。如果数据库挂了,但操作系统没挂,依旧可以保证事务的持久性
48 |
49 | 上面三个参数的安全性和性能的关系:
50 |
51 | - 安全:1 > 2 > 0
52 | - 性能:0 > 2 > 1
53 |
54 | **重点:**对于安全性要求高的系统,只能选择 1;对于可以接受 1s 数据丢失的信息,可以选择 0;如果既要求性能也要保证一定的安全性,可以选择 2,折中方案
55 |
56 | ### redo log 文件组
57 |
58 | 当 log buffer 触发刷盘时,会存到 redo log 文件中,它是以日志文件组的形式出现,即:一组中有多个大小相等的日志文件,默认情况下有两个文件:ib_logfile0 和 ib_logfile1
59 |
60 | redo log 是为了记录内存中还没有刷盘的脏页,防止当 MySQL 挂了后脏页丢失,导致修改数据的丢失。所以当脏页已经被刷盘,那么对应的 redo log 就没有用
61 |
62 | 随着系统的运行,redo log 只会越来越多,而日志文件组的数量和大小都是固定的,所以它采用循环写的方式,从头开始写,当写到末尾又回到开头,这样可以在有限的日志文件组中无限的写入 redo log
63 |
64 | 之所以可以覆盖日志文件组开头的数据,是因为开头的数据可能会随着脏页的刷盘而变成无用。用 write pos 表示新 redo log 刷盘时要写入的位置;用 checkpoint 表示当前要擦除的位置
65 |
66 | 
67 |
68 | 图中:
69 |
70 | - write pos 和 checkpoint 都是顺时针移动
71 | - write pos - checkpoint 之间的部分 (红色),用来存新的 redo log
72 | - checkpoint - write pos 之间的部分 (蓝色),表示待刷盘的脏页对应的 redo log
73 |
74 | 当 write pos 追上 checkpoint 时,表示 redo log 文件组满了,不能再将 redo log 刷盘到文件组中
75 |
76 | 此时 MySQL 会阻塞,将 Buffer Pool 中的脏页刷新到磁盘,然后标记 redo log 文件组可以被擦除的部分,最后将可以被擦除的部分擦除,更新 checkpoint (顺时针向前移动)
77 |
78 | 所以,一次 checkpoint 的过程就是将脏页刷新到磁盘中,更新 redo log 日志组中可以被覆盖的位置
--------------------------------------------------------------------------------
/markdown/MySQL/两阶段提交.md:
--------------------------------------------------------------------------------
1 | # 两阶段提交
2 |
3 | ### 分布式事务
4 |
5 | MySQL 分为 server 层和存储引擎层,事务由存储引擎层实现。如果修改服务器 A 中数据库的数据的同时也需要修改服务器 B 中数据库的数据,这两个操作必须同时成功或者失败,也就是必须保证原子性
6 |
7 | 而这两个操作属于两个不同的数据库,存储引擎也不是同一个,无法保证两个操作的原子性。这个时候就需要一个全局事务,由若干个小事务组成,这个全局事务也被称作分布式事务
8 |
9 | ### XA 规范
10 |
11 | 有一个名叫 X/Open 的组织提出了 XA 的规范,用于规范分布式事务,也就是不同的存储引擎只要符合 XA 规范,就可以放到一个分布式事务中管理
12 |
13 | XA 规范提出了两个角色
14 |
15 | - **资源管理器:**全局事务中每一个小事务
16 | - **事务管理器:**管理全局事务中每一个小事务 (后文称之为协调者)
17 |
18 | 要提交一个全局事务,就必须保证所有小事务都要能顺利提交,否则所有事务都应该回滚。XA 规范指出,要提交一个全局事务,必须分两步:(点题)
19 |
20 | - **prepare 阶段:**每个小事务在该阶段会执行各自的事务,并将事务产生的 redo log 刷新到磁盘中,做好提交的准备
21 | - **commit 阶段:**协调者准备提交前,会询问每个小事务是否做好了提交的准备,如果都准备好了就直接提交,否则全部回滚
22 |
23 | ### 外部 XA 事务
24 |
25 | 在外部 XA 事务中,每个小事务在分布在不同的数据库服务器中。在 MySQL 使用 XA 事务的一些操作如下:
26 |
27 | - `XA {start|begin} xid`:开启一个 XA 事务,此时该 XA 事务处于 active 状态。xid 表示每个事务唯一的 id
28 |
29 | - `XA end xid`:告知服务器有 xid 标识的 XA 事务的所有语句全部输入,此时该 XA 事务处于 idle 状态
30 |
31 | - `XA prepare xid`:应用程序让处于 idle 状态的 XA 事务将产生的 redo log 刷新到磁盘中,做好提交的准备,此时该 XA 事务处于 prepare 状态
32 |
33 | - `XA commit xid [one phase]`:对于处于 prepare 状态的 XA 事务,应用程序可以发送`XA commit xid`让服务器提交,此时该 XA 事务处于 commit 状态
34 |
35 | - `XA rollback xid`:应用程序通过该语句让服务器回滚 xid 所标识的 XA 事务,此时该 XA 事务处于 abort 状态
36 |
37 | - `XA recover`:应用程序可以通过该语句查看处于 prepare 状态的 XA 事务
38 |
39 | 下面给出 XA 事务的状态转换图
40 |
41 | 
42 |
43 | ### 内部 XA 事务
44 |
45 | 在内部 XA 事务中,每个小事务可能分布在同一个数据库服务器的不同存储引擎中,或者在存储引擎和插件之间。下面以最典型的 binlog 和 redo log 展开讨论内部 XA 事务
46 |
47 | redo log 以 mtr 为单位添加到 redo log buffer 中,在事务提交时会刷盘,在事务提交前后台线程每隔 1s 刷盘;bilog 以事务为单位先添加到 binlog cache 中,等事务提交后刷新到磁盘中
48 |
49 | 由于 redo log 是存储引擎生成,binlog 是 server 层生成,无法保证这两个刷盘操作的原子性,而这两个操作必须要保证原子性,否则会出现一致性问题
50 |
51 | - 如果 redo log 刷盘成功,binlog 没有刷盘成功,在主从复制的架构中会导致主库和从库数据不一致,因为从库是根据 binlog 来复制数据
52 | - 如果 redo log 没有刷盘成功,binlog 刷盘成功,在主从复制的架构中会导致主库和从库数据不一致,因为主库是根据 redo log 来恢复数据
53 |
54 | 在客户端执行 commit 或者自动提交事务的情况下,MySQL 内部开启一个 XA 事务保证 redo log 和 binlog 刷盘的原子性,binlog 作为协调者,存储引擎作为参与者
55 |
56 | 
57 |
58 | 从上图可以看出,将 redo log 持久化拆分成两个阶段:prepare 和 commit,binlog 在中间穿插写入
59 |
60 | - **prepare 阶段:**先将 XID 写入到 redo log 中,然后将 redo log 刷盘,最后将 redo log 对应的事务设置为 prepare 状态
61 | - **commit 阶段:**先将 XID 写入到 binlog 中,然后将 binlog 刷盘,接着调用存储引擎提交事务接口将 redo log 状态设置为 commit,此状态不需要持久化,可以根据 binlog 中是否存在 XID 判断 redo log 状态
62 |
63 | 假设时刻 1 (redo log 刷盘成功,binlog 刷盘失败) 或者时刻 2 (redo log 和 binlog 都刷盘成功,但还没有写入 commit 标识) 系统挂了,此时的 redo log 都处于 prapare 阶段
64 |
65 | 在 MySQL 重启后会重写扫描 redo log 文件,碰到处于 prepare 状态的 redo log,就会去检查 binlog 中是否存在和 redo log 相同的 XID
66 |
67 | - 如果 binlog 中不存在相同 XID,表示 binlog 没有刷盘成功,直接回滚事务 (对应时刻 1)
68 | - 如果 binlog 中存在相同 XID,表示 binlog 刷盘成功,直接提交事务 (对应时刻 2)
69 |
70 | **总结:**是否回滚事务完全取决于 binlog 是否存在和 redo log 中相同的 XID,如果不存在就需要回滚,否则直接提交即可
71 |
--------------------------------------------------------------------------------
/markdown/MySQL/分库分表.md:
--------------------------------------------------------------------------------
1 | # 分库分表
2 |
3 | 本篇文章主要整理关于 MySQL 分库分表的一些概述,并没有很深入,主要是因为某人多次的拜托 (是谁我不说,自己发现叭)~~
4 |
5 | ### 分库分表判断标准
6 |
7 | 先开门见山,给出写本篇文章的导火索,分库分表的标准是什么?
8 |
9 | 其实分库分表的标准在阿里巴巴 Java 开发手册中提到过:**单表行数超过 500 万行或者单表容量超过 2GB,才推荐进行分库分表**
10 |
11 | **问题一:**是否当单表行数超过 500 万行或者单表容量超过 2GB,才开始分库分表?
12 |
13 | - 不是,如果可以预计 3 年后数据会超过这个量级,就应该在创建表的时候就进行分库分表
14 |
15 | **问题二:**如果 MySQL 服务器配置较好,是否可以超过 500 万这个量级?
16 |
17 | - 虽然服务器配置更好后,数据量过大时,性能也不错,但以发展的眼光看待,考虑分库分表更佳
18 |
19 | 下面主要介绍一下分库分表到底是什么?什么情况下会考虑分库分表?分库分表的方式有哪些?
20 |
21 | ### 什么是分库分表
22 |
23 | **分库**,顾名思义是将一个数据库中的表拆分到多个数据库中,如下图所示:
24 |
25 | 
26 |
27 | 每个数据库连接数都有限制,当并发量过大时,数据库连接数也会增大,这是决定是否分库的直接原因,如果连接数成为数据库的瓶颈时就需要考虑分库
28 |
29 | **分表**,顾名思义是将一个表拆分成多个表,如下图所示:
30 |
31 | 
32 |
33 | 阿里巴巴 Java 开发手册中推荐:单表行数超过 500 万行或者单表容量超过 2GB,才推荐进行分库分表,所以决定是否分表的标准是表中记录数和容量,如果当一个表中数据量过大时就需要考虑分表
34 |
35 | 其实,还可能同时分库分表,这就是既存在并发量过大,又存在单表容量过大的情况~
36 |
37 | **总结:**
38 |
39 | | 切分方案 | 解决问题 |
40 | | :----------: | :------------------------------------: |
41 | | 只分库不分表 | 数据库读/写 QPS 过高;数据库连接数不足 |
42 | | 只分表不分库 | 单表数据量过大,存储性能遇到瓶颈 |
43 | | 既分库又分表 | 连接数不足 + 单表数据量过大 |
44 |
45 |
46 |
47 | ### 如何分库分表
48 |
49 | 上一部分只是介绍了在何种情况下会考虑分库分表,那如果决定了要分库分表,该如何分呢??
50 |
51 | 其实分库分表都有两种不同的分法,垂直和水平,排列组合一下就有四种:垂直分表、水平分表、垂直分库、水平分库
52 |
53 | #### 垂直分表
54 |
55 | 将一张表按照字段切分成多个表,通常是根据字段的关系密集程度进行切分,也可以按照常用字段和不常用字段切分,如下图所示:
56 |
57 | 
58 |
59 | #### 水平分表
60 |
61 | 水平分表又被称为 Sharding,它是将同一个表中的记录拆分到多个结构相同的表中,如下图所示:
62 |
63 | 
64 |
65 | 当一个表中数据不断增多时,水平分表是必然的选择,它可以将数据分布到集群的不同节点上,从而缓解单个数据库的压力
66 |
67 | #### 垂直分库
68 |
69 | 按照业务将表进行分类,分布到不同的数据库中,每个数据库可以放到不同的服务器上,如下图所示:
70 |
71 | 
72 |
73 | #### 水平分库
74 |
75 | 把同一个表的数据按照一定规则拆分到不同的数据库中,每个数据库可以放到不同的服务器上。假设按照表中 id 的奇偶性将数据拆分到不同的数据库中,如下图所示:
76 |
77 | 
78 |
--------------------------------------------------------------------------------
/markdown/Network/DNS.md:
--------------------------------------------------------------------------------
1 | # DNS
2 |
3 | 每一台公网服务器都有一个公网 IP,通过 IP 可以访问它,但世界上服务器那么多,而且 IP 是一串数字,难免不容易记住对应的 IP 地址,所以就有了 DNS (Domain Name System,域名系统)
4 |
5 | DNS 记录了 IP 和域名的对应关系,在通信时需要使用 IP 地址,而域名更便于用户记住,所以用户通过域名访问一个网站时,域名服务器会自动将域名转换成 IP 地址
6 |
7 | 在配置计算机的 IP 相关信息时,往往会配置一个 DNS 服务器的 IP 地址,可以将它称之为本地 DNS 服务器,我们是借助它来获取域名对应的 IP 地址
8 |
9 | ### DNS 结构
10 |
11 | 所有的 DNS 域名服务器是一个树状结构,最上层的是根域,如下图所示:
12 |
13 | 
14 |
15 | ### IP 查询过程
16 |
17 | 下面模拟`www.baidu.com`的查询过程!先给出过程图:
18 |
19 | 
20 |
21 | **第一步:**询问配置的本地 DNS 服务器,`www.baidu.com`的 IP 地址是多少?如果本地 DNS 服务器发现自己本地缓存中没有对应的域名就去根域名服务器询问,如果有缓存中有直接返回给计算机
22 |
23 | **第二步:**本地 DNS 服务器询问根域名服务器,根域名服务器会让本地 DNS 服务器去询问`com`域名服务器
24 |
25 | **第三步:**本地 DNS 服务器询问`com`域名服务器,`com`域名服务器会让本地 DNS 服务器去询问`baidu`域名服务器
26 |
27 | **第四步:**本地 DNS 服务器询问`baidu`域名服务器,`baidu`域名服务器会让本地 DNS 服务器去询问`www`域名服务器
28 |
29 | **第五步:**本地 DNS 服务器询问`www`域名服务器,`www`域名服务直接返回对应的 IP 地址,本地 DNS 服务器会缓存「域名-IP」对应关系,但该缓存有时间期限,一段时间会过期
--------------------------------------------------------------------------------
/markdown/Network/GET-POST请求.md:
--------------------------------------------------------------------------------
1 | # GET && POST 请求
2 |
3 | 在 HTPP/1.1 中,一共有 get、post、put、head、delete、potions、trace、connect 八种不同的请求方法,但本篇文章只介绍最常用的两种 get 和 post
4 |
5 | ### GET
6 |
7 | GET 请求是**从服务器获取指定资源**,指定的资源经服务器返回给客户端,资源可以是静态文本、页面、图片视频等
8 |
9 | GET 请求的参数位置一般写在 URL 中,URL 只能支持 ASCII,所以 GET 请求的参数只允许是 ASCII 字符,而且浏览器会对 URL 长度有限制,HTTP 协议本身没有对 URL 长度做任何规定
10 |
11 | 下面给出一个 GET 请求的示例:`https://www.test.com/get?xxx=111&yyy=222`。该请求中有两个参数:`xxx = 111`和`yyy = 222`
12 |
13 | ### POST
14 |
15 | POST 请求是根据请求负载对指定资源做出处理,一般请求携带的数据会写在消息体中,消息体中的数据可以是任意格式,且浏览器不会限制消息体大小
16 |
17 | GET 请求侧重于获取指定的资源,而 POST 请求侧重于传输实体到服务器进行处理,如登陆时提交表格信息
18 |
19 | 下面给出一个 post 请求的示例:
20 |
21 | ```
22 | https://www.test.com/post
23 |
24 | xxx = 111
25 | yyy = 222
26 | ```
27 |
28 | 该请求体中有两个参数:`xxx = 111`和`yyy = 222`
29 |
30 | ### 安全和幂等
31 |
32 | 首先说一下安全和幂等着两个概念:
33 |
34 | - **安全:**在 HTTP 协议里,安全表示不会修改服务器中的数据,类似于只读操作
35 | - **幂等:**多次请求操作结果相同
36 |
37 | 很显然,GET 请求是安全且幂等的,而 POST 是不安全且不幂等的。所以 GET 请求返回的结果可以被缓存,而 POST 请求返回的结果不可以被缓存
38 |
--------------------------------------------------------------------------------
/markdown/Network/HTTP-状态码.md:
--------------------------------------------------------------------------------
1 | # HTTP 状态码
2 |
3 | 简单来讲,HTTP 状态码的作用是服务器告诉客户端当前请求**响应**的状态,通过状态码就能判断和分析服务器的运行状态
4 |
5 |
114 |
115 | 文件类型(每行第一个字母):目录(d)、文件(-)、字符型文件(c)、块设备(b)、软链接(l)
116 |
117 | 文件的权限:rwx | rwx | r-x -> 属主权限 | 属组权限 | 其他人权限 (r:读 w:写 x:执行 -:无权限)
118 |
119 | 文件的硬链接总数 [传送门](./Linux硬链接和软连接的区别与总结.html)
120 |
121 | 文件属主的用户名
122 |
123 | 文件属组的组名
124 |
125 | 文件的大小(以字节为单位)
126 |
127 | 文件上次修改时间
128 |
129 | 文件名或目录名
130 |
131 |
--------------------------------------------------------------------------------
/markdown/Mac/Mac 快捷键.md:
--------------------------------------------------------------------------------
1 | # Mac 快捷键
2 |
3 |
4 |
5 | 软件最大化:control + command + F
6 |
7 | 软件最小化:command + M
8 |
9 | 软件关闭:command + Q
10 |
11 |
--------------------------------------------------------------------------------
/markdown/MySQL/MySQL索引.md:
--------------------------------------------------------------------------------
1 | # MySQL 索引
2 |
3 | 由于本篇文章侧重于 MySQL 索引的应用,所以并没有完全详细的介绍 B+ 树索引,但 B+ 树索引又是 MySQL 中默认使用的索引,所以**关于 B+ 树索引细节介绍可见 [B+ 树索引](./B+树索引.html)**
4 |
5 | ### 索引介绍
6 |
7 | **索引是一种用于快速查询和检索数据的数据结构,其本质可以看作是一种排好序的数据结构**
8 |
9 | 索引类似于书的目录,如果一本书没有目录,那么对于读者来说就是一场噩梦,目录可以加快我们查找的速度和效率,索引的作用也一样
10 |
11 | 索引底层数据结构有很多种类型,常见的索引结构:B 树、**[B+ 树](./B+树索引.html)**、Hash 表、红黑树。在 MySQL 中,无论是 InnoDB 存储引擎,还是 MyISAM 存储引擎,使用的都是 **[B+ 树索引](./B+树索引.html)**
12 |
13 | ### 索引优缺点
14 |
15 | 优点:
16 |
17 | - 加快查询检索数据的速度
18 | - 可以通过创建唯一索引保证数据的唯一性
19 |
20 | 缺点:
21 |
22 | - 空间成本:MySQL 中每一个索引都对应一个 B+ 树,需要一定的页来存储索引
23 | - 时间成本:在执行增删改操作时,需要维护索引的正确性,会消耗一定时间
24 |
25 | **注意:**有时候「二级索引 + 回表」的速度并不一定比「全表扫描」快,因为可能回表次数过多,而且页在物理存储上较为分散,需要进行多次磁盘 IO 将对应页加载到内存中,耗时大
26 |
27 | ### 索引底层数据结构
28 |
29 | #### Hash 表
30 |
31 | 将索引列映射到哈希表中,即:key = 索引列的值,value = 记录的位置,通过 key 可以快速获取记录的位置,在没有哈希冲突的情况下时间复杂度 O(1),可以用链地址法或开放定址法解决哈希冲突
32 |
33 | MySQL 之所以没有使用 Hash 表作为索引的底层实现,是因为 Hash 表不支持顺序查询和范围查询,只支持每次查询一个
34 |
35 | #### B 树 & B+ 树
36 |
37 | B 树也称 B- 树,全程为**多路平衡查找树**,B+ 树是 B 树的一个变体。B 树和 B+ 树中的 B 是`Balanced`的意思。目前大部分数据库系统及文件系统都采用 B- 树或其变体 B+ 树作为索引底层实现
38 |
39 | **B 树和 B+ 树的区别:**
40 |
41 | - B 树的所有节点既存放键 (key),也存放数据 (data);而 B+ 树只有叶子节点存放 key 和 data,其它非叶子节点只存放 key
42 | - B 树的叶子节点都是独立的;B+ 树的叶子节点间通过双向链表连接
43 | - B 树的检索过程相当于对范围内的每个节点的关键字做二分查找,可能还没到叶子节点就结束了;而 B+ 树的检索过程很稳定,任何查找都是从根节点到叶子节点
44 |
45 | ### 索引的类型
46 |
47 | **从数据结构维度划分:**
48 |
49 | - **[B+ 树索引](./B+树索引.html#innodb-中的索引方案)**:MySQL 中默认的索引结构,同层节点间双向链表连接,节点内单向链表连接
50 | - Hash 索引:通过键值对的形式,一次即可定位
51 |
52 | **从底层存储方式划分:**
53 |
54 | - **[聚簇索引](./B+树索引.html#聚簇索引)**:InnoDB 中的主键索引就属于聚簇索引,叶子节点存放完成用户记录,非叶子节点存放目录项纪录。数据和索引在一起,索引即数据,数据即索引
55 | - 非聚簇索引:数据和索引分开存储,**[二级索引](./B+树索引.html#二级索引)** 就属于非聚簇索引。MySQL 中的 **[MyISAM](./B+树索引.html#一页面至少存-2-条纪录)** 都是非聚簇索引
56 |
57 | **从应用维度划分:**
58 |
59 | - 主键索引:InnoDB 中的主键索引就属于聚簇索引,表中只会有一个主键索引,主键具有的特性该主键索引都具有,如:值唯一,且不为 NULL
60 | - 普通索引:InnoDB 中的普通索引就属于 **[二级索引](./B+树索引.html#二级索引)**
61 | - 唯一索引:值唯一,可以有 NULL
62 | - **[覆盖索引](./覆盖索引-索引条件下推.html#覆盖索引)**:索引列包含查询列表
63 | - **[联合索引](./B+树索引.html#联合索引)**:索引包含多个列
64 | - 前缀索引:为了降低索引占用的空间,可以只将一个字段的前缀作为索引
65 | - 全文索引:对文本的内容进行分词,然后搜索
66 |
67 | ### 使用索引的建议
68 |
69 | - **选择合适的字段建立索引:**频繁根据该字段查询
70 | - **频繁更新的字段慎重建立索引:**维护成本大
71 | - **限制每张表索引数量 (5 个):**索引会占用一定空间,虽然可以加快查询,但会减慢更新插入
72 | - **尽可能建立联合索引而非单列索引:**索引需要占用空间,联合索引可以减少空间的使用
73 | - **注意避免冗余索引:**比如建立了联合索引 (a, b),又建立了 单列索引 (a),就会出现冗余
74 | - **字符串类型字段尽量使用前缀索引:**可以减少空间的使用
75 | - **避免索引失效:**虽然建立了索引,但是没有使用使用,可以通过`explain`查看执行计划
76 | - **删除长期未使用的索引**
--------------------------------------------------------------------------------
/markdown/MySQL/RR隔离级别下彻底解决幻读了吗.md:
--------------------------------------------------------------------------------
1 | # RR 隔离级别下彻底解决幻读了吗?
2 |
3 | **[幻读](./MySQL事务.html#幻读-phantom)** 指在同一个事务中,同一个查询语句,前后两次执行得到的结果集不同,如:第一次查询得到六条记录,第二次查询得到七条数据
4 |
5 | **结论:**RR 隔离级别下只能最大程度的避免幻读现象的出现,但无法彻底解决幻读现象!!
6 |
7 | MySQL 中有两种读:快照读和锁定读
8 |
9 | - **快照读:**通过 **[MVCC](./MVCC.html)** 可以最大程度避免幻读,每次都只能看到生成 ReadView 之前已经提交事务修改的数据,所以在事务执行过程中多次读的结果是一致的
10 | - **锁定读:**通过加锁可以最大程度避免欢度,在 RR 下会为每个查询时符合条件的记录加 **[Next-Key Lock](./锁.html#next-key-lock)**,既不允许修改记录,也不允许在记录前的间隙插入新记录,所以在事务中多次读的结果是一致的
11 |
12 | ### 快照读 -- 出现幻读的情况
13 |
14 | 
15 |
16 | `update`语句修改的是最新数据。在时刻 4,由于事务 A 修改了`id = 3`的记录,记录中`trx_id`由 200 变成 100,所以该记录对事务 A 可见
17 |
18 | ### 锁定读 -- 出现幻读的情况
19 |
20 | 
21 |
22 | `select * from t`是快照读,不会对记录加锁,通过 MVCC 控制;`select * from t for update`是当前读,读最新的数据,而且会对记录加 **[Next-Key Lock](./锁.html#next-key-lock)**
23 |
24 | **建议:**在开启事务后,立马执行`select ... for update`,对记录加 **[Next-Key Lock](./锁.html#next-key-lock)**,可以最大程度避免幻读
--------------------------------------------------------------------------------
/markdown/MySQL/redo-log.md:
--------------------------------------------------------------------------------
1 | # redo log
2 |
3 | ### redo log 是什么?
4 |
5 | InnoDB 是以页为基本单位来管理内存空间,为了减少磁盘 IO 的开销,增加了 **[Buffer Pool](./InnoDB的Buffer-Pool.html)**,每次访问页面后不着急刷新回磁盘,而是缓存到 Buffer Pool 中,以便下次继续访问
6 |
7 | Buffer Pool 在内存中,所以会导致后续对页面的修改并不能及时刷新回磁盘,如果发生断电或者一些其它的原因会使内存中的数据丢失,重启后啥也没了,必须持久化到磁盘才安全
8 |
9 | 一个很简单的方法就是每次修改后立刻将页面刷新回磁盘,这样做的弊端在于:
10 |
11 | - 如果是少量的修改就刷新一个页面回磁盘,太过于浪费
12 | - 一个修改可能会牵连多个页面的变化,而且这些页面物理上极大可能不在一起,这样刷新回磁盘需要进行很多随机 IO,开销更大
13 |
14 | 基于上面的场景,就有了 redo log (重做日志),它记录了**对哪个表空间哪个页进行了哪些修改**,可以简单理解为就算数据丢失,但只要有对应的 redo log,也可以恢复丢失的数据
15 |
16 | redo log 也需要及时的刷新回磁盘,但它相比于刷新整个页面的优势在于:
17 |
18 | - redo log 占用的空间非常小
19 | - redo log 是顺序写入磁盘,比随机 IO 快很多
20 |
21 | ### redo log 写入过程
22 |
23 | 为了更好的管理 redo log,InnoDB 将 redo log 存储到大小为 512 字节的 block 中 (block 可以理解为页) 的 log blcok body 部分。每个 block 的结构如下所示:
24 |
25 | 
26 |
27 | 和 Buffer Pool 一样,为了缓解磁盘 IO 速度慢的问题,InnoDB 引入了 log buffer,它是内存中一片连续的区域,默认大小为 16MB
28 |
29 | redo log 是顺序写入 log buffer 中,从前往后,有一个 buf_free 指向空闲区域的起始位置,具体结构如下图所示:
30 |
31 | 
32 |
33 | ### redo log 刷盘时机
34 |
35 | log buffer 在内存中,如果不及时的将 log buffer 刷盘,也会导致 redo log 丢失,所以 log buffer 会在出现下面情况时刷盘
36 |
37 | - **log buffer 空间不足时:**如果 redo log 已经占满了 log buffer 一半的空间,就会把 redo log 刷新回磁盘
38 | - **事务提交时:**在事务提交时,将对应的 redo log 刷新回磁盘。由于 redo log 是顺序写入,所以之前的也会一起刷新回磁盘,不可能只刷新回某一个事务的 redo log
39 | - **脏页刷新回磁盘时:**将某个脏页刷新回磁盘时,会保证先将该脏页对应的 redo log 刷新回磁盘
40 | - 后台线程每隔 1s 将 log buffer 中的 redo log 刷新回磁盘
41 | - MySQL 正常关闭时也会将 buffer log 刷新回磁盘
42 |
43 | 对于上面第二点刷盘情况:**事务提交时**,由于这个要求过于严格,会降低数据库新能,所以可以通过参数`innodb_flush_log_at_trx_commit`调整:
44 |
45 | - **0:**每次事务提交时,不主动刷盘,交由后台线程来处理,所以可能丢失上一秒所有事务的数据
46 | - **1:**每次事务提交时,都将 redo log 同步到磁盘,可以保证事务的持久性 (默认值)
47 | - **2:**每次事务提交时,都只把 redo log 写入到 page cache (操作系统的缓存)。如果数据库挂了,但操作系统没挂,依旧可以保证事务的持久性
48 |
49 | 上面三个参数的安全性和性能的关系:
50 |
51 | - 安全:1 > 2 > 0
52 | - 性能:0 > 2 > 1
53 |
54 | **重点:**对于安全性要求高的系统,只能选择 1;对于可以接受 1s 数据丢失的信息,可以选择 0;如果既要求性能也要保证一定的安全性,可以选择 2,折中方案
55 |
56 | ### redo log 文件组
57 |
58 | 当 log buffer 触发刷盘时,会存到 redo log 文件中,它是以日志文件组的形式出现,即:一组中有多个大小相等的日志文件,默认情况下有两个文件:ib_logfile0 和 ib_logfile1
59 |
60 | redo log 是为了记录内存中还没有刷盘的脏页,防止当 MySQL 挂了后脏页丢失,导致修改数据的丢失。所以当脏页已经被刷盘,那么对应的 redo log 就没有用
61 |
62 | 随着系统的运行,redo log 只会越来越多,而日志文件组的数量和大小都是固定的,所以它采用循环写的方式,从头开始写,当写到末尾又回到开头,这样可以在有限的日志文件组中无限的写入 redo log
63 |
64 | 之所以可以覆盖日志文件组开头的数据,是因为开头的数据可能会随着脏页的刷盘而变成无用。用 write pos 表示新 redo log 刷盘时要写入的位置;用 checkpoint 表示当前要擦除的位置
65 |
66 | 
67 |
68 | 图中:
69 |
70 | - write pos 和 checkpoint 都是顺时针移动
71 | - write pos - checkpoint 之间的部分 (红色),用来存新的 redo log
72 | - checkpoint - write pos 之间的部分 (蓝色),表示待刷盘的脏页对应的 redo log
73 |
74 | 当 write pos 追上 checkpoint 时,表示 redo log 文件组满了,不能再将 redo log 刷盘到文件组中
75 |
76 | 此时 MySQL 会阻塞,将 Buffer Pool 中的脏页刷新到磁盘,然后标记 redo log 文件组可以被擦除的部分,最后将可以被擦除的部分擦除,更新 checkpoint (顺时针向前移动)
77 |
78 | 所以,一次 checkpoint 的过程就是将脏页刷新到磁盘中,更新 redo log 日志组中可以被覆盖的位置
--------------------------------------------------------------------------------
/markdown/MySQL/两阶段提交.md:
--------------------------------------------------------------------------------
1 | # 两阶段提交
2 |
3 | ### 分布式事务
4 |
5 | MySQL 分为 server 层和存储引擎层,事务由存储引擎层实现。如果修改服务器 A 中数据库的数据的同时也需要修改服务器 B 中数据库的数据,这两个操作必须同时成功或者失败,也就是必须保证原子性
6 |
7 | 而这两个操作属于两个不同的数据库,存储引擎也不是同一个,无法保证两个操作的原子性。这个时候就需要一个全局事务,由若干个小事务组成,这个全局事务也被称作分布式事务
8 |
9 | ### XA 规范
10 |
11 | 有一个名叫 X/Open 的组织提出了 XA 的规范,用于规范分布式事务,也就是不同的存储引擎只要符合 XA 规范,就可以放到一个分布式事务中管理
12 |
13 | XA 规范提出了两个角色
14 |
15 | - **资源管理器:**全局事务中每一个小事务
16 | - **事务管理器:**管理全局事务中每一个小事务 (后文称之为协调者)
17 |
18 | 要提交一个全局事务,就必须保证所有小事务都要能顺利提交,否则所有事务都应该回滚。XA 规范指出,要提交一个全局事务,必须分两步:(点题)
19 |
20 | - **prepare 阶段:**每个小事务在该阶段会执行各自的事务,并将事务产生的 redo log 刷新到磁盘中,做好提交的准备
21 | - **commit 阶段:**协调者准备提交前,会询问每个小事务是否做好了提交的准备,如果都准备好了就直接提交,否则全部回滚
22 |
23 | ### 外部 XA 事务
24 |
25 | 在外部 XA 事务中,每个小事务在分布在不同的数据库服务器中。在 MySQL 使用 XA 事务的一些操作如下:
26 |
27 | - `XA {start|begin} xid`:开启一个 XA 事务,此时该 XA 事务处于 active 状态。xid 表示每个事务唯一的 id
28 |
29 | - `XA end xid`:告知服务器有 xid 标识的 XA 事务的所有语句全部输入,此时该 XA 事务处于 idle 状态
30 |
31 | - `XA prepare xid`:应用程序让处于 idle 状态的 XA 事务将产生的 redo log 刷新到磁盘中,做好提交的准备,此时该 XA 事务处于 prepare 状态
32 |
33 | - `XA commit xid [one phase]`:对于处于 prepare 状态的 XA 事务,应用程序可以发送`XA commit xid`让服务器提交,此时该 XA 事务处于 commit 状态
34 |
35 | - `XA rollback xid`:应用程序通过该语句让服务器回滚 xid 所标识的 XA 事务,此时该 XA 事务处于 abort 状态
36 |
37 | - `XA recover`:应用程序可以通过该语句查看处于 prepare 状态的 XA 事务
38 |
39 | 下面给出 XA 事务的状态转换图
40 |
41 | 
42 |
43 | ### 内部 XA 事务
44 |
45 | 在内部 XA 事务中,每个小事务可能分布在同一个数据库服务器的不同存储引擎中,或者在存储引擎和插件之间。下面以最典型的 binlog 和 redo log 展开讨论内部 XA 事务
46 |
47 | redo log 以 mtr 为单位添加到 redo log buffer 中,在事务提交时会刷盘,在事务提交前后台线程每隔 1s 刷盘;bilog 以事务为单位先添加到 binlog cache 中,等事务提交后刷新到磁盘中
48 |
49 | 由于 redo log 是存储引擎生成,binlog 是 server 层生成,无法保证这两个刷盘操作的原子性,而这两个操作必须要保证原子性,否则会出现一致性问题
50 |
51 | - 如果 redo log 刷盘成功,binlog 没有刷盘成功,在主从复制的架构中会导致主库和从库数据不一致,因为从库是根据 binlog 来复制数据
52 | - 如果 redo log 没有刷盘成功,binlog 刷盘成功,在主从复制的架构中会导致主库和从库数据不一致,因为主库是根据 redo log 来恢复数据
53 |
54 | 在客户端执行 commit 或者自动提交事务的情况下,MySQL 内部开启一个 XA 事务保证 redo log 和 binlog 刷盘的原子性,binlog 作为协调者,存储引擎作为参与者
55 |
56 | 
57 |
58 | 从上图可以看出,将 redo log 持久化拆分成两个阶段:prepare 和 commit,binlog 在中间穿插写入
59 |
60 | - **prepare 阶段:**先将 XID 写入到 redo log 中,然后将 redo log 刷盘,最后将 redo log 对应的事务设置为 prepare 状态
61 | - **commit 阶段:**先将 XID 写入到 binlog 中,然后将 binlog 刷盘,接着调用存储引擎提交事务接口将 redo log 状态设置为 commit,此状态不需要持久化,可以根据 binlog 中是否存在 XID 判断 redo log 状态
62 |
63 | 假设时刻 1 (redo log 刷盘成功,binlog 刷盘失败) 或者时刻 2 (redo log 和 binlog 都刷盘成功,但还没有写入 commit 标识) 系统挂了,此时的 redo log 都处于 prapare 阶段
64 |
65 | 在 MySQL 重启后会重写扫描 redo log 文件,碰到处于 prepare 状态的 redo log,就会去检查 binlog 中是否存在和 redo log 相同的 XID
66 |
67 | - 如果 binlog 中不存在相同 XID,表示 binlog 没有刷盘成功,直接回滚事务 (对应时刻 1)
68 | - 如果 binlog 中存在相同 XID,表示 binlog 刷盘成功,直接提交事务 (对应时刻 2)
69 |
70 | **总结:**是否回滚事务完全取决于 binlog 是否存在和 redo log 中相同的 XID,如果不存在就需要回滚,否则直接提交即可
71 |
--------------------------------------------------------------------------------
/markdown/MySQL/分库分表.md:
--------------------------------------------------------------------------------
1 | # 分库分表
2 |
3 | 本篇文章主要整理关于 MySQL 分库分表的一些概述,并没有很深入,主要是因为某人多次的拜托 (是谁我不说,自己发现叭)~~
4 |
5 | ### 分库分表判断标准
6 |
7 | 先开门见山,给出写本篇文章的导火索,分库分表的标准是什么?
8 |
9 | 其实分库分表的标准在阿里巴巴 Java 开发手册中提到过:**单表行数超过 500 万行或者单表容量超过 2GB,才推荐进行分库分表**
10 |
11 | **问题一:**是否当单表行数超过 500 万行或者单表容量超过 2GB,才开始分库分表?
12 |
13 | - 不是,如果可以预计 3 年后数据会超过这个量级,就应该在创建表的时候就进行分库分表
14 |
15 | **问题二:**如果 MySQL 服务器配置较好,是否可以超过 500 万这个量级?
16 |
17 | - 虽然服务器配置更好后,数据量过大时,性能也不错,但以发展的眼光看待,考虑分库分表更佳
18 |
19 | 下面主要介绍一下分库分表到底是什么?什么情况下会考虑分库分表?分库分表的方式有哪些?
20 |
21 | ### 什么是分库分表
22 |
23 | **分库**,顾名思义是将一个数据库中的表拆分到多个数据库中,如下图所示:
24 |
25 | 
26 |
27 | 每个数据库连接数都有限制,当并发量过大时,数据库连接数也会增大,这是决定是否分库的直接原因,如果连接数成为数据库的瓶颈时就需要考虑分库
28 |
29 | **分表**,顾名思义是将一个表拆分成多个表,如下图所示:
30 |
31 | 
32 |
33 | 阿里巴巴 Java 开发手册中推荐:单表行数超过 500 万行或者单表容量超过 2GB,才推荐进行分库分表,所以决定是否分表的标准是表中记录数和容量,如果当一个表中数据量过大时就需要考虑分表
34 |
35 | 其实,还可能同时分库分表,这就是既存在并发量过大,又存在单表容量过大的情况~
36 |
37 | **总结:**
38 |
39 | | 切分方案 | 解决问题 |
40 | | :----------: | :------------------------------------: |
41 | | 只分库不分表 | 数据库读/写 QPS 过高;数据库连接数不足 |
42 | | 只分表不分库 | 单表数据量过大,存储性能遇到瓶颈 |
43 | | 既分库又分表 | 连接数不足 + 单表数据量过大 |
44 |
45 |
46 |
47 | ### 如何分库分表
48 |
49 | 上一部分只是介绍了在何种情况下会考虑分库分表,那如果决定了要分库分表,该如何分呢??
50 |
51 | 其实分库分表都有两种不同的分法,垂直和水平,排列组合一下就有四种:垂直分表、水平分表、垂直分库、水平分库
52 |
53 | #### 垂直分表
54 |
55 | 将一张表按照字段切分成多个表,通常是根据字段的关系密集程度进行切分,也可以按照常用字段和不常用字段切分,如下图所示:
56 |
57 | 
58 |
59 | #### 水平分表
60 |
61 | 水平分表又被称为 Sharding,它是将同一个表中的记录拆分到多个结构相同的表中,如下图所示:
62 |
63 | 
64 |
65 | 当一个表中数据不断增多时,水平分表是必然的选择,它可以将数据分布到集群的不同节点上,从而缓解单个数据库的压力
66 |
67 | #### 垂直分库
68 |
69 | 按照业务将表进行分类,分布到不同的数据库中,每个数据库可以放到不同的服务器上,如下图所示:
70 |
71 | 
72 |
73 | #### 水平分库
74 |
75 | 把同一个表的数据按照一定规则拆分到不同的数据库中,每个数据库可以放到不同的服务器上。假设按照表中 id 的奇偶性将数据拆分到不同的数据库中,如下图所示:
76 |
77 | 
78 |
--------------------------------------------------------------------------------
/markdown/Network/DNS.md:
--------------------------------------------------------------------------------
1 | # DNS
2 |
3 | 每一台公网服务器都有一个公网 IP,通过 IP 可以访问它,但世界上服务器那么多,而且 IP 是一串数字,难免不容易记住对应的 IP 地址,所以就有了 DNS (Domain Name System,域名系统)
4 |
5 | DNS 记录了 IP 和域名的对应关系,在通信时需要使用 IP 地址,而域名更便于用户记住,所以用户通过域名访问一个网站时,域名服务器会自动将域名转换成 IP 地址
6 |
7 | 在配置计算机的 IP 相关信息时,往往会配置一个 DNS 服务器的 IP 地址,可以将它称之为本地 DNS 服务器,我们是借助它来获取域名对应的 IP 地址
8 |
9 | ### DNS 结构
10 |
11 | 所有的 DNS 域名服务器是一个树状结构,最上层的是根域,如下图所示:
12 |
13 | 
14 |
15 | ### IP 查询过程
16 |
17 | 下面模拟`www.baidu.com`的查询过程!先给出过程图:
18 |
19 | 
20 |
21 | **第一步:**询问配置的本地 DNS 服务器,`www.baidu.com`的 IP 地址是多少?如果本地 DNS 服务器发现自己本地缓存中没有对应的域名就去根域名服务器询问,如果有缓存中有直接返回给计算机
22 |
23 | **第二步:**本地 DNS 服务器询问根域名服务器,根域名服务器会让本地 DNS 服务器去询问`com`域名服务器
24 |
25 | **第三步:**本地 DNS 服务器询问`com`域名服务器,`com`域名服务器会让本地 DNS 服务器去询问`baidu`域名服务器
26 |
27 | **第四步:**本地 DNS 服务器询问`baidu`域名服务器,`baidu`域名服务器会让本地 DNS 服务器去询问`www`域名服务器
28 |
29 | **第五步:**本地 DNS 服务器询问`www`域名服务器,`www`域名服务直接返回对应的 IP 地址,本地 DNS 服务器会缓存「域名-IP」对应关系,但该缓存有时间期限,一段时间会过期
--------------------------------------------------------------------------------
/markdown/Network/GET-POST请求.md:
--------------------------------------------------------------------------------
1 | # GET && POST 请求
2 |
3 | 在 HTPP/1.1 中,一共有 get、post、put、head、delete、potions、trace、connect 八种不同的请求方法,但本篇文章只介绍最常用的两种 get 和 post
4 |
5 | ### GET
6 |
7 | GET 请求是**从服务器获取指定资源**,指定的资源经服务器返回给客户端,资源可以是静态文本、页面、图片视频等
8 |
9 | GET 请求的参数位置一般写在 URL 中,URL 只能支持 ASCII,所以 GET 请求的参数只允许是 ASCII 字符,而且浏览器会对 URL 长度有限制,HTTP 协议本身没有对 URL 长度做任何规定
10 |
11 | 下面给出一个 GET 请求的示例:`https://www.test.com/get?xxx=111&yyy=222`。该请求中有两个参数:`xxx = 111`和`yyy = 222`
12 |
13 | ### POST
14 |
15 | POST 请求是根据请求负载对指定资源做出处理,一般请求携带的数据会写在消息体中,消息体中的数据可以是任意格式,且浏览器不会限制消息体大小
16 |
17 | GET 请求侧重于获取指定的资源,而 POST 请求侧重于传输实体到服务器进行处理,如登陆时提交表格信息
18 |
19 | 下面给出一个 post 请求的示例:
20 |
21 | ```
22 | https://www.test.com/post
23 |
24 | xxx = 111
25 | yyy = 222
26 | ```
27 |
28 | 该请求体中有两个参数:`xxx = 111`和`yyy = 222`
29 |
30 | ### 安全和幂等
31 |
32 | 首先说一下安全和幂等着两个概念:
33 |
34 | - **安全:**在 HTTP 协议里,安全表示不会修改服务器中的数据,类似于只读操作
35 | - **幂等:**多次请求操作结果相同
36 |
37 | 很显然,GET 请求是安全且幂等的,而 POST 是不安全且不幂等的。所以 GET 请求返回的结果可以被缓存,而 POST 请求返回的结果不可以被缓存
38 |
--------------------------------------------------------------------------------
/markdown/Network/HTTP-状态码.md:
--------------------------------------------------------------------------------
1 | # HTTP 状态码
2 |
3 | 简单来讲,HTTP 状态码的作用是服务器告诉客户端当前请求**响应**的状态,通过状态码就能判断和分析服务器的运行状态
4 |
5 |  6 |
7 | 状态码的第一位数字表示状态类型,第二、三位数字表示具体的情况
8 |
9 | - **1xx:**表示接收的请求正在处理
10 | - **2xx:**表示请求正常处理完毕 (成功)
11 | - **3xx:**表示重定向
12 | - **4xx:**表示客户端错误
13 | - **5xx:**表示服务端错误
14 |
15 | ### 1xx
16 |
17 | 表示请求已被接受,需要继续处理。这类响应是临时响应,只包含「状态行」和某些可选的响应「头信息」,并以空行结束
18 |
19 | 常见的有:
20 |
21 | - **100 (继续):**这个为临时响应,表示迄今为止的所有内容都是可行的,客户端应该继续发送剩余请求,如果已经完成,则忽略它
22 | - **101 (切换协议):**服务器根据客户端的请求切换协议,主要用于 websocket 或 http2 升级
23 |
24 | ### 2xx
25 |
26 | 表示请求已成功被服务器接收、理解、并接受
27 |
28 | 常见的有:
29 |
30 | - **200 (成功):**请求已成功,请求所希望的响应头或数据体将随此响应返回
31 | - **201 (已创建):**请求成功并且服务器创建了新的资源
32 | - **202 (已创建):**服务器已经接收请求,但尚未处理
33 | - **203 (非授权信息):**服务器已成功处理请求,但返回的信息可能来自另一来源
34 | - **204 (无内容):**服务器成功处理请求,但没有返回任何内容。例如:删除请求或请求是通过表单发送的,响应不应导致刷新表单或加载新页面
35 | - **205 (重置内容):**将文档重置为原始状态。例如,清除表单
36 | - **206 (部分内容):**服务器成功处理了部分请求 (范围请求,服务器成功执行了该范围内的请求)
37 |
38 | ### 3xx
39 |
40 | 表示要完成请求,需要进一步操作。 通常,这些状态代码用来重定向
41 |
42 | 常见的有:
43 |
44 | - **300 (多种选择):**针对请求,服务器可执行多种操作。 服务器可根据请求者 (user agent) 选择一项操作,或提供操作列表供请求者选择
45 | - **301 (永久重定向):**请求的网页已永久移动到新位置。 服务器返回此响应 (对 GET 或 HEAD 请求的响应)时,会自动将请求者转到新位置
46 | - **302 (临时重定向):**服务器目前从不同位置的网页响应请求,但请求者应继续使用原有位置来进行以后的请求
47 | - **303 (查看其它位置):**请求者应当对不同的位置使用单独的 GET 请求来检索响应时,服务器返回此代码
48 | - **304 (缓存重定向):**表示资源没有被修改,可以重定向到缓存文件
49 | - **305 (使用代理):**请求者只能使用代理访问请求的网页。 如果服务器返回此响应,还表示请求者应使用代理
50 | - **307 (临时重定向):**服务器目前从不同位置的网页响应请求,但请求者应继续使用原有位置来进行以后的请求 (和 302 相同)
51 |
52 | ### 4xx
53 |
54 | 表示客户端有错误,妨碍了服务器的处理
55 |
56 | 常见的有:
57 |
58 | - **400 (错误请求):**请求报文中存在语法错误
59 | - **401 (未授权):**请求要求身份验证。对于需要登录的网页,服务器可能返回此响应
60 | - **403 (禁止):**服务器拒绝请求
61 | - **404 (未找到):**服务器找不到请求的网页
62 | - **405 (方法禁用):**禁用请求中指定的方法
63 | - **406 (不接受):**无法使用请求的内容特性响应请求的网页
64 | - **407 (需要代理授权):**此状态代码与 401 (未授权)类似,但指定请求者应当授权使用代理
65 | - **408 (请求超时):**服务器等候请求时发生超时
66 |
67 | ### 5xx
68 |
69 | 表示服务器有错误,在处理请求的过程中有错误或者异常状态发生
70 |
71 | 常见的有:
72 |
73 | - **500 (服务器内部错误):**服务器遇到错误,无法完成请求
74 | - **501 (尚未实施):**服务器不具备完成请求的功能。 例如,服务器无法识别请求方法时可能会返回此代码
75 | - **502 (错误网关):**服务器作为网关或代理,从上游服务器收到无效响应
76 | - **503 (服务不可用):**服务器目前无法使用 (由于超载或停机维护)
77 | - **504 (网关超时):**服务器作为网关或代理,但是没有及时从上游服务器收到请求
78 | - **505 (HTTP 版本不受支持):**服务器不支持请求中所用的 HTTP 协议版本
79 |
80 | ### 适用场景
81 |
82 | **100:**客户端在发送 POST 数据给服务器前,征询服务器情况,看服务器是否处理POST的数据,如果不处理,客户端则不上传 POST 数据,如果处理,则 POST 上传数据。常用于 POST 大数据传输
83 |
84 | **206:**一般用来做断点续传,或者是视频文件等大文件的加载
85 |
86 | **301:**永久重定向会缓存。新域名替换旧域名,旧的域名不再使用时,用户访问旧域名时用 301 就重定向到新的域名
87 |
88 | **302:**临时重定向不会缓存,常用 于未登陆的用户访问用户中心重定向到登录页面
89 |
90 | **304:**协商缓存,告诉客户端有缓存,直接使用缓存中的数据,返回页面的只有头部信息,是没有内容部分
91 |
92 | **400:**参数有误,请求无法被服务器识别
93 |
94 | **403:**告诉客户端进制访问该站点或者资源,如在外网环境下,然后访问只有内网 IP 才能访问的时候则返回
95 |
96 | **404:**服务器找不到资源时,或者服务器拒绝请求又不想说明理由时
97 |
98 | **503:**服务器停机维护时,主动用 503 响应请求或 Nginx 设置限速,超过限速,会返回 503
99 |
100 | **504:**网关超时
--------------------------------------------------------------------------------
/markdown/Network/HTTP-缓存策略.md:
--------------------------------------------------------------------------------
1 | # HTTP 缓存策略
2 |
3 | 当使用浏览器访问一个 Web 资源时,为了提高访问效率,往往会在浏览器和服务器之间增加本地缓存
4 |
5 | 对于首次访问,会将服务器响应的数据缓存到本地;对于后续的访问,会根据缓存策略决定是否直接使用本地缓存。简化的流程如下图所示:
6 |
7 | 
8 |
9 | **注意:**缓存策略完全是根据服务器响应消息的头信息来决定滴!!
10 |
11 | ### 与缓存有关的消息头字段
12 |
13 | 先给出与缓存有关的消息头字段的一些说明:
14 |
15 | 
16 |
17 | ### 强制缓存
18 |
19 | 顾名思义,强制缓存不需要服务器的参与,浏览器可以自己决策是否使用缓存,决策规则如下:
20 |
21 | - 如果本地缓存中不存在要请求的资源,浏览器会直接将请求发送到服务器,完成首次资源请求,根据服务器响应的消息保存相关信息
22 | - 如果本地缓存中存在要请求的资源,先判断缓存是否过期,如果没有过期直接使用本地缓存,如果过期就需要根据下面要介绍的协商缓存进行处理
23 |
24 | 在响应消息中,Expires 是根据 Last-Modified 和 max-age 计算出来的,max-age 表示存活多少秒后过期,而 Last-Modified 表示最后的修改时间
25 |
26 | 如果一个请求直接强制使用缓存,那么该请求会显示`200 OK (from disk cache)`,如下所示:
27 |
28 | ```
29 | Request URL: http://192.168.124.13:8080/index.html
30 | Request Method: GET
31 | Status Code: 200 OK (from disk cache)
32 | Remote Address: 192.168.124.13:8080
33 | Referrer Policy: strict-origin-when-cross-origin
34 | ```
35 |
36 | ### 协商缓存
37 |
38 | 顾名思义,协商缓存是浏览器和服务器共同协商是否使用本地缓存,浏览器负责提供本地缓存的信息,如:最后修改时间和唯一标识,添加在请求消息头中,服务器收到消息后来决策是否允许浏览器使用本地缓存
39 |
40 | If-Modified-Since 和 If-None-Match 是在浏览器第一次发送请求到服务器时,从服务器的响应消息保存。如果浏览器发现本地缓存中不存在要请求的资源,会直接将请求发送到服务器
41 |
42 | 协商缓存基于两种消息头字段实现:
43 |
44 | - **第一种:**请求头中的 If-Modified-Since 和响应头中的 Last-Modified
45 | - **第二种:**请求头中的 If-None-Match 和响应头中的 Etag
46 |
47 | 对于第一种,如果 If-Modified-Since 时间小于 Last-Modified,表示本地缓存中是旧数据,不可以使用本地缓存中的数据,否则可以使用缓存
48 |
49 | 对于第二种,如果 If-None-Match 和 Etag 不相等,表示本地缓存中是旧数据,不可以使用本地缓存中的数据,否则可以使用缓存
50 |
51 | 如果一个请求消息头中同时包含 If-Modified-Since 和 If-None-Match 字段,那么 If-None-Match 优先级更高。先判断 If-None-Match,如果不匹配直接无法使用缓存,如果匹配,再根据 If-Modified-Since 判断
52 |
53 | **问题:**为什么 Etag 的优先级更高??
54 |
55 | Etag 是服务器中资源的唯一标识,它可以解决一些 Last-Modified 难以解决的问题
56 |
57 | - 可能存在文件没有被修改,但修改时间却发生了改变的情况
58 | - Last-Modified 的精度是秒,对于秒以内的变化,Last-Modified 无法感知;但 Etag 却可以保证秒以内多次修改都可以被感知
59 |
60 | **强制缓存和协商缓存区别:**强制缓存不需要将请求发送给服务器,浏览器自己可以决策;协商缓存需要将请求先发送给服务器,由服务器决策,如果可以使用缓存会响应一个 **[304](./HTTP-状态码.html#3xx)** 的消息,表示缓存重定向
61 |
62 | ### 总流程图
63 |
64 | 下面给出缓存策略的总体流程图:
65 |
66 | 
67 |
68 | **注意:**
69 |
70 | - 使用 F5 刷新网页时,跳过强制缓存,但会检查协商缓存
71 | - 使用 ctrl + F5 刷新页面时,直接从服务器加载,跳过强制缓存和协商缓存
72 |
73 | ### 参考文章
74 |
75 | - **[HTTP 缓存技术](https://xiaolincoding.com/network/2_http/http_interview.html#http-缓存技术)**
76 | - **[彻底弄懂浏览器缓存策略](https://mp.weixin.qq.com/s/Ui7Q9k4faiD5mv_LfB4Rrw)**
77 | - **[Cache-Control在请求头和响应头里的区别](https://juejin.cn/post/6960988505816186894)**
78 | - **[为什么我的缓存设置在 chrome 中不生效](https://xie.infoq.cn/article/70b359ab1210efb6f5b253e24)**
79 | - **[Cache-Control和Expires无效的原因](https://www.cnblogs.com/jimaww/p/10234074.html)**
--------------------------------------------------------------------------------
/markdown/Network/SYN-泛洪攻击.md:
--------------------------------------------------------------------------------
1 | # SYN 泛洪攻击
2 |
3 | ### 半连接 & 全连接
4 |
5 | 在 TCP 三次握手的时候,Linux 内核会维护两个队列:
6 |
7 | - 半连接队列,也称 SYN 队列,只进行了一次握手的连接
8 | - 全连接队列,也称 Accept 队列,进行了三次握手的连接
9 |
10 | 
11 |
12 | 关于出队和入队的详细流程如下:
13 |
14 | - 当服务器收到客户端的 SYN 报文时,会创建一个半连接对象,并加入到内核的 SYN 队列中
15 | - 接着服务器发送 SYN-ACK 报文给客户端,等待客户端的 ACK 报文
16 | - 当服务器收到客户端的 ACK 报文时,会取出一个半连接对象,然后创建一个新的连接对象加入 Accept 队列中
17 | - 应用程序通过调用 Socket 提供的`accept()`方法,从 Accept 队列中取出一个连接对象
18 |
19 | **注意:**不管是半连接队列还是全连接队列,都有最大长度限制,超过限制时都会丢弃报文!!
20 |
21 | ### SYN 泛洪攻击是什么
22 |
23 | 客户端和服务器使用 TCP 协议通信前需要进行三次握手建立连接,当服务器收到客户端第一次握手的 SYN 报文后,会发送 SYN-ACK 报文,之后服务器处于 SYN_RECV 状态。**更详细可见 [三次握手](./TCP-三次握手-四次挥手.html#tcp-三次握手过程)**
24 |
25 | **SYN 泛洪攻击:**攻击者会伪造大量不同 IP 的 SYN 报文,服务器收到 SYN 报文后会向客户端发送 SYN-ACK 报文,但攻击者不会回应该报文,这样会逐渐占满半连接队列,使得后续正常连接请求直接被丢弃
26 |
27 | ### 如何避免 SYN 泛洪攻击
28 |
29 | #### 方法一:调大 netdev_max_backlog
30 |
31 | 当网卡接收数据的速度大于内核处理的速度时,会有一个队列保存这些数据包。控制该队列的大小,默认值为 1000,可以通过参数调整为 100000
32 |
33 | ```bash
34 | net.core.netdev_max_backlog = 10000
35 | ```
36 | #### 方法二:增加 TCP 半连接队列大小
37 |
38 | 增大 TCP 半连接队列,要同时增大下面这三个参数:
39 |
40 | - 增大 net.ipv4.tcp_max_syn_backlog
41 | - 增大 listen() 函数中的 backlog
42 | - 增大 net.core.somaxconn
43 |
44 | #### 方法三:开启 net.ipv4.tcp_syncookies
45 |
46 | 开启 net.ipv4.tcp_syncookies 后可以不需要加入到 SYN 半连接队列中,也可以成功建立连接
47 |
48 | #### 方法四:减少 SYN + ACK 重发次数
49 |
50 | 攻击者不会回应服务器的 SYN-ACK 包,服务器会超时重发,在 Linux 默认重发 5 次,可以适当降低重发的次数使处于 SYN_RECV 状态的服务器尽快断开连接
--------------------------------------------------------------------------------
/markdown/Network/Solutions-7th-Edition.docx:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/LFool/LFool-Notes/8d4b7b3aa2f91cd51aa57427d016d86db8712e05/markdown/Network/Solutions-7th-Edition.docx
--------------------------------------------------------------------------------
/markdown/Network/网络层那点事儿.md:
--------------------------------------------------------------------------------
1 | # 网络层那点事儿~
2 |
3 | ### 网络层和链路层
4 |
5 | 传输层提供端到端的可靠传输,也就是不同主机中的进程间通信,通过端口唯一确认主机中的进程,TCP 报文首部也有端口字段,**详情可见 [TCP 报文段格式](./TCP-三次握手-四次挥手.html)**
6 |
7 | 网络层负责将数据从一台主机传输到另一台主机,往往这两台主机在物理上没有直接相连;而链路层也是负责将数据从一台主机传输到另一台主机,往往这两台主机在物理上直接相连
8 |
9 | 下面主要介绍网络层和链路层是如何相互配合将数据从一台主机传输到另一台主机。网络层通过 IP 地址定义一台主机,链路层通过 MAC 地址定位一台主机。下面模拟一种场景,如下图所示:
10 |
11 | 
12 |
13 | **注意:**路由器的每个端口都有一个 IP 地址和 MAC 地址
14 |
15 | 主机 A 向主机 B 发送数据,它们俩在物理上没有直接相连,需要依赖网络层将数据从主机 A 发送到主机 B
16 |
17 | - **第一步:**主机 A 将数据包发送给路由器,此时会通过 ARP 协议获取路由器的 MAC 地址,将报文中的源 MAC 地址设置为主机 A,目标 MAC 地址设置为路由器。链路层根据源/目标 MAC 地址将数据包从主机 A 发送给路由器,因为它俩在物理上直接相连
18 | - **第二步:**路由器将数据包发送给主机 B,将报文中的源 MAC 地址设置为路由器,目标 MAC 地址设置为主机 B。链路层根据源/目标 MAC 地址将数据包从路由器发送给主机 B,因为它俩在物理上直接相连
19 |
20 | 可以看出数据包在传输过程中,报文的源/目标 IP 地址始终保持不变,分别为:`10.0.1.2`和`10.0.5.6`,变化的是 MAC 地址。网络层负责根据 IP 地址寻址➕路由,而链路层负责将数据在两个物理上相邻的节点中传输!!
21 |
22 | **注意:**由于 MAC 地址在网络层封装,所以有些说法认为 ARP 属于网络层,有些说法认为 ARP 属于链路层,但这不重要,只要理解这个过程即可
23 |
24 | ### IP 分类
25 |
26 | IP 主要分为五类:A 类地址、B 类地址、C 类地址、D 类地址、E 类地址,但这里只想简单给出公有 IP 和私有 IP 的分类
27 |
28 | 简单来说,公有 IP 是网络中所有人都可以访问的 IP,而私有 IP 只有在同一个局域网中的人才可以访问。公有 IP 不允许重复;同一个局域网中的私有 IP 不允许重复,但在不同的局域网中可以重复
29 |
30 | 私有 IP 只有三种范围,如下:
31 |
32 | - 10.0.0.0 - 10.255.255.255
33 | - 172.16.0.0 - 172.31.255.255
34 | - 192.168.0.0 - 192.168.255.255
35 |
36 | 在这三个范围之外的所有 IP 都是公有 IP!!
37 |
38 | ### 路由控制
39 |
40 | 上文说:网络层负责将数据从一台主机传输到另一台主机,往往这两台主机在物理上没有直接相连。那么它是如何将数据从一台主机传输到另一台主机呢?
41 |
42 | 网络层有一个重要的设备:路由器,它内部有一张路由转发表,根据目标 IP 地址可以知道该数据包从路由器的哪一个端口转发出去。回到第一部分的例子中,先将例子扩展的更丰富一些,如下图所示:
43 |
44 | 
45 |
46 | 上图中 IP 数据包的源 IP 地址为`10.1.1.30`,目标 IP 地址为`10.1.2.10`
47 |
48 | **第一步:**主机 A 根据目标 IP 地址匹配到`0.0.0.0/0`,那么下一跳就是`10.1.1.1`。这里的`0.0.0.0/0`就是默认路由,在没有匹配到其它路由时就会匹配默认路由,默认路由的下一跳就是默认网关
49 |
50 | **第二步:**路由器根据目标 IP 地址匹配到`10.1.2.0/24`,那么下一跳就是`10.1.0.2`
51 |
52 | **第三步:**路由器根据目标 IP 地址匹配到`10.1.2.0/24`,那么下一跳就是`10.1.2.1`,最终通过交换机将数据发送给目标主机
53 |
54 | ### IP 分片与重组
55 |
56 | 数据链路层的传输单位是帧,不同的数据链路有不同的最大传输单元 (MTU),以太网的 MTU 是 1500 字节。换句话说,MTU = IP 首部 + TCP 首部 + 数据,一旦「IP 首部 + TCP 首部 + 数据」超过了 MTU,那么就会分片
57 |
58 | 在 TCP 中,如果数据长度 > MTU - IP 首部 - TCP 首部,就会进行分片;在网络层中,如果 TCP 首部 + 数据 > MTU - IP 首部,也会进行分片
59 |
60 | 如果 TCP 不分片,仅仅在网络层分片,那么一旦某个分片数据丢失,TCP 需要重传整个数据,因为 TCP 需要保证数据的可靠性,而网络层不需要保证数据的可靠性
61 |
62 | 所以 TCP 也会进行分片,如果某个分片数据在传输过程中丢失,那么只需要重传该分片数据即可,不需要重传所有数据
63 |
64 | 一般来说,TCP 分片已经考虑了 IP 首部的长度,所以在网络层不会超过长度,也就不会再进行分片,但存在一些特殊情况需要在 TCP 分片后,网络层还需要继续分片,如传输链路中存在更小的 MTU
65 |
66 | **详情分析可见 [TCP分段了,IP层就一定不会分片了吗?](https://zhuanlan.zhihu.com/p/372863051)**
--------------------------------------------------------------------------------
/markdown/Network/计算机网络(top-down)-习题&实验.md:
--------------------------------------------------------------------------------
1 | # 计算机网络(top-down) - 习题 & 实验
2 |
3 | ## 第一章
4 |
5 | ### 习题
6 |
7 | 1. “主机”和“端系统”之间有什么不同?列举几种不同类型的端系统。Web 服务器是一种端系统吗?
8 |
9 |
10 |
11 | 2.
12 |
13 | ### 实验
14 |
15 |
--------------------------------------------------------------------------------
/markdown/OS/CPU缓存一致性.md:
--------------------------------------------------------------------------------
1 | # CPU 缓存一致性
2 |
3 | ### 存储器层次结构
4 |
5 | 在计算机系统中,最常见的存储器有内存和磁盘。一个进程运行过程中往往需要将磁盘中的数据加载到内存中才可以访问
6 |
7 | CPU 的运算速度和内存的访问速度相差过大,为了缓解这种差距,在 CPU 和内存之间增加了高速缓存。由于 CPU 是基于寄存器的指令集,所以在 CPU 和高速缓存之间还存在寄存器
8 |
9 | 存储器离 CPU 越近,那么读写速度就越快,但能存储的容量也就越小。一个存储器的层次结构如下图所示:
10 |
11 | 
12 |
13 | 在现在的 CPU 中一般都有多个核心,寄存器、L1 高速缓存、L2 高速缓存都是每个核心独有,而 L3 高速缓存是 CPU 独有,如下图所示:
14 |
15 | 
16 |
17 | ### CPU Cache 结构
18 |
19 | 每个 CPU Cache 都是由缓存行构成,而且 CPU 和 CPU Cache 的交互单位也是缓存行,也就是如果 Cache 中没有数据,CPU 会一次性从内存中读取和缓存行相同大小的数据存入 Cache 中
20 |
21 | CPU Cache 的结构如下图所示:
22 |
23 | 
24 |
25 | 在使用 CPU Cache 的过程中,可能会出现伪共享问题,这也是下面要介绍的 MESI 协议导致的。**关于伪共享的分析可见 [伪共享](../java/伪共享.html)**
26 |
27 | ### CPU Cache 数据写入
28 |
29 | 对于读操作来说很简单,每次先去 Cache 中检查是否有数据,如果有数据就直接返回,如果没有数据就去内存中读,并将读到的数据加到 Cache 中以便下次可以快速读
30 |
31 | 但是对于写操作可能就麻烦一点,这里可以借鉴 **[Redis 缓存更新策略](../redis/Redis缓存更新策略.html)**,下面主要介绍两种写入策略:
32 |
33 | - **写穿透 (Write Through):**如果 Cache 中有数据,先更新 Cache,后更新内存;如果 Cache 中没有数据,直接更新内存
34 | - **写回 (Write Back):**先只更新 Cache,随后异步更新内存
35 |
36 | ### CPU 缓存一致性问题
37 |
38 | 不同线程在不同核心上执行,每个核心存在自己独有的 Cache。由于不可见性,同一个共享变量,可能出现在不同 Cache 中不一致的问题,**原理可见 [处理器重排序](../java/Java内存模型.html#处理器重排序)**
39 |
40 | 要解决缓存不一致的问题,必须保证下面两点:
41 |
42 | - 某个 CPU 核心更新 Cache 中的数据时,其它 CPU 核心必须知道该数据被更新了,这被称为**写传播 (Write Propagation)**
43 | - 所有 CPU 核心看到 Cache 中数据的修改操作顺序必须是一致性的,这被称为**事务的串行化 (Transaction Serialization)**
44 |
45 | 对于第一点使用总线嗅探机制,当某个 CPU 核心更新 Cache 中的数据时,会向总线广播这一事件,所有 CPU 核心都会监听总线上的广播事件,当发现广播事件中包含的数据也存在于自己的 Cache 中时,就会将自己 Cache 中的数据更新成广播中的数据
46 |
47 | 但仅仅做到第一点并不能完全解决缓存不一致的问题,假设存在两个 CPU 核心先后将`i`修改成 100 和 200,但无法保证这两个修改的广播事件的先后顺序,可能出现某个 CPU 核心看到的顺序:先将`i`修改为 200,再将`i`修改为 100,这也是第二点要保证事务串行化执行的原因
48 |
49 | ### MESI 协议
50 |
51 | MESI 协议基于总线嗅探机制实现了事务串行化,该协议保证了缓存一致性。首先,MESI 协议规定了四种状态:
52 |
53 | - **Modified** 已修改:表示 Cache 中的数据已经被修改过,也就是脏数据
54 | - **Exclusive** 独占:表示 Cache 中的数据被自己独占,其它 CPU Cache 中没有该数据,此时数据是干净的
55 | - **Shared** 共享:表示多个 CPU Cache 中都有该数据,此时数据是干净的
56 | - **Invalidated** 已失效:表示 Cache 中的数据无效
57 |
58 | 下面通过表格给出这四种状态之间的转化关系:
59 |
60 | 
61 |
62 | **注意:**如果在独占状态或者已修改状态下写数据,不需要广播该事件。如果是独占状态,表示其它核心的 Cache 中没有该数据,所以不需要广播;如果是已修改状态,表示包含该数据的核心的 Cache 中对应的 Cache Line 已经是已失效状态,所以也不需要广播
63 |
64 | 这里推荐一个可视化网站,可以看到 Cache 四个状态的转换 **[VivioJS MESI animation help](https://www.scss.tcd.ie/Jeremy.Jones/VivioJS/caches/MESIHelp.htm)**
--------------------------------------------------------------------------------
/markdown/OS/中断.md:
--------------------------------------------------------------------------------
1 | # 中断
2 |
3 | ### 用户态 & 内核态
4 |
5 | 用户进程不可以直接操作系统资源,因为如果给予进程的权利过大,可能会出现一些非法的访问,导致系统处于不安全的状态。基于这种原因,将系统所处状态分为用户态和内核态:
6 |
7 | - **用户态:**CPU 只能受限的访问内存,并且不允许访问敏感的系统资源,如:I/O 设备
8 | - **内核态:**CPU 可以访问任意数据,包括系统资源,还可以决定切换进程
9 |
10 | 当一个用户进程需要访问硬件资源时,需要进行系统调用,让操作系统去访问硬件资源,然后将结果返回给用户进程。系统调用相当于内核提供给用户的一套 API,通过 API 可以间接完成对硬件的访问
11 |
12 | 在系统启动时内核会设置好陷阱表,该表中存放了陷阱类型和内核代码位置的对应关系,也就是如果执行到陷阱 A,就会去执行陷阱 A 对应的内核代码
13 |
14 | 当用户线程系统调用时,会执行特殊的陷阱指令,该指令会从用户态转化到内核态,进而去执行该陷阱对应的内核代码。当操作系统执行完对应代码后,会从内核态转化到用户态
15 |
16 | 操作系统也算是一种软件,在单核 CPU 中,如果用户进程在 CPU 上执行,那么操作系统是无法执行滴,只有当用户态转化到内核态,操作系统才可以在 CPU 上执行。所以系统调用不仅从用户态转化到内核态,而且还相当于进行了一次上下文切换,从用户进程切换到操作系统进程
17 |
18 | 下面是通过系统调用完成上下文切换的过程:
19 |
20 | 
21 |
22 | ### 时钟中断
23 |
24 | 对系统资源的访问、上下文切换等操作都需要操作系统来执行。系统调用可以从用户态切换到内核态,让控制权重新回到操作系统手中,但如果一个进程始终都不进行系统调用呢?那就会出现一直不能切换到内核态,从而卡死的情况
25 |
26 | 为了避免这种情况的发生,提出了时钟中断。时钟设备可以每隔几毫秒就生成一次中断,中断产生时,当前正在运行的程序停止,操作系统中预先配置的中断程序会运行,此时操作系统重新获得了 CPU 的控制权
27 |
28 | 下面是通过时钟中断完成上下文切换的过程:
29 |
30 | 
31 |
32 | ### 软中断
33 |
34 | 在处理中断时,中断处理程序会将中断关闭,如果处理时间过长,可能会丢失其它设备的中断信号。为了避免丢失中断信号,将原来的整个中断过程分为两部分:
35 |
36 | - **第一部分:**快速处理中断,该阶段会暂时关闭中断,但一般该阶段耗时较短,只会处理与硬件相关敏感的事情
37 | - **第二部分:**交由操作系统完成中断剩余工作,该阶段会将中断打开,不会丢失中断信号
38 |
39 | 可以将第一部分看作是硬中断,也就是会关闭中断的中断;可以将第二部分看作是软中断,也就是不会关闭中断的中断。软中断可以大大降低中断信号丢失的风险
40 |
41 | ### 参考文章
42 |
43 | - **操作系统导论**
44 | - **[什么是软中断?](https://xiaolincoding.com/os/1_hardware/soft_interrupt.html)**
--------------------------------------------------------------------------------
/markdown/Redis/Redis缓存更新策略.md:
--------------------------------------------------------------------------------
1 | # Redis 缓存更新策略
2 |
3 | 缓存能够有效地加速应用的读写速度,因为它基于内存,减少了磁盘 IO 的开销。但它也存在数据不一致的问题,因为缓存层和存储层的数据存在着一定**时间窗口**的不一致性
4 |
5 | 给出加入缓存层的结构图:
6 |
7 | 
8 |
9 | 下面介绍三种缓存更新策略,没有最优,只有根据业务场景最合适!!
10 |
11 | ### 旁路缓存模式 (Cache Aside Pattern)
12 |
13 | 旁路缓存模式是平时使用较多的一个读写缓存模式,比较**适合于读请求较多的场景**
14 |
15 | 写操作的步骤:
16 |
17 | - 更新 DB
18 | - 直接删除 Cache
19 |
20 | 读操作的步骤:
21 |
22 | - 从 Cache 中读取数据,读取到就直接返回
23 | - 如果 Cache 读取不到,从 DB 中读取数据返回
24 | - 将 DB 中读取到的数据写入 Cache 中
25 |
26 | 
27 |
28 | **问题一:先更新 DB,再删除 Cache,能保证数据一致性吗?**
29 |
30 | 理论上来说还是可能会出现数据不一致的问题,但概率很小,因为删除 Cache 的操作速度快,使 Cache 中和 DB 中数据不一致的时间窗口很短
31 |
32 | 只有在不一致时间窗口内读数据才会出现数据不一致问题,即:读到旧值,如下图
33 |
34 | 
35 |
36 | 下面举一个数据不一致的例子:线程 1 写数据 A,随后线程 2 读数据 A。正确的情况下线程 2 读到的应该是数据 A 的新值,但如果以下面的顺序执行:
37 |
38 | - 线程 1 更新 DB
39 | - 线程 2 读数据 A,直接从缓存中读取并返回,但缓存中是旧值
40 | - 线程 1 删除 Cache
41 |
42 | 此时线程 2 读到的是数据 A 的旧值
43 |
44 | **问题二:为什么删除 Cache,而不是更新 Cache?**
45 |
46 | - 浪费服务端资源:不确定新写入的数据是否会被访问,而且 Cache 存放的数据一般需要经过服务端大量的计算。如果不会被访问又进行了大量的计算,无疑是白白浪费资源
47 | - 增加数据不一致的概率:更新 Cache 比 删除 Cache 更加耗时,所以会增大不一致时间窗口的大小,进而提高数据不一致性的概率
48 |
49 | 
50 |
51 | **问题三:可以先删除 Cache,后更新 DB 吗?**
52 |
53 | 显然不可以,这样会导致数据不一致的时间窗口变大,进而增加了出现数据不一致问题的概率
54 |
55 | 
56 |
57 | 下面举一个数据不一致的例子:线程 1 写数据 A,随后线程 2 读数据 A。正确的情况下线程 2 读到的应该是数据 A 的新值,但如果以下面的顺序执行:
58 |
59 | - 线程 1 删除 Cache
60 | - 线程 2 读数据 A,此时缓存中没有数据,从 DB 中读取并返回,同时存入 Cache 中,Cache 中存入的是旧值
61 | - 线程 1 更新 DB
62 |
63 | 此时线程 2 读到的是数据 A 的旧值,而且 Cache 存入的也是旧值。如果 Cache 没有设置过期时间且未来一段时间没有新的写操作,那么后面读数据 A 时全都是 Cache 中的旧值!!
64 |
65 | **缺陷一:首次请求数据不在 Cache 中**
66 |
67 | - 可以提前将热点数据放入 Cache 中
68 |
69 | **缺陷二:写操作频繁会导致 Cache 中数据频繁被删,会影响命中率?**
70 |
71 | - 对于要求数据强一致性的场景:更新 DB 的同时更新 Cache,但需要用分布式锁保证这两个更新的原子性,否则存在线程安全问题
72 | - 对于可接受短暂数据不一致的场景:更新 DB 的同时更新 Cache,为 Cache 设置一个较短的过期时间
73 |
74 | ### 读写穿透 (Read/Write Through Pattern)
75 |
76 | **核心思想:**更新 DB,缓存存在就更新,不存在就不管
77 |
78 | 读写穿透将 Cache 作为主要的数据存储,从中读取并将数据写入其中,Cache 服务自己负责将此数据读取和写入 DB,从而减轻了程序员的职责
79 |
80 | 这种模式平时使用很少,大概率因为 Redis 分布式缓存并没有提供 Cache 将数据写入 DB 的功能
81 |
82 | 写操作的步骤:
83 |
84 | - 先检查 Cache,如果 Cache 没有,直接更新 DB
85 | - 如果 Cache 中存在,直接更新 Cache,然后 Cache 服务会自己更新 DB
86 |
87 | 读操作的步骤:
88 |
89 | - 从 Cache 中读取数据,读取到就直接返回
90 | - 如果 Cache 读取不到,先从 DB 中加载,写入 Cache 后返回
91 |
92 | 
93 |
94 | ### 异步缓存写入 (Write Back Pattern)
95 |
96 | **核心思想:**只更新缓存,异步更新 DB
97 |
98 | 异步缓存写入和读写穿透很相似,两者都是由 Cache 服务来负责 Cache 和 DB 的读写。它们俩最大的不同在于:读写穿透是同步更新 Cache 和 DB;而异步缓存写入是异步更新 DB
99 |
100 | 消息队列中消息的异步写入磁盘、MySQL 的 InnoDB Buffer Pool 机制都用到了这种策略
101 |
102 | 异步缓存写入下 DB 的写性能非常高,非常适合一些数据经常变化又对数据一致性没有那么高的要求的场景,如:浏览量、点赞量等
--------------------------------------------------------------------------------
/markdown/Redis/Redis阻塞.md:
--------------------------------------------------------------------------------
1 | # Redis 阻塞
2 |
3 | Redis 是典型的单线程架构,所有的读写操作都是在一条主线程中完成,所以如果主线程被阻塞,就会直接影响到应用系统。本篇文章来盘点一下 Redis 中阻塞的常见情况
4 |
5 | ### 命令阻塞
6 |
7 | 虽然 Redis 是基于内存的数据库,但如果执行的命令时间复杂度过高,就会导致主线程阻塞。下面命令的时间复杂度均为`O(n)`,随着数据规模的增加,执行时间也会变长
8 |
9 | - `keys *`:获取所有的 key
10 | - `hgetall`:获取哈希表中所有
6 |
7 | 状态码的第一位数字表示状态类型,第二、三位数字表示具体的情况
8 |
9 | - **1xx:**表示接收的请求正在处理
10 | - **2xx:**表示请求正常处理完毕 (成功)
11 | - **3xx:**表示重定向
12 | - **4xx:**表示客户端错误
13 | - **5xx:**表示服务端错误
14 |
15 | ### 1xx
16 |
17 | 表示请求已被接受,需要继续处理。这类响应是临时响应,只包含「状态行」和某些可选的响应「头信息」,并以空行结束
18 |
19 | 常见的有:
20 |
21 | - **100 (继续):**这个为临时响应,表示迄今为止的所有内容都是可行的,客户端应该继续发送剩余请求,如果已经完成,则忽略它
22 | - **101 (切换协议):**服务器根据客户端的请求切换协议,主要用于 websocket 或 http2 升级
23 |
24 | ### 2xx
25 |
26 | 表示请求已成功被服务器接收、理解、并接受
27 |
28 | 常见的有:
29 |
30 | - **200 (成功):**请求已成功,请求所希望的响应头或数据体将随此响应返回
31 | - **201 (已创建):**请求成功并且服务器创建了新的资源
32 | - **202 (已创建):**服务器已经接收请求,但尚未处理
33 | - **203 (非授权信息):**服务器已成功处理请求,但返回的信息可能来自另一来源
34 | - **204 (无内容):**服务器成功处理请求,但没有返回任何内容。例如:删除请求或请求是通过表单发送的,响应不应导致刷新表单或加载新页面
35 | - **205 (重置内容):**将文档重置为原始状态。例如,清除表单
36 | - **206 (部分内容):**服务器成功处理了部分请求 (范围请求,服务器成功执行了该范围内的请求)
37 |
38 | ### 3xx
39 |
40 | 表示要完成请求,需要进一步操作。 通常,这些状态代码用来重定向
41 |
42 | 常见的有:
43 |
44 | - **300 (多种选择):**针对请求,服务器可执行多种操作。 服务器可根据请求者 (user agent) 选择一项操作,或提供操作列表供请求者选择
45 | - **301 (永久重定向):**请求的网页已永久移动到新位置。 服务器返回此响应 (对 GET 或 HEAD 请求的响应)时,会自动将请求者转到新位置
46 | - **302 (临时重定向):**服务器目前从不同位置的网页响应请求,但请求者应继续使用原有位置来进行以后的请求
47 | - **303 (查看其它位置):**请求者应当对不同的位置使用单独的 GET 请求来检索响应时,服务器返回此代码
48 | - **304 (缓存重定向):**表示资源没有被修改,可以重定向到缓存文件
49 | - **305 (使用代理):**请求者只能使用代理访问请求的网页。 如果服务器返回此响应,还表示请求者应使用代理
50 | - **307 (临时重定向):**服务器目前从不同位置的网页响应请求,但请求者应继续使用原有位置来进行以后的请求 (和 302 相同)
51 |
52 | ### 4xx
53 |
54 | 表示客户端有错误,妨碍了服务器的处理
55 |
56 | 常见的有:
57 |
58 | - **400 (错误请求):**请求报文中存在语法错误
59 | - **401 (未授权):**请求要求身份验证。对于需要登录的网页,服务器可能返回此响应
60 | - **403 (禁止):**服务器拒绝请求
61 | - **404 (未找到):**服务器找不到请求的网页
62 | - **405 (方法禁用):**禁用请求中指定的方法
63 | - **406 (不接受):**无法使用请求的内容特性响应请求的网页
64 | - **407 (需要代理授权):**此状态代码与 401 (未授权)类似,但指定请求者应当授权使用代理
65 | - **408 (请求超时):**服务器等候请求时发生超时
66 |
67 | ### 5xx
68 |
69 | 表示服务器有错误,在处理请求的过程中有错误或者异常状态发生
70 |
71 | 常见的有:
72 |
73 | - **500 (服务器内部错误):**服务器遇到错误,无法完成请求
74 | - **501 (尚未实施):**服务器不具备完成请求的功能。 例如,服务器无法识别请求方法时可能会返回此代码
75 | - **502 (错误网关):**服务器作为网关或代理,从上游服务器收到无效响应
76 | - **503 (服务不可用):**服务器目前无法使用 (由于超载或停机维护)
77 | - **504 (网关超时):**服务器作为网关或代理,但是没有及时从上游服务器收到请求
78 | - **505 (HTTP 版本不受支持):**服务器不支持请求中所用的 HTTP 协议版本
79 |
80 | ### 适用场景
81 |
82 | **100:**客户端在发送 POST 数据给服务器前,征询服务器情况,看服务器是否处理POST的数据,如果不处理,客户端则不上传 POST 数据,如果处理,则 POST 上传数据。常用于 POST 大数据传输
83 |
84 | **206:**一般用来做断点续传,或者是视频文件等大文件的加载
85 |
86 | **301:**永久重定向会缓存。新域名替换旧域名,旧的域名不再使用时,用户访问旧域名时用 301 就重定向到新的域名
87 |
88 | **302:**临时重定向不会缓存,常用 于未登陆的用户访问用户中心重定向到登录页面
89 |
90 | **304:**协商缓存,告诉客户端有缓存,直接使用缓存中的数据,返回页面的只有头部信息,是没有内容部分
91 |
92 | **400:**参数有误,请求无法被服务器识别
93 |
94 | **403:**告诉客户端进制访问该站点或者资源,如在外网环境下,然后访问只有内网 IP 才能访问的时候则返回
95 |
96 | **404:**服务器找不到资源时,或者服务器拒绝请求又不想说明理由时
97 |
98 | **503:**服务器停机维护时,主动用 503 响应请求或 Nginx 设置限速,超过限速,会返回 503
99 |
100 | **504:**网关超时
--------------------------------------------------------------------------------
/markdown/Network/HTTP-缓存策略.md:
--------------------------------------------------------------------------------
1 | # HTTP 缓存策略
2 |
3 | 当使用浏览器访问一个 Web 资源时,为了提高访问效率,往往会在浏览器和服务器之间增加本地缓存
4 |
5 | 对于首次访问,会将服务器响应的数据缓存到本地;对于后续的访问,会根据缓存策略决定是否直接使用本地缓存。简化的流程如下图所示:
6 |
7 | 
8 |
9 | **注意:**缓存策略完全是根据服务器响应消息的头信息来决定滴!!
10 |
11 | ### 与缓存有关的消息头字段
12 |
13 | 先给出与缓存有关的消息头字段的一些说明:
14 |
15 | 
16 |
17 | ### 强制缓存
18 |
19 | 顾名思义,强制缓存不需要服务器的参与,浏览器可以自己决策是否使用缓存,决策规则如下:
20 |
21 | - 如果本地缓存中不存在要请求的资源,浏览器会直接将请求发送到服务器,完成首次资源请求,根据服务器响应的消息保存相关信息
22 | - 如果本地缓存中存在要请求的资源,先判断缓存是否过期,如果没有过期直接使用本地缓存,如果过期就需要根据下面要介绍的协商缓存进行处理
23 |
24 | 在响应消息中,Expires 是根据 Last-Modified 和 max-age 计算出来的,max-age 表示存活多少秒后过期,而 Last-Modified 表示最后的修改时间
25 |
26 | 如果一个请求直接强制使用缓存,那么该请求会显示`200 OK (from disk cache)`,如下所示:
27 |
28 | ```
29 | Request URL: http://192.168.124.13:8080/index.html
30 | Request Method: GET
31 | Status Code: 200 OK (from disk cache)
32 | Remote Address: 192.168.124.13:8080
33 | Referrer Policy: strict-origin-when-cross-origin
34 | ```
35 |
36 | ### 协商缓存
37 |
38 | 顾名思义,协商缓存是浏览器和服务器共同协商是否使用本地缓存,浏览器负责提供本地缓存的信息,如:最后修改时间和唯一标识,添加在请求消息头中,服务器收到消息后来决策是否允许浏览器使用本地缓存
39 |
40 | If-Modified-Since 和 If-None-Match 是在浏览器第一次发送请求到服务器时,从服务器的响应消息保存。如果浏览器发现本地缓存中不存在要请求的资源,会直接将请求发送到服务器
41 |
42 | 协商缓存基于两种消息头字段实现:
43 |
44 | - **第一种:**请求头中的 If-Modified-Since 和响应头中的 Last-Modified
45 | - **第二种:**请求头中的 If-None-Match 和响应头中的 Etag
46 |
47 | 对于第一种,如果 If-Modified-Since 时间小于 Last-Modified,表示本地缓存中是旧数据,不可以使用本地缓存中的数据,否则可以使用缓存
48 |
49 | 对于第二种,如果 If-None-Match 和 Etag 不相等,表示本地缓存中是旧数据,不可以使用本地缓存中的数据,否则可以使用缓存
50 |
51 | 如果一个请求消息头中同时包含 If-Modified-Since 和 If-None-Match 字段,那么 If-None-Match 优先级更高。先判断 If-None-Match,如果不匹配直接无法使用缓存,如果匹配,再根据 If-Modified-Since 判断
52 |
53 | **问题:**为什么 Etag 的优先级更高??
54 |
55 | Etag 是服务器中资源的唯一标识,它可以解决一些 Last-Modified 难以解决的问题
56 |
57 | - 可能存在文件没有被修改,但修改时间却发生了改变的情况
58 | - Last-Modified 的精度是秒,对于秒以内的变化,Last-Modified 无法感知;但 Etag 却可以保证秒以内多次修改都可以被感知
59 |
60 | **强制缓存和协商缓存区别:**强制缓存不需要将请求发送给服务器,浏览器自己可以决策;协商缓存需要将请求先发送给服务器,由服务器决策,如果可以使用缓存会响应一个 **[304](./HTTP-状态码.html#3xx)** 的消息,表示缓存重定向
61 |
62 | ### 总流程图
63 |
64 | 下面给出缓存策略的总体流程图:
65 |
66 | 
67 |
68 | **注意:**
69 |
70 | - 使用 F5 刷新网页时,跳过强制缓存,但会检查协商缓存
71 | - 使用 ctrl + F5 刷新页面时,直接从服务器加载,跳过强制缓存和协商缓存
72 |
73 | ### 参考文章
74 |
75 | - **[HTTP 缓存技术](https://xiaolincoding.com/network/2_http/http_interview.html#http-缓存技术)**
76 | - **[彻底弄懂浏览器缓存策略](https://mp.weixin.qq.com/s/Ui7Q9k4faiD5mv_LfB4Rrw)**
77 | - **[Cache-Control在请求头和响应头里的区别](https://juejin.cn/post/6960988505816186894)**
78 | - **[为什么我的缓存设置在 chrome 中不生效](https://xie.infoq.cn/article/70b359ab1210efb6f5b253e24)**
79 | - **[Cache-Control和Expires无效的原因](https://www.cnblogs.com/jimaww/p/10234074.html)**
--------------------------------------------------------------------------------
/markdown/Network/SYN-泛洪攻击.md:
--------------------------------------------------------------------------------
1 | # SYN 泛洪攻击
2 |
3 | ### 半连接 & 全连接
4 |
5 | 在 TCP 三次握手的时候,Linux 内核会维护两个队列:
6 |
7 | - 半连接队列,也称 SYN 队列,只进行了一次握手的连接
8 | - 全连接队列,也称 Accept 队列,进行了三次握手的连接
9 |
10 | 
11 |
12 | 关于出队和入队的详细流程如下:
13 |
14 | - 当服务器收到客户端的 SYN 报文时,会创建一个半连接对象,并加入到内核的 SYN 队列中
15 | - 接着服务器发送 SYN-ACK 报文给客户端,等待客户端的 ACK 报文
16 | - 当服务器收到客户端的 ACK 报文时,会取出一个半连接对象,然后创建一个新的连接对象加入 Accept 队列中
17 | - 应用程序通过调用 Socket 提供的`accept()`方法,从 Accept 队列中取出一个连接对象
18 |
19 | **注意:**不管是半连接队列还是全连接队列,都有最大长度限制,超过限制时都会丢弃报文!!
20 |
21 | ### SYN 泛洪攻击是什么
22 |
23 | 客户端和服务器使用 TCP 协议通信前需要进行三次握手建立连接,当服务器收到客户端第一次握手的 SYN 报文后,会发送 SYN-ACK 报文,之后服务器处于 SYN_RECV 状态。**更详细可见 [三次握手](./TCP-三次握手-四次挥手.html#tcp-三次握手过程)**
24 |
25 | **SYN 泛洪攻击:**攻击者会伪造大量不同 IP 的 SYN 报文,服务器收到 SYN 报文后会向客户端发送 SYN-ACK 报文,但攻击者不会回应该报文,这样会逐渐占满半连接队列,使得后续正常连接请求直接被丢弃
26 |
27 | ### 如何避免 SYN 泛洪攻击
28 |
29 | #### 方法一:调大 netdev_max_backlog
30 |
31 | 当网卡接收数据的速度大于内核处理的速度时,会有一个队列保存这些数据包。控制该队列的大小,默认值为 1000,可以通过参数调整为 100000
32 |
33 | ```bash
34 | net.core.netdev_max_backlog = 10000
35 | ```
36 | #### 方法二:增加 TCP 半连接队列大小
37 |
38 | 增大 TCP 半连接队列,要同时增大下面这三个参数:
39 |
40 | - 增大 net.ipv4.tcp_max_syn_backlog
41 | - 增大 listen() 函数中的 backlog
42 | - 增大 net.core.somaxconn
43 |
44 | #### 方法三:开启 net.ipv4.tcp_syncookies
45 |
46 | 开启 net.ipv4.tcp_syncookies 后可以不需要加入到 SYN 半连接队列中,也可以成功建立连接
47 |
48 | #### 方法四:减少 SYN + ACK 重发次数
49 |
50 | 攻击者不会回应服务器的 SYN-ACK 包,服务器会超时重发,在 Linux 默认重发 5 次,可以适当降低重发的次数使处于 SYN_RECV 状态的服务器尽快断开连接
--------------------------------------------------------------------------------
/markdown/Network/Solutions-7th-Edition.docx:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/LFool/LFool-Notes/8d4b7b3aa2f91cd51aa57427d016d86db8712e05/markdown/Network/Solutions-7th-Edition.docx
--------------------------------------------------------------------------------
/markdown/Network/网络层那点事儿.md:
--------------------------------------------------------------------------------
1 | # 网络层那点事儿~
2 |
3 | ### 网络层和链路层
4 |
5 | 传输层提供端到端的可靠传输,也就是不同主机中的进程间通信,通过端口唯一确认主机中的进程,TCP 报文首部也有端口字段,**详情可见 [TCP 报文段格式](./TCP-三次握手-四次挥手.html)**
6 |
7 | 网络层负责将数据从一台主机传输到另一台主机,往往这两台主机在物理上没有直接相连;而链路层也是负责将数据从一台主机传输到另一台主机,往往这两台主机在物理上直接相连
8 |
9 | 下面主要介绍网络层和链路层是如何相互配合将数据从一台主机传输到另一台主机。网络层通过 IP 地址定义一台主机,链路层通过 MAC 地址定位一台主机。下面模拟一种场景,如下图所示:
10 |
11 | 
12 |
13 | **注意:**路由器的每个端口都有一个 IP 地址和 MAC 地址
14 |
15 | 主机 A 向主机 B 发送数据,它们俩在物理上没有直接相连,需要依赖网络层将数据从主机 A 发送到主机 B
16 |
17 | - **第一步:**主机 A 将数据包发送给路由器,此时会通过 ARP 协议获取路由器的 MAC 地址,将报文中的源 MAC 地址设置为主机 A,目标 MAC 地址设置为路由器。链路层根据源/目标 MAC 地址将数据包从主机 A 发送给路由器,因为它俩在物理上直接相连
18 | - **第二步:**路由器将数据包发送给主机 B,将报文中的源 MAC 地址设置为路由器,目标 MAC 地址设置为主机 B。链路层根据源/目标 MAC 地址将数据包从路由器发送给主机 B,因为它俩在物理上直接相连
19 |
20 | 可以看出数据包在传输过程中,报文的源/目标 IP 地址始终保持不变,分别为:`10.0.1.2`和`10.0.5.6`,变化的是 MAC 地址。网络层负责根据 IP 地址寻址➕路由,而链路层负责将数据在两个物理上相邻的节点中传输!!
21 |
22 | **注意:**由于 MAC 地址在网络层封装,所以有些说法认为 ARP 属于网络层,有些说法认为 ARP 属于链路层,但这不重要,只要理解这个过程即可
23 |
24 | ### IP 分类
25 |
26 | IP 主要分为五类:A 类地址、B 类地址、C 类地址、D 类地址、E 类地址,但这里只想简单给出公有 IP 和私有 IP 的分类
27 |
28 | 简单来说,公有 IP 是网络中所有人都可以访问的 IP,而私有 IP 只有在同一个局域网中的人才可以访问。公有 IP 不允许重复;同一个局域网中的私有 IP 不允许重复,但在不同的局域网中可以重复
29 |
30 | 私有 IP 只有三种范围,如下:
31 |
32 | - 10.0.0.0 - 10.255.255.255
33 | - 172.16.0.0 - 172.31.255.255
34 | - 192.168.0.0 - 192.168.255.255
35 |
36 | 在这三个范围之外的所有 IP 都是公有 IP!!
37 |
38 | ### 路由控制
39 |
40 | 上文说:网络层负责将数据从一台主机传输到另一台主机,往往这两台主机在物理上没有直接相连。那么它是如何将数据从一台主机传输到另一台主机呢?
41 |
42 | 网络层有一个重要的设备:路由器,它内部有一张路由转发表,根据目标 IP 地址可以知道该数据包从路由器的哪一个端口转发出去。回到第一部分的例子中,先将例子扩展的更丰富一些,如下图所示:
43 |
44 | 
45 |
46 | 上图中 IP 数据包的源 IP 地址为`10.1.1.30`,目标 IP 地址为`10.1.2.10`
47 |
48 | **第一步:**主机 A 根据目标 IP 地址匹配到`0.0.0.0/0`,那么下一跳就是`10.1.1.1`。这里的`0.0.0.0/0`就是默认路由,在没有匹配到其它路由时就会匹配默认路由,默认路由的下一跳就是默认网关
49 |
50 | **第二步:**路由器根据目标 IP 地址匹配到`10.1.2.0/24`,那么下一跳就是`10.1.0.2`
51 |
52 | **第三步:**路由器根据目标 IP 地址匹配到`10.1.2.0/24`,那么下一跳就是`10.1.2.1`,最终通过交换机将数据发送给目标主机
53 |
54 | ### IP 分片与重组
55 |
56 | 数据链路层的传输单位是帧,不同的数据链路有不同的最大传输单元 (MTU),以太网的 MTU 是 1500 字节。换句话说,MTU = IP 首部 + TCP 首部 + 数据,一旦「IP 首部 + TCP 首部 + 数据」超过了 MTU,那么就会分片
57 |
58 | 在 TCP 中,如果数据长度 > MTU - IP 首部 - TCP 首部,就会进行分片;在网络层中,如果 TCP 首部 + 数据 > MTU - IP 首部,也会进行分片
59 |
60 | 如果 TCP 不分片,仅仅在网络层分片,那么一旦某个分片数据丢失,TCP 需要重传整个数据,因为 TCP 需要保证数据的可靠性,而网络层不需要保证数据的可靠性
61 |
62 | 所以 TCP 也会进行分片,如果某个分片数据在传输过程中丢失,那么只需要重传该分片数据即可,不需要重传所有数据
63 |
64 | 一般来说,TCP 分片已经考虑了 IP 首部的长度,所以在网络层不会超过长度,也就不会再进行分片,但存在一些特殊情况需要在 TCP 分片后,网络层还需要继续分片,如传输链路中存在更小的 MTU
65 |
66 | **详情分析可见 [TCP分段了,IP层就一定不会分片了吗?](https://zhuanlan.zhihu.com/p/372863051)**
--------------------------------------------------------------------------------
/markdown/Network/计算机网络(top-down)-习题&实验.md:
--------------------------------------------------------------------------------
1 | # 计算机网络(top-down) - 习题 & 实验
2 |
3 | ## 第一章
4 |
5 | ### 习题
6 |
7 | 1. “主机”和“端系统”之间有什么不同?列举几种不同类型的端系统。Web 服务器是一种端系统吗?
8 |
9 |
10 |
11 | 2.
12 |
13 | ### 实验
14 |
15 |
--------------------------------------------------------------------------------
/markdown/OS/CPU缓存一致性.md:
--------------------------------------------------------------------------------
1 | # CPU 缓存一致性
2 |
3 | ### 存储器层次结构
4 |
5 | 在计算机系统中,最常见的存储器有内存和磁盘。一个进程运行过程中往往需要将磁盘中的数据加载到内存中才可以访问
6 |
7 | CPU 的运算速度和内存的访问速度相差过大,为了缓解这种差距,在 CPU 和内存之间增加了高速缓存。由于 CPU 是基于寄存器的指令集,所以在 CPU 和高速缓存之间还存在寄存器
8 |
9 | 存储器离 CPU 越近,那么读写速度就越快,但能存储的容量也就越小。一个存储器的层次结构如下图所示:
10 |
11 | 
12 |
13 | 在现在的 CPU 中一般都有多个核心,寄存器、L1 高速缓存、L2 高速缓存都是每个核心独有,而 L3 高速缓存是 CPU 独有,如下图所示:
14 |
15 | 
16 |
17 | ### CPU Cache 结构
18 |
19 | 每个 CPU Cache 都是由缓存行构成,而且 CPU 和 CPU Cache 的交互单位也是缓存行,也就是如果 Cache 中没有数据,CPU 会一次性从内存中读取和缓存行相同大小的数据存入 Cache 中
20 |
21 | CPU Cache 的结构如下图所示:
22 |
23 | 
24 |
25 | 在使用 CPU Cache 的过程中,可能会出现伪共享问题,这也是下面要介绍的 MESI 协议导致的。**关于伪共享的分析可见 [伪共享](../java/伪共享.html)**
26 |
27 | ### CPU Cache 数据写入
28 |
29 | 对于读操作来说很简单,每次先去 Cache 中检查是否有数据,如果有数据就直接返回,如果没有数据就去内存中读,并将读到的数据加到 Cache 中以便下次可以快速读
30 |
31 | 但是对于写操作可能就麻烦一点,这里可以借鉴 **[Redis 缓存更新策略](../redis/Redis缓存更新策略.html)**,下面主要介绍两种写入策略:
32 |
33 | - **写穿透 (Write Through):**如果 Cache 中有数据,先更新 Cache,后更新内存;如果 Cache 中没有数据,直接更新内存
34 | - **写回 (Write Back):**先只更新 Cache,随后异步更新内存
35 |
36 | ### CPU 缓存一致性问题
37 |
38 | 不同线程在不同核心上执行,每个核心存在自己独有的 Cache。由于不可见性,同一个共享变量,可能出现在不同 Cache 中不一致的问题,**原理可见 [处理器重排序](../java/Java内存模型.html#处理器重排序)**
39 |
40 | 要解决缓存不一致的问题,必须保证下面两点:
41 |
42 | - 某个 CPU 核心更新 Cache 中的数据时,其它 CPU 核心必须知道该数据被更新了,这被称为**写传播 (Write Propagation)**
43 | - 所有 CPU 核心看到 Cache 中数据的修改操作顺序必须是一致性的,这被称为**事务的串行化 (Transaction Serialization)**
44 |
45 | 对于第一点使用总线嗅探机制,当某个 CPU 核心更新 Cache 中的数据时,会向总线广播这一事件,所有 CPU 核心都会监听总线上的广播事件,当发现广播事件中包含的数据也存在于自己的 Cache 中时,就会将自己 Cache 中的数据更新成广播中的数据
46 |
47 | 但仅仅做到第一点并不能完全解决缓存不一致的问题,假设存在两个 CPU 核心先后将`i`修改成 100 和 200,但无法保证这两个修改的广播事件的先后顺序,可能出现某个 CPU 核心看到的顺序:先将`i`修改为 200,再将`i`修改为 100,这也是第二点要保证事务串行化执行的原因
48 |
49 | ### MESI 协议
50 |
51 | MESI 协议基于总线嗅探机制实现了事务串行化,该协议保证了缓存一致性。首先,MESI 协议规定了四种状态:
52 |
53 | - **Modified** 已修改:表示 Cache 中的数据已经被修改过,也就是脏数据
54 | - **Exclusive** 独占:表示 Cache 中的数据被自己独占,其它 CPU Cache 中没有该数据,此时数据是干净的
55 | - **Shared** 共享:表示多个 CPU Cache 中都有该数据,此时数据是干净的
56 | - **Invalidated** 已失效:表示 Cache 中的数据无效
57 |
58 | 下面通过表格给出这四种状态之间的转化关系:
59 |
60 | 
61 |
62 | **注意:**如果在独占状态或者已修改状态下写数据,不需要广播该事件。如果是独占状态,表示其它核心的 Cache 中没有该数据,所以不需要广播;如果是已修改状态,表示包含该数据的核心的 Cache 中对应的 Cache Line 已经是已失效状态,所以也不需要广播
63 |
64 | 这里推荐一个可视化网站,可以看到 Cache 四个状态的转换 **[VivioJS MESI animation help](https://www.scss.tcd.ie/Jeremy.Jones/VivioJS/caches/MESIHelp.htm)**
--------------------------------------------------------------------------------
/markdown/OS/中断.md:
--------------------------------------------------------------------------------
1 | # 中断
2 |
3 | ### 用户态 & 内核态
4 |
5 | 用户进程不可以直接操作系统资源,因为如果给予进程的权利过大,可能会出现一些非法的访问,导致系统处于不安全的状态。基于这种原因,将系统所处状态分为用户态和内核态:
6 |
7 | - **用户态:**CPU 只能受限的访问内存,并且不允许访问敏感的系统资源,如:I/O 设备
8 | - **内核态:**CPU 可以访问任意数据,包括系统资源,还可以决定切换进程
9 |
10 | 当一个用户进程需要访问硬件资源时,需要进行系统调用,让操作系统去访问硬件资源,然后将结果返回给用户进程。系统调用相当于内核提供给用户的一套 API,通过 API 可以间接完成对硬件的访问
11 |
12 | 在系统启动时内核会设置好陷阱表,该表中存放了陷阱类型和内核代码位置的对应关系,也就是如果执行到陷阱 A,就会去执行陷阱 A 对应的内核代码
13 |
14 | 当用户线程系统调用时,会执行特殊的陷阱指令,该指令会从用户态转化到内核态,进而去执行该陷阱对应的内核代码。当操作系统执行完对应代码后,会从内核态转化到用户态
15 |
16 | 操作系统也算是一种软件,在单核 CPU 中,如果用户进程在 CPU 上执行,那么操作系统是无法执行滴,只有当用户态转化到内核态,操作系统才可以在 CPU 上执行。所以系统调用不仅从用户态转化到内核态,而且还相当于进行了一次上下文切换,从用户进程切换到操作系统进程
17 |
18 | 下面是通过系统调用完成上下文切换的过程:
19 |
20 | 
21 |
22 | ### 时钟中断
23 |
24 | 对系统资源的访问、上下文切换等操作都需要操作系统来执行。系统调用可以从用户态切换到内核态,让控制权重新回到操作系统手中,但如果一个进程始终都不进行系统调用呢?那就会出现一直不能切换到内核态,从而卡死的情况
25 |
26 | 为了避免这种情况的发生,提出了时钟中断。时钟设备可以每隔几毫秒就生成一次中断,中断产生时,当前正在运行的程序停止,操作系统中预先配置的中断程序会运行,此时操作系统重新获得了 CPU 的控制权
27 |
28 | 下面是通过时钟中断完成上下文切换的过程:
29 |
30 | 
31 |
32 | ### 软中断
33 |
34 | 在处理中断时,中断处理程序会将中断关闭,如果处理时间过长,可能会丢失其它设备的中断信号。为了避免丢失中断信号,将原来的整个中断过程分为两部分:
35 |
36 | - **第一部分:**快速处理中断,该阶段会暂时关闭中断,但一般该阶段耗时较短,只会处理与硬件相关敏感的事情
37 | - **第二部分:**交由操作系统完成中断剩余工作,该阶段会将中断打开,不会丢失中断信号
38 |
39 | 可以将第一部分看作是硬中断,也就是会关闭中断的中断;可以将第二部分看作是软中断,也就是不会关闭中断的中断。软中断可以大大降低中断信号丢失的风险
40 |
41 | ### 参考文章
42 |
43 | - **操作系统导论**
44 | - **[什么是软中断?](https://xiaolincoding.com/os/1_hardware/soft_interrupt.html)**
--------------------------------------------------------------------------------
/markdown/Redis/Redis缓存更新策略.md:
--------------------------------------------------------------------------------
1 | # Redis 缓存更新策略
2 |
3 | 缓存能够有效地加速应用的读写速度,因为它基于内存,减少了磁盘 IO 的开销。但它也存在数据不一致的问题,因为缓存层和存储层的数据存在着一定**时间窗口**的不一致性
4 |
5 | 给出加入缓存层的结构图:
6 |
7 | 
8 |
9 | 下面介绍三种缓存更新策略,没有最优,只有根据业务场景最合适!!
10 |
11 | ### 旁路缓存模式 (Cache Aside Pattern)
12 |
13 | 旁路缓存模式是平时使用较多的一个读写缓存模式,比较**适合于读请求较多的场景**
14 |
15 | 写操作的步骤:
16 |
17 | - 更新 DB
18 | - 直接删除 Cache
19 |
20 | 读操作的步骤:
21 |
22 | - 从 Cache 中读取数据,读取到就直接返回
23 | - 如果 Cache 读取不到,从 DB 中读取数据返回
24 | - 将 DB 中读取到的数据写入 Cache 中
25 |
26 | 
27 |
28 | **问题一:先更新 DB,再删除 Cache,能保证数据一致性吗?**
29 |
30 | 理论上来说还是可能会出现数据不一致的问题,但概率很小,因为删除 Cache 的操作速度快,使 Cache 中和 DB 中数据不一致的时间窗口很短
31 |
32 | 只有在不一致时间窗口内读数据才会出现数据不一致问题,即:读到旧值,如下图
33 |
34 | 
35 |
36 | 下面举一个数据不一致的例子:线程 1 写数据 A,随后线程 2 读数据 A。正确的情况下线程 2 读到的应该是数据 A 的新值,但如果以下面的顺序执行:
37 |
38 | - 线程 1 更新 DB
39 | - 线程 2 读数据 A,直接从缓存中读取并返回,但缓存中是旧值
40 | - 线程 1 删除 Cache
41 |
42 | 此时线程 2 读到的是数据 A 的旧值
43 |
44 | **问题二:为什么删除 Cache,而不是更新 Cache?**
45 |
46 | - 浪费服务端资源:不确定新写入的数据是否会被访问,而且 Cache 存放的数据一般需要经过服务端大量的计算。如果不会被访问又进行了大量的计算,无疑是白白浪费资源
47 | - 增加数据不一致的概率:更新 Cache 比 删除 Cache 更加耗时,所以会增大不一致时间窗口的大小,进而提高数据不一致性的概率
48 |
49 | 
50 |
51 | **问题三:可以先删除 Cache,后更新 DB 吗?**
52 |
53 | 显然不可以,这样会导致数据不一致的时间窗口变大,进而增加了出现数据不一致问题的概率
54 |
55 | 
56 |
57 | 下面举一个数据不一致的例子:线程 1 写数据 A,随后线程 2 读数据 A。正确的情况下线程 2 读到的应该是数据 A 的新值,但如果以下面的顺序执行:
58 |
59 | - 线程 1 删除 Cache
60 | - 线程 2 读数据 A,此时缓存中没有数据,从 DB 中读取并返回,同时存入 Cache 中,Cache 中存入的是旧值
61 | - 线程 1 更新 DB
62 |
63 | 此时线程 2 读到的是数据 A 的旧值,而且 Cache 存入的也是旧值。如果 Cache 没有设置过期时间且未来一段时间没有新的写操作,那么后面读数据 A 时全都是 Cache 中的旧值!!
64 |
65 | **缺陷一:首次请求数据不在 Cache 中**
66 |
67 | - 可以提前将热点数据放入 Cache 中
68 |
69 | **缺陷二:写操作频繁会导致 Cache 中数据频繁被删,会影响命中率?**
70 |
71 | - 对于要求数据强一致性的场景:更新 DB 的同时更新 Cache,但需要用分布式锁保证这两个更新的原子性,否则存在线程安全问题
72 | - 对于可接受短暂数据不一致的场景:更新 DB 的同时更新 Cache,为 Cache 设置一个较短的过期时间
73 |
74 | ### 读写穿透 (Read/Write Through Pattern)
75 |
76 | **核心思想:**更新 DB,缓存存在就更新,不存在就不管
77 |
78 | 读写穿透将 Cache 作为主要的数据存储,从中读取并将数据写入其中,Cache 服务自己负责将此数据读取和写入 DB,从而减轻了程序员的职责
79 |
80 | 这种模式平时使用很少,大概率因为 Redis 分布式缓存并没有提供 Cache 将数据写入 DB 的功能
81 |
82 | 写操作的步骤:
83 |
84 | - 先检查 Cache,如果 Cache 没有,直接更新 DB
85 | - 如果 Cache 中存在,直接更新 Cache,然后 Cache 服务会自己更新 DB
86 |
87 | 读操作的步骤:
88 |
89 | - 从 Cache 中读取数据,读取到就直接返回
90 | - 如果 Cache 读取不到,先从 DB 中加载,写入 Cache 后返回
91 |
92 | 
93 |
94 | ### 异步缓存写入 (Write Back Pattern)
95 |
96 | **核心思想:**只更新缓存,异步更新 DB
97 |
98 | 异步缓存写入和读写穿透很相似,两者都是由 Cache 服务来负责 Cache 和 DB 的读写。它们俩最大的不同在于:读写穿透是同步更新 Cache 和 DB;而异步缓存写入是异步更新 DB
99 |
100 | 消息队列中消息的异步写入磁盘、MySQL 的 InnoDB Buffer Pool 机制都用到了这种策略
101 |
102 | 异步缓存写入下 DB 的写性能非常高,非常适合一些数据经常变化又对数据一致性没有那么高的要求的场景,如:浏览量、点赞量等
--------------------------------------------------------------------------------
/markdown/Redis/Redis阻塞.md:
--------------------------------------------------------------------------------
1 | # Redis 阻塞
2 |
3 | Redis 是典型的单线程架构,所有的读写操作都是在一条主线程中完成,所以如果主线程被阻塞,就会直接影响到应用系统。本篇文章来盘点一下 Redis 中阻塞的常见情况
4 |
5 | ### 命令阻塞
6 |
7 | 虽然 Redis 是基于内存的数据库,但如果执行的命令时间复杂度过高,就会导致主线程阻塞。下面命令的时间复杂度均为`O(n)`,随着数据规模的增加,执行时间也会变长
8 |
9 | - `keys *`:获取所有的 key
10 | - `hgetall`:获取哈希表中所有