├── 01 sum_tree ├── README.md ├── images │ ├── 1_init_01.PNG │ ├── 1_init_02.PNG │ ├── 2_update_01.PNG │ ├── 2_update_02.PNG │ ├── 2_update_03.PNG │ ├── 2_update_04.PNG │ ├── 2_update_05.PNG │ ├── 2_update_06.PNG │ ├── 2_update_07.PNG │ ├── 2_update_08.PNG │ ├── 2_update_09.PNG │ ├── 3_search_01.PNG │ ├── 3_search_02.PNG │ ├── 3_search_03.PNG │ ├── 4_finish_01.png │ ├── README.md │ ├── data_100.png │ ├── data_1000.png │ ├── data_10000.png │ ├── data_1000000.png │ └── data_origin.png └── sum_tree.py ├── 02 KNN & KD-tree ├── README.md ├── kd_tree.py └── knn_basic.py ├── 03 min_tree ├── README.md └── min_tree.py ├── 04 max_tree ├── README.md └── max_tree.py └── README.md /01 sum_tree/README.md: -------------------------------------------------------------------------------- 1 | # Sum Tree 2 | * sum tree는 binary tree 구조로 sampling에 있어서 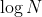![equation](https://latex.codecogs.com/gif.latex?%5Clog%20N) 을 보장한다. 3 | * ex) 1,000,000 개의 데이터일경우 마지막 data를 단순 서치하면 1,000,000 인데, ![equation](https://latex.codecogs.com/gif.latex?%5Clog%201000000%20%3D%206)이다. 4 | * 재밌는 특징으로 단순히 leaf node까지의 search만으로 확률적 특성이 반영된 sampling이 가능하다. 5 | - - - 6 | 7 | ### 1. Initialize 8 | * replay buffer와 sum tree를 표현할 Array를 0으로 초기화 해준다. 9 | * replay buffer의 size는 buffer_size. 10 | * sum tree의 size는 (buffer_size * 2) - 1. ex) buffer_size = 8, sum_tree size = 16 - 1 = 15 = 총 node 수. 11 | ```python 12 | self.replay_buffer = [0 for i in range(buffer_size)] # set rplay buffer size. 13 | self.array_tree = [0 for i in range((buffer_size * 2) - 1)] # set sum_tree size (double of buffer size) 14 | ``` 15 |

16 |

17 |

18 |

19 | 20 | - - - 21 | 22 | ### 2. Add 23 | * replay buffer의 시작 index는 0 이다. 24 | * sum tree의 시작 index는 buffer_size - 1 이다. (첫번째 leaf node의 index) 25 | ```python 26 | self.tree_index = buffer_size - 1 # define sum_tree leaf node index. 27 | self.buffer_index = 0 # define replay buffer index. 28 | ``` 29 | * 만약 둘다 정해준 maximum size에 도달한다면, replay buffer는 0으로, sum tree는 buffer_size - 1의 위치로 다시 이동한다. 30 | ```python 31 | if self.tree_index == (self.buffer_size * 2) - 1: # if sum tree index achive last index. 32 | self.tree_index = self.buffer_size - 1 # change frist leaf node index. 33 | if self.buffer_index == self.buffer_size: # if replay buffer index achive last index. 34 | self.buffer_index = 0 # change first index (0 zero) 35 | ``` 36 | * 코드상에서 현재 위치를 기록하는 self.buffer_index와 self.tree_index에 해당하는 위치에 data와 priority를 각각 저장한다. 37 | ```python 38 | self.replay_buffer[self.buffer_index] = data # append data at current replay buffer index. 39 | self.array_tree[self.tree_index] = priority # append priority at current sum_tree leaf node index. 40 | 41 | ``` 42 | 43 | - - - 44 | 45 | ### 3. Update 46 | * Add에서 새로운 data가 추가되면, sum tree의 leaf node중 변경된 leaf node로 부터 root까지 sum tree의 node들을 update해줘야 한다. 47 | * leaf node의 parent node는 parent node = left node + right node의 수식으로 update 된다. 48 | * root에 도달하면 종료된다. 여기서는 tree index가 0가 된다면 종료된다. 49 | #### 1. tree index 7 update 과정 (첫 시작 leaf node). 50 |

51 |

52 |

53 |

54 |

55 |

56 |

57 |

58 | 59 | #### 2. tree index 8 update 과정. 60 |

61 |

62 |

63 |

64 |

65 |

66 |

67 |

68 | 69 | #### 3. 최종 sum tree. 70 |

71 |

72 |

100 |

101 |

102 |

103 |

104 |

105 |

106 | 107 | - - - 108 | 109 | ### 5. Result & Test 110 | * 실제 priority에 맞게 sampling이 되는 지, 확인하기 위해 discrete uniform distribution(0 ~ 99)에서 100, 1000, 10000, 1000000 총 4개의 data set을 통해 평가했다. 111 | * 여기서 정한 priority는 [5, 5, 10, 2, 8, 20, 15, 35] 0부터 시작하므로 [6%, 5%, 10%, 2%, 8%, 20%, 15%, 34%]의 확률 값을 가진다. 112 | * test를 통해 정해진 priority 확률분포에 맞게 sampling 되는 것을 확인 할 수 있다. 113 | 114 | #### 1. 최종 Array 정보 & 원본 Data 분포. 115 |

116 |

117 |

118 |

119 | 120 | #### 2. sum tree 실험(100, 1000, 10000, 1000000). 121 |

122 |

123 |

124 |

125 |

126 |

127 |

128 |

129 | -------------------------------------------------------------------------------- /01 sum_tree/images/1_init_01.PNG: -------------------------------------------------------------------------------- https://raw.githubusercontent.com/LeejwUniverse/Algorithm_For_RL/26cf5fb207c9eca5c9ff47512f6fc595565b3fd6/01 sum_tree/images/1_init_01.PNG -------------------------------------------------------------------------------- /01 sum_tree/images/1_init_02.PNG: -------------------------------------------------------------------------------- https://raw.githubusercontent.com/LeejwUniverse/Algorithm_For_RL/26cf5fb207c9eca5c9ff47512f6fc595565b3fd6/01 sum_tree/images/1_init_02.PNG -------------------------------------------------------------------------------- /01 sum_tree/images/2_update_01.PNG: -------------------------------------------------------------------------------- https://raw.githubusercontent.com/LeejwUniverse/Algorithm_For_RL/26cf5fb207c9eca5c9ff47512f6fc595565b3fd6/01 sum_tree/images/2_update_01.PNG -------------------------------------------------------------------------------- /01 sum_tree/images/2_update_02.PNG: -------------------------------------------------------------------------------- https://raw.githubusercontent.com/LeejwUniverse/Algorithm_For_RL/26cf5fb207c9eca5c9ff47512f6fc595565b3fd6/01 sum_tree/images/2_update_02.PNG -------------------------------------------------------------------------------- /01 sum_tree/images/2_update_03.PNG: -------------------------------------------------------------------------------- https://raw.githubusercontent.com/LeejwUniverse/Algorithm_For_RL/26cf5fb207c9eca5c9ff47512f6fc595565b3fd6/01 sum_tree/images/2_update_03.PNG -------------------------------------------------------------------------------- /01 sum_tree/images/2_update_04.PNG: -------------------------------------------------------------------------------- https://raw.githubusercontent.com/LeejwUniverse/Algorithm_For_RL/26cf5fb207c9eca5c9ff47512f6fc595565b3fd6/01 sum_tree/images/2_update_04.PNG -------------------------------------------------------------------------------- /01 sum_tree/images/2_update_05.PNG: -------------------------------------------------------------------------------- https://raw.githubusercontent.com/LeejwUniverse/Algorithm_For_RL/26cf5fb207c9eca5c9ff47512f6fc595565b3fd6/01 sum_tree/images/2_update_05.PNG -------------------------------------------------------------------------------- /01 sum_tree/images/2_update_06.PNG: -------------------------------------------------------------------------------- https://raw.githubusercontent.com/LeejwUniverse/Algorithm_For_RL/26cf5fb207c9eca5c9ff47512f6fc595565b3fd6/01 sum_tree/images/2_update_06.PNG -------------------------------------------------------------------------------- /01 sum_tree/images/2_update_07.PNG: -------------------------------------------------------------------------------- https://raw.githubusercontent.com/LeejwUniverse/Algorithm_For_RL/26cf5fb207c9eca5c9ff47512f6fc595565b3fd6/01 sum_tree/images/2_update_07.PNG -------------------------------------------------------------------------------- /01 sum_tree/images/2_update_08.PNG: -------------------------------------------------------------------------------- https://raw.githubusercontent.com/LeejwUniverse/Algorithm_For_RL/26cf5fb207c9eca5c9ff47512f6fc595565b3fd6/01 sum_tree/images/2_update_08.PNG -------------------------------------------------------------------------------- /01 sum_tree/images/2_update_09.PNG: -------------------------------------------------------------------------------- https://raw.githubusercontent.com/LeejwUniverse/Algorithm_For_RL/26cf5fb207c9eca5c9ff47512f6fc595565b3fd6/01 sum_tree/images/2_update_09.PNG -------------------------------------------------------------------------------- /01 sum_tree/images/3_search_01.PNG: -------------------------------------------------------------------------------- https://raw.githubusercontent.com/LeejwUniverse/Algorithm_For_RL/26cf5fb207c9eca5c9ff47512f6fc595565b3fd6/01 sum_tree/images/3_search_01.PNG -------------------------------------------------------------------------------- /01 sum_tree/images/3_search_02.PNG: -------------------------------------------------------------------------------- https://raw.githubusercontent.com/LeejwUniverse/Algorithm_For_RL/26cf5fb207c9eca5c9ff47512f6fc595565b3fd6/01 sum_tree/images/3_search_02.PNG -------------------------------------------------------------------------------- /01 sum_tree/images/3_search_03.PNG: -------------------------------------------------------------------------------- https://raw.githubusercontent.com/LeejwUniverse/Algorithm_For_RL/26cf5fb207c9eca5c9ff47512f6fc595565b3fd6/01 sum_tree/images/3_search_03.PNG -------------------------------------------------------------------------------- /01 sum_tree/images/4_finish_01.png: -------------------------------------------------------------------------------- https://raw.githubusercontent.com/LeejwUniverse/Algorithm_For_RL/26cf5fb207c9eca5c9ff47512f6fc595565b3fd6/01 sum_tree/images/4_finish_01.png -------------------------------------------------------------------------------- /01 sum_tree/images/README.md: -------------------------------------------------------------------------------- 1 | 2 | -------------------------------------------------------------------------------- /01 sum_tree/images/data_100.png: -------------------------------------------------------------------------------- https://raw.githubusercontent.com/LeejwUniverse/Algorithm_For_RL/26cf5fb207c9eca5c9ff47512f6fc595565b3fd6/01 sum_tree/images/data_100.png -------------------------------------------------------------------------------- /01 sum_tree/images/data_1000.png: -------------------------------------------------------------------------------- https://raw.githubusercontent.com/LeejwUniverse/Algorithm_For_RL/26cf5fb207c9eca5c9ff47512f6fc595565b3fd6/01 sum_tree/images/data_1000.png -------------------------------------------------------------------------------- /01 sum_tree/images/data_10000.png: -------------------------------------------------------------------------------- https://raw.githubusercontent.com/LeejwUniverse/Algorithm_For_RL/26cf5fb207c9eca5c9ff47512f6fc595565b3fd6/01 sum_tree/images/data_10000.png -------------------------------------------------------------------------------- /01 sum_tree/images/data_1000000.png: -------------------------------------------------------------------------------- https://raw.githubusercontent.com/LeejwUniverse/Algorithm_For_RL/26cf5fb207c9eca5c9ff47512f6fc595565b3fd6/01 sum_tree/images/data_1000000.png -------------------------------------------------------------------------------- /01 sum_tree/images/data_origin.png: -------------------------------------------------------------------------------- https://raw.githubusercontent.com/LeejwUniverse/Algorithm_For_RL/26cf5fb207c9eca5c9ff47512f6fc595565b3fd6/01 sum_tree/images/data_origin.png -------------------------------------------------------------------------------- /01 sum_tree/sum_tree.py: -------------------------------------------------------------------------------- 1 | import numpy as np 2 | from collections import deque 3 | import matplotlib.pyplot as plt 4 | 5 | class sum_tree(): 6 | def __init__(self, buffer_size): 7 | self.tree_index = buffer_size - 1 # define sum_tree leaf node index. 8 | self.buffer_index = 0 # define replay buffer index. 9 | 10 | self.replay_buffer = [0 for i in range(buffer_size)] # set rplay buffer size. 11 | self.array_tree = [0 for i in range((buffer_size * 2) - 1)] # set sum_tree size (double of buffer size) 12 | self.buffer_size = buffer_size 13 | 14 | def update_tree(self, index): 15 | # index is a starting leaf node point. 16 | while True: 17 | index = (index - 1)//2 # parent node index. 18 | left = (index * 2) + 1 # left child node inex. 19 | right = (index * 2) + 2 # right child node index 20 | self.array_tree[index] = self.array_tree[left] + self.array_tree[right] # sum both child node. 21 | if index == 0: ## if index is a root node. 22 | break 23 | 24 | def add_data(self, data, priority): 25 | if self.tree_index == (self.buffer_size * 2) - 1: # if sum tree index achive last index. 26 | self.tree_index = self.buffer_size - 1 # change frist leaf node index. 27 | if self.buffer_index == self.buffer_size: # if replay buffer index achive last index. 28 | self.buffer_index = 0 # change first index (0 zero) 29 | 30 | self.replay_buffer[self.buffer_index] = data # append data at current replay buffer index. 31 | self.array_tree[self.tree_index] = priority # append priority at current sum_tree leaf node index. 32 | 33 | self.update_tree(self.tree_index) # update sum_tree node. propagate from leaf node to root node. 34 | 35 | self.tree_index += 1 # count current sum_tree index 36 | self.buffer_index += 1 # count current replay buffer index 37 | 38 | def search(self, num): 39 | index = 0 # always start from root index. 40 | while True: 41 | left = (index * 2) + 1 42 | right = (index * 2) + 2 43 | if num <= self.array_tree[left]: # if child left node is over current value. 44 | index = left # go to the left direction. 45 | else: 46 | num -= self.array_tree[left] # if child left node is under current value. 47 | index = right # go to the right direction. 48 | if index >= self.buffer_size - 1: # if current node is leaf node, break! 49 | break 50 | 51 | return index - (self.buffer_size - 1) # return real index in replay buffer. 52 | 53 | def main(): 54 | buffer_size = 8 55 | store_kv = {} # test 8 leaf node. 56 | data_list = ['a','b','c','d','e','f','g','h'] # data list 57 | priority_list = [5,5,10,2,8,20,15,35] # priority list 58 | Sum_tree = sum_tree(buffer_size) # sum_tree. 59 | 60 | for d,p in zip(data_list, priority_list): # add 8 test data and priority. 61 | Sum_tree.add_data(d,p) 62 | 63 | print(Sum_tree.array_tree) # check. array sum_tree 64 | print(Sum_tree.replay_buffer) # check. replay buffer. 65 | print() 66 | test_random_set = np.random.randint(100, size=10000) # generate test number set from discrete uniform distribution. 67 | print(test_random_set) 68 | for i in test_random_set: # test sampling according to sum_tree. 69 | index = Sum_tree.search(i) 70 | if str(data_list[index]) not in store_kv: 71 | store_kv[str(data_list[index])] = 0 72 | store_kv[str(data_list[index])] += 1 73 | print(store_kv) 74 | store_kv = sorted(store_kv.items(),key=lambda x : x[0]) 75 | x = [] 76 | y = [] 77 | x_p = [] 78 | y_p = [] 79 | for i, j in store_kv: 80 | x.append(i) 81 | y.append(j) 82 | x_p.append(i) 83 | y_p.append((j/10000) * 100) 84 | fig, axes = plt.subplots(1, 2) 85 | axes[0].bar(x,y,color='red') 86 | axes[0].set_xlabel('data') 87 | axes[0].set_ylabel('count of sampling data') 88 | axes[0].set_title('sampling data (10000)') 89 | axes[1].bar(x_p,y_p,color='blue') 90 | axes[1].set_xlabel('data') 91 | axes[1].set_ylabel('percentage') 92 | axes[1].set_title('sampling data (10000)') 93 | 94 | plt.tight_layout() 95 | plt.show() 96 | if __name__ == '__main__': 97 | main() 98 | -------------------------------------------------------------------------------- /02 KNN & KD-tree/README.md: -------------------------------------------------------------------------------- 1 | # KNN & KD-tree 2 | 3 | --- 4 | 5 | # Todo list 6 | - [X] Implementation basic KNN (calculate all data points using euclidean distance) 7 | - [X] Implementation KNN with KD-tree (using median) 8 | 9 | 1. K-NN with Kd-tree 10 | - [X] Complete Search function.(K-NN with KD Tree, In case of finding closest data point.) 11 | - [ ] Implementation a pruning policy. (Approximate K-NN with KD Tree) 12 | - [ ] Write README.md for explaining algorithm. 13 | -------------------------------------------------------------------------------- /02 KNN & KD-tree/kd_tree.py: -------------------------------------------------------------------------------- 1 | import numpy as np 2 | from collections import deque 3 | import matplotlib.pyplot as plt 4 | import math 5 | 6 | class Node(): 7 | def __init__(self, axis_data, cur_dim, data_set, left_node, right_node): 8 | self.parent = axis_data 9 | self.dim = cur_dim 10 | self.left_child = left_node 11 | self.right_child = right_node 12 | self.data_set = data_set 13 | 14 | class kd_tree(): 15 | def __init__(self, k_dim): 16 | self.k = k_dim 17 | 18 | def euclidean_distance(self, a, b): 19 | distance = 0 20 | for i,j in zip(a,b): 21 | distance+= (i - j)**2 22 | return math.sqrt(distance) 23 | 24 | def add_node(self, data_set, level): 25 | data_len = len(data_set) 26 | cur_dim = level % self.k # start from level 0 (root point). 27 | 28 | if data_len == 1: # only one data point is stored at the parent node. both child nodes store None. 29 | return Node(data_set[0], cur_dim, data_set, None, None) 30 | data_set = sorted(data_set, key=lambda x: x[cur_dim]) # have to sort every time, because dimention of axis is always changed. 31 | 32 | if data_len == 2: # In case of two data points, bigger data point is stored at the parent node and second data point is stored at the left child node. 33 | return Node(data_set[1], cur_dim, data_set, self.add_node(data_set[:1], level + 1), None) 34 | 35 | left_mid = len(data_set)//2 36 | right_mid = len(data_set)//2 + 1 37 | # median data point is stored at the parent node, the left child node stores data points under median point, the right childe node stores data points over median point. 38 | return Node(data_set[left_mid], cur_dim, data_set, self.add_node(data_set[:left_mid], level + 1), self.add_node(data_set[right_mid:], level + 1)) 39 | 40 | def construct_kdtree(self, data_set): 41 | kdtree = self.add_node(data_set, 0) 42 | return kdtree 43 | 44 | def search(self, x, kdtree): 45 | # find closest neighbor data point. And calculate distance. 46 | cur_node = kdtree 47 | while True: 48 | if cur_node.parent[cur_node.dim] > x[cur_node.dim]: 49 | if cur_node.left_child != None: 50 | cur_node = cur_node.left_child 51 | else: 52 | break 53 | else: 54 | if cur_node.right_child != None: 55 | cur_node = cur_node.right_child 56 | else: 57 | break 58 | 59 | return cur_node.parent, self.euclidean_distance(x, cur_node.parent) 60 | 61 | def preorder(self, store_node, cur_node, level): 62 | # traversal tree. 63 | store_node.append([level,cur_node.parent]) 64 | if cur_node.left_child != None: 65 | self.preorder(store_node, cur_node.left_child, level+1) 66 | else: 67 | store_node.append([level+1, None]) 68 | if cur_node.right_child != None: 69 | self.preorder(store_node, cur_node.right_child, level+1) 70 | else: 71 | store_node.append([level+1, None]) 72 | return store_node 73 | 74 | def print_all(self, kd_tree): 75 | store_node = [] 76 | cur_node = kd_tree 77 | level = 0 78 | store_node = self.preorder(store_node, cur_node, level) 79 | print(store_node) 80 | 81 | def main(): 82 | kdtree = kd_tree(2) 83 | list_temp=[] 84 | gen_x = np.random.randint(100, size=10) 85 | gen_y = np.random.randint(100, size=10) 86 | 87 | for i, j in zip(gen_x, gen_y): 88 | list_temp.append([i,j]) 89 | print(list_temp) 90 | print(list_temp[0:5]) 91 | print() 92 | ##list_temp = [[7,2],[5,4],[9,6],[2,3],[4,7],[8,1]] 93 | kd = kdtree.construct_kdtree(list_temp) 94 | kdtree.print_all(kd) 95 | x = [10,2] 96 | print(kdtree.search(x,kd)) 97 | if __name__ == '__main__': 98 | main() -------------------------------------------------------------------------------- /02 KNN & KD-tree/knn_basic.py: -------------------------------------------------------------------------------- 1 | import numpy as np 2 | from collections import deque 3 | import matplotlib.pyplot as plt 4 | import math 5 | 6 | class KNN(): 7 | def __init__(self, k, data): 8 | self.k = k 9 | self.data = data 10 | 11 | def euclidean_distance(self, a, b): 12 | distance = 0 13 | for i,j in zip(a,b): 14 | distance+= (i - j)**2 15 | return math.sqrt(distance) 16 | 17 | def query(self, x): 18 | nn_dis=[] 19 | for i in self.data: 20 | distance = self.euclidean_distance(x, i) 21 | nn_dis.append([distance,i]) 22 | nn_dis = sorted(nn_dis, key=lambda x: x[0]) 23 | nn_dis = np.array(nn_dis) 24 | return nn_dis[:self.k,1:], nn_dis[:self.k,0] 25 | 26 | 27 | def main(): 28 | k = 5 29 | data_set = [] 30 | gen_x = np.random.randint(1000, size=50) 31 | gen_y = np.random.randint(1000, size=50) 32 | for i, j in zip(gen_x, gen_y): 33 | data_set.append([i,j]) 34 | knn = KNN(k, data_set) 35 | 36 | 37 | x = [500,500] 38 | nearest_neighbor, distance = knn.query(x) 39 | print(nearest_neighbor) 40 | print(distance) 41 | if __name__ == '__main__': 42 | main() -------------------------------------------------------------------------------- /03 min_tree/README.md: -------------------------------------------------------------------------------- 1 | # Min Tree 2 | * min tree는 root node가 항상 전체 data set 중 가장 작은 값을 가지고 있다. 3 | * data가 추가 되고 삭제 될 때마다, 최솟값을 알아야 하는 경우에 유용하게 사용할 수 있다. 4 | - - - 5 | -------------------------------------------------------------------------------- /03 min_tree/min_tree.py: -------------------------------------------------------------------------------- 1 | import numpy as np 2 | from collections import deque 3 | import matplotlib.pyplot as plt 4 | 5 | class min_tree(): 6 | def __init__(self, buffer_size): 7 | self.tree_index = buffer_size - 1 # define min_tree leaf node index. 8 | self.array_tree = [0 for i in range((buffer_size * 2) - 1)] # set min_tree size (double of buffer size) 9 | self.buffer_size = buffer_size 10 | 11 | def update_tree(self, index): 12 | # index is a starting leaf node point. 13 | while True: 14 | index = (index - 1)//2 # parent node index. 15 | left = (index * 2) + 1 # left child node inex. 16 | right = (index * 2) + 2 # right child node index 17 | if self.array_tree[left] > self.array_tree[right]: # if a right child node is smaller than left. 18 | self.array_tree[index] = self.array_tree[right] 19 | else: 20 | self.array_tree[index] = self.array_tree[left] 21 | if index == 0: ## if index is a root node. 22 | break 23 | 24 | def add_data(self, priority): 25 | if self.tree_index == (self.buffer_size * 2) - 1: # if min tree index achive last index. 26 | self.tree_index = self.buffer_size - 1 # change frist leaf node index. 27 | 28 | self.array_tree[self.tree_index] = priority # append priority at current min_tree leaf node index. 29 | self.update_tree(self.tree_index) # update min_tree node. propagate from leaf node to root node. 30 | self.tree_index += 1 # count current min_tree index 31 | 32 | def main(): 33 | buffer_size = 8 34 | priority_list = [100,5,10,2,8,1,15,35] # priority list 35 | Min_tree = min_tree(buffer_size) # min_tree. 36 | 37 | for p in priority_list: # add 8 test data and priority. 38 | Min_tree.add_data(p) 39 | cnt = 1 40 | cnt2 = 1 41 | for i,d in enumerate(Min_tree.array_tree): 42 | if i == cnt: 43 | print() 44 | cnt = cnt + np.power(2,cnt2) 45 | cnt2 +=1 46 | print(d , end=' ') 47 | print() 48 | 49 | 50 | if __name__ == '__main__': 51 | main() 52 | -------------------------------------------------------------------------------- /04 max_tree/README.md: -------------------------------------------------------------------------------- 1 | # Max tree 2 | * max tree는 root node가 항상 전체 data set 중 가장 큰 값을 가지고 있다. 3 | * data가 추가 되고 삭제 될 때마다, 최댓값을 알아야 하는 경우에 유용하게 사용할 수 있다. 4 | --- 5 | -------------------------------------------------------------------------------- /04 max_tree/max_tree.py: -------------------------------------------------------------------------------- 1 | import numpy as np 2 | from collections import deque 3 | import matplotlib.pyplot as plt 4 | 5 | class max_tree(): 6 | def __init__(self, buffer_size): 7 | self.tree_index = buffer_size - 1 # define max_tree leaf node index. 8 | self.array_tree = [0 for i in range((buffer_size * 2) - 1)] # set max_tree size (double of buffer size) 9 | self.buffer_size = buffer_size 10 | 11 | def update_tree(self, index): 12 | # index is a starting leaf node point. 13 | while True: 14 | index = (index - 1)//2 # parent node index. 15 | left = (index * 2) + 1 # left child node inex. 16 | right = (index * 2) + 2 # right child node index 17 | if self.array_tree[left] > self.array_tree[right]: # if a left child node is bigger than right. 18 | self.array_tree[index] = self.array_tree[left] 19 | else: 20 | self.array_tree[index] = self.array_tree[right] 21 | if index == 0: ## if index is a root node. 22 | break 23 | 24 | def add_data(self, priority): 25 | if self.tree_index == (self.buffer_size * 2) - 1: # if min tree index achive last index. 26 | self.tree_index = self.buffer_size - 1 # change frist leaf node index. 27 | 28 | self.array_tree[self.tree_index] = priority # append priority at current max_tree leaf node index. 29 | self.update_tree(self.tree_index) # update max_tree node. propagate from leaf node to root node. 30 | self.tree_index += 1 # count current max_tree index 31 | 32 | def main(): 33 | buffer_size = 8 34 | priority_list = [5,10,2,8,1,100,15,35] # priority list 35 | Max_tree = max_tree(buffer_size) # max_tree. 36 | 37 | for p in priority_list: # add 8 test data and priority. 38 | Max_tree.add_data(p) 39 | cnt = 1 40 | cnt2 = 1 41 | for i,d in enumerate(Max_tree.array_tree): 42 | if i == cnt: 43 | print() 44 | cnt = cnt + np.power(2,cnt2) 45 | cnt2 +=1 46 | print(d , end=' ') 47 | print() 48 | 49 | 50 | if __name__ == '__main__': 51 | main() 52 | -------------------------------------------------------------------------------- /README.md: -------------------------------------------------------------------------------- 1 | #### Algorithm for RL 2 | 3 | |Num|Name|RL| 4 | |---|---|---| 5 | |0|DP|basically all method| 6 | |1|Sum_tree|PER| 7 | |2|KD_tree|Neural Episodic Control, Never Give Up| 8 | |3|Min_tree|PER| 9 | |4|Max_tree|PER (optional)| 10 | --------------------------------------------------------------------------------