├── 1 概论.md
├── 2 频域处理.md
├── 3 图像编码.md
├── 4 图像增强.md
├── 5 图像复原.md
├── 6 图像的几何变换.md
├── 7 图像分割.md
├── 8 数学形态学.md
├── I
└── 1 概论.md
├── II
├── 2.1 频域世界与频域变换.md
├── 2.2 傅立叶变换.md
├── 2.3 频域变换的一般表达式.md
├── 2.4 离散余弦变换.md
├── 2.5 离散沃尔什-哈达玛变换(WHT).md
├── 2.6 实现图像变换的VC++编程.md
└── 2.7 小波变换简介.md
├── III
├── 3.1 图像编码概述.md
├── 3.10 预测编码.md
├── 3.11 JPEG编码.md
├── 3.12 编程实例.md
├── 3.2 Huffman编码.md
├── 3.3 香农-范诺编码.md
├── 3.4 行程编码.md
├── 3.5 LZW编码 .md
├── 3.6 算术编码.md
├── 3.7 DCT变换编码.md
├── 3.8基于小波变换编码.md
└── 3.9 混合编码.md
├── IV
├── 4.1 引言.md
├── 4.2 直方图.md
├── 4.3 灰度变换.md
├── 4.4 图像噪声.md
├── 4.5 去除噪声.md
├── 4.6 图像锐化.md
├── 4.7 图像的伪彩色处理.md
├── 4.8 常见滤波器.md
└── 4.9 编程实例.md
├── README.md
├── V
├── 5.1 图像退化与复原.md
├── 5.2 代数复原法.md
├── 5.3 逆滤波.md
├── 5.4 最小二乘滤波(维纳滤波,重点).md
├── 5.5 非线性复原方法 .md
├── 5.6 其他图像复原技术.md
└── 5.7 编程实例.md
├── VI
├── 6.1 几何变换基础.md
├── 6.2 图像比例缩放.md
├── 6.3 图像平移.md
├── 6.4 图像镜像.md
├── 6.5 图像旋转.md
├── 6.6 图像复合变换.md
├── 6.7 透视变换.md
└── 6.8 应用实例.md
├── VII
├── 7.1 图像分割.md
├── 7.2 边缘检测.md
├── 7.3 轮廓跟踪与提取.md
└── 7.4 Hough 变换.md
└── VIII
├── 8.1 引言.md
├── 8.2 二值形态学.md
├── 8.3 灰值形态学.md
├── 8.4 形态学的应用.md
└── 8.5 应用实例——细化.md
/1 概论.md:
--------------------------------------------------------------------------------
1 | [TOC]
2 |
3 | # 第一章 概论
4 |
5 | ## 1.1.什么是数字图象
6 |
7 | 数字图象是指由被称作象素的小块区域组成的二维矩阵。
8 | 对于单色即灰度图象而言,每个象素的亮度用一个数值来表示,通常数值范围在0到255之间,即可用一个字节来表示,0表示黑、255表示白,而其它表示灰度。
9 |
10 | 彩色图象可以用红、绿、蓝三元组的二维矩阵来表示。通常,三元组的每个数值也是在0到255之间,0表示相应的基色在该象素中没有,而255则代表相应的基色在该象素中取得最大值,这种情况下每个象素可用三个字节来表示。
11 |
12 | ## 1.2.数字图象处理系统的基本组成结构
13 |
14 | ```mermaid
15 | graph LR;
16 | 图像数字化设备--输入图像-->图像处理计算机--输出图像-->图像输出设备
17 | ```
18 |
19 | - 图象数字化设备:扫描仪、数码相机、 摄象机与图象采集卡等
20 |
21 | - 图象处理计算机:PC、工作站等
22 |
23 | - 图象输出设备:打印机等
24 |
25 | ## 1.3.数字图象发展
26 |
27 | > 20世纪20年代,通过海底电缆从英国伦敦向美国纽约采用数字压缩技术传输了第一幅数字照片,耗时3小时.
28 | > 1964年美国喷气式推进实验室处理了太空船“徘徊者七号”发回的月球照片,标志着第三代计算机问世后数字图像处理开始得到普遍应用.
29 | > CT的发明,应用及获得诺贝尔奖.
30 | > 2003年诺贝尔奖颁发给了核磁共振影像技术.
31 | >
32 | > 本世纪20年代,纽约-伦敦海底电缆传输数字化的新闻图片。传递时间从一个多星期减少到3个小时。
33 | >
34 | > 五十年代中期在太空计划的推动下开始这项技术的研究。重要标志是1964年美国喷气推进实验室(JPL)正式使用数字计算机对“徘徊者7号”太空船送回的四千多张月球照片进行了处理。
35 | >
36 | > 60年代末,数字图象处理形成一个比较完整的理论与技术体系,从而构成了一门独立的技术
37 | > 70年代,CT的发明,血球自动分类仪的商业化
38 | > CT发明获得1979年诺贝尔医学奖。X射线1901年物理学奖。
39 | > 70年代以来迅猛发展。广泛应用于太空探索,遥感应用,生物医学工程工业应用,军事应用等方面。
40 |
41 | ## 1.4.图象处理技术分类
42 |
43 | 模拟图象处理
44 |
45 | 数字图象处理
46 |
47 | ## 1.5. 数字图象处理特点
48 |
49 | 图象信息大
50 |
51 | 图象处理技术综合性强
52 |
53 | 图象信息理论与通信理论密切相关
54 |
55 | ## 1.6. 数字图象处理的应用
56 |
57 | 图象处理的重要应用包括:
58 |
59 | - 遥感
60 | - 视觉监视、保安
61 | - 工业检测与测量
62 | - 宇宙探险、军事侦察、高精度制导
63 | - 医疗诊断
64 | - 通讯
65 |
66 | ## 1.7.数字图像处理的主要研究内容
67 |
68 | - 按研究对象
69 | - 按应用方式
70 | - 按理论方法
71 |
72 | ### 按研究对象
73 |
74 | - 灰度图像
75 | - 二值图像
76 | - 彩色及多光谱图像
77 | - 图像序列分析
78 | - 双目图像分析
79 |
80 | ### 按应用方式
81 |
82 | 图像获取:
83 |
84 | - 摄取图像
85 | - 光电转换
86 | - 数字化
87 |
88 | 图像的数字化:如何将一幅光学图像表示成一组数字既不失真又便于计算机分析处理。主要包括的是图像的采样与量化。
89 |
90 | 图像存储:
91 |
92 | - 数据压缩
93 | - 图像格式
94 | - 图像数据库
95 |
96 | 图像的传输:
97 |
98 | - 内部传输
99 | - 外部传输
100 |
101 | 图像的恢复:
102 |
103 | 把退化、模糊了的图像复原。模糊的原因有许多种,最常见的有运动模糊,散焦模糊等等。
104 |
105 | 图像的增强:
106 |
107 | 加强图像的有用信息,消弱干扰和噪声。
108 |
109 | 图像的重建:
110 |
111 | 由二维图像重建三维图像。
112 |
113 | 图像的识别:
114 |
115 | 略
116 |
117 | 图像的理解:
118 |
119 | 略
120 |
121 | 图像分割与特征提取:
122 |
123 | 图像分割是指将一幅图像的区域根据分析对象进行分割。
124 |
125 | 图像的特征提取包括了形状特征、纹理特征、颜色特征等等。
126 |
127 | #### 图像隐藏
128 |
129 | 是指媒体信息的相互隐藏。
130 | - 数字水印
131 | - 图像的信息伪装
132 |
133 | #### 虚拟现实
134 |
135 | ### 按理论方法
136 |
137 | - 点处理,代数处理,几何处理。
138 | - 变换域处理与分析(傅立叶变换及滤波器设计分析)
139 | - 随机统计等现代信号处理方法。
140 | - 小波形态学,分形等先进数学工具。
141 | - 人工智能方法:模式识别,符号逻辑,人工神经网络。
142 |
143 | ## 1.8.数字图像处理方法
144 |
145 | - 空域法
146 | - 邻域处理法
147 | - 点处理法
148 | - 变换域法
149 |
150 | ## 1.9.几个当今热点的研究方向
151 |
152 | - 因特网上的图像检索
153 | - 图像在网上的传输
154 | - 图像的安全技术
155 | - 图像的处理技术
156 | - 图像的自动识别
157 | - 图像作为检测手段的一种
158 | - 其它视频方面的研究与需求
--------------------------------------------------------------------------------
/I/1 概论.md:
--------------------------------------------------------------------------------
1 | [TOC]
2 |
3 | # 第一章 概论
4 |
5 | ## 1.1.什么是数字图象
6 |
7 | 数字图象是指由被称作象素的小块区域组成的二维矩阵。
8 | 对于单色即灰度图象而言,每个象素的亮度用一个数值来表示,通常数值范围在0到255之间,即可用一个字节来表示,0表示黑、255表示白,而其它表示灰度。
9 |
10 | 彩色图象可以用红、绿、蓝三元组的二维矩阵来表示。通常,三元组的每个数值也是在0到255之间,0表示相应的基色在该象素中没有,而255则代表相应的基色在该象素中取得最大值,这种情况下每个象素可用三个字节来表示。
11 |
12 | ## 1.2.数字图象处理系统的基本组成结构
13 |
14 | ```mermaid
15 | graph LR;
16 | 图像数字化设备--输入图像-->图像处理计算机--输出图像-->图像输出设备
17 | ```
18 |
19 | - 图象数字化设备:扫描仪、数码相机、 摄象机与图象采集卡等
20 |
21 | - 图象处理计算机:PC、工作站等
22 |
23 | - 图象输出设备:打印机等
24 |
25 | ## 1.3.数字图象发展
26 |
27 | > 20世纪20年代,通过海底电缆从英国伦敦向美国纽约采用数字压缩技术传输了第一幅数字照片,耗时3小时.
28 | > 1964年美国喷气式推进实验室处理了太空船“徘徊者七号”发回的月球照片,标志着第三代计算机问世后数字图像处理开始得到普遍应用.
29 | > CT的发明,应用及获得诺贝尔奖.
30 | > 2003年诺贝尔奖颁发给了核磁共振影像技术.
31 | >
32 | > 本世纪20年代,纽约-伦敦海底电缆传输数字化的新闻图片。传递时间从一个多星期减少到3个小时。
33 | >
34 | > 五十年代中期在太空计划的推动下开始这项技术的研究。重要标志是1964年美国喷气推进实验室(JPL)正式使用数字计算机对“徘徊者7号”太空船送回的四千多张月球照片进行了处理。
35 | >
36 | > 60年代末,数字图象处理形成一个比较完整的理论与技术体系,从而构成了一门独立的技术
37 | > 70年代,CT的发明,血球自动分类仪的商业化
38 | > CT发明获得1979年诺贝尔医学奖。X射线1901年物理学奖。
39 | > 70年代以来迅猛发展。广泛应用于太空探索,遥感应用,生物医学工程工业应用,军事应用等方面。
40 |
41 | ## 1.4.图象处理技术分类
42 |
43 | 模拟图象处理
44 |
45 | 数字图象处理
46 |
47 | ## 1.5. 数字图象处理特点
48 |
49 | 图象信息大
50 |
51 | 图象处理技术综合性强
52 |
53 | 图象信息理论与通信理论密切相关
54 |
55 | ## 1.6. 数字图象处理的应用
56 |
57 | 图象处理的重要应用包括:
58 |
59 | - 遥感
60 | - 视觉监视、保安
61 | - 工业检测与测量
62 | - 宇宙探险、军事侦察、高精度制导
63 | - 医疗诊断
64 | - 通讯
65 |
66 | ## 1.7.数字图像处理的主要研究内容
67 |
68 | - 按研究对象
69 | - 按应用方式
70 | - 按理论方法
71 |
72 | ### 按研究对象
73 |
74 | - 灰度图像
75 | - 二值图像
76 | - 彩色及多光谱图像
77 | - 图像序列分析
78 | - 双目图像分析
79 |
80 | ### 按应用方式
81 |
82 | 图像获取:
83 |
84 | - 摄取图像
85 | - 光电转换
86 | - 数字化
87 |
88 | 图像的数字化:如何将一幅光学图像表示成一组数字既不失真又便于计算机分析处理。主要包括的是图像的采样与量化。
89 |
90 | 图像存储:
91 |
92 | - 数据压缩
93 | - 图像格式
94 | - 图像数据库
95 |
96 | 图像的传输:
97 |
98 | - 内部传输
99 | - 外部传输
100 |
101 | 图像的恢复:
102 |
103 | 把退化、模糊了的图像复原。模糊的原因有许多种,最常见的有运动模糊,散焦模糊等等。
104 |
105 | 图像的增强:
106 |
107 | 加强图像的有用信息,消弱干扰和噪声。
108 |
109 | 图像的重建:
110 |
111 | 由二维图像重建三维图像。
112 |
113 | 图像的识别:
114 |
115 | 略
116 |
117 | 图像的理解:
118 |
119 | 略
120 |
121 | 图像分割与特征提取:
122 |
123 | 图像分割是指将一幅图像的区域根据分析对象进行分割。
124 |
125 | 图像的特征提取包括了形状特征、纹理特征、颜色特征等等。
126 |
127 | #### 图像隐藏
128 |
129 | 是指媒体信息的相互隐藏。
130 |
131 | - 数字水印
132 | - 图像的信息伪装
133 |
134 | #### 虚拟现实
135 |
136 | ### 按理论方法
137 |
138 | - 点处理,代数处理,几何处理。
139 | - 变换域处理与分析(傅立叶变换及滤波器设计分析)
140 | - 随机统计等现代信号处理方法。
141 | - 小波形态学,分形等先进数学工具。
142 | - 人工智能方法:模式识别,符号逻辑,人工神经网络。
143 |
144 | ## 1.8.数字图像处理方法
145 |
146 | - 空域法
147 | - 邻域处理法
148 | - 点处理法
149 | - 变换域法
150 |
151 | ## 1.9.几个当今热点的研究方向
152 |
153 | - 因特网上的图像检索
154 | - 图像在网上的传输
155 | - 图像的安全技术
156 | - 图像的处理技术
157 | - 图像的自动识别
158 | - 图像作为检测手段的一种
159 | - 其它视频方面的研究与需求
--------------------------------------------------------------------------------
/II/2.1 频域世界与频域变换.md:
--------------------------------------------------------------------------------
1 | # 2.1 频域世界与频域变换
2 |
3 |  4 |
5 | 图2-1 任意波形可分解为正弦波的加权和
6 |
7 | 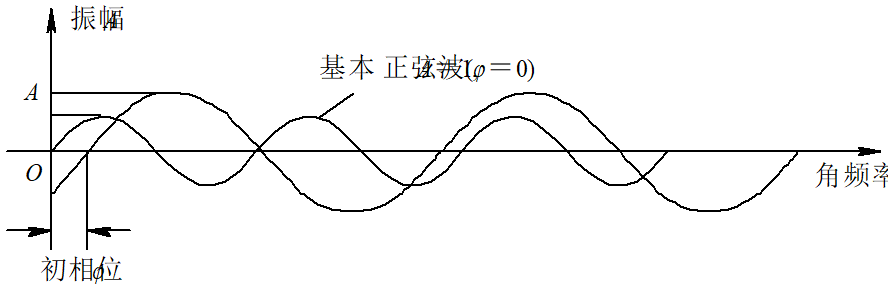
8 |
9 | 图2-2 正弦波的振幅 $A$ 和相位 $\varphi$
10 |
11 |
4 |
5 | 图2-1 任意波形可分解为正弦波的加权和
6 |
7 | 
8 |
9 | 图2-2 正弦波的振幅 $A$ 和相位 $\varphi$
10 |
11 | 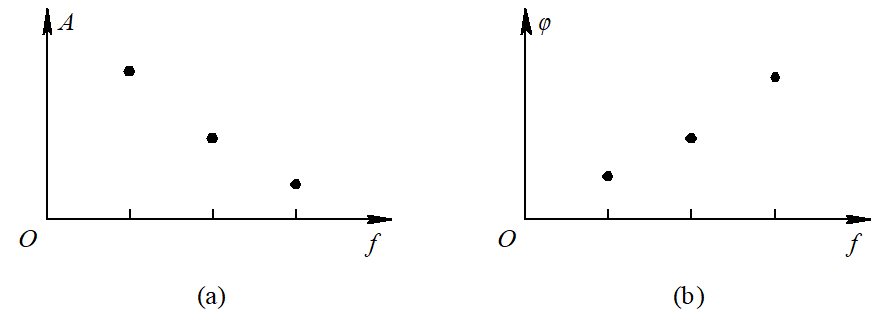 12 |
13 | 图2-3 图2-1(a)波形的频域表示
14 | (a) 幅频特性; (b) 相频特性
15 |
16 | 时域和频域之间的变换可用数学公式表示如下:
17 | $$
18 | f(f){\Leftrightarrow} A(f), \Phi(f)\tag{2-1}
19 | $$
20 | 为能同时表示信号的振幅和相位,通常采用复数表示法,因此式(2-1)可用复数表示为
21 | $$
22 | f(f)\Leftrightarrow F(f)\tag{2-2}
23 | $$
24 | 完成这种变换,一般采用的方法是线性正交变换。
25 |
--------------------------------------------------------------------------------
/II/2.3 频域变换的一般表达式.md:
--------------------------------------------------------------------------------
1 | # 2.3 频域变换的一般表达式
2 |
3 | ## 2.3.1 可分离变换
4 |
5 | 二维傅立叶变换可用通用的关系式来表示:
6 | $$
7 | F(u, v)=\sum_{x=0}^{M-1} \sum_{y=0}^{N-1} f(x, y) g(x, y, u, v)
8 |
9 | \tag{2-36}
10 | $$
11 | $$
12 | f(x, y)=\sum_{u=0}^{M-1} \sum_{v=0}^{N-1} F(u, v) h(x, y, u, v)\tag{2-37}
13 | $$
14 |
15 | 式中:$x, u=0, 1, 2, …, M-1$;$y, v=0, 1, 2, …, N-1$;$g(x,y,u,v)$和$h(x,y,u,v)$分别称为正向变换核和反向变换核。
16 |
17 | 如果
18 | $$
19 | g(x, y, u, v)=g_1(x, u) g_2(y, v)\tag{2-38}
20 | $$
21 |
22 | $$
23 | h(x, y, u, v)=h_1(x, u) h_2(y, v)\tag{2-39}
24 | $$
25 |
26 | 则称正、反变换核是可分离的。进一步,如果$g_1$和$g_2$,$h_1$和$h_2$在函数形式上一样,则称该变换核是对称的。
27 |
28 | 二维傅立叶变换对是式(2-36)和式(2-37)的一个特殊情况, 它们的核为
29 | $$
30 | g(x, y, u, v)=e^{-j 2 \pi\left(\dfrac{u x}{M}+\dfrac{v y}{N}\right)}=e^{-j 2 \pi \dfrac{u x}{M}} \cdot e^{-j 2 \pi \dfrac{v y}{N}} \tag{2-40}
31 | $$
32 | $$
33 | h(x, y, u, v)=\frac{1}{M N} e^{j 2 \pi\left(\dfrac{u x}{M}+\dfrac{v y}{N}\right)}=\frac{1}{M} e^{j 2 \pi \dfrac{u x}{M}} \cdot \frac{1}{N} e^{j 2 \pi \dfrac{v y}{N}}\tag{2-41}
34 | $$
35 |
36 | 可见,它们都是可分离的和对称的。
37 |
38 | 如前所述,二维傅立叶变换可以利用变换核的可分离性, 用两次一维变换来实现,即可先对$f(x, y)$的每一行进行一维变换得到$F(x, v)$,再沿$F(x, v)$每一列取一维变换得到变换结果$F(u, v)
39 | $。对于其他的图像变换,只要其变换核是可分离的,同样也可用两次一维变换来实现。
40 |
41 | 如果先对$f(x, y)$的每一列进行一维变换得到$F(y, u)$,再沿$F(y, u)$每一行取一维变换得到$F(u, v)$,其最终结果是一样的。该结论对反变换核也适用。
42 |
43 | ## 2.3.2 图像变换的矩阵表示
44 |
45 | 数字图像都是实数矩阵, 设$f(x, y)$为$M\times N$的图像灰度矩阵, 通常为了分析、推导方便,可将可分离变换写成矩阵的形式:
46 | $$
47 | F=P f Q\tag{2-42}
48 | $$
49 |
50 | $$
51 | F=P^{-1} F Q^{-1}\tag{2-43}
52 | $$
53 |
54 | 其中,$F$、$f$是二维$M\times N$的矩阵;$P$是$M\times M$矩阵;$Q$是$N\times N$矩阵。
55 | $$
56 | F(u, v)=\sum_{x=0}^{M-1} \sum_{y=0}^{N-1} P(x, u) f(x, y) Q(y, v)\tag{2-44}
57 | $$
58 | 式中,$u=0, 1, 2, …, M-1,v=0, 1, 2, …, N-1$。对二维离散傅立叶变换,则有
59 | $$
60 | P(x, u)=g_1(x, u)=e^{-j 2 \pi u x / M}\tag{2-45}
61 | $$
62 |
63 | $$
64 | P(y, v)=g_2(x, v)=e^{-j 2 \pi v / N}\tag{2-46}
65 | $$
66 |
67 | 实践中,除了DFT变换之外,还采用许多其他的正交变换。例如:离散余弦变换、沃尔什-哈达玛变换、K-L变换等,下面将对常用的变换作一简要介绍。
68 |
--------------------------------------------------------------------------------
/II/2.4 离散余弦变换.md:
--------------------------------------------------------------------------------
1 | # 2.4 离散余弦变换(DCT)
2 |
3 | 离散余弦变换(Discrete Cosine Transform, DCT)的变换核为余弦函数。DCT除了具有一般的正交变换性质外, 它的变换阵的基向量能很好地描述人类语音信号和图像信号的相关特征。
4 |
5 | 因此,在对语音信号、图像信号的变换中,DCT变换被认为是一种准最佳变换。近年颁布的一系列视频压缩编码的国际标准建议中, 都把DCT作为其中的一个基本处理模块。除此之外, DCT 还是一种可分离的变换。
6 |
7 | ## 2.4.1 一维离散余弦变换
8 |
9 | 一维DCT的变换核定义为
10 |
11 | $$
12 | g(x, u)=C(u) \sqrt{\frac{2}{N}} \cos \frac{(2 x+1) u \pi}{2 N}\tag{2-47}
13 | $$
14 |
15 | 式中, $x, u=0,1,2, \ldots, N-1$;
16 | $$
17 | C(u)= \begin{cases}\frac{1}{\sqrt{2}} & u=0 \\ 1 & \text { 其他 }\end{cases}\tag{2-48}
18 | $$
19 |
20 | 一维DCT定义如下: 设 $\{f(x) \mid x=0,1, \ldots, N-1\}$ 为离散的信号列。
21 |
22 | $$
23 | F(u)=C(u) \sqrt{\frac{2}{N}} \sum_{x=0}^{N-1} f(x) \cos \frac{(2 x+1) u \pi}{2 N}\tag{2-49}
24 | $$
25 |
26 | 式中, $u, x=0,1,2, \ldots, N-1$ 。
27 |
28 | 将变换式展开整理后,可以㝍成矩阵的形式,即
29 | $$
30 | F=G f\tag{2-50}
31 | $$
32 |
33 | 其中
34 | $$
35 | G=
36 | \left[
37 | \begin{array}{}
38 | \dfrac{1}{\sqrt{N}}&[&1 &1 &\cdots &1 &]\\
39 | \sqrt{\dfrac{2}{N}}&[&\cos(\dfrac{\pi}{2N}) &\cos(\dfrac{3\pi}{2N}) &\cdots&\cos(\dfrac{(2N-1)\pi}{2N})&]\\
40 | \sqrt{\dfrac{2}{N}}&[&\cos(\dfrac{\pi}{2N}) &\cos(\dfrac{6\pi}{2N}) &\cdots &\cos(\dfrac{(2N-1)\pi}{2N})&]\\
41 | \vdots\\
42 | \sqrt{\dfrac{2}{N}}&[&\cos((N-1)\dfrac{\pi}{2N}) &\cos((N-1)\dfrac{3\pi}{2N}) &\cdots &\cos((N-1)\dfrac{(2N-1)\pi}{2N})&]\\
43 | \end{array}
44 | \right]\tag{2-51}
45 | $$
46 | 一维DCT的逆变换IDCT定义为
47 |
48 | $$
49 | f(x)=\sqrt{\frac{2}{N}} \sum_{u=0}^{N-1} C(u) F(u) \cos \frac{(2 x+1) u \pi}{2 N}\tag{2-52}
50 | $$
51 |
52 | 式中, $x, u=0,1,2, \ldots, N-1$ 。可见一维DCT的逆变换核与正变换核是相同的。
53 |
54 | ## 2.4.2二维离散余弦变换
55 |
56 | 考虑到两个变量, 很容易将一维DCT的定义推广到二维DCT。其正变换核为
57 | $$
58 | g(x, y, u, v)=\frac{2}{\sqrt{M N}} C(u) C(v) \cos \frac{(2 x+1) u \pi}{2 M} \cos \frac{(2 y+1) v \pi}{2 N}\tag{2-53}
59 | $$
60 |
61 |
62 | 式中, $C(u)$ 和 $C(v)$ 的定义同式 (2-48) ; $x, u=0,1,2, \ldots, M-1$;
63 |
64 | $y, v=0,1,2, \ldots, N-1$ 。
65 |
66 | 二维DCT定义如下: 设 $f(x, y)$ 为 $M \times N$ 的数字图像矩阵, 则
67 |
68 | $$
69 | F(u, v)=\frac{2}{\sqrt{M N}} \sum_{x=0}^{M-1 N-1} f(x, y) C(u) C(v) \cos \frac{(2 x+1) u \pi}{2 M} \cos \frac{(2 y+1) v \pi}{2 N}\tag{2-54}
70 | $$
71 |
72 | 式中: $x, u=0,1,2, \ldots, M-1 ; y, v=0,1,2, \ldots, N-1$ 。
73 |
74 | 二维DCT逆变换定义如下:
75 | $$
76 | f(x, y)=\frac{2}{\sqrt{M N}} \sum_{u=0}^{M-1 N-1} \sum_{v=0} C(u) C(v) F(u, v) \cos \frac{(2 x+1) u \pi}{2 M} \cos \frac{(2 y+1) v \pi}{2 N}\tag{2-55}
77 | $$
78 |
79 | 式中: $x, u=0,1,2, \ldots, M-1 ; y, v=0,1,2, \ldots, N-1$ 。
80 |
81 | 类似一维矩阵形式的DCT, 可以写出二维DCT的矩阵形式
82 |
83 | 如下:
84 |
85 | $$
86 | F=G f G^{T}\tag{2-56}
87 | $$
88 |
89 | 同时, 由式(2-55)和式(2-54)可知二维DCT的逆变换核与正变换核相同, 且是可分离的, 即
90 |
91 | $$
92 | \begin{aligned}
93 | g(x, y, u, v) & =g_{1}(x, u) g_{2}(y, v) \\
94 | & =\frac{2}{\sqrt{M}} C(u) \cos \frac{(2 x+1) u \pi}{2 M} \cdot \frac{2}{\sqrt{N}} C(v) \cos \frac{(2 y+1) v \pi}{2 N}
95 | \end{aligned}\tag{2-57}
96 | $$
97 |
98 | 式中: $C(u)$ 和 $C(v)$ 的定义同式 (2-48); $x, u=0,1,2, \ldots, M-1;y, v=0,1,2, \ldots, N-1$ 。
99 |
100 | 通常根据可分离性,二维DCT可用两次一维DCT来完成,其算法流程与DFT类似,即
101 | $$
102 | \begin{align}
103 | f(x, y) &\rightarrow F_{行 }[f(x, y)]=F(x, v)\\
104 | &\stackrel{转置}{\rightarrow} F(x, v)^{T} \rightarrow F_{\text {列 }}\left[F(x, v)^{T}\right]=F(u, v)^{T}\\
105 | &\stackrel{转置}{\rightarrow}F(u, v)
106 | \end{align}\tag{2-58}
107 | $$
108 |
109 |
110 | ## 2.4.3 快速离散余弦变换
111 |
112 | 离散余弦变换的计算量相当大, 在实用中非常不方便, 也需要研究相应的快速算法。目前已有多种快速DCT(FCT), 在此介绍一种由FFT的思路发展起来的FCT。
113 |
114 | 首先, 将 $f(x)$ 延拓为
115 |
116 | $$
117 | f_{e}(x)= \begin{cases}f(x) & x=0,1,2, \ldots, N-1 \\ 0 & x=N, \quad N+1, \ldots, 2 N-1\end{cases}\tag{2-59}
118 | $$
119 |
120 | 按照一维DCT的定义, $f_{e}(x)$ 的DCT为
121 |
122 | $$
123 | F(0)=\frac{1}{\sqrt{N}} \sum_{x=0}^{N-1} f_{e}(x)\tag{2-60}
124 | $$
125 |
126 |
127 |
128 | $$
129 | \begin{aligned}
130 | F(u)
131 | &=\sqrt{\frac{2}{N}} \sum_{x=0}^{N-1} f(x) \cos \frac{(2 x+1) u \pi}{2 N} \\
132 | & =\sqrt{\frac{2}{N}} \sum_{x=0}^{N-1} f(x) \cos \frac{(2 x+1) u \pi}{2 N}+\sqrt{\frac{2}{N}} \sum_{x=N}^{2 N-1} 0 \cdot \cos \frac{(2 x+1) u \pi}{2 N} \\
133 | & =\sqrt{\frac{2}{N}} \sum_{x=0}^{N-1} f_{e}(x) \cos \frac{(2 x+1) u \pi}{2 N}+\sqrt{\frac{2}{N}} \sum_{x=N}^{2 N-1} f_{e}(x) \cdot \cos \frac{(2 x+1) u \pi}{2 N} \\
134 | & =\sqrt{\frac{2}{N}} \sum_{x=0}^{2 N-1} f_{e}(x) \cos \frac{(2 x+1) u \pi}{2 N} \\
135 | & =\sqrt{\frac{2}{N}} \operatorname{Re}\left\{\sum_{x=0}^{2 N-1} f_{e}(x) e^{-j \frac{(2 x+1) u \pi}{2 N}}\right\} \\
136 | & =\sqrt{\frac{2}{N}} \operatorname{Re}\left\{e^{-j \frac{u \pi}{2 N}} \cdot \sum_{x=0}^{2 N-1} f_{e}(x) e^{-j \frac{2 x u \pi}{2 N}}\right\}
137 | \end{aligned}\tag{2-61}
138 | $$
139 |
140 | 式中,$Re\{\cdot\}$表示取复数的实部
141 |
142 | 由于
143 | $$
144 | \sum_{e}^{2 N-1} f_{e}(x) e^{-j \dfrac{2 x u \pi}{2 N}}
145 | $$
146 | 因此,在作DFT时,可把长度为 $N$ 的 $f(x)$ 的长度延拓为 $2 N$ 点的序列 $f_{e}(x)$, 然后对 $f_{e}(x)$ 作 $DFT$ ,最后取DFT的实部便可得到DCT的结果。
147 |
148 | 同理对于离散余弦逆变换IDCT,可首先将 $F(u)$ 延拓为
149 |
150 | $$
151 | F_{e}(u)= \begin{cases}F(u) & u=0,1,2, \ldots, N-1 \\ 0 & u=N, N+1, \ldots, 2 N-1\end{cases}\tag{2-62}
152 | $$
153 |
154 |
155 |
156 | 由式(2-52)可得, DCT的IDCT为
157 |
158 | $$
159 | \begin{aligned}
160 | f(x)&=\sqrt{\frac{1}{N}} F_{e}(0)+\sqrt{\frac{2}{N}} \sum_{u=1}^{2 N-1} F_{e}(u) \cos \frac{(2 x+1) u \pi}{2 N} \\
161 | & =\sqrt{\frac{1}{N}} F_{e}(0)+\sqrt{\frac{2}{N}} \operatorname{Re}\left\{\sum_{u=1}^{2 N-1} F_{e}(u) e^{j \dfrac{(2 x+1) u \pi}{2 N}}\right\} \\
162 | & =\left(\sqrt{\frac{1}{N}}-\sqrt{\frac{2}{N}}\right) F_{e}(0)+\sqrt{\frac{2}{N}} \operatorname{Re}\left\{\sum_{u=0}^{2 N-1}\left[F_{e}(u) e^{j \dfrac{u \pi}{2 N}}\right] e^{j \dfrac{(2 x+1) u \pi}{2 N}}\right\}
163 | \end{aligned}\tag{2-63}
164 | $$
165 |
166 | 由式 (2-63) 可见, IDCT可由 $F_e(u) e^{j \frac{u \pi}{2 N}}$ 的 $2 N$ 点的IDFT来实现。
167 |
168 | 最后要注意的是二维DCT的频谱分布, 其谱域分布与DFT相差一倍, 如图2-11所示。
169 |
170 | 从图中可以看出, 对于DCT而言, $(0,0)$ 点对应于频谱的低频成分, $(N-1, N-1)$ 点对应于高频成分, 而同阶的DFT中, $(N / 2$, $N / 2$ )点对应于高频成分 (注: 此频谱图中末作频谱中心平移)。
171 |
172 | 由于DFT和IDFT已有快速算法FFT和IFFT, 因此可用它们实现快速DCT和IDCT算法FCT及IFCT。不过, 由于FFT及IFFT中要涉及到复数运算, 因此这种FCT及IFCT算法并不是最佳的。
173 |
174 |
12 |
13 | 图2-3 图2-1(a)波形的频域表示
14 | (a) 幅频特性; (b) 相频特性
15 |
16 | 时域和频域之间的变换可用数学公式表示如下:
17 | $$
18 | f(f){\Leftrightarrow} A(f), \Phi(f)\tag{2-1}
19 | $$
20 | 为能同时表示信号的振幅和相位,通常采用复数表示法,因此式(2-1)可用复数表示为
21 | $$
22 | f(f)\Leftrightarrow F(f)\tag{2-2}
23 | $$
24 | 完成这种变换,一般采用的方法是线性正交变换。
25 |
--------------------------------------------------------------------------------
/II/2.3 频域变换的一般表达式.md:
--------------------------------------------------------------------------------
1 | # 2.3 频域变换的一般表达式
2 |
3 | ## 2.3.1 可分离变换
4 |
5 | 二维傅立叶变换可用通用的关系式来表示:
6 | $$
7 | F(u, v)=\sum_{x=0}^{M-1} \sum_{y=0}^{N-1} f(x, y) g(x, y, u, v)
8 |
9 | \tag{2-36}
10 | $$
11 | $$
12 | f(x, y)=\sum_{u=0}^{M-1} \sum_{v=0}^{N-1} F(u, v) h(x, y, u, v)\tag{2-37}
13 | $$
14 |
15 | 式中:$x, u=0, 1, 2, …, M-1$;$y, v=0, 1, 2, …, N-1$;$g(x,y,u,v)$和$h(x,y,u,v)$分别称为正向变换核和反向变换核。
16 |
17 | 如果
18 | $$
19 | g(x, y, u, v)=g_1(x, u) g_2(y, v)\tag{2-38}
20 | $$
21 |
22 | $$
23 | h(x, y, u, v)=h_1(x, u) h_2(y, v)\tag{2-39}
24 | $$
25 |
26 | 则称正、反变换核是可分离的。进一步,如果$g_1$和$g_2$,$h_1$和$h_2$在函数形式上一样,则称该变换核是对称的。
27 |
28 | 二维傅立叶变换对是式(2-36)和式(2-37)的一个特殊情况, 它们的核为
29 | $$
30 | g(x, y, u, v)=e^{-j 2 \pi\left(\dfrac{u x}{M}+\dfrac{v y}{N}\right)}=e^{-j 2 \pi \dfrac{u x}{M}} \cdot e^{-j 2 \pi \dfrac{v y}{N}} \tag{2-40}
31 | $$
32 | $$
33 | h(x, y, u, v)=\frac{1}{M N} e^{j 2 \pi\left(\dfrac{u x}{M}+\dfrac{v y}{N}\right)}=\frac{1}{M} e^{j 2 \pi \dfrac{u x}{M}} \cdot \frac{1}{N} e^{j 2 \pi \dfrac{v y}{N}}\tag{2-41}
34 | $$
35 |
36 | 可见,它们都是可分离的和对称的。
37 |
38 | 如前所述,二维傅立叶变换可以利用变换核的可分离性, 用两次一维变换来实现,即可先对$f(x, y)$的每一行进行一维变换得到$F(x, v)$,再沿$F(x, v)$每一列取一维变换得到变换结果$F(u, v)
39 | $。对于其他的图像变换,只要其变换核是可分离的,同样也可用两次一维变换来实现。
40 |
41 | 如果先对$f(x, y)$的每一列进行一维变换得到$F(y, u)$,再沿$F(y, u)$每一行取一维变换得到$F(u, v)$,其最终结果是一样的。该结论对反变换核也适用。
42 |
43 | ## 2.3.2 图像变换的矩阵表示
44 |
45 | 数字图像都是实数矩阵, 设$f(x, y)$为$M\times N$的图像灰度矩阵, 通常为了分析、推导方便,可将可分离变换写成矩阵的形式:
46 | $$
47 | F=P f Q\tag{2-42}
48 | $$
49 |
50 | $$
51 | F=P^{-1} F Q^{-1}\tag{2-43}
52 | $$
53 |
54 | 其中,$F$、$f$是二维$M\times N$的矩阵;$P$是$M\times M$矩阵;$Q$是$N\times N$矩阵。
55 | $$
56 | F(u, v)=\sum_{x=0}^{M-1} \sum_{y=0}^{N-1} P(x, u) f(x, y) Q(y, v)\tag{2-44}
57 | $$
58 | 式中,$u=0, 1, 2, …, M-1,v=0, 1, 2, …, N-1$。对二维离散傅立叶变换,则有
59 | $$
60 | P(x, u)=g_1(x, u)=e^{-j 2 \pi u x / M}\tag{2-45}
61 | $$
62 |
63 | $$
64 | P(y, v)=g_2(x, v)=e^{-j 2 \pi v / N}\tag{2-46}
65 | $$
66 |
67 | 实践中,除了DFT变换之外,还采用许多其他的正交变换。例如:离散余弦变换、沃尔什-哈达玛变换、K-L变换等,下面将对常用的变换作一简要介绍。
68 |
--------------------------------------------------------------------------------
/II/2.4 离散余弦变换.md:
--------------------------------------------------------------------------------
1 | # 2.4 离散余弦变换(DCT)
2 |
3 | 离散余弦变换(Discrete Cosine Transform, DCT)的变换核为余弦函数。DCT除了具有一般的正交变换性质外, 它的变换阵的基向量能很好地描述人类语音信号和图像信号的相关特征。
4 |
5 | 因此,在对语音信号、图像信号的变换中,DCT变换被认为是一种准最佳变换。近年颁布的一系列视频压缩编码的国际标准建议中, 都把DCT作为其中的一个基本处理模块。除此之外, DCT 还是一种可分离的变换。
6 |
7 | ## 2.4.1 一维离散余弦变换
8 |
9 | 一维DCT的变换核定义为
10 |
11 | $$
12 | g(x, u)=C(u) \sqrt{\frac{2}{N}} \cos \frac{(2 x+1) u \pi}{2 N}\tag{2-47}
13 | $$
14 |
15 | 式中, $x, u=0,1,2, \ldots, N-1$;
16 | $$
17 | C(u)= \begin{cases}\frac{1}{\sqrt{2}} & u=0 \\ 1 & \text { 其他 }\end{cases}\tag{2-48}
18 | $$
19 |
20 | 一维DCT定义如下: 设 $\{f(x) \mid x=0,1, \ldots, N-1\}$ 为离散的信号列。
21 |
22 | $$
23 | F(u)=C(u) \sqrt{\frac{2}{N}} \sum_{x=0}^{N-1} f(x) \cos \frac{(2 x+1) u \pi}{2 N}\tag{2-49}
24 | $$
25 |
26 | 式中, $u, x=0,1,2, \ldots, N-1$ 。
27 |
28 | 将变换式展开整理后,可以㝍成矩阵的形式,即
29 | $$
30 | F=G f\tag{2-50}
31 | $$
32 |
33 | 其中
34 | $$
35 | G=
36 | \left[
37 | \begin{array}{}
38 | \dfrac{1}{\sqrt{N}}&[&1 &1 &\cdots &1 &]\\
39 | \sqrt{\dfrac{2}{N}}&[&\cos(\dfrac{\pi}{2N}) &\cos(\dfrac{3\pi}{2N}) &\cdots&\cos(\dfrac{(2N-1)\pi}{2N})&]\\
40 | \sqrt{\dfrac{2}{N}}&[&\cos(\dfrac{\pi}{2N}) &\cos(\dfrac{6\pi}{2N}) &\cdots &\cos(\dfrac{(2N-1)\pi}{2N})&]\\
41 | \vdots\\
42 | \sqrt{\dfrac{2}{N}}&[&\cos((N-1)\dfrac{\pi}{2N}) &\cos((N-1)\dfrac{3\pi}{2N}) &\cdots &\cos((N-1)\dfrac{(2N-1)\pi}{2N})&]\\
43 | \end{array}
44 | \right]\tag{2-51}
45 | $$
46 | 一维DCT的逆变换IDCT定义为
47 |
48 | $$
49 | f(x)=\sqrt{\frac{2}{N}} \sum_{u=0}^{N-1} C(u) F(u) \cos \frac{(2 x+1) u \pi}{2 N}\tag{2-52}
50 | $$
51 |
52 | 式中, $x, u=0,1,2, \ldots, N-1$ 。可见一维DCT的逆变换核与正变换核是相同的。
53 |
54 | ## 2.4.2二维离散余弦变换
55 |
56 | 考虑到两个变量, 很容易将一维DCT的定义推广到二维DCT。其正变换核为
57 | $$
58 | g(x, y, u, v)=\frac{2}{\sqrt{M N}} C(u) C(v) \cos \frac{(2 x+1) u \pi}{2 M} \cos \frac{(2 y+1) v \pi}{2 N}\tag{2-53}
59 | $$
60 |
61 |
62 | 式中, $C(u)$ 和 $C(v)$ 的定义同式 (2-48) ; $x, u=0,1,2, \ldots, M-1$;
63 |
64 | $y, v=0,1,2, \ldots, N-1$ 。
65 |
66 | 二维DCT定义如下: 设 $f(x, y)$ 为 $M \times N$ 的数字图像矩阵, 则
67 |
68 | $$
69 | F(u, v)=\frac{2}{\sqrt{M N}} \sum_{x=0}^{M-1 N-1} f(x, y) C(u) C(v) \cos \frac{(2 x+1) u \pi}{2 M} \cos \frac{(2 y+1) v \pi}{2 N}\tag{2-54}
70 | $$
71 |
72 | 式中: $x, u=0,1,2, \ldots, M-1 ; y, v=0,1,2, \ldots, N-1$ 。
73 |
74 | 二维DCT逆变换定义如下:
75 | $$
76 | f(x, y)=\frac{2}{\sqrt{M N}} \sum_{u=0}^{M-1 N-1} \sum_{v=0} C(u) C(v) F(u, v) \cos \frac{(2 x+1) u \pi}{2 M} \cos \frac{(2 y+1) v \pi}{2 N}\tag{2-55}
77 | $$
78 |
79 | 式中: $x, u=0,1,2, \ldots, M-1 ; y, v=0,1,2, \ldots, N-1$ 。
80 |
81 | 类似一维矩阵形式的DCT, 可以写出二维DCT的矩阵形式
82 |
83 | 如下:
84 |
85 | $$
86 | F=G f G^{T}\tag{2-56}
87 | $$
88 |
89 | 同时, 由式(2-55)和式(2-54)可知二维DCT的逆变换核与正变换核相同, 且是可分离的, 即
90 |
91 | $$
92 | \begin{aligned}
93 | g(x, y, u, v) & =g_{1}(x, u) g_{2}(y, v) \\
94 | & =\frac{2}{\sqrt{M}} C(u) \cos \frac{(2 x+1) u \pi}{2 M} \cdot \frac{2}{\sqrt{N}} C(v) \cos \frac{(2 y+1) v \pi}{2 N}
95 | \end{aligned}\tag{2-57}
96 | $$
97 |
98 | 式中: $C(u)$ 和 $C(v)$ 的定义同式 (2-48); $x, u=0,1,2, \ldots, M-1;y, v=0,1,2, \ldots, N-1$ 。
99 |
100 | 通常根据可分离性,二维DCT可用两次一维DCT来完成,其算法流程与DFT类似,即
101 | $$
102 | \begin{align}
103 | f(x, y) &\rightarrow F_{行 }[f(x, y)]=F(x, v)\\
104 | &\stackrel{转置}{\rightarrow} F(x, v)^{T} \rightarrow F_{\text {列 }}\left[F(x, v)^{T}\right]=F(u, v)^{T}\\
105 | &\stackrel{转置}{\rightarrow}F(u, v)
106 | \end{align}\tag{2-58}
107 | $$
108 |
109 |
110 | ## 2.4.3 快速离散余弦变换
111 |
112 | 离散余弦变换的计算量相当大, 在实用中非常不方便, 也需要研究相应的快速算法。目前已有多种快速DCT(FCT), 在此介绍一种由FFT的思路发展起来的FCT。
113 |
114 | 首先, 将 $f(x)$ 延拓为
115 |
116 | $$
117 | f_{e}(x)= \begin{cases}f(x) & x=0,1,2, \ldots, N-1 \\ 0 & x=N, \quad N+1, \ldots, 2 N-1\end{cases}\tag{2-59}
118 | $$
119 |
120 | 按照一维DCT的定义, $f_{e}(x)$ 的DCT为
121 |
122 | $$
123 | F(0)=\frac{1}{\sqrt{N}} \sum_{x=0}^{N-1} f_{e}(x)\tag{2-60}
124 | $$
125 |
126 |
127 |
128 | $$
129 | \begin{aligned}
130 | F(u)
131 | &=\sqrt{\frac{2}{N}} \sum_{x=0}^{N-1} f(x) \cos \frac{(2 x+1) u \pi}{2 N} \\
132 | & =\sqrt{\frac{2}{N}} \sum_{x=0}^{N-1} f(x) \cos \frac{(2 x+1) u \pi}{2 N}+\sqrt{\frac{2}{N}} \sum_{x=N}^{2 N-1} 0 \cdot \cos \frac{(2 x+1) u \pi}{2 N} \\
133 | & =\sqrt{\frac{2}{N}} \sum_{x=0}^{N-1} f_{e}(x) \cos \frac{(2 x+1) u \pi}{2 N}+\sqrt{\frac{2}{N}} \sum_{x=N}^{2 N-1} f_{e}(x) \cdot \cos \frac{(2 x+1) u \pi}{2 N} \\
134 | & =\sqrt{\frac{2}{N}} \sum_{x=0}^{2 N-1} f_{e}(x) \cos \frac{(2 x+1) u \pi}{2 N} \\
135 | & =\sqrt{\frac{2}{N}} \operatorname{Re}\left\{\sum_{x=0}^{2 N-1} f_{e}(x) e^{-j \frac{(2 x+1) u \pi}{2 N}}\right\} \\
136 | & =\sqrt{\frac{2}{N}} \operatorname{Re}\left\{e^{-j \frac{u \pi}{2 N}} \cdot \sum_{x=0}^{2 N-1} f_{e}(x) e^{-j \frac{2 x u \pi}{2 N}}\right\}
137 | \end{aligned}\tag{2-61}
138 | $$
139 |
140 | 式中,$Re\{\cdot\}$表示取复数的实部
141 |
142 | 由于
143 | $$
144 | \sum_{e}^{2 N-1} f_{e}(x) e^{-j \dfrac{2 x u \pi}{2 N}}
145 | $$
146 | 因此,在作DFT时,可把长度为 $N$ 的 $f(x)$ 的长度延拓为 $2 N$ 点的序列 $f_{e}(x)$, 然后对 $f_{e}(x)$ 作 $DFT$ ,最后取DFT的实部便可得到DCT的结果。
147 |
148 | 同理对于离散余弦逆变换IDCT,可首先将 $F(u)$ 延拓为
149 |
150 | $$
151 | F_{e}(u)= \begin{cases}F(u) & u=0,1,2, \ldots, N-1 \\ 0 & u=N, N+1, \ldots, 2 N-1\end{cases}\tag{2-62}
152 | $$
153 |
154 |
155 |
156 | 由式(2-52)可得, DCT的IDCT为
157 |
158 | $$
159 | \begin{aligned}
160 | f(x)&=\sqrt{\frac{1}{N}} F_{e}(0)+\sqrt{\frac{2}{N}} \sum_{u=1}^{2 N-1} F_{e}(u) \cos \frac{(2 x+1) u \pi}{2 N} \\
161 | & =\sqrt{\frac{1}{N}} F_{e}(0)+\sqrt{\frac{2}{N}} \operatorname{Re}\left\{\sum_{u=1}^{2 N-1} F_{e}(u) e^{j \dfrac{(2 x+1) u \pi}{2 N}}\right\} \\
162 | & =\left(\sqrt{\frac{1}{N}}-\sqrt{\frac{2}{N}}\right) F_{e}(0)+\sqrt{\frac{2}{N}} \operatorname{Re}\left\{\sum_{u=0}^{2 N-1}\left[F_{e}(u) e^{j \dfrac{u \pi}{2 N}}\right] e^{j \dfrac{(2 x+1) u \pi}{2 N}}\right\}
163 | \end{aligned}\tag{2-63}
164 | $$
165 |
166 | 由式 (2-63) 可见, IDCT可由 $F_e(u) e^{j \frac{u \pi}{2 N}}$ 的 $2 N$ 点的IDFT来实现。
167 |
168 | 最后要注意的是二维DCT的频谱分布, 其谱域分布与DFT相差一倍, 如图2-11所示。
169 |
170 | 从图中可以看出, 对于DCT而言, $(0,0)$ 点对应于频谱的低频成分, $(N-1, N-1)$ 点对应于高频成分, 而同阶的DFT中, $(N / 2$, $N / 2$ )点对应于高频成分 (注: 此频谱图中末作频谱中心平移)。
171 |
172 | 由于DFT和IDFT已有快速算法FFT和IFFT, 因此可用它们实现快速DCT和IDCT算法FCT及IFCT。不过, 由于FFT及IFFT中要涉及到复数运算, 因此这种FCT及IFCT算法并不是最佳的。
173 |
174 |  175 |
176 | 图2-11 DFT和DCT的频谱分布
177 |
178 | (a)DFT频谱分布; (b) DCT频谱分布
179 |
--------------------------------------------------------------------------------
/II/2.5 离散沃尔什-哈达玛变换(WHT).md:
--------------------------------------------------------------------------------
1 | # 2.5 离散沃尔什-哈达玛变换(WHT)
2 |
3 | ## 2.5.1 一维离散沃尔什-哈达玛变换
4 |
5 | ### 沃尔什函数
6 |
7 | 沃尔什函数是1923年由美国数学家沃尔什提出的。沃尔什函数系是一个完备正交函数系, 其值只能取 +1 和 -1 。从排列次序上可将沃尔什函数分为三种定义方法: 一种是按照沃尔什排列来定义 (按列率排序) ; 另一种是按照佩利排列来定义(按自然排序);第三种是按照哈达玛排列来定义。由于哈达玛排序的沃尔什函数是由 $2^{n}(n=0,1,2, \ldots)$ 阶哈达玛矩阵 (Hadamard Matrix) 得到的, 而哈达玛矩阵的最大优点在于它具有简单的递推关系, 即高阶矩阵可用两个低阶矩阵的克罗内克积求得, 因此在此只介绍哈达玛排列定义的沃尔什变换。
8 |
9 | $N=2^{n}(n=0,1,2, \ldots)$ 阶哈达玛矩阵每一行的符号变化规律对应于某一个沃尔什函数的符号变化规律, 即 $N=2 n(n=0,1,2, \ldots)$ 阶哈达玛矩阵的每一行对应于一个离散沃尔什函数, 哈达玛矩阵与沃尔什函数系不同之处仅仅是行的次序不同。 $2^{n}$ 阶哈达玛矩阵有如下形式:
10 | $$
11 | H_{1}=\text { [1] }\tag{2-64}
12 | $$
13 |
14 | $$
15 | H_{2}=\left[\begin{array}{rr}
16 | 1 & 1 \\
17 | 1 & -1
18 | \end{array}\right]\tag{2-65}
19 | $$
20 |
21 | $$
22 | H_{4}=\left[\begin{array}{rr}
23 | H_{2} & H_{2} \\
24 | H_{2} & -H_{2}
25 | \end{array}\right]=\left[\begin{array}{rrrr}
26 | 1 & 1 & 1 & 1 \\
27 | 1 & -1 & 1 & -1 \\
28 | 1 & 1 & -1 & -1 \\
29 | 1 & -1 & -1 & 1
30 | \end{array}\right]\tag{2-66}
31 | $$
32 |
33 | 哈达玛矩阵的阶数是按 $N=2^{n}(n=0,1,2, \ldots)$ 规律排列的, 阶数较高的哈达玛矩阵, 可以利用矩阵的克罗内克积运算, 由低阶哈达玛矩阵递推得到, 即
34 |
35 | $$
36 | H_{N}=H_{2^{n}}=H_{2} \otimes H_{2^{n-1}}=\left[\begin{array}{cc}
37 | H_{2^{n-1}} & H_{2^{n-1}} \\
38 | H_{2^{n-1}} & -H_{2^{n-1}}
39 | \end{array}\right]=\left[\begin{array}{cc}
40 | H_{\frac{N}{2}} & H_{\frac{N}{2}} \\
41 | H_{\frac{N}{2}} & -H_{\frac{N}{2}}
42 | \end{array}\right]\tag{2-67}
43 | $$
44 |
45 |
46 |
47 | 矩阵的克罗内克积 (Kronecker Product) 运算用符号记作$A \odot B$, 其运算规律如下:
48 |
49 | 设
50 |
51 | $$
52 | A=\left[\begin{array}{llll}
53 | a_{11} & a_{12} & \cdots & a_{1 n} \\
54 | a_{21} & a_{22} & \cdots & a_{2 n} \\
55 | \vdots & \vdots & \ddots & \vdots \\
56 | a_{m 1} & a_{m 2} & \cdots & a_{mn}
57 | \end{array}\right]&&
58 | B=\left[\begin{array}{rrrr}
59 | b_{11} & b_{12} & \cdots & b_{1 j} \\
60 | b_{21} & b_{22} & \cdots & a_{2 j} \\
61 | \vdots & \vdots & \ddots & \vdots \\
62 | b_{i 1} & b_{i 2} & \cdots & b_{i j}
63 | \end{array}\right]
64 | $$
65 |
66 | $$
67 |
68 | $$
69 |
70 | 则
71 |
72 | $$
73 | A \otimes B=\left[\begin{array}{llll}
74 | a_{11} B & a_{12} B & \cdots & a_{1 n} B \\
75 | a_{21} B & a_{22} B & \cdots & a_{2 n} B \\
76 | \vdots & \vdots & \ddots & \vdots \\
77 | a_{m 1} B & a_{m 2} B & \cdots & a_{m n} B
78 | \end{array}\right] \\
79 |
80 | \tag{2-68}
81 | $$
82 |
83 | $$
84 | B \otimes A=\left[\begin{array}{cccc}
85 | b_{11} A & b_{12} A & \cdots & b_{1 j} A \\
86 | b_{21} A & b_{22} A & \cdots & b_{2 j} A \\
87 | \vdots & \vdots & \ddots & \vdots \\
88 | b_{i 1} A & a_{i 2} A & \cdots & b_{i j} A
89 | \end{array}\right]\tag{2-69}
90 | $$
91 |
92 |
93 |
94 | ### 离散沃尔什-哈达玛变换
95 |
96 | 一维离散沃尔什变换定义为
97 |
98 | $$
99 | W(u)=\frac{1}{N} \sum_{x=0}^{N-1} f(x) W a l s h(u, x)\tag{2-70}
100 | $$
101 |
102 | 一维离散沃尔什逆变换定义为
103 |
104 | $$
105 | f(x)=\sum_{u=0}^{N-1} W(u) W a l s h(u, x)\tag{2-71}
106 | $$
107 |
108 | 式中, $\operatorname{Walsh}(u, x)$ 为沃尔什函数。若将 $W a l s h(u, x)$ 用哈达玛矩阵表示, 并将变换表达式写成矩阵形式, 则式(2-70)和式(2-71) 分别为
109 |
110 | $$
111 | \left[\begin{array}{c}
112 | W(0) \\
113 | W(1) \\
114 | \vdots \\
115 | W(N-1)
116 | \end{array}\right]=\frac{1}{N}\left[H_{N}\right]\left[\begin{array}{c}
117 | f(0) \\
118 | f(1) \\
119 | \vdots \\
120 | f(N-1)
121 | \end{array}\right]\tag{2-72}
122 | $$
123 |
124 | 和
125 |
126 | $$
127 | \left[\begin{array}{c}
128 | f(0) \\
129 | f(1) \\
130 | \vdots \\
131 | f(N-1)
132 | \end{array}\right]=\left[H_{N}\right]\left[\begin{array}{c}
133 | W(0) \\
134 | W(1) \\
135 | \vdots \\
136 | W(N-1)
137 | \end{array}\right]\tag{2-73}
138 | $$
139 |
140 | 式中, $\left[H_{N}\right]$ 为 $N$ 阶哈达玛矩阵。 由哈达玛矩阵的特点可知, 沃尔什-哈达玛变换的本质上是
141 |
142 | 由哈达玛矩阵的特点可知,沃尔什-哈达玛变换的本质上是将离散序列 $f(x)$ 的各项值的符号按一定规律改变后, 进行加减运算, 因此, 它比采用复数运算的DFT和采用余弦运算的DCT要简单得多。
143 |
144 |
145 |
146 | ## 2.5.2 二维离散沃尔什变换
147 |
148 | 很容易将一维WHT的定义推广到二维WHT。二维WHT的正变换核和逆变换核分别为
149 |
150 | $$
151 | W(u, v)=\frac{1}{M N} \sum_{x=0}^{M-1} \sum_{y=0}^{N-1} f(x, y) W a l s h(u, x) W slsh(v, y)\tag{2-74}
152 | $$
153 |
154 | 和
155 |
156 | $$
157 | f(x, y)=\sum_{u=0}^{M-1} \sum_{v=0}^{N-1} W(u, v) W a l s h(u, x) W s
158 | lsh(v, y)\tag{2-75}
159 | $$
160 |
161 | 式中: $x, u=0,1,2, \ldots, M-1 ; y, v=0,1,2, \ldots, N-1$ 。
162 |
163 | ---
164 |
165 | 二维离散沃尔什变换的矩阵形式表达式为
166 | $$
167 | f_{1}=\left[\begin{array}{llll}1 & 3 & 3 & 1 \\ 1 & 3 & 3 & 1 \\ 1 & 3 & 3 & 1 \\ 1 & 3 & 3 & 1\end{array}\right]
168 | $$
169 | 和
170 | $$
171 | f_{1}=\left[\begin{array}{llll}1 & 1 & 1 & 1 \\ 1 & 1 & 1 & 1 \\ 1 & 1 & 1 & 1 \\ 1 & 1 & 1 & 1\end{array}\right]
172 | $$
173 |
174 | 求这两个信号的二维WHT。
175 |
176 | 根据题意, 式 (2-76) 中的 $M=N=4$, 其二维WHT变换核为
177 | $$
178 | H_{4}=\left[\begin{array}{rrrr}
179 | 1 & 1 & 1 & 1 \\
180 | 1 & -1 & 1 & -1 \\
181 | 1 & 1 & -1 & -1 \\
182 | 1 & -1 & -1 & 1
183 | \end{array}\right]
184 | $$
185 |
186 | 所以
187 |
188 | $$
189 | \begin{aligned}
190 | W_{1} & =\frac{1}{4^{2}}\left[\begin{array}{rrrr}
191 | 1 & 1 & 1 & 1 \\
192 | 1 & -1 & 1 & -1 \\
193 | 1 & 1 & -1 & -1 \\
194 | 1 & -1 & -1 & 1
195 | \end{array}\right]\left[\begin{array}{rrrr}
196 | 1 & 3 & 3 & 1 \\
197 | 1 & 3 & 3 & 1 \\
198 | 1 & 3 & 3 & 1 \\
199 | 1 & 3 & 3 & 1
200 | \end{array}\right]\left[\begin{array}{rrrr}
201 | 1 & 1 & 1 & 1 \\
202 | 1 & -1 & 1 & -1 \\
203 | 1 & 1 & -1 & -1 \\
204 | 1 & -1 & -1 & 1
205 | \end{array}\right]
206 | =\left[\begin{array}{rrrr}
207 | 2 & 0 & 0 & -1 \\
208 | 0 & 0 & 0 & 0 \\
209 | 0 & 0 & 0 & 0 \\
210 | 0 & 0 & 0 & 0
211 | \end{array}\right]
212 | \end{aligned}
213 | $$
214 |
215 |
216 |
217 | $$
218 | W_{2}=\frac{1}{4^{2}}\left[\begin{array}{rrrr}
219 | 1 & 1 & 1 & 1 \\
220 | 1 & -1 & 1 & -1 \\
221 | 1 & 1 & -1 & -1 \\
222 | 1 & -1 & -1 & 1
223 | \end{array}\right]\left[\begin{array}{rrrr}
224 | 1 & 1 & 1 & 1 \\
225 | 1 & 1 & 1 & 1 \\
226 | 1 & 1 & 1 & 1 \\
227 | 1 & 1 & 1 & 1
228 | \end{array}\right]\left[\begin{array}{rrrr}
229 | 1 & 1 & 1 & 1 \\
230 | 1 & -1 & 1 & -1 \\
231 | 1 & 1 & -1 & -1 \\
232 | 1 & -1 & -1 & 1
233 | \end{array}\right]
234 |
235 | =\left[\begin{array}{rrrr}
236 | 1 & 0 & 0 & 0 \\
237 | 0 & 0 & 0 & 0 \\
238 | 0 & 0 & 0 & 0 \\
239 | 0 & 0 & 0 & 0
240 | \end{array}\right]
241 | $$
242 |
243 | ---
244 |
245 | 再如, 图2-12是一幅数字图像及对其进行二维WHT变换的结果。
246 |
247 |
175 |
176 | 图2-11 DFT和DCT的频谱分布
177 |
178 | (a)DFT频谱分布; (b) DCT频谱分布
179 |
--------------------------------------------------------------------------------
/II/2.5 离散沃尔什-哈达玛变换(WHT).md:
--------------------------------------------------------------------------------
1 | # 2.5 离散沃尔什-哈达玛变换(WHT)
2 |
3 | ## 2.5.1 一维离散沃尔什-哈达玛变换
4 |
5 | ### 沃尔什函数
6 |
7 | 沃尔什函数是1923年由美国数学家沃尔什提出的。沃尔什函数系是一个完备正交函数系, 其值只能取 +1 和 -1 。从排列次序上可将沃尔什函数分为三种定义方法: 一种是按照沃尔什排列来定义 (按列率排序) ; 另一种是按照佩利排列来定义(按自然排序);第三种是按照哈达玛排列来定义。由于哈达玛排序的沃尔什函数是由 $2^{n}(n=0,1,2, \ldots)$ 阶哈达玛矩阵 (Hadamard Matrix) 得到的, 而哈达玛矩阵的最大优点在于它具有简单的递推关系, 即高阶矩阵可用两个低阶矩阵的克罗内克积求得, 因此在此只介绍哈达玛排列定义的沃尔什变换。
8 |
9 | $N=2^{n}(n=0,1,2, \ldots)$ 阶哈达玛矩阵每一行的符号变化规律对应于某一个沃尔什函数的符号变化规律, 即 $N=2 n(n=0,1,2, \ldots)$ 阶哈达玛矩阵的每一行对应于一个离散沃尔什函数, 哈达玛矩阵与沃尔什函数系不同之处仅仅是行的次序不同。 $2^{n}$ 阶哈达玛矩阵有如下形式:
10 | $$
11 | H_{1}=\text { [1] }\tag{2-64}
12 | $$
13 |
14 | $$
15 | H_{2}=\left[\begin{array}{rr}
16 | 1 & 1 \\
17 | 1 & -1
18 | \end{array}\right]\tag{2-65}
19 | $$
20 |
21 | $$
22 | H_{4}=\left[\begin{array}{rr}
23 | H_{2} & H_{2} \\
24 | H_{2} & -H_{2}
25 | \end{array}\right]=\left[\begin{array}{rrrr}
26 | 1 & 1 & 1 & 1 \\
27 | 1 & -1 & 1 & -1 \\
28 | 1 & 1 & -1 & -1 \\
29 | 1 & -1 & -1 & 1
30 | \end{array}\right]\tag{2-66}
31 | $$
32 |
33 | 哈达玛矩阵的阶数是按 $N=2^{n}(n=0,1,2, \ldots)$ 规律排列的, 阶数较高的哈达玛矩阵, 可以利用矩阵的克罗内克积运算, 由低阶哈达玛矩阵递推得到, 即
34 |
35 | $$
36 | H_{N}=H_{2^{n}}=H_{2} \otimes H_{2^{n-1}}=\left[\begin{array}{cc}
37 | H_{2^{n-1}} & H_{2^{n-1}} \\
38 | H_{2^{n-1}} & -H_{2^{n-1}}
39 | \end{array}\right]=\left[\begin{array}{cc}
40 | H_{\frac{N}{2}} & H_{\frac{N}{2}} \\
41 | H_{\frac{N}{2}} & -H_{\frac{N}{2}}
42 | \end{array}\right]\tag{2-67}
43 | $$
44 |
45 |
46 |
47 | 矩阵的克罗内克积 (Kronecker Product) 运算用符号记作$A \odot B$, 其运算规律如下:
48 |
49 | 设
50 |
51 | $$
52 | A=\left[\begin{array}{llll}
53 | a_{11} & a_{12} & \cdots & a_{1 n} \\
54 | a_{21} & a_{22} & \cdots & a_{2 n} \\
55 | \vdots & \vdots & \ddots & \vdots \\
56 | a_{m 1} & a_{m 2} & \cdots & a_{mn}
57 | \end{array}\right]&&
58 | B=\left[\begin{array}{rrrr}
59 | b_{11} & b_{12} & \cdots & b_{1 j} \\
60 | b_{21} & b_{22} & \cdots & a_{2 j} \\
61 | \vdots & \vdots & \ddots & \vdots \\
62 | b_{i 1} & b_{i 2} & \cdots & b_{i j}
63 | \end{array}\right]
64 | $$
65 |
66 | $$
67 |
68 | $$
69 |
70 | 则
71 |
72 | $$
73 | A \otimes B=\left[\begin{array}{llll}
74 | a_{11} B & a_{12} B & \cdots & a_{1 n} B \\
75 | a_{21} B & a_{22} B & \cdots & a_{2 n} B \\
76 | \vdots & \vdots & \ddots & \vdots \\
77 | a_{m 1} B & a_{m 2} B & \cdots & a_{m n} B
78 | \end{array}\right] \\
79 |
80 | \tag{2-68}
81 | $$
82 |
83 | $$
84 | B \otimes A=\left[\begin{array}{cccc}
85 | b_{11} A & b_{12} A & \cdots & b_{1 j} A \\
86 | b_{21} A & b_{22} A & \cdots & b_{2 j} A \\
87 | \vdots & \vdots & \ddots & \vdots \\
88 | b_{i 1} A & a_{i 2} A & \cdots & b_{i j} A
89 | \end{array}\right]\tag{2-69}
90 | $$
91 |
92 |
93 |
94 | ### 离散沃尔什-哈达玛变换
95 |
96 | 一维离散沃尔什变换定义为
97 |
98 | $$
99 | W(u)=\frac{1}{N} \sum_{x=0}^{N-1} f(x) W a l s h(u, x)\tag{2-70}
100 | $$
101 |
102 | 一维离散沃尔什逆变换定义为
103 |
104 | $$
105 | f(x)=\sum_{u=0}^{N-1} W(u) W a l s h(u, x)\tag{2-71}
106 | $$
107 |
108 | 式中, $\operatorname{Walsh}(u, x)$ 为沃尔什函数。若将 $W a l s h(u, x)$ 用哈达玛矩阵表示, 并将变换表达式写成矩阵形式, 则式(2-70)和式(2-71) 分别为
109 |
110 | $$
111 | \left[\begin{array}{c}
112 | W(0) \\
113 | W(1) \\
114 | \vdots \\
115 | W(N-1)
116 | \end{array}\right]=\frac{1}{N}\left[H_{N}\right]\left[\begin{array}{c}
117 | f(0) \\
118 | f(1) \\
119 | \vdots \\
120 | f(N-1)
121 | \end{array}\right]\tag{2-72}
122 | $$
123 |
124 | 和
125 |
126 | $$
127 | \left[\begin{array}{c}
128 | f(0) \\
129 | f(1) \\
130 | \vdots \\
131 | f(N-1)
132 | \end{array}\right]=\left[H_{N}\right]\left[\begin{array}{c}
133 | W(0) \\
134 | W(1) \\
135 | \vdots \\
136 | W(N-1)
137 | \end{array}\right]\tag{2-73}
138 | $$
139 |
140 | 式中, $\left[H_{N}\right]$ 为 $N$ 阶哈达玛矩阵。 由哈达玛矩阵的特点可知, 沃尔什-哈达玛变换的本质上是
141 |
142 | 由哈达玛矩阵的特点可知,沃尔什-哈达玛变换的本质上是将离散序列 $f(x)$ 的各项值的符号按一定规律改变后, 进行加减运算, 因此, 它比采用复数运算的DFT和采用余弦运算的DCT要简单得多。
143 |
144 |
145 |
146 | ## 2.5.2 二维离散沃尔什变换
147 |
148 | 很容易将一维WHT的定义推广到二维WHT。二维WHT的正变换核和逆变换核分别为
149 |
150 | $$
151 | W(u, v)=\frac{1}{M N} \sum_{x=0}^{M-1} \sum_{y=0}^{N-1} f(x, y) W a l s h(u, x) W slsh(v, y)\tag{2-74}
152 | $$
153 |
154 | 和
155 |
156 | $$
157 | f(x, y)=\sum_{u=0}^{M-1} \sum_{v=0}^{N-1} W(u, v) W a l s h(u, x) W s
158 | lsh(v, y)\tag{2-75}
159 | $$
160 |
161 | 式中: $x, u=0,1,2, \ldots, M-1 ; y, v=0,1,2, \ldots, N-1$ 。
162 |
163 | ---
164 |
165 | 二维离散沃尔什变换的矩阵形式表达式为
166 | $$
167 | f_{1}=\left[\begin{array}{llll}1 & 3 & 3 & 1 \\ 1 & 3 & 3 & 1 \\ 1 & 3 & 3 & 1 \\ 1 & 3 & 3 & 1\end{array}\right]
168 | $$
169 | 和
170 | $$
171 | f_{1}=\left[\begin{array}{llll}1 & 1 & 1 & 1 \\ 1 & 1 & 1 & 1 \\ 1 & 1 & 1 & 1 \\ 1 & 1 & 1 & 1\end{array}\right]
172 | $$
173 |
174 | 求这两个信号的二维WHT。
175 |
176 | 根据题意, 式 (2-76) 中的 $M=N=4$, 其二维WHT变换核为
177 | $$
178 | H_{4}=\left[\begin{array}{rrrr}
179 | 1 & 1 & 1 & 1 \\
180 | 1 & -1 & 1 & -1 \\
181 | 1 & 1 & -1 & -1 \\
182 | 1 & -1 & -1 & 1
183 | \end{array}\right]
184 | $$
185 |
186 | 所以
187 |
188 | $$
189 | \begin{aligned}
190 | W_{1} & =\frac{1}{4^{2}}\left[\begin{array}{rrrr}
191 | 1 & 1 & 1 & 1 \\
192 | 1 & -1 & 1 & -1 \\
193 | 1 & 1 & -1 & -1 \\
194 | 1 & -1 & -1 & 1
195 | \end{array}\right]\left[\begin{array}{rrrr}
196 | 1 & 3 & 3 & 1 \\
197 | 1 & 3 & 3 & 1 \\
198 | 1 & 3 & 3 & 1 \\
199 | 1 & 3 & 3 & 1
200 | \end{array}\right]\left[\begin{array}{rrrr}
201 | 1 & 1 & 1 & 1 \\
202 | 1 & -1 & 1 & -1 \\
203 | 1 & 1 & -1 & -1 \\
204 | 1 & -1 & -1 & 1
205 | \end{array}\right]
206 | =\left[\begin{array}{rrrr}
207 | 2 & 0 & 0 & -1 \\
208 | 0 & 0 & 0 & 0 \\
209 | 0 & 0 & 0 & 0 \\
210 | 0 & 0 & 0 & 0
211 | \end{array}\right]
212 | \end{aligned}
213 | $$
214 |
215 |
216 |
217 | $$
218 | W_{2}=\frac{1}{4^{2}}\left[\begin{array}{rrrr}
219 | 1 & 1 & 1 & 1 \\
220 | 1 & -1 & 1 & -1 \\
221 | 1 & 1 & -1 & -1 \\
222 | 1 & -1 & -1 & 1
223 | \end{array}\right]\left[\begin{array}{rrrr}
224 | 1 & 1 & 1 & 1 \\
225 | 1 & 1 & 1 & 1 \\
226 | 1 & 1 & 1 & 1 \\
227 | 1 & 1 & 1 & 1
228 | \end{array}\right]\left[\begin{array}{rrrr}
229 | 1 & 1 & 1 & 1 \\
230 | 1 & -1 & 1 & -1 \\
231 | 1 & 1 & -1 & -1 \\
232 | 1 & -1 & -1 & 1
233 | \end{array}\right]
234 |
235 | =\left[\begin{array}{rrrr}
236 | 1 & 0 & 0 & 0 \\
237 | 0 & 0 & 0 & 0 \\
238 | 0 & 0 & 0 & 0 \\
239 | 0 & 0 & 0 & 0
240 | \end{array}\right]
241 | $$
242 |
243 | ---
244 |
245 | 再如, 图2-12是一幅数字图像及对其进行二维WHT变换的结果。
246 |
247 |  248 |
249 | 图2-12二维WHT结果
250 | (a)原图像;(b) WHT结果
251 |
252 | 注: 图2-12中的结果是按哈达玛变换后再用沃尔什排序的结果。
253 |
254 | 从以上例子可看出, 二维WHT具有能量集中的特性, 而且原始数据中数字越是均匀分布, 经变换后的数据越集中于矩阵的边角上。因此,二维WHT可用于压缩图像信息。
255 |
256 | ## 2.5.3 快速沃尔什变换(FWHT)
257 |
258 | 类似于FFT, WHT也有快速算法FWHT, 也可将输入序列 $f(x)$ 按奇偶进行分组, 分别进行WHT。FWHT的基本关系为
259 |
260 | $$
261 | \left\{\begin{array}{l}
262 | W(u)=\dfrac{1}{2}\left[W_{e}(u)+W_{o}(u)\right] \\
263 | W\left(u+\frac{N}{2}\right)=\dfrac{1}{2}\left[W_{e}(u)-W_{o}(u)\right]
264 | \end{array}\right.\tag{2-78}
265 | $$
266 |
267 | WHT的变换核是可分离和对称的, 因此二维WHT也可分为两个一维的WHT分别用FWHT进行变换而得到最终结果, 由此便可实现二维的FWHT。
268 |
269 | 综上所述, WHT是将一个函数变换成取值为 +1 或 -1 的基本函数构成的级数, 用它来逼近数字脉冲信号时要比FFT有利。
270 |
271 | 同时, WHT只需要进行实数运算, 存储量比FFT要少得多,运算速度也快得多。因此, WHT在图像传输、通信技术和数据压缩中被广泛使用。
--------------------------------------------------------------------------------
/II/2.6 实现图像变换的VC++编程.md:
--------------------------------------------------------------------------------
1 | # 2.6 用Matrix \C++ 库实现图像变换的VC++编程
2 |
3 | ## 2.6.1 Matrix\简介及其与VC++工程的集成
4 |
5 | ### Matrix\简介
6 |
7 | Matrix\C++数学库是MathTools公司利用Matcom技术开发的一个面向专业从事工程技术和科学计算人员的矩阵运算动态链接库。这个C++库提供了绝大多数的关于矩阵类、矩阵操作、 数值计算等函数的定义,它提供了一个双精度Matrix类型——Mm, 它可以定义的矩阵是复数矩阵、实数矩阵、稀疏矩阵甚至n维矩阵。同时还提供了近千个与矩阵运算相关的函数,并对如+、-、 *、 /、 ()等操作符进行了重载。库中所提供的函数涉及线性代数、多项式数学、信号处理、文件输入/输出、绘图等各个方面。充分利用这些库函数, 便可完成数字图像变换的各种操作。
8 |
9 | ### 在C++工程中集成Matrix\C++数学库
10 |
11 | 为了将Matrix\C++库集成到C++的工程文件中,需要做如下的操作:
12 |
13 | (1) 将库文件v4501v.lib库文件添加到C++的工程中;
14 | (2) 将库声明头文件matlib.h包含到工程中;
15 | (3) 初始化库;
16 | (4) 创建矩阵变量;
17 | (5) 访问矩阵单元;
18 | (6) 调用Matrix\C++库函数完成矩阵操作。
19 |
20 | 为了使读者掌握如何在VC++中使用Matrix\C++数学库的方法,下面详细介绍从创建工程到最后调用Matrix\C++库函数的全过程。
21 | 1) 创建一个新的VC++工程[HTSS]
22 | 在VC++中,采用默认选项创建一个MDI MFC工程。当然MatrixC++库可以用在任何其他类型的工程中,如Console 、 OWL、ActiveX等。
23 |
24 | 2) 将库文件添加到工程中
25 | 为使C++编译器能够将Matrix\C++库链接到最后的执行文件中去,必须将MatrixC++库加入到C++的工程文件中。用菜单命令Project/Add to Project/Files…将C:\matcom45\lib\v4501v.lib(如果v4501v.lib存在不同的文件夹中,请选择正确的路径)加入到C++工程中。
26 |
27 | 3) 包含matlib.h头文件
28 | 在要使用Matrix\C++库的.h或.cpp文件的头部, 将matlib.h头文件包含到工程中,即在使用Matrix\C++库的.h或.cpp文件头部添加如下代码:
29 |
30 |
31 | ```c++
32 | #include"matlib.h"
33 | ```
34 |
35 | 同时用菜单命令Tools/Options…/Directories设置matlib.h所在的路径,以便编译器能找到相应的头文件。
36 |
37 | 4. 初始化Matrix\C++库
38 |
39 | 调用Matrix\C++库函数之前,要用initM(MATCOM_VERSION)函数来初始化类库调用,并用exitM()函数来结束类库调用, 故还应在.cpp 中加入下列代码:
40 |
41 | ```c++
42 | initM(MATCOM_VERSION);
43 | ...//用MatrixC++库函数的调用完成矩阵操作
44 | exitM();
45 | ```
46 |
47 | 当然可以在一个类的构造函数中添加
48 |
49 | ```c++
50 | initM(MATCOM_VERSION);
51 | ```
52 |
53 | 以完成类库的初始化工作。
54 |
55 | 可在该类的析构函数中添加
56 |
57 | ```c++
58 | exitM()
59 | ```
60 |
61 | 以完成结束类库调用的工作。
62 |
63 | MATCOM_VERSION参数是一个在matlib.h头文件中定义的值为4501的常量(不同版本其值有所差异), 它保证了动态链接库与matlib.h的匹配。
64 |
65 | 5) 创建矩阵变量
66 |
67 | 添加了Matrix\C++库后,可用关键字Mm来定义中矩阵类型变量, 例如:
68 |
69 | ```c++
70 | Mm a,b,x;
71 | ```
72 |
73 | 这条VC++语句在当前工程文件中创建了a、b、x三个矩阵变量,但这时a、b和x还只是空的矩阵, 它们的矩阵单元还不包含任何的值。
74 |
75 | 6) 访问矩阵单元
76 |
77 | 矩阵单元的访问包括读和写操作,主要有:通过.r()来访问矩阵的实部,通过.i()来访问矩阵的虚部; 通过BR()函数把一个数据列表赋给矩阵各个单元;通过.addr()或.addi()返回矩阵变量的实部或虚部的内存指针来完成对矩阵单元的访问。
78 |
79 | ### 安装与Matrix\C++库对应的动态链接库
80 |
81 | 当采用Matrix\C++数学库完成矩阵的运算时, 要求系统中有相关的ago4501.dll, v4501v.dll, opengl32.dll和glu32.dll四个动态链接库文件。如果系统中安装有Matcom4.5,这些动态链接库文件将会自动安装在window\system\或window\system32\下, 如果系统没有安装Matcom4.5, 只需将这四个动态链接库文件拷贝到相应目录下即可。
82 |
83 | ## 2.6.2 创建图像数据矩阵
84 |
85 | 为利用矩阵运算完成图像变换, 首先应将其图像数据赋给矩阵变量。
86 |
87 | 设指针pBits指向读入内存中的图像数据首地址, 可用如下代码将图像数据赋给矩阵变量(为简单起见, 设图像为8位灰度图像)。
88 |
89 | ### 在类定义头文件.h中定义矩阵变量
90 |
91 | ```c++
92 | Mm m_matBits;
93 | ```
94 |
95 | ### 在类实现文件.cpp中完成对矩阵变量的赋值操作
96 |
97 | ```c++
98 | //图像数据总字节数, 其中nWidthBytes为每行图像数据占用的字节数
99 | DWORD SizeImage = nWidthBytes * nHeight;
100 | //通过创建一个1×SizeImage的一维0矩阵, 为矩阵变量分配内存
101 | m_matBits = zeros(1, SizeImage);
102 | //将矩阵由double型转换为unsigned char型, 以便将图像数据赋给矩阵
103 | m_matBits = muint8(m_matBits);
104 | //首先利用m_matBits.addr()获得矩阵实部的内存指针, 然后利用memcpy()将图像数据一次性
105 |
106 | //赋给矩阵变量
107 | memcpy(m_matBits.addr(), pBits, SizeImage);
108 | //由于Mm型的矩阵在内存中是按先列后行的顺序存储的, 因此, 应先用MatrixC++的库
109 | //函数reshape()将一维矩阵m_matBits变为nHeight×nWidthBytes的二维矩阵, 再用rot90()函数
110 |
111 | //将其逆时针旋转90°, 将矩阵变为nWidthBytes×nHeight的二维矩阵
112 | m_matBits = rot90(reshape(m_matBits, nWidthBytes, nHeight));
113 | //若图像宽度与其字节宽度不同, 则将由系统补齐的每行字节数为4的整数倍的各列0删除,以减小矩阵大小加快处理速度
114 | if(nWidthBytes != nWidth)
115 | {
116 | m_matBits = m_matBits(c_p, colon(1, 1, nWidth));
117 | }
118 | //将矩阵由unsigned char型转换为double型, 以便进行运算
119 | m_matBits = mdouble(m_matBits);
120 | ```
121 |
122 | ## 2.6.3 将矩阵数据赋给图像数据区
123 |
124 | 为使数据符合图像文件格式,还应将处理后的矩阵数据赋给图像数据区,其代码如下:
125 |
126 | ```c++
127 | //检查m_matBits矩阵是否为空
128 | if(isempty(m_matBits) == 1)
129 | {
130 | return FALSE;
131 | }
132 | //将矩阵数据范围限定于0~255之间
133 | m_matBits = mabs(m_matBits);
134 | Mm L = m_matBits > 255.0;
135 | Mm NotL = !L;
136 | m_matBits = times(m_matBits, NotL) + L * 255.0;
137 |
138 | //将矩阵由double型转换为unsigned char型, 以便将图像数据赋给矩阵
139 | m_matBits = muint8(m_matBits);
140 | //计算nWidth/4的余数
141 | int nTmp = (int)rem(nWidth, 4);
142 | int nPadding;
143 | //为矩阵各列补0, 以使其为符合4的整数倍
144 | if(nTmp > 0)
145 | {
146 | nPadding = 4 - nTmp;
147 | m_matBits = cat(2, m_matBits,
148 | repmat(muint8(0), (BR(size(m_matBits, 1)), nPadding)));
149 | }
150 | //将矩阵顺时针旋转90°
151 | m_matBits = rot90(m_matBits, -1);
152 | //将图像数据赋绘矩阵
153 | memcpy(pBits, m_matBits.addr(), (nWidthBytes * nHeight)*sizeof(unsigned char));
154 | ```
155 |
156 | ## 2.6.4 利用矩阵运算进行图像变换
157 |
158 | 图像数据矩阵建立后,便可利用Matrix\C++的库函数通过各种矩阵运算完成图像变换的工作。
159 | ### 离散傅立叶变换
160 |
161 | trix\C++的库提供了函数dft()、fft()和fft2()分别用于完成一维DFT、 一维FFT和二维FFT运算,函数ifft()和ifft2()用于完成一维FFT和二维FFT的逆傅立叶变换。在图像处理中常用的函数是fft2()和ifft2(),利用这两个函数便可分别完成图像的正、反傅立叶变换。其核心代码如下:
162 |
163 | ```c++
164 | //调用MatrixC++库函数fft2()完成二维离散傅立叶变换
165 | Mm ff = fft2(m_matBits);
166 | //调用MatrixC++库函数fftshift()将频域中心移到矩阵中心
167 | ff = fftshift(ff);
168 | //调用MatrixC++库函数mabs()计算频谱
169 | m_matBits = mabs(ff);
170 | ```
171 |
172 | ### 离散余弦变换
173 |
174 | 在Matrix\C++库中并未提供离散余弦变换函数,因此需要编写相应的变换函数。由式(7-61)和式(7-63)可知, 利用离散傅立叶正反变换便可完成离散余弦正反变换,实际上Matlab提供的dct()、 idct()、 dct2()和idct2()函数就是如此完成离散余弦正反变换的。仔细阅读相应的.m文件便可得出其实现变换的过程, 这样就可以编写用以完成一维DCT函数dct()的代码。完成一维离散余弦变换函数dct()后,利用二维DCT的可分离性,便可方便的编制出用于二维离散余弦变换函数dct2()。其核心代码为
175 |
176 | ```c++
177 | b = transpose(dct(transpose(dct(arg1))));
178 | ```
179 |
180 | 其中, arg1为待变换矩阵。
181 |
182 | 同理, 可编制出一维IDCT函数变换idct()和二维IDCT函数idct2()。
183 |
184 | 与图像的离散傅立叶变换类似, 实现图像的离散余弦变换的代码如下:
185 |
186 | ```c++
187 | Mm ff = dct2(m_matBits);
188 | //调用MatrixC++库函数mabs()计算频谱
189 | m_matBits = mabs(ff);
190 | ```
191 |
192 | ### 离散沃尔什-哈达玛变换
193 |
194 | 同样,在Matri\C++库中并未提供离散沃尔什-哈达玛变换的函数,但它提供了用于产生哈达玛矩阵的函数hadamard(), 其语法为
195 |
196 | ```c++
197 | H=hadamard(N);
198 | ```
199 |
200 | 其中的元素为1或-1, 注意该矩阵只有当n或n/12或n/20为2的整次幂时才存在。
201 |
202 | 利用矩阵形式的WHT, 可由如下代码完成离散沃尔什-哈达玛变换:
203 |
204 | ```c++
205 | //获得矩阵的行数和列数
206 | Mm mSize = size(m_matBits);
207 | //生成哈达玛矩阵
208 | Mm HColum = hadamard(mSize.r(1, 1));
209 | Mm HRow = hadamard(mSize.r(1, 2));
210 | //进行离散哈达玛变换
211 | Mm ff = HRow * m_matBits * HColum;
212 | //调整系数以便以图像方式显示结果
213 | ff = ff * 1000/(mSize.r(1, 1)*mSize.r(1, 2));
214 | //调用MatrixC++库函数mabs()计算频谱
215 | m_matBits = mabs(ff);
216 | ```
--------------------------------------------------------------------------------
/II/2.7 小波变换简介.md:
--------------------------------------------------------------------------------
1 | # 2.7 小波变换简介
2 |
3 | ## 2.7.1 小波变换的理论基础
4 |
5 | 本质:任何信号都是由低频+高频信号合成可进一步分解
6 |
7 | 信号分析是为了获得时间和频率之间的相互关系。傅立叶变换提供了有关频率域的信息, 但有关时间的局部化信息却基本丢失。与傅立叶变换不同, 小波变换是通过缩放母小波 (Mother wavelet)的宽度来获得信号的频率特征, 通过平移母小波来获得信号的时间信息。对母小波的缩放和平移操作是为了计算小波系数, 这些小波系数反映了小波和局部信号之间的相关程度。
8 |
9 | ### 连续小波变换(CWT)
10 |
11 | 像傅立叶分析一样, 小波分析就是把一个信号分解为将母小波经过缩放和平移之后的一系列小波, 因此小波是小波变换的基函数。小波变换可以理解为用经过缩放和平移的一系列小波函数代替傅立叶变换的正弦波和余弦波进行傅立叶变换的结果。
12 |
13 | 图7-13表示了正弦波和小波的区别, 由此可以看出, 正弦波从负无穷一直延续到正无穷, 正弦波是平滑而且是可预测的, 而小波是一类在有限区间内快速衰减到 0 的函数, 其平均值为 0 , 小波趋于不规则、不对称。
14 |
15 |
248 |
249 | 图2-12二维WHT结果
250 | (a)原图像;(b) WHT结果
251 |
252 | 注: 图2-12中的结果是按哈达玛变换后再用沃尔什排序的结果。
253 |
254 | 从以上例子可看出, 二维WHT具有能量集中的特性, 而且原始数据中数字越是均匀分布, 经变换后的数据越集中于矩阵的边角上。因此,二维WHT可用于压缩图像信息。
255 |
256 | ## 2.5.3 快速沃尔什变换(FWHT)
257 |
258 | 类似于FFT, WHT也有快速算法FWHT, 也可将输入序列 $f(x)$ 按奇偶进行分组, 分别进行WHT。FWHT的基本关系为
259 |
260 | $$
261 | \left\{\begin{array}{l}
262 | W(u)=\dfrac{1}{2}\left[W_{e}(u)+W_{o}(u)\right] \\
263 | W\left(u+\frac{N}{2}\right)=\dfrac{1}{2}\left[W_{e}(u)-W_{o}(u)\right]
264 | \end{array}\right.\tag{2-78}
265 | $$
266 |
267 | WHT的变换核是可分离和对称的, 因此二维WHT也可分为两个一维的WHT分别用FWHT进行变换而得到最终结果, 由此便可实现二维的FWHT。
268 |
269 | 综上所述, WHT是将一个函数变换成取值为 +1 或 -1 的基本函数构成的级数, 用它来逼近数字脉冲信号时要比FFT有利。
270 |
271 | 同时, WHT只需要进行实数运算, 存储量比FFT要少得多,运算速度也快得多。因此, WHT在图像传输、通信技术和数据压缩中被广泛使用。
--------------------------------------------------------------------------------
/II/2.6 实现图像变换的VC++编程.md:
--------------------------------------------------------------------------------
1 | # 2.6 用Matrix \C++ 库实现图像变换的VC++编程
2 |
3 | ## 2.6.1 Matrix\简介及其与VC++工程的集成
4 |
5 | ### Matrix\简介
6 |
7 | Matrix\C++数学库是MathTools公司利用Matcom技术开发的一个面向专业从事工程技术和科学计算人员的矩阵运算动态链接库。这个C++库提供了绝大多数的关于矩阵类、矩阵操作、 数值计算等函数的定义,它提供了一个双精度Matrix类型——Mm, 它可以定义的矩阵是复数矩阵、实数矩阵、稀疏矩阵甚至n维矩阵。同时还提供了近千个与矩阵运算相关的函数,并对如+、-、 *、 /、 ()等操作符进行了重载。库中所提供的函数涉及线性代数、多项式数学、信号处理、文件输入/输出、绘图等各个方面。充分利用这些库函数, 便可完成数字图像变换的各种操作。
8 |
9 | ### 在C++工程中集成Matrix\C++数学库
10 |
11 | 为了将Matrix\C++库集成到C++的工程文件中,需要做如下的操作:
12 |
13 | (1) 将库文件v4501v.lib库文件添加到C++的工程中;
14 | (2) 将库声明头文件matlib.h包含到工程中;
15 | (3) 初始化库;
16 | (4) 创建矩阵变量;
17 | (5) 访问矩阵单元;
18 | (6) 调用Matrix\C++库函数完成矩阵操作。
19 |
20 | 为了使读者掌握如何在VC++中使用Matrix\C++数学库的方法,下面详细介绍从创建工程到最后调用Matrix\C++库函数的全过程。
21 | 1) 创建一个新的VC++工程[HTSS]
22 | 在VC++中,采用默认选项创建一个MDI MFC工程。当然MatrixC++库可以用在任何其他类型的工程中,如Console 、 OWL、ActiveX等。
23 |
24 | 2) 将库文件添加到工程中
25 | 为使C++编译器能够将Matrix\C++库链接到最后的执行文件中去,必须将MatrixC++库加入到C++的工程文件中。用菜单命令Project/Add to Project/Files…将C:\matcom45\lib\v4501v.lib(如果v4501v.lib存在不同的文件夹中,请选择正确的路径)加入到C++工程中。
26 |
27 | 3) 包含matlib.h头文件
28 | 在要使用Matrix\C++库的.h或.cpp文件的头部, 将matlib.h头文件包含到工程中,即在使用Matrix\C++库的.h或.cpp文件头部添加如下代码:
29 |
30 |
31 | ```c++
32 | #include"matlib.h"
33 | ```
34 |
35 | 同时用菜单命令Tools/Options…/Directories设置matlib.h所在的路径,以便编译器能找到相应的头文件。
36 |
37 | 4. 初始化Matrix\C++库
38 |
39 | 调用Matrix\C++库函数之前,要用initM(MATCOM_VERSION)函数来初始化类库调用,并用exitM()函数来结束类库调用, 故还应在.cpp 中加入下列代码:
40 |
41 | ```c++
42 | initM(MATCOM_VERSION);
43 | ...//用MatrixC++库函数的调用完成矩阵操作
44 | exitM();
45 | ```
46 |
47 | 当然可以在一个类的构造函数中添加
48 |
49 | ```c++
50 | initM(MATCOM_VERSION);
51 | ```
52 |
53 | 以完成类库的初始化工作。
54 |
55 | 可在该类的析构函数中添加
56 |
57 | ```c++
58 | exitM()
59 | ```
60 |
61 | 以完成结束类库调用的工作。
62 |
63 | MATCOM_VERSION参数是一个在matlib.h头文件中定义的值为4501的常量(不同版本其值有所差异), 它保证了动态链接库与matlib.h的匹配。
64 |
65 | 5) 创建矩阵变量
66 |
67 | 添加了Matrix\C++库后,可用关键字Mm来定义中矩阵类型变量, 例如:
68 |
69 | ```c++
70 | Mm a,b,x;
71 | ```
72 |
73 | 这条VC++语句在当前工程文件中创建了a、b、x三个矩阵变量,但这时a、b和x还只是空的矩阵, 它们的矩阵单元还不包含任何的值。
74 |
75 | 6) 访问矩阵单元
76 |
77 | 矩阵单元的访问包括读和写操作,主要有:通过.r()来访问矩阵的实部,通过.i()来访问矩阵的虚部; 通过BR()函数把一个数据列表赋给矩阵各个单元;通过.addr()或.addi()返回矩阵变量的实部或虚部的内存指针来完成对矩阵单元的访问。
78 |
79 | ### 安装与Matrix\C++库对应的动态链接库
80 |
81 | 当采用Matrix\C++数学库完成矩阵的运算时, 要求系统中有相关的ago4501.dll, v4501v.dll, opengl32.dll和glu32.dll四个动态链接库文件。如果系统中安装有Matcom4.5,这些动态链接库文件将会自动安装在window\system\或window\system32\下, 如果系统没有安装Matcom4.5, 只需将这四个动态链接库文件拷贝到相应目录下即可。
82 |
83 | ## 2.6.2 创建图像数据矩阵
84 |
85 | 为利用矩阵运算完成图像变换, 首先应将其图像数据赋给矩阵变量。
86 |
87 | 设指针pBits指向读入内存中的图像数据首地址, 可用如下代码将图像数据赋给矩阵变量(为简单起见, 设图像为8位灰度图像)。
88 |
89 | ### 在类定义头文件.h中定义矩阵变量
90 |
91 | ```c++
92 | Mm m_matBits;
93 | ```
94 |
95 | ### 在类实现文件.cpp中完成对矩阵变量的赋值操作
96 |
97 | ```c++
98 | //图像数据总字节数, 其中nWidthBytes为每行图像数据占用的字节数
99 | DWORD SizeImage = nWidthBytes * nHeight;
100 | //通过创建一个1×SizeImage的一维0矩阵, 为矩阵变量分配内存
101 | m_matBits = zeros(1, SizeImage);
102 | //将矩阵由double型转换为unsigned char型, 以便将图像数据赋给矩阵
103 | m_matBits = muint8(m_matBits);
104 | //首先利用m_matBits.addr()获得矩阵实部的内存指针, 然后利用memcpy()将图像数据一次性
105 |
106 | //赋给矩阵变量
107 | memcpy(m_matBits.addr(), pBits, SizeImage);
108 | //由于Mm型的矩阵在内存中是按先列后行的顺序存储的, 因此, 应先用MatrixC++的库
109 | //函数reshape()将一维矩阵m_matBits变为nHeight×nWidthBytes的二维矩阵, 再用rot90()函数
110 |
111 | //将其逆时针旋转90°, 将矩阵变为nWidthBytes×nHeight的二维矩阵
112 | m_matBits = rot90(reshape(m_matBits, nWidthBytes, nHeight));
113 | //若图像宽度与其字节宽度不同, 则将由系统补齐的每行字节数为4的整数倍的各列0删除,以减小矩阵大小加快处理速度
114 | if(nWidthBytes != nWidth)
115 | {
116 | m_matBits = m_matBits(c_p, colon(1, 1, nWidth));
117 | }
118 | //将矩阵由unsigned char型转换为double型, 以便进行运算
119 | m_matBits = mdouble(m_matBits);
120 | ```
121 |
122 | ## 2.6.3 将矩阵数据赋给图像数据区
123 |
124 | 为使数据符合图像文件格式,还应将处理后的矩阵数据赋给图像数据区,其代码如下:
125 |
126 | ```c++
127 | //检查m_matBits矩阵是否为空
128 | if(isempty(m_matBits) == 1)
129 | {
130 | return FALSE;
131 | }
132 | //将矩阵数据范围限定于0~255之间
133 | m_matBits = mabs(m_matBits);
134 | Mm L = m_matBits > 255.0;
135 | Mm NotL = !L;
136 | m_matBits = times(m_matBits, NotL) + L * 255.0;
137 |
138 | //将矩阵由double型转换为unsigned char型, 以便将图像数据赋给矩阵
139 | m_matBits = muint8(m_matBits);
140 | //计算nWidth/4的余数
141 | int nTmp = (int)rem(nWidth, 4);
142 | int nPadding;
143 | //为矩阵各列补0, 以使其为符合4的整数倍
144 | if(nTmp > 0)
145 | {
146 | nPadding = 4 - nTmp;
147 | m_matBits = cat(2, m_matBits,
148 | repmat(muint8(0), (BR(size(m_matBits, 1)), nPadding)));
149 | }
150 | //将矩阵顺时针旋转90°
151 | m_matBits = rot90(m_matBits, -1);
152 | //将图像数据赋绘矩阵
153 | memcpy(pBits, m_matBits.addr(), (nWidthBytes * nHeight)*sizeof(unsigned char));
154 | ```
155 |
156 | ## 2.6.4 利用矩阵运算进行图像变换
157 |
158 | 图像数据矩阵建立后,便可利用Matrix\C++的库函数通过各种矩阵运算完成图像变换的工作。
159 | ### 离散傅立叶变换
160 |
161 | trix\C++的库提供了函数dft()、fft()和fft2()分别用于完成一维DFT、 一维FFT和二维FFT运算,函数ifft()和ifft2()用于完成一维FFT和二维FFT的逆傅立叶变换。在图像处理中常用的函数是fft2()和ifft2(),利用这两个函数便可分别完成图像的正、反傅立叶变换。其核心代码如下:
162 |
163 | ```c++
164 | //调用MatrixC++库函数fft2()完成二维离散傅立叶变换
165 | Mm ff = fft2(m_matBits);
166 | //调用MatrixC++库函数fftshift()将频域中心移到矩阵中心
167 | ff = fftshift(ff);
168 | //调用MatrixC++库函数mabs()计算频谱
169 | m_matBits = mabs(ff);
170 | ```
171 |
172 | ### 离散余弦变换
173 |
174 | 在Matrix\C++库中并未提供离散余弦变换函数,因此需要编写相应的变换函数。由式(7-61)和式(7-63)可知, 利用离散傅立叶正反变换便可完成离散余弦正反变换,实际上Matlab提供的dct()、 idct()、 dct2()和idct2()函数就是如此完成离散余弦正反变换的。仔细阅读相应的.m文件便可得出其实现变换的过程, 这样就可以编写用以完成一维DCT函数dct()的代码。完成一维离散余弦变换函数dct()后,利用二维DCT的可分离性,便可方便的编制出用于二维离散余弦变换函数dct2()。其核心代码为
175 |
176 | ```c++
177 | b = transpose(dct(transpose(dct(arg1))));
178 | ```
179 |
180 | 其中, arg1为待变换矩阵。
181 |
182 | 同理, 可编制出一维IDCT函数变换idct()和二维IDCT函数idct2()。
183 |
184 | 与图像的离散傅立叶变换类似, 实现图像的离散余弦变换的代码如下:
185 |
186 | ```c++
187 | Mm ff = dct2(m_matBits);
188 | //调用MatrixC++库函数mabs()计算频谱
189 | m_matBits = mabs(ff);
190 | ```
191 |
192 | ### 离散沃尔什-哈达玛变换
193 |
194 | 同样,在Matri\C++库中并未提供离散沃尔什-哈达玛变换的函数,但它提供了用于产生哈达玛矩阵的函数hadamard(), 其语法为
195 |
196 | ```c++
197 | H=hadamard(N);
198 | ```
199 |
200 | 其中的元素为1或-1, 注意该矩阵只有当n或n/12或n/20为2的整次幂时才存在。
201 |
202 | 利用矩阵形式的WHT, 可由如下代码完成离散沃尔什-哈达玛变换:
203 |
204 | ```c++
205 | //获得矩阵的行数和列数
206 | Mm mSize = size(m_matBits);
207 | //生成哈达玛矩阵
208 | Mm HColum = hadamard(mSize.r(1, 1));
209 | Mm HRow = hadamard(mSize.r(1, 2));
210 | //进行离散哈达玛变换
211 | Mm ff = HRow * m_matBits * HColum;
212 | //调整系数以便以图像方式显示结果
213 | ff = ff * 1000/(mSize.r(1, 1)*mSize.r(1, 2));
214 | //调用MatrixC++库函数mabs()计算频谱
215 | m_matBits = mabs(ff);
216 | ```
--------------------------------------------------------------------------------
/II/2.7 小波变换简介.md:
--------------------------------------------------------------------------------
1 | # 2.7 小波变换简介
2 |
3 | ## 2.7.1 小波变换的理论基础
4 |
5 | 本质:任何信号都是由低频+高频信号合成可进一步分解
6 |
7 | 信号分析是为了获得时间和频率之间的相互关系。傅立叶变换提供了有关频率域的信息, 但有关时间的局部化信息却基本丢失。与傅立叶变换不同, 小波变换是通过缩放母小波 (Mother wavelet)的宽度来获得信号的频率特征, 通过平移母小波来获得信号的时间信息。对母小波的缩放和平移操作是为了计算小波系数, 这些小波系数反映了小波和局部信号之间的相关程度。
8 |
9 | ### 连续小波变换(CWT)
10 |
11 | 像傅立叶分析一样, 小波分析就是把一个信号分解为将母小波经过缩放和平移之后的一系列小波, 因此小波是小波变换的基函数。小波变换可以理解为用经过缩放和平移的一系列小波函数代替傅立叶变换的正弦波和余弦波进行傅立叶变换的结果。
12 |
13 | 图7-13表示了正弦波和小波的区别, 由此可以看出, 正弦波从负无穷一直延续到正无穷, 正弦波是平滑而且是可预测的, 而小波是一类在有限区间内快速衰减到 0 的函数, 其平均值为 0 , 小波趋于不规则、不对称。
14 |
15 | 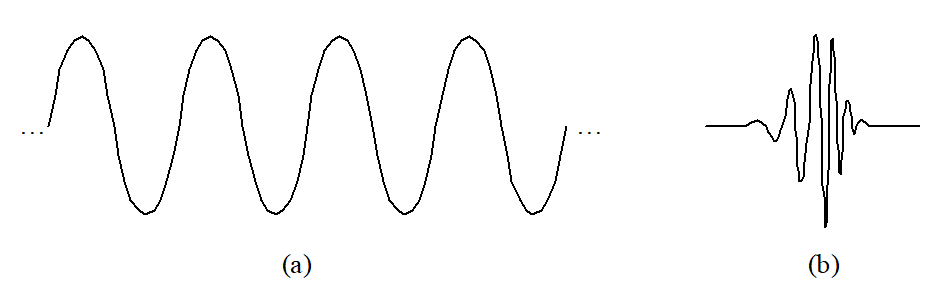 16 |
17 | 图2-13 正弦波和小波
18 | (a)正弦波曲线; (b) 小波曲线
19 |
20 | 从小波和正弦波的形状可以看出, 变化剧烈的信号, 用不规则的小波进行分析比用平滑的正弦波更好, 即用小波更能描述信号的局部特征。
21 |
22 | 连续小波变换 (Continuous Wavelet Transform, CWT) 用下式表示:
23 |
24 | $$
25 | C(\text { scale, position })=\int_{-\infty}^{+\infty} f(t) \psi( { scale, position, } t) d t
26 | $$
27 |
28 | 式 (2-79) 表示小波变换是信号 $f(x)$ 与被缩放和平移的小波函数 $\psi()$ 之积在信号存在的整个期间里求和的结果。CWT的变换结果是许多小波系数 $C$, 这些系数是缩放因子 (scale) 和平移 (positon) 的函数。
29 |
30 | 基本小波函数 $\psi()$ 的缩放和平移操作含义如下:
31 |
32 | 图2-14 小波的缩放操作
33 |
34 | (2) 平移。简单地讲, 平移就是小波的延迟或超前。在数学上, 函数 $f(t)$ 延迟 $k$ 的表达式为 $f(t-k)$, 如图2-15所示。
35 |
36 |
16 |
17 | 图2-13 正弦波和小波
18 | (a)正弦波曲线; (b) 小波曲线
19 |
20 | 从小波和正弦波的形状可以看出, 变化剧烈的信号, 用不规则的小波进行分析比用平滑的正弦波更好, 即用小波更能描述信号的局部特征。
21 |
22 | 连续小波变换 (Continuous Wavelet Transform, CWT) 用下式表示:
23 |
24 | $$
25 | C(\text { scale, position })=\int_{-\infty}^{+\infty} f(t) \psi( { scale, position, } t) d t
26 | $$
27 |
28 | 式 (2-79) 表示小波变换是信号 $f(x)$ 与被缩放和平移的小波函数 $\psi()$ 之积在信号存在的整个期间里求和的结果。CWT的变换结果是许多小波系数 $C$, 这些系数是缩放因子 (scale) 和平移 (positon) 的函数。
29 |
30 | 基本小波函数 $\psi()$ 的缩放和平移操作含义如下:
31 |
32 | 图2-14 小波的缩放操作
33 |
34 | (2) 平移。简单地讲, 平移就是小波的延迟或超前。在数学上, 函数 $f(t)$ 延迟 $k$ 的表达式为 $f(t-k)$, 如图2-15所示。
35 |
36 | 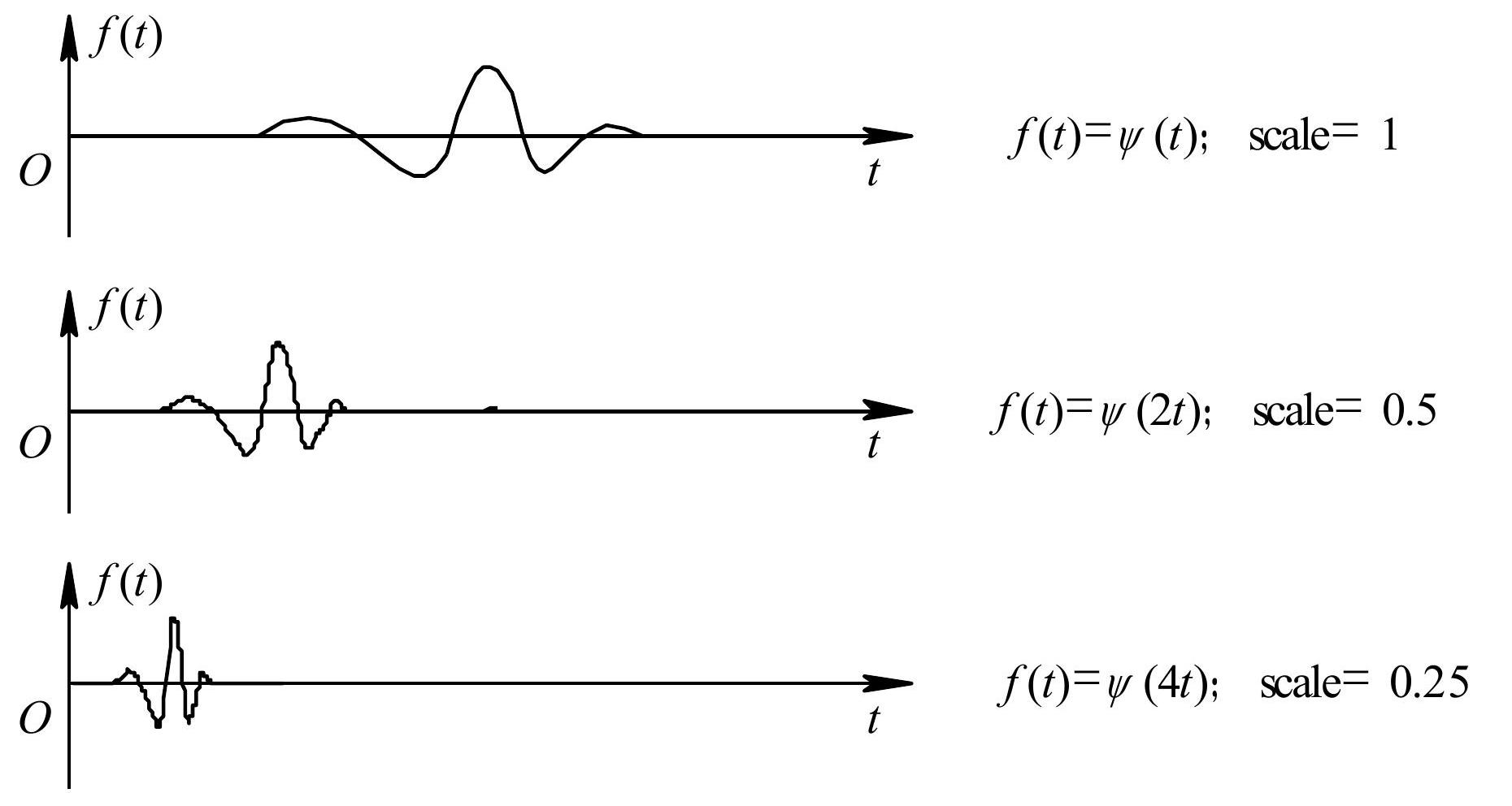 37 |
38 |
37 |
38 | 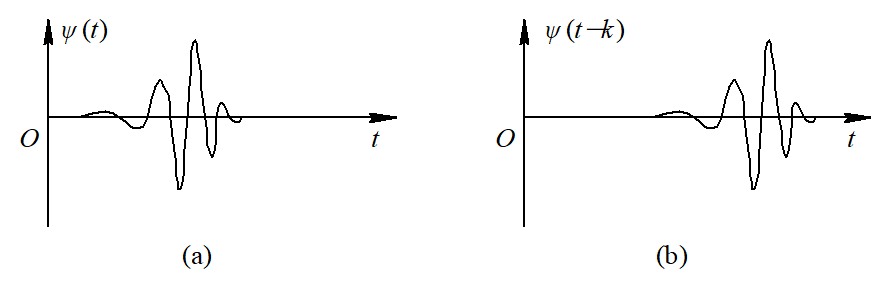 39 |
40 | 图2-15 小波的平移操作
41 |
42 | (a) 小波函数 $\psi(t)$; (b) 位移后的小波函数 $\psi(t-k)$
43 |
44 | CWT计算主要有如下五个步骤:
45 |
46 | 1. 取一个小波, 将其与原始信号的开始一节进行比较。
47 |
48 | 2. 计算数值C, C表示小波与所取一节信号的相似程度, 计算结果取决于所选小波的形状, 如图2-16所示。
49 |
50 | 3. 向右移动小波, 重复第一步和第二步, 直至覆盖整个信号, 如图2-17所示。
51 |
52 | 4. 伸展小波, 重复第一步至第三步, 如图2-18所示。
53 |
54 |
39 |
40 | 图2-15 小波的平移操作
41 |
42 | (a) 小波函数 $\psi(t)$; (b) 位移后的小波函数 $\psi(t-k)$
43 |
44 | CWT计算主要有如下五个步骤:
45 |
46 | 1. 取一个小波, 将其与原始信号的开始一节进行比较。
47 |
48 | 2. 计算数值C, C表示小波与所取一节信号的相似程度, 计算结果取决于所选小波的形状, 如图2-16所示。
49 |
50 | 3. 向右移动小波, 重复第一步和第二步, 直至覆盖整个信号, 如图2-17所示。
51 |
52 | 4. 伸展小波, 重复第一步至第三步, 如图2-18所示。
53 |
54 |  55 |
56 | 图2-16 计算系数值 $C$
57 |
58 |
55 |
56 | 图2-16 计算系数值 $C$
57 |
58 |  59 |
60 | 图2-17 计算平移后系数值 $C$
61 |
62 |
63 |
64 |
59 |
60 | 图2-17 计算平移后系数值 $C$
61 |
62 |
63 |
64 |  65 |
66 | 图2-18 计算尺度后系数值 $C$
67 |
68 | 5. 对于所有缩放,重复第一步至第四步。
69 |
70 | 小波的缩放因子与信号频率之间的关系是:缩放因子 scale
71 | 越小, 表示小波越窄, 度量的是信号的细节变化, 表示信号频率越高; 缩放因子scale越大, 表示小波越宽, 度量的是信号的粗䊁程度,表示信号频率越低。
72 |
73 | ### 离散小波变换(DWT)
74 |
75 | 在每个可能的缩放因子和平移参数下计算小波系数, 其计算量相当大, 将产生惊人的数据量, 而且有许多数据是无用的。如果缩放因子和平移参数都选择为 $2^{j}(j>0$ 且为整数) 的倍数,即只选择部分缩放因子和平移参数来进行计算, 就会使分析的数据量大大减少。使用这样的缩放因子和平移参数的小波变换称为双尺度小波变换(Dyadic Wavelet Transform),它是离散小波变换(Discrete Wavelet Transform,DWT)的一种形式。通常离散小波变换就是指双尺度小波变换。
76 |
77 | 执行离散小波变换的有效方法是使用滤波器, 该方法是Mallat于1988年提出的,称为Mallat算法。这种方法实际上是一种信号分解的方法, 在数字信号处理中常称为双通道子带编码。
78 |
79 | 用滤波器执行离散小波变换的概念如图2-19所示。S表示原始的输入信号, 通过两个互补的滤波器组, 其中一个滤波器为低通滤波器, 通过该滤波器可得到信号的近似值 $A$(Approximations), 另一个为高通滤波器, 通过该滤波器可得到信号的细节值$D$(Detail)。
80 |
81 |
82 |
83 |
65 |
66 | 图2-18 计算尺度后系数值 $C$
67 |
68 | 5. 对于所有缩放,重复第一步至第四步。
69 |
70 | 小波的缩放因子与信号频率之间的关系是:缩放因子 scale
71 | 越小, 表示小波越窄, 度量的是信号的细节变化, 表示信号频率越高; 缩放因子scale越大, 表示小波越宽, 度量的是信号的粗䊁程度,表示信号频率越低。
72 |
73 | ### 离散小波变换(DWT)
74 |
75 | 在每个可能的缩放因子和平移参数下计算小波系数, 其计算量相当大, 将产生惊人的数据量, 而且有许多数据是无用的。如果缩放因子和平移参数都选择为 $2^{j}(j>0$ 且为整数) 的倍数,即只选择部分缩放因子和平移参数来进行计算, 就会使分析的数据量大大减少。使用这样的缩放因子和平移参数的小波变换称为双尺度小波变换(Dyadic Wavelet Transform),它是离散小波变换(Discrete Wavelet Transform,DWT)的一种形式。通常离散小波变换就是指双尺度小波变换。
76 |
77 | 执行离散小波变换的有效方法是使用滤波器, 该方法是Mallat于1988年提出的,称为Mallat算法。这种方法实际上是一种信号分解的方法, 在数字信号处理中常称为双通道子带编码。
78 |
79 | 用滤波器执行离散小波变换的概念如图2-19所示。S表示原始的输入信号, 通过两个互补的滤波器组, 其中一个滤波器为低通滤波器, 通过该滤波器可得到信号的近似值 $A$(Approximations), 另一个为高通滤波器, 通过该滤波器可得到信号的细节值$D$(Detail)。
80 |
81 |
82 |
83 |  84 |
85 | 图2-19 小波分解示意图
86 |
87 | 在小波分析中,近似值是大的缩放因子计算的系数,表示信号的低频分量, 而细节值是小的缩放因子计算的系数, 表示信号的高频分量。实际应用中, 信号的低频分量往往是最重要的, 而高频分量只起一个修饰的作用。如同一个人的声音一样, 把高频分量去掉后, 听起来声音会发生改变, 但还能听出说的是什么内容, 但如果把低频分量删除后, 就会什么内容也听不出来了。
88 |
89 | 由图2-19可以看出离散小波变换可以表示成由低通滤波器和高通滤波器组成的一棵树。原始信号经过一对互补的滤波器组进行的分解称为一级分解, 信号的分解过程也可以不断进行下去, 也就是说可以进行多级分解。如果对信号的高频分量不再分解, 而对低频分量进行连续分解, 就可以得到信号不同分辨率下的低频分量, 这也称为信号的多分辨率分析。如此进行下去, 就会形成图2-20所示的一棵比较大的分解树, 称其为信号的小波分解树 (Wavelet Decomposition Tree)。实际中,分解的级数取决于要分析的信号数据特征及用户的具体需要。
90 |
91 |
84 |
85 | 图2-19 小波分解示意图
86 |
87 | 在小波分析中,近似值是大的缩放因子计算的系数,表示信号的低频分量, 而细节值是小的缩放因子计算的系数, 表示信号的高频分量。实际应用中, 信号的低频分量往往是最重要的, 而高频分量只起一个修饰的作用。如同一个人的声音一样, 把高频分量去掉后, 听起来声音会发生改变, 但还能听出说的是什么内容, 但如果把低频分量删除后, 就会什么内容也听不出来了。
88 |
89 | 由图2-19可以看出离散小波变换可以表示成由低通滤波器和高通滤波器组成的一棵树。原始信号经过一对互补的滤波器组进行的分解称为一级分解, 信号的分解过程也可以不断进行下去, 也就是说可以进行多级分解。如果对信号的高频分量不再分解, 而对低频分量进行连续分解, 就可以得到信号不同分辨率下的低频分量, 这也称为信号的多分辨率分析。如此进行下去, 就会形成图2-20所示的一棵比较大的分解树, 称其为信号的小波分解树 (Wavelet Decomposition Tree)。实际中,分解的级数取决于要分析的信号数据特征及用户的具体需要。
90 |
91 |  92 |
93 | 图2-20 多级信号分解示意图
94 | (a) 信号分解; (b) 小波分数; (c)小波分解树
95 |
96 |
92 |
93 | 图2-20 多级信号分解示意图
94 | (a) 信号分解; (b) 小波分数; (c)小波分解树
95 |
96 |  97 |
98 | 图2-21 小波分解下采样示意图
99 |
100 | ### 小波重构
101 |
102 | 将信号的小波分解的分量进行处理后, 一般还要根据需要
103 |
104 | 把信号恢复出来, 也就是利用信号的小波分解的系数还原出原始信号, 这一过程称为小波重构(Wavelet Reconstruction)或叫做小波合成(Wavelet Synthesis)。这一合成过程的数学运算叫做逆离散小波变换 ( Inverse Discrete Wavelet Transform, IDWT)。
105 |
106 |
97 |
98 | 图2-21 小波分解下采样示意图
99 |
100 | ### 小波重构
101 |
102 | 将信号的小波分解的分量进行处理后, 一般还要根据需要
103 |
104 | 把信号恢复出来, 也就是利用信号的小波分解的系数还原出原始信号, 这一过程称为小波重构(Wavelet Reconstruction)或叫做小波合成(Wavelet Synthesis)。这一合成过程的数学运算叫做逆离散小波变换 ( Inverse Discrete Wavelet Transform, IDWT)。
105 |
106 |  107 |
108 | 图2-22 小波重构算法示意图
109 |
110 | #### 重构近似信号与细节信号
111 |
112 | 由图2-22可知, 由小波分解的近似系数和细节系数可以重构出原始信号。同样, 可由近似系数和细节系数分别重构出信号的近似值或细节值, 这时只要近似系数或细节系数置为零即可。
113 |
114 | 图2-23是对第一层近似信号或细节信号进行重构的示意图。
115 |
116 |
107 |
108 | 图2-22 小波重构算法示意图
109 |
110 | #### 重构近似信号与细节信号
111 |
112 | 由图2-22可知, 由小波分解的近似系数和细节系数可以重构出原始信号。同样, 可由近似系数和细节系数分别重构出信号的近似值或细节值, 这时只要近似系数或细节系数置为零即可。
113 |
114 | 图2-23是对第一层近似信号或细节信号进行重构的示意图。
115 |
116 | 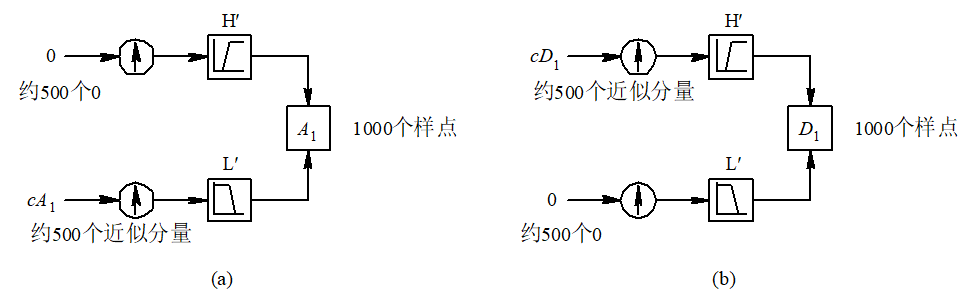 117 |
118 | 图2-23 重构近似和细节信号示意
119 |
120 | (a)重构近似信号; (b) 重构细节信号
121 |
122 | #### 多层重构
123 |
124 | 在图2-23中, 重构出信号的近似值 $A_{1}$ 与细节值 $D_{1}$ 之后, 则原信号可用 $A_{1}+D_{1}=S$ 重构出来。对应于信号的多层小波分解, 小波的多层重构如图2-24所示。由图2-24可见重构过程为:
125 | $$
126 | A_3+D_3=A_2\\
127 | A_2+D_2=A_1\\
128 | A_1+D_1=S
129 | $$
130 | 信号重构中, 滤波器的选择非常重要, 关系到能否重构出满意的原始信号。低通分解滤波器 (L) 和高通分解滤波器 (H) 及重构滤波器组 $\left(L^{\prime}\right.$ 和 $\left.H^{\prime}\right)$ 构成一个系统, 这个系统称为正交镜像滤波器(Quadrature Mirror Filters, QMF)系统, 如图7-25 所示。
131 |
132 |
117 |
118 | 图2-23 重构近似和细节信号示意
119 |
120 | (a)重构近似信号; (b) 重构细节信号
121 |
122 | #### 多层重构
123 |
124 | 在图2-23中, 重构出信号的近似值 $A_{1}$ 与细节值 $D_{1}$ 之后, 则原信号可用 $A_{1}+D_{1}=S$ 重构出来。对应于信号的多层小波分解, 小波的多层重构如图2-24所示。由图2-24可见重构过程为:
125 | $$
126 | A_3+D_3=A_2\\
127 | A_2+D_2=A_1\\
128 | A_1+D_1=S
129 | $$
130 | 信号重构中, 滤波器的选择非常重要, 关系到能否重构出满意的原始信号。低通分解滤波器 (L) 和高通分解滤波器 (H) 及重构滤波器组 $\left(L^{\prime}\right.$ 和 $\left.H^{\prime}\right)$ 构成一个系统, 这个系统称为正交镜像滤波器(Quadrature Mirror Filters, QMF)系统, 如图7-25 所示。
131 |
132 | 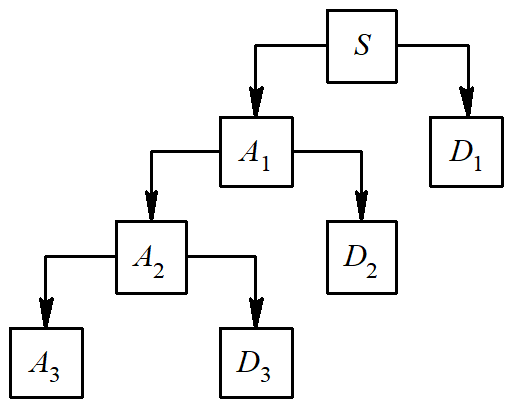 133 |
134 | 图2-24 多层小波重构示意图
135 |
136 | 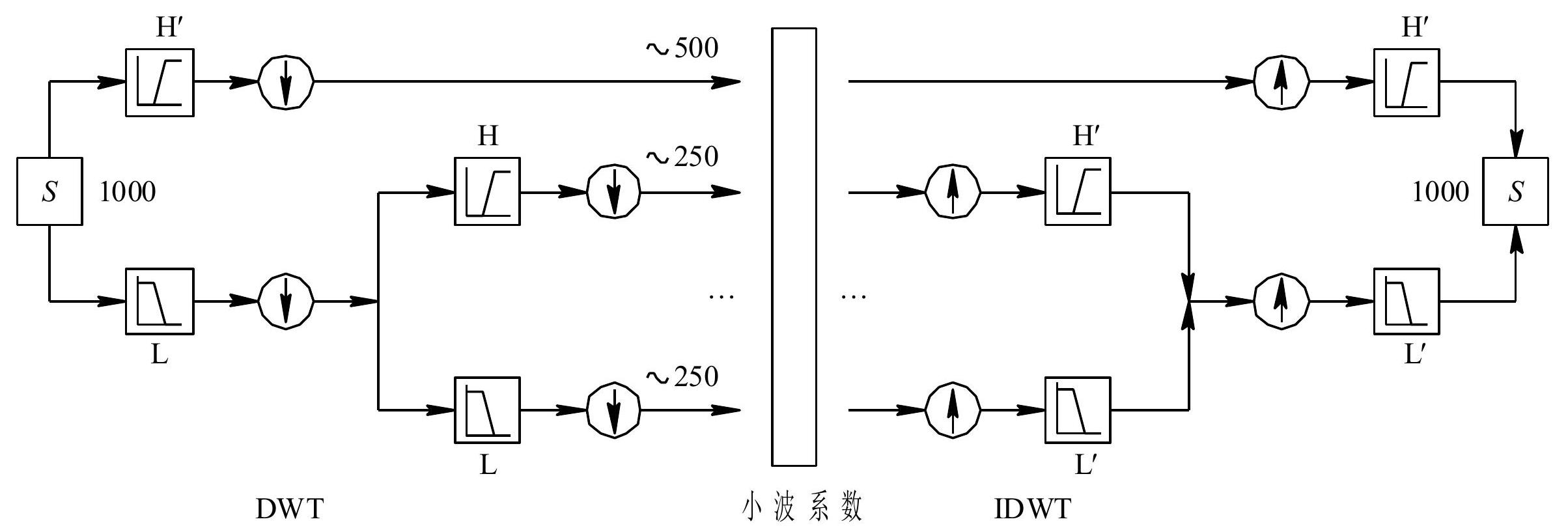
137 |
138 | 图2-25 多层小波分解和重构示意图
139 |
140 | ### 小波包分析
141 |
142 | 小波分析是将信号分解为近似与细节两部分, 近似部分又可以分解成第二层近似与细节, 可以这样重复下去。对于一个 $N$层分解来说, 有 $N+1$ 个分解信号的途径。而小波包分析的细节与近似部分一样, 也可以分解, 对于 $N$层分解, 它产生 $2 N$ 个不同的途径, 图2-26是一个小波包分解示意图。
143 |
144 |
133 |
134 | 图2-24 多层小波重构示意图
135 |
136 | 
137 |
138 | 图2-25 多层小波分解和重构示意图
139 |
140 | ### 小波包分析
141 |
142 | 小波分析是将信号分解为近似与细节两部分, 近似部分又可以分解成第二层近似与细节, 可以这样重复下去。对于一个 $N$层分解来说, 有 $N+1$ 个分解信号的途径。而小波包分析的细节与近似部分一样, 也可以分解, 对于 $N$层分解, 它产生 $2 N$ 个不同的途径, 图2-26是一个小波包分解示意图。
143 |
144 |  145 |
146 | 图2-26 小波包分解示意图
147 |
148 | 小波包分解也可得到一个分解树,称其为小波包分解树(Wavelet Packet Decomposition Tree),\cjkstart这种树是一个完整的二义树。小波包分解方法是小波分解的一般化,可为信号分析提供更丰富和更详细的信息。信号 $S$ 可表示为$AA_2+ADA_3+DDA_3+D_1$等。
149 |
150 | ### 二维离散小波变换
151 |
152 | 二维离散小波变换是一维离散小波变换的推广,其实质上是将二维信号在不同尺度上的分解, 得到原始信号的近似值和细节值。由于信号是二维的, 因此分解也是二维的。分解的结果为:近似分量cA、水平细节分量 $cH$ 、垂直细节分量cV和对角细节分量cD。同样也可以利用二维小波分解的结果在不同尺度上重构信号。二维小波分解和重构过程如图2-27所示。
153 |
154 |
145 |
146 | 图2-26 小波包分解示意图
147 |
148 | 小波包分解也可得到一个分解树,称其为小波包分解树(Wavelet Packet Decomposition Tree),\cjkstart这种树是一个完整的二义树。小波包分解方法是小波分解的一般化,可为信号分析提供更丰富和更详细的信息。信号 $S$ 可表示为$AA_2+ADA_3+DDA_3+D_1$等。
149 |
150 | ### 二维离散小波变换
151 |
152 | 二维离散小波变换是一维离散小波变换的推广,其实质上是将二维信号在不同尺度上的分解, 得到原始信号的近似值和细节值。由于信号是二维的, 因此分解也是二维的。分解的结果为:近似分量cA、水平细节分量 $cH$ 、垂直细节分量cV和对角细节分量cD。同样也可以利用二维小波分解的结果在不同尺度上重构信号。二维小波分解和重构过程如图2-27所示。
153 |
154 |  155 |
156 | 图2-27二维小波分解和重构过程示意图
157 | (a)二维DWT; (b) 二维IDWT
158 |
159 | ## 2.7.2 离散小波变换在图像处理中的应用简介
160 |
161 | ### 用小波变换进行图像分解
162 |
163 | 使用小波变换完成图像分解的方法很多,例如,均匀分解 ( Uniform decomposition ) 、非均匀分解 ( Non-uniform decomposition)、八带分解(Octave-band decomposition)、小波包分解 (Wavelet-packer decomposition) 等。其中八带分解是使用最广的一种分解方法, 这种分解方法把低频部分分解成比较窄的频带, 而对每一级分解得到的高频部分不再进一步进行分解。 图2-28为八带分解示意图, 用于分解的原始图像采用Matlab提供的预存图像文件woman2.mat,小波基函数为 “haar"小波。图228 (c)是用Matlab的小波工具箱编程进行分解得到的图像。
164 |
165 | 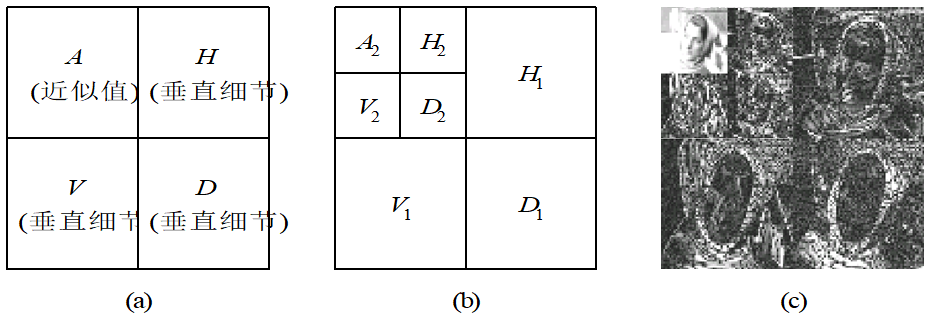
166 |
167 | 图2-28 八带分解示意图
168 |
169 | (a) 一次二维DWT; (b) 两次二维DWT; (c) Woman二级分解图
170 |
171 | ### 用小波变换进行图像处理
172 |
173 | 对静态二维数字图像,可先对其进行若干次二维DWT变换,
174 |
175 | 将图像信息分解为高频成分 $H 、 V$ 和 $D$ 和低频成分 $A$ 。对低频部分
176 |
177 | A,由于它对压缩的结果影响很大,因此可采用无损编码方法,
178 |
179 | 如Huffman、DPCM等;对 $H 、 V$ 和 $D$ 部分,可对不同的层次采用不同策略的向量量化编码方法, 这样便可大大减少数据量, 而图像的解码过程冈好相反。整个编码、解码流程如图2-29所示。
180 |
181 | 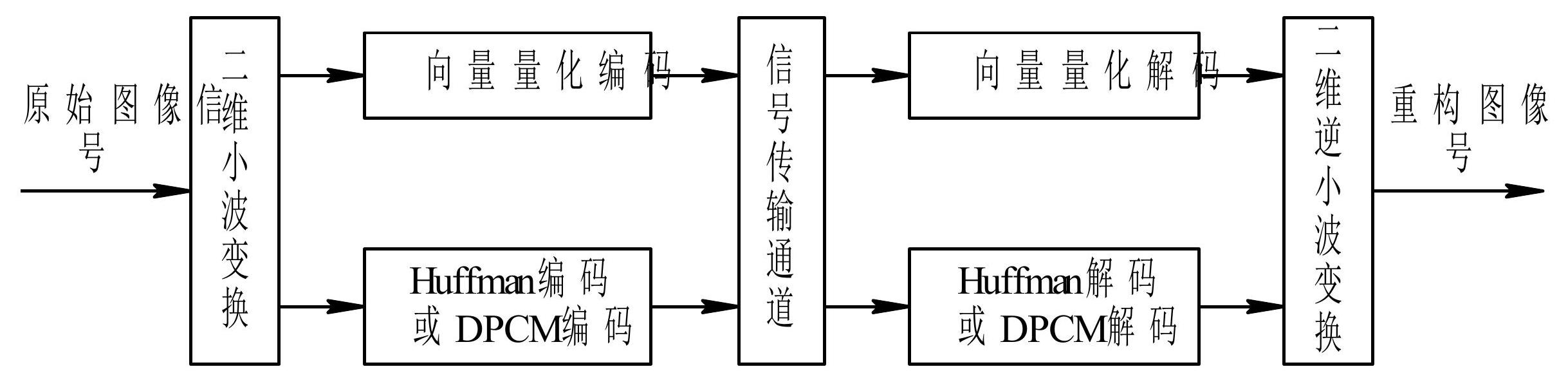
182 |
183 | 图2-29 图像压缩编码、解码流程此外,还可以在对 $A 、 H 、 V$ 和 $D$ 部分编码后加上一个反馈环节,获取误差图像,并对其编码。这样压缩效果会更好。
184 |
185 | 近年来,基于小波变换发展起来的图像编码有嵌入式零树小波编码EZW(Embedded Zerotree Wavelet)及在EZW算法基础上改进的层树分级编码SPIHT( Set Parition In HierarchicalTrees) 和最佳截断嵌入码块编码EBCOT (Embedded Block Coding with Optimized Truncation ) 等。ISO/IEC JTC1 SC29 小组制定的 JPEG2000静态图像编码标准中的图像变换技术就采用了离散小波变换,这些编码的最大特点是在不丢失重要信息的同时,能以较高的比率压缩图像数据,并且其算法计算量小。
--------------------------------------------------------------------------------
/III/3.1 图像编码概述.md:
--------------------------------------------------------------------------------
1 | [TOC]
2 |
3 | # 3.1 图像编码概述
4 |
5 | ## 3.1.1 图像编码基本原理
6 |
7 | 虽然表示图像需要大量的数据, 但图像数据是高度相关的, 或者说存在冗余 (Redundancy) 信息, 去掉这些冗余信息后可以有效压缩图像, 同时又不会损害图像的有效信息。数字图像的写余主要表现为以下几种形式: 空间几余、时间冗余、视觉杂、 信息熵咒余、结构冗余和知识冗余。
8 |
9 | - 空间冗余:图像内部相邻像素之间存在较强的相关性所造成的咒余。
10 |
11 | - 时间写余: 视频图像序列中的不同帧之间的相关性所造成的写余。
12 |
13 | - 视觉冗余: 是指人眼不能感知或不敏感的那部分图像信息。
14 |
15 | - 信息熵冗余: 也称编码冗余,如果图像中平均每个像素使用的比特数大于该图像的信息熵, 则图像中存在咒余, 这种冗余称为信息熵冗余。
16 |
17 | - 结构冗余:是指图像中存在很强的纹理结构或自相似性。
18 |
19 | - 知识冗余: 是指在有些图像中还包含与某些先验知识有关的信息。
20 |
21 | 图像数据的这些冗余信息为图像压缩编码提供了依据。如, 利用人眼对蓝光不敏感的视觉特性, 在对彩色图像编码时, 就可以用较低的精度对蓝色分量进行编码。图像编码的目的就是充分利用图像中存在的各种呪余信息, 特别是空间几余、时间冗余以及视觉冗余, 以尽量少的比特数来表示图像。利用各种冗余信息, 压缩编码技术能够很好地解决在将模拟信号转换为数字信号后所产生的带宽需求增加的问题, 它是使数字信号走上实用化的关键技术之一, 表3-1中列出了几种常见应用的码率。
22 | $$
23 | \begin{array}{|c|c|c|c|c|c|c|c|}
24 | \hline \text { 应用场合 } & \text { 比特/像素 } & \text { 像索数/行 } & \text { 行数/帧 } & \text { 帧数/秒 } & \text { 亮色比 } & \text { 比特/秒(压缩前) } & \text { 比特/秒(压缩后) } \\
25 | \hline \text { 高清晰电视 } & 8 & 1920 & 1080 & 30 & 4: 1: 1 & 1.18 ~Gb / s & 20 \sim 25 Mb / s \\
26 | \hline \text { 普通电视 } & 8 & 720 & 480 & 30 & 4: 1: 1 & 167 Mb / s & 4 \sim 8 Mb / s \\
27 | \hline \text { 会议电视 } & 8 & 352 & 288 & 30 & 4: 1: 1 & 36.5 Mb / s & 1.5 \sim 2 Mb / s \\
28 | \hline \text { 桌上电视 } & 8 & 176 & 144 & 30 & 4: 1: 1 & 9.1 Mb / s & 128 ~Kb / s \\
29 | \hline \text { 电视电话 } & 8 & 128 & 112 & 30 & 4: 1: 1 & 5.2 Mb / s & 56 ~Kb / s \\
30 | \hline
31 | \end{array}
32 | $$
33 | 表3-1 几种常见应用的码率
34 |
35 | ## 3.1.2 图像编码的方法
36 |
37 | 根据编码过程中是否存在信息损耗可将图像编码分为有损压缩和无损压缩。
38 |
39 | - 无损压缩: 无信息损失, 解压缩时能够从压缩数据精确地恢复原始图像;
40 |
41 | - 有损压缩:不能精确重建原始图像, 存在一定程度的失真。
42 |
43 | 图像冗余有损压缩的原理
44 | $$
45 | \begin{array}{|l|l|l|l|l|}
46 | \hline 36 & 35 & 34 & 34 & 34 \\
47 | \hline 34 & 34 & 32 & 34 & 34 \\
48 | \hline 33 & 37 & 30 & 34 & 34 \\
49 | \hline 34 & 34 & 34 & 34 & 34 \\
50 | \hline 34 & 35 & 34 & 34 & 31 \\
51 | \hline
52 | \end{array}
53 | \Rightarrow
54 | \begin{array}{|l|l|l|l|l|}
55 | \hline 34 & 34 & 34 & 34 & 34 \\
56 | \hline 34 & 34 & 34 & 34 & 34 \\
57 | \hline 34 & 34 & 34 & 34 & 34 \\
58 | \hline 34 & 34 & 34 & 34 & 34 \\
59 | \hline 34 & 34 & 34 & 34 & 34 \\
60 | \hline
61 | \end{array}
62 | \Rightarrow
63 | \begin{array}{|l|l|}
64 | \hline 25 &34\\
65 | \hline
66 | \end{array}
67 | $$
68 | 图像冗余无损压缩的原理
69 | $$
70 | \begin{array}{|l|l|l|l|}
71 | \hline\quad & \quad&\quad &\quad\\
72 | \hline & & &\\
73 | \hline & & &\\
74 | \hline & & &\\
75 | \hline
76 | \end{array}
77 | \Rightarrow
78 | \begin{array}{|l|l|l|l|}
79 | \hline \text { RGB } & \text { RGB } & \text { RGB } & \text { RGB } \\
80 | \hline \text { RGB } & \text { RGB } & \text { RGB } & \text { RGB } \\
81 | \hline \text { RGB } & \text { RGB } & \text { RGB } & \text { RGB } \\
82 | \hline \text { RGB } & \text { RGB } & \text { RGB } & \text { RGB } \\
83 | \hline
84 | \end{array}
85 | \Rightarrow
86 | \begin{array}{|c|c|}
87 | \hline 16 & RGB \\
88 | \hline
89 | \end{array}
90 | $$
91 |
92 |
93 | - 第一代压缩编码
94 |
95 | 八十年代以前, 主要是根据传统的信源编码方法。
96 |
97 |
155 |
156 | 图2-27二维小波分解和重构过程示意图
157 | (a)二维DWT; (b) 二维IDWT
158 |
159 | ## 2.7.2 离散小波变换在图像处理中的应用简介
160 |
161 | ### 用小波变换进行图像分解
162 |
163 | 使用小波变换完成图像分解的方法很多,例如,均匀分解 ( Uniform decomposition ) 、非均匀分解 ( Non-uniform decomposition)、八带分解(Octave-band decomposition)、小波包分解 (Wavelet-packer decomposition) 等。其中八带分解是使用最广的一种分解方法, 这种分解方法把低频部分分解成比较窄的频带, 而对每一级分解得到的高频部分不再进一步进行分解。 图2-28为八带分解示意图, 用于分解的原始图像采用Matlab提供的预存图像文件woman2.mat,小波基函数为 “haar"小波。图228 (c)是用Matlab的小波工具箱编程进行分解得到的图像。
164 |
165 | 
166 |
167 | 图2-28 八带分解示意图
168 |
169 | (a) 一次二维DWT; (b) 两次二维DWT; (c) Woman二级分解图
170 |
171 | ### 用小波变换进行图像处理
172 |
173 | 对静态二维数字图像,可先对其进行若干次二维DWT变换,
174 |
175 | 将图像信息分解为高频成分 $H 、 V$ 和 $D$ 和低频成分 $A$ 。对低频部分
176 |
177 | A,由于它对压缩的结果影响很大,因此可采用无损编码方法,
178 |
179 | 如Huffman、DPCM等;对 $H 、 V$ 和 $D$ 部分,可对不同的层次采用不同策略的向量量化编码方法, 这样便可大大减少数据量, 而图像的解码过程冈好相反。整个编码、解码流程如图2-29所示。
180 |
181 | 
182 |
183 | 图2-29 图像压缩编码、解码流程此外,还可以在对 $A 、 H 、 V$ 和 $D$ 部分编码后加上一个反馈环节,获取误差图像,并对其编码。这样压缩效果会更好。
184 |
185 | 近年来,基于小波变换发展起来的图像编码有嵌入式零树小波编码EZW(Embedded Zerotree Wavelet)及在EZW算法基础上改进的层树分级编码SPIHT( Set Parition In HierarchicalTrees) 和最佳截断嵌入码块编码EBCOT (Embedded Block Coding with Optimized Truncation ) 等。ISO/IEC JTC1 SC29 小组制定的 JPEG2000静态图像编码标准中的图像变换技术就采用了离散小波变换,这些编码的最大特点是在不丢失重要信息的同时,能以较高的比率压缩图像数据,并且其算法计算量小。
--------------------------------------------------------------------------------
/III/3.1 图像编码概述.md:
--------------------------------------------------------------------------------
1 | [TOC]
2 |
3 | # 3.1 图像编码概述
4 |
5 | ## 3.1.1 图像编码基本原理
6 |
7 | 虽然表示图像需要大量的数据, 但图像数据是高度相关的, 或者说存在冗余 (Redundancy) 信息, 去掉这些冗余信息后可以有效压缩图像, 同时又不会损害图像的有效信息。数字图像的写余主要表现为以下几种形式: 空间几余、时间冗余、视觉杂、 信息熵咒余、结构冗余和知识冗余。
8 |
9 | - 空间冗余:图像内部相邻像素之间存在较强的相关性所造成的咒余。
10 |
11 | - 时间写余: 视频图像序列中的不同帧之间的相关性所造成的写余。
12 |
13 | - 视觉冗余: 是指人眼不能感知或不敏感的那部分图像信息。
14 |
15 | - 信息熵冗余: 也称编码冗余,如果图像中平均每个像素使用的比特数大于该图像的信息熵, 则图像中存在咒余, 这种冗余称为信息熵冗余。
16 |
17 | - 结构冗余:是指图像中存在很强的纹理结构或自相似性。
18 |
19 | - 知识冗余: 是指在有些图像中还包含与某些先验知识有关的信息。
20 |
21 | 图像数据的这些冗余信息为图像压缩编码提供了依据。如, 利用人眼对蓝光不敏感的视觉特性, 在对彩色图像编码时, 就可以用较低的精度对蓝色分量进行编码。图像编码的目的就是充分利用图像中存在的各种呪余信息, 特别是空间几余、时间冗余以及视觉冗余, 以尽量少的比特数来表示图像。利用各种冗余信息, 压缩编码技术能够很好地解决在将模拟信号转换为数字信号后所产生的带宽需求增加的问题, 它是使数字信号走上实用化的关键技术之一, 表3-1中列出了几种常见应用的码率。
22 | $$
23 | \begin{array}{|c|c|c|c|c|c|c|c|}
24 | \hline \text { 应用场合 } & \text { 比特/像素 } & \text { 像索数/行 } & \text { 行数/帧 } & \text { 帧数/秒 } & \text { 亮色比 } & \text { 比特/秒(压缩前) } & \text { 比特/秒(压缩后) } \\
25 | \hline \text { 高清晰电视 } & 8 & 1920 & 1080 & 30 & 4: 1: 1 & 1.18 ~Gb / s & 20 \sim 25 Mb / s \\
26 | \hline \text { 普通电视 } & 8 & 720 & 480 & 30 & 4: 1: 1 & 167 Mb / s & 4 \sim 8 Mb / s \\
27 | \hline \text { 会议电视 } & 8 & 352 & 288 & 30 & 4: 1: 1 & 36.5 Mb / s & 1.5 \sim 2 Mb / s \\
28 | \hline \text { 桌上电视 } & 8 & 176 & 144 & 30 & 4: 1: 1 & 9.1 Mb / s & 128 ~Kb / s \\
29 | \hline \text { 电视电话 } & 8 & 128 & 112 & 30 & 4: 1: 1 & 5.2 Mb / s & 56 ~Kb / s \\
30 | \hline
31 | \end{array}
32 | $$
33 | 表3-1 几种常见应用的码率
34 |
35 | ## 3.1.2 图像编码的方法
36 |
37 | 根据编码过程中是否存在信息损耗可将图像编码分为有损压缩和无损压缩。
38 |
39 | - 无损压缩: 无信息损失, 解压缩时能够从压缩数据精确地恢复原始图像;
40 |
41 | - 有损压缩:不能精确重建原始图像, 存在一定程度的失真。
42 |
43 | 图像冗余有损压缩的原理
44 | $$
45 | \begin{array}{|l|l|l|l|l|}
46 | \hline 36 & 35 & 34 & 34 & 34 \\
47 | \hline 34 & 34 & 32 & 34 & 34 \\
48 | \hline 33 & 37 & 30 & 34 & 34 \\
49 | \hline 34 & 34 & 34 & 34 & 34 \\
50 | \hline 34 & 35 & 34 & 34 & 31 \\
51 | \hline
52 | \end{array}
53 | \Rightarrow
54 | \begin{array}{|l|l|l|l|l|}
55 | \hline 34 & 34 & 34 & 34 & 34 \\
56 | \hline 34 & 34 & 34 & 34 & 34 \\
57 | \hline 34 & 34 & 34 & 34 & 34 \\
58 | \hline 34 & 34 & 34 & 34 & 34 \\
59 | \hline 34 & 34 & 34 & 34 & 34 \\
60 | \hline
61 | \end{array}
62 | \Rightarrow
63 | \begin{array}{|l|l|}
64 | \hline 25 &34\\
65 | \hline
66 | \end{array}
67 | $$
68 | 图像冗余无损压缩的原理
69 | $$
70 | \begin{array}{|l|l|l|l|}
71 | \hline\quad & \quad&\quad &\quad\\
72 | \hline & & &\\
73 | \hline & & &\\
74 | \hline & & &\\
75 | \hline
76 | \end{array}
77 | \Rightarrow
78 | \begin{array}{|l|l|l|l|}
79 | \hline \text { RGB } & \text { RGB } & \text { RGB } & \text { RGB } \\
80 | \hline \text { RGB } & \text { RGB } & \text { RGB } & \text { RGB } \\
81 | \hline \text { RGB } & \text { RGB } & \text { RGB } & \text { RGB } \\
82 | \hline \text { RGB } & \text { RGB } & \text { RGB } & \text { RGB } \\
83 | \hline
84 | \end{array}
85 | \Rightarrow
86 | \begin{array}{|c|c|}
87 | \hline 16 & RGB \\
88 | \hline
89 | \end{array}
90 | $$
91 |
92 |
93 | - 第一代压缩编码
94 |
95 | 八十年代以前, 主要是根据传统的信源编码方法。
96 |
97 |  98 |
99 | - 第二代压缩编码
100 |
101 | 八十年代以后, 突破信源编码理论, 结合分形、 模型基、神经网络、小波变换等数学工具, 充分利用视觉系统生理心理特性和图像信源的各种特性。
102 |
103 |
98 |
99 | - 第二代压缩编码
100 |
101 | 八十年代以后, 突破信源编码理论, 结合分形、 模型基、神经网络、小波变换等数学工具, 充分利用视觉系统生理心理特性和图像信源的各种特性。
102 |
103 |  104 |
105 | 根据编码原理可以将图像编码分为熵编码、预测编码、变换编码和混合编码等。
106 |
107 | 图像压缩编码系统原理框图
108 |
109 | 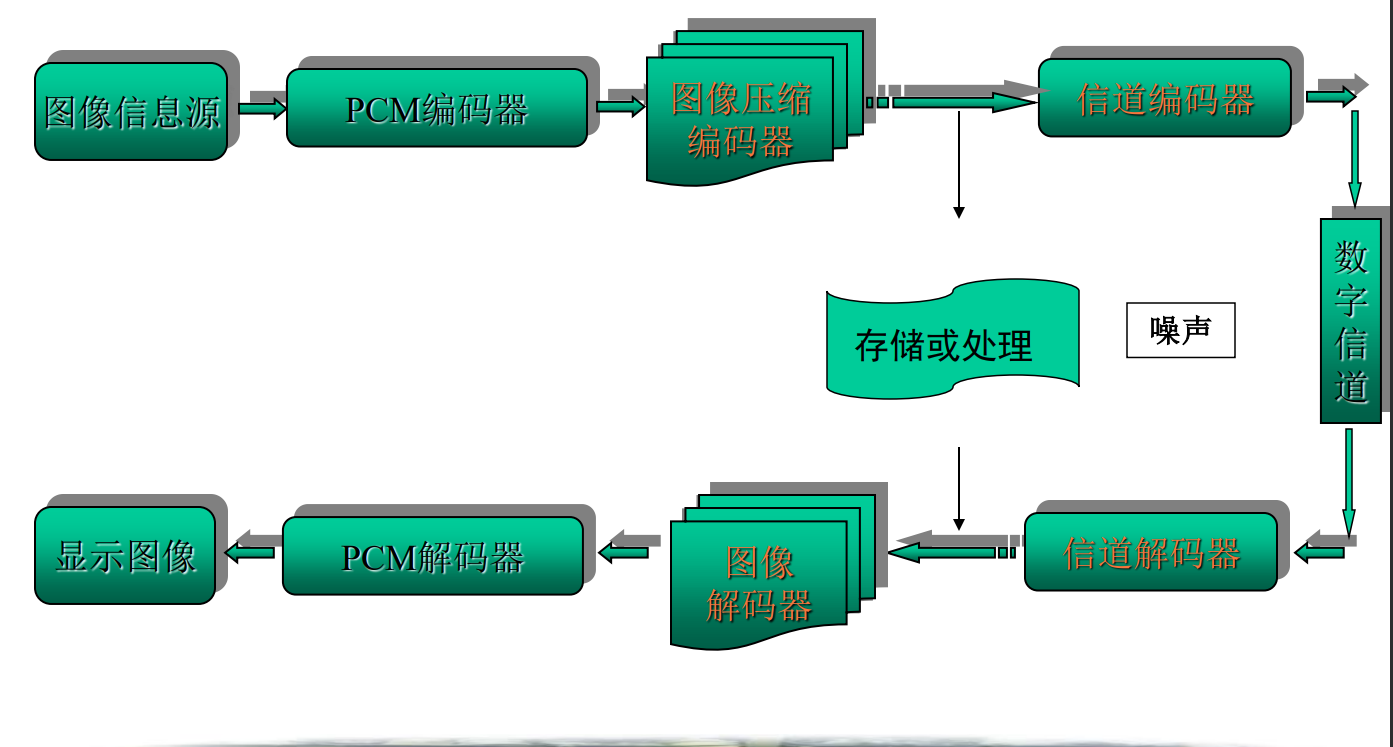
110 |
111 | (1) 熵编码。熵编码是纯粹基于信号统计特性的编码技术, 是一种无损编码。熵编码的基本原理是给出现概率较大的符号赋予一个短码字, 而给出现概率较小的符号赋予一个长码字, 从而使得最终的平均码长很小。 常见的熵编码方法有行程编码 (Run Length Encoding)、哈夫曼编码和算术编码。
112 |
113 | (2)预测编码。预测编码是基于图像数据的空间或时间冗余特性, 用相邻的已知像素(或像素块)来预测当前像素(或像素块)的取值, 然后再对预测误差进行量化和编码。预测编码可分为帧内预测和帧间预测, 常用的预测编码有差分脉码调制(Differential Pulse Code Modulation,DPCM)和运动补偿法。
114 |
115 | (3)变换编码。变换编码通常是将空间域上的图像经过正交变换映射到另一变换域上, 使变换后的系数之间的相关性降低。 图像变换本身并不能压缩数据, 但变换后图像的大部分能量只集中到少数几个变换系数上, 采用适当的量化和熵编码就可以有效地压缩图像。
116 |
117 | (4) 混合编码。混合编码是指综合了熵编码、变换编码或预测编码的编码方法, 如JPEG标准和MPEG标准。
118 |
119 | 根据对压缩编码后的图像进行重建的准确程度, 可将常用的图像编码方法分为三类:
120 |
121 | (1)信息保持编码: 也称无失真编码, 它要求在编解码过程中保证图像信息不丢失, 从而可以完整地重建图像。信息保持编码的压缩比较低, 一般不超过3: 1, 主要应用在图像的数字存储方面, 常用于医学图像编码中。
122 |
123 | (2)保真度编码: 主要利用人眼的视觉特性, 在允许的失真 (Lossy) 条件下或一定的保真度准则下, 最大限度地压缩图像。保真度编码可以实现较大的压缩比, 主要用于数字电视技术、静止图像通信、娱乐等方面。对于这些图像,过高的空间分辨率和过多的灰度层次, 不仅增加了数据量, 而且人眼也接收不到。因此在编码过程中, 可以丢掉一些人眼不敏感的信息, 在保证一定的视觉效果条件下提高压缩比。
124 |
125 | (3) 特征提取: 在图像识别、分析和分类等技术中, 往往并不需要全部图像信息, 而只要对感兴趣的部分特征信息进行编码即可压缩数据。例如, 对遥感图像进行农作物分类时,就只需对用于区别农作物与非农作物, 以及农作物类别之间的特征进行编码, 而可以忽略道路、河流、建筑物等其他背景信息。
126 |
127 | ## 3.1.3 图像编码新技术
128 |
129 | 图像编码已经发展了几十年, 人们不断提出新的压缩方法。如, 利用人工神经网络 (Artificial Neural Network, ANN) 的压缩编码、分形编码(Fractal Coding)、小波编码(Wavelet Coding)、基于对象的压缩编码(Object Based Coding)和基于模型的压缩编码(Model Based Coding)等等。
130 |
131 | 1)分形编码
132 |
133 | 分形编码是在波兰美籍数学家B.B.Mandelbrot建立的分形几何理论的基础上发展起来的一种编码方法。分形编码最大限度地利用了图像在空间域上的自相似性(即局部与整体之间存在某种相似性),通过消除图像的几何几穴余来压缩数据。 M.Barnsley将迭代函数系统 (Iterate Function System,IFS) 用于描述图像的自相似性, 并将其用于图像编码, 对某些特定图像获得了10 000: 1的压缩比。分形编码过程十分复杂, 而解码过程却很简单, 故通常用于对图像编码一次, 而需译码多次的信息传播应用中。
134 |
135 | 2)小波编码
136 |
137 | 1989年, S.G.Mallat首次将小波变换用于图像编码。经过小波变换后的图像, 具有良好的空间方向选择性, 而且是多分辨率的, 能够保持原图像在各种分辨率下的精细结构, 与人的视觉特性十分吻合。
138 |
139 | 3)模型编码
140 |
141 | 模型编码是近几年发展起来的一种很有前途的低比特率编码方法, 其基本出发点是在编、解码两端分别建立起相同的模型,编码时利用先验模型抽取图像中的主要信息并用模型参数的形式表示,解码时则利用所接收的模型参数重建图像。
142 |
143 | ## 4.1.4 图像编码评价
144 |
145 | 随着众多图像压缩算法的出现, 如何评价图像压缩算法就成为重要的课题。一般说来, 评价图像压缩算法的优劣主要有以下4个参数。
146 |
147 | 1)算法的编码效率
148 |
149 | 算法的编码效率通常有几种表现形式: 平均码字长度(R), 图像的压缩比 (rate, $r$ ), 每秒钟所需的传输比特数 (bits per second, bps), 图像熵与平均码长之比 $(\eta)$, 这些表现形式很容易相互转换。下面给出与图像编码效率有关的几个定义。 设一幅灰度级为 $N$ 的图像, 图像中第 $k$ 级灰度出现的概率为 $P_{k}$,
150 |
151 | 图像大小为 $N_{x} \times N_{y}$, 每个像素用 $d$ 比特表示, 每两帧图像间隔 $\Delta t$, 则按信息论中信息熵的定义, 数字图像的熵 $H$ 由下式定义:
152 |
153 | $$
154 | H=-\sum_{k=1}^{N} P_{k} 1 b P_{k}\tag{3-1}
155 | $$
156 |
157 | 由此可见, 图像熵 $H$ 表示各灰度级比特数的统计平均值。
158 |
159 | 对于一种图像编码方法, 设第 $k$ 级灰度的码字长度为 $B_{k}$, 则该图像的平均码字长度 $R$ 为
160 |
161 | $$
162 | R=\sum_{k=1}^{N} B_{k} P_{k}\tag{3-2}
163 | $$
164 |
165 | 于是,可定义编码效率 $\eta$ 为
166 |
167 | $$
168 | \eta=\frac{H}{R} \times 100 \%\tag{3-3}
169 | $$
170 |
171 | 每秒钟所需的传输比特数bps为
172 |
173 | $$
174 | b p s=\frac{N_{x} N_{y} R}{\Delta t}\tag{3-4}
175 | $$
176 |
177 | 压缩比 $r$ 为
178 | $$
179 | r=\frac{d}{R}\tag{3-5}
180 | $$
181 | 由于同一压缩算法对不同图像的编码效率会有所不同, 因此常需定义一些 “标准图像”,如国际上流行的三幅图像Lena、Barbara和Mandrill。一般通过测量不同压缩算法对同一组 “标准图像”的编码性能来评价各图像压缩算法的编码效率。
182 |
183 | 2)编码图像的质量
184 |
185 | 图像质量评价可分为客观质量评价和主观质量评价。最常用
186 |
187 | 的客观质量评价指标是均方误差 (MSE) 和峰值信噪比
188 |
189 | (PSNR),其定义如下:
190 |
191 | $$
192 | M S E=\frac{1}{N_{x} N_{y}} \sum_{i=0}^{N_{x}} \sum_{j=0}^{N_{y}}[f(i, j)-\hat{f}(i, j)]^{2} \tag{3-6}
193 | $$
194 |
195 | $$
196 | P S N R=10 \lg \left(\frac{255 \times 255}{M S E}\right)\tag{3-7}
197 | $$
198 |
199 | 主观质量评价是指由一批观察者对编码图像进行观察并打分, 然后综合所有人的评判结果, 给出图像的质量评价。客观质量评价能够快速有效地评价编码图像的质量, 但符合客观质量评价指标的图像不一定具有较好的主观质量。主观质量评价能够与人的视觉效果相匹配, 但其评判过程缓慢费时。
200 |
201 | 3)算法的适用范围
202 |
203 | 特定的图像编码算法具有其相应的适用范围, 并不对所有图像都有效。一般说来, 大多数基于图像信息统计特性的压缩算法具有较广的适用范围, 而一些特定的编码算法的适用范围较窄, 如分形编码主要用于自相似性高的图像。
204 |
205 | 4)算法的复杂度
206 |
207 | 算法的复杂度即指完成图像压缩和解压缩所需的运算量和硬件实现该算法的难易程度。优秀的压缩算法要求有较高的压缩比, 压缩和解压缩快, 算法简单, 易于硬件实现, 还要求解压缩后的图像质量较好。选用编码方法时一定要考虑图像信源本身的统计特性、多媒体系统(硬件和软件产品)的适应能力、应用环境以及技术标准。
--------------------------------------------------------------------------------
/III/3.10 预测编码.md:
--------------------------------------------------------------------------------
1 | # 3.10预测编码
2 |
3 | 利用图象局部邻域象素的可预测性来进行圧缩.
4 | 设: $f(n, m)$ 为 $(n, m)$ 点的灰度值; $f(n-i, m-j),(i, j) \in A$, 为邻域A内某点的灰度值,则:
5 | $$
6 | \hat{f}(n, m)=L(f(n-i, m-j),(i, j) \in A,(i, j) \neq(0,0)
7 | $$
8 | L为预测值,通常取为囱口 $A$ 内象素点恢度值的线性函数.如图所示, 即由㳡去的 $f_r(n-i, m-j)$ 来预测 $f(n, m)$ :
9 |
10 | 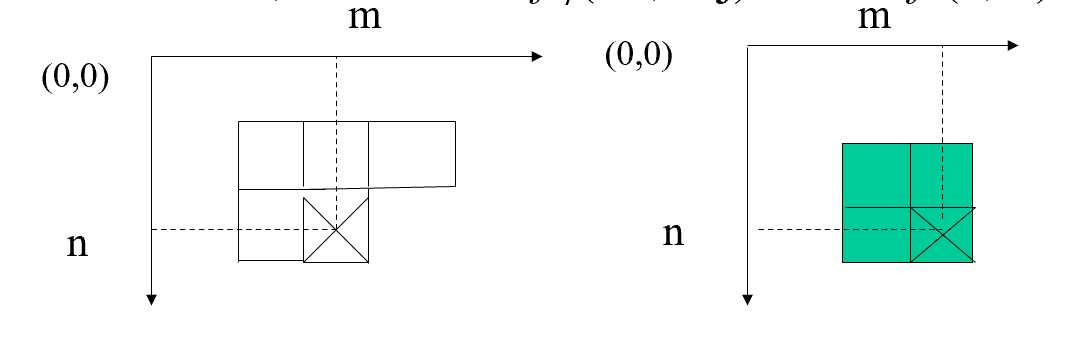
11 | $$
12 | \hat{f}(n, m)=L\left(f_r(n-i, m-j)\right) \quad(i, j) \in A
13 | $$
14 | 因此可以建立一种递归预测编码技术,对应的误差为:
15 | $$
16 | \begin{aligned}
17 | & e_q(n, m)=f(n, m)-\hat{f}(n, m) \\
18 | & f(n, m)=L\left(f_r(n-i, m-j)\right)+e_q(n, m)
19 | \end{aligned}
20 | $$
21 | 即 $\mathbf{f}(\mathbf{n}, \mathbf{m})$ 由 $\mathbf{e}(\mathbf{n}, \mathbf{m})$ 代替, 如果预测 $\hat{f}(n, m)$ 效果好, 则误差项的动态范围很小, 可以有较小的码字来编码,这样便得到显著的压缩效果.
22 |
23 | 为了重建图象,需要传输预测系数和误差编码,这种编码方式称为预测脉冲编码调制(DPCM),如图:
24 |
25 | 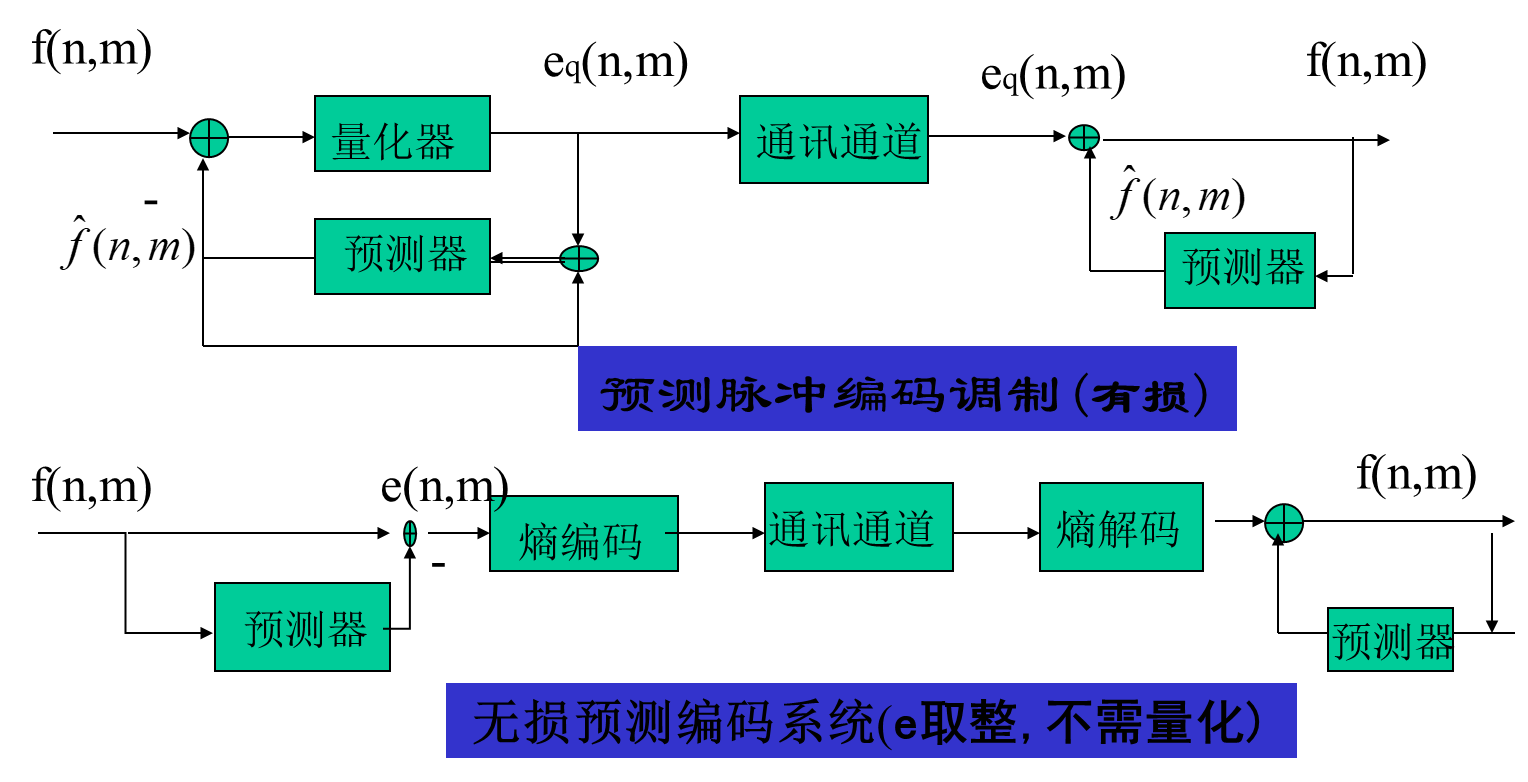
26 |
27 | 假设图象的某一行 $f(n, m)(f(n, m)$ 记为 $f(m))$ 可用一平稳自相关AR过程表示:
28 | $$
29 | f(m)=\sum_{k=1}^p a(k) f(m-k)+e(m) \quad E\left[e^2(m)\right]=\sigma^2
30 | $$
31 | 其中e $(m)$ 为一个与 $f(m)$ 不相关的高斯白噪声, 则预测器:
32 | $$
33 | \hat{f}(m)=\sum_{k=1}^P a(k) \hat{f}_r(m-k)
34 | $$
35 | 预测器系数构成一向量 $a=(a(1), a(2) \ldots, a(P))^{\top}, \quad$ 预测窗口A内重建象素 $\left\{f_r(m-1), \ldots, f_r(m-P)\right.$, 量化误差:
36 | $$
37 | e_q(m)=Q(e(m))=Q[f(m)-\hat{f}(m)]
38 | $$
39 | 重建图象行: $f_r(m)=\sum_{k=1}^p a(k) f_r(m-k)+e_q(m)$
40 |
41 | 预测系数通过下式求解
42 | $$
43 | \left[\begin{array}{cccc}
44 | R(0) & R(1) & \cdots & R(P-1) \\
45 | R(1) & R(2) & \cdots & R(P-2) \\
46 | \vdots & \vdots & \vdots & \vdots \\
47 | R(P-1) & R(P-2) & \cdots & R(0)
48 | \end{array}\right]\left[\begin{array}{c}
49 | a(1) \\
50 | a(2) \\
51 | \vdots \\
52 | a(P)
53 | \end{array}\right]=\left[\begin{array}{c}
54 | R(1) \\
55 | R(2) \\
56 | \vdots \\
57 | R(P)
58 | \end{array}\right]
59 | $$
60 |
61 | ## 预测编码(最佳线性预测)
62 |
63 | 二维模型:
64 | $$
65 | \hat{f}(n, m)=\sum \sum_{(i j) \in A}^P a(i, j) \hat{f}_r(n-i, m-j)
66 | $$
67 | 通过求解E最小:
68 | $$
69 | \left.\left.E\left[\mid f(n, m)-\sum \sum_{(i, j) \in A} a(i, j) f(n-i), m-j\right)\right|^2\right]
70 | $$
71 | 得: $\left.\quad R(k, l)=\sum \sum_{(i, j) \in A} a(i, j) R(n-i), m-j\right)$
72 | 求解上式得到 $a(i, j)$, 再得到:
73 | $$
74 | e(n, m)=f(n, m)-\hat{f}(n, m)
75 | $$
76 | 接收端得: $f_r(n, m)=\sum \sum_{(i j) \in A}^P a(i, j) \hat{f}_r(n-i, m-j)+e_q(n, m)$
--------------------------------------------------------------------------------
/III/3.11 JPEG编码.md:
--------------------------------------------------------------------------------
1 | # 3.11 JPEG 编码
2 |
3 | ## 3.11 JPEG基本系统编码
4 |
5 | JPEG是面向静态图像编码的国际标准。在相同图像质量条件下, JPEG文件拥有比其他图像文件格式更高的压缩比。JPEG目前被广泛应用于多媒体和网络程序中,是现今万维网中使用最广泛的两种图像文件格式之一。JPEG是一种有损压缩, 即在压缩过程中会丢失数据,每次编辑JPEG图像后,图像就会被重复压缩一次, 损失就会有所增加。
6 |
7 | JPEG允许四种编码模式:
8 | (1) 顺序式(Sequential)DCT方式:从左到右、从上到下对图像顺序进行基于离散余弦变换(DCT)的编码。DCT理论上是可逆的,但在计算时存在误差,因而基于DCT的编码模式是一种有损编码。
9 |
10 | (2) 渐进式(Progressive)DCT方式:基于DCT,对图像分层次进行处理,从模糊到清晰地传输图像(与GIF文件的交错方式类似)。有两种实现方法,一种是频谱选择法,即按Z形扫描的序号将DCT量化序数分成几个频段,每个频段对应一次扫描, 每块均先传送低频扫描数据,得到原图概貌,再依次传送高频扫描数据,使图像逐渐清晰;另一种是逐次逼近法,即每次扫描全部DCT量化序数,但每次的表示精度逐渐提高。
11 | (3) 无失真(Lossless)方式: 使用线性预测器,如DPCM, 而不是基于DCT。
12 |
13 | (4) 分层(Hierarchical)方式: 在空间域将源图像以不同的分辨率表示,每个分辨率对应一次扫描, 处理时可以基于DCT或预测编码,可以是渐进式,也可以是顺序式。
14 | JPEG定义了三种系统:基本系统(Baseline System)、扩展系统(Extended System)和无失真压缩系统(Lossless System)。一个符合JPEG标准的编解码器至少要满足基本系统的技术指标。
15 | 基本的JPEG算法属于变换类编码,下面针对基于DCT的顺序式基本系统编码来说明JPEG的编码方法。
16 |
17 | 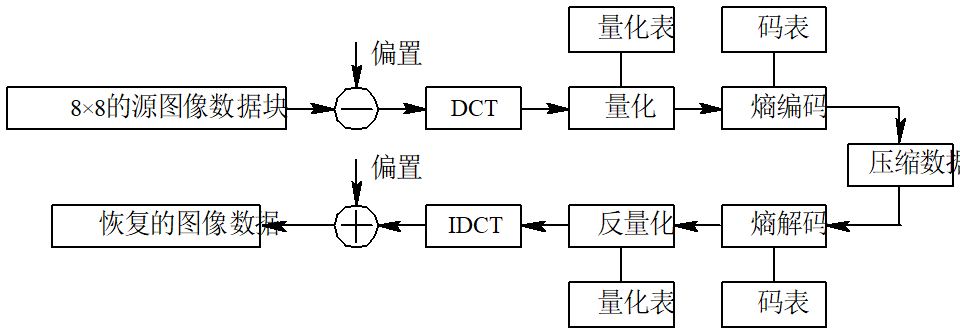
18 |
19 | 图3-3 JPEG 编码流程图
20 |
21 | 1) 数据分块
22 | 对图像进行编码前, 将每个分量图像分割成不重叠的 $8 \times 8$ 像素块, 每一个 $8 \times 8$ 像素块称为一个数据单元 (DU)。在彩色图像中, JPEG分别压缩图像的每个彩色分量。虽然JPEG可以压缩通常的红绿蓝分量, 但在 $Y_{b} C_{r}$ 空间的压缩效果会更好。 这是因为人眼对色彩的变化不如对亮度的变化敏感, 因而对色彩的编码可以比对亮度的编码粗糙些, 这主要体现在不同的采样频率和量化精度上。因此, 编码前一般先将图像从RGB空间转换到 $YC_{b} C_{i}$ 空间,再把各分量图像分割成 $8 \times 8$ 数据块。
23 |
24 | 在对图像采样时, 可以采用不同的采样频率, 这种技术称为二次采样。由于亮度比色彩更重要, 因而对 $Y$ 分量的采样频率可高于对 $C_{b} 、 C_{r}$ 的采样频率, 这样有利于节省存储空间。常用的采样方案有YUV422和YUV411。把采样频率最低的分量图像中一个DU所对应的像区上覆盖的所有各分量上的DU按顺序编组为一个最小编码单元 (MCU)。对灰度图像而言, 只有一个Y分量, MCU就是一个数据单元。而对彩色图像而言, 以 4:1:1的采样方案为例, 则一个MCU由4个 4 分量的DU、 1 个 $C_{b}$ 分量的DU和1个 $C_{r}$ 分量的DU组成。
25 |
26 | 2) DCT处理
27 | 图像数据块分割后, 即以 MCU为单位顺序将DU进行二维离散余弦变换。对以无符号数表示的具有 $P$ 位精度的输入数据, 在DCT前要减去 $2^{P-1}$, 转换成有符号数, 而在IDCT后, 应加上 $2^{P-1}$, 转换成无符号数。对每个 $8 \times 8$ 的数据块 $DU$ 进行 $DCT$ 后, 得到的64个系数代表了该图像块的频率成分,其中低频分量集中在左上角, 高频分量分布在右下角。系数矩阵左上角的叫做直流(DC)系数,它代表了该数据块的平均值, 其余 63 个叫交流(AC)系数。
28 |
29 | 3) 系数量化
30 | 在DCT处理中得到的64个系数中,低频分量包含了图像亮度等主要信息。在从空间域到频域的变换中,图像中的缓慢变化比快速变化更易引起人眼的注意, 所以在重建图像时,低频分量的重要性高于高频分量。因而在编码时可以忽略高频分量, 从而达到压缩的目的,这也是量化的根据和目的。
31 |
32 | 在JPEG标准中,用具有64个独立元素的量化表来规定DCT域中相应的64个系数的量化精度,使得对某个系数的具体量化阶取决于人眼对该频率分量的视觉敏感程度。理论上,对不同的空间分辨率、数据精度等情况,应该有不同的量化表。不过,一般采用图3-4和图3-5所示的量化表,可取得较好的视觉效果。之所以用两张量化表,是因为Y分量比Cb和Cr更重要些,因而对Y采用细量化,而对Cb和Cr采用粗量化。量化就是用DCT变换后的系数除以量化表中相对应的量化阶后四舍五入取整。由于量化表中左上角的值较小,而右下角的值较大, 因而起到了保持低频分量、 抑制高频分量的作用。
33 |
34 | 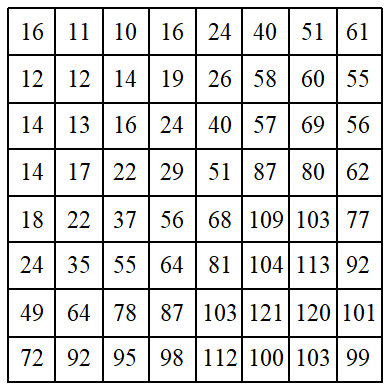
35 |
36 | 图3-4 亮度量化表
37 |
38 | 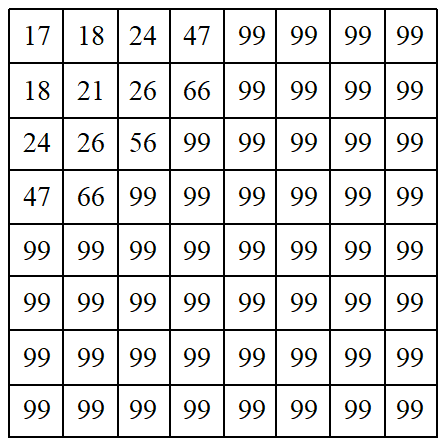
39 |
40 | 图3-5 色度量化表
41 |
42 | 4) Z形扫描
43 | DCT系数量化后,构成一个稀疏矩阵,用Z(Zigzag)形扫描将其变成一维数列,将有利于熵编码。Z形扫描的顺序如图3-6所示。
44 |
45 | 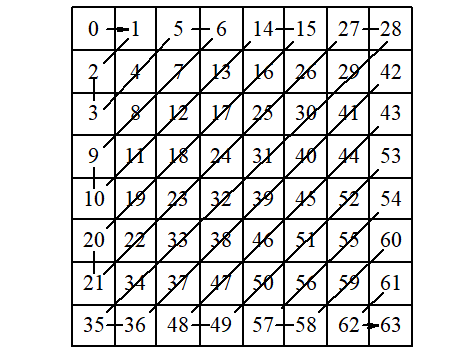
46 |
47 | 图3-6 DCT系数的Z形扫描顺序
48 |
49 | 5) DC系数编码
50 |
51 | DC系数反映了一个8×8数据块的平均亮度,一般与相邻块有较大的相关性。JPEG对DC系数作差分编码,即用前一数据块的同一分量的DC系数作为当前块的预测值,再对当前块的实际值与预测值的差值作哈夫曼编码。
52 |
53 | 若DC系数的动态范围为-1024~+1024,则差值的动态范围为-2047~+2047。如果为每个差值赋予一个码字, 则码表过于庞大。因此,JPEG对码表进行了简化,采用“前缀码(SSSS)+尾码”来表示。前缀码指明了尾码的有效位数B, 可以根据DIFF从表3-8中查出前缀码对应的哈夫曼编码。尾码的取值取决于DC系数的差值和前缀码。如果DC系数的差值DIFF大于等于0,则尾码的码字为DIFF的B位原码;否则,取DIFF的B位反码。
54 |
55 | 表3-8 图像分量为8位时DC系数差值的典型哈夫曼编码表
56 |
57 | 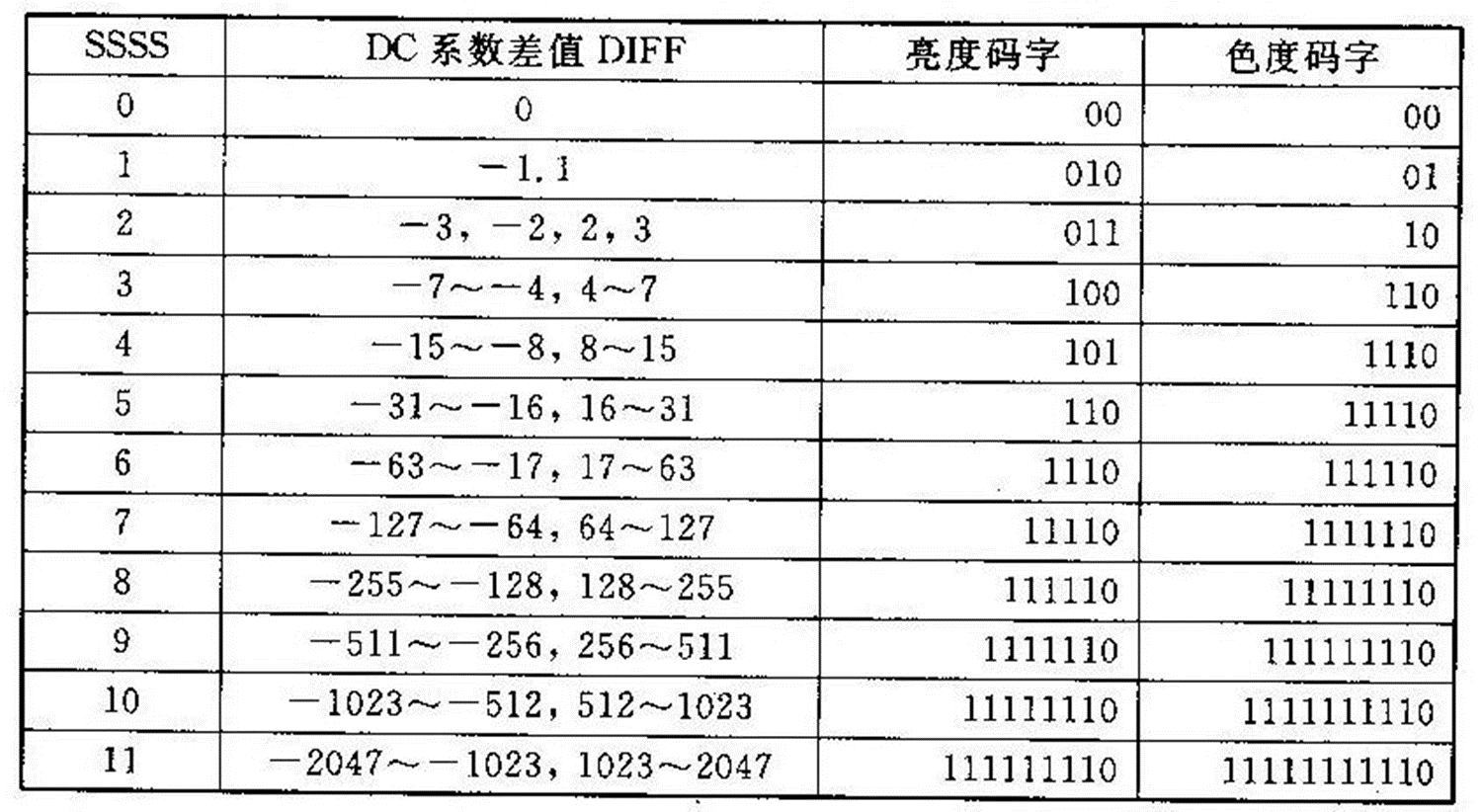
58 |
59 | 6) AC系数编码
60 | 经Z形排列后的AC系数,更有可能出现连续0组成的字符串, 从而对其进行行程编码将有利于压缩数据。JPEG将一个非零DC系数及其前面的0行程长度(连续0的个数)的组合称为一个事件。将每个事件编码表示为“NNNN/SSSS+尾码”, 其中, NNNN为0行程的长度,SSSS表示尾码的有效位数B(即当前非0系数所占的比特数),如果非零AC系数大于等于0, 则尾码的码字为该系数的B位原码, 否则, 取该系数的B位反码。
61 | 由于只用4位表示0行程的长度,故在JPEG编码中,最大0行程只能等于15。当0行程长度大于16时,需要将其分开多次编码, 即对前面的每16个0以“F/0”表示,对剩余的继续编码。
62 |
63 | 表3-9 AC系数的尾码位数表
64 |
65 | | SSSS | AC系数的尾码位数表 |
66 | | ---- | -------------------- |
67 | | 0 | 0 |
68 | | 1 | -1,1 |
69 | | 2 | -3, -2, 2, 3 |
70 | | 3 | -7~-4, 4~7 |
71 | | 4 | -15~-8, 8~15 |
72 | | 5 | -31~-16, 16~31 |
73 | | 6 | -63~-17, 17~63 |
74 | | 7 | -127~-64, 64~127 |
75 | | 8 | -255~-128, 128~255 |
76 | | 9 | -511~256, 256~511 |
77 | | 10 | -1023~-512, 512~1023 |
78 |
79 | 表3-10 亮度AC系数码表
80 |
81 | 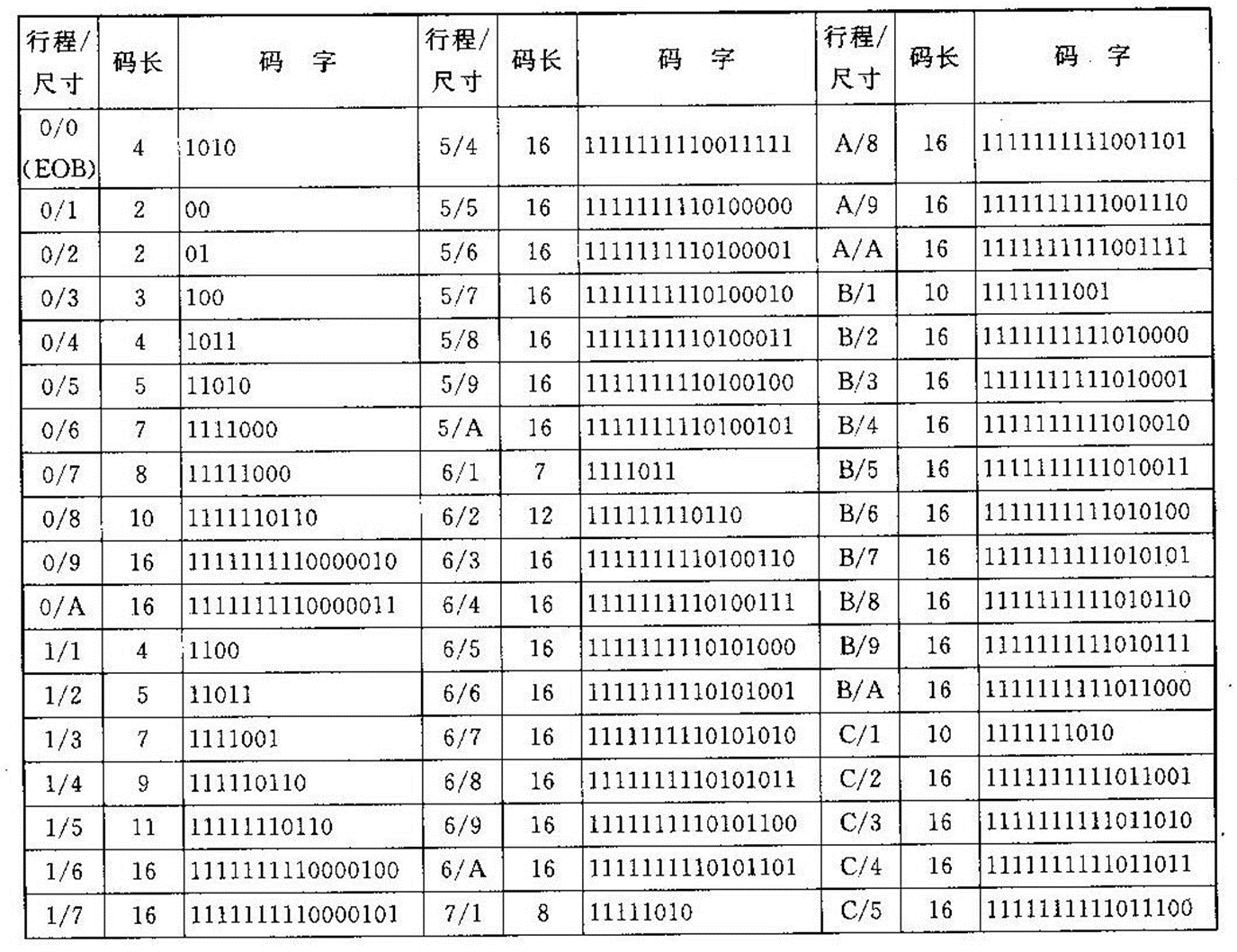
82 |
83 | 
84 |
85 | 
86 |
87 | 表3-11 色差AC系数编码
88 |
89 | 
90 |
91 | 
92 |
93 | 
94 |
95 | 3.11.2 JPEG编码实例
96 | 下面结合一个实例来讲述JPEG基本系统的编码过程。设有一图像亮度数据块如图3-7所示,对其进行离散余弦变换后, 用图3-4所示的亮度量化表对系数矩阵量化后的结果如图3-8所示。对量化结果按图3-6所示的顺序进行Z形扫描, 并对扫描结果的DC及AC系数进行编码的结果见表3-12。由于数据较多, 为简便起见, 这里只对几个系数的编码加以说明。
97 |
98 | 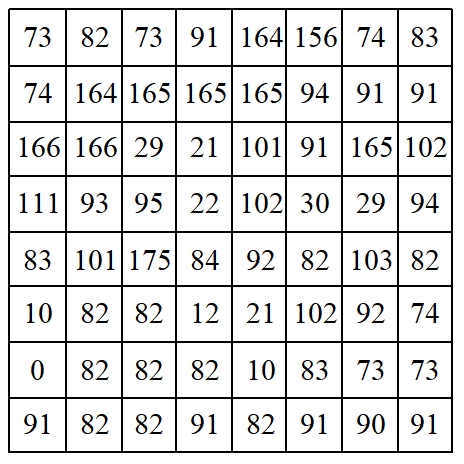
99 |
100 | 图3-7 源图像亮度数据块
101 |
102 | 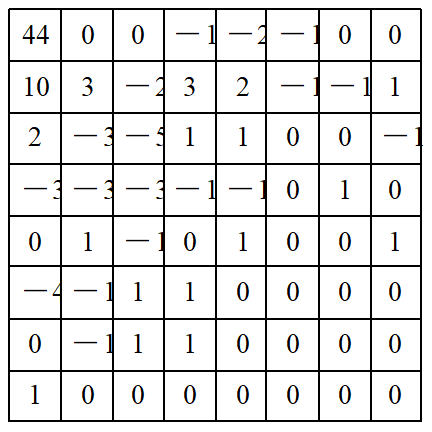
103 |
104 | 图3-8 量化结果
105 |
106 | 表3-12 Zigzag排列及行程编码与哈夫曼编码(VLC)结果
107 |
108 | 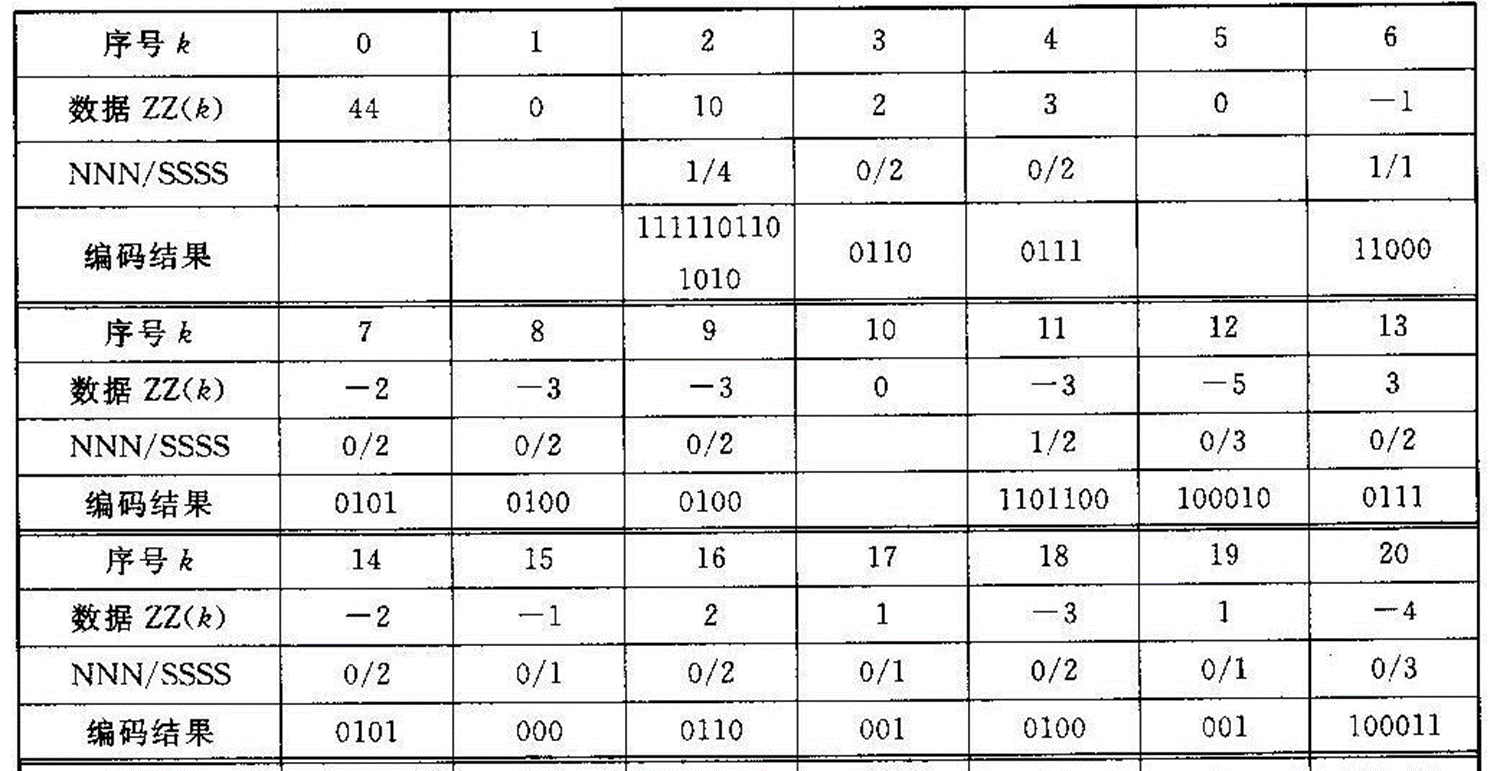
109 |
110 | 表3-12 Zigzag排列及行程编码与哈夫曼编码(VLC)结果
111 |
112 | 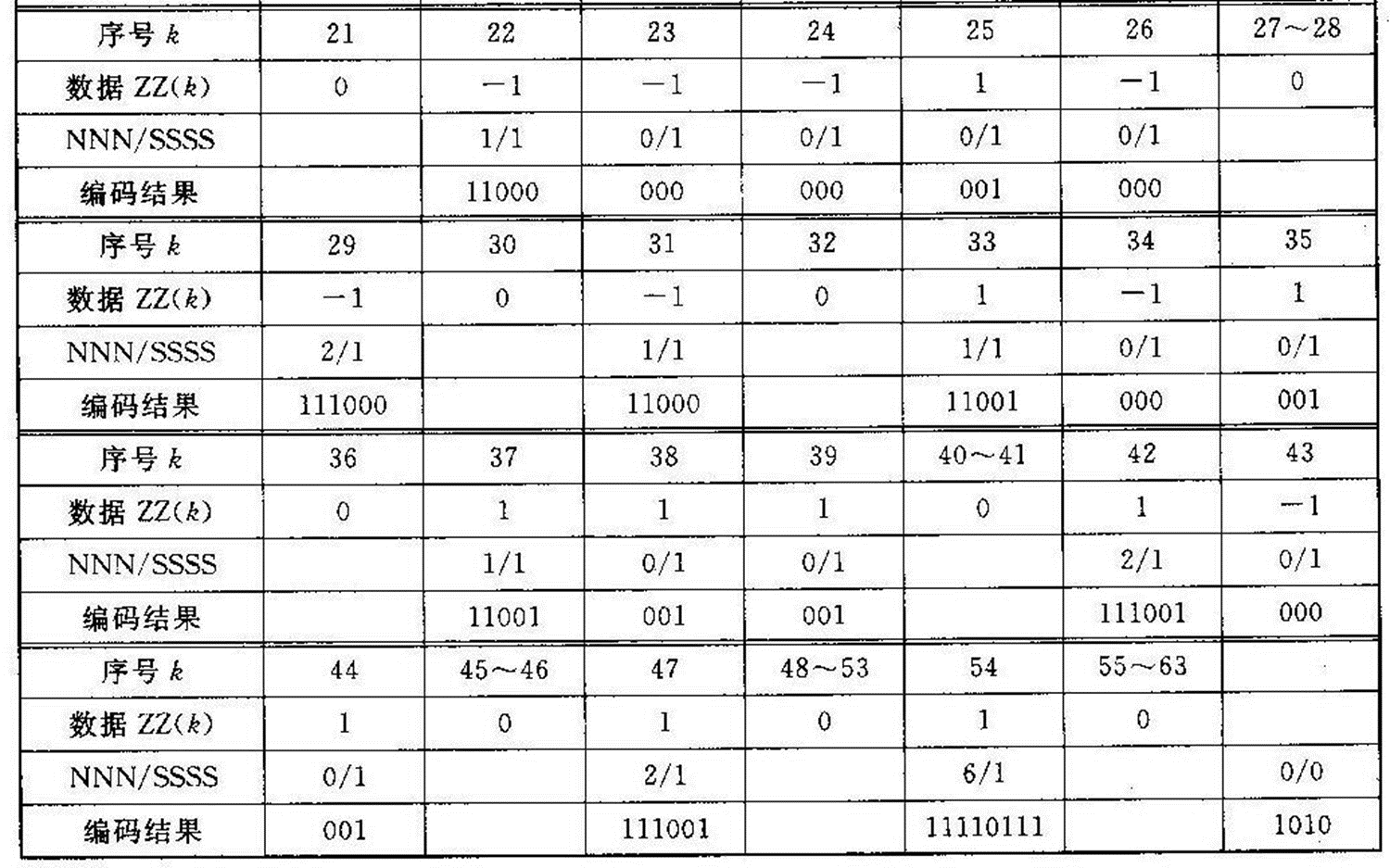
113 |
114 | 1) DC系数的编码
115 | 在量化系数矩阵的Z形扫描结果中,第一个系数为DC系数。假设前一亮度数据块的DC系数为40, 则差值DIFF=44-40=4, 因4在(-7~-4, 4~7)范围内, 由表3-8查得SSSS=3,其前缀码字为“100”, 3位尾码即为4的二进制原码“100”, 从而DC系数的编码为“100100”。如果前一数据块的DC系数为48, 则DIFF=-4, 由表10-8查得SSSS及前缀码字同上,其3位尾码即-4的反码“011”, 因此DC系数的编码为“100011”。解码时, 由前缀码“100”可知尾码有3位,若前缀码字是“100”, 因其最高位为1,故可得DC系数的差值为4; 若前缀码字为“011”,因最高位为0,知其为负, 故取反后可得差值为-4。
116 |
117 | 2) AC系数的编码
118 | 在Z形扫描结果中,第一个非零AC系数为10。在它前面的连零个数为1, 即NNNN=1。根据AC系数10从表3-9查得SSSS=4, 由NNNN/SSSS=1/4从表3-10查得其哈夫曼码字为“111110110”, 而10的二进制码为“1010”, 因此该AC系数的编码为“1111101101010”。由于篇幅所限,其他AC系数的编码就不再赘述, 结果见表10-12。在Z形扫描结果中的末尾,除第54个系数非零外, 其他系数全为零, 故直接用一个结束块“EOB(0/0)”结束本块,由表3-10查得其码字为“1010”。于是,最后该亮度块的编码为(其中,假定差值为4)100100111110110101001100111110000101010001001101100100010011101010000110001010000110001111000000000001000111000110001100100000111001001001111001000001111001111101111010,共用了168位,而原始图像块需8×8×8=512位,因此压缩比为3.048。
119 |
120 | JPEG压缩编码示例
121 |
122 | 
--------------------------------------------------------------------------------
/III/3.12 编程实例.md:
--------------------------------------------------------------------------------
1 | # 3.12 编程实例
2 |
3 | 实现哈夫曼编码的过程实际是构造一个哈夫曼二叉树, 它可分为两大部分:构造哈夫曼树和在哈夫曼树上求叶节点的编码。在构造哈夫曼树时,可设置一个结构数组HuffmanNode保存哈夫曼树中各节点的信息。结构数组元素定义如下:
4 |
5 | ```c++
6 | typedef struct
7 | {
8 | int Weight; //保存哈夫曼树节点的权值, 在此是指频数
9 | int Flag; //当Flag=0时, 表示该节点未加入树中, 为1时表示已加入树中
10 | int Parent; //存放节点的父节点在节点数组中的序号
11 | int LChild; //存放节点的左子节点在节点数组中的序号
12 | int RChild; //存放节点的右子节点在节点数组中的序号
13 | } HuffmanNode;
14 |
15 | ```
16 |
17 | 对于一幅BMP图像,调用CpointPro类下的GetHistogram()成员函数可获得图像的直方图数据m_fFreq,这些数据即各灰度出现的频数。利用这些数据可直接进行哈夫曼编码。哈夫曼编码的代码如下:
18 |
19 | ```C++
20 | void CDlgHuffman::Huffman()
21 | {
22 | CString str;
23 | int i, j, x1, x2, c, p;
24 | int m1, m2;
25 | LV_ITEM lvitem; // ListCtrl的ITEM
26 | int iActualItem; //中间变量, 用于保存ListCtrl中添加的ITEM编号
27 | HuffmanNode *huffNode; //存放哈夫曼树的节点
28 | CString *strCode; //指向各字符的哈夫曼编码的指针
29 | int *iMap; //位置映射指针
30 | int iNumNode = 0; //频数不为零的节点数(或灰度数)
31 | //统计直方图数据中频数不为零的灰度数, 并只对不为零的节点编码
32 | for(i = 0; i < m_iLeafNum; i++)
33 | {
34 | if (m_fFreq[i + m_ChannelSel * m_iLeafNum] != 0)
35 | iNumNode++;
36 | }
37 | //对于具有iNumNode个叶节点的哈夫曼树, 它具有2 iNumNode -1个节点
38 | huffNode = new HuffmanNode[iNumNode * 2 - 1];
39 | strCode = new CString[iNumNode]
40 | iMap = new int[iNumNode];
41 | //初始化huffNode中的各节点
42 | for(i = 0; i < iNumNode * 2 - 1; i++)
43 | {
44 | huffNode[i].Weight = 0;
45 | huffNode[i].Parent = 0;
46 | huffNode[i].Flag = 0;
47 | huffNode[i].LChild = -1;
48 | huffNode[i].RChild = -1;
49 | }
50 | //输入iNumNode个叶节点的权值即频数, iMap存放的是频数不为零的灰度值
51 | j = 0;
52 |
53 | for(i = 0; i < m_iLeafNum; i++)
54 | {
55 | if (m_fFreq[i + m_ChannelSel * m_iLeafNum] != 0)
56 | {
57 | huffNode[j].Weight = m_fFreq[i + m_ChannelSel * m_iLeafNum];
58 | iMap[j] = i;
59 | j++;
60 | }
61 | }
62 | //构造哈夫曼树, 对iNumNode个叶节点, 需构造iNumNode-1次
63 | for(i = 0; i < iNumNode - 1; i++)
64 | {
65 | //对Flag为0的节点比较排序, 选出两个权值最小的子树, x1和x2用于确定
66 | //两子树在数组中的序号, m1和m2用于存放最小两子树的权值
67 | m1 = m2 = m_iSizeImage;
68 | x1 = x2 = 0;
69 | for (j = 0; j < iNumNode + i; j++)
70 | {
71 | if (huffNode[j].Weight < m1 && huffNode[j].Flag = = 0)
72 | {
73 | m2 = m1;
74 | x2 = x1;
75 | m1 = huffNode[j].Weight;
76 | x1 = j;
77 | }
78 | else if (huffNode[j].Weight < m2 && huffNode[j].Flag = = 0)
79 | {
80 | m2 = huffNode[j].Weight;
81 | x2 = j;
82 | }
83 | }
84 | //将找出的两棵最小子树合并为一棵子树
85 | huffNode[x1].Parent = iNumNode + i;
86 | huffNode[x2].Parent = iNumNode + i;
87 | // Flag为1, 说明该节点已经成为其他节点的子节点
88 | huffNode[x1].Flag = 1;
89 | huffNode[x2].Flag = 1;
90 | huffNode[iNumNode + i].Weight = huffNode[x1].Weight + huffNode[x2].Weight;
91 | //权值较小的子树作为右子树
92 | huffNode[iNumNode + i].LChild = x2;
93 | huffNode[iNumNode + i].RChild = x1;
94 | }
95 | //求每个叶节点的哈夫曼编码
96 | for(i = 0; i < iNumNode; i++)
97 | {
98 | c = i;
99 | p = huffNode[c].Parent;
100 | //由叶节点上溯到树根
101 | while (p != 0)
102 | {
103 | //如果是左子树, 则代码的高一位添加0, 否则添加1
104 | if (huffNode[p].LChild = = c)
105 | strCode[i] = "0" + strCode[i];
106 | else
107 | strCode[i] = "1" + strCode[i];
108 | c = p;
109 | p = huffNode[c].Parent;
110 | }
111 | }
112 | //计算平均码字长度和图像熵
113 | int CodeLen = 0;
114 | m_fEntropy = 0.0;
115 | for(i = 0; i < iNumNode; i ++
116 | {
117 | CodeLen += huffNode[i].Weight * strCode[i].GetLength();
118 | m_fEntropy -= ((double)huffNode[i].Weight / m_iSizeImage) *
119 | log((double)huffNode[i].Weight / m_iSizeImage) / log(2.0);
120 | }
121 | //计算平均码字长度
122 | m_fAvCodeLen = (double)CodeLen/m_iSizeImage;
123 | // 计算编码效率
124 | m_fCodeEfficiency = m_fEntropy / m_fAvCodeLen;
125 | //更新对话框上的文本框中的内容
126 | UpdateData(FALSE);
127 | lvitem.mask = LVIF_TEXT;
128 | //输出哈夫曼编码结果
129 | for (i = 0; i < iNumNode; i ++)
130 | {
131 | if (huffNode[i].Weight > 0)
132 | {
133 | // 添加一项
134 | lvitem.iItem = m_lstTable.GetItemCount();
135 | str.Format("%u", iMap[i]);
136 | lvitem.iSubItem = 0;
137 | lvitem.pszText = (LPTSTR)(LPCTSTR)str;
138 | iActualItem = m_lstTable.InsertItem(&lvitem);
139 | // 添加其他列
140 | lvitem.iItem = iActualItem;
141 | // 添加灰度值出现的频率
142 | lvitem.iSubItem = 1;
143 | str.Format("%f", (float)huffNode[i].Weight / m_iSizeImage);
144 | lvitem.pszText = (LPTSTR)(LPCTSTR)str;
145 | m_lstTable.SetItem(&lvitem);
146 | // 添加哈夫曼编码
147 | lvitem.iSubItem = 2;
148 | lvitem.pszText = (LPTSTR)(LPCTSTR)strCode[i];
149 | m_lstTable.SetItem(&lvitem);
150 | // 添加码字长度
151 | lvitem.iSubItem = 3;
152 | str.Format("%u", strCode[i].GetLength());
153 | lvitem.pszText = (LPTSTR)(LPCTSTR)str;
154 | m_lstTable.SetItem(&lvitem);
155 | }
156 | }
157 | delete[] huffNode;
158 | delete[] strCode;
159 | delete[] iMap;
160 | }
161 | ```
162 |
163 |
--------------------------------------------------------------------------------
/III/3.2 Huffman编码.md:
--------------------------------------------------------------------------------
1 | # 3.2 Huffman 编码(熵编码)
2 |
3 | 图象熵:
4 | 图像灰度集合为 $\left(x_1, x_2, \ldots, x_{M}\right)$, , 对应的概率 $P_1$, $P_2, \ldots, \mathbf{P}_{M}$
5 | 则图象熵: $\quad H=-\sum_{k=1}^M P_k \log P_k$
6 | 平均码长:
7 | 设 $\beta_{k}$ 为图像第 $k$ 个码长 $C_{k}$ 的长度, 对应的概率为 $P_{k}$, 则该图象所赋予的码长的平均长度为:
8 | $$
9 | R=\sum_{k=1}^M \beta_k P_k
10 | $$
11 | 编码效率
12 | $$
13 | \eta=\frac{H}{R}
14 | $$
15 | 变长最佳编码定理
16 | 在变长编码中, 对图像中出现频度大的像素值赋予短码字, 对出现频度小的像数值赋予长码字。 如果严格按照所对应符号出现概率大小逆序排列, 则编码结果平均码长一定小于任何其它排列方式。
17 | Huffman 编码
18 | 根据变长最佳编码定理, 应用Huffman算法的一种编码方法。
19 |
20 | 举例:
21 | $$
22 | \frac{\text { aaaa }}{4} \frac{bbb}{3} \frac{cc}{2} \frac{d}{1} \frac{\text { eeeee }}{5} \frac{\text { fffffff }}{7} \text { (共22*8=176 bits) }
23 | $$
24 | 编码: $f=0 \quad e=10 \quad a=110 \quad ~b=1111 \quad c=11100 \quad ~d=11101$
25 |
26 | 11011011011011111111111111100111001110110101010100000000
27 | (共 $7 * 1+5 * 2+4 * 3+3 * 4+2 * 5+1 * 5=56$ bits)
28 |
29 | Huffman 编码步骤:
30 | 1、先将图象灰度级按出现的概率由大到小顺序排列;
31 | 2、将最小两个概率相加, 形成一个新的概率集合, 再按第 (1) 步方法重排, 如此重复进行直到只有两个概率为止;
32 | 3、分配码长。码长分配从最后一步开始反向进行, 对最后两个概率一个赋予“0”, 一个赋予“1”
33 |
34 | 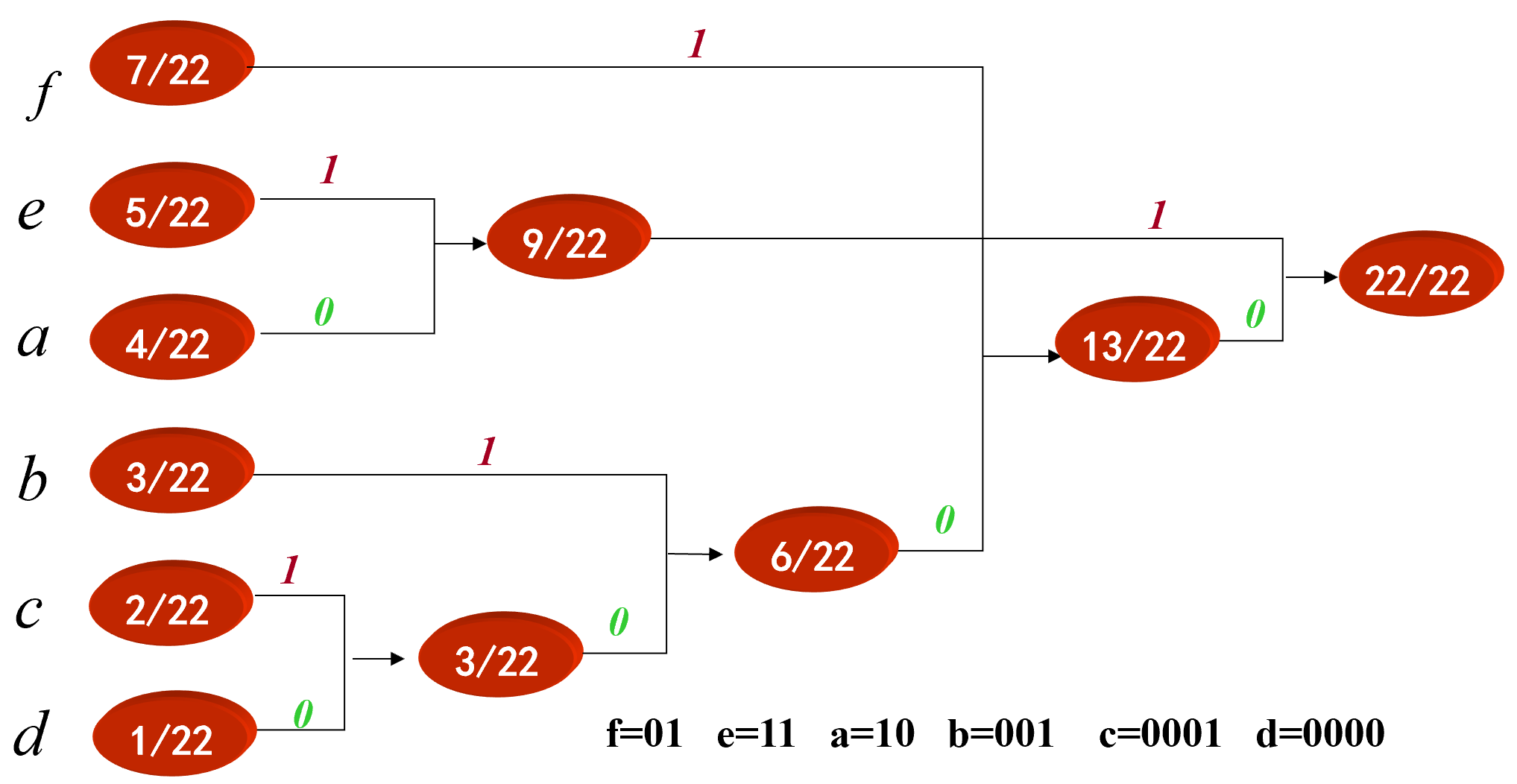
35 |
36 | 整理:
37 |
38 | 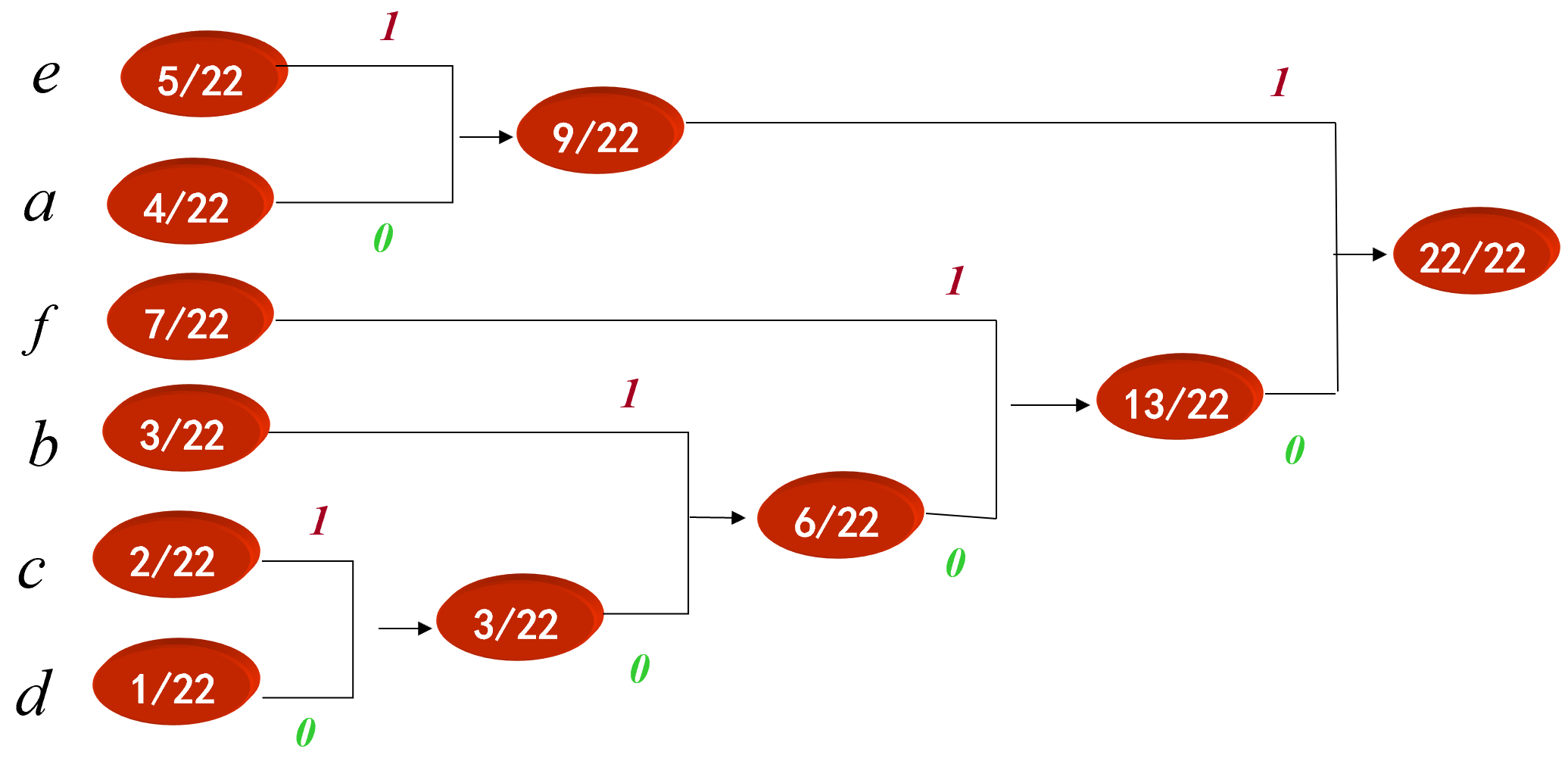
39 |
40 | f=01 e=11 a=10 b=001 c=0001 d=0000
41 | $$
42 | \frac{\text { aaaa }}{4} \frac{bbb}{3} \frac{cc}{2} \frac{d}{1} \frac{\text { eeeee }}{5} \frac{\text { fffffff }}{7} \text { (共22*8=176 bits) }
43 | $$
44 | 经过Huffman编码之后的数据为:
45 |
46 | 1010101010001001001000100010000111111111101010101010101
47 |
48 | (共 $7 * 2+5 * 2+4 * 2+3 * 3+2 * 4+1 * 4=53$ bits)
49 | 比前面我们给出的编码得到的56bits的数据量还小
50 |
51 | Huffman编码在图像压缩中的实现
52 | 我们知道, 对一幅图像进行编码时, 如果图像的大小大于 256 时, 这幅图像的不同的码字就有可能是很大, 例如极限为 256 个不同的码字。
53 | 对整幅图直接进行Huffman编码时, 小分布的灰度值, 就有可能具有很长的编码。
54 | 如: 100位以上, 这样不但达不到压缩的效果反而会使数据量加大, 应该如何处理?
55 |
56 | 常用的且有效的方法是:
57 | 将图像分割成若干的小块, 对每块进行独立的Huffman编码。例如: 分成$8\times 8$的子块, 就可以大大降低不同灰度值的个数(最多是64而不是256)。
--------------------------------------------------------------------------------
/III/3.3 香农-范诺编码.md:
--------------------------------------------------------------------------------
1 | # 3.3 香农-范诺编码
2 |
3 | 香农-范诺 (Shannon-Fannon) 编码也是一种常见的可变字长编码。与哈夫曼编码相似, 当信源符号出现的概率正好为 $2^{-i}$ $(i<0)$ 时, 采用香农-范诺编码同样能够达到 $100 \%$ 的编码效率。 香农-范诺编码的理论基础是符号的码字长度 $N_i$ 完全由该符号出现的概率来决定, 即
4 | $$
5 | -\log _D P_i \leq N_i \leq-\log _D P_i+1\tag{3-8}
6 | $$
7 | 式中,D为编码所用的数制。
8 |
9 | 香农-范诺编码的步骤如下:
10 | (1)将信源符号按其出现概率从大到小排序;
11 | (2)按照式 (3-8) 计算出各概率对应的码字长度 $N_i$;
12 | (3)计算累加概率 $A_i$, 即
13 | $$
14 | A_i=A_{i-1}+P_{i-1} \quad i=1,2, \ldots, N-1 ; \quad A_0=0\tag{3-9}
15 | $$
16 | (4) 把各个累加概率 $A_i$ 由十进制转化为二进制, 取该二进制数的前 $N_i$ 位作为对应信源符号的码字。
17 |
18 | 为便于比较, 仍以例4-1中图像为对象, 对其进行香农-范诺编码, 结果如表3-3所示。由于在此采用二进制对码字赋值, 故在利用式 (3-9) 计算码字长度 $N_i$ 时, $D$ 取为 2 。以符号 $S_4$ 为例, 其出现概率为 0.07 , 按照式 (3-9) 计算得到它的码字长度应为 4 , 按式 (3-10) 计算得到它的累加概率 $A_4$ 为 0.78 , 将 0.78 转化为二进制并取其前 4 位即得符号 $S_4$ 的码字为 1100 (省去了 “0.”, 有的浮点数不能完全转化, 转化时只需完成前 $N_i$ 位即可)。
19 |
20 | 表3-3 香农-范诺编码
21 |
22 | $$
23 | 平均码长 R=3.17 \quad图像熵 H=2.55 \quad \text { 编㐷效率 } \eta=80.4 \%\\
24 | \begin{array}{|c|c|c|c|c|c|}
25 | \hline \text { 信源符号 } & \text { 出现概率 } P_i & \text { 码字长度 } N_i & \text { 蔂加概率 } A_i & \text { 转换为二进制 } & \text { 分配码字 } B_i \\
26 | \hline S_0 & 0.40 & 2 & 0 & 0 & 00 \\
27 | \hline S_1 & 0.18 & 3 & 0.40 & 01100 & 011 \\
28 | \hline S_2 & 0.10 & 4 & 0.58 & 10010 & 1001 \\
29 | \hline S_3 & 0.10 & 4 & 0.68 & 10100 & 1010 \\
30 | \hline S_4 & 0.07 & 4 & 0.78 & 11000 & 1100 \\
31 | \hline S_5 & 0.06 & 5 & 0.85 & 1101100 & 11011 \\
32 | \hline S_6 & 0.05 & 5 & 0.91 & 1110100 & 11101 \\
33 | \hline S_7 & 0.04 & 5 & 0.96 & 1111010 & 11110 \\
34 | \hline
35 | \end{array}\\
36 |
37 |
38 |
39 | $$
40 | 除此之外, 还有二分法香农-范诺编码方法。其步骤如下:
41 | (1) 首先统计出每个符号出现的概率;
42 | (2) 从左到右对上述概率从大到小排序;
43 | (3) 从这个概率集合中的某个位置将其分为两个子集合,并尽量使两个子集合的概率和近似相等,给前面一个子集合赋值为0, 后面一个子集合赋值为1;
44 | (4) 重复步骤3,直到各个子集合中只有一个元素为止;
45 | (5) 将每个元素所属的子集合的值依次串起来,即可得到各个元素的香农-范诺编码。
46 |
47 | 表3-4 二分法香农-范诺编码
48 |
49 | 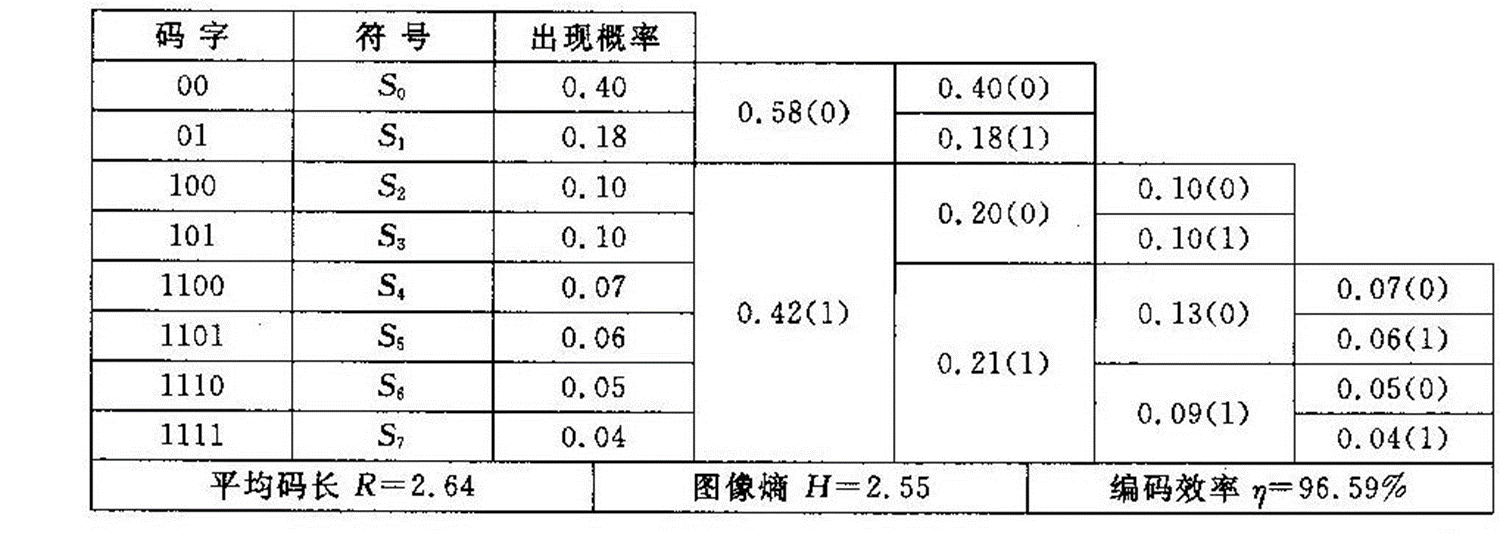
--------------------------------------------------------------------------------
/III/3.4 行程编码.md:
--------------------------------------------------------------------------------
1 | # 3.4 行程编码
2 |
3 | ## 3.4.1 行程编码基本方法
4 |
5 | 行程编码又称行程长度编码(Run Length Encoding, RLE), 是一种熵编码,其编码原理相当简单,即将具有相同值的连续串用其串长和一个代表值来代替, 该连续串就称为行程,串长称为行程长度。例如,有一字符串“aabbbcddddd”, 则经行程长度编码后, 该字符串可以只用“2a3b1c5d”来表示。
6 | 行程编码分为定长和不定长编码两种。定长编码是指编码的行程长度所用的二进制位数固定,而变长行程编码是指对不同范围的行程长度使用不同位数的二进制位数进行编码。使用变长行程编码需要增加标志位来表明所使用的二进制位数。
7 |
8 | 行程编码比较适合于二值图像的编码,一般用于量化后出现大量零系数连续的场合,用行程来表示连零码。如果图像是由很多块颜色或灰度相同的大面积区域组成的,那么采用行程编码可以达到很高的压缩比。如果图像中的数据非常分散,则行程编码不但不能压缩数据,反而会增加图像文件的大小。为了达到较好的压缩效果,一般不单独采用行程编码, 而是和其他编码方法结合使用。例如, 在JPEG中, 就综合使用了行程编码、DCT、量化编码以及哈夫曼编码, 先对图像作分块处理, 再对这些分块图像进行离散余弦变换(DCT), 对变换后的频域数据进行量化并作Z字形扫描,接着对扫描结果作行程编码, 对行程编码后的结果再作哈夫曼编码。
9 |
10 | ## 3.4.2 PCX文件中的行程编码
11 |
12 | PCX文件分为文件头和图像压缩数据两个部分。如果是256色图像,则还有一个256色调色板存于文件尾部。文件头全长128字节,包含了图像的大小和颜色以及PCX文件的版本标识等信息,图像压缩数据紧跟在文件头之后。如果没有使用调色板, 那么图像压缩数据存储的是实际像素值;否则,存储的是调色板的索引值。当压缩数据是实际的像素值时,它们按颜色平面和扫描行存储,即每行先存储所有R分量,再存储所有G分量, 最后存储所有B分量,一行数据存储完后,接着存储下一行数据。如果使用了调色板,则不会分解为单独的颜色平面存储。读者可以查阅图像文件格式的相关书籍了解PCX文件的详细格式。下面以256色PCX文件为例, 说明PCX文件中的行程编码。
13 |
14 | 在256色PCX文件中,每个像素占一字节, 压缩数据以字节为单位逐行进行编码,每行填充到偶数字节。PCX文件规定编码时的最大行程长度为63,如果行程长度大于63,则必须分多次存储。对于长度大于1的行程,编码时先存入其行程长度(长度L加上192即0xC0),再存入该行程的代表值,行程长度和行程的代表值分别占一字节。对于长度为1的行程,即单个像素, 如果该像素的值小于或等于0xC0, 则编码时直接存入该像素值, 而不存储长度信息;否则,先存入0xC1,再存入该像素值,这样做的目的是为了避免该像素值被误认为长度信息。例如,连续100个灰度值为0x80的像素, 其编码(以十六进制表示)应为FF 80 25 80。上面的编码中出现FF的长度信息是由63与0xC0相加所得。
15 |
16 | 对256色PCX文件解码时,首先从压缩数据部分读取一个字节,判断该值是否大于0xC0,如果是,则表明该字节是行程长度信息, 取其低六位(相当于减去0xC0)作为行程长度L,读取下一个字节作为像素值并重复L次存入图像数据缓冲区;否则, 直接将该字节存入图像数据缓冲区。
17 |
18 | 虽然几乎所有的图像应用软件都支持PCX文件格式,但由于它的压缩比不高, 因而现在用得不是很多。
--------------------------------------------------------------------------------
/III/3.5 LZW编码 .md:
--------------------------------------------------------------------------------
1 | # 3.5LZW编码
2 |
3 | ## 3.5.1LZW编码方法
4 |
5 | LZW(Lempel-Ziv&Welch)编码又称字串表编码,属于一种无损编码,是Welch将Lempel和Ziv所提出的无损压缩技术改进后的压缩方法。LZW编码与行程编码类似,也是对字符串进行编码从而实现压缩,但它在编码的同时还生成了特定字符串以及与之对应的索引字符串表。
6 |
7 | LZW编码的基本思想是:在编码过程中,将所遇到的字符串建立一个字符串表,表中的每个字符串都对应一个索引,编码时用该字符串在字串表中的索引来代替原始的数据串。例如,一幅8位的灰度图像,我们可以采用12位来表示每个字符串的索引,前256个索引用于对应可能出现的256种灰度,由此可建立一个初始的字符串表,而剩余的3840个索引就可分配给在压缩过程中出现的新字符串,这样就生成了一个完整的字符串表,压缩数据就可以只保存它在字符串表中的索引,从而达到压缩数据的目的。字符串表是在压缩过程中动态生成的,不必将它保存在压缩文件里,因为解压缩时字符串表可以由压缩文件中的信息重新生成。
8 |
9 | GIF(GraphicsInterchangeFormat)最初是由美国CompuServe于1987年开发的一种压缩位图格式。它可支持多达256种的颜色,具有极佳的压缩效率,已成为Internet上一种流行的文件格式。GIF图像文件采用的是一种改良的LZW压缩算法,通常称为GIF-LZW压缩算法。GIF图像文件以块(又称为区域结构)的方式来存储图像相关的信息,具体的文件格式可参考图像文件格式的相关书籍。下面简要介绍GIF-LZW的编码方法。
10 |
11 | 设S1、S2为两个存放字符串的临时变量,LZW_CLEAR和LZW_EOI分别为字符表初始化标志和编码结束标志,GIF-LZW的编码步骤如下:
12 |
13 | (1)根据图像中使用的颜色数初始化一个字串表,字串表中的每个颜色对应一个索引。在初始字串表的末尾再添加两个符号(LZW_CLEAR和LZW_EOI)的索引。设置字符串变量S1、S2并初始化为空。
14 |
15 | (2)接着输出LZW_CLEAR在字串表中的索引。
16 |
17 | (3)从图像数据流中第一个字符(假设数据以字符串表示)开始,每次读取一个字符,将其赋给字符串变量S2。
18 |
19 | (4)判断“S1+S2”是否已存在于字串表中。如果字串表中存在“S1+S2”,则S1=S1+S2;否则,输出S1在字串表中的索引,并在字串表末尾为“S1+S2”添加索引,同时,S1=S2。
20 |
21 | (5)重复第3和第4步,直到所有字符读完为止。
22 |
23 | (6)输出S1中的字符串在字串表中的索引,然后输出结束标志LZW_EOI的索引,编码完毕。
24 |
25 | GIF-LZW的解码过程比较复杂,它和编码过程正好相反,即将编码后的码字转换成对应的字符串,重新生成字串表,然后依次输出对应的字符串即可。GIF-LZW的解码流程如图3-2所示,表中的Code和OldCode是两个存放索引的临时变量。
26 |
27 | 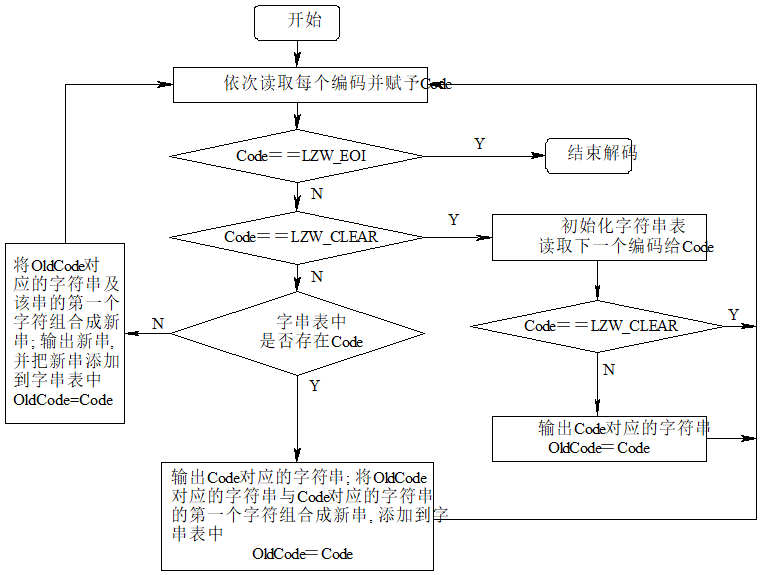
28 |
29 | 图3-2GIF-LZW解码流程
30 |
31 | ## 3.5.2LZW编码实例
32 |
33 | 设有一来源于4色(以a、b、c、d表示)图像的数据流aabcabbbbd,现对其进行LZW编码。编码过程如下:
34 | 编码前,首先需要初始化一个字符串表。由于图像中只有四种颜色,因而我们可以只用4比特表示字符串表中每个字符串的索引,表中的前4项代表4种颜色,后两项分别表示初始化和图像结束标志,建立的初始化字符串表如表3-5所示。接着把S1和S2初始化为空(即NULL),输出LZW_CLEAR的在字符串表中的索引值4H,接下来是对图像数据的编码。
35 |
36 | 表3-5初始化字符串表
37 | $$
38 | \begin{array}{|c|c|}
39 | \hline \text{字符串}&\text{索引}\\
40 | \hline a&0H\\
41 | \hline b&1H\\
42 | \hline c&2H\\
43 | \hline d&3H\\
44 | \hline \text{LZW\_CLEAR}&4H\\
45 | \hline \text{LZW\_EOI}&5H\\
46 | \hline
47 | \end{array}
48 | $$
49 |
50 |
51 | 读取图像数据流的第一个字符“a”,赋给S2,因S1+S2=“a”已存在字串表中,所以S1=S1+S2=“a”。
52 | 接着读入下一个字符“a”赋给S2,因S1+S2=“aa”不存在于字串表中,所以输出S1=“a”的索引0H,同时在字符串表末尾添加新字符串“aa”的索引6H,并使S1=S2=“a”。
53 | 依次读取数据流中的每个字符,如果S1+S2没有出现在字符串表中,则输出S1中的字符串的索引,并在字符串表末尾为新字符串S1+S2添加索引,并使S1=S2;否则,不输出任何结果,只是使S1=S1+S2。所有字符处理完毕后,输出S1中的字符串的索引,最后输出结束标志LZW_EOI的索引。至此,编码完毕,完整的编码过程如表3-6所示,最后的编码结果为“4001271B35”(以十六进制表示)。
54 |
55 | 表3-6GIF-LZW编码过程
56 | $$
57 | \begin{array}{|c|c|c|c|c|}
58 | \hline \text { 输入数据 S2 } & \text { S1+S2 } & \text { 输出结果 } & \text { S1 } & \text { 生成的新字符串及索引 } \\
59 | \hline \text { NULL } & \text { NULL } & 4 H & \text { NULL } & \\
60 | \hline a & a & & a & \\
61 | \hline a & aa & 0 H & a & aa<6 H> \\
62 | \hline b & ab & 0 H & a & ab<7 H> \\
63 | \hline c & bc & 1 H & c & ca<9 H> \\
64 | \hline a & ca & 2 H & a & \\
65 | \hline b & ab & & ab & abb \\
66 | \hline b & abb & 7 H & b & bb \\
67 | \hline b & bb & 1 H & b & \\
68 | \hline b & bb & & bb & bbd \\
69 | \hline d & bbd & BH & d & \\
70 | \hline & & 3 H & & \\
71 | \hline & & 5 H & & \\
72 | \hline
73 | \end{array}
74 | $$
75 | 下面对上述编码结果“4001271B35”进行解码。按图3-2的解码流程,首先读取第一个编码Code=4H,由于它为LZW_CLEAR,因此需初始化字符串表,结果如表3-5所示(在实际应用中,可根据文件头中给定的信息建立初始字符串表)。
76 |
77 | 读入下一个编码Code=0H,由于它不等于LZW_CLEAR,因此输出字串表中0H对应的字符串“a”,同时使OldCode=Code=0H。
78 |
79 | 读入下一个编码Code=0H,由于字串表中存在该索引,因此输出0H所对应的字符串“a”,然后将OldCode=0H所对应的字符串“a”加上Code=0H所对应的字符串的第一个字符“a”,即“aa”添加到字串表中,其索引为6H,同时使ldCode=Code=0H。
80 |
81 | 读入下一个编码Code=1H,由于字串表中存在该索引,因此输出1H所对应的字符串“b”,然后将OldCode=0H所对应的字符串“a”加上Code=1H所对应的字符串的第一个字符“b”,即“ab”添加到字串表中,其索引为7H,同时使OldCode=Code=1H。
82 |
83 | 读入下一个编码Code=2H,由于字串表中存在该索引,因此输出2H所对应的字符串“c”,然后将OldCode=1H所对应的字符串“b”加上Code=2H所对应的字符串的第一个字符“c”,即“bc”添加到字串表中,其索引为8H,同时使OldCode=Code=2H。
84 |
85 | 读入下一个编码Code=7H,由于字串表中存在该索引,因此输出7H所对应的字符串“ab”,然后将OldCode=2H所对应的字符串“c”加上Code=7H所对应的字符串的第一个字符“a”,即“ca”添加到字串表中,其索引为9H,同时使OldCode=Code=7H。
86 |
87 | 读入下一个编码Code=1H,由于字串表中存在该索引,因此输出1H所对应的字符串“b”,然后将OldCode=7H所对应的字符串“ab”加上Code=1H所对应的字符串的第一个字符“b”,即“abb”添加到字串表中,其索引为AH,同时使OldCode=Code=1H。
88 |
89 | 读入下一个编码Code=BH,由于字串表中不存在该索引,因此输出OldCode=1H所对应的字符串“b”加上该字符串的第一个字符“b”,即“bb”,同时将“aa”添加到字串表中,其索引为BH,同时使OldCode=Code=BH。
90 |
91 | 读入下一个编码Code=3H,由于字串表中存在该索引,因此输出其对应的字符串“d”,然后将OldCode=BH所对应的字符串“bb”加上Code=3H所对应的字符串的第一个字符“d”,即“bbd”添加到字串表中,其索引为CH,同时使OldCode=Code=3H。读入下一个编码Code=5H,它等于LZW_EOI,数据解码完毕,最后的解码结果为aabcabbbbd。为清晰起见,完整的解码过程如表3-7所示。
92 |
93 | 表3-7GIF-LZW解码过程
94 | $$
95 | \begin{array}{|c|c|c|c|c|}
96 | \hline \text { 输入数据 Code } & \text { 新字符串的来源 } & \text { 输出结果 } & \text { OldCode } & \text { 生成的新串及索引 } \\
97 | \hline 4 H & & & & \\
98 | \hline 0 H & & a & 0 H & \\
99 | \hline 0 H & \text { Str(OldCode)+FirstStr(Code) }=aa & a & 0 H & aa<6 H> \\
100 | \hline 1 H & \text { Str(OldCode)+FirstStr(Code) }=ab & b & 1 H & ab<7 H> \\
101 | \hline 2 H & \text { Str(OldCode)+FirstStr(Code) }=bc & c & 2 H & bc<8 H> \\
102 | \hline 7 H & \text { Str(OldCode)+FirstStr(Code) }=ca & ab & 7 H & ca<9 H> \\
103 | \hline 1 H & \text { Str(OldCode)+FirstStr(Code) }=abb & b & 1 H & abb \\
104 | \hline BH & \text { Str(OldCode)+FirstStr(OldCode) }=bb & bb & BH & bb \\
105 | \hline 3 H & \text { Str(OldCode)+FirstStr(Code) }=bbd & d & 3 H & bbd \\
106 | \hline 5 H & & & & \\
107 | \hline
108 | \end{array}
109 | $$
--------------------------------------------------------------------------------
/III/3.6 算术编码.md:
--------------------------------------------------------------------------------
1 | # 3.6 算术编码
2 |
3 | 算术编码有两种模式:一种是基于信源概率统计特性的固定编码模式,另一种是针对未知信源概率模型的自适应模式。自适应模式中各个符号的概率初始值都相同, 它们依据出现的符号而相应地改变。只要编码器和解码器都使用相同的初始值和相同的改变值的方法,那么它们的概率模型将保持一致。上述两种形式的算术编码均可用硬件实现,其中自适应模式适用于不进行概率统计的场合。有关实验数据表明,在未知信源概率分布的情况下, 算术编码一般要优于Huffman编码。在JPEG扩展系统中,就用算术编码取代了哈夫曼编码。
4 |
5 | 下面结合一个实例来阐述固定模式的算术编码的具体方法。 设一待编码的数据序列 (即信源) 为 “ dacab", 信源中各符号出现的概率依次为 $P(a)=0.4, P(b)=0.2, P(c)=0.2, \quad P(d)=0.2$ 。
6 | 首先, 数据序列中的各数据符号在区间 $[0,1]$ 内的间隔 (赋值范围)设定为 $a=[0,0.4), b=[0.4,0.6), c=[0.6,0.8)$ , $d=[0.8,1.0)$
7 | 为便于讨论, 再给出一组关系式:
8 | $$
9 | \left\{\begin{array}{l}
10 | \operatorname{Start}_{N}=\operatorname{Start}_{B}+\operatorname{Left}_{C} \times L \\
11 | \operatorname{End}_{N}=\operatorname{Start}_{B}+\operatorname{Right}_{C} \times L
12 | \end{array}\right.
13 | $$
14 | 式中, $\operatorname{Start}_{\mathbb{N}} 、 End_{\mathbb{N}}$ 分别表示新间隔 (或称之为区间)的起始位置和结束位置, Start ${ }_{B}$ 表示前一间隔的起始位置, $L$ 为前一间隔的长度, Left $_C 、$ Right $_C$ 分别表示当前编码符号的初始区间的左端和右端。
15 | 第一个被压缩的符号为 “ $d$ ",其初始间隔为 $[0.8,1.0)$;
16 | 第二个被压缩的符号为 “ $a$ ", 由于前面的符号 “ $d^{\prime \prime}$ 的取值区间被限制在 $[0.8,1.0$ )范围内, 所以 “ $a$ ”的取值范围应在前一符号间隔 $[0.8,1.0)$ 的 $[0,0.4)$ 子区间内, 根据上式可知
17 | $$
18 | \begin{aligned}
19 | & \text { Start }_{N}=0.8+0 \times(1.0-0.8)=0.8 \\
20 | & \text { End }_{N}=0.8+0.4 \times(1.0-0.8)=0.88
21 | \end{aligned}
22 | $$
23 | 即 “ $a$ ”的实际编码区间在 $[0.8,0.88)$ 之间。
24 |
25 | 第三个被压缩的符号为 “ $c^{\prime \prime}$, 其编码取值范围应在 $[0.8$, $0.88)$ 区间的 $[0.6,0.8)$ 的子区间内, 据上式可知
26 | $$
27 | \begin{aligned}
28 | & \text { Start }_N=0.8+0.6 \times(0.88-0.8)=0.848 \\
29 | & \text { End }_N=0.8+0.8 \times(0.88-0.8)=0.864
30 | \end{aligned}
31 | $$
32 | 第四个被压缩的符号为 “ $a$ ”, 同理, 根据上式可知
33 | $$
34 | \begin{aligned}
35 | & \operatorname{Start}_{N}=0.848+0 \times(0.864-0.848)=0.848 \\
36 | & \operatorname{End}_{N}=0.848+0.4 \times(0.864-0.848)=0.8544
37 | \end{aligned}
38 | $$
39 | 第五个被压缩的符号为 “ $b$ ”, 同理, 根据上式可知
40 | $$
41 | \begin{aligned}
42 | & \text { Start }_{N}=0.848+0.4 \times(0.8544-0.848)=0.84856 \\
43 | & \text { End }_{N}=0.848+0.6 \times(0.8544-0.848)=0.85144
44 | \end{aligned}
45 | $$
46 | 至此, 数据序列 “dacab"已被描述为一个实数区间 $[0.85056$, $0.85184]$, 或者说在此区间内的任一实数值都惟一对应该数据序列。这样, 就可以用一个实数表示这一数据序列。我们把区间 [0. 850 56,0.851 84] 用二进制形式表示为 $[0.110110011011$, $0.110110100001]$ 。
47 |
48 | 从这个区间可以看出,0.1101101位于这个区间内并且其编码最短, 故把其作为数据序列“dacab”的编码输出。考虑到算术编码中任一数据序列的编码都含有“0.”,所以在编码时,可以不考虑“0.”,于是把1101101作为本例中的数据序列的算术编码。由此可见, 数据序列“dacab”用7比特的二进制代码就可以表示, 平均码长为1.4比特/字符。
49 |
50 | 解码是编码的逆过程,根据编码时的概率分配表和压缩后数据代码所在的范围,确定代码所对应的每一个数据符号。由此可见,算术编码的实现方法要比哈夫曼编码复杂一些。
--------------------------------------------------------------------------------
/III/3.7 DCT变换编码.md:
--------------------------------------------------------------------------------
1 | # 3.7 DCT变换编码
2 |
3 | 注意
4 | 作DCT变换时,一般不是对整个图象作一次变换,而是将图象划为8*8或16*16的子图象,然后对各个子图象作DCT变换.
5 |
6 | 采用快速DCT变换
7 |
8 |
104 |
105 | 根据编码原理可以将图像编码分为熵编码、预测编码、变换编码和混合编码等。
106 |
107 | 图像压缩编码系统原理框图
108 |
109 | 
110 |
111 | (1) 熵编码。熵编码是纯粹基于信号统计特性的编码技术, 是一种无损编码。熵编码的基本原理是给出现概率较大的符号赋予一个短码字, 而给出现概率较小的符号赋予一个长码字, 从而使得最终的平均码长很小。 常见的熵编码方法有行程编码 (Run Length Encoding)、哈夫曼编码和算术编码。
112 |
113 | (2)预测编码。预测编码是基于图像数据的空间或时间冗余特性, 用相邻的已知像素(或像素块)来预测当前像素(或像素块)的取值, 然后再对预测误差进行量化和编码。预测编码可分为帧内预测和帧间预测, 常用的预测编码有差分脉码调制(Differential Pulse Code Modulation,DPCM)和运动补偿法。
114 |
115 | (3)变换编码。变换编码通常是将空间域上的图像经过正交变换映射到另一变换域上, 使变换后的系数之间的相关性降低。 图像变换本身并不能压缩数据, 但变换后图像的大部分能量只集中到少数几个变换系数上, 采用适当的量化和熵编码就可以有效地压缩图像。
116 |
117 | (4) 混合编码。混合编码是指综合了熵编码、变换编码或预测编码的编码方法, 如JPEG标准和MPEG标准。
118 |
119 | 根据对压缩编码后的图像进行重建的准确程度, 可将常用的图像编码方法分为三类:
120 |
121 | (1)信息保持编码: 也称无失真编码, 它要求在编解码过程中保证图像信息不丢失, 从而可以完整地重建图像。信息保持编码的压缩比较低, 一般不超过3: 1, 主要应用在图像的数字存储方面, 常用于医学图像编码中。
122 |
123 | (2)保真度编码: 主要利用人眼的视觉特性, 在允许的失真 (Lossy) 条件下或一定的保真度准则下, 最大限度地压缩图像。保真度编码可以实现较大的压缩比, 主要用于数字电视技术、静止图像通信、娱乐等方面。对于这些图像,过高的空间分辨率和过多的灰度层次, 不仅增加了数据量, 而且人眼也接收不到。因此在编码过程中, 可以丢掉一些人眼不敏感的信息, 在保证一定的视觉效果条件下提高压缩比。
124 |
125 | (3) 特征提取: 在图像识别、分析和分类等技术中, 往往并不需要全部图像信息, 而只要对感兴趣的部分特征信息进行编码即可压缩数据。例如, 对遥感图像进行农作物分类时,就只需对用于区别农作物与非农作物, 以及农作物类别之间的特征进行编码, 而可以忽略道路、河流、建筑物等其他背景信息。
126 |
127 | ## 3.1.3 图像编码新技术
128 |
129 | 图像编码已经发展了几十年, 人们不断提出新的压缩方法。如, 利用人工神经网络 (Artificial Neural Network, ANN) 的压缩编码、分形编码(Fractal Coding)、小波编码(Wavelet Coding)、基于对象的压缩编码(Object Based Coding)和基于模型的压缩编码(Model Based Coding)等等。
130 |
131 | 1)分形编码
132 |
133 | 分形编码是在波兰美籍数学家B.B.Mandelbrot建立的分形几何理论的基础上发展起来的一种编码方法。分形编码最大限度地利用了图像在空间域上的自相似性(即局部与整体之间存在某种相似性),通过消除图像的几何几穴余来压缩数据。 M.Barnsley将迭代函数系统 (Iterate Function System,IFS) 用于描述图像的自相似性, 并将其用于图像编码, 对某些特定图像获得了10 000: 1的压缩比。分形编码过程十分复杂, 而解码过程却很简单, 故通常用于对图像编码一次, 而需译码多次的信息传播应用中。
134 |
135 | 2)小波编码
136 |
137 | 1989年, S.G.Mallat首次将小波变换用于图像编码。经过小波变换后的图像, 具有良好的空间方向选择性, 而且是多分辨率的, 能够保持原图像在各种分辨率下的精细结构, 与人的视觉特性十分吻合。
138 |
139 | 3)模型编码
140 |
141 | 模型编码是近几年发展起来的一种很有前途的低比特率编码方法, 其基本出发点是在编、解码两端分别建立起相同的模型,编码时利用先验模型抽取图像中的主要信息并用模型参数的形式表示,解码时则利用所接收的模型参数重建图像。
142 |
143 | ## 4.1.4 图像编码评价
144 |
145 | 随着众多图像压缩算法的出现, 如何评价图像压缩算法就成为重要的课题。一般说来, 评价图像压缩算法的优劣主要有以下4个参数。
146 |
147 | 1)算法的编码效率
148 |
149 | 算法的编码效率通常有几种表现形式: 平均码字长度(R), 图像的压缩比 (rate, $r$ ), 每秒钟所需的传输比特数 (bits per second, bps), 图像熵与平均码长之比 $(\eta)$, 这些表现形式很容易相互转换。下面给出与图像编码效率有关的几个定义。 设一幅灰度级为 $N$ 的图像, 图像中第 $k$ 级灰度出现的概率为 $P_{k}$,
150 |
151 | 图像大小为 $N_{x} \times N_{y}$, 每个像素用 $d$ 比特表示, 每两帧图像间隔 $\Delta t$, 则按信息论中信息熵的定义, 数字图像的熵 $H$ 由下式定义:
152 |
153 | $$
154 | H=-\sum_{k=1}^{N} P_{k} 1 b P_{k}\tag{3-1}
155 | $$
156 |
157 | 由此可见, 图像熵 $H$ 表示各灰度级比特数的统计平均值。
158 |
159 | 对于一种图像编码方法, 设第 $k$ 级灰度的码字长度为 $B_{k}$, 则该图像的平均码字长度 $R$ 为
160 |
161 | $$
162 | R=\sum_{k=1}^{N} B_{k} P_{k}\tag{3-2}
163 | $$
164 |
165 | 于是,可定义编码效率 $\eta$ 为
166 |
167 | $$
168 | \eta=\frac{H}{R} \times 100 \%\tag{3-3}
169 | $$
170 |
171 | 每秒钟所需的传输比特数bps为
172 |
173 | $$
174 | b p s=\frac{N_{x} N_{y} R}{\Delta t}\tag{3-4}
175 | $$
176 |
177 | 压缩比 $r$ 为
178 | $$
179 | r=\frac{d}{R}\tag{3-5}
180 | $$
181 | 由于同一压缩算法对不同图像的编码效率会有所不同, 因此常需定义一些 “标准图像”,如国际上流行的三幅图像Lena、Barbara和Mandrill。一般通过测量不同压缩算法对同一组 “标准图像”的编码性能来评价各图像压缩算法的编码效率。
182 |
183 | 2)编码图像的质量
184 |
185 | 图像质量评价可分为客观质量评价和主观质量评价。最常用
186 |
187 | 的客观质量评价指标是均方误差 (MSE) 和峰值信噪比
188 |
189 | (PSNR),其定义如下:
190 |
191 | $$
192 | M S E=\frac{1}{N_{x} N_{y}} \sum_{i=0}^{N_{x}} \sum_{j=0}^{N_{y}}[f(i, j)-\hat{f}(i, j)]^{2} \tag{3-6}
193 | $$
194 |
195 | $$
196 | P S N R=10 \lg \left(\frac{255 \times 255}{M S E}\right)\tag{3-7}
197 | $$
198 |
199 | 主观质量评价是指由一批观察者对编码图像进行观察并打分, 然后综合所有人的评判结果, 给出图像的质量评价。客观质量评价能够快速有效地评价编码图像的质量, 但符合客观质量评价指标的图像不一定具有较好的主观质量。主观质量评价能够与人的视觉效果相匹配, 但其评判过程缓慢费时。
200 |
201 | 3)算法的适用范围
202 |
203 | 特定的图像编码算法具有其相应的适用范围, 并不对所有图像都有效。一般说来, 大多数基于图像信息统计特性的压缩算法具有较广的适用范围, 而一些特定的编码算法的适用范围较窄, 如分形编码主要用于自相似性高的图像。
204 |
205 | 4)算法的复杂度
206 |
207 | 算法的复杂度即指完成图像压缩和解压缩所需的运算量和硬件实现该算法的难易程度。优秀的压缩算法要求有较高的压缩比, 压缩和解压缩快, 算法简单, 易于硬件实现, 还要求解压缩后的图像质量较好。选用编码方法时一定要考虑图像信源本身的统计特性、多媒体系统(硬件和软件产品)的适应能力、应用环境以及技术标准。
--------------------------------------------------------------------------------
/III/3.10 预测编码.md:
--------------------------------------------------------------------------------
1 | # 3.10预测编码
2 |
3 | 利用图象局部邻域象素的可预测性来进行圧缩.
4 | 设: $f(n, m)$ 为 $(n, m)$ 点的灰度值; $f(n-i, m-j),(i, j) \in A$, 为邻域A内某点的灰度值,则:
5 | $$
6 | \hat{f}(n, m)=L(f(n-i, m-j),(i, j) \in A,(i, j) \neq(0,0)
7 | $$
8 | L为预测值,通常取为囱口 $A$ 内象素点恢度值的线性函数.如图所示, 即由㳡去的 $f_r(n-i, m-j)$ 来预测 $f(n, m)$ :
9 |
10 | 
11 | $$
12 | \hat{f}(n, m)=L\left(f_r(n-i, m-j)\right) \quad(i, j) \in A
13 | $$
14 | 因此可以建立一种递归预测编码技术,对应的误差为:
15 | $$
16 | \begin{aligned}
17 | & e_q(n, m)=f(n, m)-\hat{f}(n, m) \\
18 | & f(n, m)=L\left(f_r(n-i, m-j)\right)+e_q(n, m)
19 | \end{aligned}
20 | $$
21 | 即 $\mathbf{f}(\mathbf{n}, \mathbf{m})$ 由 $\mathbf{e}(\mathbf{n}, \mathbf{m})$ 代替, 如果预测 $\hat{f}(n, m)$ 效果好, 则误差项的动态范围很小, 可以有较小的码字来编码,这样便得到显著的压缩效果.
22 |
23 | 为了重建图象,需要传输预测系数和误差编码,这种编码方式称为预测脉冲编码调制(DPCM),如图:
24 |
25 | 
26 |
27 | 假设图象的某一行 $f(n, m)(f(n, m)$ 记为 $f(m))$ 可用一平稳自相关AR过程表示:
28 | $$
29 | f(m)=\sum_{k=1}^p a(k) f(m-k)+e(m) \quad E\left[e^2(m)\right]=\sigma^2
30 | $$
31 | 其中e $(m)$ 为一个与 $f(m)$ 不相关的高斯白噪声, 则预测器:
32 | $$
33 | \hat{f}(m)=\sum_{k=1}^P a(k) \hat{f}_r(m-k)
34 | $$
35 | 预测器系数构成一向量 $a=(a(1), a(2) \ldots, a(P))^{\top}, \quad$ 预测窗口A内重建象素 $\left\{f_r(m-1), \ldots, f_r(m-P)\right.$, 量化误差:
36 | $$
37 | e_q(m)=Q(e(m))=Q[f(m)-\hat{f}(m)]
38 | $$
39 | 重建图象行: $f_r(m)=\sum_{k=1}^p a(k) f_r(m-k)+e_q(m)$
40 |
41 | 预测系数通过下式求解
42 | $$
43 | \left[\begin{array}{cccc}
44 | R(0) & R(1) & \cdots & R(P-1) \\
45 | R(1) & R(2) & \cdots & R(P-2) \\
46 | \vdots & \vdots & \vdots & \vdots \\
47 | R(P-1) & R(P-2) & \cdots & R(0)
48 | \end{array}\right]\left[\begin{array}{c}
49 | a(1) \\
50 | a(2) \\
51 | \vdots \\
52 | a(P)
53 | \end{array}\right]=\left[\begin{array}{c}
54 | R(1) \\
55 | R(2) \\
56 | \vdots \\
57 | R(P)
58 | \end{array}\right]
59 | $$
60 |
61 | ## 预测编码(最佳线性预测)
62 |
63 | 二维模型:
64 | $$
65 | \hat{f}(n, m)=\sum \sum_{(i j) \in A}^P a(i, j) \hat{f}_r(n-i, m-j)
66 | $$
67 | 通过求解E最小:
68 | $$
69 | \left.\left.E\left[\mid f(n, m)-\sum \sum_{(i, j) \in A} a(i, j) f(n-i), m-j\right)\right|^2\right]
70 | $$
71 | 得: $\left.\quad R(k, l)=\sum \sum_{(i, j) \in A} a(i, j) R(n-i), m-j\right)$
72 | 求解上式得到 $a(i, j)$, 再得到:
73 | $$
74 | e(n, m)=f(n, m)-\hat{f}(n, m)
75 | $$
76 | 接收端得: $f_r(n, m)=\sum \sum_{(i j) \in A}^P a(i, j) \hat{f}_r(n-i, m-j)+e_q(n, m)$
--------------------------------------------------------------------------------
/III/3.11 JPEG编码.md:
--------------------------------------------------------------------------------
1 | # 3.11 JPEG 编码
2 |
3 | ## 3.11 JPEG基本系统编码
4 |
5 | JPEG是面向静态图像编码的国际标准。在相同图像质量条件下, JPEG文件拥有比其他图像文件格式更高的压缩比。JPEG目前被广泛应用于多媒体和网络程序中,是现今万维网中使用最广泛的两种图像文件格式之一。JPEG是一种有损压缩, 即在压缩过程中会丢失数据,每次编辑JPEG图像后,图像就会被重复压缩一次, 损失就会有所增加。
6 |
7 | JPEG允许四种编码模式:
8 | (1) 顺序式(Sequential)DCT方式:从左到右、从上到下对图像顺序进行基于离散余弦变换(DCT)的编码。DCT理论上是可逆的,但在计算时存在误差,因而基于DCT的编码模式是一种有损编码。
9 |
10 | (2) 渐进式(Progressive)DCT方式:基于DCT,对图像分层次进行处理,从模糊到清晰地传输图像(与GIF文件的交错方式类似)。有两种实现方法,一种是频谱选择法,即按Z形扫描的序号将DCT量化序数分成几个频段,每个频段对应一次扫描, 每块均先传送低频扫描数据,得到原图概貌,再依次传送高频扫描数据,使图像逐渐清晰;另一种是逐次逼近法,即每次扫描全部DCT量化序数,但每次的表示精度逐渐提高。
11 | (3) 无失真(Lossless)方式: 使用线性预测器,如DPCM, 而不是基于DCT。
12 |
13 | (4) 分层(Hierarchical)方式: 在空间域将源图像以不同的分辨率表示,每个分辨率对应一次扫描, 处理时可以基于DCT或预测编码,可以是渐进式,也可以是顺序式。
14 | JPEG定义了三种系统:基本系统(Baseline System)、扩展系统(Extended System)和无失真压缩系统(Lossless System)。一个符合JPEG标准的编解码器至少要满足基本系统的技术指标。
15 | 基本的JPEG算法属于变换类编码,下面针对基于DCT的顺序式基本系统编码来说明JPEG的编码方法。
16 |
17 | 
18 |
19 | 图3-3 JPEG 编码流程图
20 |
21 | 1) 数据分块
22 | 对图像进行编码前, 将每个分量图像分割成不重叠的 $8 \times 8$ 像素块, 每一个 $8 \times 8$ 像素块称为一个数据单元 (DU)。在彩色图像中, JPEG分别压缩图像的每个彩色分量。虽然JPEG可以压缩通常的红绿蓝分量, 但在 $Y_{b} C_{r}$ 空间的压缩效果会更好。 这是因为人眼对色彩的变化不如对亮度的变化敏感, 因而对色彩的编码可以比对亮度的编码粗糙些, 这主要体现在不同的采样频率和量化精度上。因此, 编码前一般先将图像从RGB空间转换到 $YC_{b} C_{i}$ 空间,再把各分量图像分割成 $8 \times 8$ 数据块。
23 |
24 | 在对图像采样时, 可以采用不同的采样频率, 这种技术称为二次采样。由于亮度比色彩更重要, 因而对 $Y$ 分量的采样频率可高于对 $C_{b} 、 C_{r}$ 的采样频率, 这样有利于节省存储空间。常用的采样方案有YUV422和YUV411。把采样频率最低的分量图像中一个DU所对应的像区上覆盖的所有各分量上的DU按顺序编组为一个最小编码单元 (MCU)。对灰度图像而言, 只有一个Y分量, MCU就是一个数据单元。而对彩色图像而言, 以 4:1:1的采样方案为例, 则一个MCU由4个 4 分量的DU、 1 个 $C_{b}$ 分量的DU和1个 $C_{r}$ 分量的DU组成。
25 |
26 | 2) DCT处理
27 | 图像数据块分割后, 即以 MCU为单位顺序将DU进行二维离散余弦变换。对以无符号数表示的具有 $P$ 位精度的输入数据, 在DCT前要减去 $2^{P-1}$, 转换成有符号数, 而在IDCT后, 应加上 $2^{P-1}$, 转换成无符号数。对每个 $8 \times 8$ 的数据块 $DU$ 进行 $DCT$ 后, 得到的64个系数代表了该图像块的频率成分,其中低频分量集中在左上角, 高频分量分布在右下角。系数矩阵左上角的叫做直流(DC)系数,它代表了该数据块的平均值, 其余 63 个叫交流(AC)系数。
28 |
29 | 3) 系数量化
30 | 在DCT处理中得到的64个系数中,低频分量包含了图像亮度等主要信息。在从空间域到频域的变换中,图像中的缓慢变化比快速变化更易引起人眼的注意, 所以在重建图像时,低频分量的重要性高于高频分量。因而在编码时可以忽略高频分量, 从而达到压缩的目的,这也是量化的根据和目的。
31 |
32 | 在JPEG标准中,用具有64个独立元素的量化表来规定DCT域中相应的64个系数的量化精度,使得对某个系数的具体量化阶取决于人眼对该频率分量的视觉敏感程度。理论上,对不同的空间分辨率、数据精度等情况,应该有不同的量化表。不过,一般采用图3-4和图3-5所示的量化表,可取得较好的视觉效果。之所以用两张量化表,是因为Y分量比Cb和Cr更重要些,因而对Y采用细量化,而对Cb和Cr采用粗量化。量化就是用DCT变换后的系数除以量化表中相对应的量化阶后四舍五入取整。由于量化表中左上角的值较小,而右下角的值较大, 因而起到了保持低频分量、 抑制高频分量的作用。
33 |
34 | 
35 |
36 | 图3-4 亮度量化表
37 |
38 | 
39 |
40 | 图3-5 色度量化表
41 |
42 | 4) Z形扫描
43 | DCT系数量化后,构成一个稀疏矩阵,用Z(Zigzag)形扫描将其变成一维数列,将有利于熵编码。Z形扫描的顺序如图3-6所示。
44 |
45 | 
46 |
47 | 图3-6 DCT系数的Z形扫描顺序
48 |
49 | 5) DC系数编码
50 |
51 | DC系数反映了一个8×8数据块的平均亮度,一般与相邻块有较大的相关性。JPEG对DC系数作差分编码,即用前一数据块的同一分量的DC系数作为当前块的预测值,再对当前块的实际值与预测值的差值作哈夫曼编码。
52 |
53 | 若DC系数的动态范围为-1024~+1024,则差值的动态范围为-2047~+2047。如果为每个差值赋予一个码字, 则码表过于庞大。因此,JPEG对码表进行了简化,采用“前缀码(SSSS)+尾码”来表示。前缀码指明了尾码的有效位数B, 可以根据DIFF从表3-8中查出前缀码对应的哈夫曼编码。尾码的取值取决于DC系数的差值和前缀码。如果DC系数的差值DIFF大于等于0,则尾码的码字为DIFF的B位原码;否则,取DIFF的B位反码。
54 |
55 | 表3-8 图像分量为8位时DC系数差值的典型哈夫曼编码表
56 |
57 | 
58 |
59 | 6) AC系数编码
60 | 经Z形排列后的AC系数,更有可能出现连续0组成的字符串, 从而对其进行行程编码将有利于压缩数据。JPEG将一个非零DC系数及其前面的0行程长度(连续0的个数)的组合称为一个事件。将每个事件编码表示为“NNNN/SSSS+尾码”, 其中, NNNN为0行程的长度,SSSS表示尾码的有效位数B(即当前非0系数所占的比特数),如果非零AC系数大于等于0, 则尾码的码字为该系数的B位原码, 否则, 取该系数的B位反码。
61 | 由于只用4位表示0行程的长度,故在JPEG编码中,最大0行程只能等于15。当0行程长度大于16时,需要将其分开多次编码, 即对前面的每16个0以“F/0”表示,对剩余的继续编码。
62 |
63 | 表3-9 AC系数的尾码位数表
64 |
65 | | SSSS | AC系数的尾码位数表 |
66 | | ---- | -------------------- |
67 | | 0 | 0 |
68 | | 1 | -1,1 |
69 | | 2 | -3, -2, 2, 3 |
70 | | 3 | -7~-4, 4~7 |
71 | | 4 | -15~-8, 8~15 |
72 | | 5 | -31~-16, 16~31 |
73 | | 6 | -63~-17, 17~63 |
74 | | 7 | -127~-64, 64~127 |
75 | | 8 | -255~-128, 128~255 |
76 | | 9 | -511~256, 256~511 |
77 | | 10 | -1023~-512, 512~1023 |
78 |
79 | 表3-10 亮度AC系数码表
80 |
81 | 
82 |
83 | 
84 |
85 | 
86 |
87 | 表3-11 色差AC系数编码
88 |
89 | 
90 |
91 | 
92 |
93 | 
94 |
95 | 3.11.2 JPEG编码实例
96 | 下面结合一个实例来讲述JPEG基本系统的编码过程。设有一图像亮度数据块如图3-7所示,对其进行离散余弦变换后, 用图3-4所示的亮度量化表对系数矩阵量化后的结果如图3-8所示。对量化结果按图3-6所示的顺序进行Z形扫描, 并对扫描结果的DC及AC系数进行编码的结果见表3-12。由于数据较多, 为简便起见, 这里只对几个系数的编码加以说明。
97 |
98 | 
99 |
100 | 图3-7 源图像亮度数据块
101 |
102 | 
103 |
104 | 图3-8 量化结果
105 |
106 | 表3-12 Zigzag排列及行程编码与哈夫曼编码(VLC)结果
107 |
108 | 
109 |
110 | 表3-12 Zigzag排列及行程编码与哈夫曼编码(VLC)结果
111 |
112 | 
113 |
114 | 1) DC系数的编码
115 | 在量化系数矩阵的Z形扫描结果中,第一个系数为DC系数。假设前一亮度数据块的DC系数为40, 则差值DIFF=44-40=4, 因4在(-7~-4, 4~7)范围内, 由表3-8查得SSSS=3,其前缀码字为“100”, 3位尾码即为4的二进制原码“100”, 从而DC系数的编码为“100100”。如果前一数据块的DC系数为48, 则DIFF=-4, 由表10-8查得SSSS及前缀码字同上,其3位尾码即-4的反码“011”, 因此DC系数的编码为“100011”。解码时, 由前缀码“100”可知尾码有3位,若前缀码字是“100”, 因其最高位为1,故可得DC系数的差值为4; 若前缀码字为“011”,因最高位为0,知其为负, 故取反后可得差值为-4。
116 |
117 | 2) AC系数的编码
118 | 在Z形扫描结果中,第一个非零AC系数为10。在它前面的连零个数为1, 即NNNN=1。根据AC系数10从表3-9查得SSSS=4, 由NNNN/SSSS=1/4从表3-10查得其哈夫曼码字为“111110110”, 而10的二进制码为“1010”, 因此该AC系数的编码为“1111101101010”。由于篇幅所限,其他AC系数的编码就不再赘述, 结果见表10-12。在Z形扫描结果中的末尾,除第54个系数非零外, 其他系数全为零, 故直接用一个结束块“EOB(0/0)”结束本块,由表3-10查得其码字为“1010”。于是,最后该亮度块的编码为(其中,假定差值为4)100100111110110101001100111110000101010001001101100100010011101010000110001010000110001111000000000001000111000110001100100000111001001001111001000001111001111101111010,共用了168位,而原始图像块需8×8×8=512位,因此压缩比为3.048。
119 |
120 | JPEG压缩编码示例
121 |
122 | 
--------------------------------------------------------------------------------
/III/3.12 编程实例.md:
--------------------------------------------------------------------------------
1 | # 3.12 编程实例
2 |
3 | 实现哈夫曼编码的过程实际是构造一个哈夫曼二叉树, 它可分为两大部分:构造哈夫曼树和在哈夫曼树上求叶节点的编码。在构造哈夫曼树时,可设置一个结构数组HuffmanNode保存哈夫曼树中各节点的信息。结构数组元素定义如下:
4 |
5 | ```c++
6 | typedef struct
7 | {
8 | int Weight; //保存哈夫曼树节点的权值, 在此是指频数
9 | int Flag; //当Flag=0时, 表示该节点未加入树中, 为1时表示已加入树中
10 | int Parent; //存放节点的父节点在节点数组中的序号
11 | int LChild; //存放节点的左子节点在节点数组中的序号
12 | int RChild; //存放节点的右子节点在节点数组中的序号
13 | } HuffmanNode;
14 |
15 | ```
16 |
17 | 对于一幅BMP图像,调用CpointPro类下的GetHistogram()成员函数可获得图像的直方图数据m_fFreq,这些数据即各灰度出现的频数。利用这些数据可直接进行哈夫曼编码。哈夫曼编码的代码如下:
18 |
19 | ```C++
20 | void CDlgHuffman::Huffman()
21 | {
22 | CString str;
23 | int i, j, x1, x2, c, p;
24 | int m1, m2;
25 | LV_ITEM lvitem; // ListCtrl的ITEM
26 | int iActualItem; //中间变量, 用于保存ListCtrl中添加的ITEM编号
27 | HuffmanNode *huffNode; //存放哈夫曼树的节点
28 | CString *strCode; //指向各字符的哈夫曼编码的指针
29 | int *iMap; //位置映射指针
30 | int iNumNode = 0; //频数不为零的节点数(或灰度数)
31 | //统计直方图数据中频数不为零的灰度数, 并只对不为零的节点编码
32 | for(i = 0; i < m_iLeafNum; i++)
33 | {
34 | if (m_fFreq[i + m_ChannelSel * m_iLeafNum] != 0)
35 | iNumNode++;
36 | }
37 | //对于具有iNumNode个叶节点的哈夫曼树, 它具有2 iNumNode -1个节点
38 | huffNode = new HuffmanNode[iNumNode * 2 - 1];
39 | strCode = new CString[iNumNode]
40 | iMap = new int[iNumNode];
41 | //初始化huffNode中的各节点
42 | for(i = 0; i < iNumNode * 2 - 1; i++)
43 | {
44 | huffNode[i].Weight = 0;
45 | huffNode[i].Parent = 0;
46 | huffNode[i].Flag = 0;
47 | huffNode[i].LChild = -1;
48 | huffNode[i].RChild = -1;
49 | }
50 | //输入iNumNode个叶节点的权值即频数, iMap存放的是频数不为零的灰度值
51 | j = 0;
52 |
53 | for(i = 0; i < m_iLeafNum; i++)
54 | {
55 | if (m_fFreq[i + m_ChannelSel * m_iLeafNum] != 0)
56 | {
57 | huffNode[j].Weight = m_fFreq[i + m_ChannelSel * m_iLeafNum];
58 | iMap[j] = i;
59 | j++;
60 | }
61 | }
62 | //构造哈夫曼树, 对iNumNode个叶节点, 需构造iNumNode-1次
63 | for(i = 0; i < iNumNode - 1; i++)
64 | {
65 | //对Flag为0的节点比较排序, 选出两个权值最小的子树, x1和x2用于确定
66 | //两子树在数组中的序号, m1和m2用于存放最小两子树的权值
67 | m1 = m2 = m_iSizeImage;
68 | x1 = x2 = 0;
69 | for (j = 0; j < iNumNode + i; j++)
70 | {
71 | if (huffNode[j].Weight < m1 && huffNode[j].Flag = = 0)
72 | {
73 | m2 = m1;
74 | x2 = x1;
75 | m1 = huffNode[j].Weight;
76 | x1 = j;
77 | }
78 | else if (huffNode[j].Weight < m2 && huffNode[j].Flag = = 0)
79 | {
80 | m2 = huffNode[j].Weight;
81 | x2 = j;
82 | }
83 | }
84 | //将找出的两棵最小子树合并为一棵子树
85 | huffNode[x1].Parent = iNumNode + i;
86 | huffNode[x2].Parent = iNumNode + i;
87 | // Flag为1, 说明该节点已经成为其他节点的子节点
88 | huffNode[x1].Flag = 1;
89 | huffNode[x2].Flag = 1;
90 | huffNode[iNumNode + i].Weight = huffNode[x1].Weight + huffNode[x2].Weight;
91 | //权值较小的子树作为右子树
92 | huffNode[iNumNode + i].LChild = x2;
93 | huffNode[iNumNode + i].RChild = x1;
94 | }
95 | //求每个叶节点的哈夫曼编码
96 | for(i = 0; i < iNumNode; i++)
97 | {
98 | c = i;
99 | p = huffNode[c].Parent;
100 | //由叶节点上溯到树根
101 | while (p != 0)
102 | {
103 | //如果是左子树, 则代码的高一位添加0, 否则添加1
104 | if (huffNode[p].LChild = = c)
105 | strCode[i] = "0" + strCode[i];
106 | else
107 | strCode[i] = "1" + strCode[i];
108 | c = p;
109 | p = huffNode[c].Parent;
110 | }
111 | }
112 | //计算平均码字长度和图像熵
113 | int CodeLen = 0;
114 | m_fEntropy = 0.0;
115 | for(i = 0; i < iNumNode; i ++
116 | {
117 | CodeLen += huffNode[i].Weight * strCode[i].GetLength();
118 | m_fEntropy -= ((double)huffNode[i].Weight / m_iSizeImage) *
119 | log((double)huffNode[i].Weight / m_iSizeImage) / log(2.0);
120 | }
121 | //计算平均码字长度
122 | m_fAvCodeLen = (double)CodeLen/m_iSizeImage;
123 | // 计算编码效率
124 | m_fCodeEfficiency = m_fEntropy / m_fAvCodeLen;
125 | //更新对话框上的文本框中的内容
126 | UpdateData(FALSE);
127 | lvitem.mask = LVIF_TEXT;
128 | //输出哈夫曼编码结果
129 | for (i = 0; i < iNumNode; i ++)
130 | {
131 | if (huffNode[i].Weight > 0)
132 | {
133 | // 添加一项
134 | lvitem.iItem = m_lstTable.GetItemCount();
135 | str.Format("%u", iMap[i]);
136 | lvitem.iSubItem = 0;
137 | lvitem.pszText = (LPTSTR)(LPCTSTR)str;
138 | iActualItem = m_lstTable.InsertItem(&lvitem);
139 | // 添加其他列
140 | lvitem.iItem = iActualItem;
141 | // 添加灰度值出现的频率
142 | lvitem.iSubItem = 1;
143 | str.Format("%f", (float)huffNode[i].Weight / m_iSizeImage);
144 | lvitem.pszText = (LPTSTR)(LPCTSTR)str;
145 | m_lstTable.SetItem(&lvitem);
146 | // 添加哈夫曼编码
147 | lvitem.iSubItem = 2;
148 | lvitem.pszText = (LPTSTR)(LPCTSTR)strCode[i];
149 | m_lstTable.SetItem(&lvitem);
150 | // 添加码字长度
151 | lvitem.iSubItem = 3;
152 | str.Format("%u", strCode[i].GetLength());
153 | lvitem.pszText = (LPTSTR)(LPCTSTR)str;
154 | m_lstTable.SetItem(&lvitem);
155 | }
156 | }
157 | delete[] huffNode;
158 | delete[] strCode;
159 | delete[] iMap;
160 | }
161 | ```
162 |
163 |
--------------------------------------------------------------------------------
/III/3.2 Huffman编码.md:
--------------------------------------------------------------------------------
1 | # 3.2 Huffman 编码(熵编码)
2 |
3 | 图象熵:
4 | 图像灰度集合为 $\left(x_1, x_2, \ldots, x_{M}\right)$, , 对应的概率 $P_1$, $P_2, \ldots, \mathbf{P}_{M}$
5 | 则图象熵: $\quad H=-\sum_{k=1}^M P_k \log P_k$
6 | 平均码长:
7 | 设 $\beta_{k}$ 为图像第 $k$ 个码长 $C_{k}$ 的长度, 对应的概率为 $P_{k}$, 则该图象所赋予的码长的平均长度为:
8 | $$
9 | R=\sum_{k=1}^M \beta_k P_k
10 | $$
11 | 编码效率
12 | $$
13 | \eta=\frac{H}{R}
14 | $$
15 | 变长最佳编码定理
16 | 在变长编码中, 对图像中出现频度大的像素值赋予短码字, 对出现频度小的像数值赋予长码字。 如果严格按照所对应符号出现概率大小逆序排列, 则编码结果平均码长一定小于任何其它排列方式。
17 | Huffman 编码
18 | 根据变长最佳编码定理, 应用Huffman算法的一种编码方法。
19 |
20 | 举例:
21 | $$
22 | \frac{\text { aaaa }}{4} \frac{bbb}{3} \frac{cc}{2} \frac{d}{1} \frac{\text { eeeee }}{5} \frac{\text { fffffff }}{7} \text { (共22*8=176 bits) }
23 | $$
24 | 编码: $f=0 \quad e=10 \quad a=110 \quad ~b=1111 \quad c=11100 \quad ~d=11101$
25 |
26 | 11011011011011111111111111100111001110110101010100000000
27 | (共 $7 * 1+5 * 2+4 * 3+3 * 4+2 * 5+1 * 5=56$ bits)
28 |
29 | Huffman 编码步骤:
30 | 1、先将图象灰度级按出现的概率由大到小顺序排列;
31 | 2、将最小两个概率相加, 形成一个新的概率集合, 再按第 (1) 步方法重排, 如此重复进行直到只有两个概率为止;
32 | 3、分配码长。码长分配从最后一步开始反向进行, 对最后两个概率一个赋予“0”, 一个赋予“1”
33 |
34 | 
35 |
36 | 整理:
37 |
38 | 
39 |
40 | f=01 e=11 a=10 b=001 c=0001 d=0000
41 | $$
42 | \frac{\text { aaaa }}{4} \frac{bbb}{3} \frac{cc}{2} \frac{d}{1} \frac{\text { eeeee }}{5} \frac{\text { fffffff }}{7} \text { (共22*8=176 bits) }
43 | $$
44 | 经过Huffman编码之后的数据为:
45 |
46 | 1010101010001001001000100010000111111111101010101010101
47 |
48 | (共 $7 * 2+5 * 2+4 * 2+3 * 3+2 * 4+1 * 4=53$ bits)
49 | 比前面我们给出的编码得到的56bits的数据量还小
50 |
51 | Huffman编码在图像压缩中的实现
52 | 我们知道, 对一幅图像进行编码时, 如果图像的大小大于 256 时, 这幅图像的不同的码字就有可能是很大, 例如极限为 256 个不同的码字。
53 | 对整幅图直接进行Huffman编码时, 小分布的灰度值, 就有可能具有很长的编码。
54 | 如: 100位以上, 这样不但达不到压缩的效果反而会使数据量加大, 应该如何处理?
55 |
56 | 常用的且有效的方法是:
57 | 将图像分割成若干的小块, 对每块进行独立的Huffman编码。例如: 分成$8\times 8$的子块, 就可以大大降低不同灰度值的个数(最多是64而不是256)。
--------------------------------------------------------------------------------
/III/3.3 香农-范诺编码.md:
--------------------------------------------------------------------------------
1 | # 3.3 香农-范诺编码
2 |
3 | 香农-范诺 (Shannon-Fannon) 编码也是一种常见的可变字长编码。与哈夫曼编码相似, 当信源符号出现的概率正好为 $2^{-i}$ $(i<0)$ 时, 采用香农-范诺编码同样能够达到 $100 \%$ 的编码效率。 香农-范诺编码的理论基础是符号的码字长度 $N_i$ 完全由该符号出现的概率来决定, 即
4 | $$
5 | -\log _D P_i \leq N_i \leq-\log _D P_i+1\tag{3-8}
6 | $$
7 | 式中,D为编码所用的数制。
8 |
9 | 香农-范诺编码的步骤如下:
10 | (1)将信源符号按其出现概率从大到小排序;
11 | (2)按照式 (3-8) 计算出各概率对应的码字长度 $N_i$;
12 | (3)计算累加概率 $A_i$, 即
13 | $$
14 | A_i=A_{i-1}+P_{i-1} \quad i=1,2, \ldots, N-1 ; \quad A_0=0\tag{3-9}
15 | $$
16 | (4) 把各个累加概率 $A_i$ 由十进制转化为二进制, 取该二进制数的前 $N_i$ 位作为对应信源符号的码字。
17 |
18 | 为便于比较, 仍以例4-1中图像为对象, 对其进行香农-范诺编码, 结果如表3-3所示。由于在此采用二进制对码字赋值, 故在利用式 (3-9) 计算码字长度 $N_i$ 时, $D$ 取为 2 。以符号 $S_4$ 为例, 其出现概率为 0.07 , 按照式 (3-9) 计算得到它的码字长度应为 4 , 按式 (3-10) 计算得到它的累加概率 $A_4$ 为 0.78 , 将 0.78 转化为二进制并取其前 4 位即得符号 $S_4$ 的码字为 1100 (省去了 “0.”, 有的浮点数不能完全转化, 转化时只需完成前 $N_i$ 位即可)。
19 |
20 | 表3-3 香农-范诺编码
21 |
22 | $$
23 | 平均码长 R=3.17 \quad图像熵 H=2.55 \quad \text { 编㐷效率 } \eta=80.4 \%\\
24 | \begin{array}{|c|c|c|c|c|c|}
25 | \hline \text { 信源符号 } & \text { 出现概率 } P_i & \text { 码字长度 } N_i & \text { 蔂加概率 } A_i & \text { 转换为二进制 } & \text { 分配码字 } B_i \\
26 | \hline S_0 & 0.40 & 2 & 0 & 0 & 00 \\
27 | \hline S_1 & 0.18 & 3 & 0.40 & 01100 & 011 \\
28 | \hline S_2 & 0.10 & 4 & 0.58 & 10010 & 1001 \\
29 | \hline S_3 & 0.10 & 4 & 0.68 & 10100 & 1010 \\
30 | \hline S_4 & 0.07 & 4 & 0.78 & 11000 & 1100 \\
31 | \hline S_5 & 0.06 & 5 & 0.85 & 1101100 & 11011 \\
32 | \hline S_6 & 0.05 & 5 & 0.91 & 1110100 & 11101 \\
33 | \hline S_7 & 0.04 & 5 & 0.96 & 1111010 & 11110 \\
34 | \hline
35 | \end{array}\\
36 |
37 |
38 |
39 | $$
40 | 除此之外, 还有二分法香农-范诺编码方法。其步骤如下:
41 | (1) 首先统计出每个符号出现的概率;
42 | (2) 从左到右对上述概率从大到小排序;
43 | (3) 从这个概率集合中的某个位置将其分为两个子集合,并尽量使两个子集合的概率和近似相等,给前面一个子集合赋值为0, 后面一个子集合赋值为1;
44 | (4) 重复步骤3,直到各个子集合中只有一个元素为止;
45 | (5) 将每个元素所属的子集合的值依次串起来,即可得到各个元素的香农-范诺编码。
46 |
47 | 表3-4 二分法香农-范诺编码
48 |
49 | 
--------------------------------------------------------------------------------
/III/3.4 行程编码.md:
--------------------------------------------------------------------------------
1 | # 3.4 行程编码
2 |
3 | ## 3.4.1 行程编码基本方法
4 |
5 | 行程编码又称行程长度编码(Run Length Encoding, RLE), 是一种熵编码,其编码原理相当简单,即将具有相同值的连续串用其串长和一个代表值来代替, 该连续串就称为行程,串长称为行程长度。例如,有一字符串“aabbbcddddd”, 则经行程长度编码后, 该字符串可以只用“2a3b1c5d”来表示。
6 | 行程编码分为定长和不定长编码两种。定长编码是指编码的行程长度所用的二进制位数固定,而变长行程编码是指对不同范围的行程长度使用不同位数的二进制位数进行编码。使用变长行程编码需要增加标志位来表明所使用的二进制位数。
7 |
8 | 行程编码比较适合于二值图像的编码,一般用于量化后出现大量零系数连续的场合,用行程来表示连零码。如果图像是由很多块颜色或灰度相同的大面积区域组成的,那么采用行程编码可以达到很高的压缩比。如果图像中的数据非常分散,则行程编码不但不能压缩数据,反而会增加图像文件的大小。为了达到较好的压缩效果,一般不单独采用行程编码, 而是和其他编码方法结合使用。例如, 在JPEG中, 就综合使用了行程编码、DCT、量化编码以及哈夫曼编码, 先对图像作分块处理, 再对这些分块图像进行离散余弦变换(DCT), 对变换后的频域数据进行量化并作Z字形扫描,接着对扫描结果作行程编码, 对行程编码后的结果再作哈夫曼编码。
9 |
10 | ## 3.4.2 PCX文件中的行程编码
11 |
12 | PCX文件分为文件头和图像压缩数据两个部分。如果是256色图像,则还有一个256色调色板存于文件尾部。文件头全长128字节,包含了图像的大小和颜色以及PCX文件的版本标识等信息,图像压缩数据紧跟在文件头之后。如果没有使用调色板, 那么图像压缩数据存储的是实际像素值;否则,存储的是调色板的索引值。当压缩数据是实际的像素值时,它们按颜色平面和扫描行存储,即每行先存储所有R分量,再存储所有G分量, 最后存储所有B分量,一行数据存储完后,接着存储下一行数据。如果使用了调色板,则不会分解为单独的颜色平面存储。读者可以查阅图像文件格式的相关书籍了解PCX文件的详细格式。下面以256色PCX文件为例, 说明PCX文件中的行程编码。
13 |
14 | 在256色PCX文件中,每个像素占一字节, 压缩数据以字节为单位逐行进行编码,每行填充到偶数字节。PCX文件规定编码时的最大行程长度为63,如果行程长度大于63,则必须分多次存储。对于长度大于1的行程,编码时先存入其行程长度(长度L加上192即0xC0),再存入该行程的代表值,行程长度和行程的代表值分别占一字节。对于长度为1的行程,即单个像素, 如果该像素的值小于或等于0xC0, 则编码时直接存入该像素值, 而不存储长度信息;否则,先存入0xC1,再存入该像素值,这样做的目的是为了避免该像素值被误认为长度信息。例如,连续100个灰度值为0x80的像素, 其编码(以十六进制表示)应为FF 80 25 80。上面的编码中出现FF的长度信息是由63与0xC0相加所得。
15 |
16 | 对256色PCX文件解码时,首先从压缩数据部分读取一个字节,判断该值是否大于0xC0,如果是,则表明该字节是行程长度信息, 取其低六位(相当于减去0xC0)作为行程长度L,读取下一个字节作为像素值并重复L次存入图像数据缓冲区;否则, 直接将该字节存入图像数据缓冲区。
17 |
18 | 虽然几乎所有的图像应用软件都支持PCX文件格式,但由于它的压缩比不高, 因而现在用得不是很多。
--------------------------------------------------------------------------------
/III/3.5 LZW编码 .md:
--------------------------------------------------------------------------------
1 | # 3.5LZW编码
2 |
3 | ## 3.5.1LZW编码方法
4 |
5 | LZW(Lempel-Ziv&Welch)编码又称字串表编码,属于一种无损编码,是Welch将Lempel和Ziv所提出的无损压缩技术改进后的压缩方法。LZW编码与行程编码类似,也是对字符串进行编码从而实现压缩,但它在编码的同时还生成了特定字符串以及与之对应的索引字符串表。
6 |
7 | LZW编码的基本思想是:在编码过程中,将所遇到的字符串建立一个字符串表,表中的每个字符串都对应一个索引,编码时用该字符串在字串表中的索引来代替原始的数据串。例如,一幅8位的灰度图像,我们可以采用12位来表示每个字符串的索引,前256个索引用于对应可能出现的256种灰度,由此可建立一个初始的字符串表,而剩余的3840个索引就可分配给在压缩过程中出现的新字符串,这样就生成了一个完整的字符串表,压缩数据就可以只保存它在字符串表中的索引,从而达到压缩数据的目的。字符串表是在压缩过程中动态生成的,不必将它保存在压缩文件里,因为解压缩时字符串表可以由压缩文件中的信息重新生成。
8 |
9 | GIF(GraphicsInterchangeFormat)最初是由美国CompuServe于1987年开发的一种压缩位图格式。它可支持多达256种的颜色,具有极佳的压缩效率,已成为Internet上一种流行的文件格式。GIF图像文件采用的是一种改良的LZW压缩算法,通常称为GIF-LZW压缩算法。GIF图像文件以块(又称为区域结构)的方式来存储图像相关的信息,具体的文件格式可参考图像文件格式的相关书籍。下面简要介绍GIF-LZW的编码方法。
10 |
11 | 设S1、S2为两个存放字符串的临时变量,LZW_CLEAR和LZW_EOI分别为字符表初始化标志和编码结束标志,GIF-LZW的编码步骤如下:
12 |
13 | (1)根据图像中使用的颜色数初始化一个字串表,字串表中的每个颜色对应一个索引。在初始字串表的末尾再添加两个符号(LZW_CLEAR和LZW_EOI)的索引。设置字符串变量S1、S2并初始化为空。
14 |
15 | (2)接着输出LZW_CLEAR在字串表中的索引。
16 |
17 | (3)从图像数据流中第一个字符(假设数据以字符串表示)开始,每次读取一个字符,将其赋给字符串变量S2。
18 |
19 | (4)判断“S1+S2”是否已存在于字串表中。如果字串表中存在“S1+S2”,则S1=S1+S2;否则,输出S1在字串表中的索引,并在字串表末尾为“S1+S2”添加索引,同时,S1=S2。
20 |
21 | (5)重复第3和第4步,直到所有字符读完为止。
22 |
23 | (6)输出S1中的字符串在字串表中的索引,然后输出结束标志LZW_EOI的索引,编码完毕。
24 |
25 | GIF-LZW的解码过程比较复杂,它和编码过程正好相反,即将编码后的码字转换成对应的字符串,重新生成字串表,然后依次输出对应的字符串即可。GIF-LZW的解码流程如图3-2所示,表中的Code和OldCode是两个存放索引的临时变量。
26 |
27 | 
28 |
29 | 图3-2GIF-LZW解码流程
30 |
31 | ## 3.5.2LZW编码实例
32 |
33 | 设有一来源于4色(以a、b、c、d表示)图像的数据流aabcabbbbd,现对其进行LZW编码。编码过程如下:
34 | 编码前,首先需要初始化一个字符串表。由于图像中只有四种颜色,因而我们可以只用4比特表示字符串表中每个字符串的索引,表中的前4项代表4种颜色,后两项分别表示初始化和图像结束标志,建立的初始化字符串表如表3-5所示。接着把S1和S2初始化为空(即NULL),输出LZW_CLEAR的在字符串表中的索引值4H,接下来是对图像数据的编码。
35 |
36 | 表3-5初始化字符串表
37 | $$
38 | \begin{array}{|c|c|}
39 | \hline \text{字符串}&\text{索引}\\
40 | \hline a&0H\\
41 | \hline b&1H\\
42 | \hline c&2H\\
43 | \hline d&3H\\
44 | \hline \text{LZW\_CLEAR}&4H\\
45 | \hline \text{LZW\_EOI}&5H\\
46 | \hline
47 | \end{array}
48 | $$
49 |
50 |
51 | 读取图像数据流的第一个字符“a”,赋给S2,因S1+S2=“a”已存在字串表中,所以S1=S1+S2=“a”。
52 | 接着读入下一个字符“a”赋给S2,因S1+S2=“aa”不存在于字串表中,所以输出S1=“a”的索引0H,同时在字符串表末尾添加新字符串“aa”的索引6H,并使S1=S2=“a”。
53 | 依次读取数据流中的每个字符,如果S1+S2没有出现在字符串表中,则输出S1中的字符串的索引,并在字符串表末尾为新字符串S1+S2添加索引,并使S1=S2;否则,不输出任何结果,只是使S1=S1+S2。所有字符处理完毕后,输出S1中的字符串的索引,最后输出结束标志LZW_EOI的索引。至此,编码完毕,完整的编码过程如表3-6所示,最后的编码结果为“4001271B35”(以十六进制表示)。
54 |
55 | 表3-6GIF-LZW编码过程
56 | $$
57 | \begin{array}{|c|c|c|c|c|}
58 | \hline \text { 输入数据 S2 } & \text { S1+S2 } & \text { 输出结果 } & \text { S1 } & \text { 生成的新字符串及索引 } \\
59 | \hline \text { NULL } & \text { NULL } & 4 H & \text { NULL } & \\
60 | \hline a & a & & a & \\
61 | \hline a & aa & 0 H & a & aa<6 H> \\
62 | \hline b & ab & 0 H & a & ab<7 H> \\
63 | \hline c & bc & 1 H & c & ca<9 H> \\
64 | \hline a & ca & 2 H & a & \\
65 | \hline b & ab & & ab & abb \\
66 | \hline b & abb & 7 H & b & bb \\
67 | \hline b & bb & 1 H & b & \\
68 | \hline b & bb & & bb & bbd \\
69 | \hline d & bbd & BH & d & \\
70 | \hline & & 3 H & & \\
71 | \hline & & 5 H & & \\
72 | \hline
73 | \end{array}
74 | $$
75 | 下面对上述编码结果“4001271B35”进行解码。按图3-2的解码流程,首先读取第一个编码Code=4H,由于它为LZW_CLEAR,因此需初始化字符串表,结果如表3-5所示(在实际应用中,可根据文件头中给定的信息建立初始字符串表)。
76 |
77 | 读入下一个编码Code=0H,由于它不等于LZW_CLEAR,因此输出字串表中0H对应的字符串“a”,同时使OldCode=Code=0H。
78 |
79 | 读入下一个编码Code=0H,由于字串表中存在该索引,因此输出0H所对应的字符串“a”,然后将OldCode=0H所对应的字符串“a”加上Code=0H所对应的字符串的第一个字符“a”,即“aa”添加到字串表中,其索引为6H,同时使ldCode=Code=0H。
80 |
81 | 读入下一个编码Code=1H,由于字串表中存在该索引,因此输出1H所对应的字符串“b”,然后将OldCode=0H所对应的字符串“a”加上Code=1H所对应的字符串的第一个字符“b”,即“ab”添加到字串表中,其索引为7H,同时使OldCode=Code=1H。
82 |
83 | 读入下一个编码Code=2H,由于字串表中存在该索引,因此输出2H所对应的字符串“c”,然后将OldCode=1H所对应的字符串“b”加上Code=2H所对应的字符串的第一个字符“c”,即“bc”添加到字串表中,其索引为8H,同时使OldCode=Code=2H。
84 |
85 | 读入下一个编码Code=7H,由于字串表中存在该索引,因此输出7H所对应的字符串“ab”,然后将OldCode=2H所对应的字符串“c”加上Code=7H所对应的字符串的第一个字符“a”,即“ca”添加到字串表中,其索引为9H,同时使OldCode=Code=7H。
86 |
87 | 读入下一个编码Code=1H,由于字串表中存在该索引,因此输出1H所对应的字符串“b”,然后将OldCode=7H所对应的字符串“ab”加上Code=1H所对应的字符串的第一个字符“b”,即“abb”添加到字串表中,其索引为AH,同时使OldCode=Code=1H。
88 |
89 | 读入下一个编码Code=BH,由于字串表中不存在该索引,因此输出OldCode=1H所对应的字符串“b”加上该字符串的第一个字符“b”,即“bb”,同时将“aa”添加到字串表中,其索引为BH,同时使OldCode=Code=BH。
90 |
91 | 读入下一个编码Code=3H,由于字串表中存在该索引,因此输出其对应的字符串“d”,然后将OldCode=BH所对应的字符串“bb”加上Code=3H所对应的字符串的第一个字符“d”,即“bbd”添加到字串表中,其索引为CH,同时使OldCode=Code=3H。读入下一个编码Code=5H,它等于LZW_EOI,数据解码完毕,最后的解码结果为aabcabbbbd。为清晰起见,完整的解码过程如表3-7所示。
92 |
93 | 表3-7GIF-LZW解码过程
94 | $$
95 | \begin{array}{|c|c|c|c|c|}
96 | \hline \text { 输入数据 Code } & \text { 新字符串的来源 } & \text { 输出结果 } & \text { OldCode } & \text { 生成的新串及索引 } \\
97 | \hline 4 H & & & & \\
98 | \hline 0 H & & a & 0 H & \\
99 | \hline 0 H & \text { Str(OldCode)+FirstStr(Code) }=aa & a & 0 H & aa<6 H> \\
100 | \hline 1 H & \text { Str(OldCode)+FirstStr(Code) }=ab & b & 1 H & ab<7 H> \\
101 | \hline 2 H & \text { Str(OldCode)+FirstStr(Code) }=bc & c & 2 H & bc<8 H> \\
102 | \hline 7 H & \text { Str(OldCode)+FirstStr(Code) }=ca & ab & 7 H & ca<9 H> \\
103 | \hline 1 H & \text { Str(OldCode)+FirstStr(Code) }=abb & b & 1 H & abb \\
104 | \hline BH & \text { Str(OldCode)+FirstStr(OldCode) }=bb & bb & BH & bb \\
105 | \hline 3 H & \text { Str(OldCode)+FirstStr(Code) }=bbd & d & 3 H & bbd \\
106 | \hline 5 H & & & & \\
107 | \hline
108 | \end{array}
109 | $$
--------------------------------------------------------------------------------
/III/3.6 算术编码.md:
--------------------------------------------------------------------------------
1 | # 3.6 算术编码
2 |
3 | 算术编码有两种模式:一种是基于信源概率统计特性的固定编码模式,另一种是针对未知信源概率模型的自适应模式。自适应模式中各个符号的概率初始值都相同, 它们依据出现的符号而相应地改变。只要编码器和解码器都使用相同的初始值和相同的改变值的方法,那么它们的概率模型将保持一致。上述两种形式的算术编码均可用硬件实现,其中自适应模式适用于不进行概率统计的场合。有关实验数据表明,在未知信源概率分布的情况下, 算术编码一般要优于Huffman编码。在JPEG扩展系统中,就用算术编码取代了哈夫曼编码。
4 |
5 | 下面结合一个实例来阐述固定模式的算术编码的具体方法。 设一待编码的数据序列 (即信源) 为 “ dacab", 信源中各符号出现的概率依次为 $P(a)=0.4, P(b)=0.2, P(c)=0.2, \quad P(d)=0.2$ 。
6 | 首先, 数据序列中的各数据符号在区间 $[0,1]$ 内的间隔 (赋值范围)设定为 $a=[0,0.4), b=[0.4,0.6), c=[0.6,0.8)$ , $d=[0.8,1.0)$
7 | 为便于讨论, 再给出一组关系式:
8 | $$
9 | \left\{\begin{array}{l}
10 | \operatorname{Start}_{N}=\operatorname{Start}_{B}+\operatorname{Left}_{C} \times L \\
11 | \operatorname{End}_{N}=\operatorname{Start}_{B}+\operatorname{Right}_{C} \times L
12 | \end{array}\right.
13 | $$
14 | 式中, $\operatorname{Start}_{\mathbb{N}} 、 End_{\mathbb{N}}$ 分别表示新间隔 (或称之为区间)的起始位置和结束位置, Start ${ }_{B}$ 表示前一间隔的起始位置, $L$ 为前一间隔的长度, Left $_C 、$ Right $_C$ 分别表示当前编码符号的初始区间的左端和右端。
15 | 第一个被压缩的符号为 “ $d$ ",其初始间隔为 $[0.8,1.0)$;
16 | 第二个被压缩的符号为 “ $a$ ", 由于前面的符号 “ $d^{\prime \prime}$ 的取值区间被限制在 $[0.8,1.0$ )范围内, 所以 “ $a$ ”的取值范围应在前一符号间隔 $[0.8,1.0)$ 的 $[0,0.4)$ 子区间内, 根据上式可知
17 | $$
18 | \begin{aligned}
19 | & \text { Start }_{N}=0.8+0 \times(1.0-0.8)=0.8 \\
20 | & \text { End }_{N}=0.8+0.4 \times(1.0-0.8)=0.88
21 | \end{aligned}
22 | $$
23 | 即 “ $a$ ”的实际编码区间在 $[0.8,0.88)$ 之间。
24 |
25 | 第三个被压缩的符号为 “ $c^{\prime \prime}$, 其编码取值范围应在 $[0.8$, $0.88)$ 区间的 $[0.6,0.8)$ 的子区间内, 据上式可知
26 | $$
27 | \begin{aligned}
28 | & \text { Start }_N=0.8+0.6 \times(0.88-0.8)=0.848 \\
29 | & \text { End }_N=0.8+0.8 \times(0.88-0.8)=0.864
30 | \end{aligned}
31 | $$
32 | 第四个被压缩的符号为 “ $a$ ”, 同理, 根据上式可知
33 | $$
34 | \begin{aligned}
35 | & \operatorname{Start}_{N}=0.848+0 \times(0.864-0.848)=0.848 \\
36 | & \operatorname{End}_{N}=0.848+0.4 \times(0.864-0.848)=0.8544
37 | \end{aligned}
38 | $$
39 | 第五个被压缩的符号为 “ $b$ ”, 同理, 根据上式可知
40 | $$
41 | \begin{aligned}
42 | & \text { Start }_{N}=0.848+0.4 \times(0.8544-0.848)=0.84856 \\
43 | & \text { End }_{N}=0.848+0.6 \times(0.8544-0.848)=0.85144
44 | \end{aligned}
45 | $$
46 | 至此, 数据序列 “dacab"已被描述为一个实数区间 $[0.85056$, $0.85184]$, 或者说在此区间内的任一实数值都惟一对应该数据序列。这样, 就可以用一个实数表示这一数据序列。我们把区间 [0. 850 56,0.851 84] 用二进制形式表示为 $[0.110110011011$, $0.110110100001]$ 。
47 |
48 | 从这个区间可以看出,0.1101101位于这个区间内并且其编码最短, 故把其作为数据序列“dacab”的编码输出。考虑到算术编码中任一数据序列的编码都含有“0.”,所以在编码时,可以不考虑“0.”,于是把1101101作为本例中的数据序列的算术编码。由此可见, 数据序列“dacab”用7比特的二进制代码就可以表示, 平均码长为1.4比特/字符。
49 |
50 | 解码是编码的逆过程,根据编码时的概率分配表和压缩后数据代码所在的范围,确定代码所对应的每一个数据符号。由此可见,算术编码的实现方法要比哈夫曼编码复杂一些。
--------------------------------------------------------------------------------
/III/3.7 DCT变换编码.md:
--------------------------------------------------------------------------------
1 | # 3.7 DCT变换编码
2 |
3 | 注意
4 | 作DCT变换时,一般不是对整个图象作一次变换,而是将图象划为8*8或16*16的子图象,然后对各个子图象作DCT变换.
5 |
6 | 采用快速DCT变换
7 |
8 |  --------------------------------------------------------------------------------
/III/3.8基于小波变换编码.md:
--------------------------------------------------------------------------------
1 | # 3.8基于小波变换编码
2 |
3 | ## 一维小波变换
4 |
5 | 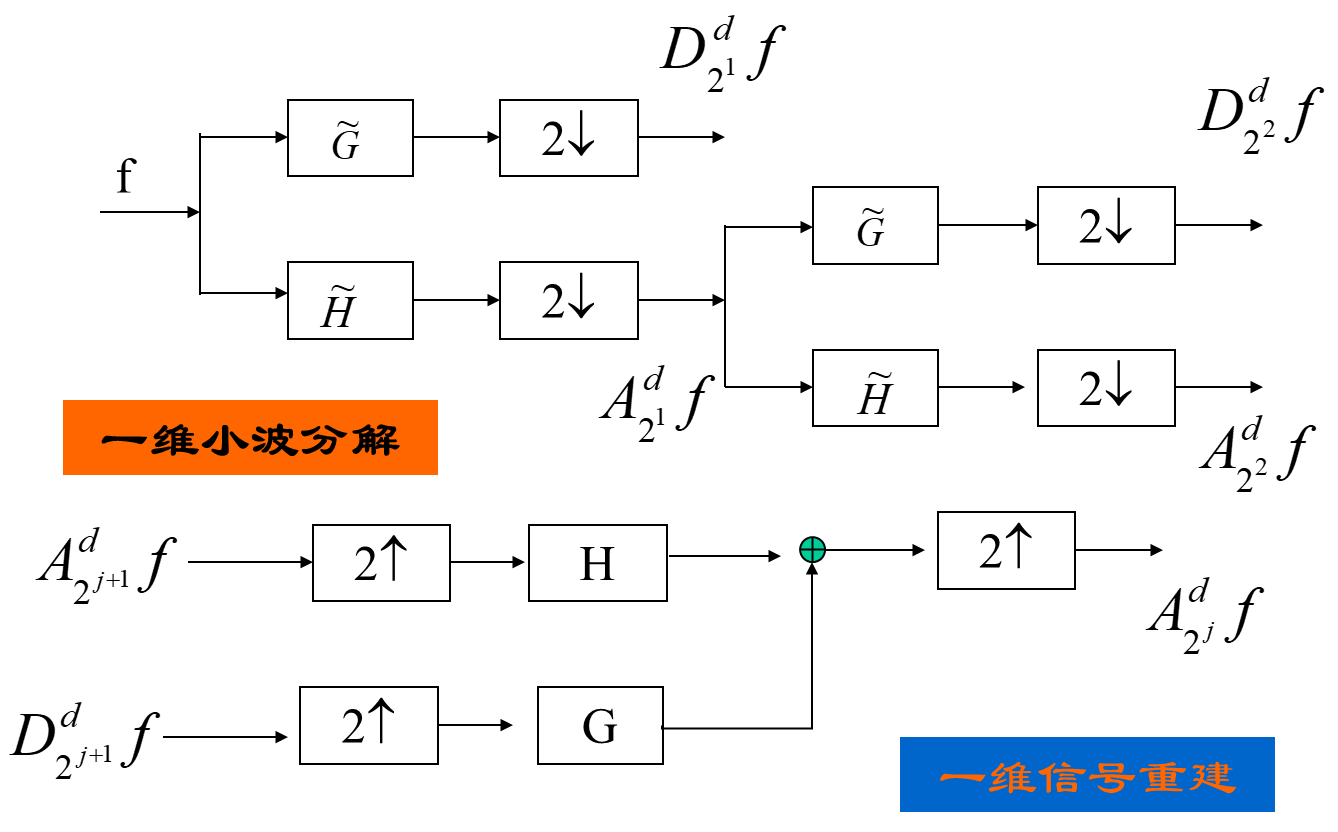
6 |
7 | 二维小波变换
8 | 一愊图象经小波变换成 $(3 ~J+1)$ 个离笃图象
9 | $$
10 | \left\{A_J^d f, D_j^1 f, D_j^2 f, D_j^3 f\right\} \quad 1 \leq j \leq J
11 | $$
12 | 其中 $A_j^d f$ 是 $f$ 在J级分辡卒的低频分量, $D_j^1 f, D_j^2 f$ 分别是水平、坚直方向的细节, $D_j^3 f$ 主要对应 45 度和 135 度方向的高频分量。
13 |
14 | 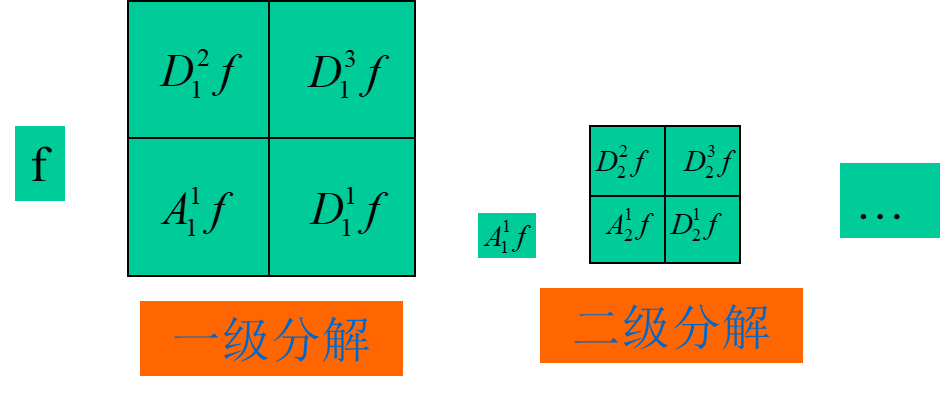
15 |
16 | 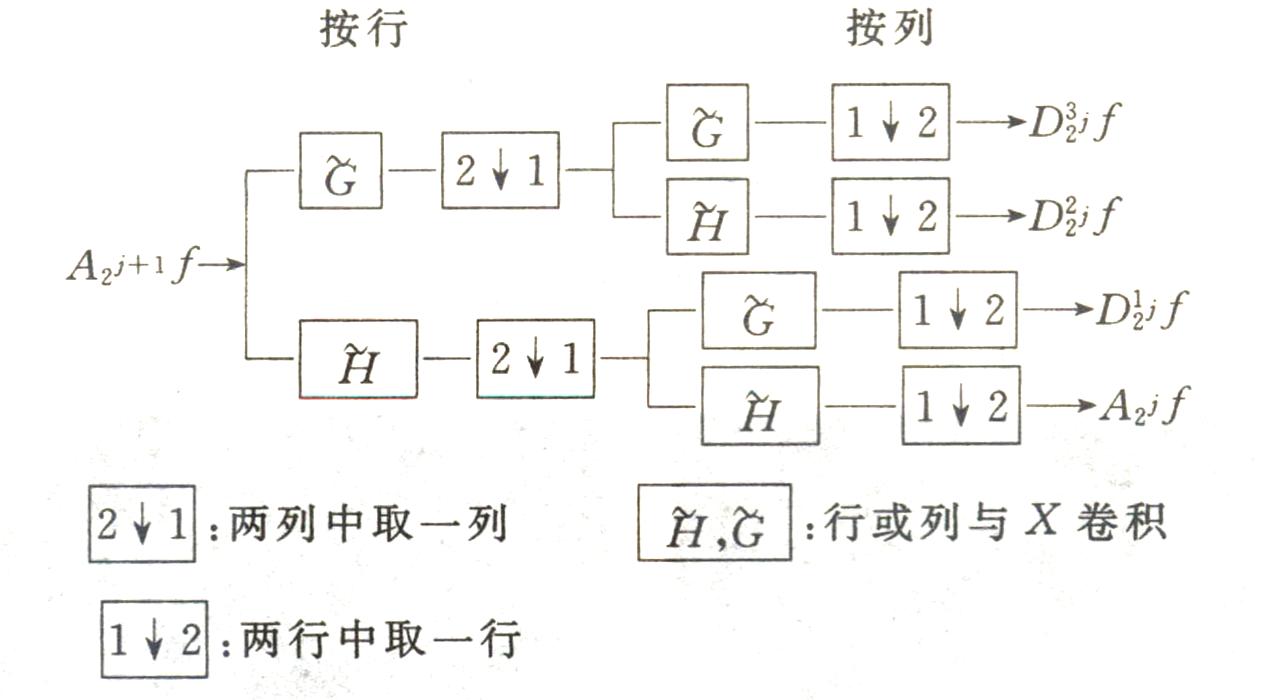
17 |
18 | 二维小波分解
19 |
20 | 
21 |
22 | 二维小波重建
23 |
24 | 基于小波变换编码原理
25 | 图象的最终目的是让人看, 而人的视觉系统对高频分量不敏感, 因此高频分量可以粗略编码, 而对图象的质量影响不大,并且高频部分有很高的相似性。由于细节部分对应于图象的高频分量, 考虎视觉特点, 它可以用较高的厓缩比编码, 而 $A_J^d f$ 象素个数小, 反映图象的整体轮廓, 对其直接编码, 以保证恢复图象的质量,而对整幅图象的编码圧缩比影响不大。
26 |
27 | 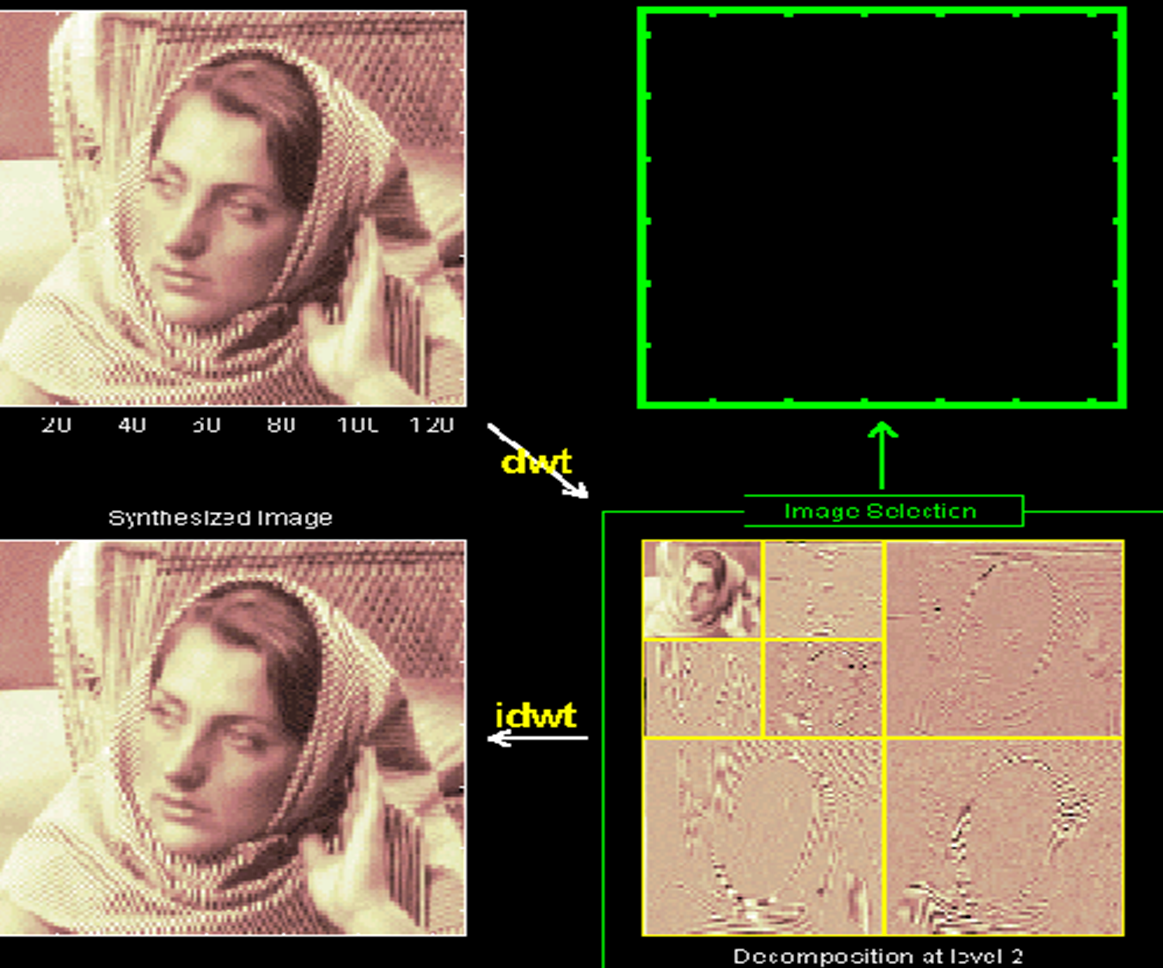
--------------------------------------------------------------------------------
/III/3.9 混合编码.md:
--------------------------------------------------------------------------------
1 | # 3.9 混合编码
2 |
3 | 混合编码实现的可能性及有效性:
4 |
5 | 回顾一下讲过的几个内容的特点
6 | 1. 行程编码:擅长于重复数字的压缩。
7 | 2. Huffman编码:擅长于像素个数的不同编码。
8 | 4. DCT变换:擅长将高频部分分离出来。
9 |
10 | 例:
11 | $$
12 | \frac{aaaa}{4}\frac{bbb}{3}\frac{cc}{2}\frac{d}{1}\frac{eeeee}{5}\frac{fffffff}{7}
13 | $$
14 | 行程编码:
15 | $$
16 | 4a3b2c1d5e7f \\
17 | $$
18 | 共$6\times(8+3)= 66Bits$
19 |
20 | Huffman编码:
21 | $$
22 | f=01\quad e=11 \quad a=10 \quad b=001\quad c=0001\quad d=0000\\
23 |
24 | $$
25 | 编码为
26 | $$
27 | 1010101010001001001000100010000111111111101010101010101
28 | $$
29 | 共$7\times2+5\times2+4\times2+3\times3+2\times4+1\times4=53 bits$
30 |
31 | Hufman与行程编码混合:
32 | $$
33 | 41030012000110000511701
34 | $$
35 | 共:$3+2+3+3+3+4+3+4+3+2+3+2=35 bits$
36 |
37 | ## 图像压缩的实例
38 |
39 | 一:
40 |
41 | 一次小波变换+DCT变换.行程编码+Huffman编码
42 |
43 | 二:
44 |
45 | 一次小波变换+差值编码+变字长行程编码+Huffman编码
46 |
47 | ### 算法 1
48 |
49 | | 原图 | 复原图 |
50 | | ------------------------------------------------------------ | ------------------------------------------------------------ |
51 | |
--------------------------------------------------------------------------------
/III/3.8基于小波变换编码.md:
--------------------------------------------------------------------------------
1 | # 3.8基于小波变换编码
2 |
3 | ## 一维小波变换
4 |
5 | 
6 |
7 | 二维小波变换
8 | 一愊图象经小波变换成 $(3 ~J+1)$ 个离笃图象
9 | $$
10 | \left\{A_J^d f, D_j^1 f, D_j^2 f, D_j^3 f\right\} \quad 1 \leq j \leq J
11 | $$
12 | 其中 $A_j^d f$ 是 $f$ 在J级分辡卒的低频分量, $D_j^1 f, D_j^2 f$ 分别是水平、坚直方向的细节, $D_j^3 f$ 主要对应 45 度和 135 度方向的高频分量。
13 |
14 | 
15 |
16 | 
17 |
18 | 二维小波分解
19 |
20 | 
21 |
22 | 二维小波重建
23 |
24 | 基于小波变换编码原理
25 | 图象的最终目的是让人看, 而人的视觉系统对高频分量不敏感, 因此高频分量可以粗略编码, 而对图象的质量影响不大,并且高频部分有很高的相似性。由于细节部分对应于图象的高频分量, 考虎视觉特点, 它可以用较高的厓缩比编码, 而 $A_J^d f$ 象素个数小, 反映图象的整体轮廓, 对其直接编码, 以保证恢复图象的质量,而对整幅图象的编码圧缩比影响不大。
26 |
27 | 
--------------------------------------------------------------------------------
/III/3.9 混合编码.md:
--------------------------------------------------------------------------------
1 | # 3.9 混合编码
2 |
3 | 混合编码实现的可能性及有效性:
4 |
5 | 回顾一下讲过的几个内容的特点
6 | 1. 行程编码:擅长于重复数字的压缩。
7 | 2. Huffman编码:擅长于像素个数的不同编码。
8 | 4. DCT变换:擅长将高频部分分离出来。
9 |
10 | 例:
11 | $$
12 | \frac{aaaa}{4}\frac{bbb}{3}\frac{cc}{2}\frac{d}{1}\frac{eeeee}{5}\frac{fffffff}{7}
13 | $$
14 | 行程编码:
15 | $$
16 | 4a3b2c1d5e7f \\
17 | $$
18 | 共$6\times(8+3)= 66Bits$
19 |
20 | Huffman编码:
21 | $$
22 | f=01\quad e=11 \quad a=10 \quad b=001\quad c=0001\quad d=0000\\
23 |
24 | $$
25 | 编码为
26 | $$
27 | 1010101010001001001000100010000111111111101010101010101
28 | $$
29 | 共$7\times2+5\times2+4\times2+3\times3+2\times4+1\times4=53 bits$
30 |
31 | Hufman与行程编码混合:
32 | $$
33 | 41030012000110000511701
34 | $$
35 | 共:$3+2+3+3+3+4+3+4+3+2+3+2=35 bits$
36 |
37 | ## 图像压缩的实例
38 |
39 | 一:
40 |
41 | 一次小波变换+DCT变换.行程编码+Huffman编码
42 |
43 | 二:
44 |
45 | 一次小波变换+差值编码+变字长行程编码+Huffman编码
46 |
47 | ### 算法 1
48 |
49 | | 原图 | 复原图 |
50 | | ------------------------------------------------------------ | ------------------------------------------------------------ |
51 | |  |
|  |
52 |
53 | 信噪比:66.02
54 |
55 | 压缩比:11.83:1
56 |
57 | ### 算法 2
58 |
59 | | 原图 | 复原图 |
60 | | ------------------------------------------------------------ | ------------------------------------------------------------ |
61 | |
|
52 |
53 | 信噪比:66.02
54 |
55 | 压缩比:11.83:1
56 |
57 | ### 算法 2
58 |
59 | | 原图 | 复原图 |
60 | | ------------------------------------------------------------ | ------------------------------------------------------------ |
61 | |  |
|  |
62 |
63 | 信噪比:64.55
64 |
65 | 压缩比:26.50:1
--------------------------------------------------------------------------------
/IV/4.1 引言.md:
--------------------------------------------------------------------------------
1 | # 4.1 引言
2 |
3 | 通过一些运算来突出图像的某些信息,如轮廓等.但通过运算的图像不一定逼近原图像.
4 | 图像增强:
5 |
6 | - 空间域法
7 |
8 | $$
9 | g(x,y)=h(x,y)*f(x,y)
10 | $$
11 | - 频域法
12 |
13 | $$
14 | \stackrel{F(x, y)}{\longrightarrow} \boxed{正交变换} \stackrel{F(u, v)}{\longrightarrow} \boxed{修正H(u,v)} \stackrel{G(u, v)}{\longrightarrow} \boxed{逆变换} \stackrel{G(x, y)}{\longrightarrow}
15 | $$
16 |
--------------------------------------------------------------------------------
/IV/4.3 灰度变换.md:
--------------------------------------------------------------------------------
1 | # 4.3 灰度变换
2 |
3 | ## 4.2.1 灰度线性变换
4 |
5 | 假定原图像 $f(x, y)$ 的灰度范围为 $[a, b]$, 希望变换后图像 $g(x$, $y)$ 的灰度范围扩展至 $[c, d]$, 则线性变换可表示为
6 | $$
7 | g(x, y)=\frac{d-c}{b-a}[f(x, y)-a]+c\tag{4-12}
8 | $$
9 | 此式用图4-12表示。若图像灰度在 $0 \sim M_f$ 范围内, 其中大部分像素的灰度级分布在区间 $[a, b]$, 很小部分的灰度级超出了此区间, 为改善增强的效果, 可令:
10 | $$
11 | g(x, y)= \begin{cases}c & 0 \leq f(x, y)
43 |
44 | 图4-15 常见的几种非线性变换函数
45 |
46 | 式(4-16)对灰度区间$ [0, a]$和$[b, M_f]$加以压缩,对灰度区间[a, b]进行扩展。通过细心调整折线拐点的位置及控制分段直线的斜率,可对任一灰度区间进行扩展或压缩。这种变换适用于在黑色或白色附近有噪声干扰的情况。例如, 照片中的划痕, 由于变换后在[0, a]以及[b, $M_f$ ]之间的灰度受到压缩, 因而使污斑得到减弱。
47 |
48 | ## 4.2.3 非线性变换
49 |
50 |
|
62 |
63 | 信噪比:64.55
64 |
65 | 压缩比:26.50:1
--------------------------------------------------------------------------------
/IV/4.1 引言.md:
--------------------------------------------------------------------------------
1 | # 4.1 引言
2 |
3 | 通过一些运算来突出图像的某些信息,如轮廓等.但通过运算的图像不一定逼近原图像.
4 | 图像增强:
5 |
6 | - 空间域法
7 |
8 | $$
9 | g(x,y)=h(x,y)*f(x,y)
10 | $$
11 | - 频域法
12 |
13 | $$
14 | \stackrel{F(x, y)}{\longrightarrow} \boxed{正交变换} \stackrel{F(u, v)}{\longrightarrow} \boxed{修正H(u,v)} \stackrel{G(u, v)}{\longrightarrow} \boxed{逆变换} \stackrel{G(x, y)}{\longrightarrow}
15 | $$
16 |
--------------------------------------------------------------------------------
/IV/4.3 灰度变换.md:
--------------------------------------------------------------------------------
1 | # 4.3 灰度变换
2 |
3 | ## 4.2.1 灰度线性变换
4 |
5 | 假定原图像 $f(x, y)$ 的灰度范围为 $[a, b]$, 希望变换后图像 $g(x$, $y)$ 的灰度范围扩展至 $[c, d]$, 则线性变换可表示为
6 | $$
7 | g(x, y)=\frac{d-c}{b-a}[f(x, y)-a]+c\tag{4-12}
8 | $$
9 | 此式用图4-12表示。若图像灰度在 $0 \sim M_f$ 范围内, 其中大部分像素的灰度级分布在区间 $[a, b]$, 很小部分的灰度级超出了此区间, 为改善增强的效果, 可令:
10 | $$
11 | g(x, y)= \begin{cases}c & 0 \leq f(x, y)
43 |
44 | 图4-15 常见的几种非线性变换函数
45 |
46 | 式(4-16)对灰度区间$ [0, a]$和$[b, M_f]$加以压缩,对灰度区间[a, b]进行扩展。通过细心调整折线拐点的位置及控制分段直线的斜率,可对任一灰度区间进行扩展或压缩。这种变换适用于在黑色或白色附近有噪声干扰的情况。例如, 照片中的划痕, 由于变换后在[0, a]以及[b, $M_f$ ]之间的灰度受到压缩, 因而使污斑得到减弱。
47 |
48 | ## 4.2.3 非线性变换
49 |
50 | 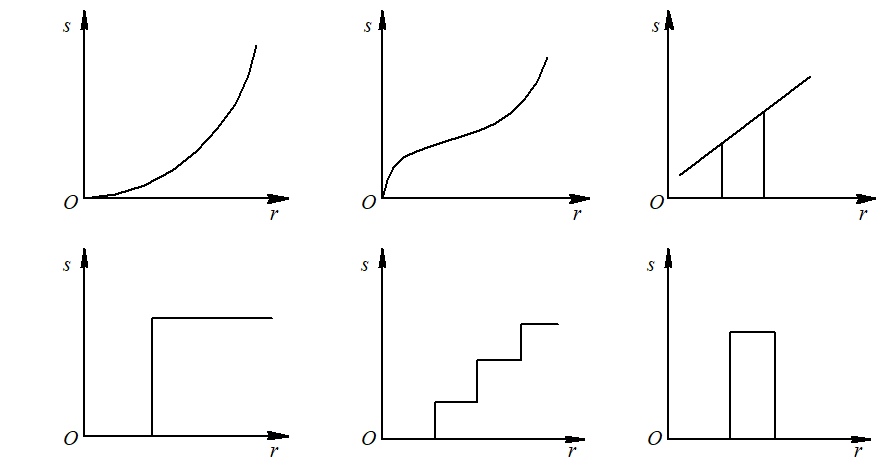 51 |
52 | ### S型函数
53 |
54 | $$
55 | \begin{aligned}
56 | & T(x)=\frac{L}{2}\left\{1+\frac{1}{\sin \left(\alpha \frac{\pi}{2}\right)} \sin \left[\alpha \pi\left(\frac{r}{L}-\frac{1}{2}\right)\right]\right\}
57 | & 0<\alpha<1 \\
58 | & ~T(x)=\frac{D_m}{2}\left\{1+\frac{1}{\tan \left(\alpha \frac{\pi}{2}\right)} \tan \left[\alpha \pi\left(\frac{x}{D_m}-\frac{1}{2}\right)\right]\right\}
59 | & 0<\alpha<1
60 | \end{aligned}
61 | $$
62 |
63 | ### 指数变换
64 |
65 | $$
66 | s=c y^\gamma
67 | $$
68 |
69 | $c$ 和 $y$ 为常数。
70 | 当 $\gamma<1$ 时, 具有扩展低亮度区、压缩高亮度区的效果;
71 | 当 $\gamma>1$ 时, 性能正好相反,具有压缩低亮度区、扩展高亮度区的效果。
72 | 而当 $c=\gamma=1$ 时, 输出正比与输入, 图像无变化。
73 | “ $\gamma$ 校正"(伽马校正),CRT显示器
74 |
75 | ### 显示器校正
76 |
77 | 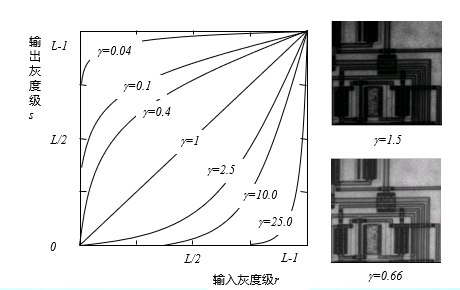
78 |
79 | 图6-23 不同$\gamma$的$s=cr^{\gamma}$曲线及图像变换结果
80 |
81 | 组合灰度变换效果与直方图变图像增强与平滑化
82 |
83 | ### 组合灰度变换效果与直方图变化
84 |
85 |
51 |
52 | ### S型函数
53 |
54 | $$
55 | \begin{aligned}
56 | & T(x)=\frac{L}{2}\left\{1+\frac{1}{\sin \left(\alpha \frac{\pi}{2}\right)} \sin \left[\alpha \pi\left(\frac{r}{L}-\frac{1}{2}\right)\right]\right\}
57 | & 0<\alpha<1 \\
58 | & ~T(x)=\frac{D_m}{2}\left\{1+\frac{1}{\tan \left(\alpha \frac{\pi}{2}\right)} \tan \left[\alpha \pi\left(\frac{x}{D_m}-\frac{1}{2}\right)\right]\right\}
59 | & 0<\alpha<1
60 | \end{aligned}
61 | $$
62 |
63 | ### 指数变换
64 |
65 | $$
66 | s=c y^\gamma
67 | $$
68 |
69 | $c$ 和 $y$ 为常数。
70 | 当 $\gamma<1$ 时, 具有扩展低亮度区、压缩高亮度区的效果;
71 | 当 $\gamma>1$ 时, 性能正好相反,具有压缩低亮度区、扩展高亮度区的效果。
72 | 而当 $c=\gamma=1$ 时, 输出正比与输入, 图像无变化。
73 | “ $\gamma$ 校正"(伽马校正),CRT显示器
74 |
75 | ### 显示器校正
76 |
77 | 
78 |
79 | 图6-23 不同$\gamma$的$s=cr^{\gamma}$曲线及图像变换结果
80 |
81 | 组合灰度变换效果与直方图变图像增强与平滑化
82 |
83 | ### 组合灰度变换效果与直方图变化
84 |
85 | 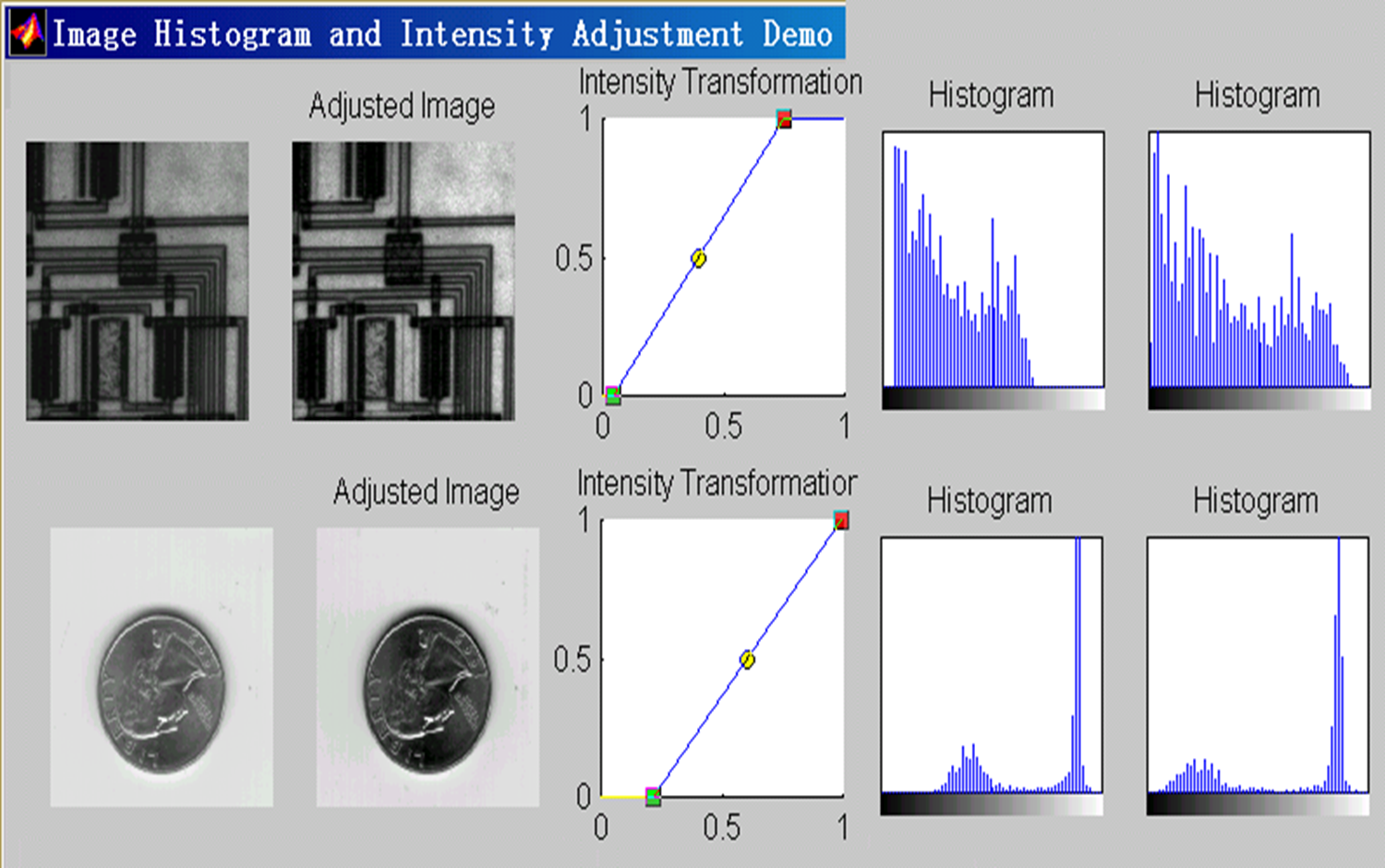 86 |
87 | ### 分段线性变换
88 |
89 | 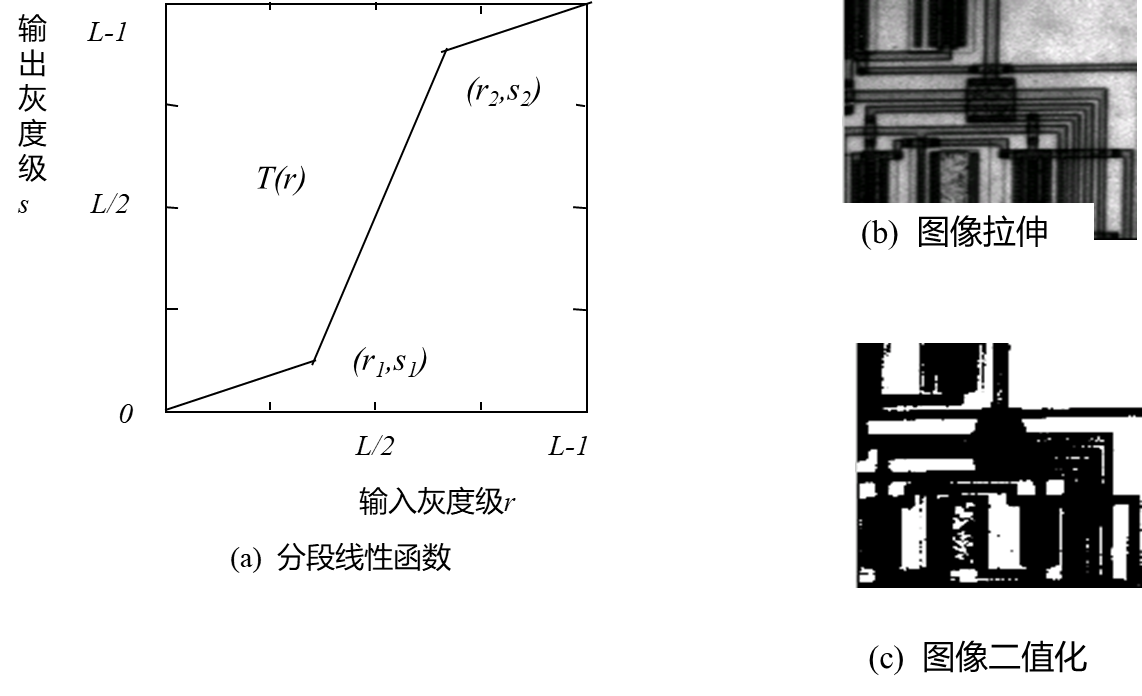
--------------------------------------------------------------------------------
/IV/4.4 图像噪声.md:
--------------------------------------------------------------------------------
1 | # 4.4 图像噪声
2 |
3 | 重点:均值滤波法s
4 |
5 | ## 4.4.1 概述
6 |
7 | 噪声可以理解为“妨碍人们感觉器官对所接收的信源信息理解的因素” 。例如,一幅黑白图像,其亮度分布假定为$f (x, y)$, 那么对其起干扰作用的亮度分布$R(x, y)$便称为图像噪声。噪声在理论上可以定义为“不可预测, 只能用概率统计方法来认识的随机误差” 。因此,将图像噪声看成是多维随机过程是合适的, 描述噪声的方法完全可以借用随机过程及其概率分布函数和概率密度函数。但在很多情况下,这种描述方法很复杂,甚至不可能,而且实际应用往往也不必要,通常是用其数字特征,即均值方差、相关函数等进行处理。
8 |
9 | 目前,大多数数字图像系统中,输入光图像都是采用先冻结再扫描方式将多维图像变成一维电信号,再对其进行处理、存储、 传输等加工,最后往往还要再组成多维图像信号。图像噪声同样也受到这样的分解和合成,在这些过程中电气系统和外界影响将使得图像噪声的精确分析变得十分复杂。另一方面, 对图像信息的认识和理解是由人的视觉系统所决定的。不同的图像噪声,人的感觉(理解)程度是不同的,这就是所谓人的噪声视觉特性问题。该方面虽早已进行研究,但终因人的视觉系统本身未搞清楚而未获得解决。尽管如此,图像噪声在数字图像处理技术中的重要性却愈加明显。例如,高放大倍数遥感图片的判读,X射线图像系统中的噪声去除等都已成为不可缺少的技术。
10 |
11 | ## 4.4.2 图像噪声分类
12 |
13 | 图像噪声按其产生的原因可分为外部噪声和内部噪声。
14 |
15 | 外部噪声是指系统外部干扰从电磁波或经电源传进系统内部而引起的噪声,如电气设备、天体放电现象等引起的噪声。 主要外部干扰如下:
16 |
17 | (1) 由光和电的基本性质所引起的噪声。
18 |
19 | (2) 电器的机械运动产生的噪声。如, 各种接头因抖动引起的电流变化所产生的噪声;磁头、磁带抖动引起的抖动噪声等。
20 |
21 | (3) 元器件材料本身引起的噪声。如, 磁带、磁盘表面缺陷所产生的噪声。
22 |
23 | (4) 系统内部设备电路所引起的噪声。如, 电源系统引入的交流噪声,偏转系统和箝位电路引起的噪声等。
24 |
25 | 图像噪声从统计特性可分为平稳噪声和非平稳噪声两种。 统计特性不随时间变化的噪声称为平稳噪声;统计特性随时间变化的噪声称为非平稳噪声
26 |
27 | 另外, 按噪声和信号之间的关系可分为加性噪声和乘性噪声。假定信号为 $S(t)$, 噪声为 $n(t)$, 如果混合叠加波形是 $S(t)+n(t)$ 形式, 则称其为加性噪声; 如果叠加波形为 $S(t)[1+n(t)]$ 形式, 则称其为乘性噪声。为了分析处理方便, 往往将乘性噪声近似认为加性噪声, 而且总是假定信号和噪声是互相独立的。
28 |
29 | ## 4.4.3 图像系统噪声特点
30 |
31 | 如图4-16是一幅含有噪声的图像, 由此可知图像中的噪声有以下三个特点。
32 |
33 | 1. 噪声在图像中的分布和大小不规则
34 | 2. 噪声与图像之间具有相关性
35 | 3. 噪声具有叠加性
36 |
37 | 
38 |
39 | 图4-16 有噪声的图像
--------------------------------------------------------------------------------
/IV/4.6 图像锐化.md:
--------------------------------------------------------------------------------
1 | # 4.6 图像锐化
2 |
3 | 需要使用高通滤波器,此时变化大的点为感兴趣的点
4 |
5 | **所谓锐化算法,就是利用图像的一阶微分信息,得到想要的信息**
6 |
7 | ## 4.6.1 微分法
8 |
9 | ### 梯度法
10 |
11 | 对于图像函数 $f(x, y)$, 它在点 $(x, y)$ 处的梯度是一个矢量, 定义为
12 | $$
13 | G[f(x, y)]=\left[\begin{array}{l}
14 | \frac{\partial f}{\partial x} \\
15 | \frac{\partial f}{\partial y}
16 | \end{array}\right] \tag{4-27}
17 | $$
18 | 梯度的两个重要性质是:
19 |
20 | (1) 梯度的方向在函数$f(x, y)$最大变化率的方向上。
21 |
22 | (2) 梯度的幅度用 $G[f(x, y)]$ 表示, 并由下式算出:
23 | $$
24 | G[f(x, y)]=\left[\left(\frac{\partial f}{\partial x}\right)^2+\left(\frac{\partial f}{\partial y}\right)^2\right]^{1 / 2}\tag{4-28}
25 | $$
26 | 由上式可知, 梯度的数值就是 $f(x, y)$ 在其最大变化率方向上的单位距离所增加的量。对于数字图像而言, 式(4-28)可以近似为
27 | $$
28 | G[f(x, y)]=\left\{[f(i, j)-f(i+1, j)]^2+[f(i, j)-f(i, j+1)]^2\right\}^{1 / 2}\tag{4-29}
29 | $$
30 | 式中: 各像素的位置如图4-28(a)所示。
31 |
32 | 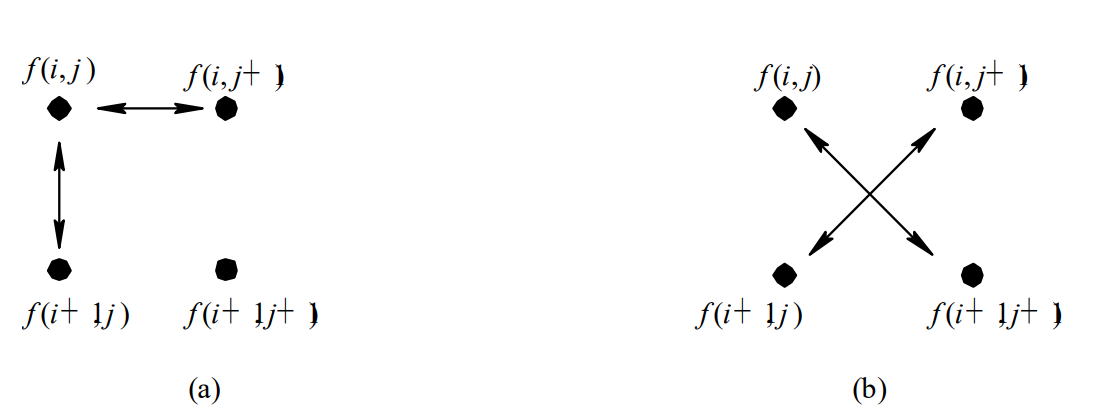
33 |
34 | 图4-28 求梯度的两种差分运算
35 |
36 | 式(4-29)可简化成为
37 | $$
38 | G[f(x, y)]=\left|f(i, j)-f(i+1, j)\right|+\left|f(i, j)-f(i, j+1)\right| \tag{4-30}
39 | $$
40 | 以上梯度法又称为水平垂直差分法。另一种梯度法叫做罗伯特梯度法 (Robert Gradient), 它是一种交叉差分计算法, 如图4-28(b)所示。其数学表达式为
41 | $$
42 | G[f(x, y)]=\left\{[f(i, j)-f(i+1, j+1)]^2+[f(i+1, j)-f(i, j+1)]^2\right\}^{1 / 2}\tag{4-31}
43 | $$
44 | 同样可近似为
45 | $$
46 | G[f(x, y)]=\mid\left[f(i, j)-f\left(i+1, j^{+1)}|+| f(i+1, j)-f(i, j+1)\right.\right.\tag{4-32}
47 | $$
48 | 以上两种梯度近似算法在图像的最后一行和最后一列的各像素的梯度无法求得,一般就用前一行和前一列的梯度值近似代替。
49 | 由梯度的计算可知,图像中灰度变化较大的边缘区域其梯度值大,在灰度变化平缓的区域其梯度值较小,而在灰度均匀区域其梯度值为零。图4-29(b)是采用水平垂直差分法对图4-29(a)锐化的结果,锐化后仅留下灰度值急剧变化的边沿处的点
50 |
51 | 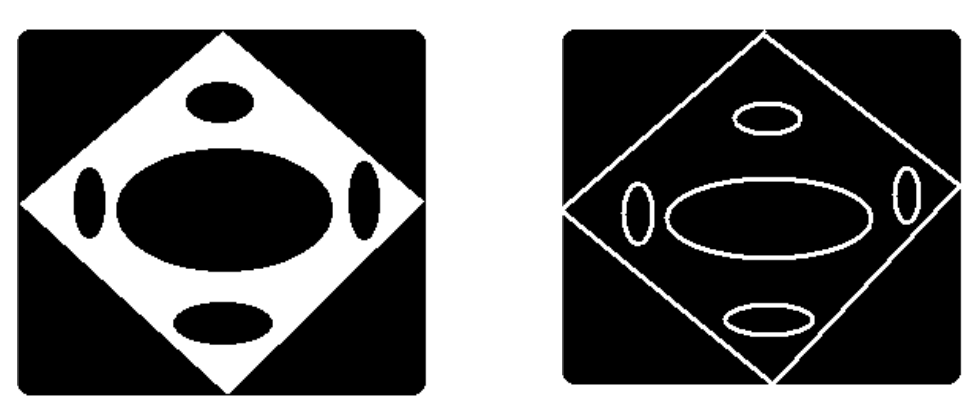
52 |
53 | 图4-29 图像梯度锐化结果
54 |
55 | (a) 二值图像; (b) 梯度运算结果
56 |
57 | 当梯度计算完之后,可以根据需要生成不同的梯度增强图像。 第一种是使各点的灰度$g(x, y)$等于该点的梯度幅度,即
58 | $$
59 | g(x, y)=G[f(x, y)]\tag{4-33}
60 | $$
61 | 此法的缺点是增强的图像仅显示灰度变化比较陡的边缘轮廓, 而灰度变化平缓的区域则呈黑色
62 |
63 | 第二种增强的图像是使
64 | $$
65 | g(x, y)= \begin{cases}G[f(x, y)] & G[f(x, y)] \geq T \\ f(x, y) & \text {其他 }\end{cases}\tag{4-34}
66 | $$
67 | 式中: $T$ 是一个非负的阈值, 适当选取 $T$, 即可使明显的边缘轮廓得到突出, 又不会破坏原灰度变化比较平缓的背景。
68 |
69 | 第三种增强图像是使
70 | $$
71 | g(x, y)= \begin{cases}L_G & G[f(x, y)] \geq T \\ f(x, y) & \text {其他 }\end{cases}\tag{4-35}
72 | $$
73 | 式中: $T$ 是根据需要指定的一个灰度级, 它将明显边缘用一固定的灰度级 $L_G$ 来实现。
74 |
75 | 第四种增强图像是使
76 | $$
77 | g(x, y)= \begin{cases}G[f(x, y)] & G[f(x, y)] \geq T \\ L_G & \text { 其他 }\end{cases}\tag{4-36}
78 | $$
79 | 此法将背景用一个固定灰度级 $L_G$ 来实现, 便于研究边缘灰度的变化。
80 |
81 | 第五种增强图像是使
82 | $$
83 | g(x, y)= \begin{cases}L_G & G[f(x, y)] \geq T \\ L_B & \text { 其他 }\end{cases}\tag{4-37}
84 | $$
85 | 此法将背景和边缘用二值图像表示, 便于研究边缘所在位置。
86 |
87 | ### Sobel算子
88 |
89 | 重点,很常用,目前国际上占据主流
90 |
91 | 采用梯度微分锐化图像,同时会使噪声、条纹等得到增强, Sobel算子则在一定程度上克服了这个问题。Sobel算子法的基本原理是: 按式(4-38)计算3×3窗口(如图4-30所示)的灰度, 将其作为变换后图像f(i, j)的灰度。
92 |
93 | 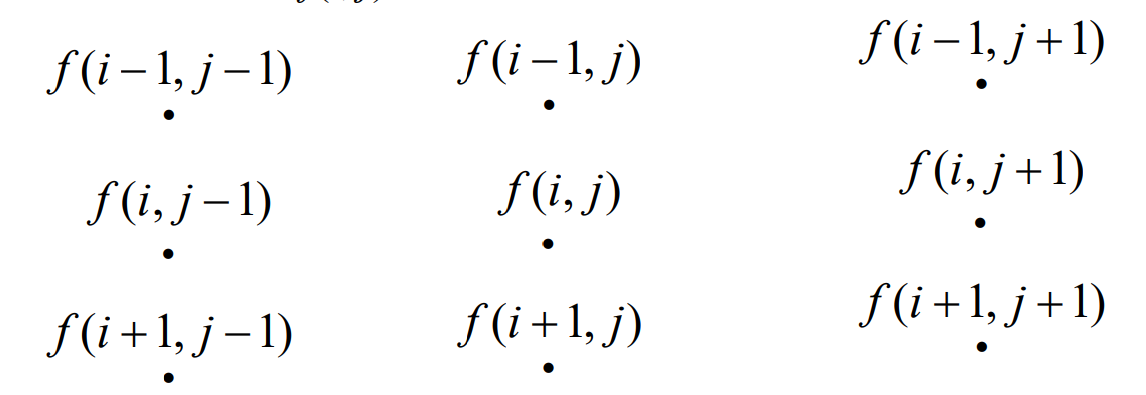
94 |
95 | 图4-30 Sobel算子图像坐标
96 | $$
97 | g=\sqrt{S_x^2+S_y^2}\tag{4-38}
98 | $$
99 | 式中:
100 | $$
101 | \begin{aligned}
102 | S_x & =[f(i+1, j-1)+2 f(i+1, j)+f(i+1, j+1)] \\
103 | & -[f(i-1, j-1)+2 f(i-1, j)+f(i-1, j+1)] \\
104 | S_y & =[f(i-1, j+1)+2 f(i, j+1)+f(i+1, j+1)] \\
105 | & -[f(i-1, j-1)+2 f(i, j-1)+f(i+1, j-1)]
106 | \end{aligned}
107 | $$
108 | 为简化计算, 可用 $\left.g=\left|S_{x}\right|\right]+\left|S_{y}\right|$ 来代替式(4-38), 从而得到锐化后的图像。Sobel算子不像普通梯度算子那样用两个像素的差值, 这就导致了以下两个优点:
109 | (1) 由于引入了平均因素, 因而对图像中的随机噪声有一定的平滑作用。
110 | (2) 由于它是相隔两行或两列之差分, 故边缘两侧元素得到了增强, 边缘显得粗而亮。
111 |
112 | Sobel锐化算法
113 | $$
114 | d_x=\left[\begin{array}{rrr}
115 | -1 & 0 & 1 \\
116 | -2 & 0 & 2 \\
117 | -1 & 0 & 1
118 | \end{array}\right]&d_y=\left[\begin{array}{ccc}
119 | -1 & -2 & -1 \\
120 | 0 & 0 & 0 \\
121 | 1 & 2 & 1
122 | \end{array}\right]\tag{4-39}
123 | $$
124 |
125 | $$
126 |
127 | $$
128 |
129 | Roberts梯度锐化效果图例
130 |
131 | 
132 |
133 | 为简化计算, 可用 $g=\left|S_{x}\right|+\left|S_{y}\right|$ 来代替式(4-38), 从而得到锐化后的图像。Sobel算子不像普通梯度算子那样用两个像素的差值, 这就导致了以下两个优点:
134 | (1) 由于引入了平均因素, 因而对图像中的随机噪声有一定的平滑作用。
135 | (2) 由于它是相隔两行或两列之差分, 故边缘两侧元素得到了增强, 边缘显得粗而亮。
136 |
137 | Roberts梯度锐化效果图例
138 |
139 |
86 |
87 | ### 分段线性变换
88 |
89 | 
--------------------------------------------------------------------------------
/IV/4.4 图像噪声.md:
--------------------------------------------------------------------------------
1 | # 4.4 图像噪声
2 |
3 | 重点:均值滤波法s
4 |
5 | ## 4.4.1 概述
6 |
7 | 噪声可以理解为“妨碍人们感觉器官对所接收的信源信息理解的因素” 。例如,一幅黑白图像,其亮度分布假定为$f (x, y)$, 那么对其起干扰作用的亮度分布$R(x, y)$便称为图像噪声。噪声在理论上可以定义为“不可预测, 只能用概率统计方法来认识的随机误差” 。因此,将图像噪声看成是多维随机过程是合适的, 描述噪声的方法完全可以借用随机过程及其概率分布函数和概率密度函数。但在很多情况下,这种描述方法很复杂,甚至不可能,而且实际应用往往也不必要,通常是用其数字特征,即均值方差、相关函数等进行处理。
8 |
9 | 目前,大多数数字图像系统中,输入光图像都是采用先冻结再扫描方式将多维图像变成一维电信号,再对其进行处理、存储、 传输等加工,最后往往还要再组成多维图像信号。图像噪声同样也受到这样的分解和合成,在这些过程中电气系统和外界影响将使得图像噪声的精确分析变得十分复杂。另一方面, 对图像信息的认识和理解是由人的视觉系统所决定的。不同的图像噪声,人的感觉(理解)程度是不同的,这就是所谓人的噪声视觉特性问题。该方面虽早已进行研究,但终因人的视觉系统本身未搞清楚而未获得解决。尽管如此,图像噪声在数字图像处理技术中的重要性却愈加明显。例如,高放大倍数遥感图片的判读,X射线图像系统中的噪声去除等都已成为不可缺少的技术。
10 |
11 | ## 4.4.2 图像噪声分类
12 |
13 | 图像噪声按其产生的原因可分为外部噪声和内部噪声。
14 |
15 | 外部噪声是指系统外部干扰从电磁波或经电源传进系统内部而引起的噪声,如电气设备、天体放电现象等引起的噪声。 主要外部干扰如下:
16 |
17 | (1) 由光和电的基本性质所引起的噪声。
18 |
19 | (2) 电器的机械运动产生的噪声。如, 各种接头因抖动引起的电流变化所产生的噪声;磁头、磁带抖动引起的抖动噪声等。
20 |
21 | (3) 元器件材料本身引起的噪声。如, 磁带、磁盘表面缺陷所产生的噪声。
22 |
23 | (4) 系统内部设备电路所引起的噪声。如, 电源系统引入的交流噪声,偏转系统和箝位电路引起的噪声等。
24 |
25 | 图像噪声从统计特性可分为平稳噪声和非平稳噪声两种。 统计特性不随时间变化的噪声称为平稳噪声;统计特性随时间变化的噪声称为非平稳噪声
26 |
27 | 另外, 按噪声和信号之间的关系可分为加性噪声和乘性噪声。假定信号为 $S(t)$, 噪声为 $n(t)$, 如果混合叠加波形是 $S(t)+n(t)$ 形式, 则称其为加性噪声; 如果叠加波形为 $S(t)[1+n(t)]$ 形式, 则称其为乘性噪声。为了分析处理方便, 往往将乘性噪声近似认为加性噪声, 而且总是假定信号和噪声是互相独立的。
28 |
29 | ## 4.4.3 图像系统噪声特点
30 |
31 | 如图4-16是一幅含有噪声的图像, 由此可知图像中的噪声有以下三个特点。
32 |
33 | 1. 噪声在图像中的分布和大小不规则
34 | 2. 噪声与图像之间具有相关性
35 | 3. 噪声具有叠加性
36 |
37 | 
38 |
39 | 图4-16 有噪声的图像
--------------------------------------------------------------------------------
/IV/4.6 图像锐化.md:
--------------------------------------------------------------------------------
1 | # 4.6 图像锐化
2 |
3 | 需要使用高通滤波器,此时变化大的点为感兴趣的点
4 |
5 | **所谓锐化算法,就是利用图像的一阶微分信息,得到想要的信息**
6 |
7 | ## 4.6.1 微分法
8 |
9 | ### 梯度法
10 |
11 | 对于图像函数 $f(x, y)$, 它在点 $(x, y)$ 处的梯度是一个矢量, 定义为
12 | $$
13 | G[f(x, y)]=\left[\begin{array}{l}
14 | \frac{\partial f}{\partial x} \\
15 | \frac{\partial f}{\partial y}
16 | \end{array}\right] \tag{4-27}
17 | $$
18 | 梯度的两个重要性质是:
19 |
20 | (1) 梯度的方向在函数$f(x, y)$最大变化率的方向上。
21 |
22 | (2) 梯度的幅度用 $G[f(x, y)]$ 表示, 并由下式算出:
23 | $$
24 | G[f(x, y)]=\left[\left(\frac{\partial f}{\partial x}\right)^2+\left(\frac{\partial f}{\partial y}\right)^2\right]^{1 / 2}\tag{4-28}
25 | $$
26 | 由上式可知, 梯度的数值就是 $f(x, y)$ 在其最大变化率方向上的单位距离所增加的量。对于数字图像而言, 式(4-28)可以近似为
27 | $$
28 | G[f(x, y)]=\left\{[f(i, j)-f(i+1, j)]^2+[f(i, j)-f(i, j+1)]^2\right\}^{1 / 2}\tag{4-29}
29 | $$
30 | 式中: 各像素的位置如图4-28(a)所示。
31 |
32 | 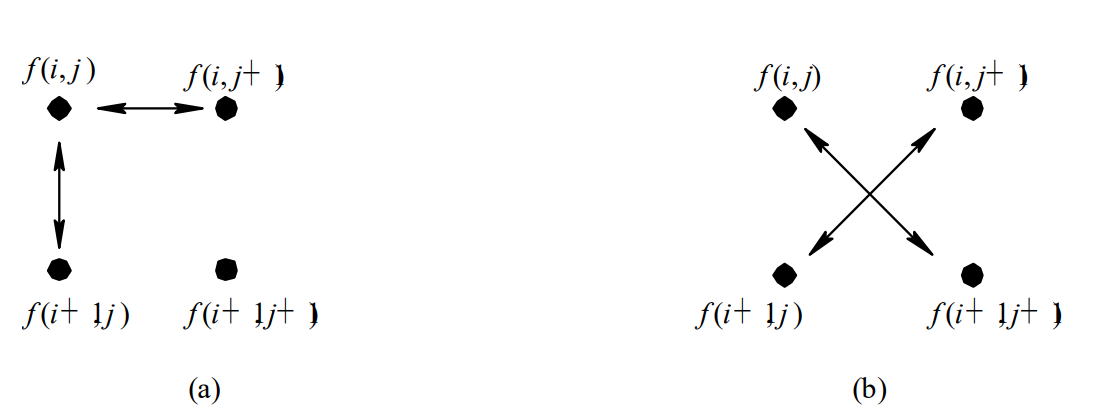
33 |
34 | 图4-28 求梯度的两种差分运算
35 |
36 | 式(4-29)可简化成为
37 | $$
38 | G[f(x, y)]=\left|f(i, j)-f(i+1, j)\right|+\left|f(i, j)-f(i, j+1)\right| \tag{4-30}
39 | $$
40 | 以上梯度法又称为水平垂直差分法。另一种梯度法叫做罗伯特梯度法 (Robert Gradient), 它是一种交叉差分计算法, 如图4-28(b)所示。其数学表达式为
41 | $$
42 | G[f(x, y)]=\left\{[f(i, j)-f(i+1, j+1)]^2+[f(i+1, j)-f(i, j+1)]^2\right\}^{1 / 2}\tag{4-31}
43 | $$
44 | 同样可近似为
45 | $$
46 | G[f(x, y)]=\mid\left[f(i, j)-f\left(i+1, j^{+1)}|+| f(i+1, j)-f(i, j+1)\right.\right.\tag{4-32}
47 | $$
48 | 以上两种梯度近似算法在图像的最后一行和最后一列的各像素的梯度无法求得,一般就用前一行和前一列的梯度值近似代替。
49 | 由梯度的计算可知,图像中灰度变化较大的边缘区域其梯度值大,在灰度变化平缓的区域其梯度值较小,而在灰度均匀区域其梯度值为零。图4-29(b)是采用水平垂直差分法对图4-29(a)锐化的结果,锐化后仅留下灰度值急剧变化的边沿处的点
50 |
51 | 
52 |
53 | 图4-29 图像梯度锐化结果
54 |
55 | (a) 二值图像; (b) 梯度运算结果
56 |
57 | 当梯度计算完之后,可以根据需要生成不同的梯度增强图像。 第一种是使各点的灰度$g(x, y)$等于该点的梯度幅度,即
58 | $$
59 | g(x, y)=G[f(x, y)]\tag{4-33}
60 | $$
61 | 此法的缺点是增强的图像仅显示灰度变化比较陡的边缘轮廓, 而灰度变化平缓的区域则呈黑色
62 |
63 | 第二种增强的图像是使
64 | $$
65 | g(x, y)= \begin{cases}G[f(x, y)] & G[f(x, y)] \geq T \\ f(x, y) & \text {其他 }\end{cases}\tag{4-34}
66 | $$
67 | 式中: $T$ 是一个非负的阈值, 适当选取 $T$, 即可使明显的边缘轮廓得到突出, 又不会破坏原灰度变化比较平缓的背景。
68 |
69 | 第三种增强图像是使
70 | $$
71 | g(x, y)= \begin{cases}L_G & G[f(x, y)] \geq T \\ f(x, y) & \text {其他 }\end{cases}\tag{4-35}
72 | $$
73 | 式中: $T$ 是根据需要指定的一个灰度级, 它将明显边缘用一固定的灰度级 $L_G$ 来实现。
74 |
75 | 第四种增强图像是使
76 | $$
77 | g(x, y)= \begin{cases}G[f(x, y)] & G[f(x, y)] \geq T \\ L_G & \text { 其他 }\end{cases}\tag{4-36}
78 | $$
79 | 此法将背景用一个固定灰度级 $L_G$ 来实现, 便于研究边缘灰度的变化。
80 |
81 | 第五种增强图像是使
82 | $$
83 | g(x, y)= \begin{cases}L_G & G[f(x, y)] \geq T \\ L_B & \text { 其他 }\end{cases}\tag{4-37}
84 | $$
85 | 此法将背景和边缘用二值图像表示, 便于研究边缘所在位置。
86 |
87 | ### Sobel算子
88 |
89 | 重点,很常用,目前国际上占据主流
90 |
91 | 采用梯度微分锐化图像,同时会使噪声、条纹等得到增强, Sobel算子则在一定程度上克服了这个问题。Sobel算子法的基本原理是: 按式(4-38)计算3×3窗口(如图4-30所示)的灰度, 将其作为变换后图像f(i, j)的灰度。
92 |
93 | 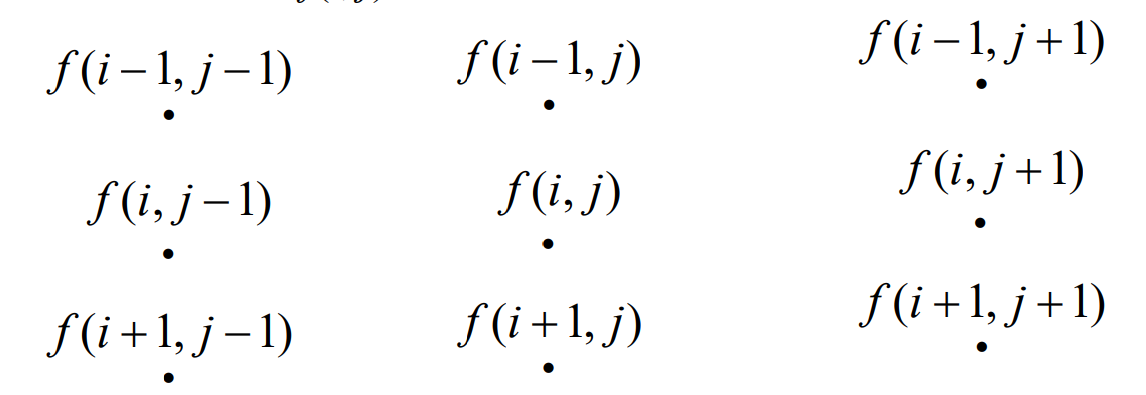
94 |
95 | 图4-30 Sobel算子图像坐标
96 | $$
97 | g=\sqrt{S_x^2+S_y^2}\tag{4-38}
98 | $$
99 | 式中:
100 | $$
101 | \begin{aligned}
102 | S_x & =[f(i+1, j-1)+2 f(i+1, j)+f(i+1, j+1)] \\
103 | & -[f(i-1, j-1)+2 f(i-1, j)+f(i-1, j+1)] \\
104 | S_y & =[f(i-1, j+1)+2 f(i, j+1)+f(i+1, j+1)] \\
105 | & -[f(i-1, j-1)+2 f(i, j-1)+f(i+1, j-1)]
106 | \end{aligned}
107 | $$
108 | 为简化计算, 可用 $\left.g=\left|S_{x}\right|\right]+\left|S_{y}\right|$ 来代替式(4-38), 从而得到锐化后的图像。Sobel算子不像普通梯度算子那样用两个像素的差值, 这就导致了以下两个优点:
109 | (1) 由于引入了平均因素, 因而对图像中的随机噪声有一定的平滑作用。
110 | (2) 由于它是相隔两行或两列之差分, 故边缘两侧元素得到了增强, 边缘显得粗而亮。
111 |
112 | Sobel锐化算法
113 | $$
114 | d_x=\left[\begin{array}{rrr}
115 | -1 & 0 & 1 \\
116 | -2 & 0 & 2 \\
117 | -1 & 0 & 1
118 | \end{array}\right]&d_y=\left[\begin{array}{ccc}
119 | -1 & -2 & -1 \\
120 | 0 & 0 & 0 \\
121 | 1 & 2 & 1
122 | \end{array}\right]\tag{4-39}
123 | $$
124 |
125 | $$
126 |
127 | $$
128 |
129 | Roberts梯度锐化效果图例
130 |
131 | 
132 |
133 | 为简化计算, 可用 $g=\left|S_{x}\right|+\left|S_{y}\right|$ 来代替式(4-38), 从而得到锐化后的图像。Sobel算子不像普通梯度算子那样用两个像素的差值, 这就导致了以下两个优点:
134 | (1) 由于引入了平均因素, 因而对图像中的随机噪声有一定的平滑作用。
135 | (2) 由于它是相隔两行或两列之差分, 故边缘两侧元素得到了增强, 边缘显得粗而亮。
136 |
137 | Roberts梯度锐化效果图例
138 |
139 |  140 |
141 | Priwitt锐化算法
142 | $$
143 | g(i, j)=\left\{d_x^2(i, j)+d_y^2(i, j)\right\}^{\frac{1}{2}}\tag{4-40}\\
144 | $$
145 | $$
146 | d_x=\left[\begin{array}{ccc}
147 | -1 & 0 & 1 \\
148 | -1 & 0 & 1 \\
149 | -1 & 0 & 1
150 | \end{array}\right]
151 | &d_y=\left[\begin{array}{ccc}
152 | -1 & -1 & -1 \\
153 | 0 & 0 & 0 \\
154 | 1 & 1 & 1
155 | \end{array}\right]
156 | $$
157 |
158 | 表4-2 常用的梯度算子
159 | $$
160 | \begin{array}{|l|l|l|ll|}
161 | \hline \text { 算子名称 } & H_1 & H_2 & \text { 特 } & \text { 点 } \\
162 | \hline \text { Roberts } & {\left[\begin{array}{cc}
163 | 0 * & 1 \\
164 | -1 & 0
165 | \end{array}\right]} & {\left[\begin{array}{cc}
166 | 1 * & 0 \\
167 | 0 & -1
168 | \end{array}\right]} & \text { 边缘定位准,但对噪声敏感 } \\
169 | \hline \text { Prewitt } & {\left[\begin{array}{ccc}
170 | -1 & 0 & 1 \\
171 | -1 & 0 * & 1 \\
172 | -1 & 0 & 1
173 | \end{array}\right]} & {\left[\begin{array}{ccc}
174 | -1 & -1 & 1 \\
175 | 0 & 0 * & 0 \\
176 | 1 & 1 & 1
177 | \end{array}\right]} & \text { 平均、微分对噪声有抑制作用 } \\
178 | \hline \text {Sobel } & {\left[\begin{array}{ccc}
179 | -1 & 0 & 1 \\
180 | -2 & 0 * & 2 \\
181 | -1 & 0 & 1
182 | \end{array}\right]} & {\left[\begin{array}{ccc}
183 | -1 & -1 & 1 \\
184 | 0 & 0 * & 0 \\
185 | 1 & 2 & 1
186 | \end{array}\right]} & 加权平均边宽 \geqslant 2 像素 \\
187 | \hline \text { Krisch } & {\left[\begin{array}{ccc}
188 | 5 & 5 & 5 \\
189 | -3 & 0 * & -3 \\
190 | -3 & -3 & -3
191 | \end{array}\right]} & {\left[\begin{array}{ccc}
192 | -3 & -3 & 5 \\
193 | -3 & 0 * & 5 \\
194 | -3 & -3 & 5
195 | \end{array}\right]} & 对噪声有较好地抑制作用。该算子需求出 f(x, y) 在 8 个方向上的平均差分的最大值, 这里只给出了 2 个方向的模板 \\
196 | \hline \text { Isotropic Sobel } & {\left[\begin{array}{ccc}
197 | -1 & 0 & 1 \\
198 | -\sqrt{2} & 0 * & \sqrt{2} \\
199 | -1 & 0 & 1
200 | \end{array}\right]} & {\left[\begin{array}{ccc}
201 | -1 & -1 & 1 \\
202 | 0 & 0 * & 0 \\
203 | 1 & \sqrt{2} & 1
204 | \end{array}\right]} & \text { 权值反比于领点与中心点的距离, 检测沿不同方向边缘时梯度幅度一致 } \\
205 | \hline
206 | \end{array}
207 | $$
208 | Prewitt锐化效果图例
209 |
210 | 
211 |
212 | 其他
213 |
214 | 一、单方向的一阶梯度算法(浮雕效果)
215 |
216 | 水平方向的锐化
217 |
218 | 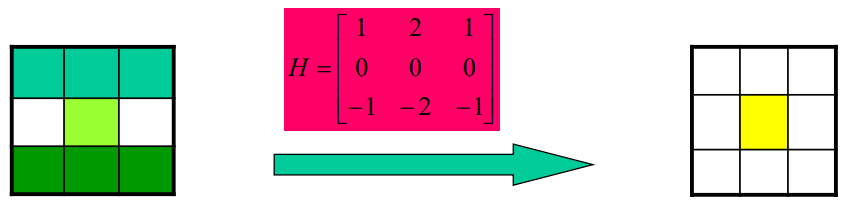
219 |
220 | 一阶水平方向锐化效果
221 |
222 | 
223 |
224 | 2. 垂直方向的锐化
225 |
226 | 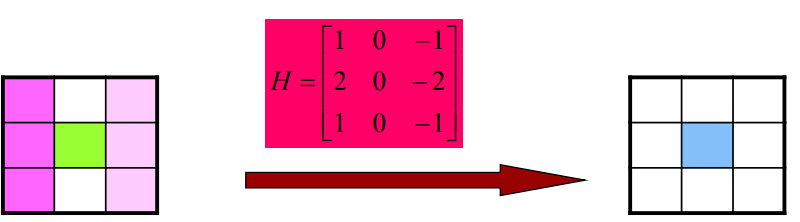
227 |
228 | 单方向一阶锐化效果图例
229 |
230 | 
231 |
232 |
140 |
141 | Priwitt锐化算法
142 | $$
143 | g(i, j)=\left\{d_x^2(i, j)+d_y^2(i, j)\right\}^{\frac{1}{2}}\tag{4-40}\\
144 | $$
145 | $$
146 | d_x=\left[\begin{array}{ccc}
147 | -1 & 0 & 1 \\
148 | -1 & 0 & 1 \\
149 | -1 & 0 & 1
150 | \end{array}\right]
151 | &d_y=\left[\begin{array}{ccc}
152 | -1 & -1 & -1 \\
153 | 0 & 0 & 0 \\
154 | 1 & 1 & 1
155 | \end{array}\right]
156 | $$
157 |
158 | 表4-2 常用的梯度算子
159 | $$
160 | \begin{array}{|l|l|l|ll|}
161 | \hline \text { 算子名称 } & H_1 & H_2 & \text { 特 } & \text { 点 } \\
162 | \hline \text { Roberts } & {\left[\begin{array}{cc}
163 | 0 * & 1 \\
164 | -1 & 0
165 | \end{array}\right]} & {\left[\begin{array}{cc}
166 | 1 * & 0 \\
167 | 0 & -1
168 | \end{array}\right]} & \text { 边缘定位准,但对噪声敏感 } \\
169 | \hline \text { Prewitt } & {\left[\begin{array}{ccc}
170 | -1 & 0 & 1 \\
171 | -1 & 0 * & 1 \\
172 | -1 & 0 & 1
173 | \end{array}\right]} & {\left[\begin{array}{ccc}
174 | -1 & -1 & 1 \\
175 | 0 & 0 * & 0 \\
176 | 1 & 1 & 1
177 | \end{array}\right]} & \text { 平均、微分对噪声有抑制作用 } \\
178 | \hline \text {Sobel } & {\left[\begin{array}{ccc}
179 | -1 & 0 & 1 \\
180 | -2 & 0 * & 2 \\
181 | -1 & 0 & 1
182 | \end{array}\right]} & {\left[\begin{array}{ccc}
183 | -1 & -1 & 1 \\
184 | 0 & 0 * & 0 \\
185 | 1 & 2 & 1
186 | \end{array}\right]} & 加权平均边宽 \geqslant 2 像素 \\
187 | \hline \text { Krisch } & {\left[\begin{array}{ccc}
188 | 5 & 5 & 5 \\
189 | -3 & 0 * & -3 \\
190 | -3 & -3 & -3
191 | \end{array}\right]} & {\left[\begin{array}{ccc}
192 | -3 & -3 & 5 \\
193 | -3 & 0 * & 5 \\
194 | -3 & -3 & 5
195 | \end{array}\right]} & 对噪声有较好地抑制作用。该算子需求出 f(x, y) 在 8 个方向上的平均差分的最大值, 这里只给出了 2 个方向的模板 \\
196 | \hline \text { Isotropic Sobel } & {\left[\begin{array}{ccc}
197 | -1 & 0 & 1 \\
198 | -\sqrt{2} & 0 * & \sqrt{2} \\
199 | -1 & 0 & 1
200 | \end{array}\right]} & {\left[\begin{array}{ccc}
201 | -1 & -1 & 1 \\
202 | 0 & 0 * & 0 \\
203 | 1 & \sqrt{2} & 1
204 | \end{array}\right]} & \text { 权值反比于领点与中心点的距离, 检测沿不同方向边缘时梯度幅度一致 } \\
205 | \hline
206 | \end{array}
207 | $$
208 | Prewitt锐化效果图例
209 |
210 | 
211 |
212 | 其他
213 |
214 | 一、单方向的一阶梯度算法(浮雕效果)
215 |
216 | 水平方向的锐化
217 |
218 | 
219 |
220 | 一阶水平方向锐化效果
221 |
222 | 
223 |
224 | 2. 垂直方向的锐化
225 |
226 | 
227 |
228 | 单方向一阶锐化效果图例
229 |
230 | 
231 |
232 |  233 |
234 | ## 4.6.2 拉普拉斯运算
235 |
236 | 拉普拉斯算子是常用的边缘增强算子,拉普拉斯运算也是偏导数运算的线性组合运算,而且是一种各向同性(旋转不变性)的线性运算。拉普拉斯算子为
237 | $$
238 | \nabla^2 f=\frac{\partial^2 f}{\partial x^2}+\frac{\partial^2 f}{\partial y^2}\tag{4-41}
239 | $$
240 | 如果图像的模糊是由扩散现象引起的 (如胶片颗粒化学扩散等), 则锐化后的图像 $g$ 为
241 | $$
242 | g=f-k \nabla^2 f\tag{4-42}
243 | $$
244 | 式中: $f 、 g$ 分别为锐化前后的图像, $k$ 为与扩散效应有关的系数。
245 |
246 | 式(4-42)表示模糊图像经拉普拉斯算子锐化以后得到新图像 $g \circ k$ 的选择要合理, 太大会使图像中的轮廓边缘产生过冲; $k$ 太小,锐化不明显。
247 | 对数字图像来讲, $f(x, y)$ 的二阶偏导数可表示为
248 | $$
249 | \begin{aligned}
250 | \frac{\partial^2 f(x, y)}{\partial x^2} & =\nabla_x f(i+1, j)-\nabla_x f(i, j) \\
251 | & =[f(i+1, j)-f(i, j)]-[f(i, j)-f(i-1), j] \\
252 | & =f(i+1, j)+f(i-1, j)-2 f(i, j) \\
253 | \end{aligned}
254 | $$
255 | $$
256 | \frac{\partial^2 f(x, y)}{\partial y^2} =f(i, j+1)+f(i, j-1)-2 f(i, j)\tag{4-43}
257 | $$
258 |
259 | 为此, 拉普拉斯算子 $\nabla^2 f$ 为
260 | $$
261 | \begin{aligned}
262 | \nabla^2 f & =\frac{\partial^2 f(x, y)}{\partial x^2}+\frac{\partial^2 f(x, y)}{\partial y^2} \\
263 | & =f(i+1, j)+f(i-1, j)+f(i, j+1)+f(i, j-1)-4 f(i, j) \\
264 | & =-5\left\{f(i, j)-\frac{1}{5}[f(i+1, j)+f(i-1, j)+f(i, j+1)\right. \\
265 | & +f(i, j-1)+f(i, j)]\}
266 | \end{aligned}\tag{4-44}
267 | $$
268 | 可见, 数字图像在 $(i, j)$ 点的拉普拉斯算子, 可以由 $(i, j)$ 点灰度值减去该点邻域平均灰度值来求得。当 $k=1$ 时, 拉普拉斯锐化后的图像为
269 | $$
270 | \begin{aligned}
271 | g(i, j) & =f(i, j)-\nabla^2 f(i, j) \\
272 | & =5 f(i, j)-f(i+1, j)-f(i-1, j)-f(i, j+1)-f(i, j-1)
273 | \end{aligned}\tag{4-45}
274 | $$
275 | ### Laplacian锐化算子
276 |
277 | 写成模板系数形式形式即为Laplacian算子:
278 | $$
279 | H_1=\left[\begin{array}{ccc}
280 | 0 & -1 & 0 \\
281 | -1 & 4 & -1 \\
282 | 0 & -1 & 0
283 | \end{array}\right]
284 | $$
285 | ### Laplacian变形算子
286 |
287 | $$
288 | H_2=\left[\begin{array}{ccc}
289 | -1 & -1 & -1 \\
290 | -1 & 8 & -1 \\
291 | -1 & -1 & -1
292 | \end{array}\right] \quad H_3=\left[\begin{array}{ccc}
293 | 1 & -2 & 1 \\
294 | -2 & 4 & -2 \\
295 | 1 & -2 & 1
296 | \end{array}\right] \quad H_4=\left[\begin{array}{ccc}
297 | 0 & -1 & 0 \\
298 | -1 & 5 & -1 \\
299 | 0 & -1 & 0
300 | \end{array}\right]
301 | $$
302 | 例:
303 |
304 | 设有 $1 \times n$ 的数字图像 $f(i, j)$, 其各点的灰度如下:
305 |
306 | $$
307 | \ldots, 0,0,0,1,2,3,4,5,5,5,5,5,5,6,6,6,6,6,6,3,3,3,3,3
308 | $$
309 |
310 | 计算 $\nabla^2 f$ 及锐化后的各点灰度值 $g$ (设 $\left.k=1\right)$ 。
311 |
312 | - 首先按式 (4-44)计算各点的 $\nabla^2 f$ 。例如:
313 |
314 | 第3点:
315 |
316 | $$
317 | \quad \nabla^2 f=-3\left[0-\frac{1}{3}(0+0+1)\right]=1
318 | $$
319 |
320 | 第8点:
321 |
322 | $$
323 | \quad \nabla^2 f=-3\left[5-\frac{1}{3}(4+4+5)\right]=-1
324 | $$
325 |
326 |
327 |
328 | 各点拉普拉斯算子如下:
329 |
330 | $$
331 | \ldots, 0,0,1,0,0,0,0,-1,0,0,0,0,1,-1,0,0,0,0,-3,3,0,0,0, \ldots
332 | $$
333 |
334 | - 按式(4-42)计算 $g=f-2 f$ 。例如:
335 |
336 | $$
337 | \begin{aligned}
338 | &第3点: g=f-\nabla^2 f=0-1=-1\\
339 | &\vdots \\
340 | &第8点: g=5-(-1)=6
341 | \end{aligned}
342 | $$
343 |
344 | 锐化后各点的灰度值如下:
345 |
346 | $$
347 | \ldots, 0,0,-1,1,2,3,4,6,5,5,5,5,4,7,6,6,6,6,9,0,3,3,3, \ldots
348 | $$
349 |
350 | 从上例可以看出,在灰度级斜坡底部(如第3点)和界线的低灰度级侧(如第13、20点)形成下冲。在灰度级斜坡顶部(如第8点)和界线的高灰度级侧(如第14、 19点)形成上冲。在灰度级平坦区域(如第9~12点, 第15~18点), 运算前后没有变化。如图4-31所示。
351 |
352 |
233 |
234 | ## 4.6.2 拉普拉斯运算
235 |
236 | 拉普拉斯算子是常用的边缘增强算子,拉普拉斯运算也是偏导数运算的线性组合运算,而且是一种各向同性(旋转不变性)的线性运算。拉普拉斯算子为
237 | $$
238 | \nabla^2 f=\frac{\partial^2 f}{\partial x^2}+\frac{\partial^2 f}{\partial y^2}\tag{4-41}
239 | $$
240 | 如果图像的模糊是由扩散现象引起的 (如胶片颗粒化学扩散等), 则锐化后的图像 $g$ 为
241 | $$
242 | g=f-k \nabla^2 f\tag{4-42}
243 | $$
244 | 式中: $f 、 g$ 分别为锐化前后的图像, $k$ 为与扩散效应有关的系数。
245 |
246 | 式(4-42)表示模糊图像经拉普拉斯算子锐化以后得到新图像 $g \circ k$ 的选择要合理, 太大会使图像中的轮廓边缘产生过冲; $k$ 太小,锐化不明显。
247 | 对数字图像来讲, $f(x, y)$ 的二阶偏导数可表示为
248 | $$
249 | \begin{aligned}
250 | \frac{\partial^2 f(x, y)}{\partial x^2} & =\nabla_x f(i+1, j)-\nabla_x f(i, j) \\
251 | & =[f(i+1, j)-f(i, j)]-[f(i, j)-f(i-1), j] \\
252 | & =f(i+1, j)+f(i-1, j)-2 f(i, j) \\
253 | \end{aligned}
254 | $$
255 | $$
256 | \frac{\partial^2 f(x, y)}{\partial y^2} =f(i, j+1)+f(i, j-1)-2 f(i, j)\tag{4-43}
257 | $$
258 |
259 | 为此, 拉普拉斯算子 $\nabla^2 f$ 为
260 | $$
261 | \begin{aligned}
262 | \nabla^2 f & =\frac{\partial^2 f(x, y)}{\partial x^2}+\frac{\partial^2 f(x, y)}{\partial y^2} \\
263 | & =f(i+1, j)+f(i-1, j)+f(i, j+1)+f(i, j-1)-4 f(i, j) \\
264 | & =-5\left\{f(i, j)-\frac{1}{5}[f(i+1, j)+f(i-1, j)+f(i, j+1)\right. \\
265 | & +f(i, j-1)+f(i, j)]\}
266 | \end{aligned}\tag{4-44}
267 | $$
268 | 可见, 数字图像在 $(i, j)$ 点的拉普拉斯算子, 可以由 $(i, j)$ 点灰度值减去该点邻域平均灰度值来求得。当 $k=1$ 时, 拉普拉斯锐化后的图像为
269 | $$
270 | \begin{aligned}
271 | g(i, j) & =f(i, j)-\nabla^2 f(i, j) \\
272 | & =5 f(i, j)-f(i+1, j)-f(i-1, j)-f(i, j+1)-f(i, j-1)
273 | \end{aligned}\tag{4-45}
274 | $$
275 | ### Laplacian锐化算子
276 |
277 | 写成模板系数形式形式即为Laplacian算子:
278 | $$
279 | H_1=\left[\begin{array}{ccc}
280 | 0 & -1 & 0 \\
281 | -1 & 4 & -1 \\
282 | 0 & -1 & 0
283 | \end{array}\right]
284 | $$
285 | ### Laplacian变形算子
286 |
287 | $$
288 | H_2=\left[\begin{array}{ccc}
289 | -1 & -1 & -1 \\
290 | -1 & 8 & -1 \\
291 | -1 & -1 & -1
292 | \end{array}\right] \quad H_3=\left[\begin{array}{ccc}
293 | 1 & -2 & 1 \\
294 | -2 & 4 & -2 \\
295 | 1 & -2 & 1
296 | \end{array}\right] \quad H_4=\left[\begin{array}{ccc}
297 | 0 & -1 & 0 \\
298 | -1 & 5 & -1 \\
299 | 0 & -1 & 0
300 | \end{array}\right]
301 | $$
302 | 例:
303 |
304 | 设有 $1 \times n$ 的数字图像 $f(i, j)$, 其各点的灰度如下:
305 |
306 | $$
307 | \ldots, 0,0,0,1,2,3,4,5,5,5,5,5,5,6,6,6,6,6,6,3,3,3,3,3
308 | $$
309 |
310 | 计算 $\nabla^2 f$ 及锐化后的各点灰度值 $g$ (设 $\left.k=1\right)$ 。
311 |
312 | - 首先按式 (4-44)计算各点的 $\nabla^2 f$ 。例如:
313 |
314 | 第3点:
315 |
316 | $$
317 | \quad \nabla^2 f=-3\left[0-\frac{1}{3}(0+0+1)\right]=1
318 | $$
319 |
320 | 第8点:
321 |
322 | $$
323 | \quad \nabla^2 f=-3\left[5-\frac{1}{3}(4+4+5)\right]=-1
324 | $$
325 |
326 |
327 |
328 | 各点拉普拉斯算子如下:
329 |
330 | $$
331 | \ldots, 0,0,1,0,0,0,0,-1,0,0,0,0,1,-1,0,0,0,0,-3,3,0,0,0, \ldots
332 | $$
333 |
334 | - 按式(4-42)计算 $g=f-2 f$ 。例如:
335 |
336 | $$
337 | \begin{aligned}
338 | &第3点: g=f-\nabla^2 f=0-1=-1\\
339 | &\vdots \\
340 | &第8点: g=5-(-1)=6
341 | \end{aligned}
342 | $$
343 |
344 | 锐化后各点的灰度值如下:
345 |
346 | $$
347 | \ldots, 0,0,-1,1,2,3,4,6,5,5,5,5,4,7,6,6,6,6,9,0,3,3,3, \ldots
348 | $$
349 |
350 | 从上例可以看出,在灰度级斜坡底部(如第3点)和界线的低灰度级侧(如第13、20点)形成下冲。在灰度级斜坡顶部(如第8点)和界线的高灰度级侧(如第14、 19点)形成上冲。在灰度级平坦区域(如第9~12点, 第15~18点), 运算前后没有变化。如图4-31所示。
351 |
352 |  353 |
354 | 图4-31 拉普拉斯锐化前、 后图像的灰度
355 | (a) 原图像灰度; (b) 拉普拉斯锐化后图像的灰度
356 |
357 |
353 |
354 | 图4-31 拉普拉斯锐化前、 后图像的灰度
355 | (a) 原图像灰度; (b) 拉普拉斯锐化后图像的灰度
356 |
357 |  358 |
359 | 图4-33 拉普拉斯锐化结果
360 | (a) 二值图像; (b) 拉普拉斯运算结果
361 |
362 | Laplacian锐化算子效果
363 |
364 | 
365 |
366 | 
367 |
368 | Wallis算子
369 | $$
370 | g(i, j)=\log [f(i, j)]-\frac{1}{4} s \\
371 | s=[\log f(i-1, j)+\log f(i+1, j)+\log f(i, j-1)+\log f(i, j+1)
372 | $$
373 | 它可以看作是校正了视觉的指数特性后的Laplacian运算。
374 | $$
375 | H_1=\left[\begin{array}{ccc}
376 | 0 & -1 & 0 \\
377 | -1 & 4 & -1 \\
378 | 0 & -1 & 0
379 | \end{array}\right]
380 | \Rightarrow
381 | H_1=\left[\begin{array}{ccc}
382 | 0 & -\dfrac{1}{4} & 0 \\
383 | -\dfrac{1}{4} & 1 & -\dfrac{1}{4} \\
384 | 0 & -\dfrac{1}{4} & 0
385 | \end{array}\right]
386 | $$
387 | Wallis算法效果图
388 |
389 |
358 |
359 | 图4-33 拉普拉斯锐化结果
360 | (a) 二值图像; (b) 拉普拉斯运算结果
361 |
362 | Laplacian锐化算子效果
363 |
364 | 
365 |
366 | 
367 |
368 | Wallis算子
369 | $$
370 | g(i, j)=\log [f(i, j)]-\frac{1}{4} s \\
371 | s=[\log f(i-1, j)+\log f(i+1, j)+\log f(i, j-1)+\log f(i, j+1)
372 | $$
373 | 它可以看作是校正了视觉的指数特性后的Laplacian运算。
374 | $$
375 | H_1=\left[\begin{array}{ccc}
376 | 0 & -1 & 0 \\
377 | -1 & 4 & -1 \\
378 | 0 & -1 & 0
379 | \end{array}\right]
380 | \Rightarrow
381 | H_1=\left[\begin{array}{ccc}
382 | 0 & -\dfrac{1}{4} & 0 \\
383 | -\dfrac{1}{4} & 1 & -\dfrac{1}{4} \\
384 | 0 & -\dfrac{1}{4} & 0
385 | \end{array}\right]
386 | $$
387 | Wallis算法效果图
388 |
389 |  390 |
391 | 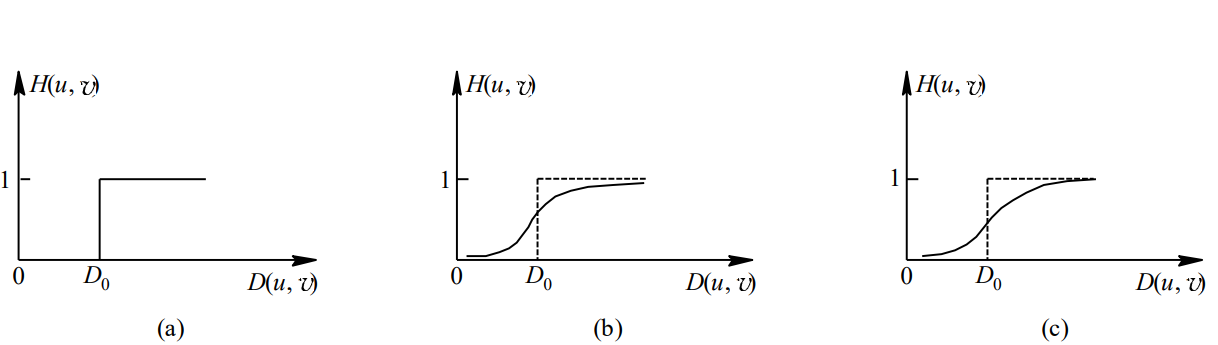
392 |
393 | 图4-34 3种频域高通滤波特性曲线
394 | (a) IHPF特征曲线; (b) BHPF特征曲线; (c) EHPF特征曲线
--------------------------------------------------------------------------------
/IV/4.7 图像的伪彩色处理.md:
--------------------------------------------------------------------------------
1 | # 4.7 图像的伪彩色处理
2 |
3 | ## 4.7.1 密度分割
4 |
5 | 密度分割是伪彩色处理技术中最简单的一种。设一幅灰度图像 $f(x, y)$, 在某一个灰度级 (如 $\left.f(x, y)=L_1\right)$ 上设置一个平行于 $x y$ 平面的切割平面, 如图4-35所示。灰度图像被切割成只有两个灰度级, 对切割平面以下的 (灰度级小于 $L_1$ ) 像素分配给一种颜色 (如蓝色), 对切割平面以上的像素分配给另一种颜色 (如红色)。这样切割结果就可以将灰度图像变为只有两个颜色的伪彩色图像。
6 |
7 | 若将灰度图像级用 $M$ 个切割平面去切割。就会得到 $M+1$ 个不同灰度级的区域 $S_1, S_2, \ldots, S_{M}, S_{M+1}$ 。对这 $M+1$ 个区域中的像素人为分配给 $M+1$ 种不同颜色, 就可以得到具有 $M+1$ 种颜色的伪彩色图像, 如图4-36所示。密度分割伪彩色处理的优点是简单易行, 便于用软件或硬件实现。还可以扩大它的用途, 如计算图像中某灰度级面积等。
8 |
9 |
390 |
391 | 
392 |
393 | 图4-34 3种频域高通滤波特性曲线
394 | (a) IHPF特征曲线; (b) BHPF特征曲线; (c) EHPF特征曲线
--------------------------------------------------------------------------------
/IV/4.7 图像的伪彩色处理.md:
--------------------------------------------------------------------------------
1 | # 4.7 图像的伪彩色处理
2 |
3 | ## 4.7.1 密度分割
4 |
5 | 密度分割是伪彩色处理技术中最简单的一种。设一幅灰度图像 $f(x, y)$, 在某一个灰度级 (如 $\left.f(x, y)=L_1\right)$ 上设置一个平行于 $x y$ 平面的切割平面, 如图4-35所示。灰度图像被切割成只有两个灰度级, 对切割平面以下的 (灰度级小于 $L_1$ ) 像素分配给一种颜色 (如蓝色), 对切割平面以上的像素分配给另一种颜色 (如红色)。这样切割结果就可以将灰度图像变为只有两个颜色的伪彩色图像。
6 |
7 | 若将灰度图像级用 $M$ 个切割平面去切割。就会得到 $M+1$ 个不同灰度级的区域 $S_1, S_2, \ldots, S_{M}, S_{M+1}$ 。对这 $M+1$ 个区域中的像素人为分配给 $M+1$ 种不同颜色, 就可以得到具有 $M+1$ 种颜色的伪彩色图像, 如图4-36所示。密度分割伪彩色处理的优点是简单易行, 便于用软件或硬件实现。还可以扩大它的用途, 如计算图像中某灰度级面积等。
8 |
9 | 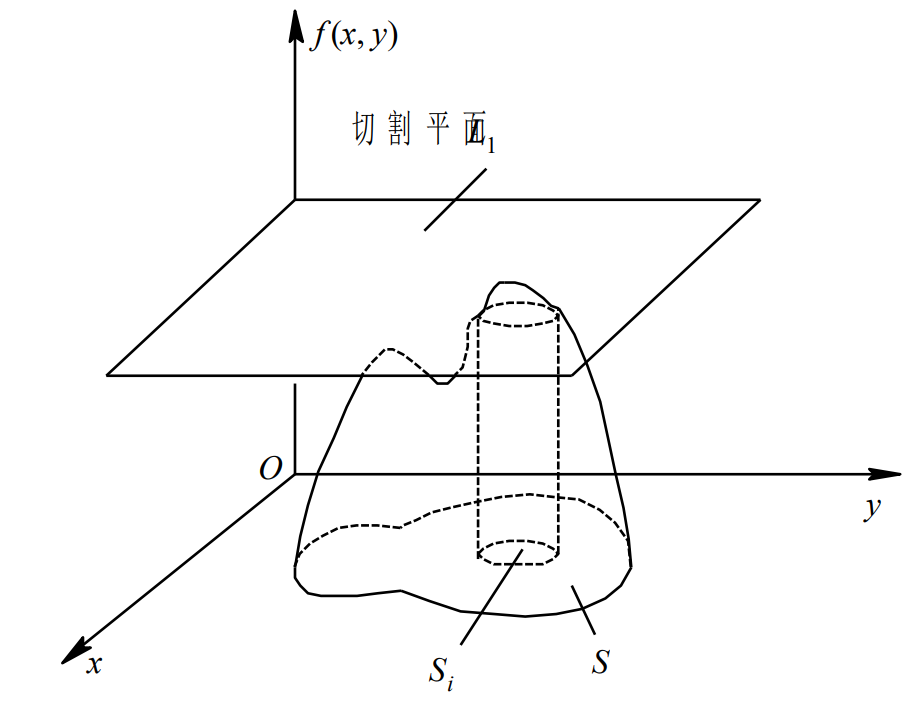 10 |
11 | 图4-35 密度分割示意图
12 |
13 |
10 |
11 | 图4-35 密度分割示意图
12 |
13 | 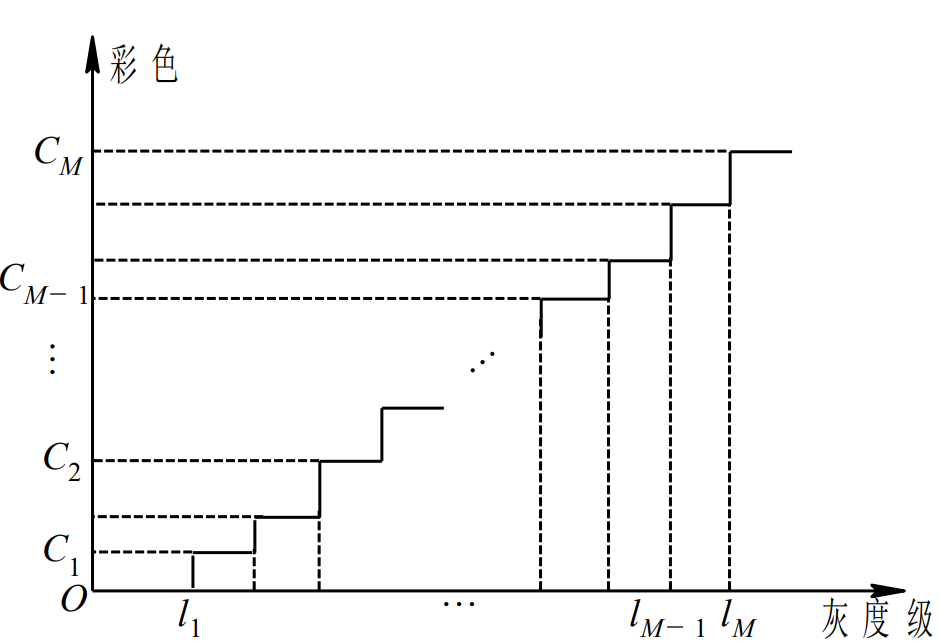 14 |
15 | 图4-36 多灰度伪彩色分割示意图
16 |
17 | ## 4.7.2 灰度级彩色变换
18 |
19 | 这种伪彩色处理技术(在遥感技术中常称为假彩色合成方法),可以将灰度图像变为具有多种颜色渐变的连续彩色图像, 实际图像的连续伪彩色变换如图4-37所示。其变换过程为:将灰度图像送入具有不同变换特性的红、绿、蓝3个变换器,再将3 个变换器的不同输出分别送到彩色显像管的红、绿、蓝电子枪。 同一灰度由3个变换器对其实施不同变换, 而使3个变换器输出不同,从而在彩色显像管里合成某种色彩。可见,不同大小灰度级一定可以合成不同色彩。
20 |
21 | 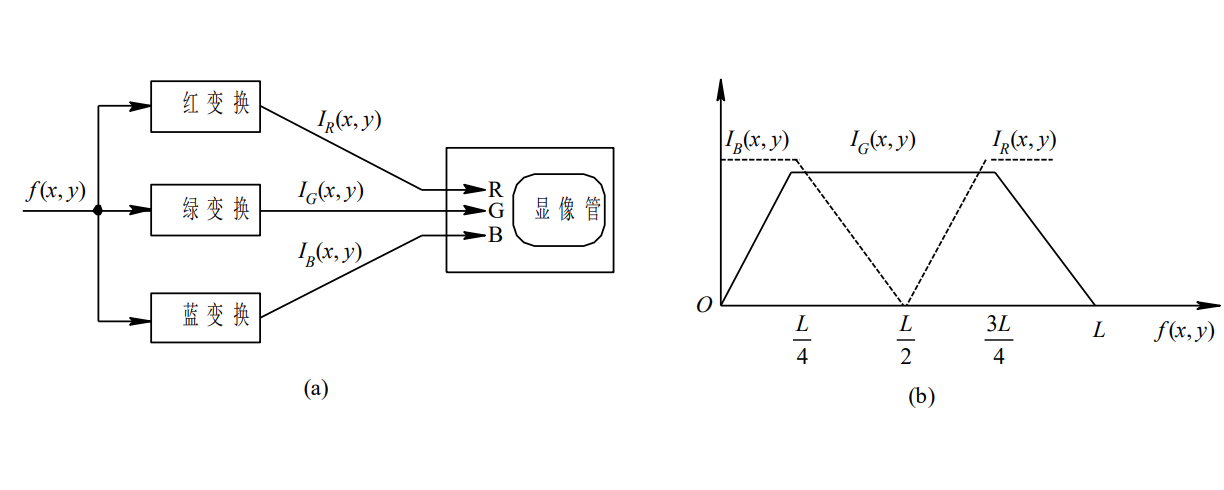
22 |
23 | 图4-37 伪彩色变换
24 |
25 | 从图中可见, 若 $f(x, y)=0$, 则 $I_B(x, y)=L, I_R(x, y)=I_{G}(x, y)=0$, 从而显示蓝色。同样, 若 $f(x, y)=L / 2$, 则 $I_G(x, y)=L, I_R(x, y)=I_G(x$, $y)=0$, 从而显示绿色。若 $f(x, y)=L$, 则 $I_R(x, y)=L, I_B(x, y)=I_G(x$, $y)=0$, 从而显示红色。
26 | 因此不难理解, 若灰度图像 $f(x, y)$ 灰度级在 $0 \sim L$ 之间变化, $I_R 、 I_B 、 I_G$ 会有不同输出, 从而合成不同的彩色图像。
27 |
28 | ## 4.7.3 滤波法
29 |
30 | 这是一种在频率域进行伪彩色处理的技术,与上面不同的是输出图像的伪彩色与图像的灰度级无关, 而是取决于图像中不同空间频率域成分。如, 为了突出图像中高频成分(图像细节)将其变为红色,只要将红色通道滤波器设计成高通特性即可。而且可以结合其他处理方法,在附加处理中实施(如直方图修正等),使其彩色对比度更强。如果要抑制图像中某种频率成分,可以设计一个带阻滤波器。其过程如图4-38所示,从3个不同频率的滤波器输出的信号再经过傅立叶反变换,可以对其做进一步的处理,如直方图均衡化。最后把它们作为三基色分别加到彩色显像管的红、绿、蓝显示通道,从而实现频率域的伪彩色处理。
31 |
32 |
14 |
15 | 图4-36 多灰度伪彩色分割示意图
16 |
17 | ## 4.7.2 灰度级彩色变换
18 |
19 | 这种伪彩色处理技术(在遥感技术中常称为假彩色合成方法),可以将灰度图像变为具有多种颜色渐变的连续彩色图像, 实际图像的连续伪彩色变换如图4-37所示。其变换过程为:将灰度图像送入具有不同变换特性的红、绿、蓝3个变换器,再将3 个变换器的不同输出分别送到彩色显像管的红、绿、蓝电子枪。 同一灰度由3个变换器对其实施不同变换, 而使3个变换器输出不同,从而在彩色显像管里合成某种色彩。可见,不同大小灰度级一定可以合成不同色彩。
20 |
21 | 
22 |
23 | 图4-37 伪彩色变换
24 |
25 | 从图中可见, 若 $f(x, y)=0$, 则 $I_B(x, y)=L, I_R(x, y)=I_{G}(x, y)=0$, 从而显示蓝色。同样, 若 $f(x, y)=L / 2$, 则 $I_G(x, y)=L, I_R(x, y)=I_G(x$, $y)=0$, 从而显示绿色。若 $f(x, y)=L$, 则 $I_R(x, y)=L, I_B(x, y)=I_G(x$, $y)=0$, 从而显示红色。
26 | 因此不难理解, 若灰度图像 $f(x, y)$ 灰度级在 $0 \sim L$ 之间变化, $I_R 、 I_B 、 I_G$ 会有不同输出, 从而合成不同的彩色图像。
27 |
28 | ## 4.7.3 滤波法
29 |
30 | 这是一种在频率域进行伪彩色处理的技术,与上面不同的是输出图像的伪彩色与图像的灰度级无关, 而是取决于图像中不同空间频率域成分。如, 为了突出图像中高频成分(图像细节)将其变为红色,只要将红色通道滤波器设计成高通特性即可。而且可以结合其他处理方法,在附加处理中实施(如直方图修正等),使其彩色对比度更强。如果要抑制图像中某种频率成分,可以设计一个带阻滤波器。其过程如图4-38所示,从3个不同频率的滤波器输出的信号再经过傅立叶反变换,可以对其做进一步的处理,如直方图均衡化。最后把它们作为三基色分别加到彩色显像管的红、绿、蓝显示通道,从而实现频率域的伪彩色处理。
31 |
32 | 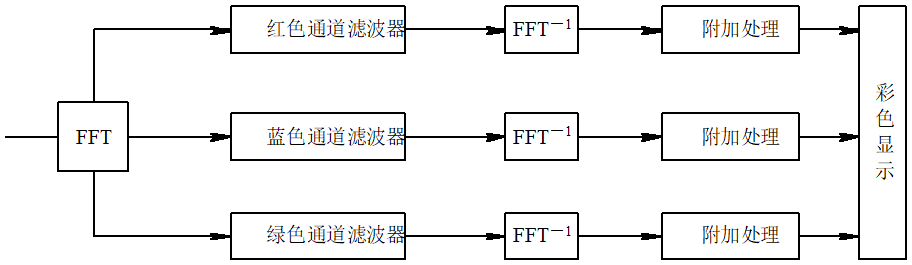 33 |
34 | 图4-38 频率域伪彩色增强处理
--------------------------------------------------------------------------------
/IV/4.8 常见滤波器.md:
--------------------------------------------------------------------------------
1 | # 4.8常见滤波器
2 |
3 | ## 4.8.1频域低通滤波
4 |
5 | ### ILPF
6 |
7 | $$
8 | \begin{aligned}
9 | & H(u, v)=\left\{\begin{array}{l}
10 | 1, \text { ifD }(u, v) \leq D_0 \\
11 | 0, \text { ifD }(u, v)>D_0
12 | \end{array}\right. \\
13 | & D(u, v)=\sqrt{u^2+v^2}
14 | \end{aligned}
15 | $$
16 |
17 |
33 |
34 | 图4-38 频率域伪彩色增强处理
--------------------------------------------------------------------------------
/IV/4.8 常见滤波器.md:
--------------------------------------------------------------------------------
1 | # 4.8常见滤波器
2 |
3 | ## 4.8.1频域低通滤波
4 |
5 | ### ILPF
6 |
7 | $$
8 | \begin{aligned}
9 | & H(u, v)=\left\{\begin{array}{l}
10 | 1, \text { ifD }(u, v) \leq D_0 \\
11 | 0, \text { ifD }(u, v)>D_0
12 | \end{array}\right. \\
13 | & D(u, v)=\sqrt{u^2+v^2}
14 | \end{aligned}
15 | $$
16 |
17 | 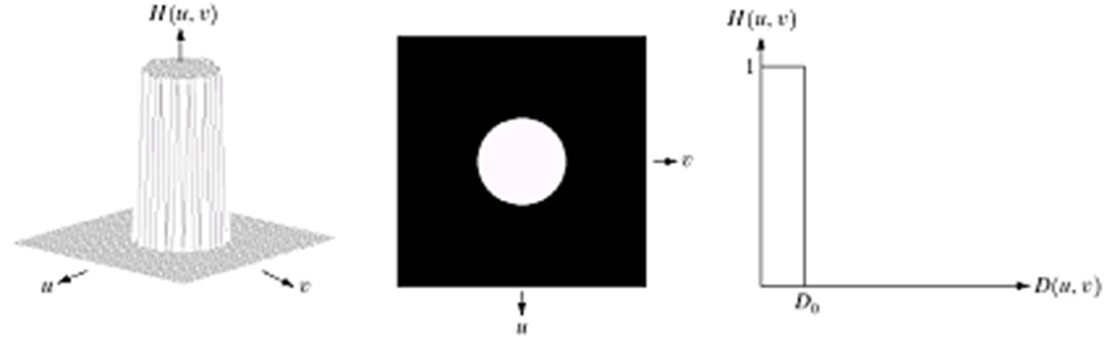 18 |
19 | 图4-39理想低通滤波器(a)变换函数透视图;(b)图像方式显示的滤波器(c)滤波器的剖面图
20 |
21 | 截止频率与所保留能量的关系
22 | $$
23 | E_T=\sum_{u=0}^{N-1} \sum_{v=0}^{N-1} E(u, v) \\
24 | E(u, v)=R^2(u, v)+I^2(u, v) \\
25 | \beta=100\left[\sum_u \sum_v E(u, v) / E_T\right] \\
26 | $$
27 |
18 |
19 | 图4-39理想低通滤波器(a)变换函数透视图;(b)图像方式显示的滤波器(c)滤波器的剖面图
20 |
21 | 截止频率与所保留能量的关系
22 | $$
23 | E_T=\sum_{u=0}^{N-1} \sum_{v=0}^{N-1} E(u, v) \\
24 | E(u, v)=R^2(u, v)+I^2(u, v) \\
25 | \beta=100\left[\sum_u \sum_v E(u, v) / E_T\right] \\
26 | $$
27 |  28 |
29 |
30 |
31 | 图4-40低通滤波器的能量与$D_0$的关系(a)尺寸为$500\times500$像素的图像(b)图像的Fourier谱。叠加的圆环分别具有5、15、30、80、230像素的半径,分别包含的能量为90.0%、94.6%、96.4%、98.0%、99.55%
32 |
33 | IHPF的图像处理效果
34 |
35 | 
36 |
37 | 图4-41 图像4-39(a)经过理想低通滤波器的结果,
38 | 对应的半径分别为15、30、80,滤去的能量为5.4%、3.6%、2%。
39 |
40 | ### 振铃效应
41 |
42 | $$
43 | G(u,v)=H(u,v)F(u,v)\\
44 | g(x,y)=h(x,y)*f(x,y)
45 | $$
46 |
47 |
48 |
49 |
28 |
29 |
30 |
31 | 图4-40低通滤波器的能量与$D_0$的关系(a)尺寸为$500\times500$像素的图像(b)图像的Fourier谱。叠加的圆环分别具有5、15、30、80、230像素的半径,分别包含的能量为90.0%、94.6%、96.4%、98.0%、99.55%
32 |
33 | IHPF的图像处理效果
34 |
35 | 
36 |
37 | 图4-41 图像4-39(a)经过理想低通滤波器的结果,
38 | 对应的半径分别为15、30、80,滤去的能量为5.4%、3.6%、2%。
39 |
40 | ### 振铃效应
41 |
42 | $$
43 | G(u,v)=H(u,v)F(u,v)\\
44 | g(x,y)=h(x,y)*f(x,y)
45 | $$
46 |
47 |
48 |
49 |  50 |
51 | 图4-42(a)半径为5的脉冲图像 (b)相应的空间滤波器
52 |
53 | (c)空域的5个脉冲(d)滤波结果
54 |
55 | 滤波器1
56 |
57 |
50 |
51 | 图4-42(a)半径为5的脉冲图像 (b)相应的空间滤波器
52 |
53 | (c)空域的5个脉冲(d)滤波结果
54 |
55 | 滤波器1
56 |
57 | 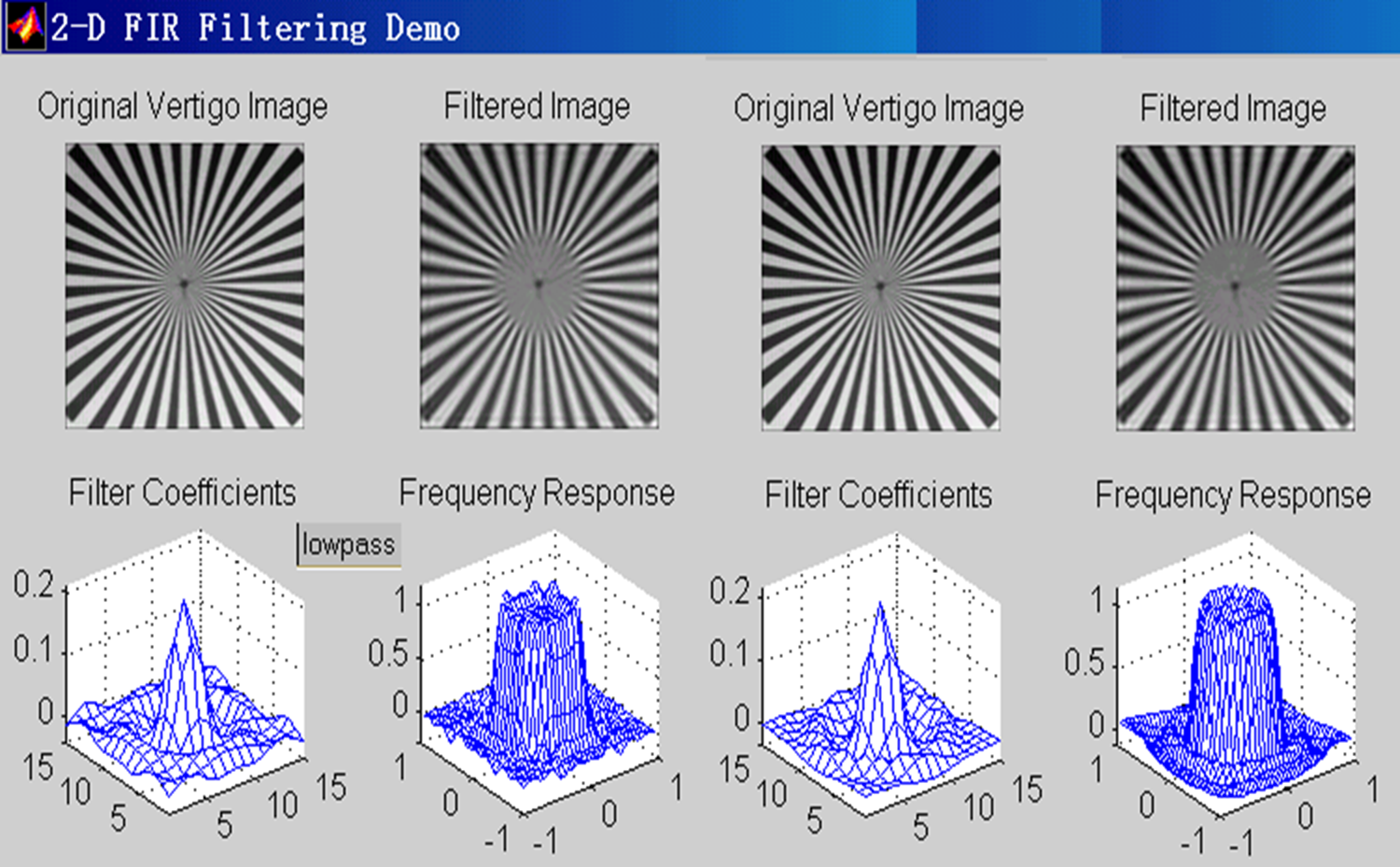 58 |
59 | 滤波器2
60 |
61 |
58 |
59 | 滤波器2
60 |
61 |  62 |
63 | ### 巴特沃思滤波器Butterworth
64 |
65 | BLPF:
66 | $$
67 | H(u, v)=\frac{1}{1+\left[D(u, v) / D_0\right]^{2 n}}
68 | $$
69 | 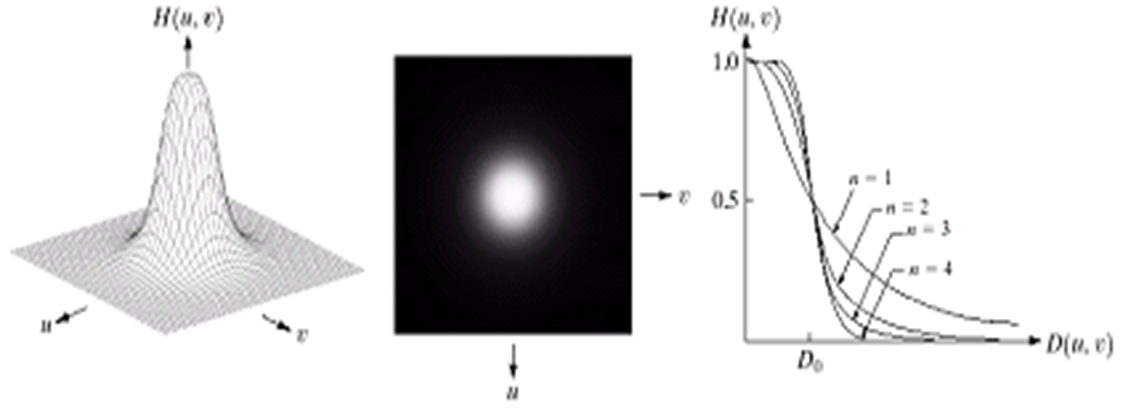
70 |
71 | 图4-43 BLPF特性曲线
72 |
73 | BLPF的滤波结果
74 |
75 |
62 |
63 | ### 巴特沃思滤波器Butterworth
64 |
65 | BLPF:
66 | $$
67 | H(u, v)=\frac{1}{1+\left[D(u, v) / D_0\right]^{2 n}}
68 | $$
69 | 
70 |
71 | 图4-43 BLPF特性曲线
72 |
73 | BLPF的滤波结果
74 |
75 |  76 |
77 | 图4-44 二阶BLPF滤波的结果(a)原图像,
78 | (b)半径15,(b)半径30,(d)半径80
79 |
80 | ### 指数滤波器或高斯滤波器
81 |
82 | ELPF:
83 | $$
84 | H(u, v)=e^{-\left[D(u, v) / D_0\right]^n}
85 | $$
86 |
76 |
77 | 图4-44 二阶BLPF滤波的结果(a)原图像,
78 | (b)半径15,(b)半径30,(d)半径80
79 |
80 | ### 指数滤波器或高斯滤波器
81 |
82 | ELPF:
83 | $$
84 | H(u, v)=e^{-\left[D(u, v) / D_0\right]^n}
85 | $$
86 |  87 |
88 | 图4-45高斯滤波器(a)传递函数的透视图;(b)图像形式;(c)径向剖面图
89 |
90 | ELPF的滤波效果
91 |
92 |
87 |
88 | 图4-45高斯滤波器(a)传递函数的透视图;(b)图像形式;(c)径向剖面图
89 |
90 | ELPF的滤波效果
91 |
92 |  93 |
94 | 图4-46 高斯滤波器的处理效果,
95 | 从左到右依次为原图、半径15、30、80
96 |
97 | ## 4.8.2高通滤波器
98 |
99 |
93 |
94 | 图4-46 高斯滤波器的处理效果,
95 | 从左到右依次为原图、半径15、30、80
96 |
97 | ## 4.8.2高通滤波器
98 |
99 | 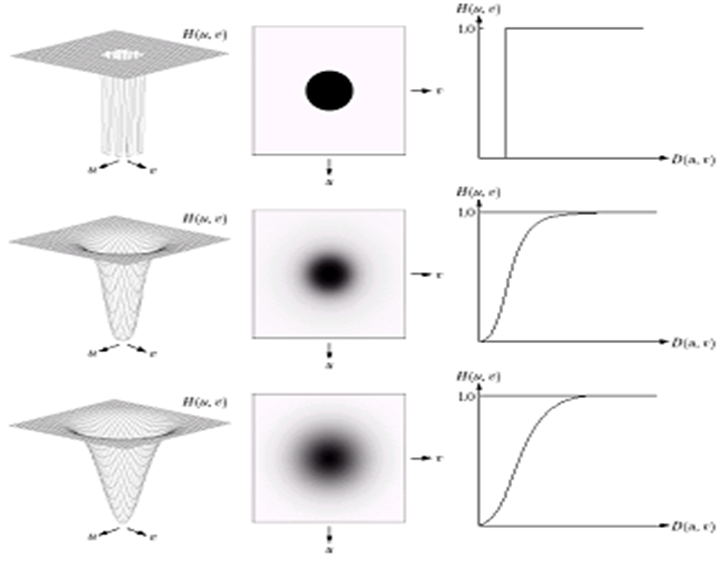 100 |
101 | 图4-47 三种典型的高通滤波器,从上到下依次为理想高通滤波器、巴特沃思高通滤波器、指数滤波器。
102 |
103 | ### 高通滤波器定义
104 |
105 | IHPF:
106 | $$
107 | H(u, v)=\left\{\begin{array}{l}
108 | 0, \text { if } D(u, v) \leq D_{0 ;} \\
109 | 1, \text { if } D(u, v)>D_0 .
110 | \end{array} \quad D(u, v)=\sqrt{u^2+v^2}\right.\\
111 | $$
112 | BHPF:
113 | $$
114 | H(u, v)=\frac{1}{1+\left[D_0 / D(u, v)\right]^{2 n}}
115 | $$
116 | EHPF:
117 | $$
118 | H(u, v)=e^{-\left[D_0 / D(u, v)\right]^{n}}
119 | $$
120 | THPF:
121 | $$
122 | H(u, v)=\left\{\begin{array}{lr}
123 | 0 & D(u, v)D_1
126 | \end{array}\right.
127 | $$
128 | HPF比较
129 |
130 |
100 |
101 | 图4-47 三种典型的高通滤波器,从上到下依次为理想高通滤波器、巴特沃思高通滤波器、指数滤波器。
102 |
103 | ### 高通滤波器定义
104 |
105 | IHPF:
106 | $$
107 | H(u, v)=\left\{\begin{array}{l}
108 | 0, \text { if } D(u, v) \leq D_{0 ;} \\
109 | 1, \text { if } D(u, v)>D_0 .
110 | \end{array} \quad D(u, v)=\sqrt{u^2+v^2}\right.\\
111 | $$
112 | BHPF:
113 | $$
114 | H(u, v)=\frac{1}{1+\left[D_0 / D(u, v)\right]^{2 n}}
115 | $$
116 | EHPF:
117 | $$
118 | H(u, v)=e^{-\left[D_0 / D(u, v)\right]^{n}}
119 | $$
120 | THPF:
121 | $$
122 | H(u, v)=\left\{\begin{array}{lr}
123 | 0 & D(u, v)D_1
126 | \end{array}\right.
127 | $$
128 | HPF比较
129 |
130 | 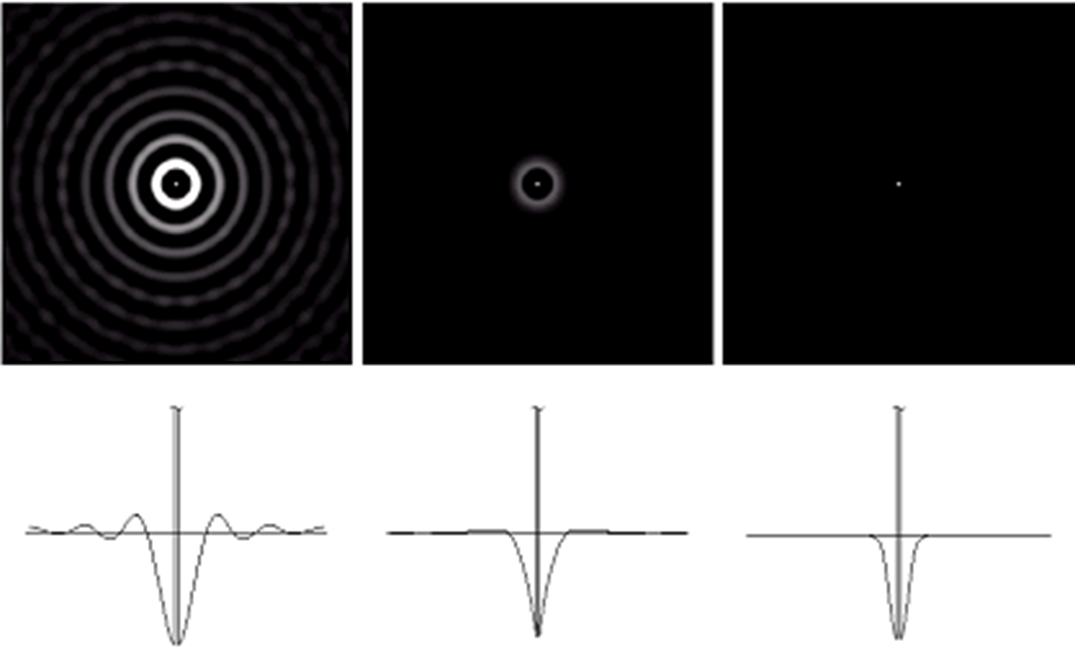 131 |
132 | 高通滤波器效果
133 |
134 |
131 |
132 | 高通滤波器效果
133 |
134 |  135 |
136 | 图4-48 理想高通滤波效果,从左到右依次为$D_0$=15,30,80。越小,振铃效应越明显
137 |
138 |
135 |
136 | 图4-48 理想高通滤波效果,从左到右依次为$D_0$=15,30,80。越小,振铃效应越明显
137 |
138 |  139 |
140 | 图4-49 BHPF效果,从左到右依次为$D_0$=15,30,80。比IHPF的结果平滑得多
141 |
142 |
139 |
140 | 图4-49 BHPF效果,从左到右依次为$D_0$=15,30,80。比IHPF的结果平滑得多
141 |
142 |  143 |
144 | 图5-50高斯高通滤波效果,从左到右依次为$D_0$=15,30,80。
145 |
146 | ### 高频加强
147 |
148 | $$
149 | \begin{aligned}
150 | & H^{\prime}(u, v)=H(u, v)+c, 0
156 |
157 | 图4-51 X光片原图;高通滤波效果;高频增强效果;直方图均衡化效果
158 |
159 | ## 4.8.3带通(带阻)滤波器
160 |
161 | 抑制以点 $(u 0, v 0)$ 为中心, $D 0$ 为半径的邻域中所有频率的理想带阻滤波器 (IBPF) 的转移函数为:
162 | $$
163 | H(u, v)=\left\{\begin{array}{lll}
164 | 0, & \text { if } & D(u, v) \leq D_0 \\
165 | 1, & \text { if } & D(u, v)>D_0
166 | \end{array}\right.\\
167 | D(u, v)=\left\{\left(u-u_0\right)^2+\left(v-v_0\right)^2\right\}^{1 / 2}
168 | $$
169 |
143 |
144 | 图5-50高斯高通滤波效果,从左到右依次为$D_0$=15,30,80。
145 |
146 | ### 高频加强
147 |
148 | $$
149 | \begin{aligned}
150 | & H^{\prime}(u, v)=H(u, v)+c, 0
156 |
157 | 图4-51 X光片原图;高通滤波效果;高频增强效果;直方图均衡化效果
158 |
159 | ## 4.8.3带通(带阻)滤波器
160 |
161 | 抑制以点 $(u 0, v 0)$ 为中心, $D 0$ 为半径的邻域中所有频率的理想带阻滤波器 (IBPF) 的转移函数为:
162 | $$
163 | H(u, v)=\left\{\begin{array}{lll}
164 | 0, & \text { if } & D(u, v) \leq D_0 \\
165 | 1, & \text { if } & D(u, v)>D_0
166 | \end{array}\right.\\
167 | D(u, v)=\left\{\left(u-u_0\right)^2+\left(v-v_0\right)^2\right\}^{1 / 2}
168 | $$
169 | 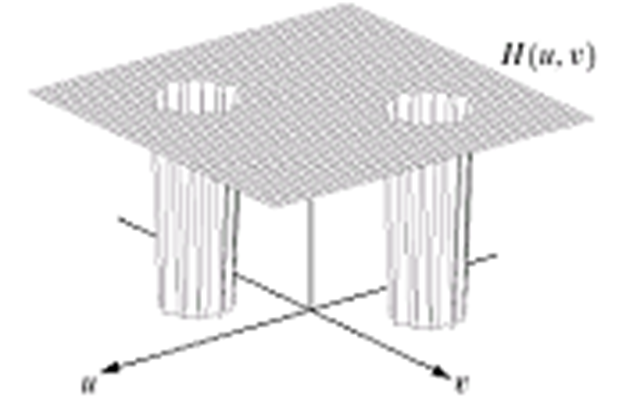 170 |
171 | ### 不围绕原点的情况
172 |
173 | $$
174 | H(u,v)=\begin{cases}
175 | 0 &&if\,\,D_1(u,v)\leq D_0 \,\,or\,\, D_2(u,v)\leq D_0\\
176 | 1&& else
177 | \end{cases}
178 | $$
179 |
180 |
181 | $$
182 | \begin{aligned}
183 | &\begin{aligned}
184 | & D_1(u, v)=\left\{\left(u-u_0\right)^2+\left(v-v_0\right)^2\right\}^{1 / 2} \\
185 | &
186 | \end{aligned}\\
187 | &D_2(u, v)=\left\{\left(u+u_0\right)^2+\left(v+v_0\right)^2\right\}^{1 / 2}
188 | \end{aligned}
189 | $$
190 |
191 | ### 围绕原点的模型
192 |
193 | 为消去围绕原点的一个频带,必须考虑周期性和对称性。一个径向对称(放射对称)的理想带阻滤波器
194 | $$
195 | H(u, v)=\left\{\begin{array}{rr}
196 | 1, & \text { if } D(u, v)D_0+\frac{W}{2}
199 | \end{array}\right.
200 | $$
201 | 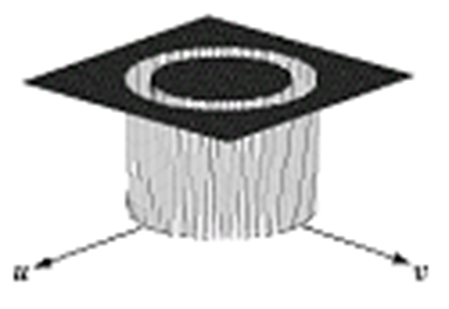
202 |
203 | ### 巴特沃思带阻滤波器用于去噪声
204 |
205 |
170 |
171 | ### 不围绕原点的情况
172 |
173 | $$
174 | H(u,v)=\begin{cases}
175 | 0 &&if\,\,D_1(u,v)\leq D_0 \,\,or\,\, D_2(u,v)\leq D_0\\
176 | 1&& else
177 | \end{cases}
178 | $$
179 |
180 |
181 | $$
182 | \begin{aligned}
183 | &\begin{aligned}
184 | & D_1(u, v)=\left\{\left(u-u_0\right)^2+\left(v-v_0\right)^2\right\}^{1 / 2} \\
185 | &
186 | \end{aligned}\\
187 | &D_2(u, v)=\left\{\left(u+u_0\right)^2+\left(v+v_0\right)^2\right\}^{1 / 2}
188 | \end{aligned}
189 | $$
190 |
191 | ### 围绕原点的模型
192 |
193 | 为消去围绕原点的一个频带,必须考虑周期性和对称性。一个径向对称(放射对称)的理想带阻滤波器
194 | $$
195 | H(u, v)=\left\{\begin{array}{rr}
196 | 1, & \text { if } D(u, v)D_0+\frac{W}{2}
199 | \end{array}\right.
200 | $$
201 | 
202 |
203 | ### 巴特沃思带阻滤波器用于去噪声
204 |
205 |  206 |
207 | (a)被正弦噪声污染的图像 (b)图像(a)的频谱 (c)巴特沃思带阻滤波器 (d)图像(a)的滤波效果
208 |
209 | ## 频域滤波小结
210 |
211 | 物理可实现的低通滤波器的传递函数必须是连续的。如果处处可导,滤波后的图像就不会出现振铃效应;
212 |
213 | 频域低通滤波器的效果是去除图像中的高频噪声,去噪声的能力与滤波器的形式以及截止频率有关;
214 |
215 | 频域低通滤波器在滤除噪声的同时会造成图像模糊,图像模糊的程度与截止频率有关;
216 |
217 | 高通滤波器可以增强图像的边缘,是实现图像边缘检测的基础;
218 |
219 | 高通滤波器基本上抑制了图像中的平滑信息,因此如要在保持图像基本信息的基础上实现锐化,就需要采用高频加强技术;
220 |
221 | 带通和带阻滤波器在消除特定类型的噪声上有很好的效果,它们也是彩色图像增强的技术基础;
222 |
223 | 同态滤波是一类利用图像的照明反射模型,同时实现亮度动态范围压缩和图像对比度增强的技术
--------------------------------------------------------------------------------
/IV/4.9 编程实例.md:
--------------------------------------------------------------------------------
1 | # 4.9 编程实例
2 |
3 | ## 4.7.1 编程绘制灰度直方图
4 |
5 | ### 1. 创建灰度直方图数据
6 |
7 | ```c++
8 | //*******************************************
9 | //函数名称: CreateHistogram()
10 | //参数说明: nX1、 nY1、 nX2、 nY2为需创建直方图图像区域坐标, 默认为- // 1。pData、pPalette、 nWidthBytes为位图数据指针、调色板指
11 | // 针、 图像行字节宽度
12 | //返回值: int型数组指针*pBuffer。在数组中依次存储亮度、红、绿、蓝分量
13 | // 的直方图数据, 每个分量各占256个元素[FK)]
14 | //基本功能:创建指定的图像对象的直方图数据。如果未给定坐标,则针对整 个图像
15 | //****************************************
16 | int *CPointPro:: CreateHistogram(int nX1, int nY1, int nX2, int nY2,
17 | unsigned char *pData, RGBQUAD *pPalette, int nWidthBytes)
18 | {
19 | //图像指针为空, 无法操作返回
20 | if(m_pDibObject == NULL) return(FALSE);
21 | //分配直方图数据缓存区(数组)
22 | int *pBuffer = new int [256 * 4];
23 | //分配直方图数据缓存区失败
24 | if(pBuffer == NULL) return( NULL );
25 | //直方图数据缓存区清零
26 | memset(pBuffer, 0, (256 * 4) * sizeof(int));
27 | //变量定义
28 | DWORD dwGray;
29 | int x, y;
30 | unsigned char *pTemp, ucRed, ucGreen, ucBlue;
31 | //图像的高度
32 | int nHeight = m_pDibObject->GetHeight();
33 | switch(m_pDibObject->GetNumBits())
34 | {
35 | case 24:
36 | for(y = nY1; y < nY2; y++)
37 | {
38 | //数据指针定位到图像数据起始位置
39 | pTemp = pData;
40 | //数据指针定位到图像数据每行的起始零位置
41 | pTemp += (( nHeight - 1 - y) * nWidthBytes);
42 | //数据指针定位到图像数据每行的起始nX1位置
43 | pTemp += (nX1 * 3);
44 | for(x=nX1; x<=nX2; x++)
45 | {
46 | //获取像素颜色的三原色
47 | ucRed = pTemp[x * 3 + 2];
48 | ucGreen = pTemp[x * 3 + 1];
49 | ucBlue = pTemp[x * 3];
50 | //按关系L=0.3R+0.59G+0.11B, 得到亮度值
51 | dwGray = (DWORD) (ucRed * 30 + ucGreen * 59 + ucBlue * 11) / 100;
52 | dwGray &= 0x000000ff;
53 | //亮度直方图数据
54 | pBuffer[dwGray]++;
55 | //红色直方图数据
56 | pBuffer[256 + ucRed]++;
57 | //绿色直方图数据
58 | pBuffer[512 + ucGreen]++;
59 | //蓝色直方图数据
60 | pBuffer[768 + ucBlue]++;
61 | //数据指针加3
62 | pTemp += 3;
63 | }
64 | }
65 | break;
66 | }
67 | return( pBuffer );
68 | }
69 | ```
70 |
71 | ### 2.定制灰度直方图对话框
72 |
73 | 定制一个直方图对话框并创建一个CDlgIntensity类, 在它的构造函数中初始化成员变量(例如, 初始化直方图数据指针m_pnHistogram = NULL), 添加WM_PAINT的消息映射函数OnPaint(), 然后在消息映射函数中绘制直方图数据。
74 |
75 | ### 3. 显示直方图
76 |
77 | ```c++
78 | void CDipView:: OnViewHist()
79 | {
80 | CDipDoc* pDoc = GetDocument();
81 | ASSERT_VALID(pDoc);
82 | //判断当前是否有图像对象
83 | if( pDoc->m_pDibObject = = NULL ) return;
84 | //在点处理CPointPro类中创建用来绘制直方图的数据
85 | CPointPro PointOperation( pDoc->m_pDibObject );
86 | int *pHistogram = PointOperation.GetHistogram();
87 | //生成一个对话框CDlgIntensity类的实例
88 | CDlgIntensity HistDlg;
89 | //将直方图数据传给CDlgIntensity的成员变量m_pnHistogram
90 | if( pHistogram != NULL )
91 | {
92 | //设置直方图数据指针
93 | HistDlg.m_pnHistogram = pHistogram;
94 | //设置当前像素值为0的像素数
95 | HistDlg.m_nCurrentPiexsNum = pHistogram[0];
96 | //设置是否为256级灰度图像
97 | HistDlg.m_bIsGray256 = PointOperation.IsGray256();
98 | }
99 | //显示对话框
100 | if ( HistDlg.DoModal() != IDOK) return;
101 | delete [] pHistogram;
102 | }
103 |
104 | ```
105 |
106 | ## 4.7.2 中值滤波的VC++编程实现
107 |
108 | 下面以3×3矩形窗口为例来说明8位灰度图像的中值滤波的主要算法。
109 |
110 | ```c++
111 | for(y = nY1; y < nY2; y++)
112 | {
113 | // pOldBits和pNewBits分别为指向源图像和新图像的图像数据指针
114 | pOldTemp = pOldBits;
115 | pOldTemp += ((nHeight-1-y-1)*nWidthBytes);
116 | pOldTemp += nX1-1;
117 | pNewTemp = pNewBits;
118 | pNewTemp += ((nHeight-1-y-1)*nWidthBytes);
119 | pNewTemp += nX1;
120 | k = 0;
121 | for(x = nX1; xj; k- -)
158 | {
159 | dwMedianList[k] = dwMedianList[k-1
160 | nLoc[k] = nLoc[k-1];
161 | }
162 | dwMedianList[j] = dwTmp;
163 | nLoc[j]= nTmp;
164 | break;
165 | }
166 | }
167 | }
168 | // 取得3×3邻域排序结果的中间值在原图像中的索引, 并给新图赋值
169 | Data = pOldTemp[nLoc[4]];
170 | *pNewTemp++ = (unsigned char) m_pDibObject->GetNearestIndex
171 | (pNewPalette[Data].rgbRed, pNewPalette[Data].rgbGreen,
172 | pNewPalette[Data].rgbBlue, pNewPalette, nNumColors );
173 | k++;
174 | }
175 | }
176 |
177 | ```
178 |
179 | ## 4.7.3 图像平滑的VC++编程实现
180 |
181 | 1. 设计模板对话框
182 | 图像平滑实际上可以看作是卷积运算, 因此图像平滑的关键在于模板窗口的设计。本例首先定制了如图4-39所示的对话框, 并创建了与之对应的CDlgSmooth类。除了可以使用平均模板和高斯模板外, 还可自定义模板, 模板的大小被限制在5×5内。
183 |
184 |
206 |
207 | (a)被正弦噪声污染的图像 (b)图像(a)的频谱 (c)巴特沃思带阻滤波器 (d)图像(a)的滤波效果
208 |
209 | ## 频域滤波小结
210 |
211 | 物理可实现的低通滤波器的传递函数必须是连续的。如果处处可导,滤波后的图像就不会出现振铃效应;
212 |
213 | 频域低通滤波器的效果是去除图像中的高频噪声,去噪声的能力与滤波器的形式以及截止频率有关;
214 |
215 | 频域低通滤波器在滤除噪声的同时会造成图像模糊,图像模糊的程度与截止频率有关;
216 |
217 | 高通滤波器可以增强图像的边缘,是实现图像边缘检测的基础;
218 |
219 | 高通滤波器基本上抑制了图像中的平滑信息,因此如要在保持图像基本信息的基础上实现锐化,就需要采用高频加强技术;
220 |
221 | 带通和带阻滤波器在消除特定类型的噪声上有很好的效果,它们也是彩色图像增强的技术基础;
222 |
223 | 同态滤波是一类利用图像的照明反射模型,同时实现亮度动态范围压缩和图像对比度增强的技术
--------------------------------------------------------------------------------
/IV/4.9 编程实例.md:
--------------------------------------------------------------------------------
1 | # 4.9 编程实例
2 |
3 | ## 4.7.1 编程绘制灰度直方图
4 |
5 | ### 1. 创建灰度直方图数据
6 |
7 | ```c++
8 | //*******************************************
9 | //函数名称: CreateHistogram()
10 | //参数说明: nX1、 nY1、 nX2、 nY2为需创建直方图图像区域坐标, 默认为- // 1。pData、pPalette、 nWidthBytes为位图数据指针、调色板指
11 | // 针、 图像行字节宽度
12 | //返回值: int型数组指针*pBuffer。在数组中依次存储亮度、红、绿、蓝分量
13 | // 的直方图数据, 每个分量各占256个元素[FK)]
14 | //基本功能:创建指定的图像对象的直方图数据。如果未给定坐标,则针对整 个图像
15 | //****************************************
16 | int *CPointPro:: CreateHistogram(int nX1, int nY1, int nX2, int nY2,
17 | unsigned char *pData, RGBQUAD *pPalette, int nWidthBytes)
18 | {
19 | //图像指针为空, 无法操作返回
20 | if(m_pDibObject == NULL) return(FALSE);
21 | //分配直方图数据缓存区(数组)
22 | int *pBuffer = new int [256 * 4];
23 | //分配直方图数据缓存区失败
24 | if(pBuffer == NULL) return( NULL );
25 | //直方图数据缓存区清零
26 | memset(pBuffer, 0, (256 * 4) * sizeof(int));
27 | //变量定义
28 | DWORD dwGray;
29 | int x, y;
30 | unsigned char *pTemp, ucRed, ucGreen, ucBlue;
31 | //图像的高度
32 | int nHeight = m_pDibObject->GetHeight();
33 | switch(m_pDibObject->GetNumBits())
34 | {
35 | case 24:
36 | for(y = nY1; y < nY2; y++)
37 | {
38 | //数据指针定位到图像数据起始位置
39 | pTemp = pData;
40 | //数据指针定位到图像数据每行的起始零位置
41 | pTemp += (( nHeight - 1 - y) * nWidthBytes);
42 | //数据指针定位到图像数据每行的起始nX1位置
43 | pTemp += (nX1 * 3);
44 | for(x=nX1; x<=nX2; x++)
45 | {
46 | //获取像素颜色的三原色
47 | ucRed = pTemp[x * 3 + 2];
48 | ucGreen = pTemp[x * 3 + 1];
49 | ucBlue = pTemp[x * 3];
50 | //按关系L=0.3R+0.59G+0.11B, 得到亮度值
51 | dwGray = (DWORD) (ucRed * 30 + ucGreen * 59 + ucBlue * 11) / 100;
52 | dwGray &= 0x000000ff;
53 | //亮度直方图数据
54 | pBuffer[dwGray]++;
55 | //红色直方图数据
56 | pBuffer[256 + ucRed]++;
57 | //绿色直方图数据
58 | pBuffer[512 + ucGreen]++;
59 | //蓝色直方图数据
60 | pBuffer[768 + ucBlue]++;
61 | //数据指针加3
62 | pTemp += 3;
63 | }
64 | }
65 | break;
66 | }
67 | return( pBuffer );
68 | }
69 | ```
70 |
71 | ### 2.定制灰度直方图对话框
72 |
73 | 定制一个直方图对话框并创建一个CDlgIntensity类, 在它的构造函数中初始化成员变量(例如, 初始化直方图数据指针m_pnHistogram = NULL), 添加WM_PAINT的消息映射函数OnPaint(), 然后在消息映射函数中绘制直方图数据。
74 |
75 | ### 3. 显示直方图
76 |
77 | ```c++
78 | void CDipView:: OnViewHist()
79 | {
80 | CDipDoc* pDoc = GetDocument();
81 | ASSERT_VALID(pDoc);
82 | //判断当前是否有图像对象
83 | if( pDoc->m_pDibObject = = NULL ) return;
84 | //在点处理CPointPro类中创建用来绘制直方图的数据
85 | CPointPro PointOperation( pDoc->m_pDibObject );
86 | int *pHistogram = PointOperation.GetHistogram();
87 | //生成一个对话框CDlgIntensity类的实例
88 | CDlgIntensity HistDlg;
89 | //将直方图数据传给CDlgIntensity的成员变量m_pnHistogram
90 | if( pHistogram != NULL )
91 | {
92 | //设置直方图数据指针
93 | HistDlg.m_pnHistogram = pHistogram;
94 | //设置当前像素值为0的像素数
95 | HistDlg.m_nCurrentPiexsNum = pHistogram[0];
96 | //设置是否为256级灰度图像
97 | HistDlg.m_bIsGray256 = PointOperation.IsGray256();
98 | }
99 | //显示对话框
100 | if ( HistDlg.DoModal() != IDOK) return;
101 | delete [] pHistogram;
102 | }
103 |
104 | ```
105 |
106 | ## 4.7.2 中值滤波的VC++编程实现
107 |
108 | 下面以3×3矩形窗口为例来说明8位灰度图像的中值滤波的主要算法。
109 |
110 | ```c++
111 | for(y = nY1; y < nY2; y++)
112 | {
113 | // pOldBits和pNewBits分别为指向源图像和新图像的图像数据指针
114 | pOldTemp = pOldBits;
115 | pOldTemp += ((nHeight-1-y-1)*nWidthBytes);
116 | pOldTemp += nX1-1;
117 | pNewTemp = pNewBits;
118 | pNewTemp += ((nHeight-1-y-1)*nWidthBytes);
119 | pNewTemp += nX1;
120 | k = 0;
121 | for(x = nX1; xj; k- -)
158 | {
159 | dwMedianList[k] = dwMedianList[k-1
160 | nLoc[k] = nLoc[k-1];
161 | }
162 | dwMedianList[j] = dwTmp;
163 | nLoc[j]= nTmp;
164 | break;
165 | }
166 | }
167 | }
168 | // 取得3×3邻域排序结果的中间值在原图像中的索引, 并给新图赋值
169 | Data = pOldTemp[nLoc[4]];
170 | *pNewTemp++ = (unsigned char) m_pDibObject->GetNearestIndex
171 | (pNewPalette[Data].rgbRed, pNewPalette[Data].rgbGreen,
172 | pNewPalette[Data].rgbBlue, pNewPalette, nNumColors );
173 | k++;
174 | }
175 | }
176 |
177 | ```
178 |
179 | ## 4.7.3 图像平滑的VC++编程实现
180 |
181 | 1. 设计模板对话框
182 | 图像平滑实际上可以看作是卷积运算, 因此图像平滑的关键在于模板窗口的设计。本例首先定制了如图4-39所示的对话框, 并创建了与之对应的CDlgSmooth类。除了可以使用平均模板和高斯模板外, 还可自定义模板, 模板的大小被限制在5×5内。
183 |
184 |  185 |
186 | 图4-39 图像平滑模板设置对话框
187 |
188 | 利用类向导为对话框的相应控件添加成员变量,如模板类型、模板高度、模板宽度、模板中心元素X坐标、模板中心元素Y坐标对应的成员变量分别定义为整型变量m_intType、m_iTempH、m_iTempW、m_iTempMX、m_iTempMY, 而模板系数对应浮点型的变量m_fTempC,另外还定义了一个模板元素数组指针m_fpArray。
189 | 为3个单选按钮分别定义一个单击事件的消息映射,在映射函数中给模板元素m_fpArray及其他成员变量赋值。
190 |
191 | 2. 获取图像数据
192 | 对每个像素的邻域用选定的模板作卷积运算, 就可以得到平滑后的图像。下面给出了卷积运算的源代码。
193 | 卷积函数中的各参数的含义如下: fpData为被卷积的数组, fpKernel为卷积核数组,fCoef为卷积系数,nSize为卷积尺寸, nResult为卷积结果。
194 |
195 | ```c++
196 | void CAreaPro:: Convolution(float *fpData, float *fpKernel, float fCoef,
197 | int nSize, unsigned char *nResult)
198 | {
199 | int i;
200 | float Sum = 0, fResult;
201 | //计算卷积
202 | for(i = 0; i < nSize; i++)
203 | {
204 | Sum += fpData[i] * fpKernel[i];
205 | }
206 | //执行卷积后的结果
207 | fResult = Sum / fCoef;
208 | //求绝对值
209 | fResult = (float)fabs(fResult);
210 | //判断是否超过255
211 | if(fResult > 255.0 )
212 | {
213 | // 直接赋值为255
214 | fResult = 255.0;
215 | }
216 | //对卷积结果四舍五入, 并转换成unsigned char类型作为最后返回结果
217 | *nResult = (unsigned char) (fResult + 0.5);
218 | }
219 |
220 | ```
221 |
222 | 接着就是对原图像的每个像素作卷积运算,运算后的结果赋予新图像,其中图像边界像素不作处理,代码实现在CAreaPro:: Smoothing()中。
--------------------------------------------------------------------------------
/README.md:
--------------------------------------------------------------------------------
1 | # Digital-mage-Processing
2 | 数字图像处理笔记,整理张航老师的数字图像处理课件,推荐教材是冈萨雷斯第四版
3 |
4 | 现在已经初步整理完毕,但不排除个别地方仍然有细微错误。
--------------------------------------------------------------------------------
/V/5.1 图像退化与复原.md:
--------------------------------------------------------------------------------
1 | # 5.1 图像退化与复原
2 |
3 | 数字图像在获取的过程中,由于光学系统的像差、 光学成像衍射、 成像系统的非线性畸变、 摄影胶片的感光的非线性、 成像过程的相对运动、 大气的湍流效应、环境随机噪声等原因, 图像会产生一定程度的退化。因此,必须采取一定的方法尽可能地减少或消除图像质量的下降,恢复图像的本来面目,这就是图像复原, 也称为图像恢复。
4 |
5 | 图像复原与图像增强有类似的地方, 都是为了改善图像。但是它们又有着明显的不同。图像复原是试图利用退化过程的先验知识使已退化的图像恢复本来面目,即根据退化的原因, 分析引起退化的环境因素,建立相应的数学模型, 并沿着使图像降质的逆过程恢复图像。从图像质量评价的角度来看, 图像复原就是提高图像的可理解性。而图像增强的目的是提高视感质量,图像增强的过程基本上是一个探索的过程, 它利用人的心理状态和视觉系统去控制图像质量, 直到人们的视觉系统满意为止。
6 |
7 | 图像复原是利用退化现象的某种先验知识,建立退化现象的数学模型,再根据模型进行反向的推演运算,以恢复原来的景图像。因而,图像复原可以理解为图像降质过程的反向过程。建立图像复原的反向过程的数学模型,就是图像复原的主要务。经过反向过程的数学模型的运算,要想恢复全真的景物图像比较困难。所以, 图像复原本身往往需要有一个质量准, 即衡量接近全真景物图像的程度,或者说,对原图像的估计是否到达最佳的程度。
8 |
9 | 由于引起退化的因素众多而且性质不同,为了描述图像退化过程所建立的数学模型往往多种多样,而恢复的质量标准也往存在差异性,因此图像复原是一个复杂的数学过程,图像复原的方法、技术也各不相同。
10 |
11 | ## 5.1.1 图像降质的数学模型
12 |
13 | 图像复原处理的关键问题在于建立退化模型。输入图像f(x, y)经过某个退化系统后输出的是一幅退化的图像。为了讨论方便, 把噪声引起的退化即噪声对图像的影响一般作为加性噪声考虑, 这也与许多实际应用情况一致,如图像数字化时的量化噪声、 随机噪声等就可以作为加性噪声,即使不是加性噪声而是乘性噪声, 也可以用对数方式将其转化为相加形式。
14 |
15 | 原始图像 $f(x, y)$ 经过一个退化算子或退化系统 $H(x, y)$ 的作用, 再和噪声 $n(x, y)$ 进行叠加, 形成退化后的图像 $g(x, y)$ 。图11-1表示退化过程的输入和输出的关系, 其中 $H(x, y)$ 概括了退化系统的物理过程, 就是所要寻找的退化数学模型。
16 |
17 | 此处是进行了简化,因为乘法噪声可以转化为加法噪声
18 |
19 | 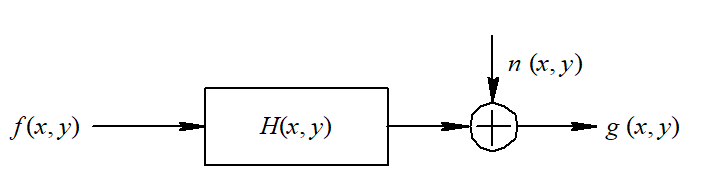
20 |
21 | 数字图像的图像恢复问题可看作是: 根据退化图像 $g(x, y)$ 和退化算子 $H(x, y)$ 的形式, 沿着反向过程去求解原始图像 $f(x, y)$, 或者说是逆向地寻找原始图像的最佳近似估计。图像退化的过程可以用数学表达式写成如下的形式:
22 | $$
23 | g(x, y)=H[f(x, y)]+n(x, y)\tag{5-1}
24 | $$
25 | 在这里, $n(x, y)$ 是一种统计性质的信息。在实际应用中, 往往假设噪声是白噪声, 即它的频谱密度为常数, 并且与图像不相关。
26 |
27 | 在图像复原处理中, 尽管非线性、 时变和空间变化的系统模型更具有普遍性和准确性,更与复杂的退化环境相接近,但它给实际处理工作带来了巨大的困难, 常常找不到解或者很难用计算机来处理。因此,在图像复原处理中, 往往用线性系统和空间不变系统模型来加以近似。这种近似的优点使得线性系统中的许多理论可直接用于解决图像复原问题,同时又不失可用性。
28 |
29 | 一幅连续图像 $f(x, y)$ 可以看作是由一系列点源组成的。因此, $f(x, y)$ 可以通过点源函数的卷积来表示。即
30 | $$
31 | f(x, y)=\int_{-\infty}^{+\infty} \int_{-\infty}^{+\infty} f(\alpha, \beta) \delta(x-\alpha, y-\beta) d \alpha d \beta\tag{5-2}
32 | $$
33 | 式中, $\delta$ 函数为点源函数, 表示空间上的点脉冲。
34 | 在不考虑噪声的一般情况下, 连续图像经过退化系统 $H$ 后的输出为
35 |
36 | $$
37 | \quad g(x, y)=H[f(x, y)]\tag{5-3}
38 | $$
39 |
40 | 把式(5-2)代入式(5-3)得
41 |
42 | $$
43 | \begin{gathered}
44 | g(x, y)=H[f(x, y)]=H\left[\int_{-\infty}^{+\infty} \int_{-\infty}^{+\infty} f(\alpha, \beta) \delta(x-\alpha, y-\beta) d \alpha d \beta\right]
45 | \end{gathered}\tag{5-4}
46 | $$
47 |
48 | 在线性和空间不变系统的情况下, 退化算子 $H$ 具有如下性质:
49 | (1) 线性: 设 $f_1(x, y)$ 和 $f_2(x, y)$ 为两幅输入图像, $k_1$ 和 $k_2$ 为常数, 则
50 |
51 | $$
52 | H\left[k_1 f_1(x, y)+k_2 f_2(x, y)\right]=k_1 H\left[f_1(x, y)\right]+k_2 H\left[f_2(x, y)\right]\tag{5-5}
53 | $$
54 |
55 | 由该性质还可推出下面两个结论:
56 | (1) 当 $k_1=k_2=1$ 时, 式(11-5)变为
57 |
58 | $$
59 | H\left[f_1(x, y)+f_2(x, y)\right]=H\left[f_1(x, y)\right]+H\left[f_2(x, y)\right]\tag{5-6}
60 | $$
61 |
62 | (2) 如果 $f_2(x, y)=0$, 则式 (11-5) 变为
63 |
64 | $$
65 | H\left[k_1 f_1(x, y)\right]=k_1 H\left[f_1(x, y)\right]\tag{5-7}
66 | $$
67 |
68 | (2) 空间不变性: 如果对任意 $f(x, y)$ 以及 $a$ 和 $b$, 有
69 |
70 | $$
71 | H[f(x-a, y-b)]=g(x-a, y-b)\tag{5-8}
72 | $$
73 |
74 | 则对于线性空间不变系统, 输入图像经退化后的输出为
75 |
76 | $$
77 | \begin{aligned}
78 | g(x, y) & =H[f(x, y)]=H\left[\int_{-\infty}^{+\infty} \int_{-\infty}^{+\infty} f(\alpha, \beta) \delta(x-\alpha, y-\beta) d \alpha d \beta\right] \\
79 | & =\int_{-\infty}^{+\infty} \int_{-\infty}^{+\infty} f(\alpha, \beta) H[\delta(x-\alpha, y-\beta)] d \alpha d \beta \\
80 | & =\int_{-\infty}^{+\infty} \int_{-\infty}^{+\infty} f(\alpha, \beta) h(x-\alpha, y-\beta) d \alpha d \beta
81 | \end{aligned}\tag{5-9}
82 | $$
83 |
84 | 式中, $h(x-\alpha, y-\beta)$ 为该退化系统的点扩展函数, 或叫系统的冲激响应函数。它表示系统对坐标为 $(a, \beta)$ 处的冲激函数 $\delta(x-\alpha, y-\beta)$ 的响应。也就是说, 只要系统对冲激函数的响应为已知, 那么就可以清楚图像退化是如何形成的。因为对于任一输入 $f(a, \beta)$ 的响应, 都可以通过上式计算出来。
85 | 此时, 退化系统的输出就是输入图像信号 $f(x, y)$ 与点扩展函数 $h(x, y)$ 的卷积, 即
86 |
87 | $$
88 | g(x, y)=\int_{-\infty}^{+\infty} \int_{-\infty}^{+\infty} f(\alpha, \beta) h(x-\alpha, y-\beta) d \alpha d \beta=f(x, y) * h(x, y)\tag{5-10}
89 | $$
90 |
91 | 图像退化除了受到成像系统本身的影响外, 有时还要受到噪声的影响。假设噪声 $n(x, y)$ 是加性白噪声, 这时上式可写成
92 |
93 | $$
94 | \begin{aligned}
95 | g(x, y) & =\int_{-\infty}^{+\infty} \int_{-\infty}^{+\infty} f(\alpha, \beta) h(x-\alpha, y-\beta) d \alpha d \beta+n(x, y) \\
96 | & =f(x, y) * h(x, y)+n(x, y)
97 | \end{aligned}\tag{5-11}
98 | $$
99 |
100 | 在频域上, 式(11-11)可以写成
101 |
102 | $$
103 | G(u, v)=F(u, v) H(u, v)+N(u, v)\tag{5-12}
104 | $$
105 |
106 | 其中, $G(u, v) 、 F(u, v) 、 N(u, v)$ 分别是退化图像 $g(x, y)$ 、原图像 $f(x, y)$、噪声信号 $n(x, y)$ 的傅立叶变换; $H(u, v)$ 是系统的点冲激响应函数 $h(x, y)$ 的傅立叶变换, 称为系统在频率域上的传递函数。
107 |
108 | 式(5-11)和式(5-12)就是连续函数的退化模型。可见, 图像复原实际上就是已知 $g(x, y)$ 求 $f(x, y)$ 的问题或已知 $G(u, v)$ 求 $F(u, v)$ 的问题, 它们的不同之处在于一个是在空域,一个是在频域。
109 | 显然, 进行图像复原的关键问题是寻找降质系统在空间域上的冲激响应函数 $h(x, y)$, 或者降质系统在频率域上的传递函数 $H(u$, $v)$ 。一般来说, 传递函数比较容易求得。因此, 在进行图像复原之前, 一般应设法求得完全的或近似的降质系统传递函数, 要想得到 $h(x, y)$, 只需对 $H(u, v)$ 求傅立叶逆变换即可。
110 |
111 | ## 5.1.2 离散图像退化的数学模型
112 |
113 | 1. 一维离散退化模型
114 | 设 $f(x)$ 为具有 $A$ 个采样值的离散输入函数, $h(x)$ 为具有 $B$ 个采样值的退化系统的冲激响应函数, 则经退化系统后的离散输出函数 $g(x)$ 为输入 $f(x)$ 和冲激响应 $h(x)$ 的卷积, 即
115 | $$
116 | g(x)=f(x)^* h(x)
117 | $$
118 | 为了避免上述卷积所产生的各个周期重叠(设每个采样函数的周期为 $M)$ ,分别对 $f(x)$ 和 $h(x)$ 用添零延伸的方法扩展成周期 $M=A+B-1$ 的周期函数, 即
119 | $$
120 | f_e(x)=\left\{\begin{array}{cc}
121 | f(x) & 0 \leq x \leq A-1 \\
122 | 0 & A \leq x \leq M-1
123 | \end{array}\right. \tag{5-13a}
124 | $$
125 | $$
126 | h_e(x)=\left\{\begin{array}{cc}
127 | h(x) & 0 \leq x \leq B-1 \\
128 | 0 & B \leq x \leq M-1
129 | \end{array}\right.\tag{5-13b}
130 | $$
131 | 输出为
132 | $$
133 | g_e(x)=f_e(x) * h_e(x)=\sum_{m=0}^{M-1} f_e(m) h_e(x-m)\tag{5-14}
134 | $$
135 | 式中, $x=0,1,2, \ldots, M-1$ 。
136 |
137 | 因为 $f_{e}(x)$ 和 $h_{e}(x)$ 已扩展成周期函数, 故 $g_{e}(x)$ 也是周期性函数, 用矩阵表示为
138 | $$
139 | \left[\begin{array}{c}
140 | g(0) \\
141 | g(1) \\
142 | g(2) \\
143 | M \\
144 | g(M-1)
145 | \end{array}\right]=\left[\begin{array}{cccc}
146 | h_e(0) & h_e(-1) & \Lambda & h_e(-M+1) \\
147 | h_e(1) & h_e(0) & \Lambda & h_e(-M+2) \\
148 | h_e(2) & h_e(1) & \Lambda & h_e(-M+3) \\
149 | M & M & M & M \\
150 | h_e(M-1) & h_e(M-2) & \Lambda & h_e(0)
151 | \end{array}\right]\left[\begin{array}{c}
152 | f_e(0) \\
153 | f_e(1) \\
154 | f_e(2) \\
155 | M \\
156 | f_e(M-1)
157 | \end{array}\right]\tag{5-15}
158 | $$
159 | 因为 $h_{e}(x)$ 的周期为 $M$, 所以 $h_{e}(x)=h_{e}(x+M)$, 即
160 | $$
161 | \begin{gathered}
162 | h_e(-1)=h_e(M-1) \\
163 | h_e(-2)=h_e(M-2) \\
164 | h_e(-3)=h_e(M-3) \\
165 | M \\
166 | h_e(-M+1)=h_e(1)
167 | \end{gathered}
168 | $$
169 | $M \times M$ 阶矩阵 $\boldsymbol{H}$ 可写为
170 | $$
171 | H=\left[\begin{array}{cccc}
172 | h_e(0) & h_e(-1) & \Lambda & h_e(1) \\
173 | h_e(1) & h_e(0) & \Lambda & h_e(2) \\
174 | h_e(2) & h_e(1) & \Lambda & h_e(3) \\
175 | M & M & \Lambda & \Lambda \\
176 | h_e(M-1) & h_e(M-2) & h_e(0)
177 | \end{array}\right]\tag{5-16}
178 | $$
179 | 可将式(5-15)写成更简洁的形式,即
180 | $$
181 | g=H f\tag{5-17}
182 | $$
183 | 式中, $\boldsymbol{g} 、 \boldsymbol{f}$ 都是 $M$ 维列向量, $\boldsymbol{H}$ 是 $M \times M$ 阶矩阵, 矩阵中的每一行元素均相同, 只是每行以循环方式右移一位, 因此矩阵 $\boldsymbol{H}$ 是循环矩阵。循环矩阵相加或相乘得到的还是循环矩阵。
184 |
185 | 2. 二维离散模型
186 | 设输入的数字图像 $f(x, y)$ 大小为 $A \times B$, 点扩展函数 $h(x, y)$ 被均匀采样为 $C \times D$ 大小。为避免交叠误差, 仍用添零扩展的方法, 将它们扩展成 $M=A+C-1$ 和 $N=B+D-1$ 个元素的周期函数。
187 |
188 | $$
189 | f_e(x, y)=\left\{\begin{array}{cc}
190 | f(x, y) & 0 \leq x \leq A-1 \text { 且 } 0 \leq y \leq B-1 \\
191 | 0 & \text { 其他 }
192 | \end{array}\right. \tag{5-18a}
193 | $$
194 | $$
195 | h_e(x, y)=\left\{\begin{array}{cc}
196 | h(x, y) & 0 \leq x \leq C-1 \text { 且 } 0 \leq y \leq D-1 \\
197 | 0 & \text { 其他 }
198 | \end{array}\right.\tag{5-18b}
199 | $$
200 |
201 | 则输出的降质数字图像为
202 | $$
203 | g_e(x, y)=\sum_{m=0}^{M-1} \sum_{n=0}^{N-1} f_e(m, n) h_e(x-m, y-n)=f(x, y)^* h(x, y)\tag{5-19}
204 | $$
205 | 式中: $x=0,1,2, \ldots, M-1 ; y=0,1,2, \ldots, N-1$ 。
206 | 式(5-19)的二维离散退化模型同样可以用式 (5-17) 所示的矩阵形式表示, 即
207 | $$
208 | g=H f
209 | $$
210 | 式中, $g 、 f$ 是 $M N \times 1$ 维列向量, $H$ 是 $M N \times M N$ 维矩阵。其方法是将 $g(x, y)$ 和 $f(x, y)$ 中的元素排成列向量。
211 | $$
212 | f_1=\left[\underbrace{f_1(0,0),f_1(0,1),\cdots,f_1(0,N-1)}_{第0行元素},\underbrace{f_1(1,0),f_1(1,1),\cdots,f_1(1,N-1)}_{第1行元素},\cdots,\underbrace{f_1(M-1,0),f_1(M-1,1),\cdots,f_1(M-1,N-1)}_{第M-1行元素}\right]^T\\
213 | g_1=\left[\underbrace{g_1(0,0),g_1(0,1),\cdots,g_1(0,N-1)}_{第0行元素},\underbrace{g_1(1,0),g_1(1,1),\cdots,g_1(1,N-1)}_{第1行元素},.\cdots,\underbrace{g_1(M-1,0),g_1(M-1,1),\cdots,g_1(M-1,N-1)}_{第M-1行元素}\right]^T
214 | \tag{5-20}
215 | $$
216 |
217 | $$
218 | H=\left[\begin{array}{cccc}
219 | H_0 & H_{M-1} & H_{M-2} & \cdots& H_1 \\
220 | H_1 & H_0 & H_{M-1} & \cdots& H_2 \\
221 | \vdots & \vdots & \vdots & \ddots&\vdots \\
222 | H_{M-1} & H_{M-2} & H_{M-3} & \cdots &H_0
223 | \end{array}\right]
224 | \tag{5-21}
225 | $$
226 | $H_i(i=0,1,2, \ldots, M-1)$ 为子矩阵, 大小为 $N \times N$, 即 $H$ 矩阵由 $M \times M$ 个大小为 $N \times N$ 的子矩阵组成, 称为分块循环矩阵。分块矩阵是由延拓函数 $h_{e}(x, y)$ 的第 $j$ 行构成的, 构成方法如下:
227 | $$
228 | H=\left[\begin{array}{cccc}
229 | h_e(j, 0) & h_e(j, N-1) & h_e(j, N-2) & \cdots& h_e(j, 1) \\
230 | h_e(j, 1) & h_e(j, 0) & h_e(j, N-1) & \cdots &h_e(j, 0) \\
231 | \vdots & \vdots & \vdots &\ddots &\vdots \\
232 | h_e(j, N-1) & h_e(j, N-2) & h_e(j, N-3) & \cdots &h_e(j, 0)
233 | \end{array}\right]
234 | \tag{5-22}
235 | $$
236 | 若把噪声考虑进去, 则离散图像退化模型为
237 | $$
238 | g_e(x, y)=\sum_{m=0}^{M-1} \sum_{n=0}^{N-1} f_e(m, n) h_e(x-m, y-n)+n_e(x, y)
239 | \tag{5-23}
240 | $$
241 | 写成矩阵形式为
242 | $$
243 | g=H f+n\tag{5-24}
244 | $$
245 | 上述线性空间不变退化模型表明, 在给定了 $g(x, y)$, 并且知道退化系统的点扩展函数 $h(x, y)$ 和噪声分布 $n(x, y)$ 的情况下, 可估计出原始图像 $f(x, y)$ 。
246 | 假设图像大小 $M=N=512$, 相应矩阵 $M H$ 的大小为 $M N \times M N=262144 \times 262144$, 这意味着要解出 $f(x, y)$ 需要解262 144 个联立方程组, 其计算量十分惊人。
247 |
248 | 图像恢复目的是在给定的 $g(x, y), h(x, y), n(x, y)$ 情况下, 求 $f(x, y)$. 由于 $G , F$ 维数很大, 通过解方程组不可能进行图像恢复.
249 | 1. 代数复原方法:寻找一个估计 $f(x, y)$.
250 | - 非约束复原方法
251 | - 约束复原方法
252 | 2.逆滤波方法
253 |
254 |
--------------------------------------------------------------------------------
/V/5.2 代数复原法.md:
--------------------------------------------------------------------------------
1 | # 5.2 代数复原法
2 |
3 | ## 5.2.1非约束复原方法
4 |
5 | 由式(5-24)可得
6 | $$
7 | n=g-H f\tag{5-25}
8 | $$
9 | 在对 $n$ 没有先验知识的情况下, 可以依据这样的最优准则, 即寻找一个 $\hat{f}$, 使得 $H \hat{f}$ 在最小二乘方误差的意义下最按近 $g$, 即要使 $n$ 的模或范数 (norm) 最小:
10 | $$
11 | \|n\|^2=n^T n=\|g-H \hat{f}\|^2=(g-H \hat{f})^T(g-\hat{H f})\tag{5-26}
12 | $$
13 | 即优化目标为:
14 | $$
15 | L(\hat{f})=\|g-H \hat{f}\|^2\tag{5-27}
16 | $$
17 | 如果我们在求最小值的过程中, 不做任何约束, 称这种复原为非约束复原。由极值条件
18 | $$
19 | \frac{\partial L(\hat{f})}{\partial \hat{f}}=0 \Rightarrow H^T(g-H \hat{f})=0\tag{5-28}
20 | $$
21 | 解出 $\hat{f}$ 为
22 | $$
23 | \hat{f}=\left(H^T H\right)^{-1} H^T g\tag{5-29}
24 | $$
25 |
26 | ## 5.2.2 约束复原法
27 |
28 | 非约束复原是指除了使准则函数 $L(\hat{f})=\|g-\hat{H f}\|^2$ 最小外, 再没有其他的约束条件。因此只需了解降质系统的传递函数或点扩展函数, 就能利用如前所述的方法进行复原。但是由于传递函数存在病态问题, 复原只能局限在靠近原点的有限区域内进行, 这使得非约束图像复原具有相当大的局限性。
29 |
30 | 最小二乘类约束复原是指除了要求了解关于退化系统的传递函数之外, 还需要知道某些噪声的统计特性或噪声与图像的某些相关情况。根据所了解的噪声的先验知识的不同, 采用不同的约束条件, 可得到不同的图像复原技术。在最小二乘类约束复原中, 要设法寻找一个最优估计 $\hat{f}$, 使得形式为 $\|Q \hat{f}\|^2=\|n\|^2$ 的函数最小化。求这类问题的最小化, 常采用拉格朗日乘子算法。也就说, 要寻找一个 $\hat{f}$, 使得优化目标函数:
31 | $$
32 | J(\hat{f})=\|\hat{O \hat{f}}\|^2+\alpha\left(\|g-H \hat{f}\|^2-\|n\|^2\right)\tag{5-30}
33 | $$
34 | 为最小。式中, $Q$ 为 $\hat{f}$ 的线性算子, $\alpha$ 为一常数, 称为拉格朗日乘子。对式(5-30)求导得
35 | $$
36 | \begin{aligned}
37 | & \frac{\partial J(\hat{f})}{\partial f}=0 \\
38 | & Q^T Q \hat{f}-\alpha H^T(g-H \hat{f})=0
39 | \end{aligned}
40 | $$
41 | 求解 $\hat{f}$ 得到
42 | $$
43 | \hat{f}=\left(H^T H+\gamma Q^T Q\right)^{-1} H^T g\tag{5-31}
44 | $$
--------------------------------------------------------------------------------
/V/5.3 逆滤波.md:
--------------------------------------------------------------------------------
1 | # 5.3 逆滤波
2 |
3 | 只能接近,无法完全恢复
4 |
5 | 1.逆滤波基本原理
6 | 由退化图像的付里叶变换求得图像的付里叶变换的估计方法称为逆滤波.
7 |
8 | 逆滤波
9 | $$
10 | \begin{aligned}
11 | \overline{g(x, y)}= & \int_{-\infty}^{\infty} \int_{-\infty}^{\infty} f(x, A) h(x-\imath v, y-A) d x d, \partial+n(x, y) \\
12 | & G(u, v)=F(u, v) H(u, v)+N(u, v)
13 | \end{aligned}
14 | $$
15 | 不考虑噪声:
16 |
17 | $$
18 | \begin{aligned} F(u, v) & =\frac{G(u, v)}{H(u, v)} \\ f(x, y) & =\mathcal{G}^{-1}[F(u, v)]\end{aligned}
19 | $$
20 | 有噪声:
21 | $$
22 | \begin{aligned}
23 | & F(u, v)=\frac{G(u, v)}{H(u, v)}-\frac{N(u, v)}{H(u, v)} \\
24 | & f(x, y)=\xi^{-1}[F(u, v)]
25 | \end{aligned}
26 | $$
27 |
28 |
29 |
30 |
31 | 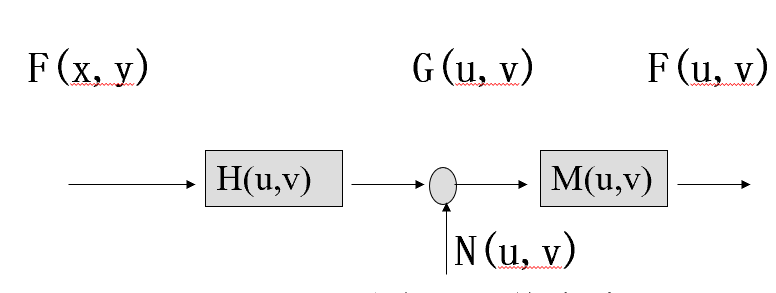
32 |
33 | 图5.2 逆滤波
34 |
35 | 逆滤波
36 | 2.去除由均匀直线运动引起的模糊
37 | - 模糊模型
38 | $$
39 | g(x, y)=\int_0^T f\left[x-x_0(t), y-y_0(t)\right] d t
40 | $$
41 | $f(x, y)$ : 原图像; $g(x, y)$ : 模糊图像; $T$ : 暴光时间
42 | - 图像恢复 $G(u, v)=H(u, v) F(u, v)$
43 | 其中: $H(u, v)=\int_0^T \exp \left\{-j 2 \pi\left[u x_0(t)+v y_0(t)\right]\right\} d t$
44 |
45 | ## 用途
46 |
47 | 在实验室中,可以反复做实验的情景
--------------------------------------------------------------------------------
/V/5.4 最小二乘滤波(维纳滤波,重点).md:
--------------------------------------------------------------------------------
1 |
2 |
3 | # 5.4 最小二乘方滤波(维纳滤波)
4 |
5 | **重点**
6 |
7 | 知道图像,知道有关分布特征
8 |
9 | 1.最小二乘方滤波
10 | 设原始图像, 退化图像和噪声分别为 $f(x, y), g(x, y)$ 和 $n(x, y)$, 则 :
11 |
12 | $$
13 | g(x, y)=H[f(x, y)]=H\left[\int_{-\infty}^{+\infty} \int_{-\infty}^{+\infty} f(\alpha, \beta) \delta(x-\alpha, y-\beta) d \alpha d \beta\right]+n(x, y)$ 在给定的 $g(x, y)$ 时, 找出 $f(x, y)$ 的估计 $f(x, y)
14 | $$
15 | 使:
16 | $$
17 | e^2=E\left\{[f(x, y)-\hat{f}(x, y)]^2\right\}
18 | $$
19 | 最小.
20 |
21 | 设
22 | $$
23 | \quad \hat{f}(x, y)=\iint m(x, y, \alpha, \beta) g(\alpha, \beta) d \alpha d \beta
24 | $$
25 | 2. 求解
26 | 如果 $f(x, y), g(x, y)$ 和 $n(x, y)$ 是均匀随机场, 则 :
27 | $$
28 | \hat{f}(x, y)=\iint m(x-\alpha, y-\beta) g(\alpha, \beta) d \alpha d \beta
29 | $$
30 | 因此图像恢复就是确定m $m, y)$. 通过求解得:
31 | $$
32 | \begin{aligned}
33 | M(u, v) & =\left[\frac{H^*(u, v)}{|H(u, v)|^2+\left[S_n(u, v) / S_f(u, v)\right]}\right] \\
34 | & =\left[\frac{1}{H(u, v)} \cdot \frac{|H(u, v)|^2}{\left|H(u, v)^2\right|+\left[S_n(u, v) / S_f(u, v)\right]}\right]
35 | \end{aligned}
36 | $$
37 | $H(u, v)$ 是的h $(x, y)$ 付里叶变换.
38 | $S_f, S_n$ 分别是 $f(x, y), n(x, y)$ 的谱密度
39 |
40 | 于是:
41 | $$
42 | \begin{aligned}
43 | \hat{F}(u, v) & =\left[\frac{H^*(u, v)}{|H(u, v)|^2+\left[S_n(u, v) / S_f(u, v)\right]}\right] G(u, v) \\
44 | & =\left[\frac{1}{H(u, v)} \cdot \frac{|H(u, v)|^2}{\left|H(u, v)^2\right|+\left[S_n(u, v) / S_f(u, v)\right]}\right] G(u, v)
45 | \end{aligned}\tag{5-32}
46 | $$
47 | 式中,
48 | $$
49 | u, v=0,1,2, \ldots, N-1,|H(u, v)|^2=H^*(u, v) H(u, v)
50 | $$
51 |
52 | 3. 讨论
53 | - $S_n=0$ 时, 是理想的逆滤波器
54 | -若随机过程的统计特性不知道, 可采用:
55 | $$
56 | M(u, v)=\frac{1}{H(u, v)} \frac{|H(u, v)|^2}{|H(u, v)|^2+\Gamma}
57 | $$
58 | 式中 $\Gamma$ 是噪声对信号的功率密度比.
59 |
60 | - 维纳滤波器是假设线性系统, 实际上图像的记录和评价图像的视觉系统都是非线性系统.
61 | - 维纳滤波器是根据最小均方差设计的,这个准则不见得与人的视觉判决准则相符.
62 | - 维纳滤波器是基于平稳随机过程的模型,实际图像不一定符合这一条件.
63 |
64 | ## 几种最小二乘方滤波器
65 |
66 | (仅供了解)
67 |
68 | 1.图像功率谱滤波器
69 | $$
70 | H_{R}(u, v)=\left[\frac{W_{FI}(u, v)}{\left|H_{D}(u, v)\right|^2 W_{F 1}(u, v)+W_{N}(u, v)}\right]^{\frac{1}{2}}
71 | $$
72 | 式中 $H_{D}(u, v)$ 是图像退化的传递函数。 $W_{F 1}(u, v)$ 代表滤波器输出功率频谱,
73 | $$
74 | W_{FI}(u, v)=\left|H_{D}(u, v)\right|^2 W_{FO}(u, v)
75 | $$
76 | 式中 $W_{FO}(u, v)$ 代表观测的功率频谱。它与理想图像的功率频谱的关系是
77 | $$
78 | W_{FO}(u, v)=\left|H_{D}(u, v)\right|^2 \cdot W_{FI}(u, v)+W_{N}(u, v)
79 | $$
80 | 式中 $W_{N}(u, v)$ 是噪声功率频谱。
81 |
82 | 2.几何平均滤波器.
83 |
84 | 几何平均滤波器的传递函数由下式表示:
85 | $$
86 | H_{R}(u, v)=\left[H_{D}(u, v)\right]^{-s}\left[\frac{H_{D}^*(u, v) W_{FI}(u, v)}{\left|H_{D}(u, v)\right|^2 W_{FI}(u, v)+W_{N}(u, v)}\right]^{1-s}
87 | $$
88 | S是一个参数
89 |
90 | 3.约束最小方滤波器
91 |
92 | 约束最小方滤波器的传递函数如下:
93 | $$
94 | H_{\mathrm{R}}(u, v)=\frac{H_{\mathrm{D}}^*(u, v)}{\left|H_{\mathrm{D}}(u, v)\right|^2+r|L(u, v)|^2}
95 | $$
96 | $r$是一个参数,$L(u,v)$是一个频率参数。$r=1$为维纳滤波器
--------------------------------------------------------------------------------
/V/5.5 非线性复原方法 .md:
--------------------------------------------------------------------------------
1 | # 5.5 非线性复原方法(仅供了解)
2 |
3 | ## 5.5.1 最大后验复原
4 |
5 | 最大后验复原是一种统计方法, 它把原图像 $f(x, y)$ 和退化图像 $g(x, y)$ 都作为随机场, 在已知 $g(x, y)$ 的前提下, 求出后验条件概率密度函数 $P(f(x, y) / g(x, y))$ 。若 $\hat{f}(x, y)$ 使式
6 | $$
7 | \max _{f} p(f \mid g)=\max _f p(g \mid f) p(f) / p(g)=\max _f p(g \mid f) p(f)\tag{5-33}
8 | $$
9 | 最大, 则 $\hat{f}(x, y)$ 就代表已知退化图像 $g(x, y)$ 时, 最可能的原始图像 $f(x, y)$ 。这种图像方法称之为最大后验图像复原方法。
10 |
11 | 最大后验图像复原方法把图像看作是非平稳随机场, 把图像模型表示成一个平稳随机过程对于一个不平稳的均值作零均值Gauss起伏, 可得出求解迭代序列:
12 | $$
13 | \hat{f}_{k+1}=\hat{f}_k-h^* \sigma_n^{-2}\left(g-h^* \hat{f}_k\right)-\sigma_n^{-2}\left(\hat{f}_k-\bar{f}\right)\tag{5-34}
14 | $$
15 | 其中, $k$ 为迭代次数, $\sigma_n^{-2}$ 和 $\sigma_f^{-2}$ 分别为 $f$ 和 $n$ 的方差的倒数, $f$ 是随空间而变的均值, 它是一个常数, 但要经过多次迭代才能收敛到最后的解。
16 |
17 | ## 5.5.2 最大熵复原
18 |
19 | 最大熵复原方法是通过最大化某种反映图像平滑性的准则函数来作约束条件, 以解决图像复原中反向滤波法存在的病态问题。
20 | 首先简单介绍一下熵的概念。
21 | 熵的定义为
22 | $$
23 | H=-\int_{-\infty}^{+\infty} P(x) \ln P(x) d x\tag{5-35}
24 | $$
25 | 式中, $P(x)$ 为随机变量 $x$ 的概率密度。
26 | 对于离散信号, 熵的定义为
27 | $$
28 | H=-\sum_{k=1}^M P(k) \ln P(k)\tag{5-36}
29 | $$
30 | 熵是表征随机变量集合的随机程度的量度。当所有随机变量等可能性时, 也就是说 $P_1=P_2=\ldots=P_{m}$ 时熵最大, 为 $H=\ln M$ 。由于概率 $P(k)$ 介于 $0 \sim 1$ 之间, 因此最大熵的范围为 $0 \sim \ln M, H$ 不可能出现负值。
31 | 在二维数字图像中, 熵的定义为
32 | $$
33 | H_f=-\sum_{m=1}^M \sum_{n=1}^N f(m, n) \ln f(m, n)\tag{5-37}
34 | $$
35 | 最大熵复原的原理是将 $f(x, y)$ 写成随机变量的统计模型,然后在一定的约束条件下,找出用随机变量形式表示的熵的表达式, 运用求极大值的方法, 求得最优估计解 $\hat{f}(x, y)$ 。最大熵复原的含义是对 $\hat{f}(x, y)$ 的最大平滑估计。 最大熵复原常用Friend和Burg两种方法, 这两种方法基本原理相同, 这里仅介绍Friend法。
36 |
37 | 首先定义一幅大小为 $M \times N$ 的图像 $f(x, y)$, 显然 $f(x, y)$ 非负。 图像的总能量 $E$ 和熵分别为
38 | $$
39 | E=\sum_{i=j}^M \sum_{j=1}^N f\left(x_i, y_j\right)\tag{5-38}
40 | $$
41 | 和
42 | $$
43 | H_f=\sum_{i=j}^M \sum_{j=1}^N f\left(x_i, y_j\right) \operatorname{lnf}\left(x_i, y_j\right)\tag{5-39}
44 | $$
45 | 类似地可定义噪声的熵 $H_n$ :
46 | $$
47 | H_n=-\sum_{i=1}^M \sum_{j=1}^N n^{\prime}\left(x_i, y_j\right) 1 n n^{\prime}\left(x_i, y_j\right)\tag{5-40}
48 | $$
49 | 式中: $n^{\prime}(x, y)=n(x, y)+B, B$ 为最大噪声负值。
50 |
51 | 恢复就是在满足式(5-38) 和图像退化模型的约束条件下, 使恢复后的图像熵和噪声熵达到最大。熵通常取决于 $f$ 的形状, 当图像具有均匀的灰度时熵最大。因此用最大熵恢复图像具有某种平滑性。
52 | 引入拉格朗日 (Lagrange) 函数
53 | $$
54 | \begin{aligned}
55 | R & =H_f+\rho H_n+\sum_{m=1}^N \sum_{n=1}^N \lambda_{m m}\left\{\sum_{x=1}^N \sum_{n=1}^N h(m-x, n-y) f(x, y)+n_T(m, n)-B-g(m, n)\right. \\
56 | & +\beta\left\{\sum_{x=1}^N \sum_{y=1}^N f(x, y)-E\right\}
57 | \end{aligned}\tag{5-41}
58 | $$
59 | 式中: $\lambda_{m n}(m, n=1,2, \ldots, N)$ 和 $\beta$ 是拉格朗日乘子, $\rho$ 是加权因子,表示 $H_f$ 和 $H_n$ 相互之间的权重。
60 |
61 | $\hat{f}(x, y)$ 和 $\hat{n}(m, n)$ 分别表示 $f(x, y)$ 和 $n^{\prime}(x, y)$ 的估计值, 则有
62 | $$
63 | \frac{\partial R}{\partial f(x, y)}=0 \tag{5-42}
64 | $$
65 |
66 | $$
67 | \frac{\partial R}{\partial n^{\prime}(x, y)}=0\tag{5-43}
68 | $$
69 | 把式(5-41)分别代入式(5-42)和式(5-43), 可得
70 | $$
71 | \hat{f}(x, y)=\exp \left[-1+\beta+\sum_{m=1}^N \sum_{n=1}^N \lambda_{m m} h(m-x, n-y)\right] \quad x, y=1,2, \ldots, N \tag{5-44}
72 | $$
73 | $$
74 | \hat{n}(m, n)=\exp \left(-1+\frac{\lambda_{m n}}{\rho}\right) \quad \quad m, n=1,2, \ldots, N\tag{5-45}
75 | $$
76 |
77 | 并且$\hat{f}(x,y)$和$\hat{n}(m,n)$满足下列约束条件
78 | $$
79 | \sum_{x=1}^N \sum_{y=1}^N f(x, y)=E\tag{5-46}
80 | $$
81 |
82 | $$
83 | \sum_{x=1}^N \sum_{y=1}^N h(m-x, n-y) f(x, y)+\hat{n}(m, n)-\beta=g(m, n)\tag{5-47}
84 | $$
85 |
86 | 式(5-44)为图像恢复函数。把式(5-44)和式(5-45)代入式(5$46)$ 和式(5-47)可得 $\left(N^2+1\right)$ 个方程。由此联立方程组可解得 $\left(N^2+1\right)$ 个末知数解 $\lambda_{m n}(m, n=1,2, \ldots, N)$, 解上述方程组可求得 $\hat{f}(x, y)$ 的值。
87 |
88 | ## 投影复原
89 |
90 | 投影复原法是用代数方程组来描述线性和非线性退化系统的。该系统可用下式描述:
91 | $$
92 | g(x, y)=H[f(x, y)]+n(x, y)
93 | $$
94 | 其中: $f(x, y)$ 是原始图像, $g(x, y)$ 是退化图像, $n(x, y)$ 是系统噪声, $H$ 是退化算子,表示对图像进行某种运算。
95 | 在使用投影复原法进行图像复原时, 引进一些先验信息附加的约束条件, 可改善图像复原效果。
96 |
97 | ### 投影复原法
98 |
99 | $$
100 | g(x, y)=H[f(x, y)]+n(x, y)
101 | $$
102 | 投影复原方法就是迭代方法之一。设初始估值 $f^0(x, y)$, 然后进行迭代运算.
103 | 设 $f^0(x, y)=g(x, y)$
104 | 设 $H$ 是非线性的, 并忽略噪声, 则上式写成:
105 | $$
106 | \begin{array}{ll}
107 | a_{11} f_1+a_{12} f_2+\ldots & a_{1 N} f_N=g_1 \\
108 | a_{21} f_1+a_{22} f_2+\ldots & a_{2 N} f_N=g_2 \\
109 | \ldots & \\
110 | a_{M 1} f_1+a_{M 2} f_2+\ldots & a_{M N} f_N=g_M
111 | \end{array}\tag{5-48}
112 | $$
113 | $$
114 | f=\left[f_1 \ldots f_N\right]
115 | $$
116 | 取
117 | $$
118 | f^{(0)}=\left[f_1^{(0)}, f_2^{(0)}, \ldots f_N^{(0)}\right]
119 | $$
120 | $$
121 | f^{(0)}=\left[g_1, g_2, \ldots g_N\right]
122 | $$
123 | $f^{(1)}$ 取 $f^{(0)}$ 在第一个超平面$a_{11} f_1+a_{12} f_2+\ldots \quad a_{1 N} f_{N}=g_1$上的投影。
124 |
125 | 即:
126 |
127 | $$
128 | f^{(1)}=f^{(0)}-\frac{f^{(0)} \cdot a_1-g_1}{a_1 \bullet a_2} a_1\tag{5-49}
129 | $$
130 |
131 | $f^{(2)}$ 取 $f^{(1)}$ 在第二个超平面$a_{21} f_1+a_{22} f_2+\ldots \quad a_{2 N} f_{N}=g_2$ 上的投影。
132 |
133 | 依次继续下去, 直到满足 $( 5 . 4 8 )$ 式中最后一个方程式。这就实现了迭代的第一个循环然后再从 (5.48)式中第一个方程式开始第二次迭代。即取 $f^{(M)}$ 在第一个超平面$a_{11} f_1+a_{12} f_2+\ldots a_{1 N} f_{N}=g_1$上的投影。并称之为 $f^{(M+1)}$ 。依次继续, 直到
134 | $$
135 | f^{(k+1)}=f^{(k)}\tag{5-50}
136 | $$
137 | 则:
138 | $$
139 | f^{(k)}=f\tag{5-51}
140 | $$
141 |
--------------------------------------------------------------------------------
/V/5.6 其他图像复原技术.md:
--------------------------------------------------------------------------------
1 | # 5.6 其他图像复原技术
2 |
3 | ## 5.6 几何畸变校正
4 |
5 | 数字图像在获取过程中,由于成像系统的非线性,成像后的图像与原景物图像相比,会产生比例失调,甚至扭曲,我们把这类图像退化现象称之为几何畸变。典型的几何失真如图5-4所示。
6 |
7 |
185 |
186 | 图4-39 图像平滑模板设置对话框
187 |
188 | 利用类向导为对话框的相应控件添加成员变量,如模板类型、模板高度、模板宽度、模板中心元素X坐标、模板中心元素Y坐标对应的成员变量分别定义为整型变量m_intType、m_iTempH、m_iTempW、m_iTempMX、m_iTempMY, 而模板系数对应浮点型的变量m_fTempC,另外还定义了一个模板元素数组指针m_fpArray。
189 | 为3个单选按钮分别定义一个单击事件的消息映射,在映射函数中给模板元素m_fpArray及其他成员变量赋值。
190 |
191 | 2. 获取图像数据
192 | 对每个像素的邻域用选定的模板作卷积运算, 就可以得到平滑后的图像。下面给出了卷积运算的源代码。
193 | 卷积函数中的各参数的含义如下: fpData为被卷积的数组, fpKernel为卷积核数组,fCoef为卷积系数,nSize为卷积尺寸, nResult为卷积结果。
194 |
195 | ```c++
196 | void CAreaPro:: Convolution(float *fpData, float *fpKernel, float fCoef,
197 | int nSize, unsigned char *nResult)
198 | {
199 | int i;
200 | float Sum = 0, fResult;
201 | //计算卷积
202 | for(i = 0; i < nSize; i++)
203 | {
204 | Sum += fpData[i] * fpKernel[i];
205 | }
206 | //执行卷积后的结果
207 | fResult = Sum / fCoef;
208 | //求绝对值
209 | fResult = (float)fabs(fResult);
210 | //判断是否超过255
211 | if(fResult > 255.0 )
212 | {
213 | // 直接赋值为255
214 | fResult = 255.0;
215 | }
216 | //对卷积结果四舍五入, 并转换成unsigned char类型作为最后返回结果
217 | *nResult = (unsigned char) (fResult + 0.5);
218 | }
219 |
220 | ```
221 |
222 | 接着就是对原图像的每个像素作卷积运算,运算后的结果赋予新图像,其中图像边界像素不作处理,代码实现在CAreaPro:: Smoothing()中。
--------------------------------------------------------------------------------
/README.md:
--------------------------------------------------------------------------------
1 | # Digital-mage-Processing
2 | 数字图像处理笔记,整理张航老师的数字图像处理课件,推荐教材是冈萨雷斯第四版
3 |
4 | 现在已经初步整理完毕,但不排除个别地方仍然有细微错误。
--------------------------------------------------------------------------------
/V/5.1 图像退化与复原.md:
--------------------------------------------------------------------------------
1 | # 5.1 图像退化与复原
2 |
3 | 数字图像在获取的过程中,由于光学系统的像差、 光学成像衍射、 成像系统的非线性畸变、 摄影胶片的感光的非线性、 成像过程的相对运动、 大气的湍流效应、环境随机噪声等原因, 图像会产生一定程度的退化。因此,必须采取一定的方法尽可能地减少或消除图像质量的下降,恢复图像的本来面目,这就是图像复原, 也称为图像恢复。
4 |
5 | 图像复原与图像增强有类似的地方, 都是为了改善图像。但是它们又有着明显的不同。图像复原是试图利用退化过程的先验知识使已退化的图像恢复本来面目,即根据退化的原因, 分析引起退化的环境因素,建立相应的数学模型, 并沿着使图像降质的逆过程恢复图像。从图像质量评价的角度来看, 图像复原就是提高图像的可理解性。而图像增强的目的是提高视感质量,图像增强的过程基本上是一个探索的过程, 它利用人的心理状态和视觉系统去控制图像质量, 直到人们的视觉系统满意为止。
6 |
7 | 图像复原是利用退化现象的某种先验知识,建立退化现象的数学模型,再根据模型进行反向的推演运算,以恢复原来的景图像。因而,图像复原可以理解为图像降质过程的反向过程。建立图像复原的反向过程的数学模型,就是图像复原的主要务。经过反向过程的数学模型的运算,要想恢复全真的景物图像比较困难。所以, 图像复原本身往往需要有一个质量准, 即衡量接近全真景物图像的程度,或者说,对原图像的估计是否到达最佳的程度。
8 |
9 | 由于引起退化的因素众多而且性质不同,为了描述图像退化过程所建立的数学模型往往多种多样,而恢复的质量标准也往存在差异性,因此图像复原是一个复杂的数学过程,图像复原的方法、技术也各不相同。
10 |
11 | ## 5.1.1 图像降质的数学模型
12 |
13 | 图像复原处理的关键问题在于建立退化模型。输入图像f(x, y)经过某个退化系统后输出的是一幅退化的图像。为了讨论方便, 把噪声引起的退化即噪声对图像的影响一般作为加性噪声考虑, 这也与许多实际应用情况一致,如图像数字化时的量化噪声、 随机噪声等就可以作为加性噪声,即使不是加性噪声而是乘性噪声, 也可以用对数方式将其转化为相加形式。
14 |
15 | 原始图像 $f(x, y)$ 经过一个退化算子或退化系统 $H(x, y)$ 的作用, 再和噪声 $n(x, y)$ 进行叠加, 形成退化后的图像 $g(x, y)$ 。图11-1表示退化过程的输入和输出的关系, 其中 $H(x, y)$ 概括了退化系统的物理过程, 就是所要寻找的退化数学模型。
16 |
17 | 此处是进行了简化,因为乘法噪声可以转化为加法噪声
18 |
19 | 
20 |
21 | 数字图像的图像恢复问题可看作是: 根据退化图像 $g(x, y)$ 和退化算子 $H(x, y)$ 的形式, 沿着反向过程去求解原始图像 $f(x, y)$, 或者说是逆向地寻找原始图像的最佳近似估计。图像退化的过程可以用数学表达式写成如下的形式:
22 | $$
23 | g(x, y)=H[f(x, y)]+n(x, y)\tag{5-1}
24 | $$
25 | 在这里, $n(x, y)$ 是一种统计性质的信息。在实际应用中, 往往假设噪声是白噪声, 即它的频谱密度为常数, 并且与图像不相关。
26 |
27 | 在图像复原处理中, 尽管非线性、 时变和空间变化的系统模型更具有普遍性和准确性,更与复杂的退化环境相接近,但它给实际处理工作带来了巨大的困难, 常常找不到解或者很难用计算机来处理。因此,在图像复原处理中, 往往用线性系统和空间不变系统模型来加以近似。这种近似的优点使得线性系统中的许多理论可直接用于解决图像复原问题,同时又不失可用性。
28 |
29 | 一幅连续图像 $f(x, y)$ 可以看作是由一系列点源组成的。因此, $f(x, y)$ 可以通过点源函数的卷积来表示。即
30 | $$
31 | f(x, y)=\int_{-\infty}^{+\infty} \int_{-\infty}^{+\infty} f(\alpha, \beta) \delta(x-\alpha, y-\beta) d \alpha d \beta\tag{5-2}
32 | $$
33 | 式中, $\delta$ 函数为点源函数, 表示空间上的点脉冲。
34 | 在不考虑噪声的一般情况下, 连续图像经过退化系统 $H$ 后的输出为
35 |
36 | $$
37 | \quad g(x, y)=H[f(x, y)]\tag{5-3}
38 | $$
39 |
40 | 把式(5-2)代入式(5-3)得
41 |
42 | $$
43 | \begin{gathered}
44 | g(x, y)=H[f(x, y)]=H\left[\int_{-\infty}^{+\infty} \int_{-\infty}^{+\infty} f(\alpha, \beta) \delta(x-\alpha, y-\beta) d \alpha d \beta\right]
45 | \end{gathered}\tag{5-4}
46 | $$
47 |
48 | 在线性和空间不变系统的情况下, 退化算子 $H$ 具有如下性质:
49 | (1) 线性: 设 $f_1(x, y)$ 和 $f_2(x, y)$ 为两幅输入图像, $k_1$ 和 $k_2$ 为常数, 则
50 |
51 | $$
52 | H\left[k_1 f_1(x, y)+k_2 f_2(x, y)\right]=k_1 H\left[f_1(x, y)\right]+k_2 H\left[f_2(x, y)\right]\tag{5-5}
53 | $$
54 |
55 | 由该性质还可推出下面两个结论:
56 | (1) 当 $k_1=k_2=1$ 时, 式(11-5)变为
57 |
58 | $$
59 | H\left[f_1(x, y)+f_2(x, y)\right]=H\left[f_1(x, y)\right]+H\left[f_2(x, y)\right]\tag{5-6}
60 | $$
61 |
62 | (2) 如果 $f_2(x, y)=0$, 则式 (11-5) 变为
63 |
64 | $$
65 | H\left[k_1 f_1(x, y)\right]=k_1 H\left[f_1(x, y)\right]\tag{5-7}
66 | $$
67 |
68 | (2) 空间不变性: 如果对任意 $f(x, y)$ 以及 $a$ 和 $b$, 有
69 |
70 | $$
71 | H[f(x-a, y-b)]=g(x-a, y-b)\tag{5-8}
72 | $$
73 |
74 | 则对于线性空间不变系统, 输入图像经退化后的输出为
75 |
76 | $$
77 | \begin{aligned}
78 | g(x, y) & =H[f(x, y)]=H\left[\int_{-\infty}^{+\infty} \int_{-\infty}^{+\infty} f(\alpha, \beta) \delta(x-\alpha, y-\beta) d \alpha d \beta\right] \\
79 | & =\int_{-\infty}^{+\infty} \int_{-\infty}^{+\infty} f(\alpha, \beta) H[\delta(x-\alpha, y-\beta)] d \alpha d \beta \\
80 | & =\int_{-\infty}^{+\infty} \int_{-\infty}^{+\infty} f(\alpha, \beta) h(x-\alpha, y-\beta) d \alpha d \beta
81 | \end{aligned}\tag{5-9}
82 | $$
83 |
84 | 式中, $h(x-\alpha, y-\beta)$ 为该退化系统的点扩展函数, 或叫系统的冲激响应函数。它表示系统对坐标为 $(a, \beta)$ 处的冲激函数 $\delta(x-\alpha, y-\beta)$ 的响应。也就是说, 只要系统对冲激函数的响应为已知, 那么就可以清楚图像退化是如何形成的。因为对于任一输入 $f(a, \beta)$ 的响应, 都可以通过上式计算出来。
85 | 此时, 退化系统的输出就是输入图像信号 $f(x, y)$ 与点扩展函数 $h(x, y)$ 的卷积, 即
86 |
87 | $$
88 | g(x, y)=\int_{-\infty}^{+\infty} \int_{-\infty}^{+\infty} f(\alpha, \beta) h(x-\alpha, y-\beta) d \alpha d \beta=f(x, y) * h(x, y)\tag{5-10}
89 | $$
90 |
91 | 图像退化除了受到成像系统本身的影响外, 有时还要受到噪声的影响。假设噪声 $n(x, y)$ 是加性白噪声, 这时上式可写成
92 |
93 | $$
94 | \begin{aligned}
95 | g(x, y) & =\int_{-\infty}^{+\infty} \int_{-\infty}^{+\infty} f(\alpha, \beta) h(x-\alpha, y-\beta) d \alpha d \beta+n(x, y) \\
96 | & =f(x, y) * h(x, y)+n(x, y)
97 | \end{aligned}\tag{5-11}
98 | $$
99 |
100 | 在频域上, 式(11-11)可以写成
101 |
102 | $$
103 | G(u, v)=F(u, v) H(u, v)+N(u, v)\tag{5-12}
104 | $$
105 |
106 | 其中, $G(u, v) 、 F(u, v) 、 N(u, v)$ 分别是退化图像 $g(x, y)$ 、原图像 $f(x, y)$、噪声信号 $n(x, y)$ 的傅立叶变换; $H(u, v)$ 是系统的点冲激响应函数 $h(x, y)$ 的傅立叶变换, 称为系统在频率域上的传递函数。
107 |
108 | 式(5-11)和式(5-12)就是连续函数的退化模型。可见, 图像复原实际上就是已知 $g(x, y)$ 求 $f(x, y)$ 的问题或已知 $G(u, v)$ 求 $F(u, v)$ 的问题, 它们的不同之处在于一个是在空域,一个是在频域。
109 | 显然, 进行图像复原的关键问题是寻找降质系统在空间域上的冲激响应函数 $h(x, y)$, 或者降质系统在频率域上的传递函数 $H(u$, $v)$ 。一般来说, 传递函数比较容易求得。因此, 在进行图像复原之前, 一般应设法求得完全的或近似的降质系统传递函数, 要想得到 $h(x, y)$, 只需对 $H(u, v)$ 求傅立叶逆变换即可。
110 |
111 | ## 5.1.2 离散图像退化的数学模型
112 |
113 | 1. 一维离散退化模型
114 | 设 $f(x)$ 为具有 $A$ 个采样值的离散输入函数, $h(x)$ 为具有 $B$ 个采样值的退化系统的冲激响应函数, 则经退化系统后的离散输出函数 $g(x)$ 为输入 $f(x)$ 和冲激响应 $h(x)$ 的卷积, 即
115 | $$
116 | g(x)=f(x)^* h(x)
117 | $$
118 | 为了避免上述卷积所产生的各个周期重叠(设每个采样函数的周期为 $M)$ ,分别对 $f(x)$ 和 $h(x)$ 用添零延伸的方法扩展成周期 $M=A+B-1$ 的周期函数, 即
119 | $$
120 | f_e(x)=\left\{\begin{array}{cc}
121 | f(x) & 0 \leq x \leq A-1 \\
122 | 0 & A \leq x \leq M-1
123 | \end{array}\right. \tag{5-13a}
124 | $$
125 | $$
126 | h_e(x)=\left\{\begin{array}{cc}
127 | h(x) & 0 \leq x \leq B-1 \\
128 | 0 & B \leq x \leq M-1
129 | \end{array}\right.\tag{5-13b}
130 | $$
131 | 输出为
132 | $$
133 | g_e(x)=f_e(x) * h_e(x)=\sum_{m=0}^{M-1} f_e(m) h_e(x-m)\tag{5-14}
134 | $$
135 | 式中, $x=0,1,2, \ldots, M-1$ 。
136 |
137 | 因为 $f_{e}(x)$ 和 $h_{e}(x)$ 已扩展成周期函数, 故 $g_{e}(x)$ 也是周期性函数, 用矩阵表示为
138 | $$
139 | \left[\begin{array}{c}
140 | g(0) \\
141 | g(1) \\
142 | g(2) \\
143 | M \\
144 | g(M-1)
145 | \end{array}\right]=\left[\begin{array}{cccc}
146 | h_e(0) & h_e(-1) & \Lambda & h_e(-M+1) \\
147 | h_e(1) & h_e(0) & \Lambda & h_e(-M+2) \\
148 | h_e(2) & h_e(1) & \Lambda & h_e(-M+3) \\
149 | M & M & M & M \\
150 | h_e(M-1) & h_e(M-2) & \Lambda & h_e(0)
151 | \end{array}\right]\left[\begin{array}{c}
152 | f_e(0) \\
153 | f_e(1) \\
154 | f_e(2) \\
155 | M \\
156 | f_e(M-1)
157 | \end{array}\right]\tag{5-15}
158 | $$
159 | 因为 $h_{e}(x)$ 的周期为 $M$, 所以 $h_{e}(x)=h_{e}(x+M)$, 即
160 | $$
161 | \begin{gathered}
162 | h_e(-1)=h_e(M-1) \\
163 | h_e(-2)=h_e(M-2) \\
164 | h_e(-3)=h_e(M-3) \\
165 | M \\
166 | h_e(-M+1)=h_e(1)
167 | \end{gathered}
168 | $$
169 | $M \times M$ 阶矩阵 $\boldsymbol{H}$ 可写为
170 | $$
171 | H=\left[\begin{array}{cccc}
172 | h_e(0) & h_e(-1) & \Lambda & h_e(1) \\
173 | h_e(1) & h_e(0) & \Lambda & h_e(2) \\
174 | h_e(2) & h_e(1) & \Lambda & h_e(3) \\
175 | M & M & \Lambda & \Lambda \\
176 | h_e(M-1) & h_e(M-2) & h_e(0)
177 | \end{array}\right]\tag{5-16}
178 | $$
179 | 可将式(5-15)写成更简洁的形式,即
180 | $$
181 | g=H f\tag{5-17}
182 | $$
183 | 式中, $\boldsymbol{g} 、 \boldsymbol{f}$ 都是 $M$ 维列向量, $\boldsymbol{H}$ 是 $M \times M$ 阶矩阵, 矩阵中的每一行元素均相同, 只是每行以循环方式右移一位, 因此矩阵 $\boldsymbol{H}$ 是循环矩阵。循环矩阵相加或相乘得到的还是循环矩阵。
184 |
185 | 2. 二维离散模型
186 | 设输入的数字图像 $f(x, y)$ 大小为 $A \times B$, 点扩展函数 $h(x, y)$ 被均匀采样为 $C \times D$ 大小。为避免交叠误差, 仍用添零扩展的方法, 将它们扩展成 $M=A+C-1$ 和 $N=B+D-1$ 个元素的周期函数。
187 |
188 | $$
189 | f_e(x, y)=\left\{\begin{array}{cc}
190 | f(x, y) & 0 \leq x \leq A-1 \text { 且 } 0 \leq y \leq B-1 \\
191 | 0 & \text { 其他 }
192 | \end{array}\right. \tag{5-18a}
193 | $$
194 | $$
195 | h_e(x, y)=\left\{\begin{array}{cc}
196 | h(x, y) & 0 \leq x \leq C-1 \text { 且 } 0 \leq y \leq D-1 \\
197 | 0 & \text { 其他 }
198 | \end{array}\right.\tag{5-18b}
199 | $$
200 |
201 | 则输出的降质数字图像为
202 | $$
203 | g_e(x, y)=\sum_{m=0}^{M-1} \sum_{n=0}^{N-1} f_e(m, n) h_e(x-m, y-n)=f(x, y)^* h(x, y)\tag{5-19}
204 | $$
205 | 式中: $x=0,1,2, \ldots, M-1 ; y=0,1,2, \ldots, N-1$ 。
206 | 式(5-19)的二维离散退化模型同样可以用式 (5-17) 所示的矩阵形式表示, 即
207 | $$
208 | g=H f
209 | $$
210 | 式中, $g 、 f$ 是 $M N \times 1$ 维列向量, $H$ 是 $M N \times M N$ 维矩阵。其方法是将 $g(x, y)$ 和 $f(x, y)$ 中的元素排成列向量。
211 | $$
212 | f_1=\left[\underbrace{f_1(0,0),f_1(0,1),\cdots,f_1(0,N-1)}_{第0行元素},\underbrace{f_1(1,0),f_1(1,1),\cdots,f_1(1,N-1)}_{第1行元素},\cdots,\underbrace{f_1(M-1,0),f_1(M-1,1),\cdots,f_1(M-1,N-1)}_{第M-1行元素}\right]^T\\
213 | g_1=\left[\underbrace{g_1(0,0),g_1(0,1),\cdots,g_1(0,N-1)}_{第0行元素},\underbrace{g_1(1,0),g_1(1,1),\cdots,g_1(1,N-1)}_{第1行元素},.\cdots,\underbrace{g_1(M-1,0),g_1(M-1,1),\cdots,g_1(M-1,N-1)}_{第M-1行元素}\right]^T
214 | \tag{5-20}
215 | $$
216 |
217 | $$
218 | H=\left[\begin{array}{cccc}
219 | H_0 & H_{M-1} & H_{M-2} & \cdots& H_1 \\
220 | H_1 & H_0 & H_{M-1} & \cdots& H_2 \\
221 | \vdots & \vdots & \vdots & \ddots&\vdots \\
222 | H_{M-1} & H_{M-2} & H_{M-3} & \cdots &H_0
223 | \end{array}\right]
224 | \tag{5-21}
225 | $$
226 | $H_i(i=0,1,2, \ldots, M-1)$ 为子矩阵, 大小为 $N \times N$, 即 $H$ 矩阵由 $M \times M$ 个大小为 $N \times N$ 的子矩阵组成, 称为分块循环矩阵。分块矩阵是由延拓函数 $h_{e}(x, y)$ 的第 $j$ 行构成的, 构成方法如下:
227 | $$
228 | H=\left[\begin{array}{cccc}
229 | h_e(j, 0) & h_e(j, N-1) & h_e(j, N-2) & \cdots& h_e(j, 1) \\
230 | h_e(j, 1) & h_e(j, 0) & h_e(j, N-1) & \cdots &h_e(j, 0) \\
231 | \vdots & \vdots & \vdots &\ddots &\vdots \\
232 | h_e(j, N-1) & h_e(j, N-2) & h_e(j, N-3) & \cdots &h_e(j, 0)
233 | \end{array}\right]
234 | \tag{5-22}
235 | $$
236 | 若把噪声考虑进去, 则离散图像退化模型为
237 | $$
238 | g_e(x, y)=\sum_{m=0}^{M-1} \sum_{n=0}^{N-1} f_e(m, n) h_e(x-m, y-n)+n_e(x, y)
239 | \tag{5-23}
240 | $$
241 | 写成矩阵形式为
242 | $$
243 | g=H f+n\tag{5-24}
244 | $$
245 | 上述线性空间不变退化模型表明, 在给定了 $g(x, y)$, 并且知道退化系统的点扩展函数 $h(x, y)$ 和噪声分布 $n(x, y)$ 的情况下, 可估计出原始图像 $f(x, y)$ 。
246 | 假设图像大小 $M=N=512$, 相应矩阵 $M H$ 的大小为 $M N \times M N=262144 \times 262144$, 这意味着要解出 $f(x, y)$ 需要解262 144 个联立方程组, 其计算量十分惊人。
247 |
248 | 图像恢复目的是在给定的 $g(x, y), h(x, y), n(x, y)$ 情况下, 求 $f(x, y)$. 由于 $G , F$ 维数很大, 通过解方程组不可能进行图像恢复.
249 | 1. 代数复原方法:寻找一个估计 $f(x, y)$.
250 | - 非约束复原方法
251 | - 约束复原方法
252 | 2.逆滤波方法
253 |
254 |
--------------------------------------------------------------------------------
/V/5.2 代数复原法.md:
--------------------------------------------------------------------------------
1 | # 5.2 代数复原法
2 |
3 | ## 5.2.1非约束复原方法
4 |
5 | 由式(5-24)可得
6 | $$
7 | n=g-H f\tag{5-25}
8 | $$
9 | 在对 $n$ 没有先验知识的情况下, 可以依据这样的最优准则, 即寻找一个 $\hat{f}$, 使得 $H \hat{f}$ 在最小二乘方误差的意义下最按近 $g$, 即要使 $n$ 的模或范数 (norm) 最小:
10 | $$
11 | \|n\|^2=n^T n=\|g-H \hat{f}\|^2=(g-H \hat{f})^T(g-\hat{H f})\tag{5-26}
12 | $$
13 | 即优化目标为:
14 | $$
15 | L(\hat{f})=\|g-H \hat{f}\|^2\tag{5-27}
16 | $$
17 | 如果我们在求最小值的过程中, 不做任何约束, 称这种复原为非约束复原。由极值条件
18 | $$
19 | \frac{\partial L(\hat{f})}{\partial \hat{f}}=0 \Rightarrow H^T(g-H \hat{f})=0\tag{5-28}
20 | $$
21 | 解出 $\hat{f}$ 为
22 | $$
23 | \hat{f}=\left(H^T H\right)^{-1} H^T g\tag{5-29}
24 | $$
25 |
26 | ## 5.2.2 约束复原法
27 |
28 | 非约束复原是指除了使准则函数 $L(\hat{f})=\|g-\hat{H f}\|^2$ 最小外, 再没有其他的约束条件。因此只需了解降质系统的传递函数或点扩展函数, 就能利用如前所述的方法进行复原。但是由于传递函数存在病态问题, 复原只能局限在靠近原点的有限区域内进行, 这使得非约束图像复原具有相当大的局限性。
29 |
30 | 最小二乘类约束复原是指除了要求了解关于退化系统的传递函数之外, 还需要知道某些噪声的统计特性或噪声与图像的某些相关情况。根据所了解的噪声的先验知识的不同, 采用不同的约束条件, 可得到不同的图像复原技术。在最小二乘类约束复原中, 要设法寻找一个最优估计 $\hat{f}$, 使得形式为 $\|Q \hat{f}\|^2=\|n\|^2$ 的函数最小化。求这类问题的最小化, 常采用拉格朗日乘子算法。也就说, 要寻找一个 $\hat{f}$, 使得优化目标函数:
31 | $$
32 | J(\hat{f})=\|\hat{O \hat{f}}\|^2+\alpha\left(\|g-H \hat{f}\|^2-\|n\|^2\right)\tag{5-30}
33 | $$
34 | 为最小。式中, $Q$ 为 $\hat{f}$ 的线性算子, $\alpha$ 为一常数, 称为拉格朗日乘子。对式(5-30)求导得
35 | $$
36 | \begin{aligned}
37 | & \frac{\partial J(\hat{f})}{\partial f}=0 \\
38 | & Q^T Q \hat{f}-\alpha H^T(g-H \hat{f})=0
39 | \end{aligned}
40 | $$
41 | 求解 $\hat{f}$ 得到
42 | $$
43 | \hat{f}=\left(H^T H+\gamma Q^T Q\right)^{-1} H^T g\tag{5-31}
44 | $$
--------------------------------------------------------------------------------
/V/5.3 逆滤波.md:
--------------------------------------------------------------------------------
1 | # 5.3 逆滤波
2 |
3 | 只能接近,无法完全恢复
4 |
5 | 1.逆滤波基本原理
6 | 由退化图像的付里叶变换求得图像的付里叶变换的估计方法称为逆滤波.
7 |
8 | 逆滤波
9 | $$
10 | \begin{aligned}
11 | \overline{g(x, y)}= & \int_{-\infty}^{\infty} \int_{-\infty}^{\infty} f(x, A) h(x-\imath v, y-A) d x d, \partial+n(x, y) \\
12 | & G(u, v)=F(u, v) H(u, v)+N(u, v)
13 | \end{aligned}
14 | $$
15 | 不考虑噪声:
16 |
17 | $$
18 | \begin{aligned} F(u, v) & =\frac{G(u, v)}{H(u, v)} \\ f(x, y) & =\mathcal{G}^{-1}[F(u, v)]\end{aligned}
19 | $$
20 | 有噪声:
21 | $$
22 | \begin{aligned}
23 | & F(u, v)=\frac{G(u, v)}{H(u, v)}-\frac{N(u, v)}{H(u, v)} \\
24 | & f(x, y)=\xi^{-1}[F(u, v)]
25 | \end{aligned}
26 | $$
27 |
28 |
29 |
30 |
31 | 
32 |
33 | 图5.2 逆滤波
34 |
35 | 逆滤波
36 | 2.去除由均匀直线运动引起的模糊
37 | - 模糊模型
38 | $$
39 | g(x, y)=\int_0^T f\left[x-x_0(t), y-y_0(t)\right] d t
40 | $$
41 | $f(x, y)$ : 原图像; $g(x, y)$ : 模糊图像; $T$ : 暴光时间
42 | - 图像恢复 $G(u, v)=H(u, v) F(u, v)$
43 | 其中: $H(u, v)=\int_0^T \exp \left\{-j 2 \pi\left[u x_0(t)+v y_0(t)\right]\right\} d t$
44 |
45 | ## 用途
46 |
47 | 在实验室中,可以反复做实验的情景
--------------------------------------------------------------------------------
/V/5.4 最小二乘滤波(维纳滤波,重点).md:
--------------------------------------------------------------------------------
1 |
2 |
3 | # 5.4 最小二乘方滤波(维纳滤波)
4 |
5 | **重点**
6 |
7 | 知道图像,知道有关分布特征
8 |
9 | 1.最小二乘方滤波
10 | 设原始图像, 退化图像和噪声分别为 $f(x, y), g(x, y)$ 和 $n(x, y)$, 则 :
11 |
12 | $$
13 | g(x, y)=H[f(x, y)]=H\left[\int_{-\infty}^{+\infty} \int_{-\infty}^{+\infty} f(\alpha, \beta) \delta(x-\alpha, y-\beta) d \alpha d \beta\right]+n(x, y)$ 在给定的 $g(x, y)$ 时, 找出 $f(x, y)$ 的估计 $f(x, y)
14 | $$
15 | 使:
16 | $$
17 | e^2=E\left\{[f(x, y)-\hat{f}(x, y)]^2\right\}
18 | $$
19 | 最小.
20 |
21 | 设
22 | $$
23 | \quad \hat{f}(x, y)=\iint m(x, y, \alpha, \beta) g(\alpha, \beta) d \alpha d \beta
24 | $$
25 | 2. 求解
26 | 如果 $f(x, y), g(x, y)$ 和 $n(x, y)$ 是均匀随机场, 则 :
27 | $$
28 | \hat{f}(x, y)=\iint m(x-\alpha, y-\beta) g(\alpha, \beta) d \alpha d \beta
29 | $$
30 | 因此图像恢复就是确定m $m, y)$. 通过求解得:
31 | $$
32 | \begin{aligned}
33 | M(u, v) & =\left[\frac{H^*(u, v)}{|H(u, v)|^2+\left[S_n(u, v) / S_f(u, v)\right]}\right] \\
34 | & =\left[\frac{1}{H(u, v)} \cdot \frac{|H(u, v)|^2}{\left|H(u, v)^2\right|+\left[S_n(u, v) / S_f(u, v)\right]}\right]
35 | \end{aligned}
36 | $$
37 | $H(u, v)$ 是的h $(x, y)$ 付里叶变换.
38 | $S_f, S_n$ 分别是 $f(x, y), n(x, y)$ 的谱密度
39 |
40 | 于是:
41 | $$
42 | \begin{aligned}
43 | \hat{F}(u, v) & =\left[\frac{H^*(u, v)}{|H(u, v)|^2+\left[S_n(u, v) / S_f(u, v)\right]}\right] G(u, v) \\
44 | & =\left[\frac{1}{H(u, v)} \cdot \frac{|H(u, v)|^2}{\left|H(u, v)^2\right|+\left[S_n(u, v) / S_f(u, v)\right]}\right] G(u, v)
45 | \end{aligned}\tag{5-32}
46 | $$
47 | 式中,
48 | $$
49 | u, v=0,1,2, \ldots, N-1,|H(u, v)|^2=H^*(u, v) H(u, v)
50 | $$
51 |
52 | 3. 讨论
53 | - $S_n=0$ 时, 是理想的逆滤波器
54 | -若随机过程的统计特性不知道, 可采用:
55 | $$
56 | M(u, v)=\frac{1}{H(u, v)} \frac{|H(u, v)|^2}{|H(u, v)|^2+\Gamma}
57 | $$
58 | 式中 $\Gamma$ 是噪声对信号的功率密度比.
59 |
60 | - 维纳滤波器是假设线性系统, 实际上图像的记录和评价图像的视觉系统都是非线性系统.
61 | - 维纳滤波器是根据最小均方差设计的,这个准则不见得与人的视觉判决准则相符.
62 | - 维纳滤波器是基于平稳随机过程的模型,实际图像不一定符合这一条件.
63 |
64 | ## 几种最小二乘方滤波器
65 |
66 | (仅供了解)
67 |
68 | 1.图像功率谱滤波器
69 | $$
70 | H_{R}(u, v)=\left[\frac{W_{FI}(u, v)}{\left|H_{D}(u, v)\right|^2 W_{F 1}(u, v)+W_{N}(u, v)}\right]^{\frac{1}{2}}
71 | $$
72 | 式中 $H_{D}(u, v)$ 是图像退化的传递函数。 $W_{F 1}(u, v)$ 代表滤波器输出功率频谱,
73 | $$
74 | W_{FI}(u, v)=\left|H_{D}(u, v)\right|^2 W_{FO}(u, v)
75 | $$
76 | 式中 $W_{FO}(u, v)$ 代表观测的功率频谱。它与理想图像的功率频谱的关系是
77 | $$
78 | W_{FO}(u, v)=\left|H_{D}(u, v)\right|^2 \cdot W_{FI}(u, v)+W_{N}(u, v)
79 | $$
80 | 式中 $W_{N}(u, v)$ 是噪声功率频谱。
81 |
82 | 2.几何平均滤波器.
83 |
84 | 几何平均滤波器的传递函数由下式表示:
85 | $$
86 | H_{R}(u, v)=\left[H_{D}(u, v)\right]^{-s}\left[\frac{H_{D}^*(u, v) W_{FI}(u, v)}{\left|H_{D}(u, v)\right|^2 W_{FI}(u, v)+W_{N}(u, v)}\right]^{1-s}
87 | $$
88 | S是一个参数
89 |
90 | 3.约束最小方滤波器
91 |
92 | 约束最小方滤波器的传递函数如下:
93 | $$
94 | H_{\mathrm{R}}(u, v)=\frac{H_{\mathrm{D}}^*(u, v)}{\left|H_{\mathrm{D}}(u, v)\right|^2+r|L(u, v)|^2}
95 | $$
96 | $r$是一个参数,$L(u,v)$是一个频率参数。$r=1$为维纳滤波器
--------------------------------------------------------------------------------
/V/5.5 非线性复原方法 .md:
--------------------------------------------------------------------------------
1 | # 5.5 非线性复原方法(仅供了解)
2 |
3 | ## 5.5.1 最大后验复原
4 |
5 | 最大后验复原是一种统计方法, 它把原图像 $f(x, y)$ 和退化图像 $g(x, y)$ 都作为随机场, 在已知 $g(x, y)$ 的前提下, 求出后验条件概率密度函数 $P(f(x, y) / g(x, y))$ 。若 $\hat{f}(x, y)$ 使式
6 | $$
7 | \max _{f} p(f \mid g)=\max _f p(g \mid f) p(f) / p(g)=\max _f p(g \mid f) p(f)\tag{5-33}
8 | $$
9 | 最大, 则 $\hat{f}(x, y)$ 就代表已知退化图像 $g(x, y)$ 时, 最可能的原始图像 $f(x, y)$ 。这种图像方法称之为最大后验图像复原方法。
10 |
11 | 最大后验图像复原方法把图像看作是非平稳随机场, 把图像模型表示成一个平稳随机过程对于一个不平稳的均值作零均值Gauss起伏, 可得出求解迭代序列:
12 | $$
13 | \hat{f}_{k+1}=\hat{f}_k-h^* \sigma_n^{-2}\left(g-h^* \hat{f}_k\right)-\sigma_n^{-2}\left(\hat{f}_k-\bar{f}\right)\tag{5-34}
14 | $$
15 | 其中, $k$ 为迭代次数, $\sigma_n^{-2}$ 和 $\sigma_f^{-2}$ 分别为 $f$ 和 $n$ 的方差的倒数, $f$ 是随空间而变的均值, 它是一个常数, 但要经过多次迭代才能收敛到最后的解。
16 |
17 | ## 5.5.2 最大熵复原
18 |
19 | 最大熵复原方法是通过最大化某种反映图像平滑性的准则函数来作约束条件, 以解决图像复原中反向滤波法存在的病态问题。
20 | 首先简单介绍一下熵的概念。
21 | 熵的定义为
22 | $$
23 | H=-\int_{-\infty}^{+\infty} P(x) \ln P(x) d x\tag{5-35}
24 | $$
25 | 式中, $P(x)$ 为随机变量 $x$ 的概率密度。
26 | 对于离散信号, 熵的定义为
27 | $$
28 | H=-\sum_{k=1}^M P(k) \ln P(k)\tag{5-36}
29 | $$
30 | 熵是表征随机变量集合的随机程度的量度。当所有随机变量等可能性时, 也就是说 $P_1=P_2=\ldots=P_{m}$ 时熵最大, 为 $H=\ln M$ 。由于概率 $P(k)$ 介于 $0 \sim 1$ 之间, 因此最大熵的范围为 $0 \sim \ln M, H$ 不可能出现负值。
31 | 在二维数字图像中, 熵的定义为
32 | $$
33 | H_f=-\sum_{m=1}^M \sum_{n=1}^N f(m, n) \ln f(m, n)\tag{5-37}
34 | $$
35 | 最大熵复原的原理是将 $f(x, y)$ 写成随机变量的统计模型,然后在一定的约束条件下,找出用随机变量形式表示的熵的表达式, 运用求极大值的方法, 求得最优估计解 $\hat{f}(x, y)$ 。最大熵复原的含义是对 $\hat{f}(x, y)$ 的最大平滑估计。 最大熵复原常用Friend和Burg两种方法, 这两种方法基本原理相同, 这里仅介绍Friend法。
36 |
37 | 首先定义一幅大小为 $M \times N$ 的图像 $f(x, y)$, 显然 $f(x, y)$ 非负。 图像的总能量 $E$ 和熵分别为
38 | $$
39 | E=\sum_{i=j}^M \sum_{j=1}^N f\left(x_i, y_j\right)\tag{5-38}
40 | $$
41 | 和
42 | $$
43 | H_f=\sum_{i=j}^M \sum_{j=1}^N f\left(x_i, y_j\right) \operatorname{lnf}\left(x_i, y_j\right)\tag{5-39}
44 | $$
45 | 类似地可定义噪声的熵 $H_n$ :
46 | $$
47 | H_n=-\sum_{i=1}^M \sum_{j=1}^N n^{\prime}\left(x_i, y_j\right) 1 n n^{\prime}\left(x_i, y_j\right)\tag{5-40}
48 | $$
49 | 式中: $n^{\prime}(x, y)=n(x, y)+B, B$ 为最大噪声负值。
50 |
51 | 恢复就是在满足式(5-38) 和图像退化模型的约束条件下, 使恢复后的图像熵和噪声熵达到最大。熵通常取决于 $f$ 的形状, 当图像具有均匀的灰度时熵最大。因此用最大熵恢复图像具有某种平滑性。
52 | 引入拉格朗日 (Lagrange) 函数
53 | $$
54 | \begin{aligned}
55 | R & =H_f+\rho H_n+\sum_{m=1}^N \sum_{n=1}^N \lambda_{m m}\left\{\sum_{x=1}^N \sum_{n=1}^N h(m-x, n-y) f(x, y)+n_T(m, n)-B-g(m, n)\right. \\
56 | & +\beta\left\{\sum_{x=1}^N \sum_{y=1}^N f(x, y)-E\right\}
57 | \end{aligned}\tag{5-41}
58 | $$
59 | 式中: $\lambda_{m n}(m, n=1,2, \ldots, N)$ 和 $\beta$ 是拉格朗日乘子, $\rho$ 是加权因子,表示 $H_f$ 和 $H_n$ 相互之间的权重。
60 |
61 | $\hat{f}(x, y)$ 和 $\hat{n}(m, n)$ 分别表示 $f(x, y)$ 和 $n^{\prime}(x, y)$ 的估计值, 则有
62 | $$
63 | \frac{\partial R}{\partial f(x, y)}=0 \tag{5-42}
64 | $$
65 |
66 | $$
67 | \frac{\partial R}{\partial n^{\prime}(x, y)}=0\tag{5-43}
68 | $$
69 | 把式(5-41)分别代入式(5-42)和式(5-43), 可得
70 | $$
71 | \hat{f}(x, y)=\exp \left[-1+\beta+\sum_{m=1}^N \sum_{n=1}^N \lambda_{m m} h(m-x, n-y)\right] \quad x, y=1,2, \ldots, N \tag{5-44}
72 | $$
73 | $$
74 | \hat{n}(m, n)=\exp \left(-1+\frac{\lambda_{m n}}{\rho}\right) \quad \quad m, n=1,2, \ldots, N\tag{5-45}
75 | $$
76 |
77 | 并且$\hat{f}(x,y)$和$\hat{n}(m,n)$满足下列约束条件
78 | $$
79 | \sum_{x=1}^N \sum_{y=1}^N f(x, y)=E\tag{5-46}
80 | $$
81 |
82 | $$
83 | \sum_{x=1}^N \sum_{y=1}^N h(m-x, n-y) f(x, y)+\hat{n}(m, n)-\beta=g(m, n)\tag{5-47}
84 | $$
85 |
86 | 式(5-44)为图像恢复函数。把式(5-44)和式(5-45)代入式(5$46)$ 和式(5-47)可得 $\left(N^2+1\right)$ 个方程。由此联立方程组可解得 $\left(N^2+1\right)$ 个末知数解 $\lambda_{m n}(m, n=1,2, \ldots, N)$, 解上述方程组可求得 $\hat{f}(x, y)$ 的值。
87 |
88 | ## 投影复原
89 |
90 | 投影复原法是用代数方程组来描述线性和非线性退化系统的。该系统可用下式描述:
91 | $$
92 | g(x, y)=H[f(x, y)]+n(x, y)
93 | $$
94 | 其中: $f(x, y)$ 是原始图像, $g(x, y)$ 是退化图像, $n(x, y)$ 是系统噪声, $H$ 是退化算子,表示对图像进行某种运算。
95 | 在使用投影复原法进行图像复原时, 引进一些先验信息附加的约束条件, 可改善图像复原效果。
96 |
97 | ### 投影复原法
98 |
99 | $$
100 | g(x, y)=H[f(x, y)]+n(x, y)
101 | $$
102 | 投影复原方法就是迭代方法之一。设初始估值 $f^0(x, y)$, 然后进行迭代运算.
103 | 设 $f^0(x, y)=g(x, y)$
104 | 设 $H$ 是非线性的, 并忽略噪声, 则上式写成:
105 | $$
106 | \begin{array}{ll}
107 | a_{11} f_1+a_{12} f_2+\ldots & a_{1 N} f_N=g_1 \\
108 | a_{21} f_1+a_{22} f_2+\ldots & a_{2 N} f_N=g_2 \\
109 | \ldots & \\
110 | a_{M 1} f_1+a_{M 2} f_2+\ldots & a_{M N} f_N=g_M
111 | \end{array}\tag{5-48}
112 | $$
113 | $$
114 | f=\left[f_1 \ldots f_N\right]
115 | $$
116 | 取
117 | $$
118 | f^{(0)}=\left[f_1^{(0)}, f_2^{(0)}, \ldots f_N^{(0)}\right]
119 | $$
120 | $$
121 | f^{(0)}=\left[g_1, g_2, \ldots g_N\right]
122 | $$
123 | $f^{(1)}$ 取 $f^{(0)}$ 在第一个超平面$a_{11} f_1+a_{12} f_2+\ldots \quad a_{1 N} f_{N}=g_1$上的投影。
124 |
125 | 即:
126 |
127 | $$
128 | f^{(1)}=f^{(0)}-\frac{f^{(0)} \cdot a_1-g_1}{a_1 \bullet a_2} a_1\tag{5-49}
129 | $$
130 |
131 | $f^{(2)}$ 取 $f^{(1)}$ 在第二个超平面$a_{21} f_1+a_{22} f_2+\ldots \quad a_{2 N} f_{N}=g_2$ 上的投影。
132 |
133 | 依次继续下去, 直到满足 $( 5 . 4 8 )$ 式中最后一个方程式。这就实现了迭代的第一个循环然后再从 (5.48)式中第一个方程式开始第二次迭代。即取 $f^{(M)}$ 在第一个超平面$a_{11} f_1+a_{12} f_2+\ldots a_{1 N} f_{N}=g_1$上的投影。并称之为 $f^{(M+1)}$ 。依次继续, 直到
134 | $$
135 | f^{(k+1)}=f^{(k)}\tag{5-50}
136 | $$
137 | 则:
138 | $$
139 | f^{(k)}=f\tag{5-51}
140 | $$
141 |
--------------------------------------------------------------------------------
/V/5.6 其他图像复原技术.md:
--------------------------------------------------------------------------------
1 | # 5.6 其他图像复原技术
2 |
3 | ## 5.6 几何畸变校正
4 |
5 | 数字图像在获取过程中,由于成像系统的非线性,成像后的图像与原景物图像相比,会产生比例失调,甚至扭曲,我们把这类图像退化现象称之为几何畸变。典型的几何失真如图5-4所示。
6 |
7 |  8 |
9 | 图5-4 几种典型的几何失真
10 | (a) 原图像; (b) 梯形失真; (c) 枕形失真; (d) 桶形失真
11 |
12 | 一般,几何畸变校正要对失真的图像进行精确的几何校正, 通常是先确定一幅图像为基准,然后去校正另一幅图像的几何形状。因此,几何畸变校正一般分两步来做:第一步是图像空间坐标的变换;第二步是重新确定在校正空间各像素点的取值。
13 |
14 | ### 空间几何坐标变换
15 |
16 | 按照一幅标准图像 $g(u, v)$ 或一组基准点去校正另一幅几何失真图像 $f(x, y)$, 称之为空间几何坐标变换。根据两幅图像的一些 已知对应点对(也称为控制点对)建立起函数关系式, 将失真图像的 $x-y$ 坐标系变换到标准图像 $u-v$ 坐标系, 从而实现失真图像按标准图像的几何位置校正, 使 $f(x, y)$ 中的每一像点都可在 $g(u, v)$ 中找到对应像点。
17 |
18 | ### 三角形线性法
19 |
20 | 图像的几何失真虽然是非线性的,但在一个局部小区域内可近似认为是线性的,基于这一假设,将标准图像和被校正图像之间的对应点对划分成一系列小三角形区域,三角形顶点为三个控制点, 在三角形区内满足以下线性关系:
21 | $$
22 | \left\{\begin{array}{l}
23 | x=a u+b v+c \\
24 | y=d u+e v+f
25 | \end{array}\right.\tag{5-52}
26 | $$
27 | 若三对控制点在两个坐标系中的位置分别为 $\left(x_1, y_1\right) 、\left(x_2, y_2\right)$ 、 $\left(x_3, y_3\right)$ 和 $\left(u_1, v_1\right) 、\left(u_2, v_2\right) 、\left(u_3, v_3\right)$, 则可建立两级方程组:
28 | $$
29 | \left\{\begin{array}{l}
30 | x_1=a u_1+b v_1+c \\
31 | x_2=a u_2+b v_2+c \\
32 | x_3=a u_3+b v_3+c
33 | \end{array}\right.\tag{5-53a}
34 | $$
35 |
36 | $$
37 | \left\{\begin{array}{l}
38 | y_1=d u_1+e v_1+f \\
39 | y_2=d u_2+e v_2+f \\
40 | y_3=d u_3+e v_3+f
41 | \end{array}\right.\tag{5-53b}
42 | $$
43 |
44 | 解方程组(5-53),可求出a, b, c, d, e, f六个系数。用式(5-53)可实现该三角形区内其他像点的坐标变换。对于不同的三角形控制区域,这六个系数的值是不同的。
45 | 三角形线性法简单,能满足一定的精度要求,这是因它是以局部范围内的线性失真去处理大范围内的非线性失真, 所以选择的控制点对越多,分布越均匀,三角形区域的面积越小, 则变换的精度越高。但是控制点过多又会导致计算量的增加, 因此需要综合考虑。
46 |
47 | ### 灰度值的确定
48 |
49 | 图像经几何位置校正后,在校正空间中各像点的灰度值等于被校正图像对应点的灰度值。一般校正后的图像某些像素点可能挤压在一起,或者分散开,不会恰好落在坐标点上,因此常采用内插法来求得这些像素点的灰度值。经常使用的方法有如下两种。
50 |
51 | 1) 最近邻点法
52 | 最近邻点法是取与像素点相邻的4个点中距离最近的邻点灰度值作为该点的灰度值。如图5-5所示。显然,最近邻点法计算简单,但精度不高,同时校正后的图像亮度有明显的不连续性。
53 |
54 |
8 |
9 | 图5-4 几种典型的几何失真
10 | (a) 原图像; (b) 梯形失真; (c) 枕形失真; (d) 桶形失真
11 |
12 | 一般,几何畸变校正要对失真的图像进行精确的几何校正, 通常是先确定一幅图像为基准,然后去校正另一幅图像的几何形状。因此,几何畸变校正一般分两步来做:第一步是图像空间坐标的变换;第二步是重新确定在校正空间各像素点的取值。
13 |
14 | ### 空间几何坐标变换
15 |
16 | 按照一幅标准图像 $g(u, v)$ 或一组基准点去校正另一幅几何失真图像 $f(x, y)$, 称之为空间几何坐标变换。根据两幅图像的一些 已知对应点对(也称为控制点对)建立起函数关系式, 将失真图像的 $x-y$ 坐标系变换到标准图像 $u-v$ 坐标系, 从而实现失真图像按标准图像的几何位置校正, 使 $f(x, y)$ 中的每一像点都可在 $g(u, v)$ 中找到对应像点。
17 |
18 | ### 三角形线性法
19 |
20 | 图像的几何失真虽然是非线性的,但在一个局部小区域内可近似认为是线性的,基于这一假设,将标准图像和被校正图像之间的对应点对划分成一系列小三角形区域,三角形顶点为三个控制点, 在三角形区内满足以下线性关系:
21 | $$
22 | \left\{\begin{array}{l}
23 | x=a u+b v+c \\
24 | y=d u+e v+f
25 | \end{array}\right.\tag{5-52}
26 | $$
27 | 若三对控制点在两个坐标系中的位置分别为 $\left(x_1, y_1\right) 、\left(x_2, y_2\right)$ 、 $\left(x_3, y_3\right)$ 和 $\left(u_1, v_1\right) 、\left(u_2, v_2\right) 、\left(u_3, v_3\right)$, 则可建立两级方程组:
28 | $$
29 | \left\{\begin{array}{l}
30 | x_1=a u_1+b v_1+c \\
31 | x_2=a u_2+b v_2+c \\
32 | x_3=a u_3+b v_3+c
33 | \end{array}\right.\tag{5-53a}
34 | $$
35 |
36 | $$
37 | \left\{\begin{array}{l}
38 | y_1=d u_1+e v_1+f \\
39 | y_2=d u_2+e v_2+f \\
40 | y_3=d u_3+e v_3+f
41 | \end{array}\right.\tag{5-53b}
42 | $$
43 |
44 | 解方程组(5-53),可求出a, b, c, d, e, f六个系数。用式(5-53)可实现该三角形区内其他像点的坐标变换。对于不同的三角形控制区域,这六个系数的值是不同的。
45 | 三角形线性法简单,能满足一定的精度要求,这是因它是以局部范围内的线性失真去处理大范围内的非线性失真, 所以选择的控制点对越多,分布越均匀,三角形区域的面积越小, 则变换的精度越高。但是控制点过多又会导致计算量的增加, 因此需要综合考虑。
46 |
47 | ### 灰度值的确定
48 |
49 | 图像经几何位置校正后,在校正空间中各像点的灰度值等于被校正图像对应点的灰度值。一般校正后的图像某些像素点可能挤压在一起,或者分散开,不会恰好落在坐标点上,因此常采用内插法来求得这些像素点的灰度值。经常使用的方法有如下两种。
50 |
51 | 1) 最近邻点法
52 | 最近邻点法是取与像素点相邻的4个点中距离最近的邻点灰度值作为该点的灰度值。如图5-5所示。显然,最近邻点法计算简单,但精度不高,同时校正后的图像亮度有明显的不连续性。
53 |
54 | 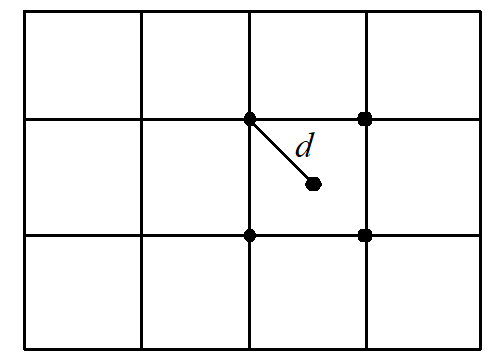 55 |
56 | 图5-5 最近邻点法
57 |
58 | 2. 内插法
59 | 用像素点周围4个邻点的灰度值加权内插作为g(u0, v0),如图5-6所示,设像素点(x0, y0)周围4个点为$(x_1, y_1), (x_1+1, y_1), (x_1, y_1+1), (x_1+1, y_1+1)$,则校正值为
60 |
61 | $$
62 | \begin{aligned}
63 | g\left(u_0, v_0\right)= & (1-\alpha)(1-\beta) f\left(x_1, y_1\right)+\alpha(1-\beta) f\left(x_1+1, y_1\right) \\
64 | & +(1-\alpha) \beta f\left(x_1, y_1+1\right)+\alpha \beta f\left(x_1+1, y_1+1\right)
65 | \end{aligned}\tag{5-54}
66 | $$
67 |
68 | 式中:
69 | $$
70 | \alpha=\left|x_0-x_1\right|, \beta=\left|y_0-y_1\right|
71 | $$
72 |
55 |
56 | 图5-5 最近邻点法
57 |
58 | 2. 内插法
59 | 用像素点周围4个邻点的灰度值加权内插作为g(u0, v0),如图5-6所示,设像素点(x0, y0)周围4个点为$(x_1, y_1), (x_1+1, y_1), (x_1, y_1+1), (x_1+1, y_1+1)$,则校正值为
60 |
61 | $$
62 | \begin{aligned}
63 | g\left(u_0, v_0\right)= & (1-\alpha)(1-\beta) f\left(x_1, y_1\right)+\alpha(1-\beta) f\left(x_1+1, y_1\right) \\
64 | & +(1-\alpha) \beta f\left(x_1, y_1+1\right)+\alpha \beta f\left(x_1+1, y_1+1\right)
65 | \end{aligned}\tag{5-54}
66 | $$
67 |
68 | 式中:
69 | $$
70 | \alpha=\left|x_0-x_1\right|, \beta=\left|y_0-y_1\right|
71 | $$
72 | 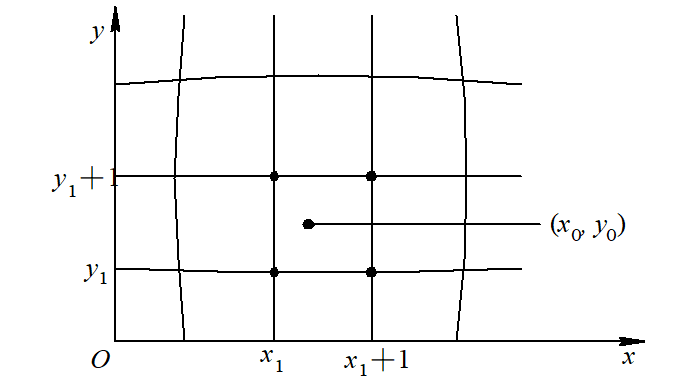 73 |
74 | 图5-6 内插法几何校正
75 |
76 | ## 5.6.2 盲目图像复原
77 |
78 | 盲目图像复原法是在没有图像退化先验知识的情况下,对观察目标的多幅图像以某种方式抽出退化信息, 从而进行图像复原的方法。
79 | 加性噪声的模糊图像复原方法一般有两种: 直接测量法和间接估计法。
80 | 用直接测量法复原图像时,需要测量图像的模糊脉冲响应和噪声功率谱或协方差函数。在所观察的景物中,点光源能量往往直接指示出冲激响应;另外,图像边缘是否陡峭也能用来推测模糊冲激响应。在背景亮度相对恒定的区域内测量图像的协方差,可以估计出观测图像的噪声协方差函数。
81 |
82 | 间接估计法复原图像类似于多图像平均法处理。如对一个景物连续拍摄 $N$ 次, 每一次获取的图像用下式表示:
83 | $$
84 | g_i(x, y)=f(x, y)+n_i(x, y) \quad i=1,2, \ldots, N\tag{5-55}
85 | $$
86 | 式中: $f(x, y)$ 是原始图像, $g_i(x, y)$ 是第次获取的图像, $n_i(x, y)$ 是第 $i$ 次的噪声函数。
87 | $$
88 | f(x, y)=\frac{1}{N} \sum_{i=1}^N g_i(x, y)-\frac{1}{N} \sum_{i=1}^N n_i(x, y)\tag{5-56}
89 | $$
90 | 当 $N$ 很大时, 上式右边的噪声项的值趋于它的数学期望 $E\{n(x$, $y)\}$ 。一般情况下白色高斯噪声在所有 $(x, y)$ 上的数学期望等于零。 因此,原始图像为
91 | $$
92 | f(x, y)=\frac{1}{N} \sum_{i=1}^N g_i(x, y)\tag{5-57}
93 | $$
94 | 盲目图像复原
95 | 若 $g_{i}(x, y)=f_{i}(x, y)^* h_{i}(x, y)$
96 | 则 $G_i(n, v)=F_i(u, v) H_{i}(u, v)$
97 | $\ln G_{i}(n, v)=\ln \left[F_{i}(u, v)\right]+\ln \left[H_{i}(u, v)\right]$
98 | 如果帧间退化冲激响应不相关, 则
99 | $$
100 | \sum_{i=1}^M \ln \left[G_i(u, v)\right]=M \ln \left[F_i(u, v)\right]+\sum_{i=1}^M \ln \left[H_i(u, v)\right]
101 | $$
102 | 当M很大时, 传递函数的对数和接近一恒定值
103 | $$
104 | \begin{gathered}
105 | K_H=\lim _{M \rightarrow \infty} \sum_{i=1}^M \ln \left[H_i(u, v)\right] \quad \hat{F}_i(u, v)=\exp \left\{\frac{k_H(u, v)}{M} \prod_{i=1}^M\left[G_i(u, v)\right]^{\frac{1}{M}}\right\} \\
106 | \hat{f}(x, y)=J^{-1}\left[\hat{F_G}(u, v)\right]
107 | \end{gathered}
108 | $$
--------------------------------------------------------------------------------
/V/5.7 编程实例.md:
--------------------------------------------------------------------------------
1 | # 5.7 编程实例
2 |
3 | 根据前面章节的讨论, 图像退化的模型为
4 | $$
5 | g(x, y)=f(x, y) * h(x, y)+n(x, y)
6 | $$
7 | 那么,图像复原的过程可认为是已知$g(x,y),h(x,y),n(x,y)$的一些先验知识,求出$f(x,y)$。对于不同的退化函数和噪声性质, 可推导出前面介绍的一些图像复原方法。本节介绍实际中经常用到的逆滤波复原图像法。
8 |
9 | 图像的点扩展函数$h$为
10 | $$
11 | h=\frac{1}{49}
12 | \left[
13 | \begin{array}{lllllll}
14 | 1 &1& 1& 1& 1& 1& 1\\
15 | 1 &1& 1& 1& 1& 1& 1\\
16 | 1 &1& 1& 1& 1& 1& 1\\
17 | 1 &1& 1& 1& 1& 1& 1\\
18 | 1 &1& 1& 1& 1& 1& 1\\
19 | 1 &1& 1& 1& 1& 1& 1\\
20 | 1 &1& 1& 1& 1& 1& 1\\
21 | \end{array}
22 | \right]
23 | $$
24 | 首先使用退化函数$h$对图像进行模糊操作, 生成一幅退化的图像,退化系统为
25 | $$
26 | g=F^{-1}(F(h) \cdot F(f))
27 | $$
28 | 上式的计算过程是,先求出图像和退化函数的傅立叶变换, 在频域相乘后,再按下式求逆傅立叶变换:
29 | $$
30 | \hat{f}=F^{-1}\left(\frac{G}{H}\right)=F^{-1}\left(\frac{F(g)}{F(h)}\right)
31 | $$
32 | 图像复原的具体实现过程如下。
33 |
34 | ## 添加菜单
35 |
36 |
73 |
74 | 图5-6 内插法几何校正
75 |
76 | ## 5.6.2 盲目图像复原
77 |
78 | 盲目图像复原法是在没有图像退化先验知识的情况下,对观察目标的多幅图像以某种方式抽出退化信息, 从而进行图像复原的方法。
79 | 加性噪声的模糊图像复原方法一般有两种: 直接测量法和间接估计法。
80 | 用直接测量法复原图像时,需要测量图像的模糊脉冲响应和噪声功率谱或协方差函数。在所观察的景物中,点光源能量往往直接指示出冲激响应;另外,图像边缘是否陡峭也能用来推测模糊冲激响应。在背景亮度相对恒定的区域内测量图像的协方差,可以估计出观测图像的噪声协方差函数。
81 |
82 | 间接估计法复原图像类似于多图像平均法处理。如对一个景物连续拍摄 $N$ 次, 每一次获取的图像用下式表示:
83 | $$
84 | g_i(x, y)=f(x, y)+n_i(x, y) \quad i=1,2, \ldots, N\tag{5-55}
85 | $$
86 | 式中: $f(x, y)$ 是原始图像, $g_i(x, y)$ 是第次获取的图像, $n_i(x, y)$ 是第 $i$ 次的噪声函数。
87 | $$
88 | f(x, y)=\frac{1}{N} \sum_{i=1}^N g_i(x, y)-\frac{1}{N} \sum_{i=1}^N n_i(x, y)\tag{5-56}
89 | $$
90 | 当 $N$ 很大时, 上式右边的噪声项的值趋于它的数学期望 $E\{n(x$, $y)\}$ 。一般情况下白色高斯噪声在所有 $(x, y)$ 上的数学期望等于零。 因此,原始图像为
91 | $$
92 | f(x, y)=\frac{1}{N} \sum_{i=1}^N g_i(x, y)\tag{5-57}
93 | $$
94 | 盲目图像复原
95 | 若 $g_{i}(x, y)=f_{i}(x, y)^* h_{i}(x, y)$
96 | 则 $G_i(n, v)=F_i(u, v) H_{i}(u, v)$
97 | $\ln G_{i}(n, v)=\ln \left[F_{i}(u, v)\right]+\ln \left[H_{i}(u, v)\right]$
98 | 如果帧间退化冲激响应不相关, 则
99 | $$
100 | \sum_{i=1}^M \ln \left[G_i(u, v)\right]=M \ln \left[F_i(u, v)\right]+\sum_{i=1}^M \ln \left[H_i(u, v)\right]
101 | $$
102 | 当M很大时, 传递函数的对数和接近一恒定值
103 | $$
104 | \begin{gathered}
105 | K_H=\lim _{M \rightarrow \infty} \sum_{i=1}^M \ln \left[H_i(u, v)\right] \quad \hat{F}_i(u, v)=\exp \left\{\frac{k_H(u, v)}{M} \prod_{i=1}^M\left[G_i(u, v)\right]^{\frac{1}{M}}\right\} \\
106 | \hat{f}(x, y)=J^{-1}\left[\hat{F_G}(u, v)\right]
107 | \end{gathered}
108 | $$
--------------------------------------------------------------------------------
/V/5.7 编程实例.md:
--------------------------------------------------------------------------------
1 | # 5.7 编程实例
2 |
3 | 根据前面章节的讨论, 图像退化的模型为
4 | $$
5 | g(x, y)=f(x, y) * h(x, y)+n(x, y)
6 | $$
7 | 那么,图像复原的过程可认为是已知$g(x,y),h(x,y),n(x,y)$的一些先验知识,求出$f(x,y)$。对于不同的退化函数和噪声性质, 可推导出前面介绍的一些图像复原方法。本节介绍实际中经常用到的逆滤波复原图像法。
8 |
9 | 图像的点扩展函数$h$为
10 | $$
11 | h=\frac{1}{49}
12 | \left[
13 | \begin{array}{lllllll}
14 | 1 &1& 1& 1& 1& 1& 1\\
15 | 1 &1& 1& 1& 1& 1& 1\\
16 | 1 &1& 1& 1& 1& 1& 1\\
17 | 1 &1& 1& 1& 1& 1& 1\\
18 | 1 &1& 1& 1& 1& 1& 1\\
19 | 1 &1& 1& 1& 1& 1& 1\\
20 | 1 &1& 1& 1& 1& 1& 1\\
21 | \end{array}
22 | \right]
23 | $$
24 | 首先使用退化函数$h$对图像进行模糊操作, 生成一幅退化的图像,退化系统为
25 | $$
26 | g=F^{-1}(F(h) \cdot F(f))
27 | $$
28 | 上式的计算过程是,先求出图像和退化函数的傅立叶变换, 在频域相乘后,再按下式求逆傅立叶变换:
29 | $$
30 | \hat{f}=F^{-1}\left(\frac{G}{H}\right)=F^{-1}\left(\frac{F(g)}{F(h)}\right)
31 | $$
32 | 图像复原的具体实现过程如下。
33 |
34 | ## 添加菜单
35 |
36 |  37 |
38 | 图11-7 图像复原菜单
39 |
40 | ## 添加消息映射
41 |
42 | 在文档类中添加两个消息映射函数, 分别是OnRestoreBlur()和OnRestoreInvfilt()。OnRestorBlur()调用图像复原类CRestore的ConvBlur()函数生成一幅退化图像。OnRestoreInvfilt()调用图像复原类CRestore的InvFilter()函数对退化图像进行复原。代码如下:
43 |
44 | ```c++
45 | void CDipDoc: : OnRestoreBlur()
46 | {
47 | // TODO: Add your command handler code here
48 | //判断当前是否载入图像
49 | if( m_pImageObject == NULL ) return; D
50 | //定义一个图像复原对象
51 | CRestore Restore( m_pImageObject );
52 | //调用卷积模糊函数
53 | Restore.ConvBlur();
54 | //更新视图
55 | UpdateAllViews(NULL);
56 | }
57 | OnRestoreInvfilt()函数主要代码如下, 其他代码与OnRestoreBlur()相同。
58 | void CDipDoc: : OnRestoreInvfilt()
59 | {
60 |
61 | //调用逆滤波复原函数
62 | Restore.InvFilter();
63 |
64 | }
65 |
66 | ```
67 |
68 | ## CRestore类介绍
69 |
70 | 功能: 实现图像复原
71 | 函数列表:
72 | ConvBlur() 对图像进行卷积模糊处理, 生成一幅待复原的退化图像;
73 | InvFilter() 逆滤波复原法, 对由卷积模糊所造成的退化图像进行复原;
74 | ConvNoiseBlur() 对图像进行卷积噪声模糊处理, 生成一幅待复原的退化图像;
75 | Wiener() 维纳滤波复原法, 对由卷积噪声所造成的退化图像进行复原。
76 |
77 | ## 函数实现代码
78 |
79 | ```c++
80 | ConvBlur()函数关键代码
81 | {
82 |
83 | //定义卷积模板, 大小为7×7
84 | Mm m_matFilter;
85 | m_matFilter=zeros(nHeight, nWidth);
86 | int i, j;
87 | for(i=1; i<7; i++)
88 | {
89 | for(j=1; j<7; j++)
90 | {
91 | m_matFilter.r(i, j)=0.02;
92 | }
93 | }
94 | // m_matBits是一个二维矩阵, 存储的是图像数据
95 | //对原图像进行快速傅立叶变换, 将图像从空域变换到频域
96 | m_matBits=fft2(m_matBits);
97 | //对模板进行快速傅立叶变换
98 | m_matFilter=fft2(m_matFilter);
99 | //频率相乘
100 | for(i=1; i<=nHeight; i++)
101 | {
102 | for(j=1; j<=nWidth; j++)
103 | {
104 | m_matBits.r(i, j)=m_matBits.r(i, j)*m_matFilter.r(i, j)-m_matBits.i(i, j)*m_matFilter.i(i, j);
105 | m_matBits.i(i, j)=m_matBits.r(i, j)*m_matFilter.i(i, j)+m_matBits.i(i, j)*m_matFilter.r(i, j);
106 | }
107 | }
108 | //对图像做逆傅立叶变换, 将图像从频域变换到空域
109 | m_matBits=ifft2(m_matBits);
110 |
111 | }
112 | InvFilter()函数关键代码
113 | {
114 | //对原图像进行快速傅立叶变换, 将图像从空域变换到频域
115 | m_matBits=fft2(m_matBits);
116 | //对模板进行快速傅立叶变换
117 | m_matFilter=fft2(m_matFilter);
118 | //频率相乘
119 | double a, b, c, d;
120 | for(i=1; i<=nHeight; i++)
121 | {
122 | for(j=1; j<=nWidth; j++)
123 | {
124 | a=m_matBits.r(i, j);
125 | b=m_matBits.i(i, j);
126 | c=m_matFilter.r(i, j);
127 | d=m_matFilter.i(i, j);
128 | if(c*c+d*d>0.003)
129 | {
130 | m_matBits.r(i, j)=(a*c+b*d)/(c*c+d*d);
131 | m_matBits.i(i, j)=(b*c-a*d)/(c*c+d*d);
132 | }
133 | }
134 | }
135 | //对图像进行快速逆傅立叶变换, 将图像从频域变换到空域
136 | m_matBits=ifft2(m_matBits);
137 | }
138 |
139 | ```
140 |
141 |
37 |
38 | 图11-7 图像复原菜单
39 |
40 | ## 添加消息映射
41 |
42 | 在文档类中添加两个消息映射函数, 分别是OnRestoreBlur()和OnRestoreInvfilt()。OnRestorBlur()调用图像复原类CRestore的ConvBlur()函数生成一幅退化图像。OnRestoreInvfilt()调用图像复原类CRestore的InvFilter()函数对退化图像进行复原。代码如下:
43 |
44 | ```c++
45 | void CDipDoc: : OnRestoreBlur()
46 | {
47 | // TODO: Add your command handler code here
48 | //判断当前是否载入图像
49 | if( m_pImageObject == NULL ) return; D
50 | //定义一个图像复原对象
51 | CRestore Restore( m_pImageObject );
52 | //调用卷积模糊函数
53 | Restore.ConvBlur();
54 | //更新视图
55 | UpdateAllViews(NULL);
56 | }
57 | OnRestoreInvfilt()函数主要代码如下, 其他代码与OnRestoreBlur()相同。
58 | void CDipDoc: : OnRestoreInvfilt()
59 | {
60 |
61 | //调用逆滤波复原函数
62 | Restore.InvFilter();
63 |
64 | }
65 |
66 | ```
67 |
68 | ## CRestore类介绍
69 |
70 | 功能: 实现图像复原
71 | 函数列表:
72 | ConvBlur() 对图像进行卷积模糊处理, 生成一幅待复原的退化图像;
73 | InvFilter() 逆滤波复原法, 对由卷积模糊所造成的退化图像进行复原;
74 | ConvNoiseBlur() 对图像进行卷积噪声模糊处理, 生成一幅待复原的退化图像;
75 | Wiener() 维纳滤波复原法, 对由卷积噪声所造成的退化图像进行复原。
76 |
77 | ## 函数实现代码
78 |
79 | ```c++
80 | ConvBlur()函数关键代码
81 | {
82 |
83 | //定义卷积模板, 大小为7×7
84 | Mm m_matFilter;
85 | m_matFilter=zeros(nHeight, nWidth);
86 | int i, j;
87 | for(i=1; i<7; i++)
88 | {
89 | for(j=1; j<7; j++)
90 | {
91 | m_matFilter.r(i, j)=0.02;
92 | }
93 | }
94 | // m_matBits是一个二维矩阵, 存储的是图像数据
95 | //对原图像进行快速傅立叶变换, 将图像从空域变换到频域
96 | m_matBits=fft2(m_matBits);
97 | //对模板进行快速傅立叶变换
98 | m_matFilter=fft2(m_matFilter);
99 | //频率相乘
100 | for(i=1; i<=nHeight; i++)
101 | {
102 | for(j=1; j<=nWidth; j++)
103 | {
104 | m_matBits.r(i, j)=m_matBits.r(i, j)*m_matFilter.r(i, j)-m_matBits.i(i, j)*m_matFilter.i(i, j);
105 | m_matBits.i(i, j)=m_matBits.r(i, j)*m_matFilter.i(i, j)+m_matBits.i(i, j)*m_matFilter.r(i, j);
106 | }
107 | }
108 | //对图像做逆傅立叶变换, 将图像从频域变换到空域
109 | m_matBits=ifft2(m_matBits);
110 |
111 | }
112 | InvFilter()函数关键代码
113 | {
114 | //对原图像进行快速傅立叶变换, 将图像从空域变换到频域
115 | m_matBits=fft2(m_matBits);
116 | //对模板进行快速傅立叶变换
117 | m_matFilter=fft2(m_matFilter);
118 | //频率相乘
119 | double a, b, c, d;
120 | for(i=1; i<=nHeight; i++)
121 | {
122 | for(j=1; j<=nWidth; j++)
123 | {
124 | a=m_matBits.r(i, j);
125 | b=m_matBits.i(i, j);
126 | c=m_matFilter.r(i, j);
127 | d=m_matFilter.i(i, j);
128 | if(c*c+d*d>0.003)
129 | {
130 | m_matBits.r(i, j)=(a*c+b*d)/(c*c+d*d);
131 | m_matBits.i(i, j)=(b*c-a*d)/(c*c+d*d);
132 | }
133 | }
134 | }
135 | //对图像进行快速逆傅立叶变换, 将图像从频域变换到空域
136 | m_matBits=ifft2(m_matBits);
137 | }
138 |
139 | ```
140 |
141 |  142 |
143 | 图11-8 逆滤波法复原图像
144 | (a) 原始图像; (b) 退化图像; (c)复原图像
--------------------------------------------------------------------------------
/VI/6.1 几何变换基础.md:
--------------------------------------------------------------------------------
1 | # 6.1 几何变换基础
2 |
3 |
4 |
5 | ## 6.1.1 概述
6 |
7 | 图像的几何变换,是指使用户获得或设计的原始图像。按照需要产生大小、形状和位置的变化。从图像类型来分,图像的几何变换有二维平面图像的几何变换和三维图像的几何变换以及由三维向二维平面投影变换等。从变换的性质分, 图像的几何变换有平移、比例缩放、旋转、反射和错切等基本变换,透视变换等复合变换,以及插值运算等。
8 |
9 | 数字图像是把连续图像在坐标空间和性质空间离散化了的图像。例如,一幅二维数字图像就是把一幅连续的二维(2D)。图像在坐标空间XOY和性质空间F都离散化了的图像,它可以用一组二维(2D)数组f(x, y)来表示,其中x和y表示2D空间XOY中一个坐标点的位置,f代表图像在点(x, y)的某种性质F的数值,如果所处理的是一幅灰度图,这时f表示灰度值。而且此时f、x、y都在整数集合中取值。因此,除了插值运算外,常见的图像几何变换可以通过与之对应的矩阵线性变换来实现。
10 |
11 | 对于2D图像几何变换及变换中心在坐标原点的比例缩放、 反射、 错切和旋转等各种变换,都可以用2×2的矩阵表示和实现。但是一个2×2变换矩阵$T=\left[\begin{array}{ll}a & b \\ c & d\end{array}\right]$却不能实现图像的平移以及绕任意点的比例缩放、反射、错切和旋转等各种变换。因此,为了能够用统一的矩阵线性变换形式,表示和实现这些常见的图像几何变换,就需要引入一种新的坐标,即齐次坐标。利用齐次坐标来变换处理,才能实现上述各种2D图像的几何变换。
12 |
13 | ## 6.1.2 齐次坐标
14 |
15 | 现设点 $P_0\left(x_0, y_0\right)$ 进行平移后, 移到 $P(x, y)$, 其中 $x$ 方向的平移量为 $\Delta x, y$ 方向的平移量为 $\Delta y$ 。那么, 点 $P(x, y)$ 的坐标为
16 | $$
17 | \left\{\begin{array}{l}
18 | x=x_0+\Delta x \\
19 | y=y_0+\Delta y
20 | \end{array}\right.
21 | $$
22 | 如图6-1所示。这个变换用矩阵的形式可以表示为
23 | $$
24 | \left[\begin{array}{l}
25 | x \\
26 | y
27 | \end{array}\right]=\left[\begin{array}{ll}
28 | 1 & 0 \\
29 | 0 & 1
30 | \end{array}\right]\left[\begin{array}{l}
31 | x_0 \\
32 | y_0
33 | \end{array}\right]+\left[\begin{array}{l}
34 | \Delta x \\
35 | \Delta y
36 | \end{array}\right]
37 | $$
38 | 图6-1 点的平移(不再是笛卡尔坐标系)
39 |
40 | 而平面上点的变换矩阵$T=\left[\begin{array}{ll}a & b \\ c & d\end{array}\right]$中没有引入平移常量,无论$a、b、c、d$取什么值,都不能实现上述的平移变换。因此,需要使用$2\times3$阶变换矩阵,取其形式为
41 | $$
42 | T=\left[\begin{array}{ccc}
43 | 1 & 0 & \Delta x \\
44 | 0 & 1 & \Delta y
45 | \end{array}\right]
46 | $$
47 | 此矩阵的第一、二列构成单位矩阵,第三列元素为平移常量。由上述可知,对2D图像进行变换,只需要将图像的点集矩阵乘以变换矩阵即可,2D图像对应的点集矩阵是2×*n*阶的,而上式扩展后的变换矩阵是2×3阶的矩阵,这不符合矩阵相乘时要求前者的列数与后者的行数相等的规则。
48 |
49 | 所以需要在点的坐标列矩阵 $\left[\begin{array}{ll}x & y\end{array}\right]^{T}$ 中引入第三个元素, 增加一个附加坐标, 扩展为 $3 \times 1$ 的列矩阵 $\left[\begin{array}{lll}x & y & 1\end{array}\right]^{T}$, 这样用三维空间点 $(x, y, 1)$ 表示二维空间点 $(x, y)$, 即采用一种特殊的坐标,可以实现平移变换,变换结果为
50 | $$
51 | P=T \cdot P_0=\left[\begin{array}{ccc}1 & 0 & \Delta x \\ 0 & 1 & \Delta y\end{array}\right]\left[\begin{array}{l}x_0 \\ y_0 \\ 1\end{array}\right]=\left[\begin{array}{l}x_0+\Delta x \\ y_0+\Delta y\end{array}\right]=\left[\begin{array}{l}x \\ y\end{array}\right]
52 | $$
53 |
54 | 式 $\left\{\begin{array}{l}x=x_0+\Delta x \\ y=y_0+\Delta y\end{array}\right.$ 符合上述平移后的坐标位置。通常将 $2 \times 3$ 阶矩阵扩
55 | 充为 $3 \times 3$ 阶矩阵, 以拓宽功能。由此可得平移变换矩阵为
56 | $$
57 | T=\left[\begin{array}{lll}
58 | 1 & 0 & \Delta x \\
59 | 0 & 1 & \Delta y
60 | \end{array}\right] \text { a- }
61 | $$
62 | 下面再验证一下点 $P(x, y)$ 按照 $3 \times 3$ 的变换矩阵 $T$ 平移变换的结果
63 | $$
64 | P=T \cdot P_0=\left[\begin{array}{lll}
65 | 1 & 0 & \Delta x \\
66 | 0 & 1 & \Delta y \\
67 | 0 & 0 & 1
68 | \end{array}\right]\left[\begin{array}{l}
69 | x_0 \\
70 | y_0 \\
71 | 1
72 | \end{array}\right]=\left[\begin{array}{l}
73 | x_0+\Delta x \\
74 | y_0+\Delta y \\
75 | 1
76 | \end{array}\right]=\left[\begin{array}{l}
77 | x \\
78 | y \\
79 | 1
80 | \end{array}\right]
81 | $$
82 | 从上式可以看出, 引入附加坐标后, 扩充了矩阵的第 3 行, 并没有使变换结果受到影响。这种用 $n+1$ 维向量表示 $n$ 维向量的方法称为齐次坐标表示法。
83 |
84 | 因此, 2D图像中的点坐标 $(x, y)$ 通常表示成齐次坐标 $(H x, H y$, H), 其中 $H$ 表示非零的任意实数, 当 $H=1$ 时, 则 $(x, y, 1)$ 就称为点 $(x, y)$ 的规范化齐次坐标。显然规范化齐次坐标的前两个数是相应二维点的坐标, 没有变化, 仅在原坐标中增加了 $H=1$ 的附加坐标。
85 | 由点的齐次坐标 $(H x, H y, H)$ 求点的规范化齐次坐标 $(x, y,1)$, 可按如下公式进行:
86 | $$
87 | x=\frac{H x}{H} \quad y=\frac{H y}{H}
88 | $$
89 |
90 | 齐次坐标的几何意义相当于点 $(x, y)$ 落在 $3 D$ 空间 $H=1$ 的平面上, 如图6-2所示。如果将XOY 平面内的三角形 $abc$ 的各顶点表示成齐次坐标 $\left(x_i, y_i, 1\right)(i=1,2,3)$ 的形式, 就变成 $H=1$ 平面内的三角形 $a_1 b_1 c_1$ 的各顶点。
91 |
92 |
142 |
143 | 图11-8 逆滤波法复原图像
144 | (a) 原始图像; (b) 退化图像; (c)复原图像
--------------------------------------------------------------------------------
/VI/6.1 几何变换基础.md:
--------------------------------------------------------------------------------
1 | # 6.1 几何变换基础
2 |
3 |
4 |
5 | ## 6.1.1 概述
6 |
7 | 图像的几何变换,是指使用户获得或设计的原始图像。按照需要产生大小、形状和位置的变化。从图像类型来分,图像的几何变换有二维平面图像的几何变换和三维图像的几何变换以及由三维向二维平面投影变换等。从变换的性质分, 图像的几何变换有平移、比例缩放、旋转、反射和错切等基本变换,透视变换等复合变换,以及插值运算等。
8 |
9 | 数字图像是把连续图像在坐标空间和性质空间离散化了的图像。例如,一幅二维数字图像就是把一幅连续的二维(2D)。图像在坐标空间XOY和性质空间F都离散化了的图像,它可以用一组二维(2D)数组f(x, y)来表示,其中x和y表示2D空间XOY中一个坐标点的位置,f代表图像在点(x, y)的某种性质F的数值,如果所处理的是一幅灰度图,这时f表示灰度值。而且此时f、x、y都在整数集合中取值。因此,除了插值运算外,常见的图像几何变换可以通过与之对应的矩阵线性变换来实现。
10 |
11 | 对于2D图像几何变换及变换中心在坐标原点的比例缩放、 反射、 错切和旋转等各种变换,都可以用2×2的矩阵表示和实现。但是一个2×2变换矩阵$T=\left[\begin{array}{ll}a & b \\ c & d\end{array}\right]$却不能实现图像的平移以及绕任意点的比例缩放、反射、错切和旋转等各种变换。因此,为了能够用统一的矩阵线性变换形式,表示和实现这些常见的图像几何变换,就需要引入一种新的坐标,即齐次坐标。利用齐次坐标来变换处理,才能实现上述各种2D图像的几何变换。
12 |
13 | ## 6.1.2 齐次坐标
14 |
15 | 现设点 $P_0\left(x_0, y_0\right)$ 进行平移后, 移到 $P(x, y)$, 其中 $x$ 方向的平移量为 $\Delta x, y$ 方向的平移量为 $\Delta y$ 。那么, 点 $P(x, y)$ 的坐标为
16 | $$
17 | \left\{\begin{array}{l}
18 | x=x_0+\Delta x \\
19 | y=y_0+\Delta y
20 | \end{array}\right.
21 | $$
22 | 如图6-1所示。这个变换用矩阵的形式可以表示为
23 | $$
24 | \left[\begin{array}{l}
25 | x \\
26 | y
27 | \end{array}\right]=\left[\begin{array}{ll}
28 | 1 & 0 \\
29 | 0 & 1
30 | \end{array}\right]\left[\begin{array}{l}
31 | x_0 \\
32 | y_0
33 | \end{array}\right]+\left[\begin{array}{l}
34 | \Delta x \\
35 | \Delta y
36 | \end{array}\right]
37 | $$
38 | 图6-1 点的平移(不再是笛卡尔坐标系)
39 |
40 | 而平面上点的变换矩阵$T=\left[\begin{array}{ll}a & b \\ c & d\end{array}\right]$中没有引入平移常量,无论$a、b、c、d$取什么值,都不能实现上述的平移变换。因此,需要使用$2\times3$阶变换矩阵,取其形式为
41 | $$
42 | T=\left[\begin{array}{ccc}
43 | 1 & 0 & \Delta x \\
44 | 0 & 1 & \Delta y
45 | \end{array}\right]
46 | $$
47 | 此矩阵的第一、二列构成单位矩阵,第三列元素为平移常量。由上述可知,对2D图像进行变换,只需要将图像的点集矩阵乘以变换矩阵即可,2D图像对应的点集矩阵是2×*n*阶的,而上式扩展后的变换矩阵是2×3阶的矩阵,这不符合矩阵相乘时要求前者的列数与后者的行数相等的规则。
48 |
49 | 所以需要在点的坐标列矩阵 $\left[\begin{array}{ll}x & y\end{array}\right]^{T}$ 中引入第三个元素, 增加一个附加坐标, 扩展为 $3 \times 1$ 的列矩阵 $\left[\begin{array}{lll}x & y & 1\end{array}\right]^{T}$, 这样用三维空间点 $(x, y, 1)$ 表示二维空间点 $(x, y)$, 即采用一种特殊的坐标,可以实现平移变换,变换结果为
50 | $$
51 | P=T \cdot P_0=\left[\begin{array}{ccc}1 & 0 & \Delta x \\ 0 & 1 & \Delta y\end{array}\right]\left[\begin{array}{l}x_0 \\ y_0 \\ 1\end{array}\right]=\left[\begin{array}{l}x_0+\Delta x \\ y_0+\Delta y\end{array}\right]=\left[\begin{array}{l}x \\ y\end{array}\right]
52 | $$
53 |
54 | 式 $\left\{\begin{array}{l}x=x_0+\Delta x \\ y=y_0+\Delta y\end{array}\right.$ 符合上述平移后的坐标位置。通常将 $2 \times 3$ 阶矩阵扩
55 | 充为 $3 \times 3$ 阶矩阵, 以拓宽功能。由此可得平移变换矩阵为
56 | $$
57 | T=\left[\begin{array}{lll}
58 | 1 & 0 & \Delta x \\
59 | 0 & 1 & \Delta y
60 | \end{array}\right] \text { a- }
61 | $$
62 | 下面再验证一下点 $P(x, y)$ 按照 $3 \times 3$ 的变换矩阵 $T$ 平移变换的结果
63 | $$
64 | P=T \cdot P_0=\left[\begin{array}{lll}
65 | 1 & 0 & \Delta x \\
66 | 0 & 1 & \Delta y \\
67 | 0 & 0 & 1
68 | \end{array}\right]\left[\begin{array}{l}
69 | x_0 \\
70 | y_0 \\
71 | 1
72 | \end{array}\right]=\left[\begin{array}{l}
73 | x_0+\Delta x \\
74 | y_0+\Delta y \\
75 | 1
76 | \end{array}\right]=\left[\begin{array}{l}
77 | x \\
78 | y \\
79 | 1
80 | \end{array}\right]
81 | $$
82 | 从上式可以看出, 引入附加坐标后, 扩充了矩阵的第 3 行, 并没有使变换结果受到影响。这种用 $n+1$ 维向量表示 $n$ 维向量的方法称为齐次坐标表示法。
83 |
84 | 因此, 2D图像中的点坐标 $(x, y)$ 通常表示成齐次坐标 $(H x, H y$, H), 其中 $H$ 表示非零的任意实数, 当 $H=1$ 时, 则 $(x, y, 1)$ 就称为点 $(x, y)$ 的规范化齐次坐标。显然规范化齐次坐标的前两个数是相应二维点的坐标, 没有变化, 仅在原坐标中增加了 $H=1$ 的附加坐标。
85 | 由点的齐次坐标 $(H x, H y, H)$ 求点的规范化齐次坐标 $(x, y,1)$, 可按如下公式进行:
86 | $$
87 | x=\frac{H x}{H} \quad y=\frac{H y}{H}
88 | $$
89 |
90 | 齐次坐标的几何意义相当于点 $(x, y)$ 落在 $3 D$ 空间 $H=1$ 的平面上, 如图6-2所示。如果将XOY 平面内的三角形 $abc$ 的各顶点表示成齐次坐标 $\left(x_i, y_i, 1\right)(i=1,2,3)$ 的形式, 就变成 $H=1$ 平面内的三角形 $a_1 b_1 c_1$ 的各顶点。
91 |
92 | 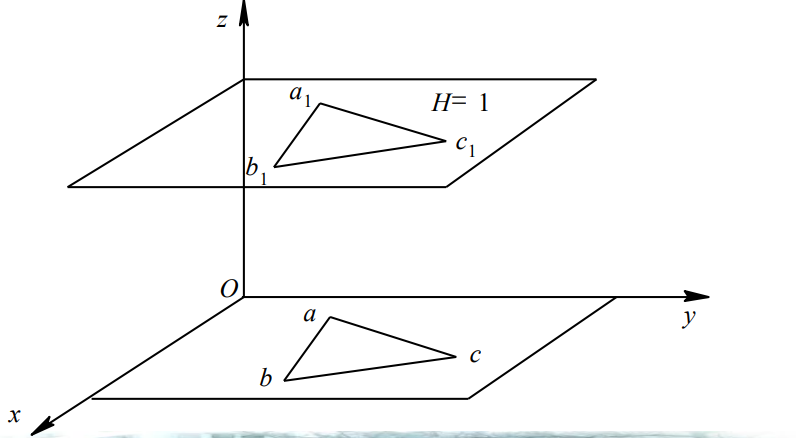 93 |
94 | 图6-2 齐次坐标的几何意义
95 |
96 | 齐次坐标在2D图像几何变换中的另一个应用是:如某点S(60 000, 40 000)在16位计算机上表示则大于32 767的最大坐标值, 需要进行复杂的操作。但如果把S的坐标形式变成(Hx, Hy, H) 形式的齐次坐标,则情况就不同了。在齐次坐标系中,设H=1 /2,则 (60 000,40 000)的齐次坐标为(1/2x, 1/2y, 1/2),那么所要表示的点变为(30 000, 20 000, 1/2),此点显然在16位计算机上二进制数所能表示的范围之内。
97 |
98 | 因此,采用齐次坐标,并将变换矩阵改成3×3阶的形式后, 便可实现所有2D图像几何变换的基本变换。
99 |
100 | ## 6.1.3 二维图像几何变换的矩阵
101 |
102 |
103 |
104 | 利用齐次坐标及改成 $3 \times 3$ 阶形式的变换矩阵, 实现 $2 D$ 图像几何变换的基本变换的一般过程是: 将 $2 \times n$ 阶的二维点集矩阵 $\left[\begin{array}{c}x_{0 i} \\ y_{0 i}\end{array}\right]_{2 \times n}$ 矩阵龶示成齐次完成, 坐标 $\left[\begin{array}{l}x_{0 i} \\ y_{0 i} \\ 1\end{array}\right]_{3 \times n}$ 的形式, 然后乘以相应的变换
105 | 变换后的点集矩阵=变换矩阵 $T \times$ 变换前的点集矩阵
106 | (图像上各点的新齐次坐标) (图像上各点的原齐次坐标)
107 |
108 | 设变换矩阵T为
109 | $$
110 | T=\left[\begin{array}{lll}
111 | a & b & p \\
112 | c & d & q \\
113 | l & m & s
114 | \end{array}\right]
115 | $$
116 | 则上述变换可以用公式表示为
117 | $$
118 | \left[\begin{array}{cccc}
119 | H x_1^{\prime} & H x_2^{\prime} & \Lambda & H x_n^{\prime} \\
120 | H y_1^{\prime} & H y_2^{\prime} & \Lambda & H y_n^{\prime} \\
121 | H & H & \Lambda & H
122 | \end{array}\right]_{3 \times n}=T \times\left[\begin{array}{llll}
123 | x_1 & x_2 & \Lambda & x_n \\
124 | y_1 & y_2 & \Lambda & y_n \\
125 | 1 & 1 & \Lambda & 1
126 | \end{array}\right]_{3 \times n}
127 | $$
128 | 图像上各点的新齐次坐标规范化后的点集矩阵为
129 | $$
130 | \left[\begin{array}{rrrr}
131 | x_1^{\prime} & x_2^{\prime} & \Lambda & x_n^{\prime} \\
132 | y_1^{\prime} & y_2^{\prime} & \Lambda & y_n^{\prime} \\
133 | 1 & 1 & \Lambda & 1
134 | \end{array}\right]_{3 \times n}
135 | $$
136 | 引入齐次坐标后,表示2D图像几何变换的3×3矩阵的功能就完善了,可以用它完成2D图像的各种几何变换。下面讨论 3×3阶变换矩阵中各元素在变换中的功能。几何变换的3×3矩阵的一般形式为
137 | $$
138 | T=\left[\begin{array}{lll}
139 | a & b & p \\
140 | c & d & q \\
141 | l & m & s
142 | \end{array}\right]
143 | $$
144 | 3×3的阶矩阵T可以分成四个子矩阵。其中,$\left[\begin{array}{ll}a & b \\ c & d\end{array}\right]_{2 \times 2}$这一子矩阵可使图像实现恒等、 比例、 反射(或镜像)、 错切和旋转变换。[l m]这一行矩阵可以使图像实现平移变换。[p q] T这一列矩阵可以使图像实现透视变换,但当p=0,q=0时它无透视作用。[s]这一元素可以使图像实现全比例变换。例如, 将图像进行全比例变换, 即
145 | $$
146 | \left[\begin{array}{lll}1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & s\end{array}\right] \times\left[\begin{array}{c}x_{0 i} \\ y_{0 i} \\ 1\end{array}\right]=\left[\begin{array}{c}x_i \\ y_i \\ s\end{array}\right]
147 | $$
148 |
149 | 将齐次坐标$[x_i \quad y_i \quad s]^T$规范化后,$[\dfrac{x_{oi}}{s} \quad \dfrac{y_{oi}}{s} \quad s]^T=[x_i \quad y_i \quad 1]^T$。 由此可见
150 |
151 | 当 $s>1$ 时, 图像按比例缩小; 当 $0
8 |
9 | 图6-3 比例缩放
10 |
11 | 比例缩放前后两点 $P_0\left(x_0, y_0\right) 、 P(x, y)$ 之间的关系用矩阵形式可以表示为
12 | $$
13 | \left[\begin{array}{l}
14 | x \\
15 | y \\
16 | 1
17 | \end{array}\right]=\left[\begin{array}{lll}
18 | f x & 0 & 0 \\
19 | 0 & f x & 0 \\
20 | 0 & 0 & 0
21 | \end{array}\right]\left[\begin{array}{l}
22 | x_0 \\
23 | y_0 \\
24 | 1
25 | \end{array}\right]\tag{6-1}
26 | $$
27 | 公式 (6-1) 的逆运算为
28 | $$
29 | \left[\begin{array}{l}
30 | x_0 \\
31 | y_0 \\
32 | 1
33 | \end{array}\right]=\left[\begin{array}{lll}
34 | \frac{1}{f x} & 0 & 0 \\
35 | 0 & \frac{1}{f x} & 0 \\
36 | 0 & 0 & 1
37 | \end{array}\right]\left[\begin{array}{l}
38 | x_0 \\
39 | y_0 \\
40 | 1
41 | \end{array}\right]
42 | $$
43 | 即
44 | $$
45 | \left\{\begin{array}{l}
46 | x_0=\frac{x}{f x} \\
47 | y_0=\frac{y}{f y}
48 | \end{array}\right.
49 | $$
50 | 比例缩放所产生的图像中的像素可能在原图像中找不到相应的像素点,这样就必须进行插值处理。插值处理常用的方法有两种, 一种是直接赋值为和它最相近的像素值, 另一种是通过一些插值算法来计算相应的像素值。前一种方法计算简单, 但会出现马赛克现象;后者处理效果要好些,但是运算量也相应增加。 在下面的算法中直接采用了前一种做法。实际上,这也是一种插值算法, 称为最邻近插值法(Nearest Neighbor Interpolation)
51 |
52 | 下面首先讨论图像的比例缩小。最简单的比例缩小是当 fx=fy=1/2时,图像被缩到一半大小,此时缩小后图像中的(0, 0)像素对应于原图像中的(0, 0)像素; (0, 1)像素对应于原图像中的(0, 2)像素; (1, 0)像素对应于原图像中的(2, 0)像素, 依此类推。图像缩小之后,因为承载的信息量小了,所以画布可相应缩小。此时, 只需在原图像基础上,每行隔一个像素取一点,每隔一行进行操作,即取原图的偶(奇)数行和偶(奇)数列构成新的图像,如图6-4所示。如果图像按任意比例缩小, 则需要计算选择的行和列
53 |
54 |
93 |
94 | 图6-2 齐次坐标的几何意义
95 |
96 | 齐次坐标在2D图像几何变换中的另一个应用是:如某点S(60 000, 40 000)在16位计算机上表示则大于32 767的最大坐标值, 需要进行复杂的操作。但如果把S的坐标形式变成(Hx, Hy, H) 形式的齐次坐标,则情况就不同了。在齐次坐标系中,设H=1 /2,则 (60 000,40 000)的齐次坐标为(1/2x, 1/2y, 1/2),那么所要表示的点变为(30 000, 20 000, 1/2),此点显然在16位计算机上二进制数所能表示的范围之内。
97 |
98 | 因此,采用齐次坐标,并将变换矩阵改成3×3阶的形式后, 便可实现所有2D图像几何变换的基本变换。
99 |
100 | ## 6.1.3 二维图像几何变换的矩阵
101 |
102 |
103 |
104 | 利用齐次坐标及改成 $3 \times 3$ 阶形式的变换矩阵, 实现 $2 D$ 图像几何变换的基本变换的一般过程是: 将 $2 \times n$ 阶的二维点集矩阵 $\left[\begin{array}{c}x_{0 i} \\ y_{0 i}\end{array}\right]_{2 \times n}$ 矩阵龶示成齐次完成, 坐标 $\left[\begin{array}{l}x_{0 i} \\ y_{0 i} \\ 1\end{array}\right]_{3 \times n}$ 的形式, 然后乘以相应的变换
105 | 变换后的点集矩阵=变换矩阵 $T \times$ 变换前的点集矩阵
106 | (图像上各点的新齐次坐标) (图像上各点的原齐次坐标)
107 |
108 | 设变换矩阵T为
109 | $$
110 | T=\left[\begin{array}{lll}
111 | a & b & p \\
112 | c & d & q \\
113 | l & m & s
114 | \end{array}\right]
115 | $$
116 | 则上述变换可以用公式表示为
117 | $$
118 | \left[\begin{array}{cccc}
119 | H x_1^{\prime} & H x_2^{\prime} & \Lambda & H x_n^{\prime} \\
120 | H y_1^{\prime} & H y_2^{\prime} & \Lambda & H y_n^{\prime} \\
121 | H & H & \Lambda & H
122 | \end{array}\right]_{3 \times n}=T \times\left[\begin{array}{llll}
123 | x_1 & x_2 & \Lambda & x_n \\
124 | y_1 & y_2 & \Lambda & y_n \\
125 | 1 & 1 & \Lambda & 1
126 | \end{array}\right]_{3 \times n}
127 | $$
128 | 图像上各点的新齐次坐标规范化后的点集矩阵为
129 | $$
130 | \left[\begin{array}{rrrr}
131 | x_1^{\prime} & x_2^{\prime} & \Lambda & x_n^{\prime} \\
132 | y_1^{\prime} & y_2^{\prime} & \Lambda & y_n^{\prime} \\
133 | 1 & 1 & \Lambda & 1
134 | \end{array}\right]_{3 \times n}
135 | $$
136 | 引入齐次坐标后,表示2D图像几何变换的3×3矩阵的功能就完善了,可以用它完成2D图像的各种几何变换。下面讨论 3×3阶变换矩阵中各元素在变换中的功能。几何变换的3×3矩阵的一般形式为
137 | $$
138 | T=\left[\begin{array}{lll}
139 | a & b & p \\
140 | c & d & q \\
141 | l & m & s
142 | \end{array}\right]
143 | $$
144 | 3×3的阶矩阵T可以分成四个子矩阵。其中,$\left[\begin{array}{ll}a & b \\ c & d\end{array}\right]_{2 \times 2}$这一子矩阵可使图像实现恒等、 比例、 反射(或镜像)、 错切和旋转变换。[l m]这一行矩阵可以使图像实现平移变换。[p q] T这一列矩阵可以使图像实现透视变换,但当p=0,q=0时它无透视作用。[s]这一元素可以使图像实现全比例变换。例如, 将图像进行全比例变换, 即
145 | $$
146 | \left[\begin{array}{lll}1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & s\end{array}\right] \times\left[\begin{array}{c}x_{0 i} \\ y_{0 i} \\ 1\end{array}\right]=\left[\begin{array}{c}x_i \\ y_i \\ s\end{array}\right]
147 | $$
148 |
149 | 将齐次坐标$[x_i \quad y_i \quad s]^T$规范化后,$[\dfrac{x_{oi}}{s} \quad \dfrac{y_{oi}}{s} \quad s]^T=[x_i \quad y_i \quad 1]^T$。 由此可见
150 |
151 | 当 $s>1$ 时, 图像按比例缩小; 当 $0
8 |
9 | 图6-3 比例缩放
10 |
11 | 比例缩放前后两点 $P_0\left(x_0, y_0\right) 、 P(x, y)$ 之间的关系用矩阵形式可以表示为
12 | $$
13 | \left[\begin{array}{l}
14 | x \\
15 | y \\
16 | 1
17 | \end{array}\right]=\left[\begin{array}{lll}
18 | f x & 0 & 0 \\
19 | 0 & f x & 0 \\
20 | 0 & 0 & 0
21 | \end{array}\right]\left[\begin{array}{l}
22 | x_0 \\
23 | y_0 \\
24 | 1
25 | \end{array}\right]\tag{6-1}
26 | $$
27 | 公式 (6-1) 的逆运算为
28 | $$
29 | \left[\begin{array}{l}
30 | x_0 \\
31 | y_0 \\
32 | 1
33 | \end{array}\right]=\left[\begin{array}{lll}
34 | \frac{1}{f x} & 0 & 0 \\
35 | 0 & \frac{1}{f x} & 0 \\
36 | 0 & 0 & 1
37 | \end{array}\right]\left[\begin{array}{l}
38 | x_0 \\
39 | y_0 \\
40 | 1
41 | \end{array}\right]
42 | $$
43 | 即
44 | $$
45 | \left\{\begin{array}{l}
46 | x_0=\frac{x}{f x} \\
47 | y_0=\frac{y}{f y}
48 | \end{array}\right.
49 | $$
50 | 比例缩放所产生的图像中的像素可能在原图像中找不到相应的像素点,这样就必须进行插值处理。插值处理常用的方法有两种, 一种是直接赋值为和它最相近的像素值, 另一种是通过一些插值算法来计算相应的像素值。前一种方法计算简单, 但会出现马赛克现象;后者处理效果要好些,但是运算量也相应增加。 在下面的算法中直接采用了前一种做法。实际上,这也是一种插值算法, 称为最邻近插值法(Nearest Neighbor Interpolation)
51 |
52 | 下面首先讨论图像的比例缩小。最简单的比例缩小是当 fx=fy=1/2时,图像被缩到一半大小,此时缩小后图像中的(0, 0)像素对应于原图像中的(0, 0)像素; (0, 1)像素对应于原图像中的(0, 2)像素; (1, 0)像素对应于原图像中的(2, 0)像素, 依此类推。图像缩小之后,因为承载的信息量小了,所以画布可相应缩小。此时, 只需在原图像基础上,每行隔一个像素取一点,每隔一行进行操作,即取原图的偶(奇)数行和偶(奇)数列构成新的图像,如图6-4所示。如果图像按任意比例缩小, 则需要计算选择的行和列
53 |
54 | 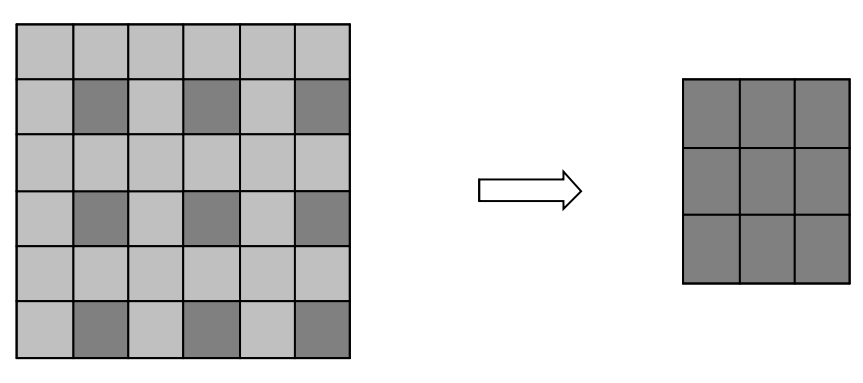 55 |
56 | 如果$M×N$大小的原图像$F(x,y)$缩小为 $kM×kN$大小$(k<1)$ 的新图像$I(x,y)$时,则
57 | $$
58 | I(x, y)=F(\operatorname{int}(c \times x), \operatorname{int}(c \times y))
59 | $$
60 | 其中, $c=1/k$。由此公式可以构造出新图像,如图6-5所示。
61 |
62 | 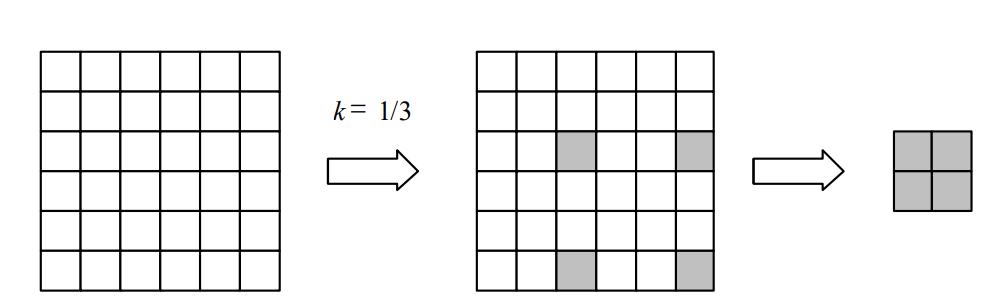
63 |
64 | 图6-5 图像按任意比例缩小
65 |
66 | 当 $f x \neq f y(f x, f y>0)$ 时, 图像不按比例缩小, 这种操作因为在 $x$ 方向和y方向的缩小比例不同, 一定会带来图像的几何畸变。图像不按比例缩小的方法是: 如果 $M \times N$ 大小的旧图 $F(x, y)$ 缩小为 $k_1 M \times k_2 N\left(k_1<1, k_2<1\right)$ 大小的新图像 $I(x, y)$ 时, 则
67 | $$
68 | I(x, y)=F\left(\operatorname{int}\left(c_1 \times x\right), \operatorname{int}\left(c_2 \times y\right)\right)
69 | $$
70 | 其中
71 | $$
72 | c=\frac{1}{k_1}, c_2=\frac{1}{k_2}
73 | $$
74 | 由此公式可以构造出新图像。
75 |
76 | 图像在缩小操作中, 是在现有的信息里如何挑选所需要的有用信息。而在图像的放大操作中, 则需要对尺寸放大后所多出来的空格填入适当的像素值, 这是信息的估计问题, 所以较图像的缩小要难一些。当 $f x=f y=2$ 时, 图像被按全比例放大 2 倍, 放大后图像中的 $(0,0)$ 像素对应于原图中的 $(0,0)$ 像素; $(0,1)$ 像素对应于原图中的 $(0,0.5)$ 像素, 该像素不存在, 可以近似为 $(0,0)$ 也可以近似 $(0,1) ; \quad(0,2)$ 像素对应于原图像中的 $(0,1)$ 像素; $(1,0)$ 像素对应于原图中的 $(0.5,0)$, 它的像素值近似于 $(0,0)$ 或 $(1,0)$ 像素; (2,0)像素对应于原图中的 $(1,0)$ 像素, 依此类推。其实这是将原图像每行中的像素重复取值一遍, 然后每行重复一次。图66是原始图像, 图6-7和图6-8是分别采用上述两种近似方法放大后的图像。
77 |
78 |
55 |
56 | 如果$M×N$大小的原图像$F(x,y)$缩小为 $kM×kN$大小$(k<1)$ 的新图像$I(x,y)$时,则
57 | $$
58 | I(x, y)=F(\operatorname{int}(c \times x), \operatorname{int}(c \times y))
59 | $$
60 | 其中, $c=1/k$。由此公式可以构造出新图像,如图6-5所示。
61 |
62 | 
63 |
64 | 图6-5 图像按任意比例缩小
65 |
66 | 当 $f x \neq f y(f x, f y>0)$ 时, 图像不按比例缩小, 这种操作因为在 $x$ 方向和y方向的缩小比例不同, 一定会带来图像的几何畸变。图像不按比例缩小的方法是: 如果 $M \times N$ 大小的旧图 $F(x, y)$ 缩小为 $k_1 M \times k_2 N\left(k_1<1, k_2<1\right)$ 大小的新图像 $I(x, y)$ 时, 则
67 | $$
68 | I(x, y)=F\left(\operatorname{int}\left(c_1 \times x\right), \operatorname{int}\left(c_2 \times y\right)\right)
69 | $$
70 | 其中
71 | $$
72 | c=\frac{1}{k_1}, c_2=\frac{1}{k_2}
73 | $$
74 | 由此公式可以构造出新图像。
75 |
76 | 图像在缩小操作中, 是在现有的信息里如何挑选所需要的有用信息。而在图像的放大操作中, 则需要对尺寸放大后所多出来的空格填入适当的像素值, 这是信息的估计问题, 所以较图像的缩小要难一些。当 $f x=f y=2$ 时, 图像被按全比例放大 2 倍, 放大后图像中的 $(0,0)$ 像素对应于原图中的 $(0,0)$ 像素; $(0,1)$ 像素对应于原图中的 $(0,0.5)$ 像素, 该像素不存在, 可以近似为 $(0,0)$ 也可以近似 $(0,1) ; \quad(0,2)$ 像素对应于原图像中的 $(0,1)$ 像素; $(1,0)$ 像素对应于原图中的 $(0.5,0)$, 它的像素值近似于 $(0,0)$ 或 $(1,0)$ 像素; (2,0)像素对应于原图中的 $(1,0)$ 像素, 依此类推。其实这是将原图像每行中的像素重复取值一遍, 然后每行重复一次。图66是原始图像, 图6-7和图6-8是分别采用上述两种近似方法放大后的图像。
77 |
78 | 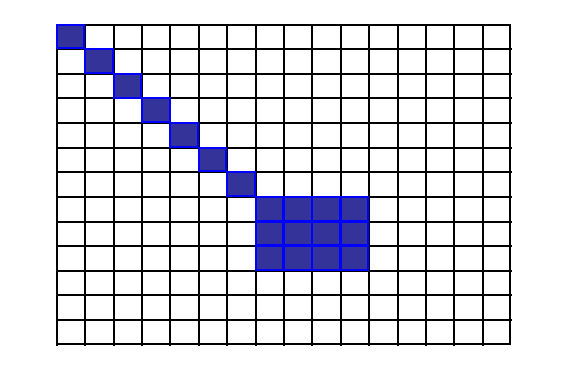 79 |
80 | 图6-6 放大前的图像
81 |
82 |
79 |
80 | 图6-6 放大前的图像
81 |
82 | 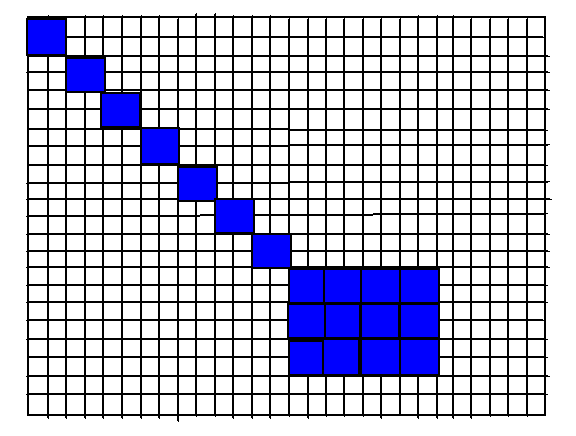 83 |
84 | 图6-7 按最近邻域法放大两倍的图像
85 |
86 |
83 |
84 | 图6-7 按最近邻域法放大两倍的图像
85 |
86 | 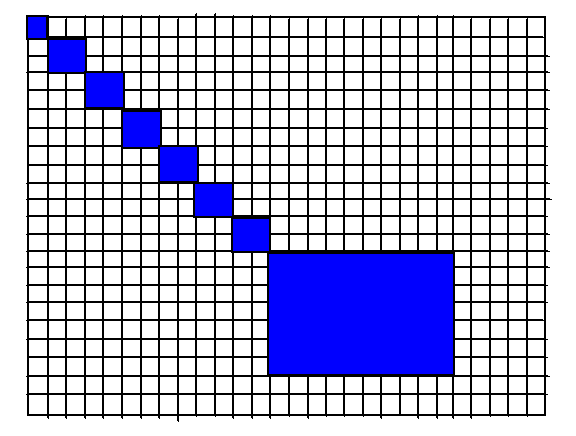 87 |
88 | 图6-8 按插值法放大两倍的图像
89 |
90 | 一般地, 按比例将原图像放大 $k$ 倍时, 如果按照最近邻域法则需要将一个像素值添在新图像的 $k \times k$ 的子块中, 如图6-9所示。 显然, 如果放大倍数太大, 按照这种方法处理会出现马赛克效应。当 $f x \neq f y(f x, f y>0)$ 时, 图像在 $x$ 方向和 $y$ 方向不按比例放大, 此时, 这种操作由于 $x$ 方向和 $y$ 方向的放大倍数不同, 一定带来图像的几何畸变。放大的方法是将原图像的一个像素添到新图像的一个 $k_1 \times k_2$ 的子块中去。为了提高几何变换后的图像质量, 常采用线性揷值法。该方法的原理是, 当求出的分数地址与像素点不一致时, 求出周围四个像素点的距离比, 根据该比率, 由四个邻域的像素灰度值进行线性揷值, 如图6-10所示。
91 |
92 |
87 |
88 | 图6-8 按插值法放大两倍的图像
89 |
90 | 一般地, 按比例将原图像放大 $k$ 倍时, 如果按照最近邻域法则需要将一个像素值添在新图像的 $k \times k$ 的子块中, 如图6-9所示。 显然, 如果放大倍数太大, 按照这种方法处理会出现马赛克效应。当 $f x \neq f y(f x, f y>0)$ 时, 图像在 $x$ 方向和 $y$ 方向不按比例放大, 此时, 这种操作由于 $x$ 方向和 $y$ 方向的放大倍数不同, 一定带来图像的几何畸变。放大的方法是将原图像的一个像素添到新图像的一个 $k_1 \times k_2$ 的子块中去。为了提高几何变换后的图像质量, 常采用线性揷值法。该方法的原理是, 当求出的分数地址与像素点不一致时, 求出周围四个像素点的距离比, 根据该比率, 由四个邻域的像素灰度值进行线性揷值, 如图6-10所示。
91 |
92 | 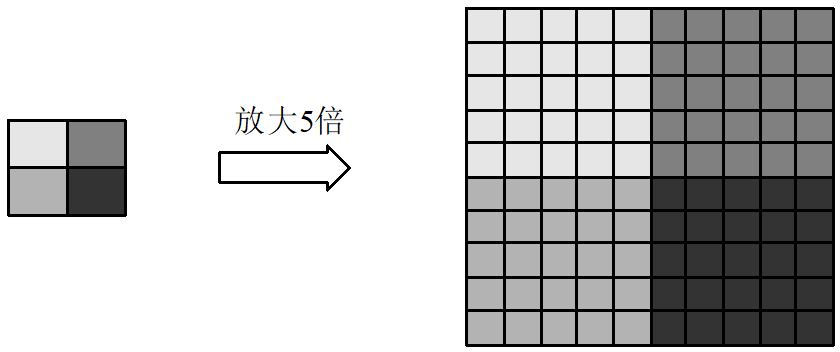 93 |
94 | 图6-9 按最近邻域法放大五倍的图像
95 |
96 |
93 |
94 | 图6-9 按最近邻域法放大五倍的图像
95 |
96 |  97 |
98 | 图6-10 线性插值法示意图
99 |
100 | 简化后的灰度值计算式如下:
101 | $$
102 | \begin{aligned}
103 | & g(x, y)=(1-q)\{(1-p) \times g([x],[y])+p \times g([x] \\
104 | & +1,[y])\}+q\{(1-p) \times g([x],[y]+1)+p \times g([x] \\
105 | & +1,[y]+1)\}
106 | \end{aligned}
107 | $$
108 | 式中: $g(x, y)$ 为坐标 $(x, y)$ 处的灰度值, $[x]$ 、 $[y]$ 分别为不大于 $x, y$ 的整数。关于这个问题的详细算法及其实现, 读者可以参考有关参考文献。
109 |
110 | ## 6.2.2 比例缩放的实现
111 |
112 |
97 |
98 | 图6-10 线性插值法示意图
99 |
100 | 简化后的灰度值计算式如下:
101 | $$
102 | \begin{aligned}
103 | & g(x, y)=(1-q)\{(1-p) \times g([x],[y])+p \times g([x] \\
104 | & +1,[y])\}+q\{(1-p) \times g([x],[y]+1)+p \times g([x] \\
105 | & +1,[y]+1)\}
106 | \end{aligned}
107 | $$
108 | 式中: $g(x, y)$ 为坐标 $(x, y)$ 处的灰度值, $[x]$ 、 $[y]$ 分别为不大于 $x, y$ 的整数。关于这个问题的详细算法及其实现, 读者可以参考有关参考文献。
109 |
110 | ## 6.2.2 比例缩放的实现
111 |
112 | 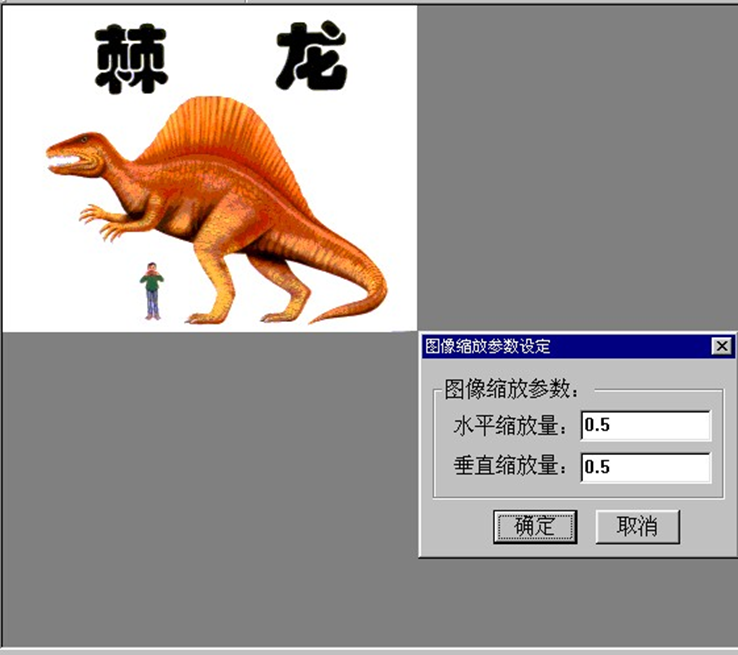 113 |
114 | 图6-11 图像比例缩放处理结果
115 |
116 | 下面给出这个函数的框架和主要算法。
117 |
118 | ```c
119 | //*****************************************
120 | //函数名称: BOOL ZoomImage()
121 | //基本功能: 本函数对传入的CDibObject对象中的图像进行缩放操作
122 | //参数说明: float fXZoomRatio X轴方向缩放比率
123 | // float fYZoomRatio Y轴方向缩放比率
124 | // BOOL bBilinear TRUE为双线性插值, FALSE为最邻近插值
125 | // CDibObject *pDibObject 默认为NULL
126 | //返回值: BOOL 成功返回TRUE, 失败返回FALSE
127 | //*****************************************
128 | BOOL CGeoTrans:: ZoomImage(float fXZoomRatio, float fYZoomRatio,
129 | BOOL bBilinear, CDibObject *pDibObject)
130 | {
131 | //获得图像宽度和高度, 计算缩放后的图像实际宽度
132 | nNewWidth = (int)(nOldWidth * fXZoomRatio + 0.5);
133 | nNewHeight = (int)(nOldHeight * fYZoomRatio + 0.5);
134 | //获取源图像指针,为新图像分配内存,用白色填充新图像数据区,调整新图像信息
135 | //由图像位数确定的移动字节数nMovedBits
136 | //针对图像每行进行操作
137 | for(y = 0; y < nNewHeight; y++)
138 | {
139 | //指向新图像第y行
140 | pNewTemp = pNewBits;
141 | pNewTemp += (nNewHeight -1[KG*3]-y) * nNewWidthBytes;
142 | //针对图像每列进行操作
143 | for(x = 0; x < nNewWidth; x++)
144 | {
145 | //计算该像素在源图像中的坐标
146 | int y0 = (long) (y/fYZoomRatio +0.5);
147 | int x0 = (long) (x/fXZoomRatio +0.5);
148 | //判断是否在源图范围内
149 | if( (x0 >= 0) && (x0 < nOldWidth) && (y0 >= 0) && (y0 < nOldHeight))
150 | {
151 | if(bBilinear)
152 | {
153 | //双线性插值
154 | }
155 | else
156 | {
157 | //指向源图像第y0行, 第x0个像素
158 | pOldTemp = pOldBits;
159 | pOldTemp += (nOldHeight - 1 - y0) * nOldWidthBytes;
160 | pOldTemp += x0 * nMovedBits;
161 | memcpy(pNewTemp, pOldTemp, nMovedBits);
162 | }
163 | }
164 | pNewTemp += nMovedBits;
165 | }
166 | }
167 | //将内存解锁和将不再使用的内存释放, 将新图像设置为当前图像
168 | return TRUE;
169 | }
170 |
171 | ```
172 |
173 |
--------------------------------------------------------------------------------
/VI/6.3 图像平移.md:
--------------------------------------------------------------------------------
1 |
2 |
3 | # 6.3 图像平移
4 |
5 | ## 6.3.1 图像平移变换
6 |
7 | 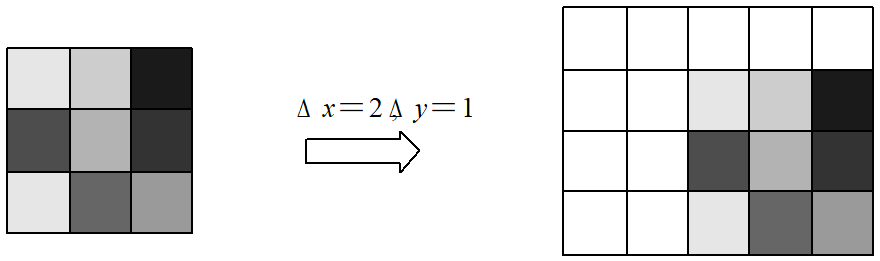
8 |
9 | 图6-12 图像平移
10 |
11 | 设点 $P_{0}\left(x_{0}, y_{0}\right)$ 进行平移后, 移到 $P(x, y)$, 其中 $x$ 方向的平移量为 $\Delta x, y$ 方向的平移量为 $\Delta y$ 。那么,点 $P(x, y)$ 的坐标为
12 |
13 | $$
14 | \left\{\begin{array}{l}
15 | x=x_{0}+\Delta x \\
16 | y=y_{0}+\Delta y
17 | \end{array}\right.
18 | $$
19 |
20 | 利用齐次坐标, 变换前后图像上的点 $P_{0}\left(x_{0}, y_{0}\right)$ 和 $P(x, y)$ 之间的关系可以用如下的矩阵变换表示为
21 |
22 | $$
23 | \left[\begin{array}{l}
24 | x \\
25 | y \\
26 | 1
27 | \end{array}\right]=\left[\begin{array}{lll}
28 | 1 & 0 & \Delta x \\
29 | 0 & 1 & \Delta y \\
30 | 0 & 0 & 1
31 | \end{array}\right]\left[\begin{array}{l}
32 | x_0 \\
33 | y_0 \\
34 | 1
35 | \end{array}\right]\tag{6-2}
36 | $$
37 | 对变换矩阵求逆, 可以得到式 (6-2) 的逆变换
38 | $$
39 | \left[\begin{array}{l}
40 | x_{0} \\
41 | y_{0} \\
42 | 1
43 | \end{array}\right]=\left[\begin{array}{ccc}
44 | 1 & 0 & -\Delta x \\
45 | 0 & 1 & -\Delta y \\
46 | 0 & 0 & 1
47 | \end{array}\right]\left[\begin{array}{l}
48 | x \\
49 | y \\
50 | 1
51 | \end{array}\right]
52 | $$
53 |
54 | 即
55 |
56 | $$
57 | \left\{\begin{array}{l}
58 | x_{0}=x-\Delta x \\
59 | y_{0}=y-\Delta y
60 | \end{array}\right.
61 | $$
62 |
63 | 这样, 平移后的图像上的每一点都可以在原图像中找到对应的点。例如, 对于新图中的 $(0,0)$ 像素, 代入上面的方程组,可以求出对应原图中的像素 $(-\Delta x,-\Delta y)$ 。如果 $\Delta x$ 或 $\Delta y 大于 0$, 则点 $(-\Delta x,-\Delta y)$ 不在原图像中。对于不在原图像中的点, 可以直接将它的像素值统一设置为 0 或者255 (对于灰度图就是黑色或白色)。同样, 若有像素点不在原图像中, 也就说明原图像中有点被移出显示区域。如果不想丢失被移出的部分图像, 可以将新生成的图像宽度扩大 $|\Delta x|$, 高度扩大 $|\Delta y|$ 。
64 |
65 |
113 |
114 | 图6-11 图像比例缩放处理结果
115 |
116 | 下面给出这个函数的框架和主要算法。
117 |
118 | ```c
119 | //*****************************************
120 | //函数名称: BOOL ZoomImage()
121 | //基本功能: 本函数对传入的CDibObject对象中的图像进行缩放操作
122 | //参数说明: float fXZoomRatio X轴方向缩放比率
123 | // float fYZoomRatio Y轴方向缩放比率
124 | // BOOL bBilinear TRUE为双线性插值, FALSE为最邻近插值
125 | // CDibObject *pDibObject 默认为NULL
126 | //返回值: BOOL 成功返回TRUE, 失败返回FALSE
127 | //*****************************************
128 | BOOL CGeoTrans:: ZoomImage(float fXZoomRatio, float fYZoomRatio,
129 | BOOL bBilinear, CDibObject *pDibObject)
130 | {
131 | //获得图像宽度和高度, 计算缩放后的图像实际宽度
132 | nNewWidth = (int)(nOldWidth * fXZoomRatio + 0.5);
133 | nNewHeight = (int)(nOldHeight * fYZoomRatio + 0.5);
134 | //获取源图像指针,为新图像分配内存,用白色填充新图像数据区,调整新图像信息
135 | //由图像位数确定的移动字节数nMovedBits
136 | //针对图像每行进行操作
137 | for(y = 0; y < nNewHeight; y++)
138 | {
139 | //指向新图像第y行
140 | pNewTemp = pNewBits;
141 | pNewTemp += (nNewHeight -1[KG*3]-y) * nNewWidthBytes;
142 | //针对图像每列进行操作
143 | for(x = 0; x < nNewWidth; x++)
144 | {
145 | //计算该像素在源图像中的坐标
146 | int y0 = (long) (y/fYZoomRatio +0.5);
147 | int x0 = (long) (x/fXZoomRatio +0.5);
148 | //判断是否在源图范围内
149 | if( (x0 >= 0) && (x0 < nOldWidth) && (y0 >= 0) && (y0 < nOldHeight))
150 | {
151 | if(bBilinear)
152 | {
153 | //双线性插值
154 | }
155 | else
156 | {
157 | //指向源图像第y0行, 第x0个像素
158 | pOldTemp = pOldBits;
159 | pOldTemp += (nOldHeight - 1 - y0) * nOldWidthBytes;
160 | pOldTemp += x0 * nMovedBits;
161 | memcpy(pNewTemp, pOldTemp, nMovedBits);
162 | }
163 | }
164 | pNewTemp += nMovedBits;
165 | }
166 | }
167 | //将内存解锁和将不再使用的内存释放, 将新图像设置为当前图像
168 | return TRUE;
169 | }
170 |
171 | ```
172 |
173 |
--------------------------------------------------------------------------------
/VI/6.3 图像平移.md:
--------------------------------------------------------------------------------
1 |
2 |
3 | # 6.3 图像平移
4 |
5 | ## 6.3.1 图像平移变换
6 |
7 | 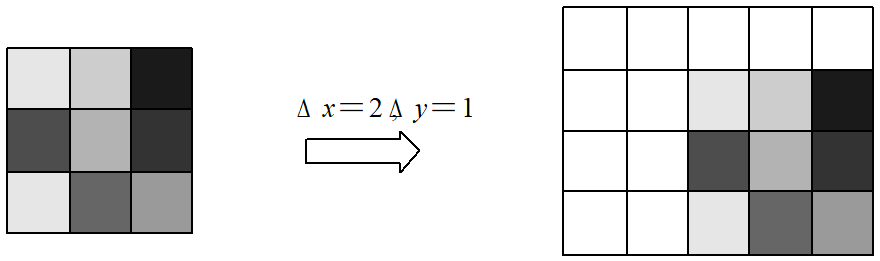
8 |
9 | 图6-12 图像平移
10 |
11 | 设点 $P_{0}\left(x_{0}, y_{0}\right)$ 进行平移后, 移到 $P(x, y)$, 其中 $x$ 方向的平移量为 $\Delta x, y$ 方向的平移量为 $\Delta y$ 。那么,点 $P(x, y)$ 的坐标为
12 |
13 | $$
14 | \left\{\begin{array}{l}
15 | x=x_{0}+\Delta x \\
16 | y=y_{0}+\Delta y
17 | \end{array}\right.
18 | $$
19 |
20 | 利用齐次坐标, 变换前后图像上的点 $P_{0}\left(x_{0}, y_{0}\right)$ 和 $P(x, y)$ 之间的关系可以用如下的矩阵变换表示为
21 |
22 | $$
23 | \left[\begin{array}{l}
24 | x \\
25 | y \\
26 | 1
27 | \end{array}\right]=\left[\begin{array}{lll}
28 | 1 & 0 & \Delta x \\
29 | 0 & 1 & \Delta y \\
30 | 0 & 0 & 1
31 | \end{array}\right]\left[\begin{array}{l}
32 | x_0 \\
33 | y_0 \\
34 | 1
35 | \end{array}\right]\tag{6-2}
36 | $$
37 | 对变换矩阵求逆, 可以得到式 (6-2) 的逆变换
38 | $$
39 | \left[\begin{array}{l}
40 | x_{0} \\
41 | y_{0} \\
42 | 1
43 | \end{array}\right]=\left[\begin{array}{ccc}
44 | 1 & 0 & -\Delta x \\
45 | 0 & 1 & -\Delta y \\
46 | 0 & 0 & 1
47 | \end{array}\right]\left[\begin{array}{l}
48 | x \\
49 | y \\
50 | 1
51 | \end{array}\right]
52 | $$
53 |
54 | 即
55 |
56 | $$
57 | \left\{\begin{array}{l}
58 | x_{0}=x-\Delta x \\
59 | y_{0}=y-\Delta y
60 | \end{array}\right.
61 | $$
62 |
63 | 这样, 平移后的图像上的每一点都可以在原图像中找到对应的点。例如, 对于新图中的 $(0,0)$ 像素, 代入上面的方程组,可以求出对应原图中的像素 $(-\Delta x,-\Delta y)$ 。如果 $\Delta x$ 或 $\Delta y 大于 0$, 则点 $(-\Delta x,-\Delta y)$ 不在原图像中。对于不在原图像中的点, 可以直接将它的像素值统一设置为 0 或者255 (对于灰度图就是黑色或白色)。同样, 若有像素点不在原图像中, 也就说明原图像中有点被移出显示区域。如果不想丢失被移出的部分图像, 可以将新生成的图像宽度扩大 $|\Delta x|$, 高度扩大 $|\Delta y|$ 。
64 |
65 |  66 |
67 | 图6-13 平移前的图像
68 |
69 |
70 |
71 |
66 |
67 | 图6-13 平移前的图像
68 |
69 |
70 |
71 |  72 |
73 | 图6-14 平移后的图像
74 |
75 |
72 |
73 | 图6-14 平移后的图像
74 |
75 |  76 |
77 | 图6-15 平移扩大后的图像
78 |
79 |
80 |
81 | ## 6.3.2 图像平移的算法
82 |
83 | 按照上述理论, 可以比较容易地用 VC++来实现图像的平移。 下面介绍灰度图像的平移, 因为灰度图像每个像素位数正好是 8 位, 即 1 个字节, 在进行图像处理时可以不用考虑拼凑字节的问题。而且由于灰度图像调色板的特殊性, 进行灰度图像处理时不必考虑调色板的问题。所以, 在介绍图像处理时,一般采用灰度图像, 以便将重点放在算法本身。由上述分析, 可以得到实现图像平移的算法如下。
84 |
85 | ```c++
86 | //*****************************************
87 | //函数名称: BOOL TranslationPixel()
88 | //基本功能: 本函数对传入的CDibObject对象中的图像进行逐点平移操作
89 | //参数说明: long lXOffset X轴平移量(像素数)
90 | // long lYOffset Y轴平移量(像素数)
91 | //返回值: BOOL 成功返回TRUE, 失败返回FALSE
92 | //注意: 该函数不会改变图像的大小, 移出的部分图像将截去, 空白部分用白色填充
93 | //*****************************************
94 | BOOL CGeoTrans:: TranslationPixel(long lXOffset, long lYOffset, CDibObject *pDibObject)
95 | {
96 | //定义变量, 获得源图像指针及其图像信息, 为新图像分配内存及用白色填充新图
97 | //由图像位数确定的移动字节数nMovedBits, 对于灰度图像有nMovedBits = 1
98 | //每行
99 | for(y = 0; y < nHeight; y++)
100 | {
101 | pNewTemp = pNewBits;
102 | pNewTemp += (nHeight -1-y) * nWidthBytes;
103 | //每列
104 | for(x = 0; x < nWidth; x++)
105 | {
106 | //指向新DIB第y行, 第x个像素的指针, 计算该像素在源DIB中的坐标
107 | int x0 = x – lXOffset;
108 | int y0 = y – lYOffset;
109 | //判断是否在源图范围内
110 | if( (x0 >= 0) && (x0 < nWidth) && (y0 >= 0) && (y0 < nHeight))
111 | {
112 | //指向源DIB第y0行, 第x0个像素的指针
113 | pOldTemp = pOldBits;
114 | pOldTemp += (nHeight -1-y0) * nWidthBytes;
115 | pOldTemp += x0 * nMovedBits;
116 | //复制像素
117 | memcpy( pNewTemp, pOldTemp, nMovedBits );
118 | }
119 | pNewTemp += nMovedBits;
120 | }
121 | }
122 | //用新图像数据填充源图像数据区
123 | memcpy( pOldBits, pNewBits, nWidthBytes * nHeight );
124 | }
125 | ```
126 |
127 |
--------------------------------------------------------------------------------
/VI/6.4 图像镜像.md:
--------------------------------------------------------------------------------
1 | # 图像镜像
2 |
3 | ## 6.4.1 图像镜像变换
4 |
5 | 图像的镜像变换不改变图像的形状。图像的镜像(Mirror)变换分为两种:一种是水平镜像,另外一种是垂直镜像。图像的水平镜像操作是将图像左半部分和右半部分以图像垂直中轴线为中心进行镜像对换;图像的垂直镜像操作是将图像上半部分和下半部分以图像水平中轴线为中心进行镜像对换,如图6-16所示
6 |
7 | 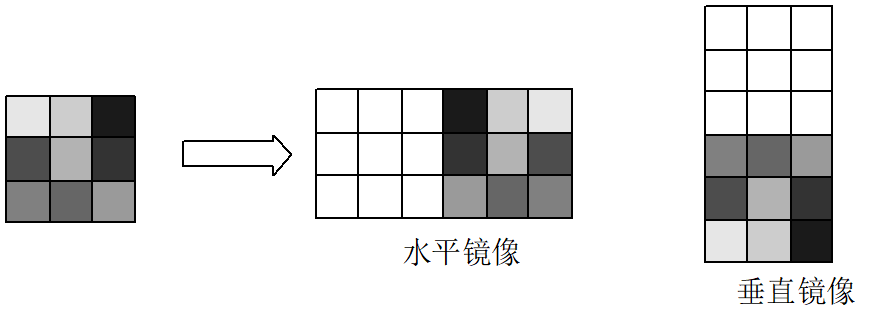
8 |
9 | 图6-16 图像的镜像
10 |
11 | 图像的镜像变换也可以用矩阵变换表示。设点 $P_{0}\left(x_{0}, y_{0}\right)$ 进行镜像后的对应点为$P(x, y)$, 图像高度为 fHeight, 宽度为fWidth,原图像中 $P_0\left(x_0, y_0\right)$ 经过水平镜像后坐标将变为 (fWidth- $\left.x_0, y_0\right)$,其矩阵表达式为
12 | $$
13 | \left[\begin{array}{l}
14 | x \\
15 | y \\
16 | 1
17 | \end{array}\right]=\left[\begin{array}{rrc}
18 | -1 & 0 & fWidth \\
19 | 0 & 1 & 0 \\
20 | 0 & 0 & 1
21 | \end{array}\right]\left[\begin{array}{l}
22 | x_{0} \\
23 | y_{0} \\
24 | 1
25 | \end{array}\right]\tag{6-3}
26 | $$
27 |
28 | 逆运算矩阵表达式为
29 |
30 | $$
31 | \left[\begin{array}{l}
32 | x_{0} \\
33 | y_{0} \\
34 | 1
35 | \end{array}\right]=\left[\begin{array}{ccc}
36 | -1 & 0 & fwidth \\
37 | 0 & 1 & 0 \\
38 | 0 & 0 & 1
39 | \end{array}\right]\left[\begin{array}{l}
40 | x \\
41 | y \\
42 | 1
43 | \end{array}\right]
44 | $$
45 |
46 | 即
47 |
48 | $$
49 | \left\{\begin{array}{l}
50 | x_{0}=f \text { Width }-x \\
51 | y_{0}=y
52 | \end{array}\right.
53 | $$
54 |
55 | 同样, $P_{0}\left(x_{0}, y_{0}\right)$ 经过垂直镜像后坐标将变为 $\left(x_{0}, f H e i g h t-y_{0}\right)$,
56 |
57 | 其矩阵表表达式为
58 |
59 | $$
60 | \left[\begin{array}{l}
61 | x \\
62 | y \\
63 | 1
64 | \end{array}\right]=\left[\begin{array}{ccc}
65 | 1 & 0 & 0 \\
66 | 0 & -1 & fHeight \\
67 | 0 & 0 & 1
68 | \end{array}\right]\left[\begin{array}{l}
69 | x_{0} \\
70 | y_{0} \\
71 | 1
72 | \end{array}\right]
73 | \tag{6-4}
74 | $$
75 |
76 | 逆运算矩阵表达式为
77 |
78 | $$
79 | \left[\begin{array}{l}
80 | x_{0} \\
81 | y_{0} \\
82 | 1
83 | \end{array}\right]=\left[\begin{array}{ccc}
84 | 1 & 0 & 0 \\
85 | 0 & -1 & \text { fHeight } \\
86 | 0 & 0 & 1
87 | \end{array}\right]\left[\begin{array}{l}
88 | x \\
89 | y \\
90 | 1
91 | \end{array}\right]
92 | $$
93 |
94 | 即
95 |
96 | $$
97 | \left\{\begin{array}{l}
98 | x_{0}=x \\
99 | y_{0}=f W i d t h-y
100 | \end{array}\right.
101 | $$
102 |
103 | ## 6.4.2 图像镜像的算法
104 |
105 | 按照上面的变换公式 (6-3) 和(6-4),可以比较简单的实现图像的水平和垂直镜像操作, 读者可以参照6.3.2中平移的算法, 写出公式 (6-3) 和 (6-4) 对应的算法。
106 |
107 | 和图像平移一样, 在垂直镜像中也可以利用位图存储的连续性整行复制图像。下面将介绍采用这种方法的算法, 其主要算法如下, bDirection为真时表示水平镜像, 否则为垂直镜像。
108 |
109 | ```c++
110 | //由图像位数确定的移动字节数nMovedBits
111 | //判断镜像方式
112 | if (bDirection)
113 | {
114 | //垂直中轴坐标
115 | int nMiddleX = nWidth / 2;
116 | //针对图像每行进行操作
117 | for(y = 0; y < nHeight; y++)
118 | {
119 | //指向图像的倒数第y行
120 | pOldTemp = pOldBits;
121 | pOldTemp += y * nWidthBytes;
122 | pNewTemp = pNewBits;
123 | pNewTemp += y * nWidthBytes;
124 | //针对每行图像左半部分进行操作
125 | for(x = 0; x <= nMiddleX; x++)
126 | {
127 | //将源图像第x个像素复制到新图像倒数第x个像素
128 | pTemp1 = pOldTemp + x * nMovedBits;
129 | pTemp2 = pNewTemp + (nWidth -1 - x) * nMovedBits;
130 | memcpy(pTemp2, pTemp1, nMovedBits);
131 | //将源图像倒数第x个像素复制到新图像第x个像素
132 | pTemp1 = pOldTemp + (nWidth -1 - x) * nMovedBits;
133 | pTemp2 = pNewTemp + x * nMovedBits;
134 | memcpy(pTemp2, pTemp1, nMovedBits);
135 | }
136 | }
137 | }
138 | else
139 | {
140 | //水平中轴坐标
141 | int nMiddleY = nHeight / 2;
142 | //针对上半图像进行操作
143 | for(y = 0; y <= nMiddleY; y++)
144 | {
145 | //指向源图像倒数第y行像素起点的指针
146 | pOldTemp = pOldBits;
147 | pOldTemp += y * nWidthBytes;
148 | //指向新图像第y行像素起点的指针
149 | pNewTemp = pNewBits;
150 | pNewTemp += (nHeight - 1 - y) * nWidthBytes;
151 | //将源图像倒数第y行像素复制到新图像第y行
152 | memcpy(pNewTemp, pOldTemp, nWidthBytes);
153 | //指向源图像第y行像素起点的指针
154 | pOldTemp = pOldBits;
155 | pOldTemp += (nHeight -1 -y) * nWidthBytes;
156 | //指向新图像倒数第y行像素起点的指针
157 | pNewTemp = pNewBits;
158 | pNewTemp += y * nWidthBytes;
159 | //将源图像第y行像素复制到新图像倒数第y行
160 | memcpy(pNewTemp, pOldTemp, nWidthBytes);
161 | }
162 | }
163 | //用新图像数据填充原图像数据区
164 | memcpy( pOldBits, pNewBits, nWidthBytes * nHeight );
165 |
166 | ```
167 |
168 |
169 |
170 |
76 |
77 | 图6-15 平移扩大后的图像
78 |
79 |
80 |
81 | ## 6.3.2 图像平移的算法
82 |
83 | 按照上述理论, 可以比较容易地用 VC++来实现图像的平移。 下面介绍灰度图像的平移, 因为灰度图像每个像素位数正好是 8 位, 即 1 个字节, 在进行图像处理时可以不用考虑拼凑字节的问题。而且由于灰度图像调色板的特殊性, 进行灰度图像处理时不必考虑调色板的问题。所以, 在介绍图像处理时,一般采用灰度图像, 以便将重点放在算法本身。由上述分析, 可以得到实现图像平移的算法如下。
84 |
85 | ```c++
86 | //*****************************************
87 | //函数名称: BOOL TranslationPixel()
88 | //基本功能: 本函数对传入的CDibObject对象中的图像进行逐点平移操作
89 | //参数说明: long lXOffset X轴平移量(像素数)
90 | // long lYOffset Y轴平移量(像素数)
91 | //返回值: BOOL 成功返回TRUE, 失败返回FALSE
92 | //注意: 该函数不会改变图像的大小, 移出的部分图像将截去, 空白部分用白色填充
93 | //*****************************************
94 | BOOL CGeoTrans:: TranslationPixel(long lXOffset, long lYOffset, CDibObject *pDibObject)
95 | {
96 | //定义变量, 获得源图像指针及其图像信息, 为新图像分配内存及用白色填充新图
97 | //由图像位数确定的移动字节数nMovedBits, 对于灰度图像有nMovedBits = 1
98 | //每行
99 | for(y = 0; y < nHeight; y++)
100 | {
101 | pNewTemp = pNewBits;
102 | pNewTemp += (nHeight -1-y) * nWidthBytes;
103 | //每列
104 | for(x = 0; x < nWidth; x++)
105 | {
106 | //指向新DIB第y行, 第x个像素的指针, 计算该像素在源DIB中的坐标
107 | int x0 = x – lXOffset;
108 | int y0 = y – lYOffset;
109 | //判断是否在源图范围内
110 | if( (x0 >= 0) && (x0 < nWidth) && (y0 >= 0) && (y0 < nHeight))
111 | {
112 | //指向源DIB第y0行, 第x0个像素的指针
113 | pOldTemp = pOldBits;
114 | pOldTemp += (nHeight -1-y0) * nWidthBytes;
115 | pOldTemp += x0 * nMovedBits;
116 | //复制像素
117 | memcpy( pNewTemp, pOldTemp, nMovedBits );
118 | }
119 | pNewTemp += nMovedBits;
120 | }
121 | }
122 | //用新图像数据填充源图像数据区
123 | memcpy( pOldBits, pNewBits, nWidthBytes * nHeight );
124 | }
125 | ```
126 |
127 |
--------------------------------------------------------------------------------
/VI/6.4 图像镜像.md:
--------------------------------------------------------------------------------
1 | # 图像镜像
2 |
3 | ## 6.4.1 图像镜像变换
4 |
5 | 图像的镜像变换不改变图像的形状。图像的镜像(Mirror)变换分为两种:一种是水平镜像,另外一种是垂直镜像。图像的水平镜像操作是将图像左半部分和右半部分以图像垂直中轴线为中心进行镜像对换;图像的垂直镜像操作是将图像上半部分和下半部分以图像水平中轴线为中心进行镜像对换,如图6-16所示
6 |
7 | 
8 |
9 | 图6-16 图像的镜像
10 |
11 | 图像的镜像变换也可以用矩阵变换表示。设点 $P_{0}\left(x_{0}, y_{0}\right)$ 进行镜像后的对应点为$P(x, y)$, 图像高度为 fHeight, 宽度为fWidth,原图像中 $P_0\left(x_0, y_0\right)$ 经过水平镜像后坐标将变为 (fWidth- $\left.x_0, y_0\right)$,其矩阵表达式为
12 | $$
13 | \left[\begin{array}{l}
14 | x \\
15 | y \\
16 | 1
17 | \end{array}\right]=\left[\begin{array}{rrc}
18 | -1 & 0 & fWidth \\
19 | 0 & 1 & 0 \\
20 | 0 & 0 & 1
21 | \end{array}\right]\left[\begin{array}{l}
22 | x_{0} \\
23 | y_{0} \\
24 | 1
25 | \end{array}\right]\tag{6-3}
26 | $$
27 |
28 | 逆运算矩阵表达式为
29 |
30 | $$
31 | \left[\begin{array}{l}
32 | x_{0} \\
33 | y_{0} \\
34 | 1
35 | \end{array}\right]=\left[\begin{array}{ccc}
36 | -1 & 0 & fwidth \\
37 | 0 & 1 & 0 \\
38 | 0 & 0 & 1
39 | \end{array}\right]\left[\begin{array}{l}
40 | x \\
41 | y \\
42 | 1
43 | \end{array}\right]
44 | $$
45 |
46 | 即
47 |
48 | $$
49 | \left\{\begin{array}{l}
50 | x_{0}=f \text { Width }-x \\
51 | y_{0}=y
52 | \end{array}\right.
53 | $$
54 |
55 | 同样, $P_{0}\left(x_{0}, y_{0}\right)$ 经过垂直镜像后坐标将变为 $\left(x_{0}, f H e i g h t-y_{0}\right)$,
56 |
57 | 其矩阵表表达式为
58 |
59 | $$
60 | \left[\begin{array}{l}
61 | x \\
62 | y \\
63 | 1
64 | \end{array}\right]=\left[\begin{array}{ccc}
65 | 1 & 0 & 0 \\
66 | 0 & -1 & fHeight \\
67 | 0 & 0 & 1
68 | \end{array}\right]\left[\begin{array}{l}
69 | x_{0} \\
70 | y_{0} \\
71 | 1
72 | \end{array}\right]
73 | \tag{6-4}
74 | $$
75 |
76 | 逆运算矩阵表达式为
77 |
78 | $$
79 | \left[\begin{array}{l}
80 | x_{0} \\
81 | y_{0} \\
82 | 1
83 | \end{array}\right]=\left[\begin{array}{ccc}
84 | 1 & 0 & 0 \\
85 | 0 & -1 & \text { fHeight } \\
86 | 0 & 0 & 1
87 | \end{array}\right]\left[\begin{array}{l}
88 | x \\
89 | y \\
90 | 1
91 | \end{array}\right]
92 | $$
93 |
94 | 即
95 |
96 | $$
97 | \left\{\begin{array}{l}
98 | x_{0}=x \\
99 | y_{0}=f W i d t h-y
100 | \end{array}\right.
101 | $$
102 |
103 | ## 6.4.2 图像镜像的算法
104 |
105 | 按照上面的变换公式 (6-3) 和(6-4),可以比较简单的实现图像的水平和垂直镜像操作, 读者可以参照6.3.2中平移的算法, 写出公式 (6-3) 和 (6-4) 对应的算法。
106 |
107 | 和图像平移一样, 在垂直镜像中也可以利用位图存储的连续性整行复制图像。下面将介绍采用这种方法的算法, 其主要算法如下, bDirection为真时表示水平镜像, 否则为垂直镜像。
108 |
109 | ```c++
110 | //由图像位数确定的移动字节数nMovedBits
111 | //判断镜像方式
112 | if (bDirection)
113 | {
114 | //垂直中轴坐标
115 | int nMiddleX = nWidth / 2;
116 | //针对图像每行进行操作
117 | for(y = 0; y < nHeight; y++)
118 | {
119 | //指向图像的倒数第y行
120 | pOldTemp = pOldBits;
121 | pOldTemp += y * nWidthBytes;
122 | pNewTemp = pNewBits;
123 | pNewTemp += y * nWidthBytes;
124 | //针对每行图像左半部分进行操作
125 | for(x = 0; x <= nMiddleX; x++)
126 | {
127 | //将源图像第x个像素复制到新图像倒数第x个像素
128 | pTemp1 = pOldTemp + x * nMovedBits;
129 | pTemp2 = pNewTemp + (nWidth -1 - x) * nMovedBits;
130 | memcpy(pTemp2, pTemp1, nMovedBits);
131 | //将源图像倒数第x个像素复制到新图像第x个像素
132 | pTemp1 = pOldTemp + (nWidth -1 - x) * nMovedBits;
133 | pTemp2 = pNewTemp + x * nMovedBits;
134 | memcpy(pTemp2, pTemp1, nMovedBits);
135 | }
136 | }
137 | }
138 | else
139 | {
140 | //水平中轴坐标
141 | int nMiddleY = nHeight / 2;
142 | //针对上半图像进行操作
143 | for(y = 0; y <= nMiddleY; y++)
144 | {
145 | //指向源图像倒数第y行像素起点的指针
146 | pOldTemp = pOldBits;
147 | pOldTemp += y * nWidthBytes;
148 | //指向新图像第y行像素起点的指针
149 | pNewTemp = pNewBits;
150 | pNewTemp += (nHeight - 1 - y) * nWidthBytes;
151 | //将源图像倒数第y行像素复制到新图像第y行
152 | memcpy(pNewTemp, pOldTemp, nWidthBytes);
153 | //指向源图像第y行像素起点的指针
154 | pOldTemp = pOldBits;
155 | pOldTemp += (nHeight -1 -y) * nWidthBytes;
156 | //指向新图像倒数第y行像素起点的指针
157 | pNewTemp = pNewBits;
158 | pNewTemp += y * nWidthBytes;
159 | //将源图像第y行像素复制到新图像倒数第y行
160 | memcpy(pNewTemp, pOldTemp, nWidthBytes);
161 | }
162 | }
163 | //用新图像数据填充原图像数据区
164 | memcpy( pOldBits, pNewBits, nWidthBytes * nHeight );
165 |
166 | ```
167 |
168 |
169 |
170 |  171 |
172 | 图6-17 镜像前的图像
173 |
174 |
171 |
172 | 图6-17 镜像前的图像
173 |
174 |  175 |
176 | 图6-18 水平镜像
177 |
178 |
175 |
176 | 图6-18 水平镜像
177 |
178 |  179 |
180 | 图6-19 垂直镜像
--------------------------------------------------------------------------------
/VI/6.5 图像旋转.md:
--------------------------------------------------------------------------------
1 | # 6.5 图像旋转
2 |
3 | ## 6.5.1 图像旋转变换
4 |
5 | 本节介绍一种相对复杂的几何变换一图像的旋转。一般图像的旋转是以图像的中心为原点, 将图像上的所有像素都旋转 一个相同的角度。图像的旋转变换是图像的位置变换, 但旋转后, 图像的大小一般会改变。和图像平移一样, 在图像旋转变 换中既可以把转出显示区域的图像截去, 也可以扩大图像范围 以显示所有的图像。如图6-20、图6-21所示。
6 |
7 |
179 |
180 | 图6-19 垂直镜像
--------------------------------------------------------------------------------
/VI/6.5 图像旋转.md:
--------------------------------------------------------------------------------
1 | # 6.5 图像旋转
2 |
3 | ## 6.5.1 图像旋转变换
4 |
5 | 本节介绍一种相对复杂的几何变换一图像的旋转。一般图像的旋转是以图像的中心为原点, 将图像上的所有像素都旋转 一个相同的角度。图像的旋转变换是图像的位置变换, 但旋转后, 图像的大小一般会改变。和图像平移一样, 在图像旋转变 换中既可以把转出显示区域的图像截去, 也可以扩大图像范围 以显示所有的图像。如图6-20、图6-21所示。
6 |
7 |  8 |
9 | 图6-20 旋转前的图像
10 | 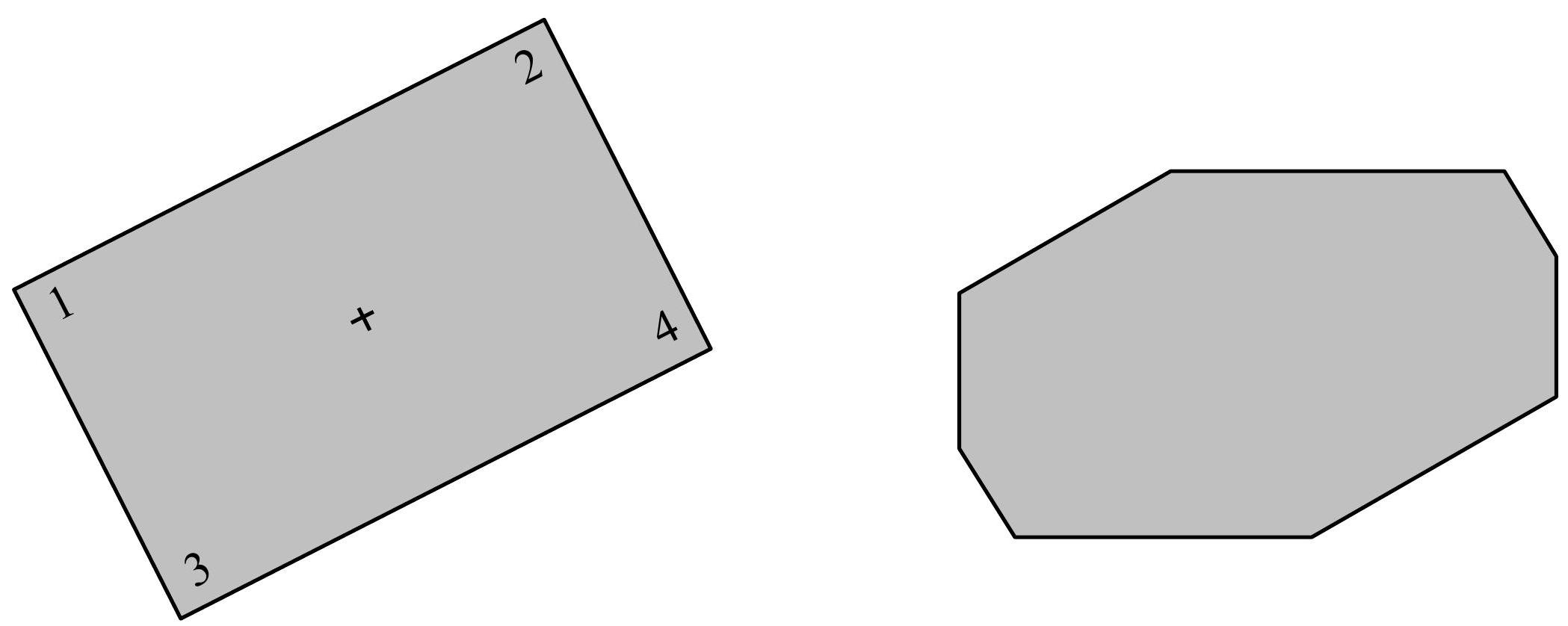
11 |
12 | 图6-21 旋转 $\theta$ 后的图像(扩大图像、转出部分被截)
13 |
14 | 同样, 图像的旋转变换也可以用矩阵变换表示。设点 $P_{0}\left(x_{0}, y_{0}\right)$旋转 $\theta$ 角后的对应点为 $P(x, y)$, 如图6-22所示。那么, 旋转前后 点 $P_{0}\left(x_{0}, y_{0}\right) 、 P(x, y)$ 的坐标分别是:
15 |
16 | 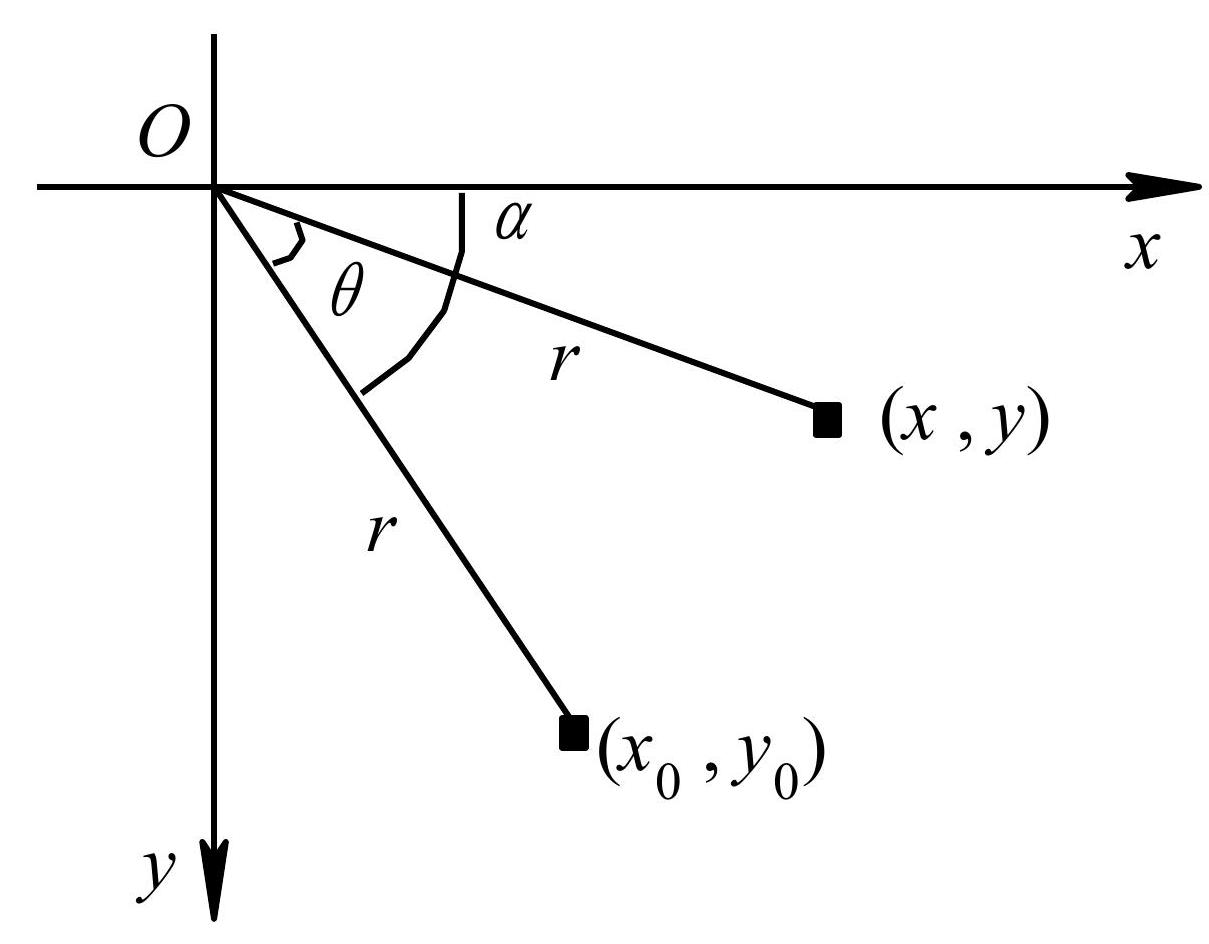
17 | 图6-22 图像旋转 $\theta$ 角
18 | $$
19 | \begin{aligned}
20 | & \left\{\begin{array}{l}
21 | x_0=r \cos \alpha \\
22 | y_0=r \sin \alpha
23 | \end{array}\right. \\
24 | & \left\{\begin{array}{l}
25 | x=r \cos (\alpha-\theta)=r \cos \alpha \cos \theta+r \sin \alpha \sin \theta=x_0 \cos \theta+y_0 \sin \theta \\
26 | y=r \sin (\alpha-\theta)=r \sin \alpha \cos \theta-r \cos \alpha \sin \theta=-x_0 \sin \theta+y_0 \cos \theta
27 | \end{array}\right.
28 | \end{aligned}
29 | $$
30 | 写成矩阵表达式为
31 | $$
32 | \left[\begin{array}{l}
33 | x \\
34 | y \\
35 | 1
36 | \end{array}\right]=\left[\begin{array}{ccc}
37 | \cos \theta & \sin \theta & 0 \\
38 | -\sin \theta & \cos \theta & 0 \\
39 | 0 & 0 & 1
40 | \end{array}\right]\left[\begin{array}{l}
41 | x_0 \\
42 | y_0 \\
43 | 1
44 | \end{array}\right]\tag{6-5}
45 | $$
46 | 其逆运算为
47 |
48 | $$
49 | \left[\begin{array}{l}
50 | x \\
51 | y \\
52 | 1
53 | \end{array}\right]=\left[\begin{array}{ccc}
54 | \cos \theta & -\sin \theta & 0 \\
55 | \sin \theta & \cos \theta & 0 \\
56 | 0 & 0 & 1
57 | \end{array}\right]\left[\begin{array}{l}
58 | x_{0} \\
59 | y_{0} \\
60 | 1
61 | \end{array}\right]
62 | $$
63 |
64 | 利用公式 (6-5) 可以确定旋转后图像上的像素。例如, 当 $\theta=30^{\circ}$ 时, 公式 (6-5) 为
65 |
66 | $$
67 | \left\{\begin{array}{l}
68 | x=0.866 x-0.5 y \\
69 | y=0.5 x+0.866
70 | \end{array}\right.
71 | $$
72 | 而且, 此时
73 |
74 | $$
75 | \begin{aligned}
76 | & x_{\min }=0.866-0.5 \times 3=-0.634 ; x_{\min }=0.866 \times 3-0.5=2.098 \\
77 | & y_{\min }=0.866+0.5=1.366 ; \quad y_{\max }=0.866 \times 3+0.5 \times 3=4.098
78 | \end{aligned}
79 | $$
80 | 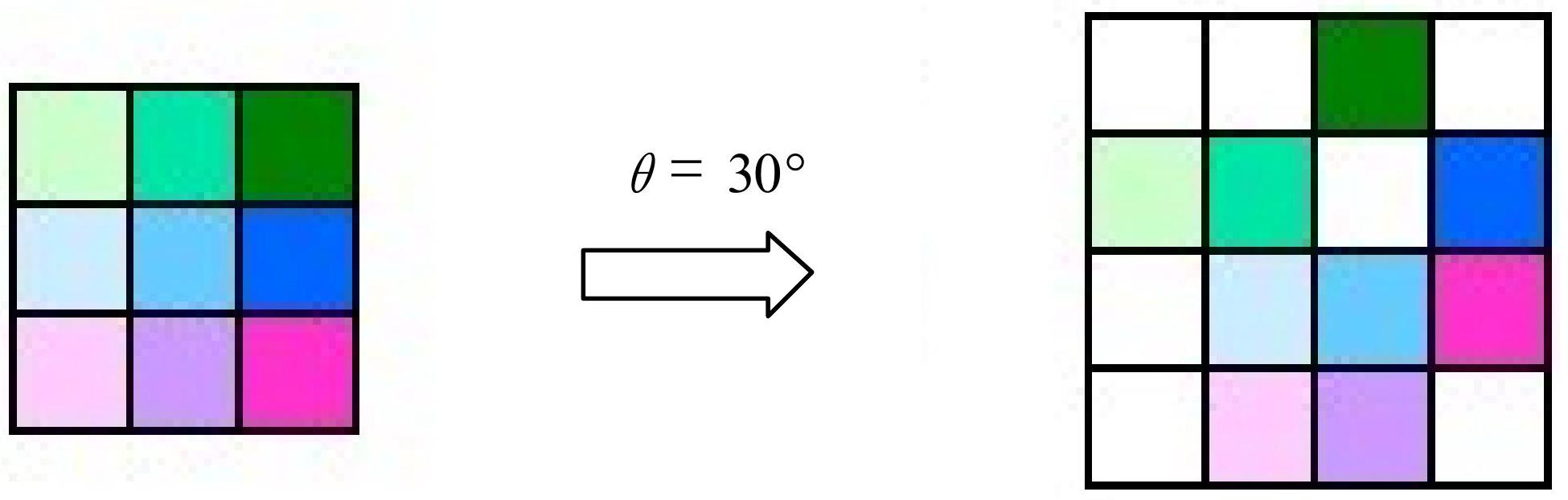
81 | 图6-23 图像旋转 $\theta$ 角
82 |
83 | 利用公式(6-5)进行图像旋转时需要注意如下两点:
84 |
85 | (1) 图像旋转之前, 为了避免信息的丢失, 一定要有坐标平移,具体的做法有如图6-24所示的两种方法。
86 | 
87 |
88 | 图6-24 图像旋转之前进行的平移 (2) 图像旋转之后, 会出现许多空洞点, 如图6-23所示。对 这些空洞点必须进行填充处理, 否则画面效果不好, 一般也称 这种操作为揷值处理。最简单的方法是行揷值方法或列揷值方 法:
89 |
90 | (1) 找出当前行的最小和最大的非白点的坐标, 记作: $(i, k 1)$ 、 $(i, k 2)$ 。
91 |
92 | (2) 在(k1, k2)范围内进行揷值, 揷值的方法是: 空点的像素 值等于前一点的像素值。
93 |
94 | (3) 同样的操作重复到所有行。经过如上的揷值处理之后, 图像效果就变得自然。如图6-25所示。列揷值方法与此类同, 请读者自己给出。
95 | 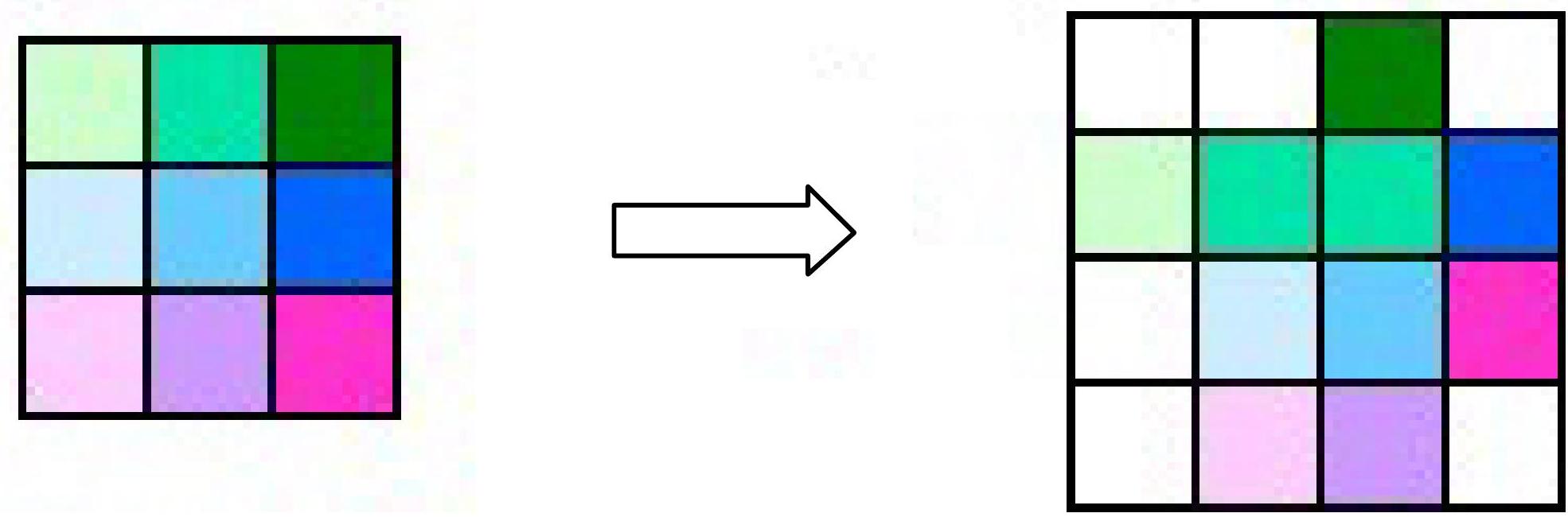
96 |
97 | 图6-25 图6-23中的图像处理后的效果
98 |
99 | ## 6.5.2 图像旋转的实现
100 |
101 | 按照上述理论,也可以用VC++编程实现图像的旋转。为了 将重点放在算法本身, 下面介绍灰度图像的旋转算法。由上面 的公式(6-6)以及产生空穴时的双线性揷值方法,可以编制一 个实现图像旋转的函数RotateDIB2()。下面给出这个函数的框架和主要算法。
102 |
103 | ```c++
104 | //*****************************************
105 | //函数名称: BOOL Rotate()
106 | //基本功能: 本函数对传入的CDibObject对象中的图像进行旋转操作
107 | //参数说明: int iRotateAngle 旋转的角度(0~360度)
108 | // BOOL bBilinear TRUE为双线性插值, FALSE为最邻近插值
109 | // CDibObject *pDibObject 默认为NULL
110 | //返回值: BOOL 成功返回TRUE, 失败返回FALSE
111 | //*****************************************
112 | BOOL CGeoTrans:: Rotate(int nRotateAngle, BOOL bBilinear, CDibObject *pDibObject)
113 | {
114 | //获得图像宽度和高度: nOldWidth、 nOldHeight
115 | //定义旋转角度(弧度)及其正弦和余弦值: fRotateAngle、 fSina、 fCosa
116 | //定义源图四个角的坐标、 旋转后四个角的坐标(以图像中心为坐标系原点)
117 | //计算旋转角度的正弦和余弦值
118 | //计算源图的四个角的坐标(以图像中心为坐标系原点)
119 | //计算新图四个角的坐标(以图像中心为坐标系原点)
120 | fDstX1 = fCosa * fSrcX1 + fSina * fSrcY1;
121 | fDstY1 = -fSina * fSrcX1 + fCosa * fSrcY1;
122 | fDstX2 = fCosa * fSrcX2 + fSina * fSrcY2;
123 | fDstY2 = -fSina * fSrcX2 + fCosa * fSrcY2;
124 | fDstX3 = fCosa * fSrcX3 + fSina * fSrcY3;
125 | fDstY3 = -fSina * fSrcX3 + fCosa * fSrcY3;
126 | fDstX4 = fCosa * fSrcX4 + fSina * fSrcY4;
127 | fDstY4 = -fSina * fSrcX4 + fCosa * fSrcY4;
128 | //计算旋转后的图像实际宽度
129 | int nNewWidth=(long)(max(fabs(fDstX4-fDstX1), fabs(fDstX3-fDstX2))+0.5);
130 | //计算旋转后的图像高度
131 | int nNewHeight=(long)(max(fabs(fDstY4-fDstY1), fabs(fDstY3-fDstY2))+0.5);
132 | //计算两个常数
133 | f1= (float) (-0.5 * (nNewWidth - 1) * fCosa - 0.5 * (nNewHeight - 1) * fSina
134 | + 0.5 * (nOldWidth - 1));
135 | f2= (float) ( 0.5 * (nNewWidth - 1) * fSina - 0.5 * (nNewHeight - 1) * fCosa
136 | + 0.5 * (nOldHeight - 1));
137 | //获取指向源图像的指针, 为旋转图像分配内存并用白色填充新图像数据区
138 | //由图像位数确定的移动字节数nMovedBits
139 | //针对图像每行进行操作
140 | for(y = 0; y < nNewHeight; y++)
141 | {
142 | //指向新图像第y行
143 | pNewTemp = pNewBits;
144 | pNewTemp += (nNewHeight - 1 - y) * nNewWidthBytes;
145 | //针对图像每列进行操作
146 | for(x = 0; x < nNewWidth; x++)
147 | {
148 | //计算该像素在源图像中的坐标
149 | int y0 = (long) (-((float) x) * fSina + ((float) y)
150 | * fCosa + f2 + 0.5);
151 | int x0 = (long) ( ((float) x) * fCosa + ((float) y)
152 | * fSina + f1 + 0.5);
153 | //判断是否在源图范围内
154 | if( (x0 >= 0) && (x0 < nOldWidth) && (y0 >= 0) && (y0 < nOldHeight))
155 | {
156 | //用双线性插值
157 | if(bBilinear)
158 | {
159 | unsigned char *pTemp = Interpolation (nOldWidth, nOldHeight,
160 | (float)x0, (float)y0, nOldWidthBytes, nMovedBits, pOldBits);
161 | //复制像素
162 | memcpy(pNewTemp, pTemp, nMovedBits);
163 | delete [] pTemp ;
164 | }
165 | else
166 | {
167 | //指向源图像第y0行, 第x0个像素
168 | pOldTemp = pOldBits;
169 | pOldTemp += (nOldHeight - 1 - y0) * nOldWidthBytes;
170 | pOldTemp += x0 * nMovedBits;
171 | //复制像素
172 | memcpy(pNewTemp, pOldTemp, nMovedBits);
173 | }
174 | }
175 | pNewTemp += nMovedBits;
176 | }
177 | }
178 | //将内存解锁和将不再使用的内存释放, 将新图像设置为当前图像
179 | return TRUE;
180 | }
181 | ```
182 |
183 |
8 |
9 | 图6-20 旋转前的图像
10 | 
11 |
12 | 图6-21 旋转 $\theta$ 后的图像(扩大图像、转出部分被截)
13 |
14 | 同样, 图像的旋转变换也可以用矩阵变换表示。设点 $P_{0}\left(x_{0}, y_{0}\right)$旋转 $\theta$ 角后的对应点为 $P(x, y)$, 如图6-22所示。那么, 旋转前后 点 $P_{0}\left(x_{0}, y_{0}\right) 、 P(x, y)$ 的坐标分别是:
15 |
16 | 
17 | 图6-22 图像旋转 $\theta$ 角
18 | $$
19 | \begin{aligned}
20 | & \left\{\begin{array}{l}
21 | x_0=r \cos \alpha \\
22 | y_0=r \sin \alpha
23 | \end{array}\right. \\
24 | & \left\{\begin{array}{l}
25 | x=r \cos (\alpha-\theta)=r \cos \alpha \cos \theta+r \sin \alpha \sin \theta=x_0 \cos \theta+y_0 \sin \theta \\
26 | y=r \sin (\alpha-\theta)=r \sin \alpha \cos \theta-r \cos \alpha \sin \theta=-x_0 \sin \theta+y_0 \cos \theta
27 | \end{array}\right.
28 | \end{aligned}
29 | $$
30 | 写成矩阵表达式为
31 | $$
32 | \left[\begin{array}{l}
33 | x \\
34 | y \\
35 | 1
36 | \end{array}\right]=\left[\begin{array}{ccc}
37 | \cos \theta & \sin \theta & 0 \\
38 | -\sin \theta & \cos \theta & 0 \\
39 | 0 & 0 & 1
40 | \end{array}\right]\left[\begin{array}{l}
41 | x_0 \\
42 | y_0 \\
43 | 1
44 | \end{array}\right]\tag{6-5}
45 | $$
46 | 其逆运算为
47 |
48 | $$
49 | \left[\begin{array}{l}
50 | x \\
51 | y \\
52 | 1
53 | \end{array}\right]=\left[\begin{array}{ccc}
54 | \cos \theta & -\sin \theta & 0 \\
55 | \sin \theta & \cos \theta & 0 \\
56 | 0 & 0 & 1
57 | \end{array}\right]\left[\begin{array}{l}
58 | x_{0} \\
59 | y_{0} \\
60 | 1
61 | \end{array}\right]
62 | $$
63 |
64 | 利用公式 (6-5) 可以确定旋转后图像上的像素。例如, 当 $\theta=30^{\circ}$ 时, 公式 (6-5) 为
65 |
66 | $$
67 | \left\{\begin{array}{l}
68 | x=0.866 x-0.5 y \\
69 | y=0.5 x+0.866
70 | \end{array}\right.
71 | $$
72 | 而且, 此时
73 |
74 | $$
75 | \begin{aligned}
76 | & x_{\min }=0.866-0.5 \times 3=-0.634 ; x_{\min }=0.866 \times 3-0.5=2.098 \\
77 | & y_{\min }=0.866+0.5=1.366 ; \quad y_{\max }=0.866 \times 3+0.5 \times 3=4.098
78 | \end{aligned}
79 | $$
80 | 
81 | 图6-23 图像旋转 $\theta$ 角
82 |
83 | 利用公式(6-5)进行图像旋转时需要注意如下两点:
84 |
85 | (1) 图像旋转之前, 为了避免信息的丢失, 一定要有坐标平移,具体的做法有如图6-24所示的两种方法。
86 | 
87 |
88 | 图6-24 图像旋转之前进行的平移 (2) 图像旋转之后, 会出现许多空洞点, 如图6-23所示。对 这些空洞点必须进行填充处理, 否则画面效果不好, 一般也称 这种操作为揷值处理。最简单的方法是行揷值方法或列揷值方 法:
89 |
90 | (1) 找出当前行的最小和最大的非白点的坐标, 记作: $(i, k 1)$ 、 $(i, k 2)$ 。
91 |
92 | (2) 在(k1, k2)范围内进行揷值, 揷值的方法是: 空点的像素 值等于前一点的像素值。
93 |
94 | (3) 同样的操作重复到所有行。经过如上的揷值处理之后, 图像效果就变得自然。如图6-25所示。列揷值方法与此类同, 请读者自己给出。
95 | 
96 |
97 | 图6-25 图6-23中的图像处理后的效果
98 |
99 | ## 6.5.2 图像旋转的实现
100 |
101 | 按照上述理论,也可以用VC++编程实现图像的旋转。为了 将重点放在算法本身, 下面介绍灰度图像的旋转算法。由上面 的公式(6-6)以及产生空穴时的双线性揷值方法,可以编制一 个实现图像旋转的函数RotateDIB2()。下面给出这个函数的框架和主要算法。
102 |
103 | ```c++
104 | //*****************************************
105 | //函数名称: BOOL Rotate()
106 | //基本功能: 本函数对传入的CDibObject对象中的图像进行旋转操作
107 | //参数说明: int iRotateAngle 旋转的角度(0~360度)
108 | // BOOL bBilinear TRUE为双线性插值, FALSE为最邻近插值
109 | // CDibObject *pDibObject 默认为NULL
110 | //返回值: BOOL 成功返回TRUE, 失败返回FALSE
111 | //*****************************************
112 | BOOL CGeoTrans:: Rotate(int nRotateAngle, BOOL bBilinear, CDibObject *pDibObject)
113 | {
114 | //获得图像宽度和高度: nOldWidth、 nOldHeight
115 | //定义旋转角度(弧度)及其正弦和余弦值: fRotateAngle、 fSina、 fCosa
116 | //定义源图四个角的坐标、 旋转后四个角的坐标(以图像中心为坐标系原点)
117 | //计算旋转角度的正弦和余弦值
118 | //计算源图的四个角的坐标(以图像中心为坐标系原点)
119 | //计算新图四个角的坐标(以图像中心为坐标系原点)
120 | fDstX1 = fCosa * fSrcX1 + fSina * fSrcY1;
121 | fDstY1 = -fSina * fSrcX1 + fCosa * fSrcY1;
122 | fDstX2 = fCosa * fSrcX2 + fSina * fSrcY2;
123 | fDstY2 = -fSina * fSrcX2 + fCosa * fSrcY2;
124 | fDstX3 = fCosa * fSrcX3 + fSina * fSrcY3;
125 | fDstY3 = -fSina * fSrcX3 + fCosa * fSrcY3;
126 | fDstX4 = fCosa * fSrcX4 + fSina * fSrcY4;
127 | fDstY4 = -fSina * fSrcX4 + fCosa * fSrcY4;
128 | //计算旋转后的图像实际宽度
129 | int nNewWidth=(long)(max(fabs(fDstX4-fDstX1), fabs(fDstX3-fDstX2))+0.5);
130 | //计算旋转后的图像高度
131 | int nNewHeight=(long)(max(fabs(fDstY4-fDstY1), fabs(fDstY3-fDstY2))+0.5);
132 | //计算两个常数
133 | f1= (float) (-0.5 * (nNewWidth - 1) * fCosa - 0.5 * (nNewHeight - 1) * fSina
134 | + 0.5 * (nOldWidth - 1));
135 | f2= (float) ( 0.5 * (nNewWidth - 1) * fSina - 0.5 * (nNewHeight - 1) * fCosa
136 | + 0.5 * (nOldHeight - 1));
137 | //获取指向源图像的指针, 为旋转图像分配内存并用白色填充新图像数据区
138 | //由图像位数确定的移动字节数nMovedBits
139 | //针对图像每行进行操作
140 | for(y = 0; y < nNewHeight; y++)
141 | {
142 | //指向新图像第y行
143 | pNewTemp = pNewBits;
144 | pNewTemp += (nNewHeight - 1 - y) * nNewWidthBytes;
145 | //针对图像每列进行操作
146 | for(x = 0; x < nNewWidth; x++)
147 | {
148 | //计算该像素在源图像中的坐标
149 | int y0 = (long) (-((float) x) * fSina + ((float) y)
150 | * fCosa + f2 + 0.5);
151 | int x0 = (long) ( ((float) x) * fCosa + ((float) y)
152 | * fSina + f1 + 0.5);
153 | //判断是否在源图范围内
154 | if( (x0 >= 0) && (x0 < nOldWidth) && (y0 >= 0) && (y0 < nOldHeight))
155 | {
156 | //用双线性插值
157 | if(bBilinear)
158 | {
159 | unsigned char *pTemp = Interpolation (nOldWidth, nOldHeight,
160 | (float)x0, (float)y0, nOldWidthBytes, nMovedBits, pOldBits);
161 | //复制像素
162 | memcpy(pNewTemp, pTemp, nMovedBits);
163 | delete [] pTemp ;
164 | }
165 | else
166 | {
167 | //指向源图像第y0行, 第x0个像素
168 | pOldTemp = pOldBits;
169 | pOldTemp += (nOldHeight - 1 - y0) * nOldWidthBytes;
170 | pOldTemp += x0 * nMovedBits;
171 | //复制像素
172 | memcpy(pNewTemp, pOldTemp, nMovedBits);
173 | }
174 | }
175 | pNewTemp += nMovedBits;
176 | }
177 | }
178 | //将内存解锁和将不再使用的内存释放, 将新图像设置为当前图像
179 | return TRUE;
180 | }
181 | ```
182 |
183 |  184 |
185 | 图6-26 旋转前的图像
186 |
187 |
188 |
189 |
184 |
185 | 图6-26 旋转前的图像
186 |
187 |
188 |
189 |  190 |
191 | 图6-27 旋转 $15^{\circ}$ 并进行揷值处理的图像
192 |
193 |
190 |
191 | 图6-27 旋转 $15^{\circ}$ 并进行揷值处理的图像
192 |
193 |  194 |
195 | 图6-28 被放大的旋转前图像
196 |
197 |
194 |
195 | 图6-28 被放大的旋转前图像
196 |
197 |  198 |
199 | 6-29 旋转300并进行揷值处理的放大图像
--------------------------------------------------------------------------------
/VI/6.6 图像复合变换.md:
--------------------------------------------------------------------------------
1 |
2 |
3 | # 6.6 图像复合变换
4 |
5 | ## 6.6.1 图像复合变换
6 |
7 | 图像的复合变换是指对给定的图像连续施行若干次如前所述的平移、镜像、比例、旋转等基本变换后所完成的变换, 图像的复合变换又叫级联变换。利用齐次坐标, 对给定的图像依次按一定顺序连续施行若干次基本变换, 其变换的矩阵仍然可以用 $3 \times 3$ 阶的矩阵表示, 而且从数学上可以证明, 复合变换的矩阵等于基本变换的矩阵按顺序依次相乘得到的组合矩阵。设对给定的图像依次进行了基本变换 $F_{1}, F_{2}, \ldots, F_{N}$, 它们的变换矩阵分别为 $T_{1}, T_{2}, \ldots, T_{N}$, 按照公式 (6-1) $\sim$ (6-6) 的表示形式, 图像复合变换的矩阵 $T$ 可以表示为: $T=T_{N} T_{N-1} \ldots T_{1}$ 。
8 |
9 | ### 复合平移
10 |
11 | 设某个图像先平移到新的位置 $P_{1}\left(x_{1}, y_{1}\right)$ 后, 再将图像平移到 $P_{2}\left(x_{2}, y_{2}\right)$ 的位置, 则复合平移矩阵为
12 |
13 | $$
14 | T=T_{1} T_{2}=\left[\begin{array}{ccc}
15 |
16 | 1 & 0 & x_{1} \\
17 |
18 | 0 & 1 & y_{1} \\
19 |
20 | 0 & 0 & 1
21 |
22 | \end{array}\right] \cdot\left[\begin{array}{ccc}
23 |
24 | 1 & 0 & x_{2} \\
25 |
26 | 0 & 1 & y_{2} \\
27 |
28 | 0 & 0 & 1
29 |
30 | \end{array}\right]=\left[\begin{array}{ccc}
31 |
32 | 1 & 0 & x_{1}+x_{2} \\
33 |
34 | 0 & 1 & y_{1}+y_{2} \\
35 |
36 | 0 & 0 & 1
37 |
38 | \end{array}\right]\tag{6-7}
39 | $$
40 |
41 | 由此可见, 尽管一些顺序的平移, 用到矩阵的乘法, 但最后合成的平移矩阵, 只需对平移常量作加法运算。
42 |
43 | ### 复合比例
44 |
45 | 同样, 对某个图像连续进行比例变换, 最后合成的复合比例矩阵, 只要对比例常量作乘法运算即可。复合比例矩阵如下:
46 |
47 | $$
48 | T=T_{1} T_{2}=\left[\begin{array}{lll}
49 |
50 | a_{1} & 0 & 0 \\
51 |
52 | 0 & d_{1} & 0 \\
53 |
54 | 0 & 0 & 1
55 |
56 | \end{array}\right] \cdot\left[\begin{array}{lll}
57 |
58 | a_{2} & 0 & 0 \\
59 |
60 | 0 & d_{2} & 0 \\
61 |
62 | 0 & 0 & 1
63 |
64 | \end{array}\right]=\left[\begin{array}{lll}
65 |
66 | a_{1} a_{2} & 0 & 0 \\
67 |
68 | 0 & d_{1} d_{2} & 0 \\
69 |
70 | 0 & 0 & 1
71 |
72 | \end{array}\right]\tag{6-8}
73 | $$
74 |
75 | ### 复合旋转
76 |
77 | 类似地, 对某个图像连续进行旋转变换, 最后合成的旋转变换矩阵等于两次旋转角度的和, 复合旋转变换矩阵如下式所示:
78 |
79 | $$
80 | \begin{aligned}
81 |
82 | T & =T_{1} T_{2}=\left[\begin{array}{ccc}
83 |
84 | \cos \theta_{1} & \sin \theta_{1} & 0 \\
85 |
86 | -\sin \theta_{1} & \cos \theta_{1} & 0 \\
87 |
88 | 0 & 0 & 1
89 |
90 | \end{array}\right] \cdot\left[\begin{array}{ccc}
91 |
92 | \cos \theta_{2} & \sin \theta_{2} & 0 \\
93 |
94 | -\sin \theta_{2} & \cos \theta_{2} & 0 \\
95 |
96 | 0 & 0 & 1
97 |
98 | \end{array}\right] \\
99 |
100 | & =\left[\begin{array}{ccc}
101 |
102 | \cos \left(\theta_{1}+\theta_{2}\right) & \sin \left(\theta_{1}+\theta_{2}\right) & 0 \\
103 |
104 | -\sin \left(\theta_{1}+\theta_{2}\right) & \cos \left(\theta_{1}+\theta_{2}\right) & 0 \\
105 |
106 | 0 & 0 & 1
107 |
108 | \end{array}\right]
109 |
110 | \end{aligned}\tag{6-9}
111 | $$
112 |
113 | 上述均为相对原点(图像中央)作比例、旋转等变换, 如果要相对某一个参考点作变换,则要使用含有不同种基本变换的图像复合变换。不同的复合变换, 其变换过程不同, 但是无论它的变换过程多么复杂, 都可以分解成一系列基本变换。相应地, 使用齐次坐标后, 图像复合变换的矩阵由一系列图像基本几何变换矩阵依次相乘而得到。下面通过一个例子讨论含有不同种基本变换的图像复合变换。
114 |
115 | 从6.2和6.5节的讨论中可以看出, 在进行图像的比例缩放、图像的旋转变换时, 整个变换过程由两部分组成, 即需要两个独立的算法。首先, 需要一个算法来完成几何变换本身, 用它描述每个像素如何从其初始位置移动到终止位置; 同时, 还需要一个用于灰度级插值的算法。这是因为, 在一般情况下, 原始 (输入) 图像的位置坐标 $(x, y)$ 为整数, 而变换后 (输出) 图像的位置坐标为非整数, 即产生 “空穴”,反过来也是如此。 因此, 一般地, 在进行图像的几何变换时, 除了要进行其本身的几何变换外,还要进行灰度级插值处理。
116 |
117 | 灰度级插值处理可采用如下两种方法。第一,可以把几何变换想像成将输入图像的灰度一个一个像素地转移到输出图像中。 如果一个输入像素被映射到四个输出像素之间的位置, 则其灰度值就按插值算法在四个输出像素之间进行分配。把这种灰度级插值处理称为像素移交 (pixel carry over) 或称为向前映射法, 如图6-30所示。
118 |
119 | 另一种更有效的灰度级插值处理方法是像素填充(pixel filling)或称为向后映射算法。在这种算法中, 输出像素一次一个地映射回到原始(输入)图像中,以便确定其灰度级。如果一个输出像素被映射到四个输出像素之间, 则其灰度值由灰度级插值决定, 如图6-30所示。向后空间变换是向前变换的逆变换。
120 |
121 | 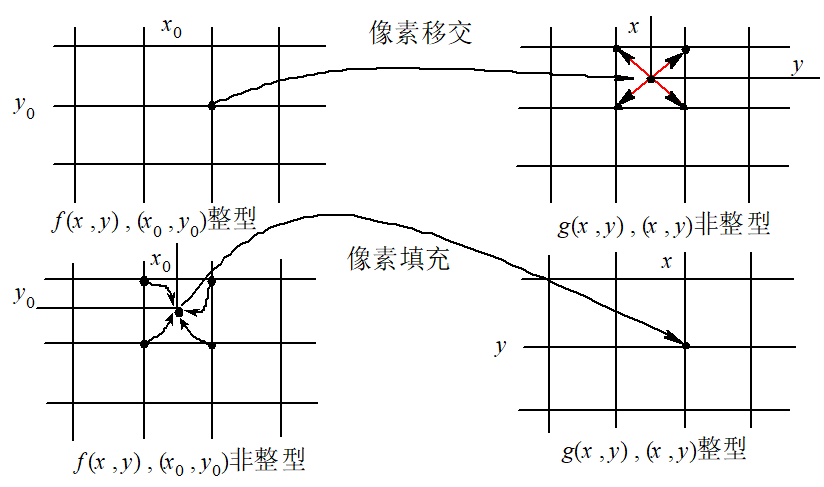
122 |
123 | 图6-30 灰度级插值处理(像素变换)
124 |
125 | 在像素填充法中,变换后(输出)图像的像素通常被映射到原始(输入)图像中的非整数位置, 即位于四个输入像素之间。因此, 为了决定与该位置相对应的灰度值, 必须进行插值运算。最简单的插值方法是零阶插值或称为最近邻插值, 也叫最近邻域法, 参见本书6.2节。一阶插值或称双线性插值法和零阶插值法相比可产生更令人满意的效果, 只是程序稍复杂一些, 运行时间稍长一些。它的原理如图6-10和图6-31所示, 插值计算公式参见6.2.1中的公式(6-2)。由于篇幅所限, 双线性插值公式的推导在此从略, 有兴趣的读者请参考书后的参考文献。
126 |
127 |
198 |
199 | 6-29 旋转300并进行揷值处理的放大图像
--------------------------------------------------------------------------------
/VI/6.6 图像复合变换.md:
--------------------------------------------------------------------------------
1 |
2 |
3 | # 6.6 图像复合变换
4 |
5 | ## 6.6.1 图像复合变换
6 |
7 | 图像的复合变换是指对给定的图像连续施行若干次如前所述的平移、镜像、比例、旋转等基本变换后所完成的变换, 图像的复合变换又叫级联变换。利用齐次坐标, 对给定的图像依次按一定顺序连续施行若干次基本变换, 其变换的矩阵仍然可以用 $3 \times 3$ 阶的矩阵表示, 而且从数学上可以证明, 复合变换的矩阵等于基本变换的矩阵按顺序依次相乘得到的组合矩阵。设对给定的图像依次进行了基本变换 $F_{1}, F_{2}, \ldots, F_{N}$, 它们的变换矩阵分别为 $T_{1}, T_{2}, \ldots, T_{N}$, 按照公式 (6-1) $\sim$ (6-6) 的表示形式, 图像复合变换的矩阵 $T$ 可以表示为: $T=T_{N} T_{N-1} \ldots T_{1}$ 。
8 |
9 | ### 复合平移
10 |
11 | 设某个图像先平移到新的位置 $P_{1}\left(x_{1}, y_{1}\right)$ 后, 再将图像平移到 $P_{2}\left(x_{2}, y_{2}\right)$ 的位置, 则复合平移矩阵为
12 |
13 | $$
14 | T=T_{1} T_{2}=\left[\begin{array}{ccc}
15 |
16 | 1 & 0 & x_{1} \\
17 |
18 | 0 & 1 & y_{1} \\
19 |
20 | 0 & 0 & 1
21 |
22 | \end{array}\right] \cdot\left[\begin{array}{ccc}
23 |
24 | 1 & 0 & x_{2} \\
25 |
26 | 0 & 1 & y_{2} \\
27 |
28 | 0 & 0 & 1
29 |
30 | \end{array}\right]=\left[\begin{array}{ccc}
31 |
32 | 1 & 0 & x_{1}+x_{2} \\
33 |
34 | 0 & 1 & y_{1}+y_{2} \\
35 |
36 | 0 & 0 & 1
37 |
38 | \end{array}\right]\tag{6-7}
39 | $$
40 |
41 | 由此可见, 尽管一些顺序的平移, 用到矩阵的乘法, 但最后合成的平移矩阵, 只需对平移常量作加法运算。
42 |
43 | ### 复合比例
44 |
45 | 同样, 对某个图像连续进行比例变换, 最后合成的复合比例矩阵, 只要对比例常量作乘法运算即可。复合比例矩阵如下:
46 |
47 | $$
48 | T=T_{1} T_{2}=\left[\begin{array}{lll}
49 |
50 | a_{1} & 0 & 0 \\
51 |
52 | 0 & d_{1} & 0 \\
53 |
54 | 0 & 0 & 1
55 |
56 | \end{array}\right] \cdot\left[\begin{array}{lll}
57 |
58 | a_{2} & 0 & 0 \\
59 |
60 | 0 & d_{2} & 0 \\
61 |
62 | 0 & 0 & 1
63 |
64 | \end{array}\right]=\left[\begin{array}{lll}
65 |
66 | a_{1} a_{2} & 0 & 0 \\
67 |
68 | 0 & d_{1} d_{2} & 0 \\
69 |
70 | 0 & 0 & 1
71 |
72 | \end{array}\right]\tag{6-8}
73 | $$
74 |
75 | ### 复合旋转
76 |
77 | 类似地, 对某个图像连续进行旋转变换, 最后合成的旋转变换矩阵等于两次旋转角度的和, 复合旋转变换矩阵如下式所示:
78 |
79 | $$
80 | \begin{aligned}
81 |
82 | T & =T_{1} T_{2}=\left[\begin{array}{ccc}
83 |
84 | \cos \theta_{1} & \sin \theta_{1} & 0 \\
85 |
86 | -\sin \theta_{1} & \cos \theta_{1} & 0 \\
87 |
88 | 0 & 0 & 1
89 |
90 | \end{array}\right] \cdot\left[\begin{array}{ccc}
91 |
92 | \cos \theta_{2} & \sin \theta_{2} & 0 \\
93 |
94 | -\sin \theta_{2} & \cos \theta_{2} & 0 \\
95 |
96 | 0 & 0 & 1
97 |
98 | \end{array}\right] \\
99 |
100 | & =\left[\begin{array}{ccc}
101 |
102 | \cos \left(\theta_{1}+\theta_{2}\right) & \sin \left(\theta_{1}+\theta_{2}\right) & 0 \\
103 |
104 | -\sin \left(\theta_{1}+\theta_{2}\right) & \cos \left(\theta_{1}+\theta_{2}\right) & 0 \\
105 |
106 | 0 & 0 & 1
107 |
108 | \end{array}\right]
109 |
110 | \end{aligned}\tag{6-9}
111 | $$
112 |
113 | 上述均为相对原点(图像中央)作比例、旋转等变换, 如果要相对某一个参考点作变换,则要使用含有不同种基本变换的图像复合变换。不同的复合变换, 其变换过程不同, 但是无论它的变换过程多么复杂, 都可以分解成一系列基本变换。相应地, 使用齐次坐标后, 图像复合变换的矩阵由一系列图像基本几何变换矩阵依次相乘而得到。下面通过一个例子讨论含有不同种基本变换的图像复合变换。
114 |
115 | 从6.2和6.5节的讨论中可以看出, 在进行图像的比例缩放、图像的旋转变换时, 整个变换过程由两部分组成, 即需要两个独立的算法。首先, 需要一个算法来完成几何变换本身, 用它描述每个像素如何从其初始位置移动到终止位置; 同时, 还需要一个用于灰度级插值的算法。这是因为, 在一般情况下, 原始 (输入) 图像的位置坐标 $(x, y)$ 为整数, 而变换后 (输出) 图像的位置坐标为非整数, 即产生 “空穴”,反过来也是如此。 因此, 一般地, 在进行图像的几何变换时, 除了要进行其本身的几何变换外,还要进行灰度级插值处理。
116 |
117 | 灰度级插值处理可采用如下两种方法。第一,可以把几何变换想像成将输入图像的灰度一个一个像素地转移到输出图像中。 如果一个输入像素被映射到四个输出像素之间的位置, 则其灰度值就按插值算法在四个输出像素之间进行分配。把这种灰度级插值处理称为像素移交 (pixel carry over) 或称为向前映射法, 如图6-30所示。
118 |
119 | 另一种更有效的灰度级插值处理方法是像素填充(pixel filling)或称为向后映射算法。在这种算法中, 输出像素一次一个地映射回到原始(输入)图像中,以便确定其灰度级。如果一个输出像素被映射到四个输出像素之间, 则其灰度值由灰度级插值决定, 如图6-30所示。向后空间变换是向前变换的逆变换。
120 |
121 | 
122 |
123 | 图6-30 灰度级插值处理(像素变换)
124 |
125 | 在像素填充法中,变换后(输出)图像的像素通常被映射到原始(输入)图像中的非整数位置, 即位于四个输入像素之间。因此, 为了决定与该位置相对应的灰度值, 必须进行插值运算。最简单的插值方法是零阶插值或称为最近邻插值, 也叫最近邻域法, 参见本书6.2节。一阶插值或称双线性插值法和零阶插值法相比可产生更令人满意的效果, 只是程序稍复杂一些, 运行时间稍长一些。它的原理如图6-10和图6-31所示, 插值计算公式参见6.2.1中的公式(6-2)。由于篇幅所限, 双线性插值公式的推导在此从略, 有兴趣的读者请参考书后的参考文献。
126 |
127 |  128 |
129 | 图6-31 双线性插值
130 |
131 | 在这里还要说明一点, 为了提高双线性插值的速度, 双线性插值也可以分解为三个线性插值来实现, 公式如下:
132 | $$
133 | \begin{aligned}
134 |
135 | & f(x, 0)=f(0,0)+x[f(1,0)-f(0,0)] \\
136 |
137 | & f(x, 1)=f(0,1)+x[f(1,1)-f(0,1)] \\
138 |
139 | & f(x, y)=f(x, 0)+y[f(x, 1)-f(x, 0)]
140 |
141 | \end{aligned}\tag{6-10}
142 | $$
143 |
144 | 因为公式(6-2)需要用到四次乘法、八次加(或减)法运算, 而公式(6-10)表示的第二种方法只需要三次乘法和六次加 (或减)法, 所以几何变换程序一般选择后者。从图6-31也可以看出双线性插值与最近邻插值的区别。
145 |
146 | 在几何运算中,双线性灰度插值的平滑作用可能会使图像的细节产生退化, 尤其是在进行放大处理时, 这种影响将更为明显。而在其他应用中, 双线性插值的斜率不连续性会产生不希望得到的结果。这两种情况都可以通过高阶插值得到修正, 当然这需要增加计算量。使用高阶插值函数的例子有:三次样条、Legendre中心函数和 $\sin (\alpha x) / \alpha$ 函数(即 $\sin (\alpha x)$ 函数)。高阶插值常用卷积来实现, 这部分内容请读者参考书后所附的参考文献。
147 |
148 | ## 6.6.2 图像复合变换的示例
149 |
150 |
128 |
129 | 图6-31 双线性插值
130 |
131 | 在这里还要说明一点, 为了提高双线性插值的速度, 双线性插值也可以分解为三个线性插值来实现, 公式如下:
132 | $$
133 | \begin{aligned}
134 |
135 | & f(x, 0)=f(0,0)+x[f(1,0)-f(0,0)] \\
136 |
137 | & f(x, 1)=f(0,1)+x[f(1,1)-f(0,1)] \\
138 |
139 | & f(x, y)=f(x, 0)+y[f(x, 1)-f(x, 0)]
140 |
141 | \end{aligned}\tag{6-10}
142 | $$
143 |
144 | 因为公式(6-2)需要用到四次乘法、八次加(或减)法运算, 而公式(6-10)表示的第二种方法只需要三次乘法和六次加 (或减)法, 所以几何变换程序一般选择后者。从图6-31也可以看出双线性插值与最近邻插值的区别。
145 |
146 | 在几何运算中,双线性灰度插值的平滑作用可能会使图像的细节产生退化, 尤其是在进行放大处理时, 这种影响将更为明显。而在其他应用中, 双线性插值的斜率不连续性会产生不希望得到的结果。这两种情况都可以通过高阶插值得到修正, 当然这需要增加计算量。使用高阶插值函数的例子有:三次样条、Legendre中心函数和 $\sin (\alpha x) / \alpha$ 函数(即 $\sin (\alpha x)$ 函数)。高阶插值常用卷积来实现, 这部分内容请读者参考书后所附的参考文献。
147 |
148 | ## 6.6.2 图像复合变换的示例
149 |
150 |  151 |
152 | 图6-32 坐标系的平移
153 |
154 | 两个坐标系之间的坐标变换矩阵表达式为:
155 | $$
156 | \left[\begin{array}{c}
157 |
158 | x_{\Pi} \\
159 |
160 | y_{\Pi} \\
161 |
162 | 1
163 |
164 | \end{array}\right]=\left[\begin{array}{ccc}
165 |
166 | 1 & 0 & -a \\
167 |
168 | 0 & -1 & b \\
169 |
170 | 0 & 0 & 1
171 |
172 | \end{array}\right] \cdot\left[\begin{array}{c}
173 |
174 | x_{I} \\
175 |
176 | y_{I} \\
177 |
178 | 1
179 |
180 | \end{array}\right]
181 | $$
182 |
183 | 它的逆变换矩阵表达式是:
184 |
185 | $$
186 | \left[\begin{array}{c}
187 |
188 | x_{I} \\
189 |
190 | y_{I} \\
191 |
192 | 1
193 |
194 | \end{array}\right]=\left[\begin{array}{ccc}
195 |
196 | 1 & 0 & a \\
197 |
198 | 0 & -1 & b \\
199 |
200 | 0 & 0 & 1
201 |
202 | \end{array}\right] \cdot\left[\begin{array}{c}
203 |
204 | x_{\Pi} \\
205 |
206 | y_{\Pi} \\
207 |
208 | 1
209 |
210 | \end{array}\right]
211 | $$
212 |
213 | 为了推导公式简单起见, 假设图像末旋转时中心坐标为 $(a,b)$, 旋转后中心坐标为 $(c, d)$ (在新的坐标系下旋转后新图像左上角为原点), 则旋转变换矩阵表达式为
214 |
215 | $$
216 | \begin{align}
217 | \left[\begin{array}{c}
218 | x \\
219 | y \\
220 | 1
221 | \end{array}\right]&=\left[\begin{array}{ccc}
222 | 1 & 0 & -c \\
223 | 0 & -1 & d \\
224 | 0 & 0 & 1
225 | \end{array}\right] \cdot\left[\begin{array}{c}
226 | x_{\Pi} \\
227 | y_{\Pi} \\
228 | 1
229 | \end{array}\right]=\left[\begin{array}{ccc}
230 | 1 & 0 & -c \\
231 | 0 & -1 & d \\
232 | 0 & 0 & 1
233 | \end{array}\right] \cdot\left[\begin{array}{ccc}
234 | \cos \theta & \sin \theta & 0 \\
235 | -\sin \theta & \cos \theta & 0 \\
236 | 0 & 0 & 1
237 | \end{array}\right]\left[\begin{array}{c}
238 | x_{\Pi} \\
239 | y_{\Pi} \\
240 | 1
241 | \end{array}\right]\\
242 | &=\left[\begin{array}{ccc}
243 | 1 & 0 & -c \\
244 | 0 & -1 & d \\
245 | 0 & 0 & 1
246 | \end{array}\right] \cdot\left[\begin{array}{ccc}
247 | \cos \theta & \sin \theta & 0 \\
248 | -\sin \theta & \cos \theta & 0 \\
249 | 0 & 0 & 1
250 | \end{array}\right] \cdot\left[\begin{array}{ccc}
251 | 1 & 0 & -a \\
252 | 0 & -1 & b \\
253 | 0 & 0 & 1
254 | \end{array}\right] \cdot\left[\begin{array}{c}
255 | x_{0} \\
256 | y_{0} \\
257 | 1
258 | \end{array}\right]
259 | \end{align}
260 | \tag{6-11}
261 | $$
262 |
263 | $$
264 |
265 | $$
266 |
267 | 其逆变换表达式为
268 |
269 | $$
270 | \left[\begin{array}{c}
271 |
272 | x_{0} \\
273 |
274 | y_{0} \\
275 |
276 | 1
277 |
278 | \end{array}\right]=\left[\begin{array}{ccc}
279 |
280 | 1 & 0 & -a \\
281 |
282 | 0 & -1 & b \\
283 |
284 | 0 & 0 & 1
285 |
286 | \end{array}\right] \cdot\left[\begin{array}{ccc}
287 |
288 | \cos \theta & \sin \theta & 0 \\
289 |
290 | -\sin \theta & \cos \theta & 0 \\
291 |
292 | 0 & 0 & 0
293 |
294 | \end{array}\right] \cdot\left[\begin{array}{ccc}
295 |
296 | 1 & 0 & -c \\
297 |
298 | 0 & -1 & d \\
299 |
300 | 0 & 0 & 1
301 |
302 | \end{array}\right] \cdot\left[\begin{array}{c}
303 |
304 | x \\
305 |
306 | y \\
307 |
308 | 1
309 |
310 | \end{array}\right]\tag{6-12}
311 | $$
312 | 即
313 | $$
314 | \left[\begin{array}{c}
315 |
316 | x_{0} \\
317 |
318 | y_{0} \\
319 |
320 | 1
321 |
322 | \end{array}\right]=\left[\begin{array}{ccc}
323 |
324 | \cos \theta & \sin \theta & -c \cos \theta-d \sin \theta+a \\
325 |
326 | -\sin \theta & \cos \theta & c \sin \theta-d \cos \theta+b \\
327 |
328 | 0 & 0 & 1
329 |
330 | \end{array}\right] \cdot\left[\begin{array}{c}
331 |
332 | x \\
333 |
334 | y \\
335 |
336 | 1
337 |
338 | \end{array}\right]\tag{6-13}
339 | $$
340 |
341 | 因此
342 |
343 | $$
344 | \left\{\begin{array}{l}
345 | x_{0}=x \cos \theta+y \sin \theta-c \cos \theta-d \sin \theta+a \\
346 | y_{0}=-x \sin \theta+y \cos \theta+c \sin \theta-d \cos \theta+b
347 | \end{array}\right.\tag{6-14}
348 | $$
349 |
350 | 公式(6-10)说明绕任意点(a,b)旋转的几何变换是由平移一旋转一平移三个基本变换所构成, 即先将坐标系平移到点( $a$,b), 再进行旋转, 然后将旋转后的图像平移回原来的坐标原点。
351 |
352 | 利用上面的转换公式 $(6-12) \sim(6-14) ,$ 就可以比较方便地编㝍出实现图像旋转的VC++函数。首先应计算出公式中需要的几个参数: $a, b, c, d$ 和旋转后新图像的高、宽度。现在已知图像的原始宽度为lWidth, 高度为lHeight, 以图像中心为坐标系原点,则原始图像四个角的坐标分别为
353 |
354 | $$
355 | \begin{aligned}
356 | & {\left[-\frac{\text { lWidth }-1}{2}, \frac{\text { lHeight }-1}{2}\right],\left[\frac{\text { lWidth }-1}{2}, \frac{\text { lHeight }-1}{2}\right]} \\
357 | & {\left[\frac{\text { lWidth }-1}{2},-\frac{\text { lHeight }-1}{2}\right],\left[-\frac{\text { lWidth }-1}{2},-\frac{\text { lHeight }-1}{2}\right]}
358 | \end{aligned}
359 | $$
360 |
361 | 按照旋转公式(6-11) (6-14), 在旋转后的新图像中, 这四个点坐标为
362 |
363 | $$
364 | \begin{aligned}
365 | & (f D s t X 1, f D s t Y 1)=\left(-\frac{l \text { Width }-1}{2} \cos \theta+\frac{\text { lHeight }-1}{2} \sin \theta,-\frac{l \text { Width }-1}{2} \sin \theta+\frac{\text { lHeight }-1}{2} \cos \theta\right) \\
366 | & (f D s t X 2, f D s t Y 2)=\left(\frac{l \text { Width }-1}{2} \cos \theta+\frac{l \text { Height }-1}{2} \sin \theta,-\frac{l \text { Width }-1}{2} \sin \theta+\frac{\text { lHeight }-1}{2} \cos \theta\right) \\
367 | & (f D s t X 3, f D s t Y 3)=\left(-\frac{l \text { Width }-1}{2} \cos \theta-\frac{l \text { Height }-1}{2} \sin \theta,-\frac{l \text { Width }-1}{2} \sin \theta-\frac{l \text { Height }-1}{2} \cos \theta\right) \\
368 | & (f D s t X 4, f D s t Y 4)=\left(-\frac{l W i d t h-1}{2} \cos \theta-\frac{l \text { Height }-1}{2} \sin \theta, \frac{l \text { Width }-1}{2} \sin \theta-\frac{l \text { Height }-1}{2} \cos \theta\right)
369 | \end{aligned}
370 | $$
371 |
372 | 则新图像的宽度lNewWidth和高度lNewHeight为
373 |
374 | $$
375 | lNewWidth =\max (|f D s t X 4-f D s t Y 1|,|f D s t X 3-f D s t Y 2|)\\
376 | lNewHeight =\max (|f D s t X 4-f D s t Y 1|,|f D s t X 3-f D s t Y 2|)
377 | $$
378 |
379 | 如果令
380 |
381 | $$
382 | \left\{\begin{array}{l}
383 | f_{1}=-c \cos \theta-d \sin \theta+a \\
384 | f_{2}=c \sin \theta-d \cos \theta+b
385 | \end{array}\right.\tag{6-15}
386 | $$
387 |
388 | 由已知及假设
389 |
390 | $$
391 | a=\frac{\text { lWidth }-1}{2}, b=\frac{\text { lHeight }-1}{2}, c=\frac{\text { lNewWidth }-1}{2}, d=\frac{\text { lNewHeight }-1}{2}
392 | $$
393 |
394 | 由公式 (6-13) 得
395 |
396 | $$
397 | \left\{\begin{array}{l}
398 | x_{0}=x \cos \theta+y \sin \theta+f_{1} \\
399 | y_{0}=-x \sin \theta+y \cos \theta+f_{2}
400 | \end{array}\right.\tag{6-16}
401 | $$
402 |
403 | 公式 (6-16)、(6-17) 便是图像绕任意点 $(a, b)$ 旋转的变换公式, 由此便可以编㝍出实现该变换的VC++程序。事
404 |
405 | 实上,只要先按上述公式计算出旋转后新图像的高度和宽度以及常数 $f 1$ 和 $f_{2}$, 并按照公式 (6-17) 计算出变换后图像上的点 $(i 0, j 0)$ :
406 |
407 | $/ /$ 计算该像素在源DIB中的坐标
408 |
409 | $$
410 | \begin{aligned}
411 | & i 0=-((\text { float }) j) * f \operatorname{sina}+((\text { float }) i) * f \operatorname{cosa}+f 2 \\
412 | & j 0=((\text { float }) j) * f \text { cosa }+((\text { float }) i) * f \sin a+f 1
413 | \end{aligned}
414 | $$
--------------------------------------------------------------------------------
/VI/6.7 透视变换.md:
--------------------------------------------------------------------------------
1 | # 6.7 透视变换
2 |
3 | ## 6.7.1 透视变换
4 |
5 | 把三维物体或对象转变为二维图形表示的过程称为投影变换。
6 |
7 | 根据视点 (投影中心) 与投影平面之间距离的不同, 投影可分为平行投影和透视投影, 透视投影即透视变换。平行投影的视点与投影平面之间的距离为无穷大, 而对透视投影(变换), 该距离是有限的。这个距离决定着透视投影的特性一透视缩小效应, 即三维物体或对象透视投影的大小与形体到视点的距离成反比。 例如, 等长的两直线段, 都平行于投影面, 但离投影中心近的线段, 其透视投影大, 而离投影中心远的线段, 透视投影小。这种效应所产生的视觉效果与照相机系统和人的视觉系统十分类似。 与平行投影相比, 透视投影的深度感更强, 看上去更真实, 但透视投影不能真实地反映物体的精确尺寸和形状。
8 |
9 | 对于透视投影,一束平行于投影面的平行线的投影可保持平行, 而不平行于投影面的平行线的投影会聚集到一个点, 这个点称为灭点 (Vanishing Point)。灭点可以看作是无限远处的一点在投影面上的投影。透视投影的灭点可以有无限多个, 不同方向的平行线在投影面上就能形成不同的灭点, 坐标轴方向的平行线在投影面上形成的灭点又称作主灭点。因为有 $x, y$ 和 $z$ 三个坐标轴, 所以主灭点最多有 3 个。透视投影是按主灭点的个数来分类的, 即按投影面与坐标轴的夹角来分类的, 可分为一点透视、二点透视和三点透视, 如图6-33 所示。
10 |
11 | 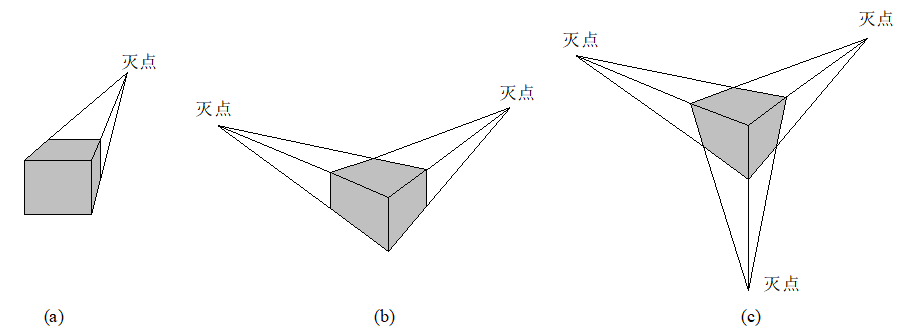
12 |
13 | 图6-33 透视变换 (a)一点透视; (b) 二点透视; (c) 三点透视
14 |
15 | 下面讨论一点透视。一点透视只有一个主灭点,即投影面与一个坐标轴正交,与另外两个坐标轴平行,如图6-33(a)所示。 进行一点透视投影变换,要很好地考虑图面布局, 以避免三维形体或对象的平面域积聚成直线或直线积聚成点而影响直观性。具体地说,就是要考虑下列几点: (1)三维形体或对象与画面 (投影面)的相对位置;(2)视距,即视点与畐面的距离;(3)视点的高度。 由此,假设视点在坐标原点, $Z$ 坐标轴方向与观察方向重合一致, 三维形体或对象上某一点为 $P(x, y, z)$, 一点透视变换后在投影面 (观察平面) $U O^{\prime} V$ 上的对应点为 $P^{\prime}\left(x^{\prime}, y^{\prime}, z^{\prime}\right)$, 投影面与 $z$ 轴垂直, 且与视点的距离为d, $z$ 轴过投影面窗口的中心,窗口是边长为 $2 S$ 的正方形, 如图6-34所示。根据相似三角形对应边成比例的关系, 有:
16 |
17 | $$
18 | \begin{gathered}
19 | \frac{x^{\prime}}{x}=\frac{y^{\prime}}{y}=\frac{z^{\prime}}{z}, z^{\prime}=d \\
20 | x^{\prime}=\frac{x}{z} d, y^{\prime}=\frac{y}{z} d, z^{\prime}=d
21 | \end{gathered}\tag{6-18}
22 | $$
23 |
24 | 利用齐次坐标, 与二维几何变换类似, 将该过程写成变换矩阵形式为
25 |
26 | $$
27 | \left[\begin{array}{l}
28 | x^{\prime} \\
29 | y^{\prime} \\
30 | z^{\prime} \\
31 | 1
32 | \end{array}\right]=\left[\begin{array}{llll}
33 | d & 0 & 0 & 0 \\
34 | 0 & d & 0 & 0 \\
35 | 0 & 0 & 0 & -1 \\
36 | 0 & 0 & 1 & 0
37 | \end{array}\right] \cdot\left[\begin{array}{l}
38 | d x \\
39 | d y \\
40 | -1 \\
41 | z
42 | \end{array}\right]\tag{6-19}
43 | $$
44 |
45 |
46 |
47 |
151 |
152 | 图6-32 坐标系的平移
153 |
154 | 两个坐标系之间的坐标变换矩阵表达式为:
155 | $$
156 | \left[\begin{array}{c}
157 |
158 | x_{\Pi} \\
159 |
160 | y_{\Pi} \\
161 |
162 | 1
163 |
164 | \end{array}\right]=\left[\begin{array}{ccc}
165 |
166 | 1 & 0 & -a \\
167 |
168 | 0 & -1 & b \\
169 |
170 | 0 & 0 & 1
171 |
172 | \end{array}\right] \cdot\left[\begin{array}{c}
173 |
174 | x_{I} \\
175 |
176 | y_{I} \\
177 |
178 | 1
179 |
180 | \end{array}\right]
181 | $$
182 |
183 | 它的逆变换矩阵表达式是:
184 |
185 | $$
186 | \left[\begin{array}{c}
187 |
188 | x_{I} \\
189 |
190 | y_{I} \\
191 |
192 | 1
193 |
194 | \end{array}\right]=\left[\begin{array}{ccc}
195 |
196 | 1 & 0 & a \\
197 |
198 | 0 & -1 & b \\
199 |
200 | 0 & 0 & 1
201 |
202 | \end{array}\right] \cdot\left[\begin{array}{c}
203 |
204 | x_{\Pi} \\
205 |
206 | y_{\Pi} \\
207 |
208 | 1
209 |
210 | \end{array}\right]
211 | $$
212 |
213 | 为了推导公式简单起见, 假设图像末旋转时中心坐标为 $(a,b)$, 旋转后中心坐标为 $(c, d)$ (在新的坐标系下旋转后新图像左上角为原点), 则旋转变换矩阵表达式为
214 |
215 | $$
216 | \begin{align}
217 | \left[\begin{array}{c}
218 | x \\
219 | y \\
220 | 1
221 | \end{array}\right]&=\left[\begin{array}{ccc}
222 | 1 & 0 & -c \\
223 | 0 & -1 & d \\
224 | 0 & 0 & 1
225 | \end{array}\right] \cdot\left[\begin{array}{c}
226 | x_{\Pi} \\
227 | y_{\Pi} \\
228 | 1
229 | \end{array}\right]=\left[\begin{array}{ccc}
230 | 1 & 0 & -c \\
231 | 0 & -1 & d \\
232 | 0 & 0 & 1
233 | \end{array}\right] \cdot\left[\begin{array}{ccc}
234 | \cos \theta & \sin \theta & 0 \\
235 | -\sin \theta & \cos \theta & 0 \\
236 | 0 & 0 & 1
237 | \end{array}\right]\left[\begin{array}{c}
238 | x_{\Pi} \\
239 | y_{\Pi} \\
240 | 1
241 | \end{array}\right]\\
242 | &=\left[\begin{array}{ccc}
243 | 1 & 0 & -c \\
244 | 0 & -1 & d \\
245 | 0 & 0 & 1
246 | \end{array}\right] \cdot\left[\begin{array}{ccc}
247 | \cos \theta & \sin \theta & 0 \\
248 | -\sin \theta & \cos \theta & 0 \\
249 | 0 & 0 & 1
250 | \end{array}\right] \cdot\left[\begin{array}{ccc}
251 | 1 & 0 & -a \\
252 | 0 & -1 & b \\
253 | 0 & 0 & 1
254 | \end{array}\right] \cdot\left[\begin{array}{c}
255 | x_{0} \\
256 | y_{0} \\
257 | 1
258 | \end{array}\right]
259 | \end{align}
260 | \tag{6-11}
261 | $$
262 |
263 | $$
264 |
265 | $$
266 |
267 | 其逆变换表达式为
268 |
269 | $$
270 | \left[\begin{array}{c}
271 |
272 | x_{0} \\
273 |
274 | y_{0} \\
275 |
276 | 1
277 |
278 | \end{array}\right]=\left[\begin{array}{ccc}
279 |
280 | 1 & 0 & -a \\
281 |
282 | 0 & -1 & b \\
283 |
284 | 0 & 0 & 1
285 |
286 | \end{array}\right] \cdot\left[\begin{array}{ccc}
287 |
288 | \cos \theta & \sin \theta & 0 \\
289 |
290 | -\sin \theta & \cos \theta & 0 \\
291 |
292 | 0 & 0 & 0
293 |
294 | \end{array}\right] \cdot\left[\begin{array}{ccc}
295 |
296 | 1 & 0 & -c \\
297 |
298 | 0 & -1 & d \\
299 |
300 | 0 & 0 & 1
301 |
302 | \end{array}\right] \cdot\left[\begin{array}{c}
303 |
304 | x \\
305 |
306 | y \\
307 |
308 | 1
309 |
310 | \end{array}\right]\tag{6-12}
311 | $$
312 | 即
313 | $$
314 | \left[\begin{array}{c}
315 |
316 | x_{0} \\
317 |
318 | y_{0} \\
319 |
320 | 1
321 |
322 | \end{array}\right]=\left[\begin{array}{ccc}
323 |
324 | \cos \theta & \sin \theta & -c \cos \theta-d \sin \theta+a \\
325 |
326 | -\sin \theta & \cos \theta & c \sin \theta-d \cos \theta+b \\
327 |
328 | 0 & 0 & 1
329 |
330 | \end{array}\right] \cdot\left[\begin{array}{c}
331 |
332 | x \\
333 |
334 | y \\
335 |
336 | 1
337 |
338 | \end{array}\right]\tag{6-13}
339 | $$
340 |
341 | 因此
342 |
343 | $$
344 | \left\{\begin{array}{l}
345 | x_{0}=x \cos \theta+y \sin \theta-c \cos \theta-d \sin \theta+a \\
346 | y_{0}=-x \sin \theta+y \cos \theta+c \sin \theta-d \cos \theta+b
347 | \end{array}\right.\tag{6-14}
348 | $$
349 |
350 | 公式(6-10)说明绕任意点(a,b)旋转的几何变换是由平移一旋转一平移三个基本变换所构成, 即先将坐标系平移到点( $a$,b), 再进行旋转, 然后将旋转后的图像平移回原来的坐标原点。
351 |
352 | 利用上面的转换公式 $(6-12) \sim(6-14) ,$ 就可以比较方便地编㝍出实现图像旋转的VC++函数。首先应计算出公式中需要的几个参数: $a, b, c, d$ 和旋转后新图像的高、宽度。现在已知图像的原始宽度为lWidth, 高度为lHeight, 以图像中心为坐标系原点,则原始图像四个角的坐标分别为
353 |
354 | $$
355 | \begin{aligned}
356 | & {\left[-\frac{\text { lWidth }-1}{2}, \frac{\text { lHeight }-1}{2}\right],\left[\frac{\text { lWidth }-1}{2}, \frac{\text { lHeight }-1}{2}\right]} \\
357 | & {\left[\frac{\text { lWidth }-1}{2},-\frac{\text { lHeight }-1}{2}\right],\left[-\frac{\text { lWidth }-1}{2},-\frac{\text { lHeight }-1}{2}\right]}
358 | \end{aligned}
359 | $$
360 |
361 | 按照旋转公式(6-11) (6-14), 在旋转后的新图像中, 这四个点坐标为
362 |
363 | $$
364 | \begin{aligned}
365 | & (f D s t X 1, f D s t Y 1)=\left(-\frac{l \text { Width }-1}{2} \cos \theta+\frac{\text { lHeight }-1}{2} \sin \theta,-\frac{l \text { Width }-1}{2} \sin \theta+\frac{\text { lHeight }-1}{2} \cos \theta\right) \\
366 | & (f D s t X 2, f D s t Y 2)=\left(\frac{l \text { Width }-1}{2} \cos \theta+\frac{l \text { Height }-1}{2} \sin \theta,-\frac{l \text { Width }-1}{2} \sin \theta+\frac{\text { lHeight }-1}{2} \cos \theta\right) \\
367 | & (f D s t X 3, f D s t Y 3)=\left(-\frac{l \text { Width }-1}{2} \cos \theta-\frac{l \text { Height }-1}{2} \sin \theta,-\frac{l \text { Width }-1}{2} \sin \theta-\frac{l \text { Height }-1}{2} \cos \theta\right) \\
368 | & (f D s t X 4, f D s t Y 4)=\left(-\frac{l W i d t h-1}{2} \cos \theta-\frac{l \text { Height }-1}{2} \sin \theta, \frac{l \text { Width }-1}{2} \sin \theta-\frac{l \text { Height }-1}{2} \cos \theta\right)
369 | \end{aligned}
370 | $$
371 |
372 | 则新图像的宽度lNewWidth和高度lNewHeight为
373 |
374 | $$
375 | lNewWidth =\max (|f D s t X 4-f D s t Y 1|,|f D s t X 3-f D s t Y 2|)\\
376 | lNewHeight =\max (|f D s t X 4-f D s t Y 1|,|f D s t X 3-f D s t Y 2|)
377 | $$
378 |
379 | 如果令
380 |
381 | $$
382 | \left\{\begin{array}{l}
383 | f_{1}=-c \cos \theta-d \sin \theta+a \\
384 | f_{2}=c \sin \theta-d \cos \theta+b
385 | \end{array}\right.\tag{6-15}
386 | $$
387 |
388 | 由已知及假设
389 |
390 | $$
391 | a=\frac{\text { lWidth }-1}{2}, b=\frac{\text { lHeight }-1}{2}, c=\frac{\text { lNewWidth }-1}{2}, d=\frac{\text { lNewHeight }-1}{2}
392 | $$
393 |
394 | 由公式 (6-13) 得
395 |
396 | $$
397 | \left\{\begin{array}{l}
398 | x_{0}=x \cos \theta+y \sin \theta+f_{1} \\
399 | y_{0}=-x \sin \theta+y \cos \theta+f_{2}
400 | \end{array}\right.\tag{6-16}
401 | $$
402 |
403 | 公式 (6-16)、(6-17) 便是图像绕任意点 $(a, b)$ 旋转的变换公式, 由此便可以编㝍出实现该变换的VC++程序。事
404 |
405 | 实上,只要先按上述公式计算出旋转后新图像的高度和宽度以及常数 $f 1$ 和 $f_{2}$, 并按照公式 (6-17) 计算出变换后图像上的点 $(i 0, j 0)$ :
406 |
407 | $/ /$ 计算该像素在源DIB中的坐标
408 |
409 | $$
410 | \begin{aligned}
411 | & i 0=-((\text { float }) j) * f \operatorname{sina}+((\text { float }) i) * f \operatorname{cosa}+f 2 \\
412 | & j 0=((\text { float }) j) * f \text { cosa }+((\text { float }) i) * f \sin a+f 1
413 | \end{aligned}
414 | $$
--------------------------------------------------------------------------------
/VI/6.7 透视变换.md:
--------------------------------------------------------------------------------
1 | # 6.7 透视变换
2 |
3 | ## 6.7.1 透视变换
4 |
5 | 把三维物体或对象转变为二维图形表示的过程称为投影变换。
6 |
7 | 根据视点 (投影中心) 与投影平面之间距离的不同, 投影可分为平行投影和透视投影, 透视投影即透视变换。平行投影的视点与投影平面之间的距离为无穷大, 而对透视投影(变换), 该距离是有限的。这个距离决定着透视投影的特性一透视缩小效应, 即三维物体或对象透视投影的大小与形体到视点的距离成反比。 例如, 等长的两直线段, 都平行于投影面, 但离投影中心近的线段, 其透视投影大, 而离投影中心远的线段, 透视投影小。这种效应所产生的视觉效果与照相机系统和人的视觉系统十分类似。 与平行投影相比, 透视投影的深度感更强, 看上去更真实, 但透视投影不能真实地反映物体的精确尺寸和形状。
8 |
9 | 对于透视投影,一束平行于投影面的平行线的投影可保持平行, 而不平行于投影面的平行线的投影会聚集到一个点, 这个点称为灭点 (Vanishing Point)。灭点可以看作是无限远处的一点在投影面上的投影。透视投影的灭点可以有无限多个, 不同方向的平行线在投影面上就能形成不同的灭点, 坐标轴方向的平行线在投影面上形成的灭点又称作主灭点。因为有 $x, y$ 和 $z$ 三个坐标轴, 所以主灭点最多有 3 个。透视投影是按主灭点的个数来分类的, 即按投影面与坐标轴的夹角来分类的, 可分为一点透视、二点透视和三点透视, 如图6-33 所示。
10 |
11 | 
12 |
13 | 图6-33 透视变换 (a)一点透视; (b) 二点透视; (c) 三点透视
14 |
15 | 下面讨论一点透视。一点透视只有一个主灭点,即投影面与一个坐标轴正交,与另外两个坐标轴平行,如图6-33(a)所示。 进行一点透视投影变换,要很好地考虑图面布局, 以避免三维形体或对象的平面域积聚成直线或直线积聚成点而影响直观性。具体地说,就是要考虑下列几点: (1)三维形体或对象与画面 (投影面)的相对位置;(2)视距,即视点与畐面的距离;(3)视点的高度。 由此,假设视点在坐标原点, $Z$ 坐标轴方向与观察方向重合一致, 三维形体或对象上某一点为 $P(x, y, z)$, 一点透视变换后在投影面 (观察平面) $U O^{\prime} V$ 上的对应点为 $P^{\prime}\left(x^{\prime}, y^{\prime}, z^{\prime}\right)$, 投影面与 $z$ 轴垂直, 且与视点的距离为d, $z$ 轴过投影面窗口的中心,窗口是边长为 $2 S$ 的正方形, 如图6-34所示。根据相似三角形对应边成比例的关系, 有:
16 |
17 | $$
18 | \begin{gathered}
19 | \frac{x^{\prime}}{x}=\frac{y^{\prime}}{y}=\frac{z^{\prime}}{z}, z^{\prime}=d \\
20 | x^{\prime}=\frac{x}{z} d, y^{\prime}=\frac{y}{z} d, z^{\prime}=d
21 | \end{gathered}\tag{6-18}
22 | $$
23 |
24 | 利用齐次坐标, 与二维几何变换类似, 将该过程写成变换矩阵形式为
25 |
26 | $$
27 | \left[\begin{array}{l}
28 | x^{\prime} \\
29 | y^{\prime} \\
30 | z^{\prime} \\
31 | 1
32 | \end{array}\right]=\left[\begin{array}{llll}
33 | d & 0 & 0 & 0 \\
34 | 0 & d & 0 & 0 \\
35 | 0 & 0 & 0 & -1 \\
36 | 0 & 0 & 1 & 0
37 | \end{array}\right] \cdot\left[\begin{array}{l}
38 | d x \\
39 | d y \\
40 | -1 \\
41 | z
42 | \end{array}\right]\tag{6-19}
43 | $$
44 |
45 |
46 |
47 | 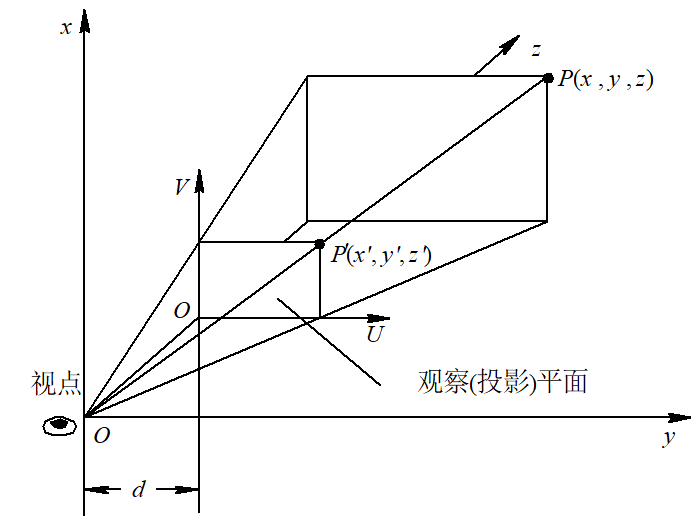 48 |
49 | 图6-34 一点透视变换
50 |
51 | 一般地, 视点不在原点, 投影平面是任意平面的情况,一点透视变换的矩阵也可以用一个 $4 \times 4$ 的矩阵表示。当根据公式 (6-19) 求出它的逆变换后, 可以用 $VC++$ 编写一个实现图像透视的程序, 实现图像的透视。
52 |
53 | ## 6.7.2 其他变换
54 |
55 | 如前所述, 齐次坐标为确定各种基本变换和复合变换公式提供了一个简单的方法。然而, 在许多图像处理与分析应用中, 所需的几何变换都相当复杂, 甚至有些无法用简便的数学式来表达。此外, 所需几何变换经常要从对实际图像的测量中获得, 因此更希望用这些测量结果而不是函数形式来描述几何变换。 例如, 在对由摄像机拍摄的有几何畸变的图像进行几何校正时, 首先应将一个矩形栅格目标数字化并显示出来。因为摄像机中有几何变形, 所显示的图案不会是准确的矩形, 因此所求几何变换应能使其栅格图案再次被复原为准确的矩形, 从而修正了摄像机产生的畸变。采用同样的几何变换可用于校正同一摄像机生成的数字化图像(假定畸变与景物无关), 由此可得到不畸变的图像。
56 |
57 | 图像几何变换的一个重要应用是消除由于摄像机导致的数字图像的几何畸变。当需要从数字图像中得到定量的空间测量数据时, 几何校正被证明是十分重要的。某些图像, 例如, 从卫星上或飞机侧视雷达上得到的图像, 都有相当严重的几何变形, 这些图像需要先经过几何校正,然后才能对其内容做出解释。一些图像系统使用非矩形的像素坐标, 例如, 极坐标、柱坐标、 球面坐标等, 用普通的显示设备观察这些图像时, 必须先对它们进行校正, 也就是说, 将其转换为矩形像素坐标。例如, 在油 (水) 井套管缺陷识别中, 有时需要将极坐标系中的内突镜图像转换为直角坐标系中的图像, 然后进行分析与处理, 如图6-35、 6-36所示。
58 |
59 |
48 |
49 | 图6-34 一点透视变换
50 |
51 | 一般地, 视点不在原点, 投影平面是任意平面的情况,一点透视变换的矩阵也可以用一个 $4 \times 4$ 的矩阵表示。当根据公式 (6-19) 求出它的逆变换后, 可以用 $VC++$ 编写一个实现图像透视的程序, 实现图像的透视。
52 |
53 | ## 6.7.2 其他变换
54 |
55 | 如前所述, 齐次坐标为确定各种基本变换和复合变换公式提供了一个简单的方法。然而, 在许多图像处理与分析应用中, 所需的几何变换都相当复杂, 甚至有些无法用简便的数学式来表达。此外, 所需几何变换经常要从对实际图像的测量中获得, 因此更希望用这些测量结果而不是函数形式来描述几何变换。 例如, 在对由摄像机拍摄的有几何畸变的图像进行几何校正时, 首先应将一个矩形栅格目标数字化并显示出来。因为摄像机中有几何变形, 所显示的图案不会是准确的矩形, 因此所求几何变换应能使其栅格图案再次被复原为准确的矩形, 从而修正了摄像机产生的畸变。采用同样的几何变换可用于校正同一摄像机生成的数字化图像(假定畸变与景物无关), 由此可得到不畸变的图像。
56 |
57 | 图像几何变换的一个重要应用是消除由于摄像机导致的数字图像的几何畸变。当需要从数字图像中得到定量的空间测量数据时, 几何校正被证明是十分重要的。某些图像, 例如, 从卫星上或飞机侧视雷达上得到的图像, 都有相当严重的几何变形, 这些图像需要先经过几何校正,然后才能对其内容做出解释。一些图像系统使用非矩形的像素坐标, 例如, 极坐标、柱坐标、 球面坐标等, 用普通的显示设备观察这些图像时, 必须先对它们进行校正, 也就是说, 将其转换为矩形像素坐标。例如, 在油 (水) 井套管缺陷识别中, 有时需要将极坐标系中的内突镜图像转换为直角坐标系中的图像, 然后进行分析与处理, 如图6-35、 6-36所示。
58 |
59 | 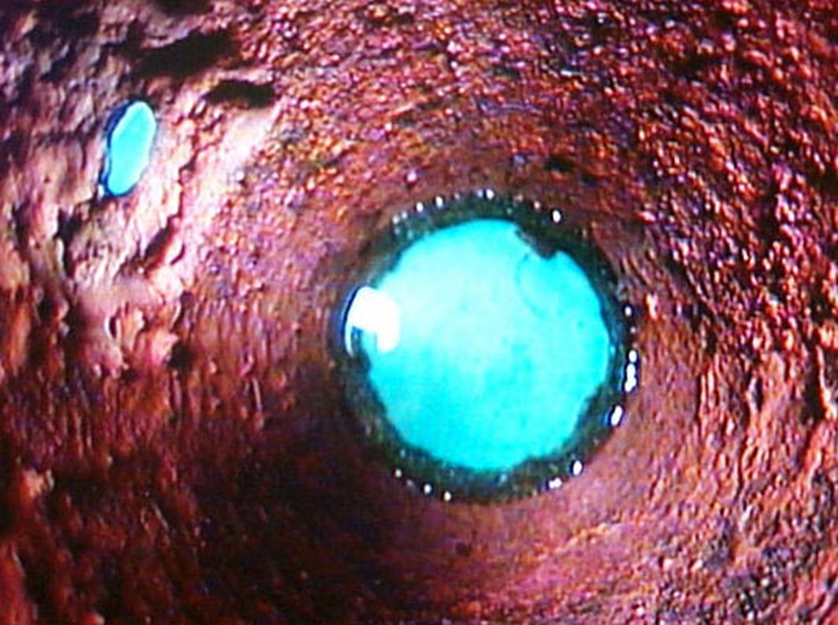 60 |
61 | 图6-35 极坐标系中的内突镜图像
62 |
63 | 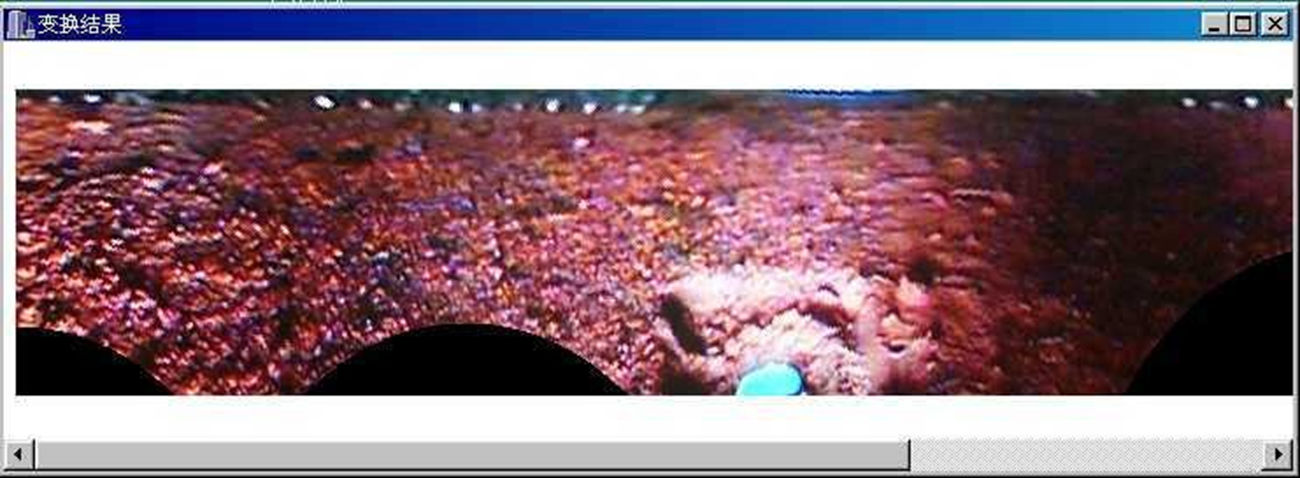
64 |
65 | 图6-36 转换为直角坐标系中的图像
66 |
67 | 有时机器人的鱼眼透镜拍摄的变形严重的一幅图像, 也可以设计一个适当的几何变换将其校正到矩形坐标系统, 这样, 可用立体视觉测距技术对机器人周围的物体进行三维空间定位。
68 |
69 | 几何变换的另一个应用是对相似的图像进行配准, 以便进行图像比较, 典型的应用是利用图像相减来检测运动或变化。 有时, 为便于解释需将图像以另一种样式表示, 这时也会用到几何变换, 地图绘制中的图像投影也会用到几何变换。例如, 在利用从宇宙飞船传回来的图像, 拼成地球、月球及行星的航拍镶嵌地图时, 就必须用几何变换。有关这些变换及其应用的详细内容请参阅书后的参考文献。
70 |
71 |
--------------------------------------------------------------------------------
/VI/6.8 应用实例.md:
--------------------------------------------------------------------------------
1 | # 6.8 应用实例
2 |
3 | 下面给出图像几何变换应用的一个例子一图像的转置。像的转置是将给定图像像素的x坐标和y坐标互换的几何变换。
4 |
5 | 图像的转置和图像的旋转不同, 而且仅仅通过旋转是不可能实现图像转置的。旋转操作与镜像操作结合才能实现图像的转置。图像转置的方法如下:
6 |
7 | 首先将图像水平镜像, 然后逆时针旋转 $90^{\circ}$ 才可以实现。设点 $P_{0}\left(x_{0}, y_{0}\right)$ 进行转置后的对应点为 $P(x, y)$, 图像高度为 $f H e i g h t$, 宽度为fWidth, 原图像中 $P_{0}\left(x_{0}, y_{0}\right)$ 经过转置后坐标将变为 $\left(y_{0}, x_{0}\right)$ 。 如果把图像转置看作是图像镜像与旋转的复合, 并且图像的水平镜像在 $x$ 方向不作平移。此时, 6.4.1中的公式 (6-4) 变为
8 | $$
9 | \left[\begin{array}{l}
10 | x \\
11 | y \\
12 | 1
13 | \end{array}\right]=\left[\begin{array}{rrr}
14 | -1 & 0 & 0 \\
15 | 0 & 1 & 0 \\
16 | 0 & 0 & 1
17 | \end{array}\right] \cdot\left[\begin{array}{l}
18 | x_{0} \\
19 | y_{0} \\
20 | 1
21 | \end{array}\right]
22 | $$
23 |
24 | 根据此式及6.5.1中的公式 (6-6) 可得
25 |
26 | $$
27 | \begin{aligned}
28 | & {\left[\begin{array}{l}
29 | x \\
30 | y \\
31 | 1
32 | \end{array}\right]=\left[\begin{array}{rrr}
33 | \cos \theta & \sin \theta & 0 \\
34 | -\sin \theta & \cos \theta & 0 \\
35 | 0 & 0 & 1
36 | \end{array}\right]\left[\begin{array}{rrr}
37 | -1 & 0 & 0 \\
38 | 0 & 1 & 0 \\
39 | 0 & 0 & 1
40 | \end{array}\right] \cdot\left[\begin{array}{l}
41 | x_{0} \\
42 | y_{0} \\
43 | 1
44 | \end{array}\right]\left(\theta=90^{\circ}\right)} \\
45 | & {\left[\begin{array}{l}
46 | x \\
47 | 1
48 | \end{array}\right]=\left[\begin{array}{rrr}
49 | 0 & 1 & 0 \\
50 | -1 & 0 & 0 \\
51 | 0 & 0 & 1
52 | \end{array}\right] \cdot\left[\begin{array}{rrr}
53 | -1 & 0 & 0 \\
54 | 0 & 1 & 0 \\
55 | 0 & 0 & 1
56 | \end{array}\right] \cdot\left[\begin{array}{l}
57 | x_{0} \\
58 | y_{0} \\
59 | 1
60 | \end{array}\right]=\left[\begin{array}{lll}
61 | 0 & 1 & 0 \\
62 | 1 & 0 & 0 \\
63 | 0 & 0 & 1
64 | \end{array}\right] \cdot\left[\begin{array}{l}
65 | x_{0} \\
66 | y_{0} \\
67 | 1
68 | \end{array}\right]}
69 | \end{aligned}\tag{6-20}
70 | $$
71 |
72 | 公式(6-20)就是图像转置的变换公式。
73 |
74 | 事实上,(6-19) 也可以直接得到, 因为原图像中 $P_{0}\left(x_{0}, y_{0}\right)$ 经过转置后坐标将变为 $P\left(y_{0}, x_{0}\right)$, 即 $x=y_{0}, y=x_{0}$, 把这个关系用齐次坐标写成矩阵形式就是式(6-20)。
75 |
76 | 图像转置的实现和图像镜像变换类似, 不同之处在于图像转置后DIB的头文件也要进行相应的改变, 主要是将头文件中图像高度和宽度信息更新。因此传递给图像转置函数的参数是直接指向DIB的指针, 而不是直接指向DIB像素的指针。下面给出实现图像转置函数TransposeDIB()的框架和主要算法。
77 |
78 | ```verilog
79 | //******************************************
80 | // 函数名称: BOOL Transpose()
81 | // 基本功能: 本函数对传入的CDibObject对象中的图像进行转置操作
82 | // 参数说明: CDibObject *pDibObject 默认为NULL
83 | // 返回值: BOOL 转置成功返回TRUE, 否则返回FALSE
84 | //******************************************
85 | BOOL CGeoTrans: : Transpose(CDibObject *pDibObject)
86 | {
87 | //定义指向源图像及新图像的指针、 位图数据指针、 调色板等指针变量
88 | //获取源图像指针及文件头、 信息头、 调色板及图像数据等信息
89 | //计算新图像大小(包括文件头、 信息头、 调色板和图像数据)
90 | //为新图像分配内存, 指定新图像的文件头、 信息头、 调色板及图像数据指针
91 | //用255填充新图像数据区, 用源图像的文件头、 信息头填充相应的新图像
92 | //调整文件总字节数、 新图像的宽度和高度等信息, 用原调色板填充新调色板
93 | //由图像位数确定的移动字节数
94 | int nMovedBits = 1;
95 | switch( m_pDibObject->GetNumBits() )
96 | {
97 | case 8:
98 | nMovedBits = 1;
99 | break;
100 | case 16:
101 | nMovedBits = 2;
102 | break;
103 | case 24:
104 | nMovedBits = 3;
105 | break;
106 | case 32:
107 | nMovedBits = 4;
108 | break;
109 | }
110 | // 针对图像每行进行操作
111 | for(y = 0; y < nOldHeight; y++)
112 | {
113 | //指向源图像第y行
114 | pOldTemp = pOldBits;
115 | pOldTemp += (nOldHeight -1 -y) * nOldWidthBytes;
116 | // 针对每行图像每列进行操作
117 | for(x = 0; x < nOldWidth; x++)
118 | {
119 | //指向转置后的图像第x行, 第y个像素的指针
120 | pNewTemp = pNewBits;
121 | pNewTemp += (nNewHeight -1 -x) * nNewWidthBytes;
122 | pNewTemp += y * nMovedBits;
123 | //复制像素
124 | memcpy(pNewTemp, pOldTemp, nMovedBits);
125 | pOldTemp += nMovedBits;
126 | }
127 | }
128 | //将内存解锁和将不再使用的内存释放,将新图像设置为当前图像,返回TRUE
129 | }
130 |
131 | ```
132 |
133 |
60 |
61 | 图6-35 极坐标系中的内突镜图像
62 |
63 | 
64 |
65 | 图6-36 转换为直角坐标系中的图像
66 |
67 | 有时机器人的鱼眼透镜拍摄的变形严重的一幅图像, 也可以设计一个适当的几何变换将其校正到矩形坐标系统, 这样, 可用立体视觉测距技术对机器人周围的物体进行三维空间定位。
68 |
69 | 几何变换的另一个应用是对相似的图像进行配准, 以便进行图像比较, 典型的应用是利用图像相减来检测运动或变化。 有时, 为便于解释需将图像以另一种样式表示, 这时也会用到几何变换, 地图绘制中的图像投影也会用到几何变换。例如, 在利用从宇宙飞船传回来的图像, 拼成地球、月球及行星的航拍镶嵌地图时, 就必须用几何变换。有关这些变换及其应用的详细内容请参阅书后的参考文献。
70 |
71 |
--------------------------------------------------------------------------------
/VI/6.8 应用实例.md:
--------------------------------------------------------------------------------
1 | # 6.8 应用实例
2 |
3 | 下面给出图像几何变换应用的一个例子一图像的转置。像的转置是将给定图像像素的x坐标和y坐标互换的几何变换。
4 |
5 | 图像的转置和图像的旋转不同, 而且仅仅通过旋转是不可能实现图像转置的。旋转操作与镜像操作结合才能实现图像的转置。图像转置的方法如下:
6 |
7 | 首先将图像水平镜像, 然后逆时针旋转 $90^{\circ}$ 才可以实现。设点 $P_{0}\left(x_{0}, y_{0}\right)$ 进行转置后的对应点为 $P(x, y)$, 图像高度为 $f H e i g h t$, 宽度为fWidth, 原图像中 $P_{0}\left(x_{0}, y_{0}\right)$ 经过转置后坐标将变为 $\left(y_{0}, x_{0}\right)$ 。 如果把图像转置看作是图像镜像与旋转的复合, 并且图像的水平镜像在 $x$ 方向不作平移。此时, 6.4.1中的公式 (6-4) 变为
8 | $$
9 | \left[\begin{array}{l}
10 | x \\
11 | y \\
12 | 1
13 | \end{array}\right]=\left[\begin{array}{rrr}
14 | -1 & 0 & 0 \\
15 | 0 & 1 & 0 \\
16 | 0 & 0 & 1
17 | \end{array}\right] \cdot\left[\begin{array}{l}
18 | x_{0} \\
19 | y_{0} \\
20 | 1
21 | \end{array}\right]
22 | $$
23 |
24 | 根据此式及6.5.1中的公式 (6-6) 可得
25 |
26 | $$
27 | \begin{aligned}
28 | & {\left[\begin{array}{l}
29 | x \\
30 | y \\
31 | 1
32 | \end{array}\right]=\left[\begin{array}{rrr}
33 | \cos \theta & \sin \theta & 0 \\
34 | -\sin \theta & \cos \theta & 0 \\
35 | 0 & 0 & 1
36 | \end{array}\right]\left[\begin{array}{rrr}
37 | -1 & 0 & 0 \\
38 | 0 & 1 & 0 \\
39 | 0 & 0 & 1
40 | \end{array}\right] \cdot\left[\begin{array}{l}
41 | x_{0} \\
42 | y_{0} \\
43 | 1
44 | \end{array}\right]\left(\theta=90^{\circ}\right)} \\
45 | & {\left[\begin{array}{l}
46 | x \\
47 | 1
48 | \end{array}\right]=\left[\begin{array}{rrr}
49 | 0 & 1 & 0 \\
50 | -1 & 0 & 0 \\
51 | 0 & 0 & 1
52 | \end{array}\right] \cdot\left[\begin{array}{rrr}
53 | -1 & 0 & 0 \\
54 | 0 & 1 & 0 \\
55 | 0 & 0 & 1
56 | \end{array}\right] \cdot\left[\begin{array}{l}
57 | x_{0} \\
58 | y_{0} \\
59 | 1
60 | \end{array}\right]=\left[\begin{array}{lll}
61 | 0 & 1 & 0 \\
62 | 1 & 0 & 0 \\
63 | 0 & 0 & 1
64 | \end{array}\right] \cdot\left[\begin{array}{l}
65 | x_{0} \\
66 | y_{0} \\
67 | 1
68 | \end{array}\right]}
69 | \end{aligned}\tag{6-20}
70 | $$
71 |
72 | 公式(6-20)就是图像转置的变换公式。
73 |
74 | 事实上,(6-19) 也可以直接得到, 因为原图像中 $P_{0}\left(x_{0}, y_{0}\right)$ 经过转置后坐标将变为 $P\left(y_{0}, x_{0}\right)$, 即 $x=y_{0}, y=x_{0}$, 把这个关系用齐次坐标写成矩阵形式就是式(6-20)。
75 |
76 | 图像转置的实现和图像镜像变换类似, 不同之处在于图像转置后DIB的头文件也要进行相应的改变, 主要是将头文件中图像高度和宽度信息更新。因此传递给图像转置函数的参数是直接指向DIB的指针, 而不是直接指向DIB像素的指针。下面给出实现图像转置函数TransposeDIB()的框架和主要算法。
77 |
78 | ```verilog
79 | //******************************************
80 | // 函数名称: BOOL Transpose()
81 | // 基本功能: 本函数对传入的CDibObject对象中的图像进行转置操作
82 | // 参数说明: CDibObject *pDibObject 默认为NULL
83 | // 返回值: BOOL 转置成功返回TRUE, 否则返回FALSE
84 | //******************************************
85 | BOOL CGeoTrans: : Transpose(CDibObject *pDibObject)
86 | {
87 | //定义指向源图像及新图像的指针、 位图数据指针、 调色板等指针变量
88 | //获取源图像指针及文件头、 信息头、 调色板及图像数据等信息
89 | //计算新图像大小(包括文件头、 信息头、 调色板和图像数据)
90 | //为新图像分配内存, 指定新图像的文件头、 信息头、 调色板及图像数据指针
91 | //用255填充新图像数据区, 用源图像的文件头、 信息头填充相应的新图像
92 | //调整文件总字节数、 新图像的宽度和高度等信息, 用原调色板填充新调色板
93 | //由图像位数确定的移动字节数
94 | int nMovedBits = 1;
95 | switch( m_pDibObject->GetNumBits() )
96 | {
97 | case 8:
98 | nMovedBits = 1;
99 | break;
100 | case 16:
101 | nMovedBits = 2;
102 | break;
103 | case 24:
104 | nMovedBits = 3;
105 | break;
106 | case 32:
107 | nMovedBits = 4;
108 | break;
109 | }
110 | // 针对图像每行进行操作
111 | for(y = 0; y < nOldHeight; y++)
112 | {
113 | //指向源图像第y行
114 | pOldTemp = pOldBits;
115 | pOldTemp += (nOldHeight -1 -y) * nOldWidthBytes;
116 | // 针对每行图像每列进行操作
117 | for(x = 0; x < nOldWidth; x++)
118 | {
119 | //指向转置后的图像第x行, 第y个像素的指针
120 | pNewTemp = pNewBits;
121 | pNewTemp += (nNewHeight -1 -x) * nNewWidthBytes;
122 | pNewTemp += y * nMovedBits;
123 | //复制像素
124 | memcpy(pNewTemp, pOldTemp, nMovedBits);
125 | pOldTemp += nMovedBits;
126 | }
127 | }
128 | //将内存解锁和将不再使用的内存释放,将新图像设置为当前图像,返回TRUE
129 | }
130 |
131 | ```
132 |
133 |  134 |
135 | 图6-37 转置后的图像
--------------------------------------------------------------------------------
/VII/7.1 图像分割.md:
--------------------------------------------------------------------------------
1 | [TOC]
2 |
3 | # 7.1 图像分割
4 |
5 | ## 7.1.1 概述
6 |
7 | 图像分割是将图像划分成若干个互不相交的小区域的过程, 小区域是某种意义下具有共同属性的像素的连通集合。如不同目标物体所占的图像区域、 前景所占的图像区域等。连通是指集合中任意两个点之间都存在着完全属于该集合的连通路径。对于离散图像而言,连通有4连通和8连通之分,如图7-1所示。
8 |
9 | 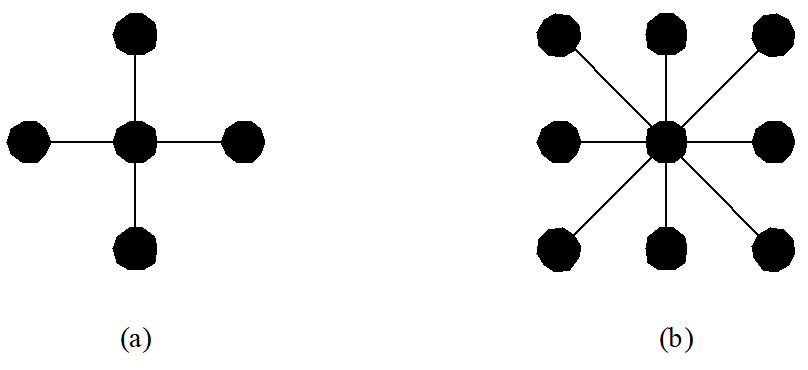
10 |
11 | 图7-1 4连通和8连通
12 |
13 | 4连通指的是从区域上一点出发,可通过4个方向,即上、 下、左、右移动的组合,在不越出区域的前提下,到达区域内的任意像素; 8连通方法指的是从区域上一点出发,可通过左、 右、上、下、左上、右上、左下、右下这8个方向的移动组合来到达区域内的任意像素。
14 |
15 | 图像分割有三种不同的途径:其一是将各像素划归到相应物体或区域的像素聚类方法, 即区域法;其二是通过直接确定区域间的边界来实现分割的边界方法;其三是首先检测边缘像素, 再将边缘像素连接起来构成边界形成分割。在图像分割技术中, 最常用的是利用阈值化处理进行的图像分割。
16 |
17 | ## 7.1.2 灰度阈值法分割
18 |
19 | 常用的图像分割方法是把图像灰度分成不同的等级, 然后用设置灰度门限 (阈值) 的方法确定有意义的区域或分割物体的边界。常用的阈值化处理就是图像的二值化处理, 即选择一阈值, 将图像转换为黑白二值图像, 用于图像分割及边缘跟踪等预处理。
20 |
21 | 图像阈值化处理的变换函数表达式为
22 |
23 | $$
24 | g(x, y)= \begin{cases}0 & f(x, y)
43 |
44 | 图7-2 阈值变换曲线
45 |
46 | 在图像的阈值化处理过程中, 选用不同的阈值其处理结果差异很大。如图7-3所示, 阈值过大, 会提取多余的部分; 而阈值过小, 又会丢失所需的部分(注意: 当前背景为黑色, 对象为白色时刚好相反)。因此, 阈值的选取非常重要。
47 |
48 | 图7-3(a)原始图像的直方图如图7-4所示。分析该直方图可知, 该直方图具有双峰特性, 图像中的目标 (细胞) 分布在较暗的灰度级上形成一个波峰, 图像中的背景分布在较亮的灰度级上形成另一个波峰。此时, 用其双峰之间的谷低处灰度值作为阈值 $T$ 进行图像的阈值化处理, 便可将目标和背景分割开来。
49 |
50 |
134 |
135 | 图6-37 转置后的图像
--------------------------------------------------------------------------------
/VII/7.1 图像分割.md:
--------------------------------------------------------------------------------
1 | [TOC]
2 |
3 | # 7.1 图像分割
4 |
5 | ## 7.1.1 概述
6 |
7 | 图像分割是将图像划分成若干个互不相交的小区域的过程, 小区域是某种意义下具有共同属性的像素的连通集合。如不同目标物体所占的图像区域、 前景所占的图像区域等。连通是指集合中任意两个点之间都存在着完全属于该集合的连通路径。对于离散图像而言,连通有4连通和8连通之分,如图7-1所示。
8 |
9 | 
10 |
11 | 图7-1 4连通和8连通
12 |
13 | 4连通指的是从区域上一点出发,可通过4个方向,即上、 下、左、右移动的组合,在不越出区域的前提下,到达区域内的任意像素; 8连通方法指的是从区域上一点出发,可通过左、 右、上、下、左上、右上、左下、右下这8个方向的移动组合来到达区域内的任意像素。
14 |
15 | 图像分割有三种不同的途径:其一是将各像素划归到相应物体或区域的像素聚类方法, 即区域法;其二是通过直接确定区域间的边界来实现分割的边界方法;其三是首先检测边缘像素, 再将边缘像素连接起来构成边界形成分割。在图像分割技术中, 最常用的是利用阈值化处理进行的图像分割。
16 |
17 | ## 7.1.2 灰度阈值法分割
18 |
19 | 常用的图像分割方法是把图像灰度分成不同的等级, 然后用设置灰度门限 (阈值) 的方法确定有意义的区域或分割物体的边界。常用的阈值化处理就是图像的二值化处理, 即选择一阈值, 将图像转换为黑白二值图像, 用于图像分割及边缘跟踪等预处理。
20 |
21 | 图像阈值化处理的变换函数表达式为
22 |
23 | $$
24 | g(x, y)= \begin{cases}0 & f(x, y)
43 |
44 | 图7-2 阈值变换曲线
45 |
46 | 在图像的阈值化处理过程中, 选用不同的阈值其处理结果差异很大。如图7-3所示, 阈值过大, 会提取多余的部分; 而阈值过小, 又会丢失所需的部分(注意: 当前背景为黑色, 对象为白色时刚好相反)。因此, 阈值的选取非常重要。
47 |
48 | 图7-3(a)原始图像的直方图如图7-4所示。分析该直方图可知, 该直方图具有双峰特性, 图像中的目标 (细胞) 分布在较暗的灰度级上形成一个波峰, 图像中的背景分布在较亮的灰度级上形成另一个波峰。此时, 用其双峰之间的谷低处灰度值作为阈值 $T$ 进行图像的阈值化处理, 便可将目标和背景分割开来。
49 |
50 |  51 |
52 | 图7-3 不同阈值对阈值化结果的影响
53 | (a) 原始图像;
54 | (b) 阈值 $T=91$;
55 | (c) 阈值 $T=130$;
56 | (d) 阈值 $T=43$
57 |
58 | 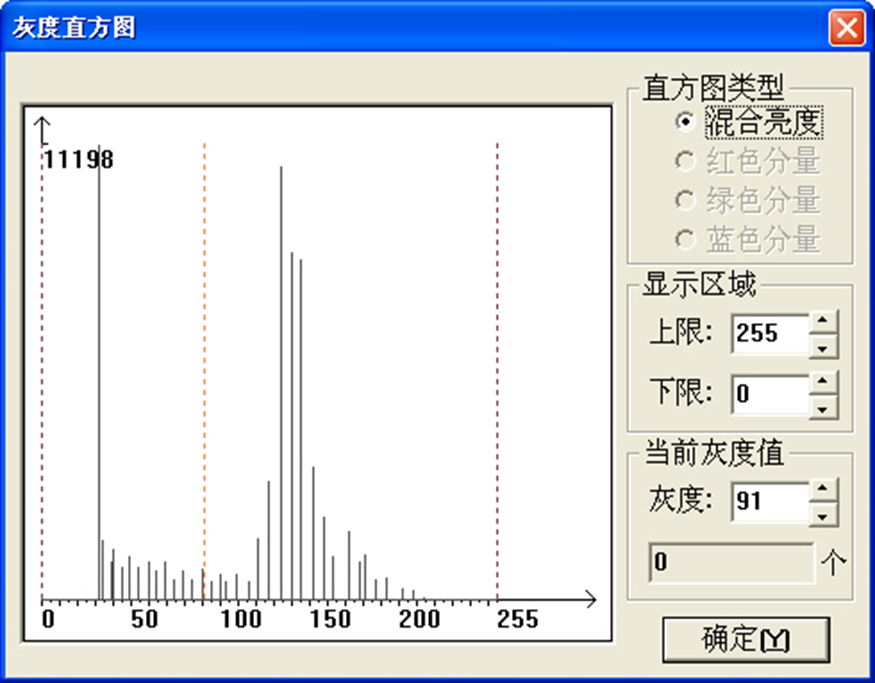
59 |
60 | 图7-4 图7-3(a)所示图像的直方图
61 |
62 | 为了有效地分割物体与背景,人们发展了各种各样的阈值处理技术,包括全局阈值、自适应阈值、最佳阈值等等。从方法分有:直方图阈值分割法, 类间方差阈值分割法,二维熵值分割法,模糊阈值分割法,共生矩阵阈值分割法.
63 |
64 |
65 | - 全局阈值
66 | 全局阈值是指整幅图象使用同一个阈值做分割处理。适用于背景和前景有明显对比的图象。 例如当直方图明显呈现双峰情况时, 可以选择两个峰值的中点作为全局阈值。
67 |
68 | - 自适应阈值
69 | 在许多情况下, 物体和背景的对比度在图象中不是各处一样的, 这时很难用统一的一个阈值将物体与背景分开。这时可以根据图象的局部特征分别采用不同的阈值进行分割。实际处理时, 需要按照具体问题将图象分成若干子区域分别选择阈值, 或者动态地根据一定的邻域范围选择每点处的阈值, 进行图象分割。
70 |
71 | - 最佳阈值
72 | 最佳阈值是使图像中目标与背景分割错误最小的阈值。
73 |
74 | 1.直方图阈值分割法
75 |
76 | 1)简单直方图分割法
77 |
78 | 基本原理: 直方图明显呈现双峰情况时,可以选择两个峰值的中点作为阈值.
79 | 
80 |
81 | 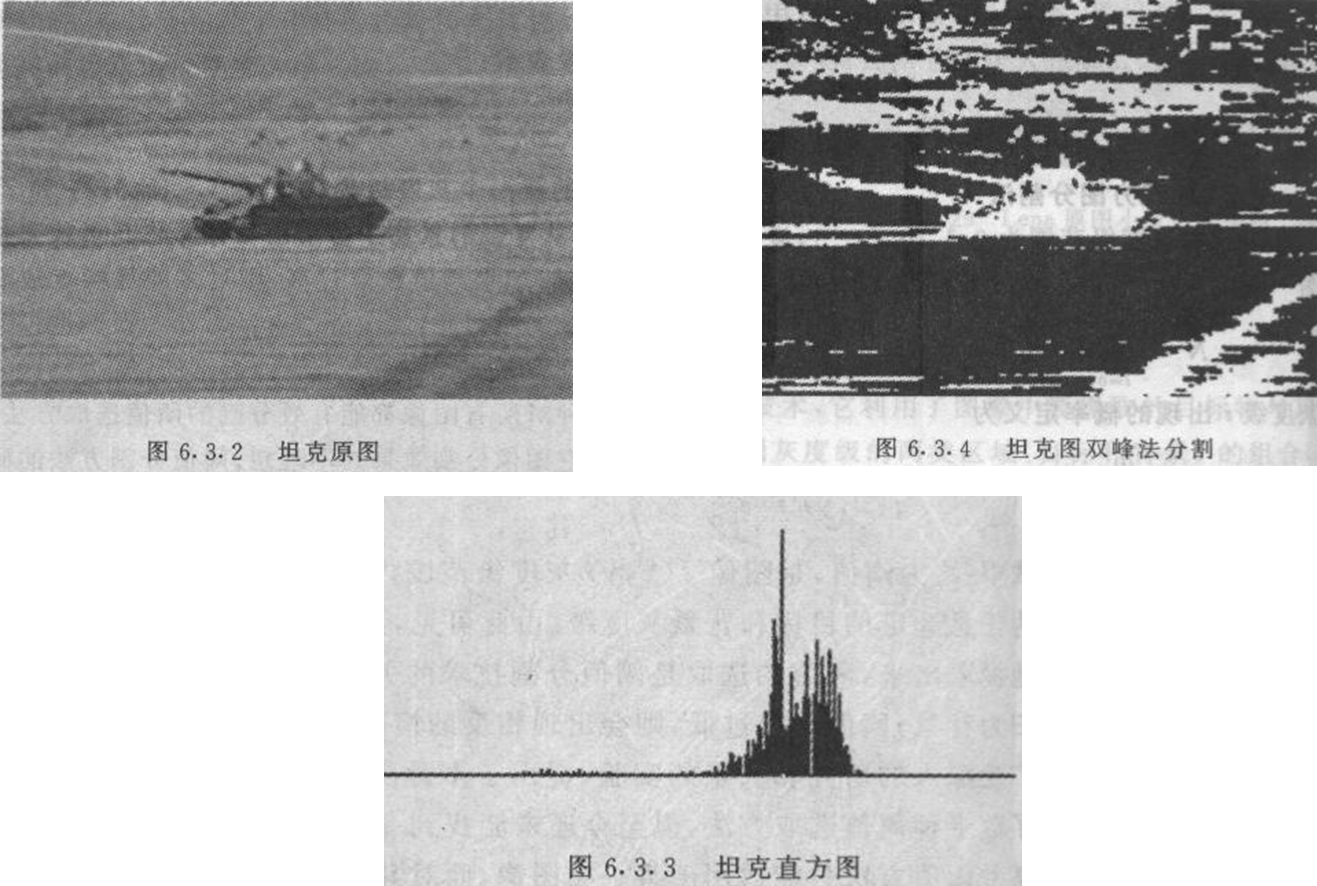
82 |
83 |
84 | 2) 最佳阈值
85 |
86 | 设一幅图像只由目标和背景组成,其灰度分布概率密度 $P_{1}(\mathbf{z})$ 和 $\mathbf{P}_{2}(\mathbf{z})$ 为正态分布,且已知目标像素占全图像像素比为 $\theta$ :
87 |
88 | $p$
89 |
90 | 
91 |
92 |
93 |
94 | $$
95 | P_{1}(Z)=\frac{1}{\sqrt{2 \pi \sigma_{1}}} \exp \left[-\frac{\left(Z-\mu_{1}\right)^{2}}{2 \sigma_{1}{ }^{2}}\right]
96 | $$
97 |
98 | $$
99 | P_{2}(Z)=\frac{1}{\sqrt{2 \pi \sigma_{2}}} \exp \left[-\frac{\left(Z-\mu_{2}\right)^{2}}{2 \sigma_{2}{ }^{2}}\right]
100 | $$
101 |
102 | 则阈值为:
103 |
104 | $$
105 | Z_{t}=\frac{\mu_{1}+\mu_{2}}{2}+\frac{\sigma^{2}}{\mu_{1}-\mu_{2}} \ln \left(\frac{1-\theta}{\theta}\right)
106 | $$
107 |
108 | 若 $\theta=0.5$
109 |
110 | 则阈值为:
111 |
112 | $$
113 | Z_{t}=\frac{\mu_{1}+\mu_{2}}{2}
114 | $$
115 |
116 |
117 |
118 | 2.类间方差阈值分割法
119 |
120 | 设一幅图像只由目标和背景组成,原图灰度级为} $L$, 灰度级为 $i$ 的像素点数为 $n_{i}$, 图像总像素点数为 $N$, 则:
121 | $$
122 | p_{i}=\frac{n_{i}}{N}
123 | $$
124 |
125 | 用阈值 $t$ 将图像分割为两类: $C_{1}=(0,1,2, \ldots, t)$ 和 $C_{2}$ $=(\mathbf{t}, \mathbf{t}+1, \mathbf{t}+2, \ldots, \mathbf{L}-1)$, 则有:
126 |
127 |
128 |
129 | $$
130 | \begin{aligned}
131 | & \omega_{1}=P_{r}\left(C_{1}\right)=\sum_{i=0}^{t} p_{i} \\
132 | & \omega_{2}=P_{r}\left(C_{2}\right)=\sum_{i=t+1}^{L-1} p_{i} \\
133 | & \mu_{1}=\sum_{i=0}^{t} i p_{i} / \omega_{1} \\
134 | & \mu_{2}=\sum_{i=t+1}^{L-1} i p_{i} / \omega_{2} \\
135 | & \sigma_{1}^{2}=\sum_{i=0}^{t}\left(i-\mu_{1}\right)^{2} p_{i} / \omega_{1} \\
136 | & \sigma_{2}^{2}=\sum_{i=t+1}^{L-1}\left(i-\mu_{2}\right)^{2} p_{i} / \omega_{2}
137 | \end{aligned}
138 | $$
139 |
140 | 类内方差:
141 |
142 | $$
143 | \sigma_{\omega}^{2}=\omega_{1} \sigma_{1}^{2}+\omega_{2} \sigma_{2}^{2}
144 | $$
145 |
146 | 类间方差:
147 |
148 | $$
149 | \sigma_{B}^{2}=\omega_{1} \omega_{2}\left(\mu_{1}-\mu_{2}\right)^{2}
150 | $$
151 |
152 | 总方差:
153 |
154 | $$
155 | \sigma_{\omega}^{2}=\sigma_{B}^{2}+\sigma_{\omega}^{2}
156 | $$
157 |
158 | 定义准则函数:
159 |
160 | $$
161 | F(t)=\sigma_{B}^{2} / \sigma_{T}^{2}
162 | $$
163 |
164 |
165 |
166 | 则使 $F(t)$ 最大的 $t$ 为最佳阈值.
167 |
168 | 
169 |
170 | 图 6.3.6 坦克图类间方差阈值分割
171 |
172 | 3二维熵值分割法
173 |
174 | 一维熵值分割法设原图灰度级为 $L$, 灰度级为 $i$ 的像素点数为 $n_{i}$, 图像总像素点数为 $\mathbf{N} \times \mathbf{N}$,则:
175 |
176 | $$
177 | p_{i}=\frac{n_{i}}{N \times N}
178 | $$
179 |
180 | 设图中灰度级低于 $t$ 的像素点构成目标区域O, 灰度级高于 $\mathbf{t}$ 的像素点构成背景区域B, 则目标区域和背景区域的熵定义为:
181 |
182 | $H_{0}(t)=-\sum_{i}\left(p_{i} / p_{t}\right) \lg \left(p_{i} / p_{t}\right) \quad i=1,2,3 \cdots t$
183 |
184 | $$
185 | H_{B}(t)=-\sum_{i}\left[p_{i} /\left(1-p_{t}\right)\right] \lg \left[p_{i} /\left(1-p_{t}\right)\right] \quad i=t+1, t+2, t+3 \cdots L-1
186 | $$
187 |
188 | 贝则熵函数定义为:
189 |
190 | $$
191 | \varphi(t)=H_{0}+H_{B}=\lg p_{t}\left(1-p_{t}\right)+\frac{H_{t}}{p_{t}}+\frac{H_{L}-H_{t}}{1-p_{t}}
192 | $$
193 |
194 | 其中:
195 |
196 | $$
197 | \begin{array}{cc}
198 | H_{t}=-\sum_{i} p_{i} \lg p_{i} & i=1,2, \cdots t \\
199 | H_{L}=-\sum_{i} p_{i} \lg p_{i} & i=1,2 \cdots L
200 | \end{array}
201 | $$
202 |
203 | 当熵函数最大时的灰度值t就为最佳阈值.
204 |
205 |
206 |
207 | 4.模糊阈值分割
208 |
209 | 1)隶属函数 $\mu\left(x_{m, n}, p, \mathbf{q}\right)$ :
210 |
211 | 设像素点 $(m, n)$ 的灰度值为 $x_{m, n}$, 则 $\mu\left(x_{m, n}, p, q\right)$ 定义为像素点 $(m, \mathbf{n})$ 属于目标的程度;
212 |
213 | $$
214 | \mu\left(x_{m, n}, p, q, r\right)=\left\{\begin{array}{cc}
215 | 0 & x_{m, n} \leq p \\
216 | 2\left[\left(x_{m, n}-p\right) /(r-p)\right]^{2} & p \leq x_{m, n} \leq q \\
217 | 1-2\left[\left(x_{m, n}-p\right) /(r-p)\right]^{2} & q_{m, n}q
228 | \end{array}\right. \\
229 | $$
230 | 或
231 | $$
232 | \mu\left(x_{m, n}, p, q, r\right)=\left\{\begin{array}{cc}
233 | 0 & x_{m, n} \leq p \\
234 | \dfrac{\left(x_{m, n}-p\right)}{q-p} & pq
236 | \end{array}\right.
237 | $$
238 | 其中 $\mathbf{q}$ 为阈值, 显然灰度值越大, 隶属函数 $\mu\left(x_{m, n}, p, q\right)$ 越大, 该点 $(\mathbf{m}, \mathbf{n})$ 属于目标的程度, 即该点越可能是目标上的点,否则该点越可能是背景上的点.
239 |
240 |
241 |
242 | 2 )模糊率、模糊熵:
243 |
244 | 模糊率
245 |
246 | $$
247 | V(q)=\frac{2}{M N} \sum_{m} \sum_{n} \min \left[\mu\left(x_{m, n}, q\right), 1-\mu\left(x_{m, n}, q\right)\right]
248 | $$
249 |
250 | 模糊熵
251 |
252 | $$
253 | \begin{aligned}
254 | & E(q)=\frac{1}{M N \ln 2} \sum_{m} \sum_{n} S_{n}\left[\mu\left(x_{m, n}, q\right)\right] \\
255 | & S_{n}\left[\mu\left(x_{m, n}, q\right)\right]=-\mu\left(x_{m, n}, q\right) \ln \mu\left(x_{m, n}, q\right)-\left(1-\mu\left(x_{m, n}, q\right) \ln \left(1-\mu\left(x_{m, n}, q\right)\right)\right.
256 | \end{aligned}
257 | $$
258 |
259 | 3)模糊阈值
260 |
261 | 当模糊率或模糊熵最大时的灰度值 $\mathbf{q}$ 就为最佳阈值.}
262 |
263 |
264 |
265 |
51 |
52 | 图7-3 不同阈值对阈值化结果的影响
53 | (a) 原始图像;
54 | (b) 阈值 $T=91$;
55 | (c) 阈值 $T=130$;
56 | (d) 阈值 $T=43$
57 |
58 | 
59 |
60 | 图7-4 图7-3(a)所示图像的直方图
61 |
62 | 为了有效地分割物体与背景,人们发展了各种各样的阈值处理技术,包括全局阈值、自适应阈值、最佳阈值等等。从方法分有:直方图阈值分割法, 类间方差阈值分割法,二维熵值分割法,模糊阈值分割法,共生矩阵阈值分割法.
63 |
64 |
65 | - 全局阈值
66 | 全局阈值是指整幅图象使用同一个阈值做分割处理。适用于背景和前景有明显对比的图象。 例如当直方图明显呈现双峰情况时, 可以选择两个峰值的中点作为全局阈值。
67 |
68 | - 自适应阈值
69 | 在许多情况下, 物体和背景的对比度在图象中不是各处一样的, 这时很难用统一的一个阈值将物体与背景分开。这时可以根据图象的局部特征分别采用不同的阈值进行分割。实际处理时, 需要按照具体问题将图象分成若干子区域分别选择阈值, 或者动态地根据一定的邻域范围选择每点处的阈值, 进行图象分割。
70 |
71 | - 最佳阈值
72 | 最佳阈值是使图像中目标与背景分割错误最小的阈值。
73 |
74 | 1.直方图阈值分割法
75 |
76 | 1)简单直方图分割法
77 |
78 | 基本原理: 直方图明显呈现双峰情况时,可以选择两个峰值的中点作为阈值.
79 | 
80 |
81 | 
82 |
83 |
84 | 2) 最佳阈值
85 |
86 | 设一幅图像只由目标和背景组成,其灰度分布概率密度 $P_{1}(\mathbf{z})$ 和 $\mathbf{P}_{2}(\mathbf{z})$ 为正态分布,且已知目标像素占全图像像素比为 $\theta$ :
87 |
88 | $p$
89 |
90 | 
91 |
92 |
93 |
94 | $$
95 | P_{1}(Z)=\frac{1}{\sqrt{2 \pi \sigma_{1}}} \exp \left[-\frac{\left(Z-\mu_{1}\right)^{2}}{2 \sigma_{1}{ }^{2}}\right]
96 | $$
97 |
98 | $$
99 | P_{2}(Z)=\frac{1}{\sqrt{2 \pi \sigma_{2}}} \exp \left[-\frac{\left(Z-\mu_{2}\right)^{2}}{2 \sigma_{2}{ }^{2}}\right]
100 | $$
101 |
102 | 则阈值为:
103 |
104 | $$
105 | Z_{t}=\frac{\mu_{1}+\mu_{2}}{2}+\frac{\sigma^{2}}{\mu_{1}-\mu_{2}} \ln \left(\frac{1-\theta}{\theta}\right)
106 | $$
107 |
108 | 若 $\theta=0.5$
109 |
110 | 则阈值为:
111 |
112 | $$
113 | Z_{t}=\frac{\mu_{1}+\mu_{2}}{2}
114 | $$
115 |
116 |
117 |
118 | 2.类间方差阈值分割法
119 |
120 | 设一幅图像只由目标和背景组成,原图灰度级为} $L$, 灰度级为 $i$ 的像素点数为 $n_{i}$, 图像总像素点数为 $N$, 则:
121 | $$
122 | p_{i}=\frac{n_{i}}{N}
123 | $$
124 |
125 | 用阈值 $t$ 将图像分割为两类: $C_{1}=(0,1,2, \ldots, t)$ 和 $C_{2}$ $=(\mathbf{t}, \mathbf{t}+1, \mathbf{t}+2, \ldots, \mathbf{L}-1)$, 则有:
126 |
127 |
128 |
129 | $$
130 | \begin{aligned}
131 | & \omega_{1}=P_{r}\left(C_{1}\right)=\sum_{i=0}^{t} p_{i} \\
132 | & \omega_{2}=P_{r}\left(C_{2}\right)=\sum_{i=t+1}^{L-1} p_{i} \\
133 | & \mu_{1}=\sum_{i=0}^{t} i p_{i} / \omega_{1} \\
134 | & \mu_{2}=\sum_{i=t+1}^{L-1} i p_{i} / \omega_{2} \\
135 | & \sigma_{1}^{2}=\sum_{i=0}^{t}\left(i-\mu_{1}\right)^{2} p_{i} / \omega_{1} \\
136 | & \sigma_{2}^{2}=\sum_{i=t+1}^{L-1}\left(i-\mu_{2}\right)^{2} p_{i} / \omega_{2}
137 | \end{aligned}
138 | $$
139 |
140 | 类内方差:
141 |
142 | $$
143 | \sigma_{\omega}^{2}=\omega_{1} \sigma_{1}^{2}+\omega_{2} \sigma_{2}^{2}
144 | $$
145 |
146 | 类间方差:
147 |
148 | $$
149 | \sigma_{B}^{2}=\omega_{1} \omega_{2}\left(\mu_{1}-\mu_{2}\right)^{2}
150 | $$
151 |
152 | 总方差:
153 |
154 | $$
155 | \sigma_{\omega}^{2}=\sigma_{B}^{2}+\sigma_{\omega}^{2}
156 | $$
157 |
158 | 定义准则函数:
159 |
160 | $$
161 | F(t)=\sigma_{B}^{2} / \sigma_{T}^{2}
162 | $$
163 |
164 |
165 |
166 | 则使 $F(t)$ 最大的 $t$ 为最佳阈值.
167 |
168 | 
169 |
170 | 图 6.3.6 坦克图类间方差阈值分割
171 |
172 | 3二维熵值分割法
173 |
174 | 一维熵值分割法设原图灰度级为 $L$, 灰度级为 $i$ 的像素点数为 $n_{i}$, 图像总像素点数为 $\mathbf{N} \times \mathbf{N}$,则:
175 |
176 | $$
177 | p_{i}=\frac{n_{i}}{N \times N}
178 | $$
179 |
180 | 设图中灰度级低于 $t$ 的像素点构成目标区域O, 灰度级高于 $\mathbf{t}$ 的像素点构成背景区域B, 则目标区域和背景区域的熵定义为:
181 |
182 | $H_{0}(t)=-\sum_{i}\left(p_{i} / p_{t}\right) \lg \left(p_{i} / p_{t}\right) \quad i=1,2,3 \cdots t$
183 |
184 | $$
185 | H_{B}(t)=-\sum_{i}\left[p_{i} /\left(1-p_{t}\right)\right] \lg \left[p_{i} /\left(1-p_{t}\right)\right] \quad i=t+1, t+2, t+3 \cdots L-1
186 | $$
187 |
188 | 贝则熵函数定义为:
189 |
190 | $$
191 | \varphi(t)=H_{0}+H_{B}=\lg p_{t}\left(1-p_{t}\right)+\frac{H_{t}}{p_{t}}+\frac{H_{L}-H_{t}}{1-p_{t}}
192 | $$
193 |
194 | 其中:
195 |
196 | $$
197 | \begin{array}{cc}
198 | H_{t}=-\sum_{i} p_{i} \lg p_{i} & i=1,2, \cdots t \\
199 | H_{L}=-\sum_{i} p_{i} \lg p_{i} & i=1,2 \cdots L
200 | \end{array}
201 | $$
202 |
203 | 当熵函数最大时的灰度值t就为最佳阈值.
204 |
205 |
206 |
207 | 4.模糊阈值分割
208 |
209 | 1)隶属函数 $\mu\left(x_{m, n}, p, \mathbf{q}\right)$ :
210 |
211 | 设像素点 $(m, n)$ 的灰度值为 $x_{m, n}$, 则 $\mu\left(x_{m, n}, p, q\right)$ 定义为像素点 $(m, \mathbf{n})$ 属于目标的程度;
212 |
213 | $$
214 | \mu\left(x_{m, n}, p, q, r\right)=\left\{\begin{array}{cc}
215 | 0 & x_{m, n} \leq p \\
216 | 2\left[\left(x_{m, n}-p\right) /(r-p)\right]^{2} & p \leq x_{m, n} \leq q \\
217 | 1-2\left[\left(x_{m, n}-p\right) /(r-p)\right]^{2} & q_{m, n}q
228 | \end{array}\right. \\
229 | $$
230 | 或
231 | $$
232 | \mu\left(x_{m, n}, p, q, r\right)=\left\{\begin{array}{cc}
233 | 0 & x_{m, n} \leq p \\
234 | \dfrac{\left(x_{m, n}-p\right)}{q-p} & pq
236 | \end{array}\right.
237 | $$
238 | 其中 $\mathbf{q}$ 为阈值, 显然灰度值越大, 隶属函数 $\mu\left(x_{m, n}, p, q\right)$ 越大, 该点 $(\mathbf{m}, \mathbf{n})$ 属于目标的程度, 即该点越可能是目标上的点,否则该点越可能是背景上的点.
239 |
240 |
241 |
242 | 2 )模糊率、模糊熵:
243 |
244 | 模糊率
245 |
246 | $$
247 | V(q)=\frac{2}{M N} \sum_{m} \sum_{n} \min \left[\mu\left(x_{m, n}, q\right), 1-\mu\left(x_{m, n}, q\right)\right]
248 | $$
249 |
250 | 模糊熵
251 |
252 | $$
253 | \begin{aligned}
254 | & E(q)=\frac{1}{M N \ln 2} \sum_{m} \sum_{n} S_{n}\left[\mu\left(x_{m, n}, q\right)\right] \\
255 | & S_{n}\left[\mu\left(x_{m, n}, q\right)\right]=-\mu\left(x_{m, n}, q\right) \ln \mu\left(x_{m, n}, q\right)-\left(1-\mu\left(x_{m, n}, q\right) \ln \left(1-\mu\left(x_{m, n}, q\right)\right)\right.
256 | \end{aligned}
257 | $$
258 |
259 | 3)模糊阈值
260 |
261 | 当模糊率或模糊熵最大时的灰度值 $\mathbf{q}$ 就为最佳阈值.}
262 |
263 |
264 |
265 |  266 |
267 | 图 6.3.13 坦克图模糊阈值法分割
268 |
269 | ## 7.1.3 区域生长
270 |
271 | 分割的目的是把一幅图像划分成一些区域,最直接的方法就是把一幅图像分成满足某种判据的区域,也就是说,把点组成区域。为了实现分组, 首先要确定区域的数目, 其次要确定一个区域与其他区域相区别的特征, 最后还要产生有意义分割的相似性判据。
272 |
273 | 分割区域的一种方法叫区域生长或区域生成。假定区域的数目以及在每个区域中单个点的位置已知, 则从一个已知点开始,加上与已知点相似的邻近点形成一个区域。相似性准则可以是灰度级、 彩色、组织、梯度或其他特性,相似性的测度可以由所确定的阈值来判定。方法是从满足检测准则的点开始, 在各个方向上生长区域, 当其邻近点满足检测准则就并入小块区域中。当新的点被合并后再用新的区域重复这一过程, 直到没有可接受的邻近点时生成过程终止。
274 |
275 | 图 7-5给出一个简单的例子。此例的相似性准则是邻近点的灰度级与物体的平均灰度级的差小于2。图中被接受的点和起始点均用下划线标出,其中(a)图是输入图像;(b)图是第一步接受的邻近点;(c)图是第二步接受的邻近点;(d) 图是从6开始生成的结果。
276 |
277 | 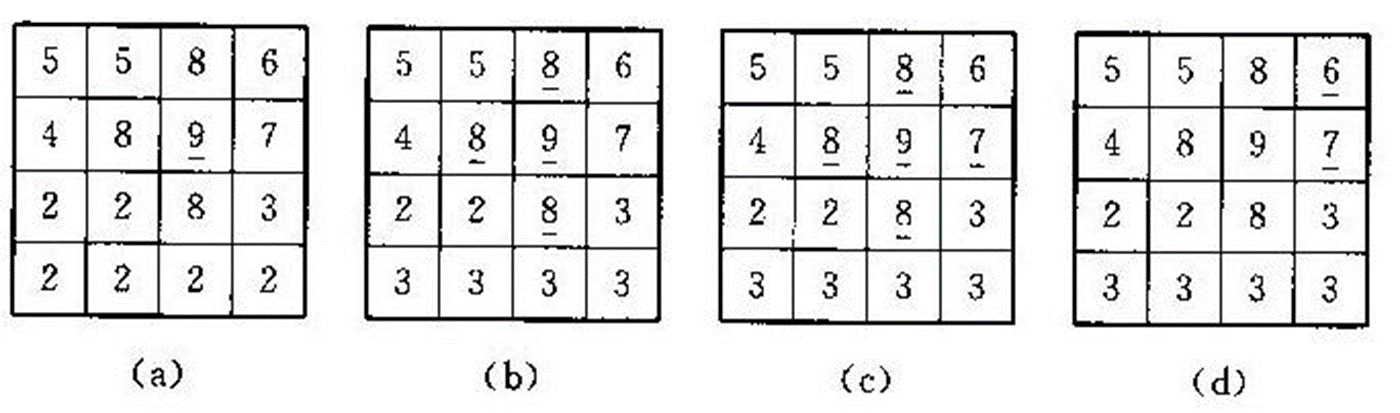
278 |
279 | 图7-5 区域生长示例
280 |
281 | 当生成任意物体时,接收准则可以结构为基础, 而不是以灰度级或对比度为基础。为了把候选的小群点包含在物体中,可以检测这些小群点, 而不是检测单个点, 如果它们的结构与物体的结构足够相似时就接受它们。
282 |
283 | ## 7.1.4 区域聚合
284 |
285 | 区域聚合可直接用于图像分割, 它要求聚合中的各个点必须在平面上相邻接而且特性相似。区域聚合的步骤是首先检查图像的测度集,以确定在测度空间中聚合的位置和数目,然后把这些聚合的定义用于图像, 以得到区域聚合。区域聚合技术可以说明如下。
286 |
287 | 首先, 在图片上定义某个等价关系。例如, 最简单的等价关系可定义为 $p(i, j)=p(k, l)$ 。也就是说, 如果 $p(i, j)=p(k, l)$, 就说明 $p(i, j)$ 与 $p(k, l)$ 等价。任何在点的格子上的等价关系又可划分为等价类。例如, $p(i, j)$ 的取值范围为 0 到 63 , 就可以产生 64 个等价类的模板。如果关系满足,它的值等于 1 ,否则为 0 。
288 |
289 | 模板的图像是两两不相交的, 那么64个模板就会充满整个格子。这些等价的类又可进一步分为最大连接的子集(连接分量)。连接性可以用点 $(i, j)$ 的邻点来定义, 如4连通邻点、8连通邻点等等。假如 $R$ 是属于格子的子集, 在 $R$ 中存在一个点序列, 第一个点是 $p_{1}$, 最后一个点是 $p_{2}$, 属于格子的子集 $R$ 的两个点 $p_{1}$ 和 $p_{2}$ 是被连接起来的, 这样, 相继的各点是 4 连接相邻的。通过这样的连接关系可以定义一个属于 $R$ 的子集, 这个子集形成一个区域, 在这个区域中, 任何点都与 $R$ 有关。利用等价模板可分成最大的连接区域, 然后, 这些最大的连接区域又可以像搭积木一样形成有意义的分割。
290 |
291 | 1970年布莱斯和芬尼玛提出一种分割方法, 如图5-6所示。图 ( $a$ ) 是具有灰度级的 $3 \times 3$ 的 $G$ 阵列, 图 (b) 是对 $G$ 的分割结果。 其中, 图像格子为 $G$, 它是大格子 $S$ 的子格子。 $G$ 为 $n \times m$ 的格子, $S$ 是 $(2 n+1) \times(2 m+1)$ 的大格子。在大格子中, $G(i, j)$ 点位于 $S$ 的 $(2 i+1,2 j+1)$ 点上。 $G$ 中的点与 $S$ 中的点相对应, 其中每一下标都是奇数, 其余的点用来代表区域的边界。以这种形式表现的区域, 产生一种寻找最大连接区域的方法。G中的点与它上边和右边的点相比较, 灰度级相同就合并, 灰度级不同就揷入边界线。把图像中的每个点都处理过之后, 整个图像就被分割成区域。 在这个例子中, 由于采用了4连通等价关系, 因此, 由图可见, 在对角线方向上的等灰度级产生了隔开的区域。
292 |
293 | 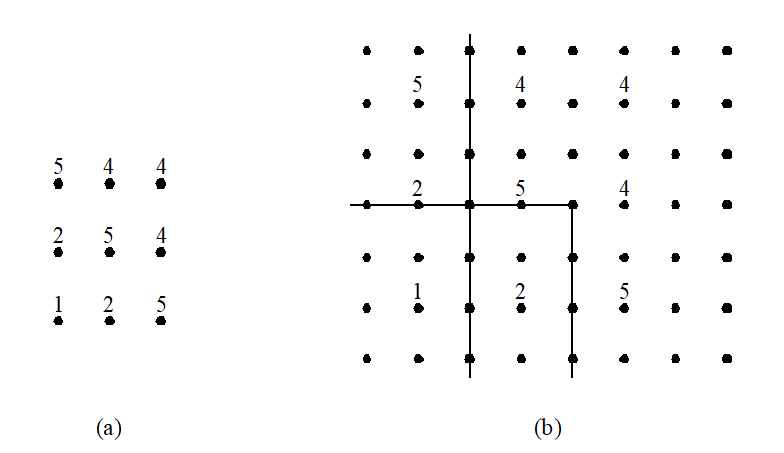
294 |
295 | 图7-6 布莱斯和芬尼玛分割方法
296 |
297 | 2 分裂合并法
298 |
299 | 实际中常先把图像分成任意大小且不重叠的区域,然后再合并或分裂这些区域以满足分割的要求, 即分裂合并法. 一致性测度可以选择基于灰度统计特征 (如同质区域中的方差),假设阈值为 $T$, 则算法步骤为:
300 |
301 | (1) 对于任一 $R_{i}$, 如果 $V\left(R_{i}\right)>T$ ,则将其分裂成互不重叠的四等分;
302 |
303 | (2) 对相邻区域 $R_{i}$ 和 $R_{j}$, 如果 $\boldsymbol{V}\left(\boldsymbol{R}_{i} \bigcup_{j} \boldsymbol{R}\right)= 2 && nCount <=6)
112 | bCondition1 = TRUE;
113 | //判断Z0(P1)=1
114 | nCount = 0;
115 | if (neighbour[1][2]==0 && neighbour[1][1] ==1)
116 | nCount++;
117 | if (neighbour[1][1] = = 0 && neighbour[2][1] = = 1)
118 | nCount++;
119 | if (neighbour[2][1] = = 0 && neighbour[3][1] = = 1)
120 | nCount++;
121 | if (neighbour[3][1] = = 0 && neighbour[3][2] = = 1)
122 | nCount++;
123 | if (neighbour[3][2] = = 0 && neighbour[3][3] = = 1)
124 | nCount++;
125 | if (neighbour[3][3] = = 0 && neighbour[2][3] = = 1)
126 | nCount++;
127 | if (neighbour[2][3] = = 0 && neighbour[1][3] = = 1)
128 | nCount++;
129 | if (neighbour[1][3] = = 0 && neighbour[1][2] = = 1)
130 | nCount++;
131 | if (nCount = = 1)
132 | bCondition2 = TRUE;
133 | //判断P2*P4*P8=0 or Z0(p2)!=1
134 | if (neighbour[1][2]*neighbour[2][1]*neighbour[2][3] = = 0)
135 | bCondition3 = TRUE;
136 | else
137 | {
138 | nCount = 0;
139 | if (neighbour[0][2] = = 0 && neighbour[0][1] = = 1)
140 | nCount++;
141 | if (neighbour[0][1] = = 0 && neighbour[1][1] = = 1)
142 | nCount++;
143 | if (neighbour[1][1] = = 0 && neighbour[2][1] = = 1)
144 | nCount++;
145 | if (neighbour[2][1] = = 0 && neighbour[2][2] = = 1)
146 | nCount++;
147 | if (neighbour[2][2 ]= = 0 && neighbour[2][3] = = 1)
148 | nCount++;
149 | if (neighbour[2][3] = = 0 && neighbour[1][3] = = 1)
150 | nCount++;
151 | if (neighbour[1][3] = = 0 && neighbour[0][3] = = 1)
152 | nCount++;
153 | if (neighbour[0][3] = = 0 && neighbour[0][2] = = 1)
154 | nCount++;
155 | if (nCount != 1)
156 | bCondition3 = TRUE;
157 | }
158 | //判断P2*P4*P6=0 or Z0(p4)!=1
159 | if (neighbour[1][2]*neighbour[2][1]*neighbour[3][2]==0)
160 | bCondition4 = TRUE;
161 | else
162 | {
163 | nCount = 0;
164 | if (neighbour[1][1] = = 0 && neighbour[1][0 ==1)
165 | nCount++;
166 | if (neighbour[1][0] = = 0 && neighbour[2][0]==1)
167 | nCount++;
168 | if (neighbour[2][0] = = 0 && neighbour[3][0]==1)
169 | nCount++;
170 | if (neighbour[3][0] = = 0 && neighbour[3][1] = = 1)
171 | nCount++;
172 | if (neighbour[3][1] = = 0 && neighbour[3][2] = = 1)
173 | nCount++;
174 | if (neighbour[3][2] = = 0 && neighbour[2][2] = = 1)
175 | nCount++;
176 | if (neighbour[2][2] = = 0 && neighbour[1][2] = = 1)
177 | nCount++;
178 | if (neighbour[1][2] = = 0 && neighbour[1][1] = = 1)
179 | nCount++;
180 | if (nCount != 1)
181 | bCondition4 = TRUE;
182 | }
183 | if(bCondition1 && bCondition2 && bCondition3 && bCondition4) {
184 | *lpDst = (unsigned char)255;
185 | bModified = TRUE;
186 | }
187 | else
188 | {
189 | *lpDst = (unsigned char)0;
190 | }
191 | }
192 | }
193 | // 复制腐蚀后的图像
194 | }
195 | // 复制腐蚀后的图像
196 | // 释放内存
197 | // 返回
198 | return TRUE;
199 | }
200 |
201 |
202 | ```
203 |
204 |
266 |
267 | 图 6.3.13 坦克图模糊阈值法分割
268 |
269 | ## 7.1.3 区域生长
270 |
271 | 分割的目的是把一幅图像划分成一些区域,最直接的方法就是把一幅图像分成满足某种判据的区域,也就是说,把点组成区域。为了实现分组, 首先要确定区域的数目, 其次要确定一个区域与其他区域相区别的特征, 最后还要产生有意义分割的相似性判据。
272 |
273 | 分割区域的一种方法叫区域生长或区域生成。假定区域的数目以及在每个区域中单个点的位置已知, 则从一个已知点开始,加上与已知点相似的邻近点形成一个区域。相似性准则可以是灰度级、 彩色、组织、梯度或其他特性,相似性的测度可以由所确定的阈值来判定。方法是从满足检测准则的点开始, 在各个方向上生长区域, 当其邻近点满足检测准则就并入小块区域中。当新的点被合并后再用新的区域重复这一过程, 直到没有可接受的邻近点时生成过程终止。
274 |
275 | 图 7-5给出一个简单的例子。此例的相似性准则是邻近点的灰度级与物体的平均灰度级的差小于2。图中被接受的点和起始点均用下划线标出,其中(a)图是输入图像;(b)图是第一步接受的邻近点;(c)图是第二步接受的邻近点;(d) 图是从6开始生成的结果。
276 |
277 | 
278 |
279 | 图7-5 区域生长示例
280 |
281 | 当生成任意物体时,接收准则可以结构为基础, 而不是以灰度级或对比度为基础。为了把候选的小群点包含在物体中,可以检测这些小群点, 而不是检测单个点, 如果它们的结构与物体的结构足够相似时就接受它们。
282 |
283 | ## 7.1.4 区域聚合
284 |
285 | 区域聚合可直接用于图像分割, 它要求聚合中的各个点必须在平面上相邻接而且特性相似。区域聚合的步骤是首先检查图像的测度集,以确定在测度空间中聚合的位置和数目,然后把这些聚合的定义用于图像, 以得到区域聚合。区域聚合技术可以说明如下。
286 |
287 | 首先, 在图片上定义某个等价关系。例如, 最简单的等价关系可定义为 $p(i, j)=p(k, l)$ 。也就是说, 如果 $p(i, j)=p(k, l)$, 就说明 $p(i, j)$ 与 $p(k, l)$ 等价。任何在点的格子上的等价关系又可划分为等价类。例如, $p(i, j)$ 的取值范围为 0 到 63 , 就可以产生 64 个等价类的模板。如果关系满足,它的值等于 1 ,否则为 0 。
288 |
289 | 模板的图像是两两不相交的, 那么64个模板就会充满整个格子。这些等价的类又可进一步分为最大连接的子集(连接分量)。连接性可以用点 $(i, j)$ 的邻点来定义, 如4连通邻点、8连通邻点等等。假如 $R$ 是属于格子的子集, 在 $R$ 中存在一个点序列, 第一个点是 $p_{1}$, 最后一个点是 $p_{2}$, 属于格子的子集 $R$ 的两个点 $p_{1}$ 和 $p_{2}$ 是被连接起来的, 这样, 相继的各点是 4 连接相邻的。通过这样的连接关系可以定义一个属于 $R$ 的子集, 这个子集形成一个区域, 在这个区域中, 任何点都与 $R$ 有关。利用等价模板可分成最大的连接区域, 然后, 这些最大的连接区域又可以像搭积木一样形成有意义的分割。
290 |
291 | 1970年布莱斯和芬尼玛提出一种分割方法, 如图5-6所示。图 ( $a$ ) 是具有灰度级的 $3 \times 3$ 的 $G$ 阵列, 图 (b) 是对 $G$ 的分割结果。 其中, 图像格子为 $G$, 它是大格子 $S$ 的子格子。 $G$ 为 $n \times m$ 的格子, $S$ 是 $(2 n+1) \times(2 m+1)$ 的大格子。在大格子中, $G(i, j)$ 点位于 $S$ 的 $(2 i+1,2 j+1)$ 点上。 $G$ 中的点与 $S$ 中的点相对应, 其中每一下标都是奇数, 其余的点用来代表区域的边界。以这种形式表现的区域, 产生一种寻找最大连接区域的方法。G中的点与它上边和右边的点相比较, 灰度级相同就合并, 灰度级不同就揷入边界线。把图像中的每个点都处理过之后, 整个图像就被分割成区域。 在这个例子中, 由于采用了4连通等价关系, 因此, 由图可见, 在对角线方向上的等灰度级产生了隔开的区域。
292 |
293 | 
294 |
295 | 图7-6 布莱斯和芬尼玛分割方法
296 |
297 | 2 分裂合并法
298 |
299 | 实际中常先把图像分成任意大小且不重叠的区域,然后再合并或分裂这些区域以满足分割的要求, 即分裂合并法. 一致性测度可以选择基于灰度统计特征 (如同质区域中的方差),假设阈值为 $T$, 则算法步骤为:
300 |
301 | (1) 对于任一 $R_{i}$, 如果 $V\left(R_{i}\right)>T$ ,则将其分裂成互不重叠的四等分;
302 |
303 | (2) 对相邻区域 $R_{i}$ 和 $R_{j}$, 如果 $\boldsymbol{V}\left(\boldsymbol{R}_{i} \bigcup_{j} \boldsymbol{R}\right)= 2 && nCount <=6)
112 | bCondition1 = TRUE;
113 | //判断Z0(P1)=1
114 | nCount = 0;
115 | if (neighbour[1][2]==0 && neighbour[1][1] ==1)
116 | nCount++;
117 | if (neighbour[1][1] = = 0 && neighbour[2][1] = = 1)
118 | nCount++;
119 | if (neighbour[2][1] = = 0 && neighbour[3][1] = = 1)
120 | nCount++;
121 | if (neighbour[3][1] = = 0 && neighbour[3][2] = = 1)
122 | nCount++;
123 | if (neighbour[3][2] = = 0 && neighbour[3][3] = = 1)
124 | nCount++;
125 | if (neighbour[3][3] = = 0 && neighbour[2][3] = = 1)
126 | nCount++;
127 | if (neighbour[2][3] = = 0 && neighbour[1][3] = = 1)
128 | nCount++;
129 | if (neighbour[1][3] = = 0 && neighbour[1][2] = = 1)
130 | nCount++;
131 | if (nCount = = 1)
132 | bCondition2 = TRUE;
133 | //判断P2*P4*P8=0 or Z0(p2)!=1
134 | if (neighbour[1][2]*neighbour[2][1]*neighbour[2][3] = = 0)
135 | bCondition3 = TRUE;
136 | else
137 | {
138 | nCount = 0;
139 | if (neighbour[0][2] = = 0 && neighbour[0][1] = = 1)
140 | nCount++;
141 | if (neighbour[0][1] = = 0 && neighbour[1][1] = = 1)
142 | nCount++;
143 | if (neighbour[1][1] = = 0 && neighbour[2][1] = = 1)
144 | nCount++;
145 | if (neighbour[2][1] = = 0 && neighbour[2][2] = = 1)
146 | nCount++;
147 | if (neighbour[2][2 ]= = 0 && neighbour[2][3] = = 1)
148 | nCount++;
149 | if (neighbour[2][3] = = 0 && neighbour[1][3] = = 1)
150 | nCount++;
151 | if (neighbour[1][3] = = 0 && neighbour[0][3] = = 1)
152 | nCount++;
153 | if (neighbour[0][3] = = 0 && neighbour[0][2] = = 1)
154 | nCount++;
155 | if (nCount != 1)
156 | bCondition3 = TRUE;
157 | }
158 | //判断P2*P4*P6=0 or Z0(p4)!=1
159 | if (neighbour[1][2]*neighbour[2][1]*neighbour[3][2]==0)
160 | bCondition4 = TRUE;
161 | else
162 | {
163 | nCount = 0;
164 | if (neighbour[1][1] = = 0 && neighbour[1][0 ==1)
165 | nCount++;
166 | if (neighbour[1][0] = = 0 && neighbour[2][0]==1)
167 | nCount++;
168 | if (neighbour[2][0] = = 0 && neighbour[3][0]==1)
169 | nCount++;
170 | if (neighbour[3][0] = = 0 && neighbour[3][1] = = 1)
171 | nCount++;
172 | if (neighbour[3][1] = = 0 && neighbour[3][2] = = 1)
173 | nCount++;
174 | if (neighbour[3][2] = = 0 && neighbour[2][2] = = 1)
175 | nCount++;
176 | if (neighbour[2][2] = = 0 && neighbour[1][2] = = 1)
177 | nCount++;
178 | if (neighbour[1][2] = = 0 && neighbour[1][1] = = 1)
179 | nCount++;
180 | if (nCount != 1)
181 | bCondition4 = TRUE;
182 | }
183 | if(bCondition1 && bCondition2 && bCondition3 && bCondition4) {
184 | *lpDst = (unsigned char)255;
185 | bModified = TRUE;
186 | }
187 | else
188 | {
189 | *lpDst = (unsigned char)0;
190 | }
191 | }
192 | }
193 | // 复制腐蚀后的图像
194 | }
195 | // 复制腐蚀后的图像
196 | // 释放内存
197 | // 返回
198 | return TRUE;
199 | }
200 |
201 |
202 | ```
203 |
204 |  205 |
206 | ### 通过开运算检测电路板
207 |
208 |
205 |
206 | ### 通过开运算检测电路板
207 |
208 |  209 |
210 |
209 |
210 |  211 |
212 | ### 肉类目标识别
213 |
214 |
211 |
212 | ### 肉类目标识别
213 |
214 |  215 |
216 |
215 |
216 |  217 |
218 |
217 |
218 |  219 |
220 | 形态学梯度,腐蚀后求取形态学梯度-分水岭算法
221 |
222 | ### MRI图像检测
223 |
224 |
219 |
220 | 形态学梯度,腐蚀后求取形态学梯度-分水岭算法
221 |
222 | ### MRI图像检测
223 |
224 |  225 |
226 |
225 |
226 |  227 |
228 | 圆盘开-重建-减去-阈值-开去掉小噪声
229 |
230 | ### 机场跑道检测
231 |
232 |
227 |
228 | 圆盘开-重建-减去-阈值-开去掉小噪声
229 |
230 | ### 机场跑道检测
231 |
232 |  233 |
234 |
233 |
234 |  235 |
236 | 圆盘开运算
237 |
238 |
235 |
236 | 圆盘开运算
237 |
238 |  239 |
240 | 阈值
241 |
242 |
239 |
240 | 阈值
241 |
242 |  243 |
244 | 细化: 红色
245 | 细化到端点检测:
246 | 绿色
247 | 开运算: 蓝色
248 |
249 |
243 |
244 | 细化: 红色
245 | 细化到端点检测:
246 | 绿色
247 | 开运算: 蓝色
248 |
249 |  250 |
251 | 重建
252 |
253 | 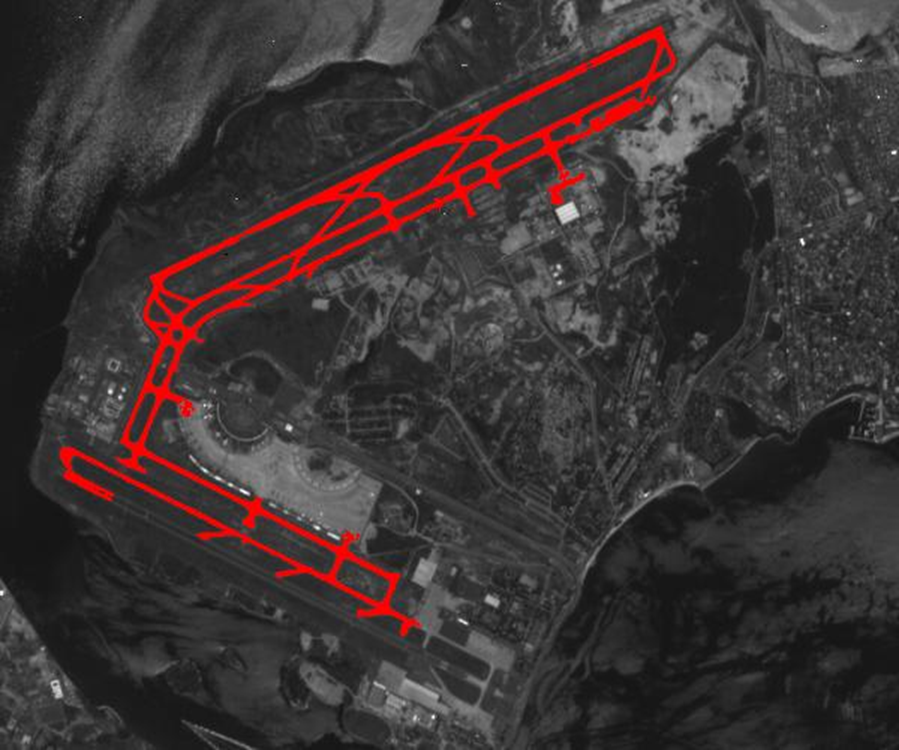
254 |
255 | 门限阈值确定
--------------------------------------------------------------------------------
250 |
251 | 重建
252 |
253 | 
254 |
255 | 门限阈值确定
--------------------------------------------------------------------------------
 16 |
17 | 图2-13 正弦波和小波
18 | (a)正弦波曲线; (b) 小波曲线
19 |
20 | 从小波和正弦波的形状可以看出, 变化剧烈的信号, 用不规则的小波进行分析比用平滑的正弦波更好, 即用小波更能描述信号的局部特征。
21 |
22 | 连续小波变换 (Continuous Wavelet Transform, CWT) 用下式表示:
23 |
24 | $$
25 | C(\text { scale, position })=\int_{-\infty}^{+\infty} f(t) \psi( { scale, position, } t) d t
26 | $$
27 |
28 | 式 (2-79) 表示小波变换是信号 $f(x)$ 与被缩放和平移的小波函数 $\psi()$ 之积在信号存在的整个期间里求和的结果。CWT的变换结果是许多小波系数 $C$, 这些系数是缩放因子 (scale) 和平移 (positon) 的函数。
29 |
30 | 基本小波函数 $\psi()$ 的缩放和平移操作含义如下:
31 |
32 | 图2-14 小波的缩放操作
33 |
34 | (2) 平移。简单地讲, 平移就是小波的延迟或超前。在数学上, 函数 $f(t)$ 延迟 $k$ 的表达式为 $f(t-k)$, 如图2-15所示。
35 |
36 |
16 |
17 | 图2-13 正弦波和小波
18 | (a)正弦波曲线; (b) 小波曲线
19 |
20 | 从小波和正弦波的形状可以看出, 变化剧烈的信号, 用不规则的小波进行分析比用平滑的正弦波更好, 即用小波更能描述信号的局部特征。
21 |
22 | 连续小波变换 (Continuous Wavelet Transform, CWT) 用下式表示:
23 |
24 | $$
25 | C(\text { scale, position })=\int_{-\infty}^{+\infty} f(t) \psi( { scale, position, } t) d t
26 | $$
27 |
28 | 式 (2-79) 表示小波变换是信号 $f(x)$ 与被缩放和平移的小波函数 $\psi()$ 之积在信号存在的整个期间里求和的结果。CWT的变换结果是许多小波系数 $C$, 这些系数是缩放因子 (scale) 和平移 (positon) 的函数。
29 |
30 | 基本小波函数 $\psi()$ 的缩放和平移操作含义如下:
31 |
32 | 图2-14 小波的缩放操作
33 |
34 | (2) 平移。简单地讲, 平移就是小波的延迟或超前。在数学上, 函数 $f(t)$ 延迟 $k$ 的表达式为 $f(t-k)$, 如图2-15所示。
35 |
36 |  37 |
38 |
37 |
38 | 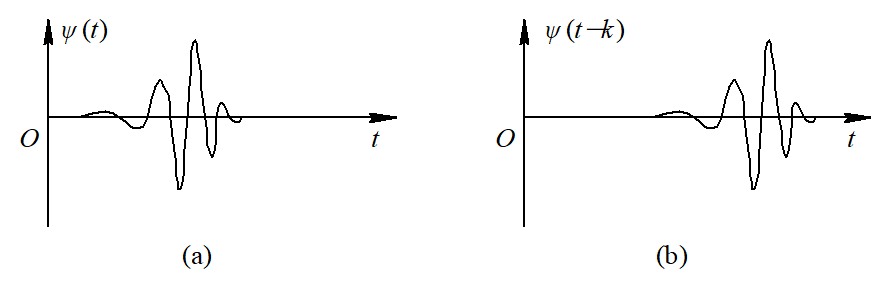 39 |
40 | 图2-15 小波的平移操作
41 |
42 | (a) 小波函数 $\psi(t)$; (b) 位移后的小波函数 $\psi(t-k)$
43 |
44 | CWT计算主要有如下五个步骤:
45 |
46 | 1. 取一个小波, 将其与原始信号的开始一节进行比较。
47 |
48 | 2. 计算数值C, C表示小波与所取一节信号的相似程度, 计算结果取决于所选小波的形状, 如图2-16所示。
49 |
50 | 3. 向右移动小波, 重复第一步和第二步, 直至覆盖整个信号, 如图2-17所示。
51 |
52 | 4. 伸展小波, 重复第一步至第三步, 如图2-18所示。
53 |
54 |
39 |
40 | 图2-15 小波的平移操作
41 |
42 | (a) 小波函数 $\psi(t)$; (b) 位移后的小波函数 $\psi(t-k)$
43 |
44 | CWT计算主要有如下五个步骤:
45 |
46 | 1. 取一个小波, 将其与原始信号的开始一节进行比较。
47 |
48 | 2. 计算数值C, C表示小波与所取一节信号的相似程度, 计算结果取决于所选小波的形状, 如图2-16所示。
49 |
50 | 3. 向右移动小波, 重复第一步和第二步, 直至覆盖整个信号, 如图2-17所示。
51 |
52 | 4. 伸展小波, 重复第一步至第三步, 如图2-18所示。
53 |
54 |  55 |
56 | 图2-16 计算系数值 $C$
57 |
58 |
55 |
56 | 图2-16 计算系数值 $C$
57 |
58 |  59 |
60 | 图2-17 计算平移后系数值 $C$
61 |
62 |
63 |
64 |
59 |
60 | 图2-17 计算平移后系数值 $C$
61 |
62 |
63 |
64 |  65 |
66 | 图2-18 计算尺度后系数值 $C$
67 |
68 | 5. 对于所有缩放,重复第一步至第四步。
69 |
70 | 小波的缩放因子与信号频率之间的关系是:缩放因子 scale
71 | 越小, 表示小波越窄, 度量的是信号的细节变化, 表示信号频率越高; 缩放因子scale越大, 表示小波越宽, 度量的是信号的粗䊁程度,表示信号频率越低。
72 |
73 | ### 离散小波变换(DWT)
74 |
75 | 在每个可能的缩放因子和平移参数下计算小波系数, 其计算量相当大, 将产生惊人的数据量, 而且有许多数据是无用的。如果缩放因子和平移参数都选择为 $2^{j}(j>0$ 且为整数) 的倍数,即只选择部分缩放因子和平移参数来进行计算, 就会使分析的数据量大大减少。使用这样的缩放因子和平移参数的小波变换称为双尺度小波变换(Dyadic Wavelet Transform),它是离散小波变换(Discrete Wavelet Transform,DWT)的一种形式。通常离散小波变换就是指双尺度小波变换。
76 |
77 | 执行离散小波变换的有效方法是使用滤波器, 该方法是Mallat于1988年提出的,称为Mallat算法。这种方法实际上是一种信号分解的方法, 在数字信号处理中常称为双通道子带编码。
78 |
79 | 用滤波器执行离散小波变换的概念如图2-19所示。S表示原始的输入信号, 通过两个互补的滤波器组, 其中一个滤波器为低通滤波器, 通过该滤波器可得到信号的近似值 $A$(Approximations), 另一个为高通滤波器, 通过该滤波器可得到信号的细节值$D$(Detail)。
80 |
81 |
82 |
83 |
65 |
66 | 图2-18 计算尺度后系数值 $C$
67 |
68 | 5. 对于所有缩放,重复第一步至第四步。
69 |
70 | 小波的缩放因子与信号频率之间的关系是:缩放因子 scale
71 | 越小, 表示小波越窄, 度量的是信号的细节变化, 表示信号频率越高; 缩放因子scale越大, 表示小波越宽, 度量的是信号的粗䊁程度,表示信号频率越低。
72 |
73 | ### 离散小波变换(DWT)
74 |
75 | 在每个可能的缩放因子和平移参数下计算小波系数, 其计算量相当大, 将产生惊人的数据量, 而且有许多数据是无用的。如果缩放因子和平移参数都选择为 $2^{j}(j>0$ 且为整数) 的倍数,即只选择部分缩放因子和平移参数来进行计算, 就会使分析的数据量大大减少。使用这样的缩放因子和平移参数的小波变换称为双尺度小波变换(Dyadic Wavelet Transform),它是离散小波变换(Discrete Wavelet Transform,DWT)的一种形式。通常离散小波变换就是指双尺度小波变换。
76 |
77 | 执行离散小波变换的有效方法是使用滤波器, 该方法是Mallat于1988年提出的,称为Mallat算法。这种方法实际上是一种信号分解的方法, 在数字信号处理中常称为双通道子带编码。
78 |
79 | 用滤波器执行离散小波变换的概念如图2-19所示。S表示原始的输入信号, 通过两个互补的滤波器组, 其中一个滤波器为低通滤波器, 通过该滤波器可得到信号的近似值 $A$(Approximations), 另一个为高通滤波器, 通过该滤波器可得到信号的细节值$D$(Detail)。
80 |
81 |
82 |
83 |  84 |
85 | 图2-19 小波分解示意图
86 |
87 | 在小波分析中,近似值是大的缩放因子计算的系数,表示信号的低频分量, 而细节值是小的缩放因子计算的系数, 表示信号的高频分量。实际应用中, 信号的低频分量往往是最重要的, 而高频分量只起一个修饰的作用。如同一个人的声音一样, 把高频分量去掉后, 听起来声音会发生改变, 但还能听出说的是什么内容, 但如果把低频分量删除后, 就会什么内容也听不出来了。
88 |
89 | 由图2-19可以看出离散小波变换可以表示成由低通滤波器和高通滤波器组成的一棵树。原始信号经过一对互补的滤波器组进行的分解称为一级分解, 信号的分解过程也可以不断进行下去, 也就是说可以进行多级分解。如果对信号的高频分量不再分解, 而对低频分量进行连续分解, 就可以得到信号不同分辨率下的低频分量, 这也称为信号的多分辨率分析。如此进行下去, 就会形成图2-20所示的一棵比较大的分解树, 称其为信号的小波分解树 (Wavelet Decomposition Tree)。实际中,分解的级数取决于要分析的信号数据特征及用户的具体需要。
90 |
91 |
84 |
85 | 图2-19 小波分解示意图
86 |
87 | 在小波分析中,近似值是大的缩放因子计算的系数,表示信号的低频分量, 而细节值是小的缩放因子计算的系数, 表示信号的高频分量。实际应用中, 信号的低频分量往往是最重要的, 而高频分量只起一个修饰的作用。如同一个人的声音一样, 把高频分量去掉后, 听起来声音会发生改变, 但还能听出说的是什么内容, 但如果把低频分量删除后, 就会什么内容也听不出来了。
88 |
89 | 由图2-19可以看出离散小波变换可以表示成由低通滤波器和高通滤波器组成的一棵树。原始信号经过一对互补的滤波器组进行的分解称为一级分解, 信号的分解过程也可以不断进行下去, 也就是说可以进行多级分解。如果对信号的高频分量不再分解, 而对低频分量进行连续分解, 就可以得到信号不同分辨率下的低频分量, 这也称为信号的多分辨率分析。如此进行下去, 就会形成图2-20所示的一棵比较大的分解树, 称其为信号的小波分解树 (Wavelet Decomposition Tree)。实际中,分解的级数取决于要分析的信号数据特征及用户的具体需要。
90 |
91 |  92 |
93 | 图2-20 多级信号分解示意图
94 | (a) 信号分解; (b) 小波分数; (c)小波分解树
95 |
96 |
92 |
93 | 图2-20 多级信号分解示意图
94 | (a) 信号分解; (b) 小波分数; (c)小波分解树
95 |
96 |  97 |
98 | 图2-21 小波分解下采样示意图
99 |
100 | ### 小波重构
101 |
102 | 将信号的小波分解的分量进行处理后, 一般还要根据需要
103 |
104 | 把信号恢复出来, 也就是利用信号的小波分解的系数还原出原始信号, 这一过程称为小波重构(Wavelet Reconstruction)或叫做小波合成(Wavelet Synthesis)。这一合成过程的数学运算叫做逆离散小波变换 ( Inverse Discrete Wavelet Transform, IDWT)。
105 |
106 |
97 |
98 | 图2-21 小波分解下采样示意图
99 |
100 | ### 小波重构
101 |
102 | 将信号的小波分解的分量进行处理后, 一般还要根据需要
103 |
104 | 把信号恢复出来, 也就是利用信号的小波分解的系数还原出原始信号, 这一过程称为小波重构(Wavelet Reconstruction)或叫做小波合成(Wavelet Synthesis)。这一合成过程的数学运算叫做逆离散小波变换 ( Inverse Discrete Wavelet Transform, IDWT)。
105 |
106 |  107 |
108 | 图2-22 小波重构算法示意图
109 |
110 | #### 重构近似信号与细节信号
111 |
112 | 由图2-22可知, 由小波分解的近似系数和细节系数可以重构出原始信号。同样, 可由近似系数和细节系数分别重构出信号的近似值或细节值, 这时只要近似系数或细节系数置为零即可。
113 |
114 | 图2-23是对第一层近似信号或细节信号进行重构的示意图。
115 |
116 |
107 |
108 | 图2-22 小波重构算法示意图
109 |
110 | #### 重构近似信号与细节信号
111 |
112 | 由图2-22可知, 由小波分解的近似系数和细节系数可以重构出原始信号。同样, 可由近似系数和细节系数分别重构出信号的近似值或细节值, 这时只要近似系数或细节系数置为零即可。
113 |
114 | 图2-23是对第一层近似信号或细节信号进行重构的示意图。
115 |
116 |  117 |
118 | 图2-23 重构近似和细节信号示意
119 |
120 | (a)重构近似信号; (b) 重构细节信号
121 |
122 | #### 多层重构
123 |
124 | 在图2-23中, 重构出信号的近似值 $A_{1}$ 与细节值 $D_{1}$ 之后, 则原信号可用 $A_{1}+D_{1}=S$ 重构出来。对应于信号的多层小波分解, 小波的多层重构如图2-24所示。由图2-24可见重构过程为:
125 | $$
126 | A_3+D_3=A_2\\
127 | A_2+D_2=A_1\\
128 | A_1+D_1=S
129 | $$
130 | 信号重构中, 滤波器的选择非常重要, 关系到能否重构出满意的原始信号。低通分解滤波器 (L) 和高通分解滤波器 (H) 及重构滤波器组 $\left(L^{\prime}\right.$ 和 $\left.H^{\prime}\right)$ 构成一个系统, 这个系统称为正交镜像滤波器(Quadrature Mirror Filters, QMF)系统, 如图7-25 所示。
131 |
132 |
117 |
118 | 图2-23 重构近似和细节信号示意
119 |
120 | (a)重构近似信号; (b) 重构细节信号
121 |
122 | #### 多层重构
123 |
124 | 在图2-23中, 重构出信号的近似值 $A_{1}$ 与细节值 $D_{1}$ 之后, 则原信号可用 $A_{1}+D_{1}=S$ 重构出来。对应于信号的多层小波分解, 小波的多层重构如图2-24所示。由图2-24可见重构过程为:
125 | $$
126 | A_3+D_3=A_2\\
127 | A_2+D_2=A_1\\
128 | A_1+D_1=S
129 | $$
130 | 信号重构中, 滤波器的选择非常重要, 关系到能否重构出满意的原始信号。低通分解滤波器 (L) 和高通分解滤波器 (H) 及重构滤波器组 $\left(L^{\prime}\right.$ 和 $\left.H^{\prime}\right)$ 构成一个系统, 这个系统称为正交镜像滤波器(Quadrature Mirror Filters, QMF)系统, 如图7-25 所示。
131 |
132 |  133 |
134 | 图2-24 多层小波重构示意图
135 |
136 | 
137 |
138 | 图2-25 多层小波分解和重构示意图
139 |
140 | ### 小波包分析
141 |
142 | 小波分析是将信号分解为近似与细节两部分, 近似部分又可以分解成第二层近似与细节, 可以这样重复下去。对于一个 $N$层分解来说, 有 $N+1$ 个分解信号的途径。而小波包分析的细节与近似部分一样, 也可以分解, 对于 $N$层分解, 它产生 $2 N$ 个不同的途径, 图2-26是一个小波包分解示意图。
143 |
144 |
133 |
134 | 图2-24 多层小波重构示意图
135 |
136 | 
137 |
138 | 图2-25 多层小波分解和重构示意图
139 |
140 | ### 小波包分析
141 |
142 | 小波分析是将信号分解为近似与细节两部分, 近似部分又可以分解成第二层近似与细节, 可以这样重复下去。对于一个 $N$层分解来说, 有 $N+1$ 个分解信号的途径。而小波包分析的细节与近似部分一样, 也可以分解, 对于 $N$层分解, 它产生 $2 N$ 个不同的途径, 图2-26是一个小波包分解示意图。
143 |
144 |  145 |
146 | 图2-26 小波包分解示意图
147 |
148 | 小波包分解也可得到一个分解树,称其为小波包分解树(Wavelet Packet Decomposition Tree),\cjkstart这种树是一个完整的二义树。小波包分解方法是小波分解的一般化,可为信号分析提供更丰富和更详细的信息。信号 $S$ 可表示为$AA_2+ADA_3+DDA_3+D_1$等。
149 |
150 | ### 二维离散小波变换
151 |
152 | 二维离散小波变换是一维离散小波变换的推广,其实质上是将二维信号在不同尺度上的分解, 得到原始信号的近似值和细节值。由于信号是二维的, 因此分解也是二维的。分解的结果为:近似分量cA、水平细节分量 $cH$ 、垂直细节分量cV和对角细节分量cD。同样也可以利用二维小波分解的结果在不同尺度上重构信号。二维小波分解和重构过程如图2-27所示。
153 |
154 |
145 |
146 | 图2-26 小波包分解示意图
147 |
148 | 小波包分解也可得到一个分解树,称其为小波包分解树(Wavelet Packet Decomposition Tree),\cjkstart这种树是一个完整的二义树。小波包分解方法是小波分解的一般化,可为信号分析提供更丰富和更详细的信息。信号 $S$ 可表示为$AA_2+ADA_3+DDA_3+D_1$等。
149 |
150 | ### 二维离散小波变换
151 |
152 | 二维离散小波变换是一维离散小波变换的推广,其实质上是将二维信号在不同尺度上的分解, 得到原始信号的近似值和细节值。由于信号是二维的, 因此分解也是二维的。分解的结果为:近似分量cA、水平细节分量 $cH$ 、垂直细节分量cV和对角细节分量cD。同样也可以利用二维小波分解的结果在不同尺度上重构信号。二维小波分解和重构过程如图2-27所示。
153 |
154 |  155 |
156 | 图2-27二维小波分解和重构过程示意图
157 | (a)二维DWT; (b) 二维IDWT
158 |
159 | ## 2.7.2 离散小波变换在图像处理中的应用简介
160 |
161 | ### 用小波变换进行图像分解
162 |
163 | 使用小波变换完成图像分解的方法很多,例如,均匀分解 ( Uniform decomposition ) 、非均匀分解 ( Non-uniform decomposition)、八带分解(Octave-band decomposition)、小波包分解 (Wavelet-packer decomposition) 等。其中八带分解是使用最广的一种分解方法, 这种分解方法把低频部分分解成比较窄的频带, 而对每一级分解得到的高频部分不再进一步进行分解。 图2-28为八带分解示意图, 用于分解的原始图像采用Matlab提供的预存图像文件woman2.mat,小波基函数为 “haar"小波。图228 (c)是用Matlab的小波工具箱编程进行分解得到的图像。
164 |
165 | 
166 |
167 | 图2-28 八带分解示意图
168 |
169 | (a) 一次二维DWT; (b) 两次二维DWT; (c) Woman二级分解图
170 |
171 | ### 用小波变换进行图像处理
172 |
173 | 对静态二维数字图像,可先对其进行若干次二维DWT变换,
174 |
175 | 将图像信息分解为高频成分 $H 、 V$ 和 $D$ 和低频成分 $A$ 。对低频部分
176 |
177 | A,由于它对压缩的结果影响很大,因此可采用无损编码方法,
178 |
179 | 如Huffman、DPCM等;对 $H 、 V$ 和 $D$ 部分,可对不同的层次采用不同策略的向量量化编码方法, 这样便可大大减少数据量, 而图像的解码过程冈好相反。整个编码、解码流程如图2-29所示。
180 |
181 | 
182 |
183 | 图2-29 图像压缩编码、解码流程此外,还可以在对 $A 、 H 、 V$ 和 $D$ 部分编码后加上一个反馈环节,获取误差图像,并对其编码。这样压缩效果会更好。
184 |
185 | 近年来,基于小波变换发展起来的图像编码有嵌入式零树小波编码EZW(Embedded Zerotree Wavelet)及在EZW算法基础上改进的层树分级编码SPIHT( Set Parition In HierarchicalTrees) 和最佳截断嵌入码块编码EBCOT (Embedded Block Coding with Optimized Truncation ) 等。ISO/IEC JTC1 SC29 小组制定的 JPEG2000静态图像编码标准中的图像变换技术就采用了离散小波变换,这些编码的最大特点是在不丢失重要信息的同时,能以较高的比率压缩图像数据,并且其算法计算量小。
--------------------------------------------------------------------------------
/III/3.1 图像编码概述.md:
--------------------------------------------------------------------------------
1 | [TOC]
2 |
3 | # 3.1 图像编码概述
4 |
5 | ## 3.1.1 图像编码基本原理
6 |
7 | 虽然表示图像需要大量的数据, 但图像数据是高度相关的, 或者说存在冗余 (Redundancy) 信息, 去掉这些冗余信息后可以有效压缩图像, 同时又不会损害图像的有效信息。数字图像的写余主要表现为以下几种形式: 空间几余、时间冗余、视觉杂、 信息熵咒余、结构冗余和知识冗余。
8 |
9 | - 空间冗余:图像内部相邻像素之间存在较强的相关性所造成的咒余。
10 |
11 | - 时间写余: 视频图像序列中的不同帧之间的相关性所造成的写余。
12 |
13 | - 视觉冗余: 是指人眼不能感知或不敏感的那部分图像信息。
14 |
15 | - 信息熵冗余: 也称编码冗余,如果图像中平均每个像素使用的比特数大于该图像的信息熵, 则图像中存在咒余, 这种冗余称为信息熵冗余。
16 |
17 | - 结构冗余:是指图像中存在很强的纹理结构或自相似性。
18 |
19 | - 知识冗余: 是指在有些图像中还包含与某些先验知识有关的信息。
20 |
21 | 图像数据的这些冗余信息为图像压缩编码提供了依据。如, 利用人眼对蓝光不敏感的视觉特性, 在对彩色图像编码时, 就可以用较低的精度对蓝色分量进行编码。图像编码的目的就是充分利用图像中存在的各种呪余信息, 特别是空间几余、时间冗余以及视觉冗余, 以尽量少的比特数来表示图像。利用各种冗余信息, 压缩编码技术能够很好地解决在将模拟信号转换为数字信号后所产生的带宽需求增加的问题, 它是使数字信号走上实用化的关键技术之一, 表3-1中列出了几种常见应用的码率。
22 | $$
23 | \begin{array}{|c|c|c|c|c|c|c|c|}
24 | \hline \text { 应用场合 } & \text { 比特/像素 } & \text { 像索数/行 } & \text { 行数/帧 } & \text { 帧数/秒 } & \text { 亮色比 } & \text { 比特/秒(压缩前) } & \text { 比特/秒(压缩后) } \\
25 | \hline \text { 高清晰电视 } & 8 & 1920 & 1080 & 30 & 4: 1: 1 & 1.18 ~Gb / s & 20 \sim 25 Mb / s \\
26 | \hline \text { 普通电视 } & 8 & 720 & 480 & 30 & 4: 1: 1 & 167 Mb / s & 4 \sim 8 Mb / s \\
27 | \hline \text { 会议电视 } & 8 & 352 & 288 & 30 & 4: 1: 1 & 36.5 Mb / s & 1.5 \sim 2 Mb / s \\
28 | \hline \text { 桌上电视 } & 8 & 176 & 144 & 30 & 4: 1: 1 & 9.1 Mb / s & 128 ~Kb / s \\
29 | \hline \text { 电视电话 } & 8 & 128 & 112 & 30 & 4: 1: 1 & 5.2 Mb / s & 56 ~Kb / s \\
30 | \hline
31 | \end{array}
32 | $$
33 | 表3-1 几种常见应用的码率
34 |
35 | ## 3.1.2 图像编码的方法
36 |
37 | 根据编码过程中是否存在信息损耗可将图像编码分为有损压缩和无损压缩。
38 |
39 | - 无损压缩: 无信息损失, 解压缩时能够从压缩数据精确地恢复原始图像;
40 |
41 | - 有损压缩:不能精确重建原始图像, 存在一定程度的失真。
42 |
43 | 图像冗余有损压缩的原理
44 | $$
45 | \begin{array}{|l|l|l|l|l|}
46 | \hline 36 & 35 & 34 & 34 & 34 \\
47 | \hline 34 & 34 & 32 & 34 & 34 \\
48 | \hline 33 & 37 & 30 & 34 & 34 \\
49 | \hline 34 & 34 & 34 & 34 & 34 \\
50 | \hline 34 & 35 & 34 & 34 & 31 \\
51 | \hline
52 | \end{array}
53 | \Rightarrow
54 | \begin{array}{|l|l|l|l|l|}
55 | \hline 34 & 34 & 34 & 34 & 34 \\
56 | \hline 34 & 34 & 34 & 34 & 34 \\
57 | \hline 34 & 34 & 34 & 34 & 34 \\
58 | \hline 34 & 34 & 34 & 34 & 34 \\
59 | \hline 34 & 34 & 34 & 34 & 34 \\
60 | \hline
61 | \end{array}
62 | \Rightarrow
63 | \begin{array}{|l|l|}
64 | \hline 25 &34\\
65 | \hline
66 | \end{array}
67 | $$
68 | 图像冗余无损压缩的原理
69 | $$
70 | \begin{array}{|l|l|l|l|}
71 | \hline\quad & \quad&\quad &\quad\\
72 | \hline & & &\\
73 | \hline & & &\\
74 | \hline & & &\\
75 | \hline
76 | \end{array}
77 | \Rightarrow
78 | \begin{array}{|l|l|l|l|}
79 | \hline \text { RGB } & \text { RGB } & \text { RGB } & \text { RGB } \\
80 | \hline \text { RGB } & \text { RGB } & \text { RGB } & \text { RGB } \\
81 | \hline \text { RGB } & \text { RGB } & \text { RGB } & \text { RGB } \\
82 | \hline \text { RGB } & \text { RGB } & \text { RGB } & \text { RGB } \\
83 | \hline
84 | \end{array}
85 | \Rightarrow
86 | \begin{array}{|c|c|}
87 | \hline 16 & RGB \\
88 | \hline
89 | \end{array}
90 | $$
91 |
92 |
93 | - 第一代压缩编码
94 |
95 | 八十年代以前, 主要是根据传统的信源编码方法。
96 |
97 |
155 |
156 | 图2-27二维小波分解和重构过程示意图
157 | (a)二维DWT; (b) 二维IDWT
158 |
159 | ## 2.7.2 离散小波变换在图像处理中的应用简介
160 |
161 | ### 用小波变换进行图像分解
162 |
163 | 使用小波变换完成图像分解的方法很多,例如,均匀分解 ( Uniform decomposition ) 、非均匀分解 ( Non-uniform decomposition)、八带分解(Octave-band decomposition)、小波包分解 (Wavelet-packer decomposition) 等。其中八带分解是使用最广的一种分解方法, 这种分解方法把低频部分分解成比较窄的频带, 而对每一级分解得到的高频部分不再进一步进行分解。 图2-28为八带分解示意图, 用于分解的原始图像采用Matlab提供的预存图像文件woman2.mat,小波基函数为 “haar"小波。图228 (c)是用Matlab的小波工具箱编程进行分解得到的图像。
164 |
165 | 
166 |
167 | 图2-28 八带分解示意图
168 |
169 | (a) 一次二维DWT; (b) 两次二维DWT; (c) Woman二级分解图
170 |
171 | ### 用小波变换进行图像处理
172 |
173 | 对静态二维数字图像,可先对其进行若干次二维DWT变换,
174 |
175 | 将图像信息分解为高频成分 $H 、 V$ 和 $D$ 和低频成分 $A$ 。对低频部分
176 |
177 | A,由于它对压缩的结果影响很大,因此可采用无损编码方法,
178 |
179 | 如Huffman、DPCM等;对 $H 、 V$ 和 $D$ 部分,可对不同的层次采用不同策略的向量量化编码方法, 这样便可大大减少数据量, 而图像的解码过程冈好相反。整个编码、解码流程如图2-29所示。
180 |
181 | 
182 |
183 | 图2-29 图像压缩编码、解码流程此外,还可以在对 $A 、 H 、 V$ 和 $D$ 部分编码后加上一个反馈环节,获取误差图像,并对其编码。这样压缩效果会更好。
184 |
185 | 近年来,基于小波变换发展起来的图像编码有嵌入式零树小波编码EZW(Embedded Zerotree Wavelet)及在EZW算法基础上改进的层树分级编码SPIHT( Set Parition In HierarchicalTrees) 和最佳截断嵌入码块编码EBCOT (Embedded Block Coding with Optimized Truncation ) 等。ISO/IEC JTC1 SC29 小组制定的 JPEG2000静态图像编码标准中的图像变换技术就采用了离散小波变换,这些编码的最大特点是在不丢失重要信息的同时,能以较高的比率压缩图像数据,并且其算法计算量小。
--------------------------------------------------------------------------------
/III/3.1 图像编码概述.md:
--------------------------------------------------------------------------------
1 | [TOC]
2 |
3 | # 3.1 图像编码概述
4 |
5 | ## 3.1.1 图像编码基本原理
6 |
7 | 虽然表示图像需要大量的数据, 但图像数据是高度相关的, 或者说存在冗余 (Redundancy) 信息, 去掉这些冗余信息后可以有效压缩图像, 同时又不会损害图像的有效信息。数字图像的写余主要表现为以下几种形式: 空间几余、时间冗余、视觉杂、 信息熵咒余、结构冗余和知识冗余。
8 |
9 | - 空间冗余:图像内部相邻像素之间存在较强的相关性所造成的咒余。
10 |
11 | - 时间写余: 视频图像序列中的不同帧之间的相关性所造成的写余。
12 |
13 | - 视觉冗余: 是指人眼不能感知或不敏感的那部分图像信息。
14 |
15 | - 信息熵冗余: 也称编码冗余,如果图像中平均每个像素使用的比特数大于该图像的信息熵, 则图像中存在咒余, 这种冗余称为信息熵冗余。
16 |
17 | - 结构冗余:是指图像中存在很强的纹理结构或自相似性。
18 |
19 | - 知识冗余: 是指在有些图像中还包含与某些先验知识有关的信息。
20 |
21 | 图像数据的这些冗余信息为图像压缩编码提供了依据。如, 利用人眼对蓝光不敏感的视觉特性, 在对彩色图像编码时, 就可以用较低的精度对蓝色分量进行编码。图像编码的目的就是充分利用图像中存在的各种呪余信息, 特别是空间几余、时间冗余以及视觉冗余, 以尽量少的比特数来表示图像。利用各种冗余信息, 压缩编码技术能够很好地解决在将模拟信号转换为数字信号后所产生的带宽需求增加的问题, 它是使数字信号走上实用化的关键技术之一, 表3-1中列出了几种常见应用的码率。
22 | $$
23 | \begin{array}{|c|c|c|c|c|c|c|c|}
24 | \hline \text { 应用场合 } & \text { 比特/像素 } & \text { 像索数/行 } & \text { 行数/帧 } & \text { 帧数/秒 } & \text { 亮色比 } & \text { 比特/秒(压缩前) } & \text { 比特/秒(压缩后) } \\
25 | \hline \text { 高清晰电视 } & 8 & 1920 & 1080 & 30 & 4: 1: 1 & 1.18 ~Gb / s & 20 \sim 25 Mb / s \\
26 | \hline \text { 普通电视 } & 8 & 720 & 480 & 30 & 4: 1: 1 & 167 Mb / s & 4 \sim 8 Mb / s \\
27 | \hline \text { 会议电视 } & 8 & 352 & 288 & 30 & 4: 1: 1 & 36.5 Mb / s & 1.5 \sim 2 Mb / s \\
28 | \hline \text { 桌上电视 } & 8 & 176 & 144 & 30 & 4: 1: 1 & 9.1 Mb / s & 128 ~Kb / s \\
29 | \hline \text { 电视电话 } & 8 & 128 & 112 & 30 & 4: 1: 1 & 5.2 Mb / s & 56 ~Kb / s \\
30 | \hline
31 | \end{array}
32 | $$
33 | 表3-1 几种常见应用的码率
34 |
35 | ## 3.1.2 图像编码的方法
36 |
37 | 根据编码过程中是否存在信息损耗可将图像编码分为有损压缩和无损压缩。
38 |
39 | - 无损压缩: 无信息损失, 解压缩时能够从压缩数据精确地恢复原始图像;
40 |
41 | - 有损压缩:不能精确重建原始图像, 存在一定程度的失真。
42 |
43 | 图像冗余有损压缩的原理
44 | $$
45 | \begin{array}{|l|l|l|l|l|}
46 | \hline 36 & 35 & 34 & 34 & 34 \\
47 | \hline 34 & 34 & 32 & 34 & 34 \\
48 | \hline 33 & 37 & 30 & 34 & 34 \\
49 | \hline 34 & 34 & 34 & 34 & 34 \\
50 | \hline 34 & 35 & 34 & 34 & 31 \\
51 | \hline
52 | \end{array}
53 | \Rightarrow
54 | \begin{array}{|l|l|l|l|l|}
55 | \hline 34 & 34 & 34 & 34 & 34 \\
56 | \hline 34 & 34 & 34 & 34 & 34 \\
57 | \hline 34 & 34 & 34 & 34 & 34 \\
58 | \hline 34 & 34 & 34 & 34 & 34 \\
59 | \hline 34 & 34 & 34 & 34 & 34 \\
60 | \hline
61 | \end{array}
62 | \Rightarrow
63 | \begin{array}{|l|l|}
64 | \hline 25 &34\\
65 | \hline
66 | \end{array}
67 | $$
68 | 图像冗余无损压缩的原理
69 | $$
70 | \begin{array}{|l|l|l|l|}
71 | \hline\quad & \quad&\quad &\quad\\
72 | \hline & & &\\
73 | \hline & & &\\
74 | \hline & & &\\
75 | \hline
76 | \end{array}
77 | \Rightarrow
78 | \begin{array}{|l|l|l|l|}
79 | \hline \text { RGB } & \text { RGB } & \text { RGB } & \text { RGB } \\
80 | \hline \text { RGB } & \text { RGB } & \text { RGB } & \text { RGB } \\
81 | \hline \text { RGB } & \text { RGB } & \text { RGB } & \text { RGB } \\
82 | \hline \text { RGB } & \text { RGB } & \text { RGB } & \text { RGB } \\
83 | \hline
84 | \end{array}
85 | \Rightarrow
86 | \begin{array}{|c|c|}
87 | \hline 16 & RGB \\
88 | \hline
89 | \end{array}
90 | $$
91 |
92 |
93 | - 第一代压缩编码
94 |
95 | 八十年代以前, 主要是根据传统的信源编码方法。
96 |
97 |  98 |
99 | - 第二代压缩编码
100 |
101 | 八十年代以后, 突破信源编码理论, 结合分形、 模型基、神经网络、小波变换等数学工具, 充分利用视觉系统生理心理特性和图像信源的各种特性。
102 |
103 |
98 |
99 | - 第二代压缩编码
100 |
101 | 八十年代以后, 突破信源编码理论, 结合分形、 模型基、神经网络、小波变换等数学工具, 充分利用视觉系统生理心理特性和图像信源的各种特性。
102 |
103 |  104 |
105 | 根据编码原理可以将图像编码分为熵编码、预测编码、变换编码和混合编码等。
106 |
107 | 图像压缩编码系统原理框图
108 |
109 | 
110 |
111 | (1) 熵编码。熵编码是纯粹基于信号统计特性的编码技术, 是一种无损编码。熵编码的基本原理是给出现概率较大的符号赋予一个短码字, 而给出现概率较小的符号赋予一个长码字, 从而使得最终的平均码长很小。 常见的熵编码方法有行程编码 (Run Length Encoding)、哈夫曼编码和算术编码。
112 |
113 | (2)预测编码。预测编码是基于图像数据的空间或时间冗余特性, 用相邻的已知像素(或像素块)来预测当前像素(或像素块)的取值, 然后再对预测误差进行量化和编码。预测编码可分为帧内预测和帧间预测, 常用的预测编码有差分脉码调制(Differential Pulse Code Modulation,DPCM)和运动补偿法。
114 |
115 | (3)变换编码。变换编码通常是将空间域上的图像经过正交变换映射到另一变换域上, 使变换后的系数之间的相关性降低。 图像变换本身并不能压缩数据, 但变换后图像的大部分能量只集中到少数几个变换系数上, 采用适当的量化和熵编码就可以有效地压缩图像。
116 |
117 | (4) 混合编码。混合编码是指综合了熵编码、变换编码或预测编码的编码方法, 如JPEG标准和MPEG标准。
118 |
119 | 根据对压缩编码后的图像进行重建的准确程度, 可将常用的图像编码方法分为三类:
120 |
121 | (1)信息保持编码: 也称无失真编码, 它要求在编解码过程中保证图像信息不丢失, 从而可以完整地重建图像。信息保持编码的压缩比较低, 一般不超过3: 1, 主要应用在图像的数字存储方面, 常用于医学图像编码中。
122 |
123 | (2)保真度编码: 主要利用人眼的视觉特性, 在允许的失真 (Lossy) 条件下或一定的保真度准则下, 最大限度地压缩图像。保真度编码可以实现较大的压缩比, 主要用于数字电视技术、静止图像通信、娱乐等方面。对于这些图像,过高的空间分辨率和过多的灰度层次, 不仅增加了数据量, 而且人眼也接收不到。因此在编码过程中, 可以丢掉一些人眼不敏感的信息, 在保证一定的视觉效果条件下提高压缩比。
124 |
125 | (3) 特征提取: 在图像识别、分析和分类等技术中, 往往并不需要全部图像信息, 而只要对感兴趣的部分特征信息进行编码即可压缩数据。例如, 对遥感图像进行农作物分类时,就只需对用于区别农作物与非农作物, 以及农作物类别之间的特征进行编码, 而可以忽略道路、河流、建筑物等其他背景信息。
126 |
127 | ## 3.1.3 图像编码新技术
128 |
129 | 图像编码已经发展了几十年, 人们不断提出新的压缩方法。如, 利用人工神经网络 (Artificial Neural Network, ANN) 的压缩编码、分形编码(Fractal Coding)、小波编码(Wavelet Coding)、基于对象的压缩编码(Object Based Coding)和基于模型的压缩编码(Model Based Coding)等等。
130 |
131 | 1)分形编码
132 |
133 | 分形编码是在波兰美籍数学家B.B.Mandelbrot建立的分形几何理论的基础上发展起来的一种编码方法。分形编码最大限度地利用了图像在空间域上的自相似性(即局部与整体之间存在某种相似性),通过消除图像的几何几穴余来压缩数据。 M.Barnsley将迭代函数系统 (Iterate Function System,IFS) 用于描述图像的自相似性, 并将其用于图像编码, 对某些特定图像获得了10 000: 1的压缩比。分形编码过程十分复杂, 而解码过程却很简单, 故通常用于对图像编码一次, 而需译码多次的信息传播应用中。
134 |
135 | 2)小波编码
136 |
137 | 1989年, S.G.Mallat首次将小波变换用于图像编码。经过小波变换后的图像, 具有良好的空间方向选择性, 而且是多分辨率的, 能够保持原图像在各种分辨率下的精细结构, 与人的视觉特性十分吻合。
138 |
139 | 3)模型编码
140 |
141 | 模型编码是近几年发展起来的一种很有前途的低比特率编码方法, 其基本出发点是在编、解码两端分别建立起相同的模型,编码时利用先验模型抽取图像中的主要信息并用模型参数的形式表示,解码时则利用所接收的模型参数重建图像。
142 |
143 | ## 4.1.4 图像编码评价
144 |
145 | 随着众多图像压缩算法的出现, 如何评价图像压缩算法就成为重要的课题。一般说来, 评价图像压缩算法的优劣主要有以下4个参数。
146 |
147 | 1)算法的编码效率
148 |
149 | 算法的编码效率通常有几种表现形式: 平均码字长度(R), 图像的压缩比 (rate, $r$ ), 每秒钟所需的传输比特数 (bits per second, bps), 图像熵与平均码长之比 $(\eta)$, 这些表现形式很容易相互转换。下面给出与图像编码效率有关的几个定义。 设一幅灰度级为 $N$ 的图像, 图像中第 $k$ 级灰度出现的概率为 $P_{k}$,
150 |
151 | 图像大小为 $N_{x} \times N_{y}$, 每个像素用 $d$ 比特表示, 每两帧图像间隔 $\Delta t$, 则按信息论中信息熵的定义, 数字图像的熵 $H$ 由下式定义:
152 |
153 | $$
154 | H=-\sum_{k=1}^{N} P_{k} 1 b P_{k}\tag{3-1}
155 | $$
156 |
157 | 由此可见, 图像熵 $H$ 表示各灰度级比特数的统计平均值。
158 |
159 | 对于一种图像编码方法, 设第 $k$ 级灰度的码字长度为 $B_{k}$, 则该图像的平均码字长度 $R$ 为
160 |
161 | $$
162 | R=\sum_{k=1}^{N} B_{k} P_{k}\tag{3-2}
163 | $$
164 |
165 | 于是,可定义编码效率 $\eta$ 为
166 |
167 | $$
168 | \eta=\frac{H}{R} \times 100 \%\tag{3-3}
169 | $$
170 |
171 | 每秒钟所需的传输比特数bps为
172 |
173 | $$
174 | b p s=\frac{N_{x} N_{y} R}{\Delta t}\tag{3-4}
175 | $$
176 |
177 | 压缩比 $r$ 为
178 | $$
179 | r=\frac{d}{R}\tag{3-5}
180 | $$
181 | 由于同一压缩算法对不同图像的编码效率会有所不同, 因此常需定义一些 “标准图像”,如国际上流行的三幅图像Lena、Barbara和Mandrill。一般通过测量不同压缩算法对同一组 “标准图像”的编码性能来评价各图像压缩算法的编码效率。
182 |
183 | 2)编码图像的质量
184 |
185 | 图像质量评价可分为客观质量评价和主观质量评价。最常用
186 |
187 | 的客观质量评价指标是均方误差 (MSE) 和峰值信噪比
188 |
189 | (PSNR),其定义如下:
190 |
191 | $$
192 | M S E=\frac{1}{N_{x} N_{y}} \sum_{i=0}^{N_{x}} \sum_{j=0}^{N_{y}}[f(i, j)-\hat{f}(i, j)]^{2} \tag{3-6}
193 | $$
194 |
195 | $$
196 | P S N R=10 \lg \left(\frac{255 \times 255}{M S E}\right)\tag{3-7}
197 | $$
198 |
199 | 主观质量评价是指由一批观察者对编码图像进行观察并打分, 然后综合所有人的评判结果, 给出图像的质量评价。客观质量评价能够快速有效地评价编码图像的质量, 但符合客观质量评价指标的图像不一定具有较好的主观质量。主观质量评价能够与人的视觉效果相匹配, 但其评判过程缓慢费时。
200 |
201 | 3)算法的适用范围
202 |
203 | 特定的图像编码算法具有其相应的适用范围, 并不对所有图像都有效。一般说来, 大多数基于图像信息统计特性的压缩算法具有较广的适用范围, 而一些特定的编码算法的适用范围较窄, 如分形编码主要用于自相似性高的图像。
204 |
205 | 4)算法的复杂度
206 |
207 | 算法的复杂度即指完成图像压缩和解压缩所需的运算量和硬件实现该算法的难易程度。优秀的压缩算法要求有较高的压缩比, 压缩和解压缩快, 算法简单, 易于硬件实现, 还要求解压缩后的图像质量较好。选用编码方法时一定要考虑图像信源本身的统计特性、多媒体系统(硬件和软件产品)的适应能力、应用环境以及技术标准。
--------------------------------------------------------------------------------
/III/3.10 预测编码.md:
--------------------------------------------------------------------------------
1 | # 3.10预测编码
2 |
3 | 利用图象局部邻域象素的可预测性来进行圧缩.
4 | 设: $f(n, m)$ 为 $(n, m)$ 点的灰度值; $f(n-i, m-j),(i, j) \in A$, 为邻域A内某点的灰度值,则:
5 | $$
6 | \hat{f}(n, m)=L(f(n-i, m-j),(i, j) \in A,(i, j) \neq(0,0)
7 | $$
8 | L为预测值,通常取为囱口 $A$ 内象素点恢度值的线性函数.如图所示, 即由㳡去的 $f_r(n-i, m-j)$ 来预测 $f(n, m)$ :
9 |
10 | 
11 | $$
12 | \hat{f}(n, m)=L\left(f_r(n-i, m-j)\right) \quad(i, j) \in A
13 | $$
14 | 因此可以建立一种递归预测编码技术,对应的误差为:
15 | $$
16 | \begin{aligned}
17 | & e_q(n, m)=f(n, m)-\hat{f}(n, m) \\
18 | & f(n, m)=L\left(f_r(n-i, m-j)\right)+e_q(n, m)
19 | \end{aligned}
20 | $$
21 | 即 $\mathbf{f}(\mathbf{n}, \mathbf{m})$ 由 $\mathbf{e}(\mathbf{n}, \mathbf{m})$ 代替, 如果预测 $\hat{f}(n, m)$ 效果好, 则误差项的动态范围很小, 可以有较小的码字来编码,这样便得到显著的压缩效果.
22 |
23 | 为了重建图象,需要传输预测系数和误差编码,这种编码方式称为预测脉冲编码调制(DPCM),如图:
24 |
25 | 
26 |
27 | 假设图象的某一行 $f(n, m)(f(n, m)$ 记为 $f(m))$ 可用一平稳自相关AR过程表示:
28 | $$
29 | f(m)=\sum_{k=1}^p a(k) f(m-k)+e(m) \quad E\left[e^2(m)\right]=\sigma^2
30 | $$
31 | 其中e $(m)$ 为一个与 $f(m)$ 不相关的高斯白噪声, 则预测器:
32 | $$
33 | \hat{f}(m)=\sum_{k=1}^P a(k) \hat{f}_r(m-k)
34 | $$
35 | 预测器系数构成一向量 $a=(a(1), a(2) \ldots, a(P))^{\top}, \quad$ 预测窗口A内重建象素 $\left\{f_r(m-1), \ldots, f_r(m-P)\right.$, 量化误差:
36 | $$
37 | e_q(m)=Q(e(m))=Q[f(m)-\hat{f}(m)]
38 | $$
39 | 重建图象行: $f_r(m)=\sum_{k=1}^p a(k) f_r(m-k)+e_q(m)$
40 |
41 | 预测系数通过下式求解
42 | $$
43 | \left[\begin{array}{cccc}
44 | R(0) & R(1) & \cdots & R(P-1) \\
45 | R(1) & R(2) & \cdots & R(P-2) \\
46 | \vdots & \vdots & \vdots & \vdots \\
47 | R(P-1) & R(P-2) & \cdots & R(0)
48 | \end{array}\right]\left[\begin{array}{c}
49 | a(1) \\
50 | a(2) \\
51 | \vdots \\
52 | a(P)
53 | \end{array}\right]=\left[\begin{array}{c}
54 | R(1) \\
55 | R(2) \\
56 | \vdots \\
57 | R(P)
58 | \end{array}\right]
59 | $$
60 |
61 | ## 预测编码(最佳线性预测)
62 |
63 | 二维模型:
64 | $$
65 | \hat{f}(n, m)=\sum \sum_{(i j) \in A}^P a(i, j) \hat{f}_r(n-i, m-j)
66 | $$
67 | 通过求解E最小:
68 | $$
69 | \left.\left.E\left[\mid f(n, m)-\sum \sum_{(i, j) \in A} a(i, j) f(n-i), m-j\right)\right|^2\right]
70 | $$
71 | 得: $\left.\quad R(k, l)=\sum \sum_{(i, j) \in A} a(i, j) R(n-i), m-j\right)$
72 | 求解上式得到 $a(i, j)$, 再得到:
73 | $$
74 | e(n, m)=f(n, m)-\hat{f}(n, m)
75 | $$
76 | 接收端得: $f_r(n, m)=\sum \sum_{(i j) \in A}^P a(i, j) \hat{f}_r(n-i, m-j)+e_q(n, m)$
--------------------------------------------------------------------------------
/III/3.11 JPEG编码.md:
--------------------------------------------------------------------------------
1 | # 3.11 JPEG 编码
2 |
3 | ## 3.11 JPEG基本系统编码
4 |
5 | JPEG是面向静态图像编码的国际标准。在相同图像质量条件下, JPEG文件拥有比其他图像文件格式更高的压缩比。JPEG目前被广泛应用于多媒体和网络程序中,是现今万维网中使用最广泛的两种图像文件格式之一。JPEG是一种有损压缩, 即在压缩过程中会丢失数据,每次编辑JPEG图像后,图像就会被重复压缩一次, 损失就会有所增加。
6 |
7 | JPEG允许四种编码模式:
8 | (1) 顺序式(Sequential)DCT方式:从左到右、从上到下对图像顺序进行基于离散余弦变换(DCT)的编码。DCT理论上是可逆的,但在计算时存在误差,因而基于DCT的编码模式是一种有损编码。
9 |
10 | (2) 渐进式(Progressive)DCT方式:基于DCT,对图像分层次进行处理,从模糊到清晰地传输图像(与GIF文件的交错方式类似)。有两种实现方法,一种是频谱选择法,即按Z形扫描的序号将DCT量化序数分成几个频段,每个频段对应一次扫描, 每块均先传送低频扫描数据,得到原图概貌,再依次传送高频扫描数据,使图像逐渐清晰;另一种是逐次逼近法,即每次扫描全部DCT量化序数,但每次的表示精度逐渐提高。
11 | (3) 无失真(Lossless)方式: 使用线性预测器,如DPCM, 而不是基于DCT。
12 |
13 | (4) 分层(Hierarchical)方式: 在空间域将源图像以不同的分辨率表示,每个分辨率对应一次扫描, 处理时可以基于DCT或预测编码,可以是渐进式,也可以是顺序式。
14 | JPEG定义了三种系统:基本系统(Baseline System)、扩展系统(Extended System)和无失真压缩系统(Lossless System)。一个符合JPEG标准的编解码器至少要满足基本系统的技术指标。
15 | 基本的JPEG算法属于变换类编码,下面针对基于DCT的顺序式基本系统编码来说明JPEG的编码方法。
16 |
17 | 
18 |
19 | 图3-3 JPEG 编码流程图
20 |
21 | 1) 数据分块
22 | 对图像进行编码前, 将每个分量图像分割成不重叠的 $8 \times 8$ 像素块, 每一个 $8 \times 8$ 像素块称为一个数据单元 (DU)。在彩色图像中, JPEG分别压缩图像的每个彩色分量。虽然JPEG可以压缩通常的红绿蓝分量, 但在 $Y_{b} C_{r}$ 空间的压缩效果会更好。 这是因为人眼对色彩的变化不如对亮度的变化敏感, 因而对色彩的编码可以比对亮度的编码粗糙些, 这主要体现在不同的采样频率和量化精度上。因此, 编码前一般先将图像从RGB空间转换到 $YC_{b} C_{i}$ 空间,再把各分量图像分割成 $8 \times 8$ 数据块。
23 |
24 | 在对图像采样时, 可以采用不同的采样频率, 这种技术称为二次采样。由于亮度比色彩更重要, 因而对 $Y$ 分量的采样频率可高于对 $C_{b} 、 C_{r}$ 的采样频率, 这样有利于节省存储空间。常用的采样方案有YUV422和YUV411。把采样频率最低的分量图像中一个DU所对应的像区上覆盖的所有各分量上的DU按顺序编组为一个最小编码单元 (MCU)。对灰度图像而言, 只有一个Y分量, MCU就是一个数据单元。而对彩色图像而言, 以 4:1:1的采样方案为例, 则一个MCU由4个 4 分量的DU、 1 个 $C_{b}$ 分量的DU和1个 $C_{r}$ 分量的DU组成。
25 |
26 | 2) DCT处理
27 | 图像数据块分割后, 即以 MCU为单位顺序将DU进行二维离散余弦变换。对以无符号数表示的具有 $P$ 位精度的输入数据, 在DCT前要减去 $2^{P-1}$, 转换成有符号数, 而在IDCT后, 应加上 $2^{P-1}$, 转换成无符号数。对每个 $8 \times 8$ 的数据块 $DU$ 进行 $DCT$ 后, 得到的64个系数代表了该图像块的频率成分,其中低频分量集中在左上角, 高频分量分布在右下角。系数矩阵左上角的叫做直流(DC)系数,它代表了该数据块的平均值, 其余 63 个叫交流(AC)系数。
28 |
29 | 3) 系数量化
30 | 在DCT处理中得到的64个系数中,低频分量包含了图像亮度等主要信息。在从空间域到频域的变换中,图像中的缓慢变化比快速变化更易引起人眼的注意, 所以在重建图像时,低频分量的重要性高于高频分量。因而在编码时可以忽略高频分量, 从而达到压缩的目的,这也是量化的根据和目的。
31 |
32 | 在JPEG标准中,用具有64个独立元素的量化表来规定DCT域中相应的64个系数的量化精度,使得对某个系数的具体量化阶取决于人眼对该频率分量的视觉敏感程度。理论上,对不同的空间分辨率、数据精度等情况,应该有不同的量化表。不过,一般采用图3-4和图3-5所示的量化表,可取得较好的视觉效果。之所以用两张量化表,是因为Y分量比Cb和Cr更重要些,因而对Y采用细量化,而对Cb和Cr采用粗量化。量化就是用DCT变换后的系数除以量化表中相对应的量化阶后四舍五入取整。由于量化表中左上角的值较小,而右下角的值较大, 因而起到了保持低频分量、 抑制高频分量的作用。
33 |
34 | 
35 |
36 | 图3-4 亮度量化表
37 |
38 | 
39 |
40 | 图3-5 色度量化表
41 |
42 | 4) Z形扫描
43 | DCT系数量化后,构成一个稀疏矩阵,用Z(Zigzag)形扫描将其变成一维数列,将有利于熵编码。Z形扫描的顺序如图3-6所示。
44 |
45 | 
46 |
47 | 图3-6 DCT系数的Z形扫描顺序
48 |
49 | 5) DC系数编码
50 |
51 | DC系数反映了一个8×8数据块的平均亮度,一般与相邻块有较大的相关性。JPEG对DC系数作差分编码,即用前一数据块的同一分量的DC系数作为当前块的预测值,再对当前块的实际值与预测值的差值作哈夫曼编码。
52 |
53 | 若DC系数的动态范围为-1024~+1024,则差值的动态范围为-2047~+2047。如果为每个差值赋予一个码字, 则码表过于庞大。因此,JPEG对码表进行了简化,采用“前缀码(SSSS)+尾码”来表示。前缀码指明了尾码的有效位数B, 可以根据DIFF从表3-8中查出前缀码对应的哈夫曼编码。尾码的取值取决于DC系数的差值和前缀码。如果DC系数的差值DIFF大于等于0,则尾码的码字为DIFF的B位原码;否则,取DIFF的B位反码。
54 |
55 | 表3-8 图像分量为8位时DC系数差值的典型哈夫曼编码表
56 |
57 | 
58 |
59 | 6) AC系数编码
60 | 经Z形排列后的AC系数,更有可能出现连续0组成的字符串, 从而对其进行行程编码将有利于压缩数据。JPEG将一个非零DC系数及其前面的0行程长度(连续0的个数)的组合称为一个事件。将每个事件编码表示为“NNNN/SSSS+尾码”, 其中, NNNN为0行程的长度,SSSS表示尾码的有效位数B(即当前非0系数所占的比特数),如果非零AC系数大于等于0, 则尾码的码字为该系数的B位原码, 否则, 取该系数的B位反码。
61 | 由于只用4位表示0行程的长度,故在JPEG编码中,最大0行程只能等于15。当0行程长度大于16时,需要将其分开多次编码, 即对前面的每16个0以“F/0”表示,对剩余的继续编码。
62 |
63 | 表3-9 AC系数的尾码位数表
64 |
65 | | SSSS | AC系数的尾码位数表 |
66 | | ---- | -------------------- |
67 | | 0 | 0 |
68 | | 1 | -1,1 |
69 | | 2 | -3, -2, 2, 3 |
70 | | 3 | -7~-4, 4~7 |
71 | | 4 | -15~-8, 8~15 |
72 | | 5 | -31~-16, 16~31 |
73 | | 6 | -63~-17, 17~63 |
74 | | 7 | -127~-64, 64~127 |
75 | | 8 | -255~-128, 128~255 |
76 | | 9 | -511~256, 256~511 |
77 | | 10 | -1023~-512, 512~1023 |
78 |
79 | 表3-10 亮度AC系数码表
80 |
81 | 
82 |
83 | 
84 |
85 | 
86 |
87 | 表3-11 色差AC系数编码
88 |
89 | 
90 |
91 | 
92 |
93 | 
94 |
95 | 3.11.2 JPEG编码实例
96 | 下面结合一个实例来讲述JPEG基本系统的编码过程。设有一图像亮度数据块如图3-7所示,对其进行离散余弦变换后, 用图3-4所示的亮度量化表对系数矩阵量化后的结果如图3-8所示。对量化结果按图3-6所示的顺序进行Z形扫描, 并对扫描结果的DC及AC系数进行编码的结果见表3-12。由于数据较多, 为简便起见, 这里只对几个系数的编码加以说明。
97 |
98 | 
99 |
100 | 图3-7 源图像亮度数据块
101 |
102 | 
103 |
104 | 图3-8 量化结果
105 |
106 | 表3-12 Zigzag排列及行程编码与哈夫曼编码(VLC)结果
107 |
108 | 
109 |
110 | 表3-12 Zigzag排列及行程编码与哈夫曼编码(VLC)结果
111 |
112 | 
113 |
114 | 1) DC系数的编码
115 | 在量化系数矩阵的Z形扫描结果中,第一个系数为DC系数。假设前一亮度数据块的DC系数为40, 则差值DIFF=44-40=4, 因4在(-7~-4, 4~7)范围内, 由表3-8查得SSSS=3,其前缀码字为“100”, 3位尾码即为4的二进制原码“100”, 从而DC系数的编码为“100100”。如果前一数据块的DC系数为48, 则DIFF=-4, 由表10-8查得SSSS及前缀码字同上,其3位尾码即-4的反码“011”, 因此DC系数的编码为“100011”。解码时, 由前缀码“100”可知尾码有3位,若前缀码字是“100”, 因其最高位为1,故可得DC系数的差值为4; 若前缀码字为“011”,因最高位为0,知其为负, 故取反后可得差值为-4。
116 |
117 | 2) AC系数的编码
118 | 在Z形扫描结果中,第一个非零AC系数为10。在它前面的连零个数为1, 即NNNN=1。根据AC系数10从表3-9查得SSSS=4, 由NNNN/SSSS=1/4从表3-10查得其哈夫曼码字为“111110110”, 而10的二进制码为“1010”, 因此该AC系数的编码为“1111101101010”。由于篇幅所限,其他AC系数的编码就不再赘述, 结果见表10-12。在Z形扫描结果中的末尾,除第54个系数非零外, 其他系数全为零, 故直接用一个结束块“EOB(0/0)”结束本块,由表3-10查得其码字为“1010”。于是,最后该亮度块的编码为(其中,假定差值为4)100100111110110101001100111110000101010001001101100100010011101010000110001010000110001111000000000001000111000110001100100000111001001001111001000001111001111101111010,共用了168位,而原始图像块需8×8×8=512位,因此压缩比为3.048。
119 |
120 | JPEG压缩编码示例
121 |
122 | 
--------------------------------------------------------------------------------
/III/3.12 编程实例.md:
--------------------------------------------------------------------------------
1 | # 3.12 编程实例
2 |
3 | 实现哈夫曼编码的过程实际是构造一个哈夫曼二叉树, 它可分为两大部分:构造哈夫曼树和在哈夫曼树上求叶节点的编码。在构造哈夫曼树时,可设置一个结构数组HuffmanNode保存哈夫曼树中各节点的信息。结构数组元素定义如下:
4 |
5 | ```c++
6 | typedef struct
7 | {
8 | int Weight; //保存哈夫曼树节点的权值, 在此是指频数
9 | int Flag; //当Flag=0时, 表示该节点未加入树中, 为1时表示已加入树中
10 | int Parent; //存放节点的父节点在节点数组中的序号
11 | int LChild; //存放节点的左子节点在节点数组中的序号
12 | int RChild; //存放节点的右子节点在节点数组中的序号
13 | } HuffmanNode;
14 |
15 | ```
16 |
17 | 对于一幅BMP图像,调用CpointPro类下的GetHistogram()成员函数可获得图像的直方图数据m_fFreq,这些数据即各灰度出现的频数。利用这些数据可直接进行哈夫曼编码。哈夫曼编码的代码如下:
18 |
19 | ```C++
20 | void CDlgHuffman::Huffman()
21 | {
22 | CString str;
23 | int i, j, x1, x2, c, p;
24 | int m1, m2;
25 | LV_ITEM lvitem; // ListCtrl的ITEM
26 | int iActualItem; //中间变量, 用于保存ListCtrl中添加的ITEM编号
27 | HuffmanNode *huffNode; //存放哈夫曼树的节点
28 | CString *strCode; //指向各字符的哈夫曼编码的指针
29 | int *iMap; //位置映射指针
30 | int iNumNode = 0; //频数不为零的节点数(或灰度数)
31 | //统计直方图数据中频数不为零的灰度数, 并只对不为零的节点编码
32 | for(i = 0; i < m_iLeafNum; i++)
33 | {
34 | if (m_fFreq[i + m_ChannelSel * m_iLeafNum] != 0)
35 | iNumNode++;
36 | }
37 | //对于具有iNumNode个叶节点的哈夫曼树, 它具有2 iNumNode -1个节点
38 | huffNode = new HuffmanNode[iNumNode * 2 - 1];
39 | strCode = new CString[iNumNode]
40 | iMap = new int[iNumNode];
41 | //初始化huffNode中的各节点
42 | for(i = 0; i < iNumNode * 2 - 1; i++)
43 | {
44 | huffNode[i].Weight = 0;
45 | huffNode[i].Parent = 0;
46 | huffNode[i].Flag = 0;
47 | huffNode[i].LChild = -1;
48 | huffNode[i].RChild = -1;
49 | }
50 | //输入iNumNode个叶节点的权值即频数, iMap存放的是频数不为零的灰度值
51 | j = 0;
52 |
53 | for(i = 0; i < m_iLeafNum; i++)
54 | {
55 | if (m_fFreq[i + m_ChannelSel * m_iLeafNum] != 0)
56 | {
57 | huffNode[j].Weight = m_fFreq[i + m_ChannelSel * m_iLeafNum];
58 | iMap[j] = i;
59 | j++;
60 | }
61 | }
62 | //构造哈夫曼树, 对iNumNode个叶节点, 需构造iNumNode-1次
63 | for(i = 0; i < iNumNode - 1; i++)
64 | {
65 | //对Flag为0的节点比较排序, 选出两个权值最小的子树, x1和x2用于确定
66 | //两子树在数组中的序号, m1和m2用于存放最小两子树的权值
67 | m1 = m2 = m_iSizeImage;
68 | x1 = x2 = 0;
69 | for (j = 0; j < iNumNode + i; j++)
70 | {
71 | if (huffNode[j].Weight < m1 && huffNode[j].Flag = = 0)
72 | {
73 | m2 = m1;
74 | x2 = x1;
75 | m1 = huffNode[j].Weight;
76 | x1 = j;
77 | }
78 | else if (huffNode[j].Weight < m2 && huffNode[j].Flag = = 0)
79 | {
80 | m2 = huffNode[j].Weight;
81 | x2 = j;
82 | }
83 | }
84 | //将找出的两棵最小子树合并为一棵子树
85 | huffNode[x1].Parent = iNumNode + i;
86 | huffNode[x2].Parent = iNumNode + i;
87 | // Flag为1, 说明该节点已经成为其他节点的子节点
88 | huffNode[x1].Flag = 1;
89 | huffNode[x2].Flag = 1;
90 | huffNode[iNumNode + i].Weight = huffNode[x1].Weight + huffNode[x2].Weight;
91 | //权值较小的子树作为右子树
92 | huffNode[iNumNode + i].LChild = x2;
93 | huffNode[iNumNode + i].RChild = x1;
94 | }
95 | //求每个叶节点的哈夫曼编码
96 | for(i = 0; i < iNumNode; i++)
97 | {
98 | c = i;
99 | p = huffNode[c].Parent;
100 | //由叶节点上溯到树根
101 | while (p != 0)
102 | {
103 | //如果是左子树, 则代码的高一位添加0, 否则添加1
104 | if (huffNode[p].LChild = = c)
105 | strCode[i] = "0" + strCode[i];
106 | else
107 | strCode[i] = "1" + strCode[i];
108 | c = p;
109 | p = huffNode[c].Parent;
110 | }
111 | }
112 | //计算平均码字长度和图像熵
113 | int CodeLen = 0;
114 | m_fEntropy = 0.0;
115 | for(i = 0; i < iNumNode; i ++
116 | {
117 | CodeLen += huffNode[i].Weight * strCode[i].GetLength();
118 | m_fEntropy -= ((double)huffNode[i].Weight / m_iSizeImage) *
119 | log((double)huffNode[i].Weight / m_iSizeImage) / log(2.0);
120 | }
121 | //计算平均码字长度
122 | m_fAvCodeLen = (double)CodeLen/m_iSizeImage;
123 | // 计算编码效率
124 | m_fCodeEfficiency = m_fEntropy / m_fAvCodeLen;
125 | //更新对话框上的文本框中的内容
126 | UpdateData(FALSE);
127 | lvitem.mask = LVIF_TEXT;
128 | //输出哈夫曼编码结果
129 | for (i = 0; i < iNumNode; i ++)
130 | {
131 | if (huffNode[i].Weight > 0)
132 | {
133 | // 添加一项
134 | lvitem.iItem = m_lstTable.GetItemCount();
135 | str.Format("%u", iMap[i]);
136 | lvitem.iSubItem = 0;
137 | lvitem.pszText = (LPTSTR)(LPCTSTR)str;
138 | iActualItem = m_lstTable.InsertItem(&lvitem);
139 | // 添加其他列
140 | lvitem.iItem = iActualItem;
141 | // 添加灰度值出现的频率
142 | lvitem.iSubItem = 1;
143 | str.Format("%f", (float)huffNode[i].Weight / m_iSizeImage);
144 | lvitem.pszText = (LPTSTR)(LPCTSTR)str;
145 | m_lstTable.SetItem(&lvitem);
146 | // 添加哈夫曼编码
147 | lvitem.iSubItem = 2;
148 | lvitem.pszText = (LPTSTR)(LPCTSTR)strCode[i];
149 | m_lstTable.SetItem(&lvitem);
150 | // 添加码字长度
151 | lvitem.iSubItem = 3;
152 | str.Format("%u", strCode[i].GetLength());
153 | lvitem.pszText = (LPTSTR)(LPCTSTR)str;
154 | m_lstTable.SetItem(&lvitem);
155 | }
156 | }
157 | delete[] huffNode;
158 | delete[] strCode;
159 | delete[] iMap;
160 | }
161 | ```
162 |
163 |
--------------------------------------------------------------------------------
/III/3.2 Huffman编码.md:
--------------------------------------------------------------------------------
1 | # 3.2 Huffman 编码(熵编码)
2 |
3 | 图象熵:
4 | 图像灰度集合为 $\left(x_1, x_2, \ldots, x_{M}\right)$, , 对应的概率 $P_1$, $P_2, \ldots, \mathbf{P}_{M}$
5 | 则图象熵: $\quad H=-\sum_{k=1}^M P_k \log P_k$
6 | 平均码长:
7 | 设 $\beta_{k}$ 为图像第 $k$ 个码长 $C_{k}$ 的长度, 对应的概率为 $P_{k}$, 则该图象所赋予的码长的平均长度为:
8 | $$
9 | R=\sum_{k=1}^M \beta_k P_k
10 | $$
11 | 编码效率
12 | $$
13 | \eta=\frac{H}{R}
14 | $$
15 | 变长最佳编码定理
16 | 在变长编码中, 对图像中出现频度大的像素值赋予短码字, 对出现频度小的像数值赋予长码字。 如果严格按照所对应符号出现概率大小逆序排列, 则编码结果平均码长一定小于任何其它排列方式。
17 | Huffman 编码
18 | 根据变长最佳编码定理, 应用Huffman算法的一种编码方法。
19 |
20 | 举例:
21 | $$
22 | \frac{\text { aaaa }}{4} \frac{bbb}{3} \frac{cc}{2} \frac{d}{1} \frac{\text { eeeee }}{5} \frac{\text { fffffff }}{7} \text { (共22*8=176 bits) }
23 | $$
24 | 编码: $f=0 \quad e=10 \quad a=110 \quad ~b=1111 \quad c=11100 \quad ~d=11101$
25 |
26 | 11011011011011111111111111100111001110110101010100000000
27 | (共 $7 * 1+5 * 2+4 * 3+3 * 4+2 * 5+1 * 5=56$ bits)
28 |
29 | Huffman 编码步骤:
30 | 1、先将图象灰度级按出现的概率由大到小顺序排列;
31 | 2、将最小两个概率相加, 形成一个新的概率集合, 再按第 (1) 步方法重排, 如此重复进行直到只有两个概率为止;
32 | 3、分配码长。码长分配从最后一步开始反向进行, 对最后两个概率一个赋予“0”, 一个赋予“1”
33 |
34 | 
35 |
36 | 整理:
37 |
38 | 
39 |
40 | f=01 e=11 a=10 b=001 c=0001 d=0000
41 | $$
42 | \frac{\text { aaaa }}{4} \frac{bbb}{3} \frac{cc}{2} \frac{d}{1} \frac{\text { eeeee }}{5} \frac{\text { fffffff }}{7} \text { (共22*8=176 bits) }
43 | $$
44 | 经过Huffman编码之后的数据为:
45 |
46 | 1010101010001001001000100010000111111111101010101010101
47 |
48 | (共 $7 * 2+5 * 2+4 * 2+3 * 3+2 * 4+1 * 4=53$ bits)
49 | 比前面我们给出的编码得到的56bits的数据量还小
50 |
51 | Huffman编码在图像压缩中的实现
52 | 我们知道, 对一幅图像进行编码时, 如果图像的大小大于 256 时, 这幅图像的不同的码字就有可能是很大, 例如极限为 256 个不同的码字。
53 | 对整幅图直接进行Huffman编码时, 小分布的灰度值, 就有可能具有很长的编码。
54 | 如: 100位以上, 这样不但达不到压缩的效果反而会使数据量加大, 应该如何处理?
55 |
56 | 常用的且有效的方法是:
57 | 将图像分割成若干的小块, 对每块进行独立的Huffman编码。例如: 分成$8\times 8$的子块, 就可以大大降低不同灰度值的个数(最多是64而不是256)。
--------------------------------------------------------------------------------
/III/3.3 香农-范诺编码.md:
--------------------------------------------------------------------------------
1 | # 3.3 香农-范诺编码
2 |
3 | 香农-范诺 (Shannon-Fannon) 编码也是一种常见的可变字长编码。与哈夫曼编码相似, 当信源符号出现的概率正好为 $2^{-i}$ $(i<0)$ 时, 采用香农-范诺编码同样能够达到 $100 \%$ 的编码效率。 香农-范诺编码的理论基础是符号的码字长度 $N_i$ 完全由该符号出现的概率来决定, 即
4 | $$
5 | -\log _D P_i \leq N_i \leq-\log _D P_i+1\tag{3-8}
6 | $$
7 | 式中,D为编码所用的数制。
8 |
9 | 香农-范诺编码的步骤如下:
10 | (1)将信源符号按其出现概率从大到小排序;
11 | (2)按照式 (3-8) 计算出各概率对应的码字长度 $N_i$;
12 | (3)计算累加概率 $A_i$, 即
13 | $$
14 | A_i=A_{i-1}+P_{i-1} \quad i=1,2, \ldots, N-1 ; \quad A_0=0\tag{3-9}
15 | $$
16 | (4) 把各个累加概率 $A_i$ 由十进制转化为二进制, 取该二进制数的前 $N_i$ 位作为对应信源符号的码字。
17 |
18 | 为便于比较, 仍以例4-1中图像为对象, 对其进行香农-范诺编码, 结果如表3-3所示。由于在此采用二进制对码字赋值, 故在利用式 (3-9) 计算码字长度 $N_i$ 时, $D$ 取为 2 。以符号 $S_4$ 为例, 其出现概率为 0.07 , 按照式 (3-9) 计算得到它的码字长度应为 4 , 按式 (3-10) 计算得到它的累加概率 $A_4$ 为 0.78 , 将 0.78 转化为二进制并取其前 4 位即得符号 $S_4$ 的码字为 1100 (省去了 “0.”, 有的浮点数不能完全转化, 转化时只需完成前 $N_i$ 位即可)。
19 |
20 | 表3-3 香农-范诺编码
21 |
22 | $$
23 | 平均码长 R=3.17 \quad图像熵 H=2.55 \quad \text { 编㐷效率 } \eta=80.4 \%\\
24 | \begin{array}{|c|c|c|c|c|c|}
25 | \hline \text { 信源符号 } & \text { 出现概率 } P_i & \text { 码字长度 } N_i & \text { 蔂加概率 } A_i & \text { 转换为二进制 } & \text { 分配码字 } B_i \\
26 | \hline S_0 & 0.40 & 2 & 0 & 0 & 00 \\
27 | \hline S_1 & 0.18 & 3 & 0.40 & 01100 & 011 \\
28 | \hline S_2 & 0.10 & 4 & 0.58 & 10010 & 1001 \\
29 | \hline S_3 & 0.10 & 4 & 0.68 & 10100 & 1010 \\
30 | \hline S_4 & 0.07 & 4 & 0.78 & 11000 & 1100 \\
31 | \hline S_5 & 0.06 & 5 & 0.85 & 1101100 & 11011 \\
32 | \hline S_6 & 0.05 & 5 & 0.91 & 1110100 & 11101 \\
33 | \hline S_7 & 0.04 & 5 & 0.96 & 1111010 & 11110 \\
34 | \hline
35 | \end{array}\\
36 |
37 |
38 |
39 | $$
40 | 除此之外, 还有二分法香农-范诺编码方法。其步骤如下:
41 | (1) 首先统计出每个符号出现的概率;
42 | (2) 从左到右对上述概率从大到小排序;
43 | (3) 从这个概率集合中的某个位置将其分为两个子集合,并尽量使两个子集合的概率和近似相等,给前面一个子集合赋值为0, 后面一个子集合赋值为1;
44 | (4) 重复步骤3,直到各个子集合中只有一个元素为止;
45 | (5) 将每个元素所属的子集合的值依次串起来,即可得到各个元素的香农-范诺编码。
46 |
47 | 表3-4 二分法香农-范诺编码
48 |
49 | 
--------------------------------------------------------------------------------
/III/3.4 行程编码.md:
--------------------------------------------------------------------------------
1 | # 3.4 行程编码
2 |
3 | ## 3.4.1 行程编码基本方法
4 |
5 | 行程编码又称行程长度编码(Run Length Encoding, RLE), 是一种熵编码,其编码原理相当简单,即将具有相同值的连续串用其串长和一个代表值来代替, 该连续串就称为行程,串长称为行程长度。例如,有一字符串“aabbbcddddd”, 则经行程长度编码后, 该字符串可以只用“2a3b1c5d”来表示。
6 | 行程编码分为定长和不定长编码两种。定长编码是指编码的行程长度所用的二进制位数固定,而变长行程编码是指对不同范围的行程长度使用不同位数的二进制位数进行编码。使用变长行程编码需要增加标志位来表明所使用的二进制位数。
7 |
8 | 行程编码比较适合于二值图像的编码,一般用于量化后出现大量零系数连续的场合,用行程来表示连零码。如果图像是由很多块颜色或灰度相同的大面积区域组成的,那么采用行程编码可以达到很高的压缩比。如果图像中的数据非常分散,则行程编码不但不能压缩数据,反而会增加图像文件的大小。为了达到较好的压缩效果,一般不单独采用行程编码, 而是和其他编码方法结合使用。例如, 在JPEG中, 就综合使用了行程编码、DCT、量化编码以及哈夫曼编码, 先对图像作分块处理, 再对这些分块图像进行离散余弦变换(DCT), 对变换后的频域数据进行量化并作Z字形扫描,接着对扫描结果作行程编码, 对行程编码后的结果再作哈夫曼编码。
9 |
10 | ## 3.4.2 PCX文件中的行程编码
11 |
12 | PCX文件分为文件头和图像压缩数据两个部分。如果是256色图像,则还有一个256色调色板存于文件尾部。文件头全长128字节,包含了图像的大小和颜色以及PCX文件的版本标识等信息,图像压缩数据紧跟在文件头之后。如果没有使用调色板, 那么图像压缩数据存储的是实际像素值;否则,存储的是调色板的索引值。当压缩数据是实际的像素值时,它们按颜色平面和扫描行存储,即每行先存储所有R分量,再存储所有G分量, 最后存储所有B分量,一行数据存储完后,接着存储下一行数据。如果使用了调色板,则不会分解为单独的颜色平面存储。读者可以查阅图像文件格式的相关书籍了解PCX文件的详细格式。下面以256色PCX文件为例, 说明PCX文件中的行程编码。
13 |
14 | 在256色PCX文件中,每个像素占一字节, 压缩数据以字节为单位逐行进行编码,每行填充到偶数字节。PCX文件规定编码时的最大行程长度为63,如果行程长度大于63,则必须分多次存储。对于长度大于1的行程,编码时先存入其行程长度(长度L加上192即0xC0),再存入该行程的代表值,行程长度和行程的代表值分别占一字节。对于长度为1的行程,即单个像素, 如果该像素的值小于或等于0xC0, 则编码时直接存入该像素值, 而不存储长度信息;否则,先存入0xC1,再存入该像素值,这样做的目的是为了避免该像素值被误认为长度信息。例如,连续100个灰度值为0x80的像素, 其编码(以十六进制表示)应为FF 80 25 80。上面的编码中出现FF的长度信息是由63与0xC0相加所得。
15 |
16 | 对256色PCX文件解码时,首先从压缩数据部分读取一个字节,判断该值是否大于0xC0,如果是,则表明该字节是行程长度信息, 取其低六位(相当于减去0xC0)作为行程长度L,读取下一个字节作为像素值并重复L次存入图像数据缓冲区;否则, 直接将该字节存入图像数据缓冲区。
17 |
18 | 虽然几乎所有的图像应用软件都支持PCX文件格式,但由于它的压缩比不高, 因而现在用得不是很多。
--------------------------------------------------------------------------------
/III/3.5 LZW编码 .md:
--------------------------------------------------------------------------------
1 | # 3.5LZW编码
2 |
3 | ## 3.5.1LZW编码方法
4 |
5 | LZW(Lempel-Ziv&Welch)编码又称字串表编码,属于一种无损编码,是Welch将Lempel和Ziv所提出的无损压缩技术改进后的压缩方法。LZW编码与行程编码类似,也是对字符串进行编码从而实现压缩,但它在编码的同时还生成了特定字符串以及与之对应的索引字符串表。
6 |
7 | LZW编码的基本思想是:在编码过程中,将所遇到的字符串建立一个字符串表,表中的每个字符串都对应一个索引,编码时用该字符串在字串表中的索引来代替原始的数据串。例如,一幅8位的灰度图像,我们可以采用12位来表示每个字符串的索引,前256个索引用于对应可能出现的256种灰度,由此可建立一个初始的字符串表,而剩余的3840个索引就可分配给在压缩过程中出现的新字符串,这样就生成了一个完整的字符串表,压缩数据就可以只保存它在字符串表中的索引,从而达到压缩数据的目的。字符串表是在压缩过程中动态生成的,不必将它保存在压缩文件里,因为解压缩时字符串表可以由压缩文件中的信息重新生成。
8 |
9 | GIF(GraphicsInterchangeFormat)最初是由美国CompuServe于1987年开发的一种压缩位图格式。它可支持多达256种的颜色,具有极佳的压缩效率,已成为Internet上一种流行的文件格式。GIF图像文件采用的是一种改良的LZW压缩算法,通常称为GIF-LZW压缩算法。GIF图像文件以块(又称为区域结构)的方式来存储图像相关的信息,具体的文件格式可参考图像文件格式的相关书籍。下面简要介绍GIF-LZW的编码方法。
10 |
11 | 设S1、S2为两个存放字符串的临时变量,LZW_CLEAR和LZW_EOI分别为字符表初始化标志和编码结束标志,GIF-LZW的编码步骤如下:
12 |
13 | (1)根据图像中使用的颜色数初始化一个字串表,字串表中的每个颜色对应一个索引。在初始字串表的末尾再添加两个符号(LZW_CLEAR和LZW_EOI)的索引。设置字符串变量S1、S2并初始化为空。
14 |
15 | (2)接着输出LZW_CLEAR在字串表中的索引。
16 |
17 | (3)从图像数据流中第一个字符(假设数据以字符串表示)开始,每次读取一个字符,将其赋给字符串变量S2。
18 |
19 | (4)判断“S1+S2”是否已存在于字串表中。如果字串表中存在“S1+S2”,则S1=S1+S2;否则,输出S1在字串表中的索引,并在字串表末尾为“S1+S2”添加索引,同时,S1=S2。
20 |
21 | (5)重复第3和第4步,直到所有字符读完为止。
22 |
23 | (6)输出S1中的字符串在字串表中的索引,然后输出结束标志LZW_EOI的索引,编码完毕。
24 |
25 | GIF-LZW的解码过程比较复杂,它和编码过程正好相反,即将编码后的码字转换成对应的字符串,重新生成字串表,然后依次输出对应的字符串即可。GIF-LZW的解码流程如图3-2所示,表中的Code和OldCode是两个存放索引的临时变量。
26 |
27 | 
28 |
29 | 图3-2GIF-LZW解码流程
30 |
31 | ## 3.5.2LZW编码实例
32 |
33 | 设有一来源于4色(以a、b、c、d表示)图像的数据流aabcabbbbd,现对其进行LZW编码。编码过程如下:
34 | 编码前,首先需要初始化一个字符串表。由于图像中只有四种颜色,因而我们可以只用4比特表示字符串表中每个字符串的索引,表中的前4项代表4种颜色,后两项分别表示初始化和图像结束标志,建立的初始化字符串表如表3-5所示。接着把S1和S2初始化为空(即NULL),输出LZW_CLEAR的在字符串表中的索引值4H,接下来是对图像数据的编码。
35 |
36 | 表3-5初始化字符串表
37 | $$
38 | \begin{array}{|c|c|}
39 | \hline \text{字符串}&\text{索引}\\
40 | \hline a&0H\\
41 | \hline b&1H\\
42 | \hline c&2H\\
43 | \hline d&3H\\
44 | \hline \text{LZW\_CLEAR}&4H\\
45 | \hline \text{LZW\_EOI}&5H\\
46 | \hline
47 | \end{array}
48 | $$
49 |
50 |
51 | 读取图像数据流的第一个字符“a”,赋给S2,因S1+S2=“a”已存在字串表中,所以S1=S1+S2=“a”。
52 | 接着读入下一个字符“a”赋给S2,因S1+S2=“aa”不存在于字串表中,所以输出S1=“a”的索引0H,同时在字符串表末尾添加新字符串“aa”的索引6H,并使S1=S2=“a”。
53 | 依次读取数据流中的每个字符,如果S1+S2没有出现在字符串表中,则输出S1中的字符串的索引,并在字符串表末尾为新字符串S1+S2添加索引,并使S1=S2;否则,不输出任何结果,只是使S1=S1+S2。所有字符处理完毕后,输出S1中的字符串的索引,最后输出结束标志LZW_EOI的索引。至此,编码完毕,完整的编码过程如表3-6所示,最后的编码结果为“4001271B35”(以十六进制表示)。
54 |
55 | 表3-6GIF-LZW编码过程
56 | $$
57 | \begin{array}{|c|c|c|c|c|}
58 | \hline \text { 输入数据 S2 } & \text { S1+S2 } & \text { 输出结果 } & \text { S1 } & \text { 生成的新字符串及索引 } \\
59 | \hline \text { NULL } & \text { NULL } & 4 H & \text { NULL } & \\
60 | \hline a & a & & a & \\
61 | \hline a & aa & 0 H & a & aa<6 H> \\
62 | \hline b & ab & 0 H & a & ab<7 H> \\
63 | \hline c & bc & 1 H & c & ca<9 H> \\
64 | \hline a & ca & 2 H & a & \\
65 | \hline b & ab & & ab & abb
104 |
105 | 根据编码原理可以将图像编码分为熵编码、预测编码、变换编码和混合编码等。
106 |
107 | 图像压缩编码系统原理框图
108 |
109 | 
110 |
111 | (1) 熵编码。熵编码是纯粹基于信号统计特性的编码技术, 是一种无损编码。熵编码的基本原理是给出现概率较大的符号赋予一个短码字, 而给出现概率较小的符号赋予一个长码字, 从而使得最终的平均码长很小。 常见的熵编码方法有行程编码 (Run Length Encoding)、哈夫曼编码和算术编码。
112 |
113 | (2)预测编码。预测编码是基于图像数据的空间或时间冗余特性, 用相邻的已知像素(或像素块)来预测当前像素(或像素块)的取值, 然后再对预测误差进行量化和编码。预测编码可分为帧内预测和帧间预测, 常用的预测编码有差分脉码调制(Differential Pulse Code Modulation,DPCM)和运动补偿法。
114 |
115 | (3)变换编码。变换编码通常是将空间域上的图像经过正交变换映射到另一变换域上, 使变换后的系数之间的相关性降低。 图像变换本身并不能压缩数据, 但变换后图像的大部分能量只集中到少数几个变换系数上, 采用适当的量化和熵编码就可以有效地压缩图像。
116 |
117 | (4) 混合编码。混合编码是指综合了熵编码、变换编码或预测编码的编码方法, 如JPEG标准和MPEG标准。
118 |
119 | 根据对压缩编码后的图像进行重建的准确程度, 可将常用的图像编码方法分为三类:
120 |
121 | (1)信息保持编码: 也称无失真编码, 它要求在编解码过程中保证图像信息不丢失, 从而可以完整地重建图像。信息保持编码的压缩比较低, 一般不超过3: 1, 主要应用在图像的数字存储方面, 常用于医学图像编码中。
122 |
123 | (2)保真度编码: 主要利用人眼的视觉特性, 在允许的失真 (Lossy) 条件下或一定的保真度准则下, 最大限度地压缩图像。保真度编码可以实现较大的压缩比, 主要用于数字电视技术、静止图像通信、娱乐等方面。对于这些图像,过高的空间分辨率和过多的灰度层次, 不仅增加了数据量, 而且人眼也接收不到。因此在编码过程中, 可以丢掉一些人眼不敏感的信息, 在保证一定的视觉效果条件下提高压缩比。
124 |
125 | (3) 特征提取: 在图像识别、分析和分类等技术中, 往往并不需要全部图像信息, 而只要对感兴趣的部分特征信息进行编码即可压缩数据。例如, 对遥感图像进行农作物分类时,就只需对用于区别农作物与非农作物, 以及农作物类别之间的特征进行编码, 而可以忽略道路、河流、建筑物等其他背景信息。
126 |
127 | ## 3.1.3 图像编码新技术
128 |
129 | 图像编码已经发展了几十年, 人们不断提出新的压缩方法。如, 利用人工神经网络 (Artificial Neural Network, ANN) 的压缩编码、分形编码(Fractal Coding)、小波编码(Wavelet Coding)、基于对象的压缩编码(Object Based Coding)和基于模型的压缩编码(Model Based Coding)等等。
130 |
131 | 1)分形编码
132 |
133 | 分形编码是在波兰美籍数学家B.B.Mandelbrot建立的分形几何理论的基础上发展起来的一种编码方法。分形编码最大限度地利用了图像在空间域上的自相似性(即局部与整体之间存在某种相似性),通过消除图像的几何几穴余来压缩数据。 M.Barnsley将迭代函数系统 (Iterate Function System,IFS) 用于描述图像的自相似性, 并将其用于图像编码, 对某些特定图像获得了10 000: 1的压缩比。分形编码过程十分复杂, 而解码过程却很简单, 故通常用于对图像编码一次, 而需译码多次的信息传播应用中。
134 |
135 | 2)小波编码
136 |
137 | 1989年, S.G.Mallat首次将小波变换用于图像编码。经过小波变换后的图像, 具有良好的空间方向选择性, 而且是多分辨率的, 能够保持原图像在各种分辨率下的精细结构, 与人的视觉特性十分吻合。
138 |
139 | 3)模型编码
140 |
141 | 模型编码是近几年发展起来的一种很有前途的低比特率编码方法, 其基本出发点是在编、解码两端分别建立起相同的模型,编码时利用先验模型抽取图像中的主要信息并用模型参数的形式表示,解码时则利用所接收的模型参数重建图像。
142 |
143 | ## 4.1.4 图像编码评价
144 |
145 | 随着众多图像压缩算法的出现, 如何评价图像压缩算法就成为重要的课题。一般说来, 评价图像压缩算法的优劣主要有以下4个参数。
146 |
147 | 1)算法的编码效率
148 |
149 | 算法的编码效率通常有几种表现形式: 平均码字长度(R), 图像的压缩比 (rate, $r$ ), 每秒钟所需的传输比特数 (bits per second, bps), 图像熵与平均码长之比 $(\eta)$, 这些表现形式很容易相互转换。下面给出与图像编码效率有关的几个定义。 设一幅灰度级为 $N$ 的图像, 图像中第 $k$ 级灰度出现的概率为 $P_{k}$,
150 |
151 | 图像大小为 $N_{x} \times N_{y}$, 每个像素用 $d$ 比特表示, 每两帧图像间隔 $\Delta t$, 则按信息论中信息熵的定义, 数字图像的熵 $H$ 由下式定义:
152 |
153 | $$
154 | H=-\sum_{k=1}^{N} P_{k} 1 b P_{k}\tag{3-1}
155 | $$
156 |
157 | 由此可见, 图像熵 $H$ 表示各灰度级比特数的统计平均值。
158 |
159 | 对于一种图像编码方法, 设第 $k$ 级灰度的码字长度为 $B_{k}$, 则该图像的平均码字长度 $R$ 为
160 |
161 | $$
162 | R=\sum_{k=1}^{N} B_{k} P_{k}\tag{3-2}
163 | $$
164 |
165 | 于是,可定义编码效率 $\eta$ 为
166 |
167 | $$
168 | \eta=\frac{H}{R} \times 100 \%\tag{3-3}
169 | $$
170 |
171 | 每秒钟所需的传输比特数bps为
172 |
173 | $$
174 | b p s=\frac{N_{x} N_{y} R}{\Delta t}\tag{3-4}
175 | $$
176 |
177 | 压缩比 $r$ 为
178 | $$
179 | r=\frac{d}{R}\tag{3-5}
180 | $$
181 | 由于同一压缩算法对不同图像的编码效率会有所不同, 因此常需定义一些 “标准图像”,如国际上流行的三幅图像Lena、Barbara和Mandrill。一般通过测量不同压缩算法对同一组 “标准图像”的编码性能来评价各图像压缩算法的编码效率。
182 |
183 | 2)编码图像的质量
184 |
185 | 图像质量评价可分为客观质量评价和主观质量评价。最常用
186 |
187 | 的客观质量评价指标是均方误差 (MSE) 和峰值信噪比
188 |
189 | (PSNR),其定义如下:
190 |
191 | $$
192 | M S E=\frac{1}{N_{x} N_{y}} \sum_{i=0}^{N_{x}} \sum_{j=0}^{N_{y}}[f(i, j)-\hat{f}(i, j)]^{2} \tag{3-6}
193 | $$
194 |
195 | $$
196 | P S N R=10 \lg \left(\frac{255 \times 255}{M S E}\right)\tag{3-7}
197 | $$
198 |
199 | 主观质量评价是指由一批观察者对编码图像进行观察并打分, 然后综合所有人的评判结果, 给出图像的质量评价。客观质量评价能够快速有效地评价编码图像的质量, 但符合客观质量评价指标的图像不一定具有较好的主观质量。主观质量评价能够与人的视觉效果相匹配, 但其评判过程缓慢费时。
200 |
201 | 3)算法的适用范围
202 |
203 | 特定的图像编码算法具有其相应的适用范围, 并不对所有图像都有效。一般说来, 大多数基于图像信息统计特性的压缩算法具有较广的适用范围, 而一些特定的编码算法的适用范围较窄, 如分形编码主要用于自相似性高的图像。
204 |
205 | 4)算法的复杂度
206 |
207 | 算法的复杂度即指完成图像压缩和解压缩所需的运算量和硬件实现该算法的难易程度。优秀的压缩算法要求有较高的压缩比, 压缩和解压缩快, 算法简单, 易于硬件实现, 还要求解压缩后的图像质量较好。选用编码方法时一定要考虑图像信源本身的统计特性、多媒体系统(硬件和软件产品)的适应能力、应用环境以及技术标准。
--------------------------------------------------------------------------------
/III/3.10 预测编码.md:
--------------------------------------------------------------------------------
1 | # 3.10预测编码
2 |
3 | 利用图象局部邻域象素的可预测性来进行圧缩.
4 | 设: $f(n, m)$ 为 $(n, m)$ 点的灰度值; $f(n-i, m-j),(i, j) \in A$, 为邻域A内某点的灰度值,则:
5 | $$
6 | \hat{f}(n, m)=L(f(n-i, m-j),(i, j) \in A,(i, j) \neq(0,0)
7 | $$
8 | L为预测值,通常取为囱口 $A$ 内象素点恢度值的线性函数.如图所示, 即由㳡去的 $f_r(n-i, m-j)$ 来预测 $f(n, m)$ :
9 |
10 | 
11 | $$
12 | \hat{f}(n, m)=L\left(f_r(n-i, m-j)\right) \quad(i, j) \in A
13 | $$
14 | 因此可以建立一种递归预测编码技术,对应的误差为:
15 | $$
16 | \begin{aligned}
17 | & e_q(n, m)=f(n, m)-\hat{f}(n, m) \\
18 | & f(n, m)=L\left(f_r(n-i, m-j)\right)+e_q(n, m)
19 | \end{aligned}
20 | $$
21 | 即 $\mathbf{f}(\mathbf{n}, \mathbf{m})$ 由 $\mathbf{e}(\mathbf{n}, \mathbf{m})$ 代替, 如果预测 $\hat{f}(n, m)$ 效果好, 则误差项的动态范围很小, 可以有较小的码字来编码,这样便得到显著的压缩效果.
22 |
23 | 为了重建图象,需要传输预测系数和误差编码,这种编码方式称为预测脉冲编码调制(DPCM),如图:
24 |
25 | 
26 |
27 | 假设图象的某一行 $f(n, m)(f(n, m)$ 记为 $f(m))$ 可用一平稳自相关AR过程表示:
28 | $$
29 | f(m)=\sum_{k=1}^p a(k) f(m-k)+e(m) \quad E\left[e^2(m)\right]=\sigma^2
30 | $$
31 | 其中e $(m)$ 为一个与 $f(m)$ 不相关的高斯白噪声, 则预测器:
32 | $$
33 | \hat{f}(m)=\sum_{k=1}^P a(k) \hat{f}_r(m-k)
34 | $$
35 | 预测器系数构成一向量 $a=(a(1), a(2) \ldots, a(P))^{\top}, \quad$ 预测窗口A内重建象素 $\left\{f_r(m-1), \ldots, f_r(m-P)\right.$, 量化误差:
36 | $$
37 | e_q(m)=Q(e(m))=Q[f(m)-\hat{f}(m)]
38 | $$
39 | 重建图象行: $f_r(m)=\sum_{k=1}^p a(k) f_r(m-k)+e_q(m)$
40 |
41 | 预测系数通过下式求解
42 | $$
43 | \left[\begin{array}{cccc}
44 | R(0) & R(1) & \cdots & R(P-1) \\
45 | R(1) & R(2) & \cdots & R(P-2) \\
46 | \vdots & \vdots & \vdots & \vdots \\
47 | R(P-1) & R(P-2) & \cdots & R(0)
48 | \end{array}\right]\left[\begin{array}{c}
49 | a(1) \\
50 | a(2) \\
51 | \vdots \\
52 | a(P)
53 | \end{array}\right]=\left[\begin{array}{c}
54 | R(1) \\
55 | R(2) \\
56 | \vdots \\
57 | R(P)
58 | \end{array}\right]
59 | $$
60 |
61 | ## 预测编码(最佳线性预测)
62 |
63 | 二维模型:
64 | $$
65 | \hat{f}(n, m)=\sum \sum_{(i j) \in A}^P a(i, j) \hat{f}_r(n-i, m-j)
66 | $$
67 | 通过求解E最小:
68 | $$
69 | \left.\left.E\left[\mid f(n, m)-\sum \sum_{(i, j) \in A} a(i, j) f(n-i), m-j\right)\right|^2\right]
70 | $$
71 | 得: $\left.\quad R(k, l)=\sum \sum_{(i, j) \in A} a(i, j) R(n-i), m-j\right)$
72 | 求解上式得到 $a(i, j)$, 再得到:
73 | $$
74 | e(n, m)=f(n, m)-\hat{f}(n, m)
75 | $$
76 | 接收端得: $f_r(n, m)=\sum \sum_{(i j) \in A}^P a(i, j) \hat{f}_r(n-i, m-j)+e_q(n, m)$
--------------------------------------------------------------------------------
/III/3.11 JPEG编码.md:
--------------------------------------------------------------------------------
1 | # 3.11 JPEG 编码
2 |
3 | ## 3.11 JPEG基本系统编码
4 |
5 | JPEG是面向静态图像编码的国际标准。在相同图像质量条件下, JPEG文件拥有比其他图像文件格式更高的压缩比。JPEG目前被广泛应用于多媒体和网络程序中,是现今万维网中使用最广泛的两种图像文件格式之一。JPEG是一种有损压缩, 即在压缩过程中会丢失数据,每次编辑JPEG图像后,图像就会被重复压缩一次, 损失就会有所增加。
6 |
7 | JPEG允许四种编码模式:
8 | (1) 顺序式(Sequential)DCT方式:从左到右、从上到下对图像顺序进行基于离散余弦变换(DCT)的编码。DCT理论上是可逆的,但在计算时存在误差,因而基于DCT的编码模式是一种有损编码。
9 |
10 | (2) 渐进式(Progressive)DCT方式:基于DCT,对图像分层次进行处理,从模糊到清晰地传输图像(与GIF文件的交错方式类似)。有两种实现方法,一种是频谱选择法,即按Z形扫描的序号将DCT量化序数分成几个频段,每个频段对应一次扫描, 每块均先传送低频扫描数据,得到原图概貌,再依次传送高频扫描数据,使图像逐渐清晰;另一种是逐次逼近法,即每次扫描全部DCT量化序数,但每次的表示精度逐渐提高。
11 | (3) 无失真(Lossless)方式: 使用线性预测器,如DPCM, 而不是基于DCT。
12 |
13 | (4) 分层(Hierarchical)方式: 在空间域将源图像以不同的分辨率表示,每个分辨率对应一次扫描, 处理时可以基于DCT或预测编码,可以是渐进式,也可以是顺序式。
14 | JPEG定义了三种系统:基本系统(Baseline System)、扩展系统(Extended System)和无失真压缩系统(Lossless System)。一个符合JPEG标准的编解码器至少要满足基本系统的技术指标。
15 | 基本的JPEG算法属于变换类编码,下面针对基于DCT的顺序式基本系统编码来说明JPEG的编码方法。
16 |
17 | 
18 |
19 | 图3-3 JPEG 编码流程图
20 |
21 | 1) 数据分块
22 | 对图像进行编码前, 将每个分量图像分割成不重叠的 $8 \times 8$ 像素块, 每一个 $8 \times 8$ 像素块称为一个数据单元 (DU)。在彩色图像中, JPEG分别压缩图像的每个彩色分量。虽然JPEG可以压缩通常的红绿蓝分量, 但在 $Y_{b} C_{r}$ 空间的压缩效果会更好。 这是因为人眼对色彩的变化不如对亮度的变化敏感, 因而对色彩的编码可以比对亮度的编码粗糙些, 这主要体现在不同的采样频率和量化精度上。因此, 编码前一般先将图像从RGB空间转换到 $YC_{b} C_{i}$ 空间,再把各分量图像分割成 $8 \times 8$ 数据块。
23 |
24 | 在对图像采样时, 可以采用不同的采样频率, 这种技术称为二次采样。由于亮度比色彩更重要, 因而对 $Y$ 分量的采样频率可高于对 $C_{b} 、 C_{r}$ 的采样频率, 这样有利于节省存储空间。常用的采样方案有YUV422和YUV411。把采样频率最低的分量图像中一个DU所对应的像区上覆盖的所有各分量上的DU按顺序编组为一个最小编码单元 (MCU)。对灰度图像而言, 只有一个Y分量, MCU就是一个数据单元。而对彩色图像而言, 以 4:1:1的采样方案为例, 则一个MCU由4个 4 分量的DU、 1 个 $C_{b}$ 分量的DU和1个 $C_{r}$ 分量的DU组成。
25 |
26 | 2) DCT处理
27 | 图像数据块分割后, 即以 MCU为单位顺序将DU进行二维离散余弦变换。对以无符号数表示的具有 $P$ 位精度的输入数据, 在DCT前要减去 $2^{P-1}$, 转换成有符号数, 而在IDCT后, 应加上 $2^{P-1}$, 转换成无符号数。对每个 $8 \times 8$ 的数据块 $DU$ 进行 $DCT$ 后, 得到的64个系数代表了该图像块的频率成分,其中低频分量集中在左上角, 高频分量分布在右下角。系数矩阵左上角的叫做直流(DC)系数,它代表了该数据块的平均值, 其余 63 个叫交流(AC)系数。
28 |
29 | 3) 系数量化
30 | 在DCT处理中得到的64个系数中,低频分量包含了图像亮度等主要信息。在从空间域到频域的变换中,图像中的缓慢变化比快速变化更易引起人眼的注意, 所以在重建图像时,低频分量的重要性高于高频分量。因而在编码时可以忽略高频分量, 从而达到压缩的目的,这也是量化的根据和目的。
31 |
32 | 在JPEG标准中,用具有64个独立元素的量化表来规定DCT域中相应的64个系数的量化精度,使得对某个系数的具体量化阶取决于人眼对该频率分量的视觉敏感程度。理论上,对不同的空间分辨率、数据精度等情况,应该有不同的量化表。不过,一般采用图3-4和图3-5所示的量化表,可取得较好的视觉效果。之所以用两张量化表,是因为Y分量比Cb和Cr更重要些,因而对Y采用细量化,而对Cb和Cr采用粗量化。量化就是用DCT变换后的系数除以量化表中相对应的量化阶后四舍五入取整。由于量化表中左上角的值较小,而右下角的值较大, 因而起到了保持低频分量、 抑制高频分量的作用。
33 |
34 | 
35 |
36 | 图3-4 亮度量化表
37 |
38 | 
39 |
40 | 图3-5 色度量化表
41 |
42 | 4) Z形扫描
43 | DCT系数量化后,构成一个稀疏矩阵,用Z(Zigzag)形扫描将其变成一维数列,将有利于熵编码。Z形扫描的顺序如图3-6所示。
44 |
45 | 
46 |
47 | 图3-6 DCT系数的Z形扫描顺序
48 |
49 | 5) DC系数编码
50 |
51 | DC系数反映了一个8×8数据块的平均亮度,一般与相邻块有较大的相关性。JPEG对DC系数作差分编码,即用前一数据块的同一分量的DC系数作为当前块的预测值,再对当前块的实际值与预测值的差值作哈夫曼编码。
52 |
53 | 若DC系数的动态范围为-1024~+1024,则差值的动态范围为-2047~+2047。如果为每个差值赋予一个码字, 则码表过于庞大。因此,JPEG对码表进行了简化,采用“前缀码(SSSS)+尾码”来表示。前缀码指明了尾码的有效位数B, 可以根据DIFF从表3-8中查出前缀码对应的哈夫曼编码。尾码的取值取决于DC系数的差值和前缀码。如果DC系数的差值DIFF大于等于0,则尾码的码字为DIFF的B位原码;否则,取DIFF的B位反码。
54 |
55 | 表3-8 图像分量为8位时DC系数差值的典型哈夫曼编码表
56 |
57 | 
58 |
59 | 6) AC系数编码
60 | 经Z形排列后的AC系数,更有可能出现连续0组成的字符串, 从而对其进行行程编码将有利于压缩数据。JPEG将一个非零DC系数及其前面的0行程长度(连续0的个数)的组合称为一个事件。将每个事件编码表示为“NNNN/SSSS+尾码”, 其中, NNNN为0行程的长度,SSSS表示尾码的有效位数B(即当前非0系数所占的比特数),如果非零AC系数大于等于0, 则尾码的码字为该系数的B位原码, 否则, 取该系数的B位反码。
61 | 由于只用4位表示0行程的长度,故在JPEG编码中,最大0行程只能等于15。当0行程长度大于16时,需要将其分开多次编码, 即对前面的每16个0以“F/0”表示,对剩余的继续编码。
62 |
63 | 表3-9 AC系数的尾码位数表
64 |
65 | | SSSS | AC系数的尾码位数表 |
66 | | ---- | -------------------- |
67 | | 0 | 0 |
68 | | 1 | -1,1 |
69 | | 2 | -3, -2, 2, 3 |
70 | | 3 | -7~-4, 4~7 |
71 | | 4 | -15~-8, 8~15 |
72 | | 5 | -31~-16, 16~31 |
73 | | 6 | -63~-17, 17~63 |
74 | | 7 | -127~-64, 64~127 |
75 | | 8 | -255~-128, 128~255 |
76 | | 9 | -511~256, 256~511 |
77 | | 10 | -1023~-512, 512~1023 |
78 |
79 | 表3-10 亮度AC系数码表
80 |
81 | 
82 |
83 | 
84 |
85 | 
86 |
87 | 表3-11 色差AC系数编码
88 |
89 | 
90 |
91 | 
92 |
93 | 
94 |
95 | 3.11.2 JPEG编码实例
96 | 下面结合一个实例来讲述JPEG基本系统的编码过程。设有一图像亮度数据块如图3-7所示,对其进行离散余弦变换后, 用图3-4所示的亮度量化表对系数矩阵量化后的结果如图3-8所示。对量化结果按图3-6所示的顺序进行Z形扫描, 并对扫描结果的DC及AC系数进行编码的结果见表3-12。由于数据较多, 为简便起见, 这里只对几个系数的编码加以说明。
97 |
98 | 
99 |
100 | 图3-7 源图像亮度数据块
101 |
102 | 
103 |
104 | 图3-8 量化结果
105 |
106 | 表3-12 Zigzag排列及行程编码与哈夫曼编码(VLC)结果
107 |
108 | 
109 |
110 | 表3-12 Zigzag排列及行程编码与哈夫曼编码(VLC)结果
111 |
112 | 
113 |
114 | 1) DC系数的编码
115 | 在量化系数矩阵的Z形扫描结果中,第一个系数为DC系数。假设前一亮度数据块的DC系数为40, 则差值DIFF=44-40=4, 因4在(-7~-4, 4~7)范围内, 由表3-8查得SSSS=3,其前缀码字为“100”, 3位尾码即为4的二进制原码“100”, 从而DC系数的编码为“100100”。如果前一数据块的DC系数为48, 则DIFF=-4, 由表10-8查得SSSS及前缀码字同上,其3位尾码即-4的反码“011”, 因此DC系数的编码为“100011”。解码时, 由前缀码“100”可知尾码有3位,若前缀码字是“100”, 因其最高位为1,故可得DC系数的差值为4; 若前缀码字为“011”,因最高位为0,知其为负, 故取反后可得差值为-4。
116 |
117 | 2) AC系数的编码
118 | 在Z形扫描结果中,第一个非零AC系数为10。在它前面的连零个数为1, 即NNNN=1。根据AC系数10从表3-9查得SSSS=4, 由NNNN/SSSS=1/4从表3-10查得其哈夫曼码字为“111110110”, 而10的二进制码为“1010”, 因此该AC系数的编码为“1111101101010”。由于篇幅所限,其他AC系数的编码就不再赘述, 结果见表10-12。在Z形扫描结果中的末尾,除第54个系数非零外, 其他系数全为零, 故直接用一个结束块“EOB(0/0)”结束本块,由表3-10查得其码字为“1010”。于是,最后该亮度块的编码为(其中,假定差值为4)100100111110110101001100111110000101010001001101100100010011101010000110001010000110001111000000000001000111000110001100100000111001001001111001000001111001111101111010,共用了168位,而原始图像块需8×8×8=512位,因此压缩比为3.048。
119 |
120 | JPEG压缩编码示例
121 |
122 | 
--------------------------------------------------------------------------------
/III/3.12 编程实例.md:
--------------------------------------------------------------------------------
1 | # 3.12 编程实例
2 |
3 | 实现哈夫曼编码的过程实际是构造一个哈夫曼二叉树, 它可分为两大部分:构造哈夫曼树和在哈夫曼树上求叶节点的编码。在构造哈夫曼树时,可设置一个结构数组HuffmanNode保存哈夫曼树中各节点的信息。结构数组元素定义如下:
4 |
5 | ```c++
6 | typedef struct
7 | {
8 | int Weight; //保存哈夫曼树节点的权值, 在此是指频数
9 | int Flag; //当Flag=0时, 表示该节点未加入树中, 为1时表示已加入树中
10 | int Parent; //存放节点的父节点在节点数组中的序号
11 | int LChild; //存放节点的左子节点在节点数组中的序号
12 | int RChild; //存放节点的右子节点在节点数组中的序号
13 | } HuffmanNode;
14 |
15 | ```
16 |
17 | 对于一幅BMP图像,调用CpointPro类下的GetHistogram()成员函数可获得图像的直方图数据m_fFreq,这些数据即各灰度出现的频数。利用这些数据可直接进行哈夫曼编码。哈夫曼编码的代码如下:
18 |
19 | ```C++
20 | void CDlgHuffman::Huffman()
21 | {
22 | CString str;
23 | int i, j, x1, x2, c, p;
24 | int m1, m2;
25 | LV_ITEM lvitem; // ListCtrl的ITEM
26 | int iActualItem; //中间变量, 用于保存ListCtrl中添加的ITEM编号
27 | HuffmanNode *huffNode; //存放哈夫曼树的节点
28 | CString *strCode; //指向各字符的哈夫曼编码的指针
29 | int *iMap; //位置映射指针
30 | int iNumNode = 0; //频数不为零的节点数(或灰度数)
31 | //统计直方图数据中频数不为零的灰度数, 并只对不为零的节点编码
32 | for(i = 0; i < m_iLeafNum; i++)
33 | {
34 | if (m_fFreq[i + m_ChannelSel * m_iLeafNum] != 0)
35 | iNumNode++;
36 | }
37 | //对于具有iNumNode个叶节点的哈夫曼树, 它具有2 iNumNode -1个节点
38 | huffNode = new HuffmanNode[iNumNode * 2 - 1];
39 | strCode = new CString[iNumNode]
40 | iMap = new int[iNumNode];
41 | //初始化huffNode中的各节点
42 | for(i = 0; i < iNumNode * 2 - 1; i++)
43 | {
44 | huffNode[i].Weight = 0;
45 | huffNode[i].Parent = 0;
46 | huffNode[i].Flag = 0;
47 | huffNode[i].LChild = -1;
48 | huffNode[i].RChild = -1;
49 | }
50 | //输入iNumNode个叶节点的权值即频数, iMap存放的是频数不为零的灰度值
51 | j = 0;
52 |
53 | for(i = 0; i < m_iLeafNum; i++)
54 | {
55 | if (m_fFreq[i + m_ChannelSel * m_iLeafNum] != 0)
56 | {
57 | huffNode[j].Weight = m_fFreq[i + m_ChannelSel * m_iLeafNum];
58 | iMap[j] = i;
59 | j++;
60 | }
61 | }
62 | //构造哈夫曼树, 对iNumNode个叶节点, 需构造iNumNode-1次
63 | for(i = 0; i < iNumNode - 1; i++)
64 | {
65 | //对Flag为0的节点比较排序, 选出两个权值最小的子树, x1和x2用于确定
66 | //两子树在数组中的序号, m1和m2用于存放最小两子树的权值
67 | m1 = m2 = m_iSizeImage;
68 | x1 = x2 = 0;
69 | for (j = 0; j < iNumNode + i; j++)
70 | {
71 | if (huffNode[j].Weight < m1 && huffNode[j].Flag = = 0)
72 | {
73 | m2 = m1;
74 | x2 = x1;
75 | m1 = huffNode[j].Weight;
76 | x1 = j;
77 | }
78 | else if (huffNode[j].Weight < m2 && huffNode[j].Flag = = 0)
79 | {
80 | m2 = huffNode[j].Weight;
81 | x2 = j;
82 | }
83 | }
84 | //将找出的两棵最小子树合并为一棵子树
85 | huffNode[x1].Parent = iNumNode + i;
86 | huffNode[x2].Parent = iNumNode + i;
87 | // Flag为1, 说明该节点已经成为其他节点的子节点
88 | huffNode[x1].Flag = 1;
89 | huffNode[x2].Flag = 1;
90 | huffNode[iNumNode + i].Weight = huffNode[x1].Weight + huffNode[x2].Weight;
91 | //权值较小的子树作为右子树
92 | huffNode[iNumNode + i].LChild = x2;
93 | huffNode[iNumNode + i].RChild = x1;
94 | }
95 | //求每个叶节点的哈夫曼编码
96 | for(i = 0; i < iNumNode; i++)
97 | {
98 | c = i;
99 | p = huffNode[c].Parent;
100 | //由叶节点上溯到树根
101 | while (p != 0)
102 | {
103 | //如果是左子树, 则代码的高一位添加0, 否则添加1
104 | if (huffNode[p].LChild = = c)
105 | strCode[i] = "0" + strCode[i];
106 | else
107 | strCode[i] = "1" + strCode[i];
108 | c = p;
109 | p = huffNode[c].Parent;
110 | }
111 | }
112 | //计算平均码字长度和图像熵
113 | int CodeLen = 0;
114 | m_fEntropy = 0.0;
115 | for(i = 0; i < iNumNode; i ++
116 | {
117 | CodeLen += huffNode[i].Weight * strCode[i].GetLength();
118 | m_fEntropy -= ((double)huffNode[i].Weight / m_iSizeImage) *
119 | log((double)huffNode[i].Weight / m_iSizeImage) / log(2.0);
120 | }
121 | //计算平均码字长度
122 | m_fAvCodeLen = (double)CodeLen/m_iSizeImage;
123 | // 计算编码效率
124 | m_fCodeEfficiency = m_fEntropy / m_fAvCodeLen;
125 | //更新对话框上的文本框中的内容
126 | UpdateData(FALSE);
127 | lvitem.mask = LVIF_TEXT;
128 | //输出哈夫曼编码结果
129 | for (i = 0; i < iNumNode; i ++)
130 | {
131 | if (huffNode[i].Weight > 0)
132 | {
133 | // 添加一项
134 | lvitem.iItem = m_lstTable.GetItemCount();
135 | str.Format("%u", iMap[i]);
136 | lvitem.iSubItem = 0;
137 | lvitem.pszText = (LPTSTR)(LPCTSTR)str;
138 | iActualItem = m_lstTable.InsertItem(&lvitem);
139 | // 添加其他列
140 | lvitem.iItem = iActualItem;
141 | // 添加灰度值出现的频率
142 | lvitem.iSubItem = 1;
143 | str.Format("%f", (float)huffNode[i].Weight / m_iSizeImage);
144 | lvitem.pszText = (LPTSTR)(LPCTSTR)str;
145 | m_lstTable.SetItem(&lvitem);
146 | // 添加哈夫曼编码
147 | lvitem.iSubItem = 2;
148 | lvitem.pszText = (LPTSTR)(LPCTSTR)strCode[i];
149 | m_lstTable.SetItem(&lvitem);
150 | // 添加码字长度
151 | lvitem.iSubItem = 3;
152 | str.Format("%u", strCode[i].GetLength());
153 | lvitem.pszText = (LPTSTR)(LPCTSTR)str;
154 | m_lstTable.SetItem(&lvitem);
155 | }
156 | }
157 | delete[] huffNode;
158 | delete[] strCode;
159 | delete[] iMap;
160 | }
161 | ```
162 |
163 |
--------------------------------------------------------------------------------
/III/3.2 Huffman编码.md:
--------------------------------------------------------------------------------
1 | # 3.2 Huffman 编码(熵编码)
2 |
3 | 图象熵:
4 | 图像灰度集合为 $\left(x_1, x_2, \ldots, x_{M}\right)$, , 对应的概率 $P_1$, $P_2, \ldots, \mathbf{P}_{M}$
5 | 则图象熵: $\quad H=-\sum_{k=1}^M P_k \log P_k$
6 | 平均码长:
7 | 设 $\beta_{k}$ 为图像第 $k$ 个码长 $C_{k}$ 的长度, 对应的概率为 $P_{k}$, 则该图象所赋予的码长的平均长度为:
8 | $$
9 | R=\sum_{k=1}^M \beta_k P_k
10 | $$
11 | 编码效率
12 | $$
13 | \eta=\frac{H}{R}
14 | $$
15 | 变长最佳编码定理
16 | 在变长编码中, 对图像中出现频度大的像素值赋予短码字, 对出现频度小的像数值赋予长码字。 如果严格按照所对应符号出现概率大小逆序排列, 则编码结果平均码长一定小于任何其它排列方式。
17 | Huffman 编码
18 | 根据变长最佳编码定理, 应用Huffman算法的一种编码方法。
19 |
20 | 举例:
21 | $$
22 | \frac{\text { aaaa }}{4} \frac{bbb}{3} \frac{cc}{2} \frac{d}{1} \frac{\text { eeeee }}{5} \frac{\text { fffffff }}{7} \text { (共22*8=176 bits) }
23 | $$
24 | 编码: $f=0 \quad e=10 \quad a=110 \quad ~b=1111 \quad c=11100 \quad ~d=11101$
25 |
26 | 11011011011011111111111111100111001110110101010100000000
27 | (共 $7 * 1+5 * 2+4 * 3+3 * 4+2 * 5+1 * 5=56$ bits)
28 |
29 | Huffman 编码步骤:
30 | 1、先将图象灰度级按出现的概率由大到小顺序排列;
31 | 2、将最小两个概率相加, 形成一个新的概率集合, 再按第 (1) 步方法重排, 如此重复进行直到只有两个概率为止;
32 | 3、分配码长。码长分配从最后一步开始反向进行, 对最后两个概率一个赋予“0”, 一个赋予“1”
33 |
34 | 
35 |
36 | 整理:
37 |
38 | 
39 |
40 | f=01 e=11 a=10 b=001 c=0001 d=0000
41 | $$
42 | \frac{\text { aaaa }}{4} \frac{bbb}{3} \frac{cc}{2} \frac{d}{1} \frac{\text { eeeee }}{5} \frac{\text { fffffff }}{7} \text { (共22*8=176 bits) }
43 | $$
44 | 经过Huffman编码之后的数据为:
45 |
46 | 1010101010001001001000100010000111111111101010101010101
47 |
48 | (共 $7 * 2+5 * 2+4 * 2+3 * 3+2 * 4+1 * 4=53$ bits)
49 | 比前面我们给出的编码得到的56bits的数据量还小
50 |
51 | Huffman编码在图像压缩中的实现
52 | 我们知道, 对一幅图像进行编码时, 如果图像的大小大于 256 时, 这幅图像的不同的码字就有可能是很大, 例如极限为 256 个不同的码字。
53 | 对整幅图直接进行Huffman编码时, 小分布的灰度值, 就有可能具有很长的编码。
54 | 如: 100位以上, 这样不但达不到压缩的效果反而会使数据量加大, 应该如何处理?
55 |
56 | 常用的且有效的方法是:
57 | 将图像分割成若干的小块, 对每块进行独立的Huffman编码。例如: 分成$8\times 8$的子块, 就可以大大降低不同灰度值的个数(最多是64而不是256)。
--------------------------------------------------------------------------------
/III/3.3 香农-范诺编码.md:
--------------------------------------------------------------------------------
1 | # 3.3 香农-范诺编码
2 |
3 | 香农-范诺 (Shannon-Fannon) 编码也是一种常见的可变字长编码。与哈夫曼编码相似, 当信源符号出现的概率正好为 $2^{-i}$ $(i<0)$ 时, 采用香农-范诺编码同样能够达到 $100 \%$ 的编码效率。 香农-范诺编码的理论基础是符号的码字长度 $N_i$ 完全由该符号出现的概率来决定, 即
4 | $$
5 | -\log _D P_i \leq N_i \leq-\log _D P_i+1\tag{3-8}
6 | $$
7 | 式中,D为编码所用的数制。
8 |
9 | 香农-范诺编码的步骤如下:
10 | (1)将信源符号按其出现概率从大到小排序;
11 | (2)按照式 (3-8) 计算出各概率对应的码字长度 $N_i$;
12 | (3)计算累加概率 $A_i$, 即
13 | $$
14 | A_i=A_{i-1}+P_{i-1} \quad i=1,2, \ldots, N-1 ; \quad A_0=0\tag{3-9}
15 | $$
16 | (4) 把各个累加概率 $A_i$ 由十进制转化为二进制, 取该二进制数的前 $N_i$ 位作为对应信源符号的码字。
17 |
18 | 为便于比较, 仍以例4-1中图像为对象, 对其进行香农-范诺编码, 结果如表3-3所示。由于在此采用二进制对码字赋值, 故在利用式 (3-9) 计算码字长度 $N_i$ 时, $D$ 取为 2 。以符号 $S_4$ 为例, 其出现概率为 0.07 , 按照式 (3-9) 计算得到它的码字长度应为 4 , 按式 (3-10) 计算得到它的累加概率 $A_4$ 为 0.78 , 将 0.78 转化为二进制并取其前 4 位即得符号 $S_4$ 的码字为 1100 (省去了 “0.”, 有的浮点数不能完全转化, 转化时只需完成前 $N_i$ 位即可)。
19 |
20 | 表3-3 香农-范诺编码
21 |
22 | $$
23 | 平均码长 R=3.17 \quad图像熵 H=2.55 \quad \text { 编㐷效率 } \eta=80.4 \%\\
24 | \begin{array}{|c|c|c|c|c|c|}
25 | \hline \text { 信源符号 } & \text { 出现概率 } P_i & \text { 码字长度 } N_i & \text { 蔂加概率 } A_i & \text { 转换为二进制 } & \text { 分配码字 } B_i \\
26 | \hline S_0 & 0.40 & 2 & 0 & 0 & 00 \\
27 | \hline S_1 & 0.18 & 3 & 0.40 & 01100 & 011 \\
28 | \hline S_2 & 0.10 & 4 & 0.58 & 10010 & 1001 \\
29 | \hline S_3 & 0.10 & 4 & 0.68 & 10100 & 1010 \\
30 | \hline S_4 & 0.07 & 4 & 0.78 & 11000 & 1100 \\
31 | \hline S_5 & 0.06 & 5 & 0.85 & 1101100 & 11011 \\
32 | \hline S_6 & 0.05 & 5 & 0.91 & 1110100 & 11101 \\
33 | \hline S_7 & 0.04 & 5 & 0.96 & 1111010 & 11110 \\
34 | \hline
35 | \end{array}\\
36 |
37 |
38 |
39 | $$
40 | 除此之外, 还有二分法香农-范诺编码方法。其步骤如下:
41 | (1) 首先统计出每个符号出现的概率;
42 | (2) 从左到右对上述概率从大到小排序;
43 | (3) 从这个概率集合中的某个位置将其分为两个子集合,并尽量使两个子集合的概率和近似相等,给前面一个子集合赋值为0, 后面一个子集合赋值为1;
44 | (4) 重复步骤3,直到各个子集合中只有一个元素为止;
45 | (5) 将每个元素所属的子集合的值依次串起来,即可得到各个元素的香农-范诺编码。
46 |
47 | 表3-4 二分法香农-范诺编码
48 |
49 | 
--------------------------------------------------------------------------------
/III/3.4 行程编码.md:
--------------------------------------------------------------------------------
1 | # 3.4 行程编码
2 |
3 | ## 3.4.1 行程编码基本方法
4 |
5 | 行程编码又称行程长度编码(Run Length Encoding, RLE), 是一种熵编码,其编码原理相当简单,即将具有相同值的连续串用其串长和一个代表值来代替, 该连续串就称为行程,串长称为行程长度。例如,有一字符串“aabbbcddddd”, 则经行程长度编码后, 该字符串可以只用“2a3b1c5d”来表示。
6 | 行程编码分为定长和不定长编码两种。定长编码是指编码的行程长度所用的二进制位数固定,而变长行程编码是指对不同范围的行程长度使用不同位数的二进制位数进行编码。使用变长行程编码需要增加标志位来表明所使用的二进制位数。
7 |
8 | 行程编码比较适合于二值图像的编码,一般用于量化后出现大量零系数连续的场合,用行程来表示连零码。如果图像是由很多块颜色或灰度相同的大面积区域组成的,那么采用行程编码可以达到很高的压缩比。如果图像中的数据非常分散,则行程编码不但不能压缩数据,反而会增加图像文件的大小。为了达到较好的压缩效果,一般不单独采用行程编码, 而是和其他编码方法结合使用。例如, 在JPEG中, 就综合使用了行程编码、DCT、量化编码以及哈夫曼编码, 先对图像作分块处理, 再对这些分块图像进行离散余弦变换(DCT), 对变换后的频域数据进行量化并作Z字形扫描,接着对扫描结果作行程编码, 对行程编码后的结果再作哈夫曼编码。
9 |
10 | ## 3.4.2 PCX文件中的行程编码
11 |
12 | PCX文件分为文件头和图像压缩数据两个部分。如果是256色图像,则还有一个256色调色板存于文件尾部。文件头全长128字节,包含了图像的大小和颜色以及PCX文件的版本标识等信息,图像压缩数据紧跟在文件头之后。如果没有使用调色板, 那么图像压缩数据存储的是实际像素值;否则,存储的是调色板的索引值。当压缩数据是实际的像素值时,它们按颜色平面和扫描行存储,即每行先存储所有R分量,再存储所有G分量, 最后存储所有B分量,一行数据存储完后,接着存储下一行数据。如果使用了调色板,则不会分解为单独的颜色平面存储。读者可以查阅图像文件格式的相关书籍了解PCX文件的详细格式。下面以256色PCX文件为例, 说明PCX文件中的行程编码。
13 |
14 | 在256色PCX文件中,每个像素占一字节, 压缩数据以字节为单位逐行进行编码,每行填充到偶数字节。PCX文件规定编码时的最大行程长度为63,如果行程长度大于63,则必须分多次存储。对于长度大于1的行程,编码时先存入其行程长度(长度L加上192即0xC0),再存入该行程的代表值,行程长度和行程的代表值分别占一字节。对于长度为1的行程,即单个像素, 如果该像素的值小于或等于0xC0, 则编码时直接存入该像素值, 而不存储长度信息;否则,先存入0xC1,再存入该像素值,这样做的目的是为了避免该像素值被误认为长度信息。例如,连续100个灰度值为0x80的像素, 其编码(以十六进制表示)应为FF 80 25 80。上面的编码中出现FF的长度信息是由63与0xC0相加所得。
15 |
16 | 对256色PCX文件解码时,首先从压缩数据部分读取一个字节,判断该值是否大于0xC0,如果是,则表明该字节是行程长度信息, 取其低六位(相当于减去0xC0)作为行程长度L,读取下一个字节作为像素值并重复L次存入图像数据缓冲区;否则, 直接将该字节存入图像数据缓冲区。
17 |
18 | 虽然几乎所有的图像应用软件都支持PCX文件格式,但由于它的压缩比不高, 因而现在用得不是很多。
--------------------------------------------------------------------------------
/III/3.5 LZW编码 .md:
--------------------------------------------------------------------------------
1 | # 3.5LZW编码
2 |
3 | ## 3.5.1LZW编码方法
4 |
5 | LZW(Lempel-Ziv&Welch)编码又称字串表编码,属于一种无损编码,是Welch将Lempel和Ziv所提出的无损压缩技术改进后的压缩方法。LZW编码与行程编码类似,也是对字符串进行编码从而实现压缩,但它在编码的同时还生成了特定字符串以及与之对应的索引字符串表。
6 |
7 | LZW编码的基本思想是:在编码过程中,将所遇到的字符串建立一个字符串表,表中的每个字符串都对应一个索引,编码时用该字符串在字串表中的索引来代替原始的数据串。例如,一幅8位的灰度图像,我们可以采用12位来表示每个字符串的索引,前256个索引用于对应可能出现的256种灰度,由此可建立一个初始的字符串表,而剩余的3840个索引就可分配给在压缩过程中出现的新字符串,这样就生成了一个完整的字符串表,压缩数据就可以只保存它在字符串表中的索引,从而达到压缩数据的目的。字符串表是在压缩过程中动态生成的,不必将它保存在压缩文件里,因为解压缩时字符串表可以由压缩文件中的信息重新生成。
8 |
9 | GIF(GraphicsInterchangeFormat)最初是由美国CompuServe于1987年开发的一种压缩位图格式。它可支持多达256种的颜色,具有极佳的压缩效率,已成为Internet上一种流行的文件格式。GIF图像文件采用的是一种改良的LZW压缩算法,通常称为GIF-LZW压缩算法。GIF图像文件以块(又称为区域结构)的方式来存储图像相关的信息,具体的文件格式可参考图像文件格式的相关书籍。下面简要介绍GIF-LZW的编码方法。
10 |
11 | 设S1、S2为两个存放字符串的临时变量,LZW_CLEAR和LZW_EOI分别为字符表初始化标志和编码结束标志,GIF-LZW的编码步骤如下:
12 |
13 | (1)根据图像中使用的颜色数初始化一个字串表,字串表中的每个颜色对应一个索引。在初始字串表的末尾再添加两个符号(LZW_CLEAR和LZW_EOI)的索引。设置字符串变量S1、S2并初始化为空。
14 |
15 | (2)接着输出LZW_CLEAR在字串表中的索引。
16 |
17 | (3)从图像数据流中第一个字符(假设数据以字符串表示)开始,每次读取一个字符,将其赋给字符串变量S2。
18 |
19 | (4)判断“S1+S2”是否已存在于字串表中。如果字串表中存在“S1+S2”,则S1=S1+S2;否则,输出S1在字串表中的索引,并在字串表末尾为“S1+S2”添加索引,同时,S1=S2。
20 |
21 | (5)重复第3和第4步,直到所有字符读完为止。
22 |
23 | (6)输出S1中的字符串在字串表中的索引,然后输出结束标志LZW_EOI的索引,编码完毕。
24 |
25 | GIF-LZW的解码过程比较复杂,它和编码过程正好相反,即将编码后的码字转换成对应的字符串,重新生成字串表,然后依次输出对应的字符串即可。GIF-LZW的解码流程如图3-2所示,表中的Code和OldCode是两个存放索引的临时变量。
26 |
27 | 
28 |
29 | 图3-2GIF-LZW解码流程
30 |
31 | ## 3.5.2LZW编码实例
32 |
33 | 设有一来源于4色(以a、b、c、d表示)图像的数据流aabcabbbbd,现对其进行LZW编码。编码过程如下:
34 | 编码前,首先需要初始化一个字符串表。由于图像中只有四种颜色,因而我们可以只用4比特表示字符串表中每个字符串的索引,表中的前4项代表4种颜色,后两项分别表示初始化和图像结束标志,建立的初始化字符串表如表3-5所示。接着把S1和S2初始化为空(即NULL),输出LZW_CLEAR的在字符串表中的索引值4H,接下来是对图像数据的编码。
35 |
36 | 表3-5初始化字符串表
37 | $$
38 | \begin{array}{|c|c|}
39 | \hline \text{字符串}&\text{索引}\\
40 | \hline a&0H\\
41 | \hline b&1H\\
42 | \hline c&2H\\
43 | \hline d&3H\\
44 | \hline \text{LZW\_CLEAR}&4H\\
45 | \hline \text{LZW\_EOI}&5H\\
46 | \hline
47 | \end{array}
48 | $$
49 |
50 |
51 | 读取图像数据流的第一个字符“a”,赋给S2,因S1+S2=“a”已存在字串表中,所以S1=S1+S2=“a”。
52 | 接着读入下一个字符“a”赋给S2,因S1+S2=“aa”不存在于字串表中,所以输出S1=“a”的索引0H,同时在字符串表末尾添加新字符串“aa”的索引6H,并使S1=S2=“a”。
53 | 依次读取数据流中的每个字符,如果S1+S2没有出现在字符串表中,则输出S1中的字符串的索引,并在字符串表末尾为新字符串S1+S2添加索引,并使S1=S2;否则,不输出任何结果,只是使S1=S1+S2。所有字符处理完毕后,输出S1中的字符串的索引,最后输出结束标志LZW_EOI的索引。至此,编码完毕,完整的编码过程如表3-6所示,最后的编码结果为“4001271B35”(以十六进制表示)。
54 |
55 | 表3-6GIF-LZW编码过程
56 | $$
57 | \begin{array}{|c|c|c|c|c|}
58 | \hline \text { 输入数据 S2 } & \text { S1+S2 } & \text { 输出结果 } & \text { S1 } & \text { 生成的新字符串及索引 } \\
59 | \hline \text { NULL } & \text { NULL } & 4 H & \text { NULL } & \\
60 | \hline a & a & & a & \\
61 | \hline a & aa & 0 H & a & aa<6 H> \\
62 | \hline b & ab & 0 H & a & ab<7 H> \\
63 | \hline c & bc & 1 H & c & ca<9 H> \\
64 | \hline a & ca & 2 H & a & \\
65 | \hline b & ab & & ab & abb --------------------------------------------------------------------------------
/III/3.8基于小波变换编码.md:
--------------------------------------------------------------------------------
1 | # 3.8基于小波变换编码
2 |
3 | ## 一维小波变换
4 |
5 | 
6 |
7 | 二维小波变换
8 | 一愊图象经小波变换成 $(3 ~J+1)$ 个离笃图象
9 | $$
10 | \left\{A_J^d f, D_j^1 f, D_j^2 f, D_j^3 f\right\} \quad 1 \leq j \leq J
11 | $$
12 | 其中 $A_j^d f$ 是 $f$ 在J级分辡卒的低频分量, $D_j^1 f, D_j^2 f$ 分别是水平、坚直方向的细节, $D_j^3 f$ 主要对应 45 度和 135 度方向的高频分量。
13 |
14 | 
15 |
16 | 
17 |
18 | 二维小波分解
19 |
20 | 
21 |
22 | 二维小波重建
23 |
24 | 基于小波变换编码原理
25 | 图象的最终目的是让人看, 而人的视觉系统对高频分量不敏感, 因此高频分量可以粗略编码, 而对图象的质量影响不大,并且高频部分有很高的相似性。由于细节部分对应于图象的高频分量, 考虎视觉特点, 它可以用较高的厓缩比编码, 而 $A_J^d f$ 象素个数小, 反映图象的整体轮廓, 对其直接编码, 以保证恢复图象的质量,而对整幅图象的编码圧缩比影响不大。
26 |
27 | 
--------------------------------------------------------------------------------
/III/3.9 混合编码.md:
--------------------------------------------------------------------------------
1 | # 3.9 混合编码
2 |
3 | 混合编码实现的可能性及有效性:
4 |
5 | 回顾一下讲过的几个内容的特点
6 | 1. 行程编码:擅长于重复数字的压缩。
7 | 2. Huffman编码:擅长于像素个数的不同编码。
8 | 4. DCT变换:擅长将高频部分分离出来。
9 |
10 | 例:
11 | $$
12 | \frac{aaaa}{4}\frac{bbb}{3}\frac{cc}{2}\frac{d}{1}\frac{eeeee}{5}\frac{fffffff}{7}
13 | $$
14 | 行程编码:
15 | $$
16 | 4a3b2c1d5e7f \\
17 | $$
18 | 共$6\times(8+3)= 66Bits$
19 |
20 | Huffman编码:
21 | $$
22 | f=01\quad e=11 \quad a=10 \quad b=001\quad c=0001\quad d=0000\\
23 |
24 | $$
25 | 编码为
26 | $$
27 | 1010101010001001001000100010000111111111101010101010101
28 | $$
29 | 共$7\times2+5\times2+4\times2+3\times3+2\times4+1\times4=53 bits$
30 |
31 | Hufman与行程编码混合:
32 | $$
33 | 41030012000110000511701
34 | $$
35 | 共:$3+2+3+3+3+4+3+4+3+2+3+2=35 bits$
36 |
37 | ## 图像压缩的实例
38 |
39 | 一:
40 |
41 | 一次小波变换+DCT变换.行程编码+Huffman编码
42 |
43 | 二:
44 |
45 | 一次小波变换+差值编码+变字长行程编码+Huffman编码
46 |
47 | ### 算法 1
48 |
49 | | 原图 | 复原图 |
50 | | ------------------------------------------------------------ | ------------------------------------------------------------ |
51 | |
--------------------------------------------------------------------------------
/III/3.8基于小波变换编码.md:
--------------------------------------------------------------------------------
1 | # 3.8基于小波变换编码
2 |
3 | ## 一维小波变换
4 |
5 | 
6 |
7 | 二维小波变换
8 | 一愊图象经小波变换成 $(3 ~J+1)$ 个离笃图象
9 | $$
10 | \left\{A_J^d f, D_j^1 f, D_j^2 f, D_j^3 f\right\} \quad 1 \leq j \leq J
11 | $$
12 | 其中 $A_j^d f$ 是 $f$ 在J级分辡卒的低频分量, $D_j^1 f, D_j^2 f$ 分别是水平、坚直方向的细节, $D_j^3 f$ 主要对应 45 度和 135 度方向的高频分量。
13 |
14 | 
15 |
16 | 
17 |
18 | 二维小波分解
19 |
20 | 
21 |
22 | 二维小波重建
23 |
24 | 基于小波变换编码原理
25 | 图象的最终目的是让人看, 而人的视觉系统对高频分量不敏感, 因此高频分量可以粗略编码, 而对图象的质量影响不大,并且高频部分有很高的相似性。由于细节部分对应于图象的高频分量, 考虎视觉特点, 它可以用较高的厓缩比编码, 而 $A_J^d f$ 象素个数小, 反映图象的整体轮廓, 对其直接编码, 以保证恢复图象的质量,而对整幅图象的编码圧缩比影响不大。
26 |
27 | 
--------------------------------------------------------------------------------
/III/3.9 混合编码.md:
--------------------------------------------------------------------------------
1 | # 3.9 混合编码
2 |
3 | 混合编码实现的可能性及有效性:
4 |
5 | 回顾一下讲过的几个内容的特点
6 | 1. 行程编码:擅长于重复数字的压缩。
7 | 2. Huffman编码:擅长于像素个数的不同编码。
8 | 4. DCT变换:擅长将高频部分分离出来。
9 |
10 | 例:
11 | $$
12 | \frac{aaaa}{4}\frac{bbb}{3}\frac{cc}{2}\frac{d}{1}\frac{eeeee}{5}\frac{fffffff}{7}
13 | $$
14 | 行程编码:
15 | $$
16 | 4a3b2c1d5e7f \\
17 | $$
18 | 共$6\times(8+3)= 66Bits$
19 |
20 | Huffman编码:
21 | $$
22 | f=01\quad e=11 \quad a=10 \quad b=001\quad c=0001\quad d=0000\\
23 |
24 | $$
25 | 编码为
26 | $$
27 | 1010101010001001001000100010000111111111101010101010101
28 | $$
29 | 共$7\times2+5\times2+4\times2+3\times3+2\times4+1\times4=53 bits$
30 |
31 | Hufman与行程编码混合:
32 | $$
33 | 41030012000110000511701
34 | $$
35 | 共:$3+2+3+3+3+4+3+4+3+2+3+2=35 bits$
36 |
37 | ## 图像压缩的实例
38 |
39 | 一:
40 |
41 | 一次小波变换+DCT变换.行程编码+Huffman编码
42 |
43 | 二:
44 |
45 | 一次小波变换+差值编码+变字长行程编码+Huffman编码
46 |
47 | ### 算法 1
48 |
49 | | 原图 | 复原图 |
50 | | ------------------------------------------------------------ | ------------------------------------------------------------ |
51 | |  |
|  |
52 |
53 | 信噪比:66.02
54 |
55 | 压缩比:11.83:1
56 |
57 | ### 算法 2
58 |
59 | | 原图 | 复原图 |
60 | | ------------------------------------------------------------ | ------------------------------------------------------------ |
61 | |
|
52 |
53 | 信噪比:66.02
54 |
55 | 压缩比:11.83:1
56 |
57 | ### 算法 2
58 |
59 | | 原图 | 复原图 |
60 | | ------------------------------------------------------------ | ------------------------------------------------------------ |
61 | |  |
|  |
62 |
63 | 信噪比:64.55
64 |
65 | 压缩比:26.50:1
--------------------------------------------------------------------------------
/IV/4.1 引言.md:
--------------------------------------------------------------------------------
1 | # 4.1 引言
2 |
3 | 通过一些运算来突出图像的某些信息,如轮廓等.但通过运算的图像不一定逼近原图像.
4 | 图像增强:
5 |
6 | - 空间域法
7 |
8 | $$
9 | g(x,y)=h(x,y)*f(x,y)
10 | $$
11 | - 频域法
12 |
13 | $$
14 | \stackrel{F(x, y)}{\longrightarrow} \boxed{正交变换} \stackrel{F(u, v)}{\longrightarrow} \boxed{修正H(u,v)} \stackrel{G(u, v)}{\longrightarrow} \boxed{逆变换} \stackrel{G(x, y)}{\longrightarrow}
15 | $$
16 |
--------------------------------------------------------------------------------
/IV/4.3 灰度变换.md:
--------------------------------------------------------------------------------
1 | # 4.3 灰度变换
2 |
3 | ## 4.2.1 灰度线性变换
4 |
5 | 假定原图像 $f(x, y)$ 的灰度范围为 $[a, b]$, 希望变换后图像 $g(x$, $y)$ 的灰度范围扩展至 $[c, d]$, 则线性变换可表示为
6 | $$
7 | g(x, y)=\frac{d-c}{b-a}[f(x, y)-a]+c\tag{4-12}
8 | $$
9 | 此式用图4-12表示。若图像灰度在 $0 \sim M_f$ 范围内, 其中大部分像素的灰度级分布在区间 $[a, b]$, 很小部分的灰度级超出了此区间, 为改善增强的效果, 可令:
10 | $$
11 | g(x, y)= \begin{cases}c & 0 \leq f(x, y)
43 |
44 | 图4-15 常见的几种非线性变换函数
45 |
46 | 式(4-16)对灰度区间$ [0, a]$和$[b, M_f]$加以压缩,对灰度区间[a, b]进行扩展。通过细心调整折线拐点的位置及控制分段直线的斜率,可对任一灰度区间进行扩展或压缩。这种变换适用于在黑色或白色附近有噪声干扰的情况。例如, 照片中的划痕, 由于变换后在[0, a]以及[b, $M_f$ ]之间的灰度受到压缩, 因而使污斑得到减弱。
47 |
48 | ## 4.2.3 非线性变换
49 |
50 |
|
62 |
63 | 信噪比:64.55
64 |
65 | 压缩比:26.50:1
--------------------------------------------------------------------------------
/IV/4.1 引言.md:
--------------------------------------------------------------------------------
1 | # 4.1 引言
2 |
3 | 通过一些运算来突出图像的某些信息,如轮廓等.但通过运算的图像不一定逼近原图像.
4 | 图像增强:
5 |
6 | - 空间域法
7 |
8 | $$
9 | g(x,y)=h(x,y)*f(x,y)
10 | $$
11 | - 频域法
12 |
13 | $$
14 | \stackrel{F(x, y)}{\longrightarrow} \boxed{正交变换} \stackrel{F(u, v)}{\longrightarrow} \boxed{修正H(u,v)} \stackrel{G(u, v)}{\longrightarrow} \boxed{逆变换} \stackrel{G(x, y)}{\longrightarrow}
15 | $$
16 |
--------------------------------------------------------------------------------
/IV/4.3 灰度变换.md:
--------------------------------------------------------------------------------
1 | # 4.3 灰度变换
2 |
3 | ## 4.2.1 灰度线性变换
4 |
5 | 假定原图像 $f(x, y)$ 的灰度范围为 $[a, b]$, 希望变换后图像 $g(x$, $y)$ 的灰度范围扩展至 $[c, d]$, 则线性变换可表示为
6 | $$
7 | g(x, y)=\frac{d-c}{b-a}[f(x, y)-a]+c\tag{4-12}
8 | $$
9 | 此式用图4-12表示。若图像灰度在 $0 \sim M_f$ 范围内, 其中大部分像素的灰度级分布在区间 $[a, b]$, 很小部分的灰度级超出了此区间, 为改善增强的效果, 可令:
10 | $$
11 | g(x, y)= \begin{cases}c & 0 \leq f(x, y)
43 |
44 | 图4-15 常见的几种非线性变换函数
45 |
46 | 式(4-16)对灰度区间$ [0, a]$和$[b, M_f]$加以压缩,对灰度区间[a, b]进行扩展。通过细心调整折线拐点的位置及控制分段直线的斜率,可对任一灰度区间进行扩展或压缩。这种变换适用于在黑色或白色附近有噪声干扰的情况。例如, 照片中的划痕, 由于变换后在[0, a]以及[b, $M_f$ ]之间的灰度受到压缩, 因而使污斑得到减弱。
47 |
48 | ## 4.2.3 非线性变换
49 |
50 |  51 |
52 | ### S型函数
53 |
54 | $$
55 | \begin{aligned}
56 | & T(x)=\frac{L}{2}\left\{1+\frac{1}{\sin \left(\alpha \frac{\pi}{2}\right)} \sin \left[\alpha \pi\left(\frac{r}{L}-\frac{1}{2}\right)\right]\right\}
57 | & 0<\alpha<1 \\
58 | & ~T(x)=\frac{D_m}{2}\left\{1+\frac{1}{\tan \left(\alpha \frac{\pi}{2}\right)} \tan \left[\alpha \pi\left(\frac{x}{D_m}-\frac{1}{2}\right)\right]\right\}
59 | & 0<\alpha<1
60 | \end{aligned}
61 | $$
62 |
63 | ### 指数变换
64 |
65 | $$
66 | s=c y^\gamma
67 | $$
68 |
69 | $c$ 和 $y$ 为常数。
70 | 当 $\gamma<1$ 时, 具有扩展低亮度区、压缩高亮度区的效果;
71 | 当 $\gamma>1$ 时, 性能正好相反,具有压缩低亮度区、扩展高亮度区的效果。
72 | 而当 $c=\gamma=1$ 时, 输出正比与输入, 图像无变化。
73 | “ $\gamma$ 校正"(伽马校正),CRT显示器
74 |
75 | ### 显示器校正
76 |
77 | 
78 |
79 | 图6-23 不同$\gamma$的$s=cr^{\gamma}$曲线及图像变换结果
80 |
81 | 组合灰度变换效果与直方图变图像增强与平滑化
82 |
83 | ### 组合灰度变换效果与直方图变化
84 |
85 |
51 |
52 | ### S型函数
53 |
54 | $$
55 | \begin{aligned}
56 | & T(x)=\frac{L}{2}\left\{1+\frac{1}{\sin \left(\alpha \frac{\pi}{2}\right)} \sin \left[\alpha \pi\left(\frac{r}{L}-\frac{1}{2}\right)\right]\right\}
57 | & 0<\alpha<1 \\
58 | & ~T(x)=\frac{D_m}{2}\left\{1+\frac{1}{\tan \left(\alpha \frac{\pi}{2}\right)} \tan \left[\alpha \pi\left(\frac{x}{D_m}-\frac{1}{2}\right)\right]\right\}
59 | & 0<\alpha<1
60 | \end{aligned}
61 | $$
62 |
63 | ### 指数变换
64 |
65 | $$
66 | s=c y^\gamma
67 | $$
68 |
69 | $c$ 和 $y$ 为常数。
70 | 当 $\gamma<1$ 时, 具有扩展低亮度区、压缩高亮度区的效果;
71 | 当 $\gamma>1$ 时, 性能正好相反,具有压缩低亮度区、扩展高亮度区的效果。
72 | 而当 $c=\gamma=1$ 时, 输出正比与输入, 图像无变化。
73 | “ $\gamma$ 校正"(伽马校正),CRT显示器
74 |
75 | ### 显示器校正
76 |
77 | 
78 |
79 | 图6-23 不同$\gamma$的$s=cr^{\gamma}$曲线及图像变换结果
80 |
81 | 组合灰度变换效果与直方图变图像增强与平滑化
82 |
83 | ### 组合灰度变换效果与直方图变化
84 |
85 |  86 |
87 | ### 分段线性变换
88 |
89 | 
--------------------------------------------------------------------------------
/IV/4.4 图像噪声.md:
--------------------------------------------------------------------------------
1 | # 4.4 图像噪声
2 |
3 | 重点:均值滤波法s
4 |
5 | ## 4.4.1 概述
6 |
7 | 噪声可以理解为“妨碍人们感觉器官对所接收的信源信息理解的因素” 。例如,一幅黑白图像,其亮度分布假定为$f (x, y)$, 那么对其起干扰作用的亮度分布$R(x, y)$便称为图像噪声。噪声在理论上可以定义为“不可预测, 只能用概率统计方法来认识的随机误差” 。因此,将图像噪声看成是多维随机过程是合适的, 描述噪声的方法完全可以借用随机过程及其概率分布函数和概率密度函数。但在很多情况下,这种描述方法很复杂,甚至不可能,而且实际应用往往也不必要,通常是用其数字特征,即均值方差、相关函数等进行处理。
8 |
9 | 目前,大多数数字图像系统中,输入光图像都是采用先冻结再扫描方式将多维图像变成一维电信号,再对其进行处理、存储、 传输等加工,最后往往还要再组成多维图像信号。图像噪声同样也受到这样的分解和合成,在这些过程中电气系统和外界影响将使得图像噪声的精确分析变得十分复杂。另一方面, 对图像信息的认识和理解是由人的视觉系统所决定的。不同的图像噪声,人的感觉(理解)程度是不同的,这就是所谓人的噪声视觉特性问题。该方面虽早已进行研究,但终因人的视觉系统本身未搞清楚而未获得解决。尽管如此,图像噪声在数字图像处理技术中的重要性却愈加明显。例如,高放大倍数遥感图片的判读,X射线图像系统中的噪声去除等都已成为不可缺少的技术。
10 |
11 | ## 4.4.2 图像噪声分类
12 |
13 | 图像噪声按其产生的原因可分为外部噪声和内部噪声。
14 |
15 | 外部噪声是指系统外部干扰从电磁波或经电源传进系统内部而引起的噪声,如电气设备、天体放电现象等引起的噪声。 主要外部干扰如下:
16 |
17 | (1) 由光和电的基本性质所引起的噪声。
18 |
19 | (2) 电器的机械运动产生的噪声。如, 各种接头因抖动引起的电流变化所产生的噪声;磁头、磁带抖动引起的抖动噪声等。
20 |
21 | (3) 元器件材料本身引起的噪声。如, 磁带、磁盘表面缺陷所产生的噪声。
22 |
23 | (4) 系统内部设备电路所引起的噪声。如, 电源系统引入的交流噪声,偏转系统和箝位电路引起的噪声等。
24 |
25 | 图像噪声从统计特性可分为平稳噪声和非平稳噪声两种。 统计特性不随时间变化的噪声称为平稳噪声;统计特性随时间变化的噪声称为非平稳噪声
26 |
27 | 另外, 按噪声和信号之间的关系可分为加性噪声和乘性噪声。假定信号为 $S(t)$, 噪声为 $n(t)$, 如果混合叠加波形是 $S(t)+n(t)$ 形式, 则称其为加性噪声; 如果叠加波形为 $S(t)[1+n(t)]$ 形式, 则称其为乘性噪声。为了分析处理方便, 往往将乘性噪声近似认为加性噪声, 而且总是假定信号和噪声是互相独立的。
28 |
29 | ## 4.4.3 图像系统噪声特点
30 |
31 | 如图4-16是一幅含有噪声的图像, 由此可知图像中的噪声有以下三个特点。
32 |
33 | 1. 噪声在图像中的分布和大小不规则
34 | 2. 噪声与图像之间具有相关性
35 | 3. 噪声具有叠加性
36 |
37 | 
38 |
39 | 图4-16 有噪声的图像
--------------------------------------------------------------------------------
/IV/4.6 图像锐化.md:
--------------------------------------------------------------------------------
1 | # 4.6 图像锐化
2 |
3 | 需要使用高通滤波器,此时变化大的点为感兴趣的点
4 |
5 | **所谓锐化算法,就是利用图像的一阶微分信息,得到想要的信息**
6 |
7 | ## 4.6.1 微分法
8 |
9 | ### 梯度法
10 |
11 | 对于图像函数 $f(x, y)$, 它在点 $(x, y)$ 处的梯度是一个矢量, 定义为
12 | $$
13 | G[f(x, y)]=\left[\begin{array}{l}
14 | \frac{\partial f}{\partial x} \\
15 | \frac{\partial f}{\partial y}
16 | \end{array}\right] \tag{4-27}
17 | $$
18 | 梯度的两个重要性质是:
19 |
20 | (1) 梯度的方向在函数$f(x, y)$最大变化率的方向上。
21 |
22 | (2) 梯度的幅度用 $G[f(x, y)]$ 表示, 并由下式算出:
23 | $$
24 | G[f(x, y)]=\left[\left(\frac{\partial f}{\partial x}\right)^2+\left(\frac{\partial f}{\partial y}\right)^2\right]^{1 / 2}\tag{4-28}
25 | $$
26 | 由上式可知, 梯度的数值就是 $f(x, y)$ 在其最大变化率方向上的单位距离所增加的量。对于数字图像而言, 式(4-28)可以近似为
27 | $$
28 | G[f(x, y)]=\left\{[f(i, j)-f(i+1, j)]^2+[f(i, j)-f(i, j+1)]^2\right\}^{1 / 2}\tag{4-29}
29 | $$
30 | 式中: 各像素的位置如图4-28(a)所示。
31 |
32 | 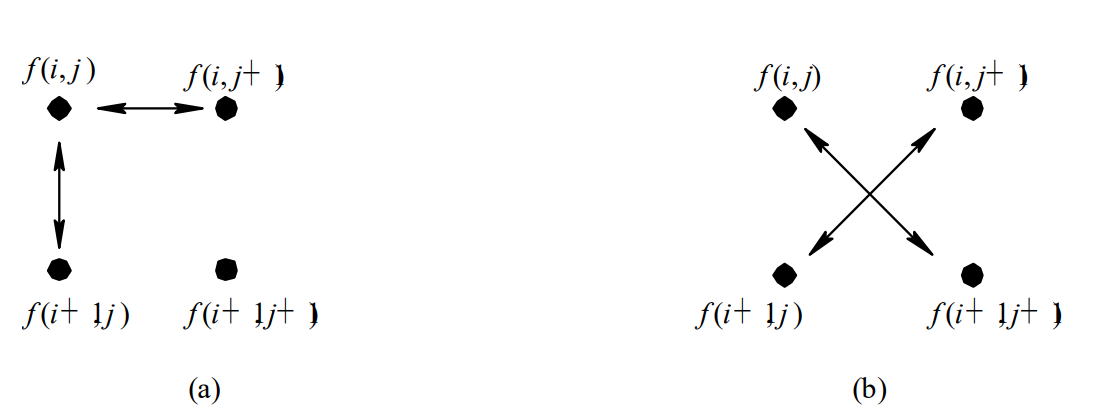
33 |
34 | 图4-28 求梯度的两种差分运算
35 |
36 | 式(4-29)可简化成为
37 | $$
38 | G[f(x, y)]=\left|f(i, j)-f(i+1, j)\right|+\left|f(i, j)-f(i, j+1)\right| \tag{4-30}
39 | $$
40 | 以上梯度法又称为水平垂直差分法。另一种梯度法叫做罗伯特梯度法 (Robert Gradient), 它是一种交叉差分计算法, 如图4-28(b)所示。其数学表达式为
41 | $$
42 | G[f(x, y)]=\left\{[f(i, j)-f(i+1, j+1)]^2+[f(i+1, j)-f(i, j+1)]^2\right\}^{1 / 2}\tag{4-31}
43 | $$
44 | 同样可近似为
45 | $$
46 | G[f(x, y)]=\mid\left[f(i, j)-f\left(i+1, j^{+1)}|+| f(i+1, j)-f(i, j+1)\right.\right.\tag{4-32}
47 | $$
48 | 以上两种梯度近似算法在图像的最后一行和最后一列的各像素的梯度无法求得,一般就用前一行和前一列的梯度值近似代替。
49 | 由梯度的计算可知,图像中灰度变化较大的边缘区域其梯度值大,在灰度变化平缓的区域其梯度值较小,而在灰度均匀区域其梯度值为零。图4-29(b)是采用水平垂直差分法对图4-29(a)锐化的结果,锐化后仅留下灰度值急剧变化的边沿处的点
50 |
51 | 
52 |
53 | 图4-29 图像梯度锐化结果
54 |
55 | (a) 二值图像; (b) 梯度运算结果
56 |
57 | 当梯度计算完之后,可以根据需要生成不同的梯度增强图像。 第一种是使各点的灰度$g(x, y)$等于该点的梯度幅度,即
58 | $$
59 | g(x, y)=G[f(x, y)]\tag{4-33}
60 | $$
61 | 此法的缺点是增强的图像仅显示灰度变化比较陡的边缘轮廓, 而灰度变化平缓的区域则呈黑色
62 |
63 | 第二种增强的图像是使
64 | $$
65 | g(x, y)= \begin{cases}G[f(x, y)] & G[f(x, y)] \geq T \\ f(x, y) & \text {其他 }\end{cases}\tag{4-34}
66 | $$
67 | 式中: $T$ 是一个非负的阈值, 适当选取 $T$, 即可使明显的边缘轮廓得到突出, 又不会破坏原灰度变化比较平缓的背景。
68 |
69 | 第三种增强图像是使
70 | $$
71 | g(x, y)= \begin{cases}L_G & G[f(x, y)] \geq T \\ f(x, y) & \text {其他 }\end{cases}\tag{4-35}
72 | $$
73 | 式中: $T$ 是根据需要指定的一个灰度级, 它将明显边缘用一固定的灰度级 $L_G$ 来实现。
74 |
75 | 第四种增强图像是使
76 | $$
77 | g(x, y)= \begin{cases}G[f(x, y)] & G[f(x, y)] \geq T \\ L_G & \text { 其他 }\end{cases}\tag{4-36}
78 | $$
79 | 此法将背景用一个固定灰度级 $L_G$ 来实现, 便于研究边缘灰度的变化。
80 |
81 | 第五种增强图像是使
82 | $$
83 | g(x, y)= \begin{cases}L_G & G[f(x, y)] \geq T \\ L_B & \text { 其他 }\end{cases}\tag{4-37}
84 | $$
85 | 此法将背景和边缘用二值图像表示, 便于研究边缘所在位置。
86 |
87 | ### Sobel算子
88 |
89 | 重点,很常用,目前国际上占据主流
90 |
91 | 采用梯度微分锐化图像,同时会使噪声、条纹等得到增强, Sobel算子则在一定程度上克服了这个问题。Sobel算子法的基本原理是: 按式(4-38)计算3×3窗口(如图4-30所示)的灰度, 将其作为变换后图像f(i, j)的灰度。
92 |
93 | 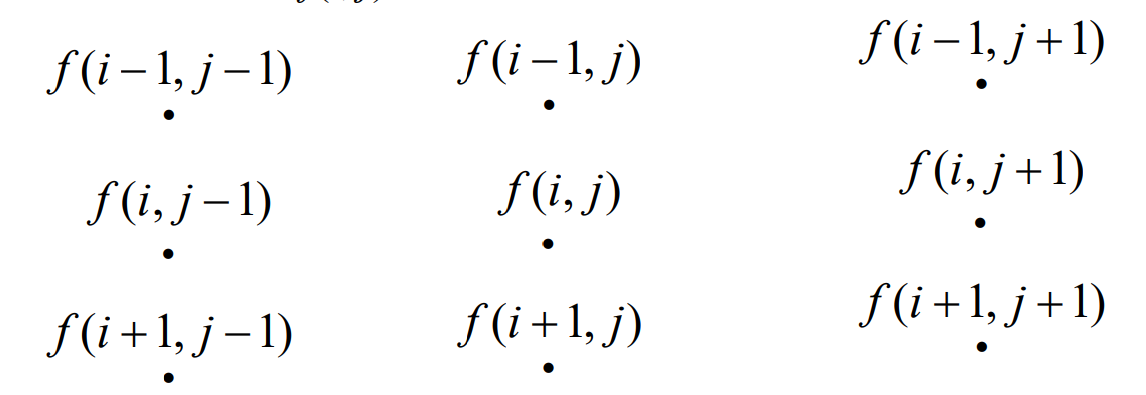
94 |
95 | 图4-30 Sobel算子图像坐标
96 | $$
97 | g=\sqrt{S_x^2+S_y^2}\tag{4-38}
98 | $$
99 | 式中:
100 | $$
101 | \begin{aligned}
102 | S_x & =[f(i+1, j-1)+2 f(i+1, j)+f(i+1, j+1)] \\
103 | & -[f(i-1, j-1)+2 f(i-1, j)+f(i-1, j+1)] \\
104 | S_y & =[f(i-1, j+1)+2 f(i, j+1)+f(i+1, j+1)] \\
105 | & -[f(i-1, j-1)+2 f(i, j-1)+f(i+1, j-1)]
106 | \end{aligned}
107 | $$
108 | 为简化计算, 可用 $\left.g=\left|S_{x}\right|\right]+\left|S_{y}\right|$ 来代替式(4-38), 从而得到锐化后的图像。Sobel算子不像普通梯度算子那样用两个像素的差值, 这就导致了以下两个优点:
109 | (1) 由于引入了平均因素, 因而对图像中的随机噪声有一定的平滑作用。
110 | (2) 由于它是相隔两行或两列之差分, 故边缘两侧元素得到了增强, 边缘显得粗而亮。
111 |
112 | Sobel锐化算法
113 | $$
114 | d_x=\left[\begin{array}{rrr}
115 | -1 & 0 & 1 \\
116 | -2 & 0 & 2 \\
117 | -1 & 0 & 1
118 | \end{array}\right]&d_y=\left[\begin{array}{ccc}
119 | -1 & -2 & -1 \\
120 | 0 & 0 & 0 \\
121 | 1 & 2 & 1
122 | \end{array}\right]\tag{4-39}
123 | $$
124 |
125 | $$
126 |
127 | $$
128 |
129 | Roberts梯度锐化效果图例
130 |
131 | 
132 |
133 | 为简化计算, 可用 $g=\left|S_{x}\right|+\left|S_{y}\right|$ 来代替式(4-38), 从而得到锐化后的图像。Sobel算子不像普通梯度算子那样用两个像素的差值, 这就导致了以下两个优点:
134 | (1) 由于引入了平均因素, 因而对图像中的随机噪声有一定的平滑作用。
135 | (2) 由于它是相隔两行或两列之差分, 故边缘两侧元素得到了增强, 边缘显得粗而亮。
136 |
137 | Roberts梯度锐化效果图例
138 |
139 |
86 |
87 | ### 分段线性变换
88 |
89 | 
--------------------------------------------------------------------------------
/IV/4.4 图像噪声.md:
--------------------------------------------------------------------------------
1 | # 4.4 图像噪声
2 |
3 | 重点:均值滤波法s
4 |
5 | ## 4.4.1 概述
6 |
7 | 噪声可以理解为“妨碍人们感觉器官对所接收的信源信息理解的因素” 。例如,一幅黑白图像,其亮度分布假定为$f (x, y)$, 那么对其起干扰作用的亮度分布$R(x, y)$便称为图像噪声。噪声在理论上可以定义为“不可预测, 只能用概率统计方法来认识的随机误差” 。因此,将图像噪声看成是多维随机过程是合适的, 描述噪声的方法完全可以借用随机过程及其概率分布函数和概率密度函数。但在很多情况下,这种描述方法很复杂,甚至不可能,而且实际应用往往也不必要,通常是用其数字特征,即均值方差、相关函数等进行处理。
8 |
9 | 目前,大多数数字图像系统中,输入光图像都是采用先冻结再扫描方式将多维图像变成一维电信号,再对其进行处理、存储、 传输等加工,最后往往还要再组成多维图像信号。图像噪声同样也受到这样的分解和合成,在这些过程中电气系统和外界影响将使得图像噪声的精确分析变得十分复杂。另一方面, 对图像信息的认识和理解是由人的视觉系统所决定的。不同的图像噪声,人的感觉(理解)程度是不同的,这就是所谓人的噪声视觉特性问题。该方面虽早已进行研究,但终因人的视觉系统本身未搞清楚而未获得解决。尽管如此,图像噪声在数字图像处理技术中的重要性却愈加明显。例如,高放大倍数遥感图片的判读,X射线图像系统中的噪声去除等都已成为不可缺少的技术。
10 |
11 | ## 4.4.2 图像噪声分类
12 |
13 | 图像噪声按其产生的原因可分为外部噪声和内部噪声。
14 |
15 | 外部噪声是指系统外部干扰从电磁波或经电源传进系统内部而引起的噪声,如电气设备、天体放电现象等引起的噪声。 主要外部干扰如下:
16 |
17 | (1) 由光和电的基本性质所引起的噪声。
18 |
19 | (2) 电器的机械运动产生的噪声。如, 各种接头因抖动引起的电流变化所产生的噪声;磁头、磁带抖动引起的抖动噪声等。
20 |
21 | (3) 元器件材料本身引起的噪声。如, 磁带、磁盘表面缺陷所产生的噪声。
22 |
23 | (4) 系统内部设备电路所引起的噪声。如, 电源系统引入的交流噪声,偏转系统和箝位电路引起的噪声等。
24 |
25 | 图像噪声从统计特性可分为平稳噪声和非平稳噪声两种。 统计特性不随时间变化的噪声称为平稳噪声;统计特性随时间变化的噪声称为非平稳噪声
26 |
27 | 另外, 按噪声和信号之间的关系可分为加性噪声和乘性噪声。假定信号为 $S(t)$, 噪声为 $n(t)$, 如果混合叠加波形是 $S(t)+n(t)$ 形式, 则称其为加性噪声; 如果叠加波形为 $S(t)[1+n(t)]$ 形式, 则称其为乘性噪声。为了分析处理方便, 往往将乘性噪声近似认为加性噪声, 而且总是假定信号和噪声是互相独立的。
28 |
29 | ## 4.4.3 图像系统噪声特点
30 |
31 | 如图4-16是一幅含有噪声的图像, 由此可知图像中的噪声有以下三个特点。
32 |
33 | 1. 噪声在图像中的分布和大小不规则
34 | 2. 噪声与图像之间具有相关性
35 | 3. 噪声具有叠加性
36 |
37 | 
38 |
39 | 图4-16 有噪声的图像
--------------------------------------------------------------------------------
/IV/4.6 图像锐化.md:
--------------------------------------------------------------------------------
1 | # 4.6 图像锐化
2 |
3 | 需要使用高通滤波器,此时变化大的点为感兴趣的点
4 |
5 | **所谓锐化算法,就是利用图像的一阶微分信息,得到想要的信息**
6 |
7 | ## 4.6.1 微分法
8 |
9 | ### 梯度法
10 |
11 | 对于图像函数 $f(x, y)$, 它在点 $(x, y)$ 处的梯度是一个矢量, 定义为
12 | $$
13 | G[f(x, y)]=\left[\begin{array}{l}
14 | \frac{\partial f}{\partial x} \\
15 | \frac{\partial f}{\partial y}
16 | \end{array}\right] \tag{4-27}
17 | $$
18 | 梯度的两个重要性质是:
19 |
20 | (1) 梯度的方向在函数$f(x, y)$最大变化率的方向上。
21 |
22 | (2) 梯度的幅度用 $G[f(x, y)]$ 表示, 并由下式算出:
23 | $$
24 | G[f(x, y)]=\left[\left(\frac{\partial f}{\partial x}\right)^2+\left(\frac{\partial f}{\partial y}\right)^2\right]^{1 / 2}\tag{4-28}
25 | $$
26 | 由上式可知, 梯度的数值就是 $f(x, y)$ 在其最大变化率方向上的单位距离所增加的量。对于数字图像而言, 式(4-28)可以近似为
27 | $$
28 | G[f(x, y)]=\left\{[f(i, j)-f(i+1, j)]^2+[f(i, j)-f(i, j+1)]^2\right\}^{1 / 2}\tag{4-29}
29 | $$
30 | 式中: 各像素的位置如图4-28(a)所示。
31 |
32 | 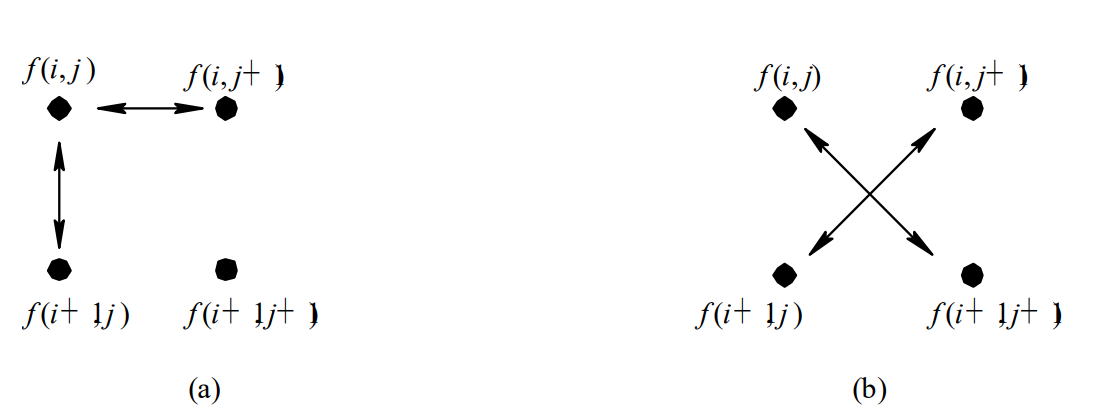
33 |
34 | 图4-28 求梯度的两种差分运算
35 |
36 | 式(4-29)可简化成为
37 | $$
38 | G[f(x, y)]=\left|f(i, j)-f(i+1, j)\right|+\left|f(i, j)-f(i, j+1)\right| \tag{4-30}
39 | $$
40 | 以上梯度法又称为水平垂直差分法。另一种梯度法叫做罗伯特梯度法 (Robert Gradient), 它是一种交叉差分计算法, 如图4-28(b)所示。其数学表达式为
41 | $$
42 | G[f(x, y)]=\left\{[f(i, j)-f(i+1, j+1)]^2+[f(i+1, j)-f(i, j+1)]^2\right\}^{1 / 2}\tag{4-31}
43 | $$
44 | 同样可近似为
45 | $$
46 | G[f(x, y)]=\mid\left[f(i, j)-f\left(i+1, j^{+1)}|+| f(i+1, j)-f(i, j+1)\right.\right.\tag{4-32}
47 | $$
48 | 以上两种梯度近似算法在图像的最后一行和最后一列的各像素的梯度无法求得,一般就用前一行和前一列的梯度值近似代替。
49 | 由梯度的计算可知,图像中灰度变化较大的边缘区域其梯度值大,在灰度变化平缓的区域其梯度值较小,而在灰度均匀区域其梯度值为零。图4-29(b)是采用水平垂直差分法对图4-29(a)锐化的结果,锐化后仅留下灰度值急剧变化的边沿处的点
50 |
51 | 
52 |
53 | 图4-29 图像梯度锐化结果
54 |
55 | (a) 二值图像; (b) 梯度运算结果
56 |
57 | 当梯度计算完之后,可以根据需要生成不同的梯度增强图像。 第一种是使各点的灰度$g(x, y)$等于该点的梯度幅度,即
58 | $$
59 | g(x, y)=G[f(x, y)]\tag{4-33}
60 | $$
61 | 此法的缺点是增强的图像仅显示灰度变化比较陡的边缘轮廓, 而灰度变化平缓的区域则呈黑色
62 |
63 | 第二种增强的图像是使
64 | $$
65 | g(x, y)= \begin{cases}G[f(x, y)] & G[f(x, y)] \geq T \\ f(x, y) & \text {其他 }\end{cases}\tag{4-34}
66 | $$
67 | 式中: $T$ 是一个非负的阈值, 适当选取 $T$, 即可使明显的边缘轮廓得到突出, 又不会破坏原灰度变化比较平缓的背景。
68 |
69 | 第三种增强图像是使
70 | $$
71 | g(x, y)= \begin{cases}L_G & G[f(x, y)] \geq T \\ f(x, y) & \text {其他 }\end{cases}\tag{4-35}
72 | $$
73 | 式中: $T$ 是根据需要指定的一个灰度级, 它将明显边缘用一固定的灰度级 $L_G$ 来实现。
74 |
75 | 第四种增强图像是使
76 | $$
77 | g(x, y)= \begin{cases}G[f(x, y)] & G[f(x, y)] \geq T \\ L_G & \text { 其他 }\end{cases}\tag{4-36}
78 | $$
79 | 此法将背景用一个固定灰度级 $L_G$ 来实现, 便于研究边缘灰度的变化。
80 |
81 | 第五种增强图像是使
82 | $$
83 | g(x, y)= \begin{cases}L_G & G[f(x, y)] \geq T \\ L_B & \text { 其他 }\end{cases}\tag{4-37}
84 | $$
85 | 此法将背景和边缘用二值图像表示, 便于研究边缘所在位置。
86 |
87 | ### Sobel算子
88 |
89 | 重点,很常用,目前国际上占据主流
90 |
91 | 采用梯度微分锐化图像,同时会使噪声、条纹等得到增强, Sobel算子则在一定程度上克服了这个问题。Sobel算子法的基本原理是: 按式(4-38)计算3×3窗口(如图4-30所示)的灰度, 将其作为变换后图像f(i, j)的灰度。
92 |
93 | 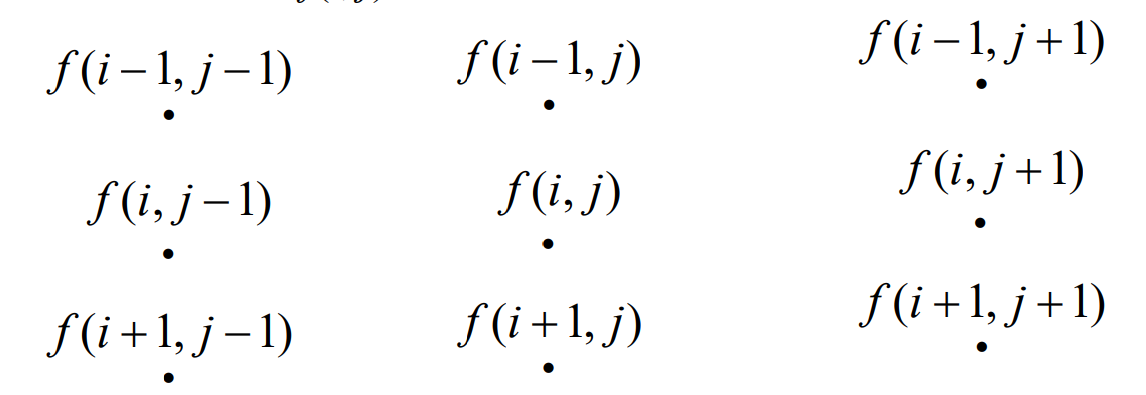
94 |
95 | 图4-30 Sobel算子图像坐标
96 | $$
97 | g=\sqrt{S_x^2+S_y^2}\tag{4-38}
98 | $$
99 | 式中:
100 | $$
101 | \begin{aligned}
102 | S_x & =[f(i+1, j-1)+2 f(i+1, j)+f(i+1, j+1)] \\
103 | & -[f(i-1, j-1)+2 f(i-1, j)+f(i-1, j+1)] \\
104 | S_y & =[f(i-1, j+1)+2 f(i, j+1)+f(i+1, j+1)] \\
105 | & -[f(i-1, j-1)+2 f(i, j-1)+f(i+1, j-1)]
106 | \end{aligned}
107 | $$
108 | 为简化计算, 可用 $\left.g=\left|S_{x}\right|\right]+\left|S_{y}\right|$ 来代替式(4-38), 从而得到锐化后的图像。Sobel算子不像普通梯度算子那样用两个像素的差值, 这就导致了以下两个优点:
109 | (1) 由于引入了平均因素, 因而对图像中的随机噪声有一定的平滑作用。
110 | (2) 由于它是相隔两行或两列之差分, 故边缘两侧元素得到了增强, 边缘显得粗而亮。
111 |
112 | Sobel锐化算法
113 | $$
114 | d_x=\left[\begin{array}{rrr}
115 | -1 & 0 & 1 \\
116 | -2 & 0 & 2 \\
117 | -1 & 0 & 1
118 | \end{array}\right]&d_y=\left[\begin{array}{ccc}
119 | -1 & -2 & -1 \\
120 | 0 & 0 & 0 \\
121 | 1 & 2 & 1
122 | \end{array}\right]\tag{4-39}
123 | $$
124 |
125 | $$
126 |
127 | $$
128 |
129 | Roberts梯度锐化效果图例
130 |
131 | 
132 |
133 | 为简化计算, 可用 $g=\left|S_{x}\right|+\left|S_{y}\right|$ 来代替式(4-38), 从而得到锐化后的图像。Sobel算子不像普通梯度算子那样用两个像素的差值, 这就导致了以下两个优点:
134 | (1) 由于引入了平均因素, 因而对图像中的随机噪声有一定的平滑作用。
135 | (2) 由于它是相隔两行或两列之差分, 故边缘两侧元素得到了增强, 边缘显得粗而亮。
136 |
137 | Roberts梯度锐化效果图例
138 |
139 |  140 |
141 | Priwitt锐化算法
142 | $$
143 | g(i, j)=\left\{d_x^2(i, j)+d_y^2(i, j)\right\}^{\frac{1}{2}}\tag{4-40}\\
144 | $$
145 | $$
146 | d_x=\left[\begin{array}{ccc}
147 | -1 & 0 & 1 \\
148 | -1 & 0 & 1 \\
149 | -1 & 0 & 1
150 | \end{array}\right]
151 | &d_y=\left[\begin{array}{ccc}
152 | -1 & -1 & -1 \\
153 | 0 & 0 & 0 \\
154 | 1 & 1 & 1
155 | \end{array}\right]
156 | $$
157 |
158 | 表4-2 常用的梯度算子
159 | $$
160 | \begin{array}{|l|l|l|ll|}
161 | \hline \text { 算子名称 } & H_1 & H_2 & \text { 特 } & \text { 点 } \\
162 | \hline \text { Roberts } & {\left[\begin{array}{cc}
163 | 0 * & 1 \\
164 | -1 & 0
165 | \end{array}\right]} & {\left[\begin{array}{cc}
166 | 1 * & 0 \\
167 | 0 & -1
168 | \end{array}\right]} & \text { 边缘定位准,但对噪声敏感 } \\
169 | \hline \text { Prewitt } & {\left[\begin{array}{ccc}
170 | -1 & 0 & 1 \\
171 | -1 & 0 * & 1 \\
172 | -1 & 0 & 1
173 | \end{array}\right]} & {\left[\begin{array}{ccc}
174 | -1 & -1 & 1 \\
175 | 0 & 0 * & 0 \\
176 | 1 & 1 & 1
177 | \end{array}\right]} & \text { 平均、微分对噪声有抑制作用 } \\
178 | \hline \text {Sobel } & {\left[\begin{array}{ccc}
179 | -1 & 0 & 1 \\
180 | -2 & 0 * & 2 \\
181 | -1 & 0 & 1
182 | \end{array}\right]} & {\left[\begin{array}{ccc}
183 | -1 & -1 & 1 \\
184 | 0 & 0 * & 0 \\
185 | 1 & 2 & 1
186 | \end{array}\right]} & 加权平均边宽 \geqslant 2 像素 \\
187 | \hline \text { Krisch } & {\left[\begin{array}{ccc}
188 | 5 & 5 & 5 \\
189 | -3 & 0 * & -3 \\
190 | -3 & -3 & -3
191 | \end{array}\right]} & {\left[\begin{array}{ccc}
192 | -3 & -3 & 5 \\
193 | -3 & 0 * & 5 \\
194 | -3 & -3 & 5
195 | \end{array}\right]} & 对噪声有较好地抑制作用。该算子需求出 f(x, y) 在 8 个方向上的平均差分的最大值, 这里只给出了 2 个方向的模板 \\
196 | \hline \text { Isotropic Sobel } & {\left[\begin{array}{ccc}
197 | -1 & 0 & 1 \\
198 | -\sqrt{2} & 0 * & \sqrt{2} \\
199 | -1 & 0 & 1
200 | \end{array}\right]} & {\left[\begin{array}{ccc}
201 | -1 & -1 & 1 \\
202 | 0 & 0 * & 0 \\
203 | 1 & \sqrt{2} & 1
204 | \end{array}\right]} & \text { 权值反比于领点与中心点的距离, 检测沿不同方向边缘时梯度幅度一致 } \\
205 | \hline
206 | \end{array}
207 | $$
208 | Prewitt锐化效果图例
209 |
210 | 
211 |
212 | 其他
213 |
214 | 一、单方向的一阶梯度算法(浮雕效果)
215 |
216 | 水平方向的锐化
217 |
218 | 
219 |
220 | 一阶水平方向锐化效果
221 |
222 | 
223 |
224 | 2. 垂直方向的锐化
225 |
226 | 
227 |
228 | 单方向一阶锐化效果图例
229 |
230 | 
231 |
232 |
140 |
141 | Priwitt锐化算法
142 | $$
143 | g(i, j)=\left\{d_x^2(i, j)+d_y^2(i, j)\right\}^{\frac{1}{2}}\tag{4-40}\\
144 | $$
145 | $$
146 | d_x=\left[\begin{array}{ccc}
147 | -1 & 0 & 1 \\
148 | -1 & 0 & 1 \\
149 | -1 & 0 & 1
150 | \end{array}\right]
151 | &d_y=\left[\begin{array}{ccc}
152 | -1 & -1 & -1 \\
153 | 0 & 0 & 0 \\
154 | 1 & 1 & 1
155 | \end{array}\right]
156 | $$
157 |
158 | 表4-2 常用的梯度算子
159 | $$
160 | \begin{array}{|l|l|l|ll|}
161 | \hline \text { 算子名称 } & H_1 & H_2 & \text { 特 } & \text { 点 } \\
162 | \hline \text { Roberts } & {\left[\begin{array}{cc}
163 | 0 * & 1 \\
164 | -1 & 0
165 | \end{array}\right]} & {\left[\begin{array}{cc}
166 | 1 * & 0 \\
167 | 0 & -1
168 | \end{array}\right]} & \text { 边缘定位准,但对噪声敏感 } \\
169 | \hline \text { Prewitt } & {\left[\begin{array}{ccc}
170 | -1 & 0 & 1 \\
171 | -1 & 0 * & 1 \\
172 | -1 & 0 & 1
173 | \end{array}\right]} & {\left[\begin{array}{ccc}
174 | -1 & -1 & 1 \\
175 | 0 & 0 * & 0 \\
176 | 1 & 1 & 1
177 | \end{array}\right]} & \text { 平均、微分对噪声有抑制作用 } \\
178 | \hline \text {Sobel } & {\left[\begin{array}{ccc}
179 | -1 & 0 & 1 \\
180 | -2 & 0 * & 2 \\
181 | -1 & 0 & 1
182 | \end{array}\right]} & {\left[\begin{array}{ccc}
183 | -1 & -1 & 1 \\
184 | 0 & 0 * & 0 \\
185 | 1 & 2 & 1
186 | \end{array}\right]} & 加权平均边宽 \geqslant 2 像素 \\
187 | \hline \text { Krisch } & {\left[\begin{array}{ccc}
188 | 5 & 5 & 5 \\
189 | -3 & 0 * & -3 \\
190 | -3 & -3 & -3
191 | \end{array}\right]} & {\left[\begin{array}{ccc}
192 | -3 & -3 & 5 \\
193 | -3 & 0 * & 5 \\
194 | -3 & -3 & 5
195 | \end{array}\right]} & 对噪声有较好地抑制作用。该算子需求出 f(x, y) 在 8 个方向上的平均差分的最大值, 这里只给出了 2 个方向的模板 \\
196 | \hline \text { Isotropic Sobel } & {\left[\begin{array}{ccc}
197 | -1 & 0 & 1 \\
198 | -\sqrt{2} & 0 * & \sqrt{2} \\
199 | -1 & 0 & 1
200 | \end{array}\right]} & {\left[\begin{array}{ccc}
201 | -1 & -1 & 1 \\
202 | 0 & 0 * & 0 \\
203 | 1 & \sqrt{2} & 1
204 | \end{array}\right]} & \text { 权值反比于领点与中心点的距离, 检测沿不同方向边缘时梯度幅度一致 } \\
205 | \hline
206 | \end{array}
207 | $$
208 | Prewitt锐化效果图例
209 |
210 | 
211 |
212 | 其他
213 |
214 | 一、单方向的一阶梯度算法(浮雕效果)
215 |
216 | 水平方向的锐化
217 |
218 | 
219 |
220 | 一阶水平方向锐化效果
221 |
222 | 
223 |
224 | 2. 垂直方向的锐化
225 |
226 | 
227 |
228 | 单方向一阶锐化效果图例
229 |
230 | 
231 |
232 |  233 |
234 | ## 4.6.2 拉普拉斯运算
235 |
236 | 拉普拉斯算子是常用的边缘增强算子,拉普拉斯运算也是偏导数运算的线性组合运算,而且是一种各向同性(旋转不变性)的线性运算。拉普拉斯算子为
237 | $$
238 | \nabla^2 f=\frac{\partial^2 f}{\partial x^2}+\frac{\partial^2 f}{\partial y^2}\tag{4-41}
239 | $$
240 | 如果图像的模糊是由扩散现象引起的 (如胶片颗粒化学扩散等), 则锐化后的图像 $g$ 为
241 | $$
242 | g=f-k \nabla^2 f\tag{4-42}
243 | $$
244 | 式中: $f 、 g$ 分别为锐化前后的图像, $k$ 为与扩散效应有关的系数。
245 |
246 | 式(4-42)表示模糊图像经拉普拉斯算子锐化以后得到新图像 $g \circ k$ 的选择要合理, 太大会使图像中的轮廓边缘产生过冲; $k$ 太小,锐化不明显。
247 | 对数字图像来讲, $f(x, y)$ 的二阶偏导数可表示为
248 | $$
249 | \begin{aligned}
250 | \frac{\partial^2 f(x, y)}{\partial x^2} & =\nabla_x f(i+1, j)-\nabla_x f(i, j) \\
251 | & =[f(i+1, j)-f(i, j)]-[f(i, j)-f(i-1), j] \\
252 | & =f(i+1, j)+f(i-1, j)-2 f(i, j) \\
253 | \end{aligned}
254 | $$
255 | $$
256 | \frac{\partial^2 f(x, y)}{\partial y^2} =f(i, j+1)+f(i, j-1)-2 f(i, j)\tag{4-43}
257 | $$
258 |
259 | 为此, 拉普拉斯算子 $\nabla^2 f$ 为
260 | $$
261 | \begin{aligned}
262 | \nabla^2 f & =\frac{\partial^2 f(x, y)}{\partial x^2}+\frac{\partial^2 f(x, y)}{\partial y^2} \\
263 | & =f(i+1, j)+f(i-1, j)+f(i, j+1)+f(i, j-1)-4 f(i, j) \\
264 | & =-5\left\{f(i, j)-\frac{1}{5}[f(i+1, j)+f(i-1, j)+f(i, j+1)\right. \\
265 | & +f(i, j-1)+f(i, j)]\}
266 | \end{aligned}\tag{4-44}
267 | $$
268 | 可见, 数字图像在 $(i, j)$ 点的拉普拉斯算子, 可以由 $(i, j)$ 点灰度值减去该点邻域平均灰度值来求得。当 $k=1$ 时, 拉普拉斯锐化后的图像为
269 | $$
270 | \begin{aligned}
271 | g(i, j) & =f(i, j)-\nabla^2 f(i, j) \\
272 | & =5 f(i, j)-f(i+1, j)-f(i-1, j)-f(i, j+1)-f(i, j-1)
273 | \end{aligned}\tag{4-45}
274 | $$
275 | ### Laplacian锐化算子
276 |
277 | 写成模板系数形式形式即为Laplacian算子:
278 | $$
279 | H_1=\left[\begin{array}{ccc}
280 | 0 & -1 & 0 \\
281 | -1 & 4 & -1 \\
282 | 0 & -1 & 0
283 | \end{array}\right]
284 | $$
285 | ### Laplacian变形算子
286 |
287 | $$
288 | H_2=\left[\begin{array}{ccc}
289 | -1 & -1 & -1 \\
290 | -1 & 8 & -1 \\
291 | -1 & -1 & -1
292 | \end{array}\right] \quad H_3=\left[\begin{array}{ccc}
293 | 1 & -2 & 1 \\
294 | -2 & 4 & -2 \\
295 | 1 & -2 & 1
296 | \end{array}\right] \quad H_4=\left[\begin{array}{ccc}
297 | 0 & -1 & 0 \\
298 | -1 & 5 & -1 \\
299 | 0 & -1 & 0
300 | \end{array}\right]
301 | $$
302 | 例:
303 |
304 | 设有 $1 \times n$ 的数字图像 $f(i, j)$, 其各点的灰度如下:
305 |
306 | $$
307 | \ldots, 0,0,0,1,2,3,4,5,5,5,5,5,5,6,6,6,6,6,6,3,3,3,3,3
308 | $$
309 |
310 | 计算 $\nabla^2 f$ 及锐化后的各点灰度值 $g$ (设 $\left.k=1\right)$ 。
311 |
312 | - 首先按式 (4-44)计算各点的 $\nabla^2 f$ 。例如:
313 |
314 | 第3点:
315 |
316 | $$
317 | \quad \nabla^2 f=-3\left[0-\frac{1}{3}(0+0+1)\right]=1
318 | $$
319 |
320 | 第8点:
321 |
322 | $$
323 | \quad \nabla^2 f=-3\left[5-\frac{1}{3}(4+4+5)\right]=-1
324 | $$
325 |
326 |
327 |
328 | 各点拉普拉斯算子如下:
329 |
330 | $$
331 | \ldots, 0,0,1,0,0,0,0,-1,0,0,0,0,1,-1,0,0,0,0,-3,3,0,0,0, \ldots
332 | $$
333 |
334 | - 按式(4-42)计算 $g=f-2 f$ 。例如:
335 |
336 | $$
337 | \begin{aligned}
338 | &第3点: g=f-\nabla^2 f=0-1=-1\\
339 | &\vdots \\
340 | &第8点: g=5-(-1)=6
341 | \end{aligned}
342 | $$
343 |
344 | 锐化后各点的灰度值如下:
345 |
346 | $$
347 | \ldots, 0,0,-1,1,2,3,4,6,5,5,5,5,4,7,6,6,6,6,9,0,3,3,3, \ldots
348 | $$
349 |
350 | 从上例可以看出,在灰度级斜坡底部(如第3点)和界线的低灰度级侧(如第13、20点)形成下冲。在灰度级斜坡顶部(如第8点)和界线的高灰度级侧(如第14、 19点)形成上冲。在灰度级平坦区域(如第9~12点, 第15~18点), 运算前后没有变化。如图4-31所示。
351 |
352 |
233 |
234 | ## 4.6.2 拉普拉斯运算
235 |
236 | 拉普拉斯算子是常用的边缘增强算子,拉普拉斯运算也是偏导数运算的线性组合运算,而且是一种各向同性(旋转不变性)的线性运算。拉普拉斯算子为
237 | $$
238 | \nabla^2 f=\frac{\partial^2 f}{\partial x^2}+\frac{\partial^2 f}{\partial y^2}\tag{4-41}
239 | $$
240 | 如果图像的模糊是由扩散现象引起的 (如胶片颗粒化学扩散等), 则锐化后的图像 $g$ 为
241 | $$
242 | g=f-k \nabla^2 f\tag{4-42}
243 | $$
244 | 式中: $f 、 g$ 分别为锐化前后的图像, $k$ 为与扩散效应有关的系数。
245 |
246 | 式(4-42)表示模糊图像经拉普拉斯算子锐化以后得到新图像 $g \circ k$ 的选择要合理, 太大会使图像中的轮廓边缘产生过冲; $k$ 太小,锐化不明显。
247 | 对数字图像来讲, $f(x, y)$ 的二阶偏导数可表示为
248 | $$
249 | \begin{aligned}
250 | \frac{\partial^2 f(x, y)}{\partial x^2} & =\nabla_x f(i+1, j)-\nabla_x f(i, j) \\
251 | & =[f(i+1, j)-f(i, j)]-[f(i, j)-f(i-1), j] \\
252 | & =f(i+1, j)+f(i-1, j)-2 f(i, j) \\
253 | \end{aligned}
254 | $$
255 | $$
256 | \frac{\partial^2 f(x, y)}{\partial y^2} =f(i, j+1)+f(i, j-1)-2 f(i, j)\tag{4-43}
257 | $$
258 |
259 | 为此, 拉普拉斯算子 $\nabla^2 f$ 为
260 | $$
261 | \begin{aligned}
262 | \nabla^2 f & =\frac{\partial^2 f(x, y)}{\partial x^2}+\frac{\partial^2 f(x, y)}{\partial y^2} \\
263 | & =f(i+1, j)+f(i-1, j)+f(i, j+1)+f(i, j-1)-4 f(i, j) \\
264 | & =-5\left\{f(i, j)-\frac{1}{5}[f(i+1, j)+f(i-1, j)+f(i, j+1)\right. \\
265 | & +f(i, j-1)+f(i, j)]\}
266 | \end{aligned}\tag{4-44}
267 | $$
268 | 可见, 数字图像在 $(i, j)$ 点的拉普拉斯算子, 可以由 $(i, j)$ 点灰度值减去该点邻域平均灰度值来求得。当 $k=1$ 时, 拉普拉斯锐化后的图像为
269 | $$
270 | \begin{aligned}
271 | g(i, j) & =f(i, j)-\nabla^2 f(i, j) \\
272 | & =5 f(i, j)-f(i+1, j)-f(i-1, j)-f(i, j+1)-f(i, j-1)
273 | \end{aligned}\tag{4-45}
274 | $$
275 | ### Laplacian锐化算子
276 |
277 | 写成模板系数形式形式即为Laplacian算子:
278 | $$
279 | H_1=\left[\begin{array}{ccc}
280 | 0 & -1 & 0 \\
281 | -1 & 4 & -1 \\
282 | 0 & -1 & 0
283 | \end{array}\right]
284 | $$
285 | ### Laplacian变形算子
286 |
287 | $$
288 | H_2=\left[\begin{array}{ccc}
289 | -1 & -1 & -1 \\
290 | -1 & 8 & -1 \\
291 | -1 & -1 & -1
292 | \end{array}\right] \quad H_3=\left[\begin{array}{ccc}
293 | 1 & -2 & 1 \\
294 | -2 & 4 & -2 \\
295 | 1 & -2 & 1
296 | \end{array}\right] \quad H_4=\left[\begin{array}{ccc}
297 | 0 & -1 & 0 \\
298 | -1 & 5 & -1 \\
299 | 0 & -1 & 0
300 | \end{array}\right]
301 | $$
302 | 例:
303 |
304 | 设有 $1 \times n$ 的数字图像 $f(i, j)$, 其各点的灰度如下:
305 |
306 | $$
307 | \ldots, 0,0,0,1,2,3,4,5,5,5,5,5,5,6,6,6,6,6,6,3,3,3,3,3
308 | $$
309 |
310 | 计算 $\nabla^2 f$ 及锐化后的各点灰度值 $g$ (设 $\left.k=1\right)$ 。
311 |
312 | - 首先按式 (4-44)计算各点的 $\nabla^2 f$ 。例如:
313 |
314 | 第3点:
315 |
316 | $$
317 | \quad \nabla^2 f=-3\left[0-\frac{1}{3}(0+0+1)\right]=1
318 | $$
319 |
320 | 第8点:
321 |
322 | $$
323 | \quad \nabla^2 f=-3\left[5-\frac{1}{3}(4+4+5)\right]=-1
324 | $$
325 |
326 |
327 |
328 | 各点拉普拉斯算子如下:
329 |
330 | $$
331 | \ldots, 0,0,1,0,0,0,0,-1,0,0,0,0,1,-1,0,0,0,0,-3,3,0,0,0, \ldots
332 | $$
333 |
334 | - 按式(4-42)计算 $g=f-2 f$ 。例如:
335 |
336 | $$
337 | \begin{aligned}
338 | &第3点: g=f-\nabla^2 f=0-1=-1\\
339 | &\vdots \\
340 | &第8点: g=5-(-1)=6
341 | \end{aligned}
342 | $$
343 |
344 | 锐化后各点的灰度值如下:
345 |
346 | $$
347 | \ldots, 0,0,-1,1,2,3,4,6,5,5,5,5,4,7,6,6,6,6,9,0,3,3,3, \ldots
348 | $$
349 |
350 | 从上例可以看出,在灰度级斜坡底部(如第3点)和界线的低灰度级侧(如第13、20点)形成下冲。在灰度级斜坡顶部(如第8点)和界线的高灰度级侧(如第14、 19点)形成上冲。在灰度级平坦区域(如第9~12点, 第15~18点), 运算前后没有变化。如图4-31所示。
351 |
352 |  353 |
354 | 图4-31 拉普拉斯锐化前、 后图像的灰度
355 | (a) 原图像灰度; (b) 拉普拉斯锐化后图像的灰度
356 |
357 |
353 |
354 | 图4-31 拉普拉斯锐化前、 后图像的灰度
355 | (a) 原图像灰度; (b) 拉普拉斯锐化后图像的灰度
356 |
357 |  358 |
359 | 图4-33 拉普拉斯锐化结果
360 | (a) 二值图像; (b) 拉普拉斯运算结果
361 |
362 | Laplacian锐化算子效果
363 |
364 | 
365 |
366 | 
367 |
368 | Wallis算子
369 | $$
370 | g(i, j)=\log [f(i, j)]-\frac{1}{4} s \\
371 | s=[\log f(i-1, j)+\log f(i+1, j)+\log f(i, j-1)+\log f(i, j+1)
372 | $$
373 | 它可以看作是校正了视觉的指数特性后的Laplacian运算。
374 | $$
375 | H_1=\left[\begin{array}{ccc}
376 | 0 & -1 & 0 \\
377 | -1 & 4 & -1 \\
378 | 0 & -1 & 0
379 | \end{array}\right]
380 | \Rightarrow
381 | H_1=\left[\begin{array}{ccc}
382 | 0 & -\dfrac{1}{4} & 0 \\
383 | -\dfrac{1}{4} & 1 & -\dfrac{1}{4} \\
384 | 0 & -\dfrac{1}{4} & 0
385 | \end{array}\right]
386 | $$
387 | Wallis算法效果图
388 |
389 |
358 |
359 | 图4-33 拉普拉斯锐化结果
360 | (a) 二值图像; (b) 拉普拉斯运算结果
361 |
362 | Laplacian锐化算子效果
363 |
364 | 
365 |
366 | 
367 |
368 | Wallis算子
369 | $$
370 | g(i, j)=\log [f(i, j)]-\frac{1}{4} s \\
371 | s=[\log f(i-1, j)+\log f(i+1, j)+\log f(i, j-1)+\log f(i, j+1)
372 | $$
373 | 它可以看作是校正了视觉的指数特性后的Laplacian运算。
374 | $$
375 | H_1=\left[\begin{array}{ccc}
376 | 0 & -1 & 0 \\
377 | -1 & 4 & -1 \\
378 | 0 & -1 & 0
379 | \end{array}\right]
380 | \Rightarrow
381 | H_1=\left[\begin{array}{ccc}
382 | 0 & -\dfrac{1}{4} & 0 \\
383 | -\dfrac{1}{4} & 1 & -\dfrac{1}{4} \\
384 | 0 & -\dfrac{1}{4} & 0
385 | \end{array}\right]
386 | $$
387 | Wallis算法效果图
388 |
389 |  390 |
391 | 
392 |
393 | 图4-34 3种频域高通滤波特性曲线
394 | (a) IHPF特征曲线; (b) BHPF特征曲线; (c) EHPF特征曲线
--------------------------------------------------------------------------------
/IV/4.7 图像的伪彩色处理.md:
--------------------------------------------------------------------------------
1 | # 4.7 图像的伪彩色处理
2 |
3 | ## 4.7.1 密度分割
4 |
5 | 密度分割是伪彩色处理技术中最简单的一种。设一幅灰度图像 $f(x, y)$, 在某一个灰度级 (如 $\left.f(x, y)=L_1\right)$ 上设置一个平行于 $x y$ 平面的切割平面, 如图4-35所示。灰度图像被切割成只有两个灰度级, 对切割平面以下的 (灰度级小于 $L_1$ ) 像素分配给一种颜色 (如蓝色), 对切割平面以上的像素分配给另一种颜色 (如红色)。这样切割结果就可以将灰度图像变为只有两个颜色的伪彩色图像。
6 |
7 | 若将灰度图像级用 $M$ 个切割平面去切割。就会得到 $M+1$ 个不同灰度级的区域 $S_1, S_2, \ldots, S_{M}, S_{M+1}$ 。对这 $M+1$ 个区域中的像素人为分配给 $M+1$ 种不同颜色, 就可以得到具有 $M+1$ 种颜色的伪彩色图像, 如图4-36所示。密度分割伪彩色处理的优点是简单易行, 便于用软件或硬件实现。还可以扩大它的用途, 如计算图像中某灰度级面积等。
8 |
9 |
390 |
391 | 
392 |
393 | 图4-34 3种频域高通滤波特性曲线
394 | (a) IHPF特征曲线; (b) BHPF特征曲线; (c) EHPF特征曲线
--------------------------------------------------------------------------------
/IV/4.7 图像的伪彩色处理.md:
--------------------------------------------------------------------------------
1 | # 4.7 图像的伪彩色处理
2 |
3 | ## 4.7.1 密度分割
4 |
5 | 密度分割是伪彩色处理技术中最简单的一种。设一幅灰度图像 $f(x, y)$, 在某一个灰度级 (如 $\left.f(x, y)=L_1\right)$ 上设置一个平行于 $x y$ 平面的切割平面, 如图4-35所示。灰度图像被切割成只有两个灰度级, 对切割平面以下的 (灰度级小于 $L_1$ ) 像素分配给一种颜色 (如蓝色), 对切割平面以上的像素分配给另一种颜色 (如红色)。这样切割结果就可以将灰度图像变为只有两个颜色的伪彩色图像。
6 |
7 | 若将灰度图像级用 $M$ 个切割平面去切割。就会得到 $M+1$ 个不同灰度级的区域 $S_1, S_2, \ldots, S_{M}, S_{M+1}$ 。对这 $M+1$ 个区域中的像素人为分配给 $M+1$ 种不同颜色, 就可以得到具有 $M+1$ 种颜色的伪彩色图像, 如图4-36所示。密度分割伪彩色处理的优点是简单易行, 便于用软件或硬件实现。还可以扩大它的用途, 如计算图像中某灰度级面积等。
8 |
9 |  10 |
11 | 图4-35 密度分割示意图
12 |
13 |
10 |
11 | 图4-35 密度分割示意图
12 |
13 |  14 |
15 | 图4-36 多灰度伪彩色分割示意图
16 |
17 | ## 4.7.2 灰度级彩色变换
18 |
19 | 这种伪彩色处理技术(在遥感技术中常称为假彩色合成方法),可以将灰度图像变为具有多种颜色渐变的连续彩色图像, 实际图像的连续伪彩色变换如图4-37所示。其变换过程为:将灰度图像送入具有不同变换特性的红、绿、蓝3个变换器,再将3 个变换器的不同输出分别送到彩色显像管的红、绿、蓝电子枪。 同一灰度由3个变换器对其实施不同变换, 而使3个变换器输出不同,从而在彩色显像管里合成某种色彩。可见,不同大小灰度级一定可以合成不同色彩。
20 |
21 | 
22 |
23 | 图4-37 伪彩色变换
24 |
25 | 从图中可见, 若 $f(x, y)=0$, 则 $I_B(x, y)=L, I_R(x, y)=I_{G}(x, y)=0$, 从而显示蓝色。同样, 若 $f(x, y)=L / 2$, 则 $I_G(x, y)=L, I_R(x, y)=I_G(x$, $y)=0$, 从而显示绿色。若 $f(x, y)=L$, 则 $I_R(x, y)=L, I_B(x, y)=I_G(x$, $y)=0$, 从而显示红色。
26 | 因此不难理解, 若灰度图像 $f(x, y)$ 灰度级在 $0 \sim L$ 之间变化, $I_R 、 I_B 、 I_G$ 会有不同输出, 从而合成不同的彩色图像。
27 |
28 | ## 4.7.3 滤波法
29 |
30 | 这是一种在频率域进行伪彩色处理的技术,与上面不同的是输出图像的伪彩色与图像的灰度级无关, 而是取决于图像中不同空间频率域成分。如, 为了突出图像中高频成分(图像细节)将其变为红色,只要将红色通道滤波器设计成高通特性即可。而且可以结合其他处理方法,在附加处理中实施(如直方图修正等),使其彩色对比度更强。如果要抑制图像中某种频率成分,可以设计一个带阻滤波器。其过程如图4-38所示,从3个不同频率的滤波器输出的信号再经过傅立叶反变换,可以对其做进一步的处理,如直方图均衡化。最后把它们作为三基色分别加到彩色显像管的红、绿、蓝显示通道,从而实现频率域的伪彩色处理。
31 |
32 |
14 |
15 | 图4-36 多灰度伪彩色分割示意图
16 |
17 | ## 4.7.2 灰度级彩色变换
18 |
19 | 这种伪彩色处理技术(在遥感技术中常称为假彩色合成方法),可以将灰度图像变为具有多种颜色渐变的连续彩色图像, 实际图像的连续伪彩色变换如图4-37所示。其变换过程为:将灰度图像送入具有不同变换特性的红、绿、蓝3个变换器,再将3 个变换器的不同输出分别送到彩色显像管的红、绿、蓝电子枪。 同一灰度由3个变换器对其实施不同变换, 而使3个变换器输出不同,从而在彩色显像管里合成某种色彩。可见,不同大小灰度级一定可以合成不同色彩。
20 |
21 | 
22 |
23 | 图4-37 伪彩色变换
24 |
25 | 从图中可见, 若 $f(x, y)=0$, 则 $I_B(x, y)=L, I_R(x, y)=I_{G}(x, y)=0$, 从而显示蓝色。同样, 若 $f(x, y)=L / 2$, 则 $I_G(x, y)=L, I_R(x, y)=I_G(x$, $y)=0$, 从而显示绿色。若 $f(x, y)=L$, 则 $I_R(x, y)=L, I_B(x, y)=I_G(x$, $y)=0$, 从而显示红色。
26 | 因此不难理解, 若灰度图像 $f(x, y)$ 灰度级在 $0 \sim L$ 之间变化, $I_R 、 I_B 、 I_G$ 会有不同输出, 从而合成不同的彩色图像。
27 |
28 | ## 4.7.3 滤波法
29 |
30 | 这是一种在频率域进行伪彩色处理的技术,与上面不同的是输出图像的伪彩色与图像的灰度级无关, 而是取决于图像中不同空间频率域成分。如, 为了突出图像中高频成分(图像细节)将其变为红色,只要将红色通道滤波器设计成高通特性即可。而且可以结合其他处理方法,在附加处理中实施(如直方图修正等),使其彩色对比度更强。如果要抑制图像中某种频率成分,可以设计一个带阻滤波器。其过程如图4-38所示,从3个不同频率的滤波器输出的信号再经过傅立叶反变换,可以对其做进一步的处理,如直方图均衡化。最后把它们作为三基色分别加到彩色显像管的红、绿、蓝显示通道,从而实现频率域的伪彩色处理。
31 |
32 |  33 |
34 | 图4-38 频率域伪彩色增强处理
--------------------------------------------------------------------------------
/IV/4.8 常见滤波器.md:
--------------------------------------------------------------------------------
1 | # 4.8常见滤波器
2 |
3 | ## 4.8.1频域低通滤波
4 |
5 | ### ILPF
6 |
7 | $$
8 | \begin{aligned}
9 | & H(u, v)=\left\{\begin{array}{l}
10 | 1, \text { ifD }(u, v) \leq D_0 \\
11 | 0, \text { ifD }(u, v)>D_0
12 | \end{array}\right. \\
13 | & D(u, v)=\sqrt{u^2+v^2}
14 | \end{aligned}
15 | $$
16 |
17 |
33 |
34 | 图4-38 频率域伪彩色增强处理
--------------------------------------------------------------------------------
/IV/4.8 常见滤波器.md:
--------------------------------------------------------------------------------
1 | # 4.8常见滤波器
2 |
3 | ## 4.8.1频域低通滤波
4 |
5 | ### ILPF
6 |
7 | $$
8 | \begin{aligned}
9 | & H(u, v)=\left\{\begin{array}{l}
10 | 1, \text { ifD }(u, v) \leq D_0 \\
11 | 0, \text { ifD }(u, v)>D_0
12 | \end{array}\right. \\
13 | & D(u, v)=\sqrt{u^2+v^2}
14 | \end{aligned}
15 | $$
16 |
17 |  18 |
19 | 图4-39理想低通滤波器(a)变换函数透视图;(b)图像方式显示的滤波器(c)滤波器的剖面图
20 |
21 | 截止频率与所保留能量的关系
22 | $$
23 | E_T=\sum_{u=0}^{N-1} \sum_{v=0}^{N-1} E(u, v) \\
24 | E(u, v)=R^2(u, v)+I^2(u, v) \\
25 | \beta=100\left[\sum_u \sum_v E(u, v) / E_T\right] \\
26 | $$
27 |
18 |
19 | 图4-39理想低通滤波器(a)变换函数透视图;(b)图像方式显示的滤波器(c)滤波器的剖面图
20 |
21 | 截止频率与所保留能量的关系
22 | $$
23 | E_T=\sum_{u=0}^{N-1} \sum_{v=0}^{N-1} E(u, v) \\
24 | E(u, v)=R^2(u, v)+I^2(u, v) \\
25 | \beta=100\left[\sum_u \sum_v E(u, v) / E_T\right] \\
26 | $$
27 |  28 |
29 |
30 |
31 | 图4-40低通滤波器的能量与$D_0$的关系(a)尺寸为$500\times500$像素的图像(b)图像的Fourier谱。叠加的圆环分别具有5、15、30、80、230像素的半径,分别包含的能量为90.0%、94.6%、96.4%、98.0%、99.55%
32 |
33 | IHPF的图像处理效果
34 |
35 | 
36 |
37 | 图4-41 图像4-39(a)经过理想低通滤波器的结果,
38 | 对应的半径分别为15、30、80,滤去的能量为5.4%、3.6%、2%。
39 |
40 | ### 振铃效应
41 |
42 | $$
43 | G(u,v)=H(u,v)F(u,v)\\
44 | g(x,y)=h(x,y)*f(x,y)
45 | $$
46 |
47 |
48 |
49 |
28 |
29 |
30 |
31 | 图4-40低通滤波器的能量与$D_0$的关系(a)尺寸为$500\times500$像素的图像(b)图像的Fourier谱。叠加的圆环分别具有5、15、30、80、230像素的半径,分别包含的能量为90.0%、94.6%、96.4%、98.0%、99.55%
32 |
33 | IHPF的图像处理效果
34 |
35 | 
36 |
37 | 图4-41 图像4-39(a)经过理想低通滤波器的结果,
38 | 对应的半径分别为15、30、80,滤去的能量为5.4%、3.6%、2%。
39 |
40 | ### 振铃效应
41 |
42 | $$
43 | G(u,v)=H(u,v)F(u,v)\\
44 | g(x,y)=h(x,y)*f(x,y)
45 | $$
46 |
47 |
48 |
49 |  50 |
51 | 图4-42(a)半径为5的脉冲图像 (b)相应的空间滤波器
52 |
53 | (c)空域的5个脉冲(d)滤波结果
54 |
55 | 滤波器1
56 |
57 |
50 |
51 | 图4-42(a)半径为5的脉冲图像 (b)相应的空间滤波器
52 |
53 | (c)空域的5个脉冲(d)滤波结果
54 |
55 | 滤波器1
56 |
57 |  58 |
59 | 滤波器2
60 |
61 |
58 |
59 | 滤波器2
60 |
61 |  62 |
63 | ### 巴特沃思滤波器Butterworth
64 |
65 | BLPF:
66 | $$
67 | H(u, v)=\frac{1}{1+\left[D(u, v) / D_0\right]^{2 n}}
68 | $$
69 | 
70 |
71 | 图4-43 BLPF特性曲线
72 |
73 | BLPF的滤波结果
74 |
75 |
62 |
63 | ### 巴特沃思滤波器Butterworth
64 |
65 | BLPF:
66 | $$
67 | H(u, v)=\frac{1}{1+\left[D(u, v) / D_0\right]^{2 n}}
68 | $$
69 | 
70 |
71 | 图4-43 BLPF特性曲线
72 |
73 | BLPF的滤波结果
74 |
75 |  76 |
77 | 图4-44 二阶BLPF滤波的结果(a)原图像,
78 | (b)半径15,(b)半径30,(d)半径80
79 |
80 | ### 指数滤波器或高斯滤波器
81 |
82 | ELPF:
83 | $$
84 | H(u, v)=e^{-\left[D(u, v) / D_0\right]^n}
85 | $$
86 |
76 |
77 | 图4-44 二阶BLPF滤波的结果(a)原图像,
78 | (b)半径15,(b)半径30,(d)半径80
79 |
80 | ### 指数滤波器或高斯滤波器
81 |
82 | ELPF:
83 | $$
84 | H(u, v)=e^{-\left[D(u, v) / D_0\right]^n}
85 | $$
86 |  87 |
88 | 图4-45高斯滤波器(a)传递函数的透视图;(b)图像形式;(c)径向剖面图
89 |
90 | ELPF的滤波效果
91 |
92 |
87 |
88 | 图4-45高斯滤波器(a)传递函数的透视图;(b)图像形式;(c)径向剖面图
89 |
90 | ELPF的滤波效果
91 |
92 |  93 |
94 | 图4-46 高斯滤波器的处理效果,
95 | 从左到右依次为原图、半径15、30、80
96 |
97 | ## 4.8.2高通滤波器
98 |
99 |
93 |
94 | 图4-46 高斯滤波器的处理效果,
95 | 从左到右依次为原图、半径15、30、80
96 |
97 | ## 4.8.2高通滤波器
98 |
99 |  100 |
101 | 图4-47 三种典型的高通滤波器,从上到下依次为理想高通滤波器、巴特沃思高通滤波器、指数滤波器。
102 |
103 | ### 高通滤波器定义
104 |
105 | IHPF:
106 | $$
107 | H(u, v)=\left\{\begin{array}{l}
108 | 0, \text { if } D(u, v) \leq D_{0 ;} \\
109 | 1, \text { if } D(u, v)>D_0 .
110 | \end{array} \quad D(u, v)=\sqrt{u^2+v^2}\right.\\
111 | $$
112 | BHPF:
113 | $$
114 | H(u, v)=\frac{1}{1+\left[D_0 / D(u, v)\right]^{2 n}}
115 | $$
116 | EHPF:
117 | $$
118 | H(u, v)=e^{-\left[D_0 / D(u, v)\right]^{n}}
119 | $$
120 | THPF:
121 | $$
122 | H(u, v)=\left\{\begin{array}{lr}
123 | 0 & D(u, v)
100 |
101 | 图4-47 三种典型的高通滤波器,从上到下依次为理想高通滤波器、巴特沃思高通滤波器、指数滤波器。
102 |
103 | ### 高通滤波器定义
104 |
105 | IHPF:
106 | $$
107 | H(u, v)=\left\{\begin{array}{l}
108 | 0, \text { if } D(u, v) \leq D_{0 ;} \\
109 | 1, \text { if } D(u, v)>D_0 .
110 | \end{array} \quad D(u, v)=\sqrt{u^2+v^2}\right.\\
111 | $$
112 | BHPF:
113 | $$
114 | H(u, v)=\frac{1}{1+\left[D_0 / D(u, v)\right]^{2 n}}
115 | $$
116 | EHPF:
117 | $$
118 | H(u, v)=e^{-\left[D_0 / D(u, v)\right]^{n}}
119 | $$
120 | THPF:
121 | $$
122 | H(u, v)=\left\{\begin{array}{lr}
123 | 0 & D(u, v) 131 |
132 | 高通滤波器效果
133 |
134 |
131 |
132 | 高通滤波器效果
133 |
134 |  135 |
136 | 图4-48 理想高通滤波效果,从左到右依次为$D_0$=15,30,80。越小,振铃效应越明显
137 |
138 |
135 |
136 | 图4-48 理想高通滤波效果,从左到右依次为$D_0$=15,30,80。越小,振铃效应越明显
137 |
138 |  139 |
140 | 图4-49 BHPF效果,从左到右依次为$D_0$=15,30,80。比IHPF的结果平滑得多
141 |
142 |
139 |
140 | 图4-49 BHPF效果,从左到右依次为$D_0$=15,30,80。比IHPF的结果平滑得多
141 |
142 |  143 |
144 | 图5-50高斯高通滤波效果,从左到右依次为$D_0$=15,30,80。
145 |
146 | ### 高频加强
147 |
148 | $$
149 | \begin{aligned}
150 | & H^{\prime}(u, v)=H(u, v)+c, 0
143 |
144 | 图5-50高斯高通滤波效果,从左到右依次为$D_0$=15,30,80。
145 |
146 | ### 高频加强
147 |
148 | $$
149 | \begin{aligned}
150 | & H^{\prime}(u, v)=H(u, v)+c, 0 170 |
171 | ### 不围绕原点的情况
172 |
173 | $$
174 | H(u,v)=\begin{cases}
175 | 0 &&if\,\,D_1(u,v)\leq D_0 \,\,or\,\, D_2(u,v)\leq D_0\\
176 | 1&& else
177 | \end{cases}
178 | $$
179 |
180 |
181 | $$
182 | \begin{aligned}
183 | &\begin{aligned}
184 | & D_1(u, v)=\left\{\left(u-u_0\right)^2+\left(v-v_0\right)^2\right\}^{1 / 2} \\
185 | &
186 | \end{aligned}\\
187 | &D_2(u, v)=\left\{\left(u+u_0\right)^2+\left(v+v_0\right)^2\right\}^{1 / 2}
188 | \end{aligned}
189 | $$
190 |
191 | ### 围绕原点的模型
192 |
193 | 为消去围绕原点的一个频带,必须考虑周期性和对称性。一个径向对称(放射对称)的理想带阻滤波器
194 | $$
195 | H(u, v)=\left\{\begin{array}{rr}
196 | 1, & \text { if } D(u, v)
170 |
171 | ### 不围绕原点的情况
172 |
173 | $$
174 | H(u,v)=\begin{cases}
175 | 0 &&if\,\,D_1(u,v)\leq D_0 \,\,or\,\, D_2(u,v)\leq D_0\\
176 | 1&& else
177 | \end{cases}
178 | $$
179 |
180 |
181 | $$
182 | \begin{aligned}
183 | &\begin{aligned}
184 | & D_1(u, v)=\left\{\left(u-u_0\right)^2+\left(v-v_0\right)^2\right\}^{1 / 2} \\
185 | &
186 | \end{aligned}\\
187 | &D_2(u, v)=\left\{\left(u+u_0\right)^2+\left(v+v_0\right)^2\right\}^{1 / 2}
188 | \end{aligned}
189 | $$
190 |
191 | ### 围绕原点的模型
192 |
193 | 为消去围绕原点的一个频带,必须考虑周期性和对称性。一个径向对称(放射对称)的理想带阻滤波器
194 | $$
195 | H(u, v)=\left\{\begin{array}{rr}
196 | 1, & \text { if } D(u, v) 206 |
207 | (a)被正弦噪声污染的图像 (b)图像(a)的频谱 (c)巴特沃思带阻滤波器 (d)图像(a)的滤波效果
208 |
209 | ## 频域滤波小结
210 |
211 | 物理可实现的低通滤波器的传递函数必须是连续的。如果处处可导,滤波后的图像就不会出现振铃效应;
212 |
213 | 频域低通滤波器的效果是去除图像中的高频噪声,去噪声的能力与滤波器的形式以及截止频率有关;
214 |
215 | 频域低通滤波器在滤除噪声的同时会造成图像模糊,图像模糊的程度与截止频率有关;
216 |
217 | 高通滤波器可以增强图像的边缘,是实现图像边缘检测的基础;
218 |
219 | 高通滤波器基本上抑制了图像中的平滑信息,因此如要在保持图像基本信息的基础上实现锐化,就需要采用高频加强技术;
220 |
221 | 带通和带阻滤波器在消除特定类型的噪声上有很好的效果,它们也是彩色图像增强的技术基础;
222 |
223 | 同态滤波是一类利用图像的照明反射模型,同时实现亮度动态范围压缩和图像对比度增强的技术
--------------------------------------------------------------------------------
/IV/4.9 编程实例.md:
--------------------------------------------------------------------------------
1 | # 4.9 编程实例
2 |
3 | ## 4.7.1 编程绘制灰度直方图
4 |
5 | ### 1. 创建灰度直方图数据
6 |
7 | ```c++
8 | //*******************************************
9 | //函数名称: CreateHistogram()
10 | //参数说明: nX1、 nY1、 nX2、 nY2为需创建直方图图像区域坐标, 默认为- // 1。pData、pPalette、 nWidthBytes为位图数据指针、调色板指
11 | // 针、 图像行字节宽度
12 | //返回值: int型数组指针*pBuffer。在数组中依次存储亮度、红、绿、蓝分量
13 | // 的直方图数据, 每个分量各占256个元素[FK)]
14 | //基本功能:创建指定的图像对象的直方图数据。如果未给定坐标,则针对整 个图像
15 | //****************************************
16 | int *CPointPro:: CreateHistogram(int nX1, int nY1, int nX2, int nY2,
17 | unsigned char *pData, RGBQUAD *pPalette, int nWidthBytes)
18 | {
19 | //图像指针为空, 无法操作返回
20 | if(m_pDibObject == NULL) return(FALSE);
21 | //分配直方图数据缓存区(数组)
22 | int *pBuffer = new int [256 * 4];
23 | //分配直方图数据缓存区失败
24 | if(pBuffer == NULL) return( NULL );
25 | //直方图数据缓存区清零
26 | memset(pBuffer, 0, (256 * 4) * sizeof(int));
27 | //变量定义
28 | DWORD dwGray;
29 | int x, y;
30 | unsigned char *pTemp, ucRed, ucGreen, ucBlue;
31 | //图像的高度
32 | int nHeight = m_pDibObject->GetHeight();
33 | switch(m_pDibObject->GetNumBits())
34 | {
35 | case 24:
36 | for(y = nY1; y < nY2; y++)
37 | {
38 | //数据指针定位到图像数据起始位置
39 | pTemp = pData;
40 | //数据指针定位到图像数据每行的起始零位置
41 | pTemp += (( nHeight - 1 - y) * nWidthBytes);
42 | //数据指针定位到图像数据每行的起始nX1位置
43 | pTemp += (nX1 * 3);
44 | for(x=nX1; x<=nX2; x++)
45 | {
46 | //获取像素颜色的三原色
47 | ucRed = pTemp[x * 3 + 2];
48 | ucGreen = pTemp[x * 3 + 1];
49 | ucBlue = pTemp[x * 3];
50 | //按关系L=0.3R+0.59G+0.11B, 得到亮度值
51 | dwGray = (DWORD) (ucRed * 30 + ucGreen * 59 + ucBlue * 11) / 100;
52 | dwGray &= 0x000000ff;
53 | //亮度直方图数据
54 | pBuffer[dwGray]++;
55 | //红色直方图数据
56 | pBuffer[256 + ucRed]++;
57 | //绿色直方图数据
58 | pBuffer[512 + ucGreen]++;
59 | //蓝色直方图数据
60 | pBuffer[768 + ucBlue]++;
61 | //数据指针加3
62 | pTemp += 3;
63 | }
64 | }
65 | break;
66 | }
67 | return( pBuffer );
68 | }
69 | ```
70 |
71 | ### 2.定制灰度直方图对话框
72 |
73 | 定制一个直方图对话框并创建一个CDlgIntensity类, 在它的构造函数中初始化成员变量(例如, 初始化直方图数据指针m_pnHistogram = NULL), 添加WM_PAINT的消息映射函数OnPaint(), 然后在消息映射函数中绘制直方图数据。
74 |
75 | ### 3. 显示直方图
76 |
77 | ```c++
78 | void CDipView:: OnViewHist()
79 | {
80 | CDipDoc* pDoc = GetDocument();
81 | ASSERT_VALID(pDoc);
82 | //判断当前是否有图像对象
83 | if( pDoc->m_pDibObject = = NULL ) return;
84 | //在点处理CPointPro类中创建用来绘制直方图的数据
85 | CPointPro PointOperation( pDoc->m_pDibObject );
86 | int *pHistogram = PointOperation.GetHistogram();
87 | //生成一个对话框CDlgIntensity类的实例
88 | CDlgIntensity HistDlg;
89 | //将直方图数据传给CDlgIntensity的成员变量m_pnHistogram
90 | if( pHistogram != NULL )
91 | {
92 | //设置直方图数据指针
93 | HistDlg.m_pnHistogram = pHistogram;
94 | //设置当前像素值为0的像素数
95 | HistDlg.m_nCurrentPiexsNum = pHistogram[0];
96 | //设置是否为256级灰度图像
97 | HistDlg.m_bIsGray256 = PointOperation.IsGray256();
98 | }
99 | //显示对话框
100 | if ( HistDlg.DoModal() != IDOK) return;
101 | delete [] pHistogram;
102 | }
103 |
104 | ```
105 |
106 | ## 4.7.2 中值滤波的VC++编程实现
107 |
108 | 下面以3×3矩形窗口为例来说明8位灰度图像的中值滤波的主要算法。
109 |
110 | ```c++
111 | for(y = nY1; y < nY2; y++)
112 | {
113 | // pOldBits和pNewBits分别为指向源图像和新图像的图像数据指针
114 | pOldTemp = pOldBits;
115 | pOldTemp += ((nHeight-1-y-1)*nWidthBytes);
116 | pOldTemp += nX1-1;
117 | pNewTemp = pNewBits;
118 | pNewTemp += ((nHeight-1-y-1)*nWidthBytes);
119 | pNewTemp += nX1;
120 | k = 0;
121 | for(x = nX1; x
206 |
207 | (a)被正弦噪声污染的图像 (b)图像(a)的频谱 (c)巴特沃思带阻滤波器 (d)图像(a)的滤波效果
208 |
209 | ## 频域滤波小结
210 |
211 | 物理可实现的低通滤波器的传递函数必须是连续的。如果处处可导,滤波后的图像就不会出现振铃效应;
212 |
213 | 频域低通滤波器的效果是去除图像中的高频噪声,去噪声的能力与滤波器的形式以及截止频率有关;
214 |
215 | 频域低通滤波器在滤除噪声的同时会造成图像模糊,图像模糊的程度与截止频率有关;
216 |
217 | 高通滤波器可以增强图像的边缘,是实现图像边缘检测的基础;
218 |
219 | 高通滤波器基本上抑制了图像中的平滑信息,因此如要在保持图像基本信息的基础上实现锐化,就需要采用高频加强技术;
220 |
221 | 带通和带阻滤波器在消除特定类型的噪声上有很好的效果,它们也是彩色图像增强的技术基础;
222 |
223 | 同态滤波是一类利用图像的照明反射模型,同时实现亮度动态范围压缩和图像对比度增强的技术
--------------------------------------------------------------------------------
/IV/4.9 编程实例.md:
--------------------------------------------------------------------------------
1 | # 4.9 编程实例
2 |
3 | ## 4.7.1 编程绘制灰度直方图
4 |
5 | ### 1. 创建灰度直方图数据
6 |
7 | ```c++
8 | //*******************************************
9 | //函数名称: CreateHistogram()
10 | //参数说明: nX1、 nY1、 nX2、 nY2为需创建直方图图像区域坐标, 默认为- // 1。pData、pPalette、 nWidthBytes为位图数据指针、调色板指
11 | // 针、 图像行字节宽度
12 | //返回值: int型数组指针*pBuffer。在数组中依次存储亮度、红、绿、蓝分量
13 | // 的直方图数据, 每个分量各占256个元素[FK)]
14 | //基本功能:创建指定的图像对象的直方图数据。如果未给定坐标,则针对整 个图像
15 | //****************************************
16 | int *CPointPro:: CreateHistogram(int nX1, int nY1, int nX2, int nY2,
17 | unsigned char *pData, RGBQUAD *pPalette, int nWidthBytes)
18 | {
19 | //图像指针为空, 无法操作返回
20 | if(m_pDibObject == NULL) return(FALSE);
21 | //分配直方图数据缓存区(数组)
22 | int *pBuffer = new int [256 * 4];
23 | //分配直方图数据缓存区失败
24 | if(pBuffer == NULL) return( NULL );
25 | //直方图数据缓存区清零
26 | memset(pBuffer, 0, (256 * 4) * sizeof(int));
27 | //变量定义
28 | DWORD dwGray;
29 | int x, y;
30 | unsigned char *pTemp, ucRed, ucGreen, ucBlue;
31 | //图像的高度
32 | int nHeight = m_pDibObject->GetHeight();
33 | switch(m_pDibObject->GetNumBits())
34 | {
35 | case 24:
36 | for(y = nY1; y < nY2; y++)
37 | {
38 | //数据指针定位到图像数据起始位置
39 | pTemp = pData;
40 | //数据指针定位到图像数据每行的起始零位置
41 | pTemp += (( nHeight - 1 - y) * nWidthBytes);
42 | //数据指针定位到图像数据每行的起始nX1位置
43 | pTemp += (nX1 * 3);
44 | for(x=nX1; x<=nX2; x++)
45 | {
46 | //获取像素颜色的三原色
47 | ucRed = pTemp[x * 3 + 2];
48 | ucGreen = pTemp[x * 3 + 1];
49 | ucBlue = pTemp[x * 3];
50 | //按关系L=0.3R+0.59G+0.11B, 得到亮度值
51 | dwGray = (DWORD) (ucRed * 30 + ucGreen * 59 + ucBlue * 11) / 100;
52 | dwGray &= 0x000000ff;
53 | //亮度直方图数据
54 | pBuffer[dwGray]++;
55 | //红色直方图数据
56 | pBuffer[256 + ucRed]++;
57 | //绿色直方图数据
58 | pBuffer[512 + ucGreen]++;
59 | //蓝色直方图数据
60 | pBuffer[768 + ucBlue]++;
61 | //数据指针加3
62 | pTemp += 3;
63 | }
64 | }
65 | break;
66 | }
67 | return( pBuffer );
68 | }
69 | ```
70 |
71 | ### 2.定制灰度直方图对话框
72 |
73 | 定制一个直方图对话框并创建一个CDlgIntensity类, 在它的构造函数中初始化成员变量(例如, 初始化直方图数据指针m_pnHistogram = NULL), 添加WM_PAINT的消息映射函数OnPaint(), 然后在消息映射函数中绘制直方图数据。
74 |
75 | ### 3. 显示直方图
76 |
77 | ```c++
78 | void CDipView:: OnViewHist()
79 | {
80 | CDipDoc* pDoc = GetDocument();
81 | ASSERT_VALID(pDoc);
82 | //判断当前是否有图像对象
83 | if( pDoc->m_pDibObject = = NULL ) return;
84 | //在点处理CPointPro类中创建用来绘制直方图的数据
85 | CPointPro PointOperation( pDoc->m_pDibObject );
86 | int *pHistogram = PointOperation.GetHistogram();
87 | //生成一个对话框CDlgIntensity类的实例
88 | CDlgIntensity HistDlg;
89 | //将直方图数据传给CDlgIntensity的成员变量m_pnHistogram
90 | if( pHistogram != NULL )
91 | {
92 | //设置直方图数据指针
93 | HistDlg.m_pnHistogram = pHistogram;
94 | //设置当前像素值为0的像素数
95 | HistDlg.m_nCurrentPiexsNum = pHistogram[0];
96 | //设置是否为256级灰度图像
97 | HistDlg.m_bIsGray256 = PointOperation.IsGray256();
98 | }
99 | //显示对话框
100 | if ( HistDlg.DoModal() != IDOK) return;
101 | delete [] pHistogram;
102 | }
103 |
104 | ```
105 |
106 | ## 4.7.2 中值滤波的VC++编程实现
107 |
108 | 下面以3×3矩形窗口为例来说明8位灰度图像的中值滤波的主要算法。
109 |
110 | ```c++
111 | for(y = nY1; y < nY2; y++)
112 | {
113 | // pOldBits和pNewBits分别为指向源图像和新图像的图像数据指针
114 | pOldTemp = pOldBits;
115 | pOldTemp += ((nHeight-1-y-1)*nWidthBytes);
116 | pOldTemp += nX1-1;
117 | pNewTemp = pNewBits;
118 | pNewTemp += ((nHeight-1-y-1)*nWidthBytes);
119 | pNewTemp += nX1;
120 | k = 0;
121 | for(x = nX1; x 185 |
186 | 图4-39 图像平滑模板设置对话框
187 |
188 | 利用类向导为对话框的相应控件添加成员变量,如模板类型、模板高度、模板宽度、模板中心元素X坐标、模板中心元素Y坐标对应的成员变量分别定义为整型变量m_intType、m_iTempH、m_iTempW、m_iTempMX、m_iTempMY, 而模板系数对应浮点型的变量m_fTempC,另外还定义了一个模板元素数组指针m_fpArray。
189 | 为3个单选按钮分别定义一个单击事件的消息映射,在映射函数中给模板元素m_fpArray及其他成员变量赋值。
190 |
191 | 2. 获取图像数据
192 | 对每个像素的邻域用选定的模板作卷积运算, 就可以得到平滑后的图像。下面给出了卷积运算的源代码。
193 | 卷积函数中的各参数的含义如下: fpData为被卷积的数组, fpKernel为卷积核数组,fCoef为卷积系数,nSize为卷积尺寸, nResult为卷积结果。
194 |
195 | ```c++
196 | void CAreaPro:: Convolution(float *fpData, float *fpKernel, float fCoef,
197 | int nSize, unsigned char *nResult)
198 | {
199 | int i;
200 | float Sum = 0, fResult;
201 | //计算卷积
202 | for(i = 0; i < nSize; i++)
203 | {
204 | Sum += fpData[i] * fpKernel[i];
205 | }
206 | //执行卷积后的结果
207 | fResult = Sum / fCoef;
208 | //求绝对值
209 | fResult = (float)fabs(fResult);
210 | //判断是否超过255
211 | if(fResult > 255.0 )
212 | {
213 | // 直接赋值为255
214 | fResult = 255.0;
215 | }
216 | //对卷积结果四舍五入, 并转换成unsigned char类型作为最后返回结果
217 | *nResult = (unsigned char) (fResult + 0.5);
218 | }
219 |
220 | ```
221 |
222 | 接着就是对原图像的每个像素作卷积运算,运算后的结果赋予新图像,其中图像边界像素不作处理,代码实现在CAreaPro:: Smoothing()中。
--------------------------------------------------------------------------------
/README.md:
--------------------------------------------------------------------------------
1 | # Digital-mage-Processing
2 | 数字图像处理笔记,整理张航老师的数字图像处理课件,推荐教材是冈萨雷斯第四版
3 |
4 | 现在已经初步整理完毕,但不排除个别地方仍然有细微错误。
--------------------------------------------------------------------------------
/V/5.1 图像退化与复原.md:
--------------------------------------------------------------------------------
1 | # 5.1 图像退化与复原
2 |
3 | 数字图像在获取的过程中,由于光学系统的像差、 光学成像衍射、 成像系统的非线性畸变、 摄影胶片的感光的非线性、 成像过程的相对运动、 大气的湍流效应、环境随机噪声等原因, 图像会产生一定程度的退化。因此,必须采取一定的方法尽可能地减少或消除图像质量的下降,恢复图像的本来面目,这就是图像复原, 也称为图像恢复。
4 |
5 | 图像复原与图像增强有类似的地方, 都是为了改善图像。但是它们又有着明显的不同。图像复原是试图利用退化过程的先验知识使已退化的图像恢复本来面目,即根据退化的原因, 分析引起退化的环境因素,建立相应的数学模型, 并沿着使图像降质的逆过程恢复图像。从图像质量评价的角度来看, 图像复原就是提高图像的可理解性。而图像增强的目的是提高视感质量,图像增强的过程基本上是一个探索的过程, 它利用人的心理状态和视觉系统去控制图像质量, 直到人们的视觉系统满意为止。
6 |
7 | 图像复原是利用退化现象的某种先验知识,建立退化现象的数学模型,再根据模型进行反向的推演运算,以恢复原来的景图像。因而,图像复原可以理解为图像降质过程的反向过程。建立图像复原的反向过程的数学模型,就是图像复原的主要务。经过反向过程的数学模型的运算,要想恢复全真的景物图像比较困难。所以, 图像复原本身往往需要有一个质量准, 即衡量接近全真景物图像的程度,或者说,对原图像的估计是否到达最佳的程度。
8 |
9 | 由于引起退化的因素众多而且性质不同,为了描述图像退化过程所建立的数学模型往往多种多样,而恢复的质量标准也往存在差异性,因此图像复原是一个复杂的数学过程,图像复原的方法、技术也各不相同。
10 |
11 | ## 5.1.1 图像降质的数学模型
12 |
13 | 图像复原处理的关键问题在于建立退化模型。输入图像f(x, y)经过某个退化系统后输出的是一幅退化的图像。为了讨论方便, 把噪声引起的退化即噪声对图像的影响一般作为加性噪声考虑, 这也与许多实际应用情况一致,如图像数字化时的量化噪声、 随机噪声等就可以作为加性噪声,即使不是加性噪声而是乘性噪声, 也可以用对数方式将其转化为相加形式。
14 |
15 | 原始图像 $f(x, y)$ 经过一个退化算子或退化系统 $H(x, y)$ 的作用, 再和噪声 $n(x, y)$ 进行叠加, 形成退化后的图像 $g(x, y)$ 。图11-1表示退化过程的输入和输出的关系, 其中 $H(x, y)$ 概括了退化系统的物理过程, 就是所要寻找的退化数学模型。
16 |
17 | 此处是进行了简化,因为乘法噪声可以转化为加法噪声
18 |
19 | 
20 |
21 | 数字图像的图像恢复问题可看作是: 根据退化图像 $g(x, y)$ 和退化算子 $H(x, y)$ 的形式, 沿着反向过程去求解原始图像 $f(x, y)$, 或者说是逆向地寻找原始图像的最佳近似估计。图像退化的过程可以用数学表达式写成如下的形式:
22 | $$
23 | g(x, y)=H[f(x, y)]+n(x, y)\tag{5-1}
24 | $$
25 | 在这里, $n(x, y)$ 是一种统计性质的信息。在实际应用中, 往往假设噪声是白噪声, 即它的频谱密度为常数, 并且与图像不相关。
26 |
27 | 在图像复原处理中, 尽管非线性、 时变和空间变化的系统模型更具有普遍性和准确性,更与复杂的退化环境相接近,但它给实际处理工作带来了巨大的困难, 常常找不到解或者很难用计算机来处理。因此,在图像复原处理中, 往往用线性系统和空间不变系统模型来加以近似。这种近似的优点使得线性系统中的许多理论可直接用于解决图像复原问题,同时又不失可用性。
28 |
29 | 一幅连续图像 $f(x, y)$ 可以看作是由一系列点源组成的。因此, $f(x, y)$ 可以通过点源函数的卷积来表示。即
30 | $$
31 | f(x, y)=\int_{-\infty}^{+\infty} \int_{-\infty}^{+\infty} f(\alpha, \beta) \delta(x-\alpha, y-\beta) d \alpha d \beta\tag{5-2}
32 | $$
33 | 式中, $\delta$ 函数为点源函数, 表示空间上的点脉冲。
34 | 在不考虑噪声的一般情况下, 连续图像经过退化系统 $H$ 后的输出为
35 |
36 | $$
37 | \quad g(x, y)=H[f(x, y)]\tag{5-3}
38 | $$
39 |
40 | 把式(5-2)代入式(5-3)得
41 |
42 | $$
43 | \begin{gathered}
44 | g(x, y)=H[f(x, y)]=H\left[\int_{-\infty}^{+\infty} \int_{-\infty}^{+\infty} f(\alpha, \beta) \delta(x-\alpha, y-\beta) d \alpha d \beta\right]
45 | \end{gathered}\tag{5-4}
46 | $$
47 |
48 | 在线性和空间不变系统的情况下, 退化算子 $H$ 具有如下性质:
49 | (1) 线性: 设 $f_1(x, y)$ 和 $f_2(x, y)$ 为两幅输入图像, $k_1$ 和 $k_2$ 为常数, 则
50 |
51 | $$
52 | H\left[k_1 f_1(x, y)+k_2 f_2(x, y)\right]=k_1 H\left[f_1(x, y)\right]+k_2 H\left[f_2(x, y)\right]\tag{5-5}
53 | $$
54 |
55 | 由该性质还可推出下面两个结论:
56 | (1) 当 $k_1=k_2=1$ 时, 式(11-5)变为
57 |
58 | $$
59 | H\left[f_1(x, y)+f_2(x, y)\right]=H\left[f_1(x, y)\right]+H\left[f_2(x, y)\right]\tag{5-6}
60 | $$
61 |
62 | (2) 如果 $f_2(x, y)=0$, 则式 (11-5) 变为
63 |
64 | $$
65 | H\left[k_1 f_1(x, y)\right]=k_1 H\left[f_1(x, y)\right]\tag{5-7}
66 | $$
67 |
68 | (2) 空间不变性: 如果对任意 $f(x, y)$ 以及 $a$ 和 $b$, 有
69 |
70 | $$
71 | H[f(x-a, y-b)]=g(x-a, y-b)\tag{5-8}
72 | $$
73 |
74 | 则对于线性空间不变系统, 输入图像经退化后的输出为
75 |
76 | $$
77 | \begin{aligned}
78 | g(x, y) & =H[f(x, y)]=H\left[\int_{-\infty}^{+\infty} \int_{-\infty}^{+\infty} f(\alpha, \beta) \delta(x-\alpha, y-\beta) d \alpha d \beta\right] \\
79 | & =\int_{-\infty}^{+\infty} \int_{-\infty}^{+\infty} f(\alpha, \beta) H[\delta(x-\alpha, y-\beta)] d \alpha d \beta \\
80 | & =\int_{-\infty}^{+\infty} \int_{-\infty}^{+\infty} f(\alpha, \beta) h(x-\alpha, y-\beta) d \alpha d \beta
81 | \end{aligned}\tag{5-9}
82 | $$
83 |
84 | 式中, $h(x-\alpha, y-\beta)$ 为该退化系统的点扩展函数, 或叫系统的冲激响应函数。它表示系统对坐标为 $(a, \beta)$ 处的冲激函数 $\delta(x-\alpha, y-\beta)$ 的响应。也就是说, 只要系统对冲激函数的响应为已知, 那么就可以清楚图像退化是如何形成的。因为对于任一输入 $f(a, \beta)$ 的响应, 都可以通过上式计算出来。
85 | 此时, 退化系统的输出就是输入图像信号 $f(x, y)$ 与点扩展函数 $h(x, y)$ 的卷积, 即
86 |
87 | $$
88 | g(x, y)=\int_{-\infty}^{+\infty} \int_{-\infty}^{+\infty} f(\alpha, \beta) h(x-\alpha, y-\beta) d \alpha d \beta=f(x, y) * h(x, y)\tag{5-10}
89 | $$
90 |
91 | 图像退化除了受到成像系统本身的影响外, 有时还要受到噪声的影响。假设噪声 $n(x, y)$ 是加性白噪声, 这时上式可写成
92 |
93 | $$
94 | \begin{aligned}
95 | g(x, y) & =\int_{-\infty}^{+\infty} \int_{-\infty}^{+\infty} f(\alpha, \beta) h(x-\alpha, y-\beta) d \alpha d \beta+n(x, y) \\
96 | & =f(x, y) * h(x, y)+n(x, y)
97 | \end{aligned}\tag{5-11}
98 | $$
99 |
100 | 在频域上, 式(11-11)可以写成
101 |
102 | $$
103 | G(u, v)=F(u, v) H(u, v)+N(u, v)\tag{5-12}
104 | $$
105 |
106 | 其中, $G(u, v) 、 F(u, v) 、 N(u, v)$ 分别是退化图像 $g(x, y)$ 、原图像 $f(x, y)$、噪声信号 $n(x, y)$ 的傅立叶变换; $H(u, v)$ 是系统的点冲激响应函数 $h(x, y)$ 的傅立叶变换, 称为系统在频率域上的传递函数。
107 |
108 | 式(5-11)和式(5-12)就是连续函数的退化模型。可见, 图像复原实际上就是已知 $g(x, y)$ 求 $f(x, y)$ 的问题或已知 $G(u, v)$ 求 $F(u, v)$ 的问题, 它们的不同之处在于一个是在空域,一个是在频域。
109 | 显然, 进行图像复原的关键问题是寻找降质系统在空间域上的冲激响应函数 $h(x, y)$, 或者降质系统在频率域上的传递函数 $H(u$, $v)$ 。一般来说, 传递函数比较容易求得。因此, 在进行图像复原之前, 一般应设法求得完全的或近似的降质系统传递函数, 要想得到 $h(x, y)$, 只需对 $H(u, v)$ 求傅立叶逆变换即可。
110 |
111 | ## 5.1.2 离散图像退化的数学模型
112 |
113 | 1. 一维离散退化模型
114 | 设 $f(x)$ 为具有 $A$ 个采样值的离散输入函数, $h(x)$ 为具有 $B$ 个采样值的退化系统的冲激响应函数, 则经退化系统后的离散输出函数 $g(x)$ 为输入 $f(x)$ 和冲激响应 $h(x)$ 的卷积, 即
115 | $$
116 | g(x)=f(x)^* h(x)
117 | $$
118 | 为了避免上述卷积所产生的各个周期重叠(设每个采样函数的周期为 $M)$ ,分别对 $f(x)$ 和 $h(x)$ 用添零延伸的方法扩展成周期 $M=A+B-1$ 的周期函数, 即
119 | $$
120 | f_e(x)=\left\{\begin{array}{cc}
121 | f(x) & 0 \leq x \leq A-1 \\
122 | 0 & A \leq x \leq M-1
123 | \end{array}\right. \tag{5-13a}
124 | $$
125 | $$
126 | h_e(x)=\left\{\begin{array}{cc}
127 | h(x) & 0 \leq x \leq B-1 \\
128 | 0 & B \leq x \leq M-1
129 | \end{array}\right.\tag{5-13b}
130 | $$
131 | 输出为
132 | $$
133 | g_e(x)=f_e(x) * h_e(x)=\sum_{m=0}^{M-1} f_e(m) h_e(x-m)\tag{5-14}
134 | $$
135 | 式中, $x=0,1,2, \ldots, M-1$ 。
136 |
137 | 因为 $f_{e}(x)$ 和 $h_{e}(x)$ 已扩展成周期函数, 故 $g_{e}(x)$ 也是周期性函数, 用矩阵表示为
138 | $$
139 | \left[\begin{array}{c}
140 | g(0) \\
141 | g(1) \\
142 | g(2) \\
143 | M \\
144 | g(M-1)
145 | \end{array}\right]=\left[\begin{array}{cccc}
146 | h_e(0) & h_e(-1) & \Lambda & h_e(-M+1) \\
147 | h_e(1) & h_e(0) & \Lambda & h_e(-M+2) \\
148 | h_e(2) & h_e(1) & \Lambda & h_e(-M+3) \\
149 | M & M & M & M \\
150 | h_e(M-1) & h_e(M-2) & \Lambda & h_e(0)
151 | \end{array}\right]\left[\begin{array}{c}
152 | f_e(0) \\
153 | f_e(1) \\
154 | f_e(2) \\
155 | M \\
156 | f_e(M-1)
157 | \end{array}\right]\tag{5-15}
158 | $$
159 | 因为 $h_{e}(x)$ 的周期为 $M$, 所以 $h_{e}(x)=h_{e}(x+M)$, 即
160 | $$
161 | \begin{gathered}
162 | h_e(-1)=h_e(M-1) \\
163 | h_e(-2)=h_e(M-2) \\
164 | h_e(-3)=h_e(M-3) \\
165 | M \\
166 | h_e(-M+1)=h_e(1)
167 | \end{gathered}
168 | $$
169 | $M \times M$ 阶矩阵 $\boldsymbol{H}$ 可写为
170 | $$
171 | H=\left[\begin{array}{cccc}
172 | h_e(0) & h_e(-1) & \Lambda & h_e(1) \\
173 | h_e(1) & h_e(0) & \Lambda & h_e(2) \\
174 | h_e(2) & h_e(1) & \Lambda & h_e(3) \\
175 | M & M & \Lambda & \Lambda \\
176 | h_e(M-1) & h_e(M-2) & h_e(0)
177 | \end{array}\right]\tag{5-16}
178 | $$
179 | 可将式(5-15)写成更简洁的形式,即
180 | $$
181 | g=H f\tag{5-17}
182 | $$
183 | 式中, $\boldsymbol{g} 、 \boldsymbol{f}$ 都是 $M$ 维列向量, $\boldsymbol{H}$ 是 $M \times M$ 阶矩阵, 矩阵中的每一行元素均相同, 只是每行以循环方式右移一位, 因此矩阵 $\boldsymbol{H}$ 是循环矩阵。循环矩阵相加或相乘得到的还是循环矩阵。
184 |
185 | 2. 二维离散模型
186 | 设输入的数字图像 $f(x, y)$ 大小为 $A \times B$, 点扩展函数 $h(x, y)$ 被均匀采样为 $C \times D$ 大小。为避免交叠误差, 仍用添零扩展的方法, 将它们扩展成 $M=A+C-1$ 和 $N=B+D-1$ 个元素的周期函数。
187 |
188 | $$
189 | f_e(x, y)=\left\{\begin{array}{cc}
190 | f(x, y) & 0 \leq x \leq A-1 \text { 且 } 0 \leq y \leq B-1 \\
191 | 0 & \text { 其他 }
192 | \end{array}\right. \tag{5-18a}
193 | $$
194 | $$
195 | h_e(x, y)=\left\{\begin{array}{cc}
196 | h(x, y) & 0 \leq x \leq C-1 \text { 且 } 0 \leq y \leq D-1 \\
197 | 0 & \text { 其他 }
198 | \end{array}\right.\tag{5-18b}
199 | $$
200 |
201 | 则输出的降质数字图像为
202 | $$
203 | g_e(x, y)=\sum_{m=0}^{M-1} \sum_{n=0}^{N-1} f_e(m, n) h_e(x-m, y-n)=f(x, y)^* h(x, y)\tag{5-19}
204 | $$
205 | 式中: $x=0,1,2, \ldots, M-1 ; y=0,1,2, \ldots, N-1$ 。
206 | 式(5-19)的二维离散退化模型同样可以用式 (5-17) 所示的矩阵形式表示, 即
207 | $$
208 | g=H f
209 | $$
210 | 式中, $g 、 f$ 是 $M N \times 1$ 维列向量, $H$ 是 $M N \times M N$ 维矩阵。其方法是将 $g(x, y)$ 和 $f(x, y)$ 中的元素排成列向量。
211 | $$
212 | f_1=\left[\underbrace{f_1(0,0),f_1(0,1),\cdots,f_1(0,N-1)}_{第0行元素},\underbrace{f_1(1,0),f_1(1,1),\cdots,f_1(1,N-1)}_{第1行元素},\cdots,\underbrace{f_1(M-1,0),f_1(M-1,1),\cdots,f_1(M-1,N-1)}_{第M-1行元素}\right]^T\\
213 | g_1=\left[\underbrace{g_1(0,0),g_1(0,1),\cdots,g_1(0,N-1)}_{第0行元素},\underbrace{g_1(1,0),g_1(1,1),\cdots,g_1(1,N-1)}_{第1行元素},.\cdots,\underbrace{g_1(M-1,0),g_1(M-1,1),\cdots,g_1(M-1,N-1)}_{第M-1行元素}\right]^T
214 | \tag{5-20}
215 | $$
216 |
217 | $$
218 | H=\left[\begin{array}{cccc}
219 | H_0 & H_{M-1} & H_{M-2} & \cdots& H_1 \\
220 | H_1 & H_0 & H_{M-1} & \cdots& H_2 \\
221 | \vdots & \vdots & \vdots & \ddots&\vdots \\
222 | H_{M-1} & H_{M-2} & H_{M-3} & \cdots &H_0
223 | \end{array}\right]
224 | \tag{5-21}
225 | $$
226 | $H_i(i=0,1,2, \ldots, M-1)$ 为子矩阵, 大小为 $N \times N$, 即 $H$ 矩阵由 $M \times M$ 个大小为 $N \times N$ 的子矩阵组成, 称为分块循环矩阵。分块矩阵是由延拓函数 $h_{e}(x, y)$ 的第 $j$ 行构成的, 构成方法如下:
227 | $$
228 | H=\left[\begin{array}{cccc}
229 | h_e(j, 0) & h_e(j, N-1) & h_e(j, N-2) & \cdots& h_e(j, 1) \\
230 | h_e(j, 1) & h_e(j, 0) & h_e(j, N-1) & \cdots &h_e(j, 0) \\
231 | \vdots & \vdots & \vdots &\ddots &\vdots \\
232 | h_e(j, N-1) & h_e(j, N-2) & h_e(j, N-3) & \cdots &h_e(j, 0)
233 | \end{array}\right]
234 | \tag{5-22}
235 | $$
236 | 若把噪声考虑进去, 则离散图像退化模型为
237 | $$
238 | g_e(x, y)=\sum_{m=0}^{M-1} \sum_{n=0}^{N-1} f_e(m, n) h_e(x-m, y-n)+n_e(x, y)
239 | \tag{5-23}
240 | $$
241 | 写成矩阵形式为
242 | $$
243 | g=H f+n\tag{5-24}
244 | $$
245 | 上述线性空间不变退化模型表明, 在给定了 $g(x, y)$, 并且知道退化系统的点扩展函数 $h(x, y)$ 和噪声分布 $n(x, y)$ 的情况下, 可估计出原始图像 $f(x, y)$ 。
246 | 假设图像大小 $M=N=512$, 相应矩阵 $M H$ 的大小为 $M N \times M N=262144 \times 262144$, 这意味着要解出 $f(x, y)$ 需要解262 144 个联立方程组, 其计算量十分惊人。
247 |
248 | 图像恢复目的是在给定的 $g(x, y), h(x, y), n(x, y)$ 情况下, 求 $f(x, y)$. 由于 $G , F$ 维数很大, 通过解方程组不可能进行图像恢复.
249 | 1. 代数复原方法:寻找一个估计 $f(x, y)$.
250 | - 非约束复原方法
251 | - 约束复原方法
252 | 2.逆滤波方法
253 |
254 |
--------------------------------------------------------------------------------
/V/5.2 代数复原法.md:
--------------------------------------------------------------------------------
1 | # 5.2 代数复原法
2 |
3 | ## 5.2.1非约束复原方法
4 |
5 | 由式(5-24)可得
6 | $$
7 | n=g-H f\tag{5-25}
8 | $$
9 | 在对 $n$ 没有先验知识的情况下, 可以依据这样的最优准则, 即寻找一个 $\hat{f}$, 使得 $H \hat{f}$ 在最小二乘方误差的意义下最按近 $g$, 即要使 $n$ 的模或范数 (norm) 最小:
10 | $$
11 | \|n\|^2=n^T n=\|g-H \hat{f}\|^2=(g-H \hat{f})^T(g-\hat{H f})\tag{5-26}
12 | $$
13 | 即优化目标为:
14 | $$
15 | L(\hat{f})=\|g-H \hat{f}\|^2\tag{5-27}
16 | $$
17 | 如果我们在求最小值的过程中, 不做任何约束, 称这种复原为非约束复原。由极值条件
18 | $$
19 | \frac{\partial L(\hat{f})}{\partial \hat{f}}=0 \Rightarrow H^T(g-H \hat{f})=0\tag{5-28}
20 | $$
21 | 解出 $\hat{f}$ 为
22 | $$
23 | \hat{f}=\left(H^T H\right)^{-1} H^T g\tag{5-29}
24 | $$
25 |
26 | ## 5.2.2 约束复原法
27 |
28 | 非约束复原是指除了使准则函数 $L(\hat{f})=\|g-\hat{H f}\|^2$ 最小外, 再没有其他的约束条件。因此只需了解降质系统的传递函数或点扩展函数, 就能利用如前所述的方法进行复原。但是由于传递函数存在病态问题, 复原只能局限在靠近原点的有限区域内进行, 这使得非约束图像复原具有相当大的局限性。
29 |
30 | 最小二乘类约束复原是指除了要求了解关于退化系统的传递函数之外, 还需要知道某些噪声的统计特性或噪声与图像的某些相关情况。根据所了解的噪声的先验知识的不同, 采用不同的约束条件, 可得到不同的图像复原技术。在最小二乘类约束复原中, 要设法寻找一个最优估计 $\hat{f}$, 使得形式为 $\|Q \hat{f}\|^2=\|n\|^2$ 的函数最小化。求这类问题的最小化, 常采用拉格朗日乘子算法。也就说, 要寻找一个 $\hat{f}$, 使得优化目标函数:
31 | $$
32 | J(\hat{f})=\|\hat{O \hat{f}}\|^2+\alpha\left(\|g-H \hat{f}\|^2-\|n\|^2\right)\tag{5-30}
33 | $$
34 | 为最小。式中, $Q$ 为 $\hat{f}$ 的线性算子, $\alpha$ 为一常数, 称为拉格朗日乘子。对式(5-30)求导得
35 | $$
36 | \begin{aligned}
37 | & \frac{\partial J(\hat{f})}{\partial f}=0 \\
38 | & Q^T Q \hat{f}-\alpha H^T(g-H \hat{f})=0
39 | \end{aligned}
40 | $$
41 | 求解 $\hat{f}$ 得到
42 | $$
43 | \hat{f}=\left(H^T H+\gamma Q^T Q\right)^{-1} H^T g\tag{5-31}
44 | $$
--------------------------------------------------------------------------------
/V/5.3 逆滤波.md:
--------------------------------------------------------------------------------
1 | # 5.3 逆滤波
2 |
3 | 只能接近,无法完全恢复
4 |
5 | 1.逆滤波基本原理
6 | 由退化图像的付里叶变换求得图像的付里叶变换的估计方法称为逆滤波.
7 |
8 | 逆滤波
9 | $$
10 | \begin{aligned}
11 | \overline{g(x, y)}= & \int_{-\infty}^{\infty} \int_{-\infty}^{\infty} f(x, A) h(x-\imath v, y-A) d x d, \partial+n(x, y) \\
12 | & G(u, v)=F(u, v) H(u, v)+N(u, v)
13 | \end{aligned}
14 | $$
15 | 不考虑噪声:
16 |
17 | $$
18 | \begin{aligned} F(u, v) & =\frac{G(u, v)}{H(u, v)} \\ f(x, y) & =\mathcal{G}^{-1}[F(u, v)]\end{aligned}
19 | $$
20 | 有噪声:
21 | $$
22 | \begin{aligned}
23 | & F(u, v)=\frac{G(u, v)}{H(u, v)}-\frac{N(u, v)}{H(u, v)} \\
24 | & f(x, y)=\xi^{-1}[F(u, v)]
25 | \end{aligned}
26 | $$
27 |
28 |
29 |
30 |
31 | 
32 |
33 | 图5.2 逆滤波
34 |
35 | 逆滤波
36 | 2.去除由均匀直线运动引起的模糊
37 | - 模糊模型
38 | $$
39 | g(x, y)=\int_0^T f\left[x-x_0(t), y-y_0(t)\right] d t
40 | $$
41 | $f(x, y)$ : 原图像; $g(x, y)$ : 模糊图像; $T$ : 暴光时间
42 | - 图像恢复 $G(u, v)=H(u, v) F(u, v)$
43 | 其中: $H(u, v)=\int_0^T \exp \left\{-j 2 \pi\left[u x_0(t)+v y_0(t)\right]\right\} d t$
44 |
45 | ## 用途
46 |
47 | 在实验室中,可以反复做实验的情景
--------------------------------------------------------------------------------
/V/5.4 最小二乘滤波(维纳滤波,重点).md:
--------------------------------------------------------------------------------
1 |
2 |
3 | # 5.4 最小二乘方滤波(维纳滤波)
4 |
5 | **重点**
6 |
7 | 知道图像,知道有关分布特征
8 |
9 | 1.最小二乘方滤波
10 | 设原始图像, 退化图像和噪声分别为 $f(x, y), g(x, y)$ 和 $n(x, y)$, 则 :
11 |
12 | $$
13 | g(x, y)=H[f(x, y)]=H\left[\int_{-\infty}^{+\infty} \int_{-\infty}^{+\infty} f(\alpha, \beta) \delta(x-\alpha, y-\beta) d \alpha d \beta\right]+n(x, y)$ 在给定的 $g(x, y)$ 时, 找出 $f(x, y)$ 的估计 $f(x, y)
14 | $$
15 | 使:
16 | $$
17 | e^2=E\left\{[f(x, y)-\hat{f}(x, y)]^2\right\}
18 | $$
19 | 最小.
20 |
21 | 设
22 | $$
23 | \quad \hat{f}(x, y)=\iint m(x, y, \alpha, \beta) g(\alpha, \beta) d \alpha d \beta
24 | $$
25 | 2. 求解
26 | 如果 $f(x, y), g(x, y)$ 和 $n(x, y)$ 是均匀随机场, 则 :
27 | $$
28 | \hat{f}(x, y)=\iint m(x-\alpha, y-\beta) g(\alpha, \beta) d \alpha d \beta
29 | $$
30 | 因此图像恢复就是确定m $m, y)$. 通过求解得:
31 | $$
32 | \begin{aligned}
33 | M(u, v) & =\left[\frac{H^*(u, v)}{|H(u, v)|^2+\left[S_n(u, v) / S_f(u, v)\right]}\right] \\
34 | & =\left[\frac{1}{H(u, v)} \cdot \frac{|H(u, v)|^2}{\left|H(u, v)^2\right|+\left[S_n(u, v) / S_f(u, v)\right]}\right]
35 | \end{aligned}
36 | $$
37 | $H(u, v)$ 是的h $(x, y)$ 付里叶变换.
38 | $S_f, S_n$ 分别是 $f(x, y), n(x, y)$ 的谱密度
39 |
40 | 于是:
41 | $$
42 | \begin{aligned}
43 | \hat{F}(u, v) & =\left[\frac{H^*(u, v)}{|H(u, v)|^2+\left[S_n(u, v) / S_f(u, v)\right]}\right] G(u, v) \\
44 | & =\left[\frac{1}{H(u, v)} \cdot \frac{|H(u, v)|^2}{\left|H(u, v)^2\right|+\left[S_n(u, v) / S_f(u, v)\right]}\right] G(u, v)
45 | \end{aligned}\tag{5-32}
46 | $$
47 | 式中,
48 | $$
49 | u, v=0,1,2, \ldots, N-1,|H(u, v)|^2=H^*(u, v) H(u, v)
50 | $$
51 |
52 | 3. 讨论
53 | - $S_n=0$ 时, 是理想的逆滤波器
54 | -若随机过程的统计特性不知道, 可采用:
55 | $$
56 | M(u, v)=\frac{1}{H(u, v)} \frac{|H(u, v)|^2}{|H(u, v)|^2+\Gamma}
57 | $$
58 | 式中 $\Gamma$ 是噪声对信号的功率密度比.
59 |
60 | - 维纳滤波器是假设线性系统, 实际上图像的记录和评价图像的视觉系统都是非线性系统.
61 | - 维纳滤波器是根据最小均方差设计的,这个准则不见得与人的视觉判决准则相符.
62 | - 维纳滤波器是基于平稳随机过程的模型,实际图像不一定符合这一条件.
63 |
64 | ## 几种最小二乘方滤波器
65 |
66 | (仅供了解)
67 |
68 | 1.图像功率谱滤波器
69 | $$
70 | H_{R}(u, v)=\left[\frac{W_{FI}(u, v)}{\left|H_{D}(u, v)\right|^2 W_{F 1}(u, v)+W_{N}(u, v)}\right]^{\frac{1}{2}}
71 | $$
72 | 式中 $H_{D}(u, v)$ 是图像退化的传递函数。 $W_{F 1}(u, v)$ 代表滤波器输出功率频谱,
73 | $$
74 | W_{FI}(u, v)=\left|H_{D}(u, v)\right|^2 W_{FO}(u, v)
75 | $$
76 | 式中 $W_{FO}(u, v)$ 代表观测的功率频谱。它与理想图像的功率频谱的关系是
77 | $$
78 | W_{FO}(u, v)=\left|H_{D}(u, v)\right|^2 \cdot W_{FI}(u, v)+W_{N}(u, v)
79 | $$
80 | 式中 $W_{N}(u, v)$ 是噪声功率频谱。
81 |
82 | 2.几何平均滤波器.
83 |
84 | 几何平均滤波器的传递函数由下式表示:
85 | $$
86 | H_{R}(u, v)=\left[H_{D}(u, v)\right]^{-s}\left[\frac{H_{D}^*(u, v) W_{FI}(u, v)}{\left|H_{D}(u, v)\right|^2 W_{FI}(u, v)+W_{N}(u, v)}\right]^{1-s}
87 | $$
88 | S是一个参数
89 |
90 | 3.约束最小方滤波器
91 |
92 | 约束最小方滤波器的传递函数如下:
93 | $$
94 | H_{\mathrm{R}}(u, v)=\frac{H_{\mathrm{D}}^*(u, v)}{\left|H_{\mathrm{D}}(u, v)\right|^2+r|L(u, v)|^2}
95 | $$
96 | $r$是一个参数,$L(u,v)$是一个频率参数。$r=1$为维纳滤波器
--------------------------------------------------------------------------------
/V/5.5 非线性复原方法 .md:
--------------------------------------------------------------------------------
1 | # 5.5 非线性复原方法(仅供了解)
2 |
3 | ## 5.5.1 最大后验复原
4 |
5 | 最大后验复原是一种统计方法, 它把原图像 $f(x, y)$ 和退化图像 $g(x, y)$ 都作为随机场, 在已知 $g(x, y)$ 的前提下, 求出后验条件概率密度函数 $P(f(x, y) / g(x, y))$ 。若 $\hat{f}(x, y)$ 使式
6 | $$
7 | \max _{f} p(f \mid g)=\max _f p(g \mid f) p(f) / p(g)=\max _f p(g \mid f) p(f)\tag{5-33}
8 | $$
9 | 最大, 则 $\hat{f}(x, y)$ 就代表已知退化图像 $g(x, y)$ 时, 最可能的原始图像 $f(x, y)$ 。这种图像方法称之为最大后验图像复原方法。
10 |
11 | 最大后验图像复原方法把图像看作是非平稳随机场, 把图像模型表示成一个平稳随机过程对于一个不平稳的均值作零均值Gauss起伏, 可得出求解迭代序列:
12 | $$
13 | \hat{f}_{k+1}=\hat{f}_k-h^* \sigma_n^{-2}\left(g-h^* \hat{f}_k\right)-\sigma_n^{-2}\left(\hat{f}_k-\bar{f}\right)\tag{5-34}
14 | $$
15 | 其中, $k$ 为迭代次数, $\sigma_n^{-2}$ 和 $\sigma_f^{-2}$ 分别为 $f$ 和 $n$ 的方差的倒数, $f$ 是随空间而变的均值, 它是一个常数, 但要经过多次迭代才能收敛到最后的解。
16 |
17 | ## 5.5.2 最大熵复原
18 |
19 | 最大熵复原方法是通过最大化某种反映图像平滑性的准则函数来作约束条件, 以解决图像复原中反向滤波法存在的病态问题。
20 | 首先简单介绍一下熵的概念。
21 | 熵的定义为
22 | $$
23 | H=-\int_{-\infty}^{+\infty} P(x) \ln P(x) d x\tag{5-35}
24 | $$
25 | 式中, $P(x)$ 为随机变量 $x$ 的概率密度。
26 | 对于离散信号, 熵的定义为
27 | $$
28 | H=-\sum_{k=1}^M P(k) \ln P(k)\tag{5-36}
29 | $$
30 | 熵是表征随机变量集合的随机程度的量度。当所有随机变量等可能性时, 也就是说 $P_1=P_2=\ldots=P_{m}$ 时熵最大, 为 $H=\ln M$ 。由于概率 $P(k)$ 介于 $0 \sim 1$ 之间, 因此最大熵的范围为 $0 \sim \ln M, H$ 不可能出现负值。
31 | 在二维数字图像中, 熵的定义为
32 | $$
33 | H_f=-\sum_{m=1}^M \sum_{n=1}^N f(m, n) \ln f(m, n)\tag{5-37}
34 | $$
35 | 最大熵复原的原理是将 $f(x, y)$ 写成随机变量的统计模型,然后在一定的约束条件下,找出用随机变量形式表示的熵的表达式, 运用求极大值的方法, 求得最优估计解 $\hat{f}(x, y)$ 。最大熵复原的含义是对 $\hat{f}(x, y)$ 的最大平滑估计。 最大熵复原常用Friend和Burg两种方法, 这两种方法基本原理相同, 这里仅介绍Friend法。
36 |
37 | 首先定义一幅大小为 $M \times N$ 的图像 $f(x, y)$, 显然 $f(x, y)$ 非负。 图像的总能量 $E$ 和熵分别为
38 | $$
39 | E=\sum_{i=j}^M \sum_{j=1}^N f\left(x_i, y_j\right)\tag{5-38}
40 | $$
41 | 和
42 | $$
43 | H_f=\sum_{i=j}^M \sum_{j=1}^N f\left(x_i, y_j\right) \operatorname{lnf}\left(x_i, y_j\right)\tag{5-39}
44 | $$
45 | 类似地可定义噪声的熵 $H_n$ :
46 | $$
47 | H_n=-\sum_{i=1}^M \sum_{j=1}^N n^{\prime}\left(x_i, y_j\right) 1 n n^{\prime}\left(x_i, y_j\right)\tag{5-40}
48 | $$
49 | 式中: $n^{\prime}(x, y)=n(x, y)+B, B$ 为最大噪声负值。
50 |
51 | 恢复就是在满足式(5-38) 和图像退化模型的约束条件下, 使恢复后的图像熵和噪声熵达到最大。熵通常取决于 $f$ 的形状, 当图像具有均匀的灰度时熵最大。因此用最大熵恢复图像具有某种平滑性。
52 | 引入拉格朗日 (Lagrange) 函数
53 | $$
54 | \begin{aligned}
55 | R & =H_f+\rho H_n+\sum_{m=1}^N \sum_{n=1}^N \lambda_{m m}\left\{\sum_{x=1}^N \sum_{n=1}^N h(m-x, n-y) f(x, y)+n_T(m, n)-B-g(m, n)\right. \\
56 | & +\beta\left\{\sum_{x=1}^N \sum_{y=1}^N f(x, y)-E\right\}
57 | \end{aligned}\tag{5-41}
58 | $$
59 | 式中: $\lambda_{m n}(m, n=1,2, \ldots, N)$ 和 $\beta$ 是拉格朗日乘子, $\rho$ 是加权因子,表示 $H_f$ 和 $H_n$ 相互之间的权重。
60 |
61 | $\hat{f}(x, y)$ 和 $\hat{n}(m, n)$ 分别表示 $f(x, y)$ 和 $n^{\prime}(x, y)$ 的估计值, 则有
62 | $$
63 | \frac{\partial R}{\partial f(x, y)}=0 \tag{5-42}
64 | $$
65 |
66 | $$
67 | \frac{\partial R}{\partial n^{\prime}(x, y)}=0\tag{5-43}
68 | $$
69 | 把式(5-41)分别代入式(5-42)和式(5-43), 可得
70 | $$
71 | \hat{f}(x, y)=\exp \left[-1+\beta+\sum_{m=1}^N \sum_{n=1}^N \lambda_{m m} h(m-x, n-y)\right] \quad x, y=1,2, \ldots, N \tag{5-44}
72 | $$
73 | $$
74 | \hat{n}(m, n)=\exp \left(-1+\frac{\lambda_{m n}}{\rho}\right) \quad \quad m, n=1,2, \ldots, N\tag{5-45}
75 | $$
76 |
77 | 并且$\hat{f}(x,y)$和$\hat{n}(m,n)$满足下列约束条件
78 | $$
79 | \sum_{x=1}^N \sum_{y=1}^N f(x, y)=E\tag{5-46}
80 | $$
81 |
82 | $$
83 | \sum_{x=1}^N \sum_{y=1}^N h(m-x, n-y) f(x, y)+\hat{n}(m, n)-\beta=g(m, n)\tag{5-47}
84 | $$
85 |
86 | 式(5-44)为图像恢复函数。把式(5-44)和式(5-45)代入式(5$46)$ 和式(5-47)可得 $\left(N^2+1\right)$ 个方程。由此联立方程组可解得 $\left(N^2+1\right)$ 个末知数解 $\lambda_{m n}(m, n=1,2, \ldots, N)$, 解上述方程组可求得 $\hat{f}(x, y)$ 的值。
87 |
88 | ## 投影复原
89 |
90 | 投影复原法是用代数方程组来描述线性和非线性退化系统的。该系统可用下式描述:
91 | $$
92 | g(x, y)=H[f(x, y)]+n(x, y)
93 | $$
94 | 其中: $f(x, y)$ 是原始图像, $g(x, y)$ 是退化图像, $n(x, y)$ 是系统噪声, $H$ 是退化算子,表示对图像进行某种运算。
95 | 在使用投影复原法进行图像复原时, 引进一些先验信息附加的约束条件, 可改善图像复原效果。
96 |
97 | ### 投影复原法
98 |
99 | $$
100 | g(x, y)=H[f(x, y)]+n(x, y)
101 | $$
102 | 投影复原方法就是迭代方法之一。设初始估值 $f^0(x, y)$, 然后进行迭代运算.
103 | 设 $f^0(x, y)=g(x, y)$
104 | 设 $H$ 是非线性的, 并忽略噪声, 则上式写成:
105 | $$
106 | \begin{array}{ll}
107 | a_{11} f_1+a_{12} f_2+\ldots & a_{1 N} f_N=g_1 \\
108 | a_{21} f_1+a_{22} f_2+\ldots & a_{2 N} f_N=g_2 \\
109 | \ldots & \\
110 | a_{M 1} f_1+a_{M 2} f_2+\ldots & a_{M N} f_N=g_M
111 | \end{array}\tag{5-48}
112 | $$
113 | $$
114 | f=\left[f_1 \ldots f_N\right]
115 | $$
116 | 取
117 | $$
118 | f^{(0)}=\left[f_1^{(0)}, f_2^{(0)}, \ldots f_N^{(0)}\right]
119 | $$
120 | $$
121 | f^{(0)}=\left[g_1, g_2, \ldots g_N\right]
122 | $$
123 | $f^{(1)}$ 取 $f^{(0)}$ 在第一个超平面$a_{11} f_1+a_{12} f_2+\ldots \quad a_{1 N} f_{N}=g_1$上的投影。
124 |
125 | 即:
126 |
127 | $$
128 | f^{(1)}=f^{(0)}-\frac{f^{(0)} \cdot a_1-g_1}{a_1 \bullet a_2} a_1\tag{5-49}
129 | $$
130 |
131 | $f^{(2)}$ 取 $f^{(1)}$ 在第二个超平面$a_{21} f_1+a_{22} f_2+\ldots \quad a_{2 N} f_{N}=g_2$ 上的投影。
132 |
133 | 依次继续下去, 直到满足 $( 5 . 4 8 )$ 式中最后一个方程式。这就实现了迭代的第一个循环然后再从 (5.48)式中第一个方程式开始第二次迭代。即取 $f^{(M)}$ 在第一个超平面$a_{11} f_1+a_{12} f_2+\ldots a_{1 N} f_{N}=g_1$上的投影。并称之为 $f^{(M+1)}$ 。依次继续, 直到
134 | $$
135 | f^{(k+1)}=f^{(k)}\tag{5-50}
136 | $$
137 | 则:
138 | $$
139 | f^{(k)}=f\tag{5-51}
140 | $$
141 |
--------------------------------------------------------------------------------
/V/5.6 其他图像复原技术.md:
--------------------------------------------------------------------------------
1 | # 5.6 其他图像复原技术
2 |
3 | ## 5.6 几何畸变校正
4 |
5 | 数字图像在获取过程中,由于成像系统的非线性,成像后的图像与原景物图像相比,会产生比例失调,甚至扭曲,我们把这类图像退化现象称之为几何畸变。典型的几何失真如图5-4所示。
6 |
7 |
185 |
186 | 图4-39 图像平滑模板设置对话框
187 |
188 | 利用类向导为对话框的相应控件添加成员变量,如模板类型、模板高度、模板宽度、模板中心元素X坐标、模板中心元素Y坐标对应的成员变量分别定义为整型变量m_intType、m_iTempH、m_iTempW、m_iTempMX、m_iTempMY, 而模板系数对应浮点型的变量m_fTempC,另外还定义了一个模板元素数组指针m_fpArray。
189 | 为3个单选按钮分别定义一个单击事件的消息映射,在映射函数中给模板元素m_fpArray及其他成员变量赋值。
190 |
191 | 2. 获取图像数据
192 | 对每个像素的邻域用选定的模板作卷积运算, 就可以得到平滑后的图像。下面给出了卷积运算的源代码。
193 | 卷积函数中的各参数的含义如下: fpData为被卷积的数组, fpKernel为卷积核数组,fCoef为卷积系数,nSize为卷积尺寸, nResult为卷积结果。
194 |
195 | ```c++
196 | void CAreaPro:: Convolution(float *fpData, float *fpKernel, float fCoef,
197 | int nSize, unsigned char *nResult)
198 | {
199 | int i;
200 | float Sum = 0, fResult;
201 | //计算卷积
202 | for(i = 0; i < nSize; i++)
203 | {
204 | Sum += fpData[i] * fpKernel[i];
205 | }
206 | //执行卷积后的结果
207 | fResult = Sum / fCoef;
208 | //求绝对值
209 | fResult = (float)fabs(fResult);
210 | //判断是否超过255
211 | if(fResult > 255.0 )
212 | {
213 | // 直接赋值为255
214 | fResult = 255.0;
215 | }
216 | //对卷积结果四舍五入, 并转换成unsigned char类型作为最后返回结果
217 | *nResult = (unsigned char) (fResult + 0.5);
218 | }
219 |
220 | ```
221 |
222 | 接着就是对原图像的每个像素作卷积运算,运算后的结果赋予新图像,其中图像边界像素不作处理,代码实现在CAreaPro:: Smoothing()中。
--------------------------------------------------------------------------------
/README.md:
--------------------------------------------------------------------------------
1 | # Digital-mage-Processing
2 | 数字图像处理笔记,整理张航老师的数字图像处理课件,推荐教材是冈萨雷斯第四版
3 |
4 | 现在已经初步整理完毕,但不排除个别地方仍然有细微错误。
--------------------------------------------------------------------------------
/V/5.1 图像退化与复原.md:
--------------------------------------------------------------------------------
1 | # 5.1 图像退化与复原
2 |
3 | 数字图像在获取的过程中,由于光学系统的像差、 光学成像衍射、 成像系统的非线性畸变、 摄影胶片的感光的非线性、 成像过程的相对运动、 大气的湍流效应、环境随机噪声等原因, 图像会产生一定程度的退化。因此,必须采取一定的方法尽可能地减少或消除图像质量的下降,恢复图像的本来面目,这就是图像复原, 也称为图像恢复。
4 |
5 | 图像复原与图像增强有类似的地方, 都是为了改善图像。但是它们又有着明显的不同。图像复原是试图利用退化过程的先验知识使已退化的图像恢复本来面目,即根据退化的原因, 分析引起退化的环境因素,建立相应的数学模型, 并沿着使图像降质的逆过程恢复图像。从图像质量评价的角度来看, 图像复原就是提高图像的可理解性。而图像增强的目的是提高视感质量,图像增强的过程基本上是一个探索的过程, 它利用人的心理状态和视觉系统去控制图像质量, 直到人们的视觉系统满意为止。
6 |
7 | 图像复原是利用退化现象的某种先验知识,建立退化现象的数学模型,再根据模型进行反向的推演运算,以恢复原来的景图像。因而,图像复原可以理解为图像降质过程的反向过程。建立图像复原的反向过程的数学模型,就是图像复原的主要务。经过反向过程的数学模型的运算,要想恢复全真的景物图像比较困难。所以, 图像复原本身往往需要有一个质量准, 即衡量接近全真景物图像的程度,或者说,对原图像的估计是否到达最佳的程度。
8 |
9 | 由于引起退化的因素众多而且性质不同,为了描述图像退化过程所建立的数学模型往往多种多样,而恢复的质量标准也往存在差异性,因此图像复原是一个复杂的数学过程,图像复原的方法、技术也各不相同。
10 |
11 | ## 5.1.1 图像降质的数学模型
12 |
13 | 图像复原处理的关键问题在于建立退化模型。输入图像f(x, y)经过某个退化系统后输出的是一幅退化的图像。为了讨论方便, 把噪声引起的退化即噪声对图像的影响一般作为加性噪声考虑, 这也与许多实际应用情况一致,如图像数字化时的量化噪声、 随机噪声等就可以作为加性噪声,即使不是加性噪声而是乘性噪声, 也可以用对数方式将其转化为相加形式。
14 |
15 | 原始图像 $f(x, y)$ 经过一个退化算子或退化系统 $H(x, y)$ 的作用, 再和噪声 $n(x, y)$ 进行叠加, 形成退化后的图像 $g(x, y)$ 。图11-1表示退化过程的输入和输出的关系, 其中 $H(x, y)$ 概括了退化系统的物理过程, 就是所要寻找的退化数学模型。
16 |
17 | 此处是进行了简化,因为乘法噪声可以转化为加法噪声
18 |
19 | 
20 |
21 | 数字图像的图像恢复问题可看作是: 根据退化图像 $g(x, y)$ 和退化算子 $H(x, y)$ 的形式, 沿着反向过程去求解原始图像 $f(x, y)$, 或者说是逆向地寻找原始图像的最佳近似估计。图像退化的过程可以用数学表达式写成如下的形式:
22 | $$
23 | g(x, y)=H[f(x, y)]+n(x, y)\tag{5-1}
24 | $$
25 | 在这里, $n(x, y)$ 是一种统计性质的信息。在实际应用中, 往往假设噪声是白噪声, 即它的频谱密度为常数, 并且与图像不相关。
26 |
27 | 在图像复原处理中, 尽管非线性、 时变和空间变化的系统模型更具有普遍性和准确性,更与复杂的退化环境相接近,但它给实际处理工作带来了巨大的困难, 常常找不到解或者很难用计算机来处理。因此,在图像复原处理中, 往往用线性系统和空间不变系统模型来加以近似。这种近似的优点使得线性系统中的许多理论可直接用于解决图像复原问题,同时又不失可用性。
28 |
29 | 一幅连续图像 $f(x, y)$ 可以看作是由一系列点源组成的。因此, $f(x, y)$ 可以通过点源函数的卷积来表示。即
30 | $$
31 | f(x, y)=\int_{-\infty}^{+\infty} \int_{-\infty}^{+\infty} f(\alpha, \beta) \delta(x-\alpha, y-\beta) d \alpha d \beta\tag{5-2}
32 | $$
33 | 式中, $\delta$ 函数为点源函数, 表示空间上的点脉冲。
34 | 在不考虑噪声的一般情况下, 连续图像经过退化系统 $H$ 后的输出为
35 |
36 | $$
37 | \quad g(x, y)=H[f(x, y)]\tag{5-3}
38 | $$
39 |
40 | 把式(5-2)代入式(5-3)得
41 |
42 | $$
43 | \begin{gathered}
44 | g(x, y)=H[f(x, y)]=H\left[\int_{-\infty}^{+\infty} \int_{-\infty}^{+\infty} f(\alpha, \beta) \delta(x-\alpha, y-\beta) d \alpha d \beta\right]
45 | \end{gathered}\tag{5-4}
46 | $$
47 |
48 | 在线性和空间不变系统的情况下, 退化算子 $H$ 具有如下性质:
49 | (1) 线性: 设 $f_1(x, y)$ 和 $f_2(x, y)$ 为两幅输入图像, $k_1$ 和 $k_2$ 为常数, 则
50 |
51 | $$
52 | H\left[k_1 f_1(x, y)+k_2 f_2(x, y)\right]=k_1 H\left[f_1(x, y)\right]+k_2 H\left[f_2(x, y)\right]\tag{5-5}
53 | $$
54 |
55 | 由该性质还可推出下面两个结论:
56 | (1) 当 $k_1=k_2=1$ 时, 式(11-5)变为
57 |
58 | $$
59 | H\left[f_1(x, y)+f_2(x, y)\right]=H\left[f_1(x, y)\right]+H\left[f_2(x, y)\right]\tag{5-6}
60 | $$
61 |
62 | (2) 如果 $f_2(x, y)=0$, 则式 (11-5) 变为
63 |
64 | $$
65 | H\left[k_1 f_1(x, y)\right]=k_1 H\left[f_1(x, y)\right]\tag{5-7}
66 | $$
67 |
68 | (2) 空间不变性: 如果对任意 $f(x, y)$ 以及 $a$ 和 $b$, 有
69 |
70 | $$
71 | H[f(x-a, y-b)]=g(x-a, y-b)\tag{5-8}
72 | $$
73 |
74 | 则对于线性空间不变系统, 输入图像经退化后的输出为
75 |
76 | $$
77 | \begin{aligned}
78 | g(x, y) & =H[f(x, y)]=H\left[\int_{-\infty}^{+\infty} \int_{-\infty}^{+\infty} f(\alpha, \beta) \delta(x-\alpha, y-\beta) d \alpha d \beta\right] \\
79 | & =\int_{-\infty}^{+\infty} \int_{-\infty}^{+\infty} f(\alpha, \beta) H[\delta(x-\alpha, y-\beta)] d \alpha d \beta \\
80 | & =\int_{-\infty}^{+\infty} \int_{-\infty}^{+\infty} f(\alpha, \beta) h(x-\alpha, y-\beta) d \alpha d \beta
81 | \end{aligned}\tag{5-9}
82 | $$
83 |
84 | 式中, $h(x-\alpha, y-\beta)$ 为该退化系统的点扩展函数, 或叫系统的冲激响应函数。它表示系统对坐标为 $(a, \beta)$ 处的冲激函数 $\delta(x-\alpha, y-\beta)$ 的响应。也就是说, 只要系统对冲激函数的响应为已知, 那么就可以清楚图像退化是如何形成的。因为对于任一输入 $f(a, \beta)$ 的响应, 都可以通过上式计算出来。
85 | 此时, 退化系统的输出就是输入图像信号 $f(x, y)$ 与点扩展函数 $h(x, y)$ 的卷积, 即
86 |
87 | $$
88 | g(x, y)=\int_{-\infty}^{+\infty} \int_{-\infty}^{+\infty} f(\alpha, \beta) h(x-\alpha, y-\beta) d \alpha d \beta=f(x, y) * h(x, y)\tag{5-10}
89 | $$
90 |
91 | 图像退化除了受到成像系统本身的影响外, 有时还要受到噪声的影响。假设噪声 $n(x, y)$ 是加性白噪声, 这时上式可写成
92 |
93 | $$
94 | \begin{aligned}
95 | g(x, y) & =\int_{-\infty}^{+\infty} \int_{-\infty}^{+\infty} f(\alpha, \beta) h(x-\alpha, y-\beta) d \alpha d \beta+n(x, y) \\
96 | & =f(x, y) * h(x, y)+n(x, y)
97 | \end{aligned}\tag{5-11}
98 | $$
99 |
100 | 在频域上, 式(11-11)可以写成
101 |
102 | $$
103 | G(u, v)=F(u, v) H(u, v)+N(u, v)\tag{5-12}
104 | $$
105 |
106 | 其中, $G(u, v) 、 F(u, v) 、 N(u, v)$ 分别是退化图像 $g(x, y)$ 、原图像 $f(x, y)$、噪声信号 $n(x, y)$ 的傅立叶变换; $H(u, v)$ 是系统的点冲激响应函数 $h(x, y)$ 的傅立叶变换, 称为系统在频率域上的传递函数。
107 |
108 | 式(5-11)和式(5-12)就是连续函数的退化模型。可见, 图像复原实际上就是已知 $g(x, y)$ 求 $f(x, y)$ 的问题或已知 $G(u, v)$ 求 $F(u, v)$ 的问题, 它们的不同之处在于一个是在空域,一个是在频域。
109 | 显然, 进行图像复原的关键问题是寻找降质系统在空间域上的冲激响应函数 $h(x, y)$, 或者降质系统在频率域上的传递函数 $H(u$, $v)$ 。一般来说, 传递函数比较容易求得。因此, 在进行图像复原之前, 一般应设法求得完全的或近似的降质系统传递函数, 要想得到 $h(x, y)$, 只需对 $H(u, v)$ 求傅立叶逆变换即可。
110 |
111 | ## 5.1.2 离散图像退化的数学模型
112 |
113 | 1. 一维离散退化模型
114 | 设 $f(x)$ 为具有 $A$ 个采样值的离散输入函数, $h(x)$ 为具有 $B$ 个采样值的退化系统的冲激响应函数, 则经退化系统后的离散输出函数 $g(x)$ 为输入 $f(x)$ 和冲激响应 $h(x)$ 的卷积, 即
115 | $$
116 | g(x)=f(x)^* h(x)
117 | $$
118 | 为了避免上述卷积所产生的各个周期重叠(设每个采样函数的周期为 $M)$ ,分别对 $f(x)$ 和 $h(x)$ 用添零延伸的方法扩展成周期 $M=A+B-1$ 的周期函数, 即
119 | $$
120 | f_e(x)=\left\{\begin{array}{cc}
121 | f(x) & 0 \leq x \leq A-1 \\
122 | 0 & A \leq x \leq M-1
123 | \end{array}\right. \tag{5-13a}
124 | $$
125 | $$
126 | h_e(x)=\left\{\begin{array}{cc}
127 | h(x) & 0 \leq x \leq B-1 \\
128 | 0 & B \leq x \leq M-1
129 | \end{array}\right.\tag{5-13b}
130 | $$
131 | 输出为
132 | $$
133 | g_e(x)=f_e(x) * h_e(x)=\sum_{m=0}^{M-1} f_e(m) h_e(x-m)\tag{5-14}
134 | $$
135 | 式中, $x=0,1,2, \ldots, M-1$ 。
136 |
137 | 因为 $f_{e}(x)$ 和 $h_{e}(x)$ 已扩展成周期函数, 故 $g_{e}(x)$ 也是周期性函数, 用矩阵表示为
138 | $$
139 | \left[\begin{array}{c}
140 | g(0) \\
141 | g(1) \\
142 | g(2) \\
143 | M \\
144 | g(M-1)
145 | \end{array}\right]=\left[\begin{array}{cccc}
146 | h_e(0) & h_e(-1) & \Lambda & h_e(-M+1) \\
147 | h_e(1) & h_e(0) & \Lambda & h_e(-M+2) \\
148 | h_e(2) & h_e(1) & \Lambda & h_e(-M+3) \\
149 | M & M & M & M \\
150 | h_e(M-1) & h_e(M-2) & \Lambda & h_e(0)
151 | \end{array}\right]\left[\begin{array}{c}
152 | f_e(0) \\
153 | f_e(1) \\
154 | f_e(2) \\
155 | M \\
156 | f_e(M-1)
157 | \end{array}\right]\tag{5-15}
158 | $$
159 | 因为 $h_{e}(x)$ 的周期为 $M$, 所以 $h_{e}(x)=h_{e}(x+M)$, 即
160 | $$
161 | \begin{gathered}
162 | h_e(-1)=h_e(M-1) \\
163 | h_e(-2)=h_e(M-2) \\
164 | h_e(-3)=h_e(M-3) \\
165 | M \\
166 | h_e(-M+1)=h_e(1)
167 | \end{gathered}
168 | $$
169 | $M \times M$ 阶矩阵 $\boldsymbol{H}$ 可写为
170 | $$
171 | H=\left[\begin{array}{cccc}
172 | h_e(0) & h_e(-1) & \Lambda & h_e(1) \\
173 | h_e(1) & h_e(0) & \Lambda & h_e(2) \\
174 | h_e(2) & h_e(1) & \Lambda & h_e(3) \\
175 | M & M & \Lambda & \Lambda \\
176 | h_e(M-1) & h_e(M-2) & h_e(0)
177 | \end{array}\right]\tag{5-16}
178 | $$
179 | 可将式(5-15)写成更简洁的形式,即
180 | $$
181 | g=H f\tag{5-17}
182 | $$
183 | 式中, $\boldsymbol{g} 、 \boldsymbol{f}$ 都是 $M$ 维列向量, $\boldsymbol{H}$ 是 $M \times M$ 阶矩阵, 矩阵中的每一行元素均相同, 只是每行以循环方式右移一位, 因此矩阵 $\boldsymbol{H}$ 是循环矩阵。循环矩阵相加或相乘得到的还是循环矩阵。
184 |
185 | 2. 二维离散模型
186 | 设输入的数字图像 $f(x, y)$ 大小为 $A \times B$, 点扩展函数 $h(x, y)$ 被均匀采样为 $C \times D$ 大小。为避免交叠误差, 仍用添零扩展的方法, 将它们扩展成 $M=A+C-1$ 和 $N=B+D-1$ 个元素的周期函数。
187 |
188 | $$
189 | f_e(x, y)=\left\{\begin{array}{cc}
190 | f(x, y) & 0 \leq x \leq A-1 \text { 且 } 0 \leq y \leq B-1 \\
191 | 0 & \text { 其他 }
192 | \end{array}\right. \tag{5-18a}
193 | $$
194 | $$
195 | h_e(x, y)=\left\{\begin{array}{cc}
196 | h(x, y) & 0 \leq x \leq C-1 \text { 且 } 0 \leq y \leq D-1 \\
197 | 0 & \text { 其他 }
198 | \end{array}\right.\tag{5-18b}
199 | $$
200 |
201 | 则输出的降质数字图像为
202 | $$
203 | g_e(x, y)=\sum_{m=0}^{M-1} \sum_{n=0}^{N-1} f_e(m, n) h_e(x-m, y-n)=f(x, y)^* h(x, y)\tag{5-19}
204 | $$
205 | 式中: $x=0,1,2, \ldots, M-1 ; y=0,1,2, \ldots, N-1$ 。
206 | 式(5-19)的二维离散退化模型同样可以用式 (5-17) 所示的矩阵形式表示, 即
207 | $$
208 | g=H f
209 | $$
210 | 式中, $g 、 f$ 是 $M N \times 1$ 维列向量, $H$ 是 $M N \times M N$ 维矩阵。其方法是将 $g(x, y)$ 和 $f(x, y)$ 中的元素排成列向量。
211 | $$
212 | f_1=\left[\underbrace{f_1(0,0),f_1(0,1),\cdots,f_1(0,N-1)}_{第0行元素},\underbrace{f_1(1,0),f_1(1,1),\cdots,f_1(1,N-1)}_{第1行元素},\cdots,\underbrace{f_1(M-1,0),f_1(M-1,1),\cdots,f_1(M-1,N-1)}_{第M-1行元素}\right]^T\\
213 | g_1=\left[\underbrace{g_1(0,0),g_1(0,1),\cdots,g_1(0,N-1)}_{第0行元素},\underbrace{g_1(1,0),g_1(1,1),\cdots,g_1(1,N-1)}_{第1行元素},.\cdots,\underbrace{g_1(M-1,0),g_1(M-1,1),\cdots,g_1(M-1,N-1)}_{第M-1行元素}\right]^T
214 | \tag{5-20}
215 | $$
216 |
217 | $$
218 | H=\left[\begin{array}{cccc}
219 | H_0 & H_{M-1} & H_{M-2} & \cdots& H_1 \\
220 | H_1 & H_0 & H_{M-1} & \cdots& H_2 \\
221 | \vdots & \vdots & \vdots & \ddots&\vdots \\
222 | H_{M-1} & H_{M-2} & H_{M-3} & \cdots &H_0
223 | \end{array}\right]
224 | \tag{5-21}
225 | $$
226 | $H_i(i=0,1,2, \ldots, M-1)$ 为子矩阵, 大小为 $N \times N$, 即 $H$ 矩阵由 $M \times M$ 个大小为 $N \times N$ 的子矩阵组成, 称为分块循环矩阵。分块矩阵是由延拓函数 $h_{e}(x, y)$ 的第 $j$ 行构成的, 构成方法如下:
227 | $$
228 | H=\left[\begin{array}{cccc}
229 | h_e(j, 0) & h_e(j, N-1) & h_e(j, N-2) & \cdots& h_e(j, 1) \\
230 | h_e(j, 1) & h_e(j, 0) & h_e(j, N-1) & \cdots &h_e(j, 0) \\
231 | \vdots & \vdots & \vdots &\ddots &\vdots \\
232 | h_e(j, N-1) & h_e(j, N-2) & h_e(j, N-3) & \cdots &h_e(j, 0)
233 | \end{array}\right]
234 | \tag{5-22}
235 | $$
236 | 若把噪声考虑进去, 则离散图像退化模型为
237 | $$
238 | g_e(x, y)=\sum_{m=0}^{M-1} \sum_{n=0}^{N-1} f_e(m, n) h_e(x-m, y-n)+n_e(x, y)
239 | \tag{5-23}
240 | $$
241 | 写成矩阵形式为
242 | $$
243 | g=H f+n\tag{5-24}
244 | $$
245 | 上述线性空间不变退化模型表明, 在给定了 $g(x, y)$, 并且知道退化系统的点扩展函数 $h(x, y)$ 和噪声分布 $n(x, y)$ 的情况下, 可估计出原始图像 $f(x, y)$ 。
246 | 假设图像大小 $M=N=512$, 相应矩阵 $M H$ 的大小为 $M N \times M N=262144 \times 262144$, 这意味着要解出 $f(x, y)$ 需要解262 144 个联立方程组, 其计算量十分惊人。
247 |
248 | 图像恢复目的是在给定的 $g(x, y), h(x, y), n(x, y)$ 情况下, 求 $f(x, y)$. 由于 $G , F$ 维数很大, 通过解方程组不可能进行图像恢复.
249 | 1. 代数复原方法:寻找一个估计 $f(x, y)$.
250 | - 非约束复原方法
251 | - 约束复原方法
252 | 2.逆滤波方法
253 |
254 |
--------------------------------------------------------------------------------
/V/5.2 代数复原法.md:
--------------------------------------------------------------------------------
1 | # 5.2 代数复原法
2 |
3 | ## 5.2.1非约束复原方法
4 |
5 | 由式(5-24)可得
6 | $$
7 | n=g-H f\tag{5-25}
8 | $$
9 | 在对 $n$ 没有先验知识的情况下, 可以依据这样的最优准则, 即寻找一个 $\hat{f}$, 使得 $H \hat{f}$ 在最小二乘方误差的意义下最按近 $g$, 即要使 $n$ 的模或范数 (norm) 最小:
10 | $$
11 | \|n\|^2=n^T n=\|g-H \hat{f}\|^2=(g-H \hat{f})^T(g-\hat{H f})\tag{5-26}
12 | $$
13 | 即优化目标为:
14 | $$
15 | L(\hat{f})=\|g-H \hat{f}\|^2\tag{5-27}
16 | $$
17 | 如果我们在求最小值的过程中, 不做任何约束, 称这种复原为非约束复原。由极值条件
18 | $$
19 | \frac{\partial L(\hat{f})}{\partial \hat{f}}=0 \Rightarrow H^T(g-H \hat{f})=0\tag{5-28}
20 | $$
21 | 解出 $\hat{f}$ 为
22 | $$
23 | \hat{f}=\left(H^T H\right)^{-1} H^T g\tag{5-29}
24 | $$
25 |
26 | ## 5.2.2 约束复原法
27 |
28 | 非约束复原是指除了使准则函数 $L(\hat{f})=\|g-\hat{H f}\|^2$ 最小外, 再没有其他的约束条件。因此只需了解降质系统的传递函数或点扩展函数, 就能利用如前所述的方法进行复原。但是由于传递函数存在病态问题, 复原只能局限在靠近原点的有限区域内进行, 这使得非约束图像复原具有相当大的局限性。
29 |
30 | 最小二乘类约束复原是指除了要求了解关于退化系统的传递函数之外, 还需要知道某些噪声的统计特性或噪声与图像的某些相关情况。根据所了解的噪声的先验知识的不同, 采用不同的约束条件, 可得到不同的图像复原技术。在最小二乘类约束复原中, 要设法寻找一个最优估计 $\hat{f}$, 使得形式为 $\|Q \hat{f}\|^2=\|n\|^2$ 的函数最小化。求这类问题的最小化, 常采用拉格朗日乘子算法。也就说, 要寻找一个 $\hat{f}$, 使得优化目标函数:
31 | $$
32 | J(\hat{f})=\|\hat{O \hat{f}}\|^2+\alpha\left(\|g-H \hat{f}\|^2-\|n\|^2\right)\tag{5-30}
33 | $$
34 | 为最小。式中, $Q$ 为 $\hat{f}$ 的线性算子, $\alpha$ 为一常数, 称为拉格朗日乘子。对式(5-30)求导得
35 | $$
36 | \begin{aligned}
37 | & \frac{\partial J(\hat{f})}{\partial f}=0 \\
38 | & Q^T Q \hat{f}-\alpha H^T(g-H \hat{f})=0
39 | \end{aligned}
40 | $$
41 | 求解 $\hat{f}$ 得到
42 | $$
43 | \hat{f}=\left(H^T H+\gamma Q^T Q\right)^{-1} H^T g\tag{5-31}
44 | $$
--------------------------------------------------------------------------------
/V/5.3 逆滤波.md:
--------------------------------------------------------------------------------
1 | # 5.3 逆滤波
2 |
3 | 只能接近,无法完全恢复
4 |
5 | 1.逆滤波基本原理
6 | 由退化图像的付里叶变换求得图像的付里叶变换的估计方法称为逆滤波.
7 |
8 | 逆滤波
9 | $$
10 | \begin{aligned}
11 | \overline{g(x, y)}= & \int_{-\infty}^{\infty} \int_{-\infty}^{\infty} f(x, A) h(x-\imath v, y-A) d x d, \partial+n(x, y) \\
12 | & G(u, v)=F(u, v) H(u, v)+N(u, v)
13 | \end{aligned}
14 | $$
15 | 不考虑噪声:
16 |
17 | $$
18 | \begin{aligned} F(u, v) & =\frac{G(u, v)}{H(u, v)} \\ f(x, y) & =\mathcal{G}^{-1}[F(u, v)]\end{aligned}
19 | $$
20 | 有噪声:
21 | $$
22 | \begin{aligned}
23 | & F(u, v)=\frac{G(u, v)}{H(u, v)}-\frac{N(u, v)}{H(u, v)} \\
24 | & f(x, y)=\xi^{-1}[F(u, v)]
25 | \end{aligned}
26 | $$
27 |
28 |
29 |
30 |
31 | 
32 |
33 | 图5.2 逆滤波
34 |
35 | 逆滤波
36 | 2.去除由均匀直线运动引起的模糊
37 | - 模糊模型
38 | $$
39 | g(x, y)=\int_0^T f\left[x-x_0(t), y-y_0(t)\right] d t
40 | $$
41 | $f(x, y)$ : 原图像; $g(x, y)$ : 模糊图像; $T$ : 暴光时间
42 | - 图像恢复 $G(u, v)=H(u, v) F(u, v)$
43 | 其中: $H(u, v)=\int_0^T \exp \left\{-j 2 \pi\left[u x_0(t)+v y_0(t)\right]\right\} d t$
44 |
45 | ## 用途
46 |
47 | 在实验室中,可以反复做实验的情景
--------------------------------------------------------------------------------
/V/5.4 最小二乘滤波(维纳滤波,重点).md:
--------------------------------------------------------------------------------
1 |
2 |
3 | # 5.4 最小二乘方滤波(维纳滤波)
4 |
5 | **重点**
6 |
7 | 知道图像,知道有关分布特征
8 |
9 | 1.最小二乘方滤波
10 | 设原始图像, 退化图像和噪声分别为 $f(x, y), g(x, y)$ 和 $n(x, y)$, 则 :
11 |
12 | $$
13 | g(x, y)=H[f(x, y)]=H\left[\int_{-\infty}^{+\infty} \int_{-\infty}^{+\infty} f(\alpha, \beta) \delta(x-\alpha, y-\beta) d \alpha d \beta\right]+n(x, y)$ 在给定的 $g(x, y)$ 时, 找出 $f(x, y)$ 的估计 $f(x, y)
14 | $$
15 | 使:
16 | $$
17 | e^2=E\left\{[f(x, y)-\hat{f}(x, y)]^2\right\}
18 | $$
19 | 最小.
20 |
21 | 设
22 | $$
23 | \quad \hat{f}(x, y)=\iint m(x, y, \alpha, \beta) g(\alpha, \beta) d \alpha d \beta
24 | $$
25 | 2. 求解
26 | 如果 $f(x, y), g(x, y)$ 和 $n(x, y)$ 是均匀随机场, 则 :
27 | $$
28 | \hat{f}(x, y)=\iint m(x-\alpha, y-\beta) g(\alpha, \beta) d \alpha d \beta
29 | $$
30 | 因此图像恢复就是确定m $m, y)$. 通过求解得:
31 | $$
32 | \begin{aligned}
33 | M(u, v) & =\left[\frac{H^*(u, v)}{|H(u, v)|^2+\left[S_n(u, v) / S_f(u, v)\right]}\right] \\
34 | & =\left[\frac{1}{H(u, v)} \cdot \frac{|H(u, v)|^2}{\left|H(u, v)^2\right|+\left[S_n(u, v) / S_f(u, v)\right]}\right]
35 | \end{aligned}
36 | $$
37 | $H(u, v)$ 是的h $(x, y)$ 付里叶变换.
38 | $S_f, S_n$ 分别是 $f(x, y), n(x, y)$ 的谱密度
39 |
40 | 于是:
41 | $$
42 | \begin{aligned}
43 | \hat{F}(u, v) & =\left[\frac{H^*(u, v)}{|H(u, v)|^2+\left[S_n(u, v) / S_f(u, v)\right]}\right] G(u, v) \\
44 | & =\left[\frac{1}{H(u, v)} \cdot \frac{|H(u, v)|^2}{\left|H(u, v)^2\right|+\left[S_n(u, v) / S_f(u, v)\right]}\right] G(u, v)
45 | \end{aligned}\tag{5-32}
46 | $$
47 | 式中,
48 | $$
49 | u, v=0,1,2, \ldots, N-1,|H(u, v)|^2=H^*(u, v) H(u, v)
50 | $$
51 |
52 | 3. 讨论
53 | - $S_n=0$ 时, 是理想的逆滤波器
54 | -若随机过程的统计特性不知道, 可采用:
55 | $$
56 | M(u, v)=\frac{1}{H(u, v)} \frac{|H(u, v)|^2}{|H(u, v)|^2+\Gamma}
57 | $$
58 | 式中 $\Gamma$ 是噪声对信号的功率密度比.
59 |
60 | - 维纳滤波器是假设线性系统, 实际上图像的记录和评价图像的视觉系统都是非线性系统.
61 | - 维纳滤波器是根据最小均方差设计的,这个准则不见得与人的视觉判决准则相符.
62 | - 维纳滤波器是基于平稳随机过程的模型,实际图像不一定符合这一条件.
63 |
64 | ## 几种最小二乘方滤波器
65 |
66 | (仅供了解)
67 |
68 | 1.图像功率谱滤波器
69 | $$
70 | H_{R}(u, v)=\left[\frac{W_{FI}(u, v)}{\left|H_{D}(u, v)\right|^2 W_{F 1}(u, v)+W_{N}(u, v)}\right]^{\frac{1}{2}}
71 | $$
72 | 式中 $H_{D}(u, v)$ 是图像退化的传递函数。 $W_{F 1}(u, v)$ 代表滤波器输出功率频谱,
73 | $$
74 | W_{FI}(u, v)=\left|H_{D}(u, v)\right|^2 W_{FO}(u, v)
75 | $$
76 | 式中 $W_{FO}(u, v)$ 代表观测的功率频谱。它与理想图像的功率频谱的关系是
77 | $$
78 | W_{FO}(u, v)=\left|H_{D}(u, v)\right|^2 \cdot W_{FI}(u, v)+W_{N}(u, v)
79 | $$
80 | 式中 $W_{N}(u, v)$ 是噪声功率频谱。
81 |
82 | 2.几何平均滤波器.
83 |
84 | 几何平均滤波器的传递函数由下式表示:
85 | $$
86 | H_{R}(u, v)=\left[H_{D}(u, v)\right]^{-s}\left[\frac{H_{D}^*(u, v) W_{FI}(u, v)}{\left|H_{D}(u, v)\right|^2 W_{FI}(u, v)+W_{N}(u, v)}\right]^{1-s}
87 | $$
88 | S是一个参数
89 |
90 | 3.约束最小方滤波器
91 |
92 | 约束最小方滤波器的传递函数如下:
93 | $$
94 | H_{\mathrm{R}}(u, v)=\frac{H_{\mathrm{D}}^*(u, v)}{\left|H_{\mathrm{D}}(u, v)\right|^2+r|L(u, v)|^2}
95 | $$
96 | $r$是一个参数,$L(u,v)$是一个频率参数。$r=1$为维纳滤波器
--------------------------------------------------------------------------------
/V/5.5 非线性复原方法 .md:
--------------------------------------------------------------------------------
1 | # 5.5 非线性复原方法(仅供了解)
2 |
3 | ## 5.5.1 最大后验复原
4 |
5 | 最大后验复原是一种统计方法, 它把原图像 $f(x, y)$ 和退化图像 $g(x, y)$ 都作为随机场, 在已知 $g(x, y)$ 的前提下, 求出后验条件概率密度函数 $P(f(x, y) / g(x, y))$ 。若 $\hat{f}(x, y)$ 使式
6 | $$
7 | \max _{f} p(f \mid g)=\max _f p(g \mid f) p(f) / p(g)=\max _f p(g \mid f) p(f)\tag{5-33}
8 | $$
9 | 最大, 则 $\hat{f}(x, y)$ 就代表已知退化图像 $g(x, y)$ 时, 最可能的原始图像 $f(x, y)$ 。这种图像方法称之为最大后验图像复原方法。
10 |
11 | 最大后验图像复原方法把图像看作是非平稳随机场, 把图像模型表示成一个平稳随机过程对于一个不平稳的均值作零均值Gauss起伏, 可得出求解迭代序列:
12 | $$
13 | \hat{f}_{k+1}=\hat{f}_k-h^* \sigma_n^{-2}\left(g-h^* \hat{f}_k\right)-\sigma_n^{-2}\left(\hat{f}_k-\bar{f}\right)\tag{5-34}
14 | $$
15 | 其中, $k$ 为迭代次数, $\sigma_n^{-2}$ 和 $\sigma_f^{-2}$ 分别为 $f$ 和 $n$ 的方差的倒数, $f$ 是随空间而变的均值, 它是一个常数, 但要经过多次迭代才能收敛到最后的解。
16 |
17 | ## 5.5.2 最大熵复原
18 |
19 | 最大熵复原方法是通过最大化某种反映图像平滑性的准则函数来作约束条件, 以解决图像复原中反向滤波法存在的病态问题。
20 | 首先简单介绍一下熵的概念。
21 | 熵的定义为
22 | $$
23 | H=-\int_{-\infty}^{+\infty} P(x) \ln P(x) d x\tag{5-35}
24 | $$
25 | 式中, $P(x)$ 为随机变量 $x$ 的概率密度。
26 | 对于离散信号, 熵的定义为
27 | $$
28 | H=-\sum_{k=1}^M P(k) \ln P(k)\tag{5-36}
29 | $$
30 | 熵是表征随机变量集合的随机程度的量度。当所有随机变量等可能性时, 也就是说 $P_1=P_2=\ldots=P_{m}$ 时熵最大, 为 $H=\ln M$ 。由于概率 $P(k)$ 介于 $0 \sim 1$ 之间, 因此最大熵的范围为 $0 \sim \ln M, H$ 不可能出现负值。
31 | 在二维数字图像中, 熵的定义为
32 | $$
33 | H_f=-\sum_{m=1}^M \sum_{n=1}^N f(m, n) \ln f(m, n)\tag{5-37}
34 | $$
35 | 最大熵复原的原理是将 $f(x, y)$ 写成随机变量的统计模型,然后在一定的约束条件下,找出用随机变量形式表示的熵的表达式, 运用求极大值的方法, 求得最优估计解 $\hat{f}(x, y)$ 。最大熵复原的含义是对 $\hat{f}(x, y)$ 的最大平滑估计。 最大熵复原常用Friend和Burg两种方法, 这两种方法基本原理相同, 这里仅介绍Friend法。
36 |
37 | 首先定义一幅大小为 $M \times N$ 的图像 $f(x, y)$, 显然 $f(x, y)$ 非负。 图像的总能量 $E$ 和熵分别为
38 | $$
39 | E=\sum_{i=j}^M \sum_{j=1}^N f\left(x_i, y_j\right)\tag{5-38}
40 | $$
41 | 和
42 | $$
43 | H_f=\sum_{i=j}^M \sum_{j=1}^N f\left(x_i, y_j\right) \operatorname{lnf}\left(x_i, y_j\right)\tag{5-39}
44 | $$
45 | 类似地可定义噪声的熵 $H_n$ :
46 | $$
47 | H_n=-\sum_{i=1}^M \sum_{j=1}^N n^{\prime}\left(x_i, y_j\right) 1 n n^{\prime}\left(x_i, y_j\right)\tag{5-40}
48 | $$
49 | 式中: $n^{\prime}(x, y)=n(x, y)+B, B$ 为最大噪声负值。
50 |
51 | 恢复就是在满足式(5-38) 和图像退化模型的约束条件下, 使恢复后的图像熵和噪声熵达到最大。熵通常取决于 $f$ 的形状, 当图像具有均匀的灰度时熵最大。因此用最大熵恢复图像具有某种平滑性。
52 | 引入拉格朗日 (Lagrange) 函数
53 | $$
54 | \begin{aligned}
55 | R & =H_f+\rho H_n+\sum_{m=1}^N \sum_{n=1}^N \lambda_{m m}\left\{\sum_{x=1}^N \sum_{n=1}^N h(m-x, n-y) f(x, y)+n_T(m, n)-B-g(m, n)\right. \\
56 | & +\beta\left\{\sum_{x=1}^N \sum_{y=1}^N f(x, y)-E\right\}
57 | \end{aligned}\tag{5-41}
58 | $$
59 | 式中: $\lambda_{m n}(m, n=1,2, \ldots, N)$ 和 $\beta$ 是拉格朗日乘子, $\rho$ 是加权因子,表示 $H_f$ 和 $H_n$ 相互之间的权重。
60 |
61 | $\hat{f}(x, y)$ 和 $\hat{n}(m, n)$ 分别表示 $f(x, y)$ 和 $n^{\prime}(x, y)$ 的估计值, 则有
62 | $$
63 | \frac{\partial R}{\partial f(x, y)}=0 \tag{5-42}
64 | $$
65 |
66 | $$
67 | \frac{\partial R}{\partial n^{\prime}(x, y)}=0\tag{5-43}
68 | $$
69 | 把式(5-41)分别代入式(5-42)和式(5-43), 可得
70 | $$
71 | \hat{f}(x, y)=\exp \left[-1+\beta+\sum_{m=1}^N \sum_{n=1}^N \lambda_{m m} h(m-x, n-y)\right] \quad x, y=1,2, \ldots, N \tag{5-44}
72 | $$
73 | $$
74 | \hat{n}(m, n)=\exp \left(-1+\frac{\lambda_{m n}}{\rho}\right) \quad \quad m, n=1,2, \ldots, N\tag{5-45}
75 | $$
76 |
77 | 并且$\hat{f}(x,y)$和$\hat{n}(m,n)$满足下列约束条件
78 | $$
79 | \sum_{x=1}^N \sum_{y=1}^N f(x, y)=E\tag{5-46}
80 | $$
81 |
82 | $$
83 | \sum_{x=1}^N \sum_{y=1}^N h(m-x, n-y) f(x, y)+\hat{n}(m, n)-\beta=g(m, n)\tag{5-47}
84 | $$
85 |
86 | 式(5-44)为图像恢复函数。把式(5-44)和式(5-45)代入式(5$46)$ 和式(5-47)可得 $\left(N^2+1\right)$ 个方程。由此联立方程组可解得 $\left(N^2+1\right)$ 个末知数解 $\lambda_{m n}(m, n=1,2, \ldots, N)$, 解上述方程组可求得 $\hat{f}(x, y)$ 的值。
87 |
88 | ## 投影复原
89 |
90 | 投影复原法是用代数方程组来描述线性和非线性退化系统的。该系统可用下式描述:
91 | $$
92 | g(x, y)=H[f(x, y)]+n(x, y)
93 | $$
94 | 其中: $f(x, y)$ 是原始图像, $g(x, y)$ 是退化图像, $n(x, y)$ 是系统噪声, $H$ 是退化算子,表示对图像进行某种运算。
95 | 在使用投影复原法进行图像复原时, 引进一些先验信息附加的约束条件, 可改善图像复原效果。
96 |
97 | ### 投影复原法
98 |
99 | $$
100 | g(x, y)=H[f(x, y)]+n(x, y)
101 | $$
102 | 投影复原方法就是迭代方法之一。设初始估值 $f^0(x, y)$, 然后进行迭代运算.
103 | 设 $f^0(x, y)=g(x, y)$
104 | 设 $H$ 是非线性的, 并忽略噪声, 则上式写成:
105 | $$
106 | \begin{array}{ll}
107 | a_{11} f_1+a_{12} f_2+\ldots & a_{1 N} f_N=g_1 \\
108 | a_{21} f_1+a_{22} f_2+\ldots & a_{2 N} f_N=g_2 \\
109 | \ldots & \\
110 | a_{M 1} f_1+a_{M 2} f_2+\ldots & a_{M N} f_N=g_M
111 | \end{array}\tag{5-48}
112 | $$
113 | $$
114 | f=\left[f_1 \ldots f_N\right]
115 | $$
116 | 取
117 | $$
118 | f^{(0)}=\left[f_1^{(0)}, f_2^{(0)}, \ldots f_N^{(0)}\right]
119 | $$
120 | $$
121 | f^{(0)}=\left[g_1, g_2, \ldots g_N\right]
122 | $$
123 | $f^{(1)}$ 取 $f^{(0)}$ 在第一个超平面$a_{11} f_1+a_{12} f_2+\ldots \quad a_{1 N} f_{N}=g_1$上的投影。
124 |
125 | 即:
126 |
127 | $$
128 | f^{(1)}=f^{(0)}-\frac{f^{(0)} \cdot a_1-g_1}{a_1 \bullet a_2} a_1\tag{5-49}
129 | $$
130 |
131 | $f^{(2)}$ 取 $f^{(1)}$ 在第二个超平面$a_{21} f_1+a_{22} f_2+\ldots \quad a_{2 N} f_{N}=g_2$ 上的投影。
132 |
133 | 依次继续下去, 直到满足 $( 5 . 4 8 )$ 式中最后一个方程式。这就实现了迭代的第一个循环然后再从 (5.48)式中第一个方程式开始第二次迭代。即取 $f^{(M)}$ 在第一个超平面$a_{11} f_1+a_{12} f_2+\ldots a_{1 N} f_{N}=g_1$上的投影。并称之为 $f^{(M+1)}$ 。依次继续, 直到
134 | $$
135 | f^{(k+1)}=f^{(k)}\tag{5-50}
136 | $$
137 | 则:
138 | $$
139 | f^{(k)}=f\tag{5-51}
140 | $$
141 |
--------------------------------------------------------------------------------
/V/5.6 其他图像复原技术.md:
--------------------------------------------------------------------------------
1 | # 5.6 其他图像复原技术
2 |
3 | ## 5.6 几何畸变校正
4 |
5 | 数字图像在获取过程中,由于成像系统的非线性,成像后的图像与原景物图像相比,会产生比例失调,甚至扭曲,我们把这类图像退化现象称之为几何畸变。典型的几何失真如图5-4所示。
6 |
7 |  8 |
9 | 图5-4 几种典型的几何失真
10 | (a) 原图像; (b) 梯形失真; (c) 枕形失真; (d) 桶形失真
11 |
12 | 一般,几何畸变校正要对失真的图像进行精确的几何校正, 通常是先确定一幅图像为基准,然后去校正另一幅图像的几何形状。因此,几何畸变校正一般分两步来做:第一步是图像空间坐标的变换;第二步是重新确定在校正空间各像素点的取值。
13 |
14 | ### 空间几何坐标变换
15 |
16 | 按照一幅标准图像 $g(u, v)$ 或一组基准点去校正另一幅几何失真图像 $f(x, y)$, 称之为空间几何坐标变换。根据两幅图像的一些 已知对应点对(也称为控制点对)建立起函数关系式, 将失真图像的 $x-y$ 坐标系变换到标准图像 $u-v$ 坐标系, 从而实现失真图像按标准图像的几何位置校正, 使 $f(x, y)$ 中的每一像点都可在 $g(u, v)$ 中找到对应像点。
17 |
18 | ### 三角形线性法
19 |
20 | 图像的几何失真虽然是非线性的,但在一个局部小区域内可近似认为是线性的,基于这一假设,将标准图像和被校正图像之间的对应点对划分成一系列小三角形区域,三角形顶点为三个控制点, 在三角形区内满足以下线性关系:
21 | $$
22 | \left\{\begin{array}{l}
23 | x=a u+b v+c \\
24 | y=d u+e v+f
25 | \end{array}\right.\tag{5-52}
26 | $$
27 | 若三对控制点在两个坐标系中的位置分别为 $\left(x_1, y_1\right) 、\left(x_2, y_2\right)$ 、 $\left(x_3, y_3\right)$ 和 $\left(u_1, v_1\right) 、\left(u_2, v_2\right) 、\left(u_3, v_3\right)$, 则可建立两级方程组:
28 | $$
29 | \left\{\begin{array}{l}
30 | x_1=a u_1+b v_1+c \\
31 | x_2=a u_2+b v_2+c \\
32 | x_3=a u_3+b v_3+c
33 | \end{array}\right.\tag{5-53a}
34 | $$
35 |
36 | $$
37 | \left\{\begin{array}{l}
38 | y_1=d u_1+e v_1+f \\
39 | y_2=d u_2+e v_2+f \\
40 | y_3=d u_3+e v_3+f
41 | \end{array}\right.\tag{5-53b}
42 | $$
43 |
44 | 解方程组(5-53),可求出a, b, c, d, e, f六个系数。用式(5-53)可实现该三角形区内其他像点的坐标变换。对于不同的三角形控制区域,这六个系数的值是不同的。
45 | 三角形线性法简单,能满足一定的精度要求,这是因它是以局部范围内的线性失真去处理大范围内的非线性失真, 所以选择的控制点对越多,分布越均匀,三角形区域的面积越小, 则变换的精度越高。但是控制点过多又会导致计算量的增加, 因此需要综合考虑。
46 |
47 | ### 灰度值的确定
48 |
49 | 图像经几何位置校正后,在校正空间中各像点的灰度值等于被校正图像对应点的灰度值。一般校正后的图像某些像素点可能挤压在一起,或者分散开,不会恰好落在坐标点上,因此常采用内插法来求得这些像素点的灰度值。经常使用的方法有如下两种。
50 |
51 | 1) 最近邻点法
52 | 最近邻点法是取与像素点相邻的4个点中距离最近的邻点灰度值作为该点的灰度值。如图5-5所示。显然,最近邻点法计算简单,但精度不高,同时校正后的图像亮度有明显的不连续性。
53 |
54 |
8 |
9 | 图5-4 几种典型的几何失真
10 | (a) 原图像; (b) 梯形失真; (c) 枕形失真; (d) 桶形失真
11 |
12 | 一般,几何畸变校正要对失真的图像进行精确的几何校正, 通常是先确定一幅图像为基准,然后去校正另一幅图像的几何形状。因此,几何畸变校正一般分两步来做:第一步是图像空间坐标的变换;第二步是重新确定在校正空间各像素点的取值。
13 |
14 | ### 空间几何坐标变换
15 |
16 | 按照一幅标准图像 $g(u, v)$ 或一组基准点去校正另一幅几何失真图像 $f(x, y)$, 称之为空间几何坐标变换。根据两幅图像的一些 已知对应点对(也称为控制点对)建立起函数关系式, 将失真图像的 $x-y$ 坐标系变换到标准图像 $u-v$ 坐标系, 从而实现失真图像按标准图像的几何位置校正, 使 $f(x, y)$ 中的每一像点都可在 $g(u, v)$ 中找到对应像点。
17 |
18 | ### 三角形线性法
19 |
20 | 图像的几何失真虽然是非线性的,但在一个局部小区域内可近似认为是线性的,基于这一假设,将标准图像和被校正图像之间的对应点对划分成一系列小三角形区域,三角形顶点为三个控制点, 在三角形区内满足以下线性关系:
21 | $$
22 | \left\{\begin{array}{l}
23 | x=a u+b v+c \\
24 | y=d u+e v+f
25 | \end{array}\right.\tag{5-52}
26 | $$
27 | 若三对控制点在两个坐标系中的位置分别为 $\left(x_1, y_1\right) 、\left(x_2, y_2\right)$ 、 $\left(x_3, y_3\right)$ 和 $\left(u_1, v_1\right) 、\left(u_2, v_2\right) 、\left(u_3, v_3\right)$, 则可建立两级方程组:
28 | $$
29 | \left\{\begin{array}{l}
30 | x_1=a u_1+b v_1+c \\
31 | x_2=a u_2+b v_2+c \\
32 | x_3=a u_3+b v_3+c
33 | \end{array}\right.\tag{5-53a}
34 | $$
35 |
36 | $$
37 | \left\{\begin{array}{l}
38 | y_1=d u_1+e v_1+f \\
39 | y_2=d u_2+e v_2+f \\
40 | y_3=d u_3+e v_3+f
41 | \end{array}\right.\tag{5-53b}
42 | $$
43 |
44 | 解方程组(5-53),可求出a, b, c, d, e, f六个系数。用式(5-53)可实现该三角形区内其他像点的坐标变换。对于不同的三角形控制区域,这六个系数的值是不同的。
45 | 三角形线性法简单,能满足一定的精度要求,这是因它是以局部范围内的线性失真去处理大范围内的非线性失真, 所以选择的控制点对越多,分布越均匀,三角形区域的面积越小, 则变换的精度越高。但是控制点过多又会导致计算量的增加, 因此需要综合考虑。
46 |
47 | ### 灰度值的确定
48 |
49 | 图像经几何位置校正后,在校正空间中各像点的灰度值等于被校正图像对应点的灰度值。一般校正后的图像某些像素点可能挤压在一起,或者分散开,不会恰好落在坐标点上,因此常采用内插法来求得这些像素点的灰度值。经常使用的方法有如下两种。
50 |
51 | 1) 最近邻点法
52 | 最近邻点法是取与像素点相邻的4个点中距离最近的邻点灰度值作为该点的灰度值。如图5-5所示。显然,最近邻点法计算简单,但精度不高,同时校正后的图像亮度有明显的不连续性。
53 |
54 |  55 |
56 | 图5-5 最近邻点法
57 |
58 | 2. 内插法
59 | 用像素点周围4个邻点的灰度值加权内插作为g(u0, v0),如图5-6所示,设像素点(x0, y0)周围4个点为$(x_1, y_1), (x_1+1, y_1), (x_1, y_1+1), (x_1+1, y_1+1)$,则校正值为
60 |
61 | $$
62 | \begin{aligned}
63 | g\left(u_0, v_0\right)= & (1-\alpha)(1-\beta) f\left(x_1, y_1\right)+\alpha(1-\beta) f\left(x_1+1, y_1\right) \\
64 | & +(1-\alpha) \beta f\left(x_1, y_1+1\right)+\alpha \beta f\left(x_1+1, y_1+1\right)
65 | \end{aligned}\tag{5-54}
66 | $$
67 |
68 | 式中:
69 | $$
70 | \alpha=\left|x_0-x_1\right|, \beta=\left|y_0-y_1\right|
71 | $$
72 |
55 |
56 | 图5-5 最近邻点法
57 |
58 | 2. 内插法
59 | 用像素点周围4个邻点的灰度值加权内插作为g(u0, v0),如图5-6所示,设像素点(x0, y0)周围4个点为$(x_1, y_1), (x_1+1, y_1), (x_1, y_1+1), (x_1+1, y_1+1)$,则校正值为
60 |
61 | $$
62 | \begin{aligned}
63 | g\left(u_0, v_0\right)= & (1-\alpha)(1-\beta) f\left(x_1, y_1\right)+\alpha(1-\beta) f\left(x_1+1, y_1\right) \\
64 | & +(1-\alpha) \beta f\left(x_1, y_1+1\right)+\alpha \beta f\left(x_1+1, y_1+1\right)
65 | \end{aligned}\tag{5-54}
66 | $$
67 |
68 | 式中:
69 | $$
70 | \alpha=\left|x_0-x_1\right|, \beta=\left|y_0-y_1\right|
71 | $$
72 |  73 |
74 | 图5-6 内插法几何校正
75 |
76 | ## 5.6.2 盲目图像复原
77 |
78 | 盲目图像复原法是在没有图像退化先验知识的情况下,对观察目标的多幅图像以某种方式抽出退化信息, 从而进行图像复原的方法。
79 | 加性噪声的模糊图像复原方法一般有两种: 直接测量法和间接估计法。
80 | 用直接测量法复原图像时,需要测量图像的模糊脉冲响应和噪声功率谱或协方差函数。在所观察的景物中,点光源能量往往直接指示出冲激响应;另外,图像边缘是否陡峭也能用来推测模糊冲激响应。在背景亮度相对恒定的区域内测量图像的协方差,可以估计出观测图像的噪声协方差函数。
81 |
82 | 间接估计法复原图像类似于多图像平均法处理。如对一个景物连续拍摄 $N$ 次, 每一次获取的图像用下式表示:
83 | $$
84 | g_i(x, y)=f(x, y)+n_i(x, y) \quad i=1,2, \ldots, N\tag{5-55}
85 | $$
86 | 式中: $f(x, y)$ 是原始图像, $g_i(x, y)$ 是第次获取的图像, $n_i(x, y)$ 是第 $i$ 次的噪声函数。
87 | $$
88 | f(x, y)=\frac{1}{N} \sum_{i=1}^N g_i(x, y)-\frac{1}{N} \sum_{i=1}^N n_i(x, y)\tag{5-56}
89 | $$
90 | 当 $N$ 很大时, 上式右边的噪声项的值趋于它的数学期望 $E\{n(x$, $y)\}$ 。一般情况下白色高斯噪声在所有 $(x, y)$ 上的数学期望等于零。 因此,原始图像为
91 | $$
92 | f(x, y)=\frac{1}{N} \sum_{i=1}^N g_i(x, y)\tag{5-57}
93 | $$
94 | 盲目图像复原
95 | 若 $g_{i}(x, y)=f_{i}(x, y)^* h_{i}(x, y)$
96 | 则 $G_i(n, v)=F_i(u, v) H_{i}(u, v)$
97 | $\ln G_{i}(n, v)=\ln \left[F_{i}(u, v)\right]+\ln \left[H_{i}(u, v)\right]$
98 | 如果帧间退化冲激响应不相关, 则
99 | $$
100 | \sum_{i=1}^M \ln \left[G_i(u, v)\right]=M \ln \left[F_i(u, v)\right]+\sum_{i=1}^M \ln \left[H_i(u, v)\right]
101 | $$
102 | 当M很大时, 传递函数的对数和接近一恒定值
103 | $$
104 | \begin{gathered}
105 | K_H=\lim _{M \rightarrow \infty} \sum_{i=1}^M \ln \left[H_i(u, v)\right] \quad \hat{F}_i(u, v)=\exp \left\{\frac{k_H(u, v)}{M} \prod_{i=1}^M\left[G_i(u, v)\right]^{\frac{1}{M}}\right\} \\
106 | \hat{f}(x, y)=J^{-1}\left[\hat{F_G}(u, v)\right]
107 | \end{gathered}
108 | $$
--------------------------------------------------------------------------------
/V/5.7 编程实例.md:
--------------------------------------------------------------------------------
1 | # 5.7 编程实例
2 |
3 | 根据前面章节的讨论, 图像退化的模型为
4 | $$
5 | g(x, y)=f(x, y) * h(x, y)+n(x, y)
6 | $$
7 | 那么,图像复原的过程可认为是已知$g(x,y),h(x,y),n(x,y)$的一些先验知识,求出$f(x,y)$。对于不同的退化函数和噪声性质, 可推导出前面介绍的一些图像复原方法。本节介绍实际中经常用到的逆滤波复原图像法。
8 |
9 | 图像的点扩展函数$h$为
10 | $$
11 | h=\frac{1}{49}
12 | \left[
13 | \begin{array}{lllllll}
14 | 1 &1& 1& 1& 1& 1& 1\\
15 | 1 &1& 1& 1& 1& 1& 1\\
16 | 1 &1& 1& 1& 1& 1& 1\\
17 | 1 &1& 1& 1& 1& 1& 1\\
18 | 1 &1& 1& 1& 1& 1& 1\\
19 | 1 &1& 1& 1& 1& 1& 1\\
20 | 1 &1& 1& 1& 1& 1& 1\\
21 | \end{array}
22 | \right]
23 | $$
24 | 首先使用退化函数$h$对图像进行模糊操作, 生成一幅退化的图像,退化系统为
25 | $$
26 | g=F^{-1}(F(h) \cdot F(f))
27 | $$
28 | 上式的计算过程是,先求出图像和退化函数的傅立叶变换, 在频域相乘后,再按下式求逆傅立叶变换:
29 | $$
30 | \hat{f}=F^{-1}\left(\frac{G}{H}\right)=F^{-1}\left(\frac{F(g)}{F(h)}\right)
31 | $$
32 | 图像复原的具体实现过程如下。
33 |
34 | ## 添加菜单
35 |
36 |
73 |
74 | 图5-6 内插法几何校正
75 |
76 | ## 5.6.2 盲目图像复原
77 |
78 | 盲目图像复原法是在没有图像退化先验知识的情况下,对观察目标的多幅图像以某种方式抽出退化信息, 从而进行图像复原的方法。
79 | 加性噪声的模糊图像复原方法一般有两种: 直接测量法和间接估计法。
80 | 用直接测量法复原图像时,需要测量图像的模糊脉冲响应和噪声功率谱或协方差函数。在所观察的景物中,点光源能量往往直接指示出冲激响应;另外,图像边缘是否陡峭也能用来推测模糊冲激响应。在背景亮度相对恒定的区域内测量图像的协方差,可以估计出观测图像的噪声协方差函数。
81 |
82 | 间接估计法复原图像类似于多图像平均法处理。如对一个景物连续拍摄 $N$ 次, 每一次获取的图像用下式表示:
83 | $$
84 | g_i(x, y)=f(x, y)+n_i(x, y) \quad i=1,2, \ldots, N\tag{5-55}
85 | $$
86 | 式中: $f(x, y)$ 是原始图像, $g_i(x, y)$ 是第次获取的图像, $n_i(x, y)$ 是第 $i$ 次的噪声函数。
87 | $$
88 | f(x, y)=\frac{1}{N} \sum_{i=1}^N g_i(x, y)-\frac{1}{N} \sum_{i=1}^N n_i(x, y)\tag{5-56}
89 | $$
90 | 当 $N$ 很大时, 上式右边的噪声项的值趋于它的数学期望 $E\{n(x$, $y)\}$ 。一般情况下白色高斯噪声在所有 $(x, y)$ 上的数学期望等于零。 因此,原始图像为
91 | $$
92 | f(x, y)=\frac{1}{N} \sum_{i=1}^N g_i(x, y)\tag{5-57}
93 | $$
94 | 盲目图像复原
95 | 若 $g_{i}(x, y)=f_{i}(x, y)^* h_{i}(x, y)$
96 | 则 $G_i(n, v)=F_i(u, v) H_{i}(u, v)$
97 | $\ln G_{i}(n, v)=\ln \left[F_{i}(u, v)\right]+\ln \left[H_{i}(u, v)\right]$
98 | 如果帧间退化冲激响应不相关, 则
99 | $$
100 | \sum_{i=1}^M \ln \left[G_i(u, v)\right]=M \ln \left[F_i(u, v)\right]+\sum_{i=1}^M \ln \left[H_i(u, v)\right]
101 | $$
102 | 当M很大时, 传递函数的对数和接近一恒定值
103 | $$
104 | \begin{gathered}
105 | K_H=\lim _{M \rightarrow \infty} \sum_{i=1}^M \ln \left[H_i(u, v)\right] \quad \hat{F}_i(u, v)=\exp \left\{\frac{k_H(u, v)}{M} \prod_{i=1}^M\left[G_i(u, v)\right]^{\frac{1}{M}}\right\} \\
106 | \hat{f}(x, y)=J^{-1}\left[\hat{F_G}(u, v)\right]
107 | \end{gathered}
108 | $$
--------------------------------------------------------------------------------
/V/5.7 编程实例.md:
--------------------------------------------------------------------------------
1 | # 5.7 编程实例
2 |
3 | 根据前面章节的讨论, 图像退化的模型为
4 | $$
5 | g(x, y)=f(x, y) * h(x, y)+n(x, y)
6 | $$
7 | 那么,图像复原的过程可认为是已知$g(x,y),h(x,y),n(x,y)$的一些先验知识,求出$f(x,y)$。对于不同的退化函数和噪声性质, 可推导出前面介绍的一些图像复原方法。本节介绍实际中经常用到的逆滤波复原图像法。
8 |
9 | 图像的点扩展函数$h$为
10 | $$
11 | h=\frac{1}{49}
12 | \left[
13 | \begin{array}{lllllll}
14 | 1 &1& 1& 1& 1& 1& 1\\
15 | 1 &1& 1& 1& 1& 1& 1\\
16 | 1 &1& 1& 1& 1& 1& 1\\
17 | 1 &1& 1& 1& 1& 1& 1\\
18 | 1 &1& 1& 1& 1& 1& 1\\
19 | 1 &1& 1& 1& 1& 1& 1\\
20 | 1 &1& 1& 1& 1& 1& 1\\
21 | \end{array}
22 | \right]
23 | $$
24 | 首先使用退化函数$h$对图像进行模糊操作, 生成一幅退化的图像,退化系统为
25 | $$
26 | g=F^{-1}(F(h) \cdot F(f))
27 | $$
28 | 上式的计算过程是,先求出图像和退化函数的傅立叶变换, 在频域相乘后,再按下式求逆傅立叶变换:
29 | $$
30 | \hat{f}=F^{-1}\left(\frac{G}{H}\right)=F^{-1}\left(\frac{F(g)}{F(h)}\right)
31 | $$
32 | 图像复原的具体实现过程如下。
33 |
34 | ## 添加菜单
35 |
36 |  37 |
38 | 图11-7 图像复原菜单
39 |
40 | ## 添加消息映射
41 |
42 | 在文档类中添加两个消息映射函数, 分别是OnRestoreBlur()和OnRestoreInvfilt()。OnRestorBlur()调用图像复原类CRestore的ConvBlur()函数生成一幅退化图像。OnRestoreInvfilt()调用图像复原类CRestore的InvFilter()函数对退化图像进行复原。代码如下:
43 |
44 | ```c++
45 | void CDipDoc: : OnRestoreBlur()
46 | {
47 | // TODO: Add your command handler code here
48 | //判断当前是否载入图像
49 | if( m_pImageObject == NULL ) return; D
50 | //定义一个图像复原对象
51 | CRestore Restore( m_pImageObject );
52 | //调用卷积模糊函数
53 | Restore.ConvBlur();
54 | //更新视图
55 | UpdateAllViews(NULL);
56 | }
57 | OnRestoreInvfilt()函数主要代码如下, 其他代码与OnRestoreBlur()相同。
58 | void CDipDoc: : OnRestoreInvfilt()
59 | {
60 |
61 | //调用逆滤波复原函数
62 | Restore.InvFilter();
63 |
64 | }
65 |
66 | ```
67 |
68 | ## CRestore类介绍
69 |
70 | 功能: 实现图像复原
71 | 函数列表:
72 | ConvBlur() 对图像进行卷积模糊处理, 生成一幅待复原的退化图像;
73 | InvFilter() 逆滤波复原法, 对由卷积模糊所造成的退化图像进行复原;
74 | ConvNoiseBlur() 对图像进行卷积噪声模糊处理, 生成一幅待复原的退化图像;
75 | Wiener() 维纳滤波复原法, 对由卷积噪声所造成的退化图像进行复原。
76 |
77 | ## 函数实现代码
78 |
79 | ```c++
80 | ConvBlur()函数关键代码
81 | {
82 |
83 | //定义卷积模板, 大小为7×7
84 | Mm m_matFilter;
85 | m_matFilter=zeros(nHeight, nWidth);
86 | int i, j;
87 | for(i=1; i<7; i++)
88 | {
89 | for(j=1; j<7; j++)
90 | {
91 | m_matFilter.r(i, j)=0.02;
92 | }
93 | }
94 | // m_matBits是一个二维矩阵, 存储的是图像数据
95 | //对原图像进行快速傅立叶变换, 将图像从空域变换到频域
96 | m_matBits=fft2(m_matBits);
97 | //对模板进行快速傅立叶变换
98 | m_matFilter=fft2(m_matFilter);
99 | //频率相乘
100 | for(i=1; i<=nHeight; i++)
101 | {
102 | for(j=1; j<=nWidth; j++)
103 | {
104 | m_matBits.r(i, j)=m_matBits.r(i, j)*m_matFilter.r(i, j)-m_matBits.i(i, j)*m_matFilter.i(i, j);
105 | m_matBits.i(i, j)=m_matBits.r(i, j)*m_matFilter.i(i, j)+m_matBits.i(i, j)*m_matFilter.r(i, j);
106 | }
107 | }
108 | //对图像做逆傅立叶变换, 将图像从频域变换到空域
109 | m_matBits=ifft2(m_matBits);
110 |
111 | }
112 | InvFilter()函数关键代码
113 | {
114 | //对原图像进行快速傅立叶变换, 将图像从空域变换到频域
115 | m_matBits=fft2(m_matBits);
116 | //对模板进行快速傅立叶变换
117 | m_matFilter=fft2(m_matFilter);
118 | //频率相乘
119 | double a, b, c, d;
120 | for(i=1; i<=nHeight; i++)
121 | {
122 | for(j=1; j<=nWidth; j++)
123 | {
124 | a=m_matBits.r(i, j);
125 | b=m_matBits.i(i, j);
126 | c=m_matFilter.r(i, j);
127 | d=m_matFilter.i(i, j);
128 | if(c*c+d*d>0.003)
129 | {
130 | m_matBits.r(i, j)=(a*c+b*d)/(c*c+d*d);
131 | m_matBits.i(i, j)=(b*c-a*d)/(c*c+d*d);
132 | }
133 | }
134 | }
135 | //对图像进行快速逆傅立叶变换, 将图像从频域变换到空域
136 | m_matBits=ifft2(m_matBits);
137 | }
138 |
139 | ```
140 |
141 |
37 |
38 | 图11-7 图像复原菜单
39 |
40 | ## 添加消息映射
41 |
42 | 在文档类中添加两个消息映射函数, 分别是OnRestoreBlur()和OnRestoreInvfilt()。OnRestorBlur()调用图像复原类CRestore的ConvBlur()函数生成一幅退化图像。OnRestoreInvfilt()调用图像复原类CRestore的InvFilter()函数对退化图像进行复原。代码如下:
43 |
44 | ```c++
45 | void CDipDoc: : OnRestoreBlur()
46 | {
47 | // TODO: Add your command handler code here
48 | //判断当前是否载入图像
49 | if( m_pImageObject == NULL ) return; D
50 | //定义一个图像复原对象
51 | CRestore Restore( m_pImageObject );
52 | //调用卷积模糊函数
53 | Restore.ConvBlur();
54 | //更新视图
55 | UpdateAllViews(NULL);
56 | }
57 | OnRestoreInvfilt()函数主要代码如下, 其他代码与OnRestoreBlur()相同。
58 | void CDipDoc: : OnRestoreInvfilt()
59 | {
60 |
61 | //调用逆滤波复原函数
62 | Restore.InvFilter();
63 |
64 | }
65 |
66 | ```
67 |
68 | ## CRestore类介绍
69 |
70 | 功能: 实现图像复原
71 | 函数列表:
72 | ConvBlur() 对图像进行卷积模糊处理, 生成一幅待复原的退化图像;
73 | InvFilter() 逆滤波复原法, 对由卷积模糊所造成的退化图像进行复原;
74 | ConvNoiseBlur() 对图像进行卷积噪声模糊处理, 生成一幅待复原的退化图像;
75 | Wiener() 维纳滤波复原法, 对由卷积噪声所造成的退化图像进行复原。
76 |
77 | ## 函数实现代码
78 |
79 | ```c++
80 | ConvBlur()函数关键代码
81 | {
82 |
83 | //定义卷积模板, 大小为7×7
84 | Mm m_matFilter;
85 | m_matFilter=zeros(nHeight, nWidth);
86 | int i, j;
87 | for(i=1; i<7; i++)
88 | {
89 | for(j=1; j<7; j++)
90 | {
91 | m_matFilter.r(i, j)=0.02;
92 | }
93 | }
94 | // m_matBits是一个二维矩阵, 存储的是图像数据
95 | //对原图像进行快速傅立叶变换, 将图像从空域变换到频域
96 | m_matBits=fft2(m_matBits);
97 | //对模板进行快速傅立叶变换
98 | m_matFilter=fft2(m_matFilter);
99 | //频率相乘
100 | for(i=1; i<=nHeight; i++)
101 | {
102 | for(j=1; j<=nWidth; j++)
103 | {
104 | m_matBits.r(i, j)=m_matBits.r(i, j)*m_matFilter.r(i, j)-m_matBits.i(i, j)*m_matFilter.i(i, j);
105 | m_matBits.i(i, j)=m_matBits.r(i, j)*m_matFilter.i(i, j)+m_matBits.i(i, j)*m_matFilter.r(i, j);
106 | }
107 | }
108 | //对图像做逆傅立叶变换, 将图像从频域变换到空域
109 | m_matBits=ifft2(m_matBits);
110 |
111 | }
112 | InvFilter()函数关键代码
113 | {
114 | //对原图像进行快速傅立叶变换, 将图像从空域变换到频域
115 | m_matBits=fft2(m_matBits);
116 | //对模板进行快速傅立叶变换
117 | m_matFilter=fft2(m_matFilter);
118 | //频率相乘
119 | double a, b, c, d;
120 | for(i=1; i<=nHeight; i++)
121 | {
122 | for(j=1; j<=nWidth; j++)
123 | {
124 | a=m_matBits.r(i, j);
125 | b=m_matBits.i(i, j);
126 | c=m_matFilter.r(i, j);
127 | d=m_matFilter.i(i, j);
128 | if(c*c+d*d>0.003)
129 | {
130 | m_matBits.r(i, j)=(a*c+b*d)/(c*c+d*d);
131 | m_matBits.i(i, j)=(b*c-a*d)/(c*c+d*d);
132 | }
133 | }
134 | }
135 | //对图像进行快速逆傅立叶变换, 将图像从频域变换到空域
136 | m_matBits=ifft2(m_matBits);
137 | }
138 |
139 | ```
140 |
141 |  142 |
143 | 图11-8 逆滤波法复原图像
144 | (a) 原始图像; (b) 退化图像; (c)复原图像
--------------------------------------------------------------------------------
/VI/6.1 几何变换基础.md:
--------------------------------------------------------------------------------
1 | # 6.1 几何变换基础
2 |
3 |
4 |
5 | ## 6.1.1 概述
6 |
7 | 图像的几何变换,是指使用户获得或设计的原始图像。按照需要产生大小、形状和位置的变化。从图像类型来分,图像的几何变换有二维平面图像的几何变换和三维图像的几何变换以及由三维向二维平面投影变换等。从变换的性质分, 图像的几何变换有平移、比例缩放、旋转、反射和错切等基本变换,透视变换等复合变换,以及插值运算等。
8 |
9 | 数字图像是把连续图像在坐标空间和性质空间离散化了的图像。例如,一幅二维数字图像就是把一幅连续的二维(2D)。图像在坐标空间XOY和性质空间F都离散化了的图像,它可以用一组二维(2D)数组f(x, y)来表示,其中x和y表示2D空间XOY中一个坐标点的位置,f代表图像在点(x, y)的某种性质F的数值,如果所处理的是一幅灰度图,这时f表示灰度值。而且此时f、x、y都在整数集合中取值。因此,除了插值运算外,常见的图像几何变换可以通过与之对应的矩阵线性变换来实现。
10 |
11 | 对于2D图像几何变换及变换中心在坐标原点的比例缩放、 反射、 错切和旋转等各种变换,都可以用2×2的矩阵表示和实现。但是一个2×2变换矩阵$T=\left[\begin{array}{ll}a & b \\ c & d\end{array}\right]$却不能实现图像的平移以及绕任意点的比例缩放、反射、错切和旋转等各种变换。因此,为了能够用统一的矩阵线性变换形式,表示和实现这些常见的图像几何变换,就需要引入一种新的坐标,即齐次坐标。利用齐次坐标来变换处理,才能实现上述各种2D图像的几何变换。
12 |
13 | ## 6.1.2 齐次坐标
14 |
15 | 现设点 $P_0\left(x_0, y_0\right)$ 进行平移后, 移到 $P(x, y)$, 其中 $x$ 方向的平移量为 $\Delta x, y$ 方向的平移量为 $\Delta y$ 。那么, 点 $P(x, y)$ 的坐标为
16 | $$
17 | \left\{\begin{array}{l}
18 | x=x_0+\Delta x \\
19 | y=y_0+\Delta y
20 | \end{array}\right.
21 | $$
22 | 如图6-1所示。这个变换用矩阵的形式可以表示为
23 | $$
24 | \left[\begin{array}{l}
25 | x \\
26 | y
27 | \end{array}\right]=\left[\begin{array}{ll}
28 | 1 & 0 \\
29 | 0 & 1
30 | \end{array}\right]\left[\begin{array}{l}
31 | x_0 \\
32 | y_0
33 | \end{array}\right]+\left[\begin{array}{l}
34 | \Delta x \\
35 | \Delta y
36 | \end{array}\right]
37 | $$
38 | 图6-1 点的平移(不再是笛卡尔坐标系)
39 |
40 | 而平面上点的变换矩阵$T=\left[\begin{array}{ll}a & b \\ c & d\end{array}\right]$中没有引入平移常量,无论$a、b、c、d$取什么值,都不能实现上述的平移变换。因此,需要使用$2\times3$阶变换矩阵,取其形式为
41 | $$
42 | T=\left[\begin{array}{ccc}
43 | 1 & 0 & \Delta x \\
44 | 0 & 1 & \Delta y
45 | \end{array}\right]
46 | $$
47 | 此矩阵的第一、二列构成单位矩阵,第三列元素为平移常量。由上述可知,对2D图像进行变换,只需要将图像的点集矩阵乘以变换矩阵即可,2D图像对应的点集矩阵是2×*n*阶的,而上式扩展后的变换矩阵是2×3阶的矩阵,这不符合矩阵相乘时要求前者的列数与后者的行数相等的规则。
48 |
49 | 所以需要在点的坐标列矩阵 $\left[\begin{array}{ll}x & y\end{array}\right]^{T}$ 中引入第三个元素, 增加一个附加坐标, 扩展为 $3 \times 1$ 的列矩阵 $\left[\begin{array}{lll}x & y & 1\end{array}\right]^{T}$, 这样用三维空间点 $(x, y, 1)$ 表示二维空间点 $(x, y)$, 即采用一种特殊的坐标,可以实现平移变换,变换结果为
50 | $$
51 | P=T \cdot P_0=\left[\begin{array}{ccc}1 & 0 & \Delta x \\ 0 & 1 & \Delta y\end{array}\right]\left[\begin{array}{l}x_0 \\ y_0 \\ 1\end{array}\right]=\left[\begin{array}{l}x_0+\Delta x \\ y_0+\Delta y\end{array}\right]=\left[\begin{array}{l}x \\ y\end{array}\right]
52 | $$
53 |
54 | 式 $\left\{\begin{array}{l}x=x_0+\Delta x \\ y=y_0+\Delta y\end{array}\right.$ 符合上述平移后的坐标位置。通常将 $2 \times 3$ 阶矩阵扩
55 | 充为 $3 \times 3$ 阶矩阵, 以拓宽功能。由此可得平移变换矩阵为
56 | $$
57 | T=\left[\begin{array}{lll}
58 | 1 & 0 & \Delta x \\
59 | 0 & 1 & \Delta y
60 | \end{array}\right] \text { a- }
61 | $$
62 | 下面再验证一下点 $P(x, y)$ 按照 $3 \times 3$ 的变换矩阵 $T$ 平移变换的结果
63 | $$
64 | P=T \cdot P_0=\left[\begin{array}{lll}
65 | 1 & 0 & \Delta x \\
66 | 0 & 1 & \Delta y \\
67 | 0 & 0 & 1
68 | \end{array}\right]\left[\begin{array}{l}
69 | x_0 \\
70 | y_0 \\
71 | 1
72 | \end{array}\right]=\left[\begin{array}{l}
73 | x_0+\Delta x \\
74 | y_0+\Delta y \\
75 | 1
76 | \end{array}\right]=\left[\begin{array}{l}
77 | x \\
78 | y \\
79 | 1
80 | \end{array}\right]
81 | $$
82 | 从上式可以看出, 引入附加坐标后, 扩充了矩阵的第 3 行, 并没有使变换结果受到影响。这种用 $n+1$ 维向量表示 $n$ 维向量的方法称为齐次坐标表示法。
83 |
84 | 因此, 2D图像中的点坐标 $(x, y)$ 通常表示成齐次坐标 $(H x, H y$, H), 其中 $H$ 表示非零的任意实数, 当 $H=1$ 时, 则 $(x, y, 1)$ 就称为点 $(x, y)$ 的规范化齐次坐标。显然规范化齐次坐标的前两个数是相应二维点的坐标, 没有变化, 仅在原坐标中增加了 $H=1$ 的附加坐标。
85 | 由点的齐次坐标 $(H x, H y, H)$ 求点的规范化齐次坐标 $(x, y,1)$, 可按如下公式进行:
86 | $$
87 | x=\frac{H x}{H} \quad y=\frac{H y}{H}
88 | $$
89 |
90 | 齐次坐标的几何意义相当于点 $(x, y)$ 落在 $3 D$ 空间 $H=1$ 的平面上, 如图6-2所示。如果将XOY 平面内的三角形 $abc$ 的各顶点表示成齐次坐标 $\left(x_i, y_i, 1\right)(i=1,2,3)$ 的形式, 就变成 $H=1$ 平面内的三角形 $a_1 b_1 c_1$ 的各顶点。
91 |
92 |
142 |
143 | 图11-8 逆滤波法复原图像
144 | (a) 原始图像; (b) 退化图像; (c)复原图像
--------------------------------------------------------------------------------
/VI/6.1 几何变换基础.md:
--------------------------------------------------------------------------------
1 | # 6.1 几何变换基础
2 |
3 |
4 |
5 | ## 6.1.1 概述
6 |
7 | 图像的几何变换,是指使用户获得或设计的原始图像。按照需要产生大小、形状和位置的变化。从图像类型来分,图像的几何变换有二维平面图像的几何变换和三维图像的几何变换以及由三维向二维平面投影变换等。从变换的性质分, 图像的几何变换有平移、比例缩放、旋转、反射和错切等基本变换,透视变换等复合变换,以及插值运算等。
8 |
9 | 数字图像是把连续图像在坐标空间和性质空间离散化了的图像。例如,一幅二维数字图像就是把一幅连续的二维(2D)。图像在坐标空间XOY和性质空间F都离散化了的图像,它可以用一组二维(2D)数组f(x, y)来表示,其中x和y表示2D空间XOY中一个坐标点的位置,f代表图像在点(x, y)的某种性质F的数值,如果所处理的是一幅灰度图,这时f表示灰度值。而且此时f、x、y都在整数集合中取值。因此,除了插值运算外,常见的图像几何变换可以通过与之对应的矩阵线性变换来实现。
10 |
11 | 对于2D图像几何变换及变换中心在坐标原点的比例缩放、 反射、 错切和旋转等各种变换,都可以用2×2的矩阵表示和实现。但是一个2×2变换矩阵$T=\left[\begin{array}{ll}a & b \\ c & d\end{array}\right]$却不能实现图像的平移以及绕任意点的比例缩放、反射、错切和旋转等各种变换。因此,为了能够用统一的矩阵线性变换形式,表示和实现这些常见的图像几何变换,就需要引入一种新的坐标,即齐次坐标。利用齐次坐标来变换处理,才能实现上述各种2D图像的几何变换。
12 |
13 | ## 6.1.2 齐次坐标
14 |
15 | 现设点 $P_0\left(x_0, y_0\right)$ 进行平移后, 移到 $P(x, y)$, 其中 $x$ 方向的平移量为 $\Delta x, y$ 方向的平移量为 $\Delta y$ 。那么, 点 $P(x, y)$ 的坐标为
16 | $$
17 | \left\{\begin{array}{l}
18 | x=x_0+\Delta x \\
19 | y=y_0+\Delta y
20 | \end{array}\right.
21 | $$
22 | 如图6-1所示。这个变换用矩阵的形式可以表示为
23 | $$
24 | \left[\begin{array}{l}
25 | x \\
26 | y
27 | \end{array}\right]=\left[\begin{array}{ll}
28 | 1 & 0 \\
29 | 0 & 1
30 | \end{array}\right]\left[\begin{array}{l}
31 | x_0 \\
32 | y_0
33 | \end{array}\right]+\left[\begin{array}{l}
34 | \Delta x \\
35 | \Delta y
36 | \end{array}\right]
37 | $$
38 | 图6-1 点的平移(不再是笛卡尔坐标系)
39 |
40 | 而平面上点的变换矩阵$T=\left[\begin{array}{ll}a & b \\ c & d\end{array}\right]$中没有引入平移常量,无论$a、b、c、d$取什么值,都不能实现上述的平移变换。因此,需要使用$2\times3$阶变换矩阵,取其形式为
41 | $$
42 | T=\left[\begin{array}{ccc}
43 | 1 & 0 & \Delta x \\
44 | 0 & 1 & \Delta y
45 | \end{array}\right]
46 | $$
47 | 此矩阵的第一、二列构成单位矩阵,第三列元素为平移常量。由上述可知,对2D图像进行变换,只需要将图像的点集矩阵乘以变换矩阵即可,2D图像对应的点集矩阵是2×*n*阶的,而上式扩展后的变换矩阵是2×3阶的矩阵,这不符合矩阵相乘时要求前者的列数与后者的行数相等的规则。
48 |
49 | 所以需要在点的坐标列矩阵 $\left[\begin{array}{ll}x & y\end{array}\right]^{T}$ 中引入第三个元素, 增加一个附加坐标, 扩展为 $3 \times 1$ 的列矩阵 $\left[\begin{array}{lll}x & y & 1\end{array}\right]^{T}$, 这样用三维空间点 $(x, y, 1)$ 表示二维空间点 $(x, y)$, 即采用一种特殊的坐标,可以实现平移变换,变换结果为
50 | $$
51 | P=T \cdot P_0=\left[\begin{array}{ccc}1 & 0 & \Delta x \\ 0 & 1 & \Delta y\end{array}\right]\left[\begin{array}{l}x_0 \\ y_0 \\ 1\end{array}\right]=\left[\begin{array}{l}x_0+\Delta x \\ y_0+\Delta y\end{array}\right]=\left[\begin{array}{l}x \\ y\end{array}\right]
52 | $$
53 |
54 | 式 $\left\{\begin{array}{l}x=x_0+\Delta x \\ y=y_0+\Delta y\end{array}\right.$ 符合上述平移后的坐标位置。通常将 $2 \times 3$ 阶矩阵扩
55 | 充为 $3 \times 3$ 阶矩阵, 以拓宽功能。由此可得平移变换矩阵为
56 | $$
57 | T=\left[\begin{array}{lll}
58 | 1 & 0 & \Delta x \\
59 | 0 & 1 & \Delta y
60 | \end{array}\right] \text { a- }
61 | $$
62 | 下面再验证一下点 $P(x, y)$ 按照 $3 \times 3$ 的变换矩阵 $T$ 平移变换的结果
63 | $$
64 | P=T \cdot P_0=\left[\begin{array}{lll}
65 | 1 & 0 & \Delta x \\
66 | 0 & 1 & \Delta y \\
67 | 0 & 0 & 1
68 | \end{array}\right]\left[\begin{array}{l}
69 | x_0 \\
70 | y_0 \\
71 | 1
72 | \end{array}\right]=\left[\begin{array}{l}
73 | x_0+\Delta x \\
74 | y_0+\Delta y \\
75 | 1
76 | \end{array}\right]=\left[\begin{array}{l}
77 | x \\
78 | y \\
79 | 1
80 | \end{array}\right]
81 | $$
82 | 从上式可以看出, 引入附加坐标后, 扩充了矩阵的第 3 行, 并没有使变换结果受到影响。这种用 $n+1$ 维向量表示 $n$ 维向量的方法称为齐次坐标表示法。
83 |
84 | 因此, 2D图像中的点坐标 $(x, y)$ 通常表示成齐次坐标 $(H x, H y$, H), 其中 $H$ 表示非零的任意实数, 当 $H=1$ 时, 则 $(x, y, 1)$ 就称为点 $(x, y)$ 的规范化齐次坐标。显然规范化齐次坐标的前两个数是相应二维点的坐标, 没有变化, 仅在原坐标中增加了 $H=1$ 的附加坐标。
85 | 由点的齐次坐标 $(H x, H y, H)$ 求点的规范化齐次坐标 $(x, y,1)$, 可按如下公式进行:
86 | $$
87 | x=\frac{H x}{H} \quad y=\frac{H y}{H}
88 | $$
89 |
90 | 齐次坐标的几何意义相当于点 $(x, y)$ 落在 $3 D$ 空间 $H=1$ 的平面上, 如图6-2所示。如果将XOY 平面内的三角形 $abc$ 的各顶点表示成齐次坐标 $\left(x_i, y_i, 1\right)(i=1,2,3)$ 的形式, 就变成 $H=1$ 平面内的三角形 $a_1 b_1 c_1$ 的各顶点。
91 |
92 |  93 |
94 | 图6-2 齐次坐标的几何意义
95 |
96 | 齐次坐标在2D图像几何变换中的另一个应用是:如某点S(60 000, 40 000)在16位计算机上表示则大于32 767的最大坐标值, 需要进行复杂的操作。但如果把S的坐标形式变成(Hx, Hy, H) 形式的齐次坐标,则情况就不同了。在齐次坐标系中,设H=1 /2,则 (60 000,40 000)的齐次坐标为(1/2x, 1/2y, 1/2),那么所要表示的点变为(30 000, 20 000, 1/2),此点显然在16位计算机上二进制数所能表示的范围之内。
97 |
98 | 因此,采用齐次坐标,并将变换矩阵改成3×3阶的形式后, 便可实现所有2D图像几何变换的基本变换。
99 |
100 | ## 6.1.3 二维图像几何变换的矩阵
101 |
102 |
103 |
104 | 利用齐次坐标及改成 $3 \times 3$ 阶形式的变换矩阵, 实现 $2 D$ 图像几何变换的基本变换的一般过程是: 将 $2 \times n$ 阶的二维点集矩阵 $\left[\begin{array}{c}x_{0 i} \\ y_{0 i}\end{array}\right]_{2 \times n}$ 矩阵龶示成齐次完成, 坐标 $\left[\begin{array}{l}x_{0 i} \\ y_{0 i} \\ 1\end{array}\right]_{3 \times n}$ 的形式, 然后乘以相应的变换
105 | 变换后的点集矩阵=变换矩阵 $T \times$ 变换前的点集矩阵
106 | (图像上各点的新齐次坐标) (图像上各点的原齐次坐标)
107 |
108 | 设变换矩阵T为
109 | $$
110 | T=\left[\begin{array}{lll}
111 | a & b & p \\
112 | c & d & q \\
113 | l & m & s
114 | \end{array}\right]
115 | $$
116 | 则上述变换可以用公式表示为
117 | $$
118 | \left[\begin{array}{cccc}
119 | H x_1^{\prime} & H x_2^{\prime} & \Lambda & H x_n^{\prime} \\
120 | H y_1^{\prime} & H y_2^{\prime} & \Lambda & H y_n^{\prime} \\
121 | H & H & \Lambda & H
122 | \end{array}\right]_{3 \times n}=T \times\left[\begin{array}{llll}
123 | x_1 & x_2 & \Lambda & x_n \\
124 | y_1 & y_2 & \Lambda & y_n \\
125 | 1 & 1 & \Lambda & 1
126 | \end{array}\right]_{3 \times n}
127 | $$
128 | 图像上各点的新齐次坐标规范化后的点集矩阵为
129 | $$
130 | \left[\begin{array}{rrrr}
131 | x_1^{\prime} & x_2^{\prime} & \Lambda & x_n^{\prime} \\
132 | y_1^{\prime} & y_2^{\prime} & \Lambda & y_n^{\prime} \\
133 | 1 & 1 & \Lambda & 1
134 | \end{array}\right]_{3 \times n}
135 | $$
136 | 引入齐次坐标后,表示2D图像几何变换的3×3矩阵的功能就完善了,可以用它完成2D图像的各种几何变换。下面讨论 3×3阶变换矩阵中各元素在变换中的功能。几何变换的3×3矩阵的一般形式为
137 | $$
138 | T=\left[\begin{array}{lll}
139 | a & b & p \\
140 | c & d & q \\
141 | l & m & s
142 | \end{array}\right]
143 | $$
144 | 3×3的阶矩阵T可以分成四个子矩阵。其中,$\left[\begin{array}{ll}a & b \\ c & d\end{array}\right]_{2 \times 2}$这一子矩阵可使图像实现恒等、 比例、 反射(或镜像)、 错切和旋转变换。[l m]这一行矩阵可以使图像实现平移变换。[p q] T这一列矩阵可以使图像实现透视变换,但当p=0,q=0时它无透视作用。[s]这一元素可以使图像实现全比例变换。例如, 将图像进行全比例变换, 即
145 | $$
146 | \left[\begin{array}{lll}1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & s\end{array}\right] \times\left[\begin{array}{c}x_{0 i} \\ y_{0 i} \\ 1\end{array}\right]=\left[\begin{array}{c}x_i \\ y_i \\ s\end{array}\right]
147 | $$
148 |
149 | 将齐次坐标$[x_i \quad y_i \quad s]^T$规范化后,$[\dfrac{x_{oi}}{s} \quad \dfrac{y_{oi}}{s} \quad s]^T=[x_i \quad y_i \quad 1]^T$。 由此可见
150 |
151 | 当 $s>1$ 时, 图像按比例缩小; 当 $0
93 |
94 | 图6-2 齐次坐标的几何意义
95 |
96 | 齐次坐标在2D图像几何变换中的另一个应用是:如某点S(60 000, 40 000)在16位计算机上表示则大于32 767的最大坐标值, 需要进行复杂的操作。但如果把S的坐标形式变成(Hx, Hy, H) 形式的齐次坐标,则情况就不同了。在齐次坐标系中,设H=1 /2,则 (60 000,40 000)的齐次坐标为(1/2x, 1/2y, 1/2),那么所要表示的点变为(30 000, 20 000, 1/2),此点显然在16位计算机上二进制数所能表示的范围之内。
97 |
98 | 因此,采用齐次坐标,并将变换矩阵改成3×3阶的形式后, 便可实现所有2D图像几何变换的基本变换。
99 |
100 | ## 6.1.3 二维图像几何变换的矩阵
101 |
102 |
103 |
104 | 利用齐次坐标及改成 $3 \times 3$ 阶形式的变换矩阵, 实现 $2 D$ 图像几何变换的基本变换的一般过程是: 将 $2 \times n$ 阶的二维点集矩阵 $\left[\begin{array}{c}x_{0 i} \\ y_{0 i}\end{array}\right]_{2 \times n}$ 矩阵龶示成齐次完成, 坐标 $\left[\begin{array}{l}x_{0 i} \\ y_{0 i} \\ 1\end{array}\right]_{3 \times n}$ 的形式, 然后乘以相应的变换
105 | 变换后的点集矩阵=变换矩阵 $T \times$ 变换前的点集矩阵
106 | (图像上各点的新齐次坐标) (图像上各点的原齐次坐标)
107 |
108 | 设变换矩阵T为
109 | $$
110 | T=\left[\begin{array}{lll}
111 | a & b & p \\
112 | c & d & q \\
113 | l & m & s
114 | \end{array}\right]
115 | $$
116 | 则上述变换可以用公式表示为
117 | $$
118 | \left[\begin{array}{cccc}
119 | H x_1^{\prime} & H x_2^{\prime} & \Lambda & H x_n^{\prime} \\
120 | H y_1^{\prime} & H y_2^{\prime} & \Lambda & H y_n^{\prime} \\
121 | H & H & \Lambda & H
122 | \end{array}\right]_{3 \times n}=T \times\left[\begin{array}{llll}
123 | x_1 & x_2 & \Lambda & x_n \\
124 | y_1 & y_2 & \Lambda & y_n \\
125 | 1 & 1 & \Lambda & 1
126 | \end{array}\right]_{3 \times n}
127 | $$
128 | 图像上各点的新齐次坐标规范化后的点集矩阵为
129 | $$
130 | \left[\begin{array}{rrrr}
131 | x_1^{\prime} & x_2^{\prime} & \Lambda & x_n^{\prime} \\
132 | y_1^{\prime} & y_2^{\prime} & \Lambda & y_n^{\prime} \\
133 | 1 & 1 & \Lambda & 1
134 | \end{array}\right]_{3 \times n}
135 | $$
136 | 引入齐次坐标后,表示2D图像几何变换的3×3矩阵的功能就完善了,可以用它完成2D图像的各种几何变换。下面讨论 3×3阶变换矩阵中各元素在变换中的功能。几何变换的3×3矩阵的一般形式为
137 | $$
138 | T=\left[\begin{array}{lll}
139 | a & b & p \\
140 | c & d & q \\
141 | l & m & s
142 | \end{array}\right]
143 | $$
144 | 3×3的阶矩阵T可以分成四个子矩阵。其中,$\left[\begin{array}{ll}a & b \\ c & d\end{array}\right]_{2 \times 2}$这一子矩阵可使图像实现恒等、 比例、 反射(或镜像)、 错切和旋转变换。[l m]这一行矩阵可以使图像实现平移变换。[p q] T这一列矩阵可以使图像实现透视变换,但当p=0,q=0时它无透视作用。[s]这一元素可以使图像实现全比例变换。例如, 将图像进行全比例变换, 即
145 | $$
146 | \left[\begin{array}{lll}1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & s\end{array}\right] \times\left[\begin{array}{c}x_{0 i} \\ y_{0 i} \\ 1\end{array}\right]=\left[\begin{array}{c}x_i \\ y_i \\ s\end{array}\right]
147 | $$
148 |
149 | 将齐次坐标$[x_i \quad y_i \quad s]^T$规范化后,$[\dfrac{x_{oi}}{s} \quad \dfrac{y_{oi}}{s} \quad s]^T=[x_i \quad y_i \quad 1]^T$。 由此可见
150 |
151 | 当 $s>1$ 时, 图像按比例缩小; 当 $0 55 |
56 | 如果$M×N$大小的原图像$F(x,y)$缩小为 $kM×kN$大小$(k<1)$ 的新图像$I(x,y)$时,则
57 | $$
58 | I(x, y)=F(\operatorname{int}(c \times x), \operatorname{int}(c \times y))
59 | $$
60 | 其中, $c=1/k$。由此公式可以构造出新图像,如图6-5所示。
61 |
62 | 
63 |
64 | 图6-5 图像按任意比例缩小
65 |
66 | 当 $f x \neq f y(f x, f y>0)$ 时, 图像不按比例缩小, 这种操作因为在 $x$ 方向和y方向的缩小比例不同, 一定会带来图像的几何畸变。图像不按比例缩小的方法是: 如果 $M \times N$ 大小的旧图 $F(x, y)$ 缩小为 $k_1 M \times k_2 N\left(k_1<1, k_2<1\right)$ 大小的新图像 $I(x, y)$ 时, 则
67 | $$
68 | I(x, y)=F\left(\operatorname{int}\left(c_1 \times x\right), \operatorname{int}\left(c_2 \times y\right)\right)
69 | $$
70 | 其中
71 | $$
72 | c=\frac{1}{k_1}, c_2=\frac{1}{k_2}
73 | $$
74 | 由此公式可以构造出新图像。
75 |
76 | 图像在缩小操作中, 是在现有的信息里如何挑选所需要的有用信息。而在图像的放大操作中, 则需要对尺寸放大后所多出来的空格填入适当的像素值, 这是信息的估计问题, 所以较图像的缩小要难一些。当 $f x=f y=2$ 时, 图像被按全比例放大 2 倍, 放大后图像中的 $(0,0)$ 像素对应于原图中的 $(0,0)$ 像素; $(0,1)$ 像素对应于原图中的 $(0,0.5)$ 像素, 该像素不存在, 可以近似为 $(0,0)$ 也可以近似 $(0,1) ; \quad(0,2)$ 像素对应于原图像中的 $(0,1)$ 像素; $(1,0)$ 像素对应于原图中的 $(0.5,0)$, 它的像素值近似于 $(0,0)$ 或 $(1,0)$ 像素; (2,0)像素对应于原图中的 $(1,0)$ 像素, 依此类推。其实这是将原图像每行中的像素重复取值一遍, 然后每行重复一次。图66是原始图像, 图6-7和图6-8是分别采用上述两种近似方法放大后的图像。
77 |
78 |
55 |
56 | 如果$M×N$大小的原图像$F(x,y)$缩小为 $kM×kN$大小$(k<1)$ 的新图像$I(x,y)$时,则
57 | $$
58 | I(x, y)=F(\operatorname{int}(c \times x), \operatorname{int}(c \times y))
59 | $$
60 | 其中, $c=1/k$。由此公式可以构造出新图像,如图6-5所示。
61 |
62 | 
63 |
64 | 图6-5 图像按任意比例缩小
65 |
66 | 当 $f x \neq f y(f x, f y>0)$ 时, 图像不按比例缩小, 这种操作因为在 $x$ 方向和y方向的缩小比例不同, 一定会带来图像的几何畸变。图像不按比例缩小的方法是: 如果 $M \times N$ 大小的旧图 $F(x, y)$ 缩小为 $k_1 M \times k_2 N\left(k_1<1, k_2<1\right)$ 大小的新图像 $I(x, y)$ 时, 则
67 | $$
68 | I(x, y)=F\left(\operatorname{int}\left(c_1 \times x\right), \operatorname{int}\left(c_2 \times y\right)\right)
69 | $$
70 | 其中
71 | $$
72 | c=\frac{1}{k_1}, c_2=\frac{1}{k_2}
73 | $$
74 | 由此公式可以构造出新图像。
75 |
76 | 图像在缩小操作中, 是在现有的信息里如何挑选所需要的有用信息。而在图像的放大操作中, 则需要对尺寸放大后所多出来的空格填入适当的像素值, 这是信息的估计问题, 所以较图像的缩小要难一些。当 $f x=f y=2$ 时, 图像被按全比例放大 2 倍, 放大后图像中的 $(0,0)$ 像素对应于原图中的 $(0,0)$ 像素; $(0,1)$ 像素对应于原图中的 $(0,0.5)$ 像素, 该像素不存在, 可以近似为 $(0,0)$ 也可以近似 $(0,1) ; \quad(0,2)$ 像素对应于原图像中的 $(0,1)$ 像素; $(1,0)$ 像素对应于原图中的 $(0.5,0)$, 它的像素值近似于 $(0,0)$ 或 $(1,0)$ 像素; (2,0)像素对应于原图中的 $(1,0)$ 像素, 依此类推。其实这是将原图像每行中的像素重复取值一遍, 然后每行重复一次。图66是原始图像, 图6-7和图6-8是分别采用上述两种近似方法放大后的图像。
77 |
78 |  79 |
80 | 图6-6 放大前的图像
81 |
82 |
79 |
80 | 图6-6 放大前的图像
81 |
82 |  83 |
84 | 图6-7 按最近邻域法放大两倍的图像
85 |
86 |
83 |
84 | 图6-7 按最近邻域法放大两倍的图像
85 |
86 |  87 |
88 | 图6-8 按插值法放大两倍的图像
89 |
90 | 一般地, 按比例将原图像放大 $k$ 倍时, 如果按照最近邻域法则需要将一个像素值添在新图像的 $k \times k$ 的子块中, 如图6-9所示。 显然, 如果放大倍数太大, 按照这种方法处理会出现马赛克效应。当 $f x \neq f y(f x, f y>0)$ 时, 图像在 $x$ 方向和 $y$ 方向不按比例放大, 此时, 这种操作由于 $x$ 方向和 $y$ 方向的放大倍数不同, 一定带来图像的几何畸变。放大的方法是将原图像的一个像素添到新图像的一个 $k_1 \times k_2$ 的子块中去。为了提高几何变换后的图像质量, 常采用线性揷值法。该方法的原理是, 当求出的分数地址与像素点不一致时, 求出周围四个像素点的距离比, 根据该比率, 由四个邻域的像素灰度值进行线性揷值, 如图6-10所示。
91 |
92 |
87 |
88 | 图6-8 按插值法放大两倍的图像
89 |
90 | 一般地, 按比例将原图像放大 $k$ 倍时, 如果按照最近邻域法则需要将一个像素值添在新图像的 $k \times k$ 的子块中, 如图6-9所示。 显然, 如果放大倍数太大, 按照这种方法处理会出现马赛克效应。当 $f x \neq f y(f x, f y>0)$ 时, 图像在 $x$ 方向和 $y$ 方向不按比例放大, 此时, 这种操作由于 $x$ 方向和 $y$ 方向的放大倍数不同, 一定带来图像的几何畸变。放大的方法是将原图像的一个像素添到新图像的一个 $k_1 \times k_2$ 的子块中去。为了提高几何变换后的图像质量, 常采用线性揷值法。该方法的原理是, 当求出的分数地址与像素点不一致时, 求出周围四个像素点的距离比, 根据该比率, 由四个邻域的像素灰度值进行线性揷值, 如图6-10所示。
91 |
92 |  93 |
94 | 图6-9 按最近邻域法放大五倍的图像
95 |
96 |
93 |
94 | 图6-9 按最近邻域法放大五倍的图像
95 |
96 |  97 |
98 | 图6-10 线性插值法示意图
99 |
100 | 简化后的灰度值计算式如下:
101 | $$
102 | \begin{aligned}
103 | & g(x, y)=(1-q)\{(1-p) \times g([x],[y])+p \times g([x] \\
104 | & +1,[y])\}+q\{(1-p) \times g([x],[y]+1)+p \times g([x] \\
105 | & +1,[y]+1)\}
106 | \end{aligned}
107 | $$
108 | 式中: $g(x, y)$ 为坐标 $(x, y)$ 处的灰度值, $[x]$ 、 $[y]$ 分别为不大于 $x, y$ 的整数。关于这个问题的详细算法及其实现, 读者可以参考有关参考文献。
109 |
110 | ## 6.2.2 比例缩放的实现
111 |
112 |
97 |
98 | 图6-10 线性插值法示意图
99 |
100 | 简化后的灰度值计算式如下:
101 | $$
102 | \begin{aligned}
103 | & g(x, y)=(1-q)\{(1-p) \times g([x],[y])+p \times g([x] \\
104 | & +1,[y])\}+q\{(1-p) \times g([x],[y]+1)+p \times g([x] \\
105 | & +1,[y]+1)\}
106 | \end{aligned}
107 | $$
108 | 式中: $g(x, y)$ 为坐标 $(x, y)$ 处的灰度值, $[x]$ 、 $[y]$ 分别为不大于 $x, y$ 的整数。关于这个问题的详细算法及其实现, 读者可以参考有关参考文献。
109 |
110 | ## 6.2.2 比例缩放的实现
111 |
112 |  113 |
114 | 图6-11 图像比例缩放处理结果
115 |
116 | 下面给出这个函数的框架和主要算法。
117 |
118 | ```c
119 | //*****************************************
120 | //函数名称: BOOL ZoomImage()
121 | //基本功能: 本函数对传入的CDibObject对象中的图像进行缩放操作
122 | //参数说明: float fXZoomRatio X轴方向缩放比率
123 | // float fYZoomRatio Y轴方向缩放比率
124 | // BOOL bBilinear TRUE为双线性插值, FALSE为最邻近插值
125 | // CDibObject *pDibObject 默认为NULL
126 | //返回值: BOOL 成功返回TRUE, 失败返回FALSE
127 | //*****************************************
128 | BOOL CGeoTrans:: ZoomImage(float fXZoomRatio, float fYZoomRatio,
129 | BOOL bBilinear, CDibObject *pDibObject)
130 | {
131 | //获得图像宽度和高度, 计算缩放后的图像实际宽度
132 | nNewWidth = (int)(nOldWidth * fXZoomRatio + 0.5);
133 | nNewHeight = (int)(nOldHeight * fYZoomRatio + 0.5);
134 | //获取源图像指针,为新图像分配内存,用白色填充新图像数据区,调整新图像信息
135 | //由图像位数确定的移动字节数nMovedBits
136 | //针对图像每行进行操作
137 | for(y = 0; y < nNewHeight; y++)
138 | {
139 | //指向新图像第y行
140 | pNewTemp = pNewBits;
141 | pNewTemp += (nNewHeight -1[KG*3]-y) * nNewWidthBytes;
142 | //针对图像每列进行操作
143 | for(x = 0; x < nNewWidth; x++)
144 | {
145 | //计算该像素在源图像中的坐标
146 | int y0 = (long) (y/fYZoomRatio +0.5);
147 | int x0 = (long) (x/fXZoomRatio +0.5);
148 | //判断是否在源图范围内
149 | if( (x0 >= 0) && (x0 < nOldWidth) && (y0 >= 0) && (y0 < nOldHeight))
150 | {
151 | if(bBilinear)
152 | {
153 | //双线性插值
154 | }
155 | else
156 | {
157 | //指向源图像第y0行, 第x0个像素
158 | pOldTemp = pOldBits;
159 | pOldTemp += (nOldHeight - 1 - y0) * nOldWidthBytes;
160 | pOldTemp += x0 * nMovedBits;
161 | memcpy(pNewTemp, pOldTemp, nMovedBits);
162 | }
163 | }
164 | pNewTemp += nMovedBits;
165 | }
166 | }
167 | //将内存解锁和将不再使用的内存释放, 将新图像设置为当前图像
168 | return TRUE;
169 | }
170 |
171 | ```
172 |
173 |
--------------------------------------------------------------------------------
/VI/6.3 图像平移.md:
--------------------------------------------------------------------------------
1 |
2 |
3 | # 6.3 图像平移
4 |
5 | ## 6.3.1 图像平移变换
6 |
7 | 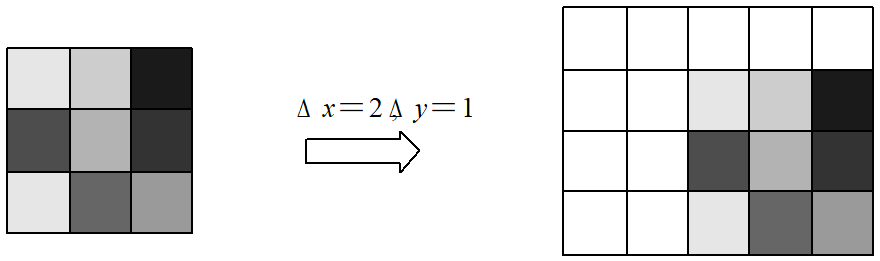
8 |
9 | 图6-12 图像平移
10 |
11 | 设点 $P_{0}\left(x_{0}, y_{0}\right)$ 进行平移后, 移到 $P(x, y)$, 其中 $x$ 方向的平移量为 $\Delta x, y$ 方向的平移量为 $\Delta y$ 。那么,点 $P(x, y)$ 的坐标为
12 |
13 | $$
14 | \left\{\begin{array}{l}
15 | x=x_{0}+\Delta x \\
16 | y=y_{0}+\Delta y
17 | \end{array}\right.
18 | $$
19 |
20 | 利用齐次坐标, 变换前后图像上的点 $P_{0}\left(x_{0}, y_{0}\right)$ 和 $P(x, y)$ 之间的关系可以用如下的矩阵变换表示为
21 |
22 | $$
23 | \left[\begin{array}{l}
24 | x \\
25 | y \\
26 | 1
27 | \end{array}\right]=\left[\begin{array}{lll}
28 | 1 & 0 & \Delta x \\
29 | 0 & 1 & \Delta y \\
30 | 0 & 0 & 1
31 | \end{array}\right]\left[\begin{array}{l}
32 | x_0 \\
33 | y_0 \\
34 | 1
35 | \end{array}\right]\tag{6-2}
36 | $$
37 | 对变换矩阵求逆, 可以得到式 (6-2) 的逆变换
38 | $$
39 | \left[\begin{array}{l}
40 | x_{0} \\
41 | y_{0} \\
42 | 1
43 | \end{array}\right]=\left[\begin{array}{ccc}
44 | 1 & 0 & -\Delta x \\
45 | 0 & 1 & -\Delta y \\
46 | 0 & 0 & 1
47 | \end{array}\right]\left[\begin{array}{l}
48 | x \\
49 | y \\
50 | 1
51 | \end{array}\right]
52 | $$
53 |
54 | 即
55 |
56 | $$
57 | \left\{\begin{array}{l}
58 | x_{0}=x-\Delta x \\
59 | y_{0}=y-\Delta y
60 | \end{array}\right.
61 | $$
62 |
63 | 这样, 平移后的图像上的每一点都可以在原图像中找到对应的点。例如, 对于新图中的 $(0,0)$ 像素, 代入上面的方程组,可以求出对应原图中的像素 $(-\Delta x,-\Delta y)$ 。如果 $\Delta x$ 或 $\Delta y 大于 0$, 则点 $(-\Delta x,-\Delta y)$ 不在原图像中。对于不在原图像中的点, 可以直接将它的像素值统一设置为 0 或者255 (对于灰度图就是黑色或白色)。同样, 若有像素点不在原图像中, 也就说明原图像中有点被移出显示区域。如果不想丢失被移出的部分图像, 可以将新生成的图像宽度扩大 $|\Delta x|$, 高度扩大 $|\Delta y|$ 。
64 |
65 |
113 |
114 | 图6-11 图像比例缩放处理结果
115 |
116 | 下面给出这个函数的框架和主要算法。
117 |
118 | ```c
119 | //*****************************************
120 | //函数名称: BOOL ZoomImage()
121 | //基本功能: 本函数对传入的CDibObject对象中的图像进行缩放操作
122 | //参数说明: float fXZoomRatio X轴方向缩放比率
123 | // float fYZoomRatio Y轴方向缩放比率
124 | // BOOL bBilinear TRUE为双线性插值, FALSE为最邻近插值
125 | // CDibObject *pDibObject 默认为NULL
126 | //返回值: BOOL 成功返回TRUE, 失败返回FALSE
127 | //*****************************************
128 | BOOL CGeoTrans:: ZoomImage(float fXZoomRatio, float fYZoomRatio,
129 | BOOL bBilinear, CDibObject *pDibObject)
130 | {
131 | //获得图像宽度和高度, 计算缩放后的图像实际宽度
132 | nNewWidth = (int)(nOldWidth * fXZoomRatio + 0.5);
133 | nNewHeight = (int)(nOldHeight * fYZoomRatio + 0.5);
134 | //获取源图像指针,为新图像分配内存,用白色填充新图像数据区,调整新图像信息
135 | //由图像位数确定的移动字节数nMovedBits
136 | //针对图像每行进行操作
137 | for(y = 0; y < nNewHeight; y++)
138 | {
139 | //指向新图像第y行
140 | pNewTemp = pNewBits;
141 | pNewTemp += (nNewHeight -1[KG*3]-y) * nNewWidthBytes;
142 | //针对图像每列进行操作
143 | for(x = 0; x < nNewWidth; x++)
144 | {
145 | //计算该像素在源图像中的坐标
146 | int y0 = (long) (y/fYZoomRatio +0.5);
147 | int x0 = (long) (x/fXZoomRatio +0.5);
148 | //判断是否在源图范围内
149 | if( (x0 >= 0) && (x0 < nOldWidth) && (y0 >= 0) && (y0 < nOldHeight))
150 | {
151 | if(bBilinear)
152 | {
153 | //双线性插值
154 | }
155 | else
156 | {
157 | //指向源图像第y0行, 第x0个像素
158 | pOldTemp = pOldBits;
159 | pOldTemp += (nOldHeight - 1 - y0) * nOldWidthBytes;
160 | pOldTemp += x0 * nMovedBits;
161 | memcpy(pNewTemp, pOldTemp, nMovedBits);
162 | }
163 | }
164 | pNewTemp += nMovedBits;
165 | }
166 | }
167 | //将内存解锁和将不再使用的内存释放, 将新图像设置为当前图像
168 | return TRUE;
169 | }
170 |
171 | ```
172 |
173 |
--------------------------------------------------------------------------------
/VI/6.3 图像平移.md:
--------------------------------------------------------------------------------
1 |
2 |
3 | # 6.3 图像平移
4 |
5 | ## 6.3.1 图像平移变换
6 |
7 | 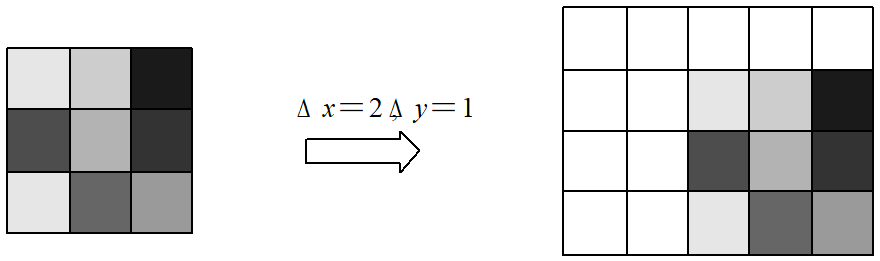
8 |
9 | 图6-12 图像平移
10 |
11 | 设点 $P_{0}\left(x_{0}, y_{0}\right)$ 进行平移后, 移到 $P(x, y)$, 其中 $x$ 方向的平移量为 $\Delta x, y$ 方向的平移量为 $\Delta y$ 。那么,点 $P(x, y)$ 的坐标为
12 |
13 | $$
14 | \left\{\begin{array}{l}
15 | x=x_{0}+\Delta x \\
16 | y=y_{0}+\Delta y
17 | \end{array}\right.
18 | $$
19 |
20 | 利用齐次坐标, 变换前后图像上的点 $P_{0}\left(x_{0}, y_{0}\right)$ 和 $P(x, y)$ 之间的关系可以用如下的矩阵变换表示为
21 |
22 | $$
23 | \left[\begin{array}{l}
24 | x \\
25 | y \\
26 | 1
27 | \end{array}\right]=\left[\begin{array}{lll}
28 | 1 & 0 & \Delta x \\
29 | 0 & 1 & \Delta y \\
30 | 0 & 0 & 1
31 | \end{array}\right]\left[\begin{array}{l}
32 | x_0 \\
33 | y_0 \\
34 | 1
35 | \end{array}\right]\tag{6-2}
36 | $$
37 | 对变换矩阵求逆, 可以得到式 (6-2) 的逆变换
38 | $$
39 | \left[\begin{array}{l}
40 | x_{0} \\
41 | y_{0} \\
42 | 1
43 | \end{array}\right]=\left[\begin{array}{ccc}
44 | 1 & 0 & -\Delta x \\
45 | 0 & 1 & -\Delta y \\
46 | 0 & 0 & 1
47 | \end{array}\right]\left[\begin{array}{l}
48 | x \\
49 | y \\
50 | 1
51 | \end{array}\right]
52 | $$
53 |
54 | 即
55 |
56 | $$
57 | \left\{\begin{array}{l}
58 | x_{0}=x-\Delta x \\
59 | y_{0}=y-\Delta y
60 | \end{array}\right.
61 | $$
62 |
63 | 这样, 平移后的图像上的每一点都可以在原图像中找到对应的点。例如, 对于新图中的 $(0,0)$ 像素, 代入上面的方程组,可以求出对应原图中的像素 $(-\Delta x,-\Delta y)$ 。如果 $\Delta x$ 或 $\Delta y 大于 0$, 则点 $(-\Delta x,-\Delta y)$ 不在原图像中。对于不在原图像中的点, 可以直接将它的像素值统一设置为 0 或者255 (对于灰度图就是黑色或白色)。同样, 若有像素点不在原图像中, 也就说明原图像中有点被移出显示区域。如果不想丢失被移出的部分图像, 可以将新生成的图像宽度扩大 $|\Delta x|$, 高度扩大 $|\Delta y|$ 。
64 |
65 |  66 |
67 | 图6-13 平移前的图像
68 |
69 |
70 |
71 |
66 |
67 | 图6-13 平移前的图像
68 |
69 |
70 |
71 |  72 |
73 | 图6-14 平移后的图像
74 |
75 |
72 |
73 | 图6-14 平移后的图像
74 |
75 |  76 |
77 | 图6-15 平移扩大后的图像
78 |
79 |
80 |
81 | ## 6.3.2 图像平移的算法
82 |
83 | 按照上述理论, 可以比较容易地用 VC++来实现图像的平移。 下面介绍灰度图像的平移, 因为灰度图像每个像素位数正好是 8 位, 即 1 个字节, 在进行图像处理时可以不用考虑拼凑字节的问题。而且由于灰度图像调色板的特殊性, 进行灰度图像处理时不必考虑调色板的问题。所以, 在介绍图像处理时,一般采用灰度图像, 以便将重点放在算法本身。由上述分析, 可以得到实现图像平移的算法如下。
84 |
85 | ```c++
86 | //*****************************************
87 | //函数名称: BOOL TranslationPixel()
88 | //基本功能: 本函数对传入的CDibObject对象中的图像进行逐点平移操作
89 | //参数说明: long lXOffset X轴平移量(像素数)
90 | // long lYOffset Y轴平移量(像素数)
91 | //返回值: BOOL 成功返回TRUE, 失败返回FALSE
92 | //注意: 该函数不会改变图像的大小, 移出的部分图像将截去, 空白部分用白色填充
93 | //*****************************************
94 | BOOL CGeoTrans:: TranslationPixel(long lXOffset, long lYOffset, CDibObject *pDibObject)
95 | {
96 | //定义变量, 获得源图像指针及其图像信息, 为新图像分配内存及用白色填充新图
97 | //由图像位数确定的移动字节数nMovedBits, 对于灰度图像有nMovedBits = 1
98 | //每行
99 | for(y = 0; y < nHeight; y++)
100 | {
101 | pNewTemp = pNewBits;
102 | pNewTemp += (nHeight -1-y) * nWidthBytes;
103 | //每列
104 | for(x = 0; x < nWidth; x++)
105 | {
106 | //指向新DIB第y行, 第x个像素的指针, 计算该像素在源DIB中的坐标
107 | int x0 = x – lXOffset;
108 | int y0 = y – lYOffset;
109 | //判断是否在源图范围内
110 | if( (x0 >= 0) && (x0 < nWidth) && (y0 >= 0) && (y0 < nHeight))
111 | {
112 | //指向源DIB第y0行, 第x0个像素的指针
113 | pOldTemp = pOldBits;
114 | pOldTemp += (nHeight -1-y0) * nWidthBytes;
115 | pOldTemp += x0 * nMovedBits;
116 | //复制像素
117 | memcpy( pNewTemp, pOldTemp, nMovedBits );
118 | }
119 | pNewTemp += nMovedBits;
120 | }
121 | }
122 | //用新图像数据填充源图像数据区
123 | memcpy( pOldBits, pNewBits, nWidthBytes * nHeight );
124 | }
125 | ```
126 |
127 |
--------------------------------------------------------------------------------
/VI/6.4 图像镜像.md:
--------------------------------------------------------------------------------
1 | # 图像镜像
2 |
3 | ## 6.4.1 图像镜像变换
4 |
5 | 图像的镜像变换不改变图像的形状。图像的镜像(Mirror)变换分为两种:一种是水平镜像,另外一种是垂直镜像。图像的水平镜像操作是将图像左半部分和右半部分以图像垂直中轴线为中心进行镜像对换;图像的垂直镜像操作是将图像上半部分和下半部分以图像水平中轴线为中心进行镜像对换,如图6-16所示
6 |
7 | 
8 |
9 | 图6-16 图像的镜像
10 |
11 | 图像的镜像变换也可以用矩阵变换表示。设点 $P_{0}\left(x_{0}, y_{0}\right)$ 进行镜像后的对应点为$P(x, y)$, 图像高度为 fHeight, 宽度为fWidth,原图像中 $P_0\left(x_0, y_0\right)$ 经过水平镜像后坐标将变为 (fWidth- $\left.x_0, y_0\right)$,其矩阵表达式为
12 | $$
13 | \left[\begin{array}{l}
14 | x \\
15 | y \\
16 | 1
17 | \end{array}\right]=\left[\begin{array}{rrc}
18 | -1 & 0 & fWidth \\
19 | 0 & 1 & 0 \\
20 | 0 & 0 & 1
21 | \end{array}\right]\left[\begin{array}{l}
22 | x_{0} \\
23 | y_{0} \\
24 | 1
25 | \end{array}\right]\tag{6-3}
26 | $$
27 |
28 | 逆运算矩阵表达式为
29 |
30 | $$
31 | \left[\begin{array}{l}
32 | x_{0} \\
33 | y_{0} \\
34 | 1
35 | \end{array}\right]=\left[\begin{array}{ccc}
36 | -1 & 0 & fwidth \\
37 | 0 & 1 & 0 \\
38 | 0 & 0 & 1
39 | \end{array}\right]\left[\begin{array}{l}
40 | x \\
41 | y \\
42 | 1
43 | \end{array}\right]
44 | $$
45 |
46 | 即
47 |
48 | $$
49 | \left\{\begin{array}{l}
50 | x_{0}=f \text { Width }-x \\
51 | y_{0}=y
52 | \end{array}\right.
53 | $$
54 |
55 | 同样, $P_{0}\left(x_{0}, y_{0}\right)$ 经过垂直镜像后坐标将变为 $\left(x_{0}, f H e i g h t-y_{0}\right)$,
56 |
57 | 其矩阵表表达式为
58 |
59 | $$
60 | \left[\begin{array}{l}
61 | x \\
62 | y \\
63 | 1
64 | \end{array}\right]=\left[\begin{array}{ccc}
65 | 1 & 0 & 0 \\
66 | 0 & -1 & fHeight \\
67 | 0 & 0 & 1
68 | \end{array}\right]\left[\begin{array}{l}
69 | x_{0} \\
70 | y_{0} \\
71 | 1
72 | \end{array}\right]
73 | \tag{6-4}
74 | $$
75 |
76 | 逆运算矩阵表达式为
77 |
78 | $$
79 | \left[\begin{array}{l}
80 | x_{0} \\
81 | y_{0} \\
82 | 1
83 | \end{array}\right]=\left[\begin{array}{ccc}
84 | 1 & 0 & 0 \\
85 | 0 & -1 & \text { fHeight } \\
86 | 0 & 0 & 1
87 | \end{array}\right]\left[\begin{array}{l}
88 | x \\
89 | y \\
90 | 1
91 | \end{array}\right]
92 | $$
93 |
94 | 即
95 |
96 | $$
97 | \left\{\begin{array}{l}
98 | x_{0}=x \\
99 | y_{0}=f W i d t h-y
100 | \end{array}\right.
101 | $$
102 |
103 | ## 6.4.2 图像镜像的算法
104 |
105 | 按照上面的变换公式 (6-3) 和(6-4),可以比较简单的实现图像的水平和垂直镜像操作, 读者可以参照6.3.2中平移的算法, 写出公式 (6-3) 和 (6-4) 对应的算法。
106 |
107 | 和图像平移一样, 在垂直镜像中也可以利用位图存储的连续性整行复制图像。下面将介绍采用这种方法的算法, 其主要算法如下, bDirection为真时表示水平镜像, 否则为垂直镜像。
108 |
109 | ```c++
110 | //由图像位数确定的移动字节数nMovedBits
111 | //判断镜像方式
112 | if (bDirection)
113 | {
114 | //垂直中轴坐标
115 | int nMiddleX = nWidth / 2;
116 | //针对图像每行进行操作
117 | for(y = 0; y < nHeight; y++)
118 | {
119 | //指向图像的倒数第y行
120 | pOldTemp = pOldBits;
121 | pOldTemp += y * nWidthBytes;
122 | pNewTemp = pNewBits;
123 | pNewTemp += y * nWidthBytes;
124 | //针对每行图像左半部分进行操作
125 | for(x = 0; x <= nMiddleX; x++)
126 | {
127 | //将源图像第x个像素复制到新图像倒数第x个像素
128 | pTemp1 = pOldTemp + x * nMovedBits;
129 | pTemp2 = pNewTemp + (nWidth -1 - x) * nMovedBits;
130 | memcpy(pTemp2, pTemp1, nMovedBits);
131 | //将源图像倒数第x个像素复制到新图像第x个像素
132 | pTemp1 = pOldTemp + (nWidth -1 - x) * nMovedBits;
133 | pTemp2 = pNewTemp + x * nMovedBits;
134 | memcpy(pTemp2, pTemp1, nMovedBits);
135 | }
136 | }
137 | }
138 | else
139 | {
140 | //水平中轴坐标
141 | int nMiddleY = nHeight / 2;
142 | //针对上半图像进行操作
143 | for(y = 0; y <= nMiddleY; y++)
144 | {
145 | //指向源图像倒数第y行像素起点的指针
146 | pOldTemp = pOldBits;
147 | pOldTemp += y * nWidthBytes;
148 | //指向新图像第y行像素起点的指针
149 | pNewTemp = pNewBits;
150 | pNewTemp += (nHeight - 1 - y) * nWidthBytes;
151 | //将源图像倒数第y行像素复制到新图像第y行
152 | memcpy(pNewTemp, pOldTemp, nWidthBytes);
153 | //指向源图像第y行像素起点的指针
154 | pOldTemp = pOldBits;
155 | pOldTemp += (nHeight -1 -y) * nWidthBytes;
156 | //指向新图像倒数第y行像素起点的指针
157 | pNewTemp = pNewBits;
158 | pNewTemp += y * nWidthBytes;
159 | //将源图像第y行像素复制到新图像倒数第y行
160 | memcpy(pNewTemp, pOldTemp, nWidthBytes);
161 | }
162 | }
163 | //用新图像数据填充原图像数据区
164 | memcpy( pOldBits, pNewBits, nWidthBytes * nHeight );
165 |
166 | ```
167 |
168 |
169 |
170 |
76 |
77 | 图6-15 平移扩大后的图像
78 |
79 |
80 |
81 | ## 6.3.2 图像平移的算法
82 |
83 | 按照上述理论, 可以比较容易地用 VC++来实现图像的平移。 下面介绍灰度图像的平移, 因为灰度图像每个像素位数正好是 8 位, 即 1 个字节, 在进行图像处理时可以不用考虑拼凑字节的问题。而且由于灰度图像调色板的特殊性, 进行灰度图像处理时不必考虑调色板的问题。所以, 在介绍图像处理时,一般采用灰度图像, 以便将重点放在算法本身。由上述分析, 可以得到实现图像平移的算法如下。
84 |
85 | ```c++
86 | //*****************************************
87 | //函数名称: BOOL TranslationPixel()
88 | //基本功能: 本函数对传入的CDibObject对象中的图像进行逐点平移操作
89 | //参数说明: long lXOffset X轴平移量(像素数)
90 | // long lYOffset Y轴平移量(像素数)
91 | //返回值: BOOL 成功返回TRUE, 失败返回FALSE
92 | //注意: 该函数不会改变图像的大小, 移出的部分图像将截去, 空白部分用白色填充
93 | //*****************************************
94 | BOOL CGeoTrans:: TranslationPixel(long lXOffset, long lYOffset, CDibObject *pDibObject)
95 | {
96 | //定义变量, 获得源图像指针及其图像信息, 为新图像分配内存及用白色填充新图
97 | //由图像位数确定的移动字节数nMovedBits, 对于灰度图像有nMovedBits = 1
98 | //每行
99 | for(y = 0; y < nHeight; y++)
100 | {
101 | pNewTemp = pNewBits;
102 | pNewTemp += (nHeight -1-y) * nWidthBytes;
103 | //每列
104 | for(x = 0; x < nWidth; x++)
105 | {
106 | //指向新DIB第y行, 第x个像素的指针, 计算该像素在源DIB中的坐标
107 | int x0 = x – lXOffset;
108 | int y0 = y – lYOffset;
109 | //判断是否在源图范围内
110 | if( (x0 >= 0) && (x0 < nWidth) && (y0 >= 0) && (y0 < nHeight))
111 | {
112 | //指向源DIB第y0行, 第x0个像素的指针
113 | pOldTemp = pOldBits;
114 | pOldTemp += (nHeight -1-y0) * nWidthBytes;
115 | pOldTemp += x0 * nMovedBits;
116 | //复制像素
117 | memcpy( pNewTemp, pOldTemp, nMovedBits );
118 | }
119 | pNewTemp += nMovedBits;
120 | }
121 | }
122 | //用新图像数据填充源图像数据区
123 | memcpy( pOldBits, pNewBits, nWidthBytes * nHeight );
124 | }
125 | ```
126 |
127 |
--------------------------------------------------------------------------------
/VI/6.4 图像镜像.md:
--------------------------------------------------------------------------------
1 | # 图像镜像
2 |
3 | ## 6.4.1 图像镜像变换
4 |
5 | 图像的镜像变换不改变图像的形状。图像的镜像(Mirror)变换分为两种:一种是水平镜像,另外一种是垂直镜像。图像的水平镜像操作是将图像左半部分和右半部分以图像垂直中轴线为中心进行镜像对换;图像的垂直镜像操作是将图像上半部分和下半部分以图像水平中轴线为中心进行镜像对换,如图6-16所示
6 |
7 | 
8 |
9 | 图6-16 图像的镜像
10 |
11 | 图像的镜像变换也可以用矩阵变换表示。设点 $P_{0}\left(x_{0}, y_{0}\right)$ 进行镜像后的对应点为$P(x, y)$, 图像高度为 fHeight, 宽度为fWidth,原图像中 $P_0\left(x_0, y_0\right)$ 经过水平镜像后坐标将变为 (fWidth- $\left.x_0, y_0\right)$,其矩阵表达式为
12 | $$
13 | \left[\begin{array}{l}
14 | x \\
15 | y \\
16 | 1
17 | \end{array}\right]=\left[\begin{array}{rrc}
18 | -1 & 0 & fWidth \\
19 | 0 & 1 & 0 \\
20 | 0 & 0 & 1
21 | \end{array}\right]\left[\begin{array}{l}
22 | x_{0} \\
23 | y_{0} \\
24 | 1
25 | \end{array}\right]\tag{6-3}
26 | $$
27 |
28 | 逆运算矩阵表达式为
29 |
30 | $$
31 | \left[\begin{array}{l}
32 | x_{0} \\
33 | y_{0} \\
34 | 1
35 | \end{array}\right]=\left[\begin{array}{ccc}
36 | -1 & 0 & fwidth \\
37 | 0 & 1 & 0 \\
38 | 0 & 0 & 1
39 | \end{array}\right]\left[\begin{array}{l}
40 | x \\
41 | y \\
42 | 1
43 | \end{array}\right]
44 | $$
45 |
46 | 即
47 |
48 | $$
49 | \left\{\begin{array}{l}
50 | x_{0}=f \text { Width }-x \\
51 | y_{0}=y
52 | \end{array}\right.
53 | $$
54 |
55 | 同样, $P_{0}\left(x_{0}, y_{0}\right)$ 经过垂直镜像后坐标将变为 $\left(x_{0}, f H e i g h t-y_{0}\right)$,
56 |
57 | 其矩阵表表达式为
58 |
59 | $$
60 | \left[\begin{array}{l}
61 | x \\
62 | y \\
63 | 1
64 | \end{array}\right]=\left[\begin{array}{ccc}
65 | 1 & 0 & 0 \\
66 | 0 & -1 & fHeight \\
67 | 0 & 0 & 1
68 | \end{array}\right]\left[\begin{array}{l}
69 | x_{0} \\
70 | y_{0} \\
71 | 1
72 | \end{array}\right]
73 | \tag{6-4}
74 | $$
75 |
76 | 逆运算矩阵表达式为
77 |
78 | $$
79 | \left[\begin{array}{l}
80 | x_{0} \\
81 | y_{0} \\
82 | 1
83 | \end{array}\right]=\left[\begin{array}{ccc}
84 | 1 & 0 & 0 \\
85 | 0 & -1 & \text { fHeight } \\
86 | 0 & 0 & 1
87 | \end{array}\right]\left[\begin{array}{l}
88 | x \\
89 | y \\
90 | 1
91 | \end{array}\right]
92 | $$
93 |
94 | 即
95 |
96 | $$
97 | \left\{\begin{array}{l}
98 | x_{0}=x \\
99 | y_{0}=f W i d t h-y
100 | \end{array}\right.
101 | $$
102 |
103 | ## 6.4.2 图像镜像的算法
104 |
105 | 按照上面的变换公式 (6-3) 和(6-4),可以比较简单的实现图像的水平和垂直镜像操作, 读者可以参照6.3.2中平移的算法, 写出公式 (6-3) 和 (6-4) 对应的算法。
106 |
107 | 和图像平移一样, 在垂直镜像中也可以利用位图存储的连续性整行复制图像。下面将介绍采用这种方法的算法, 其主要算法如下, bDirection为真时表示水平镜像, 否则为垂直镜像。
108 |
109 | ```c++
110 | //由图像位数确定的移动字节数nMovedBits
111 | //判断镜像方式
112 | if (bDirection)
113 | {
114 | //垂直中轴坐标
115 | int nMiddleX = nWidth / 2;
116 | //针对图像每行进行操作
117 | for(y = 0; y < nHeight; y++)
118 | {
119 | //指向图像的倒数第y行
120 | pOldTemp = pOldBits;
121 | pOldTemp += y * nWidthBytes;
122 | pNewTemp = pNewBits;
123 | pNewTemp += y * nWidthBytes;
124 | //针对每行图像左半部分进行操作
125 | for(x = 0; x <= nMiddleX; x++)
126 | {
127 | //将源图像第x个像素复制到新图像倒数第x个像素
128 | pTemp1 = pOldTemp + x * nMovedBits;
129 | pTemp2 = pNewTemp + (nWidth -1 - x) * nMovedBits;
130 | memcpy(pTemp2, pTemp1, nMovedBits);
131 | //将源图像倒数第x个像素复制到新图像第x个像素
132 | pTemp1 = pOldTemp + (nWidth -1 - x) * nMovedBits;
133 | pTemp2 = pNewTemp + x * nMovedBits;
134 | memcpy(pTemp2, pTemp1, nMovedBits);
135 | }
136 | }
137 | }
138 | else
139 | {
140 | //水平中轴坐标
141 | int nMiddleY = nHeight / 2;
142 | //针对上半图像进行操作
143 | for(y = 0; y <= nMiddleY; y++)
144 | {
145 | //指向源图像倒数第y行像素起点的指针
146 | pOldTemp = pOldBits;
147 | pOldTemp += y * nWidthBytes;
148 | //指向新图像第y行像素起点的指针
149 | pNewTemp = pNewBits;
150 | pNewTemp += (nHeight - 1 - y) * nWidthBytes;
151 | //将源图像倒数第y行像素复制到新图像第y行
152 | memcpy(pNewTemp, pOldTemp, nWidthBytes);
153 | //指向源图像第y行像素起点的指针
154 | pOldTemp = pOldBits;
155 | pOldTemp += (nHeight -1 -y) * nWidthBytes;
156 | //指向新图像倒数第y行像素起点的指针
157 | pNewTemp = pNewBits;
158 | pNewTemp += y * nWidthBytes;
159 | //将源图像第y行像素复制到新图像倒数第y行
160 | memcpy(pNewTemp, pOldTemp, nWidthBytes);
161 | }
162 | }
163 | //用新图像数据填充原图像数据区
164 | memcpy( pOldBits, pNewBits, nWidthBytes * nHeight );
165 |
166 | ```
167 |
168 |
169 |
170 |  171 |
172 | 图6-17 镜像前的图像
173 |
174 |
171 |
172 | 图6-17 镜像前的图像
173 |
174 |  175 |
176 | 图6-18 水平镜像
177 |
178 |
175 |
176 | 图6-18 水平镜像
177 |
178 |  179 |
180 | 图6-19 垂直镜像
--------------------------------------------------------------------------------
/VI/6.5 图像旋转.md:
--------------------------------------------------------------------------------
1 | # 6.5 图像旋转
2 |
3 | ## 6.5.1 图像旋转变换
4 |
5 | 本节介绍一种相对复杂的几何变换一图像的旋转。一般图像的旋转是以图像的中心为原点, 将图像上的所有像素都旋转 一个相同的角度。图像的旋转变换是图像的位置变换, 但旋转后, 图像的大小一般会改变。和图像平移一样, 在图像旋转变 换中既可以把转出显示区域的图像截去, 也可以扩大图像范围 以显示所有的图像。如图6-20、图6-21所示。
6 |
7 |
179 |
180 | 图6-19 垂直镜像
--------------------------------------------------------------------------------
/VI/6.5 图像旋转.md:
--------------------------------------------------------------------------------
1 | # 6.5 图像旋转
2 |
3 | ## 6.5.1 图像旋转变换
4 |
5 | 本节介绍一种相对复杂的几何变换一图像的旋转。一般图像的旋转是以图像的中心为原点, 将图像上的所有像素都旋转 一个相同的角度。图像的旋转变换是图像的位置变换, 但旋转后, 图像的大小一般会改变。和图像平移一样, 在图像旋转变 换中既可以把转出显示区域的图像截去, 也可以扩大图像范围 以显示所有的图像。如图6-20、图6-21所示。
6 |
7 |  8 |
9 | 图6-20 旋转前的图像
10 | 
11 |
12 | 图6-21 旋转 $\theta$ 后的图像(扩大图像、转出部分被截)
13 |
14 | 同样, 图像的旋转变换也可以用矩阵变换表示。设点 $P_{0}\left(x_{0}, y_{0}\right)$旋转 $\theta$ 角后的对应点为 $P(x, y)$, 如图6-22所示。那么, 旋转前后 点 $P_{0}\left(x_{0}, y_{0}\right) 、 P(x, y)$ 的坐标分别是:
15 |
16 | 
17 | 图6-22 图像旋转 $\theta$ 角
18 | $$
19 | \begin{aligned}
20 | & \left\{\begin{array}{l}
21 | x_0=r \cos \alpha \\
22 | y_0=r \sin \alpha
23 | \end{array}\right. \\
24 | & \left\{\begin{array}{l}
25 | x=r \cos (\alpha-\theta)=r \cos \alpha \cos \theta+r \sin \alpha \sin \theta=x_0 \cos \theta+y_0 \sin \theta \\
26 | y=r \sin (\alpha-\theta)=r \sin \alpha \cos \theta-r \cos \alpha \sin \theta=-x_0 \sin \theta+y_0 \cos \theta
27 | \end{array}\right.
28 | \end{aligned}
29 | $$
30 | 写成矩阵表达式为
31 | $$
32 | \left[\begin{array}{l}
33 | x \\
34 | y \\
35 | 1
36 | \end{array}\right]=\left[\begin{array}{ccc}
37 | \cos \theta & \sin \theta & 0 \\
38 | -\sin \theta & \cos \theta & 0 \\
39 | 0 & 0 & 1
40 | \end{array}\right]\left[\begin{array}{l}
41 | x_0 \\
42 | y_0 \\
43 | 1
44 | \end{array}\right]\tag{6-5}
45 | $$
46 | 其逆运算为
47 |
48 | $$
49 | \left[\begin{array}{l}
50 | x \\
51 | y \\
52 | 1
53 | \end{array}\right]=\left[\begin{array}{ccc}
54 | \cos \theta & -\sin \theta & 0 \\
55 | \sin \theta & \cos \theta & 0 \\
56 | 0 & 0 & 1
57 | \end{array}\right]\left[\begin{array}{l}
58 | x_{0} \\
59 | y_{0} \\
60 | 1
61 | \end{array}\right]
62 | $$
63 |
64 | 利用公式 (6-5) 可以确定旋转后图像上的像素。例如, 当 $\theta=30^{\circ}$ 时, 公式 (6-5) 为
65 |
66 | $$
67 | \left\{\begin{array}{l}
68 | x=0.866 x-0.5 y \\
69 | y=0.5 x+0.866
70 | \end{array}\right.
71 | $$
72 | 而且, 此时
73 |
74 | $$
75 | \begin{aligned}
76 | & x_{\min }=0.866-0.5 \times 3=-0.634 ; x_{\min }=0.866 \times 3-0.5=2.098 \\
77 | & y_{\min }=0.866+0.5=1.366 ; \quad y_{\max }=0.866 \times 3+0.5 \times 3=4.098
78 | \end{aligned}
79 | $$
80 | 
81 | 图6-23 图像旋转 $\theta$ 角
82 |
83 | 利用公式(6-5)进行图像旋转时需要注意如下两点:
84 |
85 | (1) 图像旋转之前, 为了避免信息的丢失, 一定要有坐标平移,具体的做法有如图6-24所示的两种方法。
86 | 
87 |
88 | 图6-24 图像旋转之前进行的平移 (2) 图像旋转之后, 会出现许多空洞点, 如图6-23所示。对 这些空洞点必须进行填充处理, 否则画面效果不好, 一般也称 这种操作为揷值处理。最简单的方法是行揷值方法或列揷值方 法:
89 |
90 | (1) 找出当前行的最小和最大的非白点的坐标, 记作: $(i, k 1)$ 、 $(i, k 2)$ 。
91 |
92 | (2) 在(k1, k2)范围内进行揷值, 揷值的方法是: 空点的像素 值等于前一点的像素值。
93 |
94 | (3) 同样的操作重复到所有行。经过如上的揷值处理之后, 图像效果就变得自然。如图6-25所示。列揷值方法与此类同, 请读者自己给出。
95 | 
96 |
97 | 图6-25 图6-23中的图像处理后的效果
98 |
99 | ## 6.5.2 图像旋转的实现
100 |
101 | 按照上述理论,也可以用VC++编程实现图像的旋转。为了 将重点放在算法本身, 下面介绍灰度图像的旋转算法。由上面 的公式(6-6)以及产生空穴时的双线性揷值方法,可以编制一 个实现图像旋转的函数RotateDIB2()。下面给出这个函数的框架和主要算法。
102 |
103 | ```c++
104 | //*****************************************
105 | //函数名称: BOOL Rotate()
106 | //基本功能: 本函数对传入的CDibObject对象中的图像进行旋转操作
107 | //参数说明: int iRotateAngle 旋转的角度(0~360度)
108 | // BOOL bBilinear TRUE为双线性插值, FALSE为最邻近插值
109 | // CDibObject *pDibObject 默认为NULL
110 | //返回值: BOOL 成功返回TRUE, 失败返回FALSE
111 | //*****************************************
112 | BOOL CGeoTrans:: Rotate(int nRotateAngle, BOOL bBilinear, CDibObject *pDibObject)
113 | {
114 | //获得图像宽度和高度: nOldWidth、 nOldHeight
115 | //定义旋转角度(弧度)及其正弦和余弦值: fRotateAngle、 fSina、 fCosa
116 | //定义源图四个角的坐标、 旋转后四个角的坐标(以图像中心为坐标系原点)
117 | //计算旋转角度的正弦和余弦值
118 | //计算源图的四个角的坐标(以图像中心为坐标系原点)
119 | //计算新图四个角的坐标(以图像中心为坐标系原点)
120 | fDstX1 = fCosa * fSrcX1 + fSina * fSrcY1;
121 | fDstY1 = -fSina * fSrcX1 + fCosa * fSrcY1;
122 | fDstX2 = fCosa * fSrcX2 + fSina * fSrcY2;
123 | fDstY2 = -fSina * fSrcX2 + fCosa * fSrcY2;
124 | fDstX3 = fCosa * fSrcX3 + fSina * fSrcY3;
125 | fDstY3 = -fSina * fSrcX3 + fCosa * fSrcY3;
126 | fDstX4 = fCosa * fSrcX4 + fSina * fSrcY4;
127 | fDstY4 = -fSina * fSrcX4 + fCosa * fSrcY4;
128 | //计算旋转后的图像实际宽度
129 | int nNewWidth=(long)(max(fabs(fDstX4-fDstX1), fabs(fDstX3-fDstX2))+0.5);
130 | //计算旋转后的图像高度
131 | int nNewHeight=(long)(max(fabs(fDstY4-fDstY1), fabs(fDstY3-fDstY2))+0.5);
132 | //计算两个常数
133 | f1= (float) (-0.5 * (nNewWidth - 1) * fCosa - 0.5 * (nNewHeight - 1) * fSina
134 | + 0.5 * (nOldWidth - 1));
135 | f2= (float) ( 0.5 * (nNewWidth - 1) * fSina - 0.5 * (nNewHeight - 1) * fCosa
136 | + 0.5 * (nOldHeight - 1));
137 | //获取指向源图像的指针, 为旋转图像分配内存并用白色填充新图像数据区
138 | //由图像位数确定的移动字节数nMovedBits
139 | //针对图像每行进行操作
140 | for(y = 0; y < nNewHeight; y++)
141 | {
142 | //指向新图像第y行
143 | pNewTemp = pNewBits;
144 | pNewTemp += (nNewHeight - 1 - y) * nNewWidthBytes;
145 | //针对图像每列进行操作
146 | for(x = 0; x < nNewWidth; x++)
147 | {
148 | //计算该像素在源图像中的坐标
149 | int y0 = (long) (-((float) x) * fSina + ((float) y)
150 | * fCosa + f2 + 0.5);
151 | int x0 = (long) ( ((float) x) * fCosa + ((float) y)
152 | * fSina + f1 + 0.5);
153 | //判断是否在源图范围内
154 | if( (x0 >= 0) && (x0 < nOldWidth) && (y0 >= 0) && (y0 < nOldHeight))
155 | {
156 | //用双线性插值
157 | if(bBilinear)
158 | {
159 | unsigned char *pTemp = Interpolation (nOldWidth, nOldHeight,
160 | (float)x0, (float)y0, nOldWidthBytes, nMovedBits, pOldBits);
161 | //复制像素
162 | memcpy(pNewTemp, pTemp, nMovedBits);
163 | delete [] pTemp ;
164 | }
165 | else
166 | {
167 | //指向源图像第y0行, 第x0个像素
168 | pOldTemp = pOldBits;
169 | pOldTemp += (nOldHeight - 1 - y0) * nOldWidthBytes;
170 | pOldTemp += x0 * nMovedBits;
171 | //复制像素
172 | memcpy(pNewTemp, pOldTemp, nMovedBits);
173 | }
174 | }
175 | pNewTemp += nMovedBits;
176 | }
177 | }
178 | //将内存解锁和将不再使用的内存释放, 将新图像设置为当前图像
179 | return TRUE;
180 | }
181 | ```
182 |
183 |
8 |
9 | 图6-20 旋转前的图像
10 | 
11 |
12 | 图6-21 旋转 $\theta$ 后的图像(扩大图像、转出部分被截)
13 |
14 | 同样, 图像的旋转变换也可以用矩阵变换表示。设点 $P_{0}\left(x_{0}, y_{0}\right)$旋转 $\theta$ 角后的对应点为 $P(x, y)$, 如图6-22所示。那么, 旋转前后 点 $P_{0}\left(x_{0}, y_{0}\right) 、 P(x, y)$ 的坐标分别是:
15 |
16 | 
17 | 图6-22 图像旋转 $\theta$ 角
18 | $$
19 | \begin{aligned}
20 | & \left\{\begin{array}{l}
21 | x_0=r \cos \alpha \\
22 | y_0=r \sin \alpha
23 | \end{array}\right. \\
24 | & \left\{\begin{array}{l}
25 | x=r \cos (\alpha-\theta)=r \cos \alpha \cos \theta+r \sin \alpha \sin \theta=x_0 \cos \theta+y_0 \sin \theta \\
26 | y=r \sin (\alpha-\theta)=r \sin \alpha \cos \theta-r \cos \alpha \sin \theta=-x_0 \sin \theta+y_0 \cos \theta
27 | \end{array}\right.
28 | \end{aligned}
29 | $$
30 | 写成矩阵表达式为
31 | $$
32 | \left[\begin{array}{l}
33 | x \\
34 | y \\
35 | 1
36 | \end{array}\right]=\left[\begin{array}{ccc}
37 | \cos \theta & \sin \theta & 0 \\
38 | -\sin \theta & \cos \theta & 0 \\
39 | 0 & 0 & 1
40 | \end{array}\right]\left[\begin{array}{l}
41 | x_0 \\
42 | y_0 \\
43 | 1
44 | \end{array}\right]\tag{6-5}
45 | $$
46 | 其逆运算为
47 |
48 | $$
49 | \left[\begin{array}{l}
50 | x \\
51 | y \\
52 | 1
53 | \end{array}\right]=\left[\begin{array}{ccc}
54 | \cos \theta & -\sin \theta & 0 \\
55 | \sin \theta & \cos \theta & 0 \\
56 | 0 & 0 & 1
57 | \end{array}\right]\left[\begin{array}{l}
58 | x_{0} \\
59 | y_{0} \\
60 | 1
61 | \end{array}\right]
62 | $$
63 |
64 | 利用公式 (6-5) 可以确定旋转后图像上的像素。例如, 当 $\theta=30^{\circ}$ 时, 公式 (6-5) 为
65 |
66 | $$
67 | \left\{\begin{array}{l}
68 | x=0.866 x-0.5 y \\
69 | y=0.5 x+0.866
70 | \end{array}\right.
71 | $$
72 | 而且, 此时
73 |
74 | $$
75 | \begin{aligned}
76 | & x_{\min }=0.866-0.5 \times 3=-0.634 ; x_{\min }=0.866 \times 3-0.5=2.098 \\
77 | & y_{\min }=0.866+0.5=1.366 ; \quad y_{\max }=0.866 \times 3+0.5 \times 3=4.098
78 | \end{aligned}
79 | $$
80 | 
81 | 图6-23 图像旋转 $\theta$ 角
82 |
83 | 利用公式(6-5)进行图像旋转时需要注意如下两点:
84 |
85 | (1) 图像旋转之前, 为了避免信息的丢失, 一定要有坐标平移,具体的做法有如图6-24所示的两种方法。
86 | 
87 |
88 | 图6-24 图像旋转之前进行的平移 (2) 图像旋转之后, 会出现许多空洞点, 如图6-23所示。对 这些空洞点必须进行填充处理, 否则画面效果不好, 一般也称 这种操作为揷值处理。最简单的方法是行揷值方法或列揷值方 法:
89 |
90 | (1) 找出当前行的最小和最大的非白点的坐标, 记作: $(i, k 1)$ 、 $(i, k 2)$ 。
91 |
92 | (2) 在(k1, k2)范围内进行揷值, 揷值的方法是: 空点的像素 值等于前一点的像素值。
93 |
94 | (3) 同样的操作重复到所有行。经过如上的揷值处理之后, 图像效果就变得自然。如图6-25所示。列揷值方法与此类同, 请读者自己给出。
95 | 
96 |
97 | 图6-25 图6-23中的图像处理后的效果
98 |
99 | ## 6.5.2 图像旋转的实现
100 |
101 | 按照上述理论,也可以用VC++编程实现图像的旋转。为了 将重点放在算法本身, 下面介绍灰度图像的旋转算法。由上面 的公式(6-6)以及产生空穴时的双线性揷值方法,可以编制一 个实现图像旋转的函数RotateDIB2()。下面给出这个函数的框架和主要算法。
102 |
103 | ```c++
104 | //*****************************************
105 | //函数名称: BOOL Rotate()
106 | //基本功能: 本函数对传入的CDibObject对象中的图像进行旋转操作
107 | //参数说明: int iRotateAngle 旋转的角度(0~360度)
108 | // BOOL bBilinear TRUE为双线性插值, FALSE为最邻近插值
109 | // CDibObject *pDibObject 默认为NULL
110 | //返回值: BOOL 成功返回TRUE, 失败返回FALSE
111 | //*****************************************
112 | BOOL CGeoTrans:: Rotate(int nRotateAngle, BOOL bBilinear, CDibObject *pDibObject)
113 | {
114 | //获得图像宽度和高度: nOldWidth、 nOldHeight
115 | //定义旋转角度(弧度)及其正弦和余弦值: fRotateAngle、 fSina、 fCosa
116 | //定义源图四个角的坐标、 旋转后四个角的坐标(以图像中心为坐标系原点)
117 | //计算旋转角度的正弦和余弦值
118 | //计算源图的四个角的坐标(以图像中心为坐标系原点)
119 | //计算新图四个角的坐标(以图像中心为坐标系原点)
120 | fDstX1 = fCosa * fSrcX1 + fSina * fSrcY1;
121 | fDstY1 = -fSina * fSrcX1 + fCosa * fSrcY1;
122 | fDstX2 = fCosa * fSrcX2 + fSina * fSrcY2;
123 | fDstY2 = -fSina * fSrcX2 + fCosa * fSrcY2;
124 | fDstX3 = fCosa * fSrcX3 + fSina * fSrcY3;
125 | fDstY3 = -fSina * fSrcX3 + fCosa * fSrcY3;
126 | fDstX4 = fCosa * fSrcX4 + fSina * fSrcY4;
127 | fDstY4 = -fSina * fSrcX4 + fCosa * fSrcY4;
128 | //计算旋转后的图像实际宽度
129 | int nNewWidth=(long)(max(fabs(fDstX4-fDstX1), fabs(fDstX3-fDstX2))+0.5);
130 | //计算旋转后的图像高度
131 | int nNewHeight=(long)(max(fabs(fDstY4-fDstY1), fabs(fDstY3-fDstY2))+0.5);
132 | //计算两个常数
133 | f1= (float) (-0.5 * (nNewWidth - 1) * fCosa - 0.5 * (nNewHeight - 1) * fSina
134 | + 0.5 * (nOldWidth - 1));
135 | f2= (float) ( 0.5 * (nNewWidth - 1) * fSina - 0.5 * (nNewHeight - 1) * fCosa
136 | + 0.5 * (nOldHeight - 1));
137 | //获取指向源图像的指针, 为旋转图像分配内存并用白色填充新图像数据区
138 | //由图像位数确定的移动字节数nMovedBits
139 | //针对图像每行进行操作
140 | for(y = 0; y < nNewHeight; y++)
141 | {
142 | //指向新图像第y行
143 | pNewTemp = pNewBits;
144 | pNewTemp += (nNewHeight - 1 - y) * nNewWidthBytes;
145 | //针对图像每列进行操作
146 | for(x = 0; x < nNewWidth; x++)
147 | {
148 | //计算该像素在源图像中的坐标
149 | int y0 = (long) (-((float) x) * fSina + ((float) y)
150 | * fCosa + f2 + 0.5);
151 | int x0 = (long) ( ((float) x) * fCosa + ((float) y)
152 | * fSina + f1 + 0.5);
153 | //判断是否在源图范围内
154 | if( (x0 >= 0) && (x0 < nOldWidth) && (y0 >= 0) && (y0 < nOldHeight))
155 | {
156 | //用双线性插值
157 | if(bBilinear)
158 | {
159 | unsigned char *pTemp = Interpolation (nOldWidth, nOldHeight,
160 | (float)x0, (float)y0, nOldWidthBytes, nMovedBits, pOldBits);
161 | //复制像素
162 | memcpy(pNewTemp, pTemp, nMovedBits);
163 | delete [] pTemp ;
164 | }
165 | else
166 | {
167 | //指向源图像第y0行, 第x0个像素
168 | pOldTemp = pOldBits;
169 | pOldTemp += (nOldHeight - 1 - y0) * nOldWidthBytes;
170 | pOldTemp += x0 * nMovedBits;
171 | //复制像素
172 | memcpy(pNewTemp, pOldTemp, nMovedBits);
173 | }
174 | }
175 | pNewTemp += nMovedBits;
176 | }
177 | }
178 | //将内存解锁和将不再使用的内存释放, 将新图像设置为当前图像
179 | return TRUE;
180 | }
181 | ```
182 |
183 |  184 |
185 | 图6-26 旋转前的图像
186 |
187 |
188 |
189 |
184 |
185 | 图6-26 旋转前的图像
186 |
187 |
188 |
189 |  190 |
191 | 图6-27 旋转 $15^{\circ}$ 并进行揷值处理的图像
192 |
193 |
190 |
191 | 图6-27 旋转 $15^{\circ}$ 并进行揷值处理的图像
192 |
193 |  194 |
195 | 图6-28 被放大的旋转前图像
196 |
197 |
194 |
195 | 图6-28 被放大的旋转前图像
196 |
197 |  198 |
199 | 6-29 旋转300并进行揷值处理的放大图像
--------------------------------------------------------------------------------
/VI/6.6 图像复合变换.md:
--------------------------------------------------------------------------------
1 |
2 |
3 | # 6.6 图像复合变换
4 |
5 | ## 6.6.1 图像复合变换
6 |
7 | 图像的复合变换是指对给定的图像连续施行若干次如前所述的平移、镜像、比例、旋转等基本变换后所完成的变换, 图像的复合变换又叫级联变换。利用齐次坐标, 对给定的图像依次按一定顺序连续施行若干次基本变换, 其变换的矩阵仍然可以用 $3 \times 3$ 阶的矩阵表示, 而且从数学上可以证明, 复合变换的矩阵等于基本变换的矩阵按顺序依次相乘得到的组合矩阵。设对给定的图像依次进行了基本变换 $F_{1}, F_{2}, \ldots, F_{N}$, 它们的变换矩阵分别为 $T_{1}, T_{2}, \ldots, T_{N}$, 按照公式 (6-1) $\sim$ (6-6) 的表示形式, 图像复合变换的矩阵 $T$ 可以表示为: $T=T_{N} T_{N-1} \ldots T_{1}$ 。
8 |
9 | ### 复合平移
10 |
11 | 设某个图像先平移到新的位置 $P_{1}\left(x_{1}, y_{1}\right)$ 后, 再将图像平移到 $P_{2}\left(x_{2}, y_{2}\right)$ 的位置, 则复合平移矩阵为
12 |
13 | $$
14 | T=T_{1} T_{2}=\left[\begin{array}{ccc}
15 |
16 | 1 & 0 & x_{1} \\
17 |
18 | 0 & 1 & y_{1} \\
19 |
20 | 0 & 0 & 1
21 |
22 | \end{array}\right] \cdot\left[\begin{array}{ccc}
23 |
24 | 1 & 0 & x_{2} \\
25 |
26 | 0 & 1 & y_{2} \\
27 |
28 | 0 & 0 & 1
29 |
30 | \end{array}\right]=\left[\begin{array}{ccc}
31 |
32 | 1 & 0 & x_{1}+x_{2} \\
33 |
34 | 0 & 1 & y_{1}+y_{2} \\
35 |
36 | 0 & 0 & 1
37 |
38 | \end{array}\right]\tag{6-7}
39 | $$
40 |
41 | 由此可见, 尽管一些顺序的平移, 用到矩阵的乘法, 但最后合成的平移矩阵, 只需对平移常量作加法运算。
42 |
43 | ### 复合比例
44 |
45 | 同样, 对某个图像连续进行比例变换, 最后合成的复合比例矩阵, 只要对比例常量作乘法运算即可。复合比例矩阵如下:
46 |
47 | $$
48 | T=T_{1} T_{2}=\left[\begin{array}{lll}
49 |
50 | a_{1} & 0 & 0 \\
51 |
52 | 0 & d_{1} & 0 \\
53 |
54 | 0 & 0 & 1
55 |
56 | \end{array}\right] \cdot\left[\begin{array}{lll}
57 |
58 | a_{2} & 0 & 0 \\
59 |
60 | 0 & d_{2} & 0 \\
61 |
62 | 0 & 0 & 1
63 |
64 | \end{array}\right]=\left[\begin{array}{lll}
65 |
66 | a_{1} a_{2} & 0 & 0 \\
67 |
68 | 0 & d_{1} d_{2} & 0 \\
69 |
70 | 0 & 0 & 1
71 |
72 | \end{array}\right]\tag{6-8}
73 | $$
74 |
75 | ### 复合旋转
76 |
77 | 类似地, 对某个图像连续进行旋转变换, 最后合成的旋转变换矩阵等于两次旋转角度的和, 复合旋转变换矩阵如下式所示:
78 |
79 | $$
80 | \begin{aligned}
81 |
82 | T & =T_{1} T_{2}=\left[\begin{array}{ccc}
83 |
84 | \cos \theta_{1} & \sin \theta_{1} & 0 \\
85 |
86 | -\sin \theta_{1} & \cos \theta_{1} & 0 \\
87 |
88 | 0 & 0 & 1
89 |
90 | \end{array}\right] \cdot\left[\begin{array}{ccc}
91 |
92 | \cos \theta_{2} & \sin \theta_{2} & 0 \\
93 |
94 | -\sin \theta_{2} & \cos \theta_{2} & 0 \\
95 |
96 | 0 & 0 & 1
97 |
98 | \end{array}\right] \\
99 |
100 | & =\left[\begin{array}{ccc}
101 |
102 | \cos \left(\theta_{1}+\theta_{2}\right) & \sin \left(\theta_{1}+\theta_{2}\right) & 0 \\
103 |
104 | -\sin \left(\theta_{1}+\theta_{2}\right) & \cos \left(\theta_{1}+\theta_{2}\right) & 0 \\
105 |
106 | 0 & 0 & 1
107 |
108 | \end{array}\right]
109 |
110 | \end{aligned}\tag{6-9}
111 | $$
112 |
113 | 上述均为相对原点(图像中央)作比例、旋转等变换, 如果要相对某一个参考点作变换,则要使用含有不同种基本变换的图像复合变换。不同的复合变换, 其变换过程不同, 但是无论它的变换过程多么复杂, 都可以分解成一系列基本变换。相应地, 使用齐次坐标后, 图像复合变换的矩阵由一系列图像基本几何变换矩阵依次相乘而得到。下面通过一个例子讨论含有不同种基本变换的图像复合变换。
114 |
115 | 从6.2和6.5节的讨论中可以看出, 在进行图像的比例缩放、图像的旋转变换时, 整个变换过程由两部分组成, 即需要两个独立的算法。首先, 需要一个算法来完成几何变换本身, 用它描述每个像素如何从其初始位置移动到终止位置; 同时, 还需要一个用于灰度级插值的算法。这是因为, 在一般情况下, 原始 (输入) 图像的位置坐标 $(x, y)$ 为整数, 而变换后 (输出) 图像的位置坐标为非整数, 即产生 “空穴”,反过来也是如此。 因此, 一般地, 在进行图像的几何变换时, 除了要进行其本身的几何变换外,还要进行灰度级插值处理。
116 |
117 | 灰度级插值处理可采用如下两种方法。第一,可以把几何变换想像成将输入图像的灰度一个一个像素地转移到输出图像中。 如果一个输入像素被映射到四个输出像素之间的位置, 则其灰度值就按插值算法在四个输出像素之间进行分配。把这种灰度级插值处理称为像素移交 (pixel carry over) 或称为向前映射法, 如图6-30所示。
118 |
119 | 另一种更有效的灰度级插值处理方法是像素填充(pixel filling)或称为向后映射算法。在这种算法中, 输出像素一次一个地映射回到原始(输入)图像中,以便确定其灰度级。如果一个输出像素被映射到四个输出像素之间, 则其灰度值由灰度级插值决定, 如图6-30所示。向后空间变换是向前变换的逆变换。
120 |
121 | 
122 |
123 | 图6-30 灰度级插值处理(像素变换)
124 |
125 | 在像素填充法中,变换后(输出)图像的像素通常被映射到原始(输入)图像中的非整数位置, 即位于四个输入像素之间。因此, 为了决定与该位置相对应的灰度值, 必须进行插值运算。最简单的插值方法是零阶插值或称为最近邻插值, 也叫最近邻域法, 参见本书6.2节。一阶插值或称双线性插值法和零阶插值法相比可产生更令人满意的效果, 只是程序稍复杂一些, 运行时间稍长一些。它的原理如图6-10和图6-31所示, 插值计算公式参见6.2.1中的公式(6-2)。由于篇幅所限, 双线性插值公式的推导在此从略, 有兴趣的读者请参考书后的参考文献。
126 |
127 |
198 |
199 | 6-29 旋转300并进行揷值处理的放大图像
--------------------------------------------------------------------------------
/VI/6.6 图像复合变换.md:
--------------------------------------------------------------------------------
1 |
2 |
3 | # 6.6 图像复合变换
4 |
5 | ## 6.6.1 图像复合变换
6 |
7 | 图像的复合变换是指对给定的图像连续施行若干次如前所述的平移、镜像、比例、旋转等基本变换后所完成的变换, 图像的复合变换又叫级联变换。利用齐次坐标, 对给定的图像依次按一定顺序连续施行若干次基本变换, 其变换的矩阵仍然可以用 $3 \times 3$ 阶的矩阵表示, 而且从数学上可以证明, 复合变换的矩阵等于基本变换的矩阵按顺序依次相乘得到的组合矩阵。设对给定的图像依次进行了基本变换 $F_{1}, F_{2}, \ldots, F_{N}$, 它们的变换矩阵分别为 $T_{1}, T_{2}, \ldots, T_{N}$, 按照公式 (6-1) $\sim$ (6-6) 的表示形式, 图像复合变换的矩阵 $T$ 可以表示为: $T=T_{N} T_{N-1} \ldots T_{1}$ 。
8 |
9 | ### 复合平移
10 |
11 | 设某个图像先平移到新的位置 $P_{1}\left(x_{1}, y_{1}\right)$ 后, 再将图像平移到 $P_{2}\left(x_{2}, y_{2}\right)$ 的位置, 则复合平移矩阵为
12 |
13 | $$
14 | T=T_{1} T_{2}=\left[\begin{array}{ccc}
15 |
16 | 1 & 0 & x_{1} \\
17 |
18 | 0 & 1 & y_{1} \\
19 |
20 | 0 & 0 & 1
21 |
22 | \end{array}\right] \cdot\left[\begin{array}{ccc}
23 |
24 | 1 & 0 & x_{2} \\
25 |
26 | 0 & 1 & y_{2} \\
27 |
28 | 0 & 0 & 1
29 |
30 | \end{array}\right]=\left[\begin{array}{ccc}
31 |
32 | 1 & 0 & x_{1}+x_{2} \\
33 |
34 | 0 & 1 & y_{1}+y_{2} \\
35 |
36 | 0 & 0 & 1
37 |
38 | \end{array}\right]\tag{6-7}
39 | $$
40 |
41 | 由此可见, 尽管一些顺序的平移, 用到矩阵的乘法, 但最后合成的平移矩阵, 只需对平移常量作加法运算。
42 |
43 | ### 复合比例
44 |
45 | 同样, 对某个图像连续进行比例变换, 最后合成的复合比例矩阵, 只要对比例常量作乘法运算即可。复合比例矩阵如下:
46 |
47 | $$
48 | T=T_{1} T_{2}=\left[\begin{array}{lll}
49 |
50 | a_{1} & 0 & 0 \\
51 |
52 | 0 & d_{1} & 0 \\
53 |
54 | 0 & 0 & 1
55 |
56 | \end{array}\right] \cdot\left[\begin{array}{lll}
57 |
58 | a_{2} & 0 & 0 \\
59 |
60 | 0 & d_{2} & 0 \\
61 |
62 | 0 & 0 & 1
63 |
64 | \end{array}\right]=\left[\begin{array}{lll}
65 |
66 | a_{1} a_{2} & 0 & 0 \\
67 |
68 | 0 & d_{1} d_{2} & 0 \\
69 |
70 | 0 & 0 & 1
71 |
72 | \end{array}\right]\tag{6-8}
73 | $$
74 |
75 | ### 复合旋转
76 |
77 | 类似地, 对某个图像连续进行旋转变换, 最后合成的旋转变换矩阵等于两次旋转角度的和, 复合旋转变换矩阵如下式所示:
78 |
79 | $$
80 | \begin{aligned}
81 |
82 | T & =T_{1} T_{2}=\left[\begin{array}{ccc}
83 |
84 | \cos \theta_{1} & \sin \theta_{1} & 0 \\
85 |
86 | -\sin \theta_{1} & \cos \theta_{1} & 0 \\
87 |
88 | 0 & 0 & 1
89 |
90 | \end{array}\right] \cdot\left[\begin{array}{ccc}
91 |
92 | \cos \theta_{2} & \sin \theta_{2} & 0 \\
93 |
94 | -\sin \theta_{2} & \cos \theta_{2} & 0 \\
95 |
96 | 0 & 0 & 1
97 |
98 | \end{array}\right] \\
99 |
100 | & =\left[\begin{array}{ccc}
101 |
102 | \cos \left(\theta_{1}+\theta_{2}\right) & \sin \left(\theta_{1}+\theta_{2}\right) & 0 \\
103 |
104 | -\sin \left(\theta_{1}+\theta_{2}\right) & \cos \left(\theta_{1}+\theta_{2}\right) & 0 \\
105 |
106 | 0 & 0 & 1
107 |
108 | \end{array}\right]
109 |
110 | \end{aligned}\tag{6-9}
111 | $$
112 |
113 | 上述均为相对原点(图像中央)作比例、旋转等变换, 如果要相对某一个参考点作变换,则要使用含有不同种基本变换的图像复合变换。不同的复合变换, 其变换过程不同, 但是无论它的变换过程多么复杂, 都可以分解成一系列基本变换。相应地, 使用齐次坐标后, 图像复合变换的矩阵由一系列图像基本几何变换矩阵依次相乘而得到。下面通过一个例子讨论含有不同种基本变换的图像复合变换。
114 |
115 | 从6.2和6.5节的讨论中可以看出, 在进行图像的比例缩放、图像的旋转变换时, 整个变换过程由两部分组成, 即需要两个独立的算法。首先, 需要一个算法来完成几何变换本身, 用它描述每个像素如何从其初始位置移动到终止位置; 同时, 还需要一个用于灰度级插值的算法。这是因为, 在一般情况下, 原始 (输入) 图像的位置坐标 $(x, y)$ 为整数, 而变换后 (输出) 图像的位置坐标为非整数, 即产生 “空穴”,反过来也是如此。 因此, 一般地, 在进行图像的几何变换时, 除了要进行其本身的几何变换外,还要进行灰度级插值处理。
116 |
117 | 灰度级插值处理可采用如下两种方法。第一,可以把几何变换想像成将输入图像的灰度一个一个像素地转移到输出图像中。 如果一个输入像素被映射到四个输出像素之间的位置, 则其灰度值就按插值算法在四个输出像素之间进行分配。把这种灰度级插值处理称为像素移交 (pixel carry over) 或称为向前映射法, 如图6-30所示。
118 |
119 | 另一种更有效的灰度级插值处理方法是像素填充(pixel filling)或称为向后映射算法。在这种算法中, 输出像素一次一个地映射回到原始(输入)图像中,以便确定其灰度级。如果一个输出像素被映射到四个输出像素之间, 则其灰度值由灰度级插值决定, 如图6-30所示。向后空间变换是向前变换的逆变换。
120 |
121 | 
122 |
123 | 图6-30 灰度级插值处理(像素变换)
124 |
125 | 在像素填充法中,变换后(输出)图像的像素通常被映射到原始(输入)图像中的非整数位置, 即位于四个输入像素之间。因此, 为了决定与该位置相对应的灰度值, 必须进行插值运算。最简单的插值方法是零阶插值或称为最近邻插值, 也叫最近邻域法, 参见本书6.2节。一阶插值或称双线性插值法和零阶插值法相比可产生更令人满意的效果, 只是程序稍复杂一些, 运行时间稍长一些。它的原理如图6-10和图6-31所示, 插值计算公式参见6.2.1中的公式(6-2)。由于篇幅所限, 双线性插值公式的推导在此从略, 有兴趣的读者请参考书后的参考文献。
126 |
127 |  128 |
129 | 图6-31 双线性插值
130 |
131 | 在这里还要说明一点, 为了提高双线性插值的速度, 双线性插值也可以分解为三个线性插值来实现, 公式如下:
132 | $$
133 | \begin{aligned}
134 |
135 | & f(x, 0)=f(0,0)+x[f(1,0)-f(0,0)] \\
136 |
137 | & f(x, 1)=f(0,1)+x[f(1,1)-f(0,1)] \\
138 |
139 | & f(x, y)=f(x, 0)+y[f(x, 1)-f(x, 0)]
140 |
141 | \end{aligned}\tag{6-10}
142 | $$
143 |
144 | 因为公式(6-2)需要用到四次乘法、八次加(或减)法运算, 而公式(6-10)表示的第二种方法只需要三次乘法和六次加 (或减)法, 所以几何变换程序一般选择后者。从图6-31也可以看出双线性插值与最近邻插值的区别。
145 |
146 | 在几何运算中,双线性灰度插值的平滑作用可能会使图像的细节产生退化, 尤其是在进行放大处理时, 这种影响将更为明显。而在其他应用中, 双线性插值的斜率不连续性会产生不希望得到的结果。这两种情况都可以通过高阶插值得到修正, 当然这需要增加计算量。使用高阶插值函数的例子有:三次样条、Legendre中心函数和 $\sin (\alpha x) / \alpha$ 函数(即 $\sin (\alpha x)$ 函数)。高阶插值常用卷积来实现, 这部分内容请读者参考书后所附的参考文献。
147 |
148 | ## 6.6.2 图像复合变换的示例
149 |
150 |
128 |
129 | 图6-31 双线性插值
130 |
131 | 在这里还要说明一点, 为了提高双线性插值的速度, 双线性插值也可以分解为三个线性插值来实现, 公式如下:
132 | $$
133 | \begin{aligned}
134 |
135 | & f(x, 0)=f(0,0)+x[f(1,0)-f(0,0)] \\
136 |
137 | & f(x, 1)=f(0,1)+x[f(1,1)-f(0,1)] \\
138 |
139 | & f(x, y)=f(x, 0)+y[f(x, 1)-f(x, 0)]
140 |
141 | \end{aligned}\tag{6-10}
142 | $$
143 |
144 | 因为公式(6-2)需要用到四次乘法、八次加(或减)法运算, 而公式(6-10)表示的第二种方法只需要三次乘法和六次加 (或减)法, 所以几何变换程序一般选择后者。从图6-31也可以看出双线性插值与最近邻插值的区别。
145 |
146 | 在几何运算中,双线性灰度插值的平滑作用可能会使图像的细节产生退化, 尤其是在进行放大处理时, 这种影响将更为明显。而在其他应用中, 双线性插值的斜率不连续性会产生不希望得到的结果。这两种情况都可以通过高阶插值得到修正, 当然这需要增加计算量。使用高阶插值函数的例子有:三次样条、Legendre中心函数和 $\sin (\alpha x) / \alpha$ 函数(即 $\sin (\alpha x)$ 函数)。高阶插值常用卷积来实现, 这部分内容请读者参考书后所附的参考文献。
147 |
148 | ## 6.6.2 图像复合变换的示例
149 |
150 |  151 |
152 | 图6-32 坐标系的平移
153 |
154 | 两个坐标系之间的坐标变换矩阵表达式为:
155 | $$
156 | \left[\begin{array}{c}
157 |
158 | x_{\Pi} \\
159 |
160 | y_{\Pi} \\
161 |
162 | 1
163 |
164 | \end{array}\right]=\left[\begin{array}{ccc}
165 |
166 | 1 & 0 & -a \\
167 |
168 | 0 & -1 & b \\
169 |
170 | 0 & 0 & 1
171 |
172 | \end{array}\right] \cdot\left[\begin{array}{c}
173 |
174 | x_{I} \\
175 |
176 | y_{I} \\
177 |
178 | 1
179 |
180 | \end{array}\right]
181 | $$
182 |
183 | 它的逆变换矩阵表达式是:
184 |
185 | $$
186 | \left[\begin{array}{c}
187 |
188 | x_{I} \\
189 |
190 | y_{I} \\
191 |
192 | 1
193 |
194 | \end{array}\right]=\left[\begin{array}{ccc}
195 |
196 | 1 & 0 & a \\
197 |
198 | 0 & -1 & b \\
199 |
200 | 0 & 0 & 1
201 |
202 | \end{array}\right] \cdot\left[\begin{array}{c}
203 |
204 | x_{\Pi} \\
205 |
206 | y_{\Pi} \\
207 |
208 | 1
209 |
210 | \end{array}\right]
211 | $$
212 |
213 | 为了推导公式简单起见, 假设图像末旋转时中心坐标为 $(a,b)$, 旋转后中心坐标为 $(c, d)$ (在新的坐标系下旋转后新图像左上角为原点), 则旋转变换矩阵表达式为
214 |
215 | $$
216 | \begin{align}
217 | \left[\begin{array}{c}
218 | x \\
219 | y \\
220 | 1
221 | \end{array}\right]&=\left[\begin{array}{ccc}
222 | 1 & 0 & -c \\
223 | 0 & -1 & d \\
224 | 0 & 0 & 1
225 | \end{array}\right] \cdot\left[\begin{array}{c}
226 | x_{\Pi} \\
227 | y_{\Pi} \\
228 | 1
229 | \end{array}\right]=\left[\begin{array}{ccc}
230 | 1 & 0 & -c \\
231 | 0 & -1 & d \\
232 | 0 & 0 & 1
233 | \end{array}\right] \cdot\left[\begin{array}{ccc}
234 | \cos \theta & \sin \theta & 0 \\
235 | -\sin \theta & \cos \theta & 0 \\
236 | 0 & 0 & 1
237 | \end{array}\right]\left[\begin{array}{c}
238 | x_{\Pi} \\
239 | y_{\Pi} \\
240 | 1
241 | \end{array}\right]\\
242 | &=\left[\begin{array}{ccc}
243 | 1 & 0 & -c \\
244 | 0 & -1 & d \\
245 | 0 & 0 & 1
246 | \end{array}\right] \cdot\left[\begin{array}{ccc}
247 | \cos \theta & \sin \theta & 0 \\
248 | -\sin \theta & \cos \theta & 0 \\
249 | 0 & 0 & 1
250 | \end{array}\right] \cdot\left[\begin{array}{ccc}
251 | 1 & 0 & -a \\
252 | 0 & -1 & b \\
253 | 0 & 0 & 1
254 | \end{array}\right] \cdot\left[\begin{array}{c}
255 | x_{0} \\
256 | y_{0} \\
257 | 1
258 | \end{array}\right]
259 | \end{align}
260 | \tag{6-11}
261 | $$
262 |
263 | $$
264 |
265 | $$
266 |
267 | 其逆变换表达式为
268 |
269 | $$
270 | \left[\begin{array}{c}
271 |
272 | x_{0} \\
273 |
274 | y_{0} \\
275 |
276 | 1
277 |
278 | \end{array}\right]=\left[\begin{array}{ccc}
279 |
280 | 1 & 0 & -a \\
281 |
282 | 0 & -1 & b \\
283 |
284 | 0 & 0 & 1
285 |
286 | \end{array}\right] \cdot\left[\begin{array}{ccc}
287 |
288 | \cos \theta & \sin \theta & 0 \\
289 |
290 | -\sin \theta & \cos \theta & 0 \\
291 |
292 | 0 & 0 & 0
293 |
294 | \end{array}\right] \cdot\left[\begin{array}{ccc}
295 |
296 | 1 & 0 & -c \\
297 |
298 | 0 & -1 & d \\
299 |
300 | 0 & 0 & 1
301 |
302 | \end{array}\right] \cdot\left[\begin{array}{c}
303 |
304 | x \\
305 |
306 | y \\
307 |
308 | 1
309 |
310 | \end{array}\right]\tag{6-12}
311 | $$
312 | 即
313 | $$
314 | \left[\begin{array}{c}
315 |
316 | x_{0} \\
317 |
318 | y_{0} \\
319 |
320 | 1
321 |
322 | \end{array}\right]=\left[\begin{array}{ccc}
323 |
324 | \cos \theta & \sin \theta & -c \cos \theta-d \sin \theta+a \\
325 |
326 | -\sin \theta & \cos \theta & c \sin \theta-d \cos \theta+b \\
327 |
328 | 0 & 0 & 1
329 |
330 | \end{array}\right] \cdot\left[\begin{array}{c}
331 |
332 | x \\
333 |
334 | y \\
335 |
336 | 1
337 |
338 | \end{array}\right]\tag{6-13}
339 | $$
340 |
341 | 因此
342 |
343 | $$
344 | \left\{\begin{array}{l}
345 | x_{0}=x \cos \theta+y \sin \theta-c \cos \theta-d \sin \theta+a \\
346 | y_{0}=-x \sin \theta+y \cos \theta+c \sin \theta-d \cos \theta+b
347 | \end{array}\right.\tag{6-14}
348 | $$
349 |
350 | 公式(6-10)说明绕任意点(a,b)旋转的几何变换是由平移一旋转一平移三个基本变换所构成, 即先将坐标系平移到点( $a$,b), 再进行旋转, 然后将旋转后的图像平移回原来的坐标原点。
351 |
352 | 利用上面的转换公式 $(6-12) \sim(6-14) ,$ 就可以比较方便地编㝍出实现图像旋转的VC++函数。首先应计算出公式中需要的几个参数: $a, b, c, d$ 和旋转后新图像的高、宽度。现在已知图像的原始宽度为lWidth, 高度为lHeight, 以图像中心为坐标系原点,则原始图像四个角的坐标分别为
353 |
354 | $$
355 | \begin{aligned}
356 | & {\left[-\frac{\text { lWidth }-1}{2}, \frac{\text { lHeight }-1}{2}\right],\left[\frac{\text { lWidth }-1}{2}, \frac{\text { lHeight }-1}{2}\right]} \\
357 | & {\left[\frac{\text { lWidth }-1}{2},-\frac{\text { lHeight }-1}{2}\right],\left[-\frac{\text { lWidth }-1}{2},-\frac{\text { lHeight }-1}{2}\right]}
358 | \end{aligned}
359 | $$
360 |
361 | 按照旋转公式(6-11) (6-14), 在旋转后的新图像中, 这四个点坐标为
362 |
363 | $$
364 | \begin{aligned}
365 | & (f D s t X 1, f D s t Y 1)=\left(-\frac{l \text { Width }-1}{2} \cos \theta+\frac{\text { lHeight }-1}{2} \sin \theta,-\frac{l \text { Width }-1}{2} \sin \theta+\frac{\text { lHeight }-1}{2} \cos \theta\right) \\
366 | & (f D s t X 2, f D s t Y 2)=\left(\frac{l \text { Width }-1}{2} \cos \theta+\frac{l \text { Height }-1}{2} \sin \theta,-\frac{l \text { Width }-1}{2} \sin \theta+\frac{\text { lHeight }-1}{2} \cos \theta\right) \\
367 | & (f D s t X 3, f D s t Y 3)=\left(-\frac{l \text { Width }-1}{2} \cos \theta-\frac{l \text { Height }-1}{2} \sin \theta,-\frac{l \text { Width }-1}{2} \sin \theta-\frac{l \text { Height }-1}{2} \cos \theta\right) \\
368 | & (f D s t X 4, f D s t Y 4)=\left(-\frac{l W i d t h-1}{2} \cos \theta-\frac{l \text { Height }-1}{2} \sin \theta, \frac{l \text { Width }-1}{2} \sin \theta-\frac{l \text { Height }-1}{2} \cos \theta\right)
369 | \end{aligned}
370 | $$
371 |
372 | 则新图像的宽度lNewWidth和高度lNewHeight为
373 |
374 | $$
375 | lNewWidth =\max (|f D s t X 4-f D s t Y 1|,|f D s t X 3-f D s t Y 2|)\\
376 | lNewHeight =\max (|f D s t X 4-f D s t Y 1|,|f D s t X 3-f D s t Y 2|)
377 | $$
378 |
379 | 如果令
380 |
381 | $$
382 | \left\{\begin{array}{l}
383 | f_{1}=-c \cos \theta-d \sin \theta+a \\
384 | f_{2}=c \sin \theta-d \cos \theta+b
385 | \end{array}\right.\tag{6-15}
386 | $$
387 |
388 | 由已知及假设
389 |
390 | $$
391 | a=\frac{\text { lWidth }-1}{2}, b=\frac{\text { lHeight }-1}{2}, c=\frac{\text { lNewWidth }-1}{2}, d=\frac{\text { lNewHeight }-1}{2}
392 | $$
393 |
394 | 由公式 (6-13) 得
395 |
396 | $$
397 | \left\{\begin{array}{l}
398 | x_{0}=x \cos \theta+y \sin \theta+f_{1} \\
399 | y_{0}=-x \sin \theta+y \cos \theta+f_{2}
400 | \end{array}\right.\tag{6-16}
401 | $$
402 |
403 | 公式 (6-16)、(6-17) 便是图像绕任意点 $(a, b)$ 旋转的变换公式, 由此便可以编㝍出实现该变换的VC++程序。事
404 |
405 | 实上,只要先按上述公式计算出旋转后新图像的高度和宽度以及常数 $f 1$ 和 $f_{2}$, 并按照公式 (6-17) 计算出变换后图像上的点 $(i 0, j 0)$ :
406 |
407 | $/ /$ 计算该像素在源DIB中的坐标
408 |
409 | $$
410 | \begin{aligned}
411 | & i 0=-((\text { float }) j) * f \operatorname{sina}+((\text { float }) i) * f \operatorname{cosa}+f 2 \\
412 | & j 0=((\text { float }) j) * f \text { cosa }+((\text { float }) i) * f \sin a+f 1
413 | \end{aligned}
414 | $$
--------------------------------------------------------------------------------
/VI/6.7 透视变换.md:
--------------------------------------------------------------------------------
1 | # 6.7 透视变换
2 |
3 | ## 6.7.1 透视变换
4 |
5 | 把三维物体或对象转变为二维图形表示的过程称为投影变换。
6 |
7 | 根据视点 (投影中心) 与投影平面之间距离的不同, 投影可分为平行投影和透视投影, 透视投影即透视变换。平行投影的视点与投影平面之间的距离为无穷大, 而对透视投影(变换), 该距离是有限的。这个距离决定着透视投影的特性一透视缩小效应, 即三维物体或对象透视投影的大小与形体到视点的距离成反比。 例如, 等长的两直线段, 都平行于投影面, 但离投影中心近的线段, 其透视投影大, 而离投影中心远的线段, 透视投影小。这种效应所产生的视觉效果与照相机系统和人的视觉系统十分类似。 与平行投影相比, 透视投影的深度感更强, 看上去更真实, 但透视投影不能真实地反映物体的精确尺寸和形状。
8 |
9 | 对于透视投影,一束平行于投影面的平行线的投影可保持平行, 而不平行于投影面的平行线的投影会聚集到一个点, 这个点称为灭点 (Vanishing Point)。灭点可以看作是无限远处的一点在投影面上的投影。透视投影的灭点可以有无限多个, 不同方向的平行线在投影面上就能形成不同的灭点, 坐标轴方向的平行线在投影面上形成的灭点又称作主灭点。因为有 $x, y$ 和 $z$ 三个坐标轴, 所以主灭点最多有 3 个。透视投影是按主灭点的个数来分类的, 即按投影面与坐标轴的夹角来分类的, 可分为一点透视、二点透视和三点透视, 如图6-33 所示。
10 |
11 | 
12 |
13 | 图6-33 透视变换 (a)一点透视; (b) 二点透视; (c) 三点透视
14 |
15 | 下面讨论一点透视。一点透视只有一个主灭点,即投影面与一个坐标轴正交,与另外两个坐标轴平行,如图6-33(a)所示。 进行一点透视投影变换,要很好地考虑图面布局, 以避免三维形体或对象的平面域积聚成直线或直线积聚成点而影响直观性。具体地说,就是要考虑下列几点: (1)三维形体或对象与画面 (投影面)的相对位置;(2)视距,即视点与畐面的距离;(3)视点的高度。 由此,假设视点在坐标原点, $Z$ 坐标轴方向与观察方向重合一致, 三维形体或对象上某一点为 $P(x, y, z)$, 一点透视变换后在投影面 (观察平面) $U O^{\prime} V$ 上的对应点为 $P^{\prime}\left(x^{\prime}, y^{\prime}, z^{\prime}\right)$, 投影面与 $z$ 轴垂直, 且与视点的距离为d, $z$ 轴过投影面窗口的中心,窗口是边长为 $2 S$ 的正方形, 如图6-34所示。根据相似三角形对应边成比例的关系, 有:
16 |
17 | $$
18 | \begin{gathered}
19 | \frac{x^{\prime}}{x}=\frac{y^{\prime}}{y}=\frac{z^{\prime}}{z}, z^{\prime}=d \\
20 | x^{\prime}=\frac{x}{z} d, y^{\prime}=\frac{y}{z} d, z^{\prime}=d
21 | \end{gathered}\tag{6-18}
22 | $$
23 |
24 | 利用齐次坐标, 与二维几何变换类似, 将该过程写成变换矩阵形式为
25 |
26 | $$
27 | \left[\begin{array}{l}
28 | x^{\prime} \\
29 | y^{\prime} \\
30 | z^{\prime} \\
31 | 1
32 | \end{array}\right]=\left[\begin{array}{llll}
33 | d & 0 & 0 & 0 \\
34 | 0 & d & 0 & 0 \\
35 | 0 & 0 & 0 & -1 \\
36 | 0 & 0 & 1 & 0
37 | \end{array}\right] \cdot\left[\begin{array}{l}
38 | d x \\
39 | d y \\
40 | -1 \\
41 | z
42 | \end{array}\right]\tag{6-19}
43 | $$
44 |
45 |
46 |
47 |
151 |
152 | 图6-32 坐标系的平移
153 |
154 | 两个坐标系之间的坐标变换矩阵表达式为:
155 | $$
156 | \left[\begin{array}{c}
157 |
158 | x_{\Pi} \\
159 |
160 | y_{\Pi} \\
161 |
162 | 1
163 |
164 | \end{array}\right]=\left[\begin{array}{ccc}
165 |
166 | 1 & 0 & -a \\
167 |
168 | 0 & -1 & b \\
169 |
170 | 0 & 0 & 1
171 |
172 | \end{array}\right] \cdot\left[\begin{array}{c}
173 |
174 | x_{I} \\
175 |
176 | y_{I} \\
177 |
178 | 1
179 |
180 | \end{array}\right]
181 | $$
182 |
183 | 它的逆变换矩阵表达式是:
184 |
185 | $$
186 | \left[\begin{array}{c}
187 |
188 | x_{I} \\
189 |
190 | y_{I} \\
191 |
192 | 1
193 |
194 | \end{array}\right]=\left[\begin{array}{ccc}
195 |
196 | 1 & 0 & a \\
197 |
198 | 0 & -1 & b \\
199 |
200 | 0 & 0 & 1
201 |
202 | \end{array}\right] \cdot\left[\begin{array}{c}
203 |
204 | x_{\Pi} \\
205 |
206 | y_{\Pi} \\
207 |
208 | 1
209 |
210 | \end{array}\right]
211 | $$
212 |
213 | 为了推导公式简单起见, 假设图像末旋转时中心坐标为 $(a,b)$, 旋转后中心坐标为 $(c, d)$ (在新的坐标系下旋转后新图像左上角为原点), 则旋转变换矩阵表达式为
214 |
215 | $$
216 | \begin{align}
217 | \left[\begin{array}{c}
218 | x \\
219 | y \\
220 | 1
221 | \end{array}\right]&=\left[\begin{array}{ccc}
222 | 1 & 0 & -c \\
223 | 0 & -1 & d \\
224 | 0 & 0 & 1
225 | \end{array}\right] \cdot\left[\begin{array}{c}
226 | x_{\Pi} \\
227 | y_{\Pi} \\
228 | 1
229 | \end{array}\right]=\left[\begin{array}{ccc}
230 | 1 & 0 & -c \\
231 | 0 & -1 & d \\
232 | 0 & 0 & 1
233 | \end{array}\right] \cdot\left[\begin{array}{ccc}
234 | \cos \theta & \sin \theta & 0 \\
235 | -\sin \theta & \cos \theta & 0 \\
236 | 0 & 0 & 1
237 | \end{array}\right]\left[\begin{array}{c}
238 | x_{\Pi} \\
239 | y_{\Pi} \\
240 | 1
241 | \end{array}\right]\\
242 | &=\left[\begin{array}{ccc}
243 | 1 & 0 & -c \\
244 | 0 & -1 & d \\
245 | 0 & 0 & 1
246 | \end{array}\right] \cdot\left[\begin{array}{ccc}
247 | \cos \theta & \sin \theta & 0 \\
248 | -\sin \theta & \cos \theta & 0 \\
249 | 0 & 0 & 1
250 | \end{array}\right] \cdot\left[\begin{array}{ccc}
251 | 1 & 0 & -a \\
252 | 0 & -1 & b \\
253 | 0 & 0 & 1
254 | \end{array}\right] \cdot\left[\begin{array}{c}
255 | x_{0} \\
256 | y_{0} \\
257 | 1
258 | \end{array}\right]
259 | \end{align}
260 | \tag{6-11}
261 | $$
262 |
263 | $$
264 |
265 | $$
266 |
267 | 其逆变换表达式为
268 |
269 | $$
270 | \left[\begin{array}{c}
271 |
272 | x_{0} \\
273 |
274 | y_{0} \\
275 |
276 | 1
277 |
278 | \end{array}\right]=\left[\begin{array}{ccc}
279 |
280 | 1 & 0 & -a \\
281 |
282 | 0 & -1 & b \\
283 |
284 | 0 & 0 & 1
285 |
286 | \end{array}\right] \cdot\left[\begin{array}{ccc}
287 |
288 | \cos \theta & \sin \theta & 0 \\
289 |
290 | -\sin \theta & \cos \theta & 0 \\
291 |
292 | 0 & 0 & 0
293 |
294 | \end{array}\right] \cdot\left[\begin{array}{ccc}
295 |
296 | 1 & 0 & -c \\
297 |
298 | 0 & -1 & d \\
299 |
300 | 0 & 0 & 1
301 |
302 | \end{array}\right] \cdot\left[\begin{array}{c}
303 |
304 | x \\
305 |
306 | y \\
307 |
308 | 1
309 |
310 | \end{array}\right]\tag{6-12}
311 | $$
312 | 即
313 | $$
314 | \left[\begin{array}{c}
315 |
316 | x_{0} \\
317 |
318 | y_{0} \\
319 |
320 | 1
321 |
322 | \end{array}\right]=\left[\begin{array}{ccc}
323 |
324 | \cos \theta & \sin \theta & -c \cos \theta-d \sin \theta+a \\
325 |
326 | -\sin \theta & \cos \theta & c \sin \theta-d \cos \theta+b \\
327 |
328 | 0 & 0 & 1
329 |
330 | \end{array}\right] \cdot\left[\begin{array}{c}
331 |
332 | x \\
333 |
334 | y \\
335 |
336 | 1
337 |
338 | \end{array}\right]\tag{6-13}
339 | $$
340 |
341 | 因此
342 |
343 | $$
344 | \left\{\begin{array}{l}
345 | x_{0}=x \cos \theta+y \sin \theta-c \cos \theta-d \sin \theta+a \\
346 | y_{0}=-x \sin \theta+y \cos \theta+c \sin \theta-d \cos \theta+b
347 | \end{array}\right.\tag{6-14}
348 | $$
349 |
350 | 公式(6-10)说明绕任意点(a,b)旋转的几何变换是由平移一旋转一平移三个基本变换所构成, 即先将坐标系平移到点( $a$,b), 再进行旋转, 然后将旋转后的图像平移回原来的坐标原点。
351 |
352 | 利用上面的转换公式 $(6-12) \sim(6-14) ,$ 就可以比较方便地编㝍出实现图像旋转的VC++函数。首先应计算出公式中需要的几个参数: $a, b, c, d$ 和旋转后新图像的高、宽度。现在已知图像的原始宽度为lWidth, 高度为lHeight, 以图像中心为坐标系原点,则原始图像四个角的坐标分别为
353 |
354 | $$
355 | \begin{aligned}
356 | & {\left[-\frac{\text { lWidth }-1}{2}, \frac{\text { lHeight }-1}{2}\right],\left[\frac{\text { lWidth }-1}{2}, \frac{\text { lHeight }-1}{2}\right]} \\
357 | & {\left[\frac{\text { lWidth }-1}{2},-\frac{\text { lHeight }-1}{2}\right],\left[-\frac{\text { lWidth }-1}{2},-\frac{\text { lHeight }-1}{2}\right]}
358 | \end{aligned}
359 | $$
360 |
361 | 按照旋转公式(6-11) (6-14), 在旋转后的新图像中, 这四个点坐标为
362 |
363 | $$
364 | \begin{aligned}
365 | & (f D s t X 1, f D s t Y 1)=\left(-\frac{l \text { Width }-1}{2} \cos \theta+\frac{\text { lHeight }-1}{2} \sin \theta,-\frac{l \text { Width }-1}{2} \sin \theta+\frac{\text { lHeight }-1}{2} \cos \theta\right) \\
366 | & (f D s t X 2, f D s t Y 2)=\left(\frac{l \text { Width }-1}{2} \cos \theta+\frac{l \text { Height }-1}{2} \sin \theta,-\frac{l \text { Width }-1}{2} \sin \theta+\frac{\text { lHeight }-1}{2} \cos \theta\right) \\
367 | & (f D s t X 3, f D s t Y 3)=\left(-\frac{l \text { Width }-1}{2} \cos \theta-\frac{l \text { Height }-1}{2} \sin \theta,-\frac{l \text { Width }-1}{2} \sin \theta-\frac{l \text { Height }-1}{2} \cos \theta\right) \\
368 | & (f D s t X 4, f D s t Y 4)=\left(-\frac{l W i d t h-1}{2} \cos \theta-\frac{l \text { Height }-1}{2} \sin \theta, \frac{l \text { Width }-1}{2} \sin \theta-\frac{l \text { Height }-1}{2} \cos \theta\right)
369 | \end{aligned}
370 | $$
371 |
372 | 则新图像的宽度lNewWidth和高度lNewHeight为
373 |
374 | $$
375 | lNewWidth =\max (|f D s t X 4-f D s t Y 1|,|f D s t X 3-f D s t Y 2|)\\
376 | lNewHeight =\max (|f D s t X 4-f D s t Y 1|,|f D s t X 3-f D s t Y 2|)
377 | $$
378 |
379 | 如果令
380 |
381 | $$
382 | \left\{\begin{array}{l}
383 | f_{1}=-c \cos \theta-d \sin \theta+a \\
384 | f_{2}=c \sin \theta-d \cos \theta+b
385 | \end{array}\right.\tag{6-15}
386 | $$
387 |
388 | 由已知及假设
389 |
390 | $$
391 | a=\frac{\text { lWidth }-1}{2}, b=\frac{\text { lHeight }-1}{2}, c=\frac{\text { lNewWidth }-1}{2}, d=\frac{\text { lNewHeight }-1}{2}
392 | $$
393 |
394 | 由公式 (6-13) 得
395 |
396 | $$
397 | \left\{\begin{array}{l}
398 | x_{0}=x \cos \theta+y \sin \theta+f_{1} \\
399 | y_{0}=-x \sin \theta+y \cos \theta+f_{2}
400 | \end{array}\right.\tag{6-16}
401 | $$
402 |
403 | 公式 (6-16)、(6-17) 便是图像绕任意点 $(a, b)$ 旋转的变换公式, 由此便可以编㝍出实现该变换的VC++程序。事
404 |
405 | 实上,只要先按上述公式计算出旋转后新图像的高度和宽度以及常数 $f 1$ 和 $f_{2}$, 并按照公式 (6-17) 计算出变换后图像上的点 $(i 0, j 0)$ :
406 |
407 | $/ /$ 计算该像素在源DIB中的坐标
408 |
409 | $$
410 | \begin{aligned}
411 | & i 0=-((\text { float }) j) * f \operatorname{sina}+((\text { float }) i) * f \operatorname{cosa}+f 2 \\
412 | & j 0=((\text { float }) j) * f \text { cosa }+((\text { float }) i) * f \sin a+f 1
413 | \end{aligned}
414 | $$
--------------------------------------------------------------------------------
/VI/6.7 透视变换.md:
--------------------------------------------------------------------------------
1 | # 6.7 透视变换
2 |
3 | ## 6.7.1 透视变换
4 |
5 | 把三维物体或对象转变为二维图形表示的过程称为投影变换。
6 |
7 | 根据视点 (投影中心) 与投影平面之间距离的不同, 投影可分为平行投影和透视投影, 透视投影即透视变换。平行投影的视点与投影平面之间的距离为无穷大, 而对透视投影(变换), 该距离是有限的。这个距离决定着透视投影的特性一透视缩小效应, 即三维物体或对象透视投影的大小与形体到视点的距离成反比。 例如, 等长的两直线段, 都平行于投影面, 但离投影中心近的线段, 其透视投影大, 而离投影中心远的线段, 透视投影小。这种效应所产生的视觉效果与照相机系统和人的视觉系统十分类似。 与平行投影相比, 透视投影的深度感更强, 看上去更真实, 但透视投影不能真实地反映物体的精确尺寸和形状。
8 |
9 | 对于透视投影,一束平行于投影面的平行线的投影可保持平行, 而不平行于投影面的平行线的投影会聚集到一个点, 这个点称为灭点 (Vanishing Point)。灭点可以看作是无限远处的一点在投影面上的投影。透视投影的灭点可以有无限多个, 不同方向的平行线在投影面上就能形成不同的灭点, 坐标轴方向的平行线在投影面上形成的灭点又称作主灭点。因为有 $x, y$ 和 $z$ 三个坐标轴, 所以主灭点最多有 3 个。透视投影是按主灭点的个数来分类的, 即按投影面与坐标轴的夹角来分类的, 可分为一点透视、二点透视和三点透视, 如图6-33 所示。
10 |
11 | 
12 |
13 | 图6-33 透视变换 (a)一点透视; (b) 二点透视; (c) 三点透视
14 |
15 | 下面讨论一点透视。一点透视只有一个主灭点,即投影面与一个坐标轴正交,与另外两个坐标轴平行,如图6-33(a)所示。 进行一点透视投影变换,要很好地考虑图面布局, 以避免三维形体或对象的平面域积聚成直线或直线积聚成点而影响直观性。具体地说,就是要考虑下列几点: (1)三维形体或对象与画面 (投影面)的相对位置;(2)视距,即视点与畐面的距离;(3)视点的高度。 由此,假设视点在坐标原点, $Z$ 坐标轴方向与观察方向重合一致, 三维形体或对象上某一点为 $P(x, y, z)$, 一点透视变换后在投影面 (观察平面) $U O^{\prime} V$ 上的对应点为 $P^{\prime}\left(x^{\prime}, y^{\prime}, z^{\prime}\right)$, 投影面与 $z$ 轴垂直, 且与视点的距离为d, $z$ 轴过投影面窗口的中心,窗口是边长为 $2 S$ 的正方形, 如图6-34所示。根据相似三角形对应边成比例的关系, 有:
16 |
17 | $$
18 | \begin{gathered}
19 | \frac{x^{\prime}}{x}=\frac{y^{\prime}}{y}=\frac{z^{\prime}}{z}, z^{\prime}=d \\
20 | x^{\prime}=\frac{x}{z} d, y^{\prime}=\frac{y}{z} d, z^{\prime}=d
21 | \end{gathered}\tag{6-18}
22 | $$
23 |
24 | 利用齐次坐标, 与二维几何变换类似, 将该过程写成变换矩阵形式为
25 |
26 | $$
27 | \left[\begin{array}{l}
28 | x^{\prime} \\
29 | y^{\prime} \\
30 | z^{\prime} \\
31 | 1
32 | \end{array}\right]=\left[\begin{array}{llll}
33 | d & 0 & 0 & 0 \\
34 | 0 & d & 0 & 0 \\
35 | 0 & 0 & 0 & -1 \\
36 | 0 & 0 & 1 & 0
37 | \end{array}\right] \cdot\left[\begin{array}{l}
38 | d x \\
39 | d y \\
40 | -1 \\
41 | z
42 | \end{array}\right]\tag{6-19}
43 | $$
44 |
45 |
46 |
47 |  48 |
49 | 图6-34 一点透视变换
50 |
51 | 一般地, 视点不在原点, 投影平面是任意平面的情况,一点透视变换的矩阵也可以用一个 $4 \times 4$ 的矩阵表示。当根据公式 (6-19) 求出它的逆变换后, 可以用 $VC++$ 编写一个实现图像透视的程序, 实现图像的透视。
52 |
53 | ## 6.7.2 其他变换
54 |
55 | 如前所述, 齐次坐标为确定各种基本变换和复合变换公式提供了一个简单的方法。然而, 在许多图像处理与分析应用中, 所需的几何变换都相当复杂, 甚至有些无法用简便的数学式来表达。此外, 所需几何变换经常要从对实际图像的测量中获得, 因此更希望用这些测量结果而不是函数形式来描述几何变换。 例如, 在对由摄像机拍摄的有几何畸变的图像进行几何校正时, 首先应将一个矩形栅格目标数字化并显示出来。因为摄像机中有几何变形, 所显示的图案不会是准确的矩形, 因此所求几何变换应能使其栅格图案再次被复原为准确的矩形, 从而修正了摄像机产生的畸变。采用同样的几何变换可用于校正同一摄像机生成的数字化图像(假定畸变与景物无关), 由此可得到不畸变的图像。
56 |
57 | 图像几何变换的一个重要应用是消除由于摄像机导致的数字图像的几何畸变。当需要从数字图像中得到定量的空间测量数据时, 几何校正被证明是十分重要的。某些图像, 例如, 从卫星上或飞机侧视雷达上得到的图像, 都有相当严重的几何变形, 这些图像需要先经过几何校正,然后才能对其内容做出解释。一些图像系统使用非矩形的像素坐标, 例如, 极坐标、柱坐标、 球面坐标等, 用普通的显示设备观察这些图像时, 必须先对它们进行校正, 也就是说, 将其转换为矩形像素坐标。例如, 在油 (水) 井套管缺陷识别中, 有时需要将极坐标系中的内突镜图像转换为直角坐标系中的图像, 然后进行分析与处理, 如图6-35、 6-36所示。
58 |
59 |
48 |
49 | 图6-34 一点透视变换
50 |
51 | 一般地, 视点不在原点, 投影平面是任意平面的情况,一点透视变换的矩阵也可以用一个 $4 \times 4$ 的矩阵表示。当根据公式 (6-19) 求出它的逆变换后, 可以用 $VC++$ 编写一个实现图像透视的程序, 实现图像的透视。
52 |
53 | ## 6.7.2 其他变换
54 |
55 | 如前所述, 齐次坐标为确定各种基本变换和复合变换公式提供了一个简单的方法。然而, 在许多图像处理与分析应用中, 所需的几何变换都相当复杂, 甚至有些无法用简便的数学式来表达。此外, 所需几何变换经常要从对实际图像的测量中获得, 因此更希望用这些测量结果而不是函数形式来描述几何变换。 例如, 在对由摄像机拍摄的有几何畸变的图像进行几何校正时, 首先应将一个矩形栅格目标数字化并显示出来。因为摄像机中有几何变形, 所显示的图案不会是准确的矩形, 因此所求几何变换应能使其栅格图案再次被复原为准确的矩形, 从而修正了摄像机产生的畸变。采用同样的几何变换可用于校正同一摄像机生成的数字化图像(假定畸变与景物无关), 由此可得到不畸变的图像。
56 |
57 | 图像几何变换的一个重要应用是消除由于摄像机导致的数字图像的几何畸变。当需要从数字图像中得到定量的空间测量数据时, 几何校正被证明是十分重要的。某些图像, 例如, 从卫星上或飞机侧视雷达上得到的图像, 都有相当严重的几何变形, 这些图像需要先经过几何校正,然后才能对其内容做出解释。一些图像系统使用非矩形的像素坐标, 例如, 极坐标、柱坐标、 球面坐标等, 用普通的显示设备观察这些图像时, 必须先对它们进行校正, 也就是说, 将其转换为矩形像素坐标。例如, 在油 (水) 井套管缺陷识别中, 有时需要将极坐标系中的内突镜图像转换为直角坐标系中的图像, 然后进行分析与处理, 如图6-35、 6-36所示。
58 |
59 |  60 |
61 | 图6-35 极坐标系中的内突镜图像
62 |
63 | 
64 |
65 | 图6-36 转换为直角坐标系中的图像
66 |
67 | 有时机器人的鱼眼透镜拍摄的变形严重的一幅图像, 也可以设计一个适当的几何变换将其校正到矩形坐标系统, 这样, 可用立体视觉测距技术对机器人周围的物体进行三维空间定位。
68 |
69 | 几何变换的另一个应用是对相似的图像进行配准, 以便进行图像比较, 典型的应用是利用图像相减来检测运动或变化。 有时, 为便于解释需将图像以另一种样式表示, 这时也会用到几何变换, 地图绘制中的图像投影也会用到几何变换。例如, 在利用从宇宙飞船传回来的图像, 拼成地球、月球及行星的航拍镶嵌地图时, 就必须用几何变换。有关这些变换及其应用的详细内容请参阅书后的参考文献。
70 |
71 |
--------------------------------------------------------------------------------
/VI/6.8 应用实例.md:
--------------------------------------------------------------------------------
1 | # 6.8 应用实例
2 |
3 | 下面给出图像几何变换应用的一个例子一图像的转置。像的转置是将给定图像像素的x坐标和y坐标互换的几何变换。
4 |
5 | 图像的转置和图像的旋转不同, 而且仅仅通过旋转是不可能实现图像转置的。旋转操作与镜像操作结合才能实现图像的转置。图像转置的方法如下:
6 |
7 | 首先将图像水平镜像, 然后逆时针旋转 $90^{\circ}$ 才可以实现。设点 $P_{0}\left(x_{0}, y_{0}\right)$ 进行转置后的对应点为 $P(x, y)$, 图像高度为 $f H e i g h t$, 宽度为fWidth, 原图像中 $P_{0}\left(x_{0}, y_{0}\right)$ 经过转置后坐标将变为 $\left(y_{0}, x_{0}\right)$ 。 如果把图像转置看作是图像镜像与旋转的复合, 并且图像的水平镜像在 $x$ 方向不作平移。此时, 6.4.1中的公式 (6-4) 变为
8 | $$
9 | \left[\begin{array}{l}
10 | x \\
11 | y \\
12 | 1
13 | \end{array}\right]=\left[\begin{array}{rrr}
14 | -1 & 0 & 0 \\
15 | 0 & 1 & 0 \\
16 | 0 & 0 & 1
17 | \end{array}\right] \cdot\left[\begin{array}{l}
18 | x_{0} \\
19 | y_{0} \\
20 | 1
21 | \end{array}\right]
22 | $$
23 |
24 | 根据此式及6.5.1中的公式 (6-6) 可得
25 |
26 | $$
27 | \begin{aligned}
28 | & {\left[\begin{array}{l}
29 | x \\
30 | y \\
31 | 1
32 | \end{array}\right]=\left[\begin{array}{rrr}
33 | \cos \theta & \sin \theta & 0 \\
34 | -\sin \theta & \cos \theta & 0 \\
35 | 0 & 0 & 1
36 | \end{array}\right]\left[\begin{array}{rrr}
37 | -1 & 0 & 0 \\
38 | 0 & 1 & 0 \\
39 | 0 & 0 & 1
40 | \end{array}\right] \cdot\left[\begin{array}{l}
41 | x_{0} \\
42 | y_{0} \\
43 | 1
44 | \end{array}\right]\left(\theta=90^{\circ}\right)} \\
45 | & {\left[\begin{array}{l}
46 | x \\
47 | 1
48 | \end{array}\right]=\left[\begin{array}{rrr}
49 | 0 & 1 & 0 \\
50 | -1 & 0 & 0 \\
51 | 0 & 0 & 1
52 | \end{array}\right] \cdot\left[\begin{array}{rrr}
53 | -1 & 0 & 0 \\
54 | 0 & 1 & 0 \\
55 | 0 & 0 & 1
56 | \end{array}\right] \cdot\left[\begin{array}{l}
57 | x_{0} \\
58 | y_{0} \\
59 | 1
60 | \end{array}\right]=\left[\begin{array}{lll}
61 | 0 & 1 & 0 \\
62 | 1 & 0 & 0 \\
63 | 0 & 0 & 1
64 | \end{array}\right] \cdot\left[\begin{array}{l}
65 | x_{0} \\
66 | y_{0} \\
67 | 1
68 | \end{array}\right]}
69 | \end{aligned}\tag{6-20}
70 | $$
71 |
72 | 公式(6-20)就是图像转置的变换公式。
73 |
74 | 事实上,(6-19) 也可以直接得到, 因为原图像中 $P_{0}\left(x_{0}, y_{0}\right)$ 经过转置后坐标将变为 $P\left(y_{0}, x_{0}\right)$, 即 $x=y_{0}, y=x_{0}$, 把这个关系用齐次坐标写成矩阵形式就是式(6-20)。
75 |
76 | 图像转置的实现和图像镜像变换类似, 不同之处在于图像转置后DIB的头文件也要进行相应的改变, 主要是将头文件中图像高度和宽度信息更新。因此传递给图像转置函数的参数是直接指向DIB的指针, 而不是直接指向DIB像素的指针。下面给出实现图像转置函数TransposeDIB()的框架和主要算法。
77 |
78 | ```verilog
79 | //******************************************
80 | // 函数名称: BOOL Transpose()
81 | // 基本功能: 本函数对传入的CDibObject对象中的图像进行转置操作
82 | // 参数说明: CDibObject *pDibObject 默认为NULL
83 | // 返回值: BOOL 转置成功返回TRUE, 否则返回FALSE
84 | //******************************************
85 | BOOL CGeoTrans: : Transpose(CDibObject *pDibObject)
86 | {
87 | //定义指向源图像及新图像的指针、 位图数据指针、 调色板等指针变量
88 | //获取源图像指针及文件头、 信息头、 调色板及图像数据等信息
89 | //计算新图像大小(包括文件头、 信息头、 调色板和图像数据)
90 | //为新图像分配内存, 指定新图像的文件头、 信息头、 调色板及图像数据指针
91 | //用255填充新图像数据区, 用源图像的文件头、 信息头填充相应的新图像
92 | //调整文件总字节数、 新图像的宽度和高度等信息, 用原调色板填充新调色板
93 | //由图像位数确定的移动字节数
94 | int nMovedBits = 1;
95 | switch( m_pDibObject->GetNumBits() )
96 | {
97 | case 8:
98 | nMovedBits = 1;
99 | break;
100 | case 16:
101 | nMovedBits = 2;
102 | break;
103 | case 24:
104 | nMovedBits = 3;
105 | break;
106 | case 32:
107 | nMovedBits = 4;
108 | break;
109 | }
110 | // 针对图像每行进行操作
111 | for(y = 0; y < nOldHeight; y++)
112 | {
113 | //指向源图像第y行
114 | pOldTemp = pOldBits;
115 | pOldTemp += (nOldHeight -1 -y) * nOldWidthBytes;
116 | // 针对每行图像每列进行操作
117 | for(x = 0; x < nOldWidth; x++)
118 | {
119 | //指向转置后的图像第x行, 第y个像素的指针
120 | pNewTemp = pNewBits;
121 | pNewTemp += (nNewHeight -1 -x) * nNewWidthBytes;
122 | pNewTemp += y * nMovedBits;
123 | //复制像素
124 | memcpy(pNewTemp, pOldTemp, nMovedBits);
125 | pOldTemp += nMovedBits;
126 | }
127 | }
128 | //将内存解锁和将不再使用的内存释放,将新图像设置为当前图像,返回TRUE
129 | }
130 |
131 | ```
132 |
133 |
60 |
61 | 图6-35 极坐标系中的内突镜图像
62 |
63 | 
64 |
65 | 图6-36 转换为直角坐标系中的图像
66 |
67 | 有时机器人的鱼眼透镜拍摄的变形严重的一幅图像, 也可以设计一个适当的几何变换将其校正到矩形坐标系统, 这样, 可用立体视觉测距技术对机器人周围的物体进行三维空间定位。
68 |
69 | 几何变换的另一个应用是对相似的图像进行配准, 以便进行图像比较, 典型的应用是利用图像相减来检测运动或变化。 有时, 为便于解释需将图像以另一种样式表示, 这时也会用到几何变换, 地图绘制中的图像投影也会用到几何变换。例如, 在利用从宇宙飞船传回来的图像, 拼成地球、月球及行星的航拍镶嵌地图时, 就必须用几何变换。有关这些变换及其应用的详细内容请参阅书后的参考文献。
70 |
71 |
--------------------------------------------------------------------------------
/VI/6.8 应用实例.md:
--------------------------------------------------------------------------------
1 | # 6.8 应用实例
2 |
3 | 下面给出图像几何变换应用的一个例子一图像的转置。像的转置是将给定图像像素的x坐标和y坐标互换的几何变换。
4 |
5 | 图像的转置和图像的旋转不同, 而且仅仅通过旋转是不可能实现图像转置的。旋转操作与镜像操作结合才能实现图像的转置。图像转置的方法如下:
6 |
7 | 首先将图像水平镜像, 然后逆时针旋转 $90^{\circ}$ 才可以实现。设点 $P_{0}\left(x_{0}, y_{0}\right)$ 进行转置后的对应点为 $P(x, y)$, 图像高度为 $f H e i g h t$, 宽度为fWidth, 原图像中 $P_{0}\left(x_{0}, y_{0}\right)$ 经过转置后坐标将变为 $\left(y_{0}, x_{0}\right)$ 。 如果把图像转置看作是图像镜像与旋转的复合, 并且图像的水平镜像在 $x$ 方向不作平移。此时, 6.4.1中的公式 (6-4) 变为
8 | $$
9 | \left[\begin{array}{l}
10 | x \\
11 | y \\
12 | 1
13 | \end{array}\right]=\left[\begin{array}{rrr}
14 | -1 & 0 & 0 \\
15 | 0 & 1 & 0 \\
16 | 0 & 0 & 1
17 | \end{array}\right] \cdot\left[\begin{array}{l}
18 | x_{0} \\
19 | y_{0} \\
20 | 1
21 | \end{array}\right]
22 | $$
23 |
24 | 根据此式及6.5.1中的公式 (6-6) 可得
25 |
26 | $$
27 | \begin{aligned}
28 | & {\left[\begin{array}{l}
29 | x \\
30 | y \\
31 | 1
32 | \end{array}\right]=\left[\begin{array}{rrr}
33 | \cos \theta & \sin \theta & 0 \\
34 | -\sin \theta & \cos \theta & 0 \\
35 | 0 & 0 & 1
36 | \end{array}\right]\left[\begin{array}{rrr}
37 | -1 & 0 & 0 \\
38 | 0 & 1 & 0 \\
39 | 0 & 0 & 1
40 | \end{array}\right] \cdot\left[\begin{array}{l}
41 | x_{0} \\
42 | y_{0} \\
43 | 1
44 | \end{array}\right]\left(\theta=90^{\circ}\right)} \\
45 | & {\left[\begin{array}{l}
46 | x \\
47 | 1
48 | \end{array}\right]=\left[\begin{array}{rrr}
49 | 0 & 1 & 0 \\
50 | -1 & 0 & 0 \\
51 | 0 & 0 & 1
52 | \end{array}\right] \cdot\left[\begin{array}{rrr}
53 | -1 & 0 & 0 \\
54 | 0 & 1 & 0 \\
55 | 0 & 0 & 1
56 | \end{array}\right] \cdot\left[\begin{array}{l}
57 | x_{0} \\
58 | y_{0} \\
59 | 1
60 | \end{array}\right]=\left[\begin{array}{lll}
61 | 0 & 1 & 0 \\
62 | 1 & 0 & 0 \\
63 | 0 & 0 & 1
64 | \end{array}\right] \cdot\left[\begin{array}{l}
65 | x_{0} \\
66 | y_{0} \\
67 | 1
68 | \end{array}\right]}
69 | \end{aligned}\tag{6-20}
70 | $$
71 |
72 | 公式(6-20)就是图像转置的变换公式。
73 |
74 | 事实上,(6-19) 也可以直接得到, 因为原图像中 $P_{0}\left(x_{0}, y_{0}\right)$ 经过转置后坐标将变为 $P\left(y_{0}, x_{0}\right)$, 即 $x=y_{0}, y=x_{0}$, 把这个关系用齐次坐标写成矩阵形式就是式(6-20)。
75 |
76 | 图像转置的实现和图像镜像变换类似, 不同之处在于图像转置后DIB的头文件也要进行相应的改变, 主要是将头文件中图像高度和宽度信息更新。因此传递给图像转置函数的参数是直接指向DIB的指针, 而不是直接指向DIB像素的指针。下面给出实现图像转置函数TransposeDIB()的框架和主要算法。
77 |
78 | ```verilog
79 | //******************************************
80 | // 函数名称: BOOL Transpose()
81 | // 基本功能: 本函数对传入的CDibObject对象中的图像进行转置操作
82 | // 参数说明: CDibObject *pDibObject 默认为NULL
83 | // 返回值: BOOL 转置成功返回TRUE, 否则返回FALSE
84 | //******************************************
85 | BOOL CGeoTrans: : Transpose(CDibObject *pDibObject)
86 | {
87 | //定义指向源图像及新图像的指针、 位图数据指针、 调色板等指针变量
88 | //获取源图像指针及文件头、 信息头、 调色板及图像数据等信息
89 | //计算新图像大小(包括文件头、 信息头、 调色板和图像数据)
90 | //为新图像分配内存, 指定新图像的文件头、 信息头、 调色板及图像数据指针
91 | //用255填充新图像数据区, 用源图像的文件头、 信息头填充相应的新图像
92 | //调整文件总字节数、 新图像的宽度和高度等信息, 用原调色板填充新调色板
93 | //由图像位数确定的移动字节数
94 | int nMovedBits = 1;
95 | switch( m_pDibObject->GetNumBits() )
96 | {
97 | case 8:
98 | nMovedBits = 1;
99 | break;
100 | case 16:
101 | nMovedBits = 2;
102 | break;
103 | case 24:
104 | nMovedBits = 3;
105 | break;
106 | case 32:
107 | nMovedBits = 4;
108 | break;
109 | }
110 | // 针对图像每行进行操作
111 | for(y = 0; y < nOldHeight; y++)
112 | {
113 | //指向源图像第y行
114 | pOldTemp = pOldBits;
115 | pOldTemp += (nOldHeight -1 -y) * nOldWidthBytes;
116 | // 针对每行图像每列进行操作
117 | for(x = 0; x < nOldWidth; x++)
118 | {
119 | //指向转置后的图像第x行, 第y个像素的指针
120 | pNewTemp = pNewBits;
121 | pNewTemp += (nNewHeight -1 -x) * nNewWidthBytes;
122 | pNewTemp += y * nMovedBits;
123 | //复制像素
124 | memcpy(pNewTemp, pOldTemp, nMovedBits);
125 | pOldTemp += nMovedBits;
126 | }
127 | }
128 | //将内存解锁和将不再使用的内存释放,将新图像设置为当前图像,返回TRUE
129 | }
130 |
131 | ```
132 |
133 |  134 |
135 | 图6-37 转置后的图像
--------------------------------------------------------------------------------
/VII/7.1 图像分割.md:
--------------------------------------------------------------------------------
1 | [TOC]
2 |
3 | # 7.1 图像分割
4 |
5 | ## 7.1.1 概述
6 |
7 | 图像分割是将图像划分成若干个互不相交的小区域的过程, 小区域是某种意义下具有共同属性的像素的连通集合。如不同目标物体所占的图像区域、 前景所占的图像区域等。连通是指集合中任意两个点之间都存在着完全属于该集合的连通路径。对于离散图像而言,连通有4连通和8连通之分,如图7-1所示。
8 |
9 | 
10 |
11 | 图7-1 4连通和8连通
12 |
13 | 4连通指的是从区域上一点出发,可通过4个方向,即上、 下、左、右移动的组合,在不越出区域的前提下,到达区域内的任意像素; 8连通方法指的是从区域上一点出发,可通过左、 右、上、下、左上、右上、左下、右下这8个方向的移动组合来到达区域内的任意像素。
14 |
15 | 图像分割有三种不同的途径:其一是将各像素划归到相应物体或区域的像素聚类方法, 即区域法;其二是通过直接确定区域间的边界来实现分割的边界方法;其三是首先检测边缘像素, 再将边缘像素连接起来构成边界形成分割。在图像分割技术中, 最常用的是利用阈值化处理进行的图像分割。
16 |
17 | ## 7.1.2 灰度阈值法分割
18 |
19 | 常用的图像分割方法是把图像灰度分成不同的等级, 然后用设置灰度门限 (阈值) 的方法确定有意义的区域或分割物体的边界。常用的阈值化处理就是图像的二值化处理, 即选择一阈值, 将图像转换为黑白二值图像, 用于图像分割及边缘跟踪等预处理。
20 |
21 | 图像阈值化处理的变换函数表达式为
22 |
23 | $$
24 | g(x, y)= \begin{cases}0 & f(x, y)
134 |
135 | 图6-37 转置后的图像
--------------------------------------------------------------------------------
/VII/7.1 图像分割.md:
--------------------------------------------------------------------------------
1 | [TOC]
2 |
3 | # 7.1 图像分割
4 |
5 | ## 7.1.1 概述
6 |
7 | 图像分割是将图像划分成若干个互不相交的小区域的过程, 小区域是某种意义下具有共同属性的像素的连通集合。如不同目标物体所占的图像区域、 前景所占的图像区域等。连通是指集合中任意两个点之间都存在着完全属于该集合的连通路径。对于离散图像而言,连通有4连通和8连通之分,如图7-1所示。
8 |
9 | 
10 |
11 | 图7-1 4连通和8连通
12 |
13 | 4连通指的是从区域上一点出发,可通过4个方向,即上、 下、左、右移动的组合,在不越出区域的前提下,到达区域内的任意像素; 8连通方法指的是从区域上一点出发,可通过左、 右、上、下、左上、右上、左下、右下这8个方向的移动组合来到达区域内的任意像素。
14 |
15 | 图像分割有三种不同的途径:其一是将各像素划归到相应物体或区域的像素聚类方法, 即区域法;其二是通过直接确定区域间的边界来实现分割的边界方法;其三是首先检测边缘像素, 再将边缘像素连接起来构成边界形成分割。在图像分割技术中, 最常用的是利用阈值化处理进行的图像分割。
16 |
17 | ## 7.1.2 灰度阈值法分割
18 |
19 | 常用的图像分割方法是把图像灰度分成不同的等级, 然后用设置灰度门限 (阈值) 的方法确定有意义的区域或分割物体的边界。常用的阈值化处理就是图像的二值化处理, 即选择一阈值, 将图像转换为黑白二值图像, 用于图像分割及边缘跟踪等预处理。
20 |
21 | 图像阈值化处理的变换函数表达式为
22 |
23 | $$
24 | g(x, y)= \begin{cases}0 & f(x, y) 51 |
52 | 图7-3 不同阈值对阈值化结果的影响
53 | (a) 原始图像;
54 | (b) 阈值 $T=91$;
55 | (c) 阈值 $T=130$;
56 | (d) 阈值 $T=43$
57 |
58 | 
59 |
60 | 图7-4 图7-3(a)所示图像的直方图
61 |
62 | 为了有效地分割物体与背景,人们发展了各种各样的阈值处理技术,包括全局阈值、自适应阈值、最佳阈值等等。从方法分有:直方图阈值分割法, 类间方差阈值分割法,二维熵值分割法,模糊阈值分割法,共生矩阵阈值分割法.
63 |
64 |
65 | - 全局阈值
66 | 全局阈值是指整幅图象使用同一个阈值做分割处理。适用于背景和前景有明显对比的图象。 例如当直方图明显呈现双峰情况时, 可以选择两个峰值的中点作为全局阈值。
67 |
68 | - 自适应阈值
69 | 在许多情况下, 物体和背景的对比度在图象中不是各处一样的, 这时很难用统一的一个阈值将物体与背景分开。这时可以根据图象的局部特征分别采用不同的阈值进行分割。实际处理时, 需要按照具体问题将图象分成若干子区域分别选择阈值, 或者动态地根据一定的邻域范围选择每点处的阈值, 进行图象分割。
70 |
71 | - 最佳阈值
72 | 最佳阈值是使图像中目标与背景分割错误最小的阈值。
73 |
74 | 1.直方图阈值分割法
75 |
76 | 1)简单直方图分割法
77 |
78 | 基本原理: 直方图明显呈现双峰情况时,可以选择两个峰值的中点作为阈值.
79 | 
80 |
81 | 
82 |
83 |
84 | 2) 最佳阈值
85 |
86 | 设一幅图像只由目标和背景组成,其灰度分布概率密度 $P_{1}(\mathbf{z})$ 和 $\mathbf{P}_{2}(\mathbf{z})$ 为正态分布,且已知目标像素占全图像像素比为 $\theta$ :
87 |
88 | $p$
89 |
90 | 
91 |
92 |
93 |
94 | $$
95 | P_{1}(Z)=\frac{1}{\sqrt{2 \pi \sigma_{1}}} \exp \left[-\frac{\left(Z-\mu_{1}\right)^{2}}{2 \sigma_{1}{ }^{2}}\right]
96 | $$
97 |
98 | $$
99 | P_{2}(Z)=\frac{1}{\sqrt{2 \pi \sigma_{2}}} \exp \left[-\frac{\left(Z-\mu_{2}\right)^{2}}{2 \sigma_{2}{ }^{2}}\right]
100 | $$
101 |
102 | 则阈值为:
103 |
104 | $$
105 | Z_{t}=\frac{\mu_{1}+\mu_{2}}{2}+\frac{\sigma^{2}}{\mu_{1}-\mu_{2}} \ln \left(\frac{1-\theta}{\theta}\right)
106 | $$
107 |
108 | 若 $\theta=0.5$
109 |
110 | 则阈值为:
111 |
112 | $$
113 | Z_{t}=\frac{\mu_{1}+\mu_{2}}{2}
114 | $$
115 |
116 |
117 |
118 | 2.类间方差阈值分割法
119 |
120 | 设一幅图像只由目标和背景组成,原图灰度级为} $L$, 灰度级为 $i$ 的像素点数为 $n_{i}$, 图像总像素点数为 $N$, 则:
121 | $$
122 | p_{i}=\frac{n_{i}}{N}
123 | $$
124 |
125 | 用阈值 $t$ 将图像分割为两类: $C_{1}=(0,1,2, \ldots, t)$ 和 $C_{2}$ $=(\mathbf{t}, \mathbf{t}+1, \mathbf{t}+2, \ldots, \mathbf{L}-1)$, 则有:
126 |
127 |
128 |
129 | $$
130 | \begin{aligned}
131 | & \omega_{1}=P_{r}\left(C_{1}\right)=\sum_{i=0}^{t} p_{i} \\
132 | & \omega_{2}=P_{r}\left(C_{2}\right)=\sum_{i=t+1}^{L-1} p_{i} \\
133 | & \mu_{1}=\sum_{i=0}^{t} i p_{i} / \omega_{1} \\
134 | & \mu_{2}=\sum_{i=t+1}^{L-1} i p_{i} / \omega_{2} \\
135 | & \sigma_{1}^{2}=\sum_{i=0}^{t}\left(i-\mu_{1}\right)^{2} p_{i} / \omega_{1} \\
136 | & \sigma_{2}^{2}=\sum_{i=t+1}^{L-1}\left(i-\mu_{2}\right)^{2} p_{i} / \omega_{2}
137 | \end{aligned}
138 | $$
139 |
140 | 类内方差:
141 |
142 | $$
143 | \sigma_{\omega}^{2}=\omega_{1} \sigma_{1}^{2}+\omega_{2} \sigma_{2}^{2}
144 | $$
145 |
146 | 类间方差:
147 |
148 | $$
149 | \sigma_{B}^{2}=\omega_{1} \omega_{2}\left(\mu_{1}-\mu_{2}\right)^{2}
150 | $$
151 |
152 | 总方差:
153 |
154 | $$
155 | \sigma_{\omega}^{2}=\sigma_{B}^{2}+\sigma_{\omega}^{2}
156 | $$
157 |
158 | 定义准则函数:
159 |
160 | $$
161 | F(t)=\sigma_{B}^{2} / \sigma_{T}^{2}
162 | $$
163 |
164 |
165 |
166 | 则使 $F(t)$ 最大的 $t$ 为最佳阈值.
167 |
168 | 
169 |
170 | 图 6.3.6 坦克图类间方差阈值分割
171 |
172 | 3二维熵值分割法
173 |
174 | 一维熵值分割法设原图灰度级为 $L$, 灰度级为 $i$ 的像素点数为 $n_{i}$, 图像总像素点数为 $\mathbf{N} \times \mathbf{N}$,则:
175 |
176 | $$
177 | p_{i}=\frac{n_{i}}{N \times N}
178 | $$
179 |
180 | 设图中灰度级低于 $t$ 的像素点构成目标区域O, 灰度级高于 $\mathbf{t}$ 的像素点构成背景区域B, 则目标区域和背景区域的熵定义为:
181 |
182 | $H_{0}(t)=-\sum_{i}\left(p_{i} / p_{t}\right) \lg \left(p_{i} / p_{t}\right) \quad i=1,2,3 \cdots t$
183 |
184 | $$
185 | H_{B}(t)=-\sum_{i}\left[p_{i} /\left(1-p_{t}\right)\right] \lg \left[p_{i} /\left(1-p_{t}\right)\right] \quad i=t+1, t+2, t+3 \cdots L-1
186 | $$
187 |
188 | 贝则熵函数定义为:
189 |
190 | $$
191 | \varphi(t)=H_{0}+H_{B}=\lg p_{t}\left(1-p_{t}\right)+\frac{H_{t}}{p_{t}}+\frac{H_{L}-H_{t}}{1-p_{t}}
192 | $$
193 |
194 | 其中:
195 |
196 | $$
197 | \begin{array}{cc}
198 | H_{t}=-\sum_{i} p_{i} \lg p_{i} & i=1,2, \cdots t \\
199 | H_{L}=-\sum_{i} p_{i} \lg p_{i} & i=1,2 \cdots L
200 | \end{array}
201 | $$
202 |
203 | 当熵函数最大时的灰度值t就为最佳阈值.
204 |
205 |
206 |
207 | 4.模糊阈值分割
208 |
209 | 1)隶属函数 $\mu\left(x_{m, n}, p, \mathbf{q}\right)$ :
210 |
211 | 设像素点 $(m, n)$ 的灰度值为 $x_{m, n}$, 则 $\mu\left(x_{m, n}, p, q\right)$ 定义为像素点 $(m, \mathbf{n})$ 属于目标的程度;
212 |
213 | $$
214 | \mu\left(x_{m, n}, p, q, r\right)=\left\{\begin{array}{cc}
215 | 0 & x_{m, n} \leq p \\
216 | 2\left[\left(x_{m, n}-p\right) /(r-p)\right]^{2} & p \leq x_{m, n} \leq q \\
217 | 1-2\left[\left(x_{m, n}-p\right) /(r-p)\right]^{2} & q_{m, n}
51 |
52 | 图7-3 不同阈值对阈值化结果的影响
53 | (a) 原始图像;
54 | (b) 阈值 $T=91$;
55 | (c) 阈值 $T=130$;
56 | (d) 阈值 $T=43$
57 |
58 | 
59 |
60 | 图7-4 图7-3(a)所示图像的直方图
61 |
62 | 为了有效地分割物体与背景,人们发展了各种各样的阈值处理技术,包括全局阈值、自适应阈值、最佳阈值等等。从方法分有:直方图阈值分割法, 类间方差阈值分割法,二维熵值分割法,模糊阈值分割法,共生矩阵阈值分割法.
63 |
64 |
65 | - 全局阈值
66 | 全局阈值是指整幅图象使用同一个阈值做分割处理。适用于背景和前景有明显对比的图象。 例如当直方图明显呈现双峰情况时, 可以选择两个峰值的中点作为全局阈值。
67 |
68 | - 自适应阈值
69 | 在许多情况下, 物体和背景的对比度在图象中不是各处一样的, 这时很难用统一的一个阈值将物体与背景分开。这时可以根据图象的局部特征分别采用不同的阈值进行分割。实际处理时, 需要按照具体问题将图象分成若干子区域分别选择阈值, 或者动态地根据一定的邻域范围选择每点处的阈值, 进行图象分割。
70 |
71 | - 最佳阈值
72 | 最佳阈值是使图像中目标与背景分割错误最小的阈值。
73 |
74 | 1.直方图阈值分割法
75 |
76 | 1)简单直方图分割法
77 |
78 | 基本原理: 直方图明显呈现双峰情况时,可以选择两个峰值的中点作为阈值.
79 | 
80 |
81 | 
82 |
83 |
84 | 2) 最佳阈值
85 |
86 | 设一幅图像只由目标和背景组成,其灰度分布概率密度 $P_{1}(\mathbf{z})$ 和 $\mathbf{P}_{2}(\mathbf{z})$ 为正态分布,且已知目标像素占全图像像素比为 $\theta$ :
87 |
88 | $p$
89 |
90 | 
91 |
92 |
93 |
94 | $$
95 | P_{1}(Z)=\frac{1}{\sqrt{2 \pi \sigma_{1}}} \exp \left[-\frac{\left(Z-\mu_{1}\right)^{2}}{2 \sigma_{1}{ }^{2}}\right]
96 | $$
97 |
98 | $$
99 | P_{2}(Z)=\frac{1}{\sqrt{2 \pi \sigma_{2}}} \exp \left[-\frac{\left(Z-\mu_{2}\right)^{2}}{2 \sigma_{2}{ }^{2}}\right]
100 | $$
101 |
102 | 则阈值为:
103 |
104 | $$
105 | Z_{t}=\frac{\mu_{1}+\mu_{2}}{2}+\frac{\sigma^{2}}{\mu_{1}-\mu_{2}} \ln \left(\frac{1-\theta}{\theta}\right)
106 | $$
107 |
108 | 若 $\theta=0.5$
109 |
110 | 则阈值为:
111 |
112 | $$
113 | Z_{t}=\frac{\mu_{1}+\mu_{2}}{2}
114 | $$
115 |
116 |
117 |
118 | 2.类间方差阈值分割法
119 |
120 | 设一幅图像只由目标和背景组成,原图灰度级为} $L$, 灰度级为 $i$ 的像素点数为 $n_{i}$, 图像总像素点数为 $N$, 则:
121 | $$
122 | p_{i}=\frac{n_{i}}{N}
123 | $$
124 |
125 | 用阈值 $t$ 将图像分割为两类: $C_{1}=(0,1,2, \ldots, t)$ 和 $C_{2}$ $=(\mathbf{t}, \mathbf{t}+1, \mathbf{t}+2, \ldots, \mathbf{L}-1)$, 则有:
126 |
127 |
128 |
129 | $$
130 | \begin{aligned}
131 | & \omega_{1}=P_{r}\left(C_{1}\right)=\sum_{i=0}^{t} p_{i} \\
132 | & \omega_{2}=P_{r}\left(C_{2}\right)=\sum_{i=t+1}^{L-1} p_{i} \\
133 | & \mu_{1}=\sum_{i=0}^{t} i p_{i} / \omega_{1} \\
134 | & \mu_{2}=\sum_{i=t+1}^{L-1} i p_{i} / \omega_{2} \\
135 | & \sigma_{1}^{2}=\sum_{i=0}^{t}\left(i-\mu_{1}\right)^{2} p_{i} / \omega_{1} \\
136 | & \sigma_{2}^{2}=\sum_{i=t+1}^{L-1}\left(i-\mu_{2}\right)^{2} p_{i} / \omega_{2}
137 | \end{aligned}
138 | $$
139 |
140 | 类内方差:
141 |
142 | $$
143 | \sigma_{\omega}^{2}=\omega_{1} \sigma_{1}^{2}+\omega_{2} \sigma_{2}^{2}
144 | $$
145 |
146 | 类间方差:
147 |
148 | $$
149 | \sigma_{B}^{2}=\omega_{1} \omega_{2}\left(\mu_{1}-\mu_{2}\right)^{2}
150 | $$
151 |
152 | 总方差:
153 |
154 | $$
155 | \sigma_{\omega}^{2}=\sigma_{B}^{2}+\sigma_{\omega}^{2}
156 | $$
157 |
158 | 定义准则函数:
159 |
160 | $$
161 | F(t)=\sigma_{B}^{2} / \sigma_{T}^{2}
162 | $$
163 |
164 |
165 |
166 | 则使 $F(t)$ 最大的 $t$ 为最佳阈值.
167 |
168 | 
169 |
170 | 图 6.3.6 坦克图类间方差阈值分割
171 |
172 | 3二维熵值分割法
173 |
174 | 一维熵值分割法设原图灰度级为 $L$, 灰度级为 $i$ 的像素点数为 $n_{i}$, 图像总像素点数为 $\mathbf{N} \times \mathbf{N}$,则:
175 |
176 | $$
177 | p_{i}=\frac{n_{i}}{N \times N}
178 | $$
179 |
180 | 设图中灰度级低于 $t$ 的像素点构成目标区域O, 灰度级高于 $\mathbf{t}$ 的像素点构成背景区域B, 则目标区域和背景区域的熵定义为:
181 |
182 | $H_{0}(t)=-\sum_{i}\left(p_{i} / p_{t}\right) \lg \left(p_{i} / p_{t}\right) \quad i=1,2,3 \cdots t$
183 |
184 | $$
185 | H_{B}(t)=-\sum_{i}\left[p_{i} /\left(1-p_{t}\right)\right] \lg \left[p_{i} /\left(1-p_{t}\right)\right] \quad i=t+1, t+2, t+3 \cdots L-1
186 | $$
187 |
188 | 贝则熵函数定义为:
189 |
190 | $$
191 | \varphi(t)=H_{0}+H_{B}=\lg p_{t}\left(1-p_{t}\right)+\frac{H_{t}}{p_{t}}+\frac{H_{L}-H_{t}}{1-p_{t}}
192 | $$
193 |
194 | 其中:
195 |
196 | $$
197 | \begin{array}{cc}
198 | H_{t}=-\sum_{i} p_{i} \lg p_{i} & i=1,2, \cdots t \\
199 | H_{L}=-\sum_{i} p_{i} \lg p_{i} & i=1,2 \cdots L
200 | \end{array}
201 | $$
202 |
203 | 当熵函数最大时的灰度值t就为最佳阈值.
204 |
205 |
206 |
207 | 4.模糊阈值分割
208 |
209 | 1)隶属函数 $\mu\left(x_{m, n}, p, \mathbf{q}\right)$ :
210 |
211 | 设像素点 $(m, n)$ 的灰度值为 $x_{m, n}$, 则 $\mu\left(x_{m, n}, p, q\right)$ 定义为像素点 $(m, \mathbf{n})$ 属于目标的程度;
212 |
213 | $$
214 | \mu\left(x_{m, n}, p, q, r\right)=\left\{\begin{array}{cc}
215 | 0 & x_{m, n} \leq p \\
216 | 2\left[\left(x_{m, n}-p\right) /(r-p)\right]^{2} & p \leq x_{m, n} \leq q \\
217 | 1-2\left[\left(x_{m, n}-p\right) /(r-p)\right]^{2} & q_{m, n} 266 |
267 | 图 6.3.13 坦克图模糊阈值法分割
268 |
269 | ## 7.1.3 区域生长
270 |
271 | 分割的目的是把一幅图像划分成一些区域,最直接的方法就是把一幅图像分成满足某种判据的区域,也就是说,把点组成区域。为了实现分组, 首先要确定区域的数目, 其次要确定一个区域与其他区域相区别的特征, 最后还要产生有意义分割的相似性判据。
272 |
273 | 分割区域的一种方法叫区域生长或区域生成。假定区域的数目以及在每个区域中单个点的位置已知, 则从一个已知点开始,加上与已知点相似的邻近点形成一个区域。相似性准则可以是灰度级、 彩色、组织、梯度或其他特性,相似性的测度可以由所确定的阈值来判定。方法是从满足检测准则的点开始, 在各个方向上生长区域, 当其邻近点满足检测准则就并入小块区域中。当新的点被合并后再用新的区域重复这一过程, 直到没有可接受的邻近点时生成过程终止。
274 |
275 | 图 7-5给出一个简单的例子。此例的相似性准则是邻近点的灰度级与物体的平均灰度级的差小于2。图中被接受的点和起始点均用下划线标出,其中(a)图是输入图像;(b)图是第一步接受的邻近点;(c)图是第二步接受的邻近点;(d) 图是从6开始生成的结果。
276 |
277 | 
278 |
279 | 图7-5 区域生长示例
280 |
281 | 当生成任意物体时,接收准则可以结构为基础, 而不是以灰度级或对比度为基础。为了把候选的小群点包含在物体中,可以检测这些小群点, 而不是检测单个点, 如果它们的结构与物体的结构足够相似时就接受它们。
282 |
283 | ## 7.1.4 区域聚合
284 |
285 | 区域聚合可直接用于图像分割, 它要求聚合中的各个点必须在平面上相邻接而且特性相似。区域聚合的步骤是首先检查图像的测度集,以确定在测度空间中聚合的位置和数目,然后把这些聚合的定义用于图像, 以得到区域聚合。区域聚合技术可以说明如下。
286 |
287 | 首先, 在图片上定义某个等价关系。例如, 最简单的等价关系可定义为 $p(i, j)=p(k, l)$ 。也就是说, 如果 $p(i, j)=p(k, l)$, 就说明 $p(i, j)$ 与 $p(k, l)$ 等价。任何在点的格子上的等价关系又可划分为等价类。例如, $p(i, j)$ 的取值范围为 0 到 63 , 就可以产生 64 个等价类的模板。如果关系满足,它的值等于 1 ,否则为 0 。
288 |
289 | 模板的图像是两两不相交的, 那么64个模板就会充满整个格子。这些等价的类又可进一步分为最大连接的子集(连接分量)。连接性可以用点 $(i, j)$ 的邻点来定义, 如4连通邻点、8连通邻点等等。假如 $R$ 是属于格子的子集, 在 $R$ 中存在一个点序列, 第一个点是 $p_{1}$, 最后一个点是 $p_{2}$, 属于格子的子集 $R$ 的两个点 $p_{1}$ 和 $p_{2}$ 是被连接起来的, 这样, 相继的各点是 4 连接相邻的。通过这样的连接关系可以定义一个属于 $R$ 的子集, 这个子集形成一个区域, 在这个区域中, 任何点都与 $R$ 有关。利用等价模板可分成最大的连接区域, 然后, 这些最大的连接区域又可以像搭积木一样形成有意义的分割。
290 |
291 | 1970年布莱斯和芬尼玛提出一种分割方法, 如图5-6所示。图 ( $a$ ) 是具有灰度级的 $3 \times 3$ 的 $G$ 阵列, 图 (b) 是对 $G$ 的分割结果。 其中, 图像格子为 $G$, 它是大格子 $S$ 的子格子。 $G$ 为 $n \times m$ 的格子, $S$ 是 $(2 n+1) \times(2 m+1)$ 的大格子。在大格子中, $G(i, j)$ 点位于 $S$ 的 $(2 i+1,2 j+1)$ 点上。 $G$ 中的点与 $S$ 中的点相对应, 其中每一下标都是奇数, 其余的点用来代表区域的边界。以这种形式表现的区域, 产生一种寻找最大连接区域的方法。G中的点与它上边和右边的点相比较, 灰度级相同就合并, 灰度级不同就揷入边界线。把图像中的每个点都处理过之后, 整个图像就被分割成区域。 在这个例子中, 由于采用了4连通等价关系, 因此, 由图可见, 在对角线方向上的等灰度级产生了隔开的区域。
292 |
293 | 
294 |
295 | 图7-6 布莱斯和芬尼玛分割方法
296 |
297 | 2 分裂合并法
298 |
299 | 实际中常先把图像分成任意大小且不重叠的区域,然后再合并或分裂这些区域以满足分割的要求, 即分裂合并法. 一致性测度可以选择基于灰度统计特征 (如同质区域中的方差),假设阈值为 $T$, 则算法步骤为:
300 |
301 | (1) 对于任一 $R_{i}$, 如果 $V\left(R_{i}\right)>T$ ,则将其分裂成互不重叠的四等分;
302 |
303 | (2) 对相邻区域 $R_{i}$ 和 $R_{j}$, 如果 $\boldsymbol{V}\left(\boldsymbol{R}_{i} \bigcup_{j} \boldsymbol{R}\right)
266 |
267 | 图 6.3.13 坦克图模糊阈值法分割
268 |
269 | ## 7.1.3 区域生长
270 |
271 | 分割的目的是把一幅图像划分成一些区域,最直接的方法就是把一幅图像分成满足某种判据的区域,也就是说,把点组成区域。为了实现分组, 首先要确定区域的数目, 其次要确定一个区域与其他区域相区别的特征, 最后还要产生有意义分割的相似性判据。
272 |
273 | 分割区域的一种方法叫区域生长或区域生成。假定区域的数目以及在每个区域中单个点的位置已知, 则从一个已知点开始,加上与已知点相似的邻近点形成一个区域。相似性准则可以是灰度级、 彩色、组织、梯度或其他特性,相似性的测度可以由所确定的阈值来判定。方法是从满足检测准则的点开始, 在各个方向上生长区域, 当其邻近点满足检测准则就并入小块区域中。当新的点被合并后再用新的区域重复这一过程, 直到没有可接受的邻近点时生成过程终止。
274 |
275 | 图 7-5给出一个简单的例子。此例的相似性准则是邻近点的灰度级与物体的平均灰度级的差小于2。图中被接受的点和起始点均用下划线标出,其中(a)图是输入图像;(b)图是第一步接受的邻近点;(c)图是第二步接受的邻近点;(d) 图是从6开始生成的结果。
276 |
277 | 
278 |
279 | 图7-5 区域生长示例
280 |
281 | 当生成任意物体时,接收准则可以结构为基础, 而不是以灰度级或对比度为基础。为了把候选的小群点包含在物体中,可以检测这些小群点, 而不是检测单个点, 如果它们的结构与物体的结构足够相似时就接受它们。
282 |
283 | ## 7.1.4 区域聚合
284 |
285 | 区域聚合可直接用于图像分割, 它要求聚合中的各个点必须在平面上相邻接而且特性相似。区域聚合的步骤是首先检查图像的测度集,以确定在测度空间中聚合的位置和数目,然后把这些聚合的定义用于图像, 以得到区域聚合。区域聚合技术可以说明如下。
286 |
287 | 首先, 在图片上定义某个等价关系。例如, 最简单的等价关系可定义为 $p(i, j)=p(k, l)$ 。也就是说, 如果 $p(i, j)=p(k, l)$, 就说明 $p(i, j)$ 与 $p(k, l)$ 等价。任何在点的格子上的等价关系又可划分为等价类。例如, $p(i, j)$ 的取值范围为 0 到 63 , 就可以产生 64 个等价类的模板。如果关系满足,它的值等于 1 ,否则为 0 。
288 |
289 | 模板的图像是两两不相交的, 那么64个模板就会充满整个格子。这些等价的类又可进一步分为最大连接的子集(连接分量)。连接性可以用点 $(i, j)$ 的邻点来定义, 如4连通邻点、8连通邻点等等。假如 $R$ 是属于格子的子集, 在 $R$ 中存在一个点序列, 第一个点是 $p_{1}$, 最后一个点是 $p_{2}$, 属于格子的子集 $R$ 的两个点 $p_{1}$ 和 $p_{2}$ 是被连接起来的, 这样, 相继的各点是 4 连接相邻的。通过这样的连接关系可以定义一个属于 $R$ 的子集, 这个子集形成一个区域, 在这个区域中, 任何点都与 $R$ 有关。利用等价模板可分成最大的连接区域, 然后, 这些最大的连接区域又可以像搭积木一样形成有意义的分割。
290 |
291 | 1970年布莱斯和芬尼玛提出一种分割方法, 如图5-6所示。图 ( $a$ ) 是具有灰度级的 $3 \times 3$ 的 $G$ 阵列, 图 (b) 是对 $G$ 的分割结果。 其中, 图像格子为 $G$, 它是大格子 $S$ 的子格子。 $G$ 为 $n \times m$ 的格子, $S$ 是 $(2 n+1) \times(2 m+1)$ 的大格子。在大格子中, $G(i, j)$ 点位于 $S$ 的 $(2 i+1,2 j+1)$ 点上。 $G$ 中的点与 $S$ 中的点相对应, 其中每一下标都是奇数, 其余的点用来代表区域的边界。以这种形式表现的区域, 产生一种寻找最大连接区域的方法。G中的点与它上边和右边的点相比较, 灰度级相同就合并, 灰度级不同就揷入边界线。把图像中的每个点都处理过之后, 整个图像就被分割成区域。 在这个例子中, 由于采用了4连通等价关系, 因此, 由图可见, 在对角线方向上的等灰度级产生了隔开的区域。
292 |
293 | 
294 |
295 | 图7-6 布莱斯和芬尼玛分割方法
296 |
297 | 2 分裂合并法
298 |
299 | 实际中常先把图像分成任意大小且不重叠的区域,然后再合并或分裂这些区域以满足分割的要求, 即分裂合并法. 一致性测度可以选择基于灰度统计特征 (如同质区域中的方差),假设阈值为 $T$, 则算法步骤为:
300 |
301 | (1) 对于任一 $R_{i}$, 如果 $V\left(R_{i}\right)>T$ ,则将其分裂成互不重叠的四等分;
302 |
303 | (2) 对相邻区域 $R_{i}$ 和 $R_{j}$, 如果 $\boldsymbol{V}\left(\boldsymbol{R}_{i} \bigcup_{j} \boldsymbol{R}\right) 205 |
206 | ### 通过开运算检测电路板
207 |
208 |
205 |
206 | ### 通过开运算检测电路板
207 |
208 |  209 |
210 |
209 |
210 |  211 |
212 | ### 肉类目标识别
213 |
214 |
211 |
212 | ### 肉类目标识别
213 |
214 |  215 |
216 |
215 |
216 |  217 |
218 |
217 |
218 |  219 |
220 | 形态学梯度,腐蚀后求取形态学梯度-分水岭算法
221 |
222 | ### MRI图像检测
223 |
224 |
219 |
220 | 形态学梯度,腐蚀后求取形态学梯度-分水岭算法
221 |
222 | ### MRI图像检测
223 |
224 |  225 |
226 |
225 |
226 |  227 |
228 | 圆盘开-重建-减去-阈值-开去掉小噪声
229 |
230 | ### 机场跑道检测
231 |
232 |
227 |
228 | 圆盘开-重建-减去-阈值-开去掉小噪声
229 |
230 | ### 机场跑道检测
231 |
232 |  233 |
234 |
233 |
234 |  235 |
236 | 圆盘开运算
237 |
238 |
235 |
236 | 圆盘开运算
237 |
238 |  239 |
240 | 阈值
241 |
242 |
239 |
240 | 阈值
241 |
242 |  243 |
244 | 细化: 红色
245 | 细化到端点检测:
246 | 绿色
247 | 开运算: 蓝色
248 |
249 |
243 |
244 | 细化: 红色
245 | 细化到端点检测:
246 | 绿色
247 | 开运算: 蓝色
248 |
249 |  250 |
251 | 重建
252 |
253 | 
254 |
255 | 门限阈值确定
--------------------------------------------------------------------------------
250 |
251 | 重建
252 |
253 | 
254 |
255 | 门限阈值确定
--------------------------------------------------------------------------------
 4 |
5 | 图2-1 任意波形可分解为正弦波的加权和
6 |
7 | 
8 |
9 | 图2-2 正弦波的振幅 $A$ 和相位 $\varphi$
10 |
11 |
4 |
5 | 图2-1 任意波形可分解为正弦波的加权和
6 |
7 | 
8 |
9 | 图2-2 正弦波的振幅 $A$ 和相位 $\varphi$
10 |
11 | 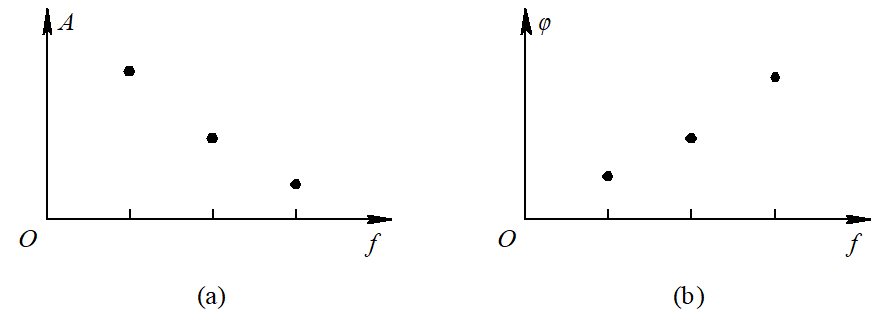 12 |
13 | 图2-3 图2-1(a)波形的频域表示
14 | (a) 幅频特性; (b) 相频特性
15 |
16 | 时域和频域之间的变换可用数学公式表示如下:
17 | $$
18 | f(f){\Leftrightarrow} A(f), \Phi(f)\tag{2-1}
19 | $$
20 | 为能同时表示信号的振幅和相位,通常采用复数表示法,因此式(2-1)可用复数表示为
21 | $$
22 | f(f)\Leftrightarrow F(f)\tag{2-2}
23 | $$
24 | 完成这种变换,一般采用的方法是线性正交变换。
25 |
--------------------------------------------------------------------------------
/II/2.3 频域变换的一般表达式.md:
--------------------------------------------------------------------------------
1 | # 2.3 频域变换的一般表达式
2 |
3 | ## 2.3.1 可分离变换
4 |
5 | 二维傅立叶变换可用通用的关系式来表示:
6 | $$
7 | F(u, v)=\sum_{x=0}^{M-1} \sum_{y=0}^{N-1} f(x, y) g(x, y, u, v)
8 |
9 | \tag{2-36}
10 | $$
11 | $$
12 | f(x, y)=\sum_{u=0}^{M-1} \sum_{v=0}^{N-1} F(u, v) h(x, y, u, v)\tag{2-37}
13 | $$
14 |
15 | 式中:$x, u=0, 1, 2, …, M-1$;$y, v=0, 1, 2, …, N-1$;$g(x,y,u,v)$和$h(x,y,u,v)$分别称为正向变换核和反向变换核。
16 |
17 | 如果
18 | $$
19 | g(x, y, u, v)=g_1(x, u) g_2(y, v)\tag{2-38}
20 | $$
21 |
22 | $$
23 | h(x, y, u, v)=h_1(x, u) h_2(y, v)\tag{2-39}
24 | $$
25 |
26 | 则称正、反变换核是可分离的。进一步,如果$g_1$和$g_2$,$h_1$和$h_2$在函数形式上一样,则称该变换核是对称的。
27 |
28 | 二维傅立叶变换对是式(2-36)和式(2-37)的一个特殊情况, 它们的核为
29 | $$
30 | g(x, y, u, v)=e^{-j 2 \pi\left(\dfrac{u x}{M}+\dfrac{v y}{N}\right)}=e^{-j 2 \pi \dfrac{u x}{M}} \cdot e^{-j 2 \pi \dfrac{v y}{N}} \tag{2-40}
31 | $$
32 | $$
33 | h(x, y, u, v)=\frac{1}{M N} e^{j 2 \pi\left(\dfrac{u x}{M}+\dfrac{v y}{N}\right)}=\frac{1}{M} e^{j 2 \pi \dfrac{u x}{M}} \cdot \frac{1}{N} e^{j 2 \pi \dfrac{v y}{N}}\tag{2-41}
34 | $$
35 |
36 | 可见,它们都是可分离的和对称的。
37 |
38 | 如前所述,二维傅立叶变换可以利用变换核的可分离性, 用两次一维变换来实现,即可先对$f(x, y)$的每一行进行一维变换得到$F(x, v)$,再沿$F(x, v)$每一列取一维变换得到变换结果$F(u, v)
39 | $。对于其他的图像变换,只要其变换核是可分离的,同样也可用两次一维变换来实现。
40 |
41 | 如果先对$f(x, y)$的每一列进行一维变换得到$F(y, u)$,再沿$F(y, u)$每一行取一维变换得到$F(u, v)$,其最终结果是一样的。该结论对反变换核也适用。
42 |
43 | ## 2.3.2 图像变换的矩阵表示
44 |
45 | 数字图像都是实数矩阵, 设$f(x, y)$为$M\times N$的图像灰度矩阵, 通常为了分析、推导方便,可将可分离变换写成矩阵的形式:
46 | $$
47 | F=P f Q\tag{2-42}
48 | $$
49 |
50 | $$
51 | F=P^{-1} F Q^{-1}\tag{2-43}
52 | $$
53 |
54 | 其中,$F$、$f$是二维$M\times N$的矩阵;$P$是$M\times M$矩阵;$Q$是$N\times N$矩阵。
55 | $$
56 | F(u, v)=\sum_{x=0}^{M-1} \sum_{y=0}^{N-1} P(x, u) f(x, y) Q(y, v)\tag{2-44}
57 | $$
58 | 式中,$u=0, 1, 2, …, M-1,v=0, 1, 2, …, N-1$。对二维离散傅立叶变换,则有
59 | $$
60 | P(x, u)=g_1(x, u)=e^{-j 2 \pi u x / M}\tag{2-45}
61 | $$
62 |
63 | $$
64 | P(y, v)=g_2(x, v)=e^{-j 2 \pi v / N}\tag{2-46}
65 | $$
66 |
67 | 实践中,除了DFT变换之外,还采用许多其他的正交变换。例如:离散余弦变换、沃尔什-哈达玛变换、K-L变换等,下面将对常用的变换作一简要介绍。
68 |
--------------------------------------------------------------------------------
/II/2.4 离散余弦变换.md:
--------------------------------------------------------------------------------
1 | # 2.4 离散余弦变换(DCT)
2 |
3 | 离散余弦变换(Discrete Cosine Transform, DCT)的变换核为余弦函数。DCT除了具有一般的正交变换性质外, 它的变换阵的基向量能很好地描述人类语音信号和图像信号的相关特征。
4 |
5 | 因此,在对语音信号、图像信号的变换中,DCT变换被认为是一种准最佳变换。近年颁布的一系列视频压缩编码的国际标准建议中, 都把DCT作为其中的一个基本处理模块。除此之外, DCT 还是一种可分离的变换。
6 |
7 | ## 2.4.1 一维离散余弦变换
8 |
9 | 一维DCT的变换核定义为
10 |
11 | $$
12 | g(x, u)=C(u) \sqrt{\frac{2}{N}} \cos \frac{(2 x+1) u \pi}{2 N}\tag{2-47}
13 | $$
14 |
15 | 式中, $x, u=0,1,2, \ldots, N-1$;
16 | $$
17 | C(u)= \begin{cases}\frac{1}{\sqrt{2}} & u=0 \\ 1 & \text { 其他 }\end{cases}\tag{2-48}
18 | $$
19 |
20 | 一维DCT定义如下: 设 $\{f(x) \mid x=0,1, \ldots, N-1\}$ 为离散的信号列。
21 |
22 | $$
23 | F(u)=C(u) \sqrt{\frac{2}{N}} \sum_{x=0}^{N-1} f(x) \cos \frac{(2 x+1) u \pi}{2 N}\tag{2-49}
24 | $$
25 |
26 | 式中, $u, x=0,1,2, \ldots, N-1$ 。
27 |
28 | 将变换式展开整理后,可以㝍成矩阵的形式,即
29 | $$
30 | F=G f\tag{2-50}
31 | $$
32 |
33 | 其中
34 | $$
35 | G=
36 | \left[
37 | \begin{array}{}
38 | \dfrac{1}{\sqrt{N}}&[&1 &1 &\cdots &1 &]\\
39 | \sqrt{\dfrac{2}{N}}&[&\cos(\dfrac{\pi}{2N}) &\cos(\dfrac{3\pi}{2N}) &\cdots&\cos(\dfrac{(2N-1)\pi}{2N})&]\\
40 | \sqrt{\dfrac{2}{N}}&[&\cos(\dfrac{\pi}{2N}) &\cos(\dfrac{6\pi}{2N}) &\cdots &\cos(\dfrac{(2N-1)\pi}{2N})&]\\
41 | \vdots\\
42 | \sqrt{\dfrac{2}{N}}&[&\cos((N-1)\dfrac{\pi}{2N}) &\cos((N-1)\dfrac{3\pi}{2N}) &\cdots &\cos((N-1)\dfrac{(2N-1)\pi}{2N})&]\\
43 | \end{array}
44 | \right]\tag{2-51}
45 | $$
46 | 一维DCT的逆变换IDCT定义为
47 |
48 | $$
49 | f(x)=\sqrt{\frac{2}{N}} \sum_{u=0}^{N-1} C(u) F(u) \cos \frac{(2 x+1) u \pi}{2 N}\tag{2-52}
50 | $$
51 |
52 | 式中, $x, u=0,1,2, \ldots, N-1$ 。可见一维DCT的逆变换核与正变换核是相同的。
53 |
54 | ## 2.4.2二维离散余弦变换
55 |
56 | 考虑到两个变量, 很容易将一维DCT的定义推广到二维DCT。其正变换核为
57 | $$
58 | g(x, y, u, v)=\frac{2}{\sqrt{M N}} C(u) C(v) \cos \frac{(2 x+1) u \pi}{2 M} \cos \frac{(2 y+1) v \pi}{2 N}\tag{2-53}
59 | $$
60 |
61 |
62 | 式中, $C(u)$ 和 $C(v)$ 的定义同式 (2-48) ; $x, u=0,1,2, \ldots, M-1$;
63 |
64 | $y, v=0,1,2, \ldots, N-1$ 。
65 |
66 | 二维DCT定义如下: 设 $f(x, y)$ 为 $M \times N$ 的数字图像矩阵, 则
67 |
68 | $$
69 | F(u, v)=\frac{2}{\sqrt{M N}} \sum_{x=0}^{M-1 N-1} f(x, y) C(u) C(v) \cos \frac{(2 x+1) u \pi}{2 M} \cos \frac{(2 y+1) v \pi}{2 N}\tag{2-54}
70 | $$
71 |
72 | 式中: $x, u=0,1,2, \ldots, M-1 ; y, v=0,1,2, \ldots, N-1$ 。
73 |
74 | 二维DCT逆变换定义如下:
75 | $$
76 | f(x, y)=\frac{2}{\sqrt{M N}} \sum_{u=0}^{M-1 N-1} \sum_{v=0} C(u) C(v) F(u, v) \cos \frac{(2 x+1) u \pi}{2 M} \cos \frac{(2 y+1) v \pi}{2 N}\tag{2-55}
77 | $$
78 |
79 | 式中: $x, u=0,1,2, \ldots, M-1 ; y, v=0,1,2, \ldots, N-1$ 。
80 |
81 | 类似一维矩阵形式的DCT, 可以写出二维DCT的矩阵形式
82 |
83 | 如下:
84 |
85 | $$
86 | F=G f G^{T}\tag{2-56}
87 | $$
88 |
89 | 同时, 由式(2-55)和式(2-54)可知二维DCT的逆变换核与正变换核相同, 且是可分离的, 即
90 |
91 | $$
92 | \begin{aligned}
93 | g(x, y, u, v) & =g_{1}(x, u) g_{2}(y, v) \\
94 | & =\frac{2}{\sqrt{M}} C(u) \cos \frac{(2 x+1) u \pi}{2 M} \cdot \frac{2}{\sqrt{N}} C(v) \cos \frac{(2 y+1) v \pi}{2 N}
95 | \end{aligned}\tag{2-57}
96 | $$
97 |
98 | 式中: $C(u)$ 和 $C(v)$ 的定义同式 (2-48); $x, u=0,1,2, \ldots, M-1;y, v=0,1,2, \ldots, N-1$ 。
99 |
100 | 通常根据可分离性,二维DCT可用两次一维DCT来完成,其算法流程与DFT类似,即
101 | $$
102 | \begin{align}
103 | f(x, y) &\rightarrow F_{行 }[f(x, y)]=F(x, v)\\
104 | &\stackrel{转置}{\rightarrow} F(x, v)^{T} \rightarrow F_{\text {列 }}\left[F(x, v)^{T}\right]=F(u, v)^{T}\\
105 | &\stackrel{转置}{\rightarrow}F(u, v)
106 | \end{align}\tag{2-58}
107 | $$
108 |
109 |
110 | ## 2.4.3 快速离散余弦变换
111 |
112 | 离散余弦变换的计算量相当大, 在实用中非常不方便, 也需要研究相应的快速算法。目前已有多种快速DCT(FCT), 在此介绍一种由FFT的思路发展起来的FCT。
113 |
114 | 首先, 将 $f(x)$ 延拓为
115 |
116 | $$
117 | f_{e}(x)= \begin{cases}f(x) & x=0,1,2, \ldots, N-1 \\ 0 & x=N, \quad N+1, \ldots, 2 N-1\end{cases}\tag{2-59}
118 | $$
119 |
120 | 按照一维DCT的定义, $f_{e}(x)$ 的DCT为
121 |
122 | $$
123 | F(0)=\frac{1}{\sqrt{N}} \sum_{x=0}^{N-1} f_{e}(x)\tag{2-60}
124 | $$
125 |
126 |
127 |
128 | $$
129 | \begin{aligned}
130 | F(u)
131 | &=\sqrt{\frac{2}{N}} \sum_{x=0}^{N-1} f(x) \cos \frac{(2 x+1) u \pi}{2 N} \\
132 | & =\sqrt{\frac{2}{N}} \sum_{x=0}^{N-1} f(x) \cos \frac{(2 x+1) u \pi}{2 N}+\sqrt{\frac{2}{N}} \sum_{x=N}^{2 N-1} 0 \cdot \cos \frac{(2 x+1) u \pi}{2 N} \\
133 | & =\sqrt{\frac{2}{N}} \sum_{x=0}^{N-1} f_{e}(x) \cos \frac{(2 x+1) u \pi}{2 N}+\sqrt{\frac{2}{N}} \sum_{x=N}^{2 N-1} f_{e}(x) \cdot \cos \frac{(2 x+1) u \pi}{2 N} \\
134 | & =\sqrt{\frac{2}{N}} \sum_{x=0}^{2 N-1} f_{e}(x) \cos \frac{(2 x+1) u \pi}{2 N} \\
135 | & =\sqrt{\frac{2}{N}} \operatorname{Re}\left\{\sum_{x=0}^{2 N-1} f_{e}(x) e^{-j \frac{(2 x+1) u \pi}{2 N}}\right\} \\
136 | & =\sqrt{\frac{2}{N}} \operatorname{Re}\left\{e^{-j \frac{u \pi}{2 N}} \cdot \sum_{x=0}^{2 N-1} f_{e}(x) e^{-j \frac{2 x u \pi}{2 N}}\right\}
137 | \end{aligned}\tag{2-61}
138 | $$
139 |
140 | 式中,$Re\{\cdot\}$表示取复数的实部
141 |
142 | 由于
143 | $$
144 | \sum_{e}^{2 N-1} f_{e}(x) e^{-j \dfrac{2 x u \pi}{2 N}}
145 | $$
146 | 因此,在作DFT时,可把长度为 $N$ 的 $f(x)$ 的长度延拓为 $2 N$ 点的序列 $f_{e}(x)$, 然后对 $f_{e}(x)$ 作 $DFT$ ,最后取DFT的实部便可得到DCT的结果。
147 |
148 | 同理对于离散余弦逆变换IDCT,可首先将 $F(u)$ 延拓为
149 |
150 | $$
151 | F_{e}(u)= \begin{cases}F(u) & u=0,1,2, \ldots, N-1 \\ 0 & u=N, N+1, \ldots, 2 N-1\end{cases}\tag{2-62}
152 | $$
153 |
154 |
155 |
156 | 由式(2-52)可得, DCT的IDCT为
157 |
158 | $$
159 | \begin{aligned}
160 | f(x)&=\sqrt{\frac{1}{N}} F_{e}(0)+\sqrt{\frac{2}{N}} \sum_{u=1}^{2 N-1} F_{e}(u) \cos \frac{(2 x+1) u \pi}{2 N} \\
161 | & =\sqrt{\frac{1}{N}} F_{e}(0)+\sqrt{\frac{2}{N}} \operatorname{Re}\left\{\sum_{u=1}^{2 N-1} F_{e}(u) e^{j \dfrac{(2 x+1) u \pi}{2 N}}\right\} \\
162 | & =\left(\sqrt{\frac{1}{N}}-\sqrt{\frac{2}{N}}\right) F_{e}(0)+\sqrt{\frac{2}{N}} \operatorname{Re}\left\{\sum_{u=0}^{2 N-1}\left[F_{e}(u) e^{j \dfrac{u \pi}{2 N}}\right] e^{j \dfrac{(2 x+1) u \pi}{2 N}}\right\}
163 | \end{aligned}\tag{2-63}
164 | $$
165 |
166 | 由式 (2-63) 可见, IDCT可由 $F_e(u) e^{j \frac{u \pi}{2 N}}$ 的 $2 N$ 点的IDFT来实现。
167 |
168 | 最后要注意的是二维DCT的频谱分布, 其谱域分布与DFT相差一倍, 如图2-11所示。
169 |
170 | 从图中可以看出, 对于DCT而言, $(0,0)$ 点对应于频谱的低频成分, $(N-1, N-1)$ 点对应于高频成分, 而同阶的DFT中, $(N / 2$, $N / 2$ )点对应于高频成分 (注: 此频谱图中末作频谱中心平移)。
171 |
172 | 由于DFT和IDFT已有快速算法FFT和IFFT, 因此可用它们实现快速DCT和IDCT算法FCT及IFCT。不过, 由于FFT及IFFT中要涉及到复数运算, 因此这种FCT及IFCT算法并不是最佳的。
173 |
174 |
12 |
13 | 图2-3 图2-1(a)波形的频域表示
14 | (a) 幅频特性; (b) 相频特性
15 |
16 | 时域和频域之间的变换可用数学公式表示如下:
17 | $$
18 | f(f){\Leftrightarrow} A(f), \Phi(f)\tag{2-1}
19 | $$
20 | 为能同时表示信号的振幅和相位,通常采用复数表示法,因此式(2-1)可用复数表示为
21 | $$
22 | f(f)\Leftrightarrow F(f)\tag{2-2}
23 | $$
24 | 完成这种变换,一般采用的方法是线性正交变换。
25 |
--------------------------------------------------------------------------------
/II/2.3 频域变换的一般表达式.md:
--------------------------------------------------------------------------------
1 | # 2.3 频域变换的一般表达式
2 |
3 | ## 2.3.1 可分离变换
4 |
5 | 二维傅立叶变换可用通用的关系式来表示:
6 | $$
7 | F(u, v)=\sum_{x=0}^{M-1} \sum_{y=0}^{N-1} f(x, y) g(x, y, u, v)
8 |
9 | \tag{2-36}
10 | $$
11 | $$
12 | f(x, y)=\sum_{u=0}^{M-1} \sum_{v=0}^{N-1} F(u, v) h(x, y, u, v)\tag{2-37}
13 | $$
14 |
15 | 式中:$x, u=0, 1, 2, …, M-1$;$y, v=0, 1, 2, …, N-1$;$g(x,y,u,v)$和$h(x,y,u,v)$分别称为正向变换核和反向变换核。
16 |
17 | 如果
18 | $$
19 | g(x, y, u, v)=g_1(x, u) g_2(y, v)\tag{2-38}
20 | $$
21 |
22 | $$
23 | h(x, y, u, v)=h_1(x, u) h_2(y, v)\tag{2-39}
24 | $$
25 |
26 | 则称正、反变换核是可分离的。进一步,如果$g_1$和$g_2$,$h_1$和$h_2$在函数形式上一样,则称该变换核是对称的。
27 |
28 | 二维傅立叶变换对是式(2-36)和式(2-37)的一个特殊情况, 它们的核为
29 | $$
30 | g(x, y, u, v)=e^{-j 2 \pi\left(\dfrac{u x}{M}+\dfrac{v y}{N}\right)}=e^{-j 2 \pi \dfrac{u x}{M}} \cdot e^{-j 2 \pi \dfrac{v y}{N}} \tag{2-40}
31 | $$
32 | $$
33 | h(x, y, u, v)=\frac{1}{M N} e^{j 2 \pi\left(\dfrac{u x}{M}+\dfrac{v y}{N}\right)}=\frac{1}{M} e^{j 2 \pi \dfrac{u x}{M}} \cdot \frac{1}{N} e^{j 2 \pi \dfrac{v y}{N}}\tag{2-41}
34 | $$
35 |
36 | 可见,它们都是可分离的和对称的。
37 |
38 | 如前所述,二维傅立叶变换可以利用变换核的可分离性, 用两次一维变换来实现,即可先对$f(x, y)$的每一行进行一维变换得到$F(x, v)$,再沿$F(x, v)$每一列取一维变换得到变换结果$F(u, v)
39 | $。对于其他的图像变换,只要其变换核是可分离的,同样也可用两次一维变换来实现。
40 |
41 | 如果先对$f(x, y)$的每一列进行一维变换得到$F(y, u)$,再沿$F(y, u)$每一行取一维变换得到$F(u, v)$,其最终结果是一样的。该结论对反变换核也适用。
42 |
43 | ## 2.3.2 图像变换的矩阵表示
44 |
45 | 数字图像都是实数矩阵, 设$f(x, y)$为$M\times N$的图像灰度矩阵, 通常为了分析、推导方便,可将可分离变换写成矩阵的形式:
46 | $$
47 | F=P f Q\tag{2-42}
48 | $$
49 |
50 | $$
51 | F=P^{-1} F Q^{-1}\tag{2-43}
52 | $$
53 |
54 | 其中,$F$、$f$是二维$M\times N$的矩阵;$P$是$M\times M$矩阵;$Q$是$N\times N$矩阵。
55 | $$
56 | F(u, v)=\sum_{x=0}^{M-1} \sum_{y=0}^{N-1} P(x, u) f(x, y) Q(y, v)\tag{2-44}
57 | $$
58 | 式中,$u=0, 1, 2, …, M-1,v=0, 1, 2, …, N-1$。对二维离散傅立叶变换,则有
59 | $$
60 | P(x, u)=g_1(x, u)=e^{-j 2 \pi u x / M}\tag{2-45}
61 | $$
62 |
63 | $$
64 | P(y, v)=g_2(x, v)=e^{-j 2 \pi v / N}\tag{2-46}
65 | $$
66 |
67 | 实践中,除了DFT变换之外,还采用许多其他的正交变换。例如:离散余弦变换、沃尔什-哈达玛变换、K-L变换等,下面将对常用的变换作一简要介绍。
68 |
--------------------------------------------------------------------------------
/II/2.4 离散余弦变换.md:
--------------------------------------------------------------------------------
1 | # 2.4 离散余弦变换(DCT)
2 |
3 | 离散余弦变换(Discrete Cosine Transform, DCT)的变换核为余弦函数。DCT除了具有一般的正交变换性质外, 它的变换阵的基向量能很好地描述人类语音信号和图像信号的相关特征。
4 |
5 | 因此,在对语音信号、图像信号的变换中,DCT变换被认为是一种准最佳变换。近年颁布的一系列视频压缩编码的国际标准建议中, 都把DCT作为其中的一个基本处理模块。除此之外, DCT 还是一种可分离的变换。
6 |
7 | ## 2.4.1 一维离散余弦变换
8 |
9 | 一维DCT的变换核定义为
10 |
11 | $$
12 | g(x, u)=C(u) \sqrt{\frac{2}{N}} \cos \frac{(2 x+1) u \pi}{2 N}\tag{2-47}
13 | $$
14 |
15 | 式中, $x, u=0,1,2, \ldots, N-1$;
16 | $$
17 | C(u)= \begin{cases}\frac{1}{\sqrt{2}} & u=0 \\ 1 & \text { 其他 }\end{cases}\tag{2-48}
18 | $$
19 |
20 | 一维DCT定义如下: 设 $\{f(x) \mid x=0,1, \ldots, N-1\}$ 为离散的信号列。
21 |
22 | $$
23 | F(u)=C(u) \sqrt{\frac{2}{N}} \sum_{x=0}^{N-1} f(x) \cos \frac{(2 x+1) u \pi}{2 N}\tag{2-49}
24 | $$
25 |
26 | 式中, $u, x=0,1,2, \ldots, N-1$ 。
27 |
28 | 将变换式展开整理后,可以㝍成矩阵的形式,即
29 | $$
30 | F=G f\tag{2-50}
31 | $$
32 |
33 | 其中
34 | $$
35 | G=
36 | \left[
37 | \begin{array}{}
38 | \dfrac{1}{\sqrt{N}}&[&1 &1 &\cdots &1 &]\\
39 | \sqrt{\dfrac{2}{N}}&[&\cos(\dfrac{\pi}{2N}) &\cos(\dfrac{3\pi}{2N}) &\cdots&\cos(\dfrac{(2N-1)\pi}{2N})&]\\
40 | \sqrt{\dfrac{2}{N}}&[&\cos(\dfrac{\pi}{2N}) &\cos(\dfrac{6\pi}{2N}) &\cdots &\cos(\dfrac{(2N-1)\pi}{2N})&]\\
41 | \vdots\\
42 | \sqrt{\dfrac{2}{N}}&[&\cos((N-1)\dfrac{\pi}{2N}) &\cos((N-1)\dfrac{3\pi}{2N}) &\cdots &\cos((N-1)\dfrac{(2N-1)\pi}{2N})&]\\
43 | \end{array}
44 | \right]\tag{2-51}
45 | $$
46 | 一维DCT的逆变换IDCT定义为
47 |
48 | $$
49 | f(x)=\sqrt{\frac{2}{N}} \sum_{u=0}^{N-1} C(u) F(u) \cos \frac{(2 x+1) u \pi}{2 N}\tag{2-52}
50 | $$
51 |
52 | 式中, $x, u=0,1,2, \ldots, N-1$ 。可见一维DCT的逆变换核与正变换核是相同的。
53 |
54 | ## 2.4.2二维离散余弦变换
55 |
56 | 考虑到两个变量, 很容易将一维DCT的定义推广到二维DCT。其正变换核为
57 | $$
58 | g(x, y, u, v)=\frac{2}{\sqrt{M N}} C(u) C(v) \cos \frac{(2 x+1) u \pi}{2 M} \cos \frac{(2 y+1) v \pi}{2 N}\tag{2-53}
59 | $$
60 |
61 |
62 | 式中, $C(u)$ 和 $C(v)$ 的定义同式 (2-48) ; $x, u=0,1,2, \ldots, M-1$;
63 |
64 | $y, v=0,1,2, \ldots, N-1$ 。
65 |
66 | 二维DCT定义如下: 设 $f(x, y)$ 为 $M \times N$ 的数字图像矩阵, 则
67 |
68 | $$
69 | F(u, v)=\frac{2}{\sqrt{M N}} \sum_{x=0}^{M-1 N-1} f(x, y) C(u) C(v) \cos \frac{(2 x+1) u \pi}{2 M} \cos \frac{(2 y+1) v \pi}{2 N}\tag{2-54}
70 | $$
71 |
72 | 式中: $x, u=0,1,2, \ldots, M-1 ; y, v=0,1,2, \ldots, N-1$ 。
73 |
74 | 二维DCT逆变换定义如下:
75 | $$
76 | f(x, y)=\frac{2}{\sqrt{M N}} \sum_{u=0}^{M-1 N-1} \sum_{v=0} C(u) C(v) F(u, v) \cos \frac{(2 x+1) u \pi}{2 M} \cos \frac{(2 y+1) v \pi}{2 N}\tag{2-55}
77 | $$
78 |
79 | 式中: $x, u=0,1,2, \ldots, M-1 ; y, v=0,1,2, \ldots, N-1$ 。
80 |
81 | 类似一维矩阵形式的DCT, 可以写出二维DCT的矩阵形式
82 |
83 | 如下:
84 |
85 | $$
86 | F=G f G^{T}\tag{2-56}
87 | $$
88 |
89 | 同时, 由式(2-55)和式(2-54)可知二维DCT的逆变换核与正变换核相同, 且是可分离的, 即
90 |
91 | $$
92 | \begin{aligned}
93 | g(x, y, u, v) & =g_{1}(x, u) g_{2}(y, v) \\
94 | & =\frac{2}{\sqrt{M}} C(u) \cos \frac{(2 x+1) u \pi}{2 M} \cdot \frac{2}{\sqrt{N}} C(v) \cos \frac{(2 y+1) v \pi}{2 N}
95 | \end{aligned}\tag{2-57}
96 | $$
97 |
98 | 式中: $C(u)$ 和 $C(v)$ 的定义同式 (2-48); $x, u=0,1,2, \ldots, M-1;y, v=0,1,2, \ldots, N-1$ 。
99 |
100 | 通常根据可分离性,二维DCT可用两次一维DCT来完成,其算法流程与DFT类似,即
101 | $$
102 | \begin{align}
103 | f(x, y) &\rightarrow F_{行 }[f(x, y)]=F(x, v)\\
104 | &\stackrel{转置}{\rightarrow} F(x, v)^{T} \rightarrow F_{\text {列 }}\left[F(x, v)^{T}\right]=F(u, v)^{T}\\
105 | &\stackrel{转置}{\rightarrow}F(u, v)
106 | \end{align}\tag{2-58}
107 | $$
108 |
109 |
110 | ## 2.4.3 快速离散余弦变换
111 |
112 | 离散余弦变换的计算量相当大, 在实用中非常不方便, 也需要研究相应的快速算法。目前已有多种快速DCT(FCT), 在此介绍一种由FFT的思路发展起来的FCT。
113 |
114 | 首先, 将 $f(x)$ 延拓为
115 |
116 | $$
117 | f_{e}(x)= \begin{cases}f(x) & x=0,1,2, \ldots, N-1 \\ 0 & x=N, \quad N+1, \ldots, 2 N-1\end{cases}\tag{2-59}
118 | $$
119 |
120 | 按照一维DCT的定义, $f_{e}(x)$ 的DCT为
121 |
122 | $$
123 | F(0)=\frac{1}{\sqrt{N}} \sum_{x=0}^{N-1} f_{e}(x)\tag{2-60}
124 | $$
125 |
126 |
127 |
128 | $$
129 | \begin{aligned}
130 | F(u)
131 | &=\sqrt{\frac{2}{N}} \sum_{x=0}^{N-1} f(x) \cos \frac{(2 x+1) u \pi}{2 N} \\
132 | & =\sqrt{\frac{2}{N}} \sum_{x=0}^{N-1} f(x) \cos \frac{(2 x+1) u \pi}{2 N}+\sqrt{\frac{2}{N}} \sum_{x=N}^{2 N-1} 0 \cdot \cos \frac{(2 x+1) u \pi}{2 N} \\
133 | & =\sqrt{\frac{2}{N}} \sum_{x=0}^{N-1} f_{e}(x) \cos \frac{(2 x+1) u \pi}{2 N}+\sqrt{\frac{2}{N}} \sum_{x=N}^{2 N-1} f_{e}(x) \cdot \cos \frac{(2 x+1) u \pi}{2 N} \\
134 | & =\sqrt{\frac{2}{N}} \sum_{x=0}^{2 N-1} f_{e}(x) \cos \frac{(2 x+1) u \pi}{2 N} \\
135 | & =\sqrt{\frac{2}{N}} \operatorname{Re}\left\{\sum_{x=0}^{2 N-1} f_{e}(x) e^{-j \frac{(2 x+1) u \pi}{2 N}}\right\} \\
136 | & =\sqrt{\frac{2}{N}} \operatorname{Re}\left\{e^{-j \frac{u \pi}{2 N}} \cdot \sum_{x=0}^{2 N-1} f_{e}(x) e^{-j \frac{2 x u \pi}{2 N}}\right\}
137 | \end{aligned}\tag{2-61}
138 | $$
139 |
140 | 式中,$Re\{\cdot\}$表示取复数的实部
141 |
142 | 由于
143 | $$
144 | \sum_{e}^{2 N-1} f_{e}(x) e^{-j \dfrac{2 x u \pi}{2 N}}
145 | $$
146 | 因此,在作DFT时,可把长度为 $N$ 的 $f(x)$ 的长度延拓为 $2 N$ 点的序列 $f_{e}(x)$, 然后对 $f_{e}(x)$ 作 $DFT$ ,最后取DFT的实部便可得到DCT的结果。
147 |
148 | 同理对于离散余弦逆变换IDCT,可首先将 $F(u)$ 延拓为
149 |
150 | $$
151 | F_{e}(u)= \begin{cases}F(u) & u=0,1,2, \ldots, N-1 \\ 0 & u=N, N+1, \ldots, 2 N-1\end{cases}\tag{2-62}
152 | $$
153 |
154 |
155 |
156 | 由式(2-52)可得, DCT的IDCT为
157 |
158 | $$
159 | \begin{aligned}
160 | f(x)&=\sqrt{\frac{1}{N}} F_{e}(0)+\sqrt{\frac{2}{N}} \sum_{u=1}^{2 N-1} F_{e}(u) \cos \frac{(2 x+1) u \pi}{2 N} \\
161 | & =\sqrt{\frac{1}{N}} F_{e}(0)+\sqrt{\frac{2}{N}} \operatorname{Re}\left\{\sum_{u=1}^{2 N-1} F_{e}(u) e^{j \dfrac{(2 x+1) u \pi}{2 N}}\right\} \\
162 | & =\left(\sqrt{\frac{1}{N}}-\sqrt{\frac{2}{N}}\right) F_{e}(0)+\sqrt{\frac{2}{N}} \operatorname{Re}\left\{\sum_{u=0}^{2 N-1}\left[F_{e}(u) e^{j \dfrac{u \pi}{2 N}}\right] e^{j \dfrac{(2 x+1) u \pi}{2 N}}\right\}
163 | \end{aligned}\tag{2-63}
164 | $$
165 |
166 | 由式 (2-63) 可见, IDCT可由 $F_e(u) e^{j \frac{u \pi}{2 N}}$ 的 $2 N$ 点的IDFT来实现。
167 |
168 | 最后要注意的是二维DCT的频谱分布, 其谱域分布与DFT相差一倍, 如图2-11所示。
169 |
170 | 从图中可以看出, 对于DCT而言, $(0,0)$ 点对应于频谱的低频成分, $(N-1, N-1)$ 点对应于高频成分, 而同阶的DFT中, $(N / 2$, $N / 2$ )点对应于高频成分 (注: 此频谱图中末作频谱中心平移)。
171 |
172 | 由于DFT和IDFT已有快速算法FFT和IFFT, 因此可用它们实现快速DCT和IDCT算法FCT及IFCT。不过, 由于FFT及IFFT中要涉及到复数运算, 因此这种FCT及IFCT算法并不是最佳的。
173 |
174 |  175 |
176 | 图2-11 DFT和DCT的频谱分布
177 |
178 | (a)DFT频谱分布; (b) DCT频谱分布
179 |
--------------------------------------------------------------------------------
/II/2.5 离散沃尔什-哈达玛变换(WHT).md:
--------------------------------------------------------------------------------
1 | # 2.5 离散沃尔什-哈达玛变换(WHT)
2 |
3 | ## 2.5.1 一维离散沃尔什-哈达玛变换
4 |
5 | ### 沃尔什函数
6 |
7 | 沃尔什函数是1923年由美国数学家沃尔什提出的。沃尔什函数系是一个完备正交函数系, 其值只能取 +1 和 -1 。从排列次序上可将沃尔什函数分为三种定义方法: 一种是按照沃尔什排列来定义 (按列率排序) ; 另一种是按照佩利排列来定义(按自然排序);第三种是按照哈达玛排列来定义。由于哈达玛排序的沃尔什函数是由 $2^{n}(n=0,1,2, \ldots)$ 阶哈达玛矩阵 (Hadamard Matrix) 得到的, 而哈达玛矩阵的最大优点在于它具有简单的递推关系, 即高阶矩阵可用两个低阶矩阵的克罗内克积求得, 因此在此只介绍哈达玛排列定义的沃尔什变换。
8 |
9 | $N=2^{n}(n=0,1,2, \ldots)$ 阶哈达玛矩阵每一行的符号变化规律对应于某一个沃尔什函数的符号变化规律, 即 $N=2 n(n=0,1,2, \ldots)$ 阶哈达玛矩阵的每一行对应于一个离散沃尔什函数, 哈达玛矩阵与沃尔什函数系不同之处仅仅是行的次序不同。 $2^{n}$ 阶哈达玛矩阵有如下形式:
10 | $$
11 | H_{1}=\text { [1] }\tag{2-64}
12 | $$
13 |
14 | $$
15 | H_{2}=\left[\begin{array}{rr}
16 | 1 & 1 \\
17 | 1 & -1
18 | \end{array}\right]\tag{2-65}
19 | $$
20 |
21 | $$
22 | H_{4}=\left[\begin{array}{rr}
23 | H_{2} & H_{2} \\
24 | H_{2} & -H_{2}
25 | \end{array}\right]=\left[\begin{array}{rrrr}
26 | 1 & 1 & 1 & 1 \\
27 | 1 & -1 & 1 & -1 \\
28 | 1 & 1 & -1 & -1 \\
29 | 1 & -1 & -1 & 1
30 | \end{array}\right]\tag{2-66}
31 | $$
32 |
33 | 哈达玛矩阵的阶数是按 $N=2^{n}(n=0,1,2, \ldots)$ 规律排列的, 阶数较高的哈达玛矩阵, 可以利用矩阵的克罗内克积运算, 由低阶哈达玛矩阵递推得到, 即
34 |
35 | $$
36 | H_{N}=H_{2^{n}}=H_{2} \otimes H_{2^{n-1}}=\left[\begin{array}{cc}
37 | H_{2^{n-1}} & H_{2^{n-1}} \\
38 | H_{2^{n-1}} & -H_{2^{n-1}}
39 | \end{array}\right]=\left[\begin{array}{cc}
40 | H_{\frac{N}{2}} & H_{\frac{N}{2}} \\
41 | H_{\frac{N}{2}} & -H_{\frac{N}{2}}
42 | \end{array}\right]\tag{2-67}
43 | $$
44 |
45 |
46 |
47 | 矩阵的克罗内克积 (Kronecker Product) 运算用符号记作$A \odot B$, 其运算规律如下:
48 |
49 | 设
50 |
51 | $$
52 | A=\left[\begin{array}{llll}
53 | a_{11} & a_{12} & \cdots & a_{1 n} \\
54 | a_{21} & a_{22} & \cdots & a_{2 n} \\
55 | \vdots & \vdots & \ddots & \vdots \\
56 | a_{m 1} & a_{m 2} & \cdots & a_{mn}
57 | \end{array}\right]&&
58 | B=\left[\begin{array}{rrrr}
59 | b_{11} & b_{12} & \cdots & b_{1 j} \\
60 | b_{21} & b_{22} & \cdots & a_{2 j} \\
61 | \vdots & \vdots & \ddots & \vdots \\
62 | b_{i 1} & b_{i 2} & \cdots & b_{i j}
63 | \end{array}\right]
64 | $$
65 |
66 | $$
67 |
68 | $$
69 |
70 | 则
71 |
72 | $$
73 | A \otimes B=\left[\begin{array}{llll}
74 | a_{11} B & a_{12} B & \cdots & a_{1 n} B \\
75 | a_{21} B & a_{22} B & \cdots & a_{2 n} B \\
76 | \vdots & \vdots & \ddots & \vdots \\
77 | a_{m 1} B & a_{m 2} B & \cdots & a_{m n} B
78 | \end{array}\right] \\
79 |
80 | \tag{2-68}
81 | $$
82 |
83 | $$
84 | B \otimes A=\left[\begin{array}{cccc}
85 | b_{11} A & b_{12} A & \cdots & b_{1 j} A \\
86 | b_{21} A & b_{22} A & \cdots & b_{2 j} A \\
87 | \vdots & \vdots & \ddots & \vdots \\
88 | b_{i 1} A & a_{i 2} A & \cdots & b_{i j} A
89 | \end{array}\right]\tag{2-69}
90 | $$
91 |
92 |
93 |
94 | ### 离散沃尔什-哈达玛变换
95 |
96 | 一维离散沃尔什变换定义为
97 |
98 | $$
99 | W(u)=\frac{1}{N} \sum_{x=0}^{N-1} f(x) W a l s h(u, x)\tag{2-70}
100 | $$
101 |
102 | 一维离散沃尔什逆变换定义为
103 |
104 | $$
105 | f(x)=\sum_{u=0}^{N-1} W(u) W a l s h(u, x)\tag{2-71}
106 | $$
107 |
108 | 式中, $\operatorname{Walsh}(u, x)$ 为沃尔什函数。若将 $W a l s h(u, x)$ 用哈达玛矩阵表示, 并将变换表达式写成矩阵形式, 则式(2-70)和式(2-71) 分别为
109 |
110 | $$
111 | \left[\begin{array}{c}
112 | W(0) \\
113 | W(1) \\
114 | \vdots \\
115 | W(N-1)
116 | \end{array}\right]=\frac{1}{N}\left[H_{N}\right]\left[\begin{array}{c}
117 | f(0) \\
118 | f(1) \\
119 | \vdots \\
120 | f(N-1)
121 | \end{array}\right]\tag{2-72}
122 | $$
123 |
124 | 和
125 |
126 | $$
127 | \left[\begin{array}{c}
128 | f(0) \\
129 | f(1) \\
130 | \vdots \\
131 | f(N-1)
132 | \end{array}\right]=\left[H_{N}\right]\left[\begin{array}{c}
133 | W(0) \\
134 | W(1) \\
135 | \vdots \\
136 | W(N-1)
137 | \end{array}\right]\tag{2-73}
138 | $$
139 |
140 | 式中, $\left[H_{N}\right]$ 为 $N$ 阶哈达玛矩阵。 由哈达玛矩阵的特点可知, 沃尔什-哈达玛变换的本质上是
141 |
142 | 由哈达玛矩阵的特点可知,沃尔什-哈达玛变换的本质上是将离散序列 $f(x)$ 的各项值的符号按一定规律改变后, 进行加减运算, 因此, 它比采用复数运算的DFT和采用余弦运算的DCT要简单得多。
143 |
144 |
145 |
146 | ## 2.5.2 二维离散沃尔什变换
147 |
148 | 很容易将一维WHT的定义推广到二维WHT。二维WHT的正变换核和逆变换核分别为
149 |
150 | $$
151 | W(u, v)=\frac{1}{M N} \sum_{x=0}^{M-1} \sum_{y=0}^{N-1} f(x, y) W a l s h(u, x) W slsh(v, y)\tag{2-74}
152 | $$
153 |
154 | 和
155 |
156 | $$
157 | f(x, y)=\sum_{u=0}^{M-1} \sum_{v=0}^{N-1} W(u, v) W a l s h(u, x) W s
158 | lsh(v, y)\tag{2-75}
159 | $$
160 |
161 | 式中: $x, u=0,1,2, \ldots, M-1 ; y, v=0,1,2, \ldots, N-1$ 。
162 |
163 | ---
164 |
165 | 二维离散沃尔什变换的矩阵形式表达式为
166 | $$
167 | f_{1}=\left[\begin{array}{llll}1 & 3 & 3 & 1 \\ 1 & 3 & 3 & 1 \\ 1 & 3 & 3 & 1 \\ 1 & 3 & 3 & 1\end{array}\right]
168 | $$
169 | 和
170 | $$
171 | f_{1}=\left[\begin{array}{llll}1 & 1 & 1 & 1 \\ 1 & 1 & 1 & 1 \\ 1 & 1 & 1 & 1 \\ 1 & 1 & 1 & 1\end{array}\right]
172 | $$
173 |
174 | 求这两个信号的二维WHT。
175 |
176 | 根据题意, 式 (2-76) 中的 $M=N=4$, 其二维WHT变换核为
177 | $$
178 | H_{4}=\left[\begin{array}{rrrr}
179 | 1 & 1 & 1 & 1 \\
180 | 1 & -1 & 1 & -1 \\
181 | 1 & 1 & -1 & -1 \\
182 | 1 & -1 & -1 & 1
183 | \end{array}\right]
184 | $$
185 |
186 | 所以
187 |
188 | $$
189 | \begin{aligned}
190 | W_{1} & =\frac{1}{4^{2}}\left[\begin{array}{rrrr}
191 | 1 & 1 & 1 & 1 \\
192 | 1 & -1 & 1 & -1 \\
193 | 1 & 1 & -1 & -1 \\
194 | 1 & -1 & -1 & 1
195 | \end{array}\right]\left[\begin{array}{rrrr}
196 | 1 & 3 & 3 & 1 \\
197 | 1 & 3 & 3 & 1 \\
198 | 1 & 3 & 3 & 1 \\
199 | 1 & 3 & 3 & 1
200 | \end{array}\right]\left[\begin{array}{rrrr}
201 | 1 & 1 & 1 & 1 \\
202 | 1 & -1 & 1 & -1 \\
203 | 1 & 1 & -1 & -1 \\
204 | 1 & -1 & -1 & 1
205 | \end{array}\right]
206 | =\left[\begin{array}{rrrr}
207 | 2 & 0 & 0 & -1 \\
208 | 0 & 0 & 0 & 0 \\
209 | 0 & 0 & 0 & 0 \\
210 | 0 & 0 & 0 & 0
211 | \end{array}\right]
212 | \end{aligned}
213 | $$
214 |
215 |
216 |
217 | $$
218 | W_{2}=\frac{1}{4^{2}}\left[\begin{array}{rrrr}
219 | 1 & 1 & 1 & 1 \\
220 | 1 & -1 & 1 & -1 \\
221 | 1 & 1 & -1 & -1 \\
222 | 1 & -1 & -1 & 1
223 | \end{array}\right]\left[\begin{array}{rrrr}
224 | 1 & 1 & 1 & 1 \\
225 | 1 & 1 & 1 & 1 \\
226 | 1 & 1 & 1 & 1 \\
227 | 1 & 1 & 1 & 1
228 | \end{array}\right]\left[\begin{array}{rrrr}
229 | 1 & 1 & 1 & 1 \\
230 | 1 & -1 & 1 & -1 \\
231 | 1 & 1 & -1 & -1 \\
232 | 1 & -1 & -1 & 1
233 | \end{array}\right]
234 |
235 | =\left[\begin{array}{rrrr}
236 | 1 & 0 & 0 & 0 \\
237 | 0 & 0 & 0 & 0 \\
238 | 0 & 0 & 0 & 0 \\
239 | 0 & 0 & 0 & 0
240 | \end{array}\right]
241 | $$
242 |
243 | ---
244 |
245 | 再如, 图2-12是一幅数字图像及对其进行二维WHT变换的结果。
246 |
247 |
175 |
176 | 图2-11 DFT和DCT的频谱分布
177 |
178 | (a)DFT频谱分布; (b) DCT频谱分布
179 |
--------------------------------------------------------------------------------
/II/2.5 离散沃尔什-哈达玛变换(WHT).md:
--------------------------------------------------------------------------------
1 | # 2.5 离散沃尔什-哈达玛变换(WHT)
2 |
3 | ## 2.5.1 一维离散沃尔什-哈达玛变换
4 |
5 | ### 沃尔什函数
6 |
7 | 沃尔什函数是1923年由美国数学家沃尔什提出的。沃尔什函数系是一个完备正交函数系, 其值只能取 +1 和 -1 。从排列次序上可将沃尔什函数分为三种定义方法: 一种是按照沃尔什排列来定义 (按列率排序) ; 另一种是按照佩利排列来定义(按自然排序);第三种是按照哈达玛排列来定义。由于哈达玛排序的沃尔什函数是由 $2^{n}(n=0,1,2, \ldots)$ 阶哈达玛矩阵 (Hadamard Matrix) 得到的, 而哈达玛矩阵的最大优点在于它具有简单的递推关系, 即高阶矩阵可用两个低阶矩阵的克罗内克积求得, 因此在此只介绍哈达玛排列定义的沃尔什变换。
8 |
9 | $N=2^{n}(n=0,1,2, \ldots)$ 阶哈达玛矩阵每一行的符号变化规律对应于某一个沃尔什函数的符号变化规律, 即 $N=2 n(n=0,1,2, \ldots)$ 阶哈达玛矩阵的每一行对应于一个离散沃尔什函数, 哈达玛矩阵与沃尔什函数系不同之处仅仅是行的次序不同。 $2^{n}$ 阶哈达玛矩阵有如下形式:
10 | $$
11 | H_{1}=\text { [1] }\tag{2-64}
12 | $$
13 |
14 | $$
15 | H_{2}=\left[\begin{array}{rr}
16 | 1 & 1 \\
17 | 1 & -1
18 | \end{array}\right]\tag{2-65}
19 | $$
20 |
21 | $$
22 | H_{4}=\left[\begin{array}{rr}
23 | H_{2} & H_{2} \\
24 | H_{2} & -H_{2}
25 | \end{array}\right]=\left[\begin{array}{rrrr}
26 | 1 & 1 & 1 & 1 \\
27 | 1 & -1 & 1 & -1 \\
28 | 1 & 1 & -1 & -1 \\
29 | 1 & -1 & -1 & 1
30 | \end{array}\right]\tag{2-66}
31 | $$
32 |
33 | 哈达玛矩阵的阶数是按 $N=2^{n}(n=0,1,2, \ldots)$ 规律排列的, 阶数较高的哈达玛矩阵, 可以利用矩阵的克罗内克积运算, 由低阶哈达玛矩阵递推得到, 即
34 |
35 | $$
36 | H_{N}=H_{2^{n}}=H_{2} \otimes H_{2^{n-1}}=\left[\begin{array}{cc}
37 | H_{2^{n-1}} & H_{2^{n-1}} \\
38 | H_{2^{n-1}} & -H_{2^{n-1}}
39 | \end{array}\right]=\left[\begin{array}{cc}
40 | H_{\frac{N}{2}} & H_{\frac{N}{2}} \\
41 | H_{\frac{N}{2}} & -H_{\frac{N}{2}}
42 | \end{array}\right]\tag{2-67}
43 | $$
44 |
45 |
46 |
47 | 矩阵的克罗内克积 (Kronecker Product) 运算用符号记作$A \odot B$, 其运算规律如下:
48 |
49 | 设
50 |
51 | $$
52 | A=\left[\begin{array}{llll}
53 | a_{11} & a_{12} & \cdots & a_{1 n} \\
54 | a_{21} & a_{22} & \cdots & a_{2 n} \\
55 | \vdots & \vdots & \ddots & \vdots \\
56 | a_{m 1} & a_{m 2} & \cdots & a_{mn}
57 | \end{array}\right]&&
58 | B=\left[\begin{array}{rrrr}
59 | b_{11} & b_{12} & \cdots & b_{1 j} \\
60 | b_{21} & b_{22} & \cdots & a_{2 j} \\
61 | \vdots & \vdots & \ddots & \vdots \\
62 | b_{i 1} & b_{i 2} & \cdots & b_{i j}
63 | \end{array}\right]
64 | $$
65 |
66 | $$
67 |
68 | $$
69 |
70 | 则
71 |
72 | $$
73 | A \otimes B=\left[\begin{array}{llll}
74 | a_{11} B & a_{12} B & \cdots & a_{1 n} B \\
75 | a_{21} B & a_{22} B & \cdots & a_{2 n} B \\
76 | \vdots & \vdots & \ddots & \vdots \\
77 | a_{m 1} B & a_{m 2} B & \cdots & a_{m n} B
78 | \end{array}\right] \\
79 |
80 | \tag{2-68}
81 | $$
82 |
83 | $$
84 | B \otimes A=\left[\begin{array}{cccc}
85 | b_{11} A & b_{12} A & \cdots & b_{1 j} A \\
86 | b_{21} A & b_{22} A & \cdots & b_{2 j} A \\
87 | \vdots & \vdots & \ddots & \vdots \\
88 | b_{i 1} A & a_{i 2} A & \cdots & b_{i j} A
89 | \end{array}\right]\tag{2-69}
90 | $$
91 |
92 |
93 |
94 | ### 离散沃尔什-哈达玛变换
95 |
96 | 一维离散沃尔什变换定义为
97 |
98 | $$
99 | W(u)=\frac{1}{N} \sum_{x=0}^{N-1} f(x) W a l s h(u, x)\tag{2-70}
100 | $$
101 |
102 | 一维离散沃尔什逆变换定义为
103 |
104 | $$
105 | f(x)=\sum_{u=0}^{N-1} W(u) W a l s h(u, x)\tag{2-71}
106 | $$
107 |
108 | 式中, $\operatorname{Walsh}(u, x)$ 为沃尔什函数。若将 $W a l s h(u, x)$ 用哈达玛矩阵表示, 并将变换表达式写成矩阵形式, 则式(2-70)和式(2-71) 分别为
109 |
110 | $$
111 | \left[\begin{array}{c}
112 | W(0) \\
113 | W(1) \\
114 | \vdots \\
115 | W(N-1)
116 | \end{array}\right]=\frac{1}{N}\left[H_{N}\right]\left[\begin{array}{c}
117 | f(0) \\
118 | f(1) \\
119 | \vdots \\
120 | f(N-1)
121 | \end{array}\right]\tag{2-72}
122 | $$
123 |
124 | 和
125 |
126 | $$
127 | \left[\begin{array}{c}
128 | f(0) \\
129 | f(1) \\
130 | \vdots \\
131 | f(N-1)
132 | \end{array}\right]=\left[H_{N}\right]\left[\begin{array}{c}
133 | W(0) \\
134 | W(1) \\
135 | \vdots \\
136 | W(N-1)
137 | \end{array}\right]\tag{2-73}
138 | $$
139 |
140 | 式中, $\left[H_{N}\right]$ 为 $N$ 阶哈达玛矩阵。 由哈达玛矩阵的特点可知, 沃尔什-哈达玛变换的本质上是
141 |
142 | 由哈达玛矩阵的特点可知,沃尔什-哈达玛变换的本质上是将离散序列 $f(x)$ 的各项值的符号按一定规律改变后, 进行加减运算, 因此, 它比采用复数运算的DFT和采用余弦运算的DCT要简单得多。
143 |
144 |
145 |
146 | ## 2.5.2 二维离散沃尔什变换
147 |
148 | 很容易将一维WHT的定义推广到二维WHT。二维WHT的正变换核和逆变换核分别为
149 |
150 | $$
151 | W(u, v)=\frac{1}{M N} \sum_{x=0}^{M-1} \sum_{y=0}^{N-1} f(x, y) W a l s h(u, x) W slsh(v, y)\tag{2-74}
152 | $$
153 |
154 | 和
155 |
156 | $$
157 | f(x, y)=\sum_{u=0}^{M-1} \sum_{v=0}^{N-1} W(u, v) W a l s h(u, x) W s
158 | lsh(v, y)\tag{2-75}
159 | $$
160 |
161 | 式中: $x, u=0,1,2, \ldots, M-1 ; y, v=0,1,2, \ldots, N-1$ 。
162 |
163 | ---
164 |
165 | 二维离散沃尔什变换的矩阵形式表达式为
166 | $$
167 | f_{1}=\left[\begin{array}{llll}1 & 3 & 3 & 1 \\ 1 & 3 & 3 & 1 \\ 1 & 3 & 3 & 1 \\ 1 & 3 & 3 & 1\end{array}\right]
168 | $$
169 | 和
170 | $$
171 | f_{1}=\left[\begin{array}{llll}1 & 1 & 1 & 1 \\ 1 & 1 & 1 & 1 \\ 1 & 1 & 1 & 1 \\ 1 & 1 & 1 & 1\end{array}\right]
172 | $$
173 |
174 | 求这两个信号的二维WHT。
175 |
176 | 根据题意, 式 (2-76) 中的 $M=N=4$, 其二维WHT变换核为
177 | $$
178 | H_{4}=\left[\begin{array}{rrrr}
179 | 1 & 1 & 1 & 1 \\
180 | 1 & -1 & 1 & -1 \\
181 | 1 & 1 & -1 & -1 \\
182 | 1 & -1 & -1 & 1
183 | \end{array}\right]
184 | $$
185 |
186 | 所以
187 |
188 | $$
189 | \begin{aligned}
190 | W_{1} & =\frac{1}{4^{2}}\left[\begin{array}{rrrr}
191 | 1 & 1 & 1 & 1 \\
192 | 1 & -1 & 1 & -1 \\
193 | 1 & 1 & -1 & -1 \\
194 | 1 & -1 & -1 & 1
195 | \end{array}\right]\left[\begin{array}{rrrr}
196 | 1 & 3 & 3 & 1 \\
197 | 1 & 3 & 3 & 1 \\
198 | 1 & 3 & 3 & 1 \\
199 | 1 & 3 & 3 & 1
200 | \end{array}\right]\left[\begin{array}{rrrr}
201 | 1 & 1 & 1 & 1 \\
202 | 1 & -1 & 1 & -1 \\
203 | 1 & 1 & -1 & -1 \\
204 | 1 & -1 & -1 & 1
205 | \end{array}\right]
206 | =\left[\begin{array}{rrrr}
207 | 2 & 0 & 0 & -1 \\
208 | 0 & 0 & 0 & 0 \\
209 | 0 & 0 & 0 & 0 \\
210 | 0 & 0 & 0 & 0
211 | \end{array}\right]
212 | \end{aligned}
213 | $$
214 |
215 |
216 |
217 | $$
218 | W_{2}=\frac{1}{4^{2}}\left[\begin{array}{rrrr}
219 | 1 & 1 & 1 & 1 \\
220 | 1 & -1 & 1 & -1 \\
221 | 1 & 1 & -1 & -1 \\
222 | 1 & -1 & -1 & 1
223 | \end{array}\right]\left[\begin{array}{rrrr}
224 | 1 & 1 & 1 & 1 \\
225 | 1 & 1 & 1 & 1 \\
226 | 1 & 1 & 1 & 1 \\
227 | 1 & 1 & 1 & 1
228 | \end{array}\right]\left[\begin{array}{rrrr}
229 | 1 & 1 & 1 & 1 \\
230 | 1 & -1 & 1 & -1 \\
231 | 1 & 1 & -1 & -1 \\
232 | 1 & -1 & -1 & 1
233 | \end{array}\right]
234 |
235 | =\left[\begin{array}{rrrr}
236 | 1 & 0 & 0 & 0 \\
237 | 0 & 0 & 0 & 0 \\
238 | 0 & 0 & 0 & 0 \\
239 | 0 & 0 & 0 & 0
240 | \end{array}\right]
241 | $$
242 |
243 | ---
244 |
245 | 再如, 图2-12是一幅数字图像及对其进行二维WHT变换的结果。
246 |
247 |  248 |
249 | 图2-12二维WHT结果
250 | (a)原图像;(b) WHT结果
251 |
252 | 注: 图2-12中的结果是按哈达玛变换后再用沃尔什排序的结果。
253 |
254 | 从以上例子可看出, 二维WHT具有能量集中的特性, 而且原始数据中数字越是均匀分布, 经变换后的数据越集中于矩阵的边角上。因此,二维WHT可用于压缩图像信息。
255 |
256 | ## 2.5.3 快速沃尔什变换(FWHT)
257 |
258 | 类似于FFT, WHT也有快速算法FWHT, 也可将输入序列 $f(x)$ 按奇偶进行分组, 分别进行WHT。FWHT的基本关系为
259 |
260 | $$
261 | \left\{\begin{array}{l}
262 | W(u)=\dfrac{1}{2}\left[W_{e}(u)+W_{o}(u)\right] \\
263 | W\left(u+\frac{N}{2}\right)=\dfrac{1}{2}\left[W_{e}(u)-W_{o}(u)\right]
264 | \end{array}\right.\tag{2-78}
265 | $$
266 |
267 | WHT的变换核是可分离和对称的, 因此二维WHT也可分为两个一维的WHT分别用FWHT进行变换而得到最终结果, 由此便可实现二维的FWHT。
268 |
269 | 综上所述, WHT是将一个函数变换成取值为 +1 或 -1 的基本函数构成的级数, 用它来逼近数字脉冲信号时要比FFT有利。
270 |
271 | 同时, WHT只需要进行实数运算, 存储量比FFT要少得多,运算速度也快得多。因此, WHT在图像传输、通信技术和数据压缩中被广泛使用。
--------------------------------------------------------------------------------
/II/2.6 实现图像变换的VC++编程.md:
--------------------------------------------------------------------------------
1 | # 2.6 用Matrix \
248 |
249 | 图2-12二维WHT结果
250 | (a)原图像;(b) WHT结果
251 |
252 | 注: 图2-12中的结果是按哈达玛变换后再用沃尔什排序的结果。
253 |
254 | 从以上例子可看出, 二维WHT具有能量集中的特性, 而且原始数据中数字越是均匀分布, 经变换后的数据越集中于矩阵的边角上。因此,二维WHT可用于压缩图像信息。
255 |
256 | ## 2.5.3 快速沃尔什变换(FWHT)
257 |
258 | 类似于FFT, WHT也有快速算法FWHT, 也可将输入序列 $f(x)$ 按奇偶进行分组, 分别进行WHT。FWHT的基本关系为
259 |
260 | $$
261 | \left\{\begin{array}{l}
262 | W(u)=\dfrac{1}{2}\left[W_{e}(u)+W_{o}(u)\right] \\
263 | W\left(u+\frac{N}{2}\right)=\dfrac{1}{2}\left[W_{e}(u)-W_{o}(u)\right]
264 | \end{array}\right.\tag{2-78}
265 | $$
266 |
267 | WHT的变换核是可分离和对称的, 因此二维WHT也可分为两个一维的WHT分别用FWHT进行变换而得到最终结果, 由此便可实现二维的FWHT。
268 |
269 | 综上所述, WHT是将一个函数变换成取值为 +1 或 -1 的基本函数构成的级数, 用它来逼近数字脉冲信号时要比FFT有利。
270 |
271 | 同时, WHT只需要进行实数运算, 存储量比FFT要少得多,运算速度也快得多。因此, WHT在图像传输、通信技术和数据压缩中被广泛使用。
--------------------------------------------------------------------------------
/II/2.6 实现图像变换的VC++编程.md:
--------------------------------------------------------------------------------
1 | # 2.6 用Matrix \