├── .gitignore
├── README.md
├── docs
├── Architecture
│ ├── chapter1.md
│ ├── chapter2.md
│ ├── chapter3.md
│ ├── chapter4.md
│ ├── chapter5.md
│ ├── chapter6.md
│ └── chapter7.md
├── ComputerNetwork
│ ├── 《计算机网络》第一次作业.md
│ ├── 《计算机网络》第三章作业.md
│ ├── 《计算机网络》第九章作业.md
│ ├── 《计算机网络》第二章作业.md
│ ├── 《计算机网络》第五章作业.md
│ ├── 《计算机网络》第六章作业.md
│ └── 《计算机网络》第四章作业.md
├── MachineLearning
│ ├── 第一章作业.md
│ ├── 第七章作业.md
│ ├── 第三章作业.md
│ ├── 第九章作业.md
│ ├── 第二章作业.md
│ ├── 第五章作业.md
│ ├── 第八章作业.md
│ ├── 第六章作业.md
│ └── 第四章作业.md
├── OperatingSystem
│ └── index.md
├── ProfessionalBasicAptitudeTest
│ └── index.md
├── SoftwareEngineering
│ ├── 软工应用分析题.md
│ └── 软工期末考试.md
└── index.md
└── mkdocs.yml
/.gitignore:
--------------------------------------------------------------------------------
1 | site
--------------------------------------------------------------------------------
/README.md:
--------------------------------------------------------------------------------
1 | # ComputerScienceCourse
2 | 重庆大学计算机学院专业课程
3 |
--------------------------------------------------------------------------------
/docs/Architecture/chapter1.md:
--------------------------------------------------------------------------------
1 | ## 背景
2 |
3 | ### big.LITTLE
4 |
5 | 大核:高性能计算;小核:低能耗
6 |
7 | 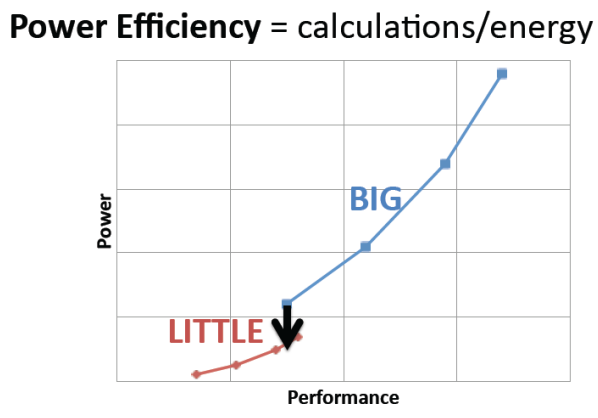
8 |
9 | ### 四堵墙
10 |
11 | - **频率墙**:工艺进入超深亚微米后,线延时超过门延时而占据主导地位;
12 |
13 | - **功耗墙**(Power Wall):漏流增大,功耗增大,导致芯片过热,器件的稳定性下降,信号噪声增大,无法正常工作;
14 |
15 | - **存储墙**(Memory Wall):通信带宽和延迟构成;
16 |
17 | - **应用墙**:每一种处理器在各自的领域内都有着很高的性能。但如果应用条件发生变化则会导致性能明显下降,导致通用微处理器并不通用。
18 |
19 | ### 基础定义
20 |
21 | 
22 |
23 |
24 |
25 | ## C&A:计算机系统结构
26 |
27 | 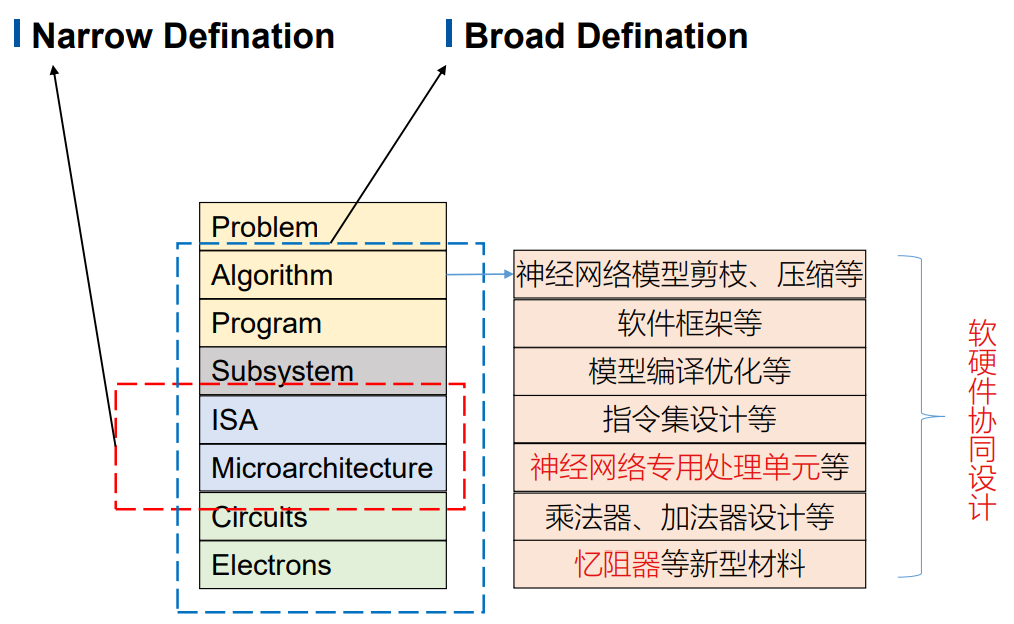
28 |
29 | - classical definition:程序员所看到的计算机的属性,即程序员编写出的能在机器上正确运行的程序所必须了解到的概念性结构和功能特性。
30 |
31 | - broadest definition:使用各种可行的制造工艺进行抽象层的设计,使得应用程序有效运行。
32 |
33 |
34 |
35 | ## 摩尔定律
36 |
37 | - **集成电路芯片上所集成的电路的数目,每隔18个月就翻一番。**
38 | - **微处理器的性能每隔18个月提高一倍,而价格下降一倍。**
39 |
40 | 
41 |
42 | ### 新摩尔定律
43 |
44 | - DLP比TLP带来的并行计算的能力增长更多
45 | - 翻倍的不再是晶体管(集成电路)和处理器速度,而是**processor的数量**,未来计算机硬件不会更快,但是会**更宽**.(比如并行处理能力)
46 |
47 |
48 |
49 | ## 冯·诺依曼计算机
50 |
51 | 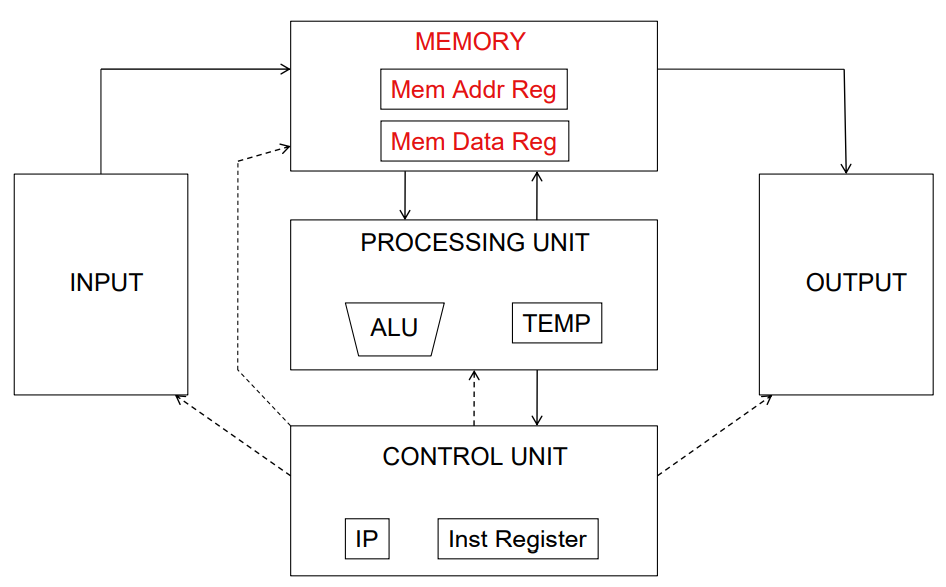
52 |
53 |
54 |
55 |
--------------------------------------------------------------------------------
/docs/Architecture/chapter2.md:
--------------------------------------------------------------------------------
1 | ## Power:功耗
2 |
3 | ### 动态功耗
4 |
5 | - traditionally dominant component:传统上占主导地位的部分?
6 | - dissipated when transitor switches :晶体管切换
7 |
8 | #### Dynamic energy
9 |
10 | Transistor switch from 0 -> 1 or 1 -> 0
11 | $$
12 | \text {Energy}_\text{dynamic} \propto \frac12 \times \text{Capacitive load} \times \text{Voltage}^2
13 | $$
14 |
15 | #### Dynamic power
16 |
17 | $$
18 | \text {Power}_\text{dynamic} \propto \frac12 \times \text{Capacitive load} \times \text{Voltage}^2 \times \text{Frequency switched}
19 | $$
20 |
21 | **ATTENTION**: Reducing clock rate reduces power, **NOT** energy.
22 |
23 | #### Techniques for reducing power
24 |
25 | - Do nothing well
26 | - Dynamic Voltage-Frequency Scaling (**DVFS**)
27 | - Low power state for DRAM, disks
28 | - Overclocking, turning off cores
29 |
30 | > 例子:DVFS is a low-power design technique that is becoming pervasive in modern processors
31 | >
32 | > If the **voltage** and **frequency** of a processing core are both **reduced by 15%** what would be the impact on dynamic power?
33 | >
34 | > 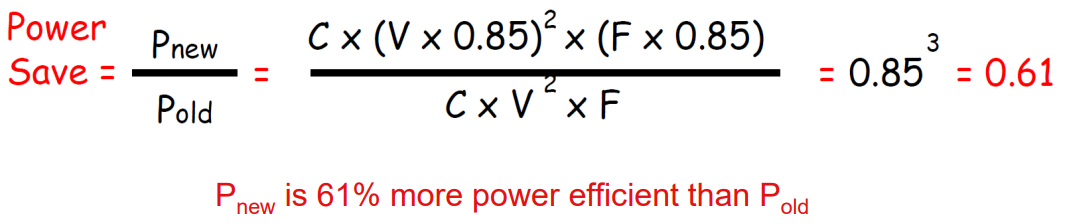
35 |
36 | ### 静态功耗
37 |
38 | - becoming more important with transitor scaling:随着晶体管规模的扩大而变得更加重要
39 | - due to "leakege current" that flows even if there is no switching activity:由于 "泄漏电流 "的存在,即使没有开关活动,也会流动
40 | - proportional to the number of transitors on the chip:与芯片上的晶体管数量成正比
41 |
42 | $$
43 | \text {Power}_\text{static} \propto \text{Current}_\text{static} \times \text{Voltage}
44 | $$
45 |
46 | - Scales with number of transistors
47 |
48 | - To reduce: power gating
49 |
50 |
51 |
52 | ## Cost:价格/成本
53 |
54 | - Cost driven down by learning curve: 成本因学习曲线而降低
55 | - Yield: 产量
56 | - DRAM: price closely tracks cost: 价格紧跟成本
57 | - Microprocessors: price depends on volume: 微处理器:价格取决于体积
58 | - 10% less for each doubling of volume
59 |
60 | ### Integrated Circuit Cost:集成电路成本
61 |
62 | - Integrated circuit
63 |
64 | $$
65 | \text{Cost of intergrated circuit} = \frac{\text{Cost of die} + \text{Cost of testing die} + \text{Cost of packaging and final test}}{\text{Final test yield}}
66 | $$
67 |
68 | $$
69 | \text{Cost of die} = \frac{\text{Cost of wafer}}{\text{Dies per wafer} \times \text{Dies yield}}
70 | $$
71 |
72 | $$
73 | \text{Dies per wafer} = \frac{\pi \times (\frac{\text{Wafer diameter}}{2})^2}{\text{Die area}} = \frac{\pi \times \text{Wafer diameter}}{\sqrt{2\times \text{Die area}}}
74 | $$
75 |
76 | - **Bose-Einstein formula**
77 |
78 | 下面的$\text{Defect per unit area}$一般为$0.016-0.057$ defects per square cm(2010);
79 |
80 | $N$为process-complexity factor = $11.5-15.5$ (40 nm, 2010)
81 |
82 | $$
83 | \text{Die yield} = \text{Wafer yield}\times \frac{1}{(1+\text{Defect per unit area}\times \text{Die area})^N}
84 | $$
85 |
86 | > 
87 |
88 | > 
89 |
90 |
91 |
92 | ## Performance:性能
93 |
94 | 评价指标:
95 |
96 | - Time to run the task:execution time(执行时间), response time(反应时间), elapsed time(经历时间), **latency**(时延)
97 | - Tasks per time unit:execution rate(执行率), bandwidth(带宽), throughput(吞吐量)
98 |
99 | ### Latency vs. Throughput
100 |
101 | #### Latency
102 |
103 | - “real” time necessary to complete a task
104 | - important when the focus is on a **single task**
105 | - a computer user who is working with a single application
106 | - a critical task of a real-time embedded system
107 |
108 | #### Throughput (aka Bandwidth)
109 |
110 | - **number of tasks completed per unit of time**
111 | - a metric independent from the exact number of executed tasks
112 | - important when the focus is on running **many tasks**
113 | - a manager of a large data-processing center is interested in the total amount of work done in a given time
114 |
115 | #### Example: Pipelining
116 |
117 | - **increases** the instruction **throughput**
118 | - does **NOT reduce** (in fact, it usually slightly increases) **the execution time of an individual instruction**
119 |
120 |
121 |
122 | ### Performance Metrics
123 |
124 | - Machine X is $n$ times faster than machine Y
125 | $$
126 | n = \frac{executionTime(Y)}{executionTime(X)}=\frac{performance(X)}{performance(Y)}
127 | $$
128 |
129 |
130 |
131 | ### Benchmark Suites:测试套件?
132 |
133 | Sets of **programs** to **simulate** typical workloads
134 |
135 | - real software applications
136 | - most accurate but typically longer to process
137 | - portability problems (OS/compiler dependencies), GUI
138 | - kernels
139 | - small, key pieces taken from real programs
140 | - limited picture, but good to isolate the performance of individual features of a machine
141 | - synthetic benchmarks
142 | - try to match the average frequency of operations on operands of a real program
143 | - try to match the average frequency of operations on operands of a real program
144 |
145 |
146 |
147 | ### Principle of Locality:局部性原理
148 |
149 | #### Temporal Locality:空间局部性
150 |
151 | a resource that is **referenced** at one point in time **will be referenced again** sometime in the near future
152 |
153 | 一个资源引用完后,旁边的资源很可能马上被用到
154 |
155 | #### Spatial Locality:时间局部性
156 |
157 | the likelihood of referencing a resource is higher if a resource **near it was just referenced**
158 |
159 | 一个资源引用完后,同一个资源很可能马上被用到
160 |
161 | #### Example: Cache
162 |
163 | - directly exploits **temporal locality** providing faster access to a smaller subset of the main memory which contains copy of data recently used
164 | - all data in the cache are not **necessarily data** that are spatially close in the main memory
165 | - when a cache miss occurs a fixed-size block of contiguous memory cells is retrieved from the main memory based on the principle of **spatial locality**
166 |
167 |
168 |
169 | ### “Make the Common Case Fast”
170 |
171 | - in making a design trade-off…
172 | - favor the frequent case rather than infrequent case
173 | - when determining how to allocate resources…
174 | - favor the frequent event rather than the rare event
175 | - when optimizing the design of a module…
176 | - target the average functional behavior
177 |
178 |
179 |
180 | ### Amdahl’s Law
181 |
182 | What is frequent case and how much performance improved by making case faster
183 |
184 | - Speedup_enhanced(增强加速比):改进部分采用改进措施后比没有采用改进措施前性能提高倍数(旧时间/新时间)
185 | $$
186 | speedup = \frac{originalExecutionTime}{originalExecutionTime}=\frac{newPerformance
187 | }{originalPerformance}
188 | $$
189 | - Fraction_enhanced(增强比例):计算机执行某个任务的总时间中可被改进部分的时间所占的百分比.
190 |
191 | If component $x$ is improved by $S_x$ and component $x$ affects a fraction $F_x$ of the overall execution time then
192 | $$
193 | speedup = \frac{1}{(1-F_x)+F_x / S_x}
194 | $$
195 |
196 | 
197 |
198 | > Example1:
199 | >
200 | > If we optimize the module for the floating-point instructions by a factor of 2, but the system will normally run programs with only 20% of floating point instructions then the speedup is only
201 | > $$
202 | > speedup = \frac{1}{(1-0.2)+0.2/2}=\frac{1}{0.9}=1.111
203 | > $$
204 |
205 | > Example2:
206 | >
207 | > 
208 |
209 | Amdahl定律告诉我们:系统中某一部件由于采用某种更快的执行方式后,整个系统性能的提高与这种执行方式的使用频率或占总执行时间的比例有关。
210 |
211 |
212 |
213 | ### CPU Time
214 |
215 | - user CPU Time
216 | - spent in the user program
217 | - system CPU Time
218 | - spent in the OS performing tasks required by the program
219 | - harder to measure and to compare across architectures
220 | - CPU performance = user CPU time on an unloaded system
221 | - CPU Time = (Clock Cycles for a Program) x (Clock Cycle Time) = (Clock Cycles for a Program) / (Clock Frequency)
222 |
223 | - IC = Instruction Count
224 | - number of instructions executed for a program
225 |
226 | - **CPI = Clock cycles Per Instruction**
227 | - average number of clock cycles per instruction of a program
228 | - IPC = Instruction Per Clock cycles
229 | - **CPU Time = IC x CPI x CCT** (CCT: Clock Cycle Time)
230 |
231 | 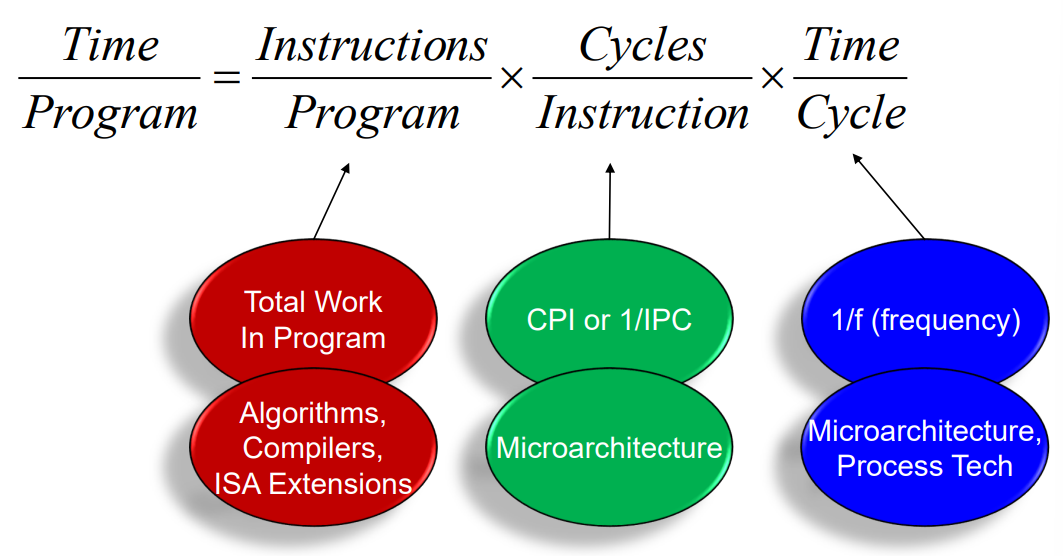
232 |
233 | 
234 | $$
235 | \text{CPU Time} = \sum_i (\text{IC}_i \times \text{CPI}_i) \times \text{CCT}
236 | $$
237 |
238 | $$
239 | \text{CPI} = \sum_i (\frac{\text{IC}_i}{\text{IC}}\times \text{CPI}_i)=\sum_i(\text{IF}\times \text{CPI}_i)
240 | $$
241 |
242 | > Example
243 | >
244 | > 
245 | >
246 | > 
247 | >
248 | > 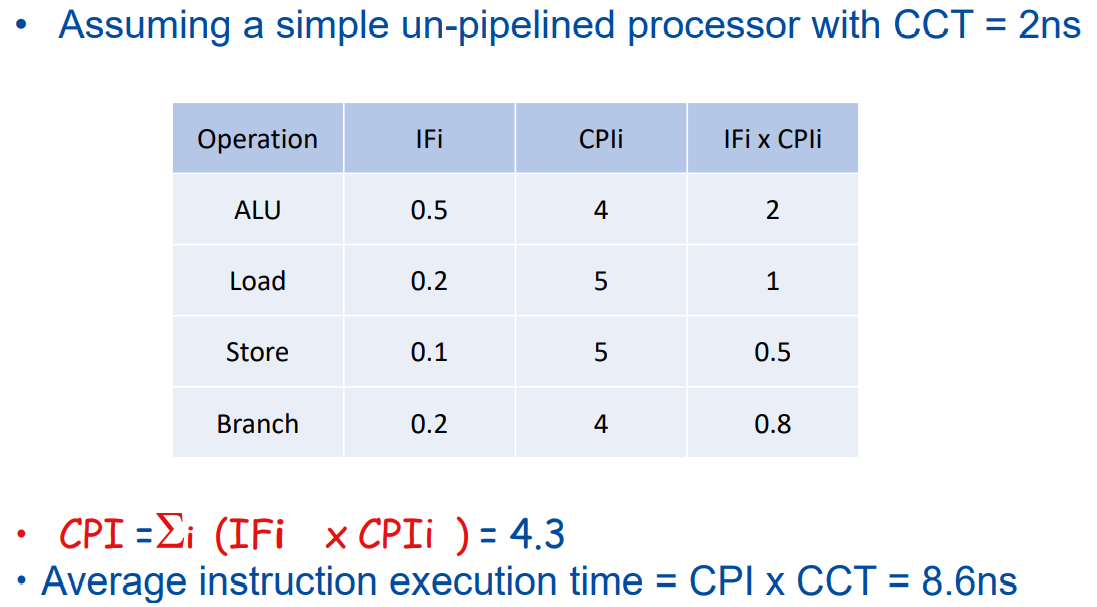
249 |
250 |
251 |
252 | ### Improving Performance by Exploiting Parallelism:并行
253 |
254 | - at the system level
255 | - use multiple processors, multiple disks
256 | - scalability is key to adaptively distribute workload in server apps
257 | - at the single microprocessor level
258 | - exploit instruction level parallelism (ILP)
259 | - e.g., pipelining overlaps the execution of instruction to reduce the overall program CPU Time
260 | - reduces CPI by overlapping instructions in time
261 | - possible because many subsequent instructions are independent
262 | - e.g. parallel computation
263 | - reduces CPI by overlapping instructions in space
264 | - duplicate hardware modules such as ALUs
265 | - at the circuit level
266 | - carry-lookahead adders speed-up sums
267 | - from linear to logarithmic
268 |
269 |
270 |
271 | ## Instruction Set Principles:ISA
272 |
273 | the computer visible to the assembler language programmer or compiler writer
274 |
275 |
276 |
277 |
278 |
279 |
280 |
281 |
282 |
283 |
284 |
285 |
286 |
287 |
288 |
289 |
290 |
291 |
292 |
293 |
294 |
295 |
296 |
297 |
298 |
299 |
300 |
301 |
302 |
303 |
304 |
305 |
306 |
307 |
308 |
309 |
--------------------------------------------------------------------------------
/docs/Architecture/chapter3.md:
--------------------------------------------------------------------------------
1 | nWhat is Instruction Set Architecture? How is it represented? * 指令集架构
2 |
3 | nRISC vs. CISC *
4 |
5 | nClassifying Instruction Set Architectures by the type of internal storage in a processor * 内部存储类型
6 |
7 | nInstruction Characteristics
8 |
9 | nEndian order * 端序/字节序 小端和大端 以及 对齐(alignment)
10 |
11 | nStructure of Recent Compilers: Multi-pass structure
12 |
13 | nMIPS Architecture & MIPS Instruction Format
14 |
15 | 什么是ISA?How is it represented(如何表示指令)?:
16 | a set of instructions,且每条指令都是由cpu硬件来执行的. 用二进制的形式存储指令集,有定长指令和不定长指令.
17 |
18 | RISC与CISC
19 | CISC:复杂指令集架构,追求更强大的指令,减少程序的指令条数,并交由硬件实现。
20 |
21 | RISC:精简指令集架构,追求更少更简单的指令和更低的CPI
22 |
23 | RISC设计原则:
24 |
25 | 简单统一的指令格式(所有指令长度均相同),减少寻址方式
26 | 每条指令的功能应尽可能简单,并在一个机器周期内完成
27 | 只有load store可以访存,其他操作都是在寄存器上
28 | 以简单有效的方式支持高级语言
29 | 强调优化编译器的作用
30 | 强调流水线技术
31 | ISA的分类(分类依据:用来存放操作数的存储单元类型):
32 |
33 |
34 | (其中寄存器型又包括r-r型和r-m型)
35 |
36 |
37 |
38 | 只有寄存器型沿用至今,区分GPR ISA的方法是看指令中mem address的个数和操作数(operands)的个数
39 |
40 |
41 |
42 | ALU指令中,存储器操作数个数和操作数个数的所有可能组合只有七种,不可能有(3,2),也就是指令有三个地址却只需要两个操作数.
43 |
44 |
45 |
46 |
47 |
48 | 小端序和大端序:
49 | 小端序:低字节保存在低地址
50 |
51 | 大端序:低字节保存在高地址
52 |
53 | 举例:
54 |
55 | var = 0x11223344,对于这个变量的最高字节为0x11,最低字节为0x44
56 |
57 | (1)大端模式存储(存储地址为16位) (2)小端模式存储(存储地址为16位)
58 |
59 | 地址 数据 地址 数据
60 |
61 | 0x0004(高地址) 0x44 0x0004(高地址) 0x11
62 |
63 | 0x0003 0x33 0x0003 0x22
64 |
65 | 0x0002 0x22 0x0002 0x33
66 |
67 | 0x0001(低地址) 0x11 0x0001(低地址) 0x44
68 |
69 |
70 | ————————————————
71 | 版权声明:本文为CSDN博主「ASR_THU」的原创文章,遵循CC 4.0 BY-SA版权协议,转载请附上原文出处链接及本声明。
72 | 原文链接:https://blog.csdn.net/zongza/article/details/83780572
--------------------------------------------------------------------------------
/docs/Architecture/chapter4.md:
--------------------------------------------------------------------------------
1 | Chapter 4 Pipelining *
2 | nConcepts and Characteristics of Pipelining * 流水线相关概念与特点
3 |
4 | nFive steps every instruction be executed in? Fill and Drain.* 流水的5个阶段;通过时间与排空时间
5 |
6 | nStructural hazards, Data hazards and Control hazards * 结构冲突、数据冲突、控制冲突
7 |
8 | nWhat is stall in pipeline? What happens when a instruction is stalled.
9 |
10 | nThree Generic Data Hazards: RAW,WAR,WAW *
11 |
12 | nHow to Avoid 3 kinds of Hazards? * 避免/解决冲突
13 |
14 | nPerformance Issues in Pipelining. ** 性能:时空图
15 |
16 | 关于流水线的几个特点:
17 |
18 |
19 | 对于每个stage时长不一样的,先把最长的那个stage(对应图中的蓝色线段)连起来,然后在每段蓝色线左右补充前后的stage
20 |
21 |
22 |
23 | 流水线的相关概念和特点:
24 | 流水线:将一个重复的时序过程分解成为若干个子过程(称为段,段数也是流水线的深度),而每个子过程都由专用功能部件实现。把多个处理过程在时间上错开,依次通过各功能段,这样不同子过程就能并行执行。流水线不会加速指令的执行时间而是改善整体的吞吐量.
25 |
26 | 流水线特点:
27 |
28 | 0--流水线定义
29 |
30 | 1--多条指令同时执行
31 |
32 | 2--每一个段只执行一条指令的一部分
33 |
34 | 3--指令沿着流水线流动一次的时间间隔就是一个机器周期(因此最慢的段决定了cycle大小)
35 |
36 | 流水线瓶颈:时间最长的段
37 |
38 | 流水线的五个阶段:
39 | IF(取指令)->ID(指令译码/取寄存器[针对分支转移指令])->EX(执行/有效地址计算)->MEM(存储器访问load或store)->WB(写到寄存器,如load或者ALU的计算结果),以RISC为例,每条指令长度4字节,每条指令执行时间至少是5 cycles
40 |
41 |
42 |
43 | 流水线的通过时间: 从任务开始到稳定工作状态(段被填满)所需要的时间
44 |
45 | 流水线的排空时间:从稳定工作状态结束到最终任务结果所需要的时间
46 |
47 |
48 |
49 |
50 |
51 | stall时发生了什么?
52 | 1--Instructions issued later than this instruction are stalled(在stall指令后的全都得一起stall)
53 |
54 | 2--Instructions issued earlier than this instruction must continue(在前的必须continue)
55 |
56 |
57 |
58 | 流水线的三个冲突:
59 | 1--结构冲突: 因硬件资源竞争引起的冲突
60 |
61 |
62 | (使用Stall解决结构冲突)
63 | (通过增加硬件解决结构冲突 比如指令cache和数据cache分离的方法(上图结构冲突由于两个指令同时需要访问cache引起,load读数据,I3取指令)
64 | 2--数据冲突: 指令在数据流中重叠执行时需要用到前面指令的结果产生的冲突
65 |
66 |
67 | (使用Stall解决数据冲突)
68 | (使用旁路技术解决数据冲突) [定向技术:使用流水线寄存器组直接向后面的指令传递结果]
69 | 定向技术检测冲突的方法是: 当硬件检测到前面某条指令的结果寄存器就是当前指令的源寄存器时,控制逻辑会将前面那条指令的结果直接从其产生的地方前递到当前指令所需的位置。定向技术的实际硬件结构如下所示
70 |
71 |
72 |
73 | 注意:
74 |
75 | load指令和其他ALU指令不同,在使用定向(解决load和其后指令的冲突)时仍有可能冲突(因为load必须得等到mem段才能得到真正的数据,其他的ALU指令可能在Ex阶段就能算出结果,load必须访存),如下,这时候需要旁路+Stall 一起用
76 |
77 |
78 |
79 | 旁路技术检测冲突在load指令RAW中的应用:在当前指令的ID段检测数据相关,可以看出只需要把load指令的结果寄存器(lw的MEM段寄存器)与load指令后的几条指令(包含当前指令sub)的(ID段)源寄存器地址进行比较,如果在同一级(如lw与and)则可以用旁路或者在后面(如lw与or)则无需操作(因为前半周期写后半周期读),如果在前面(如lw与sub)则需要stall
80 | 如果在指令中观察,则Lw的下一条指令只能stall+forward,下二条指令可以forward,下三条指令无需操作(无冲突)如下图所示
81 |
82 |
83 | 做系统结构实验的时候找到一个trick:
84 |
85 | 一般在有定向技术的情况下找RAW冲突,只需关注两条连续的指令中第一条是LW的(类似上图第二个),这种只能stall,如果两条连续指令中第一条不是LW,则可以通过定向解决,比如:
86 |
87 | ADD r1 r1 r3
88 |
89 | SW r1 0(r2)
90 |
91 | ADD写r1 SW读r1 但是ADD的EX结果可以直接传给SW的EX(如果定向机构检测到前一个ALU的计算结果写入的寄存器【对应r1】就是当前ALU的源寄存器,那么控制逻辑就选择定向的数据作为ALU的输入,而不采用从通用寄存器组读出的数据)
92 |
93 | 截图(以后补,用MIPS的模拟器)
94 |
95 | 上面举例的都是RAW,另外还有WAR和WAW冲突(但是在MIPS中也就是五段流水线里只会出现RAW):
96 |
97 |
98 |
99 |
100 |
101 |
102 |
103 |
104 |
105 |
106 |
107 | 3--控制冲突: 流水线遇到分支指令或者其他改变PC值的指令所遇到的冲突
108 |
109 |
110 | 有两个解决思路:1-更早得决定branch是否该被选中(MIPS在ID段zero test) 2-更早得计算好分支转移的地址(MIPS在ID段算转移PC)
111 |
112 | (如上右图将分支地址计算放在了ID阶段,MIPS中的branch test都是通过检测register的值是否为0,因此把zero test也一起移动到ID段(如前所示,Id段可以读寄存器)这样一旦决定转移分支就不用等到10指令的MEm走完)这样只需一个stall(若跳转,36的IF需要等10的ID出结果),相比之前的三个stall(若跳转,36的IF需要等10的MEM出结果),减少了penalty,具体如下图所示。
113 |
114 |
115 |
116 |
117 |
118 | 减少分支延迟(控制冲突)的四种方法总结:
119 |
120 | (2,3统称为分支预测,是一种静态预测,【下一章会有动态分支预测,这里静态是指预测操作是预先订好的,一定成功或者一定失败,动态则是可以根据之前的分支实际执行情况动态选择本次分支是成功还是失败】):
121 |
122 | stall一直到mem段出结果
123 | 假设分支一定not taken(也就是不跳转,接着执行下面一条指令),如果真实结果是跳转则squash(挤压,可以理解为指令作废,就是上面的idle)
124 | 假设分支一定 taken,同样需要一个stall等ID出转移地址结果,在五段流水线中,如果最后not taken,还需要转回到i+1,需要寄存器存i+1地址,相比方法2完全没有好处
125 | 延迟分支,使用编译器进行指令静态调度(调到延迟槽中)【下一章会有指令动态调度】,MIPS用的是只有一条指令的延迟槽,这种方法和2实际上几乎没区别的,只不过槽里那条指令不会被squash,也可以不是i+1(填充盐池槽的指令选择如下二图所示)
126 |
127 |
128 | 几种方法的共同特点:都属于静态方法,对分支的处理方式在程序执行过程中固定不变,要么总是预测成功,要么总是预测失败。
129 |
130 | 延迟分支几种调度策略和优缺点:
131 |
132 |
133 |
134 | 注意:
135 |
136 | 对于分支预测,无论是静态方法还是动态方法都是硬件和软件共同作用的结果!静态是说预测是提前预定好的,动态可以自我调整
137 |
138 | 对于调度,静态是指通过编译器在编译阶段进行的调度,动态是指通过硬件在执行过程中进行的调度
139 |
140 | 三种冲突的解决方法总结:
141 |
142 |
143 |
144 |
145 | 流水线性能指标:
146 |
147 |
148 | 例题1:
149 |
150 |
151 | 加速比(一定大于1):
152 |
153 |
154 | 效率:
155 | 效率相当于每一段的加速比,所以可以用总的加速比除以段数
156 |
157 |
158 |
159 |
160 |
161 | 带有stall的流水线性能:
162 | (比如:CPI,如果流水线无stall那么cpi一定是1,因为每个时钟周期流出一条指令)
163 |
164 |
165 |
166 | 例题2:
167 | 加速比除了用总时间比值也可以用平均时间(=时钟周期*平均CPI)的比值来计算
168 |
169 | 假设非流水线实现的时钟周期时间为1ns,ALU和分支指令需要4个时钟周期,访问存储器指令需5个时钟周期,
170 |
171 | 上述指令在程序中出现的相对频率分别是:40%、20%和40%。
172 |
173 | 在基本的流水线中,假设由于时钟扭曲和寄存器建立延迟等原因,流水线要在其时钟周期时间上附加0.2ns的额外开销。
174 |
175 | 现忽略任何其他延迟因素的影响,请问:相对于非流水实现而言,基本的流水线执行指令的加速比是多少?
176 |
177 |
178 |
179 |
180 |
181 |
182 |
183 |
184 |
185 |
186 |
187 |
188 |
189 |
190 |
191 | Chapter 5 ILP - 1
192 | nWhat is Instruction-Level Parallelism (ILP) and the 2 approaches to exploit ILP * 指令级并行,静态与动态
193 |
194 | nWhat is Basic Block * 基本块
195 |
196 | nData Dependence (True dependence), Name Dependence (Anti-dependence, Output dependence) , Control Dependencies * 相关(与冲突的关系)
197 |
198 | nUnrolled Loop and Minimizes Stalls * 循环展开
199 |
200 | nDynamic Branch Prediction * 动态分支预测
201 |
202 | qBranch History Table, Correlated Branch Prediction, Tournament Predictors,Branch Target Buffers 分支目标缓冲 *
203 | 什么是ILP?提高ILP的两种方法?
204 | 当指令之间不存在相关,他们在流水线中可以重叠起来并行执行,这种潜在的并行性称为指令级并行。
205 |
206 | 重叠执行指令以提高性能,两种方法:动态方法(改变硬件)软件方法(编译器调度)
207 |
208 |
209 |
210 | 什么是BB?
211 |
212 | 除入口和出口外没有其他分支(branch)的线性指令序列,BB内部的指令可能相互依赖(dependent),所以开发ILP更多是在BB之间。
213 |
214 | 比如循环级并行(loop-level parallelism):
215 |
216 | for (i=1; i<=1000; i=i+1)
217 | x[i] = x[i] + s //(一个循环中的不同循环体并行执行)
218 | 其中每个循环体就是一个BB,共有1000个BB,ILP就是使得这1000个BB能并行计算,这个具体方法叫循环展开(unrolling loop)。
219 |
220 | 动态循环展开:动态分支预测(上一章的分支预测是一种静态的)
221 | 静态循环展开:编译器静态调度指令(后面还会介绍一种动态调度)
222 |
223 |
224 | 相关与冲突的关系
225 | 相关:两条指令之间存在某种依赖关系
226 |
227 | 冲突:在具体流水线中,由于相关的存在,使得指令流中下一条指令不能在指定的时钟周期开始执行
228 |
229 | 两者之间的关系:
230 |
231 | 相关性是程序的固有属性; 冲突是流水线的特性;
232 |
233 | 相关性的存在只预示着存在有冲突的可能性。
234 |
235 |
236 |
237 | 相关的分类
238 | 数据相关:后面的指令使用了前面指令的结果
239 | 一般都是能引起RAW冲突的相关
240 |
241 |
242 |
243 | ILP的宗旨就是只在会影响结果的时候保留指令执行顺序,其他情况下尽可能改变顺序提高并行性
244 |
245 |
246 |
247 | 名相关:两条指令使用相同的寄存器名,而两者之间没有数据流动
248 | 包括反相关,一般都是能引起WAR冲突的
249 |
250 |
251 |
252 | 和输出相关,一般都是能引起WAW冲突的
253 |
254 |
255 |
256 | 反相关的解决方法:一般可以通过寄存器重命名,也可以编译器静态调度和硬件方法。
257 |
258 | 控制相关:由分支指令引起的相关
259 | 一般都是能引起控制冲突的相关
260 |
261 |
262 |
263 | 上图红字的意思是: 指令调度的时候不能跨越分支指令,也就是BNE之前的指令不能调度到BNe之后(一个特例是分支延迟中可以放在BNE的延迟槽,见后)
264 |
265 |
266 |
267 | 循环展开:
268 |
269 |
270 |
271 |
272 | 1 由上可见,BB内的指令调度能带来的ILP提升有限(虽然减少了总的cycles,但是其中真正想执行的指令只占3/7,剩下的四个都是为了分支转移)
273 |
274 | 2 同时右图中DADDUI之所以能插到L和ADD之间的stall中是因为他和L,ADD均不存在冲突!(可能有人会想他可能与L有WAR,实际上MIPS的五段流水线是不可能产生除了RAW之外的数据冲突的,原因见前,就算想冲突,L和DADDUI之间也得起码隔着两个拍才行(这样L的mem才能和DADDUI的ID冲突上))
275 |
276 | 3 此外还可以将BNE移动到S之前的一个stall中,此时S处于BNE的延迟槽中,不属于(S)跨越分支指令(BNE)的情况
277 |
278 | 由1 启发我们需要在BB之间进行调度,这种就是循环展开要做的:
279 |
280 |
281 |
282 | 重要!->总循环次数n=1000,假设每次循环展开成k=4个(如上左图所示,减少了循环控制和分支开销)然后进行寄存器重命名(避免冲突)和指令调度(如上右图所示,减少了空转周期提高效率)
283 |
284 | 实际上是先进行n mod k个loop,然后再展开成k个的大loop,对这个大loop再循环n/k次,n越大,就会有越多的时间花在循环展开后的大loop上
285 |
286 |
287 |
288 | 循环展开的优点和限制:
289 | 限制:
290 |
291 | 循环展开成大loop时,若k过大,指令cache的miss rate会增加
292 | 因为用到了重命名,寄存器可能不够
293 | 优点:
294 |
295 | 降低整体开销(通过二外的循环展开)
296 | 减少了branch的开销
297 |
298 |
299 | 动态分支预测:
300 | 动态相比静态的区别是使用从早期运行(earlier run)中收集的概要信息预测分支,并根据上次运行(last run)修改预测
301 |
302 | branch history table
303 | 1-bit的BHT存在的问题:
304 |
305 | 最后一次预测错误不可避免,因为前面分支总是成功
306 | 第一次预测错误是源于上次程序的执行,因为上一次程序最后一次分支不成功(可通过2-bit解决,见下图)
307 |
308 |
309 | Correlated Branch Prediction
310 |
311 |
312 | 2-bit的BHT存在的问题:
313 |
314 | 如果不止一个分支(branch)存在,前面的分支可能会影响后面的分支(称为相关分支,见下左图,只有b1 b2都是Not Taken,b3才能Taken)可以通过相关分支预测器解决(见下右图)
315 |
316 |
317 | 注意:2-bitBHT相当于(0,2)的相关分支预测器
318 |
319 | 例题:
320 | 一个(2,2)的分支预测器如下:求预测结果
321 |
322 |
323 |
324 | 上图中address是不同分支的地址,GBH记录了上一次run的时候两个相关分支的taken情况,根据add和GBH定位到对应的具体状态为01,则说明这次run的预测是Not Taken
325 |
326 | Tournament Predictors
327 |
328 |
329 | 其中selector 长得类似(0,2)的predictor:
330 |
331 |
332 |
333 |
334 |
335 | Branch Target Buffers
336 | BTB的思想借鉴了指令cache,他是预先把已知的是branch的指令地址和预测地址都存起来,然后将当前PC值逐一与表中的指令地址比较,若相等则说明当前PC指向的指令是一条分支指令,此后系统不再抓取PC对应的指令而是fetch与之对应的predicted PC指向的指令,如下图所示:
337 |
338 |
339 | ————————————————
340 | 版权声明:本文为CSDN博主「ASR_THU」的原创文章,遵循CC 4.0 BY-SA版权协议,转载请附上原文出处链接及本声明。
341 | 原文链接:https://blog.csdn.net/zongza/article/details/83780572
--------------------------------------------------------------------------------
/docs/Architecture/chapter5.md:
--------------------------------------------------------------------------------
1 | Chapter 5 ILP - 2
2 | nBranch Target Buffers 分支目标缓冲 *
3 |
4 | nConcept and Advantages of Dynamic Scheduling * 动态调度
5 |
6 | qScoreboard 记分牌
7 | qTomasulo
8 | qSpeculation 前瞻执行
9 | qTomasulo with ReOrder Buffer 再定序缓冲
10 | nSuperscalar and VLIW * 超标量与超长指令字
11 |
12 | 什么是动态调度?动态调度的好处?
13 | 动态是相对静态而言的,静态是指通过编译器(软件)进行调度,也就是在运行前进行调度,不可更改,动态调度是通过硬件实现在指令执行过程中的调度,同时还能保证data flow和exception behavior。
14 |
15 | 优点:
16 |
17 | 可以handle 静态调度时编译器检测不出来的相关(dependence),比如cache miss(软件方法检测不出来),在等调进cache的时候硬件调度可以使得处理器去执行别的指令。
18 | 一条指令的不同阶段可以在不同流水线中完成(尽管编译的时候他们是在同一条流水线中的)
19 | 关键思想:允许被stall的指令停顿期间执行后面的指令(顺序发射,乱序执行,乱序完成)
20 |
21 | DIVD F0,F2,F4
22 | ADDD F10,F0,F8
23 | SUBD F12,F8,F14
24 |
25 | 比如:DIVD和ADDD之间有RAW,因此ADDD被stall,此时SUBD和两者不存在任何相关和冲突,因此硬件可以在ADDD的stall期间执行SUBD
26 |
27 | 具体实现:将ID段拆成两个:Issure 和 Read operands,前者检测结构冲突,只要没有SH,该指令就能发射;后者检测数据冲突,等到没有DH就可以读操作数
28 |
29 |
30 |
31 | 但是,这种方式可能会带来WAR和WAW冲突:
32 |
33 | DIVD F10,F0,F2
34 | ADDD F10,F4,F6
35 | SUBD F6,F8,F14
36 |
37 | 如果不对ADDD和SUBD使用寄存器重命名,那么因为SUBD和ADDD存在反相关(F6)如果流水线在ADDD读出F6之前就能完成SUBD,就回出现错误。类似的,DIVD和SDDD存在输出相关,流水线必须能检测出该相关,并避免WAW冲突。(可以用寄存器重命名解决)
38 |
39 | 记分牌算法(scoreboard)
40 | 记分牌通过记录指令执行过程中指令的状态,运算部件的状态,寄存器的状态实现集中控制(centralized control),其中记分牌只记录四种指令状态:
41 |
42 |
43 |
44 | 记录的三种状态各自有一个表:如下所示
45 |
46 | 指令状态表特点:四个段 :发射 读取 执行 写回
47 | 功能部件状态表特点: 1+2+2+2
48 | 寄存器状态表特点:对应功能部件(一对一?)
49 |
50 |
51 | 下图显示了第二条LD指令准备写结果之前的三表状态:
52 |
53 | 指令状态表:
54 |
55 | 此时LD2 处于EX阶段,由于MUL SUB 与LD2有数据相关(F2,RAW)所以两者都只能过issue(无结构冲突)不能进入Read。
56 | 由于MUL和DIV有数据相关(F0,RAW)所以DIV同理也只能在Issue阶段。
57 | ADD与SUB有结构冲突(争用加法器)所以连发射都不行。
58 | 功能单元状态表:
59 |
60 | Fi 目的寄存器 Fj Fk 源寄存器 Qj Qk 源寄存器的来源(来自哪个功能部件) Rj Rk (yes表示就绪待取,no表示取完或者未就绪)
61 |
62 | Integer的Rj表示取完。
63 | Mult1的Rj表示没就绪,Rk表示就绪待取
64 | 寄存器状态表:
65 |
66 | 表示存到F0寄存器的结果来自功能部件Mult1
67 |
68 |
69 |
70 |
71 | 下图显示了MULT指令准备写结果之前的状态:
72 |
73 | 由于SUB和MUL不存在任何冲突和相关,且SUB 2cycles,MUL 10cycles 因此当MUL到了EX段,SUB一定执行完了
74 | MUL和DIV有RAW(F0),所以MUL没吧结果写到F0之前DIV只能处于Issue
75 | DIV和ADD有WAR(F6),所以DIV没读F6之前ADD必须阻塞在EX段
76 |
77 |
78 | 下图显示了DIV指令准备写结果之前的状态:
79 |
80 | DIV写结果前,前面的指令一定都完成了
81 | DIV要40个周期,ADD只要两个,因此当DIV取走F6后ADD立刻执行完全有足够的时间赶在DIV前面完成。
82 |
83 |
84 | 总结:
85 |
86 |
87 |
88 |
89 |
90 | Tomasulo算法
91 | 主要思想:
92 |
93 | 将保留站作为虚拟寄存器存储 指令和操作数,实现分布式控制和缓存
94 | 记录和检测指令相关,功能单元直接从保留站获得操作数(不再从寄存器读),操作数一旦就绪就立即执行,减少RAW(因为读操作的源已被定向(预约)到写的指令,只有操作数就绪时读才执行);
95 | 通过寄存器换名来消除WAR冲突和WAW冲突。寄存器换名是通过保留站和流出逻辑来共同完成的。(之后的写操作对保留站中的指令不再有影响,因为已换名,也就是指令中寄存器号换成了产生这个操作数的保留站标识,操作数可从CDB得到,不用再从寄存器读)
96 | 记分牌和tomasulo比较:
97 |
98 |
99 | 可见:
100 |
101 | tomasulo的控制和缓存分布在各保留站中 而 记分牌中控制和缓存集中在记分牌
102 | 使用功能单元对操作数进行计算不再是从寄存器取数(记分牌),而是从保留站的操作数缓存中取数(因此减少RAW,从寄存器读可能遇到重名的寄存器导致RAW)
103 | 寄存器换名
104 | 优点:
105 |
106 | 冲突检测逻辑是分布的(通过保留站和CDB实现)
107 | 消除了WAR和WAW冲突
108 | 缺点:
109 |
110 | 实现复杂
111 | 需要大量的高速相联存储
112 | 性能受CDB影响大(解决:多CDB)
113 |
114 |
115 | 例题:
116 | 下面是采用DLX浮点部件的Tomasulo算法执行过程中用到的状态表,试填写状态表中的相关空白。 假定:浮点流水线的延迟如下:加法2个时钟周期,乘法10个时钟周期,除法40个时钟周期。给出SUBD 将要写结果时状态表的信息。只填写相关部分空格。
117 |
118 |
119 |
120 |
121 |
122 | 指令
123 |
124 | 指令状态表
125 |
126 | IS
127 |
128 | EX
129 |
130 | WR
131 |
132 | LD F6,34(R2)
133 |
134 | √
135 |
136 | √
137 |
138 | √
139 |
140 | LD F2,45(R3)
141 |
142 | √
143 |
144 | √
145 |
146 | √
147 |
148 | MULTD FO,F2,F4
149 |
150 | √
151 |
152 |
153 |
154 |
155 |
156 | SUBD F8,F6,F2
157 |
158 | √
159 |
160 | √
161 |
162 |
163 |
164 | DIVD F10,F0,F6
165 |
166 | √
167 |
168 |
169 |
170 |
171 |
172 | ADDD F6,F8,F2
173 |
174 | √
175 |
176 | √
177 |
178 |
179 |
180 | 部件
181 |
182 | 名称
183 |
184 | 保留站
185 |
186 | Busy
187 |
188 | Op
189 |
190 | Vj
191 |
192 | Vk
193 |
194 | Qj
195 |
196 | Qk
197 |
198 | A
199 |
200 | Load1
201 |
202 | no
203 |
204 |
205 |
206 |
207 |
208 |
209 |
210 |
211 |
212 |
213 |
214 |
215 |
216 | Load2
217 |
218 | no
219 |
220 |
221 |
222 |
223 |
224 |
225 |
226 |
227 |
228 |
229 |
230 |
231 |
232 | Add1
233 |
234 | yes
235 |
236 | SUBD
237 |
238 | Mem[45+Regs[R3]]
239 |
240 | Mem[34+Regs[R2]]
241 |
242 |
243 |
244 |
245 |
246 |
247 |
248 | Add2
249 |
250 | yes
251 |
252 | ADDD
253 |
254 |
255 |
256 | Mem[45+Regs[R3]]
257 |
258 | Add1
259 |
260 |
261 |
262 |
263 |
264 | Add3
265 |
266 | no
267 |
268 |
269 |
270 |
271 |
272 |
273 |
274 |
275 |
276 |
277 |
278 |
279 |
280 | Mult1
281 |
282 | yes
283 |
284 | MULTD
285 |
286 | Mem[45+Regs[R3]]
287 |
288 | Regs[4]
289 |
290 |
291 |
292 |
293 |
294 |
295 |
296 | Mult2
297 |
298 | yes
299 |
300 | DIVD
301 |
302 |
303 |
304 | Mem[34+Regs[R2]]
305 |
306 | Mult1
307 |
308 |
309 |
310 |
311 |
312 |
313 |
314 | 结果寄存器状态表
315 |
316 | F0
317 |
318 | F2
319 |
320 | F4
321 |
322 | F6
323 |
324 | F8
325 |
326 | F10
327 |
328 | ……
329 |
330 | F30
331 |
332 | 部件名称
333 |
334 | Mult1
335 |
336 |
337 |
338 |
339 |
340 | Add2
341 |
342 | Add1
343 |
344 | Mult2
345 |
346 | ……
347 |
348 |
349 |
350 |
351 |
352 |
353 |
354 | 前瞻技术(speculation)
355 | 前瞻:循序处理器还未判断指令是否能执行之前就提前执行,以克服控制相关。他的实质是数据流执行:只要操作数就绪,指令就执行。
356 |
357 | 与流水线中的静态分支预测区别:前瞻技术是依靠硬件+动态分支预测技术+动态调度实现的。
358 |
359 |
360 |
361 | 带有前瞻的tomasulo
362 | 前瞻是为了让动态调度算法更好地处理分支指令(有控制相关)。tomasulo的指令完成和写结果都在WR段,而在前瞻执行中加以区分,分成两个不同的段:写结果,指令确认,特点是:允许指令乱序执行,但是必须顺序确认(注意不是顺序完成,确认是顺序的,但是完成可以乱序)。
363 |
364 | 写结果段:前瞻执行的结果写到ROB,并通过CDB传递ROB中的结果到需要他们的指令保留站。
365 |
366 | 指令确认段:在分支结果出来后,对相应的前瞻执行结果予以确认,如果前瞻是对的,就把ROB中的结果写到寄存器或者存储器,如果是错的,就不予以确认并从那条分支指令的另一条路径重新开始执行。
367 |
368 | ROB的每一项:
369 |
370 | 指令类型(指出该指令是分支指令、store指令或寄存器操作指令)+目标地址( 给出指令执行结果应写入的目标寄存器号(如果是 load和ALU指令)或存储器单元的地址(如果是store指令))+ 数据值字段(用来保存指令前瞻执行的结果,直到指令得到确认)+就绪字段( 指出指令是否已经完成执行并且数据已就绪)+控制字段(设置ROB的某一项是否被占用)
371 |
372 | 普通tomasulo和带有前瞻的tomasulo对比:
373 |
374 |
375 |
376 |
377 |
378 |
379 |
380 | 超标量和超长指令字
381 | 前面的方法可以提高并行度,但是CPI不可能低于1(最多就是1),想要在一个周期流出(发射)多条指令就得用多指令流出技术,包括超标量和超长指令字两种方法.
382 |
383 | 超标量和超长指令字都是指具有每个周期多指令流出能力的计算机。他们的区别在于调度方式(动态or静态)。.
384 |
385 | 静态调度超标量(顺序执行)
386 | 通过编译器进行调度+流出指令时用单独硬件检测冲突 == 静态调度+动态流出(所谓动态流出是指流出包中的指令可能不会全部流出,比如某指令与其他存在冲突,就只流出该指令之前的指令)
387 |
388 | MIPS中的静态超标量实例:
389 |
390 | 这里是2-流出超标量,每个时钟周期流出1条整型指令和1条浮点指令(load store 分支看做整型)
391 |
392 | 优点:和任意2-流出相比,对硬件要求低(比如1整+1整,就需要两套整型的硬件)
393 | 缺点1:把load归为整型,如果load是浮点load,可能会和浮点操作并行流出导致浮点寄存器访问冲突
394 | 缺点2:load有一个时钟延迟,这使得使用load的结果的指令必须和load相隔至少一个周期(在有定向的情况下),因此load之后的三条指令都不能用其结果
395 |
396 |
397 | 超标量中的循环展开:
398 |
399 | 需要考虑的问题:LD和ADD之间要有一个时钟的延迟,ADD和SD之间要有两个时钟的延迟
400 |
401 | 那么如果只展开四次ADD和SD的延迟不可避免,解决方法是进行更多的展开(5次)
402 |
403 |
404 |
405 |
406 |
407 | 动态调度超标量(乱序执行)
408 | 通过硬件进行调度+两个tomasulo控制器(整型和浮点,确保不会乱序流出)== 动态调度+动态流出
409 |
410 |
411 |
412 | 超长指令字
413 | 完全靠编译器进行调度 == 静态调度+静态流出(所谓静态流出是指每个时钟周期流出的指令数是固定的,这些指令构成一个长指令或指令包)
414 |
415 | 优点:对硬件依赖低,并行性完全由编译器挖掘。
416 | 缺点1:同一个指令包中的指令必须保证是不相关的。
417 | 缺点2:需要优秀的编译技术实现跨分支调度。
418 | 缺点3:没有冲突检测硬件,而是采用锁步机制(lockstep),某部件停顿整个处理机就停顿。
419 | 缺点4:操作槽不应定能被填满+为了提高并行性进行了过多循环展开,造成指令长度增加。
420 | 缺点5:机器代码不兼容。
421 |
422 |
423 | VLIW中的循环展开(指令包长度=2+2+1,注意其中某个指令槽不一定会被填满):
424 |
425 | 9 clocks/ 7 iterations = 1.3clock_per_interation
426 |
427 |
428 |
429 | 超标量和VILW比较(硬件和软件比较)
430 |
431 |
432 | 总结:
433 |
434 | 硬件的分支预测能力好,所需的代码少,但是需要大量的硬件
435 |
436 | 软件的推断设计简单,所需硬件少,但是代码量大
437 | ————————————————
438 | 版权声明:本文为CSDN博主「ASR_THU」的原创文章,遵循CC 4.0 BY-SA版权协议,转载请附上原文出处链接及本声明。
439 | 原文链接:https://blog.csdn.net/zongza/article/details/83933327
--------------------------------------------------------------------------------
/docs/Architecture/chapter6.md:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/MineQihang/ComputerScienceCourse/1aff4deec964c558ef93b88bd016414cc52d1634/docs/Architecture/chapter6.md
--------------------------------------------------------------------------------
/docs/Architecture/chapter7.md:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/MineQihang/ComputerScienceCourse/1aff4deec964c558ef93b88bd016414cc52d1634/docs/Architecture/chapter7.md
--------------------------------------------------------------------------------
/docs/ComputerNetwork/《计算机网络》第一次作业.md:
--------------------------------------------------------------------------------
1 | # 第一章课后思考题
2 |
3 | 1. **根据你目前的理解,请你构想一个虚拟的网络协议,并将它用你认为恰当的方式描述出来。**
4 |
5 | 答:下图描述了本虚拟网络协议的流程。主机1首先尝试与主机2建立连接,若能得到连接成功的Response则与主机2进行通信获得想获得的内容。
6 |
7 | 
8 |
9 | 本虚拟网络协议的层次结构如下,主机1可以直接将文件传入文件传送模块,并指定接收方,文件传送模块根据协议1对数据处理加上头后传输到通信服务模块,通信服务模块根据协议2加上头后传输到网络接入模块进行转发。数据到达主机2后,根据协议2进行数据解析传送到通信服务模块,再根据协议1进行解析传送到文件传送模块,从而得到发送端的源数据。
10 |
11 | 
12 |
13 | 在这个过程中,单个协议规定了数据与控制信息的结构或格式(语法),事件实现顺序(同步),“我来自”、“我要去”、“我要干嘛”等控制信息(语义)。
14 |
15 | 
16 |
17 | 2. **计算机网络体系结构分层次有什么好处?如果采用本教材的五层模型,你认为它们每个层次的主要任务是什么?**
18 |
19 | 答:(1)分层次的好处是能够①将庞大而复杂的问题转化为若干较小的局部问题,各层相互独立,易于实现和维护;②灵活性好。当任意一层改变时(接口不变),那么其他层就不会受影响;③每层结构可以分隔开,使用不同的技术架构进行开发;④能促进标准化工作。
20 |
21 | (2)**物理层**:实现比特的传输。
22 |
23 | **数据链路层**:实现两个相邻节点之间的可靠通信。
24 |
25 | **网络层**:负责为分组交换网上的不同主机提供通信服务。
26 |
27 | **运输层**:负责向向两台主机中进程间的通信提供通用的数据传输服务。
28 |
29 | **应用层**:通过应用进程间的交互来完成特定网络应用。
30 |
31 |
32 |
33 | 3. **互联网数据传输一般采用什么交换方式?它的特点是什么?**
34 |
35 | 答:分组交换。特点如下:
36 |
37 | (1)采用**存储交换**方式。将报文划分为多个小的等长数据段,并在每个数据段前加上一些必要的控制信息组成的首部后构成多个分组。发送端发出的信息会经过路由器。路由器收到一个分组,先暂时存储检查其首部,查找转发表,按照首部中的目的地址找到合适的接口转发出去。这样一步一步以存储转发的方式将分组交付到接收端。
38 |
39 | (2)分组交换的**优点**如下:**高效**:在分组传输的过程中动态分配传输带宽,对通信链路是逐段占用的;**灵活**:为每一个分组独立地选择最合适的转发路由;**迅速**:以分组作为传送单位,可以不先建立连接就能向其他主机发送分组;**可靠**:网络协议可靠、分布式多路由分组交换网保证网络很好的生存性。
40 |
41 | (3)分组交换的**缺点**如下:**时延大**:分组在各路由器存储转发时需要排队;**开销大**:分组中携带的控制信息增加了开销、分组交换网需要专门的管理和控制机制。
42 |
43 |
44 |
45 | 4. **根据你目前掌握的知识应该从哪些指标来评价一个网络的性能?**
46 |
47 | 答:(1)**速率**(数据率、比特率):数据的传输速率,往往是指而定速率或标称速率。这是网络**最重要**的一个性能指标。
48 |
49 | (2)**带宽**:①频率上,是信号具有的频带宽度,单位是赫;②时域上,是单位时间内网络中某信道所能通过的“最高数据率”,单位是比特每秒。
50 |
51 | (3)**吞吐量**:单位时间内通过某个网络(或信道、接口)的实际数据量。
52 |
53 | (4)**时延**:数据从网络的一端传送到另一端的时间。组成如下:①**发送时延**(传输时延):从发送数据帧的第一个比特算起,到该帧的最后一个比特发送完毕所需的时间;②**传播时延**:电磁波在信道中传播一定的距离需要花费的时间;③**处理时延**:主机或路由器在收到分组时,为处理分组所花费的时间;④**排队时延**:分组在路由器输入输出队列中排队等待处理和转发所经历的时延。
54 |
55 | (5)**时延带宽积**:以比特为单位的链路长度,表示从发送端发出但尚未到达接收端的比特数。
56 |
57 | (6)**往返时间RTT**:从发送方发送完数据,到发送方收到来自接收方的确认总共经历的时间。
58 |
59 | (7)**利用率**:①**信道利用率**:某信道有百分之几的时间是被利用的;②**网络利用率**:全网络的信道利用率的加权平均值。
60 |
61 |
--------------------------------------------------------------------------------
/docs/ComputerNetwork/《计算机网络》第三章作业.md:
--------------------------------------------------------------------------------
1 | # 《计算机网络》第三章作业
2 |
3 | ## 3-01
4 |
5 | **答:**
6 |
7 | - 链路(物理链路):一个节点到另一相邻节点的一段物理线路(中间无交换节点)
8 | - 数据链路(逻辑链路):物理链路上加上必要的通信协议(常使用网络适配器协调实现协议的软硬件)
9 |
10 | “电路接通了”说明物理链路接通了,并不代表“数据链路接通了”,因为有可能节点间并没有协议;“数据链路接通了”说明硬件和协议都准备好了,那么一定“电路接通了”。
11 |
12 | ## 3-04
13 |
14 | **答:**
15 |
16 | - 封装成帧:在数据前后添加首部和尾部(包含控制信息)形成一帧。这样可以保证上层能识别帧的开始和结束。
17 | - 透明传输:上层交来的数据不论何种比特组合都能正确传输。由于帧上有开始和结束的定界符,所以有可能在比特流中可能有与开始和结束定界符相同的比特组合,若不解决这个问题则会有帧定界错误的问题。
18 | - 差错检测:数据链路层对收到的数据进行差错检测(不一定要进行修复)可以有效避免资源的浪费(避免遇到错误数据还继续发送)。
19 |
20 | ## 3-07
21 |
22 | **答:**由生成多项式可知除数$P=10011$(位数为5),因此被除数还需在末尾加上4位0,使用CRC得到余数为$11010110110000\% 10011=1110$。
23 |
24 | - 若数据变为了$1101011010$,先将余数拼接后为$11010110101110$,那么$11010110101110 \% 10011= 0011$,因为余数不为0,所以此帧错误。
25 | - 若数据变为了$1101011000$,先将余数拼接后为$11010110001110$,那么$11010110001110 \% 10011= 0101$,因为余数不为0,所以此帧错误。
26 |
27 | 采用CRC检验后,数据链路层的传输并没有变为可靠的传输,因为接收方检测到错误后只是简单的丢弃,而没有进行修复,不能保证发送端和接收端的数据都是一样的。
28 |
29 | ## 3-09
30 |
31 | **答:**由字节填充的规则可知:
32 |
33 | - `0x7D 0x5E`对应的是`0x7E`;
34 | - `0x7D 0x5D`对应的是`0x7D`;
35 | - `0x7D P`对应的是`P-0x20`;
36 |
37 | 所以将题中的数据按照上述规则转化后可以得到数据为`7E FE 27 7D 7D 65 7E`。
38 |
39 | ## 3-10
40 |
41 | **答:**根据PPP协议中零比特填充规则(发送端遇到5个1就添加一个0,接收端遇到5个1就去掉后面一个0)可知:
42 |
43 | - 经过零比特填充后的数据为`01011111011111000 `;
44 | - 删除加入的零比特后数据为`0001101111111111110`。
45 |
46 | ## 3-13
47 |
48 | **答:**局域网的最主要的特点是:网络为一个单位所拥有,且地理范围和站点数目均有限,相对早期广域网有更高的数据率、更低的时延和更低的误码率。由于广域网的范围大、网络节点多,采用广播会造成很大的资源浪费,还会降低信道的有效利用率,因此不使用广播;而局域网范围小,节点少,采用广播十分方便,并且也不会有太大的资源浪费,因此局域网采用广播信道方式。
49 |
50 | ## 3-16
51 |
52 | **答:**数据率为$10\text{Mbit}$的以太网上每秒可以传输$10\times 10^6$个码元,而由于以太网采用曼彻斯特编码,所以原来的一个码元会对应曼彻斯特编码下的两个码元,因此在物理媒体上的码元传输率为$20\times 10^6$码元/秒。
53 |
54 | ## 3-20
55 |
56 | **答:**端到端传播时延为$\tau = 1 \text{km} / (2\times 10^5 \text{km/s})=5\times 10^{-6}\text{s}$,因此争用期为$2\tau=1\times 10^{-5}\text{s}$,所以在此时间内要发送$2\tau \times 1 \times 10^9 \text{bit/s}=10^4\text{bit}=1250字节$,所以此协议的最短帧长为$1250$字节。
57 |
58 | ## 3-24
59 |
60 | **答:**由于A发送的帧为以太网所容许的最短的帧,因此MAC帧大小为$64\times 8=512\text{bit}$,再加上前同步码和帧定界符($8\times8=64\text{bit}$),因此A的发送时延为$512+64=576$比特时间。设A发送的时刻为0,设B发送的时刻为$x$,由于题中要求在A发送结束前B也要发送一帧,因此B发送时还没有检测到碰撞,因此$0 \leq x < 225$,所以A检测到碰撞的时间为$x+225$。由于$x+225 < 450 < 576$,所以A在检测到和B发生碰撞之前不能把自己的数据发送完毕。
61 |
62 | 如果A在发送完毕前并没有检测到碰撞,那么$x+255 > 576$,即$x>321>225$,这说明B发送数据前就已经接收到了来自A的数据,所以A所发送的帧不会和B发送的帧发生碰撞。
63 |
64 | ## 3-25
65 |
66 | **答:**$10\text{Mbit}$的以太网上争用期时间为$512$比特时间,帧间最小间隔为$96$比特时间。题中站点A的状态如下:
67 |
68 | 1. A在传输完干扰信号后开始检测信道,直到信道空闲(B的干扰信号消失,即$273+225=498$比特时间);
69 | 2. 受以太网帧间最小间隔的影响,A需等待$96$比特时间($498+96=594$比特时间);
70 | 3. A发送数据,在$594+225=819$比特时间传输到B,在$819+576=1395$比特时间,A传输结束。
71 |
72 | 题中站点B的状态如下:
73 |
74 | 1. B在传输完干扰信号后,执行避让算法,等待$273+1\times 512=785$比特时间;
75 | 2. 受以太网帧间最小间隔的影响,B在$785 \sim 881$比特时间内先检测信道,发现在$819$比特时间时收到了来自A的数据,因此等待A传输结束;
76 | 3. 在$1395$比特时间时,A传输结束,再等待最小间隔时间后,B开始传输(即$1395+96=1491$比特时间)。
77 |
78 | 综上:A在$594$比特时间开始发送其数据帧,B在$1491$比特时间开始发送其数据帧;A重传的数据在$819$比特时间到达B;由于B在发送前检测时收到了A的数据,因此不会发送数据,所以A重传的数据不会和B重传的数据再次发生碰撞;B不会在预定的重传时间发送数据。
79 |
80 | ## 3-30
81 |
82 | **答:**主机、服务器等按照下图的方式进行通信,则每台主机或服务器的吞吐量都为$100\text{Mbit/s}$,因此总的吞吐量为$11 \times 100\text{Mbit/s} = 1100\text{Mbit/s}$。
83 |
84 | 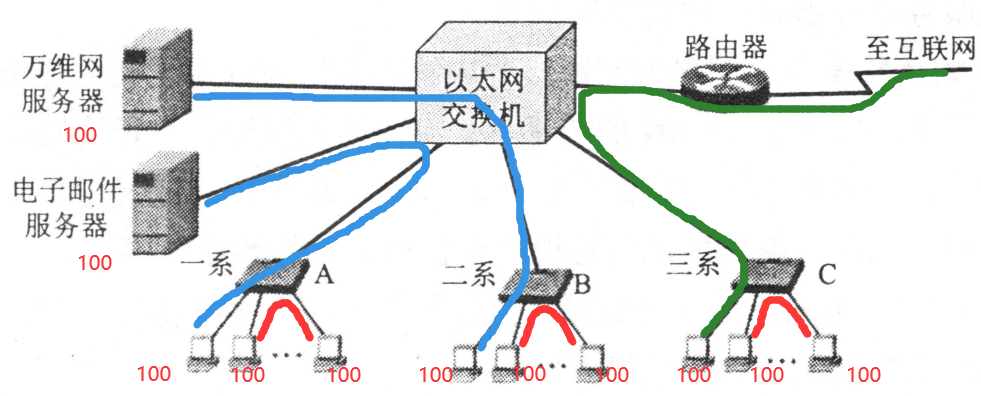
85 |
86 | ## 3-33
87 |
88 | **答:**
89 |
90 | | 动作 | 交换表的状态 | 向哪些端口转发帧 | 说明 |
91 | | ---------- | ----------------- | ---------------- | --------------------------------- |
92 | | A发送帧给D | 存储A的位置(A, 1) | 所有端口 | 交换表中此时没有D的位置,因此广播 |
93 | | D发送帧给A | 存储D的位置(D, 4) | A | 交换表中有A的位置,直接发送 |
94 | | E发送帧给A | 存储E的位置(E, 5) | A | 交换表中有A的位置,直接发送 |
95 | | A发送帧给E | 不变 | E | 交换表中有E的位置,直接发送 |
96 |
97 |
--------------------------------------------------------------------------------
/docs/ComputerNetwork/《计算机网络》第九章作业.md:
--------------------------------------------------------------------------------
1 | # 《计算机网络》第九章作业
2 |
3 | ## 9-07
4 |
5 | **答:**(1)无线局域网的MAC协议即CSMA/CA协议,特点是:
6 |
7 | ① 当某站需要发送数据时,先**检测信道**。若信道忙,则执行退避算法推迟发送;若信道空闲了一段时间(**DIFS**),那么这个站就可以发送数据。当接收站正确收到后就**响应确认帧**,接收站接收到后就说明没有发生碰撞,若没接收到则重传,直到收到确认帧或达到最大重传次数。
8 |
9 | ② 其退避算法为:第$i$次退避在时隙$\{ 0, 1, ... , 2^{2+i}-1 \}$中随机选择一个,当时隙达到$255$(对应第$6$次退避)时就不增加了。这样可以使得不同站点选择相同退避时间的概率减少。当要发送新的分组时,无需执行退避算法的情况只有**信道空闲时间超过了DIFS**。
10 |
11 | (2)不采用CSMA/CD的理由如下:
12 |
13 | ① 无线局域网适配器上,**接收信号强度远小于发送信号强度**,因此要实现碰撞检测,必须让接收信号强度提升,这就意味着硬件成本的提高。所以,无线局域网一般不使用碰撞检测。
14 |
15 | ② 无线局域网中一个站点**无法听到**其他站点是否在发送数据,因此无法碰撞检测,所以站点在发送数据时只能先把它发送完毕,如果没收到确认就表明刚才发送的数据帧出错,于是重传。为了减少碰撞的概率,无线局域网采用**碰撞避免**的方式,尽量减少碰撞的概率。
16 |
17 |
18 |
19 | ## 9-09
20 |
21 | **答:** **隐蔽站问题:**未能检测出信道上其他站点信号的问题;**暴露站问题:**一个站点向作用范围内一站点发送数据会影响作用范围内其他站点接受数据的问题。
22 |
23 | (1)使用RTS帧和CTS帧可以解决以上问题。在源站发送数据帧之前先发送一个短的控制帧(请求发送RTS),其中包括源地址、目的地址和这次通信所需的持续时间。若信道空闲,目的站B就响应一个控制帧(允许发送CTS),其中也包括持续时间。源站收到CTS帧就可以向目的站发送数据帧。这样在源站点和目的站点的作用范围内的所有其他站点都能得到控制帧,从而不会检测不出信道上有其他信号正在传输(解决了隐蔽站问题),也不会影响源站作用范围内其他站点接收数据(解决了暴露站问题)。
24 |
25 | (2)RTS/CTS帧并非强制使用。如果无线局域网工作环境中碰撞产生的不多,那就可以不采用这种方法。因为使用RTS/CST帧就意味着增加开销,而且还不一定能得到更好的效果。
26 |
27 |
28 |
29 | ## 9-14
30 |
31 | **答:**保证各站点公平地发送数据。如果不执行退避算法就会导致这个站在较长时间垄断数据传输。
32 |
33 |
34 |
35 | ## 9-27
36 |
37 | **答:**(1)在第一个时隙:A发送报文,B接收报文;在第二个时隙:B发送报文,C接收报文。因此,两个时隙传输了一个报文,最大数据报文传输速率为1/2(报文/时隙)。
38 |
39 | (2)在第一个时隙:A发送报文,B接受报文;D发送报文,C接受报文。因此,一个时隙传输了两个报文,最大数据报文传输速率为2(报文/时隙)。
40 |
41 | (3)如果A、C同时发送报文会存在碰撞(隐蔽站问题)。因此只能顺序执行。在第一个时隙:A发送报文,B接收报文;在第二个时隙:C发送数据,D接收数据。因此,两个时隙传输了两个报文,最大数据报文传输速率为1(报文/时隙)。
42 |
43 | (4)① C可以直接传输给A。最大数据报文传输速率为1(报文/时隙)。
44 |
45 | ② 同时传输。最大数据报文传输速率为2(报文/时隙)。
46 |
47 | ③ 同时传输。最大数据报文传输速率为2(报文/时隙)。
48 |
49 | (5)① 在(1)的基础上3、4两个时隙发送回ACK。因此最大数据报文传输速率为1/4(报文/时隙)。
50 |
51 | ② 在(2)的基础上2、3两个时隙发送回ACK(因为存在隐蔽站问题,不能同时发送)。因此最大数据报文传输速率为2/3(报文/时隙)。
52 |
53 | ③ 在(3)的基础上2、3两个时隙发送回ACK(注意第2个时隙同时发送B->A的ACK和C->D的报文)。因此最大数据报文传输速率为2/3(报文/时隙)。
54 |
--------------------------------------------------------------------------------
/docs/ComputerNetwork/《计算机网络》第二章作业.md:
--------------------------------------------------------------------------------
1 | # 《计算机网络》第二章作业
2 |
3 | ## 2-01
4 |
5 | **物理层要解决哪些问题?物理层的主要特点是什么?**
6 |
7 | 答:物理层要解决怎样才能在连接各种计算机的传输媒体上传输数据比特流(即如何透明地传送比特流)。
8 |
9 | 物理层的主要特点是:
10 |
11 | - 由于传输媒体、连接方式很多,因此物理层协议比较复杂;
12 | - 物理层确定与传输媒体的接口相关的一些特征;
13 | - 物理层上数据逐个比特按照时间顺序传输。
14 |
15 |
16 |
17 | ## 2-05
18 |
19 | **物理层的接口有哪几个方面的特征?包含什么内容?**
20 |
21 | 答:物理层的接口有以下四方面的特性:
22 |
23 | - **机械特性**:指明接口所用**接线器的形状和尺寸**、**引脚数目和排列**、**固定和锁定装置**等。平时常见的各种规格的接插件都有严格的标准化的规定。
24 | - **电气特性**:指明在接口电缆的各条线上出现的**电压的范围**。
25 | - **功能特性**:指明某条线上出现的某一**电平的电压的意义**。
26 | - **过程特性**:指明对于不同功能的各种可能事件的出现**顺序**。
27 |
28 |
29 |
30 | ## 2-09
31 |
32 | **用香农公式计算一下,假定信道带宽为$3100\text{Hz}$,最大信息传输速率为$35\text{kbit/s}$,那么若想使最大信息传输速率增加$60\%$,问信噪比$S/N$应增大到多少倍?如果在刚才计算出的基础上将信噪比$S/N$再增大到10倍,问最大信息传输速率是否能增加$20\%$?**
33 |
34 | 答:已知
35 | $$
36 | \begin{equation}
37 | 35 \text{kbit/s}=3100\text{Hz} \times \log_2(1+S/N) \tag{1}
38 | \end{equation}
39 | $$
40 | 设增加最大信息传输速率后的信噪比为$k\times S/N$,因此
41 | $$
42 | \begin{equation}
43 | 1.6 \times 35\text{kbit/s}=3100\text{Hz} \times \log_2(1+k \times S/N) \tag{2}
44 | \end{equation}
45 | $$
46 | 联立(1)(2)两式可得
47 | $$
48 | k=\frac{2^{\frac{1.6\times35000}{3100}}-1}{2^{\frac{35000}{3100}}-1}=109.49828285511174
49 | $$
50 | 由此,信噪比$S/N$应增大到约$109.5$倍。
51 |
52 | 若信噪比为$10\times k \times S/N$,设此信噪比下的最大信息传输速率为$r \times 1.6 \times 35\text{kbit/s}$,则
53 | $$
54 | \begin{equation}
55 | r\times 1.6 \times 35\text{kbit/s}=3100\text{Hz} \times \log_2(1+10 \times k \times S/N)
56 | \tag{3}
57 | \end{equation}
58 | $$
59 | 联立(2)(3)两式得
60 | $$
61 | r=\log_2\left[ 10\times \left(2^{\frac{1.6\times 35000}{3100}}-1 \right)+1 \right]\times3100/(1.6\times35000)=1.183892185911328
62 | $$
63 | 由此,最大信息传输速率能增加$18.4\%$。
64 |
65 |
66 |
67 | ## 2-13
68 |
69 | **为什么要使用信道复用技术?常用的信道复用技术有哪些?**
70 |
71 | 答:可以实现多用户共同使用一个共享信道来进行通信,提高信道利用率。
72 |
73 | 常见的信道复用技术如下:
74 |
75 | - **频分复用**:各路信号在同样的时间占用不同的带宽资源;
76 | - **时分复用**:所有用户在不同时间占用相同的频带宽度,包括统计时分复用;
77 | - **波分复用**:光的频分复用,使用一根光纤来同时传输多个频率很接近得光载波信号,包括密集波复用、稀疏波复用;
78 | - **码分复用**:多个不同地址得用户共享一条码分复用信道。
79 |
80 |
81 |
82 | ## 2-16
83 |
84 | **共有四个站进行码分复用CDMA通信。四个站的码片序列为:**
85 |
86 | - **A: (-1, -1, -1, +1, +1, -1, +1, +1)**
87 | - **B: (-1, -1, +1, -1, +1, +1, +1, -1)**
88 | - **C: (-1, +1, -1, +1, +1, +1, -1, -1)**
89 | - **D: (-1, +1, -1, -1, -1, -1, +1, -1)**
90 |
91 | **现收到这样的码片序列(-1, +1, -3, +1, -1, -3, +1, +1)。问哪个站发送了数据?发送数据的站发送的是1还是0?**
92 |
93 | 答:由CDMA码片设计的正交性,使用收到的码片序列与发送站的码片序列进行内积即可得出结果。
94 |
95 | 对A站:
96 | $$
97 | (-1, -1, -1, +1, +1, -1, +1, +1) \cdot (-1, +1, -3, +1, -1, -3, +1, +1) = 8
98 | $$
99 | 由于$8/8=1$,因此A站发送1;
100 |
101 | 对B站:
102 | $$
103 | (-1, -1, +1, -1, +1, +1, +1, -1) \cdot (-1, +1, -3, +1, -1, -3, +1, +1) = -8
104 | $$
105 | 由于$-8/8=-1$,因此B站发送0;
106 |
107 | 对C站:
108 | $$
109 | (-1, +1, -1, +1, +1, +1, -1, -1) \cdot (-1, +1, -3, +1, -1, -3, +1, +1) = 0
110 | $$
111 | 由于$0/8=0$,因此C站未发送数据;
112 |
113 | 对D站:
114 | $$
115 | (-1, +1, -1, -1, -1, -1, +1, -1) \cdot (-1, +1, -3, +1, -1, -3, +1, +1) = 8
116 | $$
117 | 由于$8/8=1$,因此D站发送1。
118 |
119 |
--------------------------------------------------------------------------------
/docs/ComputerNetwork/《计算机网络》第五章作业.md:
--------------------------------------------------------------------------------
1 | # 《计算机网络》第五章作业
2 |
3 | ## 5-08
4 |
5 | 因为UDP对应用程序交下来的报文,在添加首部后就向下交付IP层,不合并也不拆分,直接保留这些报文的边界,因此UDP是面向报文的。而TCP需要先进行三次握手建立连接后才可以发送数据,在同一层上看,建立连接后,数据好像就是流式传输的,TCP无需知道上层传下来的数据是什么格式的,仅仅将其看作是一串无结构的字节流,因此TCP是面向字节流的。
6 |
7 |
8 |
9 | ## 5-17
10 |
11 | 不可行。比如,接收端收到了发送端发送的报文段$M_0$,并向发送端发送确认收到的信息,这时该确认信息丢失了,那么发送端在超过规定时间后便会超时重传,接收端不予理睬的话,发送端就会因为收不到确认信息而一直超时重传,从而使得传输失败。
12 |
13 |
14 |
15 | ## 5-18
16 |
17 | 
18 |
19 | 可以看到,后一次接收到的$M_0$是旧的,协议失败了。
20 |
21 |
22 |
23 | ## 5-21
24 |
25 | (1)假定接收方之前没有收到过对发送窗口内分组的确认,那么此时窗口序号为[2, 3, 4];
26 |
27 | 假定接收方之前只收到过对发送窗口内一个分组的确认,那么此时窗口序号为[3, 4, 5];
28 |
29 | 假定接收方之前收到过对发送窗口内两个分组的确认,那么此时窗口序号为[4, 5, 6];
30 |
31 | 假定接收方受到过5之前的所有分组的确认,那么此时窗口序号为[5, 6, 7]。
32 |
33 | (2)由上题的分析,发送窗口最前在[2, 3, 4],因此接收方可能发送了对2,3,4分组的确认,这些确认可能还滞留在网络中。这些确认是用来对2,3,4之前的分组进行的确认。
34 |
35 |
36 |
37 | ## 5-22
38 |
39 | (1)TCP规定的序号数量为$2^{32}$个,由于一个TCP连接中传送的字节流中的每一个字节都按顺序编号,因此文件的最长长度为$2^{32}\text{B}=1\text{GB}$。
40 |
41 | (2)一共需要发送$\lceil 2^{32}/1460 \rceil=2,941,759$个帧,帧首部的字节数总和为$66\times2,941,759=194,156,094\text{B}$,传输的总字节数为$2^{32}+194,156,094=4,489,123,390\text{B}$,因此发送所需时间为$\frac{4,489,123,390\text{B}}{10\times 10^{6} / 8 \text{B/s}}=3591.3\text{s}$,即$59.9\text{min}$。
42 |
43 |
44 |
45 | ## 5-27
46 |
47 | 由于IP数据报最大长度为$65535$字节,TCP首部最小为$20$字节,IP首部最小为$20$字节,因此数据部分最多为$65535-20-20=65495$字节。当传送数据字节长度超过TCP报文段中可编出的最大序号时,依然可以使用TCP传输,因为编号是循环的,但需要注意发送TCP数据报的时候不要让编号混乱。
48 |
49 |
50 |
51 | ## 5-32
52 |
53 | Karn算法:在计算加权平均$\text{RTT}_S$时,只要报文段重传了,就不采用其往返时间样本。
54 |
55 | 如果不采用Karn算法,而是在收到确认时都认为是对重传报文段的确认,那么如果有一个报文在$t=r+\epsilon$到达(其中,$r$表示当前超时重传规定时间,$\epsilon$为一个极小值),这时算得的$\text{RTT}=\epsilon$。因此,如果大多数情况都像这样,那么最后就会使得重传时间减少到几乎为0。
56 |
57 |
58 |
59 | ## 5-35
60 |
61 | 广域网两节点间的传播时延为$1500(\text{km})/150000(\text{km/s})=0.01\text{s}=10\text{ms}$;每一个节点的发送时延为$960(\text{bit})/48(\text{kbit/s})=20\text{ms}$,因此单程端到端时延为$20\times 5+ 10\times 3+250\times2=630\text{ms}$。
62 |
63 |
64 |
65 | ## 5-36
66 |
67 | 因为有一个广域网传播时延为$150\text{ms}$,因此端到端时延为$20\times 4+ 10\times 3 + 150+250\times2=760\text{ms}$。
68 |
69 |
70 |
71 | ## 5-39
72 |
73 | (1)
74 |
75 | 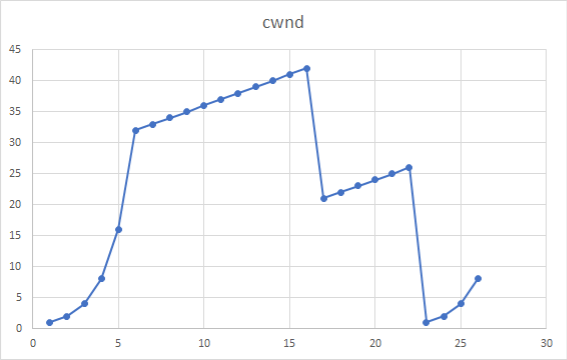
76 |
77 | (2)慢开始:[1, 6], [24, 26]。
78 |
79 | (3)拥塞避免:[6, 16], [17, 22]。
80 |
81 | (4)从16到17得过程中cwnd减半,因此是采用了快恢复算法,说明是收到了三个重复确认。从22到23直接减为1,因此是采用了慢开始算法,说明是通过超时检测到丢失报文段。
82 |
83 | (5)第1轮次是32,第18轮次设置为21(拥塞窗口42的一半),第24轮次重新设置为13(拥塞窗口26的一般)。
84 |
85 | (6)第1轮发送前1个报文段,第2轮发送完前3个报文段,第3轮发送完前7个报文段,第4轮发送完前15个报文段,第5段发送完前31个报文段,第6轮发送完前63个报文段,第7轮发送完前96个报文段,因此第70报文段是在**第7轮**发送出的。
86 |
87 | (7)此时执行快恢复算法,cwnd设置为$8/2=4$。ssthresh设置为拥塞窗口的一半,即$8/2=4$。
88 |
89 |
90 |
91 | ## 5-41
92 |
93 | 
94 |
95 |
96 |
97 | ## 5-46
98 |
99 | 如果仅进行一次握手,由于接收端无需返回确认信息,那么如果发送端发送的报文丢失,发送端也不知道。因此不能仅进行一次握手。
100 |
101 | 如果进行两次握手,由于发送端无需返回对接收端发送来报文的确认信息,那么如果接收端发给发送端的确认信息在传输中丢失了,此时接收端仍认为已经建立连接,并等待发送端向其发送数据,而发送端由于没收到确认信息,因此也不会发送数据,此时接收端就会一直等待。
102 |
103 | 如果进行大于三次握手,那么相对于三次握手来说效率就有所下降了,因此连接建立需要进行三报文握手。
104 |
105 | 或者考虑另一种情况,如果在网络中滞留着上一次TCP连接中的报文,那么如果这个报文突然传到接收端了,那么接收端就会认为发送端请求建立连接,于是就分配资源等待接收端发送数据,而发送端并没有想建立连接,这就会导致接收端资源浪费。而由于三次握手中如果发送端接收到了接收端的确认信息发现不对,那就会发送复位报文段,告诉接收端拒绝了连接,这样就不会导致上述的问题了。
106 |
107 |
108 |
109 | ## 5-61
110 |
111 | 下方**可用窗口的位置为发送窗口内白色的区域**。
112 |
113 | (1)A发送数据不会对发送窗口造成影响。
114 |
115 |  116 |
117 | (2)A把数据发完。
118 |
119 |
116 |
117 | (2)A把数据发完。
118 |
119 |  120 |
121 | (3)收到确认1000号,因此窗口移到1001以后。
122 |
123 |
120 |
121 | (3)收到确认1000号,因此窗口移到1001以后。
122 |
123 |  124 |
125 | (4)再发送850B。
126 |
127 |
124 |
125 | (4)再发送850B。
126 |
127 |  128 |
129 | (5)发送方收到的ack已经不在窗口了,所以不变化.
130 |
131 |
128 |
129 | (5)发送方收到的ack已经不在窗口了,所以不变化.
130 |
131 |  132 |
133 | (6)收到确认2047号,因此窗口移到2048以后。
134 |
135 |
132 |
133 | (6)收到确认2047号,因此窗口移到2048以后。
134 |
135 |  136 |
137 | (7)A把数据发完。由于数据总大小为3kB,因此最多就到3072以前。
138 |
139 |
136 |
137 | (7)A把数据发完。由于数据总大小为3kB,因此最多就到3072以前。
138 |
139 | 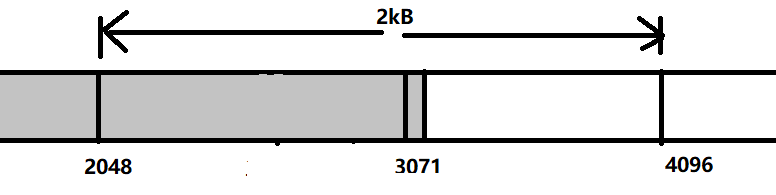 140 |
141 | (8)全部都接收到了,窗口移到3072以后。
142 |
143 |
140 |
141 | (8)全部都接收到了,窗口移到3072以后。
142 |
143 |  144 |
145 |
146 |
147 | ## 5-68
148 |
149 | 假设A是发送端(主动打开连接的一方),B是接收端(被动打开连接的一方)。那么在TCP的连接建立过程中,如果第三个报文丢失,那么A就会建立TCP连接,B还是在SYN-RCVD阶段。
150 |
151 | - 如果此时A没有紧接着发送数据,那么B经过一段时间后就会回到CLOSED状态,需要重新建立连接。
152 | - 如果此时A紧接着发送数据,那么此时A发送的数据报中自己的序号没有改变,与丢失的确认帧序号相同,且确认位ACK=1,确认号也是B选择的初始序号加1。当B接收到此报文段后就进入ESTABLISHED状态,继续接收A发送的数据。此时,第三个报文丢失不会对TCP建立造成影响。
153 |
154 | 综上,第三个报文段不确认对于在A建立连接后长时间不传输数据会有影响,而对于A建立连接后立即开始传输数据不会有什么影响。
155 |
156 |
157 |
158 |
--------------------------------------------------------------------------------
/docs/ComputerNetwork/《计算机网络》第六章作业.md:
--------------------------------------------------------------------------------
1 | # 《计算机网络》第六章作业
2 |
3 | ## 6-02
4 |
5 | **答:**域名系统是互联网使用的命名系统,其主要功能就是把域名解析为IP地址。四类域名服务器的区别如下:
6 |
7 | | 域名服务器 | 说明 |
8 | | -------------- | ------------------------------------------------------------ |
9 | | 本地域名服务器 | 离用户较近;主机发出DNS查询时,首先发给本地域名服务器 |
10 | | 根域名服务器 | 最高层次、最重要的域名服务器;根域名服务器知道所有顶级域名服务器的域名和IP地址;当本地域名服务器无法解析时,首先求助于根域名服务器 |
11 | | 顶级域名服务器 | 负责管理该顶级域名服务器注册的所有二级域名;收到查询请求后就给出相应回答 |
12 | | 权限域名服务器 | 负责一个区的域名服务器;当权限域名服务器无法给出最后的回答时,会告诉请求方下一步找哪个权限域名服务器 |
13 |
14 |
15 |
16 | ## 6-15
17 |
18 | **答:**解析IP地址的时间为$\sum_{i=1}^n \text{RTT}_i$,建立TCP连接时间为$\text{RTT}_w$,请求万维网文档时间为$\text{RTT}_w$,因此,总时间为$\sum_{i=1}^n \text{RTT}_i + 2\text{RTT}_w$ 。
19 |
20 |
21 |
22 | ## 6-23
23 |
24 | **答:**1. **连接建立**:发件人将邮件发到发送方邮件服务器缓存中,SMTP客户每隔一段时间对邮件缓存扫描一次,若有邮件,就使用25端口于接收方邮件服务器的SMTP服务器建立TCP连接。
25 |
26 | 2. **邮件传送**:(1)发送MAIL命令:命令后有发件人的地址,若SMTP服务器已准备好接收,则回复OK,不然就返回一个代码指出原因。(2)发送一个或多个RCPT命令(取决于把同一个邮件发送给一个还是多个收件人):先弄清接收方是否已准备好接收邮件,然后再发送邮件(避免浪费通信资源)。(3)发送DATA命令:开始传送邮件的内容。
27 | 3. **连接释放**:邮件发送完毕后,SMTP客户发送QUIT命令,SMTP服务器同意释放TCP连接后即断开TCP连接。
28 |
29 |
30 |
31 | ## 6-32
32 |
33 | **答:**DHCP用在计算机加入新的网络时获取这台计算机的IP地址。DHCP提供了即插即用联网机制,允许一台计算机加入新的网络和获取IP地址而不用手工参与。
34 |
35 | 当一台计算机第一次运行引导程序时,ROM中**没有**该计算机的IP地址、子网掩码和某个域名服务器的IP地址。
36 |
37 |
38 |
39 | ## 6-46
40 |
41 | **答:**(1)有的协议追求可靠连接,因此需要使用TCP协议。有的协议追求开销小,而TCP进行传送开销太大了(需要建立连接、释放连接等),因此采用UDP来减小开销。
42 |
43 | (2)MIME不是一个独立的邮件传送协议,它是SMTP上的一个协议,其首部中说明了邮件的数据类型,下图说明了MIME与SMTP的关系。
44 |
45 |
144 |
145 |
146 |
147 | ## 5-68
148 |
149 | 假设A是发送端(主动打开连接的一方),B是接收端(被动打开连接的一方)。那么在TCP的连接建立过程中,如果第三个报文丢失,那么A就会建立TCP连接,B还是在SYN-RCVD阶段。
150 |
151 | - 如果此时A没有紧接着发送数据,那么B经过一段时间后就会回到CLOSED状态,需要重新建立连接。
152 | - 如果此时A紧接着发送数据,那么此时A发送的数据报中自己的序号没有改变,与丢失的确认帧序号相同,且确认位ACK=1,确认号也是B选择的初始序号加1。当B接收到此报文段后就进入ESTABLISHED状态,继续接收A发送的数据。此时,第三个报文丢失不会对TCP建立造成影响。
153 |
154 | 综上,第三个报文段不确认对于在A建立连接后长时间不传输数据会有影响,而对于A建立连接后立即开始传输数据不会有什么影响。
155 |
156 |
157 |
158 |
--------------------------------------------------------------------------------
/docs/ComputerNetwork/《计算机网络》第六章作业.md:
--------------------------------------------------------------------------------
1 | # 《计算机网络》第六章作业
2 |
3 | ## 6-02
4 |
5 | **答:**域名系统是互联网使用的命名系统,其主要功能就是把域名解析为IP地址。四类域名服务器的区别如下:
6 |
7 | | 域名服务器 | 说明 |
8 | | -------------- | ------------------------------------------------------------ |
9 | | 本地域名服务器 | 离用户较近;主机发出DNS查询时,首先发给本地域名服务器 |
10 | | 根域名服务器 | 最高层次、最重要的域名服务器;根域名服务器知道所有顶级域名服务器的域名和IP地址;当本地域名服务器无法解析时,首先求助于根域名服务器 |
11 | | 顶级域名服务器 | 负责管理该顶级域名服务器注册的所有二级域名;收到查询请求后就给出相应回答 |
12 | | 权限域名服务器 | 负责一个区的域名服务器;当权限域名服务器无法给出最后的回答时,会告诉请求方下一步找哪个权限域名服务器 |
13 |
14 |
15 |
16 | ## 6-15
17 |
18 | **答:**解析IP地址的时间为$\sum_{i=1}^n \text{RTT}_i$,建立TCP连接时间为$\text{RTT}_w$,请求万维网文档时间为$\text{RTT}_w$,因此,总时间为$\sum_{i=1}^n \text{RTT}_i + 2\text{RTT}_w$ 。
19 |
20 |
21 |
22 | ## 6-23
23 |
24 | **答:**1. **连接建立**:发件人将邮件发到发送方邮件服务器缓存中,SMTP客户每隔一段时间对邮件缓存扫描一次,若有邮件,就使用25端口于接收方邮件服务器的SMTP服务器建立TCP连接。
25 |
26 | 2. **邮件传送**:(1)发送MAIL命令:命令后有发件人的地址,若SMTP服务器已准备好接收,则回复OK,不然就返回一个代码指出原因。(2)发送一个或多个RCPT命令(取决于把同一个邮件发送给一个还是多个收件人):先弄清接收方是否已准备好接收邮件,然后再发送邮件(避免浪费通信资源)。(3)发送DATA命令:开始传送邮件的内容。
27 | 3. **连接释放**:邮件发送完毕后,SMTP客户发送QUIT命令,SMTP服务器同意释放TCP连接后即断开TCP连接。
28 |
29 |
30 |
31 | ## 6-32
32 |
33 | **答:**DHCP用在计算机加入新的网络时获取这台计算机的IP地址。DHCP提供了即插即用联网机制,允许一台计算机加入新的网络和获取IP地址而不用手工参与。
34 |
35 | 当一台计算机第一次运行引导程序时,ROM中**没有**该计算机的IP地址、子网掩码和某个域名服务器的IP地址。
36 |
37 |
38 |
39 | ## 6-46
40 |
41 | **答:**(1)有的协议追求可靠连接,因此需要使用TCP协议。有的协议追求开销小,而TCP进行传送开销太大了(需要建立连接、释放连接等),因此采用UDP来减小开销。
42 |
43 | (2)MIME不是一个独立的邮件传送协议,它是SMTP上的一个协议,其首部中说明了邮件的数据类型,下图说明了MIME与SMTP的关系。
44 |
45 | 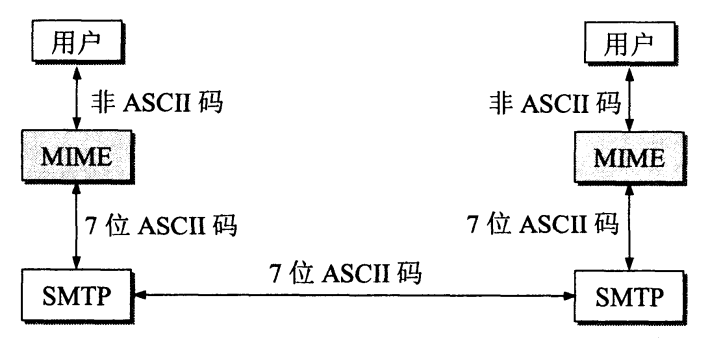 46 |
47 | (3)RIP协议使用了UDP传送数据,因此RIP在UDP之上,属于应用层。
48 |
49 |
50 |
51 |
--------------------------------------------------------------------------------
/docs/ComputerNetwork/《计算机网络》第四章作业.md:
--------------------------------------------------------------------------------
1 | # 《计算机网络》第四章作业
2 |
3 | ## 4-01
4 |
5 | **答:**一种是面向连接的服务(虚电路服务),一种是无连接的服务(数据报服务)。
6 |
7 | 面向连接的服务(可靠通信由网络保证):
8 |
9 | - 优点:分组开销小;分组无差错。
10 | - 缺点:网络成本高;若某一节点出错,所有通过该节点的虚电路都不能正常工作。
11 |
12 | 无连接的服务(可靠通信由用户主机保证):
13 |
14 | - 优点:网络成本低;某一节点出错时,路由可能变化,数据报可能仍然可以传输。
15 | - 缺点:尽力交付,可能会出现数据报异常情况。
16 |
17 | ## 4-03
18 |
19 | **答:**他们都起到连接网络的作用,但处在不同的网络体系结构层级。转发器在物理层,网桥在数据链路层,路由器在网络层,而网关在运输层及应用层(路由器也可以表示网关)。
20 |
21 | ## 4-07
22 |
23 | **答:**IP地址是网络层及以上使用的逻辑地址,而硬件地址是物理层及数据链路层使用的地址。由于不同国家、区域等有着不同的网络结构,其中的主机都有不同形式的硬件地址,因此若需要跨域传输时,会存在复杂的硬件地址转换。使用统一的IP地址可以使用户间的通信好像在一个网络上一样。IP地址与硬件地址的转换也相对硬件地址与硬件地址的转换要方便许多。
24 |
25 | ## 4-10
26 |
27 | **答:**(1)**10**000000.00100100.11000111.00000011,为B类地址;
28 |
29 | (2)**0**0010101.00001100.11110000.00010001,为A类地址;
30 |
31 | (3)**10**110111.11000010.01001100.11111101,为B类地址;
32 |
33 | (4)**110**00000.00001100.01000101.11111000,为C类地址;
34 |
35 | (5)**0**1011001.00000011.00000000.00000001,为A类地址;
36 |
37 | (6)**110**01000.00000011.00000110.00000010,为C类地址。
38 |
39 | ## 4-11
40 |
41 | **答:**好处是减小开销(加快检验、转发分组更快);坏处是在网络层传输的过程中就算数据发生了错误,也无法识别并中止传输,需要到达终点后在主机上(运输层)才能进行校验。
42 |
43 | ## 4-15
44 |
45 | **答:**MTU是一个数据帧中数据字段的最大长度。当一个IP数据报封装成数据链路层的帧的时候,数据报的总长度一定不能超过MTU。MTU与IP数据报首部中的总长度字段有关系,MTU是该字段的上限值。
46 |
47 | ## 4-18
48 |
49 | **答:**(1)数据链路层只能接触到MAC帧,如果ARP在数据链路层,那么MAC帧中就需要有IP地址,这不符合数据链路层对MAC帧的结构定义。
50 |
51 | (2)当网络中IP地址与硬件地址的映射发生变化时,ARP高速缓存中对应项就需要改变。超时时间设置太短会使ARP请求和响应分组的通信太频繁,若设置太长会使得硬件地址变化的主机迟迟无法与网络上其他主机通信。设置10~20分钟主要是因为在这样的一段时间段内更换网卡是很合理的。
52 |
53 | (3)①源主机的ARP高速缓存中已经有了目的主机的MAC地址;②源主机发送的是广播分组;③源主机与目的主机间使用点对点链路。
54 |
55 | ## 4-24
56 |
57 | **答:**A类子网划分对应数目的子网,子网掩码第一个字节需要全为1。若需要划分为n个A类子网,主机号部分的1的个数为$\lceil \log_2(n + 2) \rceil$(去除了全0和全1的子网数)。
58 |
59 | (1)$n=2$,主机号部分1的数量为2,因此子网掩码为255.192.0.0;
60 |
61 | (2)$n=6$,主机号部分1的数量为3,因此子网掩码为255.224.0.0;
62 |
63 | (3)$n=30$,主机号部分1的数量为5,因此子网掩码为255.248.0.0;
64 |
65 | (4)$n=62$,主机号部分1的数量为6,因此子网掩码为255.252.0.0;
66 |
67 | (5)$n=122$,主机号部分1的数量为7,因此子网掩码为255.254.0.0(实际有126个子网);
68 |
69 | (6)$n=250$,主机号部分1的数量为8,因此子网掩码为255.255.0.0(实际有254个子网);
70 |
71 | ## 4-25
72 |
73 | **答:**(1)10110000.0.0.0,其中1不是连续的,不推荐使用;
74 |
75 | (2)01100000.0.0.0,首位不是1(1前面有0),不推荐使用;
76 |
77 | (3)01111111.11000000.0.0,首位不是1(1前面有0),不推荐使用;
78 |
79 | (4)11111111.10000000.0.0,合理,推荐使用。
80 |
81 | ## 4-31
82 |
83 | **答:**86.32/12的网络前缀为0101 0110 0010。
84 |
85 | (1)86.33.224.123的前12位为0101 0110 0010,与上述网络前缀匹配。
86 |
87 | (2)86.79.65.216的前12位为0101 0110 0100,与上述网络前缀不匹配。
88 |
89 | (3)86.58.119.74的前12位为0101 0110 0011,与上述网络前缀不匹配。
90 |
91 | (4)86.68.206.154的前12位为0101 0110 0100,与上述网络前缀不匹配。
92 |
93 | ## 4-35
94 |
95 | **答:**转化为二进制为**10001100.01111000.0101**0100.00011000。
96 |
97 | 最大地址:**10001100.01111000.0101**1111.11111111,即140.120.95.255/20;
98 |
99 | 最小地址:**10001100.01111000.0101**0000.00000000,即140.120.80.0/20;
100 |
101 | 地址掩码:255.255.240.0;
102 |
103 | 地址块中共有$2^{12}=4096$个地址;
104 |
105 | 相当于$2^{24-20}=2^4=16$个C类地址。
106 |
107 | ## 4-38
108 |
109 | **答:**IGP是内部网关协议,是在一个自治系统内部使用的路由选择协议;EGP是外部网关协议,是在不同的自治系统间使用的路由选择协议。
110 |
111 | ## 4-39
112 |
113 | **答:**RIP协议是一种分布式的基于距离向量的路由选择协议,是互联网的标准协议,其最大优点就是简单,其主要特点为:
114 |
115 | - 仅和相邻路由器交换信息;
116 | - 路由器交换的信息是本路由器所知道的全部信息;
117 | - 按固定的时间间隔交换路由信息。
118 |
119 | OSPF使用分布式的链路状态协议,其主要特点为:
120 |
121 | - 使用洪泛法向本自治系统中所有路由器发送信息;
122 | - 发送的信息就是与本路由器相邻的所有路由器的链路状态,但这只是路由器所知道的部分信息;
123 | - 当链路状态变化或每隔一段时间,路由器向所有路由器用洪泛法发送链路状态信息;
124 | - 对于不同类型的业务可计算出不同的路由;
125 | - 多路径间存在负载均衡;
126 | - 所有在OSPF路由器之间交换的分组都具有鉴别功能;
127 | - 支持可变长度的子网划分和无分类的编址CIDR;
128 | - 每一个链路状态都会带上一个32位的序号,序号越大状态就越新。
129 |
130 | BGP是不同自治系统的路由器之间交换路由信息的协议,它采用路径向量路由选择协议,其主要特点为:
131 |
132 | - BGP在自治系统之问交换“可达性”信息;
133 | - BGP只能是力求寻找一条能够到达目的网络且比较好的路由(不能兜圈子),而并非要寻找一条最佳路由;
134 | - BGP的路由选择有很多策略,如选择本地偏好值最高的路由、选择AS跳数最少的路由、使用热土豆算法等;
135 | - BGP有四种报文,在不同的场合使用不同的报文。
136 |
137 | ## 4-43
138 |
139 | **答:**IGMP协议是让连接在本地局域网上的多播路由器知道本局域网上是否有主机(严格讲,是主机上的某个进
140 | 程)参加或退出了某个多播组。IGMP协议的要点主要体现在两个阶段:
141 |
142 | - 当某个主机加入新的多播组时,该主机应向多播组的多播地址发送一个IGMP报文,声明自己要成为该组的成员。本地的多播路由器收到IGMP报文后,还要利用多播路由选择协议把这种组成员关系转发给互联网上的其他多播路由器。
143 | - 本地多播路由器要周期性地探询本地局域网上的主机,以便知道这些主机是否还继续是组的成员。只要有一个主机对某个组响应,那么多播路由器就认为这个组是活跃的。但一个组在经过几次的探询后仍然没有一个主机响应,多播路由器就认为本网络上的主机已经都离开了这个组,因此也就不再把这个组的成员关系转发给其他
144 | 的多播路由器。
145 |
146 | 当两个多播网络之间的网络不支持多播时,会使用隧道技术。在这种情况下,发送方网络路由器会对多播数据进行再次封装,加上普通数据报首部,使之变成单播数据报,这样就能通过中间网络(此时相当于构建了一个隧道)传输到另一个多播网络,目的网络路由器收到此数据报后先剥去其首部,变成原来的多播数据报后再进行传输。
147 |
148 | ## 4-48
149 |
150 | **答:**146.102.29.0的二进制为10010010.01100110.00011101.00000000;
151 |
152 | 146.102.32.255的二进制为10010010.01100110.00100000.11111111;
153 |
154 | 从146.102.29.0(含)到146.102.29.255(含)有$256$个地址。而146.102.29.255(不含)到146.102.32.255(含)有$3\times 256$个地址,因此总共有$4\times 256=1024$个地址。
155 |
156 | ## 4-65
157 |
158 | **答:**(1)0000 : 0000 : 0000 : 0000 : 0000 : 0000 : 0000 : 0000
159 |
160 | (2)0000 : 00AA : 0000 : 0000 : 0000 : 0000 : 0000 : 0000
161 |
162 | (3)0000 : 1234 : 0000 : 0000 : 0000 : 0000 : 0000 : 0003
163 |
164 | (4)0123 : 0000 : 0000 : 0000 : 0000 : 0000 : 0001 : 0002
--------------------------------------------------------------------------------
/docs/MachineLearning/第一章作业.md:
--------------------------------------------------------------------------------
1 | # 《机器学习》第一章作业
2 |
3 | ## 1.1
4 |
5 | 表1.1中若只包含编号为1和4的两个样例,即如下表所示:
6 |
7 | | 编号 | 色泽 | 根蒂 | 敲声 | 好瓜 |
8 | | ---- | ---- | ---- | ---- | ---- |
9 | | 1 | 青绿 | 蜷缩 | 浊响 | 是 |
10 | | 4 | 乌黑 | 稍蜷 | 沉闷 | 否 |
11 |
12 | 则其版本空间如下图所示:
13 |
14 | 
15 |
16 | ## 1.3
17 |
18 | 对于所有假设,选择满足最多样本的假设。若有多个,则选择尽可能一般的假设(即属性值为任意的数量尽可能多)。若还有多个,随机选择一个即可。
19 |
20 |
21 |
22 | ## 1.5
23 |
24 | 1. 对欲搜索文本进行分词,提取关键词并分析语义后进行检索;
25 | 2. 对搜索文本和数据库中相关信息进行匹配并排序;
26 | 3. 在拥有用户信息和使用习惯的数据后,可以智能推荐搜索结果;
27 | 4. 实现对图片、视频等多媒体数据进行分析后,给出搜索结果(如百度识图);
28 | 5. 对搜索出的结果进行无效信息、重复信息的过滤;
29 | 6. 建立知识图谱,能精确给出搜索结果的梗概(或者与其他概念的关系)。
30 |
31 |
--------------------------------------------------------------------------------
/docs/MachineLearning/第七章作业.md:
--------------------------------------------------------------------------------
1 | # 《机器学习基础》第七章作业
2 |
3 | ## 7.1
4 |
5 | **答:**使用极大似然法得到的类条件概率估计表达式为
6 | $$
7 | P(x_i=t_{ij}|c) = \frac{|D_{c,x_i, t_{ij}}|}{|D_c|}
8 | $$
9 | 其中,$|D_c|$表示训练集$D$中$c$类样本的数量,$|D_{c, x_i, t_{ij}}|$表示训练集中$c$类元素属性$x_i$为$t_{ij}$的数量的元素。由此根据西瓜数据集即可得出类条件概率如下:
10 |
11 | | 属性 | 属性取值 | 好瓜($c_0$) | 坏瓜($c_1$) |
12 | | ----------- | -------------- | ----------- | ----------- |
13 | | 色泽($x_0$) | 青绿($t_{00}$) | $\frac38$ | $\frac13$ |
14 | | | 乌黑($t_{01}$) | $\frac12$ | $\frac29$ |
15 | | | 浅白($t_{02}$) | $\frac18$ | $\frac49$ |
16 | | 根蒂($x_1$) | 蜷缩($t_{10}$) | $\frac58$ | $\frac13$ |
17 | | | 稍蜷($t_{11}$) | $\frac38$ | $\frac49$ |
18 | | | 硬挺($t_{12}$) | $0$ | $\frac29$ |
19 | | 敲声($x_2$) | 浊响($t_{20}$) | $\frac34$ | $\frac49$ |
20 | | | 沉闷($t_{21}$) | $\frac14$ | $\frac13$ |
21 | | | 清脆($t_{22}$) | $0$ | $\frac29$ |
22 |
23 |
24 |
25 | ## 7.3
26 |
27 | ### 1. 环境及数据准备
28 | ```python
29 | import numpy as np
30 | import pandas as pd
31 | import scipy.stats as st
32 |
33 | df = pd.read_csv('./watermelon3.csv', index_col=0) # 西瓜数据集3.0
34 | X = np.array(df.iloc[:, :-1]) # 属性
35 | y = np.array(df.iloc[:, -1])[None].T # 标签
36 | ```
37 |
38 | ### 2. 定义模型
39 | ```python
40 | class NaiveBayes:
41 | def __init__(self) -> None:
42 | pass
43 |
44 | def get_prob(self, X, x, x_i, N): # 拉普拉斯修正
45 | return ((X[:, x] == x_i).sum() + 1) / (X.shape[0] + N)
46 |
47 | def get_dis_prob(self, X, y): # 离散概率
48 | p = []
49 | for i, c in enumerate(self.label):
50 | temp = X[(y == c).ravel()]
51 | lst = []
52 | for x in range(temp.shape[1]):
53 | dct = {}
54 | uni = np.unique(X[:, x])
55 | for x_i in uni:
56 | dct[x_i] = self.get_prob(temp, x, x_i, uni.shape[0])
57 | lst.insert(x, dct)
58 | p.insert(i, lst)
59 | return p
60 |
61 | def get_con_prob(self, X, x, x_i): # 连续概率
62 | return st.norm.pdf(x_i, loc=X[:, x].mean(), scale=X[:, x].std())
63 |
64 | def train(self, X, y):
65 | self.X, self.y = X, y
66 | self.con_col = [i for i in range(X.shape[1]) if type(X[0][i]) == float] # 连续值所在位置
67 | dis_X = np.delete(X, self.con_col, axis=1) # 提取离散值
68 | con_X = X[:, self.con_col] # 提取连续值
69 | self.label = np.unique(y) # 将label的类型取出来
70 | self.dis_p = self.get_dis_prob(dis_X, y)
71 | self.P_c = ((self.label == y).sum(axis=0) + 1) / (df.shape[0] + self.label.shape[0])
72 |
73 | def predict(self, X_pre):
74 | y_pre = np.ones(X_pre.shape[0], dtype='object')
75 | for j, X in enumerate(X_pre):
76 | maxn = 0
77 | res_c = 0
78 | for i, c in enumerate(self.label):
79 | res = 1
80 | temp_X = self.X[(self.y == c).ravel()]
81 | a = 0
82 | for x in range(X.shape[0]):
83 | if x in self.con_col: # 连续
84 | res *= self.get_con_prob(temp_X, x, X[x])
85 | else: # 离散
86 | res *= (self.dis_p[i][a][X[x]])
87 | a += 1
88 | res *= self.P_c[i]
89 | if res > maxn:
90 | maxn = res
91 | res_c = c
92 | y_pre[j] = res_c
93 | return y_pre[None].T
94 | ```
95 | ### 3. 模型测试
96 | ```python
97 | model = NaiveBayes()
98 | model.train(X, y)
99 | test_X = np.array(['青绿', '蜷缩', '浊响', '清晰', '凹陷', '硬滑', 0.697, 0.460], dtype='object')
100 | print(model.predict(test_X[None])[0][0])
101 | ```
102 |
103 | 是
104 |
105 |
106 |
107 | ## 7.4
108 |
109 | **答:**由于$P(x_i|c)\leq 1$,因此$\prod_{i=1}^{d} P(x_i|c)$很可能因为非常接近$0$而造成下溢,可以采用对此公式求对数的方式将正小数转化为负正数从而解决数据可能下溢的问题,即转化为$\sum_{i=1}^{d} \log P(x_i|c)$。
110 |
111 |
112 |
113 | ## 7.5
114 |
115 | **答:**对于贝叶斯最优分类器来说,其欲最大化的目标为
116 | $$
117 | P(c | \boldsymbol x) = \frac{P(c)P(\boldsymbol x | c)}{P(\boldsymbol x)}
118 | $$
119 |
120 | 因为$P(\boldsymbol x)$是常量,因此也就是最大化
121 | $$
122 | P(c)P(\boldsymbol x | c)
123 | $$
124 | 因为数据服从高斯分布,因此上式等价于
125 | $$
126 | P(c)\frac{1}{(2\pi)^{n/2}|\boldsymbol \Sigma |^{1/2} } \exp \left( -\frac12 (\boldsymbol x - \boldsymbol \mu_c)^\text T \boldsymbol \Sigma_c^{-1} (\boldsymbol x - \boldsymbol \mu_c)\right)
127 | $$
128 | 由题中条件“假设同先验”,因此在二分类任务中,上式等价于最大化
129 | $$
130 | \max(-\frac12 (\boldsymbol x - \boldsymbol \mu_0)^\text T \boldsymbol \Sigma_0^{-1} (\boldsymbol x - \boldsymbol \mu_0), -\frac12 (\boldsymbol x - \boldsymbol \mu_1)^\text T \boldsymbol \Sigma_1^{-1} (\boldsymbol x - \boldsymbol \mu_1))
131 | $$
132 | 由此可知,贝叶斯最优分类器的决策平面为
133 | $$
134 | \boldsymbol x ^ \text T \boldsymbol \Sigma^{-1}(\boldsymbol \mu_1 - \boldsymbol \mu_0) - \frac 12 (\boldsymbol \mu_1 + \boldsymbol \mu_0)^ \text T \boldsymbol\Sigma^{-1}(\boldsymbol \mu_1 - \boldsymbol \mu_0)
135 | $$
136 | 对于线性判别分析来说,其欲最大化的目标为
137 | $$
138 | J = \frac{\boldsymbol{w}^\text{T}(\boldsymbol\mu_0-\boldsymbol\mu_1)(\boldsymbol\mu_0-\boldsymbol\mu_1)^\text T \boldsymbol{w}}{\boldsymbol{w} ^\text{T} (\boldsymbol\Sigma_0 + \boldsymbol\Sigma_1)\boldsymbol{w}}
139 | $$
140 | 其中,$\boldsymbol w$为直线$y=\boldsymbol w ^ \text T \boldsymbol x$中的系数项,$\boldsymbol \mu_i, \boldsymbol \Sigma_i$为第$i \in \{0, 1\}$类的均值向量、协方差矩阵。由于两类数据满足高斯分布且方差相同,因此其决策平面由两数据均值点的中点$\frac 12 (\boldsymbol \mu_0 + \boldsymbol \mu_1)$和法向量$\boldsymbol w$唯一确定,而将此带入贝叶斯最优分类器的决策平面均成立,因此线性判别分析的决策平面与此重合。因此,二分类任务中两类数据满足高斯分布且方差相同时,线性判别分析产生贝叶斯最优分类器。
141 |
142 |
143 |
144 |
145 | ## 7.7
146 |
147 | **答:**由题意,对于一个二分类问题,需要估算一个二值属性对应的先验概率$P(c, x_i)$则需要$30\times 2 \times 2=120$个样例(因为$c$和$x_i$的取值均有两种)。如果第二个二值属性在上述样例上对应的$c$和$x_i$的取值均相同,那么就无需增加样例;如果第二个二值属性在上述样例上的取值只有一个,那么还需要$30\times 2=60$个样例(另一个取值在$c$两取值上的个数)。
148 |
149 | 因此,当扩展到有$d$个二值属性时,最好情况不需要在第一个的基础上添加任何样例,因此样例数为$120$;最坏情况下,每一次添加属性均会添加$60$个样例,因此样例数为$120+60\times (d-1) = 60 \times (d + 1)$。
150 |
151 |
--------------------------------------------------------------------------------
/docs/MachineLearning/第三章作业.md:
--------------------------------------------------------------------------------
1 | # 《机器学习》第三章作业
2 |
3 | ## 3.1
4 |
5 | 答:(1)该模型中$b$与输入没有关系时或模型函数一定过原点时;(2)该模型只用于差分分析时,因为假设取两实例$\boldsymbol{x}_i$和$\boldsymbol{x}_j(i\neq j)$,$f(\boldsymbol{x}_i) - f(\boldsymbol{x}_j ) = \boldsymbol{w}^\text{T}(\boldsymbol{x}_i - \boldsymbol{x}_j)$是与$b$无关的。
6 |
7 | ## 3.3
8 |
9 | ### 1.准备数据
10 |
11 | ```python
12 | import numpy as np
13 | from sklearn.model_selection import train_test_split
14 |
15 | data = np.array([[0.697, 0.460, 1],
16 | [0.774, 0.376, 1],
17 | [0.634, 0.264, 1],
18 | [0.608, 0.318, 1],
19 | [0.556, 0.215, 1],
20 | [0.403, 0.237, 1],
21 | [0.481, 0.149, 1],
22 | [0.437, 0.211, 1],
23 | [0.666, 0.091, 0],
24 | [0.243, 0.267, 0],
25 | [0.245, 0.057, 0],
26 | [0.343, 0.099, 0],
27 | [0.639, 0.161, 0],
28 | [0.657, 0.198, 0],
29 | [0.360, 0.370, 0],
30 | [0.593, 0.042, 0],
31 | [0.719, 0.103, 0]]) # 西瓜数据集3.0alpha
32 | X = data[:, 0:2] # 属性
33 | y = data[:, -1] # 标签
34 | X_train,X_test,y_train,y_test=train_test_split(X,y,test_size=0.3) #随机划分训练集和测试集
35 | ```
36 |
37 | ### 2.定义模型
38 |
39 | ```python
40 | class LogisticRegression:
41 | def __int__(self):
42 | pass
43 |
44 | def fit(self, X_, y_):
45 | # 数据调整为x_bar和\beta, 便于操作
46 | n, m = X_.shape
47 | m += 1
48 | X = np.append(X_, np.ones(n).reshape((n, 1)), axis=1).T
49 | y = y_.copy()
50 | beta = np.random.random(size=(m, 1))
51 | # 牛顿迭代法
52 | epoch = 20
53 | for i in range(epoch):
54 | mul = beta.T @ X
55 | p1 = np.exp(mul) / (1 + np.exp(mul)) # 计算p1的公式
56 | fd = -np.sum(X * (y - p1), axis=1) # 计算牛顿迭代中的一阶导数
57 | sd = np.zeros((m, m)) # 计算牛顿迭代中的二阶导数
58 | for i in range(n):
59 | sd += X[:, i:i+1] @ X[:, i:i+1].T * (p1[0, i] * (1 - p1[0, i]))
60 | beta = beta - (np.linalg.inv(sd) @ fd).reshape((m, 1)) # 一次迭代
61 | # 训练结果分析
62 | ans = (beta.T @ X) > 1
63 | self.beta = beta
64 | print("训练集准确率: ", 1 - np.sum(np.abs(ans - y)) / n)
65 |
66 | def predict(self, X_, y_):
67 | # 测试结果分析
68 | n = X_.shape[0]
69 | X = np.append(X_, np.ones(n).reshape((n, 1)), axis=1).T
70 | y = y_.copy()
71 | ans = (self.beta.T @ X) > 1
72 | print("测试集准确率: ", 1 - np.sum(np.abs(ans - y)) / n)
73 |
74 | ```
75 |
76 | ### 3.使用模型进行训练和预测
77 |
78 | ```python
79 | model = LogisticRegression()
80 | model.fit(X_train, y_train)
81 | model.predict(X_test, y_test)
82 | ```
83 |
84 | 训练集准确率: 0.7272727272727273
85 | 测试集准确率: 0.8333333333333334
86 |
87 | ## 3.5
88 |
89 | ### 1.准备数据
90 |
91 | 同3.3
92 |
93 | ### 2.定义模型计算𝜔
94 |
95 | ```python
96 | class LDA:
97 | def __init__(self):
98 | pass
99 |
100 | def fit(self, X, y):
101 | X0 = X[y == 0] # 坏瓜
102 | X1 = X[y == 1] # 好瓜
103 | mu0 = np.mean(X0, axis=0).reshape((-1, 1)) # 坏瓜均值
104 | mu1 = np.mean(X1, axis=0).reshape((-1, 1)) # 好瓜均值
105 | cov0 = np.cov(X0, rowvar=False) # 坏瓜协方差
106 | cov1 = np.cov(X1, rowvar=False) # 好瓜协方差
107 | S_w = np.mat(cov0 + cov1) # S_w
108 | U,Sigma,V = np.linalg.svd(S_w,full_matrices=False) # 奇异值分解
109 | self.omega = V.T @ np.linalg.inv(np.diag(Sigma)) @ U.T @ (mu0 - mu1) # /omega
110 | # 输出结果
111 | ans = self.omega.T @ X.T < 0
112 | acc = 1 - np.sum(np.abs(ans - y)) / y.shape[0]
113 | print("训练集准确率:", acc)
114 |
115 | def predict(self, X, y):
116 | # 输出结果
117 | ans = self.omega.T @ X.T < 0
118 | acc = 1- np.sum(np.abs(ans - y)) / y.shape[0]
119 | print("测试集准确率:", acc)
120 |
121 | ```
122 |
123 | ### 3.使用模型进行训练和预测
124 |
125 | ```python
126 | model = LDA()
127 | model.fit(X_train, y_train)
128 | model.predict(X_test, y_test)
129 | ```
130 |
131 | 训练集准确率: 0.9090909090909091
132 | 测试集准确率: 0.6666666666666667
133 |
134 | ## 3.7
135 |
136 | 答:给出汉明距离意义下理论最优的ECOC二元码:
137 |
138 | | | $f_1$ | $f_2$ | $f_3$ | $f_4$ | $f_5$ | $f_6$ | $f_7$ | $f_8$ | $f_9$ |
139 | | ----- | ----- | ----- | ----- | ---- | ---- | ------- | ---- | ---- | ---- |
140 | | $C_1$ | +1 | -1 | -1 | -1 | +1 | +1 | +1 | +1 | -1 |
141 | | $C_2$ | -1 | +1 | -1 | -1 | +1 | -1 | -1 | +1 | -1 |
142 | | $C_3$ | -1 | -1 | +1 | -1 | -1 | +1 | -1 | +1 | -1 |
143 | | $C_4$ | -1 | -1 | -1 | +1 | -1 | -1 | +1 | +1 | -1 |
144 |
145 | 证明如下:
146 |
147 | 注意到性质:若两个分类器$f_i$和$f_j(i \neq j)$对样例的分类互为反码[如$(-1,-1,1,1)$和$(1,1,-1,-1)$],由于很多算法对待0-1分类是对称的(即如果将0-1类互换,最终训练出的模型是一样的)。这样一对分类器实际上可以简化为一个分类器,因此可以计算出在不出现互为反码的情况下,最优的ECOC编码长度为
148 | $$
149 | \binom{4}{1} + \frac{\binom{4}{2}}{2}=7
150 | $$
151 | 由于可以向编码中加入冗余,即可以在最短编码长度的情况下加入互为反码的一对分类器,因此只要保证编码长度为$7+2n(n为自然数)$即可保证得出的ECOC编码是最优的。
152 |
153 | 综上,由于$9=7+2\times 1$($f_8$和$f_9$是加入的冗余分类器),因此上述给出的ECOC二元码是理论最优的。
154 |
155 | ## 3.9
156 |
157 | 答:对OvR、MvM 来说,由于**对每个类进行了相同的处理**,其拆解出的二分类任务中类别不平衡的影响会相互抵消,因此通常不需专门处理。
158 |
--------------------------------------------------------------------------------
/docs/MachineLearning/第九章作业.md:
--------------------------------------------------------------------------------
1 | # 《机器学习基础》第九章作业
2 |
3 | ## 9.1
4 |
5 | **(1)首先证明闵可夫斯基距离满足非负性,同一性和对称性。**
6 |
7 | 由于
8 | $$
9 | \text{dist}_\text{mk} (x_i, x_j) = \left( \sum_{u=1}^n |x_{iu}-x_{ju}|^p \right)^\frac 1p \ge 0
10 | $$
11 | 因此,闵可夫斯基距离满足非负性。当且仅当$x_i = x_j$时,$\text{dist}_\text{mk} (x_i, x_j)=0$,因此闵可夫斯基距离满足同一性。由于绝对值中减数和被减数可以调换位置,所以$\text{dist}_\text{mk} (x_i, x_j) = \text{dist}_\text{mk} (x_j, x_i)$,因此闵可夫斯基距离满足对称性。
12 |
13 | **(2)下面证明当$p\ge 1$时,闵可夫斯基距离满足直递性。**
14 |
15 | 显然$p=1$时,可由三角不等式证明。因此下面$p>1$。
16 |
17 | 令$a_i=|x_{iu}-x_{ku}|,b_i=|x_{ku}-x_{ju}|$,那么要证$\text{dist}_\text{mk} (x_i, x_j) \leq \text{dist}_\text{mk} (x_i, x_k) + \text{dist}_\text{mk} (x_k, x_j)$,即证
18 | $$
19 | \left(\sum_{i=1}^{n}|a_i+b_i|^p\right)^\frac 1p \leq \left(\sum_{i=1}^{n}a_i^p \right)^\frac 1p + \left(\sum_{i=1}^{n}b_i^p \right)^\frac 1p
20 | $$
21 | 由于
22 | $$
23 | \begin{align}
24 | \left(\sum_{i=1}^{n}|a_i+b_i|^p\right)^\frac 1p &\leq \sum_{i=1}^{n}|a_i+b_i|^p \\
25 | &= \sum_{i=1}^{n}|a_i+b_i||a_i+b_i|^{p-1} \\
26 | &\leq \sum_{i=1}^{n}(|a_i|+|b_i|)|a_i+b_i|^{p-1} \\
27 | &= \sum_{i=1}^{n}(|a_i||a_i+b_i|^{p-1}+|b_i||a_i+b_i|^{p-1})
28 | \end{align}
29 | $$
30 | 由赫尔德不等式$\sum_i^na_ib_i \leq (\sum_{i=1}^n a_i^p)^\frac1p(\sum_{i=1}^nb_i^q)^\frac1q \ \ (p, q > 1) $可得
31 | $$
32 | \begin{align}
33 | \sum_{i=1}^{n}(|a_i||a_i+b_i|^{p-1}+|b_i||a_i+b_i|^{p-1}) &\leq \left(\sum_{i=1}^{n}|a_i|^p \right)^{\frac1p} \left(\sum_{i=1}^{n}|a_i+b_i|^{(p-1)q}\right)^{\frac1q} + \left(\sum_{i=1}^{n}|b_i|^p\right)^{\frac1p} \left(\sum_{i=1}^{n}|a_i+b_i|^{(p-1)q}\right)^{\frac1q} \\
34 | &= \left(\left(\sum_{i=1}^{n}|a_i|^p\right)^{\frac1p} + \left(\sum_{i=1}^{n}|b_i|^p\right)^{\frac1p} \right) \left(\sum_{i=1}^{n}|a_i+b_i|^{p}\right)^{\frac1q} \\
35 | &\leq \left(\sum_{i=1}^{n}|a_i|^p\right)^{\frac1p} + \left(\sum_{i=1}^{n}|b_i|^p\right)^{\frac1p}
36 | \end{align}
37 | $$
38 | 其中$q=\frac{p}{p-1}$,于是原不等式成立,因此,当$p \ge 1$时闵可夫斯基距离满足直递性。
39 |
40 | **(3)下面证明当$0 \leq p < 1$时,闵可夫斯基距离不满足直递性。**
41 |
42 | 和(2)类似的,只需证明下式即可证明原命题。
43 | $$
44 | \left(\sum_{i=1}^{n}|a_i+b_i|^p\right)^\frac 1p \ge \left(\sum_{i=1}^{n}a_i^p \right)^\frac 1p + \left(\sum_{i=1}^{n}b_i^p \right)^\frac 1p
45 | $$
46 | 由于
47 | $$
48 | \begin{align}
49 | \sum_{i=1}^{n}|a_i+b_i|^p &= \sum_{i=1}^{n}|t\frac{a_i}{t}+(1-t)\frac{b_i}{1-t}|^p \\
50 | &\ge t^{1-p}\sum_{i=1}^{n}|a_i|^p+(1-t)^{1-p}\sum_{i=1}^{n}|b_i|^p
51 | \end{align}
52 | $$
53 | 其中
54 | $$
55 | t=\frac{\left(\sum_{i=1}^{n}a_i^p \right)^\frac 1p}{\left(\sum_{i=1}^{n}a_i^p \right)^\frac 1p + \left(\sum_{i=1}^{n}b_i^p \right)^\frac 1p}
56 | $$
57 | 于是有
58 | $$
59 | \begin{align}
60 | t^{1-p}\sum_{i=1}^{n}|a_i|^p+(1-t)^{1-p}\sum_{i=1}^{n}|b_i|^p &= \left(\left(\sum_{i=1}^{n}a_i^p \right)^\frac 1p + \left(\sum_{i=1}^{n}b_i^p \right)^\frac 1p\right)^p
61 | \end{align}
62 | $$
63 | 综上即可证明原不等式成立,闵可夫斯基距离不满足直递性。
64 |
65 | **(4)下面证明$p$趋向无穷大时,闵可夫斯基距离等于对应分量的最大绝对距离。**
66 |
67 | 闵可夫斯基距离公式可以转换如下:
68 | $$
69 | \text{dist}_\text{mk} (x_i, x_j) = \left( \sum_{u=1}^n |x_{iu}-x_{ju}|^p \right)^\frac 1p = \max_u|x_{iu}-x_{ju}| \left( \sum_{u=1}^n \left(\frac{|x_{iu}-x_{ju}|}{\max_u|x_{iu}-x_{ju}|}\right)^p \right)^\frac 1p
70 | $$
71 | 令
72 | $$
73 | t_u = \frac{|x_{iu}-x_{ju}|}{\max_u|x_{iu}-x_{ju}|}\leq 1
74 | $$
75 | 当$p \rarr +\infin$时
76 | $$
77 | \left( \sum_{u=1}^n t_u^p \right)^\frac 1p \rarr1
78 | $$
79 | 因此
80 | $$
81 | \text{dist}_\text{mk} (x_i, x_j) \rarr \max_u|x_{iu}-x_{ju}|
82 | $$
83 | 综上得证。
84 |
85 |
86 |
87 | ## 9.2
88 |
89 | 显然,豪斯多夫距离满足非负性和对称性,这里不过多证明。
90 |
91 | (1)下面证明豪斯多夫距离满足同一性。
92 |
93 | ①当$X=Z$时,$\text{dist}_\text{h}(X, Z) = \text{dist}_\text{h}(Z, X) = 0$,因此$\text{dist}_\text{H}(X, Z) = 0$。
94 |
95 | ②当$\text{dist}_\text{H}(X, Z) = 0$时,$\text{dist}_\text{h}(X, Z) = \text{dist}_\text{h}(Z, X) = 0$,这说明任意$x\in X$,存在$z\in Z$使得距离为0,因此$X \subset Z$,同时也说明任意$z\in Z$,存在$x\in X$使得距离为0,因此$Z \subset X$,所以$X=Z$。
96 |
97 | 综上得证。
98 |
99 | (2)下面证明豪斯多夫距离满足直递性。
100 |
101 | 欲证
102 | $$
103 | \text{dist}_\text{H}(X, Z) \leq \text{dist}_\text{H}(X, Y) + \text{dist}_\text{H}(Y, Z)
104 | $$
105 |
106 | 由于
107 | $$
108 | \text{dist}_\text{H}(X, Z) = \max(\text{dist}_\text{h}(X, Z), \text{dist}_\text{h}(Z, X))
109 | $$
110 | 因此,可以转化为求证
111 | $$
112 | \text{dist}_\text{h}(X, Z) \leq \text{dist}_\text{h}(X, Y) + \text{dist}_\text{h}(Y, Z)
113 | $$
114 | 由于
115 | $$
116 | \begin{align}
117 | \min_{z\in Z} ||x - z||_2 &= \min_{z \in Z} ||x + y+y-z||_2, \forall y\in Y \\
118 | &\leq \min_{z \in Z} (||x + y||_2+||y-z||_2), \forall y\in Y \\
119 | &= ||x+y||_2 + \min_{z \in Z} ||y-z||_2, \forall y\in Y \\
120 | &\leq ||x+y||_2 + \max_{y \in Y}\min_{z \in Z} ||y-z||_2, \forall y\in Y \\
121 | &= ||x+y||_2 + \text{dist}_\text{h}(Y, Z), \forall y\in Y \\
122 | &\leq \min_{y \in Y} ||x+y||_2 + \text{dist}_\text{h}(Y, Z)
123 | \end{align}
124 | $$
125 | 对不等式左右两边取$\max_{x\in X}$得到
126 | $$
127 | \max_{x\in X}\min_{z\in Z} ||x - z||_2 \leq \max_{x\in X}\min_{y \in Y} ||x+y||_2 + \text{dist}_\text{h}(Y, Z)
128 | $$
129 | 即
130 | $$
131 | \text{dist}_\text{h}(X, Z) \leq \text{dist}_\text{h}(X, Y) + \text{dist}_\text{h}(Y, Z)
132 | $$
133 | 综上得证。
134 |
135 |
136 |
137 |
138 | ## 9.3
139 |
140 | 不一定能。由于求解式(9.24)的最优解是一个NP-hard问题,k均值算法只是基于贪心思想通过迭代进行近似求解得到的局部最优解,不一定能得到式子的全局最优解。
141 |
142 |
143 |
144 | ## 9.4
145 |
146 | ### 1 导入库
147 | ```python
148 | from sklearn.cluster import KMeans
149 | import pandas as pd
150 | import numpy as np
151 | from matplotlib import pyplot as plt
152 | ```
153 |
154 | ### 2 导入数据集
155 | ```python
156 | df = pd.read_csv("./4.0.csv", header=None)
157 | X = df.values
158 | ```
159 |
160 | ### 3 测试不同k值的影响
161 | > 选定数据集中前k个点作为初始中心点
162 | ```python
163 | for k in range(2, 5):
164 | model = KMeans(k, init=[X[i, :] for i in range(k)], n_init=1)
165 | model.fit(X)
166 | ans = model.predict(X)
167 | print(model.cluster_centers_)
168 | plt.title(f"KMeans [k={k}]")
169 | plt.scatter(X[:, 0], X[:, 1], c=ans)
170 | plt.show()
171 | ```
172 |
173 | ```
174 | [[0.62371429 0.37435714]
175 | [0.44675 0.1875 ]]
176 | ```
177 |
178 | 
179 |
180 | ```
181 | [[0.471 0.39928571]
182 | [0.68138462 0.28446154]
183 | [0.3725 0.1748 ]]
184 | ```
185 |
186 | 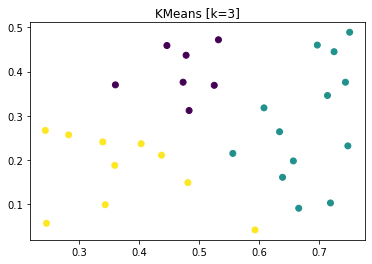
187 |
188 | ```
189 | [[0.67625 0.4665 ]
190 | [0.6896 0.3072 ]
191 | [0.61585714 0.137 ]
192 | [0.38685714 0.27714286]]
193 | ```
194 |
195 | 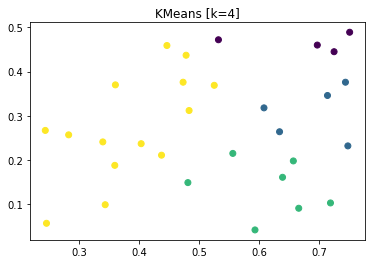
196 |
197 |
198 |
199 | ### 4 测试不同初始中心点的影响
200 |
201 | > 选定k=3
202 |
203 | ```python
204 | Xs = [[[0, 0], [0, 0], [0, 0]], # 全都在一个点
205 | [[0.5, 0.1], [0.5, 0.25], [0.5, 0.4]], # y轴分散
206 | [[0.3, 0.3], [0.5, 0.3], [0.7, 0.3]]] # x轴分散
207 |
208 | for centers in Xs:
209 | model = KMeans(3, init=centers, n_init=1)
210 | model.fit(X)
211 | ans = model.predict(X)
212 | print(model.cluster_centers_)
213 | # plt.title(f"KMeans [k={k}]")
214 | plt.scatter(X[:, 0], X[:, 1], c=ans)
215 | plt.show()
216 | ```
217 |
218 | ```
219 | [[0.36136364 0.21709091]
220 | [0.60845455 0.41336364]
221 | [0.6515 0.16325 ]]
222 | ```
223 |
224 | 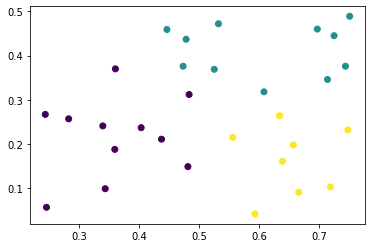
225 |
226 | ```
227 | [[0.63255556 0.16166667]
228 | [0.33455556 0.21411111]
229 | [0.598 0.40491667]]
230 | ```
231 |
232 | 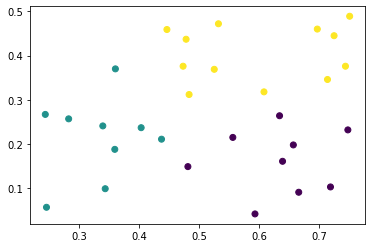
233 |
234 | ```
235 | [[0.348 0.18955556]
236 | [0.471 0.39928571]
237 | [0.67507143 0.26714286]]
238 | ```
239 |
240 | 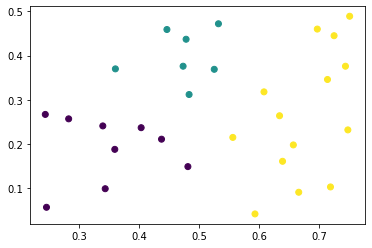
241 |
242 | ### 5 分析
243 |
244 | 1. 对比不同k值得到的结果可以看出,不是k越大越好,而是需要根据经验去确定簇的数量,这样才能达到不错的聚类效果。
245 | 2. 对比不同初始值的结果可以看出,初始中心点也很大程度上影响到了聚类的效果,选定的三组初始中心点各有特征,可以看出在选定初始中心点在x轴上分散分布时,效果比较不错,说明数据集在x轴方向上有比较好的可分性。由于KMeans基于贪心算法,只能得到局部最优解,因此根据经验选择符合数据集特征的初始中心点对聚类效果有显著影响。
246 |
247 |
248 |
249 | ## 9.5
250 |
251 | (1)连接性。设$x_k$为集合$X$中的核心对象,设$x_i \in X, x_j \in X$。由于集合$X$是由$x_k$密度可达的所有样本构成的,那么$x_i,x_j$均由$x_k$密度可达,因此$x_i$与$x_j$密度相连。由此证明连接性。
252 |
253 | (2)最大性。设$x_k$为集合$X$中的核心对象,设$x_i \in C$,那么$x_i$由$x_k$密度可达。如果$x_j$由$x_i$密度可达,由于密度可达关系满足直递性,$x_j$由$x_k$密度可达,因此$x_j\in C$。由此证明最大性。
254 |
255 |
256 |
257 |
--------------------------------------------------------------------------------
/docs/MachineLearning/第二章作业.md:
--------------------------------------------------------------------------------
1 | # 《机器学习》第二章作业
2 |
3 | ## 2.1
4 |
5 | 答:由留出法定义,单次划分(分层抽样)中训练集中正例应当有$500 \times 70 \%=350$个样本,负例应当有$500 \times 70 \%=350$个样本,从所有样本中选取训练集后,剩余的作为测试集即可。因此,划分方式数为:
6 | $$
7 | \binom{500}{350} \times \binom{500}{350}=2.56 \times 10^{289}
8 | $$
9 |
10 | ## 2.3
11 |
12 | 答:**若学习器A的F1值比学习器B的高,A的BEP不一定比B高**。由于$BEP=P=R$,而$F1=\frac{2\times P' \times R'}{P' + R'}$,其中$P$不一定等于$P'$,$R$也不一定等于$R'$。因此若已知学习器A的F1值比学习器B的高,也无法推算出A的BEP值和B的BEP值之间的关系。
13 |
14 | ## 2.5
15 |
16 | 答:设$\boldsymbol{x}^+$为正例,$\boldsymbol{x}^-$为负例,那么:
17 |
18 | - $f(\boldsymbol{x}^+) > f(\boldsymbol{x}^-)$表示两者都预测正确;
19 |
20 | - $f(\boldsymbol{x}^+) = f(\boldsymbol{x}^-)$表示$\boldsymbol{x}^+$预测成功,而$\boldsymbol{x}^-$预测失败或者$\boldsymbol{x}^-$预测成功,而$\boldsymbol{x}^+$预测失败;
21 | - $f(\boldsymbol{x}^+) < f(\boldsymbol{x}^-)$表示两者都预测错误;
22 |
23 | 因此根据$\text{AUC}$的几何意义,可以对其公式进行改写:
24 | $$
25 | \begin{align}
26 | \text{AUC} &= \sum_{\boldsymbol{x}^+ \in D^+} \frac12 · \frac{1}{m^+} \left[ \frac{2}{m^-} \sum_{\boldsymbol{x}^- \in D^-} \mathbb{I}\left(f(\boldsymbol{x}^+) > f(\boldsymbol{x}^-)\right) + \frac1{m^-} \sum_{\boldsymbol{x}^- \in D^-} \mathbb{I}\left(f(\boldsymbol{x}^+) = f(\boldsymbol{x}^-)\right) \right] \\
27 | &= \frac{1}{m^+m^-} \sum_{\boldsymbol{x}^+ \in D^+} \sum_{\boldsymbol{x}^- \in D^-} \left( \mathbb{I}\left(f(\boldsymbol{x}^+) > f(\boldsymbol{x}^-)\right) + \frac12 \mathbb{I}\left(f(\boldsymbol{x}^+) = f(\boldsymbol{x}^-)\right) \right) \\
28 |
29 | \end{align}
30 | $$
31 | 因此:
32 | $$
33 | \begin{align}
34 | \text{AUC} + \ell_{\rank} &= \frac{1}{m^+m^-} \sum_{\boldsymbol{x}^+ \in D^+} \sum_{\boldsymbol{x}^- \in D^-} \left( \mathbb{I}\left(f(\boldsymbol{x}^+) < f(\boldsymbol{x}^-)\right) + \mathbb{I}\left(f(\boldsymbol{x}^+) > f(\boldsymbol{x}^-)\right) + \mathbb{I}\left(f(\boldsymbol{x}^+) = f(\boldsymbol{x}^-)\right) \right) \\
35 | &= \frac{1}{m^+m^-} \sum_{\boldsymbol{x}^+ \in D^+} \sum_{\boldsymbol{x}^- \in D^-} (1) \\
36 | &= 1
37 | \end{align}
38 | $$
39 | 原式得证。
40 |
41 | ## 2.7
42 |
43 | 答:由于ROC曲线上的点为$(\text{FPR}, \text{TPR})$,且有$\text{TPR} + \text{FNR} = 1$,所以由ROC曲线上一点能确定代价曲线图中$(0, \text{FPR})$和$(1, \text{FNR})$两点,并由此得到连接两点的线段。将ROC曲线上所有的点对应到代价曲线图的所有线段,取所有线段的公共下界即可得到唯一的代价曲线。
44 |
45 | 反之,代价曲线(折线)的每个分段可以对应一条直线,从而得到直线与$x=0$和$x=1$的交点$(0, \text{FPR})$和$(1, \text{FNR})$,这两点可以对应ROC曲线上的一点,由此即可确定一条ROC曲线(不是唯一的,因为可能存在在代价曲线上方而不与曲线相交的线段,这可能也会对应ROC曲线上的一个点)。
46 |
47 | ## 2.9
48 |
49 | 卡方检验就是统计样本的实际观测值与理论推断值之间的偏离程度,卡方值越大,越不符合;卡方值越小,越趋于符合。检验过程如下:
50 |
51 | 1. 写出假设和备择假设;
52 |
53 | 2. 计算卡方值
54 | $$
55 | \chi^2 = \sum_{i=1}^n \frac{(x_i - \hat{x}_i)^2}{\hat{x}_i}
56 | $$
57 | 其中,$x_i$表示观测值,而$\hat{x}_i$表示预期值;
58 |
59 | 3. 计算卡方分布的自由度(若为$R \times C$的列联表,自由度为$(R-1)(C - 1)$);
60 |
61 | 4. 确定显著水平并根据自由度查表得到卡方检验值,将其与计算出的卡方值进行比较;
62 |
63 | 5. 若计算出的卡方值比检验值小,那么无法拒绝原假设,反之拒绝原假设。
64 |
65 |
--------------------------------------------------------------------------------
/docs/MachineLearning/第五章作业.md:
--------------------------------------------------------------------------------
1 | # 《机器学习》第五章作业
2 |
3 | ## 5.1
4 |
5 | **答**:虽然线性函数相对阶跃函数是连续的,但它不能将输入值压缩到$(0,1)$输出值范围内,这使得后续过程中神经元受变量值相对较大的属性影响更大,不利于参数收敛。而且,使用线性函数作为激活函数时,输入值经过每一层的传播后的输出值是输入值的线性组合,此时等价于线性回归。
6 |
7 | ## 5.2
8 |
9 | **答**:在使用Sigmoid函数作为激活函数的每个神经元的输出都是
10 | $$
11 | y=\frac{1}{1+e^{-\left( \sum_{i=1}^nw_i x_i-\theta \right)}}
12 | $$
13 | 对数几率回归的输出为
14 | $$
15 | y=
16 | \left\{
17 | \begin{array}{}
18 | 0, & z<0 \\
19 | 0.5, & z=0 \\
20 | 1, & z>0
21 | \end{array}
22 | \right.
23 | $$
24 | 其中
25 | $$
26 | z=\frac1{1+e^{-\left( \boldsymbol w^\text T \boldsymbol x + b \right)}}
27 | $$
28 | 可以看到,神经元的$y$函数和对数几率回归的$z$函数是相等的。不过神经元的输出不对Sigmoid函数的输出做任何变换,而对数几率回归由于需要判别,因此在输出后加入了分段函数。同时可以发现,如果神经网络中神经元除了输出的激活函数为Sigmoid函数,其他激活函数均为线性函数的话,此神经网络就等价于对数几率回归。
29 |
30 | ## 5.3
31 |
32 | **答**:对于$v_{ih}$,其更新公式为
33 | $$
34 | \Delta v_{ih} = -\eta \frac{\partial E_k}{\partial v_{ih}}
35 | $$
36 | 其中
37 | $$
38 | \frac{\partial E_k}{\partial v_{ih}} = \frac{\partial E_k}{\partial b_h}
39 | \frac{\partial b_h}{\partial \alpha_h} \frac{\partial \alpha_h}{\partial v_{ih}}
40 | $$
41 | 由于
42 | $$
43 | \frac{\partial \alpha_h}{\partial v_{ih}} = x_i \\
44 | e_h = -\frac{\partial E_k}{\partial b_h}
45 | \frac{\partial b_h}{\partial \alpha_h}
46 | $$
47 | 所以
48 | $$
49 | \Delta v_{ih} = -\eta \frac{\partial E_k}{\partial v_{ih}} = -\eta \frac{\partial E_k}{\partial b_h}
50 | \frac{\partial b_h}{\partial \alpha_h} \frac{\partial \alpha_h}{\partial v_{ih}} = \eta e_h x_i
51 | $$
52 | 此即书中式(5.13),证毕。
53 |
54 | ## 5.4
55 |
56 | **答**:若学习率过低,会导致模型收敛过慢,而学习率过高又可能会导致震荡而使模型无法收敛到最优解。可以考虑使用Adam算法等设定合适的初始学习率后,在迭代过程中自动调整学习率。
57 |
58 | ## 5.5
59 |
60 | ### 1. 环境及数据准备
61 |
62 | ```python
63 | import numpy as np
64 | import pandas as pd
65 | from matplotlib import pyplot as plt
66 | from sklearn.model_selection import train_test_split
67 | from sklearn.preprocessing import LabelEncoder
68 |
69 | df = pd.read_csv('./watermelon3.csv', index_col=0) # 西瓜数据集3.0
70 | for label in df.columns: # 离散值预处理为整数
71 | if df[label].dtype == object:
72 | df[label] = LabelEncoder().fit(df[label]).transform(df[label])
73 | df
74 | ```
75 |
76 | | | 色泽 | 根蒂 | 敲声 | 纹理 | 脐部 | 触感 | 密度 | 含糖率 | 好瓜 |
77 | | ---: | ---: | ---: | ---: | ---: | ---: | ---: | ----: | -----: | ---: |
78 | | 编号 | | | | | | | | | |
79 | | 1 | 2 | 2 | 1 | 1 | 0 | 0 | 0.697 | 0.460 | 1 |
80 | | 2 | 0 | 2 | 0 | 1 | 0 | 0 | 0.774 | 0.376 | 1 |
81 | | 3 | 0 | 2 | 1 | 1 | 0 | 0 | 0.634 | 0.264 | 1 |
82 | | 4 | 2 | 2 | 0 | 1 | 0 | 0 | 0.608 | 0.318 | 1 |
83 | | 5 | 1 | 2 | 1 | 1 | 0 | 0 | 0.556 | 0.215 | 1 |
84 | | 6 | 2 | 1 | 1 | 1 | 2 | 1 | 0.403 | 0.237 | 1 |
85 | | 7 | 0 | 1 | 1 | 2 | 2 | 1 | 0.481 | 0.149 | 1 |
86 | | 8 | 0 | 1 | 1 | 1 | 2 | 0 | 0.437 | 0.211 | 1 |
87 | | 9 | 0 | 1 | 0 | 2 | 2 | 0 | 0.666 | 0.091 | 0 |
88 | | 10 | 2 | 0 | 2 | 1 | 1 | 1 | 0.243 | 0.267 | 0 |
89 | | 11 | 1 | 0 | 2 | 0 | 1 | 0 | 0.245 | 0.057 | 0 |
90 | | 12 | 1 | 2 | 1 | 0 | 1 | 1 | 0.343 | 0.099 | 0 |
91 | | 13 | 2 | 1 | 1 | 2 | 0 | 0 | 0.639 | 0.161 | 0 |
92 | | 14 | 1 | 1 | 0 | 2 | 0 | 0 | 0.657 | 0.198 | 0 |
93 | | 15 | 0 | 1 | 1 | 1 | 2 | 1 | 0.360 | 0.370 | 0 |
94 | | 16 | 1 | 2 | 1 | 0 | 1 | 0 | 0.593 | 0.042 | 0 |
95 | | 17 | 2 | 2 | 0 | 2 | 2 | 0 | 0.719 | 0.103 | 0 |
96 |
97 | ```python
98 | X = df.iloc[:, :-1] # 属性
99 | y = df.iloc[:, -1] # 标签
100 | X_train,X_test,y_train,y_test=train_test_split(X,y,test_size=0.3) #随机划分训练集和测试集
101 | ```
102 |
103 | ### 2. 定义模型
104 |
105 | ```python
106 | class BPNN:
107 | def __init__(self):
108 | pass
109 |
110 | def __init(self, X, y, q):
111 | '''
112 | @param: X: 训练集属性
113 | @param: y: 训练集输出
114 | @param: q: 隐层神经元数量
115 | '''
116 | self.v = np.random.uniform(size=(X.shape[1], q))
117 | self.w = np.random.uniform(size=(q, 1))
118 |
119 | def __sigmoid(self, x):
120 | return 1 / (1 + np.exp(-x))
121 |
122 | def __sgd(self, X, y, lr, epoch):
123 | # 标准BP算法, 对每一个样本进行一次权重更新
124 | self.loss = []
125 | for ep in range(1, epoch+1):
126 | sum_ek = 0
127 | idx = list(range(X.shape[0]))
128 | np.random.shuffle(idx)
129 | X, y = X[idx], y[idx]
130 | for i in range(X.shape[0]):
131 | # 前向传播
132 | self.alpha = X[i:i+1] @ self.v
133 | self.b = self.__sigmoid(self.alpha)
134 | self.beta = self.b @ self.w
135 | self.py = self.__sigmoid(self.beta)
136 | # 计算误差
137 | ek = np.power(self.py - y[i], 2) / 2
138 | sum_ek += np.average(ek)
139 | # 后向更新
140 | g = self.py * (1 - self.py) * (y[i] - self.py)
141 | delta_w = self.eta * (self.b.T @ g)
142 | e = self.b * (1 - self.b) * np.sum(self.w @ g, axis=1)
143 | delta_v = self.eta * (X[i:i+1].T @ e)
144 | self.w += delta_w
145 | self.v += delta_v
146 | self.loss.append(sum_ek/X.shape[0])
147 |
148 | def __bgd(self, X, y, lr, epoch):
149 | # 累积BP算法, 对所有样本都进行一次权重更新
150 | self.loss = []
151 | y = y.reshape((-1, 1))
152 | for ep in range(1, epoch+1):
153 | # 前向传播
154 | self.alpha = X @ self.v
155 | self.b = self.__sigmoid(self.alpha)
156 | self.beta = self.b @ self.w
157 | self.py = self.__sigmoid(self.beta)
158 | # 计算误差
159 | ek = np.power(self.py - y, 2) / 2
160 | self.loss.append(np.average(ek))
161 | # 后向更新
162 | g = self.py * (1 - self.py) * (y - self.py)
163 | delta_w = self.eta * (self.b.T @ g)
164 | e = self.b * (1 - self.b) * (g @ self.w.T)
165 | delta_v = self.eta * (X.T @ e) # (8, 17) (17, 10)
166 | self.w += delta_w
167 | self.v += delta_v
168 |
169 | def fit(self, X, y, lr, epoch, algo="sgd"):
170 | X = np.array(X)
171 | y = np.array(y)
172 | self.eta = lr
173 | self.__init(X, y, 10)
174 | # 标准BP算法
175 | if algo.lower() == "sgd":
176 | self.__sgd(X, y, lr, epoch)
177 | # 累积BP算法
178 | elif algo.lower() == "bgd":
179 | self.__bgd(X, y, lr, epoch)
180 |
181 | def predict(self, X, y):
182 | X = np.array(X)
183 | y = np.array(y)
184 | # 前向传播
185 | alpha = X @ self.v
186 | b = self.__sigmoid(alpha)
187 | beta = b @ self.w
188 | py = self.__sigmoid(beta)
189 | return np.array(py > 0.5).astype(np.int32).reshape(1, -1)[0]
190 |
191 | def accuracy(self, X, y):
192 | ans = self.predict(X, y)
193 | return 1 - np.sum(np.abs(ans - y)) / X.shape[0]
194 | ```
195 |
196 | ### 3. 模型测试
197 |
198 | ```python
199 | model = BPNN()
200 | model.fit(X, y, 0.2, 500, algo="sgd")
201 | print("使用SGD训练后的准确度为:", model.accuracy(X, y))
202 | plt.plot(model.loss, label="sgd")
203 | model.fit(X, y, 0.2, 500, algo="bgd")
204 | plt.plot(model.loss, label="bgd")
205 | print("使用BGD训练后的准确度为:", model.accuracy(X, y))
206 | plt.legend()
207 | ```
208 |
209 | ```
210 | 使用SGD训练后的准确度为: 1.0
211 | 使用BGD训练后的准确度为: 1.0
212 | ```
213 |
214 | 
215 |
216 | 可以看到,由于sgd每次迭代是对每个样本依次更新权重,因此在中间会出现抖动,但总体是朝着最优解的。从计算用时来看,sgd显然时间会更长,而bgd一次对所有损失更新权重,因此用时相对少一些。
217 |
--------------------------------------------------------------------------------
/docs/MachineLearning/第八章作业.md:
--------------------------------------------------------------------------------
1 | # 《机器学习基础》第八章作业
2 |
3 | ## 8.1
4 |
5 | 使用简单投票法的集成学习预测错误,意味着少于半数的基学习器预测正确。那么,集成学习的错误率就是少于半数的基学习器预测正确的概率。这等价于抛$T$次硬币,有少于$\lfloor T/2 \rfloor$的硬币朝上的概率(这里硬币朝上的概率为$1-\epsilon$,也就是一个基学习器预测正确的概率)。预测正确的基学习器数量为
6 | $$
7 | g(x) = \sum_{i=0}^{T} \mathbb I (h_i(x)=f(x))
8 | $$
9 | 那么$g(x) \leq \lfloor T / 2 \rfloor$的概率为
10 | $$
11 | P(g(x) \leq \lfloor T/2 \rfloor)=\sum_{k=0}^{\lfloor T/2 \rfloor}\binom{T}{k}(1-\epsilon)^k\epsilon^{T-k}
12 | $$
13 | 这就是式(8.3)的左半部分$P(H(x)\neq f(x))$,由题中给出的定义可得$\lfloor T/2 \rfloor= (\epsilon - \delta)T$,于是$\delta = \epsilon - \lfloor T/2 \rfloor/T \ge \epsilon - 1/2$,由Hoeffding不等式得
14 | $$
15 | P(H(x)\neq f(x)) \leq \exp\left( -2 \left( \epsilon - \frac12 \right)^2 T \right) = \exp\left( -\frac12 T \left( 1 - 2\epsilon \right)^2 \right)
16 | $$
17 | 式(8.3)得证。
18 |
19 |
20 |
21 | ## 8.2
22 |
23 | 我们需要最小化的就是$\mathbb E_{x\in D}[\ell(-f(x) H(x))]$,考虑对$H(x)$进行求偏导,得到
24 | $$
25 | -P(f(x)=1|x) \ell(-H(x)) +P(f(x)=-1|x) \ell(H(x))
26 | $$
27 | 令其为0得到
28 | $$
29 | \frac{P(f(x)=-1|x)}{P(f(x)=1|x)} = \frac{\ell(H(x))}{\ell(-H(x))}
30 | $$
31 | 当$P(f(x)=-1|x) > P(f(x)=1|x)$时,$\ell(H(x)) > \ell(-H(x))$,由于$\ell(-f(x)H(x))$关于$H(x)$递减,因此
32 | $$
33 | H(x) < -H(x)
34 | $$
35 | 所以$H(x)<0$。同理,当$P(f(x)=-1|x) < P(f(x)=1|x)$时,$H(x)>0$。
36 |
37 | 综上:$\text{sign}(H(x))=\arg \max_{y\in (-1, 1)}P(f(x)=y|x)$,这意味着$\text{sign}(H(x))$达到了贝叶斯最优错误率。这说明此损失函数是分类任务原本0/1损失函数得一致性替代函数。
38 |
39 |
40 |
41 | ## 8.3
42 |
43 | 使用`sklean.ensemble`中的`AdaBoostClassifier`实现即可(默认采用决策树模型作为基学习器),代码如下:
44 |
45 | ```python
46 | from sklearn.ensemble import AdaBoostClassifier
47 | import pandas as pd
48 | from matplotlib import pyplot as plt
49 | import numpy as np
50 |
51 | # 加载数据
52 | df = pd.read_csv("./3.0a.csv", index_col=0)
53 | X = df.iloc[:, :2].values
54 | y = df.iloc[:, -1].values
55 |
56 | # 模型训练与预测
57 | model = AdaBoostClassifier(n_estimators=1, random_state=0)
58 | model.fit(X, y)
59 | pred = model.predict(X)
60 | print("错误分类数量:", np.sum(np.abs(pred - y)))
61 |
62 | # 画图
63 | plt.scatter(X[:, 0], X[:, 1], c=pred)
64 | ```
65 |
66 | 基学习器数量为1时:
67 |
68 | 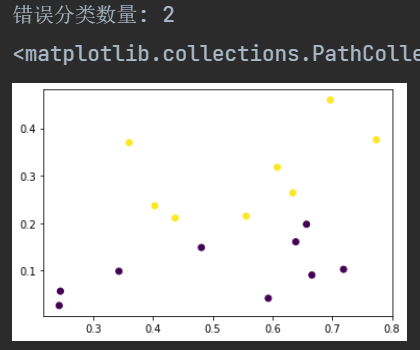
69 |
70 | 基学习器数量为2时:
71 |
72 | 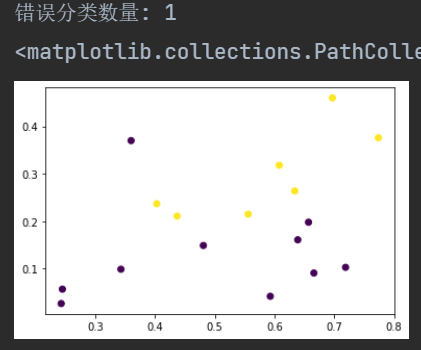
73 |
74 | 基学习器数量超过3时:
75 |
76 | 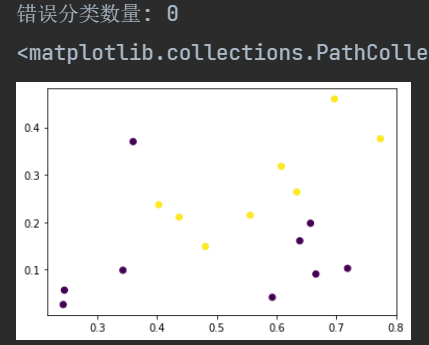
77 |
78 | 可以发现,当基学习器变多的时候分类效果得到了提升,并且很稳定!
79 |
80 |
81 |
82 | ## 8.5
83 |
84 | 使用`sklean.ensemble`中的`BaggingClassifier`实现即可(默认采用决策树模型作为基学习器),代码如下:
85 |
86 | ```python
87 | from sklearn.ensemble import BaggingClassifier
88 | import pandas as pd
89 | from matplotlib import pyplot as plt
90 | import numpy as np
91 |
92 | # 加载数据
93 | df = pd.read_csv("./3.0a.csv", index_col=0)
94 | X = df.iloc[:, :2].values
95 | y = df.iloc[:, -1].values
96 |
97 | # 模型训练与预测
98 | model = BaggingClassifier(n_estimators=1, random_state=0)
99 | model.fit(X, y)
100 | pred = model.predict(X)
101 | print(np.sum(np.abs(pred - y)))
102 |
103 | # 画图
104 | plt.scatter(X[:, 0], X[:, 1], c=pred)
105 | ```
106 |
107 | 基学习器数量为1时:
108 |
109 | 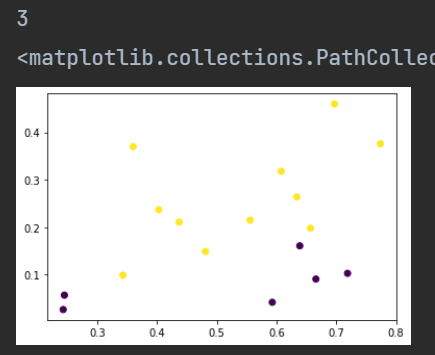
110 |
111 | 基学习器数量为2,3,4时:
112 |
113 | 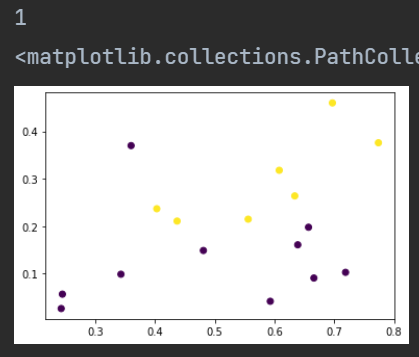
114 |
115 | 基学习器数量为7时:
116 |
117 | 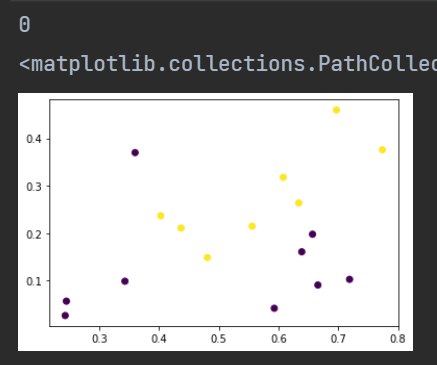
118 |
119 | 可以发现,当基学习器变多的时候分类效果不一定得到提升,在分类器数量较小时,变化比较不稳定。
120 |
121 |
122 |
123 | ## 8.6
124 |
125 | Bagging方法使用自助采样,简单高效,但考虑到“误差-分歧分解”,Bagging方法中个体学习器的多样性较低。朴素贝叶斯属于稳定基学习器,对数据样本的扰动不敏感,对这类基学习器进行集成往往需要使用输入属性扰动等其他扰动,而Bagging方法做不到,因此,Bagging方法通常很难提升朴素贝叶斯分类器的性能。
126 |
127 |
--------------------------------------------------------------------------------
/docs/MachineLearning/第六章作业.md:
--------------------------------------------------------------------------------
1 | # 《机器学习》第六章作业
2 |
3 | ## 6.1
4 |
5 | **答**:设超平面上任意一点为$\boldsymbol{y}$,满足$\boldsymbol{w}^{\text T} \boldsymbol{y} + b = 0$,那么$\boldsymbol{x}$与$\boldsymbol{y}$的距离为$|\boldsymbol{x} - \boldsymbol{y}|$。由几何关系可知,只有当$\boldsymbol{x} - \boldsymbol{y}$与超平面垂直时,才能满足$\boldsymbol{x}$与超平面的距离为$|\boldsymbol{x} - \boldsymbol{y}|$,又因为$\boldsymbol{w}$与超平面垂直,因此
6 | $$
7 | \boldsymbol{x} - \boldsymbol{y} = \pm |\boldsymbol{x} - \boldsymbol{y}| \frac{\boldsymbol{w}}{||\boldsymbol{w}||}
8 | $$
9 | 两边同时左乘$\boldsymbol w^{\text T}$可得
10 | $$
11 | \boldsymbol w^{\text T} \boldsymbol{x} - \boldsymbol w^{\text T} \boldsymbol{y} &= \pm |\boldsymbol{x} - \boldsymbol{y}| \frac{\boldsymbol w^{\text T}\boldsymbol{w}}{||\boldsymbol{w}||} \\
12 | \boldsymbol w^{\text T} \boldsymbol{x} + b &= \pm |\boldsymbol{x} - \boldsymbol{y}| \times ||\boldsymbol w||
13 | $$
14 | 即
15 | $$
16 | r = |\boldsymbol{x} - \boldsymbol{y}| = \frac{|\boldsymbol w^{\text T} \boldsymbol{x} + b|}{||\boldsymbol w||}
17 | $$
18 |
19 | ## 6.2
20 |
21 | ### 1. 搭建环境
22 |
23 |
24 | ```python
25 | import pandas as pd
26 | import numpy as np
27 | from matplotlib import pyplot as plt
28 | from sklearn import svm
29 | ```
30 |
31 | ### 2. 导入数据
32 |
33 |
34 | ```python
35 | df = pd.read_csv("./3.0a.csv", index_col=0)
36 | X = df.iloc[:, :2].values
37 | y = df.iloc[:, -1].values
38 | ```
39 |
40 | ### 3. 使用线性核训练一个SVM
41 |
42 |
43 | ```python
44 | model = svm.SVC(C=1000, kernel='linear') # C高一些,对误差的容忍度低
45 | model.fit(X, y)
46 | model.score(X, y)
47 | ```
48 |
49 |
50 | 0.8235294117647058
51 |
52 |
53 | ```python
54 | # 绘制支持向量
55 | idx = model.support_
56 | plt.scatter(X[:, 0], X[:, 1], c=y, s=30)
57 | plt.scatter(X[idx][:, 0], X[idx][:, 1], c=y[idx], edgecolors='r', s=100)
58 | plt.show()
59 | ```
60 |
61 |
62 | 
63 |
64 |
65 | ### 4. 使用高斯核训练一个SVM
66 |
67 |
68 | ```python
69 | model = svm.SVC(C=1000, kernel='rbf') # C高一些,对误差的容忍度低
70 | model.fit(X, y)
71 | model.score(X, y)
72 | ```
73 |
74 | ```
75 | 1.0
76 | ```
77 |
78 |
79 | ```python
80 | # 绘制支持向量
81 | idx = model.support_
82 | plt.scatter(X[:, 0], X[:, 1], c=y, s=30)
83 | plt.scatter(X[idx][:, 0], X[idx][:, 1], c=y[idx], edgecolors='r', s=100)
84 | plt.show()
85 | ```
86 |
87 | 
88 |
89 | ### 5. 对比分析
90 |
91 | 在对误差容忍度比较高的情况下,高斯核SVM可以完全拟合数据,而且支持向量也比较少。但由于数据线性不可分,线性核SVM不论设置多高的容忍度仍不能很好地区分数据,且支持向量也较多。
92 |
93 | ## 6.3
94 |
95 | ### 1. 搭建环境
96 |
97 |
98 | ```python
99 | import numpy as np
100 | from matplotlib import pyplot as plt
101 | from sklearn.model_selection import train_test_split
102 | from sklearn.datasets import load_iris, load_breast_cancer
103 | from sklearn.svm import SVC # 支持向量机
104 | from sklearn.neural_network import MLPClassifier # BP神经网络
105 | from sklearn.tree import DecisionTreeClassifier # 决策树
106 | ```
107 |
108 | ### 2. 构建数据集
109 |
110 |
111 | ```python
112 | X_iris, y_iris = load_iris(return_X_y=True) # 鸢尾花数据集
113 | X_bc, y_bc = load_breast_cancer(return_X_y=True) # 乳腺癌数据集
114 | # 划分训练集和测试集
115 | X_iris_train, X_iris_test, y_iris_train, y_iris_test = train_test_split(X_iris, y_iris, test_size=0.2, random_state=0)
116 | X_bc_train, X_bc_test, y_bc_train, y_bc_test = train_test_split(X_bc, y_bc, test_size=0.2, random_state=0)
117 | ```
118 |
119 | ### 3. 定义各种模型函数
120 |
121 |
122 | ```python
123 | def svm(X_train, X_test, y_train, y_test, kernel="linear"):
124 | model = SVC(C=1, kernel=kernel)
125 | model.fit(X_train, y_train)
126 | print(f"[SVM with {kernel} kernel]Accuracy: {model.score(X_test, y_test)*100: .2f}%")
127 | ```
128 |
129 |
130 | ```python
131 | def mlp(X_train, X_test, y_train, y_test, activation="logistic"):
132 | model = MLPClassifier(max_iter=1000, activation=activation, random_state=0)
133 | model.fit(X_train, y_train)
134 | print(f"[BP Neural Network with {activation}]Accuracy: {model.score(X_test, y_test)*100: .2f}%")
135 | ```
136 |
137 |
138 | ```python
139 | def dt(X_train, X_test, y_train, y_test, criterion="entropy"):
140 | model = DecisionTreeClassifier(criterion=criterion, random_state=0)
141 | model.fit(X_train, y_train)
142 | print(f"[Decision Tree with {criterion}]Accuracy: {model.score(X_test, y_test)*100: .2f}%")
143 | ```
144 |
145 | ### 4. 在鸢尾花数据集上测试
146 |
147 |
148 | ```python
149 | svm(X_iris_train, X_iris_test, y_iris_train, y_iris_test, kernel="linear")
150 | svm(X_iris_train, X_iris_test, y_iris_train, y_iris_test, kernel="rbf")
151 | mlp(X_iris_train, X_iris_test, y_iris_train, y_iris_test, activation="logistic")
152 | mlp(X_iris_train, X_iris_test, y_iris_train, y_iris_test, activation="relu")
153 | dt(X_iris_train, X_iris_test, y_iris_train, y_iris_test, criterion="entropy")
154 | dt(X_iris_train, X_iris_test, y_iris_train, y_iris_test, criterion="gini")
155 | ```
156 |
157 | [SVM with linear kernel]Accuracy: 100.00%
158 | [SVM with rbf kernel]Accuracy: 100.00%
159 | [BP Neural Network with logistic]Accuracy: 100.00%
160 | [BP Neural Network with relu]Accuracy: 100.00%
161 | [Decision Tree with entropy]Accuracy: 100.00%
162 | [Decision Tree with gini]Accuracy: 100.00%
163 |
164 |
165 | ### 5. 在乳腺癌数据集上测试
166 |
167 |
168 | ```python
169 | svm(X_bc_train, X_bc_test, y_bc_train, y_bc_test, kernel="linear")
170 | svm(X_bc_train, X_bc_test, y_bc_train, y_bc_test, kernel="rbf")
171 | mlp(X_bc_train, X_bc_test, y_bc_train, y_bc_test, activation="logistic")
172 | mlp(X_bc_train, X_bc_test, y_bc_train, y_bc_test, activation="relu")
173 | dt(X_bc_train, X_bc_test, y_bc_train, y_bc_test, criterion="entropy")
174 | dt(X_bc_train, X_bc_test, y_bc_train, y_bc_test, criterion="gini")
175 | ```
176 |
177 | [SVM with linear kernel]Accuracy: 95.61%
178 | [SVM with rbf kernel]Accuracy: 92.98%
179 | [BP Neural Network with logistic]Accuracy: 91.23%
180 | [BP Neural Network with relu]Accuracy: 94.74%
181 | [Decision Tree with entropy]Accuracy: 92.98%
182 | [Decision Tree with gini]Accuracy: 91.23%
183 |
184 | ### 6. 分析
185 |
186 | 针对不同的数据集特征可以选择不同的算法。通过针对不同数据集对不同算法的参数进行调节,很多模型都能很好地拟合数据。
187 |
188 | ## 6.4
189 |
190 | **答**:线性判别分析是将$n$维的数据投影到$n-1$维上的一个超平面后再来分类,可以支持多分类;而线性核的SVM是在$n$维的数据中寻找一个$n-1$的超平面来分隔数据,是解决的二分类问题。因此,若需线性判别分析与线性核等价,一定要满足都是在**解决二分类问题**上(不考虑使用OvR等使SVM解决多分类)。
191 |
192 | 由于线性判别分析关键在找到映射平面,线性核的SVM关键在找分类超平面。考虑两者的关系,可以想到若**两平面垂直**时,如果线性判别分析能达成分类任务,那么在映射平面的两类之间取一条直线,并以这条直线和映射平面的法向量相交做一个平面,一定可以分隔样本。而这个样本就可以作为线性核SVM的分类超平面。
193 |
194 | 综上所述,线性判别分析与线性核支持向量机满足以下两个条件时等价:
195 |
196 | - 解决的问题是二分类问题;
197 | - 线性判别分析的映射超平面和线性核支持向量机的分类超平面垂直。
198 |
199 | ## 6.6
200 |
201 | **答**:对于硬间隔支持向量机,若噪声样本出现在支持向量中,会使决策超平面变化,间隔变小,使得SVM的泛化能力变弱、检测精度降低;对于软间隔支持向量机,噪声样本的出现会使目标函数中的损失项显著提高,使SVM决策受到影响。因此SVM对噪声敏感。
202 |
--------------------------------------------------------------------------------
/docs/MachineLearning/第四章作业.md:
--------------------------------------------------------------------------------
1 | # 《机器学习》第四章作业
2 |
3 | ## 4.1
4 |
5 | **证明**:假设在题目条件下,不存在于与训练集一致的决策树,那么一定存在一个中间节点使得经过此节点后分出的叶子节点中包含不一样标签的样本。而由于不含冲突数据,因此在此叶子节点中标签不同的样本一定还有特征是不相同的,也就是说,此叶子节点还可以根据不同的属性进行下一步决策,使得标签不同的样本完全分离,从而使得训练误差为0。因此得证:**对于不含冲突数据的训练集,必存在与训练集一致的决策树。**
6 |
7 | ## 4.3
8 |
9 | ### 1. 准备数据
10 |
11 | ```python
12 | import numpy as np
13 | import pandas as pd
14 | from sklearn.model_selection import train_test_split
15 | from sklearn.preprocessing import LabelEncoder
16 |
17 | df = pd.read_csv('./watermelon3.csv', index_col=0) # 西瓜数据集3.0
18 | for label in df.columns: # 离散值预处理为整数
19 | if df[label].dtype == object:
20 | df[label] = LabelEncoder().fit(df[label]).transform(df[label])
21 | df
22 | ```
23 |
24 | | | 色泽 | 根蒂 | 敲声 | 纹理 | 脐部 | 触感 | 密度 | 含糖率 | 好瓜 |
25 | | ---: | ---: | ---: | ---: | ---: | ---: | ---: | ----: | -----: | ---: |
26 | | 编号 | | | | | | | | | |
27 | | 1 | 2 | 2 | 1 | 1 | 0 | 0 | 0.697 | 0.460 | 1 |
28 | | 2 | 0 | 2 | 0 | 1 | 0 | 0 | 0.774 | 0.376 | 1 |
29 | | 3 | 0 | 2 | 1 | 1 | 0 | 0 | 0.634 | 0.264 | 1 |
30 | | 4 | 2 | 2 | 0 | 1 | 0 | 0 | 0.608 | 0.318 | 1 |
31 | | 5 | 1 | 2 | 1 | 1 | 0 | 0 | 0.556 | 0.215 | 1 |
32 | | 6 | 2 | 1 | 1 | 1 | 2 | 1 | 0.403 | 0.237 | 1 |
33 | | 7 | 0 | 1 | 1 | 2 | 2 | 1 | 0.481 | 0.149 | 1 |
34 | | 8 | 0 | 1 | 1 | 1 | 2 | 0 | 0.437 | 0.211 | 1 |
35 | | 9 | 0 | 1 | 0 | 2 | 2 | 0 | 0.666 | 0.091 | 0 |
36 | | 10 | 2 | 0 | 2 | 1 | 1 | 1 | 0.243 | 0.267 | 0 |
37 | | 11 | 1 | 0 | 2 | 0 | 1 | 0 | 0.245 | 0.057 | 0 |
38 | | 12 | 1 | 2 | 1 | 0 | 1 | 1 | 0.343 | 0.099 | 0 |
39 | | 13 | 2 | 1 | 1 | 2 | 0 | 0 | 0.639 | 0.161 | 0 |
40 | | 14 | 1 | 1 | 0 | 2 | 0 | 0 | 0.657 | 0.198 | 0 |
41 | | 15 | 0 | 1 | 1 | 1 | 2 | 1 | 0.360 | 0.370 | 0 |
42 | | 16 | 1 | 2 | 1 | 0 | 1 | 0 | 0.593 | 0.042 | 0 |
43 | | 17 | 2 | 2 | 0 | 2 | 2 | 0 | 0.719 | 0.103 | 0 |
44 |
45 | ```python
46 | X = df.iloc[:, :-1] # 属性
47 | y = df.iloc[:, -1] # 标签
48 | X_train,X_test,y_train,y_test=train_test_split(X,y,test_size=0.3) #随机划分训练集和测试集
49 | ```
50 |
51 | ### 2. 定义节点
52 |
53 | ```python
54 | class TreeNode:
55 | def __init__(self, tp=0, label=0, decide=0, compare=0):
56 | self.nxt = dict() # 儿子节点(属性值:节点)(中间节点特有)
57 | self.type = tp # 0->叶子, 1->中间节点
58 | self.label = label # 0->坏瓜, 1->好瓜
59 | self.decide = decide # 划分属性(中间节点特有)
60 | self.compare = compare # 判断值(连续节点特有)
61 | ```
62 |
63 | ### 3. 定义决策树模型
64 |
65 | ```python
66 | class DecisionTree:
67 | def __init__(self):
68 | pass
69 |
70 | def __Ent(self, y):
71 | p = pd.value_counts(y) / len(y)
72 | return -np.sum(p * np.log2(p))
73 |
74 | def __choose(self, D, A):
75 | EntD = self.__Ent(D[-1])
76 | calc1 = lambda x : x.shape[0] / D[0].shape[0] * self.__Ent(x) # 计算信息熵
77 | calc2 = lambda x : x.shape[0] / D[0].shape[0] * np.log2(x.shape[0] / D[0].shape[0]) # 计算IV
78 | mp = dict()
79 | for attr in A:
80 | v = None # 记录连续值判别的值
81 | if self.attr_type[attr]: # 连续值
82 | gain = 0
83 | iv = 0x3f3f3f3f
84 | for value in sorted(np.unique(D[0][:, attr])):
85 | Dv1 = D[-1][D[0][:, attr] <= value]
86 | Dv2 = D[-1][D[0][:, attr] > value]
87 | temp = EntD - (calc1(Dv1) + calc1(Dv2))
88 | if temp > gain:
89 | gain = temp
90 | iv = -calc2(Dv1)-calc2(Dv2)
91 | v = value
92 | # print("iv=", iv)
93 | else: # 离散值
94 | sm = 0
95 | iv = 1
96 | for value in np.unique(D[0][:, attr]):
97 | Dv = D[-1][D[0][:, attr] == value]
98 | sm += calc1(Dv)
99 | iv += -calc2(Dv)
100 | gain = EntD - sm
101 | # print(gain, iv)
102 | gain_ratio = gain / iv
103 | mp[attr] = (gain, 2, v) # 去除gain_ratio的影响
104 | # print(mp)
105 | temp = sorted(list(mp.items()), key=lambda x : (-x[-1][0], -x[-1][1]))[0]
106 | return temp[0],temp[-1][-1]
107 |
108 | def __generate(self, D, A):
109 | node = TreeNode()
110 | if np.unique(D[-1]).shape[0] <= 1:
111 | return TreeNode(tp=0, label=D[-1][0])
112 | if len(A) == 0 or np.unique(D[0][:, A], axis=0).shape[0] <= 1:
113 | return TreeNode(tp=0, label=np.argmax(np.bincount(D[1])))
114 | attr, v = self.__choose(D, A)
115 | # print(attr)
116 | node.decide = attr
117 | node.type = 1
118 | node.label = np.argmax(np.bincount([int(x) for x in D[1]]))
119 | if self.attr_type[attr]: # 连续值
120 | Dv = D[0][D[0][:, attr] <= v]
121 | # print(Dv)
122 | if Dv.shape[0] == 0:
123 | node.nxt[0] = TreeNode(tp=0, label=node.label)
124 | else:
125 | node.nxt[1] = self.__generate((Dv, D[1][D[0][:, attr] <= v]), [x for x in A if x != attr])
126 | Dv = D[0][D[0][:, attr] > v]
127 | # print(Dv)
128 | if Dv.shape[0] == 0:
129 | node.nxt[0] = TreeNode(tp=0, label=node.label)
130 | else:
131 | node.nxt[1] = self.__generate((Dv, D[1][D[0][:, attr] > v]), [x for x in A if x != attr])
132 | else: # 离散值
133 | for value in np.unique(D[0][:, attr]):
134 | Dv = D[0][D[0][:, attr] == value]
135 | if Dv.shape[0] == 0:
136 | node.nxt[value] = TreeNode(tp=0, label=node.label)
137 | else:
138 | node.nxt[value] = self.__generate((Dv, D[1][D[0][:, attr] == value]), [x for x in A if x != attr])
139 | return node
140 |
141 | def calc(self, X, y): # 将数据通过决策树,得出结果,返回准确率
142 | n = X.shape[0]
143 | lst = []
144 | for i in range(X.shape[0]):
145 | x = X[i, :]
146 | node = self.root
147 | while node.type == 1:
148 | if self.attr_type[node.decide]:
149 | if x[node.decide] <= node.compare:
150 | node = node.nxt[0]
151 | else:
152 | node = node.nxt[1]
153 | else:
154 | if x[node.decide] not in node.nxt.keys():
155 | break
156 | node = node.nxt[x[node.decide]]
157 | lst.append(node.label)
158 | ans = np.array(lst)
159 | acc = 1- np.sum(np.abs(ans - y)) / y.shape[0]
160 | return acc
161 |
162 | def fit(self, X, y):
163 | A = [i for i in range(X.values.shape[1])]
164 | self.attr_type = [X[label].dtype == float for label in X.columns] # 是否是连续值
165 | self.root = self.__generate((X.values, y.values), A)
166 | ans = self.calc(X.values, y.values)
167 | print(f"训练集准确率:{ans: .2f}")
168 |
169 | def predict(self, X, y):
170 | ans = self.calc(X.values, y.values)
171 | print(f"测试集准确率:{ans: .2f}")
172 | ```
173 |
174 | ### 4. 训练、测试
175 |
176 | ```python
177 | model = DecisionTree()
178 | model.fit(X_train, y_train)
179 | model.predict(X_test, y_test)
180 | ```
181 |
182 | 训练集准确率: 1.00
183 | 测试集准确率: 0.67
184 |
185 | ### 5. 讨论
186 |
187 | 本题中由于数据量较少,所以建立的决策树模型可以无需使用gain_ratio,实验发现:在本数据集中使用gain_ratio效果还没有gain好。
188 |
189 | ### 6. 决策树
190 |
191 | 
192 |
193 |
194 |
195 | ## 4.5
196 |
197 | 本题目中仅有决策树模型中`__choose`函数与上题不同。下面是本题的`__choose`函数
198 |
199 | ```python
200 | def __choose(self, D, A):
201 | mp = {}
202 | for attr in A:
203 | X = D[0][:, attr:attr+1]
204 | y = D[1]
205 | v = None
206 | if self.attr_type[attr]:
207 | X_ = X.copy()
208 | ans = -1
209 | for value in np.unique(X):
210 | X_ = X < value
211 | model = LogisticRegression()
212 | model.fit(X_, y)
213 | t = model.score(X_, y)
214 | if t > ans:
215 | ans = t
216 | v = value
217 | else:
218 | model = LogisticRegression()
219 | # print(X, y)
220 | model.fit(X, y)
221 | ans = model.score(X, y)
222 | mp[attr] = (ans, v)
223 | temp = sorted(list(mp.items()), key=lambda x : -x[1][0])
224 | return temp[0][0], temp[0][1][1]
225 | ```
226 |
227 | 训练集准确率: 1.00
228 | 测试集准确率: 0.83
229 |
230 | ### 决策树
231 |
232 | 
233 |
234 | ## 4.7
235 |
236 | **输入**:训练集$D={(\boldsymbol{x}_1, y_1),(\boldsymbol{x}_2, y_2),...,(\boldsymbol{x}_m, y_m)}$;属性集$A={a_1, a_2, ..., a_d}$
237 |
238 | **过程**:函数$\text{TreeGenerate}(D, A)$
239 |
240 | 1. 生成根节点$\text{root}$;用于存储中间节点的队列$\text{queue}$;
241 | 2. 将$(\text{root}, D, A)$放入队列$\text{queue}$中;
242 | 3. $\bold{while}$ $\text{queue}$不为空 $\bold{do}$
243 | 4. 从$\text{queue}$中取出节点$\text{node}$、训练集$D$和属性集$A$;
244 | 5. $\bold{if}$ $D$中样本全属于同一类别$C$ $\bold{then}$
245 | 6. 将$\text{node}$标记为$C$类叶节点; $\bold{continue}$
246 | 7. $\bold{end}\ \bold{if}$
247 | 8. $\bold{if}$ $A = \varnothing$ $\bold{OR}$ $D$中样本在$A$上取值相同 $\bold{then}$
248 | 9. 将$\text{node}$标记为叶节点,其类型标记为$D$中样本数最多的类; $\bold{continue}$
249 | 10. $\bold{end}\ \bold{if}$
250 | 11. 从$A$中选择最优划分属性$a_*$;
251 | 12. $\bold{for}$ $a_*$的每一个值$a_*^v$ $\bold{do}$
252 | 13. 为$\text{node}$生成一个分支节点$\text{branch}$;令$D_v$表示$D$中在$a_*$上取值为$a_*^v$的样本子集;
253 | 14. $\bold{if}$ $D_v$为空 $\bold{then}$
254 | 15. 将分支节点$\text{branch}$标记为叶节点,其类型标记为$D$中样本最多的类;
255 | 16. $\bold{else}$
256 | 17. 将$(\text{branch}, D_v, A\backslash \{ a_* \})$放入队列$\text{queue}$中;
257 | 18. $\bold{end}\ \bold{if}$
258 | 19. $\bold{end}\ \bold{for}$
259 | 20. $\bold{end}\ \bold{while}$
260 |
261 | **输出**:以$\text{root}$为根节点的一棵决策树
262 |
263 |
264 |
265 | ## 4.9
266 |
267 | **答**:在含缺失值的样本中进行划分属性的选择,只需要将包含所有样本的集合$D$转化为只包含在属性$a$上非缺失值样本的集合$\tilde{D}$,并乘上权重即可。具体来说,计算基尼指数的公式如下:
268 | $$
269 | \text{Gini\_index}(D, a)=\rho \times \sum_{v=1}^{V} \tilde r_v \frac{|\tilde D^v|}{|\tilde D|}\text{Gini}(\tilde D^v)
270 | $$
271 | 其中,
272 | $$
273 | \begin{align}
274 | \text{Gini}(\tilde D) &= 1-\sum_{k=1}^{|\mathcal Y|}\tilde p_k^2, \\
275 | \rho &= \frac {\sum_{\boldsymbol x \in\tilde D} w_{\boldsymbol x}} {\sum_{\boldsymbol x \in D} w_{\boldsymbol x}}, \\
276 | \tilde p_k &= \frac {\sum_{\boldsymbol x \in\tilde D_k} w_{\boldsymbol x}} {\sum_{\boldsymbol x \in D} w_{\boldsymbol x}} (1 \leq k \leq |\mathcal Y |),\\
277 | \tilde r_v &= \frac {\sum_{\boldsymbol x \in\tilde D^v} w_{\boldsymbol x}} {\sum_{\boldsymbol x \in D} w_{\boldsymbol x}} (1\leq v \leq V),
278 | \end{align}
279 | $$
280 |
281 |
--------------------------------------------------------------------------------
/docs/OperatingSystem/index.md:
--------------------------------------------------------------------------------
1 | # 暂无
--------------------------------------------------------------------------------
/docs/SoftwareEngineering/软工应用分析题.md:
--------------------------------------------------------------------------------
1 | 前面的结构化分析和面向对象分析建模看实验指导书和UML的PPT即可。这个文件请重点参考后面两种测试中涉及的方法。
2 |
3 | # 一、结构化分析
4 |
5 | ## 1. 数据流图【重要】
6 |
7 | 参考PPT和实验文档即可。
8 |
9 | ## 2. 数据字典【重要】
10 |
11 | 参考PPT和实验文档即可。
12 |
13 | ## 3. 控制流建模
14 |
15 | 不重要。考到就看PPT。
16 |
17 |
18 |
19 | # 二、面向对象分析
20 |
21 | ## 1. 用例图【重要】
22 |
23 | **请参考UML的PPT。**
24 |
25 | 分析用例实现中,对象之间的交互行为,核心是时序图、状态图等
26 |
27 | 【用例建模】
28 |
29 | · 用例表示从执行者的角度观察到系统的功能和外部行为。
30 |
31 | · 用例图主要描述用户需求,强调谁在使用系统,系统可以实现哪些功能目标。
32 |
33 | · 用例特征
34 |
35 | · 用例都是动宾结构
36 |
37 | · 用例是相互独立的
38 |
39 | · 用例由参与者启动
40 |
41 | · 有可观测的执行结果
42 |
43 | 【识别用例】
44 |
45 | 识别用例最好的方法就是从分析系统的参与者(可以是角色、外部系统、设备甚至时钟信号等)开始,考虑每一个参与者是如何使用系统的。
46 |
47 | **【用例图】**
48 |
49 | 用例模型主要包含4种元素:执行者、用例,执行者与用例间关联、用例间关系。
50 |
51 | 【用例间关系】
52 |
53 | 《include》关系
54 |
55 | 父用例执行过程中会用到子用例(无条件执行)。
56 |
57 | 子用例一般表示为公共功能。
58 |
59 | 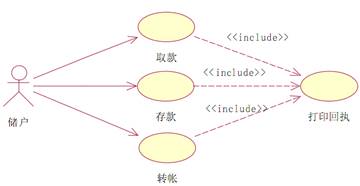
60 |
61 | 《extend》关系
62 |
63 | 父用例在特定情况下(称为扩展点)会用到子用例(有条件执行)
64 |
65 | 子用例一般表示为异常功能。
66 |
67 | 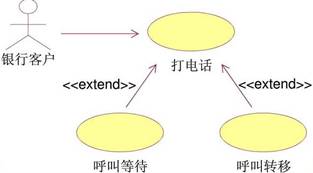
68 |
69 | 泛化(generalization)关系
70 |
71 | 当多个用例共同拥有一种类似的行为时,可以将它们的共性抽象成为父用例,其他用例作为子用例。
72 |
73 | 该关系也可存在于参与者之间。
74 |
75 | 
76 |
77 | 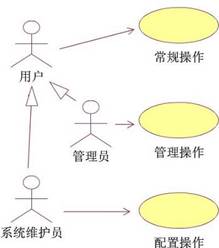
78 |
79 | 【用例描述】
80 |
81 | 单纯的用例图并不能描述完整的信息,需要用文字描述不能反映在图形上的信息。
82 |
83 | 用例描述是将用例发生的各种场景描述出来,表示参与者与系统交互时双方的行为,即参与者做什么,系统做什么反应。
84 |
85 | 场景能真实反映参与者在用例执行中可能遇到的
86 |
87 | 各种情形。
88 |
89 | 可以使用**用例模版**或**活动图**描述用例执行中的各种场景。
90 |
91 | 【用例模板】
92 |
93 | 用例描述模版的内容大致包括:用例名、参与者,前置条件,后置条件,事件流等。
94 |
95 | 用例的事件流
96 |
97 | 说明参与者与系统之间的交互过程;
98 |
99 | 说明用例在不同条件下可以选择执行的多种方案;
100 |
101 | 分为基本流和备选流两类
102 |
103 | 基本流:描述该用例正常执行的一种场景,系统执行一系列活动步骤来响应参与者提出的服务请求;
104 |
105 | 备选流:描述用例执行过程中异常的或偶尔发生的一些情况。
106 |
107 | 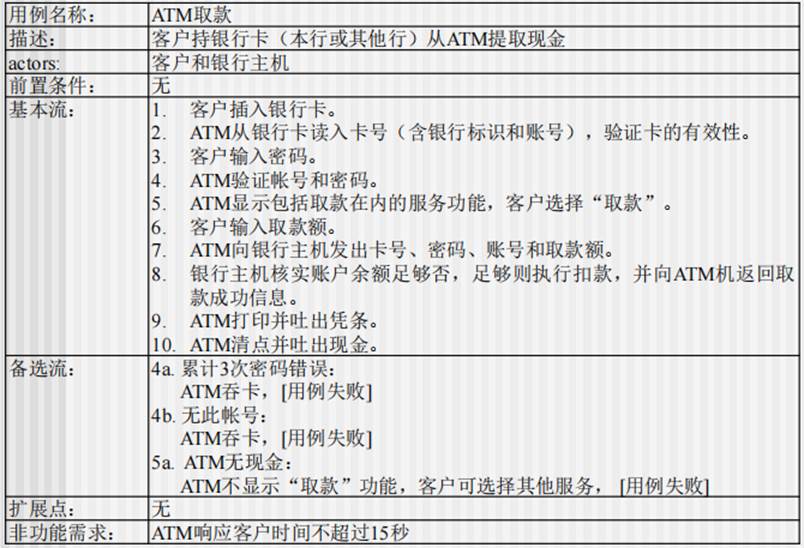
108 |
109 |
110 |
111 |
112 |
113 | ## 2. 类图【重要】
114 |
115 | **请参考UML的PPT。**
116 |
117 | 【类图】
118 |
119 | (具体画法参考实验文档)
120 |
121 | 目标是对领域内的概念类进行分析,并抽象出对应的类及其关系等。
122 |
123 | 具体包括三个步骤:
124 |
125 | 1. 从用例场景中寻找概念类
126 |
127 | (1) 分析用例场景
128 |
129 | (2) 找出其中的名词或名词短语作为分析类备选
130 |
131 | (3) 如何判断分离出的词是否是分析类?
132 |
133 | 
134 |
135 | 2. 细化概念类,识别其类型(如边界类、实体类等)
136 |
137 | 例子:学生选课用例
138 |
139 | 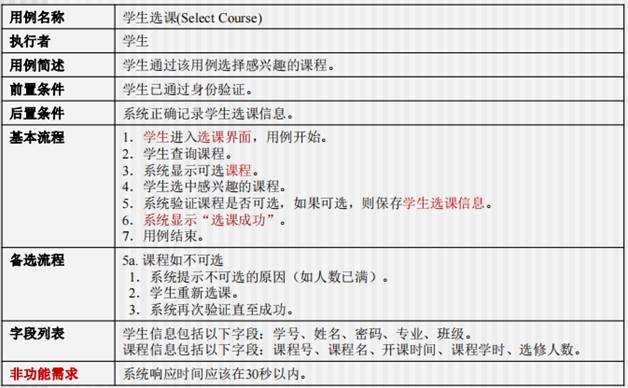
140 |
141 | 通过分析,可以确定以下分析类:
142 |
143 | 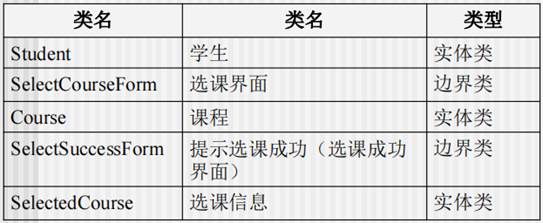
144 |
145 | 分析类是概念层次的东西,源于问题空间,与实现方式无关。
146 |
147 | 类的类型:
148 |
149 | 《Entity》 classes 表示系统中的持久信息或贯穿应用的数据封装
150 |
151 | 《Boundary》 classes 实现用户与系统的交互,如用户界面或外部接口
152 |
153 | 《Control》 classes 实现对用例行为的封装,管理、调度其它类
154 |
155 | 3. 为概念类定义属性及行为
156 |
157 | 属性描述了一个已被选择以包含在分析模型中的类。
158 |
159 | 要识别类所属行为,可以对处理叙述进行语法解析,看看动词;还可以结合动态(交互)建模,识别分析类的行为。
160 |
161 | 例子:
162 |
163 | 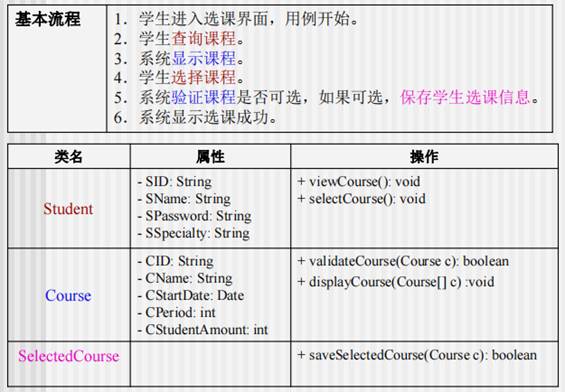
164 |
165 | 4. 定义关系
166 |
167 | (1) 关联关系:关联关系可以使一个类可以引用另一个类的属性和方法。一般使用成员变量来实现。
168 |
169 | 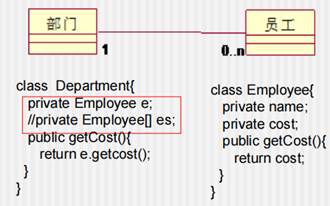
170 |
171 | (2) 聚合关系:表示整体和部分的关系,整体与部分可以分开,使用带空心菱形的实线来表示。
172 |
173 | 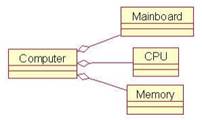
174 |
175 | (3) 组合关系:也是整体与部分的关系,但是整体与部分不可以分开,使用实心带菱形的实线来表示。组合关系中整体类和部分类必须有相同的生命周期。
176 |
177 | 
178 |
179 | (4) 依赖关系:即一个类的实现需要另一个类的协助。多数情况下,依赖关系表现在某个类的方法使用另一个类的对象作为参数。
180 |
181 | 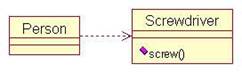
182 |
183 | (5) 泛化关系:表示类与类、接口与接口之间的继承关系
184 |
185 | 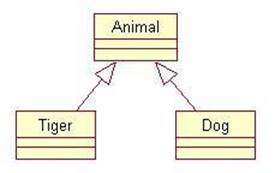
186 |
187 | 实例:
188 |
189 | 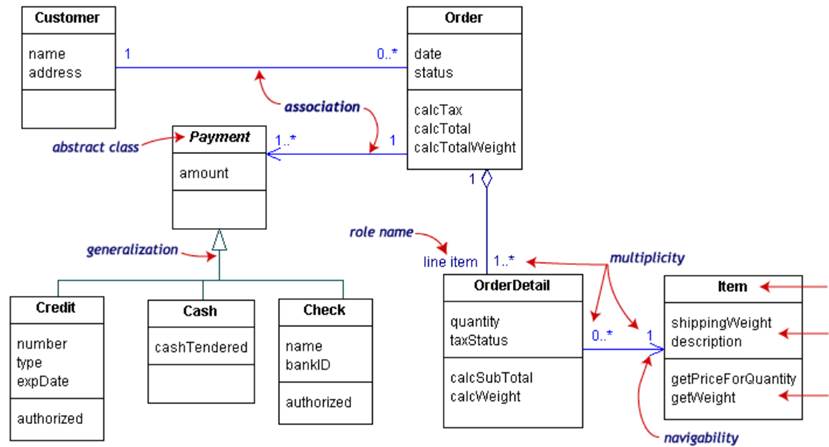
190 |
191 |
192 |
193 | ## 3. 时序图(顺序图)【重要】
194 |
195 | **请参考UML的PPT。**
196 |
197 | 【时序图】
198 |
199 | 时序图建模步骤
200 |
201 | (1)对每个用例,建立系统时序图(可选)
202 |
203 | (2)建立对象时序图
204 |
205 | (3)从图中确定分析类的行为
206 |
207 | 主要步骤
208 |
209 | 按从左到右的顺序
210 |
211 | 1、列出启动该用例的参与者;
212 |
213 | 2、列出参与者使用的边界类;
214 |
215 | 3、列出管理该用例的控制类;
216 |
217 | 4、根据用例的执行流程,按时间顺序列出分析类之间的消息序列。
218 |
219 | **例子:****还书用例**
220 |
221 | 1. 借阅者点击还书按钮向系统申请还书
222 | 2. 系统提示借阅者输入还书号等信息
223 | 3. 借阅者输入还书信息后,系统查询该书是否已超期。
224 | 4. 如果未超期,则记录用户还书信息并更新图书可借状态,并返回借阅者成功还书信息。
225 | 5. 如果已超期,则系统提示超期、罚款金额等信息。
226 | 6. 借阅者如果认可,并确认缴纳罚款,则系统执行扣款并还书,返回借阅者成功还书信息。
227 |
228 | 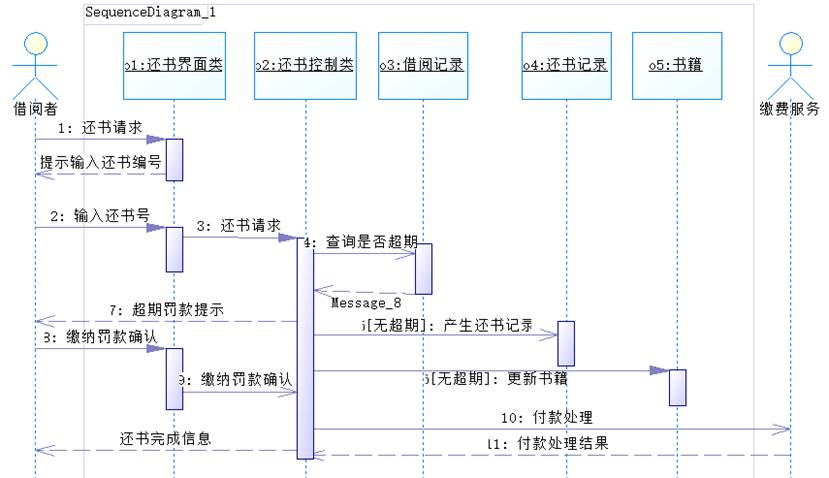
229 |
230 | ## 4. 状态图
231 |
232 | 请参考UML的PPT。
233 |
234 | 【状态图】
235 |
236 | 状态图描述了一个对象生命周期内所经历的状态序列,以及引起状态转移的外部事件。
237 |
238 | 状态图的主要作用:
239 |
240 | 描述多个状态之间的转换顺序,即事件的执行顺序,避免非法的事件序列。(如: 必须先付款进入“已付款”状态,才能执行发货进入“已发货”状态。)
241 |
242 | 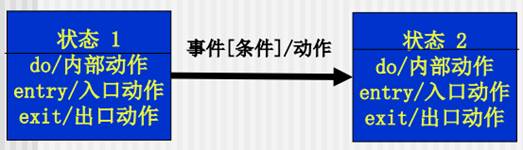
243 |
244 | 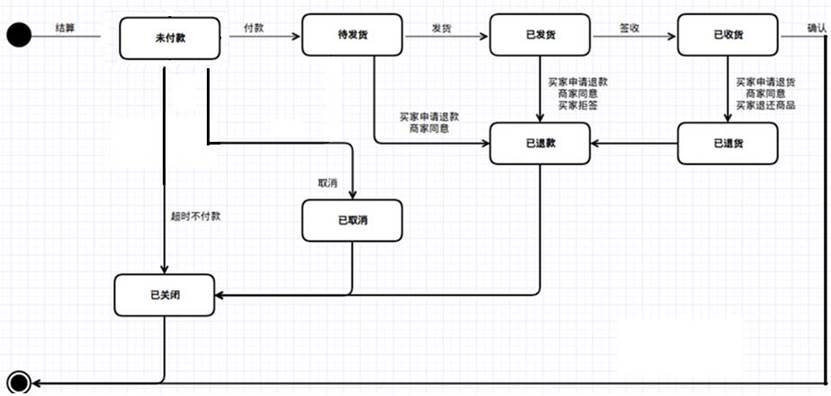
245 |
246 | ## 5. 其他
247 |
248 | ### 5.1. 活动图
249 |
250 | 【活动图】
251 |
252 | 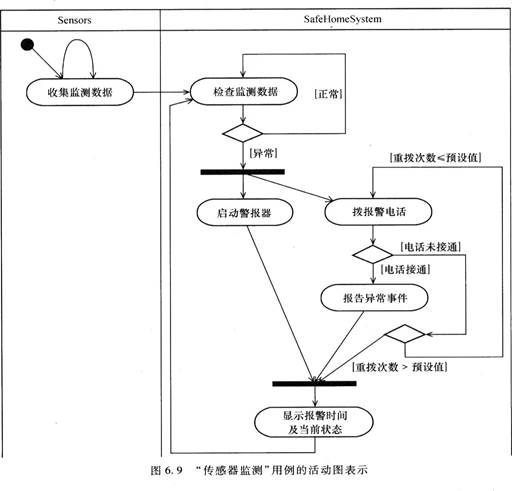
253 |
254 |
255 |
256 | ### 5.2. ER图
257 |
258 | 【ER图】
259 |
260 | 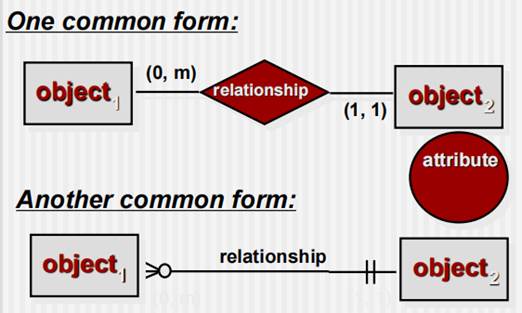
261 |
262 | 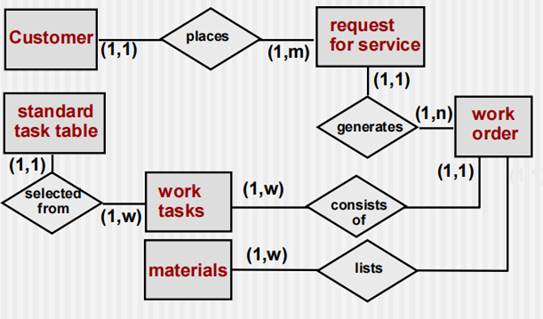
263 |
264 | ### 5.3. CRC模型
265 |
266 | 【CRC模型, Class-responsibility-collaborator】
267 |
268 | 作用:帮助补充、完善、优化分析类(属性、行为)
269 |
270 | 职责:职责是与类相关的属性和操作。
271 |
272 | 简单的说,职责就是“类所知道的或能做的任何事情”,可理解为类的能力。
273 |
274 | 例如,顾客有名字、地址和电话号码,这是顾客知道的东西。顾客要借书和还书,这是顾客要完成的事情。
275 |
276 | 分配职责的指导原则:属性和与之相关的行为应该在同一个类中。
277 |
278 | 类主要通过两种方式实现其职责:
279 |
280 | 通过自己内部的行为,实现特定的职责
281 |
282 | 请求其它类的协作
283 |
284 | 如果某个对象请求协作,就会向其它对象发送消息。
285 |
286 | 消息接收者作为服务方,通过自己的服务作为对消息发送者的回应。
287 |
288 | 职责是一种较高层次的抽象,其在设计过程中可能细化为一到多个具体的行为。
289 |
290 | 例子:用户登录用例中,登录控制类的职责之一是“身份验证” 。该职责在设计阶段,可以被细化为多个具体方法:getUser(),getRole(),getGroup(),check()
291 |
292 | 
293 |
294 |
295 |
296 | ### 5.4. 包图
297 |
298 | 【包图】
299 |
300 | 对于较大的项目,由于有很多的类和用例,常常会使系统结构看起非常复杂。
301 |
302 | 通过包图,庞大系统之间的关系变得更简单,整个系统的架构一目了然。
303 |
304 | 原则:将概念上或语义上相近的类纳入一个包
305 |
306 | 包之间的主要关系是依赖关系。
307 |
308 | 意味着两个Package内的元素之间存在着一个或多个依赖
309 |
310 | 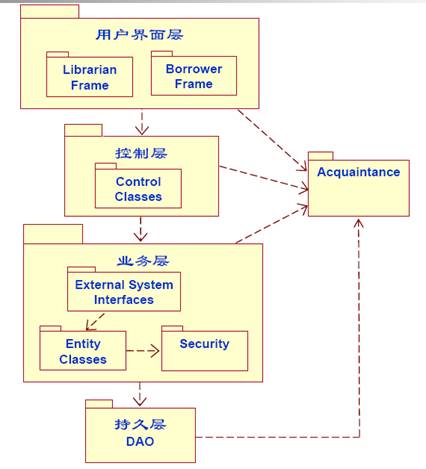
311 |
312 | 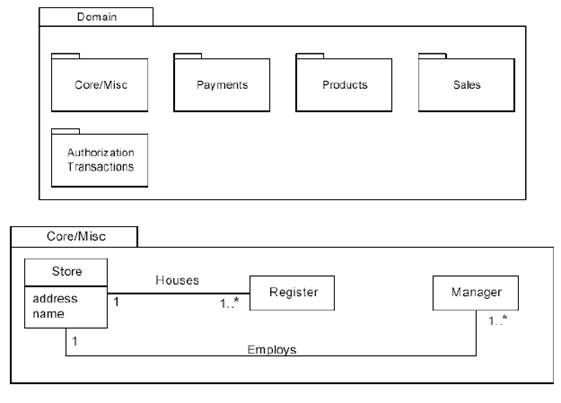
313 |
314 |
315 |
316 |
317 |
318 |
319 |
320 |
321 |
322 |
323 |
324 |
325 |
326 |
327 |
328 | # 三、白盒测试
329 |
330 | ## 1. 基本路径测试法【重要】
331 |
332 | 参考视频:https://www.bilibili.com/video/BV13V4y1g7tc/?share_source=copy_web&vd_source=7ba452d8ee6f8b8a4b8ef831bf573bda
333 |
334 | 步骤:
335 |
336 | - **(1) 画出控制流图**
337 |
338 | 流程图用来描述程序控制结构。可将流程图映射到一个相应的流图(假设流程图的菱形决定框中不包含复合条件)。
339 |
340 | - 在流图中,每一个圆,称为流图的**结点**,代表一个或多个语句。一个处理方框序列和一个菱形决策框可被映射为一个结点 。
341 | - 流图中的箭头,称为**边或连接**, 代表控制流 , 类似于流程图中的箭头 。一条边必须终止于一个结点 , 即使该结点并不代表任何语句(例如:if-else-then结构)。
342 | - 由边和结点限定的范围称为**区域** 。
343 |
344 | 控制流图基本结构:
345 |
346 |
46 |
47 | (3)RIP协议使用了UDP传送数据,因此RIP在UDP之上,属于应用层。
48 |
49 |
50 |
51 |
--------------------------------------------------------------------------------
/docs/ComputerNetwork/《计算机网络》第四章作业.md:
--------------------------------------------------------------------------------
1 | # 《计算机网络》第四章作业
2 |
3 | ## 4-01
4 |
5 | **答:**一种是面向连接的服务(虚电路服务),一种是无连接的服务(数据报服务)。
6 |
7 | 面向连接的服务(可靠通信由网络保证):
8 |
9 | - 优点:分组开销小;分组无差错。
10 | - 缺点:网络成本高;若某一节点出错,所有通过该节点的虚电路都不能正常工作。
11 |
12 | 无连接的服务(可靠通信由用户主机保证):
13 |
14 | - 优点:网络成本低;某一节点出错时,路由可能变化,数据报可能仍然可以传输。
15 | - 缺点:尽力交付,可能会出现数据报异常情况。
16 |
17 | ## 4-03
18 |
19 | **答:**他们都起到连接网络的作用,但处在不同的网络体系结构层级。转发器在物理层,网桥在数据链路层,路由器在网络层,而网关在运输层及应用层(路由器也可以表示网关)。
20 |
21 | ## 4-07
22 |
23 | **答:**IP地址是网络层及以上使用的逻辑地址,而硬件地址是物理层及数据链路层使用的地址。由于不同国家、区域等有着不同的网络结构,其中的主机都有不同形式的硬件地址,因此若需要跨域传输时,会存在复杂的硬件地址转换。使用统一的IP地址可以使用户间的通信好像在一个网络上一样。IP地址与硬件地址的转换也相对硬件地址与硬件地址的转换要方便许多。
24 |
25 | ## 4-10
26 |
27 | **答:**(1)**10**000000.00100100.11000111.00000011,为B类地址;
28 |
29 | (2)**0**0010101.00001100.11110000.00010001,为A类地址;
30 |
31 | (3)**10**110111.11000010.01001100.11111101,为B类地址;
32 |
33 | (4)**110**00000.00001100.01000101.11111000,为C类地址;
34 |
35 | (5)**0**1011001.00000011.00000000.00000001,为A类地址;
36 |
37 | (6)**110**01000.00000011.00000110.00000010,为C类地址。
38 |
39 | ## 4-11
40 |
41 | **答:**好处是减小开销(加快检验、转发分组更快);坏处是在网络层传输的过程中就算数据发生了错误,也无法识别并中止传输,需要到达终点后在主机上(运输层)才能进行校验。
42 |
43 | ## 4-15
44 |
45 | **答:**MTU是一个数据帧中数据字段的最大长度。当一个IP数据报封装成数据链路层的帧的时候,数据报的总长度一定不能超过MTU。MTU与IP数据报首部中的总长度字段有关系,MTU是该字段的上限值。
46 |
47 | ## 4-18
48 |
49 | **答:**(1)数据链路层只能接触到MAC帧,如果ARP在数据链路层,那么MAC帧中就需要有IP地址,这不符合数据链路层对MAC帧的结构定义。
50 |
51 | (2)当网络中IP地址与硬件地址的映射发生变化时,ARP高速缓存中对应项就需要改变。超时时间设置太短会使ARP请求和响应分组的通信太频繁,若设置太长会使得硬件地址变化的主机迟迟无法与网络上其他主机通信。设置10~20分钟主要是因为在这样的一段时间段内更换网卡是很合理的。
52 |
53 | (3)①源主机的ARP高速缓存中已经有了目的主机的MAC地址;②源主机发送的是广播分组;③源主机与目的主机间使用点对点链路。
54 |
55 | ## 4-24
56 |
57 | **答:**A类子网划分对应数目的子网,子网掩码第一个字节需要全为1。若需要划分为n个A类子网,主机号部分的1的个数为$\lceil \log_2(n + 2) \rceil$(去除了全0和全1的子网数)。
58 |
59 | (1)$n=2$,主机号部分1的数量为2,因此子网掩码为255.192.0.0;
60 |
61 | (2)$n=6$,主机号部分1的数量为3,因此子网掩码为255.224.0.0;
62 |
63 | (3)$n=30$,主机号部分1的数量为5,因此子网掩码为255.248.0.0;
64 |
65 | (4)$n=62$,主机号部分1的数量为6,因此子网掩码为255.252.0.0;
66 |
67 | (5)$n=122$,主机号部分1的数量为7,因此子网掩码为255.254.0.0(实际有126个子网);
68 |
69 | (6)$n=250$,主机号部分1的数量为8,因此子网掩码为255.255.0.0(实际有254个子网);
70 |
71 | ## 4-25
72 |
73 | **答:**(1)10110000.0.0.0,其中1不是连续的,不推荐使用;
74 |
75 | (2)01100000.0.0.0,首位不是1(1前面有0),不推荐使用;
76 |
77 | (3)01111111.11000000.0.0,首位不是1(1前面有0),不推荐使用;
78 |
79 | (4)11111111.10000000.0.0,合理,推荐使用。
80 |
81 | ## 4-31
82 |
83 | **答:**86.32/12的网络前缀为0101 0110 0010。
84 |
85 | (1)86.33.224.123的前12位为0101 0110 0010,与上述网络前缀匹配。
86 |
87 | (2)86.79.65.216的前12位为0101 0110 0100,与上述网络前缀不匹配。
88 |
89 | (3)86.58.119.74的前12位为0101 0110 0011,与上述网络前缀不匹配。
90 |
91 | (4)86.68.206.154的前12位为0101 0110 0100,与上述网络前缀不匹配。
92 |
93 | ## 4-35
94 |
95 | **答:**转化为二进制为**10001100.01111000.0101**0100.00011000。
96 |
97 | 最大地址:**10001100.01111000.0101**1111.11111111,即140.120.95.255/20;
98 |
99 | 最小地址:**10001100.01111000.0101**0000.00000000,即140.120.80.0/20;
100 |
101 | 地址掩码:255.255.240.0;
102 |
103 | 地址块中共有$2^{12}=4096$个地址;
104 |
105 | 相当于$2^{24-20}=2^4=16$个C类地址。
106 |
107 | ## 4-38
108 |
109 | **答:**IGP是内部网关协议,是在一个自治系统内部使用的路由选择协议;EGP是外部网关协议,是在不同的自治系统间使用的路由选择协议。
110 |
111 | ## 4-39
112 |
113 | **答:**RIP协议是一种分布式的基于距离向量的路由选择协议,是互联网的标准协议,其最大优点就是简单,其主要特点为:
114 |
115 | - 仅和相邻路由器交换信息;
116 | - 路由器交换的信息是本路由器所知道的全部信息;
117 | - 按固定的时间间隔交换路由信息。
118 |
119 | OSPF使用分布式的链路状态协议,其主要特点为:
120 |
121 | - 使用洪泛法向本自治系统中所有路由器发送信息;
122 | - 发送的信息就是与本路由器相邻的所有路由器的链路状态,但这只是路由器所知道的部分信息;
123 | - 当链路状态变化或每隔一段时间,路由器向所有路由器用洪泛法发送链路状态信息;
124 | - 对于不同类型的业务可计算出不同的路由;
125 | - 多路径间存在负载均衡;
126 | - 所有在OSPF路由器之间交换的分组都具有鉴别功能;
127 | - 支持可变长度的子网划分和无分类的编址CIDR;
128 | - 每一个链路状态都会带上一个32位的序号,序号越大状态就越新。
129 |
130 | BGP是不同自治系统的路由器之间交换路由信息的协议,它采用路径向量路由选择协议,其主要特点为:
131 |
132 | - BGP在自治系统之问交换“可达性”信息;
133 | - BGP只能是力求寻找一条能够到达目的网络且比较好的路由(不能兜圈子),而并非要寻找一条最佳路由;
134 | - BGP的路由选择有很多策略,如选择本地偏好值最高的路由、选择AS跳数最少的路由、使用热土豆算法等;
135 | - BGP有四种报文,在不同的场合使用不同的报文。
136 |
137 | ## 4-43
138 |
139 | **答:**IGMP协议是让连接在本地局域网上的多播路由器知道本局域网上是否有主机(严格讲,是主机上的某个进
140 | 程)参加或退出了某个多播组。IGMP协议的要点主要体现在两个阶段:
141 |
142 | - 当某个主机加入新的多播组时,该主机应向多播组的多播地址发送一个IGMP报文,声明自己要成为该组的成员。本地的多播路由器收到IGMP报文后,还要利用多播路由选择协议把这种组成员关系转发给互联网上的其他多播路由器。
143 | - 本地多播路由器要周期性地探询本地局域网上的主机,以便知道这些主机是否还继续是组的成员。只要有一个主机对某个组响应,那么多播路由器就认为这个组是活跃的。但一个组在经过几次的探询后仍然没有一个主机响应,多播路由器就认为本网络上的主机已经都离开了这个组,因此也就不再把这个组的成员关系转发给其他
144 | 的多播路由器。
145 |
146 | 当两个多播网络之间的网络不支持多播时,会使用隧道技术。在这种情况下,发送方网络路由器会对多播数据进行再次封装,加上普通数据报首部,使之变成单播数据报,这样就能通过中间网络(此时相当于构建了一个隧道)传输到另一个多播网络,目的网络路由器收到此数据报后先剥去其首部,变成原来的多播数据报后再进行传输。
147 |
148 | ## 4-48
149 |
150 | **答:**146.102.29.0的二进制为10010010.01100110.00011101.00000000;
151 |
152 | 146.102.32.255的二进制为10010010.01100110.00100000.11111111;
153 |
154 | 从146.102.29.0(含)到146.102.29.255(含)有$256$个地址。而146.102.29.255(不含)到146.102.32.255(含)有$3\times 256$个地址,因此总共有$4\times 256=1024$个地址。
155 |
156 | ## 4-65
157 |
158 | **答:**(1)0000 : 0000 : 0000 : 0000 : 0000 : 0000 : 0000 : 0000
159 |
160 | (2)0000 : 00AA : 0000 : 0000 : 0000 : 0000 : 0000 : 0000
161 |
162 | (3)0000 : 1234 : 0000 : 0000 : 0000 : 0000 : 0000 : 0003
163 |
164 | (4)0123 : 0000 : 0000 : 0000 : 0000 : 0000 : 0001 : 0002
--------------------------------------------------------------------------------
/docs/MachineLearning/第一章作业.md:
--------------------------------------------------------------------------------
1 | # 《机器学习》第一章作业
2 |
3 | ## 1.1
4 |
5 | 表1.1中若只包含编号为1和4的两个样例,即如下表所示:
6 |
7 | | 编号 | 色泽 | 根蒂 | 敲声 | 好瓜 |
8 | | ---- | ---- | ---- | ---- | ---- |
9 | | 1 | 青绿 | 蜷缩 | 浊响 | 是 |
10 | | 4 | 乌黑 | 稍蜷 | 沉闷 | 否 |
11 |
12 | 则其版本空间如下图所示:
13 |
14 | 
15 |
16 | ## 1.3
17 |
18 | 对于所有假设,选择满足最多样本的假设。若有多个,则选择尽可能一般的假设(即属性值为任意的数量尽可能多)。若还有多个,随机选择一个即可。
19 |
20 |
21 |
22 | ## 1.5
23 |
24 | 1. 对欲搜索文本进行分词,提取关键词并分析语义后进行检索;
25 | 2. 对搜索文本和数据库中相关信息进行匹配并排序;
26 | 3. 在拥有用户信息和使用习惯的数据后,可以智能推荐搜索结果;
27 | 4. 实现对图片、视频等多媒体数据进行分析后,给出搜索结果(如百度识图);
28 | 5. 对搜索出的结果进行无效信息、重复信息的过滤;
29 | 6. 建立知识图谱,能精确给出搜索结果的梗概(或者与其他概念的关系)。
30 |
31 |
--------------------------------------------------------------------------------
/docs/MachineLearning/第七章作业.md:
--------------------------------------------------------------------------------
1 | # 《机器学习基础》第七章作业
2 |
3 | ## 7.1
4 |
5 | **答:**使用极大似然法得到的类条件概率估计表达式为
6 | $$
7 | P(x_i=t_{ij}|c) = \frac{|D_{c,x_i, t_{ij}}|}{|D_c|}
8 | $$
9 | 其中,$|D_c|$表示训练集$D$中$c$类样本的数量,$|D_{c, x_i, t_{ij}}|$表示训练集中$c$类元素属性$x_i$为$t_{ij}$的数量的元素。由此根据西瓜数据集即可得出类条件概率如下:
10 |
11 | | 属性 | 属性取值 | 好瓜($c_0$) | 坏瓜($c_1$) |
12 | | ----------- | -------------- | ----------- | ----------- |
13 | | 色泽($x_0$) | 青绿($t_{00}$) | $\frac38$ | $\frac13$ |
14 | | | 乌黑($t_{01}$) | $\frac12$ | $\frac29$ |
15 | | | 浅白($t_{02}$) | $\frac18$ | $\frac49$ |
16 | | 根蒂($x_1$) | 蜷缩($t_{10}$) | $\frac58$ | $\frac13$ |
17 | | | 稍蜷($t_{11}$) | $\frac38$ | $\frac49$ |
18 | | | 硬挺($t_{12}$) | $0$ | $\frac29$ |
19 | | 敲声($x_2$) | 浊响($t_{20}$) | $\frac34$ | $\frac49$ |
20 | | | 沉闷($t_{21}$) | $\frac14$ | $\frac13$ |
21 | | | 清脆($t_{22}$) | $0$ | $\frac29$ |
22 |
23 |
24 |
25 | ## 7.3
26 |
27 | ### 1. 环境及数据准备
28 | ```python
29 | import numpy as np
30 | import pandas as pd
31 | import scipy.stats as st
32 |
33 | df = pd.read_csv('./watermelon3.csv', index_col=0) # 西瓜数据集3.0
34 | X = np.array(df.iloc[:, :-1]) # 属性
35 | y = np.array(df.iloc[:, -1])[None].T # 标签
36 | ```
37 |
38 | ### 2. 定义模型
39 | ```python
40 | class NaiveBayes:
41 | def __init__(self) -> None:
42 | pass
43 |
44 | def get_prob(self, X, x, x_i, N): # 拉普拉斯修正
45 | return ((X[:, x] == x_i).sum() + 1) / (X.shape[0] + N)
46 |
47 | def get_dis_prob(self, X, y): # 离散概率
48 | p = []
49 | for i, c in enumerate(self.label):
50 | temp = X[(y == c).ravel()]
51 | lst = []
52 | for x in range(temp.shape[1]):
53 | dct = {}
54 | uni = np.unique(X[:, x])
55 | for x_i in uni:
56 | dct[x_i] = self.get_prob(temp, x, x_i, uni.shape[0])
57 | lst.insert(x, dct)
58 | p.insert(i, lst)
59 | return p
60 |
61 | def get_con_prob(self, X, x, x_i): # 连续概率
62 | return st.norm.pdf(x_i, loc=X[:, x].mean(), scale=X[:, x].std())
63 |
64 | def train(self, X, y):
65 | self.X, self.y = X, y
66 | self.con_col = [i for i in range(X.shape[1]) if type(X[0][i]) == float] # 连续值所在位置
67 | dis_X = np.delete(X, self.con_col, axis=1) # 提取离散值
68 | con_X = X[:, self.con_col] # 提取连续值
69 | self.label = np.unique(y) # 将label的类型取出来
70 | self.dis_p = self.get_dis_prob(dis_X, y)
71 | self.P_c = ((self.label == y).sum(axis=0) + 1) / (df.shape[0] + self.label.shape[0])
72 |
73 | def predict(self, X_pre):
74 | y_pre = np.ones(X_pre.shape[0], dtype='object')
75 | for j, X in enumerate(X_pre):
76 | maxn = 0
77 | res_c = 0
78 | for i, c in enumerate(self.label):
79 | res = 1
80 | temp_X = self.X[(self.y == c).ravel()]
81 | a = 0
82 | for x in range(X.shape[0]):
83 | if x in self.con_col: # 连续
84 | res *= self.get_con_prob(temp_X, x, X[x])
85 | else: # 离散
86 | res *= (self.dis_p[i][a][X[x]])
87 | a += 1
88 | res *= self.P_c[i]
89 | if res > maxn:
90 | maxn = res
91 | res_c = c
92 | y_pre[j] = res_c
93 | return y_pre[None].T
94 | ```
95 | ### 3. 模型测试
96 | ```python
97 | model = NaiveBayes()
98 | model.train(X, y)
99 | test_X = np.array(['青绿', '蜷缩', '浊响', '清晰', '凹陷', '硬滑', 0.697, 0.460], dtype='object')
100 | print(model.predict(test_X[None])[0][0])
101 | ```
102 |
103 | 是
104 |
105 |
106 |
107 | ## 7.4
108 |
109 | **答:**由于$P(x_i|c)\leq 1$,因此$\prod_{i=1}^{d} P(x_i|c)$很可能因为非常接近$0$而造成下溢,可以采用对此公式求对数的方式将正小数转化为负正数从而解决数据可能下溢的问题,即转化为$\sum_{i=1}^{d} \log P(x_i|c)$。
110 |
111 |
112 |
113 | ## 7.5
114 |
115 | **答:**对于贝叶斯最优分类器来说,其欲最大化的目标为
116 | $$
117 | P(c | \boldsymbol x) = \frac{P(c)P(\boldsymbol x | c)}{P(\boldsymbol x)}
118 | $$
119 |
120 | 因为$P(\boldsymbol x)$是常量,因此也就是最大化
121 | $$
122 | P(c)P(\boldsymbol x | c)
123 | $$
124 | 因为数据服从高斯分布,因此上式等价于
125 | $$
126 | P(c)\frac{1}{(2\pi)^{n/2}|\boldsymbol \Sigma |^{1/2} } \exp \left( -\frac12 (\boldsymbol x - \boldsymbol \mu_c)^\text T \boldsymbol \Sigma_c^{-1} (\boldsymbol x - \boldsymbol \mu_c)\right)
127 | $$
128 | 由题中条件“假设同先验”,因此在二分类任务中,上式等价于最大化
129 | $$
130 | \max(-\frac12 (\boldsymbol x - \boldsymbol \mu_0)^\text T \boldsymbol \Sigma_0^{-1} (\boldsymbol x - \boldsymbol \mu_0), -\frac12 (\boldsymbol x - \boldsymbol \mu_1)^\text T \boldsymbol \Sigma_1^{-1} (\boldsymbol x - \boldsymbol \mu_1))
131 | $$
132 | 由此可知,贝叶斯最优分类器的决策平面为
133 | $$
134 | \boldsymbol x ^ \text T \boldsymbol \Sigma^{-1}(\boldsymbol \mu_1 - \boldsymbol \mu_0) - \frac 12 (\boldsymbol \mu_1 + \boldsymbol \mu_0)^ \text T \boldsymbol\Sigma^{-1}(\boldsymbol \mu_1 - \boldsymbol \mu_0)
135 | $$
136 | 对于线性判别分析来说,其欲最大化的目标为
137 | $$
138 | J = \frac{\boldsymbol{w}^\text{T}(\boldsymbol\mu_0-\boldsymbol\mu_1)(\boldsymbol\mu_0-\boldsymbol\mu_1)^\text T \boldsymbol{w}}{\boldsymbol{w} ^\text{T} (\boldsymbol\Sigma_0 + \boldsymbol\Sigma_1)\boldsymbol{w}}
139 | $$
140 | 其中,$\boldsymbol w$为直线$y=\boldsymbol w ^ \text T \boldsymbol x$中的系数项,$\boldsymbol \mu_i, \boldsymbol \Sigma_i$为第$i \in \{0, 1\}$类的均值向量、协方差矩阵。由于两类数据满足高斯分布且方差相同,因此其决策平面由两数据均值点的中点$\frac 12 (\boldsymbol \mu_0 + \boldsymbol \mu_1)$和法向量$\boldsymbol w$唯一确定,而将此带入贝叶斯最优分类器的决策平面均成立,因此线性判别分析的决策平面与此重合。因此,二分类任务中两类数据满足高斯分布且方差相同时,线性判别分析产生贝叶斯最优分类器。
141 |
142 |
143 |
144 |
145 | ## 7.7
146 |
147 | **答:**由题意,对于一个二分类问题,需要估算一个二值属性对应的先验概率$P(c, x_i)$则需要$30\times 2 \times 2=120$个样例(因为$c$和$x_i$的取值均有两种)。如果第二个二值属性在上述样例上对应的$c$和$x_i$的取值均相同,那么就无需增加样例;如果第二个二值属性在上述样例上的取值只有一个,那么还需要$30\times 2=60$个样例(另一个取值在$c$两取值上的个数)。
148 |
149 | 因此,当扩展到有$d$个二值属性时,最好情况不需要在第一个的基础上添加任何样例,因此样例数为$120$;最坏情况下,每一次添加属性均会添加$60$个样例,因此样例数为$120+60\times (d-1) = 60 \times (d + 1)$。
150 |
151 |
--------------------------------------------------------------------------------
/docs/MachineLearning/第三章作业.md:
--------------------------------------------------------------------------------
1 | # 《机器学习》第三章作业
2 |
3 | ## 3.1
4 |
5 | 答:(1)该模型中$b$与输入没有关系时或模型函数一定过原点时;(2)该模型只用于差分分析时,因为假设取两实例$\boldsymbol{x}_i$和$\boldsymbol{x}_j(i\neq j)$,$f(\boldsymbol{x}_i) - f(\boldsymbol{x}_j ) = \boldsymbol{w}^\text{T}(\boldsymbol{x}_i - \boldsymbol{x}_j)$是与$b$无关的。
6 |
7 | ## 3.3
8 |
9 | ### 1.准备数据
10 |
11 | ```python
12 | import numpy as np
13 | from sklearn.model_selection import train_test_split
14 |
15 | data = np.array([[0.697, 0.460, 1],
16 | [0.774, 0.376, 1],
17 | [0.634, 0.264, 1],
18 | [0.608, 0.318, 1],
19 | [0.556, 0.215, 1],
20 | [0.403, 0.237, 1],
21 | [0.481, 0.149, 1],
22 | [0.437, 0.211, 1],
23 | [0.666, 0.091, 0],
24 | [0.243, 0.267, 0],
25 | [0.245, 0.057, 0],
26 | [0.343, 0.099, 0],
27 | [0.639, 0.161, 0],
28 | [0.657, 0.198, 0],
29 | [0.360, 0.370, 0],
30 | [0.593, 0.042, 0],
31 | [0.719, 0.103, 0]]) # 西瓜数据集3.0alpha
32 | X = data[:, 0:2] # 属性
33 | y = data[:, -1] # 标签
34 | X_train,X_test,y_train,y_test=train_test_split(X,y,test_size=0.3) #随机划分训练集和测试集
35 | ```
36 |
37 | ### 2.定义模型
38 |
39 | ```python
40 | class LogisticRegression:
41 | def __int__(self):
42 | pass
43 |
44 | def fit(self, X_, y_):
45 | # 数据调整为x_bar和\beta, 便于操作
46 | n, m = X_.shape
47 | m += 1
48 | X = np.append(X_, np.ones(n).reshape((n, 1)), axis=1).T
49 | y = y_.copy()
50 | beta = np.random.random(size=(m, 1))
51 | # 牛顿迭代法
52 | epoch = 20
53 | for i in range(epoch):
54 | mul = beta.T @ X
55 | p1 = np.exp(mul) / (1 + np.exp(mul)) # 计算p1的公式
56 | fd = -np.sum(X * (y - p1), axis=1) # 计算牛顿迭代中的一阶导数
57 | sd = np.zeros((m, m)) # 计算牛顿迭代中的二阶导数
58 | for i in range(n):
59 | sd += X[:, i:i+1] @ X[:, i:i+1].T * (p1[0, i] * (1 - p1[0, i]))
60 | beta = beta - (np.linalg.inv(sd) @ fd).reshape((m, 1)) # 一次迭代
61 | # 训练结果分析
62 | ans = (beta.T @ X) > 1
63 | self.beta = beta
64 | print("训练集准确率: ", 1 - np.sum(np.abs(ans - y)) / n)
65 |
66 | def predict(self, X_, y_):
67 | # 测试结果分析
68 | n = X_.shape[0]
69 | X = np.append(X_, np.ones(n).reshape((n, 1)), axis=1).T
70 | y = y_.copy()
71 | ans = (self.beta.T @ X) > 1
72 | print("测试集准确率: ", 1 - np.sum(np.abs(ans - y)) / n)
73 |
74 | ```
75 |
76 | ### 3.使用模型进行训练和预测
77 |
78 | ```python
79 | model = LogisticRegression()
80 | model.fit(X_train, y_train)
81 | model.predict(X_test, y_test)
82 | ```
83 |
84 | 训练集准确率: 0.7272727272727273
85 | 测试集准确率: 0.8333333333333334
86 |
87 | ## 3.5
88 |
89 | ### 1.准备数据
90 |
91 | 同3.3
92 |
93 | ### 2.定义模型计算𝜔
94 |
95 | ```python
96 | class LDA:
97 | def __init__(self):
98 | pass
99 |
100 | def fit(self, X, y):
101 | X0 = X[y == 0] # 坏瓜
102 | X1 = X[y == 1] # 好瓜
103 | mu0 = np.mean(X0, axis=0).reshape((-1, 1)) # 坏瓜均值
104 | mu1 = np.mean(X1, axis=0).reshape((-1, 1)) # 好瓜均值
105 | cov0 = np.cov(X0, rowvar=False) # 坏瓜协方差
106 | cov1 = np.cov(X1, rowvar=False) # 好瓜协方差
107 | S_w = np.mat(cov0 + cov1) # S_w
108 | U,Sigma,V = np.linalg.svd(S_w,full_matrices=False) # 奇异值分解
109 | self.omega = V.T @ np.linalg.inv(np.diag(Sigma)) @ U.T @ (mu0 - mu1) # /omega
110 | # 输出结果
111 | ans = self.omega.T @ X.T < 0
112 | acc = 1 - np.sum(np.abs(ans - y)) / y.shape[0]
113 | print("训练集准确率:", acc)
114 |
115 | def predict(self, X, y):
116 | # 输出结果
117 | ans = self.omega.T @ X.T < 0
118 | acc = 1- np.sum(np.abs(ans - y)) / y.shape[0]
119 | print("测试集准确率:", acc)
120 |
121 | ```
122 |
123 | ### 3.使用模型进行训练和预测
124 |
125 | ```python
126 | model = LDA()
127 | model.fit(X_train, y_train)
128 | model.predict(X_test, y_test)
129 | ```
130 |
131 | 训练集准确率: 0.9090909090909091
132 | 测试集准确率: 0.6666666666666667
133 |
134 | ## 3.7
135 |
136 | 答:给出汉明距离意义下理论最优的ECOC二元码:
137 |
138 | | | $f_1$ | $f_2$ | $f_3$ | $f_4$ | $f_5$ | $f_6$ | $f_7$ | $f_8$ | $f_9$ |
139 | | ----- | ----- | ----- | ----- | ---- | ---- | ------- | ---- | ---- | ---- |
140 | | $C_1$ | +1 | -1 | -1 | -1 | +1 | +1 | +1 | +1 | -1 |
141 | | $C_2$ | -1 | +1 | -1 | -1 | +1 | -1 | -1 | +1 | -1 |
142 | | $C_3$ | -1 | -1 | +1 | -1 | -1 | +1 | -1 | +1 | -1 |
143 | | $C_4$ | -1 | -1 | -1 | +1 | -1 | -1 | +1 | +1 | -1 |
144 |
145 | 证明如下:
146 |
147 | 注意到性质:若两个分类器$f_i$和$f_j(i \neq j)$对样例的分类互为反码[如$(-1,-1,1,1)$和$(1,1,-1,-1)$],由于很多算法对待0-1分类是对称的(即如果将0-1类互换,最终训练出的模型是一样的)。这样一对分类器实际上可以简化为一个分类器,因此可以计算出在不出现互为反码的情况下,最优的ECOC编码长度为
148 | $$
149 | \binom{4}{1} + \frac{\binom{4}{2}}{2}=7
150 | $$
151 | 由于可以向编码中加入冗余,即可以在最短编码长度的情况下加入互为反码的一对分类器,因此只要保证编码长度为$7+2n(n为自然数)$即可保证得出的ECOC编码是最优的。
152 |
153 | 综上,由于$9=7+2\times 1$($f_8$和$f_9$是加入的冗余分类器),因此上述给出的ECOC二元码是理论最优的。
154 |
155 | ## 3.9
156 |
157 | 答:对OvR、MvM 来说,由于**对每个类进行了相同的处理**,其拆解出的二分类任务中类别不平衡的影响会相互抵消,因此通常不需专门处理。
158 |
--------------------------------------------------------------------------------
/docs/MachineLearning/第九章作业.md:
--------------------------------------------------------------------------------
1 | # 《机器学习基础》第九章作业
2 |
3 | ## 9.1
4 |
5 | **(1)首先证明闵可夫斯基距离满足非负性,同一性和对称性。**
6 |
7 | 由于
8 | $$
9 | \text{dist}_\text{mk} (x_i, x_j) = \left( \sum_{u=1}^n |x_{iu}-x_{ju}|^p \right)^\frac 1p \ge 0
10 | $$
11 | 因此,闵可夫斯基距离满足非负性。当且仅当$x_i = x_j$时,$\text{dist}_\text{mk} (x_i, x_j)=0$,因此闵可夫斯基距离满足同一性。由于绝对值中减数和被减数可以调换位置,所以$\text{dist}_\text{mk} (x_i, x_j) = \text{dist}_\text{mk} (x_j, x_i)$,因此闵可夫斯基距离满足对称性。
12 |
13 | **(2)下面证明当$p\ge 1$时,闵可夫斯基距离满足直递性。**
14 |
15 | 显然$p=1$时,可由三角不等式证明。因此下面$p>1$。
16 |
17 | 令$a_i=|x_{iu}-x_{ku}|,b_i=|x_{ku}-x_{ju}|$,那么要证$\text{dist}_\text{mk} (x_i, x_j) \leq \text{dist}_\text{mk} (x_i, x_k) + \text{dist}_\text{mk} (x_k, x_j)$,即证
18 | $$
19 | \left(\sum_{i=1}^{n}|a_i+b_i|^p\right)^\frac 1p \leq \left(\sum_{i=1}^{n}a_i^p \right)^\frac 1p + \left(\sum_{i=1}^{n}b_i^p \right)^\frac 1p
20 | $$
21 | 由于
22 | $$
23 | \begin{align}
24 | \left(\sum_{i=1}^{n}|a_i+b_i|^p\right)^\frac 1p &\leq \sum_{i=1}^{n}|a_i+b_i|^p \\
25 | &= \sum_{i=1}^{n}|a_i+b_i||a_i+b_i|^{p-1} \\
26 | &\leq \sum_{i=1}^{n}(|a_i|+|b_i|)|a_i+b_i|^{p-1} \\
27 | &= \sum_{i=1}^{n}(|a_i||a_i+b_i|^{p-1}+|b_i||a_i+b_i|^{p-1})
28 | \end{align}
29 | $$
30 | 由赫尔德不等式$\sum_i^na_ib_i \leq (\sum_{i=1}^n a_i^p)^\frac1p(\sum_{i=1}^nb_i^q)^\frac1q \ \ (p, q > 1) $可得
31 | $$
32 | \begin{align}
33 | \sum_{i=1}^{n}(|a_i||a_i+b_i|^{p-1}+|b_i||a_i+b_i|^{p-1}) &\leq \left(\sum_{i=1}^{n}|a_i|^p \right)^{\frac1p} \left(\sum_{i=1}^{n}|a_i+b_i|^{(p-1)q}\right)^{\frac1q} + \left(\sum_{i=1}^{n}|b_i|^p\right)^{\frac1p} \left(\sum_{i=1}^{n}|a_i+b_i|^{(p-1)q}\right)^{\frac1q} \\
34 | &= \left(\left(\sum_{i=1}^{n}|a_i|^p\right)^{\frac1p} + \left(\sum_{i=1}^{n}|b_i|^p\right)^{\frac1p} \right) \left(\sum_{i=1}^{n}|a_i+b_i|^{p}\right)^{\frac1q} \\
35 | &\leq \left(\sum_{i=1}^{n}|a_i|^p\right)^{\frac1p} + \left(\sum_{i=1}^{n}|b_i|^p\right)^{\frac1p}
36 | \end{align}
37 | $$
38 | 其中$q=\frac{p}{p-1}$,于是原不等式成立,因此,当$p \ge 1$时闵可夫斯基距离满足直递性。
39 |
40 | **(3)下面证明当$0 \leq p < 1$时,闵可夫斯基距离不满足直递性。**
41 |
42 | 和(2)类似的,只需证明下式即可证明原命题。
43 | $$
44 | \left(\sum_{i=1}^{n}|a_i+b_i|^p\right)^\frac 1p \ge \left(\sum_{i=1}^{n}a_i^p \right)^\frac 1p + \left(\sum_{i=1}^{n}b_i^p \right)^\frac 1p
45 | $$
46 | 由于
47 | $$
48 | \begin{align}
49 | \sum_{i=1}^{n}|a_i+b_i|^p &= \sum_{i=1}^{n}|t\frac{a_i}{t}+(1-t)\frac{b_i}{1-t}|^p \\
50 | &\ge t^{1-p}\sum_{i=1}^{n}|a_i|^p+(1-t)^{1-p}\sum_{i=1}^{n}|b_i|^p
51 | \end{align}
52 | $$
53 | 其中
54 | $$
55 | t=\frac{\left(\sum_{i=1}^{n}a_i^p \right)^\frac 1p}{\left(\sum_{i=1}^{n}a_i^p \right)^\frac 1p + \left(\sum_{i=1}^{n}b_i^p \right)^\frac 1p}
56 | $$
57 | 于是有
58 | $$
59 | \begin{align}
60 | t^{1-p}\sum_{i=1}^{n}|a_i|^p+(1-t)^{1-p}\sum_{i=1}^{n}|b_i|^p &= \left(\left(\sum_{i=1}^{n}a_i^p \right)^\frac 1p + \left(\sum_{i=1}^{n}b_i^p \right)^\frac 1p\right)^p
61 | \end{align}
62 | $$
63 | 综上即可证明原不等式成立,闵可夫斯基距离不满足直递性。
64 |
65 | **(4)下面证明$p$趋向无穷大时,闵可夫斯基距离等于对应分量的最大绝对距离。**
66 |
67 | 闵可夫斯基距离公式可以转换如下:
68 | $$
69 | \text{dist}_\text{mk} (x_i, x_j) = \left( \sum_{u=1}^n |x_{iu}-x_{ju}|^p \right)^\frac 1p = \max_u|x_{iu}-x_{ju}| \left( \sum_{u=1}^n \left(\frac{|x_{iu}-x_{ju}|}{\max_u|x_{iu}-x_{ju}|}\right)^p \right)^\frac 1p
70 | $$
71 | 令
72 | $$
73 | t_u = \frac{|x_{iu}-x_{ju}|}{\max_u|x_{iu}-x_{ju}|}\leq 1
74 | $$
75 | 当$p \rarr +\infin$时
76 | $$
77 | \left( \sum_{u=1}^n t_u^p \right)^\frac 1p \rarr1
78 | $$
79 | 因此
80 | $$
81 | \text{dist}_\text{mk} (x_i, x_j) \rarr \max_u|x_{iu}-x_{ju}|
82 | $$
83 | 综上得证。
84 |
85 |
86 |
87 | ## 9.2
88 |
89 | 显然,豪斯多夫距离满足非负性和对称性,这里不过多证明。
90 |
91 | (1)下面证明豪斯多夫距离满足同一性。
92 |
93 | ①当$X=Z$时,$\text{dist}_\text{h}(X, Z) = \text{dist}_\text{h}(Z, X) = 0$,因此$\text{dist}_\text{H}(X, Z) = 0$。
94 |
95 | ②当$\text{dist}_\text{H}(X, Z) = 0$时,$\text{dist}_\text{h}(X, Z) = \text{dist}_\text{h}(Z, X) = 0$,这说明任意$x\in X$,存在$z\in Z$使得距离为0,因此$X \subset Z$,同时也说明任意$z\in Z$,存在$x\in X$使得距离为0,因此$Z \subset X$,所以$X=Z$。
96 |
97 | 综上得证。
98 |
99 | (2)下面证明豪斯多夫距离满足直递性。
100 |
101 | 欲证
102 | $$
103 | \text{dist}_\text{H}(X, Z) \leq \text{dist}_\text{H}(X, Y) + \text{dist}_\text{H}(Y, Z)
104 | $$
105 |
106 | 由于
107 | $$
108 | \text{dist}_\text{H}(X, Z) = \max(\text{dist}_\text{h}(X, Z), \text{dist}_\text{h}(Z, X))
109 | $$
110 | 因此,可以转化为求证
111 | $$
112 | \text{dist}_\text{h}(X, Z) \leq \text{dist}_\text{h}(X, Y) + \text{dist}_\text{h}(Y, Z)
113 | $$
114 | 由于
115 | $$
116 | \begin{align}
117 | \min_{z\in Z} ||x - z||_2 &= \min_{z \in Z} ||x + y+y-z||_2, \forall y\in Y \\
118 | &\leq \min_{z \in Z} (||x + y||_2+||y-z||_2), \forall y\in Y \\
119 | &= ||x+y||_2 + \min_{z \in Z} ||y-z||_2, \forall y\in Y \\
120 | &\leq ||x+y||_2 + \max_{y \in Y}\min_{z \in Z} ||y-z||_2, \forall y\in Y \\
121 | &= ||x+y||_2 + \text{dist}_\text{h}(Y, Z), \forall y\in Y \\
122 | &\leq \min_{y \in Y} ||x+y||_2 + \text{dist}_\text{h}(Y, Z)
123 | \end{align}
124 | $$
125 | 对不等式左右两边取$\max_{x\in X}$得到
126 | $$
127 | \max_{x\in X}\min_{z\in Z} ||x - z||_2 \leq \max_{x\in X}\min_{y \in Y} ||x+y||_2 + \text{dist}_\text{h}(Y, Z)
128 | $$
129 | 即
130 | $$
131 | \text{dist}_\text{h}(X, Z) \leq \text{dist}_\text{h}(X, Y) + \text{dist}_\text{h}(Y, Z)
132 | $$
133 | 综上得证。
134 |
135 |
136 |
137 |
138 | ## 9.3
139 |
140 | 不一定能。由于求解式(9.24)的最优解是一个NP-hard问题,k均值算法只是基于贪心思想通过迭代进行近似求解得到的局部最优解,不一定能得到式子的全局最优解。
141 |
142 |
143 |
144 | ## 9.4
145 |
146 | ### 1 导入库
147 | ```python
148 | from sklearn.cluster import KMeans
149 | import pandas as pd
150 | import numpy as np
151 | from matplotlib import pyplot as plt
152 | ```
153 |
154 | ### 2 导入数据集
155 | ```python
156 | df = pd.read_csv("./4.0.csv", header=None)
157 | X = df.values
158 | ```
159 |
160 | ### 3 测试不同k值的影响
161 | > 选定数据集中前k个点作为初始中心点
162 | ```python
163 | for k in range(2, 5):
164 | model = KMeans(k, init=[X[i, :] for i in range(k)], n_init=1)
165 | model.fit(X)
166 | ans = model.predict(X)
167 | print(model.cluster_centers_)
168 | plt.title(f"KMeans [k={k}]")
169 | plt.scatter(X[:, 0], X[:, 1], c=ans)
170 | plt.show()
171 | ```
172 |
173 | ```
174 | [[0.62371429 0.37435714]
175 | [0.44675 0.1875 ]]
176 | ```
177 |
178 | 
179 |
180 | ```
181 | [[0.471 0.39928571]
182 | [0.68138462 0.28446154]
183 | [0.3725 0.1748 ]]
184 | ```
185 |
186 | 
187 |
188 | ```
189 | [[0.67625 0.4665 ]
190 | [0.6896 0.3072 ]
191 | [0.61585714 0.137 ]
192 | [0.38685714 0.27714286]]
193 | ```
194 |
195 | 
196 |
197 |
198 |
199 | ### 4 测试不同初始中心点的影响
200 |
201 | > 选定k=3
202 |
203 | ```python
204 | Xs = [[[0, 0], [0, 0], [0, 0]], # 全都在一个点
205 | [[0.5, 0.1], [0.5, 0.25], [0.5, 0.4]], # y轴分散
206 | [[0.3, 0.3], [0.5, 0.3], [0.7, 0.3]]] # x轴分散
207 |
208 | for centers in Xs:
209 | model = KMeans(3, init=centers, n_init=1)
210 | model.fit(X)
211 | ans = model.predict(X)
212 | print(model.cluster_centers_)
213 | # plt.title(f"KMeans [k={k}]")
214 | plt.scatter(X[:, 0], X[:, 1], c=ans)
215 | plt.show()
216 | ```
217 |
218 | ```
219 | [[0.36136364 0.21709091]
220 | [0.60845455 0.41336364]
221 | [0.6515 0.16325 ]]
222 | ```
223 |
224 | 
225 |
226 | ```
227 | [[0.63255556 0.16166667]
228 | [0.33455556 0.21411111]
229 | [0.598 0.40491667]]
230 | ```
231 |
232 | 
233 |
234 | ```
235 | [[0.348 0.18955556]
236 | [0.471 0.39928571]
237 | [0.67507143 0.26714286]]
238 | ```
239 |
240 | 
241 |
242 | ### 5 分析
243 |
244 | 1. 对比不同k值得到的结果可以看出,不是k越大越好,而是需要根据经验去确定簇的数量,这样才能达到不错的聚类效果。
245 | 2. 对比不同初始值的结果可以看出,初始中心点也很大程度上影响到了聚类的效果,选定的三组初始中心点各有特征,可以看出在选定初始中心点在x轴上分散分布时,效果比较不错,说明数据集在x轴方向上有比较好的可分性。由于KMeans基于贪心算法,只能得到局部最优解,因此根据经验选择符合数据集特征的初始中心点对聚类效果有显著影响。
246 |
247 |
248 |
249 | ## 9.5
250 |
251 | (1)连接性。设$x_k$为集合$X$中的核心对象,设$x_i \in X, x_j \in X$。由于集合$X$是由$x_k$密度可达的所有样本构成的,那么$x_i,x_j$均由$x_k$密度可达,因此$x_i$与$x_j$密度相连。由此证明连接性。
252 |
253 | (2)最大性。设$x_k$为集合$X$中的核心对象,设$x_i \in C$,那么$x_i$由$x_k$密度可达。如果$x_j$由$x_i$密度可达,由于密度可达关系满足直递性,$x_j$由$x_k$密度可达,因此$x_j\in C$。由此证明最大性。
254 |
255 |
256 |
257 |
--------------------------------------------------------------------------------
/docs/MachineLearning/第二章作业.md:
--------------------------------------------------------------------------------
1 | # 《机器学习》第二章作业
2 |
3 | ## 2.1
4 |
5 | 答:由留出法定义,单次划分(分层抽样)中训练集中正例应当有$500 \times 70 \%=350$个样本,负例应当有$500 \times 70 \%=350$个样本,从所有样本中选取训练集后,剩余的作为测试集即可。因此,划分方式数为:
6 | $$
7 | \binom{500}{350} \times \binom{500}{350}=2.56 \times 10^{289}
8 | $$
9 |
10 | ## 2.3
11 |
12 | 答:**若学习器A的F1值比学习器B的高,A的BEP不一定比B高**。由于$BEP=P=R$,而$F1=\frac{2\times P' \times R'}{P' + R'}$,其中$P$不一定等于$P'$,$R$也不一定等于$R'$。因此若已知学习器A的F1值比学习器B的高,也无法推算出A的BEP值和B的BEP值之间的关系。
13 |
14 | ## 2.5
15 |
16 | 答:设$\boldsymbol{x}^+$为正例,$\boldsymbol{x}^-$为负例,那么:
17 |
18 | - $f(\boldsymbol{x}^+) > f(\boldsymbol{x}^-)$表示两者都预测正确;
19 |
20 | - $f(\boldsymbol{x}^+) = f(\boldsymbol{x}^-)$表示$\boldsymbol{x}^+$预测成功,而$\boldsymbol{x}^-$预测失败或者$\boldsymbol{x}^-$预测成功,而$\boldsymbol{x}^+$预测失败;
21 | - $f(\boldsymbol{x}^+) < f(\boldsymbol{x}^-)$表示两者都预测错误;
22 |
23 | 因此根据$\text{AUC}$的几何意义,可以对其公式进行改写:
24 | $$
25 | \begin{align}
26 | \text{AUC} &= \sum_{\boldsymbol{x}^+ \in D^+} \frac12 · \frac{1}{m^+} \left[ \frac{2}{m^-} \sum_{\boldsymbol{x}^- \in D^-} \mathbb{I}\left(f(\boldsymbol{x}^+) > f(\boldsymbol{x}^-)\right) + \frac1{m^-} \sum_{\boldsymbol{x}^- \in D^-} \mathbb{I}\left(f(\boldsymbol{x}^+) = f(\boldsymbol{x}^-)\right) \right] \\
27 | &= \frac{1}{m^+m^-} \sum_{\boldsymbol{x}^+ \in D^+} \sum_{\boldsymbol{x}^- \in D^-} \left( \mathbb{I}\left(f(\boldsymbol{x}^+) > f(\boldsymbol{x}^-)\right) + \frac12 \mathbb{I}\left(f(\boldsymbol{x}^+) = f(\boldsymbol{x}^-)\right) \right) \\
28 |
29 | \end{align}
30 | $$
31 | 因此:
32 | $$
33 | \begin{align}
34 | \text{AUC} + \ell_{\rank} &= \frac{1}{m^+m^-} \sum_{\boldsymbol{x}^+ \in D^+} \sum_{\boldsymbol{x}^- \in D^-} \left( \mathbb{I}\left(f(\boldsymbol{x}^+) < f(\boldsymbol{x}^-)\right) + \mathbb{I}\left(f(\boldsymbol{x}^+) > f(\boldsymbol{x}^-)\right) + \mathbb{I}\left(f(\boldsymbol{x}^+) = f(\boldsymbol{x}^-)\right) \right) \\
35 | &= \frac{1}{m^+m^-} \sum_{\boldsymbol{x}^+ \in D^+} \sum_{\boldsymbol{x}^- \in D^-} (1) \\
36 | &= 1
37 | \end{align}
38 | $$
39 | 原式得证。
40 |
41 | ## 2.7
42 |
43 | 答:由于ROC曲线上的点为$(\text{FPR}, \text{TPR})$,且有$\text{TPR} + \text{FNR} = 1$,所以由ROC曲线上一点能确定代价曲线图中$(0, \text{FPR})$和$(1, \text{FNR})$两点,并由此得到连接两点的线段。将ROC曲线上所有的点对应到代价曲线图的所有线段,取所有线段的公共下界即可得到唯一的代价曲线。
44 |
45 | 反之,代价曲线(折线)的每个分段可以对应一条直线,从而得到直线与$x=0$和$x=1$的交点$(0, \text{FPR})$和$(1, \text{FNR})$,这两点可以对应ROC曲线上的一点,由此即可确定一条ROC曲线(不是唯一的,因为可能存在在代价曲线上方而不与曲线相交的线段,这可能也会对应ROC曲线上的一个点)。
46 |
47 | ## 2.9
48 |
49 | 卡方检验就是统计样本的实际观测值与理论推断值之间的偏离程度,卡方值越大,越不符合;卡方值越小,越趋于符合。检验过程如下:
50 |
51 | 1. 写出假设和备择假设;
52 |
53 | 2. 计算卡方值
54 | $$
55 | \chi^2 = \sum_{i=1}^n \frac{(x_i - \hat{x}_i)^2}{\hat{x}_i}
56 | $$
57 | 其中,$x_i$表示观测值,而$\hat{x}_i$表示预期值;
58 |
59 | 3. 计算卡方分布的自由度(若为$R \times C$的列联表,自由度为$(R-1)(C - 1)$);
60 |
61 | 4. 确定显著水平并根据自由度查表得到卡方检验值,将其与计算出的卡方值进行比较;
62 |
63 | 5. 若计算出的卡方值比检验值小,那么无法拒绝原假设,反之拒绝原假设。
64 |
65 |
--------------------------------------------------------------------------------
/docs/MachineLearning/第五章作业.md:
--------------------------------------------------------------------------------
1 | # 《机器学习》第五章作业
2 |
3 | ## 5.1
4 |
5 | **答**:虽然线性函数相对阶跃函数是连续的,但它不能将输入值压缩到$(0,1)$输出值范围内,这使得后续过程中神经元受变量值相对较大的属性影响更大,不利于参数收敛。而且,使用线性函数作为激活函数时,输入值经过每一层的传播后的输出值是输入值的线性组合,此时等价于线性回归。
6 |
7 | ## 5.2
8 |
9 | **答**:在使用Sigmoid函数作为激活函数的每个神经元的输出都是
10 | $$
11 | y=\frac{1}{1+e^{-\left( \sum_{i=1}^nw_i x_i-\theta \right)}}
12 | $$
13 | 对数几率回归的输出为
14 | $$
15 | y=
16 | \left\{
17 | \begin{array}{}
18 | 0, & z<0 \\
19 | 0.5, & z=0 \\
20 | 1, & z>0
21 | \end{array}
22 | \right.
23 | $$
24 | 其中
25 | $$
26 | z=\frac1{1+e^{-\left( \boldsymbol w^\text T \boldsymbol x + b \right)}}
27 | $$
28 | 可以看到,神经元的$y$函数和对数几率回归的$z$函数是相等的。不过神经元的输出不对Sigmoid函数的输出做任何变换,而对数几率回归由于需要判别,因此在输出后加入了分段函数。同时可以发现,如果神经网络中神经元除了输出的激活函数为Sigmoid函数,其他激活函数均为线性函数的话,此神经网络就等价于对数几率回归。
29 |
30 | ## 5.3
31 |
32 | **答**:对于$v_{ih}$,其更新公式为
33 | $$
34 | \Delta v_{ih} = -\eta \frac{\partial E_k}{\partial v_{ih}}
35 | $$
36 | 其中
37 | $$
38 | \frac{\partial E_k}{\partial v_{ih}} = \frac{\partial E_k}{\partial b_h}
39 | \frac{\partial b_h}{\partial \alpha_h} \frac{\partial \alpha_h}{\partial v_{ih}}
40 | $$
41 | 由于
42 | $$
43 | \frac{\partial \alpha_h}{\partial v_{ih}} = x_i \\
44 | e_h = -\frac{\partial E_k}{\partial b_h}
45 | \frac{\partial b_h}{\partial \alpha_h}
46 | $$
47 | 所以
48 | $$
49 | \Delta v_{ih} = -\eta \frac{\partial E_k}{\partial v_{ih}} = -\eta \frac{\partial E_k}{\partial b_h}
50 | \frac{\partial b_h}{\partial \alpha_h} \frac{\partial \alpha_h}{\partial v_{ih}} = \eta e_h x_i
51 | $$
52 | 此即书中式(5.13),证毕。
53 |
54 | ## 5.4
55 |
56 | **答**:若学习率过低,会导致模型收敛过慢,而学习率过高又可能会导致震荡而使模型无法收敛到最优解。可以考虑使用Adam算法等设定合适的初始学习率后,在迭代过程中自动调整学习率。
57 |
58 | ## 5.5
59 |
60 | ### 1. 环境及数据准备
61 |
62 | ```python
63 | import numpy as np
64 | import pandas as pd
65 | from matplotlib import pyplot as plt
66 | from sklearn.model_selection import train_test_split
67 | from sklearn.preprocessing import LabelEncoder
68 |
69 | df = pd.read_csv('./watermelon3.csv', index_col=0) # 西瓜数据集3.0
70 | for label in df.columns: # 离散值预处理为整数
71 | if df[label].dtype == object:
72 | df[label] = LabelEncoder().fit(df[label]).transform(df[label])
73 | df
74 | ```
75 |
76 | | | 色泽 | 根蒂 | 敲声 | 纹理 | 脐部 | 触感 | 密度 | 含糖率 | 好瓜 |
77 | | ---: | ---: | ---: | ---: | ---: | ---: | ---: | ----: | -----: | ---: |
78 | | 编号 | | | | | | | | | |
79 | | 1 | 2 | 2 | 1 | 1 | 0 | 0 | 0.697 | 0.460 | 1 |
80 | | 2 | 0 | 2 | 0 | 1 | 0 | 0 | 0.774 | 0.376 | 1 |
81 | | 3 | 0 | 2 | 1 | 1 | 0 | 0 | 0.634 | 0.264 | 1 |
82 | | 4 | 2 | 2 | 0 | 1 | 0 | 0 | 0.608 | 0.318 | 1 |
83 | | 5 | 1 | 2 | 1 | 1 | 0 | 0 | 0.556 | 0.215 | 1 |
84 | | 6 | 2 | 1 | 1 | 1 | 2 | 1 | 0.403 | 0.237 | 1 |
85 | | 7 | 0 | 1 | 1 | 2 | 2 | 1 | 0.481 | 0.149 | 1 |
86 | | 8 | 0 | 1 | 1 | 1 | 2 | 0 | 0.437 | 0.211 | 1 |
87 | | 9 | 0 | 1 | 0 | 2 | 2 | 0 | 0.666 | 0.091 | 0 |
88 | | 10 | 2 | 0 | 2 | 1 | 1 | 1 | 0.243 | 0.267 | 0 |
89 | | 11 | 1 | 0 | 2 | 0 | 1 | 0 | 0.245 | 0.057 | 0 |
90 | | 12 | 1 | 2 | 1 | 0 | 1 | 1 | 0.343 | 0.099 | 0 |
91 | | 13 | 2 | 1 | 1 | 2 | 0 | 0 | 0.639 | 0.161 | 0 |
92 | | 14 | 1 | 1 | 0 | 2 | 0 | 0 | 0.657 | 0.198 | 0 |
93 | | 15 | 0 | 1 | 1 | 1 | 2 | 1 | 0.360 | 0.370 | 0 |
94 | | 16 | 1 | 2 | 1 | 0 | 1 | 0 | 0.593 | 0.042 | 0 |
95 | | 17 | 2 | 2 | 0 | 2 | 2 | 0 | 0.719 | 0.103 | 0 |
96 |
97 | ```python
98 | X = df.iloc[:, :-1] # 属性
99 | y = df.iloc[:, -1] # 标签
100 | X_train,X_test,y_train,y_test=train_test_split(X,y,test_size=0.3) #随机划分训练集和测试集
101 | ```
102 |
103 | ### 2. 定义模型
104 |
105 | ```python
106 | class BPNN:
107 | def __init__(self):
108 | pass
109 |
110 | def __init(self, X, y, q):
111 | '''
112 | @param: X: 训练集属性
113 | @param: y: 训练集输出
114 | @param: q: 隐层神经元数量
115 | '''
116 | self.v = np.random.uniform(size=(X.shape[1], q))
117 | self.w = np.random.uniform(size=(q, 1))
118 |
119 | def __sigmoid(self, x):
120 | return 1 / (1 + np.exp(-x))
121 |
122 | def __sgd(self, X, y, lr, epoch):
123 | # 标准BP算法, 对每一个样本进行一次权重更新
124 | self.loss = []
125 | for ep in range(1, epoch+1):
126 | sum_ek = 0
127 | idx = list(range(X.shape[0]))
128 | np.random.shuffle(idx)
129 | X, y = X[idx], y[idx]
130 | for i in range(X.shape[0]):
131 | # 前向传播
132 | self.alpha = X[i:i+1] @ self.v
133 | self.b = self.__sigmoid(self.alpha)
134 | self.beta = self.b @ self.w
135 | self.py = self.__sigmoid(self.beta)
136 | # 计算误差
137 | ek = np.power(self.py - y[i], 2) / 2
138 | sum_ek += np.average(ek)
139 | # 后向更新
140 | g = self.py * (1 - self.py) * (y[i] - self.py)
141 | delta_w = self.eta * (self.b.T @ g)
142 | e = self.b * (1 - self.b) * np.sum(self.w @ g, axis=1)
143 | delta_v = self.eta * (X[i:i+1].T @ e)
144 | self.w += delta_w
145 | self.v += delta_v
146 | self.loss.append(sum_ek/X.shape[0])
147 |
148 | def __bgd(self, X, y, lr, epoch):
149 | # 累积BP算法, 对所有样本都进行一次权重更新
150 | self.loss = []
151 | y = y.reshape((-1, 1))
152 | for ep in range(1, epoch+1):
153 | # 前向传播
154 | self.alpha = X @ self.v
155 | self.b = self.__sigmoid(self.alpha)
156 | self.beta = self.b @ self.w
157 | self.py = self.__sigmoid(self.beta)
158 | # 计算误差
159 | ek = np.power(self.py - y, 2) / 2
160 | self.loss.append(np.average(ek))
161 | # 后向更新
162 | g = self.py * (1 - self.py) * (y - self.py)
163 | delta_w = self.eta * (self.b.T @ g)
164 | e = self.b * (1 - self.b) * (g @ self.w.T)
165 | delta_v = self.eta * (X.T @ e) # (8, 17) (17, 10)
166 | self.w += delta_w
167 | self.v += delta_v
168 |
169 | def fit(self, X, y, lr, epoch, algo="sgd"):
170 | X = np.array(X)
171 | y = np.array(y)
172 | self.eta = lr
173 | self.__init(X, y, 10)
174 | # 标准BP算法
175 | if algo.lower() == "sgd":
176 | self.__sgd(X, y, lr, epoch)
177 | # 累积BP算法
178 | elif algo.lower() == "bgd":
179 | self.__bgd(X, y, lr, epoch)
180 |
181 | def predict(self, X, y):
182 | X = np.array(X)
183 | y = np.array(y)
184 | # 前向传播
185 | alpha = X @ self.v
186 | b = self.__sigmoid(alpha)
187 | beta = b @ self.w
188 | py = self.__sigmoid(beta)
189 | return np.array(py > 0.5).astype(np.int32).reshape(1, -1)[0]
190 |
191 | def accuracy(self, X, y):
192 | ans = self.predict(X, y)
193 | return 1 - np.sum(np.abs(ans - y)) / X.shape[0]
194 | ```
195 |
196 | ### 3. 模型测试
197 |
198 | ```python
199 | model = BPNN()
200 | model.fit(X, y, 0.2, 500, algo="sgd")
201 | print("使用SGD训练后的准确度为:", model.accuracy(X, y))
202 | plt.plot(model.loss, label="sgd")
203 | model.fit(X, y, 0.2, 500, algo="bgd")
204 | plt.plot(model.loss, label="bgd")
205 | print("使用BGD训练后的准确度为:", model.accuracy(X, y))
206 | plt.legend()
207 | ```
208 |
209 | ```
210 | 使用SGD训练后的准确度为: 1.0
211 | 使用BGD训练后的准确度为: 1.0
212 | ```
213 |
214 | 
215 |
216 | 可以看到,由于sgd每次迭代是对每个样本依次更新权重,因此在中间会出现抖动,但总体是朝着最优解的。从计算用时来看,sgd显然时间会更长,而bgd一次对所有损失更新权重,因此用时相对少一些。
217 |
--------------------------------------------------------------------------------
/docs/MachineLearning/第八章作业.md:
--------------------------------------------------------------------------------
1 | # 《机器学习基础》第八章作业
2 |
3 | ## 8.1
4 |
5 | 使用简单投票法的集成学习预测错误,意味着少于半数的基学习器预测正确。那么,集成学习的错误率就是少于半数的基学习器预测正确的概率。这等价于抛$T$次硬币,有少于$\lfloor T/2 \rfloor$的硬币朝上的概率(这里硬币朝上的概率为$1-\epsilon$,也就是一个基学习器预测正确的概率)。预测正确的基学习器数量为
6 | $$
7 | g(x) = \sum_{i=0}^{T} \mathbb I (h_i(x)=f(x))
8 | $$
9 | 那么$g(x) \leq \lfloor T / 2 \rfloor$的概率为
10 | $$
11 | P(g(x) \leq \lfloor T/2 \rfloor)=\sum_{k=0}^{\lfloor T/2 \rfloor}\binom{T}{k}(1-\epsilon)^k\epsilon^{T-k}
12 | $$
13 | 这就是式(8.3)的左半部分$P(H(x)\neq f(x))$,由题中给出的定义可得$\lfloor T/2 \rfloor= (\epsilon - \delta)T$,于是$\delta = \epsilon - \lfloor T/2 \rfloor/T \ge \epsilon - 1/2$,由Hoeffding不等式得
14 | $$
15 | P(H(x)\neq f(x)) \leq \exp\left( -2 \left( \epsilon - \frac12 \right)^2 T \right) = \exp\left( -\frac12 T \left( 1 - 2\epsilon \right)^2 \right)
16 | $$
17 | 式(8.3)得证。
18 |
19 |
20 |
21 | ## 8.2
22 |
23 | 我们需要最小化的就是$\mathbb E_{x\in D}[\ell(-f(x) H(x))]$,考虑对$H(x)$进行求偏导,得到
24 | $$
25 | -P(f(x)=1|x) \ell(-H(x)) +P(f(x)=-1|x) \ell(H(x))
26 | $$
27 | 令其为0得到
28 | $$
29 | \frac{P(f(x)=-1|x)}{P(f(x)=1|x)} = \frac{\ell(H(x))}{\ell(-H(x))}
30 | $$
31 | 当$P(f(x)=-1|x) > P(f(x)=1|x)$时,$\ell(H(x)) > \ell(-H(x))$,由于$\ell(-f(x)H(x))$关于$H(x)$递减,因此
32 | $$
33 | H(x) < -H(x)
34 | $$
35 | 所以$H(x)<0$。同理,当$P(f(x)=-1|x) < P(f(x)=1|x)$时,$H(x)>0$。
36 |
37 | 综上:$\text{sign}(H(x))=\arg \max_{y\in (-1, 1)}P(f(x)=y|x)$,这意味着$\text{sign}(H(x))$达到了贝叶斯最优错误率。这说明此损失函数是分类任务原本0/1损失函数得一致性替代函数。
38 |
39 |
40 |
41 | ## 8.3
42 |
43 | 使用`sklean.ensemble`中的`AdaBoostClassifier`实现即可(默认采用决策树模型作为基学习器),代码如下:
44 |
45 | ```python
46 | from sklearn.ensemble import AdaBoostClassifier
47 | import pandas as pd
48 | from matplotlib import pyplot as plt
49 | import numpy as np
50 |
51 | # 加载数据
52 | df = pd.read_csv("./3.0a.csv", index_col=0)
53 | X = df.iloc[:, :2].values
54 | y = df.iloc[:, -1].values
55 |
56 | # 模型训练与预测
57 | model = AdaBoostClassifier(n_estimators=1, random_state=0)
58 | model.fit(X, y)
59 | pred = model.predict(X)
60 | print("错误分类数量:", np.sum(np.abs(pred - y)))
61 |
62 | # 画图
63 | plt.scatter(X[:, 0], X[:, 1], c=pred)
64 | ```
65 |
66 | 基学习器数量为1时:
67 |
68 | 
69 |
70 | 基学习器数量为2时:
71 |
72 | 
73 |
74 | 基学习器数量超过3时:
75 |
76 | 
77 |
78 | 可以发现,当基学习器变多的时候分类效果得到了提升,并且很稳定!
79 |
80 |
81 |
82 | ## 8.5
83 |
84 | 使用`sklean.ensemble`中的`BaggingClassifier`实现即可(默认采用决策树模型作为基学习器),代码如下:
85 |
86 | ```python
87 | from sklearn.ensemble import BaggingClassifier
88 | import pandas as pd
89 | from matplotlib import pyplot as plt
90 | import numpy as np
91 |
92 | # 加载数据
93 | df = pd.read_csv("./3.0a.csv", index_col=0)
94 | X = df.iloc[:, :2].values
95 | y = df.iloc[:, -1].values
96 |
97 | # 模型训练与预测
98 | model = BaggingClassifier(n_estimators=1, random_state=0)
99 | model.fit(X, y)
100 | pred = model.predict(X)
101 | print(np.sum(np.abs(pred - y)))
102 |
103 | # 画图
104 | plt.scatter(X[:, 0], X[:, 1], c=pred)
105 | ```
106 |
107 | 基学习器数量为1时:
108 |
109 | 
110 |
111 | 基学习器数量为2,3,4时:
112 |
113 | 
114 |
115 | 基学习器数量为7时:
116 |
117 | 
118 |
119 | 可以发现,当基学习器变多的时候分类效果不一定得到提升,在分类器数量较小时,变化比较不稳定。
120 |
121 |
122 |
123 | ## 8.6
124 |
125 | Bagging方法使用自助采样,简单高效,但考虑到“误差-分歧分解”,Bagging方法中个体学习器的多样性较低。朴素贝叶斯属于稳定基学习器,对数据样本的扰动不敏感,对这类基学习器进行集成往往需要使用输入属性扰动等其他扰动,而Bagging方法做不到,因此,Bagging方法通常很难提升朴素贝叶斯分类器的性能。
126 |
127 |
--------------------------------------------------------------------------------
/docs/MachineLearning/第六章作业.md:
--------------------------------------------------------------------------------
1 | # 《机器学习》第六章作业
2 |
3 | ## 6.1
4 |
5 | **答**:设超平面上任意一点为$\boldsymbol{y}$,满足$\boldsymbol{w}^{\text T} \boldsymbol{y} + b = 0$,那么$\boldsymbol{x}$与$\boldsymbol{y}$的距离为$|\boldsymbol{x} - \boldsymbol{y}|$。由几何关系可知,只有当$\boldsymbol{x} - \boldsymbol{y}$与超平面垂直时,才能满足$\boldsymbol{x}$与超平面的距离为$|\boldsymbol{x} - \boldsymbol{y}|$,又因为$\boldsymbol{w}$与超平面垂直,因此
6 | $$
7 | \boldsymbol{x} - \boldsymbol{y} = \pm |\boldsymbol{x} - \boldsymbol{y}| \frac{\boldsymbol{w}}{||\boldsymbol{w}||}
8 | $$
9 | 两边同时左乘$\boldsymbol w^{\text T}$可得
10 | $$
11 | \boldsymbol w^{\text T} \boldsymbol{x} - \boldsymbol w^{\text T} \boldsymbol{y} &= \pm |\boldsymbol{x} - \boldsymbol{y}| \frac{\boldsymbol w^{\text T}\boldsymbol{w}}{||\boldsymbol{w}||} \\
12 | \boldsymbol w^{\text T} \boldsymbol{x} + b &= \pm |\boldsymbol{x} - \boldsymbol{y}| \times ||\boldsymbol w||
13 | $$
14 | 即
15 | $$
16 | r = |\boldsymbol{x} - \boldsymbol{y}| = \frac{|\boldsymbol w^{\text T} \boldsymbol{x} + b|}{||\boldsymbol w||}
17 | $$
18 |
19 | ## 6.2
20 |
21 | ### 1. 搭建环境
22 |
23 |
24 | ```python
25 | import pandas as pd
26 | import numpy as np
27 | from matplotlib import pyplot as plt
28 | from sklearn import svm
29 | ```
30 |
31 | ### 2. 导入数据
32 |
33 |
34 | ```python
35 | df = pd.read_csv("./3.0a.csv", index_col=0)
36 | X = df.iloc[:, :2].values
37 | y = df.iloc[:, -1].values
38 | ```
39 |
40 | ### 3. 使用线性核训练一个SVM
41 |
42 |
43 | ```python
44 | model = svm.SVC(C=1000, kernel='linear') # C高一些,对误差的容忍度低
45 | model.fit(X, y)
46 | model.score(X, y)
47 | ```
48 |
49 |
50 | 0.8235294117647058
51 |
52 |
53 | ```python
54 | # 绘制支持向量
55 | idx = model.support_
56 | plt.scatter(X[:, 0], X[:, 1], c=y, s=30)
57 | plt.scatter(X[idx][:, 0], X[idx][:, 1], c=y[idx], edgecolors='r', s=100)
58 | plt.show()
59 | ```
60 |
61 |
62 | 
63 |
64 |
65 | ### 4. 使用高斯核训练一个SVM
66 |
67 |
68 | ```python
69 | model = svm.SVC(C=1000, kernel='rbf') # C高一些,对误差的容忍度低
70 | model.fit(X, y)
71 | model.score(X, y)
72 | ```
73 |
74 | ```
75 | 1.0
76 | ```
77 |
78 |
79 | ```python
80 | # 绘制支持向量
81 | idx = model.support_
82 | plt.scatter(X[:, 0], X[:, 1], c=y, s=30)
83 | plt.scatter(X[idx][:, 0], X[idx][:, 1], c=y[idx], edgecolors='r', s=100)
84 | plt.show()
85 | ```
86 |
87 | 
88 |
89 | ### 5. 对比分析
90 |
91 | 在对误差容忍度比较高的情况下,高斯核SVM可以完全拟合数据,而且支持向量也比较少。但由于数据线性不可分,线性核SVM不论设置多高的容忍度仍不能很好地区分数据,且支持向量也较多。
92 |
93 | ## 6.3
94 |
95 | ### 1. 搭建环境
96 |
97 |
98 | ```python
99 | import numpy as np
100 | from matplotlib import pyplot as plt
101 | from sklearn.model_selection import train_test_split
102 | from sklearn.datasets import load_iris, load_breast_cancer
103 | from sklearn.svm import SVC # 支持向量机
104 | from sklearn.neural_network import MLPClassifier # BP神经网络
105 | from sklearn.tree import DecisionTreeClassifier # 决策树
106 | ```
107 |
108 | ### 2. 构建数据集
109 |
110 |
111 | ```python
112 | X_iris, y_iris = load_iris(return_X_y=True) # 鸢尾花数据集
113 | X_bc, y_bc = load_breast_cancer(return_X_y=True) # 乳腺癌数据集
114 | # 划分训练集和测试集
115 | X_iris_train, X_iris_test, y_iris_train, y_iris_test = train_test_split(X_iris, y_iris, test_size=0.2, random_state=0)
116 | X_bc_train, X_bc_test, y_bc_train, y_bc_test = train_test_split(X_bc, y_bc, test_size=0.2, random_state=0)
117 | ```
118 |
119 | ### 3. 定义各种模型函数
120 |
121 |
122 | ```python
123 | def svm(X_train, X_test, y_train, y_test, kernel="linear"):
124 | model = SVC(C=1, kernel=kernel)
125 | model.fit(X_train, y_train)
126 | print(f"[SVM with {kernel} kernel]Accuracy: {model.score(X_test, y_test)*100: .2f}%")
127 | ```
128 |
129 |
130 | ```python
131 | def mlp(X_train, X_test, y_train, y_test, activation="logistic"):
132 | model = MLPClassifier(max_iter=1000, activation=activation, random_state=0)
133 | model.fit(X_train, y_train)
134 | print(f"[BP Neural Network with {activation}]Accuracy: {model.score(X_test, y_test)*100: .2f}%")
135 | ```
136 |
137 |
138 | ```python
139 | def dt(X_train, X_test, y_train, y_test, criterion="entropy"):
140 | model = DecisionTreeClassifier(criterion=criterion, random_state=0)
141 | model.fit(X_train, y_train)
142 | print(f"[Decision Tree with {criterion}]Accuracy: {model.score(X_test, y_test)*100: .2f}%")
143 | ```
144 |
145 | ### 4. 在鸢尾花数据集上测试
146 |
147 |
148 | ```python
149 | svm(X_iris_train, X_iris_test, y_iris_train, y_iris_test, kernel="linear")
150 | svm(X_iris_train, X_iris_test, y_iris_train, y_iris_test, kernel="rbf")
151 | mlp(X_iris_train, X_iris_test, y_iris_train, y_iris_test, activation="logistic")
152 | mlp(X_iris_train, X_iris_test, y_iris_train, y_iris_test, activation="relu")
153 | dt(X_iris_train, X_iris_test, y_iris_train, y_iris_test, criterion="entropy")
154 | dt(X_iris_train, X_iris_test, y_iris_train, y_iris_test, criterion="gini")
155 | ```
156 |
157 | [SVM with linear kernel]Accuracy: 100.00%
158 | [SVM with rbf kernel]Accuracy: 100.00%
159 | [BP Neural Network with logistic]Accuracy: 100.00%
160 | [BP Neural Network with relu]Accuracy: 100.00%
161 | [Decision Tree with entropy]Accuracy: 100.00%
162 | [Decision Tree with gini]Accuracy: 100.00%
163 |
164 |
165 | ### 5. 在乳腺癌数据集上测试
166 |
167 |
168 | ```python
169 | svm(X_bc_train, X_bc_test, y_bc_train, y_bc_test, kernel="linear")
170 | svm(X_bc_train, X_bc_test, y_bc_train, y_bc_test, kernel="rbf")
171 | mlp(X_bc_train, X_bc_test, y_bc_train, y_bc_test, activation="logistic")
172 | mlp(X_bc_train, X_bc_test, y_bc_train, y_bc_test, activation="relu")
173 | dt(X_bc_train, X_bc_test, y_bc_train, y_bc_test, criterion="entropy")
174 | dt(X_bc_train, X_bc_test, y_bc_train, y_bc_test, criterion="gini")
175 | ```
176 |
177 | [SVM with linear kernel]Accuracy: 95.61%
178 | [SVM with rbf kernel]Accuracy: 92.98%
179 | [BP Neural Network with logistic]Accuracy: 91.23%
180 | [BP Neural Network with relu]Accuracy: 94.74%
181 | [Decision Tree with entropy]Accuracy: 92.98%
182 | [Decision Tree with gini]Accuracy: 91.23%
183 |
184 | ### 6. 分析
185 |
186 | 针对不同的数据集特征可以选择不同的算法。通过针对不同数据集对不同算法的参数进行调节,很多模型都能很好地拟合数据。
187 |
188 | ## 6.4
189 |
190 | **答**:线性判别分析是将$n$维的数据投影到$n-1$维上的一个超平面后再来分类,可以支持多分类;而线性核的SVM是在$n$维的数据中寻找一个$n-1$的超平面来分隔数据,是解决的二分类问题。因此,若需线性判别分析与线性核等价,一定要满足都是在**解决二分类问题**上(不考虑使用OvR等使SVM解决多分类)。
191 |
192 | 由于线性判别分析关键在找到映射平面,线性核的SVM关键在找分类超平面。考虑两者的关系,可以想到若**两平面垂直**时,如果线性判别分析能达成分类任务,那么在映射平面的两类之间取一条直线,并以这条直线和映射平面的法向量相交做一个平面,一定可以分隔样本。而这个样本就可以作为线性核SVM的分类超平面。
193 |
194 | 综上所述,线性判别分析与线性核支持向量机满足以下两个条件时等价:
195 |
196 | - 解决的问题是二分类问题;
197 | - 线性判别分析的映射超平面和线性核支持向量机的分类超平面垂直。
198 |
199 | ## 6.6
200 |
201 | **答**:对于硬间隔支持向量机,若噪声样本出现在支持向量中,会使决策超平面变化,间隔变小,使得SVM的泛化能力变弱、检测精度降低;对于软间隔支持向量机,噪声样本的出现会使目标函数中的损失项显著提高,使SVM决策受到影响。因此SVM对噪声敏感。
202 |
--------------------------------------------------------------------------------
/docs/MachineLearning/第四章作业.md:
--------------------------------------------------------------------------------
1 | # 《机器学习》第四章作业
2 |
3 | ## 4.1
4 |
5 | **证明**:假设在题目条件下,不存在于与训练集一致的决策树,那么一定存在一个中间节点使得经过此节点后分出的叶子节点中包含不一样标签的样本。而由于不含冲突数据,因此在此叶子节点中标签不同的样本一定还有特征是不相同的,也就是说,此叶子节点还可以根据不同的属性进行下一步决策,使得标签不同的样本完全分离,从而使得训练误差为0。因此得证:**对于不含冲突数据的训练集,必存在与训练集一致的决策树。**
6 |
7 | ## 4.3
8 |
9 | ### 1. 准备数据
10 |
11 | ```python
12 | import numpy as np
13 | import pandas as pd
14 | from sklearn.model_selection import train_test_split
15 | from sklearn.preprocessing import LabelEncoder
16 |
17 | df = pd.read_csv('./watermelon3.csv', index_col=0) # 西瓜数据集3.0
18 | for label in df.columns: # 离散值预处理为整数
19 | if df[label].dtype == object:
20 | df[label] = LabelEncoder().fit(df[label]).transform(df[label])
21 | df
22 | ```
23 |
24 | | | 色泽 | 根蒂 | 敲声 | 纹理 | 脐部 | 触感 | 密度 | 含糖率 | 好瓜 |
25 | | ---: | ---: | ---: | ---: | ---: | ---: | ---: | ----: | -----: | ---: |
26 | | 编号 | | | | | | | | | |
27 | | 1 | 2 | 2 | 1 | 1 | 0 | 0 | 0.697 | 0.460 | 1 |
28 | | 2 | 0 | 2 | 0 | 1 | 0 | 0 | 0.774 | 0.376 | 1 |
29 | | 3 | 0 | 2 | 1 | 1 | 0 | 0 | 0.634 | 0.264 | 1 |
30 | | 4 | 2 | 2 | 0 | 1 | 0 | 0 | 0.608 | 0.318 | 1 |
31 | | 5 | 1 | 2 | 1 | 1 | 0 | 0 | 0.556 | 0.215 | 1 |
32 | | 6 | 2 | 1 | 1 | 1 | 2 | 1 | 0.403 | 0.237 | 1 |
33 | | 7 | 0 | 1 | 1 | 2 | 2 | 1 | 0.481 | 0.149 | 1 |
34 | | 8 | 0 | 1 | 1 | 1 | 2 | 0 | 0.437 | 0.211 | 1 |
35 | | 9 | 0 | 1 | 0 | 2 | 2 | 0 | 0.666 | 0.091 | 0 |
36 | | 10 | 2 | 0 | 2 | 1 | 1 | 1 | 0.243 | 0.267 | 0 |
37 | | 11 | 1 | 0 | 2 | 0 | 1 | 0 | 0.245 | 0.057 | 0 |
38 | | 12 | 1 | 2 | 1 | 0 | 1 | 1 | 0.343 | 0.099 | 0 |
39 | | 13 | 2 | 1 | 1 | 2 | 0 | 0 | 0.639 | 0.161 | 0 |
40 | | 14 | 1 | 1 | 0 | 2 | 0 | 0 | 0.657 | 0.198 | 0 |
41 | | 15 | 0 | 1 | 1 | 1 | 2 | 1 | 0.360 | 0.370 | 0 |
42 | | 16 | 1 | 2 | 1 | 0 | 1 | 0 | 0.593 | 0.042 | 0 |
43 | | 17 | 2 | 2 | 0 | 2 | 2 | 0 | 0.719 | 0.103 | 0 |
44 |
45 | ```python
46 | X = df.iloc[:, :-1] # 属性
47 | y = df.iloc[:, -1] # 标签
48 | X_train,X_test,y_train,y_test=train_test_split(X,y,test_size=0.3) #随机划分训练集和测试集
49 | ```
50 |
51 | ### 2. 定义节点
52 |
53 | ```python
54 | class TreeNode:
55 | def __init__(self, tp=0, label=0, decide=0, compare=0):
56 | self.nxt = dict() # 儿子节点(属性值:节点)(中间节点特有)
57 | self.type = tp # 0->叶子, 1->中间节点
58 | self.label = label # 0->坏瓜, 1->好瓜
59 | self.decide = decide # 划分属性(中间节点特有)
60 | self.compare = compare # 判断值(连续节点特有)
61 | ```
62 |
63 | ### 3. 定义决策树模型
64 |
65 | ```python
66 | class DecisionTree:
67 | def __init__(self):
68 | pass
69 |
70 | def __Ent(self, y):
71 | p = pd.value_counts(y) / len(y)
72 | return -np.sum(p * np.log2(p))
73 |
74 | def __choose(self, D, A):
75 | EntD = self.__Ent(D[-1])
76 | calc1 = lambda x : x.shape[0] / D[0].shape[0] * self.__Ent(x) # 计算信息熵
77 | calc2 = lambda x : x.shape[0] / D[0].shape[0] * np.log2(x.shape[0] / D[0].shape[0]) # 计算IV
78 | mp = dict()
79 | for attr in A:
80 | v = None # 记录连续值判别的值
81 | if self.attr_type[attr]: # 连续值
82 | gain = 0
83 | iv = 0x3f3f3f3f
84 | for value in sorted(np.unique(D[0][:, attr])):
85 | Dv1 = D[-1][D[0][:, attr] <= value]
86 | Dv2 = D[-1][D[0][:, attr] > value]
87 | temp = EntD - (calc1(Dv1) + calc1(Dv2))
88 | if temp > gain:
89 | gain = temp
90 | iv = -calc2(Dv1)-calc2(Dv2)
91 | v = value
92 | # print("iv=", iv)
93 | else: # 离散值
94 | sm = 0
95 | iv = 1
96 | for value in np.unique(D[0][:, attr]):
97 | Dv = D[-1][D[0][:, attr] == value]
98 | sm += calc1(Dv)
99 | iv += -calc2(Dv)
100 | gain = EntD - sm
101 | # print(gain, iv)
102 | gain_ratio = gain / iv
103 | mp[attr] = (gain, 2, v) # 去除gain_ratio的影响
104 | # print(mp)
105 | temp = sorted(list(mp.items()), key=lambda x : (-x[-1][0], -x[-1][1]))[0]
106 | return temp[0],temp[-1][-1]
107 |
108 | def __generate(self, D, A):
109 | node = TreeNode()
110 | if np.unique(D[-1]).shape[0] <= 1:
111 | return TreeNode(tp=0, label=D[-1][0])
112 | if len(A) == 0 or np.unique(D[0][:, A], axis=0).shape[0] <= 1:
113 | return TreeNode(tp=0, label=np.argmax(np.bincount(D[1])))
114 | attr, v = self.__choose(D, A)
115 | # print(attr)
116 | node.decide = attr
117 | node.type = 1
118 | node.label = np.argmax(np.bincount([int(x) for x in D[1]]))
119 | if self.attr_type[attr]: # 连续值
120 | Dv = D[0][D[0][:, attr] <= v]
121 | # print(Dv)
122 | if Dv.shape[0] == 0:
123 | node.nxt[0] = TreeNode(tp=0, label=node.label)
124 | else:
125 | node.nxt[1] = self.__generate((Dv, D[1][D[0][:, attr] <= v]), [x for x in A if x != attr])
126 | Dv = D[0][D[0][:, attr] > v]
127 | # print(Dv)
128 | if Dv.shape[0] == 0:
129 | node.nxt[0] = TreeNode(tp=0, label=node.label)
130 | else:
131 | node.nxt[1] = self.__generate((Dv, D[1][D[0][:, attr] > v]), [x for x in A if x != attr])
132 | else: # 离散值
133 | for value in np.unique(D[0][:, attr]):
134 | Dv = D[0][D[0][:, attr] == value]
135 | if Dv.shape[0] == 0:
136 | node.nxt[value] = TreeNode(tp=0, label=node.label)
137 | else:
138 | node.nxt[value] = self.__generate((Dv, D[1][D[0][:, attr] == value]), [x for x in A if x != attr])
139 | return node
140 |
141 | def calc(self, X, y): # 将数据通过决策树,得出结果,返回准确率
142 | n = X.shape[0]
143 | lst = []
144 | for i in range(X.shape[0]):
145 | x = X[i, :]
146 | node = self.root
147 | while node.type == 1:
148 | if self.attr_type[node.decide]:
149 | if x[node.decide] <= node.compare:
150 | node = node.nxt[0]
151 | else:
152 | node = node.nxt[1]
153 | else:
154 | if x[node.decide] not in node.nxt.keys():
155 | break
156 | node = node.nxt[x[node.decide]]
157 | lst.append(node.label)
158 | ans = np.array(lst)
159 | acc = 1- np.sum(np.abs(ans - y)) / y.shape[0]
160 | return acc
161 |
162 | def fit(self, X, y):
163 | A = [i for i in range(X.values.shape[1])]
164 | self.attr_type = [X[label].dtype == float for label in X.columns] # 是否是连续值
165 | self.root = self.__generate((X.values, y.values), A)
166 | ans = self.calc(X.values, y.values)
167 | print(f"训练集准确率:{ans: .2f}")
168 |
169 | def predict(self, X, y):
170 | ans = self.calc(X.values, y.values)
171 | print(f"测试集准确率:{ans: .2f}")
172 | ```
173 |
174 | ### 4. 训练、测试
175 |
176 | ```python
177 | model = DecisionTree()
178 | model.fit(X_train, y_train)
179 | model.predict(X_test, y_test)
180 | ```
181 |
182 | 训练集准确率: 1.00
183 | 测试集准确率: 0.67
184 |
185 | ### 5. 讨论
186 |
187 | 本题中由于数据量较少,所以建立的决策树模型可以无需使用gain_ratio,实验发现:在本数据集中使用gain_ratio效果还没有gain好。
188 |
189 | ### 6. 决策树
190 |
191 | 
192 |
193 |
194 |
195 | ## 4.5
196 |
197 | 本题目中仅有决策树模型中`__choose`函数与上题不同。下面是本题的`__choose`函数
198 |
199 | ```python
200 | def __choose(self, D, A):
201 | mp = {}
202 | for attr in A:
203 | X = D[0][:, attr:attr+1]
204 | y = D[1]
205 | v = None
206 | if self.attr_type[attr]:
207 | X_ = X.copy()
208 | ans = -1
209 | for value in np.unique(X):
210 | X_ = X < value
211 | model = LogisticRegression()
212 | model.fit(X_, y)
213 | t = model.score(X_, y)
214 | if t > ans:
215 | ans = t
216 | v = value
217 | else:
218 | model = LogisticRegression()
219 | # print(X, y)
220 | model.fit(X, y)
221 | ans = model.score(X, y)
222 | mp[attr] = (ans, v)
223 | temp = sorted(list(mp.items()), key=lambda x : -x[1][0])
224 | return temp[0][0], temp[0][1][1]
225 | ```
226 |
227 | 训练集准确率: 1.00
228 | 测试集准确率: 0.83
229 |
230 | ### 决策树
231 |
232 | 
233 |
234 | ## 4.7
235 |
236 | **输入**:训练集$D={(\boldsymbol{x}_1, y_1),(\boldsymbol{x}_2, y_2),...,(\boldsymbol{x}_m, y_m)}$;属性集$A={a_1, a_2, ..., a_d}$
237 |
238 | **过程**:函数$\text{TreeGenerate}(D, A)$
239 |
240 | 1. 生成根节点$\text{root}$;用于存储中间节点的队列$\text{queue}$;
241 | 2. 将$(\text{root}, D, A)$放入队列$\text{queue}$中;
242 | 3. $\bold{while}$ $\text{queue}$不为空 $\bold{do}$
243 | 4. 从$\text{queue}$中取出节点$\text{node}$、训练集$D$和属性集$A$;
244 | 5. $\bold{if}$ $D$中样本全属于同一类别$C$ $\bold{then}$
245 | 6. 将$\text{node}$标记为$C$类叶节点; $\bold{continue}$
246 | 7. $\bold{end}\ \bold{if}$
247 | 8. $\bold{if}$ $A = \varnothing$ $\bold{OR}$ $D$中样本在$A$上取值相同 $\bold{then}$
248 | 9. 将$\text{node}$标记为叶节点,其类型标记为$D$中样本数最多的类; $\bold{continue}$
249 | 10. $\bold{end}\ \bold{if}$
250 | 11. 从$A$中选择最优划分属性$a_*$;
251 | 12. $\bold{for}$ $a_*$的每一个值$a_*^v$ $\bold{do}$
252 | 13. 为$\text{node}$生成一个分支节点$\text{branch}$;令$D_v$表示$D$中在$a_*$上取值为$a_*^v$的样本子集;
253 | 14. $\bold{if}$ $D_v$为空 $\bold{then}$
254 | 15. 将分支节点$\text{branch}$标记为叶节点,其类型标记为$D$中样本最多的类;
255 | 16. $\bold{else}$
256 | 17. 将$(\text{branch}, D_v, A\backslash \{ a_* \})$放入队列$\text{queue}$中;
257 | 18. $\bold{end}\ \bold{if}$
258 | 19. $\bold{end}\ \bold{for}$
259 | 20. $\bold{end}\ \bold{while}$
260 |
261 | **输出**:以$\text{root}$为根节点的一棵决策树
262 |
263 |
264 |
265 | ## 4.9
266 |
267 | **答**:在含缺失值的样本中进行划分属性的选择,只需要将包含所有样本的集合$D$转化为只包含在属性$a$上非缺失值样本的集合$\tilde{D}$,并乘上权重即可。具体来说,计算基尼指数的公式如下:
268 | $$
269 | \text{Gini\_index}(D, a)=\rho \times \sum_{v=1}^{V} \tilde r_v \frac{|\tilde D^v|}{|\tilde D|}\text{Gini}(\tilde D^v)
270 | $$
271 | 其中,
272 | $$
273 | \begin{align}
274 | \text{Gini}(\tilde D) &= 1-\sum_{k=1}^{|\mathcal Y|}\tilde p_k^2, \\
275 | \rho &= \frac {\sum_{\boldsymbol x \in\tilde D} w_{\boldsymbol x}} {\sum_{\boldsymbol x \in D} w_{\boldsymbol x}}, \\
276 | \tilde p_k &= \frac {\sum_{\boldsymbol x \in\tilde D_k} w_{\boldsymbol x}} {\sum_{\boldsymbol x \in D} w_{\boldsymbol x}} (1 \leq k \leq |\mathcal Y |),\\
277 | \tilde r_v &= \frac {\sum_{\boldsymbol x \in\tilde D^v} w_{\boldsymbol x}} {\sum_{\boldsymbol x \in D} w_{\boldsymbol x}} (1\leq v \leq V),
278 | \end{align}
279 | $$
280 |
281 |
--------------------------------------------------------------------------------
/docs/OperatingSystem/index.md:
--------------------------------------------------------------------------------
1 | # 暂无
--------------------------------------------------------------------------------
/docs/SoftwareEngineering/软工应用分析题.md:
--------------------------------------------------------------------------------
1 | 前面的结构化分析和面向对象分析建模看实验指导书和UML的PPT即可。这个文件请重点参考后面两种测试中涉及的方法。
2 |
3 | # 一、结构化分析
4 |
5 | ## 1. 数据流图【重要】
6 |
7 | 参考PPT和实验文档即可。
8 |
9 | ## 2. 数据字典【重要】
10 |
11 | 参考PPT和实验文档即可。
12 |
13 | ## 3. 控制流建模
14 |
15 | 不重要。考到就看PPT。
16 |
17 |
18 |
19 | # 二、面向对象分析
20 |
21 | ## 1. 用例图【重要】
22 |
23 | **请参考UML的PPT。**
24 |
25 | 分析用例实现中,对象之间的交互行为,核心是时序图、状态图等
26 |
27 | 【用例建模】
28 |
29 | · 用例表示从执行者的角度观察到系统的功能和外部行为。
30 |
31 | · 用例图主要描述用户需求,强调谁在使用系统,系统可以实现哪些功能目标。
32 |
33 | · 用例特征
34 |
35 | · 用例都是动宾结构
36 |
37 | · 用例是相互独立的
38 |
39 | · 用例由参与者启动
40 |
41 | · 有可观测的执行结果
42 |
43 | 【识别用例】
44 |
45 | 识别用例最好的方法就是从分析系统的参与者(可以是角色、外部系统、设备甚至时钟信号等)开始,考虑每一个参与者是如何使用系统的。
46 |
47 | **【用例图】**
48 |
49 | 用例模型主要包含4种元素:执行者、用例,执行者与用例间关联、用例间关系。
50 |
51 | 【用例间关系】
52 |
53 | 《include》关系
54 |
55 | 父用例执行过程中会用到子用例(无条件执行)。
56 |
57 | 子用例一般表示为公共功能。
58 |
59 | 
60 |
61 | 《extend》关系
62 |
63 | 父用例在特定情况下(称为扩展点)会用到子用例(有条件执行)
64 |
65 | 子用例一般表示为异常功能。
66 |
67 | 
68 |
69 | 泛化(generalization)关系
70 |
71 | 当多个用例共同拥有一种类似的行为时,可以将它们的共性抽象成为父用例,其他用例作为子用例。
72 |
73 | 该关系也可存在于参与者之间。
74 |
75 | 
76 |
77 | 
78 |
79 | 【用例描述】
80 |
81 | 单纯的用例图并不能描述完整的信息,需要用文字描述不能反映在图形上的信息。
82 |
83 | 用例描述是将用例发生的各种场景描述出来,表示参与者与系统交互时双方的行为,即参与者做什么,系统做什么反应。
84 |
85 | 场景能真实反映参与者在用例执行中可能遇到的
86 |
87 | 各种情形。
88 |
89 | 可以使用**用例模版**或**活动图**描述用例执行中的各种场景。
90 |
91 | 【用例模板】
92 |
93 | 用例描述模版的内容大致包括:用例名、参与者,前置条件,后置条件,事件流等。
94 |
95 | 用例的事件流
96 |
97 | 说明参与者与系统之间的交互过程;
98 |
99 | 说明用例在不同条件下可以选择执行的多种方案;
100 |
101 | 分为基本流和备选流两类
102 |
103 | 基本流:描述该用例正常执行的一种场景,系统执行一系列活动步骤来响应参与者提出的服务请求;
104 |
105 | 备选流:描述用例执行过程中异常的或偶尔发生的一些情况。
106 |
107 | 
108 |
109 |
110 |
111 |
112 |
113 | ## 2. 类图【重要】
114 |
115 | **请参考UML的PPT。**
116 |
117 | 【类图】
118 |
119 | (具体画法参考实验文档)
120 |
121 | 目标是对领域内的概念类进行分析,并抽象出对应的类及其关系等。
122 |
123 | 具体包括三个步骤:
124 |
125 | 1. 从用例场景中寻找概念类
126 |
127 | (1) 分析用例场景
128 |
129 | (2) 找出其中的名词或名词短语作为分析类备选
130 |
131 | (3) 如何判断分离出的词是否是分析类?
132 |
133 | 
134 |
135 | 2. 细化概念类,识别其类型(如边界类、实体类等)
136 |
137 | 例子:学生选课用例
138 |
139 | 
140 |
141 | 通过分析,可以确定以下分析类:
142 |
143 | 
144 |
145 | 分析类是概念层次的东西,源于问题空间,与实现方式无关。
146 |
147 | 类的类型:
148 |
149 | 《Entity》 classes 表示系统中的持久信息或贯穿应用的数据封装
150 |
151 | 《Boundary》 classes 实现用户与系统的交互,如用户界面或外部接口
152 |
153 | 《Control》 classes 实现对用例行为的封装,管理、调度其它类
154 |
155 | 3. 为概念类定义属性及行为
156 |
157 | 属性描述了一个已被选择以包含在分析模型中的类。
158 |
159 | 要识别类所属行为,可以对处理叙述进行语法解析,看看动词;还可以结合动态(交互)建模,识别分析类的行为。
160 |
161 | 例子:
162 |
163 | 
164 |
165 | 4. 定义关系
166 |
167 | (1) 关联关系:关联关系可以使一个类可以引用另一个类的属性和方法。一般使用成员变量来实现。
168 |
169 | 
170 |
171 | (2) 聚合关系:表示整体和部分的关系,整体与部分可以分开,使用带空心菱形的实线来表示。
172 |
173 | 
174 |
175 | (3) 组合关系:也是整体与部分的关系,但是整体与部分不可以分开,使用实心带菱形的实线来表示。组合关系中整体类和部分类必须有相同的生命周期。
176 |
177 | 
178 |
179 | (4) 依赖关系:即一个类的实现需要另一个类的协助。多数情况下,依赖关系表现在某个类的方法使用另一个类的对象作为参数。
180 |
181 | 
182 |
183 | (5) 泛化关系:表示类与类、接口与接口之间的继承关系
184 |
185 | 
186 |
187 | 实例:
188 |
189 | 
190 |
191 |
192 |
193 | ## 3. 时序图(顺序图)【重要】
194 |
195 | **请参考UML的PPT。**
196 |
197 | 【时序图】
198 |
199 | 时序图建模步骤
200 |
201 | (1)对每个用例,建立系统时序图(可选)
202 |
203 | (2)建立对象时序图
204 |
205 | (3)从图中确定分析类的行为
206 |
207 | 主要步骤
208 |
209 | 按从左到右的顺序
210 |
211 | 1、列出启动该用例的参与者;
212 |
213 | 2、列出参与者使用的边界类;
214 |
215 | 3、列出管理该用例的控制类;
216 |
217 | 4、根据用例的执行流程,按时间顺序列出分析类之间的消息序列。
218 |
219 | **例子:****还书用例**
220 |
221 | 1. 借阅者点击还书按钮向系统申请还书
222 | 2. 系统提示借阅者输入还书号等信息
223 | 3. 借阅者输入还书信息后,系统查询该书是否已超期。
224 | 4. 如果未超期,则记录用户还书信息并更新图书可借状态,并返回借阅者成功还书信息。
225 | 5. 如果已超期,则系统提示超期、罚款金额等信息。
226 | 6. 借阅者如果认可,并确认缴纳罚款,则系统执行扣款并还书,返回借阅者成功还书信息。
227 |
228 | 
229 |
230 | ## 4. 状态图
231 |
232 | 请参考UML的PPT。
233 |
234 | 【状态图】
235 |
236 | 状态图描述了一个对象生命周期内所经历的状态序列,以及引起状态转移的外部事件。
237 |
238 | 状态图的主要作用:
239 |
240 | 描述多个状态之间的转换顺序,即事件的执行顺序,避免非法的事件序列。(如: 必须先付款进入“已付款”状态,才能执行发货进入“已发货”状态。)
241 |
242 | 
243 |
244 | 
245 |
246 | ## 5. 其他
247 |
248 | ### 5.1. 活动图
249 |
250 | 【活动图】
251 |
252 | 
253 |
254 |
255 |
256 | ### 5.2. ER图
257 |
258 | 【ER图】
259 |
260 | 
261 |
262 | 
263 |
264 | ### 5.3. CRC模型
265 |
266 | 【CRC模型, Class-responsibility-collaborator】
267 |
268 | 作用:帮助补充、完善、优化分析类(属性、行为)
269 |
270 | 职责:职责是与类相关的属性和操作。
271 |
272 | 简单的说,职责就是“类所知道的或能做的任何事情”,可理解为类的能力。
273 |
274 | 例如,顾客有名字、地址和电话号码,这是顾客知道的东西。顾客要借书和还书,这是顾客要完成的事情。
275 |
276 | 分配职责的指导原则:属性和与之相关的行为应该在同一个类中。
277 |
278 | 类主要通过两种方式实现其职责:
279 |
280 | 通过自己内部的行为,实现特定的职责
281 |
282 | 请求其它类的协作
283 |
284 | 如果某个对象请求协作,就会向其它对象发送消息。
285 |
286 | 消息接收者作为服务方,通过自己的服务作为对消息发送者的回应。
287 |
288 | 职责是一种较高层次的抽象,其在设计过程中可能细化为一到多个具体的行为。
289 |
290 | 例子:用户登录用例中,登录控制类的职责之一是“身份验证” 。该职责在设计阶段,可以被细化为多个具体方法:getUser(),getRole(),getGroup(),check()
291 |
292 | 
293 |
294 |
295 |
296 | ### 5.4. 包图
297 |
298 | 【包图】
299 |
300 | 对于较大的项目,由于有很多的类和用例,常常会使系统结构看起非常复杂。
301 |
302 | 通过包图,庞大系统之间的关系变得更简单,整个系统的架构一目了然。
303 |
304 | 原则:将概念上或语义上相近的类纳入一个包
305 |
306 | 包之间的主要关系是依赖关系。
307 |
308 | 意味着两个Package内的元素之间存在着一个或多个依赖
309 |
310 | 
311 |
312 | 
313 |
314 |
315 |
316 |
317 |
318 |
319 |
320 |
321 |
322 |
323 |
324 |
325 |
326 |
327 |
328 | # 三、白盒测试
329 |
330 | ## 1. 基本路径测试法【重要】
331 |
332 | 参考视频:https://www.bilibili.com/video/BV13V4y1g7tc/?share_source=copy_web&vd_source=7ba452d8ee6f8b8a4b8ef831bf573bda
333 |
334 | 步骤:
335 |
336 | - **(1) 画出控制流图**
337 |
338 | 流程图用来描述程序控制结构。可将流程图映射到一个相应的流图(假设流程图的菱形决定框中不包含复合条件)。
339 |
340 | - 在流图中,每一个圆,称为流图的**结点**,代表一个或多个语句。一个处理方框序列和一个菱形决策框可被映射为一个结点 。
341 | - 流图中的箭头,称为**边或连接**, 代表控制流 , 类似于流程图中的箭头 。一条边必须终止于一个结点 , 即使该结点并不代表任何语句(例如:if-else-then结构)。
342 | - 由边和结点限定的范围称为**区域** 。
343 |
344 | 控制流图基本结构:
345 |
346 | 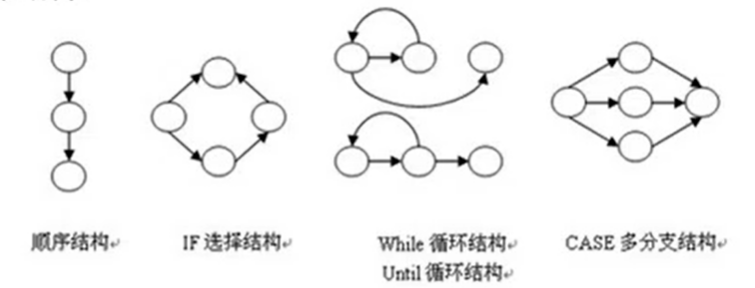 347 |
348 | 在将程序流程图简化成控制流图时 , 应注意 :
349 |
350 | - 在选择或多分支结构中 , 分支的**汇聚处应有一个汇聚结点**;
351 | - 边和结点圈定的区域叫做区域 , 当对区域计数时 , **图形外的区域也应记为一个区域**。
352 |
353 | > 例子:
354 | >
355 | >
347 |
348 | 在将程序流程图简化成控制流图时 , 应注意 :
349 |
350 | - 在选择或多分支结构中 , 分支的**汇聚处应有一个汇聚结点**;
351 | - 边和结点圈定的区域叫做区域 , 当对区域计数时 , **图形外的区域也应记为一个区域**。
352 |
353 | > 例子:
354 | >
355 | > 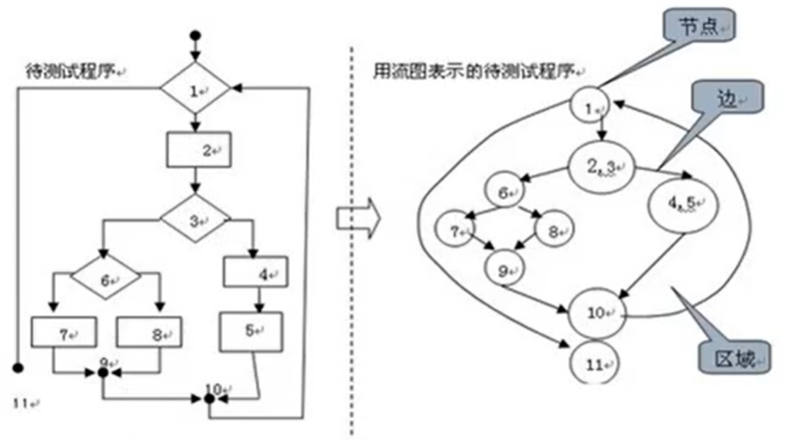 356 |
357 | 如果遇到一个条件表达式有多个逻辑运算符,则需改为一系列只有单条件的嵌套的判断:
358 |
359 |
356 |
357 | 如果遇到一个条件表达式有多个逻辑运算符,则需改为一系列只有单条件的嵌套的判断:
358 |
359 | 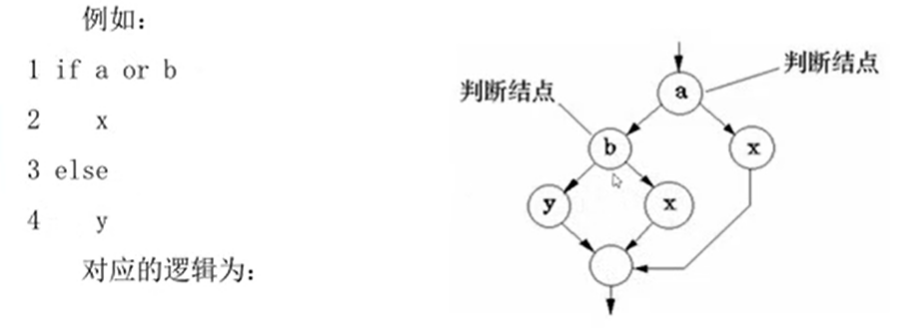 360 |
361 | > 例子:
362 | >
363 | >
360 |
361 | > 例子:
362 | >
363 | > 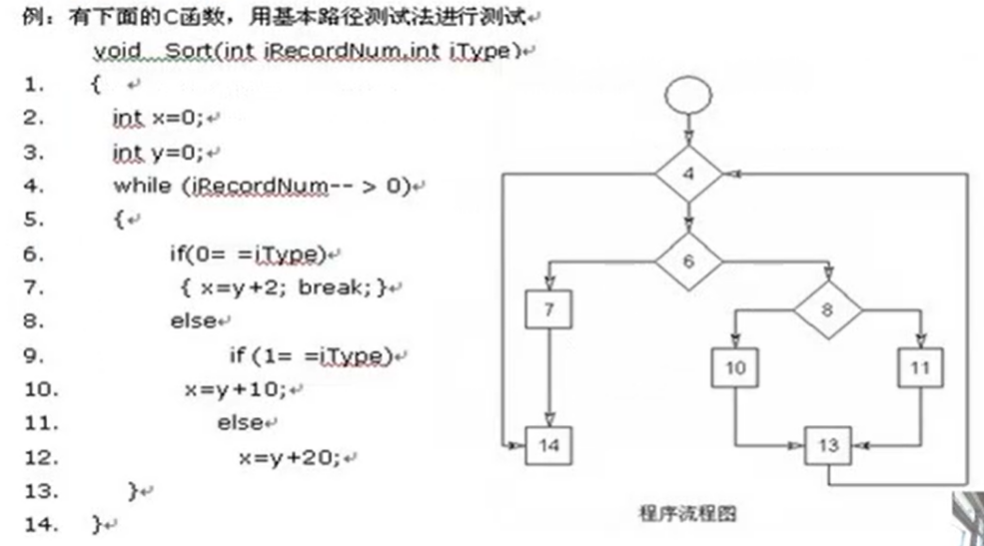 364 | >
365 | >
364 | >
365 | > 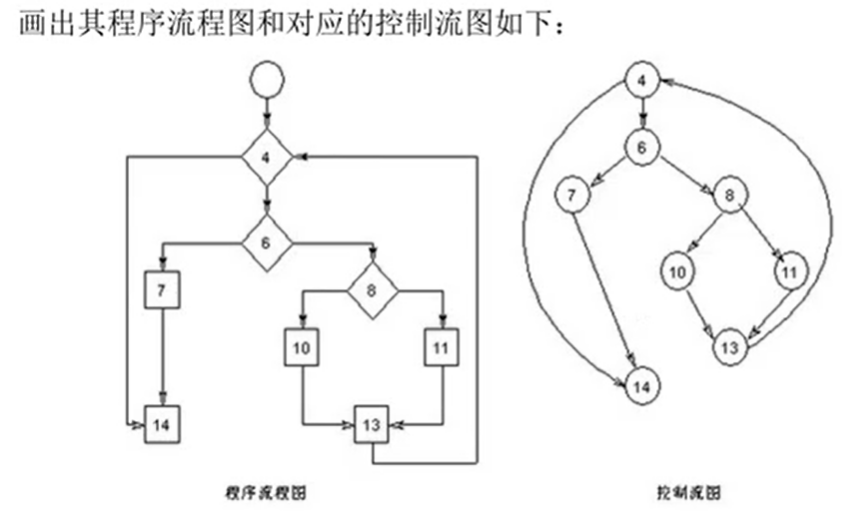 366 |
367 | - **(2)计算环路复杂度(圈复杂度或McCabe复杂度)**
368 |
369 | 圈复杂度是一种为程序逻辑复杂性提供定量测度的软件度量, 将该度量用于计算程序的基本的独立路径数目 ,为确保所有语句至少执行一次的测试数量的上界。独立路径必须包含一条在定义之前不曾用到的边。
370 | 有以下三种方法计算圈复杂度:
371 |
372 | - 流图中区域的数量对应于环型的复杂性;
373 | - 给定流图$G$的圈复杂度$V(G)$, 定义为$V(G) = E - N + 2$,$E$是流图中边的数量,$N$是流图中结点的数量;
374 | - 给定流图 G 的圈复杂度$V(G)$, 定义为$V(G) = P + 1$, P 是流图$G$中判定结点的数量。
375 |
376 | > 例子(接上):
377 | >
378 | >
366 |
367 | - **(2)计算环路复杂度(圈复杂度或McCabe复杂度)**
368 |
369 | 圈复杂度是一种为程序逻辑复杂性提供定量测度的软件度量, 将该度量用于计算程序的基本的独立路径数目 ,为确保所有语句至少执行一次的测试数量的上界。独立路径必须包含一条在定义之前不曾用到的边。
370 | 有以下三种方法计算圈复杂度:
371 |
372 | - 流图中区域的数量对应于环型的复杂性;
373 | - 给定流图$G$的圈复杂度$V(G)$, 定义为$V(G) = E - N + 2$,$E$是流图中边的数量,$N$是流图中结点的数量;
374 | - 给定流图 G 的圈复杂度$V(G)$, 定义为$V(G) = P + 1$, P 是流图$G$中判定结点的数量。
375 |
376 | > 例子(接上):
377 | >
378 | > 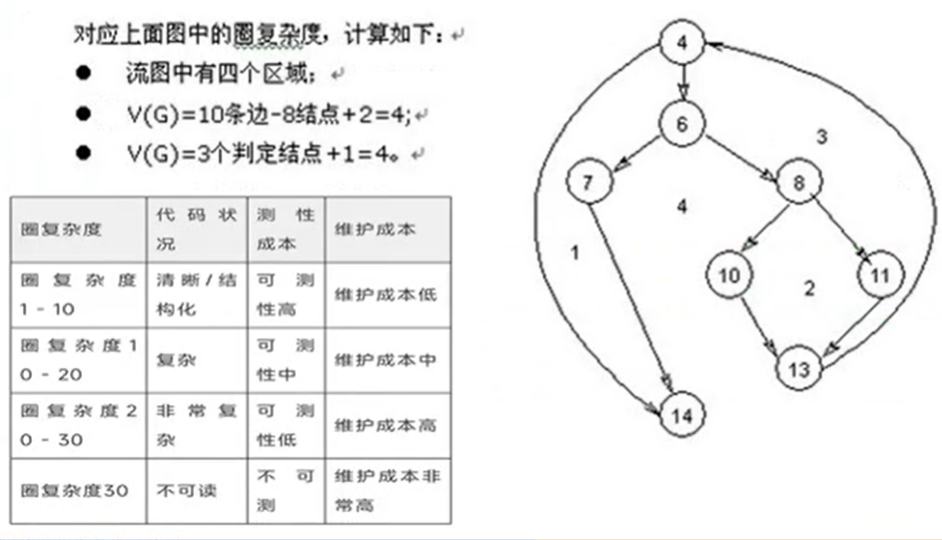 379 |
380 | - **确定独立路径**
381 |
382 | 一条独立路径是指与其他的独立路径相比,至少引入一个新处理语句或一个新判断的程序通路。**$V(G)$值正好等于该程序的独立路径的条数。**
383 |
384 | > 例子(接上):
385 | >
386 | > 根据上面的计算方法,可得出四条独立的路径。
387 | > 路径1: 4 一 14
388 | > 路径2: 4 一 6 一 7 一 14
389 | > 路径3: 4 一 6 一 8 一 10 一 13 一 4 一 14
390 | > 路径4: 4 一 6 一 8 一 11 一 13 一 4 一 14
391 | > 根据上而的独立路径 , 去设计输入数据 , 使程序分别执行到上面四条路径 。
392 |
393 | - **准备测试用例**
394 |
395 | 为了确保基本路径集中的每一条路径的执行,根据判断结点给出的条件,选择适当的数据以保证某一条路径可以被测试到。
396 |
397 | > 例子(接上):
398 | >
399 | > 满足上面例子基本路径集的测试用例是 :
400 | >
401 | >
379 |
380 | - **确定独立路径**
381 |
382 | 一条独立路径是指与其他的独立路径相比,至少引入一个新处理语句或一个新判断的程序通路。**$V(G)$值正好等于该程序的独立路径的条数。**
383 |
384 | > 例子(接上):
385 | >
386 | > 根据上面的计算方法,可得出四条独立的路径。
387 | > 路径1: 4 一 14
388 | > 路径2: 4 一 6 一 7 一 14
389 | > 路径3: 4 一 6 一 8 一 10 一 13 一 4 一 14
390 | > 路径4: 4 一 6 一 8 一 11 一 13 一 4 一 14
391 | > 根据上而的独立路径 , 去设计输入数据 , 使程序分别执行到上面四条路径 。
392 |
393 | - **准备测试用例**
394 |
395 | 为了确保基本路径集中的每一条路径的执行,根据判断结点给出的条件,选择适当的数据以保证某一条路径可以被测试到。
396 |
397 | > 例子(接上):
398 | >
399 | > 满足上面例子基本路径集的测试用例是 :
400 | >
401 | >  402 |
403 | ### 实例1
404 |
405 | **题目**:判断任意年份是否为闰年,需要满足以下条件中的任意一个:
406 |
407 | - 该年份能被4整除同时不能被100整除;
408 | - 该年份能被400整除。
409 |
410 | 代码如下:
411 |
412 | ```c
413 | int isLeap (int year) {
414 | if(year % 4 == 0) { // 1
415 | if(year % 100 == 0) { // 3
416 | if(year % 400 == 0) { // 4
417 | leap = 1; // 6
418 | } else {
419 | leap = 0; // 7
420 | }
421 | } else {
422 | leap = 1; // 5
423 | }
424 | } else {
425 | leap = 0; // 2
426 | }
427 | return leap; // 8
428 | }
429 | ```
430 |
431 | 请采用基本路径测试法设计上述程序的测试用例。要求:
432 |
433 | (1)画出流图;
434 |
435 | (2)计算环路复杂度;
436 |
437 | (3)给出基本路径;
438 |
439 | (4)给出满足基本路径测试标准的最小测试用例集。(提示:测试用例= 测试输入+预期输出。)
440 |
441 | **解答**:
442 |
443 | (1)画出流图
444 |
445 |
402 |
403 | ### 实例1
404 |
405 | **题目**:判断任意年份是否为闰年,需要满足以下条件中的任意一个:
406 |
407 | - 该年份能被4整除同时不能被100整除;
408 | - 该年份能被400整除。
409 |
410 | 代码如下:
411 |
412 | ```c
413 | int isLeap (int year) {
414 | if(year % 4 == 0) { // 1
415 | if(year % 100 == 0) { // 3
416 | if(year % 400 == 0) { // 4
417 | leap = 1; // 6
418 | } else {
419 | leap = 0; // 7
420 | }
421 | } else {
422 | leap = 1; // 5
423 | }
424 | } else {
425 | leap = 0; // 2
426 | }
427 | return leap; // 8
428 | }
429 | ```
430 |
431 | 请采用基本路径测试法设计上述程序的测试用例。要求:
432 |
433 | (1)画出流图;
434 |
435 | (2)计算环路复杂度;
436 |
437 | (3)给出基本路径;
438 |
439 | (4)给出满足基本路径测试标准的最小测试用例集。(提示:测试用例= 测试输入+预期输出。)
440 |
441 | **解答**:
442 |
443 | (1)画出流图
444 |
445 | 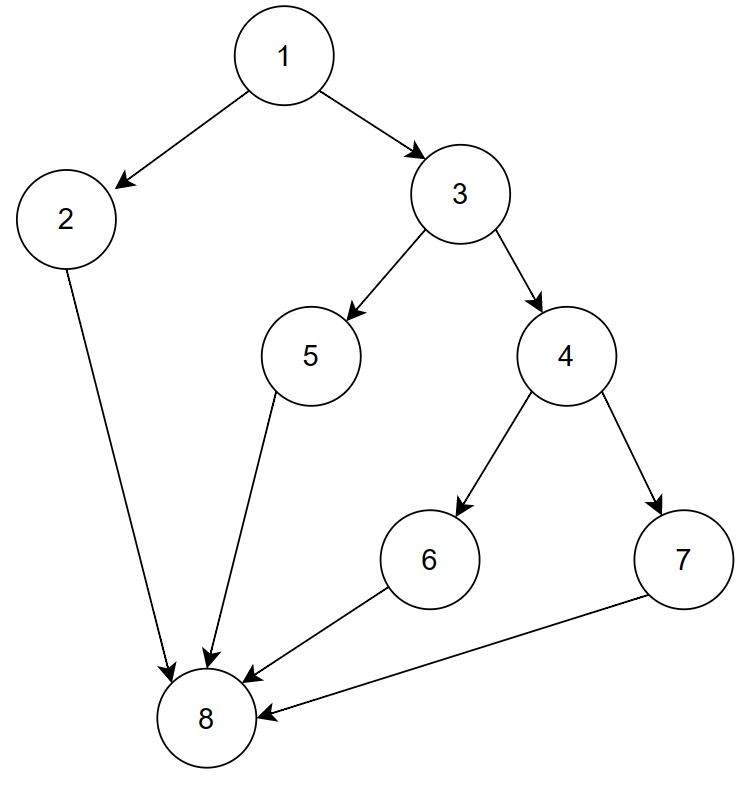 446 |
447 | (2)计算环路复杂度
448 |
449 | (方法一)一共有4个区域,因此$V(G)=4$。
450 |
451 | (方法二)一共有8个节点,10条边,因此$V(G) = E - N + 2=10-8+2=4$。
452 |
453 | (方法三)一共有三个判定节点:1、3、4,因此$V(G) = 3 + 1 = 4$。
454 |
455 | (3)写出基本路径
456 |
457 | 路径1:1-2-8
458 |
459 | 路径2:1-3-5-8
460 |
461 | 路径3:1-3-4-6-8
462 |
463 | 路径4:1-3-4-7-8
464 |
465 | (4)给出满足基本路径测试标准的最小测试用例集
466 |
467 | | 覆盖路径 | 测试输入 | 测试输出 | 说明 |
468 | | -------- | ---------- | -------- | ------------------------------- |
469 | | 1 | year = 1 | 0 | 不能被4整除 |
470 | | 2 | year = 4 | 1 | 能被4整除,但不能被100整除 |
471 | | 3 | year = 400 | 1 | 能被4,100,400整除 |
472 | | 4 | year = 200 | 0 | 能被4,100整除,但不能被400整除 |
473 |
474 |
475 |
476 | ### 实例2
477 |
478 | **题目**: 请采用基本路径测试法设计下列伪码程序的测试用例。 要求:
479 |
480 | (1)画出流图;
481 |
482 | (2)计算环路复杂度;
483 |
484 | (3)给出基本路径;
485 |
486 | (4)给出满足基本路径测试标准的最小测试用例集。(提示:测试用例= 测试输入+预期输出。)
487 |
488 | ```
489 | 1: Start Input(a,b,c,d)
490 | 2: If(a>0)
491 | 3: and (b>0)
492 | 4: Then x=a+b
493 | 5: Else x=a-b
494 | 6: End if
495 | 7: If (c>a)
496 | 8: or (d
506 |
507 | (2)计算环路复杂度
508 |
509 | (方法一)一共有5个区域,因此$V(G)=5$。
510 |
511 | (方法二)一共有12个节点,15条边,因此$V(G) = E - N + 2=15-12+2=5$。
512 |
513 | (方法三)一共有三个判定节点:2、3、7、8,因此$V(G) = 4 + 1 = 5$。
514 |
515 | (3)写出基本路径
516 |
517 | 路径1:1-2-5-6-7-9-11-12
518 |
519 | 路径2:1-2-3-5-6-7-9-11-12
520 |
521 | 路径3:1-2-3-4-6-7-9-11-12
522 |
523 | 路径4:1-2-5-6-7-8-9-11-12
524 |
525 | 路径4:1-2-5-6-7-8-10-11-12
526 |
527 | (4)给出满足基本路径测试标准的最小测试用例集
528 |
529 | | 覆盖路径 | 测试输入(a,b,c,d) | 测试输出(x,y) | 说明 |
530 | | -------- | ----------------- | ------------- | -------------------------- |
531 | | 1 | (0, 0, 1, 0) | (0, 1) | a <= 0 && c > a |
532 | | 2 | (1, 0, 2, 0) | (1, 2) | a > 0 && b <= 0 && c > a |
533 | | 3 | (1, 1, 2, 0) | (2, 2) | a > 0 && b > 0 && c > a |
534 | | 4 | (0, 0, 0, -1) | (0, 1) | a <= 0 && c <= a && d < b |
535 | | 5 | (0, 0, 0, 0) | (0, 0) | a <= 0 && c <= a && d >= b |
536 |
537 |
538 |
539 | ## 2. 控制结构测试法(逻辑覆盖法)
540 |
541 | 参考视频:https://www.bilibili.com/video/BV1zL4y1A785
542 |
543 | 以下面这个代码来解释:
544 |
545 | ```
546 | if A and B
547 | then action1
548 | if C or D
549 | then action2
550 | ```
551 |
552 | - **语句覆盖**:语句至少被执行一次
553 |
554 | 要让`action1`和`action2`被走过。
555 |
556 | `action1`: `A and B = T` => `A = T, B = T`;
557 |
558 | `action2`: `C or D = T` => `C = T`。
559 |
560 | 因此设计测试用例为:`A = T, B = T, C = T`。
561 |
562 | - **判定覆盖**:判定至少真假一次
563 |
564 | if后的所有就是判定,比如上述的`A and B`和`C or D`。
565 |
566 | ```
567 | A and B = T => A = T, B = T // (1)
568 | A and B = F => A = T, B = F // (2)
569 | C or D = T => C = T, D = F // (3)
570 | C or D = F => C = F, D = F // (4)
571 | ```
572 |
573 | 设计测试样例为
574 |
575 | ```
576 | test1: A = T, B = T, C = T, D = F // (1) & (3)
577 | test2: A = T, B = F, C = F, D = F // (2) & (4)
578 | ```
579 |
580 | - **条件覆盖**:条件至少真假一次
581 |
582 | 判定中的条件,比如上述的`A`、`B`、`C`、`D`。
583 |
584 | ```
585 | (5) (6)
586 | A T F
587 | B T F
588 | C T F
589 | D T F
590 | ```
591 |
592 | 设计测试样例为
593 |
594 | ```
595 | test1: A = T, B = T, C = T, D = T // (5)
596 | test2: A = F, B = F, C = F, D = F // (6)
597 | ```
598 |
599 | - **判定条件覆盖**
600 |
601 | 就是要同时覆盖`(1)~(6)`。
602 |
603 | ```
604 | test1: A = T, B = T, C = T, D = T // (1) & (3) & (5)
605 | test2: A = F, B = F, C = F, D = F // (2) & (4) & (6)
606 | ```
607 |
608 | - **组合覆盖**(条件组合覆盖)
609 |
610 | 要让一个判定中的每个条件的各种组合至少一次。
611 |
612 | ```
613 | A B | C D
614 | test1: T T | T T
615 | test2: T F | T F
616 | test3: F T | F T
617 | test4: F F | F F
618 | ```
619 |
620 | - **路径覆盖**
621 |
622 |
446 |
447 | (2)计算环路复杂度
448 |
449 | (方法一)一共有4个区域,因此$V(G)=4$。
450 |
451 | (方法二)一共有8个节点,10条边,因此$V(G) = E - N + 2=10-8+2=4$。
452 |
453 | (方法三)一共有三个判定节点:1、3、4,因此$V(G) = 3 + 1 = 4$。
454 |
455 | (3)写出基本路径
456 |
457 | 路径1:1-2-8
458 |
459 | 路径2:1-3-5-8
460 |
461 | 路径3:1-3-4-6-8
462 |
463 | 路径4:1-3-4-7-8
464 |
465 | (4)给出满足基本路径测试标准的最小测试用例集
466 |
467 | | 覆盖路径 | 测试输入 | 测试输出 | 说明 |
468 | | -------- | ---------- | -------- | ------------------------------- |
469 | | 1 | year = 1 | 0 | 不能被4整除 |
470 | | 2 | year = 4 | 1 | 能被4整除,但不能被100整除 |
471 | | 3 | year = 400 | 1 | 能被4,100,400整除 |
472 | | 4 | year = 200 | 0 | 能被4,100整除,但不能被400整除 |
473 |
474 |
475 |
476 | ### 实例2
477 |
478 | **题目**: 请采用基本路径测试法设计下列伪码程序的测试用例。 要求:
479 |
480 | (1)画出流图;
481 |
482 | (2)计算环路复杂度;
483 |
484 | (3)给出基本路径;
485 |
486 | (4)给出满足基本路径测试标准的最小测试用例集。(提示:测试用例= 测试输入+预期输出。)
487 |
488 | ```
489 | 1: Start Input(a,b,c,d)
490 | 2: If(a>0)
491 | 3: and (b>0)
492 | 4: Then x=a+b
493 | 5: Else x=a-b
494 | 6: End if
495 | 7: If (c>a)
496 | 8: or (d
506 |
507 | (2)计算环路复杂度
508 |
509 | (方法一)一共有5个区域,因此$V(G)=5$。
510 |
511 | (方法二)一共有12个节点,15条边,因此$V(G) = E - N + 2=15-12+2=5$。
512 |
513 | (方法三)一共有三个判定节点:2、3、7、8,因此$V(G) = 4 + 1 = 5$。
514 |
515 | (3)写出基本路径
516 |
517 | 路径1:1-2-5-6-7-9-11-12
518 |
519 | 路径2:1-2-3-5-6-7-9-11-12
520 |
521 | 路径3:1-2-3-4-6-7-9-11-12
522 |
523 | 路径4:1-2-5-6-7-8-9-11-12
524 |
525 | 路径4:1-2-5-6-7-8-10-11-12
526 |
527 | (4)给出满足基本路径测试标准的最小测试用例集
528 |
529 | | 覆盖路径 | 测试输入(a,b,c,d) | 测试输出(x,y) | 说明 |
530 | | -------- | ----------------- | ------------- | -------------------------- |
531 | | 1 | (0, 0, 1, 0) | (0, 1) | a <= 0 && c > a |
532 | | 2 | (1, 0, 2, 0) | (1, 2) | a > 0 && b <= 0 && c > a |
533 | | 3 | (1, 1, 2, 0) | (2, 2) | a > 0 && b > 0 && c > a |
534 | | 4 | (0, 0, 0, -1) | (0, 1) | a <= 0 && c <= a && d < b |
535 | | 5 | (0, 0, 0, 0) | (0, 0) | a <= 0 && c <= a && d >= b |
536 |
537 |
538 |
539 | ## 2. 控制结构测试法(逻辑覆盖法)
540 |
541 | 参考视频:https://www.bilibili.com/video/BV1zL4y1A785
542 |
543 | 以下面这个代码来解释:
544 |
545 | ```
546 | if A and B
547 | then action1
548 | if C or D
549 | then action2
550 | ```
551 |
552 | - **语句覆盖**:语句至少被执行一次
553 |
554 | 要让`action1`和`action2`被走过。
555 |
556 | `action1`: `A and B = T` => `A = T, B = T`;
557 |
558 | `action2`: `C or D = T` => `C = T`。
559 |
560 | 因此设计测试用例为:`A = T, B = T, C = T`。
561 |
562 | - **判定覆盖**:判定至少真假一次
563 |
564 | if后的所有就是判定,比如上述的`A and B`和`C or D`。
565 |
566 | ```
567 | A and B = T => A = T, B = T // (1)
568 | A and B = F => A = T, B = F // (2)
569 | C or D = T => C = T, D = F // (3)
570 | C or D = F => C = F, D = F // (4)
571 | ```
572 |
573 | 设计测试样例为
574 |
575 | ```
576 | test1: A = T, B = T, C = T, D = F // (1) & (3)
577 | test2: A = T, B = F, C = F, D = F // (2) & (4)
578 | ```
579 |
580 | - **条件覆盖**:条件至少真假一次
581 |
582 | 判定中的条件,比如上述的`A`、`B`、`C`、`D`。
583 |
584 | ```
585 | (5) (6)
586 | A T F
587 | B T F
588 | C T F
589 | D T F
590 | ```
591 |
592 | 设计测试样例为
593 |
594 | ```
595 | test1: A = T, B = T, C = T, D = T // (5)
596 | test2: A = F, B = F, C = F, D = F // (6)
597 | ```
598 |
599 | - **判定条件覆盖**
600 |
601 | 就是要同时覆盖`(1)~(6)`。
602 |
603 | ```
604 | test1: A = T, B = T, C = T, D = T // (1) & (3) & (5)
605 | test2: A = F, B = F, C = F, D = F // (2) & (4) & (6)
606 | ```
607 |
608 | - **组合覆盖**(条件组合覆盖)
609 |
610 | 要让一个判定中的每个条件的各种组合至少一次。
611 |
612 | ```
613 | A B | C D
614 | test1: T T | T T
615 | test2: T F | T F
616 | test3: F T | F T
617 | test4: F F | F F
618 | ```
619 |
620 | - **路径覆盖**
621 |
622 | 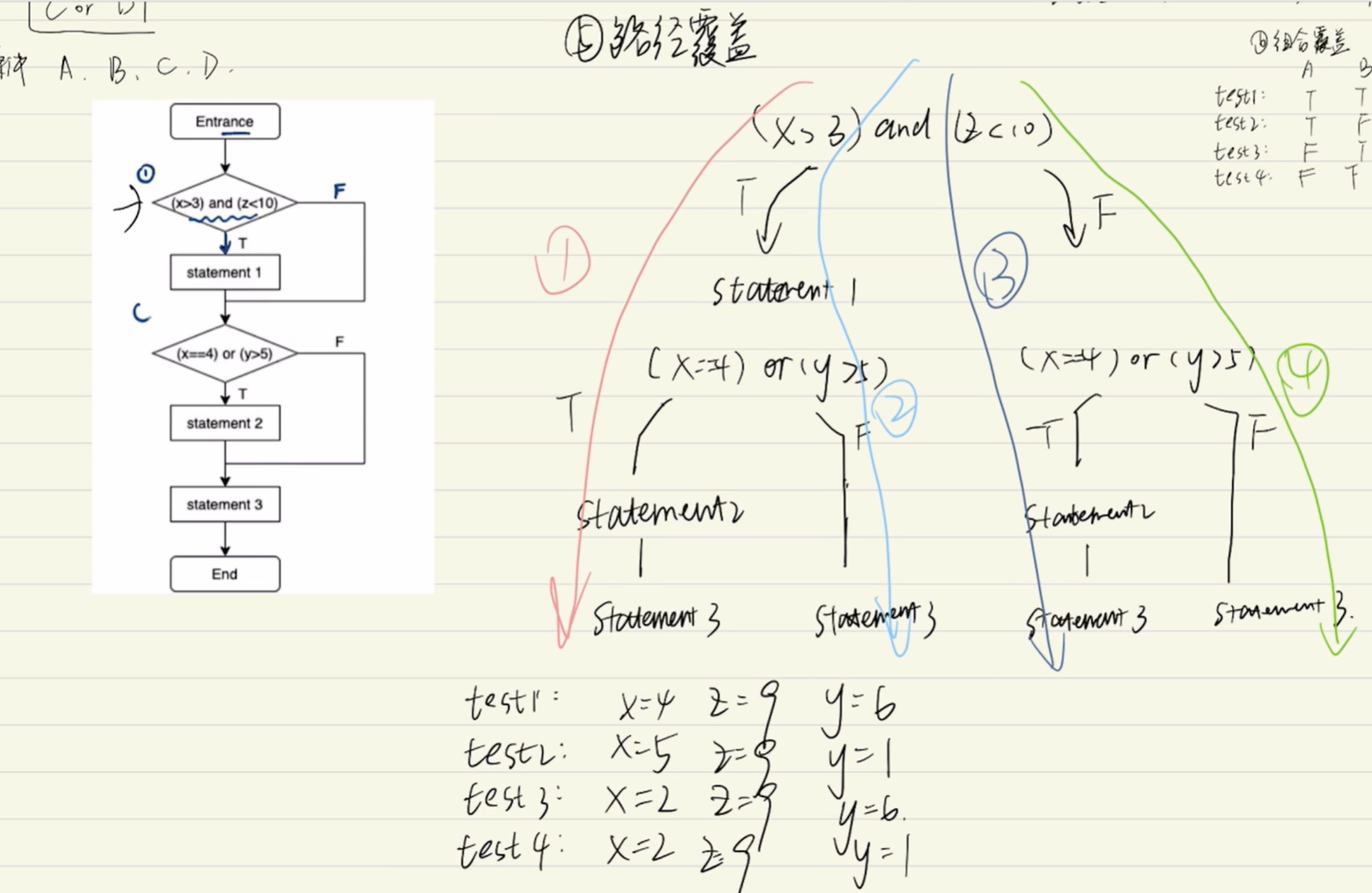 623 |
624 |
625 |
626 | # 四、黑盒测试
627 |
628 | ## 1.等价类划分
629 |
630 | 参考视频:https://www.bilibili.com/video/BV1MT411M7EC/?share_source=copy_web&vd_source=7ba452d8ee6f8b8a4b8ef831bf573bda
631 |
632 | 把被测对象的输入域划分为有限个等价区段“等价类”, 以有针对性的等价类少量测试,代替漫无边际的、数量较大的 “ 穷尽 ” 测试或随机测试。每个等价类的典型值的测试作用,可以代表这一类的所有其它数据。
633 |
634 | 等价类分为:
635 |
636 | - 有效等价类:对于程序的规格说明是合理、有意义的输入数据的集合
637 | - 无效等价类:对于程序的规格说明是不合理的、没有意义的输入数据的集合
638 |
639 | 步骤:
640 |
641 | - **划分“等价类”**
642 |
643 | 应按照输入条件(如输入值的范围、值的个数、 值的集合 、输入条件)划分为有效等价类和无效等价类。
644 |
645 | > 例1:每个学生可选修1-3门课程
646 | >
647 | > - 可以划分一个有效等价类:选修1-3门课程。
648 | > - 可以划分两个无效等价类:未选择选修课,选修课超过3门 。
649 | >
650 | > 例2:标识符的第一个字符必须是字母
651 | >
652 | > 可以划分为一个有效等价类:第一个字符是字母
653 | >
654 | > (或两个有效等价类:第一个字母是大写字母 / 小写字母) 。
655 | >
656 | > 可以划分一个无效等价类 : 第一个字符不是字母 。
657 |
658 | 等价法划分类的启发式规则:
659 |
660 | - 如果规定了输入值的范围 , 则可划分出一个有效的等价类 ( 输入值在此范围内 ) 和两个无效的等价类 ( 输入值小于最小值或大于最大值 ) 。
661 | - 如果规定了输入数据的个数 , 则类似地可以划分出一个有效的等价类和两个无效的等价类 。
662 | - 如果规定了输入数据的一组值 , 而且程序对不同输入值做不同处理 , 则每个允许的输入值是一个有效的等价类 , 此外还有一个无效的等价类 ( 任意一个不允许的输入值 ) 。
663 | - 若规定了输入数据的规则 , 则可以划分出一个有效的等价类 ( 符合规则 ) 和若干个无效的等价类 ( 从各种不同角度违反规则 )
664 | - 若规定了输入数据为整型 , 则可以划分出正整数 、 零和负整数等三个有效等价类 。
665 | - 若处理对象是表格 , 则应该使用空表以及含一项或多项的表 。
666 |
667 | - **选择测试用例**
668 | - 为每个等价类编号;
669 | - 使一个测试用例尽可能覆盖多个有效等价类;
670 | - 特别要注意的是:**一个测试用例只能覆盖一个无效等价类**;**每一个无效等价类都需要测试用例**。
671 |
672 |
673 |
674 | ### 实例1
675 |
676 | **题目**:在某一 PASCAL 语言版本中规定:在同一说明语句中 , 标识符至少必须有一个,标识符是由字母开头 、 后跟字母或数字的任意组合构成 。 有效字符数为 1 个 ,最大字符数为 80 个 。 并且规定:标识符必须先说明,再使用 。请使用等价划分法进行测试用例设计。
677 |
678 | **解答**:为用等价类划分的方法得到上述规格说明所规定的要求 , 本着前述的划分原则 ,建立等价类表 , 如表所示 ( 表中括中的数为等价类编号 ) 。
679 |
680 |
623 |
624 |
625 |
626 | # 四、黑盒测试
627 |
628 | ## 1.等价类划分
629 |
630 | 参考视频:https://www.bilibili.com/video/BV1MT411M7EC/?share_source=copy_web&vd_source=7ba452d8ee6f8b8a4b8ef831bf573bda
631 |
632 | 把被测对象的输入域划分为有限个等价区段“等价类”, 以有针对性的等价类少量测试,代替漫无边际的、数量较大的 “ 穷尽 ” 测试或随机测试。每个等价类的典型值的测试作用,可以代表这一类的所有其它数据。
633 |
634 | 等价类分为:
635 |
636 | - 有效等价类:对于程序的规格说明是合理、有意义的输入数据的集合
637 | - 无效等价类:对于程序的规格说明是不合理的、没有意义的输入数据的集合
638 |
639 | 步骤:
640 |
641 | - **划分“等价类”**
642 |
643 | 应按照输入条件(如输入值的范围、值的个数、 值的集合 、输入条件)划分为有效等价类和无效等价类。
644 |
645 | > 例1:每个学生可选修1-3门课程
646 | >
647 | > - 可以划分一个有效等价类:选修1-3门课程。
648 | > - 可以划分两个无效等价类:未选择选修课,选修课超过3门 。
649 | >
650 | > 例2:标识符的第一个字符必须是字母
651 | >
652 | > 可以划分为一个有效等价类:第一个字符是字母
653 | >
654 | > (或两个有效等价类:第一个字母是大写字母 / 小写字母) 。
655 | >
656 | > 可以划分一个无效等价类 : 第一个字符不是字母 。
657 |
658 | 等价法划分类的启发式规则:
659 |
660 | - 如果规定了输入值的范围 , 则可划分出一个有效的等价类 ( 输入值在此范围内 ) 和两个无效的等价类 ( 输入值小于最小值或大于最大值 ) 。
661 | - 如果规定了输入数据的个数 , 则类似地可以划分出一个有效的等价类和两个无效的等价类 。
662 | - 如果规定了输入数据的一组值 , 而且程序对不同输入值做不同处理 , 则每个允许的输入值是一个有效的等价类 , 此外还有一个无效的等价类 ( 任意一个不允许的输入值 ) 。
663 | - 若规定了输入数据的规则 , 则可以划分出一个有效的等价类 ( 符合规则 ) 和若干个无效的等价类 ( 从各种不同角度违反规则 )
664 | - 若规定了输入数据为整型 , 则可以划分出正整数 、 零和负整数等三个有效等价类 。
665 | - 若处理对象是表格 , 则应该使用空表以及含一项或多项的表 。
666 |
667 | - **选择测试用例**
668 | - 为每个等价类编号;
669 | - 使一个测试用例尽可能覆盖多个有效等价类;
670 | - 特别要注意的是:**一个测试用例只能覆盖一个无效等价类**;**每一个无效等价类都需要测试用例**。
671 |
672 |
673 |
674 | ### 实例1
675 |
676 | **题目**:在某一 PASCAL 语言版本中规定:在同一说明语句中 , 标识符至少必须有一个,标识符是由字母开头 、 后跟字母或数字的任意组合构成 。 有效字符数为 1 个 ,最大字符数为 80 个 。 并且规定:标识符必须先说明,再使用 。请使用等价划分法进行测试用例设计。
677 |
678 | **解答**:为用等价类划分的方法得到上述规格说明所规定的要求 , 本着前述的划分原则 ,建立等价类表 , 如表所示 ( 表中括中的数为等价类编号 ) 。
679 |
680 | 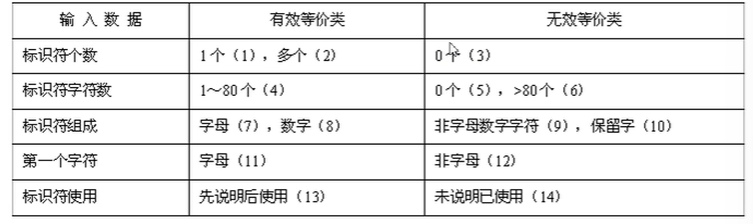 681 |
682 | 下面选取了8个测试用例,它们覆盖了所有的等价类。
683 |
684 |
681 |
682 | 下面选取了8个测试用例,它们覆盖了所有的等价类。
683 |
684 |  685 |
686 |
687 |
688 | ### 实例2
689 |
690 | **题目**:下面以测试`NextDate`函数的具体实例为出发点 , 讲解使用等价类划分法的细节 。 输入 3 个变量 ( 年 、 月 、 日 ) , 函数返回输入日期后面一天的日期 :1<=月<=12 , 1 <=日<=31 , 1812<=年<=2012 。 给出等价类划分表并设计测试用例 。
691 | **解答**:**(1)划分等价类 , 得到等价类划分表** , 如下表所示 。
692 |
693 |
685 |
686 |
687 |
688 | ### 实例2
689 |
690 | **题目**:下面以测试`NextDate`函数的具体实例为出发点 , 讲解使用等价类划分法的细节 。 输入 3 个变量 ( 年 、 月 、 日 ) , 函数返回输入日期后面一天的日期 :1<=月<=12 , 1 <=日<=31 , 1812<=年<=2012 。 给出等价类划分表并设计测试用例 。
691 | **解答**:**(1)划分等价类 , 得到等价类划分表** , 如下表所示 。
692 |
693 | 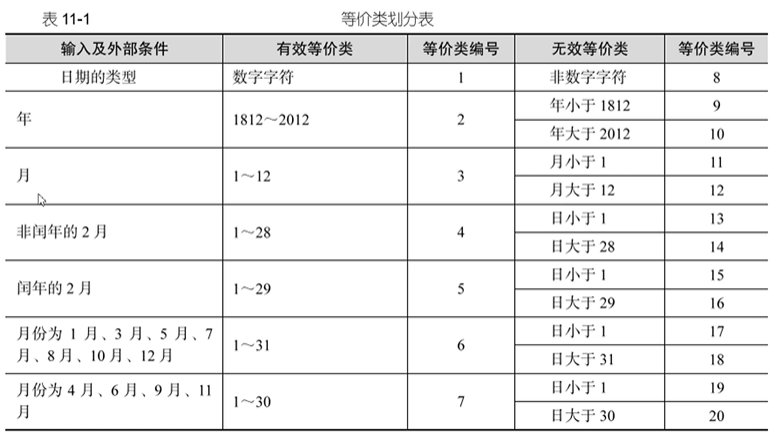 694 |
695 | (2)为**有效等价类**设计测试用例,如下表所示。
696 |
697 |
694 |
695 | (2)为**有效等价类**设计测试用例,如下表所示。
696 |
697 | 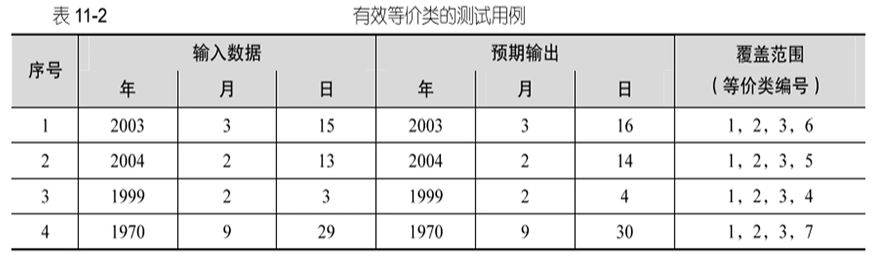 698 |
699 | (3)为**无效等价类**设计测试用例,如下表所示。
700 |
701 |
698 |
699 | (3)为**无效等价类**设计测试用例,如下表所示。
700 |
701 | 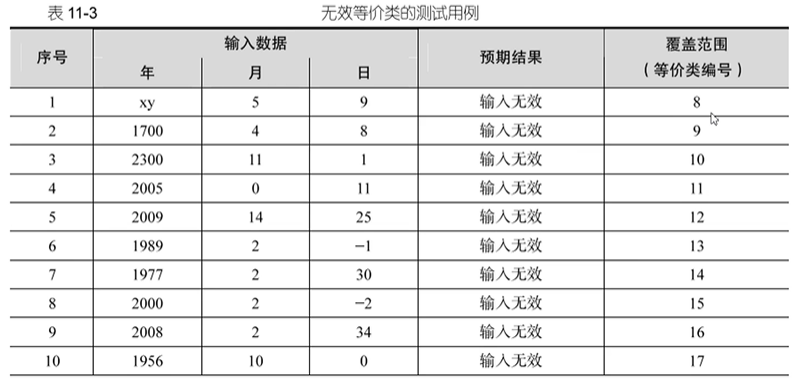 702 |
703 |
702 |
703 | 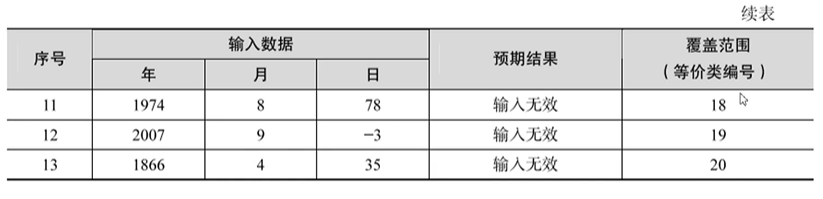 704 |
705 |
706 |
707 | ## 2. 边界值分析
708 |
709 | 经验表明,处理边界情况时程序最容易发生错误
710 |
711 | **边界类型:下标 、 数据结构 、 循环 、 选择等的边界附近**
712 |
713 | ——使程序运行在边界附近的测试方案 , 更容易暴露程序错误
714 |
715 | 通常选用**等价类边界值**作为边界值测试的数据
716 |
717 | 取值:按照边界值分析法 , 一般选取**刚好等于、稍小于和稍大于**等价类边界值的数据作为测试数据 。
718 |
719 | 一般边界值分析法作为等价类划分法的补充与细化 。
720 |
721 | **边界值分析法应当遵循的原则**:
722 |
723 | - 按照输入值范围的边界 。
724 |
725 | 例如:输入值的范围是$-1.0$至$1.0$,则设计用例:$-1.0,1.0,-1.001,1.001$。
726 |
727 | - 按照输入 / 输出值个数的边界 。
728 |
729 | 例如: 输入文件可有1-255个记录,则设计用例:文件的记录数为$0, 1, 255, 256$。
730 |
731 | - 输出值域的边界 。
732 |
733 | 例如:检索文献摘要,最多4篇,则设计用例:可检索篇数:$0,1,4,5$ 。
734 |
735 | - 输入/输出有序集(如顺序文件 、 线性表)的边界 。
736 |
737 | 应选择第一个元素和最后一个元素 。
738 |
739 |
740 |
741 | ### 实例
742 |
743 | 在上面实例2的基础上,使用边界值分析法设计测试用例。通常 , 设计测试方案时会联合使用等价类划分和边界值分析两种技术 。以上一节的`NextDate`函数为例 , 除了用等价类划分法设计出的测试方案外 ,还应该用边界值分析法补充以下测试方案 。
744 |
745 |
704 |
705 |
706 |
707 | ## 2. 边界值分析
708 |
709 | 经验表明,处理边界情况时程序最容易发生错误
710 |
711 | **边界类型:下标 、 数据结构 、 循环 、 选择等的边界附近**
712 |
713 | ——使程序运行在边界附近的测试方案 , 更容易暴露程序错误
714 |
715 | 通常选用**等价类边界值**作为边界值测试的数据
716 |
717 | 取值:按照边界值分析法 , 一般选取**刚好等于、稍小于和稍大于**等价类边界值的数据作为测试数据 。
718 |
719 | 一般边界值分析法作为等价类划分法的补充与细化 。
720 |
721 | **边界值分析法应当遵循的原则**:
722 |
723 | - 按照输入值范围的边界 。
724 |
725 | 例如:输入值的范围是$-1.0$至$1.0$,则设计用例:$-1.0,1.0,-1.001,1.001$。
726 |
727 | - 按照输入 / 输出值个数的边界 。
728 |
729 | 例如: 输入文件可有1-255个记录,则设计用例:文件的记录数为$0, 1, 255, 256$。
730 |
731 | - 输出值域的边界 。
732 |
733 | 例如:检索文献摘要,最多4篇,则设计用例:可检索篇数:$0,1,4,5$ 。
734 |
735 | - 输入/输出有序集(如顺序文件 、 线性表)的边界 。
736 |
737 | 应选择第一个元素和最后一个元素 。
738 |
739 |
740 |
741 | ### 实例
742 |
743 | 在上面实例2的基础上,使用边界值分析法设计测试用例。通常 , 设计测试方案时会联合使用等价类划分和边界值分析两种技术 。以上一节的`NextDate`函数为例 , 除了用等价类划分法设计出的测试方案外 ,还应该用边界值分析法补充以下测试方案 。
744 |
745 | 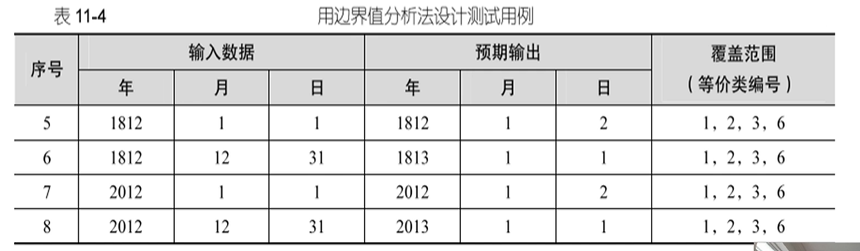 746 |
747 |
748 |
749 | ## 3. 正交表法
750 |
751 | 详见PPT.C18.25-26
752 | $$
753 | 测试用例数量 = 变量个数 \times (变量最大取值数目-1) + 1
754 | $$
755 | 例如:某大学刚考完某门课程考试,想通过“性别”、“班级”、“成绩”三个查询条件对这门课程的成绩进行查询,查询条件包括:
756 |
757 | - “性别” = “男、女”
758 | - “班级” = “1班、2班”
759 | - “成绩” = “及格、不及格”
760 |
761 | 一般来说是设计$2\times 2 \times 2 = 8$个测试用例。但如果使用正交数组法(正交表)法则只需要$3\times (2-1)+1 = 4$个测试用例。
762 |
763 |
--------------------------------------------------------------------------------
/docs/SoftwareEngineering/软工期末考试.md:
--------------------------------------------------------------------------------
1 |
746 |
747 |
748 |
749 | ## 3. 正交表法
750 |
751 | 详见PPT.C18.25-26
752 | $$
753 | 测试用例数量 = 变量个数 \times (变量最大取值数目-1) + 1
754 | $$
755 | 例如:某大学刚考完某门课程考试,想通过“性别”、“班级”、“成绩”三个查询条件对这门课程的成绩进行查询,查询条件包括:
756 |
757 | - “性别” = “男、女”
758 | - “班级” = “1班、2班”
759 | - “成绩” = “及格、不及格”
760 |
761 | 一般来说是设计$2\times 2 \times 2 = 8$个测试用例。但如果使用正交数组法(正交表)法则只需要$3\times (2-1)+1 = 4$个测试用例。
762 |
763 |
--------------------------------------------------------------------------------
/docs/SoftwareEngineering/软工期末考试.md:
--------------------------------------------------------------------------------
1 | 软件工程期末考试复习
2 |
3 | ## 一、填空题(10空,每空2分,共20分)
4 |
5 | ### (一)软件与软件工程
6 |
7 | - 软件的定义:P3
8 | - 软件的特点:PPT.C1.3
9 | - 软件发展:PPT.C1.5
10 | - 软件危机的定义与表现:PPT.C1.6
11 | - 软件危机产生的原因:PPT.C1.8
12 | - 7个软件应用领域:P4-5
13 | - 四大类软件:P6-8
14 |
15 | - 软件工程的定义:P11
16 |
17 | - 软件工程的层次(核心要素):PPT.C1.10-14,P11
18 |
19 |  20 |
21 | - 质量关注点:支持软件工程的**根基**在于**质量关注点**。P11
22 | - 过程:软件工程的**基础**。P11
23 | - 方法:解决方案。P11
24 | - 工具:自动化/半自动化支持。P11
25 |
26 | - 过程框架及其通用的5个框架活动:PPT.C1.15-16,P12
27 |
28 | - 框架性活动
29 | - 普适性活动:包括的8项活动:P12-13
30 |
31 | - George Polya提出的4个软件工程**实践的精髓**:P14
32 | - David Hooker提出的7个关注软件工程整体**实践的原则**:P15
33 | - 三个软件开发神话:P16-17
34 |
35 |
36 |
37 | ### (二)过程模型
38 |
39 | - 软件过程的定义:PPT.C2.2,P22
40 | - 每个框架活动由一系列软件工程动作构成;每个软件工程动作由**任务集**来定义。P23
41 | - 四种过程流:P23-24
42 | - 任务集所需要包括的四个组成成分:P24
43 | - 需求获取的任务集需要包括的内容(包括小型或大型项目):P25
44 | - Ambler提出的过程模式的描述模板:P26
45 | - Ambler模板中的三种模式类型:P26
46 | - Ambler模板中的步骤模式沟通中的一组任务模式:P26
47 | - Howard Baetjer Jr提出的软件资产:P22
48 |
49 |
50 |
51 | - 过程模型需要包含的5个方面:PPT.C2.6
52 |
53 | - **瀑布模型**(经典生命周期):PPT.C2.7-8,P30-32
54 |
55 |
20 |
21 | - 质量关注点:支持软件工程的**根基**在于**质量关注点**。P11
22 | - 过程:软件工程的**基础**。P11
23 | - 方法:解决方案。P11
24 | - 工具:自动化/半自动化支持。P11
25 |
26 | - 过程框架及其通用的5个框架活动:PPT.C1.15-16,P12
27 |
28 | - 框架性活动
29 | - 普适性活动:包括的8项活动:P12-13
30 |
31 | - George Polya提出的4个软件工程**实践的精髓**:P14
32 | - David Hooker提出的7个关注软件工程整体**实践的原则**:P15
33 | - 三个软件开发神话:P16-17
34 |
35 |
36 |
37 | ### (二)过程模型
38 |
39 | - 软件过程的定义:PPT.C2.2,P22
40 | - 每个框架活动由一系列软件工程动作构成;每个软件工程动作由**任务集**来定义。P23
41 | - 四种过程流:P23-24
42 | - 任务集所需要包括的四个组成成分:P24
43 | - 需求获取的任务集需要包括的内容(包括小型或大型项目):P25
44 | - Ambler提出的过程模式的描述模板:P26
45 | - Ambler模板中的三种模式类型:P26
46 | - Ambler模板中的步骤模式沟通中的一组任务模式:P26
47 | - Howard Baetjer Jr提出的软件资产:P22
48 |
49 |
50 |
51 | - 过程模型需要包含的5个方面:PPT.C2.6
52 |
53 | - **瀑布模型**(经典生命周期):PPT.C2.7-8,P30-32
54 |
55 | 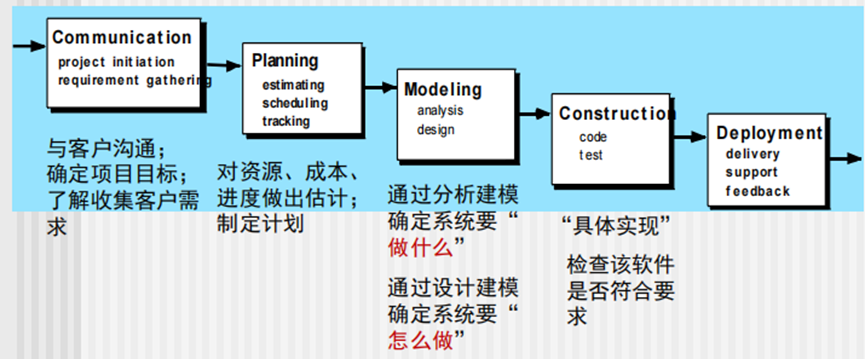 56 |
57 | - 3个特点:PPT.C2.7
58 | - 4个问题:PPT.C2.8,P31
59 | - **适合于:**PPT.C2.8
60 | - **需求稳定的项目**
61 | - **开发团队对该应用领域非常熟悉**
62 |
63 | - **增量模型**:PPT.C2.9,P32
64 |
65 |
56 |
57 | - 3个特点:PPT.C2.7
58 | - 4个问题:PPT.C2.8,P31
59 | - **适合于:**PPT.C2.8
60 | - **需求稳定的项目**
61 | - **开发团队对该应用领域非常熟悉**
62 |
63 | - **增量模型**:PPT.C2.9,P32
64 |
65 | 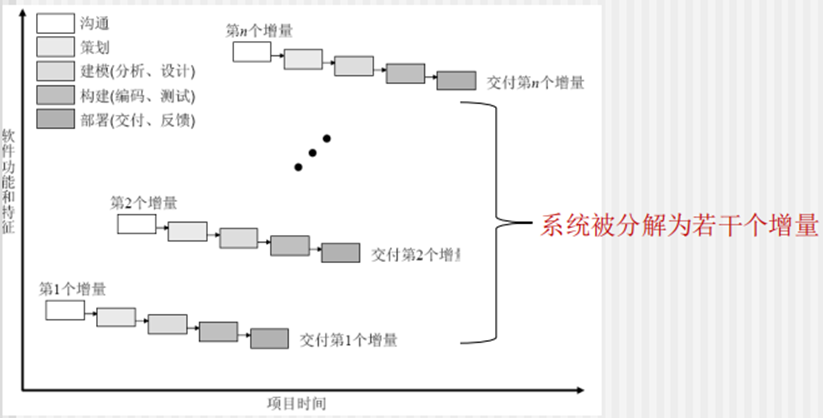 66 |
67 | - 特点:PPT.C2.9-10
68 | - 综合了线性过程流和并行过程流的特征。
69 | - 每个阶段都运用线性序列。
70 | - 第一个增量往往是核心产品。
71 | - 客户使用核心产品并进行评估。
72 | - 开发人员根据评估结果指定下一个增量计划。计划中需要说明对核心产品进行的修改,以便更好地满足客户的要求,也应说明需要增加的特性和功能。
73 | - 优势:PPT.C2.10
74 | - 可提高对用户需求或市场需求的响应。
75 | - 通过将不确定、不完全掌握相关技术的功能放在后续增量开发,可减轻技术风险。
76 | - **适合于:**
77 | - **团队成员不足以支持项目完整开发。**
78 | - **迫切需要为用户迅速提供一套功能有限的软件产品,然后再进行细化和拓展功能。**
79 |
80 | - **演化模型——原型法**:PPT.C2.12
81 |
82 | - 本质:通过迭代中一系列活动的重复应用,使软件持续改进。PPT.C2.12
83 | - 特点:PPT.C2.11
84 | - 让“系统”快速可见
85 | - 减少分析、设计过程中的不确定性
86 | - 类型:PPT.C2.11
87 | - 抛弃型:一种识别软件需求的机制
88 | - 演化型:慢慢发展成实际的系统
89 | - 问题:PPT.C2.15
90 |
91 | - **演化模型——螺旋法**:PPT.C2.16
92 |
93 |
66 |
67 | - 特点:PPT.C2.9-10
68 | - 综合了线性过程流和并行过程流的特征。
69 | - 每个阶段都运用线性序列。
70 | - 第一个增量往往是核心产品。
71 | - 客户使用核心产品并进行评估。
72 | - 开发人员根据评估结果指定下一个增量计划。计划中需要说明对核心产品进行的修改,以便更好地满足客户的要求,也应说明需要增加的特性和功能。
73 | - 优势:PPT.C2.10
74 | - 可提高对用户需求或市场需求的响应。
75 | - 通过将不确定、不完全掌握相关技术的功能放在后续增量开发,可减轻技术风险。
76 | - **适合于:**
77 | - **团队成员不足以支持项目完整开发。**
78 | - **迫切需要为用户迅速提供一套功能有限的软件产品,然后再进行细化和拓展功能。**
79 |
80 | - **演化模型——原型法**:PPT.C2.12
81 |
82 | - 本质:通过迭代中一系列活动的重复应用,使软件持续改进。PPT.C2.12
83 | - 特点:PPT.C2.11
84 | - 让“系统”快速可见
85 | - 减少分析、设计过程中的不确定性
86 | - 类型:PPT.C2.11
87 | - 抛弃型:一种识别软件需求的机制
88 | - 演化型:慢慢发展成实际的系统
89 | - 问题:PPT.C2.15
90 |
91 | - **演化模型——螺旋法**:PPT.C2.16
92 |
93 | 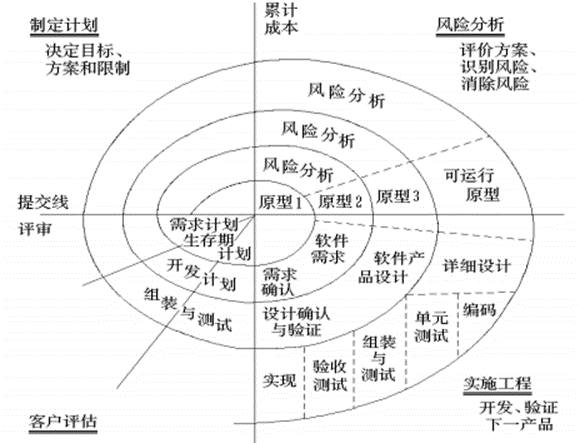 94 |
95 | - 结合了原型模型的迭代特性和瀑布模型的系统性和可控性,是一种风险驱动的过程模型。
96 | - 说明:PPT.C2.17
97 | - 早期的内圈,可能仅仅产生产品的规格说明或一个简单原型;
98 | - 后期每一圈,逐渐演化产生软件产品的初始版本,更完善的新版本……
99 | - 特点:PPT.C2.18
100 | - 结合了原型模型的迭代特征和瀑布模型的系统性和可控性,是一种风险驱动的过程模型。
101 | - 是开发大型系统和软件的很实际的方法。
102 | - 把原型作为降低风险的机制。
103 | - 保留了经典生命周期模型中系统逐步细化的方法,但是把它纳入一种迭代框架之中,这种迭代方式与真实世界更加吻合。
104 | - **适合于:**PPT.C2.18
105 | - **大规模软件项目**
106 | - **高风险项目**
107 |
108 | - 并发模型:P36-37
109 | - 统一过程模型(UP):PPT.C2.19-24,P40-42
110 | - 四个阶段:初始,细化,构建,交付。PPT.C2.19
111 | - 在UP**初始**阶段的迭代中,项目组必须:PPT.C2.21
112 | - 到了**细化**阶段的迭代,需要:PPT.C2.22
113 | - 进入**构建**阶段后,核心是所有功能的实现、测试,为应用部署做好准备。PPT.C2.23
114 | - 最后到了**交付**阶段,核心是部署、系统上线、运行和维护。PPT.C2.23
115 | - 特点:PPT.C2.20
116 | - UP裁剪:PPT.C2.24
117 |
118 |
119 |
120 | ### (三)敏捷开发与华为云平台
121 |
122 |
123 |
124 |
125 |
126 |
127 |
128 |
129 |
130 | ### (四)需求——需求工程
131 |
132 | - 理解需求困难的原因:PPT.C5.2
133 | - 【软件需求(SR)】是从软件外部可见的,软件所具有的、满足用户特点的功能及其它属性的集合。PPT.C5.5
134 | - 软件需求通常表达“做什么”,而不是“如何做”
135 | - 软件需求描述**应该满足**:**清晰、简洁、一致且无二义性**
136 |
137 | - 【最主要的需求来源】用户和产品经理,其他。PPT.C5.6
138 |
139 | - 各种需求。PPT.C5.6-8
140 |
141 | - 【需求工程的七项需明确的任务】
142 |
143 | - 起始:提出一系列的问题,以建立对问题的基本理解。PPT.C5.10
144 |
145 | 1. 收集客户的资料,了解系统的背景,进行初步的可行性分析,确定项目范围。
146 | 2. 确定干系人
147 | 3. 识别多个观点
148 | 4. 致力于协作
149 |
150 | 确定有共同点的地区和发生冲突的地区
151 |
152 | - 导出:引出所有利益相关者的需求。PPT.C5.11
153 |
154 | **【需求获取的主要方式】**
155 |
156 | - 需求讨论会。PPT.C5.12-13
157 | - 由软件工程师和客户主持和参加
158 | - 提出议程(确定议程,准备调研提纲)
159 | - 调解人控制全场
160 | - 可由客户方的情况介绍开始,分析人员逐渐成为主导,有效的引导和把握调研的重点和方向。
161 | - 从业务流程入手,采用IPO(Input Process Output)的思想获取需求
162 | - **软件需求分两个层次:用户需求与功能需求**。由用户需求导出功能需求。
163 | - 满足用户需求如果有多种备选方案,可以**协商**不同的方法,提出一套解决方案的要素。
164 |
165 | - 头脑风暴法。PPT.C5.14
166 | - 该方法对**需求不确定**的情况非常适用。
167 | - 调查问卷。PPT.C5.14
168 | - 适合于**需求调研的后期**,用于对前期发现的一些不确定或不一致的地方进行确认。
169 |
170 | - 场景分析法。PPT.C5.15-16
171 | - 场景分析核心是3个维度的梳理:角色、场景、方案。
172 | - 第一人称视角感受考察。PPT.C5.17
173 | - 基于自己的实际使用需求提出产品需求。
174 | - 原型法。PPT.C5.17
175 | - 高保真方式(只包含前端的界面和交互)
176 | - 低保真方式(手绘)
177 |
178 | > 【Experience】
179 | >
180 | > (1) 调研前做好必要的相关背景知识准备
181 | >
182 | > (2) 通过用户获取重要的原始资料(如表单,文件)
183 | >
184 | > (3) 渐进、反复的进行
185 | >
186 | > 访谈后,要及时对需求整理、分类,以便在下次与用户见面时由用户确认;
187 | >
188 | > 同时,准备下一次访谈时更细节的问题。
189 | >
190 | > (4) 根据需求的重要性划优先等级
191 |
192 | - 精化:创建一个可以识别数据、功能和行为需求的分析模型。PPT.C5.22-25
193 |
194 | - 通过分析建模,得到精确的需求模型,用以说明软件的功能、特征和数据等各个方面。
195 |
196 | **【分析模型的元素】**
197 |
198 | - 基于场景的元素——用例图
199 | - 基于类的元素——类图
200 | - 行为元素——状态图
201 | - 流元素——数据流图
202 | - E-R模型
203 |
204 | - 协商:就开发人员和客户现实的可交付系统达成一致。PPT.C5.26
205 |
206 | - 确定关键利益相关者:这些是将参与谈判的人
207 | - 确定每个利益相关者“赢条件”
208 | - 谈判:工作朝着一系列导致“双赢”的要求
209 |
210 | - 规格说明(Software Requirement Specification, SRS)。PPT.C5.27-29
211 |
212 | - **定义:**规格说明可以是一份写好的文档、一套图形化的模型、一组使用场景、一个原型或上述各项的任意组合。PPT.C5.27
213 | - 对大型系统而言,规范、标准的文档和图形化模型是最佳选择;
214 | - 对于技术环节明确的小型系统而言,使用场景可能就足够了。
215 | - **作用:**PPT.C5.28
216 | - **主要内容**:PPT.C5.28-29
217 |
218 | - 确认:审查机制。PPT.C5.30-31
219 | - 参与者:需求分析员、开发人员、测试人员、客户代表、项目经理、产品经理……
220 | - 需求评审要点:
221 | 1. 是否在适当的抽象级别上指定了所有的需求?
222 | 2. 这个要求对系统的目标真的是必要的吗?
223 | 3. 每个要求是否都是有界限和明确的?
224 | 4. 每个要求都有属性吗?
225 | 5. 是否有任何要求与其他要求相冲突?
226 | 6. 在技术环境中是否可满足每个要求?
227 | 7. 每个需求一旦实现,是否可测试?
228 |
229 | ### (五)需求——需求建模:面向对象分析方法
230 |
231 | - 【OOA分析模型分类】
232 | - 用例模型、(静态)领域模型、(动态)行为模型
233 |
234 | - 【分析过程】
235 |
236 |
94 |
95 | - 结合了原型模型的迭代特性和瀑布模型的系统性和可控性,是一种风险驱动的过程模型。
96 | - 说明:PPT.C2.17
97 | - 早期的内圈,可能仅仅产生产品的规格说明或一个简单原型;
98 | - 后期每一圈,逐渐演化产生软件产品的初始版本,更完善的新版本……
99 | - 特点:PPT.C2.18
100 | - 结合了原型模型的迭代特征和瀑布模型的系统性和可控性,是一种风险驱动的过程模型。
101 | - 是开发大型系统和软件的很实际的方法。
102 | - 把原型作为降低风险的机制。
103 | - 保留了经典生命周期模型中系统逐步细化的方法,但是把它纳入一种迭代框架之中,这种迭代方式与真实世界更加吻合。
104 | - **适合于:**PPT.C2.18
105 | - **大规模软件项目**
106 | - **高风险项目**
107 |
108 | - 并发模型:P36-37
109 | - 统一过程模型(UP):PPT.C2.19-24,P40-42
110 | - 四个阶段:初始,细化,构建,交付。PPT.C2.19
111 | - 在UP**初始**阶段的迭代中,项目组必须:PPT.C2.21
112 | - 到了**细化**阶段的迭代,需要:PPT.C2.22
113 | - 进入**构建**阶段后,核心是所有功能的实现、测试,为应用部署做好准备。PPT.C2.23
114 | - 最后到了**交付**阶段,核心是部署、系统上线、运行和维护。PPT.C2.23
115 | - 特点:PPT.C2.20
116 | - UP裁剪:PPT.C2.24
117 |
118 |
119 |
120 | ### (三)敏捷开发与华为云平台
121 |
122 |
123 |
124 |
125 |
126 |
127 |
128 |
129 |
130 | ### (四)需求——需求工程
131 |
132 | - 理解需求困难的原因:PPT.C5.2
133 | - 【软件需求(SR)】是从软件外部可见的,软件所具有的、满足用户特点的功能及其它属性的集合。PPT.C5.5
134 | - 软件需求通常表达“做什么”,而不是“如何做”
135 | - 软件需求描述**应该满足**:**清晰、简洁、一致且无二义性**
136 |
137 | - 【最主要的需求来源】用户和产品经理,其他。PPT.C5.6
138 |
139 | - 各种需求。PPT.C5.6-8
140 |
141 | - 【需求工程的七项需明确的任务】
142 |
143 | - 起始:提出一系列的问题,以建立对问题的基本理解。PPT.C5.10
144 |
145 | 1. 收集客户的资料,了解系统的背景,进行初步的可行性分析,确定项目范围。
146 | 2. 确定干系人
147 | 3. 识别多个观点
148 | 4. 致力于协作
149 |
150 | 确定有共同点的地区和发生冲突的地区
151 |
152 | - 导出:引出所有利益相关者的需求。PPT.C5.11
153 |
154 | **【需求获取的主要方式】**
155 |
156 | - 需求讨论会。PPT.C5.12-13
157 | - 由软件工程师和客户主持和参加
158 | - 提出议程(确定议程,准备调研提纲)
159 | - 调解人控制全场
160 | - 可由客户方的情况介绍开始,分析人员逐渐成为主导,有效的引导和把握调研的重点和方向。
161 | - 从业务流程入手,采用IPO(Input Process Output)的思想获取需求
162 | - **软件需求分两个层次:用户需求与功能需求**。由用户需求导出功能需求。
163 | - 满足用户需求如果有多种备选方案,可以**协商**不同的方法,提出一套解决方案的要素。
164 |
165 | - 头脑风暴法。PPT.C5.14
166 | - 该方法对**需求不确定**的情况非常适用。
167 | - 调查问卷。PPT.C5.14
168 | - 适合于**需求调研的后期**,用于对前期发现的一些不确定或不一致的地方进行确认。
169 |
170 | - 场景分析法。PPT.C5.15-16
171 | - 场景分析核心是3个维度的梳理:角色、场景、方案。
172 | - 第一人称视角感受考察。PPT.C5.17
173 | - 基于自己的实际使用需求提出产品需求。
174 | - 原型法。PPT.C5.17
175 | - 高保真方式(只包含前端的界面和交互)
176 | - 低保真方式(手绘)
177 |
178 | > 【Experience】
179 | >
180 | > (1) 调研前做好必要的相关背景知识准备
181 | >
182 | > (2) 通过用户获取重要的原始资料(如表单,文件)
183 | >
184 | > (3) 渐进、反复的进行
185 | >
186 | > 访谈后,要及时对需求整理、分类,以便在下次与用户见面时由用户确认;
187 | >
188 | > 同时,准备下一次访谈时更细节的问题。
189 | >
190 | > (4) 根据需求的重要性划优先等级
191 |
192 | - 精化:创建一个可以识别数据、功能和行为需求的分析模型。PPT.C5.22-25
193 |
194 | - 通过分析建模,得到精确的需求模型,用以说明软件的功能、特征和数据等各个方面。
195 |
196 | **【分析模型的元素】**
197 |
198 | - 基于场景的元素——用例图
199 | - 基于类的元素——类图
200 | - 行为元素——状态图
201 | - 流元素——数据流图
202 | - E-R模型
203 |
204 | - 协商:就开发人员和客户现实的可交付系统达成一致。PPT.C5.26
205 |
206 | - 确定关键利益相关者:这些是将参与谈判的人
207 | - 确定每个利益相关者“赢条件”
208 | - 谈判:工作朝着一系列导致“双赢”的要求
209 |
210 | - 规格说明(Software Requirement Specification, SRS)。PPT.C5.27-29
211 |
212 | - **定义:**规格说明可以是一份写好的文档、一套图形化的模型、一组使用场景、一个原型或上述各项的任意组合。PPT.C5.27
213 | - 对大型系统而言,规范、标准的文档和图形化模型是最佳选择;
214 | - 对于技术环节明确的小型系统而言,使用场景可能就足够了。
215 | - **作用:**PPT.C5.28
216 | - **主要内容**:PPT.C5.28-29
217 |
218 | - 确认:审查机制。PPT.C5.30-31
219 | - 参与者:需求分析员、开发人员、测试人员、客户代表、项目经理、产品经理……
220 | - 需求评审要点:
221 | 1. 是否在适当的抽象级别上指定了所有的需求?
222 | 2. 这个要求对系统的目标真的是必要的吗?
223 | 3. 每个要求是否都是有界限和明确的?
224 | 4. 每个要求都有属性吗?
225 | 5. 是否有任何要求与其他要求相冲突?
226 | 6. 在技术环境中是否可满足每个要求?
227 | 7. 每个需求一旦实现,是否可测试?
228 |
229 | ### (五)需求——需求建模:面向对象分析方法
230 |
231 | - 【OOA分析模型分类】
232 | - 用例模型、(静态)领域模型、(动态)行为模型
233 |
234 | - 【分析过程】
235 |
236 |  237 |
238 | 1. 建立用例模型
239 |
240 | 从不同用户的角度获取并描述功能需求,核心是用例。
241 |
242 | 2. 建立领域模型
243 |
244 | 发现和描述用例中涉及的对象和概念,核心是类图
245 |
246 | 3. 建立动态(交互)模型
247 |
248 |
249 |
250 | 【数据建模】
251 |
252 | 将注意力集中在数据域上
253 |
254 | 在客户的抽象级别上创建一个模型
255 |
256 | 指示数据对象之间如何相互关联
257 |
258 | 【数据对象】
259 |
260 | 一种几乎所有必须被软件理解的复合信息的表示。
261 |
262 | 可以是外部实体、事物、事件、角色、组织单元、地点或结构。
263 |
264 | 数据对象的描述包含了数据对象及其所有属性。数据对象包含一组作为对象的方面、质量、特征或描述符的属性。
265 |
266 | 【数据对象间的关系】
267 |
268 | 数据对象以不同的方式相互连接。
269 |
270 | 在人和车之间建立了一个连接,因为这两个对象是相关的。
271 |
272 | 一个人拥有一辆车
273 |
274 | 一个人可以驾驶汽车
275 |
276 | 关系“拥有”和“驾驶”定义人和汽车之间的相关联系。
277 |
278 | 对象可以通过多种不同的方式进行关联
279 |
280 | 
281 |
282 |
283 |
284 | 【领域建模】
285 |
286 | 领域模型分析以用例模型作为输入,将系统分解为一组相互协作的概念类(也称分析类) 。
287 |
288 | 分析类具有突出业务领域、突出概念性的特征,主要针对问题和职责,不涉及细节。
289 |
290 | 设计阶段,分析类可进一步演化为设计类,提供更多设计表达。
291 |
292 | 领域模型包括:**类图**、**CRC****模型**、**包图**
293 |
294 |
295 |
296 |
297 |
298 |
299 |
300 | 【行为建模】
301 |
302 | 行为模型显示了软件如何对外部事件或激励做出响应。
303 |
304 | 该模型通常描述一个用例中,系统在接收到特定事件后,所涉及的对象以及这些对象之间的交互(消息传递)过程。
305 |
306 | 行为模型主要包括:时序图、协作图、状态图。
307 |
308 |
309 |
310 | 【状态图 vs 时序图】
311 |
312 | (1)状态图针对单个类,跨多个用例。时序图针对的是一个用例。
313 |
314 | (2)状态图中的行为不仅与事件有关,还与对象所处状态有关。
315 |
316 | 【时序图 vs 协作图】
317 |
318 | (1)时序图可等价的转化为协作图
319 |
320 | (2)协作图更侧重表达对象间的关联关系,而非消息传递的时间先后。
321 |
322 | 
323 |
324 |
325 |
326 |
327 |
328 | ### (六)需求——需求建模:结构化分析方法
329 |
330 | 【结构化分析方法(SA)】又称面向数据流的分析方法。主要是创建基于数据流的模型,通过分析数据流发现系统功能和行为,并对其进行划分。
331 |
332 | SA主要构建四种分析模型
333 |
334 | · 数据流图(Data Flow Diagram)——功能视角
335 |
336 | · 数据字典
337 |
338 | · 实体关系图——数据视角
339 |
340 | · 状态迁移图——行为视角
341 |
342 |
343 |
344 | 【控制流建模】
345 |
346 | 一些应用程序是由事件而不是数据“驱动”的,产生控制信息而不是报告或显示,以及处理严重关注时间和性能的信息。
347 |
348 | 适合对实时系统、控制类系统等建模。
349 |
350 | 以状态图为主,描述系统对外部事件响应的行为模型。
351 |
352 | 
353 |
354 |
355 |
356 | ### (五)设计
357 |
358 | **7.** **设计概念**
359 |
360 | 【软件设计】即根据软件需求,产生一个软件内部逻辑表示的过程。这种更接近于软件的逻辑表达或模型,提供了软件系统关心的体系结构、数据结构、接口和构件等细节。
361 |
362 | 对比:
363 |
364 | 需求分析偏重于问题域,描述软件要做什么。
365 |
366 | 软件设计则偏重于解决方案,描述软件究竟要如何做。
367 |
368 | 【软件设计的价值】
369 |
370 | 1. 设计是需求与实现代码之间的“桥梁”
371 |
372 | (1) 设计本质是满足需求,并对方案优中选优的过程。
373 |
374 | (2) 设计模型比代码更易评估、更易修改。
375 |
376 | 2. 设计是软件质量形成的关键,软件质量依赖于设计的结果
377 |
378 | (1) 如软件质量中的效率、可靠性、高并发等。
379 |
380 | **例子:****对含有上百亿信息的数据库,如何满足用户的高并发访问需求?**
381 |
382 | 设计方案:分库分表、读写分离。
383 |
384 | 【好的设计】
385 |
386 | 设计必须实现分析模型中的明确需求,包括客户期望的隐性需求。(承上)
387 |
388 | 对后续的编码、测试以及维护人员,设计必须是可读、可理解的指南。(启下)
389 |
390 | 设计必须提供未来软件的全貌,从实现的角度说明其数据域、功能域和行为域。
391 |
392 | 例子:自动排课是系统的功能需求之一,那么设计要解决数据存储问题(排课信息保存)、界面显示问题(排课及结果显示)、算法逻辑问题(排课算法)等。
393 |
394 | 【实施软件设计】
395 |
396 | 软件设计是一个迭代的过程。
397 |
398 | (1)初始时,设计者应关注系统的整体架构(如架构风格、主要构件、连接关系)等,对应于**体系结构设计阶段**。
399 |
400 | (2)随着设计迭代的开始,更多的细节被关注(如数据、构件)等,对应于**构件设计或详细设计阶段**。
401 |
402 | 【软件设计任务集】
403 |
404 | 
405 |
406 | (1) 体系结构设计:定义软件的主要元素(构件)以及元素之间的联系
407 |
408 | 
409 |
410 | (2) 数据/类设计:将分析类模型转化为设计类以及软件所需要的数据结构
411 |
412 | 
413 |
414 | (3) 接口设计:定义软件与协作系统之间、软件与用户之间的通信
415 |
416 | (4) 构件设计或详细设计:定义软件元素(构件)的内部细节,如内部数据结构、算法等
417 |
418 | (5) 部署设计:定义软件元素在物理拓扑结构中的分布
419 |
420 |
421 |
422 | 【应该遵循什么原则才能保证设计质量?】
423 |
424 | 1. 抽象
425 |
426 | 抽象的本质:强调关键特征,忽略无关细节。
427 |
428 | 过程抽象:具有明确和有限功能的指令序列。
429 |
430 | 数据抽象:描述数据对象的具名数据集合。
431 |
432 | 2. 体系结构
433 |
434 | 软件体系结构设计,即找到一种最佳的方式对系统进行划分,标识其中的构件,构件之间的联系等。
435 |
436 | 设计应该先勾勒全貌,不能一开始就跳入细节。
437 |
438 | 3. 模式
439 | 4. 关注点分离
440 | 5. 模块化
441 |
442 | 庞大的系统不便于并行开发,软件工程师也难以理解和把握。
443 |
444 | 采用分治策略,将大系统分解为若干更小、更简单的模块。这样,问题理解变得更加容易,开发成本也会减小。
445 |
446 | 6. 信息隐蔽
447 |
448 | 每个模块都对其它模块隐藏自己的设计细节(就像黑盒子),这样如果模块内部发生变化,外部受到的影响最小。
449 |
450 | **7.** **功能独立**
451 |
452 | 功能独立性是指:模块化设计时,希望每个模块尽可能功能专一,同时避免与其它模块过多交互。
453 |
454 | Cohesion(内聚): 表示模块内相关功能的强度
455 |
456 | 内聚性强的模块通常只完成一件事情。
457 |
458 | Coupling (耦合) :表示模块之间的相互依赖性
459 |
460 | 模块的耦合性取决于模块之间接口的复杂性、引用方式、传递数据的复杂性等。
461 |
462 | 功能独立意味着:**高内聚、低耦合**
463 |
464 | 功能独立的优势:
465 |
466 | · 更容易开发。因为每个功能均有效分隔,且接口简单。
467 |
468 | · 更容易维护。因为修改代码引起的副作用被限制,减少错误扩散。
469 |
470 | · 复用性更好。
471 |
472 | 8. 逐步求精
473 |
474 | 随着设计的深入,设计者不能老是停留在抽象层级,而应逐步揭示底层的细节。
475 |
476 | 9. 方面
477 | 10. 重构
478 |
479 | 在不改变代码的外部行为的前提下,优化内部结构的过程。
480 |
481 | 例子:早期设计中发现某构件的内聚性较差,在保持接口不变的情况下,可通过重构将其分解为两个独立的构件,每个新的构件内聚性得以增强。
482 |
483 | 11. 面向对象的设计概念
484 | 12. 设计类
485 |
486 | 分析类只与业务领域有关,和具体实现技术无关。
487 |
488 | 设计类则面向实现,通过对分析类的细化设计,达到能提供给构造阶段编码实现的目的。
489 |
490 | 定义设计类的两种方式:
491 |
492 | (1) 通过对分析类提供细节设计。
493 |
494 | (2) 创建新的设计类,该设计类提供软件的基础设施以支持业务解决方案。
495 |
496 | 改进:基于工厂模式
497 |
498 |
499 |
500 | **8.** **体系结构设计**
501 |
502 | 【软件体系结构】是软件的一种划分形式,从较高抽象层次定义系统的构件、构件之间的连接,以及由构件与构件连接形成的拓扑结构。
503 |
504 | 【体系结构设计的必要性】
505 |
506 | · 体系结构设计决定了系统的主体结构,结构优劣对软件质量具有重要影响。
507 |
508 | · 针对安全需求,可以考虑采用分层结构,将重要资源置于内层保护。
509 |
510 | · 针对可用性需求,可以考虑冗余设计。
511 |
512 | 【软件体系结构设计的关键决策】
513 |
514 | · 系统的基本构造单元是什么?
515 |
516 | · 这些构造单元连接方式?
517 |
518 | · 最终形成怎样的拓扑结构?
519 |
520 | · 有哪些体系结构风格可供系统借鉴?
521 |
522 | · 对于目标系统,如何基于一般性的体系结构进行适应性改造?
523 |
524 | · 如何评估体系结构设计?
525 |
526 | 【体系结构风格】
527 |
528 | 众多系统所共有的结构和特性(如构件类型、交互机制、拓扑、约束),可以指导同类型应用的体系结构设计。
529 |
530 | · 数据中心结构
531 |
532 | 该结构适合于:数据由一个构件(模块)产生,而由其它构件使用的情形。
533 |
534 | 缺点:一旦中心数据存储出现问题会影响整个系统。
535 |
536 | 如电子白板系统、管理信息系统(MIS) 。
537 |
538 | 
539 |
540 | · 管道-过滤器结构
541 |
542 | 系统由若干构件(过滤器)按一定顺序组合而成,一个构件的输出是另一个构件的输入。
543 |
544 | 适合于批处理系统,不适用于交互式应用系统。
545 |
546 | 编译器就是一种管道-过滤器系统,包括词法分析、语法分析、字节码生成等。
547 |
548 | 图像处理系统等也大多采用该风格。
549 |
550 | 
551 |
552 | 
553 |
554 | · 调用返回结构
555 |
556 | (1) 主程序/子程序结构
557 |
558 | 
559 |
560 | (2) 远程过程调用结构:主程序/子程序中的构件分布在网络中的多台计算机。
561 |
562 | 如:如分布式计算系统Hadoop。
563 |
564 | 
565 |
566 | 调用返回结构缺点:
567 |
568 | 主构件需要预先知道被调子构件的接口标识。
569 |
570 | 构件接口标识的更改会影响所有调用它的其它构件,而且这种现象还会进行传递,导致更大的负面影响。
571 |
572 | · 面向对象结构
573 |
574 | 构造单元:类和对象
575 |
576 | 连接:基于消息机制。
577 |
578 | 拓扑结构:不同对象之间是平级的,没有主次之分
579 |
580 | 
581 |
582 | · 消息总线结构
583 |
584 | 构件不直接调用其它构件,而是广播一个或多个事件。
585 |
586 | 系统中的构件注册(监听)一个或多个事件源;
587 |
588 | 当一个事件被广播,系统自动调用该事件中注册的构件。
589 |
590 | 
591 |
592 | 消息总线风格逐渐演变为**消息中间件**。消息中间件应用场景:系统解耦、异步通讯、削峰。
593 |
594 | 下图为传统方式下系统B、C与A之间的通信连接,随着新的D、E、F、G系统的增加,必然导致巨大的维护成本(加入或退出均需要维护A)。
595 |
596 | 
597 |
598 | 优点:扩展简单。系统无须知道其他子系统接口名、位置的情况下,就可以激活其它子系统。
599 |
600 | 消息中间件产品:ActiveMQ、RabbitMQ
601 |
602 | 
603 |
604 | 
605 |
606 | · 层次化结构
607 |
608 | 系统被组织成若干个层次,每层都由一系列构件组成。
609 |
610 | 同层内构件可相互调用。
611 |
612 | 层之间存在调用接口,但只限于相邻层,下层可为上层服务,并作为再下一层客户。
613 |
614 | 
615 |
616 | · 客户-服务器结构
617 |
618 | 源于计算任务和计算资源的能力差异。
619 |
620 | 构件分布在两台或多台计算环境中。
621 |
622 | 演变:三层,多层C/S,B/S体系结构
623 |
624 | · MVC(Model-View-Controller)
625 |
626 | 常用于Web应用系统。
627 |
628 | 将系统分解为应用逻辑、用户界面、控制逻辑等不同构件类型。
629 |
630 | 优势:
631 |
632 | ·任何一种构件的改变都不会对其它构件造成影响。
633 |
634 | ·一个模型能为多个视图提供数据。
635 |
636 | 
637 |
638 | · 微服务架构
639 |
640 | 单体架构:应用打包(如war)部署为一个独立的单元,通过一个进程方式运行。
641 |
642 | 微服务架构:
643 |
644 | · 应用(功能)被分割成更小的、独立的服务,各个微服务之间的关联通过RPC(同步调用)或MQ(异步调用)实现。
645 |
646 | · 独立的微服务不需要部署在同一个虚拟机或应用服务器中。
647 |
648 | 
649 |
650 | · 混合风格
651 |
652 | 大规模系统往往包括多种体系结构风格
653 |
654 | 
655 |
656 |
657 |
658 | 【体系结构描述】
659 |
660 | 关注点:为谁描述哪些内容?用什么符号体系或描述语言?
661 |
662 | 程序员说:体系结构就是要决定需要编写哪些类、使用哪些现成框架。
663 |
664 | 程序经理说:体系结构就是模块的划分和接口的定义。
665 |
666 | 数据库工程师说:体系结构规定了持久化数据的结构,其他不过是对数据的操作而已。
667 |
668 | 用户说:体系结构就是决定一个个功能子系统如何划分。
669 |
670 | 这些描述我们都需要。每个视角代表一类利益相关者,反应了系统结构的一个侧面。
671 |
672 | 系统体系结构多从逻辑架构、物理架构和开发架构等视角描述。
673 |
674 | **·** **逻辑架构**关注的是功能构件,包含用户可见的功能构件,以及不可见的功能构件。
675 |
676 | **·** **物理架构**关注网络、服务器等基础设施及其拓扑结构。
677 |
678 | · **开发架构**更关注程序包,除自己写的程序外,还包括应用程序依赖的SDK、第三方类库等。
679 |
680 | 【体系结构设计方法】
681 |
682 | 基本设计思路:
683 |
684 | 
685 |
686 | 包括:
687 |
688 | · 面向对象体系结构设计
689 |
690 | · 传统结构化设计
691 |
692 | 【面向对象体系结构设计方法】
693 |
694 | 1. 定义系统交互的外部环境和交互特性
695 |
696 | (1) 目的是识别系统的外部实体与接口,定义接口构件
697 |
698 | 2. 识别一组结构原型(archetypes)
699 |
700 | (1) 原型是系统中最核心的抽象类或模式,目标系统的体系结构可由这些原型组成。
701 |
702 | (2) 原型是系统中最稳定的元素,可以基于系统行为以不同方式对这些元素实例化。
703 |
704 | (3) 多数情况下,原型可以通过分析类来获得。
705 |
706 | 3. 对每个结构原型进一步细化,以完善系统结构。
707 |
708 | 例子:对图书管理系统体系结构设计
709 |
710 | (1) 先采用“包图”划分子系统。
711 |
712 | 
713 |
714 | (2) 针对“借书”需求,识别结构原型
715 |
716 | 
717 |
718 | (3) 对“借书”构件,采取MVC风格进行细化
719 |
720 | 
721 |
722 | 【结构化体系结构设计方法】
723 |
724 | 目标:根据DFD的不同类型,通过对系统中模块的合理划分,得到软件体系结构图
725 |
726 | 体系结构风格:主程序/子程序风格
727 |
728 | 1. 将系统分割为多个功能模块
729 | 2. 确定各个模块之间的调用关系
730 | 3. 用系统结构图表示设计模型
731 |
732 | 步骤:
733 |
734 | (1) 分析确定数据流图类型。
735 |
736 | (2) 标识输入、输出流边界。
737 |
738 | (3) 依据变化或事务分析规则,将DFD图映射为顶层和第一层模块结构。
739 |
740 | (4) 对第一层中的模块继续细化和分解。
741 |
742 | (5) 利用启发式规则优化初始系统结构图。
743 |
744 | 变换分析和事务分析实例见PPT【体系结构设计】末尾
745 |
746 | 9. 构件级设计
747 |
748 | 【构件设计】是在体系结构设计的基础上,对其中每个构件内部构成的进一步设计。
749 |
750 | 体系结构设计相当于确定了计算机的部件组成,连接关系等。
751 |
752 | 构件设计则着重于设计每个部件的**内部细节**,如运算器的内部电路和元件等。
753 |
754 | 面向对象视角:
755 |
756 | 确定设计类并对其细化的过程。
757 |
758 | 结构化视角:
759 |
760 | 细化模块内部的数据结构、算法和接口的过程。
761 |
762 | 【构件】是计算机软件中的一个模块化的构造块。它部件**封装**了实现并暴露一系列**接口**。
763 |
764 | 面向对象视角:
765 |
766 | 构件封装了一组相互协作的类(也可以是一个类)。
767 |
768 | 结构化视角:
769 |
770 | 构件也称功能模块(如系统中图像读入模块、图像压缩模块)
771 |
772 | 封装了数据结构、算法和接口
773 |
774 | 【面向对象构件构成】
775 |
776 | 面向对象构件可能由多个设计类构成
777 |
778 | (1) 构件接口与实现需要严格分离。
779 |
780 | (2) 基于设计框架,一个构件需要分解为多个设计类。
781 |
782 | 【面向对象构建设计关键问题】
783 |
784 | 1. 构件由哪些设计类组成?
785 | 2. 设计类之间是什么关系,如何优化?
786 | 3. 构件提供的接口是什么?
787 | 4. 每个设计类的详细构成(属性和方法)?
788 |
789 | 前3个问题都与设计优化原则相关
790 |
791 | 通过设计优化,可以提高构件复用性,灵活适应系统变更,并减少副作用的传播。
792 |
793 | 【构件设计指导原则】
794 |
795 | 1. 开闭原则(OCP)
796 |
797 | 对扩展开放:构件的行为是可扩展或改变的
798 |
799 | 对修改关闭:当构件改变行为时,不要修改其源码
800 |
801 | 实现途径:用抽象构建框架,用继承/实现扩展细节。
802 |
803 | 需求变化时,不是通过修改类本身来完成,而是通过扩展一个子类来改变构件的行为。
804 |
805 | 优点:尽量不修改原有的代码,实现一个热插拔的效果。
806 |
807 | 2. Liskov替换原则(LSP)
808 |
809 | LSP 原则用来指导继承关系中子类该如何设计,子类的设计要保证在替换父类的时候,不改变原有程序的逻辑以及不破坏原有程序的正确性。
810 |
811 | 简单理解:子类可以扩展父类的功能,但不能改变父类原有的功能。
812 |
813 | LSP原则能减少代码冗余,避免运行期的类型判别(实现动态加载)。
814 |
815 | 3. 依赖倒置原则
816 |
817 | 依赖于抽象,而非具体实现。 具体方法是:首先,分离接口和实现。将类之间的依赖关系建立在高层抽象(如抽象类、接口)基础上。
818 |
819 | 优点:减少类间的耦合性,提高系统的稳定性
820 |
821 | 4. 接口分离原则
822 |
823 | 建立单一接口,不要建立臃肿庞大的接口。即:接口尽量细化,同时接口中的时间尽量少。
824 |
825 | 5. 单一职责原则:一个类或接口只承担一类责任。
826 | 6. 迪米特法则:尽量减少对象之间的交互,从而减小类之间的耦合。
827 |
828 | 内聚性和耦合性
829 |
830 | **内聚性**意味着构件只封装那些密切相关的类,或者类只封装自身密切相关的属性和操作。
831 |
832 | 根据程度可细分为:功能内聚、分层内聚、通信内聚等
833 |
834 | **耦合性**是类之间彼此联系程度的一种定性度量。
835 |
836 | 根据程度可细分为:内容耦合、共用耦合、控制耦合、标记耦合……
837 |
838 | 【面向对象构件设计过程】
839 |
840 | 1. 识别构件中与问题域相对应的设计类。包括界面类、控制类、实体类。
841 |
842 | (1) 一般可为每个用例设计一个控制类。如果多个用例中任务较为相似,也可以公用一个控制类。
843 |
844 | (2) 如果实体类的职责比较单一,直接将其映射为设计类;
845 |
846 | (3) 如果某类的职责过于复杂,应该将其分解为多个设计类(单一职责)。
847 |
848 | 2. 识别构件中与基础设施相对应的设计类。 这些设计类往往在分析模型中并没有定义。
849 | 3. 细化所有的设计类,定义该类中所有的接口、属性和操作。
850 |
851 | (1) 通过设计时序图或协作图说明协作细节。
852 |
853 | 将时序图中职责分解为具体操作,并分配给相关类;
854 |
855 | 定义操作对应的方法名,方法参数,返回值、可见性等。
856 |
857 | (2) 为每个构件确定合适的接口。
858 |
859 | 简单构件可直接定义public方法作为接口;
860 |
861 | 复杂构件单独定义接口类,构件负责实现接口;
862 |
863 | 确定接口的参数;
864 |
865 | (3) 细化属性,并定义相应的数据类型和数据结构。
866 |
867 | (4) 描述类成员方法中的处理逻辑。绘制程序流程图或活动图。
868 |
869 | 4. 说明持久数据源 (数据库或文件),并确定管理数据源所需要的类。
870 |
871 | (1) 对象可暂存于内存中,但要持久保存,需要通过数据存储实现。
872 |
873 | (2) 可以通过对象关系映射(ORM)将类映射为表,以简化数据库使用。
874 |
875 | 5. 细化**部署图**以提供额外的实现细节。
876 |
877 | (1) 为系统选择硬件配置和运行平台;
878 |
879 | (2) 将类、包、子系统分配到各个硬件结点上。
880 |
881 | 构建设计实例见PPT【构件级设计】中的实例部分
882 |
883 | 【传统构件设计过程】
884 |
885 | · 确定每个模块的算法,用工具描述算法逻辑。
886 |
887 | · 确定每一模块的数据结构。
888 |
889 | · 确定模块接口细节。
890 |
891 | 常用算法描述工具包括
892 |
893 | · 程序流程图
894 |
895 | · 问题分析图(PAD)
896 |
897 | 
898 |
899 | · 盒图(N-S图)
900 |
901 | 
902 |
903 | · 伪代码(PDL)
904 |
905 |
906 |
907 | 10. 用户界面设计
908 |
909 | 【UI设计】
910 |
911 | 软件强大的计算能力和功能,最终要通过界面来表现。
912 |
913 | 用户界面是软件的直观形象,直接影响用户对软件的体验。
914 |
915 | 用户通常从用户界面(而非功能)的好坏来评价软件的质量。
916 |
917 | 【常见UI设计错误】
918 |
919 | · 缺乏一致性
920 |
921 | · 太多需要记忆的
922 |
923 | · 没有指导和帮助
924 |
925 | · 没有上下文敏感性
926 |
927 | · 无意义的反馈
928 |
929 | · 界面复杂
930 |
931 | 【黄金法则】(这部分看书P198)
932 |
933 | 1. 把控制权交给用户(让用户掌握一切)
934 |
935 | (1) 提供灵活的交互。允许用户选择使用键盘、语音、鼠标等多种交互方式。
936 |
937 | (2) 允许用户交互被中断和撤销。如在手机编写短信时,允许接听电话,并能找到之前正在编写的短信。
938 |
939 | (3) 允许定制交互。
940 |
941 | (4) 将用户和内部技术细节隔离开。
942 |
943 | (5) 设计应允许用户与出现在屏幕上的对象直接交互。
944 |
945 | 2. 减轻用户的记忆负担
946 |
947 | 经验表明,需要记住的东西越多,交互出错的概率越大。
948 |
949 | (1) 减少对短期记忆的要求。
950 |
951 | (2) 建立有意义的默认设置。
952 |
953 | (3) 定义直观的快捷方式。
954 |
955 | (4) 界面的视觉布局应该基于真实世界的象征。
956 |
957 | (5) 以一种渐进的方式揭示信息。
958 |
959 | 3. 保持界面一致
960 |
961 | (1) 在完整的产品线上保持设计规则的一致性。
962 |
963 | (2) 如果过去的交互方式已经建立起用户期望,除非有不得已的理由,否则不要改变它。
964 |
965 | 4. 补充规则
966 |
967 | (1) 反馈:对用户的操作,应该给予及时、明确的反馈,并提供上下文帮助。
968 |
969 | (2) 宽容性:允许用户犯错,并能帮助用户从错误中及时恢复出来。
970 |
971 | (3) 个性化:允许用户根据自己的喜好定制界面元素、布局等。
972 |
973 | (4) 美观性
974 |
975 | 【UI设计过程】
976 |
977 | 
978 |
979 | 【接口/界面分析】
980 |
981 | 接口分析是指理解
982 |
983 | (1) 通过接口与系统交互的人员(最终用户);
984 |
985 | (2) 终端用户完成工作必须执行的任务;
986 |
987 | (3) 作为接口一部分呈现的内容;
988 |
989 | (4) 这些任务将被执行的环境。
990 |
991 | 成分:
992 |
993 | 1. 用户分析(看书P203)
994 | 2. 任务分析与建模
995 |
996 | 根据用例模型中的场景描述,将其映射为人机界面上的一组子任务
997 |
998 | 3. 显示内容分析
999 |
1000 | 根据每项任务确定其呈现的界面内容。
1001 |
1002 | 【界面设计】
1003 |
1004 | 对每项任务对应的界面进行**交互设计**和**视觉设计**。
1005 |
1006 | 交互设计的重点包括:交互流程、交互方式。
1007 |
1008 | 【交互流程设计】
1009 |
1010 | 1. 定义界面对象和动作
1011 | 2. 定义可能导致界面变化的事件
1012 | 3. 界面应该如何变化
1013 | 4. 想告诉用户什么?
1014 |
1015 | 好的交互方式可以让用户更简单、方便的使用产品。
1016 |
1017 | 【视觉设计】
1018 |
1019 | 视觉设计是指:针对眼睛的主观形式的表现手段和结果。
1020 |
1021 | 主要考虑界面的布局、数据的呈现方式、色彩搭配等
1022 |
1023 | 【界面设计工具】
1024 |
1025 | Visio、Axure
1026 |
1027 | 【设计评审】
1028 |
1029 | 所有设计工作完成后,为保证设计质量,需要对所有设计成果,包括**体系结构、构件、接口、数据模型**等进行综合设计评审。
1030 |
1031 |
1032 |
1033 |
1034 |
1035 | ### (六)测试
1036 |
1037 | 11. 软件测试策略
1038 |
1039 | 【测试的目的】
1040 |
1041 | 测试是选择适当的测试用例并执行被测程序的过程。
1042 |
1043 | 目的在于**发现错误**,而不是为了验证程序不存在错误。
1044 |
1045 | 好的测试用例可以发现今未发现的错误。
1046 |
1047 | 【测试策略】
1048 |
1049 | 一般特征:
1050 |
1051 | · 未完成有效的测试,应该进行有效的、正式的技术评审。通过评审,许多错误可以在测试开始之前排除。
1052 |
1053 | · 测试开始于构件层,然后向外“延申”到整个基于计算机系统的继承中。
1054 |
1055 | · 不同的测试技术适用于不同的软件工程方法和不同的时间点。
1056 |
1057 | · 测试由软件开发人员和(对大型项目而言)独立的测试组执行。
1058 |
1059 | · 测试和调试是不同的活动,但任何测试策略都必须包括调试。
1060 |
1061 | 策略:
1062 |
1063 | 1. 测试不能取代评审
1064 |
1065 | 据说,检验项目质量的标准之一:质量 = 项目review时骂的次数 / 项目review时间。
1066 |
1067 | 被骂的次数越多,评审耗时越短,质量越可靠。
1068 |
1069 | 2. 谁来测试?
1070 |
1071 | (1) 开发者:对系统很了解,但由于急于交付,测试比较“gentle”
1072 |
1073 | (2) 独立测试人员:虽然对系统没有特别了解,但为了质量会尝试尽可能找出所有问题
1074 |
1075 | 3. 测试什么时候开始?
1076 |
1077 | 软件测试**不是在编码阶段**才开始,软件测试从**项目确立**时就开始了,主要经过以下环节:
1078 |
1079 | 需求分析→测试计划→测试设计→测试环境搭建→测试执行→测试记录。
1080 |
1081 | 4. 测试流程
1082 |
1083 | 从模块由小到大进行测试。
1084 |
1085 | 
1086 |
1087 | 【传统软件的测试策略:单元测试】(参考书P251-253)
1088 |
1089 | 目的:验证开发人员编写的模块或单元是否符合预期。
1090 |
1091 | 单元测试问题:
1092 |
1093 | · 说明不正确或不一致;
1094 |
1095 | · 初始化或缺省值错误;
1096 |
1097 | · 数据类型不相容;
1098 |
1099 | · 上溢、下溢或地址错误等。
1100 |
1101 | · 全局数据与模块的相互影响。
1102 |
1103 | 单元测试环境:
1104 |
1105 | 
1106 |
1107 | 驱动模块:用来模拟被测模块的上级调用模块。
1108 |
1109 | 桩模块:模拟被测试模块所调用的模块,返回被测模块所需的信息。
1110 |
1111 | 【传统软件的测试策略:集成测试】
1112 |
1113 | 通过单元测试的模块集成在一起,仍然可能无法正常工作,因为模块相互调用时仍然可能出错。
1114 |
1115 | 集成测试:旨在发现与调用接口相关的错误。
1116 |
1117 | **自顶向下集成**:
1118 |
1119 | 
1120 |
1121 | **自底向上集成**:
1122 |
1123 | 
1124 |
1125 | **三明治集成**:
1126 |
1127 | 
1128 |
1129 | **回归测试:**
1130 |
1131 | 集成测试中每加入新的模块,都会导致软件发生变更,这些变更可能使得原本正常工作的模块产生问题。
1132 |
1133 | 回归测试就是重新执行已经测试过的某些子集,以确保变更不会引入新的或额外的错误。
1134 |
1135 | 回归测试可以复用之前的测试用例和测试脚本。
1136 |
1137 | 可以使用自动测试工具提高回归测试效率。
1138 |
1139 | 捕获-回放工具(如WinRunner)能够捕获在测试过程中传递给软件的输入数据,生成执行的脚本,并且在回归测试中,重复执行该过程。
1140 |
1141 | **冒烟测试:**
1142 |
1143 | 冒烟测试也是一种特殊的集成测试,指完成一个新版本的集成、构建后,对该版本最基本的功能进行测试,目的是**保证基本的功能和流程能走通**。
1144 |
1145 | 如果通不过,则打回开发部门重新开发;如果通过测试,才会进行下一步的测试(功能测试,集成测试,系统测试等)。
1146 |
1147 | 例如,冒烟测试内容:
1148 |
1149 | 检查被测系统或模块能否正常启动和退出;
1150 |
1151 | 数据库能否正常连接,控件能否正常加载;
1152 |
1153 | 是否存在严重错误或者数据严重丢失等。
1154 |
1155 | 【面向对象的单元与集成测试】
1156 |
1157 | 类测试相当于单元测试。我们将测试该类内的操作。
1158 |
1159 | 集成采用了三种不同的策略。传统的自顶向下或自底向上的集成测试策略在面向对象软
1160 |
1161 | 件的集成测试中无意义。
1162 |
1163 | 1. 基于类之间的协作关系进行集成。
1164 | 2. 基于线程的测试—集成了响应一个输入或事件所需的类集。
1165 | 3. 基于使用的测试——从测试独立类开始,然后测试使用独立类的依赖类。
1166 |
1167 | 【确认测试】
1168 |
1169 | 确认测试:检验所开发的软件是否满足需求规格说明中的各种功能和性能需求,以及软件配置是否完全和正确。
1170 |
1171 | α测试是由用户在开发环境下进行的测试;β测试是由软件的多个用户在实际使用环境下进行的测试。可归为确认测试,产品正式发布前的测试,由用户主导。
1172 |
1173 | 【系统测试】
1174 |
1175 | 系统测试是将软件与其它系统部分(如外部系统,硬件设计等)结合进行的整体测试。其关注非功能性需求。
1176 |
1177 | 系统测试主要包括一下几种类型:
1178 |
1179 | 1. 恢复测试:有些系统失效后必须在规定时间段内被恢复,否则将会导致严重的经济损失。关注导致软件运行失败的各种条件,并验证其恢复过程能否正确执行。(如:系统供电故障后的恢复、日志处理恢复能力、程序运行崩溃后恢复能力)
1180 | 2. 安全测试:检测系统对非法侵入的防范能力。如口令截取或破译等。
1181 |
1182 | IBM AppScan,包括众多的安全扫描产品,如针对源代码扫描的AppScan source edition, 针对WEB应用扫描的AppScan standard edition,进行安全管理和汇总整合的AppScan enterprise Editio。
1183 |
1184 | 3. 压力测试
1185 |
1186 | 压力测试目的是为了发现系统能支持的最大负载等,前提是系统性能处在可以接受的范围内,如规定的3秒钟内响应。
1187 |
1188 | 压力测试通过不断对系统增加压力,确定一个系统的瓶颈或者不能接受的性能点,从而获得系统最大负载能力。
1189 |
1190 | 压力测试工具WebRunner:RadView公司推出的一个性能测试和分析工具,它让web应用开发者自动执行压力测试;webload通过模拟真实用户的操作,生成压力负载来测试web的性能。
1191 |
1192 | 4. 性能测试
1193 |
1194 | 通过测试确定系统(常态下)运行时的性能表现,如运行速度、响应时间、占有系统资源等方面的系统数据。
1195 |
1196 | 性能测试工具LoadRunner:它能预测系统行为,优化性能。它通过模拟实际用户的操作行为和实行实时性能监测。
1197 |
1198 | 【软件调试】
1199 |
1200 | 调试目标:定位错误发生的原因和位置。
1201 |
1202 | 调试技巧:
1203 |
1204 | (1)暴力法:一种比较简单,但效率较低的方法。包括:
1205 |
1206 | ① 主存信息输出法。
1207 |
1208 | 将计算机存储器和寄存器的全部内容打印出来。
1209 |
1210 | ② 关键部分设置打印语句。
1211 |
1212 | ③ 使用自动调试工具。
1213 |
1214 | (2)反向跟踪:是从可能的错误征兆处逐步向回追溯,直到找准错误,纠正为止。
1215 |
1216 | (3)归纳法:从线索(错误征兆出发),通过分析这些线索之间的关系找出故障。主要有4步:
1217 |
1218 | ① 收集数据。列出已知的测试用例和执行结果。
1219 |
1220 | ② 整理分析数据,以便发现规律,即“什么条件下出现错误,什么条件下不出现错误”。如:字符计数程序对“输入型”文本正确,对“拷贝型”文本错误。
1221 |
1222 | ③ 导出假设。分析线索之间的关系,提出关于错误的一个或多个假设。
1223 |
1224 | ④ 证明假设。证实提出的假设是导致错误发生的真正原因。
1225 |
1226 | (4)演绎法
1227 |
1228 | ① 设想出所有可能的出错原因;
1229 |
1230 | ② 试图用测试来排除每一个假设的原因,如果测试表明某个假设的原因可能是真的原因,则对数据进行细化以确定位错误。
1231 |
1232 |
1233 |
1234 | 12. 传统应用测试
1235 |
1236 | 【关于测试的两个问题】
1237 |
1238 | 1. 经过测试没有发现错误的软件就一定正确吗?错误。测试只能证明软件是有错的,不能证明软件是没有错误的。
1239 | 2. 可以通过穷举方式测试软件吗?一般不行,因为分支或循环太多会导致所需测试样例的数量呈指数型增长。
1240 |
1241 | 【如何设计好的测试用例?】
1242 |
1243 | 测试的有效性很大程度取决于选取的测试用例。
1244 |
1245 | 一个好的测试有很高的概率找到一个错误的;测试不是冗余的;一个好的测试应该是“最好的品种”。
1246 |
1247 | 【测试用例设计方法】
1248 |
1249 | 黑盒法:测试者把测试对象看作一黑盒子,仅依据程序的功能需求,设计测试用例并推断测试结果。
1250 |
1251 | 白盒法:按照程序内部逻辑结构,设计测试数据并完成测试的一种测试方法。
1252 |
1253 | 【白盒测试】
1254 |
1255 | 该方法把测试对象看做一个透明的盒子,它允许测试人员利用程序内部的逻辑结构及有关信息,设计或选择测试用例。
1256 |
1257 | 目标是使得程序中各元素(如语句、判定)尽可能被覆盖到。
1258 |
1259 | 白盒测试一般在测试过程的早期执行。
1260 |
1261 | 方法:
1262 |
1263 | 1. 语句覆盖:指选择足够的测试用例,使得被测程序中每条语句至少执行一次。是一种比较弱的测试标准。
1264 | 2. 基本路径测试
1265 |
1266 | 如果程序中含有循环结构,完全的路径覆盖是不可能的。
1267 |
1268 | **基本路径法**:在程序控制流图的基础上,通过导出基本可执行路径(注: 不是所有可能路径)集合,从而设计测试用例。
1269 |
1270 | 【重点掌握,见PPT(传统应用测试)】
1271 |
1272 | 3. 控制结构测试
1273 |
1274 | (1) 条件测试:一种测试程序模块中包含的逻辑条件的测试用例设计方法
1275 |
1276 | 设计测试用例确保至少条件C为真为假执行各一次。如果C是复合条件,则同时还要满足每个简单条件至少执行一次。
1277 |
1278 | 
1279 |
1280 | (2) 数据流测试:根据程序中定义的位置和变量的使用情况来选择程序的测试路径
1281 |
1282 | 设计测试用例使得每个变量定义-使用链至少覆盖一次。
1283 |
1284 | 
1285 |
1286 | (3) 循环测试:分为简单循环、嵌套循环、串接循环、非结构化循环。
1287 |
1288 | 对于简单循环,下列测试集可以用于简单循环:
1289 |
1290 |
1291 |
1292 | 
1293 |
1294 | 【黑盒测试】
1295 |
1296 | 这种方法是把测试对象看做一个黑盒子,测试人员完全不考虑程序内部的逻辑结构,只依据需求规格说明书,检查程序的功能是否符合它的功能说明。
1297 |
1298 | 黑盒测试一般在应用于测试的后期阶段。
1299 |
1300 | 1. 等价类划分
1301 |
1302 | 等价类划分法:将程序的输入域划分为若干个数据类,从中生成测试用例。
1303 |
1304 | 假定:对等价类中的代表值测试就等于对这一类值的测试。
1305 |
1306 | 
1307 |
1308 | 基本步骤: (1)确定等价类;(2)为等价类选择一个测试用例
1309 |
1310 | 例子:某城市的电话号码由3部分组成。假定被测程序能接收一切符合下述规定的电话号码,拒绝所有不符合规定的电话号码。
1311 |
1312 | 地区码:空白或3位数字;
1313 |
1314 | 前缀:非‘0’或‘1’开头的3位数字;
1315 |
1316 | 后缀:4位数字。
1317 |
1318 | (1) 确定等价类
1319 |
1320 | 
1321 |
1322 | (2) 设计测试用例
1323 |
1324 | 设计测试用例,使其尽可能多的覆盖到尚未覆盖的有效等价类
1325 |
1326 | 设计测试用例,使其只覆盖一个尚未被覆盖的无效等价类
1327 |
1328 | 
1329 |
1330 | 2. 边界值分析
1331 |
1332 | (1) 边界值应该尽可能选择等于边界,略小于边界,略大于边界的值
1333 |
1334 | (2) 边界值法可与等价类划分法结合,作为对其的一种补充。
1335 |
1336 | 例子: 一个输入文件应该包含1~255条记录,则应用边界值分析法设计测试用例。
1337 |
1338 | 可以用4组数据进行测试:
1339 |
1340 | 含1条记录的文件
1341 |
1342 | 含2条记录的文件
1343 |
1344 | 含254条记录的文件
1345 |
1346 | 含255条记录的文件
1347 |
1348 | 3. 正交阵列测试
1349 |
1350 | (1) 正交数组测试通过挑选适量的、有代表性的点进行试验,能有效地减少测试用例数,节约测试成本。
1351 |
1352 | (2) 该方法由日本口玄一博士提出并导出正交数组,从而使得测试数据具有“均匀分散、整齐可比”的特点。
1353 |
1354 | 例子:某大学刚考完某门课程,想通过“性别”、“班级”和“成绩”这3个查询条件对这门课程的成绩查询,查询条件包括:
1355 |
1356 | “性别”=“男,女”
1357 |
1358 | “班级”=“1班,2班”
1359 |
1360 | “成绩”=“及格,不及格”
1361 |
1362 | 一般需要设计2X2X2=8个测试用例。
1363 |
1364 | 
1365 |
1366 | 【基于模型的测试】
1367 |
1368 | 1. 分析软件的现有行为模型或创建一个。
1369 | 2. 穿越行为模型,并指定迫使软件从状态转换到另一个状态的输入。
1370 |
1371 | (1) 输入将触发将导致转换发生的事件。
1372 |
1373 | 3. 回顾行为模型,并注意到软件从状态过渡到状态时的预期输出。
1374 | 4. 执行测试用例。
1375 |
1376 | 
1377 |
1378 |
1379 |
1380 |
1381 |
1382 | ### 例题
1383 |
1384 | 1. 过程框架至少定义了五种框架活动分别是( )。
1385 |
1386 | 2. 类-职责-协作者模型又称为( )建模。
1387 |
1388 | 3. 软件工程层次图中,支持软件工程的根基在于( )。
1389 | 4. 填空题:在UML模型中,( )图用于描述系统与外部系统及用户之间的交互;( )图用于按时间顺序描述对象间的交互。
1390 | 5. 基于大量构件共同使用一个全局变量时所发生的耦合称为( )耦合。
1391 | 6. 华为云(DevCloud)是一个一站式、全流程、安全可信的( )平台。
1392 | 7. 华为云(DevCloud)敏捷开发的“看板”核心元素包括分层、( )、列、价值流、在制品(WIP)、风险&瓶颈、拉动式开发等核心元素。
1393 | 8. 顺序图(时序图)的构成元素主要包括: ( )、生命线、激活和( )。
1394 | 9. 汽车类与方向盘类之间的关系是( )关系。
1395 |
1396 | **重庆大学《软件工程》课程试卷(A 卷) 2019 — 2020 学年 第 2 学期**
1397 |
1398 | 1. FURPS 质量属性分别是指:功能性、( )、( )、性能和( )。
1399 |
1400 | 2. 在基于类的需求建模中,类可分为: ( )、( )和( )。
1401 |
1402 | 3. 需求工程是指( )。
1403 |
1404 | 4. 软件质量的成本包括:( )、( )和( )。
1405 |
1406 | 5. 一个通用的软件工程过程框架通常包含 沟通、( )、建模、( ) 和( )。
1407 |
1408 | 6. 开闭原则是指模块或构件应该对外延具有开放性,对( )具有封 闭性。
1409 |
1410 | 7. 需求模型必须实现的三个主要目标有: ( )、( )、定义在软 件完成后可以被确认的一组需求
1411 |
1412 | 8. OMG 定义构件是:系统中( )、可部署的和可替换的部件。
1413 |
1414 | 9. 用户满意度=合格的产品+( ) +( ) 10.CRC 卡中 CRC 的中文全称( )。
1415 |
1416 | > **参考答案**
1417 | >
1418 | > 1. (易用性)、(可靠性)、(可支持性)
1419 | > 2. (实体类)、(边界类)、(控制类)
1420 | > 3. (致力于不断理解需求的大量任务和技术)
1421 | > 4. (预防成本)、(评估成本)、(失效成本)
1422 | > 5. (策划)、(构建)、(部署)
1423 | > 6. ( 修改 )
1424 | > 7. (描述客户需要什么)、(为软件设计奠定基础)
1425 | > 8. (模块化的)
1426 | > 9. (好的质量)、(按预算和进度安排交付)
1427 | > 10. (类-职责-协作者)
1428 |
1429 | ## 二、单选题 (10个,每个2分,共20分)
1430 |
1431 | 看填空题的索引
1432 |
1433 | ### 需要理解的内容
1434 |
1435 | 1. 如何判断什么时候该用什么样的过程模型。
1436 |
1437 |
1438 |
1439 |
1440 |
1441 |
1442 |
1443 | ### 例题
1444 |
1445 | 1. 某软件公司欲开发一个基于Web的考勤管理系统。在项目初期,客户对系统的基本功能、表现形式等要求并不明确,在这种情况下,采用( )开发方法比较合适。
1446 |
1447 | A、瀑布模型
1448 |
1449 | B、形式化
1450 |
1451 | C、结构化
1452 |
1453 | D、极限编程
1454 |
1455 | 2. 在类图中下列哪个符号表示的是泛化关系是( )
1456 |
1457 | A、实线实心箭头
1458 |
1459 | B、虚线实心箭头
1460 |
1461 | C、实线空心箭头
1462 |
1463 | D、实线空心菱形
1464 |
1465 | 3. 在设计模式中“依赖于抽象,而非具体的实现”指的是( )
1466 |
1467 | A、开闭原则
1468 |
1469 | B、Liskov替换原则
1470 |
1471 | C、依赖倒置原则
1472 |
1473 | D、接口分离原则
1474 |
1475 | 4. 软件质量是一个重要的问题贯穿了软件的( )
1476 |
1477 | A、生存周期
1478 |
1479 | B、设计阶段
1480 |
1481 | C、编码阶段
1482 |
1483 | D、测试阶段
1484 |
1485 | ## 三、判断题 (5个,每个2分,共10分)
1486 |
1487 |
1488 |
1489 |
1490 |
1491 | ### 例题
1492 |
1493 | 1. 软件工程是一种结构化的技术。( )
1494 | 2. 每个应用系统只能使用一种体系结构风格。( )
1495 | 3.
1496 |
1497 |
1498 |
1499 |
1500 |
1501 | ## 四、简答题 (4个,每个5分,共20分)
1502 |
1503 | 看填空题的索引即可
1504 |
1505 |
1506 |
1507 | ### 例题
1508 |
1509 | 1. 简述David Hooker提出的7个关注软件工程整体实践的原则。(要点+一两句的补充说明)。
1510 | 2. 简述模块独立性的两个定量准则及模块独立性的好处。
1511 |
1512 |
1513 |
1514 |
1515 |
1516 | ## 五、应用分析题(2个,每个15分,共30分)
1517 |
1518 | ### (一)需求建模
1519 |
1520 | 1. 结构化分析——数据流图
1521 |
1522 | https://www.bilibili.com/video/BV1Jt411d7nR
1523 |
1524 |
1525 |
1526 | > #### 例题
1527 | >
1528 | > 某时装邮购提供商拟开发订单处理系统,用于处理客户通过电话、传真、邮件或Web站点所下订单。其主要功能如下:
1529 | >
1530 | > (1)增加客户记录。将新客户信息添加到客户文件,并分配一个客户号以备后续使用。
1531 | >
1532 | > (2)查询商品信息。接收客户提交商品信息请求,从商品文件中查询商品的价格和可订购数量等商品信息,返回给客户。
1533 | >
1534 | > (3)增加订单记录。根据客户的订购请求及该客户记录的相关信息,产生订单并添加到订单文件中。
1535 | >
1536 | > (4)产生配货单。根据订单记录产生配货单,并将配货单发送给仓库进行备货;备好货后,发送备货就绪通知。如果现货不足,则需向供应商订货。
1537 | >
1538 | > (5)准备发货单。从订单文件中获取订单记录,从客户文件中获取客户记录,并产生发货单。
1539 | >
1540 | > (6)发货。当收到仓库发送的备货就绪通知后,根据发货单给客户发货;产生装运单并发送给客户。
1541 | >
1542 | > (7)创建客户账单。根据订单文件中的订单记录和客户文件中的客户记录,产生并发送客户账单,同时更新商品文件中的商品数量和订单文件中的订单状态。
1543 | >
1544 | > (8)产生应收账户。根据客户记录和订单文件中的订单信息,产生并发送给财务部门应收账户报表。
1545 | >
1546 | > 问题:
1547 | >
1548 | > 1.使用说明中的词语,给出图1-1中的实体E1~E3的名称。
1549 | >
1550 | > 2.使用说明中的词语,给出图1-2中的数据存储D1~D3的名称。
1551 | >
1552 | > 3.(1)给出图1-2中处理(加工)P1和P2的名称及其相应的输入、输出流。(2)除加工P1和P2的输入输出流外,图1-2还缺失了1条数据流,请给出其起点和终点。
1553 | >
1554 | > 
1555 | >
1556 | > 
1557 |
1558 |
1559 |
1560 | 2. 面向对象分析——类图
1561 |
1562 | https://www.bilibili.com/video/BV1Jt411d7PR
1563 |
1564 |
1565 |
1566 | > #### 例题
1567 | >
1568 | > 某网上药店允许顾客凭借医生开具的处方,通过网络在该药店购买处方上的药品。该网上药店的基本功能描述如下:
1569 | >
1570 | > (1)注册。顾客在买药之前,必须先在网上药店注册。注册过程中需填写顾客资料以及付款方式(信用卡或者支付宝账户)。此外顾客必须与药店签订一份授权协议书,授权药店可以向其医生确认处方的真伪。
1571 | >
1572 | > (2)登录。已经注册的顾客可以登录到网上药房购买药品。如果是没有注册的顾客,系统将拒绝其登录。
1573 | >
1574 | > (3)录入及提交处方。登录成功后,顾客按照“处方录入界面”显示的信息,填写开具处方的医生的信息以及处方,上的药品信息。填写完成后,提交该处方。
1575 | >
1576 | > (4)验证**处方**。对于**已经提交的处方**(系统将其状态设置为“处方已提交”),其验证过程为:
1577 | >
1578 | > ①**核实医生信息**。如果医生信息不正确,该处方的状态被设置为“**医生信息无效**”,并取消这个处方的购买请求;如果医生信息是正确的,系统给该医生发送处方确认请求,并将处方状态修改为“审核中”。
1579 | >
1580 | > ②如果医生回复处方无效,系统取消处方,并将处方状态设置为**“无效处方**”。如果医生没有在7天内给出确认答复,系统也会取消处方,并将处方状态设置为“**无法审核**”。
1581 | >
1582 | > ③如果医生在7天内给出了确认答复,该处方的状态被修改为“准许付款”。系统取消所有未通过验证的处方,并自动发送一封电子邮件给顾客,通知顾客处方被取消以及取消的原因。
1583 | >
1584 | > (5)对于通过验证的处方,系统自动计算药品的价格并邮寄药品给已经付款的顾客。该网上药店:采用面向对象方法开发,使用UML进行建模。系统的类图如图3-1所示。
1585 | >
1586 | > 问题:
1587 | >
1588 | > 1. 根据说明中的描述,给出图3-1中缺少的C1~C5所对应的类名。
1589 | > 2. 图3-2给出了“处方”的部分状态图。根据说明中的描述,给出图3-2中缺少的S1 ~S4所对应的状态名以及(7)~(10)处所对应的迁移(transition) 名。
1590 | >
1591 | > 
1592 | >
1593 | > 
1594 |
1595 | 3. 面向对象分析——用例图
1596 |
1597 | 【例】
1598 |
1599 |
1600 |
1601 |
1602 |
1603 | > #### 例题
1604 | >
1605 | > 阅读下列说明和图,完善用例图A1、A2及U1~U3。
1606 | >
1607 | > 某网上购物平台的主要功能如下:
1608 | >
1609 | > (1)**创建订单**。**顾客**(Customer)在线创建订单(Order),主要操作是向订单中添加项目,从订单中删除项目。订单中应列出所订购的商品(Product)及其数量(Quantities)
1610 | >
1611 | > (2)提交订单。订单通过网络提交。在提交订单时,顾客需要提供其姓名(name)、收货地址(address)、付款方式(Payment)(预付卡、现金或信用卡)。
1612 | >
1613 | > (3)处理订单。**订单处理人员**接收来自系统的订单,根据订单内容,安排配货,制定送货计划。
1614 | >
1615 | > (4)派单。订单处理人员将已配好货的订单转交给派送人员。
1616 | >
1617 | > (5)**送货**/**收货**。派送人员将货物送到顾客指定的收货地址。顾客需在运货单上签收。签收后的运货单最终需交还给订单处理人员。
1618 | >
1619 | > (6)收货确认。当订单处理人员收到签收过的运货单后,会和顾客进行一次再确认。
1620 | >
1621 | > 
1622 |
1623 |
1624 |
1625 | 4. 面向对象分析——状态图
1626 |
1627 | 【例】
1628 |
1629 |
1630 |
1631 |
1632 |
1633 | 5. 面向对象分析——时序图
1634 |
1635 | 【例】
1636 |
1637 |
1638 |
1639 |
1640 |
1641 |
1642 |
1643 | ### (二)软件测试
1644 |
1645 | #### 2.1 测试用例的设计——白盒法
1646 |
1647 | ##### 2.1.1 控制结构测试
1648 |
1649 | 【软件工程——11-白盒测试】 https://www.bilibili.com/video/BV1wG41137Hs/?share_source=copy_web&vd_source=7ba452d8ee6f8b8a4b8ef831bf573bda
1650 |
1651 | 【白盒测试so easy!】 https://www.bilibili.com/video/BV1zL4y1A785/?share_source=copy_web&vd_source=7ba452d8ee6f8b8a4b8ef831bf573bda
1652 |
1653 | ##### 2.1.2 基本路径测试
1654 |
1655 | 【软件工程——11-基本路径测试法】 https://www.bilibili.com/video/BV13V4y1g7tc/?share_source=copy_web&vd_source=7ba452d8ee6f8b8a4b8ef831bf573bda
1656 |
1657 | #### 2.2 测试用例的设计——黑盒法
1658 |
1659 | ##### 2.2.1 等价类划分法
1660 |
1661 | 【软件工程——11-等价类划分.mp4】 https://www.bilibili.com/video/BV1MT411M7EC/?share_source=copy_web&vd_source=7ba452d8ee6f8b8a4b8ef831bf573bda
1662 |
1663 | ##### 2.2.2 边界值分析法
1664 |
1665 | 【软件工程——11-边界值及错误推测法】 https://www.bilibili.com/video/BV1nV4y1g7ig/?share_source=copy_web&vd_source=7ba452d8ee6f8b8a4b8ef831bf573bda
--------------------------------------------------------------------------------
/docs/index.md:
--------------------------------------------------------------------------------
1 | Hello world !!
--------------------------------------------------------------------------------
/mkdocs.yml:
--------------------------------------------------------------------------------
1 | site_name: Mine_qihang's Docs
2 | theme:
3 | name: "material"
4 | features:
5 | #- navigation.instant # 点击内部链接时,不用全部刷新页面
6 | - navigation.tracking # 在url中使用标题定位锚点
7 | - navigation.tabs # 顶部显示导航顶层nav(也就是第一个节点)
8 | - navigation.tabs.sticky # 滚动是隐藏顶部nav,需要配合navigation.tabs使用
9 | - navigation.sections # nav节点缩进
10 | - navigation.expand # 不折叠左侧nav节点
11 | - navigation.indexes # 指定节点index pages ,跟instant不兼容
12 | - toc.integrate # 右侧生产目录
13 | - navigation.top # 一键回顶部
14 | # plugins:
15 | # - search:
16 | # lang: jp
17 | markdown_extensions:
18 | - pymdownx.highlight # code hilight
19 | - pymdownx.superfences
20 | - pymdownx.arithmatex:
21 | generic: true
22 | extra_javascript:
23 | - javascripts/config.js
24 | - https://polyfill.io/v3/polyfill.min.js?features=es6
25 | - https://cdn.jsdelivr.net/npm/mathjax@3/es5/tex-mml-chtml.js
26 | nav:
27 | - 计算机系统结构:
28 | - Introduction: Architecture/chapter1.md
29 | - Principles of Quantitative Analysis; MIPS: Architecture/chapter2.md
30 | - Pipelining, Hazards, Implementation Issues: Architecture/chapter3.md
31 | - Instruction-Level Parallelism (ILP), Tomasulo: Architecture/chapter4.md
32 | - Memory-Hierarchy Design, Cache Optimization: Architecture/chapter5.md
33 | - ILP; Branch Prediction, Superscalars: Architecture/chapter6.md
34 | - Memory Hierarchy Design, Virtual Memory: Architecture/chapter7.md
35 | - 软件工程:
36 | - 软工期末考试: SoftwareEngineering/软工期末考试.md
37 | - 软工应用分析题: SoftwareEngineering/软工应用分析题.md
38 | - 计算机网络:
39 | - 第一次作业: ComputerNetwork/《计算机网络》第一次作业.md
40 | - 第二章作业: ComputerNetwork/《计算机网络》第二章作业.md
41 | - 第三章作业: ComputerNetwork/《计算机网络》第三章作业.md
42 | - 第四章作业: ComputerNetwork/《计算机网络》第四章作业.md
43 | - 第五章作业: ComputerNetwork/《计算机网络》第五章作业.md
44 | - 第六章作业: ComputerNetwork/《计算机网络》第六章作业.md
45 | - 第九章作业: ComputerNetwork/《计算机网络》第九章作业.md
46 | - 操作系统原理: OperatingSystem/index.md
47 | - 机器学习基础:
48 | - 第一章作业: MachineLearning/第一章作业.md
49 | - 第二章作业: MachineLearning/第二章作业.md
50 | - 第三章作业: MachineLearning/第三章作业.md
51 | - 第四章作业: MachineLearning/第四章作业.md
52 | - 第五章作业: MachineLearning/第五章作业.md
53 | - 第六章作业: MachineLearning/第六章作业.md
54 | - 第七章作业: MachineLearning/第七章作业.md
55 | - 第八章作业: MachineLearning/第八章作业.md
56 | - 第九章作业: MachineLearning/第九章作业.md
57 | - 自然语言处理: index.md
58 | - 专业基本能力测试: ProfessionalBasicAptitudeTest/index.md
--------------------------------------------------------------------------------
237 |
238 | 1. 建立用例模型
239 |
240 | 从不同用户的角度获取并描述功能需求,核心是用例。
241 |
242 | 2. 建立领域模型
243 |
244 | 发现和描述用例中涉及的对象和概念,核心是类图
245 |
246 | 3. 建立动态(交互)模型
247 |
248 |
249 |
250 | 【数据建模】
251 |
252 | 将注意力集中在数据域上
253 |
254 | 在客户的抽象级别上创建一个模型
255 |
256 | 指示数据对象之间如何相互关联
257 |
258 | 【数据对象】
259 |
260 | 一种几乎所有必须被软件理解的复合信息的表示。
261 |
262 | 可以是外部实体、事物、事件、角色、组织单元、地点或结构。
263 |
264 | 数据对象的描述包含了数据对象及其所有属性。数据对象包含一组作为对象的方面、质量、特征或描述符的属性。
265 |
266 | 【数据对象间的关系】
267 |
268 | 数据对象以不同的方式相互连接。
269 |
270 | 在人和车之间建立了一个连接,因为这两个对象是相关的。
271 |
272 | 一个人拥有一辆车
273 |
274 | 一个人可以驾驶汽车
275 |
276 | 关系“拥有”和“驾驶”定义人和汽车之间的相关联系。
277 |
278 | 对象可以通过多种不同的方式进行关联
279 |
280 | 
281 |
282 |
283 |
284 | 【领域建模】
285 |
286 | 领域模型分析以用例模型作为输入,将系统分解为一组相互协作的概念类(也称分析类) 。
287 |
288 | 分析类具有突出业务领域、突出概念性的特征,主要针对问题和职责,不涉及细节。
289 |
290 | 设计阶段,分析类可进一步演化为设计类,提供更多设计表达。
291 |
292 | 领域模型包括:**类图**、**CRC****模型**、**包图**
293 |
294 |
295 |
296 |
297 |
298 |
299 |
300 | 【行为建模】
301 |
302 | 行为模型显示了软件如何对外部事件或激励做出响应。
303 |
304 | 该模型通常描述一个用例中,系统在接收到特定事件后,所涉及的对象以及这些对象之间的交互(消息传递)过程。
305 |
306 | 行为模型主要包括:时序图、协作图、状态图。
307 |
308 |
309 |
310 | 【状态图 vs 时序图】
311 |
312 | (1)状态图针对单个类,跨多个用例。时序图针对的是一个用例。
313 |
314 | (2)状态图中的行为不仅与事件有关,还与对象所处状态有关。
315 |
316 | 【时序图 vs 协作图】
317 |
318 | (1)时序图可等价的转化为协作图
319 |
320 | (2)协作图更侧重表达对象间的关联关系,而非消息传递的时间先后。
321 |
322 | 
323 |
324 |
325 |
326 |
327 |
328 | ### (六)需求——需求建模:结构化分析方法
329 |
330 | 【结构化分析方法(SA)】又称面向数据流的分析方法。主要是创建基于数据流的模型,通过分析数据流发现系统功能和行为,并对其进行划分。
331 |
332 | SA主要构建四种分析模型
333 |
334 | · 数据流图(Data Flow Diagram)——功能视角
335 |
336 | · 数据字典
337 |
338 | · 实体关系图——数据视角
339 |
340 | · 状态迁移图——行为视角
341 |
342 |
343 |
344 | 【控制流建模】
345 |
346 | 一些应用程序是由事件而不是数据“驱动”的,产生控制信息而不是报告或显示,以及处理严重关注时间和性能的信息。
347 |
348 | 适合对实时系统、控制类系统等建模。
349 |
350 | 以状态图为主,描述系统对外部事件响应的行为模型。
351 |
352 | 
353 |
354 |
355 |
356 | ### (五)设计
357 |
358 | **7.** **设计概念**
359 |
360 | 【软件设计】即根据软件需求,产生一个软件内部逻辑表示的过程。这种更接近于软件的逻辑表达或模型,提供了软件系统关心的体系结构、数据结构、接口和构件等细节。
361 |
362 | 对比:
363 |
364 | 需求分析偏重于问题域,描述软件要做什么。
365 |
366 | 软件设计则偏重于解决方案,描述软件究竟要如何做。
367 |
368 | 【软件设计的价值】
369 |
370 | 1. 设计是需求与实现代码之间的“桥梁”
371 |
372 | (1) 设计本质是满足需求,并对方案优中选优的过程。
373 |
374 | (2) 设计模型比代码更易评估、更易修改。
375 |
376 | 2. 设计是软件质量形成的关键,软件质量依赖于设计的结果
377 |
378 | (1) 如软件质量中的效率、可靠性、高并发等。
379 |
380 | **例子:****对含有上百亿信息的数据库,如何满足用户的高并发访问需求?**
381 |
382 | 设计方案:分库分表、读写分离。
383 |
384 | 【好的设计】
385 |
386 | 设计必须实现分析模型中的明确需求,包括客户期望的隐性需求。(承上)
387 |
388 | 对后续的编码、测试以及维护人员,设计必须是可读、可理解的指南。(启下)
389 |
390 | 设计必须提供未来软件的全貌,从实现的角度说明其数据域、功能域和行为域。
391 |
392 | 例子:自动排课是系统的功能需求之一,那么设计要解决数据存储问题(排课信息保存)、界面显示问题(排课及结果显示)、算法逻辑问题(排课算法)等。
393 |
394 | 【实施软件设计】
395 |
396 | 软件设计是一个迭代的过程。
397 |
398 | (1)初始时,设计者应关注系统的整体架构(如架构风格、主要构件、连接关系)等,对应于**体系结构设计阶段**。
399 |
400 | (2)随着设计迭代的开始,更多的细节被关注(如数据、构件)等,对应于**构件设计或详细设计阶段**。
401 |
402 | 【软件设计任务集】
403 |
404 | 
405 |
406 | (1) 体系结构设计:定义软件的主要元素(构件)以及元素之间的联系
407 |
408 | 
409 |
410 | (2) 数据/类设计:将分析类模型转化为设计类以及软件所需要的数据结构
411 |
412 | 
413 |
414 | (3) 接口设计:定义软件与协作系统之间、软件与用户之间的通信
415 |
416 | (4) 构件设计或详细设计:定义软件元素(构件)的内部细节,如内部数据结构、算法等
417 |
418 | (5) 部署设计:定义软件元素在物理拓扑结构中的分布
419 |
420 |
421 |
422 | 【应该遵循什么原则才能保证设计质量?】
423 |
424 | 1. 抽象
425 |
426 | 抽象的本质:强调关键特征,忽略无关细节。
427 |
428 | 过程抽象:具有明确和有限功能的指令序列。
429 |
430 | 数据抽象:描述数据对象的具名数据集合。
431 |
432 | 2. 体系结构
433 |
434 | 软件体系结构设计,即找到一种最佳的方式对系统进行划分,标识其中的构件,构件之间的联系等。
435 |
436 | 设计应该先勾勒全貌,不能一开始就跳入细节。
437 |
438 | 3. 模式
439 | 4. 关注点分离
440 | 5. 模块化
441 |
442 | 庞大的系统不便于并行开发,软件工程师也难以理解和把握。
443 |
444 | 采用分治策略,将大系统分解为若干更小、更简单的模块。这样,问题理解变得更加容易,开发成本也会减小。
445 |
446 | 6. 信息隐蔽
447 |
448 | 每个模块都对其它模块隐藏自己的设计细节(就像黑盒子),这样如果模块内部发生变化,外部受到的影响最小。
449 |
450 | **7.** **功能独立**
451 |
452 | 功能独立性是指:模块化设计时,希望每个模块尽可能功能专一,同时避免与其它模块过多交互。
453 |
454 | Cohesion(内聚): 表示模块内相关功能的强度
455 |
456 | 内聚性强的模块通常只完成一件事情。
457 |
458 | Coupling (耦合) :表示模块之间的相互依赖性
459 |
460 | 模块的耦合性取决于模块之间接口的复杂性、引用方式、传递数据的复杂性等。
461 |
462 | 功能独立意味着:**高内聚、低耦合**
463 |
464 | 功能独立的优势:
465 |
466 | · 更容易开发。因为每个功能均有效分隔,且接口简单。
467 |
468 | · 更容易维护。因为修改代码引起的副作用被限制,减少错误扩散。
469 |
470 | · 复用性更好。
471 |
472 | 8. 逐步求精
473 |
474 | 随着设计的深入,设计者不能老是停留在抽象层级,而应逐步揭示底层的细节。
475 |
476 | 9. 方面
477 | 10. 重构
478 |
479 | 在不改变代码的外部行为的前提下,优化内部结构的过程。
480 |
481 | 例子:早期设计中发现某构件的内聚性较差,在保持接口不变的情况下,可通过重构将其分解为两个独立的构件,每个新的构件内聚性得以增强。
482 |
483 | 11. 面向对象的设计概念
484 | 12. 设计类
485 |
486 | 分析类只与业务领域有关,和具体实现技术无关。
487 |
488 | 设计类则面向实现,通过对分析类的细化设计,达到能提供给构造阶段编码实现的目的。
489 |
490 | 定义设计类的两种方式:
491 |
492 | (1) 通过对分析类提供细节设计。
493 |
494 | (2) 创建新的设计类,该设计类提供软件的基础设施以支持业务解决方案。
495 |
496 | 改进:基于工厂模式
497 |
498 |
499 |
500 | **8.** **体系结构设计**
501 |
502 | 【软件体系结构】是软件的一种划分形式,从较高抽象层次定义系统的构件、构件之间的连接,以及由构件与构件连接形成的拓扑结构。
503 |
504 | 【体系结构设计的必要性】
505 |
506 | · 体系结构设计决定了系统的主体结构,结构优劣对软件质量具有重要影响。
507 |
508 | · 针对安全需求,可以考虑采用分层结构,将重要资源置于内层保护。
509 |
510 | · 针对可用性需求,可以考虑冗余设计。
511 |
512 | 【软件体系结构设计的关键决策】
513 |
514 | · 系统的基本构造单元是什么?
515 |
516 | · 这些构造单元连接方式?
517 |
518 | · 最终形成怎样的拓扑结构?
519 |
520 | · 有哪些体系结构风格可供系统借鉴?
521 |
522 | · 对于目标系统,如何基于一般性的体系结构进行适应性改造?
523 |
524 | · 如何评估体系结构设计?
525 |
526 | 【体系结构风格】
527 |
528 | 众多系统所共有的结构和特性(如构件类型、交互机制、拓扑、约束),可以指导同类型应用的体系结构设计。
529 |
530 | · 数据中心结构
531 |
532 | 该结构适合于:数据由一个构件(模块)产生,而由其它构件使用的情形。
533 |
534 | 缺点:一旦中心数据存储出现问题会影响整个系统。
535 |
536 | 如电子白板系统、管理信息系统(MIS) 。
537 |
538 | 
539 |
540 | · 管道-过滤器结构
541 |
542 | 系统由若干构件(过滤器)按一定顺序组合而成,一个构件的输出是另一个构件的输入。
543 |
544 | 适合于批处理系统,不适用于交互式应用系统。
545 |
546 | 编译器就是一种管道-过滤器系统,包括词法分析、语法分析、字节码生成等。
547 |
548 | 图像处理系统等也大多采用该风格。
549 |
550 | 
551 |
552 | 
553 |
554 | · 调用返回结构
555 |
556 | (1) 主程序/子程序结构
557 |
558 | 
559 |
560 | (2) 远程过程调用结构:主程序/子程序中的构件分布在网络中的多台计算机。
561 |
562 | 如:如分布式计算系统Hadoop。
563 |
564 | 
565 |
566 | 调用返回结构缺点:
567 |
568 | 主构件需要预先知道被调子构件的接口标识。
569 |
570 | 构件接口标识的更改会影响所有调用它的其它构件,而且这种现象还会进行传递,导致更大的负面影响。
571 |
572 | · 面向对象结构
573 |
574 | 构造单元:类和对象
575 |
576 | 连接:基于消息机制。
577 |
578 | 拓扑结构:不同对象之间是平级的,没有主次之分
579 |
580 | 
581 |
582 | · 消息总线结构
583 |
584 | 构件不直接调用其它构件,而是广播一个或多个事件。
585 |
586 | 系统中的构件注册(监听)一个或多个事件源;
587 |
588 | 当一个事件被广播,系统自动调用该事件中注册的构件。
589 |
590 | 
591 |
592 | 消息总线风格逐渐演变为**消息中间件**。消息中间件应用场景:系统解耦、异步通讯、削峰。
593 |
594 | 下图为传统方式下系统B、C与A之间的通信连接,随着新的D、E、F、G系统的增加,必然导致巨大的维护成本(加入或退出均需要维护A)。
595 |
596 | 
597 |
598 | 优点:扩展简单。系统无须知道其他子系统接口名、位置的情况下,就可以激活其它子系统。
599 |
600 | 消息中间件产品:ActiveMQ、RabbitMQ
601 |
602 | 
603 |
604 | 
605 |
606 | · 层次化结构
607 |
608 | 系统被组织成若干个层次,每层都由一系列构件组成。
609 |
610 | 同层内构件可相互调用。
611 |
612 | 层之间存在调用接口,但只限于相邻层,下层可为上层服务,并作为再下一层客户。
613 |
614 | 
615 |
616 | · 客户-服务器结构
617 |
618 | 源于计算任务和计算资源的能力差异。
619 |
620 | 构件分布在两台或多台计算环境中。
621 |
622 | 演变:三层,多层C/S,B/S体系结构
623 |
624 | · MVC(Model-View-Controller)
625 |
626 | 常用于Web应用系统。
627 |
628 | 将系统分解为应用逻辑、用户界面、控制逻辑等不同构件类型。
629 |
630 | 优势:
631 |
632 | ·任何一种构件的改变都不会对其它构件造成影响。
633 |
634 | ·一个模型能为多个视图提供数据。
635 |
636 | 
637 |
638 | · 微服务架构
639 |
640 | 单体架构:应用打包(如war)部署为一个独立的单元,通过一个进程方式运行。
641 |
642 | 微服务架构:
643 |
644 | · 应用(功能)被分割成更小的、独立的服务,各个微服务之间的关联通过RPC(同步调用)或MQ(异步调用)实现。
645 |
646 | · 独立的微服务不需要部署在同一个虚拟机或应用服务器中。
647 |
648 | 
649 |
650 | · 混合风格
651 |
652 | 大规模系统往往包括多种体系结构风格
653 |
654 | 
655 |
656 |
657 |
658 | 【体系结构描述】
659 |
660 | 关注点:为谁描述哪些内容?用什么符号体系或描述语言?
661 |
662 | 程序员说:体系结构就是要决定需要编写哪些类、使用哪些现成框架。
663 |
664 | 程序经理说:体系结构就是模块的划分和接口的定义。
665 |
666 | 数据库工程师说:体系结构规定了持久化数据的结构,其他不过是对数据的操作而已。
667 |
668 | 用户说:体系结构就是决定一个个功能子系统如何划分。
669 |
670 | 这些描述我们都需要。每个视角代表一类利益相关者,反应了系统结构的一个侧面。
671 |
672 | 系统体系结构多从逻辑架构、物理架构和开发架构等视角描述。
673 |
674 | **·** **逻辑架构**关注的是功能构件,包含用户可见的功能构件,以及不可见的功能构件。
675 |
676 | **·** **物理架构**关注网络、服务器等基础设施及其拓扑结构。
677 |
678 | · **开发架构**更关注程序包,除自己写的程序外,还包括应用程序依赖的SDK、第三方类库等。
679 |
680 | 【体系结构设计方法】
681 |
682 | 基本设计思路:
683 |
684 | 
685 |
686 | 包括:
687 |
688 | · 面向对象体系结构设计
689 |
690 | · 传统结构化设计
691 |
692 | 【面向对象体系结构设计方法】
693 |
694 | 1. 定义系统交互的外部环境和交互特性
695 |
696 | (1) 目的是识别系统的外部实体与接口,定义接口构件
697 |
698 | 2. 识别一组结构原型(archetypes)
699 |
700 | (1) 原型是系统中最核心的抽象类或模式,目标系统的体系结构可由这些原型组成。
701 |
702 | (2) 原型是系统中最稳定的元素,可以基于系统行为以不同方式对这些元素实例化。
703 |
704 | (3) 多数情况下,原型可以通过分析类来获得。
705 |
706 | 3. 对每个结构原型进一步细化,以完善系统结构。
707 |
708 | 例子:对图书管理系统体系结构设计
709 |
710 | (1) 先采用“包图”划分子系统。
711 |
712 | 
713 |
714 | (2) 针对“借书”需求,识别结构原型
715 |
716 | 
717 |
718 | (3) 对“借书”构件,采取MVC风格进行细化
719 |
720 | 
721 |
722 | 【结构化体系结构设计方法】
723 |
724 | 目标:根据DFD的不同类型,通过对系统中模块的合理划分,得到软件体系结构图
725 |
726 | 体系结构风格:主程序/子程序风格
727 |
728 | 1. 将系统分割为多个功能模块
729 | 2. 确定各个模块之间的调用关系
730 | 3. 用系统结构图表示设计模型
731 |
732 | 步骤:
733 |
734 | (1) 分析确定数据流图类型。
735 |
736 | (2) 标识输入、输出流边界。
737 |
738 | (3) 依据变化或事务分析规则,将DFD图映射为顶层和第一层模块结构。
739 |
740 | (4) 对第一层中的模块继续细化和分解。
741 |
742 | (5) 利用启发式规则优化初始系统结构图。
743 |
744 | 变换分析和事务分析实例见PPT【体系结构设计】末尾
745 |
746 | 9. 构件级设计
747 |
748 | 【构件设计】是在体系结构设计的基础上,对其中每个构件内部构成的进一步设计。
749 |
750 | 体系结构设计相当于确定了计算机的部件组成,连接关系等。
751 |
752 | 构件设计则着重于设计每个部件的**内部细节**,如运算器的内部电路和元件等。
753 |
754 | 面向对象视角:
755 |
756 | 确定设计类并对其细化的过程。
757 |
758 | 结构化视角:
759 |
760 | 细化模块内部的数据结构、算法和接口的过程。
761 |
762 | 【构件】是计算机软件中的一个模块化的构造块。它部件**封装**了实现并暴露一系列**接口**。
763 |
764 | 面向对象视角:
765 |
766 | 构件封装了一组相互协作的类(也可以是一个类)。
767 |
768 | 结构化视角:
769 |
770 | 构件也称功能模块(如系统中图像读入模块、图像压缩模块)
771 |
772 | 封装了数据结构、算法和接口
773 |
774 | 【面向对象构件构成】
775 |
776 | 面向对象构件可能由多个设计类构成
777 |
778 | (1) 构件接口与实现需要严格分离。
779 |
780 | (2) 基于设计框架,一个构件需要分解为多个设计类。
781 |
782 | 【面向对象构建设计关键问题】
783 |
784 | 1. 构件由哪些设计类组成?
785 | 2. 设计类之间是什么关系,如何优化?
786 | 3. 构件提供的接口是什么?
787 | 4. 每个设计类的详细构成(属性和方法)?
788 |
789 | 前3个问题都与设计优化原则相关
790 |
791 | 通过设计优化,可以提高构件复用性,灵活适应系统变更,并减少副作用的传播。
792 |
793 | 【构件设计指导原则】
794 |
795 | 1. 开闭原则(OCP)
796 |
797 | 对扩展开放:构件的行为是可扩展或改变的
798 |
799 | 对修改关闭:当构件改变行为时,不要修改其源码
800 |
801 | 实现途径:用抽象构建框架,用继承/实现扩展细节。
802 |
803 | 需求变化时,不是通过修改类本身来完成,而是通过扩展一个子类来改变构件的行为。
804 |
805 | 优点:尽量不修改原有的代码,实现一个热插拔的效果。
806 |
807 | 2. Liskov替换原则(LSP)
808 |
809 | LSP 原则用来指导继承关系中子类该如何设计,子类的设计要保证在替换父类的时候,不改变原有程序的逻辑以及不破坏原有程序的正确性。
810 |
811 | 简单理解:子类可以扩展父类的功能,但不能改变父类原有的功能。
812 |
813 | LSP原则能减少代码冗余,避免运行期的类型判别(实现动态加载)。
814 |
815 | 3. 依赖倒置原则
816 |
817 | 依赖于抽象,而非具体实现。 具体方法是:首先,分离接口和实现。将类之间的依赖关系建立在高层抽象(如抽象类、接口)基础上。
818 |
819 | 优点:减少类间的耦合性,提高系统的稳定性
820 |
821 | 4. 接口分离原则
822 |
823 | 建立单一接口,不要建立臃肿庞大的接口。即:接口尽量细化,同时接口中的时间尽量少。
824 |
825 | 5. 单一职责原则:一个类或接口只承担一类责任。
826 | 6. 迪米特法则:尽量减少对象之间的交互,从而减小类之间的耦合。
827 |
828 | 内聚性和耦合性
829 |
830 | **内聚性**意味着构件只封装那些密切相关的类,或者类只封装自身密切相关的属性和操作。
831 |
832 | 根据程度可细分为:功能内聚、分层内聚、通信内聚等
833 |
834 | **耦合性**是类之间彼此联系程度的一种定性度量。
835 |
836 | 根据程度可细分为:内容耦合、共用耦合、控制耦合、标记耦合……
837 |
838 | 【面向对象构件设计过程】
839 |
840 | 1. 识别构件中与问题域相对应的设计类。包括界面类、控制类、实体类。
841 |
842 | (1) 一般可为每个用例设计一个控制类。如果多个用例中任务较为相似,也可以公用一个控制类。
843 |
844 | (2) 如果实体类的职责比较单一,直接将其映射为设计类;
845 |
846 | (3) 如果某类的职责过于复杂,应该将其分解为多个设计类(单一职责)。
847 |
848 | 2. 识别构件中与基础设施相对应的设计类。 这些设计类往往在分析模型中并没有定义。
849 | 3. 细化所有的设计类,定义该类中所有的接口、属性和操作。
850 |
851 | (1) 通过设计时序图或协作图说明协作细节。
852 |
853 | 将时序图中职责分解为具体操作,并分配给相关类;
854 |
855 | 定义操作对应的方法名,方法参数,返回值、可见性等。
856 |
857 | (2) 为每个构件确定合适的接口。
858 |
859 | 简单构件可直接定义public方法作为接口;
860 |
861 | 复杂构件单独定义接口类,构件负责实现接口;
862 |
863 | 确定接口的参数;
864 |
865 | (3) 细化属性,并定义相应的数据类型和数据结构。
866 |
867 | (4) 描述类成员方法中的处理逻辑。绘制程序流程图或活动图。
868 |
869 | 4. 说明持久数据源 (数据库或文件),并确定管理数据源所需要的类。
870 |
871 | (1) 对象可暂存于内存中,但要持久保存,需要通过数据存储实现。
872 |
873 | (2) 可以通过对象关系映射(ORM)将类映射为表,以简化数据库使用。
874 |
875 | 5. 细化**部署图**以提供额外的实现细节。
876 |
877 | (1) 为系统选择硬件配置和运行平台;
878 |
879 | (2) 将类、包、子系统分配到各个硬件结点上。
880 |
881 | 构建设计实例见PPT【构件级设计】中的实例部分
882 |
883 | 【传统构件设计过程】
884 |
885 | · 确定每个模块的算法,用工具描述算法逻辑。
886 |
887 | · 确定每一模块的数据结构。
888 |
889 | · 确定模块接口细节。
890 |
891 | 常用算法描述工具包括
892 |
893 | · 程序流程图
894 |
895 | · 问题分析图(PAD)
896 |
897 | 
898 |
899 | · 盒图(N-S图)
900 |
901 | 
902 |
903 | · 伪代码(PDL)
904 |
905 |
906 |
907 | 10. 用户界面设计
908 |
909 | 【UI设计】
910 |
911 | 软件强大的计算能力和功能,最终要通过界面来表现。
912 |
913 | 用户界面是软件的直观形象,直接影响用户对软件的体验。
914 |
915 | 用户通常从用户界面(而非功能)的好坏来评价软件的质量。
916 |
917 | 【常见UI设计错误】
918 |
919 | · 缺乏一致性
920 |
921 | · 太多需要记忆的
922 |
923 | · 没有指导和帮助
924 |
925 | · 没有上下文敏感性
926 |
927 | · 无意义的反馈
928 |
929 | · 界面复杂
930 |
931 | 【黄金法则】(这部分看书P198)
932 |
933 | 1. 把控制权交给用户(让用户掌握一切)
934 |
935 | (1) 提供灵活的交互。允许用户选择使用键盘、语音、鼠标等多种交互方式。
936 |
937 | (2) 允许用户交互被中断和撤销。如在手机编写短信时,允许接听电话,并能找到之前正在编写的短信。
938 |
939 | (3) 允许定制交互。
940 |
941 | (4) 将用户和内部技术细节隔离开。
942 |
943 | (5) 设计应允许用户与出现在屏幕上的对象直接交互。
944 |
945 | 2. 减轻用户的记忆负担
946 |
947 | 经验表明,需要记住的东西越多,交互出错的概率越大。
948 |
949 | (1) 减少对短期记忆的要求。
950 |
951 | (2) 建立有意义的默认设置。
952 |
953 | (3) 定义直观的快捷方式。
954 |
955 | (4) 界面的视觉布局应该基于真实世界的象征。
956 |
957 | (5) 以一种渐进的方式揭示信息。
958 |
959 | 3. 保持界面一致
960 |
961 | (1) 在完整的产品线上保持设计规则的一致性。
962 |
963 | (2) 如果过去的交互方式已经建立起用户期望,除非有不得已的理由,否则不要改变它。
964 |
965 | 4. 补充规则
966 |
967 | (1) 反馈:对用户的操作,应该给予及时、明确的反馈,并提供上下文帮助。
968 |
969 | (2) 宽容性:允许用户犯错,并能帮助用户从错误中及时恢复出来。
970 |
971 | (3) 个性化:允许用户根据自己的喜好定制界面元素、布局等。
972 |
973 | (4) 美观性
974 |
975 | 【UI设计过程】
976 |
977 | 
978 |
979 | 【接口/界面分析】
980 |
981 | 接口分析是指理解
982 |
983 | (1) 通过接口与系统交互的人员(最终用户);
984 |
985 | (2) 终端用户完成工作必须执行的任务;
986 |
987 | (3) 作为接口一部分呈现的内容;
988 |
989 | (4) 这些任务将被执行的环境。
990 |
991 | 成分:
992 |
993 | 1. 用户分析(看书P203)
994 | 2. 任务分析与建模
995 |
996 | 根据用例模型中的场景描述,将其映射为人机界面上的一组子任务
997 |
998 | 3. 显示内容分析
999 |
1000 | 根据每项任务确定其呈现的界面内容。
1001 |
1002 | 【界面设计】
1003 |
1004 | 对每项任务对应的界面进行**交互设计**和**视觉设计**。
1005 |
1006 | 交互设计的重点包括:交互流程、交互方式。
1007 |
1008 | 【交互流程设计】
1009 |
1010 | 1. 定义界面对象和动作
1011 | 2. 定义可能导致界面变化的事件
1012 | 3. 界面应该如何变化
1013 | 4. 想告诉用户什么?
1014 |
1015 | 好的交互方式可以让用户更简单、方便的使用产品。
1016 |
1017 | 【视觉设计】
1018 |
1019 | 视觉设计是指:针对眼睛的主观形式的表现手段和结果。
1020 |
1021 | 主要考虑界面的布局、数据的呈现方式、色彩搭配等
1022 |
1023 | 【界面设计工具】
1024 |
1025 | Visio、Axure
1026 |
1027 | 【设计评审】
1028 |
1029 | 所有设计工作完成后,为保证设计质量,需要对所有设计成果,包括**体系结构、构件、接口、数据模型**等进行综合设计评审。
1030 |
1031 |
1032 |
1033 |
1034 |
1035 | ### (六)测试
1036 |
1037 | 11. 软件测试策略
1038 |
1039 | 【测试的目的】
1040 |
1041 | 测试是选择适当的测试用例并执行被测程序的过程。
1042 |
1043 | 目的在于**发现错误**,而不是为了验证程序不存在错误。
1044 |
1045 | 好的测试用例可以发现今未发现的错误。
1046 |
1047 | 【测试策略】
1048 |
1049 | 一般特征:
1050 |
1051 | · 未完成有效的测试,应该进行有效的、正式的技术评审。通过评审,许多错误可以在测试开始之前排除。
1052 |
1053 | · 测试开始于构件层,然后向外“延申”到整个基于计算机系统的继承中。
1054 |
1055 | · 不同的测试技术适用于不同的软件工程方法和不同的时间点。
1056 |
1057 | · 测试由软件开发人员和(对大型项目而言)独立的测试组执行。
1058 |
1059 | · 测试和调试是不同的活动,但任何测试策略都必须包括调试。
1060 |
1061 | 策略:
1062 |
1063 | 1. 测试不能取代评审
1064 |
1065 | 据说,检验项目质量的标准之一:质量 = 项目review时骂的次数 / 项目review时间。
1066 |
1067 | 被骂的次数越多,评审耗时越短,质量越可靠。
1068 |
1069 | 2. 谁来测试?
1070 |
1071 | (1) 开发者:对系统很了解,但由于急于交付,测试比较“gentle”
1072 |
1073 | (2) 独立测试人员:虽然对系统没有特别了解,但为了质量会尝试尽可能找出所有问题
1074 |
1075 | 3. 测试什么时候开始?
1076 |
1077 | 软件测试**不是在编码阶段**才开始,软件测试从**项目确立**时就开始了,主要经过以下环节:
1078 |
1079 | 需求分析→测试计划→测试设计→测试环境搭建→测试执行→测试记录。
1080 |
1081 | 4. 测试流程
1082 |
1083 | 从模块由小到大进行测试。
1084 |
1085 | 
1086 |
1087 | 【传统软件的测试策略:单元测试】(参考书P251-253)
1088 |
1089 | 目的:验证开发人员编写的模块或单元是否符合预期。
1090 |
1091 | 单元测试问题:
1092 |
1093 | · 说明不正确或不一致;
1094 |
1095 | · 初始化或缺省值错误;
1096 |
1097 | · 数据类型不相容;
1098 |
1099 | · 上溢、下溢或地址错误等。
1100 |
1101 | · 全局数据与模块的相互影响。
1102 |
1103 | 单元测试环境:
1104 |
1105 | 
1106 |
1107 | 驱动模块:用来模拟被测模块的上级调用模块。
1108 |
1109 | 桩模块:模拟被测试模块所调用的模块,返回被测模块所需的信息。
1110 |
1111 | 【传统软件的测试策略:集成测试】
1112 |
1113 | 通过单元测试的模块集成在一起,仍然可能无法正常工作,因为模块相互调用时仍然可能出错。
1114 |
1115 | 集成测试:旨在发现与调用接口相关的错误。
1116 |
1117 | **自顶向下集成**:
1118 |
1119 | 
1120 |
1121 | **自底向上集成**:
1122 |
1123 | 
1124 |
1125 | **三明治集成**:
1126 |
1127 | 
1128 |
1129 | **回归测试:**
1130 |
1131 | 集成测试中每加入新的模块,都会导致软件发生变更,这些变更可能使得原本正常工作的模块产生问题。
1132 |
1133 | 回归测试就是重新执行已经测试过的某些子集,以确保变更不会引入新的或额外的错误。
1134 |
1135 | 回归测试可以复用之前的测试用例和测试脚本。
1136 |
1137 | 可以使用自动测试工具提高回归测试效率。
1138 |
1139 | 捕获-回放工具(如WinRunner)能够捕获在测试过程中传递给软件的输入数据,生成执行的脚本,并且在回归测试中,重复执行该过程。
1140 |
1141 | **冒烟测试:**
1142 |
1143 | 冒烟测试也是一种特殊的集成测试,指完成一个新版本的集成、构建后,对该版本最基本的功能进行测试,目的是**保证基本的功能和流程能走通**。
1144 |
1145 | 如果通不过,则打回开发部门重新开发;如果通过测试,才会进行下一步的测试(功能测试,集成测试,系统测试等)。
1146 |
1147 | 例如,冒烟测试内容:
1148 |
1149 | 检查被测系统或模块能否正常启动和退出;
1150 |
1151 | 数据库能否正常连接,控件能否正常加载;
1152 |
1153 | 是否存在严重错误或者数据严重丢失等。
1154 |
1155 | 【面向对象的单元与集成测试】
1156 |
1157 | 类测试相当于单元测试。我们将测试该类内的操作。
1158 |
1159 | 集成采用了三种不同的策略。传统的自顶向下或自底向上的集成测试策略在面向对象软
1160 |
1161 | 件的集成测试中无意义。
1162 |
1163 | 1. 基于类之间的协作关系进行集成。
1164 | 2. 基于线程的测试—集成了响应一个输入或事件所需的类集。
1165 | 3. 基于使用的测试——从测试独立类开始,然后测试使用独立类的依赖类。
1166 |
1167 | 【确认测试】
1168 |
1169 | 确认测试:检验所开发的软件是否满足需求规格说明中的各种功能和性能需求,以及软件配置是否完全和正确。
1170 |
1171 | α测试是由用户在开发环境下进行的测试;β测试是由软件的多个用户在实际使用环境下进行的测试。可归为确认测试,产品正式发布前的测试,由用户主导。
1172 |
1173 | 【系统测试】
1174 |
1175 | 系统测试是将软件与其它系统部分(如外部系统,硬件设计等)结合进行的整体测试。其关注非功能性需求。
1176 |
1177 | 系统测试主要包括一下几种类型:
1178 |
1179 | 1. 恢复测试:有些系统失效后必须在规定时间段内被恢复,否则将会导致严重的经济损失。关注导致软件运行失败的各种条件,并验证其恢复过程能否正确执行。(如:系统供电故障后的恢复、日志处理恢复能力、程序运行崩溃后恢复能力)
1180 | 2. 安全测试:检测系统对非法侵入的防范能力。如口令截取或破译等。
1181 |
1182 | IBM AppScan,包括众多的安全扫描产品,如针对源代码扫描的AppScan source edition, 针对WEB应用扫描的AppScan standard edition,进行安全管理和汇总整合的AppScan enterprise Editio。
1183 |
1184 | 3. 压力测试
1185 |
1186 | 压力测试目的是为了发现系统能支持的最大负载等,前提是系统性能处在可以接受的范围内,如规定的3秒钟内响应。
1187 |
1188 | 压力测试通过不断对系统增加压力,确定一个系统的瓶颈或者不能接受的性能点,从而获得系统最大负载能力。
1189 |
1190 | 压力测试工具WebRunner:RadView公司推出的一个性能测试和分析工具,它让web应用开发者自动执行压力测试;webload通过模拟真实用户的操作,生成压力负载来测试web的性能。
1191 |
1192 | 4. 性能测试
1193 |
1194 | 通过测试确定系统(常态下)运行时的性能表现,如运行速度、响应时间、占有系统资源等方面的系统数据。
1195 |
1196 | 性能测试工具LoadRunner:它能预测系统行为,优化性能。它通过模拟实际用户的操作行为和实行实时性能监测。
1197 |
1198 | 【软件调试】
1199 |
1200 | 调试目标:定位错误发生的原因和位置。
1201 |
1202 | 调试技巧:
1203 |
1204 | (1)暴力法:一种比较简单,但效率较低的方法。包括:
1205 |
1206 | ① 主存信息输出法。
1207 |
1208 | 将计算机存储器和寄存器的全部内容打印出来。
1209 |
1210 | ② 关键部分设置打印语句。
1211 |
1212 | ③ 使用自动调试工具。
1213 |
1214 | (2)反向跟踪:是从可能的错误征兆处逐步向回追溯,直到找准错误,纠正为止。
1215 |
1216 | (3)归纳法:从线索(错误征兆出发),通过分析这些线索之间的关系找出故障。主要有4步:
1217 |
1218 | ① 收集数据。列出已知的测试用例和执行结果。
1219 |
1220 | ② 整理分析数据,以便发现规律,即“什么条件下出现错误,什么条件下不出现错误”。如:字符计数程序对“输入型”文本正确,对“拷贝型”文本错误。
1221 |
1222 | ③ 导出假设。分析线索之间的关系,提出关于错误的一个或多个假设。
1223 |
1224 | ④ 证明假设。证实提出的假设是导致错误发生的真正原因。
1225 |
1226 | (4)演绎法
1227 |
1228 | ① 设想出所有可能的出错原因;
1229 |
1230 | ② 试图用测试来排除每一个假设的原因,如果测试表明某个假设的原因可能是真的原因,则对数据进行细化以确定位错误。
1231 |
1232 |
1233 |
1234 | 12. 传统应用测试
1235 |
1236 | 【关于测试的两个问题】
1237 |
1238 | 1. 经过测试没有发现错误的软件就一定正确吗?错误。测试只能证明软件是有错的,不能证明软件是没有错误的。
1239 | 2. 可以通过穷举方式测试软件吗?一般不行,因为分支或循环太多会导致所需测试样例的数量呈指数型增长。
1240 |
1241 | 【如何设计好的测试用例?】
1242 |
1243 | 测试的有效性很大程度取决于选取的测试用例。
1244 |
1245 | 一个好的测试有很高的概率找到一个错误的;测试不是冗余的;一个好的测试应该是“最好的品种”。
1246 |
1247 | 【测试用例设计方法】
1248 |
1249 | 黑盒法:测试者把测试对象看作一黑盒子,仅依据程序的功能需求,设计测试用例并推断测试结果。
1250 |
1251 | 白盒法:按照程序内部逻辑结构,设计测试数据并完成测试的一种测试方法。
1252 |
1253 | 【白盒测试】
1254 |
1255 | 该方法把测试对象看做一个透明的盒子,它允许测试人员利用程序内部的逻辑结构及有关信息,设计或选择测试用例。
1256 |
1257 | 目标是使得程序中各元素(如语句、判定)尽可能被覆盖到。
1258 |
1259 | 白盒测试一般在测试过程的早期执行。
1260 |
1261 | 方法:
1262 |
1263 | 1. 语句覆盖:指选择足够的测试用例,使得被测程序中每条语句至少执行一次。是一种比较弱的测试标准。
1264 | 2. 基本路径测试
1265 |
1266 | 如果程序中含有循环结构,完全的路径覆盖是不可能的。
1267 |
1268 | **基本路径法**:在程序控制流图的基础上,通过导出基本可执行路径(注: 不是所有可能路径)集合,从而设计测试用例。
1269 |
1270 | 【重点掌握,见PPT(传统应用测试)】
1271 |
1272 | 3. 控制结构测试
1273 |
1274 | (1) 条件测试:一种测试程序模块中包含的逻辑条件的测试用例设计方法
1275 |
1276 | 设计测试用例确保至少条件C为真为假执行各一次。如果C是复合条件,则同时还要满足每个简单条件至少执行一次。
1277 |
1278 | 
1279 |
1280 | (2) 数据流测试:根据程序中定义的位置和变量的使用情况来选择程序的测试路径
1281 |
1282 | 设计测试用例使得每个变量定义-使用链至少覆盖一次。
1283 |
1284 | 
1285 |
1286 | (3) 循环测试:分为简单循环、嵌套循环、串接循环、非结构化循环。
1287 |
1288 | 对于简单循环,下列测试集可以用于简单循环:
1289 |
1290 |
1291 |
1292 | 
1293 |
1294 | 【黑盒测试】
1295 |
1296 | 这种方法是把测试对象看做一个黑盒子,测试人员完全不考虑程序内部的逻辑结构,只依据需求规格说明书,检查程序的功能是否符合它的功能说明。
1297 |
1298 | 黑盒测试一般在应用于测试的后期阶段。
1299 |
1300 | 1. 等价类划分
1301 |
1302 | 等价类划分法:将程序的输入域划分为若干个数据类,从中生成测试用例。
1303 |
1304 | 假定:对等价类中的代表值测试就等于对这一类值的测试。
1305 |
1306 | 
1307 |
1308 | 基本步骤: (1)确定等价类;(2)为等价类选择一个测试用例
1309 |
1310 | 例子:某城市的电话号码由3部分组成。假定被测程序能接收一切符合下述规定的电话号码,拒绝所有不符合规定的电话号码。
1311 |
1312 | 地区码:空白或3位数字;
1313 |
1314 | 前缀:非‘0’或‘1’开头的3位数字;
1315 |
1316 | 后缀:4位数字。
1317 |
1318 | (1) 确定等价类
1319 |
1320 | 
1321 |
1322 | (2) 设计测试用例
1323 |
1324 | 设计测试用例,使其尽可能多的覆盖到尚未覆盖的有效等价类
1325 |
1326 | 设计测试用例,使其只覆盖一个尚未被覆盖的无效等价类
1327 |
1328 | 
1329 |
1330 | 2. 边界值分析
1331 |
1332 | (1) 边界值应该尽可能选择等于边界,略小于边界,略大于边界的值
1333 |
1334 | (2) 边界值法可与等价类划分法结合,作为对其的一种补充。
1335 |
1336 | 例子: 一个输入文件应该包含1~255条记录,则应用边界值分析法设计测试用例。
1337 |
1338 | 可以用4组数据进行测试:
1339 |
1340 | 含1条记录的文件
1341 |
1342 | 含2条记录的文件
1343 |
1344 | 含254条记录的文件
1345 |
1346 | 含255条记录的文件
1347 |
1348 | 3. 正交阵列测试
1349 |
1350 | (1) 正交数组测试通过挑选适量的、有代表性的点进行试验,能有效地减少测试用例数,节约测试成本。
1351 |
1352 | (2) 该方法由日本口玄一博士提出并导出正交数组,从而使得测试数据具有“均匀分散、整齐可比”的特点。
1353 |
1354 | 例子:某大学刚考完某门课程,想通过“性别”、“班级”和“成绩”这3个查询条件对这门课程的成绩查询,查询条件包括:
1355 |
1356 | “性别”=“男,女”
1357 |
1358 | “班级”=“1班,2班”
1359 |
1360 | “成绩”=“及格,不及格”
1361 |
1362 | 一般需要设计2X2X2=8个测试用例。
1363 |
1364 | 
1365 |
1366 | 【基于模型的测试】
1367 |
1368 | 1. 分析软件的现有行为模型或创建一个。
1369 | 2. 穿越行为模型,并指定迫使软件从状态转换到另一个状态的输入。
1370 |
1371 | (1) 输入将触发将导致转换发生的事件。
1372 |
1373 | 3. 回顾行为模型,并注意到软件从状态过渡到状态时的预期输出。
1374 | 4. 执行测试用例。
1375 |
1376 | 
1377 |
1378 |
1379 |
1380 |
1381 |
1382 | ### 例题
1383 |
1384 | 1. 过程框架至少定义了五种框架活动分别是( )。
1385 |
1386 | 2. 类-职责-协作者模型又称为( )建模。
1387 |
1388 | 3. 软件工程层次图中,支持软件工程的根基在于( )。
1389 | 4. 填空题:在UML模型中,( )图用于描述系统与外部系统及用户之间的交互;( )图用于按时间顺序描述对象间的交互。
1390 | 5. 基于大量构件共同使用一个全局变量时所发生的耦合称为( )耦合。
1391 | 6. 华为云(DevCloud)是一个一站式、全流程、安全可信的( )平台。
1392 | 7. 华为云(DevCloud)敏捷开发的“看板”核心元素包括分层、( )、列、价值流、在制品(WIP)、风险&瓶颈、拉动式开发等核心元素。
1393 | 8. 顺序图(时序图)的构成元素主要包括: ( )、生命线、激活和( )。
1394 | 9. 汽车类与方向盘类之间的关系是( )关系。
1395 |
1396 | **重庆大学《软件工程》课程试卷(A 卷) 2019 — 2020 学年 第 2 学期**
1397 |
1398 | 1. FURPS 质量属性分别是指:功能性、( )、( )、性能和( )。
1399 |
1400 | 2. 在基于类的需求建模中,类可分为: ( )、( )和( )。
1401 |
1402 | 3. 需求工程是指( )。
1403 |
1404 | 4. 软件质量的成本包括:( )、( )和( )。
1405 |
1406 | 5. 一个通用的软件工程过程框架通常包含 沟通、( )、建模、( ) 和( )。
1407 |
1408 | 6. 开闭原则是指模块或构件应该对外延具有开放性,对( )具有封 闭性。
1409 |
1410 | 7. 需求模型必须实现的三个主要目标有: ( )、( )、定义在软 件完成后可以被确认的一组需求
1411 |
1412 | 8. OMG 定义构件是:系统中( )、可部署的和可替换的部件。
1413 |
1414 | 9. 用户满意度=合格的产品+( ) +( ) 10.CRC 卡中 CRC 的中文全称( )。
1415 |
1416 | > **参考答案**
1417 | >
1418 | > 1. (易用性)、(可靠性)、(可支持性)
1419 | > 2. (实体类)、(边界类)、(控制类)
1420 | > 3. (致力于不断理解需求的大量任务和技术)
1421 | > 4. (预防成本)、(评估成本)、(失效成本)
1422 | > 5. (策划)、(构建)、(部署)
1423 | > 6. ( 修改 )
1424 | > 7. (描述客户需要什么)、(为软件设计奠定基础)
1425 | > 8. (模块化的)
1426 | > 9. (好的质量)、(按预算和进度安排交付)
1427 | > 10. (类-职责-协作者)
1428 |
1429 | ## 二、单选题 (10个,每个2分,共20分)
1430 |
1431 | 看填空题的索引
1432 |
1433 | ### 需要理解的内容
1434 |
1435 | 1. 如何判断什么时候该用什么样的过程模型。
1436 |
1437 |
1438 |
1439 |
1440 |
1441 |
1442 |
1443 | ### 例题
1444 |
1445 | 1. 某软件公司欲开发一个基于Web的考勤管理系统。在项目初期,客户对系统的基本功能、表现形式等要求并不明确,在这种情况下,采用( )开发方法比较合适。
1446 |
1447 | A、瀑布模型
1448 |
1449 | B、形式化
1450 |
1451 | C、结构化
1452 |
1453 | D、极限编程
1454 |
1455 | 2. 在类图中下列哪个符号表示的是泛化关系是( )
1456 |
1457 | A、实线实心箭头
1458 |
1459 | B、虚线实心箭头
1460 |
1461 | C、实线空心箭头
1462 |
1463 | D、实线空心菱形
1464 |
1465 | 3. 在设计模式中“依赖于抽象,而非具体的实现”指的是( )
1466 |
1467 | A、开闭原则
1468 |
1469 | B、Liskov替换原则
1470 |
1471 | C、依赖倒置原则
1472 |
1473 | D、接口分离原则
1474 |
1475 | 4. 软件质量是一个重要的问题贯穿了软件的( )
1476 |
1477 | A、生存周期
1478 |
1479 | B、设计阶段
1480 |
1481 | C、编码阶段
1482 |
1483 | D、测试阶段
1484 |
1485 | ## 三、判断题 (5个,每个2分,共10分)
1486 |
1487 |
1488 |
1489 |
1490 |
1491 | ### 例题
1492 |
1493 | 1. 软件工程是一种结构化的技术。( )
1494 | 2. 每个应用系统只能使用一种体系结构风格。( )
1495 | 3.
1496 |
1497 |
1498 |
1499 |
1500 |
1501 | ## 四、简答题 (4个,每个5分,共20分)
1502 |
1503 | 看填空题的索引即可
1504 |
1505 |
1506 |
1507 | ### 例题
1508 |
1509 | 1. 简述David Hooker提出的7个关注软件工程整体实践的原则。(要点+一两句的补充说明)。
1510 | 2. 简述模块独立性的两个定量准则及模块独立性的好处。
1511 |
1512 |
1513 |
1514 |
1515 |
1516 | ## 五、应用分析题(2个,每个15分,共30分)
1517 |
1518 | ### (一)需求建模
1519 |
1520 | 1. 结构化分析——数据流图
1521 |
1522 | https://www.bilibili.com/video/BV1Jt411d7nR
1523 |
1524 |
1525 |
1526 | > #### 例题
1527 | >
1528 | > 某时装邮购提供商拟开发订单处理系统,用于处理客户通过电话、传真、邮件或Web站点所下订单。其主要功能如下:
1529 | >
1530 | > (1)增加客户记录。将新客户信息添加到客户文件,并分配一个客户号以备后续使用。
1531 | >
1532 | > (2)查询商品信息。接收客户提交商品信息请求,从商品文件中查询商品的价格和可订购数量等商品信息,返回给客户。
1533 | >
1534 | > (3)增加订单记录。根据客户的订购请求及该客户记录的相关信息,产生订单并添加到订单文件中。
1535 | >
1536 | > (4)产生配货单。根据订单记录产生配货单,并将配货单发送给仓库进行备货;备好货后,发送备货就绪通知。如果现货不足,则需向供应商订货。
1537 | >
1538 | > (5)准备发货单。从订单文件中获取订单记录,从客户文件中获取客户记录,并产生发货单。
1539 | >
1540 | > (6)发货。当收到仓库发送的备货就绪通知后,根据发货单给客户发货;产生装运单并发送给客户。
1541 | >
1542 | > (7)创建客户账单。根据订单文件中的订单记录和客户文件中的客户记录,产生并发送客户账单,同时更新商品文件中的商品数量和订单文件中的订单状态。
1543 | >
1544 | > (8)产生应收账户。根据客户记录和订单文件中的订单信息,产生并发送给财务部门应收账户报表。
1545 | >
1546 | > 问题:
1547 | >
1548 | > 1.使用说明中的词语,给出图1-1中的实体E1~E3的名称。
1549 | >
1550 | > 2.使用说明中的词语,给出图1-2中的数据存储D1~D3的名称。
1551 | >
1552 | > 3.(1)给出图1-2中处理(加工)P1和P2的名称及其相应的输入、输出流。(2)除加工P1和P2的输入输出流外,图1-2还缺失了1条数据流,请给出其起点和终点。
1553 | >
1554 | > 
1555 | >
1556 | > 
1557 |
1558 |
1559 |
1560 | 2. 面向对象分析——类图
1561 |
1562 | https://www.bilibili.com/video/BV1Jt411d7PR
1563 |
1564 |
1565 |
1566 | > #### 例题
1567 | >
1568 | > 某网上药店允许顾客凭借医生开具的处方,通过网络在该药店购买处方上的药品。该网上药店的基本功能描述如下:
1569 | >
1570 | > (1)注册。顾客在买药之前,必须先在网上药店注册。注册过程中需填写顾客资料以及付款方式(信用卡或者支付宝账户)。此外顾客必须与药店签订一份授权协议书,授权药店可以向其医生确认处方的真伪。
1571 | >
1572 | > (2)登录。已经注册的顾客可以登录到网上药房购买药品。如果是没有注册的顾客,系统将拒绝其登录。
1573 | >
1574 | > (3)录入及提交处方。登录成功后,顾客按照“处方录入界面”显示的信息,填写开具处方的医生的信息以及处方,上的药品信息。填写完成后,提交该处方。
1575 | >
1576 | > (4)验证**处方**。对于**已经提交的处方**(系统将其状态设置为“处方已提交”),其验证过程为:
1577 | >
1578 | > ①**核实医生信息**。如果医生信息不正确,该处方的状态被设置为“**医生信息无效**”,并取消这个处方的购买请求;如果医生信息是正确的,系统给该医生发送处方确认请求,并将处方状态修改为“审核中”。
1579 | >
1580 | > ②如果医生回复处方无效,系统取消处方,并将处方状态设置为**“无效处方**”。如果医生没有在7天内给出确认答复,系统也会取消处方,并将处方状态设置为“**无法审核**”。
1581 | >
1582 | > ③如果医生在7天内给出了确认答复,该处方的状态被修改为“准许付款”。系统取消所有未通过验证的处方,并自动发送一封电子邮件给顾客,通知顾客处方被取消以及取消的原因。
1583 | >
1584 | > (5)对于通过验证的处方,系统自动计算药品的价格并邮寄药品给已经付款的顾客。该网上药店:采用面向对象方法开发,使用UML进行建模。系统的类图如图3-1所示。
1585 | >
1586 | > 问题:
1587 | >
1588 | > 1. 根据说明中的描述,给出图3-1中缺少的C1~C5所对应的类名。
1589 | > 2. 图3-2给出了“处方”的部分状态图。根据说明中的描述,给出图3-2中缺少的S1 ~S4所对应的状态名以及(7)~(10)处所对应的迁移(transition) 名。
1590 | >
1591 | > 
1592 | >
1593 | > 
1594 |
1595 | 3. 面向对象分析——用例图
1596 |
1597 | 【例】
1598 |
1599 |
1600 |
1601 |
1602 |
1603 | > #### 例题
1604 | >
1605 | > 阅读下列说明和图,完善用例图A1、A2及U1~U3。
1606 | >
1607 | > 某网上购物平台的主要功能如下:
1608 | >
1609 | > (1)**创建订单**。**顾客**(Customer)在线创建订单(Order),主要操作是向订单中添加项目,从订单中删除项目。订单中应列出所订购的商品(Product)及其数量(Quantities)
1610 | >
1611 | > (2)提交订单。订单通过网络提交。在提交订单时,顾客需要提供其姓名(name)、收货地址(address)、付款方式(Payment)(预付卡、现金或信用卡)。
1612 | >
1613 | > (3)处理订单。**订单处理人员**接收来自系统的订单,根据订单内容,安排配货,制定送货计划。
1614 | >
1615 | > (4)派单。订单处理人员将已配好货的订单转交给派送人员。
1616 | >
1617 | > (5)**送货**/**收货**。派送人员将货物送到顾客指定的收货地址。顾客需在运货单上签收。签收后的运货单最终需交还给订单处理人员。
1618 | >
1619 | > (6)收货确认。当订单处理人员收到签收过的运货单后,会和顾客进行一次再确认。
1620 | >
1621 | > 
1622 |
1623 |
1624 |
1625 | 4. 面向对象分析——状态图
1626 |
1627 | 【例】
1628 |
1629 |
1630 |
1631 |
1632 |
1633 | 5. 面向对象分析——时序图
1634 |
1635 | 【例】
1636 |
1637 |
1638 |
1639 |
1640 |
1641 |
1642 |
1643 | ### (二)软件测试
1644 |
1645 | #### 2.1 测试用例的设计——白盒法
1646 |
1647 | ##### 2.1.1 控制结构测试
1648 |
1649 | 【软件工程——11-白盒测试】 https://www.bilibili.com/video/BV1wG41137Hs/?share_source=copy_web&vd_source=7ba452d8ee6f8b8a4b8ef831bf573bda
1650 |
1651 | 【白盒测试so easy!】 https://www.bilibili.com/video/BV1zL4y1A785/?share_source=copy_web&vd_source=7ba452d8ee6f8b8a4b8ef831bf573bda
1652 |
1653 | ##### 2.1.2 基本路径测试
1654 |
1655 | 【软件工程——11-基本路径测试法】 https://www.bilibili.com/video/BV13V4y1g7tc/?share_source=copy_web&vd_source=7ba452d8ee6f8b8a4b8ef831bf573bda
1656 |
1657 | #### 2.2 测试用例的设计——黑盒法
1658 |
1659 | ##### 2.2.1 等价类划分法
1660 |
1661 | 【软件工程——11-等价类划分.mp4】 https://www.bilibili.com/video/BV1MT411M7EC/?share_source=copy_web&vd_source=7ba452d8ee6f8b8a4b8ef831bf573bda
1662 |
1663 | ##### 2.2.2 边界值分析法
1664 |
1665 | 【软件工程——11-边界值及错误推测法】 https://www.bilibili.com/video/BV1nV4y1g7ig/?share_source=copy_web&vd_source=7ba452d8ee6f8b8a4b8ef831bf573bda
--------------------------------------------------------------------------------
/docs/index.md:
--------------------------------------------------------------------------------
1 | Hello world !!
--------------------------------------------------------------------------------
/mkdocs.yml:
--------------------------------------------------------------------------------
1 | site_name: Mine_qihang's Docs
2 | theme:
3 | name: "material"
4 | features:
5 | #- navigation.instant # 点击内部链接时,不用全部刷新页面
6 | - navigation.tracking # 在url中使用标题定位锚点
7 | - navigation.tabs # 顶部显示导航顶层nav(也就是第一个节点)
8 | - navigation.tabs.sticky # 滚动是隐藏顶部nav,需要配合navigation.tabs使用
9 | - navigation.sections # nav节点缩进
10 | - navigation.expand # 不折叠左侧nav节点
11 | - navigation.indexes # 指定节点index pages ,跟instant不兼容
12 | - toc.integrate # 右侧生产目录
13 | - navigation.top # 一键回顶部
14 | # plugins:
15 | # - search:
16 | # lang: jp
17 | markdown_extensions:
18 | - pymdownx.highlight # code hilight
19 | - pymdownx.superfences
20 | - pymdownx.arithmatex:
21 | generic: true
22 | extra_javascript:
23 | - javascripts/config.js
24 | - https://polyfill.io/v3/polyfill.min.js?features=es6
25 | - https://cdn.jsdelivr.net/npm/mathjax@3/es5/tex-mml-chtml.js
26 | nav:
27 | - 计算机系统结构:
28 | - Introduction: Architecture/chapter1.md
29 | - Principles of Quantitative Analysis; MIPS: Architecture/chapter2.md
30 | - Pipelining, Hazards, Implementation Issues: Architecture/chapter3.md
31 | - Instruction-Level Parallelism (ILP), Tomasulo: Architecture/chapter4.md
32 | - Memory-Hierarchy Design, Cache Optimization: Architecture/chapter5.md
33 | - ILP; Branch Prediction, Superscalars: Architecture/chapter6.md
34 | - Memory Hierarchy Design, Virtual Memory: Architecture/chapter7.md
35 | - 软件工程:
36 | - 软工期末考试: SoftwareEngineering/软工期末考试.md
37 | - 软工应用分析题: SoftwareEngineering/软工应用分析题.md
38 | - 计算机网络:
39 | - 第一次作业: ComputerNetwork/《计算机网络》第一次作业.md
40 | - 第二章作业: ComputerNetwork/《计算机网络》第二章作业.md
41 | - 第三章作业: ComputerNetwork/《计算机网络》第三章作业.md
42 | - 第四章作业: ComputerNetwork/《计算机网络》第四章作业.md
43 | - 第五章作业: ComputerNetwork/《计算机网络》第五章作业.md
44 | - 第六章作业: ComputerNetwork/《计算机网络》第六章作业.md
45 | - 第九章作业: ComputerNetwork/《计算机网络》第九章作业.md
46 | - 操作系统原理: OperatingSystem/index.md
47 | - 机器学习基础:
48 | - 第一章作业: MachineLearning/第一章作业.md
49 | - 第二章作业: MachineLearning/第二章作业.md
50 | - 第三章作业: MachineLearning/第三章作业.md
51 | - 第四章作业: MachineLearning/第四章作业.md
52 | - 第五章作业: MachineLearning/第五章作业.md
53 | - 第六章作业: MachineLearning/第六章作业.md
54 | - 第七章作业: MachineLearning/第七章作业.md
55 | - 第八章作业: MachineLearning/第八章作业.md
56 | - 第九章作业: MachineLearning/第九章作业.md
57 | - 自然语言处理: index.md
58 | - 专业基本能力测试: ProfessionalBasicAptitudeTest/index.md
--------------------------------------------------------------------------------
 116 |
117 | (2)A把数据发完。
118 |
119 |
116 |
117 | (2)A把数据发完。
118 |
119 |  120 |
121 | (3)收到确认1000号,因此窗口移到1001以后。
122 |
123 |
120 |
121 | (3)收到确认1000号,因此窗口移到1001以后。
122 |
123 |  124 |
125 | (4)再发送850B。
126 |
127 |
124 |
125 | (4)再发送850B。
126 |
127 |  128 |
129 | (5)发送方收到的ack已经不在窗口了,所以不变化.
130 |
131 |
128 |
129 | (5)发送方收到的ack已经不在窗口了,所以不变化.
130 |
131 |  132 |
133 | (6)收到确认2047号,因此窗口移到2048以后。
134 |
135 |
132 |
133 | (6)收到确认2047号,因此窗口移到2048以后。
134 |
135 |  136 |
137 | (7)A把数据发完。由于数据总大小为3kB,因此最多就到3072以前。
138 |
139 |
136 |
137 | (7)A把数据发完。由于数据总大小为3kB,因此最多就到3072以前。
138 |
139 |  140 |
141 | (8)全部都接收到了,窗口移到3072以后。
142 |
143 |
140 |
141 | (8)全部都接收到了,窗口移到3072以后。
142 |
143 |  144 |
145 |
146 |
147 | ## 5-68
148 |
149 | 假设A是发送端(主动打开连接的一方),B是接收端(被动打开连接的一方)。那么在TCP的连接建立过程中,如果第三个报文丢失,那么A就会建立TCP连接,B还是在SYN-RCVD阶段。
150 |
151 | - 如果此时A没有紧接着发送数据,那么B经过一段时间后就会回到CLOSED状态,需要重新建立连接。
152 | - 如果此时A紧接着发送数据,那么此时A发送的数据报中自己的序号没有改变,与丢失的确认帧序号相同,且确认位ACK=1,确认号也是B选择的初始序号加1。当B接收到此报文段后就进入ESTABLISHED状态,继续接收A发送的数据。此时,第三个报文丢失不会对TCP建立造成影响。
153 |
154 | 综上,第三个报文段不确认对于在A建立连接后长时间不传输数据会有影响,而对于A建立连接后立即开始传输数据不会有什么影响。
155 |
156 |
157 |
158 |
--------------------------------------------------------------------------------
/docs/ComputerNetwork/《计算机网络》第六章作业.md:
--------------------------------------------------------------------------------
1 | # 《计算机网络》第六章作业
2 |
3 | ## 6-02
4 |
5 | **答:**域名系统是互联网使用的命名系统,其主要功能就是把域名解析为IP地址。四类域名服务器的区别如下:
6 |
7 | | 域名服务器 | 说明 |
8 | | -------------- | ------------------------------------------------------------ |
9 | | 本地域名服务器 | 离用户较近;主机发出DNS查询时,首先发给本地域名服务器 |
10 | | 根域名服务器 | 最高层次、最重要的域名服务器;根域名服务器知道所有顶级域名服务器的域名和IP地址;当本地域名服务器无法解析时,首先求助于根域名服务器 |
11 | | 顶级域名服务器 | 负责管理该顶级域名服务器注册的所有二级域名;收到查询请求后就给出相应回答 |
12 | | 权限域名服务器 | 负责一个区的域名服务器;当权限域名服务器无法给出最后的回答时,会告诉请求方下一步找哪个权限域名服务器 |
13 |
14 |
15 |
16 | ## 6-15
17 |
18 | **答:**解析IP地址的时间为$\sum_{i=1}^n \text{RTT}_i$,建立TCP连接时间为$\text{RTT}_w$,请求万维网文档时间为$\text{RTT}_w$,因此,总时间为$\sum_{i=1}^n \text{RTT}_i + 2\text{RTT}_w$ 。
19 |
20 |
21 |
22 | ## 6-23
23 |
24 | **答:**1. **连接建立**:发件人将邮件发到发送方邮件服务器缓存中,SMTP客户每隔一段时间对邮件缓存扫描一次,若有邮件,就使用25端口于接收方邮件服务器的SMTP服务器建立TCP连接。
25 |
26 | 2. **邮件传送**:(1)发送MAIL命令:命令后有发件人的地址,若SMTP服务器已准备好接收,则回复OK,不然就返回一个代码指出原因。(2)发送一个或多个RCPT命令(取决于把同一个邮件发送给一个还是多个收件人):先弄清接收方是否已准备好接收邮件,然后再发送邮件(避免浪费通信资源)。(3)发送DATA命令:开始传送邮件的内容。
27 | 3. **连接释放**:邮件发送完毕后,SMTP客户发送QUIT命令,SMTP服务器同意释放TCP连接后即断开TCP连接。
28 |
29 |
30 |
31 | ## 6-32
32 |
33 | **答:**DHCP用在计算机加入新的网络时获取这台计算机的IP地址。DHCP提供了即插即用联网机制,允许一台计算机加入新的网络和获取IP地址而不用手工参与。
34 |
35 | 当一台计算机第一次运行引导程序时,ROM中**没有**该计算机的IP地址、子网掩码和某个域名服务器的IP地址。
36 |
37 |
38 |
39 | ## 6-46
40 |
41 | **答:**(1)有的协议追求可靠连接,因此需要使用TCP协议。有的协议追求开销小,而TCP进行传送开销太大了(需要建立连接、释放连接等),因此采用UDP来减小开销。
42 |
43 | (2)MIME不是一个独立的邮件传送协议,它是SMTP上的一个协议,其首部中说明了邮件的数据类型,下图说明了MIME与SMTP的关系。
44 |
45 |
144 |
145 |
146 |
147 | ## 5-68
148 |
149 | 假设A是发送端(主动打开连接的一方),B是接收端(被动打开连接的一方)。那么在TCP的连接建立过程中,如果第三个报文丢失,那么A就会建立TCP连接,B还是在SYN-RCVD阶段。
150 |
151 | - 如果此时A没有紧接着发送数据,那么B经过一段时间后就会回到CLOSED状态,需要重新建立连接。
152 | - 如果此时A紧接着发送数据,那么此时A发送的数据报中自己的序号没有改变,与丢失的确认帧序号相同,且确认位ACK=1,确认号也是B选择的初始序号加1。当B接收到此报文段后就进入ESTABLISHED状态,继续接收A发送的数据。此时,第三个报文丢失不会对TCP建立造成影响。
153 |
154 | 综上,第三个报文段不确认对于在A建立连接后长时间不传输数据会有影响,而对于A建立连接后立即开始传输数据不会有什么影响。
155 |
156 |
157 |
158 |
--------------------------------------------------------------------------------
/docs/ComputerNetwork/《计算机网络》第六章作业.md:
--------------------------------------------------------------------------------
1 | # 《计算机网络》第六章作业
2 |
3 | ## 6-02
4 |
5 | **答:**域名系统是互联网使用的命名系统,其主要功能就是把域名解析为IP地址。四类域名服务器的区别如下:
6 |
7 | | 域名服务器 | 说明 |
8 | | -------------- | ------------------------------------------------------------ |
9 | | 本地域名服务器 | 离用户较近;主机发出DNS查询时,首先发给本地域名服务器 |
10 | | 根域名服务器 | 最高层次、最重要的域名服务器;根域名服务器知道所有顶级域名服务器的域名和IP地址;当本地域名服务器无法解析时,首先求助于根域名服务器 |
11 | | 顶级域名服务器 | 负责管理该顶级域名服务器注册的所有二级域名;收到查询请求后就给出相应回答 |
12 | | 权限域名服务器 | 负责一个区的域名服务器;当权限域名服务器无法给出最后的回答时,会告诉请求方下一步找哪个权限域名服务器 |
13 |
14 |
15 |
16 | ## 6-15
17 |
18 | **答:**解析IP地址的时间为$\sum_{i=1}^n \text{RTT}_i$,建立TCP连接时间为$\text{RTT}_w$,请求万维网文档时间为$\text{RTT}_w$,因此,总时间为$\sum_{i=1}^n \text{RTT}_i + 2\text{RTT}_w$ 。
19 |
20 |
21 |
22 | ## 6-23
23 |
24 | **答:**1. **连接建立**:发件人将邮件发到发送方邮件服务器缓存中,SMTP客户每隔一段时间对邮件缓存扫描一次,若有邮件,就使用25端口于接收方邮件服务器的SMTP服务器建立TCP连接。
25 |
26 | 2. **邮件传送**:(1)发送MAIL命令:命令后有发件人的地址,若SMTP服务器已准备好接收,则回复OK,不然就返回一个代码指出原因。(2)发送一个或多个RCPT命令(取决于把同一个邮件发送给一个还是多个收件人):先弄清接收方是否已准备好接收邮件,然后再发送邮件(避免浪费通信资源)。(3)发送DATA命令:开始传送邮件的内容。
27 | 3. **连接释放**:邮件发送完毕后,SMTP客户发送QUIT命令,SMTP服务器同意释放TCP连接后即断开TCP连接。
28 |
29 |
30 |
31 | ## 6-32
32 |
33 | **答:**DHCP用在计算机加入新的网络时获取这台计算机的IP地址。DHCP提供了即插即用联网机制,允许一台计算机加入新的网络和获取IP地址而不用手工参与。
34 |
35 | 当一台计算机第一次运行引导程序时,ROM中**没有**该计算机的IP地址、子网掩码和某个域名服务器的IP地址。
36 |
37 |
38 |
39 | ## 6-46
40 |
41 | **答:**(1)有的协议追求可靠连接,因此需要使用TCP协议。有的协议追求开销小,而TCP进行传送开销太大了(需要建立连接、释放连接等),因此采用UDP来减小开销。
42 |
43 | (2)MIME不是一个独立的邮件传送协议,它是SMTP上的一个协议,其首部中说明了邮件的数据类型,下图说明了MIME与SMTP的关系。
44 |
45 |  46 |
47 | (3)RIP协议使用了UDP传送数据,因此RIP在UDP之上,属于应用层。
48 |
49 |
50 |
51 |
--------------------------------------------------------------------------------
/docs/ComputerNetwork/《计算机网络》第四章作业.md:
--------------------------------------------------------------------------------
1 | # 《计算机网络》第四章作业
2 |
3 | ## 4-01
4 |
5 | **答:**一种是面向连接的服务(虚电路服务),一种是无连接的服务(数据报服务)。
6 |
7 | 面向连接的服务(可靠通信由网络保证):
8 |
9 | - 优点:分组开销小;分组无差错。
10 | - 缺点:网络成本高;若某一节点出错,所有通过该节点的虚电路都不能正常工作。
11 |
12 | 无连接的服务(可靠通信由用户主机保证):
13 |
14 | - 优点:网络成本低;某一节点出错时,路由可能变化,数据报可能仍然可以传输。
15 | - 缺点:尽力交付,可能会出现数据报异常情况。
16 |
17 | ## 4-03
18 |
19 | **答:**他们都起到连接网络的作用,但处在不同的网络体系结构层级。转发器在物理层,网桥在数据链路层,路由器在网络层,而网关在运输层及应用层(路由器也可以表示网关)。
20 |
21 | ## 4-07
22 |
23 | **答:**IP地址是网络层及以上使用的逻辑地址,而硬件地址是物理层及数据链路层使用的地址。由于不同国家、区域等有着不同的网络结构,其中的主机都有不同形式的硬件地址,因此若需要跨域传输时,会存在复杂的硬件地址转换。使用统一的IP地址可以使用户间的通信好像在一个网络上一样。IP地址与硬件地址的转换也相对硬件地址与硬件地址的转换要方便许多。
24 |
25 | ## 4-10
26 |
27 | **答:**(1)**10**000000.00100100.11000111.00000011,为B类地址;
28 |
29 | (2)**0**0010101.00001100.11110000.00010001,为A类地址;
30 |
31 | (3)**10**110111.11000010.01001100.11111101,为B类地址;
32 |
33 | (4)**110**00000.00001100.01000101.11111000,为C类地址;
34 |
35 | (5)**0**1011001.00000011.00000000.00000001,为A类地址;
36 |
37 | (6)**110**01000.00000011.00000110.00000010,为C类地址。
38 |
39 | ## 4-11
40 |
41 | **答:**好处是减小开销(加快检验、转发分组更快);坏处是在网络层传输的过程中就算数据发生了错误,也无法识别并中止传输,需要到达终点后在主机上(运输层)才能进行校验。
42 |
43 | ## 4-15
44 |
45 | **答:**MTU是一个数据帧中数据字段的最大长度。当一个IP数据报封装成数据链路层的帧的时候,数据报的总长度一定不能超过MTU。MTU与IP数据报首部中的总长度字段有关系,MTU是该字段的上限值。
46 |
47 | ## 4-18
48 |
49 | **答:**(1)数据链路层只能接触到MAC帧,如果ARP在数据链路层,那么MAC帧中就需要有IP地址,这不符合数据链路层对MAC帧的结构定义。
50 |
51 | (2)当网络中IP地址与硬件地址的映射发生变化时,ARP高速缓存中对应项就需要改变。超时时间设置太短会使ARP请求和响应分组的通信太频繁,若设置太长会使得硬件地址变化的主机迟迟无法与网络上其他主机通信。设置10~20分钟主要是因为在这样的一段时间段内更换网卡是很合理的。
52 |
53 | (3)①源主机的ARP高速缓存中已经有了目的主机的MAC地址;②源主机发送的是广播分组;③源主机与目的主机间使用点对点链路。
54 |
55 | ## 4-24
56 |
57 | **答:**A类子网划分对应数目的子网,子网掩码第一个字节需要全为1。若需要划分为n个A类子网,主机号部分的1的个数为$\lceil \log_2(n + 2) \rceil$(去除了全0和全1的子网数)。
58 |
59 | (1)$n=2$,主机号部分1的数量为2,因此子网掩码为255.192.0.0;
60 |
61 | (2)$n=6$,主机号部分1的数量为3,因此子网掩码为255.224.0.0;
62 |
63 | (3)$n=30$,主机号部分1的数量为5,因此子网掩码为255.248.0.0;
64 |
65 | (4)$n=62$,主机号部分1的数量为6,因此子网掩码为255.252.0.0;
66 |
67 | (5)$n=122$,主机号部分1的数量为7,因此子网掩码为255.254.0.0(实际有126个子网);
68 |
69 | (6)$n=250$,主机号部分1的数量为8,因此子网掩码为255.255.0.0(实际有254个子网);
70 |
71 | ## 4-25
72 |
73 | **答:**(1)10110000.0.0.0,其中1不是连续的,不推荐使用;
74 |
75 | (2)01100000.0.0.0,首位不是1(1前面有0),不推荐使用;
76 |
77 | (3)01111111.11000000.0.0,首位不是1(1前面有0),不推荐使用;
78 |
79 | (4)11111111.10000000.0.0,合理,推荐使用。
80 |
81 | ## 4-31
82 |
83 | **答:**86.32/12的网络前缀为0101 0110 0010。
84 |
85 | (1)86.33.224.123的前12位为0101 0110 0010,与上述网络前缀匹配。
86 |
87 | (2)86.79.65.216的前12位为0101 0110 0100,与上述网络前缀不匹配。
88 |
89 | (3)86.58.119.74的前12位为0101 0110 0011,与上述网络前缀不匹配。
90 |
91 | (4)86.68.206.154的前12位为0101 0110 0100,与上述网络前缀不匹配。
92 |
93 | ## 4-35
94 |
95 | **答:**转化为二进制为**10001100.01111000.0101**0100.00011000。
96 |
97 | 最大地址:**10001100.01111000.0101**1111.11111111,即140.120.95.255/20;
98 |
99 | 最小地址:**10001100.01111000.0101**0000.00000000,即140.120.80.0/20;
100 |
101 | 地址掩码:255.255.240.0;
102 |
103 | 地址块中共有$2^{12}=4096$个地址;
104 |
105 | 相当于$2^{24-20}=2^4=16$个C类地址。
106 |
107 | ## 4-38
108 |
109 | **答:**IGP是内部网关协议,是在一个自治系统内部使用的路由选择协议;EGP是外部网关协议,是在不同的自治系统间使用的路由选择协议。
110 |
111 | ## 4-39
112 |
113 | **答:**RIP协议是一种分布式的基于距离向量的路由选择协议,是互联网的标准协议,其最大优点就是简单,其主要特点为:
114 |
115 | - 仅和相邻路由器交换信息;
116 | - 路由器交换的信息是本路由器所知道的全部信息;
117 | - 按固定的时间间隔交换路由信息。
118 |
119 | OSPF使用分布式的链路状态协议,其主要特点为:
120 |
121 | - 使用洪泛法向本自治系统中所有路由器发送信息;
122 | - 发送的信息就是与本路由器相邻的所有路由器的链路状态,但这只是路由器所知道的部分信息;
123 | - 当链路状态变化或每隔一段时间,路由器向所有路由器用洪泛法发送链路状态信息;
124 | - 对于不同类型的业务可计算出不同的路由;
125 | - 多路径间存在负载均衡;
126 | - 所有在OSPF路由器之间交换的分组都具有鉴别功能;
127 | - 支持可变长度的子网划分和无分类的编址CIDR;
128 | - 每一个链路状态都会带上一个32位的序号,序号越大状态就越新。
129 |
130 | BGP是不同自治系统的路由器之间交换路由信息的协议,它采用路径向量路由选择协议,其主要特点为:
131 |
132 | - BGP在自治系统之问交换“可达性”信息;
133 | - BGP只能是力求寻找一条能够到达目的网络且比较好的路由(不能兜圈子),而并非要寻找一条最佳路由;
134 | - BGP的路由选择有很多策略,如选择本地偏好值最高的路由、选择AS跳数最少的路由、使用热土豆算法等;
135 | - BGP有四种报文,在不同的场合使用不同的报文。
136 |
137 | ## 4-43
138 |
139 | **答:**IGMP协议是让连接在本地局域网上的多播路由器知道本局域网上是否有主机(严格讲,是主机上的某个进
140 | 程)参加或退出了某个多播组。IGMP协议的要点主要体现在两个阶段:
141 |
142 | - 当某个主机加入新的多播组时,该主机应向多播组的多播地址发送一个IGMP报文,声明自己要成为该组的成员。本地的多播路由器收到IGMP报文后,还要利用多播路由选择协议把这种组成员关系转发给互联网上的其他多播路由器。
143 | - 本地多播路由器要周期性地探询本地局域网上的主机,以便知道这些主机是否还继续是组的成员。只要有一个主机对某个组响应,那么多播路由器就认为这个组是活跃的。但一个组在经过几次的探询后仍然没有一个主机响应,多播路由器就认为本网络上的主机已经都离开了这个组,因此也就不再把这个组的成员关系转发给其他
144 | 的多播路由器。
145 |
146 | 当两个多播网络之间的网络不支持多播时,会使用隧道技术。在这种情况下,发送方网络路由器会对多播数据进行再次封装,加上普通数据报首部,使之变成单播数据报,这样就能通过中间网络(此时相当于构建了一个隧道)传输到另一个多播网络,目的网络路由器收到此数据报后先剥去其首部,变成原来的多播数据报后再进行传输。
147 |
148 | ## 4-48
149 |
150 | **答:**146.102.29.0的二进制为10010010.01100110.00011101.00000000;
151 |
152 | 146.102.32.255的二进制为10010010.01100110.00100000.11111111;
153 |
154 | 从146.102.29.0(含)到146.102.29.255(含)有$256$个地址。而146.102.29.255(不含)到146.102.32.255(含)有$3\times 256$个地址,因此总共有$4\times 256=1024$个地址。
155 |
156 | ## 4-65
157 |
158 | **答:**(1)0000 : 0000 : 0000 : 0000 : 0000 : 0000 : 0000 : 0000
159 |
160 | (2)0000 : 00AA : 0000 : 0000 : 0000 : 0000 : 0000 : 0000
161 |
162 | (3)0000 : 1234 : 0000 : 0000 : 0000 : 0000 : 0000 : 0003
163 |
164 | (4)0123 : 0000 : 0000 : 0000 : 0000 : 0000 : 0001 : 0002
--------------------------------------------------------------------------------
/docs/MachineLearning/第一章作业.md:
--------------------------------------------------------------------------------
1 | # 《机器学习》第一章作业
2 |
3 | ## 1.1
4 |
5 | 表1.1中若只包含编号为1和4的两个样例,即如下表所示:
6 |
7 | | 编号 | 色泽 | 根蒂 | 敲声 | 好瓜 |
8 | | ---- | ---- | ---- | ---- | ---- |
9 | | 1 | 青绿 | 蜷缩 | 浊响 | 是 |
10 | | 4 | 乌黑 | 稍蜷 | 沉闷 | 否 |
11 |
12 | 则其版本空间如下图所示:
13 |
14 | 
15 |
16 | ## 1.3
17 |
18 | 对于所有假设,选择满足最多样本的假设。若有多个,则选择尽可能一般的假设(即属性值为任意的数量尽可能多)。若还有多个,随机选择一个即可。
19 |
20 |
21 |
22 | ## 1.5
23 |
24 | 1. 对欲搜索文本进行分词,提取关键词并分析语义后进行检索;
25 | 2. 对搜索文本和数据库中相关信息进行匹配并排序;
26 | 3. 在拥有用户信息和使用习惯的数据后,可以智能推荐搜索结果;
27 | 4. 实现对图片、视频等多媒体数据进行分析后,给出搜索结果(如百度识图);
28 | 5. 对搜索出的结果进行无效信息、重复信息的过滤;
29 | 6. 建立知识图谱,能精确给出搜索结果的梗概(或者与其他概念的关系)。
30 |
31 |
--------------------------------------------------------------------------------
/docs/MachineLearning/第七章作业.md:
--------------------------------------------------------------------------------
1 | # 《机器学习基础》第七章作业
2 |
3 | ## 7.1
4 |
5 | **答:**使用极大似然法得到的类条件概率估计表达式为
6 | $$
7 | P(x_i=t_{ij}|c) = \frac{|D_{c,x_i, t_{ij}}|}{|D_c|}
8 | $$
9 | 其中,$|D_c|$表示训练集$D$中$c$类样本的数量,$|D_{c, x_i, t_{ij}}|$表示训练集中$c$类元素属性$x_i$为$t_{ij}$的数量的元素。由此根据西瓜数据集即可得出类条件概率如下:
10 |
11 | | 属性 | 属性取值 | 好瓜($c_0$) | 坏瓜($c_1$) |
12 | | ----------- | -------------- | ----------- | ----------- |
13 | | 色泽($x_0$) | 青绿($t_{00}$) | $\frac38$ | $\frac13$ |
14 | | | 乌黑($t_{01}$) | $\frac12$ | $\frac29$ |
15 | | | 浅白($t_{02}$) | $\frac18$ | $\frac49$ |
16 | | 根蒂($x_1$) | 蜷缩($t_{10}$) | $\frac58$ | $\frac13$ |
17 | | | 稍蜷($t_{11}$) | $\frac38$ | $\frac49$ |
18 | | | 硬挺($t_{12}$) | $0$ | $\frac29$ |
19 | | 敲声($x_2$) | 浊响($t_{20}$) | $\frac34$ | $\frac49$ |
20 | | | 沉闷($t_{21}$) | $\frac14$ | $\frac13$ |
21 | | | 清脆($t_{22}$) | $0$ | $\frac29$ |
22 |
23 |
24 |
25 | ## 7.3
26 |
27 | ### 1. 环境及数据准备
28 | ```python
29 | import numpy as np
30 | import pandas as pd
31 | import scipy.stats as st
32 |
33 | df = pd.read_csv('./watermelon3.csv', index_col=0) # 西瓜数据集3.0
34 | X = np.array(df.iloc[:, :-1]) # 属性
35 | y = np.array(df.iloc[:, -1])[None].T # 标签
36 | ```
37 |
38 | ### 2. 定义模型
39 | ```python
40 | class NaiveBayes:
41 | def __init__(self) -> None:
42 | pass
43 |
44 | def get_prob(self, X, x, x_i, N): # 拉普拉斯修正
45 | return ((X[:, x] == x_i).sum() + 1) / (X.shape[0] + N)
46 |
47 | def get_dis_prob(self, X, y): # 离散概率
48 | p = []
49 | for i, c in enumerate(self.label):
50 | temp = X[(y == c).ravel()]
51 | lst = []
52 | for x in range(temp.shape[1]):
53 | dct = {}
54 | uni = np.unique(X[:, x])
55 | for x_i in uni:
56 | dct[x_i] = self.get_prob(temp, x, x_i, uni.shape[0])
57 | lst.insert(x, dct)
58 | p.insert(i, lst)
59 | return p
60 |
61 | def get_con_prob(self, X, x, x_i): # 连续概率
62 | return st.norm.pdf(x_i, loc=X[:, x].mean(), scale=X[:, x].std())
63 |
64 | def train(self, X, y):
65 | self.X, self.y = X, y
66 | self.con_col = [i for i in range(X.shape[1]) if type(X[0][i]) == float] # 连续值所在位置
67 | dis_X = np.delete(X, self.con_col, axis=1) # 提取离散值
68 | con_X = X[:, self.con_col] # 提取连续值
69 | self.label = np.unique(y) # 将label的类型取出来
70 | self.dis_p = self.get_dis_prob(dis_X, y)
71 | self.P_c = ((self.label == y).sum(axis=0) + 1) / (df.shape[0] + self.label.shape[0])
72 |
73 | def predict(self, X_pre):
74 | y_pre = np.ones(X_pre.shape[0], dtype='object')
75 | for j, X in enumerate(X_pre):
76 | maxn = 0
77 | res_c = 0
78 | for i, c in enumerate(self.label):
79 | res = 1
80 | temp_X = self.X[(self.y == c).ravel()]
81 | a = 0
82 | for x in range(X.shape[0]):
83 | if x in self.con_col: # 连续
84 | res *= self.get_con_prob(temp_X, x, X[x])
85 | else: # 离散
86 | res *= (self.dis_p[i][a][X[x]])
87 | a += 1
88 | res *= self.P_c[i]
89 | if res > maxn:
90 | maxn = res
91 | res_c = c
92 | y_pre[j] = res_c
93 | return y_pre[None].T
94 | ```
95 | ### 3. 模型测试
96 | ```python
97 | model = NaiveBayes()
98 | model.train(X, y)
99 | test_X = np.array(['青绿', '蜷缩', '浊响', '清晰', '凹陷', '硬滑', 0.697, 0.460], dtype='object')
100 | print(model.predict(test_X[None])[0][0])
101 | ```
102 |
103 | 是
104 |
105 |
106 |
107 | ## 7.4
108 |
109 | **答:**由于$P(x_i|c)\leq 1$,因此$\prod_{i=1}^{d} P(x_i|c)$很可能因为非常接近$0$而造成下溢,可以采用对此公式求对数的方式将正小数转化为负正数从而解决数据可能下溢的问题,即转化为$\sum_{i=1}^{d} \log P(x_i|c)$。
110 |
111 |
112 |
113 | ## 7.5
114 |
115 | **答:**对于贝叶斯最优分类器来说,其欲最大化的目标为
116 | $$
117 | P(c | \boldsymbol x) = \frac{P(c)P(\boldsymbol x | c)}{P(\boldsymbol x)}
118 | $$
119 |
120 | 因为$P(\boldsymbol x)$是常量,因此也就是最大化
121 | $$
122 | P(c)P(\boldsymbol x | c)
123 | $$
124 | 因为数据服从高斯分布,因此上式等价于
125 | $$
126 | P(c)\frac{1}{(2\pi)^{n/2}|\boldsymbol \Sigma |^{1/2} } \exp \left( -\frac12 (\boldsymbol x - \boldsymbol \mu_c)^\text T \boldsymbol \Sigma_c^{-1} (\boldsymbol x - \boldsymbol \mu_c)\right)
127 | $$
128 | 由题中条件“假设同先验”,因此在二分类任务中,上式等价于最大化
129 | $$
130 | \max(-\frac12 (\boldsymbol x - \boldsymbol \mu_0)^\text T \boldsymbol \Sigma_0^{-1} (\boldsymbol x - \boldsymbol \mu_0), -\frac12 (\boldsymbol x - \boldsymbol \mu_1)^\text T \boldsymbol \Sigma_1^{-1} (\boldsymbol x - \boldsymbol \mu_1))
131 | $$
132 | 由此可知,贝叶斯最优分类器的决策平面为
133 | $$
134 | \boldsymbol x ^ \text T \boldsymbol \Sigma^{-1}(\boldsymbol \mu_1 - \boldsymbol \mu_0) - \frac 12 (\boldsymbol \mu_1 + \boldsymbol \mu_0)^ \text T \boldsymbol\Sigma^{-1}(\boldsymbol \mu_1 - \boldsymbol \mu_0)
135 | $$
136 | 对于线性判别分析来说,其欲最大化的目标为
137 | $$
138 | J = \frac{\boldsymbol{w}^\text{T}(\boldsymbol\mu_0-\boldsymbol\mu_1)(\boldsymbol\mu_0-\boldsymbol\mu_1)^\text T \boldsymbol{w}}{\boldsymbol{w} ^\text{T} (\boldsymbol\Sigma_0 + \boldsymbol\Sigma_1)\boldsymbol{w}}
139 | $$
140 | 其中,$\boldsymbol w$为直线$y=\boldsymbol w ^ \text T \boldsymbol x$中的系数项,$\boldsymbol \mu_i, \boldsymbol \Sigma_i$为第$i \in \{0, 1\}$类的均值向量、协方差矩阵。由于两类数据满足高斯分布且方差相同,因此其决策平面由两数据均值点的中点$\frac 12 (\boldsymbol \mu_0 + \boldsymbol \mu_1)$和法向量$\boldsymbol w$唯一确定,而将此带入贝叶斯最优分类器的决策平面均成立,因此线性判别分析的决策平面与此重合。因此,二分类任务中两类数据满足高斯分布且方差相同时,线性判别分析产生贝叶斯最优分类器。
141 |
142 |
143 |
144 |
145 | ## 7.7
146 |
147 | **答:**由题意,对于一个二分类问题,需要估算一个二值属性对应的先验概率$P(c, x_i)$则需要$30\times 2 \times 2=120$个样例(因为$c$和$x_i$的取值均有两种)。如果第二个二值属性在上述样例上对应的$c$和$x_i$的取值均相同,那么就无需增加样例;如果第二个二值属性在上述样例上的取值只有一个,那么还需要$30\times 2=60$个样例(另一个取值在$c$两取值上的个数)。
148 |
149 | 因此,当扩展到有$d$个二值属性时,最好情况不需要在第一个的基础上添加任何样例,因此样例数为$120$;最坏情况下,每一次添加属性均会添加$60$个样例,因此样例数为$120+60\times (d-1) = 60 \times (d + 1)$。
150 |
151 |
--------------------------------------------------------------------------------
/docs/MachineLearning/第三章作业.md:
--------------------------------------------------------------------------------
1 | # 《机器学习》第三章作业
2 |
3 | ## 3.1
4 |
5 | 答:(1)该模型中$b$与输入没有关系时或模型函数一定过原点时;(2)该模型只用于差分分析时,因为假设取两实例$\boldsymbol{x}_i$和$\boldsymbol{x}_j(i\neq j)$,$f(\boldsymbol{x}_i) - f(\boldsymbol{x}_j ) = \boldsymbol{w}^\text{T}(\boldsymbol{x}_i - \boldsymbol{x}_j)$是与$b$无关的。
6 |
7 | ## 3.3
8 |
9 | ### 1.准备数据
10 |
11 | ```python
12 | import numpy as np
13 | from sklearn.model_selection import train_test_split
14 |
15 | data = np.array([[0.697, 0.460, 1],
16 | [0.774, 0.376, 1],
17 | [0.634, 0.264, 1],
18 | [0.608, 0.318, 1],
19 | [0.556, 0.215, 1],
20 | [0.403, 0.237, 1],
21 | [0.481, 0.149, 1],
22 | [0.437, 0.211, 1],
23 | [0.666, 0.091, 0],
24 | [0.243, 0.267, 0],
25 | [0.245, 0.057, 0],
26 | [0.343, 0.099, 0],
27 | [0.639, 0.161, 0],
28 | [0.657, 0.198, 0],
29 | [0.360, 0.370, 0],
30 | [0.593, 0.042, 0],
31 | [0.719, 0.103, 0]]) # 西瓜数据集3.0alpha
32 | X = data[:, 0:2] # 属性
33 | y = data[:, -1] # 标签
34 | X_train,X_test,y_train,y_test=train_test_split(X,y,test_size=0.3) #随机划分训练集和测试集
35 | ```
36 |
37 | ### 2.定义模型
38 |
39 | ```python
40 | class LogisticRegression:
41 | def __int__(self):
42 | pass
43 |
44 | def fit(self, X_, y_):
45 | # 数据调整为x_bar和\beta, 便于操作
46 | n, m = X_.shape
47 | m += 1
48 | X = np.append(X_, np.ones(n).reshape((n, 1)), axis=1).T
49 | y = y_.copy()
50 | beta = np.random.random(size=(m, 1))
51 | # 牛顿迭代法
52 | epoch = 20
53 | for i in range(epoch):
54 | mul = beta.T @ X
55 | p1 = np.exp(mul) / (1 + np.exp(mul)) # 计算p1的公式
56 | fd = -np.sum(X * (y - p1), axis=1) # 计算牛顿迭代中的一阶导数
57 | sd = np.zeros((m, m)) # 计算牛顿迭代中的二阶导数
58 | for i in range(n):
59 | sd += X[:, i:i+1] @ X[:, i:i+1].T * (p1[0, i] * (1 - p1[0, i]))
60 | beta = beta - (np.linalg.inv(sd) @ fd).reshape((m, 1)) # 一次迭代
61 | # 训练结果分析
62 | ans = (beta.T @ X) > 1
63 | self.beta = beta
64 | print("训练集准确率: ", 1 - np.sum(np.abs(ans - y)) / n)
65 |
66 | def predict(self, X_, y_):
67 | # 测试结果分析
68 | n = X_.shape[0]
69 | X = np.append(X_, np.ones(n).reshape((n, 1)), axis=1).T
70 | y = y_.copy()
71 | ans = (self.beta.T @ X) > 1
72 | print("测试集准确率: ", 1 - np.sum(np.abs(ans - y)) / n)
73 |
74 | ```
75 |
76 | ### 3.使用模型进行训练和预测
77 |
78 | ```python
79 | model = LogisticRegression()
80 | model.fit(X_train, y_train)
81 | model.predict(X_test, y_test)
82 | ```
83 |
84 | 训练集准确率: 0.7272727272727273
85 | 测试集准确率: 0.8333333333333334
86 |
87 | ## 3.5
88 |
89 | ### 1.准备数据
90 |
91 | 同3.3
92 |
93 | ### 2.定义模型计算𝜔
94 |
95 | ```python
96 | class LDA:
97 | def __init__(self):
98 | pass
99 |
100 | def fit(self, X, y):
101 | X0 = X[y == 0] # 坏瓜
102 | X1 = X[y == 1] # 好瓜
103 | mu0 = np.mean(X0, axis=0).reshape((-1, 1)) # 坏瓜均值
104 | mu1 = np.mean(X1, axis=0).reshape((-1, 1)) # 好瓜均值
105 | cov0 = np.cov(X0, rowvar=False) # 坏瓜协方差
106 | cov1 = np.cov(X1, rowvar=False) # 好瓜协方差
107 | S_w = np.mat(cov0 + cov1) # S_w
108 | U,Sigma,V = np.linalg.svd(S_w,full_matrices=False) # 奇异值分解
109 | self.omega = V.T @ np.linalg.inv(np.diag(Sigma)) @ U.T @ (mu0 - mu1) # /omega
110 | # 输出结果
111 | ans = self.omega.T @ X.T < 0
112 | acc = 1 - np.sum(np.abs(ans - y)) / y.shape[0]
113 | print("训练集准确率:", acc)
114 |
115 | def predict(self, X, y):
116 | # 输出结果
117 | ans = self.omega.T @ X.T < 0
118 | acc = 1- np.sum(np.abs(ans - y)) / y.shape[0]
119 | print("测试集准确率:", acc)
120 |
121 | ```
122 |
123 | ### 3.使用模型进行训练和预测
124 |
125 | ```python
126 | model = LDA()
127 | model.fit(X_train, y_train)
128 | model.predict(X_test, y_test)
129 | ```
130 |
131 | 训练集准确率: 0.9090909090909091
132 | 测试集准确率: 0.6666666666666667
133 |
134 | ## 3.7
135 |
136 | 答:给出汉明距离意义下理论最优的ECOC二元码:
137 |
138 | | | $f_1$ | $f_2$ | $f_3$ | $f_4$ | $f_5$ | $f_6$ | $f_7$ | $f_8$ | $f_9$ |
139 | | ----- | ----- | ----- | ----- | ---- | ---- | ------- | ---- | ---- | ---- |
140 | | $C_1$ | +1 | -1 | -1 | -1 | +1 | +1 | +1 | +1 | -1 |
141 | | $C_2$ | -1 | +1 | -1 | -1 | +1 | -1 | -1 | +1 | -1 |
142 | | $C_3$ | -1 | -1 | +1 | -1 | -1 | +1 | -1 | +1 | -1 |
143 | | $C_4$ | -1 | -1 | -1 | +1 | -1 | -1 | +1 | +1 | -1 |
144 |
145 | 证明如下:
146 |
147 | 注意到性质:若两个分类器$f_i$和$f_j(i \neq j)$对样例的分类互为反码[如$(-1,-1,1,1)$和$(1,1,-1,-1)$],由于很多算法对待0-1分类是对称的(即如果将0-1类互换,最终训练出的模型是一样的)。这样一对分类器实际上可以简化为一个分类器,因此可以计算出在不出现互为反码的情况下,最优的ECOC编码长度为
148 | $$
149 | \binom{4}{1} + \frac{\binom{4}{2}}{2}=7
150 | $$
151 | 由于可以向编码中加入冗余,即可以在最短编码长度的情况下加入互为反码的一对分类器,因此只要保证编码长度为$7+2n(n为自然数)$即可保证得出的ECOC编码是最优的。
152 |
153 | 综上,由于$9=7+2\times 1$($f_8$和$f_9$是加入的冗余分类器),因此上述给出的ECOC二元码是理论最优的。
154 |
155 | ## 3.9
156 |
157 | 答:对OvR、MvM 来说,由于**对每个类进行了相同的处理**,其拆解出的二分类任务中类别不平衡的影响会相互抵消,因此通常不需专门处理。
158 |
--------------------------------------------------------------------------------
/docs/MachineLearning/第九章作业.md:
--------------------------------------------------------------------------------
1 | # 《机器学习基础》第九章作业
2 |
3 | ## 9.1
4 |
5 | **(1)首先证明闵可夫斯基距离满足非负性,同一性和对称性。**
6 |
7 | 由于
8 | $$
9 | \text{dist}_\text{mk} (x_i, x_j) = \left( \sum_{u=1}^n |x_{iu}-x_{ju}|^p \right)^\frac 1p \ge 0
10 | $$
11 | 因此,闵可夫斯基距离满足非负性。当且仅当$x_i = x_j$时,$\text{dist}_\text{mk} (x_i, x_j)=0$,因此闵可夫斯基距离满足同一性。由于绝对值中减数和被减数可以调换位置,所以$\text{dist}_\text{mk} (x_i, x_j) = \text{dist}_\text{mk} (x_j, x_i)$,因此闵可夫斯基距离满足对称性。
12 |
13 | **(2)下面证明当$p\ge 1$时,闵可夫斯基距离满足直递性。**
14 |
15 | 显然$p=1$时,可由三角不等式证明。因此下面$p>1$。
16 |
17 | 令$a_i=|x_{iu}-x_{ku}|,b_i=|x_{ku}-x_{ju}|$,那么要证$\text{dist}_\text{mk} (x_i, x_j) \leq \text{dist}_\text{mk} (x_i, x_k) + \text{dist}_\text{mk} (x_k, x_j)$,即证
18 | $$
19 | \left(\sum_{i=1}^{n}|a_i+b_i|^p\right)^\frac 1p \leq \left(\sum_{i=1}^{n}a_i^p \right)^\frac 1p + \left(\sum_{i=1}^{n}b_i^p \right)^\frac 1p
20 | $$
21 | 由于
22 | $$
23 | \begin{align}
24 | \left(\sum_{i=1}^{n}|a_i+b_i|^p\right)^\frac 1p &\leq \sum_{i=1}^{n}|a_i+b_i|^p \\
25 | &= \sum_{i=1}^{n}|a_i+b_i||a_i+b_i|^{p-1} \\
26 | &\leq \sum_{i=1}^{n}(|a_i|+|b_i|)|a_i+b_i|^{p-1} \\
27 | &= \sum_{i=1}^{n}(|a_i||a_i+b_i|^{p-1}+|b_i||a_i+b_i|^{p-1})
28 | \end{align}
29 | $$
30 | 由赫尔德不等式$\sum_i^na_ib_i \leq (\sum_{i=1}^n a_i^p)^\frac1p(\sum_{i=1}^nb_i^q)^\frac1q \ \ (p, q > 1) $可得
31 | $$
32 | \begin{align}
33 | \sum_{i=1}^{n}(|a_i||a_i+b_i|^{p-1}+|b_i||a_i+b_i|^{p-1}) &\leq \left(\sum_{i=1}^{n}|a_i|^p \right)^{\frac1p} \left(\sum_{i=1}^{n}|a_i+b_i|^{(p-1)q}\right)^{\frac1q} + \left(\sum_{i=1}^{n}|b_i|^p\right)^{\frac1p} \left(\sum_{i=1}^{n}|a_i+b_i|^{(p-1)q}\right)^{\frac1q} \\
34 | &= \left(\left(\sum_{i=1}^{n}|a_i|^p\right)^{\frac1p} + \left(\sum_{i=1}^{n}|b_i|^p\right)^{\frac1p} \right) \left(\sum_{i=1}^{n}|a_i+b_i|^{p}\right)^{\frac1q} \\
35 | &\leq \left(\sum_{i=1}^{n}|a_i|^p\right)^{\frac1p} + \left(\sum_{i=1}^{n}|b_i|^p\right)^{\frac1p}
36 | \end{align}
37 | $$
38 | 其中$q=\frac{p}{p-1}$,于是原不等式成立,因此,当$p \ge 1$时闵可夫斯基距离满足直递性。
39 |
40 | **(3)下面证明当$0 \leq p < 1$时,闵可夫斯基距离不满足直递性。**
41 |
42 | 和(2)类似的,只需证明下式即可证明原命题。
43 | $$
44 | \left(\sum_{i=1}^{n}|a_i+b_i|^p\right)^\frac 1p \ge \left(\sum_{i=1}^{n}a_i^p \right)^\frac 1p + \left(\sum_{i=1}^{n}b_i^p \right)^\frac 1p
45 | $$
46 | 由于
47 | $$
48 | \begin{align}
49 | \sum_{i=1}^{n}|a_i+b_i|^p &= \sum_{i=1}^{n}|t\frac{a_i}{t}+(1-t)\frac{b_i}{1-t}|^p \\
50 | &\ge t^{1-p}\sum_{i=1}^{n}|a_i|^p+(1-t)^{1-p}\sum_{i=1}^{n}|b_i|^p
51 | \end{align}
52 | $$
53 | 其中
54 | $$
55 | t=\frac{\left(\sum_{i=1}^{n}a_i^p \right)^\frac 1p}{\left(\sum_{i=1}^{n}a_i^p \right)^\frac 1p + \left(\sum_{i=1}^{n}b_i^p \right)^\frac 1p}
56 | $$
57 | 于是有
58 | $$
59 | \begin{align}
60 | t^{1-p}\sum_{i=1}^{n}|a_i|^p+(1-t)^{1-p}\sum_{i=1}^{n}|b_i|^p &= \left(\left(\sum_{i=1}^{n}a_i^p \right)^\frac 1p + \left(\sum_{i=1}^{n}b_i^p \right)^\frac 1p\right)^p
61 | \end{align}
62 | $$
63 | 综上即可证明原不等式成立,闵可夫斯基距离不满足直递性。
64 |
65 | **(4)下面证明$p$趋向无穷大时,闵可夫斯基距离等于对应分量的最大绝对距离。**
66 |
67 | 闵可夫斯基距离公式可以转换如下:
68 | $$
69 | \text{dist}_\text{mk} (x_i, x_j) = \left( \sum_{u=1}^n |x_{iu}-x_{ju}|^p \right)^\frac 1p = \max_u|x_{iu}-x_{ju}| \left( \sum_{u=1}^n \left(\frac{|x_{iu}-x_{ju}|}{\max_u|x_{iu}-x_{ju}|}\right)^p \right)^\frac 1p
70 | $$
71 | 令
72 | $$
73 | t_u = \frac{|x_{iu}-x_{ju}|}{\max_u|x_{iu}-x_{ju}|}\leq 1
74 | $$
75 | 当$p \rarr +\infin$时
76 | $$
77 | \left( \sum_{u=1}^n t_u^p \right)^\frac 1p \rarr1
78 | $$
79 | 因此
80 | $$
81 | \text{dist}_\text{mk} (x_i, x_j) \rarr \max_u|x_{iu}-x_{ju}|
82 | $$
83 | 综上得证。
84 |
85 |
86 |
87 | ## 9.2
88 |
89 | 显然,豪斯多夫距离满足非负性和对称性,这里不过多证明。
90 |
91 | (1)下面证明豪斯多夫距离满足同一性。
92 |
93 | ①当$X=Z$时,$\text{dist}_\text{h}(X, Z) = \text{dist}_\text{h}(Z, X) = 0$,因此$\text{dist}_\text{H}(X, Z) = 0$。
94 |
95 | ②当$\text{dist}_\text{H}(X, Z) = 0$时,$\text{dist}_\text{h}(X, Z) = \text{dist}_\text{h}(Z, X) = 0$,这说明任意$x\in X$,存在$z\in Z$使得距离为0,因此$X \subset Z$,同时也说明任意$z\in Z$,存在$x\in X$使得距离为0,因此$Z \subset X$,所以$X=Z$。
96 |
97 | 综上得证。
98 |
99 | (2)下面证明豪斯多夫距离满足直递性。
100 |
101 | 欲证
102 | $$
103 | \text{dist}_\text{H}(X, Z) \leq \text{dist}_\text{H}(X, Y) + \text{dist}_\text{H}(Y, Z)
104 | $$
105 |
106 | 由于
107 | $$
108 | \text{dist}_\text{H}(X, Z) = \max(\text{dist}_\text{h}(X, Z), \text{dist}_\text{h}(Z, X))
109 | $$
110 | 因此,可以转化为求证
111 | $$
112 | \text{dist}_\text{h}(X, Z) \leq \text{dist}_\text{h}(X, Y) + \text{dist}_\text{h}(Y, Z)
113 | $$
114 | 由于
115 | $$
116 | \begin{align}
117 | \min_{z\in Z} ||x - z||_2 &= \min_{z \in Z} ||x + y+y-z||_2, \forall y\in Y \\
118 | &\leq \min_{z \in Z} (||x + y||_2+||y-z||_2), \forall y\in Y \\
119 | &= ||x+y||_2 + \min_{z \in Z} ||y-z||_2, \forall y\in Y \\
120 | &\leq ||x+y||_2 + \max_{y \in Y}\min_{z \in Z} ||y-z||_2, \forall y\in Y \\
121 | &= ||x+y||_2 + \text{dist}_\text{h}(Y, Z), \forall y\in Y \\
122 | &\leq \min_{y \in Y} ||x+y||_2 + \text{dist}_\text{h}(Y, Z)
123 | \end{align}
124 | $$
125 | 对不等式左右两边取$\max_{x\in X}$得到
126 | $$
127 | \max_{x\in X}\min_{z\in Z} ||x - z||_2 \leq \max_{x\in X}\min_{y \in Y} ||x+y||_2 + \text{dist}_\text{h}(Y, Z)
128 | $$
129 | 即
130 | $$
131 | \text{dist}_\text{h}(X, Z) \leq \text{dist}_\text{h}(X, Y) + \text{dist}_\text{h}(Y, Z)
132 | $$
133 | 综上得证。
134 |
135 |
136 |
137 |
138 | ## 9.3
139 |
140 | 不一定能。由于求解式(9.24)的最优解是一个NP-hard问题,k均值算法只是基于贪心思想通过迭代进行近似求解得到的局部最优解,不一定能得到式子的全局最优解。
141 |
142 |
143 |
144 | ## 9.4
145 |
146 | ### 1 导入库
147 | ```python
148 | from sklearn.cluster import KMeans
149 | import pandas as pd
150 | import numpy as np
151 | from matplotlib import pyplot as plt
152 | ```
153 |
154 | ### 2 导入数据集
155 | ```python
156 | df = pd.read_csv("./4.0.csv", header=None)
157 | X = df.values
158 | ```
159 |
160 | ### 3 测试不同k值的影响
161 | > 选定数据集中前k个点作为初始中心点
162 | ```python
163 | for k in range(2, 5):
164 | model = KMeans(k, init=[X[i, :] for i in range(k)], n_init=1)
165 | model.fit(X)
166 | ans = model.predict(X)
167 | print(model.cluster_centers_)
168 | plt.title(f"KMeans [k={k}]")
169 | plt.scatter(X[:, 0], X[:, 1], c=ans)
170 | plt.show()
171 | ```
172 |
173 | ```
174 | [[0.62371429 0.37435714]
175 | [0.44675 0.1875 ]]
176 | ```
177 |
178 | 
179 |
180 | ```
181 | [[0.471 0.39928571]
182 | [0.68138462 0.28446154]
183 | [0.3725 0.1748 ]]
184 | ```
185 |
186 | 
187 |
188 | ```
189 | [[0.67625 0.4665 ]
190 | [0.6896 0.3072 ]
191 | [0.61585714 0.137 ]
192 | [0.38685714 0.27714286]]
193 | ```
194 |
195 | 
196 |
197 |
198 |
199 | ### 4 测试不同初始中心点的影响
200 |
201 | > 选定k=3
202 |
203 | ```python
204 | Xs = [[[0, 0], [0, 0], [0, 0]], # 全都在一个点
205 | [[0.5, 0.1], [0.5, 0.25], [0.5, 0.4]], # y轴分散
206 | [[0.3, 0.3], [0.5, 0.3], [0.7, 0.3]]] # x轴分散
207 |
208 | for centers in Xs:
209 | model = KMeans(3, init=centers, n_init=1)
210 | model.fit(X)
211 | ans = model.predict(X)
212 | print(model.cluster_centers_)
213 | # plt.title(f"KMeans [k={k}]")
214 | plt.scatter(X[:, 0], X[:, 1], c=ans)
215 | plt.show()
216 | ```
217 |
218 | ```
219 | [[0.36136364 0.21709091]
220 | [0.60845455 0.41336364]
221 | [0.6515 0.16325 ]]
222 | ```
223 |
224 | 
225 |
226 | ```
227 | [[0.63255556 0.16166667]
228 | [0.33455556 0.21411111]
229 | [0.598 0.40491667]]
230 | ```
231 |
232 | 
233 |
234 | ```
235 | [[0.348 0.18955556]
236 | [0.471 0.39928571]
237 | [0.67507143 0.26714286]]
238 | ```
239 |
240 | 
241 |
242 | ### 5 分析
243 |
244 | 1. 对比不同k值得到的结果可以看出,不是k越大越好,而是需要根据经验去确定簇的数量,这样才能达到不错的聚类效果。
245 | 2. 对比不同初始值的结果可以看出,初始中心点也很大程度上影响到了聚类的效果,选定的三组初始中心点各有特征,可以看出在选定初始中心点在x轴上分散分布时,效果比较不错,说明数据集在x轴方向上有比较好的可分性。由于KMeans基于贪心算法,只能得到局部最优解,因此根据经验选择符合数据集特征的初始中心点对聚类效果有显著影响。
246 |
247 |
248 |
249 | ## 9.5
250 |
251 | (1)连接性。设$x_k$为集合$X$中的核心对象,设$x_i \in X, x_j \in X$。由于集合$X$是由$x_k$密度可达的所有样本构成的,那么$x_i,x_j$均由$x_k$密度可达,因此$x_i$与$x_j$密度相连。由此证明连接性。
252 |
253 | (2)最大性。设$x_k$为集合$X$中的核心对象,设$x_i \in C$,那么$x_i$由$x_k$密度可达。如果$x_j$由$x_i$密度可达,由于密度可达关系满足直递性,$x_j$由$x_k$密度可达,因此$x_j\in C$。由此证明最大性。
254 |
255 |
256 |
257 |
--------------------------------------------------------------------------------
/docs/MachineLearning/第二章作业.md:
--------------------------------------------------------------------------------
1 | # 《机器学习》第二章作业
2 |
3 | ## 2.1
4 |
5 | 答:由留出法定义,单次划分(分层抽样)中训练集中正例应当有$500 \times 70 \%=350$个样本,负例应当有$500 \times 70 \%=350$个样本,从所有样本中选取训练集后,剩余的作为测试集即可。因此,划分方式数为:
6 | $$
7 | \binom{500}{350} \times \binom{500}{350}=2.56 \times 10^{289}
8 | $$
9 |
10 | ## 2.3
11 |
12 | 答:**若学习器A的F1值比学习器B的高,A的BEP不一定比B高**。由于$BEP=P=R$,而$F1=\frac{2\times P' \times R'}{P' + R'}$,其中$P$不一定等于$P'$,$R$也不一定等于$R'$。因此若已知学习器A的F1值比学习器B的高,也无法推算出A的BEP值和B的BEP值之间的关系。
13 |
14 | ## 2.5
15 |
16 | 答:设$\boldsymbol{x}^+$为正例,$\boldsymbol{x}^-$为负例,那么:
17 |
18 | - $f(\boldsymbol{x}^+) > f(\boldsymbol{x}^-)$表示两者都预测正确;
19 |
20 | - $f(\boldsymbol{x}^+) = f(\boldsymbol{x}^-)$表示$\boldsymbol{x}^+$预测成功,而$\boldsymbol{x}^-$预测失败或者$\boldsymbol{x}^-$预测成功,而$\boldsymbol{x}^+$预测失败;
21 | - $f(\boldsymbol{x}^+) < f(\boldsymbol{x}^-)$表示两者都预测错误;
22 |
23 | 因此根据$\text{AUC}$的几何意义,可以对其公式进行改写:
24 | $$
25 | \begin{align}
26 | \text{AUC} &= \sum_{\boldsymbol{x}^+ \in D^+} \frac12 · \frac{1}{m^+} \left[ \frac{2}{m^-} \sum_{\boldsymbol{x}^- \in D^-} \mathbb{I}\left(f(\boldsymbol{x}^+) > f(\boldsymbol{x}^-)\right) + \frac1{m^-} \sum_{\boldsymbol{x}^- \in D^-} \mathbb{I}\left(f(\boldsymbol{x}^+) = f(\boldsymbol{x}^-)\right) \right] \\
27 | &= \frac{1}{m^+m^-} \sum_{\boldsymbol{x}^+ \in D^+} \sum_{\boldsymbol{x}^- \in D^-} \left( \mathbb{I}\left(f(\boldsymbol{x}^+) > f(\boldsymbol{x}^-)\right) + \frac12 \mathbb{I}\left(f(\boldsymbol{x}^+) = f(\boldsymbol{x}^-)\right) \right) \\
28 |
29 | \end{align}
30 | $$
31 | 因此:
32 | $$
33 | \begin{align}
34 | \text{AUC} + \ell_{\rank} &= \frac{1}{m^+m^-} \sum_{\boldsymbol{x}^+ \in D^+} \sum_{\boldsymbol{x}^- \in D^-} \left( \mathbb{I}\left(f(\boldsymbol{x}^+) < f(\boldsymbol{x}^-)\right) + \mathbb{I}\left(f(\boldsymbol{x}^+) > f(\boldsymbol{x}^-)\right) + \mathbb{I}\left(f(\boldsymbol{x}^+) = f(\boldsymbol{x}^-)\right) \right) \\
35 | &= \frac{1}{m^+m^-} \sum_{\boldsymbol{x}^+ \in D^+} \sum_{\boldsymbol{x}^- \in D^-} (1) \\
36 | &= 1
37 | \end{align}
38 | $$
39 | 原式得证。
40 |
41 | ## 2.7
42 |
43 | 答:由于ROC曲线上的点为$(\text{FPR}, \text{TPR})$,且有$\text{TPR} + \text{FNR} = 1$,所以由ROC曲线上一点能确定代价曲线图中$(0, \text{FPR})$和$(1, \text{FNR})$两点,并由此得到连接两点的线段。将ROC曲线上所有的点对应到代价曲线图的所有线段,取所有线段的公共下界即可得到唯一的代价曲线。
44 |
45 | 反之,代价曲线(折线)的每个分段可以对应一条直线,从而得到直线与$x=0$和$x=1$的交点$(0, \text{FPR})$和$(1, \text{FNR})$,这两点可以对应ROC曲线上的一点,由此即可确定一条ROC曲线(不是唯一的,因为可能存在在代价曲线上方而不与曲线相交的线段,这可能也会对应ROC曲线上的一个点)。
46 |
47 | ## 2.9
48 |
49 | 卡方检验就是统计样本的实际观测值与理论推断值之间的偏离程度,卡方值越大,越不符合;卡方值越小,越趋于符合。检验过程如下:
50 |
51 | 1. 写出假设和备择假设;
52 |
53 | 2. 计算卡方值
54 | $$
55 | \chi^2 = \sum_{i=1}^n \frac{(x_i - \hat{x}_i)^2}{\hat{x}_i}
56 | $$
57 | 其中,$x_i$表示观测值,而$\hat{x}_i$表示预期值;
58 |
59 | 3. 计算卡方分布的自由度(若为$R \times C$的列联表,自由度为$(R-1)(C - 1)$);
60 |
61 | 4. 确定显著水平并根据自由度查表得到卡方检验值,将其与计算出的卡方值进行比较;
62 |
63 | 5. 若计算出的卡方值比检验值小,那么无法拒绝原假设,反之拒绝原假设。
64 |
65 |
--------------------------------------------------------------------------------
/docs/MachineLearning/第五章作业.md:
--------------------------------------------------------------------------------
1 | # 《机器学习》第五章作业
2 |
3 | ## 5.1
4 |
5 | **答**:虽然线性函数相对阶跃函数是连续的,但它不能将输入值压缩到$(0,1)$输出值范围内,这使得后续过程中神经元受变量值相对较大的属性影响更大,不利于参数收敛。而且,使用线性函数作为激活函数时,输入值经过每一层的传播后的输出值是输入值的线性组合,此时等价于线性回归。
6 |
7 | ## 5.2
8 |
9 | **答**:在使用Sigmoid函数作为激活函数的每个神经元的输出都是
10 | $$
11 | y=\frac{1}{1+e^{-\left( \sum_{i=1}^nw_i x_i-\theta \right)}}
12 | $$
13 | 对数几率回归的输出为
14 | $$
15 | y=
16 | \left\{
17 | \begin{array}{}
18 | 0, & z<0 \\
19 | 0.5, & z=0 \\
20 | 1, & z>0
21 | \end{array}
22 | \right.
23 | $$
24 | 其中
25 | $$
26 | z=\frac1{1+e^{-\left( \boldsymbol w^\text T \boldsymbol x + b \right)}}
27 | $$
28 | 可以看到,神经元的$y$函数和对数几率回归的$z$函数是相等的。不过神经元的输出不对Sigmoid函数的输出做任何变换,而对数几率回归由于需要判别,因此在输出后加入了分段函数。同时可以发现,如果神经网络中神经元除了输出的激活函数为Sigmoid函数,其他激活函数均为线性函数的话,此神经网络就等价于对数几率回归。
29 |
30 | ## 5.3
31 |
32 | **答**:对于$v_{ih}$,其更新公式为
33 | $$
34 | \Delta v_{ih} = -\eta \frac{\partial E_k}{\partial v_{ih}}
35 | $$
36 | 其中
37 | $$
38 | \frac{\partial E_k}{\partial v_{ih}} = \frac{\partial E_k}{\partial b_h}
39 | \frac{\partial b_h}{\partial \alpha_h} \frac{\partial \alpha_h}{\partial v_{ih}}
40 | $$
41 | 由于
42 | $$
43 | \frac{\partial \alpha_h}{\partial v_{ih}} = x_i \\
44 | e_h = -\frac{\partial E_k}{\partial b_h}
45 | \frac{\partial b_h}{\partial \alpha_h}
46 | $$
47 | 所以
48 | $$
49 | \Delta v_{ih} = -\eta \frac{\partial E_k}{\partial v_{ih}} = -\eta \frac{\partial E_k}{\partial b_h}
50 | \frac{\partial b_h}{\partial \alpha_h} \frac{\partial \alpha_h}{\partial v_{ih}} = \eta e_h x_i
51 | $$
52 | 此即书中式(5.13),证毕。
53 |
54 | ## 5.4
55 |
56 | **答**:若学习率过低,会导致模型收敛过慢,而学习率过高又可能会导致震荡而使模型无法收敛到最优解。可以考虑使用Adam算法等设定合适的初始学习率后,在迭代过程中自动调整学习率。
57 |
58 | ## 5.5
59 |
60 | ### 1. 环境及数据准备
61 |
62 | ```python
63 | import numpy as np
64 | import pandas as pd
65 | from matplotlib import pyplot as plt
66 | from sklearn.model_selection import train_test_split
67 | from sklearn.preprocessing import LabelEncoder
68 |
69 | df = pd.read_csv('./watermelon3.csv', index_col=0) # 西瓜数据集3.0
70 | for label in df.columns: # 离散值预处理为整数
71 | if df[label].dtype == object:
72 | df[label] = LabelEncoder().fit(df[label]).transform(df[label])
73 | df
74 | ```
75 |
76 | | | 色泽 | 根蒂 | 敲声 | 纹理 | 脐部 | 触感 | 密度 | 含糖率 | 好瓜 |
77 | | ---: | ---: | ---: | ---: | ---: | ---: | ---: | ----: | -----: | ---: |
78 | | 编号 | | | | | | | | | |
79 | | 1 | 2 | 2 | 1 | 1 | 0 | 0 | 0.697 | 0.460 | 1 |
80 | | 2 | 0 | 2 | 0 | 1 | 0 | 0 | 0.774 | 0.376 | 1 |
81 | | 3 | 0 | 2 | 1 | 1 | 0 | 0 | 0.634 | 0.264 | 1 |
82 | | 4 | 2 | 2 | 0 | 1 | 0 | 0 | 0.608 | 0.318 | 1 |
83 | | 5 | 1 | 2 | 1 | 1 | 0 | 0 | 0.556 | 0.215 | 1 |
84 | | 6 | 2 | 1 | 1 | 1 | 2 | 1 | 0.403 | 0.237 | 1 |
85 | | 7 | 0 | 1 | 1 | 2 | 2 | 1 | 0.481 | 0.149 | 1 |
86 | | 8 | 0 | 1 | 1 | 1 | 2 | 0 | 0.437 | 0.211 | 1 |
87 | | 9 | 0 | 1 | 0 | 2 | 2 | 0 | 0.666 | 0.091 | 0 |
88 | | 10 | 2 | 0 | 2 | 1 | 1 | 1 | 0.243 | 0.267 | 0 |
89 | | 11 | 1 | 0 | 2 | 0 | 1 | 0 | 0.245 | 0.057 | 0 |
90 | | 12 | 1 | 2 | 1 | 0 | 1 | 1 | 0.343 | 0.099 | 0 |
91 | | 13 | 2 | 1 | 1 | 2 | 0 | 0 | 0.639 | 0.161 | 0 |
92 | | 14 | 1 | 1 | 0 | 2 | 0 | 0 | 0.657 | 0.198 | 0 |
93 | | 15 | 0 | 1 | 1 | 1 | 2 | 1 | 0.360 | 0.370 | 0 |
94 | | 16 | 1 | 2 | 1 | 0 | 1 | 0 | 0.593 | 0.042 | 0 |
95 | | 17 | 2 | 2 | 0 | 2 | 2 | 0 | 0.719 | 0.103 | 0 |
96 |
97 | ```python
98 | X = df.iloc[:, :-1] # 属性
99 | y = df.iloc[:, -1] # 标签
100 | X_train,X_test,y_train,y_test=train_test_split(X,y,test_size=0.3) #随机划分训练集和测试集
101 | ```
102 |
103 | ### 2. 定义模型
104 |
105 | ```python
106 | class BPNN:
107 | def __init__(self):
108 | pass
109 |
110 | def __init(self, X, y, q):
111 | '''
112 | @param: X: 训练集属性
113 | @param: y: 训练集输出
114 | @param: q: 隐层神经元数量
115 | '''
116 | self.v = np.random.uniform(size=(X.shape[1], q))
117 | self.w = np.random.uniform(size=(q, 1))
118 |
119 | def __sigmoid(self, x):
120 | return 1 / (1 + np.exp(-x))
121 |
122 | def __sgd(self, X, y, lr, epoch):
123 | # 标准BP算法, 对每一个样本进行一次权重更新
124 | self.loss = []
125 | for ep in range(1, epoch+1):
126 | sum_ek = 0
127 | idx = list(range(X.shape[0]))
128 | np.random.shuffle(idx)
129 | X, y = X[idx], y[idx]
130 | for i in range(X.shape[0]):
131 | # 前向传播
132 | self.alpha = X[i:i+1] @ self.v
133 | self.b = self.__sigmoid(self.alpha)
134 | self.beta = self.b @ self.w
135 | self.py = self.__sigmoid(self.beta)
136 | # 计算误差
137 | ek = np.power(self.py - y[i], 2) / 2
138 | sum_ek += np.average(ek)
139 | # 后向更新
140 | g = self.py * (1 - self.py) * (y[i] - self.py)
141 | delta_w = self.eta * (self.b.T @ g)
142 | e = self.b * (1 - self.b) * np.sum(self.w @ g, axis=1)
143 | delta_v = self.eta * (X[i:i+1].T @ e)
144 | self.w += delta_w
145 | self.v += delta_v
146 | self.loss.append(sum_ek/X.shape[0])
147 |
148 | def __bgd(self, X, y, lr, epoch):
149 | # 累积BP算法, 对所有样本都进行一次权重更新
150 | self.loss = []
151 | y = y.reshape((-1, 1))
152 | for ep in range(1, epoch+1):
153 | # 前向传播
154 | self.alpha = X @ self.v
155 | self.b = self.__sigmoid(self.alpha)
156 | self.beta = self.b @ self.w
157 | self.py = self.__sigmoid(self.beta)
158 | # 计算误差
159 | ek = np.power(self.py - y, 2) / 2
160 | self.loss.append(np.average(ek))
161 | # 后向更新
162 | g = self.py * (1 - self.py) * (y - self.py)
163 | delta_w = self.eta * (self.b.T @ g)
164 | e = self.b * (1 - self.b) * (g @ self.w.T)
165 | delta_v = self.eta * (X.T @ e) # (8, 17) (17, 10)
166 | self.w += delta_w
167 | self.v += delta_v
168 |
169 | def fit(self, X, y, lr, epoch, algo="sgd"):
170 | X = np.array(X)
171 | y = np.array(y)
172 | self.eta = lr
173 | self.__init(X, y, 10)
174 | # 标准BP算法
175 | if algo.lower() == "sgd":
176 | self.__sgd(X, y, lr, epoch)
177 | # 累积BP算法
178 | elif algo.lower() == "bgd":
179 | self.__bgd(X, y, lr, epoch)
180 |
181 | def predict(self, X, y):
182 | X = np.array(X)
183 | y = np.array(y)
184 | # 前向传播
185 | alpha = X @ self.v
186 | b = self.__sigmoid(alpha)
187 | beta = b @ self.w
188 | py = self.__sigmoid(beta)
189 | return np.array(py > 0.5).astype(np.int32).reshape(1, -1)[0]
190 |
191 | def accuracy(self, X, y):
192 | ans = self.predict(X, y)
193 | return 1 - np.sum(np.abs(ans - y)) / X.shape[0]
194 | ```
195 |
196 | ### 3. 模型测试
197 |
198 | ```python
199 | model = BPNN()
200 | model.fit(X, y, 0.2, 500, algo="sgd")
201 | print("使用SGD训练后的准确度为:", model.accuracy(X, y))
202 | plt.plot(model.loss, label="sgd")
203 | model.fit(X, y, 0.2, 500, algo="bgd")
204 | plt.plot(model.loss, label="bgd")
205 | print("使用BGD训练后的准确度为:", model.accuracy(X, y))
206 | plt.legend()
207 | ```
208 |
209 | ```
210 | 使用SGD训练后的准确度为: 1.0
211 | 使用BGD训练后的准确度为: 1.0
212 | ```
213 |
214 | 
215 |
216 | 可以看到,由于sgd每次迭代是对每个样本依次更新权重,因此在中间会出现抖动,但总体是朝着最优解的。从计算用时来看,sgd显然时间会更长,而bgd一次对所有损失更新权重,因此用时相对少一些。
217 |
--------------------------------------------------------------------------------
/docs/MachineLearning/第八章作业.md:
--------------------------------------------------------------------------------
1 | # 《机器学习基础》第八章作业
2 |
3 | ## 8.1
4 |
5 | 使用简单投票法的集成学习预测错误,意味着少于半数的基学习器预测正确。那么,集成学习的错误率就是少于半数的基学习器预测正确的概率。这等价于抛$T$次硬币,有少于$\lfloor T/2 \rfloor$的硬币朝上的概率(这里硬币朝上的概率为$1-\epsilon$,也就是一个基学习器预测正确的概率)。预测正确的基学习器数量为
6 | $$
7 | g(x) = \sum_{i=0}^{T} \mathbb I (h_i(x)=f(x))
8 | $$
9 | 那么$g(x) \leq \lfloor T / 2 \rfloor$的概率为
10 | $$
11 | P(g(x) \leq \lfloor T/2 \rfloor)=\sum_{k=0}^{\lfloor T/2 \rfloor}\binom{T}{k}(1-\epsilon)^k\epsilon^{T-k}
12 | $$
13 | 这就是式(8.3)的左半部分$P(H(x)\neq f(x))$,由题中给出的定义可得$\lfloor T/2 \rfloor= (\epsilon - \delta)T$,于是$\delta = \epsilon - \lfloor T/2 \rfloor/T \ge \epsilon - 1/2$,由Hoeffding不等式得
14 | $$
15 | P(H(x)\neq f(x)) \leq \exp\left( -2 \left( \epsilon - \frac12 \right)^2 T \right) = \exp\left( -\frac12 T \left( 1 - 2\epsilon \right)^2 \right)
16 | $$
17 | 式(8.3)得证。
18 |
19 |
20 |
21 | ## 8.2
22 |
23 | 我们需要最小化的就是$\mathbb E_{x\in D}[\ell(-f(x) H(x))]$,考虑对$H(x)$进行求偏导,得到
24 | $$
25 | -P(f(x)=1|x) \ell(-H(x)) +P(f(x)=-1|x) \ell(H(x))
26 | $$
27 | 令其为0得到
28 | $$
29 | \frac{P(f(x)=-1|x)}{P(f(x)=1|x)} = \frac{\ell(H(x))}{\ell(-H(x))}
30 | $$
31 | 当$P(f(x)=-1|x) > P(f(x)=1|x)$时,$\ell(H(x)) > \ell(-H(x))$,由于$\ell(-f(x)H(x))$关于$H(x)$递减,因此
32 | $$
33 | H(x) < -H(x)
34 | $$
35 | 所以$H(x)<0$。同理,当$P(f(x)=-1|x) < P(f(x)=1|x)$时,$H(x)>0$。
36 |
37 | 综上:$\text{sign}(H(x))=\arg \max_{y\in (-1, 1)}P(f(x)=y|x)$,这意味着$\text{sign}(H(x))$达到了贝叶斯最优错误率。这说明此损失函数是分类任务原本0/1损失函数得一致性替代函数。
38 |
39 |
40 |
41 | ## 8.3
42 |
43 | 使用`sklean.ensemble`中的`AdaBoostClassifier`实现即可(默认采用决策树模型作为基学习器),代码如下:
44 |
45 | ```python
46 | from sklearn.ensemble import AdaBoostClassifier
47 | import pandas as pd
48 | from matplotlib import pyplot as plt
49 | import numpy as np
50 |
51 | # 加载数据
52 | df = pd.read_csv("./3.0a.csv", index_col=0)
53 | X = df.iloc[:, :2].values
54 | y = df.iloc[:, -1].values
55 |
56 | # 模型训练与预测
57 | model = AdaBoostClassifier(n_estimators=1, random_state=0)
58 | model.fit(X, y)
59 | pred = model.predict(X)
60 | print("错误分类数量:", np.sum(np.abs(pred - y)))
61 |
62 | # 画图
63 | plt.scatter(X[:, 0], X[:, 1], c=pred)
64 | ```
65 |
66 | 基学习器数量为1时:
67 |
68 | 
69 |
70 | 基学习器数量为2时:
71 |
72 | 
73 |
74 | 基学习器数量超过3时:
75 |
76 | 
77 |
78 | 可以发现,当基学习器变多的时候分类效果得到了提升,并且很稳定!
79 |
80 |
81 |
82 | ## 8.5
83 |
84 | 使用`sklean.ensemble`中的`BaggingClassifier`实现即可(默认采用决策树模型作为基学习器),代码如下:
85 |
86 | ```python
87 | from sklearn.ensemble import BaggingClassifier
88 | import pandas as pd
89 | from matplotlib import pyplot as plt
90 | import numpy as np
91 |
92 | # 加载数据
93 | df = pd.read_csv("./3.0a.csv", index_col=0)
94 | X = df.iloc[:, :2].values
95 | y = df.iloc[:, -1].values
96 |
97 | # 模型训练与预测
98 | model = BaggingClassifier(n_estimators=1, random_state=0)
99 | model.fit(X, y)
100 | pred = model.predict(X)
101 | print(np.sum(np.abs(pred - y)))
102 |
103 | # 画图
104 | plt.scatter(X[:, 0], X[:, 1], c=pred)
105 | ```
106 |
107 | 基学习器数量为1时:
108 |
109 | 
110 |
111 | 基学习器数量为2,3,4时:
112 |
113 | 
114 |
115 | 基学习器数量为7时:
116 |
117 | 
118 |
119 | 可以发现,当基学习器变多的时候分类效果不一定得到提升,在分类器数量较小时,变化比较不稳定。
120 |
121 |
122 |
123 | ## 8.6
124 |
125 | Bagging方法使用自助采样,简单高效,但考虑到“误差-分歧分解”,Bagging方法中个体学习器的多样性较低。朴素贝叶斯属于稳定基学习器,对数据样本的扰动不敏感,对这类基学习器进行集成往往需要使用输入属性扰动等其他扰动,而Bagging方法做不到,因此,Bagging方法通常很难提升朴素贝叶斯分类器的性能。
126 |
127 |
--------------------------------------------------------------------------------
/docs/MachineLearning/第六章作业.md:
--------------------------------------------------------------------------------
1 | # 《机器学习》第六章作业
2 |
3 | ## 6.1
4 |
5 | **答**:设超平面上任意一点为$\boldsymbol{y}$,满足$\boldsymbol{w}^{\text T} \boldsymbol{y} + b = 0$,那么$\boldsymbol{x}$与$\boldsymbol{y}$的距离为$|\boldsymbol{x} - \boldsymbol{y}|$。由几何关系可知,只有当$\boldsymbol{x} - \boldsymbol{y}$与超平面垂直时,才能满足$\boldsymbol{x}$与超平面的距离为$|\boldsymbol{x} - \boldsymbol{y}|$,又因为$\boldsymbol{w}$与超平面垂直,因此
6 | $$
7 | \boldsymbol{x} - \boldsymbol{y} = \pm |\boldsymbol{x} - \boldsymbol{y}| \frac{\boldsymbol{w}}{||\boldsymbol{w}||}
8 | $$
9 | 两边同时左乘$\boldsymbol w^{\text T}$可得
10 | $$
11 | \boldsymbol w^{\text T} \boldsymbol{x} - \boldsymbol w^{\text T} \boldsymbol{y} &= \pm |\boldsymbol{x} - \boldsymbol{y}| \frac{\boldsymbol w^{\text T}\boldsymbol{w}}{||\boldsymbol{w}||} \\
12 | \boldsymbol w^{\text T} \boldsymbol{x} + b &= \pm |\boldsymbol{x} - \boldsymbol{y}| \times ||\boldsymbol w||
13 | $$
14 | 即
15 | $$
16 | r = |\boldsymbol{x} - \boldsymbol{y}| = \frac{|\boldsymbol w^{\text T} \boldsymbol{x} + b|}{||\boldsymbol w||}
17 | $$
18 |
19 | ## 6.2
20 |
21 | ### 1. 搭建环境
22 |
23 |
24 | ```python
25 | import pandas as pd
26 | import numpy as np
27 | from matplotlib import pyplot as plt
28 | from sklearn import svm
29 | ```
30 |
31 | ### 2. 导入数据
32 |
33 |
34 | ```python
35 | df = pd.read_csv("./3.0a.csv", index_col=0)
36 | X = df.iloc[:, :2].values
37 | y = df.iloc[:, -1].values
38 | ```
39 |
40 | ### 3. 使用线性核训练一个SVM
41 |
42 |
43 | ```python
44 | model = svm.SVC(C=1000, kernel='linear') # C高一些,对误差的容忍度低
45 | model.fit(X, y)
46 | model.score(X, y)
47 | ```
48 |
49 |
50 | 0.8235294117647058
51 |
52 |
53 | ```python
54 | # 绘制支持向量
55 | idx = model.support_
56 | plt.scatter(X[:, 0], X[:, 1], c=y, s=30)
57 | plt.scatter(X[idx][:, 0], X[idx][:, 1], c=y[idx], edgecolors='r', s=100)
58 | plt.show()
59 | ```
60 |
61 |
62 | 
63 |
64 |
65 | ### 4. 使用高斯核训练一个SVM
66 |
67 |
68 | ```python
69 | model = svm.SVC(C=1000, kernel='rbf') # C高一些,对误差的容忍度低
70 | model.fit(X, y)
71 | model.score(X, y)
72 | ```
73 |
74 | ```
75 | 1.0
76 | ```
77 |
78 |
79 | ```python
80 | # 绘制支持向量
81 | idx = model.support_
82 | plt.scatter(X[:, 0], X[:, 1], c=y, s=30)
83 | plt.scatter(X[idx][:, 0], X[idx][:, 1], c=y[idx], edgecolors='r', s=100)
84 | plt.show()
85 | ```
86 |
87 | 
88 |
89 | ### 5. 对比分析
90 |
91 | 在对误差容忍度比较高的情况下,高斯核SVM可以完全拟合数据,而且支持向量也比较少。但由于数据线性不可分,线性核SVM不论设置多高的容忍度仍不能很好地区分数据,且支持向量也较多。
92 |
93 | ## 6.3
94 |
95 | ### 1. 搭建环境
96 |
97 |
98 | ```python
99 | import numpy as np
100 | from matplotlib import pyplot as plt
101 | from sklearn.model_selection import train_test_split
102 | from sklearn.datasets import load_iris, load_breast_cancer
103 | from sklearn.svm import SVC # 支持向量机
104 | from sklearn.neural_network import MLPClassifier # BP神经网络
105 | from sklearn.tree import DecisionTreeClassifier # 决策树
106 | ```
107 |
108 | ### 2. 构建数据集
109 |
110 |
111 | ```python
112 | X_iris, y_iris = load_iris(return_X_y=True) # 鸢尾花数据集
113 | X_bc, y_bc = load_breast_cancer(return_X_y=True) # 乳腺癌数据集
114 | # 划分训练集和测试集
115 | X_iris_train, X_iris_test, y_iris_train, y_iris_test = train_test_split(X_iris, y_iris, test_size=0.2, random_state=0)
116 | X_bc_train, X_bc_test, y_bc_train, y_bc_test = train_test_split(X_bc, y_bc, test_size=0.2, random_state=0)
117 | ```
118 |
119 | ### 3. 定义各种模型函数
120 |
121 |
122 | ```python
123 | def svm(X_train, X_test, y_train, y_test, kernel="linear"):
124 | model = SVC(C=1, kernel=kernel)
125 | model.fit(X_train, y_train)
126 | print(f"[SVM with {kernel} kernel]Accuracy: {model.score(X_test, y_test)*100: .2f}%")
127 | ```
128 |
129 |
130 | ```python
131 | def mlp(X_train, X_test, y_train, y_test, activation="logistic"):
132 | model = MLPClassifier(max_iter=1000, activation=activation, random_state=0)
133 | model.fit(X_train, y_train)
134 | print(f"[BP Neural Network with {activation}]Accuracy: {model.score(X_test, y_test)*100: .2f}%")
135 | ```
136 |
137 |
138 | ```python
139 | def dt(X_train, X_test, y_train, y_test, criterion="entropy"):
140 | model = DecisionTreeClassifier(criterion=criterion, random_state=0)
141 | model.fit(X_train, y_train)
142 | print(f"[Decision Tree with {criterion}]Accuracy: {model.score(X_test, y_test)*100: .2f}%")
143 | ```
144 |
145 | ### 4. 在鸢尾花数据集上测试
146 |
147 |
148 | ```python
149 | svm(X_iris_train, X_iris_test, y_iris_train, y_iris_test, kernel="linear")
150 | svm(X_iris_train, X_iris_test, y_iris_train, y_iris_test, kernel="rbf")
151 | mlp(X_iris_train, X_iris_test, y_iris_train, y_iris_test, activation="logistic")
152 | mlp(X_iris_train, X_iris_test, y_iris_train, y_iris_test, activation="relu")
153 | dt(X_iris_train, X_iris_test, y_iris_train, y_iris_test, criterion="entropy")
154 | dt(X_iris_train, X_iris_test, y_iris_train, y_iris_test, criterion="gini")
155 | ```
156 |
157 | [SVM with linear kernel]Accuracy: 100.00%
158 | [SVM with rbf kernel]Accuracy: 100.00%
159 | [BP Neural Network with logistic]Accuracy: 100.00%
160 | [BP Neural Network with relu]Accuracy: 100.00%
161 | [Decision Tree with entropy]Accuracy: 100.00%
162 | [Decision Tree with gini]Accuracy: 100.00%
163 |
164 |
165 | ### 5. 在乳腺癌数据集上测试
166 |
167 |
168 | ```python
169 | svm(X_bc_train, X_bc_test, y_bc_train, y_bc_test, kernel="linear")
170 | svm(X_bc_train, X_bc_test, y_bc_train, y_bc_test, kernel="rbf")
171 | mlp(X_bc_train, X_bc_test, y_bc_train, y_bc_test, activation="logistic")
172 | mlp(X_bc_train, X_bc_test, y_bc_train, y_bc_test, activation="relu")
173 | dt(X_bc_train, X_bc_test, y_bc_train, y_bc_test, criterion="entropy")
174 | dt(X_bc_train, X_bc_test, y_bc_train, y_bc_test, criterion="gini")
175 | ```
176 |
177 | [SVM with linear kernel]Accuracy: 95.61%
178 | [SVM with rbf kernel]Accuracy: 92.98%
179 | [BP Neural Network with logistic]Accuracy: 91.23%
180 | [BP Neural Network with relu]Accuracy: 94.74%
181 | [Decision Tree with entropy]Accuracy: 92.98%
182 | [Decision Tree with gini]Accuracy: 91.23%
183 |
184 | ### 6. 分析
185 |
186 | 针对不同的数据集特征可以选择不同的算法。通过针对不同数据集对不同算法的参数进行调节,很多模型都能很好地拟合数据。
187 |
188 | ## 6.4
189 |
190 | **答**:线性判别分析是将$n$维的数据投影到$n-1$维上的一个超平面后再来分类,可以支持多分类;而线性核的SVM是在$n$维的数据中寻找一个$n-1$的超平面来分隔数据,是解决的二分类问题。因此,若需线性判别分析与线性核等价,一定要满足都是在**解决二分类问题**上(不考虑使用OvR等使SVM解决多分类)。
191 |
192 | 由于线性判别分析关键在找到映射平面,线性核的SVM关键在找分类超平面。考虑两者的关系,可以想到若**两平面垂直**时,如果线性判别分析能达成分类任务,那么在映射平面的两类之间取一条直线,并以这条直线和映射平面的法向量相交做一个平面,一定可以分隔样本。而这个样本就可以作为线性核SVM的分类超平面。
193 |
194 | 综上所述,线性判别分析与线性核支持向量机满足以下两个条件时等价:
195 |
196 | - 解决的问题是二分类问题;
197 | - 线性判别分析的映射超平面和线性核支持向量机的分类超平面垂直。
198 |
199 | ## 6.6
200 |
201 | **答**:对于硬间隔支持向量机,若噪声样本出现在支持向量中,会使决策超平面变化,间隔变小,使得SVM的泛化能力变弱、检测精度降低;对于软间隔支持向量机,噪声样本的出现会使目标函数中的损失项显著提高,使SVM决策受到影响。因此SVM对噪声敏感。
202 |
--------------------------------------------------------------------------------
/docs/MachineLearning/第四章作业.md:
--------------------------------------------------------------------------------
1 | # 《机器学习》第四章作业
2 |
3 | ## 4.1
4 |
5 | **证明**:假设在题目条件下,不存在于与训练集一致的决策树,那么一定存在一个中间节点使得经过此节点后分出的叶子节点中包含不一样标签的样本。而由于不含冲突数据,因此在此叶子节点中标签不同的样本一定还有特征是不相同的,也就是说,此叶子节点还可以根据不同的属性进行下一步决策,使得标签不同的样本完全分离,从而使得训练误差为0。因此得证:**对于不含冲突数据的训练集,必存在与训练集一致的决策树。**
6 |
7 | ## 4.3
8 |
9 | ### 1. 准备数据
10 |
11 | ```python
12 | import numpy as np
13 | import pandas as pd
14 | from sklearn.model_selection import train_test_split
15 | from sklearn.preprocessing import LabelEncoder
16 |
17 | df = pd.read_csv('./watermelon3.csv', index_col=0) # 西瓜数据集3.0
18 | for label in df.columns: # 离散值预处理为整数
19 | if df[label].dtype == object:
20 | df[label] = LabelEncoder().fit(df[label]).transform(df[label])
21 | df
22 | ```
23 |
24 | | | 色泽 | 根蒂 | 敲声 | 纹理 | 脐部 | 触感 | 密度 | 含糖率 | 好瓜 |
25 | | ---: | ---: | ---: | ---: | ---: | ---: | ---: | ----: | -----: | ---: |
26 | | 编号 | | | | | | | | | |
27 | | 1 | 2 | 2 | 1 | 1 | 0 | 0 | 0.697 | 0.460 | 1 |
28 | | 2 | 0 | 2 | 0 | 1 | 0 | 0 | 0.774 | 0.376 | 1 |
29 | | 3 | 0 | 2 | 1 | 1 | 0 | 0 | 0.634 | 0.264 | 1 |
30 | | 4 | 2 | 2 | 0 | 1 | 0 | 0 | 0.608 | 0.318 | 1 |
31 | | 5 | 1 | 2 | 1 | 1 | 0 | 0 | 0.556 | 0.215 | 1 |
32 | | 6 | 2 | 1 | 1 | 1 | 2 | 1 | 0.403 | 0.237 | 1 |
33 | | 7 | 0 | 1 | 1 | 2 | 2 | 1 | 0.481 | 0.149 | 1 |
34 | | 8 | 0 | 1 | 1 | 1 | 2 | 0 | 0.437 | 0.211 | 1 |
35 | | 9 | 0 | 1 | 0 | 2 | 2 | 0 | 0.666 | 0.091 | 0 |
36 | | 10 | 2 | 0 | 2 | 1 | 1 | 1 | 0.243 | 0.267 | 0 |
37 | | 11 | 1 | 0 | 2 | 0 | 1 | 0 | 0.245 | 0.057 | 0 |
38 | | 12 | 1 | 2 | 1 | 0 | 1 | 1 | 0.343 | 0.099 | 0 |
39 | | 13 | 2 | 1 | 1 | 2 | 0 | 0 | 0.639 | 0.161 | 0 |
40 | | 14 | 1 | 1 | 0 | 2 | 0 | 0 | 0.657 | 0.198 | 0 |
41 | | 15 | 0 | 1 | 1 | 1 | 2 | 1 | 0.360 | 0.370 | 0 |
42 | | 16 | 1 | 2 | 1 | 0 | 1 | 0 | 0.593 | 0.042 | 0 |
43 | | 17 | 2 | 2 | 0 | 2 | 2 | 0 | 0.719 | 0.103 | 0 |
44 |
45 | ```python
46 | X = df.iloc[:, :-1] # 属性
47 | y = df.iloc[:, -1] # 标签
48 | X_train,X_test,y_train,y_test=train_test_split(X,y,test_size=0.3) #随机划分训练集和测试集
49 | ```
50 |
51 | ### 2. 定义节点
52 |
53 | ```python
54 | class TreeNode:
55 | def __init__(self, tp=0, label=0, decide=0, compare=0):
56 | self.nxt = dict() # 儿子节点(属性值:节点)(中间节点特有)
57 | self.type = tp # 0->叶子, 1->中间节点
58 | self.label = label # 0->坏瓜, 1->好瓜
59 | self.decide = decide # 划分属性(中间节点特有)
60 | self.compare = compare # 判断值(连续节点特有)
61 | ```
62 |
63 | ### 3. 定义决策树模型
64 |
65 | ```python
66 | class DecisionTree:
67 | def __init__(self):
68 | pass
69 |
70 | def __Ent(self, y):
71 | p = pd.value_counts(y) / len(y)
72 | return -np.sum(p * np.log2(p))
73 |
74 | def __choose(self, D, A):
75 | EntD = self.__Ent(D[-1])
76 | calc1 = lambda x : x.shape[0] / D[0].shape[0] * self.__Ent(x) # 计算信息熵
77 | calc2 = lambda x : x.shape[0] / D[0].shape[0] * np.log2(x.shape[0] / D[0].shape[0]) # 计算IV
78 | mp = dict()
79 | for attr in A:
80 | v = None # 记录连续值判别的值
81 | if self.attr_type[attr]: # 连续值
82 | gain = 0
83 | iv = 0x3f3f3f3f
84 | for value in sorted(np.unique(D[0][:, attr])):
85 | Dv1 = D[-1][D[0][:, attr] <= value]
86 | Dv2 = D[-1][D[0][:, attr] > value]
87 | temp = EntD - (calc1(Dv1) + calc1(Dv2))
88 | if temp > gain:
89 | gain = temp
90 | iv = -calc2(Dv1)-calc2(Dv2)
91 | v = value
92 | # print("iv=", iv)
93 | else: # 离散值
94 | sm = 0
95 | iv = 1
96 | for value in np.unique(D[0][:, attr]):
97 | Dv = D[-1][D[0][:, attr] == value]
98 | sm += calc1(Dv)
99 | iv += -calc2(Dv)
100 | gain = EntD - sm
101 | # print(gain, iv)
102 | gain_ratio = gain / iv
103 | mp[attr] = (gain, 2, v) # 去除gain_ratio的影响
104 | # print(mp)
105 | temp = sorted(list(mp.items()), key=lambda x : (-x[-1][0], -x[-1][1]))[0]
106 | return temp[0],temp[-1][-1]
107 |
108 | def __generate(self, D, A):
109 | node = TreeNode()
110 | if np.unique(D[-1]).shape[0] <= 1:
111 | return TreeNode(tp=0, label=D[-1][0])
112 | if len(A) == 0 or np.unique(D[0][:, A], axis=0).shape[0] <= 1:
113 | return TreeNode(tp=0, label=np.argmax(np.bincount(D[1])))
114 | attr, v = self.__choose(D, A)
115 | # print(attr)
116 | node.decide = attr
117 | node.type = 1
118 | node.label = np.argmax(np.bincount([int(x) for x in D[1]]))
119 | if self.attr_type[attr]: # 连续值
120 | Dv = D[0][D[0][:, attr] <= v]
121 | # print(Dv)
122 | if Dv.shape[0] == 0:
123 | node.nxt[0] = TreeNode(tp=0, label=node.label)
124 | else:
125 | node.nxt[1] = self.__generate((Dv, D[1][D[0][:, attr] <= v]), [x for x in A if x != attr])
126 | Dv = D[0][D[0][:, attr] > v]
127 | # print(Dv)
128 | if Dv.shape[0] == 0:
129 | node.nxt[0] = TreeNode(tp=0, label=node.label)
130 | else:
131 | node.nxt[1] = self.__generate((Dv, D[1][D[0][:, attr] > v]), [x for x in A if x != attr])
132 | else: # 离散值
133 | for value in np.unique(D[0][:, attr]):
134 | Dv = D[0][D[0][:, attr] == value]
135 | if Dv.shape[0] == 0:
136 | node.nxt[value] = TreeNode(tp=0, label=node.label)
137 | else:
138 | node.nxt[value] = self.__generate((Dv, D[1][D[0][:, attr] == value]), [x for x in A if x != attr])
139 | return node
140 |
141 | def calc(self, X, y): # 将数据通过决策树,得出结果,返回准确率
142 | n = X.shape[0]
143 | lst = []
144 | for i in range(X.shape[0]):
145 | x = X[i, :]
146 | node = self.root
147 | while node.type == 1:
148 | if self.attr_type[node.decide]:
149 | if x[node.decide] <= node.compare:
150 | node = node.nxt[0]
151 | else:
152 | node = node.nxt[1]
153 | else:
154 | if x[node.decide] not in node.nxt.keys():
155 | break
156 | node = node.nxt[x[node.decide]]
157 | lst.append(node.label)
158 | ans = np.array(lst)
159 | acc = 1- np.sum(np.abs(ans - y)) / y.shape[0]
160 | return acc
161 |
162 | def fit(self, X, y):
163 | A = [i for i in range(X.values.shape[1])]
164 | self.attr_type = [X[label].dtype == float for label in X.columns] # 是否是连续值
165 | self.root = self.__generate((X.values, y.values), A)
166 | ans = self.calc(X.values, y.values)
167 | print(f"训练集准确率:{ans: .2f}")
168 |
169 | def predict(self, X, y):
170 | ans = self.calc(X.values, y.values)
171 | print(f"测试集准确率:{ans: .2f}")
172 | ```
173 |
174 | ### 4. 训练、测试
175 |
176 | ```python
177 | model = DecisionTree()
178 | model.fit(X_train, y_train)
179 | model.predict(X_test, y_test)
180 | ```
181 |
182 | 训练集准确率: 1.00
183 | 测试集准确率: 0.67
184 |
185 | ### 5. 讨论
186 |
187 | 本题中由于数据量较少,所以建立的决策树模型可以无需使用gain_ratio,实验发现:在本数据集中使用gain_ratio效果还没有gain好。
188 |
189 | ### 6. 决策树
190 |
191 | 
192 |
193 |
194 |
195 | ## 4.5
196 |
197 | 本题目中仅有决策树模型中`__choose`函数与上题不同。下面是本题的`__choose`函数
198 |
199 | ```python
200 | def __choose(self, D, A):
201 | mp = {}
202 | for attr in A:
203 | X = D[0][:, attr:attr+1]
204 | y = D[1]
205 | v = None
206 | if self.attr_type[attr]:
207 | X_ = X.copy()
208 | ans = -1
209 | for value in np.unique(X):
210 | X_ = X < value
211 | model = LogisticRegression()
212 | model.fit(X_, y)
213 | t = model.score(X_, y)
214 | if t > ans:
215 | ans = t
216 | v = value
217 | else:
218 | model = LogisticRegression()
219 | # print(X, y)
220 | model.fit(X, y)
221 | ans = model.score(X, y)
222 | mp[attr] = (ans, v)
223 | temp = sorted(list(mp.items()), key=lambda x : -x[1][0])
224 | return temp[0][0], temp[0][1][1]
225 | ```
226 |
227 | 训练集准确率: 1.00
228 | 测试集准确率: 0.83
229 |
230 | ### 决策树
231 |
232 | 
233 |
234 | ## 4.7
235 |
236 | **输入**:训练集$D={(\boldsymbol{x}_1, y_1),(\boldsymbol{x}_2, y_2),...,(\boldsymbol{x}_m, y_m)}$;属性集$A={a_1, a_2, ..., a_d}$
237 |
238 | **过程**:函数$\text{TreeGenerate}(D, A)$
239 |
240 | 1. 生成根节点$\text{root}$;用于存储中间节点的队列$\text{queue}$;
241 | 2. 将$(\text{root}, D, A)$放入队列$\text{queue}$中;
242 | 3. $\bold{while}$ $\text{queue}$不为空 $\bold{do}$
243 | 4. 从$\text{queue}$中取出节点$\text{node}$、训练集$D$和属性集$A$;
244 | 5. $\bold{if}$ $D$中样本全属于同一类别$C$ $\bold{then}$
245 | 6. 将$\text{node}$标记为$C$类叶节点; $\bold{continue}$
246 | 7. $\bold{end}\ \bold{if}$
247 | 8. $\bold{if}$ $A = \varnothing$ $\bold{OR}$ $D$中样本在$A$上取值相同 $\bold{then}$
248 | 9. 将$\text{node}$标记为叶节点,其类型标记为$D$中样本数最多的类; $\bold{continue}$
249 | 10. $\bold{end}\ \bold{if}$
250 | 11. 从$A$中选择最优划分属性$a_*$;
251 | 12. $\bold{for}$ $a_*$的每一个值$a_*^v$ $\bold{do}$
252 | 13. 为$\text{node}$生成一个分支节点$\text{branch}$;令$D_v$表示$D$中在$a_*$上取值为$a_*^v$的样本子集;
253 | 14. $\bold{if}$ $D_v$为空 $\bold{then}$
254 | 15. 将分支节点$\text{branch}$标记为叶节点,其类型标记为$D$中样本最多的类;
255 | 16. $\bold{else}$
256 | 17. 将$(\text{branch}, D_v, A\backslash \{ a_* \})$放入队列$\text{queue}$中;
257 | 18. $\bold{end}\ \bold{if}$
258 | 19. $\bold{end}\ \bold{for}$
259 | 20. $\bold{end}\ \bold{while}$
260 |
261 | **输出**:以$\text{root}$为根节点的一棵决策树
262 |
263 |
264 |
265 | ## 4.9
266 |
267 | **答**:在含缺失值的样本中进行划分属性的选择,只需要将包含所有样本的集合$D$转化为只包含在属性$a$上非缺失值样本的集合$\tilde{D}$,并乘上权重即可。具体来说,计算基尼指数的公式如下:
268 | $$
269 | \text{Gini\_index}(D, a)=\rho \times \sum_{v=1}^{V} \tilde r_v \frac{|\tilde D^v|}{|\tilde D|}\text{Gini}(\tilde D^v)
270 | $$
271 | 其中,
272 | $$
273 | \begin{align}
274 | \text{Gini}(\tilde D) &= 1-\sum_{k=1}^{|\mathcal Y|}\tilde p_k^2, \\
275 | \rho &= \frac {\sum_{\boldsymbol x \in\tilde D} w_{\boldsymbol x}} {\sum_{\boldsymbol x \in D} w_{\boldsymbol x}}, \\
276 | \tilde p_k &= \frac {\sum_{\boldsymbol x \in\tilde D_k} w_{\boldsymbol x}} {\sum_{\boldsymbol x \in D} w_{\boldsymbol x}} (1 \leq k \leq |\mathcal Y |),\\
277 | \tilde r_v &= \frac {\sum_{\boldsymbol x \in\tilde D^v} w_{\boldsymbol x}} {\sum_{\boldsymbol x \in D} w_{\boldsymbol x}} (1\leq v \leq V),
278 | \end{align}
279 | $$
280 |
281 |
--------------------------------------------------------------------------------
/docs/OperatingSystem/index.md:
--------------------------------------------------------------------------------
1 | # 暂无
--------------------------------------------------------------------------------
/docs/SoftwareEngineering/软工应用分析题.md:
--------------------------------------------------------------------------------
1 | 前面的结构化分析和面向对象分析建模看实验指导书和UML的PPT即可。这个文件请重点参考后面两种测试中涉及的方法。
2 |
3 | # 一、结构化分析
4 |
5 | ## 1. 数据流图【重要】
6 |
7 | 参考PPT和实验文档即可。
8 |
9 | ## 2. 数据字典【重要】
10 |
11 | 参考PPT和实验文档即可。
12 |
13 | ## 3. 控制流建模
14 |
15 | 不重要。考到就看PPT。
16 |
17 |
18 |
19 | # 二、面向对象分析
20 |
21 | ## 1. 用例图【重要】
22 |
23 | **请参考UML的PPT。**
24 |
25 | 分析用例实现中,对象之间的交互行为,核心是时序图、状态图等
26 |
27 | 【用例建模】
28 |
29 | · 用例表示从执行者的角度观察到系统的功能和外部行为。
30 |
31 | · 用例图主要描述用户需求,强调谁在使用系统,系统可以实现哪些功能目标。
32 |
33 | · 用例特征
34 |
35 | · 用例都是动宾结构
36 |
37 | · 用例是相互独立的
38 |
39 | · 用例由参与者启动
40 |
41 | · 有可观测的执行结果
42 |
43 | 【识别用例】
44 |
45 | 识别用例最好的方法就是从分析系统的参与者(可以是角色、外部系统、设备甚至时钟信号等)开始,考虑每一个参与者是如何使用系统的。
46 |
47 | **【用例图】**
48 |
49 | 用例模型主要包含4种元素:执行者、用例,执行者与用例间关联、用例间关系。
50 |
51 | 【用例间关系】
52 |
53 | 《include》关系
54 |
55 | 父用例执行过程中会用到子用例(无条件执行)。
56 |
57 | 子用例一般表示为公共功能。
58 |
59 | 
60 |
61 | 《extend》关系
62 |
63 | 父用例在特定情况下(称为扩展点)会用到子用例(有条件执行)
64 |
65 | 子用例一般表示为异常功能。
66 |
67 | 
68 |
69 | 泛化(generalization)关系
70 |
71 | 当多个用例共同拥有一种类似的行为时,可以将它们的共性抽象成为父用例,其他用例作为子用例。
72 |
73 | 该关系也可存在于参与者之间。
74 |
75 | 
76 |
77 | 
78 |
79 | 【用例描述】
80 |
81 | 单纯的用例图并不能描述完整的信息,需要用文字描述不能反映在图形上的信息。
82 |
83 | 用例描述是将用例发生的各种场景描述出来,表示参与者与系统交互时双方的行为,即参与者做什么,系统做什么反应。
84 |
85 | 场景能真实反映参与者在用例执行中可能遇到的
86 |
87 | 各种情形。
88 |
89 | 可以使用**用例模版**或**活动图**描述用例执行中的各种场景。
90 |
91 | 【用例模板】
92 |
93 | 用例描述模版的内容大致包括:用例名、参与者,前置条件,后置条件,事件流等。
94 |
95 | 用例的事件流
96 |
97 | 说明参与者与系统之间的交互过程;
98 |
99 | 说明用例在不同条件下可以选择执行的多种方案;
100 |
101 | 分为基本流和备选流两类
102 |
103 | 基本流:描述该用例正常执行的一种场景,系统执行一系列活动步骤来响应参与者提出的服务请求;
104 |
105 | 备选流:描述用例执行过程中异常的或偶尔发生的一些情况。
106 |
107 | 
108 |
109 |
110 |
111 |
112 |
113 | ## 2. 类图【重要】
114 |
115 | **请参考UML的PPT。**
116 |
117 | 【类图】
118 |
119 | (具体画法参考实验文档)
120 |
121 | 目标是对领域内的概念类进行分析,并抽象出对应的类及其关系等。
122 |
123 | 具体包括三个步骤:
124 |
125 | 1. 从用例场景中寻找概念类
126 |
127 | (1) 分析用例场景
128 |
129 | (2) 找出其中的名词或名词短语作为分析类备选
130 |
131 | (3) 如何判断分离出的词是否是分析类?
132 |
133 | 
134 |
135 | 2. 细化概念类,识别其类型(如边界类、实体类等)
136 |
137 | 例子:学生选课用例
138 |
139 | 
140 |
141 | 通过分析,可以确定以下分析类:
142 |
143 | 
144 |
145 | 分析类是概念层次的东西,源于问题空间,与实现方式无关。
146 |
147 | 类的类型:
148 |
149 | 《Entity》 classes 表示系统中的持久信息或贯穿应用的数据封装
150 |
151 | 《Boundary》 classes 实现用户与系统的交互,如用户界面或外部接口
152 |
153 | 《Control》 classes 实现对用例行为的封装,管理、调度其它类
154 |
155 | 3. 为概念类定义属性及行为
156 |
157 | 属性描述了一个已被选择以包含在分析模型中的类。
158 |
159 | 要识别类所属行为,可以对处理叙述进行语法解析,看看动词;还可以结合动态(交互)建模,识别分析类的行为。
160 |
161 | 例子:
162 |
163 | 
164 |
165 | 4. 定义关系
166 |
167 | (1) 关联关系:关联关系可以使一个类可以引用另一个类的属性和方法。一般使用成员变量来实现。
168 |
169 | 
170 |
171 | (2) 聚合关系:表示整体和部分的关系,整体与部分可以分开,使用带空心菱形的实线来表示。
172 |
173 | 
174 |
175 | (3) 组合关系:也是整体与部分的关系,但是整体与部分不可以分开,使用实心带菱形的实线来表示。组合关系中整体类和部分类必须有相同的生命周期。
176 |
177 | 
178 |
179 | (4) 依赖关系:即一个类的实现需要另一个类的协助。多数情况下,依赖关系表现在某个类的方法使用另一个类的对象作为参数。
180 |
181 | 
182 |
183 | (5) 泛化关系:表示类与类、接口与接口之间的继承关系
184 |
185 | 
186 |
187 | 实例:
188 |
189 | 
190 |
191 |
192 |
193 | ## 3. 时序图(顺序图)【重要】
194 |
195 | **请参考UML的PPT。**
196 |
197 | 【时序图】
198 |
199 | 时序图建模步骤
200 |
201 | (1)对每个用例,建立系统时序图(可选)
202 |
203 | (2)建立对象时序图
204 |
205 | (3)从图中确定分析类的行为
206 |
207 | 主要步骤
208 |
209 | 按从左到右的顺序
210 |
211 | 1、列出启动该用例的参与者;
212 |
213 | 2、列出参与者使用的边界类;
214 |
215 | 3、列出管理该用例的控制类;
216 |
217 | 4、根据用例的执行流程,按时间顺序列出分析类之间的消息序列。
218 |
219 | **例子:****还书用例**
220 |
221 | 1. 借阅者点击还书按钮向系统申请还书
222 | 2. 系统提示借阅者输入还书号等信息
223 | 3. 借阅者输入还书信息后,系统查询该书是否已超期。
224 | 4. 如果未超期,则记录用户还书信息并更新图书可借状态,并返回借阅者成功还书信息。
225 | 5. 如果已超期,则系统提示超期、罚款金额等信息。
226 | 6. 借阅者如果认可,并确认缴纳罚款,则系统执行扣款并还书,返回借阅者成功还书信息。
227 |
228 | 
229 |
230 | ## 4. 状态图
231 |
232 | 请参考UML的PPT。
233 |
234 | 【状态图】
235 |
236 | 状态图描述了一个对象生命周期内所经历的状态序列,以及引起状态转移的外部事件。
237 |
238 | 状态图的主要作用:
239 |
240 | 描述多个状态之间的转换顺序,即事件的执行顺序,避免非法的事件序列。(如: 必须先付款进入“已付款”状态,才能执行发货进入“已发货”状态。)
241 |
242 | 
243 |
244 | 
245 |
246 | ## 5. 其他
247 |
248 | ### 5.1. 活动图
249 |
250 | 【活动图】
251 |
252 | 
253 |
254 |
255 |
256 | ### 5.2. ER图
257 |
258 | 【ER图】
259 |
260 | 
261 |
262 | 
263 |
264 | ### 5.3. CRC模型
265 |
266 | 【CRC模型, Class-responsibility-collaborator】
267 |
268 | 作用:帮助补充、完善、优化分析类(属性、行为)
269 |
270 | 职责:职责是与类相关的属性和操作。
271 |
272 | 简单的说,职责就是“类所知道的或能做的任何事情”,可理解为类的能力。
273 |
274 | 例如,顾客有名字、地址和电话号码,这是顾客知道的东西。顾客要借书和还书,这是顾客要完成的事情。
275 |
276 | 分配职责的指导原则:属性和与之相关的行为应该在同一个类中。
277 |
278 | 类主要通过两种方式实现其职责:
279 |
280 | 通过自己内部的行为,实现特定的职责
281 |
282 | 请求其它类的协作
283 |
284 | 如果某个对象请求协作,就会向其它对象发送消息。
285 |
286 | 消息接收者作为服务方,通过自己的服务作为对消息发送者的回应。
287 |
288 | 职责是一种较高层次的抽象,其在设计过程中可能细化为一到多个具体的行为。
289 |
290 | 例子:用户登录用例中,登录控制类的职责之一是“身份验证” 。该职责在设计阶段,可以被细化为多个具体方法:getUser(),getRole(),getGroup(),check()
291 |
292 | 
293 |
294 |
295 |
296 | ### 5.4. 包图
297 |
298 | 【包图】
299 |
300 | 对于较大的项目,由于有很多的类和用例,常常会使系统结构看起非常复杂。
301 |
302 | 通过包图,庞大系统之间的关系变得更简单,整个系统的架构一目了然。
303 |
304 | 原则:将概念上或语义上相近的类纳入一个包
305 |
306 | 包之间的主要关系是依赖关系。
307 |
308 | 意味着两个Package内的元素之间存在着一个或多个依赖
309 |
310 | 
311 |
312 | 
313 |
314 |
315 |
316 |
317 |
318 |
319 |
320 |
321 |
322 |
323 |
324 |
325 |
326 |
327 |
328 | # 三、白盒测试
329 |
330 | ## 1. 基本路径测试法【重要】
331 |
332 | 参考视频:https://www.bilibili.com/video/BV13V4y1g7tc/?share_source=copy_web&vd_source=7ba452d8ee6f8b8a4b8ef831bf573bda
333 |
334 | 步骤:
335 |
336 | - **(1) 画出控制流图**
337 |
338 | 流程图用来描述程序控制结构。可将流程图映射到一个相应的流图(假设流程图的菱形决定框中不包含复合条件)。
339 |
340 | - 在流图中,每一个圆,称为流图的**结点**,代表一个或多个语句。一个处理方框序列和一个菱形决策框可被映射为一个结点 。
341 | - 流图中的箭头,称为**边或连接**, 代表控制流 , 类似于流程图中的箭头 。一条边必须终止于一个结点 , 即使该结点并不代表任何语句(例如:if-else-then结构)。
342 | - 由边和结点限定的范围称为**区域** 。
343 |
344 | 控制流图基本结构:
345 |
346 |
46 |
47 | (3)RIP协议使用了UDP传送数据,因此RIP在UDP之上,属于应用层。
48 |
49 |
50 |
51 |
--------------------------------------------------------------------------------
/docs/ComputerNetwork/《计算机网络》第四章作业.md:
--------------------------------------------------------------------------------
1 | # 《计算机网络》第四章作业
2 |
3 | ## 4-01
4 |
5 | **答:**一种是面向连接的服务(虚电路服务),一种是无连接的服务(数据报服务)。
6 |
7 | 面向连接的服务(可靠通信由网络保证):
8 |
9 | - 优点:分组开销小;分组无差错。
10 | - 缺点:网络成本高;若某一节点出错,所有通过该节点的虚电路都不能正常工作。
11 |
12 | 无连接的服务(可靠通信由用户主机保证):
13 |
14 | - 优点:网络成本低;某一节点出错时,路由可能变化,数据报可能仍然可以传输。
15 | - 缺点:尽力交付,可能会出现数据报异常情况。
16 |
17 | ## 4-03
18 |
19 | **答:**他们都起到连接网络的作用,但处在不同的网络体系结构层级。转发器在物理层,网桥在数据链路层,路由器在网络层,而网关在运输层及应用层(路由器也可以表示网关)。
20 |
21 | ## 4-07
22 |
23 | **答:**IP地址是网络层及以上使用的逻辑地址,而硬件地址是物理层及数据链路层使用的地址。由于不同国家、区域等有着不同的网络结构,其中的主机都有不同形式的硬件地址,因此若需要跨域传输时,会存在复杂的硬件地址转换。使用统一的IP地址可以使用户间的通信好像在一个网络上一样。IP地址与硬件地址的转换也相对硬件地址与硬件地址的转换要方便许多。
24 |
25 | ## 4-10
26 |
27 | **答:**(1)**10**000000.00100100.11000111.00000011,为B类地址;
28 |
29 | (2)**0**0010101.00001100.11110000.00010001,为A类地址;
30 |
31 | (3)**10**110111.11000010.01001100.11111101,为B类地址;
32 |
33 | (4)**110**00000.00001100.01000101.11111000,为C类地址;
34 |
35 | (5)**0**1011001.00000011.00000000.00000001,为A类地址;
36 |
37 | (6)**110**01000.00000011.00000110.00000010,为C类地址。
38 |
39 | ## 4-11
40 |
41 | **答:**好处是减小开销(加快检验、转发分组更快);坏处是在网络层传输的过程中就算数据发生了错误,也无法识别并中止传输,需要到达终点后在主机上(运输层)才能进行校验。
42 |
43 | ## 4-15
44 |
45 | **答:**MTU是一个数据帧中数据字段的最大长度。当一个IP数据报封装成数据链路层的帧的时候,数据报的总长度一定不能超过MTU。MTU与IP数据报首部中的总长度字段有关系,MTU是该字段的上限值。
46 |
47 | ## 4-18
48 |
49 | **答:**(1)数据链路层只能接触到MAC帧,如果ARP在数据链路层,那么MAC帧中就需要有IP地址,这不符合数据链路层对MAC帧的结构定义。
50 |
51 | (2)当网络中IP地址与硬件地址的映射发生变化时,ARP高速缓存中对应项就需要改变。超时时间设置太短会使ARP请求和响应分组的通信太频繁,若设置太长会使得硬件地址变化的主机迟迟无法与网络上其他主机通信。设置10~20分钟主要是因为在这样的一段时间段内更换网卡是很合理的。
52 |
53 | (3)①源主机的ARP高速缓存中已经有了目的主机的MAC地址;②源主机发送的是广播分组;③源主机与目的主机间使用点对点链路。
54 |
55 | ## 4-24
56 |
57 | **答:**A类子网划分对应数目的子网,子网掩码第一个字节需要全为1。若需要划分为n个A类子网,主机号部分的1的个数为$\lceil \log_2(n + 2) \rceil$(去除了全0和全1的子网数)。
58 |
59 | (1)$n=2$,主机号部分1的数量为2,因此子网掩码为255.192.0.0;
60 |
61 | (2)$n=6$,主机号部分1的数量为3,因此子网掩码为255.224.0.0;
62 |
63 | (3)$n=30$,主机号部分1的数量为5,因此子网掩码为255.248.0.0;
64 |
65 | (4)$n=62$,主机号部分1的数量为6,因此子网掩码为255.252.0.0;
66 |
67 | (5)$n=122$,主机号部分1的数量为7,因此子网掩码为255.254.0.0(实际有126个子网);
68 |
69 | (6)$n=250$,主机号部分1的数量为8,因此子网掩码为255.255.0.0(实际有254个子网);
70 |
71 | ## 4-25
72 |
73 | **答:**(1)10110000.0.0.0,其中1不是连续的,不推荐使用;
74 |
75 | (2)01100000.0.0.0,首位不是1(1前面有0),不推荐使用;
76 |
77 | (3)01111111.11000000.0.0,首位不是1(1前面有0),不推荐使用;
78 |
79 | (4)11111111.10000000.0.0,合理,推荐使用。
80 |
81 | ## 4-31
82 |
83 | **答:**86.32/12的网络前缀为0101 0110 0010。
84 |
85 | (1)86.33.224.123的前12位为0101 0110 0010,与上述网络前缀匹配。
86 |
87 | (2)86.79.65.216的前12位为0101 0110 0100,与上述网络前缀不匹配。
88 |
89 | (3)86.58.119.74的前12位为0101 0110 0011,与上述网络前缀不匹配。
90 |
91 | (4)86.68.206.154的前12位为0101 0110 0100,与上述网络前缀不匹配。
92 |
93 | ## 4-35
94 |
95 | **答:**转化为二进制为**10001100.01111000.0101**0100.00011000。
96 |
97 | 最大地址:**10001100.01111000.0101**1111.11111111,即140.120.95.255/20;
98 |
99 | 最小地址:**10001100.01111000.0101**0000.00000000,即140.120.80.0/20;
100 |
101 | 地址掩码:255.255.240.0;
102 |
103 | 地址块中共有$2^{12}=4096$个地址;
104 |
105 | 相当于$2^{24-20}=2^4=16$个C类地址。
106 |
107 | ## 4-38
108 |
109 | **答:**IGP是内部网关协议,是在一个自治系统内部使用的路由选择协议;EGP是外部网关协议,是在不同的自治系统间使用的路由选择协议。
110 |
111 | ## 4-39
112 |
113 | **答:**RIP协议是一种分布式的基于距离向量的路由选择协议,是互联网的标准协议,其最大优点就是简单,其主要特点为:
114 |
115 | - 仅和相邻路由器交换信息;
116 | - 路由器交换的信息是本路由器所知道的全部信息;
117 | - 按固定的时间间隔交换路由信息。
118 |
119 | OSPF使用分布式的链路状态协议,其主要特点为:
120 |
121 | - 使用洪泛法向本自治系统中所有路由器发送信息;
122 | - 发送的信息就是与本路由器相邻的所有路由器的链路状态,但这只是路由器所知道的部分信息;
123 | - 当链路状态变化或每隔一段时间,路由器向所有路由器用洪泛法发送链路状态信息;
124 | - 对于不同类型的业务可计算出不同的路由;
125 | - 多路径间存在负载均衡;
126 | - 所有在OSPF路由器之间交换的分组都具有鉴别功能;
127 | - 支持可变长度的子网划分和无分类的编址CIDR;
128 | - 每一个链路状态都会带上一个32位的序号,序号越大状态就越新。
129 |
130 | BGP是不同自治系统的路由器之间交换路由信息的协议,它采用路径向量路由选择协议,其主要特点为:
131 |
132 | - BGP在自治系统之问交换“可达性”信息;
133 | - BGP只能是力求寻找一条能够到达目的网络且比较好的路由(不能兜圈子),而并非要寻找一条最佳路由;
134 | - BGP的路由选择有很多策略,如选择本地偏好值最高的路由、选择AS跳数最少的路由、使用热土豆算法等;
135 | - BGP有四种报文,在不同的场合使用不同的报文。
136 |
137 | ## 4-43
138 |
139 | **答:**IGMP协议是让连接在本地局域网上的多播路由器知道本局域网上是否有主机(严格讲,是主机上的某个进
140 | 程)参加或退出了某个多播组。IGMP协议的要点主要体现在两个阶段:
141 |
142 | - 当某个主机加入新的多播组时,该主机应向多播组的多播地址发送一个IGMP报文,声明自己要成为该组的成员。本地的多播路由器收到IGMP报文后,还要利用多播路由选择协议把这种组成员关系转发给互联网上的其他多播路由器。
143 | - 本地多播路由器要周期性地探询本地局域网上的主机,以便知道这些主机是否还继续是组的成员。只要有一个主机对某个组响应,那么多播路由器就认为这个组是活跃的。但一个组在经过几次的探询后仍然没有一个主机响应,多播路由器就认为本网络上的主机已经都离开了这个组,因此也就不再把这个组的成员关系转发给其他
144 | 的多播路由器。
145 |
146 | 当两个多播网络之间的网络不支持多播时,会使用隧道技术。在这种情况下,发送方网络路由器会对多播数据进行再次封装,加上普通数据报首部,使之变成单播数据报,这样就能通过中间网络(此时相当于构建了一个隧道)传输到另一个多播网络,目的网络路由器收到此数据报后先剥去其首部,变成原来的多播数据报后再进行传输。
147 |
148 | ## 4-48
149 |
150 | **答:**146.102.29.0的二进制为10010010.01100110.00011101.00000000;
151 |
152 | 146.102.32.255的二进制为10010010.01100110.00100000.11111111;
153 |
154 | 从146.102.29.0(含)到146.102.29.255(含)有$256$个地址。而146.102.29.255(不含)到146.102.32.255(含)有$3\times 256$个地址,因此总共有$4\times 256=1024$个地址。
155 |
156 | ## 4-65
157 |
158 | **答:**(1)0000 : 0000 : 0000 : 0000 : 0000 : 0000 : 0000 : 0000
159 |
160 | (2)0000 : 00AA : 0000 : 0000 : 0000 : 0000 : 0000 : 0000
161 |
162 | (3)0000 : 1234 : 0000 : 0000 : 0000 : 0000 : 0000 : 0003
163 |
164 | (4)0123 : 0000 : 0000 : 0000 : 0000 : 0000 : 0001 : 0002
--------------------------------------------------------------------------------
/docs/MachineLearning/第一章作业.md:
--------------------------------------------------------------------------------
1 | # 《机器学习》第一章作业
2 |
3 | ## 1.1
4 |
5 | 表1.1中若只包含编号为1和4的两个样例,即如下表所示:
6 |
7 | | 编号 | 色泽 | 根蒂 | 敲声 | 好瓜 |
8 | | ---- | ---- | ---- | ---- | ---- |
9 | | 1 | 青绿 | 蜷缩 | 浊响 | 是 |
10 | | 4 | 乌黑 | 稍蜷 | 沉闷 | 否 |
11 |
12 | 则其版本空间如下图所示:
13 |
14 | 
15 |
16 | ## 1.3
17 |
18 | 对于所有假设,选择满足最多样本的假设。若有多个,则选择尽可能一般的假设(即属性值为任意的数量尽可能多)。若还有多个,随机选择一个即可。
19 |
20 |
21 |
22 | ## 1.5
23 |
24 | 1. 对欲搜索文本进行分词,提取关键词并分析语义后进行检索;
25 | 2. 对搜索文本和数据库中相关信息进行匹配并排序;
26 | 3. 在拥有用户信息和使用习惯的数据后,可以智能推荐搜索结果;
27 | 4. 实现对图片、视频等多媒体数据进行分析后,给出搜索结果(如百度识图);
28 | 5. 对搜索出的结果进行无效信息、重复信息的过滤;
29 | 6. 建立知识图谱,能精确给出搜索结果的梗概(或者与其他概念的关系)。
30 |
31 |
--------------------------------------------------------------------------------
/docs/MachineLearning/第七章作业.md:
--------------------------------------------------------------------------------
1 | # 《机器学习基础》第七章作业
2 |
3 | ## 7.1
4 |
5 | **答:**使用极大似然法得到的类条件概率估计表达式为
6 | $$
7 | P(x_i=t_{ij}|c) = \frac{|D_{c,x_i, t_{ij}}|}{|D_c|}
8 | $$
9 | 其中,$|D_c|$表示训练集$D$中$c$类样本的数量,$|D_{c, x_i, t_{ij}}|$表示训练集中$c$类元素属性$x_i$为$t_{ij}$的数量的元素。由此根据西瓜数据集即可得出类条件概率如下:
10 |
11 | | 属性 | 属性取值 | 好瓜($c_0$) | 坏瓜($c_1$) |
12 | | ----------- | -------------- | ----------- | ----------- |
13 | | 色泽($x_0$) | 青绿($t_{00}$) | $\frac38$ | $\frac13$ |
14 | | | 乌黑($t_{01}$) | $\frac12$ | $\frac29$ |
15 | | | 浅白($t_{02}$) | $\frac18$ | $\frac49$ |
16 | | 根蒂($x_1$) | 蜷缩($t_{10}$) | $\frac58$ | $\frac13$ |
17 | | | 稍蜷($t_{11}$) | $\frac38$ | $\frac49$ |
18 | | | 硬挺($t_{12}$) | $0$ | $\frac29$ |
19 | | 敲声($x_2$) | 浊响($t_{20}$) | $\frac34$ | $\frac49$ |
20 | | | 沉闷($t_{21}$) | $\frac14$ | $\frac13$ |
21 | | | 清脆($t_{22}$) | $0$ | $\frac29$ |
22 |
23 |
24 |
25 | ## 7.3
26 |
27 | ### 1. 环境及数据准备
28 | ```python
29 | import numpy as np
30 | import pandas as pd
31 | import scipy.stats as st
32 |
33 | df = pd.read_csv('./watermelon3.csv', index_col=0) # 西瓜数据集3.0
34 | X = np.array(df.iloc[:, :-1]) # 属性
35 | y = np.array(df.iloc[:, -1])[None].T # 标签
36 | ```
37 |
38 | ### 2. 定义模型
39 | ```python
40 | class NaiveBayes:
41 | def __init__(self) -> None:
42 | pass
43 |
44 | def get_prob(self, X, x, x_i, N): # 拉普拉斯修正
45 | return ((X[:, x] == x_i).sum() + 1) / (X.shape[0] + N)
46 |
47 | def get_dis_prob(self, X, y): # 离散概率
48 | p = []
49 | for i, c in enumerate(self.label):
50 | temp = X[(y == c).ravel()]
51 | lst = []
52 | for x in range(temp.shape[1]):
53 | dct = {}
54 | uni = np.unique(X[:, x])
55 | for x_i in uni:
56 | dct[x_i] = self.get_prob(temp, x, x_i, uni.shape[0])
57 | lst.insert(x, dct)
58 | p.insert(i, lst)
59 | return p
60 |
61 | def get_con_prob(self, X, x, x_i): # 连续概率
62 | return st.norm.pdf(x_i, loc=X[:, x].mean(), scale=X[:, x].std())
63 |
64 | def train(self, X, y):
65 | self.X, self.y = X, y
66 | self.con_col = [i for i in range(X.shape[1]) if type(X[0][i]) == float] # 连续值所在位置
67 | dis_X = np.delete(X, self.con_col, axis=1) # 提取离散值
68 | con_X = X[:, self.con_col] # 提取连续值
69 | self.label = np.unique(y) # 将label的类型取出来
70 | self.dis_p = self.get_dis_prob(dis_X, y)
71 | self.P_c = ((self.label == y).sum(axis=0) + 1) / (df.shape[0] + self.label.shape[0])
72 |
73 | def predict(self, X_pre):
74 | y_pre = np.ones(X_pre.shape[0], dtype='object')
75 | for j, X in enumerate(X_pre):
76 | maxn = 0
77 | res_c = 0
78 | for i, c in enumerate(self.label):
79 | res = 1
80 | temp_X = self.X[(self.y == c).ravel()]
81 | a = 0
82 | for x in range(X.shape[0]):
83 | if x in self.con_col: # 连续
84 | res *= self.get_con_prob(temp_X, x, X[x])
85 | else: # 离散
86 | res *= (self.dis_p[i][a][X[x]])
87 | a += 1
88 | res *= self.P_c[i]
89 | if res > maxn:
90 | maxn = res
91 | res_c = c
92 | y_pre[j] = res_c
93 | return y_pre[None].T
94 | ```
95 | ### 3. 模型测试
96 | ```python
97 | model = NaiveBayes()
98 | model.train(X, y)
99 | test_X = np.array(['青绿', '蜷缩', '浊响', '清晰', '凹陷', '硬滑', 0.697, 0.460], dtype='object')
100 | print(model.predict(test_X[None])[0][0])
101 | ```
102 |
103 | 是
104 |
105 |
106 |
107 | ## 7.4
108 |
109 | **答:**由于$P(x_i|c)\leq 1$,因此$\prod_{i=1}^{d} P(x_i|c)$很可能因为非常接近$0$而造成下溢,可以采用对此公式求对数的方式将正小数转化为负正数从而解决数据可能下溢的问题,即转化为$\sum_{i=1}^{d} \log P(x_i|c)$。
110 |
111 |
112 |
113 | ## 7.5
114 |
115 | **答:**对于贝叶斯最优分类器来说,其欲最大化的目标为
116 | $$
117 | P(c | \boldsymbol x) = \frac{P(c)P(\boldsymbol x | c)}{P(\boldsymbol x)}
118 | $$
119 |
120 | 因为$P(\boldsymbol x)$是常量,因此也就是最大化
121 | $$
122 | P(c)P(\boldsymbol x | c)
123 | $$
124 | 因为数据服从高斯分布,因此上式等价于
125 | $$
126 | P(c)\frac{1}{(2\pi)^{n/2}|\boldsymbol \Sigma |^{1/2} } \exp \left( -\frac12 (\boldsymbol x - \boldsymbol \mu_c)^\text T \boldsymbol \Sigma_c^{-1} (\boldsymbol x - \boldsymbol \mu_c)\right)
127 | $$
128 | 由题中条件“假设同先验”,因此在二分类任务中,上式等价于最大化
129 | $$
130 | \max(-\frac12 (\boldsymbol x - \boldsymbol \mu_0)^\text T \boldsymbol \Sigma_0^{-1} (\boldsymbol x - \boldsymbol \mu_0), -\frac12 (\boldsymbol x - \boldsymbol \mu_1)^\text T \boldsymbol \Sigma_1^{-1} (\boldsymbol x - \boldsymbol \mu_1))
131 | $$
132 | 由此可知,贝叶斯最优分类器的决策平面为
133 | $$
134 | \boldsymbol x ^ \text T \boldsymbol \Sigma^{-1}(\boldsymbol \mu_1 - \boldsymbol \mu_0) - \frac 12 (\boldsymbol \mu_1 + \boldsymbol \mu_0)^ \text T \boldsymbol\Sigma^{-1}(\boldsymbol \mu_1 - \boldsymbol \mu_0)
135 | $$
136 | 对于线性判别分析来说,其欲最大化的目标为
137 | $$
138 | J = \frac{\boldsymbol{w}^\text{T}(\boldsymbol\mu_0-\boldsymbol\mu_1)(\boldsymbol\mu_0-\boldsymbol\mu_1)^\text T \boldsymbol{w}}{\boldsymbol{w} ^\text{T} (\boldsymbol\Sigma_0 + \boldsymbol\Sigma_1)\boldsymbol{w}}
139 | $$
140 | 其中,$\boldsymbol w$为直线$y=\boldsymbol w ^ \text T \boldsymbol x$中的系数项,$\boldsymbol \mu_i, \boldsymbol \Sigma_i$为第$i \in \{0, 1\}$类的均值向量、协方差矩阵。由于两类数据满足高斯分布且方差相同,因此其决策平面由两数据均值点的中点$\frac 12 (\boldsymbol \mu_0 + \boldsymbol \mu_1)$和法向量$\boldsymbol w$唯一确定,而将此带入贝叶斯最优分类器的决策平面均成立,因此线性判别分析的决策平面与此重合。因此,二分类任务中两类数据满足高斯分布且方差相同时,线性判别分析产生贝叶斯最优分类器。
141 |
142 |
143 |
144 |
145 | ## 7.7
146 |
147 | **答:**由题意,对于一个二分类问题,需要估算一个二值属性对应的先验概率$P(c, x_i)$则需要$30\times 2 \times 2=120$个样例(因为$c$和$x_i$的取值均有两种)。如果第二个二值属性在上述样例上对应的$c$和$x_i$的取值均相同,那么就无需增加样例;如果第二个二值属性在上述样例上的取值只有一个,那么还需要$30\times 2=60$个样例(另一个取值在$c$两取值上的个数)。
148 |
149 | 因此,当扩展到有$d$个二值属性时,最好情况不需要在第一个的基础上添加任何样例,因此样例数为$120$;最坏情况下,每一次添加属性均会添加$60$个样例,因此样例数为$120+60\times (d-1) = 60 \times (d + 1)$。
150 |
151 |
--------------------------------------------------------------------------------
/docs/MachineLearning/第三章作业.md:
--------------------------------------------------------------------------------
1 | # 《机器学习》第三章作业
2 |
3 | ## 3.1
4 |
5 | 答:(1)该模型中$b$与输入没有关系时或模型函数一定过原点时;(2)该模型只用于差分分析时,因为假设取两实例$\boldsymbol{x}_i$和$\boldsymbol{x}_j(i\neq j)$,$f(\boldsymbol{x}_i) - f(\boldsymbol{x}_j ) = \boldsymbol{w}^\text{T}(\boldsymbol{x}_i - \boldsymbol{x}_j)$是与$b$无关的。
6 |
7 | ## 3.3
8 |
9 | ### 1.准备数据
10 |
11 | ```python
12 | import numpy as np
13 | from sklearn.model_selection import train_test_split
14 |
15 | data = np.array([[0.697, 0.460, 1],
16 | [0.774, 0.376, 1],
17 | [0.634, 0.264, 1],
18 | [0.608, 0.318, 1],
19 | [0.556, 0.215, 1],
20 | [0.403, 0.237, 1],
21 | [0.481, 0.149, 1],
22 | [0.437, 0.211, 1],
23 | [0.666, 0.091, 0],
24 | [0.243, 0.267, 0],
25 | [0.245, 0.057, 0],
26 | [0.343, 0.099, 0],
27 | [0.639, 0.161, 0],
28 | [0.657, 0.198, 0],
29 | [0.360, 0.370, 0],
30 | [0.593, 0.042, 0],
31 | [0.719, 0.103, 0]]) # 西瓜数据集3.0alpha
32 | X = data[:, 0:2] # 属性
33 | y = data[:, -1] # 标签
34 | X_train,X_test,y_train,y_test=train_test_split(X,y,test_size=0.3) #随机划分训练集和测试集
35 | ```
36 |
37 | ### 2.定义模型
38 |
39 | ```python
40 | class LogisticRegression:
41 | def __int__(self):
42 | pass
43 |
44 | def fit(self, X_, y_):
45 | # 数据调整为x_bar和\beta, 便于操作
46 | n, m = X_.shape
47 | m += 1
48 | X = np.append(X_, np.ones(n).reshape((n, 1)), axis=1).T
49 | y = y_.copy()
50 | beta = np.random.random(size=(m, 1))
51 | # 牛顿迭代法
52 | epoch = 20
53 | for i in range(epoch):
54 | mul = beta.T @ X
55 | p1 = np.exp(mul) / (1 + np.exp(mul)) # 计算p1的公式
56 | fd = -np.sum(X * (y - p1), axis=1) # 计算牛顿迭代中的一阶导数
57 | sd = np.zeros((m, m)) # 计算牛顿迭代中的二阶导数
58 | for i in range(n):
59 | sd += X[:, i:i+1] @ X[:, i:i+1].T * (p1[0, i] * (1 - p1[0, i]))
60 | beta = beta - (np.linalg.inv(sd) @ fd).reshape((m, 1)) # 一次迭代
61 | # 训练结果分析
62 | ans = (beta.T @ X) > 1
63 | self.beta = beta
64 | print("训练集准确率: ", 1 - np.sum(np.abs(ans - y)) / n)
65 |
66 | def predict(self, X_, y_):
67 | # 测试结果分析
68 | n = X_.shape[0]
69 | X = np.append(X_, np.ones(n).reshape((n, 1)), axis=1).T
70 | y = y_.copy()
71 | ans = (self.beta.T @ X) > 1
72 | print("测试集准确率: ", 1 - np.sum(np.abs(ans - y)) / n)
73 |
74 | ```
75 |
76 | ### 3.使用模型进行训练和预测
77 |
78 | ```python
79 | model = LogisticRegression()
80 | model.fit(X_train, y_train)
81 | model.predict(X_test, y_test)
82 | ```
83 |
84 | 训练集准确率: 0.7272727272727273
85 | 测试集准确率: 0.8333333333333334
86 |
87 | ## 3.5
88 |
89 | ### 1.准备数据
90 |
91 | 同3.3
92 |
93 | ### 2.定义模型计算𝜔
94 |
95 | ```python
96 | class LDA:
97 | def __init__(self):
98 | pass
99 |
100 | def fit(self, X, y):
101 | X0 = X[y == 0] # 坏瓜
102 | X1 = X[y == 1] # 好瓜
103 | mu0 = np.mean(X0, axis=0).reshape((-1, 1)) # 坏瓜均值
104 | mu1 = np.mean(X1, axis=0).reshape((-1, 1)) # 好瓜均值
105 | cov0 = np.cov(X0, rowvar=False) # 坏瓜协方差
106 | cov1 = np.cov(X1, rowvar=False) # 好瓜协方差
107 | S_w = np.mat(cov0 + cov1) # S_w
108 | U,Sigma,V = np.linalg.svd(S_w,full_matrices=False) # 奇异值分解
109 | self.omega = V.T @ np.linalg.inv(np.diag(Sigma)) @ U.T @ (mu0 - mu1) # /omega
110 | # 输出结果
111 | ans = self.omega.T @ X.T < 0
112 | acc = 1 - np.sum(np.abs(ans - y)) / y.shape[0]
113 | print("训练集准确率:", acc)
114 |
115 | def predict(self, X, y):
116 | # 输出结果
117 | ans = self.omega.T @ X.T < 0
118 | acc = 1- np.sum(np.abs(ans - y)) / y.shape[0]
119 | print("测试集准确率:", acc)
120 |
121 | ```
122 |
123 | ### 3.使用模型进行训练和预测
124 |
125 | ```python
126 | model = LDA()
127 | model.fit(X_train, y_train)
128 | model.predict(X_test, y_test)
129 | ```
130 |
131 | 训练集准确率: 0.9090909090909091
132 | 测试集准确率: 0.6666666666666667
133 |
134 | ## 3.7
135 |
136 | 答:给出汉明距离意义下理论最优的ECOC二元码:
137 |
138 | | | $f_1$ | $f_2$ | $f_3$ | $f_4$ | $f_5$ | $f_6$ | $f_7$ | $f_8$ | $f_9$ |
139 | | ----- | ----- | ----- | ----- | ---- | ---- | ------- | ---- | ---- | ---- |
140 | | $C_1$ | +1 | -1 | -1 | -1 | +1 | +1 | +1 | +1 | -1 |
141 | | $C_2$ | -1 | +1 | -1 | -1 | +1 | -1 | -1 | +1 | -1 |
142 | | $C_3$ | -1 | -1 | +1 | -1 | -1 | +1 | -1 | +1 | -1 |
143 | | $C_4$ | -1 | -1 | -1 | +1 | -1 | -1 | +1 | +1 | -1 |
144 |
145 | 证明如下:
146 |
147 | 注意到性质:若两个分类器$f_i$和$f_j(i \neq j)$对样例的分类互为反码[如$(-1,-1,1,1)$和$(1,1,-1,-1)$],由于很多算法对待0-1分类是对称的(即如果将0-1类互换,最终训练出的模型是一样的)。这样一对分类器实际上可以简化为一个分类器,因此可以计算出在不出现互为反码的情况下,最优的ECOC编码长度为
148 | $$
149 | \binom{4}{1} + \frac{\binom{4}{2}}{2}=7
150 | $$
151 | 由于可以向编码中加入冗余,即可以在最短编码长度的情况下加入互为反码的一对分类器,因此只要保证编码长度为$7+2n(n为自然数)$即可保证得出的ECOC编码是最优的。
152 |
153 | 综上,由于$9=7+2\times 1$($f_8$和$f_9$是加入的冗余分类器),因此上述给出的ECOC二元码是理论最优的。
154 |
155 | ## 3.9
156 |
157 | 答:对OvR、MvM 来说,由于**对每个类进行了相同的处理**,其拆解出的二分类任务中类别不平衡的影响会相互抵消,因此通常不需专门处理。
158 |
--------------------------------------------------------------------------------
/docs/MachineLearning/第九章作业.md:
--------------------------------------------------------------------------------
1 | # 《机器学习基础》第九章作业
2 |
3 | ## 9.1
4 |
5 | **(1)首先证明闵可夫斯基距离满足非负性,同一性和对称性。**
6 |
7 | 由于
8 | $$
9 | \text{dist}_\text{mk} (x_i, x_j) = \left( \sum_{u=1}^n |x_{iu}-x_{ju}|^p \right)^\frac 1p \ge 0
10 | $$
11 | 因此,闵可夫斯基距离满足非负性。当且仅当$x_i = x_j$时,$\text{dist}_\text{mk} (x_i, x_j)=0$,因此闵可夫斯基距离满足同一性。由于绝对值中减数和被减数可以调换位置,所以$\text{dist}_\text{mk} (x_i, x_j) = \text{dist}_\text{mk} (x_j, x_i)$,因此闵可夫斯基距离满足对称性。
12 |
13 | **(2)下面证明当$p\ge 1$时,闵可夫斯基距离满足直递性。**
14 |
15 | 显然$p=1$时,可由三角不等式证明。因此下面$p>1$。
16 |
17 | 令$a_i=|x_{iu}-x_{ku}|,b_i=|x_{ku}-x_{ju}|$,那么要证$\text{dist}_\text{mk} (x_i, x_j) \leq \text{dist}_\text{mk} (x_i, x_k) + \text{dist}_\text{mk} (x_k, x_j)$,即证
18 | $$
19 | \left(\sum_{i=1}^{n}|a_i+b_i|^p\right)^\frac 1p \leq \left(\sum_{i=1}^{n}a_i^p \right)^\frac 1p + \left(\sum_{i=1}^{n}b_i^p \right)^\frac 1p
20 | $$
21 | 由于
22 | $$
23 | \begin{align}
24 | \left(\sum_{i=1}^{n}|a_i+b_i|^p\right)^\frac 1p &\leq \sum_{i=1}^{n}|a_i+b_i|^p \\
25 | &= \sum_{i=1}^{n}|a_i+b_i||a_i+b_i|^{p-1} \\
26 | &\leq \sum_{i=1}^{n}(|a_i|+|b_i|)|a_i+b_i|^{p-1} \\
27 | &= \sum_{i=1}^{n}(|a_i||a_i+b_i|^{p-1}+|b_i||a_i+b_i|^{p-1})
28 | \end{align}
29 | $$
30 | 由赫尔德不等式$\sum_i^na_ib_i \leq (\sum_{i=1}^n a_i^p)^\frac1p(\sum_{i=1}^nb_i^q)^\frac1q \ \ (p, q > 1) $可得
31 | $$
32 | \begin{align}
33 | \sum_{i=1}^{n}(|a_i||a_i+b_i|^{p-1}+|b_i||a_i+b_i|^{p-1}) &\leq \left(\sum_{i=1}^{n}|a_i|^p \right)^{\frac1p} \left(\sum_{i=1}^{n}|a_i+b_i|^{(p-1)q}\right)^{\frac1q} + \left(\sum_{i=1}^{n}|b_i|^p\right)^{\frac1p} \left(\sum_{i=1}^{n}|a_i+b_i|^{(p-1)q}\right)^{\frac1q} \\
34 | &= \left(\left(\sum_{i=1}^{n}|a_i|^p\right)^{\frac1p} + \left(\sum_{i=1}^{n}|b_i|^p\right)^{\frac1p} \right) \left(\sum_{i=1}^{n}|a_i+b_i|^{p}\right)^{\frac1q} \\
35 | &\leq \left(\sum_{i=1}^{n}|a_i|^p\right)^{\frac1p} + \left(\sum_{i=1}^{n}|b_i|^p\right)^{\frac1p}
36 | \end{align}
37 | $$
38 | 其中$q=\frac{p}{p-1}$,于是原不等式成立,因此,当$p \ge 1$时闵可夫斯基距离满足直递性。
39 |
40 | **(3)下面证明当$0 \leq p < 1$时,闵可夫斯基距离不满足直递性。**
41 |
42 | 和(2)类似的,只需证明下式即可证明原命题。
43 | $$
44 | \left(\sum_{i=1}^{n}|a_i+b_i|^p\right)^\frac 1p \ge \left(\sum_{i=1}^{n}a_i^p \right)^\frac 1p + \left(\sum_{i=1}^{n}b_i^p \right)^\frac 1p
45 | $$
46 | 由于
47 | $$
48 | \begin{align}
49 | \sum_{i=1}^{n}|a_i+b_i|^p &= \sum_{i=1}^{n}|t\frac{a_i}{t}+(1-t)\frac{b_i}{1-t}|^p \\
50 | &\ge t^{1-p}\sum_{i=1}^{n}|a_i|^p+(1-t)^{1-p}\sum_{i=1}^{n}|b_i|^p
51 | \end{align}
52 | $$
53 | 其中
54 | $$
55 | t=\frac{\left(\sum_{i=1}^{n}a_i^p \right)^\frac 1p}{\left(\sum_{i=1}^{n}a_i^p \right)^\frac 1p + \left(\sum_{i=1}^{n}b_i^p \right)^\frac 1p}
56 | $$
57 | 于是有
58 | $$
59 | \begin{align}
60 | t^{1-p}\sum_{i=1}^{n}|a_i|^p+(1-t)^{1-p}\sum_{i=1}^{n}|b_i|^p &= \left(\left(\sum_{i=1}^{n}a_i^p \right)^\frac 1p + \left(\sum_{i=1}^{n}b_i^p \right)^\frac 1p\right)^p
61 | \end{align}
62 | $$
63 | 综上即可证明原不等式成立,闵可夫斯基距离不满足直递性。
64 |
65 | **(4)下面证明$p$趋向无穷大时,闵可夫斯基距离等于对应分量的最大绝对距离。**
66 |
67 | 闵可夫斯基距离公式可以转换如下:
68 | $$
69 | \text{dist}_\text{mk} (x_i, x_j) = \left( \sum_{u=1}^n |x_{iu}-x_{ju}|^p \right)^\frac 1p = \max_u|x_{iu}-x_{ju}| \left( \sum_{u=1}^n \left(\frac{|x_{iu}-x_{ju}|}{\max_u|x_{iu}-x_{ju}|}\right)^p \right)^\frac 1p
70 | $$
71 | 令
72 | $$
73 | t_u = \frac{|x_{iu}-x_{ju}|}{\max_u|x_{iu}-x_{ju}|}\leq 1
74 | $$
75 | 当$p \rarr +\infin$时
76 | $$
77 | \left( \sum_{u=1}^n t_u^p \right)^\frac 1p \rarr1
78 | $$
79 | 因此
80 | $$
81 | \text{dist}_\text{mk} (x_i, x_j) \rarr \max_u|x_{iu}-x_{ju}|
82 | $$
83 | 综上得证。
84 |
85 |
86 |
87 | ## 9.2
88 |
89 | 显然,豪斯多夫距离满足非负性和对称性,这里不过多证明。
90 |
91 | (1)下面证明豪斯多夫距离满足同一性。
92 |
93 | ①当$X=Z$时,$\text{dist}_\text{h}(X, Z) = \text{dist}_\text{h}(Z, X) = 0$,因此$\text{dist}_\text{H}(X, Z) = 0$。
94 |
95 | ②当$\text{dist}_\text{H}(X, Z) = 0$时,$\text{dist}_\text{h}(X, Z) = \text{dist}_\text{h}(Z, X) = 0$,这说明任意$x\in X$,存在$z\in Z$使得距离为0,因此$X \subset Z$,同时也说明任意$z\in Z$,存在$x\in X$使得距离为0,因此$Z \subset X$,所以$X=Z$。
96 |
97 | 综上得证。
98 |
99 | (2)下面证明豪斯多夫距离满足直递性。
100 |
101 | 欲证
102 | $$
103 | \text{dist}_\text{H}(X, Z) \leq \text{dist}_\text{H}(X, Y) + \text{dist}_\text{H}(Y, Z)
104 | $$
105 |
106 | 由于
107 | $$
108 | \text{dist}_\text{H}(X, Z) = \max(\text{dist}_\text{h}(X, Z), \text{dist}_\text{h}(Z, X))
109 | $$
110 | 因此,可以转化为求证
111 | $$
112 | \text{dist}_\text{h}(X, Z) \leq \text{dist}_\text{h}(X, Y) + \text{dist}_\text{h}(Y, Z)
113 | $$
114 | 由于
115 | $$
116 | \begin{align}
117 | \min_{z\in Z} ||x - z||_2 &= \min_{z \in Z} ||x + y+y-z||_2, \forall y\in Y \\
118 | &\leq \min_{z \in Z} (||x + y||_2+||y-z||_2), \forall y\in Y \\
119 | &= ||x+y||_2 + \min_{z \in Z} ||y-z||_2, \forall y\in Y \\
120 | &\leq ||x+y||_2 + \max_{y \in Y}\min_{z \in Z} ||y-z||_2, \forall y\in Y \\
121 | &= ||x+y||_2 + \text{dist}_\text{h}(Y, Z), \forall y\in Y \\
122 | &\leq \min_{y \in Y} ||x+y||_2 + \text{dist}_\text{h}(Y, Z)
123 | \end{align}
124 | $$
125 | 对不等式左右两边取$\max_{x\in X}$得到
126 | $$
127 | \max_{x\in X}\min_{z\in Z} ||x - z||_2 \leq \max_{x\in X}\min_{y \in Y} ||x+y||_2 + \text{dist}_\text{h}(Y, Z)
128 | $$
129 | 即
130 | $$
131 | \text{dist}_\text{h}(X, Z) \leq \text{dist}_\text{h}(X, Y) + \text{dist}_\text{h}(Y, Z)
132 | $$
133 | 综上得证。
134 |
135 |
136 |
137 |
138 | ## 9.3
139 |
140 | 不一定能。由于求解式(9.24)的最优解是一个NP-hard问题,k均值算法只是基于贪心思想通过迭代进行近似求解得到的局部最优解,不一定能得到式子的全局最优解。
141 |
142 |
143 |
144 | ## 9.4
145 |
146 | ### 1 导入库
147 | ```python
148 | from sklearn.cluster import KMeans
149 | import pandas as pd
150 | import numpy as np
151 | from matplotlib import pyplot as plt
152 | ```
153 |
154 | ### 2 导入数据集
155 | ```python
156 | df = pd.read_csv("./4.0.csv", header=None)
157 | X = df.values
158 | ```
159 |
160 | ### 3 测试不同k值的影响
161 | > 选定数据集中前k个点作为初始中心点
162 | ```python
163 | for k in range(2, 5):
164 | model = KMeans(k, init=[X[i, :] for i in range(k)], n_init=1)
165 | model.fit(X)
166 | ans = model.predict(X)
167 | print(model.cluster_centers_)
168 | plt.title(f"KMeans [k={k}]")
169 | plt.scatter(X[:, 0], X[:, 1], c=ans)
170 | plt.show()
171 | ```
172 |
173 | ```
174 | [[0.62371429 0.37435714]
175 | [0.44675 0.1875 ]]
176 | ```
177 |
178 | 
179 |
180 | ```
181 | [[0.471 0.39928571]
182 | [0.68138462 0.28446154]
183 | [0.3725 0.1748 ]]
184 | ```
185 |
186 | 
187 |
188 | ```
189 | [[0.67625 0.4665 ]
190 | [0.6896 0.3072 ]
191 | [0.61585714 0.137 ]
192 | [0.38685714 0.27714286]]
193 | ```
194 |
195 | 
196 |
197 |
198 |
199 | ### 4 测试不同初始中心点的影响
200 |
201 | > 选定k=3
202 |
203 | ```python
204 | Xs = [[[0, 0], [0, 0], [0, 0]], # 全都在一个点
205 | [[0.5, 0.1], [0.5, 0.25], [0.5, 0.4]], # y轴分散
206 | [[0.3, 0.3], [0.5, 0.3], [0.7, 0.3]]] # x轴分散
207 |
208 | for centers in Xs:
209 | model = KMeans(3, init=centers, n_init=1)
210 | model.fit(X)
211 | ans = model.predict(X)
212 | print(model.cluster_centers_)
213 | # plt.title(f"KMeans [k={k}]")
214 | plt.scatter(X[:, 0], X[:, 1], c=ans)
215 | plt.show()
216 | ```
217 |
218 | ```
219 | [[0.36136364 0.21709091]
220 | [0.60845455 0.41336364]
221 | [0.6515 0.16325 ]]
222 | ```
223 |
224 | 
225 |
226 | ```
227 | [[0.63255556 0.16166667]
228 | [0.33455556 0.21411111]
229 | [0.598 0.40491667]]
230 | ```
231 |
232 | 
233 |
234 | ```
235 | [[0.348 0.18955556]
236 | [0.471 0.39928571]
237 | [0.67507143 0.26714286]]
238 | ```
239 |
240 | 
241 |
242 | ### 5 分析
243 |
244 | 1. 对比不同k值得到的结果可以看出,不是k越大越好,而是需要根据经验去确定簇的数量,这样才能达到不错的聚类效果。
245 | 2. 对比不同初始值的结果可以看出,初始中心点也很大程度上影响到了聚类的效果,选定的三组初始中心点各有特征,可以看出在选定初始中心点在x轴上分散分布时,效果比较不错,说明数据集在x轴方向上有比较好的可分性。由于KMeans基于贪心算法,只能得到局部最优解,因此根据经验选择符合数据集特征的初始中心点对聚类效果有显著影响。
246 |
247 |
248 |
249 | ## 9.5
250 |
251 | (1)连接性。设$x_k$为集合$X$中的核心对象,设$x_i \in X, x_j \in X$。由于集合$X$是由$x_k$密度可达的所有样本构成的,那么$x_i,x_j$均由$x_k$密度可达,因此$x_i$与$x_j$密度相连。由此证明连接性。
252 |
253 | (2)最大性。设$x_k$为集合$X$中的核心对象,设$x_i \in C$,那么$x_i$由$x_k$密度可达。如果$x_j$由$x_i$密度可达,由于密度可达关系满足直递性,$x_j$由$x_k$密度可达,因此$x_j\in C$。由此证明最大性。
254 |
255 |
256 |
257 |
--------------------------------------------------------------------------------
/docs/MachineLearning/第二章作业.md:
--------------------------------------------------------------------------------
1 | # 《机器学习》第二章作业
2 |
3 | ## 2.1
4 |
5 | 答:由留出法定义,单次划分(分层抽样)中训练集中正例应当有$500 \times 70 \%=350$个样本,负例应当有$500 \times 70 \%=350$个样本,从所有样本中选取训练集后,剩余的作为测试集即可。因此,划分方式数为:
6 | $$
7 | \binom{500}{350} \times \binom{500}{350}=2.56 \times 10^{289}
8 | $$
9 |
10 | ## 2.3
11 |
12 | 答:**若学习器A的F1值比学习器B的高,A的BEP不一定比B高**。由于$BEP=P=R$,而$F1=\frac{2\times P' \times R'}{P' + R'}$,其中$P$不一定等于$P'$,$R$也不一定等于$R'$。因此若已知学习器A的F1值比学习器B的高,也无法推算出A的BEP值和B的BEP值之间的关系。
13 |
14 | ## 2.5
15 |
16 | 答:设$\boldsymbol{x}^+$为正例,$\boldsymbol{x}^-$为负例,那么:
17 |
18 | - $f(\boldsymbol{x}^+) > f(\boldsymbol{x}^-)$表示两者都预测正确;
19 |
20 | - $f(\boldsymbol{x}^+) = f(\boldsymbol{x}^-)$表示$\boldsymbol{x}^+$预测成功,而$\boldsymbol{x}^-$预测失败或者$\boldsymbol{x}^-$预测成功,而$\boldsymbol{x}^+$预测失败;
21 | - $f(\boldsymbol{x}^+) < f(\boldsymbol{x}^-)$表示两者都预测错误;
22 |
23 | 因此根据$\text{AUC}$的几何意义,可以对其公式进行改写:
24 | $$
25 | \begin{align}
26 | \text{AUC} &= \sum_{\boldsymbol{x}^+ \in D^+} \frac12 · \frac{1}{m^+} \left[ \frac{2}{m^-} \sum_{\boldsymbol{x}^- \in D^-} \mathbb{I}\left(f(\boldsymbol{x}^+) > f(\boldsymbol{x}^-)\right) + \frac1{m^-} \sum_{\boldsymbol{x}^- \in D^-} \mathbb{I}\left(f(\boldsymbol{x}^+) = f(\boldsymbol{x}^-)\right) \right] \\
27 | &= \frac{1}{m^+m^-} \sum_{\boldsymbol{x}^+ \in D^+} \sum_{\boldsymbol{x}^- \in D^-} \left( \mathbb{I}\left(f(\boldsymbol{x}^+) > f(\boldsymbol{x}^-)\right) + \frac12 \mathbb{I}\left(f(\boldsymbol{x}^+) = f(\boldsymbol{x}^-)\right) \right) \\
28 |
29 | \end{align}
30 | $$
31 | 因此:
32 | $$
33 | \begin{align}
34 | \text{AUC} + \ell_{\rank} &= \frac{1}{m^+m^-} \sum_{\boldsymbol{x}^+ \in D^+} \sum_{\boldsymbol{x}^- \in D^-} \left( \mathbb{I}\left(f(\boldsymbol{x}^+) < f(\boldsymbol{x}^-)\right) + \mathbb{I}\left(f(\boldsymbol{x}^+) > f(\boldsymbol{x}^-)\right) + \mathbb{I}\left(f(\boldsymbol{x}^+) = f(\boldsymbol{x}^-)\right) \right) \\
35 | &= \frac{1}{m^+m^-} \sum_{\boldsymbol{x}^+ \in D^+} \sum_{\boldsymbol{x}^- \in D^-} (1) \\
36 | &= 1
37 | \end{align}
38 | $$
39 | 原式得证。
40 |
41 | ## 2.7
42 |
43 | 答:由于ROC曲线上的点为$(\text{FPR}, \text{TPR})$,且有$\text{TPR} + \text{FNR} = 1$,所以由ROC曲线上一点能确定代价曲线图中$(0, \text{FPR})$和$(1, \text{FNR})$两点,并由此得到连接两点的线段。将ROC曲线上所有的点对应到代价曲线图的所有线段,取所有线段的公共下界即可得到唯一的代价曲线。
44 |
45 | 反之,代价曲线(折线)的每个分段可以对应一条直线,从而得到直线与$x=0$和$x=1$的交点$(0, \text{FPR})$和$(1, \text{FNR})$,这两点可以对应ROC曲线上的一点,由此即可确定一条ROC曲线(不是唯一的,因为可能存在在代价曲线上方而不与曲线相交的线段,这可能也会对应ROC曲线上的一个点)。
46 |
47 | ## 2.9
48 |
49 | 卡方检验就是统计样本的实际观测值与理论推断值之间的偏离程度,卡方值越大,越不符合;卡方值越小,越趋于符合。检验过程如下:
50 |
51 | 1. 写出假设和备择假设;
52 |
53 | 2. 计算卡方值
54 | $$
55 | \chi^2 = \sum_{i=1}^n \frac{(x_i - \hat{x}_i)^2}{\hat{x}_i}
56 | $$
57 | 其中,$x_i$表示观测值,而$\hat{x}_i$表示预期值;
58 |
59 | 3. 计算卡方分布的自由度(若为$R \times C$的列联表,自由度为$(R-1)(C - 1)$);
60 |
61 | 4. 确定显著水平并根据自由度查表得到卡方检验值,将其与计算出的卡方值进行比较;
62 |
63 | 5. 若计算出的卡方值比检验值小,那么无法拒绝原假设,反之拒绝原假设。
64 |
65 |
--------------------------------------------------------------------------------
/docs/MachineLearning/第五章作业.md:
--------------------------------------------------------------------------------
1 | # 《机器学习》第五章作业
2 |
3 | ## 5.1
4 |
5 | **答**:虽然线性函数相对阶跃函数是连续的,但它不能将输入值压缩到$(0,1)$输出值范围内,这使得后续过程中神经元受变量值相对较大的属性影响更大,不利于参数收敛。而且,使用线性函数作为激活函数时,输入值经过每一层的传播后的输出值是输入值的线性组合,此时等价于线性回归。
6 |
7 | ## 5.2
8 |
9 | **答**:在使用Sigmoid函数作为激活函数的每个神经元的输出都是
10 | $$
11 | y=\frac{1}{1+e^{-\left( \sum_{i=1}^nw_i x_i-\theta \right)}}
12 | $$
13 | 对数几率回归的输出为
14 | $$
15 | y=
16 | \left\{
17 | \begin{array}{}
18 | 0, & z<0 \\
19 | 0.5, & z=0 \\
20 | 1, & z>0
21 | \end{array}
22 | \right.
23 | $$
24 | 其中
25 | $$
26 | z=\frac1{1+e^{-\left( \boldsymbol w^\text T \boldsymbol x + b \right)}}
27 | $$
28 | 可以看到,神经元的$y$函数和对数几率回归的$z$函数是相等的。不过神经元的输出不对Sigmoid函数的输出做任何变换,而对数几率回归由于需要判别,因此在输出后加入了分段函数。同时可以发现,如果神经网络中神经元除了输出的激活函数为Sigmoid函数,其他激活函数均为线性函数的话,此神经网络就等价于对数几率回归。
29 |
30 | ## 5.3
31 |
32 | **答**:对于$v_{ih}$,其更新公式为
33 | $$
34 | \Delta v_{ih} = -\eta \frac{\partial E_k}{\partial v_{ih}}
35 | $$
36 | 其中
37 | $$
38 | \frac{\partial E_k}{\partial v_{ih}} = \frac{\partial E_k}{\partial b_h}
39 | \frac{\partial b_h}{\partial \alpha_h} \frac{\partial \alpha_h}{\partial v_{ih}}
40 | $$
41 | 由于
42 | $$
43 | \frac{\partial \alpha_h}{\partial v_{ih}} = x_i \\
44 | e_h = -\frac{\partial E_k}{\partial b_h}
45 | \frac{\partial b_h}{\partial \alpha_h}
46 | $$
47 | 所以
48 | $$
49 | \Delta v_{ih} = -\eta \frac{\partial E_k}{\partial v_{ih}} = -\eta \frac{\partial E_k}{\partial b_h}
50 | \frac{\partial b_h}{\partial \alpha_h} \frac{\partial \alpha_h}{\partial v_{ih}} = \eta e_h x_i
51 | $$
52 | 此即书中式(5.13),证毕。
53 |
54 | ## 5.4
55 |
56 | **答**:若学习率过低,会导致模型收敛过慢,而学习率过高又可能会导致震荡而使模型无法收敛到最优解。可以考虑使用Adam算法等设定合适的初始学习率后,在迭代过程中自动调整学习率。
57 |
58 | ## 5.5
59 |
60 | ### 1. 环境及数据准备
61 |
62 | ```python
63 | import numpy as np
64 | import pandas as pd
65 | from matplotlib import pyplot as plt
66 | from sklearn.model_selection import train_test_split
67 | from sklearn.preprocessing import LabelEncoder
68 |
69 | df = pd.read_csv('./watermelon3.csv', index_col=0) # 西瓜数据集3.0
70 | for label in df.columns: # 离散值预处理为整数
71 | if df[label].dtype == object:
72 | df[label] = LabelEncoder().fit(df[label]).transform(df[label])
73 | df
74 | ```
75 |
76 | | | 色泽 | 根蒂 | 敲声 | 纹理 | 脐部 | 触感 | 密度 | 含糖率 | 好瓜 |
77 | | ---: | ---: | ---: | ---: | ---: | ---: | ---: | ----: | -----: | ---: |
78 | | 编号 | | | | | | | | | |
79 | | 1 | 2 | 2 | 1 | 1 | 0 | 0 | 0.697 | 0.460 | 1 |
80 | | 2 | 0 | 2 | 0 | 1 | 0 | 0 | 0.774 | 0.376 | 1 |
81 | | 3 | 0 | 2 | 1 | 1 | 0 | 0 | 0.634 | 0.264 | 1 |
82 | | 4 | 2 | 2 | 0 | 1 | 0 | 0 | 0.608 | 0.318 | 1 |
83 | | 5 | 1 | 2 | 1 | 1 | 0 | 0 | 0.556 | 0.215 | 1 |
84 | | 6 | 2 | 1 | 1 | 1 | 2 | 1 | 0.403 | 0.237 | 1 |
85 | | 7 | 0 | 1 | 1 | 2 | 2 | 1 | 0.481 | 0.149 | 1 |
86 | | 8 | 0 | 1 | 1 | 1 | 2 | 0 | 0.437 | 0.211 | 1 |
87 | | 9 | 0 | 1 | 0 | 2 | 2 | 0 | 0.666 | 0.091 | 0 |
88 | | 10 | 2 | 0 | 2 | 1 | 1 | 1 | 0.243 | 0.267 | 0 |
89 | | 11 | 1 | 0 | 2 | 0 | 1 | 0 | 0.245 | 0.057 | 0 |
90 | | 12 | 1 | 2 | 1 | 0 | 1 | 1 | 0.343 | 0.099 | 0 |
91 | | 13 | 2 | 1 | 1 | 2 | 0 | 0 | 0.639 | 0.161 | 0 |
92 | | 14 | 1 | 1 | 0 | 2 | 0 | 0 | 0.657 | 0.198 | 0 |
93 | | 15 | 0 | 1 | 1 | 1 | 2 | 1 | 0.360 | 0.370 | 0 |
94 | | 16 | 1 | 2 | 1 | 0 | 1 | 0 | 0.593 | 0.042 | 0 |
95 | | 17 | 2 | 2 | 0 | 2 | 2 | 0 | 0.719 | 0.103 | 0 |
96 |
97 | ```python
98 | X = df.iloc[:, :-1] # 属性
99 | y = df.iloc[:, -1] # 标签
100 | X_train,X_test,y_train,y_test=train_test_split(X,y,test_size=0.3) #随机划分训练集和测试集
101 | ```
102 |
103 | ### 2. 定义模型
104 |
105 | ```python
106 | class BPNN:
107 | def __init__(self):
108 | pass
109 |
110 | def __init(self, X, y, q):
111 | '''
112 | @param: X: 训练集属性
113 | @param: y: 训练集输出
114 | @param: q: 隐层神经元数量
115 | '''
116 | self.v = np.random.uniform(size=(X.shape[1], q))
117 | self.w = np.random.uniform(size=(q, 1))
118 |
119 | def __sigmoid(self, x):
120 | return 1 / (1 + np.exp(-x))
121 |
122 | def __sgd(self, X, y, lr, epoch):
123 | # 标准BP算法, 对每一个样本进行一次权重更新
124 | self.loss = []
125 | for ep in range(1, epoch+1):
126 | sum_ek = 0
127 | idx = list(range(X.shape[0]))
128 | np.random.shuffle(idx)
129 | X, y = X[idx], y[idx]
130 | for i in range(X.shape[0]):
131 | # 前向传播
132 | self.alpha = X[i:i+1] @ self.v
133 | self.b = self.__sigmoid(self.alpha)
134 | self.beta = self.b @ self.w
135 | self.py = self.__sigmoid(self.beta)
136 | # 计算误差
137 | ek = np.power(self.py - y[i], 2) / 2
138 | sum_ek += np.average(ek)
139 | # 后向更新
140 | g = self.py * (1 - self.py) * (y[i] - self.py)
141 | delta_w = self.eta * (self.b.T @ g)
142 | e = self.b * (1 - self.b) * np.sum(self.w @ g, axis=1)
143 | delta_v = self.eta * (X[i:i+1].T @ e)
144 | self.w += delta_w
145 | self.v += delta_v
146 | self.loss.append(sum_ek/X.shape[0])
147 |
148 | def __bgd(self, X, y, lr, epoch):
149 | # 累积BP算法, 对所有样本都进行一次权重更新
150 | self.loss = []
151 | y = y.reshape((-1, 1))
152 | for ep in range(1, epoch+1):
153 | # 前向传播
154 | self.alpha = X @ self.v
155 | self.b = self.__sigmoid(self.alpha)
156 | self.beta = self.b @ self.w
157 | self.py = self.__sigmoid(self.beta)
158 | # 计算误差
159 | ek = np.power(self.py - y, 2) / 2
160 | self.loss.append(np.average(ek))
161 | # 后向更新
162 | g = self.py * (1 - self.py) * (y - self.py)
163 | delta_w = self.eta * (self.b.T @ g)
164 | e = self.b * (1 - self.b) * (g @ self.w.T)
165 | delta_v = self.eta * (X.T @ e) # (8, 17) (17, 10)
166 | self.w += delta_w
167 | self.v += delta_v
168 |
169 | def fit(self, X, y, lr, epoch, algo="sgd"):
170 | X = np.array(X)
171 | y = np.array(y)
172 | self.eta = lr
173 | self.__init(X, y, 10)
174 | # 标准BP算法
175 | if algo.lower() == "sgd":
176 | self.__sgd(X, y, lr, epoch)
177 | # 累积BP算法
178 | elif algo.lower() == "bgd":
179 | self.__bgd(X, y, lr, epoch)
180 |
181 | def predict(self, X, y):
182 | X = np.array(X)
183 | y = np.array(y)
184 | # 前向传播
185 | alpha = X @ self.v
186 | b = self.__sigmoid(alpha)
187 | beta = b @ self.w
188 | py = self.__sigmoid(beta)
189 | return np.array(py > 0.5).astype(np.int32).reshape(1, -1)[0]
190 |
191 | def accuracy(self, X, y):
192 | ans = self.predict(X, y)
193 | return 1 - np.sum(np.abs(ans - y)) / X.shape[0]
194 | ```
195 |
196 | ### 3. 模型测试
197 |
198 | ```python
199 | model = BPNN()
200 | model.fit(X, y, 0.2, 500, algo="sgd")
201 | print("使用SGD训练后的准确度为:", model.accuracy(X, y))
202 | plt.plot(model.loss, label="sgd")
203 | model.fit(X, y, 0.2, 500, algo="bgd")
204 | plt.plot(model.loss, label="bgd")
205 | print("使用BGD训练后的准确度为:", model.accuracy(X, y))
206 | plt.legend()
207 | ```
208 |
209 | ```
210 | 使用SGD训练后的准确度为: 1.0
211 | 使用BGD训练后的准确度为: 1.0
212 | ```
213 |
214 | 
215 |
216 | 可以看到,由于sgd每次迭代是对每个样本依次更新权重,因此在中间会出现抖动,但总体是朝着最优解的。从计算用时来看,sgd显然时间会更长,而bgd一次对所有损失更新权重,因此用时相对少一些。
217 |
--------------------------------------------------------------------------------
/docs/MachineLearning/第八章作业.md:
--------------------------------------------------------------------------------
1 | # 《机器学习基础》第八章作业
2 |
3 | ## 8.1
4 |
5 | 使用简单投票法的集成学习预测错误,意味着少于半数的基学习器预测正确。那么,集成学习的错误率就是少于半数的基学习器预测正确的概率。这等价于抛$T$次硬币,有少于$\lfloor T/2 \rfloor$的硬币朝上的概率(这里硬币朝上的概率为$1-\epsilon$,也就是一个基学习器预测正确的概率)。预测正确的基学习器数量为
6 | $$
7 | g(x) = \sum_{i=0}^{T} \mathbb I (h_i(x)=f(x))
8 | $$
9 | 那么$g(x) \leq \lfloor T / 2 \rfloor$的概率为
10 | $$
11 | P(g(x) \leq \lfloor T/2 \rfloor)=\sum_{k=0}^{\lfloor T/2 \rfloor}\binom{T}{k}(1-\epsilon)^k\epsilon^{T-k}
12 | $$
13 | 这就是式(8.3)的左半部分$P(H(x)\neq f(x))$,由题中给出的定义可得$\lfloor T/2 \rfloor= (\epsilon - \delta)T$,于是$\delta = \epsilon - \lfloor T/2 \rfloor/T \ge \epsilon - 1/2$,由Hoeffding不等式得
14 | $$
15 | P(H(x)\neq f(x)) \leq \exp\left( -2 \left( \epsilon - \frac12 \right)^2 T \right) = \exp\left( -\frac12 T \left( 1 - 2\epsilon \right)^2 \right)
16 | $$
17 | 式(8.3)得证。
18 |
19 |
20 |
21 | ## 8.2
22 |
23 | 我们需要最小化的就是$\mathbb E_{x\in D}[\ell(-f(x) H(x))]$,考虑对$H(x)$进行求偏导,得到
24 | $$
25 | -P(f(x)=1|x) \ell(-H(x)) +P(f(x)=-1|x) \ell(H(x))
26 | $$
27 | 令其为0得到
28 | $$
29 | \frac{P(f(x)=-1|x)}{P(f(x)=1|x)} = \frac{\ell(H(x))}{\ell(-H(x))}
30 | $$
31 | 当$P(f(x)=-1|x) > P(f(x)=1|x)$时,$\ell(H(x)) > \ell(-H(x))$,由于$\ell(-f(x)H(x))$关于$H(x)$递减,因此
32 | $$
33 | H(x) < -H(x)
34 | $$
35 | 所以$H(x)<0$。同理,当$P(f(x)=-1|x) < P(f(x)=1|x)$时,$H(x)>0$。
36 |
37 | 综上:$\text{sign}(H(x))=\arg \max_{y\in (-1, 1)}P(f(x)=y|x)$,这意味着$\text{sign}(H(x))$达到了贝叶斯最优错误率。这说明此损失函数是分类任务原本0/1损失函数得一致性替代函数。
38 |
39 |
40 |
41 | ## 8.3
42 |
43 | 使用`sklean.ensemble`中的`AdaBoostClassifier`实现即可(默认采用决策树模型作为基学习器),代码如下:
44 |
45 | ```python
46 | from sklearn.ensemble import AdaBoostClassifier
47 | import pandas as pd
48 | from matplotlib import pyplot as plt
49 | import numpy as np
50 |
51 | # 加载数据
52 | df = pd.read_csv("./3.0a.csv", index_col=0)
53 | X = df.iloc[:, :2].values
54 | y = df.iloc[:, -1].values
55 |
56 | # 模型训练与预测
57 | model = AdaBoostClassifier(n_estimators=1, random_state=0)
58 | model.fit(X, y)
59 | pred = model.predict(X)
60 | print("错误分类数量:", np.sum(np.abs(pred - y)))
61 |
62 | # 画图
63 | plt.scatter(X[:, 0], X[:, 1], c=pred)
64 | ```
65 |
66 | 基学习器数量为1时:
67 |
68 | 
69 |
70 | 基学习器数量为2时:
71 |
72 | 
73 |
74 | 基学习器数量超过3时:
75 |
76 | 
77 |
78 | 可以发现,当基学习器变多的时候分类效果得到了提升,并且很稳定!
79 |
80 |
81 |
82 | ## 8.5
83 |
84 | 使用`sklean.ensemble`中的`BaggingClassifier`实现即可(默认采用决策树模型作为基学习器),代码如下:
85 |
86 | ```python
87 | from sklearn.ensemble import BaggingClassifier
88 | import pandas as pd
89 | from matplotlib import pyplot as plt
90 | import numpy as np
91 |
92 | # 加载数据
93 | df = pd.read_csv("./3.0a.csv", index_col=0)
94 | X = df.iloc[:, :2].values
95 | y = df.iloc[:, -1].values
96 |
97 | # 模型训练与预测
98 | model = BaggingClassifier(n_estimators=1, random_state=0)
99 | model.fit(X, y)
100 | pred = model.predict(X)
101 | print(np.sum(np.abs(pred - y)))
102 |
103 | # 画图
104 | plt.scatter(X[:, 0], X[:, 1], c=pred)
105 | ```
106 |
107 | 基学习器数量为1时:
108 |
109 | 
110 |
111 | 基学习器数量为2,3,4时:
112 |
113 | 
114 |
115 | 基学习器数量为7时:
116 |
117 | 
118 |
119 | 可以发现,当基学习器变多的时候分类效果不一定得到提升,在分类器数量较小时,变化比较不稳定。
120 |
121 |
122 |
123 | ## 8.6
124 |
125 | Bagging方法使用自助采样,简单高效,但考虑到“误差-分歧分解”,Bagging方法中个体学习器的多样性较低。朴素贝叶斯属于稳定基学习器,对数据样本的扰动不敏感,对这类基学习器进行集成往往需要使用输入属性扰动等其他扰动,而Bagging方法做不到,因此,Bagging方法通常很难提升朴素贝叶斯分类器的性能。
126 |
127 |
--------------------------------------------------------------------------------
/docs/MachineLearning/第六章作业.md:
--------------------------------------------------------------------------------
1 | # 《机器学习》第六章作业
2 |
3 | ## 6.1
4 |
5 | **答**:设超平面上任意一点为$\boldsymbol{y}$,满足$\boldsymbol{w}^{\text T} \boldsymbol{y} + b = 0$,那么$\boldsymbol{x}$与$\boldsymbol{y}$的距离为$|\boldsymbol{x} - \boldsymbol{y}|$。由几何关系可知,只有当$\boldsymbol{x} - \boldsymbol{y}$与超平面垂直时,才能满足$\boldsymbol{x}$与超平面的距离为$|\boldsymbol{x} - \boldsymbol{y}|$,又因为$\boldsymbol{w}$与超平面垂直,因此
6 | $$
7 | \boldsymbol{x} - \boldsymbol{y} = \pm |\boldsymbol{x} - \boldsymbol{y}| \frac{\boldsymbol{w}}{||\boldsymbol{w}||}
8 | $$
9 | 两边同时左乘$\boldsymbol w^{\text T}$可得
10 | $$
11 | \boldsymbol w^{\text T} \boldsymbol{x} - \boldsymbol w^{\text T} \boldsymbol{y} &= \pm |\boldsymbol{x} - \boldsymbol{y}| \frac{\boldsymbol w^{\text T}\boldsymbol{w}}{||\boldsymbol{w}||} \\
12 | \boldsymbol w^{\text T} \boldsymbol{x} + b &= \pm |\boldsymbol{x} - \boldsymbol{y}| \times ||\boldsymbol w||
13 | $$
14 | 即
15 | $$
16 | r = |\boldsymbol{x} - \boldsymbol{y}| = \frac{|\boldsymbol w^{\text T} \boldsymbol{x} + b|}{||\boldsymbol w||}
17 | $$
18 |
19 | ## 6.2
20 |
21 | ### 1. 搭建环境
22 |
23 |
24 | ```python
25 | import pandas as pd
26 | import numpy as np
27 | from matplotlib import pyplot as plt
28 | from sklearn import svm
29 | ```
30 |
31 | ### 2. 导入数据
32 |
33 |
34 | ```python
35 | df = pd.read_csv("./3.0a.csv", index_col=0)
36 | X = df.iloc[:, :2].values
37 | y = df.iloc[:, -1].values
38 | ```
39 |
40 | ### 3. 使用线性核训练一个SVM
41 |
42 |
43 | ```python
44 | model = svm.SVC(C=1000, kernel='linear') # C高一些,对误差的容忍度低
45 | model.fit(X, y)
46 | model.score(X, y)
47 | ```
48 |
49 |
50 | 0.8235294117647058
51 |
52 |
53 | ```python
54 | # 绘制支持向量
55 | idx = model.support_
56 | plt.scatter(X[:, 0], X[:, 1], c=y, s=30)
57 | plt.scatter(X[idx][:, 0], X[idx][:, 1], c=y[idx], edgecolors='r', s=100)
58 | plt.show()
59 | ```
60 |
61 |
62 | 
63 |
64 |
65 | ### 4. 使用高斯核训练一个SVM
66 |
67 |
68 | ```python
69 | model = svm.SVC(C=1000, kernel='rbf') # C高一些,对误差的容忍度低
70 | model.fit(X, y)
71 | model.score(X, y)
72 | ```
73 |
74 | ```
75 | 1.0
76 | ```
77 |
78 |
79 | ```python
80 | # 绘制支持向量
81 | idx = model.support_
82 | plt.scatter(X[:, 0], X[:, 1], c=y, s=30)
83 | plt.scatter(X[idx][:, 0], X[idx][:, 1], c=y[idx], edgecolors='r', s=100)
84 | plt.show()
85 | ```
86 |
87 | 
88 |
89 | ### 5. 对比分析
90 |
91 | 在对误差容忍度比较高的情况下,高斯核SVM可以完全拟合数据,而且支持向量也比较少。但由于数据线性不可分,线性核SVM不论设置多高的容忍度仍不能很好地区分数据,且支持向量也较多。
92 |
93 | ## 6.3
94 |
95 | ### 1. 搭建环境
96 |
97 |
98 | ```python
99 | import numpy as np
100 | from matplotlib import pyplot as plt
101 | from sklearn.model_selection import train_test_split
102 | from sklearn.datasets import load_iris, load_breast_cancer
103 | from sklearn.svm import SVC # 支持向量机
104 | from sklearn.neural_network import MLPClassifier # BP神经网络
105 | from sklearn.tree import DecisionTreeClassifier # 决策树
106 | ```
107 |
108 | ### 2. 构建数据集
109 |
110 |
111 | ```python
112 | X_iris, y_iris = load_iris(return_X_y=True) # 鸢尾花数据集
113 | X_bc, y_bc = load_breast_cancer(return_X_y=True) # 乳腺癌数据集
114 | # 划分训练集和测试集
115 | X_iris_train, X_iris_test, y_iris_train, y_iris_test = train_test_split(X_iris, y_iris, test_size=0.2, random_state=0)
116 | X_bc_train, X_bc_test, y_bc_train, y_bc_test = train_test_split(X_bc, y_bc, test_size=0.2, random_state=0)
117 | ```
118 |
119 | ### 3. 定义各种模型函数
120 |
121 |
122 | ```python
123 | def svm(X_train, X_test, y_train, y_test, kernel="linear"):
124 | model = SVC(C=1, kernel=kernel)
125 | model.fit(X_train, y_train)
126 | print(f"[SVM with {kernel} kernel]Accuracy: {model.score(X_test, y_test)*100: .2f}%")
127 | ```
128 |
129 |
130 | ```python
131 | def mlp(X_train, X_test, y_train, y_test, activation="logistic"):
132 | model = MLPClassifier(max_iter=1000, activation=activation, random_state=0)
133 | model.fit(X_train, y_train)
134 | print(f"[BP Neural Network with {activation}]Accuracy: {model.score(X_test, y_test)*100: .2f}%")
135 | ```
136 |
137 |
138 | ```python
139 | def dt(X_train, X_test, y_train, y_test, criterion="entropy"):
140 | model = DecisionTreeClassifier(criterion=criterion, random_state=0)
141 | model.fit(X_train, y_train)
142 | print(f"[Decision Tree with {criterion}]Accuracy: {model.score(X_test, y_test)*100: .2f}%")
143 | ```
144 |
145 | ### 4. 在鸢尾花数据集上测试
146 |
147 |
148 | ```python
149 | svm(X_iris_train, X_iris_test, y_iris_train, y_iris_test, kernel="linear")
150 | svm(X_iris_train, X_iris_test, y_iris_train, y_iris_test, kernel="rbf")
151 | mlp(X_iris_train, X_iris_test, y_iris_train, y_iris_test, activation="logistic")
152 | mlp(X_iris_train, X_iris_test, y_iris_train, y_iris_test, activation="relu")
153 | dt(X_iris_train, X_iris_test, y_iris_train, y_iris_test, criterion="entropy")
154 | dt(X_iris_train, X_iris_test, y_iris_train, y_iris_test, criterion="gini")
155 | ```
156 |
157 | [SVM with linear kernel]Accuracy: 100.00%
158 | [SVM with rbf kernel]Accuracy: 100.00%
159 | [BP Neural Network with logistic]Accuracy: 100.00%
160 | [BP Neural Network with relu]Accuracy: 100.00%
161 | [Decision Tree with entropy]Accuracy: 100.00%
162 | [Decision Tree with gini]Accuracy: 100.00%
163 |
164 |
165 | ### 5. 在乳腺癌数据集上测试
166 |
167 |
168 | ```python
169 | svm(X_bc_train, X_bc_test, y_bc_train, y_bc_test, kernel="linear")
170 | svm(X_bc_train, X_bc_test, y_bc_train, y_bc_test, kernel="rbf")
171 | mlp(X_bc_train, X_bc_test, y_bc_train, y_bc_test, activation="logistic")
172 | mlp(X_bc_train, X_bc_test, y_bc_train, y_bc_test, activation="relu")
173 | dt(X_bc_train, X_bc_test, y_bc_train, y_bc_test, criterion="entropy")
174 | dt(X_bc_train, X_bc_test, y_bc_train, y_bc_test, criterion="gini")
175 | ```
176 |
177 | [SVM with linear kernel]Accuracy: 95.61%
178 | [SVM with rbf kernel]Accuracy: 92.98%
179 | [BP Neural Network with logistic]Accuracy: 91.23%
180 | [BP Neural Network with relu]Accuracy: 94.74%
181 | [Decision Tree with entropy]Accuracy: 92.98%
182 | [Decision Tree with gini]Accuracy: 91.23%
183 |
184 | ### 6. 分析
185 |
186 | 针对不同的数据集特征可以选择不同的算法。通过针对不同数据集对不同算法的参数进行调节,很多模型都能很好地拟合数据。
187 |
188 | ## 6.4
189 |
190 | **答**:线性判别分析是将$n$维的数据投影到$n-1$维上的一个超平面后再来分类,可以支持多分类;而线性核的SVM是在$n$维的数据中寻找一个$n-1$的超平面来分隔数据,是解决的二分类问题。因此,若需线性判别分析与线性核等价,一定要满足都是在**解决二分类问题**上(不考虑使用OvR等使SVM解决多分类)。
191 |
192 | 由于线性判别分析关键在找到映射平面,线性核的SVM关键在找分类超平面。考虑两者的关系,可以想到若**两平面垂直**时,如果线性判别分析能达成分类任务,那么在映射平面的两类之间取一条直线,并以这条直线和映射平面的法向量相交做一个平面,一定可以分隔样本。而这个样本就可以作为线性核SVM的分类超平面。
193 |
194 | 综上所述,线性判别分析与线性核支持向量机满足以下两个条件时等价:
195 |
196 | - 解决的问题是二分类问题;
197 | - 线性判别分析的映射超平面和线性核支持向量机的分类超平面垂直。
198 |
199 | ## 6.6
200 |
201 | **答**:对于硬间隔支持向量机,若噪声样本出现在支持向量中,会使决策超平面变化,间隔变小,使得SVM的泛化能力变弱、检测精度降低;对于软间隔支持向量机,噪声样本的出现会使目标函数中的损失项显著提高,使SVM决策受到影响。因此SVM对噪声敏感。
202 |
--------------------------------------------------------------------------------
/docs/MachineLearning/第四章作业.md:
--------------------------------------------------------------------------------
1 | # 《机器学习》第四章作业
2 |
3 | ## 4.1
4 |
5 | **证明**:假设在题目条件下,不存在于与训练集一致的决策树,那么一定存在一个中间节点使得经过此节点后分出的叶子节点中包含不一样标签的样本。而由于不含冲突数据,因此在此叶子节点中标签不同的样本一定还有特征是不相同的,也就是说,此叶子节点还可以根据不同的属性进行下一步决策,使得标签不同的样本完全分离,从而使得训练误差为0。因此得证:**对于不含冲突数据的训练集,必存在与训练集一致的决策树。**
6 |
7 | ## 4.3
8 |
9 | ### 1. 准备数据
10 |
11 | ```python
12 | import numpy as np
13 | import pandas as pd
14 | from sklearn.model_selection import train_test_split
15 | from sklearn.preprocessing import LabelEncoder
16 |
17 | df = pd.read_csv('./watermelon3.csv', index_col=0) # 西瓜数据集3.0
18 | for label in df.columns: # 离散值预处理为整数
19 | if df[label].dtype == object:
20 | df[label] = LabelEncoder().fit(df[label]).transform(df[label])
21 | df
22 | ```
23 |
24 | | | 色泽 | 根蒂 | 敲声 | 纹理 | 脐部 | 触感 | 密度 | 含糖率 | 好瓜 |
25 | | ---: | ---: | ---: | ---: | ---: | ---: | ---: | ----: | -----: | ---: |
26 | | 编号 | | | | | | | | | |
27 | | 1 | 2 | 2 | 1 | 1 | 0 | 0 | 0.697 | 0.460 | 1 |
28 | | 2 | 0 | 2 | 0 | 1 | 0 | 0 | 0.774 | 0.376 | 1 |
29 | | 3 | 0 | 2 | 1 | 1 | 0 | 0 | 0.634 | 0.264 | 1 |
30 | | 4 | 2 | 2 | 0 | 1 | 0 | 0 | 0.608 | 0.318 | 1 |
31 | | 5 | 1 | 2 | 1 | 1 | 0 | 0 | 0.556 | 0.215 | 1 |
32 | | 6 | 2 | 1 | 1 | 1 | 2 | 1 | 0.403 | 0.237 | 1 |
33 | | 7 | 0 | 1 | 1 | 2 | 2 | 1 | 0.481 | 0.149 | 1 |
34 | | 8 | 0 | 1 | 1 | 1 | 2 | 0 | 0.437 | 0.211 | 1 |
35 | | 9 | 0 | 1 | 0 | 2 | 2 | 0 | 0.666 | 0.091 | 0 |
36 | | 10 | 2 | 0 | 2 | 1 | 1 | 1 | 0.243 | 0.267 | 0 |
37 | | 11 | 1 | 0 | 2 | 0 | 1 | 0 | 0.245 | 0.057 | 0 |
38 | | 12 | 1 | 2 | 1 | 0 | 1 | 1 | 0.343 | 0.099 | 0 |
39 | | 13 | 2 | 1 | 1 | 2 | 0 | 0 | 0.639 | 0.161 | 0 |
40 | | 14 | 1 | 1 | 0 | 2 | 0 | 0 | 0.657 | 0.198 | 0 |
41 | | 15 | 0 | 1 | 1 | 1 | 2 | 1 | 0.360 | 0.370 | 0 |
42 | | 16 | 1 | 2 | 1 | 0 | 1 | 0 | 0.593 | 0.042 | 0 |
43 | | 17 | 2 | 2 | 0 | 2 | 2 | 0 | 0.719 | 0.103 | 0 |
44 |
45 | ```python
46 | X = df.iloc[:, :-1] # 属性
47 | y = df.iloc[:, -1] # 标签
48 | X_train,X_test,y_train,y_test=train_test_split(X,y,test_size=0.3) #随机划分训练集和测试集
49 | ```
50 |
51 | ### 2. 定义节点
52 |
53 | ```python
54 | class TreeNode:
55 | def __init__(self, tp=0, label=0, decide=0, compare=0):
56 | self.nxt = dict() # 儿子节点(属性值:节点)(中间节点特有)
57 | self.type = tp # 0->叶子, 1->中间节点
58 | self.label = label # 0->坏瓜, 1->好瓜
59 | self.decide = decide # 划分属性(中间节点特有)
60 | self.compare = compare # 判断值(连续节点特有)
61 | ```
62 |
63 | ### 3. 定义决策树模型
64 |
65 | ```python
66 | class DecisionTree:
67 | def __init__(self):
68 | pass
69 |
70 | def __Ent(self, y):
71 | p = pd.value_counts(y) / len(y)
72 | return -np.sum(p * np.log2(p))
73 |
74 | def __choose(self, D, A):
75 | EntD = self.__Ent(D[-1])
76 | calc1 = lambda x : x.shape[0] / D[0].shape[0] * self.__Ent(x) # 计算信息熵
77 | calc2 = lambda x : x.shape[0] / D[0].shape[0] * np.log2(x.shape[0] / D[0].shape[0]) # 计算IV
78 | mp = dict()
79 | for attr in A:
80 | v = None # 记录连续值判别的值
81 | if self.attr_type[attr]: # 连续值
82 | gain = 0
83 | iv = 0x3f3f3f3f
84 | for value in sorted(np.unique(D[0][:, attr])):
85 | Dv1 = D[-1][D[0][:, attr] <= value]
86 | Dv2 = D[-1][D[0][:, attr] > value]
87 | temp = EntD - (calc1(Dv1) + calc1(Dv2))
88 | if temp > gain:
89 | gain = temp
90 | iv = -calc2(Dv1)-calc2(Dv2)
91 | v = value
92 | # print("iv=", iv)
93 | else: # 离散值
94 | sm = 0
95 | iv = 1
96 | for value in np.unique(D[0][:, attr]):
97 | Dv = D[-1][D[0][:, attr] == value]
98 | sm += calc1(Dv)
99 | iv += -calc2(Dv)
100 | gain = EntD - sm
101 | # print(gain, iv)
102 | gain_ratio = gain / iv
103 | mp[attr] = (gain, 2, v) # 去除gain_ratio的影响
104 | # print(mp)
105 | temp = sorted(list(mp.items()), key=lambda x : (-x[-1][0], -x[-1][1]))[0]
106 | return temp[0],temp[-1][-1]
107 |
108 | def __generate(self, D, A):
109 | node = TreeNode()
110 | if np.unique(D[-1]).shape[0] <= 1:
111 | return TreeNode(tp=0, label=D[-1][0])
112 | if len(A) == 0 or np.unique(D[0][:, A], axis=0).shape[0] <= 1:
113 | return TreeNode(tp=0, label=np.argmax(np.bincount(D[1])))
114 | attr, v = self.__choose(D, A)
115 | # print(attr)
116 | node.decide = attr
117 | node.type = 1
118 | node.label = np.argmax(np.bincount([int(x) for x in D[1]]))
119 | if self.attr_type[attr]: # 连续值
120 | Dv = D[0][D[0][:, attr] <= v]
121 | # print(Dv)
122 | if Dv.shape[0] == 0:
123 | node.nxt[0] = TreeNode(tp=0, label=node.label)
124 | else:
125 | node.nxt[1] = self.__generate((Dv, D[1][D[0][:, attr] <= v]), [x for x in A if x != attr])
126 | Dv = D[0][D[0][:, attr] > v]
127 | # print(Dv)
128 | if Dv.shape[0] == 0:
129 | node.nxt[0] = TreeNode(tp=0, label=node.label)
130 | else:
131 | node.nxt[1] = self.__generate((Dv, D[1][D[0][:, attr] > v]), [x for x in A if x != attr])
132 | else: # 离散值
133 | for value in np.unique(D[0][:, attr]):
134 | Dv = D[0][D[0][:, attr] == value]
135 | if Dv.shape[0] == 0:
136 | node.nxt[value] = TreeNode(tp=0, label=node.label)
137 | else:
138 | node.nxt[value] = self.__generate((Dv, D[1][D[0][:, attr] == value]), [x for x in A if x != attr])
139 | return node
140 |
141 | def calc(self, X, y): # 将数据通过决策树,得出结果,返回准确率
142 | n = X.shape[0]
143 | lst = []
144 | for i in range(X.shape[0]):
145 | x = X[i, :]
146 | node = self.root
147 | while node.type == 1:
148 | if self.attr_type[node.decide]:
149 | if x[node.decide] <= node.compare:
150 | node = node.nxt[0]
151 | else:
152 | node = node.nxt[1]
153 | else:
154 | if x[node.decide] not in node.nxt.keys():
155 | break
156 | node = node.nxt[x[node.decide]]
157 | lst.append(node.label)
158 | ans = np.array(lst)
159 | acc = 1- np.sum(np.abs(ans - y)) / y.shape[0]
160 | return acc
161 |
162 | def fit(self, X, y):
163 | A = [i for i in range(X.values.shape[1])]
164 | self.attr_type = [X[label].dtype == float for label in X.columns] # 是否是连续值
165 | self.root = self.__generate((X.values, y.values), A)
166 | ans = self.calc(X.values, y.values)
167 | print(f"训练集准确率:{ans: .2f}")
168 |
169 | def predict(self, X, y):
170 | ans = self.calc(X.values, y.values)
171 | print(f"测试集准确率:{ans: .2f}")
172 | ```
173 |
174 | ### 4. 训练、测试
175 |
176 | ```python
177 | model = DecisionTree()
178 | model.fit(X_train, y_train)
179 | model.predict(X_test, y_test)
180 | ```
181 |
182 | 训练集准确率: 1.00
183 | 测试集准确率: 0.67
184 |
185 | ### 5. 讨论
186 |
187 | 本题中由于数据量较少,所以建立的决策树模型可以无需使用gain_ratio,实验发现:在本数据集中使用gain_ratio效果还没有gain好。
188 |
189 | ### 6. 决策树
190 |
191 | 
192 |
193 |
194 |
195 | ## 4.5
196 |
197 | 本题目中仅有决策树模型中`__choose`函数与上题不同。下面是本题的`__choose`函数
198 |
199 | ```python
200 | def __choose(self, D, A):
201 | mp = {}
202 | for attr in A:
203 | X = D[0][:, attr:attr+1]
204 | y = D[1]
205 | v = None
206 | if self.attr_type[attr]:
207 | X_ = X.copy()
208 | ans = -1
209 | for value in np.unique(X):
210 | X_ = X < value
211 | model = LogisticRegression()
212 | model.fit(X_, y)
213 | t = model.score(X_, y)
214 | if t > ans:
215 | ans = t
216 | v = value
217 | else:
218 | model = LogisticRegression()
219 | # print(X, y)
220 | model.fit(X, y)
221 | ans = model.score(X, y)
222 | mp[attr] = (ans, v)
223 | temp = sorted(list(mp.items()), key=lambda x : -x[1][0])
224 | return temp[0][0], temp[0][1][1]
225 | ```
226 |
227 | 训练集准确率: 1.00
228 | 测试集准确率: 0.83
229 |
230 | ### 决策树
231 |
232 | 
233 |
234 | ## 4.7
235 |
236 | **输入**:训练集$D={(\boldsymbol{x}_1, y_1),(\boldsymbol{x}_2, y_2),...,(\boldsymbol{x}_m, y_m)}$;属性集$A={a_1, a_2, ..., a_d}$
237 |
238 | **过程**:函数$\text{TreeGenerate}(D, A)$
239 |
240 | 1. 生成根节点$\text{root}$;用于存储中间节点的队列$\text{queue}$;
241 | 2. 将$(\text{root}, D, A)$放入队列$\text{queue}$中;
242 | 3. $\bold{while}$ $\text{queue}$不为空 $\bold{do}$
243 | 4. 从$\text{queue}$中取出节点$\text{node}$、训练集$D$和属性集$A$;
244 | 5. $\bold{if}$ $D$中样本全属于同一类别$C$ $\bold{then}$
245 | 6. 将$\text{node}$标记为$C$类叶节点; $\bold{continue}$
246 | 7. $\bold{end}\ \bold{if}$
247 | 8. $\bold{if}$ $A = \varnothing$ $\bold{OR}$ $D$中样本在$A$上取值相同 $\bold{then}$
248 | 9. 将$\text{node}$标记为叶节点,其类型标记为$D$中样本数最多的类; $\bold{continue}$
249 | 10. $\bold{end}\ \bold{if}$
250 | 11. 从$A$中选择最优划分属性$a_*$;
251 | 12. $\bold{for}$ $a_*$的每一个值$a_*^v$ $\bold{do}$
252 | 13. 为$\text{node}$生成一个分支节点$\text{branch}$;令$D_v$表示$D$中在$a_*$上取值为$a_*^v$的样本子集;
253 | 14. $\bold{if}$ $D_v$为空 $\bold{then}$
254 | 15. 将分支节点$\text{branch}$标记为叶节点,其类型标记为$D$中样本最多的类;
255 | 16. $\bold{else}$
256 | 17. 将$(\text{branch}, D_v, A\backslash \{ a_* \})$放入队列$\text{queue}$中;
257 | 18. $\bold{end}\ \bold{if}$
258 | 19. $\bold{end}\ \bold{for}$
259 | 20. $\bold{end}\ \bold{while}$
260 |
261 | **输出**:以$\text{root}$为根节点的一棵决策树
262 |
263 |
264 |
265 | ## 4.9
266 |
267 | **答**:在含缺失值的样本中进行划分属性的选择,只需要将包含所有样本的集合$D$转化为只包含在属性$a$上非缺失值样本的集合$\tilde{D}$,并乘上权重即可。具体来说,计算基尼指数的公式如下:
268 | $$
269 | \text{Gini\_index}(D, a)=\rho \times \sum_{v=1}^{V} \tilde r_v \frac{|\tilde D^v|}{|\tilde D|}\text{Gini}(\tilde D^v)
270 | $$
271 | 其中,
272 | $$
273 | \begin{align}
274 | \text{Gini}(\tilde D) &= 1-\sum_{k=1}^{|\mathcal Y|}\tilde p_k^2, \\
275 | \rho &= \frac {\sum_{\boldsymbol x \in\tilde D} w_{\boldsymbol x}} {\sum_{\boldsymbol x \in D} w_{\boldsymbol x}}, \\
276 | \tilde p_k &= \frac {\sum_{\boldsymbol x \in\tilde D_k} w_{\boldsymbol x}} {\sum_{\boldsymbol x \in D} w_{\boldsymbol x}} (1 \leq k \leq |\mathcal Y |),\\
277 | \tilde r_v &= \frac {\sum_{\boldsymbol x \in\tilde D^v} w_{\boldsymbol x}} {\sum_{\boldsymbol x \in D} w_{\boldsymbol x}} (1\leq v \leq V),
278 | \end{align}
279 | $$
280 |
281 |
--------------------------------------------------------------------------------
/docs/OperatingSystem/index.md:
--------------------------------------------------------------------------------
1 | # 暂无
--------------------------------------------------------------------------------
/docs/SoftwareEngineering/软工应用分析题.md:
--------------------------------------------------------------------------------
1 | 前面的结构化分析和面向对象分析建模看实验指导书和UML的PPT即可。这个文件请重点参考后面两种测试中涉及的方法。
2 |
3 | # 一、结构化分析
4 |
5 | ## 1. 数据流图【重要】
6 |
7 | 参考PPT和实验文档即可。
8 |
9 | ## 2. 数据字典【重要】
10 |
11 | 参考PPT和实验文档即可。
12 |
13 | ## 3. 控制流建模
14 |
15 | 不重要。考到就看PPT。
16 |
17 |
18 |
19 | # 二、面向对象分析
20 |
21 | ## 1. 用例图【重要】
22 |
23 | **请参考UML的PPT。**
24 |
25 | 分析用例实现中,对象之间的交互行为,核心是时序图、状态图等
26 |
27 | 【用例建模】
28 |
29 | · 用例表示从执行者的角度观察到系统的功能和外部行为。
30 |
31 | · 用例图主要描述用户需求,强调谁在使用系统,系统可以实现哪些功能目标。
32 |
33 | · 用例特征
34 |
35 | · 用例都是动宾结构
36 |
37 | · 用例是相互独立的
38 |
39 | · 用例由参与者启动
40 |
41 | · 有可观测的执行结果
42 |
43 | 【识别用例】
44 |
45 | 识别用例最好的方法就是从分析系统的参与者(可以是角色、外部系统、设备甚至时钟信号等)开始,考虑每一个参与者是如何使用系统的。
46 |
47 | **【用例图】**
48 |
49 | 用例模型主要包含4种元素:执行者、用例,执行者与用例间关联、用例间关系。
50 |
51 | 【用例间关系】
52 |
53 | 《include》关系
54 |
55 | 父用例执行过程中会用到子用例(无条件执行)。
56 |
57 | 子用例一般表示为公共功能。
58 |
59 | 
60 |
61 | 《extend》关系
62 |
63 | 父用例在特定情况下(称为扩展点)会用到子用例(有条件执行)
64 |
65 | 子用例一般表示为异常功能。
66 |
67 | 
68 |
69 | 泛化(generalization)关系
70 |
71 | 当多个用例共同拥有一种类似的行为时,可以将它们的共性抽象成为父用例,其他用例作为子用例。
72 |
73 | 该关系也可存在于参与者之间。
74 |
75 | 
76 |
77 | 
78 |
79 | 【用例描述】
80 |
81 | 单纯的用例图并不能描述完整的信息,需要用文字描述不能反映在图形上的信息。
82 |
83 | 用例描述是将用例发生的各种场景描述出来,表示参与者与系统交互时双方的行为,即参与者做什么,系统做什么反应。
84 |
85 | 场景能真实反映参与者在用例执行中可能遇到的
86 |
87 | 各种情形。
88 |
89 | 可以使用**用例模版**或**活动图**描述用例执行中的各种场景。
90 |
91 | 【用例模板】
92 |
93 | 用例描述模版的内容大致包括:用例名、参与者,前置条件,后置条件,事件流等。
94 |
95 | 用例的事件流
96 |
97 | 说明参与者与系统之间的交互过程;
98 |
99 | 说明用例在不同条件下可以选择执行的多种方案;
100 |
101 | 分为基本流和备选流两类
102 |
103 | 基本流:描述该用例正常执行的一种场景,系统执行一系列活动步骤来响应参与者提出的服务请求;
104 |
105 | 备选流:描述用例执行过程中异常的或偶尔发生的一些情况。
106 |
107 | 
108 |
109 |
110 |
111 |
112 |
113 | ## 2. 类图【重要】
114 |
115 | **请参考UML的PPT。**
116 |
117 | 【类图】
118 |
119 | (具体画法参考实验文档)
120 |
121 | 目标是对领域内的概念类进行分析,并抽象出对应的类及其关系等。
122 |
123 | 具体包括三个步骤:
124 |
125 | 1. 从用例场景中寻找概念类
126 |
127 | (1) 分析用例场景
128 |
129 | (2) 找出其中的名词或名词短语作为分析类备选
130 |
131 | (3) 如何判断分离出的词是否是分析类?
132 |
133 | 
134 |
135 | 2. 细化概念类,识别其类型(如边界类、实体类等)
136 |
137 | 例子:学生选课用例
138 |
139 | 
140 |
141 | 通过分析,可以确定以下分析类:
142 |
143 | 
144 |
145 | 分析类是概念层次的东西,源于问题空间,与实现方式无关。
146 |
147 | 类的类型:
148 |
149 | 《Entity》 classes 表示系统中的持久信息或贯穿应用的数据封装
150 |
151 | 《Boundary》 classes 实现用户与系统的交互,如用户界面或外部接口
152 |
153 | 《Control》 classes 实现对用例行为的封装,管理、调度其它类
154 |
155 | 3. 为概念类定义属性及行为
156 |
157 | 属性描述了一个已被选择以包含在分析模型中的类。
158 |
159 | 要识别类所属行为,可以对处理叙述进行语法解析,看看动词;还可以结合动态(交互)建模,识别分析类的行为。
160 |
161 | 例子:
162 |
163 | 
164 |
165 | 4. 定义关系
166 |
167 | (1) 关联关系:关联关系可以使一个类可以引用另一个类的属性和方法。一般使用成员变量来实现。
168 |
169 | 
170 |
171 | (2) 聚合关系:表示整体和部分的关系,整体与部分可以分开,使用带空心菱形的实线来表示。
172 |
173 | 
174 |
175 | (3) 组合关系:也是整体与部分的关系,但是整体与部分不可以分开,使用实心带菱形的实线来表示。组合关系中整体类和部分类必须有相同的生命周期。
176 |
177 | 
178 |
179 | (4) 依赖关系:即一个类的实现需要另一个类的协助。多数情况下,依赖关系表现在某个类的方法使用另一个类的对象作为参数。
180 |
181 | 
182 |
183 | (5) 泛化关系:表示类与类、接口与接口之间的继承关系
184 |
185 | 
186 |
187 | 实例:
188 |
189 | 
190 |
191 |
192 |
193 | ## 3. 时序图(顺序图)【重要】
194 |
195 | **请参考UML的PPT。**
196 |
197 | 【时序图】
198 |
199 | 时序图建模步骤
200 |
201 | (1)对每个用例,建立系统时序图(可选)
202 |
203 | (2)建立对象时序图
204 |
205 | (3)从图中确定分析类的行为
206 |
207 | 主要步骤
208 |
209 | 按从左到右的顺序
210 |
211 | 1、列出启动该用例的参与者;
212 |
213 | 2、列出参与者使用的边界类;
214 |
215 | 3、列出管理该用例的控制类;
216 |
217 | 4、根据用例的执行流程,按时间顺序列出分析类之间的消息序列。
218 |
219 | **例子:****还书用例**
220 |
221 | 1. 借阅者点击还书按钮向系统申请还书
222 | 2. 系统提示借阅者输入还书号等信息
223 | 3. 借阅者输入还书信息后,系统查询该书是否已超期。
224 | 4. 如果未超期,则记录用户还书信息并更新图书可借状态,并返回借阅者成功还书信息。
225 | 5. 如果已超期,则系统提示超期、罚款金额等信息。
226 | 6. 借阅者如果认可,并确认缴纳罚款,则系统执行扣款并还书,返回借阅者成功还书信息。
227 |
228 | 
229 |
230 | ## 4. 状态图
231 |
232 | 请参考UML的PPT。
233 |
234 | 【状态图】
235 |
236 | 状态图描述了一个对象生命周期内所经历的状态序列,以及引起状态转移的外部事件。
237 |
238 | 状态图的主要作用:
239 |
240 | 描述多个状态之间的转换顺序,即事件的执行顺序,避免非法的事件序列。(如: 必须先付款进入“已付款”状态,才能执行发货进入“已发货”状态。)
241 |
242 | 
243 |
244 | 
245 |
246 | ## 5. 其他
247 |
248 | ### 5.1. 活动图
249 |
250 | 【活动图】
251 |
252 | 
253 |
254 |
255 |
256 | ### 5.2. ER图
257 |
258 | 【ER图】
259 |
260 | 
261 |
262 | 
263 |
264 | ### 5.3. CRC模型
265 |
266 | 【CRC模型, Class-responsibility-collaborator】
267 |
268 | 作用:帮助补充、完善、优化分析类(属性、行为)
269 |
270 | 职责:职责是与类相关的属性和操作。
271 |
272 | 简单的说,职责就是“类所知道的或能做的任何事情”,可理解为类的能力。
273 |
274 | 例如,顾客有名字、地址和电话号码,这是顾客知道的东西。顾客要借书和还书,这是顾客要完成的事情。
275 |
276 | 分配职责的指导原则:属性和与之相关的行为应该在同一个类中。
277 |
278 | 类主要通过两种方式实现其职责:
279 |
280 | 通过自己内部的行为,实现特定的职责
281 |
282 | 请求其它类的协作
283 |
284 | 如果某个对象请求协作,就会向其它对象发送消息。
285 |
286 | 消息接收者作为服务方,通过自己的服务作为对消息发送者的回应。
287 |
288 | 职责是一种较高层次的抽象,其在设计过程中可能细化为一到多个具体的行为。
289 |
290 | 例子:用户登录用例中,登录控制类的职责之一是“身份验证” 。该职责在设计阶段,可以被细化为多个具体方法:getUser(),getRole(),getGroup(),check()
291 |
292 | 
293 |
294 |
295 |
296 | ### 5.4. 包图
297 |
298 | 【包图】
299 |
300 | 对于较大的项目,由于有很多的类和用例,常常会使系统结构看起非常复杂。
301 |
302 | 通过包图,庞大系统之间的关系变得更简单,整个系统的架构一目了然。
303 |
304 | 原则:将概念上或语义上相近的类纳入一个包
305 |
306 | 包之间的主要关系是依赖关系。
307 |
308 | 意味着两个Package内的元素之间存在着一个或多个依赖
309 |
310 | 
311 |
312 | 
313 |
314 |
315 |
316 |
317 |
318 |
319 |
320 |
321 |
322 |
323 |
324 |
325 |
326 |
327 |
328 | # 三、白盒测试
329 |
330 | ## 1. 基本路径测试法【重要】
331 |
332 | 参考视频:https://www.bilibili.com/video/BV13V4y1g7tc/?share_source=copy_web&vd_source=7ba452d8ee6f8b8a4b8ef831bf573bda
333 |
334 | 步骤:
335 |
336 | - **(1) 画出控制流图**
337 |
338 | 流程图用来描述程序控制结构。可将流程图映射到一个相应的流图(假设流程图的菱形决定框中不包含复合条件)。
339 |
340 | - 在流图中,每一个圆,称为流图的**结点**,代表一个或多个语句。一个处理方框序列和一个菱形决策框可被映射为一个结点 。
341 | - 流图中的箭头,称为**边或连接**, 代表控制流 , 类似于流程图中的箭头 。一条边必须终止于一个结点 , 即使该结点并不代表任何语句(例如:if-else-then结构)。
342 | - 由边和结点限定的范围称为**区域** 。
343 |
344 | 控制流图基本结构:
345 |
346 |  347 |
348 | 在将程序流程图简化成控制流图时 , 应注意 :
349 |
350 | - 在选择或多分支结构中 , 分支的**汇聚处应有一个汇聚结点**;
351 | - 边和结点圈定的区域叫做区域 , 当对区域计数时 , **图形外的区域也应记为一个区域**。
352 |
353 | > 例子:
354 | >
355 | >
347 |
348 | 在将程序流程图简化成控制流图时 , 应注意 :
349 |
350 | - 在选择或多分支结构中 , 分支的**汇聚处应有一个汇聚结点**;
351 | - 边和结点圈定的区域叫做区域 , 当对区域计数时 , **图形外的区域也应记为一个区域**。
352 |
353 | > 例子:
354 | >
355 | >  356 |
357 | 如果遇到一个条件表达式有多个逻辑运算符,则需改为一系列只有单条件的嵌套的判断:
358 |
359 |
356 |
357 | 如果遇到一个条件表达式有多个逻辑运算符,则需改为一系列只有单条件的嵌套的判断:
358 |
359 |  360 |
361 | > 例子:
362 | >
363 | >
360 |
361 | > 例子:
362 | >
363 | >  364 | >
365 | >
364 | >
365 | >  366 |
367 | - **(2)计算环路复杂度(圈复杂度或McCabe复杂度)**
368 |
369 | 圈复杂度是一种为程序逻辑复杂性提供定量测度的软件度量, 将该度量用于计算程序的基本的独立路径数目 ,为确保所有语句至少执行一次的测试数量的上界。独立路径必须包含一条在定义之前不曾用到的边。
370 | 有以下三种方法计算圈复杂度:
371 |
372 | - 流图中区域的数量对应于环型的复杂性;
373 | - 给定流图$G$的圈复杂度$V(G)$, 定义为$V(G) = E - N + 2$,$E$是流图中边的数量,$N$是流图中结点的数量;
374 | - 给定流图 G 的圈复杂度$V(G)$, 定义为$V(G) = P + 1$, P 是流图$G$中判定结点的数量。
375 |
376 | > 例子(接上):
377 | >
378 | >
366 |
367 | - **(2)计算环路复杂度(圈复杂度或McCabe复杂度)**
368 |
369 | 圈复杂度是一种为程序逻辑复杂性提供定量测度的软件度量, 将该度量用于计算程序的基本的独立路径数目 ,为确保所有语句至少执行一次的测试数量的上界。独立路径必须包含一条在定义之前不曾用到的边。
370 | 有以下三种方法计算圈复杂度:
371 |
372 | - 流图中区域的数量对应于环型的复杂性;
373 | - 给定流图$G$的圈复杂度$V(G)$, 定义为$V(G) = E - N + 2$,$E$是流图中边的数量,$N$是流图中结点的数量;
374 | - 给定流图 G 的圈复杂度$V(G)$, 定义为$V(G) = P + 1$, P 是流图$G$中判定结点的数量。
375 |
376 | > 例子(接上):
377 | >
378 | >  379 |
380 | - **确定独立路径**
381 |
382 | 一条独立路径是指与其他的独立路径相比,至少引入一个新处理语句或一个新判断的程序通路。**$V(G)$值正好等于该程序的独立路径的条数。**
383 |
384 | > 例子(接上):
385 | >
386 | > 根据上面的计算方法,可得出四条独立的路径。
387 | > 路径1: 4 一 14
388 | > 路径2: 4 一 6 一 7 一 14
389 | > 路径3: 4 一 6 一 8 一 10 一 13 一 4 一 14
390 | > 路径4: 4 一 6 一 8 一 11 一 13 一 4 一 14
391 | > 根据上而的独立路径 , 去设计输入数据 , 使程序分别执行到上面四条路径 。
392 |
393 | - **准备测试用例**
394 |
395 | 为了确保基本路径集中的每一条路径的执行,根据判断结点给出的条件,选择适当的数据以保证某一条路径可以被测试到。
396 |
397 | > 例子(接上):
398 | >
399 | > 满足上面例子基本路径集的测试用例是 :
400 | >
401 | >
379 |
380 | - **确定独立路径**
381 |
382 | 一条独立路径是指与其他的独立路径相比,至少引入一个新处理语句或一个新判断的程序通路。**$V(G)$值正好等于该程序的独立路径的条数。**
383 |
384 | > 例子(接上):
385 | >
386 | > 根据上面的计算方法,可得出四条独立的路径。
387 | > 路径1: 4 一 14
388 | > 路径2: 4 一 6 一 7 一 14
389 | > 路径3: 4 一 6 一 8 一 10 一 13 一 4 一 14
390 | > 路径4: 4 一 6 一 8 一 11 一 13 一 4 一 14
391 | > 根据上而的独立路径 , 去设计输入数据 , 使程序分别执行到上面四条路径 。
392 |
393 | - **准备测试用例**
394 |
395 | 为了确保基本路径集中的每一条路径的执行,根据判断结点给出的条件,选择适当的数据以保证某一条路径可以被测试到。
396 |
397 | > 例子(接上):
398 | >
399 | > 满足上面例子基本路径集的测试用例是 :
400 | >
401 | >  402 |
403 | ### 实例1
404 |
405 | **题目**:判断任意年份是否为闰年,需要满足以下条件中的任意一个:
406 |
407 | - 该年份能被4整除同时不能被100整除;
408 | - 该年份能被400整除。
409 |
410 | 代码如下:
411 |
412 | ```c
413 | int isLeap (int year) {
414 | if(year % 4 == 0) { // 1
415 | if(year % 100 == 0) { // 3
416 | if(year % 400 == 0) { // 4
417 | leap = 1; // 6
418 | } else {
419 | leap = 0; // 7
420 | }
421 | } else {
422 | leap = 1; // 5
423 | }
424 | } else {
425 | leap = 0; // 2
426 | }
427 | return leap; // 8
428 | }
429 | ```
430 |
431 | 请采用基本路径测试法设计上述程序的测试用例。要求:
432 |
433 | (1)画出流图;
434 |
435 | (2)计算环路复杂度;
436 |
437 | (3)给出基本路径;
438 |
439 | (4)给出满足基本路径测试标准的最小测试用例集。(提示:测试用例= 测试输入+预期输出。)
440 |
441 | **解答**:
442 |
443 | (1)画出流图
444 |
445 |
402 |
403 | ### 实例1
404 |
405 | **题目**:判断任意年份是否为闰年,需要满足以下条件中的任意一个:
406 |
407 | - 该年份能被4整除同时不能被100整除;
408 | - 该年份能被400整除。
409 |
410 | 代码如下:
411 |
412 | ```c
413 | int isLeap (int year) {
414 | if(year % 4 == 0) { // 1
415 | if(year % 100 == 0) { // 3
416 | if(year % 400 == 0) { // 4
417 | leap = 1; // 6
418 | } else {
419 | leap = 0; // 7
420 | }
421 | } else {
422 | leap = 1; // 5
423 | }
424 | } else {
425 | leap = 0; // 2
426 | }
427 | return leap; // 8
428 | }
429 | ```
430 |
431 | 请采用基本路径测试法设计上述程序的测试用例。要求:
432 |
433 | (1)画出流图;
434 |
435 | (2)计算环路复杂度;
436 |
437 | (3)给出基本路径;
438 |
439 | (4)给出满足基本路径测试标准的最小测试用例集。(提示:测试用例= 测试输入+预期输出。)
440 |
441 | **解答**:
442 |
443 | (1)画出流图
444 |
445 |  446 |
447 | (2)计算环路复杂度
448 |
449 | (方法一)一共有4个区域,因此$V(G)=4$。
450 |
451 | (方法二)一共有8个节点,10条边,因此$V(G) = E - N + 2=10-8+2=4$。
452 |
453 | (方法三)一共有三个判定节点:1、3、4,因此$V(G) = 3 + 1 = 4$。
454 |
455 | (3)写出基本路径
456 |
457 | 路径1:1-2-8
458 |
459 | 路径2:1-3-5-8
460 |
461 | 路径3:1-3-4-6-8
462 |
463 | 路径4:1-3-4-7-8
464 |
465 | (4)给出满足基本路径测试标准的最小测试用例集
466 |
467 | | 覆盖路径 | 测试输入 | 测试输出 | 说明 |
468 | | -------- | ---------- | -------- | ------------------------------- |
469 | | 1 | year = 1 | 0 | 不能被4整除 |
470 | | 2 | year = 4 | 1 | 能被4整除,但不能被100整除 |
471 | | 3 | year = 400 | 1 | 能被4,100,400整除 |
472 | | 4 | year = 200 | 0 | 能被4,100整除,但不能被400整除 |
473 |
474 |
475 |
476 | ### 实例2
477 |
478 | **题目**: 请采用基本路径测试法设计下列伪码程序的测试用例。 要求:
479 |
480 | (1)画出流图;
481 |
482 | (2)计算环路复杂度;
483 |
484 | (3)给出基本路径;
485 |
486 | (4)给出满足基本路径测试标准的最小测试用例集。(提示:测试用例= 测试输入+预期输出。)
487 |
488 | ```
489 | 1: Start Input(a,b,c,d)
490 | 2: If(a>0)
491 | 3: and (b>0)
492 | 4: Then x=a+b
493 | 5: Else x=a-b
494 | 6: End if
495 | 7: If (c>a)
496 | 8: or (d
446 |
447 | (2)计算环路复杂度
448 |
449 | (方法一)一共有4个区域,因此$V(G)=4$。
450 |
451 | (方法二)一共有8个节点,10条边,因此$V(G) = E - N + 2=10-8+2=4$。
452 |
453 | (方法三)一共有三个判定节点:1、3、4,因此$V(G) = 3 + 1 = 4$。
454 |
455 | (3)写出基本路径
456 |
457 | 路径1:1-2-8
458 |
459 | 路径2:1-3-5-8
460 |
461 | 路径3:1-3-4-6-8
462 |
463 | 路径4:1-3-4-7-8
464 |
465 | (4)给出满足基本路径测试标准的最小测试用例集
466 |
467 | | 覆盖路径 | 测试输入 | 测试输出 | 说明 |
468 | | -------- | ---------- | -------- | ------------------------------- |
469 | | 1 | year = 1 | 0 | 不能被4整除 |
470 | | 2 | year = 4 | 1 | 能被4整除,但不能被100整除 |
471 | | 3 | year = 400 | 1 | 能被4,100,400整除 |
472 | | 4 | year = 200 | 0 | 能被4,100整除,但不能被400整除 |
473 |
474 |
475 |
476 | ### 实例2
477 |
478 | **题目**: 请采用基本路径测试法设计下列伪码程序的测试用例。 要求:
479 |
480 | (1)画出流图;
481 |
482 | (2)计算环路复杂度;
483 |
484 | (3)给出基本路径;
485 |
486 | (4)给出满足基本路径测试标准的最小测试用例集。(提示:测试用例= 测试输入+预期输出。)
487 |
488 | ```
489 | 1: Start Input(a,b,c,d)
490 | 2: If(a>0)
491 | 3: and (b>0)
492 | 4: Then x=a+b
493 | 5: Else x=a-b
494 | 6: End if
495 | 7: If (c>a)
496 | 8: or (d 623 |
624 |
625 |
626 | # 四、黑盒测试
627 |
628 | ## 1.等价类划分
629 |
630 | 参考视频:https://www.bilibili.com/video/BV1MT411M7EC/?share_source=copy_web&vd_source=7ba452d8ee6f8b8a4b8ef831bf573bda
631 |
632 | 把被测对象的输入域划分为有限个等价区段“等价类”, 以有针对性的等价类少量测试,代替漫无边际的、数量较大的 “ 穷尽 ” 测试或随机测试。每个等价类的典型值的测试作用,可以代表这一类的所有其它数据。
633 |
634 | 等价类分为:
635 |
636 | - 有效等价类:对于程序的规格说明是合理、有意义的输入数据的集合
637 | - 无效等价类:对于程序的规格说明是不合理的、没有意义的输入数据的集合
638 |
639 | 步骤:
640 |
641 | - **划分“等价类”**
642 |
643 | 应按照输入条件(如输入值的范围、值的个数、 值的集合 、输入条件)划分为有效等价类和无效等价类。
644 |
645 | > 例1:每个学生可选修1-3门课程
646 | >
647 | > - 可以划分一个有效等价类:选修1-3门课程。
648 | > - 可以划分两个无效等价类:未选择选修课,选修课超过3门 。
649 | >
650 | > 例2:标识符的第一个字符必须是字母
651 | >
652 | > 可以划分为一个有效等价类:第一个字符是字母
653 | >
654 | > (或两个有效等价类:第一个字母是大写字母 / 小写字母) 。
655 | >
656 | > 可以划分一个无效等价类 : 第一个字符不是字母 。
657 |
658 | 等价法划分类的启发式规则:
659 |
660 | - 如果规定了输入值的范围 , 则可划分出一个有效的等价类 ( 输入值在此范围内 ) 和两个无效的等价类 ( 输入值小于最小值或大于最大值 ) 。
661 | - 如果规定了输入数据的个数 , 则类似地可以划分出一个有效的等价类和两个无效的等价类 。
662 | - 如果规定了输入数据的一组值 , 而且程序对不同输入值做不同处理 , 则每个允许的输入值是一个有效的等价类 , 此外还有一个无效的等价类 ( 任意一个不允许的输入值 ) 。
663 | - 若规定了输入数据的规则 , 则可以划分出一个有效的等价类 ( 符合规则 ) 和若干个无效的等价类 ( 从各种不同角度违反规则 )
664 | - 若规定了输入数据为整型 , 则可以划分出正整数 、 零和负整数等三个有效等价类 。
665 | - 若处理对象是表格 , 则应该使用空表以及含一项或多项的表 。
666 |
667 | - **选择测试用例**
668 | - 为每个等价类编号;
669 | - 使一个测试用例尽可能覆盖多个有效等价类;
670 | - 特别要注意的是:**一个测试用例只能覆盖一个无效等价类**;**每一个无效等价类都需要测试用例**。
671 |
672 |
673 |
674 | ### 实例1
675 |
676 | **题目**:在某一 PASCAL 语言版本中规定:在同一说明语句中 , 标识符至少必须有一个,标识符是由字母开头 、 后跟字母或数字的任意组合构成 。 有效字符数为 1 个 ,最大字符数为 80 个 。 并且规定:标识符必须先说明,再使用 。请使用等价划分法进行测试用例设计。
677 |
678 | **解答**:为用等价类划分的方法得到上述规格说明所规定的要求 , 本着前述的划分原则 ,建立等价类表 , 如表所示 ( 表中括中的数为等价类编号 ) 。
679 |
680 |
623 |
624 |
625 |
626 | # 四、黑盒测试
627 |
628 | ## 1.等价类划分
629 |
630 | 参考视频:https://www.bilibili.com/video/BV1MT411M7EC/?share_source=copy_web&vd_source=7ba452d8ee6f8b8a4b8ef831bf573bda
631 |
632 | 把被测对象的输入域划分为有限个等价区段“等价类”, 以有针对性的等价类少量测试,代替漫无边际的、数量较大的 “ 穷尽 ” 测试或随机测试。每个等价类的典型值的测试作用,可以代表这一类的所有其它数据。
633 |
634 | 等价类分为:
635 |
636 | - 有效等价类:对于程序的规格说明是合理、有意义的输入数据的集合
637 | - 无效等价类:对于程序的规格说明是不合理的、没有意义的输入数据的集合
638 |
639 | 步骤:
640 |
641 | - **划分“等价类”**
642 |
643 | 应按照输入条件(如输入值的范围、值的个数、 值的集合 、输入条件)划分为有效等价类和无效等价类。
644 |
645 | > 例1:每个学生可选修1-3门课程
646 | >
647 | > - 可以划分一个有效等价类:选修1-3门课程。
648 | > - 可以划分两个无效等价类:未选择选修课,选修课超过3门 。
649 | >
650 | > 例2:标识符的第一个字符必须是字母
651 | >
652 | > 可以划分为一个有效等价类:第一个字符是字母
653 | >
654 | > (或两个有效等价类:第一个字母是大写字母 / 小写字母) 。
655 | >
656 | > 可以划分一个无效等价类 : 第一个字符不是字母 。
657 |
658 | 等价法划分类的启发式规则:
659 |
660 | - 如果规定了输入值的范围 , 则可划分出一个有效的等价类 ( 输入值在此范围内 ) 和两个无效的等价类 ( 输入值小于最小值或大于最大值 ) 。
661 | - 如果规定了输入数据的个数 , 则类似地可以划分出一个有效的等价类和两个无效的等价类 。
662 | - 如果规定了输入数据的一组值 , 而且程序对不同输入值做不同处理 , 则每个允许的输入值是一个有效的等价类 , 此外还有一个无效的等价类 ( 任意一个不允许的输入值 ) 。
663 | - 若规定了输入数据的规则 , 则可以划分出一个有效的等价类 ( 符合规则 ) 和若干个无效的等价类 ( 从各种不同角度违反规则 )
664 | - 若规定了输入数据为整型 , 则可以划分出正整数 、 零和负整数等三个有效等价类 。
665 | - 若处理对象是表格 , 则应该使用空表以及含一项或多项的表 。
666 |
667 | - **选择测试用例**
668 | - 为每个等价类编号;
669 | - 使一个测试用例尽可能覆盖多个有效等价类;
670 | - 特别要注意的是:**一个测试用例只能覆盖一个无效等价类**;**每一个无效等价类都需要测试用例**。
671 |
672 |
673 |
674 | ### 实例1
675 |
676 | **题目**:在某一 PASCAL 语言版本中规定:在同一说明语句中 , 标识符至少必须有一个,标识符是由字母开头 、 后跟字母或数字的任意组合构成 。 有效字符数为 1 个 ,最大字符数为 80 个 。 并且规定:标识符必须先说明,再使用 。请使用等价划分法进行测试用例设计。
677 |
678 | **解答**:为用等价类划分的方法得到上述规格说明所规定的要求 , 本着前述的划分原则 ,建立等价类表 , 如表所示 ( 表中括中的数为等价类编号 ) 。
679 |
680 |  681 |
682 | 下面选取了8个测试用例,它们覆盖了所有的等价类。
683 |
684 |
681 |
682 | 下面选取了8个测试用例,它们覆盖了所有的等价类。
683 |
684 |  685 |
686 |
687 |
688 | ### 实例2
689 |
690 | **题目**:下面以测试`NextDate`函数的具体实例为出发点 , 讲解使用等价类划分法的细节 。 输入 3 个变量 ( 年 、 月 、 日 ) , 函数返回输入日期后面一天的日期 :1<=月<=12 , 1 <=日<=31 , 1812<=年<=2012 。 给出等价类划分表并设计测试用例 。
691 | **解答**:**(1)划分等价类 , 得到等价类划分表** , 如下表所示 。
692 |
693 |
685 |
686 |
687 |
688 | ### 实例2
689 |
690 | **题目**:下面以测试`NextDate`函数的具体实例为出发点 , 讲解使用等价类划分法的细节 。 输入 3 个变量 ( 年 、 月 、 日 ) , 函数返回输入日期后面一天的日期 :1<=月<=12 , 1 <=日<=31 , 1812<=年<=2012 。 给出等价类划分表并设计测试用例 。
691 | **解答**:**(1)划分等价类 , 得到等价类划分表** , 如下表所示 。
692 |
693 |  694 |
695 | (2)为**有效等价类**设计测试用例,如下表所示。
696 |
697 |
694 |
695 | (2)为**有效等价类**设计测试用例,如下表所示。
696 |
697 |  698 |
699 | (3)为**无效等价类**设计测试用例,如下表所示。
700 |
701 |
698 |
699 | (3)为**无效等价类**设计测试用例,如下表所示。
700 |
701 |  702 |
703 |
702 |
703 |  704 |
705 |
706 |
707 | ## 2. 边界值分析
708 |
709 | 经验表明,处理边界情况时程序最容易发生错误
710 |
711 | **边界类型:下标 、 数据结构 、 循环 、 选择等的边界附近**
712 |
713 | ——使程序运行在边界附近的测试方案 , 更容易暴露程序错误
714 |
715 | 通常选用**等价类边界值**作为边界值测试的数据
716 |
717 | 取值:按照边界值分析法 , 一般选取**刚好等于、稍小于和稍大于**等价类边界值的数据作为测试数据 。
718 |
719 | 一般边界值分析法作为等价类划分法的补充与细化 。
720 |
721 | **边界值分析法应当遵循的原则**:
722 |
723 | - 按照输入值范围的边界 。
724 |
725 | 例如:输入值的范围是$-1.0$至$1.0$,则设计用例:$-1.0,1.0,-1.001,1.001$。
726 |
727 | - 按照输入 / 输出值个数的边界 。
728 |
729 | 例如: 输入文件可有1-255个记录,则设计用例:文件的记录数为$0, 1, 255, 256$。
730 |
731 | - 输出值域的边界 。
732 |
733 | 例如:检索文献摘要,最多4篇,则设计用例:可检索篇数:$0,1,4,5$ 。
734 |
735 | - 输入/输出有序集(如顺序文件 、 线性表)的边界 。
736 |
737 | 应选择第一个元素和最后一个元素 。
738 |
739 |
740 |
741 | ### 实例
742 |
743 | 在上面实例2的基础上,使用边界值分析法设计测试用例。通常 , 设计测试方案时会联合使用等价类划分和边界值分析两种技术 。以上一节的`NextDate`函数为例 , 除了用等价类划分法设计出的测试方案外 ,还应该用边界值分析法补充以下测试方案 。
744 |
745 |
704 |
705 |
706 |
707 | ## 2. 边界值分析
708 |
709 | 经验表明,处理边界情况时程序最容易发生错误
710 |
711 | **边界类型:下标 、 数据结构 、 循环 、 选择等的边界附近**
712 |
713 | ——使程序运行在边界附近的测试方案 , 更容易暴露程序错误
714 |
715 | 通常选用**等价类边界值**作为边界值测试的数据
716 |
717 | 取值:按照边界值分析法 , 一般选取**刚好等于、稍小于和稍大于**等价类边界值的数据作为测试数据 。
718 |
719 | 一般边界值分析法作为等价类划分法的补充与细化 。
720 |
721 | **边界值分析法应当遵循的原则**:
722 |
723 | - 按照输入值范围的边界 。
724 |
725 | 例如:输入值的范围是$-1.0$至$1.0$,则设计用例:$-1.0,1.0,-1.001,1.001$。
726 |
727 | - 按照输入 / 输出值个数的边界 。
728 |
729 | 例如: 输入文件可有1-255个记录,则设计用例:文件的记录数为$0, 1, 255, 256$。
730 |
731 | - 输出值域的边界 。
732 |
733 | 例如:检索文献摘要,最多4篇,则设计用例:可检索篇数:$0,1,4,5$ 。
734 |
735 | - 输入/输出有序集(如顺序文件 、 线性表)的边界 。
736 |
737 | 应选择第一个元素和最后一个元素 。
738 |
739 |
740 |
741 | ### 实例
742 |
743 | 在上面实例2的基础上,使用边界值分析法设计测试用例。通常 , 设计测试方案时会联合使用等价类划分和边界值分析两种技术 。以上一节的`NextDate`函数为例 , 除了用等价类划分法设计出的测试方案外 ,还应该用边界值分析法补充以下测试方案 。
744 |
745 |  746 |
747 |
748 |
749 | ## 3. 正交表法
750 |
751 | 详见PPT.C18.25-26
752 | $$
753 | 测试用例数量 = 变量个数 \times (变量最大取值数目-1) + 1
754 | $$
755 | 例如:某大学刚考完某门课程考试,想通过“性别”、“班级”、“成绩”三个查询条件对这门课程的成绩进行查询,查询条件包括:
756 |
757 | - “性别” = “男、女”
758 | - “班级” = “1班、2班”
759 | - “成绩” = “及格、不及格”
760 |
761 | 一般来说是设计$2\times 2 \times 2 = 8$个测试用例。但如果使用正交数组法(正交表)法则只需要$3\times (2-1)+1 = 4$个测试用例。
762 |
763 |
--------------------------------------------------------------------------------
/docs/SoftwareEngineering/软工期末考试.md:
--------------------------------------------------------------------------------
1 |
746 |
747 |
748 |
749 | ## 3. 正交表法
750 |
751 | 详见PPT.C18.25-26
752 | $$
753 | 测试用例数量 = 变量个数 \times (变量最大取值数目-1) + 1
754 | $$
755 | 例如:某大学刚考完某门课程考试,想通过“性别”、“班级”、“成绩”三个查询条件对这门课程的成绩进行查询,查询条件包括:
756 |
757 | - “性别” = “男、女”
758 | - “班级” = “1班、2班”
759 | - “成绩” = “及格、不及格”
760 |
761 | 一般来说是设计$2\times 2 \times 2 = 8$个测试用例。但如果使用正交数组法(正交表)法则只需要$3\times (2-1)+1 = 4$个测试用例。
762 |
763 |
--------------------------------------------------------------------------------
/docs/SoftwareEngineering/软工期末考试.md:
--------------------------------------------------------------------------------
1 |  20 |
21 | - 质量关注点:支持软件工程的**根基**在于**质量关注点**。P11
22 | - 过程:软件工程的**基础**。P11
23 | - 方法:解决方案。P11
24 | - 工具:自动化/半自动化支持。P11
25 |
26 | - 过程框架及其通用的5个框架活动:PPT.C1.15-16,P12
27 |
28 | - 框架性活动
29 | - 普适性活动:包括的8项活动:P12-13
30 |
31 | - George Polya提出的4个软件工程**实践的精髓**:P14
32 | - David Hooker提出的7个关注软件工程整体**实践的原则**:P15
33 | - 三个软件开发神话:P16-17
34 |
35 |
36 |
37 | ### (二)过程模型
38 |
39 | - 软件过程的定义:PPT.C2.2,P22
40 | - 每个框架活动由一系列软件工程动作构成;每个软件工程动作由**任务集**来定义。P23
41 | - 四种过程流:P23-24
42 | - 任务集所需要包括的四个组成成分:P24
43 | - 需求获取的任务集需要包括的内容(包括小型或大型项目):P25
44 | - Ambler提出的过程模式的描述模板:P26
45 | - Ambler模板中的三种模式类型:P26
46 | - Ambler模板中的步骤模式沟通中的一组任务模式:P26
47 | - Howard Baetjer Jr提出的软件资产:P22
48 |
49 |
50 |
51 | - 过程模型需要包含的5个方面:PPT.C2.6
52 |
53 | - **瀑布模型**(经典生命周期):PPT.C2.7-8,P30-32
54 |
55 |
20 |
21 | - 质量关注点:支持软件工程的**根基**在于**质量关注点**。P11
22 | - 过程:软件工程的**基础**。P11
23 | - 方法:解决方案。P11
24 | - 工具:自动化/半自动化支持。P11
25 |
26 | - 过程框架及其通用的5个框架活动:PPT.C1.15-16,P12
27 |
28 | - 框架性活动
29 | - 普适性活动:包括的8项活动:P12-13
30 |
31 | - George Polya提出的4个软件工程**实践的精髓**:P14
32 | - David Hooker提出的7个关注软件工程整体**实践的原则**:P15
33 | - 三个软件开发神话:P16-17
34 |
35 |
36 |
37 | ### (二)过程模型
38 |
39 | - 软件过程的定义:PPT.C2.2,P22
40 | - 每个框架活动由一系列软件工程动作构成;每个软件工程动作由**任务集**来定义。P23
41 | - 四种过程流:P23-24
42 | - 任务集所需要包括的四个组成成分:P24
43 | - 需求获取的任务集需要包括的内容(包括小型或大型项目):P25
44 | - Ambler提出的过程模式的描述模板:P26
45 | - Ambler模板中的三种模式类型:P26
46 | - Ambler模板中的步骤模式沟通中的一组任务模式:P26
47 | - Howard Baetjer Jr提出的软件资产:P22
48 |
49 |
50 |
51 | - 过程模型需要包含的5个方面:PPT.C2.6
52 |
53 | - **瀑布模型**(经典生命周期):PPT.C2.7-8,P30-32
54 |
55 |  56 |
57 | - 3个特点:PPT.C2.7
58 | - 4个问题:PPT.C2.8,P31
59 | - **适合于:**PPT.C2.8
60 | - **需求稳定的项目**
61 | - **开发团队对该应用领域非常熟悉**
62 |
63 | - **增量模型**:PPT.C2.9,P32
64 |
65 |
56 |
57 | - 3个特点:PPT.C2.7
58 | - 4个问题:PPT.C2.8,P31
59 | - **适合于:**PPT.C2.8
60 | - **需求稳定的项目**
61 | - **开发团队对该应用领域非常熟悉**
62 |
63 | - **增量模型**:PPT.C2.9,P32
64 |
65 |  66 |
67 | - 特点:PPT.C2.9-10
68 | - 综合了线性过程流和并行过程流的特征。
69 | - 每个阶段都运用线性序列。
70 | - 第一个增量往往是核心产品。
71 | - 客户使用核心产品并进行评估。
72 | - 开发人员根据评估结果指定下一个增量计划。计划中需要说明对核心产品进行的修改,以便更好地满足客户的要求,也应说明需要增加的特性和功能。
73 | - 优势:PPT.C2.10
74 | - 可提高对用户需求或市场需求的响应。
75 | - 通过将不确定、不完全掌握相关技术的功能放在后续增量开发,可减轻技术风险。
76 | - **适合于:**
77 | - **团队成员不足以支持项目完整开发。**
78 | - **迫切需要为用户迅速提供一套功能有限的软件产品,然后再进行细化和拓展功能。**
79 |
80 | - **演化模型——原型法**:PPT.C2.12
81 |
82 | - 本质:通过迭代中一系列活动的重复应用,使软件持续改进。PPT.C2.12
83 | - 特点:PPT.C2.11
84 | - 让“系统”快速可见
85 | - 减少分析、设计过程中的不确定性
86 | - 类型:PPT.C2.11
87 | - 抛弃型:一种识别软件需求的机制
88 | - 演化型:慢慢发展成实际的系统
89 | - 问题:PPT.C2.15
90 |
91 | - **演化模型——螺旋法**:PPT.C2.16
92 |
93 |
66 |
67 | - 特点:PPT.C2.9-10
68 | - 综合了线性过程流和并行过程流的特征。
69 | - 每个阶段都运用线性序列。
70 | - 第一个增量往往是核心产品。
71 | - 客户使用核心产品并进行评估。
72 | - 开发人员根据评估结果指定下一个增量计划。计划中需要说明对核心产品进行的修改,以便更好地满足客户的要求,也应说明需要增加的特性和功能。
73 | - 优势:PPT.C2.10
74 | - 可提高对用户需求或市场需求的响应。
75 | - 通过将不确定、不完全掌握相关技术的功能放在后续增量开发,可减轻技术风险。
76 | - **适合于:**
77 | - **团队成员不足以支持项目完整开发。**
78 | - **迫切需要为用户迅速提供一套功能有限的软件产品,然后再进行细化和拓展功能。**
79 |
80 | - **演化模型——原型法**:PPT.C2.12
81 |
82 | - 本质:通过迭代中一系列活动的重复应用,使软件持续改进。PPT.C2.12
83 | - 特点:PPT.C2.11
84 | - 让“系统”快速可见
85 | - 减少分析、设计过程中的不确定性
86 | - 类型:PPT.C2.11
87 | - 抛弃型:一种识别软件需求的机制
88 | - 演化型:慢慢发展成实际的系统
89 | - 问题:PPT.C2.15
90 |
91 | - **演化模型——螺旋法**:PPT.C2.16
92 |
93 |  94 |
95 | - 结合了原型模型的迭代特性和瀑布模型的系统性和可控性,是一种风险驱动的过程模型。
96 | - 说明:PPT.C2.17
97 | - 早期的内圈,可能仅仅产生产品的规格说明或一个简单原型;
98 | - 后期每一圈,逐渐演化产生软件产品的初始版本,更完善的新版本……
99 | - 特点:PPT.C2.18
100 | - 结合了原型模型的迭代特征和瀑布模型的系统性和可控性,是一种风险驱动的过程模型。
101 | - 是开发大型系统和软件的很实际的方法。
102 | - 把原型作为降低风险的机制。
103 | - 保留了经典生命周期模型中系统逐步细化的方法,但是把它纳入一种迭代框架之中,这种迭代方式与真实世界更加吻合。
104 | - **适合于:**PPT.C2.18
105 | - **大规模软件项目**
106 | - **高风险项目**
107 |
108 | - 并发模型:P36-37
109 | - 统一过程模型(UP):PPT.C2.19-24,P40-42
110 | - 四个阶段:初始,细化,构建,交付。PPT.C2.19
111 | - 在UP**初始**阶段的迭代中,项目组必须:PPT.C2.21
112 | - 到了**细化**阶段的迭代,需要:PPT.C2.22
113 | - 进入**构建**阶段后,核心是所有功能的实现、测试,为应用部署做好准备。PPT.C2.23
114 | - 最后到了**交付**阶段,核心是部署、系统上线、运行和维护。PPT.C2.23
115 | - 特点:PPT.C2.20
116 | - UP裁剪:PPT.C2.24
117 |
118 |
119 |
120 | ### (三)敏捷开发与华为云平台
121 |
122 |
123 |
124 |
125 |
126 |
127 |
128 |
129 |
130 | ### (四)需求——需求工程
131 |
132 | - 理解需求困难的原因:PPT.C5.2
133 | - 【软件需求(SR)】是从软件外部可见的,软件所具有的、满足用户特点的功能及其它属性的集合。PPT.C5.5
134 | - 软件需求通常表达“做什么”,而不是“如何做”
135 | - 软件需求描述**应该满足**:**清晰、简洁、一致且无二义性**
136 |
137 | - 【最主要的需求来源】用户和产品经理,其他。PPT.C5.6
138 |
139 | - 各种需求。PPT.C5.6-8
140 |
141 | - 【需求工程的七项需明确的任务】
142 |
143 | - 起始:提出一系列的问题,以建立对问题的基本理解。PPT.C5.10
144 |
145 | 1. 收集客户的资料,了解系统的背景,进行初步的可行性分析,确定项目范围。
146 | 2. 确定干系人
147 | 3. 识别多个观点
148 | 4. 致力于协作
149 |
150 | 确定有共同点的地区和发生冲突的地区
151 |
152 | - 导出:引出所有利益相关者的需求。PPT.C5.11
153 |
154 | **【需求获取的主要方式】**
155 |
156 | - 需求讨论会。PPT.C5.12-13
157 | - 由软件工程师和客户主持和参加
158 | - 提出议程(确定议程,准备调研提纲)
159 | - 调解人控制全场
160 | - 可由客户方的情况介绍开始,分析人员逐渐成为主导,有效的引导和把握调研的重点和方向。
161 | - 从业务流程入手,采用IPO(Input Process Output)的思想获取需求
162 | - **软件需求分两个层次:用户需求与功能需求**。由用户需求导出功能需求。
163 | - 满足用户需求如果有多种备选方案,可以**协商**不同的方法,提出一套解决方案的要素。
164 |
165 | - 头脑风暴法。PPT.C5.14
166 | - 该方法对**需求不确定**的情况非常适用。
167 | - 调查问卷。PPT.C5.14
168 | - 适合于**需求调研的后期**,用于对前期发现的一些不确定或不一致的地方进行确认。
169 |
170 | - 场景分析法。PPT.C5.15-16
171 | - 场景分析核心是3个维度的梳理:角色、场景、方案。
172 | - 第一人称视角感受考察。PPT.C5.17
173 | - 基于自己的实际使用需求提出产品需求。
174 | - 原型法。PPT.C5.17
175 | - 高保真方式(只包含前端的界面和交互)
176 | - 低保真方式(手绘)
177 |
178 | > 【Experience】
179 | >
180 | > (1) 调研前做好必要的相关背景知识准备
181 | >
182 | > (2) 通过用户获取重要的原始资料(如表单,文件)
183 | >
184 | > (3) 渐进、反复的进行
185 | >
186 | > 访谈后,要及时对需求整理、分类,以便在下次与用户见面时由用户确认;
187 | >
188 | > 同时,准备下一次访谈时更细节的问题。
189 | >
190 | > (4) 根据需求的重要性划优先等级
191 |
192 | - 精化:创建一个可以识别数据、功能和行为需求的分析模型。PPT.C5.22-25
193 |
194 | - 通过分析建模,得到精确的需求模型,用以说明软件的功能、特征和数据等各个方面。
195 |
196 | **【分析模型的元素】**
197 |
198 | - 基于场景的元素——用例图
199 | - 基于类的元素——类图
200 | - 行为元素——状态图
201 | - 流元素——数据流图
202 | - E-R模型
203 |
204 | - 协商:就开发人员和客户现实的可交付系统达成一致。PPT.C5.26
205 |
206 | - 确定关键利益相关者:这些是将参与谈判的人
207 | - 确定每个利益相关者“赢条件”
208 | - 谈判:工作朝着一系列导致“双赢”的要求
209 |
210 | - 规格说明(Software Requirement Specification, SRS)。PPT.C5.27-29
211 |
212 | - **定义:**规格说明可以是一份写好的文档、一套图形化的模型、一组使用场景、一个原型或上述各项的任意组合。PPT.C5.27
213 | - 对大型系统而言,规范、标准的文档和图形化模型是最佳选择;
214 | - 对于技术环节明确的小型系统而言,使用场景可能就足够了。
215 | - **作用:**PPT.C5.28
216 | - **主要内容**:PPT.C5.28-29
217 |
218 | - 确认:审查机制。PPT.C5.30-31
219 | - 参与者:需求分析员、开发人员、测试人员、客户代表、项目经理、产品经理……
220 | - 需求评审要点:
221 | 1. 是否在适当的抽象级别上指定了所有的需求?
222 | 2. 这个要求对系统的目标真的是必要的吗?
223 | 3. 每个要求是否都是有界限和明确的?
224 | 4. 每个要求都有属性吗?
225 | 5. 是否有任何要求与其他要求相冲突?
226 | 6. 在技术环境中是否可满足每个要求?
227 | 7. 每个需求一旦实现,是否可测试?
228 |
229 | ### (五)需求——需求建模:面向对象分析方法
230 |
231 | - 【OOA分析模型分类】
232 | - 用例模型、(静态)领域模型、(动态)行为模型
233 |
234 | - 【分析过程】
235 |
236 |
94 |
95 | - 结合了原型模型的迭代特性和瀑布模型的系统性和可控性,是一种风险驱动的过程模型。
96 | - 说明:PPT.C2.17
97 | - 早期的内圈,可能仅仅产生产品的规格说明或一个简单原型;
98 | - 后期每一圈,逐渐演化产生软件产品的初始版本,更完善的新版本……
99 | - 特点:PPT.C2.18
100 | - 结合了原型模型的迭代特征和瀑布模型的系统性和可控性,是一种风险驱动的过程模型。
101 | - 是开发大型系统和软件的很实际的方法。
102 | - 把原型作为降低风险的机制。
103 | - 保留了经典生命周期模型中系统逐步细化的方法,但是把它纳入一种迭代框架之中,这种迭代方式与真实世界更加吻合。
104 | - **适合于:**PPT.C2.18
105 | - **大规模软件项目**
106 | - **高风险项目**
107 |
108 | - 并发模型:P36-37
109 | - 统一过程模型(UP):PPT.C2.19-24,P40-42
110 | - 四个阶段:初始,细化,构建,交付。PPT.C2.19
111 | - 在UP**初始**阶段的迭代中,项目组必须:PPT.C2.21
112 | - 到了**细化**阶段的迭代,需要:PPT.C2.22
113 | - 进入**构建**阶段后,核心是所有功能的实现、测试,为应用部署做好准备。PPT.C2.23
114 | - 最后到了**交付**阶段,核心是部署、系统上线、运行和维护。PPT.C2.23
115 | - 特点:PPT.C2.20
116 | - UP裁剪:PPT.C2.24
117 |
118 |
119 |
120 | ### (三)敏捷开发与华为云平台
121 |
122 |
123 |
124 |
125 |
126 |
127 |
128 |
129 |
130 | ### (四)需求——需求工程
131 |
132 | - 理解需求困难的原因:PPT.C5.2
133 | - 【软件需求(SR)】是从软件外部可见的,软件所具有的、满足用户特点的功能及其它属性的集合。PPT.C5.5
134 | - 软件需求通常表达“做什么”,而不是“如何做”
135 | - 软件需求描述**应该满足**:**清晰、简洁、一致且无二义性**
136 |
137 | - 【最主要的需求来源】用户和产品经理,其他。PPT.C5.6
138 |
139 | - 各种需求。PPT.C5.6-8
140 |
141 | - 【需求工程的七项需明确的任务】
142 |
143 | - 起始:提出一系列的问题,以建立对问题的基本理解。PPT.C5.10
144 |
145 | 1. 收集客户的资料,了解系统的背景,进行初步的可行性分析,确定项目范围。
146 | 2. 确定干系人
147 | 3. 识别多个观点
148 | 4. 致力于协作
149 |
150 | 确定有共同点的地区和发生冲突的地区
151 |
152 | - 导出:引出所有利益相关者的需求。PPT.C5.11
153 |
154 | **【需求获取的主要方式】**
155 |
156 | - 需求讨论会。PPT.C5.12-13
157 | - 由软件工程师和客户主持和参加
158 | - 提出议程(确定议程,准备调研提纲)
159 | - 调解人控制全场
160 | - 可由客户方的情况介绍开始,分析人员逐渐成为主导,有效的引导和把握调研的重点和方向。
161 | - 从业务流程入手,采用IPO(Input Process Output)的思想获取需求
162 | - **软件需求分两个层次:用户需求与功能需求**。由用户需求导出功能需求。
163 | - 满足用户需求如果有多种备选方案,可以**协商**不同的方法,提出一套解决方案的要素。
164 |
165 | - 头脑风暴法。PPT.C5.14
166 | - 该方法对**需求不确定**的情况非常适用。
167 | - 调查问卷。PPT.C5.14
168 | - 适合于**需求调研的后期**,用于对前期发现的一些不确定或不一致的地方进行确认。
169 |
170 | - 场景分析法。PPT.C5.15-16
171 | - 场景分析核心是3个维度的梳理:角色、场景、方案。
172 | - 第一人称视角感受考察。PPT.C5.17
173 | - 基于自己的实际使用需求提出产品需求。
174 | - 原型法。PPT.C5.17
175 | - 高保真方式(只包含前端的界面和交互)
176 | - 低保真方式(手绘)
177 |
178 | > 【Experience】
179 | >
180 | > (1) 调研前做好必要的相关背景知识准备
181 | >
182 | > (2) 通过用户获取重要的原始资料(如表单,文件)
183 | >
184 | > (3) 渐进、反复的进行
185 | >
186 | > 访谈后,要及时对需求整理、分类,以便在下次与用户见面时由用户确认;
187 | >
188 | > 同时,准备下一次访谈时更细节的问题。
189 | >
190 | > (4) 根据需求的重要性划优先等级
191 |
192 | - 精化:创建一个可以识别数据、功能和行为需求的分析模型。PPT.C5.22-25
193 |
194 | - 通过分析建模,得到精确的需求模型,用以说明软件的功能、特征和数据等各个方面。
195 |
196 | **【分析模型的元素】**
197 |
198 | - 基于场景的元素——用例图
199 | - 基于类的元素——类图
200 | - 行为元素——状态图
201 | - 流元素——数据流图
202 | - E-R模型
203 |
204 | - 协商:就开发人员和客户现实的可交付系统达成一致。PPT.C5.26
205 |
206 | - 确定关键利益相关者:这些是将参与谈判的人
207 | - 确定每个利益相关者“赢条件”
208 | - 谈判:工作朝着一系列导致“双赢”的要求
209 |
210 | - 规格说明(Software Requirement Specification, SRS)。PPT.C5.27-29
211 |
212 | - **定义:**规格说明可以是一份写好的文档、一套图形化的模型、一组使用场景、一个原型或上述各项的任意组合。PPT.C5.27
213 | - 对大型系统而言,规范、标准的文档和图形化模型是最佳选择;
214 | - 对于技术环节明确的小型系统而言,使用场景可能就足够了。
215 | - **作用:**PPT.C5.28
216 | - **主要内容**:PPT.C5.28-29
217 |
218 | - 确认:审查机制。PPT.C5.30-31
219 | - 参与者:需求分析员、开发人员、测试人员、客户代表、项目经理、产品经理……
220 | - 需求评审要点:
221 | 1. 是否在适当的抽象级别上指定了所有的需求?
222 | 2. 这个要求对系统的目标真的是必要的吗?
223 | 3. 每个要求是否都是有界限和明确的?
224 | 4. 每个要求都有属性吗?
225 | 5. 是否有任何要求与其他要求相冲突?
226 | 6. 在技术环境中是否可满足每个要求?
227 | 7. 每个需求一旦实现,是否可测试?
228 |
229 | ### (五)需求——需求建模:面向对象分析方法
230 |
231 | - 【OOA分析模型分类】
232 | - 用例模型、(静态)领域模型、(动态)行为模型
233 |
234 | - 【分析过程】
235 |
236 |  237 |
238 | 1. 建立用例模型
239 |
240 | 从不同用户的角度获取并描述功能需求,核心是用例。
241 |
242 | 2. 建立领域模型
243 |
244 | 发现和描述用例中涉及的对象和概念,核心是类图
245 |
246 | 3. 建立动态(交互)模型
247 |
248 |
249 |
250 | 【数据建模】
251 |
252 | 将注意力集中在数据域上
253 |
254 | 在客户的抽象级别上创建一个模型
255 |
256 | 指示数据对象之间如何相互关联
257 |
258 | 【数据对象】
259 |
260 | 一种几乎所有必须被软件理解的复合信息的表示。
261 |
262 | 可以是外部实体、事物、事件、角色、组织单元、地点或结构。
263 |
264 | 数据对象的描述包含了数据对象及其所有属性。数据对象包含一组作为对象的方面、质量、特征或描述符的属性。
265 |
266 | 【数据对象间的关系】
267 |
268 | 数据对象以不同的方式相互连接。
269 |
270 | 在人和车之间建立了一个连接,因为这两个对象是相关的。
271 |
272 | 一个人拥有一辆车
273 |
274 | 一个人可以驾驶汽车
275 |
276 | 关系“拥有”和“驾驶”定义人和汽车之间的相关联系。
277 |
278 | 对象可以通过多种不同的方式进行关联
279 |
280 | 
281 |
282 |
283 |
284 | 【领域建模】
285 |
286 | 领域模型分析以用例模型作为输入,将系统分解为一组相互协作的概念类(也称分析类) 。
287 |
288 | 分析类具有突出业务领域、突出概念性的特征,主要针对问题和职责,不涉及细节。
289 |
290 | 设计阶段,分析类可进一步演化为设计类,提供更多设计表达。
291 |
292 | 领域模型包括:**类图**、**CRC****模型**、**包图**
293 |
294 |
295 |
296 |
297 |
298 |
299 |
300 | 【行为建模】
301 |
302 | 行为模型显示了软件如何对外部事件或激励做出响应。
303 |
304 | 该模型通常描述一个用例中,系统在接收到特定事件后,所涉及的对象以及这些对象之间的交互(消息传递)过程。
305 |
306 | 行为模型主要包括:时序图、协作图、状态图。
307 |
308 |
309 |
310 | 【状态图 vs 时序图】
311 |
312 | (1)状态图针对单个类,跨多个用例。时序图针对的是一个用例。
313 |
314 | (2)状态图中的行为不仅与事件有关,还与对象所处状态有关。
315 |
316 | 【时序图 vs 协作图】
317 |
318 | (1)时序图可等价的转化为协作图
319 |
320 | (2)协作图更侧重表达对象间的关联关系,而非消息传递的时间先后。
321 |
322 | 
323 |
324 |
325 |
326 |
327 |
328 | ### (六)需求——需求建模:结构化分析方法
329 |
330 | 【结构化分析方法(SA)】又称面向数据流的分析方法。主要是创建基于数据流的模型,通过分析数据流发现系统功能和行为,并对其进行划分。
331 |
332 | SA主要构建四种分析模型
333 |
334 | · 数据流图(Data Flow Diagram)——功能视角
335 |
336 | · 数据字典
337 |
338 | · 实体关系图——数据视角
339 |
340 | · 状态迁移图——行为视角
341 |
342 |
343 |
344 | 【控制流建模】
345 |
346 | 一些应用程序是由事件而不是数据“驱动”的,产生控制信息而不是报告或显示,以及处理严重关注时间和性能的信息。
347 |
348 | 适合对实时系统、控制类系统等建模。
349 |
350 | 以状态图为主,描述系统对外部事件响应的行为模型。
351 |
352 | 
353 |
354 |
355 |
356 | ### (五)设计
357 |
358 | **7.** **设计概念**
359 |
360 | 【软件设计】即根据软件需求,产生一个软件内部逻辑表示的过程。这种更接近于软件的逻辑表达或模型,提供了软件系统关心的体系结构、数据结构、接口和构件等细节。
361 |
362 | 对比:
363 |
364 | 需求分析偏重于问题域,描述软件要做什么。
365 |
366 | 软件设计则偏重于解决方案,描述软件究竟要如何做。
367 |
368 | 【软件设计的价值】
369 |
370 | 1. 设计是需求与实现代码之间的“桥梁”
371 |
372 | (1) 设计本质是满足需求,并对方案优中选优的过程。
373 |
374 | (2) 设计模型比代码更易评估、更易修改。
375 |
376 | 2. 设计是软件质量形成的关键,软件质量依赖于设计的结果
377 |
378 | (1) 如软件质量中的效率、可靠性、高并发等。
379 |
380 | **例子:****对含有上百亿信息的数据库,如何满足用户的高并发访问需求?**
381 |
382 | 设计方案:分库分表、读写分离。
383 |
384 | 【好的设计】
385 |
386 | 设计必须实现分析模型中的明确需求,包括客户期望的隐性需求。(承上)
387 |
388 | 对后续的编码、测试以及维护人员,设计必须是可读、可理解的指南。(启下)
389 |
390 | 设计必须提供未来软件的全貌,从实现的角度说明其数据域、功能域和行为域。
391 |
392 | 例子:自动排课是系统的功能需求之一,那么设计要解决数据存储问题(排课信息保存)、界面显示问题(排课及结果显示)、算法逻辑问题(排课算法)等。
393 |
394 | 【实施软件设计】
395 |
396 | 软件设计是一个迭代的过程。
397 |
398 | (1)初始时,设计者应关注系统的整体架构(如架构风格、主要构件、连接关系)等,对应于**体系结构设计阶段**。
399 |
400 | (2)随着设计迭代的开始,更多的细节被关注(如数据、构件)等,对应于**构件设计或详细设计阶段**。
401 |
402 | 【软件设计任务集】
403 |
404 | 
405 |
406 | (1) 体系结构设计:定义软件的主要元素(构件)以及元素之间的联系
407 |
408 | 
409 |
410 | (2) 数据/类设计:将分析类模型转化为设计类以及软件所需要的数据结构
411 |
412 | 
413 |
414 | (3) 接口设计:定义软件与协作系统之间、软件与用户之间的通信
415 |
416 | (4) 构件设计或详细设计:定义软件元素(构件)的内部细节,如内部数据结构、算法等
417 |
418 | (5) 部署设计:定义软件元素在物理拓扑结构中的分布
419 |
420 |
421 |
422 | 【应该遵循什么原则才能保证设计质量?】
423 |
424 | 1. 抽象
425 |
426 | 抽象的本质:强调关键特征,忽略无关细节。
427 |
428 | 过程抽象:具有明确和有限功能的指令序列。
429 |
430 | 数据抽象:描述数据对象的具名数据集合。
431 |
432 | 2. 体系结构
433 |
434 | 软件体系结构设计,即找到一种最佳的方式对系统进行划分,标识其中的构件,构件之间的联系等。
435 |
436 | 设计应该先勾勒全貌,不能一开始就跳入细节。
437 |
438 | 3. 模式
439 | 4. 关注点分离
440 | 5. 模块化
441 |
442 | 庞大的系统不便于并行开发,软件工程师也难以理解和把握。
443 |
444 | 采用分治策略,将大系统分解为若干更小、更简单的模块。这样,问题理解变得更加容易,开发成本也会减小。
445 |
446 | 6. 信息隐蔽
447 |
448 | 每个模块都对其它模块隐藏自己的设计细节(就像黑盒子),这样如果模块内部发生变化,外部受到的影响最小。
449 |
450 | **7.** **功能独立**
451 |
452 | 功能独立性是指:模块化设计时,希望每个模块尽可能功能专一,同时避免与其它模块过多交互。
453 |
454 | Cohesion(内聚): 表示模块内相关功能的强度
455 |
456 | 内聚性强的模块通常只完成一件事情。
457 |
458 | Coupling (耦合) :表示模块之间的相互依赖性
459 |
460 | 模块的耦合性取决于模块之间接口的复杂性、引用方式、传递数据的复杂性等。
461 |
462 | 功能独立意味着:**高内聚、低耦合**
463 |
464 | 功能独立的优势:
465 |
466 | · 更容易开发。因为每个功能均有效分隔,且接口简单。
467 |
468 | · 更容易维护。因为修改代码引起的副作用被限制,减少错误扩散。
469 |
470 | · 复用性更好。
471 |
472 | 8. 逐步求精
473 |
474 | 随着设计的深入,设计者不能老是停留在抽象层级,而应逐步揭示底层的细节。
475 |
476 | 9. 方面
477 | 10. 重构
478 |
479 | 在不改变代码的外部行为的前提下,优化内部结构的过程。
480 |
481 | 例子:早期设计中发现某构件的内聚性较差,在保持接口不变的情况下,可通过重构将其分解为两个独立的构件,每个新的构件内聚性得以增强。
482 |
483 | 11. 面向对象的设计概念
484 | 12. 设计类
485 |
486 | 分析类只与业务领域有关,和具体实现技术无关。
487 |
488 | 设计类则面向实现,通过对分析类的细化设计,达到能提供给构造阶段编码实现的目的。
489 |
490 | 定义设计类的两种方式:
491 |
492 | (1) 通过对分析类提供细节设计。
493 |
494 | (2) 创建新的设计类,该设计类提供软件的基础设施以支持业务解决方案。
495 |
496 | 改进:基于工厂模式
497 |
498 |
499 |
500 | **8.** **体系结构设计**
501 |
502 | 【软件体系结构】是软件的一种划分形式,从较高抽象层次定义系统的构件、构件之间的连接,以及由构件与构件连接形成的拓扑结构。
503 |
504 | 【体系结构设计的必要性】
505 |
506 | · 体系结构设计决定了系统的主体结构,结构优劣对软件质量具有重要影响。
507 |
508 | · 针对安全需求,可以考虑采用分层结构,将重要资源置于内层保护。
509 |
510 | · 针对可用性需求,可以考虑冗余设计。
511 |
512 | 【软件体系结构设计的关键决策】
513 |
514 | · 系统的基本构造单元是什么?
515 |
516 | · 这些构造单元连接方式?
517 |
518 | · 最终形成怎样的拓扑结构?
519 |
520 | · 有哪些体系结构风格可供系统借鉴?
521 |
522 | · 对于目标系统,如何基于一般性的体系结构进行适应性改造?
523 |
524 | · 如何评估体系结构设计?
525 |
526 | 【体系结构风格】
527 |
528 | 众多系统所共有的结构和特性(如构件类型、交互机制、拓扑、约束),可以指导同类型应用的体系结构设计。
529 |
530 | · 数据中心结构
531 |
532 | 该结构适合于:数据由一个构件(模块)产生,而由其它构件使用的情形。
533 |
534 | 缺点:一旦中心数据存储出现问题会影响整个系统。
535 |
536 | 如电子白板系统、管理信息系统(MIS) 。
537 |
538 | 
539 |
540 | · 管道-过滤器结构
541 |
542 | 系统由若干构件(过滤器)按一定顺序组合而成,一个构件的输出是另一个构件的输入。
543 |
544 | 适合于批处理系统,不适用于交互式应用系统。
545 |
546 | 编译器就是一种管道-过滤器系统,包括词法分析、语法分析、字节码生成等。
547 |
548 | 图像处理系统等也大多采用该风格。
549 |
550 | 
551 |
552 | 
553 |
554 | · 调用返回结构
555 |
556 | (1) 主程序/子程序结构
557 |
558 | 
559 |
560 | (2) 远程过程调用结构:主程序/子程序中的构件分布在网络中的多台计算机。
561 |
562 | 如:如分布式计算系统Hadoop。
563 |
564 | 
565 |
566 | 调用返回结构缺点:
567 |
568 | 主构件需要预先知道被调子构件的接口标识。
569 |
570 | 构件接口标识的更改会影响所有调用它的其它构件,而且这种现象还会进行传递,导致更大的负面影响。
571 |
572 | · 面向对象结构
573 |
574 | 构造单元:类和对象
575 |
576 | 连接:基于消息机制。
577 |
578 | 拓扑结构:不同对象之间是平级的,没有主次之分
579 |
580 | 
581 |
582 | · 消息总线结构
583 |
584 | 构件不直接调用其它构件,而是广播一个或多个事件。
585 |
586 | 系统中的构件注册(监听)一个或多个事件源;
587 |
588 | 当一个事件被广播,系统自动调用该事件中注册的构件。
589 |
590 | 
591 |
592 | 消息总线风格逐渐演变为**消息中间件**。消息中间件应用场景:系统解耦、异步通讯、削峰。
593 |
594 | 下图为传统方式下系统B、C与A之间的通信连接,随着新的D、E、F、G系统的增加,必然导致巨大的维护成本(加入或退出均需要维护A)。
595 |
596 | 
597 |
598 | 优点:扩展简单。系统无须知道其他子系统接口名、位置的情况下,就可以激活其它子系统。
599 |
600 | 消息中间件产品:ActiveMQ、RabbitMQ
601 |
602 | 
603 |
604 | 
605 |
606 | · 层次化结构
607 |
608 | 系统被组织成若干个层次,每层都由一系列构件组成。
609 |
610 | 同层内构件可相互调用。
611 |
612 | 层之间存在调用接口,但只限于相邻层,下层可为上层服务,并作为再下一层客户。
613 |
614 | 
615 |
616 | · 客户-服务器结构
617 |
618 | 源于计算任务和计算资源的能力差异。
619 |
620 | 构件分布在两台或多台计算环境中。
621 |
622 | 演变:三层,多层C/S,B/S体系结构
623 |
624 | · MVC(Model-View-Controller)
625 |
626 | 常用于Web应用系统。
627 |
628 | 将系统分解为应用逻辑、用户界面、控制逻辑等不同构件类型。
629 |
630 | 优势:
631 |
632 | ·任何一种构件的改变都不会对其它构件造成影响。
633 |
634 | ·一个模型能为多个视图提供数据。
635 |
636 | 
637 |
638 | · 微服务架构
639 |
640 | 单体架构:应用打包(如war)部署为一个独立的单元,通过一个进程方式运行。
641 |
642 | 微服务架构:
643 |
644 | · 应用(功能)被分割成更小的、独立的服务,各个微服务之间的关联通过RPC(同步调用)或MQ(异步调用)实现。
645 |
646 | · 独立的微服务不需要部署在同一个虚拟机或应用服务器中。
647 |
648 | 
649 |
650 | · 混合风格
651 |
652 | 大规模系统往往包括多种体系结构风格
653 |
654 | 
655 |
656 |
657 |
658 | 【体系结构描述】
659 |
660 | 关注点:为谁描述哪些内容?用什么符号体系或描述语言?
661 |
662 | 程序员说:体系结构就是要决定需要编写哪些类、使用哪些现成框架。
663 |
664 | 程序经理说:体系结构就是模块的划分和接口的定义。
665 |
666 | 数据库工程师说:体系结构规定了持久化数据的结构,其他不过是对数据的操作而已。
667 |
668 | 用户说:体系结构就是决定一个个功能子系统如何划分。
669 |
670 | 这些描述我们都需要。每个视角代表一类利益相关者,反应了系统结构的一个侧面。
671 |
672 | 系统体系结构多从逻辑架构、物理架构和开发架构等视角描述。
673 |
674 | **·** **逻辑架构**关注的是功能构件,包含用户可见的功能构件,以及不可见的功能构件。
675 |
676 | **·** **物理架构**关注网络、服务器等基础设施及其拓扑结构。
677 |
678 | · **开发架构**更关注程序包,除自己写的程序外,还包括应用程序依赖的SDK、第三方类库等。
679 |
680 | 【体系结构设计方法】
681 |
682 | 基本设计思路:
683 |
684 | 
685 |
686 | 包括:
687 |
688 | · 面向对象体系结构设计
689 |
690 | · 传统结构化设计
691 |
692 | 【面向对象体系结构设计方法】
693 |
694 | 1. 定义系统交互的外部环境和交互特性
695 |
696 | (1) 目的是识别系统的外部实体与接口,定义接口构件
697 |
698 | 2. 识别一组结构原型(archetypes)
699 |
700 | (1) 原型是系统中最核心的抽象类或模式,目标系统的体系结构可由这些原型组成。
701 |
702 | (2) 原型是系统中最稳定的元素,可以基于系统行为以不同方式对这些元素实例化。
703 |
704 | (3) 多数情况下,原型可以通过分析类来获得。
705 |
706 | 3. 对每个结构原型进一步细化,以完善系统结构。
707 |
708 | 例子:对图书管理系统体系结构设计
709 |
710 | (1) 先采用“包图”划分子系统。
711 |
712 | 
713 |
714 | (2) 针对“借书”需求,识别结构原型
715 |
716 | 
717 |
718 | (3) 对“借书”构件,采取MVC风格进行细化
719 |
720 | 
721 |
722 | 【结构化体系结构设计方法】
723 |
724 | 目标:根据DFD的不同类型,通过对系统中模块的合理划分,得到软件体系结构图
725 |
726 | 体系结构风格:主程序/子程序风格
727 |
728 | 1. 将系统分割为多个功能模块
729 | 2. 确定各个模块之间的调用关系
730 | 3. 用系统结构图表示设计模型
731 |
732 | 步骤:
733 |
734 | (1) 分析确定数据流图类型。
735 |
736 | (2) 标识输入、输出流边界。
737 |
738 | (3) 依据变化或事务分析规则,将DFD图映射为顶层和第一层模块结构。
739 |
740 | (4) 对第一层中的模块继续细化和分解。
741 |
742 | (5) 利用启发式规则优化初始系统结构图。
743 |
744 | 变换分析和事务分析实例见PPT【体系结构设计】末尾
745 |
746 | 9. 构件级设计
747 |
748 | 【构件设计】是在体系结构设计的基础上,对其中每个构件内部构成的进一步设计。
749 |
750 | 体系结构设计相当于确定了计算机的部件组成,连接关系等。
751 |
752 | 构件设计则着重于设计每个部件的**内部细节**,如运算器的内部电路和元件等。
753 |
754 | 面向对象视角:
755 |
756 | 确定设计类并对其细化的过程。
757 |
758 | 结构化视角:
759 |
760 | 细化模块内部的数据结构、算法和接口的过程。
761 |
762 | 【构件】是计算机软件中的一个模块化的构造块。它部件**封装**了实现并暴露一系列**接口**。
763 |
764 | 面向对象视角:
765 |
766 | 构件封装了一组相互协作的类(也可以是一个类)。
767 |
768 | 结构化视角:
769 |
770 | 构件也称功能模块(如系统中图像读入模块、图像压缩模块)
771 |
772 | 封装了数据结构、算法和接口
773 |
774 | 【面向对象构件构成】
775 |
776 | 面向对象构件可能由多个设计类构成
777 |
778 | (1) 构件接口与实现需要严格分离。
779 |
780 | (2) 基于设计框架,一个构件需要分解为多个设计类。
781 |
782 | 【面向对象构建设计关键问题】
783 |
784 | 1. 构件由哪些设计类组成?
785 | 2. 设计类之间是什么关系,如何优化?
786 | 3. 构件提供的接口是什么?
787 | 4. 每个设计类的详细构成(属性和方法)?
788 |
789 | 前3个问题都与设计优化原则相关
790 |
791 | 通过设计优化,可以提高构件复用性,灵活适应系统变更,并减少副作用的传播。
792 |
793 | 【构件设计指导原则】
794 |
795 | 1. 开闭原则(OCP)
796 |
797 | 对扩展开放:构件的行为是可扩展或改变的
798 |
799 | 对修改关闭:当构件改变行为时,不要修改其源码
800 |
801 | 实现途径:用抽象构建框架,用继承/实现扩展细节。
802 |
803 | 需求变化时,不是通过修改类本身来完成,而是通过扩展一个子类来改变构件的行为。
804 |
805 | 优点:尽量不修改原有的代码,实现一个热插拔的效果。
806 |
807 | 2. Liskov替换原则(LSP)
808 |
809 | LSP 原则用来指导继承关系中子类该如何设计,子类的设计要保证在替换父类的时候,不改变原有程序的逻辑以及不破坏原有程序的正确性。
810 |
811 | 简单理解:子类可以扩展父类的功能,但不能改变父类原有的功能。
812 |
813 | LSP原则能减少代码冗余,避免运行期的类型判别(实现动态加载)。
814 |
815 | 3. 依赖倒置原则
816 |
817 | 依赖于抽象,而非具体实现。 具体方法是:首先,分离接口和实现。将类之间的依赖关系建立在高层抽象(如抽象类、接口)基础上。
818 |
819 | 优点:减少类间的耦合性,提高系统的稳定性
820 |
821 | 4. 接口分离原则
822 |
823 | 建立单一接口,不要建立臃肿庞大的接口。即:接口尽量细化,同时接口中的时间尽量少。
824 |
825 | 5. 单一职责原则:一个类或接口只承担一类责任。
826 | 6. 迪米特法则:尽量减少对象之间的交互,从而减小类之间的耦合。
827 |
828 | 内聚性和耦合性
829 |
830 | **内聚性**意味着构件只封装那些密切相关的类,或者类只封装自身密切相关的属性和操作。
831 |
832 | 根据程度可细分为:功能内聚、分层内聚、通信内聚等
833 |
834 | **耦合性**是类之间彼此联系程度的一种定性度量。
835 |
836 | 根据程度可细分为:内容耦合、共用耦合、控制耦合、标记耦合……
837 |
838 | 【面向对象构件设计过程】
839 |
840 | 1. 识别构件中与问题域相对应的设计类。包括界面类、控制类、实体类。
841 |
842 | (1) 一般可为每个用例设计一个控制类。如果多个用例中任务较为相似,也可以公用一个控制类。
843 |
844 | (2) 如果实体类的职责比较单一,直接将其映射为设计类;
845 |
846 | (3) 如果某类的职责过于复杂,应该将其分解为多个设计类(单一职责)。
847 |
848 | 2. 识别构件中与基础设施相对应的设计类。 这些设计类往往在分析模型中并没有定义。
849 | 3. 细化所有的设计类,定义该类中所有的接口、属性和操作。
850 |
851 | (1) 通过设计时序图或协作图说明协作细节。
852 |
853 | 将时序图中职责分解为具体操作,并分配给相关类;
854 |
855 | 定义操作对应的方法名,方法参数,返回值、可见性等。
856 |
857 | (2) 为每个构件确定合适的接口。
858 |
859 | 简单构件可直接定义public方法作为接口;
860 |
861 | 复杂构件单独定义接口类,构件负责实现接口;
862 |
863 | 确定接口的参数;
864 |
865 | (3) 细化属性,并定义相应的数据类型和数据结构。
866 |
867 | (4) 描述类成员方法中的处理逻辑。绘制程序流程图或活动图。
868 |
869 | 4. 说明持久数据源 (数据库或文件),并确定管理数据源所需要的类。
870 |
871 | (1) 对象可暂存于内存中,但要持久保存,需要通过数据存储实现。
872 |
873 | (2) 可以通过对象关系映射(ORM)将类映射为表,以简化数据库使用。
874 |
875 | 5. 细化**部署图**以提供额外的实现细节。
876 |
877 | (1) 为系统选择硬件配置和运行平台;
878 |
879 | (2) 将类、包、子系统分配到各个硬件结点上。
880 |
881 | 构建设计实例见PPT【构件级设计】中的实例部分
882 |
883 | 【传统构件设计过程】
884 |
885 | · 确定每个模块的算法,用工具描述算法逻辑。
886 |
887 | · 确定每一模块的数据结构。
888 |
889 | · 确定模块接口细节。
890 |
891 | 常用算法描述工具包括
892 |
893 | · 程序流程图
894 |
895 | · 问题分析图(PAD)
896 |
897 | 
898 |
899 | · 盒图(N-S图)
900 |
901 | 
902 |
903 | · 伪代码(PDL)
904 |
905 |
906 |
907 | 10. 用户界面设计
908 |
909 | 【UI设计】
910 |
911 | 软件强大的计算能力和功能,最终要通过界面来表现。
912 |
913 | 用户界面是软件的直观形象,直接影响用户对软件的体验。
914 |
915 | 用户通常从用户界面(而非功能)的好坏来评价软件的质量。
916 |
917 | 【常见UI设计错误】
918 |
919 | · 缺乏一致性
920 |
921 | · 太多需要记忆的
922 |
923 | · 没有指导和帮助
924 |
925 | · 没有上下文敏感性
926 |
927 | · 无意义的反馈
928 |
929 | · 界面复杂
930 |
931 | 【黄金法则】(这部分看书P198)
932 |
933 | 1. 把控制权交给用户(让用户掌握一切)
934 |
935 | (1) 提供灵活的交互。允许用户选择使用键盘、语音、鼠标等多种交互方式。
936 |
937 | (2) 允许用户交互被中断和撤销。如在手机编写短信时,允许接听电话,并能找到之前正在编写的短信。
938 |
939 | (3) 允许定制交互。
940 |
941 | (4) 将用户和内部技术细节隔离开。
942 |
943 | (5) 设计应允许用户与出现在屏幕上的对象直接交互。
944 |
945 | 2. 减轻用户的记忆负担
946 |
947 | 经验表明,需要记住的东西越多,交互出错的概率越大。
948 |
949 | (1) 减少对短期记忆的要求。
950 |
951 | (2) 建立有意义的默认设置。
952 |
953 | (3) 定义直观的快捷方式。
954 |
955 | (4) 界面的视觉布局应该基于真实世界的象征。
956 |
957 | (5) 以一种渐进的方式揭示信息。
958 |
959 | 3. 保持界面一致
960 |
961 | (1) 在完整的产品线上保持设计规则的一致性。
962 |
963 | (2) 如果过去的交互方式已经建立起用户期望,除非有不得已的理由,否则不要改变它。
964 |
965 | 4. 补充规则
966 |
967 | (1) 反馈:对用户的操作,应该给予及时、明确的反馈,并提供上下文帮助。
968 |
969 | (2) 宽容性:允许用户犯错,并能帮助用户从错误中及时恢复出来。
970 |
971 | (3) 个性化:允许用户根据自己的喜好定制界面元素、布局等。
972 |
973 | (4) 美观性
974 |
975 | 【UI设计过程】
976 |
977 | 
978 |
979 | 【接口/界面分析】
980 |
981 | 接口分析是指理解
982 |
983 | (1) 通过接口与系统交互的人员(最终用户);
984 |
985 | (2) 终端用户完成工作必须执行的任务;
986 |
987 | (3) 作为接口一部分呈现的内容;
988 |
989 | (4) 这些任务将被执行的环境。
990 |
991 | 成分:
992 |
993 | 1. 用户分析(看书P203)
994 | 2. 任务分析与建模
995 |
996 | 根据用例模型中的场景描述,将其映射为人机界面上的一组子任务
997 |
998 | 3. 显示内容分析
999 |
1000 | 根据每项任务确定其呈现的界面内容。
1001 |
1002 | 【界面设计】
1003 |
1004 | 对每项任务对应的界面进行**交互设计**和**视觉设计**。
1005 |
1006 | 交互设计的重点包括:交互流程、交互方式。
1007 |
1008 | 【交互流程设计】
1009 |
1010 | 1. 定义界面对象和动作
1011 | 2. 定义可能导致界面变化的事件
1012 | 3. 界面应该如何变化
1013 | 4. 想告诉用户什么?
1014 |
1015 | 好的交互方式可以让用户更简单、方便的使用产品。
1016 |
1017 | 【视觉设计】
1018 |
1019 | 视觉设计是指:针对眼睛的主观形式的表现手段和结果。
1020 |
1021 | 主要考虑界面的布局、数据的呈现方式、色彩搭配等
1022 |
1023 | 【界面设计工具】
1024 |
1025 | Visio、Axure
1026 |
1027 | 【设计评审】
1028 |
1029 | 所有设计工作完成后,为保证设计质量,需要对所有设计成果,包括**体系结构、构件、接口、数据模型**等进行综合设计评审。
1030 |
1031 |
1032 |
1033 |
1034 |
1035 | ### (六)测试
1036 |
1037 | 11. 软件测试策略
1038 |
1039 | 【测试的目的】
1040 |
1041 | 测试是选择适当的测试用例并执行被测程序的过程。
1042 |
1043 | 目的在于**发现错误**,而不是为了验证程序不存在错误。
1044 |
1045 | 好的测试用例可以发现今未发现的错误。
1046 |
1047 | 【测试策略】
1048 |
1049 | 一般特征:
1050 |
1051 | · 未完成有效的测试,应该进行有效的、正式的技术评审。通过评审,许多错误可以在测试开始之前排除。
1052 |
1053 | · 测试开始于构件层,然后向外“延申”到整个基于计算机系统的继承中。
1054 |
1055 | · 不同的测试技术适用于不同的软件工程方法和不同的时间点。
1056 |
1057 | · 测试由软件开发人员和(对大型项目而言)独立的测试组执行。
1058 |
1059 | · 测试和调试是不同的活动,但任何测试策略都必须包括调试。
1060 |
1061 | 策略:
1062 |
1063 | 1. 测试不能取代评审
1064 |
1065 | 据说,检验项目质量的标准之一:质量 = 项目review时骂的次数 / 项目review时间。
1066 |
1067 | 被骂的次数越多,评审耗时越短,质量越可靠。
1068 |
1069 | 2. 谁来测试?
1070 |
1071 | (1) 开发者:对系统很了解,但由于急于交付,测试比较“gentle”
1072 |
1073 | (2) 独立测试人员:虽然对系统没有特别了解,但为了质量会尝试尽可能找出所有问题
1074 |
1075 | 3. 测试什么时候开始?
1076 |
1077 | 软件测试**不是在编码阶段**才开始,软件测试从**项目确立**时就开始了,主要经过以下环节:
1078 |
1079 | 需求分析→测试计划→测试设计→测试环境搭建→测试执行→测试记录。
1080 |
1081 | 4. 测试流程
1082 |
1083 | 从模块由小到大进行测试。
1084 |
1085 | 
1086 |
1087 | 【传统软件的测试策略:单元测试】(参考书P251-253)
1088 |
1089 | 目的:验证开发人员编写的模块或单元是否符合预期。
1090 |
1091 | 单元测试问题:
1092 |
1093 | · 说明不正确或不一致;
1094 |
1095 | · 初始化或缺省值错误;
1096 |
1097 | · 数据类型不相容;
1098 |
1099 | · 上溢、下溢或地址错误等。
1100 |
1101 | · 全局数据与模块的相互影响。
1102 |
1103 | 单元测试环境:
1104 |
1105 | 
1106 |
1107 | 驱动模块:用来模拟被测模块的上级调用模块。
1108 |
1109 | 桩模块:模拟被测试模块所调用的模块,返回被测模块所需的信息。
1110 |
1111 | 【传统软件的测试策略:集成测试】
1112 |
1113 | 通过单元测试的模块集成在一起,仍然可能无法正常工作,因为模块相互调用时仍然可能出错。
1114 |
1115 | 集成测试:旨在发现与调用接口相关的错误。
1116 |
1117 | **自顶向下集成**:
1118 |
1119 | 
1120 |
1121 | **自底向上集成**:
1122 |
1123 | 
1124 |
1125 | **三明治集成**:
1126 |
1127 | 
1128 |
1129 | **回归测试:**
1130 |
1131 | 集成测试中每加入新的模块,都会导致软件发生变更,这些变更可能使得原本正常工作的模块产生问题。
1132 |
1133 | 回归测试就是重新执行已经测试过的某些子集,以确保变更不会引入新的或额外的错误。
1134 |
1135 | 回归测试可以复用之前的测试用例和测试脚本。
1136 |
1137 | 可以使用自动测试工具提高回归测试效率。
1138 |
1139 | 捕获-回放工具(如WinRunner)能够捕获在测试过程中传递给软件的输入数据,生成执行的脚本,并且在回归测试中,重复执行该过程。
1140 |
1141 | **冒烟测试:**
1142 |
1143 | 冒烟测试也是一种特殊的集成测试,指完成一个新版本的集成、构建后,对该版本最基本的功能进行测试,目的是**保证基本的功能和流程能走通**。
1144 |
1145 | 如果通不过,则打回开发部门重新开发;如果通过测试,才会进行下一步的测试(功能测试,集成测试,系统测试等)。
1146 |
1147 | 例如,冒烟测试内容:
1148 |
1149 | 检查被测系统或模块能否正常启动和退出;
1150 |
1151 | 数据库能否正常连接,控件能否正常加载;
1152 |
1153 | 是否存在严重错误或者数据严重丢失等。
1154 |
1155 | 【面向对象的单元与集成测试】
1156 |
1157 | 类测试相当于单元测试。我们将测试该类内的操作。
1158 |
1159 | 集成采用了三种不同的策略。传统的自顶向下或自底向上的集成测试策略在面向对象软
1160 |
1161 | 件的集成测试中无意义。
1162 |
1163 | 1. 基于类之间的协作关系进行集成。
1164 | 2. 基于线程的测试—集成了响应一个输入或事件所需的类集。
1165 | 3. 基于使用的测试——从测试独立类开始,然后测试使用独立类的依赖类。
1166 |
1167 | 【确认测试】
1168 |
1169 | 确认测试:检验所开发的软件是否满足需求规格说明中的各种功能和性能需求,以及软件配置是否完全和正确。
1170 |
1171 | α测试是由用户在开发环境下进行的测试;β测试是由软件的多个用户在实际使用环境下进行的测试。可归为确认测试,产品正式发布前的测试,由用户主导。
1172 |
1173 | 【系统测试】
1174 |
1175 | 系统测试是将软件与其它系统部分(如外部系统,硬件设计等)结合进行的整体测试。其关注非功能性需求。
1176 |
1177 | 系统测试主要包括一下几种类型:
1178 |
1179 | 1. 恢复测试:有些系统失效后必须在规定时间段内被恢复,否则将会导致严重的经济损失。关注导致软件运行失败的各种条件,并验证其恢复过程能否正确执行。(如:系统供电故障后的恢复、日志处理恢复能力、程序运行崩溃后恢复能力)
1180 | 2. 安全测试:检测系统对非法侵入的防范能力。如口令截取或破译等。
1181 |
1182 | IBM AppScan,包括众多的安全扫描产品,如针对源代码扫描的AppScan source edition, 针对WEB应用扫描的AppScan standard edition,进行安全管理和汇总整合的AppScan enterprise Editio。
1183 |
1184 | 3. 压力测试
1185 |
1186 | 压力测试目的是为了发现系统能支持的最大负载等,前提是系统性能处在可以接受的范围内,如规定的3秒钟内响应。
1187 |
1188 | 压力测试通过不断对系统增加压力,确定一个系统的瓶颈或者不能接受的性能点,从而获得系统最大负载能力。
1189 |
1190 | 压力测试工具WebRunner:RadView公司推出的一个性能测试和分析工具,它让web应用开发者自动执行压力测试;webload通过模拟真实用户的操作,生成压力负载来测试web的性能。
1191 |
1192 | 4. 性能测试
1193 |
1194 | 通过测试确定系统(常态下)运行时的性能表现,如运行速度、响应时间、占有系统资源等方面的系统数据。
1195 |
1196 | 性能测试工具LoadRunner:它能预测系统行为,优化性能。它通过模拟实际用户的操作行为和实行实时性能监测。
1197 |
1198 | 【软件调试】
1199 |
1200 | 调试目标:定位错误发生的原因和位置。
1201 |
1202 | 调试技巧:
1203 |
1204 | (1)暴力法:一种比较简单,但效率较低的方法。包括:
1205 |
1206 | ① 主存信息输出法。
1207 |
1208 | 将计算机存储器和寄存器的全部内容打印出来。
1209 |
1210 | ② 关键部分设置打印语句。
1211 |
1212 | ③ 使用自动调试工具。
1213 |
1214 | (2)反向跟踪:是从可能的错误征兆处逐步向回追溯,直到找准错误,纠正为止。
1215 |
1216 | (3)归纳法:从线索(错误征兆出发),通过分析这些线索之间的关系找出故障。主要有4步:
1217 |
1218 | ① 收集数据。列出已知的测试用例和执行结果。
1219 |
1220 | ② 整理分析数据,以便发现规律,即“什么条件下出现错误,什么条件下不出现错误”。如:字符计数程序对“输入型”文本正确,对“拷贝型”文本错误。
1221 |
1222 | ③ 导出假设。分析线索之间的关系,提出关于错误的一个或多个假设。
1223 |
1224 | ④ 证明假设。证实提出的假设是导致错误发生的真正原因。
1225 |
1226 | (4)演绎法
1227 |
1228 | ① 设想出所有可能的出错原因;
1229 |
1230 | ② 试图用测试来排除每一个假设的原因,如果测试表明某个假设的原因可能是真的原因,则对数据进行细化以确定位错误。
1231 |
1232 |
1233 |
1234 | 12. 传统应用测试
1235 |
1236 | 【关于测试的两个问题】
1237 |
1238 | 1. 经过测试没有发现错误的软件就一定正确吗?错误。测试只能证明软件是有错的,不能证明软件是没有错误的。
1239 | 2. 可以通过穷举方式测试软件吗?一般不行,因为分支或循环太多会导致所需测试样例的数量呈指数型增长。
1240 |
1241 | 【如何设计好的测试用例?】
1242 |
1243 | 测试的有效性很大程度取决于选取的测试用例。
1244 |
1245 | 一个好的测试有很高的概率找到一个错误的;测试不是冗余的;一个好的测试应该是“最好的品种”。
1246 |
1247 | 【测试用例设计方法】
1248 |
1249 | 黑盒法:测试者把测试对象看作一黑盒子,仅依据程序的功能需求,设计测试用例并推断测试结果。
1250 |
1251 | 白盒法:按照程序内部逻辑结构,设计测试数据并完成测试的一种测试方法。
1252 |
1253 | 【白盒测试】
1254 |
1255 | 该方法把测试对象看做一个透明的盒子,它允许测试人员利用程序内部的逻辑结构及有关信息,设计或选择测试用例。
1256 |
1257 | 目标是使得程序中各元素(如语句、判定)尽可能被覆盖到。
1258 |
1259 | 白盒测试一般在测试过程的早期执行。
1260 |
1261 | 方法:
1262 |
1263 | 1. 语句覆盖:指选择足够的测试用例,使得被测程序中每条语句至少执行一次。是一种比较弱的测试标准。
1264 | 2. 基本路径测试
1265 |
1266 | 如果程序中含有循环结构,完全的路径覆盖是不可能的。
1267 |
1268 | **基本路径法**:在程序控制流图的基础上,通过导出基本可执行路径(注: 不是所有可能路径)集合,从而设计测试用例。
1269 |
1270 | 【重点掌握,见PPT(传统应用测试)】
1271 |
1272 | 3. 控制结构测试
1273 |
1274 | (1) 条件测试:一种测试程序模块中包含的逻辑条件的测试用例设计方法
1275 |
1276 | 设计测试用例确保至少条件C为真为假执行各一次。如果C是复合条件,则同时还要满足每个简单条件至少执行一次。
1277 |
1278 | 
1279 |
1280 | (2) 数据流测试:根据程序中定义的位置和变量的使用情况来选择程序的测试路径
1281 |
1282 | 设计测试用例使得每个变量定义-使用链至少覆盖一次。
1283 |
1284 | 
1285 |
1286 | (3) 循环测试:分为简单循环、嵌套循环、串接循环、非结构化循环。
1287 |
1288 | 对于简单循环,下列测试集可以用于简单循环:
1289 |
1290 |
1291 |
1292 | 
1293 |
1294 | 【黑盒测试】
1295 |
1296 | 这种方法是把测试对象看做一个黑盒子,测试人员完全不考虑程序内部的逻辑结构,只依据需求规格说明书,检查程序的功能是否符合它的功能说明。
1297 |
1298 | 黑盒测试一般在应用于测试的后期阶段。
1299 |
1300 | 1. 等价类划分
1301 |
1302 | 等价类划分法:将程序的输入域划分为若干个数据类,从中生成测试用例。
1303 |
1304 | 假定:对等价类中的代表值测试就等于对这一类值的测试。
1305 |
1306 | 
1307 |
1308 | 基本步骤: (1)确定等价类;(2)为等价类选择一个测试用例
1309 |
1310 | 例子:某城市的电话号码由3部分组成。假定被测程序能接收一切符合下述规定的电话号码,拒绝所有不符合规定的电话号码。
1311 |
1312 | 地区码:空白或3位数字;
1313 |
1314 | 前缀:非‘0’或‘1’开头的3位数字;
1315 |
1316 | 后缀:4位数字。
1317 |
1318 | (1) 确定等价类
1319 |
1320 | 
1321 |
1322 | (2) 设计测试用例
1323 |
1324 | 设计测试用例,使其尽可能多的覆盖到尚未覆盖的有效等价类
1325 |
1326 | 设计测试用例,使其只覆盖一个尚未被覆盖的无效等价类
1327 |
1328 | 
1329 |
1330 | 2. 边界值分析
1331 |
1332 | (1) 边界值应该尽可能选择等于边界,略小于边界,略大于边界的值
1333 |
1334 | (2) 边界值法可与等价类划分法结合,作为对其的一种补充。
1335 |
1336 | 例子: 一个输入文件应该包含1~255条记录,则应用边界值分析法设计测试用例。
1337 |
1338 | 可以用4组数据进行测试:
1339 |
1340 | 含1条记录的文件
1341 |
1342 | 含2条记录的文件
1343 |
1344 | 含254条记录的文件
1345 |
1346 | 含255条记录的文件
1347 |
1348 | 3. 正交阵列测试
1349 |
1350 | (1) 正交数组测试通过挑选适量的、有代表性的点进行试验,能有效地减少测试用例数,节约测试成本。
1351 |
1352 | (2) 该方法由日本口玄一博士提出并导出正交数组,从而使得测试数据具有“均匀分散、整齐可比”的特点。
1353 |
1354 | 例子:某大学刚考完某门课程,想通过“性别”、“班级”和“成绩”这3个查询条件对这门课程的成绩查询,查询条件包括:
1355 |
1356 | “性别”=“男,女”
1357 |
1358 | “班级”=“1班,2班”
1359 |
1360 | “成绩”=“及格,不及格”
1361 |
1362 | 一般需要设计2X2X2=8个测试用例。
1363 |
1364 | 
1365 |
1366 | 【基于模型的测试】
1367 |
1368 | 1. 分析软件的现有行为模型或创建一个。
1369 | 2. 穿越行为模型,并指定迫使软件从状态转换到另一个状态的输入。
1370 |
1371 | (1) 输入将触发将导致转换发生的事件。
1372 |
1373 | 3. 回顾行为模型,并注意到软件从状态过渡到状态时的预期输出。
1374 | 4. 执行测试用例。
1375 |
1376 | 
1377 |
1378 |
1379 |
1380 |
1381 |
1382 | ### 例题
1383 |
1384 | 1. 过程框架至少定义了五种框架活动分别是( )。
1385 |
1386 | 2. 类-职责-协作者模型又称为( )建模。
1387 |
1388 | 3. 软件工程层次图中,支持软件工程的根基在于( )。
1389 | 4. 填空题:在UML模型中,( )图用于描述系统与外部系统及用户之间的交互;( )图用于按时间顺序描述对象间的交互。
1390 | 5. 基于大量构件共同使用一个全局变量时所发生的耦合称为( )耦合。
1391 | 6. 华为云(DevCloud)是一个一站式、全流程、安全可信的( )平台。
1392 | 7. 华为云(DevCloud)敏捷开发的“看板”核心元素包括分层、( )、列、价值流、在制品(WIP)、风险&瓶颈、拉动式开发等核心元素。
1393 | 8. 顺序图(时序图)的构成元素主要包括: ( )、生命线、激活和( )。
1394 | 9. 汽车类与方向盘类之间的关系是( )关系。
1395 |
1396 | **重庆大学《软件工程》课程试卷(A 卷) 2019 — 2020 学年 第 2 学期**
1397 |
1398 | 1. FURPS 质量属性分别是指:功能性、( )、( )、性能和( )。
1399 |
1400 | 2. 在基于类的需求建模中,类可分为: ( )、( )和( )。
1401 |
1402 | 3. 需求工程是指( )。
1403 |
1404 | 4. 软件质量的成本包括:( )、( )和( )。
1405 |
1406 | 5. 一个通用的软件工程过程框架通常包含 沟通、( )、建模、( ) 和( )。
1407 |
1408 | 6. 开闭原则是指模块或构件应该对外延具有开放性,对( )具有封 闭性。
1409 |
1410 | 7. 需求模型必须实现的三个主要目标有: ( )、( )、定义在软 件完成后可以被确认的一组需求
1411 |
1412 | 8. OMG 定义构件是:系统中( )、可部署的和可替换的部件。
1413 |
1414 | 9. 用户满意度=合格的产品+( ) +( ) 10.CRC 卡中 CRC 的中文全称( )。
1415 |
1416 | > **参考答案**
1417 | >
1418 | > 1. (易用性)、(可靠性)、(可支持性)
1419 | > 2. (实体类)、(边界类)、(控制类)
1420 | > 3. (致力于不断理解需求的大量任务和技术)
1421 | > 4. (预防成本)、(评估成本)、(失效成本)
1422 | > 5. (策划)、(构建)、(部署)
1423 | > 6. ( 修改 )
1424 | > 7. (描述客户需要什么)、(为软件设计奠定基础)
1425 | > 8. (模块化的)
1426 | > 9. (好的质量)、(按预算和进度安排交付)
1427 | > 10. (类-职责-协作者)
1428 |
1429 | ## 二、单选题 (10个,每个2分,共20分)
1430 |
1431 | 看填空题的索引
1432 |
1433 | ### 需要理解的内容
1434 |
1435 | 1. 如何判断什么时候该用什么样的过程模型。
1436 |
1437 |
1438 |
1439 |
1440 |
1441 |
1442 |
1443 | ### 例题
1444 |
1445 | 1. 某软件公司欲开发一个基于Web的考勤管理系统。在项目初期,客户对系统的基本功能、表现形式等要求并不明确,在这种情况下,采用( )开发方法比较合适。
1446 |
1447 | A、瀑布模型
1448 |
1449 | B、形式化
1450 |
1451 | C、结构化
1452 |
1453 | D、极限编程
1454 |
1455 | 2. 在类图中下列哪个符号表示的是泛化关系是( )
1456 |
1457 | A、实线实心箭头
1458 |
1459 | B、虚线实心箭头
1460 |
1461 | C、实线空心箭头
1462 |
1463 | D、实线空心菱形
1464 |
1465 | 3. 在设计模式中“依赖于抽象,而非具体的实现”指的是( )
1466 |
1467 | A、开闭原则
1468 |
1469 | B、Liskov替换原则
1470 |
1471 | C、依赖倒置原则
1472 |
1473 | D、接口分离原则
1474 |
1475 | 4. 软件质量是一个重要的问题贯穿了软件的( )
1476 |
1477 | A、生存周期
1478 |
1479 | B、设计阶段
1480 |
1481 | C、编码阶段
1482 |
1483 | D、测试阶段
1484 |
1485 | ## 三、判断题 (5个,每个2分,共10分)
1486 |
1487 |
1488 |
1489 |
1490 |
1491 | ### 例题
1492 |
1493 | 1. 软件工程是一种结构化的技术。( )
1494 | 2. 每个应用系统只能使用一种体系结构风格。( )
1495 | 3.
1496 |
1497 |
1498 |
1499 |
1500 |
1501 | ## 四、简答题 (4个,每个5分,共20分)
1502 |
1503 | 看填空题的索引即可
1504 |
1505 |
1506 |
1507 | ### 例题
1508 |
1509 | 1. 简述David Hooker提出的7个关注软件工程整体实践的原则。(要点+一两句的补充说明)。
1510 | 2. 简述模块独立性的两个定量准则及模块独立性的好处。
1511 |
1512 |
1513 |
1514 |
1515 |
1516 | ## 五、应用分析题(2个,每个15分,共30分)
1517 |
1518 | ### (一)需求建模
1519 |
1520 | 1. 结构化分析——数据流图
1521 |
1522 | https://www.bilibili.com/video/BV1Jt411d7nR
1523 |
1524 |
1525 |
1526 | > #### 例题
1527 | >
1528 | > 某时装邮购提供商拟开发订单处理系统,用于处理客户通过电话、传真、邮件或Web站点所下订单。其主要功能如下:
1529 | >
1530 | > (1)增加客户记录。将新客户信息添加到客户文件,并分配一个客户号以备后续使用。
1531 | >
1532 | > (2)查询商品信息。接收客户提交商品信息请求,从商品文件中查询商品的价格和可订购数量等商品信息,返回给客户。
1533 | >
1534 | > (3)增加订单记录。根据客户的订购请求及该客户记录的相关信息,产生订单并添加到订单文件中。
1535 | >
1536 | > (4)产生配货单。根据订单记录产生配货单,并将配货单发送给仓库进行备货;备好货后,发送备货就绪通知。如果现货不足,则需向供应商订货。
1537 | >
1538 | > (5)准备发货单。从订单文件中获取订单记录,从客户文件中获取客户记录,并产生发货单。
1539 | >
1540 | > (6)发货。当收到仓库发送的备货就绪通知后,根据发货单给客户发货;产生装运单并发送给客户。
1541 | >
1542 | > (7)创建客户账单。根据订单文件中的订单记录和客户文件中的客户记录,产生并发送客户账单,同时更新商品文件中的商品数量和订单文件中的订单状态。
1543 | >
1544 | > (8)产生应收账户。根据客户记录和订单文件中的订单信息,产生并发送给财务部门应收账户报表。
1545 | >
1546 | > 问题:
1547 | >
1548 | > 1.使用说明中的词语,给出图1-1中的实体E1~E3的名称。
1549 | >
1550 | > 2.使用说明中的词语,给出图1-2中的数据存储D1~D3的名称。
1551 | >
1552 | > 3.(1)给出图1-2中处理(加工)P1和P2的名称及其相应的输入、输出流。(2)除加工P1和P2的输入输出流外,图1-2还缺失了1条数据流,请给出其起点和终点。
1553 | >
1554 | > 
1555 | >
1556 | > 
1557 |
1558 |
1559 |
1560 | 2. 面向对象分析——类图
1561 |
1562 | https://www.bilibili.com/video/BV1Jt411d7PR
1563 |
1564 |
1565 |
1566 | > #### 例题
1567 | >
1568 | > 某网上药店允许顾客凭借医生开具的处方,通过网络在该药店购买处方上的药品。该网上药店的基本功能描述如下:
1569 | >
1570 | > (1)注册。顾客在买药之前,必须先在网上药店注册。注册过程中需填写顾客资料以及付款方式(信用卡或者支付宝账户)。此外顾客必须与药店签订一份授权协议书,授权药店可以向其医生确认处方的真伪。
1571 | >
1572 | > (2)登录。已经注册的顾客可以登录到网上药房购买药品。如果是没有注册的顾客,系统将拒绝其登录。
1573 | >
1574 | > (3)录入及提交处方。登录成功后,顾客按照“处方录入界面”显示的信息,填写开具处方的医生的信息以及处方,上的药品信息。填写完成后,提交该处方。
1575 | >
1576 | > (4)验证**处方**。对于**已经提交的处方**(系统将其状态设置为“处方已提交”),其验证过程为:
1577 | >
1578 | > ①**核实医生信息**。如果医生信息不正确,该处方的状态被设置为“**医生信息无效**”,并取消这个处方的购买请求;如果医生信息是正确的,系统给该医生发送处方确认请求,并将处方状态修改为“审核中”。
1579 | >
1580 | > ②如果医生回复处方无效,系统取消处方,并将处方状态设置为**“无效处方**”。如果医生没有在7天内给出确认答复,系统也会取消处方,并将处方状态设置为“**无法审核**”。
1581 | >
1582 | > ③如果医生在7天内给出了确认答复,该处方的状态被修改为“准许付款”。系统取消所有未通过验证的处方,并自动发送一封电子邮件给顾客,通知顾客处方被取消以及取消的原因。
1583 | >
1584 | > (5)对于通过验证的处方,系统自动计算药品的价格并邮寄药品给已经付款的顾客。该网上药店:采用面向对象方法开发,使用UML进行建模。系统的类图如图3-1所示。
1585 | >
1586 | > 问题:
1587 | >
1588 | > 1. 根据说明中的描述,给出图3-1中缺少的C1~C5所对应的类名。
1589 | > 2. 图3-2给出了“处方”的部分状态图。根据说明中的描述,给出图3-2中缺少的S1 ~S4所对应的状态名以及(7)~(10)处所对应的迁移(transition) 名。
1590 | >
1591 | > 
1592 | >
1593 | > 
1594 |
1595 | 3. 面向对象分析——用例图
1596 |
1597 | 【例】
1598 |
1599 |
1600 |
1601 |
1602 |
1603 | > #### 例题
1604 | >
1605 | > 阅读下列说明和图,完善用例图A1、A2及U1~U3。
1606 | >
1607 | > 某网上购物平台的主要功能如下:
1608 | >
1609 | > (1)**创建订单**。**顾客**(Customer)在线创建订单(Order),主要操作是向订单中添加项目,从订单中删除项目。订单中应列出所订购的商品(Product)及其数量(Quantities)
1610 | >
1611 | > (2)提交订单。订单通过网络提交。在提交订单时,顾客需要提供其姓名(name)、收货地址(address)、付款方式(Payment)(预付卡、现金或信用卡)。
1612 | >
1613 | > (3)处理订单。**订单处理人员**接收来自系统的订单,根据订单内容,安排配货,制定送货计划。
1614 | >
1615 | > (4)派单。订单处理人员将已配好货的订单转交给派送人员。
1616 | >
1617 | > (5)**送货**/**收货**。派送人员将货物送到顾客指定的收货地址。顾客需在运货单上签收。签收后的运货单最终需交还给订单处理人员。
1618 | >
1619 | > (6)收货确认。当订单处理人员收到签收过的运货单后,会和顾客进行一次再确认。
1620 | >
1621 | > 
1622 |
1623 |
1624 |
1625 | 4. 面向对象分析——状态图
1626 |
1627 | 【例】
1628 |
1629 |
1630 |
1631 |
1632 |
1633 | 5. 面向对象分析——时序图
1634 |
1635 | 【例】
1636 |
1637 |
1638 |
1639 |
1640 |
1641 |
1642 |
1643 | ### (二)软件测试
1644 |
1645 | #### 2.1 测试用例的设计——白盒法
1646 |
1647 | ##### 2.1.1 控制结构测试
1648 |
1649 | 【软件工程——11-白盒测试】 https://www.bilibili.com/video/BV1wG41137Hs/?share_source=copy_web&vd_source=7ba452d8ee6f8b8a4b8ef831bf573bda
1650 |
1651 | 【白盒测试so easy!】 https://www.bilibili.com/video/BV1zL4y1A785/?share_source=copy_web&vd_source=7ba452d8ee6f8b8a4b8ef831bf573bda
1652 |
1653 | ##### 2.1.2 基本路径测试
1654 |
1655 | 【软件工程——11-基本路径测试法】 https://www.bilibili.com/video/BV13V4y1g7tc/?share_source=copy_web&vd_source=7ba452d8ee6f8b8a4b8ef831bf573bda
1656 |
1657 | #### 2.2 测试用例的设计——黑盒法
1658 |
1659 | ##### 2.2.1 等价类划分法
1660 |
1661 | 【软件工程——11-等价类划分.mp4】 https://www.bilibili.com/video/BV1MT411M7EC/?share_source=copy_web&vd_source=7ba452d8ee6f8b8a4b8ef831bf573bda
1662 |
1663 | ##### 2.2.2 边界值分析法
1664 |
1665 | 【软件工程——11-边界值及错误推测法】 https://www.bilibili.com/video/BV1nV4y1g7ig/?share_source=copy_web&vd_source=7ba452d8ee6f8b8a4b8ef831bf573bda
--------------------------------------------------------------------------------
/docs/index.md:
--------------------------------------------------------------------------------
1 | Hello world !!
--------------------------------------------------------------------------------
/mkdocs.yml:
--------------------------------------------------------------------------------
1 | site_name: Mine_qihang's Docs
2 | theme:
3 | name: "material"
4 | features:
5 | #- navigation.instant # 点击内部链接时,不用全部刷新页面
6 | - navigation.tracking # 在url中使用标题定位锚点
7 | - navigation.tabs # 顶部显示导航顶层nav(也就是第一个节点)
8 | - navigation.tabs.sticky # 滚动是隐藏顶部nav,需要配合navigation.tabs使用
9 | - navigation.sections # nav节点缩进
10 | - navigation.expand # 不折叠左侧nav节点
11 | - navigation.indexes # 指定节点index pages ,跟instant不兼容
12 | - toc.integrate # 右侧生产目录
13 | - navigation.top # 一键回顶部
14 | # plugins:
15 | # - search:
16 | # lang: jp
17 | markdown_extensions:
18 | - pymdownx.highlight # code hilight
19 | - pymdownx.superfences
20 | - pymdownx.arithmatex:
21 | generic: true
22 | extra_javascript:
23 | - javascripts/config.js
24 | - https://polyfill.io/v3/polyfill.min.js?features=es6
25 | - https://cdn.jsdelivr.net/npm/mathjax@3/es5/tex-mml-chtml.js
26 | nav:
27 | - 计算机系统结构:
28 | - Introduction: Architecture/chapter1.md
29 | - Principles of Quantitative Analysis; MIPS: Architecture/chapter2.md
30 | - Pipelining, Hazards, Implementation Issues: Architecture/chapter3.md
31 | - Instruction-Level Parallelism (ILP), Tomasulo: Architecture/chapter4.md
32 | - Memory-Hierarchy Design, Cache Optimization: Architecture/chapter5.md
33 | - ILP; Branch Prediction, Superscalars: Architecture/chapter6.md
34 | - Memory Hierarchy Design, Virtual Memory: Architecture/chapter7.md
35 | - 软件工程:
36 | - 软工期末考试: SoftwareEngineering/软工期末考试.md
37 | - 软工应用分析题: SoftwareEngineering/软工应用分析题.md
38 | - 计算机网络:
39 | - 第一次作业: ComputerNetwork/《计算机网络》第一次作业.md
40 | - 第二章作业: ComputerNetwork/《计算机网络》第二章作业.md
41 | - 第三章作业: ComputerNetwork/《计算机网络》第三章作业.md
42 | - 第四章作业: ComputerNetwork/《计算机网络》第四章作业.md
43 | - 第五章作业: ComputerNetwork/《计算机网络》第五章作业.md
44 | - 第六章作业: ComputerNetwork/《计算机网络》第六章作业.md
45 | - 第九章作业: ComputerNetwork/《计算机网络》第九章作业.md
46 | - 操作系统原理: OperatingSystem/index.md
47 | - 机器学习基础:
48 | - 第一章作业: MachineLearning/第一章作业.md
49 | - 第二章作业: MachineLearning/第二章作业.md
50 | - 第三章作业: MachineLearning/第三章作业.md
51 | - 第四章作业: MachineLearning/第四章作业.md
52 | - 第五章作业: MachineLearning/第五章作业.md
53 | - 第六章作业: MachineLearning/第六章作业.md
54 | - 第七章作业: MachineLearning/第七章作业.md
55 | - 第八章作业: MachineLearning/第八章作业.md
56 | - 第九章作业: MachineLearning/第九章作业.md
57 | - 自然语言处理: index.md
58 | - 专业基本能力测试: ProfessionalBasicAptitudeTest/index.md
--------------------------------------------------------------------------------
237 |
238 | 1. 建立用例模型
239 |
240 | 从不同用户的角度获取并描述功能需求,核心是用例。
241 |
242 | 2. 建立领域模型
243 |
244 | 发现和描述用例中涉及的对象和概念,核心是类图
245 |
246 | 3. 建立动态(交互)模型
247 |
248 |
249 |
250 | 【数据建模】
251 |
252 | 将注意力集中在数据域上
253 |
254 | 在客户的抽象级别上创建一个模型
255 |
256 | 指示数据对象之间如何相互关联
257 |
258 | 【数据对象】
259 |
260 | 一种几乎所有必须被软件理解的复合信息的表示。
261 |
262 | 可以是外部实体、事物、事件、角色、组织单元、地点或结构。
263 |
264 | 数据对象的描述包含了数据对象及其所有属性。数据对象包含一组作为对象的方面、质量、特征或描述符的属性。
265 |
266 | 【数据对象间的关系】
267 |
268 | 数据对象以不同的方式相互连接。
269 |
270 | 在人和车之间建立了一个连接,因为这两个对象是相关的。
271 |
272 | 一个人拥有一辆车
273 |
274 | 一个人可以驾驶汽车
275 |
276 | 关系“拥有”和“驾驶”定义人和汽车之间的相关联系。
277 |
278 | 对象可以通过多种不同的方式进行关联
279 |
280 | 
281 |
282 |
283 |
284 | 【领域建模】
285 |
286 | 领域模型分析以用例模型作为输入,将系统分解为一组相互协作的概念类(也称分析类) 。
287 |
288 | 分析类具有突出业务领域、突出概念性的特征,主要针对问题和职责,不涉及细节。
289 |
290 | 设计阶段,分析类可进一步演化为设计类,提供更多设计表达。
291 |
292 | 领域模型包括:**类图**、**CRC****模型**、**包图**
293 |
294 |
295 |
296 |
297 |
298 |
299 |
300 | 【行为建模】
301 |
302 | 行为模型显示了软件如何对外部事件或激励做出响应。
303 |
304 | 该模型通常描述一个用例中,系统在接收到特定事件后,所涉及的对象以及这些对象之间的交互(消息传递)过程。
305 |
306 | 行为模型主要包括:时序图、协作图、状态图。
307 |
308 |
309 |
310 | 【状态图 vs 时序图】
311 |
312 | (1)状态图针对单个类,跨多个用例。时序图针对的是一个用例。
313 |
314 | (2)状态图中的行为不仅与事件有关,还与对象所处状态有关。
315 |
316 | 【时序图 vs 协作图】
317 |
318 | (1)时序图可等价的转化为协作图
319 |
320 | (2)协作图更侧重表达对象间的关联关系,而非消息传递的时间先后。
321 |
322 | 
323 |
324 |
325 |
326 |
327 |
328 | ### (六)需求——需求建模:结构化分析方法
329 |
330 | 【结构化分析方法(SA)】又称面向数据流的分析方法。主要是创建基于数据流的模型,通过分析数据流发现系统功能和行为,并对其进行划分。
331 |
332 | SA主要构建四种分析模型
333 |
334 | · 数据流图(Data Flow Diagram)——功能视角
335 |
336 | · 数据字典
337 |
338 | · 实体关系图——数据视角
339 |
340 | · 状态迁移图——行为视角
341 |
342 |
343 |
344 | 【控制流建模】
345 |
346 | 一些应用程序是由事件而不是数据“驱动”的,产生控制信息而不是报告或显示,以及处理严重关注时间和性能的信息。
347 |
348 | 适合对实时系统、控制类系统等建模。
349 |
350 | 以状态图为主,描述系统对外部事件响应的行为模型。
351 |
352 | 
353 |
354 |
355 |
356 | ### (五)设计
357 |
358 | **7.** **设计概念**
359 |
360 | 【软件设计】即根据软件需求,产生一个软件内部逻辑表示的过程。这种更接近于软件的逻辑表达或模型,提供了软件系统关心的体系结构、数据结构、接口和构件等细节。
361 |
362 | 对比:
363 |
364 | 需求分析偏重于问题域,描述软件要做什么。
365 |
366 | 软件设计则偏重于解决方案,描述软件究竟要如何做。
367 |
368 | 【软件设计的价值】
369 |
370 | 1. 设计是需求与实现代码之间的“桥梁”
371 |
372 | (1) 设计本质是满足需求,并对方案优中选优的过程。
373 |
374 | (2) 设计模型比代码更易评估、更易修改。
375 |
376 | 2. 设计是软件质量形成的关键,软件质量依赖于设计的结果
377 |
378 | (1) 如软件质量中的效率、可靠性、高并发等。
379 |
380 | **例子:****对含有上百亿信息的数据库,如何满足用户的高并发访问需求?**
381 |
382 | 设计方案:分库分表、读写分离。
383 |
384 | 【好的设计】
385 |
386 | 设计必须实现分析模型中的明确需求,包括客户期望的隐性需求。(承上)
387 |
388 | 对后续的编码、测试以及维护人员,设计必须是可读、可理解的指南。(启下)
389 |
390 | 设计必须提供未来软件的全貌,从实现的角度说明其数据域、功能域和行为域。
391 |
392 | 例子:自动排课是系统的功能需求之一,那么设计要解决数据存储问题(排课信息保存)、界面显示问题(排课及结果显示)、算法逻辑问题(排课算法)等。
393 |
394 | 【实施软件设计】
395 |
396 | 软件设计是一个迭代的过程。
397 |
398 | (1)初始时,设计者应关注系统的整体架构(如架构风格、主要构件、连接关系)等,对应于**体系结构设计阶段**。
399 |
400 | (2)随着设计迭代的开始,更多的细节被关注(如数据、构件)等,对应于**构件设计或详细设计阶段**。
401 |
402 | 【软件设计任务集】
403 |
404 | 
405 |
406 | (1) 体系结构设计:定义软件的主要元素(构件)以及元素之间的联系
407 |
408 | 
409 |
410 | (2) 数据/类设计:将分析类模型转化为设计类以及软件所需要的数据结构
411 |
412 | 
413 |
414 | (3) 接口设计:定义软件与协作系统之间、软件与用户之间的通信
415 |
416 | (4) 构件设计或详细设计:定义软件元素(构件)的内部细节,如内部数据结构、算法等
417 |
418 | (5) 部署设计:定义软件元素在物理拓扑结构中的分布
419 |
420 |
421 |
422 | 【应该遵循什么原则才能保证设计质量?】
423 |
424 | 1. 抽象
425 |
426 | 抽象的本质:强调关键特征,忽略无关细节。
427 |
428 | 过程抽象:具有明确和有限功能的指令序列。
429 |
430 | 数据抽象:描述数据对象的具名数据集合。
431 |
432 | 2. 体系结构
433 |
434 | 软件体系结构设计,即找到一种最佳的方式对系统进行划分,标识其中的构件,构件之间的联系等。
435 |
436 | 设计应该先勾勒全貌,不能一开始就跳入细节。
437 |
438 | 3. 模式
439 | 4. 关注点分离
440 | 5. 模块化
441 |
442 | 庞大的系统不便于并行开发,软件工程师也难以理解和把握。
443 |
444 | 采用分治策略,将大系统分解为若干更小、更简单的模块。这样,问题理解变得更加容易,开发成本也会减小。
445 |
446 | 6. 信息隐蔽
447 |
448 | 每个模块都对其它模块隐藏自己的设计细节(就像黑盒子),这样如果模块内部发生变化,外部受到的影响最小。
449 |
450 | **7.** **功能独立**
451 |
452 | 功能独立性是指:模块化设计时,希望每个模块尽可能功能专一,同时避免与其它模块过多交互。
453 |
454 | Cohesion(内聚): 表示模块内相关功能的强度
455 |
456 | 内聚性强的模块通常只完成一件事情。
457 |
458 | Coupling (耦合) :表示模块之间的相互依赖性
459 |
460 | 模块的耦合性取决于模块之间接口的复杂性、引用方式、传递数据的复杂性等。
461 |
462 | 功能独立意味着:**高内聚、低耦合**
463 |
464 | 功能独立的优势:
465 |
466 | · 更容易开发。因为每个功能均有效分隔,且接口简单。
467 |
468 | · 更容易维护。因为修改代码引起的副作用被限制,减少错误扩散。
469 |
470 | · 复用性更好。
471 |
472 | 8. 逐步求精
473 |
474 | 随着设计的深入,设计者不能老是停留在抽象层级,而应逐步揭示底层的细节。
475 |
476 | 9. 方面
477 | 10. 重构
478 |
479 | 在不改变代码的外部行为的前提下,优化内部结构的过程。
480 |
481 | 例子:早期设计中发现某构件的内聚性较差,在保持接口不变的情况下,可通过重构将其分解为两个独立的构件,每个新的构件内聚性得以增强。
482 |
483 | 11. 面向对象的设计概念
484 | 12. 设计类
485 |
486 | 分析类只与业务领域有关,和具体实现技术无关。
487 |
488 | 设计类则面向实现,通过对分析类的细化设计,达到能提供给构造阶段编码实现的目的。
489 |
490 | 定义设计类的两种方式:
491 |
492 | (1) 通过对分析类提供细节设计。
493 |
494 | (2) 创建新的设计类,该设计类提供软件的基础设施以支持业务解决方案。
495 |
496 | 改进:基于工厂模式
497 |
498 |
499 |
500 | **8.** **体系结构设计**
501 |
502 | 【软件体系结构】是软件的一种划分形式,从较高抽象层次定义系统的构件、构件之间的连接,以及由构件与构件连接形成的拓扑结构。
503 |
504 | 【体系结构设计的必要性】
505 |
506 | · 体系结构设计决定了系统的主体结构,结构优劣对软件质量具有重要影响。
507 |
508 | · 针对安全需求,可以考虑采用分层结构,将重要资源置于内层保护。
509 |
510 | · 针对可用性需求,可以考虑冗余设计。
511 |
512 | 【软件体系结构设计的关键决策】
513 |
514 | · 系统的基本构造单元是什么?
515 |
516 | · 这些构造单元连接方式?
517 |
518 | · 最终形成怎样的拓扑结构?
519 |
520 | · 有哪些体系结构风格可供系统借鉴?
521 |
522 | · 对于目标系统,如何基于一般性的体系结构进行适应性改造?
523 |
524 | · 如何评估体系结构设计?
525 |
526 | 【体系结构风格】
527 |
528 | 众多系统所共有的结构和特性(如构件类型、交互机制、拓扑、约束),可以指导同类型应用的体系结构设计。
529 |
530 | · 数据中心结构
531 |
532 | 该结构适合于:数据由一个构件(模块)产生,而由其它构件使用的情形。
533 |
534 | 缺点:一旦中心数据存储出现问题会影响整个系统。
535 |
536 | 如电子白板系统、管理信息系统(MIS) 。
537 |
538 | 
539 |
540 | · 管道-过滤器结构
541 |
542 | 系统由若干构件(过滤器)按一定顺序组合而成,一个构件的输出是另一个构件的输入。
543 |
544 | 适合于批处理系统,不适用于交互式应用系统。
545 |
546 | 编译器就是一种管道-过滤器系统,包括词法分析、语法分析、字节码生成等。
547 |
548 | 图像处理系统等也大多采用该风格。
549 |
550 | 
551 |
552 | 
553 |
554 | · 调用返回结构
555 |
556 | (1) 主程序/子程序结构
557 |
558 | 
559 |
560 | (2) 远程过程调用结构:主程序/子程序中的构件分布在网络中的多台计算机。
561 |
562 | 如:如分布式计算系统Hadoop。
563 |
564 | 
565 |
566 | 调用返回结构缺点:
567 |
568 | 主构件需要预先知道被调子构件的接口标识。
569 |
570 | 构件接口标识的更改会影响所有调用它的其它构件,而且这种现象还会进行传递,导致更大的负面影响。
571 |
572 | · 面向对象结构
573 |
574 | 构造单元:类和对象
575 |
576 | 连接:基于消息机制。
577 |
578 | 拓扑结构:不同对象之间是平级的,没有主次之分
579 |
580 | 
581 |
582 | · 消息总线结构
583 |
584 | 构件不直接调用其它构件,而是广播一个或多个事件。
585 |
586 | 系统中的构件注册(监听)一个或多个事件源;
587 |
588 | 当一个事件被广播,系统自动调用该事件中注册的构件。
589 |
590 | 
591 |
592 | 消息总线风格逐渐演变为**消息中间件**。消息中间件应用场景:系统解耦、异步通讯、削峰。
593 |
594 | 下图为传统方式下系统B、C与A之间的通信连接,随着新的D、E、F、G系统的增加,必然导致巨大的维护成本(加入或退出均需要维护A)。
595 |
596 | 
597 |
598 | 优点:扩展简单。系统无须知道其他子系统接口名、位置的情况下,就可以激活其它子系统。
599 |
600 | 消息中间件产品:ActiveMQ、RabbitMQ
601 |
602 | 
603 |
604 | 
605 |
606 | · 层次化结构
607 |
608 | 系统被组织成若干个层次,每层都由一系列构件组成。
609 |
610 | 同层内构件可相互调用。
611 |
612 | 层之间存在调用接口,但只限于相邻层,下层可为上层服务,并作为再下一层客户。
613 |
614 | 
615 |
616 | · 客户-服务器结构
617 |
618 | 源于计算任务和计算资源的能力差异。
619 |
620 | 构件分布在两台或多台计算环境中。
621 |
622 | 演变:三层,多层C/S,B/S体系结构
623 |
624 | · MVC(Model-View-Controller)
625 |
626 | 常用于Web应用系统。
627 |
628 | 将系统分解为应用逻辑、用户界面、控制逻辑等不同构件类型。
629 |
630 | 优势:
631 |
632 | ·任何一种构件的改变都不会对其它构件造成影响。
633 |
634 | ·一个模型能为多个视图提供数据。
635 |
636 | 
637 |
638 | · 微服务架构
639 |
640 | 单体架构:应用打包(如war)部署为一个独立的单元,通过一个进程方式运行。
641 |
642 | 微服务架构:
643 |
644 | · 应用(功能)被分割成更小的、独立的服务,各个微服务之间的关联通过RPC(同步调用)或MQ(异步调用)实现。
645 |
646 | · 独立的微服务不需要部署在同一个虚拟机或应用服务器中。
647 |
648 | 
649 |
650 | · 混合风格
651 |
652 | 大规模系统往往包括多种体系结构风格
653 |
654 | 
655 |
656 |
657 |
658 | 【体系结构描述】
659 |
660 | 关注点:为谁描述哪些内容?用什么符号体系或描述语言?
661 |
662 | 程序员说:体系结构就是要决定需要编写哪些类、使用哪些现成框架。
663 |
664 | 程序经理说:体系结构就是模块的划分和接口的定义。
665 |
666 | 数据库工程师说:体系结构规定了持久化数据的结构,其他不过是对数据的操作而已。
667 |
668 | 用户说:体系结构就是决定一个个功能子系统如何划分。
669 |
670 | 这些描述我们都需要。每个视角代表一类利益相关者,反应了系统结构的一个侧面。
671 |
672 | 系统体系结构多从逻辑架构、物理架构和开发架构等视角描述。
673 |
674 | **·** **逻辑架构**关注的是功能构件,包含用户可见的功能构件,以及不可见的功能构件。
675 |
676 | **·** **物理架构**关注网络、服务器等基础设施及其拓扑结构。
677 |
678 | · **开发架构**更关注程序包,除自己写的程序外,还包括应用程序依赖的SDK、第三方类库等。
679 |
680 | 【体系结构设计方法】
681 |
682 | 基本设计思路:
683 |
684 | 
685 |
686 | 包括:
687 |
688 | · 面向对象体系结构设计
689 |
690 | · 传统结构化设计
691 |
692 | 【面向对象体系结构设计方法】
693 |
694 | 1. 定义系统交互的外部环境和交互特性
695 |
696 | (1) 目的是识别系统的外部实体与接口,定义接口构件
697 |
698 | 2. 识别一组结构原型(archetypes)
699 |
700 | (1) 原型是系统中最核心的抽象类或模式,目标系统的体系结构可由这些原型组成。
701 |
702 | (2) 原型是系统中最稳定的元素,可以基于系统行为以不同方式对这些元素实例化。
703 |
704 | (3) 多数情况下,原型可以通过分析类来获得。
705 |
706 | 3. 对每个结构原型进一步细化,以完善系统结构。
707 |
708 | 例子:对图书管理系统体系结构设计
709 |
710 | (1) 先采用“包图”划分子系统。
711 |
712 | 
713 |
714 | (2) 针对“借书”需求,识别结构原型
715 |
716 | 
717 |
718 | (3) 对“借书”构件,采取MVC风格进行细化
719 |
720 | 
721 |
722 | 【结构化体系结构设计方法】
723 |
724 | 目标:根据DFD的不同类型,通过对系统中模块的合理划分,得到软件体系结构图
725 |
726 | 体系结构风格:主程序/子程序风格
727 |
728 | 1. 将系统分割为多个功能模块
729 | 2. 确定各个模块之间的调用关系
730 | 3. 用系统结构图表示设计模型
731 |
732 | 步骤:
733 |
734 | (1) 分析确定数据流图类型。
735 |
736 | (2) 标识输入、输出流边界。
737 |
738 | (3) 依据变化或事务分析规则,将DFD图映射为顶层和第一层模块结构。
739 |
740 | (4) 对第一层中的模块继续细化和分解。
741 |
742 | (5) 利用启发式规则优化初始系统结构图。
743 |
744 | 变换分析和事务分析实例见PPT【体系结构设计】末尾
745 |
746 | 9. 构件级设计
747 |
748 | 【构件设计】是在体系结构设计的基础上,对其中每个构件内部构成的进一步设计。
749 |
750 | 体系结构设计相当于确定了计算机的部件组成,连接关系等。
751 |
752 | 构件设计则着重于设计每个部件的**内部细节**,如运算器的内部电路和元件等。
753 |
754 | 面向对象视角:
755 |
756 | 确定设计类并对其细化的过程。
757 |
758 | 结构化视角:
759 |
760 | 细化模块内部的数据结构、算法和接口的过程。
761 |
762 | 【构件】是计算机软件中的一个模块化的构造块。它部件**封装**了实现并暴露一系列**接口**。
763 |
764 | 面向对象视角:
765 |
766 | 构件封装了一组相互协作的类(也可以是一个类)。
767 |
768 | 结构化视角:
769 |
770 | 构件也称功能模块(如系统中图像读入模块、图像压缩模块)
771 |
772 | 封装了数据结构、算法和接口
773 |
774 | 【面向对象构件构成】
775 |
776 | 面向对象构件可能由多个设计类构成
777 |
778 | (1) 构件接口与实现需要严格分离。
779 |
780 | (2) 基于设计框架,一个构件需要分解为多个设计类。
781 |
782 | 【面向对象构建设计关键问题】
783 |
784 | 1. 构件由哪些设计类组成?
785 | 2. 设计类之间是什么关系,如何优化?
786 | 3. 构件提供的接口是什么?
787 | 4. 每个设计类的详细构成(属性和方法)?
788 |
789 | 前3个问题都与设计优化原则相关
790 |
791 | 通过设计优化,可以提高构件复用性,灵活适应系统变更,并减少副作用的传播。
792 |
793 | 【构件设计指导原则】
794 |
795 | 1. 开闭原则(OCP)
796 |
797 | 对扩展开放:构件的行为是可扩展或改变的
798 |
799 | 对修改关闭:当构件改变行为时,不要修改其源码
800 |
801 | 实现途径:用抽象构建框架,用继承/实现扩展细节。
802 |
803 | 需求变化时,不是通过修改类本身来完成,而是通过扩展一个子类来改变构件的行为。
804 |
805 | 优点:尽量不修改原有的代码,实现一个热插拔的效果。
806 |
807 | 2. Liskov替换原则(LSP)
808 |
809 | LSP 原则用来指导继承关系中子类该如何设计,子类的设计要保证在替换父类的时候,不改变原有程序的逻辑以及不破坏原有程序的正确性。
810 |
811 | 简单理解:子类可以扩展父类的功能,但不能改变父类原有的功能。
812 |
813 | LSP原则能减少代码冗余,避免运行期的类型判别(实现动态加载)。
814 |
815 | 3. 依赖倒置原则
816 |
817 | 依赖于抽象,而非具体实现。 具体方法是:首先,分离接口和实现。将类之间的依赖关系建立在高层抽象(如抽象类、接口)基础上。
818 |
819 | 优点:减少类间的耦合性,提高系统的稳定性
820 |
821 | 4. 接口分离原则
822 |
823 | 建立单一接口,不要建立臃肿庞大的接口。即:接口尽量细化,同时接口中的时间尽量少。
824 |
825 | 5. 单一职责原则:一个类或接口只承担一类责任。
826 | 6. 迪米特法则:尽量减少对象之间的交互,从而减小类之间的耦合。
827 |
828 | 内聚性和耦合性
829 |
830 | **内聚性**意味着构件只封装那些密切相关的类,或者类只封装自身密切相关的属性和操作。
831 |
832 | 根据程度可细分为:功能内聚、分层内聚、通信内聚等
833 |
834 | **耦合性**是类之间彼此联系程度的一种定性度量。
835 |
836 | 根据程度可细分为:内容耦合、共用耦合、控制耦合、标记耦合……
837 |
838 | 【面向对象构件设计过程】
839 |
840 | 1. 识别构件中与问题域相对应的设计类。包括界面类、控制类、实体类。
841 |
842 | (1) 一般可为每个用例设计一个控制类。如果多个用例中任务较为相似,也可以公用一个控制类。
843 |
844 | (2) 如果实体类的职责比较单一,直接将其映射为设计类;
845 |
846 | (3) 如果某类的职责过于复杂,应该将其分解为多个设计类(单一职责)。
847 |
848 | 2. 识别构件中与基础设施相对应的设计类。 这些设计类往往在分析模型中并没有定义。
849 | 3. 细化所有的设计类,定义该类中所有的接口、属性和操作。
850 |
851 | (1) 通过设计时序图或协作图说明协作细节。
852 |
853 | 将时序图中职责分解为具体操作,并分配给相关类;
854 |
855 | 定义操作对应的方法名,方法参数,返回值、可见性等。
856 |
857 | (2) 为每个构件确定合适的接口。
858 |
859 | 简单构件可直接定义public方法作为接口;
860 |
861 | 复杂构件单独定义接口类,构件负责实现接口;
862 |
863 | 确定接口的参数;
864 |
865 | (3) 细化属性,并定义相应的数据类型和数据结构。
866 |
867 | (4) 描述类成员方法中的处理逻辑。绘制程序流程图或活动图。
868 |
869 | 4. 说明持久数据源 (数据库或文件),并确定管理数据源所需要的类。
870 |
871 | (1) 对象可暂存于内存中,但要持久保存,需要通过数据存储实现。
872 |
873 | (2) 可以通过对象关系映射(ORM)将类映射为表,以简化数据库使用。
874 |
875 | 5. 细化**部署图**以提供额外的实现细节。
876 |
877 | (1) 为系统选择硬件配置和运行平台;
878 |
879 | (2) 将类、包、子系统分配到各个硬件结点上。
880 |
881 | 构建设计实例见PPT【构件级设计】中的实例部分
882 |
883 | 【传统构件设计过程】
884 |
885 | · 确定每个模块的算法,用工具描述算法逻辑。
886 |
887 | · 确定每一模块的数据结构。
888 |
889 | · 确定模块接口细节。
890 |
891 | 常用算法描述工具包括
892 |
893 | · 程序流程图
894 |
895 | · 问题分析图(PAD)
896 |
897 | 
898 |
899 | · 盒图(N-S图)
900 |
901 | 
902 |
903 | · 伪代码(PDL)
904 |
905 |
906 |
907 | 10. 用户界面设计
908 |
909 | 【UI设计】
910 |
911 | 软件强大的计算能力和功能,最终要通过界面来表现。
912 |
913 | 用户界面是软件的直观形象,直接影响用户对软件的体验。
914 |
915 | 用户通常从用户界面(而非功能)的好坏来评价软件的质量。
916 |
917 | 【常见UI设计错误】
918 |
919 | · 缺乏一致性
920 |
921 | · 太多需要记忆的
922 |
923 | · 没有指导和帮助
924 |
925 | · 没有上下文敏感性
926 |
927 | · 无意义的反馈
928 |
929 | · 界面复杂
930 |
931 | 【黄金法则】(这部分看书P198)
932 |
933 | 1. 把控制权交给用户(让用户掌握一切)
934 |
935 | (1) 提供灵活的交互。允许用户选择使用键盘、语音、鼠标等多种交互方式。
936 |
937 | (2) 允许用户交互被中断和撤销。如在手机编写短信时,允许接听电话,并能找到之前正在编写的短信。
938 |
939 | (3) 允许定制交互。
940 |
941 | (4) 将用户和内部技术细节隔离开。
942 |
943 | (5) 设计应允许用户与出现在屏幕上的对象直接交互。
944 |
945 | 2. 减轻用户的记忆负担
946 |
947 | 经验表明,需要记住的东西越多,交互出错的概率越大。
948 |
949 | (1) 减少对短期记忆的要求。
950 |
951 | (2) 建立有意义的默认设置。
952 |
953 | (3) 定义直观的快捷方式。
954 |
955 | (4) 界面的视觉布局应该基于真实世界的象征。
956 |
957 | (5) 以一种渐进的方式揭示信息。
958 |
959 | 3. 保持界面一致
960 |
961 | (1) 在完整的产品线上保持设计规则的一致性。
962 |
963 | (2) 如果过去的交互方式已经建立起用户期望,除非有不得已的理由,否则不要改变它。
964 |
965 | 4. 补充规则
966 |
967 | (1) 反馈:对用户的操作,应该给予及时、明确的反馈,并提供上下文帮助。
968 |
969 | (2) 宽容性:允许用户犯错,并能帮助用户从错误中及时恢复出来。
970 |
971 | (3) 个性化:允许用户根据自己的喜好定制界面元素、布局等。
972 |
973 | (4) 美观性
974 |
975 | 【UI设计过程】
976 |
977 | 
978 |
979 | 【接口/界面分析】
980 |
981 | 接口分析是指理解
982 |
983 | (1) 通过接口与系统交互的人员(最终用户);
984 |
985 | (2) 终端用户完成工作必须执行的任务;
986 |
987 | (3) 作为接口一部分呈现的内容;
988 |
989 | (4) 这些任务将被执行的环境。
990 |
991 | 成分:
992 |
993 | 1. 用户分析(看书P203)
994 | 2. 任务分析与建模
995 |
996 | 根据用例模型中的场景描述,将其映射为人机界面上的一组子任务
997 |
998 | 3. 显示内容分析
999 |
1000 | 根据每项任务确定其呈现的界面内容。
1001 |
1002 | 【界面设计】
1003 |
1004 | 对每项任务对应的界面进行**交互设计**和**视觉设计**。
1005 |
1006 | 交互设计的重点包括:交互流程、交互方式。
1007 |
1008 | 【交互流程设计】
1009 |
1010 | 1. 定义界面对象和动作
1011 | 2. 定义可能导致界面变化的事件
1012 | 3. 界面应该如何变化
1013 | 4. 想告诉用户什么?
1014 |
1015 | 好的交互方式可以让用户更简单、方便的使用产品。
1016 |
1017 | 【视觉设计】
1018 |
1019 | 视觉设计是指:针对眼睛的主观形式的表现手段和结果。
1020 |
1021 | 主要考虑界面的布局、数据的呈现方式、色彩搭配等
1022 |
1023 | 【界面设计工具】
1024 |
1025 | Visio、Axure
1026 |
1027 | 【设计评审】
1028 |
1029 | 所有设计工作完成后,为保证设计质量,需要对所有设计成果,包括**体系结构、构件、接口、数据模型**等进行综合设计评审。
1030 |
1031 |
1032 |
1033 |
1034 |
1035 | ### (六)测试
1036 |
1037 | 11. 软件测试策略
1038 |
1039 | 【测试的目的】
1040 |
1041 | 测试是选择适当的测试用例并执行被测程序的过程。
1042 |
1043 | 目的在于**发现错误**,而不是为了验证程序不存在错误。
1044 |
1045 | 好的测试用例可以发现今未发现的错误。
1046 |
1047 | 【测试策略】
1048 |
1049 | 一般特征:
1050 |
1051 | · 未完成有效的测试,应该进行有效的、正式的技术评审。通过评审,许多错误可以在测试开始之前排除。
1052 |
1053 | · 测试开始于构件层,然后向外“延申”到整个基于计算机系统的继承中。
1054 |
1055 | · 不同的测试技术适用于不同的软件工程方法和不同的时间点。
1056 |
1057 | · 测试由软件开发人员和(对大型项目而言)独立的测试组执行。
1058 |
1059 | · 测试和调试是不同的活动,但任何测试策略都必须包括调试。
1060 |
1061 | 策略:
1062 |
1063 | 1. 测试不能取代评审
1064 |
1065 | 据说,检验项目质量的标准之一:质量 = 项目review时骂的次数 / 项目review时间。
1066 |
1067 | 被骂的次数越多,评审耗时越短,质量越可靠。
1068 |
1069 | 2. 谁来测试?
1070 |
1071 | (1) 开发者:对系统很了解,但由于急于交付,测试比较“gentle”
1072 |
1073 | (2) 独立测试人员:虽然对系统没有特别了解,但为了质量会尝试尽可能找出所有问题
1074 |
1075 | 3. 测试什么时候开始?
1076 |
1077 | 软件测试**不是在编码阶段**才开始,软件测试从**项目确立**时就开始了,主要经过以下环节:
1078 |
1079 | 需求分析→测试计划→测试设计→测试环境搭建→测试执行→测试记录。
1080 |
1081 | 4. 测试流程
1082 |
1083 | 从模块由小到大进行测试。
1084 |
1085 | 
1086 |
1087 | 【传统软件的测试策略:单元测试】(参考书P251-253)
1088 |
1089 | 目的:验证开发人员编写的模块或单元是否符合预期。
1090 |
1091 | 单元测试问题:
1092 |
1093 | · 说明不正确或不一致;
1094 |
1095 | · 初始化或缺省值错误;
1096 |
1097 | · 数据类型不相容;
1098 |
1099 | · 上溢、下溢或地址错误等。
1100 |
1101 | · 全局数据与模块的相互影响。
1102 |
1103 | 单元测试环境:
1104 |
1105 | 
1106 |
1107 | 驱动模块:用来模拟被测模块的上级调用模块。
1108 |
1109 | 桩模块:模拟被测试模块所调用的模块,返回被测模块所需的信息。
1110 |
1111 | 【传统软件的测试策略:集成测试】
1112 |
1113 | 通过单元测试的模块集成在一起,仍然可能无法正常工作,因为模块相互调用时仍然可能出错。
1114 |
1115 | 集成测试:旨在发现与调用接口相关的错误。
1116 |
1117 | **自顶向下集成**:
1118 |
1119 | 
1120 |
1121 | **自底向上集成**:
1122 |
1123 | 
1124 |
1125 | **三明治集成**:
1126 |
1127 | 
1128 |
1129 | **回归测试:**
1130 |
1131 | 集成测试中每加入新的模块,都会导致软件发生变更,这些变更可能使得原本正常工作的模块产生问题。
1132 |
1133 | 回归测试就是重新执行已经测试过的某些子集,以确保变更不会引入新的或额外的错误。
1134 |
1135 | 回归测试可以复用之前的测试用例和测试脚本。
1136 |
1137 | 可以使用自动测试工具提高回归测试效率。
1138 |
1139 | 捕获-回放工具(如WinRunner)能够捕获在测试过程中传递给软件的输入数据,生成执行的脚本,并且在回归测试中,重复执行该过程。
1140 |
1141 | **冒烟测试:**
1142 |
1143 | 冒烟测试也是一种特殊的集成测试,指完成一个新版本的集成、构建后,对该版本最基本的功能进行测试,目的是**保证基本的功能和流程能走通**。
1144 |
1145 | 如果通不过,则打回开发部门重新开发;如果通过测试,才会进行下一步的测试(功能测试,集成测试,系统测试等)。
1146 |
1147 | 例如,冒烟测试内容:
1148 |
1149 | 检查被测系统或模块能否正常启动和退出;
1150 |
1151 | 数据库能否正常连接,控件能否正常加载;
1152 |
1153 | 是否存在严重错误或者数据严重丢失等。
1154 |
1155 | 【面向对象的单元与集成测试】
1156 |
1157 | 类测试相当于单元测试。我们将测试该类内的操作。
1158 |
1159 | 集成采用了三种不同的策略。传统的自顶向下或自底向上的集成测试策略在面向对象软
1160 |
1161 | 件的集成测试中无意义。
1162 |
1163 | 1. 基于类之间的协作关系进行集成。
1164 | 2. 基于线程的测试—集成了响应一个输入或事件所需的类集。
1165 | 3. 基于使用的测试——从测试独立类开始,然后测试使用独立类的依赖类。
1166 |
1167 | 【确认测试】
1168 |
1169 | 确认测试:检验所开发的软件是否满足需求规格说明中的各种功能和性能需求,以及软件配置是否完全和正确。
1170 |
1171 | α测试是由用户在开发环境下进行的测试;β测试是由软件的多个用户在实际使用环境下进行的测试。可归为确认测试,产品正式发布前的测试,由用户主导。
1172 |
1173 | 【系统测试】
1174 |
1175 | 系统测试是将软件与其它系统部分(如外部系统,硬件设计等)结合进行的整体测试。其关注非功能性需求。
1176 |
1177 | 系统测试主要包括一下几种类型:
1178 |
1179 | 1. 恢复测试:有些系统失效后必须在规定时间段内被恢复,否则将会导致严重的经济损失。关注导致软件运行失败的各种条件,并验证其恢复过程能否正确执行。(如:系统供电故障后的恢复、日志处理恢复能力、程序运行崩溃后恢复能力)
1180 | 2. 安全测试:检测系统对非法侵入的防范能力。如口令截取或破译等。
1181 |
1182 | IBM AppScan,包括众多的安全扫描产品,如针对源代码扫描的AppScan source edition, 针对WEB应用扫描的AppScan standard edition,进行安全管理和汇总整合的AppScan enterprise Editio。
1183 |
1184 | 3. 压力测试
1185 |
1186 | 压力测试目的是为了发现系统能支持的最大负载等,前提是系统性能处在可以接受的范围内,如规定的3秒钟内响应。
1187 |
1188 | 压力测试通过不断对系统增加压力,确定一个系统的瓶颈或者不能接受的性能点,从而获得系统最大负载能力。
1189 |
1190 | 压力测试工具WebRunner:RadView公司推出的一个性能测试和分析工具,它让web应用开发者自动执行压力测试;webload通过模拟真实用户的操作,生成压力负载来测试web的性能。
1191 |
1192 | 4. 性能测试
1193 |
1194 | 通过测试确定系统(常态下)运行时的性能表现,如运行速度、响应时间、占有系统资源等方面的系统数据。
1195 |
1196 | 性能测试工具LoadRunner:它能预测系统行为,优化性能。它通过模拟实际用户的操作行为和实行实时性能监测。
1197 |
1198 | 【软件调试】
1199 |
1200 | 调试目标:定位错误发生的原因和位置。
1201 |
1202 | 调试技巧:
1203 |
1204 | (1)暴力法:一种比较简单,但效率较低的方法。包括:
1205 |
1206 | ① 主存信息输出法。
1207 |
1208 | 将计算机存储器和寄存器的全部内容打印出来。
1209 |
1210 | ② 关键部分设置打印语句。
1211 |
1212 | ③ 使用自动调试工具。
1213 |
1214 | (2)反向跟踪:是从可能的错误征兆处逐步向回追溯,直到找准错误,纠正为止。
1215 |
1216 | (3)归纳法:从线索(错误征兆出发),通过分析这些线索之间的关系找出故障。主要有4步:
1217 |
1218 | ① 收集数据。列出已知的测试用例和执行结果。
1219 |
1220 | ② 整理分析数据,以便发现规律,即“什么条件下出现错误,什么条件下不出现错误”。如:字符计数程序对“输入型”文本正确,对“拷贝型”文本错误。
1221 |
1222 | ③ 导出假设。分析线索之间的关系,提出关于错误的一个或多个假设。
1223 |
1224 | ④ 证明假设。证实提出的假设是导致错误发生的真正原因。
1225 |
1226 | (4)演绎法
1227 |
1228 | ① 设想出所有可能的出错原因;
1229 |
1230 | ② 试图用测试来排除每一个假设的原因,如果测试表明某个假设的原因可能是真的原因,则对数据进行细化以确定位错误。
1231 |
1232 |
1233 |
1234 | 12. 传统应用测试
1235 |
1236 | 【关于测试的两个问题】
1237 |
1238 | 1. 经过测试没有发现错误的软件就一定正确吗?错误。测试只能证明软件是有错的,不能证明软件是没有错误的。
1239 | 2. 可以通过穷举方式测试软件吗?一般不行,因为分支或循环太多会导致所需测试样例的数量呈指数型增长。
1240 |
1241 | 【如何设计好的测试用例?】
1242 |
1243 | 测试的有效性很大程度取决于选取的测试用例。
1244 |
1245 | 一个好的测试有很高的概率找到一个错误的;测试不是冗余的;一个好的测试应该是“最好的品种”。
1246 |
1247 | 【测试用例设计方法】
1248 |
1249 | 黑盒法:测试者把测试对象看作一黑盒子,仅依据程序的功能需求,设计测试用例并推断测试结果。
1250 |
1251 | 白盒法:按照程序内部逻辑结构,设计测试数据并完成测试的一种测试方法。
1252 |
1253 | 【白盒测试】
1254 |
1255 | 该方法把测试对象看做一个透明的盒子,它允许测试人员利用程序内部的逻辑结构及有关信息,设计或选择测试用例。
1256 |
1257 | 目标是使得程序中各元素(如语句、判定)尽可能被覆盖到。
1258 |
1259 | 白盒测试一般在测试过程的早期执行。
1260 |
1261 | 方法:
1262 |
1263 | 1. 语句覆盖:指选择足够的测试用例,使得被测程序中每条语句至少执行一次。是一种比较弱的测试标准。
1264 | 2. 基本路径测试
1265 |
1266 | 如果程序中含有循环结构,完全的路径覆盖是不可能的。
1267 |
1268 | **基本路径法**:在程序控制流图的基础上,通过导出基本可执行路径(注: 不是所有可能路径)集合,从而设计测试用例。
1269 |
1270 | 【重点掌握,见PPT(传统应用测试)】
1271 |
1272 | 3. 控制结构测试
1273 |
1274 | (1) 条件测试:一种测试程序模块中包含的逻辑条件的测试用例设计方法
1275 |
1276 | 设计测试用例确保至少条件C为真为假执行各一次。如果C是复合条件,则同时还要满足每个简单条件至少执行一次。
1277 |
1278 | 
1279 |
1280 | (2) 数据流测试:根据程序中定义的位置和变量的使用情况来选择程序的测试路径
1281 |
1282 | 设计测试用例使得每个变量定义-使用链至少覆盖一次。
1283 |
1284 | 
1285 |
1286 | (3) 循环测试:分为简单循环、嵌套循环、串接循环、非结构化循环。
1287 |
1288 | 对于简单循环,下列测试集可以用于简单循环:
1289 |
1290 |
1291 |
1292 | 
1293 |
1294 | 【黑盒测试】
1295 |
1296 | 这种方法是把测试对象看做一个黑盒子,测试人员完全不考虑程序内部的逻辑结构,只依据需求规格说明书,检查程序的功能是否符合它的功能说明。
1297 |
1298 | 黑盒测试一般在应用于测试的后期阶段。
1299 |
1300 | 1. 等价类划分
1301 |
1302 | 等价类划分法:将程序的输入域划分为若干个数据类,从中生成测试用例。
1303 |
1304 | 假定:对等价类中的代表值测试就等于对这一类值的测试。
1305 |
1306 | 
1307 |
1308 | 基本步骤: (1)确定等价类;(2)为等价类选择一个测试用例
1309 |
1310 | 例子:某城市的电话号码由3部分组成。假定被测程序能接收一切符合下述规定的电话号码,拒绝所有不符合规定的电话号码。
1311 |
1312 | 地区码:空白或3位数字;
1313 |
1314 | 前缀:非‘0’或‘1’开头的3位数字;
1315 |
1316 | 后缀:4位数字。
1317 |
1318 | (1) 确定等价类
1319 |
1320 | 
1321 |
1322 | (2) 设计测试用例
1323 |
1324 | 设计测试用例,使其尽可能多的覆盖到尚未覆盖的有效等价类
1325 |
1326 | 设计测试用例,使其只覆盖一个尚未被覆盖的无效等价类
1327 |
1328 | 
1329 |
1330 | 2. 边界值分析
1331 |
1332 | (1) 边界值应该尽可能选择等于边界,略小于边界,略大于边界的值
1333 |
1334 | (2) 边界值法可与等价类划分法结合,作为对其的一种补充。
1335 |
1336 | 例子: 一个输入文件应该包含1~255条记录,则应用边界值分析法设计测试用例。
1337 |
1338 | 可以用4组数据进行测试:
1339 |
1340 | 含1条记录的文件
1341 |
1342 | 含2条记录的文件
1343 |
1344 | 含254条记录的文件
1345 |
1346 | 含255条记录的文件
1347 |
1348 | 3. 正交阵列测试
1349 |
1350 | (1) 正交数组测试通过挑选适量的、有代表性的点进行试验,能有效地减少测试用例数,节约测试成本。
1351 |
1352 | (2) 该方法由日本口玄一博士提出并导出正交数组,从而使得测试数据具有“均匀分散、整齐可比”的特点。
1353 |
1354 | 例子:某大学刚考完某门课程,想通过“性别”、“班级”和“成绩”这3个查询条件对这门课程的成绩查询,查询条件包括:
1355 |
1356 | “性别”=“男,女”
1357 |
1358 | “班级”=“1班,2班”
1359 |
1360 | “成绩”=“及格,不及格”
1361 |
1362 | 一般需要设计2X2X2=8个测试用例。
1363 |
1364 | 
1365 |
1366 | 【基于模型的测试】
1367 |
1368 | 1. 分析软件的现有行为模型或创建一个。
1369 | 2. 穿越行为模型,并指定迫使软件从状态转换到另一个状态的输入。
1370 |
1371 | (1) 输入将触发将导致转换发生的事件。
1372 |
1373 | 3. 回顾行为模型,并注意到软件从状态过渡到状态时的预期输出。
1374 | 4. 执行测试用例。
1375 |
1376 | 
1377 |
1378 |
1379 |
1380 |
1381 |
1382 | ### 例题
1383 |
1384 | 1. 过程框架至少定义了五种框架活动分别是( )。
1385 |
1386 | 2. 类-职责-协作者模型又称为( )建模。
1387 |
1388 | 3. 软件工程层次图中,支持软件工程的根基在于( )。
1389 | 4. 填空题:在UML模型中,( )图用于描述系统与外部系统及用户之间的交互;( )图用于按时间顺序描述对象间的交互。
1390 | 5. 基于大量构件共同使用一个全局变量时所发生的耦合称为( )耦合。
1391 | 6. 华为云(DevCloud)是一个一站式、全流程、安全可信的( )平台。
1392 | 7. 华为云(DevCloud)敏捷开发的“看板”核心元素包括分层、( )、列、价值流、在制品(WIP)、风险&瓶颈、拉动式开发等核心元素。
1393 | 8. 顺序图(时序图)的构成元素主要包括: ( )、生命线、激活和( )。
1394 | 9. 汽车类与方向盘类之间的关系是( )关系。
1395 |
1396 | **重庆大学《软件工程》课程试卷(A 卷) 2019 — 2020 学年 第 2 学期**
1397 |
1398 | 1. FURPS 质量属性分别是指:功能性、( )、( )、性能和( )。
1399 |
1400 | 2. 在基于类的需求建模中,类可分为: ( )、( )和( )。
1401 |
1402 | 3. 需求工程是指( )。
1403 |
1404 | 4. 软件质量的成本包括:( )、( )和( )。
1405 |
1406 | 5. 一个通用的软件工程过程框架通常包含 沟通、( )、建模、( ) 和( )。
1407 |
1408 | 6. 开闭原则是指模块或构件应该对外延具有开放性,对( )具有封 闭性。
1409 |
1410 | 7. 需求模型必须实现的三个主要目标有: ( )、( )、定义在软 件完成后可以被确认的一组需求
1411 |
1412 | 8. OMG 定义构件是:系统中( )、可部署的和可替换的部件。
1413 |
1414 | 9. 用户满意度=合格的产品+( ) +( ) 10.CRC 卡中 CRC 的中文全称( )。
1415 |
1416 | > **参考答案**
1417 | >
1418 | > 1. (易用性)、(可靠性)、(可支持性)
1419 | > 2. (实体类)、(边界类)、(控制类)
1420 | > 3. (致力于不断理解需求的大量任务和技术)
1421 | > 4. (预防成本)、(评估成本)、(失效成本)
1422 | > 5. (策划)、(构建)、(部署)
1423 | > 6. ( 修改 )
1424 | > 7. (描述客户需要什么)、(为软件设计奠定基础)
1425 | > 8. (模块化的)
1426 | > 9. (好的质量)、(按预算和进度安排交付)
1427 | > 10. (类-职责-协作者)
1428 |
1429 | ## 二、单选题 (10个,每个2分,共20分)
1430 |
1431 | 看填空题的索引
1432 |
1433 | ### 需要理解的内容
1434 |
1435 | 1. 如何判断什么时候该用什么样的过程模型。
1436 |
1437 |
1438 |
1439 |
1440 |
1441 |
1442 |
1443 | ### 例题
1444 |
1445 | 1. 某软件公司欲开发一个基于Web的考勤管理系统。在项目初期,客户对系统的基本功能、表现形式等要求并不明确,在这种情况下,采用( )开发方法比较合适。
1446 |
1447 | A、瀑布模型
1448 |
1449 | B、形式化
1450 |
1451 | C、结构化
1452 |
1453 | D、极限编程
1454 |
1455 | 2. 在类图中下列哪个符号表示的是泛化关系是( )
1456 |
1457 | A、实线实心箭头
1458 |
1459 | B、虚线实心箭头
1460 |
1461 | C、实线空心箭头
1462 |
1463 | D、实线空心菱形
1464 |
1465 | 3. 在设计模式中“依赖于抽象,而非具体的实现”指的是( )
1466 |
1467 | A、开闭原则
1468 |
1469 | B、Liskov替换原则
1470 |
1471 | C、依赖倒置原则
1472 |
1473 | D、接口分离原则
1474 |
1475 | 4. 软件质量是一个重要的问题贯穿了软件的( )
1476 |
1477 | A、生存周期
1478 |
1479 | B、设计阶段
1480 |
1481 | C、编码阶段
1482 |
1483 | D、测试阶段
1484 |
1485 | ## 三、判断题 (5个,每个2分,共10分)
1486 |
1487 |
1488 |
1489 |
1490 |
1491 | ### 例题
1492 |
1493 | 1. 软件工程是一种结构化的技术。( )
1494 | 2. 每个应用系统只能使用一种体系结构风格。( )
1495 | 3.
1496 |
1497 |
1498 |
1499 |
1500 |
1501 | ## 四、简答题 (4个,每个5分,共20分)
1502 |
1503 | 看填空题的索引即可
1504 |
1505 |
1506 |
1507 | ### 例题
1508 |
1509 | 1. 简述David Hooker提出的7个关注软件工程整体实践的原则。(要点+一两句的补充说明)。
1510 | 2. 简述模块独立性的两个定量准则及模块独立性的好处。
1511 |
1512 |
1513 |
1514 |
1515 |
1516 | ## 五、应用分析题(2个,每个15分,共30分)
1517 |
1518 | ### (一)需求建模
1519 |
1520 | 1. 结构化分析——数据流图
1521 |
1522 | https://www.bilibili.com/video/BV1Jt411d7nR
1523 |
1524 |
1525 |
1526 | > #### 例题
1527 | >
1528 | > 某时装邮购提供商拟开发订单处理系统,用于处理客户通过电话、传真、邮件或Web站点所下订单。其主要功能如下:
1529 | >
1530 | > (1)增加客户记录。将新客户信息添加到客户文件,并分配一个客户号以备后续使用。
1531 | >
1532 | > (2)查询商品信息。接收客户提交商品信息请求,从商品文件中查询商品的价格和可订购数量等商品信息,返回给客户。
1533 | >
1534 | > (3)增加订单记录。根据客户的订购请求及该客户记录的相关信息,产生订单并添加到订单文件中。
1535 | >
1536 | > (4)产生配货单。根据订单记录产生配货单,并将配货单发送给仓库进行备货;备好货后,发送备货就绪通知。如果现货不足,则需向供应商订货。
1537 | >
1538 | > (5)准备发货单。从订单文件中获取订单记录,从客户文件中获取客户记录,并产生发货单。
1539 | >
1540 | > (6)发货。当收到仓库发送的备货就绪通知后,根据发货单给客户发货;产生装运单并发送给客户。
1541 | >
1542 | > (7)创建客户账单。根据订单文件中的订单记录和客户文件中的客户记录,产生并发送客户账单,同时更新商品文件中的商品数量和订单文件中的订单状态。
1543 | >
1544 | > (8)产生应收账户。根据客户记录和订单文件中的订单信息,产生并发送给财务部门应收账户报表。
1545 | >
1546 | > 问题:
1547 | >
1548 | > 1.使用说明中的词语,给出图1-1中的实体E1~E3的名称。
1549 | >
1550 | > 2.使用说明中的词语,给出图1-2中的数据存储D1~D3的名称。
1551 | >
1552 | > 3.(1)给出图1-2中处理(加工)P1和P2的名称及其相应的输入、输出流。(2)除加工P1和P2的输入输出流外,图1-2还缺失了1条数据流,请给出其起点和终点。
1553 | >
1554 | > 
1555 | >
1556 | > 
1557 |
1558 |
1559 |
1560 | 2. 面向对象分析——类图
1561 |
1562 | https://www.bilibili.com/video/BV1Jt411d7PR
1563 |
1564 |
1565 |
1566 | > #### 例题
1567 | >
1568 | > 某网上药店允许顾客凭借医生开具的处方,通过网络在该药店购买处方上的药品。该网上药店的基本功能描述如下:
1569 | >
1570 | > (1)注册。顾客在买药之前,必须先在网上药店注册。注册过程中需填写顾客资料以及付款方式(信用卡或者支付宝账户)。此外顾客必须与药店签订一份授权协议书,授权药店可以向其医生确认处方的真伪。
1571 | >
1572 | > (2)登录。已经注册的顾客可以登录到网上药房购买药品。如果是没有注册的顾客,系统将拒绝其登录。
1573 | >
1574 | > (3)录入及提交处方。登录成功后,顾客按照“处方录入界面”显示的信息,填写开具处方的医生的信息以及处方,上的药品信息。填写完成后,提交该处方。
1575 | >
1576 | > (4)验证**处方**。对于**已经提交的处方**(系统将其状态设置为“处方已提交”),其验证过程为:
1577 | >
1578 | > ①**核实医生信息**。如果医生信息不正确,该处方的状态被设置为“**医生信息无效**”,并取消这个处方的购买请求;如果医生信息是正确的,系统给该医生发送处方确认请求,并将处方状态修改为“审核中”。
1579 | >
1580 | > ②如果医生回复处方无效,系统取消处方,并将处方状态设置为**“无效处方**”。如果医生没有在7天内给出确认答复,系统也会取消处方,并将处方状态设置为“**无法审核**”。
1581 | >
1582 | > ③如果医生在7天内给出了确认答复,该处方的状态被修改为“准许付款”。系统取消所有未通过验证的处方,并自动发送一封电子邮件给顾客,通知顾客处方被取消以及取消的原因。
1583 | >
1584 | > (5)对于通过验证的处方,系统自动计算药品的价格并邮寄药品给已经付款的顾客。该网上药店:采用面向对象方法开发,使用UML进行建模。系统的类图如图3-1所示。
1585 | >
1586 | > 问题:
1587 | >
1588 | > 1. 根据说明中的描述,给出图3-1中缺少的C1~C5所对应的类名。
1589 | > 2. 图3-2给出了“处方”的部分状态图。根据说明中的描述,给出图3-2中缺少的S1 ~S4所对应的状态名以及(7)~(10)处所对应的迁移(transition) 名。
1590 | >
1591 | > 
1592 | >
1593 | > 
1594 |
1595 | 3. 面向对象分析——用例图
1596 |
1597 | 【例】
1598 |
1599 |
1600 |
1601 |
1602 |
1603 | > #### 例题
1604 | >
1605 | > 阅读下列说明和图,完善用例图A1、A2及U1~U3。
1606 | >
1607 | > 某网上购物平台的主要功能如下:
1608 | >
1609 | > (1)**创建订单**。**顾客**(Customer)在线创建订单(Order),主要操作是向订单中添加项目,从订单中删除项目。订单中应列出所订购的商品(Product)及其数量(Quantities)
1610 | >
1611 | > (2)提交订单。订单通过网络提交。在提交订单时,顾客需要提供其姓名(name)、收货地址(address)、付款方式(Payment)(预付卡、现金或信用卡)。
1612 | >
1613 | > (3)处理订单。**订单处理人员**接收来自系统的订单,根据订单内容,安排配货,制定送货计划。
1614 | >
1615 | > (4)派单。订单处理人员将已配好货的订单转交给派送人员。
1616 | >
1617 | > (5)**送货**/**收货**。派送人员将货物送到顾客指定的收货地址。顾客需在运货单上签收。签收后的运货单最终需交还给订单处理人员。
1618 | >
1619 | > (6)收货确认。当订单处理人员收到签收过的运货单后,会和顾客进行一次再确认。
1620 | >
1621 | > 
1622 |
1623 |
1624 |
1625 | 4. 面向对象分析——状态图
1626 |
1627 | 【例】
1628 |
1629 |
1630 |
1631 |
1632 |
1633 | 5. 面向对象分析——时序图
1634 |
1635 | 【例】
1636 |
1637 |
1638 |
1639 |
1640 |
1641 |
1642 |
1643 | ### (二)软件测试
1644 |
1645 | #### 2.1 测试用例的设计——白盒法
1646 |
1647 | ##### 2.1.1 控制结构测试
1648 |
1649 | 【软件工程——11-白盒测试】 https://www.bilibili.com/video/BV1wG41137Hs/?share_source=copy_web&vd_source=7ba452d8ee6f8b8a4b8ef831bf573bda
1650 |
1651 | 【白盒测试so easy!】 https://www.bilibili.com/video/BV1zL4y1A785/?share_source=copy_web&vd_source=7ba452d8ee6f8b8a4b8ef831bf573bda
1652 |
1653 | ##### 2.1.2 基本路径测试
1654 |
1655 | 【软件工程——11-基本路径测试法】 https://www.bilibili.com/video/BV13V4y1g7tc/?share_source=copy_web&vd_source=7ba452d8ee6f8b8a4b8ef831bf573bda
1656 |
1657 | #### 2.2 测试用例的设计——黑盒法
1658 |
1659 | ##### 2.2.1 等价类划分法
1660 |
1661 | 【软件工程——11-等价类划分.mp4】 https://www.bilibili.com/video/BV1MT411M7EC/?share_source=copy_web&vd_source=7ba452d8ee6f8b8a4b8ef831bf573bda
1662 |
1663 | ##### 2.2.2 边界值分析法
1664 |
1665 | 【软件工程——11-边界值及错误推测法】 https://www.bilibili.com/video/BV1nV4y1g7ig/?share_source=copy_web&vd_source=7ba452d8ee6f8b8a4b8ef831bf573bda
--------------------------------------------------------------------------------
/docs/index.md:
--------------------------------------------------------------------------------
1 | Hello world !!
--------------------------------------------------------------------------------
/mkdocs.yml:
--------------------------------------------------------------------------------
1 | site_name: Mine_qihang's Docs
2 | theme:
3 | name: "material"
4 | features:
5 | #- navigation.instant # 点击内部链接时,不用全部刷新页面
6 | - navigation.tracking # 在url中使用标题定位锚点
7 | - navigation.tabs # 顶部显示导航顶层nav(也就是第一个节点)
8 | - navigation.tabs.sticky # 滚动是隐藏顶部nav,需要配合navigation.tabs使用
9 | - navigation.sections # nav节点缩进
10 | - navigation.expand # 不折叠左侧nav节点
11 | - navigation.indexes # 指定节点index pages ,跟instant不兼容
12 | - toc.integrate # 右侧生产目录
13 | - navigation.top # 一键回顶部
14 | # plugins:
15 | # - search:
16 | # lang: jp
17 | markdown_extensions:
18 | - pymdownx.highlight # code hilight
19 | - pymdownx.superfences
20 | - pymdownx.arithmatex:
21 | generic: true
22 | extra_javascript:
23 | - javascripts/config.js
24 | - https://polyfill.io/v3/polyfill.min.js?features=es6
25 | - https://cdn.jsdelivr.net/npm/mathjax@3/es5/tex-mml-chtml.js
26 | nav:
27 | - 计算机系统结构:
28 | - Introduction: Architecture/chapter1.md
29 | - Principles of Quantitative Analysis; MIPS: Architecture/chapter2.md
30 | - Pipelining, Hazards, Implementation Issues: Architecture/chapter3.md
31 | - Instruction-Level Parallelism (ILP), Tomasulo: Architecture/chapter4.md
32 | - Memory-Hierarchy Design, Cache Optimization: Architecture/chapter5.md
33 | - ILP; Branch Prediction, Superscalars: Architecture/chapter6.md
34 | - Memory Hierarchy Design, Virtual Memory: Architecture/chapter7.md
35 | - 软件工程:
36 | - 软工期末考试: SoftwareEngineering/软工期末考试.md
37 | - 软工应用分析题: SoftwareEngineering/软工应用分析题.md
38 | - 计算机网络:
39 | - 第一次作业: ComputerNetwork/《计算机网络》第一次作业.md
40 | - 第二章作业: ComputerNetwork/《计算机网络》第二章作业.md
41 | - 第三章作业: ComputerNetwork/《计算机网络》第三章作业.md
42 | - 第四章作业: ComputerNetwork/《计算机网络》第四章作业.md
43 | - 第五章作业: ComputerNetwork/《计算机网络》第五章作业.md
44 | - 第六章作业: ComputerNetwork/《计算机网络》第六章作业.md
45 | - 第九章作业: ComputerNetwork/《计算机网络》第九章作业.md
46 | - 操作系统原理: OperatingSystem/index.md
47 | - 机器学习基础:
48 | - 第一章作业: MachineLearning/第一章作业.md
49 | - 第二章作业: MachineLearning/第二章作业.md
50 | - 第三章作业: MachineLearning/第三章作业.md
51 | - 第四章作业: MachineLearning/第四章作业.md
52 | - 第五章作业: MachineLearning/第五章作业.md
53 | - 第六章作业: MachineLearning/第六章作业.md
54 | - 第七章作业: MachineLearning/第七章作业.md
55 | - 第八章作业: MachineLearning/第八章作业.md
56 | - 第九章作业: MachineLearning/第九章作业.md
57 | - 自然语言处理: index.md
58 | - 专业基本能力测试: ProfessionalBasicAptitudeTest/index.md
--------------------------------------------------------------------------------