├── leetcode
├── README.md
├── 48 Rotate Image.cpp
├── 238 Product of Array Except Self.cpp
├── 142 Linked List Cycle II.cpp
├── 852 Peak Index in a Mountain Array.cpp
├── 75 Sort Colors.cpp
├── 54 Spiral Matrix.cpp
├── 2 Add Two Numbers.cpp
├── 442 Find All Duplicates in an Array.cpp
├── 494 Target Sum.cpp
├── 16 3Sum Closest.cpp
├── 287 Find the Duplicate Number.cpp
├── 1456 Maximum Number of Vowels in a Substring of Given Length.cpp
└── 73 Set Matrix Zeroes.cpp
├── 07_Disjoint_Sets
├── disjoint_sets_using_arrays.cpp
└── README.md
├── Algorithms
├── 5_Miscellaneous
│ ├── README.md
│ ├── ministry.c
│ ├── fibonacci.cpp
│ └── kadanes.cpp
├── 3_Dynamic_Programming
│ ├── Sliding Window
│ │ └── README.md
│ ├── longest_common_sequence.cpp
│ ├── coin_change.cpp
│ ├── knapsack_limited.cpp
│ ├── optimal_alignment.cpp
│ ├── substring_sum.cpp
│ ├── placing_parentheses.cpp
│ └── Readme.md
├── 2_Divide_and_Conquer
│ ├── Readme.md
│ ├── polynomial_multiplication_karatsuba.cpp
│ ├── polynomial_multiplication_naive.cpp
│ └── counting_inversions.cpp
├── 1_Greedy_Algorithms
│ ├── huffman.cpp
│ └── Readme.md
├── 0_Recursion
│ ├── test.c
│ ├── pallindrome.cpp
│ ├── tower_of_hanoi.cpp
│ └── README.md
└── 4_Sorting
│ ├── selection_sort.cpp
│ ├── count_sort.cpp
│ ├── comb_sort.cpp
│ ├── merge_sort.cpp
│ ├── quick_sort.cpp
│ ├── randomized_quick_sort.cpp
│ ├── Readme.md
│ └── heap_sort.cpp
├── assets
├── arrays.png
├── bottom-up.png
├── memoization.png
├── output_10_0.png
├── output_12_0.png
├── output_15_0.png
├── output_18_0.png
├── output_20_0.png
├── output_22_0.png
├── output_24_0.png
├── output_26_0.png
├── output_28_0.png
├── output_30_0.png
├── output_32_0.png
├── output_34_0.png
├── output_36_0.png
├── output_38_0.png
├── output_5_0.png
├── output_7_0.png
├── heap_example.png
├── linked-lists.png
├── heap_properties.png
├── amortized_analysis.png
├── bankers_amortized.png
├── Graph_Representations.png
├── aggregate_amortized.png
├── djikstras intuition.png
├── physicist_amortized_1.png
├── physicist_amortized_2.png
├── physicist_amortized_3.png
├── physicist_amortized_4.png
└── Floyd Cycle Detection.jpeg
├── 03_Queues
├── Queue_using_arrays
│ ├── circular_queue.cpp
│ ├── readme.md
│ ├── Queue_using_two_pointer.cpp
│ └── Queue_using_one_pointer.cpp
├── Miscellaneous
│ ├── readme.md
│ └── Queue_using_2_stacks.cpp
├── Queue_using_Linked_list
│ ├── readme.md
│ └── simple_queue.cpp
└── readme.md
├── v2
└── Graphs
│ └── README.md
├── 02_Stack
├── Miscellaneous
│ ├── README.md
│ └── Balancing_brackets.cpp
├── README.md
├── stack.cpp
└── minimum_element.cpp
├── hanoi.cpp
├── LICENSE
├── 09_Graphs
├── djikstras.cpp
├── bellman-ford.cpp
├── adj_matrix.cpp
├── topological_sort.cpp
├── adj_list.cpp
├── dag.cpp
├── dfs.cpp
├── bfs.cpp
└── README.md
├── 06_Priority_Queues_and_Heaps
├── README.md
└── max_heap.cpp
├── 04_Linked List
├── linked_list.cpp
├── readme.md
└── floyd_cycle_detection_algorithm.cpp
├── 01_Arrays
├── dynamic_array.c
└── README.md
├── 08_Hashing
├── hashmap.c
└── README.md
├── 05_Trees
├── README.md
├── tree_traversal.cpp
└── avl.cpp
└── Data Structures
├── Arrays
└── README.md
└── Linked Lists
├── floyd_cycle_detection_algorithm.cpp
└── README.md
/leetcode/README.md:
--------------------------------------------------------------------------------
1 |
--------------------------------------------------------------------------------
/07_Disjoint_Sets/disjoint_sets_using_arrays.cpp:
--------------------------------------------------------------------------------
1 |
--------------------------------------------------------------------------------
/07_Disjoint_Sets/README.md:
--------------------------------------------------------------------------------
1 | ## Disjoint Sets
2 |
--------------------------------------------------------------------------------
/Algorithms/5_Miscellaneous/README.md:
--------------------------------------------------------------------------------
1 | ## Miscellaneous Algorithms
2 |
3 |
--------------------------------------------------------------------------------
/assets/arrays.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/PritK99/data-structures-and-algorithms/HEAD/assets/arrays.png
--------------------------------------------------------------------------------
/assets/bottom-up.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/PritK99/data-structures-and-algorithms/HEAD/assets/bottom-up.png
--------------------------------------------------------------------------------
/assets/memoization.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/PritK99/data-structures-and-algorithms/HEAD/assets/memoization.png
--------------------------------------------------------------------------------
/assets/output_10_0.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/PritK99/data-structures-and-algorithms/HEAD/assets/output_10_0.png
--------------------------------------------------------------------------------
/assets/output_12_0.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/PritK99/data-structures-and-algorithms/HEAD/assets/output_12_0.png
--------------------------------------------------------------------------------
/assets/output_15_0.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/PritK99/data-structures-and-algorithms/HEAD/assets/output_15_0.png
--------------------------------------------------------------------------------
/assets/output_18_0.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/PritK99/data-structures-and-algorithms/HEAD/assets/output_18_0.png
--------------------------------------------------------------------------------
/assets/output_20_0.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/PritK99/data-structures-and-algorithms/HEAD/assets/output_20_0.png
--------------------------------------------------------------------------------
/assets/output_22_0.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/PritK99/data-structures-and-algorithms/HEAD/assets/output_22_0.png
--------------------------------------------------------------------------------
/assets/output_24_0.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/PritK99/data-structures-and-algorithms/HEAD/assets/output_24_0.png
--------------------------------------------------------------------------------
/assets/output_26_0.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/PritK99/data-structures-and-algorithms/HEAD/assets/output_26_0.png
--------------------------------------------------------------------------------
/assets/output_28_0.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/PritK99/data-structures-and-algorithms/HEAD/assets/output_28_0.png
--------------------------------------------------------------------------------
/assets/output_30_0.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/PritK99/data-structures-and-algorithms/HEAD/assets/output_30_0.png
--------------------------------------------------------------------------------
/assets/output_32_0.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/PritK99/data-structures-and-algorithms/HEAD/assets/output_32_0.png
--------------------------------------------------------------------------------
/assets/output_34_0.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/PritK99/data-structures-and-algorithms/HEAD/assets/output_34_0.png
--------------------------------------------------------------------------------
/assets/output_36_0.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/PritK99/data-structures-and-algorithms/HEAD/assets/output_36_0.png
--------------------------------------------------------------------------------
/assets/output_38_0.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/PritK99/data-structures-and-algorithms/HEAD/assets/output_38_0.png
--------------------------------------------------------------------------------
/assets/output_5_0.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/PritK99/data-structures-and-algorithms/HEAD/assets/output_5_0.png
--------------------------------------------------------------------------------
/assets/output_7_0.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/PritK99/data-structures-and-algorithms/HEAD/assets/output_7_0.png
--------------------------------------------------------------------------------
/assets/heap_example.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/PritK99/data-structures-and-algorithms/HEAD/assets/heap_example.png
--------------------------------------------------------------------------------
/assets/linked-lists.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/PritK99/data-structures-and-algorithms/HEAD/assets/linked-lists.png
--------------------------------------------------------------------------------
/assets/heap_properties.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/PritK99/data-structures-and-algorithms/HEAD/assets/heap_properties.png
--------------------------------------------------------------------------------
/assets/amortized_analysis.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/PritK99/data-structures-and-algorithms/HEAD/assets/amortized_analysis.png
--------------------------------------------------------------------------------
/assets/bankers_amortized.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/PritK99/data-structures-and-algorithms/HEAD/assets/bankers_amortized.png
--------------------------------------------------------------------------------
/assets/Graph_Representations.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/PritK99/data-structures-and-algorithms/HEAD/assets/Graph_Representations.png
--------------------------------------------------------------------------------
/assets/aggregate_amortized.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/PritK99/data-structures-and-algorithms/HEAD/assets/aggregate_amortized.png
--------------------------------------------------------------------------------
/assets/djikstras intuition.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/PritK99/data-structures-and-algorithms/HEAD/assets/djikstras intuition.png
--------------------------------------------------------------------------------
/assets/physicist_amortized_1.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/PritK99/data-structures-and-algorithms/HEAD/assets/physicist_amortized_1.png
--------------------------------------------------------------------------------
/assets/physicist_amortized_2.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/PritK99/data-structures-and-algorithms/HEAD/assets/physicist_amortized_2.png
--------------------------------------------------------------------------------
/assets/physicist_amortized_3.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/PritK99/data-structures-and-algorithms/HEAD/assets/physicist_amortized_3.png
--------------------------------------------------------------------------------
/assets/physicist_amortized_4.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/PritK99/data-structures-and-algorithms/HEAD/assets/physicist_amortized_4.png
--------------------------------------------------------------------------------
/assets/Floyd Cycle Detection.jpeg:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/PritK99/data-structures-and-algorithms/HEAD/assets/Floyd Cycle Detection.jpeg
--------------------------------------------------------------------------------
/03_Queues/Queue_using_arrays/circular_queue.cpp:
--------------------------------------------------------------------------------
1 | #include
2 |
3 | using namespace std;
4 |
5 | int main ()
6 | {
7 | cout << "Hi" ;
8 | }
--------------------------------------------------------------------------------
/v2/Graphs/README.md:
--------------------------------------------------------------------------------
1 | # Graphs
2 |
3 | A graph is a data structure that can be used to define relationships between objects. Formaly, a graph is a collection of vertices (objects) and their edges (relationships).
4 |
5 |
--------------------------------------------------------------------------------
/Algorithms/5_Miscellaneous/ministry.c:
--------------------------------------------------------------------------------
1 | #include
2 |
3 | int q = 500;
4 |
5 | void func(int **p)
6 | {
7 | *p = &q;
8 | }
9 |
10 | int main ()
11 | {
12 | int* p ;
13 | func(&p);
14 | printf("%d", *p);
15 | return 0;
16 | }
--------------------------------------------------------------------------------
/Algorithms/3_Dynamic_Programming/Sliding Window/README.md:
--------------------------------------------------------------------------------
1 | # Sliding Window
2 |
3 | ## Introduction
4 |
5 | Sliding Window is a technique we use to often find a specific subarray from a gicen array. The brute force approach for such problems can be to check all possible subarrays. Sliding window technique offers a dynamic programming approach to the problem. Essentially there is a subset of elements you consider from the array and make decision.
6 |
--------------------------------------------------------------------------------
/Algorithms/2_Divide_and_Conquer/Readme.md:
--------------------------------------------------------------------------------
1 | ## Divide & Conquer
2 |
3 | ## Master Theorem
4 | Master theorem helps us to calculate time complexity for divide and conquer algorithms easily.
5 |
6 | 
7 |
8 | ## List of problems implemented
9 |
10 | * ```counting_inversions.cpp```
11 | * ```polynomial_multiplication_naive.cpp```
12 |
--------------------------------------------------------------------------------
/03_Queues/Miscellaneous/readme.md:
--------------------------------------------------------------------------------
1 | # Miscellaneous Contents
2 |
3 | ## 1) Queue using two stacks
4 | Here, we make use of 2 stacks to implement basic operations of queue such as enqueue and dequeue. In this method, in enqueue operation, the new element is always pushed on stack1. In de-queue operation, if stack2 is empty then all the elements in stack1 are moved to stack2 and finally stack2 is popped. This way we are able to implement FIFO using LIFO property of stacks.
5 |
--------------------------------------------------------------------------------
/Algorithms/1_Greedy_Algorithms/huffman.cpp:
--------------------------------------------------------------------------------
1 | /*******************************************************
2 | @brief Huffman encoding using greedy strategy
3 | *******************************************************/
4 |
5 | #include
6 | #include
7 |
8 | using namespace std;
9 |
10 | void huffman(string s)
11 | {
12 |
13 | }
14 |
15 | int main()
16 | {
17 | string s ;
18 | cout << "Please enter the message: " ;
19 | cin >> s ;
20 | cout << "Sending message to reciever: " ;
21 | huffman(s) ;
22 |
23 | }
--------------------------------------------------------------------------------
/02_Stack/Miscellaneous/README.md:
--------------------------------------------------------------------------------
1 | # Miscellaneous Contents
2 |
3 | ## 1) Bracket Balancing
4 | Here, we are trying to implement a code to test if the brackets are balanced.
5 |
6 | This code not only inform the user that there is an error in the usage of brackets, but also point to the exact place in the code with the problematic bracket.
7 | First priority is to find the first unmatched closing bracket which either doesn’t have an opening bracket before it. Apart from the brackets, code can contain big and small latin letters, digits and punctuation marks.
8 |
--------------------------------------------------------------------------------
/Algorithms/0_Recursion/test.c:
--------------------------------------------------------------------------------
1 | #include
2 | #define N 5
3 |
4 | int update(int arr[], int i) {
5 |
6 | //Base Case
7 | if (i == 0){
8 | return arr[0];
9 | }
10 |
11 | arr[i] = arr[i] + update(arr, i-1);
12 | }
13 |
14 | int main() {
15 | int arr[N];
16 |
17 | for (int i = 0; i < N; i++)
18 | {
19 | scanf("%d", &arr[i]);
20 | }
21 |
22 | int i = N-1;
23 | update(arr, i);
24 |
25 | for (int i = 0; i < N; i++)
26 | {
27 | printf("%d ", arr[i]);
28 | }
29 |
30 | return 0;
31 | }
--------------------------------------------------------------------------------
/Algorithms/1_Greedy_Algorithms/Readme.md:
--------------------------------------------------------------------------------
1 | ## Greedy Algorithms
2 |
3 | ## Introduction
4 | A greedy algorithm builds a solution piece by piece and at each step, chooses the most profitable piece. Some of the algorithms based on greedy choice are Kruskal's Algorithm, Prim's Algorithm, Dijkstra's Algorithm.
5 |
6 | A greedy algorithm chooses the local optimals in hope of finding the global global. Greedy algorithms sometimes fail to find the globally optimal solution because they usually do not operate exhaustively on all the data. They can make commitments to certain choices too early, preventing them from finding the best overall solution later.
7 |
8 | ## List of problems implemented
9 |
--------------------------------------------------------------------------------
/leetcode/48 Rotate Image.cpp:
--------------------------------------------------------------------------------
1 | /*
2 | Approach 1: DFS & Backtracking with pruning strategies
3 | Runtime: 0ms
4 | Memory: 7.25MB
5 | Time Complexity: O(m*n*(3^w)), where m*n is dimension of board and w is length of word
6 | */
7 |
8 | class Solution {
9 | public:
10 | void rotate(vector>& matrix) {
11 | for (int i = 0; i < matrix.size(); i++)
12 | {
13 | for(int j = 0; j < matrix.size(); j++)
14 | {
15 | if (i > j)
16 | {
17 | swap(matrix[i][j], matrix[j][i]);
18 | }
19 | }
20 | }
21 |
22 | for (int i = 0; i < matrix.size(); i++)
23 | {
24 | reverse(matrix[i].begin(), matrix[i].end());
25 | }
26 | }
27 | };
--------------------------------------------------------------------------------
/leetcode/238 Product of Array Except Self.cpp:
--------------------------------------------------------------------------------
1 | /*
2 | Approach 1: Maitaining succesor and predecessor product
3 | Runtime: 16ms
4 | Memory: 25.3MB
5 | Time Complexity: O(n)
6 | */
7 |
8 | class Solution {
9 | public:
10 | vector productExceptSelf(vector& nums) {
11 | int n = nums.size();
12 | vector pred (n);
13 | vector succ (n);
14 | pred[0]=1;
15 | succ[n-1]=1;
16 | for (int i = 1; i < n; i++)
17 | {
18 | pred[i] = nums[i-1]*pred[i-1];
19 | }
20 |
21 | for (int i = n-2; i >= 0; i--)
22 | {
23 | succ[i] = nums[i+1]*succ[i+1];
24 | }
25 |
26 | for (int i = 0; i < n; i++)
27 | {
28 | nums[i] = pred[i]*succ[i];
29 | }
30 |
31 | return nums;
32 | }
33 | };
--------------------------------------------------------------------------------
/02_Stack/README.md:
--------------------------------------------------------------------------------
1 | # Stack
2 |
3 | ## Introduction
4 | Stack is a linear data structure which follows LIFO manner i.e. Last-In-First-Out. This means that the element to enter the stack last, will be the first element to be removed.
5 |
6 |  7 |
8 | ## Basic operations on stack
9 | 1) Push: This function adds an element to the top of the Stack.
10 | 2) Pop: This function removes the topmost element from the stack.
11 | 3) IsEmpty: Checks whether the stack is empty.
12 | 4) IsFull: Checks whether the stack is full.
13 |
14 |
7 |
8 | ## Basic operations on stack
9 | 1) Push: This function adds an element to the top of the Stack.
10 | 2) Pop: This function removes the topmost element from the stack.
11 | 3) IsEmpty: Checks whether the stack is empty.
12 | 4) IsFull: Checks whether the stack is full.
13 |
14 | 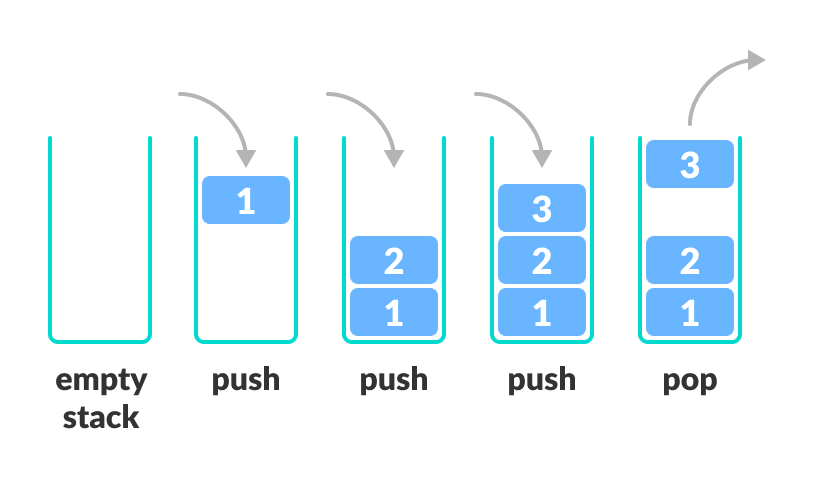 15 |
--------------------------------------------------------------------------------
/hanoi.cpp:
--------------------------------------------------------------------------------
1 | #include
2 | #include
3 |
4 | using namespace std;
5 |
6 | // Defining Source, Destination and Extra Peg
7 | stack S;
8 | stack D;
9 | stack E;
10 |
11 | void shift_upper(stack source, stack dest, stack extra)
12 | {
13 |
14 | }
15 |
16 | void hanoi(stack source, stack dest, stack extra)
17 | {
18 | if (source.empty())
19 | {
20 | cout << "Source Peg is Empty\n";
21 | return;
22 | }
23 | else if (source.size() == 1)
24 | {
25 | int x = source.top();
26 | source.pop();
27 | dest.push(x);
28 | }
29 | else
30 | {
31 | shift_upper(source, extra, dest);
32 | int x = source.top();
33 | source.pop();
34 | dest.push(x);
35 | }
36 | }
37 |
38 | int main()
39 | {
40 |
41 | }
--------------------------------------------------------------------------------
/Algorithms/2_Divide_and_Conquer/polynomial_multiplication_karatsuba.cpp:
--------------------------------------------------------------------------------
1 | #include
2 | #include
3 | #include
4 |
5 | using namespace std;
6 |
7 | int *Multiply(vector &A, vector &B, int left1, int right1, int left2, int right2)
8 | {
9 | if (right1 - left1 == 1 )
10 | {
11 |
12 | }
13 | }
14 |
15 | int main()
16 | {
17 | int n;
18 | cout << "Please enter the maximum degree of polynomial : ";
19 | cin >> n;
20 |
21 | vector A(n + 1), B(n + 1);
22 |
23 | cout << "Please enter coefficients for first polynomial : ";
24 |
25 | for (int i = 0; i < n + 1; i++)
26 | {
27 | cin >> A[i];
28 | }
29 |
30 | cout << "Please enter coefficients for second polynomial : ";
31 |
32 | for (int i = 0; i < n + 1; i++)
33 | {
34 | cin >> B[i];
35 | }
36 |
37 | Multiply(A, B, 0, n, 0, n);
38 |
39 | int C[2 * n + 1] = {0};
40 |
41 | return 0 ;
42 | }
--------------------------------------------------------------------------------
/03_Queues/Queue_using_Linked_list/readme.md:
--------------------------------------------------------------------------------
1 | # Queue using Linked List
2 |
3 | Here , we make use of two pointers called front and rear. Rear pointer is where insertion of element takes place and front is where deletion takes place.
4 | Initially the front pointer points to the first element of queue. During deletion, value is deleted dynamically using delete keyword and the front pointer is incremented. Thus the time complexity is in terms of O(1).
5 | Also , during insertion , a new node is created dynamically using malloc() function rear pointer is made to point at this new node
6 | It is very important to delete the node during dequeue() , since not doing so may lead to memory-leak.
7 | Also, we reset both front and rear pointers in case of queue being empty.
8 |
9 | While using Linked-List , since we deal with heaps and dynamic memory , generally we can create as many nodes we want , till the heap memory gets finished.
10 |
11 | Thus the advantages of using a linked list over array is that both insertion and deletion takes place in O(1) time complexity and the memory is dynamic in nature.
12 |
--------------------------------------------------------------------------------
/LICENSE:
--------------------------------------------------------------------------------
1 | MIT License
2 |
3 | Copyright (c) 2022 PritK99
4 |
5 | Permission is hereby granted, free of charge, to any person obtaining a copy
6 | of this software and associated documentation files (the "Software"), to deal
7 | in the Software without restriction, including without limitation the rights
8 | to use, copy, modify, merge, publish, distribute, sublicense, and/or sell
9 | copies of the Software, and to permit persons to whom the Software is
10 | furnished to do so, subject to the following conditions:
11 |
12 | The above copyright notice and this permission notice shall be included in all
13 | copies or substantial portions of the Software.
14 |
15 | THE SOFTWARE IS PROVIDED "AS IS", WITHOUT WARRANTY OF ANY KIND, EXPRESS OR
16 | IMPLIED, INCLUDING BUT NOT LIMITED TO THE WARRANTIES OF MERCHANTABILITY,
17 | FITNESS FOR A PARTICULAR PURPOSE AND NONINFRINGEMENT. IN NO EVENT SHALL THE
18 | AUTHORS OR COPYRIGHT HOLDERS BE LIABLE FOR ANY CLAIM, DAMAGES OR OTHER
19 | LIABILITY, WHETHER IN AN ACTION OF CONTRACT, TORT OR OTHERWISE, ARISING FROM,
20 | OUT OF OR IN CONNECTION WITH THE SOFTWARE OR THE USE OR OTHER DEALINGS IN THE
21 | SOFTWARE.
22 |
--------------------------------------------------------------------------------
/leetcode/142 Linked List Cycle II.cpp:
--------------------------------------------------------------------------------
1 | /*
2 | Approach 1: DFS & Backtracking with pruning strategies
3 | Runtime: 3ms
4 | Memory: 7.97MB
5 | Time Complexity: O(n), where n is length of linkedlist
6 | */
7 | /**
8 | * Definition for singly-linked list.
9 | * struct ListNode {
10 | * int val;
11 | * ListNode *next;
12 | * ListNode(int x) : val(x), next(NULL) {}
13 | * };
14 | */
15 | class Solution {
16 | public:
17 | ListNode *detectCycle(ListNode *head) {
18 | if (head == NULL)
19 | {
20 | return NULL;
21 | }
22 | ListNode* slow = head;
23 | ListNode* fast = head;
24 |
25 | do
26 | {
27 | if (fast->next != NULL && fast->next->next != NULL)
28 | {
29 | slow = slow->next;
30 | fast = fast->next->next;
31 | }
32 | else
33 | {
34 | return NULL;
35 | }
36 | }
37 | while (slow != fast);
38 |
39 | fast = head;
40 | while (slow != fast)
41 | {
42 | slow = slow->next;
43 | fast = fast->next;
44 | }
45 |
46 | return slow;
47 |
48 | }
49 | };
--------------------------------------------------------------------------------
/Algorithms/0_Recursion/pallindrome.cpp:
--------------------------------------------------------------------------------
1 | /*********************************************************************
2 | @brief Checking if the given string is a pallindrome or not
3 | **********************************************************************/
4 | #include
5 | using namespace std;
6 |
7 | /*
8 | * Function Name: isPallindrome
9 | * Input: Takes the struct as input
10 | * Output: returns boolean true if given string is a pallindrome, else false.
11 | * Logic: This function recursively checks if given string is a pallindrome
12 | * Example Call: isPallindrome(s)
13 | */
14 | bool isPallindrome(string s)
15 | {
16 | int n = s.size() - 1 ;
17 |
18 | // Base Case
19 | if (n == 0 || n == 1)
20 | {
21 | return true ;
22 | }
23 |
24 | // Recursive case
25 | if (s.front() == s.back())
26 | {
27 | return isPallindrome(s.substr(1, n-1)) ;
28 | }
29 | else
30 | {
31 | return false ;
32 | }
33 | }
34 |
35 | int main ()
36 | {
37 | string s ;
38 | cout << "Enter a string: " ;
39 | cin >> s ;
40 | cout << isPallindrome(s) ;
41 |
42 | return 0;
43 | }
44 | /*
45 | Analysis: The above algorithm runs in O(n)
46 | */
--------------------------------------------------------------------------------
/leetcode/852 Peak Index in a Mountain Array.cpp:
--------------------------------------------------------------------------------
1 | /*
2 | Approach 1: Static Sliding Window of size 3
3 | Runtime: 89ms
4 | Memory: 59.95MB
5 | Time Complexity: O(n)
6 | */
7 | class Solution {
8 | public:
9 | int peakIndexInMountainArray(vector& arr) {
10 | int n = arr.size();
11 | for (int i = 1; i < n-1; i++)
12 | {
13 | if (arr[i]>arr[i+1] && arr[i]>arr[i-1])
14 | {
15 | return i;
16 | }
17 | }
18 | return 0;
19 | }
20 | };
21 |
22 | /*
23 | Approach 1: Binary Search
24 | Runtime: 74ms
25 | Memory: 59.97MB
26 | Time Complexity: O(log(n))
27 | */
28 | class Solution {
29 | public:
30 | int peakIndexInMountainArray(vector& arr) {
31 | int start = 0;
32 | int end = arr.size()-1;
33 | int i = 0;
34 |
35 | while(end > start)
36 | {
37 | i = (start+end) / 2;
38 |
39 | if (arr[i]>arr[i+1] && arr[i]>arr[i-1])
40 | {
41 | return i;
42 | }
43 | else if (arr[i]>arr[i-1] && arr[i]
5 | #include
6 | #include
7 |
8 | using namespace std;
9 |
10 | int main()
11 | {
12 | string s;
13 | getline(cin, s);
14 |
15 | int num = 0;
16 | vector v;
17 |
18 | /*Taking input from the user and storing it in a vector of int*/
19 | for (int i = 0; i < s.size(); ++i)
20 | {
21 | if (s[i] == ' ')
22 | v.push_back(num), num = 0;
23 | else
24 | num = num * 10 + (s[i] - '0');
25 | }
26 | v.push_back(num);
27 |
28 | auto iter = v.begin();
29 |
30 | while (iter != v.end())
31 | {
32 | auto min = min_element(iter, v.end());
33 | int min_index = distance(v.begin(), min);
34 |
35 | /*Swapping the first value of remaining array with minimum value present in the remaining array*/
36 | int temp = v[min_index];
37 | v[min_index] = *iter;
38 | *iter = temp;
39 |
40 | iter++;
41 | }
42 |
43 | cout << "The sorted array using selection sort is : ";
44 | for (int i = 0; i < v.size(); i++)
45 | {
46 | cout << v[i] << " ";
47 | }
48 |
49 | return 0;
50 | }
51 | /*
52 | Analysis: The above algorithn runs in O(n^2)
53 | */
--------------------------------------------------------------------------------
/Algorithms/2_Divide_and_Conquer/polynomial_multiplication_naive.cpp:
--------------------------------------------------------------------------------
1 | /******************************************************************
2 | @brief Naive implementation of polynomial multiplication
3 | *******************************************************************/
4 | #include
5 |
6 | using namespace std ;
7 |
8 | int main ()
9 | {
10 | int n ;
11 | cout << "Please enter the maximum degree of polynomial : " ;
12 | cin >> n ;
13 |
14 | int A[n+1] , B[n+1] ;
15 |
16 | cout << "Please enter coefficients for first polynomial : " ;
17 |
18 | for (int i = 0 ; i < n+1 ; i++ )
19 | {
20 | cin >> A[i] ;
21 | }
22 |
23 | cout << "Please enter coefficients for second polynomial : " ;
24 |
25 | for (int i = 0 ; i < n+1 ; i++ )
26 | {
27 | cin >> B[i] ;
28 | }
29 |
30 | int C[2*n+1] = {0} ;
31 |
32 | for (int i = 0 ; i < n+1 ; i ++)
33 | {
34 | for (int j = 0 ; j < n+1 ; j++)
35 | {
36 | C[i+j] = C[i+j] + A[i]*B[j];
37 | }
38 | }
39 |
40 | cout << "The coefficients of final polynomial are: (" ;
41 |
42 | for (int i = 0 ; i < 2*n + 1 ; i++)
43 | {
44 | if (i == 2*n)
45 | {
46 | cout << C[i] ;
47 | continue ;
48 | }
49 | cout << C[i] << ", " ;
50 | }
51 | cout << ")" << endl ;
52 | }
53 | /*
54 | Analysis: The above code runs in O(n^2).
55 | */
--------------------------------------------------------------------------------
/Algorithms/0_Recursion/tower_of_hanoi.cpp:
--------------------------------------------------------------------------------
1 | /***************************************************
2 | @brief Solving the Tower of Hanoi problem
3 | ****************************************************/
4 | #include
5 | #include
6 |
7 | using namespace std;
8 |
9 | /*
10 | * Function Name: towerOfHanoi
11 | * Input: Requires number of disks, source, destination and extra rod
12 | * Logic: Transfers disks from source to destination using extra rod.
13 | * Example Call: towerOfHanoi(n, source, destination, extra) ;
14 | */
15 | void towerOfHanoi(int n, stack &source, stack &destination, stack &extra)
16 | {
17 | if (n <= 0)
18 | {
19 | return;
20 | }
21 |
22 | towerOfHanoi(n - 1, source, extra, destination); // Move n-1 disks to extra rod
23 | int x = source.top();
24 | source.pop();
25 | destination.push(x);
26 | towerOfHanoi(n - 1, extra, destination, source); // For recursively treating the rest n-1 disks
27 | }
28 |
29 | int main()
30 | {
31 | stack source, destination, extra;
32 |
33 | int n = 4;
34 |
35 | // Filling source stack with initial discs where numbers denote size of disk
36 | source.push(4);
37 | source.push(3);
38 | source.push(2);
39 | source.push(1);
40 |
41 | towerOfHanoi(n, source, destination, extra);
42 |
43 | for (int i = 0; i < n; i++)
44 | {
45 | int x = destination.top();
46 | destination.pop();
47 | cout << x << " ";
48 | }
49 |
50 | return 0;
51 | }
52 | /*
53 | Analysis: The above code runs in O(2^n), where n is the number of disks
54 | */
55 |
56 |
--------------------------------------------------------------------------------
/Algorithms/3_Dynamic_Programming/longest_common_sequence.cpp:
--------------------------------------------------------------------------------
1 | #include
2 | #include
3 | #include
4 |
5 | using namespace std;
6 |
7 | /*
8 | * Function Name: LCS
9 | * Input: 2 strings
10 | * Output: Returns the length of longest common substring in two strings
11 | * Logic: Creates a 2D matrix and calculates longest common substring using dynamic programming
12 | * Example Call: LCS(string1, string2)
13 | */
14 | int LCS(string string1, string string2)
15 | {
16 | int x = string1.length();
17 | int y = string2.length();
18 | int matrix[x + 1][y + 1] = {0};
19 |
20 | for (int i = 0; i < x + 1; i++)
21 | {
22 | matrix[i][0] = 0;
23 | }
24 |
25 | for (int j = 0; j < y + 1; j++)
26 | {
27 | matrix[0][j] = 0;
28 | }
29 |
30 | for (int i = 1; i < x + 1; i++)
31 | {
32 | for (int j = 1; j < y + 1; j++)
33 | {
34 | if (string1[i - 1] == string2[j - 1])
35 | {
36 | matrix[i][j] = matrix[i - 1][j - 1] + 1;
37 | }
38 | else
39 | {
40 | matrix[i][j] = max(matrix[i][j - 1], matrix[i - 1][j]);
41 | }
42 | }
43 | }
44 |
45 | return matrix[x][y];
46 | }
47 |
48 | int main()
49 | {
50 |
51 | string string1;
52 | cout << "Please enter first sequence: " ;
53 | cin >> string1;
54 |
55 | string string2;
56 | cout << "Please enter second sequence: " ;
57 | cin >> string2;
58 |
59 | int lcs = LCS(string1, string2);
60 |
61 | cout << "The longest common sequence among two strings is of length: " << lcs ;
62 |
63 | return 0;
64 | }
--------------------------------------------------------------------------------
/Algorithms/4_Sorting/count_sort.cpp:
--------------------------------------------------------------------------------
1 | /****************************************
2 | @brief Implementing Count Sort
3 | *****************************************/
4 | #include
5 | #include
6 | #include
7 |
8 | using namespace std;
9 |
10 | int main()
11 | {
12 | int n;
13 |
14 | string s;
15 | getline(cin, s);
16 |
17 | int num = 0;
18 | vector v;
19 |
20 | // Taking input from the user and storing it in a vector of int
21 | for (int i = 0; i < s.size(); ++i)
22 | {
23 | if (s[i] == ' ')
24 | v.push_back(num), num = 0;
25 | else
26 | num = num * 10 + (s[i] - '0');
27 | }
28 | v.push_back(num);
29 |
30 | int max = *max_element(v.begin(), v.end());
31 | vector range(max + 1, 0);
32 |
33 | // This calculates the number of occurences
34 | for (int i = 0; i < v.size(); i++)
35 | {
36 | range[v[i]]++;
37 | }
38 |
39 | /*This calculates the starting position of each integer*/
40 | for (int i = 1; i < range.size(); i++)
41 | {
42 | range[i] = range[i] + range[i - 1];
43 | }
44 |
45 | // Shift the array to left side
46 | rotate(range.begin(), range.begin() + range.size() - 1, range.end());
47 | range[0] = 0;
48 |
49 | // copy the elements from v to result vector as per their positions
50 | vector result(v.size());
51 | for (int i = 0; i < v.size(); i++)
52 | {
53 | result[range[v[i]]] = v[i];
54 | range[v[i]]++;
55 | }
56 |
57 | for (int i = 0; i < result.size(); i++)
58 | {
59 | cout << result[i] << " ";
60 | }
61 | cout << endl;
62 | }
63 | /*
64 | Analysis: The above algorithn runs in O(n)
65 | */
--------------------------------------------------------------------------------
/leetcode/75 Sort Colors.cpp:
--------------------------------------------------------------------------------
1 | /*
2 | Approach 1: count number of 0s, 1s and 2s and then edit the array in next pass
3 | Runtime: 0ms
4 | Memory: 8.50MB
5 | Time Complexity: O(n)
6 | */
7 |
8 | class Solution {
9 | public:
10 | void sortColors(vector& nums) {
11 | int red = 0;
12 | int white = 0;
13 |
14 | for (int i = 0; i < nums.size(); i++)
15 | {
16 | if (nums[i] == 0)
17 | {
18 | red++;
19 | }
20 | else if (nums[i] == 1)
21 | {
22 | white++;
23 | }
24 | }
25 |
26 | for (int i = 0; i < nums.size(); i++)
27 | {
28 | if (red > 0)
29 | {
30 | red--;
31 | nums[i] = 0;
32 | }
33 | else if (white > 0)
34 | {
35 | white--;
36 | nums[i] = 1;
37 | }
38 | else
39 | {
40 | nums[i]=2;
41 | }
42 | }
43 | }
44 | };
45 |
46 | /*
47 | Approach 2: One pass algorithm using two pointers
48 | Runtime: 4ms
49 | Memory: 8.43MB
50 | Time Complexity: O(n)
51 | */
52 | class Solution {
53 | public:
54 | void sortColors(vector& nums) {
55 | int x = 0, i = 0, y = nums.size()-1;
56 |
57 | while (i <= y)
58 | {
59 | if (nums[i] == 0)
60 | {
61 | swap(nums[i], nums[x]);
62 | i++;
63 | x++;
64 | }
65 | else if (nums[i] == 2)
66 | {
67 | swap(nums[y], nums[i]);
68 | y--;
69 | }
70 | else
71 | {
72 | i++;
73 | }
74 | }
75 | }
76 | };
--------------------------------------------------------------------------------
/Algorithms/5_Miscellaneous/fibonacci.cpp:
--------------------------------------------------------------------------------
1 | #include
2 |
3 | using namespace std;
4 |
5 | long long int fibonacci(int n)
6 | {
7 | int temp = n - 1;
8 |
9 | long long int matrix[2][2] = {1, 1, 1, 0};
10 | long long int matrix_result[2][2] = {0};
11 |
12 | while (temp != 1)
13 | {
14 | for (int i = 0; i < 2; i++)
15 | {
16 | for (int j = 0; j < 2; j++)
17 | {
18 | for (int k = 0; k < 2; k++)
19 | {
20 | matrix_result[i][k] += matrix[i][j] * matrix[j][k];
21 | }
22 | }
23 | }
24 |
25 | if (temp % 2 != 0)
26 | {
27 | long long int A[2][2] = {1, 1, 1, 0};
28 |
29 | for (int i = 0; i < 2; i++)
30 | {
31 | for (int j = 0; j < 2; j++)
32 | {
33 | for (int k = 0; k < 2; k++)
34 | {
35 | matrix_result[i][k] += A[i][j] * matrix[j][k];
36 | }
37 | }
38 | }
39 | }
40 |
41 | for (int i = 0; i < 2; i++)
42 | {
43 | for (int j = 0; j < 2; j++)
44 | {
45 | matrix[i][j] = matrix_result[i][j];
46 | matrix_result[i][j] = 0;
47 | }
48 | }
49 |
50 | temp = temp / 2;
51 | }
52 |
53 | for (int i = 0; i < 2; i++)
54 | {
55 | for (int j = 0; j < 2; j++)
56 | {
57 | cout << matrix[i][j] << " ";
58 | }
59 | cout << endl;
60 | }
61 |
62 | return matrix[0][0];
63 | }
64 |
65 | int main()
66 | {
67 | int n;
68 | cout << "Please enter the value of n: ";
69 | cin >> n;
70 |
71 | long long int answer = fibonacci(n);
72 | cout << answer;
73 | }
--------------------------------------------------------------------------------
/Algorithms/4_Sorting/comb_sort.cpp:
--------------------------------------------------------------------------------
1 | /***************************************
2 | @brief Implementing Comb Sort
3 | ****************************************/
4 | #include
5 | #include
6 | #include
7 |
8 | using namespace std;
9 |
10 | /*
11 | * Function Name: comb_sort
12 | * Input: unsorted vector
13 | * Output: sorted vector
14 | * Example Call: comb_sort(v)
15 | */
16 | vector comb_sort (vector v)
17 | {
18 | // Defining the gap value
19 | int gap = int(v.size() / 1.3);
20 | bool is_swap = 1;
21 |
22 | while (!((gap==1) && (is_swap==0)))
23 | {
24 | // Reset the value of is_swap
25 | is_swap = 0;
26 | for (int i = 0; i < v.size()-gap; i++)
27 | {
28 | if (v[i] > v[i+gap])
29 | {
30 | is_swap = 1;
31 | int temp = v[i];
32 | v[i] = v[i+gap];
33 | v[i+gap] = temp;
34 | }
35 | }
36 |
37 | // Update the value of gap using previous
38 | gap = max(int(gap / 1.3),1);
39 | }
40 |
41 | return v;
42 | }
43 |
44 | int main()
45 | {
46 | int n;
47 |
48 | string s;
49 | getline(cin, s);
50 |
51 | int num = 0;
52 | vector v;
53 |
54 | // Taking input from the user and storing it in a vector of int
55 | for (int i = 0; i < s.size(); ++i)
56 | {
57 | if (s[i] == ' ')
58 | v.push_back(num), num = 0;
59 | else
60 | num = num * 10 + (s[i] - '0');
61 | }
62 | v.push_back(num);
63 |
64 | vector result = comb_sort(v);
65 |
66 | for (int i = 0; i < result.size(); i++)
67 | {
68 | cout << result[i] << " ";
69 | }
70 | cout << endl;
71 |
72 | return 0;
73 | }
74 | /*
75 | Analysis: The above algorithn runs in O(n^2).
76 | */
--------------------------------------------------------------------------------
/03_Queues/readme.md:
--------------------------------------------------------------------------------
1 | # Introduction
2 | A queue is defined as a linear data structure that is open at both ends and the operations are performed in First In First Out (FIFO) order. One end is always used to insert data (enqueue) and the other is used to remove data (dequeue).
3 |
4 |
15 |
--------------------------------------------------------------------------------
/hanoi.cpp:
--------------------------------------------------------------------------------
1 | #include
2 | #include
3 |
4 | using namespace std;
5 |
6 | // Defining Source, Destination and Extra Peg
7 | stack S;
8 | stack D;
9 | stack E;
10 |
11 | void shift_upper(stack source, stack dest, stack extra)
12 | {
13 |
14 | }
15 |
16 | void hanoi(stack source, stack dest, stack extra)
17 | {
18 | if (source.empty())
19 | {
20 | cout << "Source Peg is Empty\n";
21 | return;
22 | }
23 | else if (source.size() == 1)
24 | {
25 | int x = source.top();
26 | source.pop();
27 | dest.push(x);
28 | }
29 | else
30 | {
31 | shift_upper(source, extra, dest);
32 | int x = source.top();
33 | source.pop();
34 | dest.push(x);
35 | }
36 | }
37 |
38 | int main()
39 | {
40 |
41 | }
--------------------------------------------------------------------------------
/Algorithms/2_Divide_and_Conquer/polynomial_multiplication_karatsuba.cpp:
--------------------------------------------------------------------------------
1 | #include
2 | #include
3 | #include
4 |
5 | using namespace std;
6 |
7 | int *Multiply(vector &A, vector &B, int left1, int right1, int left2, int right2)
8 | {
9 | if (right1 - left1 == 1 )
10 | {
11 |
12 | }
13 | }
14 |
15 | int main()
16 | {
17 | int n;
18 | cout << "Please enter the maximum degree of polynomial : ";
19 | cin >> n;
20 |
21 | vector A(n + 1), B(n + 1);
22 |
23 | cout << "Please enter coefficients for first polynomial : ";
24 |
25 | for (int i = 0; i < n + 1; i++)
26 | {
27 | cin >> A[i];
28 | }
29 |
30 | cout << "Please enter coefficients for second polynomial : ";
31 |
32 | for (int i = 0; i < n + 1; i++)
33 | {
34 | cin >> B[i];
35 | }
36 |
37 | Multiply(A, B, 0, n, 0, n);
38 |
39 | int C[2 * n + 1] = {0};
40 |
41 | return 0 ;
42 | }
--------------------------------------------------------------------------------
/03_Queues/Queue_using_Linked_list/readme.md:
--------------------------------------------------------------------------------
1 | # Queue using Linked List
2 |
3 | Here , we make use of two pointers called front and rear. Rear pointer is where insertion of element takes place and front is where deletion takes place.
4 | Initially the front pointer points to the first element of queue. During deletion, value is deleted dynamically using delete keyword and the front pointer is incremented. Thus the time complexity is in terms of O(1).
5 | Also , during insertion , a new node is created dynamically using malloc() function rear pointer is made to point at this new node
6 | It is very important to delete the node during dequeue() , since not doing so may lead to memory-leak.
7 | Also, we reset both front and rear pointers in case of queue being empty.
8 |
9 | While using Linked-List , since we deal with heaps and dynamic memory , generally we can create as many nodes we want , till the heap memory gets finished.
10 |
11 | Thus the advantages of using a linked list over array is that both insertion and deletion takes place in O(1) time complexity and the memory is dynamic in nature.
12 |
--------------------------------------------------------------------------------
/LICENSE:
--------------------------------------------------------------------------------
1 | MIT License
2 |
3 | Copyright (c) 2022 PritK99
4 |
5 | Permission is hereby granted, free of charge, to any person obtaining a copy
6 | of this software and associated documentation files (the "Software"), to deal
7 | in the Software without restriction, including without limitation the rights
8 | to use, copy, modify, merge, publish, distribute, sublicense, and/or sell
9 | copies of the Software, and to permit persons to whom the Software is
10 | furnished to do so, subject to the following conditions:
11 |
12 | The above copyright notice and this permission notice shall be included in all
13 | copies or substantial portions of the Software.
14 |
15 | THE SOFTWARE IS PROVIDED "AS IS", WITHOUT WARRANTY OF ANY KIND, EXPRESS OR
16 | IMPLIED, INCLUDING BUT NOT LIMITED TO THE WARRANTIES OF MERCHANTABILITY,
17 | FITNESS FOR A PARTICULAR PURPOSE AND NONINFRINGEMENT. IN NO EVENT SHALL THE
18 | AUTHORS OR COPYRIGHT HOLDERS BE LIABLE FOR ANY CLAIM, DAMAGES OR OTHER
19 | LIABILITY, WHETHER IN AN ACTION OF CONTRACT, TORT OR OTHERWISE, ARISING FROM,
20 | OUT OF OR IN CONNECTION WITH THE SOFTWARE OR THE USE OR OTHER DEALINGS IN THE
21 | SOFTWARE.
22 |
--------------------------------------------------------------------------------
/leetcode/142 Linked List Cycle II.cpp:
--------------------------------------------------------------------------------
1 | /*
2 | Approach 1: DFS & Backtracking with pruning strategies
3 | Runtime: 3ms
4 | Memory: 7.97MB
5 | Time Complexity: O(n), where n is length of linkedlist
6 | */
7 | /**
8 | * Definition for singly-linked list.
9 | * struct ListNode {
10 | * int val;
11 | * ListNode *next;
12 | * ListNode(int x) : val(x), next(NULL) {}
13 | * };
14 | */
15 | class Solution {
16 | public:
17 | ListNode *detectCycle(ListNode *head) {
18 | if (head == NULL)
19 | {
20 | return NULL;
21 | }
22 | ListNode* slow = head;
23 | ListNode* fast = head;
24 |
25 | do
26 | {
27 | if (fast->next != NULL && fast->next->next != NULL)
28 | {
29 | slow = slow->next;
30 | fast = fast->next->next;
31 | }
32 | else
33 | {
34 | return NULL;
35 | }
36 | }
37 | while (slow != fast);
38 |
39 | fast = head;
40 | while (slow != fast)
41 | {
42 | slow = slow->next;
43 | fast = fast->next;
44 | }
45 |
46 | return slow;
47 |
48 | }
49 | };
--------------------------------------------------------------------------------
/Algorithms/0_Recursion/pallindrome.cpp:
--------------------------------------------------------------------------------
1 | /*********************************************************************
2 | @brief Checking if the given string is a pallindrome or not
3 | **********************************************************************/
4 | #include
5 | using namespace std;
6 |
7 | /*
8 | * Function Name: isPallindrome
9 | * Input: Takes the struct as input
10 | * Output: returns boolean true if given string is a pallindrome, else false.
11 | * Logic: This function recursively checks if given string is a pallindrome
12 | * Example Call: isPallindrome(s)
13 | */
14 | bool isPallindrome(string s)
15 | {
16 | int n = s.size() - 1 ;
17 |
18 | // Base Case
19 | if (n == 0 || n == 1)
20 | {
21 | return true ;
22 | }
23 |
24 | // Recursive case
25 | if (s.front() == s.back())
26 | {
27 | return isPallindrome(s.substr(1, n-1)) ;
28 | }
29 | else
30 | {
31 | return false ;
32 | }
33 | }
34 |
35 | int main ()
36 | {
37 | string s ;
38 | cout << "Enter a string: " ;
39 | cin >> s ;
40 | cout << isPallindrome(s) ;
41 |
42 | return 0;
43 | }
44 | /*
45 | Analysis: The above algorithm runs in O(n)
46 | */
--------------------------------------------------------------------------------
/leetcode/852 Peak Index in a Mountain Array.cpp:
--------------------------------------------------------------------------------
1 | /*
2 | Approach 1: Static Sliding Window of size 3
3 | Runtime: 89ms
4 | Memory: 59.95MB
5 | Time Complexity: O(n)
6 | */
7 | class Solution {
8 | public:
9 | int peakIndexInMountainArray(vector& arr) {
10 | int n = arr.size();
11 | for (int i = 1; i < n-1; i++)
12 | {
13 | if (arr[i]>arr[i+1] && arr[i]>arr[i-1])
14 | {
15 | return i;
16 | }
17 | }
18 | return 0;
19 | }
20 | };
21 |
22 | /*
23 | Approach 1: Binary Search
24 | Runtime: 74ms
25 | Memory: 59.97MB
26 | Time Complexity: O(log(n))
27 | */
28 | class Solution {
29 | public:
30 | int peakIndexInMountainArray(vector& arr) {
31 | int start = 0;
32 | int end = arr.size()-1;
33 | int i = 0;
34 |
35 | while(end > start)
36 | {
37 | i = (start+end) / 2;
38 |
39 | if (arr[i]>arr[i+1] && arr[i]>arr[i-1])
40 | {
41 | return i;
42 | }
43 | else if (arr[i]>arr[i-1] && arr[i]
5 | #include
6 | #include
7 |
8 | using namespace std;
9 |
10 | int main()
11 | {
12 | string s;
13 | getline(cin, s);
14 |
15 | int num = 0;
16 | vector v;
17 |
18 | /*Taking input from the user and storing it in a vector of int*/
19 | for (int i = 0; i < s.size(); ++i)
20 | {
21 | if (s[i] == ' ')
22 | v.push_back(num), num = 0;
23 | else
24 | num = num * 10 + (s[i] - '0');
25 | }
26 | v.push_back(num);
27 |
28 | auto iter = v.begin();
29 |
30 | while (iter != v.end())
31 | {
32 | auto min = min_element(iter, v.end());
33 | int min_index = distance(v.begin(), min);
34 |
35 | /*Swapping the first value of remaining array with minimum value present in the remaining array*/
36 | int temp = v[min_index];
37 | v[min_index] = *iter;
38 | *iter = temp;
39 |
40 | iter++;
41 | }
42 |
43 | cout << "The sorted array using selection sort is : ";
44 | for (int i = 0; i < v.size(); i++)
45 | {
46 | cout << v[i] << " ";
47 | }
48 |
49 | return 0;
50 | }
51 | /*
52 | Analysis: The above algorithn runs in O(n^2)
53 | */
--------------------------------------------------------------------------------
/Algorithms/2_Divide_and_Conquer/polynomial_multiplication_naive.cpp:
--------------------------------------------------------------------------------
1 | /******************************************************************
2 | @brief Naive implementation of polynomial multiplication
3 | *******************************************************************/
4 | #include
5 |
6 | using namespace std ;
7 |
8 | int main ()
9 | {
10 | int n ;
11 | cout << "Please enter the maximum degree of polynomial : " ;
12 | cin >> n ;
13 |
14 | int A[n+1] , B[n+1] ;
15 |
16 | cout << "Please enter coefficients for first polynomial : " ;
17 |
18 | for (int i = 0 ; i < n+1 ; i++ )
19 | {
20 | cin >> A[i] ;
21 | }
22 |
23 | cout << "Please enter coefficients for second polynomial : " ;
24 |
25 | for (int i = 0 ; i < n+1 ; i++ )
26 | {
27 | cin >> B[i] ;
28 | }
29 |
30 | int C[2*n+1] = {0} ;
31 |
32 | for (int i = 0 ; i < n+1 ; i ++)
33 | {
34 | for (int j = 0 ; j < n+1 ; j++)
35 | {
36 | C[i+j] = C[i+j] + A[i]*B[j];
37 | }
38 | }
39 |
40 | cout << "The coefficients of final polynomial are: (" ;
41 |
42 | for (int i = 0 ; i < 2*n + 1 ; i++)
43 | {
44 | if (i == 2*n)
45 | {
46 | cout << C[i] ;
47 | continue ;
48 | }
49 | cout << C[i] << ", " ;
50 | }
51 | cout << ")" << endl ;
52 | }
53 | /*
54 | Analysis: The above code runs in O(n^2).
55 | */
--------------------------------------------------------------------------------
/Algorithms/0_Recursion/tower_of_hanoi.cpp:
--------------------------------------------------------------------------------
1 | /***************************************************
2 | @brief Solving the Tower of Hanoi problem
3 | ****************************************************/
4 | #include
5 | #include
6 |
7 | using namespace std;
8 |
9 | /*
10 | * Function Name: towerOfHanoi
11 | * Input: Requires number of disks, source, destination and extra rod
12 | * Logic: Transfers disks from source to destination using extra rod.
13 | * Example Call: towerOfHanoi(n, source, destination, extra) ;
14 | */
15 | void towerOfHanoi(int n, stack &source, stack &destination, stack &extra)
16 | {
17 | if (n <= 0)
18 | {
19 | return;
20 | }
21 |
22 | towerOfHanoi(n - 1, source, extra, destination); // Move n-1 disks to extra rod
23 | int x = source.top();
24 | source.pop();
25 | destination.push(x);
26 | towerOfHanoi(n - 1, extra, destination, source); // For recursively treating the rest n-1 disks
27 | }
28 |
29 | int main()
30 | {
31 | stack source, destination, extra;
32 |
33 | int n = 4;
34 |
35 | // Filling source stack with initial discs where numbers denote size of disk
36 | source.push(4);
37 | source.push(3);
38 | source.push(2);
39 | source.push(1);
40 |
41 | towerOfHanoi(n, source, destination, extra);
42 |
43 | for (int i = 0; i < n; i++)
44 | {
45 | int x = destination.top();
46 | destination.pop();
47 | cout << x << " ";
48 | }
49 |
50 | return 0;
51 | }
52 | /*
53 | Analysis: The above code runs in O(2^n), where n is the number of disks
54 | */
55 |
56 |
--------------------------------------------------------------------------------
/Algorithms/3_Dynamic_Programming/longest_common_sequence.cpp:
--------------------------------------------------------------------------------
1 | #include
2 | #include
3 | #include
4 |
5 | using namespace std;
6 |
7 | /*
8 | * Function Name: LCS
9 | * Input: 2 strings
10 | * Output: Returns the length of longest common substring in two strings
11 | * Logic: Creates a 2D matrix and calculates longest common substring using dynamic programming
12 | * Example Call: LCS(string1, string2)
13 | */
14 | int LCS(string string1, string string2)
15 | {
16 | int x = string1.length();
17 | int y = string2.length();
18 | int matrix[x + 1][y + 1] = {0};
19 |
20 | for (int i = 0; i < x + 1; i++)
21 | {
22 | matrix[i][0] = 0;
23 | }
24 |
25 | for (int j = 0; j < y + 1; j++)
26 | {
27 | matrix[0][j] = 0;
28 | }
29 |
30 | for (int i = 1; i < x + 1; i++)
31 | {
32 | for (int j = 1; j < y + 1; j++)
33 | {
34 | if (string1[i - 1] == string2[j - 1])
35 | {
36 | matrix[i][j] = matrix[i - 1][j - 1] + 1;
37 | }
38 | else
39 | {
40 | matrix[i][j] = max(matrix[i][j - 1], matrix[i - 1][j]);
41 | }
42 | }
43 | }
44 |
45 | return matrix[x][y];
46 | }
47 |
48 | int main()
49 | {
50 |
51 | string string1;
52 | cout << "Please enter first sequence: " ;
53 | cin >> string1;
54 |
55 | string string2;
56 | cout << "Please enter second sequence: " ;
57 | cin >> string2;
58 |
59 | int lcs = LCS(string1, string2);
60 |
61 | cout << "The longest common sequence among two strings is of length: " << lcs ;
62 |
63 | return 0;
64 | }
--------------------------------------------------------------------------------
/Algorithms/4_Sorting/count_sort.cpp:
--------------------------------------------------------------------------------
1 | /****************************************
2 | @brief Implementing Count Sort
3 | *****************************************/
4 | #include
5 | #include
6 | #include
7 |
8 | using namespace std;
9 |
10 | int main()
11 | {
12 | int n;
13 |
14 | string s;
15 | getline(cin, s);
16 |
17 | int num = 0;
18 | vector v;
19 |
20 | // Taking input from the user and storing it in a vector of int
21 | for (int i = 0; i < s.size(); ++i)
22 | {
23 | if (s[i] == ' ')
24 | v.push_back(num), num = 0;
25 | else
26 | num = num * 10 + (s[i] - '0');
27 | }
28 | v.push_back(num);
29 |
30 | int max = *max_element(v.begin(), v.end());
31 | vector range(max + 1, 0);
32 |
33 | // This calculates the number of occurences
34 | for (int i = 0; i < v.size(); i++)
35 | {
36 | range[v[i]]++;
37 | }
38 |
39 | /*This calculates the starting position of each integer*/
40 | for (int i = 1; i < range.size(); i++)
41 | {
42 | range[i] = range[i] + range[i - 1];
43 | }
44 |
45 | // Shift the array to left side
46 | rotate(range.begin(), range.begin() + range.size() - 1, range.end());
47 | range[0] = 0;
48 |
49 | // copy the elements from v to result vector as per their positions
50 | vector result(v.size());
51 | for (int i = 0; i < v.size(); i++)
52 | {
53 | result[range[v[i]]] = v[i];
54 | range[v[i]]++;
55 | }
56 |
57 | for (int i = 0; i < result.size(); i++)
58 | {
59 | cout << result[i] << " ";
60 | }
61 | cout << endl;
62 | }
63 | /*
64 | Analysis: The above algorithn runs in O(n)
65 | */
--------------------------------------------------------------------------------
/leetcode/75 Sort Colors.cpp:
--------------------------------------------------------------------------------
1 | /*
2 | Approach 1: count number of 0s, 1s and 2s and then edit the array in next pass
3 | Runtime: 0ms
4 | Memory: 8.50MB
5 | Time Complexity: O(n)
6 | */
7 |
8 | class Solution {
9 | public:
10 | void sortColors(vector& nums) {
11 | int red = 0;
12 | int white = 0;
13 |
14 | for (int i = 0; i < nums.size(); i++)
15 | {
16 | if (nums[i] == 0)
17 | {
18 | red++;
19 | }
20 | else if (nums[i] == 1)
21 | {
22 | white++;
23 | }
24 | }
25 |
26 | for (int i = 0; i < nums.size(); i++)
27 | {
28 | if (red > 0)
29 | {
30 | red--;
31 | nums[i] = 0;
32 | }
33 | else if (white > 0)
34 | {
35 | white--;
36 | nums[i] = 1;
37 | }
38 | else
39 | {
40 | nums[i]=2;
41 | }
42 | }
43 | }
44 | };
45 |
46 | /*
47 | Approach 2: One pass algorithm using two pointers
48 | Runtime: 4ms
49 | Memory: 8.43MB
50 | Time Complexity: O(n)
51 | */
52 | class Solution {
53 | public:
54 | void sortColors(vector& nums) {
55 | int x = 0, i = 0, y = nums.size()-1;
56 |
57 | while (i <= y)
58 | {
59 | if (nums[i] == 0)
60 | {
61 | swap(nums[i], nums[x]);
62 | i++;
63 | x++;
64 | }
65 | else if (nums[i] == 2)
66 | {
67 | swap(nums[y], nums[i]);
68 | y--;
69 | }
70 | else
71 | {
72 | i++;
73 | }
74 | }
75 | }
76 | };
--------------------------------------------------------------------------------
/Algorithms/5_Miscellaneous/fibonacci.cpp:
--------------------------------------------------------------------------------
1 | #include
2 |
3 | using namespace std;
4 |
5 | long long int fibonacci(int n)
6 | {
7 | int temp = n - 1;
8 |
9 | long long int matrix[2][2] = {1, 1, 1, 0};
10 | long long int matrix_result[2][2] = {0};
11 |
12 | while (temp != 1)
13 | {
14 | for (int i = 0; i < 2; i++)
15 | {
16 | for (int j = 0; j < 2; j++)
17 | {
18 | for (int k = 0; k < 2; k++)
19 | {
20 | matrix_result[i][k] += matrix[i][j] * matrix[j][k];
21 | }
22 | }
23 | }
24 |
25 | if (temp % 2 != 0)
26 | {
27 | long long int A[2][2] = {1, 1, 1, 0};
28 |
29 | for (int i = 0; i < 2; i++)
30 | {
31 | for (int j = 0; j < 2; j++)
32 | {
33 | for (int k = 0; k < 2; k++)
34 | {
35 | matrix_result[i][k] += A[i][j] * matrix[j][k];
36 | }
37 | }
38 | }
39 | }
40 |
41 | for (int i = 0; i < 2; i++)
42 | {
43 | for (int j = 0; j < 2; j++)
44 | {
45 | matrix[i][j] = matrix_result[i][j];
46 | matrix_result[i][j] = 0;
47 | }
48 | }
49 |
50 | temp = temp / 2;
51 | }
52 |
53 | for (int i = 0; i < 2; i++)
54 | {
55 | for (int j = 0; j < 2; j++)
56 | {
57 | cout << matrix[i][j] << " ";
58 | }
59 | cout << endl;
60 | }
61 |
62 | return matrix[0][0];
63 | }
64 |
65 | int main()
66 | {
67 | int n;
68 | cout << "Please enter the value of n: ";
69 | cin >> n;
70 |
71 | long long int answer = fibonacci(n);
72 | cout << answer;
73 | }
--------------------------------------------------------------------------------
/Algorithms/4_Sorting/comb_sort.cpp:
--------------------------------------------------------------------------------
1 | /***************************************
2 | @brief Implementing Comb Sort
3 | ****************************************/
4 | #include
5 | #include
6 | #include
7 |
8 | using namespace std;
9 |
10 | /*
11 | * Function Name: comb_sort
12 | * Input: unsorted vector
13 | * Output: sorted vector
14 | * Example Call: comb_sort(v)
15 | */
16 | vector comb_sort (vector v)
17 | {
18 | // Defining the gap value
19 | int gap = int(v.size() / 1.3);
20 | bool is_swap = 1;
21 |
22 | while (!((gap==1) && (is_swap==0)))
23 | {
24 | // Reset the value of is_swap
25 | is_swap = 0;
26 | for (int i = 0; i < v.size()-gap; i++)
27 | {
28 | if (v[i] > v[i+gap])
29 | {
30 | is_swap = 1;
31 | int temp = v[i];
32 | v[i] = v[i+gap];
33 | v[i+gap] = temp;
34 | }
35 | }
36 |
37 | // Update the value of gap using previous
38 | gap = max(int(gap / 1.3),1);
39 | }
40 |
41 | return v;
42 | }
43 |
44 | int main()
45 | {
46 | int n;
47 |
48 | string s;
49 | getline(cin, s);
50 |
51 | int num = 0;
52 | vector v;
53 |
54 | // Taking input from the user and storing it in a vector of int
55 | for (int i = 0; i < s.size(); ++i)
56 | {
57 | if (s[i] == ' ')
58 | v.push_back(num), num = 0;
59 | else
60 | num = num * 10 + (s[i] - '0');
61 | }
62 | v.push_back(num);
63 |
64 | vector result = comb_sort(v);
65 |
66 | for (int i = 0; i < result.size(); i++)
67 | {
68 | cout << result[i] << " ";
69 | }
70 | cout << endl;
71 |
72 | return 0;
73 | }
74 | /*
75 | Analysis: The above algorithn runs in O(n^2).
76 | */
--------------------------------------------------------------------------------
/03_Queues/readme.md:
--------------------------------------------------------------------------------
1 | # Introduction
2 | A queue is defined as a linear data structure that is open at both ends and the operations are performed in First In First Out (FIFO) order. One end is always used to insert data (enqueue) and the other is used to remove data (dequeue).
3 |
4 |  5 |
6 | ## Types of Queue
7 | 1) Simple Queue
8 | 2) Circular Queue
9 | 3) Priority Queue (PQ)
10 | 4) Double ended Queue (DEQUE)
11 |
12 | ## Data we need for Queues
13 | 1) Space for storing elements
14 | 2) Front pointer - usually for deletion
15 | 3) Rear pointer - usually for insertion
16 |
17 |
5 |
6 | ## Types of Queue
7 | 1) Simple Queue
8 | 2) Circular Queue
9 | 3) Priority Queue (PQ)
10 | 4) Double ended Queue (DEQUE)
11 |
12 | ## Data we need for Queues
13 | 1) Space for storing elements
14 | 2) Front pointer - usually for deletion
15 | 3) Rear pointer - usually for insertion
16 |
17 |  18 |
19 | ## Basic operations on Queue
20 | 1) Enqueue() : To insert an element to queue
21 | 2) Dequeue() : To delete an element from to queue
22 | 3) IsEmpty() : To check if queue is empty
23 | 4) IsFull() : To check if queue is full
24 |
25 | ## Implenting Queues
26 | There are two methods to implement queues
27 | 1) Using arrays
28 | 2) Using Linked List
29 |
30 | # Circular Queues
31 |
32 | # DEQueues
33 | Double-Ended-Queues (DEQueues) are a type of queue, which do not follow FIFO exactly.In simple queues, front is used to delete an element and rear is used to insert an element. However, Double-Ended-Queue allow insertion and deletion at both ends , front and rear.
34 | Further subtypes of DEQueue :-
35 | 1) Input-Resticted-Dequeue - Insertion only takes place at rear end, while deletion can take place at either of ends
36 | 2) Output-Resticted-Dequeue - Deletion only takes place at front end, while insertion can take place at either of ends
37 |
38 | # Priority Queues
39 | Refer ```6_Heaps``` for implementation of Priority queues.
40 |
--------------------------------------------------------------------------------
/09_Graphs/djikstras.cpp:
--------------------------------------------------------------------------------
1 | #include
2 | #include
3 | #include
4 | #include
5 |
6 | using namespace std;
7 |
8 | vector djikstras(vector> &adj, vector> &cost, int s)
9 | {
10 | vector distance(adj.size(), LLONG_MAX);
11 | vector visited(adj.size(), false);
12 |
13 | distance[s] = 0;
14 | priority_queue> pq;
15 | pq.push({0, s});
16 |
17 | while (!pq.empty())
18 | {
19 | int u = pq.top().second;
20 | pq.pop();
21 |
22 | if (visited[u])
23 | {
24 | continue;
25 | }
26 | visited[u] = true;
27 |
28 | for (int i = 0; i < adj[u].size(); i++)
29 | {
30 | int v = adj[u][i];
31 | int weight = cost[u][i];
32 |
33 | if (!visited[v] && distance[u] + weight < distance[v])
34 | {
35 | distance[v] = distance[u] + weight;
36 | pq.push({-distance[v], v});
37 | }
38 | }
39 | }
40 |
41 | return distance;
42 | }
43 |
44 | int main()
45 | {
46 | int num_vertices, num_edges;
47 | cin >> num_vertices >> num_edges;
48 |
49 | vector> adj(num_vertices, vector());
50 | vector> cost(num_vertices, vector());
51 |
52 | for (int i = 0; i < num_edges; i++)
53 | {
54 | int x, y, w;
55 | cin >> x >> y >> w;
56 | adj[x - 1].push_back(y - 1);
57 | cost[x - 1].push_back(w);
58 | }
59 |
60 | int s, t;
61 | cin >> s >> t;
62 | vector shortest_path = djikstras(adj, cost, s - 1);
63 |
64 | if (shortest_path[t - 1] == LLONG_MAX)
65 | {
66 | cout << -1;
67 | }
68 | else
69 | {
70 | cout << shortest_path[t - 1];
71 | }
72 |
73 | return 0;
74 | }
--------------------------------------------------------------------------------
/leetcode/54 Spiral Matrix.cpp:
--------------------------------------------------------------------------------
1 | /*
2 | Approach 1: Spiral Traversal
3 | Runtime: 0ms
4 | Memory: 7.31MB
5 | Time Complexity: O(m*n), where m*n is dimension of matrix
6 | */
7 | class Solution {
8 | public:
9 | vector spiralOrder(vector>& matrix) {
10 | int row = matrix.size()-1;
11 | int col = matrix[0].size()-1;
12 | vector answer;
13 |
14 | int start_row = 0;
15 | int start_col = 0;
16 | while (start_row < row && start_col < col)
17 | {
18 | //Top Sequence
19 | for (int i = start_col; i < col; i++)
20 | {
21 | answer.push_back(matrix[start_row][i]);
22 | }
23 |
24 | //Right Sequence
25 | for (int i = start_row; i < row; i++)
26 | {
27 | answer.push_back(matrix[i][col]);
28 | }
29 |
30 | //Bottom Sequence
31 | for (int i = start_col; i < col; i++)
32 | {
33 | answer.push_back(matrix[row][matrix[0].size()-1-i]);
34 | }
35 |
36 | //Left Sequence
37 | for (int i = start_row; i < row; i++)
38 | {
39 | answer.push_back(matrix[matrix.size()-1-i][start_col]);
40 | }
41 |
42 | row--;
43 | col--;
44 | start_row++;
45 | start_col++;
46 | }
47 |
48 | if (row == start_row)
49 | {
50 | for (int i = start_col; i <= col; i++)
51 | {
52 | answer.push_back(matrix[row][i]);
53 | }
54 | }
55 | else if (col == start_col)
56 | {
57 | for (int i = start_row; i <= row; i++)
58 | {
59 | answer.push_back(matrix[i][col]);
60 | }
61 | }
62 | return answer;
63 | }
64 | };
--------------------------------------------------------------------------------
/leetcode/2 Add Two Numbers.cpp:
--------------------------------------------------------------------------------
1 | /*
2 | Approach 1: traverse and add
3 | Runtime: 18ms
4 | Memory: 71.71MB
5 | Time Complexity: O(n)
6 | */
7 | /**
8 | * Definition for singly-linked list.
9 | * struct ListNode {
10 | * int val;
11 | * ListNode *next;
12 | * ListNode() : val(0), next(nullptr) {}
13 | * ListNode(int x) : val(x), next(nullptr) {}
14 | * ListNode(int x, ListNode *next) : val(x), next(next) {}
15 | * };
16 | */
17 | class Solution {
18 | public:
19 | ListNode* addTwoNumbers(ListNode* l1, ListNode* l2) {
20 | ListNode* l3 = NULL;
21 | ListNode* head = NULL;
22 | int carry = 0;
23 | while(l1 != NULL || l2 != NULL)
24 | {
25 | if (l3 == NULL)
26 | {
27 | l3 = new ListNode;
28 | }
29 | else
30 | {
31 | l3->next = new ListNode;
32 | l3 = l3->next;
33 | }
34 |
35 | if (head == NULL)
36 | {
37 | head = l3;
38 | }
39 |
40 | int value = 0;
41 | if (l1 == NULL)
42 | {
43 | value = l2->val + carry;
44 | l2 = l2->next;
45 | }
46 | else if (l2 == NULL)
47 | {
48 | value = l1->val + carry;;
49 | l1 = l1->next;
50 | }
51 | else
52 | {
53 | value = l1->val + l2->val + carry;
54 | l1 = l1->next;
55 | l2 = l2->next;
56 | }
57 | carry = value / 10;
58 | l3->val = value % 10;
59 | }
60 |
61 | if (carry != 0)
62 | {
63 | l3->next = new ListNode;
64 | l3 = l3->next;
65 | l3->val = carry;
66 | }
67 | return head;
68 | }
69 | };
--------------------------------------------------------------------------------
/leetcode/442 Find All Duplicates in an Array.cpp:
--------------------------------------------------------------------------------
1 | /*
2 | Approach 1: Sort and find duplicates
3 | Runtime: 44ms
4 | Memory: 33.9MB
5 | Time Complexity: O(nlogn)
6 | Space Complexity: 0(1)
7 | */
8 | class Solution {
9 | public:
10 | vector findDuplicates(vector& nums) {
11 | int n = nums.size();
12 | sort(nums.begin(), nums.end());
13 | vector answer;
14 | for (int i = 1; i < n; i++)
15 | {
16 | if (nums[i] == nums[i-1])
17 | {
18 | answer.push_back(nums[i]);
19 | }
20 | }
21 | return answer;
22 | }
23 | };
24 |
25 | /*
26 | Approach 2: Using unordered maps
27 | Runtime: 74ms
28 | Memory: 44.96MB
29 | Time Complexity: O(n)
30 | Space Complexity: 0(n)
31 | */
32 | class Solution {
33 | public:
34 | vector findDuplicates(vector& nums) {
35 | unordered_map umap;
36 | vector ans;
37 | for (int i = 0; i< nums.size(); i++)
38 | {
39 | if (umap[nums[i]] == 1)
40 | {
41 | ans.push_back(nums[i]);
42 | }
43 | umap[nums[i]]++;
44 | }
45 | return ans;
46 | }
47 | };
48 |
49 | /*
50 | Approach 3: Using array indices itself to track if the number has appeared before.
51 | Runtime: 36ms
52 | Memory: 33.85MB
53 | Time Complexity: O(n)
54 | Space Complexity: 0(1)
55 | */
56 | class Solution {
57 | public:
58 | vector findDuplicates(vector& nums) {
59 | int n = nums.size();
60 | vector ans;
61 | for (int i = 0; i
6 | #include
7 |
8 | using namespace std;
9 |
10 | /*
11 | * Function Name: minCoins
12 | * Input: Requires an vector of denominations and the value for which change is required
13 | * Output: returns the minimum number of coins require
14 | * Logic: Finds the optimal minimum solution using bottom-to-top method of dynamic programming
15 | * Example Call: minCoins(denomination, change)
16 | */
17 | int minCoins(vector denomination, vector change)
18 | {
19 | for (int i = 1; i < change.size(); i++)
20 | {
21 | int coinsRequired = INT_MAX;
22 | for (int j = 0; j < denomination.size(); j++)
23 | {
24 | if (i >= denomination[j])
25 | {
26 | if (change[i - denomination[j]] + 1 < coinsRequired)
27 | {
28 | change[i] = change[i - denomination[j]] + 1;
29 | coinsRequired = change[i];
30 | }
31 | }
32 | }
33 | }
34 |
35 | return change[change.size() - 1];
36 | }
37 |
38 | int main()
39 | {
40 | vector denomination = {1, 6, 10}; // denominations
41 | cout << "Please enter the change required: ";
42 | int N;
43 | cin >> N;
44 | vector change(N + 1);
45 | change[0] = 0; // It takes 0 coins to change 0 cents
46 | int coinsRequired = minCoins(denomination, change);
47 |
48 | if (coinsRequired == 0)
49 | {
50 | cout << "The given value can not be changed with the current denomination.";
51 | }
52 | else
53 | {
54 | cout << "Minimum coins required are " << coinsRequired;
55 | }
56 |
57 | return 0;
58 | }
59 | /*
60 | Analysis: The above code runs in O(m*n), where n is the value of change required and m is the number of denominations
61 | */
--------------------------------------------------------------------------------
/06_Priority_Queues_and_Heaps/README.md:
--------------------------------------------------------------------------------
1 | # Priority Queues and Heaps
2 |
3 | ## Priority Queue
4 |
5 | A priority queue data structure is a generalization of the standard queue data structure. In the priority queue data structure, there is no such thing as the beginning or the end of a queue. Instead we have just a bag of elements, but each element is assigned a priority. When a new element arrives, we just put it inside this bag by calling the method Insert. However, when we need to process the next element from this bag, we call the method ExtractMax which is supposed to find an element inside this bag whose priority is currently maximum.
6 |
7 | Priority queues are generally used in a lot of places such as in Prim's algorithm, Huffman's encoding algorithm etc.
8 |
9 | ## Naive implementation of Priority Queues
10 |
11 | We can implement a priority queue using a simple array or linked list. One approach is, we always insert the element at end. Thus insertion takes O(1). But then to extract max element, we traverse throught the entire array thus leading to O(n). Another way is to use a sorted array. Thus, here extracting max element requires O(1), however insertion requires O(n), since first it has to locate the position using binary search and then shift to right all the elements by 1.
12 |
13 | Thus, we introduce the data structure heap to implement priority queues mor efficiently.
14 |
15 | ## Heaps
16 |
17 | Heaps is a beautiful data structure that allow to store the contents of a priority queue in a complete binary tree, which is in turn stored just as an array.
18 |
19 | In a max heap, for all non-leaf node, the value stored in parent is always greater than or equal to value stored in child node.
20 |
21 |
18 |
19 | ## Basic operations on Queue
20 | 1) Enqueue() : To insert an element to queue
21 | 2) Dequeue() : To delete an element from to queue
22 | 3) IsEmpty() : To check if queue is empty
23 | 4) IsFull() : To check if queue is full
24 |
25 | ## Implenting Queues
26 | There are two methods to implement queues
27 | 1) Using arrays
28 | 2) Using Linked List
29 |
30 | # Circular Queues
31 |
32 | # DEQueues
33 | Double-Ended-Queues (DEQueues) are a type of queue, which do not follow FIFO exactly.In simple queues, front is used to delete an element and rear is used to insert an element. However, Double-Ended-Queue allow insertion and deletion at both ends , front and rear.
34 | Further subtypes of DEQueue :-
35 | 1) Input-Resticted-Dequeue - Insertion only takes place at rear end, while deletion can take place at either of ends
36 | 2) Output-Resticted-Dequeue - Deletion only takes place at front end, while insertion can take place at either of ends
37 |
38 | # Priority Queues
39 | Refer ```6_Heaps``` for implementation of Priority queues.
40 |
--------------------------------------------------------------------------------
/09_Graphs/djikstras.cpp:
--------------------------------------------------------------------------------
1 | #include
2 | #include
3 | #include
4 | #include
5 |
6 | using namespace std;
7 |
8 | vector djikstras(vector> &adj, vector> &cost, int s)
9 | {
10 | vector distance(adj.size(), LLONG_MAX);
11 | vector visited(adj.size(), false);
12 |
13 | distance[s] = 0;
14 | priority_queue> pq;
15 | pq.push({0, s});
16 |
17 | while (!pq.empty())
18 | {
19 | int u = pq.top().second;
20 | pq.pop();
21 |
22 | if (visited[u])
23 | {
24 | continue;
25 | }
26 | visited[u] = true;
27 |
28 | for (int i = 0; i < adj[u].size(); i++)
29 | {
30 | int v = adj[u][i];
31 | int weight = cost[u][i];
32 |
33 | if (!visited[v] && distance[u] + weight < distance[v])
34 | {
35 | distance[v] = distance[u] + weight;
36 | pq.push({-distance[v], v});
37 | }
38 | }
39 | }
40 |
41 | return distance;
42 | }
43 |
44 | int main()
45 | {
46 | int num_vertices, num_edges;
47 | cin >> num_vertices >> num_edges;
48 |
49 | vector> adj(num_vertices, vector());
50 | vector> cost(num_vertices, vector());
51 |
52 | for (int i = 0; i < num_edges; i++)
53 | {
54 | int x, y, w;
55 | cin >> x >> y >> w;
56 | adj[x - 1].push_back(y - 1);
57 | cost[x - 1].push_back(w);
58 | }
59 |
60 | int s, t;
61 | cin >> s >> t;
62 | vector shortest_path = djikstras(adj, cost, s - 1);
63 |
64 | if (shortest_path[t - 1] == LLONG_MAX)
65 | {
66 | cout << -1;
67 | }
68 | else
69 | {
70 | cout << shortest_path[t - 1];
71 | }
72 |
73 | return 0;
74 | }
--------------------------------------------------------------------------------
/leetcode/54 Spiral Matrix.cpp:
--------------------------------------------------------------------------------
1 | /*
2 | Approach 1: Spiral Traversal
3 | Runtime: 0ms
4 | Memory: 7.31MB
5 | Time Complexity: O(m*n), where m*n is dimension of matrix
6 | */
7 | class Solution {
8 | public:
9 | vector spiralOrder(vector>& matrix) {
10 | int row = matrix.size()-1;
11 | int col = matrix[0].size()-1;
12 | vector answer;
13 |
14 | int start_row = 0;
15 | int start_col = 0;
16 | while (start_row < row && start_col < col)
17 | {
18 | //Top Sequence
19 | for (int i = start_col; i < col; i++)
20 | {
21 | answer.push_back(matrix[start_row][i]);
22 | }
23 |
24 | //Right Sequence
25 | for (int i = start_row; i < row; i++)
26 | {
27 | answer.push_back(matrix[i][col]);
28 | }
29 |
30 | //Bottom Sequence
31 | for (int i = start_col; i < col; i++)
32 | {
33 | answer.push_back(matrix[row][matrix[0].size()-1-i]);
34 | }
35 |
36 | //Left Sequence
37 | for (int i = start_row; i < row; i++)
38 | {
39 | answer.push_back(matrix[matrix.size()-1-i][start_col]);
40 | }
41 |
42 | row--;
43 | col--;
44 | start_row++;
45 | start_col++;
46 | }
47 |
48 | if (row == start_row)
49 | {
50 | for (int i = start_col; i <= col; i++)
51 | {
52 | answer.push_back(matrix[row][i]);
53 | }
54 | }
55 | else if (col == start_col)
56 | {
57 | for (int i = start_row; i <= row; i++)
58 | {
59 | answer.push_back(matrix[i][col]);
60 | }
61 | }
62 | return answer;
63 | }
64 | };
--------------------------------------------------------------------------------
/leetcode/2 Add Two Numbers.cpp:
--------------------------------------------------------------------------------
1 | /*
2 | Approach 1: traverse and add
3 | Runtime: 18ms
4 | Memory: 71.71MB
5 | Time Complexity: O(n)
6 | */
7 | /**
8 | * Definition for singly-linked list.
9 | * struct ListNode {
10 | * int val;
11 | * ListNode *next;
12 | * ListNode() : val(0), next(nullptr) {}
13 | * ListNode(int x) : val(x), next(nullptr) {}
14 | * ListNode(int x, ListNode *next) : val(x), next(next) {}
15 | * };
16 | */
17 | class Solution {
18 | public:
19 | ListNode* addTwoNumbers(ListNode* l1, ListNode* l2) {
20 | ListNode* l3 = NULL;
21 | ListNode* head = NULL;
22 | int carry = 0;
23 | while(l1 != NULL || l2 != NULL)
24 | {
25 | if (l3 == NULL)
26 | {
27 | l3 = new ListNode;
28 | }
29 | else
30 | {
31 | l3->next = new ListNode;
32 | l3 = l3->next;
33 | }
34 |
35 | if (head == NULL)
36 | {
37 | head = l3;
38 | }
39 |
40 | int value = 0;
41 | if (l1 == NULL)
42 | {
43 | value = l2->val + carry;
44 | l2 = l2->next;
45 | }
46 | else if (l2 == NULL)
47 | {
48 | value = l1->val + carry;;
49 | l1 = l1->next;
50 | }
51 | else
52 | {
53 | value = l1->val + l2->val + carry;
54 | l1 = l1->next;
55 | l2 = l2->next;
56 | }
57 | carry = value / 10;
58 | l3->val = value % 10;
59 | }
60 |
61 | if (carry != 0)
62 | {
63 | l3->next = new ListNode;
64 | l3 = l3->next;
65 | l3->val = carry;
66 | }
67 | return head;
68 | }
69 | };
--------------------------------------------------------------------------------
/leetcode/442 Find All Duplicates in an Array.cpp:
--------------------------------------------------------------------------------
1 | /*
2 | Approach 1: Sort and find duplicates
3 | Runtime: 44ms
4 | Memory: 33.9MB
5 | Time Complexity: O(nlogn)
6 | Space Complexity: 0(1)
7 | */
8 | class Solution {
9 | public:
10 | vector findDuplicates(vector& nums) {
11 | int n = nums.size();
12 | sort(nums.begin(), nums.end());
13 | vector answer;
14 | for (int i = 1; i < n; i++)
15 | {
16 | if (nums[i] == nums[i-1])
17 | {
18 | answer.push_back(nums[i]);
19 | }
20 | }
21 | return answer;
22 | }
23 | };
24 |
25 | /*
26 | Approach 2: Using unordered maps
27 | Runtime: 74ms
28 | Memory: 44.96MB
29 | Time Complexity: O(n)
30 | Space Complexity: 0(n)
31 | */
32 | class Solution {
33 | public:
34 | vector findDuplicates(vector& nums) {
35 | unordered_map umap;
36 | vector ans;
37 | for (int i = 0; i< nums.size(); i++)
38 | {
39 | if (umap[nums[i]] == 1)
40 | {
41 | ans.push_back(nums[i]);
42 | }
43 | umap[nums[i]]++;
44 | }
45 | return ans;
46 | }
47 | };
48 |
49 | /*
50 | Approach 3: Using array indices itself to track if the number has appeared before.
51 | Runtime: 36ms
52 | Memory: 33.85MB
53 | Time Complexity: O(n)
54 | Space Complexity: 0(1)
55 | */
56 | class Solution {
57 | public:
58 | vector findDuplicates(vector& nums) {
59 | int n = nums.size();
60 | vector ans;
61 | for (int i = 0; i
6 | #include
7 |
8 | using namespace std;
9 |
10 | /*
11 | * Function Name: minCoins
12 | * Input: Requires an vector of denominations and the value for which change is required
13 | * Output: returns the minimum number of coins require
14 | * Logic: Finds the optimal minimum solution using bottom-to-top method of dynamic programming
15 | * Example Call: minCoins(denomination, change)
16 | */
17 | int minCoins(vector denomination, vector change)
18 | {
19 | for (int i = 1; i < change.size(); i++)
20 | {
21 | int coinsRequired = INT_MAX;
22 | for (int j = 0; j < denomination.size(); j++)
23 | {
24 | if (i >= denomination[j])
25 | {
26 | if (change[i - denomination[j]] + 1 < coinsRequired)
27 | {
28 | change[i] = change[i - denomination[j]] + 1;
29 | coinsRequired = change[i];
30 | }
31 | }
32 | }
33 | }
34 |
35 | return change[change.size() - 1];
36 | }
37 |
38 | int main()
39 | {
40 | vector denomination = {1, 6, 10}; // denominations
41 | cout << "Please enter the change required: ";
42 | int N;
43 | cin >> N;
44 | vector change(N + 1);
45 | change[0] = 0; // It takes 0 coins to change 0 cents
46 | int coinsRequired = minCoins(denomination, change);
47 |
48 | if (coinsRequired == 0)
49 | {
50 | cout << "The given value can not be changed with the current denomination.";
51 | }
52 | else
53 | {
54 | cout << "Minimum coins required are " << coinsRequired;
55 | }
56 |
57 | return 0;
58 | }
59 | /*
60 | Analysis: The above code runs in O(m*n), where n is the value of change required and m is the number of denominations
61 | */
--------------------------------------------------------------------------------
/06_Priority_Queues_and_Heaps/README.md:
--------------------------------------------------------------------------------
1 | # Priority Queues and Heaps
2 |
3 | ## Priority Queue
4 |
5 | A priority queue data structure is a generalization of the standard queue data structure. In the priority queue data structure, there is no such thing as the beginning or the end of a queue. Instead we have just a bag of elements, but each element is assigned a priority. When a new element arrives, we just put it inside this bag by calling the method Insert. However, when we need to process the next element from this bag, we call the method ExtractMax which is supposed to find an element inside this bag whose priority is currently maximum.
6 |
7 | Priority queues are generally used in a lot of places such as in Prim's algorithm, Huffman's encoding algorithm etc.
8 |
9 | ## Naive implementation of Priority Queues
10 |
11 | We can implement a priority queue using a simple array or linked list. One approach is, we always insert the element at end. Thus insertion takes O(1). But then to extract max element, we traverse throught the entire array thus leading to O(n). Another way is to use a sorted array. Thus, here extracting max element requires O(1), however insertion requires O(n), since first it has to locate the position using binary search and then shift to right all the elements by 1.
12 |
13 | Thus, we introduce the data structure heap to implement priority queues mor efficiently.
14 |
15 | ## Heaps
16 |
17 | Heaps is a beautiful data structure that allow to store the contents of a priority queue in a complete binary tree, which is in turn stored just as an array.
18 |
19 | In a max heap, for all non-leaf node, the value stored in parent is always greater than or equal to value stored in child node.
20 |
21 |  22 |
23 | Here, insertion and extracting maximum element both takes O(log(n)). During insertion, we can insert the new element as a leaf node and then shift it in tree as per the properties of heap. This is implemented by basic operations such as ```siftUp()``` and ```siftDown()```.
24 |
25 | Further, this entire structure can be unwrapped as an array.
26 |
27 |
22 |
23 | Here, insertion and extracting maximum element both takes O(log(n)). During insertion, we can insert the new element as a leaf node and then shift it in tree as per the properties of heap. This is implemented by basic operations such as ```siftUp()``` and ```siftDown()```.
24 |
25 | Further, this entire structure can be unwrapped as an array.
26 |
27 |  28 |
29 |
--------------------------------------------------------------------------------
/09_Graphs/bellman-ford.cpp:
--------------------------------------------------------------------------------
1 | #include
2 | #include
3 | #include
4 |
5 | using std::vector;
6 |
7 | vector negative_cycle(vector> &adj, vector> &cost, int s)
8 | {
9 | int v = adj.size();
10 | vector visited(v);
11 |
12 | vector dist(v, INT_MAX);
13 | dist[s] = 0;
14 |
15 | for (int k = 0; k < v - 1; k++)
16 | {
17 | // Run v-1 interations
18 |
19 | for (int i = 0; i < v; i++)
20 | {
21 | for (int j = 0; j < adj[i].size(); j++)
22 | {
23 | if (dist[i] + cost[i][j] < dist[adj[i][j]] && dist[i] != INT_MAX)
24 | {
25 | dist[adj[i][j]] = dist[i] + cost[i][j];
26 | }
27 | }
28 | }
29 | }
30 |
31 | while (1)
32 | {
33 | vector temp = dist;
34 | for (int i = 0; i < v; i++)
35 | {
36 | for (int j = 0; j < adj[i].size(); j++)
37 | {
38 | if (dist[i] == INT_MIN || dist[i] + cost[i][j] < dist[adj[i][j]])
39 | {
40 | dist[adj[i][j]] = INT_MIN;
41 | }
42 | }
43 | }
44 | if (temp == dist)
45 | {
46 | break;
47 | }
48 | }
49 |
50 | return dist;
51 | }
52 |
53 | int main()
54 | {
55 | int n, m;
56 | std::cin >> n >> m;
57 | vector> adj(n, vector());
58 | vector> cost(n, vector());
59 | for (int i = 0; i < m; i++)
60 | {
61 | int x, y, w;
62 | std::cin >> x >> y >> w;
63 | adj[x - 1].push_back(y - 1);
64 | cost[x - 1].push_back(w);
65 | }
66 | int s;
67 | std::cin >> s;
68 | vector dist = negative_cycle(adj, cost, s - 1);
69 |
70 | for (int i = 0; i < dist.size(); i++)
71 | {
72 | if (dist[i] == INT_MAX)
73 | {
74 | std::cout << "*";
75 | }
76 | else if (dist[i] == INT_MIN)
77 | {
78 | std::cout << "-";
79 | }
80 | else
81 | {
82 | std::cout << dist[i];
83 | }
84 | std::cout << std::endl;
85 | }
86 | }
87 |
--------------------------------------------------------------------------------
/leetcode/494 Target Sum.cpp:
--------------------------------------------------------------------------------
1 | /*
2 | Approach 1: Brute force method to try and test all possible combinations
3 | TLE
4 | Time Complexity: O(2^n)
5 | */
6 | class Solution {
7 | public:
8 | int count = 0;
9 | void eval(vector &mask,vector& nums, int pos, int target)
10 | {
11 | int sum = 0;
12 | for (int i = 0; i < mask.size(); i++)
13 | {
14 | if (mask[i] == 0)
15 | {
16 | sum+=nums[i];
17 | }
18 | else
19 | {
20 | sum-=nums[i];
21 | }
22 | }
23 | if (sum == target)
24 | {
25 | count++;
26 | }
27 | }
28 |
29 | void gen (vector &mask, vector& nums, int pos, int target)
30 | {
31 | //base case
32 | if (pos == mask.size())
33 | {
34 | eval(mask, nums, pos, target);
35 | return;
36 | }
37 | // mask will be 0
38 | gen(mask, nums, pos+1, target);
39 | //mask will be 1
40 | mask[pos]=1;
41 | gen(mask, nums, pos+1, target);
42 | mask[pos]=0;
43 | }
44 | int findTargetSumWays(vector& nums, int target) {
45 | vector mask (nums.size());
46 | gen(mask, nums, 0, target);
47 | return count;
48 | }
49 | };
50 |
51 | /*
52 | Approach 2: Brute Force Recursion with better method to obtain sum
53 | TLE
54 | Time Complexity: O(2^n), where m*n is dimension of board and w is length of word
55 | */
56 | class Solution {
57 | public:
58 | int count = 0;
59 | void gen (vector &mask, vector& nums, int pos, int target, int sum)
60 | {
61 | //base case
62 | if (pos == mask.size())
63 | {
64 | if (sum == target)
65 | {
66 | count++;
67 | }
68 | return;
69 | }
70 |
71 | //rec case
72 |
73 | // mask will be 0
74 | gen(mask, nums, pos+1, target, sum+nums[pos]);
75 | //mask will be 1
76 | mask[pos]=1;
77 | gen(mask, nums, pos+1, target, sum-nums[pos]);
78 | mask[pos]=0;
79 | }
80 | int findTargetSumWays(vector& nums, int target) {
81 | vector mask (nums.size());
82 | gen(mask, nums, 0, target, 0);
83 | return count;
84 | }
85 | };
--------------------------------------------------------------------------------
/04_Linked List/linked_list.cpp:
--------------------------------------------------------------------------------
1 | #include
2 |
3 | using namespace std;
4 |
5 | class Node
6 | {
7 | public:
8 | int data;
9 | Node* next;
10 | Node(int data)
11 | {
12 | this->data = data;
13 | next = NULL;
14 | }
15 | };
16 |
17 | class LinkedList
18 | {
19 | public:
20 | Node* head = NULL;
21 | void insert(int data);
22 | void print();
23 | void remove(int data);
24 | };
25 |
26 | void LinkedList::insert(int data)
27 | {
28 | if (head == NULL)
29 | {
30 | head = new Node(data);
31 | }
32 | else
33 | {
34 | Node* temp = head;
35 | while (temp->next != NULL)
36 | {
37 | temp = temp->next;
38 | }
39 | temp->next = new Node(data);
40 | }
41 | }
42 |
43 | void LinkedList::print()
44 | {
45 | if (head == NULL)
46 | {
47 | cout << "Linked List is Empty" << endl;
48 | }
49 | else
50 | {
51 | Node* temp = head;
52 | while (temp != NULL)
53 | {
54 | cout << temp->data << " -> ";
55 | temp = temp->next;
56 | }
57 | cout << "NULL" << endl;
58 | }
59 | }
60 |
61 | void LinkedList::remove(int key)
62 | {
63 | if (head == NULL)
64 | {
65 | cout << "Linked List is Empty" << endl;
66 | }
67 | else if(head->data == key)
68 | {
69 | Node* temp = head;
70 | temp = head->next;
71 | free(head);
72 | head = temp;
73 | }
74 | else
75 | {
76 | bool flag = 0;
77 | Node* temp = head;
78 | while (temp->next != NULL)
79 | {
80 | if (temp->next->data == key)
81 | {
82 | flag = 1;
83 | Node* p = temp->next;
84 | temp->next = temp->next->next;
85 | free(p);
86 | break;
87 | }
88 | else
89 | {
90 | temp = temp->next;
91 | }
92 | }
93 | if (flag == 0)
94 | {
95 | cout << "Key Not Found" << endl;
96 | }
97 | }
98 | }
99 |
100 | int main()
101 | {
102 | LinkedList L;
103 | L.insert(3);
104 | L.insert(6);
105 | L.insert(9);
106 | L.print();
107 | L.remove(9);
108 | L.print();
109 | return 0;
110 | }
--------------------------------------------------------------------------------
/Algorithms/0_Recursion/README.md:
--------------------------------------------------------------------------------
1 | # Recursion
2 |
3 | ## Introduction
4 |
5 | Recursion is when a function calls itself either directly or indirectly. Typically the function performs some part of the task and rest is delegated to the recursive call of the same function. Hence, there are multiple instances of same function each performing some part of the overall task. Function stops calling itself when a terminating condition is reached.
6 |
7 | The core intuition is that if we are able to express a problem in terms of smaller instances of the itself, then we can solve the problem using recursion.
8 |
9 | The two components of recursion are:-
10 |
11 | * Base case: This is the terminating case.
12 | * Recursive case: Recursive function performs some part of task and delegate rest of it to the recursive call.
13 |
14 | ## How Recursion looks in Memory
15 |
16 | When a program, represented by an executable (```.exe``` or ```.out```), is executed, it becomes a process and is allocated space in RAM known as the Process Address Space. This is managed by the operating system and is divided into four main segments:
17 |
18 | * Code Segment: This is the segment where the executable code is stored. The size of CS is fixed during load time.
19 |
20 | * Data Segment: This is the segment where the global and static variables are stored. These values, if not initialized, are initialized with zero. The size of DS is fixed during load time and does not change during execution. Here, the variables are divided into two categories: initialized and uninitialized. The uninitialized variables are initialized with zeros together at the load time.
21 |
22 | * Stack Segment: This contains the activation of all active functions. Main is also a function and is always called first. The OS calls the main function. The activation record holds metadata of the function such as parameters, return value, calling function, etc. The size of stacks keeps changing during execution. The uninitialized variables are assigned garbage value here. The rationale behind not initializing local variables is to avoid unnecessary overhead, as initializing every variable would incur a performance cost. This is different from DS, where it takes the compiler only one memset call to initialize all variables to zeros if uninitialized.
23 |
24 | * Heap Segment: This is the segment where dynamic memory is allocated. The size of the Heap is not fixed during load time. Both the stack and heap share a common area in memory, where they grow towards each other.
--------------------------------------------------------------------------------
/01_Arrays/dynamic_array.c:
--------------------------------------------------------------------------------
1 | /***********************************************************
2 | @brief Implementing dynamic arrays (Vectors) in C
3 | *************************************************************/
4 |
5 | #include
6 | #include
7 |
8 | typedef struct Vector
9 | {
10 | int capacity;
11 | int size;
12 | int *arr;
13 | } Vector;
14 |
15 | /*
16 | * Function Name: PushBack
17 | * Input: Requires The element, pointer to array, capacity and size of object
18 | * Output: returns the modified array after insertion
19 | * Logic: Inserts an element to array and resizes the array if required
20 | * Example Call: PushBack(num, v.arr, &v.capacity, &v.size)
21 | */
22 | int *PushBack(int element, int *arr, int *capacity, int *size)
23 | {
24 | if (*size == *capacity) // Resizing the array is it is full
25 | {
26 | *capacity *= 2;
27 | int *temp = (int *)malloc(sizeof(int) * (*capacity));
28 |
29 | for (int i = 0; i < *size; i++)
30 | {
31 | temp[i] = arr[i];
32 | }
33 |
34 | free(arr);
35 | arr = temp;
36 | }
37 | arr[*size] = element;
38 | (*size)++;
39 |
40 | return arr;
41 | }
42 |
43 | int main()
44 | {
45 | Vector v; // Creating an object of struct Vector
46 | v.capacity = 2; // Initializing the values for object
47 | v.size = 0;
48 | v.arr = (int *)malloc(v.capacity * sizeof(int));
49 |
50 | while (1)
51 | {
52 | printf("Please enter 1 to insert an element, 2 to display an element and 3 to quit: ");
53 | int choice;
54 | scanf("%d", &choice);
55 |
56 | if (choice == 1)
57 | {
58 | int num;
59 | printf("Please enter the element: ");
60 | scanf("%d", &num);
61 | v.arr = PushBack(num, v.arr, &v.capacity, &v.size);
62 | }
63 | else if (choice == 2)
64 | {
65 | int index;
66 | printf("Enter the index: ");
67 | scanf("%d", &index);
68 | if (index < 0 || index >= v.size)
69 | {
70 | printf("Index is out of bounds\n");
71 | continue;
72 | }
73 | printf("The element is: %d", v.arr[index]);
74 | }
75 | else
76 | {
77 | break;
78 | }
79 | }
80 | return 0;
81 | }
82 |
83 | /*
84 | Analysis: The above code runs in O(1) for inserting an element and displaying an element, using amortized analysis.
85 | */
--------------------------------------------------------------------------------
/09_Graphs/adj_matrix.cpp:
--------------------------------------------------------------------------------
1 | /*
2 | Code to create a graph using Adjacency Matrix representation
3 | We consider the graph to be directed graph and non-weighted with no self loops
4 | */
5 | #include
6 |
7 | using namespace std;
8 |
9 | class Graph
10 | {
11 | private:
12 | int no_of_vertices;
13 | bool **adj_matrix;
14 |
15 | public:
16 | void make_graph(int no_of_vertices);
17 | void display();
18 | void add_edge();
19 | };
20 |
21 | /*
22 | This function is used to create a graph
23 | parameters : no_of_vertices
24 | Returns : void
25 | */
26 | void Graph ::make_graph(int no_of_vertices)
27 | {
28 | this->no_of_vertices = no_of_vertices;
29 |
30 | // creating a graph
31 | adj_matrix = new bool *[no_of_vertices];
32 | for (int i = 0; i < no_of_vertices; i++)
33 | {
34 | adj_matrix[i] = new bool[no_of_vertices];
35 | // initializing all the elements of graph
36 | for (int j = 0; j < no_of_vertices; j++)
37 | {
38 | adj_matrix[i][j] = 0;
39 | }
40 | }
41 | }
42 | // end of function
43 |
44 | /*
45 | This function is used to display the graph
46 | parameters : void
47 | Returns : void
48 | */
49 | void Graph ::display()
50 | {
51 | cout << "The adjacency matrix representation is :-\n";
52 | for (int i = 0; i < no_of_vertices; i++)
53 | {
54 | for (int j = 0; j < no_of_vertices; j++)
55 | {
56 | cout << adj_matrix[i][j] << " ";
57 | }
58 | cout << "\n";
59 | }
60 | }
61 | // end of function
62 |
63 | /*
64 | This function iterates over all the possible edges and asks user if they want the edge to exsist or not
65 | parameters : void
66 | Returns : void
67 | */
68 | void Graph ::add_edge()
69 | {
70 | for (int i = 0; i < no_of_vertices; i++)
71 | {
72 | for (int j = 0; j < no_of_vertices; j++)
73 | {
74 | if (i != j)
75 | {
76 | char choice;
77 | cout << "Are vertices " << i << " and " << j << " adjacent? (Y/N) : ";
78 | cin >> choice;
79 |
80 | if (toupper(choice) == 'Y')
81 | {
82 | adj_matrix[i][j] = 1;
83 | }
84 | }
85 | }
86 | }
87 | }
88 | // end of function
89 |
90 | // main function starts here
91 | int main()
92 | {
93 | Graph g;
94 | int no_of_vertices;
95 | cout << "Enter the number of vertices : ";
96 | cin >> no_of_vertices;
97 |
98 | g.make_graph(no_of_vertices);
99 | g.add_edge();
100 | g.display();
101 |
102 | return 0;
103 | }
104 | // end of main
--------------------------------------------------------------------------------
/Algorithms/2_Divide_and_Conquer/counting_inversions.cpp:
--------------------------------------------------------------------------------
1 | /**************************************************************************
2 | @brief Counting the total number of inversions in an given array
3 | **************************************************************************/
4 | #include
5 | #include
6 | #include
7 | #include
8 |
9 | int global_count = 0;
10 |
11 | using namespace std;
12 |
13 | /*
14 | * Function Name: Merge
15 | * Input: Requires two sorted portions of array defined by left, mid and right
16 | * Output: returns the merged vector which is sorted
17 | * Logic: This function merges two sorted arrays and counts the number of inversions
18 | * Example Call: Merge(A, 0, 4, 2)
19 | */
20 | void Merge(vector &A, int left, int right, int mid)
21 | {
22 | int p = left;
23 | int q = mid;
24 |
25 | vector merged;
26 |
27 | while (p < mid && q < right)
28 | {
29 | if (A[p] <= A[q])
30 | {
31 | merged.push_back(A[p]);
32 | p++;
33 | }
34 | else
35 | {
36 | merged.push_back(A[q]);
37 | global_count += mid - p; // Inversions
38 | q++;
39 | }
40 | }
41 |
42 | while (p < mid)
43 | {
44 | merged.push_back(A[p]);
45 | p++;
46 | }
47 | while (q < right)
48 | {
49 | merged.push_back(A[q]);
50 | q++;
51 | }
52 |
53 | for (int i = 0; i < merged.size(); i++)
54 | {
55 | A[left + i] = merged[i];
56 | }
57 | }
58 |
59 | /*
60 | * Function Name: MergeSort
61 | * Input: Requires a vector, starting index and ending index
62 | * Output: returns the sorted array
63 | * Logic: Recursively divides the given vector in two halves and passes them to merge function
64 | * Example Call: MergeSort(A, 0, 5)
65 | */
66 | void MergeSort(vector &A, int begin, int end)
67 | {
68 | if (end - begin == 1)
69 | {
70 | return;
71 | }
72 | int mid = floor((end - begin) / 2);
73 | MergeSort(A, begin, begin + mid);
74 | MergeSort(A, begin + mid, end);
75 | Merge(A, begin, end, begin + mid);
76 | }
77 |
78 | int main()
79 | {
80 | int n;
81 | cout << "Enter number of elements: " ;
82 | cin >> n;
83 | vector v(n);
84 |
85 | cout << "Enter elements of array: " ;
86 | for (int i = 0; i < n; i++)
87 | {
88 | cin >> v[i];
89 | }
90 |
91 | MergeSort(v, 0, v.size());
92 |
93 | cout << "Total number of inversions: " << global_count;
94 |
95 | return 0;
96 | }
97 | /*
98 | Analysis: The above code runs in O(nlog(n)). The implementation is same as merge sort except for the step where we count number of inversions.
99 | */
--------------------------------------------------------------------------------
/Algorithms/4_Sorting/merge_sort.cpp:
--------------------------------------------------------------------------------
1 | /****************************************
2 | @brief Implementing Merge Sort
3 | *****************************************/
4 | #include
5 | #include
6 | #include
7 | #include
8 |
9 | using namespace std;
10 |
11 | /*
12 | * Function Name: Merge
13 | * Input: Requires two sorted portions of array defined by left, mid and right
14 | * Output: returns the merged vector which is sorted
15 | * Logic: This function merges two sorted arrays and counts the number of inversions
16 | * Example Call: Merge(A, 0, 4, 2)
17 | */
18 | void Merge(vector &A, int left, int right, int mid)
19 | {
20 | int p = left;
21 | int q = mid;
22 |
23 | vector merged;
24 |
25 | while (p < mid && q < right)
26 | {
27 | if (A[p] <= A[q])
28 | {
29 | merged.push_back(A[p]);
30 | p++;
31 | }
32 | else
33 | {
34 | merged.push_back(A[q]);
35 | q++;
36 | }
37 | }
38 |
39 | while (p < mid)
40 | {
41 | merged.push_back(A[p]);
42 | p++;
43 | }
44 | while (q < right)
45 | {
46 | merged.push_back(A[q]);
47 | q++;
48 | }
49 |
50 | for (int i = 0; i < merged.size(); i++)
51 | {
52 | A[left + i] = merged[i];
53 | }
54 | }
55 |
56 | /*
57 | * Function Name: MergeSort
58 | * Input: Requires a vector, starting index and ending index
59 | * Output: returns the sorted array
60 | * Logic: Recursively divides the given vector in two halves and passes them to merge function
61 | * Example Call: MergeSort(A, 0, 5)
62 | */
63 | void MergeSort(vector &A, int begin, int end)
64 | {
65 | if (end - begin == 1)
66 | {
67 | return;
68 | }
69 | int mid = floor((end - begin) / 2);
70 | MergeSort(A, begin, begin + mid);
71 | MergeSort(A, begin + mid, end);
72 | Merge(A, begin, end, begin + mid);
73 | }
74 |
75 | int main()
76 | {
77 | cout << "Enter the elements: " ;
78 |
79 | string s;
80 | getline(cin, s);
81 |
82 | int num = 0;
83 | vector v;
84 |
85 | /*Taking input from the user and storing it in a vector of int*/
86 | for (int i = 0; i < s.size(); ++i)
87 | {
88 | if (s[i] == ' ')
89 | v.push_back(num), num = 0;
90 | else
91 | num = num * 10 + (s[i] - '0');
92 | }
93 | v.push_back(num);
94 |
95 | MergeSort(v, 0, v.size());
96 |
97 | cout << "The sorted array is: ";
98 | for (int i = 0; i < v.size(); i++)
99 | {
100 | cout << v[i] << " ";
101 | }
102 | }
103 | /*
104 | Analysis: The above code runs in O(nlog(n))
105 | */
--------------------------------------------------------------------------------
/Algorithms/4_Sorting/quick_sort.cpp:
--------------------------------------------------------------------------------
1 | /****************************************
2 | @brief Implementing Quick Sort
3 | *****************************************/
4 | #include
5 | #include
6 | #include
7 |
8 | using namespace std;
9 |
10 | void Swap(int &i, int &j)
11 | {
12 | int temp = i;
13 | i = j;
14 | j = temp;
15 | }
16 |
17 | /*
18 | * Function Name: Parition
19 | * Input: Requires a vector, index of pivot element, starting index and ending element
20 | * Output: returns the position of pivot element in sorted array
21 | * Logic: Keeps elements smaller than pivot to its left and larger to its right
22 | * Example Call: Partition(v, 0, 0, v.size()-1)
23 | */
24 | int Partition(vector &v, int pivot, int i, int j)
25 | {
26 | if (i == j)
27 | {
28 | return i;
29 | }
30 |
31 | while (i <= j)
32 | {
33 | if (v[i] > v[pivot] && v[j] < v[pivot])
34 | {
35 | swap(v[i], v[j]);
36 | i++;
37 | j--;
38 | }
39 | else if (v[i] <= v[pivot])
40 | {
41 | i++;
42 | }
43 | else if (v[j] >= v[pivot])
44 | {
45 | j--;
46 | }
47 | }
48 |
49 | Swap(v[pivot], v[i - 1]);
50 | return i - 1;
51 | }
52 |
53 | /*
54 | * Function Name: QuickSort
55 | * Input: Requires a vector, index of pivot element, starting element and ending element
56 | * Logic: Divides the array as per partition by pivot and creates a sorted array
57 | * Example Call: QuickSort(v, pivot, 0, v.size() - 1)
58 | */
59 | void QuickSort(vector &v, int pivot, int begin, int end)
60 | {
61 | if (end <= begin)
62 | {
63 | return;
64 | }
65 |
66 | int m = Partition(v, pivot, begin, end); // m represents position of partition
67 |
68 | QuickSort(v, begin, begin, m - 1);
69 | QuickSort(v, m + 1, m + 1, end);
70 | }
71 |
72 | int main()
73 | {
74 | string s;
75 | getline(cin, s);
76 |
77 | int num = 0;
78 | vector v;
79 |
80 | /*Taking input from the user and storing it in a vector of int*/
81 | for (int i = 0; i < s.size(); ++i)
82 | {
83 | if (s[i] == ' ')
84 | v.push_back(num), num = 0;
85 | else
86 | num = num * 10 + (s[i] - '0');
87 | }
88 | v.push_back(num);
89 |
90 | int pivot = 0; // Initially the pivot element is element at 0th index
91 |
92 | QuickSort(v, pivot, 0, v.size() - 1);
93 |
94 | for (int i = 0; i < v.size(); i++)
95 | {
96 | cout << v[i] << " ";
97 | }
98 |
99 | return 0;
100 | }
101 | /*
102 | Analysis: The above code runs averagely in O(nlog(n)) and O(n^2) in worst cases
103 | */
--------------------------------------------------------------------------------
/leetcode/16 3Sum Closest.cpp:
--------------------------------------------------------------------------------
1 | /*
2 | Approach 1: Checking all possible combinations after sorting
3 | Runtime: 44ms
4 | Memory: 10.50MB
5 | Time Complexity: O(nlog(n) + n^2) or O(n^2) //Sorting + linear search for all elements
6 | */
7 | class Solution {
8 | public:
9 | int threeSumClosest(vector& nums, int target) {
10 | sort(nums.begin(),nums.end());
11 | int n = nums.size();
12 | int sum = 0, curr = 9999999;
13 |
14 | for (int i = 0; i < n-2; i++)
15 | {
16 | int start = i+1;
17 | int end = n-1;
18 | while(end>start)
19 | {
20 | int temp = nums[start]+nums[end]+nums[i];
21 | if (abs(temp-target)target)
27 | {
28 | end--;
29 | }
30 | else
31 | {
32 | start++;
33 | }
34 | }
35 | }
36 | return sum;
37 | }
38 | };
39 |
40 | /*
41 | Approach 2: Checking all possible combinations after sorting with better pruning strategies
42 | Runtime: 4ms
43 | Memory: 10.45MB
44 | Time Complexity: O(nlog(n) + n^2) or O(n^2) //Sorting + linear search for all elements
45 | */
46 | class Solution {
47 | public:
48 | int threeSumClosest(vector& nums, int target) {
49 | std::sort(nums.begin(), nums.end());
50 |
51 | if (nums[0] + nums[1] + nums[2] >= target) {
52 | return nums[0] + nums[1] + nums[2];
53 | }
54 | if (nums[nums.size() - 1] + nums[nums.size() - 2] + nums[nums.size() - 3] <= target) {
55 | return nums[nums.size() - 1] + nums[nums.size() - 2] + nums[nums.size() - 3];
56 | }
57 |
58 | int closest = nums[0] + nums[1] + nums[2];
59 | int n = nums.size();
60 | for (int i = 0; i < n - 2; ++i) {
61 | int j = i + 1, k = nums.size() - 1;
62 | while (j < k) {
63 | int sum = nums[i] + nums[j] + nums[k];
64 | if (abs(sum - target) < abs(closest - target)) {
65 | closest =sum;
66 | }
67 | if (sum < target) {
68 | while (j + 1 < k && nums[j] == nums[j + 1]) {
69 | ++j;
70 | }
71 | ++j;
72 | } else if (sum > target) {
73 | while (k - 1 > j && nums[k] == nums[k - 1]) {
74 | --k;
75 | }
76 | --k;
77 | } else {
78 | return target;
79 | }
80 | }
81 | }
82 | return closest;
83 | }
84 | };
--------------------------------------------------------------------------------
/04_Linked List/readme.md:
--------------------------------------------------------------------------------
1 | # Linked Lists
2 |
3 | ## Why Linked lists ?
4 |
5 | Stacks and Queues are great data structures to store data. However, there are a few limitations to use of stacks and queues. Both stacks and queues are statically allocated memory, which means that the amount of memory allocated to stack or queue is fixed and cannot be changed.
6 |
7 | Imagine that you allocate an array of MAX_SIZE 100 to a stack. Now, even if there are 20 elements in your stack, the remaining space of 80 elements can not be used by the program. Tommorow, if you want to insert the 101th element, it is not possible to insert it directly since you are out of space. Linked Lists solve this problem using dynamic memory allocation. Whenever we need to store an element, we create a node in linked list using malloc() / new function and once we are done with the element, we destroy the node using free() / delete() functions, hence making that memory usable by program for other tasks.
8 |
9 | ## Introduction
10 |
11 | Every element in a Linked list is stored in the form of a node. A node comprises of two things, data and the the address of the next node. We also have an external pointer called head pointing at the first node of linked list. Optionally, we can have a tail pointer which points at the last element of linked list to optimize operations such as adding an element to the end.
12 |
13 | ## Types of Linked List
14 | 1) Singly Linked List
15 | 2) Doubly Linked List
16 | 3) Circular Linked List
17 | 4) Circular Doubly Linked List
18 |
19 | ## Proof for Floyd Cycle Detection Algorithm
20 |
21 |
28 |
29 |
--------------------------------------------------------------------------------
/09_Graphs/bellman-ford.cpp:
--------------------------------------------------------------------------------
1 | #include
2 | #include
3 | #include
4 |
5 | using std::vector;
6 |
7 | vector negative_cycle(vector> &adj, vector> &cost, int s)
8 | {
9 | int v = adj.size();
10 | vector visited(v);
11 |
12 | vector dist(v, INT_MAX);
13 | dist[s] = 0;
14 |
15 | for (int k = 0; k < v - 1; k++)
16 | {
17 | // Run v-1 interations
18 |
19 | for (int i = 0; i < v; i++)
20 | {
21 | for (int j = 0; j < adj[i].size(); j++)
22 | {
23 | if (dist[i] + cost[i][j] < dist[adj[i][j]] && dist[i] != INT_MAX)
24 | {
25 | dist[adj[i][j]] = dist[i] + cost[i][j];
26 | }
27 | }
28 | }
29 | }
30 |
31 | while (1)
32 | {
33 | vector temp = dist;
34 | for (int i = 0; i < v; i++)
35 | {
36 | for (int j = 0; j < adj[i].size(); j++)
37 | {
38 | if (dist[i] == INT_MIN || dist[i] + cost[i][j] < dist[adj[i][j]])
39 | {
40 | dist[adj[i][j]] = INT_MIN;
41 | }
42 | }
43 | }
44 | if (temp == dist)
45 | {
46 | break;
47 | }
48 | }
49 |
50 | return dist;
51 | }
52 |
53 | int main()
54 | {
55 | int n, m;
56 | std::cin >> n >> m;
57 | vector> adj(n, vector());
58 | vector> cost(n, vector());
59 | for (int i = 0; i < m; i++)
60 | {
61 | int x, y, w;
62 | std::cin >> x >> y >> w;
63 | adj[x - 1].push_back(y - 1);
64 | cost[x - 1].push_back(w);
65 | }
66 | int s;
67 | std::cin >> s;
68 | vector dist = negative_cycle(adj, cost, s - 1);
69 |
70 | for (int i = 0; i < dist.size(); i++)
71 | {
72 | if (dist[i] == INT_MAX)
73 | {
74 | std::cout << "*";
75 | }
76 | else if (dist[i] == INT_MIN)
77 | {
78 | std::cout << "-";
79 | }
80 | else
81 | {
82 | std::cout << dist[i];
83 | }
84 | std::cout << std::endl;
85 | }
86 | }
87 |
--------------------------------------------------------------------------------
/leetcode/494 Target Sum.cpp:
--------------------------------------------------------------------------------
1 | /*
2 | Approach 1: Brute force method to try and test all possible combinations
3 | TLE
4 | Time Complexity: O(2^n)
5 | */
6 | class Solution {
7 | public:
8 | int count = 0;
9 | void eval(vector &mask,vector& nums, int pos, int target)
10 | {
11 | int sum = 0;
12 | for (int i = 0; i < mask.size(); i++)
13 | {
14 | if (mask[i] == 0)
15 | {
16 | sum+=nums[i];
17 | }
18 | else
19 | {
20 | sum-=nums[i];
21 | }
22 | }
23 | if (sum == target)
24 | {
25 | count++;
26 | }
27 | }
28 |
29 | void gen (vector &mask, vector& nums, int pos, int target)
30 | {
31 | //base case
32 | if (pos == mask.size())
33 | {
34 | eval(mask, nums, pos, target);
35 | return;
36 | }
37 | // mask will be 0
38 | gen(mask, nums, pos+1, target);
39 | //mask will be 1
40 | mask[pos]=1;
41 | gen(mask, nums, pos+1, target);
42 | mask[pos]=0;
43 | }
44 | int findTargetSumWays(vector& nums, int target) {
45 | vector mask (nums.size());
46 | gen(mask, nums, 0, target);
47 | return count;
48 | }
49 | };
50 |
51 | /*
52 | Approach 2: Brute Force Recursion with better method to obtain sum
53 | TLE
54 | Time Complexity: O(2^n), where m*n is dimension of board and w is length of word
55 | */
56 | class Solution {
57 | public:
58 | int count = 0;
59 | void gen (vector &mask, vector& nums, int pos, int target, int sum)
60 | {
61 | //base case
62 | if (pos == mask.size())
63 | {
64 | if (sum == target)
65 | {
66 | count++;
67 | }
68 | return;
69 | }
70 |
71 | //rec case
72 |
73 | // mask will be 0
74 | gen(mask, nums, pos+1, target, sum+nums[pos]);
75 | //mask will be 1
76 | mask[pos]=1;
77 | gen(mask, nums, pos+1, target, sum-nums[pos]);
78 | mask[pos]=0;
79 | }
80 | int findTargetSumWays(vector& nums, int target) {
81 | vector mask (nums.size());
82 | gen(mask, nums, 0, target, 0);
83 | return count;
84 | }
85 | };
--------------------------------------------------------------------------------
/04_Linked List/linked_list.cpp:
--------------------------------------------------------------------------------
1 | #include
2 |
3 | using namespace std;
4 |
5 | class Node
6 | {
7 | public:
8 | int data;
9 | Node* next;
10 | Node(int data)
11 | {
12 | this->data = data;
13 | next = NULL;
14 | }
15 | };
16 |
17 | class LinkedList
18 | {
19 | public:
20 | Node* head = NULL;
21 | void insert(int data);
22 | void print();
23 | void remove(int data);
24 | };
25 |
26 | void LinkedList::insert(int data)
27 | {
28 | if (head == NULL)
29 | {
30 | head = new Node(data);
31 | }
32 | else
33 | {
34 | Node* temp = head;
35 | while (temp->next != NULL)
36 | {
37 | temp = temp->next;
38 | }
39 | temp->next = new Node(data);
40 | }
41 | }
42 |
43 | void LinkedList::print()
44 | {
45 | if (head == NULL)
46 | {
47 | cout << "Linked List is Empty" << endl;
48 | }
49 | else
50 | {
51 | Node* temp = head;
52 | while (temp != NULL)
53 | {
54 | cout << temp->data << " -> ";
55 | temp = temp->next;
56 | }
57 | cout << "NULL" << endl;
58 | }
59 | }
60 |
61 | void LinkedList::remove(int key)
62 | {
63 | if (head == NULL)
64 | {
65 | cout << "Linked List is Empty" << endl;
66 | }
67 | else if(head->data == key)
68 | {
69 | Node* temp = head;
70 | temp = head->next;
71 | free(head);
72 | head = temp;
73 | }
74 | else
75 | {
76 | bool flag = 0;
77 | Node* temp = head;
78 | while (temp->next != NULL)
79 | {
80 | if (temp->next->data == key)
81 | {
82 | flag = 1;
83 | Node* p = temp->next;
84 | temp->next = temp->next->next;
85 | free(p);
86 | break;
87 | }
88 | else
89 | {
90 | temp = temp->next;
91 | }
92 | }
93 | if (flag == 0)
94 | {
95 | cout << "Key Not Found" << endl;
96 | }
97 | }
98 | }
99 |
100 | int main()
101 | {
102 | LinkedList L;
103 | L.insert(3);
104 | L.insert(6);
105 | L.insert(9);
106 | L.print();
107 | L.remove(9);
108 | L.print();
109 | return 0;
110 | }
--------------------------------------------------------------------------------
/Algorithms/0_Recursion/README.md:
--------------------------------------------------------------------------------
1 | # Recursion
2 |
3 | ## Introduction
4 |
5 | Recursion is when a function calls itself either directly or indirectly. Typically the function performs some part of the task and rest is delegated to the recursive call of the same function. Hence, there are multiple instances of same function each performing some part of the overall task. Function stops calling itself when a terminating condition is reached.
6 |
7 | The core intuition is that if we are able to express a problem in terms of smaller instances of the itself, then we can solve the problem using recursion.
8 |
9 | The two components of recursion are:-
10 |
11 | * Base case: This is the terminating case.
12 | * Recursive case: Recursive function performs some part of task and delegate rest of it to the recursive call.
13 |
14 | ## How Recursion looks in Memory
15 |
16 | When a program, represented by an executable (```.exe``` or ```.out```), is executed, it becomes a process and is allocated space in RAM known as the Process Address Space. This is managed by the operating system and is divided into four main segments:
17 |
18 | * Code Segment: This is the segment where the executable code is stored. The size of CS is fixed during load time.
19 |
20 | * Data Segment: This is the segment where the global and static variables are stored. These values, if not initialized, are initialized with zero. The size of DS is fixed during load time and does not change during execution. Here, the variables are divided into two categories: initialized and uninitialized. The uninitialized variables are initialized with zeros together at the load time.
21 |
22 | * Stack Segment: This contains the activation of all active functions. Main is also a function and is always called first. The OS calls the main function. The activation record holds metadata of the function such as parameters, return value, calling function, etc. The size of stacks keeps changing during execution. The uninitialized variables are assigned garbage value here. The rationale behind not initializing local variables is to avoid unnecessary overhead, as initializing every variable would incur a performance cost. This is different from DS, where it takes the compiler only one memset call to initialize all variables to zeros if uninitialized.
23 |
24 | * Heap Segment: This is the segment where dynamic memory is allocated. The size of the Heap is not fixed during load time. Both the stack and heap share a common area in memory, where they grow towards each other.
--------------------------------------------------------------------------------
/01_Arrays/dynamic_array.c:
--------------------------------------------------------------------------------
1 | /***********************************************************
2 | @brief Implementing dynamic arrays (Vectors) in C
3 | *************************************************************/
4 |
5 | #include
6 | #include
7 |
8 | typedef struct Vector
9 | {
10 | int capacity;
11 | int size;
12 | int *arr;
13 | } Vector;
14 |
15 | /*
16 | * Function Name: PushBack
17 | * Input: Requires The element, pointer to array, capacity and size of object
18 | * Output: returns the modified array after insertion
19 | * Logic: Inserts an element to array and resizes the array if required
20 | * Example Call: PushBack(num, v.arr, &v.capacity, &v.size)
21 | */
22 | int *PushBack(int element, int *arr, int *capacity, int *size)
23 | {
24 | if (*size == *capacity) // Resizing the array is it is full
25 | {
26 | *capacity *= 2;
27 | int *temp = (int *)malloc(sizeof(int) * (*capacity));
28 |
29 | for (int i = 0; i < *size; i++)
30 | {
31 | temp[i] = arr[i];
32 | }
33 |
34 | free(arr);
35 | arr = temp;
36 | }
37 | arr[*size] = element;
38 | (*size)++;
39 |
40 | return arr;
41 | }
42 |
43 | int main()
44 | {
45 | Vector v; // Creating an object of struct Vector
46 | v.capacity = 2; // Initializing the values for object
47 | v.size = 0;
48 | v.arr = (int *)malloc(v.capacity * sizeof(int));
49 |
50 | while (1)
51 | {
52 | printf("Please enter 1 to insert an element, 2 to display an element and 3 to quit: ");
53 | int choice;
54 | scanf("%d", &choice);
55 |
56 | if (choice == 1)
57 | {
58 | int num;
59 | printf("Please enter the element: ");
60 | scanf("%d", &num);
61 | v.arr = PushBack(num, v.arr, &v.capacity, &v.size);
62 | }
63 | else if (choice == 2)
64 | {
65 | int index;
66 | printf("Enter the index: ");
67 | scanf("%d", &index);
68 | if (index < 0 || index >= v.size)
69 | {
70 | printf("Index is out of bounds\n");
71 | continue;
72 | }
73 | printf("The element is: %d", v.arr[index]);
74 | }
75 | else
76 | {
77 | break;
78 | }
79 | }
80 | return 0;
81 | }
82 |
83 | /*
84 | Analysis: The above code runs in O(1) for inserting an element and displaying an element, using amortized analysis.
85 | */
--------------------------------------------------------------------------------
/09_Graphs/adj_matrix.cpp:
--------------------------------------------------------------------------------
1 | /*
2 | Code to create a graph using Adjacency Matrix representation
3 | We consider the graph to be directed graph and non-weighted with no self loops
4 | */
5 | #include
6 |
7 | using namespace std;
8 |
9 | class Graph
10 | {
11 | private:
12 | int no_of_vertices;
13 | bool **adj_matrix;
14 |
15 | public:
16 | void make_graph(int no_of_vertices);
17 | void display();
18 | void add_edge();
19 | };
20 |
21 | /*
22 | This function is used to create a graph
23 | parameters : no_of_vertices
24 | Returns : void
25 | */
26 | void Graph ::make_graph(int no_of_vertices)
27 | {
28 | this->no_of_vertices = no_of_vertices;
29 |
30 | // creating a graph
31 | adj_matrix = new bool *[no_of_vertices];
32 | for (int i = 0; i < no_of_vertices; i++)
33 | {
34 | adj_matrix[i] = new bool[no_of_vertices];
35 | // initializing all the elements of graph
36 | for (int j = 0; j < no_of_vertices; j++)
37 | {
38 | adj_matrix[i][j] = 0;
39 | }
40 | }
41 | }
42 | // end of function
43 |
44 | /*
45 | This function is used to display the graph
46 | parameters : void
47 | Returns : void
48 | */
49 | void Graph ::display()
50 | {
51 | cout << "The adjacency matrix representation is :-\n";
52 | for (int i = 0; i < no_of_vertices; i++)
53 | {
54 | for (int j = 0; j < no_of_vertices; j++)
55 | {
56 | cout << adj_matrix[i][j] << " ";
57 | }
58 | cout << "\n";
59 | }
60 | }
61 | // end of function
62 |
63 | /*
64 | This function iterates over all the possible edges and asks user if they want the edge to exsist or not
65 | parameters : void
66 | Returns : void
67 | */
68 | void Graph ::add_edge()
69 | {
70 | for (int i = 0; i < no_of_vertices; i++)
71 | {
72 | for (int j = 0; j < no_of_vertices; j++)
73 | {
74 | if (i != j)
75 | {
76 | char choice;
77 | cout << "Are vertices " << i << " and " << j << " adjacent? (Y/N) : ";
78 | cin >> choice;
79 |
80 | if (toupper(choice) == 'Y')
81 | {
82 | adj_matrix[i][j] = 1;
83 | }
84 | }
85 | }
86 | }
87 | }
88 | // end of function
89 |
90 | // main function starts here
91 | int main()
92 | {
93 | Graph g;
94 | int no_of_vertices;
95 | cout << "Enter the number of vertices : ";
96 | cin >> no_of_vertices;
97 |
98 | g.make_graph(no_of_vertices);
99 | g.add_edge();
100 | g.display();
101 |
102 | return 0;
103 | }
104 | // end of main
--------------------------------------------------------------------------------
/Algorithms/2_Divide_and_Conquer/counting_inversions.cpp:
--------------------------------------------------------------------------------
1 | /**************************************************************************
2 | @brief Counting the total number of inversions in an given array
3 | **************************************************************************/
4 | #include
5 | #include
6 | #include
7 | #include
8 |
9 | int global_count = 0;
10 |
11 | using namespace std;
12 |
13 | /*
14 | * Function Name: Merge
15 | * Input: Requires two sorted portions of array defined by left, mid and right
16 | * Output: returns the merged vector which is sorted
17 | * Logic: This function merges two sorted arrays and counts the number of inversions
18 | * Example Call: Merge(A, 0, 4, 2)
19 | */
20 | void Merge(vector &A, int left, int right, int mid)
21 | {
22 | int p = left;
23 | int q = mid;
24 |
25 | vector merged;
26 |
27 | while (p < mid && q < right)
28 | {
29 | if (A[p] <= A[q])
30 | {
31 | merged.push_back(A[p]);
32 | p++;
33 | }
34 | else
35 | {
36 | merged.push_back(A[q]);
37 | global_count += mid - p; // Inversions
38 | q++;
39 | }
40 | }
41 |
42 | while (p < mid)
43 | {
44 | merged.push_back(A[p]);
45 | p++;
46 | }
47 | while (q < right)
48 | {
49 | merged.push_back(A[q]);
50 | q++;
51 | }
52 |
53 | for (int i = 0; i < merged.size(); i++)
54 | {
55 | A[left + i] = merged[i];
56 | }
57 | }
58 |
59 | /*
60 | * Function Name: MergeSort
61 | * Input: Requires a vector, starting index and ending index
62 | * Output: returns the sorted array
63 | * Logic: Recursively divides the given vector in two halves and passes them to merge function
64 | * Example Call: MergeSort(A, 0, 5)
65 | */
66 | void MergeSort(vector &A, int begin, int end)
67 | {
68 | if (end - begin == 1)
69 | {
70 | return;
71 | }
72 | int mid = floor((end - begin) / 2);
73 | MergeSort(A, begin, begin + mid);
74 | MergeSort(A, begin + mid, end);
75 | Merge(A, begin, end, begin + mid);
76 | }
77 |
78 | int main()
79 | {
80 | int n;
81 | cout << "Enter number of elements: " ;
82 | cin >> n;
83 | vector v(n);
84 |
85 | cout << "Enter elements of array: " ;
86 | for (int i = 0; i < n; i++)
87 | {
88 | cin >> v[i];
89 | }
90 |
91 | MergeSort(v, 0, v.size());
92 |
93 | cout << "Total number of inversions: " << global_count;
94 |
95 | return 0;
96 | }
97 | /*
98 | Analysis: The above code runs in O(nlog(n)). The implementation is same as merge sort except for the step where we count number of inversions.
99 | */
--------------------------------------------------------------------------------
/Algorithms/4_Sorting/merge_sort.cpp:
--------------------------------------------------------------------------------
1 | /****************************************
2 | @brief Implementing Merge Sort
3 | *****************************************/
4 | #include
5 | #include
6 | #include
7 | #include
8 |
9 | using namespace std;
10 |
11 | /*
12 | * Function Name: Merge
13 | * Input: Requires two sorted portions of array defined by left, mid and right
14 | * Output: returns the merged vector which is sorted
15 | * Logic: This function merges two sorted arrays and counts the number of inversions
16 | * Example Call: Merge(A, 0, 4, 2)
17 | */
18 | void Merge(vector &A, int left, int right, int mid)
19 | {
20 | int p = left;
21 | int q = mid;
22 |
23 | vector merged;
24 |
25 | while (p < mid && q < right)
26 | {
27 | if (A[p] <= A[q])
28 | {
29 | merged.push_back(A[p]);
30 | p++;
31 | }
32 | else
33 | {
34 | merged.push_back(A[q]);
35 | q++;
36 | }
37 | }
38 |
39 | while (p < mid)
40 | {
41 | merged.push_back(A[p]);
42 | p++;
43 | }
44 | while (q < right)
45 | {
46 | merged.push_back(A[q]);
47 | q++;
48 | }
49 |
50 | for (int i = 0; i < merged.size(); i++)
51 | {
52 | A[left + i] = merged[i];
53 | }
54 | }
55 |
56 | /*
57 | * Function Name: MergeSort
58 | * Input: Requires a vector, starting index and ending index
59 | * Output: returns the sorted array
60 | * Logic: Recursively divides the given vector in two halves and passes them to merge function
61 | * Example Call: MergeSort(A, 0, 5)
62 | */
63 | void MergeSort(vector &A, int begin, int end)
64 | {
65 | if (end - begin == 1)
66 | {
67 | return;
68 | }
69 | int mid = floor((end - begin) / 2);
70 | MergeSort(A, begin, begin + mid);
71 | MergeSort(A, begin + mid, end);
72 | Merge(A, begin, end, begin + mid);
73 | }
74 |
75 | int main()
76 | {
77 | cout << "Enter the elements: " ;
78 |
79 | string s;
80 | getline(cin, s);
81 |
82 | int num = 0;
83 | vector v;
84 |
85 | /*Taking input from the user and storing it in a vector of int*/
86 | for (int i = 0; i < s.size(); ++i)
87 | {
88 | if (s[i] == ' ')
89 | v.push_back(num), num = 0;
90 | else
91 | num = num * 10 + (s[i] - '0');
92 | }
93 | v.push_back(num);
94 |
95 | MergeSort(v, 0, v.size());
96 |
97 | cout << "The sorted array is: ";
98 | for (int i = 0; i < v.size(); i++)
99 | {
100 | cout << v[i] << " ";
101 | }
102 | }
103 | /*
104 | Analysis: The above code runs in O(nlog(n))
105 | */
--------------------------------------------------------------------------------
/Algorithms/4_Sorting/quick_sort.cpp:
--------------------------------------------------------------------------------
1 | /****************************************
2 | @brief Implementing Quick Sort
3 | *****************************************/
4 | #include
5 | #include
6 | #include
7 |
8 | using namespace std;
9 |
10 | void Swap(int &i, int &j)
11 | {
12 | int temp = i;
13 | i = j;
14 | j = temp;
15 | }
16 |
17 | /*
18 | * Function Name: Parition
19 | * Input: Requires a vector, index of pivot element, starting index and ending element
20 | * Output: returns the position of pivot element in sorted array
21 | * Logic: Keeps elements smaller than pivot to its left and larger to its right
22 | * Example Call: Partition(v, 0, 0, v.size()-1)
23 | */
24 | int Partition(vector &v, int pivot, int i, int j)
25 | {
26 | if (i == j)
27 | {
28 | return i;
29 | }
30 |
31 | while (i <= j)
32 | {
33 | if (v[i] > v[pivot] && v[j] < v[pivot])
34 | {
35 | swap(v[i], v[j]);
36 | i++;
37 | j--;
38 | }
39 | else if (v[i] <= v[pivot])
40 | {
41 | i++;
42 | }
43 | else if (v[j] >= v[pivot])
44 | {
45 | j--;
46 | }
47 | }
48 |
49 | Swap(v[pivot], v[i - 1]);
50 | return i - 1;
51 | }
52 |
53 | /*
54 | * Function Name: QuickSort
55 | * Input: Requires a vector, index of pivot element, starting element and ending element
56 | * Logic: Divides the array as per partition by pivot and creates a sorted array
57 | * Example Call: QuickSort(v, pivot, 0, v.size() - 1)
58 | */
59 | void QuickSort(vector &v, int pivot, int begin, int end)
60 | {
61 | if (end <= begin)
62 | {
63 | return;
64 | }
65 |
66 | int m = Partition(v, pivot, begin, end); // m represents position of partition
67 |
68 | QuickSort(v, begin, begin, m - 1);
69 | QuickSort(v, m + 1, m + 1, end);
70 | }
71 |
72 | int main()
73 | {
74 | string s;
75 | getline(cin, s);
76 |
77 | int num = 0;
78 | vector v;
79 |
80 | /*Taking input from the user and storing it in a vector of int*/
81 | for (int i = 0; i < s.size(); ++i)
82 | {
83 | if (s[i] == ' ')
84 | v.push_back(num), num = 0;
85 | else
86 | num = num * 10 + (s[i] - '0');
87 | }
88 | v.push_back(num);
89 |
90 | int pivot = 0; // Initially the pivot element is element at 0th index
91 |
92 | QuickSort(v, pivot, 0, v.size() - 1);
93 |
94 | for (int i = 0; i < v.size(); i++)
95 | {
96 | cout << v[i] << " ";
97 | }
98 |
99 | return 0;
100 | }
101 | /*
102 | Analysis: The above code runs averagely in O(nlog(n)) and O(n^2) in worst cases
103 | */
--------------------------------------------------------------------------------
/leetcode/16 3Sum Closest.cpp:
--------------------------------------------------------------------------------
1 | /*
2 | Approach 1: Checking all possible combinations after sorting
3 | Runtime: 44ms
4 | Memory: 10.50MB
5 | Time Complexity: O(nlog(n) + n^2) or O(n^2) //Sorting + linear search for all elements
6 | */
7 | class Solution {
8 | public:
9 | int threeSumClosest(vector& nums, int target) {
10 | sort(nums.begin(),nums.end());
11 | int n = nums.size();
12 | int sum = 0, curr = 9999999;
13 |
14 | for (int i = 0; i < n-2; i++)
15 | {
16 | int start = i+1;
17 | int end = n-1;
18 | while(end>start)
19 | {
20 | int temp = nums[start]+nums[end]+nums[i];
21 | if (abs(temp-target)target)
27 | {
28 | end--;
29 | }
30 | else
31 | {
32 | start++;
33 | }
34 | }
35 | }
36 | return sum;
37 | }
38 | };
39 |
40 | /*
41 | Approach 2: Checking all possible combinations after sorting with better pruning strategies
42 | Runtime: 4ms
43 | Memory: 10.45MB
44 | Time Complexity: O(nlog(n) + n^2) or O(n^2) //Sorting + linear search for all elements
45 | */
46 | class Solution {
47 | public:
48 | int threeSumClosest(vector& nums, int target) {
49 | std::sort(nums.begin(), nums.end());
50 |
51 | if (nums[0] + nums[1] + nums[2] >= target) {
52 | return nums[0] + nums[1] + nums[2];
53 | }
54 | if (nums[nums.size() - 1] + nums[nums.size() - 2] + nums[nums.size() - 3] <= target) {
55 | return nums[nums.size() - 1] + nums[nums.size() - 2] + nums[nums.size() - 3];
56 | }
57 |
58 | int closest = nums[0] + nums[1] + nums[2];
59 | int n = nums.size();
60 | for (int i = 0; i < n - 2; ++i) {
61 | int j = i + 1, k = nums.size() - 1;
62 | while (j < k) {
63 | int sum = nums[i] + nums[j] + nums[k];
64 | if (abs(sum - target) < abs(closest - target)) {
65 | closest =sum;
66 | }
67 | if (sum < target) {
68 | while (j + 1 < k && nums[j] == nums[j + 1]) {
69 | ++j;
70 | }
71 | ++j;
72 | } else if (sum > target) {
73 | while (k - 1 > j && nums[k] == nums[k - 1]) {
74 | --k;
75 | }
76 | --k;
77 | } else {
78 | return target;
79 | }
80 | }
81 | }
82 | return closest;
83 | }
84 | };
--------------------------------------------------------------------------------
/04_Linked List/readme.md:
--------------------------------------------------------------------------------
1 | # Linked Lists
2 |
3 | ## Why Linked lists ?
4 |
5 | Stacks and Queues are great data structures to store data. However, there are a few limitations to use of stacks and queues. Both stacks and queues are statically allocated memory, which means that the amount of memory allocated to stack or queue is fixed and cannot be changed.
6 |
7 | Imagine that you allocate an array of MAX_SIZE 100 to a stack. Now, even if there are 20 elements in your stack, the remaining space of 80 elements can not be used by the program. Tommorow, if you want to insert the 101th element, it is not possible to insert it directly since you are out of space. Linked Lists solve this problem using dynamic memory allocation. Whenever we need to store an element, we create a node in linked list using malloc() / new function and once we are done with the element, we destroy the node using free() / delete() functions, hence making that memory usable by program for other tasks.
8 |
9 | ## Introduction
10 |
11 | Every element in a Linked list is stored in the form of a node. A node comprises of two things, data and the the address of the next node. We also have an external pointer called head pointing at the first node of linked list. Optionally, we can have a tail pointer which points at the last element of linked list to optimize operations such as adding an element to the end.
12 |
13 | ## Types of Linked List
14 | 1) Singly Linked List
15 | 2) Doubly Linked List
16 | 3) Circular Linked List
17 | 4) Circular Doubly Linked List
18 |
19 | ## Proof for Floyd Cycle Detection Algorithm
20 |
21 |  22 |
23 | Here, we know that ```k``` has to be a node in the loop, only then can the slow pointer and fast pointer intersect. Now, the slow pointer may take ```m + Al + k``` steps and fast pointer may take ```m + Bl + k``` steps where ```A``` and ```B``` are constants which can be any number. The idea being that the slow or fast pointer might have to move full loops ```A``` or ```B``` times respectively before intersection, where ```B > A```. But we also know that,
24 | ```
25 | fast = 2*slow
26 | ```
27 | ```
28 | m + Bl + k = 2*(m + Al + k)
29 | ```
30 | ```
31 | (B - 2A)l = m+k
32 | ```
33 | ```
34 | constant*l = m+k
35 | ```
36 | Thus, ```m+k = c*l```, where c is an integer constant.
37 |
38 | This signifies that ```m+k``` steps are equivalent to looping ```c``` number of times in the loop and coming back to same position.
39 |
40 | Now as per algorithm, we reset fast pointer to head, and make it now behave like slow. Doing this, it is guranteed that the next intersection point is the node which marks the start of cycle.
41 |
42 | This is because, now the fast pointer has to take ```m``` steps to reach the first node of cycle. Thus, the slow pointer will make ```c*l - k``` steps. This ensures that the position of slow pointer after ```c*l - k``` steps will be the first node of cycle.
43 |
--------------------------------------------------------------------------------
/02_Stack/stack.cpp:
--------------------------------------------------------------------------------
1 | /*******************************************************************
2 | @brief Implementing stack and performing basic operations
3 | ********************************************************************/
4 |
5 | #include
6 | #define MAX_SIZE 100 // The maximum number of elements our stack can hold is 100
7 | using namespace std;
8 |
9 | class Stack
10 | {
11 | private:
12 | int stack[MAX_SIZE];
13 | int top = -1;
14 |
15 | public:
16 | void push(int element);
17 | int pop();
18 | int peek();
19 | };
20 |
21 | /*
22 | * Function Name: push
23 | * Input: Integer element which is to be pushed
24 | * Output: None
25 | * Logic: This function allows us to insert an element in stack
26 | * Example Call: push(5)
27 | */
28 | void Stack ::push(int element)
29 | {
30 | if (top != MAX_SIZE - 1) // We can not push anymore elements if the stack is full
31 | {
32 | top++;
33 | stack[top] = element;
34 | }
35 | else
36 | {
37 | cout << "The stack is full\n";
38 | }
39 | }
40 |
41 | /*
42 | * Function Name: pop
43 | * Input: None
44 | * Output: Returns the topmost element of stack or -1 if stack is empty
45 | * Logic: This function allows us to remove an element from stack
46 | * Example Call: pop()
47 | */
48 | int Stack ::pop()
49 | {
50 | if (top != -1)
51 | {
52 | return stack[top--];
53 | /* We need to do top-- above itself cause the staements below the return statement are not executed*/
54 | }
55 | else
56 | {
57 | cout << "The stack is empty\n";
58 | return -1; // just to avoid the warning of control reaches end of non-void function
59 | }
60 | }
61 |
62 | /*
63 | * Function Name: peek
64 | * Input: None
65 | * Output: Returns the topmost element of stack or -1 if stack is empty without deleting it
66 | * Logic: This function allows us to remove an element from stack without deleting it
67 | * Example Call: peek()
68 | */
69 | int Stack ::peek()
70 | {
71 | if (top != -1)
72 | {
73 | return stack[top]; // here, we simply return the topmost element and not decrement top
74 | }
75 | else
76 | {
77 | cout << "The stack is empty\n";
78 | return -1; // just to avoid the warning of control reaches end of non-void function
79 | }
80 | }
81 |
82 | int main()
83 | {
84 | Stack s1;
85 | int x;
86 |
87 | s1.push(50);
88 | s1.push(100);
89 | s1.push(150);
90 |
91 | x = s1.peek();
92 | cout << x << "\n";
93 |
94 | x = s1.pop();
95 | cout << x << "\n";
96 | x = s1.pop();
97 | cout << x << "\n";
98 | x = s1.pop();
99 | cout << x << "\n";
100 |
101 | x = s1.pop();
102 | cout << x << "\n";
103 |
104 | return 0;
105 | }
106 |
107 | /*
108 | Analysis: The above code runs in O(1) for push, pop and peek.
109 | */
--------------------------------------------------------------------------------
/08_Hashing/hashmap.c:
--------------------------------------------------------------------------------
1 | /**************************************
2 | @brief Implementing HashMaps
3 | ***************************************/
4 | #include
5 | #include
6 |
7 | //defining chain structure to hold name and value
8 | struct list{
9 | int val;
10 | char* name;
11 | struct list* next;
12 | };
13 |
14 | //simple hash function which assigns value as per last digit in number
15 | int hash(int key)
16 | {
17 | return key%10;
18 | }
19 |
20 | void setKey(int key, char* name, struct list* hashmap[10])
21 | {
22 | int hashVal = hash(key);
23 | if (hashmap[hashVal] == NULL)
24 | {
25 | hashmap[hashVal] = (struct list *)malloc(sizeof(struct list));
26 | hashmap[hashVal]->val = key;
27 | hashmap[hashVal]->name = name;
28 | hashmap[hashVal]->next = NULL;
29 | }
30 | else
31 | {
32 | int isFound = 0;
33 | struct list *chain = hashmap[hashVal];
34 | while(chain != NULL)
35 | {
36 | if (chain->val == key)
37 | {
38 | isFound = 1;
39 | chain->name = name;
40 | break;
41 | }
42 | chain = chain->next;
43 | }
44 | if (isFound == 0)
45 | {
46 | chain = (struct list *)malloc(sizeof(struct list));
47 | chain->val = key;
48 | chain->name = name;
49 | chain->next = NULL;
50 | }
51 | }
52 | }
53 |
54 | void GetKey(int key, struct list* hashmap[10])
55 | {
56 | int hashVal = hash(key);
57 | if (hashmap[hashVal] == NULL)
58 | {
59 | printf("Value Not Found\n");
60 | }
61 | else
62 | {
63 | int isFound = 0;
64 | struct list *chain = hashmap[hashVal];
65 | while(chain != NULL)
66 | {
67 | if (chain->val == key)
68 | {
69 | isFound = 1;
70 | printf("%s\n", chain->name);
71 | break;
72 | }
73 | chain = chain->next;
74 | }
75 | if (isFound == 0)
76 | {
77 | printf("Value Not Found\n");
78 | }
79 | }
80 | }
81 |
82 | int main()
83 | {
84 | struct list* hashmap[10];
85 |
86 | //initialize all pointers as NULL
87 | for (int i = 0 ; i < 10 ; i++)
88 | {
89 | hashmap[i] = NULL;
90 | }
91 |
92 | setKey(0, "Orange", hashmap);
93 | setKey(9, "Apple", hashmap);
94 | setKey(0, "Custurd Apple", hashmap);
95 | setKey(5, "Mango", hashmap);
96 |
97 | GetKey(0, hashmap);
98 | GetKey(1, hashmap);
99 | GetKey(5, hashmap);
100 | GetKey(9, hashmap);
101 |
102 | return 0;
103 | }
104 | /*
105 | Analysis: The above algorithm runs in O(m+n) time complexity for setKey and getKey, where m is cardinality of hash table and n is the number of objects
106 | */
--------------------------------------------------------------------------------
/03_Queues/Miscellaneous/Queue_using_2_stacks.cpp:
--------------------------------------------------------------------------------
1 | /*This code implements queue using 2 stacks*/
2 | #include
3 | #define MAX_SIZE 100 // The maximum number of elements a stack can hold is 100
4 |
5 | using namespace std;
6 |
7 | class Stack
8 | {
9 | private:
10 | int stack[MAX_SIZE];
11 | int top = -1;
12 |
13 | public:
14 | void push(int element);
15 | int pop();
16 | int peek();
17 | };
18 |
19 | /*This function allows us to insert an element in stack*/
20 | void Stack ::push(int element)
21 | {
22 | if (top != MAX_SIZE - 1) // We can not push anymore elements if the stack is full
23 | {
24 | top++;
25 | stack[top] = element;
26 | }
27 | else
28 | {
29 | cout << "The stack is full\n";
30 | }
31 | }
32 | // end of function
33 |
34 | /*This function removes the topmost element of stack
35 | if the function returns -1 , it implies stack is empty*/
36 | int Stack ::pop() // We can not pop any elements if the stack is empty
37 | {
38 | if (top != -1)
39 | {
40 | return stack[top--];
41 | /* We need to do top-- above itself cause the staements below the return statement are not executed*/
42 | }
43 | else
44 | {
45 | return -1;
46 | }
47 | }
48 | // end of function
49 |
50 | /*This function simply returns the topmost element of stack without deleting it from the stack
51 | if the function returns -1 , it implies stack is empty*/
52 | int Stack ::peek()
53 | {
54 | if (top != -1)
55 | {
56 | return stack[top]; // here, we simply return the topmost element and not decrement top
57 | }
58 | else
59 | {
60 | return -1;
61 | }
62 | }
63 | // end of function
64 |
65 | /*Enqueue function is ued to insert element in queue
66 | while enqueueing, we always insert the element in stack 1*/
67 | void enqueue(Stack *s1, int element)
68 | {
69 | s1->push(element);
70 | }
71 | // end of function
72 |
73 | /*dequeue function is ued to insert element in queue
74 | while dequeuing, if stack2 is not empty, we pop it
75 | else, we transfer contents of stack1 to stack2 and then pop stack2*/
76 | int dequeue(Stack *s1, Stack *s2)
77 | {
78 | int x;
79 |
80 | if (s2->peek() == -1) // if stack2 is not empty, directly pop from it
81 | {
82 | while (s1->peek() != -1) // transferring contents of stack1 in stack2
83 | {
84 | s2->push(s1->pop());
85 | }
86 | }
87 | x = s2->pop();
88 |
89 | return x;
90 | }
91 | // end of function
92 |
93 | int main()
94 | {
95 | Stack s1, s2;
96 | int x;
97 |
98 | enqueue(&s1, 50);
99 | enqueue(&s1, 250);
100 |
101 | x = dequeue(&s1 , &s2) ;
102 | cout << x << "\n";
103 |
104 | x = dequeue(&s1 , &s2) ;
105 | cout << x << "\n";
106 |
107 | x = dequeue(&s1 , &s2) ;
108 | cout << x << "\n";
109 |
110 | return 0;
111 | }
112 | // end of main
--------------------------------------------------------------------------------
/Algorithms/5_Miscellaneous/kadanes.cpp:
--------------------------------------------------------------------------------
1 | /**********************************
2 | @brief Kadanes Algorithm
3 | ***********************************/
4 | #include
5 | #include
6 | #include
7 |
8 | using namespace std ;
9 |
10 | struct solution {
11 | int max ;
12 | int max_i ;
13 | int max_j ;
14 | } ;
15 |
16 | /*
17 | * Function Name: maxSubArray
18 | * Input: Takes the array as input
19 | * Output: return struct solution
20 | * Logic: This function finds the subarray with maximum sum
21 | * Example Call: maxSubArray(nums)
22 | */
23 | struct solution maxSubArray(vector& nums) {
24 | struct solution max_solution ;
25 | max_solution.max_i = 0;
26 | max_solution.max_j = 0;
27 | max_solution.max = 0;
28 |
29 | bool reset = 0;
30 | bool super_reset = 0;
31 | bool init = 0 ;
32 | int temp_i = 0;
33 |
34 | int curr = 0;
35 |
36 | int n = nums.size() ;
37 |
38 | for (int i = 0; i < n ; i++)
39 | {
40 | curr = curr + nums[i];
41 | if (reset == 1)
42 | {
43 | reset = 0;
44 | super_reset = 1;
45 | temp_i = i;
46 | }
47 | if (curr <= 0)
48 | {
49 | curr = 0 ;
50 | reset = 1 ;
51 | }
52 | if (curr > max_solution.max)
53 | {
54 | max_solution.max = curr;
55 | if (max_solution.max_i == 0 && max_solution.max_j == 0 && init == 0)
56 | {
57 | init = 1 ;
58 | max_solution.max_i = max_solution.max_j = i ;
59 | }
60 | else if (super_reset == 1)
61 | {
62 | max_solution.max_i = temp_i;
63 | max_solution.max_j = i ;
64 | super_reset = 0 ;
65 | }
66 | else
67 | {
68 | max_solution.max_j = i ;
69 | }
70 | }
71 | }
72 |
73 | if (max_solution.max == 0)
74 | {
75 | max_solution.max = *max_element(nums.begin(), nums.end()) ;
76 | }
77 |
78 | return max_solution;
79 | }
80 |
81 | int main()
82 | {
83 | int n;
84 | cout << "Please enter the length of array: ";
85 | cin >> n;
86 | vector nums(n) ;
87 | cout << "Please enter the array: " ;
88 | for (int i = 0 ; i < n ; i++)
89 | {
90 | cin >> nums[i] ;
91 | }
92 |
93 | struct solution max_solution = maxSubArray(nums);
94 |
95 | cout << "The maximum value of subarray is: " << max_solution.max << endl ;
96 | cout << "The maximum subarray goes from " << max_solution.max_i << " to " << max_solution.max_j << endl ;
97 | return 0;
98 | }
99 | /*
100 | Analysis: The above algorithm runs in O(n)
101 | */
--------------------------------------------------------------------------------
/leetcode/287 Find the Duplicate Number.cpp:
--------------------------------------------------------------------------------
1 | /*
2 | Approach 1: Compare each element with all elements of array
3 | Runtime: TLE
4 | Time Complexity: O(n^2)
5 | */
6 | class Solution {
7 | public:
8 | int findDuplicate(vector& nums) {
9 | int n = nums.size();
10 | for (int i = 0; i < n; i++)
11 | {
12 | for (int j = i+1; j< n; j++)
13 | {
14 | if (nums[i]==nums[j])
15 | {
16 | return nums[i];
17 | }
18 | }
19 | }
20 | return 0;
21 | }
22 | };
23 |
24 | /*
25 | Approach 2: Linear search maintaing count for all numbers in [1,n]
26 | Runtime: TLE
27 | Time Complexity: O(n^2)
28 | */
29 | class Solution {
30 | public:
31 | int findDuplicate(vector& nums) {
32 | int n = nums.size();
33 |
34 | for (int j = 1; j <= n; j++)
35 | {
36 | int count = 0;
37 | for (int i = 0; i < n; i++)
38 | {
39 | if (j >= nums[i])
40 | {
41 | count++;
42 | }
43 | }
44 | if (count > j)
45 | {
46 | return j;
47 | }
48 | }
49 | return 0;
50 | }
51 | };
52 |
53 | /*
54 | Approach 3: Using binary search and maintaining count
55 | Runtime: 122ms
56 | Memory: 61.56MB
57 | Time Complexity: O(nlog(n))
58 | */
59 | class Solution {
60 | public:
61 | int findDuplicate(vector& nums) {
62 | int n = nums.size();
63 | int start = 1;
64 | int end = n;
65 | int mid = 0;
66 | int duplicate = -1;
67 |
68 | while (end >= start)
69 | {
70 | mid = (end + start)/2;
71 | int count = 0;
72 | for (int i = 0; i < n; i++)
73 | {
74 | if (mid >= nums[i])
75 | {
76 | count++;
77 | }
78 | }
79 | if (count > mid)
80 | {
81 | duplicate = mid;
82 | end = mid-1;
83 | }
84 | else
85 | {
86 | start = mid+1;
87 | }
88 | }
89 |
90 | return duplicate;
91 | }
92 | };
93 |
94 | /*
95 | Approach 4: Using flyod cycle detection algorithm using fast and slow pointers
96 | Runtime: 81ms
97 | Memory: 61.64MB
98 | Time Complexity: O(n)
99 | */
100 | class Solution {
101 | public:
102 | int findDuplicate(vector& num) {
103 | int slow = 0;
104 | int fast = 0;
105 |
106 | do
107 | {
108 | slow = num[slow];
109 | fast = num[num[fast]];
110 | }
111 | while (slow != fast);
112 | cout << slow << fast ;
113 | fast = 0;
114 |
115 | while(slow != fast)
116 | {
117 | fast = num[fast];
118 | slow=num[slow];
119 | }
120 |
121 | return slow;
122 | }
123 | };
--------------------------------------------------------------------------------
/08_Hashing/README.md:
--------------------------------------------------------------------------------
1 | # Hashing
2 |
3 | Hashing is a technique where we use a data structure to store the mapping from one entity to other.
4 |
5 | A hash table is an implementation of hashing by map or set by any method.```unordered_set``` and ```unordered_map``` are examples of set and map in ``c++``
6 |
7 | ## Direct Addressing
8 |
9 | The direct address approach requires that the hash function is a one-to-one mapping for each K integer. Such a function is known as a perfect hashing function: it maps each key to a distinct integer within some manageable range and enables us to trivially build an O(1) search time table.
10 |
11 | The problem however is the amount of memory it requires to hold this hash table. There might be several buckets in this case which might not be used throught the execution, but they still hold memory.
12 |
13 | ## Chaining
14 |
15 | The problem with direct addressing is that the memory required is quite high. Rather, we would want an implementation which would use only hashing for the objects present in our universe.
16 |
17 | For example, if we have two numbers say {12,999}, then rather than creating hash table for 1000 numbers, we should just create it for 2 numbers. For this, we require some function to convert the numbers to different numbers, say here {2,9} if we consider hash buckets formed of last digits of number. This is done by hash function.
18 |
19 | However, this may lead to collisions according to pigeonhole principle. This is because the cardinality of the hash buckets is finite, and we wish to fit all objects in our universe in those buckets. Thus we make use of chaining to avoid these collisions. Linked List is the underlying data structure used in chaining.
20 |
21 | ## Hash functions
22 |
23 | Hash Functions are responsible for mapping of objects to [1,m] where m is cardinality of hash table. Thus, we need to choose our hash function such that,
24 |
25 | * It doesn't require lot of computation to calculate the hash value
26 | * Objects are evenly distributed
27 |
28 | One of the possible hash function that satisfies above conditions is to randomly assign hash value. However this is non deterministic. But this does indicate that random choice is indeed helpful, like choosing random pivot in quick sort. Hence we use the idea of randomness and dynamic array and create hash table using universal family of hash function.
29 |
30 | ### Universal family of hash functions
31 |
32 | 
33 |
34 |
35 | Consider U as finite universe of all objects. For eg. in case of phone numbers, U represents all possible phone numbers. H is the hash function we randomly choose from the universal hash function family. This function H maps U to V, where V is hash table with cardinality n.
36 |
37 | ### Hashing Integers
38 |
39 | 
40 |
41 | ### Hashing Strings
42 |
43 | 
44 |
45 |
--------------------------------------------------------------------------------
/05_Trees/README.md:
--------------------------------------------------------------------------------
1 | # Trees
2 |
3 |
22 |
23 | Here, we know that ```k``` has to be a node in the loop, only then can the slow pointer and fast pointer intersect. Now, the slow pointer may take ```m + Al + k``` steps and fast pointer may take ```m + Bl + k``` steps where ```A``` and ```B``` are constants which can be any number. The idea being that the slow or fast pointer might have to move full loops ```A``` or ```B``` times respectively before intersection, where ```B > A```. But we also know that,
24 | ```
25 | fast = 2*slow
26 | ```
27 | ```
28 | m + Bl + k = 2*(m + Al + k)
29 | ```
30 | ```
31 | (B - 2A)l = m+k
32 | ```
33 | ```
34 | constant*l = m+k
35 | ```
36 | Thus, ```m+k = c*l```, where c is an integer constant.
37 |
38 | This signifies that ```m+k``` steps are equivalent to looping ```c``` number of times in the loop and coming back to same position.
39 |
40 | Now as per algorithm, we reset fast pointer to head, and make it now behave like slow. Doing this, it is guranteed that the next intersection point is the node which marks the start of cycle.
41 |
42 | This is because, now the fast pointer has to take ```m``` steps to reach the first node of cycle. Thus, the slow pointer will make ```c*l - k``` steps. This ensures that the position of slow pointer after ```c*l - k``` steps will be the first node of cycle.
43 |
--------------------------------------------------------------------------------
/02_Stack/stack.cpp:
--------------------------------------------------------------------------------
1 | /*******************************************************************
2 | @brief Implementing stack and performing basic operations
3 | ********************************************************************/
4 |
5 | #include
6 | #define MAX_SIZE 100 // The maximum number of elements our stack can hold is 100
7 | using namespace std;
8 |
9 | class Stack
10 | {
11 | private:
12 | int stack[MAX_SIZE];
13 | int top = -1;
14 |
15 | public:
16 | void push(int element);
17 | int pop();
18 | int peek();
19 | };
20 |
21 | /*
22 | * Function Name: push
23 | * Input: Integer element which is to be pushed
24 | * Output: None
25 | * Logic: This function allows us to insert an element in stack
26 | * Example Call: push(5)
27 | */
28 | void Stack ::push(int element)
29 | {
30 | if (top != MAX_SIZE - 1) // We can not push anymore elements if the stack is full
31 | {
32 | top++;
33 | stack[top] = element;
34 | }
35 | else
36 | {
37 | cout << "The stack is full\n";
38 | }
39 | }
40 |
41 | /*
42 | * Function Name: pop
43 | * Input: None
44 | * Output: Returns the topmost element of stack or -1 if stack is empty
45 | * Logic: This function allows us to remove an element from stack
46 | * Example Call: pop()
47 | */
48 | int Stack ::pop()
49 | {
50 | if (top != -1)
51 | {
52 | return stack[top--];
53 | /* We need to do top-- above itself cause the staements below the return statement are not executed*/
54 | }
55 | else
56 | {
57 | cout << "The stack is empty\n";
58 | return -1; // just to avoid the warning of control reaches end of non-void function
59 | }
60 | }
61 |
62 | /*
63 | * Function Name: peek
64 | * Input: None
65 | * Output: Returns the topmost element of stack or -1 if stack is empty without deleting it
66 | * Logic: This function allows us to remove an element from stack without deleting it
67 | * Example Call: peek()
68 | */
69 | int Stack ::peek()
70 | {
71 | if (top != -1)
72 | {
73 | return stack[top]; // here, we simply return the topmost element and not decrement top
74 | }
75 | else
76 | {
77 | cout << "The stack is empty\n";
78 | return -1; // just to avoid the warning of control reaches end of non-void function
79 | }
80 | }
81 |
82 | int main()
83 | {
84 | Stack s1;
85 | int x;
86 |
87 | s1.push(50);
88 | s1.push(100);
89 | s1.push(150);
90 |
91 | x = s1.peek();
92 | cout << x << "\n";
93 |
94 | x = s1.pop();
95 | cout << x << "\n";
96 | x = s1.pop();
97 | cout << x << "\n";
98 | x = s1.pop();
99 | cout << x << "\n";
100 |
101 | x = s1.pop();
102 | cout << x << "\n";
103 |
104 | return 0;
105 | }
106 |
107 | /*
108 | Analysis: The above code runs in O(1) for push, pop and peek.
109 | */
--------------------------------------------------------------------------------
/08_Hashing/hashmap.c:
--------------------------------------------------------------------------------
1 | /**************************************
2 | @brief Implementing HashMaps
3 | ***************************************/
4 | #include
5 | #include
6 |
7 | //defining chain structure to hold name and value
8 | struct list{
9 | int val;
10 | char* name;
11 | struct list* next;
12 | };
13 |
14 | //simple hash function which assigns value as per last digit in number
15 | int hash(int key)
16 | {
17 | return key%10;
18 | }
19 |
20 | void setKey(int key, char* name, struct list* hashmap[10])
21 | {
22 | int hashVal = hash(key);
23 | if (hashmap[hashVal] == NULL)
24 | {
25 | hashmap[hashVal] = (struct list *)malloc(sizeof(struct list));
26 | hashmap[hashVal]->val = key;
27 | hashmap[hashVal]->name = name;
28 | hashmap[hashVal]->next = NULL;
29 | }
30 | else
31 | {
32 | int isFound = 0;
33 | struct list *chain = hashmap[hashVal];
34 | while(chain != NULL)
35 | {
36 | if (chain->val == key)
37 | {
38 | isFound = 1;
39 | chain->name = name;
40 | break;
41 | }
42 | chain = chain->next;
43 | }
44 | if (isFound == 0)
45 | {
46 | chain = (struct list *)malloc(sizeof(struct list));
47 | chain->val = key;
48 | chain->name = name;
49 | chain->next = NULL;
50 | }
51 | }
52 | }
53 |
54 | void GetKey(int key, struct list* hashmap[10])
55 | {
56 | int hashVal = hash(key);
57 | if (hashmap[hashVal] == NULL)
58 | {
59 | printf("Value Not Found\n");
60 | }
61 | else
62 | {
63 | int isFound = 0;
64 | struct list *chain = hashmap[hashVal];
65 | while(chain != NULL)
66 | {
67 | if (chain->val == key)
68 | {
69 | isFound = 1;
70 | printf("%s\n", chain->name);
71 | break;
72 | }
73 | chain = chain->next;
74 | }
75 | if (isFound == 0)
76 | {
77 | printf("Value Not Found\n");
78 | }
79 | }
80 | }
81 |
82 | int main()
83 | {
84 | struct list* hashmap[10];
85 |
86 | //initialize all pointers as NULL
87 | for (int i = 0 ; i < 10 ; i++)
88 | {
89 | hashmap[i] = NULL;
90 | }
91 |
92 | setKey(0, "Orange", hashmap);
93 | setKey(9, "Apple", hashmap);
94 | setKey(0, "Custurd Apple", hashmap);
95 | setKey(5, "Mango", hashmap);
96 |
97 | GetKey(0, hashmap);
98 | GetKey(1, hashmap);
99 | GetKey(5, hashmap);
100 | GetKey(9, hashmap);
101 |
102 | return 0;
103 | }
104 | /*
105 | Analysis: The above algorithm runs in O(m+n) time complexity for setKey and getKey, where m is cardinality of hash table and n is the number of objects
106 | */
--------------------------------------------------------------------------------
/03_Queues/Miscellaneous/Queue_using_2_stacks.cpp:
--------------------------------------------------------------------------------
1 | /*This code implements queue using 2 stacks*/
2 | #include
3 | #define MAX_SIZE 100 // The maximum number of elements a stack can hold is 100
4 |
5 | using namespace std;
6 |
7 | class Stack
8 | {
9 | private:
10 | int stack[MAX_SIZE];
11 | int top = -1;
12 |
13 | public:
14 | void push(int element);
15 | int pop();
16 | int peek();
17 | };
18 |
19 | /*This function allows us to insert an element in stack*/
20 | void Stack ::push(int element)
21 | {
22 | if (top != MAX_SIZE - 1) // We can not push anymore elements if the stack is full
23 | {
24 | top++;
25 | stack[top] = element;
26 | }
27 | else
28 | {
29 | cout << "The stack is full\n";
30 | }
31 | }
32 | // end of function
33 |
34 | /*This function removes the topmost element of stack
35 | if the function returns -1 , it implies stack is empty*/
36 | int Stack ::pop() // We can not pop any elements if the stack is empty
37 | {
38 | if (top != -1)
39 | {
40 | return stack[top--];
41 | /* We need to do top-- above itself cause the staements below the return statement are not executed*/
42 | }
43 | else
44 | {
45 | return -1;
46 | }
47 | }
48 | // end of function
49 |
50 | /*This function simply returns the topmost element of stack without deleting it from the stack
51 | if the function returns -1 , it implies stack is empty*/
52 | int Stack ::peek()
53 | {
54 | if (top != -1)
55 | {
56 | return stack[top]; // here, we simply return the topmost element and not decrement top
57 | }
58 | else
59 | {
60 | return -1;
61 | }
62 | }
63 | // end of function
64 |
65 | /*Enqueue function is ued to insert element in queue
66 | while enqueueing, we always insert the element in stack 1*/
67 | void enqueue(Stack *s1, int element)
68 | {
69 | s1->push(element);
70 | }
71 | // end of function
72 |
73 | /*dequeue function is ued to insert element in queue
74 | while dequeuing, if stack2 is not empty, we pop it
75 | else, we transfer contents of stack1 to stack2 and then pop stack2*/
76 | int dequeue(Stack *s1, Stack *s2)
77 | {
78 | int x;
79 |
80 | if (s2->peek() == -1) // if stack2 is not empty, directly pop from it
81 | {
82 | while (s1->peek() != -1) // transferring contents of stack1 in stack2
83 | {
84 | s2->push(s1->pop());
85 | }
86 | }
87 | x = s2->pop();
88 |
89 | return x;
90 | }
91 | // end of function
92 |
93 | int main()
94 | {
95 | Stack s1, s2;
96 | int x;
97 |
98 | enqueue(&s1, 50);
99 | enqueue(&s1, 250);
100 |
101 | x = dequeue(&s1 , &s2) ;
102 | cout << x << "\n";
103 |
104 | x = dequeue(&s1 , &s2) ;
105 | cout << x << "\n";
106 |
107 | x = dequeue(&s1 , &s2) ;
108 | cout << x << "\n";
109 |
110 | return 0;
111 | }
112 | // end of main
--------------------------------------------------------------------------------
/Algorithms/5_Miscellaneous/kadanes.cpp:
--------------------------------------------------------------------------------
1 | /**********************************
2 | @brief Kadanes Algorithm
3 | ***********************************/
4 | #include
5 | #include
6 | #include
7 |
8 | using namespace std ;
9 |
10 | struct solution {
11 | int max ;
12 | int max_i ;
13 | int max_j ;
14 | } ;
15 |
16 | /*
17 | * Function Name: maxSubArray
18 | * Input: Takes the array as input
19 | * Output: return struct solution
20 | * Logic: This function finds the subarray with maximum sum
21 | * Example Call: maxSubArray(nums)
22 | */
23 | struct solution maxSubArray(vector& nums) {
24 | struct solution max_solution ;
25 | max_solution.max_i = 0;
26 | max_solution.max_j = 0;
27 | max_solution.max = 0;
28 |
29 | bool reset = 0;
30 | bool super_reset = 0;
31 | bool init = 0 ;
32 | int temp_i = 0;
33 |
34 | int curr = 0;
35 |
36 | int n = nums.size() ;
37 |
38 | for (int i = 0; i < n ; i++)
39 | {
40 | curr = curr + nums[i];
41 | if (reset == 1)
42 | {
43 | reset = 0;
44 | super_reset = 1;
45 | temp_i = i;
46 | }
47 | if (curr <= 0)
48 | {
49 | curr = 0 ;
50 | reset = 1 ;
51 | }
52 | if (curr > max_solution.max)
53 | {
54 | max_solution.max = curr;
55 | if (max_solution.max_i == 0 && max_solution.max_j == 0 && init == 0)
56 | {
57 | init = 1 ;
58 | max_solution.max_i = max_solution.max_j = i ;
59 | }
60 | else if (super_reset == 1)
61 | {
62 | max_solution.max_i = temp_i;
63 | max_solution.max_j = i ;
64 | super_reset = 0 ;
65 | }
66 | else
67 | {
68 | max_solution.max_j = i ;
69 | }
70 | }
71 | }
72 |
73 | if (max_solution.max == 0)
74 | {
75 | max_solution.max = *max_element(nums.begin(), nums.end()) ;
76 | }
77 |
78 | return max_solution;
79 | }
80 |
81 | int main()
82 | {
83 | int n;
84 | cout << "Please enter the length of array: ";
85 | cin >> n;
86 | vector nums(n) ;
87 | cout << "Please enter the array: " ;
88 | for (int i = 0 ; i < n ; i++)
89 | {
90 | cin >> nums[i] ;
91 | }
92 |
93 | struct solution max_solution = maxSubArray(nums);
94 |
95 | cout << "The maximum value of subarray is: " << max_solution.max << endl ;
96 | cout << "The maximum subarray goes from " << max_solution.max_i << " to " << max_solution.max_j << endl ;
97 | return 0;
98 | }
99 | /*
100 | Analysis: The above algorithm runs in O(n)
101 | */
--------------------------------------------------------------------------------
/leetcode/287 Find the Duplicate Number.cpp:
--------------------------------------------------------------------------------
1 | /*
2 | Approach 1: Compare each element with all elements of array
3 | Runtime: TLE
4 | Time Complexity: O(n^2)
5 | */
6 | class Solution {
7 | public:
8 | int findDuplicate(vector& nums) {
9 | int n = nums.size();
10 | for (int i = 0; i < n; i++)
11 | {
12 | for (int j = i+1; j< n; j++)
13 | {
14 | if (nums[i]==nums[j])
15 | {
16 | return nums[i];
17 | }
18 | }
19 | }
20 | return 0;
21 | }
22 | };
23 |
24 | /*
25 | Approach 2: Linear search maintaing count for all numbers in [1,n]
26 | Runtime: TLE
27 | Time Complexity: O(n^2)
28 | */
29 | class Solution {
30 | public:
31 | int findDuplicate(vector& nums) {
32 | int n = nums.size();
33 |
34 | for (int j = 1; j <= n; j++)
35 | {
36 | int count = 0;
37 | for (int i = 0; i < n; i++)
38 | {
39 | if (j >= nums[i])
40 | {
41 | count++;
42 | }
43 | }
44 | if (count > j)
45 | {
46 | return j;
47 | }
48 | }
49 | return 0;
50 | }
51 | };
52 |
53 | /*
54 | Approach 3: Using binary search and maintaining count
55 | Runtime: 122ms
56 | Memory: 61.56MB
57 | Time Complexity: O(nlog(n))
58 | */
59 | class Solution {
60 | public:
61 | int findDuplicate(vector& nums) {
62 | int n = nums.size();
63 | int start = 1;
64 | int end = n;
65 | int mid = 0;
66 | int duplicate = -1;
67 |
68 | while (end >= start)
69 | {
70 | mid = (end + start)/2;
71 | int count = 0;
72 | for (int i = 0; i < n; i++)
73 | {
74 | if (mid >= nums[i])
75 | {
76 | count++;
77 | }
78 | }
79 | if (count > mid)
80 | {
81 | duplicate = mid;
82 | end = mid-1;
83 | }
84 | else
85 | {
86 | start = mid+1;
87 | }
88 | }
89 |
90 | return duplicate;
91 | }
92 | };
93 |
94 | /*
95 | Approach 4: Using flyod cycle detection algorithm using fast and slow pointers
96 | Runtime: 81ms
97 | Memory: 61.64MB
98 | Time Complexity: O(n)
99 | */
100 | class Solution {
101 | public:
102 | int findDuplicate(vector& num) {
103 | int slow = 0;
104 | int fast = 0;
105 |
106 | do
107 | {
108 | slow = num[slow];
109 | fast = num[num[fast]];
110 | }
111 | while (slow != fast);
112 | cout << slow << fast ;
113 | fast = 0;
114 |
115 | while(slow != fast)
116 | {
117 | fast = num[fast];
118 | slow=num[slow];
119 | }
120 |
121 | return slow;
122 | }
123 | };
--------------------------------------------------------------------------------
/08_Hashing/README.md:
--------------------------------------------------------------------------------
1 | # Hashing
2 |
3 | Hashing is a technique where we use a data structure to store the mapping from one entity to other.
4 |
5 | A hash table is an implementation of hashing by map or set by any method.```unordered_set``` and ```unordered_map``` are examples of set and map in ``c++``
6 |
7 | ## Direct Addressing
8 |
9 | The direct address approach requires that the hash function is a one-to-one mapping for each K integer. Such a function is known as a perfect hashing function: it maps each key to a distinct integer within some manageable range and enables us to trivially build an O(1) search time table.
10 |
11 | The problem however is the amount of memory it requires to hold this hash table. There might be several buckets in this case which might not be used throught the execution, but they still hold memory.
12 |
13 | ## Chaining
14 |
15 | The problem with direct addressing is that the memory required is quite high. Rather, we would want an implementation which would use only hashing for the objects present in our universe.
16 |
17 | For example, if we have two numbers say {12,999}, then rather than creating hash table for 1000 numbers, we should just create it for 2 numbers. For this, we require some function to convert the numbers to different numbers, say here {2,9} if we consider hash buckets formed of last digits of number. This is done by hash function.
18 |
19 | However, this may lead to collisions according to pigeonhole principle. This is because the cardinality of the hash buckets is finite, and we wish to fit all objects in our universe in those buckets. Thus we make use of chaining to avoid these collisions. Linked List is the underlying data structure used in chaining.
20 |
21 | ## Hash functions
22 |
23 | Hash Functions are responsible for mapping of objects to [1,m] where m is cardinality of hash table. Thus, we need to choose our hash function such that,
24 |
25 | * It doesn't require lot of computation to calculate the hash value
26 | * Objects are evenly distributed
27 |
28 | One of the possible hash function that satisfies above conditions is to randomly assign hash value. However this is non deterministic. But this does indicate that random choice is indeed helpful, like choosing random pivot in quick sort. Hence we use the idea of randomness and dynamic array and create hash table using universal family of hash function.
29 |
30 | ### Universal family of hash functions
31 |
32 | 
33 |
34 |
35 | Consider U as finite universe of all objects. For eg. in case of phone numbers, U represents all possible phone numbers. H is the hash function we randomly choose from the universal hash function family. This function H maps U to V, where V is hash table with cardinality n.
36 |
37 | ### Hashing Integers
38 |
39 | 
40 |
41 | ### Hashing Strings
42 |
43 | 
44 |
45 |
--------------------------------------------------------------------------------
/05_Trees/README.md:
--------------------------------------------------------------------------------
1 | # Trees
2 |
3 |  4 |
5 | ## Introduction
6 | A tree is a data structure similar to a linked list but instead of each node pointing simply to the next node in a linear fashion, each node points to a number of nodes. Tree is an example of a non linear data structure.
7 | A tree structure is a way of representing the hierarchical nature of a structure in a graphical form.
8 |
9 | ## Basic Terminology
10 |
11 | 
12 |
13 | 1) The set of all nodes at a given depth is called the level of the tree. The root node is at level zero (eg. Nodes B, C and D lie at level 1)
14 | 2) The depth of a node is the length of the path from the root to the node (eg. depth of G is 2, A – C – G).
15 | 3) The height of a node is the length of the path from that node to the deepest node. The height of a tree is the length of the path from the root to the deepest node in the tree(eg. the height of B is 2, B – F – J)
16 | 4) Height of the tree is the maximum height among all the nodes in the tree and depth of the tree is the maximum depth among all the nodes in the tree. For a given tree, depth and height returns the same value. But for individual nodes we may get different results.
17 | 5) If every node in a tree has only one child (except leaf nodes) then we call such trees skew trees. If every node has only left child then we call them left skew trees. Similarly, if every node has only right child then we call them right skew trees.
18 |
19 | ## Tree Traversals
20 |
21 | * Preorder
22 | * Inorder
23 | * Postorder
24 | * Levelorder
25 |
26 | ## Binary Trees
27 | A tree is called binary tree if each node has zero child, one child or two children.
28 |
29 | ## AVL Trees
30 |
31 | The tree data structure proves to be effective only when the tree is a balanced in nature.
32 |
33 | The runtime of the tree depends upon the depth of the tree. Only when the tree is a balance binary tree, we can perform the operations such as insertion, deletion, search, range, etc. in O(log(n)) time.
34 |
35 | Else, the time complexity moves to O(n). In the worst case, the tree data structure is skewed and simply behaves like a sorted linked-list. Thus, inorder to keep our runtimes limited to O(log(n)), we must ensure our tree are balanced at all times.
36 |
37 | Height of a given tree helps to define the balance parameter. In general, for any given node, if it satisfies the given property, it is an AVL tree or a balanced binary tree
38 |
39 | ```|(Height of left subtree) - (Height of right subtree)| <= 1```
40 |
41 | ## Other Notes
42 |
43 | * Solving tree always involves some sort of traversal with something in Pre or Post section
44 | * Always mention in comments your base case and rec case
45 | * In trees, you cant have a parent pointer as such. But then you can make use of recursion, you can return it and treat that as a parent link. Essentially the recursion is the link between children and parent. For tree, call left, call right, return, get their results and club them up in parent
--------------------------------------------------------------------------------
/Algorithms/4_Sorting/randomized_quick_sort.cpp:
--------------------------------------------------------------------------------
1 | /***************************************************
2 | @brief Implementing Randomized Quick Sort
3 | ****************************************************/
4 | #include
5 | #include
6 | #include
7 | #include
8 |
9 | using namespace std;
10 |
11 | void Swap(int &i, int &j)
12 | {
13 | int temp = i;
14 | i = j;
15 | j = temp;
16 | }
17 |
18 | void random(int l, int r, vector &v)
19 | {
20 | srand((unsigned)time(NULL));
21 |
22 | int random = l + (rand() % r);
23 |
24 | int temp = v[random] ;
25 | v[random] = v[l] ;
26 | v[l] = temp ;
27 | }
28 |
29 | /*
30 | * Function Name: Parition
31 | * Input: Requires a vector, index of pivot element, starting index and ending element
32 | * Output: returns the position of pivot element in sorted array
33 | * Logic: Keeps elements smaller than pivot to its left and larger to its right
34 | * Example Call: Partition(v, 0, 0, v.size()-1)
35 | */
36 | int Partition(vector &v, int pivot, int i, int j)
37 | {
38 | if (i == j)
39 | {
40 | return i;
41 | }
42 |
43 | while (i <= j)
44 | {
45 | if (v[i] > v[pivot] && v[j] < v[pivot])
46 | {
47 | swap(v[i], v[j]);
48 | i++;
49 | j--;
50 | }
51 | else if (v[i] <= v[pivot])
52 | {
53 | i++;
54 | }
55 | else if (v[j] >= v[pivot])
56 | {
57 | j--;
58 | }
59 | }
60 |
61 | Swap(v[pivot], v[i - 1]);
62 | return i - 1;
63 | }
64 |
65 | /*
66 | * Function Name: QuickSort
67 | * Input: Requires a vector, index of pivot element, starting element and ending element
68 | * Logic: Divides the array as per partition by pivot and creates a sorted array
69 | * Example Call: QuickSort(v, pivot, 0, v.size() - 1)
70 | */
71 | void QuickSort(vector &v, int pivot, int begin, int end)
72 | {
73 | if (end <= begin)
74 | {
75 | return;
76 | }
77 |
78 | int m = Partition(v, pivot, begin, end); // m represents position of partition
79 |
80 | random(begin, m, v) ;
81 | QuickSort(v, begin, begin, m - 1);
82 |
83 | // random(m+1, end+1, v) ;
84 | QuickSort(v, m + 1, m + 1, end);
85 | }
86 |
87 | int main()
88 | {
89 | string s;
90 | getline(cin, s);
91 |
92 | int num = 0;
93 | vector v;
94 |
95 | /*Taking input from the user and storing it in a vector of int*/
96 | for (int i = 0; i < s.size(); ++i)
97 | {
98 | if (s[i] == ' ')
99 | v.push_back(num), num = 0;
100 | else
101 | num = num * 10 + (s[i] - '0');
102 | }
103 | v.push_back(num);
104 |
105 | random(0, v.size(), v) ;
106 |
107 | int pivot = 0;
108 |
109 | cout << endl ;
110 |
111 | QuickSort(v, pivot, 0, v.size() - 1);
112 |
113 | for (int i = 0; i < v.size(); i++)
114 | {
115 | cout << v[i] << " ";
116 | }
117 |
118 | return 0;
119 | }
120 | /*
121 | Analysis: The above code runs averagely in O(nlog(n)) and O(n^2) in worst cases
122 | */
--------------------------------------------------------------------------------
/Algorithms/3_Dynamic_Programming/knapsack_limited.cpp:
--------------------------------------------------------------------------------
1 | /***************************************************************************
2 | @brief Using dynamic programming for 0/1 Knapsack_limited problem
3 | ****************************************************************************/
4 | #include
5 | #include
6 | #include
7 |
8 | using namespace std;
9 |
10 | /*
11 | * Function Name: knapsack
12 | * Input: Requires an vector of price, weights, status and values of capacity and n
13 | * Output: returns the maximum profit
14 | * Logic: Finds the optimal solution using bottom-to-top method of dynamic programming
15 | * Example Call: knapsack(price, weight, capacity, n - 1, status)
16 | */
17 | int knapsack(vector price, vector weight, int capacity, int n, vector &status)
18 | {
19 | vector> matrix(weight.size() + 1, vector(capacity + 1, 0));
20 |
21 | for (int i = 1; i < matrix.size(); i++)
22 | {
23 | for (int j = 1; j < matrix[0].size(); j++)
24 | {
25 | if (weight[i - 1] <= j)
26 | {
27 | matrix[i][j] = max(matrix[i - 1][j], price[i - 1] + matrix[i - 1][j - weight[i - 1]]);
28 | }
29 | else
30 | {
31 | matrix[i][j] = matrix[i - 1][j];
32 | }
33 | }
34 | }
35 |
36 | int x = weight.size();
37 | int y = capacity;
38 | int index = status.size() - 1;
39 |
40 | while (x != 0)
41 | {
42 | if (matrix[x][y] == matrix[x - 1][y])
43 | {
44 | status[index] = false;
45 | x = x - 1;
46 | index--;
47 | }
48 | else
49 | {
50 | status[index] = true;
51 | x = x - 1;
52 | y = y - weight[x];
53 | index--;
54 | }
55 | }
56 |
57 | return matrix[weight.size()][capacity];
58 | }
59 |
60 | int main()
61 | {
62 | int capacity;
63 | cout << "Enter the capacity of Knapsack: ";
64 | cin >> capacity;
65 | int n;
66 | cout << "Enter the total number of distinct elements: ";
67 | cin >> n;
68 | vector price(n);
69 | vector weight(n);
70 | vector status(n, false);
71 |
72 | for (int i = 0; i < n; i++)
73 | {
74 | cout << "Enter weight of item " << i + 1 << " : ";
75 | cin >> weight[i];
76 | cout << "Enter price of item " << i + 1 << " : ";
77 | cin >> price[i];
78 | }
79 |
80 | int answer = knapsack(price, weight, capacity, n - 1, status);
81 |
82 | for (int i = 0; i < status.size(); i++)
83 | {
84 | if (status[i] == true)
85 | {
86 | cout << "Item " << i + 1 << " : Taken";
87 | }
88 | else
89 | {
90 | cout << "Item " << i + 1 << " : Not Taken";
91 | }
92 | cout << endl;
93 | }
94 | cout << "Maximum profit is: " << answer << endl;
95 |
96 | return 0;
97 | }
98 | /*
99 | Analysis: The above code runs in O(m*n), where n is the number of different object required and m is the capacity of knapsack
100 | */
--------------------------------------------------------------------------------
/03_Queues/Queue_using_Linked_list/simple_queue.cpp:
--------------------------------------------------------------------------------
1 | /*******************************************************
2 | @brief Implementing queue using a linked list
3 | ********************************************************/
4 |
5 | #include
6 |
7 | using namespace std;
8 |
9 | void enqueue(int element);
10 | void display();
11 |
12 | struct Node
13 | {
14 | int data;
15 | class Node *next; // next is a pointer of type Node which points towards the next Node
16 | };
17 | /*initially both the pointers are NULL*/
18 | struct Node *front = NULL;
19 | struct Node *rear = NULL;
20 |
21 | /*
22 | * Function Name: enqueue
23 | * Input: Integer element which is to be inserted
24 | * Output: None
25 | * Logic: This function allows us to insert an element in queue
26 | * Example Call: enqueue(5)
27 | */
28 | void enqueue(int element)
29 | {
30 | Node *temp = (Node *)malloc(sizeof(Node)); // dynamic allocation of memory
31 | if (temp == NULL)
32 | {
33 | cout << "Queue is full";
34 | }
35 | else if (front == NULL) // or rear == NULL, both conditions work
36 | {
37 | front = rear = temp;
38 | temp->data = element;
39 | temp->next = NULL;
40 | }
41 | else
42 | {
43 | rear->next = temp; // the next of the rear node should point at new node temp
44 | temp->data = element;
45 | temp->next = NULL;
46 | rear = temp; // rear should point to the new node formed
47 | }
48 | }
49 |
50 | /*
51 | * Function Name: dequeue
52 | * Input: None
53 | * Output: Returns the first element of queue
54 | * Logic: This function allows us to remove the first element of queue
55 | * Example Call: dequeue()
56 | */
57 | void dequeue()
58 | {
59 | if (front == NULL)
60 | {
61 | cout << "Queue is empty!";
62 | }
63 | else
64 | {
65 | cout << front->data << "\n";
66 |
67 | Node *temp = front;
68 | front = front->next;
69 | delete temp; // Deallocating the memory given to node
70 | }
71 | }
72 |
73 | /*
74 | * Function Name: display
75 | * Input: None
76 | * Output: Prints all the elements in the queue
77 | * Logic: This function allows us to print the elements currently in queue
78 | * Example Call: display()
79 | */
80 | void display()
81 | {
82 | Node *temp = front;
83 | if (front == NULL)
84 | {
85 | cout << "Queue is empty!";
86 | }
87 | else if (front == rear) // incase of only one element in queue
88 | {
89 | cout << "The elements in queue are : " << front->data ;
90 | struct Node *front = NULL;
91 | struct Node *rear = NULL;
92 | }
93 | else
94 | {
95 | cout << "The elements in queue are : ";
96 | while (temp != NULL)
97 | {
98 | cout << temp->data << " "; // prints data in all nodes
99 | temp = temp->next;
100 | }
101 | }
102 |
103 | cout << "\n";
104 | }
105 |
106 | int main()
107 | {
108 | enqueue(5);
109 | enqueue(10);
110 | enqueue(15);
111 | display();
112 | dequeue();
113 | display();
114 | dequeue();
115 | display();
116 | dequeue();
117 | display();
118 |
119 | return 0;
120 | }
121 |
--------------------------------------------------------------------------------
/09_Graphs/topological_sort.cpp:
--------------------------------------------------------------------------------
1 | #include
2 | #include
3 |
4 | using namespace std;
5 |
6 | #define VERTICES 100
7 |
8 | class Graph
9 | {
10 | private:
11 | struct Node
12 | {
13 | int data;
14 | struct Node *next;
15 | };
16 | int no_of_vertices;
17 | struct Node **adj_list;
18 | vector order ;
19 |
20 | public:
21 | bool visited[VERTICES] = {0};
22 | void make_graph(int no_of_vertices);
23 | void display();
24 | void add_edge();
25 | void dfs(int v);
26 | };
27 |
28 | void Graph ::add_edge()
29 | {
30 | for (int i = 0; i < no_of_vertices; i++)
31 | {
32 | for (int j = 0; j < no_of_vertices; j++)
33 | {
34 | if (i != j)
35 | {
36 | char choice;
37 | cout << "Are vertices " << i << " and " << j << " adjacent? (Y/N) : ";
38 | cin >> choice;
39 |
40 | if (toupper(choice) == 'Y')
41 | {
42 | if (adj_list[i] == NULL)
43 | {
44 | adj_list[i] = new struct Node;
45 | adj_list[i]->data = j;
46 | adj_list[i]->next = NULL;
47 | continue;
48 | }
49 | struct Node *temp;
50 | temp = adj_list[i];
51 | while (temp->next != NULL)
52 | {
53 | temp = temp->next;
54 | }
55 | temp->next = new struct Node;
56 | temp->next->data = j;
57 | temp->next->next = NULL;
58 | }
59 | }
60 | }
61 | }
62 | }
63 | // end of function
64 |
65 | void Graph ::dfs(int v)
66 | {
67 | visited[v] = 1;
68 |
69 | struct Node *temp;
70 | temp = adj_list[v];
71 |
72 | while (temp != NULL)
73 | {
74 | if (visited[temp->data] == 0)
75 | {
76 | dfs(temp->data);
77 | }
78 | temp = temp->next;
79 | }
80 | // cout << v ;
81 | order.push_back(v) ;
82 | }
83 |
84 | void Graph ::make_graph(int no_of_vertices)
85 | {
86 | this->no_of_vertices = no_of_vertices;
87 | // creating a graph
88 | adj_list = new struct Node *[no_of_vertices];
89 | for (int i = 0; i < no_of_vertices; i++)
90 | {
91 | adj_list[i] = NULL;
92 | }
93 | }
94 |
95 | void Graph ::display()
96 | {
97 | cout << "The topological sorted order is: ";
98 | cout << order.size() << endl ;
99 | for (int i = 0 ; i < order.size(); i++)
100 | {
101 | cout << order[order.size() - 1 - i] << " " ;
102 | }
103 | cout << endl ;
104 | }
105 |
106 | int main()
107 | {
108 | Graph g;
109 | int no_of_vertices;
110 | cout << "Enter the number of vertices : ";
111 | cin >> no_of_vertices;
112 |
113 | g.make_graph(no_of_vertices);
114 | g.add_edge();
115 |
116 | for (int v = 0; v < no_of_vertices; v++)
117 | {
118 | if (g.visited[v] == 0)
119 | {
120 | g.dfs(v);
121 | }
122 | }
123 |
124 | g.display();
125 |
126 | return 0;
127 | }
128 | // end of main
129 |
--------------------------------------------------------------------------------
/01_Arrays/README.md:
--------------------------------------------------------------------------------
1 | # Arrays
2 |
3 | ## Introduction
4 |
5 | An array is a contiguous block of memory that holds elements of the same data type and is accessed using indices.
6 |
7 | ## Dynamic Arrays
8 |
9 | The problem with static arrays is that their size in memory is fixed. For example, if we're reading a sequence of numbers but don't know in advance how many there will be, we can't define a fixed-size array. We only know that some marker will indicate the end of the input.
10 |
11 | So we use Dynamic arrays or Resizable arrays. Vectors are an example of dynamic arrays in `C++`.
12 |
13 | ## Amortized Analysis
14 |
15 | For the dynamic array, we only resize every so often. Most of the time, we're doing a constant time operation, just adding an element. It's only when we fully reach the capacity, that we have to resize. It is true that the worst case for PushBack() operation is O(n), but we have to bear this cost only when we reach to full capacity of array.
16 |
17 |
4 |
5 | ## Introduction
6 | A tree is a data structure similar to a linked list but instead of each node pointing simply to the next node in a linear fashion, each node points to a number of nodes. Tree is an example of a non linear data structure.
7 | A tree structure is a way of representing the hierarchical nature of a structure in a graphical form.
8 |
9 | ## Basic Terminology
10 |
11 | 
12 |
13 | 1) The set of all nodes at a given depth is called the level of the tree. The root node is at level zero (eg. Nodes B, C and D lie at level 1)
14 | 2) The depth of a node is the length of the path from the root to the node (eg. depth of G is 2, A – C – G).
15 | 3) The height of a node is the length of the path from that node to the deepest node. The height of a tree is the length of the path from the root to the deepest node in the tree(eg. the height of B is 2, B – F – J)
16 | 4) Height of the tree is the maximum height among all the nodes in the tree and depth of the tree is the maximum depth among all the nodes in the tree. For a given tree, depth and height returns the same value. But for individual nodes we may get different results.
17 | 5) If every node in a tree has only one child (except leaf nodes) then we call such trees skew trees. If every node has only left child then we call them left skew trees. Similarly, if every node has only right child then we call them right skew trees.
18 |
19 | ## Tree Traversals
20 |
21 | * Preorder
22 | * Inorder
23 | * Postorder
24 | * Levelorder
25 |
26 | ## Binary Trees
27 | A tree is called binary tree if each node has zero child, one child or two children.
28 |
29 | ## AVL Trees
30 |
31 | The tree data structure proves to be effective only when the tree is a balanced in nature.
32 |
33 | The runtime of the tree depends upon the depth of the tree. Only when the tree is a balance binary tree, we can perform the operations such as insertion, deletion, search, range, etc. in O(log(n)) time.
34 |
35 | Else, the time complexity moves to O(n). In the worst case, the tree data structure is skewed and simply behaves like a sorted linked-list. Thus, inorder to keep our runtimes limited to O(log(n)), we must ensure our tree are balanced at all times.
36 |
37 | Height of a given tree helps to define the balance parameter. In general, for any given node, if it satisfies the given property, it is an AVL tree or a balanced binary tree
38 |
39 | ```|(Height of left subtree) - (Height of right subtree)| <= 1```
40 |
41 | ## Other Notes
42 |
43 | * Solving tree always involves some sort of traversal with something in Pre or Post section
44 | * Always mention in comments your base case and rec case
45 | * In trees, you cant have a parent pointer as such. But then you can make use of recursion, you can return it and treat that as a parent link. Essentially the recursion is the link between children and parent. For tree, call left, call right, return, get their results and club them up in parent
--------------------------------------------------------------------------------
/Algorithms/4_Sorting/randomized_quick_sort.cpp:
--------------------------------------------------------------------------------
1 | /***************************************************
2 | @brief Implementing Randomized Quick Sort
3 | ****************************************************/
4 | #include
5 | #include
6 | #include
7 | #include
8 |
9 | using namespace std;
10 |
11 | void Swap(int &i, int &j)
12 | {
13 | int temp = i;
14 | i = j;
15 | j = temp;
16 | }
17 |
18 | void random(int l, int r, vector &v)
19 | {
20 | srand((unsigned)time(NULL));
21 |
22 | int random = l + (rand() % r);
23 |
24 | int temp = v[random] ;
25 | v[random] = v[l] ;
26 | v[l] = temp ;
27 | }
28 |
29 | /*
30 | * Function Name: Parition
31 | * Input: Requires a vector, index of pivot element, starting index and ending element
32 | * Output: returns the position of pivot element in sorted array
33 | * Logic: Keeps elements smaller than pivot to its left and larger to its right
34 | * Example Call: Partition(v, 0, 0, v.size()-1)
35 | */
36 | int Partition(vector &v, int pivot, int i, int j)
37 | {
38 | if (i == j)
39 | {
40 | return i;
41 | }
42 |
43 | while (i <= j)
44 | {
45 | if (v[i] > v[pivot] && v[j] < v[pivot])
46 | {
47 | swap(v[i], v[j]);
48 | i++;
49 | j--;
50 | }
51 | else if (v[i] <= v[pivot])
52 | {
53 | i++;
54 | }
55 | else if (v[j] >= v[pivot])
56 | {
57 | j--;
58 | }
59 | }
60 |
61 | Swap(v[pivot], v[i - 1]);
62 | return i - 1;
63 | }
64 |
65 | /*
66 | * Function Name: QuickSort
67 | * Input: Requires a vector, index of pivot element, starting element and ending element
68 | * Logic: Divides the array as per partition by pivot and creates a sorted array
69 | * Example Call: QuickSort(v, pivot, 0, v.size() - 1)
70 | */
71 | void QuickSort(vector &v, int pivot, int begin, int end)
72 | {
73 | if (end <= begin)
74 | {
75 | return;
76 | }
77 |
78 | int m = Partition(v, pivot, begin, end); // m represents position of partition
79 |
80 | random(begin, m, v) ;
81 | QuickSort(v, begin, begin, m - 1);
82 |
83 | // random(m+1, end+1, v) ;
84 | QuickSort(v, m + 1, m + 1, end);
85 | }
86 |
87 | int main()
88 | {
89 | string s;
90 | getline(cin, s);
91 |
92 | int num = 0;
93 | vector v;
94 |
95 | /*Taking input from the user and storing it in a vector of int*/
96 | for (int i = 0; i < s.size(); ++i)
97 | {
98 | if (s[i] == ' ')
99 | v.push_back(num), num = 0;
100 | else
101 | num = num * 10 + (s[i] - '0');
102 | }
103 | v.push_back(num);
104 |
105 | random(0, v.size(), v) ;
106 |
107 | int pivot = 0;
108 |
109 | cout << endl ;
110 |
111 | QuickSort(v, pivot, 0, v.size() - 1);
112 |
113 | for (int i = 0; i < v.size(); i++)
114 | {
115 | cout << v[i] << " ";
116 | }
117 |
118 | return 0;
119 | }
120 | /*
121 | Analysis: The above code runs averagely in O(nlog(n)) and O(n^2) in worst cases
122 | */
--------------------------------------------------------------------------------
/Algorithms/3_Dynamic_Programming/knapsack_limited.cpp:
--------------------------------------------------------------------------------
1 | /***************************************************************************
2 | @brief Using dynamic programming for 0/1 Knapsack_limited problem
3 | ****************************************************************************/
4 | #include
5 | #include
6 | #include
7 |
8 | using namespace std;
9 |
10 | /*
11 | * Function Name: knapsack
12 | * Input: Requires an vector of price, weights, status and values of capacity and n
13 | * Output: returns the maximum profit
14 | * Logic: Finds the optimal solution using bottom-to-top method of dynamic programming
15 | * Example Call: knapsack(price, weight, capacity, n - 1, status)
16 | */
17 | int knapsack(vector price, vector weight, int capacity, int n, vector &status)
18 | {
19 | vector> matrix(weight.size() + 1, vector(capacity + 1, 0));
20 |
21 | for (int i = 1; i < matrix.size(); i++)
22 | {
23 | for (int j = 1; j < matrix[0].size(); j++)
24 | {
25 | if (weight[i - 1] <= j)
26 | {
27 | matrix[i][j] = max(matrix[i - 1][j], price[i - 1] + matrix[i - 1][j - weight[i - 1]]);
28 | }
29 | else
30 | {
31 | matrix[i][j] = matrix[i - 1][j];
32 | }
33 | }
34 | }
35 |
36 | int x = weight.size();
37 | int y = capacity;
38 | int index = status.size() - 1;
39 |
40 | while (x != 0)
41 | {
42 | if (matrix[x][y] == matrix[x - 1][y])
43 | {
44 | status[index] = false;
45 | x = x - 1;
46 | index--;
47 | }
48 | else
49 | {
50 | status[index] = true;
51 | x = x - 1;
52 | y = y - weight[x];
53 | index--;
54 | }
55 | }
56 |
57 | return matrix[weight.size()][capacity];
58 | }
59 |
60 | int main()
61 | {
62 | int capacity;
63 | cout << "Enter the capacity of Knapsack: ";
64 | cin >> capacity;
65 | int n;
66 | cout << "Enter the total number of distinct elements: ";
67 | cin >> n;
68 | vector price(n);
69 | vector weight(n);
70 | vector status(n, false);
71 |
72 | for (int i = 0; i < n; i++)
73 | {
74 | cout << "Enter weight of item " << i + 1 << " : ";
75 | cin >> weight[i];
76 | cout << "Enter price of item " << i + 1 << " : ";
77 | cin >> price[i];
78 | }
79 |
80 | int answer = knapsack(price, weight, capacity, n - 1, status);
81 |
82 | for (int i = 0; i < status.size(); i++)
83 | {
84 | if (status[i] == true)
85 | {
86 | cout << "Item " << i + 1 << " : Taken";
87 | }
88 | else
89 | {
90 | cout << "Item " << i + 1 << " : Not Taken";
91 | }
92 | cout << endl;
93 | }
94 | cout << "Maximum profit is: " << answer << endl;
95 |
96 | return 0;
97 | }
98 | /*
99 | Analysis: The above code runs in O(m*n), where n is the number of different object required and m is the capacity of knapsack
100 | */
--------------------------------------------------------------------------------
/03_Queues/Queue_using_Linked_list/simple_queue.cpp:
--------------------------------------------------------------------------------
1 | /*******************************************************
2 | @brief Implementing queue using a linked list
3 | ********************************************************/
4 |
5 | #include
6 |
7 | using namespace std;
8 |
9 | void enqueue(int element);
10 | void display();
11 |
12 | struct Node
13 | {
14 | int data;
15 | class Node *next; // next is a pointer of type Node which points towards the next Node
16 | };
17 | /*initially both the pointers are NULL*/
18 | struct Node *front = NULL;
19 | struct Node *rear = NULL;
20 |
21 | /*
22 | * Function Name: enqueue
23 | * Input: Integer element which is to be inserted
24 | * Output: None
25 | * Logic: This function allows us to insert an element in queue
26 | * Example Call: enqueue(5)
27 | */
28 | void enqueue(int element)
29 | {
30 | Node *temp = (Node *)malloc(sizeof(Node)); // dynamic allocation of memory
31 | if (temp == NULL)
32 | {
33 | cout << "Queue is full";
34 | }
35 | else if (front == NULL) // or rear == NULL, both conditions work
36 | {
37 | front = rear = temp;
38 | temp->data = element;
39 | temp->next = NULL;
40 | }
41 | else
42 | {
43 | rear->next = temp; // the next of the rear node should point at new node temp
44 | temp->data = element;
45 | temp->next = NULL;
46 | rear = temp; // rear should point to the new node formed
47 | }
48 | }
49 |
50 | /*
51 | * Function Name: dequeue
52 | * Input: None
53 | * Output: Returns the first element of queue
54 | * Logic: This function allows us to remove the first element of queue
55 | * Example Call: dequeue()
56 | */
57 | void dequeue()
58 | {
59 | if (front == NULL)
60 | {
61 | cout << "Queue is empty!";
62 | }
63 | else
64 | {
65 | cout << front->data << "\n";
66 |
67 | Node *temp = front;
68 | front = front->next;
69 | delete temp; // Deallocating the memory given to node
70 | }
71 | }
72 |
73 | /*
74 | * Function Name: display
75 | * Input: None
76 | * Output: Prints all the elements in the queue
77 | * Logic: This function allows us to print the elements currently in queue
78 | * Example Call: display()
79 | */
80 | void display()
81 | {
82 | Node *temp = front;
83 | if (front == NULL)
84 | {
85 | cout << "Queue is empty!";
86 | }
87 | else if (front == rear) // incase of only one element in queue
88 | {
89 | cout << "The elements in queue are : " << front->data ;
90 | struct Node *front = NULL;
91 | struct Node *rear = NULL;
92 | }
93 | else
94 | {
95 | cout << "The elements in queue are : ";
96 | while (temp != NULL)
97 | {
98 | cout << temp->data << " "; // prints data in all nodes
99 | temp = temp->next;
100 | }
101 | }
102 |
103 | cout << "\n";
104 | }
105 |
106 | int main()
107 | {
108 | enqueue(5);
109 | enqueue(10);
110 | enqueue(15);
111 | display();
112 | dequeue();
113 | display();
114 | dequeue();
115 | display();
116 | dequeue();
117 | display();
118 |
119 | return 0;
120 | }
121 |
--------------------------------------------------------------------------------
/09_Graphs/topological_sort.cpp:
--------------------------------------------------------------------------------
1 | #include
2 | #include
3 |
4 | using namespace std;
5 |
6 | #define VERTICES 100
7 |
8 | class Graph
9 | {
10 | private:
11 | struct Node
12 | {
13 | int data;
14 | struct Node *next;
15 | };
16 | int no_of_vertices;
17 | struct Node **adj_list;
18 | vector order ;
19 |
20 | public:
21 | bool visited[VERTICES] = {0};
22 | void make_graph(int no_of_vertices);
23 | void display();
24 | void add_edge();
25 | void dfs(int v);
26 | };
27 |
28 | void Graph ::add_edge()
29 | {
30 | for (int i = 0; i < no_of_vertices; i++)
31 | {
32 | for (int j = 0; j < no_of_vertices; j++)
33 | {
34 | if (i != j)
35 | {
36 | char choice;
37 | cout << "Are vertices " << i << " and " << j << " adjacent? (Y/N) : ";
38 | cin >> choice;
39 |
40 | if (toupper(choice) == 'Y')
41 | {
42 | if (adj_list[i] == NULL)
43 | {
44 | adj_list[i] = new struct Node;
45 | adj_list[i]->data = j;
46 | adj_list[i]->next = NULL;
47 | continue;
48 | }
49 | struct Node *temp;
50 | temp = adj_list[i];
51 | while (temp->next != NULL)
52 | {
53 | temp = temp->next;
54 | }
55 | temp->next = new struct Node;
56 | temp->next->data = j;
57 | temp->next->next = NULL;
58 | }
59 | }
60 | }
61 | }
62 | }
63 | // end of function
64 |
65 | void Graph ::dfs(int v)
66 | {
67 | visited[v] = 1;
68 |
69 | struct Node *temp;
70 | temp = adj_list[v];
71 |
72 | while (temp != NULL)
73 | {
74 | if (visited[temp->data] == 0)
75 | {
76 | dfs(temp->data);
77 | }
78 | temp = temp->next;
79 | }
80 | // cout << v ;
81 | order.push_back(v) ;
82 | }
83 |
84 | void Graph ::make_graph(int no_of_vertices)
85 | {
86 | this->no_of_vertices = no_of_vertices;
87 | // creating a graph
88 | adj_list = new struct Node *[no_of_vertices];
89 | for (int i = 0; i < no_of_vertices; i++)
90 | {
91 | adj_list[i] = NULL;
92 | }
93 | }
94 |
95 | void Graph ::display()
96 | {
97 | cout << "The topological sorted order is: ";
98 | cout << order.size() << endl ;
99 | for (int i = 0 ; i < order.size(); i++)
100 | {
101 | cout << order[order.size() - 1 - i] << " " ;
102 | }
103 | cout << endl ;
104 | }
105 |
106 | int main()
107 | {
108 | Graph g;
109 | int no_of_vertices;
110 | cout << "Enter the number of vertices : ";
111 | cin >> no_of_vertices;
112 |
113 | g.make_graph(no_of_vertices);
114 | g.add_edge();
115 |
116 | for (int v = 0; v < no_of_vertices; v++)
117 | {
118 | if (g.visited[v] == 0)
119 | {
120 | g.dfs(v);
121 | }
122 | }
123 |
124 | g.display();
125 |
126 | return 0;
127 | }
128 | // end of main
129 |
--------------------------------------------------------------------------------
/01_Arrays/README.md:
--------------------------------------------------------------------------------
1 | # Arrays
2 |
3 | ## Introduction
4 |
5 | An array is a contiguous block of memory that holds elements of the same data type and is accessed using indices.
6 |
7 | ## Dynamic Arrays
8 |
9 | The problem with static arrays is that their size in memory is fixed. For example, if we're reading a sequence of numbers but don't know in advance how many there will be, we can't define a fixed-size array. We only know that some marker will indicate the end of the input.
10 |
11 | So we use Dynamic arrays or Resizable arrays. Vectors are an example of dynamic arrays in `C++`.
12 |
13 | ## Amortized Analysis
14 |
15 | For the dynamic array, we only resize every so often. Most of the time, we're doing a constant time operation, just adding an element. It's only when we fully reach the capacity, that we have to resize. It is true that the worst case for PushBack() operation is O(n), but we have to bear this cost only when we reach to full capacity of array.
16 |
17 |  18 |
19 | Amortized analysis is a method for analyzing a given algorithm's complexity, or how much of a resource, especially time or memory, it takes to execute. The motivation for amortized analysis is that looking at the worst-case run time can be too pessimistic. Instead, amortized analysis averages the running times of operations and considers both the expensive and cheap operations together over the whole sequence of operations.
20 |
21 | ### Aggregate Method
22 |
23 |
18 |
19 | Amortized analysis is a method for analyzing a given algorithm's complexity, or how much of a resource, especially time or memory, it takes to execute. The motivation for amortized analysis is that looking at the worst-case run time can be too pessimistic. Instead, amortized analysis averages the running times of operations and considers both the expensive and cheap operations together over the whole sequence of operations.
20 |
21 | ### Aggregate Method
22 |
23 |  24 |
25 | ### Banker Method
26 |
27 | In Bankers method, we associate certain fixed extra cost for all cheap operations, which will then compensate for the expensive operation.
28 |
29 |
24 |
25 | ### Banker Method
26 |
27 | In Bankers method, we associate certain fixed extra cost for all cheap operations, which will then compensate for the expensive operation.
28 |
29 |  30 |
31 | Thus, associating cost of 3 with each cheap operation allows us to ignore the cost during resizing. Overall, we can claim that the cost for each operation is 3, or O(1).
32 |
33 | ### Physicist Method
34 |
35 | This method is very similar to the concept of potential energy. If we go from lower level to higher level, potential energy increases. In a similar fashion, we have a potential function here. We expend ```h(t) - h (t-1)``` amount of work every time inserting an element.
36 |
37 |
30 |
31 | Thus, associating cost of 3 with each cheap operation allows us to ignore the cost during resizing. Overall, we can claim that the cost for each operation is 3, or O(1).
32 |
33 | ### Physicist Method
34 |
35 | This method is very similar to the concept of potential energy. If we go from lower level to higher level, potential energy increases. In a similar fashion, we have a potential function here. We expend ```h(t) - h (t-1)``` amount of work every time inserting an element.
36 |
37 |  38 |
39 | The choice of potential function is important here. It should be made such that is ```Ct``` is small, potential function should increase at each step.
40 |
38 |
39 | The choice of potential function is important here. It should be made such that is ```Ct``` is small, potential function should increase at each step.
40 |  41 |
42 | The general cost without resizing is:
43 |
41 |
42 | The general cost without resizing is:
43 |  44 | The general cost with resizing is:
45 |
44 | The general cost with resizing is:
45 |  46 |
47 |
48 |
49 | ## Points to note
50 |
51 | * It is important to resize the array by constant factor, say twice the bigger, rather than constant amount, say by 10 always. This is because if we increase by constant amount, the expensive operations can no more be compensated by cheap operations and runtime jumps to O(n)
52 | * ```*size ++``` implies that size pointer should be incremented and then its value should be dereferenced, while ```(*size)++``` implies, increment the value stored in size.
53 |
--------------------------------------------------------------------------------
/leetcode/1456 Maximum Number of Vowels in a Substring of Given Length.cpp:
--------------------------------------------------------------------------------
1 | /*
2 | Approach 1: sliding a static window of size k over string and checking maximum everytime
3 | Runtime: 2077ms
4 | Memory: 10.20MB
5 | Time Complexity: O(n*k)
6 | */
7 | class Solution {
8 | public:
9 | int maxVowels(string s, int k) {
10 | int l = s.length();
11 | int max = 0;
12 | for (int i = 0; i <= l - k && max != k; i++)
13 | {
14 | int curr = 0;
15 | //if a vowel is hit
16 | if (s[i] == 'a' || s[i] == 'e' || s[i] == 'i' || s[i] == 'o' || s[i] == 'u')
17 | {
18 | curr++;
19 | for (int j = i+1; j < k+i; j++)
20 | {
21 | if (s[j] == 'a' || s[j] == 'e' || s[j] == 'i' || s[j] == 'o' || s[j] == 'u')
22 | {
23 | curr++;
24 | }
25 | }
26 | if (curr > max)
27 | {
28 | max = curr;
29 | }
30 | }
31 | }
32 | int curr = 0;
33 | for (int j = l-k+1; j < l && max!=k; j++)
34 | {
35 | if (s[j] == 'a' || s[j] == 'e' || s[j] == 'i' || s[j] == 'o' || s[j] == 'u')
36 | {
37 | curr++;
38 | }
39 | }
40 | if (curr > max)
41 | {
42 | max = curr;
43 | }
44 | return max;
45 | }
46 | };
47 |
48 | /*Approach 2: sliding a static window of size k over string and tracking vowels which came in and went out of window
49 | Runtime: 15ms
50 | Memory: 10.26MB
51 | Time Complexity: O(n+k)
52 | */
53 | class Solution {
54 | public:
55 | int maxVowels(string s, int k) {
56 | int l = s.length();
57 | //case1
58 | if (l <= k)
59 | {
60 | int curr = 0;
61 | for (int i = 0; i < l; i++)
62 | {
63 | if (s[i] == 'a' || s[i] == 'e' || s[i] == 'i' || s[i] == 'o' || s[i] == 'u')
64 | {
65 | curr++;
66 | }
67 | }
68 | return curr;
69 | }
70 | else
71 | {
72 | int max = 0;
73 | int curr = 0;
74 | //check first k letters as baseline
75 | for (int i = 0; i < k; i++)
76 | {
77 | if (s[i] == 'a' || s[i] == 'e' || s[i] == 'i' || s[i] == 'o' || s[i] == 'u')
78 | {
79 | max++;
80 | }
81 | }
82 | curr = max;
83 | for (int i = 1; i <= l-k; i++)
84 | {
85 | //if we a vowel was dropped from sliding window
86 | if (s[i-1] == 'a' || s[i-1] == 'e' || s[i-1] == 'i' || s[i-1] == 'o' || s[i-1] == 'u')
87 | {
88 | curr--;
89 | }
90 | //if new letter of window is a vowel
91 | if (s[i+k-1] == 'a' || s[i+k-1] == 'e' || s[i+k-1] == 'i' || s[i+k-1] == 'o' || s[i+k-1] == 'u')
92 | {
93 | curr++;
94 | }
95 | if (curr > max)
96 | {
97 | max = curr;
98 | }
99 | }
100 | return max;
101 | }
102 | }
103 | };
--------------------------------------------------------------------------------
/02_Stack/Miscellaneous/Balancing_brackets.cpp:
--------------------------------------------------------------------------------
1 | /*******************************************
2 | @brief Balancing brackets in text
3 | ********************************************/
4 |
5 | #include
6 | #define MAX_SIZE 10000
7 | using namespace std;
8 |
9 | class Stack
10 | {
11 | private:
12 | char stack[MAX_SIZE];
13 | int top = -1;
14 |
15 | public:
16 | void push(char element);
17 | char pop();
18 | char peek();
19 | };
20 |
21 | /*
22 | * Function Name: push
23 | * Input: Integer element which is to be pushed
24 | * Output: None
25 | * Logic: This function allows us to insert an element in stack
26 | * Example Call: push(5)
27 | */
28 | void Stack ::push(char element)
29 | {
30 | if (top != MAX_SIZE - 1) // We can not push anymore elements if the stack is full
31 | {
32 | top++;
33 | stack[top] = element;
34 | }
35 | }
36 |
37 | /*
38 | * Function Name: pop
39 | * Input: None
40 | * Output: Returns the topmost element of stack or -1 if stack is empty
41 | * Logic: This function allows us to remove an element from stack
42 | * Example Call: pop()
43 | */
44 | char Stack ::pop()
45 | {
46 | if (top != -1)
47 | {
48 | return stack[top--];
49 | /* We need to do top-- above itself cause the staements below the return statement are not executed*/
50 | }
51 | else
52 | {
53 | return 'X';
54 | }
55 | }
56 | // end of function
57 |
58 | /*
59 | * Function Name: peek
60 | * Input: None
61 | * Output: Returns the topmost element of stack or -1 if stack is empty without deleting it
62 | * Logic: This function allows us to remove an element from stack without deleting it
63 | * Example Call: peek()
64 | */
65 | char Stack ::peek()
66 | {
67 | if (top != -1)
68 | {
69 | return stack[top]; // here, we simply return the topmost element and not decrement top
70 | }
71 | else
72 | {
73 | return 'X';
74 | }
75 | }
76 |
77 | int main()
78 | {
79 | Stack s1;
80 |
81 | string s;
82 | getline(cin, s);
83 | for (int i = 0; i < s.length(); i++)
84 | {
85 | if (s[i] == '(' || s[i] == '[' || s[i] == '{' || s[i] == '}' || s[i] == ']' || s[i] == ')')
86 | {
87 | if (s[i] == ')' && s1.peek() == '(')
88 | {
89 | char x;
90 | x = s1.pop();
91 | }
92 | else if (s[i] == ']' && s1.peek() == '[')
93 | {
94 | char x;
95 | x = s1.pop();
96 | }
97 | else if (s[i] == '}' && s1.peek() == '{')
98 | {
99 | char x;
100 | x = s1.pop();
101 | }
102 | else
103 | {
104 | s1.push(s[i]);
105 | }
106 | }
107 | }
108 |
109 | // if stack is empty by now, the expression is valid
110 | char x;
111 | x = s1.peek();
112 | if (x == 'X')
113 | {
114 | cout << "Success"<<"\n";
115 | }
116 | else
117 | {
118 | x = s1.peek() ;
119 | for (int i = 0 ; i < s.length() ; i++)
120 | {
121 | if (x == s[i])
122 | {
123 | cout << i+1 ; //to print location of error
124 | break ;
125 | }
126 | }
127 | }
128 |
129 | return 0;
130 | }
131 | // end of main
--------------------------------------------------------------------------------
/09_Graphs/adj_list.cpp:
--------------------------------------------------------------------------------
1 | /*
2 | Code to create a graph using Adjacency listrepresentation
3 | We consider the graph to be directed graph and non-weighted with no self loops
4 | */
5 | #include
6 |
7 | using namespace std;
8 |
9 | class Graph
10 | {
11 | private:
12 | struct Node
13 | {
14 | int data;
15 | struct Node *next;
16 | };
17 | int no_of_vertices;
18 | struct Node **adj_list;
19 |
20 | public:
21 | void make_graph(int no_of_vertices);
22 | void display();
23 | void add_edge();
24 | };
25 |
26 | /*
27 | This function is used to create a graph
28 | parameters : no_of_vertices
29 | Returns : void
30 | */
31 | void Graph ::make_graph(int no_of_vertices)
32 | {
33 | this->no_of_vertices = no_of_vertices;
34 | // creating a graph
35 | adj_list = new struct Node *[no_of_vertices];
36 | for (int i = 0; i < no_of_vertices; i++)
37 | {
38 | adj_list[i] = NULL;
39 | }
40 | }
41 | // end of function
42 |
43 | /*
44 | This function is used to display the graph
45 | parameters : void
46 | Returns : void
47 | */
48 | void Graph ::display()
49 | {
50 | cout << "The adjacency list representation is :-\n";
51 | for (int i = 0; i < no_of_vertices; i++)
52 | {
53 | cout << i << " : ";
54 | if (adj_list[i] != NULL)
55 | {
56 | struct Node *temp;
57 | temp = adj_list[i];
58 | while (temp->next != NULL)
59 | {
60 | cout << temp->data << " -> ";
61 | temp = temp->next;
62 | }
63 | cout << temp->data;
64 | }
65 | cout << "\n";
66 | }
67 | }
68 | // end of function
69 |
70 | /*
71 | This function iterates over all the possible edges and asks user if they want the edge to exist or not
72 | parameters : void
73 | Returns : void
74 | */
75 | void Graph ::add_edge()
76 | {
77 | for (int i = 0; i < no_of_vertices; i++)
78 | {
79 | for (int j = 0; j < no_of_vertices; j++)
80 | {
81 | if (i != j)
82 | {
83 | char choice;
84 | cout << "Are vertices " << i << " and " << j << " adjacent? (Y/N) : ";
85 | cin >> choice;
86 |
87 | if (toupper(choice) == 'Y')
88 | {
89 | if (adj_list[i] == NULL)
90 | {
91 | adj_list[i] = new struct Node;
92 | adj_list[i]->data = j;
93 | adj_list[i]->next = NULL;
94 | continue;
95 | }
96 | struct Node *temp;
97 | temp = adj_list[i];
98 | while (temp->next != NULL)
99 | {
100 | temp = temp->next;
101 | }
102 | temp->next = new struct Node;
103 | temp->next->data = j;
104 | temp->next->next = NULL;
105 | }
106 | }
107 | }
108 | }
109 | }
110 | // end of function
111 |
112 | // main function starts here
113 | int main()
114 | {
115 | Graph g;
116 | int no_of_vertices;
117 | cout << "Enter the number of vertices : ";
118 | cin >> no_of_vertices;
119 |
120 | g.make_graph(no_of_vertices);
121 | g.add_edge();
122 | g.display();
123 | return 0;
124 | }
125 | // end of main
--------------------------------------------------------------------------------
/05_Trees/tree_traversal.cpp:
--------------------------------------------------------------------------------
1 | /********************************************************************
2 | @brief Implementing binary trees and performing traversals
3 | *********************************************************************/
4 | #include
5 |
6 | using namespace std;
7 |
8 | class Tree
9 | {
10 | struct node
11 | {
12 | int data;
13 | struct node *left = NULL;
14 | struct node *right = NULL;
15 | };
16 |
17 | public:
18 | struct node *root = NULL; // The pointer to the staring node . for now this is null and will point to the root node when created
19 | void insert(struct node *&node, int element);
20 | void inorder(struct node *root);
21 | void preorder(struct node *root);
22 | void postorder(struct node *root);
23 | };
24 |
25 | /*
26 | * Function Name: insert
27 | * Input: a pointer to root node and the element to be inserted
28 | * Output: None
29 | * Logic: Inserts a node in the binary tree
30 | * Example Call: insert(root, 5)
31 | */
32 | void Tree ::insert(struct node *&node, int element)
33 | {
34 | if (node == NULL) // if there is no root node i.e. the tree is empty
35 | {
36 | struct node *temp = (struct node *)malloc(sizeof(struct node)); // creating a memory in heap consisting a node
37 | node = temp;
38 | node->data = element;
39 | node->left = NULL;
40 | node->right = NULL; // here we create a new node
41 | }
42 | else if (element > node->data) // insert in right tree
43 | {
44 | insert(node->right, element);
45 | }
46 | else // insert in left tree
47 | {
48 | insert(node->left, element);
49 | }
50 | }
51 |
52 | /*
53 | * Function Name: inorder
54 | * Input: a pointer to root node
55 | * Output: Prints inorder traversal of tree
56 | * Example Call: inorder(root)
57 | */
58 | void Tree ::inorder(struct node *root)
59 | {
60 | if (root != NULL)
61 | {
62 | inorder(root->left);
63 | printf("%d ", root->data);
64 | inorder(root->right);
65 | }
66 | }
67 |
68 | /*
69 | * Function Name: preorder
70 | * Input: a pointer to root node
71 | * Output: Prints preorder traversal of tree
72 | * Example Call: preorder(root)
73 | */
74 | void Tree ::preorder(struct node *root)
75 | {
76 | if (root != NULL)
77 | {
78 | printf("%d ", root->data);
79 | preorder(root->left);
80 | preorder(root->right);
81 | }
82 | }
83 |
84 | /*
85 | * Function Name: postorder
86 | * Input: a pointer to root node
87 | * Output: Prints postorder traversal of tree
88 | * Example Call: postorder(root)
89 | */
90 | void Tree ::postorder(struct node *root)
91 | {
92 | if (root != NULL)
93 | {
94 | postorder(root->left);
95 | postorder(root->right);
96 | printf("%d ", root->data);
97 | }
98 | }
99 |
100 | int main()
101 | {
102 | Tree t;
103 | /*insertion*/
104 | t.insert(t.root, 15);
105 | t.insert(t.root, 5);
106 | t.insert(t.root, 2);
107 | t.insert(t.root, 40);
108 | t.insert(t.root, 80);
109 | t.insert(t.root, 20);
110 | t.insert(t.root, 1);
111 | t.insert(t.root, 3);
112 |
113 | /*traversing*/
114 | printf("The inorder Traversal is : ");
115 | t.inorder(t.root);
116 | printf("\n");
117 | printf("The preorder Traversal is : ");
118 | t.preorder(t.root);
119 | printf("\n");
120 | printf("The postorder Traversal is : ");
121 | t.postorder(t.root);
122 | printf("\n");
123 | }
124 | /*
125 | Analysis: The above algorithm runs in O(n) for traversal and O(nlog(n)) for insertion
126 | */
127 |
--------------------------------------------------------------------------------
/Algorithms/4_Sorting/Readme.md:
--------------------------------------------------------------------------------
1 | # Sorting
2 |
3 | 
4 |
5 | ## Table of Contents
6 |
7 | * Introduction
8 | * Sorting Algorithms
9 | * Selection Sort
10 | * Merge Sort
11 | * Count Sort
12 | * Quick Sort
13 | * Heap Sort
14 | * Comb Sort
15 | * Conclusion
16 |
17 | ## Sorting Algorithms
18 |
19 | Sorting algorithms are mainly of two types: comparison based and non-comparison based. It is proven mathematically that a comparison based sorting algorithm requires atleast O(nlon(n)).
20 |
21 | ### 1) Selection Sort
22 |
23 | Selection sort is a comparison based sorting algorithm.
24 |
25 | In selection sort,we first find the minimum element in the given array. Then we swap the minimum element with the first element.We then repeat the above steps for remaining array.
26 |
27 |
28 | ### 2) Merge Sort
29 | Merge sort is a comparison based sorting algorithm based on divide and conquer technique.
30 |
31 | In merge sort, we split the given array recursively and then sort them indivisually and merge them back.
32 |
33 | ### 3) Count Sort
34 | Count sort is a Non-comparison based sorting algorithm and has better time complexity than comparison based algorithms in general.
35 |
36 | However, for this algorithm to work, we need to deal with a fixed range of integers only, say I know my input is a mix of integers in range 0-100, then count sort is appropriate.
37 |
38 | ### 4) Quick Sort
39 | Quick sort is a Comparison based sorting algorithm. The runtime of this algorithm depends on the partitions which are created. If the partitions are always created at the center, the algorithm works in O(nlog(n)). However, if we were to assume the worst case, it would work in O(n^2).
40 |
41 | In Quick sort, we can prove that choosing a random element as a pivot is generally a good choice which increases our probability to get the partitions which lead to O(nlog(n)) time complexity. The same is depicted in ```randomized_quick_sort.cpp```.
42 |
43 | ### 5) Heap Sort
44 |
45 | In order to implement Heap sort, we can simply convert the given array into a Max-Heap and perform extract-max on it and place the maximum element so recieved at the end of array.
46 |
47 | We can create a new priority queue and store elements in the new array one by one, maintaining the heap property. However this requires extra space. Thus, we can rather convert the given array into a priority queue itself, avoiding use of extra space.
48 |
49 | Heap sort works in O(nlog(n)) and is a comparison based algorithm.
50 |
51 | ### 6) Comb Sort
52 |
53 | Comb Sort is like a smarter version of Bubble Sort. In Bubble Sort, we always check and swap neighboring elements. So, if a small number is at the end, it takes a long time to move to the front.
54 |
55 | In Comb Sort, we introduce a gap between elements we compare. At first, this gap is quite large, which lets us compare elements that are far apart. After each pass through the list, we shrink this gap by a factor (usually 1.3). Eventually, the gap becomes 1, and Comb Sort behaves just like Bubble Sort, checking only adjacent elements. While Comb Sort is usually faster than Bubble Sort on average, worst case remains O(n^2).
56 |
57 | ## Conclusion
58 |
59 | The time complexities of a few sorting algorithms are given below
60 |
61 | 
62 |
63 | For visualization of the above sorting algorithms, refer : https://www.toptal.com/developers/sorting-algorithms and https://www.cs.usfca.edu/~galles/visualization/ComparisonSort.html.
64 |
65 |
66 |
67 |
68 |
69 |
70 |
71 |
72 |
73 | ##
74 |
--------------------------------------------------------------------------------
/Data Structures/Arrays/README.md:
--------------------------------------------------------------------------------
1 | # Arrays
2 |
3 |
46 |
47 |
48 |
49 | ## Points to note
50 |
51 | * It is important to resize the array by constant factor, say twice the bigger, rather than constant amount, say by 10 always. This is because if we increase by constant amount, the expensive operations can no more be compensated by cheap operations and runtime jumps to O(n)
52 | * ```*size ++``` implies that size pointer should be incremented and then its value should be dereferenced, while ```(*size)++``` implies, increment the value stored in size.
53 |
--------------------------------------------------------------------------------
/leetcode/1456 Maximum Number of Vowels in a Substring of Given Length.cpp:
--------------------------------------------------------------------------------
1 | /*
2 | Approach 1: sliding a static window of size k over string and checking maximum everytime
3 | Runtime: 2077ms
4 | Memory: 10.20MB
5 | Time Complexity: O(n*k)
6 | */
7 | class Solution {
8 | public:
9 | int maxVowels(string s, int k) {
10 | int l = s.length();
11 | int max = 0;
12 | for (int i = 0; i <= l - k && max != k; i++)
13 | {
14 | int curr = 0;
15 | //if a vowel is hit
16 | if (s[i] == 'a' || s[i] == 'e' || s[i] == 'i' || s[i] == 'o' || s[i] == 'u')
17 | {
18 | curr++;
19 | for (int j = i+1; j < k+i; j++)
20 | {
21 | if (s[j] == 'a' || s[j] == 'e' || s[j] == 'i' || s[j] == 'o' || s[j] == 'u')
22 | {
23 | curr++;
24 | }
25 | }
26 | if (curr > max)
27 | {
28 | max = curr;
29 | }
30 | }
31 | }
32 | int curr = 0;
33 | for (int j = l-k+1; j < l && max!=k; j++)
34 | {
35 | if (s[j] == 'a' || s[j] == 'e' || s[j] == 'i' || s[j] == 'o' || s[j] == 'u')
36 | {
37 | curr++;
38 | }
39 | }
40 | if (curr > max)
41 | {
42 | max = curr;
43 | }
44 | return max;
45 | }
46 | };
47 |
48 | /*Approach 2: sliding a static window of size k over string and tracking vowels which came in and went out of window
49 | Runtime: 15ms
50 | Memory: 10.26MB
51 | Time Complexity: O(n+k)
52 | */
53 | class Solution {
54 | public:
55 | int maxVowels(string s, int k) {
56 | int l = s.length();
57 | //case1
58 | if (l <= k)
59 | {
60 | int curr = 0;
61 | for (int i = 0; i < l; i++)
62 | {
63 | if (s[i] == 'a' || s[i] == 'e' || s[i] == 'i' || s[i] == 'o' || s[i] == 'u')
64 | {
65 | curr++;
66 | }
67 | }
68 | return curr;
69 | }
70 | else
71 | {
72 | int max = 0;
73 | int curr = 0;
74 | //check first k letters as baseline
75 | for (int i = 0; i < k; i++)
76 | {
77 | if (s[i] == 'a' || s[i] == 'e' || s[i] == 'i' || s[i] == 'o' || s[i] == 'u')
78 | {
79 | max++;
80 | }
81 | }
82 | curr = max;
83 | for (int i = 1; i <= l-k; i++)
84 | {
85 | //if we a vowel was dropped from sliding window
86 | if (s[i-1] == 'a' || s[i-1] == 'e' || s[i-1] == 'i' || s[i-1] == 'o' || s[i-1] == 'u')
87 | {
88 | curr--;
89 | }
90 | //if new letter of window is a vowel
91 | if (s[i+k-1] == 'a' || s[i+k-1] == 'e' || s[i+k-1] == 'i' || s[i+k-1] == 'o' || s[i+k-1] == 'u')
92 | {
93 | curr++;
94 | }
95 | if (curr > max)
96 | {
97 | max = curr;
98 | }
99 | }
100 | return max;
101 | }
102 | }
103 | };
--------------------------------------------------------------------------------
/02_Stack/Miscellaneous/Balancing_brackets.cpp:
--------------------------------------------------------------------------------
1 | /*******************************************
2 | @brief Balancing brackets in text
3 | ********************************************/
4 |
5 | #include
6 | #define MAX_SIZE 10000
7 | using namespace std;
8 |
9 | class Stack
10 | {
11 | private:
12 | char stack[MAX_SIZE];
13 | int top = -1;
14 |
15 | public:
16 | void push(char element);
17 | char pop();
18 | char peek();
19 | };
20 |
21 | /*
22 | * Function Name: push
23 | * Input: Integer element which is to be pushed
24 | * Output: None
25 | * Logic: This function allows us to insert an element in stack
26 | * Example Call: push(5)
27 | */
28 | void Stack ::push(char element)
29 | {
30 | if (top != MAX_SIZE - 1) // We can not push anymore elements if the stack is full
31 | {
32 | top++;
33 | stack[top] = element;
34 | }
35 | }
36 |
37 | /*
38 | * Function Name: pop
39 | * Input: None
40 | * Output: Returns the topmost element of stack or -1 if stack is empty
41 | * Logic: This function allows us to remove an element from stack
42 | * Example Call: pop()
43 | */
44 | char Stack ::pop()
45 | {
46 | if (top != -1)
47 | {
48 | return stack[top--];
49 | /* We need to do top-- above itself cause the staements below the return statement are not executed*/
50 | }
51 | else
52 | {
53 | return 'X';
54 | }
55 | }
56 | // end of function
57 |
58 | /*
59 | * Function Name: peek
60 | * Input: None
61 | * Output: Returns the topmost element of stack or -1 if stack is empty without deleting it
62 | * Logic: This function allows us to remove an element from stack without deleting it
63 | * Example Call: peek()
64 | */
65 | char Stack ::peek()
66 | {
67 | if (top != -1)
68 | {
69 | return stack[top]; // here, we simply return the topmost element and not decrement top
70 | }
71 | else
72 | {
73 | return 'X';
74 | }
75 | }
76 |
77 | int main()
78 | {
79 | Stack s1;
80 |
81 | string s;
82 | getline(cin, s);
83 | for (int i = 0; i < s.length(); i++)
84 | {
85 | if (s[i] == '(' || s[i] == '[' || s[i] == '{' || s[i] == '}' || s[i] == ']' || s[i] == ')')
86 | {
87 | if (s[i] == ')' && s1.peek() == '(')
88 | {
89 | char x;
90 | x = s1.pop();
91 | }
92 | else if (s[i] == ']' && s1.peek() == '[')
93 | {
94 | char x;
95 | x = s1.pop();
96 | }
97 | else if (s[i] == '}' && s1.peek() == '{')
98 | {
99 | char x;
100 | x = s1.pop();
101 | }
102 | else
103 | {
104 | s1.push(s[i]);
105 | }
106 | }
107 | }
108 |
109 | // if stack is empty by now, the expression is valid
110 | char x;
111 | x = s1.peek();
112 | if (x == 'X')
113 | {
114 | cout << "Success"<<"\n";
115 | }
116 | else
117 | {
118 | x = s1.peek() ;
119 | for (int i = 0 ; i < s.length() ; i++)
120 | {
121 | if (x == s[i])
122 | {
123 | cout << i+1 ; //to print location of error
124 | break ;
125 | }
126 | }
127 | }
128 |
129 | return 0;
130 | }
131 | // end of main
--------------------------------------------------------------------------------
/09_Graphs/adj_list.cpp:
--------------------------------------------------------------------------------
1 | /*
2 | Code to create a graph using Adjacency listrepresentation
3 | We consider the graph to be directed graph and non-weighted with no self loops
4 | */
5 | #include
6 |
7 | using namespace std;
8 |
9 | class Graph
10 | {
11 | private:
12 | struct Node
13 | {
14 | int data;
15 | struct Node *next;
16 | };
17 | int no_of_vertices;
18 | struct Node **adj_list;
19 |
20 | public:
21 | void make_graph(int no_of_vertices);
22 | void display();
23 | void add_edge();
24 | };
25 |
26 | /*
27 | This function is used to create a graph
28 | parameters : no_of_vertices
29 | Returns : void
30 | */
31 | void Graph ::make_graph(int no_of_vertices)
32 | {
33 | this->no_of_vertices = no_of_vertices;
34 | // creating a graph
35 | adj_list = new struct Node *[no_of_vertices];
36 | for (int i = 0; i < no_of_vertices; i++)
37 | {
38 | adj_list[i] = NULL;
39 | }
40 | }
41 | // end of function
42 |
43 | /*
44 | This function is used to display the graph
45 | parameters : void
46 | Returns : void
47 | */
48 | void Graph ::display()
49 | {
50 | cout << "The adjacency list representation is :-\n";
51 | for (int i = 0; i < no_of_vertices; i++)
52 | {
53 | cout << i << " : ";
54 | if (adj_list[i] != NULL)
55 | {
56 | struct Node *temp;
57 | temp = adj_list[i];
58 | while (temp->next != NULL)
59 | {
60 | cout << temp->data << " -> ";
61 | temp = temp->next;
62 | }
63 | cout << temp->data;
64 | }
65 | cout << "\n";
66 | }
67 | }
68 | // end of function
69 |
70 | /*
71 | This function iterates over all the possible edges and asks user if they want the edge to exist or not
72 | parameters : void
73 | Returns : void
74 | */
75 | void Graph ::add_edge()
76 | {
77 | for (int i = 0; i < no_of_vertices; i++)
78 | {
79 | for (int j = 0; j < no_of_vertices; j++)
80 | {
81 | if (i != j)
82 | {
83 | char choice;
84 | cout << "Are vertices " << i << " and " << j << " adjacent? (Y/N) : ";
85 | cin >> choice;
86 |
87 | if (toupper(choice) == 'Y')
88 | {
89 | if (adj_list[i] == NULL)
90 | {
91 | adj_list[i] = new struct Node;
92 | adj_list[i]->data = j;
93 | adj_list[i]->next = NULL;
94 | continue;
95 | }
96 | struct Node *temp;
97 | temp = adj_list[i];
98 | while (temp->next != NULL)
99 | {
100 | temp = temp->next;
101 | }
102 | temp->next = new struct Node;
103 | temp->next->data = j;
104 | temp->next->next = NULL;
105 | }
106 | }
107 | }
108 | }
109 | }
110 | // end of function
111 |
112 | // main function starts here
113 | int main()
114 | {
115 | Graph g;
116 | int no_of_vertices;
117 | cout << "Enter the number of vertices : ";
118 | cin >> no_of_vertices;
119 |
120 | g.make_graph(no_of_vertices);
121 | g.add_edge();
122 | g.display();
123 | return 0;
124 | }
125 | // end of main
--------------------------------------------------------------------------------
/05_Trees/tree_traversal.cpp:
--------------------------------------------------------------------------------
1 | /********************************************************************
2 | @brief Implementing binary trees and performing traversals
3 | *********************************************************************/
4 | #include
5 |
6 | using namespace std;
7 |
8 | class Tree
9 | {
10 | struct node
11 | {
12 | int data;
13 | struct node *left = NULL;
14 | struct node *right = NULL;
15 | };
16 |
17 | public:
18 | struct node *root = NULL; // The pointer to the staring node . for now this is null and will point to the root node when created
19 | void insert(struct node *&node, int element);
20 | void inorder(struct node *root);
21 | void preorder(struct node *root);
22 | void postorder(struct node *root);
23 | };
24 |
25 | /*
26 | * Function Name: insert
27 | * Input: a pointer to root node and the element to be inserted
28 | * Output: None
29 | * Logic: Inserts a node in the binary tree
30 | * Example Call: insert(root, 5)
31 | */
32 | void Tree ::insert(struct node *&node, int element)
33 | {
34 | if (node == NULL) // if there is no root node i.e. the tree is empty
35 | {
36 | struct node *temp = (struct node *)malloc(sizeof(struct node)); // creating a memory in heap consisting a node
37 | node = temp;
38 | node->data = element;
39 | node->left = NULL;
40 | node->right = NULL; // here we create a new node
41 | }
42 | else if (element > node->data) // insert in right tree
43 | {
44 | insert(node->right, element);
45 | }
46 | else // insert in left tree
47 | {
48 | insert(node->left, element);
49 | }
50 | }
51 |
52 | /*
53 | * Function Name: inorder
54 | * Input: a pointer to root node
55 | * Output: Prints inorder traversal of tree
56 | * Example Call: inorder(root)
57 | */
58 | void Tree ::inorder(struct node *root)
59 | {
60 | if (root != NULL)
61 | {
62 | inorder(root->left);
63 | printf("%d ", root->data);
64 | inorder(root->right);
65 | }
66 | }
67 |
68 | /*
69 | * Function Name: preorder
70 | * Input: a pointer to root node
71 | * Output: Prints preorder traversal of tree
72 | * Example Call: preorder(root)
73 | */
74 | void Tree ::preorder(struct node *root)
75 | {
76 | if (root != NULL)
77 | {
78 | printf("%d ", root->data);
79 | preorder(root->left);
80 | preorder(root->right);
81 | }
82 | }
83 |
84 | /*
85 | * Function Name: postorder
86 | * Input: a pointer to root node
87 | * Output: Prints postorder traversal of tree
88 | * Example Call: postorder(root)
89 | */
90 | void Tree ::postorder(struct node *root)
91 | {
92 | if (root != NULL)
93 | {
94 | postorder(root->left);
95 | postorder(root->right);
96 | printf("%d ", root->data);
97 | }
98 | }
99 |
100 | int main()
101 | {
102 | Tree t;
103 | /*insertion*/
104 | t.insert(t.root, 15);
105 | t.insert(t.root, 5);
106 | t.insert(t.root, 2);
107 | t.insert(t.root, 40);
108 | t.insert(t.root, 80);
109 | t.insert(t.root, 20);
110 | t.insert(t.root, 1);
111 | t.insert(t.root, 3);
112 |
113 | /*traversing*/
114 | printf("The inorder Traversal is : ");
115 | t.inorder(t.root);
116 | printf("\n");
117 | printf("The preorder Traversal is : ");
118 | t.preorder(t.root);
119 | printf("\n");
120 | printf("The postorder Traversal is : ");
121 | t.postorder(t.root);
122 | printf("\n");
123 | }
124 | /*
125 | Analysis: The above algorithm runs in O(n) for traversal and O(nlog(n)) for insertion
126 | */
127 |
--------------------------------------------------------------------------------
/Algorithms/4_Sorting/Readme.md:
--------------------------------------------------------------------------------
1 | # Sorting
2 |
3 | 
4 |
5 | ## Table of Contents
6 |
7 | * Introduction
8 | * Sorting Algorithms
9 | * Selection Sort
10 | * Merge Sort
11 | * Count Sort
12 | * Quick Sort
13 | * Heap Sort
14 | * Comb Sort
15 | * Conclusion
16 |
17 | ## Sorting Algorithms
18 |
19 | Sorting algorithms are mainly of two types: comparison based and non-comparison based. It is proven mathematically that a comparison based sorting algorithm requires atleast O(nlon(n)).
20 |
21 | ### 1) Selection Sort
22 |
23 | Selection sort is a comparison based sorting algorithm.
24 |
25 | In selection sort,we first find the minimum element in the given array. Then we swap the minimum element with the first element.We then repeat the above steps for remaining array.
26 |
27 |
28 | ### 2) Merge Sort
29 | Merge sort is a comparison based sorting algorithm based on divide and conquer technique.
30 |
31 | In merge sort, we split the given array recursively and then sort them indivisually and merge them back.
32 |
33 | ### 3) Count Sort
34 | Count sort is a Non-comparison based sorting algorithm and has better time complexity than comparison based algorithms in general.
35 |
36 | However, for this algorithm to work, we need to deal with a fixed range of integers only, say I know my input is a mix of integers in range 0-100, then count sort is appropriate.
37 |
38 | ### 4) Quick Sort
39 | Quick sort is a Comparison based sorting algorithm. The runtime of this algorithm depends on the partitions which are created. If the partitions are always created at the center, the algorithm works in O(nlog(n)). However, if we were to assume the worst case, it would work in O(n^2).
40 |
41 | In Quick sort, we can prove that choosing a random element as a pivot is generally a good choice which increases our probability to get the partitions which lead to O(nlog(n)) time complexity. The same is depicted in ```randomized_quick_sort.cpp```.
42 |
43 | ### 5) Heap Sort
44 |
45 | In order to implement Heap sort, we can simply convert the given array into a Max-Heap and perform extract-max on it and place the maximum element so recieved at the end of array.
46 |
47 | We can create a new priority queue and store elements in the new array one by one, maintaining the heap property. However this requires extra space. Thus, we can rather convert the given array into a priority queue itself, avoiding use of extra space.
48 |
49 | Heap sort works in O(nlog(n)) and is a comparison based algorithm.
50 |
51 | ### 6) Comb Sort
52 |
53 | Comb Sort is like a smarter version of Bubble Sort. In Bubble Sort, we always check and swap neighboring elements. So, if a small number is at the end, it takes a long time to move to the front.
54 |
55 | In Comb Sort, we introduce a gap between elements we compare. At first, this gap is quite large, which lets us compare elements that are far apart. After each pass through the list, we shrink this gap by a factor (usually 1.3). Eventually, the gap becomes 1, and Comb Sort behaves just like Bubble Sort, checking only adjacent elements. While Comb Sort is usually faster than Bubble Sort on average, worst case remains O(n^2).
56 |
57 | ## Conclusion
58 |
59 | The time complexities of a few sorting algorithms are given below
60 |
61 | 
62 |
63 | For visualization of the above sorting algorithms, refer : https://www.toptal.com/developers/sorting-algorithms and https://www.cs.usfca.edu/~galles/visualization/ComparisonSort.html.
64 |
65 |
66 |
67 |
68 |
69 |
70 |
71 |
72 |
73 | ##
74 |
--------------------------------------------------------------------------------
/Data Structures/Arrays/README.md:
--------------------------------------------------------------------------------
1 | # Arrays
2 |
3 |  4 |
5 | ## Introduction
6 |
7 | Arrays are a collection of elements stored in a contiguous block of memory, where all elements are of the same data type and are indexed by contiguous integers. This structure allows for quick access to elements, as both reading and writing can be done in constant time. Adding or removing an element at the end of the array is also a constant time operation. However, inserting or removing elements at the beginning or in the middle of an array takes linear time, i.e., `O(n)`, since elements need to be shifted. Additionally, arrays require a contiguous block of memory, which can be a limitation in some cases.
8 |
9 | ## Dynamic Arrays
10 |
11 | The problem with static arrays is that they static. If we are reading a bunch of numbers and we need to put it in an array. But we don't know how many numbers there'll be. we just know there'll be some mark at the end that says we're done with the numbers.
12 |
13 | So we use Dynamic arrays or Resizable arrays. Vectors are an example of dynamic arrays in `c++`
14 |
15 | ## Amortized Analysis
16 |
17 | For the dynamic array, we only resize every so often. Most of the time, we're doing a constant time operation, just adding an element. It's only when we fully reach the capacity, that we have to resize. It is true that the worst case for PushBack() operation is O(n), but we have to bear this cost only when we reach to full capacity of array.
18 |
19 |
4 |
5 | ## Introduction
6 |
7 | Arrays are a collection of elements stored in a contiguous block of memory, where all elements are of the same data type and are indexed by contiguous integers. This structure allows for quick access to elements, as both reading and writing can be done in constant time. Adding or removing an element at the end of the array is also a constant time operation. However, inserting or removing elements at the beginning or in the middle of an array takes linear time, i.e., `O(n)`, since elements need to be shifted. Additionally, arrays require a contiguous block of memory, which can be a limitation in some cases.
8 |
9 | ## Dynamic Arrays
10 |
11 | The problem with static arrays is that they static. If we are reading a bunch of numbers and we need to put it in an array. But we don't know how many numbers there'll be. we just know there'll be some mark at the end that says we're done with the numbers.
12 |
13 | So we use Dynamic arrays or Resizable arrays. Vectors are an example of dynamic arrays in `c++`
14 |
15 | ## Amortized Analysis
16 |
17 | For the dynamic array, we only resize every so often. Most of the time, we're doing a constant time operation, just adding an element. It's only when we fully reach the capacity, that we have to resize. It is true that the worst case for PushBack() operation is O(n), but we have to bear this cost only when we reach to full capacity of array.
18 |
19 |  20 |
21 | Amortized analysis is a method for analyzing a given algorithm's complexity, or how much of a resource, especially time or memory, it takes to execute. The motivation for amortized analysis is that looking at the worst-case run time can be too pessimistic. Instead, amortized analysis averages the running times of operations and considers both the expensive and cheap operations together over the whole sequence of operations.
22 |
23 | ### Aggregate Method
24 |
25 |
20 |
21 | Amortized analysis is a method for analyzing a given algorithm's complexity, or how much of a resource, especially time or memory, it takes to execute. The motivation for amortized analysis is that looking at the worst-case run time can be too pessimistic. Instead, amortized analysis averages the running times of operations and considers both the expensive and cheap operations together over the whole sequence of operations.
22 |
23 | ### Aggregate Method
24 |
25 |  26 |
27 | ### Banker Method
28 |
29 | In Bankers method, we associate certain fixed extra cost for all cheap operations, which will then compensate for the expensive operation.
30 |
31 |
26 |
27 | ### Banker Method
28 |
29 | In Bankers method, we associate certain fixed extra cost for all cheap operations, which will then compensate for the expensive operation.
30 |
31 |  32 |
33 | Thus, associating cost of 3 with each cheap operation allows us to ignore the cost during resizing. Overall, we can claim that the cost for each operation is 3, or O(1).
34 |
35 | ### Physicist Method
36 |
37 | This method is very similar to the concept of potential energy. If we go from lower level to higher level, potential energy increases. In a similar fashion, we have a potential function here. We expend ```h(t) - h (t-1)``` amount of work every time inserting an element.
38 |
39 |
32 |
33 | Thus, associating cost of 3 with each cheap operation allows us to ignore the cost during resizing. Overall, we can claim that the cost for each operation is 3, or O(1).
34 |
35 | ### Physicist Method
36 |
37 | This method is very similar to the concept of potential energy. If we go from lower level to higher level, potential energy increases. In a similar fashion, we have a potential function here. We expend ```h(t) - h (t-1)``` amount of work every time inserting an element.
38 |
39 |  40 |
41 | The choice of potential function is important here. It should be made such that is ```Ct``` is small, potential function should increase at each step.
42 |
40 |
41 | The choice of potential function is important here. It should be made such that is ```Ct``` is small, potential function should increase at each step.
42 |  43 |
44 | The general cost without resizing is:
45 |
43 |
44 | The general cost without resizing is:
45 |  46 | The general cost with resizing is:
47 |
46 | The general cost with resizing is:
47 |  48 |
49 | ## Points to note
50 |
51 | * It is important to resize the array by constant factor, say twice the bigger, rather than constant amount, say by 10 always. This is because if we increase by constant amount, the expensive operations can no more be compensated by cheap operations and runtime jumps to O(n).
52 |
53 | * ```*size ++``` implies that size pointer should be incremented and then its value should be dereferenced, while ```(*size)++``` implies, increment the value stored in size.
--------------------------------------------------------------------------------
/Algorithms/3_Dynamic_Programming/optimal_alignment.cpp:
--------------------------------------------------------------------------------
1 | /***********************************************************************************
2 | @brief Using dynamic programming for optimal alignment of 2 strings along with edit distance
3 | ************************************************************************************/
4 |
5 | #include
6 | #include
7 | #include
8 |
9 | using namespace std;
10 |
11 | /*
12 | * Function Name: min
13 | * Input: 3 int values which are to be compared
14 | * Output: Returns the minimum of 3 numbers
15 | * Logic: To get the minimum of 3 given numbers
16 | * Example Call: min(5, 8, 18)
17 | */
18 | int min(int x, int y, int z)
19 | {
20 | if (x <= y && x <= z)
21 | {
22 | return x;
23 | }
24 | else
25 | {
26 | return min(y, z);
27 | }
28 | }
29 |
30 | /*
31 | * Function Name: edit_distance
32 | * Input: 2 strings
33 | * Output: Optimal alignment between two strings along with their edit distance
34 | * Logic: Creates a 2D matrix to calculate edit distance and then backtracks to find the optimal alignment
35 | * Example Call: edit_distance(string1, string2)
36 | */
37 | void edit_distance(string string1, string string2)
38 | {
39 | string result1 = "", result2 = "";
40 |
41 | int x = string1.length();
42 | int y = string2.length();
43 | int matrix[x + 1][y + 1] = {0};
44 |
45 | for (int i = 0; i < x + 1; i++)
46 | {
47 | matrix[i][0] = i;
48 | }
49 |
50 | for (int j = 0; j < y + 1; j++)
51 | {
52 | matrix[0][j] = j;
53 | }
54 |
55 | for (int i = 1; i < x + 1; i++)
56 | {
57 | for (int j = 1; j < y + 1; j++)
58 | {
59 | if (string1[i - 1] == string2[j - 1])
60 | {
61 | matrix[i][j] = min(matrix[i - 1][j - 1], matrix[i][j - 1] + 1, matrix[i - 1][j] + 1);
62 | }
63 | else
64 | {
65 | matrix[i][j] = min(matrix[i - 1][j - 1], matrix[i][j - 1], matrix[i - 1][j]) + 1;
66 | }
67 | }
68 | }
69 |
70 | int i = x, j = y, counter = 0;
71 | while (i > 0 || j > 0)
72 | {
73 | int temp = matrix[i][j];
74 |
75 | if (i == 0)
76 | {
77 | result2 = result2 + string2[j - 1];
78 | result1 = result1 + "_";
79 | j = j - 1;
80 | }
81 | else if (j == 0)
82 | {
83 | result1 = result1 + string1[i - 1];
84 | result2 = result2 + "_";
85 | i = i - 1;
86 | }
87 | else
88 | {
89 | int x = min(matrix[i - 1][j], matrix[i - 1][j - 1], matrix[i][j - 1]);
90 | if (matrix[i - 1][j - 1] == x)
91 | {
92 | result1 = result1 + string1[i - 1];
93 | result2 = result2 + string2[j - 1];
94 | i--;
95 | j--;
96 | }
97 | else if (matrix[i][j - 1] == x)
98 | {
99 | result2 = result2 + string2[j - 1];
100 | result1 = result1 + "_";
101 | j = j - 1;
102 | }
103 | else
104 | {
105 | result1 = result1 + string1[i - 1];
106 | result2 = result2 + "_";
107 | i = i - 1;
108 | }
109 | }
110 | }
111 |
112 | cout << "edit distance is: " << matrix[x][y] << endl;
113 | cout << result1 << endl
114 | << result2;
115 | }
116 |
117 | int main()
118 | {
119 | string string1, string2;
120 |
121 | cin >> string1;
122 | cin >> string2;
123 |
124 | edit_distance(string1, string2);
125 |
126 | return 0;
127 | }
128 |
129 | /*
130 | Analysis: The above code runs in O(m*n), where m and n are length of string1 and string2 respectively.
131 | */
--------------------------------------------------------------------------------
/09_Graphs/dag.cpp:
--------------------------------------------------------------------------------
1 | #include
2 |
3 | using namespace std;
4 |
5 | #define VERTICES 100
6 |
7 | class Graph
8 | {
9 | private:
10 | struct Node
11 | {
12 | int data;
13 | struct Node *next;
14 | };
15 | int no_of_vertices;
16 | struct Node **adj_list;
17 |
18 | public:
19 | bool visited[VERTICES] = {0};
20 | bool inStack[VERTICES] = {0};
21 | bool isCycle = false;
22 | void make_graph(int no_of_vertices);
23 | void display();
24 | void add_edge();
25 | void dfs(int v);
26 | };
27 |
28 | void Graph ::add_edge()
29 | {
30 | for (int i = 0; i < no_of_vertices; i++)
31 | {
32 | for (int j = 0; j < no_of_vertices; j++)
33 | {
34 | if (i != j)
35 | {
36 | char choice;
37 | cout << "Are vertices " << i << " and " << j << " adjacent? (Y/N) : ";
38 | cin >> choice;
39 |
40 | if (toupper(choice) == 'Y')
41 | {
42 | if (adj_list[i] == NULL)
43 | {
44 | adj_list[i] = new struct Node;
45 | adj_list[i]->data = j;
46 | adj_list[i]->next = NULL;
47 | continue;
48 | }
49 | struct Node *temp;
50 | temp = adj_list[i];
51 | while (temp->next != NULL)
52 | {
53 | temp = temp->next;
54 | }
55 | temp->next = new struct Node;
56 | temp->next->data = j;
57 | temp->next->next = NULL;
58 | }
59 | }
60 | }
61 | }
62 | }
63 | // end of function
64 |
65 | void Graph ::dfs(int v)
66 | {
67 | visited[v] = 1;
68 | inStack[v] = 1;
69 | cout << v << " ";
70 |
71 | struct Node *temp;
72 | temp = adj_list[v];
73 |
74 | while (temp != NULL)
75 | {
76 | if (visited[temp->data] == 0)
77 | {
78 | dfs(temp->data);
79 | }
80 | else if (visited[temp->data] == 1 && inStack[temp->data] == 1)
81 | {
82 | isCycle = true;
83 | }
84 | temp = temp->next;
85 | }
86 |
87 | inStack[v] = 0;
88 | }
89 | // end of function
90 |
91 | void Graph ::make_graph(int no_of_vertices)
92 | {
93 | this->no_of_vertices = no_of_vertices;
94 | // creating a graph
95 | adj_list = new struct Node *[no_of_vertices];
96 | for (int i = 0; i < no_of_vertices; i++)
97 | {
98 | adj_list[i] = NULL;
99 | }
100 | }
101 | // end of function
102 |
103 | void Graph ::display()
104 | {
105 | cout << "The adjacency list representation is :-\n";
106 | for (int i = 0; i < no_of_vertices; i++)
107 | {
108 | cout << i << " : ";
109 | if (adj_list[i] != NULL)
110 | {
111 | struct Node *temp;
112 | temp = adj_list[i];
113 | while (temp->next != NULL)
114 | {
115 | cout << temp->data << " -> ";
116 | temp = temp->next;
117 | }
118 | cout << temp->data;
119 | }
120 | cout << "\n";
121 | }
122 | }
123 | // end of function
124 |
125 | // main function starts here
126 | int main()
127 | {
128 | Graph g;
129 | int no_of_vertices;
130 | cout << "Enter the number of vertices : ";
131 | cin >> no_of_vertices;
132 |
133 | g.make_graph(no_of_vertices);
134 | g.add_edge();
135 |
136 | for (int v = 0; v < no_of_vertices; v++)
137 | {
138 | if (g.visited[v] == 0)
139 | {
140 | g.dfs(v);
141 | }
142 | if (g.isCycle == true)
143 | {
144 | cout << "Cycle detected";
145 | break;
146 | }
147 | }
148 |
149 | return 0;
150 | }
151 | // end of main
152 |
--------------------------------------------------------------------------------
/04_Linked List/floyd_cycle_detection_algorithm.cpp:
--------------------------------------------------------------------------------
1 | #include
2 |
3 | using namespace std;
4 |
5 | class Node
6 | {
7 | public:
8 | int data;
9 | Node* next;
10 | Node(int data)
11 | {
12 | this->data = data;
13 | next = NULL;
14 | }
15 | };
16 |
17 | class LinkedList
18 | {
19 | public:
20 | Node* head = NULL;
21 | void insert(int data); //To insert data at the end of linked list
22 | void insert(Node* node); //To point at an existing node
23 | void print();
24 | void detect_cycle();
25 | void remove(int data);
26 | };
27 |
28 | void LinkedList::insert(int data)
29 | {
30 | if (head == NULL)
31 | {
32 | head = new Node(data);
33 | }
34 | else
35 | {
36 | Node* temp = head;
37 | while (temp->next != NULL)
38 | {
39 | temp = temp->next;
40 | }
41 | temp->next = new Node(data);
42 | }
43 | }
44 |
45 | void LinkedList::insert(Node* node)
46 | {
47 | if (head == NULL)
48 | {
49 | head = node;
50 | }
51 | else
52 | {
53 | Node* temp = head;
54 | while (temp->next != NULL)
55 | {
56 | temp = temp->next;
57 | }
58 | temp->next = node;
59 | }
60 | }
61 |
62 | void LinkedList::print()
63 | {
64 | if (head == NULL)
65 | {
66 | cout << "Linked List is Empty" << endl;
67 | }
68 | else
69 | {
70 | Node* temp = head;
71 | while (temp != NULL)
72 | {
73 | cout << temp->data << " -> ";
74 | temp = temp->next;
75 | }
76 | cout << "NULL" << endl;
77 | }
78 | }
79 |
80 | void LinkedList::detect_cycle()
81 | {
82 | Node* slow = head;
83 | Node* fast = head;
84 |
85 | if (head == NULL)
86 | {
87 | cout << "Linked List is Empty" << endl;
88 | }
89 | else
90 | {
91 | do
92 | {
93 | if (fast->next != NULL && fast->next->next != NULL)
94 | {
95 | fast = fast->next->next;
96 | slow=slow->next;
97 | }
98 | else
99 | {
100 | cout << "No Cycle Detected";
101 | return;
102 | }
103 | } while (slow != fast);
104 |
105 | fast = head;
106 |
107 | while (slow != fast)
108 | {
109 | slow=slow->next;
110 | fast=fast->next;
111 | }
112 |
113 | cout << "Cycle detected at: " << slow->data << endl;
114 | }
115 | }
116 |
117 | void LinkedList::remove(int key)
118 | {
119 | if (head == NULL)
120 | {
121 | cout << "Linked List is Empty" << endl;
122 | }
123 | else if(head->data == key)
124 | {
125 | Node* temp = head;
126 | temp = head->next;
127 | free(head);
128 | head = temp;
129 | }
130 | else
131 | {
132 | bool flag = 0;
133 | Node* temp = head;
134 | while (temp->next != NULL)
135 | {
136 | if (temp->next->data == key)
137 | {
138 | flag = 1;
139 | Node* p = temp->next;
140 | temp->next = temp->next->next;
141 | free(p);
142 | break;
143 | }
144 | else
145 | {
146 | temp = temp->next;
147 | }
148 | }
149 | if (flag == 0)
150 | {
151 | cout << "Key Not Found" << endl;
152 | }
153 | }
154 | }
155 |
156 | int main()
157 | {
158 | LinkedList L1;
159 | L1.insert(3);
160 | L1.insert(6);
161 | L1.insert(9);
162 | L1.insert(12);
163 | Node* p = L1.head->next;
164 | L1.insert(p); //Creating a cycle in linked list
165 | L1.detect_cycle();
166 | LinkedList L2;
167 | L2.insert(5);
168 | L2.insert(10);
169 | L2.detect_cycle();
170 | return 0;
171 | }
--------------------------------------------------------------------------------
/Data Structures/Linked Lists/floyd_cycle_detection_algorithm.cpp:
--------------------------------------------------------------------------------
1 | #include
2 |
3 | using namespace std;
4 |
5 | class Node
6 | {
7 | public:
8 | int data;
9 | Node* next;
10 | Node(int data)
11 | {
12 | this->data = data;
13 | next = NULL;
14 | }
15 | };
16 |
17 | class LinkedList
18 | {
19 | public:
20 | Node* head = NULL;
21 | void insert(int data); //To insert data at the end of linked list
22 | void insert(Node* node); //To point at an existing node
23 | void print();
24 | void detect_cycle();
25 | void remove(int data);
26 | };
27 |
28 | void LinkedList::insert(int data)
29 | {
30 | if (head == NULL)
31 | {
32 | head = new Node(data);
33 | }
34 | else
35 | {
36 | Node* temp = head;
37 | while (temp->next != NULL)
38 | {
39 | temp = temp->next;
40 | }
41 | temp->next = new Node(data);
42 | }
43 | }
44 |
45 | void LinkedList::insert(Node* node)
46 | {
47 | if (head == NULL)
48 | {
49 | head = node;
50 | }
51 | else
52 | {
53 | Node* temp = head;
54 | while (temp->next != NULL)
55 | {
56 | temp = temp->next;
57 | }
58 | temp->next = node;
59 | }
60 | }
61 |
62 | void LinkedList::print()
63 | {
64 | if (head == NULL)
65 | {
66 | cout << "Linked List is Empty" << endl;
67 | }
68 | else
69 | {
70 | Node* temp = head;
71 | while (temp != NULL)
72 | {
73 | cout << temp->data << " -> ";
74 | temp = temp->next;
75 | }
76 | cout << "NULL" << endl;
77 | }
78 | }
79 |
80 | void LinkedList::detect_cycle()
81 | {
82 | Node* slow = head;
83 | Node* fast = head;
84 |
85 | if (head == NULL)
86 | {
87 | cout << "Linked List is Empty" << endl;
88 | }
89 | else
90 | {
91 | do
92 | {
93 | if (fast->next != NULL && fast->next->next != NULL)
94 | {
95 | fast = fast->next->next;
96 | slow=slow->next;
97 | }
98 | else
99 | {
100 | cout << "No Cycle Detected";
101 | return;
102 | }
103 | } while (slow != fast);
104 |
105 | fast = head;
106 |
107 | while (slow != fast)
108 | {
109 | slow=slow->next;
110 | fast=fast->next;
111 | }
112 |
113 | cout << "Cycle detected at: " << slow->data << endl;
114 | }
115 | }
116 |
117 | void LinkedList::remove(int key)
118 | {
119 | if (head == NULL)
120 | {
121 | cout << "Linked List is Empty" << endl;
122 | }
123 | else if(head->data == key)
124 | {
125 | Node* temp = head;
126 | temp = head->next;
127 | free(head);
128 | head = temp;
129 | }
130 | else
131 | {
132 | bool flag = 0;
133 | Node* temp = head;
134 | while (temp->next != NULL)
135 | {
136 | if (temp->next->data == key)
137 | {
138 | flag = 1;
139 | Node* p = temp->next;
140 | temp->next = temp->next->next;
141 | free(p);
142 | break;
143 | }
144 | else
145 | {
146 | temp = temp->next;
147 | }
148 | }
149 | if (flag == 0)
150 | {
151 | cout << "Key Not Found" << endl;
152 | }
153 | }
154 | }
155 |
156 | int main()
157 | {
158 | LinkedList L1;
159 | L1.insert(3);
160 | L1.insert(6);
161 | L1.insert(9);
162 | L1.insert(12);
163 | Node* p = L1.head->next;
164 | L1.insert(p); //Creating a cycle in linked list
165 | L1.detect_cycle();
166 | LinkedList L2;
167 | L2.insert(5);
168 | L2.insert(10);
169 | L2.detect_cycle();
170 | return 0;
171 | }
--------------------------------------------------------------------------------
/09_Graphs/dfs.cpp:
--------------------------------------------------------------------------------
1 | #include
2 |
3 | using namespace std;
4 |
5 | #define VERTICES 100
6 |
7 | class Graph
8 | {
9 | private:
10 | struct Node
11 | {
12 | int data;
13 | struct Node *next;
14 | };
15 | int no_of_vertices;
16 | struct Node **adj_list;
17 |
18 | public:
19 | bool visited[VERTICES] = {0};
20 | void make_graph(int no_of_vertices);
21 | void display();
22 | void add_edge();
23 | void dfs(int v);
24 | };
25 |
26 | /*
27 | This function iterates over all the possible edges and asks user if they want the edge to exist or not
28 | parameters : void
29 | Returns : void
30 | */
31 | void Graph ::add_edge()
32 | {
33 | for (int i = 0; i < no_of_vertices; i++)
34 | {
35 | for (int j = 0; j < no_of_vertices; j++)
36 | {
37 | if (i != j)
38 | {
39 | char choice;
40 | cout << "Are vertices " << i << " and " << j << " adjacent? (Y/N) : ";
41 | cin >> choice;
42 |
43 | if (toupper(choice) == 'Y')
44 | {
45 | if (adj_list[i] == NULL)
46 | {
47 | adj_list[i] = new struct Node;
48 | adj_list[i]->data = j;
49 | adj_list[i]->next = NULL;
50 | continue;
51 | }
52 | struct Node *temp;
53 | temp = adj_list[i];
54 | while (temp->next != NULL)
55 | {
56 | temp = temp->next;
57 | }
58 | temp->next = new struct Node;
59 | temp->next->data = j;
60 | temp->next->next = NULL;
61 | }
62 | }
63 | }
64 | }
65 | }
66 | // end of function
67 |
68 | /*
69 | Performs DFS traversal
70 | parameters : vertex on which dfs is called
71 | Returns : void
72 | */
73 | void Graph ::dfs(int v)
74 | {
75 | visited[v] = 1;
76 | cout << v << " ";
77 |
78 | struct Node *temp;
79 | temp = adj_list[v];
80 |
81 | while (temp != NULL)
82 | {
83 | if (visited[temp->data] == 0)
84 | {
85 | dfs(temp->data);
86 | }
87 | temp = temp->next;
88 | }
89 | }
90 | // end of function
91 |
92 | /*
93 | This function is used to create a graph
94 | parameters : no_of_vertices
95 | Returns : void
96 | */
97 | void Graph ::make_graph(int no_of_vertices)
98 | {
99 | this->no_of_vertices = no_of_vertices;
100 | // creating a graph
101 | adj_list = new struct Node *[no_of_vertices];
102 | for (int i = 0; i < no_of_vertices; i++)
103 | {
104 | adj_list[i] = NULL;
105 | }
106 | }
107 | // end of function
108 |
109 | /*
110 | This function is used to display the graph
111 | parameters : void
112 | Returns : void
113 | */
114 | void Graph ::display()
115 | {
116 | cout << "The adjacency list representation is :-\n";
117 | for (int i = 0; i < no_of_vertices; i++)
118 | {
119 | cout << i << " : ";
120 | if (adj_list[i] != NULL)
121 | {
122 | struct Node *temp;
123 | temp = adj_list[i];
124 | while (temp->next != NULL)
125 | {
126 | cout << temp->data << " -> ";
127 | temp = temp->next;
128 | }
129 | cout << temp->data;
130 | }
131 | cout << "\n";
132 | }
133 | }
134 | // end of function
135 |
136 | // main function starts here
137 | int main()
138 | {
139 | Graph g;
140 | int no_of_vertices;
141 | cout << "Enter the number of vertices : ";
142 | cin >> no_of_vertices;
143 |
144 | g.make_graph(no_of_vertices);
145 | g.add_edge();
146 | g.display();
147 |
148 | for (int v = 0; v < no_of_vertices; v++)
149 | {
150 | if (g.visited[v] == 0)
151 | {
152 | g.dfs(v);
153 | }
154 | }
155 |
156 | return 0;
157 | }
158 | // end of main
159 |
--------------------------------------------------------------------------------
/02_Stack/minimum_element.cpp:
--------------------------------------------------------------------------------
1 | /******************************************************************
2 | @brief Implementing stack and extracting minimum element
3 | *******************************************************************/
4 |
5 | #include
6 | #define MAX_SIZE 100 // The maximum number of elements our stack can hold is 100
7 | using namespace std;
8 |
9 | class Stack
10 | {
11 | private:
12 | int stack[MAX_SIZE];
13 | int top = -1;
14 | int min = INT_MAX;
15 | int max = INT_MIN;
16 |
17 | public:
18 | void push(int element);
19 | int pop();
20 | int peek();
21 | int get_min();
22 | };
23 |
24 | /*
25 | * Function Name: push
26 | * Input: Integer element which is to be pushed
27 | * Output: None
28 | * Logic: This function allows us to insert an element in stack
29 | * Example Call: push(5)
30 | */
31 | void Stack ::push(int element)
32 | {
33 | if (top != MAX_SIZE - 1) // We can not push anymore elements if the stack is full
34 | {
35 | if (top == -1)
36 | {
37 | min = element ;
38 | }
39 | if (element < min && top != -1)
40 | {
41 | int temp = element ;
42 | element = element - min ;
43 | min = temp ;
44 | }
45 | top++;
46 | stack[top] = element;
47 | }
48 | else
49 | {
50 | cout << "The stack is full\n";
51 | }
52 | }
53 |
54 | /*
55 | * Function Name: pop
56 | * Input: None
57 | * Output: Returns the topmost element of stack or -1 if stack is empty
58 | * Logic: This function allows us to remove an element from stack
59 | * Example Call: pop()
60 | */
61 | int Stack ::pop()
62 | {
63 | if (top != -1)
64 | {
65 | if (peek() < min)
66 | {
67 | int temp = min ;
68 | min = temp - peek() ;
69 | // cout << "min is: " << min << endl ;
70 | top -- ;
71 | return temp ;
72 | }
73 | return stack[top--];
74 | /* We need to do top-- above itself cause the staements below the return statement are not executed*/
75 | }
76 | else
77 | {
78 | cout << "The stack is empty\n";
79 | return -1; // just to avoid the warning of control reaches end of non-void function
80 | }
81 | }
82 |
83 | /*
84 | * Function Name: peek
85 | * Input: None
86 | * Output: Returns the topmost element of stack or -1 if stack is empty without deleting it
87 | * Logic: This function allows us to remove an element from stack without deleting it
88 | * Example Call: peek()
89 | */
90 | int Stack ::peek()
91 | {
92 | if (top != -1)
93 | {
94 | return stack[top]; // here, we simply return the topmost element and not decrement top
95 | }
96 | else
97 | {
98 | cout << "The stack is empty\n";
99 | return -1; // just to avoid the warning of control reaches end of non-void function
100 | }
101 | }
102 |
103 | int Stack:: get_min ()
104 | {
105 | if (top == -1)
106 | {
107 | return -1 ;
108 | }
109 | return min ;
110 | }
111 |
112 | int main()
113 | {
114 | int n ;
115 | cin >> n ;
116 | Stack s1;
117 | int x;
118 |
119 | for (int i = 0 ; i < n ; i++)
120 | {
121 | int choice ;
122 | cin >> choice ;
123 |
124 | if (choice == 1)
125 | {
126 | int element ;
127 | cin >> element ;
128 | s1.push(element) ;
129 | }
130 | else if(choice == 2)
131 | {
132 | s1.pop() ;
133 | }
134 | else
135 | {
136 | x = s1.get_min() ;
137 | cout << x << "\n";
138 | }
139 | }
140 |
141 | return 0;
142 | }
143 |
144 | /*
145 | Analysis: The above code runs in O(1) for extracting minimum element.
146 |
147 | Aliter: The same thing can be implemented by using 3 stacks, one to hold elements, one for maximum element and one for minimum element.
148 |
149 | Note: The same code works for extracting maximum element by modifying few conditions.
150 | */
--------------------------------------------------------------------------------
/Algorithms/4_Sorting/heap_sort.cpp:
--------------------------------------------------------------------------------
1 | /***************************************
2 | @brief Implementing Heap Sort
3 | ****************************************/
4 | #include
5 | #include
6 |
7 | using namespace std;
8 |
9 | /*
10 | * Function Name: parent
11 | * Input: Index of the element
12 | * Output: Returns the index of parent
13 | * Example Call: parent(5)
14 | */
15 | int parent(int index)
16 | {
17 | int parent = 0;
18 | if (index % 2 == 0)
19 | {
20 | parent = (index - 1) / 2;
21 | }
22 | else
23 | {
24 | parent = index / 2;
25 | }
26 |
27 | return parent;
28 | }
29 |
30 | /*
31 | * Function Name: left_child
32 | * Input: Index of the element
33 | * Output: Returns the index of the left child
34 | * Example Call: left_child(5)
35 | */
36 | int left_child(int index, int *n)
37 | {
38 | int left = 2 * index + 1;
39 | if (left >= *n)
40 | {
41 | return -1;
42 | }
43 | return left;
44 | }
45 |
46 | /*
47 | * Function Name: right_child
48 | * Input: Index of the element
49 | * Output: Returns the index of the right child
50 | * Example Call: right_child(5)
51 | */
52 | int right_child(int index, int *n)
53 | {
54 | int right = 2 * index + 2;
55 | if (right >= *n)
56 | {
57 | return -1;
58 | }
59 | return right;
60 | }
61 |
62 | /*
63 | * Function Name: siftDown
64 | * Input: Takes the array, current size of array, and index of element
65 | * Output: None
66 | * Logic: This function shifts the element down the heap to its correct position
67 | * Example Call: SiftDown(maxHeap, 5, &temp)
68 | */
69 | void siftDown(int maxHeap[], int index, int *n)
70 | {
71 | while (1)
72 | {
73 | if (maxHeap[left_child(index, n)] > maxHeap[right_child(index, n)] && (maxHeap[index] < maxHeap[left_child(index, n)]) && left_child(index, n) != -1)
74 | {
75 | swap(maxHeap[index], maxHeap[left_child(index, n)]);
76 | index = left_child(index, n);
77 | }
78 | else if (maxHeap[left_child(index, n)] < maxHeap[right_child(index, n)] && (maxHeap[index] < maxHeap[right_child(index, n)]) && right_child(index, n) != -1)
79 | {
80 | swap(maxHeap[index], maxHeap[right_child(index, n)]);
81 | index = right_child(index, n);
82 | }
83 | else
84 | {
85 | break;
86 | }
87 | }
88 | }
89 |
90 | /*
91 | * Function Name: extractMax
92 | * Input: Takes the array, and index of element
93 | * Output: Returns the maximum element i.e. root element of heap
94 | * Example Call: extractMax(maxHeap, 5)
95 | */
96 | int extractMax(int maxHeap[], int *n)
97 | {
98 | int temp = maxHeap[0];
99 | (*n)--;
100 | maxHeap[0] = maxHeap[(*n)];
101 | siftDown(maxHeap, 0, n);
102 | return temp;
103 | }
104 |
105 | /*
106 | * Function Name: Heapify
107 | * Input: Takes the array, and size of array by reference
108 | * Output: None
109 | * Logic: This function creates heap out of given array without taking any extra space
110 | * Example Call: Heapify(maxHeap, max_size)
111 | */
112 | void Heapify(int maxHeap[], int *n)
113 | {
114 | for (int i = (*n) / 2; i >= 0; i--)
115 | {
116 | siftDown(maxHeap, i, n);
117 | }
118 | }
119 |
120 | int main()
121 | {
122 | int max_size, temp = 0;
123 | cout << "Please enter the total number of elements: ";
124 | cin >> max_size;
125 | temp = max_size;
126 | int maxHeap[max_size] = {0};
127 |
128 | for (int i = 0; i < max_size; i++)
129 | {
130 | cin >> maxHeap[i];
131 | }
132 |
133 | //Creating heap from the given array
134 | Heapify(maxHeap, &max_size);
135 |
136 | //Sorting
137 | for (int i = 0; i < temp; i++)
138 | {
139 | int element;
140 | element = extractMax(maxHeap, &max_size);
141 | maxHeap[max_size] = element;
142 | }
143 |
144 | for (int i = 0; i < temp; i++)
145 | {
146 | cout << maxHeap[i] << " ";
147 | }
148 | }
149 | /*
150 | Analysis: The above algorithn runs in O(nlog(n))
151 | */
--------------------------------------------------------------------------------
/Algorithms/3_Dynamic_Programming/substring_sum.cpp:
--------------------------------------------------------------------------------
1 | /***********************************************************************************
2 | @brief Finding the longest substring such that sum of digits in first half and second half are equal.
3 | ************************************************************************************/
4 | #include
5 | #include
6 | #include
7 |
8 | using namespace std;
9 |
10 | /*
11 | * Function Name: check
12 | * Input: string and start and end indices
13 | * Output: True if the sum of digits in first half and second half are equal
14 | * Logic: To evaluate a substring. This is used only for recursive approach.
15 | * Example Call: check("9036", 0, 3)
16 | */
17 | bool check(string s, int start, int end)
18 | {
19 | int a = 0, b = 0;
20 | int mid = (start+end)/2;
21 |
22 | for (int i = start; i <= mid; i++)
23 | {
24 | a += (s[i] - '0');
25 | }
26 | for (int i = mid + 1; i <= end; i++)
27 | {
28 | b += (s[i] - '0');
29 | }
30 |
31 | if (a == b)
32 | {
33 | return true;
34 | }
35 | return false;
36 | }
37 | /*
38 | * Function Name: moveGen
39 | * Input: string s
40 | * Output: The longest substring with equal sum of digits in first half and second half
41 | * Logic: Iterates through all possible substrings and checks if their sum of digits is equal. Keeps track of the maximum valid substring found.
42 | * Example Call: moveGen("9036")
43 | */
44 | string moveGen(string s)
45 | {
46 | int max_str_i = 0, max_str_j = 0;
47 | for (int i = 0; i < s.length(); i++)
48 | {
49 | for (int j = i + 1; j < s.length(); j += 2)
50 | {
51 | if (j - i + 1 < max_str_j - max_str_i + 1)
52 | {
53 | continue;
54 | }
55 |
56 | if (check(s, i, j))
57 | {
58 | if (j - i + 1 > max_str_j - max_str_i + 1)
59 | {
60 | max_str_i = i;
61 | max_str_j = j;
62 | }
63 | }
64 | }
65 | }
66 |
67 | if (max_str_j == 0)
68 | {
69 | return "";
70 | }
71 |
72 | string max_str = s.substr(max_str_i, max_str_j - max_str_i + 1);
73 |
74 | return max_str;
75 | }
76 |
77 | /*
78 | * Function Name: dp
79 | * Input: string s
80 | * Output: The longest substring with equal sum of digits in first half and second half
81 | * Logic: Utilizes dynamic programming to efficiently compute the sum of digits in all substrings. Iterates through substrings, checks if their sum of digits is equal, and updates the maximum substring.
82 | * Example Call: dp("9036")
83 | */
84 | string dp(string s)
85 | {
86 | int max_str_i = 0, max_str_j = 0;
87 | vector> cache (s.length(), vector (s.length(), 0));
88 |
89 | for (int i = 0; i < s.length(); i++)
90 | {
91 | cache[i][i] = s[i]-'0';
92 | }
93 |
94 | for (int i = 0; i < s.length(); i++)
95 | {
96 | for (int j = i+1; j < s.length(); j++)
97 | {
98 | cache[i][j] = cache[i][j-1] + (s[j]-'0');
99 | if ((j-i)%2 != 0)
100 | {
101 | int mid = (j+i)/2;
102 | if (cache[i][mid] == (cache[i][j]/2) && j - i + 1 > max_str_j - max_str_i + 1)
103 | {
104 | max_str_i = i;
105 | max_str_j = j;
106 | }
107 | }
108 | }
109 | }
110 |
111 | if (max_str_j == 0)
112 | {
113 | return "";
114 | }
115 |
116 | string max_str = s.substr(max_str_i, max_str_j - max_str_i + 1);
117 |
118 | return max_str;
119 | }
120 |
121 | int main()
122 | {
123 | string s = "946723";
124 | // string rec_answer = moveGen(s);
125 | string dp_answer = dp(s);
126 | // cout << rec_answer << " " << rec_answer.size() << endl;
127 | cout << dp_answer << " " << dp_answer.size() << endl;
128 | return 0;
129 | }
130 |
131 | /*
132 | Analysis: The recursive code runs in O(n^3) time and the dp code runs in O(n^2) time with O(n^2) space.
133 | */
--------------------------------------------------------------------------------
/06_Priority_Queues_and_Heaps/max_heap.cpp:
--------------------------------------------------------------------------------
1 | /**************************************
2 | @brief Implementing MaxHeaps
3 | ***************************************/
4 | #include
5 | #include
6 |
7 | using namespace std;
8 |
9 | /*
10 | * Function Name: parent
11 | * Input: Index of the element
12 | * Output: Returns the index of parent
13 | * Example Call: parent(5)
14 | */
15 | int parent(int index)
16 | {
17 | int parent = 0;
18 | if (index % 2 == 0)
19 | {
20 | parent = (index - 1) / 2;
21 | }
22 | else
23 | {
24 | parent = index / 2;
25 | }
26 |
27 | return parent;
28 | }
29 |
30 | /*
31 | * Function Name: left_child
32 | * Input: Index of the element
33 | * Output: Returns the index of the left child
34 | * Example Call: left_child(5)
35 | */
36 | int left_child(int index)
37 | {
38 | int left = 2 * index + 1;
39 | return left;
40 | }
41 |
42 | /*
43 | * Function Name: right_child
44 | * Input: Index of the element
45 | * Output: Returns the index of the right child
46 | * Example Call: right_child(5)
47 | */
48 | int right_child(int index)
49 | {
50 | int right = 2 * index + 2;
51 | return right;
52 | }
53 |
54 | /*
55 | * Function Name: siftDown
56 | * Input: Takes the array, current size of array, and index of element
57 | * Output: None
58 | * Logic: This function shifts the element down the heap to its correct position
59 | * Example Call: SiftDown(maxHeap, 5, &temp)
60 | */
61 | void siftDown(int maxHeap[], int index, int *n)
62 | {
63 | while (1)
64 | {
65 | if (maxHeap[left_child(index)] > maxHeap[right_child(index)] && (maxHeap[index] < maxHeap[left_child(index)]))
66 | {
67 | swap(maxHeap[index], maxHeap[left_child(index)]);
68 | }
69 | else if (maxHeap[left_child(index)] < maxHeap[right_child(index)] && (maxHeap[index] < maxHeap[right_child(index)]))
70 | {
71 | swap(maxHeap[index], maxHeap[right_child(index)]);
72 | }
73 | else
74 | {
75 | break;
76 | }
77 | }
78 | }
79 |
80 | /*
81 | * Function Name: siftDown
82 | * Input: Takes the array, current size of array, and index of element
83 | * Output: None
84 | * Logic: This function shifts the element up the heap to its correct position
85 | * Example Call: SiftDown(maxHeap, 5, &temp)
86 | */
87 | void siftUp(int maxHeap[], int index)
88 | {
89 | while (index >= 1 && maxHeap[index] > maxHeap[parent(index)])
90 | {
91 | swap(maxHeap[index], maxHeap[parent(index)]);
92 | index = parent(index);
93 | }
94 | }
95 |
96 | /*
97 | * Function Name: extractMax
98 | * Input: Takes the array, and index of element
99 | * Output: Returns the maximum element i.e. root element of heap
100 | * Example Call: extractMax(maxHeap, 5)
101 | */
102 | int extractMax(int maxHeap[], int *n)
103 | {
104 | int temp = maxHeap[0];
105 | (*n)--;
106 | maxHeap[0] = maxHeap[(*n)];
107 | siftDown(maxHeap, 0, n);
108 | return temp;
109 | }
110 |
111 | /*
112 | * Function Name: insert
113 | * Input: Takes the array, element, max size by value and current size of array by reference
114 | * Output: None
115 | * Logic: This function allows us to insert an element into heap
116 | * Example Call: insert(maxHeap, max_size, &curr_size, element)
117 | */
118 | void insert(int maxHeap[], int max_size, int *n, int element)
119 | {
120 | if (*n < max_size)
121 | {
122 | maxHeap[*n] = element;
123 | siftUp(maxHeap, *n);
124 | (*n)++;
125 | }
126 | }
127 |
128 | int main()
129 | {
130 | int max_size, curr_size = 0;
131 | cout << "Please enter the total number of elements: ";
132 | cin >> max_size;
133 | int maxHeap[max_size] = {0};
134 |
135 | for (int i = 0; i < max_size; i++)
136 | {
137 | int element;
138 | cin >> element;
139 | insert(maxHeap, max_size, &curr_size, element);
140 | }
141 |
142 | int max;
143 | for (int i = 0; i < max_size; i++)
144 | {
145 | max = extractMax(maxHeap, &curr_size);
146 | cout << max << " ";
147 | }
148 | }
149 | /*
150 | Analysis: The above algorithm runs in O(nlog(n))
151 | */
--------------------------------------------------------------------------------
/Data Structures/Linked Lists/README.md:
--------------------------------------------------------------------------------
1 | # Linked Lists
2 |
3 |
48 |
49 | ## Points to note
50 |
51 | * It is important to resize the array by constant factor, say twice the bigger, rather than constant amount, say by 10 always. This is because if we increase by constant amount, the expensive operations can no more be compensated by cheap operations and runtime jumps to O(n).
52 |
53 | * ```*size ++``` implies that size pointer should be incremented and then its value should be dereferenced, while ```(*size)++``` implies, increment the value stored in size.
--------------------------------------------------------------------------------
/Algorithms/3_Dynamic_Programming/optimal_alignment.cpp:
--------------------------------------------------------------------------------
1 | /***********************************************************************************
2 | @brief Using dynamic programming for optimal alignment of 2 strings along with edit distance
3 | ************************************************************************************/
4 |
5 | #include
6 | #include
7 | #include
8 |
9 | using namespace std;
10 |
11 | /*
12 | * Function Name: min
13 | * Input: 3 int values which are to be compared
14 | * Output: Returns the minimum of 3 numbers
15 | * Logic: To get the minimum of 3 given numbers
16 | * Example Call: min(5, 8, 18)
17 | */
18 | int min(int x, int y, int z)
19 | {
20 | if (x <= y && x <= z)
21 | {
22 | return x;
23 | }
24 | else
25 | {
26 | return min(y, z);
27 | }
28 | }
29 |
30 | /*
31 | * Function Name: edit_distance
32 | * Input: 2 strings
33 | * Output: Optimal alignment between two strings along with their edit distance
34 | * Logic: Creates a 2D matrix to calculate edit distance and then backtracks to find the optimal alignment
35 | * Example Call: edit_distance(string1, string2)
36 | */
37 | void edit_distance(string string1, string string2)
38 | {
39 | string result1 = "", result2 = "";
40 |
41 | int x = string1.length();
42 | int y = string2.length();
43 | int matrix[x + 1][y + 1] = {0};
44 |
45 | for (int i = 0; i < x + 1; i++)
46 | {
47 | matrix[i][0] = i;
48 | }
49 |
50 | for (int j = 0; j < y + 1; j++)
51 | {
52 | matrix[0][j] = j;
53 | }
54 |
55 | for (int i = 1; i < x + 1; i++)
56 | {
57 | for (int j = 1; j < y + 1; j++)
58 | {
59 | if (string1[i - 1] == string2[j - 1])
60 | {
61 | matrix[i][j] = min(matrix[i - 1][j - 1], matrix[i][j - 1] + 1, matrix[i - 1][j] + 1);
62 | }
63 | else
64 | {
65 | matrix[i][j] = min(matrix[i - 1][j - 1], matrix[i][j - 1], matrix[i - 1][j]) + 1;
66 | }
67 | }
68 | }
69 |
70 | int i = x, j = y, counter = 0;
71 | while (i > 0 || j > 0)
72 | {
73 | int temp = matrix[i][j];
74 |
75 | if (i == 0)
76 | {
77 | result2 = result2 + string2[j - 1];
78 | result1 = result1 + "_";
79 | j = j - 1;
80 | }
81 | else if (j == 0)
82 | {
83 | result1 = result1 + string1[i - 1];
84 | result2 = result2 + "_";
85 | i = i - 1;
86 | }
87 | else
88 | {
89 | int x = min(matrix[i - 1][j], matrix[i - 1][j - 1], matrix[i][j - 1]);
90 | if (matrix[i - 1][j - 1] == x)
91 | {
92 | result1 = result1 + string1[i - 1];
93 | result2 = result2 + string2[j - 1];
94 | i--;
95 | j--;
96 | }
97 | else if (matrix[i][j - 1] == x)
98 | {
99 | result2 = result2 + string2[j - 1];
100 | result1 = result1 + "_";
101 | j = j - 1;
102 | }
103 | else
104 | {
105 | result1 = result1 + string1[i - 1];
106 | result2 = result2 + "_";
107 | i = i - 1;
108 | }
109 | }
110 | }
111 |
112 | cout << "edit distance is: " << matrix[x][y] << endl;
113 | cout << result1 << endl
114 | << result2;
115 | }
116 |
117 | int main()
118 | {
119 | string string1, string2;
120 |
121 | cin >> string1;
122 | cin >> string2;
123 |
124 | edit_distance(string1, string2);
125 |
126 | return 0;
127 | }
128 |
129 | /*
130 | Analysis: The above code runs in O(m*n), where m and n are length of string1 and string2 respectively.
131 | */
--------------------------------------------------------------------------------
/09_Graphs/dag.cpp:
--------------------------------------------------------------------------------
1 | #include
2 |
3 | using namespace std;
4 |
5 | #define VERTICES 100
6 |
7 | class Graph
8 | {
9 | private:
10 | struct Node
11 | {
12 | int data;
13 | struct Node *next;
14 | };
15 | int no_of_vertices;
16 | struct Node **adj_list;
17 |
18 | public:
19 | bool visited[VERTICES] = {0};
20 | bool inStack[VERTICES] = {0};
21 | bool isCycle = false;
22 | void make_graph(int no_of_vertices);
23 | void display();
24 | void add_edge();
25 | void dfs(int v);
26 | };
27 |
28 | void Graph ::add_edge()
29 | {
30 | for (int i = 0; i < no_of_vertices; i++)
31 | {
32 | for (int j = 0; j < no_of_vertices; j++)
33 | {
34 | if (i != j)
35 | {
36 | char choice;
37 | cout << "Are vertices " << i << " and " << j << " adjacent? (Y/N) : ";
38 | cin >> choice;
39 |
40 | if (toupper(choice) == 'Y')
41 | {
42 | if (adj_list[i] == NULL)
43 | {
44 | adj_list[i] = new struct Node;
45 | adj_list[i]->data = j;
46 | adj_list[i]->next = NULL;
47 | continue;
48 | }
49 | struct Node *temp;
50 | temp = adj_list[i];
51 | while (temp->next != NULL)
52 | {
53 | temp = temp->next;
54 | }
55 | temp->next = new struct Node;
56 | temp->next->data = j;
57 | temp->next->next = NULL;
58 | }
59 | }
60 | }
61 | }
62 | }
63 | // end of function
64 |
65 | void Graph ::dfs(int v)
66 | {
67 | visited[v] = 1;
68 | inStack[v] = 1;
69 | cout << v << " ";
70 |
71 | struct Node *temp;
72 | temp = adj_list[v];
73 |
74 | while (temp != NULL)
75 | {
76 | if (visited[temp->data] == 0)
77 | {
78 | dfs(temp->data);
79 | }
80 | else if (visited[temp->data] == 1 && inStack[temp->data] == 1)
81 | {
82 | isCycle = true;
83 | }
84 | temp = temp->next;
85 | }
86 |
87 | inStack[v] = 0;
88 | }
89 | // end of function
90 |
91 | void Graph ::make_graph(int no_of_vertices)
92 | {
93 | this->no_of_vertices = no_of_vertices;
94 | // creating a graph
95 | adj_list = new struct Node *[no_of_vertices];
96 | for (int i = 0; i < no_of_vertices; i++)
97 | {
98 | adj_list[i] = NULL;
99 | }
100 | }
101 | // end of function
102 |
103 | void Graph ::display()
104 | {
105 | cout << "The adjacency list representation is :-\n";
106 | for (int i = 0; i < no_of_vertices; i++)
107 | {
108 | cout << i << " : ";
109 | if (adj_list[i] != NULL)
110 | {
111 | struct Node *temp;
112 | temp = adj_list[i];
113 | while (temp->next != NULL)
114 | {
115 | cout << temp->data << " -> ";
116 | temp = temp->next;
117 | }
118 | cout << temp->data;
119 | }
120 | cout << "\n";
121 | }
122 | }
123 | // end of function
124 |
125 | // main function starts here
126 | int main()
127 | {
128 | Graph g;
129 | int no_of_vertices;
130 | cout << "Enter the number of vertices : ";
131 | cin >> no_of_vertices;
132 |
133 | g.make_graph(no_of_vertices);
134 | g.add_edge();
135 |
136 | for (int v = 0; v < no_of_vertices; v++)
137 | {
138 | if (g.visited[v] == 0)
139 | {
140 | g.dfs(v);
141 | }
142 | if (g.isCycle == true)
143 | {
144 | cout << "Cycle detected";
145 | break;
146 | }
147 | }
148 |
149 | return 0;
150 | }
151 | // end of main
152 |
--------------------------------------------------------------------------------
/04_Linked List/floyd_cycle_detection_algorithm.cpp:
--------------------------------------------------------------------------------
1 | #include
2 |
3 | using namespace std;
4 |
5 | class Node
6 | {
7 | public:
8 | int data;
9 | Node* next;
10 | Node(int data)
11 | {
12 | this->data = data;
13 | next = NULL;
14 | }
15 | };
16 |
17 | class LinkedList
18 | {
19 | public:
20 | Node* head = NULL;
21 | void insert(int data); //To insert data at the end of linked list
22 | void insert(Node* node); //To point at an existing node
23 | void print();
24 | void detect_cycle();
25 | void remove(int data);
26 | };
27 |
28 | void LinkedList::insert(int data)
29 | {
30 | if (head == NULL)
31 | {
32 | head = new Node(data);
33 | }
34 | else
35 | {
36 | Node* temp = head;
37 | while (temp->next != NULL)
38 | {
39 | temp = temp->next;
40 | }
41 | temp->next = new Node(data);
42 | }
43 | }
44 |
45 | void LinkedList::insert(Node* node)
46 | {
47 | if (head == NULL)
48 | {
49 | head = node;
50 | }
51 | else
52 | {
53 | Node* temp = head;
54 | while (temp->next != NULL)
55 | {
56 | temp = temp->next;
57 | }
58 | temp->next = node;
59 | }
60 | }
61 |
62 | void LinkedList::print()
63 | {
64 | if (head == NULL)
65 | {
66 | cout << "Linked List is Empty" << endl;
67 | }
68 | else
69 | {
70 | Node* temp = head;
71 | while (temp != NULL)
72 | {
73 | cout << temp->data << " -> ";
74 | temp = temp->next;
75 | }
76 | cout << "NULL" << endl;
77 | }
78 | }
79 |
80 | void LinkedList::detect_cycle()
81 | {
82 | Node* slow = head;
83 | Node* fast = head;
84 |
85 | if (head == NULL)
86 | {
87 | cout << "Linked List is Empty" << endl;
88 | }
89 | else
90 | {
91 | do
92 | {
93 | if (fast->next != NULL && fast->next->next != NULL)
94 | {
95 | fast = fast->next->next;
96 | slow=slow->next;
97 | }
98 | else
99 | {
100 | cout << "No Cycle Detected";
101 | return;
102 | }
103 | } while (slow != fast);
104 |
105 | fast = head;
106 |
107 | while (slow != fast)
108 | {
109 | slow=slow->next;
110 | fast=fast->next;
111 | }
112 |
113 | cout << "Cycle detected at: " << slow->data << endl;
114 | }
115 | }
116 |
117 | void LinkedList::remove(int key)
118 | {
119 | if (head == NULL)
120 | {
121 | cout << "Linked List is Empty" << endl;
122 | }
123 | else if(head->data == key)
124 | {
125 | Node* temp = head;
126 | temp = head->next;
127 | free(head);
128 | head = temp;
129 | }
130 | else
131 | {
132 | bool flag = 0;
133 | Node* temp = head;
134 | while (temp->next != NULL)
135 | {
136 | if (temp->next->data == key)
137 | {
138 | flag = 1;
139 | Node* p = temp->next;
140 | temp->next = temp->next->next;
141 | free(p);
142 | break;
143 | }
144 | else
145 | {
146 | temp = temp->next;
147 | }
148 | }
149 | if (flag == 0)
150 | {
151 | cout << "Key Not Found" << endl;
152 | }
153 | }
154 | }
155 |
156 | int main()
157 | {
158 | LinkedList L1;
159 | L1.insert(3);
160 | L1.insert(6);
161 | L1.insert(9);
162 | L1.insert(12);
163 | Node* p = L1.head->next;
164 | L1.insert(p); //Creating a cycle in linked list
165 | L1.detect_cycle();
166 | LinkedList L2;
167 | L2.insert(5);
168 | L2.insert(10);
169 | L2.detect_cycle();
170 | return 0;
171 | }
--------------------------------------------------------------------------------
/Data Structures/Linked Lists/floyd_cycle_detection_algorithm.cpp:
--------------------------------------------------------------------------------
1 | #include
2 |
3 | using namespace std;
4 |
5 | class Node
6 | {
7 | public:
8 | int data;
9 | Node* next;
10 | Node(int data)
11 | {
12 | this->data = data;
13 | next = NULL;
14 | }
15 | };
16 |
17 | class LinkedList
18 | {
19 | public:
20 | Node* head = NULL;
21 | void insert(int data); //To insert data at the end of linked list
22 | void insert(Node* node); //To point at an existing node
23 | void print();
24 | void detect_cycle();
25 | void remove(int data);
26 | };
27 |
28 | void LinkedList::insert(int data)
29 | {
30 | if (head == NULL)
31 | {
32 | head = new Node(data);
33 | }
34 | else
35 | {
36 | Node* temp = head;
37 | while (temp->next != NULL)
38 | {
39 | temp = temp->next;
40 | }
41 | temp->next = new Node(data);
42 | }
43 | }
44 |
45 | void LinkedList::insert(Node* node)
46 | {
47 | if (head == NULL)
48 | {
49 | head = node;
50 | }
51 | else
52 | {
53 | Node* temp = head;
54 | while (temp->next != NULL)
55 | {
56 | temp = temp->next;
57 | }
58 | temp->next = node;
59 | }
60 | }
61 |
62 | void LinkedList::print()
63 | {
64 | if (head == NULL)
65 | {
66 | cout << "Linked List is Empty" << endl;
67 | }
68 | else
69 | {
70 | Node* temp = head;
71 | while (temp != NULL)
72 | {
73 | cout << temp->data << " -> ";
74 | temp = temp->next;
75 | }
76 | cout << "NULL" << endl;
77 | }
78 | }
79 |
80 | void LinkedList::detect_cycle()
81 | {
82 | Node* slow = head;
83 | Node* fast = head;
84 |
85 | if (head == NULL)
86 | {
87 | cout << "Linked List is Empty" << endl;
88 | }
89 | else
90 | {
91 | do
92 | {
93 | if (fast->next != NULL && fast->next->next != NULL)
94 | {
95 | fast = fast->next->next;
96 | slow=slow->next;
97 | }
98 | else
99 | {
100 | cout << "No Cycle Detected";
101 | return;
102 | }
103 | } while (slow != fast);
104 |
105 | fast = head;
106 |
107 | while (slow != fast)
108 | {
109 | slow=slow->next;
110 | fast=fast->next;
111 | }
112 |
113 | cout << "Cycle detected at: " << slow->data << endl;
114 | }
115 | }
116 |
117 | void LinkedList::remove(int key)
118 | {
119 | if (head == NULL)
120 | {
121 | cout << "Linked List is Empty" << endl;
122 | }
123 | else if(head->data == key)
124 | {
125 | Node* temp = head;
126 | temp = head->next;
127 | free(head);
128 | head = temp;
129 | }
130 | else
131 | {
132 | bool flag = 0;
133 | Node* temp = head;
134 | while (temp->next != NULL)
135 | {
136 | if (temp->next->data == key)
137 | {
138 | flag = 1;
139 | Node* p = temp->next;
140 | temp->next = temp->next->next;
141 | free(p);
142 | break;
143 | }
144 | else
145 | {
146 | temp = temp->next;
147 | }
148 | }
149 | if (flag == 0)
150 | {
151 | cout << "Key Not Found" << endl;
152 | }
153 | }
154 | }
155 |
156 | int main()
157 | {
158 | LinkedList L1;
159 | L1.insert(3);
160 | L1.insert(6);
161 | L1.insert(9);
162 | L1.insert(12);
163 | Node* p = L1.head->next;
164 | L1.insert(p); //Creating a cycle in linked list
165 | L1.detect_cycle();
166 | LinkedList L2;
167 | L2.insert(5);
168 | L2.insert(10);
169 | L2.detect_cycle();
170 | return 0;
171 | }
--------------------------------------------------------------------------------
/09_Graphs/dfs.cpp:
--------------------------------------------------------------------------------
1 | #include
2 |
3 | using namespace std;
4 |
5 | #define VERTICES 100
6 |
7 | class Graph
8 | {
9 | private:
10 | struct Node
11 | {
12 | int data;
13 | struct Node *next;
14 | };
15 | int no_of_vertices;
16 | struct Node **adj_list;
17 |
18 | public:
19 | bool visited[VERTICES] = {0};
20 | void make_graph(int no_of_vertices);
21 | void display();
22 | void add_edge();
23 | void dfs(int v);
24 | };
25 |
26 | /*
27 | This function iterates over all the possible edges and asks user if they want the edge to exist or not
28 | parameters : void
29 | Returns : void
30 | */
31 | void Graph ::add_edge()
32 | {
33 | for (int i = 0; i < no_of_vertices; i++)
34 | {
35 | for (int j = 0; j < no_of_vertices; j++)
36 | {
37 | if (i != j)
38 | {
39 | char choice;
40 | cout << "Are vertices " << i << " and " << j << " adjacent? (Y/N) : ";
41 | cin >> choice;
42 |
43 | if (toupper(choice) == 'Y')
44 | {
45 | if (adj_list[i] == NULL)
46 | {
47 | adj_list[i] = new struct Node;
48 | adj_list[i]->data = j;
49 | adj_list[i]->next = NULL;
50 | continue;
51 | }
52 | struct Node *temp;
53 | temp = adj_list[i];
54 | while (temp->next != NULL)
55 | {
56 | temp = temp->next;
57 | }
58 | temp->next = new struct Node;
59 | temp->next->data = j;
60 | temp->next->next = NULL;
61 | }
62 | }
63 | }
64 | }
65 | }
66 | // end of function
67 |
68 | /*
69 | Performs DFS traversal
70 | parameters : vertex on which dfs is called
71 | Returns : void
72 | */
73 | void Graph ::dfs(int v)
74 | {
75 | visited[v] = 1;
76 | cout << v << " ";
77 |
78 | struct Node *temp;
79 | temp = adj_list[v];
80 |
81 | while (temp != NULL)
82 | {
83 | if (visited[temp->data] == 0)
84 | {
85 | dfs(temp->data);
86 | }
87 | temp = temp->next;
88 | }
89 | }
90 | // end of function
91 |
92 | /*
93 | This function is used to create a graph
94 | parameters : no_of_vertices
95 | Returns : void
96 | */
97 | void Graph ::make_graph(int no_of_vertices)
98 | {
99 | this->no_of_vertices = no_of_vertices;
100 | // creating a graph
101 | adj_list = new struct Node *[no_of_vertices];
102 | for (int i = 0; i < no_of_vertices; i++)
103 | {
104 | adj_list[i] = NULL;
105 | }
106 | }
107 | // end of function
108 |
109 | /*
110 | This function is used to display the graph
111 | parameters : void
112 | Returns : void
113 | */
114 | void Graph ::display()
115 | {
116 | cout << "The adjacency list representation is :-\n";
117 | for (int i = 0; i < no_of_vertices; i++)
118 | {
119 | cout << i << " : ";
120 | if (adj_list[i] != NULL)
121 | {
122 | struct Node *temp;
123 | temp = adj_list[i];
124 | while (temp->next != NULL)
125 | {
126 | cout << temp->data << " -> ";
127 | temp = temp->next;
128 | }
129 | cout << temp->data;
130 | }
131 | cout << "\n";
132 | }
133 | }
134 | // end of function
135 |
136 | // main function starts here
137 | int main()
138 | {
139 | Graph g;
140 | int no_of_vertices;
141 | cout << "Enter the number of vertices : ";
142 | cin >> no_of_vertices;
143 |
144 | g.make_graph(no_of_vertices);
145 | g.add_edge();
146 | g.display();
147 |
148 | for (int v = 0; v < no_of_vertices; v++)
149 | {
150 | if (g.visited[v] == 0)
151 | {
152 | g.dfs(v);
153 | }
154 | }
155 |
156 | return 0;
157 | }
158 | // end of main
159 |
--------------------------------------------------------------------------------
/02_Stack/minimum_element.cpp:
--------------------------------------------------------------------------------
1 | /******************************************************************
2 | @brief Implementing stack and extracting minimum element
3 | *******************************************************************/
4 |
5 | #include
6 | #define MAX_SIZE 100 // The maximum number of elements our stack can hold is 100
7 | using namespace std;
8 |
9 | class Stack
10 | {
11 | private:
12 | int stack[MAX_SIZE];
13 | int top = -1;
14 | int min = INT_MAX;
15 | int max = INT_MIN;
16 |
17 | public:
18 | void push(int element);
19 | int pop();
20 | int peek();
21 | int get_min();
22 | };
23 |
24 | /*
25 | * Function Name: push
26 | * Input: Integer element which is to be pushed
27 | * Output: None
28 | * Logic: This function allows us to insert an element in stack
29 | * Example Call: push(5)
30 | */
31 | void Stack ::push(int element)
32 | {
33 | if (top != MAX_SIZE - 1) // We can not push anymore elements if the stack is full
34 | {
35 | if (top == -1)
36 | {
37 | min = element ;
38 | }
39 | if (element < min && top != -1)
40 | {
41 | int temp = element ;
42 | element = element - min ;
43 | min = temp ;
44 | }
45 | top++;
46 | stack[top] = element;
47 | }
48 | else
49 | {
50 | cout << "The stack is full\n";
51 | }
52 | }
53 |
54 | /*
55 | * Function Name: pop
56 | * Input: None
57 | * Output: Returns the topmost element of stack or -1 if stack is empty
58 | * Logic: This function allows us to remove an element from stack
59 | * Example Call: pop()
60 | */
61 | int Stack ::pop()
62 | {
63 | if (top != -1)
64 | {
65 | if (peek() < min)
66 | {
67 | int temp = min ;
68 | min = temp - peek() ;
69 | // cout << "min is: " << min << endl ;
70 | top -- ;
71 | return temp ;
72 | }
73 | return stack[top--];
74 | /* We need to do top-- above itself cause the staements below the return statement are not executed*/
75 | }
76 | else
77 | {
78 | cout << "The stack is empty\n";
79 | return -1; // just to avoid the warning of control reaches end of non-void function
80 | }
81 | }
82 |
83 | /*
84 | * Function Name: peek
85 | * Input: None
86 | * Output: Returns the topmost element of stack or -1 if stack is empty without deleting it
87 | * Logic: This function allows us to remove an element from stack without deleting it
88 | * Example Call: peek()
89 | */
90 | int Stack ::peek()
91 | {
92 | if (top != -1)
93 | {
94 | return stack[top]; // here, we simply return the topmost element and not decrement top
95 | }
96 | else
97 | {
98 | cout << "The stack is empty\n";
99 | return -1; // just to avoid the warning of control reaches end of non-void function
100 | }
101 | }
102 |
103 | int Stack:: get_min ()
104 | {
105 | if (top == -1)
106 | {
107 | return -1 ;
108 | }
109 | return min ;
110 | }
111 |
112 | int main()
113 | {
114 | int n ;
115 | cin >> n ;
116 | Stack s1;
117 | int x;
118 |
119 | for (int i = 0 ; i < n ; i++)
120 | {
121 | int choice ;
122 | cin >> choice ;
123 |
124 | if (choice == 1)
125 | {
126 | int element ;
127 | cin >> element ;
128 | s1.push(element) ;
129 | }
130 | else if(choice == 2)
131 | {
132 | s1.pop() ;
133 | }
134 | else
135 | {
136 | x = s1.get_min() ;
137 | cout << x << "\n";
138 | }
139 | }
140 |
141 | return 0;
142 | }
143 |
144 | /*
145 | Analysis: The above code runs in O(1) for extracting minimum element.
146 |
147 | Aliter: The same thing can be implemented by using 3 stacks, one to hold elements, one for maximum element and one for minimum element.
148 |
149 | Note: The same code works for extracting maximum element by modifying few conditions.
150 | */
--------------------------------------------------------------------------------
/Algorithms/4_Sorting/heap_sort.cpp:
--------------------------------------------------------------------------------
1 | /***************************************
2 | @brief Implementing Heap Sort
3 | ****************************************/
4 | #include
5 | #include
6 |
7 | using namespace std;
8 |
9 | /*
10 | * Function Name: parent
11 | * Input: Index of the element
12 | * Output: Returns the index of parent
13 | * Example Call: parent(5)
14 | */
15 | int parent(int index)
16 | {
17 | int parent = 0;
18 | if (index % 2 == 0)
19 | {
20 | parent = (index - 1) / 2;
21 | }
22 | else
23 | {
24 | parent = index / 2;
25 | }
26 |
27 | return parent;
28 | }
29 |
30 | /*
31 | * Function Name: left_child
32 | * Input: Index of the element
33 | * Output: Returns the index of the left child
34 | * Example Call: left_child(5)
35 | */
36 | int left_child(int index, int *n)
37 | {
38 | int left = 2 * index + 1;
39 | if (left >= *n)
40 | {
41 | return -1;
42 | }
43 | return left;
44 | }
45 |
46 | /*
47 | * Function Name: right_child
48 | * Input: Index of the element
49 | * Output: Returns the index of the right child
50 | * Example Call: right_child(5)
51 | */
52 | int right_child(int index, int *n)
53 | {
54 | int right = 2 * index + 2;
55 | if (right >= *n)
56 | {
57 | return -1;
58 | }
59 | return right;
60 | }
61 |
62 | /*
63 | * Function Name: siftDown
64 | * Input: Takes the array, current size of array, and index of element
65 | * Output: None
66 | * Logic: This function shifts the element down the heap to its correct position
67 | * Example Call: SiftDown(maxHeap, 5, &temp)
68 | */
69 | void siftDown(int maxHeap[], int index, int *n)
70 | {
71 | while (1)
72 | {
73 | if (maxHeap[left_child(index, n)] > maxHeap[right_child(index, n)] && (maxHeap[index] < maxHeap[left_child(index, n)]) && left_child(index, n) != -1)
74 | {
75 | swap(maxHeap[index], maxHeap[left_child(index, n)]);
76 | index = left_child(index, n);
77 | }
78 | else if (maxHeap[left_child(index, n)] < maxHeap[right_child(index, n)] && (maxHeap[index] < maxHeap[right_child(index, n)]) && right_child(index, n) != -1)
79 | {
80 | swap(maxHeap[index], maxHeap[right_child(index, n)]);
81 | index = right_child(index, n);
82 | }
83 | else
84 | {
85 | break;
86 | }
87 | }
88 | }
89 |
90 | /*
91 | * Function Name: extractMax
92 | * Input: Takes the array, and index of element
93 | * Output: Returns the maximum element i.e. root element of heap
94 | * Example Call: extractMax(maxHeap, 5)
95 | */
96 | int extractMax(int maxHeap[], int *n)
97 | {
98 | int temp = maxHeap[0];
99 | (*n)--;
100 | maxHeap[0] = maxHeap[(*n)];
101 | siftDown(maxHeap, 0, n);
102 | return temp;
103 | }
104 |
105 | /*
106 | * Function Name: Heapify
107 | * Input: Takes the array, and size of array by reference
108 | * Output: None
109 | * Logic: This function creates heap out of given array without taking any extra space
110 | * Example Call: Heapify(maxHeap, max_size)
111 | */
112 | void Heapify(int maxHeap[], int *n)
113 | {
114 | for (int i = (*n) / 2; i >= 0; i--)
115 | {
116 | siftDown(maxHeap, i, n);
117 | }
118 | }
119 |
120 | int main()
121 | {
122 | int max_size, temp = 0;
123 | cout << "Please enter the total number of elements: ";
124 | cin >> max_size;
125 | temp = max_size;
126 | int maxHeap[max_size] = {0};
127 |
128 | for (int i = 0; i < max_size; i++)
129 | {
130 | cin >> maxHeap[i];
131 | }
132 |
133 | //Creating heap from the given array
134 | Heapify(maxHeap, &max_size);
135 |
136 | //Sorting
137 | for (int i = 0; i < temp; i++)
138 | {
139 | int element;
140 | element = extractMax(maxHeap, &max_size);
141 | maxHeap[max_size] = element;
142 | }
143 |
144 | for (int i = 0; i < temp; i++)
145 | {
146 | cout << maxHeap[i] << " ";
147 | }
148 | }
149 | /*
150 | Analysis: The above algorithn runs in O(nlog(n))
151 | */
--------------------------------------------------------------------------------
/Algorithms/3_Dynamic_Programming/substring_sum.cpp:
--------------------------------------------------------------------------------
1 | /***********************************************************************************
2 | @brief Finding the longest substring such that sum of digits in first half and second half are equal.
3 | ************************************************************************************/
4 | #include
5 | #include
6 | #include
7 |
8 | using namespace std;
9 |
10 | /*
11 | * Function Name: check
12 | * Input: string and start and end indices
13 | * Output: True if the sum of digits in first half and second half are equal
14 | * Logic: To evaluate a substring. This is used only for recursive approach.
15 | * Example Call: check("9036", 0, 3)
16 | */
17 | bool check(string s, int start, int end)
18 | {
19 | int a = 0, b = 0;
20 | int mid = (start+end)/2;
21 |
22 | for (int i = start; i <= mid; i++)
23 | {
24 | a += (s[i] - '0');
25 | }
26 | for (int i = mid + 1; i <= end; i++)
27 | {
28 | b += (s[i] - '0');
29 | }
30 |
31 | if (a == b)
32 | {
33 | return true;
34 | }
35 | return false;
36 | }
37 | /*
38 | * Function Name: moveGen
39 | * Input: string s
40 | * Output: The longest substring with equal sum of digits in first half and second half
41 | * Logic: Iterates through all possible substrings and checks if their sum of digits is equal. Keeps track of the maximum valid substring found.
42 | * Example Call: moveGen("9036")
43 | */
44 | string moveGen(string s)
45 | {
46 | int max_str_i = 0, max_str_j = 0;
47 | for (int i = 0; i < s.length(); i++)
48 | {
49 | for (int j = i + 1; j < s.length(); j += 2)
50 | {
51 | if (j - i + 1 < max_str_j - max_str_i + 1)
52 | {
53 | continue;
54 | }
55 |
56 | if (check(s, i, j))
57 | {
58 | if (j - i + 1 > max_str_j - max_str_i + 1)
59 | {
60 | max_str_i = i;
61 | max_str_j = j;
62 | }
63 | }
64 | }
65 | }
66 |
67 | if (max_str_j == 0)
68 | {
69 | return "";
70 | }
71 |
72 | string max_str = s.substr(max_str_i, max_str_j - max_str_i + 1);
73 |
74 | return max_str;
75 | }
76 |
77 | /*
78 | * Function Name: dp
79 | * Input: string s
80 | * Output: The longest substring with equal sum of digits in first half and second half
81 | * Logic: Utilizes dynamic programming to efficiently compute the sum of digits in all substrings. Iterates through substrings, checks if their sum of digits is equal, and updates the maximum substring.
82 | * Example Call: dp("9036")
83 | */
84 | string dp(string s)
85 | {
86 | int max_str_i = 0, max_str_j = 0;
87 | vector> cache (s.length(), vector (s.length(), 0));
88 |
89 | for (int i = 0; i < s.length(); i++)
90 | {
91 | cache[i][i] = s[i]-'0';
92 | }
93 |
94 | for (int i = 0; i < s.length(); i++)
95 | {
96 | for (int j = i+1; j < s.length(); j++)
97 | {
98 | cache[i][j] = cache[i][j-1] + (s[j]-'0');
99 | if ((j-i)%2 != 0)
100 | {
101 | int mid = (j+i)/2;
102 | if (cache[i][mid] == (cache[i][j]/2) && j - i + 1 > max_str_j - max_str_i + 1)
103 | {
104 | max_str_i = i;
105 | max_str_j = j;
106 | }
107 | }
108 | }
109 | }
110 |
111 | if (max_str_j == 0)
112 | {
113 | return "";
114 | }
115 |
116 | string max_str = s.substr(max_str_i, max_str_j - max_str_i + 1);
117 |
118 | return max_str;
119 | }
120 |
121 | int main()
122 | {
123 | string s = "946723";
124 | // string rec_answer = moveGen(s);
125 | string dp_answer = dp(s);
126 | // cout << rec_answer << " " << rec_answer.size() << endl;
127 | cout << dp_answer << " " << dp_answer.size() << endl;
128 | return 0;
129 | }
130 |
131 | /*
132 | Analysis: The recursive code runs in O(n^3) time and the dp code runs in O(n^2) time with O(n^2) space.
133 | */
--------------------------------------------------------------------------------
/06_Priority_Queues_and_Heaps/max_heap.cpp:
--------------------------------------------------------------------------------
1 | /**************************************
2 | @brief Implementing MaxHeaps
3 | ***************************************/
4 | #include
5 | #include
6 |
7 | using namespace std;
8 |
9 | /*
10 | * Function Name: parent
11 | * Input: Index of the element
12 | * Output: Returns the index of parent
13 | * Example Call: parent(5)
14 | */
15 | int parent(int index)
16 | {
17 | int parent = 0;
18 | if (index % 2 == 0)
19 | {
20 | parent = (index - 1) / 2;
21 | }
22 | else
23 | {
24 | parent = index / 2;
25 | }
26 |
27 | return parent;
28 | }
29 |
30 | /*
31 | * Function Name: left_child
32 | * Input: Index of the element
33 | * Output: Returns the index of the left child
34 | * Example Call: left_child(5)
35 | */
36 | int left_child(int index)
37 | {
38 | int left = 2 * index + 1;
39 | return left;
40 | }
41 |
42 | /*
43 | * Function Name: right_child
44 | * Input: Index of the element
45 | * Output: Returns the index of the right child
46 | * Example Call: right_child(5)
47 | */
48 | int right_child(int index)
49 | {
50 | int right = 2 * index + 2;
51 | return right;
52 | }
53 |
54 | /*
55 | * Function Name: siftDown
56 | * Input: Takes the array, current size of array, and index of element
57 | * Output: None
58 | * Logic: This function shifts the element down the heap to its correct position
59 | * Example Call: SiftDown(maxHeap, 5, &temp)
60 | */
61 | void siftDown(int maxHeap[], int index, int *n)
62 | {
63 | while (1)
64 | {
65 | if (maxHeap[left_child(index)] > maxHeap[right_child(index)] && (maxHeap[index] < maxHeap[left_child(index)]))
66 | {
67 | swap(maxHeap[index], maxHeap[left_child(index)]);
68 | }
69 | else if (maxHeap[left_child(index)] < maxHeap[right_child(index)] && (maxHeap[index] < maxHeap[right_child(index)]))
70 | {
71 | swap(maxHeap[index], maxHeap[right_child(index)]);
72 | }
73 | else
74 | {
75 | break;
76 | }
77 | }
78 | }
79 |
80 | /*
81 | * Function Name: siftDown
82 | * Input: Takes the array, current size of array, and index of element
83 | * Output: None
84 | * Logic: This function shifts the element up the heap to its correct position
85 | * Example Call: SiftDown(maxHeap, 5, &temp)
86 | */
87 | void siftUp(int maxHeap[], int index)
88 | {
89 | while (index >= 1 && maxHeap[index] > maxHeap[parent(index)])
90 | {
91 | swap(maxHeap[index], maxHeap[parent(index)]);
92 | index = parent(index);
93 | }
94 | }
95 |
96 | /*
97 | * Function Name: extractMax
98 | * Input: Takes the array, and index of element
99 | * Output: Returns the maximum element i.e. root element of heap
100 | * Example Call: extractMax(maxHeap, 5)
101 | */
102 | int extractMax(int maxHeap[], int *n)
103 | {
104 | int temp = maxHeap[0];
105 | (*n)--;
106 | maxHeap[0] = maxHeap[(*n)];
107 | siftDown(maxHeap, 0, n);
108 | return temp;
109 | }
110 |
111 | /*
112 | * Function Name: insert
113 | * Input: Takes the array, element, max size by value and current size of array by reference
114 | * Output: None
115 | * Logic: This function allows us to insert an element into heap
116 | * Example Call: insert(maxHeap, max_size, &curr_size, element)
117 | */
118 | void insert(int maxHeap[], int max_size, int *n, int element)
119 | {
120 | if (*n < max_size)
121 | {
122 | maxHeap[*n] = element;
123 | siftUp(maxHeap, *n);
124 | (*n)++;
125 | }
126 | }
127 |
128 | int main()
129 | {
130 | int max_size, curr_size = 0;
131 | cout << "Please enter the total number of elements: ";
132 | cin >> max_size;
133 | int maxHeap[max_size] = {0};
134 |
135 | for (int i = 0; i < max_size; i++)
136 | {
137 | int element;
138 | cin >> element;
139 | insert(maxHeap, max_size, &curr_size, element);
140 | }
141 |
142 | int max;
143 | for (int i = 0; i < max_size; i++)
144 | {
145 | max = extractMax(maxHeap, &curr_size);
146 | cout << max << " ";
147 | }
148 | }
149 | /*
150 | Analysis: The above algorithm runs in O(nlog(n))
151 | */
--------------------------------------------------------------------------------
/Data Structures/Linked Lists/README.md:
--------------------------------------------------------------------------------
1 | # Linked Lists
2 |
3 |  4 |
5 | ## Introduction
6 |
7 | Think of a traditional array where you allocate a fixed amount of space, like 100 elements, for your data. Even if you only use 20 elements, the other 80 spaces are wasted, and the size of the array can't change. If you need to add more data later, you could run out of space and have to resize the entire array, which can be inefficient and tricky.
8 |
9 | A Linked List solves this problem. Instead of having a fixed-size block of memory, it allocates memory dynamically as needed. Each element in the list (called a "node") is created separately in memory, and each node contains two things:
10 |
11 | * Data: the actual value the node holds.
12 | * Pointer: the memory address of the next node in the list.
13 |
14 | This way, a linked list can grow or shrink as needed without wasting memory, and you can insert or remove elements without worrying about resizing an array.
15 |
16 | ## Advantages & Disadvantages
17 |
18 | Linked lists are not fixed in size. You can add or remove nodes at any time without worrying about running out of space or wasting memory. Also, inserting or deleting an element doesn't require shifting the entire structure (like in arrays). You just need to update a few pointers, making these operations fast.
19 |
20 | However, each node requires extra memory for the pointer (address of the next node), which can make them more memory-hungry than arrays, especially for small data. To find an element, you have to start at the beginning and follow the links until you reach it. This is slower than accessing elements directly by index in an array.
21 |
22 | Linked lists are a great choice when the size of the data is unknown or changes frequently. Since they can dynamically grow and shrink as needed, linked lists prevent the waste of memory that can occur in arrays, where you have to allocate a fixed amount of space. Additionally, linked lists are ideal for scenarios where fast insertions or deletions are required, especially when elements need to be added or removed in the middle of the list. Unlike arrays, which require shifting elements when inserting or deleting, linked lists only need to update a few pointers, making these operations more efficient.
23 |
24 | Linked lists may not be the best option when fast access by index is a priority. In arrays, you can directly access any element using its index, but in a linked list, you have to traverse the list from the beginning to find the desired element, which can be slow. Furthermore, linked lists may not be ideal when memory is a concern. Each node in a linked list requires additional memory for the pointer, which can add up, especially in systems with limited memory or where extra space is at a premium.
25 |
26 | ## Types of Linked List
27 |
28 | 1) Singly Linked List
29 | 2) Doubly Linked List
30 | 3) Circular Linked List
31 | 4) Circular Doubly Linked List
32 |
33 | ## Proof for Floyd Cycle Detection Algorithm
34 |
35 |
4 |
5 | ## Introduction
6 |
7 | Think of a traditional array where you allocate a fixed amount of space, like 100 elements, for your data. Even if you only use 20 elements, the other 80 spaces are wasted, and the size of the array can't change. If you need to add more data later, you could run out of space and have to resize the entire array, which can be inefficient and tricky.
8 |
9 | A Linked List solves this problem. Instead of having a fixed-size block of memory, it allocates memory dynamically as needed. Each element in the list (called a "node") is created separately in memory, and each node contains two things:
10 |
11 | * Data: the actual value the node holds.
12 | * Pointer: the memory address of the next node in the list.
13 |
14 | This way, a linked list can grow or shrink as needed without wasting memory, and you can insert or remove elements without worrying about resizing an array.
15 |
16 | ## Advantages & Disadvantages
17 |
18 | Linked lists are not fixed in size. You can add or remove nodes at any time without worrying about running out of space or wasting memory. Also, inserting or deleting an element doesn't require shifting the entire structure (like in arrays). You just need to update a few pointers, making these operations fast.
19 |
20 | However, each node requires extra memory for the pointer (address of the next node), which can make them more memory-hungry than arrays, especially for small data. To find an element, you have to start at the beginning and follow the links until you reach it. This is slower than accessing elements directly by index in an array.
21 |
22 | Linked lists are a great choice when the size of the data is unknown or changes frequently. Since they can dynamically grow and shrink as needed, linked lists prevent the waste of memory that can occur in arrays, where you have to allocate a fixed amount of space. Additionally, linked lists are ideal for scenarios where fast insertions or deletions are required, especially when elements need to be added or removed in the middle of the list. Unlike arrays, which require shifting elements when inserting or deleting, linked lists only need to update a few pointers, making these operations more efficient.
23 |
24 | Linked lists may not be the best option when fast access by index is a priority. In arrays, you can directly access any element using its index, but in a linked list, you have to traverse the list from the beginning to find the desired element, which can be slow. Furthermore, linked lists may not be ideal when memory is a concern. Each node in a linked list requires additional memory for the pointer, which can add up, especially in systems with limited memory or where extra space is at a premium.
25 |
26 | ## Types of Linked List
27 |
28 | 1) Singly Linked List
29 | 2) Doubly Linked List
30 | 3) Circular Linked List
31 | 4) Circular Doubly Linked List
32 |
33 | ## Proof for Floyd Cycle Detection Algorithm
34 |
35 |  36 |
37 | Here, we know that ```k``` has to be a node in the loop, only then can the slow pointer and fast pointer intersect. Now, the slow pointer may take ```m + Al + k``` steps and fast pointer may take ```m + Bl + k``` steps where ```A``` and ```B``` are constants which can be any number. The idea being that the slow or fast pointer might have to move full loops ```A``` or ```B``` times respectively before intersection, where ```B > A```. But we also know that,
38 | ```
39 | fast = 2*slow
40 | ```
41 | ```
42 | m + Bl + k = 2*(m + Al + k)
43 | ```
44 | ```
45 | (B - 2A)l = m+k
46 | ```
47 | ```
48 | constant*l = m+k
49 | ```
50 | Thus, ```m+k = c*l```, where c is an integer constant.
51 |
52 | This signifies that ```m+k``` steps are equivalent to looping ```c``` number of times in the loop and coming back to same position.
53 |
54 | Now as per algorithm, we reset fast pointer to head, and make it now behave like slow. Doing this, it is guranteed that the next intersection point is the node which marks the start of cycle.
55 |
56 | This is because, now the fast pointer has to take ```m``` steps to reach the first node of cycle. Thus, the slow pointer will make ```c*l - k``` steps. This ensures that the position of slow pointer after ```c*l - k``` steps will be the first node of cycle.
--------------------------------------------------------------------------------
/09_Graphs/bfs.cpp:
--------------------------------------------------------------------------------
1 | #include
2 |
3 | using namespace std;
4 |
5 | #define VERTICES 99999
6 |
7 | class Graph
8 | {
9 | private:
10 | struct Node
11 | {
12 | int data;
13 | struct Node *next;
14 | };
15 | int no_of_vertices;
16 | struct Node **adj_list;
17 | int *queue = NULL;
18 | int *head = NULL;
19 | int *tail = NULL;
20 |
21 | public:
22 | bool visited[VERTICES] = {0};
23 | void make_graph(int no_of_vertices);
24 | void display();
25 | void add_edge();
26 | void bfs(int v);
27 | };
28 |
29 | /*
30 | This function is used to create a graph
31 | parameters : no_of_vertices
32 | Returns : void
33 | */
34 | void Graph ::make_graph(int no_of_vertices)
35 | {
36 | this->no_of_vertices = no_of_vertices;
37 | adj_list = new struct Node *[no_of_vertices];
38 | queue = new int[no_of_vertices];
39 | head = &queue[0];
40 | tail = &queue[0];
41 | for (int i = 0; i < no_of_vertices; i++)
42 | {
43 | adj_list[i] = NULL;
44 | }
45 | }
46 |
47 | /*
48 | This function iterates over all the possible edges and asks user if they want the edge to exist or not
49 | parameters : void
50 | Returns : void
51 | */
52 | void Graph ::add_edge()
53 | {
54 | for (int i = 0; i < no_of_vertices; i++)
55 | {
56 | for (int j = 0; j < no_of_vertices; j++)
57 | {
58 | if (i != j)
59 | {
60 | char choice;
61 | cout << "Are vertices " << i << " and " << j << " adjacent? (Y/N) : ";
62 | cin >> choice;
63 |
64 | if (toupper(choice) == 'Y')
65 | {
66 | if (adj_list[i] == NULL)
67 | {
68 | adj_list[i] = new struct Node;
69 | adj_list[i]->data = j;
70 | adj_list[i]->next = NULL;
71 | continue;
72 | }
73 | struct Node *temp;
74 | temp = adj_list[i];
75 | while (temp->next != NULL)
76 | {
77 | temp = temp->next;
78 | }
79 | temp->next = new struct Node;
80 | temp->next->data = j;
81 | temp->next->next = NULL;
82 | }
83 | }
84 | }
85 | }
86 | }
87 | // end of function
88 |
89 | /*
90 | Performs BFS traversal
91 | parameters : vertex on which bfs is called
92 | Returns : void
93 | */
94 | void Graph ::bfs(int v)
95 | {
96 | *tail = v;
97 | tail++;
98 | visited[v] = 1 ;
99 |
100 | while (head != tail)
101 | {
102 | struct Node *temp;
103 | cout << *head << " ";
104 | temp = adj_list[*head];
105 | head++;
106 |
107 | while (temp != NULL)
108 | {
109 | if (visited[temp->data] == 0)
110 | {
111 | *tail = temp->data;
112 | visited[temp->data] = 1 ;
113 | tail++;
114 | }
115 | temp = temp->next;
116 | }
117 | }
118 | }
119 |
120 | /*
121 | This function is used to display the graph
122 | parameters : void
123 | Returns : void
124 | */
125 | void Graph ::display()
126 | {
127 | cout << "The adjacency list representation is :-\n";
128 | for (int i = 0; i < no_of_vertices; i++)
129 | {
130 | cout << i << " : ";
131 | if (adj_list[i] != NULL)
132 | {
133 | struct Node *temp;
134 | temp = adj_list[i];
135 | while (temp->next != NULL)
136 | {
137 | cout << temp->data << " -> ";
138 | temp = temp->next;
139 | }
140 | cout << temp->data;
141 | }
142 | cout << "\n";
143 | }
144 | }
145 | // end of function
146 |
147 | // main function starts here
148 | int main()
149 | {
150 | Graph g;
151 | int no_of_vertices;
152 | cout << "Enter the number of vertices : ";
153 | cin >> no_of_vertices;
154 |
155 | g.make_graph(no_of_vertices);
156 | g.add_edge();
157 |
158 | int source;
159 | cout << "Enter the source node: ";
160 | cin >> source;
161 |
162 | g.bfs(source);
163 |
164 | return 0;
165 | }
166 | // end of main
167 |
--------------------------------------------------------------------------------
/03_Queues/Queue_using_arrays/Queue_using_two_pointer.cpp:
--------------------------------------------------------------------------------
1 | /*******************************************************************
2 | @brief Implementing queue using a array and a two pointer
3 | ********************************************************************/
4 | #include
5 | #define MAX_SIZE 10
6 | using namespace std;
7 |
8 | class Queue
9 | {
10 | private:
11 | int queue[MAX_SIZE];
12 | int *rear = NULL;
13 | int *front = NULL; // initially , the pointers points to NULL
14 |
15 | public:
16 | void enqueue(int element);
17 | void dequeue();
18 | bool isEmpty();
19 | bool isFull();
20 | void display();
21 | };
22 |
23 | /*
24 | * Function Name: enqueue
25 | * Input: Integer element which is to be inserted
26 | * Output: None
27 | * Logic: This function allows us to insert an element in queue
28 | * Example Call: enqueue(5)
29 | */
30 | void Queue ::enqueue(int element)
31 | {
32 | if (!isFull()) // insert element only if queue is not full
33 | {
34 | if (rear == NULL) // if the queue is empty , and the element is first to be inserted
35 | {
36 | rear = queue; // points to the first element in queue
37 | front = queue;
38 | queue[0] = element;
39 | }
40 | else
41 | {
42 | rear++; // increment the pointer to next position
43 | *rear = element; // change the value of next position
44 | }
45 | }
46 | else
47 | {
48 | cout << "queue is full!\n";
49 | }
50 | }
51 |
52 | /*
53 | * Function Name: dequeue
54 | * Input: None
55 | * Output: Returns the first element of queue
56 | * Logic: This function allows us to remove the first element of queue
57 | * Example Call: dequeue()
58 | */
59 | void Queue ::dequeue()
60 | {
61 | if (!isEmpty()) // we check if queue is not empty
62 | {
63 | cout << *front << "\n";
64 | front++; // incrementing the front the pointer to previous position
65 | // for dequeue , we first delete the element to which the front is pointing , then we increment front
66 | }
67 | else
68 | {
69 | cout << "The queue is empty!\n";
70 | }
71 | }
72 |
73 | /*
74 | * Function Name: display
75 | * Input: None
76 | * Output: Prints all the elements in the queue
77 | * Logic: This function allows us to print the elements currently in queue
78 | * Example Call: display()
79 | */
80 | void Queue ::display()
81 | {
82 | if (!isEmpty())
83 | {
84 | cout << "The elements of queue are : ";
85 | for (int i = 0; front + i <= rear; i++) // here , we print the element in queue till address of queue's last element matches with address at which rear points
86 | {
87 | cout << *(front + i) << " ";
88 | }
89 | cout << "\n";
90 | }
91 | else
92 | {
93 | cout << "The queue is empty!\n";
94 | }
95 | }
96 |
97 | /*
98 | * Function Name: isFull
99 | * Input: None
100 | * Output: Returns a boolean true if the queue is full
101 | * Logic: This function allows us to check if the queue is full
102 | * Example Call: isFull()
103 | */
104 | bool Queue ::isFull()
105 | {
106 | if (rear >= &queue[MAX_SIZE - 1])
107 | {
108 | return true; // we return false since the queue had 1 element left and is not yet empty
109 | }
110 | else
111 | {
112 | return false; // for all other cases , queue is not empty
113 | }
114 | }
115 |
116 | /*
117 | * Function Name: isEmpty
118 | * Input: None
119 | * Output: Returns a boolean true if the queue is empty
120 | * Logic: This function allows us to check if the queue is empty
121 | * Example Call: isEmpty()
122 | */
123 | bool Queue ::isEmpty()
124 | {
125 | if (rear < front || rear == NULL) // when the queue is empty , ether the front pointer is ahead of the rear pointer , or the rear pointer is null
126 | {
127 | return true;
128 | }
129 | else
130 | {
131 | return false; // for all other cases , queue is not empty
132 | }
133 | }
134 |
135 | int main()
136 | {
137 | class Queue Queue1; // creating an object Queue1 of class Queue
138 |
139 | Queue1.enqueue(34);
140 | Queue1.enqueue(55);
141 | Queue1.enqueue(10);
142 | Queue1.display();
143 | // Queue1.dequeue();
144 | // Queue1.display();
145 | // Queue1.dequeue();
146 | // Queue1.display();
147 | // Queue1.dequeue();
148 | // Queue1.display();
149 |
150 | return 0;
151 | }
152 |
--------------------------------------------------------------------------------
/Algorithms/3_Dynamic_Programming/placing_parentheses.cpp:
--------------------------------------------------------------------------------
1 | /***********************************************************************************
2 | @brief Placing parentheses to obtain maximum value of given arithmetic expression
3 | ************************************************************************************/
4 | #include
5 | #include
6 |
7 | using namespace std;
8 |
9 | struct minmax
10 | {
11 | long long int min = 999999999;
12 | long long int max = -999999999;
13 | };
14 |
15 | long long int maximum(long long int a, long long int b, long long int c, long long int d)
16 | {
17 | if (a > b && a > c && a > d)
18 | {
19 | return a;
20 | }
21 | else if (b > c && b > d)
22 | {
23 | return b;
24 | }
25 | else if (c > d)
26 | {
27 | return c;
28 | }
29 | return d;
30 | }
31 | long long int minimum(long long int a, long long int b, long long int c, long long int d)
32 | {
33 | if (a < b && a < c && a < d)
34 | {
35 | return a;
36 | }
37 | else if (b < c && b < d)
38 | {
39 | return b;
40 | }
41 | else if (c < d)
42 | {
43 | return c;
44 | }
45 | return d;
46 | }
47 |
48 | struct minmax min_and_max(vector> maxima, vector> minima, vector operand, vector operation, long long int i, long long int j, struct minmax h)
49 | {
50 | for (long long int k = i; k < j; k++)
51 | {
52 | long long int a, b, c, d;
53 | if (operation[k] == '+')
54 | {
55 | a = maxima[i][k] + maxima[k+1][j];
56 | b = maxima[i][k] + minima[k+1][j];
57 | c = minima[i][k] + maxima[k+1][j];
58 | d = minima[i][k] + minima[k+1][j];
59 | }
60 | else if (operation[k] == '-')
61 | {
62 | a = maxima[i][k] - maxima[k+1][j];
63 | b = maxima[i][k] - minima[k+1][j];
64 | c = minima[i][k] - maxima[k+1][j];
65 | d = minima[i][k] - minima[k+1][j];
66 | }
67 | else
68 | {
69 | a = maxima[i][k] * maxima[k+1][j];
70 | b = maxima[i][k] * minima[k+1][j];
71 | c = minima[i][k] * maxima[k+1][j];
72 | d = minima[i][k] * minima[k+1][j];
73 | }
74 |
75 | long long int x = maximum(a,b,c,d) ;
76 | long long int y = minimum(a,b,c,d) ;
77 | if ( x > h.max)
78 | {
79 | h.max = x ;
80 | }
81 | if ( y < h.min)
82 | {
83 | h.min = y ;
84 | }
85 | }
86 |
87 | return h;
88 | }
89 |
90 | long long int get_val(vector operand, vector operation)
91 | {
92 | long long int n = operand.size();
93 | vector> maxima(n, vector(n, 0));
94 | vector> minima(n, vector(n, 0));
95 |
96 | for (long long int i = 0; i < n; i++)
97 | {
98 | minima[i][i] = maxima[i][i] = operand[i];
99 | }
100 |
101 | for (long long int d = 1; d < n; d++)
102 | {
103 | for (long long int i = 0, j = i + d; j < n; i++, j++)
104 | {
105 | minmax h;
106 | h = min_and_max(maxima, minima, operand, operation, i, j, h);
107 | maxima[i][j] = h.max;
108 | minima[i][j] = h.min;
109 | }
110 | }
111 |
112 | return maxima[0][maxima.size()-1];
113 | }
114 |
115 | int main()
116 | {
117 | string s;
118 | cout << "Please enter your arithmetic expression: " ;
119 | cin >> s;
120 | vector operand;
121 | vector operation;
122 |
123 | int index = 0;
124 | bool input_flag = 1;
125 | for (int i = 0; i < s.length(); i++)
126 | {
127 | if (s[index] == '+' || s[index] == '-' || s[index] == '*' || s[index] == '/')
128 | {
129 | operation.push_back(s[index]);
130 | input_flag = 1;
131 | }
132 | else
133 | {
134 | if (input_flag == 1)
135 | {
136 | operand.push_back(s[index] - '0');
137 | }
138 | else
139 | {
140 | operand[operand.size() - 1] = 10 * operand[operand.size() - 1] + (s[index] - '0');
141 | }
142 | input_flag = 0;
143 | }
144 | index++;
145 | }
146 |
147 | long long int x = get_val(operand, operation) ;
148 | cout << "The maximum value of expression is: " << x ;
149 |
150 | return 0;
151 | }
--------------------------------------------------------------------------------
/03_Queues/Queue_using_arrays/Queue_using_one_pointer.cpp:
--------------------------------------------------------------------------------
1 | /**********************************************************************
2 | @brief Implementing queue using a array and a single pointer
3 | ***********************************************************************/
4 | #include
5 | #define MAX_SIZE 10
6 | using namespace std;
7 |
8 | class Queue
9 | {
10 | private:
11 | int queue[MAX_SIZE];
12 | int *rear = NULL; // initially , the pointer points to NULL
13 |
14 | public:
15 | void enqueue(int element);
16 | void dequeue();
17 | bool isEmpty();
18 | bool isFull();
19 | void display();
20 | };
21 |
22 | /*
23 | * Function Name: enqueue
24 | * Input: Integer element which is to be inserted
25 | * Output: None
26 | * Logic: This function allows us to insert an element in queue
27 | * Example Call: enqueue(5)
28 | */
29 | void Queue ::enqueue(int element)
30 | {
31 | if (!isFull()) // insert element only if queue is not full
32 | {
33 | if (rear == NULL) // if the queue is empty , and the element is first to be inserted
34 | {
35 | rear = queue; // points to the first element in queue
36 | queue[0] = element;
37 | }
38 | else
39 | {
40 | rear++; // increment the pointer to next position
41 | *rear = element; // change the value of next position
42 | }
43 | }
44 | else
45 | {
46 | cout << "queue is full!\n";
47 | }
48 | }
49 |
50 | /*
51 | * Function Name: dequeue
52 | * Input: None
53 | * Output: Returns the first element of queue
54 | * Logic: This function allows us to remove the first element of queue
55 | * Example Call: dequeue()
56 | */
57 | void Queue ::dequeue()
58 | {
59 | if (rear == &queue[0]) // considering the case if only one element is present
60 | {
61 | cout << queue[0] << "\n";
62 | rear = NULL;
63 | }
64 | else if (!isEmpty()) // we check if queue is not empty
65 | {
66 | cout << queue[0] << "\n"; // print the first element i.e. 0th index in array
67 |
68 | for (int i = 0; &queue[i] < rear; i++) // here , we go till the second last element of queue
69 | {
70 | queue[i] = queue[i + 1];
71 | }
72 |
73 | rear--; // decrementing the pointer to previous position
74 | }
75 | else
76 | {
77 | cout << "The queue is empty!\n";
78 | }
79 | }
80 |
81 | /*
82 | * Function Name: display
83 | * Input: None
84 | * Output: Prints all the elements in the queue
85 | * Logic: This function allows us to print the elements currently in queue
86 | * Example Call: display()
87 | */
88 | void Queue ::display()
89 | {
90 | if (rear != NULL)
91 | {
92 | cout << "The elements of queue are : ";
93 | for (int i = 0; &queue[i] <= rear; i++) // here , we print the element in queue till address of queue's last element matches with address at which rear points
94 | {
95 | cout << queue[i] << " ";
96 | }
97 | cout << "\n";
98 | }
99 | else
100 | {
101 | cout << "The queue is empty!\n";
102 | }
103 | }
104 |
105 | /*
106 | * Function Name: isEmpty
107 | * Input: None
108 | * Output: Returns a boolean true if the queue is empty
109 | * Logic: This function allows us to check if the queue is empty
110 | * Example Call: isEmpty()
111 | */
112 | bool Queue ::isEmpty()
113 | {
114 | if (rear == &queue[0])
115 | {
116 | rear = NULL;
117 | return false; // we return false since the queue had 1 element left and is not yet empty
118 | }
119 | else if (rear == NULL)
120 | {
121 | return true;
122 | }
123 | else
124 | {
125 | return false; // for all other cases , queue is not empty
126 | }
127 | }
128 |
129 | /*
130 | * Function Name: isFull
131 | * Input: None
132 | * Output: Returns a boolean true if the queue is full
133 | * Logic: This function allows us to check if the queue is full
134 | * Example Call: isFull()
135 | */
136 | bool Queue ::isFull()
137 | {
138 | if (rear == &queue[MAX_SIZE - 1])
139 | {
140 | return true; // we return true since the rear already points at last element and there is no space ahead
141 | }
142 | else
143 | {
144 | return false; // for all other cases , queue is not empty
145 | }
146 | }
147 |
148 | int main()
149 | {
150 | class Queue Queue1; // creating an object Queue1 of class Queue
151 |
152 | Queue1.enqueue(34);
153 | Queue1.enqueue(55);
154 | Queue1.enqueue(10);
155 | Queue1.display();
156 | Queue1.dequeue();
157 | Queue1.display();
158 | Queue1.dequeue();
159 | Queue1.display();
160 | Queue1.dequeue();
161 | Queue1.display();
162 |
163 | return 0;
164 | }
165 |
--------------------------------------------------------------------------------
/09_Graphs/README.md:
--------------------------------------------------------------------------------
1 | # Graphs
2 |
36 |
37 | Here, we know that ```k``` has to be a node in the loop, only then can the slow pointer and fast pointer intersect. Now, the slow pointer may take ```m + Al + k``` steps and fast pointer may take ```m + Bl + k``` steps where ```A``` and ```B``` are constants which can be any number. The idea being that the slow or fast pointer might have to move full loops ```A``` or ```B``` times respectively before intersection, where ```B > A```. But we also know that,
38 | ```
39 | fast = 2*slow
40 | ```
41 | ```
42 | m + Bl + k = 2*(m + Al + k)
43 | ```
44 | ```
45 | (B - 2A)l = m+k
46 | ```
47 | ```
48 | constant*l = m+k
49 | ```
50 | Thus, ```m+k = c*l```, where c is an integer constant.
51 |
52 | This signifies that ```m+k``` steps are equivalent to looping ```c``` number of times in the loop and coming back to same position.
53 |
54 | Now as per algorithm, we reset fast pointer to head, and make it now behave like slow. Doing this, it is guranteed that the next intersection point is the node which marks the start of cycle.
55 |
56 | This is because, now the fast pointer has to take ```m``` steps to reach the first node of cycle. Thus, the slow pointer will make ```c*l - k``` steps. This ensures that the position of slow pointer after ```c*l - k``` steps will be the first node of cycle.
--------------------------------------------------------------------------------
/09_Graphs/bfs.cpp:
--------------------------------------------------------------------------------
1 | #include
2 |
3 | using namespace std;
4 |
5 | #define VERTICES 99999
6 |
7 | class Graph
8 | {
9 | private:
10 | struct Node
11 | {
12 | int data;
13 | struct Node *next;
14 | };
15 | int no_of_vertices;
16 | struct Node **adj_list;
17 | int *queue = NULL;
18 | int *head = NULL;
19 | int *tail = NULL;
20 |
21 | public:
22 | bool visited[VERTICES] = {0};
23 | void make_graph(int no_of_vertices);
24 | void display();
25 | void add_edge();
26 | void bfs(int v);
27 | };
28 |
29 | /*
30 | This function is used to create a graph
31 | parameters : no_of_vertices
32 | Returns : void
33 | */
34 | void Graph ::make_graph(int no_of_vertices)
35 | {
36 | this->no_of_vertices = no_of_vertices;
37 | adj_list = new struct Node *[no_of_vertices];
38 | queue = new int[no_of_vertices];
39 | head = &queue[0];
40 | tail = &queue[0];
41 | for (int i = 0; i < no_of_vertices; i++)
42 | {
43 | adj_list[i] = NULL;
44 | }
45 | }
46 |
47 | /*
48 | This function iterates over all the possible edges and asks user if they want the edge to exist or not
49 | parameters : void
50 | Returns : void
51 | */
52 | void Graph ::add_edge()
53 | {
54 | for (int i = 0; i < no_of_vertices; i++)
55 | {
56 | for (int j = 0; j < no_of_vertices; j++)
57 | {
58 | if (i != j)
59 | {
60 | char choice;
61 | cout << "Are vertices " << i << " and " << j << " adjacent? (Y/N) : ";
62 | cin >> choice;
63 |
64 | if (toupper(choice) == 'Y')
65 | {
66 | if (adj_list[i] == NULL)
67 | {
68 | adj_list[i] = new struct Node;
69 | adj_list[i]->data = j;
70 | adj_list[i]->next = NULL;
71 | continue;
72 | }
73 | struct Node *temp;
74 | temp = adj_list[i];
75 | while (temp->next != NULL)
76 | {
77 | temp = temp->next;
78 | }
79 | temp->next = new struct Node;
80 | temp->next->data = j;
81 | temp->next->next = NULL;
82 | }
83 | }
84 | }
85 | }
86 | }
87 | // end of function
88 |
89 | /*
90 | Performs BFS traversal
91 | parameters : vertex on which bfs is called
92 | Returns : void
93 | */
94 | void Graph ::bfs(int v)
95 | {
96 | *tail = v;
97 | tail++;
98 | visited[v] = 1 ;
99 |
100 | while (head != tail)
101 | {
102 | struct Node *temp;
103 | cout << *head << " ";
104 | temp = adj_list[*head];
105 | head++;
106 |
107 | while (temp != NULL)
108 | {
109 | if (visited[temp->data] == 0)
110 | {
111 | *tail = temp->data;
112 | visited[temp->data] = 1 ;
113 | tail++;
114 | }
115 | temp = temp->next;
116 | }
117 | }
118 | }
119 |
120 | /*
121 | This function is used to display the graph
122 | parameters : void
123 | Returns : void
124 | */
125 | void Graph ::display()
126 | {
127 | cout << "The adjacency list representation is :-\n";
128 | for (int i = 0; i < no_of_vertices; i++)
129 | {
130 | cout << i << " : ";
131 | if (adj_list[i] != NULL)
132 | {
133 | struct Node *temp;
134 | temp = adj_list[i];
135 | while (temp->next != NULL)
136 | {
137 | cout << temp->data << " -> ";
138 | temp = temp->next;
139 | }
140 | cout << temp->data;
141 | }
142 | cout << "\n";
143 | }
144 | }
145 | // end of function
146 |
147 | // main function starts here
148 | int main()
149 | {
150 | Graph g;
151 | int no_of_vertices;
152 | cout << "Enter the number of vertices : ";
153 | cin >> no_of_vertices;
154 |
155 | g.make_graph(no_of_vertices);
156 | g.add_edge();
157 |
158 | int source;
159 | cout << "Enter the source node: ";
160 | cin >> source;
161 |
162 | g.bfs(source);
163 |
164 | return 0;
165 | }
166 | // end of main
167 |
--------------------------------------------------------------------------------
/03_Queues/Queue_using_arrays/Queue_using_two_pointer.cpp:
--------------------------------------------------------------------------------
1 | /*******************************************************************
2 | @brief Implementing queue using a array and a two pointer
3 | ********************************************************************/
4 | #include
5 | #define MAX_SIZE 10
6 | using namespace std;
7 |
8 | class Queue
9 | {
10 | private:
11 | int queue[MAX_SIZE];
12 | int *rear = NULL;
13 | int *front = NULL; // initially , the pointers points to NULL
14 |
15 | public:
16 | void enqueue(int element);
17 | void dequeue();
18 | bool isEmpty();
19 | bool isFull();
20 | void display();
21 | };
22 |
23 | /*
24 | * Function Name: enqueue
25 | * Input: Integer element which is to be inserted
26 | * Output: None
27 | * Logic: This function allows us to insert an element in queue
28 | * Example Call: enqueue(5)
29 | */
30 | void Queue ::enqueue(int element)
31 | {
32 | if (!isFull()) // insert element only if queue is not full
33 | {
34 | if (rear == NULL) // if the queue is empty , and the element is first to be inserted
35 | {
36 | rear = queue; // points to the first element in queue
37 | front = queue;
38 | queue[0] = element;
39 | }
40 | else
41 | {
42 | rear++; // increment the pointer to next position
43 | *rear = element; // change the value of next position
44 | }
45 | }
46 | else
47 | {
48 | cout << "queue is full!\n";
49 | }
50 | }
51 |
52 | /*
53 | * Function Name: dequeue
54 | * Input: None
55 | * Output: Returns the first element of queue
56 | * Logic: This function allows us to remove the first element of queue
57 | * Example Call: dequeue()
58 | */
59 | void Queue ::dequeue()
60 | {
61 | if (!isEmpty()) // we check if queue is not empty
62 | {
63 | cout << *front << "\n";
64 | front++; // incrementing the front the pointer to previous position
65 | // for dequeue , we first delete the element to which the front is pointing , then we increment front
66 | }
67 | else
68 | {
69 | cout << "The queue is empty!\n";
70 | }
71 | }
72 |
73 | /*
74 | * Function Name: display
75 | * Input: None
76 | * Output: Prints all the elements in the queue
77 | * Logic: This function allows us to print the elements currently in queue
78 | * Example Call: display()
79 | */
80 | void Queue ::display()
81 | {
82 | if (!isEmpty())
83 | {
84 | cout << "The elements of queue are : ";
85 | for (int i = 0; front + i <= rear; i++) // here , we print the element in queue till address of queue's last element matches with address at which rear points
86 | {
87 | cout << *(front + i) << " ";
88 | }
89 | cout << "\n";
90 | }
91 | else
92 | {
93 | cout << "The queue is empty!\n";
94 | }
95 | }
96 |
97 | /*
98 | * Function Name: isFull
99 | * Input: None
100 | * Output: Returns a boolean true if the queue is full
101 | * Logic: This function allows us to check if the queue is full
102 | * Example Call: isFull()
103 | */
104 | bool Queue ::isFull()
105 | {
106 | if (rear >= &queue[MAX_SIZE - 1])
107 | {
108 | return true; // we return false since the queue had 1 element left and is not yet empty
109 | }
110 | else
111 | {
112 | return false; // for all other cases , queue is not empty
113 | }
114 | }
115 |
116 | /*
117 | * Function Name: isEmpty
118 | * Input: None
119 | * Output: Returns a boolean true if the queue is empty
120 | * Logic: This function allows us to check if the queue is empty
121 | * Example Call: isEmpty()
122 | */
123 | bool Queue ::isEmpty()
124 | {
125 | if (rear < front || rear == NULL) // when the queue is empty , ether the front pointer is ahead of the rear pointer , or the rear pointer is null
126 | {
127 | return true;
128 | }
129 | else
130 | {
131 | return false; // for all other cases , queue is not empty
132 | }
133 | }
134 |
135 | int main()
136 | {
137 | class Queue Queue1; // creating an object Queue1 of class Queue
138 |
139 | Queue1.enqueue(34);
140 | Queue1.enqueue(55);
141 | Queue1.enqueue(10);
142 | Queue1.display();
143 | // Queue1.dequeue();
144 | // Queue1.display();
145 | // Queue1.dequeue();
146 | // Queue1.display();
147 | // Queue1.dequeue();
148 | // Queue1.display();
149 |
150 | return 0;
151 | }
152 |
--------------------------------------------------------------------------------
/Algorithms/3_Dynamic_Programming/placing_parentheses.cpp:
--------------------------------------------------------------------------------
1 | /***********************************************************************************
2 | @brief Placing parentheses to obtain maximum value of given arithmetic expression
3 | ************************************************************************************/
4 | #include
5 | #include
6 |
7 | using namespace std;
8 |
9 | struct minmax
10 | {
11 | long long int min = 999999999;
12 | long long int max = -999999999;
13 | };
14 |
15 | long long int maximum(long long int a, long long int b, long long int c, long long int d)
16 | {
17 | if (a > b && a > c && a > d)
18 | {
19 | return a;
20 | }
21 | else if (b > c && b > d)
22 | {
23 | return b;
24 | }
25 | else if (c > d)
26 | {
27 | return c;
28 | }
29 | return d;
30 | }
31 | long long int minimum(long long int a, long long int b, long long int c, long long int d)
32 | {
33 | if (a < b && a < c && a < d)
34 | {
35 | return a;
36 | }
37 | else if (b < c && b < d)
38 | {
39 | return b;
40 | }
41 | else if (c < d)
42 | {
43 | return c;
44 | }
45 | return d;
46 | }
47 |
48 | struct minmax min_and_max(vector> maxima, vector> minima, vector operand, vector operation, long long int i, long long int j, struct minmax h)
49 | {
50 | for (long long int k = i; k < j; k++)
51 | {
52 | long long int a, b, c, d;
53 | if (operation[k] == '+')
54 | {
55 | a = maxima[i][k] + maxima[k+1][j];
56 | b = maxima[i][k] + minima[k+1][j];
57 | c = minima[i][k] + maxima[k+1][j];
58 | d = minima[i][k] + minima[k+1][j];
59 | }
60 | else if (operation[k] == '-')
61 | {
62 | a = maxima[i][k] - maxima[k+1][j];
63 | b = maxima[i][k] - minima[k+1][j];
64 | c = minima[i][k] - maxima[k+1][j];
65 | d = minima[i][k] - minima[k+1][j];
66 | }
67 | else
68 | {
69 | a = maxima[i][k] * maxima[k+1][j];
70 | b = maxima[i][k] * minima[k+1][j];
71 | c = minima[i][k] * maxima[k+1][j];
72 | d = minima[i][k] * minima[k+1][j];
73 | }
74 |
75 | long long int x = maximum(a,b,c,d) ;
76 | long long int y = minimum(a,b,c,d) ;
77 | if ( x > h.max)
78 | {
79 | h.max = x ;
80 | }
81 | if ( y < h.min)
82 | {
83 | h.min = y ;
84 | }
85 | }
86 |
87 | return h;
88 | }
89 |
90 | long long int get_val(vector operand, vector operation)
91 | {
92 | long long int n = operand.size();
93 | vector> maxima(n, vector(n, 0));
94 | vector> minima(n, vector(n, 0));
95 |
96 | for (long long int i = 0; i < n; i++)
97 | {
98 | minima[i][i] = maxima[i][i] = operand[i];
99 | }
100 |
101 | for (long long int d = 1; d < n; d++)
102 | {
103 | for (long long int i = 0, j = i + d; j < n; i++, j++)
104 | {
105 | minmax h;
106 | h = min_and_max(maxima, minima, operand, operation, i, j, h);
107 | maxima[i][j] = h.max;
108 | minima[i][j] = h.min;
109 | }
110 | }
111 |
112 | return maxima[0][maxima.size()-1];
113 | }
114 |
115 | int main()
116 | {
117 | string s;
118 | cout << "Please enter your arithmetic expression: " ;
119 | cin >> s;
120 | vector operand;
121 | vector operation;
122 |
123 | int index = 0;
124 | bool input_flag = 1;
125 | for (int i = 0; i < s.length(); i++)
126 | {
127 | if (s[index] == '+' || s[index] == '-' || s[index] == '*' || s[index] == '/')
128 | {
129 | operation.push_back(s[index]);
130 | input_flag = 1;
131 | }
132 | else
133 | {
134 | if (input_flag == 1)
135 | {
136 | operand.push_back(s[index] - '0');
137 | }
138 | else
139 | {
140 | operand[operand.size() - 1] = 10 * operand[operand.size() - 1] + (s[index] - '0');
141 | }
142 | input_flag = 0;
143 | }
144 | index++;
145 | }
146 |
147 | long long int x = get_val(operand, operation) ;
148 | cout << "The maximum value of expression is: " << x ;
149 |
150 | return 0;
151 | }
--------------------------------------------------------------------------------
/03_Queues/Queue_using_arrays/Queue_using_one_pointer.cpp:
--------------------------------------------------------------------------------
1 | /**********************************************************************
2 | @brief Implementing queue using a array and a single pointer
3 | ***********************************************************************/
4 | #include
5 | #define MAX_SIZE 10
6 | using namespace std;
7 |
8 | class Queue
9 | {
10 | private:
11 | int queue[MAX_SIZE];
12 | int *rear = NULL; // initially , the pointer points to NULL
13 |
14 | public:
15 | void enqueue(int element);
16 | void dequeue();
17 | bool isEmpty();
18 | bool isFull();
19 | void display();
20 | };
21 |
22 | /*
23 | * Function Name: enqueue
24 | * Input: Integer element which is to be inserted
25 | * Output: None
26 | * Logic: This function allows us to insert an element in queue
27 | * Example Call: enqueue(5)
28 | */
29 | void Queue ::enqueue(int element)
30 | {
31 | if (!isFull()) // insert element only if queue is not full
32 | {
33 | if (rear == NULL) // if the queue is empty , and the element is first to be inserted
34 | {
35 | rear = queue; // points to the first element in queue
36 | queue[0] = element;
37 | }
38 | else
39 | {
40 | rear++; // increment the pointer to next position
41 | *rear = element; // change the value of next position
42 | }
43 | }
44 | else
45 | {
46 | cout << "queue is full!\n";
47 | }
48 | }
49 |
50 | /*
51 | * Function Name: dequeue
52 | * Input: None
53 | * Output: Returns the first element of queue
54 | * Logic: This function allows us to remove the first element of queue
55 | * Example Call: dequeue()
56 | */
57 | void Queue ::dequeue()
58 | {
59 | if (rear == &queue[0]) // considering the case if only one element is present
60 | {
61 | cout << queue[0] << "\n";
62 | rear = NULL;
63 | }
64 | else if (!isEmpty()) // we check if queue is not empty
65 | {
66 | cout << queue[0] << "\n"; // print the first element i.e. 0th index in array
67 |
68 | for (int i = 0; &queue[i] < rear; i++) // here , we go till the second last element of queue
69 | {
70 | queue[i] = queue[i + 1];
71 | }
72 |
73 | rear--; // decrementing the pointer to previous position
74 | }
75 | else
76 | {
77 | cout << "The queue is empty!\n";
78 | }
79 | }
80 |
81 | /*
82 | * Function Name: display
83 | * Input: None
84 | * Output: Prints all the elements in the queue
85 | * Logic: This function allows us to print the elements currently in queue
86 | * Example Call: display()
87 | */
88 | void Queue ::display()
89 | {
90 | if (rear != NULL)
91 | {
92 | cout << "The elements of queue are : ";
93 | for (int i = 0; &queue[i] <= rear; i++) // here , we print the element in queue till address of queue's last element matches with address at which rear points
94 | {
95 | cout << queue[i] << " ";
96 | }
97 | cout << "\n";
98 | }
99 | else
100 | {
101 | cout << "The queue is empty!\n";
102 | }
103 | }
104 |
105 | /*
106 | * Function Name: isEmpty
107 | * Input: None
108 | * Output: Returns a boolean true if the queue is empty
109 | * Logic: This function allows us to check if the queue is empty
110 | * Example Call: isEmpty()
111 | */
112 | bool Queue ::isEmpty()
113 | {
114 | if (rear == &queue[0])
115 | {
116 | rear = NULL;
117 | return false; // we return false since the queue had 1 element left and is not yet empty
118 | }
119 | else if (rear == NULL)
120 | {
121 | return true;
122 | }
123 | else
124 | {
125 | return false; // for all other cases , queue is not empty
126 | }
127 | }
128 |
129 | /*
130 | * Function Name: isFull
131 | * Input: None
132 | * Output: Returns a boolean true if the queue is full
133 | * Logic: This function allows us to check if the queue is full
134 | * Example Call: isFull()
135 | */
136 | bool Queue ::isFull()
137 | {
138 | if (rear == &queue[MAX_SIZE - 1])
139 | {
140 | return true; // we return true since the rear already points at last element and there is no space ahead
141 | }
142 | else
143 | {
144 | return false; // for all other cases , queue is not empty
145 | }
146 | }
147 |
148 | int main()
149 | {
150 | class Queue Queue1; // creating an object Queue1 of class Queue
151 |
152 | Queue1.enqueue(34);
153 | Queue1.enqueue(55);
154 | Queue1.enqueue(10);
155 | Queue1.display();
156 | Queue1.dequeue();
157 | Queue1.display();
158 | Queue1.dequeue();
159 | Queue1.display();
160 | Queue1.dequeue();
161 | Queue1.display();
162 |
163 | return 0;
164 | }
165 |
--------------------------------------------------------------------------------
/09_Graphs/README.md:
--------------------------------------------------------------------------------
1 | # Graphs
2 |  3 |
4 | # Introduction
5 |
6 | A Graph is a data structure which represents connections between objects. It is a pair (V, E), where V is a set of nodes, called vertices (which represent objects), and E is a collection of pairs of vertices, called edges (which represent connections).
7 |
8 | For example, the Internet often can be thought of as a graph, where web pages are connected to each other by links.
9 |
10 | Another example is maps, you can think of maps as a graph, sort of where you have intersections that are connected by roads. For example, we might be interested in questions like: “What’s the fastest way to go from home to college?” or “What is the cheapest way to go from home to college”. Graphs are data structures used for solving these kinds of problems.
11 |
12 | # Graph Representation
13 | Three ways to represent a graph are :-
14 |
15 | ## 1) Edge list
16 | ## 2) Adjacency Matrix
17 |
18 | In this method, we use a matrix with size V × V. The values of matrix are boolean. The value of matrix[u][v] is set to 1 if there is an edge from vertex u to vertex v.
19 |
20 | Adjacency matrix are useful to represent dense graphs.
21 |
22 | ## 3) Adjacency List
23 |
24 | In this representation all the vertices connected to a vertex v are listed on A linked list for that vertex v.
25 |
26 | Adjacency list are useful to represent sparse graphs.
27 |
28 |
3 |
4 | # Introduction
5 |
6 | A Graph is a data structure which represents connections between objects. It is a pair (V, E), where V is a set of nodes, called vertices (which represent objects), and E is a collection of pairs of vertices, called edges (which represent connections).
7 |
8 | For example, the Internet often can be thought of as a graph, where web pages are connected to each other by links.
9 |
10 | Another example is maps, you can think of maps as a graph, sort of where you have intersections that are connected by roads. For example, we might be interested in questions like: “What’s the fastest way to go from home to college?” or “What is the cheapest way to go from home to college”. Graphs are data structures used for solving these kinds of problems.
11 |
12 | # Graph Representation
13 | Three ways to represent a graph are :-
14 |
15 | ## 1) Edge list
16 | ## 2) Adjacency Matrix
17 |
18 | In this method, we use a matrix with size V × V. The values of matrix are boolean. The value of matrix[u][v] is set to 1 if there is an edge from vertex u to vertex v.
19 |
20 | Adjacency matrix are useful to represent dense graphs.
21 |
22 | ## 3) Adjacency List
23 |
24 | In this representation all the vertices connected to a vertex v are listed on A linked list for that vertex v.
25 |
26 | Adjacency list are useful to represent sparse graphs.
27 |
28 |  29 |
30 | # Graph Traversals
31 | Two ways to traverse a graph are :-
32 |
33 | 1) DFS
34 | 2) BFS
35 |
36 | Every problem of graph is simply a modification of DFS and BFS algorithm. Whenever we try to solve graph problems, we need to think to traversal which fits the best for problem statement and the modifications which we need to make to the traversal. For eg. maintaining a simple counter during dfs previsit and postvisit allows us to count number of connected components in graph.
37 |
38 | # Dijkstra's Algorithm
39 |
40 | Dijkstra's Algorithm is essentially BFS + Heuristics. It allows us to calculate shortest path from a given source node to all other nodes in the graph.
41 |
42 |
29 |
30 | # Graph Traversals
31 | Two ways to traverse a graph are :-
32 |
33 | 1) DFS
34 | 2) BFS
35 |
36 | Every problem of graph is simply a modification of DFS and BFS algorithm. Whenever we try to solve graph problems, we need to think to traversal which fits the best for problem statement and the modifications which we need to make to the traversal. For eg. maintaining a simple counter during dfs previsit and postvisit allows us to count number of connected components in graph.
37 |
38 | # Dijkstra's Algorithm
39 |
40 | Dijkstra's Algorithm is essentially BFS + Heuristics. It allows us to calculate shortest path from a given source node to all other nodes in the graph.
41 |
42 |  43 |
44 | Consider we are at a node A, which is connected to node B and C by weights 3 and 5 respectively. Here, we can not be sure that distance between A and C i.e. 5, is the shortest one between A and C. This is beacuse, chances are B and C might be connected by weight 1, which makes shortest path between A and C as A -> B -> C of length 4. However, we can be sure, that the distance between A and B is the shortest possible distance between A and B. This is because there is no other possibility which can give path shorter than A -> B directly. Here A -> C -> B will definitely be more expensive since A -> C itself is more expensive than A -> B.
45 |
46 | A naive approach can be to keep on relaxing edges in a while loop till there comes a state where no edge is relaxed in the entire loop. However, the above intuition allows us to relax edges in certain order.
47 |
48 | The time complexity of Dijkstra's algorithm depends on the underlying data structure. If our priority queue is based on heap, the Time Complexity is ```O((|V| + |E|)log(|V|))```. On the other hand, if our priority queue is array bases, it takes ```O(|V|^2)```. It is important to note that in case of dense graphs, array implementation of Priority Queue works better than Heap implementation. Thus, the choice of data structure depends on the sparsity of graph.
49 |
50 | # Bellman-Ford Algorithm
51 |
52 | The intuition which we had for dijkstra's algorithm fails when we take negative edges in account. Because now for the above example, A -> C -> B can be cheaper than A -> B, if C -> B were to become negative. Hence for graphs with negative weights, we use Bellman Ford Algorithm.
53 |
54 | The idea behind bellman ford algorithm is a naive version of Dijkstra's algorithm. It doesnt follow any sense of heuristic to relax edges. We keep on relaxing all the edges in the graph for |V|-1 times. Thus the time complexity is ```O(|V||E|)```. However, this algorithm currently works only for graphs with no negative cycles. In presence of negative cycles, the distances can be relaxed infinitely. Thus we slightly modify the code to accommodate negative distances as well.
55 |
56 | # Minimum Spanning Tree
57 |
58 | A minimum spanning tree (MST) of a connected, undirected graph G(V, E) is a subset of the edges E' that forms a tree (i.e., it is connected and acyclic) and spans all the vertices in V. Furthermore, the sum of the weights of the edges in the minimum spanning tree is minimized.
59 |
60 | # Kruskal Algorithm
61 |
62 | The core idea is indeed to add edges to the growing minimum spanning tree in increasing order of their weights, as long as adding the edge does not form a cycle.
63 |
64 | # Prims Algorithm
65 |
--------------------------------------------------------------------------------
/leetcode/73 Set Matrix Zeroes.cpp:
--------------------------------------------------------------------------------
1 | /*
2 | Approach 1: Store all locations of 0s in a vector and then set zero for all rows and columns
3 | Runtime: 12ms
4 | Memory: 13.8MB
5 | Time Complexity: O((m*n)(m+n)), where m*n is dimension of board. The worst case can be when the entire matrix is filled with zeros and each zero requires (m+n) time complexity to SetZero.
6 | */
7 | class Solution {
8 | public:
9 | void setZero(vector>& matrix, int i, int j)
10 | {
11 | for (int x = 0; x < matrix.size(); x++ )
12 | {
13 | matrix[x][j] = 0;
14 | }
15 |
16 | for (int x = 0; x < matrix[0].size(); x++ )
17 | {
18 | matrix[i][x] = 0;
19 | }
20 | }
21 | void setZeroes(vector>& matrix) {
22 | vector > v;
23 | for (int i = 0; i < matrix.size(); i++)
24 | {
25 | for (int j = 0; j < matrix[0].size(); j++)
26 | {
27 | if (matrix[i][j] == 0)
28 | {
29 | pair p;
30 | p.first = i;
31 | p.second = j;
32 | v.push_back(p);
33 | }
34 | }
35 | }
36 |
37 | for (int i = 0; i < v.size(); i++)
38 | {
39 | setZero(matrix, v[i].first, v[i].second);
40 | }
41 | }
42 | };
43 |
44 | /*
45 | Approach 2: Store all rows and cols of 0s in a set and then set zero for all rows and columns
46 | Runtime: 7ms
47 | Memory: 13.92MB
48 | Time Complexity: O(m^2 + n^2 + m*n), where m*n is dimension of board. The worst case can be when the entire matrix is filled with zeros and each zero requires (m+n) time complexity to SetZero.
49 | */
50 | class Solution {
51 | public:
52 | void setZeroes(vector>& matrix) {
53 | set row;
54 | set col;
55 | for (int i = 0; i < matrix.size(); i++)
56 | {
57 | for (int j = 0; j < matrix[0].size(); j++)
58 | {
59 | if (matrix[i][j] == 0)
60 | {
61 | row.insert(i);
62 | col.insert(j);
63 | }
64 | }
65 | }
66 | //row sweeper
67 | for (auto i : row)
68 | {
69 | for (int x = 0; x < matrix[0].size(); x++)
70 | {
71 | matrix[i][x]=0;
72 | }
73 | }
74 | //col sweeper
75 | for (auto i : col)
76 | {
77 | for (int x = 0; x < matrix.size(); x++)
78 | {
79 | matrix[x][i]=0;
80 | }
81 | }
82 | }
83 | };
84 |
85 | /*
86 | Approach 3: Without using additional memory by using matrix first row and first column itself as flag.
87 | Runtime: 16ms
88 | Memory: 13.6MB
89 | Time Complexity: O(m^2 + n^2 + m*n), where m*n is dimension of board. The worst case can be when the entire matrix is filled with zeros and each zero requires (m+n) time complexity to SetZero.
90 | */
91 | class Solution {
92 | public:
93 | void setZeroes(vector>& matrix) {
94 | bool special_row = 0, special_col = 0;
95 |
96 | for (int i = 0; i < matrix.size(); i++)
97 | {
98 | for (int j = 0; j < matrix[0].size(); j++)
99 | {
100 | if (matrix[i][j] == 0)
101 | {
102 | if (i == 0)
103 | {
104 | special_row = 1;
105 | }
106 | if (j == 0)
107 | {
108 | special_col = 1;
109 | }
110 | matrix[i][0]=0;
111 | matrix[0][j]=0;
112 | }
113 | }
114 | }
115 |
116 | //row sweeper
117 | for (int x = 1; x < matrix.size(); x++)
118 | {
119 | if (matrix[x][0]==0)
120 | {
121 | for (int i = 1; i < matrix[0].size(); i++)
122 | {
123 | matrix[x][i]=0;
124 | }
125 | }
126 | }
127 | //col sweeper
128 | for (int x = 1; x < matrix[0].size(); x++)
129 | {
130 | if (matrix[0][x]==0)
131 | {
132 | for (int i = 1; i < matrix.size(); i++)
133 | {
134 | matrix[i][x]=0;
135 | }
136 | }
137 | }
138 | //special check for first row and first col
139 | if (special_row)
140 | {
141 | for (int i = 1; i < matrix[0].size(); i++)
142 | {
143 | matrix[0][i]=0;
144 | }
145 | }
146 | if (special_col)
147 | {
148 | for (int i = 1; i < matrix.size(); i++)
149 | {
150 | matrix[i][0]=0;
151 | }
152 | }
153 | }
154 | };
--------------------------------------------------------------------------------
/05_Trees/avl.cpp:
--------------------------------------------------------------------------------
1 | /***************************************
2 | @brief Implementing AVL trees
3 | ****************************************/
4 | #include
5 | #include
6 |
7 | using namespace std;
8 |
9 | class Tree
10 | {
11 | struct node
12 | {
13 | int data;
14 | int height;
15 | struct node *parent = NULL;
16 | struct node *left = NULL;
17 | struct node *right = NULL;
18 | };
19 | void insert(int element);
20 | struct node *find(struct node *&node, int key);
21 | void rebalance(struct node *&node) ;
22 | void rebalanceRight(struct node *&node) ;
23 | void rebalanceLeft(struct node *&node) ;
24 |
25 | public:
26 | struct node *root = NULL; // The pointer to the root node.
27 | void AVLinsert(int element);
28 | void adjustHeight(struct node *&node) ;
29 | void preorder(struct node *&node);
30 | };
31 |
32 | void Tree::adjustHeight(struct node *&node)
33 | {
34 | struct node* p = node->parent ;
35 | int left = 0, right = 0;
36 |
37 | if (node->left != NULL)
38 | {
39 | left = node->left->height ;
40 | }
41 | if (node->right != NULL)
42 | {
43 | left = node->right->height ;
44 | }
45 |
46 | node->height = 1+ max(left, right) ;
47 |
48 | if (p != NULL)
49 | {
50 | adjustHeight(p) ;
51 | }
52 |
53 | }
54 |
55 | void Tree::rebalanceRight(struct node *&node)
56 | {
57 | struct node * l = node->left ;
58 |
59 | if (l->left->height < l->right->height)
60 | {
61 |
62 | }
63 | }
64 |
65 | void Tree::rebalanceLeft(struct node *&node)
66 | {
67 | // cout << "Rebalance right"<< endl ;
68 | }
69 |
70 | void Tree::AVLinsert(int element)
71 | {
72 | insert(element) ;
73 | struct node* x = find(root, element) ;
74 | rebalance(x) ;
75 | }
76 |
77 | void Tree::rebalance(struct node *&node)
78 | {
79 | struct node* p = node->parent ;
80 | int left = 0, right = 0;
81 |
82 | if (node->left != NULL)
83 | {
84 | left = node->left->height ;
85 | }
86 | if (node->right != NULL)
87 | {
88 | right = node->right->height ;
89 | }
90 |
91 | if (left > right+1)
92 | {
93 | rebalanceRight(node) ;
94 | }
95 | else if (right > left+1)
96 | {
97 | rebalanceLeft(node) ;
98 | }
99 |
100 | adjustHeight(node) ;
101 |
102 | if (p != NULL)
103 | {
104 | rebalance(p) ;
105 | }
106 | }
107 |
108 | struct Tree::node *Tree::find(struct node *&node, int key)
109 | {
110 | if (node != NULL)
111 | {
112 | if (key == node->data)
113 | {
114 | return node;
115 | }
116 | else if (key > node->data)
117 | {
118 | return find(node->right, key);
119 | }
120 | else
121 | {
122 | return find(node->left, key);
123 | }
124 | }
125 | return NULL;
126 | }
127 |
128 | void Tree::insert(int element)
129 | {
130 | if (root == NULL)
131 | {
132 | // Special case for root node
133 | root = (struct node *)malloc(sizeof(node));
134 | root->data = element;
135 | root->parent = NULL;
136 | root->left = NULL;
137 | root->right = NULL;
138 | }
139 | else
140 | {
141 | struct node *node = root; // Creating a traversing pointer
142 | bool inserted = 0;
143 | while (!inserted)
144 | {
145 | if (element > node->data)
146 | {
147 | if (node->right == NULL)
148 | {
149 | node->right = (struct node *)malloc(sizeof(struct node));
150 | node->right->parent = node;
151 | node->right->data = element;
152 | node->right->left = NULL;
153 | node->right->right = NULL;
154 | inserted = 1;
155 | continue;
156 | }
157 | else
158 | {
159 | node = node->right;
160 | }
161 | }
162 | else
163 | {
164 | if (node->left == NULL)
165 | {
166 | node->left = (struct node *)malloc(sizeof(struct node));
167 | node->left->parent = node;
168 | node->left->data = element;
169 | node->left->left = NULL;
170 | node->left->right = NULL;
171 | inserted = 1;
172 | continue;
173 | }
174 | else
175 | {
176 | node = node->left;
177 | }
178 | }
179 | }
180 | }
181 | }
182 |
183 | void Tree::preorder(struct node *&node)
184 | {
185 | if (node != NULL)
186 | {
187 | cout << node->data << " ";
188 | preorder(node->left);
189 | preorder(node->right);
190 | }
191 | }
192 |
193 | int main()
194 | {
195 | Tree t;
196 | int x;
197 |
198 | // Insertion
199 | t.AVLinsert(15);
200 | t.AVLinsert(33);
201 | t.AVLinsert(45);
202 | t.AVLinsert(34);
203 | t.AVLinsert(1);
204 | t.AVLinsert(35);
205 |
206 | t.preorder(t.root) ;
207 |
208 | return 0;
209 | }
210 |
211 |
--------------------------------------------------------------------------------
/Algorithms/3_Dynamic_Programming/Readme.md:
--------------------------------------------------------------------------------
1 | ## Dynamic Programming
2 |
3 | ```
4 | Thus, I thought dynamic programming was a good name. It was something not even a Congressman could object to.
5 |
6 | ~ Richard Bellman
7 | ```
8 |
9 | ### Why Dynamic Programming ?
10 |
11 | The greedy approach, though is very easy to think, does not always work. Another approach is a recursive way to solve problems, but this approach at time leads to very bad time complexities. The problem with this approach is that we solve the same sub-problems several times.
12 |
13 | Thus we go for dynamic programming, which is essentially performing recursion smartly.
14 |
15 | # Solving a Dynamic Programming Problem
16 |
17 | ## Step I: Identifying a Dynamic Programming Problem
18 |
19 | There are two properties a problem should hold for dynamic programming to work:
20 |
21 | * Optimal Substructure
22 | * Overlapping Solutions
23 |
24 | ### Optimal Substructure
25 |
26 | Optimal substructure means that the optimal solution to a problem of size n is based on an optimal solution of same problem of smaller size, say n-1. In other words, while building the solution for a problem of size n, we can make use of the solution to a problem of size k, where k < n.
27 |
28 | Consider the example of finding shortest path. If there is a shortest path between node A and node C, given it passes from node B, we know shortest path from A to C is sum of shortest path from A to B and shortest path from B to C. Thus, somewhere we are able to use this smaller instances of problem (A-B and B-C) in order to find the shortest path from A to C. Thus, we can pose Shortest Path Problem as Dynamic Programming problem.
29 |
30 | This same thing is not applicable for finding longest path. If there is a longest path between node A and node C, given it passes from node B, we can not say that that longest path between A and C is sum of longest path between A and B and longest path between B and C. Hence this problem can not be posed as a dynamic programming problem.
31 |
32 | ### Overlapping Solutions
33 |
34 | Overlapping solutions are found when recursive function is called with exactly same parameters more than once. In this case we say that a subproblem is solved multiple times. Had we been solving a subproblem only once, the code would have been really fast, even if we are using recursion. Memoization, Dynamic programming and Greedy approach are techniques used to solve this classic problem.
35 |
36 | ## Step II: Develop a Recursive Formula to solve the problem
37 |
38 | ## Step III: Use Dynamic Programming
39 |
40 | There are two approach in dynamic programming:-
41 |
42 | * Memoization
43 | * Bottom-up approach
44 |
45 | ### Memoization
46 |
47 | The first approach is top-down with memoization. This approach is used only when we have identified overlapping subproblems in the problem. In this approach, we write the procedure recursively in a natural manner, but modified to save the result of each subproblem in some cache. The procedure now first checks to see whether it has previously solved this subproblem. If so, it returns the saved value, saving further computation at this level; if not, the procedure computes the value in the usual manner. We say that the recursive procedure has been memoized; it “remembers” what results it has computed previously.
48 |
49 | Deciding data structure of cache is important step in memoization. The cache should be capable of storing results of all subproblems. Usually cache is an array or hash table. If our problem has only one parameter, then we can go for 1D-Arrays. However, if there are multiple parameters to be considered, we use multi-dimensional array.
50 |
51 | ```Memoization = Recursion + Cache - Overlapping Subproblems```
52 |
53 |
43 |
44 | Consider we are at a node A, which is connected to node B and C by weights 3 and 5 respectively. Here, we can not be sure that distance between A and C i.e. 5, is the shortest one between A and C. This is beacuse, chances are B and C might be connected by weight 1, which makes shortest path between A and C as A -> B -> C of length 4. However, we can be sure, that the distance between A and B is the shortest possible distance between A and B. This is because there is no other possibility which can give path shorter than A -> B directly. Here A -> C -> B will definitely be more expensive since A -> C itself is more expensive than A -> B.
45 |
46 | A naive approach can be to keep on relaxing edges in a while loop till there comes a state where no edge is relaxed in the entire loop. However, the above intuition allows us to relax edges in certain order.
47 |
48 | The time complexity of Dijkstra's algorithm depends on the underlying data structure. If our priority queue is based on heap, the Time Complexity is ```O((|V| + |E|)log(|V|))```. On the other hand, if our priority queue is array bases, it takes ```O(|V|^2)```. It is important to note that in case of dense graphs, array implementation of Priority Queue works better than Heap implementation. Thus, the choice of data structure depends on the sparsity of graph.
49 |
50 | # Bellman-Ford Algorithm
51 |
52 | The intuition which we had for dijkstra's algorithm fails when we take negative edges in account. Because now for the above example, A -> C -> B can be cheaper than A -> B, if C -> B were to become negative. Hence for graphs with negative weights, we use Bellman Ford Algorithm.
53 |
54 | The idea behind bellman ford algorithm is a naive version of Dijkstra's algorithm. It doesnt follow any sense of heuristic to relax edges. We keep on relaxing all the edges in the graph for |V|-1 times. Thus the time complexity is ```O(|V||E|)```. However, this algorithm currently works only for graphs with no negative cycles. In presence of negative cycles, the distances can be relaxed infinitely. Thus we slightly modify the code to accommodate negative distances as well.
55 |
56 | # Minimum Spanning Tree
57 |
58 | A minimum spanning tree (MST) of a connected, undirected graph G(V, E) is a subset of the edges E' that forms a tree (i.e., it is connected and acyclic) and spans all the vertices in V. Furthermore, the sum of the weights of the edges in the minimum spanning tree is minimized.
59 |
60 | # Kruskal Algorithm
61 |
62 | The core idea is indeed to add edges to the growing minimum spanning tree in increasing order of their weights, as long as adding the edge does not form a cycle.
63 |
64 | # Prims Algorithm
65 |
--------------------------------------------------------------------------------
/leetcode/73 Set Matrix Zeroes.cpp:
--------------------------------------------------------------------------------
1 | /*
2 | Approach 1: Store all locations of 0s in a vector and then set zero for all rows and columns
3 | Runtime: 12ms
4 | Memory: 13.8MB
5 | Time Complexity: O((m*n)(m+n)), where m*n is dimension of board. The worst case can be when the entire matrix is filled with zeros and each zero requires (m+n) time complexity to SetZero.
6 | */
7 | class Solution {
8 | public:
9 | void setZero(vector>& matrix, int i, int j)
10 | {
11 | for (int x = 0; x < matrix.size(); x++ )
12 | {
13 | matrix[x][j] = 0;
14 | }
15 |
16 | for (int x = 0; x < matrix[0].size(); x++ )
17 | {
18 | matrix[i][x] = 0;
19 | }
20 | }
21 | void setZeroes(vector>& matrix) {
22 | vector > v;
23 | for (int i = 0; i < matrix.size(); i++)
24 | {
25 | for (int j = 0; j < matrix[0].size(); j++)
26 | {
27 | if (matrix[i][j] == 0)
28 | {
29 | pair p;
30 | p.first = i;
31 | p.second = j;
32 | v.push_back(p);
33 | }
34 | }
35 | }
36 |
37 | for (int i = 0; i < v.size(); i++)
38 | {
39 | setZero(matrix, v[i].first, v[i].second);
40 | }
41 | }
42 | };
43 |
44 | /*
45 | Approach 2: Store all rows and cols of 0s in a set and then set zero for all rows and columns
46 | Runtime: 7ms
47 | Memory: 13.92MB
48 | Time Complexity: O(m^2 + n^2 + m*n), where m*n is dimension of board. The worst case can be when the entire matrix is filled with zeros and each zero requires (m+n) time complexity to SetZero.
49 | */
50 | class Solution {
51 | public:
52 | void setZeroes(vector>& matrix) {
53 | set row;
54 | set col;
55 | for (int i = 0; i < matrix.size(); i++)
56 | {
57 | for (int j = 0; j < matrix[0].size(); j++)
58 | {
59 | if (matrix[i][j] == 0)
60 | {
61 | row.insert(i);
62 | col.insert(j);
63 | }
64 | }
65 | }
66 | //row sweeper
67 | for (auto i : row)
68 | {
69 | for (int x = 0; x < matrix[0].size(); x++)
70 | {
71 | matrix[i][x]=0;
72 | }
73 | }
74 | //col sweeper
75 | for (auto i : col)
76 | {
77 | for (int x = 0; x < matrix.size(); x++)
78 | {
79 | matrix[x][i]=0;
80 | }
81 | }
82 | }
83 | };
84 |
85 | /*
86 | Approach 3: Without using additional memory by using matrix first row and first column itself as flag.
87 | Runtime: 16ms
88 | Memory: 13.6MB
89 | Time Complexity: O(m^2 + n^2 + m*n), where m*n is dimension of board. The worst case can be when the entire matrix is filled with zeros and each zero requires (m+n) time complexity to SetZero.
90 | */
91 | class Solution {
92 | public:
93 | void setZeroes(vector>& matrix) {
94 | bool special_row = 0, special_col = 0;
95 |
96 | for (int i = 0; i < matrix.size(); i++)
97 | {
98 | for (int j = 0; j < matrix[0].size(); j++)
99 | {
100 | if (matrix[i][j] == 0)
101 | {
102 | if (i == 0)
103 | {
104 | special_row = 1;
105 | }
106 | if (j == 0)
107 | {
108 | special_col = 1;
109 | }
110 | matrix[i][0]=0;
111 | matrix[0][j]=0;
112 | }
113 | }
114 | }
115 |
116 | //row sweeper
117 | for (int x = 1; x < matrix.size(); x++)
118 | {
119 | if (matrix[x][0]==0)
120 | {
121 | for (int i = 1; i < matrix[0].size(); i++)
122 | {
123 | matrix[x][i]=0;
124 | }
125 | }
126 | }
127 | //col sweeper
128 | for (int x = 1; x < matrix[0].size(); x++)
129 | {
130 | if (matrix[0][x]==0)
131 | {
132 | for (int i = 1; i < matrix.size(); i++)
133 | {
134 | matrix[i][x]=0;
135 | }
136 | }
137 | }
138 | //special check for first row and first col
139 | if (special_row)
140 | {
141 | for (int i = 1; i < matrix[0].size(); i++)
142 | {
143 | matrix[0][i]=0;
144 | }
145 | }
146 | if (special_col)
147 | {
148 | for (int i = 1; i < matrix.size(); i++)
149 | {
150 | matrix[i][0]=0;
151 | }
152 | }
153 | }
154 | };
--------------------------------------------------------------------------------
/05_Trees/avl.cpp:
--------------------------------------------------------------------------------
1 | /***************************************
2 | @brief Implementing AVL trees
3 | ****************************************/
4 | #include
5 | #include
6 |
7 | using namespace std;
8 |
9 | class Tree
10 | {
11 | struct node
12 | {
13 | int data;
14 | int height;
15 | struct node *parent = NULL;
16 | struct node *left = NULL;
17 | struct node *right = NULL;
18 | };
19 | void insert(int element);
20 | struct node *find(struct node *&node, int key);
21 | void rebalance(struct node *&node) ;
22 | void rebalanceRight(struct node *&node) ;
23 | void rebalanceLeft(struct node *&node) ;
24 |
25 | public:
26 | struct node *root = NULL; // The pointer to the root node.
27 | void AVLinsert(int element);
28 | void adjustHeight(struct node *&node) ;
29 | void preorder(struct node *&node);
30 | };
31 |
32 | void Tree::adjustHeight(struct node *&node)
33 | {
34 | struct node* p = node->parent ;
35 | int left = 0, right = 0;
36 |
37 | if (node->left != NULL)
38 | {
39 | left = node->left->height ;
40 | }
41 | if (node->right != NULL)
42 | {
43 | left = node->right->height ;
44 | }
45 |
46 | node->height = 1+ max(left, right) ;
47 |
48 | if (p != NULL)
49 | {
50 | adjustHeight(p) ;
51 | }
52 |
53 | }
54 |
55 | void Tree::rebalanceRight(struct node *&node)
56 | {
57 | struct node * l = node->left ;
58 |
59 | if (l->left->height < l->right->height)
60 | {
61 |
62 | }
63 | }
64 |
65 | void Tree::rebalanceLeft(struct node *&node)
66 | {
67 | // cout << "Rebalance right"<< endl ;
68 | }
69 |
70 | void Tree::AVLinsert(int element)
71 | {
72 | insert(element) ;
73 | struct node* x = find(root, element) ;
74 | rebalance(x) ;
75 | }
76 |
77 | void Tree::rebalance(struct node *&node)
78 | {
79 | struct node* p = node->parent ;
80 | int left = 0, right = 0;
81 |
82 | if (node->left != NULL)
83 | {
84 | left = node->left->height ;
85 | }
86 | if (node->right != NULL)
87 | {
88 | right = node->right->height ;
89 | }
90 |
91 | if (left > right+1)
92 | {
93 | rebalanceRight(node) ;
94 | }
95 | else if (right > left+1)
96 | {
97 | rebalanceLeft(node) ;
98 | }
99 |
100 | adjustHeight(node) ;
101 |
102 | if (p != NULL)
103 | {
104 | rebalance(p) ;
105 | }
106 | }
107 |
108 | struct Tree::node *Tree::find(struct node *&node, int key)
109 | {
110 | if (node != NULL)
111 | {
112 | if (key == node->data)
113 | {
114 | return node;
115 | }
116 | else if (key > node->data)
117 | {
118 | return find(node->right, key);
119 | }
120 | else
121 | {
122 | return find(node->left, key);
123 | }
124 | }
125 | return NULL;
126 | }
127 |
128 | void Tree::insert(int element)
129 | {
130 | if (root == NULL)
131 | {
132 | // Special case for root node
133 | root = (struct node *)malloc(sizeof(node));
134 | root->data = element;
135 | root->parent = NULL;
136 | root->left = NULL;
137 | root->right = NULL;
138 | }
139 | else
140 | {
141 | struct node *node = root; // Creating a traversing pointer
142 | bool inserted = 0;
143 | while (!inserted)
144 | {
145 | if (element > node->data)
146 | {
147 | if (node->right == NULL)
148 | {
149 | node->right = (struct node *)malloc(sizeof(struct node));
150 | node->right->parent = node;
151 | node->right->data = element;
152 | node->right->left = NULL;
153 | node->right->right = NULL;
154 | inserted = 1;
155 | continue;
156 | }
157 | else
158 | {
159 | node = node->right;
160 | }
161 | }
162 | else
163 | {
164 | if (node->left == NULL)
165 | {
166 | node->left = (struct node *)malloc(sizeof(struct node));
167 | node->left->parent = node;
168 | node->left->data = element;
169 | node->left->left = NULL;
170 | node->left->right = NULL;
171 | inserted = 1;
172 | continue;
173 | }
174 | else
175 | {
176 | node = node->left;
177 | }
178 | }
179 | }
180 | }
181 | }
182 |
183 | void Tree::preorder(struct node *&node)
184 | {
185 | if (node != NULL)
186 | {
187 | cout << node->data << " ";
188 | preorder(node->left);
189 | preorder(node->right);
190 | }
191 | }
192 |
193 | int main()
194 | {
195 | Tree t;
196 | int x;
197 |
198 | // Insertion
199 | t.AVLinsert(15);
200 | t.AVLinsert(33);
201 | t.AVLinsert(45);
202 | t.AVLinsert(34);
203 | t.AVLinsert(1);
204 | t.AVLinsert(35);
205 |
206 | t.preorder(t.root) ;
207 |
208 | return 0;
209 | }
210 |
211 |
--------------------------------------------------------------------------------
/Algorithms/3_Dynamic_Programming/Readme.md:
--------------------------------------------------------------------------------
1 | ## Dynamic Programming
2 |
3 | ```
4 | Thus, I thought dynamic programming was a good name. It was something not even a Congressman could object to.
5 |
6 | ~ Richard Bellman
7 | ```
8 |
9 | ### Why Dynamic Programming ?
10 |
11 | The greedy approach, though is very easy to think, does not always work. Another approach is a recursive way to solve problems, but this approach at time leads to very bad time complexities. The problem with this approach is that we solve the same sub-problems several times.
12 |
13 | Thus we go for dynamic programming, which is essentially performing recursion smartly.
14 |
15 | # Solving a Dynamic Programming Problem
16 |
17 | ## Step I: Identifying a Dynamic Programming Problem
18 |
19 | There are two properties a problem should hold for dynamic programming to work:
20 |
21 | * Optimal Substructure
22 | * Overlapping Solutions
23 |
24 | ### Optimal Substructure
25 |
26 | Optimal substructure means that the optimal solution to a problem of size n is based on an optimal solution of same problem of smaller size, say n-1. In other words, while building the solution for a problem of size n, we can make use of the solution to a problem of size k, where k < n.
27 |
28 | Consider the example of finding shortest path. If there is a shortest path between node A and node C, given it passes from node B, we know shortest path from A to C is sum of shortest path from A to B and shortest path from B to C. Thus, somewhere we are able to use this smaller instances of problem (A-B and B-C) in order to find the shortest path from A to C. Thus, we can pose Shortest Path Problem as Dynamic Programming problem.
29 |
30 | This same thing is not applicable for finding longest path. If there is a longest path between node A and node C, given it passes from node B, we can not say that that longest path between A and C is sum of longest path between A and B and longest path between B and C. Hence this problem can not be posed as a dynamic programming problem.
31 |
32 | ### Overlapping Solutions
33 |
34 | Overlapping solutions are found when recursive function is called with exactly same parameters more than once. In this case we say that a subproblem is solved multiple times. Had we been solving a subproblem only once, the code would have been really fast, even if we are using recursion. Memoization, Dynamic programming and Greedy approach are techniques used to solve this classic problem.
35 |
36 | ## Step II: Develop a Recursive Formula to solve the problem
37 |
38 | ## Step III: Use Dynamic Programming
39 |
40 | There are two approach in dynamic programming:-
41 |
42 | * Memoization
43 | * Bottom-up approach
44 |
45 | ### Memoization
46 |
47 | The first approach is top-down with memoization. This approach is used only when we have identified overlapping subproblems in the problem. In this approach, we write the procedure recursively in a natural manner, but modified to save the result of each subproblem in some cache. The procedure now first checks to see whether it has previously solved this subproblem. If so, it returns the saved value, saving further computation at this level; if not, the procedure computes the value in the usual manner. We say that the recursive procedure has been memoized; it “remembers” what results it has computed previously.
48 |
49 | Deciding data structure of cache is important step in memoization. The cache should be capable of storing results of all subproblems. Usually cache is an array or hash table. If our problem has only one parameter, then we can go for 1D-Arrays. However, if there are multiple parameters to be considered, we use multi-dimensional array.
50 |
51 | ```Memoization = Recursion + Cache - Overlapping Subproblems```
52 |
53 |  54 |
55 | ### Bottom-Up approach
56 |
57 | The second approach is the bottom-up method. This approach typically depends on some natural notion of the “size” of a subproblem, such that solving any particular subproblem depends only on solving “smaller” subproblems. We sort the subproblems by size and solve them in size order, smallest first. When solving a particular subproblem, we have already solved all of the smaller subproblems its solution depends upon, and we have saved their solutions. We solve each subproblem only once, and when we first see it, we have already solved all of its prerequisite subproblems.
58 |
59 | Even without any overlapping subproblems, Memoization requires recursion, which is expensive in terms of both memory and time. Each AR creation and removal adds overhead. In fact, without overlapping subproblem, Memoization is simply recursion. The core idea in bottom-up is to unroll recursion and solve it in opposite direction. The time complexity for many problems using bottom-up approach will be similar to that using memoization, but it is better since no recursion is involved and only single AR is created.
60 |
61 |
54 |
55 | ### Bottom-Up approach
56 |
57 | The second approach is the bottom-up method. This approach typically depends on some natural notion of the “size” of a subproblem, such that solving any particular subproblem depends only on solving “smaller” subproblems. We sort the subproblems by size and solve them in size order, smallest first. When solving a particular subproblem, we have already solved all of the smaller subproblems its solution depends upon, and we have saved their solutions. We solve each subproblem only once, and when we first see it, we have already solved all of its prerequisite subproblems.
58 |
59 | Even without any overlapping subproblems, Memoization requires recursion, which is expensive in terms of both memory and time. Each AR creation and removal adds overhead. In fact, without overlapping subproblem, Memoization is simply recursion. The core idea in bottom-up is to unroll recursion and solve it in opposite direction. The time complexity for many problems using bottom-up approach will be similar to that using memoization, but it is better since no recursion is involved and only single AR is created.
60 |
61 |  62 |
63 | Dynamic programming thus uses additional memory to save computation time; it serves an example of a time-memory trade-off. The savings however are massive: an exponential-time solution may be transformed into a polynomial-time solution.
64 |
65 | ## List of problems implemented
66 |
67 | * ```coin_change.cpp```
68 | * ```knapsack_limited.cpp```
69 | * ```longest_common_sequence.cpp```
70 | * ```optimal_alignment.cpp```
71 | * ```placing_parentheses.cpp```
72 |
--------------------------------------------------------------------------------
62 |
63 | Dynamic programming thus uses additional memory to save computation time; it serves an example of a time-memory trade-off. The savings however are massive: an exponential-time solution may be transformed into a polynomial-time solution.
64 |
65 | ## List of problems implemented
66 |
67 | * ```coin_change.cpp```
68 | * ```knapsack_limited.cpp```
69 | * ```longest_common_sequence.cpp```
70 | * ```optimal_alignment.cpp```
71 | * ```placing_parentheses.cpp```
72 |
--------------------------------------------------------------------------------
 7 |
8 | ## Basic operations on stack
9 | 1) Push: This function adds an element to the top of the Stack.
10 | 2) Pop: This function removes the topmost element from the stack.
11 | 3) IsEmpty: Checks whether the stack is empty.
12 | 4) IsFull: Checks whether the stack is full.
13 |
14 |
7 |
8 | ## Basic operations on stack
9 | 1) Push: This function adds an element to the top of the Stack.
10 | 2) Pop: This function removes the topmost element from the stack.
11 | 3) IsEmpty: Checks whether the stack is empty.
12 | 4) IsFull: Checks whether the stack is full.
13 |
14 |  15 |
--------------------------------------------------------------------------------
/hanoi.cpp:
--------------------------------------------------------------------------------
1 | #include
15 |
--------------------------------------------------------------------------------
/hanoi.cpp:
--------------------------------------------------------------------------------
1 | #include  18 |
19 | ## Basic operations on Queue
20 | 1) Enqueue() : To insert an element to queue
21 | 2) Dequeue() : To delete an element from to queue
22 | 3) IsEmpty() : To check if queue is empty
23 | 4) IsFull() : To check if queue is full
24 |
25 | ## Implenting Queues
26 | There are two methods to implement queues
27 | 1) Using arrays
28 | 2) Using Linked List
29 |
30 | # Circular Queues
31 |
32 | # DEQueues
33 | Double-Ended-Queues (DEQueues) are a type of queue, which do not follow FIFO exactly.In simple queues, front is used to delete an element and rear is used to insert an element. However, Double-Ended-Queue allow insertion and deletion at both ends , front and rear.
34 | Further subtypes of DEQueue :-
35 | 1) Input-Resticted-Dequeue - Insertion only takes place at rear end, while deletion can take place at either of ends
36 | 2) Output-Resticted-Dequeue - Deletion only takes place at front end, while insertion can take place at either of ends
37 |
38 | # Priority Queues
39 | Refer ```6_Heaps``` for implementation of Priority queues.
40 |
--------------------------------------------------------------------------------
/09_Graphs/djikstras.cpp:
--------------------------------------------------------------------------------
1 | #include
18 |
19 | ## Basic operations on Queue
20 | 1) Enqueue() : To insert an element to queue
21 | 2) Dequeue() : To delete an element from to queue
22 | 3) IsEmpty() : To check if queue is empty
23 | 4) IsFull() : To check if queue is full
24 |
25 | ## Implenting Queues
26 | There are two methods to implement queues
27 | 1) Using arrays
28 | 2) Using Linked List
29 |
30 | # Circular Queues
31 |
32 | # DEQueues
33 | Double-Ended-Queues (DEQueues) are a type of queue, which do not follow FIFO exactly.In simple queues, front is used to delete an element and rear is used to insert an element. However, Double-Ended-Queue allow insertion and deletion at both ends , front and rear.
34 | Further subtypes of DEQueue :-
35 | 1) Input-Resticted-Dequeue - Insertion only takes place at rear end, while deletion can take place at either of ends
36 | 2) Output-Resticted-Dequeue - Deletion only takes place at front end, while insertion can take place at either of ends
37 |
38 | # Priority Queues
39 | Refer ```6_Heaps``` for implementation of Priority queues.
40 |
--------------------------------------------------------------------------------
/09_Graphs/djikstras.cpp:
--------------------------------------------------------------------------------
1 | #include  22 |
23 | Here, insertion and extracting maximum element both takes O(log(n)). During insertion, we can insert the new element as a leaf node and then shift it in tree as per the properties of heap. This is implemented by basic operations such as ```siftUp()``` and ```siftDown()```.
24 |
25 | Further, this entire structure can be unwrapped as an array.
26 |
27 |
22 |
23 | Here, insertion and extracting maximum element both takes O(log(n)). During insertion, we can insert the new element as a leaf node and then shift it in tree as per the properties of heap. This is implemented by basic operations such as ```siftUp()``` and ```siftDown()```.
24 |
25 | Further, this entire structure can be unwrapped as an array.
26 |
27 |  28 |
29 |
--------------------------------------------------------------------------------
/09_Graphs/bellman-ford.cpp:
--------------------------------------------------------------------------------
1 | #include
28 |
29 |
--------------------------------------------------------------------------------
/09_Graphs/bellman-ford.cpp:
--------------------------------------------------------------------------------
1 | #include  22 |
23 | Here, we know that ```k``` has to be a node in the loop, only then can the slow pointer and fast pointer intersect. Now, the slow pointer may take ```m + Al + k``` steps and fast pointer may take ```m + Bl + k``` steps where ```A``` and ```B``` are constants which can be any number. The idea being that the slow or fast pointer might have to move full loops ```A``` or ```B``` times respectively before intersection, where ```B > A```. But we also know that,
24 | ```
25 | fast = 2*slow
26 | ```
27 | ```
28 | m + Bl + k = 2*(m + Al + k)
29 | ```
30 | ```
31 | (B - 2A)l = m+k
32 | ```
33 | ```
34 | constant*l = m+k
35 | ```
36 | Thus, ```m+k = c*l```, where c is an integer constant.
37 |
38 | This signifies that ```m+k``` steps are equivalent to looping ```c``` number of times in the loop and coming back to same position.
39 |
40 | Now as per algorithm, we reset fast pointer to head, and make it now behave like slow. Doing this, it is guranteed that the next intersection point is the node which marks the start of cycle.
41 |
42 | This is because, now the fast pointer has to take ```m``` steps to reach the first node of cycle. Thus, the slow pointer will make ```c*l - k``` steps. This ensures that the position of slow pointer after ```c*l - k``` steps will be the first node of cycle.
43 |
--------------------------------------------------------------------------------
/02_Stack/stack.cpp:
--------------------------------------------------------------------------------
1 | /*******************************************************************
2 | @brief Implementing stack and performing basic operations
3 | ********************************************************************/
4 |
5 | #include
22 |
23 | Here, we know that ```k``` has to be a node in the loop, only then can the slow pointer and fast pointer intersect. Now, the slow pointer may take ```m + Al + k``` steps and fast pointer may take ```m + Bl + k``` steps where ```A``` and ```B``` are constants which can be any number. The idea being that the slow or fast pointer might have to move full loops ```A``` or ```B``` times respectively before intersection, where ```B > A```. But we also know that,
24 | ```
25 | fast = 2*slow
26 | ```
27 | ```
28 | m + Bl + k = 2*(m + Al + k)
29 | ```
30 | ```
31 | (B - 2A)l = m+k
32 | ```
33 | ```
34 | constant*l = m+k
35 | ```
36 | Thus, ```m+k = c*l```, where c is an integer constant.
37 |
38 | This signifies that ```m+k``` steps are equivalent to looping ```c``` number of times in the loop and coming back to same position.
39 |
40 | Now as per algorithm, we reset fast pointer to head, and make it now behave like slow. Doing this, it is guranteed that the next intersection point is the node which marks the start of cycle.
41 |
42 | This is because, now the fast pointer has to take ```m``` steps to reach the first node of cycle. Thus, the slow pointer will make ```c*l - k``` steps. This ensures that the position of slow pointer after ```c*l - k``` steps will be the first node of cycle.
43 |
--------------------------------------------------------------------------------
/02_Stack/stack.cpp:
--------------------------------------------------------------------------------
1 | /*******************************************************************
2 | @brief Implementing stack and performing basic operations
3 | ********************************************************************/
4 |
5 | #include  18 |
19 | Amortized analysis is a method for analyzing a given algorithm's complexity, or how much of a resource, especially time or memory, it takes to execute. The motivation for amortized analysis is that looking at the worst-case run time can be too pessimistic. Instead, amortized analysis averages the running times of operations and considers both the expensive and cheap operations together over the whole sequence of operations.
20 |
21 | ### Aggregate Method
22 |
23 |
18 |
19 | Amortized analysis is a method for analyzing a given algorithm's complexity, or how much of a resource, especially time or memory, it takes to execute. The motivation for amortized analysis is that looking at the worst-case run time can be too pessimistic. Instead, amortized analysis averages the running times of operations and considers both the expensive and cheap operations together over the whole sequence of operations.
20 |
21 | ### Aggregate Method
22 |
23 |  24 |
25 | ### Banker Method
26 |
27 | In Bankers method, we associate certain fixed extra cost for all cheap operations, which will then compensate for the expensive operation.
28 |
29 |
24 |
25 | ### Banker Method
26 |
27 | In Bankers method, we associate certain fixed extra cost for all cheap operations, which will then compensate for the expensive operation.
28 |
29 |  30 |
31 | Thus, associating cost of 3 with each cheap operation allows us to ignore the cost during resizing. Overall, we can claim that the cost for each operation is 3, or O(1).
32 |
33 | ### Physicist Method
34 |
35 | This method is very similar to the concept of potential energy. If we go from lower level to higher level, potential energy increases. In a similar fashion, we have a potential function here. We expend ```h(t) - h (t-1)``` amount of work every time inserting an element.
36 |
37 |
30 |
31 | Thus, associating cost of 3 with each cheap operation allows us to ignore the cost during resizing. Overall, we can claim that the cost for each operation is 3, or O(1).
32 |
33 | ### Physicist Method
34 |
35 | This method is very similar to the concept of potential energy. If we go from lower level to higher level, potential energy increases. In a similar fashion, we have a potential function here. We expend ```h(t) - h (t-1)``` amount of work every time inserting an element.
36 |
37 |  38 |
39 | The choice of potential function is important here. It should be made such that is ```Ct``` is small, potential function should increase at each step.
40 |
38 |
39 | The choice of potential function is important here. It should be made such that is ```Ct``` is small, potential function should increase at each step.
40 |  41 |
42 | The general cost without resizing is:
43 |
41 |
42 | The general cost without resizing is:
43 |  44 | The general cost with resizing is:
45 |
44 | The general cost with resizing is:
45 |  46 |
47 |
48 |
49 | ## Points to note
50 |
51 | * It is important to resize the array by constant factor, say twice the bigger, rather than constant amount, say by 10 always. This is because if we increase by constant amount, the expensive operations can no more be compensated by cheap operations and runtime jumps to O(n)
52 | * ```*size ++``` implies that size pointer should be incremented and then its value should be dereferenced, while ```(*size)++``` implies, increment the value stored in size.
53 |
--------------------------------------------------------------------------------
/leetcode/1456 Maximum Number of Vowels in a Substring of Given Length.cpp:
--------------------------------------------------------------------------------
1 | /*
2 | Approach 1: sliding a static window of size k over string and checking maximum everytime
3 | Runtime: 2077ms
4 | Memory: 10.20MB
5 | Time Complexity: O(n*k)
6 | */
7 | class Solution {
8 | public:
9 | int maxVowels(string s, int k) {
10 | int l = s.length();
11 | int max = 0;
12 | for (int i = 0; i <= l - k && max != k; i++)
13 | {
14 | int curr = 0;
15 | //if a vowel is hit
16 | if (s[i] == 'a' || s[i] == 'e' || s[i] == 'i' || s[i] == 'o' || s[i] == 'u')
17 | {
18 | curr++;
19 | for (int j = i+1; j < k+i; j++)
20 | {
21 | if (s[j] == 'a' || s[j] == 'e' || s[j] == 'i' || s[j] == 'o' || s[j] == 'u')
22 | {
23 | curr++;
24 | }
25 | }
26 | if (curr > max)
27 | {
28 | max = curr;
29 | }
30 | }
31 | }
32 | int curr = 0;
33 | for (int j = l-k+1; j < l && max!=k; j++)
34 | {
35 | if (s[j] == 'a' || s[j] == 'e' || s[j] == 'i' || s[j] == 'o' || s[j] == 'u')
36 | {
37 | curr++;
38 | }
39 | }
40 | if (curr > max)
41 | {
42 | max = curr;
43 | }
44 | return max;
45 | }
46 | };
47 |
48 | /*Approach 2: sliding a static window of size k over string and tracking vowels which came in and went out of window
49 | Runtime: 15ms
50 | Memory: 10.26MB
51 | Time Complexity: O(n+k)
52 | */
53 | class Solution {
54 | public:
55 | int maxVowels(string s, int k) {
56 | int l = s.length();
57 | //case1
58 | if (l <= k)
59 | {
60 | int curr = 0;
61 | for (int i = 0; i < l; i++)
62 | {
63 | if (s[i] == 'a' || s[i] == 'e' || s[i] == 'i' || s[i] == 'o' || s[i] == 'u')
64 | {
65 | curr++;
66 | }
67 | }
68 | return curr;
69 | }
70 | else
71 | {
72 | int max = 0;
73 | int curr = 0;
74 | //check first k letters as baseline
75 | for (int i = 0; i < k; i++)
76 | {
77 | if (s[i] == 'a' || s[i] == 'e' || s[i] == 'i' || s[i] == 'o' || s[i] == 'u')
78 | {
79 | max++;
80 | }
81 | }
82 | curr = max;
83 | for (int i = 1; i <= l-k; i++)
84 | {
85 | //if we a vowel was dropped from sliding window
86 | if (s[i-1] == 'a' || s[i-1] == 'e' || s[i-1] == 'i' || s[i-1] == 'o' || s[i-1] == 'u')
87 | {
88 | curr--;
89 | }
90 | //if new letter of window is a vowel
91 | if (s[i+k-1] == 'a' || s[i+k-1] == 'e' || s[i+k-1] == 'i' || s[i+k-1] == 'o' || s[i+k-1] == 'u')
92 | {
93 | curr++;
94 | }
95 | if (curr > max)
96 | {
97 | max = curr;
98 | }
99 | }
100 | return max;
101 | }
102 | }
103 | };
--------------------------------------------------------------------------------
/02_Stack/Miscellaneous/Balancing_brackets.cpp:
--------------------------------------------------------------------------------
1 | /*******************************************
2 | @brief Balancing brackets in text
3 | ********************************************/
4 |
5 | #include
46 |
47 |
48 |
49 | ## Points to note
50 |
51 | * It is important to resize the array by constant factor, say twice the bigger, rather than constant amount, say by 10 always. This is because if we increase by constant amount, the expensive operations can no more be compensated by cheap operations and runtime jumps to O(n)
52 | * ```*size ++``` implies that size pointer should be incremented and then its value should be dereferenced, while ```(*size)++``` implies, increment the value stored in size.
53 |
--------------------------------------------------------------------------------
/leetcode/1456 Maximum Number of Vowels in a Substring of Given Length.cpp:
--------------------------------------------------------------------------------
1 | /*
2 | Approach 1: sliding a static window of size k over string and checking maximum everytime
3 | Runtime: 2077ms
4 | Memory: 10.20MB
5 | Time Complexity: O(n*k)
6 | */
7 | class Solution {
8 | public:
9 | int maxVowels(string s, int k) {
10 | int l = s.length();
11 | int max = 0;
12 | for (int i = 0; i <= l - k && max != k; i++)
13 | {
14 | int curr = 0;
15 | //if a vowel is hit
16 | if (s[i] == 'a' || s[i] == 'e' || s[i] == 'i' || s[i] == 'o' || s[i] == 'u')
17 | {
18 | curr++;
19 | for (int j = i+1; j < k+i; j++)
20 | {
21 | if (s[j] == 'a' || s[j] == 'e' || s[j] == 'i' || s[j] == 'o' || s[j] == 'u')
22 | {
23 | curr++;
24 | }
25 | }
26 | if (curr > max)
27 | {
28 | max = curr;
29 | }
30 | }
31 | }
32 | int curr = 0;
33 | for (int j = l-k+1; j < l && max!=k; j++)
34 | {
35 | if (s[j] == 'a' || s[j] == 'e' || s[j] == 'i' || s[j] == 'o' || s[j] == 'u')
36 | {
37 | curr++;
38 | }
39 | }
40 | if (curr > max)
41 | {
42 | max = curr;
43 | }
44 | return max;
45 | }
46 | };
47 |
48 | /*Approach 2: sliding a static window of size k over string and tracking vowels which came in and went out of window
49 | Runtime: 15ms
50 | Memory: 10.26MB
51 | Time Complexity: O(n+k)
52 | */
53 | class Solution {
54 | public:
55 | int maxVowels(string s, int k) {
56 | int l = s.length();
57 | //case1
58 | if (l <= k)
59 | {
60 | int curr = 0;
61 | for (int i = 0; i < l; i++)
62 | {
63 | if (s[i] == 'a' || s[i] == 'e' || s[i] == 'i' || s[i] == 'o' || s[i] == 'u')
64 | {
65 | curr++;
66 | }
67 | }
68 | return curr;
69 | }
70 | else
71 | {
72 | int max = 0;
73 | int curr = 0;
74 | //check first k letters as baseline
75 | for (int i = 0; i < k; i++)
76 | {
77 | if (s[i] == 'a' || s[i] == 'e' || s[i] == 'i' || s[i] == 'o' || s[i] == 'u')
78 | {
79 | max++;
80 | }
81 | }
82 | curr = max;
83 | for (int i = 1; i <= l-k; i++)
84 | {
85 | //if we a vowel was dropped from sliding window
86 | if (s[i-1] == 'a' || s[i-1] == 'e' || s[i-1] == 'i' || s[i-1] == 'o' || s[i-1] == 'u')
87 | {
88 | curr--;
89 | }
90 | //if new letter of window is a vowel
91 | if (s[i+k-1] == 'a' || s[i+k-1] == 'e' || s[i+k-1] == 'i' || s[i+k-1] == 'o' || s[i+k-1] == 'u')
92 | {
93 | curr++;
94 | }
95 | if (curr > max)
96 | {
97 | max = curr;
98 | }
99 | }
100 | return max;
101 | }
102 | }
103 | };
--------------------------------------------------------------------------------
/02_Stack/Miscellaneous/Balancing_brackets.cpp:
--------------------------------------------------------------------------------
1 | /*******************************************
2 | @brief Balancing brackets in text
3 | ********************************************/
4 |
5 | #include  4 |
5 | ## Introduction
6 |
7 | Arrays are a collection of elements stored in a contiguous block of memory, where all elements are of the same data type and are indexed by contiguous integers. This structure allows for quick access to elements, as both reading and writing can be done in constant time. Adding or removing an element at the end of the array is also a constant time operation. However, inserting or removing elements at the beginning or in the middle of an array takes linear time, i.e., `O(n)`, since elements need to be shifted. Additionally, arrays require a contiguous block of memory, which can be a limitation in some cases.
8 |
9 | ## Dynamic Arrays
10 |
11 | The problem with static arrays is that they static. If we are reading a bunch of numbers and we need to put it in an array. But we don't know how many numbers there'll be. we just know there'll be some mark at the end that says we're done with the numbers.
12 |
13 | So we use Dynamic arrays or Resizable arrays. Vectors are an example of dynamic arrays in `c++`
14 |
15 | ## Amortized Analysis
16 |
17 | For the dynamic array, we only resize every so often. Most of the time, we're doing a constant time operation, just adding an element. It's only when we fully reach the capacity, that we have to resize. It is true that the worst case for PushBack() operation is O(n), but we have to bear this cost only when we reach to full capacity of array.
18 |
19 |
4 |
5 | ## Introduction
6 |
7 | Arrays are a collection of elements stored in a contiguous block of memory, where all elements are of the same data type and are indexed by contiguous integers. This structure allows for quick access to elements, as both reading and writing can be done in constant time. Adding or removing an element at the end of the array is also a constant time operation. However, inserting or removing elements at the beginning or in the middle of an array takes linear time, i.e., `O(n)`, since elements need to be shifted. Additionally, arrays require a contiguous block of memory, which can be a limitation in some cases.
8 |
9 | ## Dynamic Arrays
10 |
11 | The problem with static arrays is that they static. If we are reading a bunch of numbers and we need to put it in an array. But we don't know how many numbers there'll be. we just know there'll be some mark at the end that says we're done with the numbers.
12 |
13 | So we use Dynamic arrays or Resizable arrays. Vectors are an example of dynamic arrays in `c++`
14 |
15 | ## Amortized Analysis
16 |
17 | For the dynamic array, we only resize every so often. Most of the time, we're doing a constant time operation, just adding an element. It's only when we fully reach the capacity, that we have to resize. It is true that the worst case for PushBack() operation is O(n), but we have to bear this cost only when we reach to full capacity of array.
18 |
19 |  20 |
21 | Amortized analysis is a method for analyzing a given algorithm's complexity, or how much of a resource, especially time or memory, it takes to execute. The motivation for amortized analysis is that looking at the worst-case run time can be too pessimistic. Instead, amortized analysis averages the running times of operations and considers both the expensive and cheap operations together over the whole sequence of operations.
22 |
23 | ### Aggregate Method
24 |
25 |
20 |
21 | Amortized analysis is a method for analyzing a given algorithm's complexity, or how much of a resource, especially time or memory, it takes to execute. The motivation for amortized analysis is that looking at the worst-case run time can be too pessimistic. Instead, amortized analysis averages the running times of operations and considers both the expensive and cheap operations together over the whole sequence of operations.
22 |
23 | ### Aggregate Method
24 |
25 |  26 |
27 | ### Banker Method
28 |
29 | In Bankers method, we associate certain fixed extra cost for all cheap operations, which will then compensate for the expensive operation.
30 |
31 |
26 |
27 | ### Banker Method
28 |
29 | In Bankers method, we associate certain fixed extra cost for all cheap operations, which will then compensate for the expensive operation.
30 |
31 |  32 |
33 | Thus, associating cost of 3 with each cheap operation allows us to ignore the cost during resizing. Overall, we can claim that the cost for each operation is 3, or O(1).
34 |
35 | ### Physicist Method
36 |
37 | This method is very similar to the concept of potential energy. If we go from lower level to higher level, potential energy increases. In a similar fashion, we have a potential function here. We expend ```h(t) - h (t-1)``` amount of work every time inserting an element.
38 |
39 |
32 |
33 | Thus, associating cost of 3 with each cheap operation allows us to ignore the cost during resizing. Overall, we can claim that the cost for each operation is 3, or O(1).
34 |
35 | ### Physicist Method
36 |
37 | This method is very similar to the concept of potential energy. If we go from lower level to higher level, potential energy increases. In a similar fashion, we have a potential function here. We expend ```h(t) - h (t-1)``` amount of work every time inserting an element.
38 |
39 |  40 |
41 | The choice of potential function is important here. It should be made such that is ```Ct``` is small, potential function should increase at each step.
42 |
40 |
41 | The choice of potential function is important here. It should be made such that is ```Ct``` is small, potential function should increase at each step.
42 |  43 |
44 | The general cost without resizing is:
45 |
43 |
44 | The general cost without resizing is:
45 |  46 | The general cost with resizing is:
47 |
46 | The general cost with resizing is:
47 |  48 |
49 | ## Points to note
50 |
51 | * It is important to resize the array by constant factor, say twice the bigger, rather than constant amount, say by 10 always. This is because if we increase by constant amount, the expensive operations can no more be compensated by cheap operations and runtime jumps to O(n).
52 |
53 | * ```*size ++``` implies that size pointer should be incremented and then its value should be dereferenced, while ```(*size)++``` implies, increment the value stored in size.
--------------------------------------------------------------------------------
/Algorithms/3_Dynamic_Programming/optimal_alignment.cpp:
--------------------------------------------------------------------------------
1 | /***********************************************************************************
2 | @brief Using dynamic programming for optimal alignment of 2 strings along with edit distance
3 | ************************************************************************************/
4 |
5 | #include
48 |
49 | ## Points to note
50 |
51 | * It is important to resize the array by constant factor, say twice the bigger, rather than constant amount, say by 10 always. This is because if we increase by constant amount, the expensive operations can no more be compensated by cheap operations and runtime jumps to O(n).
52 |
53 | * ```*size ++``` implies that size pointer should be incremented and then its value should be dereferenced, while ```(*size)++``` implies, increment the value stored in size.
--------------------------------------------------------------------------------
/Algorithms/3_Dynamic_Programming/optimal_alignment.cpp:
--------------------------------------------------------------------------------
1 | /***********************************************************************************
2 | @brief Using dynamic programming for optimal alignment of 2 strings along with edit distance
3 | ************************************************************************************/
4 |
5 | #include  4 |
5 | ## Introduction
6 |
7 | Think of a traditional array where you allocate a fixed amount of space, like 100 elements, for your data. Even if you only use 20 elements, the other 80 spaces are wasted, and the size of the array can't change. If you need to add more data later, you could run out of space and have to resize the entire array, which can be inefficient and tricky.
8 |
9 | A Linked List solves this problem. Instead of having a fixed-size block of memory, it allocates memory dynamically as needed. Each element in the list (called a "node") is created separately in memory, and each node contains two things:
10 |
11 | * Data: the actual value the node holds.
12 | * Pointer: the memory address of the next node in the list.
13 |
14 | This way, a linked list can grow or shrink as needed without wasting memory, and you can insert or remove elements without worrying about resizing an array.
15 |
16 | ## Advantages & Disadvantages
17 |
18 | Linked lists are not fixed in size. You can add or remove nodes at any time without worrying about running out of space or wasting memory. Also, inserting or deleting an element doesn't require shifting the entire structure (like in arrays). You just need to update a few pointers, making these operations fast.
19 |
20 | However, each node requires extra memory for the pointer (address of the next node), which can make them more memory-hungry than arrays, especially for small data. To find an element, you have to start at the beginning and follow the links until you reach it. This is slower than accessing elements directly by index in an array.
21 |
22 | Linked lists are a great choice when the size of the data is unknown or changes frequently. Since they can dynamically grow and shrink as needed, linked lists prevent the waste of memory that can occur in arrays, where you have to allocate a fixed amount of space. Additionally, linked lists are ideal for scenarios where fast insertions or deletions are required, especially when elements need to be added or removed in the middle of the list. Unlike arrays, which require shifting elements when inserting or deleting, linked lists only need to update a few pointers, making these operations more efficient.
23 |
24 | Linked lists may not be the best option when fast access by index is a priority. In arrays, you can directly access any element using its index, but in a linked list, you have to traverse the list from the beginning to find the desired element, which can be slow. Furthermore, linked lists may not be ideal when memory is a concern. Each node in a linked list requires additional memory for the pointer, which can add up, especially in systems with limited memory or where extra space is at a premium.
25 |
26 | ## Types of Linked List
27 |
28 | 1) Singly Linked List
29 | 2) Doubly Linked List
30 | 3) Circular Linked List
31 | 4) Circular Doubly Linked List
32 |
33 | ## Proof for Floyd Cycle Detection Algorithm
34 |
35 |
4 |
5 | ## Introduction
6 |
7 | Think of a traditional array where you allocate a fixed amount of space, like 100 elements, for your data. Even if you only use 20 elements, the other 80 spaces are wasted, and the size of the array can't change. If you need to add more data later, you could run out of space and have to resize the entire array, which can be inefficient and tricky.
8 |
9 | A Linked List solves this problem. Instead of having a fixed-size block of memory, it allocates memory dynamically as needed. Each element in the list (called a "node") is created separately in memory, and each node contains two things:
10 |
11 | * Data: the actual value the node holds.
12 | * Pointer: the memory address of the next node in the list.
13 |
14 | This way, a linked list can grow or shrink as needed without wasting memory, and you can insert or remove elements without worrying about resizing an array.
15 |
16 | ## Advantages & Disadvantages
17 |
18 | Linked lists are not fixed in size. You can add or remove nodes at any time without worrying about running out of space or wasting memory. Also, inserting or deleting an element doesn't require shifting the entire structure (like in arrays). You just need to update a few pointers, making these operations fast.
19 |
20 | However, each node requires extra memory for the pointer (address of the next node), which can make them more memory-hungry than arrays, especially for small data. To find an element, you have to start at the beginning and follow the links until you reach it. This is slower than accessing elements directly by index in an array.
21 |
22 | Linked lists are a great choice when the size of the data is unknown or changes frequently. Since they can dynamically grow and shrink as needed, linked lists prevent the waste of memory that can occur in arrays, where you have to allocate a fixed amount of space. Additionally, linked lists are ideal for scenarios where fast insertions or deletions are required, especially when elements need to be added or removed in the middle of the list. Unlike arrays, which require shifting elements when inserting or deleting, linked lists only need to update a few pointers, making these operations more efficient.
23 |
24 | Linked lists may not be the best option when fast access by index is a priority. In arrays, you can directly access any element using its index, but in a linked list, you have to traverse the list from the beginning to find the desired element, which can be slow. Furthermore, linked lists may not be ideal when memory is a concern. Each node in a linked list requires additional memory for the pointer, which can add up, especially in systems with limited memory or where extra space is at a premium.
25 |
26 | ## Types of Linked List
27 |
28 | 1) Singly Linked List
29 | 2) Doubly Linked List
30 | 3) Circular Linked List
31 | 4) Circular Doubly Linked List
32 |
33 | ## Proof for Floyd Cycle Detection Algorithm
34 |
35 |  36 |
37 | Here, we know that ```k``` has to be a node in the loop, only then can the slow pointer and fast pointer intersect. Now, the slow pointer may take ```m + Al + k``` steps and fast pointer may take ```m + Bl + k``` steps where ```A``` and ```B``` are constants which can be any number. The idea being that the slow or fast pointer might have to move full loops ```A``` or ```B``` times respectively before intersection, where ```B > A```. But we also know that,
38 | ```
39 | fast = 2*slow
40 | ```
41 | ```
42 | m + Bl + k = 2*(m + Al + k)
43 | ```
44 | ```
45 | (B - 2A)l = m+k
46 | ```
47 | ```
48 | constant*l = m+k
49 | ```
50 | Thus, ```m+k = c*l```, where c is an integer constant.
51 |
52 | This signifies that ```m+k``` steps are equivalent to looping ```c``` number of times in the loop and coming back to same position.
53 |
54 | Now as per algorithm, we reset fast pointer to head, and make it now behave like slow. Doing this, it is guranteed that the next intersection point is the node which marks the start of cycle.
55 |
56 | This is because, now the fast pointer has to take ```m``` steps to reach the first node of cycle. Thus, the slow pointer will make ```c*l - k``` steps. This ensures that the position of slow pointer after ```c*l - k``` steps will be the first node of cycle.
--------------------------------------------------------------------------------
/09_Graphs/bfs.cpp:
--------------------------------------------------------------------------------
1 | #include
36 |
37 | Here, we know that ```k``` has to be a node in the loop, only then can the slow pointer and fast pointer intersect. Now, the slow pointer may take ```m + Al + k``` steps and fast pointer may take ```m + Bl + k``` steps where ```A``` and ```B``` are constants which can be any number. The idea being that the slow or fast pointer might have to move full loops ```A``` or ```B``` times respectively before intersection, where ```B > A```. But we also know that,
38 | ```
39 | fast = 2*slow
40 | ```
41 | ```
42 | m + Bl + k = 2*(m + Al + k)
43 | ```
44 | ```
45 | (B - 2A)l = m+k
46 | ```
47 | ```
48 | constant*l = m+k
49 | ```
50 | Thus, ```m+k = c*l```, where c is an integer constant.
51 |
52 | This signifies that ```m+k``` steps are equivalent to looping ```c``` number of times in the loop and coming back to same position.
53 |
54 | Now as per algorithm, we reset fast pointer to head, and make it now behave like slow. Doing this, it is guranteed that the next intersection point is the node which marks the start of cycle.
55 |
56 | This is because, now the fast pointer has to take ```m``` steps to reach the first node of cycle. Thus, the slow pointer will make ```c*l - k``` steps. This ensures that the position of slow pointer after ```c*l - k``` steps will be the first node of cycle.
--------------------------------------------------------------------------------
/09_Graphs/bfs.cpp:
--------------------------------------------------------------------------------
1 | #include  3 |
4 | # Introduction
5 |
6 | A Graph is a data structure which represents connections between objects. It is a pair (V, E), where V is a set of nodes, called vertices (which represent objects), and E is a collection of pairs of vertices, called edges (which represent connections).
7 |
8 | For example, the Internet often can be thought of as a graph, where web pages are connected to each other by links.
9 |
10 | Another example is maps, you can think of maps as a graph, sort of where you have intersections that are connected by roads. For example, we might be interested in questions like: “What’s the fastest way to go from home to college?” or “What is the cheapest way to go from home to college”. Graphs are data structures used for solving these kinds of problems.
11 |
12 | # Graph Representation
13 | Three ways to represent a graph are :-
14 |
15 | ## 1) Edge list
16 | ## 2) Adjacency Matrix
17 |
18 | In this method, we use a matrix with size V × V. The values of matrix are boolean. The value of matrix[u][v] is set to 1 if there is an edge from vertex u to vertex v.
19 |
20 | Adjacency matrix are useful to represent dense graphs.
21 |
22 | ## 3) Adjacency List
23 |
24 | In this representation all the vertices connected to a vertex v are listed on A linked list for that vertex v.
25 |
26 | Adjacency list are useful to represent sparse graphs.
27 |
28 |
3 |
4 | # Introduction
5 |
6 | A Graph is a data structure which represents connections between objects. It is a pair (V, E), where V is a set of nodes, called vertices (which represent objects), and E is a collection of pairs of vertices, called edges (which represent connections).
7 |
8 | For example, the Internet often can be thought of as a graph, where web pages are connected to each other by links.
9 |
10 | Another example is maps, you can think of maps as a graph, sort of where you have intersections that are connected by roads. For example, we might be interested in questions like: “What’s the fastest way to go from home to college?” or “What is the cheapest way to go from home to college”. Graphs are data structures used for solving these kinds of problems.
11 |
12 | # Graph Representation
13 | Three ways to represent a graph are :-
14 |
15 | ## 1) Edge list
16 | ## 2) Adjacency Matrix
17 |
18 | In this method, we use a matrix with size V × V. The values of matrix are boolean. The value of matrix[u][v] is set to 1 if there is an edge from vertex u to vertex v.
19 |
20 | Adjacency matrix are useful to represent dense graphs.
21 |
22 | ## 3) Adjacency List
23 |
24 | In this representation all the vertices connected to a vertex v are listed on A linked list for that vertex v.
25 |
26 | Adjacency list are useful to represent sparse graphs.
27 |
28 |  29 |
30 | # Graph Traversals
31 | Two ways to traverse a graph are :-
32 |
33 | 1) DFS
34 | 2) BFS
35 |
36 | Every problem of graph is simply a modification of DFS and BFS algorithm. Whenever we try to solve graph problems, we need to think to traversal which fits the best for problem statement and the modifications which we need to make to the traversal. For eg. maintaining a simple counter during dfs previsit and postvisit allows us to count number of connected components in graph.
37 |
38 | # Dijkstra's Algorithm
39 |
40 | Dijkstra's Algorithm is essentially BFS + Heuristics. It allows us to calculate shortest path from a given source node to all other nodes in the graph.
41 |
42 |
29 |
30 | # Graph Traversals
31 | Two ways to traverse a graph are :-
32 |
33 | 1) DFS
34 | 2) BFS
35 |
36 | Every problem of graph is simply a modification of DFS and BFS algorithm. Whenever we try to solve graph problems, we need to think to traversal which fits the best for problem statement and the modifications which we need to make to the traversal. For eg. maintaining a simple counter during dfs previsit and postvisit allows us to count number of connected components in graph.
37 |
38 | # Dijkstra's Algorithm
39 |
40 | Dijkstra's Algorithm is essentially BFS + Heuristics. It allows us to calculate shortest path from a given source node to all other nodes in the graph.
41 |
42 |  43 |
44 | Consider we are at a node A, which is connected to node B and C by weights 3 and 5 respectively. Here, we can not be sure that distance between A and C i.e. 5, is the shortest one between A and C. This is beacuse, chances are B and C might be connected by weight 1, which makes shortest path between A and C as A -> B -> C of length 4. However, we can be sure, that the distance between A and B is the shortest possible distance between A and B. This is because there is no other possibility which can give path shorter than A -> B directly. Here A -> C -> B will definitely be more expensive since A -> C itself is more expensive than A -> B.
45 |
46 | A naive approach can be to keep on relaxing edges in a while loop till there comes a state where no edge is relaxed in the entire loop. However, the above intuition allows us to relax edges in certain order.
47 |
48 | The time complexity of Dijkstra's algorithm depends on the underlying data structure. If our priority queue is based on heap, the Time Complexity is ```O((|V| + |E|)log(|V|))```. On the other hand, if our priority queue is array bases, it takes ```O(|V|^2)```. It is important to note that in case of dense graphs, array implementation of Priority Queue works better than Heap implementation. Thus, the choice of data structure depends on the sparsity of graph.
49 |
50 | # Bellman-Ford Algorithm
51 |
52 | The intuition which we had for dijkstra's algorithm fails when we take negative edges in account. Because now for the above example, A -> C -> B can be cheaper than A -> B, if C -> B were to become negative. Hence for graphs with negative weights, we use Bellman Ford Algorithm.
53 |
54 | The idea behind bellman ford algorithm is a naive version of Dijkstra's algorithm. It doesnt follow any sense of heuristic to relax edges. We keep on relaxing all the edges in the graph for |V|-1 times. Thus the time complexity is ```O(|V||E|)```. However, this algorithm currently works only for graphs with no negative cycles. In presence of negative cycles, the distances can be relaxed infinitely. Thus we slightly modify the code to accommodate negative distances as well.
55 |
56 | # Minimum Spanning Tree
57 |
58 | A minimum spanning tree (MST) of a connected, undirected graph G(V, E) is a subset of the edges E' that forms a tree (i.e., it is connected and acyclic) and spans all the vertices in V. Furthermore, the sum of the weights of the edges in the minimum spanning tree is minimized.
59 |
60 | # Kruskal Algorithm
61 |
62 | The core idea is indeed to add edges to the growing minimum spanning tree in increasing order of their weights, as long as adding the edge does not form a cycle.
63 |
64 | # Prims Algorithm
65 |
--------------------------------------------------------------------------------
/leetcode/73 Set Matrix Zeroes.cpp:
--------------------------------------------------------------------------------
1 | /*
2 | Approach 1: Store all locations of 0s in a vector and then set zero for all rows and columns
3 | Runtime: 12ms
4 | Memory: 13.8MB
5 | Time Complexity: O((m*n)(m+n)), where m*n is dimension of board. The worst case can be when the entire matrix is filled with zeros and each zero requires (m+n) time complexity to SetZero.
6 | */
7 | class Solution {
8 | public:
9 | void setZero(vector
43 |
44 | Consider we are at a node A, which is connected to node B and C by weights 3 and 5 respectively. Here, we can not be sure that distance between A and C i.e. 5, is the shortest one between A and C. This is beacuse, chances are B and C might be connected by weight 1, which makes shortest path between A and C as A -> B -> C of length 4. However, we can be sure, that the distance between A and B is the shortest possible distance between A and B. This is because there is no other possibility which can give path shorter than A -> B directly. Here A -> C -> B will definitely be more expensive since A -> C itself is more expensive than A -> B.
45 |
46 | A naive approach can be to keep on relaxing edges in a while loop till there comes a state where no edge is relaxed in the entire loop. However, the above intuition allows us to relax edges in certain order.
47 |
48 | The time complexity of Dijkstra's algorithm depends on the underlying data structure. If our priority queue is based on heap, the Time Complexity is ```O((|V| + |E|)log(|V|))```. On the other hand, if our priority queue is array bases, it takes ```O(|V|^2)```. It is important to note that in case of dense graphs, array implementation of Priority Queue works better than Heap implementation. Thus, the choice of data structure depends on the sparsity of graph.
49 |
50 | # Bellman-Ford Algorithm
51 |
52 | The intuition which we had for dijkstra's algorithm fails when we take negative edges in account. Because now for the above example, A -> C -> B can be cheaper than A -> B, if C -> B were to become negative. Hence for graphs with negative weights, we use Bellman Ford Algorithm.
53 |
54 | The idea behind bellman ford algorithm is a naive version of Dijkstra's algorithm. It doesnt follow any sense of heuristic to relax edges. We keep on relaxing all the edges in the graph for |V|-1 times. Thus the time complexity is ```O(|V||E|)```. However, this algorithm currently works only for graphs with no negative cycles. In presence of negative cycles, the distances can be relaxed infinitely. Thus we slightly modify the code to accommodate negative distances as well.
55 |
56 | # Minimum Spanning Tree
57 |
58 | A minimum spanning tree (MST) of a connected, undirected graph G(V, E) is a subset of the edges E' that forms a tree (i.e., it is connected and acyclic) and spans all the vertices in V. Furthermore, the sum of the weights of the edges in the minimum spanning tree is minimized.
59 |
60 | # Kruskal Algorithm
61 |
62 | The core idea is indeed to add edges to the growing minimum spanning tree in increasing order of their weights, as long as adding the edge does not form a cycle.
63 |
64 | # Prims Algorithm
65 |
--------------------------------------------------------------------------------
/leetcode/73 Set Matrix Zeroes.cpp:
--------------------------------------------------------------------------------
1 | /*
2 | Approach 1: Store all locations of 0s in a vector and then set zero for all rows and columns
3 | Runtime: 12ms
4 | Memory: 13.8MB
5 | Time Complexity: O((m*n)(m+n)), where m*n is dimension of board. The worst case can be when the entire matrix is filled with zeros and each zero requires (m+n) time complexity to SetZero.
6 | */
7 | class Solution {
8 | public:
9 | void setZero(vector 54 |
55 | ### Bottom-Up approach
56 |
57 | The second approach is the bottom-up method. This approach typically depends on some natural notion of the “size” of a subproblem, such that solving any particular subproblem depends only on solving “smaller” subproblems. We sort the subproblems by size and solve them in size order, smallest first. When solving a particular subproblem, we have already solved all of the smaller subproblems its solution depends upon, and we have saved their solutions. We solve each subproblem only once, and when we first see it, we have already solved all of its prerequisite subproblems.
58 |
59 | Even without any overlapping subproblems, Memoization requires recursion, which is expensive in terms of both memory and time. Each AR creation and removal adds overhead. In fact, without overlapping subproblem, Memoization is simply recursion. The core idea in bottom-up is to unroll recursion and solve it in opposite direction. The time complexity for many problems using bottom-up approach will be similar to that using memoization, but it is better since no recursion is involved and only single AR is created.
60 |
61 |
54 |
55 | ### Bottom-Up approach
56 |
57 | The second approach is the bottom-up method. This approach typically depends on some natural notion of the “size” of a subproblem, such that solving any particular subproblem depends only on solving “smaller” subproblems. We sort the subproblems by size and solve them in size order, smallest first. When solving a particular subproblem, we have already solved all of the smaller subproblems its solution depends upon, and we have saved their solutions. We solve each subproblem only once, and when we first see it, we have already solved all of its prerequisite subproblems.
58 |
59 | Even without any overlapping subproblems, Memoization requires recursion, which is expensive in terms of both memory and time. Each AR creation and removal adds overhead. In fact, without overlapping subproblem, Memoization is simply recursion. The core idea in bottom-up is to unroll recursion and solve it in opposite direction. The time complexity for many problems using bottom-up approach will be similar to that using memoization, but it is better since no recursion is involved and only single AR is created.
60 |
61 |  62 |
63 | Dynamic programming thus uses additional memory to save computation time; it serves an example of a time-memory trade-off. The savings however are massive: an exponential-time solution may be transformed into a polynomial-time solution.
64 |
65 | ## List of problems implemented
66 |
67 | * ```coin_change.cpp```
68 | * ```knapsack_limited.cpp```
69 | * ```longest_common_sequence.cpp```
70 | * ```optimal_alignment.cpp```
71 | * ```placing_parentheses.cpp```
72 |
--------------------------------------------------------------------------------
62 |
63 | Dynamic programming thus uses additional memory to save computation time; it serves an example of a time-memory trade-off. The savings however are massive: an exponential-time solution may be transformed into a polynomial-time solution.
64 |
65 | ## List of problems implemented
66 |
67 | * ```coin_change.cpp```
68 | * ```knapsack_limited.cpp```
69 | * ```longest_common_sequence.cpp```
70 | * ```optimal_alignment.cpp```
71 | * ```placing_parentheses.cpp```
72 |
--------------------------------------------------------------------------------