├── .github
└── workflows
│ └── ci.yml
├── .gitignore
├── .rspec
├── .rubocop.yml
├── CHANGES.md
├── CODE_OF_CONDUCT.md
├── Gemfile
├── LICENSE
├── README.md
├── Rakefile
├── ed25519.gemspec
├── ed25519.png
├── ext
├── ed25519_jruby
│ ├── LICENSE.txt
│ ├── README.md
│ ├── net
│ │ └── i2p
│ │ │ └── crypto
│ │ │ └── eddsa
│ │ │ ├── EdDSAEngine.java
│ │ │ ├── EdDSAKey.java
│ │ │ ├── EdDSAPrivateKey.java
│ │ │ ├── EdDSAPublicKey.java
│ │ │ ├── EdDSASecurityProvider.java
│ │ │ ├── KeyFactory.java
│ │ │ ├── KeyPairGenerator.java
│ │ │ ├── Utils.java
│ │ │ ├── math
│ │ │ ├── Constants.java
│ │ │ ├── Curve.java
│ │ │ ├── Encoding.java
│ │ │ ├── Field.java
│ │ │ ├── FieldElement.java
│ │ │ ├── GroupElement.java
│ │ │ ├── ScalarOps.java
│ │ │ ├── bigint
│ │ │ │ ├── BigIntegerFieldElement.java
│ │ │ │ ├── BigIntegerLittleEndianEncoding.java
│ │ │ │ ├── BigIntegerScalarOps.java
│ │ │ │ └── package.html
│ │ │ └── ed25519
│ │ │ │ ├── Ed25519FieldElement.java
│ │ │ │ ├── Ed25519LittleEndianEncoding.java
│ │ │ │ └── Ed25519ScalarOps.java
│ │ │ └── spec
│ │ │ ├── EdDSAGenParameterSpec.java
│ │ │ ├── EdDSANamedCurveSpec.java
│ │ │ ├── EdDSANamedCurveTable.java
│ │ │ ├── EdDSAParameterSpec.java
│ │ │ ├── EdDSAPrivateKeySpec.java
│ │ │ └── EdDSAPublicKeySpec.java
│ └── org
│ │ └── cryptorb
│ │ └── Ed25519Provider.java
└── ed25519_ref10
│ ├── api.h
│ ├── base.h
│ ├── base2.h
│ ├── d.h
│ ├── d2.h
│ ├── ed25519_ref10.c
│ ├── ed25519_ref10.h
│ ├── extconf.rb
│ ├── fe.c
│ ├── fe.h
│ ├── ge.c
│ ├── ge.h
│ ├── ge_add.h
│ ├── ge_madd.h
│ ├── ge_msub.h
│ ├── ge_p2_dbl.h
│ ├── ge_sub.h
│ ├── keypair.c
│ ├── open.c
│ ├── pow22523.h
│ ├── pow225521.h
│ ├── sc.h
│ ├── sc_muladd.c
│ ├── sc_reduce.c
│ ├── sha512.c
│ ├── sha512.h
│ ├── sign.c
│ ├── sqrtm1.h
│ └── verify.c
├── lib
├── ed25519.rb
└── ed25519
│ ├── signing_key.rb
│ ├── verify_key.rb
│ └── version.rb
└── spec
├── ed25519
├── provider
│ ├── jruby_spec.rb
│ └── ref10_spec.rb
├── signing_key_spec.rb
├── test_vectors_spec.rb
└── verify_key_spec.rb
├── spec_helper.rb
└── support
└── provider_examples.rb
/.github/workflows/ci.yml:
--------------------------------------------------------------------------------
1 | name: CI
2 |
3 | on:
4 | push:
5 | branches: [main]
6 |
7 | pull_request:
8 | branches: [main]
9 |
10 | jobs:
11 | test:
12 | strategy:
13 | fail-fast: false
14 | matrix:
15 | ruby:
16 | [
17 | ruby-3.0,
18 | ruby-3.1,
19 | ruby-3.2,
20 | ruby-3.3,
21 | ruby-3.4,
22 | jruby-9.4.12,
23 | jruby-10.0.0,
24 | truffleruby,
25 | ]
26 | os: [ubuntu-latest, windows-latest]
27 | exclude:
28 | - { ruby: truffleruby, os: windows-latest }
29 | - { ruby: jruby-10.0.0, os: windows-latest }
30 |
31 | runs-on: ${{ matrix.os }}
32 |
33 | steps:
34 | - uses: actions/checkout@v3
35 |
36 | - uses: ruby/setup-ruby@v1
37 | with:
38 | ruby-version: ${{ matrix.ruby }}
39 |
40 | - uses: actions/cache@v3
41 | with:
42 | path: vendor/bundle
43 | key: bundle-use-ruby-${{ matrix.os }}-${{ matrix.ruby }}-${{ hashFiles('**/Gemfile.lock') }}
44 | restore-keys: bundle-use-ruby-${{ matrix.os }}-${{ matrix.ruby }}-
45 |
46 | - name: bundle install
47 | run: |
48 | bundle config path vendor/bundle
49 | bundle install --jobs 4 --retry 3
50 |
51 | - run: bundle exec rake compile spec
52 |
53 | lint:
54 | runs-on: ubuntu-latest
55 |
56 | steps:
57 | - uses: actions/checkout@v2
58 |
59 | - uses: ruby/setup-ruby@v1
60 | with:
61 | ruby-version: 3.0
62 | bundler: 2.5.23
63 |
64 | - uses: actions/cache@v3
65 | with:
66 | path: vendor/bundle
67 | key: bundle-use-ruby-lint-${{ hashFiles('**/Gemfile.lock') }}
68 | restore-keys: bundle-use-ruby-lint-
69 |
70 | - name: bundle install
71 | run: |
72 | bundle config path vendor/bundle
73 | bundle install --jobs 4 --retry 3
74 |
75 | - run: bundle exec rake rubocop
76 |
--------------------------------------------------------------------------------
/.gitignore:
--------------------------------------------------------------------------------
1 | /Gemfile.lock
2 | /.bundle/
3 | /.yardoc
4 | /_yardoc/
5 | /coverage/
6 | /doc/
7 | /pkg/
8 | /spec/reports/
9 | /tmp/
10 | *.o
11 | *.so
12 | *.bundle
13 | *.jar
14 | .rspec_status
15 | .rakeTasks
16 |
--------------------------------------------------------------------------------
/.rspec:
--------------------------------------------------------------------------------
1 | --color
2 | --format documentation
3 | --order random
4 | --warnings
5 | --require spec_helper
6 |
--------------------------------------------------------------------------------
/.rubocop.yml:
--------------------------------------------------------------------------------
1 | plugins:
2 | - rubocop-packaging
3 |
4 | AllCops:
5 | TargetRubyVersion: 3.0
6 | DisplayCopNames: true
7 | NewCops: enable
8 |
9 | #
10 | # Gemspec
11 | #
12 |
13 | Gemspec/DuplicatedAssignment:
14 | Enabled: false
15 |
16 | Gemspec/DevelopmentDependencies:
17 | Enabled: false
18 |
19 | Gemspec/RequireMFA:
20 | Enabled: false
21 |
22 | #
23 | # Layout
24 | #
25 |
26 | Layout/LineLength:
27 | Max: 128
28 |
29 | #
30 | # Lint
31 | #
32 |
33 | Lint/SuppressedException:
34 | Enabled: false
35 |
36 | Lint/UselessAssignment:
37 | Enabled: false
38 |
39 | #
40 | # Metrics
41 | #
42 |
43 | Metrics/AbcSize:
44 | Enabled: false
45 |
46 | Metrics/CyclomaticComplexity:
47 | Enabled: false
48 |
49 | Metrics/PerceivedComplexity:
50 | Enabled: false
51 |
52 | Metrics/BlockLength:
53 | Max: 100
54 |
55 | Metrics/ClassLength:
56 | Max: 100
57 |
58 | Metrics/MethodLength:
59 | Max: 25
60 |
61 | #
62 | # Naming
63 | #
64 |
65 | Naming/RescuedExceptionsVariableName:
66 | Enabled: false
67 |
68 | #
69 | # Style
70 | #
71 |
72 | Style/StringLiterals:
73 | EnforcedStyle: double_quotes
74 |
--------------------------------------------------------------------------------
/CHANGES.md:
--------------------------------------------------------------------------------
1 | ## [1.4.0] (2022-01-16)
2 |
3 | [1.4.0]: https://github.com/RubyCrypto/ed25519/compare/v1.3.0...v1.4.0
4 |
5 | - Use append_cflags instead of modifying CFLAGS directly ([#45])
6 |
7 | [#45]: https://github.com/RubyCrypto/ed25519/pull/45
8 |
9 | ## [1.3.0] (2022-01-16)
10 |
11 | [1.3.0]: https://github.com/RubyCrypto/ed25519/compare/v1.2.4...v1.3.0
12 |
13 | - Bump rubocop dependencies. ([#30])
14 | - Add support for Ruby 3 & JRuby 9.3.0. ([#31])
15 |
16 | [#30]: https://github.com/RubyCrypto/ed25519/pull/30
17 | [#31]: https://github.com/RubyCrypto/ed25519/pull/31
18 |
19 | ## [1.2.4] (2018-01-04)
20 |
21 | [1.2.4]: https://github.com/RubyCrypto/ed25519/compare/v1.2.3...v1.2.4
22 |
23 | * Fix JRuby platform name
24 | * Add license information to gemspec
25 |
26 | ## [1.2.3] (2017-12-31)
27 |
28 | [1.2.3]: https://github.com/RubyCrypto/ed25519/compare/v1.2.2...v1.2.3
29 |
30 | * [#18](https://github.com/RubyCrypto/ed25519/pull/18)
31 | `ext/ed25519_ref10`: Consolidate fe.c and ge.c
32 |
33 | ## [1.2.2] (2017-12-31)
34 |
35 | [1.2.2]: https://github.com/RubyCrypto/ed25519/compare/v1.2.1...v1.2.2
36 |
37 | * [#17](https://github.com/RubyCrypto/ed25519/pull/17)
38 | Test against Ruby 2.5.0
39 |
40 | * [#16](https://github.com/RubyCrypto/ed25519/pull/16)
41 | Move project to the RubyCrypto GitHub organization
42 |
43 | ## [1.2.1] (2017-12-15)
44 |
45 | [1.2.1]: https://github.com/RubyCrypto/ed25519/compare/v1.2.0...v1.2.1
46 |
47 | * [#14](https://github.com/RubyCrypto/ed25519/pull/14)
48 | Support MRI 2.0+
49 |
50 | ## [1.2.0] (2017-12-15)
51 |
52 | [1.2.0]: https://github.com/RubyCrypto/ed25519/compare/v1.1.0...v1.2.0
53 |
54 | * [#13](https://github.com/RubyCrypto/ed25519/pull/13)
55 | Add `Ed25519::SigningKey.from_keypair`
56 |
57 | * [#12](https://github.com/RubyCrypto/ed25519/pull/12)
58 | Add `Ed25519.validate_key_bytes` method
59 |
60 | ## [1.1.0] (2017-12-13)
61 |
62 | [1.1.0]: https://github.com/RubyCrypto/ed25519/compare/v1.0.0...v1.1.0
63 |
64 | * [#11](https://github.com/RubyCrypto/ed25519/pull/11)
65 | ext/ed25519_java: switch to str4d/ed25519-java implementation (fixes #4)
66 |
67 | * [#9](https://github.com/RubyCrypto/ed25519/pull/9)
68 | Implement Java backend as a proper JRuby extension
69 |
70 | * [#8](https://github.com/RubyCrypto/ed25519/pull/8)
71 | Use an attr_accessor for Ed25519.provider
72 |
73 | ## [1.0.0] (2017-12-12)
74 |
75 | [1.0.0]: https://github.com/RubyCrypto/ed25519/compare/v0.1.0...v1.0.0
76 |
77 | * [#7](https://github.com/RubyCrypto/ed25519/pull/7)
78 | Keypair refactor
79 |
80 | * [#6](https://github.com/RubyCrypto/ed25519/pull/6)
81 | Switch from "ref" C implementation to SUPERCOP "ref10"
82 |
83 | * [#5](https://github.com/RubyCrypto/ed25519/pull/5)
84 | Raise Ed25519::VerifyError if signature verification fails
85 |
86 | # 0.1.0 (2017-12-11)
87 |
88 | * Initial release
89 |
--------------------------------------------------------------------------------
/CODE_OF_CONDUCT.md:
--------------------------------------------------------------------------------
1 | # Contributor Covenant Code of Conduct
2 |
3 | ## Our Pledge
4 |
5 | In the interest of fostering an open and welcoming environment, we as
6 | contributors and maintainers pledge to making participation in our project and
7 | our community a harassment-free experience for everyone, regardless of age, body
8 | size, disability, ethnicity, gender identity and expression, level of experience,
9 | nationality, personal appearance, race, religion, or sexual identity and
10 | orientation.
11 |
12 | ## Our Standards
13 |
14 | Examples of behavior that contributes to creating a positive environment
15 | include:
16 |
17 | * Using welcoming and inclusive language
18 | * Being respectful of differing viewpoints and experiences
19 | * Gracefully accepting constructive criticism
20 | * Focusing on what is best for the community
21 | * Showing empathy towards other community members
22 |
23 | Examples of unacceptable behavior by participants include:
24 |
25 | * The use of sexualized language or imagery and unwelcome sexual attention or
26 | advances
27 | * Trolling, insulting/derogatory comments, and personal or political attacks
28 | * Public or private harassment
29 | * Publishing others' private information, such as a physical or electronic
30 | address, without explicit permission
31 | * Other conduct which could reasonably be considered inappropriate in a
32 | professional setting
33 |
34 | ## Our Responsibilities
35 |
36 | Project maintainers are responsible for clarifying the standards of acceptable
37 | behavior and are expected to take appropriate and fair corrective action in
38 | response to any instances of unacceptable behavior.
39 |
40 | Project maintainers have the right and responsibility to remove, edit, or
41 | reject comments, commits, code, wiki edits, issues, and other contributions
42 | that are not aligned to this Code of Conduct, or to ban temporarily or
43 | permanently any contributor for other behaviors that they deem inappropriate,
44 | threatening, offensive, or harmful.
45 |
46 | ## Scope
47 |
48 | This Code of Conduct applies both within project spaces and in public spaces
49 | when an individual is representing the project or its community. Examples of
50 | representing a project or community include using an official project e-mail
51 | address, posting via an official social media account, or acting as an appointed
52 | representative at an online or offline event. Representation of a project may be
53 | further defined and clarified by project maintainers.
54 |
55 | ## Enforcement
56 |
57 | Instances of abusive, harassing, or otherwise unacceptable behavior may be
58 | reported by contacting the project team at bascule@gmail.com. All
59 | complaints will be reviewed and investigated and will result in a response that
60 | is deemed necessary and appropriate to the circumstances. The project team is
61 | obligated to maintain confidentiality with regard to the reporter of an incident.
62 | Further details of specific enforcement policies may be posted separately.
63 |
64 | Project maintainers who do not follow or enforce the Code of Conduct in good
65 | faith may face temporary or permanent repercussions as determined by other
66 | members of the project's leadership.
67 |
68 | ## Attribution
69 |
70 | This Code of Conduct is adapted from the [Contributor Covenant][homepage], version 1.4,
71 | available at [http://contributor-covenant.org/version/1/4][version]
72 |
73 | [homepage]: http://contributor-covenant.org
74 | [version]: http://contributor-covenant.org/version/1/4/
75 |
--------------------------------------------------------------------------------
/Gemfile:
--------------------------------------------------------------------------------
1 | # frozen_string_literal: true
2 |
3 | source "https://rubygems.org"
4 |
5 | gemspec
6 |
7 | group :development, :test do
8 | gem "coveralls", require: false
9 | gem "rake", require: false
10 | gem "rake-compiler", "~> 1.0", require: false
11 | gem "rspec", "~> 3.7", require: false
12 | gem "rubocop", "~> 1.75.4", require: false
13 | gem "rubocop-packaging", "~> 0.6.0", require: false
14 | end
15 |
--------------------------------------------------------------------------------
/LICENSE:
--------------------------------------------------------------------------------
1 | Copyright (c) 2012-2025 Tony Arcieri
2 |
3 | MIT License
4 |
5 | Permission is hereby granted, free of charge, to any person obtaining
6 | a copy of this software and associated documentation files (the
7 | "Software"), to deal in the Software without restriction, including
8 | without limitation the rights to use, copy, modify, merge, publish,
9 | distribute, sublicense, and/or sell copies of the Software, and to
10 | permit persons to whom the Software is furnished to do so, subject to
11 | the following conditions:
12 |
13 | The above copyright notice and this permission notice shall be
14 | included in all copies or substantial portions of the Software.
15 |
16 | THE SOFTWARE IS PROVIDED "AS IS", WITHOUT WARRANTY OF ANY KIND,
17 | EXPRESS OR IMPLIED, INCLUDING BUT NOT LIMITED TO THE WARRANTIES OF
18 | MERCHANTABILITY, FITNESS FOR A PARTICULAR PURPOSE AND
19 | NONINFRINGEMENT. IN NO EVENT SHALL THE AUTHORS OR COPYRIGHT HOLDERS BE
20 | LIABLE FOR ANY CLAIM, DAMAGES OR OTHER LIABILITY, WHETHER IN AN ACTION
21 | OF CONTRACT, TORT OR OTHERWISE, ARISING FROM, OUT OF OR IN CONNECTION
22 | WITH THE SOFTWARE OR THE USE OR OTHER DEALINGS IN THE SOFTWARE.
23 |
--------------------------------------------------------------------------------
/README.md:
--------------------------------------------------------------------------------
1 | # ed25519.rb [![Latest Version][gem-shield]][gem-link] [![Yard Docs][docs-image]][docs-link] [![License: MIT][license-image]][license-link] [![CI Status][ci-image]][ci-link]
2 |
3 | [gem-shield]: https://img.shields.io/gem/v/ed25519?logo=ruby
4 | [gem-link]: https://rubygems.org/gems/ed25519
5 | [ci-image]: https://github.com/RubyCrypto/ed25519/workflows/CI/badge.svg
6 | [ci-link]: https://github.com/RubyCrypto/ed25519/actions?query=workflow%3ACI+branch%3Amaster
7 | [docs-image]: https://img.shields.io/badge/yard-docs-blue.svg
8 | [docs-link]: http://www.rubydoc.info/gems/ed25519/1.4.0
9 | [license-image]: https://img.shields.io/badge/license-MIT-blue.svg
10 | [license-link]: https://github.com/RubyCrypto/ed25519/blob/master/LICENSE
11 |
12 | A Ruby binding to the Ed25519 elliptic curve public-key signature system
13 | described in [RFC 8032].
14 |
15 | Two implementations are provided: a MRI C extension which uses the "ref10"
16 | implementation from the SUPERCOP benchmark suite, and a pure Java version
17 | based on [str4d/ed25519-java].
18 |
19 | Ed25519 is one of two notable algorithms implemented atop the Curve25519
20 | elliptic curve. The [x25519 gem] is a related project of this one,
21 | and implements the X25519 Diffie-Hellman key exchange algorithm on the
22 | Montgomery form of Curve25519.
23 |
24 | [RFC 8032]: https://tools.ietf.org/html/rfc8032
25 | [str4d/ed25519-java]: https://github.com/str4d/ed25519-java
26 | [x25519 gem]: https://github.com/RubyCrypto/x25519
27 |
28 | ## What is Ed25519?
29 |
30 | Ed25519 is a modern implementation of a [Schnorr signature] system using
31 | elliptic curve groups.
32 |
33 | Ed25519 provides a 128-bit security level, that is to say, all known attacks
34 | take at least 2^128 operations, providing the same security level as AES-128,
35 | NIST P-256, and RSA-3072.
36 |
37 | 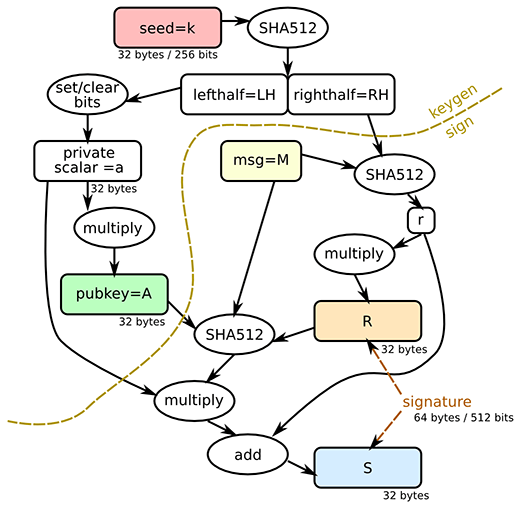
38 |
39 | Ed25519 has a number of unique properties that make it one of the best-in-class
40 | digital signature algorithms:
41 |
42 | * ***Small keys***: Ed25519 keys are only 256-bits (32 bytes), making them
43 | small enough to easily copy around. Ed25519 also allows the public key
44 | to be derived from the private key, meaning that it doesn't need to be
45 | included in a serialized private key in cases you want both.
46 | * ***Small signatures***: Ed25519 signatures are only 512-bits (64 bytes),
47 | one of the smallest signature sizes available.
48 | * ***Deterministic***: Unlike (EC)DSA, Ed25519 does not rely on an entropy
49 | source when signing messages. This can be a potential attack vector if
50 | the entropy source is not generating good random numbers. Ed25519 avoids
51 | this problem entirely and will always generate the same signature for the
52 | same data.
53 | * ***Collision Resistant***: Hash-function collisions do not break this
54 | system. This adds a layer of defense against the possibility of weakness
55 | in the selected hash function.
56 |
57 | You can read more on [Dan Bernstein's Ed25519 site](http://ed25519.cr.yp.to/).
58 |
59 | [Schnorr signature]: https://en.wikipedia.org/wiki/Schnorr_signature
60 |
61 | ### Is it any good?
62 |
63 | [Yes.](http://news.ycombinator.com/item?id=3067434)
64 |
65 | ## Help and Discussion
66 |
67 | Have questions? Want to suggest a feature or change? Join a discussion group:
68 |
69 | * [Crypto.rb Gitter]: web-based chat about Ruby crypto projects including **ed25519**.
70 | * [Crypto.rb Google Group]: join via web or email ([crypto-rb+subscribe@googlegroups.com])
71 |
72 | [Crypto.rb Gitter]: https://gitter.im/crypto-rb/Lobby
73 | [Crypto.rb Google Group]: https://groups.google.com/forum/#!forum/crypto-rb
74 | [crypto-rb+subscribe@googlegroups.com]: mailto:crypto-rb+subscribe@googlegroups.com?subject=subscribe
75 |
76 | ## Requirements
77 |
78 | **ed25519.rb** is supported on and tested against the following platforms:
79 |
80 | - MRI 3.0, 3.1, 3.2, 3.3, 3.4
81 | - JRuby 9.4.12, 10.0.0
82 |
83 | ## Installation
84 |
85 | Add this line to your application's Gemfile:
86 |
87 | gem 'ed25519'
88 |
89 | And then execute:
90 |
91 | $ bundle
92 |
93 | Or install it yourself as:
94 |
95 | $ gem install ed25519
96 |
97 | # Usage
98 |
99 | Require **ed25519.rb** in your Ruby program:
100 |
101 | ```ruby
102 | require "ed25519"
103 | ```
104 |
105 | Generate a new random signing key:
106 |
107 | ```ruby
108 | signing_key = Ed25519::SigningKey.generate
109 | ```
110 |
111 | Sign a message with the signing key:
112 |
113 | ```ruby
114 | signature = signing_key.sign(message)
115 | ```
116 |
117 | Obtain the verify key for a given signing key:
118 |
119 | ```ruby
120 | verify_key = signing_key.verify_key
121 | ```
122 |
123 | Check the validity of a signature:
124 |
125 | ```ruby
126 | verify_key.verify(signature, message)
127 | ```
128 |
129 | The verify method will return `true` if the signature verifies, or raise
130 | `Ed25519::VerifyError` if verification fails.
131 |
132 | ### Serializing Keys
133 |
134 | Keys can be serialized as 32-byte binary strings as follows:
135 |
136 | ```ruby
137 | signature_key_bytes = signing_key.to_bytes
138 | verify_key_bytes = verify_key.to_bytes
139 | ```
140 |
141 | The binary serialization can be passed directly into the constructor for a given key type:
142 |
143 | ```ruby
144 | signing_key = Ed25519::SigningKey.new(signature_key_bytes)
145 | verify_key = Ed25519::VerifyKey.new(verify_key_bytes)
146 | ```
147 |
148 | ## Security Notes
149 |
150 | The Ed25519 "ref10" implementation from SUPERCOP was lovingly crafted by expert
151 | security boffins with great care taken to prevent timing attacks. The same
152 | cannot be said for the C code used in the **ed25519.rb** C extension or in the
153 | entirety of the provided Java implementation.
154 |
155 | Care should be taken to avoid leaking to the attacker how long it takes to
156 | generate keys or sign messages (at least until **ed25519.rb** itself can be audited
157 | by experts who can fix any potential timing vulnerabilities)
158 |
159 | **ed25519.rb** relies on a strong `SecureRandom` for key generation.
160 | Weaknesses in the random number source can potentially result in insecure keys.
161 |
162 | ## Contributing
163 |
164 | Bug reports and pull requests are welcome on GitHub at https://github.com/RubyCrypto/ed25519.
165 | This project is intended to be a safe, welcoming space for collaboration,
166 | and contributors areexpected to adhere to the [Contributor Covenant](http://contributor-covenant.org)
167 | code of conduct.
168 |
169 | ## License
170 |
171 | Copyright (c) 2012-2025 Tony Arcieri. Distributed under the MIT License. See
172 | [LICENSE] for further details.
173 |
174 | [LICENSE]: https://github.com/RubyCrypto/ed25519/blob/master/LICENSE
175 |
176 | ## Code of Conduct
177 |
178 | Everyone interacting in the **ed25519.rb** project’s codebases, issue trackers, chat
179 | rooms and mailing lists is expected to follow the [code of conduct].
180 |
181 | [code of conduct]: https://github.com/RubyCrypto/ed25519/blob/master/CODE_OF_CONDUCT.md
182 |
--------------------------------------------------------------------------------
/Rakefile:
--------------------------------------------------------------------------------
1 | # frozen_string_literal: true
2 |
3 | require "bundler/gem_tasks"
4 |
5 | require "rake/clean"
6 | CLEAN.include("**/*.o", "**/*.so", "**/*.bundle", "*.jar", "pkg", "tmp")
7 |
8 | if defined? JRUBY_VERSION
9 | require "rake/javaextensiontask"
10 | Rake::JavaExtensionTask.new("ed25519_jruby") do |ext|
11 | ext.ext_dir = "ext/ed25519_jruby"
12 | end
13 | else
14 | require "rake/extensiontask"
15 |
16 | Rake::ExtensionTask.new("ed25519_ref10") do |ext|
17 | ext.ext_dir = "ext/ed25519_ref10"
18 | end
19 | end
20 |
21 | require "rspec/core/rake_task"
22 | RSpec::Core::RakeTask.new
23 |
24 | require "rubocop/rake_task"
25 | RuboCop::RakeTask.new
26 |
27 | task default: %w[compile spec rubocop]
28 |
--------------------------------------------------------------------------------
/ed25519.gemspec:
--------------------------------------------------------------------------------
1 | # frozen_string_literal: true
2 |
3 | require File.expand_path("lib/ed25519/version", __dir__)
4 |
5 | Gem::Specification.new do |spec|
6 | spec.name = "ed25519"
7 | spec.version = Ed25519::VERSION
8 | spec.authors = ["Tony Arcieri"]
9 | spec.email = ["tony.arcieri@gmail.com"]
10 | spec.summary = "An efficient digital signature library providing the Ed25519 algorithm"
11 | spec.description = <<-DESCRIPTION.strip.gsub(/\s+/, " ")
12 | A Ruby binding to the Ed25519 elliptic curve public-key signature system
13 | described in RFC 8032.
14 | DESCRIPTION
15 | spec.homepage = "https://github.com/RubyCrypto/ed25519"
16 | spec.license = "MIT"
17 | spec.files = Dir["{ext,lib}/**/*", "CHANGES.md", "LICENSE"]
18 | spec.bindir = "exe"
19 | spec.require_paths = ["lib"]
20 | spec.extra_rdoc_files = ["README.md", "ed25519.png"]
21 |
22 | if defined? JRUBY_VERSION
23 | spec.platform = "java"
24 | spec.files << "lib/ed25519_jruby.jar"
25 | else
26 | spec.platform = Gem::Platform::RUBY
27 | spec.extensions = ["ext/ed25519_ref10/extconf.rb"]
28 | end
29 |
30 | spec.required_ruby_version = ">= 3.0"
31 | spec.add_development_dependency "bundler"
32 | end
33 |
--------------------------------------------------------------------------------
/ed25519.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/RubyCrypto/ed25519/bc96e3417c0c293062e3408dd0e67751052ecc89/ed25519.png
--------------------------------------------------------------------------------
/ext/ed25519_jruby/LICENSE.txt:
--------------------------------------------------------------------------------
1 | Creative Commons Legal Code
2 |
3 | CC0 1.0 Universal
4 |
5 | CREATIVE COMMONS CORPORATION IS NOT A LAW FIRM AND DOES NOT PROVIDE
6 | LEGAL SERVICES. DISTRIBUTION OF THIS DOCUMENT DOES NOT CREATE AN
7 | ATTORNEY-CLIENT RELATIONSHIP. CREATIVE COMMONS PROVIDES THIS
8 | INFORMATION ON AN "AS-IS" BASIS. CREATIVE COMMONS MAKES NO WARRANTIES
9 | REGARDING THE USE OF THIS DOCUMENT OR THE INFORMATION OR WORKS
10 | PROVIDED HEREUNDER, AND DISCLAIMS LIABILITY FOR DAMAGES RESULTING FROM
11 | THE USE OF THIS DOCUMENT OR THE INFORMATION OR WORKS PROVIDED
12 | HEREUNDER.
13 |
14 | Statement of Purpose
15 |
16 | The laws of most jurisdictions throughout the world automatically confer
17 | exclusive Copyright and Related Rights (defined below) upon the creator
18 | and subsequent owner(s) (each and all, an "owner") of an original work of
19 | authorship and/or a database (each, a "Work").
20 |
21 | Certain owners wish to permanently relinquish those rights to a Work for
22 | the purpose of contributing to a commons of creative, cultural and
23 | scientific works ("Commons") that the public can reliably and without fear
24 | of later claims of infringement build upon, modify, incorporate in other
25 | works, reuse and redistribute as freely as possible in any form whatsoever
26 | and for any purposes, including without limitation commercial purposes.
27 | These owners may contribute to the Commons to promote the ideal of a free
28 | culture and the further production of creative, cultural and scientific
29 | works, or to gain reputation or greater distribution for their Work in
30 | part through the use and efforts of others.
31 |
32 | For these and/or other purposes and motivations, and without any
33 | expectation of additional consideration or compensation, the person
34 | associating CC0 with a Work (the "Affirmer"), to the extent that he or she
35 | is an owner of Copyright and Related Rights in the Work, voluntarily
36 | elects to apply CC0 to the Work and publicly distribute the Work under its
37 | terms, with knowledge of his or her Copyright and Related Rights in the
38 | Work and the meaning and intended legal effect of CC0 on those rights.
39 |
40 | 1. Copyright and Related Rights. A Work made available under CC0 may be
41 | protected by copyright and related or neighboring rights ("Copyright and
42 | Related Rights"). Copyright and Related Rights include, but are not
43 | limited to, the following:
44 |
45 | i. the right to reproduce, adapt, distribute, perform, display,
46 | communicate, and translate a Work;
47 | ii. moral rights retained by the original author(s) and/or performer(s);
48 | iii. publicity and privacy rights pertaining to a person's image or
49 | likeness depicted in a Work;
50 | iv. rights protecting against unfair competition in regards to a Work,
51 | subject to the limitations in paragraph 4(a), below;
52 | v. rights protecting the extraction, dissemination, use and reuse of data
53 | in a Work;
54 | vi. database rights (such as those arising under Directive 96/9/EC of the
55 | European Parliament and of the Council of 11 March 1996 on the legal
56 | protection of databases, and under any national implementation
57 | thereof, including any amended or successor version of such
58 | directive); and
59 | vii. other similar, equivalent or corresponding rights throughout the
60 | world based on applicable law or treaty, and any national
61 | implementations thereof.
62 |
63 | 2. Waiver. To the greatest extent permitted by, but not in contravention
64 | of, applicable law, Affirmer hereby overtly, fully, permanently,
65 | irrevocably and unconditionally waives, abandons, and surrenders all of
66 | Affirmer's Copyright and Related Rights and associated claims and causes
67 | of action, whether now known or unknown (including existing as well as
68 | future claims and causes of action), in the Work (i) in all territories
69 | worldwide, (ii) for the maximum duration provided by applicable law or
70 | treaty (including future time extensions), (iii) in any current or future
71 | medium and for any number of copies, and (iv) for any purpose whatsoever,
72 | including without limitation commercial, advertising or promotional
73 | purposes (the "Waiver"). Affirmer makes the Waiver for the benefit of each
74 | member of the public at large and to the detriment of Affirmer's heirs and
75 | successors, fully intending that such Waiver shall not be subject to
76 | revocation, rescission, cancellation, termination, or any other legal or
77 | equitable action to disrupt the quiet enjoyment of the Work by the public
78 | as contemplated by Affirmer's express Statement of Purpose.
79 |
80 | 3. Public License Fallback. Should any part of the Waiver for any reason
81 | be judged legally invalid or ineffective under applicable law, then the
82 | Waiver shall be preserved to the maximum extent permitted taking into
83 | account Affirmer's express Statement of Purpose. In addition, to the
84 | extent the Waiver is so judged Affirmer hereby grants to each affected
85 | person a royalty-free, non transferable, non sublicensable, non exclusive,
86 | irrevocable and unconditional license to exercise Affirmer's Copyright and
87 | Related Rights in the Work (i) in all territories worldwide, (ii) for the
88 | maximum duration provided by applicable law or treaty (including future
89 | time extensions), (iii) in any current or future medium and for any number
90 | of copies, and (iv) for any purpose whatsoever, including without
91 | limitation commercial, advertising or promotional purposes (the
92 | "License"). The License shall be deemed effective as of the date CC0 was
93 | applied by Affirmer to the Work. Should any part of the License for any
94 | reason be judged legally invalid or ineffective under applicable law, such
95 | partial invalidity or ineffectiveness shall not invalidate the remainder
96 | of the License, and in such case Affirmer hereby affirms that he or she
97 | will not (i) exercise any of his or her remaining Copyright and Related
98 | Rights in the Work or (ii) assert any associated claims and causes of
99 | action with respect to the Work, in either case contrary to Affirmer's
100 | express Statement of Purpose.
101 |
102 | 4. Limitations and Disclaimers.
103 |
104 | a. No trademark or patent rights held by Affirmer are waived, abandoned,
105 | surrendered, licensed or otherwise affected by this document.
106 | b. Affirmer offers the Work as-is and makes no representations or
107 | warranties of any kind concerning the Work, express, implied,
108 | statutory or otherwise, including without limitation warranties of
109 | title, merchantability, fitness for a particular purpose, non
110 | infringement, or the absence of latent or other defects, accuracy, or
111 | the present or absence of errors, whether or not discoverable, all to
112 | the greatest extent permissible under applicable law.
113 | c. Affirmer disclaims responsibility for clearing rights of other persons
114 | that may apply to the Work or any use thereof, including without
115 | limitation any person's Copyright and Related Rights in the Work.
116 | Further, Affirmer disclaims responsibility for obtaining any necessary
117 | consents, permissions or other rights required for any use of the
118 | Work.
119 | d. Affirmer understands and acknowledges that Creative Commons is not a
120 | party to this document and has no duty or obligation with respect to
121 | this CC0 or use of the Work.
122 |
123 | For more information, please see https://creativecommons.org/publicdomain/zero/1.0/
124 |
--------------------------------------------------------------------------------
/ext/ed25519_jruby/README.md:
--------------------------------------------------------------------------------
1 | EdDSA-Java
2 | ==========
3 |
4 | [](https://travis-ci.org/str4d/ed25519-java)
5 |
6 | This is an implementation of EdDSA in Java. Structurally, it is based on the ref10 implementation in SUPERCOP (see https://ed25519.cr.yp.to/software.html).
7 |
8 | There are two internal implementations:
9 | * A port of the radix-2^51 operations in ref10 - fast and constant-time, but only useful for Ed25519.
10 | * A generic version using BigIntegers for calculation - a bit slower and not constant-time, but compatible with any EdDSA parameter specification.
11 |
12 |
13 | To use
14 | ------
15 |
16 | Download the latest .jar from the releases tab and place it in your classpath.
17 |
18 | Gradle users:
19 |
20 | ```
21 | compile 'net.i2p.crypto:eddsa:0.2.0'
22 | ```
23 |
24 | The code requires Java 6 (for e.g. the `Arrays.copyOfRange()` calls in `EdDSAEngine.engineVerify()`).
25 |
26 | The JUnit4 tests require the Hamcrest library `hamcrest-all.jar`.
27 |
28 | This code is released to the public domain and can be used for any purpose. See `LICENSE.txt` for details.
29 |
30 | Disclaimer
31 | ----------
32 |
33 | There are **no** guarantees that this is secure for all cases, and users should
34 | review the code themselves before depending on it. PRs that fix bugs or improve
35 | reviewability are very welcome. Additionally:
36 |
37 | - The unit test suite includes tests against
38 | [the data from the original Python implementation](https://ed25519.cr.yp.to/python/sign.input).
39 | - The code (as of 97cea3f0d910fc627c7b57b1bc4d783cdd0c2a4a) was reviewed by
40 | [an independent developer](https://github.com/BloodyRookie).
41 | - The code (as of dc9f58f2c874463c15465326efc040d17a627b3a) was audited by an independent third party,
42 | and the one issue found [was fixed](https://github.com/str4d/ed25519-java/pull/31).
43 |
44 | Code comparison
45 | ---------------
46 |
47 | For ease of following, here are the main methods in ref10 and their equivalents in this codebase:
48 |
49 | | EdDSA Operation | ref10 function | Java function |
50 | | --------------- | -------------- | ------------- |
51 | | Generate keypair | `crypto_sign_keypair` | `EdDSAPrivateKeySpec` constructor |
52 | | Sign message | `crypto_sign` | `EdDSAEngine.engineSign` |
53 | | Verify signature | `crypto_sign_open` | `EdDSAEngine.engineVerify` |
54 |
55 | | EdDSA point arithmetic | ref10 function | Java function |
56 | | ---------------------- | -------------- | ------------- |
57 | | `R = b * B` | `ge_scalarmult_base` | `GroupElement.scalarMultiply` |
58 | | `R = a*A + b*B` | `ge_double_scalarmult_vartime` | `GroupElement.doubleScalarMultiplyVariableTime` |
59 | | `R = 2 * P` | `ge_p2_dbl` | `GroupElement.dbl` |
60 | | `R = P + Q` | `ge_madd`, `ge_add` | `GroupElement.madd`, `GroupElement.add` |
61 | | `R = P - Q` | `ge_msub`, `ge_sub` | `GroupElement.msub`, `GroupElement.sub` |
62 |
63 |
64 | Important changes
65 | -----------------
66 |
67 | ### 0.2.0
68 |
69 | - Ed25519 is now named `Ed25519` in `EdDSANamedCurveTable`, and the previous public constant
70 | (containing the older inaccurate name) has been removed.
71 |
72 | Credits
73 | -------
74 |
75 | * The Ed25519 class was originally ported by k3d3 from [the Python Ed25519 reference implementation](https://ed25519.cr.yp.to/python/ed25519.py).
76 | * Useful comments and tweaks were found in [the GNUnet implementation of Ed25519](https://gnunet.org/svn/gnunet-java/src/main/java/org/gnunet/util/crypto/) (based on k3d3's class).
77 | * [BloodyRookie](https://github.com/BloodyRookie) reviewed the code, adding many useful comments, unit tests and literature.
78 |
--------------------------------------------------------------------------------
/ext/ed25519_jruby/net/i2p/crypto/eddsa/EdDSAKey.java:
--------------------------------------------------------------------------------
1 | /**
2 | * EdDSA-Java by str4d
3 | *
4 | * To the extent possible under law, the person who associated CC0 with
5 | * EdDSA-Java has waived all copyright and related or neighboring rights
6 | * to EdDSA-Java.
7 | *
8 | * You should have received a copy of the CC0 legalcode along with this
9 | * work. If not, see
27 | * Warning: Private key encoding is based on the current curdle WG draft,
28 | * and is subject to change. See getEncoded().
29 | *
30 | * For compatibility with older releases, decoding supports both the old and new
31 | * draft specifications. See decode().
32 | *
33 | * Ref: https://tools.ietf.org/html/draft-ietf-curdle-pkix-04
34 | *
35 | * Old Ref: https://tools.ietf.org/html/draft-josefsson-pkix-eddsa-04
36 | *
37 | * @author str4d
38 | *
39 | */
40 | public class EdDSAPrivateKey implements EdDSAKey, PrivateKey {
41 | private static final long serialVersionUID = 23495873459878957L;
42 | private final byte[] seed;
43 | private final byte[] h;
44 | private final byte[] a;
45 | private final GroupElement A;
46 | private final byte[] Abyte;
47 | private final EdDSAParameterSpec edDsaSpec;
48 |
49 | // OID 1.3.101.xxx
50 | private static final int OID_OLD = 100;
51 | private static final int OID_ED25519 = 112;
52 | private static final int OID_BYTE = 11;
53 | private static final int IDLEN_BYTE = 6;
54 |
55 | public EdDSAPrivateKey(EdDSAPrivateKeySpec spec) {
56 | this.seed = spec.getSeed();
57 | this.h = spec.getH();
58 | this.a = spec.geta();
59 | this.A = spec.getA();
60 | this.Abyte = this.A.toByteArray();
61 | this.edDsaSpec = spec.getParams();
62 | }
63 |
64 | public EdDSAPrivateKey(PKCS8EncodedKeySpec spec) throws InvalidKeySpecException {
65 | this(new EdDSAPrivateKeySpec(decode(spec.getEncoded()),
66 | EdDSANamedCurveTable.getByName(EdDSANamedCurveTable.ED_25519)));
67 | }
68 |
69 | @Override
70 | public String getAlgorithm() {
71 | return KEY_ALGORITHM;
72 | }
73 |
74 | @Override
75 | public String getFormat() {
76 | return "PKCS#8";
77 | }
78 |
79 | /**
80 | * Returns the public key in its canonical encoding.
81 | *
82 | * This implements the following specs:
83 | *
84 | * General encoding: https://tools.ietf.org/html/draft-ietf-curdle-pkix-04
85 | *
86 | * Key encoding: https://tools.ietf.org/html/rfc8032
87 | *
89 | * This encodes the seed. It will return null if constructed from
90 | * a spec which was directly constructed from H, in which case seed is null.
91 | *
92 | * For keys in older formats, decoding and then re-encoding is sufficient to
93 | * migrate them to the canonical encoding.
94 | *
95 | * Relevant spec quotes:
96 | *
97 | * OneAsymmetricKey ::= SEQUENCE {
98 | * version Version,
99 | * privateKeyAlgorithm PrivateKeyAlgorithmIdentifier,
100 | * privateKey PrivateKey,
101 | * attributes [0] Attributes OPTIONAL,
102 | * ...,
103 | * [[2: publicKey [1] PublicKey OPTIONAL ]],
104 | * ...
105 | * }
106 | *
107 | * Version ::= INTEGER
108 | * PrivateKeyAlgorithmIdentifier ::= AlgorithmIdentifier
109 | * PrivateKey ::= OCTET STRING
110 | * PublicKey ::= OCTET STRING
111 | * Attributes ::= SET OF Attribute
112 | *
113 | *
114 | *
115 | * ... when encoding a OneAsymmetricKey object, the private key is wrapped
116 | * in a CurvePrivateKey object and wrapped by the OCTET STRING of the
117 | * 'privateKey' field.
118 | *
119 | * CurvePrivateKey ::= OCTET STRING
120 | *
121 | *
122 | *
123 | * AlgorithmIdentifier ::= SEQUENCE {
124 | * algorithm OBJECT IDENTIFIER,
125 | * parameters ANY DEFINED BY algorithm OPTIONAL
126 | * }
127 | *
128 | * For all of the OIDs, the parameters MUST be absent.
129 | *
130 | *
131 | *
132 | * id-Ed25519 OBJECT IDENTIFIER ::= { 1 3 101 112 }
133 | *
134 | *
135 | * @return 48 bytes for Ed25519, null for other curves
136 | */
137 | @Override
138 | public byte[] getEncoded() {
139 | if (!edDsaSpec.equals(EdDSANamedCurveTable.getByName(EdDSANamedCurveTable.ED_25519)))
140 | return null;
141 | if (seed == null)
142 | return null;
143 | int totlen = 16 + seed.length;
144 | byte[] rv = new byte[totlen];
145 | int idx = 0;
146 | // sequence
147 | rv[idx++] = 0x30;
148 | rv[idx++] = (byte) (totlen - 2);
149 | // version
150 | rv[idx++] = 0x02;
151 | rv[idx++] = 1;
152 | // v1 - no public key included
153 | rv[idx++] = 0;
154 | // Algorithm Identifier
155 | // sequence
156 | rv[idx++] = 0x30;
157 | rv[idx++] = 5;
158 | // OID
159 | // https://msdn.microsoft.com/en-us/library/windows/desktop/bb540809%28v=vs.85%29.aspx
160 | rv[idx++] = 0x06;
161 | rv[idx++] = 3;
162 | rv[idx++] = (1 * 40) + 3;
163 | rv[idx++] = 101;
164 | rv[idx++] = (byte) OID_ED25519;
165 | // params - absent
166 | // PrivateKey
167 | rv[idx++] = 0x04; // octet string
168 | rv[idx++] = (byte) (2 + seed.length);
169 | // CurvePrivateKey
170 | rv[idx++] = 0x04; // octet string
171 | rv[idx++] = (byte) seed.length;
172 | // the key
173 | System.arraycopy(seed, 0, rv, idx, seed.length);
174 | return rv;
175 | }
176 |
177 | /**
178 | * Extracts the private key bytes from the provided encoding.
179 | *
180 | * This will decode data conforming to the current spec at
181 | * https://tools.ietf.org/html/draft-ietf-curdle-pkix-04
182 | * or as inferred from the old spec at
183 | * https://tools.ietf.org/html/draft-josefsson-pkix-eddsa-04.
184 | *
185 | * Contrary to draft-ietf-curdle-pkix-04, it WILL accept a parameter value
186 | * of NULL, as it is required for interoperability with the default Java
187 | * keystore. Other implementations MUST NOT copy this behaviour from here
188 | * unless they also need to read keys from the default Java keystore.
189 | *
190 | * This is really dumb for now. It does not use a general-purpose ASN.1 decoder.
191 | * See also getEncoded().
192 | *
193 | * @return 32 bytes for Ed25519, throws for other curves
194 | */
195 | private static byte[] decode(byte[] d) throws InvalidKeySpecException {
196 | try {
197 | //
198 | // Setup and OID check
199 | //
200 | int totlen = 48;
201 | int idlen = 5;
202 | int doid = d[OID_BYTE];
203 | if (doid == OID_OLD) {
204 | totlen = 49;
205 | idlen = 8;
206 | } else if (doid == OID_ED25519) {
207 | // Detect parameter value of NULL
208 | if (d[IDLEN_BYTE] == 7) {
209 | totlen = 50;
210 | idlen = 7;
211 | }
212 | } else {
213 | throw new InvalidKeySpecException("unsupported key spec");
214 | }
215 |
216 | //
217 | // Pre-decoding check
218 | //
219 | if (d.length != totlen) {
220 | throw new InvalidKeySpecException("invalid key spec length");
221 | }
222 |
223 | //
224 | // Decoding
225 | //
226 | int idx = 0;
227 | if (d[idx++] != 0x30 ||
228 | d[idx++] != (totlen - 2) ||
229 | d[idx++] != 0x02 ||
230 | d[idx++] != 1 ||
231 | d[idx++] != 0 ||
232 | d[idx++] != 0x30 ||
233 | d[idx++] != idlen ||
234 | d[idx++] != 0x06 ||
235 | d[idx++] != 3 ||
236 | d[idx++] != (1 * 40) + 3 ||
237 | d[idx++] != 101) {
238 | throw new InvalidKeySpecException("unsupported key spec");
239 | }
240 | idx++; // OID, checked above
241 | // parameters only with old OID
242 | if (doid == OID_OLD) {
243 | if (d[idx++] != 0x0a ||
244 | d[idx++] != 1 ||
245 | d[idx++] != 1) {
246 | throw new InvalidKeySpecException("unsupported key spec");
247 | }
248 | } else {
249 | // Handle parameter value of NULL
250 | //
251 | // Quote https://tools.ietf.org/html/draft-ietf-curdle-pkix-04 :
252 | // For all of the OIDs, the parameters MUST be absent.
253 | // Regardless of the defect in the original 1997 syntax,
254 | // implementations MUST NOT accept a parameters value of NULL.
255 | //
256 | // But Java's default keystore puts it in (when decoding as
257 | // PKCS8 and then re-encoding to pass on), so we must accept it.
258 | if (idlen == 7) {
259 | if (d[idx++] != 0x05 ||
260 | d[idx++] != 0) {
261 | throw new InvalidKeySpecException("unsupported key spec");
262 | }
263 | }
264 | // PrivateKey wrapping the CurvePrivateKey
265 | if (d[idx++] != 0x04 ||
266 | d[idx++] != 34) {
267 | throw new InvalidKeySpecException("unsupported key spec");
268 | }
269 | }
270 | if (d[idx++] != 0x04 ||
271 | d[idx++] != 32) {
272 | throw new InvalidKeySpecException("unsupported key spec");
273 | }
274 | byte[] rv = new byte[32];
275 | System.arraycopy(d, idx, rv, 0, 32);
276 | return rv;
277 | } catch (IndexOutOfBoundsException ioobe) {
278 | throw new InvalidKeySpecException(ioobe);
279 | }
280 | }
281 |
282 | @Override
283 | public EdDSAParameterSpec getParams() {
284 | return edDsaSpec;
285 | }
286 |
287 | /**
288 | * @return will be null if constructed from a spec which was
289 | * directly constructed from H
290 | */
291 | public byte[] getSeed() {
292 | return seed;
293 | }
294 |
295 | /**
296 | * @return the hash of the seed
297 | */
298 | public byte[] getH() {
299 | return h;
300 | }
301 |
302 | /**
303 | * @return the private key
304 | */
305 | public byte[] geta() {
306 | return a;
307 | }
308 |
309 | /**
310 | * @return the public key
311 | */
312 | public GroupElement getA() {
313 | return A;
314 | }
315 |
316 | /**
317 | * @return the public key
318 | */
319 | public byte[] getAbyte() {
320 | return Abyte;
321 | }
322 |
323 | @Override
324 | public int hashCode() {
325 | return Arrays.hashCode(seed);
326 | }
327 |
328 | @Override
329 | public boolean equals(Object o) {
330 | if (o == this)
331 | return true;
332 | if (!(o instanceof EdDSAPrivateKey))
333 | return false;
334 | EdDSAPrivateKey pk = (EdDSAPrivateKey) o;
335 | return Arrays.equals(seed, pk.getSeed()) &&
336 | edDsaSpec.equals(pk.getParams());
337 | }
338 | }
339 |
--------------------------------------------------------------------------------
/ext/ed25519_jruby/net/i2p/crypto/eddsa/EdDSAPublicKey.java:
--------------------------------------------------------------------------------
1 | /**
2 | * EdDSA-Java by str4d
3 | *
4 | * To the extent possible under law, the person who associated CC0 with
5 | * EdDSA-Java has waived all copyright and related or neighboring rights
6 | * to EdDSA-Java.
7 | *
8 | * You should have received a copy of the CC0 legalcode along with this
9 | * work. If not, see
27 | * Warning: Public key encoding is is based on the current curdle WG draft,
28 | * and is subject to change. See getEncoded().
29 | *
30 | * For compatibility with older releases, decoding supports both the old and new
31 | * draft specifications. See decode().
32 | *
33 | * Ref: https://tools.ietf.org/html/draft-ietf-curdle-pkix-04
34 | *
35 | * Old Ref: https://tools.ietf.org/html/draft-josefsson-pkix-eddsa-04
36 | *
37 | * @author str4d
38 | *
39 | */
40 | public class EdDSAPublicKey implements EdDSAKey, PublicKey {
41 | private static final long serialVersionUID = 9837459837498475L;
42 | private final GroupElement A;
43 | private final GroupElement Aneg;
44 | private final byte[] Abyte;
45 | private final EdDSAParameterSpec edDsaSpec;
46 |
47 | // OID 1.3.101.xxx
48 | private static final int OID_OLD = 100;
49 | private static final int OID_ED25519 = 112;
50 | private static final int OID_BYTE = 8;
51 | private static final int IDLEN_BYTE = 3;
52 |
53 | public EdDSAPublicKey(EdDSAPublicKeySpec spec) {
54 | this.A = spec.getA();
55 | this.Aneg = spec.getNegativeA();
56 | this.Abyte = this.A.toByteArray();
57 | this.edDsaSpec = spec.getParams();
58 | }
59 |
60 | public EdDSAPublicKey(X509EncodedKeySpec spec) throws InvalidKeySpecException {
61 | this(new EdDSAPublicKeySpec(decode(spec.getEncoded()),
62 | EdDSANamedCurveTable.getByName(EdDSANamedCurveTable.ED_25519)));
63 | }
64 |
65 | @Override
66 | public String getAlgorithm() {
67 | return KEY_ALGORITHM;
68 | }
69 |
70 | @Override
71 | public String getFormat() {
72 | return "X.509";
73 | }
74 |
75 | /**
76 | * Returns the public key in its canonical encoding.
77 | *
78 | * This implements the following specs:
79 | *
80 | * General encoding: https://tools.ietf.org/html/draft-ietf-curdle-pkix-04
81 | *
82 | * Key encoding: https://tools.ietf.org/html/rfc8032
83 | *
85 | * For keys in older formats, decoding and then re-encoding is sufficient to
86 | * migrate them to the canonical encoding.
87 | *
88 | * Relevant spec quotes:
89 | *
90 | * In the X.509 certificate, the subjectPublicKeyInfo field has the
91 | * SubjectPublicKeyInfo type, which has the following ASN.1 syntax:
92 | *
93 | * SubjectPublicKeyInfo ::= SEQUENCE {
94 | * algorithm AlgorithmIdentifier,
95 | * subjectPublicKey BIT STRING
96 | * }
97 | *
98 | *
99 | *
100 | * AlgorithmIdentifier ::= SEQUENCE {
101 | * algorithm OBJECT IDENTIFIER,
102 | * parameters ANY DEFINED BY algorithm OPTIONAL
103 | * }
104 | *
105 | * For all of the OIDs, the parameters MUST be absent.
106 | *
107 | *
108 | *
109 | * id-Ed25519 OBJECT IDENTIFIER ::= { 1 3 101 112 }
110 | *
111 | *
112 | * @return 44 bytes for Ed25519, null for other curves
113 | */
114 | @Override
115 | public byte[] getEncoded() {
116 | if (!edDsaSpec.equals(EdDSANamedCurveTable.getByName(EdDSANamedCurveTable.ED_25519)))
117 | return null;
118 | int totlen = 12 + Abyte.length;
119 | byte[] rv = new byte[totlen];
120 | int idx = 0;
121 | // sequence
122 | rv[idx++] = 0x30;
123 | rv[idx++] = (byte) (totlen - 2);
124 | // Algorithm Identifier
125 | // sequence
126 | rv[idx++] = 0x30;
127 | rv[idx++] = 5;
128 | // OID
129 | // https://msdn.microsoft.com/en-us/library/windows/desktop/bb540809%28v=vs.85%29.aspx
130 | rv[idx++] = 0x06;
131 | rv[idx++] = 3;
132 | rv[idx++] = (1 * 40) + 3;
133 | rv[idx++] = 101;
134 | rv[idx++] = (byte) OID_ED25519;
135 | // params - absent
136 | // the key
137 | rv[idx++] = 0x03; // bit string
138 | rv[idx++] = (byte) (1 + Abyte.length);
139 | rv[idx++] = 0; // number of trailing unused bits
140 | System.arraycopy(Abyte, 0, rv, idx, Abyte.length);
141 | return rv;
142 | }
143 |
144 | /**
145 | * Extracts the public key bytes from the provided encoding.
146 | *
147 | * This will decode data conforming to the current spec at
148 | * https://tools.ietf.org/html/draft-ietf-curdle-pkix-04
149 | * or the old spec at
150 | * https://tools.ietf.org/html/draft-josefsson-pkix-eddsa-04.
151 | *
152 | * Contrary to draft-ietf-curdle-pkix-04, it WILL accept a parameter value
153 | * of NULL, as it is required for interoperability with the default Java
154 | * keystore. Other implementations MUST NOT copy this behaviour from here
155 | * unless they also need to read keys from the default Java keystore.
156 | *
157 | * This is really dumb for now. It does not use a general-purpose ASN.1 decoder.
158 | * See also getEncoded().
159 | *
160 | *
161 | * @return 32 bytes for Ed25519, throws for other curves
162 | */
163 | private static byte[] decode(byte[] d) throws InvalidKeySpecException {
164 | try {
165 | //
166 | // Setup and OID check
167 | //
168 | int totlen = 44;
169 | int idlen = 5;
170 | int doid = d[OID_BYTE];
171 | if (doid == OID_OLD) {
172 | totlen = 47;
173 | idlen = 8;
174 | } else if (doid == OID_ED25519) {
175 | // Detect parameter value of NULL
176 | if (d[IDLEN_BYTE] == 7) {
177 | totlen = 46;
178 | idlen = 7;
179 | }
180 | } else {
181 | throw new InvalidKeySpecException("unsupported key spec");
182 | }
183 |
184 | //
185 | // Pre-decoding check
186 | //
187 | if (d.length != totlen) {
188 | throw new InvalidKeySpecException("invalid key spec length");
189 | }
190 |
191 | //
192 | // Decoding
193 | //
194 | int idx = 0;
195 | if (d[idx++] != 0x30 ||
196 | d[idx++] != (totlen - 2) ||
197 | d[idx++] != 0x30 ||
198 | d[idx++] != idlen ||
199 | d[idx++] != 0x06 ||
200 | d[idx++] != 3 ||
201 | d[idx++] != (1 * 40) + 3 ||
202 | d[idx++] != 101) {
203 | throw new InvalidKeySpecException("unsupported key spec");
204 | }
205 | idx++; // OID, checked above
206 | // parameters only with old OID
207 | if (doid == OID_OLD) {
208 | if (d[idx++] != 0x0a ||
209 | d[idx++] != 1 ||
210 | d[idx++] != 1) {
211 | throw new InvalidKeySpecException("unsupported key spec");
212 | }
213 | } else {
214 | // Handle parameter value of NULL
215 | //
216 | // Quote https://tools.ietf.org/html/draft-ietf-curdle-pkix-04 :
217 | // For all of the OIDs, the parameters MUST be absent.
218 | // Regardless of the defect in the original 1997 syntax,
219 | // implementations MUST NOT accept a parameters value of NULL.
220 | //
221 | // But Java's default keystore puts it in (when decoding as
222 | // PKCS8 and then re-encoding to pass on), so we must accept it.
223 | if (idlen == 7) {
224 | if (d[idx++] != 0x05 ||
225 | d[idx++] != 0) {
226 | throw new InvalidKeySpecException("unsupported key spec");
227 | }
228 | }
229 | }
230 | if (d[idx++] != 0x03 ||
231 | d[idx++] != 33 ||
232 | d[idx++] != 0) {
233 | throw new InvalidKeySpecException("unsupported key spec");
234 | }
235 | byte[] rv = new byte[32];
236 | System.arraycopy(d, idx, rv, 0, 32);
237 | return rv;
238 | } catch (IndexOutOfBoundsException ioobe) {
239 | throw new InvalidKeySpecException(ioobe);
240 | }
241 | }
242 |
243 | @Override
244 | public EdDSAParameterSpec getParams() {
245 | return edDsaSpec;
246 | }
247 |
248 | public GroupElement getA() {
249 | return A;
250 | }
251 |
252 | public GroupElement getNegativeA() {
253 | return Aneg;
254 | }
255 |
256 | public byte[] getAbyte() {
257 | return Abyte;
258 | }
259 |
260 | @Override
261 | public int hashCode() {
262 | return Arrays.hashCode(Abyte);
263 | }
264 |
265 | @Override
266 | public boolean equals(Object o) {
267 | if (o == this)
268 | return true;
269 | if (!(o instanceof EdDSAPublicKey))
270 | return false;
271 | EdDSAPublicKey pk = (EdDSAPublicKey) o;
272 | return Arrays.equals(Abyte, pk.getAbyte()) &&
273 | edDsaSpec.equals(pk.getParams());
274 | }
275 | }
276 |
--------------------------------------------------------------------------------
/ext/ed25519_jruby/net/i2p/crypto/eddsa/EdDSASecurityProvider.java:
--------------------------------------------------------------------------------
1 | /**
2 | * EdDSA-Java by str4d
3 | *
4 | * To the extent possible under law, the person who associated CC0 with
5 | * EdDSA-Java has waived all copyright and related or neighboring rights
6 | * to EdDSA-Java.
7 | *
8 | * You should have received a copy of the CC0 legalcode along with this
9 | * work. If not, see () {
32 | @Override
33 | public Object run() {
34 | setup();
35 | return null;
36 | }
37 | });
38 | }
39 |
40 | protected void setup() {
41 | // See https://docs.oracle.com/javase/8/docs/technotes/guides/security/crypto/HowToImplAProvider.html
42 | put("KeyFactory." + EdDSAKey.KEY_ALGORITHM, "net.i2p.crypto.eddsa.KeyFactory");
43 | put("KeyPairGenerator." + EdDSAKey.KEY_ALGORITHM, "net.i2p.crypto.eddsa.KeyPairGenerator");
44 | put("Signature." + EdDSAEngine.SIGNATURE_ALGORITHM, "net.i2p.crypto.eddsa.EdDSAEngine");
45 |
46 | // OID Mappings
47 | // See section "Mapping from OID to name".
48 | // The Key* -> OID mappings correspond to the default algorithm in KeyPairGenerator.
49 | //
50 | // From draft-ieft-curdle-pkix-04:
51 | // id-Ed25519 OBJECT IDENTIFIER ::= { 1 3 101 112 }
52 | put("Alg.Alias.KeyFactory.1.3.101.112", EdDSAKey.KEY_ALGORITHM);
53 | put("Alg.Alias.KeyFactory.OID.1.3.101.112", EdDSAKey.KEY_ALGORITHM);
54 | put("Alg.Alias.KeyPairGenerator.1.3.101.112", EdDSAKey.KEY_ALGORITHM);
55 | put("Alg.Alias.KeyPairGenerator.OID.1.3.101.112", EdDSAKey.KEY_ALGORITHM);
56 | put("Alg.Alias.Signature.1.3.101.112", EdDSAEngine.SIGNATURE_ALGORITHM);
57 | put("Alg.Alias.Signature.OID.1.3.101.112", EdDSAEngine.SIGNATURE_ALGORITHM);
58 | }
59 | }
60 |
--------------------------------------------------------------------------------
/ext/ed25519_jruby/net/i2p/crypto/eddsa/KeyFactory.java:
--------------------------------------------------------------------------------
1 | /**
2 | * EdDSA-Java by str4d
3 | *
4 | * To the extent possible under law, the person who associated CC0 with
5 | * EdDSA-Java has waived all copyright and related or neighboring rights
6 | * to EdDSA-Java.
7 | *
8 | * You should have received a copy of the CC0 legalcode along with this
9 | * work. If not, see T engineGetKeySpec(Key key, Class keySpec)
57 | throws InvalidKeySpecException {
58 | if (keySpec.isAssignableFrom(EdDSAPublicKeySpec.class) && key instanceof EdDSAPublicKey) {
59 | EdDSAPublicKey k = (EdDSAPublicKey) key;
60 | if (k.getParams() != null) {
61 | return (T) new EdDSAPublicKeySpec(k.getA(), k.getParams());
62 | }
63 | } else if (keySpec.isAssignableFrom(EdDSAPrivateKeySpec.class) && key instanceof EdDSAPrivateKey) {
64 | EdDSAPrivateKey k = (EdDSAPrivateKey) key;
65 | if (k.getParams() != null) {
66 | return (T) new EdDSAPrivateKeySpec(k.getSeed(), k.getH(), k.geta(), k.getA(), k.getParams());
67 | }
68 | }
69 | throw new InvalidKeySpecException("not implemented yet " + key + " " + keySpec);
70 | }
71 |
72 | protected Key engineTranslateKey(Key key) throws InvalidKeyException {
73 | throw new InvalidKeyException("No other EdDSA key providers known");
74 | }
75 | }
76 |
--------------------------------------------------------------------------------
/ext/ed25519_jruby/net/i2p/crypto/eddsa/KeyPairGenerator.java:
--------------------------------------------------------------------------------
1 | /**
2 | * EdDSA-Java by str4d
3 | *
4 | * To the extent possible under law, the person who associated CC0 with
5 | * EdDSA-Java has waived all copyright and related or neighboring rights
6 | * to EdDSA-Java.
7 | *
8 | * You should have received a copy of the CC0 legalcode along with this
9 | * work. If not, see edParameters;
39 |
40 | static {
41 | edParameters = new Hashtable();
42 |
43 | edParameters.put(Integer.valueOf(256), new EdDSAGenParameterSpec(EdDSANamedCurveTable.ED_25519));
44 | }
45 |
46 | public void initialize(int keysize, SecureRandom random) {
47 | AlgorithmParameterSpec edParams = edParameters.get(Integer.valueOf(keysize));
48 | if (edParams == null)
49 | throw new InvalidParameterException("unknown key type.");
50 | try {
51 | initialize(edParams, random);
52 | } catch (InvalidAlgorithmParameterException e) {
53 | throw new InvalidParameterException("key type not configurable.");
54 | }
55 | }
56 |
57 | @Override
58 | public void initialize(AlgorithmParameterSpec params, SecureRandom random) throws InvalidAlgorithmParameterException {
59 | if (params instanceof EdDSAParameterSpec) {
60 | edParams = (EdDSAParameterSpec) params;
61 | } else if (params instanceof EdDSAGenParameterSpec) {
62 | edParams = createNamedCurveSpec(((EdDSAGenParameterSpec) params).getName());
63 | } else
64 | throw new InvalidAlgorithmParameterException("parameter object not a EdDSAParameterSpec");
65 |
66 | this.random = random;
67 | initialized = true;
68 | }
69 |
70 | public KeyPair generateKeyPair() {
71 | if (!initialized)
72 | initialize(DEFAULT_KEYSIZE, new SecureRandom());
73 |
74 | byte[] seed = new byte[edParams.getCurve().getField().getb()/8];
75 | random.nextBytes(seed);
76 |
77 | EdDSAPrivateKeySpec privKey = new EdDSAPrivateKeySpec(seed, edParams);
78 | EdDSAPublicKeySpec pubKey = new EdDSAPublicKeySpec(privKey.getA(), edParams);
79 |
80 | return new KeyPair(new EdDSAPublicKey(pubKey), new EdDSAPrivateKey(privKey));
81 | }
82 |
83 | /**
84 | * Create an EdDSANamedCurveSpec from the provided curve name. The current
85 | * implementation fetches the pre-created curve spec from a table.
86 | * @param curveName the EdDSA named curve.
87 | * @return the specification for the named curve.
88 | * @throws InvalidAlgorithmParameterException if the named curve is unknown.
89 | */
90 | protected EdDSANamedCurveSpec createNamedCurveSpec(String curveName) throws InvalidAlgorithmParameterException {
91 | EdDSANamedCurveSpec spec = EdDSANamedCurveTable.getByName(curveName);
92 | if (spec == null) {
93 | throw new InvalidAlgorithmParameterException("unknown curve name: " + curveName);
94 | }
95 | return spec;
96 | }
97 | }
98 |
--------------------------------------------------------------------------------
/ext/ed25519_jruby/net/i2p/crypto/eddsa/Utils.java:
--------------------------------------------------------------------------------
1 | /**
2 | * EdDSA-Java by str4d
3 | *
4 | * To the extent possible under law, the person who associated CC0 with
5 | * EdDSA-Java has waived all copyright and related or neighboring rights
6 | * to EdDSA-Java.
7 | *
8 | * You should have received a copy of the CC0 legalcode along with this
9 | * work. If not, see
18 | * From the Ed25519 paper:
2 |
3 | Low-level, non-optimized implementation using BigIntegers for any curve.
4 | See the ed25519 implementation for Curve 25519.
5 |
6 |
7 |
--------------------------------------------------------------------------------
/ext/ed25519_jruby/net/i2p/crypto/eddsa/math/ed25519/Ed25519LittleEndianEncoding.java:
--------------------------------------------------------------------------------
1 | /**
2 | * EdDSA-Java by str4d
3 | *
4 | * To the extent possible under law, the person who associated CC0 with
5 | * EdDSA-Java has waived all copyright and related or neighboring rights
6 | * to EdDSA-Java.
7 | *
8 | * You should have received a copy of the CC0 legalcode along with this
9 | * work. If not, see
19 | * Reviewed/commented by Bloody Rookie (nemproject@gmx.de)
20 | */
21 | public class Ed25519LittleEndianEncoding extends Encoding {
22 | /**
23 | * Encodes a given field element in its 32 byte representation. This is done in two steps:
24 | *
25 | * Reduce the value of the field element modulo $p$.
26 | * Convert the field element to the 32 byte representation.
27 | *
28 | * The idea for the modulo $p$ reduction algorithm is as follows:
29 | *
30 | * Assumption:
31 | *
32 | * $p = 2^{255} - 19$
33 | * $h = h_0 + 2^{25} * h_1 + 2^{(26+25)} * h_2 + \dots + 2^{230} * h_9$ where $0 \le |h_i| \lt 2^{27}$ for all $i=0,\dots,9$.
34 | * $h \cong r \mod p$, i.e. $h = r + q * p$ for some suitable $0 \le r \lt p$ and an integer $q$.
35 | *
36 | * Then $q = [2^{-255} * (h + 19 * 2^{-25} * h_9 + 1/2)]$ where $[x] = floor(x)$.
37 | *
38 | * Proof:
39 | *
40 | * We begin with some very raw estimation for the bounds of some expressions:
41 | *
42 | * $$
43 | * \begin{equation}
44 | * |h| \lt 2^{230} * 2^{30} = 2^{260} \Rightarrow |r + q * p| \lt 2^{260} \Rightarrow |q| \lt 2^{10}. \\
45 | * \Rightarrow -1/4 \le a := 19^2 * 2^{-255} * q \lt 1/4. \\
46 | * |h - 2^{230} * h_9| = |h_0 + \dots + 2^{204} * h_8| \lt 2^{204} * 2^{30} = 2^{234}. \\
47 | * \Rightarrow -1/4 \le b := 19 * 2^{-255} * (h - 2^{230} * h_9) \lt 1/4
48 | * \end{equation}
49 | * $$
50 | *
51 | * Therefore $0 \lt 1/2 - a - b \lt 1$.
52 | *
53 | * Set $x := r + 19 * 2^{-255} * r + 1/2 - a - b$. Then:
54 | *
55 | * $$
56 | * 0 \le x \lt 255 - 20 + 19 + 1 = 2^{255} \\
57 | * \Rightarrow 0 \le 2^{-255} * x \lt 1.
58 | * $$
59 | *
60 | * Since $q$ is an integer we have
61 | *
62 | * $$
63 | * [q + 2^{-255} * x] = q \quad (1)
64 | * $$
65 | *
66 | * Have a closer look at $x$:
67 | *
68 | * $$
69 | * \begin{align}
70 | * x &= h - q * (2^{255} - 19) + 19 * 2^{-255} * (h - q * (2^{255} - 19)) + 1/2 - 19^2 * 2^{-255} * q - 19 * 2^{-255} * (h - 2^{230} * h_9) \\
71 | * &= h - q * 2^{255} + 19 * q + 19 * 2^{-255} * h - 19 * q + 19^2 * 2^{-255} * q + 1/2 - 19^2 * 2^{-255} * q - 19 * 2^{-255} * h + 19 * 2^{-25} * h_9 \\
72 | * &= h + 19 * 2^{-25} * h_9 + 1/2 - q^{255}.
73 | * \end{align}
74 | * $$
75 | *
76 | * Inserting the expression for $x$ into $(1)$ we get the desired expression for $q$.
77 | */
78 | public byte[] encode(FieldElement x) {
79 | int[] h = ((Ed25519FieldElement)x).t;
80 | int h0 = h[0];
81 | int h1 = h[1];
82 | int h2 = h[2];
83 | int h3 = h[3];
84 | int h4 = h[4];
85 | int h5 = h[5];
86 | int h6 = h[6];
87 | int h7 = h[7];
88 | int h8 = h[8];
89 | int h9 = h[9];
90 | int q;
91 | int carry0;
92 | int carry1;
93 | int carry2;
94 | int carry3;
95 | int carry4;
96 | int carry5;
97 | int carry6;
98 | int carry7;
99 | int carry8;
100 | int carry9;
101 |
102 | // Step 1:
103 | // Calculate q
104 | q = (19 * h9 + (1 << 24)) >> 25;
105 | q = (h0 + q) >> 26;
106 | q = (h1 + q) >> 25;
107 | q = (h2 + q) >> 26;
108 | q = (h3 + q) >> 25;
109 | q = (h4 + q) >> 26;
110 | q = (h5 + q) >> 25;
111 | q = (h6 + q) >> 26;
112 | q = (h7 + q) >> 25;
113 | q = (h8 + q) >> 26;
114 | q = (h9 + q) >> 25;
115 |
116 | // r = h - q * p = h - 2^255 * q + 19 * q
117 | // First add 19 * q then discard the bit 255
118 | h0 += 19 * q;
119 |
120 | carry0 = h0 >> 26; h1 += carry0; h0 -= carry0 << 26;
121 | carry1 = h1 >> 25; h2 += carry1; h1 -= carry1 << 25;
122 | carry2 = h2 >> 26; h3 += carry2; h2 -= carry2 << 26;
123 | carry3 = h3 >> 25; h4 += carry3; h3 -= carry3 << 25;
124 | carry4 = h4 >> 26; h5 += carry4; h4 -= carry4 << 26;
125 | carry5 = h5 >> 25; h6 += carry5; h5 -= carry5 << 25;
126 | carry6 = h6 >> 26; h7 += carry6; h6 -= carry6 << 26;
127 | carry7 = h7 >> 25; h8 += carry7; h7 -= carry7 << 25;
128 | carry8 = h8 >> 26; h9 += carry8; h8 -= carry8 << 26;
129 | carry9 = h9 >> 25; h9 -= carry9 << 25;
130 |
131 | // Step 2 (straight forward conversion):
132 | byte[] s = new byte[32];
133 | s[0] = (byte) h0;
134 | s[1] = (byte) (h0 >> 8);
135 | s[2] = (byte) (h0 >> 16);
136 | s[3] = (byte) ((h0 >> 24) | (h1 << 2));
137 | s[4] = (byte) (h1 >> 6);
138 | s[5] = (byte) (h1 >> 14);
139 | s[6] = (byte) ((h1 >> 22) | (h2 << 3));
140 | s[7] = (byte) (h2 >> 5);
141 | s[8] = (byte) (h2 >> 13);
142 | s[9] = (byte) ((h2 >> 21) | (h3 << 5));
143 | s[10] = (byte) (h3 >> 3);
144 | s[11] = (byte) (h3 >> 11);
145 | s[12] = (byte) ((h3 >> 19) | (h4 << 6));
146 | s[13] = (byte) (h4 >> 2);
147 | s[14] = (byte) (h4 >> 10);
148 | s[15] = (byte) (h4 >> 18);
149 | s[16] = (byte) h5;
150 | s[17] = (byte) (h5 >> 8);
151 | s[18] = (byte) (h5 >> 16);
152 | s[19] = (byte) ((h5 >> 24) | (h6 << 1));
153 | s[20] = (byte) (h6 >> 7);
154 | s[21] = (byte) (h6 >> 15);
155 | s[22] = (byte) ((h6 >> 23) | (h7 << 3));
156 | s[23] = (byte) (h7 >> 5);
157 | s[24] = (byte) (h7 >> 13);
158 | s[25] = (byte) ((h7 >> 21) | (h8 << 4));
159 | s[26] = (byte) (h8 >> 4);
160 | s[27] = (byte) (h8 >> 12);
161 | s[28] = (byte) ((h8 >> 20) | (h9 << 6));
162 | s[29] = (byte) (h9 >> 2);
163 | s[30] = (byte) (h9 >> 10);
164 | s[31] = (byte) (h9 >> 18);
165 | return s;
166 | }
167 |
168 | static int load_3(byte[] in, int offset) {
169 | int result = in[offset++] & 0xff;
170 | result |= (in[offset++] & 0xff) << 8;
171 | result |= (in[offset] & 0xff) << 16;
172 | return result;
173 | }
174 |
175 | static long load_4(byte[] in, int offset) {
176 | int result = in[offset++] & 0xff;
177 | result |= (in[offset++] & 0xff) << 8;
178 | result |= (in[offset++] & 0xff) << 16;
179 | result |= in[offset] << 24;
180 | return ((long)result) & 0xffffffffL;
181 | }
182 |
183 | /**
184 | * Decodes a given field element in its 10 byte $2^{25.5}$ representation.
185 | *
186 | * @param in The 32 byte representation.
187 | * @return The field element in its $2^{25.5}$ bit representation.
188 | */
189 | public FieldElement decode(byte[] in) {
190 | long h0 = load_4(in, 0);
191 | long h1 = load_3(in, 4) << 6;
192 | long h2 = load_3(in, 7) << 5;
193 | long h3 = load_3(in, 10) << 3;
194 | long h4 = load_3(in, 13) << 2;
195 | long h5 = load_4(in, 16);
196 | long h6 = load_3(in, 20) << 7;
197 | long h7 = load_3(in, 23) << 5;
198 | long h8 = load_3(in, 26) << 4;
199 | long h9 = (load_3(in, 29) & 0x7FFFFF) << 2;
200 | long carry0;
201 | long carry1;
202 | long carry2;
203 | long carry3;
204 | long carry4;
205 | long carry5;
206 | long carry6;
207 | long carry7;
208 | long carry8;
209 | long carry9;
210 |
211 | // Remember: 2^255 congruent 19 modulo p
212 | carry9 = (h9 + (long) (1<<24)) >> 25; h0 += carry9 * 19; h9 -= carry9 << 25;
213 | carry1 = (h1 + (long) (1<<24)) >> 25; h2 += carry1; h1 -= carry1 << 25;
214 | carry3 = (h3 + (long) (1<<24)) >> 25; h4 += carry3; h3 -= carry3 << 25;
215 | carry5 = (h5 + (long) (1<<24)) >> 25; h6 += carry5; h5 -= carry5 << 25;
216 | carry7 = (h7 + (long) (1<<24)) >> 25; h8 += carry7; h7 -= carry7 << 25;
217 |
218 | carry0 = (h0 + (long) (1<<25)) >> 26; h1 += carry0; h0 -= carry0 << 26;
219 | carry2 = (h2 + (long) (1<<25)) >> 26; h3 += carry2; h2 -= carry2 << 26;
220 | carry4 = (h4 + (long) (1<<25)) >> 26; h5 += carry4; h4 -= carry4 << 26;
221 | carry6 = (h6 + (long) (1<<25)) >> 26; h7 += carry6; h6 -= carry6 << 26;
222 | carry8 = (h8 + (long) (1<<25)) >> 26; h9 += carry8; h8 -= carry8 << 26;
223 |
224 | int[] h = new int[10];
225 | h[0] = (int) h0;
226 | h[1] = (int) h1;
227 | h[2] = (int) h2;
228 | h[3] = (int) h3;
229 | h[4] = (int) h4;
230 | h[5] = (int) h5;
231 | h[6] = (int) h6;
232 | h[7] = (int) h7;
233 | h[8] = (int) h8;
234 | h[9] = (int) h9;
235 | return new Ed25519FieldElement(f, h);
236 | }
237 |
238 | /**
239 | * Is the FieldElement negative in this encoding?
240 | *
241 | * Return true if $x$ is in $\{1,3,5,\dots,q-2\}$
244 | * Preconditions:
245 | *
246 | * $|x|$ bounded by $1.1*2^{26},1.1*2^{25},1.1*2^{26},1.1*2^{25}$, etc.
247 | *
248 | *
249 | * @return true if $x$ is in $\{1,3,5,\dots,q-2\}$, false otherwise.
250 | */
251 | public boolean isNegative(FieldElement x) {
252 | byte[] s = encode(x);
253 | return (s[0] & 1) != 0;
254 | }
255 |
256 | }
257 |
--------------------------------------------------------------------------------
/ext/ed25519_jruby/net/i2p/crypto/eddsa/spec/EdDSAGenParameterSpec.java:
--------------------------------------------------------------------------------
1 | /**
2 | * EdDSA-Java by str4d
3 | *
4 | * To the extent possible under law, the person who associated CC0 with
5 | * EdDSA-Java has waived all copyright and related or neighboring rights
6 | * to EdDSA-Java.
7 | *
8 | * You should have received a copy of the CC0 legalcode along with this
9 | * work. If not, see curves = new Hashtable();
50 |
51 | public static void defineCurve(EdDSANamedCurveSpec curve) {
52 | curves.put(curve.getName().toLowerCase(Locale.ENGLISH), curve);
53 | }
54 |
55 | static void defineCurveAlias(String name, String alias) {
56 | EdDSANamedCurveSpec curve = curves.get(name.toLowerCase(Locale.ENGLISH));
57 | if (curve == null) {
58 | throw new IllegalStateException();
59 | }
60 | curves.put(alias.toLowerCase(Locale.ENGLISH), curve);
61 | }
62 |
63 | static {
64 | // RFC 8032
65 | defineCurve(ed25519);
66 | }
67 |
68 | public static EdDSANamedCurveSpec getByName(String name) {
69 | return curves.get(name.toLowerCase(Locale.ENGLISH));
70 | }
71 | }
72 |
--------------------------------------------------------------------------------
/ext/ed25519_jruby/net/i2p/crypto/eddsa/spec/EdDSAParameterSpec.java:
--------------------------------------------------------------------------------
1 | /**
2 | * EdDSA-Java by str4d
3 | *
4 | * To the extent possible under law, the person who associated CC0 with
5 | * EdDSA-Java has waived all copyright and related or neighboring rights
6 | * to EdDSA-Java.
7 | *
8 | * You should have received a copy of the CC0 legalcode along with this
9 | * work. If not, see
5 |
6 | #define SECRETKEYBYTES 64
7 | #define PUBLICKEYBYTES 32
8 | #define SIGNATUREBYTES 64
9 |
10 | #define ED25519_KEYSIZE_BYTES 32
11 | typedef uint8_t ED25519_KEY[ED25519_KEYSIZE_BYTES];
12 |
13 | /* Generate an Ed25519 keypair from a seed value */
14 | int crypto_sign_ed25519_ref10_seed_keypair(uint8_t *pk, uint8_t *sk, const uint8_t *seed);
15 |
16 | /* Compute an Ed25519 signature over the given message */
17 | int crypto_sign_ed25519_ref10(
18 | uint8_t *sm, uint64_t *smlen,
19 | const uint8_t *m, uint64_t mlen,
20 | const uint8_t *sk
21 | );
22 |
23 | /* Verify the given signature is authentic */
24 | int crypto_sign_open_ed25519_ref10(
25 | uint8_t *m, uint64_t *mlen,
26 | const uint8_t *sm, uint64_t smlen,
27 | const uint8_t *pk
28 | );
29 |
30 | /* Constant-time comparison function */
31 | int crypto_verify_32(const uint8_t *x,const uint8_t *y);
32 |
33 | #endif /* ED25519_REF10_H */
34 |
--------------------------------------------------------------------------------
/ext/ed25519_ref10/extconf.rb:
--------------------------------------------------------------------------------
1 | # frozen_string_literal: true
2 |
3 | require "mkmf"
4 |
5 | append_cflags(["-Wall", "-O3", "-pedantic", "-std=c99"])
6 |
7 | create_makefile "ed25519_ref10"
8 |
--------------------------------------------------------------------------------
/ext/ed25519_ref10/fe.h:
--------------------------------------------------------------------------------
1 | #ifndef FE_H
2 | #define FE_H
3 |
4 | #include "ed25519_ref10.h"
5 |
6 | typedef int32_t fe[10];
7 |
8 | /*
9 | fe means field element.
10 | Here the field is \Z/(2^255-19).
11 | An element t, entries t[0]...t[9], represents the integer
12 | t[0]+2^26 t[1]+2^51 t[2]+2^77 t[3]+2^102 t[4]+...+2^230 t[9].
13 | Bounds on each t[i] vary depending on context.
14 | */
15 |
16 | #define fe_frombytes crypto_sign_ed25519_ref10_fe_frombytes
17 | #define fe_tobytes crypto_sign_ed25519_ref10_fe_tobytes
18 | #define fe_copy crypto_sign_ed25519_ref10_fe_copy
19 | #define fe_isnonzero crypto_sign_ed25519_ref10_fe_isnonzero
20 | #define fe_isnegative crypto_sign_ed25519_ref10_fe_isnegative
21 | #define fe_0 crypto_sign_ed25519_ref10_fe_0
22 | #define fe_1 crypto_sign_ed25519_ref10_fe_1
23 | #define fe_cswap crypto_sign_ed25519_ref10_fe_cswap
24 | #define fe_cmov crypto_sign_ed25519_ref10_fe_cmov
25 | #define fe_add crypto_sign_ed25519_ref10_fe_add
26 | #define fe_sub crypto_sign_ed25519_ref10_fe_sub
27 | #define fe_neg crypto_sign_ed25519_ref10_fe_neg
28 | #define fe_mul crypto_sign_ed25519_ref10_fe_mul
29 | #define fe_sq crypto_sign_ed25519_ref10_fe_sq
30 | #define fe_sq2 crypto_sign_ed25519_ref10_fe_sq2
31 | #define fe_mul121666 crypto_sign_ed25519_ref10_fe_mul121666
32 | #define fe_invert crypto_sign_ed25519_ref10_fe_invert
33 | #define fe_pow22523 crypto_sign_ed25519_ref10_fe_pow22523
34 |
35 | extern void fe_frombytes(fe,const unsigned char *);
36 | extern void fe_tobytes(unsigned char *,const fe);
37 |
38 | extern void fe_copy(fe,const fe);
39 | extern int fe_isnonzero(const fe);
40 | extern int fe_isnegative(const fe);
41 | extern void fe_0(fe);
42 | extern void fe_1(fe);
43 | extern void fe_cswap(fe,fe,unsigned int);
44 | extern void fe_cmov(fe,const fe,unsigned int);
45 |
46 | extern void fe_add(fe,const fe,const fe);
47 | extern void fe_sub(fe,const fe,const fe);
48 | extern void fe_neg(fe,const fe);
49 | extern void fe_mul(fe,const fe,const fe);
50 | extern void fe_sq(fe,const fe);
51 | extern void fe_sq2(fe,const fe);
52 | extern void fe_mul121666(fe,const fe);
53 | extern void fe_invert(fe,const fe);
54 | extern void fe_pow22523(fe,const fe);
55 |
56 | #endif
57 |
--------------------------------------------------------------------------------
/ext/ed25519_ref10/ge.c:
--------------------------------------------------------------------------------
1 | #include "ge.h"
2 |
3 | /*
4 | r = p + q
5 | */
6 |
7 | void ge_add(ge_p1p1 *r,const ge_p3 *p,const ge_cached *q)
8 | {
9 | fe t0;
10 | #include "ge_add.h"
11 | }
12 |
13 | static void slide(signed char *r,const unsigned char *a)
14 | {
15 | int i;
16 | int b;
17 | int k;
18 |
19 | for (i = 0;i < 256;++i)
20 | r[i] = 1 & (a[i >> 3] >> (i & 7));
21 |
22 | for (i = 0;i < 256;++i)
23 | if (r[i]) {
24 | for (b = 1;b <= 6 && i + b < 256;++b) {
25 | if (r[i + b]) {
26 | if (r[i] + (r[i + b] << b) <= 15) {
27 | r[i] += r[i + b] << b; r[i + b] = 0;
28 | } else if (r[i] - (r[i + b] << b) >= -15) {
29 | r[i] -= r[i + b] << b;
30 | for (k = i + b;k < 256;++k) {
31 | if (!r[k]) {
32 | r[k] = 1;
33 | break;
34 | }
35 | r[k] = 0;
36 | }
37 | } else
38 | break;
39 | }
40 | }
41 | }
42 |
43 | }
44 |
45 | static ge_precomp Bi[8] = {
46 | #include "base2.h"
47 | } ;
48 |
49 | /*
50 | r = a * A + b * B
51 | where a = a[0]+256*a[1]+...+256^31 a[31].
52 | and b = b[0]+256*b[1]+...+256^31 b[31].
53 | B is the Ed25519 base point (x,4/5) with x positive.
54 | */
55 |
56 | void ge_double_scalarmult_vartime(ge_p2 *r,const unsigned char *a,const ge_p3 *A,const unsigned char *b)
57 | {
58 | signed char aslide[256];
59 | signed char bslide[256];
60 | ge_cached Ai[8]; /* A,3A,5A,7A,9A,11A,13A,15A */
61 | ge_p1p1 t;
62 | ge_p3 u;
63 | ge_p3 A2;
64 | int i;
65 |
66 | slide(aslide,a);
67 | slide(bslide,b);
68 |
69 | ge_p3_to_cached(&Ai[0],A);
70 | ge_p3_dbl(&t,A); ge_p1p1_to_p3(&A2,&t);
71 | ge_add(&t,&A2,&Ai[0]); ge_p1p1_to_p3(&u,&t); ge_p3_to_cached(&Ai[1],&u);
72 | ge_add(&t,&A2,&Ai[1]); ge_p1p1_to_p3(&u,&t); ge_p3_to_cached(&Ai[2],&u);
73 | ge_add(&t,&A2,&Ai[2]); ge_p1p1_to_p3(&u,&t); ge_p3_to_cached(&Ai[3],&u);
74 | ge_add(&t,&A2,&Ai[3]); ge_p1p1_to_p3(&u,&t); ge_p3_to_cached(&Ai[4],&u);
75 | ge_add(&t,&A2,&Ai[4]); ge_p1p1_to_p3(&u,&t); ge_p3_to_cached(&Ai[5],&u);
76 | ge_add(&t,&A2,&Ai[5]); ge_p1p1_to_p3(&u,&t); ge_p3_to_cached(&Ai[6],&u);
77 | ge_add(&t,&A2,&Ai[6]); ge_p1p1_to_p3(&u,&t); ge_p3_to_cached(&Ai[7],&u);
78 |
79 | ge_p2_0(r);
80 |
81 | for (i = 255;i >= 0;--i) {
82 | if (aslide[i] || bslide[i]) break;
83 | }
84 |
85 | for (;i >= 0;--i) {
86 | ge_p2_dbl(&t,r);
87 |
88 | if (aslide[i] > 0) {
89 | ge_p1p1_to_p3(&u,&t);
90 | ge_add(&t,&u,&Ai[aslide[i]/2]);
91 | } else if (aslide[i] < 0) {
92 | ge_p1p1_to_p3(&u,&t);
93 | ge_sub(&t,&u,&Ai[(-aslide[i])/2]);
94 | }
95 |
96 | if (bslide[i] > 0) {
97 | ge_p1p1_to_p3(&u,&t);
98 | ge_madd(&t,&u,&Bi[bslide[i]/2]);
99 | } else if (bslide[i] < 0) {
100 | ge_p1p1_to_p3(&u,&t);
101 | ge_msub(&t,&u,&Bi[(-bslide[i])/2]);
102 | }
103 |
104 | ge_p1p1_to_p2(r,&t);
105 | }
106 | }
107 |
108 | static const fe d = {
109 | #include "d.h"
110 | } ;
111 |
112 | static const fe sqrtm1 = {
113 | #include "sqrtm1.h"
114 | } ;
115 |
116 | int ge_frombytes_negate_vartime(ge_p3 *h,const unsigned char *s)
117 | {
118 | fe u;
119 | fe v;
120 | fe v3;
121 | fe vxx;
122 | fe check;
123 |
124 | fe_frombytes(h->Y,s);
125 | fe_1(h->Z);
126 | fe_sq(u,h->Y);
127 | fe_mul(v,u,d);
128 | fe_sub(u,u,h->Z); /* u = y^2-1 */
129 | fe_add(v,v,h->Z); /* v = dy^2+1 */
130 |
131 | fe_sq(v3,v);
132 | fe_mul(v3,v3,v); /* v3 = v^3 */
133 | fe_sq(h->X,v3);
134 | fe_mul(h->X,h->X,v);
135 | fe_mul(h->X,h->X,u); /* x = uv^7 */
136 |
137 | fe_pow22523(h->X,h->X); /* x = (uv^7)^((q-5)/8) */
138 | fe_mul(h->X,h->X,v3);
139 | fe_mul(h->X,h->X,u); /* x = uv^3(uv^7)^((q-5)/8) */
140 |
141 | fe_sq(vxx,h->X);
142 | fe_mul(vxx,vxx,v);
143 | fe_sub(check,vxx,u); /* vx^2-u */
144 | if (fe_isnonzero(check)) {
145 | fe_add(check,vxx,u); /* vx^2+u */
146 | if (fe_isnonzero(check)) return -1;
147 | fe_mul(h->X,h->X,sqrtm1);
148 | }
149 |
150 | if (fe_isnegative(h->X) == (s[31] >> 7))
151 | fe_neg(h->X,h->X);
152 |
153 | fe_mul(h->T,h->X,h->Y);
154 | return 0;
155 | }
156 |
157 | /*
158 | r = p + q
159 | */
160 |
161 | void ge_madd(ge_p1p1 *r,const ge_p3 *p,const ge_precomp *q)
162 | {
163 | fe t0;
164 | #include "ge_madd.h"
165 | }
166 |
167 | /*
168 | r = p - q
169 | */
170 |
171 | void ge_msub(ge_p1p1 *r,const ge_p3 *p,const ge_precomp *q)
172 | {
173 | fe t0;
174 | #include "ge_msub.h"
175 | }
176 |
177 | /*
178 | r = p
179 | */
180 |
181 | extern void ge_p1p1_to_p2(ge_p2 *r,const ge_p1p1 *p)
182 | {
183 | fe_mul(r->X,p->X,p->T);
184 | fe_mul(r->Y,p->Y,p->Z);
185 | fe_mul(r->Z,p->Z,p->T);
186 | }
187 |
188 | /*
189 | r = p
190 | */
191 |
192 | extern void ge_p1p1_to_p3(ge_p3 *r,const ge_p1p1 *p)
193 | {
194 | fe_mul(r->X,p->X,p->T);
195 | fe_mul(r->Y,p->Y,p->Z);
196 | fe_mul(r->Z,p->Z,p->T);
197 | fe_mul(r->T,p->X,p->Y);
198 | }
199 |
200 | void ge_p2_0(ge_p2 *h)
201 | {
202 | fe_0(h->X);
203 | fe_1(h->Y);
204 | fe_1(h->Z);
205 | }
206 |
207 | /*
208 | r = 2 * p
209 | */
210 |
211 | void ge_p2_dbl(ge_p1p1 *r,const ge_p2 *p)
212 | {
213 | fe t0;
214 | #include "ge_p2_dbl.h"
215 | }
216 |
217 | void ge_p3_0(ge_p3 *h)
218 | {
219 | fe_0(h->X);
220 | fe_1(h->Y);
221 | fe_1(h->Z);
222 | fe_0(h->T);
223 | }
224 |
225 | /*
226 | r = 2 * p
227 | */
228 |
229 | void ge_p3_dbl(ge_p1p1 *r,const ge_p3 *p)
230 | {
231 | ge_p2 q;
232 | ge_p3_to_p2(&q,p);
233 | ge_p2_dbl(r,&q);
234 | }
235 |
236 | /*
237 | r = p
238 | */
239 |
240 | static const fe d2 = {
241 | #include "d2.h"
242 | } ;
243 |
244 | extern void ge_p3_to_cached(ge_cached *r,const ge_p3 *p)
245 | {
246 | fe_add(r->YplusX,p->Y,p->X);
247 | fe_sub(r->YminusX,p->Y,p->X);
248 | fe_copy(r->Z,p->Z);
249 | fe_mul(r->T2d,p->T,d2);
250 | }
251 |
252 | /*
253 | r = p
254 | */
255 |
256 | extern void ge_p3_to_p2(ge_p2 *r,const ge_p3 *p)
257 | {
258 | fe_copy(r->X,p->X);
259 | fe_copy(r->Y,p->Y);
260 | fe_copy(r->Z,p->Z);
261 | }
262 |
263 | void ge_p3_tobytes(unsigned char *s,const ge_p3 *h)
264 | {
265 | fe recip;
266 | fe x;
267 | fe y;
268 |
269 | fe_invert(recip,h->Z);
270 | fe_mul(x,h->X,recip);
271 | fe_mul(y,h->Y,recip);
272 | fe_tobytes(s,y);
273 | s[31] ^= fe_isnegative(x) << 7;
274 | }
275 |
276 | void ge_precomp_0(ge_precomp *h)
277 | {
278 | fe_1(h->yplusx);
279 | fe_1(h->yminusx);
280 | fe_0(h->xy2d);
281 | }
282 |
283 | static uint8_t equal(int8_t b,int8_t c)
284 | {
285 | uint8_t ub = b;
286 | uint8_t uc = c;
287 | uint8_t x = ub ^ uc; /* 0: yes; 1..255: no */
288 | uint32_t y = x; /* 0: yes; 1..255: no */
289 | y -= 1; /* 4294967295: yes; 0..254: no */
290 | y >>= 31; /* 1: yes; 0: no */
291 | return y;
292 | }
293 |
294 | static uint8_t negative(int8_t b)
295 | {
296 | unsigned long long x = b; /* 18446744073709551361..18446744073709551615: yes; 0..255: no */
297 | x >>= 63; /* 1: yes; 0: no */
298 | return x;
299 | }
300 |
301 | static void cmov(ge_precomp *t,ge_precomp *u,int8_t b)
302 | {
303 | fe_cmov(t->yplusx,u->yplusx,b);
304 | fe_cmov(t->yminusx,u->yminusx,b);
305 | fe_cmov(t->xy2d,u->xy2d,b);
306 | }
307 |
308 | /* base[i][j] = (j+1)*256^i*B */
309 | static ge_precomp base[32][8] = {
310 | #include "base.h"
311 | } ;
312 |
313 | static void select(ge_precomp *t,int pos,int8_t b)
314 | {
315 | ge_precomp minust;
316 | uint8_t bnegative = negative(b);
317 | uint8_t babs = b - (((-bnegative) & b) << 1);
318 |
319 | ge_precomp_0(t);
320 | cmov(t,&base[pos][0],equal(babs,1));
321 | cmov(t,&base[pos][1],equal(babs,2));
322 | cmov(t,&base[pos][2],equal(babs,3));
323 | cmov(t,&base[pos][3],equal(babs,4));
324 | cmov(t,&base[pos][4],equal(babs,5));
325 | cmov(t,&base[pos][5],equal(babs,6));
326 | cmov(t,&base[pos][6],equal(babs,7));
327 | cmov(t,&base[pos][7],equal(babs,8));
328 | fe_copy(minust.yplusx,t->yminusx);
329 | fe_copy(minust.yminusx,t->yplusx);
330 | fe_neg(minust.xy2d,t->xy2d);
331 | cmov(t,&minust,bnegative);
332 | }
333 |
334 | /*
335 | h = a * B
336 | where a = a[0]+256*a[1]+...+256^31 a[31]
337 | B is the Ed25519 base point (x,4/5) with x positive.
338 |
339 | Preconditions:
340 | a[31] <= 127
341 | */
342 |
343 | void ge_scalarmult_base(ge_p3 *h,const uint8_t *a)
344 | {
345 | int8_t e[64];
346 | int8_t carry;
347 | ge_p1p1 r;
348 | ge_p2 s;
349 | ge_precomp t;
350 | int i;
351 |
352 | for (i = 0;i < 32;++i) {
353 | e[2 * i + 0] = (a[i] >> 0) & 15;
354 | e[2 * i + 1] = (a[i] >> 4) & 15;
355 | }
356 | /* each e[i] is between 0 and 15 */
357 | /* e[63] is between 0 and 7 */
358 |
359 | carry = 0;
360 | for (i = 0;i < 63;++i) {
361 | e[i] += carry;
362 | carry = e[i] + 8;
363 | carry >>= 4;
364 | e[i] -= carry << 4;
365 | }
366 | e[63] += carry;
367 | /* each e[i] is between -8 and 8 */
368 |
369 | ge_p3_0(h);
370 | for (i = 1;i < 64;i += 2) {
371 | select(&t,i / 2,e[i]);
372 | ge_madd(&r,h,&t); ge_p1p1_to_p3(h,&r);
373 | }
374 |
375 | ge_p3_dbl(&r,h); ge_p1p1_to_p2(&s,&r);
376 | ge_p2_dbl(&r,&s); ge_p1p1_to_p2(&s,&r);
377 | ge_p2_dbl(&r,&s); ge_p1p1_to_p2(&s,&r);
378 | ge_p2_dbl(&r,&s); ge_p1p1_to_p3(h,&r);
379 |
380 | for (i = 0;i < 64;i += 2) {
381 | select(&t,i / 2,e[i]);
382 | ge_madd(&r,h,&t); ge_p1p1_to_p3(h,&r);
383 | }
384 | }
385 |
386 | /*
387 | r = p - q
388 | */
389 |
390 | void ge_sub(ge_p1p1 *r,const ge_p3 *p,const ge_cached *q)
391 | {
392 | fe t0;
393 | #include "ge_sub.h"
394 | }
395 |
396 | void ge_tobytes(unsigned char *s,const ge_p2 *h)
397 | {
398 | fe recip;
399 | fe x;
400 | fe y;
401 |
402 | fe_invert(recip,h->Z);
403 | fe_mul(x,h->X,recip);
404 | fe_mul(y,h->Y,recip);
405 | fe_tobytes(s,y);
406 | s[31] ^= fe_isnegative(x) << 7;
407 | }
408 |
--------------------------------------------------------------------------------
/ext/ed25519_ref10/ge.h:
--------------------------------------------------------------------------------
1 | #ifndef GE_H
2 | #define GE_H
3 |
4 | /*
5 | ge means group element.
6 |
7 | Here the group is the set of pairs (x,y) of field elements (see fe.h)
8 | satisfying -x^2 + y^2 = 1 + d x^2y^2
9 | where d = -121665/121666.
10 |
11 | Representations:
12 | ge_p2 (projective): (X:Y:Z) satisfying x=X/Z, y=Y/Z
13 | ge_p3 (extended): (X:Y:Z:T) satisfying x=X/Z, y=Y/Z, XY=ZT
14 | ge_p1p1 (completed): ((X:Z),(Y:T)) satisfying x=X/Z, y=Y/T
15 | ge_precomp (Duif): (y+x,y-x,2dxy)
16 | */
17 |
18 | #include "fe.h"
19 |
20 | typedef struct {
21 | fe X;
22 | fe Y;
23 | fe Z;
24 | } ge_p2;
25 |
26 | typedef struct {
27 | fe X;
28 | fe Y;
29 | fe Z;
30 | fe T;
31 | } ge_p3;
32 |
33 | typedef struct {
34 | fe X;
35 | fe Y;
36 | fe Z;
37 | fe T;
38 | } ge_p1p1;
39 |
40 | typedef struct {
41 | fe yplusx;
42 | fe yminusx;
43 | fe xy2d;
44 | } ge_precomp;
45 |
46 | typedef struct {
47 | fe YplusX;
48 | fe YminusX;
49 | fe Z;
50 | fe T2d;
51 | } ge_cached;
52 |
53 | #define ge_frombytes_negate_vartime crypto_sign_ed25519_ref10_ge_frombytes_negate_vartime
54 | #define ge_tobytes crypto_sign_ed25519_ref10_ge_tobytes
55 | #define ge_p3_tobytes crypto_sign_ed25519_ref10_ge_p3_tobytes
56 |
57 | #define ge_p2_0 crypto_sign_ed25519_ref10_ge_p2_0
58 | #define ge_p3_0 crypto_sign_ed25519_ref10_ge_p3_0
59 | #define ge_precomp_0 crypto_sign_ed25519_ref10_ge_precomp_0
60 | #define ge_p3_to_p2 crypto_sign_ed25519_ref10_ge_p3_to_p2
61 | #define ge_p3_to_cached crypto_sign_ed25519_ref10_ge_p3_to_cached
62 | #define ge_p1p1_to_p2 crypto_sign_ed25519_ref10_ge_p1p1_to_p2
63 | #define ge_p1p1_to_p3 crypto_sign_ed25519_ref10_ge_p1p1_to_p3
64 | #define ge_p2_dbl crypto_sign_ed25519_ref10_ge_p2_dbl
65 | #define ge_p3_dbl crypto_sign_ed25519_ref10_ge_p3_dbl
66 |
67 | #define ge_madd crypto_sign_ed25519_ref10_ge_madd
68 | #define ge_msub crypto_sign_ed25519_ref10_ge_msub
69 | #define ge_add crypto_sign_ed25519_ref10_ge_add
70 | #define ge_sub crypto_sign_ed25519_ref10_ge_sub
71 | #define ge_scalarmult_base crypto_sign_ed25519_ref10_ge_scalarmult_base
72 | #define ge_double_scalarmult_vartime crypto_sign_ed25519_ref10_ge_double_scalarmult_vartime
73 |
74 | extern void ge_tobytes(unsigned char *,const ge_p2 *);
75 | extern void ge_p3_tobytes(unsigned char *,const ge_p3 *);
76 | extern int ge_frombytes_negate_vartime(ge_p3 *,const unsigned char *);
77 |
78 | extern void ge_p2_0(ge_p2 *);
79 | extern void ge_p3_0(ge_p3 *);
80 | extern void ge_precomp_0(ge_precomp *);
81 | extern void ge_p3_to_p2(ge_p2 *,const ge_p3 *);
82 | extern void ge_p3_to_cached(ge_cached *,const ge_p3 *);
83 | extern void ge_p1p1_to_p2(ge_p2 *,const ge_p1p1 *);
84 | extern void ge_p1p1_to_p3(ge_p3 *,const ge_p1p1 *);
85 | extern void ge_p2_dbl(ge_p1p1 *,const ge_p2 *);
86 | extern void ge_p3_dbl(ge_p1p1 *,const ge_p3 *);
87 |
88 | extern void ge_madd(ge_p1p1 *,const ge_p3 *,const ge_precomp *);
89 | extern void ge_msub(ge_p1p1 *,const ge_p3 *,const ge_precomp *);
90 | extern void ge_add(ge_p1p1 *,const ge_p3 *,const ge_cached *);
91 | extern void ge_sub(ge_p1p1 *,const ge_p3 *,const ge_cached *);
92 | extern void ge_scalarmult_base(ge_p3 *,const unsigned char *);
93 | extern void ge_double_scalarmult_vartime(ge_p2 *,const unsigned char *,const ge_p3 *,const unsigned char *);
94 |
95 | #endif
96 |
--------------------------------------------------------------------------------
/ext/ed25519_ref10/ge_add.h:
--------------------------------------------------------------------------------
1 |
2 | /* qhasm: enter ge_add */
3 |
4 | /* qhasm: fe X1 */
5 |
6 | /* qhasm: fe Y1 */
7 |
8 | /* qhasm: fe Z1 */
9 |
10 | /* qhasm: fe Z2 */
11 |
12 | /* qhasm: fe T1 */
13 |
14 | /* qhasm: fe ZZ */
15 |
16 | /* qhasm: fe YpX2 */
17 |
18 | /* qhasm: fe YmX2 */
19 |
20 | /* qhasm: fe T2d2 */
21 |
22 | /* qhasm: fe X3 */
23 |
24 | /* qhasm: fe Y3 */
25 |
26 | /* qhasm: fe Z3 */
27 |
28 | /* qhasm: fe T3 */
29 |
30 | /* qhasm: fe YpX1 */
31 |
32 | /* qhasm: fe YmX1 */
33 |
34 | /* qhasm: fe A */
35 |
36 | /* qhasm: fe B */
37 |
38 | /* qhasm: fe C */
39 |
40 | /* qhasm: fe D */
41 |
42 | /* qhasm: YpX1 = Y1+X1 */
43 | /* asm 1: fe_add(>YpX1=fe#1,YpX1=r->X,Y,X); */
45 | fe_add(r->X,p->Y,p->X);
46 |
47 | /* qhasm: YmX1 = Y1-X1 */
48 | /* asm 1: fe_sub(>YmX1=fe#2,YmX1=r->Y,Y,X); */
50 | fe_sub(r->Y,p->Y,p->X);
51 |
52 | /* qhasm: A = YpX1*YpX2 */
53 | /* asm 1: fe_mul(>A=fe#3,A=r->Z,X,YplusX); */
55 | fe_mul(r->Z,r->X,q->YplusX);
56 |
57 | /* qhasm: B = YmX1*YmX2 */
58 | /* asm 1: fe_mul(>B=fe#2,B=r->Y,Y,YminusX); */
60 | fe_mul(r->Y,r->Y,q->YminusX);
61 |
62 | /* qhasm: C = T2d2*T1 */
63 | /* asm 1: fe_mul(>C=fe#4,C=r->T,T2d,T); */
65 | fe_mul(r->T,q->T2d,p->T);
66 |
67 | /* qhasm: ZZ = Z1*Z2 */
68 | /* asm 1: fe_mul(>ZZ=fe#1,ZZ=r->X,Z,Z); */
70 | fe_mul(r->X,p->Z,q->Z);
71 |
72 | /* qhasm: D = 2*ZZ */
73 | /* asm 1: fe_add(>D=fe#5,D=t0,X,X); */
75 | fe_add(t0,r->X,r->X);
76 |
77 | /* qhasm: X3 = A-B */
78 | /* asm 1: fe_sub(>X3=fe#1,X3=r->X,Z,Y); */
80 | fe_sub(r->X,r->Z,r->Y);
81 |
82 | /* qhasm: Y3 = A+B */
83 | /* asm 1: fe_add(>Y3=fe#2,Y3=r->Y,Z,Y); */
85 | fe_add(r->Y,r->Z,r->Y);
86 |
87 | /* qhasm: Z3 = D+C */
88 | /* asm 1: fe_add(>Z3=fe#3,Z3=r->Z,T); */
90 | fe_add(r->Z,t0,r->T);
91 |
92 | /* qhasm: T3 = D-C */
93 | /* asm 1: fe_sub(>T3=fe#4,T3=r->T,T); */
95 | fe_sub(r->T,t0,r->T);
96 |
97 | /* qhasm: return */
98 |
--------------------------------------------------------------------------------
/ext/ed25519_ref10/ge_madd.h:
--------------------------------------------------------------------------------
1 |
2 | /* qhasm: enter ge_madd */
3 |
4 | /* qhasm: fe X1 */
5 |
6 | /* qhasm: fe Y1 */
7 |
8 | /* qhasm: fe Z1 */
9 |
10 | /* qhasm: fe T1 */
11 |
12 | /* qhasm: fe ypx2 */
13 |
14 | /* qhasm: fe ymx2 */
15 |
16 | /* qhasm: fe xy2d2 */
17 |
18 | /* qhasm: fe X3 */
19 |
20 | /* qhasm: fe Y3 */
21 |
22 | /* qhasm: fe Z3 */
23 |
24 | /* qhasm: fe T3 */
25 |
26 | /* qhasm: fe YpX1 */
27 |
28 | /* qhasm: fe YmX1 */
29 |
30 | /* qhasm: fe A */
31 |
32 | /* qhasm: fe B */
33 |
34 | /* qhasm: fe C */
35 |
36 | /* qhasm: fe D */
37 |
38 | /* qhasm: YpX1 = Y1+X1 */
39 | /* asm 1: fe_add(>YpX1=fe#1,YpX1=r->X,Y,X); */
41 | fe_add(r->X,p->Y,p->X);
42 |
43 | /* qhasm: YmX1 = Y1-X1 */
44 | /* asm 1: fe_sub(>YmX1=fe#2,YmX1=r->Y,Y,X); */
46 | fe_sub(r->Y,p->Y,p->X);
47 |
48 | /* qhasm: A = YpX1*ypx2 */
49 | /* asm 1: fe_mul(>A=fe#3,A=r->Z,X,yplusx); */
51 | fe_mul(r->Z,r->X,q->yplusx);
52 |
53 | /* qhasm: B = YmX1*ymx2 */
54 | /* asm 1: fe_mul(>B=fe#2,B=r->Y,Y,yminusx); */
56 | fe_mul(r->Y,r->Y,q->yminusx);
57 |
58 | /* qhasm: C = xy2d2*T1 */
59 | /* asm 1: fe_mul(>C=fe#4,C=r->T,xy2d,T); */
61 | fe_mul(r->T,q->xy2d,p->T);
62 |
63 | /* qhasm: D = 2*Z1 */
64 | /* asm 1: fe_add(>D=fe#5,D=t0,Z,Z); */
66 | fe_add(t0,p->Z,p->Z);
67 |
68 | /* qhasm: X3 = A-B */
69 | /* asm 1: fe_sub(>X3=fe#1,X3=r->X,Z,Y); */
71 | fe_sub(r->X,r->Z,r->Y);
72 |
73 | /* qhasm: Y3 = A+B */
74 | /* asm 1: fe_add(>Y3=fe#2,Y3=r->Y,Z,Y); */
76 | fe_add(r->Y,r->Z,r->Y);
77 |
78 | /* qhasm: Z3 = D+C */
79 | /* asm 1: fe_add(>Z3=fe#3,Z3=r->Z,T); */
81 | fe_add(r->Z,t0,r->T);
82 |
83 | /* qhasm: T3 = D-C */
84 | /* asm 1: fe_sub(>T3=fe#4,T3=r->T,T); */
86 | fe_sub(r->T,t0,r->T);
87 |
88 | /* qhasm: return */
89 |
--------------------------------------------------------------------------------
/ext/ed25519_ref10/ge_msub.h:
--------------------------------------------------------------------------------
1 |
2 | /* qhasm: enter ge_msub */
3 |
4 | /* qhasm: fe X1 */
5 |
6 | /* qhasm: fe Y1 */
7 |
8 | /* qhasm: fe Z1 */
9 |
10 | /* qhasm: fe T1 */
11 |
12 | /* qhasm: fe ypx2 */
13 |
14 | /* qhasm: fe ymx2 */
15 |
16 | /* qhasm: fe xy2d2 */
17 |
18 | /* qhasm: fe X3 */
19 |
20 | /* qhasm: fe Y3 */
21 |
22 | /* qhasm: fe Z3 */
23 |
24 | /* qhasm: fe T3 */
25 |
26 | /* qhasm: fe YpX1 */
27 |
28 | /* qhasm: fe YmX1 */
29 |
30 | /* qhasm: fe A */
31 |
32 | /* qhasm: fe B */
33 |
34 | /* qhasm: fe C */
35 |
36 | /* qhasm: fe D */
37 |
38 | /* qhasm: YpX1 = Y1+X1 */
39 | /* asm 1: fe_add(>YpX1=fe#1,YpX1=r->X,Y,X); */
41 | fe_add(r->X,p->Y,p->X);
42 |
43 | /* qhasm: YmX1 = Y1-X1 */
44 | /* asm 1: fe_sub(>YmX1=fe#2,YmX1=r->Y,Y,X); */
46 | fe_sub(r->Y,p->Y,p->X);
47 |
48 | /* qhasm: A = YpX1*ymx2 */
49 | /* asm 1: fe_mul(>A=fe#3,A=r->Z,X,yminusx); */
51 | fe_mul(r->Z,r->X,q->yminusx);
52 |
53 | /* qhasm: B = YmX1*ypx2 */
54 | /* asm 1: fe_mul(>B=fe#2,B=r->Y,Y,yplusx); */
56 | fe_mul(r->Y,r->Y,q->yplusx);
57 |
58 | /* qhasm: C = xy2d2*T1 */
59 | /* asm 1: fe_mul(>C=fe#4,C=r->T,xy2d,T); */
61 | fe_mul(r->T,q->xy2d,p->T);
62 |
63 | /* qhasm: D = 2*Z1 */
64 | /* asm 1: fe_add(>D=fe#5,D=t0,Z,Z); */
66 | fe_add(t0,p->Z,p->Z);
67 |
68 | /* qhasm: X3 = A-B */
69 | /* asm 1: fe_sub(>X3=fe#1,X3=r->X,Z,Y); */
71 | fe_sub(r->X,r->Z,r->Y);
72 |
73 | /* qhasm: Y3 = A+B */
74 | /* asm 1: fe_add(>Y3=fe#2,Y3=r->Y,Z,Y); */
76 | fe_add(r->Y,r->Z,r->Y);
77 |
78 | /* qhasm: Z3 = D-C */
79 | /* asm 1: fe_sub(>Z3=fe#3,Z3=r->Z,T); */
81 | fe_sub(r->Z,t0,r->T);
82 |
83 | /* qhasm: T3 = D+C */
84 | /* asm 1: fe_add(>T3=fe#4,T3=r->T,T); */
86 | fe_add(r->T,t0,r->T);
87 |
88 | /* qhasm: return */
89 |
--------------------------------------------------------------------------------
/ext/ed25519_ref10/ge_p2_dbl.h:
--------------------------------------------------------------------------------
1 |
2 | /* qhasm: enter ge_p2_dbl */
3 |
4 | /* qhasm: fe X1 */
5 |
6 | /* qhasm: fe Y1 */
7 |
8 | /* qhasm: fe Z1 */
9 |
10 | /* qhasm: fe A */
11 |
12 | /* qhasm: fe AA */
13 |
14 | /* qhasm: fe XX */
15 |
16 | /* qhasm: fe YY */
17 |
18 | /* qhasm: fe B */
19 |
20 | /* qhasm: fe X3 */
21 |
22 | /* qhasm: fe Y3 */
23 |
24 | /* qhasm: fe Z3 */
25 |
26 | /* qhasm: fe T3 */
27 |
28 | /* qhasm: XX=X1^2 */
29 | /* asm 1: fe_sq(>XX=fe#1,XX=r->X,X); */
31 | fe_sq(r->X,p->X);
32 |
33 | /* qhasm: YY=Y1^2 */
34 | /* asm 1: fe_sq(>YY=fe#3,YY=r->Z,Y); */
36 | fe_sq(r->Z,p->Y);
37 |
38 | /* qhasm: B=2*Z1^2 */
39 | /* asm 1: fe_sq2(>B=fe#4,B=r->T,Z); */
41 | fe_sq2(r->T,p->Z);
42 |
43 | /* qhasm: A=X1+Y1 */
44 | /* asm 1: fe_add(>A=fe#2,A=r->Y,X,Y); */
46 | fe_add(r->Y,p->X,p->Y);
47 |
48 | /* qhasm: AA=A^2 */
49 | /* asm 1: fe_sq(>AA=fe#5,AA=t0,Y); */
51 | fe_sq(t0,r->Y);
52 |
53 | /* qhasm: Y3=YY+XX */
54 | /* asm 1: fe_add(>Y3=fe#2,Y3=r->Y,Z,X); */
56 | fe_add(r->Y,r->Z,r->X);
57 |
58 | /* qhasm: Z3=YY-XX */
59 | /* asm 1: fe_sub(>Z3=fe#3,Z3=r->Z,Z,X); */
61 | fe_sub(r->Z,r->Z,r->X);
62 |
63 | /* qhasm: X3=AA-Y3 */
64 | /* asm 1: fe_sub(>X3=fe#1,X3=r->X,Y); */
66 | fe_sub(r->X,t0,r->Y);
67 |
68 | /* qhasm: T3=B-Z3 */
69 | /* asm 1: fe_sub(>T3=fe#4,T3=r->T,T,Z); */
71 | fe_sub(r->T,r->T,r->Z);
72 |
73 | /* qhasm: return */
74 |
--------------------------------------------------------------------------------
/ext/ed25519_ref10/ge_sub.h:
--------------------------------------------------------------------------------
1 |
2 | /* qhasm: enter ge_sub */
3 |
4 | /* qhasm: fe X1 */
5 |
6 | /* qhasm: fe Y1 */
7 |
8 | /* qhasm: fe Z1 */
9 |
10 | /* qhasm: fe Z2 */
11 |
12 | /* qhasm: fe T1 */
13 |
14 | /* qhasm: fe ZZ */
15 |
16 | /* qhasm: fe YpX2 */
17 |
18 | /* qhasm: fe YmX2 */
19 |
20 | /* qhasm: fe T2d2 */
21 |
22 | /* qhasm: fe X3 */
23 |
24 | /* qhasm: fe Y3 */
25 |
26 | /* qhasm: fe Z3 */
27 |
28 | /* qhasm: fe T3 */
29 |
30 | /* qhasm: fe YpX1 */
31 |
32 | /* qhasm: fe YmX1 */
33 |
34 | /* qhasm: fe A */
35 |
36 | /* qhasm: fe B */
37 |
38 | /* qhasm: fe C */
39 |
40 | /* qhasm: fe D */
41 |
42 | /* qhasm: YpX1 = Y1+X1 */
43 | /* asm 1: fe_add(>YpX1=fe#1,YpX1=r->X,Y,X); */
45 | fe_add(r->X,p->Y,p->X);
46 |
47 | /* qhasm: YmX1 = Y1-X1 */
48 | /* asm 1: fe_sub(>YmX1=fe#2,YmX1=r->Y,Y,X); */
50 | fe_sub(r->Y,p->Y,p->X);
51 |
52 | /* qhasm: A = YpX1*YmX2 */
53 | /* asm 1: fe_mul(>A=fe#3,A=r->Z,X,YminusX); */
55 | fe_mul(r->Z,r->X,q->YminusX);
56 |
57 | /* qhasm: B = YmX1*YpX2 */
58 | /* asm 1: fe_mul(>B=fe#2,B=r->Y,Y,YplusX); */
60 | fe_mul(r->Y,r->Y,q->YplusX);
61 |
62 | /* qhasm: C = T2d2*T1 */
63 | /* asm 1: fe_mul(>C=fe#4,C=r->T,T2d,T); */
65 | fe_mul(r->T,q->T2d,p->T);
66 |
67 | /* qhasm: ZZ = Z1*Z2 */
68 | /* asm 1: fe_mul(>ZZ=fe#1,ZZ=r->X,Z,Z); */
70 | fe_mul(r->X,p->Z,q->Z);
71 |
72 | /* qhasm: D = 2*ZZ */
73 | /* asm 1: fe_add(>D=fe#5,D=t0,X,X); */
75 | fe_add(t0,r->X,r->X);
76 |
77 | /* qhasm: X3 = A-B */
78 | /* asm 1: fe_sub(>X3=fe#1,X3=r->X,Z,Y); */
80 | fe_sub(r->X,r->Z,r->Y);
81 |
82 | /* qhasm: Y3 = A+B */
83 | /* asm 1: fe_add(>Y3=fe#2,Y3=r->Y,Z,Y); */
85 | fe_add(r->Y,r->Z,r->Y);
86 |
87 | /* qhasm: Z3 = D-C */
88 | /* asm 1: fe_sub(>Z3=fe#3,Z3=r->Z,T); */
90 | fe_sub(r->Z,t0,r->T);
91 |
92 | /* qhasm: T3 = D+C */
93 | /* asm 1: fe_add(>T3=fe#4,T3=r->T,T); */
95 | fe_add(r->T,t0,r->T);
96 |
97 | /* qhasm: return */
98 |
--------------------------------------------------------------------------------
/ext/ed25519_ref10/keypair.c:
--------------------------------------------------------------------------------
1 | #include
2 | #include "ed25519_ref10.h"
3 | #include "sha512.h"
4 | #include "ge.h"
5 |
6 | int crypto_sign_ed25519_ref10_seed_keypair(uint8_t *pk, uint8_t *sk, const uint8_t *seed)
7 | {
8 | ge_p3 A;
9 |
10 | crypto_hash_sha512(sk, seed, 32);
11 | sk[0] &= 248;
12 | sk[31] &= 127;
13 | sk[31] |= 64;
14 |
15 | ge_scalarmult_base(&A, sk);
16 | ge_p3_tobytes(pk, &A);
17 |
18 | memmove(sk, seed, 32);
19 | memmove(sk + 32, pk, 32);
20 |
21 | return 0;
22 | }
23 |
--------------------------------------------------------------------------------
/ext/ed25519_ref10/open.c:
--------------------------------------------------------------------------------
1 | #include
2 | #include "sha512.h"
3 | #include "ed25519_ref10.h"
4 | #include "ge.h"
5 | #include "sc.h"
6 |
7 | int crypto_sign_open_ed25519_ref10(
8 | uint8_t *m, uint64_t *mlen,
9 | const uint8_t *sm, uint64_t smlen,
10 | const uint8_t *pk
11 | )
12 | {
13 | unsigned char pkcopy[32];
14 | unsigned char rcopy[32];
15 | unsigned char scopy[32];
16 | unsigned char h[64];
17 | unsigned char rcheck[32];
18 | ge_p3 A;
19 | ge_p2 R;
20 |
21 | if (smlen < 64) goto badsig;
22 | if (sm[63] & 224) goto badsig;
23 | if (ge_frombytes_negate_vartime(&A,pk) != 0) goto badsig;
24 |
25 | memmove(pkcopy,pk,32);
26 | memmove(rcopy,sm,32);
27 | memmove(scopy,sm + 32,32);
28 |
29 | memmove(m,sm,smlen);
30 | memmove(m + 32,pkcopy,32);
31 | crypto_hash_sha512(h,m,smlen);
32 | sc_reduce(h);
33 |
34 | ge_double_scalarmult_vartime(&R,h,&A,scopy);
35 | ge_tobytes(rcheck,&R);
36 | if (crypto_verify_32(rcheck,rcopy) == 0) {
37 | memmove(m,m + 64,smlen - 64);
38 | memset(m + smlen - 64,0,64);
39 | *mlen = smlen - 64;
40 | return 0;
41 | }
42 |
43 | badsig:
44 | *mlen = -1;
45 | memset(m,0,smlen);
46 | return -1;
47 | }
48 |
--------------------------------------------------------------------------------
/ext/ed25519_ref10/pow22523.h:
--------------------------------------------------------------------------------
1 |
2 | /* qhasm: fe z1 */
3 |
4 | /* qhasm: fe z2 */
5 |
6 | /* qhasm: fe z8 */
7 |
8 | /* qhasm: fe z9 */
9 |
10 | /* qhasm: fe z11 */
11 |
12 | /* qhasm: fe z22 */
13 |
14 | /* qhasm: fe z_5_0 */
15 |
16 | /* qhasm: fe z_10_5 */
17 |
18 | /* qhasm: fe z_10_0 */
19 |
20 | /* qhasm: fe z_20_10 */
21 |
22 | /* qhasm: fe z_20_0 */
23 |
24 | /* qhasm: fe z_40_20 */
25 |
26 | /* qhasm: fe z_40_0 */
27 |
28 | /* qhasm: fe z_50_10 */
29 |
30 | /* qhasm: fe z_50_0 */
31 |
32 | /* qhasm: fe z_100_50 */
33 |
34 | /* qhasm: fe z_100_0 */
35 |
36 | /* qhasm: fe z_200_100 */
37 |
38 | /* qhasm: fe z_200_0 */
39 |
40 | /* qhasm: fe z_250_50 */
41 |
42 | /* qhasm: fe z_250_0 */
43 |
44 | /* qhasm: fe z_252_2 */
45 |
46 | /* qhasm: fe z_252_3 */
47 |
48 | /* qhasm: enter pow22523 */
49 |
50 | /* qhasm: z2 = z1^2^1 */
51 | /* asm 1: fe_sq(>z2=fe#1,z2=fe#1,>z2=fe#1); */
52 | /* asm 2: fe_sq(>z2=t0,z2=t0,>z2=t0); */
53 | fe_sq(t0,z); for (i = 1;i < 1;++i) fe_sq(t0,t0);
54 |
55 | /* qhasm: z8 = z2^2^2 */
56 | /* asm 1: fe_sq(>z8=fe#2,z8=fe#2,>z8=fe#2); */
57 | /* asm 2: fe_sq(>z8=t1,z8=t1,>z8=t1); */
58 | fe_sq(t1,t0); for (i = 1;i < 2;++i) fe_sq(t1,t1);
59 |
60 | /* qhasm: z9 = z1*z8 */
61 | /* asm 1: fe_mul(>z9=fe#2,z9=t1,z11=fe#1,z11=t0,z22=fe#1,z22=fe#1,>z22=fe#1); */
72 | /* asm 2: fe_sq(>z22=t0,z22=t0,>z22=t0); */
73 | fe_sq(t0,t0); for (i = 1;i < 1;++i) fe_sq(t0,t0);
74 |
75 | /* qhasm: z_5_0 = z9*z22 */
76 | /* asm 1: fe_mul(>z_5_0=fe#1,z_5_0=t0,z_10_5=fe#2,z_10_5=fe#2,>z_10_5=fe#2); */
82 | /* asm 2: fe_sq(>z_10_5=t1,z_10_5=t1,>z_10_5=t1); */
83 | fe_sq(t1,t0); for (i = 1;i < 5;++i) fe_sq(t1,t1);
84 |
85 | /* qhasm: z_10_0 = z_10_5*z_5_0 */
86 | /* asm 1: fe_mul(>z_10_0=fe#1,z_10_0=t0,z_20_10=fe#2,z_20_10=fe#2,>z_20_10=fe#2); */
92 | /* asm 2: fe_sq(>z_20_10=t1,z_20_10=t1,>z_20_10=t1); */
93 | fe_sq(t1,t0); for (i = 1;i < 10;++i) fe_sq(t1,t1);
94 |
95 | /* qhasm: z_20_0 = z_20_10*z_10_0 */
96 | /* asm 1: fe_mul(>z_20_0=fe#2,z_20_0=t1,z_40_20=fe#3,z_40_20=fe#3,>z_40_20=fe#3); */
102 | /* asm 2: fe_sq(>z_40_20=t2,z_40_20=t2,>z_40_20=t2); */
103 | fe_sq(t2,t1); for (i = 1;i < 20;++i) fe_sq(t2,t2);
104 |
105 | /* qhasm: z_40_0 = z_40_20*z_20_0 */
106 | /* asm 1: fe_mul(>z_40_0=fe#2,z_40_0=t1,z_50_10=fe#2,z_50_10=fe#2,>z_50_10=fe#2); */
112 | /* asm 2: fe_sq(>z_50_10=t1,z_50_10=t1,>z_50_10=t1); */
113 | fe_sq(t1,t1); for (i = 1;i < 10;++i) fe_sq(t1,t1);
114 |
115 | /* qhasm: z_50_0 = z_50_10*z_10_0 */
116 | /* asm 1: fe_mul(>z_50_0=fe#1,z_50_0=t0,z_100_50=fe#2,z_100_50=fe#2,>z_100_50=fe#2); */
122 | /* asm 2: fe_sq(>z_100_50=t1,z_100_50=t1,>z_100_50=t1); */
123 | fe_sq(t1,t0); for (i = 1;i < 50;++i) fe_sq(t1,t1);
124 |
125 | /* qhasm: z_100_0 = z_100_50*z_50_0 */
126 | /* asm 1: fe_mul(>z_100_0=fe#2,z_100_0=t1,z_200_100=fe#3,z_200_100=fe#3,>z_200_100=fe#3); */
132 | /* asm 2: fe_sq(>z_200_100=t2,z_200_100=t2,>z_200_100=t2); */
133 | fe_sq(t2,t1); for (i = 1;i < 100;++i) fe_sq(t2,t2);
134 |
135 | /* qhasm: z_200_0 = z_200_100*z_100_0 */
136 | /* asm 1: fe_mul(>z_200_0=fe#2,z_200_0=t1,z_250_50=fe#2,z_250_50=fe#2,>z_250_50=fe#2); */
142 | /* asm 2: fe_sq(>z_250_50=t1,z_250_50=t1,>z_250_50=t1); */
143 | fe_sq(t1,t1); for (i = 1;i < 50;++i) fe_sq(t1,t1);
144 |
145 | /* qhasm: z_250_0 = z_250_50*z_50_0 */
146 | /* asm 1: fe_mul(>z_250_0=fe#1,z_250_0=t0,z_252_2=fe#1,z_252_2=fe#1,>z_252_2=fe#1); */
152 | /* asm 2: fe_sq(>z_252_2=t0,z_252_2=t0,>z_252_2=t0); */
153 | fe_sq(t0,t0); for (i = 1;i < 2;++i) fe_sq(t0,t0);
154 |
155 | /* qhasm: z_252_3 = z_252_2*z1 */
156 | /* asm 1: fe_mul(>z_252_3=fe#12,z_252_3=out,z2=fe#1,z2=fe#1,>z2=fe#1); */
52 | /* asm 2: fe_sq(>z2=t0,z2=t0,>z2=t0); */
53 | fe_sq(t0,z); for (i = 1;i < 1;++i) fe_sq(t0,t0);
54 |
55 | /* qhasm: z8 = z2^2^2 */
56 | /* asm 1: fe_sq(>z8=fe#2,z8=fe#2,>z8=fe#2); */
57 | /* asm 2: fe_sq(>z8=t1,z8=t1,>z8=t1); */
58 | fe_sq(t1,t0); for (i = 1;i < 2;++i) fe_sq(t1,t1);
59 |
60 | /* qhasm: z9 = z1*z8 */
61 | /* asm 1: fe_mul(>z9=fe#2,z9=t1,z11=fe#1,z11=t0,z22=fe#3,z22=fe#3,>z22=fe#3); */
72 | /* asm 2: fe_sq(>z22=t2,z22=t2,>z22=t2); */
73 | fe_sq(t2,t0); for (i = 1;i < 1;++i) fe_sq(t2,t2);
74 |
75 | /* qhasm: z_5_0 = z9*z22 */
76 | /* asm 1: fe_mul(>z_5_0=fe#2,z_5_0=t1,z_10_5=fe#3,z_10_5=fe#3,>z_10_5=fe#3); */
82 | /* asm 2: fe_sq(>z_10_5=t2,z_10_5=t2,>z_10_5=t2); */
83 | fe_sq(t2,t1); for (i = 1;i < 5;++i) fe_sq(t2,t2);
84 |
85 | /* qhasm: z_10_0 = z_10_5*z_5_0 */
86 | /* asm 1: fe_mul(>z_10_0=fe#2,z_10_0=t1,z_20_10=fe#3,z_20_10=fe#3,>z_20_10=fe#3); */
92 | /* asm 2: fe_sq(>z_20_10=t2,z_20_10=t2,>z_20_10=t2); */
93 | fe_sq(t2,t1); for (i = 1;i < 10;++i) fe_sq(t2,t2);
94 |
95 | /* qhasm: z_20_0 = z_20_10*z_10_0 */
96 | /* asm 1: fe_mul(>z_20_0=fe#3,z_20_0=t2,z_40_20=fe#4,z_40_20=fe#4,>z_40_20=fe#4); */
102 | /* asm 2: fe_sq(>z_40_20=t3,z_40_20=t3,>z_40_20=t3); */
103 | fe_sq(t3,t2); for (i = 1;i < 20;++i) fe_sq(t3,t3);
104 |
105 | /* qhasm: z_40_0 = z_40_20*z_20_0 */
106 | /* asm 1: fe_mul(>z_40_0=fe#3,z_40_0=t2,z_50_10=fe#3,z_50_10=fe#3,>z_50_10=fe#3); */
112 | /* asm 2: fe_sq(>z_50_10=t2,z_50_10=t2,>z_50_10=t2); */
113 | fe_sq(t2,t2); for (i = 1;i < 10;++i) fe_sq(t2,t2);
114 |
115 | /* qhasm: z_50_0 = z_50_10*z_10_0 */
116 | /* asm 1: fe_mul(>z_50_0=fe#2,z_50_0=t1,z_100_50=fe#3,z_100_50=fe#3,>z_100_50=fe#3); */
122 | /* asm 2: fe_sq(>z_100_50=t2,z_100_50=t2,>z_100_50=t2); */
123 | fe_sq(t2,t1); for (i = 1;i < 50;++i) fe_sq(t2,t2);
124 |
125 | /* qhasm: z_100_0 = z_100_50*z_50_0 */
126 | /* asm 1: fe_mul(>z_100_0=fe#3,z_100_0=t2,z_200_100=fe#4,z_200_100=fe#4,>z_200_100=fe#4); */
132 | /* asm 2: fe_sq(>z_200_100=t3,z_200_100=t3,>z_200_100=t3); */
133 | fe_sq(t3,t2); for (i = 1;i < 100;++i) fe_sq(t3,t3);
134 |
135 | /* qhasm: z_200_0 = z_200_100*z_100_0 */
136 | /* asm 1: fe_mul(>z_200_0=fe#3,z_200_0=t2,z_250_50=fe#3,z_250_50=fe#3,>z_250_50=fe#3); */
142 | /* asm 2: fe_sq(>z_250_50=t2,z_250_50=t2,>z_250_50=t2); */
143 | fe_sq(t2,t2); for (i = 1;i < 50;++i) fe_sq(t2,t2);
144 |
145 | /* qhasm: z_250_0 = z_250_50*z_50_0 */
146 | /* asm 1: fe_mul(>z_250_0=fe#2,z_250_0=t1,z_255_5=fe#2,z_255_5=fe#2,>z_255_5=fe#2); */
152 | /* asm 2: fe_sq(>z_255_5=t1,z_255_5=t1,>z_255_5=t1); */
153 | fe_sq(t1,t1); for (i = 1;i < 5;++i) fe_sq(t1,t1);
154 |
155 | /* qhasm: z_255_21 = z_255_5*z11 */
156 | /* asm 1: fe_mul(>z_255_21=fe#12,z_255_21=out,
5 |
6 | /*
7 | The set of scalars is \Z/l
8 | where l = 2^252 + 27742317777372353535851937790883648493.
9 | */
10 |
11 | #define sc_reduce crypto_sign_ed25519_ref10_sc_reduce
12 | #define sc_muladd crypto_sign_ed25519_ref10_sc_muladd
13 |
14 | extern void sc_reduce(uint8_t *);
15 | extern void sc_muladd(uint8_t *,const uint8_t *,const uint8_t *,const uint8_t *);
16 |
17 | #endif
18 |
--------------------------------------------------------------------------------
/ext/ed25519_ref10/sc_muladd.c:
--------------------------------------------------------------------------------
1 | #include "sc.h"
2 |
3 | static uint64_t load_3(const uint8_t *in)
4 | {
5 | uint64_t result;
6 | result = (uint64_t) in[0];
7 | result |= ((uint64_t) in[1]) << 8;
8 | result |= ((uint64_t) in[2]) << 16;
9 | return result;
10 | }
11 |
12 | static uint64_t load_4(const uint8_t *in)
13 | {
14 | uint64_t result;
15 | result = (uint64_t) in[0];
16 | result |= ((uint64_t) in[1]) << 8;
17 | result |= ((uint64_t) in[2]) << 16;
18 | result |= ((uint64_t) in[3]) << 24;
19 | return result;
20 | }
21 |
22 | /*
23 | Input:
24 | a[0]+256*a[1]+...+256^31*a[31] = a
25 | b[0]+256*b[1]+...+256^31*b[31] = b
26 | c[0]+256*c[1]+...+256^31*c[31] = c
27 |
28 | Output:
29 | s[0]+256*s[1]+...+256^31*s[31] = (ab+c) mod l
30 | where l = 2^252 + 27742317777372353535851937790883648493.
31 | */
32 |
33 | void sc_muladd(uint8_t *s,const uint8_t *a,const uint8_t *b,const uint8_t *c)
34 | {
35 | int64_t a0 = 2097151 & load_3(a);
36 | int64_t a1 = 2097151 & (load_4(a + 2) >> 5);
37 | int64_t a2 = 2097151 & (load_3(a + 5) >> 2);
38 | int64_t a3 = 2097151 & (load_4(a + 7) >> 7);
39 | int64_t a4 = 2097151 & (load_4(a + 10) >> 4);
40 | int64_t a5 = 2097151 & (load_3(a + 13) >> 1);
41 | int64_t a6 = 2097151 & (load_4(a + 15) >> 6);
42 | int64_t a7 = 2097151 & (load_3(a + 18) >> 3);
43 | int64_t a8 = 2097151 & load_3(a + 21);
44 | int64_t a9 = 2097151 & (load_4(a + 23) >> 5);
45 | int64_t a10 = 2097151 & (load_3(a + 26) >> 2);
46 | int64_t a11 = (load_4(a + 28) >> 7);
47 | int64_t b0 = 2097151 & load_3(b);
48 | int64_t b1 = 2097151 & (load_4(b + 2) >> 5);
49 | int64_t b2 = 2097151 & (load_3(b + 5) >> 2);
50 | int64_t b3 = 2097151 & (load_4(b + 7) >> 7);
51 | int64_t b4 = 2097151 & (load_4(b + 10) >> 4);
52 | int64_t b5 = 2097151 & (load_3(b + 13) >> 1);
53 | int64_t b6 = 2097151 & (load_4(b + 15) >> 6);
54 | int64_t b7 = 2097151 & (load_3(b + 18) >> 3);
55 | int64_t b8 = 2097151 & load_3(b + 21);
56 | int64_t b9 = 2097151 & (load_4(b + 23) >> 5);
57 | int64_t b10 = 2097151 & (load_3(b + 26) >> 2);
58 | int64_t b11 = (load_4(b + 28) >> 7);
59 | int64_t c0 = 2097151 & load_3(c);
60 | int64_t c1 = 2097151 & (load_4(c + 2) >> 5);
61 | int64_t c2 = 2097151 & (load_3(c + 5) >> 2);
62 | int64_t c3 = 2097151 & (load_4(c + 7) >> 7);
63 | int64_t c4 = 2097151 & (load_4(c + 10) >> 4);
64 | int64_t c5 = 2097151 & (load_3(c + 13) >> 1);
65 | int64_t c6 = 2097151 & (load_4(c + 15) >> 6);
66 | int64_t c7 = 2097151 & (load_3(c + 18) >> 3);
67 | int64_t c8 = 2097151 & load_3(c + 21);
68 | int64_t c9 = 2097151 & (load_4(c + 23) >> 5);
69 | int64_t c10 = 2097151 & (load_3(c + 26) >> 2);
70 | int64_t c11 = (load_4(c + 28) >> 7);
71 | int64_t s0;
72 | int64_t s1;
73 | int64_t s2;
74 | int64_t s3;
75 | int64_t s4;
76 | int64_t s5;
77 | int64_t s6;
78 | int64_t s7;
79 | int64_t s8;
80 | int64_t s9;
81 | int64_t s10;
82 | int64_t s11;
83 | int64_t s12;
84 | int64_t s13;
85 | int64_t s14;
86 | int64_t s15;
87 | int64_t s16;
88 | int64_t s17;
89 | int64_t s18;
90 | int64_t s19;
91 | int64_t s20;
92 | int64_t s21;
93 | int64_t s22;
94 | int64_t s23;
95 | int64_t carry0;
96 | int64_t carry1;
97 | int64_t carry2;
98 | int64_t carry3;
99 | int64_t carry4;
100 | int64_t carry5;
101 | int64_t carry6;
102 | int64_t carry7;
103 | int64_t carry8;
104 | int64_t carry9;
105 | int64_t carry10;
106 | int64_t carry11;
107 | int64_t carry12;
108 | int64_t carry13;
109 | int64_t carry14;
110 | int64_t carry15;
111 | int64_t carry16;
112 | int64_t carry17;
113 | int64_t carry18;
114 | int64_t carry19;
115 | int64_t carry20;
116 | int64_t carry21;
117 | int64_t carry22;
118 |
119 | /* Merry Christmas! */
120 | s0 = c0 + a0*b0;
121 | s1 = c1 + a0*b1 + a1*b0;
122 | s2 = c2 + a0*b2 + a1*b1 + a2*b0;
123 | s3 = c3 + a0*b3 + a1*b2 + a2*b1 + a3*b0;
124 | s4 = c4 + a0*b4 + a1*b3 + a2*b2 + a3*b1 + a4*b0;
125 | s5 = c5 + a0*b5 + a1*b4 + a2*b3 + a3*b2 + a4*b1 + a5*b0;
126 | s6 = c6 + a0*b6 + a1*b5 + a2*b4 + a3*b3 + a4*b2 + a5*b1 + a6*b0;
127 | s7 = c7 + a0*b7 + a1*b6 + a2*b5 + a3*b4 + a4*b3 + a5*b2 + a6*b1 + a7*b0;
128 | s8 = c8 + a0*b8 + a1*b7 + a2*b6 + a3*b5 + a4*b4 + a5*b3 + a6*b2 + a7*b1 + a8*b0;
129 | s9 = c9 + a0*b9 + a1*b8 + a2*b7 + a3*b6 + a4*b5 + a5*b4 + a6*b3 + a7*b2 + a8*b1 + a9*b0;
130 | s10 = c10 + a0*b10 + a1*b9 + a2*b8 + a3*b7 + a4*b6 + a5*b5 + a6*b4 + a7*b3 + a8*b2 + a9*b1 + a10*b0;
131 | s11 = c11 + a0*b11 + a1*b10 + a2*b9 + a3*b8 + a4*b7 + a5*b6 + a6*b5 + a7*b4 + a8*b3 + a9*b2 + a10*b1 + a11*b0;
132 | s12 = a1*b11 + a2*b10 + a3*b9 + a4*b8 + a5*b7 + a6*b6 + a7*b5 + a8*b4 + a9*b3 + a10*b2 + a11*b1;
133 | s13 = a2*b11 + a3*b10 + a4*b9 + a5*b8 + a6*b7 + a7*b6 + a8*b5 + a9*b4 + a10*b3 + a11*b2;
134 | s14 = a3*b11 + a4*b10 + a5*b9 + a6*b8 + a7*b7 + a8*b6 + a9*b5 + a10*b4 + a11*b3;
135 | s15 = a4*b11 + a5*b10 + a6*b9 + a7*b8 + a8*b7 + a9*b6 + a10*b5 + a11*b4;
136 | s16 = a5*b11 + a6*b10 + a7*b9 + a8*b8 + a9*b7 + a10*b6 + a11*b5;
137 | s17 = a6*b11 + a7*b10 + a8*b9 + a9*b8 + a10*b7 + a11*b6;
138 | s18 = a7*b11 + a8*b10 + a9*b9 + a10*b8 + a11*b7;
139 | s19 = a8*b11 + a9*b10 + a10*b9 + a11*b8;
140 | s20 = a9*b11 + a10*b10 + a11*b9;
141 | s21 = a10*b11 + a11*b10;
142 | s22 = a11*b11;
143 | s23 = 0;
144 |
145 | carry0 = (s0 + (1<<20)) >> 21; s1 += carry0; s0 -= carry0 << 21;
146 | carry2 = (s2 + (1<<20)) >> 21; s3 += carry2; s2 -= carry2 << 21;
147 | carry4 = (s4 + (1<<20)) >> 21; s5 += carry4; s4 -= carry4 << 21;
148 | carry6 = (s6 + (1<<20)) >> 21; s7 += carry6; s6 -= carry6 << 21;
149 | carry8 = (s8 + (1<<20)) >> 21; s9 += carry8; s8 -= carry8 << 21;
150 | carry10 = (s10 + (1<<20)) >> 21; s11 += carry10; s10 -= carry10 << 21;
151 | carry12 = (s12 + (1<<20)) >> 21; s13 += carry12; s12 -= carry12 << 21;
152 | carry14 = (s14 + (1<<20)) >> 21; s15 += carry14; s14 -= carry14 << 21;
153 | carry16 = (s16 + (1<<20)) >> 21; s17 += carry16; s16 -= carry16 << 21;
154 | carry18 = (s18 + (1<<20)) >> 21; s19 += carry18; s18 -= carry18 << 21;
155 | carry20 = (s20 + (1<<20)) >> 21; s21 += carry20; s20 -= carry20 << 21;
156 | carry22 = (s22 + (1<<20)) >> 21; s23 += carry22; s22 -= carry22 << 21;
157 |
158 | carry1 = (s1 + (1<<20)) >> 21; s2 += carry1; s1 -= carry1 << 21;
159 | carry3 = (s3 + (1<<20)) >> 21; s4 += carry3; s3 -= carry3 << 21;
160 | carry5 = (s5 + (1<<20)) >> 21; s6 += carry5; s5 -= carry5 << 21;
161 | carry7 = (s7 + (1<<20)) >> 21; s8 += carry7; s7 -= carry7 << 21;
162 | carry9 = (s9 + (1<<20)) >> 21; s10 += carry9; s9 -= carry9 << 21;
163 | carry11 = (s11 + (1<<20)) >> 21; s12 += carry11; s11 -= carry11 << 21;
164 | carry13 = (s13 + (1<<20)) >> 21; s14 += carry13; s13 -= carry13 << 21;
165 | carry15 = (s15 + (1<<20)) >> 21; s16 += carry15; s15 -= carry15 << 21;
166 | carry17 = (s17 + (1<<20)) >> 21; s18 += carry17; s17 -= carry17 << 21;
167 | carry19 = (s19 + (1<<20)) >> 21; s20 += carry19; s19 -= carry19 << 21;
168 | carry21 = (s21 + (1<<20)) >> 21; s22 += carry21; s21 -= carry21 << 21;
169 |
170 | s11 += s23 * 666643;
171 | s12 += s23 * 470296;
172 | s13 += s23 * 654183;
173 | s14 -= s23 * 997805;
174 | s15 += s23 * 136657;
175 | s16 -= s23 * 683901;
176 | s23 = 0;
177 |
178 | s10 += s22 * 666643;
179 | s11 += s22 * 470296;
180 | s12 += s22 * 654183;
181 | s13 -= s22 * 997805;
182 | s14 += s22 * 136657;
183 | s15 -= s22 * 683901;
184 | s22 = 0;
185 |
186 | s9 += s21 * 666643;
187 | s10 += s21 * 470296;
188 | s11 += s21 * 654183;
189 | s12 -= s21 * 997805;
190 | s13 += s21 * 136657;
191 | s14 -= s21 * 683901;
192 | s21 = 0;
193 |
194 | s8 += s20 * 666643;
195 | s9 += s20 * 470296;
196 | s10 += s20 * 654183;
197 | s11 -= s20 * 997805;
198 | s12 += s20 * 136657;
199 | s13 -= s20 * 683901;
200 | s20 = 0;
201 |
202 | s7 += s19 * 666643;
203 | s8 += s19 * 470296;
204 | s9 += s19 * 654183;
205 | s10 -= s19 * 997805;
206 | s11 += s19 * 136657;
207 | s12 -= s19 * 683901;
208 | s19 = 0;
209 |
210 | s6 += s18 * 666643;
211 | s7 += s18 * 470296;
212 | s8 += s18 * 654183;
213 | s9 -= s18 * 997805;
214 | s10 += s18 * 136657;
215 | s11 -= s18 * 683901;
216 | s18 = 0;
217 |
218 | carry6 = (s6 + (1<<20)) >> 21; s7 += carry6; s6 -= carry6 << 21;
219 | carry8 = (s8 + (1<<20)) >> 21; s9 += carry8; s8 -= carry8 << 21;
220 | carry10 = (s10 + (1<<20)) >> 21; s11 += carry10; s10 -= carry10 << 21;
221 | carry12 = (s12 + (1<<20)) >> 21; s13 += carry12; s12 -= carry12 << 21;
222 | carry14 = (s14 + (1<<20)) >> 21; s15 += carry14; s14 -= carry14 << 21;
223 | carry16 = (s16 + (1<<20)) >> 21; s17 += carry16; s16 -= carry16 << 21;
224 |
225 | carry7 = (s7 + (1<<20)) >> 21; s8 += carry7; s7 -= carry7 << 21;
226 | carry9 = (s9 + (1<<20)) >> 21; s10 += carry9; s9 -= carry9 << 21;
227 | carry11 = (s11 + (1<<20)) >> 21; s12 += carry11; s11 -= carry11 << 21;
228 | carry13 = (s13 + (1<<20)) >> 21; s14 += carry13; s13 -= carry13 << 21;
229 | carry15 = (s15 + (1<<20)) >> 21; s16 += carry15; s15 -= carry15 << 21;
230 |
231 | s5 += s17 * 666643;
232 | s6 += s17 * 470296;
233 | s7 += s17 * 654183;
234 | s8 -= s17 * 997805;
235 | s9 += s17 * 136657;
236 | s10 -= s17 * 683901;
237 | s17 = 0;
238 |
239 | s4 += s16 * 666643;
240 | s5 += s16 * 470296;
241 | s6 += s16 * 654183;
242 | s7 -= s16 * 997805;
243 | s8 += s16 * 136657;
244 | s9 -= s16 * 683901;
245 | s16 = 0;
246 |
247 | s3 += s15 * 666643;
248 | s4 += s15 * 470296;
249 | s5 += s15 * 654183;
250 | s6 -= s15 * 997805;
251 | s7 += s15 * 136657;
252 | s8 -= s15 * 683901;
253 | s15 = 0;
254 |
255 | s2 += s14 * 666643;
256 | s3 += s14 * 470296;
257 | s4 += s14 * 654183;
258 | s5 -= s14 * 997805;
259 | s6 += s14 * 136657;
260 | s7 -= s14 * 683901;
261 | s14 = 0;
262 |
263 | s1 += s13 * 666643;
264 | s2 += s13 * 470296;
265 | s3 += s13 * 654183;
266 | s4 -= s13 * 997805;
267 | s5 += s13 * 136657;
268 | s6 -= s13 * 683901;
269 | s13 = 0;
270 |
271 | s0 += s12 * 666643;
272 | s1 += s12 * 470296;
273 | s2 += s12 * 654183;
274 | s3 -= s12 * 997805;
275 | s4 += s12 * 136657;
276 | s5 -= s12 * 683901;
277 | s12 = 0;
278 |
279 | carry0 = (s0 + (1<<20)) >> 21; s1 += carry0; s0 -= carry0 << 21;
280 | carry2 = (s2 + (1<<20)) >> 21; s3 += carry2; s2 -= carry2 << 21;
281 | carry4 = (s4 + (1<<20)) >> 21; s5 += carry4; s4 -= carry4 << 21;
282 | carry6 = (s6 + (1<<20)) >> 21; s7 += carry6; s6 -= carry6 << 21;
283 | carry8 = (s8 + (1<<20)) >> 21; s9 += carry8; s8 -= carry8 << 21;
284 | carry10 = (s10 + (1<<20)) >> 21; s11 += carry10; s10 -= carry10 << 21;
285 |
286 | carry1 = (s1 + (1<<20)) >> 21; s2 += carry1; s1 -= carry1 << 21;
287 | carry3 = (s3 + (1<<20)) >> 21; s4 += carry3; s3 -= carry3 << 21;
288 | carry5 = (s5 + (1<<20)) >> 21; s6 += carry5; s5 -= carry5 << 21;
289 | carry7 = (s7 + (1<<20)) >> 21; s8 += carry7; s7 -= carry7 << 21;
290 | carry9 = (s9 + (1<<20)) >> 21; s10 += carry9; s9 -= carry9 << 21;
291 | carry11 = (s11 + (1<<20)) >> 21; s12 += carry11; s11 -= carry11 << 21;
292 |
293 | s0 += s12 * 666643;
294 | s1 += s12 * 470296;
295 | s2 += s12 * 654183;
296 | s3 -= s12 * 997805;
297 | s4 += s12 * 136657;
298 | s5 -= s12 * 683901;
299 | s12 = 0;
300 |
301 | carry0 = s0 >> 21; s1 += carry0; s0 -= carry0 << 21;
302 | carry1 = s1 >> 21; s2 += carry1; s1 -= carry1 << 21;
303 | carry2 = s2 >> 21; s3 += carry2; s2 -= carry2 << 21;
304 | carry3 = s3 >> 21; s4 += carry3; s3 -= carry3 << 21;
305 | carry4 = s4 >> 21; s5 += carry4; s4 -= carry4 << 21;
306 | carry5 = s5 >> 21; s6 += carry5; s5 -= carry5 << 21;
307 | carry6 = s6 >> 21; s7 += carry6; s6 -= carry6 << 21;
308 | carry7 = s7 >> 21; s8 += carry7; s7 -= carry7 << 21;
309 | carry8 = s8 >> 21; s9 += carry8; s8 -= carry8 << 21;
310 | carry9 = s9 >> 21; s10 += carry9; s9 -= carry9 << 21;
311 | carry10 = s10 >> 21; s11 += carry10; s10 -= carry10 << 21;
312 | carry11 = s11 >> 21; s12 += carry11; s11 -= carry11 << 21;
313 |
314 | s0 += s12 * 666643;
315 | s1 += s12 * 470296;
316 | s2 += s12 * 654183;
317 | s3 -= s12 * 997805;
318 | s4 += s12 * 136657;
319 | s5 -= s12 * 683901;
320 | s12 = 0;
321 |
322 | carry0 = s0 >> 21; s1 += carry0; s0 -= carry0 << 21;
323 | carry1 = s1 >> 21; s2 += carry1; s1 -= carry1 << 21;
324 | carry2 = s2 >> 21; s3 += carry2; s2 -= carry2 << 21;
325 | carry3 = s3 >> 21; s4 += carry3; s3 -= carry3 << 21;
326 | carry4 = s4 >> 21; s5 += carry4; s4 -= carry4 << 21;
327 | carry5 = s5 >> 21; s6 += carry5; s5 -= carry5 << 21;
328 | carry6 = s6 >> 21; s7 += carry6; s6 -= carry6 << 21;
329 | carry7 = s7 >> 21; s8 += carry7; s7 -= carry7 << 21;
330 | carry8 = s8 >> 21; s9 += carry8; s8 -= carry8 << 21;
331 | carry9 = s9 >> 21; s10 += carry9; s9 -= carry9 << 21;
332 | carry10 = s10 >> 21; s11 += carry10; s10 -= carry10 << 21;
333 |
334 | s[0] = s0 >> 0;
335 | s[1] = s0 >> 8;
336 | s[2] = (s0 >> 16) | (s1 << 5);
337 | s[3] = s1 >> 3;
338 | s[4] = s1 >> 11;
339 | s[5] = (s1 >> 19) | (s2 << 2);
340 | s[6] = s2 >> 6;
341 | s[7] = (s2 >> 14) | (s3 << 7);
342 | s[8] = s3 >> 1;
343 | s[9] = s3 >> 9;
344 | s[10] = (s3 >> 17) | (s4 << 4);
345 | s[11] = s4 >> 4;
346 | s[12] = s4 >> 12;
347 | s[13] = (s4 >> 20) | (s5 << 1);
348 | s[14] = s5 >> 7;
349 | s[15] = (s5 >> 15) | (s6 << 6);
350 | s[16] = s6 >> 2;
351 | s[17] = s6 >> 10;
352 | s[18] = (s6 >> 18) | (s7 << 3);
353 | s[19] = s7 >> 5;
354 | s[20] = s7 >> 13;
355 | s[21] = s8 >> 0;
356 | s[22] = s8 >> 8;
357 | s[23] = (s8 >> 16) | (s9 << 5);
358 | s[24] = s9 >> 3;
359 | s[25] = s9 >> 11;
360 | s[26] = (s9 >> 19) | (s10 << 2);
361 | s[27] = s10 >> 6;
362 | s[28] = (s10 >> 14) | (s11 << 7);
363 | s[29] = s11 >> 1;
364 | s[30] = s11 >> 9;
365 | s[31] = s11 >> 17;
366 | }
367 |
--------------------------------------------------------------------------------
/ext/ed25519_ref10/sc_reduce.c:
--------------------------------------------------------------------------------
1 | #include "sc.h"
2 |
3 | static uint64_t load_3(const unsigned char *in)
4 | {
5 | uint64_t result;
6 | result = (uint64_t) in[0];
7 | result |= ((uint64_t) in[1]) << 8;
8 | result |= ((uint64_t) in[2]) << 16;
9 | return result;
10 | }
11 |
12 | static uint64_t load_4(const unsigned char *in)
13 | {
14 | uint64_t result;
15 | result = (uint64_t) in[0];
16 | result |= ((uint64_t) in[1]) << 8;
17 | result |= ((uint64_t) in[2]) << 16;
18 | result |= ((uint64_t) in[3]) << 24;
19 | return result;
20 | }
21 |
22 | /*
23 | Input:
24 | s[0]+256*s[1]+...+256^63*s[63] = s
25 |
26 | Output:
27 | s[0]+256*s[1]+...+256^31*s[31] = s mod l
28 | where l = 2^252 + 27742317777372353535851937790883648493.
29 | Overwrites s in place.
30 | */
31 |
32 | void sc_reduce(uint8_t *s)
33 | {
34 | int64_t s0 = 2097151 & load_3(s);
35 | int64_t s1 = 2097151 & (load_4(s + 2) >> 5);
36 | int64_t s2 = 2097151 & (load_3(s + 5) >> 2);
37 | int64_t s3 = 2097151 & (load_4(s + 7) >> 7);
38 | int64_t s4 = 2097151 & (load_4(s + 10) >> 4);
39 | int64_t s5 = 2097151 & (load_3(s + 13) >> 1);
40 | int64_t s6 = 2097151 & (load_4(s + 15) >> 6);
41 | int64_t s7 = 2097151 & (load_3(s + 18) >> 3);
42 | int64_t s8 = 2097151 & load_3(s + 21);
43 | int64_t s9 = 2097151 & (load_4(s + 23) >> 5);
44 | int64_t s10 = 2097151 & (load_3(s + 26) >> 2);
45 | int64_t s11 = 2097151 & (load_4(s + 28) >> 7);
46 | int64_t s12 = 2097151 & (load_4(s + 31) >> 4);
47 | int64_t s13 = 2097151 & (load_3(s + 34) >> 1);
48 | int64_t s14 = 2097151 & (load_4(s + 36) >> 6);
49 | int64_t s15 = 2097151 & (load_3(s + 39) >> 3);
50 | int64_t s16 = 2097151 & load_3(s + 42);
51 | int64_t s17 = 2097151 & (load_4(s + 44) >> 5);
52 | int64_t s18 = 2097151 & (load_3(s + 47) >> 2);
53 | int64_t s19 = 2097151 & (load_4(s + 49) >> 7);
54 | int64_t s20 = 2097151 & (load_4(s + 52) >> 4);
55 | int64_t s21 = 2097151 & (load_3(s + 55) >> 1);
56 | int64_t s22 = 2097151 & (load_4(s + 57) >> 6);
57 | int64_t s23 = (load_4(s + 60) >> 3);
58 | int64_t carry0;
59 | int64_t carry1;
60 | int64_t carry2;
61 | int64_t carry3;
62 | int64_t carry4;
63 | int64_t carry5;
64 | int64_t carry6;
65 | int64_t carry7;
66 | int64_t carry8;
67 | int64_t carry9;
68 | int64_t carry10;
69 | int64_t carry11;
70 | int64_t carry12;
71 | int64_t carry13;
72 | int64_t carry14;
73 | int64_t carry15;
74 | int64_t carry16;
75 |
76 | s11 += s23 * 666643;
77 | s12 += s23 * 470296;
78 | s13 += s23 * 654183;
79 | s14 -= s23 * 997805;
80 | s15 += s23 * 136657;
81 | s16 -= s23 * 683901;
82 | s23 = 0;
83 |
84 | s10 += s22 * 666643;
85 | s11 += s22 * 470296;
86 | s12 += s22 * 654183;
87 | s13 -= s22 * 997805;
88 | s14 += s22 * 136657;
89 | s15 -= s22 * 683901;
90 | s22 = 0;
91 |
92 | s9 += s21 * 666643;
93 | s10 += s21 * 470296;
94 | s11 += s21 * 654183;
95 | s12 -= s21 * 997805;
96 | s13 += s21 * 136657;
97 | s14 -= s21 * 683901;
98 | s21 = 0;
99 |
100 | s8 += s20 * 666643;
101 | s9 += s20 * 470296;
102 | s10 += s20 * 654183;
103 | s11 -= s20 * 997805;
104 | s12 += s20 * 136657;
105 | s13 -= s20 * 683901;
106 | s20 = 0;
107 |
108 | s7 += s19 * 666643;
109 | s8 += s19 * 470296;
110 | s9 += s19 * 654183;
111 | s10 -= s19 * 997805;
112 | s11 += s19 * 136657;
113 | s12 -= s19 * 683901;
114 | s19 = 0;
115 |
116 | s6 += s18 * 666643;
117 | s7 += s18 * 470296;
118 | s8 += s18 * 654183;
119 | s9 -= s18 * 997805;
120 | s10 += s18 * 136657;
121 | s11 -= s18 * 683901;
122 | s18 = 0;
123 |
124 | carry6 = (s6 + (1<<20)) >> 21; s7 += carry6; s6 -= carry6 << 21;
125 | carry8 = (s8 + (1<<20)) >> 21; s9 += carry8; s8 -= carry8 << 21;
126 | carry10 = (s10 + (1<<20)) >> 21; s11 += carry10; s10 -= carry10 << 21;
127 | carry12 = (s12 + (1<<20)) >> 21; s13 += carry12; s12 -= carry12 << 21;
128 | carry14 = (s14 + (1<<20)) >> 21; s15 += carry14; s14 -= carry14 << 21;
129 | carry16 = (s16 + (1<<20)) >> 21; s17 += carry16; s16 -= carry16 << 21;
130 |
131 | carry7 = (s7 + (1<<20)) >> 21; s8 += carry7; s7 -= carry7 << 21;
132 | carry9 = (s9 + (1<<20)) >> 21; s10 += carry9; s9 -= carry9 << 21;
133 | carry11 = (s11 + (1<<20)) >> 21; s12 += carry11; s11 -= carry11 << 21;
134 | carry13 = (s13 + (1<<20)) >> 21; s14 += carry13; s13 -= carry13 << 21;
135 | carry15 = (s15 + (1<<20)) >> 21; s16 += carry15; s15 -= carry15 << 21;
136 |
137 | s5 += s17 * 666643;
138 | s6 += s17 * 470296;
139 | s7 += s17 * 654183;
140 | s8 -= s17 * 997805;
141 | s9 += s17 * 136657;
142 | s10 -= s17 * 683901;
143 | s17 = 0;
144 |
145 | s4 += s16 * 666643;
146 | s5 += s16 * 470296;
147 | s6 += s16 * 654183;
148 | s7 -= s16 * 997805;
149 | s8 += s16 * 136657;
150 | s9 -= s16 * 683901;
151 | s16 = 0;
152 |
153 | s3 += s15 * 666643;
154 | s4 += s15 * 470296;
155 | s5 += s15 * 654183;
156 | s6 -= s15 * 997805;
157 | s7 += s15 * 136657;
158 | s8 -= s15 * 683901;
159 | s15 = 0;
160 |
161 | s2 += s14 * 666643;
162 | s3 += s14 * 470296;
163 | s4 += s14 * 654183;
164 | s5 -= s14 * 997805;
165 | s6 += s14 * 136657;
166 | s7 -= s14 * 683901;
167 | s14 = 0;
168 |
169 | s1 += s13 * 666643;
170 | s2 += s13 * 470296;
171 | s3 += s13 * 654183;
172 | s4 -= s13 * 997805;
173 | s5 += s13 * 136657;
174 | s6 -= s13 * 683901;
175 | s13 = 0;
176 |
177 | s0 += s12 * 666643;
178 | s1 += s12 * 470296;
179 | s2 += s12 * 654183;
180 | s3 -= s12 * 997805;
181 | s4 += s12 * 136657;
182 | s5 -= s12 * 683901;
183 | s12 = 0;
184 |
185 | carry0 = (s0 + (1<<20)) >> 21; s1 += carry0; s0 -= carry0 << 21;
186 | carry2 = (s2 + (1<<20)) >> 21; s3 += carry2; s2 -= carry2 << 21;
187 | carry4 = (s4 + (1<<20)) >> 21; s5 += carry4; s4 -= carry4 << 21;
188 | carry6 = (s6 + (1<<20)) >> 21; s7 += carry6; s6 -= carry6 << 21;
189 | carry8 = (s8 + (1<<20)) >> 21; s9 += carry8; s8 -= carry8 << 21;
190 | carry10 = (s10 + (1<<20)) >> 21; s11 += carry10; s10 -= carry10 << 21;
191 |
192 | carry1 = (s1 + (1<<20)) >> 21; s2 += carry1; s1 -= carry1 << 21;
193 | carry3 = (s3 + (1<<20)) >> 21; s4 += carry3; s3 -= carry3 << 21;
194 | carry5 = (s5 + (1<<20)) >> 21; s6 += carry5; s5 -= carry5 << 21;
195 | carry7 = (s7 + (1<<20)) >> 21; s8 += carry7; s7 -= carry7 << 21;
196 | carry9 = (s9 + (1<<20)) >> 21; s10 += carry9; s9 -= carry9 << 21;
197 | carry11 = (s11 + (1<<20)) >> 21; s12 += carry11; s11 -= carry11 << 21;
198 |
199 | s0 += s12 * 666643;
200 | s1 += s12 * 470296;
201 | s2 += s12 * 654183;
202 | s3 -= s12 * 997805;
203 | s4 += s12 * 136657;
204 | s5 -= s12 * 683901;
205 | s12 = 0;
206 |
207 | carry0 = s0 >> 21; s1 += carry0; s0 -= carry0 << 21;
208 | carry1 = s1 >> 21; s2 += carry1; s1 -= carry1 << 21;
209 | carry2 = s2 >> 21; s3 += carry2; s2 -= carry2 << 21;
210 | carry3 = s3 >> 21; s4 += carry3; s3 -= carry3 << 21;
211 | carry4 = s4 >> 21; s5 += carry4; s4 -= carry4 << 21;
212 | carry5 = s5 >> 21; s6 += carry5; s5 -= carry5 << 21;
213 | carry6 = s6 >> 21; s7 += carry6; s6 -= carry6 << 21;
214 | carry7 = s7 >> 21; s8 += carry7; s7 -= carry7 << 21;
215 | carry8 = s8 >> 21; s9 += carry8; s8 -= carry8 << 21;
216 | carry9 = s9 >> 21; s10 += carry9; s9 -= carry9 << 21;
217 | carry10 = s10 >> 21; s11 += carry10; s10 -= carry10 << 21;
218 | carry11 = s11 >> 21; s12 += carry11; s11 -= carry11 << 21;
219 |
220 | s0 += s12 * 666643;
221 | s1 += s12 * 470296;
222 | s2 += s12 * 654183;
223 | s3 -= s12 * 997805;
224 | s4 += s12 * 136657;
225 | s5 -= s12 * 683901;
226 | s12 = 0;
227 |
228 | carry0 = s0 >> 21; s1 += carry0; s0 -= carry0 << 21;
229 | carry1 = s1 >> 21; s2 += carry1; s1 -= carry1 << 21;
230 | carry2 = s2 >> 21; s3 += carry2; s2 -= carry2 << 21;
231 | carry3 = s3 >> 21; s4 += carry3; s3 -= carry3 << 21;
232 | carry4 = s4 >> 21; s5 += carry4; s4 -= carry4 << 21;
233 | carry5 = s5 >> 21; s6 += carry5; s5 -= carry5 << 21;
234 | carry6 = s6 >> 21; s7 += carry6; s6 -= carry6 << 21;
235 | carry7 = s7 >> 21; s8 += carry7; s7 -= carry7 << 21;
236 | carry8 = s8 >> 21; s9 += carry8; s8 -= carry8 << 21;
237 | carry9 = s9 >> 21; s10 += carry9; s9 -= carry9 << 21;
238 | carry10 = s10 >> 21; s11 += carry10; s10 -= carry10 << 21;
239 |
240 | s[0] = s0 >> 0;
241 | s[1] = s0 >> 8;
242 | s[2] = (s0 >> 16) | (s1 << 5);
243 | s[3] = s1 >> 3;
244 | s[4] = s1 >> 11;
245 | s[5] = (s1 >> 19) | (s2 << 2);
246 | s[6] = s2 >> 6;
247 | s[7] = (s2 >> 14) | (s3 << 7);
248 | s[8] = s3 >> 1;
249 | s[9] = s3 >> 9;
250 | s[10] = (s3 >> 17) | (s4 << 4);
251 | s[11] = s4 >> 4;
252 | s[12] = s4 >> 12;
253 | s[13] = (s4 >> 20) | (s5 << 1);
254 | s[14] = s5 >> 7;
255 | s[15] = (s5 >> 15) | (s6 << 6);
256 | s[16] = s6 >> 2;
257 | s[17] = s6 >> 10;
258 | s[18] = (s6 >> 18) | (s7 << 3);
259 | s[19] = s7 >> 5;
260 | s[20] = s7 >> 13;
261 | s[21] = s8 >> 0;
262 | s[22] = s8 >> 8;
263 | s[23] = (s8 >> 16) | (s9 << 5);
264 | s[24] = s9 >> 3;
265 | s[25] = s9 >> 11;
266 | s[26] = (s9 >> 19) | (s10 << 2);
267 | s[27] = s10 >> 6;
268 | s[28] = (s10 >> 14) | (s11 << 7);
269 | s[29] = s11 >> 1;
270 | s[30] = s11 >> 9;
271 | s[31] = s11 >> 17;
272 | }
273 |
--------------------------------------------------------------------------------
/ext/ed25519_ref10/sha512.c:
--------------------------------------------------------------------------------
1 | /*
2 | 20080913
3 | D. J. Bernstein
4 | Public domain.
5 | */
6 |
7 | #include "sha512.h"
8 |
9 | static void crypto_hashblocks_sha512(uint8_t *statebytes,const uint8_t *in,uint64_t inlen);
10 |
11 | #define blocks crypto_hashblocks_sha512
12 |
13 | static const uint8_t iv[64] = {
14 | 0x6a,0x09,0xe6,0x67,0xf3,0xbc,0xc9,0x08,
15 | 0xbb,0x67,0xae,0x85,0x84,0xca,0xa7,0x3b,
16 | 0x3c,0x6e,0xf3,0x72,0xfe,0x94,0xf8,0x2b,
17 | 0xa5,0x4f,0xf5,0x3a,0x5f,0x1d,0x36,0xf1,
18 | 0x51,0x0e,0x52,0x7f,0xad,0xe6,0x82,0xd1,
19 | 0x9b,0x05,0x68,0x8c,0x2b,0x3e,0x6c,0x1f,
20 | 0x1f,0x83,0xd9,0xab,0xfb,0x41,0xbd,0x6b,
21 | 0x5b,0xe0,0xcd,0x19,0x13,0x7e,0x21,0x79
22 | };
23 |
24 | int crypto_hash_sha512(uint8_t *out,const uint8_t *in,uint64_t inlen)
25 | {
26 | uint8_t h[64];
27 | uint8_t padded[256];
28 | uint64_t i;
29 | uint64_t bytes = inlen;
30 |
31 | for (i = 0;i < 64;++i) h[i] = iv[i];
32 |
33 | blocks(h,in,inlen);
34 | in += inlen;
35 | inlen &= 127;
36 | in -= inlen;
37 |
38 | for (i = 0;i < inlen;++i) padded[i] = in[i];
39 | padded[inlen] = 0x80;
40 |
41 | if (inlen < 112) {
42 | for (i = inlen + 1;i < 119;++i) padded[i] = 0;
43 | padded[119] = bytes >> 61;
44 | padded[120] = bytes >> 53;
45 | padded[121] = bytes >> 45;
46 | padded[122] = bytes >> 37;
47 | padded[123] = bytes >> 29;
48 | padded[124] = bytes >> 21;
49 | padded[125] = bytes >> 13;
50 | padded[126] = bytes >> 5;
51 | padded[127] = bytes << 3;
52 | blocks(h,padded,128);
53 | } else {
54 | for (i = inlen + 1;i < 247;++i) padded[i] = 0;
55 | padded[247] = bytes >> 61;
56 | padded[248] = bytes >> 53;
57 | padded[249] = bytes >> 45;
58 | padded[250] = bytes >> 37;
59 | padded[251] = bytes >> 29;
60 | padded[252] = bytes >> 21;
61 | padded[253] = bytes >> 13;
62 | padded[254] = bytes >> 5;
63 | padded[255] = bytes << 3;
64 | blocks(h,padded,256);
65 | }
66 |
67 | for (i = 0;i < 64;++i) out[i] = h[i];
68 |
69 | return 0;
70 | }
71 |
72 | static uint64_t load_bigendian(const unsigned char *x)
73 | {
74 | return
75 | (uint64_t) (x[7]) \
76 | | (((uint64_t) (x[6])) << 8) \
77 | | (((uint64_t) (x[5])) << 16) \
78 | | (((uint64_t) (x[4])) << 24) \
79 | | (((uint64_t) (x[3])) << 32) \
80 | | (((uint64_t) (x[2])) << 40) \
81 | | (((uint64_t) (x[1])) << 48) \
82 | | (((uint64_t) (x[0])) << 56)
83 | ;
84 | }
85 |
86 | static void store_bigendian(unsigned char *x,uint64_t u)
87 | {
88 | x[7] = u; u >>= 8;
89 | x[6] = u; u >>= 8;
90 | x[5] = u; u >>= 8;
91 | x[4] = u; u >>= 8;
92 | x[3] = u; u >>= 8;
93 | x[2] = u; u >>= 8;
94 | x[1] = u; u >>= 8;
95 | x[0] = u;
96 | }
97 |
98 | #define SHR(x,c) ((x) >> (c))
99 | #define ROTR(x,c) (((x) >> (c)) | ((x) << (64 - (c))))
100 |
101 | #define Ch(x,y,z) ((x & y) ^ (~x & z))
102 | #define Maj(x,y,z) ((x & y) ^ (x & z) ^ (y & z))
103 | #define Sigma0(x) (ROTR(x,28) ^ ROTR(x,34) ^ ROTR(x,39))
104 | #define Sigma1(x) (ROTR(x,14) ^ ROTR(x,18) ^ ROTR(x,41))
105 | #define sigma0(x) (ROTR(x, 1) ^ ROTR(x, 8) ^ SHR(x,7))
106 | #define sigma1(x) (ROTR(x,19) ^ ROTR(x,61) ^ SHR(x,6))
107 |
108 | #define M(w0,w14,w9,w1) w0 = sigma1(w14) + w9 + sigma0(w1) + w0;
109 |
110 | #define EXPAND \
111 | M(w0 ,w14,w9 ,w1 ) \
112 | M(w1 ,w15,w10,w2 ) \
113 | M(w2 ,w0 ,w11,w3 ) \
114 | M(w3 ,w1 ,w12,w4 ) \
115 | M(w4 ,w2 ,w13,w5 ) \
116 | M(w5 ,w3 ,w14,w6 ) \
117 | M(w6 ,w4 ,w15,w7 ) \
118 | M(w7 ,w5 ,w0 ,w8 ) \
119 | M(w8 ,w6 ,w1 ,w9 ) \
120 | M(w9 ,w7 ,w2 ,w10) \
121 | M(w10,w8 ,w3 ,w11) \
122 | M(w11,w9 ,w4 ,w12) \
123 | M(w12,w10,w5 ,w13) \
124 | M(w13,w11,w6 ,w14) \
125 | M(w14,w12,w7 ,w15) \
126 | M(w15,w13,w8 ,w0 )
127 |
128 | #define F(w,k) \
129 | T1 = h + Sigma1(e) + Ch(e,f,g) + k + w; \
130 | T2 = Sigma0(a) + Maj(a,b,c); \
131 | h = g; \
132 | g = f; \
133 | f = e; \
134 | e = d + T1; \
135 | d = c; \
136 | c = b; \
137 | b = a; \
138 | a = T1 + T2;
139 |
140 | static void crypto_hashblocks_sha512(uint8_t *statebytes,const uint8_t *in,uint64_t inlen)
141 | {
142 | uint64_t state[8];
143 | uint64_t a;
144 | uint64_t b;
145 | uint64_t c;
146 | uint64_t d;
147 | uint64_t e;
148 | uint64_t f;
149 | uint64_t g;
150 | uint64_t h;
151 | uint64_t T1;
152 | uint64_t T2;
153 |
154 | a = load_bigendian(statebytes + 0); state[0] = a;
155 | b = load_bigendian(statebytes + 8); state[1] = b;
156 | c = load_bigendian(statebytes + 16); state[2] = c;
157 | d = load_bigendian(statebytes + 24); state[3] = d;
158 | e = load_bigendian(statebytes + 32); state[4] = e;
159 | f = load_bigendian(statebytes + 40); state[5] = f;
160 | g = load_bigendian(statebytes + 48); state[6] = g;
161 | h = load_bigendian(statebytes + 56); state[7] = h;
162 |
163 | while (inlen >= 128) {
164 | uint64_t w0 = load_bigendian(in + 0);
165 | uint64_t w1 = load_bigendian(in + 8);
166 | uint64_t w2 = load_bigendian(in + 16);
167 | uint64_t w3 = load_bigendian(in + 24);
168 | uint64_t w4 = load_bigendian(in + 32);
169 | uint64_t w5 = load_bigendian(in + 40);
170 | uint64_t w6 = load_bigendian(in + 48);
171 | uint64_t w7 = load_bigendian(in + 56);
172 | uint64_t w8 = load_bigendian(in + 64);
173 | uint64_t w9 = load_bigendian(in + 72);
174 | uint64_t w10 = load_bigendian(in + 80);
175 | uint64_t w11 = load_bigendian(in + 88);
176 | uint64_t w12 = load_bigendian(in + 96);
177 | uint64_t w13 = load_bigendian(in + 104);
178 | uint64_t w14 = load_bigendian(in + 112);
179 | uint64_t w15 = load_bigendian(in + 120);
180 |
181 | F(w0 ,0x428a2f98d728ae22ULL)
182 | F(w1 ,0x7137449123ef65cdULL)
183 | F(w2 ,0xb5c0fbcfec4d3b2fULL)
184 | F(w3 ,0xe9b5dba58189dbbcULL)
185 | F(w4 ,0x3956c25bf348b538ULL)
186 | F(w5 ,0x59f111f1b605d019ULL)
187 | F(w6 ,0x923f82a4af194f9bULL)
188 | F(w7 ,0xab1c5ed5da6d8118ULL)
189 | F(w8 ,0xd807aa98a3030242ULL)
190 | F(w9 ,0x12835b0145706fbeULL)
191 | F(w10,0x243185be4ee4b28cULL)
192 | F(w11,0x550c7dc3d5ffb4e2ULL)
193 | F(w12,0x72be5d74f27b896fULL)
194 | F(w13,0x80deb1fe3b1696b1ULL)
195 | F(w14,0x9bdc06a725c71235ULL)
196 | F(w15,0xc19bf174cf692694ULL)
197 |
198 | EXPAND
199 |
200 | F(w0 ,0xe49b69c19ef14ad2ULL)
201 | F(w1 ,0xefbe4786384f25e3ULL)
202 | F(w2 ,0x0fc19dc68b8cd5b5ULL)
203 | F(w3 ,0x240ca1cc77ac9c65ULL)
204 | F(w4 ,0x2de92c6f592b0275ULL)
205 | F(w5 ,0x4a7484aa6ea6e483ULL)
206 | F(w6 ,0x5cb0a9dcbd41fbd4ULL)
207 | F(w7 ,0x76f988da831153b5ULL)
208 | F(w8 ,0x983e5152ee66dfabULL)
209 | F(w9 ,0xa831c66d2db43210ULL)
210 | F(w10,0xb00327c898fb213fULL)
211 | F(w11,0xbf597fc7beef0ee4ULL)
212 | F(w12,0xc6e00bf33da88fc2ULL)
213 | F(w13,0xd5a79147930aa725ULL)
214 | F(w14,0x06ca6351e003826fULL)
215 | F(w15,0x142929670a0e6e70ULL)
216 |
217 | EXPAND
218 |
219 | F(w0 ,0x27b70a8546d22ffcULL)
220 | F(w1 ,0x2e1b21385c26c926ULL)
221 | F(w2 ,0x4d2c6dfc5ac42aedULL)
222 | F(w3 ,0x53380d139d95b3dfULL)
223 | F(w4 ,0x650a73548baf63deULL)
224 | F(w5 ,0x766a0abb3c77b2a8ULL)
225 | F(w6 ,0x81c2c92e47edaee6ULL)
226 | F(w7 ,0x92722c851482353bULL)
227 | F(w8 ,0xa2bfe8a14cf10364ULL)
228 | F(w9 ,0xa81a664bbc423001ULL)
229 | F(w10,0xc24b8b70d0f89791ULL)
230 | F(w11,0xc76c51a30654be30ULL)
231 | F(w12,0xd192e819d6ef5218ULL)
232 | F(w13,0xd69906245565a910ULL)
233 | F(w14,0xf40e35855771202aULL)
234 | F(w15,0x106aa07032bbd1b8ULL)
235 |
236 | EXPAND
237 |
238 | F(w0 ,0x19a4c116b8d2d0c8ULL)
239 | F(w1 ,0x1e376c085141ab53ULL)
240 | F(w2 ,0x2748774cdf8eeb99ULL)
241 | F(w3 ,0x34b0bcb5e19b48a8ULL)
242 | F(w4 ,0x391c0cb3c5c95a63ULL)
243 | F(w5 ,0x4ed8aa4ae3418acbULL)
244 | F(w6 ,0x5b9cca4f7763e373ULL)
245 | F(w7 ,0x682e6ff3d6b2b8a3ULL)
246 | F(w8 ,0x748f82ee5defb2fcULL)
247 | F(w9 ,0x78a5636f43172f60ULL)
248 | F(w10,0x84c87814a1f0ab72ULL)
249 | F(w11,0x8cc702081a6439ecULL)
250 | F(w12,0x90befffa23631e28ULL)
251 | F(w13,0xa4506cebde82bde9ULL)
252 | F(w14,0xbef9a3f7b2c67915ULL)
253 | F(w15,0xc67178f2e372532bULL)
254 |
255 | EXPAND
256 |
257 | F(w0 ,0xca273eceea26619cULL)
258 | F(w1 ,0xd186b8c721c0c207ULL)
259 | F(w2 ,0xeada7dd6cde0eb1eULL)
260 | F(w3 ,0xf57d4f7fee6ed178ULL)
261 | F(w4 ,0x06f067aa72176fbaULL)
262 | F(w5 ,0x0a637dc5a2c898a6ULL)
263 | F(w6 ,0x113f9804bef90daeULL)
264 | F(w7 ,0x1b710b35131c471bULL)
265 | F(w8 ,0x28db77f523047d84ULL)
266 | F(w9 ,0x32caab7b40c72493ULL)
267 | F(w10,0x3c9ebe0a15c9bebcULL)
268 | F(w11,0x431d67c49c100d4cULL)
269 | F(w12,0x4cc5d4becb3e42b6ULL)
270 | F(w13,0x597f299cfc657e2aULL)
271 | F(w14,0x5fcb6fab3ad6faecULL)
272 | F(w15,0x6c44198c4a475817ULL)
273 |
274 | a += state[0];
275 | b += state[1];
276 | c += state[2];
277 | d += state[3];
278 | e += state[4];
279 | f += state[5];
280 | g += state[6];
281 | h += state[7];
282 |
283 | state[0] = a;
284 | state[1] = b;
285 | state[2] = c;
286 | state[3] = d;
287 | state[4] = e;
288 | state[5] = f;
289 | state[6] = g;
290 | state[7] = h;
291 |
292 | in += 128;
293 | inlen -= 128;
294 | }
295 |
296 | store_bigendian(statebytes + 0,state[0]);
297 | store_bigendian(statebytes + 8,state[1]);
298 | store_bigendian(statebytes + 16,state[2]);
299 | store_bigendian(statebytes + 24,state[3]);
300 | store_bigendian(statebytes + 32,state[4]);
301 | store_bigendian(statebytes + 40,state[5]);
302 | store_bigendian(statebytes + 48,state[6]);
303 | store_bigendian(statebytes + 56,state[7]);
304 | }
305 |
--------------------------------------------------------------------------------
/ext/ed25519_ref10/sha512.h:
--------------------------------------------------------------------------------
1 | #ifndef SHA512_H
2 | #define SHA512_H
3 |
4 | #include
5 |
6 | int crypto_hash_sha512(uint8_t *out,const uint8_t *in,uint64_t inlen);
7 |
8 | #endif /* SHA512_H */
9 |
--------------------------------------------------------------------------------
/ext/ed25519_ref10/sign.c:
--------------------------------------------------------------------------------
1 | #include
2 | #include "ed25519_ref10.h"
3 | #include "sha512.h"
4 | #include "ge.h"
5 | #include "sc.h"
6 |
7 | int crypto_sign_ed25519_ref10(
8 | uint8_t *sm, uint64_t *smlen,
9 | const uint8_t *m, uint64_t mlen,
10 | const uint8_t *sk
11 | )
12 | {
13 | unsigned char pk[32];
14 | unsigned char az[64];
15 | unsigned char nonce[64];
16 | unsigned char hram[64];
17 | ge_p3 R;
18 |
19 | memmove(pk,sk + 32,32);
20 |
21 | crypto_hash_sha512(az,sk,32);
22 | az[0] &= 248;
23 | az[31] &= 63;
24 | az[31] |= 64;
25 |
26 | *smlen = mlen + 64;
27 | memmove(sm + 64,m,mlen);
28 | memmove(sm + 32,az + 32,32);
29 | crypto_hash_sha512(nonce,sm + 32,mlen + 32);
30 | memmove(sm + 32,pk,32);
31 |
32 | sc_reduce(nonce);
33 | ge_scalarmult_base(&R,nonce);
34 | ge_p3_tobytes(sm,&R);
35 |
36 | crypto_hash_sha512(hram,sm,mlen + 64);
37 | sc_reduce(hram);
38 | sc_muladd(sm + 32,hram,az,nonce);
39 |
40 | return 0;
41 | }
42 |
--------------------------------------------------------------------------------
/ext/ed25519_ref10/sqrtm1.h:
--------------------------------------------------------------------------------
1 | -32595792,-7943725,9377950,3500415,12389472,-272473,-25146209,-2005654,326686,11406482
2 |
--------------------------------------------------------------------------------
/ext/ed25519_ref10/verify.c:
--------------------------------------------------------------------------------
1 | #include "ed25519_ref10.h"
2 |
3 | int crypto_verify_32(const uint8_t *x,const uint8_t *y)
4 | {
5 | unsigned int differentbits = 0;
6 | #define F(i) differentbits |= x[i] ^ y[i];
7 | F(0)
8 | F(1)
9 | F(2)
10 | F(3)
11 | F(4)
12 | F(5)
13 | F(6)
14 | F(7)
15 | F(8)
16 | F(9)
17 | F(10)
18 | F(11)
19 | F(12)
20 | F(13)
21 | F(14)
22 | F(15)
23 | F(16)
24 | F(17)
25 | F(18)
26 | F(19)
27 | F(20)
28 | F(21)
29 | F(22)
30 | F(23)
31 | F(24)
32 | F(25)
33 | F(26)
34 | F(27)
35 | F(28)
36 | F(29)
37 | F(30)
38 | F(31)
39 | return (1 & ((differentbits - 1) >> 8)) - 1;
40 | }
41 |
--------------------------------------------------------------------------------
/lib/ed25519.rb:
--------------------------------------------------------------------------------
1 | # frozen_string_literal: true
2 |
3 | require "ed25519/version"
4 | require "ed25519/signing_key"
5 | require "ed25519/verify_key"
6 |
7 | # The Ed25519 digital signatre algorithm
8 | # rubocop:disable Layout/LineLength
9 | module Ed25519
10 | module_function
11 |
12 | # Size of an Ed25519 key (public or private) in bytes
13 | KEY_SIZE = 32
14 |
15 | # Size of an Ed25519 signature in bytes
16 | SIGNATURE_SIZE = 64
17 |
18 | # Raised when a signature fails to verify
19 | VerifyError = Class.new(StandardError)
20 |
21 | # Raised when the built-in self-test fails
22 | SelfTestFailure = Class.new(StandardError)
23 |
24 | class << self
25 | # Obtain the backend provider module used to perform signatures
26 | attr_accessor :provider
27 | end
28 |
29 | # Select the Ed25519::Provider to use based on the current environment
30 | if defined? JRUBY_VERSION
31 | require "jruby"
32 | require "ed25519_jruby"
33 | self.provider = org.cryptorb.Ed25519Provider.createEd25519Module(JRuby.runtime)
34 | else
35 | require "ed25519_ref10"
36 | self.provider = Ed25519::Provider::Ref10
37 | end
38 |
39 | # Ensure a serialized key meets the requirements
40 | def validate_key_bytes(key_bytes)
41 | raise TypeError, "expected String, got #{key_bytes.class}" unless key_bytes.is_a?(String)
42 | return true if key_bytes.bytesize == KEY_SIZE
43 |
44 | raise ArgumentError, "expected #{KEY_SIZE}-byte String, got #{key_bytes.bytesize}"
45 | end
46 |
47 | # Perform a self-test to ensure the selected provider is working
48 | def self_test
49 | signature_key = Ed25519::SigningKey.new("A" * 32)
50 | raise SelfTestFailure, "failed to generate verify key correctly" unless signature_key.verify_key.to_bytes.unpack1("H*") == "db995fe25169d141cab9bbba92baa01f9f2e1ece7df4cb2ac05190f37fcc1f9d"
51 |
52 | message = "crypto libraries should self-test on boot"
53 | signature = signature_key.sign(message)
54 | raise SelfTestFailure, "failed to generate correct signature" unless signature.unpack1("H*") == "c62c12a3a6cbfa04800d4be81468ef8aecd152a6a26a81d91257baecef13ba209531fe905a843e833c8b71cee04400fa2af3a29fef1152ece470421848758d0a"
55 |
56 | verify_key = signature_key.verify_key
57 | raise SelfTestFailure, "failed to verify a valid signature" unless verify_key.verify(signature, message)
58 |
59 | bad_signature = "#{signature[0...63]}X"
60 | ex = nil
61 | begin
62 | verify_key.verify(bad_signature, message)
63 | rescue Ed25519::VerifyError => ex
64 | end
65 |
66 | raise SelfTestFailure, "failed to detect an invalid signature" unless ex.is_a?(Ed25519::VerifyError)
67 | end
68 | end
69 | # rubocop:enable Layout/LineLength
70 |
71 | # Automatically run self-test when library loads
72 | Ed25519.self_test
73 |
--------------------------------------------------------------------------------
/lib/ed25519/signing_key.rb:
--------------------------------------------------------------------------------
1 | # frozen_string_literal: true
2 |
3 | require "securerandom"
4 |
5 | module Ed25519
6 | # Private key for producing digital signatures
7 | class SigningKey
8 | attr_reader :seed, :keypair, :verify_key
9 |
10 | # Generate a random Ed25519 signing key (i.e. private scalar)
11 | def self.generate
12 | new SecureRandom.random_bytes(Ed25519::KEY_SIZE)
13 | end
14 |
15 | # Create a SigningKey from a 64-byte Ed25519 keypair (i.e. public + private)
16 | #
17 | # @param keypair [String] 64-byte keypair value containing both seed + public key
18 | def self.from_keypair(keypair)
19 | raise TypeError, "expected String, got #{keypair.class}" unless keypair.is_a?(String)
20 | raise ArgumentError, "expected 64-byte String, got #{keypair.bytesize}" unless keypair.bytesize == 64
21 |
22 | new(keypair[0, KEY_SIZE]).tap do |key|
23 | raise ArgumentError, "corrupt keypair" unless keypair[KEY_SIZE, KEY_SIZE] == key.verify_key.to_bytes
24 | end
25 | end
26 |
27 | # Create a new Ed25519::SigningKey from the given seed value
28 | #
29 | # @param seed [String] 32-byte seed value from which the key should be derived
30 | def initialize(seed)
31 | Ed25519.validate_key_bytes(seed)
32 |
33 | @seed = seed
34 | @keypair = Ed25519.provider.create_keypair(seed)
35 | @verify_key = VerifyKey.new(@keypair[32, 32])
36 | end
37 |
38 | # Sign the given message, returning an Ed25519 signature
39 | #
40 | # @param message [String] message to be signed
41 | #
42 | # @return [String] 64-byte Ed25519 signature
43 | def sign(message)
44 | Ed25519.provider.sign(@keypair, message)
45 | end
46 |
47 | # String inspection that does not leak secret values
48 | def inspect
49 | to_s
50 | end
51 |
52 | # Return a bytestring representation of this signing key
53 | #
54 | # @return [String] signing key converted to a bytestring
55 | def to_bytes
56 | seed
57 | end
58 | alias to_str to_bytes
59 | end
60 | end
61 |
--------------------------------------------------------------------------------
/lib/ed25519/verify_key.rb:
--------------------------------------------------------------------------------
1 | # frozen_string_literal: true
2 |
3 | module Ed25519
4 | # Public key for verifying digital signatures
5 | class VerifyKey
6 | # Create a Ed25519::VerifyKey from its serialized Twisted Edwards representation
7 | #
8 | # @param key [String] 32-byte string representing a serialized public key
9 | def initialize(key)
10 | Ed25519.validate_key_bytes(key)
11 | @key_bytes = key
12 | end
13 |
14 | # Verify an Ed25519 signature against the message
15 | #
16 | # @param signature [String] 64-byte string containing an Ed25519 signature
17 | # @param message [String] string containing message to be verified
18 | #
19 | # @raise Ed25519::VerifyError signature verification failed
20 | #
21 | # @return [true] message verified successfully
22 | def verify(signature, message)
23 | if signature.length != SIGNATURE_SIZE
24 | raise ArgumentError, "expected #{SIGNATURE_SIZE} byte signature, got #{signature.length}"
25 | end
26 |
27 | return true if Ed25519.provider.verify(@key_bytes, signature, message)
28 |
29 | raise VerifyError, "signature verification failed!"
30 | end
31 |
32 | # Return a compressed twisted Edwards coordinate representing the public key
33 | #
34 | # @return [String] bytestring serialization of this public key
35 | def to_bytes
36 | @key_bytes
37 | end
38 | alias to_str to_bytes
39 |
40 | # Show hex representation of serialized coordinate in string inspection
41 | def inspect
42 | "#<#{self.class}:#{@key_bytes.unpack1('H*')}>"
43 | end
44 | end
45 | end
46 |
--------------------------------------------------------------------------------
/lib/ed25519/version.rb:
--------------------------------------------------------------------------------
1 | # frozen_string_literal: true
2 |
3 | module Ed25519
4 | VERSION = "1.4.0"
5 | end
6 |
--------------------------------------------------------------------------------
/spec/ed25519/provider/jruby_spec.rb:
--------------------------------------------------------------------------------
1 | # frozen_string_literal: true
2 |
3 | if defined?(JRUBY_VERSION)
4 | RSpec.describe Ed25519::Provider::JRuby do
5 | include_examples "Ed25519::Provider"
6 | end
7 | end
8 |
--------------------------------------------------------------------------------
/spec/ed25519/provider/ref10_spec.rb:
--------------------------------------------------------------------------------
1 | # frozen_string_literal: true
2 |
3 | unless defined?(JRUBY_VERSION)
4 | RSpec.describe Ed25519::Provider::Ref10 do
5 | include_examples "Ed25519::Provider"
6 | end
7 | end
8 |
--------------------------------------------------------------------------------
/spec/ed25519/signing_key_spec.rb:
--------------------------------------------------------------------------------
1 | # frozen_string_literal: true
2 |
3 | require "spec_helper"
4 |
5 | RSpec.describe Ed25519::SigningKey do
6 | let(:key) { described_class.generate }
7 | let(:message) { "example message" }
8 |
9 | describe ".generate" do
10 | it "generates keypairs" do
11 | expect(key).to be_a described_class
12 | expect(key.verify_key).to be_a Ed25519::VerifyKey
13 | end
14 | end
15 |
16 | describe ".from_keypair" do
17 | it "loads keypairs from bytes" do
18 | expect(described_class.from_keypair(key.keypair)).to be_a described_class
19 | end
20 |
21 | it "raises ArgumentError if given an invalid keypair" do
22 | expect { described_class.from_keypair("\0" * 64) }.to raise_error ArgumentError
23 | end
24 | end
25 |
26 | describe "#sign" do
27 | it "signs messages" do
28 | expect(key.sign(message)).to be_a String
29 | end
30 | end
31 |
32 | describe "#to_bytes" do
33 | it "serializes to bytes" do
34 | bytes = key.to_bytes
35 | expect(bytes).to be_a String
36 | expect(bytes.length).to eq Ed25519::KEY_SIZE
37 | end
38 | end
39 | end
40 |
--------------------------------------------------------------------------------
/spec/ed25519/test_vectors_spec.rb:
--------------------------------------------------------------------------------
1 | # frozen_string_literal: true
2 |
3 | # rubocop:disable Metrics/BlockLength
4 |
5 | require "spec_helper"
6 |
7 | RSpec.describe Ed25519::SigningKey do
8 | describe "RFC 8032 test vectors" do
9 | it "are handled correctly" do
10 | tests = [
11 | [<