├── .gitignore ├── .idea ├── .gitignore ├── Algorithms-DataStructures-Learning.iml ├── leetcode │ ├── editor.xml │ └── statistics.xml ├── modules.xml ├── vcs.xml └── workspace.xml ├── InterviewAlgorithm ├── InterviewAlgorithm.md ├── Interview_algorithm_01.js └── Interview_algorithm_02.js ├── LeetCodeProblems.md ├── README.md ├── count.js ├── images └── img.png └── javascript-algorithms ├── algorithm ├── .vscode │ └── settings.json ├── 1.两数之和.js ├── 10.正则表达式匹配.js ├── 104.二叉树的最大深度.js ├── 12.整数转罗马数字.js ├── 15.三数之和.js ├── 18.四数之和.js ├── 19.删除链表的倒数第-n-个结点.js ├── 2.两数相加.js ├── 20.有效的括号.js ├── 22.括号生成.js ├── 25.k-个一组翻转链表.js ├── 26.删除有序数组中的重复项.js ├── 27.移除元素.js ├── 7.整数反转.js ├── 71.简化路径.js ├── 76.最小覆盖子串.js └── 8.字符串转换整数-atoi.js ├── leetcode └── editor │ └── cn │ ├── [100]相同的树.js │ ├── [101]对称二叉树.js │ ├── [102]二叉树的层序遍历.js │ ├── [1047]删除字符串中的所有相邻重复项.js │ ├── [104]二叉树的最大深度.js │ ├── [107]二叉树的层序遍历 II.js │ ├── [108]将有序数组转换为二叉搜索树.js │ ├── [109]有序链表转换二叉搜索树.js │ ├── [110]平衡二叉树.js │ ├── [111]二叉树的最小深度.js │ ├── [112]路径总和.js │ ├── [114]二叉树展开为链表.js │ ├── [116]填充每个节点的下一个右侧节点指针.js │ ├── [117]填充每个节点的下一个右侧节点指针 II.js │ ├── [125]验证回文串.js │ ├── [131]分割回文串.js │ ├── [136]只出现一次的数字.js │ ├── [141]环形链表.js │ ├── [142]环形链表 II.js │ ├── [144]二叉树的前序遍历.js │ ├── [145]二叉树的后序遍历.js │ ├── [146]LRU 缓存.js │ ├── [150]逆波兰表达式求值.js │ ├── [151]反转字符串中的单词.js │ ├── [153]寻找旋转排序数组中的最小值.js │ ├── [15]三数之和.js │ ├── [160]相交链表.js │ ├── [17]电话号码的字母组合.js │ ├── [199]二叉树的右视图.js │ ├── [1]两数之和.js │ ├── [203]移除链表元素.js │ ├── [20]有效的括号.js │ ├── [21]合并两个有序链表.js │ ├── [222]完全二叉树的节点个数.js │ ├── [225]用队列实现栈.js │ ├── [226]翻转二叉树.js │ ├── [230]二叉搜索树中第K小的元素.js │ ├── [231]2 的幂.js │ ├── [232]用栈实现队列.js │ ├── [234]回文链表.js │ ├── [236]二叉树的最近公共祖先.js │ ├── [257]二叉树的所有路径.js │ ├── [26]删除有序数组中的重复项.js │ ├── [27]移除元素.js │ ├── [283]移动零.js │ ├── [2]两数相加.js │ ├── [300]最长递增子序列.js │ ├── [322]零钱兑换.js │ ├── [37]解数独.js │ ├── [39]组合总和.js │ ├── [404]左叶子之和.js │ ├── [429]N 叉树的层序遍历.js │ ├── [455]分发饼干.js │ ├── [46]全排列.js │ ├── [509]斐波那契数.js │ ├── [515]在每个树行中找最大值.js │ ├── [51]N 皇后.js │ ├── [543]二叉树的直径.js │ ├── [55]跳跃游戏.js │ ├── [572]另一棵树的子树.js │ ├── [617]合并二叉树.js │ ├── [637]二叉树的层平均值.js │ ├── [654]最大二叉树.js │ ├── [69]x 的平方根 .js │ ├── [700]二叉搜索树中的搜索.js │ ├── [701]二叉搜索树中的插入操作.js │ ├── [704]二分查找.js │ ├── [71]简化路径.js │ ├── [77]组合.js │ ├── [78]子集.js │ ├── [79]单词搜索.js │ ├── [860]柠檬水找零.js │ ├── [876]链表的中间结点.js │ ├── [92]反转链表 II.js │ ├── [94]二叉树的中序遍历.js │ ├── [98]验证二叉搜索树.js │ ├── [99]恢复二叉搜索树.js │ └── doc │ ├── content │ ├── [100]相同的树.md │ ├── [101]对称二叉树.md │ ├── [102]二叉树的层序遍历.md │ ├── [1047]删除字符串中的所有相邻重复项.md │ ├── [104]二叉树的最大深度.md │ ├── [107]二叉树的层序遍历 II.md │ ├── [108]将有序数组转换为二叉搜索树.md │ ├── [109]有序链表转换二叉搜索树.md │ ├── [110]平衡二叉树.md │ ├── [111]二叉树的最小深度.md │ ├── [112]路径总和.md │ ├── [114]二叉树展开为链表.md │ ├── [116]填充每个节点的下一个右侧节点指针.md │ ├── [117]填充每个节点的下一个右侧节点指针 II.md │ ├── [125]验证回文串.md │ ├── [131]分割回文串.md │ ├── [136]只出现一次的数字.md │ ├── [141]环形链表.md │ ├── [142]环形链表 II.md │ ├── [144]二叉树的前序遍历.md │ ├── [145]二叉树的后序遍历.md │ ├── [146]LRU 缓存.md │ ├── [150]逆波兰表达式求值.md │ ├── [151]反转字符串中的单词.md │ ├── [153]寻找旋转排序数组中的最小值.md │ ├── [15]三数之和.md │ ├── [160]相交链表.md │ ├── [17]电话号码的字母组合.md │ ├── [199]二叉树的右视图.md │ ├── [1]两数之和.md │ ├── [203]移除链表元素.md │ ├── [20]有效的括号.md │ ├── [21]合并两个有序链表.md │ ├── [222]完全二叉树的节点个数.md │ ├── [225]用队列实现栈.md │ ├── [226]翻转二叉树.md │ ├── [230]二叉搜索树中第K小的元素.md │ ├── [231]2 的幂.md │ ├── [232]用栈实现队列.md │ ├── [234]回文链表.md │ ├── [236]二叉树的最近公共祖先.md │ ├── [257]二叉树的所有路径.md │ ├── [26]删除有序数组中的重复项.md │ ├── [27]移除元素.md │ ├── [283]移动零.md │ ├── [2]两数相加.md │ ├── [300]最长递增子序列.md │ ├── [322]零钱兑换.md │ ├── [37]解数独.md │ ├── [39]组合总和.md │ ├── [404]左叶子之和.md │ ├── [429]N 叉树的层序遍历.md │ ├── [455]分发饼干.md │ ├── [46]全排列.md │ ├── [509]斐波那契数.md │ ├── [515]在每个树行中找最大值.md │ ├── [543]二叉树的直径.md │ ├── [55]跳跃游戏.md │ ├── [572]另一棵树的子树.md │ ├── [617]合并二叉树.md │ ├── [637]二叉树的层平均值.md │ ├── [654]最大二叉树.md │ ├── [69]x 的平方根 .md │ ├── [700]二叉搜索树中的搜索.md │ ├── [701]二叉搜索树中的插入操作.md │ ├── [704]二分查找.md │ ├── [71]简化路径.md │ ├── [77]组合.md │ ├── [78]子集.md │ ├── [79]单词搜索.md │ ├── [860]柠檬水找零.md │ ├── [876]链表的中间结点.md │ ├── [92]反转链表 II.md │ ├── [94]二叉树的中序遍历.md │ ├── [98]验证二叉搜索树.md │ └── [99]恢复二叉搜索树.md │ └── note │ └── [99]恢复二叉搜索树.md ├── linkList ├── linkList.js └── test.js └── sort ├── arr.js └── sort.js /.gitignore: -------------------------------------------------------------------------------- 1 | .DS_Store 2 | # Editor directories and files 3 | .idea 4 | .idea/ 5 | /.idea/ 6 | .vscode 7 | *.suo 8 | *.ntvs* 9 | *.njsproj 10 | *.sln 11 | -------------------------------------------------------------------------------- /.idea/.gitignore: -------------------------------------------------------------------------------- 1 | .DS_Store 2 | node_modules 3 | # local env files 4 | .env.local 5 | .env.*.local 6 | 7 | # Log files 8 | 9 | 10 | # Editor directories and files 11 | .idea 12 | .vscode 13 | *.suo 14 | *.ntvs* 15 | *.njsproj 16 | *.sln 17 | *.sw? 18 | -------------------------------------------------------------------------------- /.idea/Algorithms-DataStructures-Learning.iml: -------------------------------------------------------------------------------- 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | -------------------------------------------------------------------------------- /.idea/leetcode/statistics.xml: -------------------------------------------------------------------------------- 1 | 2 | 3 | 4 | 19 | 20 | -------------------------------------------------------------------------------- /.idea/modules.xml: -------------------------------------------------------------------------------- 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | -------------------------------------------------------------------------------- /.idea/vcs.xml: -------------------------------------------------------------------------------- 1 | 2 | 3 | 4 | 5 | 6 | -------------------------------------------------------------------------------- /InterviewAlgorithm/InterviewAlgorithm.md: -------------------------------------------------------------------------------- 1 | ### InterviewAlgorithm 2 | 3 | #### 笔试题 4 | - [设计一个大数加法：有两个特别大的数(用字符串表示)](Interview_algorithm_01.js) 5 | - [给定一个字符串str 和一个字符串列表 wordDict 作为字典。 判断是否可以利用字典中出现的单词拼接出 str](Interview_algorithm_02.js) 6 | - 7 | 8 | ### 关于 9 | 10 | 主要记录笔者自己学习算法知识和自己参加面试遇到的一些面试题，如果有错误欢迎大家提交对本仓库的改进建议~ 11 | 12 | -------------------------------------------------------------------------------- /InterviewAlgorithm/Interview_algorithm_01.js: -------------------------------------------------------------------------------- 1 | //设计一个大数加法：有两个特别大的数(用字符串表示)，设计一个add()方法； 2 | function addLargeNumber (num1, num2) { 3 | // 主要思路：如果是通过将数字转为字符串，然后字符串按位相加 4 | let result = ""; //保存最后返回结果 5 | let carry = false; //保留进位结果 6 | let tmpNum1 = num1.split("") 7 | let tmpNum2 = num2.split("") 8 | // 当数组的长度都变为0，并且最终不再进位时，结束循环 9 | //按位非运算符“~” 双非“～～” 10 | while (tmpNum1.length || tmpNum2.length ||carry){ 11 | //每次将最后的数字进行相加，使用～～的好处 即使返回值为 undefined 也能转换为0 12 | carry += ~~tmpNum1.pop() + ~~tmpNum2.pop(); 13 | 14 | //取加法的个位加入最终结果 15 | result = carry % 10 + result; 16 | 17 | //判断是否需要进位， true 和 false 的值在加法中会被转换为1和0 18 | carry = carry > 9; 19 | } 20 | return result; 21 | } 22 | console.log(addLargeNumber('23480623453457923523', '723456923458023456238045')); // '723480404081476914161568' 23 | 24 | -------------------------------------------------------------------------------- /InterviewAlgorithm/Interview_algorithm_02.js: -------------------------------------------------------------------------------- 1 | /**** 2 | 给定一个字符串str 和一个字符串列表 wordDict 作为字典。 判断是否可以利用字典中出现的单词拼接出 str。 3 | 举例: 4 | str = "faraway", wordDict = ["far", "away"] 5 | 输出: true 6 | 7 | str = "catsandog", wordDict = ["cats", "dog", "sand", "and", "cat"] 8 | 输出: false 9 | 10 | ****/ 11 | function wordBreak(str, wordDict) { 12 | const stack = [0]; 13 | const visited = new Set(); 14 | 15 | while (stack.length > 0) { 16 | const start = stack.pop(); 17 | 18 | if (!visited.has(start)) { 19 | for (let end = start + 1; end <= str.length; end++) { 20 | const subStr = str.substring(start, end); 21 | if (wordDict.includes(subStr)) { 22 | if (end === str.length) { 23 | return true; 24 | } 25 | stack.push(end); 26 | } 27 | } 28 | visited.add(start); 29 | } 30 | } 31 | 32 | return false; 33 | } 34 | 35 | const str1 = "faraway"; 36 | const wordDict1 = ["far", "away"]; 37 | console.log(wordBreak(str1, wordDict1)); 38 | -------------------------------------------------------------------------------- /README.md: -------------------------------------------------------------------------------- 1 | # Algorithms-DataStructures-Learning 2 | ## 算法学习书籍、视频资源 3 | ### 书籍资源 4 | 5 | - [算法4](https://book.douban.com/subject/19952400/) 6 | - [Hello算法](https://book.douban.com/subject/36794227/) 7 | - [labuladong的算法小抄](https://book.douban.com/subject/35252621/) 8 | - [labuladong的算法笔记](https://book.douban.com/subject/36537238/) 9 | 10 | ### 视频资源 11 | - [慕课网：算法与数据结构](https://class.imooc.com/sale/datastructure?mc_marking=847f8fb5de6faa3343df639065d45b7d&mc_channel=imoocsearch) 12 | - [Harvards Advanced Algorithms Course](https://www.youtube.com/watch?v=0JUN9aDxVmI&list=PL2SOU6wwxB0uP4rJgf5ayhHWgw7akUWSf&ab_channel=HarvardUniversity) 13 | - 14 | ## 数据结构基础 15 | - 数据结构研究的是数据如何在计算机中进行组织和存储，使得我们可以【高效】的获取数据或修改数据。 16 | 17 | * 数据结构应用场景 18 | * 数据库： 19 | * 树结构： AVL、红黑树、B类树、哈希表 20 | * 操作系统 21 | * 优先队列 22 | * 内存管理：内存堆栈 23 | * 文件管理 24 | * 文件压缩：压缩算法(哈夫曼树) 25 | * 寻路算法： 26 | * 图论算法： 27 | * DFS(深度优先遍历): 使用栈 28 | * BFS(广度优先遍历 ): 使用队列 29 | 30 | 31 | ### 线性结构 32 | * 数组 33 | * 栈 34 | * 队列 35 | * 链表 36 | * 哈希表 37 | * ...... 38 | 39 | ### 数结构 40 | * 二叉树 41 | * 二分搜索树 42 | * AVL 43 | * 红黑树 44 | * Treap 45 | * Splay 46 | * 堆 47 | * Trie 48 | * 线段树 49 | * K-D树 50 | * 并查集 51 | * 哈夫曼树 52 | * ...... 53 | 54 | ### 图结构 55 | * 邻接矩阵 56 | * 邻接表 57 | 58 | ## LeetCode Problems 59 | * [LeetCode 算法题练习](LeetCodeProblems.md) 60 | 61 | ## 关于仓库 62 | 63 | 这个仓库是笔者用来记录自己学习算法与数据结构相关知识，自己整理、记录的一些的学习笔记。加油！！！奥利给！！！ 64 | 65 | ![](images/img.png) 66 | 67 | 欢迎提交对本仓库的改进建议~ 68 | -------------------------------------------------------------------------------- /count.js: -------------------------------------------------------------------------------- 1 | //算法练习统计 2 | 3 | const fs = require('fs') 4 | const path = require('path') 5 | 6 | 7 | const dir = path.resolve(__dirname,'javascript-algorithms/leetcode/editor/cn') 8 | 9 | let files = fs.readdirSync(dir) 10 | console.log(files) 11 | 12 | // let len = files.filter(f=>/^\d+\..+\.js$/.test(f)).length 13 | let len = files.filter(f=>/^\[\d+\]..+\.js$/.test(f)).length 14 | console.log('一共刷了'+ len +'题', '加油啦！！！') 15 | -------------------------------------------------------------------------------- /images/img.png: -------------------------------------------------------------------------------- https://raw.githubusercontent.com/SincereCSL/Algorithms-DataStructures-Learning/45c5bdff2cb070b7cde598c716e97ccaf99ce8bc/images/img.png -------------------------------------------------------------------------------- /javascript-algorithms/algorithm/.vscode/settings.json: -------------------------------------------------------------------------------- 1 | { 2 | } -------------------------------------------------------------------------------- /javascript-algorithms/algorithm/1.两数之和.js: -------------------------------------------------------------------------------- 1 | /* 2 | * @lc app=leetcode.cn id=1 lang=javascript 3 | * 4 | * [1] 两数之和 5 | */ 6 | 7 | // @lc code=start 8 | /** 9 | * @param {number[]} nums 10 | * @param {number} target 11 | * @return {number[]} 12 | */ 13 | var twoSum = function (nums, target) { 14 | let obj = {}; 15 | for(let i = 0; i{ 52 | if(root1 === null && root2 === null){ 53 | return true 54 | } 55 | if(root1 ===null || root2 === null){ 56 | return false 57 | } 58 | if(root1.val === root2.val){ 59 | return travese(root1.left,root2.right) && travese(root1.right,root2.left) 60 | } 61 | return false; 62 | } 63 | return travese(root.left,root.right) 64 | }; 65 | //leetcode submit region end(Prohibit modification and deletion) 66 | -------------------------------------------------------------------------------- /javascript-algorithms/leetcode/editor/cn/[102]二叉树的层序遍历.js: -------------------------------------------------------------------------------- 1 | /** 2 | 给你二叉树的根节点 root ，返回其节点值的 层序遍历 。 （即逐层地，从左到右访问所有节点）。 3 | 4 | 5 | 6 | 示例 1： 7 | 8 | 9 | 输入：root = [3,9,20,null,null,15,7] 10 | 输出：[[3],[9,20],[15,7]] 11 | 12 | 13 | 示例 2： 14 | 15 | 16 | 输入：root = [1] 17 | 输出：[[1]] 18 | 19 | 20 | 示例 3： 21 | 22 | 23 | 输入：root = [] 24 | 输出：[] 25 | 26 | 27 | 28 | 29 | 提示： 30 | 31 | 32 | 树中节点数目在范围 [0, 2000] 内 33 | -1000 <= Node.val <= 1000 34 | 35 | 36 | Related Topics 树 广度优先搜索 二叉树 👍 1903 👎 0 37 | 38 | */ 39 | 40 | //leetcode submit region begin(Prohibit modification and deletion) 41 | /** 42 | * Definition for a binary tree node. 43 | * function TreeNode(val, left, right) { 44 | * this.val = (val===undefined ? 0 : val) 45 | * this.left = (left===undefined ? null : left) 46 | * this.right = (right===undefined ? null : right) 47 | * } 48 | */ 49 | /** 50 | * @param {TreeNode} root 51 | * @return {number[][]} 52 | */ 53 | var levelOrder = function(root) { 54 | //队列方式去解题 55 | let ret = [];// 返回的结果 56 | if(root === null){ 57 | return ret 58 | } 59 | let queue = [root]; //需要遍历的队列 60 | while (queue.length){ 61 | let len = queue.length; 62 | let curLevel = []; 63 | while (len>0){ 64 | let node = queue.shift() 65 | curLevel.push(node.val) 66 | node.left && queue.push(node.left) 67 | node.right && queue.push(node.right) 68 | len-- 69 | } 70 | ret.push(curLevel) 71 | } 72 | return ret 73 | }; 74 | //leetcode submit region end(Prohibit modification and deletion) 75 | -------------------------------------------------------------------------------- /javascript-algorithms/leetcode/editor/cn/[1047]删除字符串中的所有相邻重复项.js: -------------------------------------------------------------------------------- 1 | /** 2 | 给出由小写字母组成的字符串 S，重复项删除操作会选择两个相邻且相同的字母，并删除它们。 3 | 4 | 在 S 上反复执行重复项删除操作，直到无法继续删除。 5 | 6 | 在完成所有重复项删除操作后返回最终的字符串。答案保证唯一。 7 | 8 | 9 | 10 | 示例： 11 | 12 | 输入："abbaca" 13 | 输出："ca" 14 | 解释： 15 | 例如，在 "abbaca" 中，我们可以删除 "bb" 由于两字母相邻且相同，这是此时唯一可以执行删除操作的重复项。之后我们得到字符串 "aaca"，其中又只有 16 | "aa" 可以执行重复项删除操作，所以最后的字符串为 "ca"。 17 | 18 | 19 | 20 | 21 | 提示： 22 | 23 | 24 | 1 <= S.length <= 20000 25 | S 仅由小写英文字母组成。 26 | 27 | 28 | Related Topics 栈 字符串 👍 618 👎 0 29 | 30 | */ 31 | 32 | //leetcode submit region begin(Prohibit modification and deletion) 33 | /** 34 | * @param {string} s 35 | * @return {string} 36 | */ 37 | var removeDuplicates = function(s) { 38 | // ---- 解法1: ---- 39 | // let stack = [] 40 | // for (let i = 0;i0){ 64 | let node = queue.shift() 65 | curLevel.push(node.val) 66 | node.left && queue.push(node.left) 67 | node.right && queue.push(node.right) 68 | len-- 69 | } 70 | ret.unshift(curLevel) 71 | } 72 | return ret 73 | }; 74 | //leetcode submit region end(Prohibit modification and deletion) 75 | -------------------------------------------------------------------------------- /javascript-algorithms/leetcode/editor/cn/[108]将有序数组转换为二叉搜索树.js: -------------------------------------------------------------------------------- 1 | /** 2 | 给你一个整数数组 nums ，其中元素已经按 升序 排列，请你将其转换为一棵 高度平衡 二叉搜索树。 3 | 4 | 高度平衡 二叉树是一棵满足「每个节点的左右两个子树的高度差的绝对值不超过 1 」的二叉树。 5 | 6 | 7 | 8 | 示例 1： 9 | 10 | 11 | 输入：nums = [-10,-3,0,5,9] 12 | 输出：[0,-3,9,-10,null,5] 13 | 解释：[0,-10,5,null,-3,null,9] 也将被视为正确答案： 14 | 15 | 16 | 17 | 示例 2： 18 | 19 | 20 | 输入：nums = [1,3] 21 | 输出：[3,1] 22 | 解释：[1,null,3] 和 [3,1] 都是高度平衡二叉搜索树。 23 | 24 | 25 | 26 | 27 | 提示： 28 | 29 | 30 | 1 <= nums.length <= 10⁴ 31 | -10⁴ <= nums[i] <= 10⁴ 32 | nums 按 严格递增 顺序排列 33 | 34 | 35 | Related Topics 树 二叉搜索树 数组 分治 二叉树 👍 1478 👎 0 36 | 37 | */ 38 | 39 | //leetcode submit region begin(Prohibit modification and deletion) 40 | /** 41 | * Definition for a binary tree node. 42 | * function TreeNode(val, left, right) { 43 | * this.val = (val===undefined ? 0 : val) 44 | * this.left = (left===undefined ? null : left) 45 | * this.right = (right===undefined ? null : right) 46 | * } 47 | */ 48 | /** 49 | * @param {number[]} nums 50 | * @return {TreeNode} 51 | */ 52 | var sortedArrayToBST = function(nums) { 53 | if(!nums.length){ 54 | return null 55 | } 56 | // 二叉搜索树的中中序遍历，生序列表 57 | // 数组中间的位置，可以作为树的根节点 58 | const mid = Math.floor(nums.length/2) 59 | const root = new TreeNode(nums[mid]) 60 | root.left = sortedArrayToBST(nums.slice(0,mid)) 61 | root.right = sortedArrayToBST(nums.slice(mid+1)) 62 | return root 63 | }; 64 | //leetcode submit region end(Prohibit modification and deletion) 65 | -------------------------------------------------------------------------------- /javascript-algorithms/leetcode/editor/cn/[109]有序链表转换二叉搜索树.js: -------------------------------------------------------------------------------- 1 | /** 2 | 给定一个单链表的头节点 head ，其中的元素 按升序排序 ，将其转换为高度平衡的二叉搜索树。 3 | 4 | 本题中，一个高度平衡二叉树是指一个二叉树每个节点 的左右两个子树的高度差不超过 1。 5 | 6 | 7 | 8 | 示例 1: 9 | 10 | 11 | 12 | 13 | 输入: head = [-10,-3,0,5,9] 14 | 输出: [0,-3,9,-10,null,5] 15 | 解释: 一个可能的答案是[0，-3,9，-10,null,5]，它表示所示的高度平衡的二叉搜索树。 16 | 17 | 18 | 示例 2: 19 | 20 | 21 | 输入: head = [] 22 | 输出: [] 23 | 24 | 25 | 26 | 27 | 提示: 28 | 29 | 30 | head 中的节点数在[0, 2 * 10⁴] 范围内 31 | -10⁵ <= Node.val <= 10⁵ 32 | 33 | 34 | Related Topics 树 二叉搜索树 链表 分治 二叉树 👍 889 👎 0 35 | 36 | */ 37 | 38 | //leetcode submit region begin(Prohibit modification and deletion) 39 | /** 40 | * Definition for singly-linked list. 41 | * function ListNode(val, next) { 42 | * this.val = (val===undefined ? 0 : val) 43 | * this.next = (next===undefined ? null : next) 44 | * } 45 | */ 46 | /** 47 | * Definition for a binary tree node. 48 | * function TreeNode(val, left, right) { 49 | * this.val = (val===undefined ? 0 : val) 50 | * this.left = (left===undefined ? null : left) 51 | * this.right = (right===undefined ? null : right) 52 | * } 53 | */ 54 | /** 55 | * @param {ListNode} head 56 | * @return {TreeNode} 57 | */ 58 | var sortedListToBST = function(head) { 59 | // 快慢指针 60 | function travese(head,tail){ 61 | if(head === tail){ 62 | return null 63 | } 64 | let slow = fast = head; 65 | while (fast !== tail && fast.next !== tail){ 66 | slow = slow.next 67 | fast = fast.next.next 68 | } 69 | let root = new TreeNode(slow.val) 70 | root.left = travese(head,slow) 71 | root.right = travese(slow.next,tail) 72 | return root; 73 | } 74 | return travese(head,null) 75 | 76 | }; 77 | //leetcode submit region end(Prohibit modification and deletion) 78 | -------------------------------------------------------------------------------- /javascript-algorithms/leetcode/editor/cn/[110]平衡二叉树.js: -------------------------------------------------------------------------------- 1 | /** 2 | 给定一个二叉树，判断它是否是高度平衡的二叉树。 3 | 4 | 本题中，一棵高度平衡二叉树定义为： 5 | 6 | 7 | 一个二叉树每个节点 的左右两个子树的高度差的绝对值不超过 1 。 8 | 9 | 10 | 11 | 12 | 示例 1： 13 | 14 | 15 | 输入：root = [3,9,20,null,null,15,7] 16 | 输出：true 17 | 18 | 19 | 示例 2： 20 | 21 | 22 | 输入：root = [1,2,2,3,3,null,null,4,4] 23 | 输出：false 24 | 25 | 26 | 示例 3： 27 | 28 | 29 | 输入：root = [] 30 | 输出：true 31 | 32 | 33 | 34 | 35 | 提示： 36 | 37 | 38 | 树中的节点数在范围 [0, 5000] 内 39 | -10⁴ <= Node.val <= 10⁴ 40 | 41 | 42 | Related Topics 树 深度优先搜索 二叉树 👍 1485 👎 0 43 | 44 | */ 45 | 46 | //leetcode submit region begin(Prohibit modification and deletion) 47 | /** 48 | * Definition for a binary tree node. 49 | * function TreeNode(val, left, right) { 50 | * this.val = (val===undefined ? 0 : val) 51 | * this.left = (left===undefined ? null : left) 52 | * this.right = (right===undefined ? null : right) 53 | * } 54 | */ 55 | /** 56 | * @param {TreeNode} root 57 | * @return {boolean} 58 | */ 59 | // -1 60 | var isBalanced = function(root) { 61 | function travese(treeNode){ 62 | if(treeNode === null){ 63 | return 0 64 | } 65 | let leftDepth = travese(treeNode.left) 66 | if(leftDepth === -1){ 67 | return -1 68 | } 69 | let rightDepth = travese(treeNode.right) 70 | if(rightDepth === -1){ 71 | return -1 72 | } 73 | if(Math.abs(leftDepth-rightDepth)>1){ 74 | return -1 75 | }else{ 76 | return Math.max(leftDepth,rightDepth)+1 77 | } 78 | } 79 | return travese(root) !== -1 80 | }; 81 | //leetcode submit region end(Prohibit modification and deletion) 82 | -------------------------------------------------------------------------------- /javascript-algorithms/leetcode/editor/cn/[112]路径总和.js: -------------------------------------------------------------------------------- 1 | /** 2 | 给你二叉树的根节点 root 和一个表示目标和的整数 targetSum 。判断该树中是否存在 根节点到叶子节点 的路径，这条路径上所有节点值相加等于目标和 3 | targetSum 。如果存在，返回 true ；否则，返回 false 。 4 | 5 | 叶子节点 是指没有子节点的节点。 6 | 7 | 8 | 9 | 示例 1： 10 | 11 | 12 | 输入：root = [5,4,8,11,null,13,4,7,2,null,null,null,1], targetSum = 22 13 | 输出：true 14 | 解释：等于目标和的根节点到叶节点路径如上图所示。 15 | 16 | 17 | 示例 2： 18 | 19 | 20 | 输入：root = [1,2,3], targetSum = 5 21 | 输出：false 22 | 解释：树中存在两条根节点到叶子节点的路径： 23 | (1 --> 2): 和为 3 24 | (1 --> 3): 和为 4 25 | 不存在 sum = 5 的根节点到叶子节点的路径。 26 | 27 | 示例 3： 28 | 29 | 30 | 输入：root = [], targetSum = 0 31 | 输出：false 32 | 解释：由于树是空的，所以不存在根节点到叶子节点的路径。 33 | 34 | 35 | 36 | 37 | 提示： 38 | 39 | 40 | 树中节点的数目在范围 [0, 5000] 内 41 | -1000 <= Node.val <= 1000 42 | -1000 <= targetSum <= 1000 43 | 44 | 45 | Related Topics 树 深度优先搜索 广度优先搜索 二叉树 👍 1319 👎 0 46 | 47 | */ 48 | 49 | //leetcode submit region begin(Prohibit modification and deletion) 50 | /** 51 | * Definition for a binary tree node. 52 | * function TreeNode(val, left, right) { 53 | * this.val = (val===undefined ? 0 : val) 54 | * this.left = (left===undefined ? null : left) 55 | * this.right = (right===undefined ? null : right) 56 | * } 57 | */ 58 | /** 59 | * @param {TreeNode} root 60 | * @param {number} targetSum 61 | * @return {boolean} 62 | */ 63 | var hasPathSum = function(root, targetSum) { 64 | // 递归解法 65 | if(root === null){ 66 | return false 67 | } 68 | if(!root.left && !root.right){ 69 | return root.val === targetSum 70 | } 71 | let offset = targetSum - root.val 72 | return hasPathSum(root.left,offset) || hasPathSum(root.right,offset) 73 | }; 74 | //leetcode submit region end(Prohibit modification and deletion) 75 | -------------------------------------------------------------------------------- /javascript-algorithms/leetcode/editor/cn/[114]二叉树展开为链表.js: -------------------------------------------------------------------------------- 1 | /** 2 | 给你二叉树的根结点 root ，请你将它展开为一个单链表： 3 | 4 | 5 | 展开后的单链表应该同样使用 TreeNode ，其中 right 子指针指向链表中下一个结点，而左子指针始终为 null 。 6 | 展开后的单链表应该与二叉树 先序遍历 顺序相同。 7 | 8 | 9 | 10 | 11 | 示例 1： 12 | 13 | 14 | 输入：root = [1,2,5,3,4,null,6] 15 | 输出：[1,null,2,null,3,null,4,null,5,null,6] 16 | 17 | 18 | 示例 2： 19 | 20 | 21 | 输入：root = [] 22 | 输出：[] 23 | 24 | 25 | 示例 3： 26 | 27 | 28 | 输入：root = [0] 29 | 输出：[0] 30 | 31 | 32 | 33 | 34 | 提示： 35 | 36 | 37 | 树中结点数在范围 [0, 2000] 内 38 | -100 <= Node.val <= 100 39 | 40 | 41 | 42 | 43 | 进阶：你可以使用原地算法（O(1) 额外空间）展开这棵树吗？ 44 | 45 | Related Topics 栈 树 深度优先搜索 链表 二叉树 👍 1629 👎 0 46 | 47 | */ 48 | 49 | //leetcode submit region begin(Prohibit modification and deletion) 50 | /** 51 | * Definition for a binary tree node. 52 | * function TreeNode(val, left, right) { 53 | * this.val = (val===undefined ? 0 : val) 54 | * this.left = (left===undefined ? null : left) 55 | * this.right = (right===undefined ? null : right) 56 | * } 57 | */ 58 | /** 59 | * @param {TreeNode} root 60 | * @return {void} Do not return anything, modify root in-place instead. 61 | */ 62 | var flatten = function(root) { 63 | let list = []; 64 | prevTravese(root,list) 65 | for (let i=1;i0){ 81 | node.next = queue[0] 82 | } 83 | node.left && queue.push(node.left) 84 | node.right && queue.push(node.right) 85 | } 86 | } 87 | return root 88 | }; 89 | //leetcode submit region end(Prohibit modification and deletion) 90 | -------------------------------------------------------------------------------- /javascript-algorithms/leetcode/editor/cn/[125]验证回文串.js: -------------------------------------------------------------------------------- 1 | /** 2 | 如果在将所有大写字符转换为小写字符、并移除所有非字母数字字符之后，短语正着读和反着读都一样。则可以认为该短语是一个 回文串 。 3 | 4 | 字母和数字都属于字母数字字符。 5 | 6 | 给你一个字符串 s，如果它是 回文串 ，返回 true ；否则，返回 false 。 7 | 8 | 9 | 10 | 示例 1： 11 | 12 | 13 | 输入: s = "A man, a plan, a canal: Panama" 14 | 输出：true 15 | 解释："amanaplanacanalpanama" 是回文串。 16 | 17 | 18 | 示例 2： 19 | 20 | 21 | 输入：s = "race a car" 22 | 输出：false 23 | 解释："raceacar" 不是回文串。 24 | 25 | 26 | 示例 3： 27 | 28 | 29 | 输入：s = " " 30 | 输出：true 31 | 解释：在移除非字母数字字符之后，s 是一个空字符串 "" 。 32 | 由于空字符串正着反着读都一样，所以是回文串。 33 | 34 | 35 | 36 | 37 | 提示： 38 | 39 | 40 | 1 <= s.length <= 2 * 10⁵ 41 | s 仅由可打印的 ASCII 字符组成 42 | 43 | 44 | Related Topics 双指针 字符串 👍 742 👎 0 45 | 46 | */ 47 | 48 | //leetcode submit region begin(Prohibit modification and deletion) 49 | /** 50 | * @param {string} s 51 | * @return {boolean} 52 | */ 53 | var isPalindrome = function(s) { 54 | let str = s.replace(/[^a-z0-9]/gi,'').toLowerCase() 55 | // 暴力解法 56 | // return str.split('').reverse().join('') === str 57 | // let left = 0; 58 | // let right = s.length-1 59 | // while (left<=right){ 60 | // if(s[left] !== s[right]){ 61 | // return false 62 | // } 63 | // left++ 64 | // right-- 65 | // } 66 | // return true 67 | 68 | // ---- 解法2 69 | let left = 0; 70 | let right = str.length-1 71 | while (left<=right){ 72 | if(str[left] !== str[right]){ 73 | return false 74 | } 75 | left++ 76 | right-- 77 | } 78 | return true 79 | }; 80 | //leetcode submit region end(Prohibit modification and deletion) 81 | -------------------------------------------------------------------------------- /javascript-algorithms/leetcode/editor/cn/[131]分割回文串.js: -------------------------------------------------------------------------------- 1 | /** 2 | 给你一个字符串 s，请你将 s 分割成一些子串，使每个子串都是 回文串 。返回 s 所有可能的分割方案。 3 | 4 | 5 | 6 | 示例 1： 7 | 8 | 9 | 输入：s = "aab" 10 | 输出：[["a","a","b"],["aa","b"]] 11 | 12 | 13 | 示例 2： 14 | 15 | 16 | 输入：s = "a" 17 | 输出：[["a"]] 18 | 19 | 20 | 21 | 22 | 提示： 23 | 24 | 25 | 1 <= s.length <= 16 26 | s 仅由小写英文字母组成 27 | 28 | 29 | Related Topics 字符串 动态规划 回溯 👍 1781 👎 0 30 | 31 | */ 32 | 33 | //leetcode submit region begin(Prohibit modification and deletion) 34 | /** 35 | * @param {string} s 36 | * @return {string[][]} 37 | */ 38 | function isPalindrome(s,l,r){ 39 | for(let i =l,j=r;i=s.length){ 53 | ret.push([...path]) 54 | return 55 | } 56 | for(let j=i;j 10 55 | // 1--> 01 56 | // 2^1 = 3 -->11 57 | let tmp = 0 58 | nums.forEach(num=>{ 59 | tmp ^= num 60 | }) 61 | return tmp 62 | }; 63 | //leetcode submit region end(Prohibit modification and deletion) 64 | -------------------------------------------------------------------------------- /javascript-algorithms/leetcode/editor/cn/[141]环形链表.js: -------------------------------------------------------------------------------- 1 | /** 2 | 给你一个链表的头节点 head ，判断链表中是否有环。 3 | 4 | 如果链表中有某个节点，可以通过连续跟踪 next 指针再次到达，则链表中存在环。 为了表示给定链表中的环，评测系统内部使用整数 pos 来表示链表尾连接到链表 5 | 中的位置（索引从 0 开始）。注意：pos 不作为参数进行传递 。仅仅是为了标识链表的实际情况。 6 | 7 | 如果链表中存在环 ，则返回 true 。 否则，返回 false 。 8 | 9 | 10 | 11 | 示例 1： 12 | 13 | 14 | 15 | 16 | 输入：head = [3,2,0,-4], pos = 1 17 | 输出：true 18 | 解释：链表中有一个环，其尾部连接到第二个节点。 19 | 20 | 21 | 示例 2： 22 | 23 | 24 | 25 | 26 | 输入：head = [1,2], pos = 0 27 | 输出：true 28 | 解释：链表中有一个环，其尾部连接到第一个节点。 29 | 30 | 31 | 示例 3： 32 | 33 | 34 | 35 | 36 | 输入：head = [1], pos = -1 37 | 输出：false 38 | 解释：链表中没有环。 39 | 40 | 41 | 42 | 43 | 提示： 44 | 45 | 46 | 链表中节点的数目范围是 [0, 10⁴] 47 | -10⁵ <= Node.val <= 10⁵ 48 | pos 为 -1 或者链表中的一个 有效索引 。 49 | 50 | 51 | 52 | 53 | 进阶：你能用 O(1)（即，常量）内存解决此问题吗？ 54 | 55 | Related Topics 哈希表 链表 双指针 👍 1974 👎 0 56 | 57 | */ 58 | 59 | //leetcode submit region begin(Prohibit modification and deletion) 60 | /** 61 | * Definition for singly-linked list. 62 | * function ListNode(val) { 63 | * this.val = val; 64 | * this.next = null; 65 | * } 66 | */ 67 | 68 | /** 69 | * @param {ListNode} head 70 | * @return {boolean} 71 | */ 72 | var hasCycle = function(head) { 73 | //----方法一： 74 | // let cache = new Set() 75 | // while (head){ 76 | // if(cache.has(head)){ 77 | // return true 78 | // }else { 79 | // cache.add(head) 80 | // } 81 | // head = head.next; 82 | // } 83 | // return false 84 | 85 | // 方法二: 双指针解法 86 | let slow = head; 87 | let fast = head; 88 | while (fast && fast.next){ 89 | fast = fast.next.next; 90 | slow = slow.next; 91 | if(slow === fast) return true; 92 | } 93 | return false; 94 | 95 | // 时间复杂度都是O(n) 96 | // 空间复杂度：方法一 O(n) 方法二 O(1) 97 | }; 98 | //leetcode submit region end(Prohibit modification and deletion) 99 | -------------------------------------------------------------------------------- /javascript-algorithms/leetcode/editor/cn/[144]二叉树的前序遍历.js: -------------------------------------------------------------------------------- 1 | /** 2 | 给你二叉树的根节点 root ，返回它节点值的 前序 遍历。 3 | 4 | 5 | 6 | 示例 1： 7 | 8 | 9 | 输入：root = [1,null,2,3] 10 | 输出：[1,2,3] 11 | 12 | 13 | 示例 2： 14 | 15 | 16 | 输入：root = [] 17 | 输出：[] 18 | 19 | 20 | 示例 3： 21 | 22 | 23 | 输入：root = [1] 24 | 输出：[1] 25 | 26 | 27 | 示例 4： 28 | 29 | 30 | 输入：root = [1,2] 31 | 输出：[1,2] 32 | 33 | 34 | 示例 5： 35 | 36 | 37 | 输入：root = [1,null,2] 38 | 输出：[1,2] 39 | 40 | 41 | 42 | 43 | 提示： 44 | 45 | 46 | 树中节点数目在范围 [0, 100] 内 47 | -100 <= Node.val <= 100 48 | 49 | 50 | 51 | 52 | 进阶：递归算法很简单，你可以通过迭代算法完成吗？ 53 | 54 | Related Topics 栈 树 深度优先搜索 二叉树 👍 1218 👎 0 55 | 56 | */ 57 | 58 | //leetcode submit region begin(Prohibit modification and deletion) 59 | /** 60 | * Definition for a binary tree node. 61 | * function TreeNode(val, left, right) { 62 | * this.val = (val===undefined ? 0 : val) 63 | * this.left = (left===undefined ? null : left) 64 | * this.right = (right===undefined ? null : right) 65 | * } 66 | */ 67 | /** 68 | * @param {TreeNode} root 69 | * @return {number[]} 70 | */ 71 | var preorderTraversal = function(root) { 72 | // let arr = []; 73 | // function dfs(root){ 74 | // if(root === null){ 75 | // return 76 | // } 77 | // arr.push(root.val) 78 | // dfs(root.left) 79 | // dfs(root.right) 80 | // } 81 | // dfs(root) 82 | // return arr; 83 | 84 | //迭代解法： 85 | 86 | let res = []; 87 | if(root === null){ 88 | return res 89 | } 90 | let stack = [root]; 91 | while (stack.length){ 92 | let cur = stack.pop() 93 | res.push(cur.val) 94 | cur.right && stack.push(cur.right); 95 | cur.left && stack.push(cur.left); 96 | } 97 | return res 98 | 99 | }; 100 | //leetcode submit region end(Prohibit modification and deletion) 101 | -------------------------------------------------------------------------------- /javascript-algorithms/leetcode/editor/cn/[145]二叉树的后序遍历.js: -------------------------------------------------------------------------------- 1 | /** 2 | 给你一棵二叉树的根节点 root ，返回其节点值的 后序遍历 。 3 | 4 | 5 | 6 | 示例 1： 7 | 8 | 9 | 输入：root = [1,null,2,3] 10 | 输出：[3,2,1] 11 | 12 | 13 | 示例 2： 14 | 15 | 16 | 输入：root = [] 17 | 输出：[] 18 | 19 | 20 | 示例 3： 21 | 22 | 23 | 输入：root = [1] 24 | 输出：[1] 25 | 26 | 27 | 28 | 29 | 提示： 30 | 31 | 32 | 树中节点的数目在范围 [0, 100] 内 33 | -100 <= Node.val <= 100 34 | 35 | 36 | 37 | 38 | 进阶：递归算法很简单，你可以通过迭代算法完成吗？ 39 | 40 | Related Topics 栈 树 深度优先搜索 二叉树 👍 1144 👎 0 41 | 42 | */ 43 | 44 | //leetcode submit region begin(Prohibit modification and deletion) 45 | /** 46 | * Definition for a binary tree node. 47 | * function TreeNode(val, left, right) { 48 | * this.val = (val===undefined ? 0 : val) 49 | * this.left = (left===undefined ? null : left) 50 | * this.right = (right===undefined ? null : right) 51 | * } 52 | */ 53 | /** 54 | * @param {TreeNode} root 55 | * @return {number[]} 56 | */ 57 | var postorderTraversal = function(root) { 58 | let arr = []; 59 | function dfs(root){ 60 | if(root === null){ 61 | return 62 | } 63 | dfs(root.left) 64 | dfs(root.right) 65 | arr.push(root.val) 66 | } 67 | dfs(root) 68 | return arr; 69 | 70 | }; 71 | //leetcode submit region end(Prohibit modification and deletion) 72 | -------------------------------------------------------------------------------- /javascript-algorithms/leetcode/editor/cn/[151]反转字符串中的单词.js: -------------------------------------------------------------------------------- 1 | /** 2 | 给你一个字符串 s ，请你反转字符串中 单词 的顺序。 3 | 4 | 单词 是由非空格字符组成的字符串。s 中使用至少一个空格将字符串中的 单词 分隔开。 5 | 6 | 返回 单词 顺序颠倒且 单词 之间用单个空格连接的结果字符串。 7 | 8 | 注意：输入字符串 s中可能会存在前导空格、尾随空格或者单词间的多个空格。返回的结果字符串中，单词间应当仅用单个空格分隔，且不包含任何额外的空格。 9 | 10 | 11 | 12 | 示例 1： 13 | 14 | 15 | 输入：s = "the sky is blue" 16 | 输出："blue is sky the" 17 | 18 | 19 | 示例 2： 20 | 21 | 22 | 输入：s = "  hello world  " 23 | 输出："world hello" 24 | 解释：反转后的字符串中不能存在前导空格和尾随空格。 25 | 26 | 27 | 示例 3： 28 | 29 | 30 | 输入：s = "a good   example" 31 | 输出："example good a" 32 | 解释：如果两个单词间有多余的空格，反转后的字符串需要将单词间的空格减少到仅有一个。 33 | 34 | 35 | 36 | 37 | 提示： 38 | 39 | 40 | 1 <= s.length <= 10⁴ 41 | s 包含英文大小写字母、数字和空格 ' ' 42 | s 中 至少存在一个 单词 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 | 进阶：如果字符串在你使用的编程语言中是一种可变数据类型，请尝试使用 O(1) 额外空间复杂度的 原地 解法。 51 | 52 | Related Topics 双指针 字符串 👍 1135 👎 0 53 | 54 | */ 55 | 56 | //leetcode submit region begin(Prohibit modification and deletion) 57 | /** 58 | * @param {string} s 59 | * @return {string} 60 | */ 61 | var reverseWords = function(s) { 62 | // 技巧解法 一般不推荐 63 | // return s.trim().split(' ').filter(v =>v).reverse().join(' ') 64 | 65 | // 解法1 66 | let left = 0; 67 | let right = s.length-1; 68 | let queue = []; 69 | let word = '' 70 | while (s.charAt(left) ===' '){ 71 | left++ 72 | } 73 | while (s.charAt(right) ===' '){ 74 | right-- 75 | } 76 | while (left <= right){ 77 | let ch = s.charAt(left) 78 | if(ch===' ' && word){ 79 | queue.unshift(word) 80 | word = '' 81 | }else if(ch !==' '){ 82 | word += ch 83 | } 84 | left ++ 85 | } 86 | queue.unshift(word) 87 | return queue.join(' ') 88 | 89 | }; 90 | //leetcode submit region end(Prohibit modification and deletion) 91 | -------------------------------------------------------------------------------- /javascript-algorithms/leetcode/editor/cn/[153]寻找旋转排序数组中的最小值.js: -------------------------------------------------------------------------------- 1 | /** 2 | 已知一个长度为 n 的数组，预先按照升序排列，经由 1 到 n 次 旋转 后，得到输入数组。例如，原数组 nums = [0,1,2,4,5,6,7] 在变化后 3 | 可能得到： 4 | 5 | 6 | 若旋转 4 次，则可以得到 [4,5,6,7,0,1,2] 7 | 若旋转 7 次，则可以得到 [0,1,2,4,5,6,7] 8 | 9 | 10 | 注意，数组 [a[0], a[1], a[2], ..., a[n-1]] 旋转一次 的结果为数组 [a[n-1], a[0], a[1], a[2], .. 11 | ., a[n-2]] 。 12 | 13 | 给你一个元素值 互不相同 的数组 nums ，它原来是一个升序排列的数组，并按上述情形进行了多次旋转。请你找出并返回数组中的 最小元素 。 14 | 15 | 你必须设计一个时间复杂度为 O(log n) 的算法解决此问题。 16 | 17 | 18 | 19 | 示例 1： 20 | 21 | 22 | 输入：nums = [3,4,5,1,2] 23 | 输出：1 24 | 解释：原数组为 [1,2,3,4,5] ，旋转 3 次得到输入数组。 25 | 26 | 27 | 示例 2： 28 | 29 | 30 | 输入：nums = [4,5,6,7,0,1,2] 31 | 输出：0 32 | 解释：原数组为 [0,1,2,4,5,6,7] ，旋转 3 次得到输入数组。 33 | 34 | 35 | 示例 3： 36 | 37 | 38 | 输入：nums = [11,13,15,17] 39 | 输出：11 40 | 解释：原数组为 [11,13,15,17] ，旋转 4 次得到输入数组。 41 | 42 | 43 | 44 | 45 | 提示： 46 | 47 | 48 | n == nums.length 49 | 1 <= n <= 5000 50 | -5000 <= nums[i] <= 5000 51 | nums 中的所有整数 互不相同 52 | nums 原来是一个升序排序的数组，并进行了 1 至 n 次旋转 53 | 54 | 55 | Related Topics 数组 二分查找 👍 1089 👎 0 56 | 57 | */ 58 | 59 | //leetcode submit region begin(Prohibit modification and deletion) 60 | /** 61 | * @param {number[]} nums 62 | * @return {number} 63 | */ 64 | var findMin = function(nums) { 65 | // 66 | let left = 0 67 | let right = nums.length-1 68 | while (left>1) 70 | if(nums[mid] nums[right]){ 73 | left = mid+1 74 | } 75 | } 76 | return nums[left] 77 | }; 78 | //leetcode submit region end(Prohibit modification and deletion) 79 | -------------------------------------------------------------------------------- /javascript-algorithms/leetcode/editor/cn/[17]电话号码的字母组合.js: -------------------------------------------------------------------------------- 1 | /** 2 | 给定一个仅包含数字 2-9 的字符串，返回所有它能表示的字母组合。答案可以按 任意顺序 返回。 3 | 4 | 给出数字到字母的映射如下（与电话按键相同）。注意 1 不对应任何字母。 5 | 6 | 7 | 8 | 9 | 10 | 示例 1： 11 | 12 | 13 | 输入：digits = "23" 14 | 输出：["ad","ae","af","bd","be","bf","cd","ce","cf"] 15 | 16 | 17 | 示例 2： 18 | 19 | 20 | 输入：digits = "" 21 | 输出：[] 22 | 23 | 24 | 示例 3： 25 | 26 | 27 | 输入：digits = "2" 28 | 输出：["a","b","c"] 29 | 30 | 31 | 32 | 33 | 提示： 34 | 35 | 36 | 0 <= digits.length <= 4 37 | digits[i] 是范围 ['2', '9'] 的一个数字。 38 | 39 | 40 | Related Topics 哈希表 字符串 回溯 👍 2791 👎 0 41 | 42 | */ 43 | 44 | //leetcode submit region begin(Prohibit modification and deletion) 45 | /** 46 | * @param {string} digits 47 | * @return {string[]} 48 | */ 49 | var letterCombinations = function(digits) { 50 | let len = digits.length; 51 | const arr = ['','','abc','def','ghi','jkl','mno','pqrs','tuv','wxyz'] 52 | if(!len){ 53 | return [] 54 | } 55 | if(len===1){ 56 | console.log(arr[digits].split('')) 57 | return arr[digits].split('') 58 | } 59 | let ret = [] 60 | let path = [] 61 | backtrack(digits,len,0) 62 | return ret 63 | function backtrack(digits,l,i){ 64 | if(path.length === l){ 65 | ret.push(path.join('')) 66 | return 67 | } 68 | for(const v of arr[digits[i]]){ 69 | path.push(v) 70 | backtrack(digits,l,i+1) 71 | path.pop() 72 | } 73 | } 74 | }; 75 | //leetcode submit region end(Prohibit modification and deletion) 76 | -------------------------------------------------------------------------------- /javascript-algorithms/leetcode/editor/cn/[199]二叉树的右视图.js: -------------------------------------------------------------------------------- 1 | /** 2 | 给定一个二叉树的 根节点 root，想象自己站在它的右侧，按照从顶部到底部的顺序，返回从右侧所能看到的节点值。 3 | 4 | 5 | 6 | 示例 1: 7 | 8 | 9 | 10 | 11 | 输入: [1,2,3,null,5,null,4] 12 | 输出: [1,3,4] 13 | 14 | 15 | 示例 2: 16 | 17 | 18 | 输入: [1,null,3] 19 | 输出: [1,3] 20 | 21 | 22 | 示例 3: 23 | 24 | 25 | 输入: [] 26 | 输出: [] 27 | 28 | 29 | 30 | 31 | 提示: 32 | 33 | 34 | 二叉树的节点个数的范围是 [0,100] 35 | 36 | -100 <= Node.val <= 100 37 | 38 | 39 | Related Topics 树 深度优先搜索 广度优先搜索 二叉树 👍 1036 👎 0 40 | 41 | */ 42 | 43 | //leetcode submit region begin(Prohibit modification and deletion) 44 | /** 45 | * Definition for a binary tree node. 46 | * function TreeNode(val, left, right) { 47 | * this.val = (val===undefined ? 0 : val) 48 | * this.left = (left===undefined ? null : left) 49 | * this.right = (right===undefined ? null : right) 50 | * } 51 | */ 52 | /** 53 | * @param {TreeNode} root 54 | * @return {number[]} 55 | */ 56 | var rightSideView = function(root) { 57 | //遍历每一层最右边的一个值 58 | let ret = []; 59 | if(root === null){ 60 | return ret 61 | } 62 | let queue = [root] 63 | while (queue.length){ 64 | let len = queue.length 65 | while (len--){ 66 | let node = queue.shift() 67 | if(len === 0){ 68 | ret.push(node.val) 69 | } 70 | node.left && queue.push(node.left) 71 | node.right && queue.push(node.right) 72 | } 73 | } 74 | return ret; 75 | }; 76 | //leetcode submit region end(Prohibit modification and deletion) 77 | -------------------------------------------------------------------------------- /javascript-algorithms/leetcode/editor/cn/[1]两数之和.js: -------------------------------------------------------------------------------- 1 | /** 2 | 给定一个整数数组 nums 和一个整数目标值 target，请你在该数组中找出 和为目标值 target 的那 两个 整数，并返回它们的数组下标。 3 | 4 | 你可以假设每种输入只会对应一个答案。但是，数组中同一个元素在答案里不能重复出现。 5 | 6 | 你可以按任意顺序返回答案。 7 | 8 | 9 | 10 | 示例 1： 11 | 12 | 13 | 输入：nums = [2,7,11,15], target = 9 14 | 输出：[0,1] 15 | 解释：因为 nums[0] + nums[1] == 9 ，返回 [0, 1] 。 16 | 17 | 18 | 示例 2： 19 | 20 | 21 | 输入：nums = [3,2,4], target = 6 22 | 输出：[1,2] 23 | 24 | 25 | 示例 3： 26 | 27 | 28 | 输入：nums = [3,3], target = 6 29 | 输出：[0,1] 30 | 31 | 32 | 33 | 34 | 提示： 35 | 36 | 37 | 2 <= nums.length <= 10⁴ 38 | -10⁹ <= nums[i] <= 10⁹ 39 | -10⁹ <= target <= 10⁹ 40 | 只会存在一个有效答案 41 | 42 | 43 | 44 | 45 | 进阶：你可以想出一个时间复杂度小于 O(n²) 的算法吗？ 46 | 47 | Related Topics 数组 哈希表 👍 16275 👎 0 48 | 49 | */ 50 | 51 | //leetcode submit region begin(Prohibit modification and deletion) 52 | /** 53 | * @param {number[]} nums 54 | * @param {number} target 55 | * @return {number[]} 56 | */ 57 | var twoSum = function(nums, target) { 58 | //****解法：1 59 | // for(let i=0;i 1 =>2 =>3 =>4 63 | let ele = { 64 | next:head 65 | } 66 | let p = ele; 67 | while(p.next){ 68 | if(p.next.val === val){ 69 | p.next = p.next.next; 70 | }else{ 71 | p = p.next 72 | } 73 | } 74 | return ele.next 75 | 76 | }; 77 | //leetcode submit region end(Prohibit modification and deletion) 78 | -------------------------------------------------------------------------------- /javascript-algorithms/leetcode/editor/cn/[20]有效的括号.js: -------------------------------------------------------------------------------- 1 | /** 2 | 给定一个只包括 '('，')'，'{'，'}'，'['，']' 的字符串 s ，判断字符串是否有效。 3 | 4 | 有效字符串需满足： 5 | 6 | 7 | 左括号必须用相同类型的右括号闭合。 8 | 左括号必须以正确的顺序闭合。 9 | 每个右括号都有一个对应的相同类型的左括号。 10 | 11 | 12 | 13 | 14 | 示例 1： 15 | 16 | 17 | 输入：s = "()" 18 | 输出：true 19 | 20 | 21 | 示例 2： 22 | 23 | 24 | 输入：s = "()[]{}" 25 | 输出：true 26 | 27 | 28 | 示例 3： 29 | 30 | 31 | 输入：s = "(]" 32 | 输出：false 33 | 34 | 35 | 36 | 37 | 提示： 38 | 39 | 40 | 1 <= s.length <= 10⁴ 41 | s 仅由括号 '()[]{}' 组成 42 | 43 | 44 | Related Topics 栈 字符串 👍 4145 👎 0 45 | 46 | */ 47 | 48 | //leetcode submit region begin(Prohibit modification and deletion) 49 | /** 50 | * @param {string} s 51 | * @return {boolean} 52 | */ 53 | var isValid = function(s) { 54 | //利用数组实现--栈的功能 先入后出 ( 55 | //出现左边括号就塞进到stack中，如果出现右边括号，就利用pop 给左边最后一个给弹出来 对比是否匹配 ) 56 | let stack = [] 57 | let obj = { 58 | '(':')', 59 | '{':'}', 60 | '[':']' 61 | } 62 | for(let i= 0;i> & | 二进制位置上的计算 68 | // << 向左移动一位 乘以1 69 | // >> 向右移动一位 整除以2 70 | // & 两个同时是1的时候，结果是1否则是0 71 | // | 两个同时是0的时候，结果是0否则是1 72 | 73 | return n>0 && (n & (n-1))===0; 74 | 75 | }; 76 | //leetcode submit region end(Prohibit modification and deletion) 77 | -------------------------------------------------------------------------------- /javascript-algorithms/leetcode/editor/cn/[234]回文链表.js: -------------------------------------------------------------------------------- 1 | /** 2 | 给你一个单链表的头节点 head ，请你判断该链表是否为回文链表。如果是，返回 true ；否则，返回 false 。 3 | 4 | 5 | 6 | 示例 1： 7 | 8 | 9 | 输入：head = [1,2,2,1] 10 | 输出：true 11 | 12 | 13 | 示例 2： 14 | 15 | 16 | 输入：head = [1,2] 17 | 输出：false 18 | 19 | 20 | 21 | 22 | 提示： 23 | 24 | 25 | 链表中节点数目在范围[1, 10⁵] 内 26 | 0 <= Node.val <= 9 27 | 28 | 29 | 30 | 31 | 进阶：你能否用 O(n) 时间复杂度和 O(1) 空间复杂度解决此题？ 32 | 33 | Related Topics 栈 递归 链表 双指针 👍 1858 👎 0 34 | 35 | */ 36 | 37 | //leetcode submit region begin(Prohibit modification and deletion) 38 | /** 39 | * Definition for singly-linked list. 40 | * function ListNode(val, next) { 41 | * this.val = (val===undefined ? 0 : val) 42 | * this.next = (next===undefined ? null : next) 43 | * } 44 | */ 45 | /** 46 | * @param {ListNode} head 47 | * @return {boolean} 48 | */ 49 | var isPalindrome = function(head) { 50 | //使用双指针，先将链表前半段翻转 51 | let slow = fast = head; 52 | let prev 53 | while (fast && fast.next){ 54 | fast = fast.next.next; 55 | 56 | let next = slow.next; 57 | slow.next = prev; 58 | prev = slow; 59 | slow = next; 60 | } 61 | 62 | // slow 在中间 63 | if(fast){ 64 | slow = slow.next //奇数个节点 65 | } 66 | while (prev && slow){ 67 | if(prev.val !== slow.val){ 68 | return false 69 | } 70 | prev = prev.next; 71 | slow = slow.next 72 | } 73 | return true; 74 | }; 75 | //leetcode submit region end(Prohibit modification and deletion) 76 | -------------------------------------------------------------------------------- /javascript-algorithms/leetcode/editor/cn/[236]二叉树的最近公共祖先.js: -------------------------------------------------------------------------------- 1 | /** 2 | 给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。 3 | 4 | 百度百科中最近公共祖先的定义为：“对于有根树 T 的两个节点 p、q，最近公共祖先表示为一个节点 x，满足 x 是 p、q 的祖先且 x 的深度尽可能大（一个 5 | 节点也可以是它自己的祖先）。” 6 | 7 | 8 | 9 | 示例 1： 10 | 11 | 12 | 输入：root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1 13 | 输出：3 14 | 解释：节点 5 和节点 1 的最近公共祖先是节点 3 。 15 | 16 | 17 | 示例 2： 18 | 19 | 20 | 输入：root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 4 21 | 输出：5 22 | 解释：节点 5 和节点 4 的最近公共祖先是节点 5 。因为根据定义最近公共祖先节点可以为节点本身。 23 | 24 | 25 | 示例 3： 26 | 27 | 28 | 输入：root = [1,2], p = 1, q = 2 29 | 输出：1 30 | 31 | 32 | 33 | 34 | 提示： 35 | 36 | 37 | 树中节点数目在范围 [2, 10⁵] 内。 38 | -10⁹ <= Node.val <= 10⁹ 39 | 所有 Node.val 互不相同 。 40 | p != q 41 | p 和 q 均存在于给定的二叉树中。 42 | 43 | 44 | Related Topics 树 深度优先搜索 二叉树 👍 2611 👎 0 45 | 46 | */ 47 | 48 | //leetcode submit region begin(Prohibit modification and deletion) 49 | /** 50 | * Definition for a binary tree node. 51 | * function TreeNode(val) { 52 | * this.val = val; 53 | * this.left = this.right = null; 54 | * } 55 | */ 56 | /** 57 | * @param {TreeNode} root 58 | * @param {TreeNode} p 59 | * @param {TreeNode} q 60 | * @return {TreeNode} 61 | */ 62 | var lowestCommonAncestor = function(root, p, q) { 63 | if(root === null){ 64 | return null 65 | } 66 | if(root === p || root === q){ 67 | return root 68 | } 69 | let left = lowestCommonAncestor(root.left,p,q) 70 | let right = lowestCommonAncestor(root.right,p,q) 71 | if(left && right){ 72 | return root 73 | } 74 | return left ? left : right 75 | }; 76 | //leetcode submit region end(Prohibit modification and deletion) 77 | -------------------------------------------------------------------------------- /javascript-algorithms/leetcode/editor/cn/[26]删除有序数组中的重复项.js: -------------------------------------------------------------------------------- 1 | /** 2 | 给你一个 非严格递增排列 的数组 nums ，请你 原地 删除重复出现的元素，使每个元素 只出现一次 ，返回删除后数组的新长度。元素的 相对顺序 应该保持 一致 3 | 。然后返回 nums 中唯一元素的个数。 4 | 5 | 考虑 nums 的唯一元素的数量为 k ，你需要做以下事情确保你的题解可以被通过： 6 | 7 | 8 | 更改数组 nums ，使 nums 的前 k 个元素包含唯一元素，并按照它们最初在 nums 中出现的顺序排列。nums 的其余元素与 nums 的大小不重要 9 | 。 10 | 返回 k 。 11 | 12 | 13 | 判题标准: 14 | 15 | 系统会用下面的代码来测试你的题解: 16 | 17 | 18 | int[] nums = [...]; // 输入数组 19 | int[] expectedNums = [...]; // 长度正确的期望答案 20 | 21 | int k = removeDuplicates(nums); // 调用 22 | 23 | assert k == expectedNums.length; 24 | for (int i = 0; i < k; i++) { 25 | assert nums[i] == expectedNums[i]; 26 | } 27 | 28 | 如果所有断言都通过，那么您的题解将被 通过。 29 | 30 | 31 | 32 | 示例 1： 33 | 34 | 35 | 输入：nums = [1,1,2] 36 | 输出：2, nums = [1,2,_] 37 | 解释：函数应该返回新的长度 2 ，并且原数组 nums 的前两个元素被修改为 1, 2 。不需要考虑数组中超出新长度后面的元素。 38 | 39 | 40 | 示例 2： 41 | 42 | 43 | 输入：nums = [0,0,1,1,1,2,2,3,3,4] 44 | 输出：5, nums = [0,1,2,3,4] 45 | 解释：函数应该返回新的长度 5 ， 并且原数组 nums 的前五个元素被修改为 0, 1, 2, 3, 4 。不需要考虑数组中超出新长度后面的元素。 46 | 47 | 48 | 49 | 50 | 提示： 51 | 52 | 53 | 1 <= nums.length <= 3 * 10⁴ 54 | -10⁴ <= nums[i] <= 10⁴ 55 | nums 已按 非严格递增 排列 56 | 57 | 58 | Related Topics 数组 双指针 👍 3460 👎 0 59 | 60 | */ 61 | 62 | //leetcode submit region begin(Prohibit modification and deletion) 63 | /** 64 | * @param {number[]} nums 65 | * @return {number} 66 | */ 67 | var removeDuplicates = function(nums) { 68 | if(nums.length === 0){ 69 | return 0 70 | } 71 | let slow = 0; 72 | let fast = 0; 73 | while (fast < nums.length){ 74 | if(nums[fast] !== nums[slow]){ 75 | slow++ 76 | nums[slow] = nums[fast] 77 | } 78 | fast++ 79 | } 80 | return slow+1 81 | }; 82 | //leetcode submit region end(Prohibit modification and deletion) 83 | -------------------------------------------------------------------------------- /javascript-algorithms/leetcode/editor/cn/[27]移除元素.js: -------------------------------------------------------------------------------- 1 | /** 2 | 给你一个数组 nums 和一个值 val，你需要 原地 移除所有数值等于 val 的元素，并返回移除后数组的新长度。 3 | 4 | 不要使用额外的数组空间，你必须仅使用 O(1) 额外空间并 原地 修改输入数组。 5 | 6 | 元素的顺序可以改变。你不需要考虑数组中超出新长度后面的元素。 7 | 8 | 9 | 10 | 说明: 11 | 12 | 为什么返回数值是整数，但输出的答案是数组呢? 13 | 14 | 请注意，输入数组是以「引用」方式传递的，这意味着在函数里修改输入数组对于调用者是可见的。 15 | 16 | 你可以想象内部操作如下: 17 | 18 | 19 | // nums 是以“引用”方式传递的。也就是说，不对实参作任何拷贝 20 | int len = removeElement(nums, val); 21 | 22 | // 在函数里修改输入数组对于调用者是可见的。 23 | // 根据你的函数返回的长度, 它会打印出数组中 该长度范围内 的所有元素。 24 | for (int i = 0; i < len; i++) { 25 |     print(nums[i]); 26 | } 27 | 28 | 29 | 30 | 31 | 示例 1： 32 | 33 | 34 | 输入：nums = [3,2,2,3], val = 3 35 | 输出：2, nums = [2,2] 36 | 解释：函数应该返回新的长度 2, 并且 nums 中的前两个元素均为 2。你不需要考虑数组中超出新长度后面的元素。例如，函数返回的新长度为 2 ，而 nums 37 | = [2,2,3,3] 或 nums = [2,2,0,0]，也会被视作正确答案。 38 | 39 | 40 | 示例 2： 41 | 42 | 43 | 输入：nums = [0,1,2,2,3,0,4,2], val = 2 44 | 输出：5, nums = [0,1,3,0,4] 45 | 解释：函数应该返回新的长度 5, 并且 nums 中的前五个元素为 0, 1, 3, 0, 4。注意这五个元素可为任意顺序。你不需要考虑数组中超出新长度后面的元 46 | 素。 47 | 48 | 49 | 50 | 51 | 提示： 52 | 53 | 54 | 0 <= nums.length <= 100 55 | 0 <= nums[i] <= 50 56 | 0 <= val <= 100 57 | 58 | 59 | Related Topics 数组 双指针 👍 2142 👎 0 60 | 61 | */ 62 | 63 | //leetcode submit region begin(Prohibit modification and deletion) 64 | /** 65 | * @param {number[]} nums 66 | * @param {number} val 67 | * @return {number} 68 | */ 69 | var removeElement = function(nums, val) { 70 | let n = 0; 71 | for(let i = 0; itarget){ 63 | return // 比target大 64 | } 65 | if(sum === target){ 66 | ret.push([...path]) 67 | } 68 | for (let j =i;jtarget){ 71 | continue 72 | } 73 | path.push(num) 74 | sum += num 75 | backtrack(j,sum) 76 | path.pop() 77 | sum-=num 78 | } 79 | } 80 | }; 81 | //leetcode submit region end(Prohibit modification and deletion) 82 | -------------------------------------------------------------------------------- /javascript-algorithms/leetcode/editor/cn/[404]左叶子之和.js: -------------------------------------------------------------------------------- 1 | /** 2 | 给定二叉树的根节点 root ，返回所有左叶子之和。 3 | 4 | 5 | 6 | 示例 1： 7 | 8 | 9 | 10 | 11 | 输入: root = [3,9,20,null,null,15,7] 12 | 输出: 24 13 | 解释: 在这个二叉树中，有两个左叶子，分别是 9 和 15，所以返回 24 14 | 15 | 16 | 示例 2: 17 | 18 | 19 | 输入: root = [1] 20 | 输出: 0 21 | 22 | 23 | 24 | 25 | 提示: 26 | 27 | 28 | 节点数在 [1, 1000] 范围内 29 | -1000 <= Node.val <= 1000 30 | 31 | 32 | 33 | 34 | Related Topics 树 深度优先搜索 广度优先搜索 二叉树 👍 699 👎 0 35 | 36 | */ 37 | 38 | //leetcode submit region begin(Prohibit modification and deletion) 39 | /** 40 | * Definition for a binary tree node. 41 | * function TreeNode(val, left, right) { 42 | * this.val = (val===undefined ? 0 : val) 43 | * this.left = (left===undefined ? null : left) 44 | * this.right = (right===undefined ? null : right) 45 | * } 46 | */ 47 | /** 48 | * @param {TreeNode} root 49 | * @return {number} 50 | */ 51 | var sumOfLeftLeaves = function(root) { 52 | let leftSum = 0 53 | function travese(node){ 54 | if(node===null){ 55 | return 56 | } 57 | // 如果left是单独节点 58 | let left = node.left; 59 | if(left && !left.left && !left.right){ 60 | leftSum += left.val 61 | } 62 | // 如果left 有其他子节点 63 | travese(node.left) 64 | travese(node.right) 65 | } 66 | travese(root) 67 | return leftSum; 68 | }; 69 | //leetcode submit region end(Prohibit modification and deletion) 70 | -------------------------------------------------------------------------------- /javascript-algorithms/leetcode/editor/cn/[429]N 叉树的层序遍历.js: -------------------------------------------------------------------------------- 1 | /** 2 | 给定一个 N 叉树，返回其节点值的层序遍历。（即从左到右，逐层遍历）。 3 | 4 | 树的序列化输入是用层序遍历，每组子节点都由 null 值分隔（参见示例）。 5 | 6 | 7 | 8 | 示例 1： 9 | 10 | 11 | 12 | 13 | 输入：root = [1,null,3,2,4,null,5,6] 14 | 输出：[[1],[3,2,4],[5,6]] 15 | 16 | 17 | 示例 2： 18 | 19 | 20 | 21 | 22 | 输入：root = [1,null,2,3,4,5,null,null,6,7,null,8,null,9,10,null,null,11,null,12, 23 | null,13,null,null,14] 24 | 输出：[[1],[2,3,4,5],[6,7,8,9,10],[11,12,13],[14]] 25 | 26 | 27 | 28 | 29 | 提示： 30 | 31 | 32 | 树的高度不会超过 1000 33 | 树的节点总数在 [0, 10^4] 之间 34 | 35 | 36 | Related Topics 树 广度优先搜索 👍 452 👎 0 37 | 38 | */ 39 | 40 | //leetcode submit region begin(Prohibit modification and deletion) 41 | /** 42 | * // Definition for a Node. 43 | * function Node(val,children) { 44 | * this.val = val; 45 | * this.children = children; 46 | * }; 47 | */ 48 | 49 | /** 50 | * @param {Node|null} root 51 | * @return {number[][]} 52 | */ 53 | var levelOrder = function(root) { 54 | let ret = []; 55 | if(root === null){ 56 | return ret 57 | } 58 | let queue = [root] 59 | while (queue.length){ 60 | let curLevel = []; 61 | let len = queue.length; 62 | for(let i=0;i{ 66 | child && queue.push(child) 67 | }) 68 | } 69 | ret.push(curLevel) 70 | } 71 | return ret; 72 | }; 73 | //leetcode submit region end(Prohibit modification and deletion) 74 | -------------------------------------------------------------------------------- /javascript-algorithms/leetcode/editor/cn/[455]分发饼干.js: -------------------------------------------------------------------------------- 1 | /** 2 | 假设你是一位很棒的家长，想要给你的孩子们一些小饼干。但是，每个孩子最多只能给一块饼干。 3 | 4 | 对每个孩子 i，都有一个胃口值 g[i]，这是能让孩子们满足胃口的饼干的最小尺寸；并且每块饼干 j，都有一个尺寸 s[j] 。如果 s[j] >= g[i]， 5 | 我们可以将这个饼干 j 分配给孩子 i ，这个孩子会得到满足。你的目标是尽可能满足越多数量的孩子，并输出这个最大数值。 6 | 7 | 示例 1: 8 | 9 | 10 | 输入: g = [1,2,3], s = [1,1] 11 | 输出: 1 12 | 解释: 13 | 你有三个孩子和两块小饼干，3个孩子的胃口值分别是：1,2,3。 14 | 虽然你有两块小饼干，由于他们的尺寸都是1，你只能让胃口值是1的孩子满足。 15 | 所以你应该输出1。 16 | 17 | 18 | 示例 2: 19 | 20 | 21 | 输入: g = [1,2], s = [1,2,3] 22 | 输出: 2 23 | 解释: 24 | 你有两个孩子和三块小饼干，2个孩子的胃口值分别是1,2。 25 | 你拥有的饼干数量和尺寸都足以让所有孩子满足。 26 | 所以你应该输出2. 27 | 28 | 29 | 30 | 31 | 提示： 32 | 33 | 34 | 1 <= g.length <= 3 * 10⁴ 35 | 0 <= s.length <= 3 * 10⁴ 36 | 1 <= g[i], s[j] <= 2³¹ - 1 37 | 38 | 39 | Related Topics 贪心 数组 双指针 排序 👍 773 👎 0 40 | 41 | */ 42 | 43 | //leetcode submit region begin(Prohibit modification and deletion) 44 | /** 45 | * @param {number[]} g 46 | * @param {number[]} s 47 | * @return {number} 48 | */ 49 | var findContentChildren = function(g, s) { 50 | g = g.sort((a,b)=> a-b) 51 | s = s.sort((a,b)=> a-b) 52 | //满足尽可能胃口最大的小朋友 53 | let ret = 0; 54 | let index = s.length-1 55 | for (let i=g.length-1;i>=0;i--){ 56 | if(index>=0 && s[index] >= g[i]){ 57 | ret ++; 58 | index --; 59 | } 60 | } 61 | return ret; 62 | 63 | }; 64 | //leetcode submit region end(Prohibit modification and deletion) 65 | -------------------------------------------------------------------------------- /javascript-algorithms/leetcode/editor/cn/[46]全排列.js: -------------------------------------------------------------------------------- 1 | /** 2 | 给定一个不含重复数字的数组 nums ，返回其 所有可能的全排列 。你可以 按任意顺序 返回答案。 3 | 4 | 5 | 6 | 示例 1： 7 | 8 | 9 | 输入：nums = [1,2,3] 10 | 输出：[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]] 11 | 12 | 13 | 示例 2： 14 | 15 | 16 | 输入：nums = [0,1] 17 | 输出：[[0,1],[1,0]] 18 | 19 | 20 | 示例 3： 21 | 22 | 23 | 输入：nums = [1] 24 | 输出：[[1]] 25 | 26 | 27 | 28 | 29 | 提示： 30 | 31 | 32 | 1 <= nums.length <= 6 33 | -10 <= nums[i] <= 10 34 | nums 中的所有整数 互不相同 35 | 36 | 37 | Related Topics 数组 回溯 👍 2687 👎 0 38 | 39 | */ 40 | 41 | //leetcode submit region begin(Prohibit modification and deletion) 42 | /** 43 | * @param {number[]} nums 44 | * @return {number[][]} 45 | */ 46 | 47 | 48 | // 递归公式 49 | // 遍历到3的时候 50 | // [1,2] 51 | // [2,1] 52 | function backTrack(list,temp,nums){ 53 | // 放进去一个元素 54 | // 执行递归公式 55 | // 撤回这个不元素 56 | 57 | // 1、终止条件 58 | if(temp.length === nums.length){//已经排列完成 59 | return list.push([...temp]) 60 | } 61 | //没有终止 62 | for (let i=0;inode.val ? maxVal : node.val 63 | node.left && queue.push(node.left) 64 | node.right && queue.push(node.right) 65 | } 66 | ret.push(maxVal) 67 | } 68 | return ret 69 | }; 70 | //leetcode submit region end(Prohibit modification and deletion) 71 | -------------------------------------------------------------------------------- /javascript-algorithms/leetcode/editor/cn/[51]N 皇后.js: -------------------------------------------------------------------------------- 1 | /** 2 | 按照国际象棋的规则，皇后可以攻击与之处在同一行或同一列或同一斜线上的棋子。 3 | 4 | n 皇后问题 研究的是如何将 n 个皇后放置在 n×n 的棋盘上，并且使皇后彼此之间不能相互攻击。 5 | 6 | 给你一个整数 n ，返回所有不同的 n 皇后问题 的解决方案。 7 | 8 | 9 | 10 | 每一种解法包含一个不同的 n 皇后问题 的棋子放置方案，该方案中 'Q' 和 '.' 分别代表了皇后和空位。 11 | 12 | 13 | 14 | 15 | 16 | 示例 1： 17 | 18 | 19 | 输入：n = 4 20 | 输出：[[".Q..","...Q","Q...","..Q."],["..Q.","Q...","...Q",".Q.."]] 21 | 解释：如上图所示，4 皇后问题存在两个不同的解法。 22 | 23 | 24 | 示例 2： 25 | 26 | 27 | 输入：n = 1 28 | 输出：[["Q"]] 29 | 30 | 31 | 32 | 33 | 提示： 34 | 35 | 36 | 1 <= n <= 9 37 | 38 | 39 | Related Topics 数组 回溯 👍 2070 👎 0 40 | 41 | */ 42 | 43 | //leetcode submit region begin(Prohibit modification and deletion) 44 | /** 45 | * @param {number} n 46 | * @return {string[][]} 47 | */ 48 | var solveNQueens = function(n) { 49 | let ret = [] 50 | let path = [] 51 | backtrack(0,path) 52 | return ret 53 | function backtrack(row,tmp){ 54 | //终止条件 55 | if(row === n){ 56 | ret.push( 57 | tmp.map(c=>{ 58 | let arr = new Array(n).fill('.') 59 | arr[c] = 'Q' 60 | return arr.join('') 61 | }) 62 | ) 63 | } 64 | // row 第几行 65 | for(let col = 0; col < n; col++){ 66 | let canNotSet = tmp.some((c,r)=>{ 67 | return c === col || ((r-c) === (row-col)) || ((r+c) === (row+col)) 68 | }) 69 | if(canNotSet){ 70 | continue 71 | } 72 | backtrack(row+1,[...tmp,col]) 73 | } 74 | } 75 | }; 76 | //leetcode submit region end(Prohibit modification and deletion) 77 | -------------------------------------------------------------------------------- /javascript-algorithms/leetcode/editor/cn/[543]二叉树的直径.js: -------------------------------------------------------------------------------- 1 | /** 2 | 给你一棵二叉树的根节点，返回该树的 直径 。 3 | 4 | 二叉树的 直径 是指树中任意两个节点之间最长路径的 长度 。这条路径可能经过也可能不经过根节点 root 。 5 | 6 | 两节点之间路径的 长度 由它们之间边数表示。 7 | 8 | 9 | 10 | 示例 1： 11 | 12 | 13 | 输入：root = [1,2,3,4,5] 14 | 输出：3 15 | 解释：3 ，取路径 [4,2,1,3] 或 [5,2,1,3] 的长度。 16 | 17 | 18 | 示例 2： 19 | 20 | 21 | 输入：root = [1,2] 22 | 输出：1 23 | 24 | 25 | 26 | 27 | 提示： 28 | 29 | 30 | 树中节点数目在范围 [1, 10⁴] 内 31 | -100 <= Node.val <= 100 32 | 33 | 34 | Related Topics 树 深度优先搜索 二叉树 👍 1485 👎 0 35 | 36 | */ 37 | 38 | //leetcode submit region begin(Prohibit modification and deletion) 39 | /** 40 | * Definition for a binary tree node. 41 | * function TreeNode(val, left, right) { 42 | * this.val = (val===undefined ? 0 : val) 43 | * this.left = (left===undefined ? null : left) 44 | * this.right = (right===undefined ? null : right) 45 | * } 46 | */ 47 | /** 48 | * @param {TreeNode} root 49 | * @return {number} 50 | */ 51 | var diameterOfBinaryTree = function(root) { 52 | // 后续遍历 53 | let len = 0; 54 | function dfs(root){ 55 | if(root === null){ 56 | return null 57 | } 58 | let left = dfs(root.left) 59 | let right = dfs(root.right) 60 | len = Math.max(len,left+right) 61 | 62 | return Math.max(left,right)+1 63 | } 64 | dfs(root) 65 | return len 66 | }; 67 | //leetcode submit region end(Prohibit modification and deletion) 68 | -------------------------------------------------------------------------------- /javascript-algorithms/leetcode/editor/cn/[55]跳跃游戏.js: -------------------------------------------------------------------------------- 1 | /** 2 | 给你一个非负整数数组 nums ，你最初位于数组的 第一个下标 。数组中的每个元素代表你在该位置可以跳跃的最大长度。 3 | 4 | 判断你是否能够到达最后一个下标，如果可以，返回 true ；否则，返回 false 。 5 | 6 | 7 | 8 | 示例 1： 9 | 10 | 11 | 输入：nums = [2,3,1,1,4] 12 | 输出：true 13 | 解释：可以先跳 1 步，从下标 0 到达下标 1, 然后再从下标 1 跳 3 步到达最后一个下标。 14 | 15 | 16 | 示例 2： 17 | 18 | 19 | 输入：nums = [3,2,1,0,4] 20 | 输出：false 21 | 解释：无论怎样，总会到达下标为 3 的位置。但该下标的最大跳跃长度是 0 ， 所以永远不可能到达最后一个下标。 22 | 23 | 24 | 25 | 26 | 提示： 27 | 28 | 29 | 1 <= nums.length <= 10⁴ 30 | 0 <= nums[i] <= 10⁵ 31 | 32 | 33 | Related Topics 贪心 数组 动态规划 👍 2491 👎 0 34 | 35 | */ 36 | 37 | //leetcode submit region begin(Prohibit modification and deletion) 38 | /** 39 | * @param {number[]} nums 40 | * @return {boolean} 41 | */ 42 | var canJump = function(nums) { 43 | let cover = 0; //cover 比 nums.length-1 大 44 | for (let i=0;i<=cover;i++){ 45 | cover = Math.max(cover,i+nums[i]) 46 | if(cover >= nums.length-1){ 47 | return true; 48 | } 49 | } 50 | return false; 51 | }; 52 | //leetcode submit region end(Prohibit modification and deletion) 53 | -------------------------------------------------------------------------------- /javascript-algorithms/leetcode/editor/cn/[572]另一棵树的子树.js: -------------------------------------------------------------------------------- 1 | /** 2 | 3 | 4 | 给你两棵二叉树 root 和 subRoot 。检验 root 中是否包含和 subRoot 具有相同结构和节点值的子树。如果存在，返回 true ；否则，返 5 | 回 false 。 6 | 7 | 8 | 9 | 二叉树 tree 的一棵子树包括 tree 的某个节点和这个节点的所有后代节点。tree 也可以看做它自身的一棵子树。 10 | 11 | 12 | 13 | 示例 1： 14 | 15 | 16 | 输入：root = [3,4,5,1,2], subRoot = [4,1,2] 17 | 输出：true 18 | 19 | 20 | 示例 2： 21 | 22 | 23 | 输入：root = [3,4,5,1,2,null,null,null,null,0], subRoot = [4,1,2] 24 | 输出：false 25 | 26 | 27 | 28 | 29 | 提示： 30 | 31 | 32 | root 树上的节点数量范围是 [1, 2000] 33 | subRoot 树上的节点数量范围是 [1, 1000] 34 | -10⁴ <= root.val <= 10⁴ 35 | -10⁴ <= subRoot.val <= 10⁴ 36 | 37 | 38 | Related Topics 树 深度优先搜索 二叉树 字符串匹配 哈希函数 👍 1009 👎 0 39 | 40 | */ 41 | 42 | //leetcode submit region begin(Prohibit modification and deletion) 43 | /** 44 | * Definition for a binary tree node. 45 | * function TreeNode(val, left, right) { 46 | * this.val = (val===undefined ? 0 : val) 47 | * this.left = (left===undefined ? null : left) 48 | * this.right = (right===undefined ? null : right) 49 | * } 50 | */ 51 | /** 52 | * @param {TreeNode} root 53 | * @param {TreeNode} subRoot 54 | * @return {boolean} 55 | */ 56 | // react的虚拟Dom,树平级对比 57 | var isSubtree = function(root, subRoot) { 58 | // 不停的比较某一个子树 是不是和subRoot一样 59 | if(root === null){ 60 | return false 61 | } 62 | if(root.val === subRoot.val){ 63 | if(isSameTree(root,subRoot)){ 64 | return true 65 | } 66 | } 67 | //判断子树 68 | return isSubtree(root.left,subRoot) || isSubtree(root.right,subRoot) 69 | }; 70 | var isSameTree = function (p,q){ 71 | if(p === null && q === null){ 72 | return true 73 | } 74 | if(p === null || q === null){ 75 | return false 76 | } 77 | if(p.val !== q.val){ 78 | return false 79 | } 80 | return isSameTree(p.left,q.left) && isSameTree(p.right,q.right) 81 | } 82 | //leetcode submit region end(Prohibit modification and deletion) 83 | -------------------------------------------------------------------------------- /javascript-algorithms/leetcode/editor/cn/[617]合并二叉树.js: -------------------------------------------------------------------------------- 1 | /** 2 | 给你两棵二叉树： root1 和 root2 。 3 | 4 | 想象一下，当你将其中一棵覆盖到另一棵之上时，两棵树上的一些节点将会重叠（而另一些不会）。你需要将这两棵树合并成一棵新二叉树。合并的规则是：如果两个节点重叠，那 5 | 么将这两个节点的值相加作为合并后节点的新值；否则，不为 null 的节点将直接作为新二叉树的节点。 6 | 7 | 返回合并后的二叉树。 8 | 9 | 注意: 合并过程必须从两个树的根节点开始。 10 | 11 | 12 | 13 | 示例 1： 14 | 15 | 16 | 输入：root1 = [1,3,2,5], root2 = [2,1,3,null,4,null,7] 17 | 输出：[3,4,5,5,4,null,7] 18 | 19 | 20 | 示例 2： 21 | 22 | 23 | 输入：root1 = [1], root2 = [1,2] 24 | 输出：[2,2] 25 | 26 | 27 | 28 | 29 | 提示： 30 | 31 | 32 | 两棵树中的节点数目在范围 [0, 2000] 内 33 | -10⁴ <= Node.val <= 10⁴ 34 | 35 | 36 | Related Topics 树 深度优先搜索 广度优先搜索 二叉树 👍 1382 👎 0 37 | 38 | */ 39 | 40 | //leetcode submit region begin(Prohibit modification and deletion) 41 | /** 42 | * Definition for a binary tree node. 43 | * function TreeNode(val, left, right) { 44 | * this.val = (val===undefined ? 0 : val) 45 | * this.left = (left===undefined ? null : left) 46 | * this.right = (right===undefined ? null : right) 47 | * } 48 | */ 49 | /** 50 | * @param {TreeNode} root1 51 | * @param {TreeNode} root2 52 | * @return {TreeNode} 53 | */ 54 | var mergeTrees = function(root1, root2) { 55 | function dfs(root1,root2){ 56 | if(!root1){ 57 | return root2 58 | } 59 | if(!root2){ 60 | return root1 61 | } 62 | root1.val += root2.val 63 | root1.left = dfs(root1.left,root2.left) 64 | root1.right = dfs(root1.right,root2.right) 65 | return root1 66 | } 67 | return dfs(root1,root2) 68 | }; 69 | //leetcode submit region end(Prohibit modification and deletion) 70 | -------------------------------------------------------------------------------- /javascript-algorithms/leetcode/editor/cn/[637]二叉树的层平均值.js: -------------------------------------------------------------------------------- 1 | /** 2 | 给定一个非空二叉树的根节点 3 | root , 以数组的形式返回每一层节点的平均值。与实际答案相差 10⁻⁵ 以内的答案可以被接受。 4 | 5 | 6 | 7 | 示例 1： 8 | 9 | 10 | 11 | 12 | 输入：root = [3,9,20,null,null,15,7] 13 | 输出：[3.00000,14.50000,11.00000] 14 | 解释：第 0 层的平均值为 3,第 1 层的平均值为 14.5,第 2 层的平均值为 11 。 15 | 因此返回 [3, 14.5, 11] 。 16 | 17 | 18 | 示例 2: 19 | 20 | 21 | 22 | 23 | 输入：root = [3,9,20,15,7] 24 | 输出：[3.00000,14.50000,11.00000] 25 | 26 | 27 | 28 | 29 | 提示： 30 | 31 | 32 | 33 | 34 | 35 | 树中节点数量在 [1, 10⁴] 范围内 36 | -2³¹ <= Node.val <= 2³¹ - 1 37 | 38 | 39 | Related Topics 树 深度优先搜索 广度优先搜索 二叉树 👍 476 👎 0 40 | 41 | */ 42 | 43 | //leetcode submit region begin(Prohibit modification and deletion) 44 | /** 45 | * Definition for a binary tree node. 46 | * function TreeNode(val, left, right) { 47 | * this.val = (val===undefined ? 0 : val) 48 | * this.left = (left===undefined ? null : left) 49 | * this.right = (right===undefined ? null : right) 50 | * } 51 | */ 52 | /** 53 | * @param {TreeNode} root 54 | * @return {number[]} 55 | */ 56 | var averageOfLevels = function(root) { 57 | let ret = [] 58 | if(root === null){ 59 | return ret 60 | } 61 | let queue = [root] 62 | while (queue.length){ 63 | let len = queue.length 64 | let sum = 0 65 | for (let i=0; i> 1) 47 | if(mid*midx){ 50 | right = mid-1 51 | }else if(mid*mid===x){ 52 | return mid 53 | } 54 | } 55 | return right 56 | // return left-1 // 减去错过的位置 57 | }; 58 | //leetcode submit region end(Prohibit modification and deletion) 59 | -------------------------------------------------------------------------------- /javascript-algorithms/leetcode/editor/cn/[700]二叉搜索树中的搜索.js: -------------------------------------------------------------------------------- 1 | /** 2 | 给定二叉搜索树（BST）的根节点 3 | root 和一个整数值 4 | val。 5 | 6 | 你需要在 BST 中找到节点值等于 val 的节点。 返回以该节点为根的子树。 如果节点不存在，则返回 7 | null 。 8 | 9 | 10 | 11 | 示例 1: 12 | 13 | 14 | 15 | 16 | 17 | 输入：root = [4,2,7,1,3], val = 2 18 | 输出：[2,1,3] 19 | 20 | 21 | 示例 2: 22 | 23 | 24 | 输入：root = [4,2,7,1,3], val = 5 25 | 输出：[] 26 | 27 | 28 | 29 | 30 | 提示： 31 | 32 | 33 | 树中节点数在 [1, 5000] 范围内 34 | 1 <= Node.val <= 10⁷ 35 | root 是二叉搜索树 36 | 1 <= val <= 10⁷ 37 | 38 | 39 | Related Topics 树 二叉搜索树 二叉树 👍 462 👎 0 40 | 41 | */ 42 | 43 | //leetcode submit region begin(Prohibit modification and deletion) 44 | /** 45 | * Definition for a binary tree node. 46 | * function TreeNode(val, left, right) { 47 | * this.val = (val===undefined ? 0 : val) 48 | * this.left = (left===undefined ? null : left) 49 | * this.right = (right===undefined ? null : right) 50 | * } 51 | */ 52 | /** 53 | * @param {TreeNode} root 54 | * @param {number} val 55 | * @return {TreeNode} 56 | */ 57 | var searchBST = function(root, val) { 58 | if(root === null){ 59 | return root 60 | } 61 | if(root.val === val){ 62 | return root 63 | }else if(root.val > val){ 64 | return searchBST(root.left,val) 65 | }else if(root.val < val){ 66 | return searchBST(root.right,val) 67 | } 68 | }; 69 | //leetcode submit region end(Prohibit modification and deletion) 70 | -------------------------------------------------------------------------------- /javascript-algorithms/leetcode/editor/cn/[701]二叉搜索树中的插入操作.js: -------------------------------------------------------------------------------- 1 | /** 2 | 给定二叉搜索树（BST）的根节点 3 | root 和要插入树中的值 4 | value ，将值插入二叉搜索树。 返回插入后二叉搜索树的根节点。 输入数据 保证 ，新值和原始二叉搜索树中的任意节点值都不同。 5 | 6 | 注意，可能存在多种有效的插入方式，只要树在插入后仍保持为二叉搜索树即可。 你可以返回 任意有效的结果 。 7 | 8 | 9 | 10 | 示例 1： 11 | 12 | 13 | 输入：root = [4,2,7,1,3], val = 5 14 | 输出：[4,2,7,1,3,5] 15 | 解释：另一个满足题目要求可以通过的树是： 16 | 17 | 18 | 19 | 示例 2： 20 | 21 | 22 | 输入：root = [40,20,60,10,30,50,70], val = 25 23 | 输出：[40,20,60,10,30,50,70,null,null,25] 24 | 25 | 26 | 示例 3： 27 | 28 | 29 | 输入：root = [4,2,7,1,3,null,null,null,null,null,null], val = 5 30 | 输出：[4,2,7,1,3,5] 31 | 32 | 33 | 34 | 35 | 提示： 36 | 37 | 38 | 树中的节点数将在 39 | [0, 10⁴]的范围内。 40 | 41 | -10⁸ <= Node.val <= 10⁸ 42 | 所有值 43 | Node.val 是 独一无二 的。 44 | -10⁸ <= val <= 10⁸ 45 | 保证 val 在原始BST中不存在。 46 | 47 | 48 | Related Topics 树 二叉搜索树 二叉树 👍 553 👎 0 49 | 50 | */ 51 | 52 | //leetcode submit region begin(Prohibit modification and deletion) 53 | /** 54 | * Definition for a binary tree node. 55 | * function TreeNode(val, left, right) { 56 | * this.val = (val===undefined ? 0 : val) 57 | * this.left = (left===undefined ? null : left) 58 | * this.right = (right===undefined ? null : right) 59 | * } 60 | */ 61 | /** 62 | * @param {TreeNode} root 63 | * @param {number} val 64 | * @return {TreeNode} 65 | */ 66 | var insertIntoBST = function(root, val) { 67 | if(root === null){ 68 | return new TreeNode(val) 69 | } 70 | if(root.val > val){ 71 | root.left = insertIntoBST(root.left,val) 72 | }else if(root.val >1 // 右移一位 54 | // let mid = left + ((right-left))>>1 55 | if(nums[mid] < target){ 56 | // 在mid的右边查找 57 | left = mid+1 58 | }else if(nums[mid] > target){ 59 | // 在mid的左边查找 60 | right = mid-1 61 | }else if(nums[mid] === target){ 62 | return mid 63 | } 64 | } 65 | return -1 66 | }; 67 | //leetcode submit region end(Prohibit modification and deletion) 68 | -------------------------------------------------------------------------------- /javascript-algorithms/leetcode/editor/cn/[71]简化路径.js: -------------------------------------------------------------------------------- 1 | /** 2 | 给你一个字符串 path ，表示指向某一文件或目录的 Unix 风格 绝对路径 （以 '/' 开头），请你将其转化为更加简洁的规范路径。 3 | 4 | 在 Unix 风格的文件系统中，一个点（.）表示当前目录本身；此外，两个点 （..） 表示将目录切换到上一级（指向父目录）；两者都可以是复杂相对路径的组成部分 5 | 。任意多个连续的斜杠（即，'//'）都被视为单个斜杠 '/' 。 对于此问题，任何其他格式的点（例如，'...'）均被视为文件/目录名称。 6 | 7 | 请注意，返回的 规范路径 必须遵循下述格式： 8 | 9 | 10 | 始终以斜杠 '/' 开头。 11 | 两个目录名之间必须只有一个斜杠 '/' 。 12 | 最后一个目录名（如果存在）不能 以 '/' 结尾。 13 | 此外，路径仅包含从根目录到目标文件或目录的路径上的目录（即，不含 '.' 或 '..'）。 14 | 15 | 16 | 返回简化后得到的 规范路径 。 17 | 18 | 19 | 20 | 示例 1： 21 | 22 | 23 | 输入：path = "/home/" 24 | 输出："/home" 25 | 解释：注意，最后一个目录名后面没有斜杠。 26 | 27 | 示例 2： 28 | 29 | 30 | 输入：path = "/../" 31 | 输出："/" 32 | 解释：从根目录向上一级是不可行的，因为根目录是你可以到达的最高级。 33 | 34 | 35 | 示例 3： 36 | 37 | 38 | 输入：path = "/home//foo/" 39 | 输出："/home/foo" 40 | 解释：在规范路径中，多个连续斜杠需要用一个斜杠替换。 41 | 42 | 43 | 示例 4： 44 | 45 | 46 | 输入：path = "/a/./b/../../c/" 47 | 输出："/c" 48 | 49 | 50 | 51 | 52 | 提示： 53 | 54 | 55 | 1 <= path.length <= 3000 56 | path 由英文字母，数字，'.'，'/' 或 '_' 组成。 57 | path 是一个有效的 Unix 风格绝对路径。 58 | 59 | 60 | Related Topics 栈 字符串 👍 643 👎 0 61 | 62 | */ 63 | 64 | //leetcode submit region begin(Prohibit modification and deletion) 65 | /** 66 | * @param {string} path 67 | * @return {string} 68 | */ 69 | var simplifyPath = function(path) { 70 | // /a/./b/../../c/ 71 | //利用栈的机制进行解答 72 | let stack = []; 73 | let paths = path.split('/') 74 | // console.log(paths) 75 | for(let i=0;i= right){ 56 | return head 57 | } 58 | let dummy = { 59 | next : head 60 | } 61 | let tmp = dummy; 62 | for (let i = 0; i= node.val){ 64 | return false 65 | } 66 | prev = node.val 67 | let right = travese(node.right) 68 | return left && right 69 | } 70 | return travese(root) 71 | }; 72 | //leetcode submit region end(Prohibit modification and deletion) 73 | -------------------------------------------------------------------------------- /javascript-algorithms/leetcode/editor/cn/[99]恢复二叉搜索树.js: -------------------------------------------------------------------------------- 1 | /** 2 | 给你二叉搜索树的根节点 root ，该树中的 恰好 两个节点的值被错误地交换。请在不改变其结构的情况下，恢复这棵树 。 3 | 4 | 5 | 6 | 示例 1： 7 | 8 | 9 | 输入：root = [1,3,null,null,2] 10 | 输出：[3,1,null,null,2] 11 | 解释：3 不能是 1 的左孩子，因为 3 > 1 。交换 1 和 3 使二叉搜索树有效。 12 | 13 | 14 | 示例 2： 15 | 16 | 17 | 输入：root = [3,1,4,null,null,2] 18 | 输出：[2,1,4,null,null,3] 19 | 解释：2 不能在 3 的右子树中，因为 2 < 3 。交换 2 和 3 使二叉搜索树有效。 20 | 21 | 22 | 23 | 提示： 24 | 25 | 26 | 树上节点的数目在范围 [2, 1000] 内 27 | -2³¹ <= Node.val <= 2³¹ - 1 28 | 29 | 30 | 31 | 32 | 进阶：使用 O(n) 空间复杂度的解法很容易实现。你能想出一个只使用 O(1) 空间的解决方案吗？ 33 | 34 | Related Topics 树 深度优先搜索 二叉搜索树 二叉树 👍 939 👎 0 35 | 36 | */ 37 | 38 | //leetcode submit region begin(Prohibit modification and deletion) 39 | /** 40 | * Definition for a binary tree node. 41 | * function TreeNode(val, left, right) { 42 | * this.val = (val===undefined ? 0 : val) 43 | * this.left = (left===undefined ? null : left) 44 | * this.right = (right===undefined ? null : right) 45 | * } 46 | */ 47 | /** 48 | * @param {TreeNode} root 49 | * @return {void} Do not return anything, modify root in-place instead. 50 | */ 51 | var recoverTree = function(root) { 52 | let arr = [] 53 | let first 54 | let second 55 | function travese(node){ 56 | if(node === null){ 57 | return 58 | } 59 | travese(node.left) 60 | arr.push(node) 61 | travese(node.right) 62 | } 63 | travese(root) 64 | for(let i=0;i arr[i+1].val){ 66 | //找到两个值移动位置 67 | if(!first){ 68 | //第一次遇见 69 | first = arr[i] 70 | } 71 | second = arr[i+1] 72 | } 73 | } 74 | let tmp = first.val 75 | first.val = second.val 76 | second.val = tmp 77 | }; 78 | //leetcode submit region end(Prohibit modification and deletion) 79 | -------------------------------------------------------------------------------- /javascript-algorithms/leetcode/editor/cn/doc/content/[100]相同的树.md: -------------------------------------------------------------------------------- 1 |

给你两棵二叉树的根节点 p 和 q ，编写一个函数来检验这两棵树是否相同。

2 | 3 |

如果两个树在结构上相同，并且节点具有相同的值，则认为它们是相同的。

4 | 5 |

 

6 | 7 |

示例 1：

8 |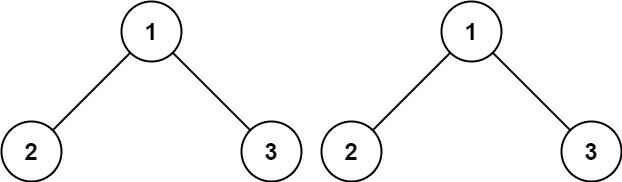 9 | 
10 | 输入：p = [1,2,3], q = [1,2,3]
11 | 输出：true
12 |
13 | 14 |

示例 2：

15 |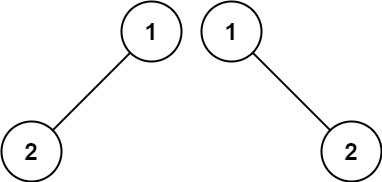 16 | 
17 | 输入：p = [1,2], q = [1,null,2]
18 | 输出：false
19 |
20 | 21 |

示例 3：

22 |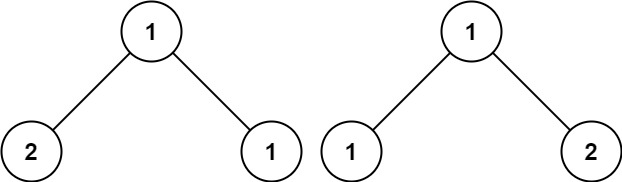 23 | 
24 | 输入：p = [1,2,1], q = [1,1,2]
25 | 输出：false
26 |
27 | 28 |

 

29 | 30 |

提示：

31 | 32 |
    33 |
  • 两棵树上的节点数目都在范围 [0, 100] 内
    • 34 |
  • -104 <= Node.val <= 104
    • 35 |
36 | 37 |
Related Topics
  • 树
  • 深度优先搜索
  • 广度优先搜索
  • 二叉树

  • 👍 1070
  • 👎 0
    • -------------------------------------------------------------------------------- /javascript-algorithms/leetcode/editor/cn/doc/content/[101]对称二叉树.md: -------------------------------------------------------------------------------- 1 |

    给你一个二叉树的根节点 root ， 检查它是否轴对称。

    2 | 3 |

     

    4 | 5 |

    示例 1：

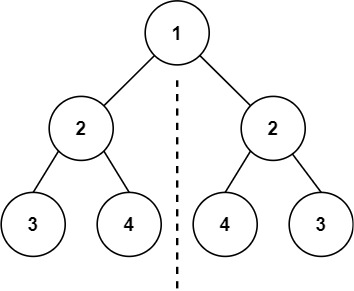    6 | 7 | 
     8 | 输入：root = [1,2,2,3,4,4,3]
 9 | 输出：true
10 |
    11 | 12 |

    示例 2：

    13 |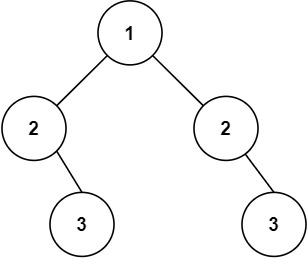 14 | 
    15 | 输入：root = [1,2,2,null,3,null,3]
16 | 输出：false
17 |
    18 | 19 |

     

    20 | 21 |

    提示：

    22 | 23 |
      24 |
    • 树中节点数目在范围 [1, 1000] 内
      • 25 |
    • -100 <= Node.val <= 100
      • 26 |
    27 | 28 |

     

    29 | 30 |

    进阶：你可以运用递归和迭代两种方法解决这个问题吗？

    31 | 32 |
    Related Topics
  • 树
  • 深度优先搜索
  • 广度优先搜索
  • 二叉树

  • 👍 2651
  • 👎 0
    • -------------------------------------------------------------------------------- /javascript-algorithms/leetcode/editor/cn/doc/content/[102]二叉树的层序遍历.md: -------------------------------------------------------------------------------- 1 |

    给你二叉树的根节点 root ，返回其节点值的 层序遍历 。 （即逐层地，从左到右访问所有节点）。

    2 | 3 |

     

    4 | 5 |

    示例 1：

    6 | 7 | 
     8 | 输入：root = [3,9,20,null,null,15,7]
 9 | 输出：[[3],[9,20],[15,7]]
10 |
    11 | 12 |

    示例 2：

    13 | 14 | 
    15 | 输入：root = [1]
16 | 输出：[[1]]
17 |
    18 | 19 |

    示例 3：

    20 | 21 | 
    22 | 输入：root = []
23 | 输出：[]
24 |
    25 | 26 |

     

    27 | 28 |

    提示：

    29 | 30 |
      31 |
    • 树中节点数目在范围 [0, 2000] 内
      • 32 |
    • -1000 <= Node.val <= 1000
      • 33 |
    34 | 35 |
    Related Topics
  • 树
  • 广度优先搜索
  • 二叉树

  • 👍 1903
  • 👎 0
    • -------------------------------------------------------------------------------- /javascript-algorithms/leetcode/editor/cn/doc/content/[1047]删除字符串中的所有相邻重复项.md: -------------------------------------------------------------------------------- 1 |

    给出由小写字母组成的字符串 S，重复项删除操作会选择两个相邻且相同的字母，并删除它们。

    2 | 3 |

    在 S 上反复执行重复项删除操作，直到无法继续删除。

    4 | 5 |

    在完成所有重复项删除操作后返回最终的字符串。答案保证唯一。

    6 | 7 |

     

    8 | 9 |

    示例：

    10 | 11 | 
    输入："abbaca"
12 | 输出："ca"
13 | 解释：
14 | 例如，在 "abbaca" 中，我们可以删除 "bb" 由于两字母相邻且相同，这是此时唯一可以执行删除操作的重复项。之后我们得到字符串 "aaca"，其中又只有 "aa" 可以执行重复项删除操作，所以最后的字符串为 "ca"。
15 |
    16 | 17 |

     

    18 | 19 |

    提示：

    20 | 21 |
      22 |
    1. 1 <= S.length <= 20000
      2. 23 |
    2. S 仅由小写英文字母组成。
      3. 24 |
    25 | 26 |
    Related Topics
  • 栈
  • 字符串

  • 👍 618
  • 👎 0
    • -------------------------------------------------------------------------------- /javascript-algorithms/leetcode/editor/cn/doc/content/[104]二叉树的最大深度.md: -------------------------------------------------------------------------------- 1 |

    给定一个二叉树 root ，返回其最大深度。

    2 | 3 |

    二叉树的 最大深度 是指从根节点到最远叶子节点的最长路径上的节点数。

    4 | 5 |

     

    6 | 7 |

    示例 1：

    8 | 9 |

    10 | 11 |

     

    12 | 13 | 
    14 | 输入：root = [3,9,20,null,null,15,7]
15 | 输出：3
16 |
    17 | 18 |

    示例 2：

    19 | 20 | 
    21 | 输入：root = [1,null,2]
22 | 输出：2
23 |
    24 | 25 |

     

    26 | 27 |

    提示：

    28 | 29 |
      30 |
    • 树中节点的数量在 [0, 104] 区间内。
      • 31 |
    • -100 <= Node.val <= 100
      • 32 |
    33 | 34 |
    Related Topics
  • 树
  • 深度优先搜索
  • 广度优先搜索
  • 二叉树

  • 👍 1686
  • 👎 0
    • -------------------------------------------------------------------------------- /javascript-algorithms/leetcode/editor/cn/doc/content/[107]二叉树的层序遍历 II.md: -------------------------------------------------------------------------------- 1 |

    给你二叉树的根节点 root ，返回其节点值 自底向上的层序遍历 。 （即按从叶子节点所在层到根节点所在的层，逐层从左向右遍历）

    2 | 3 |

     

    4 | 5 |

    示例 1：

    6 | 7 | 
     8 | 输入：root = [3,9,20,null,null,15,7]
 9 | 输出：[[15,7],[9,20],[3]]
10 |
    11 | 12 |

    示例 2：

    13 | 14 | 
    15 | 输入：root = [1]
16 | 输出：[[1]]
17 |
    18 | 19 |

    示例 3：

    20 | 21 | 
    22 | 输入：root = []
23 | 输出：[]
24 |
    25 | 26 |

     

    27 | 28 |

    提示：

    29 | 30 |
      31 |
    • 树中节点数目在范围 [0, 2000] 内
      • 32 |
    • -1000 <= Node.val <= 1000
      • 33 |
    34 | 35 |
    Related Topics
  • 树
  • 广度优先搜索
  • 二叉树

  • 👍 784
  • 👎 0
    • -------------------------------------------------------------------------------- /javascript-algorithms/leetcode/editor/cn/doc/content/[108]将有序数组转换为二叉搜索树.md: -------------------------------------------------------------------------------- 1 |

    给你一个整数数组 nums ，其中元素已经按 升序 排列，请你将其转换为一棵 高度平衡 二叉搜索树。

    2 | 3 |

    高度平衡 二叉树是一棵满足「每个节点的左右两个子树的高度差的绝对值不超过 1 」的二叉树。

    4 | 5 |

     

    6 | 7 |

    示例 1：

    8 | 9 | 
    10 | 输入：nums = [-10,-3,0,5,9]
11 | 输出：[0,-3,9,-10,null,5]
12 | 解释：[0,-10,5,null,-3,null,9] 也将被视为正确答案：
13 | 
14 |
    15 | 16 |

    示例 2：

    17 | 18 | 
    19 | 输入：nums = [1,3]
20 | 输出：[3,1]
21 | 解释：[1,null,3] 和 [3,1] 都是高度平衡二叉搜索树。
22 |
    23 | 24 |

     

    25 | 26 |

    提示：

    27 | 28 |
      29 |
    • 1 <= nums.length <= 104
      • 30 |
    • -104 <= nums[i] <= 104
      • 31 |
    • nums 按 严格递增 顺序排列
      • 32 |
    33 | 34 |
    Related Topics
  • 树
  • 二叉搜索树
  • 数组
  • 分治
  • 二叉树

  • 👍 1478
  • 👎 0
    • -------------------------------------------------------------------------------- /javascript-algorithms/leetcode/editor/cn/doc/content/[109]有序链表转换二叉搜索树.md: -------------------------------------------------------------------------------- 1 |

    给定一个单链表的头节点  head ，其中的元素 按升序排序 ，将其转换为高度平衡的二叉搜索树。

    2 | 3 |

    本题中，一个高度平衡二叉树是指一个二叉树每个节点 的左右两个子树的高度差不超过 1。

    4 | 5 |

     

    6 | 7 |

    示例 1:

    8 | 9 |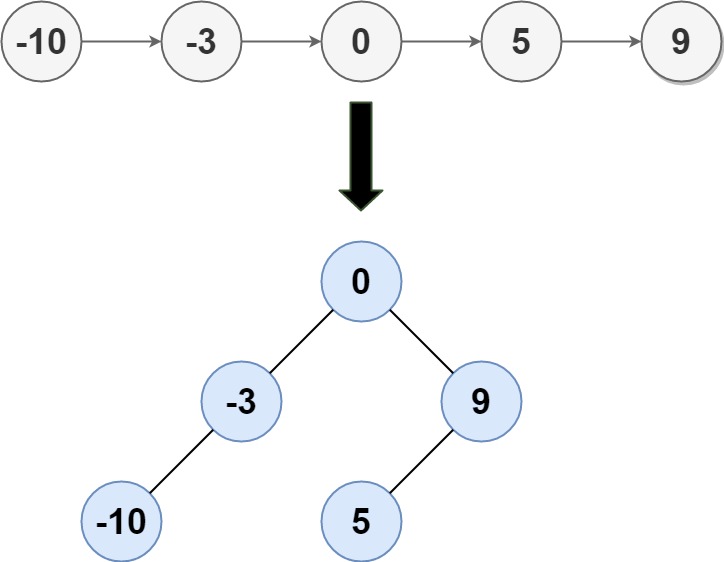

    10 | 11 | 
    12 | 输入: head = [-10,-3,0,5,9]
13 | 输出: [0,-3,9,-10,null,5]
14 | 解释: 一个可能的答案是[0，-3,9，-10,null,5]，它表示所示的高度平衡的二叉搜索树。
15 |
    16 | 17 |

    示例 2:

    18 | 19 | 
    20 | 输入: head = []
21 | 输出: []
22 |
    23 | 24 |

     

    25 | 26 |

    提示:

    27 | 28 |
      29 |
    • head 中的节点数在[0, 2 * 104] 范围内
      • 30 |
    • -105 <= Node.val <= 105
      • 31 |
    32 | 33 |
    Related Topics
  • 树
  • 二叉搜索树
  • 链表
  • 分治
  • 二叉树

  • 👍 889
  • 👎 0
    • -------------------------------------------------------------------------------- /javascript-algorithms/leetcode/editor/cn/doc/content/[110]平衡二叉树.md: -------------------------------------------------------------------------------- 1 |

    给定一个二叉树，判断它是否是高度平衡的二叉树。

    2 | 3 |

    本题中，一棵高度平衡二叉树定义为：

    4 | 5 |
    6 |

    一个二叉树每个节点 的左右两个子树的高度差的绝对值不超过 1 。

    7 |
    8 | 9 |

     

    10 | 11 |

    示例 1：

    12 | 13 | 
    14 | 输入：root = [3,9,20,null,null,15,7]
15 | 输出：true
16 |
    17 | 18 |

    示例 2：

    19 | 20 | 
    21 | 输入：root = [1,2,2,3,3,null,null,4,4]
22 | 输出：false
23 |
    24 | 25 |

    示例 3：

    26 | 27 | 
    28 | 输入：root = []
29 | 输出：true
30 |
    31 | 32 |

     

    33 | 34 |

    提示：

    35 | 36 |
      37 |
    • 树中的节点数在范围 [0, 5000] 内
      • 38 |
    • -104 <= Node.val <= 104
      • 39 |
    40 | 41 |
    Related Topics
  • 树
  • 深度优先搜索
  • 二叉树

  • 👍 1485
  • 👎 0
    • -------------------------------------------------------------------------------- /javascript-algorithms/leetcode/editor/cn/doc/content/[111]二叉树的最小深度.md: -------------------------------------------------------------------------------- 1 |

    给定一个二叉树，找出其最小深度。

    2 | 3 |

    最小深度是从根节点到最近叶子节点的最短路径上的节点数量。

    4 | 5 |

    说明：叶子节点是指没有子节点的节点。

    6 | 7 |

     

    8 | 9 |

    示例 1：

    10 | 11 | 
    12 | 输入：root = [3,9,20,null,null,15,7]
13 | 输出：2
14 |
    15 | 16 |

    示例 2：

    17 | 18 | 
    19 | 输入：root = [2,null,3,null,4,null,5,null,6]
20 | 输出：5
21 |
    22 | 23 |

     

    24 | 25 |

    提示：

    26 | 27 |
      28 |
    • 树中节点数的范围在 [0, 105] 内
      • 29 |
    • -1000 <= Node.val <= 1000
      • 30 |
    31 | 32 |
    Related Topics
  • 树
  • 深度优先搜索
  • 广度优先搜索
  • 二叉树

  • 👍 1156
  • 👎 0
    • -------------------------------------------------------------------------------- /javascript-algorithms/leetcode/editor/cn/doc/content/[112]路径总和.md: -------------------------------------------------------------------------------- 1 |

    给你二叉树的根节点 root 和一个表示目标和的整数 targetSum 。判断该树中是否存在 根节点到叶子节点 的路径，这条路径上所有节点值相加等于目标和 targetSum 。如果存在，返回 true ；否则，返回 false 。

    2 | 3 |

    叶子节点 是指没有子节点的节点。

    4 | 5 |

     

    6 | 7 |

    示例 1：

    8 | 9 | 
    10 | 输入：root = [5,4,8,11,null,13,4,7,2,null,null,null,1], targetSum = 22
11 | 输出：true
12 | 解释：等于目标和的根节点到叶节点路径如上图所示。
13 |
    14 | 15 |

    示例 2：

    16 | 17 | 
    18 | 输入：root = [1,2,3], targetSum = 5
19 | 输出：false
20 | 解释：树中存在两条根节点到叶子节点的路径：
21 | (1 --> 2): 和为 3
22 | (1 --> 3): 和为 4
23 | 不存在 sum = 5 的根节点到叶子节点的路径。
    24 | 25 |

    示例 3：

    26 | 27 | 
    28 | 输入：root = [], targetSum = 0
29 | 输出：false
30 | 解释：由于树是空的，所以不存在根节点到叶子节点的路径。
31 |
    32 | 33 |

     

    34 | 35 |

    提示：

    36 | 37 |
      38 |
    • 树中节点的数目在范围 [0, 5000] 内
      • 39 |
    • -1000 <= Node.val <= 1000
      • 40 |
    • -1000 <= targetSum <= 1000
      • 41 |
    42 | 43 |
    Related Topics
  • 树
  • 深度优先搜索
  • 广度优先搜索
  • 二叉树

  • 👍 1319
  • 👎 0
    • -------------------------------------------------------------------------------- /javascript-algorithms/leetcode/editor/cn/doc/content/[114]二叉树展开为链表.md: -------------------------------------------------------------------------------- 1 |

    给你二叉树的根结点 root ，请你将它展开为一个单链表：

    2 | 3 |
      4 |
    • 展开后的单链表应该同样使用 TreeNode ，其中 right 子指针指向链表中下一个结点，而左子指针始终为 null 。
      • 5 |
    • 展开后的单链表应该与二叉树 先序遍历 顺序相同。
      • 6 |
    7 | 8 |

     

    9 | 10 |

    示例 1：

    11 | 12 | 
    13 | 输入：root = [1,2,5,3,4,null,6]
14 | 输出：[1,null,2,null,3,null,4,null,5,null,6]
15 |
    16 | 17 |

    示例 2：

    18 | 19 | 
    20 | 输入：root = []
21 | 输出：[]
22 |
    23 | 24 |

    示例 3：

    25 | 26 | 
    27 | 输入：root = [0]
28 | 输出：[0]
29 |
    30 | 31 |

     

    32 | 33 |

    提示：

    34 | 35 |
      36 |
    • 树中结点数在范围 [0, 2000] 内
      • 37 |
    • -100 <= Node.val <= 100
      • 38 |
    39 | 40 |

     

    41 | 42 |

    进阶：你可以使用原地算法（O(1) 额外空间）展开这棵树吗？

    43 | 44 |
    Related Topics
  • 栈
  • 树
  • 深度优先搜索
  • 链表
  • 二叉树

  • 👍 1629
  • 👎 0
    • -------------------------------------------------------------------------------- /javascript-algorithms/leetcode/editor/cn/doc/content/[116]填充每个节点的下一个右侧节点指针.md: -------------------------------------------------------------------------------- 1 |

    给定一个 完美二叉树 ，其所有叶子节点都在同一层，每个父节点都有两个子节点。二叉树定义如下：

    2 | 3 | 
     4 | struct Node {
 5 |   int val;
 6 |   Node *left;
 7 |   Node *right;
 8 |   Node *next;
 9 | }
    10 | 11 |

    填充它的每个 next 指针，让这个指针指向其下一个右侧节点。如果找不到下一个右侧节点，则将 next 指针设置为 NULL。

    12 | 13 |

    初始状态下，所有 next 指针都被设置为 NULL。

    14 | 15 |

     

    16 | 17 |

    示例 1：

    18 | 19 |

    20 | 21 | 
    22 | 输入：root = [1,2,3,4,5,6,7]
23 | 输出：[1,#,2,3,#,4,5,6,7,#]
24 | 解释：给定二叉树如图 A 所示，你的函数应该填充它的每个 next 指针，以指向其下一个右侧节点，如图 B 所示。序列化的输出按层序遍历排列，同一层节点由 next 指针连接，'#' 标志着每一层的结束。
25 |
    26 | 27 |

    28 |

    29 | 30 |

    示例 2:

    31 | 32 | 
    33 | 输入：root = []
34 | 输出：[]
35 |
    36 | 37 |

     

    38 | 39 |

    提示：

    40 | 41 |
      42 |
    • 树中节点的数量在 43 |  [0, 212 - 1] 范围内
      • 44 |
    • -1000 <= node.val <= 1000
      • 45 |
    46 | 47 |

     

    48 | 49 |

    进阶：

    50 | 51 |
      52 |
    • 你只能使用常量级额外空间。
      • 53 |
    • 使用递归解题也符合要求，本题中递归程序占用的栈空间不算做额外的空间复杂度。
      • 54 |
    55 | 56 |
    Related Topics
  • 树
  • 深度优先搜索
  • 广度优先搜索
  • 链表
  • 二叉树

  • 👍 1098
  • 👎 0
    • -------------------------------------------------------------------------------- /javascript-algorithms/leetcode/editor/cn/doc/content/[117]填充每个节点的下一个右侧节点指针 II.md: -------------------------------------------------------------------------------- 1 |

    给定一个二叉树：

    2 | 3 | 
     4 | struct Node {
 5 |   int val;
 6 |   Node *left;
 7 |   Node *right;
 8 |   Node *next;
 9 | }
    10 | 11 |

    填充它的每个 next 指针，让这个指针指向其下一个右侧节点。如果找不到下一个右侧节点，则将 next 指针设置为 NULL 。

    12 | 13 |

    初始状态下，所有 next 指针都被设置为 NULL 。

    14 | 15 |

     

    16 | 17 |

    示例 1：

    18 | 19 | 
    20 | 输入：root = [1,2,3,4,5,null,7]
21 | 输出：[1,#,2,3,#,4,5,7,#]
22 | 解释：给定二叉树如图 A 所示，你的函数应该填充它的每个 next 指针，以指向其下一个右侧节点，如图 B 所示。序列化输出按层序遍历顺序（由 next 指针连接），'#' 表示每层的末尾。
    23 | 24 |

    示例 2：

    25 | 26 | 
    27 | 输入：root = []
28 | 输出：[]
29 |
    30 | 31 |

     

    32 | 33 |

    提示：

    34 | 35 |
      36 |
    • 树中的节点数在范围 [0, 6000] 内
      • 37 |
    • -100 <= Node.val <= 100
      • 38 |
    39 | 40 |

    进阶：

    41 | 42 |
      43 |
    • 你只能使用常量级额外空间。
      • 44 |
    • 使用递归解题也符合要求，本题中递归程序的隐式栈空间不计入额外空间复杂度。
      • 45 |
    46 | 47 |
      48 |
    49 | 50 |
    Related Topics
  • 树
  • 深度优先搜索
  • 广度优先搜索
  • 链表
  • 二叉树

  • 👍 830
  • 👎 0
    • -------------------------------------------------------------------------------- /javascript-algorithms/leetcode/editor/cn/doc/content/[125]验证回文串.md: -------------------------------------------------------------------------------- 1 |

    如果在将所有大写字符转换为小写字符、并移除所有非字母数字字符之后，短语正着读和反着读都一样。则可以认为该短语是一个 回文串 。

    2 | 3 |

    字母和数字都属于字母数字字符。

    4 | 5 |

    给你一个字符串 s，如果它是 回文串 ，返回 true ；否则，返回 false 。

    6 | 7 |

     

    8 | 9 |

    示例 1：

    10 | 11 | 
    12 | 输入: s = "A man, a plan, a canal: Panama"
13 | 输出：true
14 | 解释："amanaplanacanalpanama" 是回文串。
15 |
    16 | 17 |

    示例 2：

    18 | 19 | 
    20 | 输入：s = "race a car"
21 | 输出：false
22 | 解释："raceacar" 不是回文串。
23 |
    24 | 25 |

    示例 3：

    26 | 27 | 
    28 | 输入：s = " "
29 | 输出：true
30 | 解释：在移除非字母数字字符之后，s 是一个空字符串 "" 。
31 | 由于空字符串正着反着读都一样，所以是回文串。
32 |
    33 | 34 |

     

    35 | 36 |

    提示：

    37 | 38 |
      39 |
    • 1 <= s.length <= 2 * 105
      • 40 |
    • s 仅由可打印的 ASCII 字符组成
      • 41 |
    42 | 43 |
    Related Topics
  • 双指针
  • 字符串

  • 👍 742
  • 👎 0
    • -------------------------------------------------------------------------------- /javascript-algorithms/leetcode/editor/cn/doc/content/[131]分割回文串.md: -------------------------------------------------------------------------------- 1 |

    给你一个字符串 s，请你将 s 分割成一些子串，使每个子串都是 回文串 。返回 s 所有可能的分割方案。

    2 | 3 |

     

    4 | 5 |

    示例 1：

    6 | 7 | 
     8 | 输入：s = "aab"
 9 | 输出：[["a","a","b"],["aa","b"]]
10 |
    11 | 12 |

    示例 2：

    13 | 14 | 
    15 | 输入：s = "a"
16 | 输出：[["a"]]
17 |
    18 | 19 |

     

    20 | 21 |

    提示：

    22 | 23 |
      24 |
    • 1 <= s.length <= 16
      • 25 |
    • s 仅由小写英文字母组成
      • 26 |
    27 | 28 |
    Related Topics
  • 字符串
  • 动态规划
  • 回溯

  • 👍 1781
  • 👎 0
    • -------------------------------------------------------------------------------- /javascript-algorithms/leetcode/editor/cn/doc/content/[136]只出现一次的数字.md: -------------------------------------------------------------------------------- 1 |

    给你一个 非空 整数数组 nums ，除了某个元素只出现一次以外，其余每个元素均出现两次。找出那个只出现了一次的元素。

    2 | 3 |

    你必须设计并实现线性时间复杂度的算法来解决此问题，且该算法只使用常量额外空间。

    4 | 5 |
    6 |
    7 |

     

    8 |
    9 |
    10 | 11 |

    示例 1 ：

    12 | 13 | 
    14 | 输入：nums = [2,2,1]
15 | 输出：1
16 |
    17 | 18 |

    示例 2 ：

    19 | 20 | 
    21 | 输入：nums = [4,1,2,1,2]
22 | 输出：4
23 |
    24 | 25 |

    示例 3 ：

    26 | 27 | 
    28 | 输入：nums = [1]
29 | 输出：1
30 |
    31 | 32 |

     

    33 | 34 |

    提示：

    35 | 36 |
      37 |
    • 1 <= nums.length <= 3 * 104
      • 38 |
    • -3 * 104 <= nums[i] <= 3 * 104
      • 39 |
    • 除了某个元素只出现一次以外，其余每个元素均出现两次。
      • 40 |
    41 | 42 |
    Related Topics
  • 位运算
  • 数组

  • 👍 2950
  • 👎 0
    • -------------------------------------------------------------------------------- /javascript-algorithms/leetcode/editor/cn/doc/content/[141]环形链表.md: -------------------------------------------------------------------------------- 1 |

    给你一个链表的头节点 head ，判断链表中是否有环。

    2 | 3 |

    如果链表中有某个节点，可以通过连续跟踪 next 指针再次到达，则链表中存在环。 为了表示给定链表中的环，评测系统内部使用整数 pos 来表示链表尾连接到链表中的位置（索引从 0 开始）。注意：pos 不作为参数进行传递 。仅仅是为了标识链表的实际情况。

    4 | 5 |

    如果链表中存在环 ，则返回 true 。 否则，返回 false 。

    6 | 7 |

     

    8 | 9 |

    示例 1：

    10 | 11 |

    12 | 13 | 
    14 | 输入：head = [3,2,0,-4], pos = 1
15 | 输出：true
16 | 解释：链表中有一个环，其尾部连接到第二个节点。
17 |
    18 | 19 |

    示例 2：

    20 | 21 |

    22 | 23 | 
    24 | 输入：head = [1,2], pos = 0
25 | 输出：true
26 | 解释：链表中有一个环，其尾部连接到第一个节点。
27 |
    28 | 29 |

    示例 3：

    30 | 31 |

    32 | 33 | 
    34 | 输入：head = [1], pos = -1
35 | 输出：false
36 | 解释：链表中没有环。
37 |
    38 | 39 |

     

    40 | 41 |

    提示：

    42 | 43 |
      44 |
    • 链表中节点的数目范围是 [0, 104]
      • 45 |
    • -105 <= Node.val <= 105
      • 46 |
    • pos 为 -1 或者链表中的一个 有效索引 。
      • 47 |
    48 | 49 |

     

    50 | 51 |

    进阶：你能用 O(1)（即，常量）内存解决此问题吗？

    52 | 53 |
    Related Topics
  • 哈希表
  • 链表
  • 双指针

  • 👍 1974
  • 👎 0
    • -------------------------------------------------------------------------------- /javascript-algorithms/leetcode/editor/cn/doc/content/[144]二叉树的前序遍历.md: -------------------------------------------------------------------------------- 1 |

    给你二叉树的根节点 root ，返回它节点值的 前序 遍历。

    2 | 3 |

     

    4 | 5 |

    示例 1：

    6 | 7 | 
     8 | 输入：root = [1,null,2,3]
 9 | 输出：[1,2,3]
10 |
    11 | 12 |

    示例 2：

    13 | 14 | 
    15 | 输入：root = []
16 | 输出：[]
17 |
    18 | 19 |

    示例 3：

    20 | 21 | 
    22 | 输入：root = [1]
23 | 输出：[1]
24 |
    25 | 26 |

    示例 4：

    27 | 28 | 
    29 | 输入：root = [1,2]
30 | 输出：[1,2]
31 |
    32 | 33 |

    示例 5：

    34 | 35 | 
    36 | 输入：root = [1,null,2]
37 | 输出：[1,2]
38 |
    39 | 40 |

     

    41 | 42 |

    提示：

    43 | 44 |
      45 |
    • 树中节点数目在范围 [0, 100] 内
      • 46 |
    • -100 <= Node.val <= 100
      • 47 |
    48 | 49 |

     

    50 | 51 |

    进阶：递归算法很简单，你可以通过迭代算法完成吗？

    52 | 53 |
    Related Topics
  • 栈
  • 树
  • 深度优先搜索
  • 二叉树

  • 👍 1218
  • 👎 0
    • -------------------------------------------------------------------------------- /javascript-algorithms/leetcode/editor/cn/doc/content/[145]二叉树的后序遍历.md: -------------------------------------------------------------------------------- 1 |

    给你一棵二叉树的根节点 root ，返回其节点值的 后序遍历 。

    2 | 3 |

     

    4 | 5 |

    示例 1：

    6 | 7 | 
     8 | 输入：root = [1,null,2,3]
 9 | 输出：[3,2,1]
10 |
    11 | 12 |

    示例 2：

    13 | 14 | 
    15 | 输入：root = []
16 | 输出：[]
17 |
    18 | 19 |

    示例 3：

    20 | 21 | 
    22 | 输入：root = [1]
23 | 输出：[1]
24 |
    25 | 26 |

     

    27 | 28 |

    提示：

    29 | 30 |
      31 |
    • 树中节点的数目在范围 [0, 100] 内
      • 32 |
    • -100 <= Node.val <= 100
      • 33 |
    34 | 35 |

     

    36 | 37 |

    进阶：递归算法很简单，你可以通过迭代算法完成吗？

    38 | 39 |
    Related Topics
  • 栈
  • 树
  • 深度优先搜索
  • 二叉树

  • 👍 1144
  • 👎 0
    • -------------------------------------------------------------------------------- /javascript-algorithms/leetcode/editor/cn/doc/content/[151]反转字符串中的单词.md: -------------------------------------------------------------------------------- 1 |

    给你一个字符串 s ，请你反转字符串中 单词 的顺序。

    2 | 3 |

    单词 是由非空格字符组成的字符串。s 中使用至少一个空格将字符串中的 单词 分隔开。

    4 | 5 |

    返回 单词 顺序颠倒且 单词 之间用单个空格连接的结果字符串。

    6 | 7 |

    注意：输入字符串 s中可能会存在前导空格、尾随空格或者单词间的多个空格。返回的结果字符串中，单词间应当仅用单个空格分隔，且不包含任何额外的空格。

    8 | 9 |

     

    10 | 11 |

    示例 1：

    12 | 13 | 
    14 | 输入：s = "the sky is blue"
15 | 输出："blue is sky the"
16 |
    17 | 18 |

    示例 2：

    19 | 20 | 
    21 | 输入：s = "  hello world  "
22 | 输出："world hello"
23 | 解释：反转后的字符串中不能存在前导空格和尾随空格。
24 |
    25 | 26 |

    示例 3：

    27 | 28 | 
    29 | 输入：s = "a good   example"
30 | 输出："example good a"
31 | 解释：如果两个单词间有多余的空格，反转后的字符串需要将单词间的空格减少到仅有一个。
32 |
    33 | 34 |

     

    35 | 36 |

    提示：

    37 | 38 |
      39 |
    • 1 <= s.length <= 104
      • 40 |
    • s 包含英文大小写字母、数字和空格 ' '
      • 41 |
    • s 中 至少存在一个 单词
      • 42 |
    43 | 44 |
      45 |
    46 | 47 |

     

    48 | 49 |

    进阶：如果字符串在你使用的编程语言中是一种可变数据类型，请尝试使用 O(1) 额外空间复杂度的 原地 解法。

    50 | 51 |
    Related Topics
  • 双指针
  • 字符串

  • 👍 1135
  • 👎 0
    • -------------------------------------------------------------------------------- /javascript-algorithms/leetcode/editor/cn/doc/content/[153]寻找旋转排序数组中的最小值.md: -------------------------------------------------------------------------------- 1 | 已知一个长度为 n 的数组，预先按照升序排列，经由 1 到 n 次 旋转 后，得到输入数组。例如，原数组 nums = [0,1,2,4,5,6,7] 在变化后可能得到： 2 | 3 |
      4 |
    • 若旋转 4 次，则可以得到 [4,5,6,7,0,1,2]
      • 5 |
    • 若旋转 7 次，则可以得到 [0,1,2,4,5,6,7]
      • 6 |
    7 | 8 |

    注意，数组 [a[0], a[1], a[2], ..., a[n-1]] 旋转一次 的结果为数组 [a[n-1], a[0], a[1], a[2], ..., a[n-2]] 。

    9 | 10 |

    给你一个元素值 互不相同 的数组 nums ，它原来是一个升序排列的数组，并按上述情形进行了多次旋转。请你找出并返回数组中的 最小元素 。

    11 | 12 |

    你必须设计一个时间复杂度为 O(log n) 的算法解决此问题。

    13 | 14 |

     

    15 | 16 |

    示例 1：

    17 | 18 | 
    19 | 输入：nums = [3,4,5,1,2]
20 | 输出：1
21 | 解释：原数组为 [1,2,3,4,5] ，旋转 3 次得到输入数组。
22 |
    23 | 24 |

    示例 2：

    25 | 26 | 
    27 | 输入：nums = [4,5,6,7,0,1,2]
28 | 输出：0
29 | 解释：原数组为 [0,1,2,4,5,6,7] ，旋转 3 次得到输入数组。
30 |
    31 | 32 |

    示例 3：

    33 | 34 | 
    35 | 输入：nums = [11,13,15,17]
36 | 输出：11
37 | 解释：原数组为 [11,13,15,17] ，旋转 4 次得到输入数组。
38 |
    39 | 40 |

     

    41 | 42 |

    提示：

    43 | 44 |
      45 |
    • n == nums.length
      • 46 |
    • 1 <= n <= 5000
      • 47 |
    • -5000 <= nums[i] <= 5000
      • 48 |
    • nums 中的所有整数 互不相同
      • 49 |
    • nums 原来是一个升序排序的数组，并进行了 1 至 n 次旋转
      • 50 |
    51 | 52 |
    Related Topics
  • 数组
  • 二分查找

  • 👍 1089
  • 👎 0
    • -------------------------------------------------------------------------------- /javascript-algorithms/leetcode/editor/cn/doc/content/[15]三数之和.md: -------------------------------------------------------------------------------- 1 |

    给你一个整数数组 nums ，判断是否存在三元组 [nums[i], nums[j], nums[k]] 满足 i != j、i != k 且 j != k ，同时还满足 nums[i] + nums[j] + nums[k] == 0 。请

    2 | 3 |

    你返回所有和为 0 且不重复的三元组。

    4 | 5 |

    注意：答案中不可以包含重复的三元组。

    6 | 7 |

     

    8 | 9 |

     

    10 | 11 |

    示例 1：

    12 | 13 | 
    14 | 输入：nums = [-1,0,1,2,-1,-4]
15 | 输出：[[-1,-1,2],[-1,0,1]]
16 | 解释：
17 | nums[0] + nums[1] + nums[2] = (-1) + 0 + 1 = 0 。
18 | nums[1] + nums[2] + nums[4] = 0 + 1 + (-1) = 0 。
19 | nums[0] + nums[3] + nums[4] = (-1) + 2 + (-1) = 0 。
20 | 不同的三元组是 [-1,0,1] 和 [-1,-1,2] 。
21 | 注意，输出的顺序和三元组的顺序并不重要。
22 |
    23 | 24 |

    示例 2：

    25 | 26 | 
    27 | 输入：nums = [0,1,1]
28 | 输出：[]
29 | 解释：唯一可能的三元组和不为 0 。
30 |
    31 | 32 |

    示例 3：

    33 | 34 | 
    35 | 输入：nums = [0,0,0]
36 | 输出：[[0,0,0]]
37 | 解释：唯一可能的三元组和为 0 。
38 |
    39 | 40 |

     

    41 | 42 |

    提示：

    43 | 44 |
      45 |
    • 3 <= nums.length <= 3000
      • 46 |
    • -105 <= nums[i] <= 105
      • 47 |
    48 | 49 |
    Related Topics
  • 数组
  • 双指针
  • 排序

  • 👍 5526
  • 👎 0
    • -------------------------------------------------------------------------------- /javascript-algorithms/leetcode/editor/cn/doc/content/[17]电话号码的字母组合.md: -------------------------------------------------------------------------------- 1 |

    给定一个仅包含数字 2-9 的字符串，返回所有它能表示的字母组合。答案可以按 任意顺序 返回。

    2 | 3 |

    给出数字到字母的映射如下（与电话按键相同）。注意 1 不对应任何字母。

    4 | 5 |

    6 | 7 |

     

    8 | 9 |

    示例 1：

    10 | 11 | 
    12 | 输入：digits = "23"
13 | 输出：["ad","ae","af","bd","be","bf","cd","ce","cf"]
14 |
    15 | 16 |

    示例 2：

    17 | 18 | 
    19 | 输入：digits = ""
20 | 输出：[]
21 |
    22 | 23 |

    示例 3：

    24 | 25 | 
    26 | 输入：digits = "2"
27 | 输出：["a","b","c"]
28 |
    29 | 30 |

     

    31 | 32 |

    提示：

    33 | 34 |
      35 |
    • 0 <= digits.length <= 4
      • 36 |
    • digits[i] 是范围 ['2', '9'] 的一个数字。
      • 37 |
    38 | 39 |
    Related Topics
  • 哈希表
  • 字符串
  • 回溯

  • 👍 2791
  • 👎 0
    • -------------------------------------------------------------------------------- /javascript-algorithms/leetcode/editor/cn/doc/content/[199]二叉树的右视图.md: -------------------------------------------------------------------------------- 1 |

    给定一个二叉树的 根节点 root，想象自己站在它的右侧，按照从顶部到底部的顺序，返回从右侧所能看到的节点值。

    2 | 3 |

     

    4 | 5 |

    示例 1:

    6 | 7 |

    8 | 9 | 
    10 | 输入: [1,2,3,null,5,null,4]
11 | 输出: [1,3,4]
12 |
    13 | 14 |

    示例 2:

    15 | 16 | 
    17 | 输入: [1,null,3]
18 | 输出: [1,3]
19 |
    20 | 21 |

    示例 3:

    22 | 23 | 
    24 | 输入: []
25 | 输出: []
26 |
    27 | 28 |

     

    29 | 30 |

    提示:

    31 | 32 |
      33 |
    • 二叉树的节点个数的范围是 [0,100]
      • 34 |
    • 35 | -100 <= Node.val <= 100 
      • 36 |
    37 | 38 |
    Related Topics
  • 树
  • 深度优先搜索
  • 广度优先搜索
  • 二叉树

  • 👍 1036
  • 👎 0
    • -------------------------------------------------------------------------------- /javascript-algorithms/leetcode/editor/cn/doc/content/[1]两数之和.md: -------------------------------------------------------------------------------- 1 |

    给定一个整数数组 nums 和一个整数目标值 target，请你在该数组中找出 和为目标值 target  的那 两个 整数，并返回它们的数组下标。

    2 | 3 |

    你可以假设每种输入只会对应一个答案。但是，数组中同一个元素在答案里不能重复出现。

    4 | 5 |

    你可以按任意顺序返回答案。

    6 | 7 |

     

    8 | 9 |

    示例 1：

    10 | 11 | 
    12 | 输入：nums = [2,7,11,15], target = 9
13 | 输出：[0,1]
14 | 解释：因为 nums[0] + nums[1] == 9 ，返回 [0, 1] 。
15 |
    16 | 17 |

    示例 2：

    18 | 19 | 
    20 | 输入：nums = [3,2,4], target = 6
21 | 输出：[1,2]
22 |
    23 | 24 |

    示例 3：

    25 | 26 | 
    27 | 输入：nums = [3,3], target = 6
28 | 输出：[0,1]
29 |
    30 | 31 |

     

    32 | 33 |

    提示：

    34 | 35 |
      36 |
    • 2 <= nums.length <= 104
      • 37 |
    • -109 <= nums[i] <= 109
      • 38 |
    • -109 <= target <= 109
      • 39 |
    • 只会存在一个有效答案
      • 40 |
    41 | 42 |

     

    43 | 44 |

    进阶：你可以想出一个时间复杂度小于 O(n2) 的算法吗？

    45 | 46 |
    Related Topics
  • 数组
  • 哈希表

  • 👍 16275
  • 👎 0
    • -------------------------------------------------------------------------------- /javascript-algorithms/leetcode/editor/cn/doc/content/[203]移除链表元素.md: -------------------------------------------------------------------------------- 1 | 给你一个链表的头节点 head 和一个整数 val ，请你删除链表中所有满足 Node.val == val 的节点，并返回 新的头节点 。 2 | 3 |

     

    4 | 5 |

    示例 1：

    6 |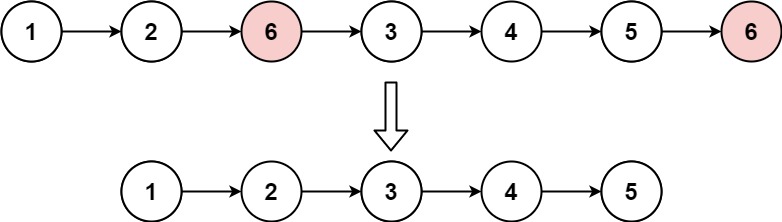 7 | 
     8 | 输入：head = [1,2,6,3,4,5,6], val = 6
 9 | 输出：[1,2,3,4,5]
10 |
    11 | 12 |

    示例 2：

    13 | 14 | 
    15 | 输入：head = [], val = 1
16 | 输出：[]
17 |
    18 | 19 |

    示例 3：

    20 | 21 | 
    22 | 输入：head = [7,7,7,7], val = 7
23 | 输出：[]
24 |
    25 | 26 |

     

    27 | 28 |

    提示：

    29 | 30 |
      31 |
    • 列表中的节点数目在范围 [0, 104] 内
      • 32 |
    • 1 <= Node.val <= 50
      • 33 |
    • 0 <= val <= 50
      • 34 |
    35 | 36 |
    Related Topics
  • 递归
  • 链表

  • 👍 1325
  • 👎 0
    • -------------------------------------------------------------------------------- /javascript-algorithms/leetcode/editor/cn/doc/content/[20]有效的括号.md: -------------------------------------------------------------------------------- 1 |

    给定一个只包括 '('，')'，'{'，'}'，'['，']' 的字符串 s ，判断字符串是否有效。

    2 | 3 |

    有效字符串需满足：

    4 | 5 |
      6 |
    1. 左括号必须用相同类型的右括号闭合。
      2. 7 |
    2. 左括号必须以正确的顺序闭合。
      3. 8 |
    3. 每个右括号都有一个对应的相同类型的左括号。
      4. 9 |
    10 | 11 |

     

    12 | 13 |

    示例 1：

    14 | 15 | 
    16 | 输入：s = "()"
17 | 输出：true
18 |
    19 | 20 |

    示例 2：

    21 | 22 | 
    23 | 输入：s = "()[]{}"
24 | 输出：true
25 |
    26 | 27 |

    示例 3：

    28 | 29 | 
    30 | 输入：s = "(]"
31 | 输出：false
32 |
    33 | 34 |

     

    35 | 36 |

    提示：

    37 | 38 |
      39 |
    • 1 <= s.length <= 104
      • 40 |
    • s 仅由括号 '()[]{}' 组成
      • 41 |
    42 | 43 |
    Related Topics
  • 栈
  • 字符串

  • 👍 4145
  • 👎 0
    • -------------------------------------------------------------------------------- /javascript-algorithms/leetcode/editor/cn/doc/content/[21]合并两个有序链表.md: -------------------------------------------------------------------------------- 1 |

    将两个升序链表合并为一个新的 升序 链表并返回。新链表是通过拼接给定的两个链表的所有节点组成的。 

    2 | 3 |

     

    4 | 5 |

    示例 1：

    6 | 7 | 
     8 | 输入：l1 = [1,2,4], l2 = [1,3,4]
 9 | 输出：[1,1,2,3,4,4]
10 |
    11 | 12 |

    示例 2：

    13 | 14 | 
    15 | 输入：l1 = [], l2 = []
16 | 输出：[]
17 |
    18 | 19 |

    示例 3：

    20 | 21 | 
    22 | 输入：l1 = [], l2 = [0]
23 | 输出：[0]
24 |
    25 | 26 |

     

    27 | 28 |

    提示：

    29 | 30 |
      31 |
    • 两个链表的节点数目范围是 [0, 50]
      • 32 |
    • -100 <= Node.val <= 100
      • 33 |
    • l1 和 l2 均按 非递减顺序 排列
      • 34 |
    35 | 36 |
    Related Topics
  • 递归
  • 链表

  • 👍 3435
  • 👎 0
    • -------------------------------------------------------------------------------- /javascript-algorithms/leetcode/editor/cn/doc/content/[222]完全二叉树的节点个数.md: -------------------------------------------------------------------------------- 1 |

    给你一棵 完全二叉树 的根节点 root ，求出该树的节点个数。

    2 | 3 |

    完全二叉树 的定义如下：在完全二叉树中，除了最底层节点可能没填满外，其余每层节点数都达到最大值，并且最下面一层的节点都集中在该层最左边的若干位置。若最底层为第 h 层，则该层包含 1~ 2h 个节点。

    4 | 5 |

     

    6 | 7 |

    示例 1：

    8 | 9 | 
    10 | 输入：root = [1,2,3,4,5,6]
11 | 输出：6
12 |
    13 | 14 |

    示例 2：

    15 | 16 | 
    17 | 输入：root = []
18 | 输出：0
19 |
    20 | 21 |

    示例 3：

    22 | 23 | 
    24 | 输入：root = [1]
25 | 输出：1
26 |
    27 | 28 |

     

    29 | 30 |

    提示：

    31 | 32 |
      33 |
    • 树中节点的数目范围是[0, 5 * 104]
      • 34 |
    • 0 <= Node.val <= 5 * 104
      • 35 |
    • 题目数据保证输入的树是 完全二叉树
      • 36 |
    37 | 38 |

     

    39 | 40 |

    进阶：遍历树来统计节点是一种时间复杂度为 O(n) 的简单解决方案。你可以设计一个更快的算法吗？

    41 | 42 |
    Related Topics
  • 位运算
  • 树
  • 二分查找
  • 二叉树

  • 👍 1095
  • 👎 0
    • -------------------------------------------------------------------------------- /javascript-algorithms/leetcode/editor/cn/doc/content/[225]用队列实现栈.md: -------------------------------------------------------------------------------- 1 |

    请你仅使用两个队列实现一个后入先出（LIFO）的栈，并支持普通栈的全部四种操作（push、top、pop 和 empty）。

    2 | 3 |

    实现 MyStack 类：

    4 | 5 |
      6 |
    • void push(int x) 将元素 x 压入栈顶。
      • 7 |
    • int pop() 移除并返回栈顶元素。
      • 8 |
    • int top() 返回栈顶元素。
      • 9 |
    • boolean empty() 如果栈是空的，返回 true ；否则，返回 false 。
      • 10 |
    11 | 12 |

     

    13 | 14 |

    注意：

    15 | 16 |
      17 |
    • 你只能使用队列的标准操作 —— 也就是 push to back、peek/pop from front、size 和 is empty 这些操作。
      • 18 |
    • 你所使用的语言也许不支持队列。 你可以使用 list （列表）或者 deque（双端队列）来模拟一个队列 , 只要是标准的队列操作即可。
      • 19 |
    20 | 21 |

     

    22 | 23 |

    示例：

    24 | 25 | 
    26 | 输入：
27 | ["MyStack", "push", "push", "top", "pop", "empty"]
28 | [[], [1], [2], [], [], []]
29 | 输出：
30 | [null, null, null, 2, 2, false]
31 | 
32 | 解释：
33 | MyStack myStack = new MyStack();
34 | myStack.push(1);
35 | myStack.push(2);
36 | myStack.top(); // 返回 2
37 | myStack.pop(); // 返回 2
38 | myStack.empty(); // 返回 False
39 |
    40 | 41 |

     

    42 | 43 |

    提示：

    44 | 45 |
      46 |
    • 1 <= x <= 9
      • 47 |
    • 最多调用100 次 push、pop、top 和 empty
      • 48 |
    • 每次调用 pop 和 top 都保证栈不为空
      • 49 |
    50 | 51 |

     

    52 | 53 |

    进阶：你能否仅用一个队列来实现栈。

    54 | 55 |
    Related Topics
  • 栈
  • 设计
  • 队列

  • 👍 868
  • 👎 0
    • -------------------------------------------------------------------------------- /javascript-algorithms/leetcode/editor/cn/doc/content/[226]翻转二叉树.md: -------------------------------------------------------------------------------- 1 |

    给你一棵二叉树的根节点 root ，翻转这棵二叉树，并返回其根节点。

    2 | 3 |

     

    4 | 5 |

    示例 1：

    6 | 7 |

    8 | 9 | 
    10 | 输入：root = [4,2,7,1,3,6,9]
11 | 输出：[4,7,2,9,6,3,1]
12 |
    13 | 14 |

    示例 2：

    15 | 16 |

    17 | 18 | 
    19 | 输入：root = [2,1,3]
20 | 输出：[2,3,1]
21 |
    22 | 23 |

    示例 3：

    24 | 25 | 
    26 | 输入：root = []
27 | 输出：[]
28 |
    29 | 30 |

     

    31 | 32 |

    提示：

    33 | 34 |
      35 |
    • 树中节点数目范围在 [0, 100] 内
      • 36 |
    • -100 <= Node.val <= 100
      • 37 |
    38 | 39 |
    Related Topics
  • 树
  • 深度优先搜索
  • 广度优先搜索
  • 二叉树

  • 👍 1670
  • 👎 0
    • -------------------------------------------------------------------------------- /javascript-algorithms/leetcode/editor/cn/doc/content/[230]二叉搜索树中第K小的元素.md: -------------------------------------------------------------------------------- 1 |

    给定一个二叉搜索树的根节点 root ，和一个整数 k ，请你设计一个算法查找其中第 k 个最小元素（从 1 开始计数）。

    2 | 3 |

     

    4 | 5 |

    示例 1：

    6 | 7 | 
     8 | 输入：root = [3,1,4,null,2], k = 1
 9 | 输出：1
10 |
    11 | 12 |

    示例 2：

    13 | 14 | 
    15 | 输入：root = [5,3,6,2,4,null,null,1], k = 3
16 | 输出：3
17 |
    18 | 19 |

     

    20 | 21 |

     

    22 | 23 |

    提示：

    24 | 25 |
      26 |
    • 树中的节点数为 n 。
      • 27 |
    • 1 <= k <= n <= 104
      • 28 |
    • 0 <= Node.val <= 104
      • 29 |
    30 | 31 |

     

    32 | 33 |

    进阶：如果二叉搜索树经常被修改（插入/删除操作）并且你需要频繁地查找第 k 小的值，你将如何优化算法？

    34 | 35 |
    Related Topics
  • 树
  • 深度优先搜索
  • 二叉搜索树
  • 二叉树

  • 👍 824
  • 👎 0
    • -------------------------------------------------------------------------------- /javascript-algorithms/leetcode/editor/cn/doc/content/[231]2 的幂.md: -------------------------------------------------------------------------------- 1 |

    给你一个整数 n，请你判断该整数是否是 2 的幂次方。如果是，返回 true ；否则，返回 false 。

    2 | 3 |

    如果存在一个整数 x 使得 n == 2x ，则认为 n 是 2 的幂次方。

    4 | 5 |

     

    6 | 7 |

    示例 1：

    8 | 9 | 
    10 | 输入：n = 1
11 | 输出：true
12 | 解释：20 = 1
13 |
    14 | 15 |

    示例 2：

    16 | 17 | 
    18 | 输入：n = 16
19 | 输出：true
20 | 解释：24 = 16
21 |
    22 | 23 |

    示例 3：

    24 | 25 | 
    26 | 输入：n = 3
27 | 输出：false
28 |
    29 | 30 |

    示例 4：

    31 | 32 | 
    33 | 输入：n = 4
34 | 输出：true
35 |
    36 | 37 |

    示例 5：

    38 | 39 | 
    40 | 输入：n = 5
41 | 输出：false
42 |
    43 | 44 |

     

    45 | 46 |

    提示：

    47 | 48 |
      49 |
    • -231 <= n <= 231 - 1
      • 50 |
    51 | 52 |

     

    53 | 54 |

    进阶：你能够不使用循环/递归解决此问题吗？

    55 | 56 |
    Related Topics
  • 位运算
  • 递归
  • 数学

  • 👍 626
  • 👎 0
    • -------------------------------------------------------------------------------- /javascript-algorithms/leetcode/editor/cn/doc/content/[234]回文链表.md: -------------------------------------------------------------------------------- 1 |

    给你一个单链表的头节点 head ，请你判断该链表是否为回文链表。如果是，返回 true ；否则，返回 false 。

    2 | 3 |

     

    4 | 5 |

    示例 1：

    6 | 7 | 
     8 | 输入：head = [1,2,2,1]
 9 | 输出：true
10 |
    11 | 12 |

    示例 2：

    13 |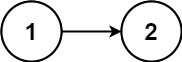 14 | 
    15 | 输入：head = [1,2]
16 | 输出：false
17 |
    18 | 19 |

     

    20 | 21 |

    提示：

    22 | 23 |
      24 |
    • 链表中节点数目在范围[1, 105] 内
      • 25 |
    • 0 <= Node.val <= 9
      • 26 |
    27 | 28 |

     

    29 | 30 |

    进阶：你能否用 O(n) 时间复杂度和 O(1) 空间复杂度解决此题？

    31 | 32 |
    Related Topics
  • 栈
  • 递归
  • 链表
  • 双指针

  • 👍 1858
  • 👎 0
    • -------------------------------------------------------------------------------- /javascript-algorithms/leetcode/editor/cn/doc/content/[236]二叉树的最近公共祖先.md: -------------------------------------------------------------------------------- 1 |

    给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。

    2 | 3 |

    百度百科中最近公共祖先的定义为：“对于有根树 T 的两个节点 p、q，最近公共祖先表示为一个节点 x，满足 x 是 p、q 的祖先且 x 的深度尽可能大（一个节点也可以是它自己的祖先）。”

    4 | 5 |

     

    6 | 7 |

    示例 1：

    8 | 9 | 
    10 | 输入：root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1
11 | 输出：3
12 | 解释：节点 5 和节点 1 的最近公共祖先是节点 3 。
13 |
    14 | 15 |

    示例 2：

    16 | 17 | 
    18 | 输入：root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 4
19 | 输出：5
20 | 解释：节点 5 和节点 4 的最近公共祖先是节点 5 。因为根据定义最近公共祖先节点可以为节点本身。
21 |
    22 | 23 |

    示例 3：

    24 | 25 | 
    26 | 输入：root = [1,2], p = 1, q = 2
27 | 输出：1
28 |
    29 | 30 |

     

    31 | 32 |

    提示：

    33 | 34 |
      35 |
    • 树中节点数目在范围 [2, 105] 内。
      • 36 |
    • -109 <= Node.val <= 109
      • 37 |
    • 所有 Node.val 互不相同 。
      • 38 |
    • p != q
      • 39 |
    • p 和 q 均存在于给定的二叉树中。
      • 40 |
    41 | 42 |
    Related Topics
  • 树
  • 深度优先搜索
  • 二叉树

  • 👍 2611
  • 👎 0
    • -------------------------------------------------------------------------------- /javascript-algorithms/leetcode/editor/cn/doc/content/[257]二叉树的所有路径.md: -------------------------------------------------------------------------------- 1 |

    给你一个二叉树的根节点 root ，按 任意顺序 ，返回所有从根节点到叶子节点的路径。

    2 | 3 |

    叶子节点 是指没有子节点的节点。

      4 | 5 |

    示例 1：

    6 |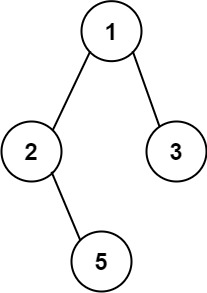 7 | 
     8 | 输入：root = [1,2,3,null,5]
 9 | 输出：["1->2->5","1->3"]
10 |
    11 | 12 |

    示例 2：

    13 | 14 | 
    15 | 输入：root = [1]
16 | 输出：["1"]
17 |
    18 | 19 |

     

    20 | 21 |

    提示：

    22 | 23 |
      24 |
    • 树中节点的数目在范围 [1, 100] 内
      • 25 |
    • -100 <= Node.val <= 100
      • 26 |
    27 | 28 |
    Related Topics
  • 树
  • 深度优先搜索
  • 字符串
  • 回溯
  • 二叉树

  • 👍 1098
  • 👎 0
    • -------------------------------------------------------------------------------- /javascript-algorithms/leetcode/editor/cn/doc/content/[283]移动零.md: -------------------------------------------------------------------------------- 1 |

    给定一个数组 nums，编写一个函数将所有 0 移动到数组的末尾，同时保持非零元素的相对顺序。

    2 | 3 |

    请注意 ，必须在不复制数组的情况下原地对数组进行操作。

    4 | 5 |

     

    6 | 7 |

    示例 1:

    8 | 9 | 
    10 | 输入: nums = [0,1,0,3,12]
11 | 输出: [1,3,12,0,0]
12 |
    13 | 14 |

    示例 2:

    15 | 16 | 
    17 | 输入: nums = [0]
18 | 输出: [0]
    19 | 20 |

     

    21 | 22 |

    提示:

    23 | 24 | 25 |
      26 |
    • 1 <= nums.length <= 104
      • 27 |
    • -231 <= nums[i] <= 231 - 1
      • 28 |
    29 | 30 |

     

    31 | 32 |

    进阶：你能尽量减少完成的操作次数吗？

    33 | 34 |
    Related Topics
  • 数组
  • 双指针

  • 👍 2299
  • 👎 0
    • -------------------------------------------------------------------------------- /javascript-algorithms/leetcode/editor/cn/doc/content/[2]两数相加.md: -------------------------------------------------------------------------------- 1 |

    给你两个 非空 的链表，表示两个非负的整数。它们每位数字都是按照 逆序 的方式存储的，并且每个节点只能存储 一位 数字。

    2 | 3 |

    请你将两个数相加，并以相同形式返回一个表示和的链表。

    4 | 5 |

    你可以假设除了数字 0 之外，这两个数都不会以 0 开头。

    6 | 7 |

     

    8 | 9 |

    示例 1：

    10 |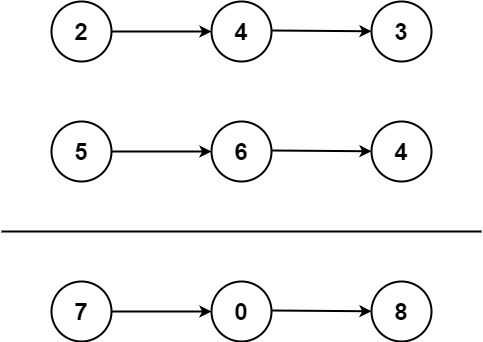 11 | 
    12 | 输入：l1 = [2,4,3], l2 = [5,6,4]
13 | 输出：[7,0,8]
14 | 解释：342 + 465 = 807.
15 |
    16 | 17 |

    示例 2：

    18 | 19 | 
    20 | 输入：l1 = [0], l2 = [0]
21 | 输出：[0]
22 |
    23 | 24 |

    示例 3：

    25 | 26 | 
    27 | 输入：l1 = [9,9,9,9,9,9,9], l2 = [9,9,9,9]
28 | 输出：[8,9,9,9,0,0,0,1]
29 |
    30 | 31 |

     

    32 | 33 |

    提示：

    34 | 35 |
      36 |
    • 每个链表中的节点数在范围 [1, 100] 内
      • 37 |
    • 0 <= Node.val <= 9
      • 38 |
    • 题目数据保证列表表示的数字不含前导零
      • 39 |
    40 | 41 |
    Related Topics
  • 递归
  • 链表
  • 数学

  • 👍 9175
  • 👎 0
    • -------------------------------------------------------------------------------- /javascript-algorithms/leetcode/editor/cn/doc/content/[300]最长递增子序列.md: -------------------------------------------------------------------------------- 1 |

    给你一个整数数组 nums ，找到其中最长严格递增子序列的长度。

    2 | 3 |

    子序列 是由数组派生而来的序列，删除（或不删除）数组中的元素而不改变其余元素的顺序。例如，[3,6,2,7] 是数组 [0,3,1,6,2,2,7] 的子序列。

      4 | 5 |

    示例 1：

    6 | 7 | 
     8 | 输入：nums = [10,9,2,5,3,7,101,18]
 9 | 输出：4
10 | 解释：最长递增子序列是 [2,3,7,101]，因此长度为 4 。
11 |
    12 | 13 |

    示例 2：

    14 | 15 | 
    16 | 输入：nums = [0,1,0,3,2,3]
17 | 输出：4
18 |
    19 | 20 |

    示例 3：

    21 | 22 | 
    23 | 输入：nums = [7,7,7,7,7,7,7]
24 | 输出：1
25 |
    26 | 27 |

     

    28 | 29 |

    提示：

    30 | 31 |
      32 |
    • 1 <= nums.length <= 2500
      • 33 |
    • -104 <= nums[i] <= 104
      • 34 |
    35 | 36 |

     

    37 | 38 |

    进阶：

    39 | 40 |
      41 |
    • 你能将算法的时间复杂度降低到 O(n log(n)) 吗?
      • 42 |
    43 | 44 |
    Related Topics
  • 数组
  • 二分查找
  • 动态规划

  • 👍 3410
  • 👎 0
    • -------------------------------------------------------------------------------- /javascript-algorithms/leetcode/editor/cn/doc/content/[322]零钱兑换.md: -------------------------------------------------------------------------------- 1 |

    给你一个整数数组 coins ，表示不同面额的硬币；以及一个整数 amount ，表示总金额。

    2 | 3 |

    计算并返回可以凑成总金额所需的 最少的硬币个数 。如果没有任何一种硬币组合能组成总金额，返回 -1 。

    4 | 5 |

    你可以认为每种硬币的数量是无限的。

    6 | 7 |

     

    8 | 9 |

    示例 1：

    10 | 11 | 
    12 | 输入：coins = [1, 2, 5], amount = 11
13 | 输出：3 
14 | 解释：11 = 5 + 5 + 1
    15 | 16 |

    示例 2：

    17 | 18 | 
    19 | 输入：coins = [2], amount = 3
20 | 输出：-1
    21 | 22 |

    示例 3：

    23 | 24 | 
    25 | 输入：coins = [1], amount = 0
26 | 输出：0
27 |
    28 | 29 |

     

    30 | 31 |

    提示：

    32 | 33 |
      34 |
    • 1 <= coins.length <= 12
      • 35 |
    • 1 <= coins[i] <= 231 - 1
      • 36 |
    • 0 <= amount <= 104
      • 37 |
    38 | 39 |
    Related Topics
  • 广度优先搜索
  • 数组
  • 动态规划

  • 👍 2588
  • 👎 0
    • -------------------------------------------------------------------------------- /javascript-algorithms/leetcode/editor/cn/doc/content/[39]组合总和.md: -------------------------------------------------------------------------------- 1 |

    给你一个 无重复元素 的整数数组 candidates 和一个目标整数 target ，找出 candidates 中可以使数字和为目标数 target 的 所有 不同组合 ，并以列表形式返回。你可以按 任意顺序 返回这些组合。

    2 | 3 |

    candidates 中的 同一个 数字可以 无限制重复被选取 。如果至少一个数字的被选数量不同，则两种组合是不同的。 

    4 | 5 |

    对于给定的输入，保证和为 target 的不同组合数少于 150 个。

    6 | 7 |

     

    8 | 9 |

    示例 1：

    10 | 11 | 
    12 | 输入：candidates = [2,3,6,7], target = 7
13 | 输出：[[2,2,3],[7]]
14 | 解释：
15 | 2 和 3 可以形成一组候选，2 + 2 + 3 = 7 。注意 2 可以使用多次。
16 | 7 也是一个候选， 7 = 7 。
17 | 仅有这两种组合。
    18 | 19 |

    示例 2：

    20 | 21 | 
    22 | 输入: candidates = [2,3,5], target = 8
23 | 输出: [[2,2,2,2],[2,3,3],[3,5]]
    24 | 25 |

    示例 3：

    26 | 27 | 
    28 | 输入: candidates = [2], target = 1
29 | 输出: []
30 |
    31 | 32 |

     

    33 | 34 |

    提示：

    35 | 36 |
      37 |
    • 1 <= candidates.length <= 30
      • 38 |
    • 2 <= candidates[i] <= 40
      • 39 |
    • candidates 的所有元素 互不相同
      • 40 |
    • 1 <= target <= 40
      • 41 |
    42 | 43 |
    Related Topics
  • 数组
  • 回溯

  • 👍 2752
  • 👎 0
    • -------------------------------------------------------------------------------- /javascript-algorithms/leetcode/editor/cn/doc/content/[404]左叶子之和.md: -------------------------------------------------------------------------------- 1 |

    给定二叉树的根节点 root ，返回所有左叶子之和。

    2 | 3 |

     

    4 | 5 |

    示例 1：

    6 | 7 |

    8 | 9 | 
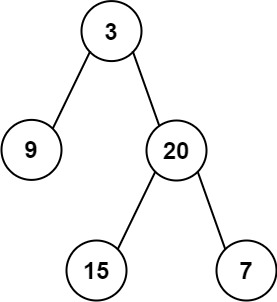
    10 | 输入: root = [3,9,20,null,null,15,7] 
11 | 输出: 24 
12 | 解释: 在这个二叉树中，有两个左叶子，分别是 9 和 15，所以返回 24
13 |
    14 | 15 |

    示例 2:

    16 | 17 | 
    18 | 输入: root = [1]
19 | 输出: 0
20 |
    21 | 22 |

     

    23 | 24 |

    提示:

    25 | 26 |
      27 |
    • 节点数在 [1, 1000] 范围内
      • 28 |
    • -1000 <= Node.val <= 1000
      • 29 |
    30 | 31 |

     

    32 | 33 |
    Related Topics
  • 树
  • 深度优先搜索
  • 广度优先搜索
  • 二叉树

  • 👍 699
  • 👎 0
    • -------------------------------------------------------------------------------- /javascript-algorithms/leetcode/editor/cn/doc/content/[429]N 叉树的层序遍历.md: -------------------------------------------------------------------------------- 1 |

    给定一个 N 叉树，返回其节点值的层序遍历。（即从左到右，逐层遍历）。

    2 | 3 |

    树的序列化输入是用层序遍历，每组子节点都由 null 值分隔（参见示例）。

    4 | 5 |

     

    6 | 7 |

    示例 1：

    8 | 9 |

    10 | 11 | 
    12 | 输入：root = [1,null,3,2,4,null,5,6]
13 | 输出：[[1],[3,2,4],[5,6]]
14 |
    15 | 16 |

    示例 2：

    17 | 18 |

    19 | 20 | 
    21 | 输入：root = [1,null,2,3,4,5,null,null,6,7,null,8,null,9,10,null,null,11,null,12,null,13,null,null,14]
22 | 输出：[[1],[2,3,4,5],[6,7,8,9,10],[11,12,13],[14]]
23 |
    24 | 25 |

     

    26 | 27 |

    提示：

    28 | 29 |
      30 |
    • 树的高度不会超过 1000
      • 31 |
    • 树的节点总数在 [0, 10^4] 之间
      • 32 |
    33 | 34 |
    Related Topics
  • 树
  • 广度优先搜索

  • 👍 452
  • 👎 0
    • -------------------------------------------------------------------------------- /javascript-algorithms/leetcode/editor/cn/doc/content/[455]分发饼干.md: -------------------------------------------------------------------------------- 1 |

    假设你是一位很棒的家长，想要给你的孩子们一些小饼干。但是，每个孩子最多只能给一块饼干。

    2 | 3 |

    对每个孩子 i，都有一个胃口值 g[i]，这是能让孩子们满足胃口的饼干的最小尺寸；并且每块饼干 j，都有一个尺寸 s[j] 。如果 s[j] >= g[i]，我们可以将这个饼干 j 分配给孩子 i ，这个孩子会得到满足。你的目标是尽可能满足越多数量的孩子，并输出这个最大数值。

      4 | 5 |

    示例 1:

    6 | 7 | 
     8 | 输入: g = [1,2,3], s = [1,1]
 9 | 输出: 1
10 | 解释: 
11 | 你有三个孩子和两块小饼干，3个孩子的胃口值分别是：1,2,3。
12 | 虽然你有两块小饼干，由于他们的尺寸都是1，你只能让胃口值是1的孩子满足。
13 | 所以你应该输出1。
14 |
    15 | 16 |

    示例 2:

    17 | 18 | 
    19 | 输入: g = [1,2], s = [1,2,3]
20 | 输出: 2
21 | 解释: 
22 | 你有两个孩子和三块小饼干，2个孩子的胃口值分别是1,2。
23 | 你拥有的饼干数量和尺寸都足以让所有孩子满足。
24 | 所以你应该输出2.
25 |
    26 | 27 |

     

    28 | 29 |

    提示：

    30 | 31 |
      32 |
    • 1 <= g.length <= 3 * 104
      • 33 |
    • 0 <= s.length <= 3 * 104
      • 34 |
    • 1 <= g[i], s[j] <= 231 - 1
      • 35 |
    36 | 37 |
    Related Topics
  • 贪心
  • 数组
  • 双指针
  • 排序

  • 👍 773
  • 👎 0
    • -------------------------------------------------------------------------------- /javascript-algorithms/leetcode/editor/cn/doc/content/[46]全排列.md: -------------------------------------------------------------------------------- 1 |

    给定一个不含重复数字的数组 nums ，返回其 所有可能的全排列 。你可以 按任意顺序 返回答案。

    2 | 3 |

     

    4 | 5 |

    示例 1：

    6 | 7 | 
     8 | 输入：nums = [1,2,3]
 9 | 输出：[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]
10 |
    11 | 12 |

    示例 2：

    13 | 14 | 
    15 | 输入：nums = [0,1]
16 | 输出：[[0,1],[1,0]]
17 |
    18 | 19 |

    示例 3：

    20 | 21 | 
    22 | 输入：nums = [1]
23 | 输出：[[1]]
24 |
    25 | 26 |

     

    27 | 28 |

    提示：

    29 | 30 |
      31 |
    • 1 <= nums.length <= 6
      • 32 |
    • -10 <= nums[i] <= 10
      • 33 |
    • nums 中的所有整数 互不相同
      • 34 |
    35 | 36 |
    Related Topics
  • 数组
  • 回溯

  • 👍 2687
  • 👎 0
    • -------------------------------------------------------------------------------- /javascript-algorithms/leetcode/editor/cn/doc/content/[509]斐波那契数.md: -------------------------------------------------------------------------------- 1 |

    斐波那契数 （通常用 F(n) 表示）形成的序列称为 斐波那契数列 。该数列由 0 和 1 开始，后面的每一项数字都是前面两项数字的和。也就是：

    2 | 3 | 
     4 | F(0) = 0，F(1) = 1
 5 | F(n) = F(n - 1) + F(n - 2)，其中 n > 1
 6 |
    7 | 8 |

    给定 n ，请计算 F(n) 。

    9 | 10 |

     

    11 | 12 |

    示例 1：

    13 | 14 | 
    15 | 输入：n = 2
16 | 输出：1
17 | 解释：F(2) = F(1) + F(0) = 1 + 0 = 1
18 |
    19 | 20 |

    示例 2：

    21 | 22 | 
    23 | 输入：n = 3
24 | 输出：2
25 | 解释：F(3) = F(2) + F(1) = 1 + 1 = 2
26 |
    27 | 28 |

    示例 3：

    29 | 30 | 
    31 | 输入：n = 4
32 | 输出：3
33 | 解释：F(4) = F(3) + F(2) = 2 + 1 = 3
34 |
    35 | 36 |

     

    37 | 38 |

    提示：

    39 | 40 |
      41 |
    • 0 <= n <= 30
      • 42 |
    43 | 44 |
    Related Topics
  • 递归
  • 记忆化搜索
  • 数学
  • 动态规划

  • 👍 694
  • 👎 0
    • -------------------------------------------------------------------------------- /javascript-algorithms/leetcode/editor/cn/doc/content/[515]在每个树行中找最大值.md: -------------------------------------------------------------------------------- 1 |

    给定一棵二叉树的根节点 root ，请找出该二叉树中每一层的最大值。

    2 | 3 |

     

    4 | 5 |

    示例1：

    6 | 7 |

    8 | 9 | 
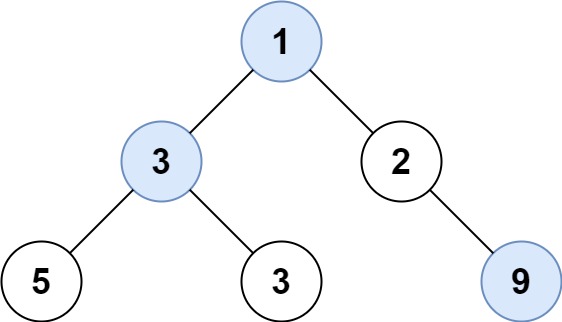
    10 | 输入: root = [1,3,2,5,3,null,9]
11 | 输出: [1,3,9]
12 |
    13 | 14 |

    示例2：

    15 | 16 | 
    17 | 输入: root = [1,2,3]
18 | 输出: [1,3]
19 |
    20 | 21 |

     

    22 | 23 |

    提示：

    24 | 25 |
      26 |
    • 二叉树的节点个数的范围是 [0,104]
      • 27 |
    • 28 | -231 <= Node.val <= 231 - 1
      • 29 |
    30 | 31 |

     

    32 | 33 |
    Related Topics
  • 树
  • 深度优先搜索
  • 广度优先搜索
  • 二叉树

  • 👍 353
  • 👎 0
    • -------------------------------------------------------------------------------- /javascript-algorithms/leetcode/editor/cn/doc/content/[543]二叉树的直径.md: -------------------------------------------------------------------------------- 1 |

    给你一棵二叉树的根节点，返回该树的 直径 。

    2 | 3 |

    二叉树的 直径 是指树中任意两个节点之间最长路径的 长度 。这条路径可能经过也可能不经过根节点 root 。

    4 | 5 |

    两节点之间路径的 长度 由它们之间边数表示。

    6 | 7 |

     

    8 | 9 |

    示例 1：

    10 | 11 | 
    12 | 输入：root = [1,2,3,4,5]
13 | 输出：3
14 | 解释：3 ，取路径 [4,2,1,3] 或 [5,2,1,3] 的长度。
15 |
    16 | 17 |

    示例 2：

    18 | 19 | 
    20 | 输入：root = [1,2]
21 | 输出：1
22 |
    23 | 24 |

     

    25 | 26 |

    提示：

    27 | 28 |
      29 |
    • 树中节点数目在范围 [1, 104] 内
      • 30 |
    • -100 <= Node.val <= 100
      • 31 |
    32 | 33 |
    Related Topics
  • 树
  • 深度优先搜索
  • 二叉树

  • 👍 1485
  • 👎 0
    • -------------------------------------------------------------------------------- /javascript-algorithms/leetcode/editor/cn/doc/content/[55]跳跃游戏.md: -------------------------------------------------------------------------------- 1 |

    给你一个非负整数数组 nums ，你最初位于数组的 第一个下标 。数组中的每个元素代表你在该位置可以跳跃的最大长度。

    2 | 3 |

    判断你是否能够到达最后一个下标，如果可以，返回 true ；否则，返回 false 。

    4 | 5 |

     

    6 | 7 |

    示例 1：

    8 | 9 | 
    10 | 输入：nums = [2,3,1,1,4]
11 | 输出：true
12 | 解释：可以先跳 1 步，从下标 0 到达下标 1, 然后再从下标 1 跳 3 步到达最后一个下标。
13 |
    14 | 15 |

    示例 2：

    16 | 17 | 
    18 | 输入：nums = [3,2,1,0,4]
19 | 输出：false
20 | 解释：无论怎样，总会到达下标为 3 的位置。但该下标的最大跳跃长度是 0 ， 所以永远不可能到达最后一个下标。
21 |
    22 | 23 |

     

    24 | 25 |

    提示：

    26 | 27 |
      28 |
    • 1 <= nums.length <= 104
      • 29 |
    • 0 <= nums[i] <= 105
      • 30 |
    31 | 32 |
    Related Topics
  • 贪心
  • 数组
  • 动态规划

  • 👍 2491
  • 👎 0
    • -------------------------------------------------------------------------------- /javascript-algorithms/leetcode/editor/cn/doc/content/[572]另一棵树的子树.md: -------------------------------------------------------------------------------- 1 |
    2 |
    3 |

    给你两棵二叉树 root 和 subRoot 。检验 root 中是否包含和 subRoot 具有相同结构和节点值的子树。如果存在，返回 true ；否则，返回 false 。

    4 |
    5 |
    6 | 7 |

    二叉树 tree 的一棵子树包括 tree 的某个节点和这个节点的所有后代节点。tree 也可以看做它自身的一棵子树。

    8 | 9 |

     

    10 | 11 |

    示例 1：

    12 |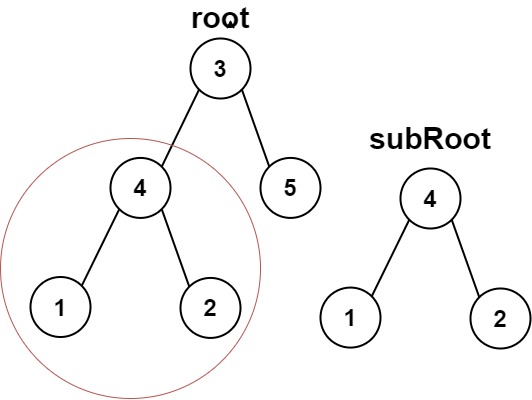 13 | 
    14 | 输入：root = [3,4,5,1,2], subRoot = [4,1,2]
15 | 输出：true
16 |
    17 | 18 |

    示例 2：

    19 |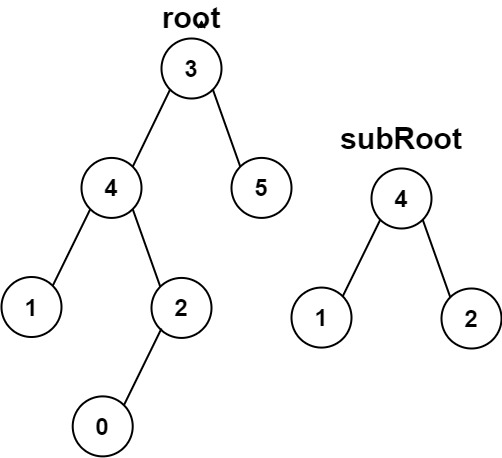 20 | 
    21 | 输入：root = [3,4,5,1,2,null,null,null,null,0], subRoot = [4,1,2]
22 | 输出：false
23 |
    24 | 25 |

     

    26 | 27 |

    提示：

    28 | 29 |
      30 |
    • root 树上的节点数量范围是 [1, 2000]
      • 31 |
    • subRoot 树上的节点数量范围是 [1, 1000]
      • 32 |
    • -104 <= root.val <= 104
      • 33 |
    • -104 <= subRoot.val <= 104
      • 34 |
    35 | 36 |
    Related Topics
  • 树
  • 深度优先搜索
  • 二叉树
  • 字符串匹配
  • 哈希函数

  • 👍 1009
  • 👎 0
    • -------------------------------------------------------------------------------- /javascript-algorithms/leetcode/editor/cn/doc/content/[617]合并二叉树.md: -------------------------------------------------------------------------------- 1 |

    给你两棵二叉树： root1 和 root2 。

    2 | 3 |

    想象一下，当你将其中一棵覆盖到另一棵之上时，两棵树上的一些节点将会重叠（而另一些不会）。你需要将这两棵树合并成一棵新二叉树。合并的规则是：如果两个节点重叠，那么将这两个节点的值相加作为合并后节点的新值；否则，不为 null 的节点将直接作为新二叉树的节点。

    4 | 5 |

    返回合并后的二叉树。

    6 | 7 |

    注意: 合并过程必须从两个树的根节点开始。

    8 | 9 |

     

    10 | 11 |

    示例 1：

    12 | 13 | 
    14 | 输入：root1 = [1,3,2,5], root2 = [2,1,3,null,4,null,7]
15 | 输出：[3,4,5,5,4,null,7]
16 |
    17 | 18 |

    示例 2：

    19 | 20 | 
    21 | 输入：root1 = [1], root2 = [1,2]
22 | 输出：[2,2]
23 |
    24 | 25 |

     

    26 | 27 |

    提示：

    28 | 29 |
      30 |
    • 两棵树中的节点数目在范围 [0, 2000] 内
      • 31 |
    • -104 <= Node.val <= 104
      • 32 |
    33 | 34 |
    Related Topics
  • 树
  • 深度优先搜索
  • 广度优先搜索
  • 二叉树

  • 👍 1382
  • 👎 0
    • -------------------------------------------------------------------------------- /javascript-algorithms/leetcode/editor/cn/doc/content/[637]二叉树的层平均值.md: -------------------------------------------------------------------------------- 1 |

    给定一个非空二叉树的根节点 2 |  root , 以数组的形式返回每一层节点的平均值。与实际答案相差 10-5 以内的答案可以被接受。

    3 | 4 |

     

    5 | 6 |

    示例 1：

    7 | 8 |

    9 | 10 | 
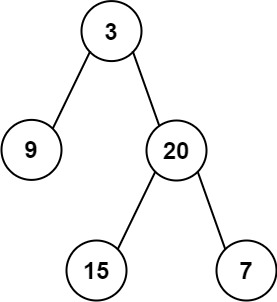
    11 | 输入：root = [3,9,20,null,null,15,7]
12 | 输出：[3.00000,14.50000,11.00000]
13 | 解释：第 0 层的平均值为 3,第 1 层的平均值为 14.5,第 2 层的平均值为 11 。
14 | 因此返回 [3, 14.5, 11] 。
15 |
    16 | 17 |

    示例 2:

    18 | 19 |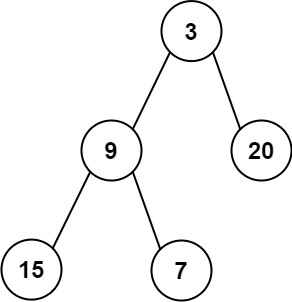

    20 | 21 | 
    22 | 输入：root = [3,9,20,15,7]
23 | 输出：[3.00000,14.50000,11.00000]
24 |
    25 | 26 |

     

    27 | 28 |

    提示：

    29 | 30 |

    31 |

    32 | 33 |
      34 |
    • 树中节点数量在 [1, 104] 范围内
      • 35 |
    • -231 <= Node.val <= 231 - 1
      • 36 |
    37 | 38 |
    Related Topics
  • 树
  • 深度优先搜索
  • 广度优先搜索
  • 二叉树

  • 👍 476
  • 👎 0
    • -------------------------------------------------------------------------------- /javascript-algorithms/leetcode/editor/cn/doc/content/[654]最大二叉树.md: -------------------------------------------------------------------------------- 1 |

    给定一个不重复的整数数组 nums 。 最大二叉树 可以用下面的算法从 nums 递归地构建:

    2 | 3 |
      4 |
    1. 创建一个根节点，其值为 nums 中的最大值。
      2. 5 |
    2. 递归地在最大值 左边 的 子数组前缀上 构建左子树。
      3. 6 |
    3. 递归地在最大值 右边 的 子数组后缀上 构建右子树。
      4. 7 |
    8 | 9 |

    返回 nums 构建的 最大二叉树 。

    10 | 11 |

     

    12 | 13 |

    示例 1：

    14 | 15 | 
    16 | 输入：nums = [3,2,1,6,0,5]
17 | 输出：[6,3,5,null,2,0,null,null,1]
18 | 解释：递归调用如下所示：
19 | - [3,2,1,6,0,5] 中的最大值是 6 ，左边部分是 [3,2,1] ，右边部分是 [0,5] 。
20 |     - [3,2,1] 中的最大值是 3 ，左边部分是 [] ，右边部分是 [2,1] 。
21 |         - 空数组，无子节点。
22 |         - [2,1] 中的最大值是 2 ，左边部分是 [] ，右边部分是 [1] 。
23 |             - 空数组，无子节点。
24 |             - 只有一个元素，所以子节点是一个值为 1 的节点。
25 |     - [0,5] 中的最大值是 5 ，左边部分是 [0] ，右边部分是 [] 。
26 |         - 只有一个元素，所以子节点是一个值为 0 的节点。
27 |         - 空数组，无子节点。
28 |
    29 | 30 |

    示例 2：

    31 | 32 | 
    33 | 输入：nums = [3,2,1]
34 | 输出：[3,null,2,null,1]
35 |
    36 | 37 |

     

    38 | 39 |

    提示：

    40 | 41 |
      42 |
    • 1 <= nums.length <= 1000
      • 43 |
    • 0 <= nums[i] <= 1000
      • 44 |
    • nums 中的所有整数 互不相同
      • 45 |
    46 | 47 |
    Related Topics
  • 栈
  • 树
  • 数组
  • 分治
  • 二叉树
  • 单调栈

  • 👍 770
  • 👎 0
    • -------------------------------------------------------------------------------- /javascript-algorithms/leetcode/editor/cn/doc/content/[69]x 的平方根 .md: -------------------------------------------------------------------------------- 1 |

    给你一个非负整数 x ，计算并返回 x 的 算术平方根 。

    2 | 3 |

    由于返回类型是整数，结果只保留 整数部分 ，小数部分将被 舍去 。

    4 | 5 |

    注意：不允许使用任何内置指数函数和算符，例如 pow(x, 0.5) 或者 x ** 0.5 。

    6 | 7 |

     

    8 | 9 |

    示例 1：

    10 | 11 | 
    12 | 输入：x = 4
13 | 输出：2
14 |
    15 | 16 |

    示例 2：

    17 | 18 | 
    19 | 输入：x = 8
20 | 输出：2
21 | 解释：8 的算术平方根是 2.82842..., 由于返回类型是整数，小数部分将被舍去。
22 |
    23 | 24 |

     

    25 | 26 |

    提示：

    27 | 28 |
      29 |
    • 0 <= x <= 231 - 1
      • 30 |
    31 | 32 |
    Related Topics
  • 数学
  • 二分查找

  • 👍 1530
  • 👎 0
    • -------------------------------------------------------------------------------- /javascript-algorithms/leetcode/editor/cn/doc/content/[700]二叉搜索树中的搜索.md: -------------------------------------------------------------------------------- 1 |

    给定二叉搜索树（BST）的根节点 2 |  root 和一个整数值 3 |  val。

    4 | 5 |

    你需要在 BST 中找到节点值等于 val 的节点。 返回以该节点为根的子树。 如果节点不存在，则返回 6 |  null 。

    7 | 8 |

     

    9 | 10 |

    示例 1:

    11 | 12 |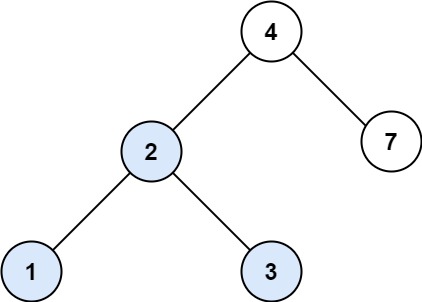

    13 |

    14 | 15 | 
    16 | 输入：root = [4,2,7,1,3], val = 2
17 | 输出：[2,1,3]
18 |
    19 | 20 |

    示例 2:

    21 |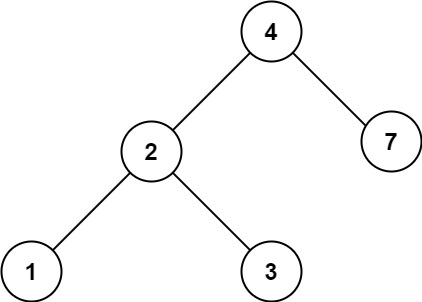 22 | 
    23 | 输入：root = [4,2,7,1,3], val = 5
24 | 输出：[]
25 |
    26 | 27 |

     

    28 | 29 |

    提示：

    30 | 31 |
      32 |
    • 树中节点数在 [1, 5000] 范围内
      • 33 |
    • 1 <= Node.val <= 107
      • 34 |
    • root 是二叉搜索树
      • 35 |
    • 1 <= val <= 107
      • 36 |
    37 | 38 |
    Related Topics
  • 树
  • 二叉搜索树
  • 二叉树

  • 👍 462
  • 👎 0
    • -------------------------------------------------------------------------------- /javascript-algorithms/leetcode/editor/cn/doc/content/[701]二叉搜索树中的插入操作.md: -------------------------------------------------------------------------------- 1 |

    给定二叉搜索树（BST）的根节点 2 |  root 和要插入树中的值 3 |  value ，将值插入二叉搜索树。 返回插入后二叉搜索树的根节点。 输入数据 保证 ，新值和原始二叉搜索树中的任意节点值都不同。

    4 | 5 |

    注意，可能存在多种有效的插入方式，只要树在插入后仍保持为二叉搜索树即可。 你可以返回 任意有效的结果 。

    6 | 7 |

     

    8 | 9 |

    示例 1：

    10 | 11 | 
    12 | 输入：root = [4,2,7,1,3], val = 5
13 | 输出：[4,2,7,1,3,5]
14 | 解释：另一个满足题目要求可以通过的树是：
15 | 
16 |
    17 | 18 |

    示例 2：

    19 | 20 | 
    21 | 输入：root = [40,20,60,10,30,50,70], val = 25
22 | 输出：[40,20,60,10,30,50,70,null,null,25]
23 |
    24 | 25 |

    示例 3：

    26 | 27 | 
    28 | 输入：root = [4,2,7,1,3,null,null,null,null,null,null], val = 5
29 | 输出：[4,2,7,1,3,5]
30 |
    31 | 32 |

     

    33 | 34 |

    提示：

    35 | 36 |
      37 |
    • 树中的节点数将在 38 |  [0, 104]的范围内。 39 |
      • 40 |
    • -108 <= Node.val <= 108
      • 41 |
    • 所有值  42 | Node.val 是 独一无二 的。
      • 43 |
    • -108 <= val <= 108
      • 44 |
    • 保证 val 在原始BST中不存在。
      • 45 |
    46 | 47 |
    Related Topics
  • 树
  • 二叉搜索树
  • 二叉树

  • 👍 553
  • 👎 0
    • -------------------------------------------------------------------------------- /javascript-algorithms/leetcode/editor/cn/doc/content/[704]二分查找.md: -------------------------------------------------------------------------------- 1 |

    给定一个 n 个元素有序的（升序）整型数组 nums 和一个目标值 target  ，写一个函数搜索 nums 中的 target，如果目标值存在返回下标，否则返回 -1。

    2 | 3 |


    示例 1:

    4 | 5 | 
    输入: nums = [-1,0,3,5,9,12], target = 9
 6 | 输出: 4
 7 | 解释: 9 出现在 nums 中并且下标为 4
 8 |
    9 | 10 |

    示例 2:

    11 | 12 | 
    输入: nums = [-1,0,3,5,9,12], target = 2
13 | 输出: -1
14 | 解释: 2 不存在 nums 中因此返回 -1
15 |
    16 | 17 |

     

    18 | 19 |

    提示：

    20 | 21 |
      22 |
    1. 你可以假设 nums 中的所有元素是不重复的。
      2. 23 |
    2. n 将在 [1, 10000]之间。
      3. 24 |
    3. nums 的每个元素都将在 [-9999, 9999]之间。
      4. 25 |
    26 | 27 |
    Related Topics
  • 数组
  • 二分查找

  • 👍 1556
  • 👎 0
    • -------------------------------------------------------------------------------- /javascript-algorithms/leetcode/editor/cn/doc/content/[71]简化路径.md: -------------------------------------------------------------------------------- 1 |

    给你一个字符串 path ，表示指向某一文件或目录的 Unix 风格 绝对路径 （以 '/' 开头），请你将其转化为更加简洁的规范路径。

    2 | 3 |

    在 Unix 风格的文件系统中，一个点（.）表示当前目录本身；此外，两个点 （..） 表示将目录切换到上一级（指向父目录）；两者都可以是复杂相对路径的组成部分。任意多个连续的斜杠（即，'//'）都被视为单个斜杠 '/' 。 对于此问题，任何其他格式的点（例如，'...'）均被视为文件/目录名称。

    4 | 5 |

    请注意，返回的 规范路径 必须遵循下述格式：

    6 | 7 |
      8 |
    • 始终以斜杠 '/' 开头。
      • 9 |
    • 两个目录名之间必须只有一个斜杠 '/' 。
      • 10 |
    • 最后一个目录名（如果存在）不能 以 '/' 结尾。
      • 11 |
    • 此外，路径仅包含从根目录到目标文件或目录的路径上的目录（即，不含 '.' 或 '..'）。
      • 12 |
    13 | 14 |

    返回简化后得到的 规范路径 。

    15 | 16 |

     

    17 | 18 |

    示例 1：

    19 | 20 | 
    21 | 输入：path = "/home/"
22 | 输出："/home"
23 | 解释：注意，最后一个目录名后面没有斜杠。
    24 | 25 |

    示例 2：

    26 | 27 | 
    28 | 输入：path = "/../"
29 | 输出："/"
30 | 解释：从根目录向上一级是不可行的，因为根目录是你可以到达的最高级。
31 |
    32 | 33 |

    示例 3：

    34 | 35 | 
    36 | 输入：path = "/home//foo/"
37 | 输出："/home/foo"
38 | 解释：在规范路径中，多个连续斜杠需要用一个斜杠替换。
39 |
    40 | 41 |

    示例 4：

    42 | 43 | 
    44 | 输入：path = "/a/./b/../../c/"
45 | 输出："/c"
46 |
    47 | 48 |

     

    49 | 50 |

    提示：

    51 | 52 |
      53 |
    • 1 <= path.length <= 3000
      • 54 |
    • path 由英文字母，数字，'.'，'/' 或 '_' 组成。
      • 55 |
    • path 是一个有效的 Unix 风格绝对路径。
      • 56 |
    57 | 58 |
    Related Topics
  • 栈
  • 字符串

  • 👍 643
  • 👎 0
    • -------------------------------------------------------------------------------- /javascript-algorithms/leetcode/editor/cn/doc/content/[77]组合.md: -------------------------------------------------------------------------------- 1 |

    给定两个整数 n 和 k，返回范围 [1, n] 中所有可能的 k 个数的组合。

    2 | 3 |

    你可以按 任何顺序 返回答案。

    4 | 5 |

     

    6 | 7 |

    示例 1：

    8 | 9 | 
    10 | 输入：n = 4, k = 2
11 | 输出：
12 | [
13 |   [2,4],
14 |   [3,4],
15 |   [2,3],
16 |   [1,2],
17 |   [1,3],
18 |   [1,4],
19 | ]
    20 | 21 |

    示例 2：

    22 | 23 | 
    24 | 输入：n = 1, k = 1
25 | 输出：[[1]]
    26 | 27 |

     

    28 | 29 |

    提示：

    30 | 31 |
      32 |
    • 1 <= n <= 20
      • 33 |
    • 1 <= k <= n
      • 34 |
    35 | 36 |
    Related Topics
  • 回溯

  • 👍 1622
  • 👎 0
    • -------------------------------------------------------------------------------- /javascript-algorithms/leetcode/editor/cn/doc/content/[78]子集.md: -------------------------------------------------------------------------------- 1 |

    给你一个整数数组 nums ，数组中的元素 互不相同 。返回该数组所有可能的子集（幂集）。

    2 | 3 |

    解集 不能 包含重复的子集。你可以按 任意顺序 返回解集。

    4 | 5 |

     

    6 | 7 |

    示例 1：

    8 | 9 | 
    10 | 输入：nums = [1,2,3]
11 | 输出：[[],[1],[2],[1,2],[3],[1,3],[2,3],[1,2,3]]
12 |
    13 | 14 |

    示例 2：

    15 | 16 | 
    17 | 输入：nums = [0]
18 | 输出：[[],[0]]
19 |
    20 | 21 |

     

    22 | 23 |

    提示：

    24 | 25 |
      26 |
    • 1 <= nums.length <= 10
      • 27 |
    • -10 <= nums[i] <= 10
      • 28 |
    • nums 中的所有元素 互不相同
      • 29 |
    30 | 31 |
    Related Topics
  • 位运算
  • 数组
  • 回溯

  • 👍 2285
  • 👎 0
    • -------------------------------------------------------------------------------- /javascript-algorithms/leetcode/editor/cn/doc/content/[79]单词搜索.md: -------------------------------------------------------------------------------- 1 |

    给定一个 m x n 二维字符网格 board 和一个字符串单词 word 。如果 word 存在于网格中，返回 true ；否则，返回 false 。

    2 | 3 |

    单词必须按照字母顺序，通过相邻的单元格内的字母构成，其中“相邻”单元格是那些水平相邻或垂直相邻的单元格。同一个单元格内的字母不允许被重复使用。

    4 | 5 |

     

    6 | 7 |

    示例 1：

    8 | 9 | 
    10 | 输入：board = [["A","B","C","E"],["S","F","C","S"],["A","D","E","E"]], word = "ABCCED"
11 | 输出：true
12 |
    13 | 14 |

    示例 2：

    15 | 16 | 
    17 | 输入：board = [["A","B","C","E"],["S","F","C","S"],["A","D","E","E"]], word = "SEE"
18 | 输出：true
19 |
    20 | 21 |

    示例 3：

    22 | 23 | 
    24 | 输入：board = [["A","B","C","E"],["S","F","C","S"],["A","D","E","E"]], word = "ABCB"
25 | 输出：false
26 |
    27 | 28 |

     

    29 | 30 |

    提示：

    31 | 32 |
      33 |
    • m == board.length
      • 34 |
    • n = board[i].length
      • 35 |
    • 1 <= m, n <= 6
      • 36 |
    • 1 <= word.length <= 15
      • 37 |
    • board 和 word 仅由大小写英文字母组成
      • 38 |
    39 | 40 |

     

    41 | 42 |

    进阶：你可以使用搜索剪枝的技术来优化解决方案，使其在 board 更大的情况下可以更快解决问题？

    43 | 44 |
    Related Topics
  • 数组
  • 回溯
  • 矩阵

  • 👍 1677
  • 👎 0
    • -------------------------------------------------------------------------------- /javascript-algorithms/leetcode/editor/cn/doc/content/[860]柠檬水找零.md: -------------------------------------------------------------------------------- 1 |

    在柠檬水摊上，每一杯柠檬水的售价为 5 美元。顾客排队购买你的产品，（按账单 bills 支付的顺序）一次购买一杯。

    2 | 3 |

    每位顾客只买一杯柠檬水，然后向你付 5 美元、10 美元或 20 美元。你必须给每个顾客正确找零，也就是说净交易是每位顾客向你支付 5 美元。

    4 | 5 |

    注意，一开始你手头没有任何零钱。

    6 | 7 |

    给你一个整数数组 bills ，其中 bills[i] 是第 i 位顾客付的账。如果你能给每位顾客正确找零，返回 true ，否则返回 false 。

    8 | 9 |

     

    10 | 11 |

    示例 1：

    12 | 13 | 
    14 | 输入：bills = [5,5,5,10,20]
15 | 输出：true
16 | 解释：
17 | 前 3 位顾客那里，我们按顺序收取 3 张 5 美元的钞票。
18 | 第 4 位顾客那里，我们收取一张 10 美元的钞票，并返还 5 美元。
19 | 第 5 位顾客那里，我们找还一张 10 美元的钞票和一张 5 美元的钞票。
20 | 由于所有客户都得到了正确的找零，所以我们输出 true。
21 |
    22 | 23 |

    示例 2：

    24 | 25 | 
    26 | 输入：bills = [5,5,10,10,20]
27 | 输出：false
28 | 解释：
29 | 前 2 位顾客那里，我们按顺序收取 2 张 5 美元的钞票。
30 | 对于接下来的 2 位顾客，我们收取一张 10 美元的钞票，然后返还 5 美元。
31 | 对于最后一位顾客，我们无法退回 15 美元，因为我们现在只有两张 10 美元的钞票。
32 | 由于不是每位顾客都得到了正确的找零，所以答案是 false。
33 |
    34 | 35 |

     

    36 | 37 |

    提示：

    38 | 39 |
      40 |
    • 1 <= bills.length <= 105
      • 41 |
    • bills[i] 不是 5 就是 10 或是 20 
      • 42 |
    43 | 44 |
    Related Topics
  • 贪心
  • 数组

  • 👍 537
  • 👎 0
    • -------------------------------------------------------------------------------- /javascript-algorithms/leetcode/editor/cn/doc/content/[876]链表的中间结点.md: -------------------------------------------------------------------------------- 1 |

    给你单链表的头结点 head ，请你找出并返回链表的中间结点。

    2 | 3 |

    如果有两个中间结点，则返回第二个中间结点。

    4 | 5 |

     

    6 | 7 |

    示例 1：

    8 | 9 | 
    10 | 输入：head = [1,2,3,4,5]
11 | 输出：[3,4,5]
12 | 解释：链表只有一个中间结点，值为 3 。
13 |
    14 | 15 |

    示例 2：

    16 | 17 | 
    18 | 输入：head = [1,2,3,4,5,6]
19 | 输出：[4,5,6]
20 | 解释：该链表有两个中间结点，值分别为 3 和 4 ，返回第二个结点。
21 |
    22 | 23 |

     

    24 | 25 |

    提示：

    26 | 27 |
      28 |
    • 链表的结点数范围是 [1, 100]
      • 29 |
    • 1 <= Node.val <= 100
      • 30 |
    31 | 32 |
    Related Topics
  • 链表
  • 双指针

  • 👍 974
  • 👎 0
    • -------------------------------------------------------------------------------- /javascript-algorithms/leetcode/editor/cn/doc/content/[92]反转链表 II.md: -------------------------------------------------------------------------------- 1 | 给你单链表的头指针 head 和两个整数 left 和 right ，其中 left <= right 。请你反转从位置 left 到位置 right 的链表节点，返回 反转后的链表 。 2 | 3 |

     

    4 | 5 |

    示例 1：

    6 |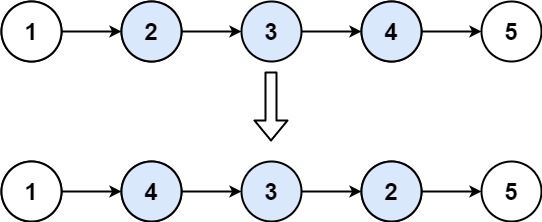 7 | 
     8 | 输入：head = [1,2,3,4,5], left = 2, right = 4
 9 | 输出：[1,4,3,2,5]
10 |
    11 | 12 |

    示例 2：

    13 | 14 | 
    15 | 输入：head = [5], left = 1, right = 1
16 | 输出：[5]
17 |
    18 | 19 |

     

    20 | 21 |

    提示：

    22 | 23 |
      24 |
    • 链表中节点数目为 n
      • 25 |
    • 1 <= n <= 500
      • 26 |
    • -500 <= Node.val <= 500
      • 27 |
    • 1 <= left <= right <= n
      • 28 |
    29 | 30 |

     

    31 | 32 |

    进阶： 你可以使用一趟扫描完成反转吗？

    33 | 34 |
    Related Topics
  • 链表

  • 👍 1733
  • 👎 0
    • -------------------------------------------------------------------------------- /javascript-algorithms/leetcode/editor/cn/doc/content/[94]二叉树的中序遍历.md: -------------------------------------------------------------------------------- 1 |

    给定一个二叉树的根节点 root ，返回 它的 中序 遍历 。

    2 | 3 |

     

    4 | 5 |

    示例 1：

    6 | 7 | 
     8 | 输入：root = [1,null,2,3]
 9 | 输出：[1,3,2]
10 |
    11 | 12 |

    示例 2：

    13 | 14 | 
    15 | 输入：root = []
16 | 输出：[]
17 |
    18 | 19 |

    示例 3：

    20 | 21 | 
    22 | 输入：root = [1]
23 | 输出：[1]
24 |
    25 | 26 |

     

    27 | 28 |

    提示：

    29 | 30 |
      31 |
    • 树中节点数目在范围 [0, 100] 内
      • 32 |
    • -100 <= Node.val <= 100
      • 33 |
    34 | 35 |

     

    36 | 37 |

    进阶: 递归算法很简单，你可以通过迭代算法完成吗？

    38 | 39 |
    Related Topics
  • 栈
  • 树
  • 深度优先搜索
  • 二叉树

  • 👍 2031
  • 👎 0
    • -------------------------------------------------------------------------------- /javascript-algorithms/leetcode/editor/cn/doc/content/[98]验证二叉搜索树.md: -------------------------------------------------------------------------------- 1 |

    给你一个二叉树的根节点 root ，判断其是否是一个有效的二叉搜索树。

    2 | 3 |

    有效 二叉搜索树定义如下：

    4 | 5 |
      6 |
    • 节点的左子树只包含 小于 当前节点的数。
      • 7 |
    • 节点的右子树只包含 大于 当前节点的数。
      • 8 |
    • 所有左子树和右子树自身必须也是二叉搜索树。
      • 9 |
    10 | 11 |

     

    12 | 13 |

    示例 1：

    14 | 15 | 
    16 | 输入：root = [2,1,3]
17 | 输出：true
18 |
    19 | 20 |

    示例 2：

    21 | 22 | 
    23 | 输入：root = [5,1,4,null,null,3,6]
24 | 输出：false
25 | 解释：根节点的值是 5 ，但是右子节点的值是 4 。
26 |
    27 | 28 |

     

    29 | 30 |

    提示：

    31 | 32 |
      33 |
    • 树中节点数目范围在[1, 104] 内
      • 34 |
    • -231 <= Node.val <= 231 - 1
      • 35 |
    36 | 37 |
    Related Topics
  • 树
  • 深度优先搜索
  • 二叉搜索树
  • 二叉树

  • 👍 2280
  • 👎 0
    • -------------------------------------------------------------------------------- /javascript-algorithms/leetcode/editor/cn/doc/content/[99]恢复二叉搜索树.md: -------------------------------------------------------------------------------- 1 |

    给你二叉搜索树的根节点 root ，该树中的 恰好 两个节点的值被错误地交换。请在不改变其结构的情况下，恢复这棵树 。

    2 | 3 |

     

    4 | 5 |

    示例 1：

    6 | 7 | 
     8 | 输入：root = [1,3,null,null,2]
 9 | 输出：[3,1,null,null,2]
10 | 解释：3 不能是 1 的左孩子，因为 3 > 1 。交换 1 和 3 使二叉搜索树有效。
11 |
    12 | 13 |

    示例 2：

    14 | 15 | 
    16 | 输入：root = [3,1,4,null,null,2]
17 | 输出：[2,1,4,null,null,3]
18 | 解释：2 不能在 3 的右子树中，因为 2 < 3 。交换 2 和 3 使二叉搜索树有效。
    19 | 20 |

     

    21 | 22 |

    提示：

    23 | 24 |
      25 |
    • 树上节点的数目在范围 [2, 1000] 内
      • 26 |
    • -231 <= Node.val <= 231 - 1
      • 27 |
    28 | 29 |

     

    30 | 31 |

    进阶：使用 O(n) 空间复杂度的解法很容易实现。你能想出一个只使用 O(1) 空间的解决方案吗？

    32 | 33 |
    Related Topics
  • 树
  • 深度优先搜索
  • 二叉搜索树
  • 二叉树

  • 👍 939
  • 👎 0
    • -------------------------------------------------------------------------------- /javascript-algorithms/leetcode/editor/cn/doc/note/[99]恢复二叉搜索树.md: -------------------------------------------------------------------------------- https://raw.githubusercontent.com/SincereCSL/Algorithms-DataStructures-Learning/45c5bdff2cb070b7cde598c716e97ccaf99ce8bc/javascript-algorithms/leetcode/editor/cn/doc/note/[99]恢复二叉搜索树.md -------------------------------------------------------------------------------- /javascript-algorithms/linkList/linkList.js: -------------------------------------------------------------------------------- 1 | 2 | class linkNode { 3 | constructor(val){ 4 | this.val = val; 5 | this.next = null; 6 | } 7 | } 8 | 9 | class linkNodeList { 10 | constructor(){ 11 | this.head = null; 12 | this.length = 0; 13 | } 14 | append(val){ 15 | let node = new linkNode(val); 16 | let p = this.head; //缓存下head节点 17 | if(this.head){ 18 | //找到链表最后一个节点，把这个节点的.next属性赋值给node 19 | while(p.next){ //链表通过while进行循环 20 | p = p.next; 21 | } 22 | p.next = node; 23 | }else{ 24 | // 如果没有head节点，链表是空的 把要创建的节点 赋值给head 25 | this.head = node; 26 | } 27 | this.length++ ; 28 | } 29 | print(){ 30 | let p = this.head; 31 | let result = ''; 32 | if(this.head){ 33 | do{ 34 | result += (p.val +'=>'); 35 | p = p.next; 36 | }while(p.next) 37 | result += p.val; 38 | console.log(result) 39 | }else{ 40 | console.log('empty') 41 | } 42 | } 43 | } 44 | 45 | // 1 => 2 => 3 => 4 46 | 47 | let linkList = new linkNodeList(); 48 | linkList.append(1); 49 | linkList.append(2); 50 | linkList.append(3); 51 | linkList.append(4); 52 | linkList.print(); 53 | console.log(linkList.length) 54 | 55 | -------------------------------------------------------------------------------- /javascript-algorithms/linkList/test.js: -------------------------------------------------------------------------------- 1 | let test = function(){ 2 | var box = document.getElementById("box"); 3 | var blocks = box.childNodes; 4 | for(var i = 0; i a-b) 8 | // console.log(array) 9 | 10 | //1.冒泡排序 11 | function bubbleSort(arr){ 12 | // 时间复杂度：O(n^2) 13 | //每一个元素和它右侧的元素进行比较，如果比它自己右侧元素大 就交换位置 否则就不动 14 | let len = arr.length-1; 15 | for(let j=0;jarr[i+1]){ 18 | // let tmp = arr[i]; 19 | // arr[i] = arr[i+1]; 20 | // arr[i+1] = tmp; 21 | [arr[i],arr[i+1]]= [arr[i+1],arr[i]] //结构赋值 22 | } 23 | } 24 | } 25 | return arr; 26 | } 27 | console.log('冒泡排序:',bubbleSort(array)) --------------------------------------------------------------------------------