├── .gitignore
├── README.md
├── assets
├── shapes.png
└── speck.png
├── examples
├── java_hash.html
├── java_hash.ipynb
└── only_for_genius.ipynb
├── exercises
├── roulette.html
├── roulette.js
├── speck.ipynb
├── sudoku.ipynb
└── xorrayhul64p-rng.ipynb
├── guide.pdf
├── install.sh
├── solutions
├── speck.ipynb
├── sudoku-solve.ipynb
└── xorrayhul64p-rng-solved.ipynb
└── z3-4.5.0-x64-win
├── LICENSE.txt
├── bin
├── Microsoft.Z3.dll
├── Microsoft.Z3.xml
├── com.microsoft.z3.jar
├── libz3.dll
├── libz3.lib
├── libz3java.dll
├── libz3java.lib
├── msvcp110.dll
├── msvcr110.dll
├── python
│ ├── example.py
│ └── z3
│ │ ├── __init__.py
│ │ ├── __init__.pyc
│ │ ├── z3.py
│ │ ├── z3.pyc
│ │ ├── z3consts.py
│ │ ├── z3consts.pyc
│ │ ├── z3core.py
│ │ ├── z3core.pyc
│ │ ├── z3num.py
│ │ ├── z3num.pyc
│ │ ├── z3poly.py
│ │ ├── z3poly.pyc
│ │ ├── z3printer.py
│ │ ├── z3printer.pyc
│ │ ├── z3rcf.py
│ │ ├── z3rcf.pyc
│ │ ├── z3types.py
│ │ ├── z3types.pyc
│ │ ├── z3util.py
│ │ └── z3util.pyc
├── vcomp110.dll
└── z3.exe
└── include
├── z3++.h
├── z3.h
├── z3_algebraic.h
├── z3_api.h
├── z3_ast_containers.h
├── z3_fixedpoint.h
├── z3_fpa.h
├── z3_interp.h
├── z3_macros.h
├── z3_optimization.h
├── z3_polynomial.h
├── z3_rcf.h
└── z3_v1.h
/.gitignore:
--------------------------------------------------------------------------------
1 | .ipynb_checkpoints
2 |
3 |
--------------------------------------------------------------------------------
/README.md:
--------------------------------------------------------------------------------
1 | # Breaking Crypto with Z3
2 |
3 | This repo holds materials for our Splash 2017 class on Z3.
4 |
5 | ## Getting started with Z3
6 |
7 | Z3 is a powerful theorem prover developed by Microsoft Research. Essentially, you can give Z3 a bunch of equations or constraints expressed in terms of variables, and it will do its best to find a solution that satisfies the constraints. Z3 is an example of an [*SMT Solver*](https://en.wikipedia.org/wiki/Satisfiability_modulo_theories). There's a rich theory underlying how to write good SMT solvers, but we're not concerned with any of that in this class. We'll just be using Z3 as a tool in order to break some cryptography.
8 |
9 | ### Installing
10 |
11 | * Once you're logged in, double-click and install Anaconda3 on the Desktop
12 | * While that's installing, navigate to https://github.com/TechSecCTF/z3_splash_class/ in a browser, and click the green "Clone or download" button.
13 | * Then click "Download Zip", then click the "Save" button on the prompt at the bottom of your screen. Once it's done downloading, click "Open".
14 | * Right-click on the big folder icon on the right, and click "Extract All"
15 | * Set it to extract to `C:\Users\espuser`.
16 | * By now, Anaconda3 should have finished installing. Once it's done, click the Windows icon on the bottom-left corner of the screen and click "Anaconda Prompt"
17 | * Finally, wait for the prompt to load and then type `jupyter notebook`
18 | * Copy the url that it gives you and paste it into your browser.
19 | * Double click on `z3_splash_class`. You should be all set.
20 |
21 | You may also be interested in installing Z3 in a different environment. We have provided an `install.sh` script which should install Z3 successfully OS X or Linux. (You'll need root access). If you want to run the jupyter notebooks, you'll need to download and install [jupyter](http://jupyter.org/install.html). You can then get rid all the path nonsense at the top of the python source code and simply include `from z3 import *`.
22 |
23 | Further installation instructions can be found [here](https://github.com/Z3Prover/z3).
24 |
25 | ### Example: ONLY FOR GENiUS
26 |
27 | This image was floating around Facebook some time ago, with the caption "ONLY FOR GENiUS". Let's find the solution using Z3.
28 |
29 | 
30 |
31 | Check out `examples/only_for_genius.py`, reproduced below:
32 |
33 | ```python
34 | from Z3 import *
35 |
36 | circle, square, triangle = Ints('circle square triangle')
37 | s = Solver()
38 | s.add(circle + circle == 10)
39 | s.add(circle * square + square == 12)
40 | s.add(circle * square - triangle * circle == circle)
41 | print s.check()
42 | print s.model()
43 | ```
44 |
45 | Let's go through it line by line:
46 |
47 | * All of our Z3 programs will start with the line `from Z3 import *`. This imports all the Z3 python bindings.
48 | * Next, we declare three integer variables, `circle`, `square` and `triangle`.
49 | * Then, we instantiate a new solver `s` and we add our three constraints.
50 | * Finally, we call the function `s.check()`. In any Z3 program, this function is doing all of the heavy lifting. It checks if a solution exists given our constraints and returns `sat` if yes, and `unsat` if no.
51 | * Once we've verified that there is at least one solution, we can get Z3 to print it for us by asking it for its model.
52 |
53 | When we run the program we see:
54 |
55 | ```
56 | sat
57 | [triangle = 1, square = 2, circle = 5]
58 | ```
59 |
60 | ## Exercise: Sudoku
61 |
62 | Let's get warmed up with a relatively easy example — Sudoku.
63 |
64 | Sudoku is just a system of equations, and it's simple for Z3 to solve.
65 |
66 | 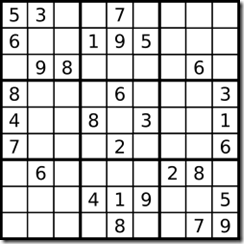
67 |
68 | We can do this solely with the Z3 `Int` and `Distinct` types, plus some basic operators `And` and `<=`.
69 |
70 | Check out `exercises/sudoku.ipynb`. Your task is to add the Z3 constraints for the individual cells, columns, and subsquares. (To get you started, we've given you the row constraints). Remember to enforce that the entries are all numbers from 1 to 9.
71 |
72 | ## Example: Weak hash function
73 |
74 | In computer science, a *hash function* is a function that takes in a string of characters (or any object really), and produces a fixed-size number (the "hash") that corresponds to that string. Importantly, the hashes of two related strings should be different. Hash functions are useful for all sorts of things in computer science (like hashtables). *Cryptographic hash functions* are a special type of hash function which also satisfies a number of properties, one of the most important of which is that given the hash of a string, it should be difficult to reconstruct the string.
75 |
76 | One area where hash functions are very useful are in password checking. When a user registers with a site, they specify a password. Suppose that the webiste records the password in their database. Later when the user logs in, they enter that password and the website checks that it matches the password in their database. But now, if the website's database gets leaked, every user's account is compromised.
77 |
78 | Suppose instead the website computes a *hash* of the password when a user registers and stores the hash in their database instead of the password itself. Then, whenever the user logs in, the website can just compute the hash of whatever password is entered and check the hash against whatever is stored in their database. If the database leaks (and the hash is cryptographically secure, and the passwords themselves are sufficiently complex) it should be difficult to easily reverse the hashes and compromise the user accounts.
79 |
80 | The problem is, many people frequently use non-cryptographically secure hash functions for password-checking. In this example, we'll reverse the hash for a website using the same hash function that Java uses for its hash tables. Check out `examples/java_hash.ipynb` and `examples/java_hash.html`.
81 |
82 | ## Exercise: Breaking 3SPECK
83 |
84 | [SPECK](https://en.wikipedia.org/wiki/Speck_(cipher)) is a lightweight block cipher developed by the NSA and published in 2013.
85 |
86 | It consists of 3 basic operations done on 64-bit numbers:
87 |
88 | ### XOR
89 | The XOR operation is very common in cryptography. It's 0 if the two input bits are the same and 1 if the two input bits are different. When applied to 64-bit numbers, the XOR is computed bit-by-bit:
90 |
91 | ```
92 | a = 0b10001111100010001 = 73489
93 | b = 0b00111001001111000 = 29304
94 | c = 0b10110110101101001 = 93545 <--- a XOR b
95 | ```
96 |
97 | In python, the XOR operation is represented by the caret symbol (^)
98 |
99 | ```python
100 | a = 73489
101 | b = 29304
102 | assert a ^ b == 93545
103 | ```
104 |
105 | ### Addition
106 | This is standard grade-school addition. The one thing to note is that if the resulting sum is greater than 64-bits, it "overflows" and we only consider the lower 64 bits.
107 |
108 | ### Rotations
109 | In a bit rotation, you literally rotate the bits of the number to the right or left by the amount specified by the operation.
110 |
111 | Here is an example of a 3 bit right rotation:
112 |
113 | ```
114 | a = 0b10001111100010001 = 73489
115 | b = 0b00110001111100010 = 25570 <-- a >>> 3
116 | ```
117 |
118 | Python doesn't have a native operation for bit rotation, but the following functions will do it for us:
119 |
120 | ```python
121 | MASK = (1 << 64) - 1
122 |
123 | # Rotate 64 bit integer x right by r
124 | def ror(x, r):
125 | return ((x >> r) | (x << (64 - r))) & MASK
126 |
127 | # Rotate 64 bit integer x left by r
128 | def rol(x, r):
129 | return ((x << r) | (x >> (64 - r))) & MASK
130 | ```
131 |
132 | ### SPECK's round function:
133 |
134 | SPECK makes heavy use of the following function `r`, which takes in three 64-bit numbers and modifies the first two numbers based on the third:
135 |
136 | ```python
137 | # SPECK round function; x, y, and k are all 64 bits
138 | def r(x, y, k):
139 | x = ror(x, 8)
140 | x += y
141 | x ^= k
142 | y = rol(y, 3)
143 | y ^= x
144 | return x, y
145 | ```
146 |
147 | SPECK (or at least the version we're interested in) operates on 128-bit plaintext blocks. This block is immediately split into two 64-bit blocks, x and y. SPECK's key is also 128 bits long and is also split up into two 64-bit blocks, a and b.
148 |
149 | In each round of SPECK, we use apply the `r` function to our plaintext (x and y) using b as the third argument. Then we modify our keys by applying the `r` function to our key (a and b) using the round number as the third argument.
150 |
151 | SPECK normally includes 32 rounds. Our variant, 3SPECK, (that Z3 is able to break in a reasonable amount of time) uses only 3 rounds.
152 |
153 | 
154 |
155 | ### Breaking 3SPECK with Z3
156 |
157 | Check out `exercises/speck.ipynb`. We've implemented the SPECK cipher for you and provided you with a plaintext / ciphertext pair which uses some unknown key. Your task is to implemented the Z3 versions of 3SPECK's encrypt and round functions in order to derive the key. Once you have the key, we'll use it to try to decrypt a new ciphertext.
158 |
159 | For this problem, the correct datatype to use are (64 bit) BitVecs, which act like Ints in many ways but support useful operations like `RotateRight` and `RotateLeft`. They also have the nice property that if you add two BitVecs that overflow, the resulting BitVec will only keep track of the last 64 bits.
160 |
161 |
162 | ## Exercise: Breaking xorrayhul64+
163 |
164 | There are many cases when writing programs that you'd want to have access to a random number generator. Psuedorandom number generators, or PRNGs for short, take a *seed* (some initial random value) and use that seed to produce an infinite stream of random-looking bytes. In contrast, true random number generators, or TRNGS, produce their randomness from environmental factors like radio noise or the weather or random keystrokes. The problem with TRNGs is that they are very slow. In practice PRNGs are usually enough.
165 |
166 | There is a special class of PRNGs called *cryptographically-secure psuedorandom number generators*, or CSPRNGs. The basic property that these generators satisfy is that even if you get access to the first N random values that it generates (but not the seed), you can't predict anything about the next N values it will generate. You can't use Z3 to break CSPRNGs (if you could, that means something has gone really really wrong with its design), but you can absolutely use Z3 to break non-cryptographically secure PRNGs. And the thing is, people misuse PSRNGs *all the time*.
167 |
168 | There's a PRNG called [`xorshift128+`](https://en.wikipedia.org/wiki/Xorshift) (it roughly stands for "XOR, Shift, 128-bits, Plus"), which is the RNG that Chrome and Firefox use for their Javascript engines. It's very fast, but it's also not cryptographically secure. Given a number of its outputs, we can clone the state of the PRNG and exactly predict the rest of the numbers it will generate. In this exercise we'll clone `xorrayhul64+` (a home-brewed variant of the real thing) using Z3 and then use our clone to win a Roulette wheel game.
169 |
170 | Check out `exercises/xorrayhul64p-rng.ipynb` and `exercises/roulette.html`.
171 |
172 | Hints:
173 |
174 | * The website computes the numbers it generates modulo 37 to select a random place on the wheel, but if you check the javascript console log, you can see the raw numbers it generates.
175 | * This PRNG uses left and right bit shifts, which are similar to left and right bit rotations, except the bits that fall off the edge don't get rotated around to the other end.
176 | * There is a difference between a *logical* right shift and an *arithmetic* right shift. The former is represented in Z3 using the function `LShR` which takes two arguments: the bit vector to be shifted and the amount to shift by. The latter is represented with the standard python operator `>>`. You'll need to user the former.
177 | * There is no difference between a logical and arithmetic left shift operator, so you should just use `<<`. Read why [here](http://teaching.idallen.com/dat2343/09f/notes/04bit_operations_shift.txt).
178 |
179 | ## Further reading
180 |
181 | * [Quick introduction into SAT/SMT solvers and symbolic execution](https://yurichev.com/writings/SAT_SMT_draft-EN.pdf) - A very good, if lengthy, book on Z3
182 | * [Hacking the Javascript Lottery](https://blog.securityevaluators.com/hacking-the-javascript-lottery-80cc437e3b7f) - Cloning Chrome's PRNG to win a javascript game
183 | * Z3 API - https://z3prover.github.io/api/html/z3.html
184 |
--------------------------------------------------------------------------------
/assets/shapes.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/TechSecCTF/z3_splash_class/b64cf9b51187c7b179b63ed4de43aa28b6a70fdb/assets/shapes.png
--------------------------------------------------------------------------------
/assets/speck.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/TechSecCTF/z3_splash_class/b64cf9b51187c7b179b63ed4de43aa28b6a70fdb/assets/speck.png
--------------------------------------------------------------------------------
/examples/java_hash.html:
--------------------------------------------------------------------------------
1 |
2 |
3 |
4 |
5 | Java Hash
6 |
7 |
8 |
9 |
10 |
LOGIN
11 |
15 |
16 |
38 |
39 |
40 |
--------------------------------------------------------------------------------
/examples/java_hash.ipynb:
--------------------------------------------------------------------------------
1 | {
2 | "cells": [
3 | {
4 | "cell_type": "code",
5 | "execution_count": null,
6 | "metadata": {},
7 | "outputs": [],
8 | "source": [
9 | "import sys\n",
10 | "sys.path.append(\"C:\\\\Users\\\\espuser\\\\z3_splash_class-master\\\\z3-4.5.0-x64-win\\\\bin\\\\python\")\n",
11 | "\n",
12 | "from z3 import *\n",
13 | "init(\"C:\\\\Users\\\\espuser\\\\z3_splash_class-master\\\\z3-4.5.0-x64-win\\\\bin\\\\libz3.dll\")\n",
14 | "\n",
15 | "def java_hash(s):\n",
16 | " m = 0\n",
17 | " for c in s:\n",
18 | " m *= 31\n",
19 | " m += ord(c)\n",
20 | " return m\n",
21 | "\n",
22 | "def z3_java_hash(s):\n",
23 | " m = 0\n",
24 | " for c in s:\n",
25 | " m *= 31\n",
26 | " m += c\n",
27 | " return m\n",
28 | "\n",
29 | "a, b, c, d, e, f, g, h = Ints('a b c d e f g h')\n",
30 | "s = Solver()\n",
31 | "s.add(And(a <= ord('z'), ord('a') <= a))\n",
32 | "s.add(And(b <= ord('z'), ord('a') <= b))\n",
33 | "s.add(And(c <= ord('z'), ord('a') <= c))\n",
34 | "s.add(And(d <= ord('z'), ord('a') <= d))\n",
35 | "s.add(And(e <= ord('z'), ord('a') <= e))\n",
36 | "s.add(And(f <= ord('z'), ord('a') <= f))\n",
37 | "s.add(And(g <= ord('z'), ord('a') <= g))\n",
38 | "s.add(And(h <= ord('z'), ord('a') <= h))\n",
39 | "s.add(z3_java_hash([a,b,c,d,e,f,g,h]) == 3229186608006)\n",
40 | "\n",
41 | "print(s.check())\n",
42 | "m = s.model()\n",
43 | "print(m)\n",
44 | "password = chr(m[a].as_long()) + chr(m[b].as_long()) + chr(m[c].as_long()) + chr(m[d].as_long()) + chr(m[e].as_long()) + chr(m[f].as_long()) + chr(m[g].as_long()) + chr(m[h].as_long())\n",
45 | "print(password)"
46 | ]
47 | },
48 | {
49 | "cell_type": "code",
50 | "execution_count": null,
51 | "metadata": {},
52 | "outputs": [],
53 | "source": []
54 | }
55 | ],
56 | "metadata": {
57 | "kernelspec": {
58 | "display_name": "Python 3",
59 | "language": "python",
60 | "name": "python3"
61 | },
62 | "language_info": {
63 | "codemirror_mode": {
64 | "name": "ipython",
65 | "version": 3
66 | },
67 | "file_extension": ".py",
68 | "mimetype": "text/x-python",
69 | "name": "python",
70 | "nbconvert_exporter": "python",
71 | "pygments_lexer": "ipython3",
72 | "version": "3.6.2"
73 | }
74 | },
75 | "nbformat": 4,
76 | "nbformat_minor": 2
77 | }
78 |
--------------------------------------------------------------------------------
/examples/only_for_genius.ipynb:
--------------------------------------------------------------------------------
1 | {
2 | "cells": [
3 | {
4 | "cell_type": "code",
5 | "execution_count": null,
6 | "metadata": {},
7 | "outputs": [],
8 | "source": [
9 | "import sys\n",
10 | "sys.path.append(\"C:\\\\Users\\\\espuser\\\\z3_splash_class-master\\\\z3-4.5.0-x64-win\\\\bin\\\\python\")\n",
11 | "\n",
12 | "from z3 import *\n",
13 | "init(\"C:\\\\Users\\\\espuser\\\\z3_splash_class-master\\\\z3-4.5.0-x64-win\\\\bin\\\\libz3.dll\")\n",
14 | "\n",
15 | "circle, square, triangle = Ints('circle square triangle')\n",
16 | "s = Solver()\n",
17 | "s.add(circle + circle == 10)\n",
18 | "s.add(circle * square + square == 12)\n",
19 | "s.add(circle * square - triangle * circle == circle)\n",
20 | "print(s.check())\n",
21 | "print(s.model())"
22 | ]
23 | }
24 | ],
25 | "metadata": {
26 | "kernelspec": {
27 | "display_name": "Python 3",
28 | "language": "python",
29 | "name": "python3"
30 | },
31 | "language_info": {
32 | "codemirror_mode": {
33 | "name": "ipython",
34 | "version": 3
35 | },
36 | "file_extension": ".py",
37 | "mimetype": "text/x-python",
38 | "name": "python",
39 | "nbconvert_exporter": "python",
40 | "pygments_lexer": "ipython3",
41 | "version": "3.6.2"
42 | }
43 | },
44 | "nbformat": 4,
45 | "nbformat_minor": 2
46 | }
47 |
--------------------------------------------------------------------------------
/exercises/roulette.html:
--------------------------------------------------------------------------------
1 |
2 |
8 |
9 |
10 |
11 |
12 |
--------------------------------------------------------------------------------
/exercises/roulette.js:
--------------------------------------------------------------------------------
1 | var options = ['0', '1', '2', '3', '4', '5', '6', '7', '8', '9', '10', '11', '12', '13', '14', '15', '16', '17', '18', '19', '20', '21', '22', '23', '24', '25', '26', '27', '28', '29', '30', '31', '32', '33', '34', '35', '36'];
2 |
3 | var startAngle = 0;
4 | var arc = Math.PI / (options.length / 2);
5 | var spinTimeout = null;
6 |
7 | var spinArcStart = 10;
8 | var spinTime = 0;
9 | var spinTimeTotal = 0;
10 | var MASK = 0xFFFFFFFF
11 |
12 | var ctx;
13 | var desiredNum = "";
14 | var wager = "";
15 | var guess = "";
16 | var bank = "";
17 |
18 | // document.getElementById("spin").addEventListener("click", spin);
19 | document.getElementById("gamble").addEventListener("click", gamble);
20 |
21 | function byte2Hex(n) {
22 | var nybHexString = "0123456789ABCDEF";
23 | return String(nybHexString.substr((n >> 4) & 0x0F, 1)) + nybHexString.substr(
24 | n & 0x0F, 1);
25 | }
26 |
27 | function RGB2Color(r, g, b) {
28 | return '#' + byte2Hex(r) + byte2Hex(g) + byte2Hex(b);
29 | }
30 |
31 | function getColor(item, maxitem) {
32 | if (item == 0){
33 | return 'green';
34 | } else if (item % 2 == 0) {
35 | return '#ee0000';
36 | } else {
37 | return '#000000';
38 | }
39 | }
40 |
41 | class XoRRayhulRNG {
42 | constructor(s0, s1) {
43 | this.s0 = s0;
44 | this.s1 = s1;
45 | }
46 |
47 | xorrayhul64p(){
48 | var s0 = (this.s0>>>0) & MASK;
49 | var s1 = (this.s1>>>0) & MASK;
50 |
51 | var r = (s0 + s1)>>>0 & MASK;
52 |
53 | s1 = ((s0 ^ s1)>>>0) & MASK;
54 | this.s0 = ((((s0 << 23)>>>0 | s0 >>> (32 - 23)) & MASK) ^ s1 ^ (s1 << 7)>>>0) & MASK;
55 | this.s1 = ((s1 << 18)>>>0 | s1 >>> (32 - 18)) & MASK;
56 | return r;
57 | }
58 |
59 | gen_rand(){
60 | var r = this.xorrayhul64p() & 0x1FFFFFF;
61 | console.log("r:", r);
62 | var index = r % 37;
63 | var text = options[index];
64 | return text;
65 | }
66 | }
67 |
68 | rng = new XoRRayhulRNG(Math.floor(Math.random()*Math.pow(2, 32)), Math.floor(Math.random()*Math.pow(2, 32)));
69 |
70 | function drawRouletteWheel() {
71 | var canvas = document.getElementById("canvas");
72 | if (canvas.getContext) {
73 | var outsideRadius = 200;
74 | var textRadius = 160;
75 | var insideRadius = 125;
76 |
77 | ctx = canvas.getContext("2d");
78 | ctx.clearRect(0, 0, 500, 500);
79 |
80 | ctx.strokeStyle = "white";
81 | ctx.lineWidth = 2;
82 |
83 | ctx.font = 'bold 12px Helvetica, Arial';
84 |
85 | for (var i = 0; i < options.length; i++) {
86 | var angle = startAngle + i * arc;
87 | //ctx.fillStyle = colors[i];
88 | ctx.fillStyle = getColor(i, options.length);
89 | ctx.beginPath();
90 | ctx.arc(250, 250, outsideRadius, angle, angle + arc, false);
91 | ctx.arc(250, 250, insideRadius, angle + arc, angle, true);
92 | ctx.stroke();
93 | ctx.fill();
94 |
95 | ctx.save();
96 | ctx.shadowOffsetX = -1;
97 | ctx.shadowOffsetY = -1;
98 | ctx.shadowBlur = 0;
99 | ctx.shadowColor = "rgb(220,220,220)";
100 | ctx.fillStyle = "black";
101 | ctx.translate(250 + Math.cos(angle + arc / 2) * textRadius,
102 | 250 + Math.sin(angle + arc / 2) * textRadius);
103 | ctx.rotate(angle + arc / 2 + Math.PI / 2);
104 | var text = options[i];
105 | // console.log("text", text, "angle", angle);
106 | ctx.fillStyle = 'white';
107 | ctx.fillText(text, -ctx.measureText(text).width / 2, 0);
108 | ctx.restore();
109 | }
110 |
111 | //Arrow
112 | ctx.fillStyle = "silver";
113 | ctx.beginPath();
114 | ctx.moveTo(250 - 4, 250 - (outsideRadius + 5));
115 | ctx.lineTo(250 + 4, 250 - (outsideRadius + 5));
116 | ctx.lineTo(250 + 4, 250 - (outsideRadius - 5));
117 | ctx.lineTo(250 + 9, 250 - (outsideRadius - 5));
118 | ctx.lineTo(250 + 0, 250 - (outsideRadius - 13));
119 | ctx.lineTo(250 - 9, 250 - (outsideRadius - 5));
120 | ctx.lineTo(250 - 4, 250 - (outsideRadius - 5));
121 | ctx.lineTo(250 - 4, 250 - (outsideRadius + 5));
122 | ctx.fill();
123 | }
124 | }
125 |
126 | function gamble(){
127 | wager = document.getElementById('wager').value;
128 | wager = parseInt(wager);
129 | if (isNaN(wager) || wager <= 0) {
130 | alert("Wager must be a positive number!");
131 | return;
132 | }
133 | guess = document.getElementById('guess').value;
134 | spin();
135 | }
136 |
137 | function spin() {
138 | spinAngleStart = 10;
139 |
140 | // Generate random number
141 | desiredNum = rng.gen_rand();
142 |
143 | spinTime = 0;
144 | spinTimeTotal = 2000;
145 | rotateWheel();
146 | }
147 |
148 | function rotateWheel(callback) {
149 | var degrees = startAngle * 180 / Math.PI + 90;
150 | var arcd = arc * 180 / Math.PI;
151 | var index = Math.floor((360 - degrees % 360) / arcd);
152 | var text = options[index];
153 |
154 | spinTime += 30;
155 |
156 | if (desiredNum == text && spinTime >= spinTimeTotal) {
157 | stopRotateWheel(function(){
158 | if (guess == desiredNum) {
159 | alert("Winner! Payout: $" + wager*35);
160 | } else {
161 | alert("You just lost $" + wager+ ". Better luck next time :(");
162 | }
163 | });
164 | return;
165 | }
166 |
167 | var spinAngle = spinAngleStart;
168 | startAngle += (spinAngle * Math.PI / 180);
169 | drawRouletteWheel();
170 | spinTimeout = setTimeout('rotateWheel()', 30);
171 | }
172 |
173 | function stopRotateWheel(callback) {
174 | clearTimeout(spinTimeout);
175 | var degrees = startAngle * 180 / Math.PI + 90;
176 | var arcd = arc * 180 / Math.PI;
177 | var index = Math.floor((360 - degrees % 360) / arcd);
178 | ctx.save();
179 | ctx.font = 'bold 30px Helvetica, Arial';
180 | var text = options[index]
181 | ctx.fillText(text, 250 - ctx.measureText(text).width / 2, 250 + 10);
182 | ctx.restore();
183 | callback();
184 | }
185 |
186 | function easeOut(t, b, c, d) {
187 | var ts = (t /= d) * t;
188 | var tc = ts * t;
189 | return b + c * (tc + -3 * ts + 3 * t);
190 | }
191 |
192 | drawRouletteWheel();
193 |
--------------------------------------------------------------------------------
/exercises/speck.ipynb:
--------------------------------------------------------------------------------
1 | {
2 | "cells": [
3 | {
4 | "cell_type": "code",
5 | "execution_count": null,
6 | "metadata": {},
7 | "outputs": [],
8 | "source": [
9 | "import sys\n",
10 | "sys.path.append(\"C:\\\\Users\\\\espuser\\\\z3_splash_class-master\\\\z3-4.5.0-x64-win\\\\bin\\\\python\")\n",
11 | "\n",
12 | "from z3 import *\n",
13 | "init(\"C:\\\\Users\\\\espuser\\\\z3_splash_class-master\\\\z3-4.5.0-x64-win\\\\bin\\\\libz3.dll\")\n",
14 | "\n",
15 | "import struct\n",
16 | "import binascii\n",
17 | "\n",
18 | "ROUNDS = 3\n",
19 | "MASK = (1 << 64) - 1\n",
20 | "\n",
21 | "#############################\n",
22 | "# SPECK functions #\n",
23 | "#############################\n",
24 | "\n",
25 | "# Rotate 64 bit integer x right by r\n",
26 | "def ror(x, r):\n",
27 | " return ((x >> r) | (x << (64 - r))) & MASK\n",
28 | "\n",
29 | "# Rotate 64 bit integer x left by r\n",
30 | "def rol(x, r):\n",
31 | " return ((x << r) | (x >> (64 - r))) & MASK\n",
32 | "\n",
33 | "# SPECK round function; x, y, and k are all 64 bits\n",
34 | "def r(x, y, k):\n",
35 | " x = ror(x, 8)\n",
36 | " x += y\n",
37 | " x &= MASK\n",
38 | " x ^= k\n",
39 | " y = rol(y, 3)\n",
40 | " y ^= x\n",
41 | " return x, y\n",
42 | "\n",
43 | "# SPECK undo round function; x, y, and k are all 64 bits\n",
44 | "def unr(x, y, k):\n",
45 | " y ^= x\n",
46 | " y = ror(y, 3)\n",
47 | " x ^= k\n",
48 | " x -= y\n",
49 | " x &= MASK\n",
50 | " x = rol(x, 8)\n",
51 | " return x, y\n",
52 | "\n",
53 | "# SPECK encrypt function; all inputs are 64 bits\n",
54 | "# x || y is the plaintext\n",
55 | "# a || b is the key\n",
56 | "def encrypt(x, y, a, b):\n",
57 | " for i in range(ROUNDS):\n",
58 | " x, y = r(x, y, b)\n",
59 | " a, b = r(a, b, i)\n",
60 | " return x, y\n",
61 | "\n",
62 | "# SPECK decrypt function; all inputs are 64 bits\n",
63 | "# x || y is the ciphertext\n",
64 | "# a || b is the key\n",
65 | "def decrypt(x, y, a, b):\n",
66 | " for i in range(ROUNDS):\n",
67 | " a, b = r(a, b, i)\n",
68 | " for i in range(ROUNDS - 1, -1, -1):\n",
69 | " a, b = unr(a, b, i)\n",
70 | " x, y = unr(x, y, b)\n",
71 | " return x, y\n",
72 | "\n",
73 | "#############################\n",
74 | "# z3 SPECK functions #\n",
75 | "#############################\n",
76 | "\n",
77 | "def z3_ror(x, r):\n",
78 | " return RotateRight(x, r)\n",
79 | "\n",
80 | "\n",
81 | "def z3_rol(x, r):\n",
82 | " return RotateLeft(x, r)\n",
83 | "\n",
84 | "# Write a z3 version of the SPECK round function, `r`\n",
85 | "# HINTS:\n",
86 | "# * Remember to use the z3 versions of `rol` and `ror`\n",
87 | "# defined just above\n",
88 | "# * z3 BitVectors already deal with overflow, so you can\n",
89 | "# ignore the MASK operation\n",
90 | "def z3_r(x, y, k):\n",
91 | " pass\n",
92 | "\n",
93 | "# Write a z3 version of the SPECK encrypt function\n",
94 | "# HINTS:\n",
95 | "# * Remember to use the z3 version of the round function you wrote\n",
96 | "def z3_encrypt(x, y, a, b):\n",
97 | " pass\n",
98 | "\n",
99 | "# Given a plaintext, ciphertext pair encrypted using 3-Round SPECK,\n",
100 | "# use z3 to derive the secret key, and then use that key to decrypt\n",
101 | "# a secret message\n",
102 | "def break_speck():\n",
103 | " plaintext = binascii.unhexlify('6c617669757165207469206564616d20')\n",
104 | " ciphertext = binascii.unhexlify('8b7de2836dece7b9a5871dfecf9d0551')\n",
105 | " p1 = struct.unpack('>Q', plaintext[:8])[0]\n",
106 | " p2 = struct.unpack('>Q', plaintext[8:])[0]\n",
107 | " c1 = struct.unpack('>Q', ciphertext[:8])[0]\n",
108 | " c2 = struct.unpack('>Q', ciphertext[8:])[0]\n",
109 | "\n",
110 | " x = BitVecVal(p1, 64)\n",
111 | " y = BitVecVal(p2, 64)\n",
112 | " a = BitVec('a', 64)\n",
113 | " b = BitVec('b', 64)\n",
114 | "\n",
115 | " try:\n",
116 | " s = Solver()\n",
117 | " o1, o2 = z3_encrypt(x, y, a, b)\n",
118 | " s.add(o1 == c1)\n",
119 | " s.add(o2 == c2)\n",
120 | " except:\n",
121 | " print('FAIL')\n",
122 | " return\n",
123 | "\n",
124 | " if s.check():\n",
125 | " print('SUCCESS')\n",
126 | " m = s.model()\n",
127 | " k1 = m[a].as_long()\n",
128 | " k2 = m[b].as_long()\n",
129 | "\n",
130 | " real_ctext = binascii.unhexlify('7625ed6dd6ee6d2c58d5ae4f217d39da')\n",
131 | " c1 = struct.unpack('>Q', real_ctext[:8])[0]\n",
132 | " c2 = struct.unpack('>Q', real_ctext[8:])[0]\n",
133 | " p1, p2 = decrypt(c1, c2, k1, k2)\n",
134 | "\n",
135 | " plaintext = struct.pack('>Q', p1) + struct.pack('>Q', p2)\n",
136 | " print(plaintext)\n",
137 | "\n",
138 | " else:\n",
139 | " print('FAIL')\n",
140 | "\n",
141 | "\n",
142 | "if __name__ == '__main__':\n",
143 | " break_speck()"
144 | ]
145 | },
146 | {
147 | "cell_type": "code",
148 | "execution_count": null,
149 | "metadata": {},
150 | "outputs": [],
151 | "source": []
152 | }
153 | ],
154 | "metadata": {
155 | "kernelspec": {
156 | "display_name": "Python 3",
157 | "language": "python",
158 | "name": "python3"
159 | },
160 | "language_info": {
161 | "codemirror_mode": {
162 | "name": "ipython",
163 | "version": 3
164 | },
165 | "file_extension": ".py",
166 | "mimetype": "text/x-python",
167 | "name": "python",
168 | "nbconvert_exporter": "python",
169 | "pygments_lexer": "ipython3",
170 | "version": "3.6.2"
171 | }
172 | },
173 | "nbformat": 4,
174 | "nbformat_minor": 1
175 | }
176 |
--------------------------------------------------------------------------------
/exercises/sudoku.ipynb:
--------------------------------------------------------------------------------
1 | {
2 | "cells": [
3 | {
4 | "cell_type": "code",
5 | "execution_count": null,
6 | "metadata": {},
7 | "outputs": [],
8 | "source": [
9 | "import sys\n",
10 | "sys.path.append(\"C:\\\\Users\\\\espuser\\\\z3_splash_class-master\\\\z3-4.5.0-x64-win\\\\bin\\\\python\")\n",
11 | "\n",
12 | "from z3 import *\n",
13 | "init(\"C:\\\\Users\\\\espuser\\\\z3_splash_class-master\\\\z3-4.5.0-x64-win\\\\bin\\\\libz3.dll\")\n",
14 | "import itertools\n",
15 | "from pprint import *\n",
16 | "\n",
17 | "\n",
18 | "s = Solver()\n",
19 | "cells=[[Int('cell_%d_%d' % (r, c)) for c in range(9)] for r in range(9)]\n",
20 | "\n",
21 | "game = \"\"\"\n",
22 | ". . 5 |3 . . |. . . \n",
23 | "8 . . |. . . |. 2 . \n",
24 | ". 7 . |. 1 . |5 . . \n",
25 | "------+------+------\n",
26 | "4 . . |. . 5 |3 . . \n",
27 | ". 1 . |. 7 . |. . 6 \n",
28 | ". . 3 |2 . . |. 8 . \n",
29 | "------+------+------\n",
30 | ". 6 . |5 . . |. . 9 \n",
31 | ". . 4 |. . . |. 3 . \n",
32 | ". . . |. . 9 |7 . . \n",
33 | "\"\"\"\n",
34 | "\n",
35 | "\n",
36 | "game = game.replace(\"|\", \"\").replace(\"-\", \"\").replace(\"+\", \"\")\n",
37 | "game = [row.split() for row in game.split(\"\\n\") if row != '']\n",
38 | "\n",
39 | "# Add cell constraints\n",
40 | "\n",
41 | "# Create row constraints\n",
42 | "for i in range(9):\n",
43 | " s.add(Distinct(cells[i]))\n",
44 | "\n",
45 | "# Create column constraints\n",
46 | "\n",
47 | "# Create subsquare constraints\n",
48 | "\n",
49 | "s.check()\n",
50 | "m = s.model()\n",
51 | "solved = [['.' for i in range(9)] for j in range(9)]\n",
52 | "for i in range(9):\n",
53 | " for j in range(9):\n",
54 | " a = m.evaluate(cells[i][j])\n",
55 | " solved[i][j] = a\n",
56 | "pprint(solved)\n"
57 | ]
58 | },
59 | {
60 | "cell_type": "code",
61 | "execution_count": null,
62 | "metadata": {},
63 | "outputs": [],
64 | "source": []
65 | }
66 | ],
67 | "metadata": {
68 | "kernelspec": {
69 | "display_name": "Python 3",
70 | "language": "python",
71 | "name": "python3"
72 | },
73 | "language_info": {
74 | "codemirror_mode": {
75 | "name": "ipython",
76 | "version": 3
77 | },
78 | "file_extension": ".py",
79 | "mimetype": "text/x-python",
80 | "name": "python",
81 | "nbconvert_exporter": "python",
82 | "pygments_lexer": "ipython3",
83 | "version": "3.6.2"
84 | }
85 | },
86 | "nbformat": 4,
87 | "nbformat_minor": 2
88 | }
89 |
--------------------------------------------------------------------------------
/exercises/xorrayhul64p-rng.ipynb:
--------------------------------------------------------------------------------
1 | {
2 | "cells": [
3 | {
4 | "cell_type": "code",
5 | "execution_count": null,
6 | "metadata": {},
7 | "outputs": [],
8 | "source": [
9 | "import sys\n",
10 | "sys.path.append(\"C:\\\\Users\\\\espuser\\\\z3_splash_class-master\\\\z3-4.5.0-x64-win\\\\bin\\\\python\")\n",
11 | "\n",
12 | "from z3 import *\n",
13 | "init(\"C:\\\\Users\\\\espuser\\\\z3_splash_class-master\\\\z3-4.5.0-x64-win\\\\bin\\\\libz3.dll\")\n",
14 | "\n",
15 | "import math\n",
16 | "import struct\n",
17 | "import random\n",
18 | "import binascii\n",
19 | "\n",
20 | "MASK = 0xFFFFFFFF\n",
21 | "\n",
22 | "\n",
23 | "def xorrayhul64p(state0, state1):\n",
24 | " s0 = state0 & MASK\n",
25 | " s1 = state1 & MASK\n",
26 | " r = (s0 + s1) & MASK\n",
27 | " s1 = (s0 ^ s1) & MASK\n",
28 | " state0 = ((((s0 << 23) | s0 >> (32 - 23)) & MASK) ^ s1 ^ (s1 << 7)) & MASK\n",
29 | " state1 = ((s1 << 18) | s1 >> (32 - 18)) & MASK\n",
30 | "\n",
31 | " return state0, state1, r\n",
32 | "\n",
33 | "# Symbolic execution of xorrayrahul64p\n",
34 | "# Add the constraint to the solver\n",
35 | "\n",
36 | "# As a note, Z3 has two right shifts — arithmetic right shift and a logical right shift. \n",
37 | "# You must use the logical shift function LShR, not the >> operator\n",
38 | "def z3_xorrayhul64p(slvr, sym_state0, sym_state1, rand_num):\n",
39 | " pass\n",
40 | "\n",
41 | "\n",
42 | "class RNG():\n",
43 | " def __init__(self, seed):\n",
44 | " self.s0 = struct.unpack('>I', seed[:4])[0]\n",
45 | " self.s1 = struct.unpack('>I', seed[4:])[0]\n",
46 | "\n",
47 | " def gen_rand(self):\n",
48 | " self.s0, self.s1, r = xorrayhul64p(self.s0, self.s1)\n",
49 | " return r & 0x1FFFFFF\n",
50 | " \n",
51 | "\n",
52 | "def break_rng():\n",
53 | " # setup symbolic state for xorshiro128+\n",
54 | " ostate0, ostate1 = BitVecs('ostate0 ostate1', 32)\n",
55 | " sym_state0 = ostate0\n",
56 | " sym_state1 = ostate1\n",
57 | " slvr = Solver()\n",
58 | " conditions = []\n",
59 | " \n",
60 | " # Fill in these random numbers from the roulette game\n",
61 | " rand_nums = [32893022, 9612492, 17187167]\n",
62 | "\n",
63 | " # run symbolic xorshiro128+ algorithm for three iterations\n",
64 | " # using the recovered numbers as constraints\n",
65 | " for r in rand_nums:\n",
66 | " sym_state0, sym_state1 = z3_xorrayhul64p(slvr, sym_state0, sym_state1, r)\n",
67 | "\n",
68 | " if slvr.check() == sat:\n",
69 | " print('SAT')\n",
70 | "\n",
71 | " # get a solved state\n",
72 | " m = slvr.model()\n",
73 | " state0 = m[ostate0].as_long()\n",
74 | " state1 = m[ostate1].as_long()\n",
75 | "\n",
76 | " # Print the next set of random numbers\n",
77 | " seed = struct.pack('>I', state0) + struct.pack('>I', state1)\n",
78 | " rng = RNG(seed)\n",
79 | " print(\"Next random numbers: \")\n",
80 | " for i in range(20): \n",
81 | " print(rng.gen_rand() % 37)\n",
82 | "\n",
83 | " else:\n",
84 | " print('UNSAT')\n",
85 | "\n",
86 | "\n",
87 | "if __name__ == '__main__':\n",
88 | " break_rng()"
89 | ]
90 | }
91 | ],
92 | "metadata": {
93 | "kernelspec": {
94 | "display_name": "Python 3",
95 | "language": "python",
96 | "name": "python3"
97 | },
98 | "language_info": {
99 | "codemirror_mode": {
100 | "name": "ipython",
101 | "version": 3
102 | },
103 | "file_extension": ".py",
104 | "mimetype": "text/x-python",
105 | "name": "python",
106 | "nbconvert_exporter": "python",
107 | "pygments_lexer": "ipython3",
108 | "version": "3.6.2"
109 | }
110 | },
111 | "nbformat": 4,
112 | "nbformat_minor": 1
113 | }
114 |
--------------------------------------------------------------------------------
/guide.pdf:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/TechSecCTF/z3_splash_class/b64cf9b51187c7b179b63ed4de43aa28b6a70fdb/guide.pdf
--------------------------------------------------------------------------------
/install.sh:
--------------------------------------------------------------------------------
1 | #!/bin/bash
2 | git clone git@github.com:Z3Prover/z3.git
3 | cd z3
4 | python scripts/mk_make.py --python
5 | cd build
6 | make -j8
7 | sudo make install
8 |
--------------------------------------------------------------------------------
/solutions/speck.ipynb:
--------------------------------------------------------------------------------
1 | {
2 | "cells": [
3 | {
4 | "cell_type": "code",
5 | "execution_count": null,
6 | "metadata": {},
7 | "outputs": [],
8 | "source": [
9 | "import sys\n",
10 | "sys.path.append(\"C:\\\\Users\\\\espuser\\\\z3_splash_class-master\\\\z3-4.5.0-x64-win\\\\bin\\\\python\")\n",
11 | "\n",
12 | "from z3 import *\n",
13 | "init(\"C:\\\\Users\\\\espuser\\\\z3_splash_class-master\\\\z3-4.5.0-x64-win\\\\bin\\\\libz3.dll\")\n",
14 | "\n",
15 | "import struct\n",
16 | "import binascii\n",
17 | "\n",
18 | "ROUNDS = 3\n",
19 | "MASK = (1 << 64) - 1\n",
20 | "\n",
21 | "#############################\n",
22 | "# SPECK functions #\n",
23 | "#############################\n",
24 | "\n",
25 | "# Rotate 64 bit integer x right by r\n",
26 | "def ror(x, r):\n",
27 | " return ((x >> r) | (x << (64 - r))) & MASK\n",
28 | "\n",
29 | "# Rotate 64 bit integer x left by r\n",
30 | "def rol(x, r):\n",
31 | " return ((x << r) | (x >> (64 - r))) & MASK\n",
32 | "\n",
33 | "# SPECK round function; x, y, and k are all 64 bits\n",
34 | "def r(x, y, k):\n",
35 | " x = ror(x, 8)\n",
36 | " x += y\n",
37 | " x &= MASK\n",
38 | " x ^= k\n",
39 | " y = rol(y, 3)\n",
40 | " y ^= x\n",
41 | " return x, y\n",
42 | "\n",
43 | "# SPECK undo round function; x, y, and k are all 64 bits\n",
44 | "def unr(x, y, k):\n",
45 | " y ^= x\n",
46 | " y = ror(y, 3)\n",
47 | " x ^= k\n",
48 | " x -= y\n",
49 | " x &= MASK\n",
50 | " x = rol(x, 8)\n",
51 | " return x, y\n",
52 | "\n",
53 | "# SPECK encrypt function; all inputs are 64 bits\n",
54 | "# x || y is the plaintext\n",
55 | "# a || b is the key\n",
56 | "def encrypt(x, y, a, b):\n",
57 | " for i in range(ROUNDS):\n",
58 | " x, y = r(x, y, b)\n",
59 | " a, b = r(a, b, i)\n",
60 | " return x, y\n",
61 | "\n",
62 | "# SPECK decrypt function; all inputs are 64 bits\n",
63 | "# x || y is the ciphertext\n",
64 | "# a || b is the key\n",
65 | "def decrypt(x, y, a, b):\n",
66 | " for i in range(ROUNDS):\n",
67 | " a, b = r(a, b, i)\n",
68 | " for i in range(ROUNDS - 1, -1, -1):\n",
69 | " a, b = unr(a, b, i)\n",
70 | " x, y = unr(x, y, b)\n",
71 | " return x, y\n",
72 | "\n",
73 | "#############################\n",
74 | "# z3 SPECK functions #\n",
75 | "#############################\n",
76 | "\n",
77 | "def z3_ror(x, r):\n",
78 | " return RotateRight(x, r)\n",
79 | "\n",
80 | "\n",
81 | "def z3_rol(x, r):\n",
82 | " return RotateLeft(x, r)\n",
83 | "\n",
84 | "# Write a z3 version of the SPECK round function, `r`\n",
85 | "# HINTS:\n",
86 | "# * Remember to use the z3 versions of `rol` and `ror`\n",
87 | "# defined just above\n",
88 | "# * z3 BitVectors already deal with overflow, so you can\n",
89 | "# ignore the MASK operation\n",
90 | "def z3_r(x, y, k):\n",
91 | " x = z3_ror(x, 8)\n",
92 | " x += y\n",
93 | " x ^= k\n",
94 | " y = z3_rol(y, 3)\n",
95 | " y ^= x\n",
96 | " return x, y\n",
97 | "\n",
98 | "# Write a z3 version of the SPECK encrypt function\n",
99 | "# HINTS:\n",
100 | "# * Remember to use the z3 version of the round function you wrote\n",
101 | "def z3_encrypt(x, y, a, b):\n",
102 | " for i in range(ROUNDS):\n",
103 | " x, y = z3_r(x, y, b)\n",
104 | " a, b = z3_r(a, b, i)\n",
105 | " return x, y\n",
106 | "\n",
107 | "# Given a plaintext, ciphertext pair encrypted using 3-Round SPECK,\n",
108 | "# use z3 to derive the secret key, and then use that key to decrypt\n",
109 | "# a secret message\n",
110 | "def break_speck():\n",
111 | " plaintext = binascii.unhexlify('6c617669757165207469206564616d20')\n",
112 | " ciphertext = binascii.unhexlify('8b7de2836dece7b9a5871dfecf9d0551')\n",
113 | " p1 = struct.unpack('>Q', plaintext[:8])[0]\n",
114 | " p2 = struct.unpack('>Q', plaintext[8:])[0]\n",
115 | " c1 = struct.unpack('>Q', ciphertext[:8])[0]\n",
116 | " c2 = struct.unpack('>Q', ciphertext[8:])[0]\n",
117 | "\n",
118 | " x = BitVecVal(p1, 64)\n",
119 | " y = BitVecVal(p2, 64)\n",
120 | " a = BitVec('a', 64)\n",
121 | " b = BitVec('b', 64)\n",
122 | "\n",
123 | " try:\n",
124 | " s = Solver()\n",
125 | " o1, o2 = z3_encrypt(x, y, a, b)\n",
126 | " s.add(o1 == c1)\n",
127 | " s.add(o2 == c2)\n",
128 | " except:\n",
129 | " print('FAIL')\n",
130 | " return\n",
131 | "\n",
132 | " if s.check():\n",
133 | " print('SUCCESS')\n",
134 | " m = s.model()\n",
135 | " k1 = m[a].as_long()\n",
136 | " k2 = m[b].as_long()\n",
137 | "\n",
138 | " real_ctext = binascii.unhexlify('7625ed6dd6ee6d2c58d5ae4f217d39da')\n",
139 | " c1 = struct.unpack('>Q', real_ctext[:8])[0]\n",
140 | " c2 = struct.unpack('>Q', real_ctext[8:])[0]\n",
141 | " p1, p2 = decrypt(c1, c2, k1, k2)\n",
142 | "\n",
143 | " plaintext = struct.pack('>Q', p1) + struct.pack('>Q', p2)\n",
144 | " print(plaintext)\n",
145 | "\n",
146 | " else:\n",
147 | " print('FAIL')\n",
148 | "\n",
149 | "\n",
150 | "if __name__ == '__main__':\n",
151 | " break_speck()"
152 | ]
153 | }
154 | ],
155 | "metadata": {
156 | "kernelspec": {
157 | "display_name": "Python 3",
158 | "language": "python",
159 | "name": "python3"
160 | },
161 | "language_info": {
162 | "codemirror_mode": {
163 | "name": "ipython",
164 | "version": 3
165 | },
166 | "file_extension": ".py",
167 | "mimetype": "text/x-python",
168 | "name": "python",
169 | "nbconvert_exporter": "python",
170 | "pygments_lexer": "ipython3",
171 | "version": "3.6.2"
172 | }
173 | },
174 | "nbformat": 4,
175 | "nbformat_minor": 2
176 | }
177 |
--------------------------------------------------------------------------------
/solutions/sudoku-solve.ipynb:
--------------------------------------------------------------------------------
1 | {
2 | "cells": [
3 | {
4 | "cell_type": "code",
5 | "execution_count": 2,
6 | "metadata": {},
7 | "outputs": [
8 | {
9 | "name": "stdout",
10 | "output_type": "stream",
11 | "text": [
12 | "count: 1\n",
13 | "[[8, 5, 2, 1, 7, 6, 9, 3, 4],\n",
14 | " [3, 4, 7, 2, 9, 8, 1, 5, 6],\n",
15 | " [9, 1, 6, 4, 3, 5, 7, 2, 8],\n",
16 | " [5, 2, 9, 8, 6, 3, 4, 7, 1],\n",
17 | " [4, 8, 3, 5, 1, 7, 6, 9, 2],\n",
18 | " [7, 6, 1, 9, 4, 2, 5, 8, 3],\n",
19 | " [2, 7, 8, 6, 5, 1, 3, 4, 9],\n",
20 | " [1, 9, 5, 3, 2, 4, 8, 6, 7],\n",
21 | " [6, 3, 4, 7, 8, 9, 2, 1, 5]]\n",
22 | "count: 2\n",
23 | "[[2, 5, 8, 1, 7, 6, 9, 3, 4],\n",
24 | " [3, 4, 7, 2, 9, 8, 1, 5, 6],\n",
25 | " [9, 1, 6, 4, 3, 5, 7, 2, 8],\n",
26 | " [5, 2, 9, 8, 6, 3, 4, 7, 1],\n",
27 | " [4, 8, 3, 5, 1, 7, 6, 9, 2],\n",
28 | " [7, 6, 1, 9, 4, 2, 5, 8, 3],\n",
29 | " [8, 7, 2, 6, 5, 1, 3, 4, 9],\n",
30 | " [1, 9, 5, 3, 2, 4, 8, 6, 7],\n",
31 | " [6, 3, 4, 7, 8, 9, 2, 1, 5]]\n"
32 | ]
33 | }
34 | ],
35 | "source": [
36 | "from z3 import *\n",
37 | "import itertools\n",
38 | "from pprint import *\n",
39 | "\n",
40 | "s = Solver()\n",
41 | "cells=[[Int('cell_%d_%d' % (r, c)) for c in range(9)] for r in range(9)]\n",
42 | "\n",
43 | "# game = \"\"\"\n",
44 | "# 8 . . . . . 9 . .\n",
45 | "# 7 . . 9 . . . 3 .\n",
46 | "# . . . . 3 . 1 . 7\n",
47 | "# . . . . . . . . .\n",
48 | "# 4 . 3 1 . . 2 5 .\n",
49 | "# . . 6 . . . . . .\n",
50 | "# . . . . . 7 . . 3\n",
51 | "# . 9 7 5 8 . . . .\n",
52 | "# . . . . . . 4 . .\n",
53 | "# \"\"\"\n",
54 | "\n",
55 | "# game = \"\"\"\n",
56 | "# 8 5 . |. . 2 |4 . . \n",
57 | "# 7 2 . |. . . |. . 9 \n",
58 | "# . . 4 |. . . |. . . \n",
59 | "# ------+------+------\n",
60 | "# . . . |1 . 7 |. . 2 \n",
61 | "# 3 . 5 |. . . |9 . . \n",
62 | "# . 4 . |. . . |. . . \n",
63 | "# ------+------+------\n",
64 | "# . . . |. 8 . |. 7 . \n",
65 | "# . 1 7 |. . . |. . . \n",
66 | "# . . . |. 3 6 |. 4 . \n",
67 | "# \"\"\"\n",
68 | "\n",
69 | "game = \"\"\"\n",
70 | ". . 5 |3 . . |. . . \n",
71 | "8 . . |. . . |. 2 . \n",
72 | ". 7 . |. 1 . |5 . . \n",
73 | "------+------+------\n",
74 | "4 . . |. . 5 |3 . . \n",
75 | ". 1 . |. 7 . |. . 6 \n",
76 | ". . 3 |2 . . |. 8 . \n",
77 | "------+------+------\n",
78 | ". 6 . |5 . . |. . 9 \n",
79 | ". . 4 |. . . |. 3 . \n",
80 | ". . . |. . 9 |7 . . \n",
81 | "\"\"\"\n",
82 | "\n",
83 | "game = \".5.1.6......2....69.6..5..8.2.....7...3..........4.5...7..5...919.3..8...3..8....\"\n",
84 | "# game = \".521.6......2....6..6..5..8.2.....7...3..........4.5...7..5...9.9.3..8...3..8....\"\n",
85 | "game = [game[9*i:9*i+9] for i in range(9)]\n",
86 | "\n",
87 | "# game = game.replace(\"|\", \"\").replace(\"-\", \"\").replace(\"+\", \"\")\n",
88 | "# game = [row.split() for row in game.split(\"\\n\") if row != '']\n",
89 | "# pprint(game)\n",
90 | "\n",
91 | "for i in range(9):\n",
92 | " for j in range(9):\n",
93 | " c = game[i][j]\n",
94 | " if c != '.':\n",
95 | " s.add(cells[i][j] == int(c))\n",
96 | "\n",
97 | "# Add cell constraints\n",
98 | "for y in range(9):\n",
99 | " for x in range(9):\n",
100 | " s.add(And(1 <= cells[x][y], cells[x][y] <= 9))\n",
101 | "\n",
102 | "# Create row constraints\n",
103 | "for row in cells:\n",
104 | " s.add(Distinct(row))\n",
105 | "\n",
106 | "# Create column constraints \n",
107 | "cols = [[row[i] for row in cells] for i in range(9)]\n",
108 | "for col in cols:\n",
109 | " s.add(Distinct(col))\n",
110 | "\n",
111 | "# Create subsquare constraints\n",
112 | "for i in range(0,9,3):\n",
113 | " for j in range(0,9,3):\n",
114 | " s.add(Distinct([cells[x][y] for x, y in itertools.product(range(i, i+3), range(j, j+3))]))\n",
115 | "\n",
116 | "def add_constraints(m):\n",
117 | " constraints = []\n",
118 | " for i in range(9):\n",
119 | " for j in range(9):\n",
120 | " c = game[i][j]\n",
121 | " if c == '.':\n",
122 | " constraints.append(cells[i][j] != m.evaluate(cells[i][j]))\n",
123 | " return constraints\n",
124 | "\n",
125 | "count = 0 \n",
126 | "while s.check() == sat:\n",
127 | " m = s.model()\n",
128 | " count+=1\n",
129 | " print(\"count:\", count)\n",
130 | "\n",
131 | " solved = [['.' for i in range(9)] for j in range(9)]\n",
132 | " for i in range(9):\n",
133 | " for j in range(9):\n",
134 | " a = m.evaluate(cells[i][j])\n",
135 | " solved[i][j] = a\n",
136 | " pprint(solved)\n",
137 | " s.add(Or(add_constraints(m))) # At least one square must be different from previous solutions"
138 | ]
139 | },
140 | {
141 | "cell_type": "code",
142 | "execution_count": null,
143 | "metadata": {},
144 | "outputs": [],
145 | "source": []
146 | }
147 | ],
148 | "metadata": {
149 | "kernelspec": {
150 | "display_name": "Python 3",
151 | "language": "python",
152 | "name": "python3"
153 | },
154 | "language_info": {
155 | "codemirror_mode": {
156 | "name": "ipython",
157 | "version": 3
158 | },
159 | "file_extension": ".py",
160 | "mimetype": "text/x-python",
161 | "name": "python",
162 | "nbconvert_exporter": "python",
163 | "pygments_lexer": "ipython3",
164 | "version": "3.6.3"
165 | }
166 | },
167 | "nbformat": 4,
168 | "nbformat_minor": 2
169 | }
170 |
--------------------------------------------------------------------------------
/solutions/xorrayhul64p-rng-solved.ipynb:
--------------------------------------------------------------------------------
1 | {
2 | "cells": [
3 | {
4 | "cell_type": "code",
5 | "execution_count": 1,
6 | "metadata": {},
7 | "outputs": [
8 | {
9 | "name": "stdout",
10 | "output_type": "stream",
11 | "text": [
12 | "SAT\n",
13 | "b\"i'J\\xcdI\\xd0\\xbb\\xee\"\n",
14 | "1764182733 1238416366\n",
15 | "33\n",
16 | "5\n",
17 | "18\n",
18 | "36\n",
19 | "0\n",
20 | "27\n",
21 | "16\n",
22 | "21\n",
23 | "24\n",
24 | "0\n",
25 | "7\n",
26 | "18\n",
27 | "34\n",
28 | "25\n",
29 | "23\n",
30 | "29\n",
31 | "23\n",
32 | "33\n",
33 | "29\n",
34 | "32\n"
35 | ]
36 | }
37 | ],
38 | "source": [
39 | "import math\n",
40 | "import struct\n",
41 | "import random\n",
42 | "import binascii\n",
43 | "from z3 import *\n",
44 | "\n",
45 | "MASK = 0xFFFFFFFF\n",
46 | "\n",
47 | "\n",
48 | "def xorrayhul64p(state0, state1):\n",
49 | " s0 = state0 & MASK\n",
50 | " s1 = state1 & MASK\n",
51 | " r = (s0 + s1) & MASK\n",
52 | " s1 = (s0 ^ s1) & MASK\n",
53 | " state0 = ((((s0 << 23) | s0 >> (32 - 23)) & MASK) ^ s1 ^ (s1 << 7)) & MASK\n",
54 | " state1 = ((s1 << 18) | s1 >> (32 - 18)) & MASK\n",
55 | "\n",
56 | " return state0, state1, r\n",
57 | "\n",
58 | "# Symbolic execution of xs128p\n",
59 | "# Add the constraint to the solver\n",
60 | "# As a note, Z3 has two right shifts — arithmetic right shift and a logical right shift. \n",
61 | "# It uses the arithmetic shift when shifting with the >> operator. must use the logical shift LShR\n",
62 | "\n",
63 | "def z3_xorrayhul64p(slvr, sym_state0, sym_state1, rand_num):\n",
64 | " slvr.add(rand_num == ((sym_state0 + sym_state1) & 0x1FFFFFF))\n",
65 | " sym_state1 = sym_state0 ^ sym_state1\n",
66 | " sym_state0 = (((sym_state0 << 23) | LShR(sym_state0, (32 - 23))) ^ sym_state1 ^ (sym_state1 << 7))\n",
67 | " sym_state1 = ((sym_state1 << 18) | LShR(sym_state1, (32 - 18)))\n",
68 | "\n",
69 | " return sym_state0, sym_state1\n",
70 | "\n",
71 | "\n",
72 | "class RNG():\n",
73 | " def __init__(self, seed):\n",
74 | " self.s0 = struct.unpack('>I', seed[:4])[0]\n",
75 | " self.s1 = struct.unpack('>I', seed[4:])[0]\n",
76 | " print(self.s0, self.s1)\n",
77 | "\n",
78 | " def gen_rand(self):\n",
79 | " self.s0, self.s1, r = xorrayhul64p(self.s0, self.s1)\n",
80 | " return r & 0x1FFFFFF\n",
81 | " \n",
82 | "\n",
83 | "def break_rng():\n",
84 | " # setup symbolic state for xorshiro128+\n",
85 | " ostate0, ostate1 = BitVecs('ostate0 ostate1', 32)\n",
86 | " sym_state0 = ostate0\n",
87 | " sym_state1 = ostate1\n",
88 | " slvr = Solver()\n",
89 | " conditions = []\n",
90 | " \n",
91 | " \n",
92 | " rand_nums = [16254651, 4749029, 16361085]\n",
93 | "\n",
94 | " # run symbolic xorshiro128+ algorithm for three iterations\n",
95 | " # using the recovered numbers as constraints\n",
96 | " for r in rand_nums:\n",
97 | " sym_state0, sym_state1 = z3_xorrayhul64p(slvr, sym_state0, sym_state1, r)\n",
98 | "\n",
99 | " if slvr.check() == sat:\n",
100 | " print('SAT')\n",
101 | "\n",
102 | " # get a solved state\n",
103 | " m = slvr.model()\n",
104 | " state0 = m[ostate0].as_long()\n",
105 | " state1 = m[ostate1].as_long()\n",
106 | "\n",
107 | " # Print the next set of random numbers\n",
108 | " seed = struct.pack('>I', state0) + struct.pack('>I', state1)\n",
109 | " print(seed)\n",
110 | " rng = RNG(seed)\n",
111 | " for i in range(20): \n",
112 | " print(rng.gen_rand() % 37)\n",
113 | "\n",
114 | " else:\n",
115 | " print('UNSAT')\n",
116 | "\n",
117 | "\n",
118 | "if __name__ == '__main__':\n",
119 | " break_rng()\n"
120 | ]
121 | }
122 | ],
123 | "metadata": {
124 | "kernelspec": {
125 | "display_name": "Python 3",
126 | "language": "python",
127 | "name": "python3"
128 | },
129 | "language_info": {
130 | "codemirror_mode": {
131 | "name": "ipython",
132 | "version": 3
133 | },
134 | "file_extension": ".py",
135 | "mimetype": "text/x-python",
136 | "name": "python",
137 | "nbconvert_exporter": "python",
138 | "pygments_lexer": "ipython3",
139 | "version": "3.6.3"
140 | }
141 | },
142 | "nbformat": 4,
143 | "nbformat_minor": 1
144 | }
145 |
--------------------------------------------------------------------------------
/z3-4.5.0-x64-win/LICENSE.txt:
--------------------------------------------------------------------------------
1 | Z3
2 | Copyright (c) Microsoft Corporation
3 | All rights reserved.
4 | MIT License
5 | Permission is hereby granted, free of charge, to any person obtaining a copy of this software and associated documentation files (the ""Software""), to deal in the Software without restriction, including without limitation the rights to use, copy, modify, merge, publish, distribute, sublicense, and/or sell copies of the Software, and to permit persons to whom the Software is furnished to do so, subject to the following conditions:
6 | The above copyright notice and this permission notice shall be included in all copies or substantial portions of the Software.
7 | THE SOFTWARE IS PROVIDED *AS IS*, WITHOUT WARRANTY OF ANY KIND, EXPRESS OR IMPLIED, INCLUDING BUT NOT LIMITED TO THE WARRANTIES OF MERCHANTABILITY, FITNESS FOR A PARTICULAR PURPOSE AND NONINFRINGEMENT. IN NO EVENT SHALL THE AUTHORS OR COPYRIGHT HOLDERS BE LIABLE FOR ANY CLAIM, DAMAGES OR OTHER LIABILITY, WHETHER IN AN ACTION OF CONTRACT, TORT OR OTHERWISE, ARISING FROM, OUT OF OR IN CONNECTION WITH THE SOFTWARE OR THE USE OR OTHER DEALINGS IN THE SOFTWARE.
8 |
--------------------------------------------------------------------------------
/z3-4.5.0-x64-win/bin/Microsoft.Z3.dll:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/TechSecCTF/z3_splash_class/b64cf9b51187c7b179b63ed4de43aa28b6a70fdb/z3-4.5.0-x64-win/bin/Microsoft.Z3.dll
--------------------------------------------------------------------------------
/z3-4.5.0-x64-win/bin/com.microsoft.z3.jar:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/TechSecCTF/z3_splash_class/b64cf9b51187c7b179b63ed4de43aa28b6a70fdb/z3-4.5.0-x64-win/bin/com.microsoft.z3.jar
--------------------------------------------------------------------------------
/z3-4.5.0-x64-win/bin/libz3.dll:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/TechSecCTF/z3_splash_class/b64cf9b51187c7b179b63ed4de43aa28b6a70fdb/z3-4.5.0-x64-win/bin/libz3.dll
--------------------------------------------------------------------------------
/z3-4.5.0-x64-win/bin/libz3.lib:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/TechSecCTF/z3_splash_class/b64cf9b51187c7b179b63ed4de43aa28b6a70fdb/z3-4.5.0-x64-win/bin/libz3.lib
--------------------------------------------------------------------------------
/z3-4.5.0-x64-win/bin/libz3java.dll:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/TechSecCTF/z3_splash_class/b64cf9b51187c7b179b63ed4de43aa28b6a70fdb/z3-4.5.0-x64-win/bin/libz3java.dll
--------------------------------------------------------------------------------
/z3-4.5.0-x64-win/bin/libz3java.lib:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/TechSecCTF/z3_splash_class/b64cf9b51187c7b179b63ed4de43aa28b6a70fdb/z3-4.5.0-x64-win/bin/libz3java.lib
--------------------------------------------------------------------------------
/z3-4.5.0-x64-win/bin/msvcp110.dll:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/TechSecCTF/z3_splash_class/b64cf9b51187c7b179b63ed4de43aa28b6a70fdb/z3-4.5.0-x64-win/bin/msvcp110.dll
--------------------------------------------------------------------------------
/z3-4.5.0-x64-win/bin/msvcr110.dll:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/TechSecCTF/z3_splash_class/b64cf9b51187c7b179b63ed4de43aa28b6a70fdb/z3-4.5.0-x64-win/bin/msvcr110.dll
--------------------------------------------------------------------------------
/z3-4.5.0-x64-win/bin/python/example.py:
--------------------------------------------------------------------------------
1 | # Copyright (c) Microsoft Corporation 2015, 2016
2 |
3 | # The Z3 Python API requires libz3.dll/.so/.dylib in the
4 | # PATH/LD_LIBRARY_PATH/DYLD_LIBRARY_PATH
5 | # environment variable and the PYTHON_PATH environment variable
6 | # needs to point to the `python' directory that contains `z3/z3.py'
7 | # (which is at bin/python in our binary releases).
8 |
9 | # If you obtained example.py as part of our binary release zip files,
10 | # which you unzipped into a directory called `MYZ3', then follow these
11 | # instructions to run the example:
12 |
13 | # Running this example on Windows:
14 | # set PATH=%PATH%;MYZ3\bin
15 | # set PYTHONPATH=MYZ3\bin\python
16 | # python example.py
17 |
18 | # Running this example on Linux:
19 | # export LD_LIBRARY_PATH=$LD_LIBRARY_PATH:MYZ3/bin
20 | # export PYTHONPATH=MYZ3/bin/python
21 | # python example.py
22 |
23 | # Running this example on OSX:
24 | # export DYLD_LIBRARY_PATH=$DYLD_LIBRARY_PATH:MYZ3/bin
25 | # export PYTHONPATH=MYZ3/bin/python
26 | # python example.py
27 |
28 |
29 | from z3 import *
30 |
31 | x = Real('x')
32 | y = Real('y')
33 | s = Solver()
34 | s.add(x + y > 5, x > 1, y > 1)
35 | print(s.check())
36 | print(s.model())
37 |
--------------------------------------------------------------------------------
/z3-4.5.0-x64-win/bin/python/z3/__init__.py:
--------------------------------------------------------------------------------
1 | from .z3 import *
2 |
3 | from . import z3num
4 | from . import z3poly
5 | from . import z3printer
6 | from . import z3rcf
7 | from . import z3types
8 | from . import z3util
9 |
10 | # generated files
11 | from . import z3core
12 | from . import z3consts
13 |
--------------------------------------------------------------------------------
/z3-4.5.0-x64-win/bin/python/z3/__init__.pyc:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/TechSecCTF/z3_splash_class/b64cf9b51187c7b179b63ed4de43aa28b6a70fdb/z3-4.5.0-x64-win/bin/python/z3/__init__.pyc
--------------------------------------------------------------------------------
/z3-4.5.0-x64-win/bin/python/z3/z3.pyc:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/TechSecCTF/z3_splash_class/b64cf9b51187c7b179b63ed4de43aa28b6a70fdb/z3-4.5.0-x64-win/bin/python/z3/z3.pyc
--------------------------------------------------------------------------------
/z3-4.5.0-x64-win/bin/python/z3/z3consts.py:
--------------------------------------------------------------------------------
1 | # Automatically generated file
2 |
3 | # enum Z3_lbool
4 | Z3_L_FALSE = -1
5 | Z3_L_UNDEF = 0
6 | Z3_L_TRUE = 1
7 |
8 | # enum Z3_symbol_kind
9 | Z3_INT_SYMBOL = 0
10 | Z3_STRING_SYMBOL = 1
11 |
12 | # enum Z3_parameter_kind
13 | Z3_PARAMETER_INT = 0
14 | Z3_PARAMETER_DOUBLE = 1
15 | Z3_PARAMETER_RATIONAL = 2
16 | Z3_PARAMETER_SYMBOL = 3
17 | Z3_PARAMETER_SORT = 4
18 | Z3_PARAMETER_AST = 5
19 | Z3_PARAMETER_FUNC_DECL = 6
20 |
21 | # enum Z3_sort_kind
22 | Z3_UNINTERPRETED_SORT = 0
23 | Z3_BOOL_SORT = 1
24 | Z3_INT_SORT = 2
25 | Z3_REAL_SORT = 3
26 | Z3_BV_SORT = 4
27 | Z3_ARRAY_SORT = 5
28 | Z3_DATATYPE_SORT = 6
29 | Z3_RELATION_SORT = 7
30 | Z3_FINITE_DOMAIN_SORT = 8
31 | Z3_FLOATING_POINT_SORT = 9
32 | Z3_ROUNDING_MODE_SORT = 10
33 | Z3_SEQ_SORT = 11
34 | Z3_RE_SORT = 12
35 | Z3_UNKNOWN_SORT = 1000
36 |
37 | # enum Z3_ast_kind
38 | Z3_NUMERAL_AST = 0
39 | Z3_APP_AST = 1
40 | Z3_VAR_AST = 2
41 | Z3_QUANTIFIER_AST = 3
42 | Z3_SORT_AST = 4
43 | Z3_FUNC_DECL_AST = 5
44 | Z3_UNKNOWN_AST = 1000
45 |
46 | # enum Z3_decl_kind
47 | Z3_OP_TRUE = 256
48 | Z3_OP_FALSE = 257
49 | Z3_OP_EQ = 258
50 | Z3_OP_DISTINCT = 259
51 | Z3_OP_ITE = 260
52 | Z3_OP_AND = 261
53 | Z3_OP_OR = 262
54 | Z3_OP_IFF = 263
55 | Z3_OP_XOR = 264
56 | Z3_OP_NOT = 265
57 | Z3_OP_IMPLIES = 266
58 | Z3_OP_OEQ = 267
59 | Z3_OP_INTERP = 268
60 | Z3_OP_ANUM = 512
61 | Z3_OP_AGNUM = 513
62 | Z3_OP_LE = 514
63 | Z3_OP_GE = 515
64 | Z3_OP_LT = 516
65 | Z3_OP_GT = 517
66 | Z3_OP_ADD = 518
67 | Z3_OP_SUB = 519
68 | Z3_OP_UMINUS = 520
69 | Z3_OP_MUL = 521
70 | Z3_OP_DIV = 522
71 | Z3_OP_IDIV = 523
72 | Z3_OP_REM = 524
73 | Z3_OP_MOD = 525
74 | Z3_OP_TO_REAL = 526
75 | Z3_OP_TO_INT = 527
76 | Z3_OP_IS_INT = 528
77 | Z3_OP_POWER = 529
78 | Z3_OP_STORE = 768
79 | Z3_OP_SELECT = 769
80 | Z3_OP_CONST_ARRAY = 770
81 | Z3_OP_ARRAY_MAP = 771
82 | Z3_OP_ARRAY_DEFAULT = 772
83 | Z3_OP_SET_UNION = 773
84 | Z3_OP_SET_INTERSECT = 774
85 | Z3_OP_SET_DIFFERENCE = 775
86 | Z3_OP_SET_COMPLEMENT = 776
87 | Z3_OP_SET_SUBSET = 777
88 | Z3_OP_AS_ARRAY = 778
89 | Z3_OP_ARRAY_EXT = 779
90 | Z3_OP_BNUM = 1024
91 | Z3_OP_BIT1 = 1025
92 | Z3_OP_BIT0 = 1026
93 | Z3_OP_BNEG = 1027
94 | Z3_OP_BADD = 1028
95 | Z3_OP_BSUB = 1029
96 | Z3_OP_BMUL = 1030
97 | Z3_OP_BSDIV = 1031
98 | Z3_OP_BUDIV = 1032
99 | Z3_OP_BSREM = 1033
100 | Z3_OP_BUREM = 1034
101 | Z3_OP_BSMOD = 1035
102 | Z3_OP_BSDIV0 = 1036
103 | Z3_OP_BUDIV0 = 1037
104 | Z3_OP_BSREM0 = 1038
105 | Z3_OP_BUREM0 = 1039
106 | Z3_OP_BSMOD0 = 1040
107 | Z3_OP_ULEQ = 1041
108 | Z3_OP_SLEQ = 1042
109 | Z3_OP_UGEQ = 1043
110 | Z3_OP_SGEQ = 1044
111 | Z3_OP_ULT = 1045
112 | Z3_OP_SLT = 1046
113 | Z3_OP_UGT = 1047
114 | Z3_OP_SGT = 1048
115 | Z3_OP_BAND = 1049
116 | Z3_OP_BOR = 1050
117 | Z3_OP_BNOT = 1051
118 | Z3_OP_BXOR = 1052
119 | Z3_OP_BNAND = 1053
120 | Z3_OP_BNOR = 1054
121 | Z3_OP_BXNOR = 1055
122 | Z3_OP_CONCAT = 1056
123 | Z3_OP_SIGN_EXT = 1057
124 | Z3_OP_ZERO_EXT = 1058
125 | Z3_OP_EXTRACT = 1059
126 | Z3_OP_REPEAT = 1060
127 | Z3_OP_BREDOR = 1061
128 | Z3_OP_BREDAND = 1062
129 | Z3_OP_BCOMP = 1063
130 | Z3_OP_BSHL = 1064
131 | Z3_OP_BLSHR = 1065
132 | Z3_OP_BASHR = 1066
133 | Z3_OP_ROTATE_LEFT = 1067
134 | Z3_OP_ROTATE_RIGHT = 1068
135 | Z3_OP_EXT_ROTATE_LEFT = 1069
136 | Z3_OP_EXT_ROTATE_RIGHT = 1070
137 | Z3_OP_INT2BV = 1071
138 | Z3_OP_BV2INT = 1072
139 | Z3_OP_CARRY = 1073
140 | Z3_OP_XOR3 = 1074
141 | Z3_OP_BSMUL_NO_OVFL = 1075
142 | Z3_OP_BUMUL_NO_OVFL = 1076
143 | Z3_OP_BSMUL_NO_UDFL = 1077
144 | Z3_OP_BSDIV_I = 1078
145 | Z3_OP_BUDIV_I = 1079
146 | Z3_OP_BSREM_I = 1080
147 | Z3_OP_BUREM_I = 1081
148 | Z3_OP_BSMOD_I = 1082
149 | Z3_OP_PR_UNDEF = 1280
150 | Z3_OP_PR_TRUE = 1281
151 | Z3_OP_PR_ASSERTED = 1282
152 | Z3_OP_PR_GOAL = 1283
153 | Z3_OP_PR_MODUS_PONENS = 1284
154 | Z3_OP_PR_REFLEXIVITY = 1285
155 | Z3_OP_PR_SYMMETRY = 1286
156 | Z3_OP_PR_TRANSITIVITY = 1287
157 | Z3_OP_PR_TRANSITIVITY_STAR = 1288
158 | Z3_OP_PR_MONOTONICITY = 1289
159 | Z3_OP_PR_QUANT_INTRO = 1290
160 | Z3_OP_PR_DISTRIBUTIVITY = 1291
161 | Z3_OP_PR_AND_ELIM = 1292
162 | Z3_OP_PR_NOT_OR_ELIM = 1293
163 | Z3_OP_PR_REWRITE = 1294
164 | Z3_OP_PR_REWRITE_STAR = 1295
165 | Z3_OP_PR_PULL_QUANT = 1296
166 | Z3_OP_PR_PULL_QUANT_STAR = 1297
167 | Z3_OP_PR_PUSH_QUANT = 1298
168 | Z3_OP_PR_ELIM_UNUSED_VARS = 1299
169 | Z3_OP_PR_DER = 1300
170 | Z3_OP_PR_QUANT_INST = 1301
171 | Z3_OP_PR_HYPOTHESIS = 1302
172 | Z3_OP_PR_LEMMA = 1303
173 | Z3_OP_PR_UNIT_RESOLUTION = 1304
174 | Z3_OP_PR_IFF_TRUE = 1305
175 | Z3_OP_PR_IFF_FALSE = 1306
176 | Z3_OP_PR_COMMUTATIVITY = 1307
177 | Z3_OP_PR_DEF_AXIOM = 1308
178 | Z3_OP_PR_DEF_INTRO = 1309
179 | Z3_OP_PR_APPLY_DEF = 1310
180 | Z3_OP_PR_IFF_OEQ = 1311
181 | Z3_OP_PR_NNF_POS = 1312
182 | Z3_OP_PR_NNF_NEG = 1313
183 | Z3_OP_PR_NNF_STAR = 1314
184 | Z3_OP_PR_CNF_STAR = 1315
185 | Z3_OP_PR_SKOLEMIZE = 1316
186 | Z3_OP_PR_MODUS_PONENS_OEQ = 1317
187 | Z3_OP_PR_TH_LEMMA = 1318
188 | Z3_OP_PR_HYPER_RESOLVE = 1319
189 | Z3_OP_RA_STORE = 1536
190 | Z3_OP_RA_EMPTY = 1537
191 | Z3_OP_RA_IS_EMPTY = 1538
192 | Z3_OP_RA_JOIN = 1539
193 | Z3_OP_RA_UNION = 1540
194 | Z3_OP_RA_WIDEN = 1541
195 | Z3_OP_RA_PROJECT = 1542
196 | Z3_OP_RA_FILTER = 1543
197 | Z3_OP_RA_NEGATION_FILTER = 1544
198 | Z3_OP_RA_RENAME = 1545
199 | Z3_OP_RA_COMPLEMENT = 1546
200 | Z3_OP_RA_SELECT = 1547
201 | Z3_OP_RA_CLONE = 1548
202 | Z3_OP_FD_CONSTANT = 1549
203 | Z3_OP_FD_LT = 1550
204 | Z3_OP_SEQ_UNIT = 1551
205 | Z3_OP_SEQ_EMPTY = 1552
206 | Z3_OP_SEQ_CONCAT = 1553
207 | Z3_OP_SEQ_PREFIX = 1554
208 | Z3_OP_SEQ_SUFFIX = 1555
209 | Z3_OP_SEQ_CONTAINS = 1556
210 | Z3_OP_SEQ_EXTRACT = 1557
211 | Z3_OP_SEQ_REPLACE = 1558
212 | Z3_OP_SEQ_AT = 1559
213 | Z3_OP_SEQ_LENGTH = 1560
214 | Z3_OP_SEQ_INDEX = 1561
215 | Z3_OP_SEQ_TO_RE = 1562
216 | Z3_OP_SEQ_IN_RE = 1563
217 | Z3_OP_RE_PLUS = 1564
218 | Z3_OP_RE_STAR = 1565
219 | Z3_OP_RE_OPTION = 1566
220 | Z3_OP_RE_CONCAT = 1567
221 | Z3_OP_RE_UNION = 1568
222 | Z3_OP_LABEL = 1792
223 | Z3_OP_LABEL_LIT = 1793
224 | Z3_OP_DT_CONSTRUCTOR = 2048
225 | Z3_OP_DT_RECOGNISER = 2049
226 | Z3_OP_DT_ACCESSOR = 2050
227 | Z3_OP_DT_UPDATE_FIELD = 2051
228 | Z3_OP_PB_AT_MOST = 2304
229 | Z3_OP_PB_LE = 2305
230 | Z3_OP_PB_GE = 2306
231 | Z3_OP_PB_EQ = 2307
232 | Z3_OP_FPA_RM_NEAREST_TIES_TO_EVEN = 2308
233 | Z3_OP_FPA_RM_NEAREST_TIES_TO_AWAY = 2309
234 | Z3_OP_FPA_RM_TOWARD_POSITIVE = 2310
235 | Z3_OP_FPA_RM_TOWARD_NEGATIVE = 2311
236 | Z3_OP_FPA_RM_TOWARD_ZERO = 2312
237 | Z3_OP_FPA_NUM = 2313
238 | Z3_OP_FPA_PLUS_INF = 2314
239 | Z3_OP_FPA_MINUS_INF = 2315
240 | Z3_OP_FPA_NAN = 2316
241 | Z3_OP_FPA_PLUS_ZERO = 2317
242 | Z3_OP_FPA_MINUS_ZERO = 2318
243 | Z3_OP_FPA_ADD = 2319
244 | Z3_OP_FPA_SUB = 2320
245 | Z3_OP_FPA_NEG = 2321
246 | Z3_OP_FPA_MUL = 2322
247 | Z3_OP_FPA_DIV = 2323
248 | Z3_OP_FPA_REM = 2324
249 | Z3_OP_FPA_ABS = 2325
250 | Z3_OP_FPA_MIN = 2326
251 | Z3_OP_FPA_MAX = 2327
252 | Z3_OP_FPA_FMA = 2328
253 | Z3_OP_FPA_SQRT = 2329
254 | Z3_OP_FPA_ROUND_TO_INTEGRAL = 2330
255 | Z3_OP_FPA_EQ = 2331
256 | Z3_OP_FPA_LT = 2332
257 | Z3_OP_FPA_GT = 2333
258 | Z3_OP_FPA_LE = 2334
259 | Z3_OP_FPA_GE = 2335
260 | Z3_OP_FPA_IS_NAN = 2336
261 | Z3_OP_FPA_IS_INF = 2337
262 | Z3_OP_FPA_IS_ZERO = 2338
263 | Z3_OP_FPA_IS_NORMAL = 2339
264 | Z3_OP_FPA_IS_SUBNORMAL = 2340
265 | Z3_OP_FPA_IS_NEGATIVE = 2341
266 | Z3_OP_FPA_IS_POSITIVE = 2342
267 | Z3_OP_FPA_FP = 2343
268 | Z3_OP_FPA_TO_FP = 2344
269 | Z3_OP_FPA_TO_FP_UNSIGNED = 2345
270 | Z3_OP_FPA_TO_UBV = 2346
271 | Z3_OP_FPA_TO_SBV = 2347
272 | Z3_OP_FPA_TO_REAL = 2348
273 | Z3_OP_FPA_TO_IEEE_BV = 2349
274 | Z3_OP_FPA_MIN_I = 2350
275 | Z3_OP_FPA_MAX_I = 2351
276 | Z3_OP_INTERNAL = 2352
277 | Z3_OP_UNINTERPRETED = 2353
278 |
279 | # enum Z3_param_kind
280 | Z3_PK_UINT = 0
281 | Z3_PK_BOOL = 1
282 | Z3_PK_DOUBLE = 2
283 | Z3_PK_SYMBOL = 3
284 | Z3_PK_STRING = 4
285 | Z3_PK_OTHER = 5
286 | Z3_PK_INVALID = 6
287 |
288 | # enum Z3_ast_print_mode
289 | Z3_PRINT_SMTLIB_FULL = 0
290 | Z3_PRINT_LOW_LEVEL = 1
291 | Z3_PRINT_SMTLIB_COMPLIANT = 2
292 | Z3_PRINT_SMTLIB2_COMPLIANT = 3
293 |
294 | # enum Z3_error_code
295 | Z3_OK = 0
296 | Z3_SORT_ERROR = 1
297 | Z3_IOB = 2
298 | Z3_INVALID_ARG = 3
299 | Z3_PARSER_ERROR = 4
300 | Z3_NO_PARSER = 5
301 | Z3_INVALID_PATTERN = 6
302 | Z3_MEMOUT_FAIL = 7
303 | Z3_FILE_ACCESS_ERROR = 8
304 | Z3_INTERNAL_FATAL = 9
305 | Z3_INVALID_USAGE = 10
306 | Z3_DEC_REF_ERROR = 11
307 | Z3_EXCEPTION = 12
308 |
309 | # enum Z3_goal_prec
310 | Z3_GOAL_PRECISE = 0
311 | Z3_GOAL_UNDER = 1
312 | Z3_GOAL_OVER = 2
313 | Z3_GOAL_UNDER_OVER = 3
314 |
315 |
--------------------------------------------------------------------------------
/z3-4.5.0-x64-win/bin/python/z3/z3consts.pyc:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/TechSecCTF/z3_splash_class/b64cf9b51187c7b179b63ed4de43aa28b6a70fdb/z3-4.5.0-x64-win/bin/python/z3/z3consts.pyc
--------------------------------------------------------------------------------
/z3-4.5.0-x64-win/bin/python/z3/z3core.pyc:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/TechSecCTF/z3_splash_class/b64cf9b51187c7b179b63ed4de43aa28b6a70fdb/z3-4.5.0-x64-win/bin/python/z3/z3core.pyc
--------------------------------------------------------------------------------
/z3-4.5.0-x64-win/bin/python/z3/z3num.py:
--------------------------------------------------------------------------------
1 | ############################################
2 | # Copyright (c) 2012 Microsoft Corporation
3 | #
4 | # Z3 Python interface for Z3 numerals
5 | #
6 | # Author: Leonardo de Moura (leonardo)
7 | ############################################
8 | from .z3 import *
9 | from .z3core import *
10 | from .z3printer import *
11 | from fractions import Fraction
12 |
13 | from .z3 import _get_ctx
14 |
15 | def _to_numeral(num, ctx=None):
16 | if isinstance(num, Numeral):
17 | return num
18 | else:
19 | return Numeral(num, ctx)
20 |
21 | class Numeral:
22 | """
23 | A Z3 numeral can be used to perform computations over arbitrary
24 | precision integers, rationals and real algebraic numbers.
25 | It also automatically converts python numeric values.
26 |
27 | >>> Numeral(2)
28 | 2
29 | >>> Numeral("3/2") + 1
30 | 5/2
31 | >>> Numeral(Sqrt(2))
32 | 1.4142135623?
33 | >>> Numeral(Sqrt(2)) + 2
34 | 3.4142135623?
35 | >>> Numeral(Sqrt(2)) + Numeral(Sqrt(3))
36 | 3.1462643699?
37 |
38 | Z3 numerals can be used to perform computations with
39 | values in a Z3 model.
40 |
41 | >>> s = Solver()
42 | >>> x = Real('x')
43 | >>> s.add(x*x == 2)
44 | >>> s.add(x > 0)
45 | >>> s.check()
46 | sat
47 | >>> m = s.model()
48 | >>> m[x]
49 | 1.4142135623?
50 | >>> m[x] + 1
51 | 1.4142135623? + 1
52 |
53 | The previous result is a Z3 expression.
54 |
55 | >>> (m[x] + 1).sexpr()
56 | '(+ (root-obj (+ (^ x 2) (- 2)) 2) 1.0)'
57 |
58 | >>> Numeral(m[x]) + 1
59 | 2.4142135623?
60 | >>> Numeral(m[x]).is_pos()
61 | True
62 | >>> Numeral(m[x])**2
63 | 2
64 |
65 | We can also isolate the roots of polynomials.
66 |
67 | >>> x0, x1, x2 = RealVarVector(3)
68 | >>> r0 = isolate_roots(x0**5 - x0 - 1)
69 | >>> r0
70 | [1.1673039782?]
71 |
72 | In the following example, we are isolating the roots
73 | of a univariate polynomial (on x1) obtained after substituting
74 | x0 -> r0[0]
75 |
76 | >>> r1 = isolate_roots(x1**2 - x0 + 1, [ r0[0] ])
77 | >>> r1
78 | [-0.4090280898?, 0.4090280898?]
79 |
80 | Similarly, in the next example we isolate the roots of
81 | a univariate polynomial (on x2) obtained after substituting
82 | x0 -> r0[0] and x1 -> r1[0]
83 |
84 | >>> isolate_roots(x1*x2 + x0, [ r0[0], r1[0] ])
85 | [2.8538479564?]
86 |
87 | """
88 | def __init__(self, num, ctx=None):
89 | if isinstance(num, Ast):
90 | self.ast = num
91 | self.ctx = _get_ctx(ctx)
92 | elif isinstance(num, RatNumRef) or isinstance(num, AlgebraicNumRef):
93 | self.ast = num.ast
94 | self.ctx = num.ctx
95 | elif isinstance(num, ArithRef):
96 | r = simplify(num)
97 | self.ast = r.ast
98 | self.ctx = r.ctx
99 | else:
100 | v = RealVal(num, ctx)
101 | self.ast = v.ast
102 | self.ctx = v.ctx
103 | Z3_inc_ref(self.ctx_ref(), self.as_ast())
104 | assert Z3_algebraic_is_value(self.ctx_ref(), self.ast)
105 |
106 | def __del__(self):
107 | Z3_dec_ref(self.ctx_ref(), self.as_ast())
108 |
109 | def is_integer(self):
110 | """ Return True if the numeral is integer.
111 |
112 | >>> Numeral(2).is_integer()
113 | True
114 | >>> (Numeral(Sqrt(2)) * Numeral(Sqrt(2))).is_integer()
115 | True
116 | >>> Numeral(Sqrt(2)).is_integer()
117 | False
118 | >>> Numeral("2/3").is_integer()
119 | False
120 | """
121 | return self.is_rational() and self.denominator() == 1
122 |
123 | def is_rational(self):
124 | """ Return True if the numeral is rational.
125 |
126 | >>> Numeral(2).is_rational()
127 | True
128 | >>> Numeral("2/3").is_rational()
129 | True
130 | >>> Numeral(Sqrt(2)).is_rational()
131 | False
132 |
133 | """
134 | return Z3_get_ast_kind(self.ctx_ref(), self.as_ast()) == Z3_NUMERAL_AST
135 |
136 | def denominator(self):
137 | """ Return the denominator if `self` is rational.
138 |
139 | >>> Numeral("2/3").denominator()
140 | 3
141 | """
142 | assert(self.is_rational())
143 | return Numeral(Z3_get_denominator(self.ctx_ref(), self.as_ast()), self.ctx)
144 |
145 | def numerator(self):
146 | """ Return the numerator if `self` is rational.
147 |
148 | >>> Numeral("2/3").numerator()
149 | 2
150 | """
151 | assert(self.is_rational())
152 | return Numeral(Z3_get_numerator(self.ctx_ref(), self.as_ast()), self.ctx)
153 |
154 |
155 | def is_irrational(self):
156 | """ Return True if the numeral is irrational.
157 |
158 | >>> Numeral(2).is_irrational()
159 | False
160 | >>> Numeral("2/3").is_irrational()
161 | False
162 | >>> Numeral(Sqrt(2)).is_irrational()
163 | True
164 | """
165 | return not self.is_rational()
166 |
167 | def as_long(self):
168 | """ Return a numeral (that is an integer) as a Python long.
169 |
170 | """
171 | assert(self.is_integer())
172 | if sys.version_info[0] >= 3:
173 | return int(Z3_get_numeral_string(self.ctx_ref(), self.as_ast()))
174 | else:
175 | return long(Z3_get_numeral_string(self.ctx_ref(), self.as_ast()))
176 |
177 | def as_fraction(self):
178 | """ Return a numeral (that is a rational) as a Python Fraction.
179 | >>> Numeral("1/5").as_fraction()
180 | Fraction(1, 5)
181 | """
182 | assert(self.is_rational())
183 | return Fraction(self.numerator().as_long(), self.denominator().as_long())
184 |
185 | def approx(self, precision=10):
186 | """Return a numeral that approximates the numeral `self`.
187 | The result `r` is such that |r - self| <= 1/10^precision
188 |
189 | If `self` is rational, then the result is `self`.
190 |
191 | >>> x = Numeral(2).root(2)
192 | >>> x.approx(20)
193 | 6838717160008073720548335/4835703278458516698824704
194 | >>> x.approx(5)
195 | 2965821/2097152
196 | >>> Numeral(2).approx(10)
197 | 2
198 | """
199 | return self.upper(precision)
200 |
201 | def upper(self, precision=10):
202 | """Return a upper bound that approximates the numeral `self`.
203 | The result `r` is such that r - self <= 1/10^precision
204 |
205 | If `self` is rational, then the result is `self`.
206 |
207 | >>> x = Numeral(2).root(2)
208 | >>> x.upper(20)
209 | 6838717160008073720548335/4835703278458516698824704
210 | >>> x.upper(5)
211 | 2965821/2097152
212 | >>> Numeral(2).upper(10)
213 | 2
214 | """
215 | if self.is_rational():
216 | return self
217 | else:
218 | return Numeral(Z3_get_algebraic_number_upper(self.ctx_ref(), self.as_ast(), precision), self.ctx)
219 |
220 | def lower(self, precision=10):
221 | """Return a lower bound that approximates the numeral `self`.
222 | The result `r` is such that self - r <= 1/10^precision
223 |
224 | If `self` is rational, then the result is `self`.
225 |
226 | >>> x = Numeral(2).root(2)
227 | >>> x.lower(20)
228 | 1709679290002018430137083/1208925819614629174706176
229 | >>> Numeral("2/3").lower(10)
230 | 2/3
231 | """
232 | if self.is_rational():
233 | return self
234 | else:
235 | return Numeral(Z3_get_algebraic_number_lower(self.ctx_ref(), self.as_ast(), precision), self.ctx)
236 |
237 | def sign(self):
238 | """ Return the sign of the numeral.
239 |
240 | >>> Numeral(2).sign()
241 | 1
242 | >>> Numeral(-3).sign()
243 | -1
244 | >>> Numeral(0).sign()
245 | 0
246 | """
247 | return Z3_algebraic_sign(self.ctx_ref(), self.ast)
248 |
249 | def is_pos(self):
250 | """ Return True if the numeral is positive.
251 |
252 | >>> Numeral(2).is_pos()
253 | True
254 | >>> Numeral(-3).is_pos()
255 | False
256 | >>> Numeral(0).is_pos()
257 | False
258 | """
259 | return Z3_algebraic_is_pos(self.ctx_ref(), self.ast)
260 |
261 | def is_neg(self):
262 | """ Return True if the numeral is negative.
263 |
264 | >>> Numeral(2).is_neg()
265 | False
266 | >>> Numeral(-3).is_neg()
267 | True
268 | >>> Numeral(0).is_neg()
269 | False
270 | """
271 | return Z3_algebraic_is_neg(self.ctx_ref(), self.ast)
272 |
273 | def is_zero(self):
274 | """ Return True if the numeral is zero.
275 |
276 | >>> Numeral(2).is_zero()
277 | False
278 | >>> Numeral(-3).is_zero()
279 | False
280 | >>> Numeral(0).is_zero()
281 | True
282 | >>> sqrt2 = Numeral(2).root(2)
283 | >>> sqrt2.is_zero()
284 | False
285 | >>> (sqrt2 - sqrt2).is_zero()
286 | True
287 | """
288 | return Z3_algebraic_is_zero(self.ctx_ref(), self.ast)
289 |
290 | def __add__(self, other):
291 | """ Return the numeral `self + other`.
292 |
293 | >>> Numeral(2) + 3
294 | 5
295 | >>> Numeral(2) + Numeral(4)
296 | 6
297 | >>> Numeral("2/3") + 1
298 | 5/3
299 | """
300 | return Numeral(Z3_algebraic_add(self.ctx_ref(), self.ast, _to_numeral(other, self.ctx).ast), self.ctx)
301 |
302 | def __radd__(self, other):
303 | """ Return the numeral `other + self`.
304 |
305 | >>> 3 + Numeral(2)
306 | 5
307 | """
308 | return Numeral(Z3_algebraic_add(self.ctx_ref(), self.ast, _to_numeral(other, self.ctx).ast), self.ctx)
309 |
310 | def __sub__(self, other):
311 | """ Return the numeral `self - other`.
312 |
313 | >>> Numeral(2) - 3
314 | -1
315 | """
316 | return Numeral(Z3_algebraic_sub(self.ctx_ref(), self.ast, _to_numeral(other, self.ctx).ast), self.ctx)
317 |
318 | def __rsub__(self, other):
319 | """ Return the numeral `other - self`.
320 |
321 | >>> 3 - Numeral(2)
322 | 1
323 | """
324 | return Numeral(Z3_algebraic_sub(self.ctx_ref(), _to_numeral(other, self.ctx).ast, self.ast), self.ctx)
325 |
326 | def __mul__(self, other):
327 | """ Return the numeral `self * other`.
328 | >>> Numeral(2) * 3
329 | 6
330 | """
331 | return Numeral(Z3_algebraic_mul(self.ctx_ref(), self.ast, _to_numeral(other, self.ctx).ast), self.ctx)
332 |
333 | def __rmul__(self, other):
334 | """ Return the numeral `other * mul`.
335 | >>> 3 * Numeral(2)
336 | 6
337 | """
338 | return Numeral(Z3_algebraic_mul(self.ctx_ref(), self.ast, _to_numeral(other, self.ctx).ast), self.ctx)
339 |
340 | def __div__(self, other):
341 | """ Return the numeral `self / other`.
342 | >>> Numeral(2) / 3
343 | 2/3
344 | >>> Numeral(2).root(2) / 3
345 | 0.4714045207?
346 | >>> Numeral(Sqrt(2)) / Numeral(Sqrt(3))
347 | 0.8164965809?
348 | """
349 | return Numeral(Z3_algebraic_div(self.ctx_ref(), self.ast, _to_numeral(other, self.ctx).ast), self.ctx)
350 |
351 | def __truediv__(self, other):
352 | return self.__div__(other)
353 |
354 | def __rdiv__(self, other):
355 | """ Return the numeral `other / self`.
356 | >>> 3 / Numeral(2)
357 | 3/2
358 | >>> 3 / Numeral(2).root(2)
359 | 2.1213203435?
360 | """
361 | return Numeral(Z3_algebraic_div(self.ctx_ref(), _to_numeral(other, self.ctx).ast, self.ast), self.ctx)
362 |
363 | def __rtruediv__(self, other):
364 | return self.__rdiv__(other)
365 |
366 | def root(self, k):
367 | """ Return the numeral `self^(1/k)`.
368 |
369 | >>> sqrt2 = Numeral(2).root(2)
370 | >>> sqrt2
371 | 1.4142135623?
372 | >>> sqrt2 * sqrt2
373 | 2
374 | >>> sqrt2 * 2 + 1
375 | 3.8284271247?
376 | >>> (sqrt2 * 2 + 1).sexpr()
377 | '(root-obj (+ (^ x 2) (* (- 2) x) (- 7)) 2)'
378 | """
379 | return Numeral(Z3_algebraic_root(self.ctx_ref(), self.ast, k), self.ctx)
380 |
381 | def power(self, k):
382 | """ Return the numeral `self^k`.
383 |
384 | >>> sqrt3 = Numeral(3).root(2)
385 | >>> sqrt3
386 | 1.7320508075?
387 | >>> sqrt3.power(2)
388 | 3
389 | """
390 | return Numeral(Z3_algebraic_power(self.ctx_ref(), self.ast, k), self.ctx)
391 |
392 | def __pow__(self, k):
393 | """ Return the numeral `self^k`.
394 |
395 | >>> sqrt3 = Numeral(3).root(2)
396 | >>> sqrt3
397 | 1.7320508075?
398 | >>> sqrt3**2
399 | 3
400 | """
401 | return self.power(k)
402 |
403 | def __lt__(self, other):
404 | """ Return True if `self < other`.
405 |
406 | >>> Numeral(Sqrt(2)) < 2
407 | True
408 | >>> Numeral(Sqrt(3)) < Numeral(Sqrt(2))
409 | False
410 | >>> Numeral(Sqrt(2)) < Numeral(Sqrt(2))
411 | False
412 | """
413 | return Z3_algebraic_lt(self.ctx_ref(), self.ast, _to_numeral(other, self.ctx).ast)
414 |
415 | def __rlt__(self, other):
416 | """ Return True if `other < self`.
417 |
418 | >>> 2 < Numeral(Sqrt(2))
419 | False
420 | """
421 | return self > other
422 |
423 | def __gt__(self, other):
424 | """ Return True if `self > other`.
425 |
426 | >>> Numeral(Sqrt(2)) > 2
427 | False
428 | >>> Numeral(Sqrt(3)) > Numeral(Sqrt(2))
429 | True
430 | >>> Numeral(Sqrt(2)) > Numeral(Sqrt(2))
431 | False
432 | """
433 | return Z3_algebraic_gt(self.ctx_ref(), self.ast, _to_numeral(other, self.ctx).ast)
434 |
435 | def __rgt__(self, other):
436 | """ Return True if `other > self`.
437 |
438 | >>> 2 > Numeral(Sqrt(2))
439 | True
440 | """
441 | return self < other
442 |
443 |
444 | def __le__(self, other):
445 | """ Return True if `self <= other`.
446 |
447 | >>> Numeral(Sqrt(2)) <= 2
448 | True
449 | >>> Numeral(Sqrt(3)) <= Numeral(Sqrt(2))
450 | False
451 | >>> Numeral(Sqrt(2)) <= Numeral(Sqrt(2))
452 | True
453 | """
454 | return Z3_algebraic_le(self.ctx_ref(), self.ast, _to_numeral(other, self.ctx).ast)
455 |
456 | def __rle__(self, other):
457 | """ Return True if `other <= self`.
458 |
459 | >>> 2 <= Numeral(Sqrt(2))
460 | False
461 | """
462 | return self >= other
463 |
464 | def __ge__(self, other):
465 | """ Return True if `self >= other`.
466 |
467 | >>> Numeral(Sqrt(2)) >= 2
468 | False
469 | >>> Numeral(Sqrt(3)) >= Numeral(Sqrt(2))
470 | True
471 | >>> Numeral(Sqrt(2)) >= Numeral(Sqrt(2))
472 | True
473 | """
474 | return Z3_algebraic_ge(self.ctx_ref(), self.ast, _to_numeral(other, self.ctx).ast)
475 |
476 | def __rge__(self, other):
477 | """ Return True if `other >= self`.
478 |
479 | >>> 2 >= Numeral(Sqrt(2))
480 | True
481 | """
482 | return self <= other
483 |
484 | def __eq__(self, other):
485 | """ Return True if `self == other`.
486 |
487 | >>> Numeral(Sqrt(2)) == 2
488 | False
489 | >>> Numeral(Sqrt(3)) == Numeral(Sqrt(2))
490 | False
491 | >>> Numeral(Sqrt(2)) == Numeral(Sqrt(2))
492 | True
493 | """
494 | return Z3_algebraic_eq(self.ctx_ref(), self.ast, _to_numeral(other, self.ctx).ast)
495 |
496 | def __ne__(self, other):
497 | """ Return True if `self != other`.
498 |
499 | >>> Numeral(Sqrt(2)) != 2
500 | True
501 | >>> Numeral(Sqrt(3)) != Numeral(Sqrt(2))
502 | True
503 | >>> Numeral(Sqrt(2)) != Numeral(Sqrt(2))
504 | False
505 | """
506 | return Z3_algebraic_neq(self.ctx_ref(), self.ast, _to_numeral(other, self.ctx).ast)
507 |
508 | def __str__(self):
509 | if Z3_is_numeral_ast(self.ctx_ref(), self.ast):
510 | return str(RatNumRef(self.ast, self.ctx))
511 | else:
512 | return str(AlgebraicNumRef(self.ast, self.ctx))
513 |
514 | def __repr__(self):
515 | return self.__str__()
516 |
517 | def sexpr(self):
518 | return Z3_ast_to_string(self.ctx_ref(), self.as_ast())
519 |
520 | def as_ast(self):
521 | return self.ast
522 |
523 | def ctx_ref(self):
524 | return self.ctx.ref()
525 |
526 | def eval_sign_at(p, vs):
527 | """
528 | Evaluate the sign of the polynomial `p` at `vs`. `p` is a Z3
529 | Expression containing arithmetic operators: +, -, *, ^k where k is
530 | an integer; and free variables x that is_var(x) is True. Moreover,
531 | all variables must be real.
532 |
533 | The result is 1 if the polynomial is positive at the given point,
534 | -1 if negative, and 0 if zero.
535 |
536 | >>> x0, x1, x2 = RealVarVector(3)
537 | >>> eval_sign_at(x0**2 + x1*x2 + 1, (Numeral(0), Numeral(1), Numeral(2)))
538 | 1
539 | >>> eval_sign_at(x0**2 - 2, [ Numeral(Sqrt(2)) ])
540 | 0
541 | >>> eval_sign_at((x0 + x1)*(x0 + x2), (Numeral(0), Numeral(Sqrt(2)), Numeral(Sqrt(3))))
542 | 1
543 | """
544 | num = len(vs)
545 | _vs = (Ast * num)()
546 | for i in range(num):
547 | _vs[i] = vs[i].ast
548 | return Z3_algebraic_eval(p.ctx_ref(), p.as_ast(), num, _vs)
549 |
550 | def isolate_roots(p, vs=[]):
551 | """
552 | Given a multivariate polynomial p(x_0, ..., x_{n-1}, x_n), returns the
553 | roots of the univariate polynomial p(vs[0], ..., vs[len(vs)-1], x_n).
554 |
555 | Remarks:
556 | * p is a Z3 expression that contains only arithmetic terms and free variables.
557 | * forall i in [0, n) vs is a numeral.
558 |
559 | The result is a list of numerals
560 |
561 | >>> x0 = RealVar(0)
562 | >>> isolate_roots(x0**5 - x0 - 1)
563 | [1.1673039782?]
564 | >>> x1 = RealVar(1)
565 | >>> isolate_roots(x0**2 - x1**4 - 1, [ Numeral(Sqrt(3)) ])
566 | [-1.1892071150?, 1.1892071150?]
567 | >>> x2 = RealVar(2)
568 | >>> isolate_roots(x2**2 + x0 - x1, [ Numeral(Sqrt(3)), Numeral(Sqrt(2)) ])
569 | []
570 | """
571 | num = len(vs)
572 | _vs = (Ast * num)()
573 | for i in range(num):
574 | _vs[i] = vs[i].ast
575 | _roots = AstVector(Z3_algebraic_roots(p.ctx_ref(), p.as_ast(), num, _vs), p.ctx)
576 | return [ Numeral(r) for r in _roots ]
577 |
578 |
--------------------------------------------------------------------------------
/z3-4.5.0-x64-win/bin/python/z3/z3num.pyc:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/TechSecCTF/z3_splash_class/b64cf9b51187c7b179b63ed4de43aa28b6a70fdb/z3-4.5.0-x64-win/bin/python/z3/z3num.pyc
--------------------------------------------------------------------------------
/z3-4.5.0-x64-win/bin/python/z3/z3poly.py:
--------------------------------------------------------------------------------
1 | ############################################
2 | # Copyright (c) 2012 Microsoft Corporation
3 | #
4 | # Z3 Python interface for Z3 polynomials
5 | #
6 | # Author: Leonardo de Moura (leonardo)
7 | ############################################
8 |
9 | from .z3 import *
10 |
11 | def subresultants(p, q, x):
12 | """
13 | Return the non-constant subresultants of 'p' and 'q' with respect to the "variable" 'x'.
14 |
15 | 'p', 'q' and 'x' are Z3 expressions where 'p' and 'q' are arithmetic terms.
16 | Note that, any subterm that cannot be viewed as a polynomial is assumed to be a variable.
17 | Example: f(a) is a considered to be a variable b in the polynomial
18 |
19 | f(a)*f(a) + 2*f(a) + 1
20 |
21 | >>> x, y = Reals('x y')
22 | >>> subresultants(2*x + y, 3*x - 2*y + 2, x)
23 | [-7*y + 4]
24 | >>> r = subresultants(3*y*x**2 + y**3 + 1, 2*x**3 + y + 3, x)
25 | >>> r[0]
26 | 4*y**9 + 12*y**6 + 27*y**5 + 162*y**4 + 255*y**3 + 4
27 | >>> r[1]
28 | -6*y**4 + -6*y
29 | """
30 | return AstVector(Z3_polynomial_subresultants(p.ctx_ref(), p.as_ast(), q.as_ast(), x.as_ast()), p.ctx)
31 |
32 | if __name__ == "__main__":
33 | import doctest
34 | if doctest.testmod().failed:
35 | exit(1)
36 |
--------------------------------------------------------------------------------
/z3-4.5.0-x64-win/bin/python/z3/z3poly.pyc:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/TechSecCTF/z3_splash_class/b64cf9b51187c7b179b63ed4de43aa28b6a70fdb/z3-4.5.0-x64-win/bin/python/z3/z3poly.pyc
--------------------------------------------------------------------------------
/z3-4.5.0-x64-win/bin/python/z3/z3printer.pyc:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/TechSecCTF/z3_splash_class/b64cf9b51187c7b179b63ed4de43aa28b6a70fdb/z3-4.5.0-x64-win/bin/python/z3/z3printer.pyc
--------------------------------------------------------------------------------
/z3-4.5.0-x64-win/bin/python/z3/z3rcf.py:
--------------------------------------------------------------------------------
1 | ############################################
2 | # Copyright (c) 2013 Microsoft Corporation
3 | #
4 | # Z3 Python interface for Z3 Real Closed Fields
5 | # that may contain
6 | # - computable transcendentals
7 | # - infinitesimals
8 | # - algebraic extensions
9 | #
10 | # Author: Leonardo de Moura (leonardo)
11 | ############################################
12 | from .z3 import *
13 | from .z3core import *
14 | from .z3printer import *
15 | from fractions import Fraction
16 |
17 | def _to_rcfnum(num, ctx=None):
18 | if isinstance(num, RCFNum):
19 | return num
20 | else:
21 | return RCFNum(num, ctx)
22 |
23 | def Pi(ctx=None):
24 | ctx = z3._get_ctx(ctx)
25 | return RCFNum(Z3_rcf_mk_pi(ctx.ref()), ctx)
26 |
27 | def E(ctx=None):
28 | ctx = z3._get_ctx(ctx)
29 | return RCFNum(Z3_rcf_mk_e(ctx.ref()), ctx)
30 |
31 | def MkInfinitesimal(name="eps", ctx=None):
32 | # Todo: remove parameter name.
33 | # For now, we keep it for backward compatibility.
34 | ctx = z3._get_ctx(ctx)
35 | return RCFNum(Z3_rcf_mk_infinitesimal(ctx.ref()), ctx)
36 |
37 | def MkRoots(p, ctx=None):
38 | ctx = z3._get_ctx(ctx)
39 | num = len(p)
40 | _tmp = []
41 | _as = (RCFNumObj * num)()
42 | _rs = (RCFNumObj * num)()
43 | for i in range(num):
44 | _a = _to_rcfnum(p[i], ctx)
45 | _tmp.append(_a) # prevent GC
46 | _as[i] = _a.num
47 | nr = Z3_rcf_mk_roots(ctx.ref(), num, _as, _rs)
48 | r = []
49 | for i in range(nr):
50 | r.append(RCFNum(_rs[i], ctx))
51 | return r
52 |
53 | class RCFNum:
54 | def __init__(self, num, ctx=None):
55 | # TODO: add support for converting AST numeral values into RCFNum
56 | if isinstance(num, RCFNumObj):
57 | self.num = num
58 | self.ctx = z3._get_ctx(ctx)
59 | else:
60 | self.ctx = z3._get_ctx(ctx)
61 | self.num = Z3_rcf_mk_rational(self.ctx_ref(), str(num))
62 |
63 | def __del__(self):
64 | Z3_rcf_del(self.ctx_ref(), self.num)
65 |
66 | def ctx_ref(self):
67 | return self.ctx.ref()
68 |
69 | def __repr__(self):
70 | return Z3_rcf_num_to_string(self.ctx_ref(), self.num, False, in_html_mode())
71 |
72 | def compact_str(self):
73 | return Z3_rcf_num_to_string(self.ctx_ref(), self.num, True, in_html_mode())
74 |
75 | def __add__(self, other):
76 | v = _to_rcfnum(other, self.ctx)
77 | return RCFNum(Z3_rcf_add(self.ctx_ref(), self.num, v.num), self.ctx)
78 |
79 | def __radd__(self, other):
80 | v = _to_rcfnum(other, self.ctx)
81 | return RCFNum(Z3_rcf_add(self.ctx_ref(), v.num, self.num), self.ctx)
82 |
83 | def __mul__(self, other):
84 | v = _to_rcfnum(other, self.ctx)
85 | return RCFNum(Z3_rcf_mul(self.ctx_ref(), self.num, v.num), self.ctx)
86 |
87 | def __rmul__(self, other):
88 | v = _to_rcfnum(other, self.ctx)
89 | return RCFNum(Z3_rcf_mul(self.ctx_ref(), v.num, self.num), self.ctx)
90 |
91 | def __sub__(self, other):
92 | v = _to_rcfnum(other, self.ctx)
93 | return RCFNum(Z3_rcf_sub(self.ctx_ref(), self.num, v.num), self.ctx)
94 |
95 | def __rsub__(self, other):
96 | v = _to_rcfnum(other, self.ctx)
97 | return RCFNum(Z3_rcf_sub(self.ctx_ref(), v.num, self.num), self.ctx)
98 |
99 | def __div__(self, other):
100 | v = _to_rcfnum(other, self.ctx)
101 | return RCFNum(Z3_rcf_div(self.ctx_ref(), self.num, v.num), self.ctx)
102 |
103 | def __rdiv__(self, other):
104 | v = _to_rcfnum(other, self.ctx)
105 | return RCFNum(Z3_rcf_div(self.ctx_ref(), v.num, self.num), self.ctx)
106 |
107 | def __neg__(self):
108 | return self.__rsub__(0)
109 |
110 | def power(self, k):
111 | return RCFNum(Z3_rcf_power(self.ctx_ref(), self.num, k), self.ctx)
112 |
113 | def __pow__(self, k):
114 | return self.power(k)
115 |
116 | def decimal(self, prec=5):
117 | return Z3_rcf_num_to_decimal_string(self.ctx_ref(), self.num, prec)
118 |
119 | def __lt__(self, other):
120 | v = _to_rcfnum(other, self.ctx)
121 | return Z3_rcf_lt(self.ctx_ref(), self.num, v.num)
122 |
123 | def __rlt__(self, other):
124 | v = _to_rcfnum(other, self.ctx)
125 | return Z3_rcf_lt(self.ctx_ref(), v.num, self.num)
126 |
127 | def __gt__(self, other):
128 | v = _to_rcfnum(other, self.ctx)
129 | return Z3_rcf_gt(self.ctx_ref(), self.num, v.num)
130 |
131 | def __rgt__(self, other):
132 | v = _to_rcfnum(other, self.ctx)
133 | return Z3_rcf_gt(self.ctx_ref(), v.num, self.num)
134 |
135 | def __le__(self, other):
136 | v = _to_rcfnum(other, self.ctx)
137 | return Z3_rcf_le(self.ctx_ref(), self.num, v.num)
138 |
139 | def __rle__(self, other):
140 | v = _to_rcfnum(other, self.ctx)
141 | return Z3_rcf_le(self.ctx_ref(), v.num, self.num)
142 |
143 | def __ge__(self, other):
144 | v = _to_rcfnum(other, self.ctx)
145 | return Z3_rcf_ge(self.ctx_ref(), self.num, v.num)
146 |
147 | def __rge__(self, other):
148 | v = _to_rcfnum(other, self.ctx)
149 | return Z3_rcf_ge(self.ctx_ref(), v.num, self.num)
150 |
151 | def __eq__(self, other):
152 | v = _to_rcfnum(other, self.ctx)
153 | return Z3_rcf_eq(self.ctx_ref(), self.num, v.num)
154 |
155 | def __ne__(self, other):
156 | v = _to_rcfnum(other, self.ctx)
157 | return Z3_rcf_neq(self.ctx_ref(), self.num, v.num)
158 |
159 | def split(self):
160 | n = (RCFNumObj * 1)()
161 | d = (RCFNumObj * 1)()
162 | Z3_rcf_get_numerator_denominator(self.ctx_ref(), self.num, n, d)
163 | return (RCFNum(n[0], self.ctx), RCFNum(d[0], self.ctx))
164 |
--------------------------------------------------------------------------------
/z3-4.5.0-x64-win/bin/python/z3/z3rcf.pyc:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/TechSecCTF/z3_splash_class/b64cf9b51187c7b179b63ed4de43aa28b6a70fdb/z3-4.5.0-x64-win/bin/python/z3/z3rcf.pyc
--------------------------------------------------------------------------------
/z3-4.5.0-x64-win/bin/python/z3/z3types.py:
--------------------------------------------------------------------------------
1 | ############################################
2 | # Copyright (c) 2012 Microsoft Corporation
3 | #
4 | # Z3 Python interface
5 | #
6 | # Author: Leonardo de Moura (leonardo)
7 | ############################################
8 |
9 | import ctypes
10 |
11 | class Z3Exception(Exception):
12 | def __init__(self, value):
13 | self.value = value
14 | def __str__(self):
15 | return str(self.value)
16 |
17 | class ContextObj(ctypes.c_void_p):
18 | def __init__(self, context): self._as_parameter_ = context
19 | def from_param(obj): return obj
20 |
21 | class Config(ctypes.c_void_p):
22 | def __init__(self, config): self._as_parameter_ = config
23 | def from_param(obj): return obj
24 |
25 | class Symbol(ctypes.c_void_p):
26 | def __init__(self, symbol): self._as_parameter_ = symbol
27 | def from_param(obj): return obj
28 |
29 | class Sort(ctypes.c_void_p):
30 | def __init__(self, sort): self._as_parameter_ = sort
31 | def from_param(obj): return obj
32 |
33 | class FuncDecl(ctypes.c_void_p):
34 | def __init__(self, decl): self._as_parameter_ = decl
35 | def from_param(obj): return obj
36 |
37 | class Ast(ctypes.c_void_p):
38 | def __init__(self, ast): self._as_parameter_ = ast
39 | def from_param(obj): return obj
40 |
41 | class Pattern(ctypes.c_void_p):
42 | def __init__(self, pattern): self._as_parameter_ = pattern
43 | def from_param(obj): return obj
44 |
45 | class Model(ctypes.c_void_p):
46 | def __init__(self, model): self._as_parameter_ = model
47 | def from_param(obj): return obj
48 |
49 | class Literals(ctypes.c_void_p):
50 | def __init__(self, literals): self._as_parameter_ = literals
51 | def from_param(obj): return obj
52 |
53 | class Constructor(ctypes.c_void_p):
54 | def __init__(self, constructor): self._as_parameter_ = constructor
55 | def from_param(obj): return obj
56 |
57 | class ConstructorList(ctypes.c_void_p):
58 | def __init__(self, constructor_list): self._as_parameter_ = constructor_list
59 | def from_param(obj): return obj
60 |
61 | class GoalObj(ctypes.c_void_p):
62 | def __init__(self, goal): self._as_parameter_ = goal
63 | def from_param(obj): return obj
64 |
65 | class TacticObj(ctypes.c_void_p):
66 | def __init__(self, tactic): self._as_parameter_ = tactic
67 | def from_param(obj): return obj
68 |
69 | class ProbeObj(ctypes.c_void_p):
70 | def __init__(self, probe): self._as_parameter_ = probe
71 | def from_param(obj): return obj
72 |
73 | class ApplyResultObj(ctypes.c_void_p):
74 | def __init__(self, obj): self._as_parameter_ = obj
75 | def from_param(obj): return obj
76 |
77 | class StatsObj(ctypes.c_void_p):
78 | def __init__(self, statistics): self._as_parameter_ = statistics
79 | def from_param(obj): return obj
80 |
81 | class SolverObj(ctypes.c_void_p):
82 | def __init__(self, solver): self._as_parameter_ = solver
83 | def from_param(obj): return obj
84 |
85 | class FixedpointObj(ctypes.c_void_p):
86 | def __init__(self, fixedpoint): self._as_parameter_ = fixedpoint
87 | def from_param(obj): return obj
88 |
89 | class OptimizeObj(ctypes.c_void_p):
90 | def __init__(self, optimize): self._as_parameter_ = optimize
91 | def from_param(obj): return obj
92 |
93 | class ModelObj(ctypes.c_void_p):
94 | def __init__(self, model): self._as_parameter_ = model
95 | def from_param(obj): return obj
96 |
97 | class AstVectorObj(ctypes.c_void_p):
98 | def __init__(self, vector): self._as_parameter_ = vector
99 | def from_param(obj): return obj
100 |
101 | class AstMapObj(ctypes.c_void_p):
102 | def __init__(self, ast_map): self._as_parameter_ = ast_map
103 | def from_param(obj): return obj
104 |
105 | class Params(ctypes.c_void_p):
106 | def __init__(self, params): self._as_parameter_ = params
107 | def from_param(obj): return obj
108 |
109 | class ParamDescrs(ctypes.c_void_p):
110 | def __init__(self, paramdescrs): self._as_parameter_ = paramdescrs
111 | def from_param(obj): return obj
112 |
113 | class FuncInterpObj(ctypes.c_void_p):
114 | def __init__(self, f): self._as_parameter_ = f
115 | def from_param(obj): return obj
116 |
117 | class FuncEntryObj(ctypes.c_void_p):
118 | def __init__(self, e): self._as_parameter_ = e
119 | def from_param(obj): return obj
120 |
121 | class RCFNumObj(ctypes.c_void_p):
122 | def __init__(self, e): self._as_parameter_ = e
123 | def from_param(obj): return obj
124 |
--------------------------------------------------------------------------------
/z3-4.5.0-x64-win/bin/python/z3/z3types.pyc:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/TechSecCTF/z3_splash_class/b64cf9b51187c7b179b63ed4de43aa28b6a70fdb/z3-4.5.0-x64-win/bin/python/z3/z3types.pyc
--------------------------------------------------------------------------------
/z3-4.5.0-x64-win/bin/python/z3/z3util.py:
--------------------------------------------------------------------------------
1 | ############################################
2 | # Copyright (c) 2012 Microsoft Corporation
3 | #
4 | # Z3 Python interface
5 | #
6 | # Authors: Leonardo de Moura (leonardo)
7 | # ThanhVu (Vu) Nguyen
8 | ############################################
9 | """
10 | Usage:
11 | import common_z3 as CM_Z3
12 | """
13 |
14 | from .z3 import *
15 |
16 | def vset(seq, idfun=None, as_list=True):
17 | # This functions preserves the order of arguments while removing duplicates.
18 | # This function is from https://code.google.com/p/common-python-vu/source/browse/vu_common.py
19 | # (Thanhu's personal code). It has been copied here to avoid a dependency on vu_common.py.
20 | """
21 | order preserving
22 |
23 | >>> vset([[11,2],1, [10,['9',1]],2, 1, [11,2],[3,3],[10,99],1,[10,['9',1]]],idfun=repr)
24 | [[11, 2], 1, [10, ['9', 1]], 2, [3, 3], [10, 99]]
25 | """
26 |
27 | def _uniq_normal(seq):
28 | d_ = {}
29 | for s in seq:
30 | if s not in d_:
31 | d_[s] = None
32 | yield s
33 |
34 | def _uniq_idfun(seq,idfun):
35 | d_ = {}
36 | for s in seq:
37 | h_ = idfun(s)
38 | if h_ not in d_:
39 | d_[h_] = None
40 | yield s
41 |
42 | if idfun is None:
43 | res = _uniq_normal(seq)
44 | else:
45 | res = _uniq_idfun(seq,idfun)
46 |
47 | return list(res) if as_list else res
48 |
49 |
50 | def get_z3_version(as_str=False):
51 | major = ctypes.c_uint(0)
52 | minor = ctypes.c_uint(0)
53 | build = ctypes.c_uint(0)
54 | rev = ctypes.c_uint(0)
55 | Z3_get_version(major,minor,build,rev)
56 | rs = map(int,(major.value,minor.value,build.value,rev.value))
57 | if as_str:
58 | return "{}.{}.{}.{}".format(*rs)
59 | else:
60 | return rs
61 |
62 |
63 | def ehash(v):
64 | """
65 | Returns a 'stronger' hash value than the default hash() method.
66 | The result from hash() is not enough to distinguish between 2
67 | z3 expressions in some cases.
68 |
69 | Note: the following doctests will fail with Python 2.x as the
70 | default formatting doesn't match that of 3.x.
71 | >>> x1 = Bool('x'); x2 = Bool('x'); x3 = Int('x')
72 | >>> print(x1.hash(),x2.hash(),x3.hash()) #BAD: all same hash values
73 | 783810685 783810685 783810685
74 | >>> print(ehash(x1), ehash(x2), ehash(x3))
75 | x_783810685_1 x_783810685_1 x_783810685_2
76 |
77 | """
78 | if __debug__:
79 | assert is_expr(v)
80 |
81 | return "{}_{}_{}".format(str(v),v.hash(),v.sort_kind())
82 |
83 |
84 | """
85 | In Z3, variables are called *uninterpreted* consts and
86 | variables are *interpreted* consts.
87 | """
88 |
89 | def is_expr_var(v):
90 | """
91 | EXAMPLES:
92 |
93 | >>> is_expr_var(Int('7'))
94 | True
95 | >>> is_expr_var(IntVal('7'))
96 | False
97 | >>> is_expr_var(Bool('y'))
98 | True
99 | >>> is_expr_var(Int('x') + 7 == Int('y'))
100 | False
101 | >>> LOnOff, (On,Off) = EnumSort("LOnOff",['On','Off'])
102 | >>> Block,Reset,SafetyInjection=Consts("Block Reset SafetyInjection",LOnOff)
103 | >>> is_expr_var(LOnOff)
104 | False
105 | >>> is_expr_var(On)
106 | False
107 | >>> is_expr_var(Block)
108 | True
109 | >>> is_expr_var(SafetyInjection)
110 | True
111 | """
112 |
113 | return is_const(v) and v.decl().kind()==Z3_OP_UNINTERPRETED
114 |
115 | def is_expr_val(v):
116 | """
117 | EXAMPLES:
118 |
119 | >>> is_expr_val(Int('7'))
120 | False
121 | >>> is_expr_val(IntVal('7'))
122 | True
123 | >>> is_expr_val(Bool('y'))
124 | False
125 | >>> is_expr_val(Int('x') + 7 == Int('y'))
126 | False
127 | >>> LOnOff, (On,Off) = EnumSort("LOnOff",['On','Off'])
128 | >>> Block,Reset,SafetyInjection=Consts("Block Reset SafetyInjection",LOnOff)
129 | >>> is_expr_val(LOnOff)
130 | False
131 | >>> is_expr_val(On)
132 | True
133 | >>> is_expr_val(Block)
134 | False
135 | >>> is_expr_val(SafetyInjection)
136 | False
137 | """
138 | return is_const(v) and v.decl().kind()!=Z3_OP_UNINTERPRETED
139 |
140 |
141 |
142 |
143 | def get_vars(f,rs=[]):
144 | """
145 | >>> x,y = Ints('x y')
146 | >>> a,b = Bools('a b')
147 | >>> get_vars(Implies(And(x+y==0,x*2==10),Or(a,Implies(a,b==False))))
148 | [x, y, a, b]
149 |
150 | """
151 | if __debug__:
152 | assert is_expr(f)
153 |
154 | if is_const(f):
155 | if is_expr_val(f):
156 | return rs
157 | else: #variable
158 | return vset(rs + [f],str)
159 |
160 | else:
161 | for f_ in f.children():
162 | rs = get_vars(f_,rs)
163 |
164 | return vset(rs,str)
165 |
166 |
167 |
168 | def mk_var(name,vsort):
169 | if vsort.kind() == Z3_INT_SORT:
170 | v = Int(name)
171 | elif vsort.kind() == Z3_REAL_SORT:
172 | v = Real(name)
173 | elif vsort.kind() == Z3_BOOL_SORT:
174 | v = Bool(name)
175 | elif vsort.kind() == Z3_DATATYPE_SORT:
176 | v = Const(name,vsort)
177 |
178 | else:
179 | assert False, 'Cannot handle this sort (s: %sid: %d)'\
180 | %(vsort,vsort.kind())
181 |
182 | return v
183 |
184 |
185 |
186 | def prove(claim,assume=None,verbose=0):
187 | """
188 | >>> r,m = prove(BoolVal(True),verbose=0); r,model_str(m,as_str=False)
189 | (True, None)
190 |
191 | #infinite counter example when proving contradiction
192 | >>> r,m = prove(BoolVal(False)); r,model_str(m,as_str=False)
193 | (False, [])
194 |
195 | >>> x,y,z=Bools('x y z')
196 | >>> r,m = prove(And(x,Not(x))); r,model_str(m,as_str=True)
197 | (False, '[]')
198 |
199 | >>> r,m = prove(True,assume=And(x,Not(x)),verbose=0)
200 | Traceback (most recent call last):
201 | ...
202 | AssertionError: Assumption is alway False!
203 |
204 | >>> r,m = prove(Implies(x,x),assume=y,verbose=2); r,model_str(m,as_str=False)
205 | assume:
206 | y
207 | claim:
208 | Implies(x, x)
209 | to_prove:
210 | Implies(y, Implies(x, x))
211 | (True, None)
212 |
213 | >>> r,m = prove(And(x,True),assume=y,verbose=0); r,model_str(m,as_str=False)
214 | (False, [(x, False), (y, True)])
215 |
216 | >>> r,m = prove(And(x,y),assume=y,verbose=0)
217 | >>> print(r)
218 | False
219 | >>> print(model_str(m,as_str=True))
220 | x = False
221 | y = True
222 |
223 | >>> a,b = Ints('a b')
224 | >>> r,m = prove(a**b == b**a,assume=None,verbose=0)
225 | E: cannot solve !
226 | >>> r is None and m is None
227 | True
228 |
229 | """
230 |
231 | if __debug__:
232 | assert not assume or is_expr(assume)
233 |
234 |
235 | to_prove = claim
236 | if assume:
237 | if __debug__:
238 | is_proved,_ = prove(Not(assume))
239 |
240 | def _f():
241 | emsg = "Assumption is alway False!"
242 | if verbose >= 2:
243 | emsg = "{}\n{}".format(assume,emsg)
244 | return emsg
245 |
246 | assert is_proved==False, _f()
247 |
248 | to_prove = Implies(assume,to_prove)
249 |
250 |
251 |
252 | if verbose >= 2:
253 | print('assume: ')
254 | print(assume)
255 | print('claim: ')
256 | print(claim)
257 | print('to_prove: ')
258 | print(to_prove)
259 |
260 | f = Not(to_prove)
261 |
262 | models = get_models(f,k=1)
263 | if models is None: #unknown
264 | print('E: cannot solve !')
265 | return None, None
266 | elif models == False: #unsat
267 | return True,None
268 | else: #sat
269 | if __debug__:
270 | assert isinstance(models,list)
271 |
272 | if models:
273 | return False, models[0] #the first counterexample
274 | else:
275 | return False, [] #infinite counterexample,models
276 |
277 |
278 | def get_models(f,k):
279 | """
280 | Returns the first k models satisfiying f.
281 | If f is not satisfiable, returns False.
282 | If f cannot be solved, returns None
283 | If f is satisfiable, returns the first k models
284 | Note that if f is a tautology, e.g.\ True, then the result is []
285 |
286 | Based on http://stackoverflow.com/questions/11867611/z3py-checking-all-solutions-for-equation
287 |
288 | EXAMPLES:
289 | >>> x, y = Ints('x y')
290 | >>> len(get_models(And(0<=x,x <= 4),k=11))
291 | 5
292 | >>> get_models(And(0<=x**y,x <= 1),k=2) is None
293 | True
294 | >>> get_models(And(0<=x,x <= -1),k=2)
295 | False
296 | >>> len(get_models(x+y==7,5))
297 | 5
298 | >>> len(get_models(And(x<=5,x>=1),7))
299 | 5
300 | >>> get_models(And(x<=0,x>=5),7)
301 | False
302 |
303 | >>> x = Bool('x')
304 | >>> get_models(And(x,Not(x)),k=1)
305 | False
306 | >>> get_models(Implies(x,x),k=1)
307 | []
308 | >>> get_models(BoolVal(True),k=1)
309 | []
310 |
311 |
312 |
313 | """
314 |
315 | if __debug__:
316 | assert is_expr(f)
317 | assert k>=1
318 |
319 |
320 |
321 | s = Solver()
322 | s.add(f)
323 |
324 | models = []
325 | i = 0
326 | while s.check() == sat and i < k:
327 | i = i + 1
328 |
329 | m = s.model()
330 |
331 | if not m: #if m == []
332 | break
333 |
334 | models.append(m)
335 |
336 |
337 | #create new constraint to block the current model
338 | block = Not(And([v() == m[v] for v in m]))
339 | s.add(block)
340 |
341 |
342 | if s.check() == unknown:
343 | return None
344 | elif s.check() == unsat and i==0:
345 | return False
346 | else:
347 | return models
348 |
349 | def is_tautology(claim,verbose=0):
350 | """
351 | >>> is_tautology(Implies(Bool('x'),Bool('x')))
352 | True
353 |
354 | >>> is_tautology(Implies(Bool('x'),Bool('y')))
355 | False
356 |
357 | >>> is_tautology(BoolVal(True))
358 | True
359 |
360 | >>> is_tautology(BoolVal(False))
361 | False
362 |
363 | """
364 | return prove(claim=claim,assume=None,verbose=verbose)[0]
365 |
366 |
367 | def is_contradiction(claim,verbose=0):
368 | """
369 | >>> x,y=Bools('x y')
370 | >>> is_contradiction(BoolVal(False))
371 | True
372 |
373 | >>> is_contradiction(BoolVal(True))
374 | False
375 |
376 | >>> is_contradiction(x)
377 | False
378 |
379 | >>> is_contradiction(Implies(x,y))
380 | False
381 |
382 | >>> is_contradiction(Implies(x,x))
383 | False
384 |
385 | >>> is_contradiction(And(x,Not(x)))
386 | True
387 | """
388 |
389 | return prove(claim=Not(claim),assume=None,verbose=verbose)[0]
390 |
391 |
392 | def exact_one_model(f):
393 | """
394 | return True if f has exactly 1 model, False otherwise.
395 |
396 | EXAMPLES:
397 |
398 | >>> x, y = Ints('x y')
399 | >>> exact_one_model(And(0<=x**y,x <= 0))
400 | False
401 |
402 | >>> exact_one_model(And(0<=x,x <= 0))
403 | True
404 |
405 | >>> exact_one_model(And(0<=x,x <= 1))
406 | False
407 |
408 | >>> exact_one_model(And(0<=x,x <= -1))
409 | False
410 | """
411 |
412 | models = get_models(f,k=2)
413 | if isinstance(models,list):
414 | return len(models)==1
415 | else:
416 | return False
417 |
418 |
419 |
420 | def myBinOp(op,*L):
421 | """
422 | >>> myAnd(*[Bool('x'),Bool('y')])
423 | And(x, y)
424 |
425 | >>> myAnd(*[Bool('x'),None])
426 | x
427 |
428 | >>> myAnd(*[Bool('x')])
429 | x
430 |
431 | >>> myAnd(*[])
432 |
433 | >>> myAnd(Bool('x'),Bool('y'))
434 | And(x, y)
435 |
436 | >>> myAnd(*[Bool('x'),Bool('y')])
437 | And(x, y)
438 |
439 | >>> myAnd([Bool('x'),Bool('y')])
440 | And(x, y)
441 |
442 | >>> myAnd((Bool('x'),Bool('y')))
443 | And(x, y)
444 |
445 | >>> myAnd(*[Bool('x'),Bool('y'),True])
446 | Traceback (most recent call last):
447 | ...
448 | AssertionError
449 | """
450 |
451 | if __debug__:
452 | assert op == Z3_OP_OR or op == Z3_OP_AND or op == Z3_OP_IMPLIES
453 |
454 | if len(L)==1 and (isinstance(L[0],list) or isinstance(L[0],tuple)):
455 | L = L[0]
456 |
457 | if __debug__:
458 | assert all(not isinstance(l,bool) for l in L)
459 |
460 | L = [l for l in L if is_expr(l)]
461 | if L:
462 | if len(L)==1:
463 | return L[0]
464 | else:
465 | if op == Z3_OP_OR:
466 | return Or(L)
467 | elif op == Z3_OP_AND:
468 | return And(L)
469 | else: #IMPLIES
470 | return Implies(L[0],L[1])
471 | else:
472 | return None
473 |
474 |
475 | def myAnd(*L): return myBinOp(Z3_OP_AND,*L)
476 | def myOr(*L): return myBinOp(Z3_OP_OR,*L)
477 | def myImplies(a,b):return myBinOp(Z3_OP_IMPLIES,[a,b])
478 |
479 |
480 |
481 | Iff = lambda f: And(Implies(f[0],f[1]),Implies(f[1],f[0]))
482 |
483 |
484 |
485 | def model_str(m,as_str=True):
486 | """
487 | Returned a 'sorted' model (so that it's easier to see)
488 | The model is sorted by its key,
489 | e.g. if the model is y = 3 , x = 10, then the result is
490 | x = 10, y = 3
491 |
492 | EXAMPLES:
493 | see doctest exampels from function prove()
494 |
495 | """
496 | if __debug__:
497 | assert m is None or m == [] or isinstance(m,ModelRef)
498 |
499 | if m :
500 | vs = [(v,m[v]) for v in m]
501 | vs = sorted(vs,key=lambda a,_: str(a))
502 | if as_str:
503 | return '\n'.join(['{} = {}'.format(k,v) for (k,v) in vs])
504 | else:
505 | return vs
506 | else:
507 | return str(m) if as_str else m
508 |
509 |
--------------------------------------------------------------------------------
/z3-4.5.0-x64-win/bin/python/z3/z3util.pyc:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/TechSecCTF/z3_splash_class/b64cf9b51187c7b179b63ed4de43aa28b6a70fdb/z3-4.5.0-x64-win/bin/python/z3/z3util.pyc
--------------------------------------------------------------------------------
/z3-4.5.0-x64-win/bin/vcomp110.dll:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/TechSecCTF/z3_splash_class/b64cf9b51187c7b179b63ed4de43aa28b6a70fdb/z3-4.5.0-x64-win/bin/vcomp110.dll
--------------------------------------------------------------------------------
/z3-4.5.0-x64-win/bin/z3.exe:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/TechSecCTF/z3_splash_class/b64cf9b51187c7b179b63ed4de43aa28b6a70fdb/z3-4.5.0-x64-win/bin/z3.exe
--------------------------------------------------------------------------------
/z3-4.5.0-x64-win/include/z3.h:
--------------------------------------------------------------------------------
1 | /*++
2 | Copyright (c) 2007 Microsoft Corporation
3 |
4 | Module Name:
5 |
6 | z3.h
7 |
8 | Abstract:
9 |
10 | Z3 API.
11 |
12 | Author:
13 |
14 | Nikolaj Bjorner (nbjorner)
15 | Leonardo de Moura (leonardo) 2007-06-8
16 |
17 | Notes:
18 |
19 | --*/
20 |
21 | #ifndef Z3_H_
22 | #define Z3_H_
23 |
24 | #include
25 | #include"z3_macros.h"
26 | #include"z3_api.h"
27 | #include"z3_ast_containers.h"
28 | #include"z3_algebraic.h"
29 | #include"z3_polynomial.h"
30 | #include"z3_rcf.h"
31 | #include"z3_fixedpoint.h"
32 | #include"z3_optimization.h"
33 | #include"z3_interp.h"
34 | #include"z3_fpa.h"
35 |
36 | #endif
37 |
38 |
--------------------------------------------------------------------------------
/z3-4.5.0-x64-win/include/z3_algebraic.h:
--------------------------------------------------------------------------------
1 | /*++
2 | Copyright (c) 2012 Microsoft Corporation
3 |
4 | Module Name:
5 |
6 | z3_algebraic.h
7 |
8 | Abstract:
9 |
10 | Additional APIs for handling Z3 algebraic numbers encoded as
11 | Z3_ASTs
12 |
13 | Author:
14 |
15 | Leonardo de Moura (leonardo) 2012-12-07
16 |
17 | Notes:
18 |
19 | --*/
20 |
21 | #ifndef Z3_ALGEBRAIC_H_
22 | #define Z3_ALGEBRAIC_H_
23 |
24 | #ifdef __cplusplus
25 | extern "C" {
26 | #endif // __cplusplus
27 |
28 | /** \defgroup capi C API */
29 | /*@{*/
30 |
31 | /** @name Algebraic Numbers */
32 | /*@{*/
33 | /**
34 | \brief Return Z3_TRUE if \c can be used as value in the Z3 real algebraic
35 | number package.
36 |
37 | def_API('Z3_algebraic_is_value', BOOL, (_in(CONTEXT), _in(AST)))
38 | */
39 | Z3_bool Z3_API Z3_algebraic_is_value(Z3_context c, Z3_ast a);
40 |
41 | /**
42 | \brief Return the Z3_TRUE if \c a is positive, and Z3_FALSE otherwise.
43 |
44 | \pre Z3_algebraic_is_value(c, a)
45 |
46 | def_API('Z3_algebraic_is_pos', BOOL, (_in(CONTEXT), _in(AST)))
47 | */
48 | Z3_bool Z3_API Z3_algebraic_is_pos(Z3_context c, Z3_ast a);
49 |
50 | /**
51 | \brief Return the Z3_TRUE if \c a is negative, and Z3_FALSE otherwise.
52 |
53 | \pre Z3_algebraic_is_value(c, a)
54 |
55 | def_API('Z3_algebraic_is_neg', BOOL, (_in(CONTEXT), _in(AST)))
56 | */
57 | Z3_bool Z3_API Z3_algebraic_is_neg(Z3_context c, Z3_ast a);
58 |
59 | /**
60 | \brief Return the Z3_TRUE if \c a is zero, and Z3_FALSE otherwise.
61 |
62 | \pre Z3_algebraic_is_value(c, a)
63 |
64 | def_API('Z3_algebraic_is_zero', BOOL, (_in(CONTEXT), _in(AST)))
65 | */
66 | Z3_bool Z3_API Z3_algebraic_is_zero(Z3_context c, Z3_ast a);
67 |
68 | /**
69 | \brief Return 1 if \c a is positive, 0 if \c a is zero, and -1 if \c a is negative.
70 |
71 | \pre Z3_algebraic_is_value(c, a)
72 |
73 | def_API('Z3_algebraic_sign', INT, (_in(CONTEXT), _in(AST)))
74 | */
75 | int Z3_API Z3_algebraic_sign(Z3_context c, Z3_ast a);
76 |
77 | /**
78 | \brief Return the value a + b.
79 |
80 | \pre Z3_algebraic_is_value(c, a)
81 | \pre Z3_algebraic_is_value(c, b)
82 | \post Z3_algebraic_is_value(c, result)
83 |
84 | def_API('Z3_algebraic_add', AST, (_in(CONTEXT), _in(AST), _in(AST)))
85 | */
86 | Z3_ast Z3_API Z3_algebraic_add(Z3_context c, Z3_ast a, Z3_ast b);
87 |
88 | /**
89 | \brief Return the value a - b.
90 |
91 | \pre Z3_algebraic_is_value(c, a)
92 | \pre Z3_algebraic_is_value(c, b)
93 | \post Z3_algebraic_is_value(c, result)
94 |
95 | def_API('Z3_algebraic_sub', AST, (_in(CONTEXT), _in(AST), _in(AST)))
96 | */
97 | Z3_ast Z3_API Z3_algebraic_sub(Z3_context c, Z3_ast a, Z3_ast b);
98 |
99 | /**
100 | \brief Return the value a * b.
101 |
102 | \pre Z3_algebraic_is_value(c, a)
103 | \pre Z3_algebraic_is_value(c, b)
104 | \post Z3_algebraic_is_value(c, result)
105 |
106 | def_API('Z3_algebraic_mul', AST, (_in(CONTEXT), _in(AST), _in(AST)))
107 | */
108 | Z3_ast Z3_API Z3_algebraic_mul(Z3_context c, Z3_ast a, Z3_ast b);
109 |
110 | /**
111 | \brief Return the value a / b.
112 |
113 | \pre Z3_algebraic_is_value(c, a)
114 | \pre Z3_algebraic_is_value(c, b)
115 | \pre !Z3_algebraic_is_zero(c, b)
116 | \post Z3_algebraic_is_value(c, result)
117 |
118 | def_API('Z3_algebraic_div', AST, (_in(CONTEXT), _in(AST), _in(AST)))
119 | */
120 | Z3_ast Z3_API Z3_algebraic_div(Z3_context c, Z3_ast a, Z3_ast b);
121 |
122 | /**
123 | \brief Return the a^(1/k)
124 |
125 | \pre Z3_algebraic_is_value(c, a)
126 | \pre k is even => !Z3_algebraic_is_neg(c, a)
127 | \post Z3_algebraic_is_value(c, result)
128 |
129 | def_API('Z3_algebraic_root', AST, (_in(CONTEXT), _in(AST), _in(UINT)))
130 | */
131 | Z3_ast Z3_API Z3_algebraic_root(Z3_context c, Z3_ast a, unsigned k);
132 |
133 | /**
134 | \brief Return the a^k
135 |
136 | \pre Z3_algebraic_is_value(c, a)
137 | \post Z3_algebraic_is_value(c, result)
138 |
139 | def_API('Z3_algebraic_power', AST, (_in(CONTEXT), _in(AST), _in(UINT)))
140 | */
141 | Z3_ast Z3_API Z3_algebraic_power(Z3_context c, Z3_ast a, unsigned k);
142 |
143 | /**
144 | \brief Return Z3_TRUE if a < b, and Z3_FALSE otherwise.
145 |
146 | \pre Z3_algebraic_is_value(c, a)
147 | \pre Z3_algebraic_is_value(c, b)
148 |
149 | def_API('Z3_algebraic_lt', BOOL, (_in(CONTEXT), _in(AST), _in(AST)))
150 | */
151 | Z3_bool Z3_API Z3_algebraic_lt(Z3_context c, Z3_ast a, Z3_ast b);
152 |
153 | /**
154 | \brief Return Z3_TRUE if a > b, and Z3_FALSE otherwise.
155 |
156 | \pre Z3_algebraic_is_value(c, a)
157 | \pre Z3_algebraic_is_value(c, b)
158 |
159 | def_API('Z3_algebraic_gt', BOOL, (_in(CONTEXT), _in(AST), _in(AST)))
160 | */
161 | Z3_bool Z3_API Z3_algebraic_gt(Z3_context c, Z3_ast a, Z3_ast b);
162 |
163 | /**
164 | \brief Return Z3_TRUE if a <= b, and Z3_FALSE otherwise.
165 |
166 | \pre Z3_algebraic_is_value(c, a)
167 | \pre Z3_algebraic_is_value(c, b)
168 |
169 | def_API('Z3_algebraic_le', BOOL, (_in(CONTEXT), _in(AST), _in(AST)))
170 | */
171 | Z3_bool Z3_API Z3_algebraic_le(Z3_context c, Z3_ast a, Z3_ast b);
172 |
173 | /**
174 | \brief Return Z3_TRUE if a >= b, and Z3_FALSE otherwise.
175 |
176 | \pre Z3_algebraic_is_value(c, a)
177 | \pre Z3_algebraic_is_value(c, b)
178 |
179 | def_API('Z3_algebraic_ge', BOOL, (_in(CONTEXT), _in(AST), _in(AST)))
180 | */
181 | Z3_bool Z3_API Z3_algebraic_ge(Z3_context c, Z3_ast a, Z3_ast b);
182 |
183 | /**
184 | \brief Return Z3_TRUE if a == b, and Z3_FALSE otherwise.
185 |
186 | \pre Z3_algebraic_is_value(c, a)
187 | \pre Z3_algebraic_is_value(c, b)
188 |
189 | def_API('Z3_algebraic_eq', BOOL, (_in(CONTEXT), _in(AST), _in(AST)))
190 | */
191 | Z3_bool Z3_API Z3_algebraic_eq(Z3_context c, Z3_ast a, Z3_ast b);
192 |
193 | /**
194 | \brief Return Z3_TRUE if a != b, and Z3_FALSE otherwise.
195 |
196 | \pre Z3_algebraic_is_value(c, a)
197 | \pre Z3_algebraic_is_value(c, b)
198 |
199 | def_API('Z3_algebraic_neq', BOOL, (_in(CONTEXT), _in(AST), _in(AST)))
200 | */
201 | Z3_bool Z3_API Z3_algebraic_neq(Z3_context c, Z3_ast a, Z3_ast b);
202 |
203 | /**
204 | \brief Given a multivariate polynomial p(x_0, ..., x_{n-1}, x_n), returns the
205 | roots of the univariate polynomial p(a[0], ..., a[n-1], x_n).
206 |
207 | \pre p is a Z3 expression that contains only arithmetic terms and free variables.
208 | \pre forall i in [0, n) Z3_algebraic_is_value(c, a[i])
209 | \post forall r in result Z3_algebraic_is_value(c, result)
210 |
211 | def_API('Z3_algebraic_roots', AST_VECTOR, (_in(CONTEXT), _in(AST), _in(UINT), _in_array(2, AST)))
212 | */
213 | Z3_ast_vector Z3_API Z3_algebraic_roots(Z3_context c, Z3_ast p, unsigned n, Z3_ast a[]);
214 |
215 | /**
216 | \brief Given a multivariate polynomial p(x_0, ..., x_{n-1}), return the
217 | sign of p(a[0], ..., a[n-1]).
218 |
219 | \pre p is a Z3 expression that contains only arithmetic terms and free variables.
220 | \pre forall i in [0, n) Z3_algebraic_is_value(c, a[i])
221 |
222 | def_API('Z3_algebraic_eval', INT, (_in(CONTEXT), _in(AST), _in(UINT), _in_array(2, AST)))
223 | */
224 | int Z3_API Z3_algebraic_eval(Z3_context c, Z3_ast p, unsigned n, Z3_ast a[]);
225 |
226 | /*@}*/
227 | /*@}*/
228 |
229 | #ifdef __cplusplus
230 | }
231 | #endif // __cplusplus
232 |
233 | #endif
234 |
--------------------------------------------------------------------------------
/z3-4.5.0-x64-win/include/z3_ast_containers.h:
--------------------------------------------------------------------------------
1 | /*++
2 | Copyright (c) 2015 Microsoft Corporation
3 |
4 | Module Name:
5 |
6 | z3_ast_containers.h
7 |
8 | Abstract:
9 |
10 | AST Containers
11 |
12 | Author:
13 |
14 | Christoph M. Wintersteiger (cwinter) 2015-12-03
15 |
16 | Notes:
17 |
18 | --*/
19 | #ifndef Z3_AST_CONTAINERS_H_
20 | #define Z3_AST_CONTAINERS_H_
21 |
22 | #ifdef __cplusplus
23 | extern "C" {
24 | #endif // __cplusplus
25 |
26 | /** \defgroup capi C API */
27 | /*@{*/
28 |
29 | /** @name AST vectors */
30 | /*@{*/
31 | /**
32 | \brief Return an empty AST vector.
33 |
34 | \remark Reference counting must be used to manage AST vectors, even when the Z3_context was
35 | created using #Z3_mk_context instead of #Z3_mk_context_rc.
36 |
37 | def_API('Z3_mk_ast_vector', AST_VECTOR, (_in(CONTEXT),))
38 | */
39 | Z3_ast_vector Z3_API Z3_mk_ast_vector(Z3_context c);
40 |
41 | /**
42 | \brief Increment the reference counter of the given AST vector.
43 |
44 | def_API('Z3_ast_vector_inc_ref', VOID, (_in(CONTEXT), _in(AST_VECTOR)))
45 | */
46 | void Z3_API Z3_ast_vector_inc_ref(Z3_context c, Z3_ast_vector v);
47 |
48 | /**
49 | \brief Decrement the reference counter of the given AST vector.
50 |
51 | def_API('Z3_ast_vector_dec_ref', VOID, (_in(CONTEXT), _in(AST_VECTOR)))
52 | */
53 | void Z3_API Z3_ast_vector_dec_ref(Z3_context c, Z3_ast_vector v);
54 |
55 | /**
56 | \brief Return the size of the given AST vector.
57 |
58 | def_API('Z3_ast_vector_size', UINT, (_in(CONTEXT), _in(AST_VECTOR)))
59 | */
60 | unsigned Z3_API Z3_ast_vector_size(Z3_context c, Z3_ast_vector v);
61 |
62 | /**
63 | \brief Return the AST at position \c i in the AST vector \c v.
64 |
65 | \pre i < Z3_ast_vector_size(c, v)
66 |
67 | def_API('Z3_ast_vector_get', AST, (_in(CONTEXT), _in(AST_VECTOR), _in(UINT)))
68 | */
69 | Z3_ast Z3_API Z3_ast_vector_get(Z3_context c, Z3_ast_vector v, unsigned i);
70 |
71 | /**
72 | \brief Update position \c i of the AST vector \c v with the AST \c a.
73 |
74 | \pre i < Z3_ast_vector_size(c, v)
75 |
76 | def_API('Z3_ast_vector_set', VOID, (_in(CONTEXT), _in(AST_VECTOR), _in(UINT), _in(AST)))
77 | */
78 | void Z3_API Z3_ast_vector_set(Z3_context c, Z3_ast_vector v, unsigned i, Z3_ast a);
79 |
80 | /**
81 | \brief Resize the AST vector \c v.
82 |
83 | def_API('Z3_ast_vector_resize', VOID, (_in(CONTEXT), _in(AST_VECTOR), _in(UINT)))
84 | */
85 | void Z3_API Z3_ast_vector_resize(Z3_context c, Z3_ast_vector v, unsigned n);
86 |
87 | /**
88 | \brief Add the AST \c a in the end of the AST vector \c v. The size of \c v is increased by one.
89 |
90 | def_API('Z3_ast_vector_push', VOID, (_in(CONTEXT), _in(AST_VECTOR), _in(AST)))
91 | */
92 | void Z3_API Z3_ast_vector_push(Z3_context c, Z3_ast_vector v, Z3_ast a);
93 |
94 | /**
95 | \brief Translate the AST vector \c v from context \c s into an AST vector in context \c t.
96 |
97 | def_API('Z3_ast_vector_translate', AST_VECTOR, (_in(CONTEXT), _in(AST_VECTOR), _in(CONTEXT)))
98 | */
99 | Z3_ast_vector Z3_API Z3_ast_vector_translate(Z3_context s, Z3_ast_vector v, Z3_context t);
100 |
101 | /**
102 | \brief Convert AST vector into a string.
103 |
104 | def_API('Z3_ast_vector_to_string', STRING, (_in(CONTEXT), _in(AST_VECTOR)))
105 | */
106 | Z3_string Z3_API Z3_ast_vector_to_string(Z3_context c, Z3_ast_vector v);
107 |
108 | /*@}*/
109 |
110 | /** @name AST maps */
111 | /*@{*/
112 | /**
113 | \brief Return an empty mapping from AST to AST
114 |
115 | \remark Reference counting must be used to manage AST maps, even when the Z3_context was
116 | created using #Z3_mk_context instead of #Z3_mk_context_rc.
117 |
118 | def_API('Z3_mk_ast_map', AST_MAP, (_in(CONTEXT),) )
119 | */
120 | Z3_ast_map Z3_API Z3_mk_ast_map(Z3_context c);
121 |
122 | /**
123 | \brief Increment the reference counter of the given AST map.
124 |
125 | def_API('Z3_ast_map_inc_ref', VOID, (_in(CONTEXT), _in(AST_MAP)))
126 | */
127 | void Z3_API Z3_ast_map_inc_ref(Z3_context c, Z3_ast_map m);
128 |
129 | /**
130 | \brief Decrement the reference counter of the given AST map.
131 |
132 | def_API('Z3_ast_map_dec_ref', VOID, (_in(CONTEXT), _in(AST_MAP)))
133 | */
134 | void Z3_API Z3_ast_map_dec_ref(Z3_context c, Z3_ast_map m);
135 |
136 | /**
137 | \brief Return true if the map \c m contains the AST key \c k.
138 |
139 | def_API('Z3_ast_map_contains', BOOL, (_in(CONTEXT), _in(AST_MAP), _in(AST)))
140 | */
141 | Z3_bool Z3_API Z3_ast_map_contains(Z3_context c, Z3_ast_map m, Z3_ast k);
142 |
143 | /**
144 | \brief Return the value associated with the key \c k.
145 |
146 | The procedure invokes the error handler if \c k is not in the map.
147 |
148 | def_API('Z3_ast_map_find', AST, (_in(CONTEXT), _in(AST_MAP), _in(AST)))
149 | */
150 | Z3_ast Z3_API Z3_ast_map_find(Z3_context c, Z3_ast_map m, Z3_ast k);
151 |
152 | /**
153 | \brief Store/Replace a new key, value pair in the given map.
154 |
155 | def_API('Z3_ast_map_insert', VOID, (_in(CONTEXT), _in(AST_MAP), _in(AST), _in(AST)))
156 | */
157 | void Z3_API Z3_ast_map_insert(Z3_context c, Z3_ast_map m, Z3_ast k, Z3_ast v);
158 |
159 | /**
160 | \brief Erase a key from the map.
161 |
162 | def_API('Z3_ast_map_erase', VOID, (_in(CONTEXT), _in(AST_MAP), _in(AST)))
163 | */
164 | void Z3_API Z3_ast_map_erase(Z3_context c, Z3_ast_map m, Z3_ast k);
165 |
166 | /**
167 | \brief Remove all keys from the given map.
168 |
169 | def_API('Z3_ast_map_reset', VOID, (_in(CONTEXT), _in(AST_MAP)))
170 | */
171 | void Z3_API Z3_ast_map_reset(Z3_context c, Z3_ast_map m);
172 |
173 | /**
174 | \brief Return the size of the given map.
175 |
176 | def_API('Z3_ast_map_size', UINT, (_in(CONTEXT), _in(AST_MAP)))
177 | */
178 | unsigned Z3_API Z3_ast_map_size(Z3_context c, Z3_ast_map m);
179 |
180 | /**
181 | \brief Return the keys stored in the given map.
182 |
183 | def_API('Z3_ast_map_keys', AST_VECTOR, (_in(CONTEXT), _in(AST_MAP)))
184 | */
185 | Z3_ast_vector Z3_API Z3_ast_map_keys(Z3_context c, Z3_ast_map m);
186 |
187 | /**
188 | \brief Convert the given map into a string.
189 |
190 | def_API('Z3_ast_map_to_string', STRING, (_in(CONTEXT), _in(AST_MAP)))
191 | */
192 | Z3_string Z3_API Z3_ast_map_to_string(Z3_context c, Z3_ast_map m);
193 | /*@}*/
194 | /*@}*/
195 |
196 | #ifdef __cplusplus
197 | }
198 | #endif // __cplusplus
199 |
200 | #endif
--------------------------------------------------------------------------------
/z3-4.5.0-x64-win/include/z3_fixedpoint.h:
--------------------------------------------------------------------------------
1 | /*++
2 | Copyright (c) 2015 Microsoft Corporation
3 |
4 | Module Name:
5 |
6 | z3_fixedpoint.h
7 |
8 | Abstract:
9 |
10 | Fixedpoint API
11 |
12 | Author:
13 |
14 | Christoph M. Wintersteiger (cwinter) 2015-12-03
15 |
16 | Notes:
17 |
18 | --*/
19 | #ifndef Z3_FIXEDPOINT_H_
20 | #define Z3_FIXEDPOINT_H_
21 |
22 | #ifdef __cplusplus
23 | extern "C" {
24 | #endif // __cplusplus
25 |
26 | /** \defgroup capi C API */
27 | /*@{*/
28 |
29 | /** @name Fixedpoint facilities */
30 | /*@{*/
31 | /**
32 | \brief Create a new fixedpoint context.
33 |
34 | \remark User must use #Z3_fixedpoint_inc_ref and #Z3_fixedpoint_dec_ref to manage fixedpoint objects.
35 | Even if the context was created using #Z3_mk_context instead of #Z3_mk_context_rc.
36 |
37 | def_API('Z3_mk_fixedpoint', FIXEDPOINT, (_in(CONTEXT), ))
38 | */
39 | Z3_fixedpoint Z3_API Z3_mk_fixedpoint(Z3_context c);
40 |
41 | /**
42 | \brief Increment the reference counter of the given fixedpoint context
43 |
44 | def_API('Z3_fixedpoint_inc_ref', VOID, (_in(CONTEXT), _in(FIXEDPOINT)))
45 | */
46 | void Z3_API Z3_fixedpoint_inc_ref(Z3_context c, Z3_fixedpoint d);
47 |
48 | /**
49 | \brief Decrement the reference counter of the given fixedpoint context.
50 |
51 | def_API('Z3_fixedpoint_dec_ref', VOID, (_in(CONTEXT), _in(FIXEDPOINT)))
52 | */
53 | void Z3_API Z3_fixedpoint_dec_ref(Z3_context c, Z3_fixedpoint d);
54 |
55 | /**
56 | \brief Add a universal Horn clause as a named rule.
57 | The \c horn_rule should be of the form:
58 |
59 | \code
60 | horn_rule ::= (forall (bound-vars) horn_rule)
61 | | (=> atoms horn_rule)
62 | | atom
63 | \endcode
64 |
65 | def_API('Z3_fixedpoint_add_rule', VOID, (_in(CONTEXT), _in(FIXEDPOINT), _in(AST), _in(SYMBOL)))
66 | */
67 | void Z3_API Z3_fixedpoint_add_rule(Z3_context c, Z3_fixedpoint d, Z3_ast rule, Z3_symbol name);
68 |
69 | /**
70 | \brief Add a Database fact.
71 |
72 | \param c - context
73 | \param d - fixed point context
74 | \param r - relation signature for the row.
75 | \param num_args - number of columns for the given row.
76 | \param args - array of the row elements.
77 |
78 | The number of arguments \c num_args should be equal to the number
79 | of sorts in the domain of \c r. Each sort in the domain should be an integral
80 | (bit-vector, Boolean or or finite domain sort).
81 |
82 | The call has the same effect as adding a rule where \c r is applied to the arguments.
83 |
84 | def_API('Z3_fixedpoint_add_fact', VOID, (_in(CONTEXT), _in(FIXEDPOINT), _in(FUNC_DECL), _in(UINT), _in_array(3, UINT)))
85 | */
86 | void Z3_API Z3_fixedpoint_add_fact(Z3_context c, Z3_fixedpoint d,
87 | Z3_func_decl r,
88 | unsigned num_args, unsigned args[]);
89 |
90 | /**
91 | \brief Assert a constraint to the fixedpoint context.
92 |
93 | The constraints are used as background axioms when the fixedpoint engine uses the PDR mode.
94 | They are ignored for standard Datalog mode.
95 |
96 | def_API('Z3_fixedpoint_assert', VOID, (_in(CONTEXT), _in(FIXEDPOINT), _in(AST)))
97 | */
98 | void Z3_API Z3_fixedpoint_assert(Z3_context c, Z3_fixedpoint d, Z3_ast axiom);
99 |
100 | /**
101 | \brief Pose a query against the asserted rules.
102 |
103 | \code
104 | query ::= (exists (bound-vars) query)
105 | | literals
106 | \endcode
107 |
108 | query returns
109 | - Z3_L_FALSE if the query is unsatisfiable.
110 | - Z3_L_TRUE if the query is satisfiable. Obtain the answer by calling #Z3_fixedpoint_get_answer.
111 | - Z3_L_UNDEF if the query was interrupted, timed out or otherwise failed.
112 |
113 | def_API('Z3_fixedpoint_query', INT, (_in(CONTEXT), _in(FIXEDPOINT), _in(AST)))
114 | */
115 | Z3_lbool Z3_API Z3_fixedpoint_query(Z3_context c, Z3_fixedpoint d, Z3_ast query);
116 |
117 | /**
118 | \brief Pose multiple queries against the asserted rules.
119 |
120 | The queries are encoded as relations (function declarations).
121 |
122 | query returns
123 | - Z3_L_FALSE if the query is unsatisfiable.
124 | - Z3_L_TRUE if the query is satisfiable. Obtain the answer by calling #Z3_fixedpoint_get_answer.
125 | - Z3_L_UNDEF if the query was interrupted, timed out or otherwise failed.
126 |
127 | def_API('Z3_fixedpoint_query_relations', INT, (_in(CONTEXT), _in(FIXEDPOINT), _in(UINT), _in_array(2, FUNC_DECL)))
128 | */
129 | Z3_lbool Z3_API Z3_fixedpoint_query_relations(
130 | Z3_context c, Z3_fixedpoint d,
131 | unsigned num_relations, Z3_func_decl const relations[]);
132 |
133 | /**
134 | \brief Retrieve a formula that encodes satisfying answers to the query.
135 |
136 |
137 | When used in Datalog mode, the returned answer is a disjunction of conjuncts.
138 | Each conjunct encodes values of the bound variables of the query that are satisfied.
139 | In PDR mode, the returned answer is a single conjunction.
140 |
141 | When used in Datalog mode the previous call to Z3_fixedpoint_query must have returned Z3_L_TRUE.
142 | When used with the PDR engine, the previous call must have been either Z3_L_TRUE or Z3_L_FALSE.
143 |
144 | def_API('Z3_fixedpoint_get_answer', AST, (_in(CONTEXT), _in(FIXEDPOINT)))
145 | */
146 | Z3_ast Z3_API Z3_fixedpoint_get_answer(Z3_context c, Z3_fixedpoint d);
147 |
148 | /**
149 | \brief Retrieve a string that describes the last status returned by #Z3_fixedpoint_query.
150 |
151 | Use this method when #Z3_fixedpoint_query returns Z3_L_UNDEF.
152 |
153 | def_API('Z3_fixedpoint_get_reason_unknown', STRING, (_in(CONTEXT), _in(FIXEDPOINT) ))
154 | */
155 | Z3_string Z3_API Z3_fixedpoint_get_reason_unknown(Z3_context c, Z3_fixedpoint d);
156 |
157 | /**
158 | \brief Update a named rule.
159 | A rule with the same name must have been previously created.
160 |
161 | def_API('Z3_fixedpoint_update_rule', VOID, (_in(CONTEXT), _in(FIXEDPOINT), _in(AST), _in(SYMBOL)))
162 | */
163 | void Z3_API Z3_fixedpoint_update_rule(Z3_context c, Z3_fixedpoint d, Z3_ast a, Z3_symbol name);
164 |
165 | /**
166 | \brief Query the PDR engine for the maximal levels properties are known about predicate.
167 |
168 | This call retrieves the maximal number of relevant unfoldings
169 | of \c pred with respect to the current exploration state.
170 | Note: this functionality is PDR specific.
171 |
172 | def_API('Z3_fixedpoint_get_num_levels', UINT, (_in(CONTEXT), _in(FIXEDPOINT), _in(FUNC_DECL)))
173 | */
174 | unsigned Z3_API Z3_fixedpoint_get_num_levels(Z3_context c, Z3_fixedpoint d, Z3_func_decl pred);
175 |
176 | /**
177 | Retrieve the current cover of \c pred up to \c level unfoldings.
178 | Return just the delta that is known at \c level. To
179 | obtain the full set of properties of \c pred one should query
180 | at \c level+1 , \c level+2 etc, and include \c level=-1.
181 |
182 | Note: this functionality is PDR specific.
183 |
184 | def_API('Z3_fixedpoint_get_cover_delta', AST, (_in(CONTEXT), _in(FIXEDPOINT), _in(INT), _in(FUNC_DECL)))
185 | */
186 | Z3_ast Z3_API Z3_fixedpoint_get_cover_delta(Z3_context c, Z3_fixedpoint d, int level, Z3_func_decl pred);
187 |
188 | /**
189 | \brief Add property about the predicate \c pred.
190 | Add a property of predicate \c pred at \c level.
191 | It gets pushed forward when possible.
192 |
193 | Note: level = -1 is treated as the fixedpoint. So passing -1 for the \c level
194 | means that the property is true of the fixed-point unfolding with respect to \c pred.
195 |
196 | Note: this functionality is PDR specific.
197 |
198 | def_API('Z3_fixedpoint_add_cover', VOID, (_in(CONTEXT), _in(FIXEDPOINT), _in(INT), _in(FUNC_DECL), _in(AST)))
199 | */
200 | void Z3_API Z3_fixedpoint_add_cover(Z3_context c, Z3_fixedpoint d, int level, Z3_func_decl pred, Z3_ast property);
201 |
202 | /**
203 | \brief Retrieve statistics information from the last call to #Z3_fixedpoint_query.
204 |
205 | def_API('Z3_fixedpoint_get_statistics', STATS, (_in(CONTEXT), _in(FIXEDPOINT)))
206 | */
207 | Z3_stats Z3_API Z3_fixedpoint_get_statistics(Z3_context c, Z3_fixedpoint d);
208 |
209 | /**
210 | \brief Register relation as Fixedpoint defined.
211 | Fixedpoint defined relations have least-fixedpoint semantics.
212 | For example, the relation is empty if it does not occur
213 | in a head or a fact.
214 |
215 | def_API('Z3_fixedpoint_register_relation', VOID, (_in(CONTEXT), _in(FIXEDPOINT), _in(FUNC_DECL)))
216 | */
217 | void Z3_API Z3_fixedpoint_register_relation(Z3_context c, Z3_fixedpoint d, Z3_func_decl f);
218 |
219 | /**
220 | \brief Configure the predicate representation.
221 |
222 | It sets the predicate to use a set of domains given by the list of symbols.
223 | The domains given by the list of symbols must belong to a set
224 | of built-in domains.
225 |
226 | def_API('Z3_fixedpoint_set_predicate_representation', VOID, (_in(CONTEXT), _in(FIXEDPOINT), _in(FUNC_DECL), _in(UINT), _in_array(3, SYMBOL)))
227 | */
228 | void Z3_API Z3_fixedpoint_set_predicate_representation(
229 | Z3_context c,
230 | Z3_fixedpoint d,
231 | Z3_func_decl f,
232 | unsigned num_relations,
233 | Z3_symbol const relation_kinds[]);
234 |
235 | /**
236 | \brief Retrieve set of rules from fixedpoint context.
237 |
238 | def_API('Z3_fixedpoint_get_rules', AST_VECTOR, (_in(CONTEXT),_in(FIXEDPOINT)))
239 | */
240 | Z3_ast_vector Z3_API Z3_fixedpoint_get_rules(
241 | Z3_context c,
242 | Z3_fixedpoint f);
243 |
244 | /**
245 | \brief Retrieve set of background assertions from fixedpoint context.
246 |
247 | def_API('Z3_fixedpoint_get_assertions', AST_VECTOR, (_in(CONTEXT),_in(FIXEDPOINT)))
248 | */
249 | Z3_ast_vector Z3_API Z3_fixedpoint_get_assertions(
250 | Z3_context c,
251 | Z3_fixedpoint f);
252 |
253 | /**
254 | \brief Set parameters on fixedpoint context.
255 |
256 | def_API('Z3_fixedpoint_set_params', VOID, (_in(CONTEXT), _in(FIXEDPOINT), _in(PARAMS)))
257 | */
258 | void Z3_API Z3_fixedpoint_set_params(Z3_context c, Z3_fixedpoint f, Z3_params p);
259 |
260 | /**
261 | \brief Return a string describing all fixedpoint available parameters.
262 |
263 | def_API('Z3_fixedpoint_get_help', STRING, (_in(CONTEXT), _in(FIXEDPOINT)))
264 | */
265 | Z3_string Z3_API Z3_fixedpoint_get_help(Z3_context c, Z3_fixedpoint f);
266 |
267 | /**
268 | \brief Return the parameter description set for the given fixedpoint object.
269 |
270 | def_API('Z3_fixedpoint_get_param_descrs', PARAM_DESCRS, (_in(CONTEXT), _in(FIXEDPOINT)))
271 | */
272 | Z3_param_descrs Z3_API Z3_fixedpoint_get_param_descrs(Z3_context c, Z3_fixedpoint f);
273 |
274 | /**
275 | \brief Print the current rules and background axioms as a string.
276 | \param c - context.
277 | \param f - fixedpoint context.
278 | \param num_queries - number of additional queries to print.
279 | \param queries - additional queries.
280 |
281 | def_API('Z3_fixedpoint_to_string', STRING, (_in(CONTEXT), _in(FIXEDPOINT), _in(UINT), _in_array(2, AST)))
282 | */
283 | Z3_string Z3_API Z3_fixedpoint_to_string(
284 | Z3_context c,
285 | Z3_fixedpoint f,
286 | unsigned num_queries,
287 | Z3_ast queries[]);
288 |
289 | /**
290 | \brief Parse an SMT-LIB2 string with fixedpoint rules.
291 | Add the rules to the current fixedpoint context.
292 | Return the set of queries in the string.
293 |
294 | \param c - context.
295 | \param f - fixedpoint context.
296 | \param s - string containing SMT2 specification.
297 |
298 | def_API('Z3_fixedpoint_from_string', AST_VECTOR, (_in(CONTEXT), _in(FIXEDPOINT), _in(STRING)))
299 | */
300 | Z3_ast_vector Z3_API Z3_fixedpoint_from_string(Z3_context c,
301 | Z3_fixedpoint f,
302 | Z3_string s);
303 |
304 | /**
305 | \brief Parse an SMT-LIB2 file with fixedpoint rules.
306 | Add the rules to the current fixedpoint context.
307 | Return the set of queries in the file.
308 |
309 | \param c - context.
310 | \param f - fixedpoint context.
311 | \param s - string containing SMT2 specification.
312 |
313 | def_API('Z3_fixedpoint_from_file', AST_VECTOR, (_in(CONTEXT), _in(FIXEDPOINT), _in(STRING)))
314 | */
315 | Z3_ast_vector Z3_API Z3_fixedpoint_from_file(Z3_context c,
316 | Z3_fixedpoint f,
317 | Z3_string s);
318 |
319 | /**
320 | \brief Create a backtracking point.
321 |
322 | The fixedpoint solver contains a set of rules, added facts and assertions.
323 | The set of rules, facts and assertions are restored upon calling #Z3_fixedpoint_pop.
324 |
325 | \sa Z3_fixedpoint_pop
326 |
327 | def_API('Z3_fixedpoint_push', VOID, (_in(CONTEXT), _in(FIXEDPOINT)))
328 | */
329 | void Z3_API Z3_fixedpoint_push(Z3_context c, Z3_fixedpoint d);
330 |
331 | /**
332 | \brief Backtrack one backtracking point.
333 |
334 | \sa Z3_fixedpoint_push
335 |
336 | \pre The number of calls to pop cannot exceed calls to push.
337 |
338 | def_API('Z3_fixedpoint_pop', VOID, (_in(CONTEXT), _in(FIXEDPOINT)))
339 | */
340 | void Z3_API Z3_fixedpoint_pop(Z3_context c, Z3_fixedpoint d);
341 |
342 | /** \brief The following utilities allows adding user-defined domains. */
343 |
344 | typedef void Z3_fixedpoint_reduce_assign_callback_fptr(
345 | void*, Z3_func_decl,
346 | unsigned, Z3_ast const [],
347 | unsigned, Z3_ast const []);
348 |
349 | typedef void Z3_fixedpoint_reduce_app_callback_fptr(
350 | void*, Z3_func_decl,
351 | unsigned, Z3_ast const [],
352 | Z3_ast*);
353 |
354 |
355 | /** \brief Initialize the context with a user-defined state. */
356 | void Z3_API Z3_fixedpoint_init(Z3_context c, Z3_fixedpoint d, void* state);
357 |
358 | /**
359 | \brief Register a callback to destructive updates.
360 |
361 | Registers are identified with terms encoded as fresh constants,
362 | */
363 | void Z3_API Z3_fixedpoint_set_reduce_assign_callback(
364 | Z3_context c ,Z3_fixedpoint d, Z3_fixedpoint_reduce_assign_callback_fptr cb);
365 |
366 | /** \brief Register a callback for buildling terms based on the relational operators. */
367 | void Z3_API Z3_fixedpoint_set_reduce_app_callback(
368 | Z3_context c, Z3_fixedpoint d, Z3_fixedpoint_reduce_app_callback_fptr cb);
369 |
370 | /*@}*/
371 | /*@}*/
372 |
373 | #ifdef __cplusplus
374 | }
375 | #endif // __cplusplus
376 |
377 | #endif
378 |
--------------------------------------------------------------------------------
/z3-4.5.0-x64-win/include/z3_fpa.h:
--------------------------------------------------------------------------------
1 | /*++
2 | Copyright (c) 2013 Microsoft Corporation
3 |
4 | Module Name:
5 |
6 | z3_fpa.h
7 |
8 | Abstract:
9 |
10 | Additional APIs for floating-point arithmetic (FP).
11 |
12 | Author:
13 |
14 | Christoph M. Wintersteiger (cwinter) 2013-06-05
15 |
16 | Notes:
17 |
18 | --*/
19 | #ifndef Z3_FPA_H_
20 | #define Z3_FPA_H_
21 |
22 | #ifdef __cplusplus
23 | extern "C" {
24 | #endif // __cplusplus
25 |
26 | /** \defgroup capi C API */
27 | /*@{*/
28 |
29 | /** @name Floating-Point Arithmetic */
30 | /*@{*/
31 | /**
32 | \brief Create the RoundingMode sort.
33 |
34 | \param c logical context
35 |
36 | def_API('Z3_mk_fpa_rounding_mode_sort', SORT, (_in(CONTEXT),))
37 | */
38 | Z3_sort Z3_API Z3_mk_fpa_rounding_mode_sort(Z3_context c);
39 |
40 | /**
41 | \brief Create a numeral of RoundingMode sort which represents the NearestTiesToEven rounding mode.
42 |
43 | \param c logical context
44 |
45 | def_API('Z3_mk_fpa_round_nearest_ties_to_even', AST, (_in(CONTEXT),))
46 | */
47 | Z3_ast Z3_API Z3_mk_fpa_round_nearest_ties_to_even(Z3_context c);
48 |
49 | /**
50 | \brief Create a numeral of RoundingMode sort which represents the NearestTiesToEven rounding mode.
51 |
52 | \param c logical context
53 |
54 | def_API('Z3_mk_fpa_rne', AST, (_in(CONTEXT),))
55 | */
56 | Z3_ast Z3_API Z3_mk_fpa_rne(Z3_context c);
57 |
58 | /**
59 | \brief Create a numeral of RoundingMode sort which represents the NearestTiesToAway rounding mode.
60 |
61 | \param c logical context
62 |
63 | def_API('Z3_mk_fpa_round_nearest_ties_to_away', AST, (_in(CONTEXT),))
64 | */
65 | Z3_ast Z3_API Z3_mk_fpa_round_nearest_ties_to_away(Z3_context c);
66 |
67 | /**
68 | \brief Create a numeral of RoundingMode sort which represents the NearestTiesToAway rounding mode.
69 |
70 | \param c logical context
71 |
72 | def_API('Z3_mk_fpa_rna', AST, (_in(CONTEXT),))
73 | */
74 | Z3_ast Z3_API Z3_mk_fpa_rna(Z3_context c);
75 |
76 | /**
77 | \brief Create a numeral of RoundingMode sort which represents the TowardPositive rounding mode.
78 |
79 | \param c logical context
80 |
81 | def_API('Z3_mk_fpa_round_toward_positive', AST, (_in(CONTEXT),))
82 | */
83 | Z3_ast Z3_API Z3_mk_fpa_round_toward_positive(Z3_context c);
84 |
85 | /**
86 | \brief Create a numeral of RoundingMode sort which represents the TowardPositive rounding mode.
87 |
88 | \param c logical context
89 |
90 | def_API('Z3_mk_fpa_rtp', AST, (_in(CONTEXT),))
91 | */
92 | Z3_ast Z3_API Z3_mk_fpa_rtp(Z3_context c);
93 |
94 | /**
95 | \brief Create a numeral of RoundingMode sort which represents the TowardNegative rounding mode.
96 |
97 | \param c logical context
98 |
99 | def_API('Z3_mk_fpa_round_toward_negative', AST, (_in(CONTEXT),))
100 | */
101 | Z3_ast Z3_API Z3_mk_fpa_round_toward_negative(Z3_context c);
102 |
103 | /**
104 | \brief Create a numeral of RoundingMode sort which represents the TowardNegative rounding mode.
105 |
106 | \param c logical context
107 |
108 | def_API('Z3_mk_fpa_rtn', AST, (_in(CONTEXT),))
109 | */
110 | Z3_ast Z3_API Z3_mk_fpa_rtn(Z3_context c);
111 |
112 | /**
113 | \brief Create a numeral of RoundingMode sort which represents the TowardZero rounding mode.
114 |
115 | \param c logical context
116 |
117 | def_API('Z3_mk_fpa_round_toward_zero', AST, (_in(CONTEXT),))
118 | */
119 | Z3_ast Z3_API Z3_mk_fpa_round_toward_zero(Z3_context c);
120 |
121 | /**
122 | \brief Create a numeral of RoundingMode sort which represents the TowardZero rounding mode.
123 |
124 | \param c logical context
125 |
126 | def_API('Z3_mk_fpa_rtz', AST, (_in(CONTEXT),))
127 | */
128 | Z3_ast Z3_API Z3_mk_fpa_rtz(Z3_context c);
129 |
130 | /**
131 | \brief Create a FloatingPoint sort.
132 |
133 | \param c logical context
134 | \param ebits number of exponent bits
135 | \param sbits number of significand bits
136 |
137 | \remark ebits must be larger than 1 and sbits must be larger than 2.
138 |
139 | def_API('Z3_mk_fpa_sort', SORT, (_in(CONTEXT), _in(UINT), _in(UINT)))
140 | */
141 | Z3_sort Z3_API Z3_mk_fpa_sort(Z3_context c, unsigned ebits, unsigned sbits);
142 |
143 | /**
144 | \brief Create the half-precision (16-bit) FloatingPoint sort.
145 |
146 | \param c logical context
147 |
148 | def_API('Z3_mk_fpa_sort_half', SORT, (_in(CONTEXT),))
149 | */
150 | Z3_sort Z3_API Z3_mk_fpa_sort_half(Z3_context c);
151 |
152 | /**
153 | \brief Create the half-precision (16-bit) FloatingPoint sort.
154 |
155 | \param c logical context
156 |
157 | def_API('Z3_mk_fpa_sort_16', SORT, (_in(CONTEXT),))
158 | */
159 | Z3_sort Z3_API Z3_mk_fpa_sort_16(Z3_context c);
160 |
161 | /**
162 | \brief Create the single-precision (32-bit) FloatingPoint sort.
163 |
164 | \param c logical context.
165 |
166 | def_API('Z3_mk_fpa_sort_single', SORT, (_in(CONTEXT),))
167 | */
168 | Z3_sort Z3_API Z3_mk_fpa_sort_single(Z3_context c);
169 |
170 | /**
171 | \brief Create the single-precision (32-bit) FloatingPoint sort.
172 |
173 | \param c logical context
174 |
175 | def_API('Z3_mk_fpa_sort_32', SORT, (_in(CONTEXT),))
176 | */
177 | Z3_sort Z3_API Z3_mk_fpa_sort_32(Z3_context c);
178 |
179 | /**
180 | \brief Create the double-precision (64-bit) FloatingPoint sort.
181 |
182 | \param c logical context
183 |
184 | def_API('Z3_mk_fpa_sort_double', SORT, (_in(CONTEXT),))
185 | */
186 | Z3_sort Z3_API Z3_mk_fpa_sort_double(Z3_context c);
187 |
188 | /**
189 | \brief Create the double-precision (64-bit) FloatingPoint sort.
190 |
191 | \param c logical context
192 |
193 | def_API('Z3_mk_fpa_sort_64', SORT, (_in(CONTEXT),))
194 | */
195 | Z3_sort Z3_API Z3_mk_fpa_sort_64(Z3_context c);
196 |
197 | /**
198 | \brief Create the quadruple-precision (128-bit) FloatingPoint sort.
199 |
200 | \param c logical context
201 |
202 | def_API('Z3_mk_fpa_sort_quadruple', SORT, (_in(CONTEXT),))
203 | */
204 | Z3_sort Z3_API Z3_mk_fpa_sort_quadruple(Z3_context c);
205 |
206 | /**
207 | \brief Create the quadruple-precision (128-bit) FloatingPoint sort.
208 |
209 | \param c logical context
210 |
211 | def_API('Z3_mk_fpa_sort_128', SORT, (_in(CONTEXT),))
212 | */
213 | Z3_sort Z3_API Z3_mk_fpa_sort_128(Z3_context c);
214 |
215 | /**
216 | \brief Create a floating-point NaN of sort s.
217 |
218 | \param c logical context
219 | \param s target sort
220 |
221 | def_API('Z3_mk_fpa_nan', AST, (_in(CONTEXT),_in(SORT)))
222 | */
223 | Z3_ast Z3_API Z3_mk_fpa_nan(Z3_context c, Z3_sort s);
224 |
225 | /**
226 | \brief Create a floating-point infinity of sort s.
227 |
228 | \param c logical context
229 | \param s target sort
230 | \param negative indicates whether the result should be negative
231 |
232 | When \c negative is true, -oo will be generated instead of +oo.
233 |
234 | def_API('Z3_mk_fpa_inf', AST, (_in(CONTEXT),_in(SORT),_in(BOOL)))
235 | */
236 | Z3_ast Z3_API Z3_mk_fpa_inf(Z3_context c, Z3_sort s, Z3_bool negative);
237 |
238 | /**
239 | \brief Create a floating-point zero of sort s.
240 |
241 | \param c logical context
242 | \param s target sort
243 | \param negative indicates whether the result should be negative
244 |
245 | When \c negative is true, -zero will be generated instead of +zero.
246 |
247 | def_API('Z3_mk_fpa_zero', AST, (_in(CONTEXT),_in(SORT),_in(BOOL)))
248 | */
249 | Z3_ast Z3_API Z3_mk_fpa_zero(Z3_context c, Z3_sort s, Z3_bool negative);
250 |
251 | /**
252 | \brief Create an expression of FloatingPoint sort from three bit-vector expressions.
253 |
254 | This is the operator named `fp' in the SMT FP theory definition.
255 | Note that \c sign is required to be a bit-vector of size 1. Significand and exponent
256 | are required to be greater than 1 and 2 respectively. The FloatingPoint sort
257 | of the resulting expression is automatically determined from the bit-vector sizes
258 | of the arguments.
259 |
260 | \param c logical context
261 | \param sgn sign
262 | \param exp exponent
263 | \param sig significand
264 |
265 | def_API('Z3_mk_fpa_fp', AST, (_in(CONTEXT), _in(AST), _in(AST), _in(AST)))
266 | */
267 | Z3_ast Z3_API Z3_mk_fpa_fp(Z3_context c, Z3_ast sgn, Z3_ast exp, Z3_ast sig);
268 |
269 | /**
270 | \brief Create a numeral of FloatingPoint sort from a float.
271 |
272 | This function is used to create numerals that fit in a float value.
273 | It is slightly faster than #Z3_mk_numeral since it is not necessary to parse a string.
274 |
275 | \param c logical context
276 | \param v value
277 | \param ty sort
278 |
279 | ty must be a FloatingPoint sort
280 |
281 | \sa Z3_mk_numeral
282 |
283 | def_API('Z3_mk_fpa_numeral_float', AST, (_in(CONTEXT), _in(FLOAT), _in(SORT)))
284 | */
285 | Z3_ast Z3_API Z3_mk_fpa_numeral_float(Z3_context c, float v, Z3_sort ty);
286 |
287 | /**
288 | \brief Create a numeral of FloatingPoint sort from a double.
289 |
290 | This function is used to create numerals that fit in a double value.
291 | It is slightly faster than #Z3_mk_numeral since it is not necessary to parse a string.
292 |
293 | \param c logical context
294 | \param v value
295 | \param ty sort
296 |
297 | ty must be a FloatingPoint sort
298 |
299 | \sa Z3_mk_numeral
300 |
301 | def_API('Z3_mk_fpa_numeral_double', AST, (_in(CONTEXT), _in(DOUBLE), _in(SORT)))
302 | */
303 | Z3_ast Z3_API Z3_mk_fpa_numeral_double(Z3_context c, double v, Z3_sort ty);
304 |
305 | /**
306 | \brief Create a numeral of FloatingPoint sort from a signed integer.
307 |
308 | \param c logical context
309 | \param v value
310 | \param ty result sort
311 |
312 | ty must be a FloatingPoint sort
313 |
314 | \sa Z3_mk_numeral
315 |
316 | def_API('Z3_mk_fpa_numeral_int', AST, (_in(CONTEXT), _in(INT), _in(SORT)))
317 | */
318 | Z3_ast Z3_API Z3_mk_fpa_numeral_int(Z3_context c, signed v, Z3_sort ty);
319 |
320 | /**
321 | \brief Create a numeral of FloatingPoint sort from a sign bit and two integers.
322 |
323 | \param c logical context
324 | \param sgn sign bit (true == negative)
325 | \param sig significand
326 | \param exp exponent
327 | \param ty result sort
328 |
329 | ty must be a FloatingPoint sort
330 |
331 | \sa Z3_mk_numeral
332 |
333 | def_API('Z3_mk_fpa_numeral_int_uint', AST, (_in(CONTEXT), _in(BOOL), _in(INT), _in(UINT), _in(SORT)))
334 | */
335 | Z3_ast Z3_API Z3_mk_fpa_numeral_int_uint(Z3_context c, Z3_bool sgn, signed exp, unsigned sig, Z3_sort ty);
336 |
337 | /**
338 | \brief Create a numeral of FloatingPoint sort from a sign bit and two 64-bit integers.
339 |
340 | \param c logical context
341 | \param sgn sign bit (true == negative)
342 | \param sig significand
343 | \param exp exponent
344 | \param ty result sort
345 |
346 | ty must be a FloatingPoint sort
347 |
348 | \sa Z3_mk_numeral
349 |
350 | def_API('Z3_mk_fpa_numeral_int64_uint64', AST, (_in(CONTEXT), _in(BOOL), _in(INT64), _in(UINT64), _in(SORT)))
351 | */
352 | Z3_ast Z3_API Z3_mk_fpa_numeral_int64_uint64(Z3_context c, Z3_bool sgn, __int64 exp, __uint64 sig, Z3_sort ty);
353 |
354 | /**
355 | \brief Floating-point absolute value
356 |
357 | \param c logical context
358 | \param t term of FloatingPoint sort
359 |
360 | def_API('Z3_mk_fpa_abs', AST, (_in(CONTEXT),_in(AST)))
361 | */
362 | Z3_ast Z3_API Z3_mk_fpa_abs(Z3_context c, Z3_ast t);
363 |
364 | /**
365 | \brief Floating-point negation
366 |
367 | \param c logical context
368 | \param t term of FloatingPoint sort
369 |
370 | def_API('Z3_mk_fpa_neg', AST, (_in(CONTEXT),_in(AST)))
371 | */
372 | Z3_ast Z3_API Z3_mk_fpa_neg(Z3_context c, Z3_ast t);
373 |
374 | /**
375 | \brief Floating-point addition
376 |
377 | \param c logical context
378 | \param rm term of RoundingMode sort
379 | \param t1 term of FloatingPoint sort
380 | \param t2 term of FloatingPoint sort
381 |
382 | rm must be of RoundingMode sort, t1 and t2 must have the same FloatingPoint sort.
383 |
384 | def_API('Z3_mk_fpa_add', AST, (_in(CONTEXT),_in(AST),_in(AST),_in(AST)))
385 | */
386 | Z3_ast Z3_API Z3_mk_fpa_add(Z3_context c, Z3_ast rm, Z3_ast t1, Z3_ast t2);
387 |
388 | /**
389 | \brief Floating-point subtraction
390 |
391 | \param c logical context
392 | \param rm term of RoundingMode sort
393 | \param t1 term of FloatingPoint sort
394 | \param t2 term of FloatingPoint sort
395 |
396 | rm must be of RoundingMode sort, t1 and t2 must have the same FloatingPoint sort.
397 |
398 | def_API('Z3_mk_fpa_sub', AST, (_in(CONTEXT),_in(AST),_in(AST),_in(AST)))
399 | */
400 | Z3_ast Z3_API Z3_mk_fpa_sub(Z3_context c, Z3_ast rm, Z3_ast t1, Z3_ast t2);
401 |
402 | /**
403 | \brief Floating-point multiplication
404 |
405 | \param c logical context
406 | \param rm term of RoundingMode sort
407 | \param t1 term of FloatingPoint sort
408 | \param t2 term of FloatingPoint sort
409 |
410 | rm must be of RoundingMode sort, t1 and t2 must have the same FloatingPoint sort.
411 |
412 | def_API('Z3_mk_fpa_mul', AST, (_in(CONTEXT),_in(AST),_in(AST),_in(AST)))
413 | */
414 | Z3_ast Z3_API Z3_mk_fpa_mul(Z3_context c, Z3_ast rm, Z3_ast t1, Z3_ast t2);
415 |
416 | /**
417 | \brief Floating-point division
418 |
419 | \param c logical context
420 | \param rm term of RoundingMode sort
421 | \param t1 term of FloatingPoint sort.
422 | \param t2 term of FloatingPoint sort
423 |
424 | The nodes rm must be of RoundingMode sort t1 and t2 must have the same FloatingPoint sort.
425 |
426 | def_API('Z3_mk_fpa_div', AST, (_in(CONTEXT),_in(AST),_in(AST),_in(AST)))
427 | */
428 | Z3_ast Z3_API Z3_mk_fpa_div(Z3_context c, Z3_ast rm, Z3_ast t1, Z3_ast t2);
429 |
430 | /**
431 | \brief Floating-point fused multiply-add.
432 |
433 | \param c logical context
434 | \param rm term of RoundingMode sort
435 | \param t1 term of FloatingPoint sort
436 | \param t2 term of FloatingPoint sor
437 | \param t3 term of FloatingPoint sort
438 |
439 | The result is round((t1 * t2) + t3)
440 |
441 | rm must be of RoundingMode sort, t1, t2, and t3 must have the same FloatingPoint sort.
442 |
443 | def_API('Z3_mk_fpa_fma', AST, (_in(CONTEXT),_in(AST),_in(AST),_in(AST),_in(AST)))
444 | */
445 | Z3_ast Z3_API Z3_mk_fpa_fma(Z3_context c, Z3_ast rm, Z3_ast t1, Z3_ast t2, Z3_ast t3);
446 |
447 | /**
448 | \brief Floating-point square root
449 |
450 | \param c logical context
451 | \param rm term of RoundingMode sort
452 | \param t term of FloatingPoint sort
453 |
454 | rm must be of RoundingMode sort, t must have FloatingPoint sort.
455 |
456 | def_API('Z3_mk_fpa_sqrt', AST, (_in(CONTEXT),_in(AST),_in(AST)))
457 | */
458 | Z3_ast Z3_API Z3_mk_fpa_sqrt(Z3_context c, Z3_ast rm, Z3_ast t);
459 |
460 | /**
461 | \brief Floating-point remainder
462 |
463 | \param c logical context
464 | \param t1 term of FloatingPoint sort
465 | \param t2 term of FloatingPoint sort
466 |
467 | t1 and t2 must have the same FloatingPoint sort.
468 |
469 | def_API('Z3_mk_fpa_rem', AST, (_in(CONTEXT),_in(AST),_in(AST)))
470 | */
471 | Z3_ast Z3_API Z3_mk_fpa_rem(Z3_context c, Z3_ast t1, Z3_ast t2);
472 |
473 | /**
474 | \brief Floating-point roundToIntegral. Rounds a floating-point number to
475 | the closest integer, again represented as a floating-point number.
476 |
477 | \param c logical context
478 | \param rm term of RoundingMode sort
479 | \param t term of FloatingPoint sort
480 |
481 | t must be of FloatingPoint sort.
482 |
483 | def_API('Z3_mk_fpa_round_to_integral', AST, (_in(CONTEXT),_in(AST),_in(AST)))
484 | */
485 | Z3_ast Z3_API Z3_mk_fpa_round_to_integral(Z3_context c, Z3_ast rm, Z3_ast t);
486 |
487 | /**
488 | \brief Minimum of floating-point numbers.
489 |
490 | \param c logical context
491 | \param t1 term of FloatingPoint sort
492 | \param t2 term of FloatingPoint sort
493 |
494 | t1, t2 must have the same FloatingPoint sort.
495 |
496 | def_API('Z3_mk_fpa_min', AST, (_in(CONTEXT),_in(AST),_in(AST)))
497 | */
498 | Z3_ast Z3_API Z3_mk_fpa_min(Z3_context c, Z3_ast t1, Z3_ast t2);
499 |
500 | /**
501 | \brief Maximum of floating-point numbers.
502 |
503 | \param c logical context
504 | \param t1 term of FloatingPoint sort
505 | \param t2 term of FloatingPoint sort
506 |
507 | t1, t2 must have the same FloatingPoint sort.
508 |
509 | def_API('Z3_mk_fpa_max', AST, (_in(CONTEXT),_in(AST),_in(AST)))
510 | */
511 | Z3_ast Z3_API Z3_mk_fpa_max(Z3_context c, Z3_ast t1, Z3_ast t2);
512 |
513 | /**
514 | \brief Floating-point less than or equal.
515 |
516 | \param c logical context
517 | \param t1 term of FloatingPoint sort
518 | \param t2 term of FloatingPoint sort
519 |
520 | t1 and t2 must have the same FloatingPoint sort.
521 |
522 | def_API('Z3_mk_fpa_leq', AST, (_in(CONTEXT),_in(AST),_in(AST)))
523 | */
524 | Z3_ast Z3_API Z3_mk_fpa_leq(Z3_context c, Z3_ast t1, Z3_ast t2);
525 |
526 | /**
527 | \brief Floating-point less than.
528 |
529 | \param c logical context
530 | \param t1 term of FloatingPoint sort
531 | \param t2 term of FloatingPoint sort
532 |
533 | t1 and t2 must have the same FloatingPoint sort.
534 |
535 | def_API('Z3_mk_fpa_lt', AST, (_in(CONTEXT),_in(AST),_in(AST)))
536 | */
537 | Z3_ast Z3_API Z3_mk_fpa_lt(Z3_context c, Z3_ast t1, Z3_ast t2);
538 |
539 | /**
540 | \brief Floating-point greater than or equal.
541 |
542 | \param c logical context
543 | \param t1 term of FloatingPoint sort
544 | \param t2 term of FloatingPoint sort
545 |
546 | t1 and t2 must have the same FloatingPoint sort.
547 |
548 | def_API('Z3_mk_fpa_geq', AST, (_in(CONTEXT),_in(AST),_in(AST)))
549 | */
550 | Z3_ast Z3_API Z3_mk_fpa_geq(Z3_context c, Z3_ast t1, Z3_ast t2);
551 |
552 | /**
553 | \brief Floating-point greater than.
554 |
555 | \param c logical context
556 | \param t1 term of FloatingPoint sort
557 | \param t2 term of FloatingPoint sort
558 |
559 | t1 and t2 must have the same FloatingPoint sort.
560 |
561 | def_API('Z3_mk_fpa_gt', AST, (_in(CONTEXT),_in(AST),_in(AST)))
562 | */
563 | Z3_ast Z3_API Z3_mk_fpa_gt(Z3_context c, Z3_ast t1, Z3_ast t2);
564 |
565 | /**
566 | \brief Floating-point equality.
567 |
568 | \param c logical context
569 | \param t1 term of FloatingPoint sort
570 | \param t2 term of FloatingPoint sort
571 |
572 | Note that this is IEEE 754 equality (as opposed to SMT-LIB =).
573 |
574 | t1 and t2 must have the same FloatingPoint sort.
575 |
576 | def_API('Z3_mk_fpa_eq', AST, (_in(CONTEXT),_in(AST),_in(AST)))
577 | */
578 | Z3_ast Z3_API Z3_mk_fpa_eq(Z3_context c, Z3_ast t1, Z3_ast t2);
579 |
580 | /**
581 | \brief Predicate indicating whether t is a normal floating-point number.
582 |
583 | \param c logical context
584 | \param t term of FloatingPoint sort
585 |
586 | t must have FloatingPoint sort.
587 |
588 | def_API('Z3_mk_fpa_is_normal', AST, (_in(CONTEXT),_in(AST)))
589 | */
590 | Z3_ast Z3_API Z3_mk_fpa_is_normal(Z3_context c, Z3_ast t);
591 |
592 | /**
593 | \brief Predicate indicating whether t is a subnormal floating-point number.
594 |
595 | \param c logical context
596 | \param t term of FloatingPoint sort
597 |
598 | t must have FloatingPoint sort.
599 |
600 | def_API('Z3_mk_fpa_is_subnormal', AST, (_in(CONTEXT),_in(AST)))
601 | */
602 | Z3_ast Z3_API Z3_mk_fpa_is_subnormal(Z3_context c, Z3_ast t);
603 |
604 | /**
605 | \brief Predicate indicating whether t is a floating-point number with zero value, i.e., +zero or -zero.
606 |
607 | \param c logical context
608 | \param t term of FloatingPoint sort
609 |
610 | t must have FloatingPoint sort.
611 |
612 | def_API('Z3_mk_fpa_is_zero', AST, (_in(CONTEXT),_in(AST)))
613 | */
614 | Z3_ast Z3_API Z3_mk_fpa_is_zero(Z3_context c, Z3_ast t);
615 |
616 | /**
617 | \brief Predicate indicating whether t is a floating-point number representing +oo or -oo.
618 |
619 | \param c logical context
620 | \param t term of FloatingPoint sort
621 |
622 | t must have FloatingPoint sort.
623 |
624 | def_API('Z3_mk_fpa_is_infinite', AST, (_in(CONTEXT),_in(AST)))
625 | */
626 | Z3_ast Z3_API Z3_mk_fpa_is_infinite(Z3_context c, Z3_ast t);
627 |
628 | /**
629 | \brief Predicate indicating whether t is a NaN.
630 |
631 | \param c logical context
632 | \param t term of FloatingPoint sort
633 |
634 | t must have FloatingPoint sort.
635 |
636 | def_API('Z3_mk_fpa_is_nan', AST, (_in(CONTEXT),_in(AST)))
637 | */
638 | Z3_ast Z3_API Z3_mk_fpa_is_nan(Z3_context c, Z3_ast t);
639 |
640 | /**
641 | \brief Predicate indicating whether t is a negative floating-point number.
642 |
643 | \param c logical context
644 | \param t term of FloatingPoint sort
645 |
646 | t must have FloatingPoint sort.
647 |
648 | def_API('Z3_mk_fpa_is_negative', AST, (_in(CONTEXT),_in(AST)))
649 | */
650 | Z3_ast Z3_API Z3_mk_fpa_is_negative(Z3_context c, Z3_ast t);
651 |
652 | /**
653 | \brief Predicate indicating whether t is a positive floating-point number.
654 |
655 | \param c logical context
656 | \param t term of FloatingPoint sort
657 |
658 | t must have FloatingPoint sort.
659 |
660 | def_API('Z3_mk_fpa_is_positive', AST, (_in(CONTEXT),_in(AST)))
661 | */
662 | Z3_ast Z3_API Z3_mk_fpa_is_positive(Z3_context c, Z3_ast t);
663 |
664 | /**
665 | \brief Conversion of a single IEEE 754-2008 bit-vector into a floating-point number.
666 |
667 | Produces a term that represents the conversion of a bit-vector term bv to a
668 | floating-point term of sort s.
669 |
670 | \param c logical context
671 | \param bv a bit-vector term
672 | \param s floating-point sort
673 |
674 | s must be a FloatingPoint sort, t must be of bit-vector sort, and the bit-vector
675 | size of bv must be equal to ebits+sbits of s. The format of the bit-vector is
676 | as defined by the IEEE 754-2008 interchange format.
677 |
678 | def_API('Z3_mk_fpa_to_fp_bv', AST, (_in(CONTEXT),_in(AST),_in(SORT)))
679 | */
680 | Z3_ast Z3_API Z3_mk_fpa_to_fp_bv(Z3_context c, Z3_ast bv, Z3_sort s);
681 |
682 | /**
683 | \brief Conversion of a FloatingPoint term into another term of different FloatingPoint sort.
684 |
685 | Produces a term that represents the conversion of a floating-point term t to a
686 | floating-point term of sort s. If necessary, the result will be rounded according
687 | to rounding mode rm.
688 |
689 | \param c logical context
690 | \param rm term of RoundingMode sort
691 | \param t term of FloatingPoint sort
692 | \param s floating-point sort
693 |
694 | s must be a FloatingPoint sort, rm must be of RoundingMode sort, t must be of floating-point sort.
695 |
696 | def_API('Z3_mk_fpa_to_fp_float', AST, (_in(CONTEXT),_in(AST),_in(AST),_in(SORT)))
697 | */
698 | Z3_ast Z3_API Z3_mk_fpa_to_fp_float(Z3_context c, Z3_ast rm, Z3_ast t, Z3_sort s);
699 |
700 | /**
701 | \brief Conversion of a term of real sort into a term of FloatingPoint sort.
702 |
703 | Produces a term that represents the conversion of term t of real sort into a
704 | floating-point term of sort s. If necessary, the result will be rounded according
705 | to rounding mode rm.
706 |
707 | \param c logical context
708 | \param rm term of RoundingMode sort
709 | \param t term of Real sort
710 | \param s floating-point sort
711 |
712 | s must be a FloatingPoint sort, rm must be of RoundingMode sort, t must be of real sort.
713 |
714 | def_API('Z3_mk_fpa_to_fp_real', AST, (_in(CONTEXT),_in(AST),_in(AST),_in(SORT)))
715 | */
716 | Z3_ast Z3_API Z3_mk_fpa_to_fp_real(Z3_context c, Z3_ast rm, Z3_ast t, Z3_sort s);
717 |
718 | /**
719 | \brief Conversion of a 2's complement signed bit-vector term into a term of FloatingPoint sort.
720 |
721 | Produces a term that represents the conversion of the bit-vector term t into a
722 | floating-point term of sort s. The bit-vector t is taken to be in signed
723 | 2's complement format. If necessary, the result will be rounded according
724 | to rounding mode rm.
725 |
726 | \param c logical context
727 | \param rm term of RoundingMode sort
728 | \param t term of bit-vector sort
729 | \param s floating-point sort
730 |
731 | s must be a FloatingPoint sort, rm must be of RoundingMode sort, t must be of bit-vector sort.
732 |
733 | def_API('Z3_mk_fpa_to_fp_signed', AST, (_in(CONTEXT),_in(AST),_in(AST),_in(SORT)))
734 | */
735 | Z3_ast Z3_API Z3_mk_fpa_to_fp_signed(Z3_context c, Z3_ast rm, Z3_ast t, Z3_sort s);
736 |
737 | /**
738 | \brief Conversion of a 2's complement unsigned bit-vector term into a term of FloatingPoint sort.
739 |
740 | Produces a term that represents the conversion of the bit-vector term t into a
741 | floating-point term of sort s. The bit-vector t is taken to be in unsigned
742 | 2's complement format. If necessary, the result will be rounded according
743 | to rounding mode rm.
744 |
745 | \param c logical context
746 | \param rm term of RoundingMode sort
747 | \param t term of bit-vector sort
748 | \param s floating-point sort
749 |
750 | s must be a FloatingPoint sort, rm must be of RoundingMode sort, t must be of bit-vector sort.
751 |
752 | def_API('Z3_mk_fpa_to_fp_unsigned', AST, (_in(CONTEXT),_in(AST),_in(AST),_in(SORT)))
753 | */
754 | Z3_ast Z3_API Z3_mk_fpa_to_fp_unsigned(Z3_context c, Z3_ast rm, Z3_ast t, Z3_sort s);
755 |
756 | /**
757 | \brief Conversion of a floating-point term into an unsigned bit-vector.
758 |
759 | Produces a term that represents the conversion of the floating-poiunt term t into a
760 | bit-vector term of size sz in unsigned 2's complement format. If necessary, the result
761 | will be rounded according to rounding mode rm.
762 |
763 | \param c logical context
764 | \param rm term of RoundingMode sort
765 | \param t term of FloatingPoint sort
766 | \param sz size of the resulting bit-vector
767 |
768 | def_API('Z3_mk_fpa_to_ubv', AST, (_in(CONTEXT),_in(AST),_in(AST),_in(UINT)))
769 | */
770 | Z3_ast Z3_API Z3_mk_fpa_to_ubv(Z3_context c, Z3_ast rm, Z3_ast t, unsigned sz);
771 |
772 | /**
773 | \brief Conversion of a floating-point term into a signed bit-vector.
774 |
775 | Produces a term that represents the conversion of the floating-poiunt term t into a
776 | bit-vector term of size sz in signed 2's complement format. If necessary, the result
777 | will be rounded according to rounding mode rm.
778 |
779 | \param c logical context
780 | \param rm term of RoundingMode sort
781 | \param t term of FloatingPoint sort
782 | \param sz size of the resulting bit-vector
783 |
784 | def_API('Z3_mk_fpa_to_sbv', AST, (_in(CONTEXT),_in(AST),_in(AST),_in(UINT)))
785 | */
786 | Z3_ast Z3_API Z3_mk_fpa_to_sbv(Z3_context c, Z3_ast rm, Z3_ast t, unsigned sz);
787 |
788 | /**
789 | \brief Conversion of a floating-point term into a real-numbered term.
790 |
791 | Produces a term that represents the conversion of the floating-poiunt term t into a
792 | real number. Note that this type of conversion will often result in non-linear
793 | constraints over real terms.
794 |
795 | \param c logical context
796 | \param t term of FloatingPoint sort
797 |
798 | def_API('Z3_mk_fpa_to_real', AST, (_in(CONTEXT),_in(AST)))
799 | */
800 | Z3_ast Z3_API Z3_mk_fpa_to_real(Z3_context c, Z3_ast t);
801 |
802 |
803 | /** @name Z3-specific floating-point extensions */
804 | /*@{*/
805 | /**
806 | \brief Retrieves the number of bits reserved for the exponent in a FloatingPoint sort.
807 |
808 | \param c logical context
809 | \param s FloatingPoint sort
810 |
811 | def_API('Z3_fpa_get_ebits', UINT, (_in(CONTEXT),_in(SORT)))
812 | */
813 | unsigned Z3_API Z3_fpa_get_ebits(Z3_context c, Z3_sort s);
814 |
815 | /**
816 | \brief Retrieves the number of bits reserved for the significand in a FloatingPoint sort.
817 |
818 | \param c logical context
819 | \param s FloatingPoint sort
820 |
821 | def_API('Z3_fpa_get_sbits', UINT, (_in(CONTEXT),_in(SORT)))
822 | */
823 | unsigned Z3_API Z3_fpa_get_sbits(Z3_context c, Z3_sort s);
824 |
825 | /**
826 | \brief Retrieves the sign of a floating-point literal.
827 |
828 | \param c logical context
829 | \param t a floating-point numeral
830 | \param sgn sign
831 |
832 | Remarks: sets \c sgn to 0 if `t' is positive and to 1 otherwise, except for
833 | NaN, which is an invalid argument.
834 |
835 | def_API('Z3_fpa_get_numeral_sign', BOOL, (_in(CONTEXT), _in(AST), _out(INT)))
836 | */
837 | Z3_bool Z3_API Z3_fpa_get_numeral_sign(Z3_context c, Z3_ast t, int * sgn);
838 |
839 | /**
840 | \brief Return the significand value of a floating-point numeral as a string.
841 |
842 | \param c logical context
843 | \param t a floating-point numeral
844 |
845 | Remarks: The significand s is always 0.0 <= s < 2.0; the resulting string is long
846 | enough to represent the real significand precisely.
847 |
848 | def_API('Z3_fpa_get_numeral_significand_string', STRING, (_in(CONTEXT), _in(AST)))
849 | */
850 | Z3_string Z3_API Z3_fpa_get_numeral_significand_string(Z3_context c, Z3_ast t);
851 |
852 | /**
853 | \brief Return the significand value of a floating-point numeral as a uint64.
854 |
855 | \param c logical context
856 | \param t a floating-point numeral
857 | \param n pointer to output uint64
858 |
859 | Remarks: This function extracts the significand bits in `t`, without the
860 | hidden bit or normalization. Sets the Z3_INVALID_ARG error code if the
861 | significand does not fit into a uint64.
862 |
863 | def_API('Z3_fpa_get_numeral_significand_uint64', BOOL, (_in(CONTEXT), _in(AST), _out(UINT64)))
864 | */
865 | Z3_bool Z3_API Z3_fpa_get_numeral_significand_uint64(Z3_context c, Z3_ast t, __uint64 * n);
866 |
867 | /**
868 | \brief Return the exponent value of a floating-point numeral as a string
869 |
870 | \param c logical context
871 | \param t a floating-point numeral
872 |
873 | Remarks: This function extracts the exponent in `t`, without normalization.
874 |
875 | def_API('Z3_fpa_get_numeral_exponent_string', STRING, (_in(CONTEXT), _in(AST)))
876 | */
877 | Z3_string Z3_API Z3_fpa_get_numeral_exponent_string(Z3_context c, Z3_ast t);
878 |
879 | /**
880 | \brief Return the exponent value of a floating-point numeral as a signed 64-bit integer
881 |
882 | \param c logical context
883 | \param t a floating-point numeral
884 | \param n exponent
885 |
886 | Remarks: This function extracts the exponent in `t`, without normalization.
887 |
888 | def_API('Z3_fpa_get_numeral_exponent_int64', BOOL, (_in(CONTEXT), _in(AST), _out(INT64)))
889 | */
890 | Z3_bool Z3_API Z3_fpa_get_numeral_exponent_int64(Z3_context c, Z3_ast t, __int64 * n);
891 |
892 | /**
893 | \brief Conversion of a floating-point term into a bit-vector term in IEEE 754-2008 format.
894 |
895 | \param c logical context
896 | \param t term of FloatingPoint sort
897 |
898 | t must have FloatingPoint sort. The size of the resulting bit-vector is automatically
899 | determined.
900 |
901 | Note that IEEE 754-2008 allows multiple different representations of NaN. This conversion
902 | knows only one NaN and it will always produce the same bit-vector represenatation of
903 | that NaN.
904 |
905 | def_API('Z3_mk_fpa_to_ieee_bv', AST, (_in(CONTEXT),_in(AST)))
906 | */
907 | Z3_ast Z3_API Z3_mk_fpa_to_ieee_bv(Z3_context c, Z3_ast t);
908 |
909 | /**
910 | \brief Conversion of a real-sorted significand and an integer-sorted exponent into a term of FloatingPoint sort.
911 |
912 | Produces a term that represents the conversion of sig * 2^exp into a
913 | floating-point term of sort s. If necessary, the result will be rounded
914 | according to rounding mode rm.
915 |
916 | \param c logical context
917 | \param rm term of RoundingMode sort
918 | \param exp exponent term of Int sort
919 | \param sig significand term of Real sort
920 | \param s FloatingPoint sort
921 |
922 | s must be a FloatingPoint sort, rm must be of RoundingMode sort, exp must be of int sort, sig must be of real sort.
923 |
924 | def_API('Z3_mk_fpa_to_fp_int_real', AST, (_in(CONTEXT),_in(AST),_in(AST),_in(AST),_in(SORT)))
925 | */
926 | Z3_ast Z3_API Z3_mk_fpa_to_fp_int_real(Z3_context c, Z3_ast rm, Z3_ast exp, Z3_ast sig, Z3_sort s);
927 | /*@}*/
928 | /*@}*/
929 | /*@}*/
930 |
931 | #ifdef __cplusplus
932 | }
933 | #endif // __cplusplus
934 |
935 | #endif
936 |
--------------------------------------------------------------------------------
/z3-4.5.0-x64-win/include/z3_interp.h:
--------------------------------------------------------------------------------
1 | /*++
2 | Copyright (c) 2014 Microsoft Corporation
3 |
4 | Module Name:
5 |
6 | z3_interp.h
7 |
8 | Abstract:
9 |
10 | API for interpolation
11 |
12 | Author:
13 |
14 | Kenneth McMillan (kenmcmil)
15 |
16 | Notes:
17 |
18 | --*/
19 | #ifndef Z3_INTERPOLATION_H_
20 | #define Z3_INTERPOLATION_H_
21 |
22 | #ifdef __cplusplus
23 | extern "C" {
24 | #endif // __cplusplus
25 |
26 | /** \defgroup capi C API */
27 | /*@{*/
28 |
29 | /** @name Interpolation facilities */
30 | /*@{*/
31 | /**
32 | \brief Create an AST node marking a formula position for interpolation.
33 |
34 | The node \c a must have Boolean sort.
35 |
36 | def_API('Z3_mk_interpolant', AST, (_in(CONTEXT), _in(AST)))
37 | */
38 | Z3_ast Z3_API Z3_mk_interpolant(Z3_context c, Z3_ast a);
39 |
40 |
41 | /** \brief This function generates a Z3 context suitable for generation of
42 | interpolants. Formulas can be generated as abstract syntax trees in
43 | this context using the Z3 C API.
44 |
45 | Interpolants are also generated as AST's in this context.
46 |
47 | If cfg is non-null, it will be used as the base configuration
48 | for the Z3 context. This makes it possible to set Z3 options
49 | to be used during interpolation. This feature should be used
50 | with some caution however, as it may be that certain Z3 options
51 | are incompatible with interpolation.
52 |
53 | def_API('Z3_mk_interpolation_context', CONTEXT, (_in(CONFIG),))
54 |
55 | */
56 |
57 | Z3_context Z3_API Z3_mk_interpolation_context(Z3_config cfg);
58 |
59 | /** Compute an interpolant from a refutation. This takes a proof of
60 | "false" from a set of formulas C, and an interpolation
61 | pattern. The pattern pat is a formula combining the formulas in C
62 | using logical conjunction and the "interp" operator (see
63 | #Z3_mk_interpolant). This interp operator is logically the identity
64 | operator. It marks the sub-formulas of the pattern for which interpolants should
65 | be computed. The interpolant is a map sigma from marked subformulas to
66 | formulas, such that, for each marked subformula phi of pat (where phi sigma
67 | is phi with sigma(psi) substituted for each subformula psi of phi such that
68 | psi in dom(sigma)):
69 |
70 | 1) phi sigma implies sigma(phi), and
71 |
72 | 2) sigma(phi) is in the common uninterpreted vocabulary between
73 | the formulas of C occurring in phi and those not occurring in
74 | phi
75 |
76 | and moreover pat sigma implies false. In the simplest case
77 | an interpolant for the pattern "(and (interp A) B)" maps A
78 | to an interpolant for A /\ B.
79 |
80 | The return value is a vector of formulas representing sigma. The
81 | vector contains sigma(phi) for each marked subformula of pat, in
82 | pre-order traversal. This means that subformulas of phi occur before phi
83 | in the vector. Also, subformulas that occur multiply in pat will
84 | occur multiply in the result vector.
85 |
86 | In particular, calling Z3_get_interpolant on a pattern of the
87 | form (interp ... (interp (and (interp A_1) A_2)) ... A_N) will
88 | result in a sequence interpolant for A_1, A_2,... A_N.
89 |
90 | Neglecting interp markers, the pattern must be a conjunction of
91 | formulas in C, the set of premises of the proof. Otherwise an
92 | error is flagged.
93 |
94 | Any premises of the proof not present in the pattern are
95 | treated as "background theory". Predicate and function symbols
96 | occurring in the background theory are treated as interpreted and
97 | thus always allowed in the interpolant.
98 |
99 | Interpolant may not necessarily be computable from all
100 | proofs. To be sure an interpolant can be computed, the proof
101 | must be generated by an SMT solver for which interpoaltion is
102 | supported, and the premises must be expressed using only
103 | theories and operators for which interpolation is supported.
104 |
105 | Currently, the only SMT solver that is supported is the legacy
106 | SMT solver. Such a solver is available as the default solver in
107 | \c Z3_context objects produced by #Z3_mk_interpolation_context.
108 | Currently, the theories supported are equality with
109 | uninterpreted functions, linear integer arithmetic, and the
110 | theory of arrays (in SMT-LIB terms, this is AUFLIA).
111 | Quantifiers are allowed. Use of any other operators (including
112 | "labels") may result in failure to compute an interpolant from a
113 | proof.
114 |
115 | Parameters:
116 |
117 | \param c logical context.
118 | \param pf a refutation from premises (assertions) C
119 | \param pat an interpolation pattern over C
120 | \param p parameters
121 |
122 | def_API('Z3_get_interpolant', AST_VECTOR, (_in(CONTEXT), _in(AST), _in(AST), _in(PARAMS)))
123 | */
124 |
125 | Z3_ast_vector Z3_API Z3_get_interpolant(Z3_context c, Z3_ast pf, Z3_ast pat, Z3_params p);
126 |
127 | /* Compute an interpolant for an unsatisfiable conjunction of formulas.
128 |
129 | This takes as an argument an interpolation pattern as in
130 | #Z3_get_interpolant. This is a conjunction, some subformulas of
131 | which are marked with the "interp" operator (see #Z3_mk_interpolant).
132 |
133 | The conjunction is first checked for unsatisfiability. The result
134 | of this check is returned in the out parameter "status". If the result
135 | is unsat, an interpolant is computed from the refutation as in #Z3_get_interpolant
136 | and returned as a vector of formulas. Otherwise the return value is
137 | an empty formula.
138 |
139 | See #Z3_get_interpolant for a discussion of supported theories.
140 |
141 | The advantage of this function over #Z3_get_interpolant is that
142 | it is not necessary to create a suitable SMT solver and generate
143 | a proof. The disadvantage is that it is not possible to use the
144 | solver incrementally.
145 |
146 | Parameters:
147 |
148 | \param c logical context.
149 | \param pat an interpolation pattern
150 | \param p parameters for solver creation
151 | \param status returns the status of the sat check
152 | \param model returns model if satisfiable
153 |
154 | Return value: status of SAT check
155 |
156 | def_API('Z3_compute_interpolant', INT, (_in(CONTEXT), _in(AST), _in(PARAMS), _out(AST_VECTOR), _out(MODEL)))
157 | */
158 |
159 | Z3_lbool Z3_API Z3_compute_interpolant(Z3_context c,
160 | Z3_ast pat,
161 | Z3_params p,
162 | Z3_ast_vector *interp,
163 | Z3_model *model);
164 |
165 | /** Return a string summarizing cumulative time used for
166 | interpolation. This string is purely for entertainment purposes
167 | and has no semantics.
168 |
169 | \param ctx The context (currently ignored)
170 |
171 |
172 | def_API('Z3_interpolation_profile', STRING, (_in(CONTEXT),))
173 | */
174 |
175 | Z3_string Z3_API Z3_interpolation_profile(Z3_context ctx);
176 |
177 | /**
178 | \brief Read an interpolation problem from file.
179 |
180 | \param ctx The Z3 context. This resets the error handler of ctx.
181 | \param filename The file name to read.
182 | \param num Returns length of sequence.
183 | \param cnsts Returns sequence of formulas (do not free)
184 | \param parents Returns the parents vector (or NULL for sequence)
185 | \param error Returns an error message in case of failure (do not free the string)
186 | \param num_theory Number of theory terms
187 | \param theory Theory terms
188 |
189 | Returns true on success.
190 |
191 | File formats: Currently two formats are supported, based on
192 | SMT-LIB2. For sequence interpolants, the sequence of constraints is
193 | represented by the sequence of "assert" commands in the file.
194 |
195 | For tree interpolants, one symbol of type bool is associated to
196 | each vertex of the tree. For each vertex v there is an "assert"
197 | of the form:
198 |
199 | (implies (and c1 ... cn f) v)
200 |
201 | where c1 .. cn are the children of v (which must precede v in the file)
202 | and f is the formula assiciated to node v. The last formula in the
203 | file is the root vertex, and is represented by the predicate "false".
204 |
205 | A solution to a tree interpolation problem can be thought of as a
206 | valuation of the vertices that makes all the implications true
207 | where each value is represented using the common symbols between
208 | the formulas in the subtree and the remainder of the formulas.
209 |
210 | def_API('Z3_read_interpolation_problem', INT, (_in(CONTEXT), _out(UINT), _out_managed_array(1, AST), _out_managed_array(1, UINT), _in(STRING), _out(STRING), _out(UINT), _out_managed_array(6, AST)))
211 |
212 | */
213 |
214 | int Z3_API Z3_read_interpolation_problem(Z3_context ctx,
215 | unsigned *num,
216 | Z3_ast *cnsts[],
217 | unsigned *parents[],
218 | Z3_string filename,
219 | Z3_string_ptr error,
220 | unsigned *num_theory,
221 | Z3_ast *theory[]);
222 |
223 |
224 |
225 | /** Check the correctness of an interpolant. The Z3 context must
226 | have no constraints asserted when this call is made. That means
227 | that after interpolating, you must first fully pop the Z3
228 | context before calling this. See Z3_interpolate for meaning of parameters.
229 |
230 | \param ctx The Z3 context. Must be generated by Z3_mk_interpolation_context
231 | \param num The number of constraints in the sequence
232 | \param cnsts Array of constraints (AST's in context ctx)
233 | \param parents The parents vector (or NULL for sequence)
234 | \param interps The interpolant to check
235 | \param error Returns an error message if interpolant incorrect (do not free the string)
236 | \param num_theory Number of theory terms
237 | \param theory Theory terms
238 |
239 | Return value is Z3_L_TRUE if interpolant is verified, Z3_L_FALSE if
240 | incorrect, and Z3_L_UNDEF if unknown.
241 |
242 | def_API('Z3_check_interpolant', INT, (_in(CONTEXT), _in(UINT), _in_array(1, AST), _in_array(1, UINT), _in_array(1, AST), _out(STRING), _in(UINT), _in_array(6, AST)))
243 | */
244 |
245 | int Z3_API Z3_check_interpolant(Z3_context ctx,
246 | unsigned num,
247 | Z3_ast cnsts[],
248 | unsigned parents[],
249 | Z3_ast *interps,
250 | Z3_string_ptr error,
251 | unsigned num_theory,
252 | Z3_ast theory[]);
253 |
254 | /** Write an interpolation problem to file suitable for reading with
255 | Z3_read_interpolation_problem. The output file is a sequence
256 | of SMT-LIB2 format commands, suitable for reading with command-line Z3
257 | or other interpolating solvers.
258 |
259 | \param ctx The Z3 context. Must be generated by z3_mk_interpolation_context
260 | \param num The number of constraints in the sequence
261 | \param cnsts Array of constraints
262 | \param parents The parents vector (or NULL for sequence)
263 | \param filename The file name to write
264 | \param num_theory Number of theory terms
265 | \param theory Theory terms
266 |
267 | def_API('Z3_write_interpolation_problem', VOID, (_in(CONTEXT), _in(UINT), _in_array(1, AST), _in_array(1, UINT), _in(STRING), _in(UINT), _in_array(5, AST)))
268 | */
269 |
270 | void Z3_API Z3_write_interpolation_problem(Z3_context ctx,
271 | unsigned num,
272 | Z3_ast cnsts[],
273 | unsigned parents[],
274 | Z3_string filename,
275 | unsigned num_theory,
276 | Z3_ast theory[]);
277 | /*@}*/
278 | /*@}*/
279 |
280 | #ifdef __cplusplus
281 | }
282 | #endif // __cplusplus
283 |
284 | #endif
285 |
--------------------------------------------------------------------------------
/z3-4.5.0-x64-win/include/z3_macros.h:
--------------------------------------------------------------------------------
1 |
2 | /*++
3 | Copyright (c) 2015 Microsoft Corporation
4 |
5 | --*/
6 |
7 | #ifndef Z3_bool_opt
8 | #define Z3_bool_opt Z3_bool
9 | #endif
10 |
11 | #ifndef Z3_API
12 | # ifdef __GNUC__
13 | # define Z3_API __attribute__ ((visibility ("default")))
14 | # else
15 | # define Z3_API
16 | # endif
17 | #endif
18 |
19 | #ifndef DEFINE_TYPE
20 | #define DEFINE_TYPE(T) typedef struct _ ## T *T
21 | #endif
22 |
23 | #ifndef DEFINE_VOID
24 | #define DEFINE_VOID(T) typedef void* T
25 | #endif
26 |
--------------------------------------------------------------------------------
/z3-4.5.0-x64-win/include/z3_optimization.h:
--------------------------------------------------------------------------------
1 | /*++
2 | Copyright (c) 2015 Microsoft Corporation
3 |
4 | Module Name:
5 |
6 | z3_optimization.h
7 |
8 | Abstract:
9 |
10 | Optimization facilities
11 |
12 | Author:
13 |
14 | Christoph M. Wintersteiger (cwinter) 2015-12-03
15 |
16 | Notes:
17 |
18 | --*/
19 | #ifndef Z3_OPTIMIZATION_H_
20 | #define Z3_OPTIMIZATION_H_
21 |
22 | #ifdef __cplusplus
23 | extern "C" {
24 | #endif // __cplusplus
25 |
26 | /** \defgroup capi C API */
27 | /*@{*/
28 |
29 | /** @name Optimization facilities */
30 | /*@{*/
31 | /**
32 | \brief Create a new optimize context.
33 |
34 | \remark User must use #Z3_optimize_inc_ref and #Z3_optimize_dec_ref to manage optimize objects.
35 | Even if the context was created using #Z3_mk_context instead of #Z3_mk_context_rc.
36 |
37 | def_API('Z3_mk_optimize', OPTIMIZE, (_in(CONTEXT), ))
38 | */
39 | Z3_optimize Z3_API Z3_mk_optimize(Z3_context c);
40 |
41 | /**
42 | \brief Increment the reference counter of the given optimize context
43 |
44 | def_API('Z3_optimize_inc_ref', VOID, (_in(CONTEXT), _in(OPTIMIZE)))
45 | */
46 | void Z3_API Z3_optimize_inc_ref(Z3_context c, Z3_optimize d);
47 |
48 | /**
49 | \brief Decrement the reference counter of the given optimize context.
50 |
51 | def_API('Z3_optimize_dec_ref', VOID, (_in(CONTEXT), _in(OPTIMIZE)))
52 | */
53 | void Z3_API Z3_optimize_dec_ref(Z3_context c, Z3_optimize d);
54 |
55 | /**
56 | \brief Assert hard constraint to the optimization context.
57 |
58 | def_API('Z3_optimize_assert', VOID, (_in(CONTEXT), _in(OPTIMIZE), _in(AST)))
59 | */
60 | void Z3_API Z3_optimize_assert(Z3_context c, Z3_optimize o, Z3_ast a);
61 |
62 | /**
63 | \brief Assert soft constraint to the optimization context.
64 | \param c - context
65 | \param o - optimization context
66 | \param a - formula
67 | \param weight - a positive weight, penalty for violating soft constraint
68 | \param id - optional identifier to group soft constraints
69 |
70 | def_API('Z3_optimize_assert_soft', UINT, (_in(CONTEXT), _in(OPTIMIZE), _in(AST), _in(STRING), _in(SYMBOL)))
71 | */
72 | unsigned Z3_API Z3_optimize_assert_soft(Z3_context c, Z3_optimize o, Z3_ast a, Z3_string weight, Z3_symbol id);
73 |
74 | /**
75 | \brief Add a maximization constraint.
76 | \param c - context
77 | \param o - optimization context
78 | \param a - arithmetical term
79 | def_API('Z3_optimize_maximize', UINT, (_in(CONTEXT), _in(OPTIMIZE), _in(AST)))
80 | */
81 | unsigned Z3_API Z3_optimize_maximize(Z3_context c, Z3_optimize o, Z3_ast t);
82 |
83 | /**
84 | \brief Add a minimization constraint.
85 | \param c - context
86 | \param o - optimization context
87 | \param a - arithmetical term
88 |
89 | def_API('Z3_optimize_minimize', UINT, (_in(CONTEXT), _in(OPTIMIZE), _in(AST)))
90 | */
91 | unsigned Z3_API Z3_optimize_minimize(Z3_context c, Z3_optimize o, Z3_ast t);
92 |
93 | /**
94 | \brief Create a backtracking point.
95 |
96 | The optimize solver contains a set of rules, added facts and assertions.
97 | The set of rules, facts and assertions are restored upon calling #Z3_optimize_pop.
98 |
99 | \sa Z3_optimize_pop
100 |
101 | def_API('Z3_optimize_push', VOID, (_in(CONTEXT), _in(OPTIMIZE)))
102 | */
103 | void Z3_API Z3_optimize_push(Z3_context c, Z3_optimize d);
104 |
105 | /**
106 | \brief Backtrack one level.
107 |
108 | \sa Z3_optimize_push
109 |
110 | \pre The number of calls to pop cannot exceed calls to push.
111 |
112 | def_API('Z3_optimize_pop', VOID, (_in(CONTEXT), _in(OPTIMIZE)))
113 | */
114 | void Z3_API Z3_optimize_pop(Z3_context c, Z3_optimize d);
115 |
116 | /**
117 | \brief Check consistency and produce optimal values.
118 | \param c - context
119 | \param o - optimization context
120 |
121 | def_API('Z3_optimize_check', INT, (_in(CONTEXT), _in(OPTIMIZE)))
122 | */
123 | Z3_lbool Z3_API Z3_optimize_check(Z3_context c, Z3_optimize o);
124 |
125 |
126 | /**
127 | \brief Retrieve a string that describes the last status returned by #Z3_optimize_check.
128 |
129 | Use this method when #Z3_optimize_check returns Z3_L_UNDEF.
130 |
131 | def_API('Z3_optimize_get_reason_unknown', STRING, (_in(CONTEXT), _in(OPTIMIZE) ))
132 | */
133 | Z3_string Z3_API Z3_optimize_get_reason_unknown(Z3_context c, Z3_optimize d);
134 |
135 | /**
136 | \brief Retrieve the model for the last #Z3_optimize_check
137 |
138 | The error handler is invoked if a model is not available because
139 | the commands above were not invoked for the given optimization
140 | solver, or if the result was \c Z3_L_FALSE.
141 |
142 | def_API('Z3_optimize_get_model', MODEL, (_in(CONTEXT), _in(OPTIMIZE)))
143 | */
144 | Z3_model Z3_API Z3_optimize_get_model(Z3_context c, Z3_optimize o);
145 |
146 | /**
147 | \brief Set parameters on optimization context.
148 |
149 | \param c - context
150 | \param o - optimization context
151 | \param p - parameters
152 |
153 | def_API('Z3_optimize_set_params', VOID, (_in(CONTEXT), _in(OPTIMIZE), _in(PARAMS)))
154 | */
155 | void Z3_API Z3_optimize_set_params(Z3_context c, Z3_optimize o, Z3_params p);
156 |
157 | /**
158 | \brief Return the parameter description set for the given optimize object.
159 |
160 | \param c - context
161 | \param o - optimization context
162 |
163 | def_API('Z3_optimize_get_param_descrs', PARAM_DESCRS, (_in(CONTEXT), _in(OPTIMIZE)))
164 | */
165 | Z3_param_descrs Z3_API Z3_optimize_get_param_descrs(Z3_context c, Z3_optimize o);
166 |
167 | /**
168 | \brief Retrieve lower bound value or approximation for the i'th optimization objective.
169 |
170 | \param c - context
171 | \param o - optimization context
172 | \param idx - index of optimization objective
173 |
174 | def_API('Z3_optimize_get_lower', AST, (_in(CONTEXT), _in(OPTIMIZE), _in(UINT)))
175 | */
176 | Z3_ast Z3_API Z3_optimize_get_lower(Z3_context c, Z3_optimize o, unsigned idx);
177 |
178 | /**
179 | \brief Retrieve upper bound value or approximation for the i'th optimization objective.
180 |
181 | \param c - context
182 | \param o - optimization context
183 | \param idx - index of optimization objective
184 |
185 | def_API('Z3_optimize_get_upper', AST, (_in(CONTEXT), _in(OPTIMIZE), _in(UINT)))
186 | */
187 | Z3_ast Z3_API Z3_optimize_get_upper(Z3_context c, Z3_optimize o, unsigned idx);
188 |
189 | /**
190 | \brief Print the current context as a string.
191 | \param c - context.
192 | \param o - optimization context.
193 |
194 | def_API('Z3_optimize_to_string', STRING, (_in(CONTEXT), _in(OPTIMIZE)))
195 | */
196 | Z3_string Z3_API Z3_optimize_to_string(Z3_context c, Z3_optimize o);
197 |
198 | /**
199 | \brief Parse an SMT-LIB2 string with assertions,
200 | soft constraints and optimization objectives.
201 | Add the parsed constraints and objectives to the optimization context.
202 |
203 | \param c - context.
204 | \param o - optimize context.
205 | \param s - string containing SMT2 specification.
206 |
207 | def_API('Z3_optimize_from_string', VOID, (_in(CONTEXT), _in(OPTIMIZE), _in(STRING)))
208 | */
209 | void Z3_API Z3_optimize_from_string(Z3_context c, Z3_optimize o, Z3_string s);
210 |
211 | /**
212 | \brief Parse an SMT-LIB2 file with assertions,
213 | soft constraints and optimization objectives.
214 | Add the parsed constraints and objectives to the optimization context.
215 |
216 | \param c - context.
217 | \param o - optimize context.
218 | \param s - string containing SMT2 specification.
219 |
220 | def_API('Z3_optimize_from_file', VOID, (_in(CONTEXT), _in(OPTIMIZE), _in(STRING)))
221 | */
222 | void Z3_API Z3_optimize_from_file(Z3_context c, Z3_optimize o, Z3_string s);
223 |
224 | /**
225 | \brief Return a string containing a description of parameters accepted by optimize.
226 |
227 | def_API('Z3_optimize_get_help', STRING, (_in(CONTEXT), _in(OPTIMIZE)))
228 | */
229 | Z3_string Z3_API Z3_optimize_get_help(Z3_context c, Z3_optimize t);
230 |
231 | /**
232 | \brief Retrieve statistics information from the last call to #Z3_optimize_check
233 |
234 | def_API('Z3_optimize_get_statistics', STATS, (_in(CONTEXT), _in(OPTIMIZE)))
235 | */
236 | Z3_stats Z3_API Z3_optimize_get_statistics(Z3_context c, Z3_optimize d);
237 |
238 | /**
239 | \brief Return the set of asserted formulas on the optimization context.
240 |
241 | def_API('Z3_optimize_get_assertions', AST_VECTOR, (_in(CONTEXT), _in(OPTIMIZE)))
242 | */
243 | Z3_ast_vector Z3_API Z3_optimize_get_assertions(Z3_context c, Z3_optimize o);
244 |
245 | /**
246 | \brief Return objectives on the optimization context.
247 | If the objective function is a max-sat objective it is returned
248 | as a Pseudo-Boolean (minimization) sum of the form (+ (if f1 w1 0) (if f2 w2 0) ...)
249 | If the objective function is entered as a maximization objective, then return
250 | the corresponding minimization objective. In this way the resulting objective
251 | function is always returned as a minimization objective.
252 |
253 | def_API('Z3_optimize_get_objectives', AST_VECTOR, (_in(CONTEXT), _in(OPTIMIZE)))
254 | */
255 | Z3_ast_vector Z3_API Z3_optimize_get_objectives(Z3_context c, Z3_optimize o);
256 |
257 | /*@}*/
258 | /*@}*/
259 |
260 | #ifdef __cplusplus
261 | }
262 | #endif // __cplusplus
263 |
264 | #endif
265 |
--------------------------------------------------------------------------------
/z3-4.5.0-x64-win/include/z3_polynomial.h:
--------------------------------------------------------------------------------
1 | /*++
2 | Copyright (c) 2012 Microsoft Corporation
3 |
4 | Module Name:
5 |
6 | z3_polynomial.h
7 |
8 | Abstract:
9 |
10 | Additional APIs for polynomials.
11 |
12 | Author:
13 |
14 | Leonardo de Moura (leonardo) 2012-12-09
15 |
16 | Notes:
17 |
18 | --*/
19 |
20 | #ifndef Z3_POLYNOMIAL_H_
21 | #define Z3_POLYNOMIAL_H_
22 |
23 | #ifdef __cplusplus
24 | extern "C" {
25 | #endif // __cplusplus
26 |
27 | /** \defgroup capi C API */
28 | /*@{*/
29 |
30 |
31 | /** @name Polynomials */
32 | /*@{*/
33 |
34 | /**
35 | \brief Return the nonzero subresultants of \c p and \c q with respect to the "variable" \c x.
36 |
37 | \pre \c p, \c q and \c x are Z3 expressions where \c p and \c q are arithmetic terms.
38 | Note that, any subterm that cannot be viewed as a polynomial is assumed to be a variable.
39 | Example: f(a) is a considered to be a variable in the polynomial
40 |
41 | f(a)*f(a) + 2*f(a) + 1
42 |
43 | def_API('Z3_polynomial_subresultants', AST_VECTOR, (_in(CONTEXT), _in(AST), _in(AST), _in(AST)))
44 | */
45 | Z3_ast_vector Z3_API Z3_polynomial_subresultants(Z3_context c, Z3_ast p, Z3_ast q, Z3_ast x);
46 |
47 |
48 | /*@}*/
49 | /*@}*/
50 |
51 | #ifdef __cplusplus
52 | }
53 | #endif // __cplusplus
54 |
55 | #endif
56 |
--------------------------------------------------------------------------------
/z3-4.5.0-x64-win/include/z3_rcf.h:
--------------------------------------------------------------------------------
1 | /*++
2 | Copyright (c) 2013 Microsoft Corporation
3 |
4 | Module Name:
5 |
6 | z3_rcf.h
7 |
8 | Abstract:
9 |
10 | Additional APIs for handling elements of the Z3 real closed field that contains:
11 | - transcendental extensions
12 | - infinitesimal extensions
13 | - algebraic extensions
14 |
15 | Author:
16 |
17 | Leonardo de Moura (leonardo) 2012-01-05
18 |
19 | Notes:
20 |
21 | --*/
22 | #ifndef Z3_RCF_H_
23 | #define Z3_RCF_H_
24 |
25 | #ifdef __cplusplus
26 | extern "C" {
27 | #endif // __cplusplus
28 |
29 | /** \defgroup capi C API */
30 | /*@{*/
31 |
32 | /** @name Real Closed Fields */
33 | /*@{*/
34 | /**
35 | \brief Delete a RCF numeral created using the RCF API.
36 |
37 | def_API('Z3_rcf_del', VOID, (_in(CONTEXT), _in(RCF_NUM)))
38 | */
39 | void Z3_API Z3_rcf_del(Z3_context c, Z3_rcf_num a);
40 |
41 | /**
42 | \brief Return a RCF rational using the given string.
43 |
44 | def_API('Z3_rcf_mk_rational', RCF_NUM, (_in(CONTEXT), _in(STRING)))
45 | */
46 | Z3_rcf_num Z3_API Z3_rcf_mk_rational(Z3_context c, Z3_string val);
47 |
48 | /**
49 | \brief Return a RCF small integer.
50 |
51 | def_API('Z3_rcf_mk_small_int', RCF_NUM, (_in(CONTEXT), _in(INT)))
52 | */
53 | Z3_rcf_num Z3_API Z3_rcf_mk_small_int(Z3_context c, int val);
54 |
55 | /**
56 | \brief Return Pi
57 |
58 | def_API('Z3_rcf_mk_pi', RCF_NUM, (_in(CONTEXT),))
59 | */
60 | Z3_rcf_num Z3_API Z3_rcf_mk_pi(Z3_context c);
61 |
62 | /**
63 | \brief Return e (Euler's constant)
64 |
65 | def_API('Z3_rcf_mk_e', RCF_NUM, (_in(CONTEXT),))
66 | */
67 | Z3_rcf_num Z3_API Z3_rcf_mk_e(Z3_context c);
68 |
69 | /**
70 | \brief Return a new infinitesimal that is smaller than all elements in the Z3 field.
71 |
72 | def_API('Z3_rcf_mk_infinitesimal', RCF_NUM, (_in(CONTEXT),))
73 | */
74 | Z3_rcf_num Z3_API Z3_rcf_mk_infinitesimal(Z3_context c);
75 |
76 | /**
77 | \brief Store in roots the roots of the polynomial a[n-1]*x^{n-1} + ... + a[0].
78 | The output vector \c roots must have size \c n.
79 | It returns the number of roots of the polynomial.
80 |
81 | \pre The input polynomial is not the zero polynomial.
82 |
83 | def_API('Z3_rcf_mk_roots', UINT, (_in(CONTEXT), _in(UINT), _in_array(1, RCF_NUM), _out_array(1, RCF_NUM)))
84 | */
85 | unsigned Z3_API Z3_rcf_mk_roots(Z3_context c, unsigned n, Z3_rcf_num const a[], Z3_rcf_num roots[]);
86 |
87 | /**
88 | \brief Return the value a + b.
89 |
90 | def_API('Z3_rcf_add', RCF_NUM, (_in(CONTEXT), _in(RCF_NUM), _in(RCF_NUM)))
91 | */
92 | Z3_rcf_num Z3_API Z3_rcf_add(Z3_context c, Z3_rcf_num a, Z3_rcf_num b);
93 |
94 | /**
95 | \brief Return the value a - b.
96 |
97 | def_API('Z3_rcf_sub', RCF_NUM, (_in(CONTEXT), _in(RCF_NUM), _in(RCF_NUM)))
98 | */
99 | Z3_rcf_num Z3_API Z3_rcf_sub(Z3_context c, Z3_rcf_num a, Z3_rcf_num b);
100 |
101 | /**
102 | \brief Return the value a * b.
103 |
104 | def_API('Z3_rcf_mul', RCF_NUM, (_in(CONTEXT), _in(RCF_NUM), _in(RCF_NUM)))
105 | */
106 | Z3_rcf_num Z3_API Z3_rcf_mul(Z3_context c, Z3_rcf_num a, Z3_rcf_num b);
107 |
108 | /**
109 | \brief Return the value a / b.
110 |
111 | def_API('Z3_rcf_div', RCF_NUM, (_in(CONTEXT), _in(RCF_NUM), _in(RCF_NUM)))
112 | */
113 | Z3_rcf_num Z3_API Z3_rcf_div(Z3_context c, Z3_rcf_num a, Z3_rcf_num b);
114 |
115 | /**
116 | \brief Return the value -a
117 |
118 | def_API('Z3_rcf_neg', RCF_NUM, (_in(CONTEXT), _in(RCF_NUM)))
119 | */
120 | Z3_rcf_num Z3_API Z3_rcf_neg(Z3_context c, Z3_rcf_num a);
121 |
122 | /**
123 | \brief Return the value 1/a
124 |
125 | def_API('Z3_rcf_inv', RCF_NUM, (_in(CONTEXT), _in(RCF_NUM)))
126 | */
127 | Z3_rcf_num Z3_API Z3_rcf_inv(Z3_context c, Z3_rcf_num a);
128 |
129 | /**
130 | \brief Return the value a^k
131 |
132 | def_API('Z3_rcf_power', RCF_NUM, (_in(CONTEXT), _in(RCF_NUM), _in(UINT)))
133 | */
134 | Z3_rcf_num Z3_API Z3_rcf_power(Z3_context c, Z3_rcf_num a, unsigned k);
135 |
136 | /**
137 | \brief Return Z3_TRUE if a < b
138 |
139 | def_API('Z3_rcf_lt', BOOL, (_in(CONTEXT), _in(RCF_NUM), _in(RCF_NUM)))
140 | */
141 | Z3_bool Z3_API Z3_rcf_lt(Z3_context c, Z3_rcf_num a, Z3_rcf_num b);
142 |
143 | /**
144 | \brief Return Z3_TRUE if a > b
145 |
146 | def_API('Z3_rcf_gt', BOOL, (_in(CONTEXT), _in(RCF_NUM), _in(RCF_NUM)))
147 | */
148 | Z3_bool Z3_API Z3_rcf_gt(Z3_context c, Z3_rcf_num a, Z3_rcf_num b);
149 |
150 | /**
151 | \brief Return Z3_TRUE if a <= b
152 |
153 | def_API('Z3_rcf_le', BOOL, (_in(CONTEXT), _in(RCF_NUM), _in(RCF_NUM)))
154 | */
155 | Z3_bool Z3_API Z3_rcf_le(Z3_context c, Z3_rcf_num a, Z3_rcf_num b);
156 |
157 | /**
158 | \brief Return Z3_TRUE if a >= b
159 |
160 | def_API('Z3_rcf_ge', BOOL, (_in(CONTEXT), _in(RCF_NUM), _in(RCF_NUM)))
161 | */
162 | Z3_bool Z3_API Z3_rcf_ge(Z3_context c, Z3_rcf_num a, Z3_rcf_num b);
163 |
164 | /**
165 | \brief Return Z3_TRUE if a == b
166 |
167 | def_API('Z3_rcf_eq', BOOL, (_in(CONTEXT), _in(RCF_NUM), _in(RCF_NUM)))
168 | */
169 | Z3_bool Z3_API Z3_rcf_eq(Z3_context c, Z3_rcf_num a, Z3_rcf_num b);
170 |
171 | /**
172 | \brief Return Z3_TRUE if a != b
173 |
174 | def_API('Z3_rcf_neq', BOOL, (_in(CONTEXT), _in(RCF_NUM), _in(RCF_NUM)))
175 | */
176 | Z3_bool Z3_API Z3_rcf_neq(Z3_context c, Z3_rcf_num a, Z3_rcf_num b);
177 |
178 | /**
179 | \brief Convert the RCF numeral into a string.
180 |
181 | def_API('Z3_rcf_num_to_string', STRING, (_in(CONTEXT), _in(RCF_NUM), _in(BOOL), _in(BOOL)))
182 | */
183 | Z3_string Z3_API Z3_rcf_num_to_string(Z3_context c, Z3_rcf_num a, Z3_bool compact, Z3_bool html);
184 |
185 | /**
186 | \brief Convert the RCF numeral into a string in decimal notation.
187 |
188 | def_API('Z3_rcf_num_to_decimal_string', STRING, (_in(CONTEXT), _in(RCF_NUM), _in(UINT)))
189 | */
190 | Z3_string Z3_API Z3_rcf_num_to_decimal_string(Z3_context c, Z3_rcf_num a, unsigned prec);
191 |
192 | /**
193 | \brief Extract the "numerator" and "denominator" of the given RCF numeral.
194 | We have that a = n/d, moreover n and d are not represented using rational functions.
195 |
196 | def_API('Z3_rcf_get_numerator_denominator', VOID, (_in(CONTEXT), _in(RCF_NUM), _out(RCF_NUM), _out(RCF_NUM)))
197 | */
198 | void Z3_API Z3_rcf_get_numerator_denominator(Z3_context c, Z3_rcf_num a, Z3_rcf_num * n, Z3_rcf_num * d);
199 |
200 | /*@}*/
201 | /*@}*/
202 |
203 | #ifdef __cplusplus
204 | }
205 | #endif // __cplusplus
206 |
207 | #endif
208 |
--------------------------------------------------------------------------------
/z3-4.5.0-x64-win/include/z3_v1.h:
--------------------------------------------------------------------------------
1 | /*++
2 | Copyright (c) 2011 Microsoft Corporation
3 |
4 | Module Name:
5 |
6 | z3_v1.h
7 |
8 | Abstract:
9 |
10 | Z3 1.x backwards compatibility macros.
11 | These macros are used to simulate the Z3 API using in the 1.x versions.
12 | This file should only be used by users still using the Z3 1.x API.
13 |
14 | Author:
15 |
16 | Leonardo de Moura (leonardo) 2011-09-22
17 |
18 | Notes:
19 |
20 | --*/
21 | #ifndef Z3_V1_H_
22 | #define Z3_V1_H_
23 |
24 | #include"z3.h"
25 |
26 | // Backwards compatibility
27 | #define Z3_type_ast Z3_sort
28 | #define Z3_const_decl_ast Z3_func_decl
29 | #define Z3_const Z3_app
30 | #define Z3_pattern_ast Z3_pattern
31 | #define Z3_UNINTERPRETED_TYPE Z3_UNINTERPRETED_SORT
32 | #define Z3_BOOL_TYPE Z3_BOOL_SORT
33 | #define Z3_INT_TYPE Z3_INT_SORT
34 | #define Z3_REAL_TYPE Z3_REAL_SORT
35 | #define Z3_BV_TYPE Z3_BV_SORT
36 | #define Z3_ARRAY_TYPE Z3_ARRAY_SORT
37 | #define Z3_TUPLE_TYPE Z3_DATATYPE_SORT
38 | #define Z3_UNKNOWN_TYPE Z3_UNKNOWN_SORT
39 | #define Z3_CONST_DECL_AST Z3_FUNC_DECL_AST
40 | #define Z3_TYPE_AST Z3_SORT_AST
41 | #define Z3_SORT_ERROR Z3_TYPE_ERROR
42 | #define Z3_mk_uninterpreted_type Z3_mk_uninterpreted_sort
43 | #define Z3_mk_bool_type Z3_mk_bool_sort
44 | #define Z3_mk_int_type Z3_mk_int_sort
45 | #define Z3_mk_real_type Z3_mk_real_sort
46 | #define Z3_mk_bv_type Z3_mk_bv_sort
47 | #define Z3_mk_array_type Z3_mk_array_sort
48 | #define Z3_mk_tuple_type Z3_mk_tuple_sort
49 | #define Z3_get_type Z3_get_sort
50 | #define Z3_get_pattern_ast Z3_get_pattern
51 | #define Z3_get_type_kind Z3_get_sort_kind
52 | #define Z3_get_type_name Z3_get_sort_name
53 | #define Z3_get_bv_type_size Z3_get_bv_sort_size
54 | #define Z3_get_array_type_domain Z3_get_array_sort_domain
55 | #define Z3_get_array_type_range Z3_get_array_sort_range
56 | #define Z3_get_tuple_type_num_fields Z3_get_tuple_sort_num_fields
57 | #define Z3_get_tuple_type_field_decl Z3_get_tuple_sort_field_decl
58 | #define Z3_get_tuple_type_mk_decl Z3_get_tuple_sort_mk_decl
59 | #define Z3_to_const_ast Z3_to_app
60 | #define Z3_get_numeral_value_string Z3_get_numeral_string
61 | #define Z3_get_const_ast_decl Z3_get_app_decl
62 | #define Z3_get_value Z3_eval_func_decl
63 |
64 | #endif
65 |
--------------------------------------------------------------------------------