├── BINK.md
├── ConfID.md
├── PKEY2005.md
├── README.md
└── images
├── ECClines.svg.png
├── Example_of_a_hyperelliptic_curve.svg.png
└── cid_screenshot.png
/BINK.md:
--------------------------------------------------------------------------------
1 | # BINK1998 and BINK2002
2 |
3 | By Endermanch and WitherOrNot
4 |
5 | ## Product ID
6 |
7 | We need to use a random Raw Product Key as a base to generate a Product ID in a form of `AAAAA-BBB-CCCCCCS-DDEEE`.
8 |
9 | | Digits | Meaning |
10 | |-------:|:----------------------|
11 | | AAAAA | OS Family constant |
12 | | BBB | Channel ID |
13 | | CCCCCC | Sequence Number |
14 | | S | Check digit |
15 | | DD | Public key index |
16 | | EEE | Random 3-digit number |
17 |
18 |
19 | The OS Family constant `AAAAA` is different for each series of Windows XP. For example, it is 76487 for SP3.
20 |
21 | The `BBB` and `CCCCCC` sections essentially encode the Raw Product Key. For example, if the first section is equal to `XXX` and the second section is equal to `YYYYYY`, the Raw Product Key will be encoded as `XXX-YYYYYY`.
22 |
23 | The check digit `S` is picked so that the sum of all `C` digits with it added makes a number divisible by 7.
24 |
25 | The public key index `DD` lets us know which public key was used to successfully verify the authenticity of our Product Key.
26 | For example, it's `22` for Professional keys and `23` for VLK keys. This value is equal to half of the BINK ID (discussed below).
27 |
28 | A random number `EEE` is used to generate a different Installation ID each time.
29 |
30 | ## Product Key
31 |
32 | The Product Key itself (not to confuse with the RPK) is in form `FFFFF-GGGGG-HHHHH-JJJJJ-KKKKK`, encoded in Base-24 with
33 | the alphabet `BCDFGHJKMPQRTVWXY2346789` to exclude any characters that can be easily confused, like `I` and `1` or `O` and `0`.
34 |
35 | As per the alphabet capacity formula, the key can at most contain 114 bits of information.
36 | $$N = \log_2(24^{25}) \approx 114$$
37 |
38 | Based on that calculation, we unpack the 114-bit Product Key into 4 ordered segments:
39 |
40 | | Segment | Capacity | Data |
41 | |-----------|----------|-------------------------------------------|
42 | | Upgrade | 1 bit | Upgrade version flag |
43 | | Serial | 30 bits | Raw Product Key (RPK) |
44 | | Hash | 28 bits | RPK hash |
45 | | Signature | 55 bits | Elliptic Curve signature for the RPK hash |
46 |
47 | For simplicity' sake, we'll combine `Upgrade` and `Serial` segments into a single segment called `Data`. By that logic we'll be able to extract the RPK by
48 | shifting `Data` right and pack it back by shifting bits left, because most a priori valid product keys I've checked had the Upgrade bit set to 1.
49 |
50 | Microsoft redid their Product Key format with Windows Server 2003 to include a backend server authentication key, which was an actually secure approach to
51 | license validation, as no one could ever make a guess on which validation algorithm they had employed on their private server. Besides adding the online
52 | validation mechanism, they also cranked up the overall arithmetic from 384 to 512 bits, and the signature scalar to 62 bits of information.
53 |
54 | | Segment | Capacity | Data |
55 | |------------|----------|-------------------------------------------|
56 | | Upgrade | 1 bit | Upgrade version flag |
57 | | Channel ID | 10 bits | The `BBB` part of the RPK |
58 | | Hash | 31 bits | RPK hash |
59 | | Signature | 62 bits | Elliptic Curve signature for the RPK hash |
60 | | Auth Key | 10 bits | Backend authentication value |
61 |
62 | However, if we generated a key without the online activation in mind, we still could generate valid keys that would let us through the setup of the operating system.
63 | And that's exactly what the code does - it generates a random 10-bit authentication key. Nowadays it doesn't matter at all, as activation servers are down and
64 | Server 2003 is considered abandonware, the same way this entire project shouldn't be considered piracy.
65 |
66 | ## Elliptic Curves
67 |
68 | Elliptic Curve Cryptography (ECC) is a type of public-key cryptographic system.
69 | This class of systems relies on challenging "one-way" math problems - easy to compute one way and intractable to solve the "other" way.
70 | Sometimes these are called "trapdoor" functions - easy to fall into, complicated to escape.[5]
71 |
72 | ECC relies on solving equations of the form
73 | $$y^2 = x^3 + ax + b$$
74 |
75 | In general, there are 2 special cases for the Elliptic Curve leveraged in cryptography - **F2m** and **Fp**.
76 | They differ only slightly. Both curves are defined over the finite field, Fp uses a prime parameter that's larger than 3,
77 | F2m assumes $p = 2m$. Microsoft used the latter in their algorithm.
78 |
79 | An elliptic curve over the finite field Fp consists of:
80 | * a set of integer coordinates ${x, y}$, such that $0 \le x, y < p$;
81 | * a set of points $y^2 = x^3 + ax + b \mod p$.
82 |
83 | **An elliptic curve over F17 would look like this:**
84 |
85 | 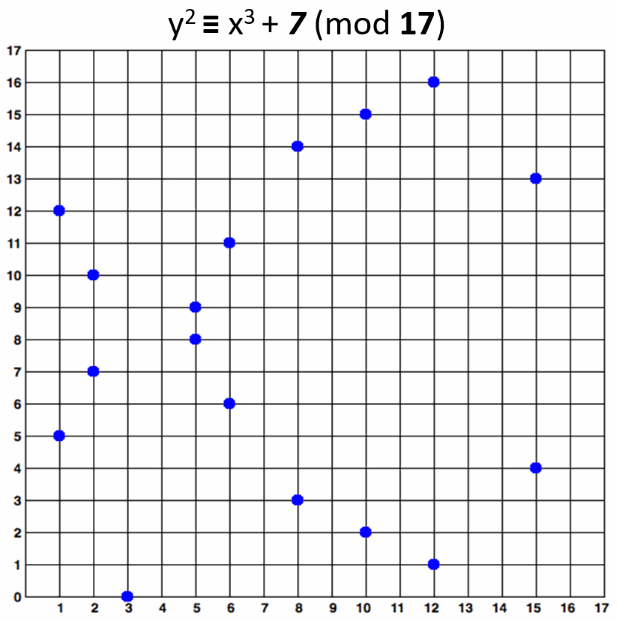
86 |
87 | The curve consists of the blue points in above image. In practice the "elliptic curves"
88 | used in cryptography are "sets of points in a square matrix".
89 |
90 | The above curve is "educational". It provides very small key length (4-5 bits).
91 | In real world situations developers typically use curves of 256-bits or more.
92 |
93 | An important concept is that addition can be defined between two points on an elliptic curve. This also allows a definition of integer multiplication ($nP$ is $P$ added to itself $n$ times).
94 |
95 | The core of elliptic curve cryptography uses this multiplication definition, as solving the equation $Q=nP$ for known points $P$ and $Q$ is difficult with known algorithms, but it is easy to compute knowing $n$ and $Q$. This allows elliptic curve multiplication to act as a trapdoor function.
96 |
97 | ## BINK resource
98 |
99 | Since it is a public-key cryptographic system, Microsoft had to share the public key with their Windows XP release to check entered product keys against.
100 | It is stored within `pidgen.dll` in a form of a BINK resource. The first set of BINK data is there to validate retail keys, the second is for the
101 | OEM keys respectively.
102 |
103 | **The structure of the BINK resource for Windows 98 and Windows XP is as follows:**
104 |
105 | | Offset | Value |
106 | |---------:|:---------------------------------------------------------------------|
107 | | `0x0000` | BINK ID |
108 | | `0x0004` | Size of BINKEY structure in bytes (always `0x16C` in practice) |
109 | | `0x0008` | Header length (always `7` in practice) |
110 | | `0x000C` | Checksum |
111 | | `0x0010` | Number-encoded date - BINKEY version (always `19980206` in practice) |
112 | | `0x0014` | ECC curve order size (always `12` in practice) |
113 | | `0x0018` | Hash length (always `28` in practice) |
114 | | `0x001C` | Signature length (always `55` in practice) |
115 | | `0x0020` | Finite Field Order `p` |
116 | | `0x005C` | Curve Parameter `a` |
117 | | `0x0098` | Curve Parameter `b` |
118 | | `0x00D4` | Base Point x-coordinate `Gx` |
119 | | `0x0110` | Base Point y-coordinate `Gy` |
120 | | `0x014C` | Public Key x-coordinate `Kx` |
121 | | `0x0188` | Public Key y-coordinate `Ky` |
122 |
123 | Each segment is marked with a different color, the BINK header values are the same.
124 |
125 | 
126 |
127 | **Windows Server 2003 and Windows XP x64 implement it differently:**
128 |
129 | | Offset | Value |
130 | |---------:|:---------------------------------------------------------------------|
131 | | `0x0000` | BINK ID |
132 | | `0x0004` | Size of BINKEY structure in bytes |
133 | | `0x0008` | Header length (always `9` in practice) |
134 | | `0x000C` | Checksum |
135 | | `0x0010` | Number-encoded date - BINKEY version (always `20020420` in practice) |
136 | | `0x0014` | ECC curve order size (always `16` in practice) |
137 | | `0x0018` | Hash length (always `31` in practice) |
138 | | `0x001C` | Signature length (always `62` in practice) |
139 | | `0x0020` | Backend authentication value length (always `12` in practice) |
140 | | `0x0024` | Product ID length (always `20` in practice) |
141 | | `0x0028` | Finite Field Order `p` |
142 | | `0x0068` | Curve Parameter `a` |
143 | | `0x00A8` | Curve Parameter `b` |
144 | | `0x00E8` | Base Point x-coordinate `Gx` |
145 | | `0x0128` | Base Point y-coordinate `Gy` |
146 | | `0x0168` | Public Key x-coordinate `Kx` |
147 | | `0x01A8` | Public Key y-coordinate `Ky` |
148 |
149 | **And here are my structure prototypes made for the BINK Reader in C:**
150 |
151 | ```c
152 | typedef struct _EC_BYTE_POINT {
153 | CHAR x[256]; // x-coordinate of the point on the elliptic curve.
154 | CHAR y[256]; // y-coordinate of the point on the elliptic curve.
155 | } EC_BYTE_POINT;
156 |
157 | typedef struct _BINKHDR {
158 | // BINK version - not stored in the resource.
159 | ULONG32 dwVersion;
160 |
161 | // Original BINK header.
162 | ULONG32 dwID;
163 | ULONG32 dwSize;
164 | ULONG32 dwHeaderLength;
165 | ULONG32 dwChecksum;
166 | ULONG32 dwDate;
167 | ULONG32 dwKeySizeInDWORDs;
168 | ULONG32 dwHashLength;
169 | ULONG32 dwSignatureLength;
170 |
171 | // Extended BINK header. (Windows Server 2003+)
172 | ULONG32 dwAuthCodeLength;
173 | ULONG32 dwProductIDLength;
174 | } BINKHDR;
175 |
176 | typedef struct _BINKDATA {
177 | CHAR p[256]; // Finite Field order p.
178 | CHAR a[256]; // Elliptic Curve parameter a.
179 | CHAR b[256]; // Elliptic Curve parameter b.
180 |
181 | EC_BYTE_POINT G; // Base point (Generator) G.
182 | EC_BYTE_POINT K; // Public key K.
183 | } BINKDATA;
184 |
185 | typedef struct _BINKEY {
186 | BINKHDR header;
187 | BINKDATA data;
188 | } BINKEY;
189 | ```
190 |
191 | ## Validating / generating product keys
192 |
193 | Please note throughout this section that whenever integers are converted to bytes or vice-versa, they are in [little-endian](https://en.wikipedia.org/wiki/Endianness#Little) byte order.
194 |
195 | First, let's define some variables used in these algorithms:
196 |
197 | - $m$, the `Data` section of the product key (Raw Product Key/Channel ID and Upgrade bit)
198 | - $h$, the `Hash` section of the product key
199 | - $s$, the `Signature` section of the product key
200 | - $k$, the private key, used to generate product keys
201 | - $a$, the `Authentication Info` section of the product key (BINK2002 only)
202 |
203 | $G$, $K$, $p$, $a$, and $b$ are constants that come from the BINK, described above.
204 |
205 | The constant $n$, not included in the BINK, is the order of the point $G$.
206 |
207 | ### BINK1998 (Windows 98/XP era)
208 |
209 | #### Validation
210 |
211 | 1. Using base-24 conversion, with the base alphabet `BCDFGHJKMPQRTVWXY2346789`, convert the product key into an integer
212 | 2. From this integer, extract the values $m$, $h$, and $s$ using bit-shifting and logical ANDs
213 | 3. Compute the elliptic curve point $R = hK + sG$
214 | 4. Compute `digest = SHA1(m || R.x || R.y)`, where `||` represents byte concatenation
215 | 5. Convert `digest` to an integer
216 | 6. Let $h_t$ be the lower 28 bits of `digest`
217 | 7. Compare $h$ and $h_t$, if they are equal, the product key is valid
218 |
219 | #### Generation
220 |
221 | 1. Compute a random number $c$
222 | 2. Compute the random point $R = cG$
223 | 3. Compute `digest = SHA1(m || R.x || R.y)`
224 | 4. Let $h$ be integer formed by the lower 28 bits of `digest`
225 | 5. Let $s = kh + c \pmod{p}$
226 | 6. Pack $s$, $h$, and $m$ into a 114-bit integer
227 | 7. Convert this integer into a product key, using base-24 conversion
228 |
229 | #### Mathematical mechanism
230 |
231 | The point $K$ is related to the point $G$ as $K=-kG$. Thus,
232 |
233 | $$ R = hK + sG = -hkG + \left(hk + c\right)G = cG $$
234 |
235 | The values $h$ and $s$ are dependent on the value of $R$ and $m$, so they can only be found by knowing the private key $k$.
236 |
237 | ### BINK2002 (Windows Server 2003/Windows XP x64 era)
238 |
239 | #### Validation
240 |
241 | 1. Using base-24 conversion, with the base alphabet `BCDFGHJKMPQRTVWXY2346789`, convert the product key into an integer
242 | 2. From this integer, extract the values $m$, $h$, and $s$ using bit-shifting and logical ANDs
243 | 3. Compute `digest1 = SHA1(5D || m || h || a || 00 00)`
244 | 4. Let $e$ be the integer formed by the lower 62 bits of `digest1`
245 | 5. Let $R = s(sG + eK)$
246 | 6. Let `digest2 = SHA1(79 || m || R.x || R.y)`
247 | 7. Let $h_t$ be the lower 31 bits of `digest2`
248 | 8. Compare $h$ and $h_t$, if they are equal, the product key is valid
249 |
250 | Afterwards, the value $a$, along with some other information, can be sent to the activation server for further validation.
251 |
252 | #### Generation
253 |
254 | 1. Compute a random number $c$
255 | 2. Compute the random point $R = cG$
256 | 3. Let `digest2 = SHA1(79 || m || R.x || R.y)`
257 | 4. Let $h$ be integer formed by the lower 31 bits of `digest2`
258 | 5. Compute `digest1 = SHA1(5D || m || h || a || 00 00)`
259 | 6. Let $e$ be the integer formed by the lower 62 bits of `digest1`
260 | 7. Let $s = \frac{-ek + \sqrt{\left(ek\right)^2 + 4c}}{2} \pmod {n}$
261 | 8. Compute $a$ by unknown algorithm
262 | 9. Pack $s$, $h$, and $m$, and $a$ into a 114-bit integer
263 | 10. Convert this integer into a product key, using base-24 conversion
264 |
265 | #### Mathematical mechanism
266 |
267 | The variables used in this algorithm are related as follows:
268 |
269 | $$ R=s(sG + eK) = {s^2}G + seK = {s^2}G - sekG = cG $$
270 |
271 | $$ \left(s^2 - eks - c\right)G = O $$
272 |
273 | $$ s^2 - eks - c = 0 $$
274 |
275 | During generation, $s$ is found as the solution to the above quadratic equation.
276 |
277 | ### Reversing the private key
278 |
279 | If we want to generate valid product keys for Windows XP, we must compute the corresponding private key using the public key supplied with `pidgen.dll`,
280 | which means we have to reverse-solve the one-way ECC task.
281 |
282 | Judging by the key located in BINK, the curve order is **384 bits** long in Windows XP and **512 bits** long in Server 2003 / XP x64 respectively.
283 | The computation difficulty using the most efficient Pollard's Rho algorithm with asymptotic complexity $O(\sqrt{n})$ would be at least $O(2^{168})$ for Windows XP, and $O(2^{256})$ for Windows Server 2003, but lucky for us,
284 | Microsoft limited the value of the signature to 55 bits in Windows XP and 62 bits in Windows Server 2003 in order to reduce the amount of matching product keys, reducing the difficulty to a far more manageable $O(2^{28})$ / $O(2^{31})$.
285 |
286 | As mentioned before, there's only one public tool that satisfies our current needs, which is the ECDLP solver by Mr. HAANDI.
287 |
288 | To compute the private key, we will need to supply the tool with the public ECC values located in the BINK resource, as well as the order `genOrder` of the base point `G(Gx; Gy)`.
289 | The order of the base point can be computed using SageMath.
290 |
291 | **Here's the basic algorithm I used to reverse the Windows 98 private key:**
292 |
293 | 1. Compute the order of the base point using **SageMath**. In SageMath, execute the following commands:
294 | 1) `E = EllipticCurve(GF(p), [0, 0, 0, a, b])`, where `p`, `a` and `b` are decimally represented elliptic curve parameters from the BINK resource.
295 | 2) `G = E(Gx, Gy)`, where `Gx` and `Gy` are decimally represented base point coordinates from the BINK resource.
296 | 3) `K = E(Kx, Ky)`, where `Kx` and `Ky` are decimally represented public key coordinates from the BINK resource.
297 | 4) `n = G.order()`, `n` will be the computed order of the base point. **It may take some time to compute, even on the newest builds.**
298 | 5) Factor the order using `factor(n)`. Microsoft used prime numbers for the point orders, so if it returns the number itself, it's completely normal.
299 | 6) Save the resulting factors of the order somewhere.
300 | 7) `-K` will give you the inverse of the public key in a projective plane with coordinates `(x : y : z)`. Save the `y` coordinate somewhere, it is required to generate a correct private key.
301 | 2. Compute the private key using **ECDLP Solver v0.2a**.
302 | 1) The tool comes with a template job `job_template.txt` and a ReadMe file. It's necessary to understand how the tool works to use it.
303 | 2) Insert all public elliptic curve values from the BINK resource, **except the `Ky` coordinate**. To generate a correct private key, **you must use the inverse coordinate `-Ky` you have calculated in SageMath earlier.**
304 | 3) Insert the factors of the base point order `n` and specify the factor count. It will very likely be `1`, as Microsoft mainly uses primes for their generator orders.
305 | 4) Run the tool ` ECDLP Solver.exe .txt` and wait until it calculates the private key `k = %d` for you.
306 |
307 | **Here's an example of the Windows XP job `job_xp.txt` that yields the correct private key for the ECDLP Solver.**
308 |
309 | ```pascal
310 | GF := GF(22604814143135632990679956684344311209819952803216271952472204855524756275151440456421260165232069708317717961315241);
311 | E := EllipticCurve([GF|1,0]);
312 | G := E![10910744922206512781156913169071750153028386884676208947062808346072531411270489432930252839559606812441712224597826,19170993669917204517491618000619818679152109690172641868349612889930480365274675096509477191800826190959228181870174];
313 | K := E![14399230353963643339712940015954061581064239835926823517419716769613937039346822269422480779920783799484349086780408,17120082747148185997450361756610881166187863099877353630300913555824935802439591336620545428308962346299700128114607];
314 | /*
315 | FactorCount:=1;
316 | 61760995553426173
317 | */
318 | ```
319 |
320 | **And the ECDLP Solver output for it:**
321 |
322 | 
323 |
324 | ## DPCDLL and Channel IDs
325 |
326 | In Windows versions before XP, the channel ID is rarely validated except in certain products, such as Windows 98 SE Select Edition.
327 | In Windows XP and Server 2003, however, the channel ID is validated to determine the license type for a specific copy.
328 | This validation is done by DPCDLL.DLL, which contains a table of signed channel ID ranges and their associated license type.
329 |
330 | For all NT 5 Windows versions except Server 2003 R2, this table has the following structure for each row:
331 |
332 | | Offset | Value |
333 | |----------|-----------------------------------|
334 | | `0x0000` | Index |
335 | | `0x0004` | BINK ID |
336 | | `0x0008` | Minimum Channel ID |
337 | | `0x000C` | Maximum Channel ID |
338 | | `0x0010` | License Type |
339 | | `0x0014` | Activation Grace Period (in days) |
340 | | `0x0018` | Evaluation Period (in days) |
341 | | `0x001C` | Signature Length |
342 | | `0x0020` | Signature |
343 |
344 | The license types are as follows:
345 |
346 | | Type | Meaning |
347 | |------|--------------------------------------------------|
348 | | 1 | Volume (VLK) |
349 | | 2 | Retail/OEM Certificate of Authenticity (OEM-COA) |
350 | | 3 | Evaluation |
351 | | 4 | Tablet |
352 | | 5 | OEM System Locked Pre-Installation (OEM-SLP) |
353 | | 6 | Embedded |
354 |
355 | For the Evaluation Period and Activation Grace Period values, the value `2147483647` is used to indicate `N/A`.
356 |
357 | When a key with an invalid channel ID and correct BINK is supplied during setup, the setup installed will accept the key since it has a valid signature.
358 | However, when attempting to login to the system, the system will prevent login until the system is activated.
359 | When attempting to activate, a non-functional OOBE Activation popup will appear, blocking login and effectively bricking the system, as shown below.
360 |
361 | 
362 |
363 | This strange behavior is most likely a bug triggered by a lack of error handling in DPCDLL's channel ID validation code.
364 |
365 | ## Literature
366 | I will add more decent reads into the bibliography in later releases.
367 |
368 | **Understanding basics of Windows XP Activation**:
369 | * [[1] Inside Windows Product Activation - Fully Licensed](https://www.licenturion.com/xp/fully-licensed-wpa.txt)
370 | * [[2] MSKey 4-in-1 ReadMe](https://malwarewatch.org/documents/MSKey4in1.pdf)
371 | * [[3] Windows序列号产生原理(椭圆曲线法)](https://blog.csdn.net/zhiyuan411/article/details/5156330)
372 |
373 | **Understanding Elliptic Curve Cryptography**:
374 | * [[4] Elliptic Curve Cryptography for Beginners - Matt Rickard](https://matt-rickard.com/elliptic-curve-cryptography)
375 | * [[5] Elliptic Curve Cryptography (ECC) - Practical Cryptography for Developers](https://cryptobook.nakov.com/asymmetric-key-ciphers/elliptic-curve-cryptography-ecc)
376 | * [[6] A (Relatively Easy To Understand) Primer on Elliptic Curve Cryptography - Cloudflare](https://blog.cloudflare.com/a-relatively-easy-to-understand-primer-on-elliptic-curve-cryptography/)
377 |
378 | **Public discussions**:
379 | * [[7] Windows 98 Equivalent // Server 2003 Algorithm](https://github.com/Endermanch/XPKeygen/issues/3)
380 | * [[8] Cracking Windows XP](https://forums.mydigitallife.net/threads/is-there-any-way-to-crack-decrypt-the-winxp-consumer-activation-system-to-generate-activation-ids.80133/)
381 |
--------------------------------------------------------------------------------
/ConfID.md:
--------------------------------------------------------------------------------
1 | # Windows XP Confirmation IDs
2 |
3 | By WitherOrNot
4 |
5 | # Background
6 |
7 | In the interest of convenience for those who would like to do further research into or implementation of the Confirmation ID system, a summary of the mathematics involved in hyperelliptic curve cryptography is provided below.
8 |
9 | If you are not interested in the mathematics, please skip to [Validation Mechanism](#Validation-Mechanism).
10 |
11 | ## Hyperelliptic Curves
12 |
13 | An imaginary hyperelliptic curve $H$ of genus $g$ is a set of points $(x,y)$ that satisfies the following relation:
14 |
15 | $$ y^2 + y \cdot h(x) \equiv F(x) \pmod {p} $$
16 |
17 | where $F(x)$ is a monic polynomial of degree $2g+1$, $h(x)$ is a polynomial of degree less than $g+2$, and $p$ is a prime number.
18 |
19 | For this write-up, we will be focusing on the curves used by the Confirmation ID system which are genus 2 curves where $h(x) = 0$, thus
20 |
21 | $$ y^2 \equiv x^5 + a_{4}x^4 + a_{3}x^3 + a_{2}x^2 + a_{1}x + a_0 \pmod {p} $$
22 |
23 | Those familiar with the related concept of elliptic curves may assume points on this curve follow a similar group law. However, the group law for hyperelliptic curves is very different.
24 |
25 | As a refresher, for points on elliptic curves, a form of addition can be done by defining the sum of 2 points to be the reflection of their third collinear point over the y-axis.
26 |
27 | 
28 |
29 | This works because any line on the projective plane (a plane with a defined point at infinity) that passes through 2 points on this curve will intersect exactly at one other point, even if the two points are identical (we define the point at infinity to be on the curve).
30 |
31 | As an exercise for the reader, see how the same property fails to hold on the following hyperelliptic curve.
32 |
33 | 
34 |
35 | Therefore, a different group representation will be needed for hyperelliptic curves.
36 |
37 | ## Divisors
38 |
39 | We define the divisor $D$ over the curve $E$ to be a formal linear combination of all $n$ points $P_i$ on the curve with weights $c_i$.
40 |
41 | $$ D = \sum_{i=1}^{n} c_{i}P_{i} $$
42 |
43 | "Formal" means that there is no actual definition of summation or scalar multiplication on points, it simply denotes the behavior we want divisors to have.
44 |
45 | The only operation that is defined on individual points is negation, which for a point $P = (x,y)$ is defined as $-P = (x,-y)$.
46 |
47 | Divisors, however, can be added and multiplied by scalars according to their definition. This allows the construction of an abelian (commutative) additive group, but this group is too large to be cryptographically useful. Therefore, we will need to consider a subset of divisors with useful properties.
48 |
49 | ## Semi-reduced and reduced divisors
50 |
51 | Semi-reduced divisors are divisors where for all $P_i$ with non-zero coefficients $c_i$, there are no two $P_a$ and $P_b$ such that $P_a = -P_b$. Thus, the divisors sum only across sets of points where no two points are negatives of each other.
52 |
53 | Reduced divisors are semi-reduced divisors where the sum of all coefficients in $D$ is less than or equal to $g$. Additionally, when added, reduced divisors undergo an additional step known as reduction.
54 |
55 | The reduction algorithm is as follows:
56 | 1. Let $v(x)$ be a polynomial such that for all $P_i=(x_i,y_i)$ in $D$, $y_i=v(x_i)$
57 | 2. Find all points $Q_i=(x_i,y_i)$ on the curve such that $q(x)=F(x)-v(x)^2=0$ for all $x_i$.
58 | - If the coefficient $c_i$ of $P_i$ is greater than 1 in $D$, $q$ must have a root of multiplicity $c_i$ at $x_i$.
59 |
60 |
61 | 3. From the set of points $Q_i$, remove all points $P_i$.
62 | 4. Let $E=-\sum Q_i$.
63 | 5. If the number of points in $E$ is less than or equal to $g$, then stop, the reduction of $D$ is $E$. Otherwise, let $D=E$ and repeat from step 1.
64 |
65 | Reduction by this method is analogous to the modulo operation for integers, in that it maps the group of all divisors to a cyclic group known as the *Jacobian* $J(H)$. The Jacobian group has similar properties to the addition group for elliptic curve points, making it useful for cryptography. Additionally, the reduction process preserves the commutativity of addition, so the Jacobian is also abelian.
66 |
67 | Some useful observations can be made about the reduction procedure. Notice first that it is necessary for the polynomial $q$ to equal 0 for all $x_i$ of the points $P_i$ in the divisor $D$, as can be seen from the curve equation and the definition of $v$. Therefore, we can let $q(x)=u(x)q'(x)$, where the polynomial $u(x)=0$ has roots $x_i$ with multiplicity $c_i$ for all the points $P_i$ in $D$.
68 |
69 | Next, it can be seen that after step 3, the x-coordinates $x_i$ of the remaining points $Q_i$ are exactly the roots of $q'(x)$.
70 |
71 | Note that in many cases, $q'(x)$ will be an irreducible (non-factorable) polynomial, so the points $Q_i$ will contain coordinates that are not integers, which makes representing reduced divisors difficult. Luckily, using the above observations, a simpler representation of semi-reduced and reduced divisors can be constructed.
72 |
73 | ## Mumford representation
74 |
75 | The Mumford representation of a semi-reduced divisor $D=\sum c_i(x_i,y_i)$ is the unique pair of polynomials $u(x)$ and $v(x)$ where:
76 |
77 | $$ u(x) = \prod_{i=1}^{n} (x-x_i)^{c_i} $$
78 |
79 | $$ v^2 \equiv F \pmod {u}$$
80 |
81 | $$\mathrm{deg}(v) \lt \mathrm{deg}(u)$$
82 |
83 | With this, the divisor can now be re-defined as $D=\langle u(x), v(x) \rangle$.
84 |
85 | From the previous observations, it can be seen that $u$ and $v$ in this representation are exactly the polynomials $u$ and $v$ from the reduction steps above. Therefore, the reduction algorithm is much more concise using the Mumford representation.
86 |
87 | Reduction algorithm for $D=\langle u,v \rangle$:
88 | 1. Let $u' = \frac{F-v^2}{u}$
89 | 2. Let $v' = -v \bmod u'$
90 | 3. If $\mathrm{deg}(u') \leq g$, then stop. $E = \left\langle u', v' \right\rangle$ is the reduction of $D$. Otherwise, let $u=u'$ and $v=v'$ and start from step 1.
91 |
92 | With the Mumford representation and reduction defined, we are ready to state the central problem of hyperelliptic curve cryptography.
93 |
94 | ## Cryptographic problem
95 |
96 | Let the scalar multiplication of a divisor $D$ by the integer $r$ be defined as follows:
97 |
98 | $$ \left[r\right]D = \overbrace{D+\ldots+D}^{r \text{ times}} $$
99 |
100 | Then the cryptographic problem for hyperelliptic curve cryptography is to find an integer $k$ such that
101 |
102 | $$ D = \left[k\right] D_2 $$
103 |
104 | given that
105 |
106 | $$ D_2 = \left[e\right] D $$
107 |
108 | for some known integer $e$ and a pair of known divisors $D$ and $D_2$.
109 |
110 | To compute $k$ from $e$, we need to know the *order* of the Jacobian $N=\\#J(H)$, which is the number of unique divisors in $J$.
111 |
112 | When this value is known, $k$ can be computed in a straightforward manner:
113 |
114 | $$ k = e^{-1} \pmod {N} $$
115 |
116 | Computation of $k$ and $\\#J(H)$ is a difficult process that warrants its own write-up, the automated method is discussed in [Parameter Extraction](#Parameter-Extraction). For now, we will go into the mechanism behind confirmation ID generation and validation.
117 |
118 | # Validation Mechanism
119 |
120 | The confirmation ID is derived directly from a value known as the *Installation ID*. This value is displayed to the user when selecting the "Telephone Activation" option when activating a product, as shown below.
121 |
122 | 
123 |
124 | As seen in the screenshot, the confirmation ID is broken into 6-digit groups. This is related to the first validation step, known as the checksum.
125 |
126 | ## Checksum
127 |
128 | Within each 6-digit group $d_1d_2d_3d_4d_5d_6$, the checksum digit $d_6$ is calculated from the others as $d_6 = (d_1 + 2d_2 + d_3 + 2d_4 + d_5) \bmod {7}$.
129 |
130 | For instance, from the screenshot above, the checksum digit for the group $154814$ is $4$, and $(1 + 2\cdot5 + 4 + 2\cdot8 + 1) \bmod {7} = 32 \bmod 7 = 4$.
131 |
132 | Once the checksums are validated for each digit group, the checksum digits are removed and the remaining digits are concatenated to form an integer that we will refer to as $C$.
133 |
134 | ## Hyperelliptic Decryption
135 |
136 | $C$ is then split into two integers $x_1$ and $x_2$ like so:
137 |
138 | $$ x_1 = \left \lfloor {\frac{C}{p+1}} \right \rfloor $$
139 |
140 | $$ x_2 = C \bmod {(p+1)} $$
141 |
142 | with $p$ being the modulus for the hyperelliptic curve used to validate the confirmation ID.
143 |
144 | Next, the divisor $D$ is constructed as follows:
145 |
146 | $\text{Let } m \text{ be the smallest integer such that } c^2 \not\equiv m \pmod {p} \text{ for all integers } c$
147 |
148 | $\text{If } x_1 \leq p \text{:}$
149 |
150 | $\quad\text{Determine } y_1 \text{ such that } (x_1, y_1) \text{ is on the curve} $
151 |
152 | $\quad\text{Determine } y_2 \text{ such that } (x_2, y_2) \text{ is on the curve} $
153 |
154 | $\quad\text{If } x_2 \lt x_1 \text{ and } y_1 \equiv y_2 \pmod {2} \text{ or } x_2 \geq x_1 \text{ and } y_1 \not\equiv y_2 \pmod {2} \text{:}$
155 |
156 | $\quad\quad y_2 = p - y_2 $
157 |
158 | $\quad \text{Let } D = (x_1, y_1) + (x_2, y_2) \text{ stored as Mumford representation}$
159 |
160 | $\text{Else:}$
161 |
162 | $\quad \text{Let } s(x)=(x+x_2)^2 - mx_1^2 $
163 |
164 | $\quad\text{Find a root } w \text{ of } s$
165 |
166 | $\quad\text{Determine } z \text{ such that } (w,z) \text{ is on the curve }$
167 |
168 | $\quad\text{Let } D = (w,z) + (w^p, z^p) \text{ stored as Mumford representation}$
169 |
170 | Next, the divisor $D_2$ is calculated as $D_2 = \left[65537\right]D$.
171 |
172 | Expressing $D_2$ as $\left\langle x^2 + u_1x + u_0, v_1x + v_0 \right\rangle$, we compute the values $t_1$ and $t_2$ over $\mathbb{F}_p$ (the integers modulo $p$) as follows:
173 |
174 | $$ t_1 = \frac{u_1}{2} $$
175 |
176 | $$ t_2 = \sqrt{\frac{t_1^2 - u_0}{m}} $$
177 |
178 | And finally, we compute the value $D_E = t_1 + p(t_2 - 1)$.
179 |
180 | ## Feistel Cipher
181 |
182 | `Note: the following information applies to MS Plus! DME, Office XP, and Windows. Office 03 and 07 use a much more complex encoding scheme that has not been fully reverse engineered as of writing.`
183 |
184 | The last step is to decrypt the data in $D_E$ using a key derived from the installation ID.
185 |
186 | The installation ID is first validated and has its checksum digits removed to form an integer, just like with the confirmation ID. Then, it is converted to a little endian byte representation and decrypted using a 4-byte key.
187 |
188 | The decryption algorithm uses a variant of a Feistel cipher. Its pseudocode is provided below:
189 |
190 | ```
191 | function decrypt_feistel(data, key):
192 | size_half := data.length / 2
193 | size_half_dwords := size_half - (size_half % 4) // Round size_half down to multiple of 4
194 | last_byte := data[2 * size_half:] // For odd lengths of data, this contains the last byte, otherwise empty
195 | data = data.slice[:2 * size_half]
196 |
197 | repeat 4 times:
198 | first_half := data[:size_half]
199 | second_half := data[size_half:]
200 | hash := SHA1(first_half + key)
201 | hash = hash[:size_half_dwords] + hash[4 + size_half_dwords - (size_half % 4):4 + size_half_dwords]
202 | data = (second_half ^ hash) + first
203 |
204 | return data + last_byte
205 | ```
206 |
207 | The decrypted IID data is either 17 or 19 bytes, with the following structure:
208 |
209 | ```c++
210 | struct DecryptedIID {
211 | byte hwid[8];
212 | // The following values correspond to the product code
213 | // rpc-chid-seq-last
214 | uint last : 17;
215 | uint version : 3; // 4 for XP RTM, 5 for XP SP1+
216 | uint seq : 24;
217 | uint chid : 10;
218 | uint rpc : 9;
219 | ushort key_hash; // Only in SP1+, contains 12 bits of product key hash
220 | }
221 | ```
222 |
223 | The IID data is then rearranged into a 16-byte key like so:
224 |
225 | ```
226 | key = hwid + bytes_from_int((chid << 58 | rpc << 41 | seq << 17 | last) & BITMASK(64))
227 | ```
228 |
229 | Finally, the value $D_E$ from the previous section is converted to little endian and decrypted with this key using the Feistel cipher.
230 |
231 | The structure of the decrypted CID data is as follows:
232 |
233 | ```c++
234 | struct DecryptedCID {
235 | byte key_hash[6]; // Genuine CIDs have bytes of the product key hash stored here, but they're usually not checked
236 | bool check_hash; // key_hash is checked only if this byte is true
237 | byte attempt; // When generating CIDs, this byte is incremented for each generation attempt, maximum of 0x80 times
238 | byte zero[6]; // Must be zeroes
239 | };
240 | ```
241 |
242 | # Parameter Extraction
243 |
244 | Other software that is known to use this confirmation ID system includes Microsoft Plus! Digital Media Edition and Microsoft Office XP through 2007. The parameters for these products have already been extracted, but the extraction procedure will be documented here for completeness.
245 |
246 | The parameters for confirmation ID generation are stored in `licdll.dll` (Windows), `MSO.DLL` (Office), or `MPA.DLL` (MS Plus). These DLLs are obfuscated, and therefore will need to be deobfuscated using AntiWPA Generic by the AntiWPA Team.
247 |
248 | 1. Download [AntiWPA Generic 2.3](https://antiwpa.planet-dl.org/Generic%20Antiwpa-2.3-WinXP-2k3.ZiP). Username and password are `planet-dl.org`.
249 | 2. Extract the DLL.
250 | 3. Under the Options menu, uncheck "Apply OOBE Fix" and "Apply WPA Fix".
251 | 4. Check "Remove selfcheck blocks" and "Remove crypt blocks". The menu that comes up after "Remove selfcheck blocks" is not important, any option can be picked.
252 | 5. Ensure that "Save decrypted code to .exe" is checked.
253 | 6. Open the DLL and click "Apply / Browse"
254 | 7. Open the decrypted DLL file in a disassembler, and search for the byte pattern "01 00 01 00" or the integer 0x10001.
255 | 8. Find an instruction fitting the pattern `mov dword ptr [esi/ebp + ??h], 10001h`.
256 | 9. Decompile the surrounding function.
257 |
258 | An example when run on Windows XP SP3's `licdll.dll` with IDA is provided below.
259 |
260 | ```c
261 | int __stdcall sub_6107FAF4(int a1)
262 | {
263 | int v1; // edi
264 | _DWORD *v2; // eax
265 |
266 | v1 = 0;
267 | *(_DWORD *)a1 = 2;
268 | *(_DWORD *)(a1 + 4) = 2;
269 | *(_DWORD *)(a1 + 8) = 4;
270 | if ( !sub_610A064B(a1) )
271 | return 14;
272 | v2 = *(_DWORD **)(a1 + 24);
273 | *(_DWORD *)(a1 + 12) = 65537;
274 | *v2 = 0x6D7F2A79;
275 | *(_DWORD *)(*(_DWORD *)(a1 + 24) + 4) = 0x16A6B03;
276 | **(_DWORD **)(a1 + 28) = 0;
277 | *(_DWORD *)(*(_DWORD *)(a1 + 28) + 4) = 0;
278 | *(_DWORD *)(*(_DWORD *)(a1 + 28) + 8) = 0x36C85381;
279 | *(_DWORD *)(*(_DWORD *)(a1 + 28) + 12) = 0x218401;
280 | *(_DWORD *)(*(_DWORD *)(a1 + 28) + 16) = 0x83892AD0;
281 | *(_DWORD *)(*(_DWORD *)(a1 + 28) + 20) = 0x44197B;
282 | *(_DWORD *)(*(_DWORD *)(a1 + 28) + 24) = 0x322B3B04;
283 | *(_DWORD *)(*(_DWORD *)(a1 + 28) + 28) = 0x1400606;
284 | *(_DWORD *)(*(_DWORD *)(a1 + 28) + 32) = 0x322B3B04;
285 | *(_DWORD *)(*(_DWORD *)(a1 + 28) + 36) = 0x1400606;
286 | *(_DWORD *)(*(_DWORD *)(a1 + 28) + 40) = 1;
287 | *(_DWORD *)(*(_DWORD *)(a1 + 28) + 44) = 0;
288 | return v1;
289 | }
290 | ```
291 |
292 | The variable `a1` is a pointer to a `WPAHyperellipticParams` struct with the following layout:
293 |
294 | ```c
295 | // BigInts are stored as 2 DWORDs in little endian order
296 | struct BigInt {
297 | uint low;
298 | uint high;
299 | };
300 |
301 | struct WPAHyperellipticParams {
302 | uint genus; // Genus of the curve, almost always 2
303 | uint modulus_size; // Size of prime modulus in DWORDs, almost always 2
304 | uint unknown;
305 | uint public_multiplier; // Value multiplied by initial divisor to verify CID
306 | uint modulus[modulus_size]; // Prime modulus of curve
307 | BigInt coefficients[6]; // Coefficients of F(x) in order of lowest to highest degree
308 | };
309 | ```
310 |
311 | Then, download the private key solver from [here](https://github.com/UMSKT/XPCIDSolver). Edit solve.py to include the parameters from the DLL, run `Install.sh`, then run `solve.py`. The solver will then output the private key for the curve, which can then be used to generate confirmation IDs.
312 |
313 | ## Credits
314 |
315 | - diamondggg, for writing and releasing the xp_activate32 source code
316 | - Pierrick Gaudry, for creating NTLJac2, off which our modified Confirmation ID parameter solver is based
317 | - david4599, for providing his modified version of NTLJac2 and assisting in Confirmation ID generation
318 | - CONIGUERO, Neo-Desktop, TheTank20, for assisting in finding parameters for non-Windows products
319 | - Microsoft :heart:
320 |
--------------------------------------------------------------------------------
/PKEY2005.md:
--------------------------------------------------------------------------------
1 | # PKEY2005 Validation
2 |
3 | By WitherOrNot
4 |
5 | > NOTE: PKEY2005 is an area of active research. The documentation contained here is likely to change as more information is discovered.
6 |
7 | ## Background
8 |
9 | This writeup assumes that you have already read the [patent for this signature scheme](https://patentimages.storage.googleapis.com/a3/27/c1/3c0948a078cb28/US7587605.pdf).
10 | The patent itself assumes decent knowledge of elliptic curve cryptography, group theory, and field theory.
11 | If you are looking to implement this system yourself and are unfamiliar with the math, please [contact the UMSKT Team](https://umskt.zulipchat.com),
12 | as there will not be sufficient room in this writeup to explain all of the math involved.
13 |
14 | ## Patent Summary
15 |
16 | The following vocabulary is borrowed from the patent.
17 |
18 | - $M$, the message, or data, to be validated
19 | - $K$, a finite field of prime order
20 | - $p$, the order of $K$
21 | - $K_3$, an extension field of $K$ of degree 3
22 | - $K_6$, an extension field of $K_3$ of degree 2
23 | - $E$, an elliptic curve of the form $y^2 = x^3 + ax + b$
24 | - $m$, the order of $E/K$
25 | - $\vec{\alpha}$, the private key vector
26 | - $H_1(M)$, a hash function which outputs a vector of dimension $n$
27 | - $H_2(M)$, a hash function which outputs a point in $E/K$
28 | - $P$, a generator of the order $m$ torsion subgroup of $E/K_6$
29 | - $S$, the signature point in $E/K$
30 | - $\vec{Q}$, a collection of $n$ points generated by $P$
31 | - $e_m(P, Q)$, a Tate pairing of order $m$ between points $P$ and $Q$
32 |
33 | In short, ignoring all of the server-side authentication mechanisms and parameter generation procedures, message validation boils down to the following as per the patent:
34 |
35 | 1. Given a message $M$, generate the hash vector $\vec{v} = H_1(M)$
36 | 2. Generate the hash point $T = H_2(M)$
37 | 3. Calculate the point $Q = \sum v_iQ_i$
38 | 4. Calculate $c_1=e_m(Q, T)$
39 | 5. Compare this value to $c=e_m(P, S)$
40 | 6. If $c = c_1$, the message is valid, otherwise the message is invalid
41 |
42 | Generation of a signature is the reverse of this process:
43 |
44 | 1. Given a message $M$, generate the hash vector $\vec{v} = H_1(M)$
45 | 2. Generate the hash point $T = H_2(M)$
46 | 3. Generate $\vec{Q}$ with $Q_i = \alpha_i P$
47 | 4. Calculate $\alpha = \sum v_i \alpha_i \pmod{m}$
48 | 5. Calculate $S = \alpha T$
49 | 6. Return the tuple $(M, S)$, and let $\vec{Q}$ be a public parameter
50 |
51 | Note that this signature scheme works due to the bilinearity of the pairing function, as
52 |
53 | $$ Q = \sum v_iQ_i = \sum v_i \alpha_i P = \left(\sum v_i \alpha_i\right) P = \alpha P $$
54 |
55 | $$ e_m(P, S) = e_m(P, \alpha T) = e_m(\alpha P, T) = e_m(Q, T) $$
56 |
57 | ## Practical Validation
58 |
59 | While the patent provides a very comprehensive description of the signature implementation, it fails to completely describe the mechanism used in PKEY2005 specifically.
60 | This section is devoted to describing the specifics of PKEY2005's validation mechanism.
61 |
62 | ### Public Key Binary Format
63 |
64 | The binary serialzed form of a PKEY2005 public key is as follows, given in [ImHex Pattern Language](https://docs.werwolv.net/pattern-language/).
65 |
66 | ```c
67 | u8 size_bignum @ 0x15;
68 |
69 | // Bignums are stored in little endian order
70 | struct bignum {
71 | u8 data[size_bignum];
72 | };
73 |
74 | struct field_data {
75 | u32 magic; // 0x00112233
76 | u16 eq256; // must be 0x0100
77 | padding[2];
78 | u8 must_be_0; // Enables use of unused values, but parser will error if nonzero
79 | u8 size_modulus; // Same as size_bignum
80 | u8 size_order;
81 | u32 ext_deg1; // Degree of first field extension
82 | u32 ext_deg2; // Degree of second field extension
83 | u32 at_0x1f; // unused
84 | u32 at_0x23; // unused
85 | u32 at_0x27; // unused
86 | u32 num_elements; // Number of points Qi and length of H1 vector
87 | u32 at_0x2f; // unused
88 | u32 at_0x33; // unused
89 | u32 at_0x37; // unused
90 | u8 max_quotient; // Can equal floor((24 ^ 25) / p) - 1, unused
91 | u8 h1_coeffs[num_elements]; // H1 radices
92 | bignum modulus; // Prime modulus of base field
93 | u8 order[size_order]; // Order of elliptic curve over base field (also a bignum)
94 | // Polynomials are stored as bytes in order of lowest to highest degree coefficients
95 | u8 ext_split_poly1[ext_deg1 + 1]; // Minimal polynomial of first field extension
96 | u8 ext_split_poly2[ext_deg2 + 1]; // Minimal polynomial of second field extension
97 | // Unused capability: y^2 = x^3 + ec_a_base * x + ec_b_base
98 | // This curve would be over the base field
99 | bignum ec_a_base;
100 | bignum ec_b_base;
101 | // Elliptic curve: y^2 = x^3 + ax + b
102 | bignum ec_a; // a coefficient
103 | bignum ec_b; // b coefficient
104 | };
105 |
106 | struct ecpoint_k3 {
107 | bignum x[3];
108 | bignum y[3];
109 | };
110 |
111 | struct Pubkey {
112 | u32 magic; // 0x44556677
113 | u16 eq256; // must be 0x0100
114 | padding[2];
115 | u32 field_data_size;
116 | field_data field;
117 | padding[field_data_size + 12 - $];
118 | ecpoint_k3 points[field.num_elements]; // Points Qi over twisted curve
119 | bignum pairing_val[field.ext_deg1 * field.ext_deg2]; // value of Tate pairing between generator P and signature base point S
120 | };
121 |
122 | Pubkey pubkey @ 0;
123 | ```
124 |
125 | In total, the public key describes the following:
126 |
127 | - The parameters of $E$: $a$, $b$, and $m$
128 | - The modulus of $K$: $p$
129 | - $F_1$, the splitting polynomial of $K_3$ over $K$
130 | - $F_2$, the splitting polynomial of $K_6$ over $K_3$
131 | - $\vec{r}$, a collection of radices used in the implementation of $H_1$
132 | - $\vec{Q}'$, a collection of points over $E/K_3$
133 | - $c$, the value of $e_m(P, S)$
134 |
135 | From this, it can already be seen that the implementation of PKEY2005's signature scheme is different from the patent.
136 |
137 | ### PKEY2005 Verification
138 |
139 | The first major departure from the patent is that $M$, the message, is never actually directly provided in practice.
140 | $M$ normally contains some digits of the product ID associated with a product key, as well as presumed authentication and upgrade bits, but the value of $M$ is never exposed to the user.
141 | This is because **all product keys are hashes of $M$**.
142 | The hash function used to derive product keys is unknown as of yet, and will be referred to as $HASH(M)$.
143 | $HASH(M)$ is decoded from the product key through conversion from base-24, with the base alphabet being `BCDFGHJKMPQRTVWXY2346789`.
144 | The value of $HASH(M)$ is given a basic check against $\vec{r}$ by checking that $\left \lfloor {\frac{HASH(M)}{p}} \right \rfloor \leq (r_2 + 1)(r_3 + 1)$.
145 |
146 | Another important note is the binary serialization of elements of extension fields.
147 | Given an extension field $K \supseteq L$, with $u$ being the primitive element of the extension, all elements $w \in K$ can be expressed as
148 |
149 | $$ w = z_0 + z_1 u + z_2 u^2 + \ldots + z_{n-1} u^{n-1} $$
150 |
151 | where $n$ is the degree of the extension and $z_i \in L$.
152 | This encoding method is used to represent elements of an extension field as arrays of elements in the base field, and is used to encode the coordinates of elliptic curve points as well.
153 |
154 | The patent also describes that points in $E/K_6$ can be represented as points in $E/K_3$ to reduce storage space.
155 | This compression method is used on the points in $\vec{Q}'$, and must be undone before pairing computation to retrieve $\vec{Q}$.
156 |
157 | The method to undo this compression is implemented as follows:
158 |
159 | 1. Let $t$ be the primitive element of the extension from $K_3$ to $K_6$.
160 | 2. Let $d = t^2$
161 | 3. Define $E' = x^3 + d^2 ax + d^3 b$
162 | 4. Define the untwist mapping $\tau : E' \rightarrow E = (x,y) \rightarrow (t^{-2}x, t^{-3}y)$
163 | 5. Given a point $R' \in E/K_3$, recover $R = \tau(R')$
164 |
165 | Since the quadratic twist on $E$ is preserved through point addition, the untwist mapping can alternatively be done on the final point $Q$ to save time.
166 |
167 | Next, the value of $H_1(M)$ is found through a meet-in-the-middle tree search. This is necessary since the value of $M$ is unavailable.
168 | Some of the elements of $H_1(M)$ are known in advance, as for $\vec{v} = H_1(M)$ and $k = \left \lfloor {\frac{HASH(M)}{p}} \right \rfloor$, $v_1 = 1$, $v_2 = k \bmod (r_2 + 1)$, and $v_3 = \left \lfloor {\frac{k}{r_2 + 1}} \right \rfloor$.
169 |
170 | The point $T = H_2(M)$ is found from $h = HASH(M)$ as $H_2(M) = lift_x\left(h \bmod p\right)$, where the function $lift_x(x)$ finds a point on $E/K$ with the x-coordinate $x$.
171 | Note that two points meet this definition, differing by the sign of their y-coordinate, the correct point is chosen by an unknown hash algorithm.
172 |
173 | Afterwards, the value of M is recovered through the following algorithm, with $\vec{v} = H_1(M)$ and $\vec{r}$ from the public key:
174 |
175 | ```py
176 | M = 0
177 | # Indexing backwards from n ... 1, ignoring the first element
178 | for i in range(len(r) - 1, 0, -1):
179 | M *= r[i]
180 | M += v[i]
181 | ```
182 |
183 | The final value of M can then be interpreted with the following bitfields:
184 |
185 | ```c
186 | struct DECODED_PKEY {
187 | uint auth : 10; // presumed to be authentication bits
188 | uint pid : 30; // middle 9 digits of Product ID
189 | bool upgrade : 1; // presumed to indicate upgrade keys
190 | }
191 | ```
192 |
193 | Finally, the reference pairing value of $c = e_m(P, S)$ is stored in the public key rather than the points $P$ and $S$, most likely to reduce storage space and computation costs.
194 |
195 | ## Practical Generation
196 |
197 | Although much of the information involved in generating a signature is not provided in public keys,
198 | it turns out that all of the information necessary to generate signatures is theoretically recoverable.
199 |
200 | The main property of PKEY2005 public keys that makes key generation theoretically possible is that the pairing value $c$ is constant.
201 | Since $P$ is a constant, and the value of $c$ depends on both $P$ and $S$, $S$ must also be effectively constant.
202 |
203 | This allows generation of product keys without needing to know the implementation of $H_2$, assuming that $\vec{\alpha}$ is known and one valid, decoded product key is available per public key.
204 |
205 | Letting $M$ be the message of the known product key and $h = HASH(M)$, $S$ can be recovered like so:
206 |
207 | $$ T = lift_x(h \bmod p) $$
208 |
209 | $$ \vec{v} = H_1(M) $$
210 |
211 | $$ \alpha = \sum v_i \alpha_i \pmod{m} $$
212 |
213 | $$ S = \alpha T $$
214 |
215 | And now with the value of $S$ known, the points $T$ can be generated without using $H_2$.
216 | This allows key generation via the following algorithm, for a given message $M$:
217 |
218 | $$ \vec{v} = H_1(M) $$
219 |
220 | $$ \alpha = \sum v_i \alpha_i \pmod{m} $$
221 |
222 | $$ \beta = \alpha^{-1} \pmod{m} $$
223 |
224 | $$ T = \beta S $$
225 |
226 | And now, the value of $HASH(M)$ can be recovered from $\vec{v}$ and the x-coordinate of $T$, then encoded into a product key.
227 |
228 | ## Current Plans
229 |
230 | As shown above, the only thing hindering product-key generation is finding the private key vector $\vec{\alpha}$, which requires the use of an ECDLP solver.
231 | We are currently in the process of creating such a solver, since readily available solvers do not support the finite field arithmetic required for our case.
232 | The group sizes at play are 112-bit, which are [within the realm of possibility](https://www.joppebos.com/presentations/112bitECDLP.pdf), especially given the [capabilities of modern GPUs](https://en.wikipedia.org/wiki/Discrete_logarithm_records#Elliptic_curves). We plan to recruit volunteers for this purpose and will
233 | be releasing a distributed solver client to let anyone participate, so stay tuned!
234 |
235 | ## Credits/Thanks
236 |
237 | - diamondggg, for providing the steps of the algorithm we hadn't reverse-engineered
238 | - CONIGUERO, Neo-Desktop, Endermanch, and TheTank20, for assisting in the reverse-engineering process
239 | - Microsoft, for making cool software worth researching :heart:
240 |
--------------------------------------------------------------------------------
/README.md:
--------------------------------------------------------------------------------
1 | # UMSKT Writeup Repository
2 |
3 | Greetings all. This repository is where you will find our documentation on the inner workings activation mechanisms.
4 |
5 | Currently, we have written documentation on the following topics:
6 |
7 | - [BINK1998 (Windows 98-XP) and BINK2002 (Server 2003/XP x64/Longhorn Pre-Reset) Product Key Validation](./BINK.md)
8 | - [Windows XP Confirmation IDs](./ConfID.md)
9 | - [PKEY2005 (Windows Vista/7) Product Key Validation](./PKEY2005.md)
10 |
11 | We do assume the reader has certain background knowledge in mathematics and programming when creating these writeups, but much of this background info is readily available on the internet.
12 |
13 | Some suggested reading for those looking to use, understand, or contribute to our documentation:
14 |
15 | - [Wikipedia - Finite field](https://en.wikipedia.org/wiki/Finite_field)
16 | - [Wikipedia - Finite field arithmetic](https://en.wikipedia.org/wiki/Finite_field_arithmetic)
17 | - [David Forney - Introduction to finite fields](http://web.stanford.edu/~marykw/classes/CS250_W18/readings/Forney_Introduction_to_Finite_Fields.pdf)
18 | - [Nick Sullivan - A (Relatively Easy To Understand) Primer on Elliptic Curve Cryptography](https://blog.cloudflare.com/a-relatively-easy-to-understand-primer-on-elliptic-curve-cryptography/)
19 | - [Wikipedia - Elliptic curve](https://en.wikipedia.org/wiki/Elliptic_curve)
20 | - [Wikipedia - Elliptic-curve cryptography](https://en.wikipedia.org/wiki/Elliptic-curve_cryptography)
21 | - [Wikipedia - Imaginary hyperelliptic curve](https://en.wikipedia.org/wiki/Imaginary_hyperelliptic_curve)
22 | - [Wikipedia - Hyperelliptic curve cryptography](https://en.wikipedia.org/wiki/Hyperelliptic_curve_cryptography)
23 | - [Craig Costello - Pairings for Beginners](https://static1.squarespace.com/static/5fdbb09f31d71c1227082339/t/5ff394720493bd28278889c6/1609798774687/PairingsForBeginners.pdf)
24 |
25 | We take care to ensure that our documentation is accurate, but if you discover any errors or insufficient explanations, please contact [the UMSKT Team](https://umskt.zulipchat.com/).
26 |
--------------------------------------------------------------------------------
/images/ECClines.svg.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/UMSKT/writeups/356e14a8daa3f59bc3ea3826ce4b23fa307e6e61/images/ECClines.svg.png
--------------------------------------------------------------------------------
/images/Example_of_a_hyperelliptic_curve.svg.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/UMSKT/writeups/356e14a8daa3f59bc3ea3826ce4b23fa307e6e61/images/Example_of_a_hyperelliptic_curve.svg.png
--------------------------------------------------------------------------------
/images/cid_screenshot.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/UMSKT/writeups/356e14a8daa3f59bc3ea3826ce4b23fa307e6e61/images/cid_screenshot.png
--------------------------------------------------------------------------------