├── .github
└── ISSUE_TEMPLATE
│ ├── bug_report.md
│ ├── feature_request.md
│ └── suggestions.md
├── .gitignore
├── CODE_OF_CONDUCT.md
├── CONTRIBUTING.md
├── LICENSE
├── README.md
├── algorithm
├── analysis.md
├── backtrace.md
├── bfs.md
├── bi-divide.md
├── big-num.md
├── dfs.md
├── dynamic programming.md
├── greedy.md
├── recursion-2.md
├── recursion.md
├── sort.md
└── string.md
├── code
├── 1.java
├── 10.java
├── 11.java
├── 12.java
├── 13.java
├── 14.java
├── 15.java
├── 16.java
├── 17.java
├── 18.java
├── 19.java
├── 2.java
├── 20.java
├── 21.java
├── 22.java
├── 23.java
├── 24.java
├── 25.java
├── 26.java
├── 27.java
├── 28.java
├── 29.java
├── 3.java
├── 30.java
├── 31.java
├── 32.java
├── 33.java
├── 34.java
├── 35.java
├── 36.java
├── 37.java
├── 38.java
├── 39.java
├── 4.java
├── 40.java
├── 41.java
├── 42.java
├── 43.java
├── 44.java
├── 45.java
├── 46.java
├── 47.java
├── 48.java
├── 49.java
├── 5.java
├── 50.java
├── 51.java
├── 52.java
├── 53.java
├── 54.java
├── 55.java
├── 56.java
├── 57.java
├── 58.java
├── 59.java
├── 6.java
├── 60.java
├── 61.java
├── 62.java
├── 63.java
├── 64.java
├── 65.java
├── 66.java
├── 67.java
├── 68.java
├── 69.java
├── 7.java
├── 70.java
├── 71.java
├── 72.java
├── 73.java
├── 74.java
├── 75.java
├── 8.java
└── 9.java
└── data-structure
├── DisjointSets.md
├── graph.md
├── heap.md
├── key-path.md
├── kruskal.md
├── line-tree.md
├── queue.md
├── stack.md
├── tree-array.md
└── tree.md
/.github/ISSUE_TEMPLATE/bug_report.md:
--------------------------------------------------------------------------------
1 | ---
2 | name: Bug report
3 | about: Create a report to help us improve
4 | title: ''
5 | labels: bug
6 | assignees: ''
7 |
8 | ---
9 |
10 | **Describe the bug**
11 | A clear and concise description of what the bug is.
12 |
13 | **To Reproduce**
14 | Steps to reproduce the behavior:
15 | 1. Go to '...'
16 | 2. Click on '....'
17 | 3. Scroll down to '....'
18 | 4. See error
19 |
20 | **Expected behavior**
21 | A clear and concise description of what you expected to happen.
22 |
23 | **Screenshots**
24 | If applicable, add screenshots to help explain your problem.
25 |
26 | **Desktop (please complete the following information):**
27 | - OS: [e.g. iOS]
28 | - Browser [e.g. chrome, safari]
29 | - Version [e.g. 22]
30 |
31 | **Smartphone (please complete the following information):**
32 | - Device: [e.g. iPhone6]
33 | - OS: [e.g. iOS8.1]
34 | - Browser [e.g. stock browser, safari]
35 | - Version [e.g. 22]
36 |
37 | **Additional context**
38 | Add any other context about the problem here.
39 |
--------------------------------------------------------------------------------
/.github/ISSUE_TEMPLATE/feature_request.md:
--------------------------------------------------------------------------------
1 | ---
2 | name: Feature request
3 | about: Suggest an idea for this project
4 | title: ''
5 | labels: enhancement
6 | assignees: ''
7 |
8 | ---
9 |
10 | **Is your feature request related to a problem? Please describe.**
11 | A clear and concise description of what the problem is. Ex. I'm always frustrated when [...]
12 |
13 | **Describe the solution you'd like**
14 | A clear and concise description of what you want to happen.
15 |
16 | **Describe alternatives you've considered**
17 | A clear and concise description of any alternative solutions or features you've considered.
18 |
19 | **Additional context**
20 | Add any other context or screenshots about the feature request here.
21 |
--------------------------------------------------------------------------------
/.github/ISSUE_TEMPLATE/suggestions.md:
--------------------------------------------------------------------------------
1 | ---
2 | name: Suggestions
3 | about: Give your ideas and suggestions.
4 | title: ''
5 | labels: question
6 | assignees: ''
7 |
8 | ---
9 |
10 |
11 |
--------------------------------------------------------------------------------
/.gitignore:
--------------------------------------------------------------------------------
1 | .DS_Store
2 |
3 |
--------------------------------------------------------------------------------
/CODE_OF_CONDUCT.md:
--------------------------------------------------------------------------------
1 | # Contributor Covenant Code of Conduct
2 |
3 | ## Our Pledge
4 |
5 | In the interest of fostering an open and welcoming environment, we as
6 | contributors and maintainers pledge to making participation in our project and
7 | our community a harassment-free experience for everyone, regardless of age, body
8 | size, disability, ethnicity, sex characteristics, gender identity and expression,
9 | level of experience, education, socio-economic status, nationality, personal
10 | appearance, race, religion, or sexual identity and orientation.
11 |
12 | ## Our Standards
13 |
14 | Examples of behavior that contributes to creating a positive environment
15 | include:
16 |
17 | * Using welcoming and inclusive language
18 | * Being respectful of differing viewpoints and experiences
19 | * Gracefully accepting constructive criticism
20 | * Focusing on what is best for the community
21 | * Showing empathy towards other community members
22 |
23 | Examples of unacceptable behavior by participants include:
24 |
25 | * The use of sexualized language or imagery and unwelcome sexual attention or
26 | advances
27 | * Trolling, insulting/derogatory comments, and personal or political attacks
28 | * Public or private harassment
29 | * Publishing others' private information, such as a physical or electronic
30 | address, without explicit permission
31 | * Other conduct which could reasonably be considered inappropriate in a
32 | professional setting
33 |
34 | ## Our Responsibilities
35 |
36 | Project maintainers are responsible for clarifying the standards of acceptable
37 | behavior and are expected to take appropriate and fair corrective action in
38 | response to any instances of unacceptable behavior.
39 |
40 | Project maintainers have the right and responsibility to remove, edit, or
41 | reject comments, commits, code, wiki edits, issues, and other contributions
42 | that are not aligned to this Code of Conduct, or to ban temporarily or
43 | permanently any contributor for other behaviors that they deem inappropriate,
44 | threatening, offensive, or harmful.
45 |
46 | ## Scope
47 |
48 | This Code of Conduct applies both within project spaces and in public spaces
49 | when an individual is representing the project or its community. Examples of
50 | representing a project or community include using an official project e-mail
51 | address, posting via an official social media account, or acting as an appointed
52 | representative at an online or offline event. Representation of a project may be
53 | further defined and clarified by project maintainers.
54 |
55 | ## Enforcement
56 |
57 | Instances of abusive, harassing, or otherwise unacceptable behavior may be
58 | reported by contacting the project team at mixdeers@gmail.com. All
59 | complaints will be reviewed and investigated and will result in a response that
60 | is deemed necessary and appropriate to the circumstances. The project team is
61 | obligated to maintain confidentiality with regard to the reporter of an incident.
62 | Further details of specific enforcement policies may be posted separately.
63 |
64 | Project maintainers who do not follow or enforce the Code of Conduct in good
65 | faith may face temporary or permanent repercussions as determined by other
66 | members of the project's leadership.
67 |
68 | ## Attribution
69 |
70 | This Code of Conduct is adapted from the [Contributor Covenant][homepage], version 1.4,
71 | available at https://www.contributor-covenant.org/version/1/4/code-of-conduct.html
72 |
73 | [homepage]: https://www.contributor-covenant.org
74 |
75 | For answers to common questions about this code of conduct, see
76 | https://www.contributor-covenant.org/faq
77 |
--------------------------------------------------------------------------------
/CONTRIBUTING.md:
--------------------------------------------------------------------------------
1 | If you want to make this repo better,welcome to give your Issues and PRs.
2 |
--------------------------------------------------------------------------------
/LICENSE:
--------------------------------------------------------------------------------
1 | Apache License
2 | Version 2.0, January 2004
3 | http://www.apache.org/licenses/
4 |
5 | TERMS AND CONDITIONS FOR USE, REPRODUCTION, AND DISTRIBUTION
6 |
7 | 1. Definitions.
8 |
9 | "License" shall mean the terms and conditions for use, reproduction,
10 | and distribution as defined by Sections 1 through 9 of this document.
11 |
12 | "Licensor" shall mean the copyright owner or entity authorized by
13 | the copyright owner that is granting the License.
14 |
15 | "Legal Entity" shall mean the union of the acting entity and all
16 | other entities that control, are controlled by, or are under common
17 | control with that entity. For the purposes of this definition,
18 | "control" means (i) the power, direct or indirect, to cause the
19 | direction or management of such entity, whether by contract or
20 | otherwise, or (ii) ownership of fifty percent (50%) or more of the
21 | outstanding shares, or (iii) beneficial ownership of such entity.
22 |
23 | "You" (or "Your") shall mean an individual or Legal Entity
24 | exercising permissions granted by this License.
25 |
26 | "Source" form shall mean the preferred form for making modifications,
27 | including but not limited to software source code, documentation
28 | source, and configuration files.
29 |
30 | "Object" form shall mean any form resulting from mechanical
31 | transformation or translation of a Source form, including but
32 | not limited to compiled object code, generated documentation,
33 | and conversions to other media types.
34 |
35 | "Work" shall mean the work of authorship, whether in Source or
36 | Object form, made available under the License, as indicated by a
37 | copyright notice that is included in or attached to the work
38 | (an example is provided in the Appendix below).
39 |
40 | "Derivative Works" shall mean any work, whether in Source or Object
41 | form, that is based on (or derived from) the Work and for which the
42 | editorial revisions, annotations, elaborations, or other modifications
43 | represent, as a whole, an original work of authorship. For the purposes
44 | of this License, Derivative Works shall not include works that remain
45 | separable from, or merely link (or bind by name) to the interfaces of,
46 | the Work and Derivative Works thereof.
47 |
48 | "Contribution" shall mean any work of authorship, including
49 | the original version of the Work and any modifications or additions
50 | to that Work or Derivative Works thereof, that is intentionally
51 | submitted to Licensor for inclusion in the Work by the copyright owner
52 | or by an individual or Legal Entity authorized to submit on behalf of
53 | the copyright owner. For the purposes of this definition, "submitted"
54 | means any form of electronic, verbal, or written communication sent
55 | to the Licensor or its representatives, including but not limited to
56 | communication on electronic mailing lists, source code control systems,
57 | and issue tracking systems that are managed by, or on behalf of, the
58 | Licensor for the purpose of discussing and improving the Work, but
59 | excluding communication that is conspicuously marked or otherwise
60 | designated in writing by the copyright owner as "Not a Contribution."
61 |
62 | "Contributor" shall mean Licensor and any individual or Legal Entity
63 | on behalf of whom a Contribution has been received by Licensor and
64 | subsequently incorporated within the Work.
65 |
66 | 2. Grant of Copyright License. Subject to the terms and conditions of
67 | this License, each Contributor hereby grants to You a perpetual,
68 | worldwide, non-exclusive, no-charge, royalty-free, irrevocable
69 | copyright license to reproduce, prepare Derivative Works of,
70 | publicly display, publicly perform, sublicense, and distribute the
71 | Work and such Derivative Works in Source or Object form.
72 |
73 | 3. Grant of Patent License. Subject to the terms and conditions of
74 | this License, each Contributor hereby grants to You a perpetual,
75 | worldwide, non-exclusive, no-charge, royalty-free, irrevocable
76 | (except as stated in this section) patent license to make, have made,
77 | use, offer to sell, sell, import, and otherwise transfer the Work,
78 | where such license applies only to those patent claims licensable
79 | by such Contributor that are necessarily infringed by their
80 | Contribution(s) alone or by combination of their Contribution(s)
81 | with the Work to which such Contribution(s) was submitted. If You
82 | institute patent litigation against any entity (including a
83 | cross-claim or counterclaim in a lawsuit) alleging that the Work
84 | or a Contribution incorporated within the Work constitutes direct
85 | or contributory patent infringement, then any patent licenses
86 | granted to You under this License for that Work shall terminate
87 | as of the date such litigation is filed.
88 |
89 | 4. Redistribution. You may reproduce and distribute copies of the
90 | Work or Derivative Works thereof in any medium, with or without
91 | modifications, and in Source or Object form, provided that You
92 | meet the following conditions:
93 |
94 | (a) You must give any other recipients of the Work or
95 | Derivative Works a copy of this License; and
96 |
97 | (b) You must cause any modified files to carry prominent notices
98 | stating that You changed the files; and
99 |
100 | (c) You must retain, in the Source form of any Derivative Works
101 | that You distribute, all copyright, patent, trademark, and
102 | attribution notices from the Source form of the Work,
103 | excluding those notices that do not pertain to any part of
104 | the Derivative Works; and
105 |
106 | (d) If the Work includes a "NOTICE" text file as part of its
107 | distribution, then any Derivative Works that You distribute must
108 | include a readable copy of the attribution notices contained
109 | within such NOTICE file, excluding those notices that do not
110 | pertain to any part of the Derivative Works, in at least one
111 | of the following places: within a NOTICE text file distributed
112 | as part of the Derivative Works; within the Source form or
113 | documentation, if provided along with the Derivative Works; or,
114 | within a display generated by the Derivative Works, if and
115 | wherever such third-party notices normally appear. The contents
116 | of the NOTICE file are for informational purposes only and
117 | do not modify the License. You may add Your own attribution
118 | notices within Derivative Works that You distribute, alongside
119 | or as an addendum to the NOTICE text from the Work, provided
120 | that such additional attribution notices cannot be construed
121 | as modifying the License.
122 |
123 | You may add Your own copyright statement to Your modifications and
124 | may provide additional or different license terms and conditions
125 | for use, reproduction, or distribution of Your modifications, or
126 | for any such Derivative Works as a whole, provided Your use,
127 | reproduction, and distribution of the Work otherwise complies with
128 | the conditions stated in this License.
129 |
130 | 5. Submission of Contributions. Unless You explicitly state otherwise,
131 | any Contribution intentionally submitted for inclusion in the Work
132 | by You to the Licensor shall be under the terms and conditions of
133 | this License, without any additional terms or conditions.
134 | Notwithstanding the above, nothing herein shall supersede or modify
135 | the terms of any separate license agreement you may have executed
136 | with Licensor regarding such Contributions.
137 |
138 | 6. Trademarks. This License does not grant permission to use the trade
139 | names, trademarks, service marks, or product names of the Licensor,
140 | except as required for reasonable and customary use in describing the
141 | origin of the Work and reproducing the content of the NOTICE file.
142 |
143 | 7. Disclaimer of Warranty. Unless required by applicable law or
144 | agreed to in writing, Licensor provides the Work (and each
145 | Contributor provides its Contributions) on an "AS IS" BASIS,
146 | WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or
147 | implied, including, without limitation, any warranties or conditions
148 | of TITLE, NON-INFRINGEMENT, MERCHANTABILITY, or FITNESS FOR A
149 | PARTICULAR PURPOSE. You are solely responsible for determining the
150 | appropriateness of using or redistributing the Work and assume any
151 | risks associated with Your exercise of permissions under this License.
152 |
153 | 8. Limitation of Liability. In no event and under no legal theory,
154 | whether in tort (including negligence), contract, or otherwise,
155 | unless required by applicable law (such as deliberate and grossly
156 | negligent acts) or agreed to in writing, shall any Contributor be
157 | liable to You for damages, including any direct, indirect, special,
158 | incidental, or consequential damages of any character arising as a
159 | result of this License or out of the use or inability to use the
160 | Work (including but not limited to damages for loss of goodwill,
161 | work stoppage, computer failure or malfunction, or any and all
162 | other commercial damages or losses), even if such Contributor
163 | has been advised of the possibility of such damages.
164 |
165 | 9. Accepting Warranty or Additional Liability. While redistributing
166 | the Work or Derivative Works thereof, You may choose to offer,
167 | and charge a fee for, acceptance of support, warranty, indemnity,
168 | or other liability obligations and/or rights consistent with this
169 | License. However, in accepting such obligations, You may act only
170 | on Your own behalf and on Your sole responsibility, not on behalf
171 | of any other Contributor, and only if You agree to indemnify,
172 | defend, and hold each Contributor harmless for any liability
173 | incurred by, or claims asserted against, such Contributor by reason
174 | of your accepting any such warranty or additional liability.
175 |
176 | END OF TERMS AND CONDITIONS
177 |
178 | APPENDIX: How to apply the Apache License to your work.
179 |
180 | To apply the Apache License to your work, attach the following
181 | boilerplate notice, with the fields enclosed by brackets "[]"
182 | replaced with your own identifying information. (Don't include
183 | the brackets!) The text should be enclosed in the appropriate
184 | comment syntax for the file format. We also recommend that a
185 | file or class name and description of purpose be included on the
186 | same "printed page" as the copyright notice for easier
187 | identification within third-party archives.
188 |
189 | Copyright [yyyy] [name of copyright owner]
190 |
191 | Licensed under the Apache License, Version 2.0 (the "License");
192 | you may not use this file except in compliance with the License.
193 | You may obtain a copy of the License at
194 |
195 | http://www.apache.org/licenses/LICENSE-2.0
196 |
197 | Unless required by applicable law or agreed to in writing, software
198 | distributed under the License is distributed on an "AS IS" BASIS,
199 | WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
200 | See the License for the specific language governing permissions and
201 | limitations under the License.
202 |
--------------------------------------------------------------------------------
/README.md:
--------------------------------------------------------------------------------
1 |
2 |
3 | Algorithm Guide
4 |
5 |
6 |
7 | 本仓库带你系统掌握程序员必知必会的**算法**和**数据结构**
8 |
9 | 本仓库主要有**两个分支**:
10 |
11 | + **master分支**:最近的新分支,也是以后日常维护的主分支,内容为算法和数据结构的教程。
12 |
13 | + **Collections 分支**:以前的主分支,整理了算法和数据结构的资料,现作为辅助分支:[这里访问](https://github.com/Xunzhuo/Algorithms-in-4-Steps/tree/Collections)
14 |
15 | > **算法部分**基本完成,**数据结构**还有很多未完成部分,空闲时会加快完善
16 |
17 | ## 目录:
18 |
19 | 1. [算法篇](#算法篇)
20 | 2. [数据结构篇](#数据结构篇)
21 | 3. [刷题练习篇](#刷题练习篇)
22 |
23 | ## 算法篇
24 |
25 | + [一、复杂度分析](algorithm/analysis.md)
26 | + [二、高精度算法](algorithm/big-num.md)
27 | + [三、排序算法](algorithm/sort.md)
28 | + [四、递推算法](algorithm/recursion.md)
29 | + [五 、递归算法](algorithm/recursion-2.md)
30 | + [六、分治算法](algorithm/bi-divide.md)
31 | + [七、贪心算法](algorithm/greedy.md)
32 | + [八、广度优先搜索算法](algorithm/bfs.md)
33 | + [九、深度优先搜索算法](algorithm/dfs.md)
34 | + [十、回溯算法](algorithm/backtrace.md)
35 | + [十一、动态规划](algorithm/dynamic%20programming.md)
36 | + [十二、字符串算法](algorithm/string.md)
37 |
38 | ## 数据结构篇
39 |
40 | + [一、栈](data-structure/stack.md)
41 | + [二、队列](data-structure/queue.md)
42 | + [三、树](data-structure/tree.md)
43 | + [四、堆](data-structure/heap.md)
44 | + [五、图论算法 ](data-structure/graph.md)
45 | + [六、并查集](data-structure/DisjointSets.md)
46 | + [七、最小生成树](data-structure/kruskal.md)
47 | + [八、拓扑排序与关键路径](data-structure/key-path.md)
48 | + [九、线段树](data-structure/line-tree.md)
49 | + [十、树状数组](data-structure/tree-array.md)
50 |
51 | ## 刷题练习篇
52 |
53 | 在掌握了重要的算法和数据结构之后,需要练习巩固
54 |
55 | #### **网站的选择?**
56 |
57 | 推荐 **LeetCode**,[这里访问](https://leetcode-cn.com/)
58 |
59 | #### **刷哪些题目?**
60 |
61 | 1. 如果你**时间紧张**:可以练习**LeetCode**的**热门推荐**:
62 |
63 | 
64 |
65 | 比如:[Leetcode 热题 Hot 100](https://leetcode-cn.com/problemset/leetcode-hot-100/) 和 [LeetCode 精选 TOP 面试题](https://leetcode-cn.com/problemset/leetcode-top/)
66 |
67 | 2. 如果你**时间充裕**:可以按以下分类,系统练习:
68 |
69 | + **专题一:数组(`Chapter1_Array`)**
70 | + **专题二:链表(`Chapter2_list`)**
71 | + **专题三:字符串(`Chapter3_String`)**
72 | + **专题四:栈(`Chapter4_Stack`)**
73 | + **专题五:树(`Chapter5_Tree`)**
74 | + **专题六:排序(`Chapter6_Sort`)**
75 | + **专题七:查找(`Chapter7_Search`)**
76 | + **专题八:暴力解法(`Chapter8_Violence`)**
77 | + **专题九:BFS(`Chapter9_BFS`)**
78 | + **专题十:DFS(`Chapter10_DFS`)**
79 | + **专题十一:分治(`Chapter11_Paritition`)**
80 | + **专题十二:贪心(`Chapter12_Greedy`)**
81 | + **专题十三:动态规划(`Chapter13_DP`)**
82 | + **专题十四:图(`Chapter14_Graph`)**
83 | + **专题十五:不定类型(`Chapter15_Unspecific`)**
84 |
85 | #### 练习策略
86 |
87 | + **第一遍**:**先思考**,如果没思路,可以看题解,结合其他人的题解刷。总结自己是否在思路上有问题,或者是否算法与数据结构基础上有问题,掌握本题的类型,思考方式,最优题解。
88 | + **第二遍**:**回忆最优解法**,**尝试直接写**,并与之前自己写过的解答作比对,总结问题和方法。
89 | + **第三遍**:提升**刷题速度**和**一题多解**,拿出一个题,就能够知道其考察重点,解题方法,在短时间内写出解答,并且思考多种解决办法。
90 |
91 |
--------------------------------------------------------------------------------
/algorithm/analysis.md:
--------------------------------------------------------------------------------
1 | # 复杂度理论
2 |
3 | ## **算法时间复杂度的数学意义**
4 |
5 | 从数学上定义,给定算法A,如果存在函数f(n),当n=k时,f(k)表示算法A在输入规模为k的情况下的运行时间,则称f(n)为算法A的时间复杂度。
6 |
7 | 其中:输入规模是指算法A所接受输入的自然独立体的大小,我们总是假设算法的输入规模是用大于零的整数表示的,即n=1,2,3,……,k,……
8 |
9 | 对于同一个算法,每次执行的时间不仅取决于输入规模,还取决于输入的特性和具体的硬件环境在某次执行时的状态。所以想要得到一个统一精确的F(n)是不可能的。为此,通常做法:
10 | 1. 忽略硬件及环境因素,假设每次执行时硬件条件和环境条件是完全一致的。
11 | 2. 对于输入特性的差异,我们将从数学上进行精确分析并带入函数解析式。
12 |
13 | **例子:**
14 |
15 | ``` c
16 | x=1;
17 | for(i=1;i<=n;i++)
18 | for(j=1;j<=i;j++)
19 | for(k=1;k<=j;k++)
20 | x++;
21 | ```
22 |
23 | 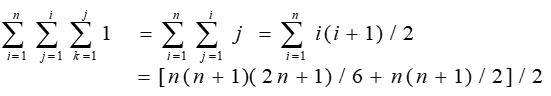
24 |
25 | ## 算法的渐近时间复杂度
26 | 很多时候,我们不需要进行如此精确的分析,究其原因:
27 | 1.在较复杂的算法中,进行精确分析是非常复杂的。
28 | 2.实际上,大多数时候我们并不关心F(n)的精确度量,而只是关心其量级。
29 |
30 | ## **算法复杂度的考察方法**
31 |
32 | (1)考察一个算法的复杂度,一般考察的是当问题复杂度n的增加时,运算所需时间、空间代价f(n)的上下界。
33 |
34 | (2)进一步而言,又分为最好情况、平均情况、最坏情况三种情况。通常最坏情况往往是我们最关注的。
35 |
36 | ### 上界函数
37 |
38 | 定义1 如果存在两个正常数c和n0,对于所有的n≥n0,有
39 |
40 | |T(n)| ≤ c|f(n)|
41 |
42 | 则记作T(n) = Ο(f(n))
43 |
44 | 含义:
45 |
46 | + 如果算法用n值不变的同一类数据在某台机器上运行时,所用的时间总是小于|f(n)|的一个常数倍。所以f(n)是计算时间T(n)的一个上界函数。
47 |
48 | + 试图求出最小的f(n),使得T(n) = Ο(f(n))。
49 |
50 | 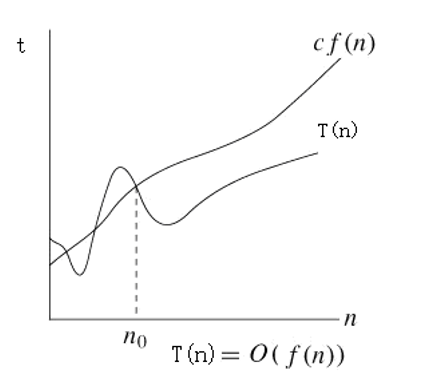
51 |
52 | 在分析算法的时间复杂度时,我们更关心最坏情况而不是最好情况,理由如下:
53 |
54 | 1. 最坏情况给出了算法执行时间的上界,我们可以确信,无论给什么输入,算法的执行时间都不会超过这个上界,这样为比较和分析提供了便利。
55 |
56 | 2. 虽然最坏情况是一种悲观估计,但是对于很多问题,平均情况和最坏情况的时间复杂度差不多,比如插入排序这个例子,平均情况和最坏情况的时间复杂度都是输入长度n的二次函数。
57 |
58 | ### 下界函数
59 |
60 | 定义1.2 如果存在两个正常数c和n0,对于所有的n≥n0,有
61 |
62 | |T(n)| ≥ c|g(n)|,则记作T(n) = Ω(g(n))
63 |
64 | 含义:
65 |
66 | + 如果算法用n值不变的同一类数据在某台机器上运行时,所用的时间总是不小于|g(n)|的一个常数倍。所以g(n)是计算时间T(n)的一个下界函数。
67 |
68 | + 试图求出“最大”的g(n),使得T(n) = Ω(g(n))。
69 |
70 | ### “平均情况”限界函数
71 |
72 | 定义1.3 如果存在正常数c1,c2和n0,对于所有的n≥n0,有
73 |
74 | ` c1|g(n)| ≤|T(n)| ≤ c2|g(n)|`
75 |
76 | 则记作
77 |
78 | 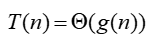
79 |
80 | 含义:
81 |
82 | + 算法在最好和最坏情况下的计算时间就一个常数因子范围内而言是相同的。可看作:
83 |
84 | 既有 T(n) = Ω(g(n)),又有T(n) = Ο(g(n))
85 |
86 | 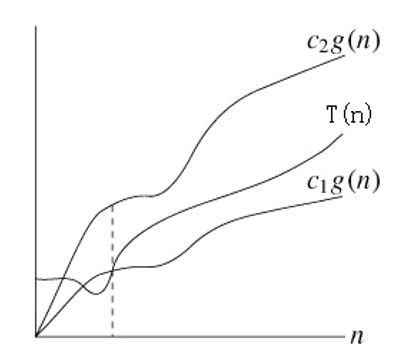
87 |
88 | ## **常见算法时间复杂度:**
89 |
90 | 1. O(1): 表示算法的运行时间为常量
91 |
92 | 2. O(n): 表示该算法是线性算法
93 |
94 | 3. O(㏒2n): 二分搜索算法
95 |
96 | 4. O(n㏒2n): 快速排序算法
97 | 5. O(n^2): 对数组进行排序的各种简单算法,例如直接插入排序的算法。
98 | 6. O(n^3): 做两个n阶矩阵的乘法运算
99 |
100 | 7. O(2^n): 求具有n个元素集合的所有子集的算法
101 |
102 | 8. O(n!): 求具有N个元素的全排列的算法
103 |
104 | 优<---------------------------<劣
105 |
106 | O(1)1
127 | X(1) = 1
128 |
129 | x(1)=1
130 | x(2)=2x(1)+1 = 2*1+1=3
131 | x(3)=2x(2)+1=2*3+1=7
132 | x(4)=2x(3)+1=2*7+1=15
133 | X(n)=2^n-1 n>0
134 | ```
135 |
136 | (2)反向替换法
137 |
138 | 例如:X(n)=x(n-1)+n
139 |
140 | 使用所讨论的递推关系,将x(n-1)表示为x(n-2)得函数,然后把这个结果代入原始方程,来把x(n)表示为x(n-2)的函数。重复这一过程。
141 |
142 | `X(n)=x(0)+1+2+3+4+5…+n=0+1+2+3=4 = n(n+1)/2`
143 |
144 | (3)换名
145 |
146 | 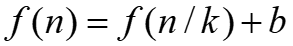
147 |
148 | 上面形式的在递推关系式,一个规模为n的问题,每一次递归调用后,都简化为n/k规模的问题,为了方便求解,我们通常设定:n=km,
149 |
150 | 则,上面的求解过程可简化为:
151 |
152 | ```
153 | f(n)= f(km-1)+b
154 |
155 | = f(km-2)+2b
156 |
157 | = …
158 |
159 | = f(k0)+mb
160 |
161 | = f(1) + blog n
162 | ```
163 |
164 | 几种常见复杂度举例:
165 |
166 | 1. O(logn):我们学过的算法,二分搜索
167 |
168 |
169 | ``` c
170 | int BinSrch(Type A[],int i, int n, Type x)
171 | //A[i..n]是非递减排列 且 1<=i<=n;
172 | {
173 | if(n==i) { if(x==A[i]) return i;
174 | else return 0; }
175 | else
176 | {
177 | int mid=(i+n)/2;
178 | if(x==A[mid]) return mid; ----基本操作
179 | else if(xA[mid]) return BinSrh(A, mid+1, n, x);——递归调用
181 | }
182 | }
183 |
184 | ```
185 |
186 | #### 递归关系式:
187 |
188 | 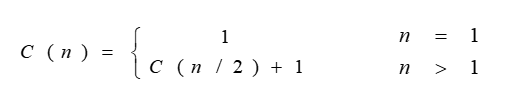
189 |
190 | 因为规模每一次递归调用后,缩减为原来的1/2,所以采用换名方法求解,设 n = 2k:
191 |
192 | ```
193 | C(n) = C(2k)= C(2k-1)+1
194 |
195 | = C(2k-2) + 2
196 |
197 | =…
198 |
199 | =C(2k-k)+k
200 |
201 | =C(1) + k
202 |
203 | = logn+1
204 | ```
205 |
206 |
207 |
208 | 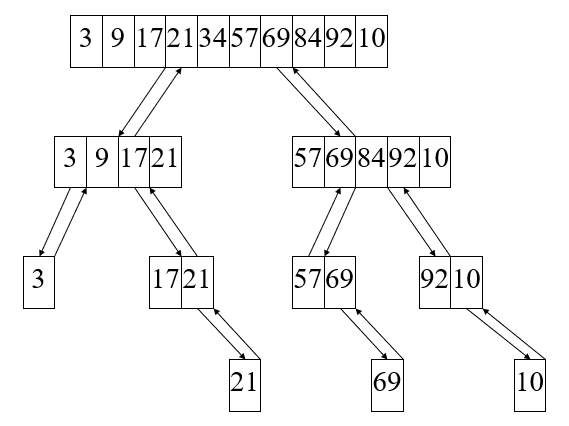
209 |
210 | 观察递归调用的过程以及递推关系式:
211 |
212 | + 在递归关系式中:递归调用共有k次,我们设n= 2k,k=logn
213 |
214 | + 递归调用的二叉树型结构中,调用次数为二叉树的深度。
215 |
216 | 2. O(n): 表示该算法是线性算法
217 |
218 | 目前所学的算法中有:线性选择算法
219 |
220 | ``` c
221 | int Select(int data[],int p,int r,int k)
222 | {
223 | if(p>r) return -1; //p不能大于r
224 | if(p==r) return data[p]; //pk)
228 | {
229 | int r1= Select(data,p,s-1,k);-----递归调用
230 | return r1;
231 | }
232 | else //s
64 |
65 | #include
66 |
67 | #include
68 |
69 | #include
70 |
71 | using namespace std;
72 |
73 | bool b[21]={0};
74 |
75 | int total=0,a[21]={0};
76 |
77 | int search(int); //回溯过程
78 |
79 | int print(); //输出方案
80 |
81 | bool pd(int,int); //判断素数
82 | int main()
83 | {
84 | search(1);
85 | cout<";
105 | for (int j=1;j<=20;j++)
106 | cout<sqrt(i)) return 1;
114 | else return 0;
115 | }
116 |
117 | ```
118 |
119 | **【例2】设有n个整数的集合{1,2,…,n},从中取出任意r个数进行排列(r
125 |
126 | #include
127 |
128 | #include
129 |
130 | using namespace std;
131 |
132 | int num=0,a[10001]={0},n,r;
133 |
134 | bool b[10001]={0};
135 |
136 | int search(int); //回溯过程
137 |
138 | int print(); //输出方案
139 |
140 |
141 |
142 | int main()
143 |
144 | {
145 |
146 | cout<<"input n,r:";
147 |
148 | cin>>n>>r;
149 |
150 | search(1);
151 |
152 | cout<<"number="<
218 | #include
219 | #include
220 | using namespace std;
221 | int a[10001]={1},n,total;
222 | int search(int,int);
223 | int print(int);
224 | int main()
225 | {
226 | cin>>n;
227 | search(n,1);
228 | //将要拆分的数n传递给s
229 | cout<<"total="<0时,继续递归
247 | s+=i;
248 | //回溯:加上拆分的数,以便产分所有可能的拆分
249 | }
250 | }
251 | int print(int t)
252 | {
253 | cout<A[J] AND ABS(I-J)<>ABS(A[I]-A[J]){I和J分别表示两个皇后的行号}
309 |
310 | ``` c
311 | #include
312 | #include
313 | #include
314 | #include
315 | using namespace std;
316 | bool d[100]={0},b[100]={0},c[100]={0};
317 | int sum=0,a[100];
318 | int search(int);
319 | int print();
320 | int main()
321 | {
322 | search(1); //从第1个皇后开始放置
323 | system("pause");
324 | }
325 | int search(int i)
326 | {
327 | int j;
328 | for (j=1;j<=8;j++) //每个皇后都有8位置(列)可以试放
329 | if ((!b[j])&&(!c[i+j])&&(!d[i-j+7])) //寻找放置皇后的位置
330 | //由于C++不能操作负数组,因此考虑加7
331 | { //放置皇后,建立相应标志值
332 | a[i]=j; //摆放皇后
333 | b[j]=1; //宣布占领第j列
334 | c[i+j]=1; //占领两个对角线
335 | d[i-j+7]=1;
336 | if (i==8) print(); //8个皇后都放置好,输出
337 | else search(i+1); //继续递归放置下一个皇后
338 | b[j]=0; //递归返回即为回溯一步,当前皇后退出
339 | c[i+j]=0;
340 | d[i-j+7]=0;
341 | }
342 | }
343 | int print()
344 | {
345 | int i;
346 | sum++; //方案数累加1
347 | cout<<"sum="<2,1->3,3->1,4->3,5->2,7->4,8…
358 |
359 | 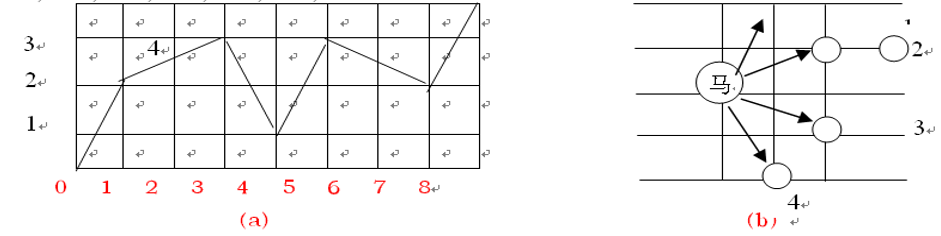
360 |
361 | **【算法分析】**
362 |
363 | 如图4(b),马最多有四个方向,若原来的横坐标为j、纵坐标为i,则四个方向的移动可表示为:
364 |
365 | 1: (i,j)→(i+2,j+1); (i<3,j<8)
366 |
367 | 2: (i,j)→(i+1,j+2); (i<4,j<7)
368 |
369 | 3: (i,j)→(i-1,j+2); (i>0,j<7)
370 |
371 | 4: (i,j)→(i-2,j+1); (i>1,j<8)
372 |
373 | 搜索策略:
374 |
375 | S1:A[1]:=(0,0);
376 |
377 | S2:从A[1]出发,按移动规则依次选定某个方向,如果达到的是(4,8)则转向S3,否则继续搜索下一个到达的顶点;
378 |
379 | S3:打印路径。
380 |
381 | ``` c
382 | #include
383 | #include
384 | #include
385 | using namespace std;
386 | int a[100][100],t=0; //路径总数和路径
387 | int x[4]={2,1,-1,-2}, //四种移动规则
388 | y[4]={1,2,2,1};
389 | int search(int); //搜索
390 | int print(int); //打印
391 | int main() //主程序
392 | {
393 | a[1][1]=0;a[1][2]=0; //从坐标(0,0)开始往右跳第二步
394 | search(2);
395 | system("pause");
396 | };
397 | int search(int i)
398 | {
399 | for (int j=0;j<=3;j++) //往4个方向跳
400 | if (a[i-1][1]+x[j]>=0&&a[i-1][1]+x[j]<=4
401 | &&a[i-1][2]+y[j]>=0&&a[i-1][2]+y[j]<=8) //判断马不越界
402 | {
403 | a[i][1]=a[i-1][1]+x[j]; //保存当前马的位置
404 | a[i][2]=a[i-1][2]+y[j];
405 | if (a[i][1]==4&&a[i][2]==8) print(i);
406 | else search(i+1); //搜索下一步
407 | }
408 | }
409 | int print(int ii)
410 | {
411 | {
412 | t++;
413 | cout<";
416 | cout<<"4,8"<
441 | #include
442 | #include
443 | #include
444 | using namespace std;
445 | int data[6][6]={{0,0,0,0,0,0},{0,13,11,10,4,7},{0,13,10,10,8,5},{0,5,9,7,7,4},{0,15,12,10,11,5},{0,10,11,8,8,4}};
446 | int max1=0,g[10],f[10];
447 | bool p[6]={0};
448 | int go(int step,int t) // step是第几个人,t是之前已得的效益
449 | {
450 | for (int i=1;i<=5;i++)
451 | if (!p[i]) //判断第i项工作没人选择
452 | {
453 | f[step]=i; //第step个人,就选第i项工作
454 | p[i]=1; //标记第i项工作被人安排了
455 | t+=data[step][i]; //计算效益值
456 | if (step<5) go(step+1,t);
457 | else if (t>max1) //保存最佳效益值
458 | {
459 | max1=t;
460 | for (int j=1;j<=5;j++)
461 | g[j]=f[j]; //保存最优效益下的工作选择方案
462 | }
463 | t-=data[step][i]; //回溯
464 | p[i]=0;
465 | }
466 | }
467 | int main()
468 | {
469 | go(1,0); //从第1个人,总效益为0开始
470 | for (int i=1;i<=5;i++)
471 | cout<
527 | #include
528 | #include
529 | using namespace std;
530 | int book[6],c;
531 | bool flag[6],like[6][6]={{0,0,0,0,0,0},{0,0,0,1,1,0},{0,1,1,0,0,1},
532 | {0,0,1,1,0,0},{0,0,0,0,1,0},{0,0,1,0,0,1}};;
533 | int search(int);
534 | int print();
535 | int main()
536 | {
537 | for (int i=1;i<=5;i++) flag[i]=1;
538 | search(1); //从第1个开始选书,递归。
539 | system("pause");
540 | }
541 | int search(int i) //递归函数
542 | {
543 | for (int j=1;j<=5; j++) //每个人都有5本书可选
544 | if (flag[j]&&like[i][j]) //满足分书的条件
545 | {
546 | flag[j]=0; //把被选中的书放入集合flag中,避免重复被选
547 | book[i]=j; //保存第i个人选中的第j本书
548 | if (i==5) print(); //i=5时,所有的人都分到书,输出结果
549 | else search(i+1); //i<5时,继续递归分书
550 | flag[j]=1; //回溯:把选中的书放回,产生其他分书的方案
551 | book[i]=0;
552 | }
553 |
554 | }
555 |
556 | int print()
557 | {
558 | c++; //方案数累加1
559 | cout <<"answer " <
593 | #include
594 | #include
595 | #include
596 | using namespace std;
597 | int u[8]={1,2,2,1,-1,-2,-2,-1}, //8个方向上的x,y增量
598 | v[8]={-2,-1,1,2,2,1,-1,-2};
599 | int a[100][100]={0},num=0; //记每一步走在棋盘的哪一格和棋盘的每一格有
600 | //没有被走过
601 | bool b[100][100]={0};
602 | int search(int,int,int); //以每一格为阶段,在每一阶段中试遍8个方向
603 | int print(); //打印方案
604 | int main()
605 | {
606 | a[1][1]=1;b[1][1]=1; //从(1,1)第一步开始走
607 | search(1,1,2); //从(1,1)开始搜第2步该怎样走
608 | cout<25) {print();return 0;} //达到最大规模打印、统计方案
615 | for (k=0;k<=7;k++) //试遍8个方向
616 | {
617 | x=i+u[k];y=j+v[k]; //走此方向,得到的新坐标
618 | if (x<=5&&x>=1&&y<=5&&y>=1&&(!b[x][y]))
619 | { //如果新坐标在棋盘上,并且这一格可以走
620 | b[x][y]=1;
621 | a[x][y]=n;
622 | search(x,y,n+1); //从(x,y)去搜下一步该如何走
623 | b[x][y]=0;
624 | a[x][y]=0;
625 | }
626 | }
627 | }
628 | int print()
629 | {
630 | num++; //统计总方案
631 | if (num<=5) //打印出前5种方案
632 | {
633 | for (int k=1;k<=5;k++) //打印本次方案
634 | {
635 | for (int kk=1;kk<=5;kk++)
636 | cout<
675 | #include
676 | #include
677 | using namespace std;
678 | int n,i,j,k,rest,sum,total;
679 | int s[7];
680 | int main()
681 | {
682 | cout << "Input n k";
683 | cin >> n >> k;
684 | total = 0; s[1] = 0;
685 | i = 1;
686 | while (i)
687 | {
688 | s[i]++;
689 | if (s[i] > n) i--;
690 | else if (i == k)
691 | {
692 | sum = 0;
693 | for (j = 1; j <= k; j++) sum += s[j];
694 | if (n == sum) total++;
695 | }
696 | else {
697 | rest -= s[i];
698 | i++;
699 | s[i] = s[i-1] - 1;
700 | }
701 | }
702 | cout << total;
703 | system("pause");
704 | return 0;
705 | }
706 |
707 | 方法2、递归,参考程序如下。
708 | #include
709 | #include
710 | #include
711 | using namespace std;
712 | int n,k;
713 | int f(int a,int b,int c)
714 | {
715 | int g = 0,i;
716 | if (b == 1) g = 1;
717 | else for (i = c; i <= a/b; i++)
718 | g += f(a-i,b-1,i);
719 | return g;
720 | }
721 | int main()
722 | {
723 | cout << "Input n,k:";
724 | cin >> n >> k;
725 | cout << f(n,k,1);
726 | system("pause");
727 | return 0;
728 | }
729 |
730 | 方法3、用动态循环穷举所有不同的分解,要注意剪枝,参考程序如下。
731 | #include
732 | #include
733 | #include
734 | using namespace std;
735 | int n,k,total;
736 | int min(int x,int y)
737 | {
738 | if (x < y) return x;
739 | else return y;
740 | }
741 | void select(int dep,int rest,int last)
742 | {
743 | int i;
744 | if (dep == 0) total++;
745 | else for (i = min(rest-dep+1,last); i >= rest/dep; i--)
746 | select(dep-1,rest-i,i);
747 | }
748 | int main()
749 | {
750 | cout << "Input n,k:";
751 | cin >> n >> k;
752 | total = 0;
753 | select(k,n,n);
754 | cout << total;
755 | system("pause");
756 | return 0;
757 | }
758 |
759 | 方法4、递推法
760 | 首先将正整数n分解成k个正整数之和的不同分解方案总数等于将正整数n-k分解成任意个不大于k的正整数之和的不同分解方案总数(可用ferror图证明之),后者的递推公式不难得到,参考程序如下。
761 | #include
762 | #include
763 | #include
764 | #include
765 | using namespace std;
766 | int i,j,k,n,x;
767 | int p[201][7];
768 | int main()
769 | {
770 | cin >> n >> k;
771 | memset(p,0,sizeof(p));
772 | p[0][0] = 1;
773 | for (i = 1; i <= n; i++) p[i][1] = 1;
774 | for (i = 1; i <= n - k; i++)
775 | for (j = 2; j <= min(i,k); j++)
776 | for (x = 1; x <= min(i,j); x++)
777 | p[i][j] += p[i-x][min(i-x,x)];
778 | cout << p[n-k][k];
779 | system("pause");
780 | return 0;
781 | }
782 |
783 | ```
784 |
785 |
--------------------------------------------------------------------------------
/algorithm/bfs.md:
--------------------------------------------------------------------------------
1 | # **广度优先搜索**
2 |
3 | ## **广度优先搜索的过程**
4 |
5 | 广度优先搜索算法(又称宽度优先搜索)是最简便的图的搜索算法之一,这一算法也是很多重要的图的算法的原型。
6 |
7 | Dijkstra单源最短路径算法和Prim最小生成树算法都采用了和宽度优先搜索类似的思想。
8 |
9 | 广度优先算法的核心思想是:从初始节点开始,应用算符生成第一层节点,检查目标节点是否在这些后继节点中,若没有,再用产生式规则将所有第一层的节点逐一扩展,得到第二层节点,并逐一检查第二层节点中是否包含目标节点。若没有,再用算符逐一扩展第二层的所有节点……,如此依次扩展,检查下去,直到发现目标节点为止。即
10 |
11 | 1. 从图中的某一顶点V0开始,先访问V0;
12 | 2. 访问所有与V0相邻接的顶点V1,V2,......,Vt;
13 | 3. 依次访问与V1,V2,......,Vt相邻接的所有未曾访问过的顶点;
14 | 4. 循此以往,直至所有的顶点都被访问过为止。
15 |
16 | 这种搜索的次序体现沿层次向横向扩展的趋势,所以称之为广度优先搜索。
17 |
18 | ## **广度优先搜索算法描述:**
19 |
20 | ``` c
21 | int Bfs()
22 | {
23 | 初始化,初始状态存入队列;
24 | 队列首指针head=0; 尾指针tail=1;
25 | do
26 | {
27 | 指针head后移一位,指向待扩展结点;
28 | for (int i=1;i<=max;++i) //max为产生子结点的规则数
29 | {
30 | if (子结点符合条件)
31 | {
32 | tail指针增1,把新结点存入列尾;
33 | if (新结点与原已产生结点重复) 删去该结点(取消入队,tail减1);
34 | else
35 | if (新结点是目标结点) 输出并退出;
36 | }
37 | }
38 | }while(head
72 | #include
73 | using namespace std;
74 | int ju[9][9]={{0,0,0,0,0,0,0,0,0},
75 | {0,1,0,0,0,1,0,1,1},
76 | {0,0,1,1,1,1,0,1,1},
77 | {0,0,1,1,0,0,1,1,1},
78 | {0,0,1,0,1,1,1,0,1},
79 | {0,1,1,0,1,1,1,0,0},
80 | {0,0,0,1,1,1,1,1,0},
81 | {0,1,1,1,0,0,1,1,0},
82 | {0,1,1,1,1,0,0,0,1}};
83 | int a[101],b[101];
84 | bool s[9]; //初始化
85 | int out(int d) //输出过程
86 | {
87 | cout<
161 | using namespace std;
162 | int dx[4]={-1,0,1,0},
163 | dy[4]={0,1,0,-1};
164 | int bz[100][100],num=0,n,m;
165 | void doit(int p,int q)
166 | {
167 | int x,y,t,w,i;
168 | int h[1000][10];
169 | num++;bz[p][q]=0;
170 | t=0;w=1;h[1][1]=p;h[1][2]=q; //遇到的第一个细胞入队
171 | do
172 | {
173 | t++; //队头指针加1
174 | for (i=0;i<=3;i++) //沿细胞的上下左右四个方向搜索细胞
175 | {
176 | x=h[t][1]+dx[i];y=h[t][2]+dy[i];
177 | if ((x>=0)&&(x=0)&&(y
280 | using namespace std;
281 | int n,m,desx,desy,soux,souy,totstep,a[51],b[51],map[51][51];
282 | bool f;
283 | int move(int x, int y,int step)
284 | {
285 | map[x][y]=step; //走一步,作标记,把步数记下来
286 | a[step]=x; b[step]=y; //记路径
287 | if ((x==desx)&&(y==desy))
288 | {
289 | f=1;
290 | totstep=step;
291 | }
292 | else
293 | {
294 | if ((y!=m)&&(map[x][y+1]==0)) move(x,y+1,step+1); //向右
295 | if ((!f)&&(x!=n)&&(map[x+1][y]==0)) move(x+1,y,step+1); //往下
296 | if ((!f)&&(y!=1)&&(map[x][y-1]==0)) move(x,y-1,step+1); //往左
297 | if ((!f)&&(x!=1)&&(map[x-1][y]==0)) move(x-1,y,step+1); //往上
298 | }
299 | }
300 | int main()
301 | {
302 | int i,j;
303 | cin>>n>>m; //n行m列的迷宫
304 | for (i=1;i<=n;i++) //读入迷宫,0表示通,-1表示不通
305 | for (j=1;j<=m;j++)
306 | cin>>map[i][j];
307 | cout<<"input the enter:";
308 | cin>>soux>>souy; //入口
309 | cout<<"input the exit:";
310 | cin>>desx>>desy; //出口
311 | f=0; //f=0表示无解;f=1表示找到了一个解
312 | move(soux,souy,1);
313 | if (f)
314 | {
315 | for (i=1;i<=totstep;i++) //输出直迷宫的路径
316 | cout<
324 | using namespace std;
325 | int u[5]={0,0,1,0,-1},
326 | w[5]={0,1,0,-1,0};
327 | int n,m,i,j,desx,desy,soux,souy,head,tail,x,y,a[51],b[51],pre[51],map[51][51];
328 | bool f;
329 | int print(int d)
330 | {
331 | if (pre[d]!=0) print (pre[d]); //递归输出路径
332 | cout<>n>>m; //n行m列的迷宫
338 | for (i=1;i<=n;i++) //读入迷宫,0表示通,-1表示不通
339 | for (j=1;j<=m;j++)
340 | cin>>map[i][j];
341 | cout<<"input the enter:";
342 | cin>>soux>>souy; //入口
343 | cout<<"input the exit:";
344 | cin>>desx>>desy; //出口
345 | head=0;
346 | tail=1;
347 | f=0;
348 | map[soux][souy]=-1;
349 | a[tail]=soux; b[tail]=souy; pre[tail]=0;
350 | while (head!=tail) //队列不为空
351 | {
352 | head++;
353 | for (i=1;i<=4;i++) //4个方向
354 | {
355 | x=a[head]+u[i]; y=b[head]+w[i];
356 | if ((x>0)&&(x<=n)&&(y>0)&&(y<=m)&&(map[x][y]==0))
357 | { //本方向上可以走
358 | tail++;
359 | a[tail]=x; b[tail]=y; pre[tail]=head;
360 | map[x][y]=-1;
361 | if ((x==desx)&&(y==desy)) //扩展出的结点为目标结点
362 | {
363 | f=1;
364 | print(tail);
365 | break;
366 | }
367 | }
368 | }
369 | if (f) break;
370 | }
371 | if (!f) cout<<"no way."<mid) {j--;} //在右半部分寻找比中间数小的数
55 |
56 | if (i<=j)
57 |
58 | { //若找到一组与排序目标不一致的数对则交换它们
59 |
60 | p=a[i];a[i]=a[j];a[j]=p;
61 |
62 | i++;j--; //继续找
63 |
64 | }
65 |
66 | }while(i<=j); //注意这里要有等号
67 |
68 | if (l
80 |
81 | using namespace std;
82 |
83 | int jc(int,int);
84 |
85 | int n,a[1000],m;
86 |
87 | int main()
88 |
89 | {
90 |
91 | int x,y,i;
92 |
93 | cin>>n;
94 |
95 | x=1;y=n;
96 |
97 | for (i=1;i<=n;i++) //输入排序好的数
98 |
99 | cin>>a[i];
100 |
101 | cin>>m; //输入要查找的数
102 |
103 | jc(x,y); //递归过程
104 |
105 | cout<y) cout<<"no find"<m) jc(x,k-1); //在前半中查找
124 | }
125 | }
126 |
127 | ```
128 |
129 | **【例3】一元三次方程求解**
130 |
131 | **有形如:ax3+bx2+cx+d=0这样的一个一元三次方程。给出该方程中各项的系数(a,b,c,d均为实数),并约定该方程存在三个不同实根(根的范围在-100至100之间),且根与根之差的绝对值≥1。**
132 |
133 | **要求由小到大依次在同一行输出这三个实根(根与根之间留有空格),并精确到小数点后2位。**
134 |
135 | `提示:记方程f(x)=0,若存在2个数x1和x2,且x10`,则确定根x不在区间[x1,x2]内,设定[x2,x2+1]为下一个搜索区间
196 | 3. `f(x1)*f(x2)<0`,则确定根x在区间[x1,x2]内。
197 |
198 | 如果确定根x在区间[x1,x2]内的话(`f(x1)*f(x2)<0`),如何在该区间找到根的确切位置。采用二分法,将区间[x1,x2]分成左右两个子区间:左子区间[x1,x]和右子区间[x,x2]:
199 |
200 | 如果`f(x1)*f(x)≤0`,则确定根在左区间[x1,x]内,将x设为该区间的右指针(x2=x),继续对左区间进行对分;如果`f(x1)*f(x)>0`,则确定根在右区间[x,x2]内,将x设为该区间的左指针(x1=x),继续对右区间进行对分;
201 |
202 | 上述对分过程一直进行到区间的间距满足精度要求为止(x2-x1<0.001)。此时确定x1为f(x)的根。
203 |
204 | ``` c
205 | 由此得出算法:
206 | 输入方程中各项的系数a,b,c,d ;
207 | {
208 | for (x=-100;x<=100;x++) //枚举每一个可能的根
209 | {
210 | x1=x;x2=x+1; //确定根的可能区间
211 | if (f(x1)==0) printf("%.2f ",x1); //若x1为根,则输出
212 | else if (f(x1)*f(x2)<0) //若根在区间[x1,x2]中
213 | {
214 | while (x2-x1>=0.001) //若区间[x1,x2]不满足精度要求,则循环
215 | {
216 | xx=(x2+x1)/2; //计算区间[x1,x2]的中间位置
217 | if ((f(x1)*f(xx))<=0) //若根在左区间,则调整右指针
218 | x2=xx;
219 | else x1=xx; //若根在右区间,则调整左指针
220 | }
221 | printf("%.2f ",x1); //区间[x1,x2]满足精度要求,确定x1为根
222 | }
223 | }
224 | cout<
308 | const int MAXN=33,MAXM=5;
309 | int matchlist[MAXN][MAXN];
310 | int m;
311 | int main()
312 | {
313 | printf("Input m:");
314 | scanf("%d",&m);
315 | int n=1<
366 | #include
367 | using namespace std;
368 | int b,p,k,a;
369 | int f(int p) //利用分治求b^p % k
370 | {
371 | if (p==0) return 1; // b^0 %k=1
372 | int tmp=f(p/2)%k;
373 | tmp=(tmp*tmp) % k; // b^p %k=(b^(p/2))^2 % k
374 | if (p%2==1) tmp=(tmp * b) %k; //如果p为奇数,则 b^p %
375 | return tmp; //k=((b^(p/2))^2)* b%k
376 |
377 | }
378 | int main()
379 | {
380 | cin>>b>>p>>k; //读入3个数
381 | int tmpb=b; //将b的值备份
382 | b%=k; //防止b太大
383 | printf("%d^%d mod %d=%d\n",tmpb,p,k,f(p)); //输出
384 | return 0;
385 | }
386 |
387 | ```
388 |
389 | **【例8】、黑白棋子的移动(chessman)**
390 |
391 | **【问题描述】**
392 |
393 | **有2n个棋子(n≥4)排成一行,开始位置为白子全部在左边,黑子全部在右边,如下图为n=5的情形:**
394 |
395 | **○○○○○●●●●●**
396 |
397 | **移动棋子的规则是:每次必须同时移动相邻的两个棋子,颜色不限,可以左移也可以右移到空位上去,但不能调换两个棋子的左右位置。每次移动必须跳过若干个棋子(不能平移),要求最后能移成黑白相间的一行棋子。如n=5时,成为:**
398 |
399 | **○●○●○●○●○●**
400 |
401 | **任务:编程打印出移动过程。**
402 |
403 | **【输入样例】chessman.in**
404 |
405 | **7**
406 |
407 | **【输出样例】chessman.out**
408 |
409 | ```
410 | step 0:ooooooo*******--
411 | step 1:oooooo--******o*
412 | step 2:oooooo******--o*
413 | step 3:ooooo--*****o*o*
414 | step 4:ooooo*****--o*o*
415 | step 5:oooo--****o*o*o*
416 | step 6:oooo****--o*o*o*
417 | step 7:ooo--***o*o*o*o*
418 | step 8:ooo*o**--*o*o*o*
419 | step 9:o--*o**oo*o*o*o*
420 | step10:o*o*o*--o*o*o*o*
421 | step11:--o*o*o*o*o*o*o*
422 | ```
423 |
424 | **【算法分析】**
425 |
426 | **我们先从n=4开始试试看,初始时:**
427 |
428 | **○○○○●●●●**
429 |
430 | **第1步:○○○——●●●○● {—表示空位}**
431 |
432 | **第2步:○○○●○●●——●**
433 |
434 | **第3步:○——●○●●○○●**
435 |
436 | **第4步:○●○●○●——○●**
437 |
438 | **第5步:——○●○●○●○●**
439 |
440 | **如果n=5呢?我们继续尝试,希望看出一些规律,初始时:**
441 |
442 | **○○○○○●●●●●**
443 |
444 | **第1步:○○○○——●●●●○●**
445 |
446 | **第2步:○○○○●●●●——○●**
447 |
448 | **这样,n=5的问题又分解成了n=4的情况,下面只要再做一下n=4的5个步骤就行了。同理,n=6的情况又可以分解成n=5的情况,……,所以,对于一个规模为n的问题,我们很容易地就把他分治成了规模为n-1的相同类型子问题。**
449 |
450 | **数据结构如下:数组c[1..max]用来作为棋子移动的场所,初始时,c[1]~c[n]存放白子(用字符o表示),c[n+1]~c[2n]存放黑子(用字符*表示),c[2n+1],c[2n+2]为空位置(用字符—表示)。最后结果在c[3]~c[2n+2]中。**
451 |
452 | ``` c
453 | #include
454 | using namespace std;
455 | int n,st,sp;
456 | char c[101];
457 | void print() //打印
458 | {
459 | int i;
460 | cout<<"step "<>n;
501 | init(n);
502 | mv(n);
503 | }
504 | ```
505 |
506 |
--------------------------------------------------------------------------------
/algorithm/big-num.md:
--------------------------------------------------------------------------------
1 | # 高精度算法
2 |
3 | ## 应用场景
4 |
5 | 利用计算机进行数值计算,有时会遇到这样的问题:有些计算要求精度高,希望计算的数的位数可达几十位甚至几百位,虽然计算机的计算精度也算较高了,但因受到硬件的限制,往往达不到实际问题所要求的精度。我们可以利用程序设计的方法去实现这样的高精度计算。
6 |
7 | > 本节介绍常用的几种高精度计算的方法。
8 |
9 | ## 算法的难点
10 |
11 | ### 1. 数据的接收方法和存贮方法
12 |
13 | 数据的接收和存贮:当输入的数很长时:
14 |
15 | + 可采用字符串方式输入,这样可输入数字很长的数,利用字符串函数和操作运算,将每一位数取出,存入数组中。
16 |
17 | ``` c++
18 | void init(int a[]) //传入一个数组
19 | {
20 | string s;
21 | cin>>s; //读入字符串s
22 | a[0]=s.length(); //用a[0]计算字符串s的位数
23 | for(i=1;i<=a[0];i++)
24 | a[i]=s[a[0]-i]-'0'; //将数串s转换为数组a,并倒序存储
25 | }
26 | ```
27 |
28 | + 另一种方法是直接用循环加数组方法输入数据。
29 |
30 | ### 2.高精度数位数的确定
31 |
32 | 位数的确定:接收时往往是用字符串的,所以它的位数就等于字符串的长度。
33 |
34 | ### 3.进位,借位处理
35 |
36 | **加法进位:**
37 |
38 | ``` c++
39 | c[i]=a[i]+b[i];
40 |
41 | if (c[i]>=10) {
42 | c[i]%=10; ++c[i+1];
43 | }
44 | ```
45 |
46 | **减法借位:**
47 |
48 | ``` c++
49 | if (a[i]
107 | #include
108 | #include
109 | using namespace std;
110 | int main()
111 | {
112 | char a1[100],b1[100];
113 | int a[100],b[100],c[100],lena,lenb,lenc,i,x;
114 | memset(a,0,sizeof(a));
115 | memset(b,0,sizeof(b));
116 | memset(c,0,sizeof(c));
117 | gets(a1);
118 | gets(b1); //输入加数与被加数
119 | lena=strlen(a1);
120 | lenb=strlen(b1);
121 | for (i=0;i<=lena-1;i++) a[lena-i]=a1[i]-48; //加数放入a数组
122 | for (i=0;i<=lenb-1;i++) b[lenb-i]=b1[i]-48; //加数放入b数组
123 | lenc =1;
124 | x=0;
125 | while (lenc <=lena||lenc <=lenb)
126 | {
127 | c[lenc]=a[lenc]+b[lenc]+x; //两数相加
128 | x=c[lenc]/10;
129 | c[lenc]%=10;
130 | lenc++;
131 | }
132 | c[lenc]=x;
133 | if (c[lenc]==0)
134 | lenc--; //处理最高进位
135 | for (i=lenc;i>=1;i--)
136 | cout<
158 | #include
159 | #include
160 | using namespace std;
161 | int main()
162 | {
163 | int a[256],b[256],c[256],lena,lenb,lenc,i;
164 | char n[256],n1[256],n2[256];
165 | memset(a,0,sizeof(a));
166 | memset(b,0,sizeof(b));
167 | memset(c,0,sizeof(c));
168 | printf("Input minuend:"); gets(n1); //输入被减数
169 | printf("Input subtrahend:"); gets(n2); //输入减数
170 | if (strlen(n1)n2时,返回正整数;n11)) lenc--; //最高位的0不输出
196 | for (i=lenc;i>=1;i--) cout<
226 | #include
227 | #include
228 | using namespace std;
229 | int main()
230 | {
231 | char a1[100],b1[100];
232 | int a[100],b[100],c[100],lena,lenb,lenc,i,j,x;
233 | memset(a,0,sizeof(a));
234 | memset(b,0,sizeof(b));
235 | memset(c,0,sizeof(c));
236 | gets(a1);gets(b1);
237 | lena=strlen(a1);lenb=strlen(b1);
238 | for (i=0;i<=lena-1;i++) a[lena-i]=a1[i]-48;
239 | for (i=0;i<=lenb-1;i++) b[lenb-i]=b1[i]-48;
240 | for (i=1;i<=lena;i++)
241 | {
242 | x=0; //用于存放进位
243 | for (j=1;j<=lenb;j++) //对乘数的每一位进行处理
244 | {
245 | c[i+j-1]=a[i]*b[j]+x+c[i+j-1]; //当前乘积+上次乘积进位+原数 x=c[i+j-1]/10;
246 | c[i+j-1] %= 10;
247 | }
248 | c[i+lenb]=x; //进位
249 | }
250 | lenc=lena+lenb;
251 | while (c[lenc]==0&&lenc>1) //删除前导0
252 | lenc--;
253 | for (i=lenc;i>=1;i--)
254 | cout<
277 | #include
278 | #include
279 | using namespace std;
280 | int main()
281 | {
282 | char a1[100],c1[100];
283 | int a[100],c[100],lena,i,x=0,lenc,b;
284 | memset(a,0,sizeof(a));
285 | memset(c,0,sizeof(c));
286 | gets(a1);
287 | cin>>b;
288 | lena=strlen(a1);
289 | for (i=0;i<=lena-1;i++)
290 | a[i+1]=a1[i]-48;
291 | for (i=1;i<=lena;i++) //按位相除
292 | {
293 | c[i]=(x*10+a[i])/b;
294 | x=(x*10+a[i])%b;
295 | }
296 | lenc=1;
297 | while (c[lenc]==0&&lenc
323 | #include
324 | using namespace std;
325 | int a[101],b[101],c[101],d,i;
326 | void init(int a[])
327 | { string s;
328 | cin>>s; //读入字符串s
329 | a[0]=s.length(); //用a[0]计算字符串 s的位数
330 | for(i=1;i<=a[0];i++)
331 | a[i]=s[a[0]-i]-'0'; //将数串s转换为数组a,并倒序存储.
332 | }
333 | void print(int a[]) //打印输出
334 | {
335 | if (a[0]==0){cout<<0<0;i--) cout<b则为1,ab[0]) return 1; //a的位数大于b则a比b大
344 | if(a[0]0;i--) //从高位到低位比较
346 | {
347 | if (a[i]>b[i]) return 1;
348 | if (a[i]0&&a[a[0]]==0) a[0]--; //修正a的位数
372 | return;
373 | }
374 | }
375 |
376 | void chugao(int a[],int b[],int c[])
377 | {
378 | int tmp[101];
379 | c[0]=a[0]-b[0]+1;
380 | for (int i=c[0];i>0;i--)
381 | {
382 | memset(tmp,0,sizeof(tmp)); //数组清零
383 | numcpy(b,tmp,i);
384 | while(compare(a,tmp)>=0){c[i]++;jian(a,tmp);} //用减法来模拟
385 | }
386 | while(c[0]>0&&c[c[0]]==0)c[0]--;
387 | return ;
388 | }
389 |
390 | int main()
391 | {
392 | memset(a,0,sizeof(a));
393 | memset(b,0,sizeof(b));
394 | memset(c,0,sizeof(c));
395 | init(a);init(b);
396 | chugao(a,b,c);
397 | print(c);
398 | print(a);
399 | return 0;
400 | }
401 | ```
--------------------------------------------------------------------------------
/algorithm/dfs.md:
--------------------------------------------------------------------------------
1 | # 深度优先搜索
2 |
3 | 从起点出发,走过的点要做标记,发现有没走过的点,就随意挑一个往前走,走不 了就回退,此种路径搜索策略就称为“深度优先搜索”,简称“深搜”。
4 |
5 | 其实称为“远度优先搜索”更容易理解些。因为这种策略能往前走一步就往前走一 步,总是试图走得更远。所谓远近(或深度),就是以距离起点的步数来衡量的。
6 |
7 | ### 代码框架
8 |
9 | ``` c
10 | void dfs(当前状态)
11 | {
12 | if(达到目标状态)
13 | {
14 | ...
15 | return;
16 | }
17 | for(遍历下一层状态)
18 | {
19 | ...
20 | dfs(下一层状态);
21 | ...
22 | }
23 | }
24 |
25 | ```
26 |
27 | ## 几个概念
28 |
29 | + 状态:对问题在某一时刻的进展情况的数学描述(如迷宫题中当前所在位置)
30 | + 状态转移:从一个状态扩展出(走出)其他状态的过程
31 | + 剪枝:去掉搜索树中不需要的状态和转移
32 | + 判重:已经搜索过的状态不再进行搜索
33 | + 搜索树:由若干状态和状态转移形成的树形结构
34 |
35 | ## 问题引入:
36 |
37 | 给出一个矩阵,1表示墙壁不能走,0表示可以走,找出一条从左上角到右下角的最短路。
38 |
39 | 
40 |
41 | 以递归的方式寻找路径,走不通就返回上一层。
42 |
43 | 1. 怎么找?一个点一个点地走。
44 | 2. 怎么判重?染色。
45 | 3. 怎么找最短?到达终点时更新答案
46 | 4. 终止条件?无路可走,到达终点
47 |
48 | 解决过程如图所示:
49 |
50 | 
51 |
52 | 实现代码如下:
53 |
54 | 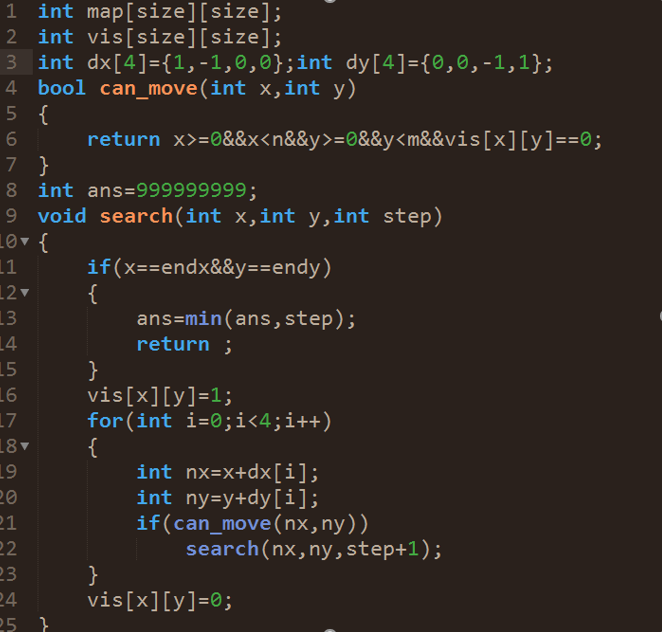
55 |
56 | 使用这种方法能解决问题:
57 |
58 | **时间复杂度:**
59 |
60 | 每个状态最多有3种扩展方式,迷宫的最大深度为nm,因此时间复杂度可能达到O(3^(nm))
61 |
62 | **空间复杂度:**
63 |
64 | 只需要记录每个节点是否被走过为O(n*m)
65 |
66 | 不过其实可以优化,这里就是接下来需要谈到的**DFS剪枝**
67 |
68 | ## **DFS剪枝**
69 |
70 | 可以在下图中看到:
71 |
72 | 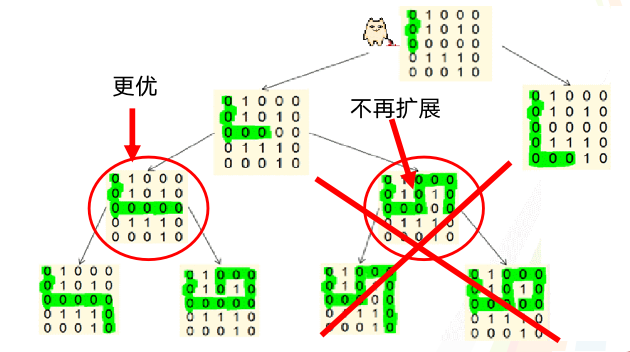
73 |
74 | **时间复杂度:**
75 |
76 | `考虑搜索树,因为不会重复经过结点,所以深度不会超过n*m。
77 | 因此,每个结点最多只会遍历n*m次。
78 | 所以,时间复杂度最多可能达到O( (n*m)^2 )`
79 |
80 | **空间复杂度:**
81 |
82 | 只需要记录到达每个节点的最小步数
83 | 复杂度为`O(n*m)`
84 |
85 | 实现代码:
86 |
87 | 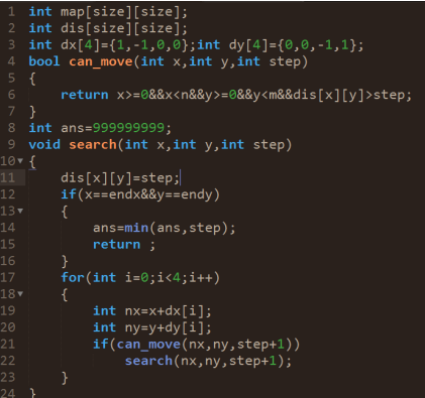
88 |
89 | 我们再用一个例子谈谈 DFS剪枝:
90 |
91 | 给出n个正整数a1,a2,a3,...,an,和一个正整数k, 问是否能从n个数中选出若干个数,使其和为k。
92 |
93 | 思路 :
94 |
95 | 每个数只有选或不选两种选择:
96 |
97 | 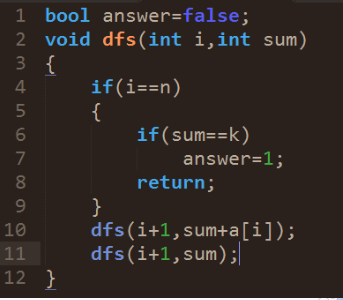
98 |
99 | 剪枝1:当sum>k时,直接返回
100 |
101 | 剪枝2:设s[i]表示第i个数到最后一个数的所有数和
102 | 当遍历到第i个数时,若此时sum加上所有剩下
103 | 的数也达不到k,即sum+s[i] DFS暂时先讲到这里,希望你有所收获。
--------------------------------------------------------------------------------
/algorithm/greedy.md:
--------------------------------------------------------------------------------
1 | # **贪心算法**
2 |
3 | ## 思路
4 |
5 | 若在求解一个问题时,能根据每次所得到的局部最优解,推导出全局最优或最优目标。
6 |
7 | 那么,我们可以根据这个策略,每次得到局部最优解答,逐步而推导出问题,这种策略称为**贪心法**
8 |
9 | **【例1】**在N行M列的正整数矩阵中,要求从每行中选出1个数,使得选出的总共N个数的和最大。
10 |
11 | **【算法分析】**
12 |
13 | 要使总和最大,则每个数要尽可能大,自然应该选每行中最大的那个数。因此,我们设计出如下算法:
14 |
15 | 读入N, M,矩阵数据;
16 |
17 | ``` c
18 | Total = 0;
19 |
20 | for (int l= 1; l<= N; ++l)
21 |
22 | { //对N行进行选择
23 |
24 | 选择第I行最大的数,记为K;
25 |
26 | Total +=K;
27 |
28 | }
29 |
30 | 输出最大总和Total;
31 | ```
32 |
33 | 从上例中我们可以看出,和递推法相仿,贪心法也是从问题的某一个初始解出发,向给定的目标递推。但不同的是,推进的每一步不是依据某一固定的递推式,而是做一个局部的最优选择,即贪心选择(在例中,这种贪心选择表现为选择一行中的最大整数),这样,不断的将问题归纳为若干相似的子问题,最终产生出一个全局最优解。
34 |
35 | 特别注意的是,局部贪心的选择是否可以得出全局最优是能否采用贪心法的关键所在。对于能否使用贪心策略,应从理论上予以证明。下面我们看看另一个问题。
36 |
37 | **【例2】部分背包问题**
38 |
39 | 给定一个最大载重量为M的卡车和N种食品,有食盐,白糖,大米等。已知第i种食品的最多拥有Wi公斤,其商品价值为Vi元/公斤,编程确定一个装货方案,使得装入卡车中的所有物品总价值最大。
40 |
41 | **【算法分析】**
42 |
43 | 因为每一个物品都可以分割成单位块,单位块的利益越大显然总收益越大,所以它局部最优满足全局最优,可以用贪心法解答,方法如下:先将单位块收益按从大到小进行排列,然后用循环从单位块收益最大的取起,直到不能取为止便得到了最优解。
44 |
45 | 因此我们非常容易设计出如下算法:
46 |
47 | 问题初始化; //读入数据
48 |
49 | 按Vi从大到小将商品排序;
50 |
51 | ``` c++
52 | i=1;
53 |
54 | do
55 |
56 | {
57 |
58 | if (m==0) break; //如果卡车满载则跳出循环
59 |
60 | m=m-w[i];
61 |
62 | if (m>=0) //将第i种商品全部装入卡车
63 |
64 | else 将(m+w[i]) 重量的物品i装入卡车;
65 |
66 | i=i+1; //选择下一种商品
67 |
68 | }while (m>0&&i<=n);
69 | ```
70 |
71 |
72 |
73 | 在解决上述问题的过程中,首先根据题设条件,找到了贪心选择标准(Vi),并依据这个标准直接逐步去求最优解,这种解题策略被称为贪心法。
74 |
75 | ## 贪心解决的问题
76 |
77 | **因此,利用贪心策略解题,需要解决两个问题:**
78 |
79 | **首先,确定问题是否能用贪心策略求解;一般来说,适用于贪心策略求解的问题具有以下特点:**
80 |
81 | **①**可通过局部的贪心选择来达到问题的全局最优解。运用贪心策略解题,一般来说需要一步步的进行多次的贪心选择。在经过一次贪心选择之后,原问题将变成一个相似的,但规模更小的问题,而后的每一步都是当前看似最佳的选择,且每一个选择都仅做一次。
82 |
83 | **②**原问题的最优解包含子问题的最优解,即问题具有最优子结构的性质。在背包问题中,第一次选择单位重量价值最大的货物,它是第一个子问题的最优解,第二次选择剩下的货物中单位重量价值最大的货物,同样是第二个子问题的最优解,依次类推。
84 |
85 | **③**其次,如何选择一个贪心标准?正确的贪心标准可以得到问题的最优解,在确定采用贪心策略解决问题时,不能随意的判断贪心标准是否正确,尤其不要被表面上看似正确的贪心标准所迷惑。在得出贪心标准之后应给予严格的数学证明。
86 |
87 | ## 例题讲解
88 |
89 | **下面来看看0-1背包问题。**
90 |
91 | 给定一个最大载重量为M的卡车和N种动物。已知第i种动物的重量为Wi,其最大价值为Vi,设定M,Wi,Vi均为整数,编程确定一个装货方案,使得装入卡车中的所有动物总价值最大。
92 |
93 | 【分析】对于n种动物,要么被装,要么不装,也就是说在满足卡车载重的条件下,如何选择动物,使得动物价值最大的问题。
94 |
95 | 即确定一组x1,x2,…,xn, xi∈{0,1}
96 |
97 | ` f(x)=max(∑xi*vi) 其中,∑(xi*wi)≦w`
98 |
99 | 从直观上来看,我们可以按照上例一样选择那些价值大,而重量轻的动物。也就是可以按价值质量比(vi/wi)的大小来进行选择。可以看出,每做一次选择,都是从剩下的动物中选择那些vi/wi最大的,这种局部最优的选择是否能满足全局最优呢?我们来看看一个简单的例子:
100 |
101 | 设n=3,卡车最大载重量是100,三种动物a、b、c的重量分别是40,50,70,其对应的总价值分别是80、100、150。
102 |
103 | 情况a:按照上述思路,三种动物的vi/wi分别为2,2,2.14。显然,我们首先选择动物c,得到价值150,然后任意选择a或b,由于卡车最大载重为100,因此卡车不能装载其他动物。
104 |
105 | 情况b:不按上述约束条件,直接选择a和b。可以得到价值80+100=180,卡车装载的重量为40+50=90。没有超过卡车的实际载重,因此也是一种可行解,显然,这种解比上一种解要优化。
106 |
107 | 问题出现在什么地方呢?我们看看图23
108 |
109 | 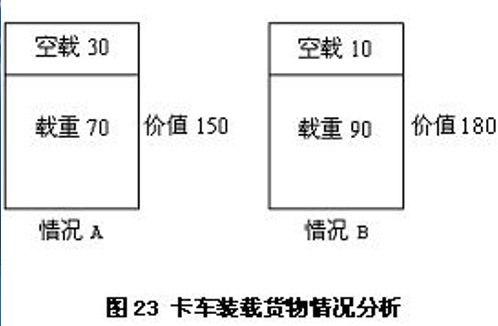
110 |
111 | 从图23中明显可以看出,情况a,卡车的空载率比情况b高。也就是说,上面的分析,只考虑了货物的价值质量比,而没有考虑到卡车的运营效率,因此,局部的最优化,不能导致全局的最优化。
112 |
113 | 因此,贪心不能简单进行,而需要全面的考虑,最后得到证明。
114 |
115 | **【例3】排队打水问题**
116 |
117 | 有N个人排队到R个水龙头去打水,他们装满水桶的时间为T1,T2,…,Tn为整数且各不相等,应如何安排他们的打水顺序才能使他们花费的时间最少?
118 |
119 | **【算法分析】**
120 |
121 | 由于排队时,越靠前面的计算的次数越多,显然越小的排在越前面得出的结果越小(可以用数学方法简单证明,这里就不再赘述),所以这道题可以用贪心法解答,基本步骤:
122 |
123 | 1. 将输入的时间按从小到大排序;
124 | 2. 将排序后的时间按顺序依次放入每个水龙头的队列中;
125 | 3. 统计,输出答案。
126 |
127 | **【样例输入】**
128 |
129 | 4 2 //4人打水,2个水龙头
130 |
131 | 2 6 4 5 //每个打水时间
132 |
133 | ### 实现代码
134 |
135 | ``` c++
136 | cin>>n>>r;
137 |
138 | memset(s,0,sizeof(s)); //初始化
139 |
140 | j=0; min=0;
141 |
142 | for (i=1;i<=n;++i) //用贪心法求解
143 |
144 | {
145 |
146 | j++;
147 |
148 | if (j==r+1) j=1;
149 |
150 | s[j]+=a[i];
151 |
152 | min+=s[j];
153 |
154 | }
155 |
156 | cout<从③取3张牌放到 ②(9 11 10 10)-> 从②取1张牌放到①(10 10 10 10)。
172 |
173 | 【输入格式】
174 |
175 | N(N 堆纸牌,1 <= N <= 100)
176 |
177 | A1 A2 … An (N 堆纸牌,每堆纸牌初始数,l<= Ai <=10000)
178 |
179 | 【输出格式】
180 |
181 | 所有堆均达到相等时的最少移动次数。
182 |
183 | 【样例输入】Playcard.in
184 |
185 | 4
186 |
187 | 9 8 17 6
188 |
189 | 【样例输出】Playcard.out
190 |
191 | 3
192 |
193 | 【算法分析】
194 |
195 | 如果你想到把每堆牌的张数减去平均张数,题目就变成移动正数,加到负数中,使大家都变成0,那就意味着成功了一半!拿例题来说,平均张数为10,原张数9,8,17,6,变为-1,-2,7,-4,其中没有为0的数,我们从左边出发:要使第1堆的牌数-1变为0,只须将-1张牌移到它的右边(第2堆)-2中;结果是-1变为0,-2变为-3,各堆牌张数变为0,-3,7,-4;同理:要使第2堆变为0,只需将-3移到它的右边(第3堆)中去,各堆牌张数变为0,0,4,-4;要使第3堆变为0,只需将第3堆中的4移到它的右边(第4堆)中去,结果为0,0,0,0,完成任务。每移动1次牌,步数加1。也许你要问,负数张牌怎么移,不违反题意吗?其实从第i堆移动-m张牌到第i+1堆,等价于从第i+1堆移动m张牌到第i堆,步数是一样的。
196 |
197 | 如果张数中本来就有为0的,怎么办呢?如0,-1,-5,6,还是从左算起(从右算起也完全一样),第1堆是0,无需移牌,余下与上相同;再比如-1,-2,3,10,-4,-6,从左算起,第1次移动的结果为0,-3,3,10,-4,-6;第2次移动的结果为0,0,0,10,-4,-6,现在第3堆已经变为0了,可节省1步,余下继续。
198 |
199 | ### 实现代码
200 |
201 | ``` c++
202 | cin>>n;
203 | ave=0;step=0;
204 | for (i=1;i<=n;++i)
205 | {
206 | cin>>a[i]; ave+=a[i]; //读入各堆牌张数,求总张数ave
207 | }
208 | ave/=n; //求牌的平均张数ave
209 | for (i=1;i<=n;++i) a[i]-=ave; //每堆牌的张数减去平均数
210 | i=1;j=n;
211 | while (a[i]==0&&i1) --j; //过滤右边的0
213 | while (in[j+1] ) { //找到第一个符合条件的
285 |
286 | for ( k=j;k导弹i的高度};l[p]←导弹i的高度)(i≤j≤k)。这样可使得一套系统拦截的导弹数尽可能增多。
346 |
347 | 依次类推,直至分析了n枚导弹的高度为止。此时得出的k便为应配备的最少系统数。
348 |
349 | ### 实现代码
350 |
351 | ``` c++
352 |
353 |
354 | k=1;l[k]=导弹1的高度;
355 |
356 | for (i=2;i<=n;++i)
357 |
358 | {
359 |
360 | p=0;
361 |
362 | for (j=1;j<=k;++j)
363 |
364 | if (l[j]>=导弹i的高度) { if (p==0) p=j;
365 |
366 | else if (l[j]
433 | using namespace std;
434 | int n,begin[1001],end[1001];
435 | void init()
436 | {
437 | cin>>n;
438 | for(int i=1;i<=n;i++)
439 | cin>>begin[i]>>end[i];
440 | }
441 | void qsort(int x,int y)
442 | {
443 | int i,j,mid,t;
444 | i=x;j=y;mid=end[(x+y)/2];
445 | while(i<=j)
446 | {
447 | while(end[i]mid) --j;
449 | if(i<=j)
450 | {
451 | t=end[j];end[j]=end[i];end[i]=t;
452 | t=begin[j];begin[j]=begin[i];begin[i]=t;
453 | ++i;j;
454 | }
455 | }
456 | if(x=t) {++ans;t=end[i];}//如果当前活动与之前最后结束的活动不冲突,
465 | 就接受当前活动。
466 | cout<
525 | using namespace std;
526 | int a[10001],b[10001],sum=0,n,m;
527 | void qsort(int x,int y) //多关键字快排
528 | {
529 | int i,j,mid1,mid2,t;
530 | i=x;j=y;mid1=b[(x+y)/2];mid2=a[(x+y)/2];
531 | while(i<=j)
532 | { while(b[i]mid1||((b[j]==mid1)&&(a[j]>mid2))) --j;
534 | if(i<=j)
535 | { t=b[j];b[j]=b[i];b[i]=t;
536 | t=a[j];a[j]=a[i];a[i]=t;
537 | ++i; --j;
538 | }
539 | }
540 | if(x>n;
546 | for(int i=1;i<=n;++i)cin>>a[i]>>b[i];
547 | qsort(1,n);
548 | for(int i=1,x=-1;i<=n;++i) //在初始化循环变量的同时,初始化x。
549 | //令x=-1可以使第一个区间与其他区间的操作
550 | 相同。
551 | {
552 | if (x>=a[i]) continue; //如果当前区间包含标记点,就跳过。
553 | ++sum; x=b[i]; //更新标记点。
554 | }
555 | cout<=1),用递归的方法计算1+2+3+4+...+(n-1)+n。**
12 |
13 | 【算法分析】
14 |
15 | 本题可以用递归方法求解,其原因在于它符合递归的三个条件:
16 |
17 | 1. 本题是累加问题:当前和=前一次和+当前项,而前一次和的计算方法与其相同,只是数据不同s(n)=s(n-1)+n;
18 | 2. 给定n,所以是有限次的递归调用;
19 | 3. 结束条件是当n=1,则s=1。
20 |
21 | ### 实现代码
22 |
23 | ``` c++
24 | #include
25 |
26 | using namespace std;
27 |
28 | int fac(int); //递归函数
29 |
30 | int main()
31 |
32 | {
33 |
34 | int t;
35 |
36 | cin>>t; //输入t的值
37 |
38 | cout<<"s="<A[MID]则到数据前半段查找:L不变,R=MID-1,计算新的MID值,并进行新的一段查找;
70 | 5. 若L>R都没有查找到,则输出“NO”。
71 |
72 | 该算法符合递归程序设计的基本规律,可以用递归方法设计。
73 |
74 | ### 实现代码:
75 |
76 | ``` c++
77 |
78 | #include
79 | #include
80 | using namespace std;
81 | int a[11];
82 | void search(int,int,int);
83 | int main() //主程序
84 | {
85 | int k,x,L=1,R=10;
86 | cout<<"输入10个从大到小顺序的数:"<>a[k];
89 | cin>>x;
90 | search(x,L,R);
91 | system("pause");
92 | }
93 | void search(int x,int top,int bot) //二分查找递归过程
94 | {
95 | int mid;
96 | if (top<=bot)
97 | {
98 | mid=(top+bot)/2; //求中间数的位置
99 | if (x==a[mid]) cout<<"YES"<C;
120 |
121 | (2)当N=2时,则需要移动三次:
122 |
123 | A------ 1 ------> B, A ------ 2 ------> C, B ------ 1------> C.
124 |
125 | (3)如果N=3,则具体移动步骤为:
126 |
127 | 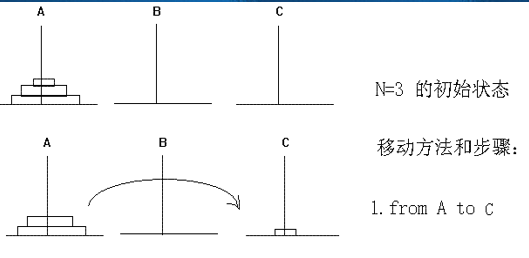
128 |
129 | 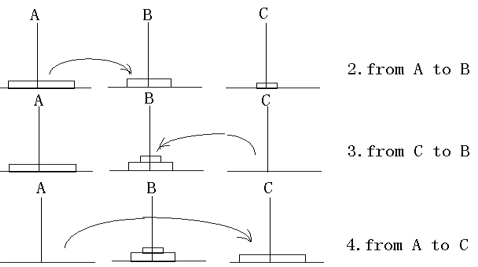
130 |
131 | 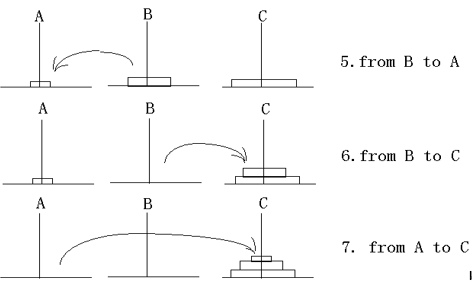
132 |
133 | 假设把第3步,第4步,第7步抽出来就相当于N=2的情况(把上面2片捆在一起,视为一片):
134 |
135 | 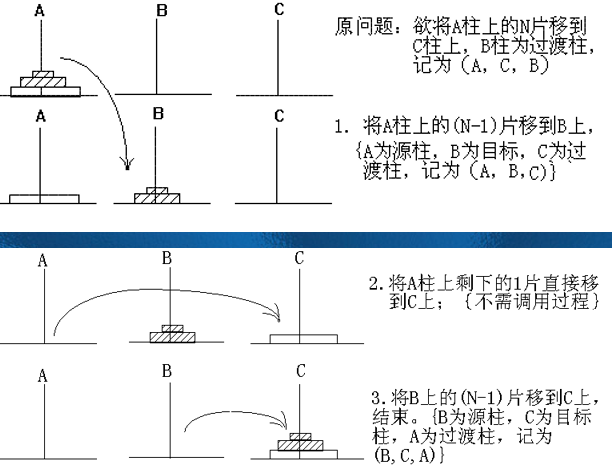
136 |
137 | 所以可按“N=2”的移动步骤设计:
138 |
139 | ①如果N=0,则退出,即结束程序;否则继续往下执行;
140 |
141 | ②用C柱作为协助过渡,将A柱上的(N-1)片移到B柱上,调用过程mov(n-1, a,b,c);
142 |
143 | ③将A柱上剩下的一片直接移到C柱上;
144 |
145 | ④用A柱作为协助过渡,将B柱上的(N-1)移到C柱上,调用过程mov (n-1,b,c,a)。
146 |
147 | ### 实现代码:
148 |
149 | ``` c++
150 | #include
151 | using namespace std;
152 | int k=0,n;
153 | void mov(int n,char a,char c,char b)
154 | //用b柱作为协助过渡,将a柱上的(n)移到c柱上
155 | {
156 | if (n==0) return; //如果n=0,则退出,即结束程序
157 | mov(n-1,a,b,c ); //用c柱作为协助过渡,将a柱上的(n-1)片移到b柱上
158 | k++;
159 | cout <"<>n;
230 | a[1]=1;a[2]=2;
231 | cout<<"x[1]="<
355 | using namespace std;
356 | int main()
357 | {
358 | long long a[101]={0},b[101]={0},i,j,x,y,z;
359 | cin>>x>>y>>z;
360 | for(i=1;i<=x;i++){a[i]=1;b[i]=0;}
361 | for(i=x+1;i<=z+1;i++) //因为要统计到第z个月后,所以要for到z+1
362 | {
363 | b[i]=y*a[i-x];
364 | a[i]=a[i-1]+b[i-2];
365 | }
366 | cout<
429 | using namespace std;
430 | int main()
431 | {
432 | int f[1001][2],n,i,x;
433 | cin>>n;
434 | f[1][1]=1;f[1][0]=9;
435 | for(i=2;i<=n;i++)
436 | {
437 | x=f[1][0];
438 | if(i==n)x--;
439 | f[i][0]=(f[i-1][0]*x+f[i-1][1])%12345;
440 | f[i][1]=(f[i-1][1]*x+f[i-1][0])%12345;
441 | }
442 | cout<0且j>0且`g[i][j]= 0`
466 |
467 | 递推边界有4个:
468 |
469 | `F[i][j] = 0 //g[i][j] = 1`
470 |
471 | ` F[i][0] = F[i-1][0] //i > 0且g[i][j] = 0`
472 |
473 | ` F[0][j] = F[0][j-1] //j > 0且g[i][j] = 0`
474 |
475 | `F[0][0] = 1`
476 |
477 | 考虑到最大情况下:n=20,m=20,路径条数可能会超过231-1,所以要用高精度。
478 |
479 |
480 |
481 | **【例7】**邮票问题
482 |
483 | **【问题描述】**
484 |
485 | 设有已知面额的邮票m种,每种有n张,用总数不超过n张的邮票,能从面额1开始,最多连续组成多少面额。(1≤m≤100,1≤n≤100,1≤邮票面额≤255)
486 |
487 | **【输入格式】**
488 |
489 | 第一行:m,n的值,中间用一空格隔开。
490 |
491 | 第二行:A[1..m](面额),每个数中间用一空格隔开。
492 |
493 | **【输出格式】**
494 |
495 | 连续面额数的最大值
496 |
497 | **【输入样例】stamp.in**
498 |
499 | 3 4
500 |
501 | 1 2 4
502 |
503 | **【输出样例】samp.out**
504 |
505 | 14
506 |
507 | ### **算法分析**
508 |
509 | 一看到这个题目,给人的第一感觉是用回溯算法,从面额1开始,每种面额都用回溯进行判断,算法复杂度并不高,但是当m,n取到极限值100时,程序明显超时,因此,回溯算法在这里并不可取。 能否用递推完成呢?我们有一个思路:从面额1开始,建立递推关系方程,就用范例来说吧,面额1,2,4只用1张邮票行了,面额3可以表示为面额1,2的邮票和1+1=2,面额5有两种表示方式min(面额1+面额4,面额2+面额3),照此类推,递推关系方程不难建立,就拿邮票问题来说,以下是递推的一种方法:
510 |
511 | ``` c++
512 | #include
513 | using namespace std;
514 | int n,m,i,j,k;
515 | int c[256]; //面额
516 | int a[31001]; //递推数组
517 | bool b1;
518 | void readfile() //读入数据
519 | {
520 | cin >> m >> n;
521 | b1 = true;
522 | for (i = 1; i <= m; i++)
523 | {
524 | cin >> c[i];
525 | if (c[i] == 1) b1 = false;
526 | }
527 | }
528 | void work()
529 | {
530 | if (b1 == true) cout << "MAX=0"; //不存在面额1时输出无解
531 | else
532 | {
533 | i = 1; a[i] = 1;
534 | do
535 | {
536 | i++;
537 | for (j = 1; j <= m; j++)
538 | if (((i % c[j] == 0) && ((i / c[j]) < a[i])) || (a[i] == 0))
539 | a[i] = i / c[j]; //判断它能否被题目给定面额整除
540 | for (j = 1; j <= i/2; j++)
541 | if (a[j] + a[i-j] < a[i])
542 | a[i] = a[j] + a[i-j]; //寻找(1<=j<=i),使a[j]+a[i-j]值最小
543 | }
544 | while ((a[i] <= n) && (a[i] != 0));
545 | cout << i-1; //输出
546 | }
547 | }
548 |
549 | int main ( )
550 | {
551 | readfile() ;
552 | work();
553 | return 0;
554 | }
555 |
556 | ```
557 |
558 | 这种递推方法虽然简单,由于1<=邮票面额<=255,1<=n<=100,因此MAX值最多可达到25500,25500次循环里必定还有嵌套循环,因此算法不加优化,很难在规定时间内得出最优值。这就需要递推的算法优化。 一味递推不寻求算法优化,速度较之搜索提高不少,但一旦数据规模过大,很难在规定时间内得出最优值。 这种递推方法原理是:对于某种要求得到的面额,判断它能否被题目给定面额整除,再寻找(1<=j<=i),使A[j]+A[i-j]值最小,求出凑成某种面额最少邮票数,算法虽然简单,但还可以进一步优化。何不将用m种面额邮票作循环,建立递推关系式:A[i]=MAX(A[I-C[j]]+1),于是当取到极限值时,程序减少了约1.6*10^8次循环,递推优化作用不言而喻。
559 |
560 | ### 下面是改进后的程序:
561 |
562 | ``` c++
563 | #include
564 | #include
565 | using namespace std;
566 | int x[256];
567 | int pieces[30001];
568 | int m,n,i,j;
569 |
570 | int main()
571 | {
572 | cin >> m >> n;
573 | for (i = 1; i <= m; i++)
574 | cin >> x[i];
575 | memset(pieces,0,sizeof(pieces));
576 | int maxx = 0;
577 | do //递推循环
578 | {
579 | maxx++;
580 | for (i = 1; i <= m; i++)
581 | if (maxx - x[i] >= 0)
582 | { //循环,建立递推关系式PIECES[i]=MAX(PIECES[I-X[j]]+1)
583 | if (pieces[maxx] == 0) pieces[maxx] = pieces[maxx-x[i]] + 1;
584 | if (pieces[maxx]>pieces[maxx-x[i]]+1) pieces[maxx] = pieces[maxx-x[i]]+1;
585 | }
586 | if ((pieces[maxx] == 0) || (pieces[maxx] > n))
587 | {
588 | cout << maxx - 1;
589 | break;
590 | }
591 |
592 | }
593 | while (true);
594 | return 0;
595 | }
596 |
597 |
598 |
599 | ```
600 |
601 |
--------------------------------------------------------------------------------
/algorithm/string.md:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/Xunzhuo/Algorithm-Guide/019eafeaa5de25e24030ea31f5c0b5d3aee982eb/algorithm/string.md
--------------------------------------------------------------------------------
/code/1.java:
--------------------------------------------------------------------------------
1 | class Solution {
2 | public int findRepeatNumber(int[] nums) {
3 | int len = nums.length;
4 | for (int i = 0; i < len; i++) {
5 | while (nums[i] != i) {//保证交换过来的新元素位置也要正确,即令:a[i]=i
6 | if (nums[i] == nums[nums[i]]) {//将每个位置的数交换映射到其对应的数组下标下面,当出现新的元素与其对应的下标中的数字相等时,即为重复数字
7 | return nums[i];
8 | }
9 | int temp = nums[i]; //交换,使对应下标的数组值与其下标值相等,即令 a[i]=i
10 | nums[i] = nums[temp];
11 | nums[temp] = temp;
12 | }
13 | }
14 | return -1;
15 | }
16 | }
--------------------------------------------------------------------------------
/code/10.java:
--------------------------------------------------------------------------------
1 | class Solution {
2 | static int[][] check ;
3 | static char[] arr;
4 |
5 | public static void main(String[] args) {
6 | char[][] board = {{'a','b'}};
7 | System.out.println(exist(board, "ba"));
8 | }
9 | public static boolean exist(char[][] board, String word) {
10 | check = new int[board.length][board[0].length];
11 | arr = word.toCharArray();
12 | int index = 0;
13 | for(int i=0; i=arr.length) return true; //递归出口
28 | if(board[i][j]!=arr[index]) return false;
29 | //boolean f1 = false, f2 = false, f3 = false, f4 = false;
30 |
31 | //向上走
32 | if(i-1>=0 && check[i-1][j]==0){
33 | check[i-1][j] = 1;
34 | if( dfs(board, i-1, j, index+1) )
35 | return true; //已经找到路径,就没有必要再进行其他方向的搜索
36 | check[i-1][j] = 0; //回溯
37 | }
38 |
39 | //向下走
40 | if(i+1=0 && check[i][j-1]==0){
49 | check[i][j-1] = 1;
50 | if(dfs(board, i, j-1, index+1))
51 | return true;
52 | check[i][j-1] = 0;
53 | }
54 |
55 | //向右走
56 | if(j+1=0 && ey>=0 && ex9)
48 | a2 = i/10%10; //获取十位上的值
49 | int b1 = j%10;
50 | int b2 = 0;
51 | if(j>9)
52 | b2 = j/10%10;
53 | if((a1+a2+b1+b2)<=K)
54 | return true;
55 | return false;
56 | }
57 | }
--------------------------------------------------------------------------------
/code/12.java:
--------------------------------------------------------------------------------
1 | class Solution {
2 | public int cuttingRope(int n) {
3 | if(n==2)
4 |
5 | {
6 | return 1;
7 |
8 | }
9 |
10 | if(n==3)
11 |
12 | {
13 | return 2;
14 |
15 | }
16 |
17 | int count1=0,count2=0;
18 |
19 | count1 = n/3;
20 |
21 | if(n-count1*3==1&&count1>0)
22 |
23 | {
24 | count1-=1;
25 |
26 | }
27 |
28 | count2 = n-count1*3;
29 |
30 | count2 /=2;
31 |
32 | int result = 1;
33 |
34 | for(int i=1;i<=count1;i++)
35 |
36 | {
37 | result*=3;
38 |
39 | }
40 |
41 | for(int i=1;i<=count2;i++)
42 |
43 | {
44 | result*=2;
45 |
46 | }
47 |
48 | return result;
49 |
50 | }
51 |
52 | }
--------------------------------------------------------------------------------
/code/13.java:
--------------------------------------------------------------------------------
1 | public class Solution {
2 | // you need to treat n as an unsigned value
3 |
4 | public int hammingWeight(int n) {
5 | int count = 0;
6 |
7 | while(n!=0)
8 |
9 | {
10 | if((n&1)==1)
11 |
12 | {
13 | count++;
14 |
15 | }
16 |
17 | n>>>=1;
18 |
19 | }
20 |
21 | return count;
22 |
23 | }
24 |
25 | }
--------------------------------------------------------------------------------
/code/14.java:
--------------------------------------------------------------------------------
1 | public class Solution {
2 | // you need to treat n as an unsigned value
3 |
4 | public int hammingWeight(int n) {
5 | int count = 0;
6 |
7 | while(n!=0)
8 |
9 | {
10 | if((n&1)==1)
11 |
12 | {
13 | count++;
14 |
15 | }
16 |
17 | n>>>=1;
18 |
19 | }
20 |
21 | return count;
22 |
23 | }
24 |
25 | }
--------------------------------------------------------------------------------
/code/15.java:
--------------------------------------------------------------------------------
1 | class Solution {
2 | public double myPow(double x, int n) {
3 | int flag = 0;
4 |
5 | if(n==0)
6 |
7 | {
8 | return 1;
9 |
10 | }
11 |
12 | else if(n<0){
13 | n=-n;
14 |
15 | flag=1;
16 |
17 | }
18 |
19 | double result = PowCorn(x,n);
20 |
21 | if(flag==1)
22 |
23 | {
24 | result = 1/result;
25 |
26 | }
27 |
28 | return result;
29 |
30 | }
31 |
32 | public double PowCorn(double x,int n)
33 |
34 | {
35 | if(n==0)
36 |
37 | {
38 | return 1;
39 |
40 | }
41 |
42 | double a = PowCorn(x,n/2);
43 |
44 | if(n%2==0)
45 |
46 | {
47 |
48 |
49 | return a*a;
50 |
51 | }
52 |
53 | else
54 |
55 | {
56 | return a*a*x;
57 |
58 | }
59 |
60 | }
61 |
62 | }
--------------------------------------------------------------------------------
/code/16.java:
--------------------------------------------------------------------------------
1 | class Solution {
2 | public int[] printNumbers(int n) {
3 | int max=0;
4 | max= (int)Math.pow(10,n)-1;
5 | int[] count=new int[max];
6 | for(int i=1;i<=max;i++){
7 | count[i-1]=i;
8 | }
9 | return count;
10 | }
11 | }
--------------------------------------------------------------------------------
/code/17.java:
--------------------------------------------------------------------------------
1 | /**
2 | * Definition for singly-linked list.
3 | * public class ListNode {
4 | * int val;
5 | * ListNode next;
6 | * ListNode(int x) { val = x; }
7 | * }
8 | */
9 | class Solution {
10 | public ListNode deleteNode(ListNode head, int val) {
11 | if (head == null)
12 | return head;
13 | if (head.val == val)
14 | return head.next;
15 | head.next = deleteNode(head.next, val);
16 | return head;
17 | }
18 | }
--------------------------------------------------------------------------------
/code/18.java:
--------------------------------------------------------------------------------
1 | class Solution {
2 | public boolean isMatch(String s, String p) {
3 | boolean dp[][] = new boolean[s.length()+1][p.length()+1];
4 |
5 | dp[0][0] = true;
6 |
7 | for(int j=1;j<=p.length();j++)
8 |
9 | {
10 |
11 | if(p.charAt(j-1)=='*'&&dp[0][j-2])
12 |
13 | dp[0][j] = true;
14 |
15 | }
16 |
17 | for(int i=1;i<=s.length();i++)
18 |
19 | {
20 | for(int j=1;j<=p.length();j++)
21 |
22 | {
23 | if(s.charAt(i-1)==p.charAt(j-1))
24 |
25 | {
26 | dp[i][j] = dp[i-1][j-1];
27 |
28 | }
29 |
30 | else if(p.charAt(j-1)=='.')
31 |
32 | {
33 | dp[i][j] = dp[i-1][j-1];
34 |
35 | }
36 |
37 | else if(p.charAt(j-1)=='*')
38 |
39 | {
40 | if(j>=2)
41 |
42 | {
43 | if(s.charAt(i-1)==p.charAt(j-2)||p.charAt(j-2)=='.')
44 |
45 | {
46 | dp[i][j] = dp[i][j-1]||dp[i][j-2]||dp[i-1][j];
47 |
48 | }
49 |
50 | else
51 |
52 | {
53 | dp[i][j] = dp[i][j-2];
54 |
55 | }
56 |
57 | }
58 |
59 |
60 |
61 | }
62 |
63 | else
64 |
65 | {
66 | dp[i][j]=false;
67 |
68 | }
69 |
70 | }
71 |
72 | }
73 |
74 | return dp[s.length()][p.length()];
75 |
76 | }
77 |
78 | }
--------------------------------------------------------------------------------
/code/19.java:
--------------------------------------------------------------------------------
1 | /*
2 | 核心: 有效数字的模式有两种:1)A[.[B]][e|EC] 2).B[e|EC]; 其中,A、C是整数,B是正整数
3 | 有A的话,有没有B都可以
4 | 没有A的话, 必须有B
5 | */
6 | class Solution {
7 | //扫描字符串时的索引
8 | int i=0;
9 | public boolean isNumber(String s) {
10 | //input check
11 | if(s==null || s.length()==0)
12 | return false;
13 | //去掉首尾的空字符
14 | s = s.trim();
15 | boolean A = scanInteger(s), B=false, C=false;
16 | //判断是否有B; 使用索引时要确保索引不越界
17 | if(i='0' && s.charAt(i)<='9'){
43 | i++;
44 | }
45 | //i>start说明扫描到了数字;
46 | //i<=start说明没有扫描到数字, 此种情况说明要么start越界, 要么s.charAt(start)不是数字
47 | return i > start;
48 | }
49 | }
--------------------------------------------------------------------------------
/code/2.java:
--------------------------------------------------------------------------------
1 | class Solution {
2 | public boolean findNumberIn2DArray(int[][] matrix, int target) {
3 | if (matrix == null || matrix.length == 0 || matrix[0].length == 0)
4 | return false;
5 | int rows = matrix.length, cols = matrix[0].length;
6 | int r = 0, c = cols - 1; // 从右上角开始
7 | while (r <= rows - 1 && c >= 0) {
8 | if (target == matrix[r][c])
9 | return true;
10 | else if (target > matrix[r][c])
11 | r++;
12 | else
13 | c--;
14 | }
15 | return false;
16 | }
17 | }
--------------------------------------------------------------------------------
/code/20.java:
--------------------------------------------------------------------------------
1 | class Solution {
2 | public int[] exchange(int[] nums) {
3 | if(nums.length==0)
4 |
5 | {
6 | return nums;
7 |
8 | }
9 |
10 | int j = nums.length-1;
11 |
12 | for(int i=0;i=j)
16 |
17 | {
18 | break;
19 |
20 | }
21 |
22 | while(nums[j]%2==0)
23 |
24 | {
25 | if(i=k;i--)
53 |
54 | {
55 | nums[count++] = matrix[matrix.length-1-k][i];
56 |
57 | }
58 |
59 | if(count==m*n) break;
60 |
61 | for(int i=matrix.length-2-k;i>k;i--)
62 |
63 | {
64 | nums[count++] = matrix[i][k];
65 |
66 | }
67 |
68 | if(count==m*n) break;
69 |
70 | k++;
71 |
72 | }
73 |
74 | return nums;
75 |
76 | }
77 |
78 | }
--------------------------------------------------------------------------------
/code/28.java:
--------------------------------------------------------------------------------
1 | class MinStack {
2 | Stack stack;
3 |
4 | Stack minstack;
5 |
6 | /** initialize your data structure here. */
7 |
8 | public MinStack() {
9 | stack = new Stack();
10 |
11 | minstack = new Stack();
12 |
13 | }
14 |
15 |
16 |
17 | public void push(int x) {
18 | stack.push(x);
19 |
20 | if(minstack.isEmpty()||x<=minstack.peek()){
21 | minstack.push(x);
22 |
23 | }else{
24 | minstack.push(minstack.peek());
25 |
26 | }
27 |
28 | }
29 |
30 | public void pop() {
31 | stack.pop();
32 |
33 | minstack.pop();
34 |
35 | }
36 |
37 |
38 |
39 | public int top() {
40 | return stack.peek();
41 |
42 | }
43 |
44 |
45 |
46 | public int min() {
47 | return minstack.peek();
48 |
49 | }
50 |
51 | }
--------------------------------------------------------------------------------
/code/29.java:
--------------------------------------------------------------------------------
1 | class Solution {
2 | public boolean validateStackSequences(int[] pushed, int[] popped) {
3 | if(pushed.length==0&&popped.length==0)
4 |
5 | {
6 | return true;
7 |
8 | }
9 |
10 | if(pushed.length!=popped.length)
11 |
12 | {
13 | return false;
14 |
15 | }
16 |
17 | Stack stack = new Stack();
18 |
19 | int i=0,j=0;
20 |
21 | while(i0&&popped[j]==pushed[i-1])
44 |
45 | {
46 | j++;
47 |
48 | stack.pop();
49 |
50 | }
51 |
52 | else if(i<=pushed.length-1)
53 |
54 | {
55 | stack.push(pushed[i++]);
56 |
57 | }
58 |
59 | else
60 |
61 | {
62 | return false;
63 |
64 | }
65 |
66 | }
67 |
68 | }
69 |
70 | while(j list = new ArrayList();
4 |
5 | Queue queue = new LinkedList<>();
6 |
7 | if(root==null) return new int[]{};
8 |
9 | queue.offer(root);
10 |
11 | while(!queue.isEmpty())
12 |
13 | {
14 | TreeNode p = queue.poll();
15 |
16 | list.add(p.val);
17 |
18 | if(p.left!=null)
19 |
20 | {
21 | queue.offer(p.left);
22 |
23 | }
24 |
25 | if(p.right!=null)
26 |
27 | {
28 | queue.offer(p.right);
29 |
30 | }
31 |
32 | }
33 |
34 | int[] res = new int[list.size()];
35 |
36 | for(int i=0; i> levelOrder(TreeNode root) {
3 | List> result = new ArrayList>();
4 |
5 | List list = new ArrayList();
6 |
7 | Deque deque = new LinkedList<>();
8 |
9 | if(root==null) return result;
10 |
11 | TreeNode flag = root;
12 |
13 | deque.offer(root);
14 |
15 | while(!deque.isEmpty())
16 |
17 | {
18 | TreeNode p = deque.poll();
19 |
20 | list.add(p.val);
21 |
22 | if(p.left!=null)
23 |
24 | {
25 | deque.offer(p.left);
26 |
27 | }
28 |
29 | if(p.right!=null)
30 |
31 | {
32 | deque.offer(p.right);
33 |
34 | }
35 |
36 | if(flag==p)
37 |
38 | {
39 | flag = deque.peekLast();
40 |
41 | result.add(list);
42 |
43 | list = new ArrayList<>();
44 |
45 | }
46 |
47 | }
48 |
49 | return result;
50 |
51 | }
52 |
53 | }
--------------------------------------------------------------------------------
/code/32.java:
--------------------------------------------------------------------------------
1 | class Solution {
2 | public List> levelOrder(TreeNode root) {
3 | List> result = new LinkedList>();
4 |
5 | if(root==null)
6 |
7 | {
8 | return result;
9 |
10 | }
11 |
12 | List list = new LinkedList();
13 |
14 | Deque deque = new LinkedList();
15 |
16 | deque.offer(root);
17 |
18 | TreeNode flag = root;
19 |
20 | int k=1;
21 |
22 | while(!deque.isEmpty())
23 |
24 | {
25 | TreeNode p =deque.poll();
26 |
27 | list.add(p.val);
28 |
29 | if(p.left!=null)
30 |
31 | {
32 | deque.offer(p.left);
33 |
34 | }
35 |
36 | if(p.right!=null)
37 |
38 | {
39 | deque.offer(p.right);
40 |
41 | }
42 |
43 | if(flag==p)
44 |
45 | {
46 | flag = deque.peekLast();
47 |
48 | if(k%2==0)
49 |
50 | {
51 | Collections.reverse(list);
52 |
53 | }
54 |
55 | result.add(list);
56 |
57 | list = new LinkedList();
58 |
59 | k++;
60 |
61 | }
62 |
63 | }
64 |
65 | return result;
66 |
67 | }
68 |
69 | }
--------------------------------------------------------------------------------
/code/33.java:
--------------------------------------------------------------------------------
1 | class Solution {
2 | public boolean verifyPostorder(int[] postorder) {
3 | if(postorder.length==0)
4 |
5 | {
6 | return true;
7 |
8 | }
9 |
10 | return find(postorder,0,postorder.length-1);
11 |
12 | }
13 |
14 | public boolean find(int[] postorder,int start,int end)
15 |
16 | {
17 | if(start>=end)
18 |
19 | {
20 | return true;
21 |
22 | }
23 |
24 | int i = start,j = end-1;
25 |
26 | while(istart&&postorder[j]>postorder[end])
34 |
35 | {
36 | j--;
37 |
38 | }
39 |
40 | if(i> result = new LinkedList>();
3 |
4 | public List> pathSum(TreeNode root, int sum) {
5 | if(root==null)
6 |
7 | {
8 | return result;
9 |
10 | }
11 |
12 | List list = new LinkedList();
13 |
14 | find(list,root,0,sum);
15 |
16 | return result;
17 |
18 | }
19 |
20 | public void find(List list,TreeNode root,int target,int sum)
21 |
22 | {
23 | if(root==null)
24 |
25 | {
26 | return;
27 |
28 | }
29 |
30 | target+=root.val;
31 |
32 | list.add(root.val);
33 |
34 | if(target==sum&&root.left==null&&root.right==null)
35 |
36 | {
37 | result.add(new LinkedList<>(list));
38 |
39 | }
40 |
41 | else
42 |
43 | {
44 | find(list,root.left,target,sum);
45 |
46 | find(list,root.right,target,sum);
47 |
48 | }
49 |
50 | list.remove(list.size()-1);
51 |
52 |
53 |
54 | }
55 |
56 | }
--------------------------------------------------------------------------------
/code/35.java:
--------------------------------------------------------------------------------
1 | class Solution {
2 | public Node copyRandomList(Node head) {
3 | if(head==null)
4 |
5 | {
6 | return head;
7 |
8 | }
9 |
10 | Node p = head;
11 |
12 | while(p!=null)
13 |
14 | {
15 | Node node = new Node(p.val);
16 |
17 | node.next = p.next;
18 |
19 | p.next = node;
20 |
21 | p = p.next.next;
22 |
23 | }
24 |
25 | p = head;
26 |
27 | while(p!=null&&p.next!=null)
28 |
29 | {
30 | if(p.random!=null)
31 |
32 | {
33 | p.next.random = p.random.next;
34 |
35 | }
36 |
37 | p = p.next.next;
38 |
39 | }
40 |
41 | Node x = head.next;
42 |
43 | Node q = head;
44 |
45 | while(q.next!=null)
46 |
47 | {
48 | Node t = q.next;
49 |
50 | q.next = q.next.next;
51 |
52 | q = t;
53 |
54 | }
55 |
56 | return x;
57 |
58 | }
59 |
60 | }
--------------------------------------------------------------------------------
/code/36.java:
--------------------------------------------------------------------------------
1 | class Solution {
2 | Node pre,head;
3 | public Node treeToDoublyList(Node root) {
4 | if(root==null) return null;
5 | dfs(root);
6 | head.left=pre;//头结点的前驱是尾结点
7 | pre.right=head;//尾结点的后继是头结点
8 | return head;
9 | }
10 | public void dfs(Node root){
11 | if(root==null){
12 | return;
13 | }
14 | dfs(root.left);
15 | //当前结点不是头结点
16 | if(pre!=null){
17 | pre.right=root;//上一个结点的后继结点设为当前结点
18 | }
19 | else{
20 | head=root;//将当前节点设为头结点
21 | }
22 | root.left=pre;//当前结点的前驱结点
23 | pre=root;//将当前结点设为最后一个结点,即下一个结点的pre
24 | dfs(root.right);
25 | return;
26 | }
27 | }
--------------------------------------------------------------------------------
/code/37.java:
--------------------------------------------------------------------------------
1 | public class Codec {
2 | // Encodes a tree to a single string.
3 | //递归; 二叉树的遍历, 采用前序遍历, 1)要保留结构信息(除了左右孩子, 还要考虑null), 2)要设置间隔符, 从而区分不同的val
4 | public String serialize(TreeNode root) {
5 | //base case
6 | if(root==null)
7 | return "#!";
8 | StringBuilder sb = new StringBuilder();
9 | sb.append(root.val).append("!");
10 | sb.append(serialize(root.left));
11 | sb.append(serialize(root.right));
12 | return sb.toString();
13 | }
14 |
15 |
16 | // Decodes your encoded data to tree.
17 | public TreeNode deserialize(String data) {
18 | String[] strs = data.split("!");
19 | return core(strs);
20 | }
21 | private int i;
22 | //二叉树的遍历, 前序遍历, 递归
23 | private TreeNode core(String[] strs){
24 | //base case
25 | if(i==strs.length)
26 | return null;
27 | if(strs[i].equals("#")){
28 | i++; //索引++
29 | return null;
30 | }
31 | TreeNode root = new TreeNode(Integer.parseInt(strs[i]));
32 | i++;
33 | root.left = core(strs);
34 | root.right = core(strs);
35 | return root;
36 | }
37 | }
--------------------------------------------------------------------------------
/code/38.java:
--------------------------------------------------------------------------------
1 | class Solution {
2 | public String[] permutation(String s) {
3 | List result = new ArrayList<>();
4 |
5 | boolean visited[] = new boolean[s.length()];
6 |
7 | char arr[] = s.toCharArray();
8 |
9 | Arrays.sort(arr);
10 |
11 | StringBuilder x = new StringBuilder();
12 |
13 | helper(result,visited,arr,x);
14 |
15 | String res[] = new String[result.size()];
16 |
17 | for(int i=0;i result,boolean visited[],char arr[],StringBuilder x){
27 | if(x.length()==arr.length){
28 | result.add(x.toString());
29 |
30 | return;
31 |
32 | }
33 |
34 | for(int i=0;i heapS;
3 | PriorityQueue heapL;
4 | /** initialize your data structure here. */
5 | public MedianFinder() {
6 | heapS = new PriorityQueue<>();
7 | heapL = new PriorityQueue<>(new Comparator(){
8 | public int compare(Integer o1, Integer o2){
9 | return o2 - o1;
10 | }
11 | });
12 | }
13 |
14 | public void addNum(int num) {
15 | //当heapS为空或者heapS和heapL的size一样时, 优先向heapS中添加元素
16 | if(heapS.isEmpty() || heapS.size()==heapL.size()){
17 | if(!heapL.isEmpty() && num < heapL.peek()){
18 | heapL.add(num);
19 | num = heapL.poll();
20 | }
21 | heapS.add(num);
22 | }else{
23 | if(!heapS.isEmpty() && num > heapS.peek()){
24 | heapS.add(num);
25 | num = heapS.poll();
26 | }
27 | heapL.add(num);
28 | }
29 | }
30 |
31 | public double findMedian() {
32 | return heapS.size()>heapL.size()? heapS.peek() : (heapL.peek() + heapS.peek())/2.0;
33 | }
34 | }
--------------------------------------------------------------------------------
/code/42.java:
--------------------------------------------------------------------------------
1 | class Solution {
2 | public int maxSubArray(int[] nums) {
3 | if(nums.length==0)
4 |
5 | {
6 | return 0;
7 |
8 | }
9 |
10 | int max = nums[0],sum = nums[0];
11 |
12 | for(int i=1;imax)
25 |
26 | {
27 | max = sum;
28 |
29 | }
30 |
31 | }
32 |
33 | return max;
34 |
35 | }
36 |
37 | }
--------------------------------------------------------------------------------
/code/43.java:
--------------------------------------------------------------------------------
1 | class Solution {
2 | private int dfs(int n) {
3 | if (n <= 0) {
4 | return 0;
5 |
6 | }
7 |
8 |
9 |
10 | String numStr = String.valueOf(n);
11 |
12 | int high = numStr.charAt(0) - '0';
13 |
14 | int pow = (int) Math.pow(10, numStr.length() - 1);
15 |
16 | int last = n - high * pow;
17 |
18 |
19 |
20 | if (high == 1) {
21 | // 最高位是1,如1234, 此时pow = 1000,那么结果由以下三部分构成:
22 |
23 | // (1) dfs(pow - 1)代表[0,999]中1的个数;
24 |
25 | // (2) dfs(last)代表234中1出现的个数;
26 |
27 | // (3) last+1代表固定高位1有多少种情况。
28 |
29 | return dfs(pow - 1) + dfs(last) + last + 1;
30 |
31 | } else {
32 | // 最高位不为1,如2234,那么结果也分成以下三部分构成:
33 |
34 | // (1) pow代表固定高位1,有多少种情况;
35 |
36 | // (2) high * dfs(pow - 1)代表999以内和1999以内低三位1出现的个数;
37 |
38 | // (3) dfs(last)同上。
39 |
40 | return pow + high * dfs(pow - 1) + dfs(last);
41 |
42 | }
43 |
44 | }
45 |
46 |
47 |
48 | // 递归求解
49 |
50 | public int countDigitOne(int n) {
51 | return dfs(n);
52 |
53 | }
54 |
55 | }
--------------------------------------------------------------------------------
/code/44.java:
--------------------------------------------------------------------------------
1 | class Solution {
2 | public int findNthDigit(int n) {
3 | if(n==0)
4 | return 0;
5 | //数字的长度为len; 从长度为1的数字开始, 也就是从个位数开始
6 | int len = 1;
7 | //长度为len的数字有count个
8 | long count = 9;
9 | //长度为len的第一个数字
10 | int start = 1;
11 | //确定第n位对应的数字的长度
12 | while(n > len*count){
13 | // n = n - len*count; //这么写会报错, 需要把count转成int
14 | n -= len*count; //这么写就不报错了
15 | //update
16 | len++;
17 | start = start*10;
18 | count = count*10;
19 | }
20 | //确定第n位对应的数字是哪个长度为len的数字
21 | start = start + (n%len==0? n/len-1 : n/len);
22 | //取出该数字的第(n-1)%len位
23 | String s = Integer.toString(start);
24 | return Character.getNumericValue(s.charAt(n%len==0? len-1 : n%len-1));
25 | }
26 | }
--------------------------------------------------------------------------------
/code/45.java:
--------------------------------------------------------------------------------
1 | class Solution {
2 | public String minNumber(int[] nums) {
3 | if(nums==null||nums.length==0)
4 |
5 | {
6 | return " ";
7 |
8 | }
9 |
10 | List list = new LinkedList<>();
11 |
12 | for(int i=0;i(){
20 | @Override
21 |
22 | public int compare(Integer o1,Integer o2)
23 |
24 | {
25 | String s1 = o1+"" +o2;
26 |
27 | String s2 = o2+""+o2;
28 |
29 | return s1.compareTo(s2);
30 |
31 | }
32 |
33 | });
34 |
35 | StringBuilder result = new StringBuilder();
36 |
37 | for(int i:list)
38 |
39 | {
40 | result.append(i);
41 |
42 | }
43 |
44 | return result.toString();
45 |
46 | }
47 |
48 | }
--------------------------------------------------------------------------------
/code/46.java:
--------------------------------------------------------------------------------
1 | class Solution {
2 | public int translateNum(int num) {
3 | if(num<0)
4 |
5 | {
6 | return 0;
7 |
8 | }
9 |
10 | if(num<10)
11 |
12 | {
13 | return 1;
14 |
15 | }
16 |
17 | int n=num,k=0;
18 |
19 | while(n!=0)
20 |
21 | {
22 | k++;
23 |
24 | n/=10;
25 |
26 | }
27 |
28 | k--;
29 |
30 | int dp[] = new int[k+1];
31 |
32 | dp[0]=1;
33 |
34 | StringBuilder sb = new StringBuilder();
35 |
36 | for(int i=k;i>=0;i--)
37 |
38 | {
39 | int x = (int)((num/Math.pow(10,i))%10);
40 |
41 | // System.out.println(x);
42 |
43 | sb.append(x);
44 |
45 | }
46 |
47 | //System.out.println(k+" "+sb);
48 |
49 | if(k>=1)
50 |
51 | {
52 | if(sb.charAt(0)=='1'||(sb.charAt(0)=='2'&&sb.charAt(1)<'6'))
53 |
54 | dp[1]=2;
55 |
56 | else
57 |
58 | dp[1]=1;
59 |
60 | }
61 |
62 | else
63 |
64 | {
65 | dp[1] = 1;
66 |
67 | }
68 |
69 | for(int i=2;i<=k;i++)
70 |
71 | {
72 | if(i>1)
73 |
74 | {
75 | if(sb.charAt(i-1)=='0'||sb.charAt(i-1)>'2')
76 |
77 | {
78 | dp[i] = dp[i-1];
79 |
80 | }
81 |
82 | else if(sb.charAt(i-1)=='2'&&sb.charAt(i)>='6')
83 |
84 | {
85 | dp[i] = dp[i-1];
86 |
87 | }
88 |
89 | else
90 |
91 | {
92 | dp[i] = dp[i-2]+dp[i-1];
93 |
94 | }
95 |
96 | }
97 |
98 | }
99 |
100 | return dp[k];
101 |
102 | }
103 |
104 | }
--------------------------------------------------------------------------------
/code/47.java:
--------------------------------------------------------------------------------
1 | class Solution {
2 | public int maxValue(int[][] grid) {
3 | if(grid.length==0 || grid[0].length==0){
4 | return 0;
5 | }
6 | int n = grid.length , m = grid[0].length;
7 | //
8 | int[][] dp = new int[n][m];
9 | dp[0][0] = grid[0][0];
10 | for(int i=1; i set = new HashSet<>();
4 |
5 | int left = 0, right = 0, max = 0;
6 |
7 | while(right < s.length()) {
8 | while(set.contains(s.charAt(right))) {
9 | set.remove(s.charAt(left));
10 |
11 | left++;
12 |
13 | }
14 |
15 | set.add(s.charAt(right));
16 |
17 | right++;
18 |
19 | max = Math.max(right - left, max);
20 |
21 | }
22 |
23 | return max;
24 |
25 | }
26 |
27 | }
--------------------------------------------------------------------------------
/code/49.java:
--------------------------------------------------------------------------------
1 | class Solution {
2 | public int nthUglyNumber(int n) {
3 | int count1=0,count2=0,count3=0;
4 |
5 | int ugly[] = new int[n];
6 |
7 | int i=1;
8 |
9 | if(n==0)
10 |
11 | {
12 | return 0;
13 |
14 | }
15 |
16 | ugly[0]=1;
17 |
18 | while(i map = new HashMap<>();//标记中序遍历
12 | int[] preorder;//保留的先序遍历
13 |
14 | public TreeNode buildTree(int[] preorder, int[] inorder) {
15 | this.preorder = preorder;
16 | for (int i = 0; i < preorder.length; i++) {
17 | map.put(inorder[i], i);
18 | }
19 | return recursive(0,0,inorder.length-1);
20 | }
21 |
22 | /**
23 | * @param pre_root_idx 先序遍历的索引
24 | * @param in_left_idx 中序遍历的索引
25 | * @param in_right_idx 中序遍历的索引
26 | */
27 | public TreeNode recursive(int pre_root_idx, int in_left_idx, int in_right_idx) {
28 | //相等就是自己
29 | if (in_left_idx > in_right_idx) {
30 | return null;
31 | }
32 | //root_idx是在先序里面的
33 | TreeNode root = new TreeNode(preorder[pre_root_idx]);
34 | // 有了先序的,再根据先序的,在中序中获 当前根的索引
35 | int idx = map.get(preorder[pre_root_idx]);
36 |
37 | //左子树的根节点就是 左子树的(前序遍历)第一个,就是+1,左边边界就是left,右边边界是中间区分的idx-1
38 | root.left = recursive(pre_root_idx + 1, in_left_idx, idx - 1);
39 |
40 | //由根节点在中序遍历的idx 区分成2段,idx 就是根
41 |
42 | //右子树的根,就是右子树(前序遍历)的第一个,就是当前根节点 加上左子树的数量
43 | // pre_root_idx 当前的根 左子树的长度 = 左子树的左边-右边 (idx-1 - in_left_idx +1) 。最后+1就是右子树的根了
44 | root.right = recursive(pre_root_idx + (idx-1 - in_left_idx +1) + 1, idx + 1, in_right_idx);
45 | return root;
46 | }
47 | }
--------------------------------------------------------------------------------
/code/50.java:
--------------------------------------------------------------------------------
1 | class Solution {
2 | public char firstUniqChar(String s) {
3 | int arr[] = new int[26];
4 |
5 | for(int i=0;i=right){
12 | return 0;
13 | }
14 | int mid = left + ((right - left)>>1);
15 | int res = mergeSort(nums, left, mid);
16 | res += mergeSort(nums, mid+1, right);
17 | res += merge(nums, left, mid, right);
18 | return res;
19 | }
20 |
21 | private int merge(int[] nums, int left, int mid, int right){
22 | int[] arr = new int[right-left+1];
23 | int p=0, p1 = left, p2=mid+1;
24 | int res = 0;
25 | while(p1<=mid && p2<=right){
26 | if(nums[p1] > nums[p2]){
27 | arr[p++] = nums[p1++];
28 | res += right - p2 + 1;
29 | }else{
30 | arr[p++] = nums[p2++];
31 | }
32 | }
33 | while(p1<=mid){
34 | arr[p++] = nums[p1++];
35 | }
36 | while(p2<=right){
37 | arr[p++] = nums[p2++];
38 | }
39 | for(int i=0; i list = helper(root);
4 | return list.get(list.size() - k);
5 | }
6 |
7 | public List helper(TreeNode root){
8 | List list = new LinkedList<>();
9 | if(root == null) return list;
10 |
11 | list.addAll(helper(root.left));
12 | list.add(root.val);
13 | list.addAll(helper(root.right));
14 |
15 | return list;
16 | }
17 | }
--------------------------------------------------------------------------------
/code/56.java:
--------------------------------------------------------------------------------
1 | class Solution {
2 | public int maxDepth(TreeNode root) {
3 | return find(root,0);
4 |
5 | }
6 |
7 | public int find(TreeNode root,int num)
8 |
9 | {
10 | if(root==null)
11 |
12 | {
13 | return num;
14 |
15 | }
16 |
17 | return Math.max(find(root.left,num+1),find(root.right,num+1));
18 |
19 | }
20 |
21 | }
--------------------------------------------------------------------------------
/code/57.java:
--------------------------------------------------------------------------------
1 | class Solution {
2 | public boolean isBalanced(TreeNode root) {
3 | return helper(root)!=-1;
4 |
5 | }
6 |
7 | public int helper(TreeNode root)
8 |
9 | {
10 | if(root == null) return 0;
11 |
12 | int left = helper(root.left);
13 |
14 | if(left == -1) return -1; //左子树不平衡直接返回-1
15 |
16 | int right = helper(root.right);
17 |
18 | if(right == -1) return -1; //右子树不平衡直接返回-1
19 |
20 | return Math.abs(left - right) > 1 ? -1 : 1 + Math.max(left, right);
21 |
22 | }
23 |
24 | }
--------------------------------------------------------------------------------
/code/58.java:
--------------------------------------------------------------------------------
1 | class Solution {
2 | public int[] singleNumbers(int[] nums) {
3 | int result=0;
4 |
5 | for(int i=0;i>i)&1)==1)
14 |
15 | {
16 | count++;
17 |
18 | }
19 |
20 | }
21 |
22 | if(count%3!=0)
23 |
24 | {
25 | result = result |(1< a;
3 | private Stack b;
4 | public CQueue() {
5 | a=new Stack();
6 | b=new Stack();
7 | }
8 |
9 | public void appendTail(int value) {
10 | a.push(value);
11 | }
12 |
13 | public int deleteHead() {
14 | if(!b.empty()){
15 | return b.pop();
16 | }
17 | else if(a.empty()){
18 | return -1;
19 | }
20 | else{
21 | while(!a.empty())
22 | b.push(a.pop());
23 | return b.pop();
24 | }
25 | }
26 | }
27 | /**
28 | * Your CQueue object will be instantiated and called as such:
29 | * CQueue obj = new CQueue();
30 | * obj.appendTail(value);
31 | * int param_2 = obj.deleteHead();
32 | */
--------------------------------------------------------------------------------
/code/60.java:
--------------------------------------------------------------------------------
1 | class Solution {
2 | public int[] twoSum(int[] nums, int target) {
3 | int left = 0,right = nums.length-1;
4 |
5 | int arr[] = new int[2];
6 |
7 | while(lefttarget)
11 |
12 | {
13 | right--;
14 |
15 | }
16 |
17 | else if(nums[left]+nums[right] list = new ArrayList<>();
4 |
5 | int left = 1,right = 2;
6 |
7 | int sum = 3;
8 |
9 | while(righttarget)
22 |
23 | {
24 | sum-=left;
25 |
26 | left++;
27 |
28 | }
29 |
30 | else{
31 | int nums[] = new int[right-left+1];
32 |
33 | for(int i=0;i<=right-left;i++)
34 |
35 | {
36 | nums[i] = left+i;
37 |
38 | }
39 |
40 | list.add(nums);
41 |
42 | right++;
43 |
44 | sum+=right;
45 |
46 | }
47 |
48 | }
49 |
50 | return list.toArray(new int[0][]);
51 |
52 | }
53 |
54 | }
--------------------------------------------------------------------------------
/code/62.java:
--------------------------------------------------------------------------------
1 | class Solution {
2 | public String reverseWords(String s) {
3 | String x = s.trim();
4 |
5 | char arr[] = s.toCharArray();
6 |
7 | StringBuilder sb = new StringBuilder();
8 |
9 | List list = new ArrayList<>();
10 |
11 | for(int i=0;i=0)
53 |
54 | {
55 | sb.append(' ');
56 |
57 | sb.append(list.get(k));
58 |
59 | k--;
60 |
61 | }
62 |
63 | return sb.toString().trim();
64 |
65 | }
66 |
67 | }
--------------------------------------------------------------------------------
/code/63.java:
--------------------------------------------------------------------------------
1 | class Solution {
2 | public String reverseLeftWords(String s, int n) {
3 | if(n>s.length()-1||n<=0)
4 |
5 | {
6 | return s;
7 |
8 | }
9 |
10 | String x = s.substring(0,n);
11 |
12 | s = s.substring(n,s.length());
13 |
14 | return s+x;
15 |
16 | }
17 |
18 | }
--------------------------------------------------------------------------------
/code/64.java:
--------------------------------------------------------------------------------
1 | class Solution {
2 | int count = 0;
3 | public int[] maxSlidingWindow(int[] nums, int k) {
4 | if(k > nums.length || nums.length == 0) return new int[0];
5 | int i = 0;
6 | int[] res = new int[nums.length - k + 1];
7 | while(i + k - 1 <= nums.length - 1){
8 | int max = nums[i];
9 | for(int j = i; j <= i + k - 1; j++){
10 | if(nums[j] > max) max = nums[j];
11 | }
12 | res[count] = max;
13 | i++; count++;
14 | }
15 | return res;
16 | }
17 | }
--------------------------------------------------------------------------------
/code/65.java:
--------------------------------------------------------------------------------
1 | class MaxQueue {
2 | LinkedList list1;
3 | LinkedList list2;
4 |
5 | public MaxQueue() {
6 | list1 = new LinkedList<>();
7 | list2 = new LinkedList<>();
8 | }
9 |
10 | public int max_value() {
11 | if(!list2.isEmpty()){
12 | return list2.peekFirst();
13 | }
14 | return -1;
15 | }
16 |
17 | public void push_back(int value) {
18 | list1.add(value);
19 | while(!list2.isEmpty() && value > list2.peekLast()){
20 | list2.removeLast();
21 | }
22 | list2.addLast(value);
23 | }
24 |
25 | public int pop_front() {
26 | if(!list1.isEmpty()){
27 | int value = list1.poll();
28 | if(value == list2.peekFirst()) list2.removeFirst();
29 | return value;
30 | }
31 | return -1;
32 | }
33 | }
--------------------------------------------------------------------------------
/code/66.java:
--------------------------------------------------------------------------------
1 | class Solution {
2 | public double[] twoSum(int n) {
3 | int dp[][] = new int[n+1][6*n+1];
4 |
5 | double result[] = new double[5*n+1];
6 |
7 | double x = Math.pow(6,n);
8 |
9 | for(int i=1;i<=6;i++)
10 |
11 | {
12 | dp[1][i]=1;
13 |
14 | }
15 |
16 | for(int i=1;i<=n;i++)
17 |
18 | {
19 | for(int j=i;j<=6*n;j++)
20 |
21 | {
22 | for(int k=1;k<=6;k++)
23 |
24 | {
25 | if(j>=k)
26 |
27 | {
28 | dp[i][j]+=dp[i-1][j-k];
29 |
30 | }
31 |
32 | if(i==n)
33 |
34 | {
35 | result[j-i]=dp[i][j]/x;
36 |
37 | }
38 |
39 | }
40 |
41 | }
42 |
43 | }
44 |
45 | return result;
46 |
47 | }
48 |
49 | }
--------------------------------------------------------------------------------
/code/67.java:
--------------------------------------------------------------------------------
1 | class Solution {
2 | public boolean isStraight(int[] nums) {
3 | Arrays.sort(nums);
4 |
5 | int i = 0,wang=0;
6 |
7 | while(nums[i]==0)
8 |
9 | {
10 | i++;
11 |
12 | wang++;
13 |
14 | }
15 |
16 | int cha=0;
17 |
18 | for(int j=i;j<4;j++)
19 |
20 | {
21 | cha+=nums[j+1]-nums[j]-1;
22 |
23 | if(nums[j]==nums[j+1]||cha>wang)
24 |
25 | {
26 | return false;
27 |
28 | }
29 |
30 | }
31 |
32 | return true;
33 |
34 | }
35 |
36 | }
--------------------------------------------------------------------------------
/code/68.java:
--------------------------------------------------------------------------------
1 | class Solution {
2 | public int lastRemaining(int n, int m) {
3 | if(n==0||m==0)
4 |
5 | {
6 | return -1;
7 |
8 | }
9 |
10 | List list = new ArrayList<>();
11 |
12 | for(int i=0;i 1 && sumNums(n - 1) > 0;
5 | res += n;
6 | return res;
7 | }
8 | }
--------------------------------------------------------------------------------
/code/71.java:
--------------------------------------------------------------------------------
1 | class Solution {
2 | public int add(int a, int b) {
3 | int sum=0;
4 |
5 | while(b!=0)
6 |
7 | {
8 | int temp = a^b;
9 |
10 | b = (a&b)<<1;
11 |
12 | a = temp;
13 |
14 | }
15 |
16 | return a;
17 |
18 | }
19 |
20 | }
--------------------------------------------------------------------------------
/code/72.java:
--------------------------------------------------------------------------------
1 | class Solution {
2 | public int[] constructArr(int[] a) {
3 |
4 |
5 | int left[] = new int[a.length];
6 |
7 | int right[] = new int[a.length];
8 |
9 | int result[] = new int[a.length];
10 |
11 | if(a.length==0)
12 |
13 | {
14 | return result;
15 |
16 | }
17 |
18 | left[0] = 1;
19 |
20 | right[a.length-1]=1;
21 |
22 | for(int i =1;i=0;i--)
30 |
31 | {
32 | right[i] = right[i+1]*a[i+1];
33 |
34 | }
35 |
36 | for(int i=0;i='0' && ch<='9'){
22 | //溢出判断
23 | if(flag==1){
24 | //res * 10 + cur > max
25 | if(res>(Integer.MAX_VALUE - (ch-'0'))/10){
26 | return Integer.MAX_VALUE;
27 | }
28 | }else{
29 | //-res * 10 - cur < min
30 | if(-res<(Integer.MIN_VALUE + ch - '0')/10){
31 | return Integer.MIN_VALUE;
32 | }
33 | }
34 | res = res*10 + ch - '0';
35 | }else{
36 | break;
37 | }
38 | }
39 | return res*flag;
40 |
41 | }
42 | }
--------------------------------------------------------------------------------
/code/74.java:
--------------------------------------------------------------------------------
1 | class Solution {
2 | public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
3 | if (root == null)
4 |
5 | return null;
6 |
7 |
8 |
9 | if (root.val > p.val && root.val > q.val)
10 |
11 | return lowestCommonAncestor(root.left, p, q);
12 |
13 | if (root.val < p.val && root.val < q.val)
14 |
15 | return lowestCommonAncestor(root.right, p, q);
16 |
17 |
18 |
19 | return root;
20 |
21 | }
22 |
23 | }
--------------------------------------------------------------------------------
/code/75.java:
--------------------------------------------------------------------------------
1 | class Solution {
2 | public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
3 | if(root == null) return null;
4 | if(root == p || root == q) return root;
5 | TreeNode left = lowestCommonAncestor(root.left, p, q);
6 | TreeNode right = lowestCommonAncestor(root.right, p, q);
7 | if(left != null && right != null) return root;
8 | return left != null ? left : right;
9 | }
10 | }
--------------------------------------------------------------------------------
/code/8.java:
--------------------------------------------------------------------------------
1 | class Solution {
2 | public int numWays(int n) {
3 | if (n == 0) return 1;
4 | if (n <= 2) return n;
5 | int[] res = new int[n + 1];
6 | res[1] = 1;
7 | res[2] = 2;
8 | for (int i = 3; i <= n; i++){
9 | res[i] = (res[i - 1] + res[i - 2]) % 1000000007;
10 | }
11 | return res[n];
12 | }
13 | }
--------------------------------------------------------------------------------
/code/9.java:
--------------------------------------------------------------------------------
1 | class Solution {
2 | public int minArray(int[] nums) {
3 | if(nums.length==0)
4 |
5 | {
6 | return 0;
7 |
8 | }
9 |
10 | int left=0,right=nums.length-1;
11 |
12 | int mid=0;
13 |
14 | while(leftnums[right])
27 |
28 | {
29 | left = mid+1;
30 |
31 | }
32 |
33 | else{
34 | right--;
35 |
36 | }
37 |
38 | }
39 |
40 | return nums[right];
41 |
42 | }
43 |
44 | }
--------------------------------------------------------------------------------
/data-structure/DisjointSets.md:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/Xunzhuo/Algorithm-Guide/019eafeaa5de25e24030ea31f5c0b5d3aee982eb/data-structure/DisjointSets.md
--------------------------------------------------------------------------------
/data-structure/graph.md:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/Xunzhuo/Algorithm-Guide/019eafeaa5de25e24030ea31f5c0b5d3aee982eb/data-structure/graph.md
--------------------------------------------------------------------------------
/data-structure/heap.md:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/Xunzhuo/Algorithm-Guide/019eafeaa5de25e24030ea31f5c0b5d3aee982eb/data-structure/heap.md
--------------------------------------------------------------------------------
/data-structure/key-path.md:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/Xunzhuo/Algorithm-Guide/019eafeaa5de25e24030ea31f5c0b5d3aee982eb/data-structure/key-path.md
--------------------------------------------------------------------------------
/data-structure/kruskal.md:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/Xunzhuo/Algorithm-Guide/019eafeaa5de25e24030ea31f5c0b5d3aee982eb/data-structure/kruskal.md
--------------------------------------------------------------------------------
/data-structure/line-tree.md:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/Xunzhuo/Algorithm-Guide/019eafeaa5de25e24030ea31f5c0b5d3aee982eb/data-structure/line-tree.md
--------------------------------------------------------------------------------
/data-structure/queue.md:
--------------------------------------------------------------------------------
1 | # 队列
2 |
3 | 队列是限定在一端进行插入,另一端进行删除特殊线性表。
4 |
5 | 就像排队买东西,排在前面的人买完东西后离开队伍(删除),而后来的人总是排在队伍未尾(插入)。
6 |
7 | 通常把队列的删除和插入分别称为出队和入队。允许出队的一端称为队头,允许入队的一端称为队尾。所有需要进队的数据项,只能从队尾进入,队列中的数据项只能从队头离去。由于总是先入队的元素先出队(先排队的人先买完东西),这种表也称为先进先出(FIFO)表。
8 |
9 | 队列可以用数组Q[m+1]来存储,数组的上界m即是队列所容许的最大容量。在队列的运算中需设两个指针:
10 |
11 | head:队头指针,指向实际队头元素的前一个位置
12 |
13 | tail:队尾指针,指向实际队尾元素所在的位置
14 |
15 | 一般情况下,两个指针的初值设为0,这时队列为空,没有元素。图1 (a)画出了一个由6个元素构成的队列,数组定义Q[11]。
16 |
17 | Q[i] i=3,4,5,6,7,8 头指针head=2,尾指针tail=8。
18 |
19 | 队列中拥有的元素个数为:L=tail-head现要让排头的元素出队,则需将头指针加1。即head=head+1这时头指针向上移动一个位置,指向Q[3],表示Q[3]已出队。见图1 (b)。
20 |
21 | 如果想让一个新元素入队,则需尾指针向上移动一个位置。即tail=tail+1这时Q[9]入队,见图1 (c)。
22 |
23 | 当队尾已经处理在最上面时,即tail=10,见图1 (d),如果还要执行入队操作,则要发生“上溢”,但实际上队列中还有三个空位置,所以这种溢出称为“假溢出”。
24 |
25 | 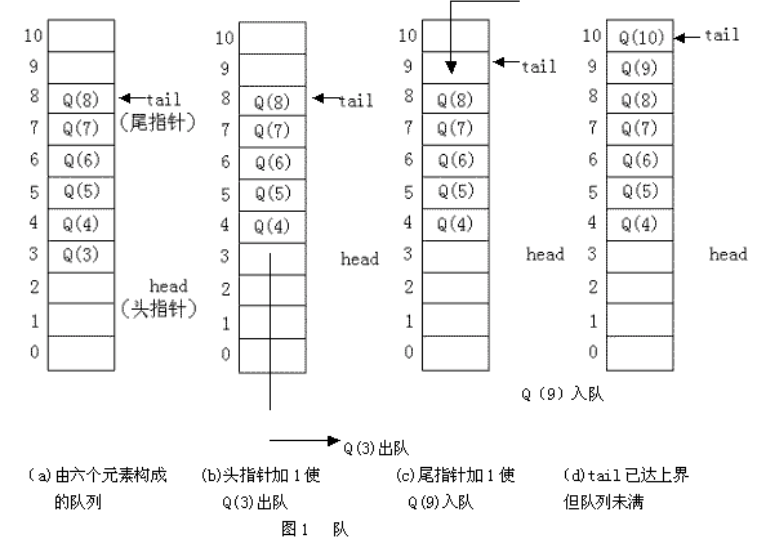
26 |
27 | 克服假溢出的方法有两种。
28 |
29 | 一种是将队列中的所有元素均向低地址区移动,显然这种方法是很浪费时间的;
30 |
31 | 另一种方法是将数组存储区看成是一个首尾相接的环形区域。当存放到n地址后,下一个地址就"翻转"为1。
32 |
33 | 在结构上采用这种技巧来存储的队列称为循环队列,见图2
34 |
35 | 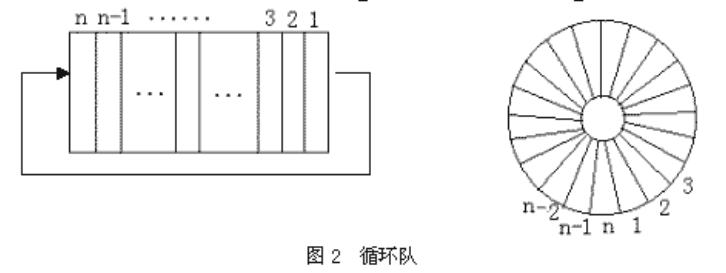
36 |
37 | 循环队的入队算法如下:
38 |
39 | 1、tail=tail+1;
40 |
41 | 2、若tail=n+1,则tail=1;
42 |
43 | 3、若head=tail尾指针与头指针重合了,表示元素已装满队列, 则作上溢出错处理;�
44 |
45 | 4、否则,Q[tail]=x,结束(x为新入出元素)。
46 |
47 | 队列和栈一样,有着非常广泛的应用。
48 |
49 | 考虑一个分时系统,如果一台计算机联有四个终端,即允许四个用户同时使用这一台计算机。
50 |
51 | 那么,计算机系统必须设立一个队列, 用以管理各终端用户使用CPU的请求。
52 |
53 | 当某个用户要求使用CPU时,相应的终端代号就入队(插入队尾),而队头的终端用户则是CPU当前服务的对象。
54 |
55 | 我们考虑最简单的情况, 对于当前用户(队头),系统每次分配一个为时间片的时间间隔,在一个时间片内,如果当前用户的作业没有结束,则该终端用户的代号出队后重新入队,插入队尾,等待下一次CPU服务。
56 |
57 | 如果某个用户的作业运行结束,则先退出,出队后不再入队,整个运行过程就是各终端代号不断地入队、出队,CPU 轮流地为n(n≤4)个终端用户服务。
58 |
59 | 由于计算机的运行速度极快,所以,对于每个终端用户来说,似乎计算机是单独在为其服务。
60 |
61 | 和线性表一样,栈和队可以采用链表存储结构,当要实现多个栈共享内存或多个队共享内存时,选择链式分配结构则更为合适。
62 |
63 | ## 例题
64 |
65 | 【例1】假设在周末舞会上,男士们和女士们进入舞厅时,各自排成一队。跳舞开始时,依次从男队和女队的队头上各出一人配成舞伴。规定每个舞曲能有一对跳舞者。若两队初始人数不相同,则较长的那一队中未配对者等待下一轮舞曲。现要求写一个程序,模拟上述舞伴配对问题。
66 |
67 | 输入:
68 |
69 | 第一行两队的人数
70 |
71 | 第二行舞曲的数目
72 |
73 | 【分析】:设计两个队列分别存放男士和女士。每对跳舞的人一旦跳完后就回到队尾等待下次被选。如m=4 n=3 k=6
74 |
75 | 
76 |
77 | ``` c
78 | 【参考程序】
79 | #include
80 | #include
81 | using namespace std;
82 | int a[10001],b[10001],k1=1,k,i,f1=1,r1,f2=1,r2;
83 | main()
84 | {
85 | int m,n;
86 | cin>>m>>n;
87 | for (i=1;i<=m;i++) a[i]=i;
88 | for (i=1;i<=n;i++) b[i]=i;
89 | cin>>k;
90 | r1=m; r2=n;
91 | while (k1<=k)
92 | {
93 | printf("%d %d\n",a[f1],b[f2]);
94 | r1++; a[r1]=a[f1]; f1++; //第一次a[m+1]=a[1]=1,第二次a[m+2]=a[2]=2,如此循环
95 | r2++; b[r2]=b[f2]; f2++; //第一次b[n+1]=b[1]=1,第二次b[n+2]=b[2]=2,如此循环。
96 | k1++;
97 | }
98 | return 0;
99 | }
100 | ```
101 |
102 | 【例2】集合的前N个元素:编一个程序,按递增次序生成集合M的最小的N个数,M的定义如下:
103 |
104 | (1)数1属于M;
105 |
106 | (2)如果X属于M,则Y=2*x+1和Z=3*x+1也属于M;
107 |
108 | (3)此外再没有别的数属于M。
109 |
110 | 【分析】
111 |
112 | 可以用两个队列a和b来存放新产生的数,然后通过比较大小决定是否输出,具体方法如下:
113 |
114 | (1)令fa和fb分别为队列a和队列b的头指针,它们的尾指针分别为ra和rb。
115 |
116 | 初始时,X=1,fa=fb=ra=rb=1;
117 |
118 | (2)将2*x+1和3*x+1分别放入队列a和队列b的队尾,尾指针加1。
119 |
120 | 即:a[r]←2*x+1,b[r]←3*x+1,r←r+1;
121 |
122 | (3)将队列a和队列b的头结点进行比较,可能有三种情况:(A)a[ha]>b[hb] (B)a[ha]=b[hb] (C)a[ha]
131 | using namespace std;
132 | int a[1001],b[1001],x=1,fa=1,fb=1,ra=0,rb=0,total=1,n,i;
133 | main()
134 | {
135 | printf("N="); scanf("%d",&n);
136 | while (total<=n)
137 | {
138 | printf("%d ",x);
139 | a[++ra]=2*x+1;
140 | b[++rb]=3*x+1;
141 | if (a[fa]>b[fb]) x=b[fb++];
142 | else if (a[fa]
174 | using namespace std;
175 | const int n=10,m=4; //设有10个人,报到4的人出列
176 | int a[n+1],j=n,k=1,p=0;
177 | main()
178 | {
179 | for (int i=1;i
222 | using namespace std;
223 | char a[51][51];
224 | bool b[51][51];
225 | int n,m,i,j,s=0,c[5]={1,0,-1,0,1};
226 | void f(int,int);
227 | main()
228 | {
229 | scanf("%d%d\n",&n,&m);
230 | for (i=0;i-1&&x+c[i]-1&&y+c[i+1]
296 | #include
297 | #include
298 | using namespace std;
299 | int dx[12]={-2,-2,-1,1,2,2,2,2,1,-1,-2,-2},
300 | dy[12]={-1,-2,-2,-2,-2,-1,1,2,2,2,2,1};
301 | int main()
302 | {
303 | int s[101][101],que[10000][4]={0},x1,y1,x2,y2;
304 | memset(s,0xff,sizeof(s)); //s数组的初始化
305 | int head=1,tail=1; //初始位置入队
306 | que[1][1]=1;que[1][2]=1;que[1][3]=0;
307 | cin>>x1>>y1>>x2>>y2; //读入黑马和白马的出发位置
308 | while(head<=tail) //若队列非空,则扩展队首结点
309 | {
310 | for(int d=0;d<=11;d++) //枚举12个扩展方向
311 | {
312 | int x=que[head][1]+dx[d]; //计算马按d方向跳跃后的位置
313 | int y=que[head][2]+dy[d];
314 | if(x>0&&y>0)
315 | if(s[x][y]==-1) //若(x,y)满足约束条件
316 | {
317 | s[x][y]=que[head][3]+1; //计算(1,1)到(x,y)的最少步数
318 | tail++; //(1,1)至(x,y)的最少步数入队
319 | que[tail][1]=x;
320 | que[tail][2]=y;
321 | que[tail][3]=s[x][y];
322 | if(s[x1][y1]>0&&s[x2][y2]>0) //输出问题的解
323 | {
324 | cout< **栈是只能在某一端插入和删除的特殊线性表。**
4 |
5 | 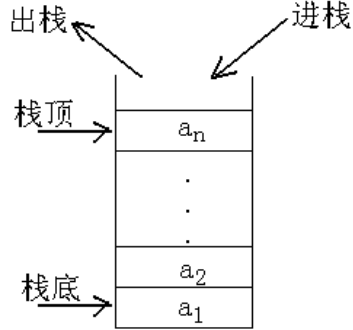
6 |
7 | 用桶堆积物品,先堆进来的压在底下,随后一件一件往上堆。取走时,只能从上面一件一件取。堆和取都在顶部进行,底部一般是不动的。
8 |
9 | 栈就是一种类似桶堆积物品的数据结构,进行删除和插入的一端称栈顶,另一堆称栈底。
10 |
11 | 插入一般称为进栈(PUSH),删除则称为退栈(POP)。 栈也称为后进先出表(LIFO表)。
12 |
13 | 一个栈可以用定长为N的数组S来表示,用一个栈指针TOP指向栈顶。
14 |
15 | 若TOP=0,表示栈空,TOP=N时栈满。进栈时TOP加1。退栈时TOP减1。
16 |
17 | 当TOP<0时为下溢。栈指针在运算中永远指向栈顶。
18 |
19 | ### 1、进栈(PUSH)算法
20 |
21 | ①若TOP≥n时,则给出溢出信息,作出错处理(进栈前首先检查栈是否已满,满则溢出;不满则作②)
22 |
23 | ②TOP++(栈指针加1,指向进栈地址);
24 |
25 | ③S[TOP]=X,结束(X为新进栈的元素);
26 |
27 | ### 2、退栈(POP)算法
28 | ①若TOP≤0,则给出下溢信息,作出错处理(退栈前先检查是否已为空栈, 空则下溢;不空则作②);
29 |
30 | ②X=S[TOP],(退栈后的元素赋给X);
31 |
32 | ③TOP--,结束(栈指针减1,指向栈顶)。
33 |
34 | 进栈、出栈的c++实现过程程序:
35 |
36 | ``` c
37 | #define n 100
38 | void push(int s[],int *top,int *x) //入栈
39 | {
40 | if (*top==n) printf("overflow");
41 | else { (*top)++; s[*top]=*x; }
42 | }
43 | void pop(int s[],int *y,int *top) //出栈
44 | {
45 | if (*top==0) printf("underflow");
46 | else { *y=s[*top]; (*top)--; }
47 | }
48 | ```
49 |
50 | 对于出栈运算中的“下溢”,程序中仅给出了一个标志信息,而在实际应用中,下溢可用来作为控制程序转移的判断标志,是十分有用的。
51 |
52 | 对于入栈运算中的“上溢”,则是一种致命的错误,将使程序无法继续运行,所以要设法避免。
53 |
54 | 堆栈的数组模拟
55 |
56 | 十进制数N和其它d进制数的转换是实现计算的基本问题,解决方法很多,下面给出一种算法原理:
57 |
58 | `N=(N / d)×d+N % d` (其中 / 为整除运算,%为求余运算)。
59 |
60 | 例如:(1348)10=(2504)8运算过程如下:
61 |
62 | 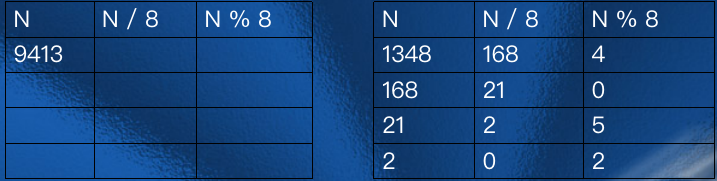
63 |
64 | ## 例题:
65 |
66 | 【例1】括号的匹配(表达式的合法性检查)
67 |
68 | 【问题描述】
69 |
70 | 假设一个表达式有英文字母(小写)、运算符(+,—,*,/)和左右小(圆)括号构成,以“@”作为表达式的结束符。请编写一个程序检查表达式中的左右圆括号是否匹配,若匹配,则返回“YES”;否则返回“NO”。假设表达式长度小于255,左圆括号少于20个。
71 |
72 | 【算法分析】
73 |
74 | 假设输入的字符串存储在c中(`char c[256]` )。
75 |
76 | 我们可以定义一个栈:`char s[maxn+1]; int top;`
77 |
78 | 用它来存放表达式中从左往右的左圆括号(maxn=20)。
79 |
80 | 算法的思路为:
81 |
82 | 顺序(从左往右)扫描表达式的每个字符c[i],若是“(”,则让它进栈;若遇到的是“)”,则让栈顶元素出栈;当栈发生下溢或当表达式处理完毕而栈非空时,都表示不匹配,返回“NO”;否则表示匹配,返回“YES”。
83 |
84 | ``` c
85 | #include
86 | #include
87 | using namespace std;
88 | #define maxn 20
89 | char c[256];
90 | bool judge(char c[256])
91 | {
92 | int top=0,i=0;
93 | while (c[i]!='@')
94 | {
95 | if (c[i]=='(') top++;
96 | if (c[i]==')')
97 | {
98 | if (top>0) top--;
99 | else return 0;
100 | }
101 | i++;
102 | }
103 | if (top!=0) return 0; //检测栈是否为空。不空则说明有未匹配的括号
104 | else return 1;
105 | }
106 | main()
107 | {
108 | scanf("%s",c);
109 | if (judge(c))printf("YES");
110 | else printf("NO");
111 | system("pause");
112 | return 0;
113 | }
114 |
115 | ```
116 |
117 |
118 |
119 | 【例2】编程求一个后缀表达式的值
120 |
121 | 【问题描述】
122 |
123 | 从键盘读入一个后缀表达式(字符串),只含有0-9组成的运算数及加(+)、减(—)、乘(`*`)、除(/)四种运算符。每个运算数之间用一个空格隔开,不需要判断给你的表达式是否合法。以@作为结束标志
124 |
125 | 【算法分析】
126 |
127 | 后缀表达式的处理过程很简单,过程如下:扫描后缀表达式,凡遇操作数则将之压进堆栈,遇运算符则从堆栈中弹出两个操作数进行该运算,将运算结果压栈,然后继续扫描,直到后缀表达式被扫描完毕为止,此时栈底元素即为该后缀表达式的值。
128 |
129 | 比如,16–9*(4+3)转换成后缀表达式为:16□9□4□3□+*–,在字符数组A中的形式为:
130 |
131 | 
132 |
133 | 栈中的变化情况:
134 |
135 | 
136 |
137 | 运行结果:-47
138 |
139 | ``` c
140 | #include
141 | #include
142 | #include
143 | #include
144 | using namespace std;
145 | int stack[101];
146 | char s[256];
147 | int comp(char s[256])
148 | {
149 | int i=0,top=0,x,y;
150 | while (i<=strlen(s)-2)
151 | {
152 | switch (s[i])
153 | {
154 | case '+':stack[--top]+=stack[top+1]; break;
155 | case '-':stack[--top]-=stack[top+1]; break;
156 | case '*':stack[--top]*=stack[top+1]; break;
157 | case '/':stack[--top]/=stack[top+1]; break;
158 | default:x=0; while (s[i]!=' ') x=x*10+s[i++]-'0'; stack[++top]=x; break;
159 | }
160 | i++;
161 | } //while
162 | return stack[top];
163 | }
164 |
165 | main()
166 | {
167 | printf("input a string(@_over):");
168 | gets(s);
169 | printf("result=%d",comp(s));
170 | system("pause");
171 | return 0;
172 | }
173 |
174 | ```
175 |
176 | 栈的用途极为广泛,在源程序编译中表达式的计算、过程的嵌套调用和递归调用等都要用到栈,下面以表达式计算为例子加以说明。
177 |
178 | 源程序编译中,若要把一个含有表达式的赋值语句翻译成正确求值的机器语言,首先应正确地解释表达式。例如,对赋值语句X=4+8×2-3; (式 11.1)
179 |
180 | 其正确的计算结果应该是17,但若在编译程序中简单地按自左向右扫描的原则进行计算,则为:X=12×2-3=24-3=21.这结果显然是错误的。
181 |
182 | 因此,为了使编译程序能够正确地求值,必须事先规定求值的顺序和规则。通常采用运算符优先数法
183 |
184 | 一般表达式中会遇到操作数、运算符和语句结束符等,以算术运算符为例,对每种运算赋予一个优先数,如:
185 |
186 | 运算符:× ÷ + -
187 |
188 | 优先数:2 2 1 1(语句结束符“;”的优先数为零)
189 |
190 | 在运算过程中,优先数高的运算符应先进行运算(但遇到括号时,应另作处理)。按这样的规定,对式(11.1)自左向右进行运算时,其计算顺序就被唯一地确定下来了。计算顺序确定后,在对表达式进行编译时,一般设立两个栈,一个称为运算符栈(OPS),另一个称为操作数栈(OVS),以便分别存放表达式中的运算符和操作数。编译程序自左向右扫描表达式直至语句结束,其处理原则是:
191 |
192 | ①凡遇到操作数,一律进入操作数栈;
193 |
194 | ②当遇到运算符时,则将运算符的优先数与运算符栈中的栈顶元素的优先
195 |
196 | 数相比较;若该运算符的优先数大,则进栈;反之,则取出栈顶的运算符,并在操作数栈中连续取出两个栈顶元素作为运算对象进行运算,并将运算结果存入操作数栈,然后继续比较该运算符与栈顶元素的优先数。
197 |
198 | 例如式(11.1)中,当扫描到“+”和“×”时都要将运算符入栈。接着扫描到“-”号, 其优先数小于乘号所以乘号退栈,并执行8×2,将结果16再存入操作数栈。
199 |
200 | 再将“-”号的优先数与运算符栈的栈顶元素“+”号的优先数相比较,两者相等,所以再将加号退栈,进行4+16,结果为20,再入栈,接着,由于运算栈已空,所以减号入栈。
201 |
202 | 当扫描到“3”时,操作数入栈。当扫描到“;”时,其优先数最低, 所以减号退栈并执行20-3,结果为17并入栈。因已扫描到语句结束符,所以表达式的求值结束,结果为17。
203 |
204 | 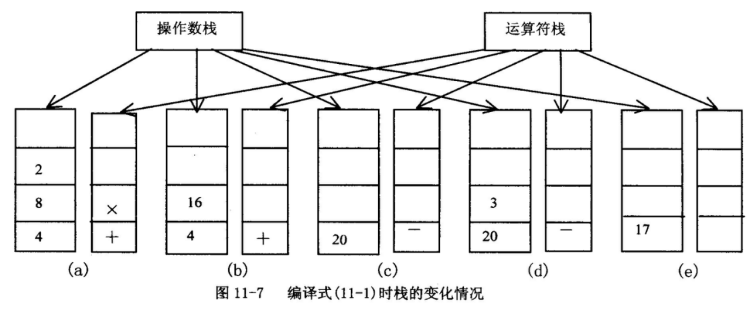
205 |
206 | 【例3】模拟计算机处理算术表达式过程。从键盘上输入算术表达式串(只含+、-、×、÷运算符,允许含括号),输出算术表达式的值。设输入的表达式串是合法的。
207 | 【算法分析】
208 | 建立两个栈,一个是操作数栈(number),一个是运算符栈(symbol),根据运算符的优先级对两个栈进行相应的操作。
209 |
210 | ``` c
211 | #include
212 | #include
213 | #include
214 | #include
215 | using namespace std;
216 | int number[101],i=0, p=1;
217 | char symbol[101],s[256], t[256];
218 | void push() //算符入栈运算
219 | {
220 | symbol[++p]=s[i];
221 | }
222 | void pop() //运算符栈顶元素出栈,并取出操作数栈元素完成相应的运算
223 | {
224 | switch (symbol[p--])
225 | {
226 | case '+':number[p]+=number[p + 1];break;
227 | case '-':number[p]-=number[p + 1];break;
228 | case '*':number[p]*=number[p + 1];break;
229 | case '/':number[p]/=number[p + 1];break;
230 | }
231 | }
232 | bool can() //判断运算符的优先级别,建立标志函数
233 | {
234 | if ((s[i]=='+'||s[i]=='-')&&symbol[p]!='(') return 1;
235 | if ((s[i]=='*'||s[i]=='/')&&(symbol[p]=='*'||symbol[p]=='/'))return 1;
236 | return 0;
237 | }
238 | main()
239 | {
240 | printf("String :");gets(s);
241 | s[strlen(s)]=')';symbol[p]='(';
242 | while (i='0'&&s[i]<='9') //取数入操作数栈
250 | x=x*10+s[i++]-'0';
251 | number[p]=x;
252 | do
253 | {
254 | if (s[i]==')') //右括号处理
255 | {
256 | while (symbol[p]!='(') pop();
257 | number[--p]=number[p + 1];
258 | }
259 | else
260 | { //根据标志函数值作运算符入栈或出栈运算处理
261 | while (can()) pop();
262 | push();
263 | }
264 | i++;
265 | }while (i