├── README.md
├── fig
├── Snipaste_2023-04-30_18-08-31.png
├── eigen.jpg
├── image-20230501195619748.png
├── image-20230501195741172.png
├── image-20230501200950919.png
├── image-20230501211952713.png
├── image-20230501213900620.png
├── image-20230501214031426.png
├── image-20230501214155104.png
├── image-20230501214253550.png
├── image-20230506102019638.png
├── image-20230508233120113.png
├── image-20230511143006297.png
├── image-20230512204137442.png
├── image-20230512204431253.png
├── image-20230512211245183.png
├── image-20230513155646122.png
├── image-20230517175030220.png
├── image-20230517234638119.png
├── image-20230518000751175.png
├── image-20230518000811831.png
├── image-20230518001043223.png
├── image-20230518005615452.png
├── image-20230518005635830.png
├── image-20230518083519018.png
├── image-20230518091103967.png
├── image-20230518091125854.png
├── image-20230518091141651.png
├── image-20230518091247684.png
├── image-20230518091310671.png
├── image-20230518172023048.png
├── image-20230518175054651.png
├── image-20230518175249315.png
├── image-20230518175339123.png
├── image-20230518204337091.png
├── image-20230518204551989.png
├── image-20230518204756111.png
├── image-20230518210627946.png
├── image-20230522010014858.png
├── image-20230628000546194.png
├── semidefinite
├── v2-198097c9d0728977c2f10f7ffd95a68f_720w.webp
├── v2-7602f389573cfa945a476c21203cb79a_720w.webp
└── v2-d7dee7938523a3c7f541b0b57a83827d_720w.webp
├── 人工智能.md
├── 数据结构与算法.md
├── 机器学习.md
├── 概率论与数理统计.md
├── 深度学习.md
├── 线性代数.md
├── 英文.md
├── 面经.md
├── 面经(分类).md
└── 面试.md
/README.md:
--------------------------------------------------------------------------------
1 | # 2023-NJUAI-open-day-review
2 |
3 | 在本repo里,将简要介绍
4 |
5 | - 2023年本人在南京大学人工智能学院(NJUAI)夏令营面试、笔试、机试的经历
6 | - 我收集到的往年经验贴汇总
7 | - 一些复习笔记和建议
8 |
9 | 如果觉得本repo的内容对你有帮助的话,请star!如果你有有用的信息想要补充,也欢迎pull request~
10 |
11 | ## 2023年NJUAI夏令营的大概流程
12 |
13 | - 6.16:报名,[南京大学人工智能学院 2023 年本科生开放日(夏令营)报名通知](https://ai.nju.edu.cn/8c/72/c53055a625778/page.htm)
14 | - 6.27:收到通过初选邮件
15 | - 7.11:面试
16 | - 7.12:上午机试+笔试,总共2h;下午各实验室宣讲,~我踏马吃吃吃~
17 | - 7.19:收到通过考核邮件,完结撒花!
18 |
19 | 如果你想加入南京大学人工智能学院的LAMDA实验室,还得参加LAMDA的额外考核:
20 |
21 | - 5.15:报名,[LAMDA2024](http://www.lamda.nju.edu.cn/recruit-2024/recruit-2024.html)
22 | - 5.21:收到通过初选邮件,通知次日一面
23 | - 5.22:一面。这个内容和时间因组而异,我们组是师兄面,师兄针对我的简历项目问了一些问题,时间5分钟左右
24 | - 5.25:收到通过一面邮件,通知次日二面
25 | - 5.26:二面。这个内容和时间也是因组而异,我们组是本校同学线下和导师面谈(三个人一起,谈了差不多2h),外校同学应该是线上
26 | - 6.1:收到通过考核邮件
27 |
28 |
29 |
30 | 考核面试150分(综合能力120,英文30分);机试50分,笔试100分。下面介绍本人的夏令营面试、机试、笔试的经历:
31 |
32 | ## 面试
33 |
34 | 7.11面试。面试是分成多组,每组四个老师对一个学生的形式,时间10分钟左右。其中一位老师负责问英文问题,其他老师问专业相关的问题。考察范围较广,问题比较灵活,每个老师会问自己更熟悉的领域里的问题。(但是好好复习可以cover到不少,不用太慌张!)
35 |
36 | 我被问到的问题有(有个别我忘掉了,就没有写):
37 |
38 | - 为什么F1 score使用precision和recall调和平均,而不是它们的算术平均?(节奏很快,根本想不出来,直接私密马赛)
39 | - SVM中被分错的向量是不是支持向量?
40 | - K-means有没有什么更好的初始化方法?
41 | - zero-shot是什么?(因为我的项目涉及到CLIP)
42 | - 斐波那契数列有什么求法,时间复杂度分别是多少?
43 | - 决策树是不是一种DP?
44 | - 特征值、特征向量的定义是什么?在线性变换的场景下有什么意义?
45 | - 常见的激活函数以及它们各自的特点
46 | - 关于我项目的英文问题(我有一个王者荣耀MARL的项目,问我MOBA指什么?如何实现多英雄合作?我还有一个与Diffusion有关的项目,老师问我Diffusion的原理)
47 |
48 | ## 机试+笔试
49 |
50 | 7.12 9:30-11:30一共两个小时,线下在机房考试。时间紧,建议拿到卷子就狂写,不会就跳,否则肯定写不完。
51 |
52 | 机试50分,一共两题,一题数据结构与算法(语言自选,C/C++,Python,Java均可),一题机器学习(Python)。有VSCode等IDE可以用。
53 |
54 | - 数据结构与算法:最长连续不重复子串,类似于力扣里[3. 无重复字符的最长子串](https://leetcode.cn/problems/longest-substring-without-repeating-characters/)(好巧之前面实习的时候做过了)
55 | - 机器学习:三小问
56 | - 实现对多个坐标组成的两个矩阵计算曼哈顿距离和欧式距离
57 | - 使用前一问的距离函数实现KNN
58 | - 实现NCM,之前没有学过但是会介绍算法。如果熟悉机器学习相关代码的实现应该不算难,但是时间来不及了qaq
59 |
60 |
61 |
62 | 笔试100分,10道填空,13道简答,用纸笔答题(听学长学姐说都是选择题,情报大错误)。涉及的范围很广,包括数据结构与算法,概率论,机器学习,凸优化,知识表示等。下面介绍一些我还记得的内容:
63 |
64 | - 数据结构与算法:题目很多,涉及树、堆、图等。题目有:写出给定数据的heap sort过程,一些关于树的计算,森林和其转化的树的x序遍历等价关系等。
65 | - 概率论:没有什么计算,主要是概念。比如说中心极限定理是什么这样的问题。
66 | - 机器学习:有一题是Adaboost训练准确率到1后可以继续训练,测试集准确率还有可能上升,对这件事归因。其他忘了,总之是除了记得书中内容之外,还需要融会贯通思考才能答出的问题。
67 | - 凸优化:给出一个函数,写出它的Dual function和KKT条件。
68 | - 知识表示:五道题,英文,主要和model与一阶逻辑有关。有一道题是给定自然语言句子用一阶逻辑表示,有一道题是判断一些statements的正误。总之不咋会,泪目了。
69 |
70 | ## 个人的一些建议
71 |
72 | 下面是个人关于准备夏令营的一些建议,仅供参考。此外我的笔记见下面的表格。
73 |
74 | ### 关于面试
75 |
76 | - 考察范围包括但不限于:机器学习、神经网络、人工智能、概率论、线性代数、数据结构和算法、凸优化、数字信号处理、离散数学、一些智力题(比如说双蛋问题)、简历上做过的项目。复习的时候尽量多看一些,面试时遇到不会的不要慌张,直接说不太会,老师会接着问其他问题的。
77 | - 英文:准备英文自我介绍,常见问题,熟悉简历上项目的英文表达。
78 |
79 | ### 关于笔试
80 |
81 | 如果时间有限,建议优先复习机器学习、数据结构与算法、概率论,这三个在考察中占比较大。
82 |
83 | - 机器学习:认真看完西瓜书前10章,不要仅局限于背记定义,尽量多多思考。在回顾西瓜书的过程中,我发现一些算法之间的联系,理解了一些公式这样设计的原因,感觉收获颇丰。
84 | - 数据结构与算法:我是用的王道计算机考研数据结构书复习的(花了五块钱买了电子书),把整本书看完+做完了书中的所有例题。个人感觉和考试的拟合程度还是比较高的。考研书中经常有一些小结论,有的恰好撞上了,也算是比较巧。如果你是和我一样有点阅读障碍、有时候会漏过重点的人,不妨在看完知识点后做一些题,这样也可以补全看漏的知识点。
85 | - 概率论:看gw老师的概率论笔记,做做上面的例题;旁听人工智能综合基础gw老师讲概率论的部分。在此之外我还做了李永乐数一660的概率论部分,不过考试时没怎么用到。
86 |
87 | - 知识表示:回顾赵老师KR的前几节课的PPT,做做他当时mock exam相应的题目。(可惜我没看)
88 | - 凸优化:复习常见的概念,比如凸函数,对偶函数,KKT条件等。这方面我没有太多经验,毕竟自己复习也没太cover到。
89 | - 此外还可以旁听人工智能综合基础课程,看它的PPT复习。
90 |
91 | ### 关于机试
92 |
93 | - 数据结构与算法的题目用[力扣](https://leetcode.cn/)刷题即可,2023的题目是力扣medium的难度。如果想系统地刷一些基础算法的题可以看看[AcWing算法基础课](https://www.acwing.com/activity/content/11/)(我还买了个号,但是没做几题,不过借给网友了所以也不算亏)。
94 | - 机器学习机试刷题可以看头歌平台上的[机器学习原理与实践](https://www.educoder.net/paths/cuhv94tf),这个课程的参考书是西瓜书,教学团队里有NJUAI的教授,内容和考核还是比较拟合的。
95 |
96 | ### 关于找导师
97 |
98 | - 今年夏令营报名时要求填写志愿导师,不过好像没什么影响。此外,学院要求通过的同学在20日内提交有一位导师签字的申请表,表示导师愿意接收你。
99 | - 据我了解NJUAI的导师人都挺好的,没有所谓的“坑导”。主要还是看导师的研究方向和风格与自己是否契合,具体可以找学长学姐咨询。
100 | - 如果目标是NJUAI的的话,可以提前联系导师进组听组会等,这样可以进一步了解组里的研究方向,认识导师和学长学姐,对未来有一定帮助。
101 | - 导师名录在[人工智能学院教师](https://ai.nju.edu.cn/people/list.htm),LAMDA导师名录在[LAMDA成员](http://www.lamda.nju.edu.cn/CH.People.ashx#教师_1),此外还有NLP、MCG、RINC等组的老师。
102 |
103 | ### 我的整理和笔记
104 |
105 | 下面是我复习中做的一些整理和笔记。请注意:这只是本人在学习过程中的一些整理,有许多地方还没有整理到,还可能会有一些纰漏,还望包涵\~
106 |
107 | | Description | Link |
108 | | --------------------------------------------------- | ------------------------------------------------------------ |
109 | | 在互联网上收集的NJUAI往年面经和链接,按照年份分类 | [面经.md](https://github.com/YuRuiii/2023-NJUAI-open-day-review/blob/main/面经.md) |
110 | | 在互联网上收集的NJUAI往年面经和链接,按照科目分类 | [面经(分类).md](https://github.com/YuRuiii/2023-NJUAI-open-day-review/blob/main/面经(分类).md) |
111 | | 根据往年/今年面经,结合我的复习,猜测整理的高频问题 | [面试.md](https://github.com/YuRuiii/2023-NJUAI-open-day-review/blob/main/面试.md) |
112 | | 个人机器学习复习整理 | [机器学习.md](https://github.com/YuRuiii/2023-NJUAI-open-day-review/blob/main/机器学习.md) |
113 | | 个人数据结构与算法复习整理 | [数据结构与算法.md](https://github.com/YuRuiii/2023-NJUAI-open-day-review/blob/main/数据结构与算法.md) |
114 | | 个人概率论与数理统计复习整理 | [概率论与数理统计.md](https://github.com/YuRuiii/2023-NJUAI-open-day-review/blob/main/概率论与数理统计.md) |
115 | | 个人人工智能复习整理 | [人工智能.md](https://github.com/YuRuiii/2023-NJUAI-open-day-review/blob/main/人工智能.md) |
116 | | 个人深度学习复习整理 | [深度学习.md](https://github.com/YuRuiii/2023-NJUAI-open-day-review/blob/main/深度学习.md) |
117 | | 个人线性代数复习整理 | [线性代数.md](https://github.com/YuRuiii/2023-NJUAI-open-day-review/blob/main/线性代数.md) |
118 | | 整理了一些常见的英文问题,但是都没用到 | [英文.md](https://github.com/YuRuiii/2023-NJUAI-open-day-review/blob/main/英文.md) |
119 |
120 | ## 致谢
121 |
122 | 感谢学长学姐们耐心的答疑解惑,感谢同学们的互相帮助,感谢朋友们一直以来的关心与支持。也希望这个repo的内容也能帮助到你。
--------------------------------------------------------------------------------
/fig/Snipaste_2023-04-30_18-08-31.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/YuRuiii/2023-NJUAI-open-day-review/05b88cc2f0fb494a804e6c21b2b99e9520ab1b3c/fig/Snipaste_2023-04-30_18-08-31.png
--------------------------------------------------------------------------------
/fig/eigen.jpg:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/YuRuiii/2023-NJUAI-open-day-review/05b88cc2f0fb494a804e6c21b2b99e9520ab1b3c/fig/eigen.jpg
--------------------------------------------------------------------------------
/fig/image-20230501195619748.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/YuRuiii/2023-NJUAI-open-day-review/05b88cc2f0fb494a804e6c21b2b99e9520ab1b3c/fig/image-20230501195619748.png
--------------------------------------------------------------------------------
/fig/image-20230501195741172.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/YuRuiii/2023-NJUAI-open-day-review/05b88cc2f0fb494a804e6c21b2b99e9520ab1b3c/fig/image-20230501195741172.png
--------------------------------------------------------------------------------
/fig/image-20230501200950919.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/YuRuiii/2023-NJUAI-open-day-review/05b88cc2f0fb494a804e6c21b2b99e9520ab1b3c/fig/image-20230501200950919.png
--------------------------------------------------------------------------------
/fig/image-20230501211952713.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/YuRuiii/2023-NJUAI-open-day-review/05b88cc2f0fb494a804e6c21b2b99e9520ab1b3c/fig/image-20230501211952713.png
--------------------------------------------------------------------------------
/fig/image-20230501213900620.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/YuRuiii/2023-NJUAI-open-day-review/05b88cc2f0fb494a804e6c21b2b99e9520ab1b3c/fig/image-20230501213900620.png
--------------------------------------------------------------------------------
/fig/image-20230501214031426.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/YuRuiii/2023-NJUAI-open-day-review/05b88cc2f0fb494a804e6c21b2b99e9520ab1b3c/fig/image-20230501214031426.png
--------------------------------------------------------------------------------
/fig/image-20230501214155104.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/YuRuiii/2023-NJUAI-open-day-review/05b88cc2f0fb494a804e6c21b2b99e9520ab1b3c/fig/image-20230501214155104.png
--------------------------------------------------------------------------------
/fig/image-20230501214253550.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/YuRuiii/2023-NJUAI-open-day-review/05b88cc2f0fb494a804e6c21b2b99e9520ab1b3c/fig/image-20230501214253550.png
--------------------------------------------------------------------------------
/fig/image-20230506102019638.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/YuRuiii/2023-NJUAI-open-day-review/05b88cc2f0fb494a804e6c21b2b99e9520ab1b3c/fig/image-20230506102019638.png
--------------------------------------------------------------------------------
/fig/image-20230508233120113.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/YuRuiii/2023-NJUAI-open-day-review/05b88cc2f0fb494a804e6c21b2b99e9520ab1b3c/fig/image-20230508233120113.png
--------------------------------------------------------------------------------
/fig/image-20230511143006297.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/YuRuiii/2023-NJUAI-open-day-review/05b88cc2f0fb494a804e6c21b2b99e9520ab1b3c/fig/image-20230511143006297.png
--------------------------------------------------------------------------------
/fig/image-20230512204137442.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/YuRuiii/2023-NJUAI-open-day-review/05b88cc2f0fb494a804e6c21b2b99e9520ab1b3c/fig/image-20230512204137442.png
--------------------------------------------------------------------------------
/fig/image-20230512204431253.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/YuRuiii/2023-NJUAI-open-day-review/05b88cc2f0fb494a804e6c21b2b99e9520ab1b3c/fig/image-20230512204431253.png
--------------------------------------------------------------------------------
/fig/image-20230512211245183.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/YuRuiii/2023-NJUAI-open-day-review/05b88cc2f0fb494a804e6c21b2b99e9520ab1b3c/fig/image-20230512211245183.png
--------------------------------------------------------------------------------
/fig/image-20230513155646122.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/YuRuiii/2023-NJUAI-open-day-review/05b88cc2f0fb494a804e6c21b2b99e9520ab1b3c/fig/image-20230513155646122.png
--------------------------------------------------------------------------------
/fig/image-20230517175030220.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/YuRuiii/2023-NJUAI-open-day-review/05b88cc2f0fb494a804e6c21b2b99e9520ab1b3c/fig/image-20230517175030220.png
--------------------------------------------------------------------------------
/fig/image-20230517234638119.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/YuRuiii/2023-NJUAI-open-day-review/05b88cc2f0fb494a804e6c21b2b99e9520ab1b3c/fig/image-20230517234638119.png
--------------------------------------------------------------------------------
/fig/image-20230518000751175.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/YuRuiii/2023-NJUAI-open-day-review/05b88cc2f0fb494a804e6c21b2b99e9520ab1b3c/fig/image-20230518000751175.png
--------------------------------------------------------------------------------
/fig/image-20230518000811831.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/YuRuiii/2023-NJUAI-open-day-review/05b88cc2f0fb494a804e6c21b2b99e9520ab1b3c/fig/image-20230518000811831.png
--------------------------------------------------------------------------------
/fig/image-20230518001043223.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/YuRuiii/2023-NJUAI-open-day-review/05b88cc2f0fb494a804e6c21b2b99e9520ab1b3c/fig/image-20230518001043223.png
--------------------------------------------------------------------------------
/fig/image-20230518005615452.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/YuRuiii/2023-NJUAI-open-day-review/05b88cc2f0fb494a804e6c21b2b99e9520ab1b3c/fig/image-20230518005615452.png
--------------------------------------------------------------------------------
/fig/image-20230518005635830.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/YuRuiii/2023-NJUAI-open-day-review/05b88cc2f0fb494a804e6c21b2b99e9520ab1b3c/fig/image-20230518005635830.png
--------------------------------------------------------------------------------
/fig/image-20230518083519018.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/YuRuiii/2023-NJUAI-open-day-review/05b88cc2f0fb494a804e6c21b2b99e9520ab1b3c/fig/image-20230518083519018.png
--------------------------------------------------------------------------------
/fig/image-20230518091103967.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/YuRuiii/2023-NJUAI-open-day-review/05b88cc2f0fb494a804e6c21b2b99e9520ab1b3c/fig/image-20230518091103967.png
--------------------------------------------------------------------------------
/fig/image-20230518091125854.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/YuRuiii/2023-NJUAI-open-day-review/05b88cc2f0fb494a804e6c21b2b99e9520ab1b3c/fig/image-20230518091125854.png
--------------------------------------------------------------------------------
/fig/image-20230518091141651.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/YuRuiii/2023-NJUAI-open-day-review/05b88cc2f0fb494a804e6c21b2b99e9520ab1b3c/fig/image-20230518091141651.png
--------------------------------------------------------------------------------
/fig/image-20230518091247684.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/YuRuiii/2023-NJUAI-open-day-review/05b88cc2f0fb494a804e6c21b2b99e9520ab1b3c/fig/image-20230518091247684.png
--------------------------------------------------------------------------------
/fig/image-20230518091310671.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/YuRuiii/2023-NJUAI-open-day-review/05b88cc2f0fb494a804e6c21b2b99e9520ab1b3c/fig/image-20230518091310671.png
--------------------------------------------------------------------------------
/fig/image-20230518172023048.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/YuRuiii/2023-NJUAI-open-day-review/05b88cc2f0fb494a804e6c21b2b99e9520ab1b3c/fig/image-20230518172023048.png
--------------------------------------------------------------------------------
/fig/image-20230518175054651.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/YuRuiii/2023-NJUAI-open-day-review/05b88cc2f0fb494a804e6c21b2b99e9520ab1b3c/fig/image-20230518175054651.png
--------------------------------------------------------------------------------
/fig/image-20230518175249315.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/YuRuiii/2023-NJUAI-open-day-review/05b88cc2f0fb494a804e6c21b2b99e9520ab1b3c/fig/image-20230518175249315.png
--------------------------------------------------------------------------------
/fig/image-20230518175339123.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/YuRuiii/2023-NJUAI-open-day-review/05b88cc2f0fb494a804e6c21b2b99e9520ab1b3c/fig/image-20230518175339123.png
--------------------------------------------------------------------------------
/fig/image-20230518204337091.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/YuRuiii/2023-NJUAI-open-day-review/05b88cc2f0fb494a804e6c21b2b99e9520ab1b3c/fig/image-20230518204337091.png
--------------------------------------------------------------------------------
/fig/image-20230518204551989.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/YuRuiii/2023-NJUAI-open-day-review/05b88cc2f0fb494a804e6c21b2b99e9520ab1b3c/fig/image-20230518204551989.png
--------------------------------------------------------------------------------
/fig/image-20230518204756111.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/YuRuiii/2023-NJUAI-open-day-review/05b88cc2f0fb494a804e6c21b2b99e9520ab1b3c/fig/image-20230518204756111.png
--------------------------------------------------------------------------------
/fig/image-20230518210627946.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/YuRuiii/2023-NJUAI-open-day-review/05b88cc2f0fb494a804e6c21b2b99e9520ab1b3c/fig/image-20230518210627946.png
--------------------------------------------------------------------------------
/fig/image-20230522010014858.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/YuRuiii/2023-NJUAI-open-day-review/05b88cc2f0fb494a804e6c21b2b99e9520ab1b3c/fig/image-20230522010014858.png
--------------------------------------------------------------------------------
/fig/image-20230628000546194.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/YuRuiii/2023-NJUAI-open-day-review/05b88cc2f0fb494a804e6c21b2b99e9520ab1b3c/fig/image-20230628000546194.png
--------------------------------------------------------------------------------
/fig/semidefinite:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/YuRuiii/2023-NJUAI-open-day-review/05b88cc2f0fb494a804e6c21b2b99e9520ab1b3c/fig/semidefinite
--------------------------------------------------------------------------------
/fig/v2-198097c9d0728977c2f10f7ffd95a68f_720w.webp:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/YuRuiii/2023-NJUAI-open-day-review/05b88cc2f0fb494a804e6c21b2b99e9520ab1b3c/fig/v2-198097c9d0728977c2f10f7ffd95a68f_720w.webp
--------------------------------------------------------------------------------
/fig/v2-7602f389573cfa945a476c21203cb79a_720w.webp:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/YuRuiii/2023-NJUAI-open-day-review/05b88cc2f0fb494a804e6c21b2b99e9520ab1b3c/fig/v2-7602f389573cfa945a476c21203cb79a_720w.webp
--------------------------------------------------------------------------------
/fig/v2-d7dee7938523a3c7f541b0b57a83827d_720w.webp:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/YuRuiii/2023-NJUAI-open-day-review/05b88cc2f0fb494a804e6c21b2b99e9520ab1b3c/fig/v2-d7dee7938523a3c7f541b0b57a83827d_720w.webp
--------------------------------------------------------------------------------
/人工智能.md:
--------------------------------------------------------------------------------
1 | # 人工智能
2 |
3 | ## 搜索
4 |
5 | DFS using stack (正常的递归)
6 |
7 | DFS using heap(循环,每次`heap.pop()`,再将pop出的节点的后继加入heap中,直到找到目标) p13
8 |
9 | General tree search
10 |
11 | General graph search:要考虑节点是否已经被访问
12 |
13 | 评估:完备性(如果有解,是否一定能找到),时间复杂度,空间复杂度,最优性
14 |
15 | ### Uniformed search
16 |
17 | 只使用问题定义中的信息
18 |
19 | $b$搜索树宽度,$d$解的深度;$m$状态空间的深度(可以是$\infty$),$g$路径开销
20 |
21 |  22 |
23 | - Breadth-first search
24 | - heap是FIFO queue
25 | - 完备性:如果$b$有限
26 | - Uniform-cost search
27 | - 解决边有权重的问题,Priority queue,权重最小先出栈
28 | - 当边权重为正时完备
29 | - 时空复杂度都是路径开销$\leq$最优解的节点个数
30 | - 最优性证明:
31 | - 它扩展最小成本的节点
32 | - 最优路径上的目标状态比任何次优路径上的目标状态具有更小的成本
33 | - 它永远不会在扩展最优路径上的目标状态之前,扩展次优路径上的目标状态
34 | - Depth-first search
35 | - heap是LIFO queue
36 | - 不完备:在无限深度空间、有环的空间中失败(如果有限、没有重复状态则完备)
37 |
38 | - Depth-limited search
39 |
40 | - Iterative deepening search
41 |
42 | - 对从0到$\infty$的depth,分别做Depth-limited search,直到找到结果
43 |
44 | - 时间复杂度(实际上重复搜索浪费的时间并不多):
45 | $$
46 | \begin{aligned}
47 | &b^0+(b^0+b^1)+\dots+(b^0+\dots+b^d)\\
48 | =&(d+1)b^0+db^1+\dots+b^d=O(b^d)
49 | \end{aligned}
50 | $$
51 |
52 | ### Informed Search
53 |
54 | - Greedy Search
55 |
56 | - heuristic function: $h(n)$ 为从$n$到最近目标的成本估计
57 | - 扩展**看起来**最接近目标的节点
58 | - 不完备(可以卡在环上),$T=O(b^m)$,$S=O(b^m)$,不最优
59 |
60 | - A\* Search
61 |
62 | - heuristic function: $f(n)=g(n)+h(n)$,其中$g(n)$为到目前为止达到$ n $的成本,$h(n)$为从$n$到最近目标的成本估计,$f(n)$为通过$ n $到达目标的路径的估计总成本
63 | - Admissible可接受:估值永远小于真实值,$0\leq h(n)\leq h^*(n)$
64 | - Consistent一致性:$h(n)\leq c(n,a',n')+h(n')$,其中$ n' $是由动作$ a' $生成的$ n $的后继,Consistent$\to$Admissible
65 | - 证明:对于树搜索,如果启发式函数是可接受的,则A\*最优**(重点理解)**
66 | - 假设$h$是admissible的,如果$A$是最优目标节点,$B $是次优目标节点,下证明:$A$会比$B$先扩展
67 | - 对于$A$的任意祖先$n$,证明:$n$会比$B$先扩展
68 | - 有$h(A)=h(B)=0$;$g(A)
31 |
32 | 找到一个从L1到L2的变换,使得P on x is yes iff Q on T(x) is yes。
33 |
34 | 例子:3SAT问题,是否存在赋值使得下式成立($d$可以是$a$或$\neg a$,但是不能是$e,f$,否则就不是3SAT问题)
35 |
36 | $$
37 | (a \or b\or c)\and(d \or e\or f) \and \cdots
38 | $$
39 |
40 | 顶点覆盖问题(Vertex Covering Problem)是一种组合优化问题,旨在寻找一个最小的顶点集合,使得图中的每条边都至少与该顶点集合中的一个顶点相邻。
41 |
42 | ### NP-hard
43 |
44 | 满足NP-complete的条件2即可。
45 |
46 | ## 排序算法
47 |
48 | ### 基本问题
49 |
50 | #### 排序为什么要稳定?
51 |
52 | 稳定性的定义:对于值相同的两个元素,排序后它们的先后顺序与原数组相同。
53 |
54 | 因为在某些情况下,我们需要保留原数数据中的元素的相对位置。比如说对多个关键字排序,先按照关键字1排序,在关键字1相同的情况下再按照关键字2排序,在这种情况下,如果排序算法是不稳定的,那么在排序关键字2时就会打乱关键字1的顺序。
55 |
56 | #### 为什么归并的最坏复杂度是$O(n\log n)$,快排是$O(n^2)$,但是大家用的都是快排?
57 |
58 | 因为实际上在大多数情况下,无论从时间复杂度还是空间复杂度的角度考虑,快排的性能均优于归并排序。
59 |
60 | 首先,从时间复杂度上看,平均情况下两者的时间复杂度都是$O(n\log n)$,但是由于归并排序需要进行分配和取消分配辅助数组等操作,其所需的常量时间更大。
61 |
62 | 其次,从空间复杂度上看,快速排序是原地排序in-place的,不需要额外的空间,而归并排序则需要额外分配数组。
63 |
64 | 最后,虽然在数组已有序的情况下,快排的最坏时间复杂度是$O(n^2)$,但是我们可以通过随机选取pivot而非直接使用最后一个元素,使得快排的时间复杂度是最坏情况的概率很小,甚至趋近于0。
65 |
66 | 此外,当数据存储在内存中时,快排更好;但是当数据存储在硬盘中时或数据是链表时,归并排序最好,因为它最小化了读写的时间。
67 |
68 | #### 快排为什么叫“快”排?
69 |
70 | 因为它可以比任何其他排序方法更快地(两到三倍)对数据元素列表进行排序。
71 |
72 | ### 选择排序
73 |
74 | **Selection sort** is a simple and efficient sorting algorithm that works by repeatedly selecting the smallest (or largest) element from the unsorted portion of the list and moving it to the sorted portion of the list. The algorithm repeatedly selects the smallest (or largest) element from the unsorted portion of the list and swaps it with the first element of the unsorted portion. This process is repeated for the remaining unsorted portion of the list until the entire list is sorted.
75 |
76 | 选择排序重复地选择从未排序的部分选择最小的元素,将其与未排序部分的第一个元素交换位置,再将未排序部分的第一个元素并入已排序部分。
77 |
78 | ### 插入排序
79 |
80 | **Insertion sort** is a simple sorting algorithm that works similar to the way you sort playing cards in your hands. The array is virtually split into a sorted and an unsorted part. Values from the unsorted part are picked and placed at the correct position in the sorted part.
81 |
82 | 插入排序是一种简单的排序算法,类似于你整理手中的扑克牌的方式。该算法将数组虚拟地分成已排序部分和未排序部分。从未排序部分中选出值,将它们放置到已排序部分的正确位置上。
83 |
84 | ```python
85 | def insertion_sort(arr):
86 | n = len(arr)
87 | for i in range(1, n):
88 | j = i
89 | while j > 0 and arr[j-1] > arr[j]:
90 | arr[j], arr[j-1] = arr[j-1], arr[j]
91 | ```
92 |
93 | ### 冒泡排序
94 |
95 | **Bubble Sort** is the simplest sorting algorithm that works by repeatedly swapping the adjacent elements if they are in the wrong order.
96 |
97 | 冒泡排序通过反复交换相邻的元素进行排序。
98 |
99 | ```python
100 | def bubble_sort(arr):
101 | n = len(arr)
102 | for i in range(n):
103 | for j in range(0, n-i-1): # Last i elements are already in place
104 | if arr[j] > arr[j+1]:
105 | arr[j], arr[j+1] = arr[j+1], arr[j]
106 | ```
107 |
108 | ### 快速排序
109 |
110 | **Quick Sort** is a sorting algorithm based on the Divide and Conquer algorithm that picks an element as a pivot and partitions the given array around the picked pivot by placing the pivot in its correct position in the sorted array.
111 |
112 | 快速排序是一个基于分治的思想的排序算法,每次选择一个元素作为pivot,然后将给定的数组围绕这个基准进行划分,将小于基准的元素放到基准的左边,将大于基准的元素放到基准的右边,最终将基准放置在排序后的正确位置上。
113 |
114 | ```python
115 | def quick_sort(arr, low, high):
116 | if low < high:
117 | pi = partition(arr, low, high)
118 | quick_sort(arr, low, pi-1)
119 | quick_sort(arr, pi+1, high)
120 |
121 | def partition(arr, low, high):
122 | pivot = arr[high]
123 | i = low - 1
124 | for j in range(low, high):
125 | if arr[j] < pivot:
126 | i += 1
127 | arr[i], arr[j] = arr[j], arr[i]
128 | arr[i+1], arr[high] = arr[high], arr[i+1]
129 | return i+1
130 | ```
131 |
132 | ### 快速排序时间复杂度证明
133 |
134 | 假设数组被分成大小为$j$和$n-j$的两部分,则时间复杂度为
135 |
136 | $$
137 | T(n)=T(j) + T(n-j) + cn
138 | $$
139 |
140 | 最好情况:
141 |
142 | $$
143 | \begin{aligned}
144 | T(n) &= 2T\left(\frac n2\right) + cn\\
145 | &=2 \left(2T\left(\frac n4\right)+c\cdot \frac{n}{2}\right) + cn\\
146 | &=\cdots\\
147 | &=2^{\log n} T(1) + c+2c + \dots + 2^{\log n}c\\
148 | &= nT(1)+n\log n=O(n\log n)
149 | \end{aligned}
150 | $$
151 |
152 | 最坏情况:
153 |
154 | $$
155 | T(n)=T(n-1)+cn = c(1+2+\dots+n)=O(n^2)
156 | $$
157 |
158 | 平均情况:
159 |
160 | 当index i是pivot时,
161 |
162 | $$
163 | T(n)=T(i)+T(n-i) +cn
164 | $$
165 |
166 | 所以平均时间复杂度是:
167 |
168 | $$
169 | T(n)=\frac1n\sum_{i=1}^{n-1} T(i)+\frac1n \sum_{i=1}^{n-1}T(n-i) +cn=\frac 2n\sum_{i=1}^{n-1}T(i)+cn
170 | $$
171 |
172 | 所以有:
173 |
174 | $$
175 | \begin{aligned}
176 | nT(n)&=2\sum_{i=1}^{n-1}T(i)+cn^2\\
177 | (n-1)T(n-1)&=2\sum_{i=1}^{n-2}+c(n-1)^2
178 | \end{aligned}
179 | $$
180 |
181 | 两式相减有:
182 |
183 | $$
184 | \begin{aligned}
185 | nT(n)-(n-1)T(n-1)&=2T(n-1)+2cn-c\\
186 | nT(n)&=(n+1)T(n-1)+2cn\quad (\text{remove constant c})
187 | \end{aligned}
188 | $$
189 |
190 | 两边同除$n(n+1)$
191 |
192 | $$
193 | \begin{aligned}
194 | \frac{T(n)}{n+1}=&\frac{T(n-1)}{n}+\frac{2c}{n+1}\\
195 | =&\frac{T(1)}{2}+2c\left(\frac12+\frac13+\dots+\frac1n+\frac1{n+1}\right)\\
196 | =&\frac{T(1)}{2}+2c\log n+C
197 | \end{aligned}
198 | $$
199 |
200 | 可得
201 |
202 | $$
203 | T(n)=O(n\log n)
204 | $$
205 |
206 | ### 归并排序
207 |
208 | **Merge sort** is defined as a sorting algorithm that works by dividing an array into smaller subarrays, sorting each subarray, and then merging the sorted subarrays back together to form the final sorted array.
209 |
210 | 快速排序是一个基于分治的思想的排序算法,每次将数组分为两个子数组,分别对子数组排序,再将两个子数组归并,形成最终的排序好的数组。
211 |
212 | ```python
213 | def merge_sort(arr, left, right):
214 | if left > right: return
215 | mid = (left + right) / 2
216 | merge_sort(arr, left, mid)
217 | merge_sort(arr, mid+1, right)
218 | merge(arr, left, mid, right)
219 |
220 | def merge(arr, left, mid, right):
221 | left_arr = arr[:mid]
222 | right_arr = arr[mid:]
223 | i = j = k = 0
224 | while i < len(left_arr) and j < len(right_arr):
225 | if left_arr[i] <= right_arr[j]:
226 | arr[k] = left_arr[i]
227 | i += 1
228 | else:
229 | arr[k] = right_arr[j]
230 | j += 1
231 | k += 1
232 | while i < len(left_arr):
233 | arr[k] = left_arr[i]
234 | i += 1
235 | k += 1
236 | while j < len(right_arr):
237 | arr[k] = right_arr[j]
238 | j += 1
239 | k += 1
240 | ```
241 |
242 | ### 堆排序
243 |
244 | Heap sort is a comparison-based sorting technique based on Binary Heap data structure.
245 |
246 | 堆排序是一种基于二叉堆数据结构的排序算法。首先根据未排序数组建立大顶堆,每次从堆中删除最大的元素(移动到数组末尾),再通过 `heapify`操作维护大顶堆的性质。`heapify`的具体操作为:如果根节点比左右子节点都大,则直接返回;否则交换根节点和值最大的节点,再递归地对原先值最大的节点调用 `heapify`。
247 |
248 | ```python
249 | def heapify(arr, N, i):
250 | largest = i
251 | l = 2 * i + 1
252 | r = 2 * i + 2
253 |
254 | if l < N and arr[largest] < arr[l]:
255 | largest = l
256 | if r < N and arr[largest] < arr[r]:
257 | largest = r
258 | if largest != i:
259 | arr[i], arr[largest] = arr[largest], arr[i]
260 | heapify(arr, N, largest)
261 |
262 | def heap_sort(arr):
263 | N = len(arr)
264 | for i in range(N//2-1, -1, -1):
265 | heapify(arr, N, i)
266 | for i in range(N-1, -, -1):
267 | arr[i], arr[0] = arr[0], arr[i]
268 | heapify(arr, i, 0)
269 | ```
270 |
271 | ### 计数排序
272 |
273 | Counting sort is a sorting technique based on keys between a specific range. It works by counting the number of objects having distinct key values (a kind of hashing). Then do some arithmetic operations to calculate the position of each object in the output sequence.
274 |
275 | 计数排序(Counting Sort)是一种针对于特定范围之间的整数进行排序的算法。它通过统计给定数组中不同元素的数量(类似于哈希映射),然后对映射后的数组进行排序输出即可。
276 |
277 | ```python
278 | def counting_sort(arr):
279 | count = [0 for i in range(m)]
280 | for e in arr:
281 | count[e] += 1
282 | for i in range(1, m):
283 | count[m] += count[m-1] # count[m]-1就是排序好的数组中m的最大idx
284 |
285 | for i in range(len(arr)-1, -1, -1): # 倒着遍历是为了保持in-place
286 | output[count[arr[i]]-1] = arr[i]
287 | count[arr[i]] - 1
288 |
289 | return output
290 | ```
291 |
292 | ### 基数排序
293 |
294 | Radix sort is a non-comparison sorting algorithm that separates the elements to be sorted into different digits, and then sorts them according to each digit. This process requires the use of buckets to store the data. Radix sort can handle positive integers, negative integers, and decimals.
295 |
296 | 基数排序(Radix Sort)是一种非比较排序算法,它将待排序的元素按照位数切割成不同的数字,然后按照每个位数分别比较排序。这个过程中需要使用到桶(bucket)来存储数据。基数排序可以处理正整数、负整数和小数,只要数据能用位数表示,且位数有限。
297 |
298 | 
299 |
300 | ### 桶排序
301 |
302 | Bucket sort is a sorting algorithm that works by distributing the elements of an array into a number of buckets. Each bucket is then sorted individually, either using a different sorting algorithm, or by recursively applying the bucket sorting algorithm.
303 |
304 | 桶排序(Bucket Sort)是一种排序算法,它将待排序数组的元素分配到一定数量的桶中。每个桶单独进行排序,可以使用不同的排序算法或者递归地应用桶排序算法。
305 |
306 | 
307 |
308 | ### 总结
309 |
310 | | 算法 | 选择排序 | 插入排序 | 归并排序 | 快速排序 | |
311 | | ---------- | ----------------------------------------- | ------------------------------ | ------------------------------------------------------------------ | ---------------- | - |
312 | | 额外空间 | $O(1)$ | $O(1)$ | $O(n)$ | $O(1)$,考虑栈$O(\log n)$ | |
313 | | 最好时间 | $O(n^2)$ | $o(n)$(已排序好) | $O(n\log n)$ | $O(n\log n)$ | |
314 | | 平均时间 | $O(n^2)$ | $O(n^2)$ | $O(n\log n)$ | $O(n\log n)$ | |
315 | | 最坏时间 | $O(n^2)$ | $O(n^2)$ | $O(n\log n)$ | $O(n^2)$ | |
316 | | 稳定性 | n | y | y | n | |
317 | | in-replace | y | y | n | y | |
318 | | 优点 | | 简单,小数组性能好,额外空间小 | 可并行,最坏性能有保障,对不同数据分布适应性好 | | |
319 | | 缺点 | cache性能不好,读写太多,不能利用有序部分 | 时间复杂度太大 | 空间复杂度高,递归算法需要调用栈,对于大数据集可能会stack overflow | 最坏复杂度无保证 | |
320 |
321 | | 算法 | 堆排序 | 计数排序 | 基数排序 | 桶排序 | |
322 | | -------- | ----------------------------- | -------- | --------------------------- | -------------------------- | - |
323 | | 额外空间 | $O(1)$ | $O(n)$ | $O(n+b)$(b是进制) | $O(n+k)$,$k$是桶数 | |
324 | | 最好时间 | $O(n\log n)$ | $O(n)$ | $O(d(n+b))$ | $O(n+k)$ | |
325 | | 平均时间 | $O(n\log n)$ | $O(n)$ | $O(d(n+b))$ | $O(n+k)$ | |
326 | | 最坏时间 | $O(n\log n)$ | $O(n)$ | $O(d(n+b))$d是位数 | $O(n+k)$ | |
327 | | 稳定性 | n,操作在heap中,可能改变顺序 | y | y | 取决于internal sorting alg | |
328 | | in-place | y | n | | n | |
329 | | 优点 | | | 快,并行,对int str快 | 并行 | |
330 | | 缺点 | | | 空间复杂度高,对float不友好 | 对不均匀分布的数据不友好 | |
331 |
332 | ### 并查集
333 |
334 |
335 |
336 | ## 图
337 |
338 | ### 定义
339 |
340 | - 连通:无向图,若从顶点v到顶点w有路径存在,则称v和w是连通的。
341 | - 连通图:图G中的任意两个顶点都是联通的,则称图G是连通图。否则称为非连通图。
342 | - 连通分量Connected components:无向图中的极大连通子图
343 | - 强连通:有向图,若从顶点v到顶点w、从顶点w到顶点v之间都有路径,则称v和w是强连通的
344 | - 强连通分量:有向图中的极大强连通子图
345 | - 极大连通子图Maximum Connected Subgraph:图中的一组节点,这些节点之间互相可达,且无法再加入其他节点使其变得更大
346 | - 极小连通子图:既要保持图连通,又要使得边数最少的子图。
347 | - 图存储:
348 |
349 | - 邻接矩阵:用二维数组存储边的信息(各顶点之间的邻接关系)
350 | - 邻接表:对每个顶点v建立单链表,存储依附于依附于v的边
351 | - 最小生成树Minimum spanning tree, MST:
352 |
353 | - 生成树是一棵包含图中所有节点的无向树,它的边数比节点数少1,且不形成环路。[求解:Prim, Kruskal]
354 | - MST:在带权连通图中使得所有边的权值之和最小的生成树。(不唯一,但是权值之和唯一)
355 | - 有向无环图Directed Acyclic Graph, DAG:不存在环的有向图
356 |
357 | ### 最小生成树算法
358 |
359 | #### 构造准则
360 |
361 | 1. 必须使用且仅使用该网络中的$ n-1 $条边来联结网络中的$ n $个顶点
362 | 2. 不能使用产生回路的边
363 | 3. 各边上的权值的总和达到最小
364 |
365 | #### Kruskal
366 |
367 | (基于边,适用于边稀疏的的网络)
368 |
369 | ```python
370 | def kruskal(V, T):
371 | T = V # 初始化树,只含顶点
372 | numS = n # 连通分量数
373 | while numS > 1:
374 | 从E中取出权值最小的边(v, u)
375 | if v和u属于T中不同的连通分量: # 用并查集的数据结构描述T
376 | T = T + {(u, v)}
377 | numS -= 1
378 | ```
379 |
380 | 时间复杂度为$O(|E|\log_2 \vert E\vert )$,适合求解边稀疏而顶点较多的图的MST
381 |
382 | #### Prim
383 |
384 | (基于顶点,适合于边稠密情形)
385 |
386 | ```python
387 | def prim(G, T):
388 | T = {} # 初始化为空树
389 | U = {w} # 添加任意一个顶点w
390 | while U != V:
391 | (u, v) satisfies: 1. u in U; 2. v in (V-U); 3. is with minimum weight
392 | T = T + {(u, v)}
393 | U = U + {v}
394 | ```
395 |
396 | 时间复杂度为$O(\vert V\vert ^2)$。
397 |
398 | ### 最短路径
399 |
400 | #### Dijkstra
401 |
402 | 边上权值非负情形的单源最短路径问题
403 |
404 | ```python
405 | def dijkstra:
406 | dist[]: 记录从源点0到其他各顶点当前的最短路径长度。
407 | path[]: path[i]表示从源点到顶点i之间的最短路径的前驱结点。算法结束时可通过其回溯最短路径。
408 | S = {0}
409 | dist[i] = arcs[0][i] if arcs[0][i] else inf
410 |
411 | for time in range(n-1):
412 | 选择j, 满足j in (V-S) and dist[j] = min(dist[i] | i in (V-S))
413 | S = S + {j}
414 | for k in (V-S): # 更新V-S中的所有顶点与0之间的距离
415 | dist[k] = max(dist[k], dist[j] + ards[j][k])
416 | ```
417 |
418 | 与Prim算法比较:也是基于贪心策略。
419 |
420 | 时间复杂度为$O(\vert V\vert ^2)$。
421 |
422 | #### Bellman-Ford
423 |
424 | 边上权值为任意值的单源最短路径问题
425 |
426 | ```python
427 | def BellmanFord(src):
428 | dist = [inf] * |V|
429 | dist[src] = 0
430 |
431 | # Step 2: Relax all edges |V| - 1 times. A simple shortest
432 | # path from src to any other vertex can have at-most |V| - 1
433 | # edges
434 | for i in range(|V|-1):
435 | for u, v, w in graph:
436 | if dist[u] != inf and dist[u] + w < dist[v]:
437 | dist[v] = dist[u] + w
438 |
439 | # Step 3: check for negative-weight cycles. The above step
440 | # guarantees shortest distances if graph doesn't contain
441 | # negative weight cycle. If we get a shorter path, then there
442 | # is a cycle.
443 | for u, v, w in self.graph:
444 | if dist[u] != float("Inf") and dist[u] + w < dist[v]:
445 | print("Graph contains negative weight cycle")
446 | return
447 | ```
448 |
449 | 时间:$O(|VE|)$
450 |
451 | #### Floyd
452 |
453 | 求所有顶点之间的最短路径
454 |
455 | ```
456 | for k=1 -> n:
457 | for i=1 -> n:
458 | for j=1 -> n:
459 | d[i,j] = min(d[i,j], d[i,k] + d[k,j])
460 | ```
461 |
462 | 只经过k的距离。
463 |
464 | 时间复杂度:$O(|V|^3)$,但是常数系数很小。
465 |
466 | ### 拓扑排序
467 |
468 | AOV网(Activity on Vertex Network):有向图,顶点表示活动的网络,用于DAG的表示和计算。每个结点表示一个任务,每条边表示结点间的依赖关系(这种前驱和后继关系有传递性)。
469 |
470 | 拓扑排序:当且仅当:1. 每个顶点出现且仅出现一次;2. 若顶点$A$在序列中排在顶点$B$前面,则在图上不存在从顶点$B$到顶点$A$的路径。每个AOV网都有一个或多个拓扑排序序列。
471 |
472 | ```python
473 | def topological_sort(V):
474 | for (u, v) in E:
475 | indegree[u] += 1
476 | parent[v].append(u)
477 | for u in V:
478 | if indegree[u] != 0:
479 | stack.append(u)
480 |
481 | cnt = 0
482 | while stack:
483 | u = stack.pop()
484 | cnt += 1
485 | for v in u.neighbor:
486 | indegree[v] -= 1
487 | if indegree[v] == 0:
488 | stack.push(v)
489 |
490 | if cnt != n:
491 | return False
492 | return True
493 | ```
494 |
495 | ### 如何判断图中是否有环?
496 |
497 | 1. 拓扑排序,最后如果还存在未被删除的顶点,则表示有环;否则没有环
498 | 2. DFS,如果在遍历的过程中,发现某个节点有一条边指向已经访问过的节点,并且这个已访问过的节点不是当前节点的父节点,则表示存在环(用黑白灰表示)
499 | 3. 对于有向图,若存在强连通分量(即存在$v_i \to v_j$的路径也存在$v_j\to v_i$的路径),图中有环。
500 |
501 | ### 欧拉图
502 |
503 | 定义:
504 |
505 | - **欧拉回路**:通过图中每条边恰好一次的回路
506 | - **欧拉通路**:通过图中每条边恰好一次的通路
507 | - **欧拉图**:具有欧拉回路的图
508 | - **半欧拉图**:具有欧拉通路但不具有欧拉回路的图
509 |
510 | 性质:
511 |
512 | 欧拉图中所有顶点的度数都是偶数。
513 |
514 | 若$G$是欧拉图,则它为若干个环的并,且每条边被包含在奇数个环内。
515 |
516 | 判断:
517 |
518 | 1. 无向图是欧拉图当且仅当:
519 | - 非零度顶点是连通的
520 | - 顶点的度数都是偶数
521 | 2. 无向图是半欧拉图当且仅当:
522 | - 非零度顶点是连通的
523 | - 恰有 0 或 2 个奇度顶点
524 | 3. 有向图是欧拉图当且仅当:
525 | - 非零度顶点是强连通的
526 | - 每个顶点的入度和出度相等
527 | 4. 有向图是半欧拉图当且仅当:
528 | - 非零度顶点是弱连通的
529 | - 至多一个顶点的出度与入度之差为 1
530 | - 至多一个顶点的入度与出度之差为 1
531 | - 其他顶点的入度和出度相等
532 |
--------------------------------------------------------------------------------
/机器学习.md:
--------------------------------------------------------------------------------
1 | # 机器学习
2 |
3 | [toc]
4 |
5 | ## 绪论
6 |
7 | ### 常见定义
8 |
9 | #### 归纳
10 |
11 | induction,从特殊到一半的泛化generalization过程,即从具体的事实归结出一般性规律。
12 |
13 | #### 演绎
14 |
15 | deduction,从一半到特殊的特化specialization过程,即从基础原理推演出具体情况。
16 |
17 | #### 假设空间
18 |
19 | 假设空间(hypothesis space)是指在机器学习算法中,所有可能的候选模型组成的集合。学习过程就是一个在所有假设组成的空间中进行搜索的过程,搜索目标是找到与训练集匹配fit的假设。
20 |
21 | #### 泛化能力
22 |
23 | 模型对未知数据的适应能力,也可以理解为模型的普适性。
24 |
25 | #### 鲁棒性
26 |
27 | 鲁棒性是指模型对于数据噪声、异常值、缺失值等干扰因素的抵抗能力,也可以说是模型对于数据变化的适应能力。
28 |
29 | ### 奥卡姆剃刀
30 |
31 | 若有多个假设与观察一致,则选最简单的那个。
32 |
33 | ### NFL定理
34 |
35 | No Free Lunch定理,如果所有“问题”出现的机会相同、或所有问题同等重要,则总误差竟然与学习算法无关。说明不存在绝对好的算法,要结合实际问题寻找算法解决方案。
36 |
37 | #### 生成式模型和判别式模型的区别?
38 |
39 | $ R $ 其他变量的集合
40 |
41 | 生成式考虑联合分布 $ P(Y,R,O) $
42 |
43 | 判别式考虑条件分布 $ P(Y,R|O) $
44 |
45 | 推断:给定观测值,从 $ P(Y,R,O),P(Y,R|O) $ 推断 $ P(Y|O) $
46 |
47 | ## 模型评估与选择
48 |
49 | 如何获得测试结果?评估方法
50 |
51 | 如何评估性能优劣?性能度量
52 |
53 | 如何判断实质差别?比较检验
54 |
55 | ### 经验误差与过拟合
56 |
57 | #### 常见定义
58 |
59 | 训练误差training error/经验误差empirical error:学习器在训练集上的误差
60 |
61 | 泛化误差generalization error:在新样本上的学习器
62 |
63 | 真实目标是最小化泛化误差,但泛化误差未知,所以大部分情况下在使经验误差最小化。
64 |
65 | #### 过拟合和欠拟合
66 |
67 | > 如何判断过拟合和欠拟合?
68 |
69 | - 过拟合:方差Variance(对不同数据集的表现差异)大,训练集的准确率高,但是测试集不高,模型的学习能力太强,泛化能力弱
70 | - 欠拟合:偏差Bias(模型预测结果与真实值的差异程度)大,训练集和测试集的准确率都不高
71 |
72 | > 为什么会过拟合?
73 |
74 | - 模型复杂度过高:学习能力过于强大, 以至于把训练样本所包含的不太一般的特性、噪声、随机性都学到了
75 | - 训练数据不足
76 | - 训练轮数过多
77 | - 特征选择不当
78 |
79 | > 为什么会欠拟合?
80 |
81 | - 模型复杂度不足,特征数量不足,数据集不足或不均衡
82 |
83 | > 预防过拟合的方法?
84 |
85 | - data augmentation:通过图像平移、翻转、缩放、切割等手段将数据库成倍扩充;语音:加入噪音。
86 | - early stopping:运行优化方法直到若干次在验证集上的验证误差没有提升时候停止。
87 | - 正则化:加上 $ L_1 $ 或 $ L_2 $ 正则化项
88 | - dropout:通过修改隐藏层神经元的个数来防止网络的过拟合。在每一批次数据被训练时,Dropout按照给定的概率p随机忽略一些神经元,只有被保留下来的神经元的参数被更新。每一批次数据,由于随机性忽略神经元,使得网络具有一定的稀疏性,从而能减轻了不同特征之间的协同效应。而且由于每次被剔除的神经元不同,所以整个网络神经元的参数也只是部分被更新,消除减弱了神经元间的联合适应性,增强了神经网络的泛化能力和鲁棒性。Dropout只在训练时使用,作为一个超参数,然而在测试集时,并不能使用。p为超参,一般置为0或1。
89 | - 简化模型:减少特征数量,或者进行特征选择,以减少模型的复杂度
90 |
91 | > 预防欠拟合的方法?
92 |
93 | - 增加模型的复杂度,增加训练数据,减少正则化参数,减少特征选择的限制,增加训练时间和迭代次数
94 |
95 | ### 评估方法
96 |
97 | #### 留出法
98 |
99 | hold out,将数据集划分为两个互斥的集合,其中一个集合作为训练集,另一个作为测试集。在训练集中训练出模型后,用测试集来评估其测试误差,作为对泛化误差的估计。
100 |
101 | > 留出法的缺点
102 |
103 | - 不同的训练集/测试集分割会导致不同的模型评估结果,单次使用留出法得到的估计结果往往不够稳定可靠。
104 | - 困境:如果训练集太小,则训练效果差;如果测试集太小,则评估结果不够稳定准确。(一般0.66-0.8)
105 |
106 | #### 交叉验证法
107 |
108 | k-fold cross validation,k折交叉验证。
109 |
110 | 先将数据集划分为 $ k $ 个大小相似、分布尽量一致的互斥子集,每次用 $ k-1 $ 个子集的并集训练,一个子集测试。最终返回的是这 $ k $ 个测试结果的均值。
111 |
112 | #### 留一法
113 |
114 | leave-one-out, LOO,交叉验证的特例,每个子集只有一个样本。
115 |
116 | > 留一法的缺点
117 |
118 | 1. 当数据集比较大时,计算开销太大
119 | 2. 不一定准确:例如随机取球问题(50红,50黑;如果leave红则会猜 黑,反之同理,准确率为0)
120 |
121 | #### 自助法
122 |
123 | 从包含 $ m $ 个样本的数据集中用自主采样法bootstrap sampling为基础采样,
124 |
125 | $$
126 | \lim_{m\to\infty}\left(1-\frac1m\right)^m\to\frac1e\approx 0.368
127 | $$
128 |
129 | 约有36.8%的样本未出现在采样数据集中,用采样数据集作为训练集,未采样到的样本作为测试集。测试结果叫做保外估计out-of-bag estimate。
130 |
131 | > 自助法的优缺点
132 |
133 | 优:
134 |
135 | 1. 对于数据集较小,难以有效划分训练/测试集的时候很有用
136 | 2. 能产生多个不同的训练集,对集成学习等方法有用处
137 |
138 | 缺:
139 |
140 | 1. 改变初始数据集的分布,引入估计偏差
141 | 2. 因此在初始数据量足够的情况下,留出法和交叉验证法更常用。
142 |
143 | #### 如何调参?
144 |
145 | 调参是指通过调整模型的超参数,以获得更好的性能和更好的泛化能力。
146 |
147 | - 网格搜索:基于一个参数网格,对每一组超参数进行训练和评估,以找到最佳的超参数组合。这种方法可以保证找到全局最优解,但需要对参数空间进行完整搜索,因此比较耗时。
148 | - 实现可视化,用TensorBoard或者Wandb去可视化训练的过程,看loss等等有没有像理想中那样收敛,这个会是调参的一个依据,如果曲线太离谱就直接停止实验。
149 | - 固定其他参数,优化单个参数
150 | - 尽量去找相关论文中给出的数值,以之初始化,再根据训练结果进行微调。如果说没有这样的参考的话,我会依据经验找一个数值,然后二分法由粗到细去调参。
151 | - 调参时可以缩小训练规模来节省时间。
152 |
153 | ### 性能度量
154 |
155 | #### 错误率
156 |
157 | $$
158 | \begin{aligned}
159 | E(f;D)&=\frac1m\sum_{i=1}^m\mathbb I(f(x_i)\neq y_i)\\
160 | &=\int_{x\sim D}\mathbb I(f(x)\neq y)p(x)\text dx
161 | \end{aligned}
162 | $$
163 |
164 | #### 精度
165 |
166 | $$
167 | \begin{aligned}
168 | acc(f;D)&=\frac1m\sum_{i=1}^m\mathbb I(f(x_i)=y_i)=1-E(f:D)\\
169 | &=\int_{x\sim D}\mathbb I(f(x)= y)p(x)\text{d}x
170 | \end{aligned}
171 | $$
172 |
173 | #### 混淆矩阵
174 |
175 |
22 |
23 | - Breadth-first search
24 | - heap是FIFO queue
25 | - 完备性:如果$b$有限
26 | - Uniform-cost search
27 | - 解决边有权重的问题,Priority queue,权重最小先出栈
28 | - 当边权重为正时完备
29 | - 时空复杂度都是路径开销$\leq$最优解的节点个数
30 | - 最优性证明:
31 | - 它扩展最小成本的节点
32 | - 最优路径上的目标状态比任何次优路径上的目标状态具有更小的成本
33 | - 它永远不会在扩展最优路径上的目标状态之前,扩展次优路径上的目标状态
34 | - Depth-first search
35 | - heap是LIFO queue
36 | - 不完备:在无限深度空间、有环的空间中失败(如果有限、没有重复状态则完备)
37 |
38 | - Depth-limited search
39 |
40 | - Iterative deepening search
41 |
42 | - 对从0到$\infty$的depth,分别做Depth-limited search,直到找到结果
43 |
44 | - 时间复杂度(实际上重复搜索浪费的时间并不多):
45 | $$
46 | \begin{aligned}
47 | &b^0+(b^0+b^1)+\dots+(b^0+\dots+b^d)\\
48 | =&(d+1)b^0+db^1+\dots+b^d=O(b^d)
49 | \end{aligned}
50 | $$
51 |
52 | ### Informed Search
53 |
54 | - Greedy Search
55 |
56 | - heuristic function: $h(n)$ 为从$n$到最近目标的成本估计
57 | - 扩展**看起来**最接近目标的节点
58 | - 不完备(可以卡在环上),$T=O(b^m)$,$S=O(b^m)$,不最优
59 |
60 | - A\* Search
61 |
62 | - heuristic function: $f(n)=g(n)+h(n)$,其中$g(n)$为到目前为止达到$ n $的成本,$h(n)$为从$n$到最近目标的成本估计,$f(n)$为通过$ n $到达目标的路径的估计总成本
63 | - Admissible可接受:估值永远小于真实值,$0\leq h(n)\leq h^*(n)$
64 | - Consistent一致性:$h(n)\leq c(n,a',n')+h(n')$,其中$ n' $是由动作$ a' $生成的$ n $的后继,Consistent$\to$Admissible
65 | - 证明:对于树搜索,如果启发式函数是可接受的,则A\*最优**(重点理解)**
66 | - 假设$h$是admissible的,如果$A$是最优目标节点,$B $是次优目标节点,下证明:$A$会比$B$先扩展
67 | - 对于$A$的任意祖先$n$,证明:$n$会比$B$先扩展
68 | - 有$h(A)=h(B)=0$;$g(A)
31 |
32 | 找到一个从L1到L2的变换,使得P on x is yes iff Q on T(x) is yes。
33 |
34 | 例子:3SAT问题,是否存在赋值使得下式成立($d$可以是$a$或$\neg a$,但是不能是$e,f$,否则就不是3SAT问题)
35 |
36 | $$
37 | (a \or b\or c)\and(d \or e\or f) \and \cdots
38 | $$
39 |
40 | 顶点覆盖问题(Vertex Covering Problem)是一种组合优化问题,旨在寻找一个最小的顶点集合,使得图中的每条边都至少与该顶点集合中的一个顶点相邻。
41 |
42 | ### NP-hard
43 |
44 | 满足NP-complete的条件2即可。
45 |
46 | ## 排序算法
47 |
48 | ### 基本问题
49 |
50 | #### 排序为什么要稳定?
51 |
52 | 稳定性的定义:对于值相同的两个元素,排序后它们的先后顺序与原数组相同。
53 |
54 | 因为在某些情况下,我们需要保留原数数据中的元素的相对位置。比如说对多个关键字排序,先按照关键字1排序,在关键字1相同的情况下再按照关键字2排序,在这种情况下,如果排序算法是不稳定的,那么在排序关键字2时就会打乱关键字1的顺序。
55 |
56 | #### 为什么归并的最坏复杂度是$O(n\log n)$,快排是$O(n^2)$,但是大家用的都是快排?
57 |
58 | 因为实际上在大多数情况下,无论从时间复杂度还是空间复杂度的角度考虑,快排的性能均优于归并排序。
59 |
60 | 首先,从时间复杂度上看,平均情况下两者的时间复杂度都是$O(n\log n)$,但是由于归并排序需要进行分配和取消分配辅助数组等操作,其所需的常量时间更大。
61 |
62 | 其次,从空间复杂度上看,快速排序是原地排序in-place的,不需要额外的空间,而归并排序则需要额外分配数组。
63 |
64 | 最后,虽然在数组已有序的情况下,快排的最坏时间复杂度是$O(n^2)$,但是我们可以通过随机选取pivot而非直接使用最后一个元素,使得快排的时间复杂度是最坏情况的概率很小,甚至趋近于0。
65 |
66 | 此外,当数据存储在内存中时,快排更好;但是当数据存储在硬盘中时或数据是链表时,归并排序最好,因为它最小化了读写的时间。
67 |
68 | #### 快排为什么叫“快”排?
69 |
70 | 因为它可以比任何其他排序方法更快地(两到三倍)对数据元素列表进行排序。
71 |
72 | ### 选择排序
73 |
74 | **Selection sort** is a simple and efficient sorting algorithm that works by repeatedly selecting the smallest (or largest) element from the unsorted portion of the list and moving it to the sorted portion of the list. The algorithm repeatedly selects the smallest (or largest) element from the unsorted portion of the list and swaps it with the first element of the unsorted portion. This process is repeated for the remaining unsorted portion of the list until the entire list is sorted.
75 |
76 | 选择排序重复地选择从未排序的部分选择最小的元素,将其与未排序部分的第一个元素交换位置,再将未排序部分的第一个元素并入已排序部分。
77 |
78 | ### 插入排序
79 |
80 | **Insertion sort** is a simple sorting algorithm that works similar to the way you sort playing cards in your hands. The array is virtually split into a sorted and an unsorted part. Values from the unsorted part are picked and placed at the correct position in the sorted part.
81 |
82 | 插入排序是一种简单的排序算法,类似于你整理手中的扑克牌的方式。该算法将数组虚拟地分成已排序部分和未排序部分。从未排序部分中选出值,将它们放置到已排序部分的正确位置上。
83 |
84 | ```python
85 | def insertion_sort(arr):
86 | n = len(arr)
87 | for i in range(1, n):
88 | j = i
89 | while j > 0 and arr[j-1] > arr[j]:
90 | arr[j], arr[j-1] = arr[j-1], arr[j]
91 | ```
92 |
93 | ### 冒泡排序
94 |
95 | **Bubble Sort** is the simplest sorting algorithm that works by repeatedly swapping the adjacent elements if they are in the wrong order.
96 |
97 | 冒泡排序通过反复交换相邻的元素进行排序。
98 |
99 | ```python
100 | def bubble_sort(arr):
101 | n = len(arr)
102 | for i in range(n):
103 | for j in range(0, n-i-1): # Last i elements are already in place
104 | if arr[j] > arr[j+1]:
105 | arr[j], arr[j+1] = arr[j+1], arr[j]
106 | ```
107 |
108 | ### 快速排序
109 |
110 | **Quick Sort** is a sorting algorithm based on the Divide and Conquer algorithm that picks an element as a pivot and partitions the given array around the picked pivot by placing the pivot in its correct position in the sorted array.
111 |
112 | 快速排序是一个基于分治的思想的排序算法,每次选择一个元素作为pivot,然后将给定的数组围绕这个基准进行划分,将小于基准的元素放到基准的左边,将大于基准的元素放到基准的右边,最终将基准放置在排序后的正确位置上。
113 |
114 | ```python
115 | def quick_sort(arr, low, high):
116 | if low < high:
117 | pi = partition(arr, low, high)
118 | quick_sort(arr, low, pi-1)
119 | quick_sort(arr, pi+1, high)
120 |
121 | def partition(arr, low, high):
122 | pivot = arr[high]
123 | i = low - 1
124 | for j in range(low, high):
125 | if arr[j] < pivot:
126 | i += 1
127 | arr[i], arr[j] = arr[j], arr[i]
128 | arr[i+1], arr[high] = arr[high], arr[i+1]
129 | return i+1
130 | ```
131 |
132 | ### 快速排序时间复杂度证明
133 |
134 | 假设数组被分成大小为$j$和$n-j$的两部分,则时间复杂度为
135 |
136 | $$
137 | T(n)=T(j) + T(n-j) + cn
138 | $$
139 |
140 | 最好情况:
141 |
142 | $$
143 | \begin{aligned}
144 | T(n) &= 2T\left(\frac n2\right) + cn\\
145 | &=2 \left(2T\left(\frac n4\right)+c\cdot \frac{n}{2}\right) + cn\\
146 | &=\cdots\\
147 | &=2^{\log n} T(1) + c+2c + \dots + 2^{\log n}c\\
148 | &= nT(1)+n\log n=O(n\log n)
149 | \end{aligned}
150 | $$
151 |
152 | 最坏情况:
153 |
154 | $$
155 | T(n)=T(n-1)+cn = c(1+2+\dots+n)=O(n^2)
156 | $$
157 |
158 | 平均情况:
159 |
160 | 当index i是pivot时,
161 |
162 | $$
163 | T(n)=T(i)+T(n-i) +cn
164 | $$
165 |
166 | 所以平均时间复杂度是:
167 |
168 | $$
169 | T(n)=\frac1n\sum_{i=1}^{n-1} T(i)+\frac1n \sum_{i=1}^{n-1}T(n-i) +cn=\frac 2n\sum_{i=1}^{n-1}T(i)+cn
170 | $$
171 |
172 | 所以有:
173 |
174 | $$
175 | \begin{aligned}
176 | nT(n)&=2\sum_{i=1}^{n-1}T(i)+cn^2\\
177 | (n-1)T(n-1)&=2\sum_{i=1}^{n-2}+c(n-1)^2
178 | \end{aligned}
179 | $$
180 |
181 | 两式相减有:
182 |
183 | $$
184 | \begin{aligned}
185 | nT(n)-(n-1)T(n-1)&=2T(n-1)+2cn-c\\
186 | nT(n)&=(n+1)T(n-1)+2cn\quad (\text{remove constant c})
187 | \end{aligned}
188 | $$
189 |
190 | 两边同除$n(n+1)$
191 |
192 | $$
193 | \begin{aligned}
194 | \frac{T(n)}{n+1}=&\frac{T(n-1)}{n}+\frac{2c}{n+1}\\
195 | =&\frac{T(1)}{2}+2c\left(\frac12+\frac13+\dots+\frac1n+\frac1{n+1}\right)\\
196 | =&\frac{T(1)}{2}+2c\log n+C
197 | \end{aligned}
198 | $$
199 |
200 | 可得
201 |
202 | $$
203 | T(n)=O(n\log n)
204 | $$
205 |
206 | ### 归并排序
207 |
208 | **Merge sort** is defined as a sorting algorithm that works by dividing an array into smaller subarrays, sorting each subarray, and then merging the sorted subarrays back together to form the final sorted array.
209 |
210 | 快速排序是一个基于分治的思想的排序算法,每次将数组分为两个子数组,分别对子数组排序,再将两个子数组归并,形成最终的排序好的数组。
211 |
212 | ```python
213 | def merge_sort(arr, left, right):
214 | if left > right: return
215 | mid = (left + right) / 2
216 | merge_sort(arr, left, mid)
217 | merge_sort(arr, mid+1, right)
218 | merge(arr, left, mid, right)
219 |
220 | def merge(arr, left, mid, right):
221 | left_arr = arr[:mid]
222 | right_arr = arr[mid:]
223 | i = j = k = 0
224 | while i < len(left_arr) and j < len(right_arr):
225 | if left_arr[i] <= right_arr[j]:
226 | arr[k] = left_arr[i]
227 | i += 1
228 | else:
229 | arr[k] = right_arr[j]
230 | j += 1
231 | k += 1
232 | while i < len(left_arr):
233 | arr[k] = left_arr[i]
234 | i += 1
235 | k += 1
236 | while j < len(right_arr):
237 | arr[k] = right_arr[j]
238 | j += 1
239 | k += 1
240 | ```
241 |
242 | ### 堆排序
243 |
244 | Heap sort is a comparison-based sorting technique based on Binary Heap data structure.
245 |
246 | 堆排序是一种基于二叉堆数据结构的排序算法。首先根据未排序数组建立大顶堆,每次从堆中删除最大的元素(移动到数组末尾),再通过 `heapify`操作维护大顶堆的性质。`heapify`的具体操作为:如果根节点比左右子节点都大,则直接返回;否则交换根节点和值最大的节点,再递归地对原先值最大的节点调用 `heapify`。
247 |
248 | ```python
249 | def heapify(arr, N, i):
250 | largest = i
251 | l = 2 * i + 1
252 | r = 2 * i + 2
253 |
254 | if l < N and arr[largest] < arr[l]:
255 | largest = l
256 | if r < N and arr[largest] < arr[r]:
257 | largest = r
258 | if largest != i:
259 | arr[i], arr[largest] = arr[largest], arr[i]
260 | heapify(arr, N, largest)
261 |
262 | def heap_sort(arr):
263 | N = len(arr)
264 | for i in range(N//2-1, -1, -1):
265 | heapify(arr, N, i)
266 | for i in range(N-1, -, -1):
267 | arr[i], arr[0] = arr[0], arr[i]
268 | heapify(arr, i, 0)
269 | ```
270 |
271 | ### 计数排序
272 |
273 | Counting sort is a sorting technique based on keys between a specific range. It works by counting the number of objects having distinct key values (a kind of hashing). Then do some arithmetic operations to calculate the position of each object in the output sequence.
274 |
275 | 计数排序(Counting Sort)是一种针对于特定范围之间的整数进行排序的算法。它通过统计给定数组中不同元素的数量(类似于哈希映射),然后对映射后的数组进行排序输出即可。
276 |
277 | ```python
278 | def counting_sort(arr):
279 | count = [0 for i in range(m)]
280 | for e in arr:
281 | count[e] += 1
282 | for i in range(1, m):
283 | count[m] += count[m-1] # count[m]-1就是排序好的数组中m的最大idx
284 |
285 | for i in range(len(arr)-1, -1, -1): # 倒着遍历是为了保持in-place
286 | output[count[arr[i]]-1] = arr[i]
287 | count[arr[i]] - 1
288 |
289 | return output
290 | ```
291 |
292 | ### 基数排序
293 |
294 | Radix sort is a non-comparison sorting algorithm that separates the elements to be sorted into different digits, and then sorts them according to each digit. This process requires the use of buckets to store the data. Radix sort can handle positive integers, negative integers, and decimals.
295 |
296 | 基数排序(Radix Sort)是一种非比较排序算法,它将待排序的元素按照位数切割成不同的数字,然后按照每个位数分别比较排序。这个过程中需要使用到桶(bucket)来存储数据。基数排序可以处理正整数、负整数和小数,只要数据能用位数表示,且位数有限。
297 |
298 | 
299 |
300 | ### 桶排序
301 |
302 | Bucket sort is a sorting algorithm that works by distributing the elements of an array into a number of buckets. Each bucket is then sorted individually, either using a different sorting algorithm, or by recursively applying the bucket sorting algorithm.
303 |
304 | 桶排序(Bucket Sort)是一种排序算法,它将待排序数组的元素分配到一定数量的桶中。每个桶单独进行排序,可以使用不同的排序算法或者递归地应用桶排序算法。
305 |
306 | 
307 |
308 | ### 总结
309 |
310 | | 算法 | 选择排序 | 插入排序 | 归并排序 | 快速排序 | |
311 | | ---------- | ----------------------------------------- | ------------------------------ | ------------------------------------------------------------------ | ---------------- | - |
312 | | 额外空间 | $O(1)$ | $O(1)$ | $O(n)$ | $O(1)$,考虑栈$O(\log n)$ | |
313 | | 最好时间 | $O(n^2)$ | $o(n)$(已排序好) | $O(n\log n)$ | $O(n\log n)$ | |
314 | | 平均时间 | $O(n^2)$ | $O(n^2)$ | $O(n\log n)$ | $O(n\log n)$ | |
315 | | 最坏时间 | $O(n^2)$ | $O(n^2)$ | $O(n\log n)$ | $O(n^2)$ | |
316 | | 稳定性 | n | y | y | n | |
317 | | in-replace | y | y | n | y | |
318 | | 优点 | | 简单,小数组性能好,额外空间小 | 可并行,最坏性能有保障,对不同数据分布适应性好 | | |
319 | | 缺点 | cache性能不好,读写太多,不能利用有序部分 | 时间复杂度太大 | 空间复杂度高,递归算法需要调用栈,对于大数据集可能会stack overflow | 最坏复杂度无保证 | |
320 |
321 | | 算法 | 堆排序 | 计数排序 | 基数排序 | 桶排序 | |
322 | | -------- | ----------------------------- | -------- | --------------------------- | -------------------------- | - |
323 | | 额外空间 | $O(1)$ | $O(n)$ | $O(n+b)$(b是进制) | $O(n+k)$,$k$是桶数 | |
324 | | 最好时间 | $O(n\log n)$ | $O(n)$ | $O(d(n+b))$ | $O(n+k)$ | |
325 | | 平均时间 | $O(n\log n)$ | $O(n)$ | $O(d(n+b))$ | $O(n+k)$ | |
326 | | 最坏时间 | $O(n\log n)$ | $O(n)$ | $O(d(n+b))$d是位数 | $O(n+k)$ | |
327 | | 稳定性 | n,操作在heap中,可能改变顺序 | y | y | 取决于internal sorting alg | |
328 | | in-place | y | n | | n | |
329 | | 优点 | | | 快,并行,对int str快 | 并行 | |
330 | | 缺点 | | | 空间复杂度高,对float不友好 | 对不均匀分布的数据不友好 | |
331 |
332 | ### 并查集
333 |
334 |
335 |
336 | ## 图
337 |
338 | ### 定义
339 |
340 | - 连通:无向图,若从顶点v到顶点w有路径存在,则称v和w是连通的。
341 | - 连通图:图G中的任意两个顶点都是联通的,则称图G是连通图。否则称为非连通图。
342 | - 连通分量Connected components:无向图中的极大连通子图
343 | - 强连通:有向图,若从顶点v到顶点w、从顶点w到顶点v之间都有路径,则称v和w是强连通的
344 | - 强连通分量:有向图中的极大强连通子图
345 | - 极大连通子图Maximum Connected Subgraph:图中的一组节点,这些节点之间互相可达,且无法再加入其他节点使其变得更大
346 | - 极小连通子图:既要保持图连通,又要使得边数最少的子图。
347 | - 图存储:
348 |
349 | - 邻接矩阵:用二维数组存储边的信息(各顶点之间的邻接关系)
350 | - 邻接表:对每个顶点v建立单链表,存储依附于依附于v的边
351 | - 最小生成树Minimum spanning tree, MST:
352 |
353 | - 生成树是一棵包含图中所有节点的无向树,它的边数比节点数少1,且不形成环路。[求解:Prim, Kruskal]
354 | - MST:在带权连通图中使得所有边的权值之和最小的生成树。(不唯一,但是权值之和唯一)
355 | - 有向无环图Directed Acyclic Graph, DAG:不存在环的有向图
356 |
357 | ### 最小生成树算法
358 |
359 | #### 构造准则
360 |
361 | 1. 必须使用且仅使用该网络中的$ n-1 $条边来联结网络中的$ n $个顶点
362 | 2. 不能使用产生回路的边
363 | 3. 各边上的权值的总和达到最小
364 |
365 | #### Kruskal
366 |
367 | (基于边,适用于边稀疏的的网络)
368 |
369 | ```python
370 | def kruskal(V, T):
371 | T = V # 初始化树,只含顶点
372 | numS = n # 连通分量数
373 | while numS > 1:
374 | 从E中取出权值最小的边(v, u)
375 | if v和u属于T中不同的连通分量: # 用并查集的数据结构描述T
376 | T = T + {(u, v)}
377 | numS -= 1
378 | ```
379 |
380 | 时间复杂度为$O(|E|\log_2 \vert E\vert )$,适合求解边稀疏而顶点较多的图的MST
381 |
382 | #### Prim
383 |
384 | (基于顶点,适合于边稠密情形)
385 |
386 | ```python
387 | def prim(G, T):
388 | T = {} # 初始化为空树
389 | U = {w} # 添加任意一个顶点w
390 | while U != V:
391 | (u, v) satisfies: 1. u in U; 2. v in (V-U); 3. is with minimum weight
392 | T = T + {(u, v)}
393 | U = U + {v}
394 | ```
395 |
396 | 时间复杂度为$O(\vert V\vert ^2)$。
397 |
398 | ### 最短路径
399 |
400 | #### Dijkstra
401 |
402 | 边上权值非负情形的单源最短路径问题
403 |
404 | ```python
405 | def dijkstra:
406 | dist[]: 记录从源点0到其他各顶点当前的最短路径长度。
407 | path[]: path[i]表示从源点到顶点i之间的最短路径的前驱结点。算法结束时可通过其回溯最短路径。
408 | S = {0}
409 | dist[i] = arcs[0][i] if arcs[0][i] else inf
410 |
411 | for time in range(n-1):
412 | 选择j, 满足j in (V-S) and dist[j] = min(dist[i] | i in (V-S))
413 | S = S + {j}
414 | for k in (V-S): # 更新V-S中的所有顶点与0之间的距离
415 | dist[k] = max(dist[k], dist[j] + ards[j][k])
416 | ```
417 |
418 | 与Prim算法比较:也是基于贪心策略。
419 |
420 | 时间复杂度为$O(\vert V\vert ^2)$。
421 |
422 | #### Bellman-Ford
423 |
424 | 边上权值为任意值的单源最短路径问题
425 |
426 | ```python
427 | def BellmanFord(src):
428 | dist = [inf] * |V|
429 | dist[src] = 0
430 |
431 | # Step 2: Relax all edges |V| - 1 times. A simple shortest
432 | # path from src to any other vertex can have at-most |V| - 1
433 | # edges
434 | for i in range(|V|-1):
435 | for u, v, w in graph:
436 | if dist[u] != inf and dist[u] + w < dist[v]:
437 | dist[v] = dist[u] + w
438 |
439 | # Step 3: check for negative-weight cycles. The above step
440 | # guarantees shortest distances if graph doesn't contain
441 | # negative weight cycle. If we get a shorter path, then there
442 | # is a cycle.
443 | for u, v, w in self.graph:
444 | if dist[u] != float("Inf") and dist[u] + w < dist[v]:
445 | print("Graph contains negative weight cycle")
446 | return
447 | ```
448 |
449 | 时间:$O(|VE|)$
450 |
451 | #### Floyd
452 |
453 | 求所有顶点之间的最短路径
454 |
455 | ```
456 | for k=1 -> n:
457 | for i=1 -> n:
458 | for j=1 -> n:
459 | d[i,j] = min(d[i,j], d[i,k] + d[k,j])
460 | ```
461 |
462 | 只经过k的距离。
463 |
464 | 时间复杂度:$O(|V|^3)$,但是常数系数很小。
465 |
466 | ### 拓扑排序
467 |
468 | AOV网(Activity on Vertex Network):有向图,顶点表示活动的网络,用于DAG的表示和计算。每个结点表示一个任务,每条边表示结点间的依赖关系(这种前驱和后继关系有传递性)。
469 |
470 | 拓扑排序:当且仅当:1. 每个顶点出现且仅出现一次;2. 若顶点$A$在序列中排在顶点$B$前面,则在图上不存在从顶点$B$到顶点$A$的路径。每个AOV网都有一个或多个拓扑排序序列。
471 |
472 | ```python
473 | def topological_sort(V):
474 | for (u, v) in E:
475 | indegree[u] += 1
476 | parent[v].append(u)
477 | for u in V:
478 | if indegree[u] != 0:
479 | stack.append(u)
480 |
481 | cnt = 0
482 | while stack:
483 | u = stack.pop()
484 | cnt += 1
485 | for v in u.neighbor:
486 | indegree[v] -= 1
487 | if indegree[v] == 0:
488 | stack.push(v)
489 |
490 | if cnt != n:
491 | return False
492 | return True
493 | ```
494 |
495 | ### 如何判断图中是否有环?
496 |
497 | 1. 拓扑排序,最后如果还存在未被删除的顶点,则表示有环;否则没有环
498 | 2. DFS,如果在遍历的过程中,发现某个节点有一条边指向已经访问过的节点,并且这个已访问过的节点不是当前节点的父节点,则表示存在环(用黑白灰表示)
499 | 3. 对于有向图,若存在强连通分量(即存在$v_i \to v_j$的路径也存在$v_j\to v_i$的路径),图中有环。
500 |
501 | ### 欧拉图
502 |
503 | 定义:
504 |
505 | - **欧拉回路**:通过图中每条边恰好一次的回路
506 | - **欧拉通路**:通过图中每条边恰好一次的通路
507 | - **欧拉图**:具有欧拉回路的图
508 | - **半欧拉图**:具有欧拉通路但不具有欧拉回路的图
509 |
510 | 性质:
511 |
512 | 欧拉图中所有顶点的度数都是偶数。
513 |
514 | 若$G$是欧拉图,则它为若干个环的并,且每条边被包含在奇数个环内。
515 |
516 | 判断:
517 |
518 | 1. 无向图是欧拉图当且仅当:
519 | - 非零度顶点是连通的
520 | - 顶点的度数都是偶数
521 | 2. 无向图是半欧拉图当且仅当:
522 | - 非零度顶点是连通的
523 | - 恰有 0 或 2 个奇度顶点
524 | 3. 有向图是欧拉图当且仅当:
525 | - 非零度顶点是强连通的
526 | - 每个顶点的入度和出度相等
527 | 4. 有向图是半欧拉图当且仅当:
528 | - 非零度顶点是弱连通的
529 | - 至多一个顶点的出度与入度之差为 1
530 | - 至多一个顶点的入度与出度之差为 1
531 | - 其他顶点的入度和出度相等
532 |
--------------------------------------------------------------------------------
/机器学习.md:
--------------------------------------------------------------------------------
1 | # 机器学习
2 |
3 | [toc]
4 |
5 | ## 绪论
6 |
7 | ### 常见定义
8 |
9 | #### 归纳
10 |
11 | induction,从特殊到一半的泛化generalization过程,即从具体的事实归结出一般性规律。
12 |
13 | #### 演绎
14 |
15 | deduction,从一半到特殊的特化specialization过程,即从基础原理推演出具体情况。
16 |
17 | #### 假设空间
18 |
19 | 假设空间(hypothesis space)是指在机器学习算法中,所有可能的候选模型组成的集合。学习过程就是一个在所有假设组成的空间中进行搜索的过程,搜索目标是找到与训练集匹配fit的假设。
20 |
21 | #### 泛化能力
22 |
23 | 模型对未知数据的适应能力,也可以理解为模型的普适性。
24 |
25 | #### 鲁棒性
26 |
27 | 鲁棒性是指模型对于数据噪声、异常值、缺失值等干扰因素的抵抗能力,也可以说是模型对于数据变化的适应能力。
28 |
29 | ### 奥卡姆剃刀
30 |
31 | 若有多个假设与观察一致,则选最简单的那个。
32 |
33 | ### NFL定理
34 |
35 | No Free Lunch定理,如果所有“问题”出现的机会相同、或所有问题同等重要,则总误差竟然与学习算法无关。说明不存在绝对好的算法,要结合实际问题寻找算法解决方案。
36 |
37 | #### 生成式模型和判别式模型的区别?
38 |
39 | $ R $ 其他变量的集合
40 |
41 | 生成式考虑联合分布 $ P(Y,R,O) $
42 |
43 | 判别式考虑条件分布 $ P(Y,R|O) $
44 |
45 | 推断:给定观测值,从 $ P(Y,R,O),P(Y,R|O) $ 推断 $ P(Y|O) $
46 |
47 | ## 模型评估与选择
48 |
49 | 如何获得测试结果?评估方法
50 |
51 | 如何评估性能优劣?性能度量
52 |
53 | 如何判断实质差别?比较检验
54 |
55 | ### 经验误差与过拟合
56 |
57 | #### 常见定义
58 |
59 | 训练误差training error/经验误差empirical error:学习器在训练集上的误差
60 |
61 | 泛化误差generalization error:在新样本上的学习器
62 |
63 | 真实目标是最小化泛化误差,但泛化误差未知,所以大部分情况下在使经验误差最小化。
64 |
65 | #### 过拟合和欠拟合
66 |
67 | > 如何判断过拟合和欠拟合?
68 |
69 | - 过拟合:方差Variance(对不同数据集的表现差异)大,训练集的准确率高,但是测试集不高,模型的学习能力太强,泛化能力弱
70 | - 欠拟合:偏差Bias(模型预测结果与真实值的差异程度)大,训练集和测试集的准确率都不高
71 |
72 | > 为什么会过拟合?
73 |
74 | - 模型复杂度过高:学习能力过于强大, 以至于把训练样本所包含的不太一般的特性、噪声、随机性都学到了
75 | - 训练数据不足
76 | - 训练轮数过多
77 | - 特征选择不当
78 |
79 | > 为什么会欠拟合?
80 |
81 | - 模型复杂度不足,特征数量不足,数据集不足或不均衡
82 |
83 | > 预防过拟合的方法?
84 |
85 | - data augmentation:通过图像平移、翻转、缩放、切割等手段将数据库成倍扩充;语音:加入噪音。
86 | - early stopping:运行优化方法直到若干次在验证集上的验证误差没有提升时候停止。
87 | - 正则化:加上 $ L_1 $ 或 $ L_2 $ 正则化项
88 | - dropout:通过修改隐藏层神经元的个数来防止网络的过拟合。在每一批次数据被训练时,Dropout按照给定的概率p随机忽略一些神经元,只有被保留下来的神经元的参数被更新。每一批次数据,由于随机性忽略神经元,使得网络具有一定的稀疏性,从而能减轻了不同特征之间的协同效应。而且由于每次被剔除的神经元不同,所以整个网络神经元的参数也只是部分被更新,消除减弱了神经元间的联合适应性,增强了神经网络的泛化能力和鲁棒性。Dropout只在训练时使用,作为一个超参数,然而在测试集时,并不能使用。p为超参,一般置为0或1。
89 | - 简化模型:减少特征数量,或者进行特征选择,以减少模型的复杂度
90 |
91 | > 预防欠拟合的方法?
92 |
93 | - 增加模型的复杂度,增加训练数据,减少正则化参数,减少特征选择的限制,增加训练时间和迭代次数
94 |
95 | ### 评估方法
96 |
97 | #### 留出法
98 |
99 | hold out,将数据集划分为两个互斥的集合,其中一个集合作为训练集,另一个作为测试集。在训练集中训练出模型后,用测试集来评估其测试误差,作为对泛化误差的估计。
100 |
101 | > 留出法的缺点
102 |
103 | - 不同的训练集/测试集分割会导致不同的模型评估结果,单次使用留出法得到的估计结果往往不够稳定可靠。
104 | - 困境:如果训练集太小,则训练效果差;如果测试集太小,则评估结果不够稳定准确。(一般0.66-0.8)
105 |
106 | #### 交叉验证法
107 |
108 | k-fold cross validation,k折交叉验证。
109 |
110 | 先将数据集划分为 $ k $ 个大小相似、分布尽量一致的互斥子集,每次用 $ k-1 $ 个子集的并集训练,一个子集测试。最终返回的是这 $ k $ 个测试结果的均值。
111 |
112 | #### 留一法
113 |
114 | leave-one-out, LOO,交叉验证的特例,每个子集只有一个样本。
115 |
116 | > 留一法的缺点
117 |
118 | 1. 当数据集比较大时,计算开销太大
119 | 2. 不一定准确:例如随机取球问题(50红,50黑;如果leave红则会猜 黑,反之同理,准确率为0)
120 |
121 | #### 自助法
122 |
123 | 从包含 $ m $ 个样本的数据集中用自主采样法bootstrap sampling为基础采样,
124 |
125 | $$
126 | \lim_{m\to\infty}\left(1-\frac1m\right)^m\to\frac1e\approx 0.368
127 | $$
128 |
129 | 约有36.8%的样本未出现在采样数据集中,用采样数据集作为训练集,未采样到的样本作为测试集。测试结果叫做保外估计out-of-bag estimate。
130 |
131 | > 自助法的优缺点
132 |
133 | 优:
134 |
135 | 1. 对于数据集较小,难以有效划分训练/测试集的时候很有用
136 | 2. 能产生多个不同的训练集,对集成学习等方法有用处
137 |
138 | 缺:
139 |
140 | 1. 改变初始数据集的分布,引入估计偏差
141 | 2. 因此在初始数据量足够的情况下,留出法和交叉验证法更常用。
142 |
143 | #### 如何调参?
144 |
145 | 调参是指通过调整模型的超参数,以获得更好的性能和更好的泛化能力。
146 |
147 | - 网格搜索:基于一个参数网格,对每一组超参数进行训练和评估,以找到最佳的超参数组合。这种方法可以保证找到全局最优解,但需要对参数空间进行完整搜索,因此比较耗时。
148 | - 实现可视化,用TensorBoard或者Wandb去可视化训练的过程,看loss等等有没有像理想中那样收敛,这个会是调参的一个依据,如果曲线太离谱就直接停止实验。
149 | - 固定其他参数,优化单个参数
150 | - 尽量去找相关论文中给出的数值,以之初始化,再根据训练结果进行微调。如果说没有这样的参考的话,我会依据经验找一个数值,然后二分法由粗到细去调参。
151 | - 调参时可以缩小训练规模来节省时间。
152 |
153 | ### 性能度量
154 |
155 | #### 错误率
156 |
157 | $$
158 | \begin{aligned}
159 | E(f;D)&=\frac1m\sum_{i=1}^m\mathbb I(f(x_i)\neq y_i)\\
160 | &=\int_{x\sim D}\mathbb I(f(x)\neq y)p(x)\text dx
161 | \end{aligned}
162 | $$
163 |
164 | #### 精度
165 |
166 | $$
167 | \begin{aligned}
168 | acc(f;D)&=\frac1m\sum_{i=1}^m\mathbb I(f(x_i)=y_i)=1-E(f:D)\\
169 | &=\int_{x\sim D}\mathbb I(f(x)= y)p(x)\text{d}x
170 | \end{aligned}
171 | $$
172 |
173 | #### 混淆矩阵
174 |
175 |  176 |
177 | #### 查准率P
178 |
179 | precision
180 |
181 | $$
182 | P=\frac{TP}{TP+FP}
183 | $$
184 |
185 | #### 查全率R
186 |
187 | Recall
188 |
189 | $$
190 | R=\frac{TP}{TP+FN}
191 | $$
192 |
193 | #### P-R曲线
194 |
195 |
176 |
177 | #### 查准率P
178 |
179 | precision
180 |
181 | $$
182 | P=\frac{TP}{TP+FP}
183 | $$
184 |
185 | #### 查全率R
186 |
187 | Recall
188 |
189 | $$
190 | R=\frac{TP}{TP+FN}
191 | $$
192 |
193 | #### P-R曲线
194 |
195 |  196 |
197 | 若一个学习器的P-R曲线被另一个学习器的曲线完全“包住”,则可断言后者的性能优于前者。如果两个学习器的P-R曲线发生了交叉,则难以一般性地断言两者孰优孰劣,只能在具体的查准率或查全率条件下进行比较。
198 |
199 | #### $ F_1 $ 度量
200 |
201 | $$
202 | F_1=\frac{2PR}{P+R}=\frac{2TP}{样例总数+TP-TN}
203 | $$
204 |
205 | (是P和R的调和平均 $ \frac1{F1}=\frac12(\frac1P+\frac1R) $ )
206 |
207 | #### $ F_\beta $ 度量
208 |
209 | 对查准率和查全率的重视程度有所不同的度量:
210 |
211 | $$
212 | F_\beta=\frac{1+\beta^2PR}{\beta^2P+R}
213 | $$
214 |
215 | $ \beta>1 $ 查全率更重要, $ \beta<1 $ 查准率更重要, $ \beta=1 $ 退化为 $ F_1 $ 。
216 |
217 | #### Macro
218 |
219 | $$
220 | \begin{aligned}
221 | \text{macro-}P&=\frac1n\sum_{i=1}^n P_i\\
222 | \text{macro-}R&=\frac1n\sum_{i=1}^n R_i\\
223 | \text{macro-}F_1&=\frac{2\times\text{macro-}P\times\text{macro-}R}{\text{macro-}P+\text{macro-}R}
224 | \end{aligned}
225 | $$
226 |
227 | #### Micro
228 |
229 | $$
230 | \begin{aligned}
231 | \text{micro-}P&=\frac{\overline {TP}}{\overline {TP}+\overline {FP}}\\
232 | \text{micro-}R&=\frac{\overline {TP}}{\overline {TP}+\overline {FN}}\\
233 | \text{micro-}F_1&=\frac{2\times\text{micro-}P\times\text{micro-}R}{\text{micro-}P+\text{micro-}R}
234 | \end{aligned}
235 | $$
236 |
237 | #### ROC & AUC
238 |
239 | 纵轴TPR,横轴FPR
240 |
241 | $$
242 | \begin{aligned}
243 | TPR&=\frac{TP}{TP+FN}\\
244 | FPR&=\frac{FP}{TN+FP}
245 | \end{aligned}
246 | $$
247 |
248 | 
249 |
250 | ROC曲线 (Receiver Operating Characteristic):若一个学习器的ROC曲线被另一个学习器的曲线完全“包住”,则可断言后者的性能优于前者;若两个学习器的ROC曲线发生交叉,则难以以般性地断言两者孰优孰劣。
251 |
252 | AUC (Area Under ROC Curve):
253 |
254 | $$
255 | \ell_{rank}=\frac1{m^+m^-}\sum_{x^+\in D^+}\sum_{x^-\in D^-}\left(\mathbb I\left((f(x^+) 存在什么问题?
277 |
278 | 1. 我们希望比较的是泛化性能,实际比较的是测试集性能,两者的对比结果不一定相同
279 | 2. 测试集性能与测试集本身的选择有很大关系
280 | 3. 很多机器学习本身有一定的随机性
281 |
282 | #### 假设检验[还没看]
283 |
284 | “假设”是对学习器泛化错误率分布的猜想,假设检验根据测试错误率估推出泛化错误率的分布。
285 |
286 | 泛化错误率 $ \epsilon $ ,测试错误率 $ \hat{\epsilon} $
287 |
288 | ### 偏差与方差
289 |
290 | #### 偏差、方差、噪声
291 |
292 | 偏差:度量了学习算法的期望预测与真实结果的偏离程度,即刻画了学习算法本身的拟合能力。
293 |
294 | 方差:度量了同样大小的训练集的变动所导致的学习性能的变化,即刻画了数据扰动所造成的影响。
295 |
296 | 噪声:表达了在当前任务上任何学习算法所能达到的期望泛化误差的下界,即刻画了学习问题本身的难度。
297 |
298 | #### 偏差-方差分解
299 |
300 | bias-variance decomposition,泛化误差可分解为偏差、方差与噪声之和。说明泛化性能是由学习算法的能力、数据的充分性以及学习任务本身的难度所共同决定的。 $ E(f:D)=bias^2(x)+var(x)+\epsilon $
301 |
302 | 以回归任务为例,学习算法的期望预测为:
303 |
304 | $$
305 | \overline f(x)=\mathbb E_D[f(x;D)]
306 | $$
307 |
308 | 使用样本数相同的不同训练集产生的方差:
309 |
310 | $$
311 | var(x)=\mathbb E_D\left[(f(x;D)-\overline f(x))^2\right]
312 | $$
313 |
314 | 噪声:
315 |
316 | $$
317 | \epsilon ^2=\mathbb E_D\left[(y_D-y)^2\right]
318 | $$
319 |
320 | 期望输出与真实标记的差别称为偏差 (bias),即
321 |
322 | $$
323 | bias^2(x)=\left(\overline f(x)-y\right)^2
324 | $$
325 |
326 | 证明:
327 |
328 | $$
329 | \begin{aligned}
330 | \mathbb E_D(f;D)=&\mathbb E_D\left[\left(f(x:D)-y_D \right)^2\right]\\
331 | =&\mathbb E_D\left[\left(f(x:D)-\overline f(x)+\overline f(x)-y_D \right)^2\right]\\
332 | =&\mathbb E_D\left[\left(f(x:D)-\overline f(x) \right)^2\right]+\mathbb E_D\left[\left(\overline f(x)-y_D \right)^2\right]\\
333 | &+\mathbb E_D\left[2\left(f(x:D)-\overline f(x) \right)\left(\overline f(x)-y_D \right)\right]\\
334 | =&\mathbb E_D\left[\left(f(x:D)-\overline f(x) \right)^2\right]+\mathbb E_D\left[\left(\overline f(x)-y_D \right)^2\right]\\
335 | =&\mathbb E_D\left[\left(f(x:D)-\overline f(x) \right)^2\right]+\mathbb E_D\left[\left(\overline f(x)-y+y-y_D \right)^2\right]\\
336 | =&\mathbb E_D\left[\left(f(x:D)-\overline f(x) \right)^2\right]+\mathbb E_D\left[\left(\overline f(x)-y \right)^2\right]\\
337 | &+\mathbb E_D\left[\left(y-y_D \right)^2\right]+\mathbb E_D\left[\left(\overline f(x)-y \right)\left(y-y_D \right)\right]\\
338 | =&\mathbb E_D\left[\left(f(x:D)-\overline f(x) \right)^2\right]+\left(\overline f(x)-y \right)^2+\mathbb E_D\left[\left(y_D-y \right)^2\right]
339 |
340 |
341 | \end{aligned}
342 | $$
343 |
344 | #### 偏差-方差困境
345 |
346 | 偏差与方差是有冲突的,这称为偏差-方差窘境 (bias-variance dilemma)。假定我们能控制学习算法的训练程度,则在训练不足时学习器的拟合能力不够强,训练数据的扰动不足以便学习器产生显著变化,此时偏差主导了泛化错误率;随着训练程度的加深,学习器的拟合能力逐渐增强,训练数据发生的扰动渐渐能被学习器学到,方差逐渐主导了泛化错误率。在训练程度充足后,学习器的拟合能力已非常强,训练数据发生的轻微扰动都会导致学习器发生显著变化,若训练数据自身的、非全局的特性被学习器学到了,则将发生过拟合。
347 |
348 |
196 |
197 | 若一个学习器的P-R曲线被另一个学习器的曲线完全“包住”,则可断言后者的性能优于前者。如果两个学习器的P-R曲线发生了交叉,则难以一般性地断言两者孰优孰劣,只能在具体的查准率或查全率条件下进行比较。
198 |
199 | #### $ F_1 $ 度量
200 |
201 | $$
202 | F_1=\frac{2PR}{P+R}=\frac{2TP}{样例总数+TP-TN}
203 | $$
204 |
205 | (是P和R的调和平均 $ \frac1{F1}=\frac12(\frac1P+\frac1R) $ )
206 |
207 | #### $ F_\beta $ 度量
208 |
209 | 对查准率和查全率的重视程度有所不同的度量:
210 |
211 | $$
212 | F_\beta=\frac{1+\beta^2PR}{\beta^2P+R}
213 | $$
214 |
215 | $ \beta>1 $ 查全率更重要, $ \beta<1 $ 查准率更重要, $ \beta=1 $ 退化为 $ F_1 $ 。
216 |
217 | #### Macro
218 |
219 | $$
220 | \begin{aligned}
221 | \text{macro-}P&=\frac1n\sum_{i=1}^n P_i\\
222 | \text{macro-}R&=\frac1n\sum_{i=1}^n R_i\\
223 | \text{macro-}F_1&=\frac{2\times\text{macro-}P\times\text{macro-}R}{\text{macro-}P+\text{macro-}R}
224 | \end{aligned}
225 | $$
226 |
227 | #### Micro
228 |
229 | $$
230 | \begin{aligned}
231 | \text{micro-}P&=\frac{\overline {TP}}{\overline {TP}+\overline {FP}}\\
232 | \text{micro-}R&=\frac{\overline {TP}}{\overline {TP}+\overline {FN}}\\
233 | \text{micro-}F_1&=\frac{2\times\text{micro-}P\times\text{micro-}R}{\text{micro-}P+\text{micro-}R}
234 | \end{aligned}
235 | $$
236 |
237 | #### ROC & AUC
238 |
239 | 纵轴TPR,横轴FPR
240 |
241 | $$
242 | \begin{aligned}
243 | TPR&=\frac{TP}{TP+FN}\\
244 | FPR&=\frac{FP}{TN+FP}
245 | \end{aligned}
246 | $$
247 |
248 | 
249 |
250 | ROC曲线 (Receiver Operating Characteristic):若一个学习器的ROC曲线被另一个学习器的曲线完全“包住”,则可断言后者的性能优于前者;若两个学习器的ROC曲线发生交叉,则难以以般性地断言两者孰优孰劣。
251 |
252 | AUC (Area Under ROC Curve):
253 |
254 | $$
255 | \ell_{rank}=\frac1{m^+m^-}\sum_{x^+\in D^+}\sum_{x^-\in D^-}\left(\mathbb I\left((f(x^+) 存在什么问题?
277 |
278 | 1. 我们希望比较的是泛化性能,实际比较的是测试集性能,两者的对比结果不一定相同
279 | 2. 测试集性能与测试集本身的选择有很大关系
280 | 3. 很多机器学习本身有一定的随机性
281 |
282 | #### 假设检验[还没看]
283 |
284 | “假设”是对学习器泛化错误率分布的猜想,假设检验根据测试错误率估推出泛化错误率的分布。
285 |
286 | 泛化错误率 $ \epsilon $ ,测试错误率 $ \hat{\epsilon} $
287 |
288 | ### 偏差与方差
289 |
290 | #### 偏差、方差、噪声
291 |
292 | 偏差:度量了学习算法的期望预测与真实结果的偏离程度,即刻画了学习算法本身的拟合能力。
293 |
294 | 方差:度量了同样大小的训练集的变动所导致的学习性能的变化,即刻画了数据扰动所造成的影响。
295 |
296 | 噪声:表达了在当前任务上任何学习算法所能达到的期望泛化误差的下界,即刻画了学习问题本身的难度。
297 |
298 | #### 偏差-方差分解
299 |
300 | bias-variance decomposition,泛化误差可分解为偏差、方差与噪声之和。说明泛化性能是由学习算法的能力、数据的充分性以及学习任务本身的难度所共同决定的。 $ E(f:D)=bias^2(x)+var(x)+\epsilon $
301 |
302 | 以回归任务为例,学习算法的期望预测为:
303 |
304 | $$
305 | \overline f(x)=\mathbb E_D[f(x;D)]
306 | $$
307 |
308 | 使用样本数相同的不同训练集产生的方差:
309 |
310 | $$
311 | var(x)=\mathbb E_D\left[(f(x;D)-\overline f(x))^2\right]
312 | $$
313 |
314 | 噪声:
315 |
316 | $$
317 | \epsilon ^2=\mathbb E_D\left[(y_D-y)^2\right]
318 | $$
319 |
320 | 期望输出与真实标记的差别称为偏差 (bias),即
321 |
322 | $$
323 | bias^2(x)=\left(\overline f(x)-y\right)^2
324 | $$
325 |
326 | 证明:
327 |
328 | $$
329 | \begin{aligned}
330 | \mathbb E_D(f;D)=&\mathbb E_D\left[\left(f(x:D)-y_D \right)^2\right]\\
331 | =&\mathbb E_D\left[\left(f(x:D)-\overline f(x)+\overline f(x)-y_D \right)^2\right]\\
332 | =&\mathbb E_D\left[\left(f(x:D)-\overline f(x) \right)^2\right]+\mathbb E_D\left[\left(\overline f(x)-y_D \right)^2\right]\\
333 | &+\mathbb E_D\left[2\left(f(x:D)-\overline f(x) \right)\left(\overline f(x)-y_D \right)\right]\\
334 | =&\mathbb E_D\left[\left(f(x:D)-\overline f(x) \right)^2\right]+\mathbb E_D\left[\left(\overline f(x)-y_D \right)^2\right]\\
335 | =&\mathbb E_D\left[\left(f(x:D)-\overline f(x) \right)^2\right]+\mathbb E_D\left[\left(\overline f(x)-y+y-y_D \right)^2\right]\\
336 | =&\mathbb E_D\left[\left(f(x:D)-\overline f(x) \right)^2\right]+\mathbb E_D\left[\left(\overline f(x)-y \right)^2\right]\\
337 | &+\mathbb E_D\left[\left(y-y_D \right)^2\right]+\mathbb E_D\left[\left(\overline f(x)-y \right)\left(y-y_D \right)\right]\\
338 | =&\mathbb E_D\left[\left(f(x:D)-\overline f(x) \right)^2\right]+\left(\overline f(x)-y \right)^2+\mathbb E_D\left[\left(y_D-y \right)^2\right]
339 |
340 |
341 | \end{aligned}
342 | $$
343 |
344 | #### 偏差-方差困境
345 |
346 | 偏差与方差是有冲突的,这称为偏差-方差窘境 (bias-variance dilemma)。假定我们能控制学习算法的训练程度,则在训练不足时学习器的拟合能力不够强,训练数据的扰动不足以便学习器产生显著变化,此时偏差主导了泛化错误率;随着训练程度的加深,学习器的拟合能力逐渐增强,训练数据发生的扰动渐渐能被学习器学到,方差逐渐主导了泛化错误率。在训练程度充足后,学习器的拟合能力已非常强,训练数据发生的轻微扰动都会导致学习器发生显著变化,若训练数据自身的、非全局的特性被学习器学到了,则将发生过拟合。
347 |
348 |  349 |
350 | ## 线性模型
351 |
352 | ### 线性回归
353 |
354 | #### 线性回归的目标
355 |
356 | $$
357 | (w^*,b^*)=\arg \min_{(w,b)}\sum_{i=1}^m(f(x_i)-y_i)^2=\arg \min_{(w,b)}\sum_{i=1}^m(y_i-wx_i-b)^2
358 | $$
359 |
360 | #### 最小二乘
361 |
362 | 最小二乘“参数估计”:求解 $ w,b $ 使 $ \mathbb E_{(w,b)}=\sum_{i=1}^m(y_i-wx_i-b)^2 $ 最小化的过程。将 $ \mathbb E_{(w,b)} $ 对 $ w,b $ 求导,令之为零后得到 $ w,b $ 最优解的闭式解。
363 |
364 | #### 对数线性回归
365 |
366 | log-linear regression, $ \ln y=w^\top x+b $
367 |
368 | #### 广义线性模型
369 |
370 | generalized linear model, $ y=g^{-1}(w^\top x+b) $ ,其中 $ g(\cdot) $ 为联系函数link function
371 |
372 | ### 逻辑斯蒂回归
373 |
374 | #### 什么是逻辑斯蒂回归?
375 |
376 | 逻辑斯蒂回归为一个分类算法,通过对输入特征进行加权求和,并将结果通过一个值域为0-1的sigmoid函数(也称为逻辑函数)进行映射,从而得到输出概率值。
377 |
378 | #### Sigmoid函数是什么?为什么要用Sigmoid函数?
379 |
380 | Sigmoid函数即形似S的函数,目的是近似不连续不可导的单位阶跃函数(值域 $ \{0,1\} $ ),作为它的替代函数surrogate function。又称对数几率函数。公式为
381 |
382 | $$
383 | y=\frac1{1+e^{-z}}
384 | $$
385 |
386 | 值域为 $ [0,1] $
387 |
388 | #### 如何求解参数?
389 |
390 | 将后验概率估计代入对数几率的式子,用极大似然法找到Loss函数。然后用梯度下降法、牛顿法等数值优化方法找到使得Loss最小的 $ \beta $ ,即可得到参数。
391 |
392 | 具体见p59。
393 |
394 | #### 梯度下降
395 |
396 | > 什么是梯度下降法?
397 |
398 | 一阶迭代数值优化算法,用于寻找可微函数的局部最小值。
399 |
400 | 更新公式:
401 |
402 | $$
403 | x_{n+1}=x_{n}-\gamma\nabla f(x_n)
404 | $$
405 |
406 | 其中, $ \gamma $ 是学习率。 $ \nabla f $ 指向函数值增长最快的方向,则 $ -\nabla f $ 指向函数值增长最快的方向。理论上当 $ \gamma $ 足够小,则 $ f(x_n)\geq f(x_{n+1}) $
407 |
408 | > 需要满足什么条件?
409 |
410 | 前提:
411 |
412 | 1. 目标函数可导
413 | 2. 目标函数是凸函数(否则可能会陷入局部最优解)
414 |
415 | > 有什么优缺点?
416 |
417 | 优点:
418 |
419 | 1. 可以应用于许多不同的优化问题(线性回归,逻辑回归,神经网络)
420 | 2. 算法简单
421 | 3. 只需要计算一阶导数,计算成本相对较低。
422 | 4. 可以在大规模数据集上进行优化。
423 |
424 | 缺点:
425 |
426 | 1. 可能会陷入局部最小值,无法得到全局最小值。
427 | 2. 当函数存在平台、峡谷和其他复杂的非凸结构时,可能会出现震荡或缓慢收敛的情况。
428 | 3. 需要选择合适的学习率,过大或过小都会影响优化结果。
429 | 4. 对于某些问题,可能需要较多的迭代次数才能达到收敛。
430 |
431 | #### 什么是牛顿迭代法?需要满足什么条件?有什么优缺点?
432 |
433 | 目的:求 $ f(x)=0 $ 的解
434 |
435 | 初始化: $ x_0 $
436 |
437 | 重复:过 $ x_i $ 求 $ f(x) $ 的切线 $ L:y=f(x_{i})+f'(x_{i})(x-x_i) $ ,与x轴交点为 $ x_{i+1}=x_i-\frac{f(x_i)}{f'(x_i)} $
438 |
439 | 迭代公式:
440 |
441 | $$
442 | x_{n+1}=x_n-\frac{f(x_n)}{f'(x_n)}
443 | $$
444 |
445 | 对于 $ \beta^*=\arg\min_{\beta}\ell(\beta) $ 的优化问题,更新公式为:
446 |
447 | $$
448 | \beta^{t+1}=\beta^t-\left(\frac{\part^2\ell(\beta)}{\part \beta\part \beta^\top}\right)^{-1}\frac{\part\ell(\beta)}{\part \beta}
449 | $$
450 |
451 | 必要条件:
452 |
453 | 1. 目标函数二价可微
454 | 2. 目标函数的海森矩阵必须正定或负定
455 |
456 | 优点:
457 |
458 | 1. 可以更快地收敛到最优解,尤其是在函数存在二阶导数且二阶导数连续的情况下。
459 | 2. 可以解决梯度下降等一阶方法无法收敛的问题。
460 | 3. 可以自动调整学习率,减少手动调参的工作量。
461 |
462 | 缺点:
463 |
464 | 1. 对于高维问题,计算海森矩阵的代价非常昂贵。
465 | 2. 当海森矩阵不正定时,可能会导致算法发散。
466 | 3. 可能会陷入局部最小值,无法得到全局最小值。
467 | 4. 由于需要计算二阶导数,所以计算成本相对较高。
468 | 5. 当函数存在平台、峡谷和其他复杂的非凸结构时,可能会出现震荡或缓慢收敛的情况。
469 |
470 | ### 线性判别分析
471 |
472 | LDA, Linear Discriminant Analysis
473 |
474 | > 什么是LDA?
475 |
476 | LDA是一种常用的分类算法和数据降维方法。它可以将一个高维数据集降到一个更低的维度,同时保持样本类别信息,从而方便后续的分类任务。
477 |
478 | LDA 假设数据符合高斯分布,且各类别的协方差矩阵相等,基于此,它通过线性变换,将数据投影到一个低维空间中,使得同一类别的数据尽可能的接近,不同类别的数据尽可能的远离。这种投影方式保留了最大的类间差异性和最小的类内差异性,因此可以有效的提高分类准确率。
479 |
480 | 具体来说,LDA 算法主要包含两个步骤:(1)计算类内散度矩阵和类间散度矩阵;(2)通过求解广义瑞利商的特征向量,得到用于投影的变换矩阵。
481 |
482 | LDA 广泛应用于图像识别、人脸识别、语音识别等领域,并且在实际应用中表现良好。
483 |
484 | > 什么是类内散度矩阵,类间散度矩阵?
485 |
486 | $ X_i,\mu_i,\Sigma_i $ :第 $ i $ 类示例的集合、均值向量、协方差矩阵。
487 |
488 | $ w^\top \mu_i,w^\top \Sigma_i w $ :投影后的结果
489 |
490 | 目标:同类样例投影点的协方差尽可能小,即 $ w^\top \Sigma_0 w+w^\top \Sigma_1 w $ 尽可能小;类中心之间的距离尽可能大,即 $ ||w^\top \mu_0-w^\top\mu_1||_2^2 $ 尽可能大。即最大化
491 |
492 | $$
493 | J=\frac{||w^\top \mu_0-w^\top\mu_1||_2^2}{w^\top \Sigma_0 w+w^\top \Sigma_1 w}=\frac{w^\top (\mu_0-\mu_1)(\mu_0-\mu_1)^\top w}{w^\top(\Sigma_0+\Sigma_1)w}
494 | $$
495 |
496 | 其中**类内散度矩阵**within-class scatter matrix:
497 |
498 | $$
499 | S_w=\Sigma_0+\Sigma_1=\sum_{x\in X_0}(x-\mu_0)(x-\mu_0)^\top+\sum_{x\in X_1}(x-\mu_1)(x-\mu_1)^\top
500 | $$
501 |
502 | **类间散度矩阵**between-class scatter matrix:
503 |
504 | $$
505 | S_b=(\mu_0-\mu_1)(\mu_0-\mu_1)^\top
506 | $$
507 |
508 | 这就是LDA想要最大化的目标,即 $ S_b,S_w $ 的广义瑞利商generalized Rayleigh quotient:
509 |
510 | $$
511 | J=\frac{w^\top S_b w}{w^\top S_w w}
512 | $$
513 |
514 | > 如何求解LDA?
515 |
516 | 即确定能最大化 $ J $ 的 $ w $
517 |
518 | 令 $ w^\top S_ww=1 $ ,原式等价于
519 |
520 | $$
521 | \begin{aligned}
522 | &\min_w &&-w^\top S_b w\\
523 | &s.t. && w^\top S_w w=1
524 | \end{aligned}
525 | $$
526 |
527 | 由拉格朗日乘子法,等价于
528 |
529 | $$
530 | S_b w=\lambda S_ww
531 | $$
532 |
533 | $ S_b w $ 方向恒等于 $ \mu_0-\mu_1 $ ,令
534 |
535 | $$
536 | S_b w=\lambda(\mu_0-\mu_1)
537 | $$
538 |
539 | 有:
540 |
541 | $$
542 | w=S_w^{-1}(\mu_0-\mu_1)
543 | $$
544 |
545 | 考虑到数值解的稳定性,在实践中通常是对 $ S_w $ 进行奇异值分解,即 $ S_w= U\Sigma V^\top $ ,这里 $ \Sigma $ 是一个实对角矩阵,其对角线上的元素是 $ S_w $ 的奇异值,然后再由 $ S_w^{-1}=V\Sigma^{-1}U^\top $ 得到 $ S_w^{-1} $
546 |
547 | > 如何推广到多分类?[再看看!]
548 |
549 | 定义全局散度矩阵( $ \mu $ 是所有示例的均值之和)
550 |
551 | $$
552 | S_t=S_b+S_w=\sum_{i=1}^m(x_i-\mu)(x_i-\mu)^\top\\
553 | S_w=\sum_{i=1}^N S_{w_i}=\sum_{i=1}^N\sum_{x\in X_i}(x-\mu_i)(x-\mu_i)^\top\\
554 | S_b=S_t-S_w=\sum_{i=1}^N m_i(\mu_i-\mu)(\mu_i-\mu)^\top
555 | $$
556 |
557 | 优化目标:
558 |
559 | $$
560 | \max_W\frac{tr(W^\top S_bW)}{tr(W^\top S_wW)}
561 | $$
562 |
563 | 通过求解 $ S_b W=\lambda S_w W $ 可得, $ W $ 的闭式解为 $ S_w^{-1}S_b $ 的 $ N-1 $ 个最大广义特征值所对应的特征向量组成的矩阵。
564 |
565 | ### 多分类学习
566 |
567 | #### 有什么拆分策略?
568 |
569 | OvO(一对一,one vs one): $ \frac{N(N-1)}{2} $ 个分类器
570 |
571 | OvR(一对剩余,one vs rest): $ N $ 个分类器,选择置信度最大的类别标记
572 |
573 | MvM(多对多,many vs many):需要用ECOC编码特殊构造。
574 |
575 | ### 类别不平衡
576 |
577 | class-imbalance
578 |
579 | #### 有什么解决方法?
580 |
581 | “再缩放”,也是“代价敏感学习”cost-sensitive learning的基础
582 |
583 | 1. 对反例进行“欠采样”
584 | 2. 对正例进行“过采样”
585 | 3. 阈值移动
586 |
587 | ## 决策树
588 |
589 | ### 基本流程
590 |
591 | #### 什么是决策树?
592 |
593 | 决策树是一种基于树结构的分类算法,其中每个内部节点表示一个属性或特征,每个叶子节点代表一个类别。该算法可以用于分类和回归问题,它通过对样本集合进行递归分治来构建决策树。
594 |
595 | 在构建决策树时,算法会选择一个最好的属性或特征,将样本集合分成更小的子集。这个过程会不断重复,直到所有的子集都属于同一个类别,或者已经达到了预先定义的最大深度。
596 |
597 | 决策树算法具有可解释性和易于理解的优点,因为它可以清楚地显示分类决策的过程,还可以处理缺失值和噪声数据。不过,决策树算法在处理高维数据时可能会遇到困难,并且容易受到过拟合和欠拟合等问题的影响。
598 |
599 | #### 决策树算法的基本流程是什么?
600 |
601 | 决策树的生成是基于分治策略的递归过程。
602 |
603 | 首先生成结点,如果训练集中的样本均属于同一类别,则将该节点标记为该类叶子结点,返回。如果属性集为空或训练集在属性集上的取值相同,则将该节点标记为叶子结点,类别为数据集中样本数最多的类,返回。如果都不满足这两种情况的话,从属性集中选择最优划分 $ a^* $ 。对最优划分中的每一个值,为结点生成一个分支,构造相应取值的样本子集。如果样本子集为空,则将该节点标记为叶子结点,类别为数据集中样本数最多的类,返回。否则递归地对样本子集和最优划分的子集生成决策树。
604 |
605 | #### 什么情况会导致递归返回?
606 |
607 | 1. 当前结点包含的样本全属于同一类别,无需划分
608 | 2. 当前属性集为空,或是所有样本在所有属性上取值相同,无法划分
609 | 3. 当前结点包含的样本集合为空,不能划分。
610 |
611 | ### 划分选择
612 |
613 | #### 有什么划分的指标?它们的具体定义?
614 |
615 | 划分选择的目标是希望决策树的分支结点所包含的样本尽可能属于同一类别,即结点的“纯度” (purity) 越来越高。
616 |
617 | 划分的指标有:(ID3)信息增益、(C4.5)增益率、(CART)基尼指数。
618 |
619 | $ p_k $ :当前样本属于第 $ k $ 类的比例
620 |
621 | 假设离散属性 $ a $ 有 $ V $ 个可能的取值 $ \{a^1,\dots,a^V\} $ ,若使用 $ a $ 来对样本集 $ D $ 进行划分,则会产生 $ V $ 个分支结点,其中第 $ v $ 个分支结点包含了 $ D $ 中所有在属性 $ a $ 上取值为 $ a^v $ 的样本,记为 $ D^v $
622 |
623 | 信息熵:值越小,纯度越高
624 |
625 | $$
626 | Ent(D)=-\sum_{k=1}^{\mathcal Y}p_k\log_2 p_k
627 | $$
628 |
629 | 信息增益:值越大,说明使用属性 $ a $ 来划分所获得的纯度提升越大。
630 |
631 | $$
632 | Gain(D,a)=Ent(D)-\sum_{v=1}^V\frac{|D^v|}{|D|}Ent(D^v)
633 | $$
634 |
635 | 增益率:信息增益准则对可取值数目较多的属性有所偏好,为减少这种偏好可能带来的不利影响,引入增益率。其中 $ IV(a) $ 为属性 $ a $ 的固有值intrinsic value
636 |
637 | $$
638 | Gain_ratio(D,a)=\frac{Gain(D,a)}{IV(a)}\\
639 | IV(a)=-\sum_{v=1}^V\frac{|D|^v}{|D|}\log_2\frac{|D|^v}{|D|}
640 | $$
641 |
642 | 基尼指数Gini index:Gini反映从数据集 $ D $ 中随机抽取两个样本,其类别标记不一致的概率。越小纯度越高
643 |
644 | $$
645 | Gini(D)=\sum_{k=1}^{|\mathcal Y|}\sum_{k'\neq k}p_kp_{k'}=1-\sum_{k=1}^{|\mathcal Y|}p_k^2\\
646 | \text{Gini_Index}(D,a) =\sum_{v=1}^V\frac{|D^v|}{|D|}Gini(D^v)
647 | $$
648 |
649 | ### 剪枝
650 |
651 | #### 简述预剪枝和后剪枝的策略?
652 |
653 | 预剪枝:基于贪心思想,如果划分后验证集精度 $ \leq $ 原来的精度,则剪枝,禁止这些分支展开。
654 |
655 | 后剪枝:生成完整决策树后,从叶子结点开始遍历,如果划分后验证集精度 $ \leq $ 原来的精度,则剪枝,禁止这些分支展开。
656 |
657 | #### 两者的优缺点?
658 |
659 | | | 预剪枝 | 后剪枝 |
660 | | ------------- | ------------------------------ | ---------------------------------- |
661 | | 时间开销 | 测试时间降低,训练时间降低 | 测试时间降低,训练时间提高 |
662 | | 过/欠拟合风险 | 过拟合风险降低,欠拟合风险增加 | 过拟合风险降低,欠拟合风险基本不变 |
663 | | 泛化性能 | | 后剪枝通常优于预剪枝 |
664 |
665 | ### 连续值与缺失值
666 |
667 | #### 如何处理连续值?
668 |
669 | 基本思路是连续属性离散化
670 |
671 | 1. 二分法
672 | 2. 对于从大到小排序好的取值 $ \{a^1,\dots,a^n\} $ ,令划分点集合为 $ T_a=\left\{\frac{a^i+a^{i+1}}2|i\leq i\leq n-1\right\} $ ,然像离散属性值一样来考察这些划分点
673 |
674 | 需注意的是,与离散属性不同,若当前结点划分属性为连续属性,该属性还 可作为其后代结点的划分属性。
675 |
676 | #### 如何处理缺失值?
677 |
678 | 需要解决 1. 训练 2. 测试时的处理
679 |
680 | 令 $ \tilde D $ 为 $ D $ 在属性 $ a $ 上没有缺失值的样本子集,定义:
681 |
682 | 无缺失值比例: $ \displaystyle \rho=\frac{\sum_{x\in\tilde D} w_x}{\sum_{x\in D} w_x} $
683 |
684 | 无缺失值样本中第 $ k $ 类的比例: $ \displaystyle \tilde p_k=\frac{\sum_{x\in\tilde D_k} w_x}{\sum_{x\in \tilde D} w_x},1\leq k\leq|\mathcal Y| $
685 |
686 | 无缺失值样本中在属性 $ a $ 上取值为 $ a^v $ 的比例: $ \displaystyle \tilde r_v=\frac{\sum_{x\in\tilde D^v} w_x}{\sum_{x\in \tilde D} w_x},1\leq v\leq V $
687 |
688 | 推广:
689 |
690 | $$
691 | Ent(\tilde D)=-\sum_{k=1}^{\mathcal Y}\tilde p_k\log_2 \tilde p_k\\
692 | Gain(D,a)=\rho \times Gain(\tilde D,a)=\rho \times\left(Ent(D)-\sum_{v=1}^V \tilde r_v Ent(D^v)\right)
693 | $$
694 |
695 | ### 多变量决策树
696 |
697 | multivariate decision tree,在多变量决策树的学习过程中, 不是为每个非叶结点寻找一个最优划分属性,而是试图建立一个合适的线性分类器。
698 |
699 | ## 神经网络
700 |
701 | ## 支持向量机
702 |
703 | ### 基本概念
704 |
705 | #### 英文介绍
706 |
707 | Support Vector Machine (SVM) is a powerful machine learning algorithm used for classification and regression analysis. SVM finds the best hyperplane that separates different classes in a high-dimensional space. The hyperplane is chosen in such a way that it maximizes the margin or the distance between the two closest points of different classes. These closest points are called support vectors, and they play a crucial role in defining the hyperplane.
708 |
709 | SVM can handle both linearly separable and non-linearly separable data by using different types of kernel functions such as linear, polynomial, radial basis function (RBF), and sigmoid. The choice of kernel function depends on the data and the problem at hand. SVM can also handle multi-class classification problems using various techniques such as one-vs-one and one-vs-all.
710 |
711 | SVM has several advantages over other classification algorithms such as logistic regression and decision trees. It is less prone to overfitting, works well with high-dimensional data, and is computationally efficient. However, SVM has some limitations, such as the need for careful selection of kernel functions and hyperparameters, and the difficulty in handling large datasets.
712 |
713 | #### SVM是什么?
714 |
715 | 支持向量机是一种可以用于解决分类和回归问题的机器学习算法,目标是在高维空间中找到最佳的超平面,以最大化间隔,也就是margin。
716 |
717 | SVM问题的基本型(是一个凸二次优化问题):
718 |
719 | $$
720 | \begin{aligned}
721 | &\min_{w,b} \quad\frac12||w||^2\\
722 | &s.t. \quad y_i(w^\top x_i+b)\geq1,i=1,\dots,m
723 | \end{aligned}
724 | $$
725 |
726 | #### SVM中的“支持向量”指什么?在SVM中如何确定支持向量?
727 |
728 | “支持向量”是指离分隔超平面最近的训练样本点。这些样本点是最能影响分隔超平面位置和方向的点,如果它们的位置发生变化,会直接影响到分隔超平面的位置和方向。
729 |
730 | 我们在SVM的训练过程中确定支持向量。在SVM的训练过程中,我们首先随机初始化超平面参数,然后迭代地优化超平面参数,直到收敛为止。在每一次迭代中,我们根据当前的超平面参数计算每个训练样本点到超平面的距离,并根据这些距离来判断哪些样本点是支持向量。
731 |
732 | #### SVM在分类问题中如何定义“边界”(decision boundary)?
733 |
734 | 在SVM中,边界(decision boundary)是指将不同类别的数据点分开的超平面(hyperplane)。SVM的目标是寻找一个最优的超平面,将不同类别的数据点分开,并且使得该超平面与最近的数据点之间的距离(即margin)最大化。
735 |
736 | #### SVM有什么优点和缺点?
737 |
738 | 优点:
739 |
740 | 1. 能有效处理高维数据,例如图像和文本分类
741 | 2. 在小数据集处理时表现优异,因为它只需要少量的支持向量来定义边界
742 | 3. SVM对数据中的噪声具有鲁棒性,因为决策边界由支持向量确定,它们是距离边界最近的数据点。
743 | 4. 泛化性好
744 |
745 | 缺点:
746 |
747 | 1. 不适用于大数据集,因为计算开销过大
748 | 2. 对核函数选择和参数选择敏感
749 | 3. 只适用于二元问题
750 | 4. 缺乏概率解释
751 | 5. 不适用于有缺失值的数据
752 |
753 | ### 原问题和对偶问题
754 |
755 | #### 如何将SVM转化为对偶问题?
756 |
757 | 对偶问题(dual problem)是指将一个优化问题的原问题(primal problem)转化为一个新的优化问题,对偶问题和原问题有相同的最优解,但对于一些问题,通过求解对偶问题可以更方便或更有效地得到原问题的解。
758 |
759 | 对偶问题一定是凸优化问题。
760 |
761 | 可以使用拉格朗日乘子法得到SVM的对偶问题:
762 |
763 | 拉格朗日函数:
764 |
765 | $$
766 | L(w,b,\alpha)=\frac12||w||^2+\sum_{i=1}^m\alpha_i(1-y_i(\omega^\top x_i+b))
767 | $$
768 |
769 | 令 $ L(w,b,\alpha) $ 对 $ \omega,b $ 的偏导为零可得:
770 |
771 | $$
772 | w=\sum_{i=1}^m\alpha_i y_ix_i\quad(1)\\
773 | 0=\sum_{i=1}^m\alpha_i y_i\quad(2)
774 | $$
775 |
776 | 将(1)代入拉格朗日函数可消去 $ w,b $ ,考虑(2)的约束可以得到对偶问题:
777 |
778 | $$
779 | \begin{aligned}
780 | &\max_{\alpha}\quad \sum_{i=1}^m\alpha_i-\frac12\sum_{i=1}^m\sum_{i=1}^m\alpha_i\alpha_jy_iy_jx_i^\top x_j\\
781 | &s.t. \quad \sum_{i=1}^m\alpha_i y_i=0,\alpha_i\geq 0,i=1,\dots,m
782 | \end{aligned}
783 | $$
784 |
785 | 要满足KKT条件:
786 |
787 | $$
788 | \left\{\begin{aligned}
789 | &\alpha_i\geq0\\
790 | &y_if(x_i)-1\geq 0\\
791 | &\alpha_i(y_if(x_i)-1)=0
792 | \end{aligned}\right.
793 | $$
794 |
795 | ##### 什么是KKT条件?[x]
796 |
797 | Karush-Kuhn-Tucker (KKT)条件是非线性规划(nonlinear programming)最佳解的必要条件。
798 |
799 | 对于Lagrangian函数
800 |
801 | $$
802 | L(x,\lambda,\mu)=f(x)+\sum_{j=1}^m\lambda_jg_j(x)+\sum_{k=1}^n\mu_kh_k(x)
803 | $$
804 |
805 | KKT条件包括:**[术语怎么说?KKT只是必要条件,要到充分条件该如何做?内点]**
806 |
807 | $$
808 | \left\{\begin{aligned}
809 | &\nabla_xL=0\\
810 | &g_j(x)=0,j = 1,\dots,m\\
811 | &h_k(x)\leq 0,\\
812 | &\mu_k\geq 0,\\
813 | &\mu_kh_k(x)=0,k=1,\dots,p
814 | \end{aligned}\right.
815 | $$
816 |
817 | #### 为什么要将SVM转化为对偶问题?
818 |
819 | 虽然原问题本身就是一个凸二次规划(convex quadratic programming)问题,可以直接用现成的优化计算包求解,但是转化为对偶问题求解更高效。
820 |
821 | 原始的SVM问题是一个凸二次规划问题,通常使用二次规划算法求解。然而,当数据集的规模很大时,使用原始问题求解SVM会变得很慢,甚至变得不可行。此外,对于非线性SVM,计算的复杂度会随着特征空间的维度增加而急剧增加。
822 |
823 | 将SVM转化为对偶问题,就可以使用SMO算法等更高效的方法求解。
824 |
825 | 对偶问题和内积有关,可以引入核函数
826 |
827 | ##### 什么是SMO算法?
828 |
829 | ##### 为什么SMO算法不能用于求解原问题?
830 |
831 | ### 核函数
832 |
833 | kernel function
834 |
835 | #### SVM中的核函数是什么?
836 |
837 | 核函数是一种常用的技巧,用于将低维空间中线性不可分的数据映射到高维空间,从而使其在高维空间中变得线性可分。
838 |
839 | 如果原始空间是有限维(属性有限),那么一定存在一个高维特征空间使样本可分。
840 |
841 | 令 $ \phi(x) $ 为将 $ x $ 映射后的特征向量,于是,在特征空间中划分超平面所对应的模型可表示为
842 |
843 | $$
844 | f(x)=w^\top\phi(x)+b
845 | $$
846 |
847 | 原问题
848 |
849 | $$
850 | \begin{aligned}&\min_{w,b} \quad\frac12||w||^2\\&s.t. \quad y_i(w^\top \phi(x_i)+b)\geq1,i=1,\dots,m\end{aligned}
851 | $$
852 |
853 | 对偶问题
854 |
855 | $$
856 | \begin{aligned}
857 | &\max_{\alpha}\quad \sum_{i=1}^m\alpha_i-\frac12\sum_{i=1}^m\sum_{i=1}^m\alpha_i\alpha_jy_iy_j\phi(x_i)^\top\phi( x_j)\\
858 | &s.t. \quad \sum_{i=1}^m\alpha_i y_i=0,\alpha_i\geq 0,i=1,\dots,m
859 | \end{aligned}
860 | $$
861 |
862 | 核函数就是 $ \kappa(x_i,x_j)=<\phi(x_i),\phi(x_j)>=\phi(x_i)^\top\phi(x_j) $
863 |
864 | #### 核函数有什么性质?
865 |
866 | **[充要条件]** $ \kappa $ 是核函数当且仅当对于任意数据 $ D={x_1,\dots,x_m} $ ,核矩阵 $ K=[\kappa(x_i,x_i)]_{m\times m} $ 总是半正定的。
867 |
868 | 也就是说,对于一个半正定的核矩阵,总能找到一个与之对于的映射 $ \phi $ 。
869 |
870 | #### 有什么常用的核函数?
871 |
872 | | 名称 | 表达式 | 参数 | 适用场景 |
873 | | ----------- | ----------------------------------------------------------- | -------------------------- | ------------------------------------------------------------------------------------------------------------------------------------------------------------ |
874 | | 线性核 | $ \kappa(x_i,x_j)=x_i^\top x_j $ | | 输入特征维度较低,数据线性可分 |
875 | | 多项式核 | $ \kappa(x_i,x_j)=(x_i^\top x_j)^d $ | $ d\geq 1 $ ,多项式次数 | 数据中存在多项式关系 |
876 | | 高斯核(RBF) | $ \kappa(x_i,x_j)=\exp(-\frac{||x_i- x_j||^2}{2\sigma^2}) $ | $ \sigma>0 $ ,高斯核的带宽 | 输入特征维度较高 |
877 | | 拉普拉斯核 | $ \kappa(x_i,x_j)=\exp(-\frac{||x_i-x_j||}{\sigma}) $ | $ \sigma>0 $ | 采用 $ L_1 $ 范数来度量两个样本点之间的距离,而高斯核函数采用 $ L_2 $ 范数来度量。可以在一定程度上克服高斯核函数中存在的过拟合问题,适用于一些噪声较多的数据集。 |
878 | | Sigmoid核 | $ \kappa(x_i,x_j)=\tanh(\beta x_i^\top x_j+\theta) $ | $ \beta>0,\theta<0 $ | 数据集合线性不可分时,将数据映射到一个非线性空间中。表现不是很好,高斯核和拉普拉斯核更常用。 |
879 |
880 | 此外,若 $ \kappa_1,\kappa_2 $ 为核函数,则
881 |
882 | - $ \gamma_1\kappa_1+\gamma_2\kappa_2 $ 也是核函数
883 | - $ \kappa_1\otimes\kappa_2(x,z)=\kappa_1(x,z)\kappa_2(x,z) $ 也是核函数
884 | - 对于任意函数 $ g(x) $ , $ g(x)\kappa_1(x,z)g(z) $ 也是核函数
885 |
886 | #### 如何选择合适的核函数?[x]
887 |
888 | **[未完善]核函数需要满足什么性质?(很好地度量在希尔伯特空间里的距离,自反性,来回一样,对于自己为0...)**
889 |
890 | 根据根据具体的问题和数据选择。
891 |
892 | ### 软间隔与正则化
893 |
894 | #### 什么是软间隔SVM?
895 |
896 | 软间隔(soft margin)SVM通过设置松弛变量(slack variable),以允许某些样本不满足约束。传统硬间隔SVM要求数据完全线性可分,然而在实际情况下,由于数据可能存在一些噪声和异常点,很难找到完全线性可分的数据集。软间隔SVM通过允许一些样本出现在超平面的错误一侧,以此来解决线性不可分的问题。
897 |
898 | 优化目标可以写为
899 |
900 | 结构风险最小化+经验风险最小化
901 |
902 | $$
903 | \min_{w,b}\quad\frac12\vert\vert w\vert\vert^2+C\sum_{i=1}^{m}\ell_{0/1}\left(y_i(\omega^\top x_i+b)-1\right)
904 | $$
905 |
906 | 其中正则化常数 $ C>0 $ , $ \ell_{0/1} $ 为“0/1损失函数”, $ \ell_{0/1}=\left\{\begin{aligned}&1&z<0\\&0&otherwise\end{aligned}\right. $
907 |
908 | $ C\to\infty $ 时,会迫使所有样本均满足约束,等价于硬间隔; $ C $ 有限值时,允许一些样本不满足约束。
909 |
910 | #### 什么是替代损失?
911 |
912 | 由于 $ \ell_{0/1} $ 非凸、不连续,数学性质不好,使得优化目标难以直接求解,于是,使用其他一些函数替代 $ \ell_{0/1} $ ,称为替代损失(surrogate loss)
913 |
914 | - hinge损失(最常用): $ \ell_{hinge}(z)=\max(0,1-z) $
915 | - 指数损失exponential loss: $ \ell_{\exp}(z)=\exp(-z) $
916 | - 对率损失logistic loss: $ \ell_{\log}=\log(1+\exp(-z)) $
917 |
918 | 若采取hinge损失,优化目标可以改写为:
919 |
920 | $$
921 | \min_{w,b}\quad\frac12\vert\vert w\vert\vert^2+C\sum_{i=1}^{m}\max\left(0,1-y_i(\omega^\top x_i+b)\right)
922 | $$
923 |
924 | ##### 为什么使用Hinge Loss?[不知道!]
925 |
926 | Hinge Loss的优点在于它可以将最小化分类错误和最大化间隔相结合,即最小化损失的同时,最大化分类间隔。相比于其他损失函数,Hinge Loss对异常值的容忍度更高,可以更好地处理噪声和异常点的情况。同时,Hinge Loss的导数在0处不连续,使得模型更加稳定,不容易陷入局部最优解。(ChatGPT的回答)
927 |
928 | #### 什么是松弛变量?
929 |
930 | 引入松弛变量(slack variables),可将优化目标重写为
931 |
932 | $$
933 | \begin{aligned}
934 | &\min_{w,b}&\frac12\vert\vert w\vert\vert^2+C\sum_{i=1}^{m}\xi_{i}\\
935 | &s.t.&y_i(w^\top x_i+b)\geq1-\xi_{i}\\
936 | &&\xi_i\geq0,i=1,\dots,m
937 | \end{aligned}
938 | $$
939 |
940 | ##### 噪声和异常点的区别?
941 |
942 | | 噪声(noise) | 异常值(outliers) |
943 | | -------------------------------------------------------------- | ---------------------------------------------------------------------------------------------------- |
944 | | 数据中存在的错误或不准确的值 | 与其他数据点不同的、明显偏离正常情况的数据点 |
945 | | 可能是由于测量设备、传输问题或人为因素导致的 | 可能是由于记录或测量错误、系统故障或自然变异等原因导致的 |
946 | | 在整个数据集中分布较均匀 | |
947 | | 可能会对模型的性能产生一定影响,但它们不一定是非常明显的异常值 | 可能会对模型的训练和预测造成不良影响,因为它们可能会导致模型的偏差和方差增大,从而影响模型的泛化性能 |
948 | | 数据清洗和预处理噪声 | 使用特定的算法或技术来检测和处理异常点 |
949 |
950 | #### 与硬间隔SVM相比有何优势和劣势?
951 |
952 | hard margin
953 |
954 | 优势:
955 |
956 | 1. 对于存在噪声或异常点的数据,软间隔SVM可以允许一些样本不满足约束条件,从而更好地适应这些数据;
957 | 2. 更好地处理线性不可分数据集。
958 |
959 | 劣势:
960 |
961 | 1. 在使用松弛变量的情况下,软间隔SVM更容易出现过拟合现象,需要谨慎调参;
962 | 2. 计算复杂度增加,需要花费更多的计算资源和时间。
963 |
964 | #### 如何在SVM中使用正则化?
965 |
966 | 正则化(regularization)问题如下:
967 |
968 | $$
969 | \min_{f}\quad\Omega(f)+C\sum_{i=1}^{m}\ell(f(x_i),y_i)
970 | $$
971 |
972 | $ \Omega(f) $ :“结构风险”structural risk,正则化项用于描述模型 $ f $ 的某些性质
973 |
974 | $ \sum_{i=1}^{m}\ell(f(x_i),y_i) $ :“经验风险”empirical risk,用于描述模型与训练数据的契合程度
975 |
976 | $ C $ :正则化常数,折中两者,C越大,表示分类错误的惩罚越严厉,对于训练集的拟合效果更好,但是可能会过拟合;C越小,则表示更容忍分类错误,对于新数据的泛化性能更好,但是可能会欠拟合。
977 |
978 | #### $ L_1 $ 和 $ L_2 $ 正则化有何区别?
979 |
980 | $ L_p $ 范数是常用的正则化项, $ L_2 $ 倾向于 $ w $ 的分量取值尽量均衡,即非零分量个数尽量稠密; $ L_0 $ 范数(向量中非0的元素的个数)和 $ L_1 $ 范数倾向于 $ w $ 的分量尽量稀疏,即非零分量个数尽量少。
981 |
982 | ### 支持向量回归
983 |
984 | (Support Vector Regression,SVR)
985 |
986 | #### 什么是SVR?
987 |
988 | 有别于传统回归模型,SVR可以容忍 $ f(x) $ 和 $ y $ 之间最多有 $ \epsilon $ 的偏差,即仅当 $ f(x) $ 与 $ y $ 之间的差别绝对值大于 $ \epsilon $ 时才计算损失。这相当于构建了一个宽度为 $ 2\epsilon $ 的间隔带,若训练样本落入此间隔带,则认为预测正确。
989 |
990 | SVR可形式化为
991 |
992 | $$
993 | \min_{w,b}\quad\frac12\vert\vert w\vert\vert^2+C\sum_{i=1}^{m}\ell_{\epsilon}\left(f(x_i)-y_i\right)
994 | $$
995 |
996 | 其中正则化常数 $ C>0 $ , $ \ell_{\epsilon} $ 为 $ \epsilon $ -不敏感损失( $ \epsilon $ -insensitive loss)函数, $ \ell_{\epsilon}=\left\{\begin{aligned}&0&|z|\leq\epsilon\\&|z|-\epsilon&otherwise\end{aligned}\right. $
997 |
998 | #### 优化目标
999 |
1000 | ### 核方法
1001 |
1002 | #### KLDA[还没写]
1003 |
1004 | ### 具体任务
1005 |
1006 | #### 百万样本量可以用SVM吗?
1007 |
1008 | 对于百万级别的样本量,求解SVM的原问题计算复杂度过大,时空开销较大,可能存在着困难。不过,存在一些优化算法,使得可以在大规模数据集上使用SVM。
1009 |
1010 | 1. 一种方法是使用随机梯度下降(SGD)算法等在线学习算法,在每次迭代中随机选择一部分数据进行训练。这种方法的计算复杂度低,但可能会影响模型的收敛性和精度。
1011 | 2. 另一种方法是使用核函数的低秩近似,例如随机核近似(RKA)或核特征映射(KFM),以降低计算复杂度。这些方法将数据集投影到一个低维空间中,从而减少了计算量。不过,这些方法可能会对模型的精度产生一定的影响。
1012 | 3. 此外,还有一些并行化的方法,例如基于GPU的实现或者分布式计算框架的使用,可以加速SVM的训练过程。
1013 |
1014 | #### 在使用SVM时,如何处理不平衡的训练数据?
1015 |
1016 | - 改变类别权重:为少数样本增加权重
1017 | - 过采样少数样本
1018 | - 欠采样多数样本
1019 |
1020 | #### SVM中如何处理非线性可分数据?
1021 |
1022 | - 使用核函数:将原始数据映射到高维特征空间,从而使得原本线性不可分的数据在新的高维空间中成为线性可分的。
1023 | - 引入软间隔:允许某些样本不符合约束。
1024 |
1025 | #### 在SVM中如何处理多分类问题?
1026 |
1027 | - One-vs-All:对于 $ k $ 类问题,训练 $ k $ 个二元分类器,每个分类器的正例为第 $ i $ 类样本,负例为其他类别的所有样本。测试时,选择具有最高决策函数值的分类器。
1028 | - One-vs-One:对于 $ k $ 类问题,在任意两类样本之间设计一个SVM,因此 $ k $ 个类别的样本就需要设计 $ k(k-1)/2 $ 个SVM。当对一个未知样本进行分类时,最后得票最多的类别即为该未知样本的类别。Libsvm中的多类分类就是根据这个方法实现的。
1029 |
1030 | #### 在SVM中如何处理缺失数据?
1031 |
1032 | 1. 删除缺失值:直接删除包含缺失数据的样本,在剩余的完整数据上进行SVM训练。但是,这种方法会损失有用的信息,并且可能导致训练数据的减少。
1033 | 2. 插值:可以使用基于均值、中位数或其他统计量的简单插值方法,也可以使用更高级的插值方法,例如多重插值或KNN插值。然后使用填充后的数据进行SVM训练。
1034 |
1035 | 都会对SVM的性能造成负面影响。
1036 |
1037 | ### 训练细节
1038 |
1039 | #### 如何解决SVM模型过拟合(overfitting)的问题?
1040 |
1041 | 1. 减少特征数:使用特征选择技术,如主成分分析(PCA),来减少特征数量。
1042 | 2. 增加正则化:惩罚过于复杂的模型,防止过拟合。
1043 | 3. 增加数据量。
1044 | 4. 调整模型参数:如惩罚参数C、核函数类型等,来寻找最优模型。
1045 | 5. 使用交叉验证:可以使用交叉验证来评估模型性能和泛化能力,并进行模型选择。
1046 |
1047 | #### SVM中如何选择合适的超参数?如何通过网格搜索来选择超参数?
1048 |
1049 | 交叉验证。
1050 |
1051 | 正则化项 $ C $ :较大的值将使模型更加倾向于正确分类每个训练样本,但也可能导致过拟合。较小的值将允许更多的分类错误,但也可能导致欠拟合。
1052 |
1053 | (RBF核) $ \gamma $ :较大的值将导致决策边界更加复杂,可能会导致过拟合。较小的值将导致决策边界更加简单,可能会导致欠拟合。
1054 |
1055 | 需要避免使用测试集来选择,应该使用验证集来选择超参数,而将测试集保留到最后评估模型的性能。
1056 |
1057 | #### SVM模型的复杂度是如何计算的?如何通过交叉验证来选择合适的SVM模型?
1058 |
1059 | - 基于训练数据集大小(训练数据集大小 $ N $ ,特征维度 $ d $ , $ O(Nd^2) $ )
1060 | - 基于支持向量的复杂度(支持向量的数量为 $ m $ , $ O(md) $ )
1061 |
1062 | ### 模型对比
1063 |
1064 | #### SVM与逻辑回归相比有哪些优势和劣势?
1065 |
1066 | | | SVM | LR |
1067 | | ---------- | ------------------------------ | ---------------------------------------------- |
1068 | | 数据特征 | 对于线性可分的数据效果往往更好 | 能够处理非线性问题,可以使用多项式特征 |
1069 | | 数据规模 | 小数据集效果好 | 需要较多数据才能获得较好分类效果 |
1070 | | 噪声数据 | 容易受影响 | 容易受影响 |
1071 | | 参数选择 | 对参数的选择比较敏感 | 参数的选择比较简单 |
1072 | | 模型复杂度 | 复杂度较高 | 训练时间和内存开销相对较小,适合处理大规模数据 |
1073 |
1074 | #### SVM与神经网络有何异同点?
1075 |
1076 | (Answered by ChatGPT)
1077 |
1078 | 1. 工作原理不同:SVM是一种基于几何距离的分类器,它通过最大化分类间隔,寻找超平面将不同类别的数据分开;而神经网络则是通过模拟生物神经元的方式,使用一系列非线性变换来构建模型,实现分类和回归等任务。
1079 | 2. 模型结构不同:SVM的模型结构比较简单,只有一个决策边界;而神经网络的模型结构比较复杂,由多个神经元和层组成。
1080 | 3. 特征处理不同:SVM通常使用核函数将数据从低维空间映射到高维空间,以便找到更好的决策边界;而神经网络则通常使用输入层、隐藏层和输出层来提取和处理特征,不需要显式的特征转换过程。
1081 | 4. 训练方法不同:SVM使用凸优化算法来训练模型,而神经网络通常使用反向传播算法来训练模型。
1082 | 5. 适用场景不同:SVM适用于小规模、高维度的数据集,特别是在样本数目相对于特征数目较小的情况下表现更好,而神经网络适用于大规模、高维度的数据集,可以处理非线性问题和复杂的关系。
1083 |
1084 | 总之,SVM和神经网络都是有效的分类算法,但它们的实现方式和适用场景有所不同,需要根据具体的问题和数据情况选择适当的算法。
1085 |
1086 | ## 贝叶斯分类
1087 |
1088 | ### 贝叶斯决策论
1089 |
1090 | Bayes decision theory
1091 |
1092 | #### 贝叶斯判定准则,贝叶斯最优分类器,贝叶斯风险
1093 |
1094 | 贝叶斯判定准则Bayes decision rule:目标是找到最小化总体风险的判定准则 $ h:\mathcal X\to\mathcal Y $ ,只需在每个样本上选择那个能使条件风险 $ R(c|x) $ 最小的类别标记,即 $ h^*(x)=\arg\min_{c\in\mathcal Y} R(c|x) $ ,这里 $ h^* $ 是贝叶斯最优分类器 (Bayes optimal classifier) ,与之对应的总体风险 $ R(h^*) $ 称为贝叶斯风险 (Bayes risk),即通过机器学习所能产生的模型精度的理论上限。
1095 |
1096 | 定义:
1097 |
1098 | - 条件风险: $ \lambda_{ij} $ 为将 $ c_j $ 类别的样本误分类为 $ c_i $ 的损失
1099 |
1100 | $$
1101 | R(c_i|x)=\sum_{j=1}^N\lambda_{ij}P(c_j|x)
1102 | $$
1103 | - 总体风险
1104 |
1105 | $$
1106 | R(h)=\mathbb E_x[R(h(x)|x)]
1107 | $$
1108 |
1109 | #### 生成式模型,判别式模型
1110 |
1111 | 然而,后验概率 $ P(c|x) $ 难以直接获得,所以学习器要基于有限的训练样本集尽可能准确地估计出后验概率。
1112 |
1113 | - 判别式:直接建模 $ P(c|x) $
1114 | - 生成式:先建模联合概率分布 $ P(x,c) $ ,也就是 $ P(c) $ (先验)和 $ P(x|c) $ (似然)再得到 $ P(c|x) $
1115 |
1116 | ### 极大似然估计
1117 |
1118 | 见概率论
1119 |
1120 | ### 朴素贝叶斯分类器
1121 |
1122 | Naive Bayes classifier
1123 |
1124 | 朴素贝叶斯分类器 (naÏve Bayes classifier) 采用了**属性条件独立性假设**(attribute conditional independence assumption):假设每个属性独立地对分类结果发生影响。简化类条件概率 $ P(x|c) $ 的建模。
1125 |
1126 | 重写贝叶斯公式: $ x_i $ 为 $ x $ 在第 $ i $ 个属性上的取值.
1127 |
1128 | 
1129 |
1130 | 基于贝叶斯判定准则,朴素贝叶斯分类器表达式:
1131 |
1132 | $$
1133 | h_{nb}(x)=\arg\max_{c\in\mathcal Y}P(c)\prod_{i=1}^d P(x_i|c)
1134 | $$
1135 |
1136 | 离散:
1137 |
1138 | $$
1139 | P(c)=\frac{|D_c|}{|D|}\quad P(x_i|c)=\frac{|D_{c,x_i}|}{|D_c|}
1140 | $$
1141 |
1142 | 拉普拉斯修正(防止训练集中某个属性值没有与某个类同时出现过, $ |D_{c,x_i}|=0 $ 带来的误差。假设了属性值与类别的均匀分布,这是额外引入的 bias。 $ N $ 类别数, $ N_i $ 第 $ i $ 个属性可能的取值数)
1143 |
1144 | $$
1145 | \hat P(c)=\frac{|D_c|+1}{|D|+N}\quad P(x_i|c)=\frac{|D_{c,x_i}|+1}{|D_c|+N_i}
1146 | $$
1147 |
1148 | 连续:考虑概率密度函数
1149 |
1150 | ### 半朴素贝叶斯分类器
1151 |
1152 | 属性条件独立性假设在现实中很难成立,于是半朴素贝叶斯分类器(semi-naïve Bayes classifiers)对属性条件独立性假设进行一定程度的放松,适当考虑一部分属性问的相互依赖信息,从而既不需进行完全联合概率计算,又不至于彻底忽略了比较强的属性依赖关系。
1153 |
1154 | 采用独依赖估计(One-Dependent Estimator ,简称 ODE),新假设:每个属性在类别之外最多仅依赖于一个其他属性
1155 |
1156 | 
1157 |
1158 | 其中 $ pa_i $ 为属性 $ x_i $ 所依赖的属性,称为 $ x_i $ 的父属性,如何确定副属性引出不同算法
1159 |
1160 | 
1161 |
1162 | #### SPODE
1163 |
1164 | super-parent ODE,假设所有属性都依赖于同一个属性,通过交叉验证等模型选择方法来确定超父属性
1165 |
1166 | #### TAN
1167 |
1168 | 
1169 |
1170 | #### ADOE
1171 |
1172 | averaged one-dependent estimator,基于集成学习,尝试将每个属性作为超父来构建SPODE,然后将那些具有足够训练数据支撑的SPODE集成起来作为最终结果。
1173 |
1174 | #### kDE
1175 |
1176 | 将属性 $ pa_i $ 替换为包含 $ k $ 个属性的集合,随着 $ k $ 的增加,准确估计概率 $ P(x_i| y ,pai ) $ 所需的训练样本数量将以指数级增加。可能又会陷入求高阶联合概率的泥沼。
1177 |
1178 | ### 贝叶斯网
1179 |
1180 | 贝叶斯图(Bayesian network),也被称为信念网络(belief network)或概率有向无环图(probabilistic directed acyclic graph,PDAG),是一种图形化的概率模型,用于描述变量之间的概率依赖关系。变量(或节点)用圆圈表示,而变量之间的概率依赖关系则用有向箭头连接。箭头从一个变量指向依赖于它的变量,表示变量之间的因果关系或条件依赖关系。
1181 |
1182 | #### 贝叶斯网的条件独立性
1183 |
1184 | 
1185 |
1186 | $$
1187 | P(x_1,x_2,x_3,x_4,x_5)=P(x_1)P(x_2)P(x_3\vert x_1)P(x_4\vert x_1,x_2)P(x_5|x_2)
1188 | $$
1189 |
1190 | 
1191 |
1192 | 一个变量取值的确定与否,能对另两个变量间的独立性发生影响
1193 |
1194 | 同父:given $ x_1 $ , $ x_3,x_4 $ 独立
1195 |
1196 | V型:给定 $ x_4 $ ,必不独立; $ x_4 $ 未知,两者独立(边际独立性marginal independence, $ x_1\perp\!\!\!\perp x_2 $ ,两个随机变量在给定其他变量的边际分布下是独立的)
1197 |
1198 | 
1199 |
1200 | #### 边际分布
1201 |
1202 | #### Gibbs采样[没看]
1203 |
1204 | ### EM算法
1205 |
1206 | EM算法(Expectation-Maximization algorithm)是一种迭代优化算法,用于在存在隐变量(或缺失数据)的概率模型中进行参数估计。它是一种常用的无监督学习方法,通常用于处理含有不完整数据或观测数据中存在隐含变量的情况。非梯度
1207 |
1208 | EM算法的基本思想是通过迭代的方式,交替进行两个步骤:E步(Expectation step)和M步(Maximization step),以较好地逼近参数的最大似然估计。
1209 |
1210 | 已观测变量 $ X $ ,隐变量(未观测变量) $ Z $ ,模型参数 $ \Theta $ ,若对 $ \Theta $ 做极大似然估计,则应该最大化对数似然(对 $ Z $ 算期望)
1211 |
1212 | $$
1213 | LL(\Theta |X)=\ln P(X|\Theta)=\ln\sum_Z P(X,Z|\Theta)
1214 | $$
1215 |
1216 | EM算法步骤
1217 |
1218 | 1. 初始化模型参数。
1219 | 2.
349 |
350 | ## 线性模型
351 |
352 | ### 线性回归
353 |
354 | #### 线性回归的目标
355 |
356 | $$
357 | (w^*,b^*)=\arg \min_{(w,b)}\sum_{i=1}^m(f(x_i)-y_i)^2=\arg \min_{(w,b)}\sum_{i=1}^m(y_i-wx_i-b)^2
358 | $$
359 |
360 | #### 最小二乘
361 |
362 | 最小二乘“参数估计”:求解 $ w,b $ 使 $ \mathbb E_{(w,b)}=\sum_{i=1}^m(y_i-wx_i-b)^2 $ 最小化的过程。将 $ \mathbb E_{(w,b)} $ 对 $ w,b $ 求导,令之为零后得到 $ w,b $ 最优解的闭式解。
363 |
364 | #### 对数线性回归
365 |
366 | log-linear regression, $ \ln y=w^\top x+b $
367 |
368 | #### 广义线性模型
369 |
370 | generalized linear model, $ y=g^{-1}(w^\top x+b) $ ,其中 $ g(\cdot) $ 为联系函数link function
371 |
372 | ### 逻辑斯蒂回归
373 |
374 | #### 什么是逻辑斯蒂回归?
375 |
376 | 逻辑斯蒂回归为一个分类算法,通过对输入特征进行加权求和,并将结果通过一个值域为0-1的sigmoid函数(也称为逻辑函数)进行映射,从而得到输出概率值。
377 |
378 | #### Sigmoid函数是什么?为什么要用Sigmoid函数?
379 |
380 | Sigmoid函数即形似S的函数,目的是近似不连续不可导的单位阶跃函数(值域 $ \{0,1\} $ ),作为它的替代函数surrogate function。又称对数几率函数。公式为
381 |
382 | $$
383 | y=\frac1{1+e^{-z}}
384 | $$
385 |
386 | 值域为 $ [0,1] $
387 |
388 | #### 如何求解参数?
389 |
390 | 将后验概率估计代入对数几率的式子,用极大似然法找到Loss函数。然后用梯度下降法、牛顿法等数值优化方法找到使得Loss最小的 $ \beta $ ,即可得到参数。
391 |
392 | 具体见p59。
393 |
394 | #### 梯度下降
395 |
396 | > 什么是梯度下降法?
397 |
398 | 一阶迭代数值优化算法,用于寻找可微函数的局部最小值。
399 |
400 | 更新公式:
401 |
402 | $$
403 | x_{n+1}=x_{n}-\gamma\nabla f(x_n)
404 | $$
405 |
406 | 其中, $ \gamma $ 是学习率。 $ \nabla f $ 指向函数值增长最快的方向,则 $ -\nabla f $ 指向函数值增长最快的方向。理论上当 $ \gamma $ 足够小,则 $ f(x_n)\geq f(x_{n+1}) $
407 |
408 | > 需要满足什么条件?
409 |
410 | 前提:
411 |
412 | 1. 目标函数可导
413 | 2. 目标函数是凸函数(否则可能会陷入局部最优解)
414 |
415 | > 有什么优缺点?
416 |
417 | 优点:
418 |
419 | 1. 可以应用于许多不同的优化问题(线性回归,逻辑回归,神经网络)
420 | 2. 算法简单
421 | 3. 只需要计算一阶导数,计算成本相对较低。
422 | 4. 可以在大规模数据集上进行优化。
423 |
424 | 缺点:
425 |
426 | 1. 可能会陷入局部最小值,无法得到全局最小值。
427 | 2. 当函数存在平台、峡谷和其他复杂的非凸结构时,可能会出现震荡或缓慢收敛的情况。
428 | 3. 需要选择合适的学习率,过大或过小都会影响优化结果。
429 | 4. 对于某些问题,可能需要较多的迭代次数才能达到收敛。
430 |
431 | #### 什么是牛顿迭代法?需要满足什么条件?有什么优缺点?
432 |
433 | 目的:求 $ f(x)=0 $ 的解
434 |
435 | 初始化: $ x_0 $
436 |
437 | 重复:过 $ x_i $ 求 $ f(x) $ 的切线 $ L:y=f(x_{i})+f'(x_{i})(x-x_i) $ ,与x轴交点为 $ x_{i+1}=x_i-\frac{f(x_i)}{f'(x_i)} $
438 |
439 | 迭代公式:
440 |
441 | $$
442 | x_{n+1}=x_n-\frac{f(x_n)}{f'(x_n)}
443 | $$
444 |
445 | 对于 $ \beta^*=\arg\min_{\beta}\ell(\beta) $ 的优化问题,更新公式为:
446 |
447 | $$
448 | \beta^{t+1}=\beta^t-\left(\frac{\part^2\ell(\beta)}{\part \beta\part \beta^\top}\right)^{-1}\frac{\part\ell(\beta)}{\part \beta}
449 | $$
450 |
451 | 必要条件:
452 |
453 | 1. 目标函数二价可微
454 | 2. 目标函数的海森矩阵必须正定或负定
455 |
456 | 优点:
457 |
458 | 1. 可以更快地收敛到最优解,尤其是在函数存在二阶导数且二阶导数连续的情况下。
459 | 2. 可以解决梯度下降等一阶方法无法收敛的问题。
460 | 3. 可以自动调整学习率,减少手动调参的工作量。
461 |
462 | 缺点:
463 |
464 | 1. 对于高维问题,计算海森矩阵的代价非常昂贵。
465 | 2. 当海森矩阵不正定时,可能会导致算法发散。
466 | 3. 可能会陷入局部最小值,无法得到全局最小值。
467 | 4. 由于需要计算二阶导数,所以计算成本相对较高。
468 | 5. 当函数存在平台、峡谷和其他复杂的非凸结构时,可能会出现震荡或缓慢收敛的情况。
469 |
470 | ### 线性判别分析
471 |
472 | LDA, Linear Discriminant Analysis
473 |
474 | > 什么是LDA?
475 |
476 | LDA是一种常用的分类算法和数据降维方法。它可以将一个高维数据集降到一个更低的维度,同时保持样本类别信息,从而方便后续的分类任务。
477 |
478 | LDA 假设数据符合高斯分布,且各类别的协方差矩阵相等,基于此,它通过线性变换,将数据投影到一个低维空间中,使得同一类别的数据尽可能的接近,不同类别的数据尽可能的远离。这种投影方式保留了最大的类间差异性和最小的类内差异性,因此可以有效的提高分类准确率。
479 |
480 | 具体来说,LDA 算法主要包含两个步骤:(1)计算类内散度矩阵和类间散度矩阵;(2)通过求解广义瑞利商的特征向量,得到用于投影的变换矩阵。
481 |
482 | LDA 广泛应用于图像识别、人脸识别、语音识别等领域,并且在实际应用中表现良好。
483 |
484 | > 什么是类内散度矩阵,类间散度矩阵?
485 |
486 | $ X_i,\mu_i,\Sigma_i $ :第 $ i $ 类示例的集合、均值向量、协方差矩阵。
487 |
488 | $ w^\top \mu_i,w^\top \Sigma_i w $ :投影后的结果
489 |
490 | 目标:同类样例投影点的协方差尽可能小,即 $ w^\top \Sigma_0 w+w^\top \Sigma_1 w $ 尽可能小;类中心之间的距离尽可能大,即 $ ||w^\top \mu_0-w^\top\mu_1||_2^2 $ 尽可能大。即最大化
491 |
492 | $$
493 | J=\frac{||w^\top \mu_0-w^\top\mu_1||_2^2}{w^\top \Sigma_0 w+w^\top \Sigma_1 w}=\frac{w^\top (\mu_0-\mu_1)(\mu_0-\mu_1)^\top w}{w^\top(\Sigma_0+\Sigma_1)w}
494 | $$
495 |
496 | 其中**类内散度矩阵**within-class scatter matrix:
497 |
498 | $$
499 | S_w=\Sigma_0+\Sigma_1=\sum_{x\in X_0}(x-\mu_0)(x-\mu_0)^\top+\sum_{x\in X_1}(x-\mu_1)(x-\mu_1)^\top
500 | $$
501 |
502 | **类间散度矩阵**between-class scatter matrix:
503 |
504 | $$
505 | S_b=(\mu_0-\mu_1)(\mu_0-\mu_1)^\top
506 | $$
507 |
508 | 这就是LDA想要最大化的目标,即 $ S_b,S_w $ 的广义瑞利商generalized Rayleigh quotient:
509 |
510 | $$
511 | J=\frac{w^\top S_b w}{w^\top S_w w}
512 | $$
513 |
514 | > 如何求解LDA?
515 |
516 | 即确定能最大化 $ J $ 的 $ w $
517 |
518 | 令 $ w^\top S_ww=1 $ ,原式等价于
519 |
520 | $$
521 | \begin{aligned}
522 | &\min_w &&-w^\top S_b w\\
523 | &s.t. && w^\top S_w w=1
524 | \end{aligned}
525 | $$
526 |
527 | 由拉格朗日乘子法,等价于
528 |
529 | $$
530 | S_b w=\lambda S_ww
531 | $$
532 |
533 | $ S_b w $ 方向恒等于 $ \mu_0-\mu_1 $ ,令
534 |
535 | $$
536 | S_b w=\lambda(\mu_0-\mu_1)
537 | $$
538 |
539 | 有:
540 |
541 | $$
542 | w=S_w^{-1}(\mu_0-\mu_1)
543 | $$
544 |
545 | 考虑到数值解的稳定性,在实践中通常是对 $ S_w $ 进行奇异值分解,即 $ S_w= U\Sigma V^\top $ ,这里 $ \Sigma $ 是一个实对角矩阵,其对角线上的元素是 $ S_w $ 的奇异值,然后再由 $ S_w^{-1}=V\Sigma^{-1}U^\top $ 得到 $ S_w^{-1} $
546 |
547 | > 如何推广到多分类?[再看看!]
548 |
549 | 定义全局散度矩阵( $ \mu $ 是所有示例的均值之和)
550 |
551 | $$
552 | S_t=S_b+S_w=\sum_{i=1}^m(x_i-\mu)(x_i-\mu)^\top\\
553 | S_w=\sum_{i=1}^N S_{w_i}=\sum_{i=1}^N\sum_{x\in X_i}(x-\mu_i)(x-\mu_i)^\top\\
554 | S_b=S_t-S_w=\sum_{i=1}^N m_i(\mu_i-\mu)(\mu_i-\mu)^\top
555 | $$
556 |
557 | 优化目标:
558 |
559 | $$
560 | \max_W\frac{tr(W^\top S_bW)}{tr(W^\top S_wW)}
561 | $$
562 |
563 | 通过求解 $ S_b W=\lambda S_w W $ 可得, $ W $ 的闭式解为 $ S_w^{-1}S_b $ 的 $ N-1 $ 个最大广义特征值所对应的特征向量组成的矩阵。
564 |
565 | ### 多分类学习
566 |
567 | #### 有什么拆分策略?
568 |
569 | OvO(一对一,one vs one): $ \frac{N(N-1)}{2} $ 个分类器
570 |
571 | OvR(一对剩余,one vs rest): $ N $ 个分类器,选择置信度最大的类别标记
572 |
573 | MvM(多对多,many vs many):需要用ECOC编码特殊构造。
574 |
575 | ### 类别不平衡
576 |
577 | class-imbalance
578 |
579 | #### 有什么解决方法?
580 |
581 | “再缩放”,也是“代价敏感学习”cost-sensitive learning的基础
582 |
583 | 1. 对反例进行“欠采样”
584 | 2. 对正例进行“过采样”
585 | 3. 阈值移动
586 |
587 | ## 决策树
588 |
589 | ### 基本流程
590 |
591 | #### 什么是决策树?
592 |
593 | 决策树是一种基于树结构的分类算法,其中每个内部节点表示一个属性或特征,每个叶子节点代表一个类别。该算法可以用于分类和回归问题,它通过对样本集合进行递归分治来构建决策树。
594 |
595 | 在构建决策树时,算法会选择一个最好的属性或特征,将样本集合分成更小的子集。这个过程会不断重复,直到所有的子集都属于同一个类别,或者已经达到了预先定义的最大深度。
596 |
597 | 决策树算法具有可解释性和易于理解的优点,因为它可以清楚地显示分类决策的过程,还可以处理缺失值和噪声数据。不过,决策树算法在处理高维数据时可能会遇到困难,并且容易受到过拟合和欠拟合等问题的影响。
598 |
599 | #### 决策树算法的基本流程是什么?
600 |
601 | 决策树的生成是基于分治策略的递归过程。
602 |
603 | 首先生成结点,如果训练集中的样本均属于同一类别,则将该节点标记为该类叶子结点,返回。如果属性集为空或训练集在属性集上的取值相同,则将该节点标记为叶子结点,类别为数据集中样本数最多的类,返回。如果都不满足这两种情况的话,从属性集中选择最优划分 $ a^* $ 。对最优划分中的每一个值,为结点生成一个分支,构造相应取值的样本子集。如果样本子集为空,则将该节点标记为叶子结点,类别为数据集中样本数最多的类,返回。否则递归地对样本子集和最优划分的子集生成决策树。
604 |
605 | #### 什么情况会导致递归返回?
606 |
607 | 1. 当前结点包含的样本全属于同一类别,无需划分
608 | 2. 当前属性集为空,或是所有样本在所有属性上取值相同,无法划分
609 | 3. 当前结点包含的样本集合为空,不能划分。
610 |
611 | ### 划分选择
612 |
613 | #### 有什么划分的指标?它们的具体定义?
614 |
615 | 划分选择的目标是希望决策树的分支结点所包含的样本尽可能属于同一类别,即结点的“纯度” (purity) 越来越高。
616 |
617 | 划分的指标有:(ID3)信息增益、(C4.5)增益率、(CART)基尼指数。
618 |
619 | $ p_k $ :当前样本属于第 $ k $ 类的比例
620 |
621 | 假设离散属性 $ a $ 有 $ V $ 个可能的取值 $ \{a^1,\dots,a^V\} $ ,若使用 $ a $ 来对样本集 $ D $ 进行划分,则会产生 $ V $ 个分支结点,其中第 $ v $ 个分支结点包含了 $ D $ 中所有在属性 $ a $ 上取值为 $ a^v $ 的样本,记为 $ D^v $
622 |
623 | 信息熵:值越小,纯度越高
624 |
625 | $$
626 | Ent(D)=-\sum_{k=1}^{\mathcal Y}p_k\log_2 p_k
627 | $$
628 |
629 | 信息增益:值越大,说明使用属性 $ a $ 来划分所获得的纯度提升越大。
630 |
631 | $$
632 | Gain(D,a)=Ent(D)-\sum_{v=1}^V\frac{|D^v|}{|D|}Ent(D^v)
633 | $$
634 |
635 | 增益率:信息增益准则对可取值数目较多的属性有所偏好,为减少这种偏好可能带来的不利影响,引入增益率。其中 $ IV(a) $ 为属性 $ a $ 的固有值intrinsic value
636 |
637 | $$
638 | Gain_ratio(D,a)=\frac{Gain(D,a)}{IV(a)}\\
639 | IV(a)=-\sum_{v=1}^V\frac{|D|^v}{|D|}\log_2\frac{|D|^v}{|D|}
640 | $$
641 |
642 | 基尼指数Gini index:Gini反映从数据集 $ D $ 中随机抽取两个样本,其类别标记不一致的概率。越小纯度越高
643 |
644 | $$
645 | Gini(D)=\sum_{k=1}^{|\mathcal Y|}\sum_{k'\neq k}p_kp_{k'}=1-\sum_{k=1}^{|\mathcal Y|}p_k^2\\
646 | \text{Gini_Index}(D,a) =\sum_{v=1}^V\frac{|D^v|}{|D|}Gini(D^v)
647 | $$
648 |
649 | ### 剪枝
650 |
651 | #### 简述预剪枝和后剪枝的策略?
652 |
653 | 预剪枝:基于贪心思想,如果划分后验证集精度 $ \leq $ 原来的精度,则剪枝,禁止这些分支展开。
654 |
655 | 后剪枝:生成完整决策树后,从叶子结点开始遍历,如果划分后验证集精度 $ \leq $ 原来的精度,则剪枝,禁止这些分支展开。
656 |
657 | #### 两者的优缺点?
658 |
659 | | | 预剪枝 | 后剪枝 |
660 | | ------------- | ------------------------------ | ---------------------------------- |
661 | | 时间开销 | 测试时间降低,训练时间降低 | 测试时间降低,训练时间提高 |
662 | | 过/欠拟合风险 | 过拟合风险降低,欠拟合风险增加 | 过拟合风险降低,欠拟合风险基本不变 |
663 | | 泛化性能 | | 后剪枝通常优于预剪枝 |
664 |
665 | ### 连续值与缺失值
666 |
667 | #### 如何处理连续值?
668 |
669 | 基本思路是连续属性离散化
670 |
671 | 1. 二分法
672 | 2. 对于从大到小排序好的取值 $ \{a^1,\dots,a^n\} $ ,令划分点集合为 $ T_a=\left\{\frac{a^i+a^{i+1}}2|i\leq i\leq n-1\right\} $ ,然像离散属性值一样来考察这些划分点
673 |
674 | 需注意的是,与离散属性不同,若当前结点划分属性为连续属性,该属性还 可作为其后代结点的划分属性。
675 |
676 | #### 如何处理缺失值?
677 |
678 | 需要解决 1. 训练 2. 测试时的处理
679 |
680 | 令 $ \tilde D $ 为 $ D $ 在属性 $ a $ 上没有缺失值的样本子集,定义:
681 |
682 | 无缺失值比例: $ \displaystyle \rho=\frac{\sum_{x\in\tilde D} w_x}{\sum_{x\in D} w_x} $
683 |
684 | 无缺失值样本中第 $ k $ 类的比例: $ \displaystyle \tilde p_k=\frac{\sum_{x\in\tilde D_k} w_x}{\sum_{x\in \tilde D} w_x},1\leq k\leq|\mathcal Y| $
685 |
686 | 无缺失值样本中在属性 $ a $ 上取值为 $ a^v $ 的比例: $ \displaystyle \tilde r_v=\frac{\sum_{x\in\tilde D^v} w_x}{\sum_{x\in \tilde D} w_x},1\leq v\leq V $
687 |
688 | 推广:
689 |
690 | $$
691 | Ent(\tilde D)=-\sum_{k=1}^{\mathcal Y}\tilde p_k\log_2 \tilde p_k\\
692 | Gain(D,a)=\rho \times Gain(\tilde D,a)=\rho \times\left(Ent(D)-\sum_{v=1}^V \tilde r_v Ent(D^v)\right)
693 | $$
694 |
695 | ### 多变量决策树
696 |
697 | multivariate decision tree,在多变量决策树的学习过程中, 不是为每个非叶结点寻找一个最优划分属性,而是试图建立一个合适的线性分类器。
698 |
699 | ## 神经网络
700 |
701 | ## 支持向量机
702 |
703 | ### 基本概念
704 |
705 | #### 英文介绍
706 |
707 | Support Vector Machine (SVM) is a powerful machine learning algorithm used for classification and regression analysis. SVM finds the best hyperplane that separates different classes in a high-dimensional space. The hyperplane is chosen in such a way that it maximizes the margin or the distance between the two closest points of different classes. These closest points are called support vectors, and they play a crucial role in defining the hyperplane.
708 |
709 | SVM can handle both linearly separable and non-linearly separable data by using different types of kernel functions such as linear, polynomial, radial basis function (RBF), and sigmoid. The choice of kernel function depends on the data and the problem at hand. SVM can also handle multi-class classification problems using various techniques such as one-vs-one and one-vs-all.
710 |
711 | SVM has several advantages over other classification algorithms such as logistic regression and decision trees. It is less prone to overfitting, works well with high-dimensional data, and is computationally efficient. However, SVM has some limitations, such as the need for careful selection of kernel functions and hyperparameters, and the difficulty in handling large datasets.
712 |
713 | #### SVM是什么?
714 |
715 | 支持向量机是一种可以用于解决分类和回归问题的机器学习算法,目标是在高维空间中找到最佳的超平面,以最大化间隔,也就是margin。
716 |
717 | SVM问题的基本型(是一个凸二次优化问题):
718 |
719 | $$
720 | \begin{aligned}
721 | &\min_{w,b} \quad\frac12||w||^2\\
722 | &s.t. \quad y_i(w^\top x_i+b)\geq1,i=1,\dots,m
723 | \end{aligned}
724 | $$
725 |
726 | #### SVM中的“支持向量”指什么?在SVM中如何确定支持向量?
727 |
728 | “支持向量”是指离分隔超平面最近的训练样本点。这些样本点是最能影响分隔超平面位置和方向的点,如果它们的位置发生变化,会直接影响到分隔超平面的位置和方向。
729 |
730 | 我们在SVM的训练过程中确定支持向量。在SVM的训练过程中,我们首先随机初始化超平面参数,然后迭代地优化超平面参数,直到收敛为止。在每一次迭代中,我们根据当前的超平面参数计算每个训练样本点到超平面的距离,并根据这些距离来判断哪些样本点是支持向量。
731 |
732 | #### SVM在分类问题中如何定义“边界”(decision boundary)?
733 |
734 | 在SVM中,边界(decision boundary)是指将不同类别的数据点分开的超平面(hyperplane)。SVM的目标是寻找一个最优的超平面,将不同类别的数据点分开,并且使得该超平面与最近的数据点之间的距离(即margin)最大化。
735 |
736 | #### SVM有什么优点和缺点?
737 |
738 | 优点:
739 |
740 | 1. 能有效处理高维数据,例如图像和文本分类
741 | 2. 在小数据集处理时表现优异,因为它只需要少量的支持向量来定义边界
742 | 3. SVM对数据中的噪声具有鲁棒性,因为决策边界由支持向量确定,它们是距离边界最近的数据点。
743 | 4. 泛化性好
744 |
745 | 缺点:
746 |
747 | 1. 不适用于大数据集,因为计算开销过大
748 | 2. 对核函数选择和参数选择敏感
749 | 3. 只适用于二元问题
750 | 4. 缺乏概率解释
751 | 5. 不适用于有缺失值的数据
752 |
753 | ### 原问题和对偶问题
754 |
755 | #### 如何将SVM转化为对偶问题?
756 |
757 | 对偶问题(dual problem)是指将一个优化问题的原问题(primal problem)转化为一个新的优化问题,对偶问题和原问题有相同的最优解,但对于一些问题,通过求解对偶问题可以更方便或更有效地得到原问题的解。
758 |
759 | 对偶问题一定是凸优化问题。
760 |
761 | 可以使用拉格朗日乘子法得到SVM的对偶问题:
762 |
763 | 拉格朗日函数:
764 |
765 | $$
766 | L(w,b,\alpha)=\frac12||w||^2+\sum_{i=1}^m\alpha_i(1-y_i(\omega^\top x_i+b))
767 | $$
768 |
769 | 令 $ L(w,b,\alpha) $ 对 $ \omega,b $ 的偏导为零可得:
770 |
771 | $$
772 | w=\sum_{i=1}^m\alpha_i y_ix_i\quad(1)\\
773 | 0=\sum_{i=1}^m\alpha_i y_i\quad(2)
774 | $$
775 |
776 | 将(1)代入拉格朗日函数可消去 $ w,b $ ,考虑(2)的约束可以得到对偶问题:
777 |
778 | $$
779 | \begin{aligned}
780 | &\max_{\alpha}\quad \sum_{i=1}^m\alpha_i-\frac12\sum_{i=1}^m\sum_{i=1}^m\alpha_i\alpha_jy_iy_jx_i^\top x_j\\
781 | &s.t. \quad \sum_{i=1}^m\alpha_i y_i=0,\alpha_i\geq 0,i=1,\dots,m
782 | \end{aligned}
783 | $$
784 |
785 | 要满足KKT条件:
786 |
787 | $$
788 | \left\{\begin{aligned}
789 | &\alpha_i\geq0\\
790 | &y_if(x_i)-1\geq 0\\
791 | &\alpha_i(y_if(x_i)-1)=0
792 | \end{aligned}\right.
793 | $$
794 |
795 | ##### 什么是KKT条件?[x]
796 |
797 | Karush-Kuhn-Tucker (KKT)条件是非线性规划(nonlinear programming)最佳解的必要条件。
798 |
799 | 对于Lagrangian函数
800 |
801 | $$
802 | L(x,\lambda,\mu)=f(x)+\sum_{j=1}^m\lambda_jg_j(x)+\sum_{k=1}^n\mu_kh_k(x)
803 | $$
804 |
805 | KKT条件包括:**[术语怎么说?KKT只是必要条件,要到充分条件该如何做?内点]**
806 |
807 | $$
808 | \left\{\begin{aligned}
809 | &\nabla_xL=0\\
810 | &g_j(x)=0,j = 1,\dots,m\\
811 | &h_k(x)\leq 0,\\
812 | &\mu_k\geq 0,\\
813 | &\mu_kh_k(x)=0,k=1,\dots,p
814 | \end{aligned}\right.
815 | $$
816 |
817 | #### 为什么要将SVM转化为对偶问题?
818 |
819 | 虽然原问题本身就是一个凸二次规划(convex quadratic programming)问题,可以直接用现成的优化计算包求解,但是转化为对偶问题求解更高效。
820 |
821 | 原始的SVM问题是一个凸二次规划问题,通常使用二次规划算法求解。然而,当数据集的规模很大时,使用原始问题求解SVM会变得很慢,甚至变得不可行。此外,对于非线性SVM,计算的复杂度会随着特征空间的维度增加而急剧增加。
822 |
823 | 将SVM转化为对偶问题,就可以使用SMO算法等更高效的方法求解。
824 |
825 | 对偶问题和内积有关,可以引入核函数
826 |
827 | ##### 什么是SMO算法?
828 |
829 | ##### 为什么SMO算法不能用于求解原问题?
830 |
831 | ### 核函数
832 |
833 | kernel function
834 |
835 | #### SVM中的核函数是什么?
836 |
837 | 核函数是一种常用的技巧,用于将低维空间中线性不可分的数据映射到高维空间,从而使其在高维空间中变得线性可分。
838 |
839 | 如果原始空间是有限维(属性有限),那么一定存在一个高维特征空间使样本可分。
840 |
841 | 令 $ \phi(x) $ 为将 $ x $ 映射后的特征向量,于是,在特征空间中划分超平面所对应的模型可表示为
842 |
843 | $$
844 | f(x)=w^\top\phi(x)+b
845 | $$
846 |
847 | 原问题
848 |
849 | $$
850 | \begin{aligned}&\min_{w,b} \quad\frac12||w||^2\\&s.t. \quad y_i(w^\top \phi(x_i)+b)\geq1,i=1,\dots,m\end{aligned}
851 | $$
852 |
853 | 对偶问题
854 |
855 | $$
856 | \begin{aligned}
857 | &\max_{\alpha}\quad \sum_{i=1}^m\alpha_i-\frac12\sum_{i=1}^m\sum_{i=1}^m\alpha_i\alpha_jy_iy_j\phi(x_i)^\top\phi( x_j)\\
858 | &s.t. \quad \sum_{i=1}^m\alpha_i y_i=0,\alpha_i\geq 0,i=1,\dots,m
859 | \end{aligned}
860 | $$
861 |
862 | 核函数就是 $ \kappa(x_i,x_j)=<\phi(x_i),\phi(x_j)>=\phi(x_i)^\top\phi(x_j) $
863 |
864 | #### 核函数有什么性质?
865 |
866 | **[充要条件]** $ \kappa $ 是核函数当且仅当对于任意数据 $ D={x_1,\dots,x_m} $ ,核矩阵 $ K=[\kappa(x_i,x_i)]_{m\times m} $ 总是半正定的。
867 |
868 | 也就是说,对于一个半正定的核矩阵,总能找到一个与之对于的映射 $ \phi $ 。
869 |
870 | #### 有什么常用的核函数?
871 |
872 | | 名称 | 表达式 | 参数 | 适用场景 |
873 | | ----------- | ----------------------------------------------------------- | -------------------------- | ------------------------------------------------------------------------------------------------------------------------------------------------------------ |
874 | | 线性核 | $ \kappa(x_i,x_j)=x_i^\top x_j $ | | 输入特征维度较低,数据线性可分 |
875 | | 多项式核 | $ \kappa(x_i,x_j)=(x_i^\top x_j)^d $ | $ d\geq 1 $ ,多项式次数 | 数据中存在多项式关系 |
876 | | 高斯核(RBF) | $ \kappa(x_i,x_j)=\exp(-\frac{||x_i- x_j||^2}{2\sigma^2}) $ | $ \sigma>0 $ ,高斯核的带宽 | 输入特征维度较高 |
877 | | 拉普拉斯核 | $ \kappa(x_i,x_j)=\exp(-\frac{||x_i-x_j||}{\sigma}) $ | $ \sigma>0 $ | 采用 $ L_1 $ 范数来度量两个样本点之间的距离,而高斯核函数采用 $ L_2 $ 范数来度量。可以在一定程度上克服高斯核函数中存在的过拟合问题,适用于一些噪声较多的数据集。 |
878 | | Sigmoid核 | $ \kappa(x_i,x_j)=\tanh(\beta x_i^\top x_j+\theta) $ | $ \beta>0,\theta<0 $ | 数据集合线性不可分时,将数据映射到一个非线性空间中。表现不是很好,高斯核和拉普拉斯核更常用。 |
879 |
880 | 此外,若 $ \kappa_1,\kappa_2 $ 为核函数,则
881 |
882 | - $ \gamma_1\kappa_1+\gamma_2\kappa_2 $ 也是核函数
883 | - $ \kappa_1\otimes\kappa_2(x,z)=\kappa_1(x,z)\kappa_2(x,z) $ 也是核函数
884 | - 对于任意函数 $ g(x) $ , $ g(x)\kappa_1(x,z)g(z) $ 也是核函数
885 |
886 | #### 如何选择合适的核函数?[x]
887 |
888 | **[未完善]核函数需要满足什么性质?(很好地度量在希尔伯特空间里的距离,自反性,来回一样,对于自己为0...)**
889 |
890 | 根据根据具体的问题和数据选择。
891 |
892 | ### 软间隔与正则化
893 |
894 | #### 什么是软间隔SVM?
895 |
896 | 软间隔(soft margin)SVM通过设置松弛变量(slack variable),以允许某些样本不满足约束。传统硬间隔SVM要求数据完全线性可分,然而在实际情况下,由于数据可能存在一些噪声和异常点,很难找到完全线性可分的数据集。软间隔SVM通过允许一些样本出现在超平面的错误一侧,以此来解决线性不可分的问题。
897 |
898 | 优化目标可以写为
899 |
900 | 结构风险最小化+经验风险最小化
901 |
902 | $$
903 | \min_{w,b}\quad\frac12\vert\vert w\vert\vert^2+C\sum_{i=1}^{m}\ell_{0/1}\left(y_i(\omega^\top x_i+b)-1\right)
904 | $$
905 |
906 | 其中正则化常数 $ C>0 $ , $ \ell_{0/1} $ 为“0/1损失函数”, $ \ell_{0/1}=\left\{\begin{aligned}&1&z<0\\&0&otherwise\end{aligned}\right. $
907 |
908 | $ C\to\infty $ 时,会迫使所有样本均满足约束,等价于硬间隔; $ C $ 有限值时,允许一些样本不满足约束。
909 |
910 | #### 什么是替代损失?
911 |
912 | 由于 $ \ell_{0/1} $ 非凸、不连续,数学性质不好,使得优化目标难以直接求解,于是,使用其他一些函数替代 $ \ell_{0/1} $ ,称为替代损失(surrogate loss)
913 |
914 | - hinge损失(最常用): $ \ell_{hinge}(z)=\max(0,1-z) $
915 | - 指数损失exponential loss: $ \ell_{\exp}(z)=\exp(-z) $
916 | - 对率损失logistic loss: $ \ell_{\log}=\log(1+\exp(-z)) $
917 |
918 | 若采取hinge损失,优化目标可以改写为:
919 |
920 | $$
921 | \min_{w,b}\quad\frac12\vert\vert w\vert\vert^2+C\sum_{i=1}^{m}\max\left(0,1-y_i(\omega^\top x_i+b)\right)
922 | $$
923 |
924 | ##### 为什么使用Hinge Loss?[不知道!]
925 |
926 | Hinge Loss的优点在于它可以将最小化分类错误和最大化间隔相结合,即最小化损失的同时,最大化分类间隔。相比于其他损失函数,Hinge Loss对异常值的容忍度更高,可以更好地处理噪声和异常点的情况。同时,Hinge Loss的导数在0处不连续,使得模型更加稳定,不容易陷入局部最优解。(ChatGPT的回答)
927 |
928 | #### 什么是松弛变量?
929 |
930 | 引入松弛变量(slack variables),可将优化目标重写为
931 |
932 | $$
933 | \begin{aligned}
934 | &\min_{w,b}&\frac12\vert\vert w\vert\vert^2+C\sum_{i=1}^{m}\xi_{i}\\
935 | &s.t.&y_i(w^\top x_i+b)\geq1-\xi_{i}\\
936 | &&\xi_i\geq0,i=1,\dots,m
937 | \end{aligned}
938 | $$
939 |
940 | ##### 噪声和异常点的区别?
941 |
942 | | 噪声(noise) | 异常值(outliers) |
943 | | -------------------------------------------------------------- | ---------------------------------------------------------------------------------------------------- |
944 | | 数据中存在的错误或不准确的值 | 与其他数据点不同的、明显偏离正常情况的数据点 |
945 | | 可能是由于测量设备、传输问题或人为因素导致的 | 可能是由于记录或测量错误、系统故障或自然变异等原因导致的 |
946 | | 在整个数据集中分布较均匀 | |
947 | | 可能会对模型的性能产生一定影响,但它们不一定是非常明显的异常值 | 可能会对模型的训练和预测造成不良影响,因为它们可能会导致模型的偏差和方差增大,从而影响模型的泛化性能 |
948 | | 数据清洗和预处理噪声 | 使用特定的算法或技术来检测和处理异常点 |
949 |
950 | #### 与硬间隔SVM相比有何优势和劣势?
951 |
952 | hard margin
953 |
954 | 优势:
955 |
956 | 1. 对于存在噪声或异常点的数据,软间隔SVM可以允许一些样本不满足约束条件,从而更好地适应这些数据;
957 | 2. 更好地处理线性不可分数据集。
958 |
959 | 劣势:
960 |
961 | 1. 在使用松弛变量的情况下,软间隔SVM更容易出现过拟合现象,需要谨慎调参;
962 | 2. 计算复杂度增加,需要花费更多的计算资源和时间。
963 |
964 | #### 如何在SVM中使用正则化?
965 |
966 | 正则化(regularization)问题如下:
967 |
968 | $$
969 | \min_{f}\quad\Omega(f)+C\sum_{i=1}^{m}\ell(f(x_i),y_i)
970 | $$
971 |
972 | $ \Omega(f) $ :“结构风险”structural risk,正则化项用于描述模型 $ f $ 的某些性质
973 |
974 | $ \sum_{i=1}^{m}\ell(f(x_i),y_i) $ :“经验风险”empirical risk,用于描述模型与训练数据的契合程度
975 |
976 | $ C $ :正则化常数,折中两者,C越大,表示分类错误的惩罚越严厉,对于训练集的拟合效果更好,但是可能会过拟合;C越小,则表示更容忍分类错误,对于新数据的泛化性能更好,但是可能会欠拟合。
977 |
978 | #### $ L_1 $ 和 $ L_2 $ 正则化有何区别?
979 |
980 | $ L_p $ 范数是常用的正则化项, $ L_2 $ 倾向于 $ w $ 的分量取值尽量均衡,即非零分量个数尽量稠密; $ L_0 $ 范数(向量中非0的元素的个数)和 $ L_1 $ 范数倾向于 $ w $ 的分量尽量稀疏,即非零分量个数尽量少。
981 |
982 | ### 支持向量回归
983 |
984 | (Support Vector Regression,SVR)
985 |
986 | #### 什么是SVR?
987 |
988 | 有别于传统回归模型,SVR可以容忍 $ f(x) $ 和 $ y $ 之间最多有 $ \epsilon $ 的偏差,即仅当 $ f(x) $ 与 $ y $ 之间的差别绝对值大于 $ \epsilon $ 时才计算损失。这相当于构建了一个宽度为 $ 2\epsilon $ 的间隔带,若训练样本落入此间隔带,则认为预测正确。
989 |
990 | SVR可形式化为
991 |
992 | $$
993 | \min_{w,b}\quad\frac12\vert\vert w\vert\vert^2+C\sum_{i=1}^{m}\ell_{\epsilon}\left(f(x_i)-y_i\right)
994 | $$
995 |
996 | 其中正则化常数 $ C>0 $ , $ \ell_{\epsilon} $ 为 $ \epsilon $ -不敏感损失( $ \epsilon $ -insensitive loss)函数, $ \ell_{\epsilon}=\left\{\begin{aligned}&0&|z|\leq\epsilon\\&|z|-\epsilon&otherwise\end{aligned}\right. $
997 |
998 | #### 优化目标
999 |
1000 | ### 核方法
1001 |
1002 | #### KLDA[还没写]
1003 |
1004 | ### 具体任务
1005 |
1006 | #### 百万样本量可以用SVM吗?
1007 |
1008 | 对于百万级别的样本量,求解SVM的原问题计算复杂度过大,时空开销较大,可能存在着困难。不过,存在一些优化算法,使得可以在大规模数据集上使用SVM。
1009 |
1010 | 1. 一种方法是使用随机梯度下降(SGD)算法等在线学习算法,在每次迭代中随机选择一部分数据进行训练。这种方法的计算复杂度低,但可能会影响模型的收敛性和精度。
1011 | 2. 另一种方法是使用核函数的低秩近似,例如随机核近似(RKA)或核特征映射(KFM),以降低计算复杂度。这些方法将数据集投影到一个低维空间中,从而减少了计算量。不过,这些方法可能会对模型的精度产生一定的影响。
1012 | 3. 此外,还有一些并行化的方法,例如基于GPU的实现或者分布式计算框架的使用,可以加速SVM的训练过程。
1013 |
1014 | #### 在使用SVM时,如何处理不平衡的训练数据?
1015 |
1016 | - 改变类别权重:为少数样本增加权重
1017 | - 过采样少数样本
1018 | - 欠采样多数样本
1019 |
1020 | #### SVM中如何处理非线性可分数据?
1021 |
1022 | - 使用核函数:将原始数据映射到高维特征空间,从而使得原本线性不可分的数据在新的高维空间中成为线性可分的。
1023 | - 引入软间隔:允许某些样本不符合约束。
1024 |
1025 | #### 在SVM中如何处理多分类问题?
1026 |
1027 | - One-vs-All:对于 $ k $ 类问题,训练 $ k $ 个二元分类器,每个分类器的正例为第 $ i $ 类样本,负例为其他类别的所有样本。测试时,选择具有最高决策函数值的分类器。
1028 | - One-vs-One:对于 $ k $ 类问题,在任意两类样本之间设计一个SVM,因此 $ k $ 个类别的样本就需要设计 $ k(k-1)/2 $ 个SVM。当对一个未知样本进行分类时,最后得票最多的类别即为该未知样本的类别。Libsvm中的多类分类就是根据这个方法实现的。
1029 |
1030 | #### 在SVM中如何处理缺失数据?
1031 |
1032 | 1. 删除缺失值:直接删除包含缺失数据的样本,在剩余的完整数据上进行SVM训练。但是,这种方法会损失有用的信息,并且可能导致训练数据的减少。
1033 | 2. 插值:可以使用基于均值、中位数或其他统计量的简单插值方法,也可以使用更高级的插值方法,例如多重插值或KNN插值。然后使用填充后的数据进行SVM训练。
1034 |
1035 | 都会对SVM的性能造成负面影响。
1036 |
1037 | ### 训练细节
1038 |
1039 | #### 如何解决SVM模型过拟合(overfitting)的问题?
1040 |
1041 | 1. 减少特征数:使用特征选择技术,如主成分分析(PCA),来减少特征数量。
1042 | 2. 增加正则化:惩罚过于复杂的模型,防止过拟合。
1043 | 3. 增加数据量。
1044 | 4. 调整模型参数:如惩罚参数C、核函数类型等,来寻找最优模型。
1045 | 5. 使用交叉验证:可以使用交叉验证来评估模型性能和泛化能力,并进行模型选择。
1046 |
1047 | #### SVM中如何选择合适的超参数?如何通过网格搜索来选择超参数?
1048 |
1049 | 交叉验证。
1050 |
1051 | 正则化项 $ C $ :较大的值将使模型更加倾向于正确分类每个训练样本,但也可能导致过拟合。较小的值将允许更多的分类错误,但也可能导致欠拟合。
1052 |
1053 | (RBF核) $ \gamma $ :较大的值将导致决策边界更加复杂,可能会导致过拟合。较小的值将导致决策边界更加简单,可能会导致欠拟合。
1054 |
1055 | 需要避免使用测试集来选择,应该使用验证集来选择超参数,而将测试集保留到最后评估模型的性能。
1056 |
1057 | #### SVM模型的复杂度是如何计算的?如何通过交叉验证来选择合适的SVM模型?
1058 |
1059 | - 基于训练数据集大小(训练数据集大小 $ N $ ,特征维度 $ d $ , $ O(Nd^2) $ )
1060 | - 基于支持向量的复杂度(支持向量的数量为 $ m $ , $ O(md) $ )
1061 |
1062 | ### 模型对比
1063 |
1064 | #### SVM与逻辑回归相比有哪些优势和劣势?
1065 |
1066 | | | SVM | LR |
1067 | | ---------- | ------------------------------ | ---------------------------------------------- |
1068 | | 数据特征 | 对于线性可分的数据效果往往更好 | 能够处理非线性问题,可以使用多项式特征 |
1069 | | 数据规模 | 小数据集效果好 | 需要较多数据才能获得较好分类效果 |
1070 | | 噪声数据 | 容易受影响 | 容易受影响 |
1071 | | 参数选择 | 对参数的选择比较敏感 | 参数的选择比较简单 |
1072 | | 模型复杂度 | 复杂度较高 | 训练时间和内存开销相对较小,适合处理大规模数据 |
1073 |
1074 | #### SVM与神经网络有何异同点?
1075 |
1076 | (Answered by ChatGPT)
1077 |
1078 | 1. 工作原理不同:SVM是一种基于几何距离的分类器,它通过最大化分类间隔,寻找超平面将不同类别的数据分开;而神经网络则是通过模拟生物神经元的方式,使用一系列非线性变换来构建模型,实现分类和回归等任务。
1079 | 2. 模型结构不同:SVM的模型结构比较简单,只有一个决策边界;而神经网络的模型结构比较复杂,由多个神经元和层组成。
1080 | 3. 特征处理不同:SVM通常使用核函数将数据从低维空间映射到高维空间,以便找到更好的决策边界;而神经网络则通常使用输入层、隐藏层和输出层来提取和处理特征,不需要显式的特征转换过程。
1081 | 4. 训练方法不同:SVM使用凸优化算法来训练模型,而神经网络通常使用反向传播算法来训练模型。
1082 | 5. 适用场景不同:SVM适用于小规模、高维度的数据集,特别是在样本数目相对于特征数目较小的情况下表现更好,而神经网络适用于大规模、高维度的数据集,可以处理非线性问题和复杂的关系。
1083 |
1084 | 总之,SVM和神经网络都是有效的分类算法,但它们的实现方式和适用场景有所不同,需要根据具体的问题和数据情况选择适当的算法。
1085 |
1086 | ## 贝叶斯分类
1087 |
1088 | ### 贝叶斯决策论
1089 |
1090 | Bayes decision theory
1091 |
1092 | #### 贝叶斯判定准则,贝叶斯最优分类器,贝叶斯风险
1093 |
1094 | 贝叶斯判定准则Bayes decision rule:目标是找到最小化总体风险的判定准则 $ h:\mathcal X\to\mathcal Y $ ,只需在每个样本上选择那个能使条件风险 $ R(c|x) $ 最小的类别标记,即 $ h^*(x)=\arg\min_{c\in\mathcal Y} R(c|x) $ ,这里 $ h^* $ 是贝叶斯最优分类器 (Bayes optimal classifier) ,与之对应的总体风险 $ R(h^*) $ 称为贝叶斯风险 (Bayes risk),即通过机器学习所能产生的模型精度的理论上限。
1095 |
1096 | 定义:
1097 |
1098 | - 条件风险: $ \lambda_{ij} $ 为将 $ c_j $ 类别的样本误分类为 $ c_i $ 的损失
1099 |
1100 | $$
1101 | R(c_i|x)=\sum_{j=1}^N\lambda_{ij}P(c_j|x)
1102 | $$
1103 | - 总体风险
1104 |
1105 | $$
1106 | R(h)=\mathbb E_x[R(h(x)|x)]
1107 | $$
1108 |
1109 | #### 生成式模型,判别式模型
1110 |
1111 | 然而,后验概率 $ P(c|x) $ 难以直接获得,所以学习器要基于有限的训练样本集尽可能准确地估计出后验概率。
1112 |
1113 | - 判别式:直接建模 $ P(c|x) $
1114 | - 生成式:先建模联合概率分布 $ P(x,c) $ ,也就是 $ P(c) $ (先验)和 $ P(x|c) $ (似然)再得到 $ P(c|x) $
1115 |
1116 | ### 极大似然估计
1117 |
1118 | 见概率论
1119 |
1120 | ### 朴素贝叶斯分类器
1121 |
1122 | Naive Bayes classifier
1123 |
1124 | 朴素贝叶斯分类器 (naÏve Bayes classifier) 采用了**属性条件独立性假设**(attribute conditional independence assumption):假设每个属性独立地对分类结果发生影响。简化类条件概率 $ P(x|c) $ 的建模。
1125 |
1126 | 重写贝叶斯公式: $ x_i $ 为 $ x $ 在第 $ i $ 个属性上的取值.
1127 |
1128 | 
1129 |
1130 | 基于贝叶斯判定准则,朴素贝叶斯分类器表达式:
1131 |
1132 | $$
1133 | h_{nb}(x)=\arg\max_{c\in\mathcal Y}P(c)\prod_{i=1}^d P(x_i|c)
1134 | $$
1135 |
1136 | 离散:
1137 |
1138 | $$
1139 | P(c)=\frac{|D_c|}{|D|}\quad P(x_i|c)=\frac{|D_{c,x_i}|}{|D_c|}
1140 | $$
1141 |
1142 | 拉普拉斯修正(防止训练集中某个属性值没有与某个类同时出现过, $ |D_{c,x_i}|=0 $ 带来的误差。假设了属性值与类别的均匀分布,这是额外引入的 bias。 $ N $ 类别数, $ N_i $ 第 $ i $ 个属性可能的取值数)
1143 |
1144 | $$
1145 | \hat P(c)=\frac{|D_c|+1}{|D|+N}\quad P(x_i|c)=\frac{|D_{c,x_i}|+1}{|D_c|+N_i}
1146 | $$
1147 |
1148 | 连续:考虑概率密度函数
1149 |
1150 | ### 半朴素贝叶斯分类器
1151 |
1152 | 属性条件独立性假设在现实中很难成立,于是半朴素贝叶斯分类器(semi-naïve Bayes classifiers)对属性条件独立性假设进行一定程度的放松,适当考虑一部分属性问的相互依赖信息,从而既不需进行完全联合概率计算,又不至于彻底忽略了比较强的属性依赖关系。
1153 |
1154 | 采用独依赖估计(One-Dependent Estimator ,简称 ODE),新假设:每个属性在类别之外最多仅依赖于一个其他属性
1155 |
1156 | 
1157 |
1158 | 其中 $ pa_i $ 为属性 $ x_i $ 所依赖的属性,称为 $ x_i $ 的父属性,如何确定副属性引出不同算法
1159 |
1160 | 
1161 |
1162 | #### SPODE
1163 |
1164 | super-parent ODE,假设所有属性都依赖于同一个属性,通过交叉验证等模型选择方法来确定超父属性
1165 |
1166 | #### TAN
1167 |
1168 | 
1169 |
1170 | #### ADOE
1171 |
1172 | averaged one-dependent estimator,基于集成学习,尝试将每个属性作为超父来构建SPODE,然后将那些具有足够训练数据支撑的SPODE集成起来作为最终结果。
1173 |
1174 | #### kDE
1175 |
1176 | 将属性 $ pa_i $ 替换为包含 $ k $ 个属性的集合,随着 $ k $ 的增加,准确估计概率 $ P(x_i| y ,pai ) $ 所需的训练样本数量将以指数级增加。可能又会陷入求高阶联合概率的泥沼。
1177 |
1178 | ### 贝叶斯网
1179 |
1180 | 贝叶斯图(Bayesian network),也被称为信念网络(belief network)或概率有向无环图(probabilistic directed acyclic graph,PDAG),是一种图形化的概率模型,用于描述变量之间的概率依赖关系。变量(或节点)用圆圈表示,而变量之间的概率依赖关系则用有向箭头连接。箭头从一个变量指向依赖于它的变量,表示变量之间的因果关系或条件依赖关系。
1181 |
1182 | #### 贝叶斯网的条件独立性
1183 |
1184 | 
1185 |
1186 | $$
1187 | P(x_1,x_2,x_3,x_4,x_5)=P(x_1)P(x_2)P(x_3\vert x_1)P(x_4\vert x_1,x_2)P(x_5|x_2)
1188 | $$
1189 |
1190 | 
1191 |
1192 | 一个变量取值的确定与否,能对另两个变量间的独立性发生影响
1193 |
1194 | 同父:given $ x_1 $ , $ x_3,x_4 $ 独立
1195 |
1196 | V型:给定 $ x_4 $ ,必不独立; $ x_4 $ 未知,两者独立(边际独立性marginal independence, $ x_1\perp\!\!\!\perp x_2 $ ,两个随机变量在给定其他变量的边际分布下是独立的)
1197 |
1198 | 
1199 |
1200 | #### 边际分布
1201 |
1202 | #### Gibbs采样[没看]
1203 |
1204 | ### EM算法
1205 |
1206 | EM算法(Expectation-Maximization algorithm)是一种迭代优化算法,用于在存在隐变量(或缺失数据)的概率模型中进行参数估计。它是一种常用的无监督学习方法,通常用于处理含有不完整数据或观测数据中存在隐含变量的情况。非梯度
1207 |
1208 | EM算法的基本思想是通过迭代的方式,交替进行两个步骤:E步(Expectation step)和M步(Maximization step),以较好地逼近参数的最大似然估计。
1209 |
1210 | 已观测变量 $ X $ ,隐变量(未观测变量) $ Z $ ,模型参数 $ \Theta $ ,若对 $ \Theta $ 做极大似然估计,则应该最大化对数似然(对 $ Z $ 算期望)
1211 |
1212 | $$
1213 | LL(\Theta |X)=\ln P(X|\Theta)=\ln\sum_Z P(X,Z|\Theta)
1214 | $$
1215 |
1216 | EM算法步骤
1217 |
1218 | 1. 初始化模型参数。
1219 | 2.  1220 | 3. 重复执行E步和M步,直到收敛或达到预定的停止条件。
1221 |
1222 | ## 集成学习
1223 |
1224 | ### 基本概念
1225 |
1226 | #### 什么是集成学习?
1227 |
1228 | 集成学习ensemble learning(读“昂”)是一种机器学习方法,首先训练一组基学习器(也称为弱学习器),再将它们的预测结果通过某种策略结合,来完成学习任务。集成学习的核心思想是通过组合多个弱学习器,来达到比单个弱学习器更好的泛化性能,从而提高模型的预测能力。
1229 |
1230 | #### 为什么集成学习需要集成“好而不同”的学习器?
1231 |
1232 | 好指的是基学习器的准确性,不同指的是基学习器间的多样性。
1233 |
1234 | 直觉上,模型的准确性当然是越高越好,基学习器的准确率较低,集成学习的预测性能也会受到影响。基学习器具有多样性意味着不同的学习器可以捕捉到数据中的不同特征,因此可以相互补充、互相弥补,从而提高整体的学习性能。
1235 |
1236 | 数学上,可以用“误差-分歧分解”(error-ambiguity decomposition)证明:个体学习器准确性越高、多样性越大,则集成越好。
1237 |
1238 | 我们通过“分歧”来反应个体学习器的多样性,分歧的定义是各个学习器预测结果与集成的MSE的加权均值。
1239 |
1240 | 学习器 $ h_i $ 的分歧: $ A(h_i|x)=(h_i(x)-H(x))^2 $
1241 |
1242 | 集成 $ H $ 的分歧: $ \overline A(h|x)=\sum_{i=1}^T w_i(h_i(x)-H(x))^2 $
1243 |
1244 | 个体学习器的平方误差: $ E(h_i|x)=(f(x)-h_i(x))^2 $
1245 |
1246 | 集成的平方误差: $ E(H|x)=(f(x)-H(x))^2 $
1247 |
1248 | 个体学习器误差的加权均值: $ \overline E(h|x)=\sum_{i=1}^T w_i E(h_i|x) $
1249 |
1250 | 有:
1251 |
1252 | $$
1253 | \begin{aligned}
1254 | \overline A (h|x)&=\sum_{i=1}^Tw_i E(h_i|x)-E(H|x)\\
1255 | &=\overline E(h|x)-E(H|x)\\
1256 | \end{aligned}
1257 | $$
1258 |
1259 | 该式对所有样本 $ x $ 均成立,令 $ p(x) $ 表示样本的概率密度,则在全样本上有:
1260 |
1261 | $$
1262 | \sum_{i=1}^Tw_i\int A(h_i|x)p(x)\text{d}x=\sum_{i=1}^Tw_i\int E(h_i|x)p(x)\text{d}x-\int E(H|x)p(x)\text{d}x
1263 | $$
1264 |
1265 | 类似地,个体学习器 $ h_i $ 在全样本上的泛化误差和分歧项、集成的泛化误差分别为:
1266 |
1267 | $$
1268 | \begin{aligned}
1269 | E_i &= \int E(h_i|x)p(x)\text{d}x\\
1270 | A_i &= \int A(h_i|x)p(x)\text{d}x\\
1271 | E &= \int E(H|x)p(x)\text{d}x
1272 | \end{aligned}
1273 | $$
1274 |
1275 | 令 $ \overline E=\sum_{i=1}^Tw_i E_i $ 表示个体学习器的泛化误差的加权均值, $ \overline A=\sum_{i=1}^T w_iA_i $ 表示个体学习器的加权分歧值。有:
1276 |
1277 | $$
1278 | E = \overline E-\overline A
1279 | $$
1280 |
1281 | 这个漂亮的式子明确提示出:个体学习器准确性越高、多样性越大,则集成越好。
1282 |
1283 | [然而,个体学习器的"准确性"和"多样性"本身就存在冲突。一般的,准确性很高之后,要增加多样性就需牺牲准确性。因此我们需要达到两者的平衡。]
1284 |
1285 | [如何产生并结合“好而不同”的个体学习器,恰是集成学习研究的核心。]
1286 |
1287 | #### 有什么集成学习的方法?
1288 |
1289 | 1. 以Boosting为代表的,个体学习器问存在强依赖关系、必须串行生成的序列化方法
1290 | 2. 以Bagging, Random Forest为代表的,个体学习器间不存在强依赖关系、可同时生成的并行化方法
1291 | 3. 两者混合的方法
1292 |
1293 | #### 学习器结合的优点?
1294 |
1295 | 1. 减小泛化性能不佳的风险
1296 | 2. 降低陷入糟糕局部极小点的风险
1297 | 3. 扩大假设空间,可以学到更好的近似
1298 |
1299 | #### 各个算法的优缺点?
1300 |
1301 | Boosting:
1302 |
1303 | 优点:准确,鲁棒,泛化能力强。
1304 |
1305 | 缺点:因为是序列化训练,所以训练时间长;对噪声敏感,可能过拟合,可以增加正则化项、减少弱分类器数量;受初始值影响较大,需要用随机化的丰富减少影响。
1306 |
1307 | Bagging:
1308 |
1309 | 优点:可并行,准确,鲁棒,泛化能力强。
1310 |
1311 | 缺点:对高偏差模型效果不明显:Bagging主要的优势在于减少方差,对于高偏差的模型并不能很好地发挥作用。可解释性差。
1312 |
1313 | #### 学习器是越多越好吗?
1314 |
1315 | 不是,根据选择性集成,给定一组个体学习器,从中选择一部分来构建集成,经常会比使 用所有个体学习器更好 (更小的存储/时间开销,更强的泛化性能)。选择过程需考虑个体性能与多样性/互补性,仅选择“精度最高的”通常不好。
1316 |
1317 | ### Boosting
1318 |
1319 | #### 什么是Boosting?
1320 |
1321 | Boosting是一组可以将弱学习器提升为强学习器的算法。工作机制为:先从初始训练集中训练出一个基学习器,再根据基学习器的表现对训练样本分布进行调整,使得先前基学习器做错的训练样本在后续受到更多关注,然后基于调整后的样本分布来训练下一个基学习器。如此重复进行,直至基学习器数目达到事先指定的值 $ T $ 。最终将这 $ T $ 个基学习器进行加权结合。
1322 |
1323 | #### AdaBoost的计算过程是什么?
1324 |
1325 | 原始的AdaBoost算法只能处理二分类问题,计算过程如下:
1326 |
1327 |
1220 | 3. 重复执行E步和M步,直到收敛或达到预定的停止条件。
1221 |
1222 | ## 集成学习
1223 |
1224 | ### 基本概念
1225 |
1226 | #### 什么是集成学习?
1227 |
1228 | 集成学习ensemble learning(读“昂”)是一种机器学习方法,首先训练一组基学习器(也称为弱学习器),再将它们的预测结果通过某种策略结合,来完成学习任务。集成学习的核心思想是通过组合多个弱学习器,来达到比单个弱学习器更好的泛化性能,从而提高模型的预测能力。
1229 |
1230 | #### 为什么集成学习需要集成“好而不同”的学习器?
1231 |
1232 | 好指的是基学习器的准确性,不同指的是基学习器间的多样性。
1233 |
1234 | 直觉上,模型的准确性当然是越高越好,基学习器的准确率较低,集成学习的预测性能也会受到影响。基学习器具有多样性意味着不同的学习器可以捕捉到数据中的不同特征,因此可以相互补充、互相弥补,从而提高整体的学习性能。
1235 |
1236 | 数学上,可以用“误差-分歧分解”(error-ambiguity decomposition)证明:个体学习器准确性越高、多样性越大,则集成越好。
1237 |
1238 | 我们通过“分歧”来反应个体学习器的多样性,分歧的定义是各个学习器预测结果与集成的MSE的加权均值。
1239 |
1240 | 学习器 $ h_i $ 的分歧: $ A(h_i|x)=(h_i(x)-H(x))^2 $
1241 |
1242 | 集成 $ H $ 的分歧: $ \overline A(h|x)=\sum_{i=1}^T w_i(h_i(x)-H(x))^2 $
1243 |
1244 | 个体学习器的平方误差: $ E(h_i|x)=(f(x)-h_i(x))^2 $
1245 |
1246 | 集成的平方误差: $ E(H|x)=(f(x)-H(x))^2 $
1247 |
1248 | 个体学习器误差的加权均值: $ \overline E(h|x)=\sum_{i=1}^T w_i E(h_i|x) $
1249 |
1250 | 有:
1251 |
1252 | $$
1253 | \begin{aligned}
1254 | \overline A (h|x)&=\sum_{i=1}^Tw_i E(h_i|x)-E(H|x)\\
1255 | &=\overline E(h|x)-E(H|x)\\
1256 | \end{aligned}
1257 | $$
1258 |
1259 | 该式对所有样本 $ x $ 均成立,令 $ p(x) $ 表示样本的概率密度,则在全样本上有:
1260 |
1261 | $$
1262 | \sum_{i=1}^Tw_i\int A(h_i|x)p(x)\text{d}x=\sum_{i=1}^Tw_i\int E(h_i|x)p(x)\text{d}x-\int E(H|x)p(x)\text{d}x
1263 | $$
1264 |
1265 | 类似地,个体学习器 $ h_i $ 在全样本上的泛化误差和分歧项、集成的泛化误差分别为:
1266 |
1267 | $$
1268 | \begin{aligned}
1269 | E_i &= \int E(h_i|x)p(x)\text{d}x\\
1270 | A_i &= \int A(h_i|x)p(x)\text{d}x\\
1271 | E &= \int E(H|x)p(x)\text{d}x
1272 | \end{aligned}
1273 | $$
1274 |
1275 | 令 $ \overline E=\sum_{i=1}^Tw_i E_i $ 表示个体学习器的泛化误差的加权均值, $ \overline A=\sum_{i=1}^T w_iA_i $ 表示个体学习器的加权分歧值。有:
1276 |
1277 | $$
1278 | E = \overline E-\overline A
1279 | $$
1280 |
1281 | 这个漂亮的式子明确提示出:个体学习器准确性越高、多样性越大,则集成越好。
1282 |
1283 | [然而,个体学习器的"准确性"和"多样性"本身就存在冲突。一般的,准确性很高之后,要增加多样性就需牺牲准确性。因此我们需要达到两者的平衡。]
1284 |
1285 | [如何产生并结合“好而不同”的个体学习器,恰是集成学习研究的核心。]
1286 |
1287 | #### 有什么集成学习的方法?
1288 |
1289 | 1. 以Boosting为代表的,个体学习器问存在强依赖关系、必须串行生成的序列化方法
1290 | 2. 以Bagging, Random Forest为代表的,个体学习器间不存在强依赖关系、可同时生成的并行化方法
1291 | 3. 两者混合的方法
1292 |
1293 | #### 学习器结合的优点?
1294 |
1295 | 1. 减小泛化性能不佳的风险
1296 | 2. 降低陷入糟糕局部极小点的风险
1297 | 3. 扩大假设空间,可以学到更好的近似
1298 |
1299 | #### 各个算法的优缺点?
1300 |
1301 | Boosting:
1302 |
1303 | 优点:准确,鲁棒,泛化能力强。
1304 |
1305 | 缺点:因为是序列化训练,所以训练时间长;对噪声敏感,可能过拟合,可以增加正则化项、减少弱分类器数量;受初始值影响较大,需要用随机化的丰富减少影响。
1306 |
1307 | Bagging:
1308 |
1309 | 优点:可并行,准确,鲁棒,泛化能力强。
1310 |
1311 | 缺点:对高偏差模型效果不明显:Bagging主要的优势在于减少方差,对于高偏差的模型并不能很好地发挥作用。可解释性差。
1312 |
1313 | #### 学习器是越多越好吗?
1314 |
1315 | 不是,根据选择性集成,给定一组个体学习器,从中选择一部分来构建集成,经常会比使 用所有个体学习器更好 (更小的存储/时间开销,更强的泛化性能)。选择过程需考虑个体性能与多样性/互补性,仅选择“精度最高的”通常不好。
1316 |
1317 | ### Boosting
1318 |
1319 | #### 什么是Boosting?
1320 |
1321 | Boosting是一组可以将弱学习器提升为强学习器的算法。工作机制为:先从初始训练集中训练出一个基学习器,再根据基学习器的表现对训练样本分布进行调整,使得先前基学习器做错的训练样本在后续受到更多关注,然后基于调整后的样本分布来训练下一个基学习器。如此重复进行,直至基学习器数目达到事先指定的值 $ T $ 。最终将这 $ T $ 个基学习器进行加权结合。
1322 |
1323 | #### AdaBoost的计算过程是什么?
1324 |
1325 | 原始的AdaBoost算法只能处理二分类问题,计算过程如下:
1326 |
1327 |  1328 |
1329 | 1. 初始化数据分布
1330 | 2. 在训练的每一轮中:
1331 | 1. 使用当前的样本权重训练基学习器
1332 | 2. 计算分类误差率
1333 | 3. 如果分类误差率大于0.5,为了避免它进一步降低整个模型的准确率,算法会从循环中退出,停止训练
1334 | 4. 计算这个基学习器的权重
1335 | 5. 基于对分类正误情况更新数据分布,增加分错样本的影响,降低分对样本的影响
1336 | 3. 最后基于各个基学习器的权重,得到最终的分类器
1337 |
1338 | #### 为什么分布这样更新?[没回答]
1339 |
1340 | #### 在AdaBoost中,如何更新数据分布?
1341 |
1342 | 1. **重赋权法re-weighting**:在训练过程的每一轮中,根据样本分布为每个训练样本重新赋一个权重
1343 | 2. **重采样法re-sampling**:(对无法接受带权样本的基学习算法)在每一轮学习中,根据样本分布对训练 集重新进行采样,再用重采样而得的样本集对基学习器进行训练
1344 | 1. 可能获得**重启动**的机会以避免训练过程过早停止,即在抛弃不满足条件的当前基学习器之后,可根据当前分布重新对训练样本进行采样,再基于新的采样结果重新训练出基学习器,从而使得学习过程可以持 续到预设的 $ T $ 轮完成。
1345 |
1346 | 一般而言,这两种做法没有显著的优劣差别。
1347 |
1348 | ### Bagging,随机森林
1349 |
1350 | #### 什么是Bagging算法?
1351 |
1352 | bootstrap aggregating
1353 |
1354 | 基于自助采样法 (bootstrap sampling),得到含 $ m $ 个样本的采样集,基于每个采样集训练出一个基学习器,再将这些基学习器进行结合。对于分类任务,使用简单投票法;对于回归任务,使用简单平均法。
1355 |
1356 | 若分类预测时出现两个类收到同样票数的情形,则最简单的做法是随机选择一个,也可进一步考察学习器投票的置信度来确定最终胜者。
1357 |
1358 | 包外估计out-of-bag estimation: bootstrap使得每个基学习器值使用了初始训练集中约63.2%的样本,剩下的样本可以作为验证集来对泛化性能进行“包外估计“。
1359 |
1360 | #### Bagging的计算复杂度?
1361 |
1362 | 假定基学习器的计算复杂度为 $ O(m) $ ,则Bagging的复杂度大致为 $ T(O(m)+O(s)) $ ,采样与投票、平均过程的复杂度 $ O(s) $ 很小。
1363 |
1364 | #### 随机森林
1365 |
1366 | Random Forest
1367 |
1368 | 在以决策树为基学习器的Bagging集成的基础上,进一步在决策树的训练中引入了随机属性选择。(传统决策树:在当前结点的属性集合中选择一个最优属性;RF:对基决策树的每个接待您,先从结点的属性集合中随机选择一个包含 $ k $ 个属性的子集,然后再从一个子集中选择一个最优属性用于划分,推荐 $ k=\log_2 d $ )
1369 |
1370 | 在Bagging仅通过样本扰动增加多样性的基础上,引入了属性的扰动。
1371 |
1372 | ### Stacking
1373 |
1374 | Stacking 先从初始数据集训练出初级学习器,然后“生成”一个新数据集用于训练次级学习器。在这个新数据集中,初级学习器的输出被当作样例输入特征,而初始样本的标记仍被当作样例标记。这里我们假定初级学习器使用不同学习算法产生,即初级集成是异质的。若直接用初级学习器的训练集来产生次级训练集,则过拟合风险会比较大,因此一般是通过使用交叉验证或留一法这样的方式,用训练初级学习器未使用的样本来产生次级学习器的训练样本。
1375 |
1376 | ### 多样性
1377 |
1378 | #### 有什么多样性度量的方法?
1379 |
1380 | | | $ h_i=+1 $ | $ h_i=-1 $ |
1381 | | ---------- | ---------- | ---------- |
1382 | | $ h_j=+1 $ | a | c |
1383 | | $ h_j=-1 $ | b | d |
1384 |
1385 | - 不合度量disagreement measure:
1386 |
1387 | $$
1388 | dis_{ij}=\frac{b+c}m
1389 | $$
1390 |
1391 | $ dis_{ij} $ 值域为 $ [0,1] $ ,值越大则多样性越大。
1392 |
1393 | - 相关系数correlation coefficient
1394 |
1395 | $$
1396 | \rho_{ij}=\frac{ad-bc}{\sqrt{(a+b)(a+c)(c+d)(b+d)}}
1397 | $$
1398 |
1399 | $ \rho_{ij} $ 的值域为 $ [-1,1] $ 。若 $ h_i $ 与 $ h_j $ 无关,则值为0;若 $ h_i $ 与 $ h_j $ 正相关,则值为正,否则为负。
1400 |
1401 | - Q-统计量 Q-statistic
1402 |
1403 | $$
1404 | Q_{ij}=\frac{ad-bc}{ad+bc}
1405 | $$
1406 |
1407 | $ Q_{ij} $ 与相关系数 $ \rho_{ij} $ 的符号相同,且 $ |Q_{ij}|\leq |\rho_{ij}| $
1408 |
1409 | - $ \kappa $ -统计量 $ \kappa $ -statistic
1410 |
1411 | $$
1412 | \kappa=\frac{p_1-p_2}{1-p_2}
1413 | $$
1414 |
1415 | 其中 $ p_1 $ 是两个分类器取得一致的概率; $ p_2 $ 是两个分类器偶然达成一致的概率,它们可以由数据集 $ D $ 估算:
1416 |
1417 | $$
1418 | \begin{aligned}
1419 | p_1&=\frac{a+d}{m}\\
1420 | p_2&=\frac{(a+b)(a+c)+(c+d)(b+d)}{m^2}
1421 | \end{aligned}
1422 | $$
1423 |
1424 | 若分类器 $ h_i $ 与 $ h_j $ 在 $ D $ 上完全一致,则 $ \kappa = 1 $ ;若它们仅是偶然达成一致,则 $ \kappa = 0 $ 。188 $ \kappa $ 通常为非负值,仅在 $ h_i $ 与 $ h_j $ 达成一致的概率甚主低于偶然性的情况下取负值。
1425 |
1426 | #### 如何增强多样性?
1427 |
1428 | 对数据样本、输入属性、输出表示、算法参数进行扰动。
1429 |
1430 | ## 聚类
1431 |
1432 | ### 聚类任务
1433 |
1434 | #### 什么是聚类任务?
1435 |
1436 | 聚类试图将数据集中的样本划分为若干个通常是不相交的“簇”(cluster)。用于找寻数据内在的分布结构,也可作为分类等其他学习任务的前驱过程。
1437 |
1438 | ### 性能度量
1439 |
1440 | #### 直观上,什么样的聚类好?
1441 |
1442 | 直观上看,我们希望“物以类聚“,即同一簇的样本尽可能彼此相似,不同簇的样本尽可能不同。换言之,聚类结果的“簇内相似度 (intra-cluster similarity) 高且“簇间相似度” (inter-cluster similarity) 低。
1443 |
1444 | #### 什么是外部指标,内部指标?具体有什么指标?
1445 |
1446 | 外部指标external index,将聚类结果与某个“参考模型”reference model进行比较:
1447 |
1448 | $ a= |SS| $ ,属于同一簇且在参考模型中也属于同一簇的样本对数
1449 |
1450 | $ b= |SD| $ ,属于同一簇但在参考模型中不属于同一簇的样本对数
1451 |
1452 | $ c= |DS| $ ,不属于同一簇但在参考模型中属于同一簇的样本对数
1453 |
1454 | $ c= |DD| $ ,不属于同一簇且在参考模型中也不属于同一簇的样本对数
1455 |
1456 | - Jaccard系数,Jaccard Coefficient, JC
1457 | - FM指数
1458 | - Rand指数(p198)
1459 |
1460 | 内部指标internal index,直接考察聚类结果而不利用任何参考模型:
1461 |
1462 | - DBI,越小越好
1463 | - Dunn,越大越好
1464 |
1465 | ### 距离计算
1466 |
1467 | #### 距离度量需要满足什么基本性质?
1468 |
1469 | 非负性,同一性(距离为零当且仅当两点相等),对称性( $ \operatorname{dist}(a,b)=\operatorname{dist}(b,a) $ ),直递性( $ \operatorname{dist}(a,b)\leq\operatorname{dist}(a,c)+\operatorname{dist}(c,b) $ )
1470 |
1471 | #### 有什么常见的距离度量?
1472 |
1473 | - 对连续属性
1474 |
1475 | 闵可夫斯基距离Minkowski distance
1476 |
1477 | $$
1478 | \operatorname{dist}_{mk}(x_i,x_j)=\left(\sum_{u=1}^n |x_{iu}-x_{ju}|^p\right)^{\frac1p}
1479 | $$
1480 |
1481 | $ p=2 $ ,欧氏距离Euclidean distance
1482 |
1483 | $ p=1 $ ,曼哈顿距离Manhattan distance
1484 |
1485 | $ p=\infty $ ,切比雪夫距离 $ =\max(|x_2-x_1|,|y_2-y_1|) $
1486 |
1487 | - 对离散属性
1488 |
1489 | - 对有序属性:接近连续
1490 | - 对无序属性:VDM, value difference metric
1491 |
1492 | $ m_{u,a} $ 在属性 $ u $ 上取值为 $ a $ 的样本数, $ m_{u,a,i} $ 在第 $ i $ 个样本簇中在属性 $ u $ 上取值为 $ a $ 的样本数, $ k $ 样本簇数
1493 |
1494 | $$
1495 | VDM_p(a,b)=\sum_{i=1}^k\left\vert\frac{m_{u,a,i}}{m_{u,a}}-\frac{m_{u,b,i}}{m_{u,b}}\right\vert^p\\
1496 | $$
1497 | - 对混合属性
1498 |
1499 | 基于闵可夫斯基距离,括号里加上无序属性的VDM。
1500 |
1501 | #### 什么是距离度量学习?
1502 |
1503 | 在现实任务中基于数据样本来确定合适的距离计算式。
1504 |
1505 | ### 常见聚类方法
1506 |
1507 | - 原型聚类
1508 |
1509 | - 亦称“基于原型的聚类”(prototype-based clustering)
1510 | - 假设:聚类结构能通过一组原型刻画
1511 | - 过程:先对原型初始化,然后对原型进行迭代更新求解
1512 | - 代表:
1513 |
1514 | - k均值聚类:找到一组原型向量来刻画聚类结构,每个簇以该簇中所有样本点的“均值”表示
1515 | - 学习向量量化(LVQ):找到一组原型向量来刻画聚类结构,假设数据样本带有类别标记
1516 | - 高斯混合聚类Gaussian Mixture Clustering:生成式模型。采用概率模型来表达聚类原型,假设样本由高斯混合过程(先选成分,再根据其概率密度函数采样)生成相应的样本。用EM算法迭代优化求解其最大对数似然。
1517 | - 密度聚类
1518 |
1519 | - 亦称“基于密度的聚类”(density-based clustering)
1520 | - 假设:聚类结构能通过样本分布的紧密程度确定
1521 | - 过程:从样本密度的角度来考察样本之间的可连接性,并基于可连接样本不断扩展聚类簇
1522 | - 代表:DBSCAN, OPTICS, DENCLUE
1523 | - 层次聚类 (hierarchical clustering)
1524 |
1525 | - 假设:能够产生不同粒度的聚类结果
1526 | - 过程:在不同层次对数据集进行划分,从而形成树形的聚类结构
1527 | - 代表:AGNES (自底向上),DIANA (自顶向下)
1528 |
1529 | ## 降维与度量学习
1530 |
1531 | ### k近邻学习
1532 |
1533 | 给定测试样本,基于某种距离度量找出训练集中与其最靠近的k个训练样本,然后基于这k个"邻居"的信息来进行预测 .
1534 |
1535 | lazy learning,即在训练阶段仅仅是把样本保存起来,训练时间开销为零,待收到测试样本后再进行处理。
1536 |
1537 | ### 维数灾难
1538 |
1539 | #### 是什么
1540 |
1541 | curse of dimensionality,高维情形下出现的数据样本稀疏、 距离计算困难等问题
1542 |
1543 | #### 解决
1544 |
1545 | 降维dimension reduction,某种数学变换将原始高维属性空间转变为一个低维子空间,在这个子空间中样本密度大幅提高,距离计算也变得更为容易。
1546 |
1547 | #### 为什么可以降维
1548 |
1549 | 与学习任务密切相关的也许仅是某个低维分布,即高维空间中的一 个低维嵌入(embedding)
1550 |
1551 | #### MDS[没看]
1552 |
1553 | 经典降维方法,要求原始空间中样本之间的距离在低维空间中得以保持
1554 |
1555 | ### 主成分分析
1556 |
1557 | Principal Component Analysis,常用降维方法
1558 |
1559 | #### 推导[自己推一遍]
1560 |
1561 | 根据**最近重构性**(样本点到这个超平面的距离都足够近)和**最大可分性**(样本点在这个超平面上的投影能尽可能分开)的两个推导
1562 |
1563 | #### 计算过程
1564 |
1565 | 中心化:
1566 |
1567 | $ x_i=x_i-\overline {x_i} $
1568 |
1569 | 优化目标:
1570 |
1571 | $$
1572 | \min_W -\text{tr}(W^\top XX^\top W)\\
1573 | s.t. W^\top W=E
1574 | $$
1575 |
1576 | 拉格朗日乘子法:
1577 |
1578 | $$
1579 | XX^\top W=\lambda W
1580 | $$
1581 |
1582 | 对 $ XX^\top $ 特征值分解并将求得的特征值从大到小排序,选择前 $ d' $ 维特征值对应的特征向量构成 $ w_1,\dots,w_{d'} $
1583 |
1584 | #### 重构维度选择
1585 |
1586 | 一般事先指定,可以通过重构阈值设置。例如 $ t=95\% $
1587 |
1588 | 选择满足 $ \displaystyle \frac{\sum_{i=1}^{d'}\lambda_i}{\sum_{i=1}^{d}\lambda_i}\geq t $ 的最小 $ d' $
1589 |
1590 | #### 与LDA, FDA
1591 |
1592 | p231
1593 |
1594 | 借鉴LDA的方法,假设每个 样本自成一个类型,那么则 希望所有样本在超平面上的 投影尽可能分开。 LDA既要优化类间散度又要 优化类内散度,PCA相当于 通过固定类内散度来限制它
1595 |
1596 | PCA - FDA => LDA PCA是无监督学习方法,FDA是监督学习方法,考虑了标记的作用
1597 |
1598 | #### 应用[没看!]
1599 |
1600 | 特征脸(eigenface) robust PCA
1601 |
1602 | ### 度量学习
1603 |
1604 | 度量学习(Metric Learning)是机器学习领域的一个子领域,旨在通过学习适当的距离或度量函数,使得在特征空间中具有类似特性的样本之间的距离更小,而不同类别之间的距离更大。
1605 |
1606 | #### 马氏距离
1607 |
1608 | 
1609 |
1610 | #### 优化目标
1611 |
1612 | 
1613 |
1614 | ## 特征选择与稀疏学习
1615 |
1616 | #### L1正则化和
1617 |
1618 | ## 计算学习理论
1619 |
1620 | ### PAC学习
1621 |
1622 | #### PAC理论
1623 |
1624 | probably approximately correct。PAC理论是机器学习中的理论框架,通过控制样本复杂度和近似误差的方式,以一定的概率保证算法学得误差满足预设上限的模型。
1625 |
1626 | #### PAC辨识
1627 |
1628 | 
1629 |
1630 | #### PAC可学习
1631 |
1632 | 一个学习问题被称为PAC可学习,当且仅当存在一个学习算法,对于给定的样本数量和质量,以一定的概率保证在未见过的数据上产生近似正确的输出。
1633 |
1634 | 
1635 |
1636 | #### PAC学习算法
1637 |
1638 | (考虑时间复杂度)
1639 |
1640 | 
1641 |
1642 | #### 样本复杂度
1643 |
1644 | 
1645 |
1646 | ## 半监督学习
1647 |
1648 | ## 概率图模型
1649 |
1650 | 用图表示变量的相关关系的概率模型,点:变量,边:变量间的概率相关关系
1651 |
1652 | 有向无环图 - 贝叶斯网 - HMM
1653 |
1654 | 无向图 - 马尔科夫网
1655 |
1656 | ### HMM
1657 |
1658 | #### 静态过程/动态过程?
1659 |
1660 | $ P(X_{t+1}|X_t) $ 是否改变
1661 |
1662 | #### 马尔科夫链
1663 |
1664 | 具有马尔科夫性,系统下一时刻的状态仅由当前状态决定,不依赖于以往的任何状态。
1665 |
1666 | 
1667 |
1668 | 简化模型,避免了维度灾难的问题。
1669 |
1670 | #### 参数?
1671 |
1672 | 
1673 |
1674 | 
1675 |
1676 | #### 三个要解决的问题?
1677 |
1678 | 问题1:Evaluation估值,评估模型与观测序列 之间的匹配程度
1679 |
1680 |
1328 |
1329 | 1. 初始化数据分布
1330 | 2. 在训练的每一轮中:
1331 | 1. 使用当前的样本权重训练基学习器
1332 | 2. 计算分类误差率
1333 | 3. 如果分类误差率大于0.5,为了避免它进一步降低整个模型的准确率,算法会从循环中退出,停止训练
1334 | 4. 计算这个基学习器的权重
1335 | 5. 基于对分类正误情况更新数据分布,增加分错样本的影响,降低分对样本的影响
1336 | 3. 最后基于各个基学习器的权重,得到最终的分类器
1337 |
1338 | #### 为什么分布这样更新?[没回答]
1339 |
1340 | #### 在AdaBoost中,如何更新数据分布?
1341 |
1342 | 1. **重赋权法re-weighting**:在训练过程的每一轮中,根据样本分布为每个训练样本重新赋一个权重
1343 | 2. **重采样法re-sampling**:(对无法接受带权样本的基学习算法)在每一轮学习中,根据样本分布对训练 集重新进行采样,再用重采样而得的样本集对基学习器进行训练
1344 | 1. 可能获得**重启动**的机会以避免训练过程过早停止,即在抛弃不满足条件的当前基学习器之后,可根据当前分布重新对训练样本进行采样,再基于新的采样结果重新训练出基学习器,从而使得学习过程可以持 续到预设的 $ T $ 轮完成。
1345 |
1346 | 一般而言,这两种做法没有显著的优劣差别。
1347 |
1348 | ### Bagging,随机森林
1349 |
1350 | #### 什么是Bagging算法?
1351 |
1352 | bootstrap aggregating
1353 |
1354 | 基于自助采样法 (bootstrap sampling),得到含 $ m $ 个样本的采样集,基于每个采样集训练出一个基学习器,再将这些基学习器进行结合。对于分类任务,使用简单投票法;对于回归任务,使用简单平均法。
1355 |
1356 | 若分类预测时出现两个类收到同样票数的情形,则最简单的做法是随机选择一个,也可进一步考察学习器投票的置信度来确定最终胜者。
1357 |
1358 | 包外估计out-of-bag estimation: bootstrap使得每个基学习器值使用了初始训练集中约63.2%的样本,剩下的样本可以作为验证集来对泛化性能进行“包外估计“。
1359 |
1360 | #### Bagging的计算复杂度?
1361 |
1362 | 假定基学习器的计算复杂度为 $ O(m) $ ,则Bagging的复杂度大致为 $ T(O(m)+O(s)) $ ,采样与投票、平均过程的复杂度 $ O(s) $ 很小。
1363 |
1364 | #### 随机森林
1365 |
1366 | Random Forest
1367 |
1368 | 在以决策树为基学习器的Bagging集成的基础上,进一步在决策树的训练中引入了随机属性选择。(传统决策树:在当前结点的属性集合中选择一个最优属性;RF:对基决策树的每个接待您,先从结点的属性集合中随机选择一个包含 $ k $ 个属性的子集,然后再从一个子集中选择一个最优属性用于划分,推荐 $ k=\log_2 d $ )
1369 |
1370 | 在Bagging仅通过样本扰动增加多样性的基础上,引入了属性的扰动。
1371 |
1372 | ### Stacking
1373 |
1374 | Stacking 先从初始数据集训练出初级学习器,然后“生成”一个新数据集用于训练次级学习器。在这个新数据集中,初级学习器的输出被当作样例输入特征,而初始样本的标记仍被当作样例标记。这里我们假定初级学习器使用不同学习算法产生,即初级集成是异质的。若直接用初级学习器的训练集来产生次级训练集,则过拟合风险会比较大,因此一般是通过使用交叉验证或留一法这样的方式,用训练初级学习器未使用的样本来产生次级学习器的训练样本。
1375 |
1376 | ### 多样性
1377 |
1378 | #### 有什么多样性度量的方法?
1379 |
1380 | | | $ h_i=+1 $ | $ h_i=-1 $ |
1381 | | ---------- | ---------- | ---------- |
1382 | | $ h_j=+1 $ | a | c |
1383 | | $ h_j=-1 $ | b | d |
1384 |
1385 | - 不合度量disagreement measure:
1386 |
1387 | $$
1388 | dis_{ij}=\frac{b+c}m
1389 | $$
1390 |
1391 | $ dis_{ij} $ 值域为 $ [0,1] $ ,值越大则多样性越大。
1392 |
1393 | - 相关系数correlation coefficient
1394 |
1395 | $$
1396 | \rho_{ij}=\frac{ad-bc}{\sqrt{(a+b)(a+c)(c+d)(b+d)}}
1397 | $$
1398 |
1399 | $ \rho_{ij} $ 的值域为 $ [-1,1] $ 。若 $ h_i $ 与 $ h_j $ 无关,则值为0;若 $ h_i $ 与 $ h_j $ 正相关,则值为正,否则为负。
1400 |
1401 | - Q-统计量 Q-statistic
1402 |
1403 | $$
1404 | Q_{ij}=\frac{ad-bc}{ad+bc}
1405 | $$
1406 |
1407 | $ Q_{ij} $ 与相关系数 $ \rho_{ij} $ 的符号相同,且 $ |Q_{ij}|\leq |\rho_{ij}| $
1408 |
1409 | - $ \kappa $ -统计量 $ \kappa $ -statistic
1410 |
1411 | $$
1412 | \kappa=\frac{p_1-p_2}{1-p_2}
1413 | $$
1414 |
1415 | 其中 $ p_1 $ 是两个分类器取得一致的概率; $ p_2 $ 是两个分类器偶然达成一致的概率,它们可以由数据集 $ D $ 估算:
1416 |
1417 | $$
1418 | \begin{aligned}
1419 | p_1&=\frac{a+d}{m}\\
1420 | p_2&=\frac{(a+b)(a+c)+(c+d)(b+d)}{m^2}
1421 | \end{aligned}
1422 | $$
1423 |
1424 | 若分类器 $ h_i $ 与 $ h_j $ 在 $ D $ 上完全一致,则 $ \kappa = 1 $ ;若它们仅是偶然达成一致,则 $ \kappa = 0 $ 。188 $ \kappa $ 通常为非负值,仅在 $ h_i $ 与 $ h_j $ 达成一致的概率甚主低于偶然性的情况下取负值。
1425 |
1426 | #### 如何增强多样性?
1427 |
1428 | 对数据样本、输入属性、输出表示、算法参数进行扰动。
1429 |
1430 | ## 聚类
1431 |
1432 | ### 聚类任务
1433 |
1434 | #### 什么是聚类任务?
1435 |
1436 | 聚类试图将数据集中的样本划分为若干个通常是不相交的“簇”(cluster)。用于找寻数据内在的分布结构,也可作为分类等其他学习任务的前驱过程。
1437 |
1438 | ### 性能度量
1439 |
1440 | #### 直观上,什么样的聚类好?
1441 |
1442 | 直观上看,我们希望“物以类聚“,即同一簇的样本尽可能彼此相似,不同簇的样本尽可能不同。换言之,聚类结果的“簇内相似度 (intra-cluster similarity) 高且“簇间相似度” (inter-cluster similarity) 低。
1443 |
1444 | #### 什么是外部指标,内部指标?具体有什么指标?
1445 |
1446 | 外部指标external index,将聚类结果与某个“参考模型”reference model进行比较:
1447 |
1448 | $ a= |SS| $ ,属于同一簇且在参考模型中也属于同一簇的样本对数
1449 |
1450 | $ b= |SD| $ ,属于同一簇但在参考模型中不属于同一簇的样本对数
1451 |
1452 | $ c= |DS| $ ,不属于同一簇但在参考模型中属于同一簇的样本对数
1453 |
1454 | $ c= |DD| $ ,不属于同一簇且在参考模型中也不属于同一簇的样本对数
1455 |
1456 | - Jaccard系数,Jaccard Coefficient, JC
1457 | - FM指数
1458 | - Rand指数(p198)
1459 |
1460 | 内部指标internal index,直接考察聚类结果而不利用任何参考模型:
1461 |
1462 | - DBI,越小越好
1463 | - Dunn,越大越好
1464 |
1465 | ### 距离计算
1466 |
1467 | #### 距离度量需要满足什么基本性质?
1468 |
1469 | 非负性,同一性(距离为零当且仅当两点相等),对称性( $ \operatorname{dist}(a,b)=\operatorname{dist}(b,a) $ ),直递性( $ \operatorname{dist}(a,b)\leq\operatorname{dist}(a,c)+\operatorname{dist}(c,b) $ )
1470 |
1471 | #### 有什么常见的距离度量?
1472 |
1473 | - 对连续属性
1474 |
1475 | 闵可夫斯基距离Minkowski distance
1476 |
1477 | $$
1478 | \operatorname{dist}_{mk}(x_i,x_j)=\left(\sum_{u=1}^n |x_{iu}-x_{ju}|^p\right)^{\frac1p}
1479 | $$
1480 |
1481 | $ p=2 $ ,欧氏距离Euclidean distance
1482 |
1483 | $ p=1 $ ,曼哈顿距离Manhattan distance
1484 |
1485 | $ p=\infty $ ,切比雪夫距离 $ =\max(|x_2-x_1|,|y_2-y_1|) $
1486 |
1487 | - 对离散属性
1488 |
1489 | - 对有序属性:接近连续
1490 | - 对无序属性:VDM, value difference metric
1491 |
1492 | $ m_{u,a} $ 在属性 $ u $ 上取值为 $ a $ 的样本数, $ m_{u,a,i} $ 在第 $ i $ 个样本簇中在属性 $ u $ 上取值为 $ a $ 的样本数, $ k $ 样本簇数
1493 |
1494 | $$
1495 | VDM_p(a,b)=\sum_{i=1}^k\left\vert\frac{m_{u,a,i}}{m_{u,a}}-\frac{m_{u,b,i}}{m_{u,b}}\right\vert^p\\
1496 | $$
1497 | - 对混合属性
1498 |
1499 | 基于闵可夫斯基距离,括号里加上无序属性的VDM。
1500 |
1501 | #### 什么是距离度量学习?
1502 |
1503 | 在现实任务中基于数据样本来确定合适的距离计算式。
1504 |
1505 | ### 常见聚类方法
1506 |
1507 | - 原型聚类
1508 |
1509 | - 亦称“基于原型的聚类”(prototype-based clustering)
1510 | - 假设:聚类结构能通过一组原型刻画
1511 | - 过程:先对原型初始化,然后对原型进行迭代更新求解
1512 | - 代表:
1513 |
1514 | - k均值聚类:找到一组原型向量来刻画聚类结构,每个簇以该簇中所有样本点的“均值”表示
1515 | - 学习向量量化(LVQ):找到一组原型向量来刻画聚类结构,假设数据样本带有类别标记
1516 | - 高斯混合聚类Gaussian Mixture Clustering:生成式模型。采用概率模型来表达聚类原型,假设样本由高斯混合过程(先选成分,再根据其概率密度函数采样)生成相应的样本。用EM算法迭代优化求解其最大对数似然。
1517 | - 密度聚类
1518 |
1519 | - 亦称“基于密度的聚类”(density-based clustering)
1520 | - 假设:聚类结构能通过样本分布的紧密程度确定
1521 | - 过程:从样本密度的角度来考察样本之间的可连接性,并基于可连接样本不断扩展聚类簇
1522 | - 代表:DBSCAN, OPTICS, DENCLUE
1523 | - 层次聚类 (hierarchical clustering)
1524 |
1525 | - 假设:能够产生不同粒度的聚类结果
1526 | - 过程:在不同层次对数据集进行划分,从而形成树形的聚类结构
1527 | - 代表:AGNES (自底向上),DIANA (自顶向下)
1528 |
1529 | ## 降维与度量学习
1530 |
1531 | ### k近邻学习
1532 |
1533 | 给定测试样本,基于某种距离度量找出训练集中与其最靠近的k个训练样本,然后基于这k个"邻居"的信息来进行预测 .
1534 |
1535 | lazy learning,即在训练阶段仅仅是把样本保存起来,训练时间开销为零,待收到测试样本后再进行处理。
1536 |
1537 | ### 维数灾难
1538 |
1539 | #### 是什么
1540 |
1541 | curse of dimensionality,高维情形下出现的数据样本稀疏、 距离计算困难等问题
1542 |
1543 | #### 解决
1544 |
1545 | 降维dimension reduction,某种数学变换将原始高维属性空间转变为一个低维子空间,在这个子空间中样本密度大幅提高,距离计算也变得更为容易。
1546 |
1547 | #### 为什么可以降维
1548 |
1549 | 与学习任务密切相关的也许仅是某个低维分布,即高维空间中的一 个低维嵌入(embedding)
1550 |
1551 | #### MDS[没看]
1552 |
1553 | 经典降维方法,要求原始空间中样本之间的距离在低维空间中得以保持
1554 |
1555 | ### 主成分分析
1556 |
1557 | Principal Component Analysis,常用降维方法
1558 |
1559 | #### 推导[自己推一遍]
1560 |
1561 | 根据**最近重构性**(样本点到这个超平面的距离都足够近)和**最大可分性**(样本点在这个超平面上的投影能尽可能分开)的两个推导
1562 |
1563 | #### 计算过程
1564 |
1565 | 中心化:
1566 |
1567 | $ x_i=x_i-\overline {x_i} $
1568 |
1569 | 优化目标:
1570 |
1571 | $$
1572 | \min_W -\text{tr}(W^\top XX^\top W)\\
1573 | s.t. W^\top W=E
1574 | $$
1575 |
1576 | 拉格朗日乘子法:
1577 |
1578 | $$
1579 | XX^\top W=\lambda W
1580 | $$
1581 |
1582 | 对 $ XX^\top $ 特征值分解并将求得的特征值从大到小排序,选择前 $ d' $ 维特征值对应的特征向量构成 $ w_1,\dots,w_{d'} $
1583 |
1584 | #### 重构维度选择
1585 |
1586 | 一般事先指定,可以通过重构阈值设置。例如 $ t=95\% $
1587 |
1588 | 选择满足 $ \displaystyle \frac{\sum_{i=1}^{d'}\lambda_i}{\sum_{i=1}^{d}\lambda_i}\geq t $ 的最小 $ d' $
1589 |
1590 | #### 与LDA, FDA
1591 |
1592 | p231
1593 |
1594 | 借鉴LDA的方法,假设每个 样本自成一个类型,那么则 希望所有样本在超平面上的 投影尽可能分开。 LDA既要优化类间散度又要 优化类内散度,PCA相当于 通过固定类内散度来限制它
1595 |
1596 | PCA - FDA => LDA PCA是无监督学习方法,FDA是监督学习方法,考虑了标记的作用
1597 |
1598 | #### 应用[没看!]
1599 |
1600 | 特征脸(eigenface) robust PCA
1601 |
1602 | ### 度量学习
1603 |
1604 | 度量学习(Metric Learning)是机器学习领域的一个子领域,旨在通过学习适当的距离或度量函数,使得在特征空间中具有类似特性的样本之间的距离更小,而不同类别之间的距离更大。
1605 |
1606 | #### 马氏距离
1607 |
1608 | 
1609 |
1610 | #### 优化目标
1611 |
1612 | 
1613 |
1614 | ## 特征选择与稀疏学习
1615 |
1616 | #### L1正则化和
1617 |
1618 | ## 计算学习理论
1619 |
1620 | ### PAC学习
1621 |
1622 | #### PAC理论
1623 |
1624 | probably approximately correct。PAC理论是机器学习中的理论框架,通过控制样本复杂度和近似误差的方式,以一定的概率保证算法学得误差满足预设上限的模型。
1625 |
1626 | #### PAC辨识
1627 |
1628 | 
1629 |
1630 | #### PAC可学习
1631 |
1632 | 一个学习问题被称为PAC可学习,当且仅当存在一个学习算法,对于给定的样本数量和质量,以一定的概率保证在未见过的数据上产生近似正确的输出。
1633 |
1634 | 
1635 |
1636 | #### PAC学习算法
1637 |
1638 | (考虑时间复杂度)
1639 |
1640 | 
1641 |
1642 | #### 样本复杂度
1643 |
1644 | 
1645 |
1646 | ## 半监督学习
1647 |
1648 | ## 概率图模型
1649 |
1650 | 用图表示变量的相关关系的概率模型,点:变量,边:变量间的概率相关关系
1651 |
1652 | 有向无环图 - 贝叶斯网 - HMM
1653 |
1654 | 无向图 - 马尔科夫网
1655 |
1656 | ### HMM
1657 |
1658 | #### 静态过程/动态过程?
1659 |
1660 | $ P(X_{t+1}|X_t) $ 是否改变
1661 |
1662 | #### 马尔科夫链
1663 |
1664 | 具有马尔科夫性,系统下一时刻的状态仅由当前状态决定,不依赖于以往的任何状态。
1665 |
1666 | 
1667 |
1668 | 简化模型,避免了维度灾难的问题。
1669 |
1670 | #### 参数?
1671 |
1672 | 
1673 |
1674 | 
1675 |
1676 | #### 三个要解决的问题?
1677 |
1678 | 问题1:Evaluation估值,评估模型与观测序列 之间的匹配程度
1679 |
1680 |  1681 |
1682 | 问题2:Decoding解码,如何根据观测序列推断出隐藏的模型状态
1683 |
1684 | 维特比算法
1685 |
1686 |
1681 |
1682 | 问题2:Decoding解码,如何根据观测序列推断出隐藏的模型状态
1683 |
1684 | 维特比算法
1685 |
1686 |  1687 |
1688 | 问题3:Learning学习,如何训练模型使其能最好地描述观测数据
1689 |
1690 | Baum-Welch算法(EM的特例)
1691 |
1692 | 前两者都是DP,计算简单
1693 |
1694 |
1687 |
1688 | 问题3:Learning学习,如何训练模型使其能最好地描述观测数据
1689 |
1690 | Baum-Welch算法(EM的特例)
1691 |
1692 | 前两者都是DP,计算简单
1693 |
1694 |  1695 |
1696 | ### 1、什么是马尔科夫过程?
1697 |
1698 | 假设一个随机过程中,t_n 时刻的状态 x_n 的条件发布,只与其前一状态x_(n-1) 相关,即:
1699 |
1700 | 
1701 |
1702 | 则将其称为 马尔可夫过程。
1703 |
1704 | ### 2、马尔科夫过程的核心思想是什么?
1705 |
1706 | 对于马尔可夫过程的思想,用一句话去概括:当前时刻状态仅与上一时刻状态相关,与其他时刻不相关。
1707 |
1708 | 可以从 马尔可夫过程图去理解,由于每个状态间是以有向直线连接,也就是当前时刻状态仅与上一时刻状态相关。
1709 |
1710 | ### 3、隐马尔可夫算法中的两个假设是什么?
1711 |
1712 | 齐次马尔可夫性假设:即假设隐藏的马尔科夫链在任意时刻 t 的状态只依赖于其前一时刻的状态,与其他时刻的状态及观测无关,也与时刻 t 无关;
1713 |
1714 | 
1715 |
1716 | 观测独立性假设:即假设任意时刻的观测只依赖于该时刻的马尔科夫链的状态,与其他观测及状态无关。
1717 |
1718 | 
1719 |
1720 | ### 4、隐马尔可夫模型三个基本问题是什么?
1721 |
1722 | (1)概率计算问题:**给定模型(A,B, $ \pi $ )和观测序列**,计算在模型下观测序列出现的概率。(直接计算法理论可行,但计算复杂度太大(O(N^2T));用前向与后向计算法)
1723 |
1724 | (2)学习问题:**已知观测序列,估计模型参数**,使得在该模型下观测序列概率最大。(极大似然估计的方法来估计参数,Baum-Welch算法(EM算法))
1725 |
1726 | (3)预测问题,也称为解码问题:已知模型和观测序列,**求对给定观测序列条件概率最大的状态序列**。(维特比算法,动态规划,核心:**边计算边删掉不可能是答案的路径,在最后剩下的路径中挑选最优路径**)
1727 |
1728 | ### 5、隐马尔可夫模型三个基本问题的联系?
1729 |
1730 | 三个基本问题 存在 渐进关系。首先,要学会用前向算法和后向算法算观测序列出现的概率,然后用Baum-Welch算法求参数的时候,某些步骤是需要用到前向算法和后向算法的,计算得到参数后,我们就可以用来做预测了。因此可以看到,三个基本问题,它们是渐进的,解决NLP问题,应用HMM模型做解码任务应该是最终的目的。
1731 |
1732 | ### 6、隐马尔可夫算法存在哪些问题?
1733 |
1734 | 因为HMM模型其实它简化了很多问题,做了某些很强的假设,如齐次马尔可夫性假设和观测独立性假设,做了假设的好处是,简化求解的难度,坏处是对真实情况的建模能力变弱了。
1735 |
1736 | 在序列标注问题中,隐状态(标注)不仅和单个观测状态相关,还和观察序列的长度、上下文等信息相关。例如词性标注问题中,一个词被标注为动词还是名词,不仅与它本身以及它前一个词的标注有关,还依赖于上下文中的其他词。可以使用最大熵马尔科夫模型进行优化。
1737 |
1738 | ## 规则学习
1739 |
1740 | ## 强化学习
1741 |
--------------------------------------------------------------------------------
/概率论与数理统计.md:
--------------------------------------------------------------------------------
1 | # 概率论与数理统计
2 |
3 | ## 提纲
4 |
5 | ### 第一章 基本概念
6 |
7 | - 概率和统计的区别
8 | - 必然现象与随机现象
9 | - 随机试验:样本点,样本空间
10 | - 事件间的关系,事件与集合的对应关系,事件的运算规律
11 | - 概率的公理化定义,概率的性质
12 | - 古典概型,几何概型
13 | - 条件概率,全概率公式和贝叶斯公式
14 | - 独立性,独立与互斥的关系
15 | - Freivalds算法
16 |
17 | ### 第二章 随机变量及其分布
18 |
19 | - 分布函数定义,性质(单调性,规范性,右连续性);概率密度函数定义,性质(单调性,规范性,连续性)
20 | - 离散随机变量:均匀分布、二项分布、几何分布(无记忆性)、负二项分布(Pascal分布)、泊松分布(泊松定理)
21 | - 连续随机变量:均匀分布、指数分布(无记忆性)、正态分布
22 | - 德国坦克问题
23 |
24 | ### 第三章 多维随机变量
25 |
26 | - 联合分布函数定义、性质(对每个变量单调不减,非负性,规范性,右连续);边缘分布与独立性
27 | - 联合概率密度定义、性质(非负性,规范性);边缘概率密度,两变量独立的等价条件
28 | - 多维随机变量函数的分布(和、差、积、商、最大、最小)
29 |
30 | ### 第四章 随机变量的数学特征
31 |
32 | - 期望,方差,协方差,Pearson相关系数
33 |
34 | ### 第五章 大数定律与中心极限定理
35 |
36 | - 大数定律,依概率收敛
37 | - 中心极限定理,依分布收敛
38 | - 局限:独立同分布假设,有界方差要求,收敛速度未知
39 |
40 | ### 第六章 集中不等式
41 |
42 | - Markov不等式、Chebyshev不等式、Hölder不等式、 Cauchy-Schwartz不等式、单边Chebyshev不等式
43 | - Chernoff方法,Chernoff引理,0/1 Chernoff界,有界Chernoff界
44 |
45 | ### 第七章 统计的基本概念
46 |
47 | - 统计学的概念和三大研究内容(抽样,参数估计,假设检验)
48 | - Beta分布, $ \Gamma $ -分布、性质、独立可加性;标准正态分布的平方 $ \Gamma(\frac12,\frac12) $ ;Dirichlet分布、性质
49 | - $ \chi^2 $ 分布, $ t $ 分布(student分布), $ F $ 分布
50 | - 常见抽样分布定理
51 |
52 | ### 第八章 参数估计
53 |
54 | - 点估计:矩估计,极大似然估计
55 | - 估计量评估:无偏性,有效性,一致性
56 |
57 | ### 第九章 假设检验
58 |
59 | - 假设检验基本思想:小概率原理(小概率事件在一次实验中不应该发生),假设检验概念,两类错误,显著性检验 ,显著性检验基本步骤
60 |
61 | ## 随机事件与概率
62 |
63 | ### 对立事件和互斥事件的区别
64 |
65 | A的对立事件指所有不属于A的基本事件,有 $ \overline A\cap A=\varnothing,\overline A\cup A=\Omega $
66 |
67 | $ A,B $ 不能同时发生,则称他们互不相容(互斥),有 $ A\cap B=\varnothing $
68 |
69 | 区别是 $ A $ 与其对立事件的交为全集, $ A $ 与其互斥事件的交不一定是。
70 |
71 | ### 频率和概率的关系
72 |
73 | 概率是对事件发生的可能性度量,基于统计数据或主观判断。
74 |
75 | 频率是指在大量重复试验中,某一事件发生的实际次数。频率和概率之间有一定的关系,随着试验次数的增加,频率会趋近于概率。
76 |
77 | ### 概率和统计的区别
78 |
79 | - **概率**:**研究事件的不确定性**,在给定数据生成过程中观察,研究数据的性质,强调**公理体系**, **推理**。
80 | - **统计**:**收集与分析数据**,根据观察的数据反思其数据生成过程,强调**归纳**。
81 | - 概率和统计的重要的区别在于公理体系化。
82 |
83 | ### 概率公理化的三条公理
84 |
85 | - **非负性**:对于任何事件 $ A $ ,均有 $ P(A)\geq0 $
86 | - **规范性**:对样本空间 $ \Omega $ 有 $ P(\Omega)=1 $
87 | - **可列可加性**:若 $ A_1,A_2,\dots ,A_n,\dots $ 是可列无穷个互不相容的事件,即 $ A_iA_j=\varnothing(i\neq j) $ ,有
88 |
89 | $$
90 | P(A_1\cup A_2\cup \dots\cup A_n\cup \dots)=P(A_1)+P(A_2)+\dots+P(A_n)+\dots
91 | $$
92 |
93 | 满足这三个条件的实数 $ P(A) $ 为随机事件 $ A $ 的概率。
94 |
95 | ### 古典概型
96 |
97 | 试验E满足:有限种可能( $ \Omega=\{\omega_1,\omega_2,\dots,\omega_n\} $ ,其中 $ \omega_i $ 为基本事件);每种结果发生的可能性相同 $ P(\{\omega_i\})=P(\{\omega_j\}) $ ,即是古典概型。抛硬币即是古典概型问题。
98 |
99 | 古典概率的计算的本质是计数。常见的计数原理有**加法原理**和**乘法原理**。
100 |
101 | ### 排列和组合的概念与应用场景
102 |
103 | 排列:从 $ n $ 个不同的元素中无放回地取出 $ r $ 个元素进行排列,既要考虑取出的元素,也要顾及其排列顺序,则有 $ \displaystyle (n)_r=n(n-1)\dots(n-r+1) $ 种不同的排列。全排列: $ r=n $ ,有 $ n! $ 种。
104 |
105 | 组合:从 $ n $ 个不同的元素中无放回地取出 $ r $ 个元素,取出的元素之间无顺序关系,共有 $ (^n_r) $ 种不同的取法,其中
106 |
107 | $$
108 | \left(\begin{aligned}n\\r\end{aligned}\right)=\frac{n!}{r!(n-r)!}
109 | $$
110 |
111 | (不用考虑顺序,所有将排列数除以 $ r! $ )
112 |
113 | 这里 $ (^n_r) $ 称为组合数或二项系数,是二项展开式 $ (a+b)^n=\sum_{r=0}^{n}(^n_r)a^rb^{n-r} $ 中项 $ a^rb^{n-r} $ 的系数。
114 |
115 | ### 几何概型
116 |
117 | 几何概型:样本空间无限可测,基本事件等可能性。常常使用几何画图的解法求解。
118 |
119 | ## 条件概率和独立性
120 |
121 | ### 条件概率
122 |
123 | 条件概率是事件 $ A $ 发生的条件下事件 $ B $ 发生的概率。
124 |
125 | The conditional probability is the probability of event B occurring given that event A has occurred.
126 |
127 | $$
128 | P(B\vert A)=\frac{P(AB)}{P(A)}
129 | $$
130 |
131 | 这种概率的计算通常需要基于已知的信息和假设,具有一定的主观性。在人工智能领域,条件概率经常用于模型训练和推断过程中,例如朴素贝叶斯分类算法、隐马尔可夫模型等。
132 |
133 | 条件概率也满足非负性、规范性、可列可加性。也满足容斥原理。
134 |
135 | ### 乘法公式
136 |
137 | the multiplication rule
138 |
139 | 当两个事件 $ A $ 和 $ B $ 发生的概率都已知时,计算两个事件同时发生的概率的公式。其计算公式为:
140 |
141 | $$
142 | \begin{aligned}
143 | P(AB)&=P(A)P(B\vert A)=P(B)P(A\vert B)\\
144 | P(A_1A_2\dots A_n)&=P(A_1)P(A_2\vert A_1)P(A_3\vert A_1 A_2)\dots P(A_n\vert A_1A_2\dots A_{n-1})
145 | \end{aligned}
146 | $$
147 |
148 | 在自然语言处理领域中,我们可以用乘法公式来计算一个词在给定上下文条件下出现的概率;在机器学习领域中,我们可以用乘法公式来计算多个特征同时出现的概率,从而进行分类或回归任务。
149 |
150 | ### 全概率公式
151 |
152 | 全概率公式将一个事件的概率分解成多个事件的概率之和,再利用乘法公式求解各个事件的概率。具体来说,若事件 $ A_1,A_2,\dots,A_n $ 为样本空间 $ \Omega $ 的一个划分,对任意事件 $ B $ , $ B $ 的概率是每个 $ A_i $ 的概率与 $ B $ given $ A_i $ 概率的乘积的和。
153 |
154 | 若事件 $ A_1,A_2,\dots,A_n $ 为样本空间 $ \Omega $ 的一个划分,对任意事件 $ B $ 有:
155 |
156 | $$
157 | P(B)=\sum_{i=1}^{n}P(BA_i)=\sum_{i=1}^n P(A_i)P(B|A_i)
158 | $$
159 |
160 | 称之为全概率公式(law of total probability)
161 |
162 | 这里划分指: $ A_i\cap A_j=\varnothing \quad (i\neq j);\Omega=\bigcup_{i=1}^{n}A_i $
163 |
164 | 全概率公式在人工智能领域中的应用非常广泛。例如,在语音识别中,我们可以将不同的语音信号看作互不重叠的事件,应用全概率公式来计算每个语音信号被识别为不同单词的概率;在图像处理中,我们可以将不同的图像特征看作互不重叠的事件,应用全概率公式来计算每个特征对目标分类的贡献等。
165 |
166 | ### 贝叶斯公式
167 |
168 | 贝叶斯公式Baye's law用于计算在某个先验条件下事件的后验概率。
169 |
170 | $$
171 | \begin{aligned}
172 | P(A\vert B)&=\frac{P(B\vert A)P(A)}{P(B)}\\
173 | P(A_i\vert B)&=\frac{P(A_i B)}{P(B)}=\frac{P(A_i)P(B\vert A_i)}{\sum_{j=1}^n P(A_j)P(B\vert A_j)}
174 | \end{aligned}
175 | $$
176 |
177 | 先验概率prior: $ \Pr (A_i) $ ,因为不用考虑任何 $ B $ 的因素。
178 |
179 | 证据概率evidence: $ P(B)=\sum_{j=1}^n P(A_j)P(B\vert A_j) $
180 |
181 | 后验概率posterior: $ \Pr(A_i\vert B) $ 为事件 $ A_i $ 在事件 $ B $ (证据)发生的情况下的后验概率
182 |
183 | 似然度likelihood: $ P(B|A_i) $
184 |
185 | $$
186 | 后验概率=\frac{先验概率\times似然度}{证据概率}=常量\times似然度
187 | $$
188 |
189 | ### 独立性
190 |
191 | #### 定义
192 |
193 | 独立:指两个事件的发生不受彼此的影响,若事件 $ A,B $ 满足 $ P(AB)=P(A)P(B) $ ,则称事件 $ A $ 与 $ B $ 相互独立。
194 |
195 | 即 $ P(AB)=P(A)P(B)\iff P(B\vert A)=P(B)\iff P(A\vert B)=P(B) $
196 |
197 | #### 与互斥事件有何区别
198 |
199 | 互斥:指两个事件不能同时发生。 $ A\cap B=\varnothing $
200 |
201 | 互斥 $ \iff $ 不独立
202 |
203 | 多个事件的独立性: $ A,B,C $ 独立 $ \iff P(AB)=P(A)P(B),P(AC)=P(A)P(C),P(BC)=P(B)P(C),$$P(ABC)=P(A)P(B)P(C) $ 。
204 |
205 | ### iid
206 |
207 | #### 定义
208 |
209 | iid: independent and identically distributed,即独立同分布假设,假设数据集中的每个样本都是从同一个概率分布中独立地随机取出的。
210 |
211 | iid假设在概率统计领域中经常使用,因为它是许多统计方法的基础前提。例如,在机器学习中,训练数据通常被假定为iid,这意味着每个样本是相互独立且来自同一概率分布的,从而使得机器学习算法能够利用数据中的统计信息进行学习和预测。另外,许多假设检验和置信区间的推断方法也需要假定数据是iid的,以确保推断结果的有效性。
212 |
213 | #### 基于iid假设的机器学习算法
214 |
215 | 很多机器学习算法都基于iid假设,比如Linear regression, logistic regression, decision tree, SVM, neural network等等。
216 |
217 | #### 不基于iid假设的机器学习算法
218 |
219 | 1. 时间序列分析算法:时间序列分析算法通常用于分析和预测时间序列数据,这些数据之间存在时间上的相关性,因此不满足独立同分布假设。常见的时间序列分析算法包括自回归模型(AR)、滑动平均模型(MA)、自回归滑动平均模型(ARMA)、自回归积分滑动平均模型(ARIMA)等。
220 | 2. 隐马尔可夫模型(Hidden Markov Model,HMM):HMM 是一种用于建模序列数据的统计模型,通常用于自然语言处理和语音识别等领域。HMM 假设序列数据是由一个不可观测的马尔可夫链和一个可观测的输出过程组成,因此不满足独立同分布假设。
221 | 3. 图模型(Graphical Model):图模型是一类用图形化方式表示变量之间关系的统计模型。常见的图模型包括贝叶斯网络、马尔可夫随机场等,这些模型通常用于分析非独立同分布的数据。
222 |
223 | #### 为什么算法要基于iid假设
224 |
225 | 因为这个假设可以简化建模过程,减小计算复杂度,使得许多统计学理论和方法可以应用于机器学习中,让机器学习算法的性质和性能更加可靠和有效。
226 |
227 | 通过假设数据独立同分布,我们不必考虑数据样本之间的依赖关系,这种简化的假设可以使我们使用更简单的模型,减少模型参数数量,降低模型的计算复杂度,并更容易处理大规模数据。例如,许多基于iid假设的分类算法(如朴素贝叶斯、支持向量机等)只需要学习一个简单的概率模型或决策边界即可,而不需要学习整个数据分布的复杂性。
228 |
229 | 另外,iid假设使得机器学习算法可以使用统计学中的一些基本理论和方法,如中心极限定理、最大似然估计、假设检验等,这些方法可以提供对机器学习算法的性能进行分析和评估的工具。
230 |
231 | 然而,iid假设并不总是成立的,尤其是在处理时序数据、空间数据等场景下。在这些情况下,我们需要使用其他适当的建模方法来处理数据中的依赖关系和非独立同分布性质。
232 |
233 | #### 如果数据分布不符合iid假设,还可以用基于iid假设的算法求解吗?
234 |
235 | 如果数据分布不符合iid假设,使用基于iid假设的算法可能会导致模型偏差和预测结果不准确。因为这些算法的基本假设是样本之间是独立同分布的,如果这个假设不成立,就会导致样本之间的相关性被忽略,进而影响模型的泛化能力和性能。比如说,可以拿线性回归来处理时间序列数据,但是结构可能会偏差和不准确,因为忽略了时间序列数据中样本之间的相关性。
236 |
237 | 如果数据分布不符合iid假设,可以尝试使用其他适当的机器学习算法或方法。例如,可以使用时间序列模型或空间模型来处理序列数据或空间数据,使用聚类模型或关联规则模型来处理数据集中的非独立同分布问题,使用分层模型或多层模型来考虑样本之间的相关性等。
238 |
239 | 此外,对于一些基于iid假设的算法,也有针对性的改进方法,例如,在训练模型时引入权重,调整样本的权重,或者使用bootstrap方法来处理样本的相关性等。这些方法可以帮助我们更准确地建模和处理非独立同分布的数据。
240 |
241 | ### 小概率原理
242 |
243 | Law of small probabilities
244 |
245 | 若事件 $ A $ 在一次试验中发生的概率非常小,但是经过多次独立地重复试验,事件 $ A $ 的发生是必然的。
246 |
247 | ## 离散型/连续型随机变量
248 |
249 | ### 期望和方差
250 |
251 | #### 期望和方差的公式
252 |
253 | 期望反应随机变量 $ X $ 的平均值,离散变量: $ \displaystyle E(X)=\sum_{k=1}^{\infty}p_kx_k $ ;连续变量: $ \displaystyle E(X)=\int_{-\infty}^{+\infty}tf(t)\text{d}t $ (若积分 $ \displaystyle \int_{-\infty}^{+\infty} xf(x)\text{d}x $ 绝对收敛)
254 |
255 | 方差反应随机变量与期望的偏离程度: $ Var(X)=E(X-E(X))^2=E(X^2)-(E(X))^2 $
256 |
257 | 连续变量:(若 $ \displaystyle \int_{-\infty}^{+\infty}(t-E(X))^2f(t)\text{d}t $ )
258 |
259 | $$
260 | \begin{aligned}
261 | Var(X)&=E(X-E(X))^2=\int_{-\infty}^{+\infty}(t-E(X))^2f(t)\text{d}t\\
262 | &=E(X^2)-(E(X))^2=\int_{-\infty}^{+\infty} t^2f(t)\text{d}t-\left(\int_{-\infty}^{+\infty} tf(t)\text{d}t\right)^2
263 | \end{aligned}
264 | $$
265 |
266 | #### 为什么要使用方差公式的等价形式?
267 |
268 | 使用第一种定义,要遍历两遍;但使用第二种定义,则只需要遍历 $ x_1,\dots,x_n $ 一遍,可在线(online)计算方差。
269 |
270 | #### 为什么样本方差(sample variance)的无偏估计分母是n-1?
271 |
272 | 方差的estimator: $ \displaystyle S_1^2=\frac1n\sum_{i=1}^{n}(X_i-\overline X)^2 $
273 |
274 | 但这个estimator有bias,因为:
275 |
276 | $$
277 | \begin{aligned}
278 | E(S_1^2)&=\frac1n\sum_{i=1}^nE\left((X_i-\overline X)^2\right)\\
279 | &=\frac1n\sum_{i=1}^nE\left((X_i-\mu+\mu-\overline X)^2\right)\\
280 | &=\frac1n\sum_{i=1}^nE\left((X_i-\mu)^2+2(X_i-\mu)(\mu-\overline X)+(\mu-\overline X)^2\right)\\
281 | &=\frac1n \sum_{i=1}^nE\left((X_i-\mu)^2\right)+\frac2n\sum_{i=1}^n(X_i-\mu)(\mu-\overline X)+E\left((\mu-\overline X)^2\right)\\
282 | &=\frac1n \sum_{i=1}^nE\left((X_i-\mu)^2\right)+E\left((\overline X-\mu)^2\right)\\
283 | &=nVar(X)-Var(\overline X)=\sigma^2-\frac{\sigma^2}{n}=\frac{n-1}{n}\sigma^2
284 | \end{aligned}
285 | $$
286 |
287 | 所以使用修正值: $ \displaystyle S_1^2=\frac1n\sum_{i=1}^{n}(X_i-\overline X)^2 $
288 |
289 | 直观理解:因为均值已经用了n个数的平均来做估计,在求方差时,只有(n-1)个数和均值信息是不相关的。而第n个数已经可以由前(n-1)个数和均值来唯一确定,实际上没有信息量。所以在计算方差时,只除以(n-1)
290 |
291 | #### 性质
292 |
293 | - 线性: $ E(aX+b)=aE(X)+b,E(\sum_{i=1}^n c_ig_i(x))=\sum_{i=1}^n c_i E(g_i(x)) $
294 | - 对非负随机变量,有 $ E[X]=\int_{0}^{+\infty}P(X>t)\text{d}t $
295 | - 若 $ \int_{-\infty}^{+\infty}g(t)f(t)\text{d}t $ 绝对可积,则 $ E(g(X))=\int_{-\infty}^{+\infty}g(t)f(t)\text{d}t=\int_{0}^{+\infty} P(g(X)>t)\text{d}t $
296 | - Jenson不等式:对离散型随机变量 $ X\in[a,b] $ 和连续凸函数 $ g:[a,b]\to\mathbb R $ ,有 $ g(E(x))\leq E(g(X)) $
297 | - $ Var(aX+b)=a^2 Var(X) $
298 | - $ Var(X)=E(X-E(X))^2\leq E(X-a)^2 $
299 | - Bhatia-Davis不等式: $ Var[X]\leq (b-E(X))(E(X)-a)\leq \frac14(b-a)^2 $
300 |
301 | #### 在人工智能领域中的作用?
302 |
303 | 在人工智能领域中的常见应用场景:
304 |
305 | 1. 数据预处理:在机器学习中,经常需要对数据进行预处理,例如归一化、标准化等。这时候,期望和方差就非常有用。例如,在标准化时,可以先计算出每个特征的均值和方差,然后将特征值减去均值并除以方差,这样可以使得不同特征之间的取值范围相同,从而更容易进行模型训练和比较。
306 | 2. 概率模型:在概率模型中,期望和方差是重要的概念。例如,在高斯分布中,期望就是分布的中心,方差则决定了分布的形状。这些信息可以用来描述数据的统计特征,从而可以构建更加准确的概率模型。
307 | 3. 模型评估:在机器学习中,需要对不同的模型进行比较和评估。期望和方差可以作为评估指标之一,例如在回归问题中,可以计算预测值与真实值之间的平均方差,从而评估模型的拟合效果。
308 | 4. 异常检测:在人工智能中,经常需要进行异常检测,例如检测网络攻击、欺诈行为等。期望和方差可以用来判断数据是否偏离正常范围,例如可以计算数据与均值之间的距离,如果距离超过一定的阈值,则认为数据是异常的。
309 |
310 | #### 没有期望的情况
311 |
312 | 1. 无限的期望:如果随机变量的分布有“重尾”现象,即存在很小的概率,使得随机变量取到极大的值,此时随机变量的期望可能不存在。例如,柯西分布的期望就不存在。
313 | 2. 不收敛的期望:如果随机变量的绝对值的期望不收敛,也就是E(|X|)无限大,此时随机变量的期望也不存在。
314 |
315 | #### 没有方差的情况
316 |
317 | 1. 不存在期望:如果随机变量的期望不存在,则方差也不存在。因为方差的定义中包含了随机变量与其期望之间的差异。
318 | 2. 方差无穷大:如果随机变量的方差为无穷大,则方差不存在。例如,柯西分布的方差不存在。
319 | 3. 不连续的随机变量:如果随机变量的概率密度函数(或概率质量函数)在某些点上不连续,则方差可能不存在。因为方差的定义中包含了随机变量的平方,如果概率密度函数在某些点上不连续,随机变量的平方可能也不连续。
320 |
321 | ### 分布函数
322 |
323 | #### 定义
324 |
325 | Distribution function
326 |
327 | 分布函数是描述随机变量的概率分布的函数,用来描述随机变量 X 小于或等于某个值 x 的概率。公式为 $ F(x)=P(X\leq x) $ 。
328 |
329 | 可以用分布函数表示随机事件的概率,例如
330 |
331 | $ P(X\geq a)=1-F(a-0) $
332 |
333 | $ P(a\leq X\leq b)=F(b)-F(a-0) $
334 |
335 | #### 性质
336 |
337 | 单调性:若 $ x_1 0\\&0&otherwise\end{aligned}\right. $ | $ \displaystyle{E(X)=\frac1\lambda\\Var(X)=\frac1{\lambda^2}} $ | 无记忆性 |
383 | | 正态分布 | $ X\sim \mathcal N(\mu,\sigma^2) $ | $ \displaystyle f(x)=\frac{1}{\sqrt{2\pi}\sigma}e^{-\frac{(x-\mu)^2}{2\sigma}} $ | | $ \displaystyle{E(X)=\mu\\Var(X)=\sigma^2} $ | |
384 |
385 | #### 正态分布的性质
386 |
387 | - **若 $ X\sim\mathcal N(\mu,\sigma^2) $ ,则 $ \displaystyle Y=\frac{X-\mu}{\sigma}\sim \mathcal N(0,1) $ ;若 $ X\sim \mathcal N(0,1) $ ,则 $ Y=\sigma X+\mu\sim \mathcal N(\mu,\sigma^2) $ **
388 |
389 | 证明
390 |
391 | - **若 $ X\sim \mathcal N(0,1) $ ,对于任意 $ \epsilon>0 $ ,有 $ \displaystyle P(X\geq \epsilon)\leq \frac12e^{-\epsilon^2/2} $ **
392 | - **[Mill 不等式] 若 $ X\sim \mathcal N(0,1) $ ,对于任意 $ \epsilon>0 $ ,有 $ \displaystyle P(X\geq \vert\epsilon\vert)\leq \frac12\min\left\{1,\sqrt\frac{2}{\pi}\frac1{\epsilon}e^{-\epsilon ^2/2}\right\} $ **
393 |
394 | 可得 $ P(u-3\sigma \leq X\leq u+3\sigma)\geq 99.7\% $ ,所以在工程中有 $ P(\vert X-\mu\vert \leq 3\sigma)\approx 1 $
395 |
396 | #### 基于正态分布的模型
397 |
398 | Models like LDA, Gaussian Naive Bayes, Logistic Regression, Linear Regression, etc., are explicitly calculated from the assumption that the distribution is a bivariate or multivariate normal. Also, *Sigmoid functions* work most naturally with normally distributed data.
399 |
400 | ### 已知连续随机变量,求解新的随机变量
401 |
402 | 已知连续随机变量 $ X $ 的概率密度函数为 $ f_X(x) $ ,求解新的随机变量 $ Y=g(X) $ 的概率密度 $ f_Y(y) $ 。
403 |
404 | 1. 求解 $ Y=g(X) $ 的分布函数 $ F_Y(y)=P(Y\leq y)=P(g(X)\leq y)=\int_{g(X)\leq y}f_X(x)\text{d}x $
405 | 2. 利用分布函数和概率密度之间的关系求解密度函数 $ f_Y(y)=F'_Y(y) $
406 |
407 | ## 多维随机变量及其分布
408 |
409 | **【还没有看完!】**
410 |
411 | ### 独立性
412 |
413 | #### 定义
414 |
415 | 对离散型随机变量 $ (X,Y) $ ,若对所有 $ (x_i,y_j) $ 有
416 |
417 | $$
418 | P(X=x_i,Y=y_j)=P(X=x_i)P(Y=y_j)
419 | $$
420 |
421 | 即 $ p_{ij}=p_ip_j $ 则称离散随机变量 $ X $ 和 $ Y $ 相互独立。
422 |
423 | ### 高维高斯分布
424 |
425 | $$
426 | f(x_1, \dots,x_n)=(2\pi)^{-n/2}\vert \Sigma\vert ^{-1/2}\exp\left(-\frac12(\xi-\mu)^\top \Sigma^{-1}(\xi-\mu)\right)
427 | $$
428 |
429 | 其中 $ \xi=(x_1,\dots,x_n)^\top $ ,则称随机变量 $ (X_1,\dots, X_n) $ 服从参数为 $ \mu $ 和 $ \Sigma $ 的多维正态分布。
430 |
431 | ### 协方差
432 |
433 | #### 定义
434 |
435 | $$
436 | Cov(X,Y)=E[(X-E(X))(Y-E(Y))]=E(XY)-E(X)E(Y)
437 | $$
438 |
439 | #### 性质
440 |
441 | 定理1
442 | $$
443 | Var(X+Y)=Var(X)+Var(Y)+2E[(X-E(X))(Y-E(Y))]
444 | $$
445 |
446 | 当 $ X $ 与 $ Y $ 独立时,有:
447 |
448 | $$
449 | Var(X+Y)=Var(X)+Var(Y)
450 | $$
451 |
452 | 所以有
453 |
454 | $$
455 | Cov(X,X)=Var(X)\\
456 | Var(X+Y)=Var(X)+Var(Y)+2Cov(X,Y)
457 | $$
458 |
459 | 性质1
460 |
461 | $$
462 | Cov(X,Y)=Cov(Y,X),\quad Cov(X,c)=0
463 | $$
464 |
465 | 性质2
466 |
467 | $$
468 | Cov(aX,bY)=abCov(X,Y),\quad Cov(X+a,Y+b)=Cov(X,Y)
469 | $$
470 |
471 | 性质3
472 |
473 | $$
474 | Cov(X_1+X_2,Y)=Cov(X_1,Y)+Cov(X_2,Y)\\
475 | Cov\left(\sum_{i}^{n}X_i,\sum_{j}^{m}Y_j\right)=\sum_{i}^n\sum_j^mCov(X_i,Y_j)\\
476 | Var(\sum_{i=1}^nX_i)=Cov(\sum_{i=1}^n X_i,\sum_{i=1}^n X_i)=\sum_{i=1}^n Var(X_i)+2\sum_{i0 $ ,则 $ X $ 与 $ Y $ 正相关
499 | - 若 $ \rho<0 $ ,则 $ X $ 与 $ Y $ 负相关
500 | - $ \rho=1\iff Y=aX+b $ ,本质上 $ \rho_{XY} $ 刻画了 $ X,Y $ 的相关线性相关程度,又称线性相关系数。
501 |
502 | 定理2
503 |
504 | $$
505 | \rho_{XY}=0\iff Cov(X,Y)=0\iff E(XY)=E(X)E(Y)\iff Var(X\pm Y)=Var(X)+Var(Y)
506 | $$
507 |
508 | ## 集中不等式Concentration
509 |
510 | ### 基础不等式
511 |
512 | | | | |
513 | | --------------- | ------------------------------------------------------------ | ------------------------------------------------------------ |
514 | | Markov不等式 | | $ \displaystyle P(X\geq\epsilon)\leq\frac{E(X)}{\epsilon} $ |
515 | | Chebyshev不等式 | $ X $ 的均值为 $ \mu $ | $ \displaystyle P(\vert X-\mu\vert \geq \epsilon)\leq \frac{Var(X)}{\epsilon^2} $ |
516 | | Young不等式 | 给定 $ a>0,b>0 $ ,对满足 $ \displaystyle \frac1p+\frac1q=1 $ 的 $ p>0,q>0 $ 有 | $ \displaystyle ab\leq\frac1pa^p+\frac1qb^q $ |
517 | | Holder不等式 | 对任意 $ X,Y $ 和满足 $ \displaystyle \frac1p+\frac1q=1 $ 的 $ p>0,q>0 $ 有 | $ E(|XY|)\leq(E(|X|^p))^{1/p}(E(|X|^q))^{1/q} $ |
518 | | Chernoff不等式 | $ X_1,\dots,X_n $ 独立且 $ X_i\in Ber(p_i) $ ,令 $ \displaystyle \mu=\sum_{i=1}^n E(X_i)=\sum_{i=1}^n p_i $ | $ \displaystyle P\left[\sum_{i=1}^n X_i\geq (1+\epsilon)\mu\right]\leq \left(\frac{e^\epsilon}{(1+\epsilon)^{1+\epsilon}}\right)^\mu $ |
519 | | Bennet不等式 | $ X_1,\dots,X_n $ 独立同分布且 $ X_i-E[X_i]\leq 1 $ ,均值 $ \mu $ ,方差 $ \sigma^2 $ | $ \displaystyle P\left[\sum_{i=1}^n (X_i-\mu)\geq \epsilon\right]\leq \exp\left(-\frac{n\epsilon^2}{2\sigma^2+2\epsilon/3}\right) $ |
520 | | Bernstein不等式 | | |
521 |
522 | ## 大数定律和中心极限定律
523 |
524 | 1. 依概率收敛:如果随着样本量的增加,随机变量序列以概率1逼近某个确定的常数,那么这个随机变量序列就被称为依概率收敛。
525 | 2. 依分布收敛:如果随着样本量的增加,随机变量序列的分布函数逐渐接近某个确定的分布函数,那么这个随机变量序列就被称为依分布收敛。
526 |
527 | ### 依概率收敛
528 |
529 | #### 依概率收敛的定义
530 |
531 | convergence in probability
532 |
533 | 是概率论中的一种收敛方式。它描述了一个随机变量序列中,随着样本数量的增加,这些随机变量逐渐趋近于某个确定的值的概率。
534 |
535 | 设 $ X_1,\dots,X_n,\dots $ 是一随机变量序列, $ a $ 常数,如果对任意 $ \epsilon>0 $ 有
536 |
537 | $$
538 | \lim_{n\to\infty}P(|X_n-a|<\epsilon)=1 \quad或\quad \lim_{n\to\infty}P(|X_n-a|>\epsilon)=0
539 | $$
540 |
541 | 则称 $ X_1,\dots,X_n,\dots $ 依概率收敛于 $ a $ ,记作 $ X_n\overset{P}\to a $
542 |
543 | #### 依概率收敛和数列极限的区别
544 |
545 | 数列极限是指一个数列中的元素随着下标的增大,越来越接近一个确定的实数L。如果这个实数L存在,那么数列就收敛于L;如果这个实数L不存在,那么数列就发散。
546 |
547 | 依概率收敛则是指一个随机变量序列中,随着样本数量的增加,这些随机变量逐渐趋近于某个确定的值的概率。也就是说,依概率收敛描述的是一个概率性的收敛性质,与数列极限不同,它涉及到随机事件的概率性质。
548 |
549 | 因此,数列极限和依概率收敛是两个不同的概念,它们描述的对象不同,数列极限描述的是确定性的数列,而依概率收敛描述的是随机变量序列的概率性质。
550 |
551 | ### 大数定律
552 |
553 | **【少:Chernoff方法】**
554 |
555 | #### 大数定律是什么
556 |
557 | Law of large numbers
558 |
559 | 大数定律是描述相当多次数重复实验的结果的定律。**它刻画了随机变量的均值依概率收敛于期望的均值。**
560 |
561 | | | | |
562 | | ---------------------- | ------------------- | ------------------------------------------------------------ |
563 | | 大数定律 | 无iid要求 | $ \displaystyle \frac1n\sum_{i=1}^{n}X_i\overset{P}\to\frac1n\sum_{i=1}^nE[X_i] $ |
564 | | Markov大数定律 | 无iid要求 | $ \displaystyle \frac1{n^2}Var\left(\sum_{i=1}^n X_i\right)\to 0,n\to\infty $ |
565 | | Chebyshev大数定律 | 相互独立 | 存在 $ c>0 $ 使得 $ Var(X_n)\leq c $ |
566 | | Khintchine辛钦大数定律 | 独立同分布 | 每个随机变量的期望 $ E[X_i]=\mu $ 存在(不要求方差一定存在) |
567 | | Bernoulli大数定律 | $ X_n\sim B(n,p) $ | $ \displaystyle \lim_{n\to\infty}P\left[\left\vert\frac{X_n}{n}-p\right\vert\geq\epsilon\right]=0 $ ,即 $ \displaystyle \frac{X_n}{n}\overset{P}\to p $ |
568 |
569 | #### 如何判断是否满足大数定律
570 |
571 | - if随机变量iid:辛钦
572 | - if非独立同分布随机变量,Markov
573 |
574 | ### 依分布收敛
575 |
576 | 设 $ F_Y(y)=P(Y\leq y) $ ,以及随机变量序列 $ Y_1,\dots,Y_n,\dots $ 的分布函数分别为 $ F_{Y_n}(y)=P(Y_n\leq y) $ ,如果
577 |
578 | $$
579 | \lim_{n\to\infty}\Pr[Y_n\leq y]=\Pr[Y\leq y],即\lim_{n\to\infty}F_{Y_n}(y)=F_Y(y)
580 | $$
581 |
582 | 则称 $ Y_1,\dots,Y_n,\dots $ 依分布收敛于 $ Y $ ,记作 $ Y_n\overset{d}\to Y $
583 |
584 | ### 中心极限定理
585 |
586 | central limit theorem, CLT
587 |
588 | **中心极限定理说明,在适当的条件下,大量相互独立随机变量的均值经适当标准化后依分布收敛于标准正态分布。**
589 |
590 | | | | |
591 | | ---------------------------- | ------------------------------------------------------------ | ------------------------------------------------------------ |
592 | | 独立同分布iid,林德贝格-勒维 | 若 $ E[X_k]=\mu,Var(X_k)=\sigma^2 $ | 则 $ \displaystyle Y_n=\frac{\sum_{i=1}^{n}X_i-n\mu}{\sigma\sqrt n}\overset d \to\mathcal N(0,1)$$\displaystyle\sum_{k=1}^{n}X_k\overset{d}\to \mathcal N(n\mu,n\sigma^2) $ |
593 | | 棣莫弗-拉普拉斯 | 若 $ X_n\sim B(n,p) $ | 则 $ \displaystyle Y_n=\frac{X_n-np}{\sqrt{np(1-p)}}\overset{d}\to \mathcal N(0,1) $ |
594 | | 独立不同分布,李雅普诺夫 | 若 $ E[X_n]=\mu_n,Var(X_n)=\sigma_n^2>0 $ ,记 $ \displaystyle B_n^2=\sum_{k=1}^n\sigma^2_k $ ,若存在 $ \delta>0 $ ,当 $ n\to\infty $ 时有 $ \displaystyle \frac{1}{B^{2+\delta}_n}\sum_{k=1}^mE\left[|X_k-\mu_k|^{2+\delta}\right]\to 0 $ | 则 $ Y_n=\displaystyle\frac{\sum_{k=1}^nX_k-\sum_{k=1}^n E(X_k)}{\sqrt{Var(\sum_{k=1}^nX_k)}}\overset{d}\to \mathcal N(0,1) $ |
595 |
596 | 大数定律给出了当 $ n\to\infty $ 时随机变量平均值 $ \frac1n\sum_{i=1}^n X_i $ 的趋势,中心极限定理给出了 $ \frac1n\sum_{i=1}^n X_i $ 的具体分布。
597 |
598 | ## 统计的基本概念
599 |
600 | ### 统计学
601 |
602 | #### 统计定义
603 |
604 | 
605 |
606 | ### 常见定义
607 |
608 | - 总体population:研究问题涉及到的对象全体;个体:总体中的每个元素
609 | - 样本sample:从总体中随机抽取的一些个体,一般表示为 $ X_1,\dots,X_n $ ,样本容量为 $ n $
610 | - 样本的二重性:(1) 确定性:就一次观测而言,样本值是确定的数;(2) 随机性:不同抽样下,样本值会发生变化,可看做随机变量。
611 | - 简单随机样本:满足 (1) 代表性: $ X_i $ 与 $ X $ 同分布;(2) 独立性: $ X_1,\dots,X_n $ 相互独立(之后考虑的所有样本均为简单随机样本)
612 | - 联合分布函数:设总体 $ X $ 的联合分布函数为 $ F(x) $ ,则 $ X_1,\dots,X_n $ 的联合分布函数为 $ F(x_1,\dots,x_n)=\prod_{i=1}^nF(x_i) $
613 | - 联合概率密度:设总体 $ X $ 的联合概率密度为 $ f(x) $ ,则 $ X_1,\dots,X_n $ 的联合分布函数为 $ f(x_1,\dots,x_n)=\prod_{i=1}^nf(x_i) $
614 | - 联合分布列:设总体 $ X $ 的联合分布函数为 $ \Pr(X=x_i) $ ,则 $ X_1,\dots,X_n $ 的联合分布列为 $ \Pr(X_1=x_1,\dots,X_n=x_n)=\prod_{i=1}^n \Pr(X_i=x_i) $
615 |
616 | ### 常见统计量
617 |
618 | #### 统计量的定义
619 |
620 | 设 $ X_1,\dots,X_n $ 为来自总体 $ X $ 的一个样本, $ g(X_1,\dots,X_n) $ 是关于 $ X_1,\dots,X_n $ 的一个连续、且不含任意参数的函数,称 $ g(X_1,\dots,X_n) $ 是一个统计量。
621 |
622 | #### 常见统计量
623 |
624 | - 样本均值: $ \displaystyle \overline X=\frac1n\sum_{i=1}^nX_i $
625 | - 样本方差: $ \displaystyle S_0^2=\frac1n\sum_{i=1}^n(X_i-\overline X)^2=\frac1n\sum_{i=1}^n X_i^2-\overline X^2 $ ,修正后的样本方差为 $ \displaystyle S^2=\frac1{n-1}\sum_{i=1}^n (X_i-\overline X)^2 $
626 | - 样本 $ k $ 阶原点矩: $ \displaystyle A_k=\frac1n\sum_{i=1}^nX_i^k $
627 | - 样本 $ k $ 阶中心矩: $ \displaystyle A_k=\frac1n\sum_{i=1}^n(X_i-\overline X)^k $
628 | - 最小次序统计量: $ X_{(1)}=\min\{X_1,\dots,X_n\} $
629 | - 最大次序统计量: $ X_{(n)}=\max\{X_1,\dots,X_n\} $
630 | - 样本极差: $ R_n=X_{(n)}-X_{(1)} $
631 |
632 | **【还有一些定理没有完善!】**
633 |
634 | ### 定理
635 |
636 | $$
637 | E(X)=\mu,Var(X)=\sigma^2\Longrightarrow E(\overline X)=\mu,Var(\overline X)=\frac{\sigma^2}{n},\overline X\overset{d}\to\mathcal N(\mu,\frac{\sigma^2}n)
638 | $$
639 |
640 |
641 |
642 | ### Beta分布, $ \Gamma $ -分布,Dirichlet分布
643 |
644 | | | | |
645 | | ---------------- | ------------------------------------------------------------ | ------------------------------------------------------------ |
646 | | Beta分布 | $ f(x)=\left\{\begin{aligned} &\displaystyle \frac{x^{\alpha_1-1}(1-x)^{\alpha_2-1}}{B(\alpha_1,\alpha_2)}&x\in(0,1)\\ &0&otherwise\end{aligned}\right. $ | $ \displaystyle E[X]=\frac{\alpha_1}{\alpha_1+\alpha_2}\\Var[X]=\frac{\alpha_1\alpha_2}{(\alpha_1+\alpha_2)^2(\alpha_1+\alpha_2+1)} $ |
647 | | $ \Gamma $ -函数 | $ f(x)=\left\{\begin{aligned} &\displaystyle \frac{\lambda^\alpha}{\Gamma(\alpha)}x^{\alpha-1}e^{-\lambda x}&x>0\\ &0&x\leq 0\end{aligned}\right. $ | $ \displaystyle E[X]=\frac{\alpha}{\lambda}\\Var[X]=\frac{\alpha}{\lambda^2} $ |
648 | | | | |
649 |
650 | #### Beta函数
651 |
652 | 对于任意给定 $ \alpha_1>0,\alpha_2>0 $
653 |
654 | $$
655 | Beta(\alpha_1,\alpha_2)=\int_0^1 x^{\alpha_1-1}(1-x)^{\alpha_2-1}\text{d}x
656 | $$
657 |
658 | 又称第一类欧拉积分函数。
659 |
660 | - 有对称性: $ Beta(\alpha_1,\alpha_2)=Beta(\alpha_2,\alpha_1) $
661 | - 定义多维Beta函数为
662 |
663 | $$
664 | Beta(\alpha_1,\dots,\alpha_k)=\frac{\Gamma(\alpha_1)\dots\Gamma(\alpha_k)}{\Gamma(\alpha_1+\dots+\alpha_k)}
665 | $$
666 |
667 | #### $ \Gamma $ -函数
668 |
669 | 对于任意给定 $ \alpha>0 $ ,
670 |
671 | $$
672 | \Gamma(\alpha)=\int_{0}^{+\infty}x^{\alpha-1}e^{-x}\text{d}x
673 | $$
674 |
675 | 又称第二类欧拉积分函数。
676 |
677 | - $ \Gamma(1)=1,\Gamma(\frac12)=\sqrt \pi $ ,对 $ \alpha>1 $ 有 $ \Gamma(\alpha)=(\alpha-1)\Gamma(\alpha-1) $ (所以对于任意正整数 $ n $ ,根据上面的性质有 $ \Gamma(n)=(n-1)! $ )
678 |
679 | #### 定理
680 |
681 | - 对于任意给定 $ \alpha_1>0,\alpha_2>0 $
682 |
683 | $$
684 | Beta(\alpha_1,\alpha_2)=\frac{\Gamma(\alpha_1)\Gamma(\alpha_2)}{\Gamma(\alpha_1+\alpha_2)}
685 | $$
686 | - 对于任意给定 $ \alpha_1>0,\alpha_2>0 $
687 |
688 | $$
689 | Beta(\alpha_1,\alpha_2)=\frac{\alpha_1-1}{\alpha_1+\alpha_2-1}Beta(\alpha_1-1,\alpha_2)
690 | $$
691 |
692 | #### Beta分布
693 |
694 | 给定 $ \alpha_1>0,\alpha_2>0 $ ,若随机变量 $ X $ 的概率密度为
695 |
696 | $$
697 | f(x)=\left\{
698 | \begin{aligned}
699 | &\displaystyle \frac{x^{\alpha_1-1}(1-x)^{\alpha_2-1}}{B(\alpha_1,\alpha_2)}&x\in(0,1)\\
700 | &0&otherwise
701 | \end{aligned}\right.
702 | $$
703 |
704 | 则称 $ X $ 服从参数为 $ \alpha_1,\alpha_2 $ 的Beta分布,记为 $ X\sim B(\alpha_1,\alpha_2) $
705 |
706 | - $ \displaystyle E[X]=\frac{\alpha_1}{\alpha_1+\alpha_2},Var[X]=\frac{\alpha_1\alpha_2}{(\alpha_1+\alpha_2)^2(\alpha_1+\alpha_2+1)} $
707 |
708 | #### $ \Gamma $ -分布
709 |
710 | 若随机变量 $ X $ 的概率密度为
711 |
712 | $$
713 | f(x)=\left\{
714 | \begin{aligned}
715 | &\displaystyle \frac{\lambda^\alpha}{\Gamma(\alpha)}x^{\alpha-1}e^{-\lambda x}&x>0\\
716 | &0&x\leq 0
717 | \end{aligned}\right.
718 | $$
719 |
720 | 其中 $ \alpha>0,\lambda>0 $ ,则称 $ X $ 服从参数为 $ \alpha,\lambda $ 的 $ \Gamma $ 分布,记为 $ X\sim \Gamma(\alpha,\lambda) $
721 |
722 | - $ \displaystyle E[X]=\frac{\alpha}{\lambda},Var[X]=\frac{\alpha}{\lambda^2} $
723 | - 若随机变量 $ X\sim\Gamma(\alpha_1,\lambda),Y\sim\Gamma(\alpha_2,\lambda) $ ,且 $ X,Y $ 相互独立,则 $ X+Y\sim\Gamma(\alpha_1+\alpha_2,\lambda) $
724 |
725 | #### Dirichlet分布
726 |
727 | 给定 $ \alpha_1,\dots,\alpha_k\in(0,+\infty) $ ,若多元随机向量 $ X=(X_1,\dots,X_k) $ 的密度函数为
728 |
729 | $$
730 | f(x_1,\dots,x_k)=\left\{
731 | \begin{aligned}
732 | &\displaystyle \frac{x_1^{\alpha_1-1}\dots x_k^{\alpha_k-1}}{B(\alpha_1,\dots,\alpha_k)}&\sum_{i=1}^k x_i=1,x_i>0\quad (i\in[k])\\
733 | &0&otherwise
734 | \end{aligned}\right.
735 | $$
736 |
737 | 则称 $ X $ 服从参数为 $ \alpha_1,\dots,\alpha_k $ 的Dirichlet分布,记为 $ X\sim Dir(\alpha_1,\dots,\alpha_k) $
738 |
739 | - Dirichlet分布是Beta分布发一种推广,当 $ k=2 $ 时Dirichlet分布退化为Beta分布
740 | - 设 $ \displaystyle \tilde{\alpha}=\sum_{i=1}^k\alpha_i,\tilde{\alpha}_i=\frac{\alpha_i}{\tilde{\alpha}} $ ,则 $ E[X_i]=\tilde{\alpha}_i,Cov(X_i,X_j)=\left\{\begin{aligned}&\displaystyle \frac{\tilde{\alpha}_i(1-\tilde{\alpha}_i)}{\tilde{\alpha}+1}&i=j\\&\displaystyle -\frac{\tilde{\alpha}_i\tilde{\alpha}_j}{\tilde{\alpha}+1}&i\neq j\end{aligned}\right. $
741 |
742 | ### 正态分布总体抽样分布定理
743 |
744 | #### $ \chi^2 $ 分布
745 |
746 | 若 $ X_1,\dots,X_n $ 是来自总体 $ X\sim\mathcal N(0,1) $ 的一个样本,称 $ Y=X_1^2+\dots+X_n^2 $ 为服从自由度为 $ n $ 的 $ \chi^2 $ 分布,记 $ Y\sim\chi^2(n) $
747 |
748 | 根据 $ X_1^2\sim\Gamma(\frac12,\frac12) $ 和 $ \Gamma $ 函数的可加性可得 $ Y\sim\Gamma(\frac n2,\frac12) $
749 |
750 | $$
751 | f_Y(y)=\left\{
752 | \begin{aligned}
753 | &\displaystyle \frac{\left(\frac12\right)^\alpha}{\Gamma(\alpha)}y^{\frac n2-1}e^{-\frac y2}&y>0\\
754 | &0&y\leq 0
755 | \end{aligned}\right.
756 | $$
757 |
758 | - 若 $ X\sim\chi^2(n) $ ,则 $ E(X)=n,Var(X)=2n $
759 | - 分布可加性:若 $ X\sim\chi^2(m),Y\sim\chi^2(n) $ ,则 $ X+Y\sim\chi^2(m+n) $
760 |
761 | #### $ t $ 分布(student distribution)
762 |
763 | 随机变量 $ X\sim\mathcal N(0,1) $ 和 $ Y\sim\chi^2(n) $ 相互独立,则随机变量
764 |
765 | $$
766 | T = \frac{X}{\sqrt{Y/n}}
767 | $$
768 |
769 | 服从自由度为 $ n $ 的 $ t $ 分布,记 $ T\sim t(n) $
770 |
771 | 概率密度函数:
772 |
773 | $$
774 | f(x)=\frac{\Gamma\left(\frac{n+1}2\right)}{\Gamma\left(\frac{n}2\right)\sqrt{n\pi}}\left(1+\frac {x^2} n\right)^{-\frac{n+1}2}
775 | $$
776 |
777 | 当 $ n\to\infty $ 时, $ f(x)\to\frac{1}{\sqrt {2\pi}}e^{-x^2/2} $
778 |
779 | #### $ F $ 分布
780 |
781 | 随机变量 $ X\sim\chi^2(m) $ 和 $ Y\sim\chi^2(n) $ 相互独立,则随机变量
782 |
783 | $$
784 | F = \frac{X/m}{Y/n}
785 | $$
786 |
787 | 服从自由度为 $ (m,n) $ 的 $ t $ 分布,记 $ F\sim F(m,n) $
788 |
789 | #### 正态分布的抽样分布定理
790 |
791 | 设 $ X_1,\dots,X_n $ 是来自总体 $ \mathcal N(\mu,\sigma^2) $ 的样本,则有
792 |
793 | - $ \displaystyle \overline{X}=\frac1n\sum_{i=1}^nX_i\sim\mathcal N(\mu,\frac{\sigma^2}{n}),\frac{\overline{X}-\mu}{\sigma/\sqrt{n}}\sim\mathcal N(0,1) $
794 | - $ \displaystyle \overline{X}=\sum_{i=1}^n\frac{X_i}{n},S^2=\frac{1}{n-1}\sum_{i=1}^n(X_i-\overline X)^2 $ 相互独立,且 $ \displaystyle \frac{(n-1)S^2}{\sigma^2}\sim\chi^2(n-1) $
795 | - $ \displaystyle \frac{\overline X-\mu}{S/\sqrt{n}}\sim t(n-1) $
796 | - 设 $ X_1,\dots,X_m $ 和 $ Y_1,\dots,Y_n $ 分别来自总体 $ \mathcal N(\mu_X,\sigma^2_X),\mathcal N(\mu_Y,\sigma^2_Y) $ 的两个独立样本,令其修正样本方差分别为 $ S_X^2,S_Y^2 $ ,则有 $ \displaystyle \frac{S_X^2/\sigma^2_X}{S_Y^2/\sigma^2_Y}\sim F(m-1,n-1) $
797 |
798 | ## 参数估计
799 |
800 | ### 参数估计定义
801 |
802 | 
803 |
804 | ### 矩估计
805 |
806 | | | |
807 | | -------------------------------------------- | ------------------------------------------------------------ |
808 | | 总体 $ X $ 的 $ k $ 阶矩 $ a_k=E[X^k] $ | 样本 $ k $ 阶矩 $ A_k=\frac1n\sum_{i=1}^n X_i^k $ |
809 | | 总体 $ X $ 的 $ k $ 阶中心矩 $ b_k = E[(X-E(X))^k] $ | 样本 $ k $ 阶中心矩 $ B_k=\frac1n\sum_{i=1}^n (X_i-\overline X)^k $ |
810 |
811 | #### 为什么要求 $ k $ 阶矩?
812 |
813 | 在概率论和统计学中,矩是一个用来描述随机变量分布的重要概念。一般地,k阶矩是指随机变量的k次幂的期望,其中k是一个非负整数。
814 |
815 | 求解矩是非常有用的,因为它可以帮助我们了解一个随机变量分布的特征。例如,均值(一阶矩)可以告诉我们这个随机变量的中心位置在哪里,方差(二阶矩)可以告诉我们这个随机变量的分布范围大小以及数据的离散程度,偏度(三阶矩)可以告诉我们这个随机变量的偏斜程度,而峰度(四阶矩)可以告诉我们这个随机变量的峰态程度。
816 |
817 | 因此,通过求解不同阶的矩,我们可以更全面地了解一个随机变量的分布特征,从而更好地理解和分析相关的问题。
818 |
819 | #### 如何进行矩估计?
820 |
821 | 可以使用中心矩估计,二阶中心距 $ B_k=\frac1n\sum_{i=1}^n (X_i-\overline X)^k=Var(X) $
822 |
823 | 
824 |
825 | ### 最大似然估计
826 |
827 | #### 定义
828 |
829 | Maximum likelihood estimation is a statistical method used to estimate the parameters of a model. The basic idea behind maximum likelihood estimation is to find the parameter values that maximize the likelihood of the observed data. In other words, we seek to find the values of the model parameters that make the observed data most probable.
830 |
831 | 极大似然估计是一种用于估计模型参数的统计方法。极大似然估计的基本思想是找到使观测数据的似然函数最大化的参数值。换句话说,我们寻找模型参数的值,使得观测数据发生的可能性最大。
832 |
833 | #### 需要满足什么假设?
834 |
835 | 样本独立同分布,参数化假设(参数可数且取值有限),可微性假设(似然函数可微),模型合适。
836 |
837 | #### 是贝叶斯学派还是频率主义学派?
838 |
839 | 频率主义学派
840 |
841 | - 频率主义学派(Frequentist)认为参数虽然未知,但却是客观存在的固定值,因此,可通过优化似然函数等准则来确定参数值
842 | - 贝叶斯学派(Bayesian)则认为参数是未观察到的随机变量,其本身也可有分布,因此,可假定参数服从一个先验分布,然后 基千观测到的数据来计算参数的后验分布
843 |
844 | #### 似然函数定义
845 |
846 | 似然函数是 $ X_1=x_1,\dots,X_n=x_n $ 的联合概率密度:
847 |
848 | $$
849 | L(\theta)= L(x_1,\dots,x_n;\theta)=\prod_{i=1}^nf(x_i;\theta)
850 | $$
851 |
852 | #### 似然函数和概率密度函数有什么区别?
853 |
854 | 似然函数和概率密度函数都是描述概率的函数,形式相似,但有不同的含义和用途。
855 |
856 | 概率密度函数描述随机变量在已知参数的条件下的概率分布,而似然函数描述参数在已知数据的条件下的可能取值。在统计建模中,我们通常使用似然函数来推断参数的取值,而使用概率密度函数来计算随机变量的概率分布。
857 |
858 | #### 如何求解最大似然估计?
859 |
860 | 
861 |
862 | $ D_c $ 训练集中第 $ c $ 类样本的集合,假设独立同分布
863 |
864 | $$
865 | LL(\theta_c)=\log P(D_c|\theta_c)=\sum_{x\in D_c}\log P(x|\theta_c)\\
866 | \hat{\theta_c}=\arg\max_{\theta_c}LL(\theta_c)
867 | $$
868 |
869 | 例:连续属性,概率密度函数 $ p(x|c)\sim\mathcal N(\mu_c,\sigma_c^2) $ , $ \mu_c,\sigma^2_c $ 的极大似然估计:
870 |
871 | 
872 |
873 | #### 在机器学习中的应用?
874 |
875 | 训练线性回归、逻辑回归、朴素贝叶斯等模型。
876 |
877 | 具体训练步骤是:
878 |
879 | 1. 定义模型的假设空间:即模型的函数形式和参数的范围。
880 | 2. 定义似然函数
881 | 3. 求解最大似然估计
882 | 4. 评估模型:交叉验证等方法
883 |
884 | #### 缺点
885 |
886 | 缺点:概率分布假设需要准确,样本需要iid,要求数据量大。
887 |
888 | #### 什么是贝叶斯估计?与极大似然估计相比,它有什么优点和缺点?
889 |
890 | 贝叶斯估计是一种利用贝叶斯定理进行参数估计的方法。在贝叶斯估计中,我们先假设参数 $ \theta $ 服从一个先验分布 $ p(\theta) $ ,然后根据观测数据 $ X $ ,计算后验分布 $ p(\theta|X) $ ,再从中选择最优的参数值作为估计结果。
891 |
892 | $$
893 | p(\theta\vert X)=\frac{p(\theta)p(X\vert\theta)}{P(X)}=\frac{p(\theta)p(X\vert\theta)}{\int_{\theta}p(\theta)p(X\vert\theta)\text{d}\theta}
894 | $$
895 |
896 | 贝叶斯估计与极大似然估计的主要区别在于它引入了先验分布,使得估计结果更加准确和稳定。
897 |
898 | 优点:
899 |
900 | 1. 贝叶斯估计可以引入先验分布,使得估计结果更加准确和稳定,特别是当数据量较少时,先验分布可以在一定程度上抵消数据的不足,避免出现过拟合的问题。
901 | 2. 贝叶斯估计可以通过后验分布来描述参数的不确定性,这对于一些需要考虑风险和可靠性的应用场景非常重要。
902 | 3. 贝叶斯估计的方法比较灵活,可以根据具体情况灵活地选择不同的先验分布和后验计算方法。
903 |
904 | 缺点:
905 |
906 | 1. 贝叶斯估计需要先假设参数的先验分布,这需要对领域知识有一定的了解或者有一些实验结果来支持。如果先验分布假设不合理或者不准确,会导致估计结果的偏差。
907 | 2. 贝叶斯估计的计算复杂度比较高,需要进行积分计算,计算量通常比极大似然估计要大得多。在大规模数据集上,贝叶斯估计可能会面临计算复杂度的问题。
908 | 3. 贝叶斯估计的结果不是唯一的,因为先验分布的不同选择会导致不同的后验分布。这可能会给结果的解释和应用带来一定的不确定性。
909 |
910 | #### 在机器学习中,为什么使用对数似然函数进行优化比使用原始似然函数更好?
911 |
912 | 对数似然函数log-likelihood function
913 |
914 | - 可以将乘积转换为求和,简化计算
915 | - 避免数值下溢:由于似然函数通常是由很多个小概率相乘得到,这容易导致数值下溢问题。而对数似然函数可以避免这种情况,因为它将乘积转换为求和,将大量小概率相加。
916 |
917 | ### 估计量评价标准
918 |
919 | #### 无偏性
920 |
921 | 设 $ X_1,\dots,X_n $ 是来自总体 $ X $ 的样本,令 $ \hat{\theta}=\hat{\theta}(X_1,\dots,X_n) $ 是 $ \theta $ 的一个估计,若
922 |
923 | $$
924 | E_{X_1,\dots,X_n}[\hat{\theta}]=E_{X_1,\dots,X_n}[\hat{\theta}(X_1,\dots,X_n)]=\theta
925 | $$
926 |
927 | 则称 $ \hat\theta $ 是 $ \theta $ 的无偏估计
928 |
929 | #### 有效性
930 |
931 | $ \hat{\theta}_1=\hat{\theta}_1(X_1,\dots,X_n) $ 和 $ \hat{\theta}_2=\hat{\theta}_2(X_1,\dots,X_n) $ 是 $ \theta $ 的两个无偏估计,若 $ Var(\hat\theta_1)\leq Var(\hat\theta_2) $ ,则称 $ \hat{\theta}_1 $ 比 $ \hat{\theta}_2 $ 有效。
932 |
933 | [Rao-Crammer不等式] 令
934 |
935 | $$
936 | Var(\theta)=\frac{1}{nE\left[\left(\frac{\part\ln f(X;\theta)}{\part\theta}\right)^2\right]}或Var(\theta)=\frac{1}{nE\left[\left(\frac{\part\ln F(X;\theta)}{\part\theta}\right)^2\right]}
937 | $$
938 |
939 | 称 $ Var_{0}(\theta) $ 为估计量 $ \hat{\theta} $ 方差的下界,对任意无偏估计量有 $ Var(\hat\theta)\geq Var_0(\theta) $ 。
940 |
941 | **有效估计量**: $ Var(\hat{\theta})=Var_0(\theta) $
942 |
943 | #### 一致性
944 |
945 | 令 $ \hat{\theta}=\hat{\theta}(X_1,\dots,X_n) $ 是 $ \theta $ 的一个估计,若当 $ n\to\infty $ 时有 $ \hat{\theta}_n\overset{P}\to\theta $ 成立,即对任意 $ \epsilon>0 $ 有
946 |
947 | $$
948 | \lim_{n\to0}\left[\left\vert\hat\theta_n-\theta\right\vert>\epsilon\right]=0
949 | $$
950 |
951 | 则称 $ \hat\theta_n $ 为 $ \theta $ 的一致估计量
952 |
953 | - **[充分性条件]** 若 $ \displaystyle \lim_{n\to\infty}E\left[\hat\theta_n\right]=\theta $ 且 $ \displaystyle \lim_{n\to\infty}Var\left(\hat\theta_n\right)=0 $ ,则 $ \hat\theta_n $ 为 $ \theta $ 的一致估计量
954 |
955 | ### 区间估计
956 |
957 | #### 置信区间和置信度
958 |
959 | 对于总体 $ X $ 的分布函数的未知参数 $ \theta $ ,有
960 |
961 | $$
962 | \Pr\left[\hat{\theta}_1<\theta<\hat{\theta}_2\right]\geq1-\alpha
963 | $$
964 |
965 | 则 $ \alpha $ 为置信度; $ \left[\hat{\theta}_1,\hat{\theta}_2\right] $ 为 $ \theta $ 的置信度为 $ 1-\alpha $ 的置信区间。
966 |
967 | ## 假设检验
968 |
969 | Hypothesis Testing
970 |
971 | ### 假设检验定义
972 |
973 | 
974 |
975 | ### 假设检验的一般步骤
976 |
977 | 
978 |
979 | ### 参数假设检验
980 |
981 | #### Z检验
982 |
983 | 
984 |
985 | #### t检验
986 |
987 | 
988 |
989 | #### $ \chi^2 $ 检验
990 |
991 | 
992 |
993 | ### 非参数假设检验
994 |
--------------------------------------------------------------------------------
/深度学习.md:
--------------------------------------------------------------------------------
1 | # 深度学习
2 |
3 | ## Transformer
4 |
5 | ### Transformer简介
6 |
7 | 是一个有Encoder和Decoder的seq2seq模型。它基于attention机制,使得模型在处理长序列数据时能够更好地捕捉全局依赖关系。最初由Google的团队提出,用于解决机器翻译任务。
8 |
9 | ### Attention
10 |
11 | Attention可以用于处理序列数据的关联性和重要性。在文中使用的是Scaled Dot-Product Attention,是对Query和Key的内积缩放后过一个softmax,再乘以V。
12 | $$
13 | \text{Attention}(Q,K,V)=\text{softmax}\left(\frac{QK^\top}{\sqrt{d_k}}\right)V
14 | $$
15 |
16 | ### Self-attention
17 |
18 | $\displaystyle\text{Attention}(Q,K,V)=\text{softmax}(\frac{QK^\top}{\sqrt {d_k}})V$,这里Q和K分别是query和key,$\sqrt{d_k}$是缩放因子,让softmax里的内容方差为1。
19 |
20 | self attention:计算每个输入的词与其他词的关联性。做法:将input喂入三个fc,生成query, key, value(目的:提升模型的拟合能力,矩阵$W$都是可以训练的,起到一个缓冲的效果)
21 |
22 | ### Cross attention
23 |
24 | cross-attention的输入来自不同的序列,而self-attention的输入则是来自一个单一的嵌入序列。Cross-attention将两个相同维度的嵌入序列不对称地组合在一起,而其中一个序列用作查询Q输入,而另一个序列用作键K和值V输入。
25 |
26 | ### Multi-head attention
27 |
28 | 让$V, K, Q$通过不同的$h$组不同的、训练出的线性层,分别通过attention层,再concat在一起。
29 |
30 | #### 作用
31 |
32 | 通过多个注意力头并行计算,模型可以从不同的子空间中学习到更多的特征表示。每个注意力头都可以关注不同的相关性和信息,从而捕捉到输入序列的多个不同方面,增强了模型的表达能力和学习能力。
33 |
34 | #### 和CNN相关的地方
35 |
36 | 和CNN中通过多个卷积核学习多个不同的特征表示有些相似。
37 |
38 | ### 每一层做什么操作?
39 |
40 | 首先过一个attention,再通过一个MLP,再做Layer Normalization。
41 |
42 | #### 为什么要做层归一化Layer Normalization?
43 |
44 | 因为输入的seq不一定定长,导致训练的时候每个batch各样本的方差较大,不稳定;测试时使用全局均值和方差,如果遇到特别长的样本则无法处理。每个样本自己做layer normalization,则样本间相对独立。
45 |
46 | #### Layer Normalization & Batch Normalization
47 |
48 | Batch normalization是在每个特征维度上进行归一化,使得特征的均值接近于0,方差接近于1。训练时使用batch均值和方差,测试时使用全局均值和方差。批归一化适用于卷积层和全连接层等具有多维特征的层。
49 |
50 | Layer normalization是对每个样本在特定维度上进行归一化。层归一化适用于RNN等逐步处理序列的层。
51 |
52 | 归一化好处:减轻输入数据的分布偏移,加速模型收敛速度,提高模型的稳定性和泛化能力,可以缓解梯度问题。
53 |
54 | ### 如何记录词的位置信息?
55 |
56 | 将Positional Encoding的信息concat到词的embedding后,一起作为模型的输入信息。
57 |
58 | 使用sin和cos函数表示,共512维:
59 | $$
60 | PE(pos, 2i)=\sin\left(\frac{pos}{10000^{2i/d_{model}}}\right)\\
61 | PE(pos, 2i+1)=\cos\left(\frac{pos}{10000^{2i/d_{model}}}\right)
62 | $$
63 |
64 | ### Decoder为什么/怎么做masking?
65 |
66 | 因为decoder要执行的任务是:given $y_1,\dots,y_i$,预测$y_{i+1}$,为了保证训练任务和测试任务一致,所以要mask掉$y_{i+1},\dots,y_n$。
67 |
68 | 将这一位加上一个很大的负数,这样softmax以后就会变成0。
69 |
70 | ### RNN & Transformer?
71 |
72 | 都用于处理序列信息。
73 |
74 | RNN:将上一时刻的输出作为下一时刻的输入
75 |
76 | Transformer:通过Attention层获得全局序列信息。
77 |
78 | ## 什么是Transformer?
79 |
80 | 是一个有Encoder和Decoder的seq2seq模型,采用了一种基于注意力机制的结构,使得模型在处理长序列数据时能够更好地捕捉全局依赖关系。
81 |
82 |
83 |
84 | 
85 |
86 | [Illustrated Guide to Transformers Neural Network: A step by step explanation - YouTube](https://www.youtube.com/watch?v=4Bdc55j80l8)
87 |
88 | - encoder
89 |
90 | - input embedding:为每个词寻找一个向量表征
91 |
92 | - positional encoding:加入位置信息(使用sin和cos函数)
93 |
94 | - encoder layer:输入序列$\to$抽象连续表征
95 |
96 | - multi-head attention + norm:输入:序列,输出:每个单词与其他词的关联度
97 |
98 | - fully connected network + norm:residual connection
99 |
100 | - decoder:生成文本序列,autoregressive,masking(只能算和过去词语的attention score)
101 |
102 | - 和encoder相似
103 | - classifier
104 |
105 | Transformer模型的核心思想是通过自注意力机制(Self-Attention)来建立输入序列的表示。自注意力机制能够计算序列中各个位置之间的相关性,并根据相关性分配不同的权重,从而更好地捕捉上下文信息。通过多层堆叠的自注意力层和前馈神经网络层,Transformer能够对输入序列进行逐层的特征提取和组合,从而获得更丰富的表示。
106 |
107 | Transformer模型的另一个重要组成部分是位置编码(Positional Encoding),用于将序列中每个位置的信息嵌入到表示中,以考虑序列的顺序信息。位置编码可以告知模型每个输入在序列中的位置,从而在没有显式顺序信息的情况下仍能正确建模序列。
108 |
109 | 由于其出色的性能和可扩展性,Transformer模型不仅在机器翻译任务中表现出色,还被广泛应用于其他NLP任务,如文本生成、命名实体识别、情感分析等。此外,Transformer的思想也被拓展到其他领域,如计算机视觉(如图像生成和图像分类)和推荐系统等,取得了很好的效果。
110 |
111 |
112 |
113 | ## 什么是LSTM?
114 |
115 | [人人都能看懂的LSTM - 知乎 (zhihu.com)](https://zhuanlan.zhihu.com/p/32085405)
116 |
117 | LSTM就是long short-term memory,是一种循环神经网络的变体,通过引入“记忆单元”来解决长序列训练过程中的梯度消失和梯度爆炸问题。
118 |
119 | - 相比RNN只有一个传递状态$h^t$,LSTM有两个传输状态,一个$c^t$(cell state),和一个$h^t$(hidden state)。其中$c^t$通常是$c^{t-1}$加上一些值,改变得很慢;$h^t$在不同结点下往往有很大区别。
120 | - 加上了门控状态:
121 | - 忘记:$z^f$ (f for forget),来控制上一个状态的$c^{t-1}$哪些留哪些忘
122 | - 选择记忆:$z^i$ (i for information),对$x^t$进行选择性的记忆。$z$作为输入
123 | - 输出:决定哪些将会被当成状态的输出,用$z^o$来进行控制,并且还对上一阶段得到的$c^0$进行了放缩。
124 |
125 | 
126 |
127 | 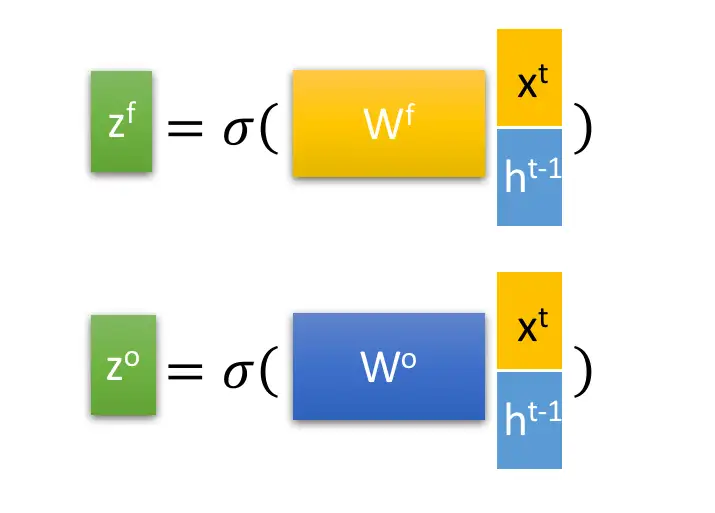
128 |
129 | 
130 |
131 | 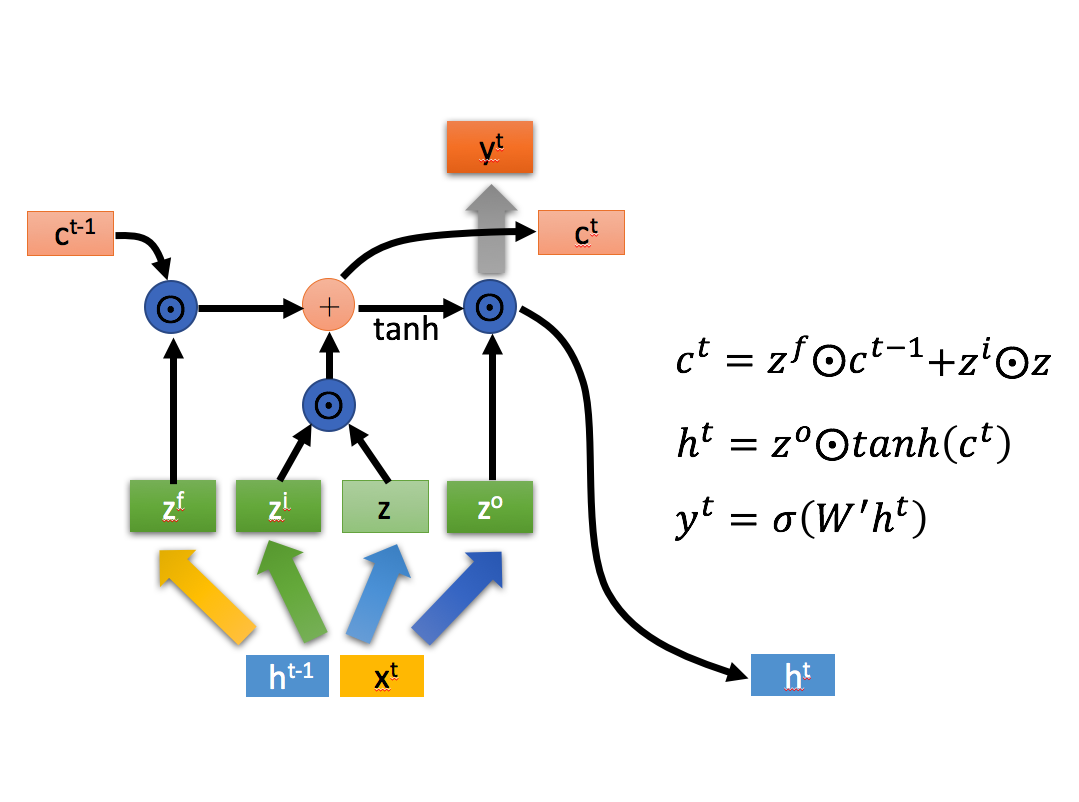
132 |
133 | ## 什么是CNN?
134 |
135 | CNN / convolutional neural networks / 卷积神经网络:用kernel对输入进行局部的特征提取
136 |
137 | 与传统的神经网络相比,CNN更加适合处理图像和语音等高维数据。
138 |
139 | CNN是一种前向反馈神经网络,主要由卷积层、池化层和全连接层等组成。在卷积层中,CNN通过卷积核对输入数据进行卷积运算,从而提取特征。卷积核可以在不同的位置进行卷积运算,这样可以检测出输入数据中的不同特征。在池化层中,CNN通过对卷积层输出进行下采样,从而降低数据维度,同时也可以减小数据量,提高模型的训练速度。在全连接层中,CNN将池化层输出的特征映射到输出层中,完成分类或回归任务。
140 |
141 | ## 什么是MLP?
142 |
143 | MLP / multi-layer perception / 多层感知器:除了输入输出层还有隐层
144 |
145 | ## 什么是GLU?
146 |
147 | GLU / Gated Linear Unit / 门控线性单元:$GLU(x,W,V,b,c)=\sigma(xW+b)\otimes (xV+c)$,其中$\sigma$是Sigmoid函数,$\otimes$是矩阵逐点相乘,总的来说效果比ReLU好。
--------------------------------------------------------------------------------
/线性代数.md:
--------------------------------------------------------------------------------
1 | # 线性代数
2 |
3 | ## 线性空间
4 |
5 | 线性空间:定义了合法加法和数乘(加法和数乘满足相应8条规则)的非空集合。
6 |
7 | 线性相关:存在一组不全为零的标量(系数),使得向量之间的线性组合等于零向量
8 |
9 | 线性无关:不线性相关,当且仅当系数均为0时,线性组合才等于零向量。说明每个向量均独立,没有冗余信息
10 |
11 | 线性空间的维度:线性空间中最大线性无关组的大小
12 |
13 | 基:1. 线性无关 2. 线性空间中任意向量都可以用它们线性表出
14 |
15 | 线性子空间:
16 |
17 | - 定义:1. 线性空间的非空子集 2. 对线性空间中的加法和数乘也构成数域上的线性空间
18 | - 性质:交也是,和也是
19 |
20 | ## 高斯空间
21 |
22 |
23 |
24 | ## 矩阵
25 |
26 | ### 秩
27 |
28 | 矩阵的秩定义为矩阵中线性无关的行或列的最大数量,记作 $\text{rank}(A)$。
29 |
30 | 1. 反应矩阵的线性相关性
31 | 2. 矩阵的逆:满秩$\iff$可逆,即有唯一逆向量
32 |
33 | ### 矩阵分解的意义?
34 |
35 | 加速计算
36 |
37 | ### 奇异值分解
38 |
39 | 可以作用与长方矩阵上,同时包含了旋转、缩放和投影三种作用。
40 |
41 | #### 什么是奇异值分解?
42 |
43 | $A=U\Sigma V^\top$,其中$U,V$均为正交矩阵,$\Sigma$为对角矩阵,对角线上的值按从大到小排列。
44 |
45 | #### 条件?
46 |
47 | $AA^\top,A^\top A$可以被特征值分解。
48 |
49 | #### 如何计算?
50 |
51 | 1. 对$A^\top A$进行特征值分解,得到特征值和特征向量。将特征值按照从大到小的顺序排列,特征向量也相应排序。$A^\top A$特征向量构成的正交矩阵,得到$V$。
52 | 2. 对$AA^\top$同理,得到$U$
53 | 3. 两次计算中的非零特征值从大到小排序,放在对角线,其他位置零。
54 |
55 | #### 应用?
56 |
57 | ### 特征值分解
58 |
59 | #### 什么是特征值和特征向量?
60 |
61 |
1695 |
1696 | ### 1、什么是马尔科夫过程?
1697 |
1698 | 假设一个随机过程中,t_n 时刻的状态 x_n 的条件发布,只与其前一状态x_(n-1) 相关,即:
1699 |
1700 | 
1701 |
1702 | 则将其称为 马尔可夫过程。
1703 |
1704 | ### 2、马尔科夫过程的核心思想是什么?
1705 |
1706 | 对于马尔可夫过程的思想,用一句话去概括:当前时刻状态仅与上一时刻状态相关,与其他时刻不相关。
1707 |
1708 | 可以从 马尔可夫过程图去理解,由于每个状态间是以有向直线连接,也就是当前时刻状态仅与上一时刻状态相关。
1709 |
1710 | ### 3、隐马尔可夫算法中的两个假设是什么?
1711 |
1712 | 齐次马尔可夫性假设:即假设隐藏的马尔科夫链在任意时刻 t 的状态只依赖于其前一时刻的状态,与其他时刻的状态及观测无关,也与时刻 t 无关;
1713 |
1714 | 
1715 |
1716 | 观测独立性假设:即假设任意时刻的观测只依赖于该时刻的马尔科夫链的状态,与其他观测及状态无关。
1717 |
1718 | 
1719 |
1720 | ### 4、隐马尔可夫模型三个基本问题是什么?
1721 |
1722 | (1)概率计算问题:**给定模型(A,B, $ \pi $ )和观测序列**,计算在模型下观测序列出现的概率。(直接计算法理论可行,但计算复杂度太大(O(N^2T));用前向与后向计算法)
1723 |
1724 | (2)学习问题:**已知观测序列,估计模型参数**,使得在该模型下观测序列概率最大。(极大似然估计的方法来估计参数,Baum-Welch算法(EM算法))
1725 |
1726 | (3)预测问题,也称为解码问题:已知模型和观测序列,**求对给定观测序列条件概率最大的状态序列**。(维特比算法,动态规划,核心:**边计算边删掉不可能是答案的路径,在最后剩下的路径中挑选最优路径**)
1727 |
1728 | ### 5、隐马尔可夫模型三个基本问题的联系?
1729 |
1730 | 三个基本问题 存在 渐进关系。首先,要学会用前向算法和后向算法算观测序列出现的概率,然后用Baum-Welch算法求参数的时候,某些步骤是需要用到前向算法和后向算法的,计算得到参数后,我们就可以用来做预测了。因此可以看到,三个基本问题,它们是渐进的,解决NLP问题,应用HMM模型做解码任务应该是最终的目的。
1731 |
1732 | ### 6、隐马尔可夫算法存在哪些问题?
1733 |
1734 | 因为HMM模型其实它简化了很多问题,做了某些很强的假设,如齐次马尔可夫性假设和观测独立性假设,做了假设的好处是,简化求解的难度,坏处是对真实情况的建模能力变弱了。
1735 |
1736 | 在序列标注问题中,隐状态(标注)不仅和单个观测状态相关,还和观察序列的长度、上下文等信息相关。例如词性标注问题中,一个词被标注为动词还是名词,不仅与它本身以及它前一个词的标注有关,还依赖于上下文中的其他词。可以使用最大熵马尔科夫模型进行优化。
1737 |
1738 | ## 规则学习
1739 |
1740 | ## 强化学习
1741 |
--------------------------------------------------------------------------------
/概率论与数理统计.md:
--------------------------------------------------------------------------------
1 | # 概率论与数理统计
2 |
3 | ## 提纲
4 |
5 | ### 第一章 基本概念
6 |
7 | - 概率和统计的区别
8 | - 必然现象与随机现象
9 | - 随机试验:样本点,样本空间
10 | - 事件间的关系,事件与集合的对应关系,事件的运算规律
11 | - 概率的公理化定义,概率的性质
12 | - 古典概型,几何概型
13 | - 条件概率,全概率公式和贝叶斯公式
14 | - 独立性,独立与互斥的关系
15 | - Freivalds算法
16 |
17 | ### 第二章 随机变量及其分布
18 |
19 | - 分布函数定义,性质(单调性,规范性,右连续性);概率密度函数定义,性质(单调性,规范性,连续性)
20 | - 离散随机变量:均匀分布、二项分布、几何分布(无记忆性)、负二项分布(Pascal分布)、泊松分布(泊松定理)
21 | - 连续随机变量:均匀分布、指数分布(无记忆性)、正态分布
22 | - 德国坦克问题
23 |
24 | ### 第三章 多维随机变量
25 |
26 | - 联合分布函数定义、性质(对每个变量单调不减,非负性,规范性,右连续);边缘分布与独立性
27 | - 联合概率密度定义、性质(非负性,规范性);边缘概率密度,两变量独立的等价条件
28 | - 多维随机变量函数的分布(和、差、积、商、最大、最小)
29 |
30 | ### 第四章 随机变量的数学特征
31 |
32 | - 期望,方差,协方差,Pearson相关系数
33 |
34 | ### 第五章 大数定律与中心极限定理
35 |
36 | - 大数定律,依概率收敛
37 | - 中心极限定理,依分布收敛
38 | - 局限:独立同分布假设,有界方差要求,收敛速度未知
39 |
40 | ### 第六章 集中不等式
41 |
42 | - Markov不等式、Chebyshev不等式、Hölder不等式、 Cauchy-Schwartz不等式、单边Chebyshev不等式
43 | - Chernoff方法,Chernoff引理,0/1 Chernoff界,有界Chernoff界
44 |
45 | ### 第七章 统计的基本概念
46 |
47 | - 统计学的概念和三大研究内容(抽样,参数估计,假设检验)
48 | - Beta分布, $ \Gamma $ -分布、性质、独立可加性;标准正态分布的平方 $ \Gamma(\frac12,\frac12) $ ;Dirichlet分布、性质
49 | - $ \chi^2 $ 分布, $ t $ 分布(student分布), $ F $ 分布
50 | - 常见抽样分布定理
51 |
52 | ### 第八章 参数估计
53 |
54 | - 点估计:矩估计,极大似然估计
55 | - 估计量评估:无偏性,有效性,一致性
56 |
57 | ### 第九章 假设检验
58 |
59 | - 假设检验基本思想:小概率原理(小概率事件在一次实验中不应该发生),假设检验概念,两类错误,显著性检验 ,显著性检验基本步骤
60 |
61 | ## 随机事件与概率
62 |
63 | ### 对立事件和互斥事件的区别
64 |
65 | A的对立事件指所有不属于A的基本事件,有 $ \overline A\cap A=\varnothing,\overline A\cup A=\Omega $
66 |
67 | $ A,B $ 不能同时发生,则称他们互不相容(互斥),有 $ A\cap B=\varnothing $
68 |
69 | 区别是 $ A $ 与其对立事件的交为全集, $ A $ 与其互斥事件的交不一定是。
70 |
71 | ### 频率和概率的关系
72 |
73 | 概率是对事件发生的可能性度量,基于统计数据或主观判断。
74 |
75 | 频率是指在大量重复试验中,某一事件发生的实际次数。频率和概率之间有一定的关系,随着试验次数的增加,频率会趋近于概率。
76 |
77 | ### 概率和统计的区别
78 |
79 | - **概率**:**研究事件的不确定性**,在给定数据生成过程中观察,研究数据的性质,强调**公理体系**, **推理**。
80 | - **统计**:**收集与分析数据**,根据观察的数据反思其数据生成过程,强调**归纳**。
81 | - 概率和统计的重要的区别在于公理体系化。
82 |
83 | ### 概率公理化的三条公理
84 |
85 | - **非负性**:对于任何事件 $ A $ ,均有 $ P(A)\geq0 $
86 | - **规范性**:对样本空间 $ \Omega $ 有 $ P(\Omega)=1 $
87 | - **可列可加性**:若 $ A_1,A_2,\dots ,A_n,\dots $ 是可列无穷个互不相容的事件,即 $ A_iA_j=\varnothing(i\neq j) $ ,有
88 |
89 | $$
90 | P(A_1\cup A_2\cup \dots\cup A_n\cup \dots)=P(A_1)+P(A_2)+\dots+P(A_n)+\dots
91 | $$
92 |
93 | 满足这三个条件的实数 $ P(A) $ 为随机事件 $ A $ 的概率。
94 |
95 | ### 古典概型
96 |
97 | 试验E满足:有限种可能( $ \Omega=\{\omega_1,\omega_2,\dots,\omega_n\} $ ,其中 $ \omega_i $ 为基本事件);每种结果发生的可能性相同 $ P(\{\omega_i\})=P(\{\omega_j\}) $ ,即是古典概型。抛硬币即是古典概型问题。
98 |
99 | 古典概率的计算的本质是计数。常见的计数原理有**加法原理**和**乘法原理**。
100 |
101 | ### 排列和组合的概念与应用场景
102 |
103 | 排列:从 $ n $ 个不同的元素中无放回地取出 $ r $ 个元素进行排列,既要考虑取出的元素,也要顾及其排列顺序,则有 $ \displaystyle (n)_r=n(n-1)\dots(n-r+1) $ 种不同的排列。全排列: $ r=n $ ,有 $ n! $ 种。
104 |
105 | 组合:从 $ n $ 个不同的元素中无放回地取出 $ r $ 个元素,取出的元素之间无顺序关系,共有 $ (^n_r) $ 种不同的取法,其中
106 |
107 | $$
108 | \left(\begin{aligned}n\\r\end{aligned}\right)=\frac{n!}{r!(n-r)!}
109 | $$
110 |
111 | (不用考虑顺序,所有将排列数除以 $ r! $ )
112 |
113 | 这里 $ (^n_r) $ 称为组合数或二项系数,是二项展开式 $ (a+b)^n=\sum_{r=0}^{n}(^n_r)a^rb^{n-r} $ 中项 $ a^rb^{n-r} $ 的系数。
114 |
115 | ### 几何概型
116 |
117 | 几何概型:样本空间无限可测,基本事件等可能性。常常使用几何画图的解法求解。
118 |
119 | ## 条件概率和独立性
120 |
121 | ### 条件概率
122 |
123 | 条件概率是事件 $ A $ 发生的条件下事件 $ B $ 发生的概率。
124 |
125 | The conditional probability is the probability of event B occurring given that event A has occurred.
126 |
127 | $$
128 | P(B\vert A)=\frac{P(AB)}{P(A)}
129 | $$
130 |
131 | 这种概率的计算通常需要基于已知的信息和假设,具有一定的主观性。在人工智能领域,条件概率经常用于模型训练和推断过程中,例如朴素贝叶斯分类算法、隐马尔可夫模型等。
132 |
133 | 条件概率也满足非负性、规范性、可列可加性。也满足容斥原理。
134 |
135 | ### 乘法公式
136 |
137 | the multiplication rule
138 |
139 | 当两个事件 $ A $ 和 $ B $ 发生的概率都已知时,计算两个事件同时发生的概率的公式。其计算公式为:
140 |
141 | $$
142 | \begin{aligned}
143 | P(AB)&=P(A)P(B\vert A)=P(B)P(A\vert B)\\
144 | P(A_1A_2\dots A_n)&=P(A_1)P(A_2\vert A_1)P(A_3\vert A_1 A_2)\dots P(A_n\vert A_1A_2\dots A_{n-1})
145 | \end{aligned}
146 | $$
147 |
148 | 在自然语言处理领域中,我们可以用乘法公式来计算一个词在给定上下文条件下出现的概率;在机器学习领域中,我们可以用乘法公式来计算多个特征同时出现的概率,从而进行分类或回归任务。
149 |
150 | ### 全概率公式
151 |
152 | 全概率公式将一个事件的概率分解成多个事件的概率之和,再利用乘法公式求解各个事件的概率。具体来说,若事件 $ A_1,A_2,\dots,A_n $ 为样本空间 $ \Omega $ 的一个划分,对任意事件 $ B $ , $ B $ 的概率是每个 $ A_i $ 的概率与 $ B $ given $ A_i $ 概率的乘积的和。
153 |
154 | 若事件 $ A_1,A_2,\dots,A_n $ 为样本空间 $ \Omega $ 的一个划分,对任意事件 $ B $ 有:
155 |
156 | $$
157 | P(B)=\sum_{i=1}^{n}P(BA_i)=\sum_{i=1}^n P(A_i)P(B|A_i)
158 | $$
159 |
160 | 称之为全概率公式(law of total probability)
161 |
162 | 这里划分指: $ A_i\cap A_j=\varnothing \quad (i\neq j);\Omega=\bigcup_{i=1}^{n}A_i $
163 |
164 | 全概率公式在人工智能领域中的应用非常广泛。例如,在语音识别中,我们可以将不同的语音信号看作互不重叠的事件,应用全概率公式来计算每个语音信号被识别为不同单词的概率;在图像处理中,我们可以将不同的图像特征看作互不重叠的事件,应用全概率公式来计算每个特征对目标分类的贡献等。
165 |
166 | ### 贝叶斯公式
167 |
168 | 贝叶斯公式Baye's law用于计算在某个先验条件下事件的后验概率。
169 |
170 | $$
171 | \begin{aligned}
172 | P(A\vert B)&=\frac{P(B\vert A)P(A)}{P(B)}\\
173 | P(A_i\vert B)&=\frac{P(A_i B)}{P(B)}=\frac{P(A_i)P(B\vert A_i)}{\sum_{j=1}^n P(A_j)P(B\vert A_j)}
174 | \end{aligned}
175 | $$
176 |
177 | 先验概率prior: $ \Pr (A_i) $ ,因为不用考虑任何 $ B $ 的因素。
178 |
179 | 证据概率evidence: $ P(B)=\sum_{j=1}^n P(A_j)P(B\vert A_j) $
180 |
181 | 后验概率posterior: $ \Pr(A_i\vert B) $ 为事件 $ A_i $ 在事件 $ B $ (证据)发生的情况下的后验概率
182 |
183 | 似然度likelihood: $ P(B|A_i) $
184 |
185 | $$
186 | 后验概率=\frac{先验概率\times似然度}{证据概率}=常量\times似然度
187 | $$
188 |
189 | ### 独立性
190 |
191 | #### 定义
192 |
193 | 独立:指两个事件的发生不受彼此的影响,若事件 $ A,B $ 满足 $ P(AB)=P(A)P(B) $ ,则称事件 $ A $ 与 $ B $ 相互独立。
194 |
195 | 即 $ P(AB)=P(A)P(B)\iff P(B\vert A)=P(B)\iff P(A\vert B)=P(B) $
196 |
197 | #### 与互斥事件有何区别
198 |
199 | 互斥:指两个事件不能同时发生。 $ A\cap B=\varnothing $
200 |
201 | 互斥 $ \iff $ 不独立
202 |
203 | 多个事件的独立性: $ A,B,C $ 独立 $ \iff P(AB)=P(A)P(B),P(AC)=P(A)P(C),P(BC)=P(B)P(C),$$P(ABC)=P(A)P(B)P(C) $ 。
204 |
205 | ### iid
206 |
207 | #### 定义
208 |
209 | iid: independent and identically distributed,即独立同分布假设,假设数据集中的每个样本都是从同一个概率分布中独立地随机取出的。
210 |
211 | iid假设在概率统计领域中经常使用,因为它是许多统计方法的基础前提。例如,在机器学习中,训练数据通常被假定为iid,这意味着每个样本是相互独立且来自同一概率分布的,从而使得机器学习算法能够利用数据中的统计信息进行学习和预测。另外,许多假设检验和置信区间的推断方法也需要假定数据是iid的,以确保推断结果的有效性。
212 |
213 | #### 基于iid假设的机器学习算法
214 |
215 | 很多机器学习算法都基于iid假设,比如Linear regression, logistic regression, decision tree, SVM, neural network等等。
216 |
217 | #### 不基于iid假设的机器学习算法
218 |
219 | 1. 时间序列分析算法:时间序列分析算法通常用于分析和预测时间序列数据,这些数据之间存在时间上的相关性,因此不满足独立同分布假设。常见的时间序列分析算法包括自回归模型(AR)、滑动平均模型(MA)、自回归滑动平均模型(ARMA)、自回归积分滑动平均模型(ARIMA)等。
220 | 2. 隐马尔可夫模型(Hidden Markov Model,HMM):HMM 是一种用于建模序列数据的统计模型,通常用于自然语言处理和语音识别等领域。HMM 假设序列数据是由一个不可观测的马尔可夫链和一个可观测的输出过程组成,因此不满足独立同分布假设。
221 | 3. 图模型(Graphical Model):图模型是一类用图形化方式表示变量之间关系的统计模型。常见的图模型包括贝叶斯网络、马尔可夫随机场等,这些模型通常用于分析非独立同分布的数据。
222 |
223 | #### 为什么算法要基于iid假设
224 |
225 | 因为这个假设可以简化建模过程,减小计算复杂度,使得许多统计学理论和方法可以应用于机器学习中,让机器学习算法的性质和性能更加可靠和有效。
226 |
227 | 通过假设数据独立同分布,我们不必考虑数据样本之间的依赖关系,这种简化的假设可以使我们使用更简单的模型,减少模型参数数量,降低模型的计算复杂度,并更容易处理大规模数据。例如,许多基于iid假设的分类算法(如朴素贝叶斯、支持向量机等)只需要学习一个简单的概率模型或决策边界即可,而不需要学习整个数据分布的复杂性。
228 |
229 | 另外,iid假设使得机器学习算法可以使用统计学中的一些基本理论和方法,如中心极限定理、最大似然估计、假设检验等,这些方法可以提供对机器学习算法的性能进行分析和评估的工具。
230 |
231 | 然而,iid假设并不总是成立的,尤其是在处理时序数据、空间数据等场景下。在这些情况下,我们需要使用其他适当的建模方法来处理数据中的依赖关系和非独立同分布性质。
232 |
233 | #### 如果数据分布不符合iid假设,还可以用基于iid假设的算法求解吗?
234 |
235 | 如果数据分布不符合iid假设,使用基于iid假设的算法可能会导致模型偏差和预测结果不准确。因为这些算法的基本假设是样本之间是独立同分布的,如果这个假设不成立,就会导致样本之间的相关性被忽略,进而影响模型的泛化能力和性能。比如说,可以拿线性回归来处理时间序列数据,但是结构可能会偏差和不准确,因为忽略了时间序列数据中样本之间的相关性。
236 |
237 | 如果数据分布不符合iid假设,可以尝试使用其他适当的机器学习算法或方法。例如,可以使用时间序列模型或空间模型来处理序列数据或空间数据,使用聚类模型或关联规则模型来处理数据集中的非独立同分布问题,使用分层模型或多层模型来考虑样本之间的相关性等。
238 |
239 | 此外,对于一些基于iid假设的算法,也有针对性的改进方法,例如,在训练模型时引入权重,调整样本的权重,或者使用bootstrap方法来处理样本的相关性等。这些方法可以帮助我们更准确地建模和处理非独立同分布的数据。
240 |
241 | ### 小概率原理
242 |
243 | Law of small probabilities
244 |
245 | 若事件 $ A $ 在一次试验中发生的概率非常小,但是经过多次独立地重复试验,事件 $ A $ 的发生是必然的。
246 |
247 | ## 离散型/连续型随机变量
248 |
249 | ### 期望和方差
250 |
251 | #### 期望和方差的公式
252 |
253 | 期望反应随机变量 $ X $ 的平均值,离散变量: $ \displaystyle E(X)=\sum_{k=1}^{\infty}p_kx_k $ ;连续变量: $ \displaystyle E(X)=\int_{-\infty}^{+\infty}tf(t)\text{d}t $ (若积分 $ \displaystyle \int_{-\infty}^{+\infty} xf(x)\text{d}x $ 绝对收敛)
254 |
255 | 方差反应随机变量与期望的偏离程度: $ Var(X)=E(X-E(X))^2=E(X^2)-(E(X))^2 $
256 |
257 | 连续变量:(若 $ \displaystyle \int_{-\infty}^{+\infty}(t-E(X))^2f(t)\text{d}t $ )
258 |
259 | $$
260 | \begin{aligned}
261 | Var(X)&=E(X-E(X))^2=\int_{-\infty}^{+\infty}(t-E(X))^2f(t)\text{d}t\\
262 | &=E(X^2)-(E(X))^2=\int_{-\infty}^{+\infty} t^2f(t)\text{d}t-\left(\int_{-\infty}^{+\infty} tf(t)\text{d}t\right)^2
263 | \end{aligned}
264 | $$
265 |
266 | #### 为什么要使用方差公式的等价形式?
267 |
268 | 使用第一种定义,要遍历两遍;但使用第二种定义,则只需要遍历 $ x_1,\dots,x_n $ 一遍,可在线(online)计算方差。
269 |
270 | #### 为什么样本方差(sample variance)的无偏估计分母是n-1?
271 |
272 | 方差的estimator: $ \displaystyle S_1^2=\frac1n\sum_{i=1}^{n}(X_i-\overline X)^2 $
273 |
274 | 但这个estimator有bias,因为:
275 |
276 | $$
277 | \begin{aligned}
278 | E(S_1^2)&=\frac1n\sum_{i=1}^nE\left((X_i-\overline X)^2\right)\\
279 | &=\frac1n\sum_{i=1}^nE\left((X_i-\mu+\mu-\overline X)^2\right)\\
280 | &=\frac1n\sum_{i=1}^nE\left((X_i-\mu)^2+2(X_i-\mu)(\mu-\overline X)+(\mu-\overline X)^2\right)\\
281 | &=\frac1n \sum_{i=1}^nE\left((X_i-\mu)^2\right)+\frac2n\sum_{i=1}^n(X_i-\mu)(\mu-\overline X)+E\left((\mu-\overline X)^2\right)\\
282 | &=\frac1n \sum_{i=1}^nE\left((X_i-\mu)^2\right)+E\left((\overline X-\mu)^2\right)\\
283 | &=nVar(X)-Var(\overline X)=\sigma^2-\frac{\sigma^2}{n}=\frac{n-1}{n}\sigma^2
284 | \end{aligned}
285 | $$
286 |
287 | 所以使用修正值: $ \displaystyle S_1^2=\frac1n\sum_{i=1}^{n}(X_i-\overline X)^2 $
288 |
289 | 直观理解:因为均值已经用了n个数的平均来做估计,在求方差时,只有(n-1)个数和均值信息是不相关的。而第n个数已经可以由前(n-1)个数和均值来唯一确定,实际上没有信息量。所以在计算方差时,只除以(n-1)
290 |
291 | #### 性质
292 |
293 | - 线性: $ E(aX+b)=aE(X)+b,E(\sum_{i=1}^n c_ig_i(x))=\sum_{i=1}^n c_i E(g_i(x)) $
294 | - 对非负随机变量,有 $ E[X]=\int_{0}^{+\infty}P(X>t)\text{d}t $
295 | - 若 $ \int_{-\infty}^{+\infty}g(t)f(t)\text{d}t $ 绝对可积,则 $ E(g(X))=\int_{-\infty}^{+\infty}g(t)f(t)\text{d}t=\int_{0}^{+\infty} P(g(X)>t)\text{d}t $
296 | - Jenson不等式:对离散型随机变量 $ X\in[a,b] $ 和连续凸函数 $ g:[a,b]\to\mathbb R $ ,有 $ g(E(x))\leq E(g(X)) $
297 | - $ Var(aX+b)=a^2 Var(X) $
298 | - $ Var(X)=E(X-E(X))^2\leq E(X-a)^2 $
299 | - Bhatia-Davis不等式: $ Var[X]\leq (b-E(X))(E(X)-a)\leq \frac14(b-a)^2 $
300 |
301 | #### 在人工智能领域中的作用?
302 |
303 | 在人工智能领域中的常见应用场景:
304 |
305 | 1. 数据预处理:在机器学习中,经常需要对数据进行预处理,例如归一化、标准化等。这时候,期望和方差就非常有用。例如,在标准化时,可以先计算出每个特征的均值和方差,然后将特征值减去均值并除以方差,这样可以使得不同特征之间的取值范围相同,从而更容易进行模型训练和比较。
306 | 2. 概率模型:在概率模型中,期望和方差是重要的概念。例如,在高斯分布中,期望就是分布的中心,方差则决定了分布的形状。这些信息可以用来描述数据的统计特征,从而可以构建更加准确的概率模型。
307 | 3. 模型评估:在机器学习中,需要对不同的模型进行比较和评估。期望和方差可以作为评估指标之一,例如在回归问题中,可以计算预测值与真实值之间的平均方差,从而评估模型的拟合效果。
308 | 4. 异常检测:在人工智能中,经常需要进行异常检测,例如检测网络攻击、欺诈行为等。期望和方差可以用来判断数据是否偏离正常范围,例如可以计算数据与均值之间的距离,如果距离超过一定的阈值,则认为数据是异常的。
309 |
310 | #### 没有期望的情况
311 |
312 | 1. 无限的期望:如果随机变量的分布有“重尾”现象,即存在很小的概率,使得随机变量取到极大的值,此时随机变量的期望可能不存在。例如,柯西分布的期望就不存在。
313 | 2. 不收敛的期望:如果随机变量的绝对值的期望不收敛,也就是E(|X|)无限大,此时随机变量的期望也不存在。
314 |
315 | #### 没有方差的情况
316 |
317 | 1. 不存在期望:如果随机变量的期望不存在,则方差也不存在。因为方差的定义中包含了随机变量与其期望之间的差异。
318 | 2. 方差无穷大:如果随机变量的方差为无穷大,则方差不存在。例如,柯西分布的方差不存在。
319 | 3. 不连续的随机变量:如果随机变量的概率密度函数(或概率质量函数)在某些点上不连续,则方差可能不存在。因为方差的定义中包含了随机变量的平方,如果概率密度函数在某些点上不连续,随机变量的平方可能也不连续。
320 |
321 | ### 分布函数
322 |
323 | #### 定义
324 |
325 | Distribution function
326 |
327 | 分布函数是描述随机变量的概率分布的函数,用来描述随机变量 X 小于或等于某个值 x 的概率。公式为 $ F(x)=P(X\leq x) $ 。
328 |
329 | 可以用分布函数表示随机事件的概率,例如
330 |
331 | $ P(X\geq a)=1-F(a-0) $
332 |
333 | $ P(a\leq X\leq b)=F(b)-F(a-0) $
334 |
335 | #### 性质
336 |
337 | 单调性:若 $ x_1 0\\&0&otherwise\end{aligned}\right. $ | $ \displaystyle{E(X)=\frac1\lambda\\Var(X)=\frac1{\lambda^2}} $ | 无记忆性 |
383 | | 正态分布 | $ X\sim \mathcal N(\mu,\sigma^2) $ | $ \displaystyle f(x)=\frac{1}{\sqrt{2\pi}\sigma}e^{-\frac{(x-\mu)^2}{2\sigma}} $ | | $ \displaystyle{E(X)=\mu\\Var(X)=\sigma^2} $ | |
384 |
385 | #### 正态分布的性质
386 |
387 | - **若 $ X\sim\mathcal N(\mu,\sigma^2) $ ,则 $ \displaystyle Y=\frac{X-\mu}{\sigma}\sim \mathcal N(0,1) $ ;若 $ X\sim \mathcal N(0,1) $ ,则 $ Y=\sigma X+\mu\sim \mathcal N(\mu,\sigma^2) $ **
388 |
389 | 证明
390 |
391 | - **若 $ X\sim \mathcal N(0,1) $ ,对于任意 $ \epsilon>0 $ ,有 $ \displaystyle P(X\geq \epsilon)\leq \frac12e^{-\epsilon^2/2} $ **
392 | - **[Mill 不等式] 若 $ X\sim \mathcal N(0,1) $ ,对于任意 $ \epsilon>0 $ ,有 $ \displaystyle P(X\geq \vert\epsilon\vert)\leq \frac12\min\left\{1,\sqrt\frac{2}{\pi}\frac1{\epsilon}e^{-\epsilon ^2/2}\right\} $ **
393 |
394 | 可得 $ P(u-3\sigma \leq X\leq u+3\sigma)\geq 99.7\% $ ,所以在工程中有 $ P(\vert X-\mu\vert \leq 3\sigma)\approx 1 $
395 |
396 | #### 基于正态分布的模型
397 |
398 | Models like LDA, Gaussian Naive Bayes, Logistic Regression, Linear Regression, etc., are explicitly calculated from the assumption that the distribution is a bivariate or multivariate normal. Also, *Sigmoid functions* work most naturally with normally distributed data.
399 |
400 | ### 已知连续随机变量,求解新的随机变量
401 |
402 | 已知连续随机变量 $ X $ 的概率密度函数为 $ f_X(x) $ ,求解新的随机变量 $ Y=g(X) $ 的概率密度 $ f_Y(y) $ 。
403 |
404 | 1. 求解 $ Y=g(X) $ 的分布函数 $ F_Y(y)=P(Y\leq y)=P(g(X)\leq y)=\int_{g(X)\leq y}f_X(x)\text{d}x $
405 | 2. 利用分布函数和概率密度之间的关系求解密度函数 $ f_Y(y)=F'_Y(y) $
406 |
407 | ## 多维随机变量及其分布
408 |
409 | **【还没有看完!】**
410 |
411 | ### 独立性
412 |
413 | #### 定义
414 |
415 | 对离散型随机变量 $ (X,Y) $ ,若对所有 $ (x_i,y_j) $ 有
416 |
417 | $$
418 | P(X=x_i,Y=y_j)=P(X=x_i)P(Y=y_j)
419 | $$
420 |
421 | 即 $ p_{ij}=p_ip_j $ 则称离散随机变量 $ X $ 和 $ Y $ 相互独立。
422 |
423 | ### 高维高斯分布
424 |
425 | $$
426 | f(x_1, \dots,x_n)=(2\pi)^{-n/2}\vert \Sigma\vert ^{-1/2}\exp\left(-\frac12(\xi-\mu)^\top \Sigma^{-1}(\xi-\mu)\right)
427 | $$
428 |
429 | 其中 $ \xi=(x_1,\dots,x_n)^\top $ ,则称随机变量 $ (X_1,\dots, X_n) $ 服从参数为 $ \mu $ 和 $ \Sigma $ 的多维正态分布。
430 |
431 | ### 协方差
432 |
433 | #### 定义
434 |
435 | $$
436 | Cov(X,Y)=E[(X-E(X))(Y-E(Y))]=E(XY)-E(X)E(Y)
437 | $$
438 |
439 | #### 性质
440 |
441 | 定理1
442 | $$
443 | Var(X+Y)=Var(X)+Var(Y)+2E[(X-E(X))(Y-E(Y))]
444 | $$
445 |
446 | 当 $ X $ 与 $ Y $ 独立时,有:
447 |
448 | $$
449 | Var(X+Y)=Var(X)+Var(Y)
450 | $$
451 |
452 | 所以有
453 |
454 | $$
455 | Cov(X,X)=Var(X)\\
456 | Var(X+Y)=Var(X)+Var(Y)+2Cov(X,Y)
457 | $$
458 |
459 | 性质1
460 |
461 | $$
462 | Cov(X,Y)=Cov(Y,X),\quad Cov(X,c)=0
463 | $$
464 |
465 | 性质2
466 |
467 | $$
468 | Cov(aX,bY)=abCov(X,Y),\quad Cov(X+a,Y+b)=Cov(X,Y)
469 | $$
470 |
471 | 性质3
472 |
473 | $$
474 | Cov(X_1+X_2,Y)=Cov(X_1,Y)+Cov(X_2,Y)\\
475 | Cov\left(\sum_{i}^{n}X_i,\sum_{j}^{m}Y_j\right)=\sum_{i}^n\sum_j^mCov(X_i,Y_j)\\
476 | Var(\sum_{i=1}^nX_i)=Cov(\sum_{i=1}^n X_i,\sum_{i=1}^n X_i)=\sum_{i=1}^n Var(X_i)+2\sum_{i0 $ ,则 $ X $ 与 $ Y $ 正相关
499 | - 若 $ \rho<0 $ ,则 $ X $ 与 $ Y $ 负相关
500 | - $ \rho=1\iff Y=aX+b $ ,本质上 $ \rho_{XY} $ 刻画了 $ X,Y $ 的相关线性相关程度,又称线性相关系数。
501 |
502 | 定理2
503 |
504 | $$
505 | \rho_{XY}=0\iff Cov(X,Y)=0\iff E(XY)=E(X)E(Y)\iff Var(X\pm Y)=Var(X)+Var(Y)
506 | $$
507 |
508 | ## 集中不等式Concentration
509 |
510 | ### 基础不等式
511 |
512 | | | | |
513 | | --------------- | ------------------------------------------------------------ | ------------------------------------------------------------ |
514 | | Markov不等式 | | $ \displaystyle P(X\geq\epsilon)\leq\frac{E(X)}{\epsilon} $ |
515 | | Chebyshev不等式 | $ X $ 的均值为 $ \mu $ | $ \displaystyle P(\vert X-\mu\vert \geq \epsilon)\leq \frac{Var(X)}{\epsilon^2} $ |
516 | | Young不等式 | 给定 $ a>0,b>0 $ ,对满足 $ \displaystyle \frac1p+\frac1q=1 $ 的 $ p>0,q>0 $ 有 | $ \displaystyle ab\leq\frac1pa^p+\frac1qb^q $ |
517 | | Holder不等式 | 对任意 $ X,Y $ 和满足 $ \displaystyle \frac1p+\frac1q=1 $ 的 $ p>0,q>0 $ 有 | $ E(|XY|)\leq(E(|X|^p))^{1/p}(E(|X|^q))^{1/q} $ |
518 | | Chernoff不等式 | $ X_1,\dots,X_n $ 独立且 $ X_i\in Ber(p_i) $ ,令 $ \displaystyle \mu=\sum_{i=1}^n E(X_i)=\sum_{i=1}^n p_i $ | $ \displaystyle P\left[\sum_{i=1}^n X_i\geq (1+\epsilon)\mu\right]\leq \left(\frac{e^\epsilon}{(1+\epsilon)^{1+\epsilon}}\right)^\mu $ |
519 | | Bennet不等式 | $ X_1,\dots,X_n $ 独立同分布且 $ X_i-E[X_i]\leq 1 $ ,均值 $ \mu $ ,方差 $ \sigma^2 $ | $ \displaystyle P\left[\sum_{i=1}^n (X_i-\mu)\geq \epsilon\right]\leq \exp\left(-\frac{n\epsilon^2}{2\sigma^2+2\epsilon/3}\right) $ |
520 | | Bernstein不等式 | | |
521 |
522 | ## 大数定律和中心极限定律
523 |
524 | 1. 依概率收敛:如果随着样本量的增加,随机变量序列以概率1逼近某个确定的常数,那么这个随机变量序列就被称为依概率收敛。
525 | 2. 依分布收敛:如果随着样本量的增加,随机变量序列的分布函数逐渐接近某个确定的分布函数,那么这个随机变量序列就被称为依分布收敛。
526 |
527 | ### 依概率收敛
528 |
529 | #### 依概率收敛的定义
530 |
531 | convergence in probability
532 |
533 | 是概率论中的一种收敛方式。它描述了一个随机变量序列中,随着样本数量的增加,这些随机变量逐渐趋近于某个确定的值的概率。
534 |
535 | 设 $ X_1,\dots,X_n,\dots $ 是一随机变量序列, $ a $ 常数,如果对任意 $ \epsilon>0 $ 有
536 |
537 | $$
538 | \lim_{n\to\infty}P(|X_n-a|<\epsilon)=1 \quad或\quad \lim_{n\to\infty}P(|X_n-a|>\epsilon)=0
539 | $$
540 |
541 | 则称 $ X_1,\dots,X_n,\dots $ 依概率收敛于 $ a $ ,记作 $ X_n\overset{P}\to a $
542 |
543 | #### 依概率收敛和数列极限的区别
544 |
545 | 数列极限是指一个数列中的元素随着下标的增大,越来越接近一个确定的实数L。如果这个实数L存在,那么数列就收敛于L;如果这个实数L不存在,那么数列就发散。
546 |
547 | 依概率收敛则是指一个随机变量序列中,随着样本数量的增加,这些随机变量逐渐趋近于某个确定的值的概率。也就是说,依概率收敛描述的是一个概率性的收敛性质,与数列极限不同,它涉及到随机事件的概率性质。
548 |
549 | 因此,数列极限和依概率收敛是两个不同的概念,它们描述的对象不同,数列极限描述的是确定性的数列,而依概率收敛描述的是随机变量序列的概率性质。
550 |
551 | ### 大数定律
552 |
553 | **【少:Chernoff方法】**
554 |
555 | #### 大数定律是什么
556 |
557 | Law of large numbers
558 |
559 | 大数定律是描述相当多次数重复实验的结果的定律。**它刻画了随机变量的均值依概率收敛于期望的均值。**
560 |
561 | | | | |
562 | | ---------------------- | ------------------- | ------------------------------------------------------------ |
563 | | 大数定律 | 无iid要求 | $ \displaystyle \frac1n\sum_{i=1}^{n}X_i\overset{P}\to\frac1n\sum_{i=1}^nE[X_i] $ |
564 | | Markov大数定律 | 无iid要求 | $ \displaystyle \frac1{n^2}Var\left(\sum_{i=1}^n X_i\right)\to 0,n\to\infty $ |
565 | | Chebyshev大数定律 | 相互独立 | 存在 $ c>0 $ 使得 $ Var(X_n)\leq c $ |
566 | | Khintchine辛钦大数定律 | 独立同分布 | 每个随机变量的期望 $ E[X_i]=\mu $ 存在(不要求方差一定存在) |
567 | | Bernoulli大数定律 | $ X_n\sim B(n,p) $ | $ \displaystyle \lim_{n\to\infty}P\left[\left\vert\frac{X_n}{n}-p\right\vert\geq\epsilon\right]=0 $ ,即 $ \displaystyle \frac{X_n}{n}\overset{P}\to p $ |
568 |
569 | #### 如何判断是否满足大数定律
570 |
571 | - if随机变量iid:辛钦
572 | - if非独立同分布随机变量,Markov
573 |
574 | ### 依分布收敛
575 |
576 | 设 $ F_Y(y)=P(Y\leq y) $ ,以及随机变量序列 $ Y_1,\dots,Y_n,\dots $ 的分布函数分别为 $ F_{Y_n}(y)=P(Y_n\leq y) $ ,如果
577 |
578 | $$
579 | \lim_{n\to\infty}\Pr[Y_n\leq y]=\Pr[Y\leq y],即\lim_{n\to\infty}F_{Y_n}(y)=F_Y(y)
580 | $$
581 |
582 | 则称 $ Y_1,\dots,Y_n,\dots $ 依分布收敛于 $ Y $ ,记作 $ Y_n\overset{d}\to Y $
583 |
584 | ### 中心极限定理
585 |
586 | central limit theorem, CLT
587 |
588 | **中心极限定理说明,在适当的条件下,大量相互独立随机变量的均值经适当标准化后依分布收敛于标准正态分布。**
589 |
590 | | | | |
591 | | ---------------------------- | ------------------------------------------------------------ | ------------------------------------------------------------ |
592 | | 独立同分布iid,林德贝格-勒维 | 若 $ E[X_k]=\mu,Var(X_k)=\sigma^2 $ | 则 $ \displaystyle Y_n=\frac{\sum_{i=1}^{n}X_i-n\mu}{\sigma\sqrt n}\overset d \to\mathcal N(0,1)$$\displaystyle\sum_{k=1}^{n}X_k\overset{d}\to \mathcal N(n\mu,n\sigma^2) $ |
593 | | 棣莫弗-拉普拉斯 | 若 $ X_n\sim B(n,p) $ | 则 $ \displaystyle Y_n=\frac{X_n-np}{\sqrt{np(1-p)}}\overset{d}\to \mathcal N(0,1) $ |
594 | | 独立不同分布,李雅普诺夫 | 若 $ E[X_n]=\mu_n,Var(X_n)=\sigma_n^2>0 $ ,记 $ \displaystyle B_n^2=\sum_{k=1}^n\sigma^2_k $ ,若存在 $ \delta>0 $ ,当 $ n\to\infty $ 时有 $ \displaystyle \frac{1}{B^{2+\delta}_n}\sum_{k=1}^mE\left[|X_k-\mu_k|^{2+\delta}\right]\to 0 $ | 则 $ Y_n=\displaystyle\frac{\sum_{k=1}^nX_k-\sum_{k=1}^n E(X_k)}{\sqrt{Var(\sum_{k=1}^nX_k)}}\overset{d}\to \mathcal N(0,1) $ |
595 |
596 | 大数定律给出了当 $ n\to\infty $ 时随机变量平均值 $ \frac1n\sum_{i=1}^n X_i $ 的趋势,中心极限定理给出了 $ \frac1n\sum_{i=1}^n X_i $ 的具体分布。
597 |
598 | ## 统计的基本概念
599 |
600 | ### 统计学
601 |
602 | #### 统计定义
603 |
604 | 
605 |
606 | ### 常见定义
607 |
608 | - 总体population:研究问题涉及到的对象全体;个体:总体中的每个元素
609 | - 样本sample:从总体中随机抽取的一些个体,一般表示为 $ X_1,\dots,X_n $ ,样本容量为 $ n $
610 | - 样本的二重性:(1) 确定性:就一次观测而言,样本值是确定的数;(2) 随机性:不同抽样下,样本值会发生变化,可看做随机变量。
611 | - 简单随机样本:满足 (1) 代表性: $ X_i $ 与 $ X $ 同分布;(2) 独立性: $ X_1,\dots,X_n $ 相互独立(之后考虑的所有样本均为简单随机样本)
612 | - 联合分布函数:设总体 $ X $ 的联合分布函数为 $ F(x) $ ,则 $ X_1,\dots,X_n $ 的联合分布函数为 $ F(x_1,\dots,x_n)=\prod_{i=1}^nF(x_i) $
613 | - 联合概率密度:设总体 $ X $ 的联合概率密度为 $ f(x) $ ,则 $ X_1,\dots,X_n $ 的联合分布函数为 $ f(x_1,\dots,x_n)=\prod_{i=1}^nf(x_i) $
614 | - 联合分布列:设总体 $ X $ 的联合分布函数为 $ \Pr(X=x_i) $ ,则 $ X_1,\dots,X_n $ 的联合分布列为 $ \Pr(X_1=x_1,\dots,X_n=x_n)=\prod_{i=1}^n \Pr(X_i=x_i) $
615 |
616 | ### 常见统计量
617 |
618 | #### 统计量的定义
619 |
620 | 设 $ X_1,\dots,X_n $ 为来自总体 $ X $ 的一个样本, $ g(X_1,\dots,X_n) $ 是关于 $ X_1,\dots,X_n $ 的一个连续、且不含任意参数的函数,称 $ g(X_1,\dots,X_n) $ 是一个统计量。
621 |
622 | #### 常见统计量
623 |
624 | - 样本均值: $ \displaystyle \overline X=\frac1n\sum_{i=1}^nX_i $
625 | - 样本方差: $ \displaystyle S_0^2=\frac1n\sum_{i=1}^n(X_i-\overline X)^2=\frac1n\sum_{i=1}^n X_i^2-\overline X^2 $ ,修正后的样本方差为 $ \displaystyle S^2=\frac1{n-1}\sum_{i=1}^n (X_i-\overline X)^2 $
626 | - 样本 $ k $ 阶原点矩: $ \displaystyle A_k=\frac1n\sum_{i=1}^nX_i^k $
627 | - 样本 $ k $ 阶中心矩: $ \displaystyle A_k=\frac1n\sum_{i=1}^n(X_i-\overline X)^k $
628 | - 最小次序统计量: $ X_{(1)}=\min\{X_1,\dots,X_n\} $
629 | - 最大次序统计量: $ X_{(n)}=\max\{X_1,\dots,X_n\} $
630 | - 样本极差: $ R_n=X_{(n)}-X_{(1)} $
631 |
632 | **【还有一些定理没有完善!】**
633 |
634 | ### 定理
635 |
636 | $$
637 | E(X)=\mu,Var(X)=\sigma^2\Longrightarrow E(\overline X)=\mu,Var(\overline X)=\frac{\sigma^2}{n},\overline X\overset{d}\to\mathcal N(\mu,\frac{\sigma^2}n)
638 | $$
639 |
640 |
641 |
642 | ### Beta分布, $ \Gamma $ -分布,Dirichlet分布
643 |
644 | | | | |
645 | | ---------------- | ------------------------------------------------------------ | ------------------------------------------------------------ |
646 | | Beta分布 | $ f(x)=\left\{\begin{aligned} &\displaystyle \frac{x^{\alpha_1-1}(1-x)^{\alpha_2-1}}{B(\alpha_1,\alpha_2)}&x\in(0,1)\\ &0&otherwise\end{aligned}\right. $ | $ \displaystyle E[X]=\frac{\alpha_1}{\alpha_1+\alpha_2}\\Var[X]=\frac{\alpha_1\alpha_2}{(\alpha_1+\alpha_2)^2(\alpha_1+\alpha_2+1)} $ |
647 | | $ \Gamma $ -函数 | $ f(x)=\left\{\begin{aligned} &\displaystyle \frac{\lambda^\alpha}{\Gamma(\alpha)}x^{\alpha-1}e^{-\lambda x}&x>0\\ &0&x\leq 0\end{aligned}\right. $ | $ \displaystyle E[X]=\frac{\alpha}{\lambda}\\Var[X]=\frac{\alpha}{\lambda^2} $ |
648 | | | | |
649 |
650 | #### Beta函数
651 |
652 | 对于任意给定 $ \alpha_1>0,\alpha_2>0 $
653 |
654 | $$
655 | Beta(\alpha_1,\alpha_2)=\int_0^1 x^{\alpha_1-1}(1-x)^{\alpha_2-1}\text{d}x
656 | $$
657 |
658 | 又称第一类欧拉积分函数。
659 |
660 | - 有对称性: $ Beta(\alpha_1,\alpha_2)=Beta(\alpha_2,\alpha_1) $
661 | - 定义多维Beta函数为
662 |
663 | $$
664 | Beta(\alpha_1,\dots,\alpha_k)=\frac{\Gamma(\alpha_1)\dots\Gamma(\alpha_k)}{\Gamma(\alpha_1+\dots+\alpha_k)}
665 | $$
666 |
667 | #### $ \Gamma $ -函数
668 |
669 | 对于任意给定 $ \alpha>0 $ ,
670 |
671 | $$
672 | \Gamma(\alpha)=\int_{0}^{+\infty}x^{\alpha-1}e^{-x}\text{d}x
673 | $$
674 |
675 | 又称第二类欧拉积分函数。
676 |
677 | - $ \Gamma(1)=1,\Gamma(\frac12)=\sqrt \pi $ ,对 $ \alpha>1 $ 有 $ \Gamma(\alpha)=(\alpha-1)\Gamma(\alpha-1) $ (所以对于任意正整数 $ n $ ,根据上面的性质有 $ \Gamma(n)=(n-1)! $ )
678 |
679 | #### 定理
680 |
681 | - 对于任意给定 $ \alpha_1>0,\alpha_2>0 $
682 |
683 | $$
684 | Beta(\alpha_1,\alpha_2)=\frac{\Gamma(\alpha_1)\Gamma(\alpha_2)}{\Gamma(\alpha_1+\alpha_2)}
685 | $$
686 | - 对于任意给定 $ \alpha_1>0,\alpha_2>0 $
687 |
688 | $$
689 | Beta(\alpha_1,\alpha_2)=\frac{\alpha_1-1}{\alpha_1+\alpha_2-1}Beta(\alpha_1-1,\alpha_2)
690 | $$
691 |
692 | #### Beta分布
693 |
694 | 给定 $ \alpha_1>0,\alpha_2>0 $ ,若随机变量 $ X $ 的概率密度为
695 |
696 | $$
697 | f(x)=\left\{
698 | \begin{aligned}
699 | &\displaystyle \frac{x^{\alpha_1-1}(1-x)^{\alpha_2-1}}{B(\alpha_1,\alpha_2)}&x\in(0,1)\\
700 | &0&otherwise
701 | \end{aligned}\right.
702 | $$
703 |
704 | 则称 $ X $ 服从参数为 $ \alpha_1,\alpha_2 $ 的Beta分布,记为 $ X\sim B(\alpha_1,\alpha_2) $
705 |
706 | - $ \displaystyle E[X]=\frac{\alpha_1}{\alpha_1+\alpha_2},Var[X]=\frac{\alpha_1\alpha_2}{(\alpha_1+\alpha_2)^2(\alpha_1+\alpha_2+1)} $
707 |
708 | #### $ \Gamma $ -分布
709 |
710 | 若随机变量 $ X $ 的概率密度为
711 |
712 | $$
713 | f(x)=\left\{
714 | \begin{aligned}
715 | &\displaystyle \frac{\lambda^\alpha}{\Gamma(\alpha)}x^{\alpha-1}e^{-\lambda x}&x>0\\
716 | &0&x\leq 0
717 | \end{aligned}\right.
718 | $$
719 |
720 | 其中 $ \alpha>0,\lambda>0 $ ,则称 $ X $ 服从参数为 $ \alpha,\lambda $ 的 $ \Gamma $ 分布,记为 $ X\sim \Gamma(\alpha,\lambda) $
721 |
722 | - $ \displaystyle E[X]=\frac{\alpha}{\lambda},Var[X]=\frac{\alpha}{\lambda^2} $
723 | - 若随机变量 $ X\sim\Gamma(\alpha_1,\lambda),Y\sim\Gamma(\alpha_2,\lambda) $ ,且 $ X,Y $ 相互独立,则 $ X+Y\sim\Gamma(\alpha_1+\alpha_2,\lambda) $
724 |
725 | #### Dirichlet分布
726 |
727 | 给定 $ \alpha_1,\dots,\alpha_k\in(0,+\infty) $ ,若多元随机向量 $ X=(X_1,\dots,X_k) $ 的密度函数为
728 |
729 | $$
730 | f(x_1,\dots,x_k)=\left\{
731 | \begin{aligned}
732 | &\displaystyle \frac{x_1^{\alpha_1-1}\dots x_k^{\alpha_k-1}}{B(\alpha_1,\dots,\alpha_k)}&\sum_{i=1}^k x_i=1,x_i>0\quad (i\in[k])\\
733 | &0&otherwise
734 | \end{aligned}\right.
735 | $$
736 |
737 | 则称 $ X $ 服从参数为 $ \alpha_1,\dots,\alpha_k $ 的Dirichlet分布,记为 $ X\sim Dir(\alpha_1,\dots,\alpha_k) $
738 |
739 | - Dirichlet分布是Beta分布发一种推广,当 $ k=2 $ 时Dirichlet分布退化为Beta分布
740 | - 设 $ \displaystyle \tilde{\alpha}=\sum_{i=1}^k\alpha_i,\tilde{\alpha}_i=\frac{\alpha_i}{\tilde{\alpha}} $ ,则 $ E[X_i]=\tilde{\alpha}_i,Cov(X_i,X_j)=\left\{\begin{aligned}&\displaystyle \frac{\tilde{\alpha}_i(1-\tilde{\alpha}_i)}{\tilde{\alpha}+1}&i=j\\&\displaystyle -\frac{\tilde{\alpha}_i\tilde{\alpha}_j}{\tilde{\alpha}+1}&i\neq j\end{aligned}\right. $
741 |
742 | ### 正态分布总体抽样分布定理
743 |
744 | #### $ \chi^2 $ 分布
745 |
746 | 若 $ X_1,\dots,X_n $ 是来自总体 $ X\sim\mathcal N(0,1) $ 的一个样本,称 $ Y=X_1^2+\dots+X_n^2 $ 为服从自由度为 $ n $ 的 $ \chi^2 $ 分布,记 $ Y\sim\chi^2(n) $
747 |
748 | 根据 $ X_1^2\sim\Gamma(\frac12,\frac12) $ 和 $ \Gamma $ 函数的可加性可得 $ Y\sim\Gamma(\frac n2,\frac12) $
749 |
750 | $$
751 | f_Y(y)=\left\{
752 | \begin{aligned}
753 | &\displaystyle \frac{\left(\frac12\right)^\alpha}{\Gamma(\alpha)}y^{\frac n2-1}e^{-\frac y2}&y>0\\
754 | &0&y\leq 0
755 | \end{aligned}\right.
756 | $$
757 |
758 | - 若 $ X\sim\chi^2(n) $ ,则 $ E(X)=n,Var(X)=2n $
759 | - 分布可加性:若 $ X\sim\chi^2(m),Y\sim\chi^2(n) $ ,则 $ X+Y\sim\chi^2(m+n) $
760 |
761 | #### $ t $ 分布(student distribution)
762 |
763 | 随机变量 $ X\sim\mathcal N(0,1) $ 和 $ Y\sim\chi^2(n) $ 相互独立,则随机变量
764 |
765 | $$
766 | T = \frac{X}{\sqrt{Y/n}}
767 | $$
768 |
769 | 服从自由度为 $ n $ 的 $ t $ 分布,记 $ T\sim t(n) $
770 |
771 | 概率密度函数:
772 |
773 | $$
774 | f(x)=\frac{\Gamma\left(\frac{n+1}2\right)}{\Gamma\left(\frac{n}2\right)\sqrt{n\pi}}\left(1+\frac {x^2} n\right)^{-\frac{n+1}2}
775 | $$
776 |
777 | 当 $ n\to\infty $ 时, $ f(x)\to\frac{1}{\sqrt {2\pi}}e^{-x^2/2} $
778 |
779 | #### $ F $ 分布
780 |
781 | 随机变量 $ X\sim\chi^2(m) $ 和 $ Y\sim\chi^2(n) $ 相互独立,则随机变量
782 |
783 | $$
784 | F = \frac{X/m}{Y/n}
785 | $$
786 |
787 | 服从自由度为 $ (m,n) $ 的 $ t $ 分布,记 $ F\sim F(m,n) $
788 |
789 | #### 正态分布的抽样分布定理
790 |
791 | 设 $ X_1,\dots,X_n $ 是来自总体 $ \mathcal N(\mu,\sigma^2) $ 的样本,则有
792 |
793 | - $ \displaystyle \overline{X}=\frac1n\sum_{i=1}^nX_i\sim\mathcal N(\mu,\frac{\sigma^2}{n}),\frac{\overline{X}-\mu}{\sigma/\sqrt{n}}\sim\mathcal N(0,1) $
794 | - $ \displaystyle \overline{X}=\sum_{i=1}^n\frac{X_i}{n},S^2=\frac{1}{n-1}\sum_{i=1}^n(X_i-\overline X)^2 $ 相互独立,且 $ \displaystyle \frac{(n-1)S^2}{\sigma^2}\sim\chi^2(n-1) $
795 | - $ \displaystyle \frac{\overline X-\mu}{S/\sqrt{n}}\sim t(n-1) $
796 | - 设 $ X_1,\dots,X_m $ 和 $ Y_1,\dots,Y_n $ 分别来自总体 $ \mathcal N(\mu_X,\sigma^2_X),\mathcal N(\mu_Y,\sigma^2_Y) $ 的两个独立样本,令其修正样本方差分别为 $ S_X^2,S_Y^2 $ ,则有 $ \displaystyle \frac{S_X^2/\sigma^2_X}{S_Y^2/\sigma^2_Y}\sim F(m-1,n-1) $
797 |
798 | ## 参数估计
799 |
800 | ### 参数估计定义
801 |
802 | 
803 |
804 | ### 矩估计
805 |
806 | | | |
807 | | -------------------------------------------- | ------------------------------------------------------------ |
808 | | 总体 $ X $ 的 $ k $ 阶矩 $ a_k=E[X^k] $ | 样本 $ k $ 阶矩 $ A_k=\frac1n\sum_{i=1}^n X_i^k $ |
809 | | 总体 $ X $ 的 $ k $ 阶中心矩 $ b_k = E[(X-E(X))^k] $ | 样本 $ k $ 阶中心矩 $ B_k=\frac1n\sum_{i=1}^n (X_i-\overline X)^k $ |
810 |
811 | #### 为什么要求 $ k $ 阶矩?
812 |
813 | 在概率论和统计学中,矩是一个用来描述随机变量分布的重要概念。一般地,k阶矩是指随机变量的k次幂的期望,其中k是一个非负整数。
814 |
815 | 求解矩是非常有用的,因为它可以帮助我们了解一个随机变量分布的特征。例如,均值(一阶矩)可以告诉我们这个随机变量的中心位置在哪里,方差(二阶矩)可以告诉我们这个随机变量的分布范围大小以及数据的离散程度,偏度(三阶矩)可以告诉我们这个随机变量的偏斜程度,而峰度(四阶矩)可以告诉我们这个随机变量的峰态程度。
816 |
817 | 因此,通过求解不同阶的矩,我们可以更全面地了解一个随机变量的分布特征,从而更好地理解和分析相关的问题。
818 |
819 | #### 如何进行矩估计?
820 |
821 | 可以使用中心矩估计,二阶中心距 $ B_k=\frac1n\sum_{i=1}^n (X_i-\overline X)^k=Var(X) $
822 |
823 | 
824 |
825 | ### 最大似然估计
826 |
827 | #### 定义
828 |
829 | Maximum likelihood estimation is a statistical method used to estimate the parameters of a model. The basic idea behind maximum likelihood estimation is to find the parameter values that maximize the likelihood of the observed data. In other words, we seek to find the values of the model parameters that make the observed data most probable.
830 |
831 | 极大似然估计是一种用于估计模型参数的统计方法。极大似然估计的基本思想是找到使观测数据的似然函数最大化的参数值。换句话说,我们寻找模型参数的值,使得观测数据发生的可能性最大。
832 |
833 | #### 需要满足什么假设?
834 |
835 | 样本独立同分布,参数化假设(参数可数且取值有限),可微性假设(似然函数可微),模型合适。
836 |
837 | #### 是贝叶斯学派还是频率主义学派?
838 |
839 | 频率主义学派
840 |
841 | - 频率主义学派(Frequentist)认为参数虽然未知,但却是客观存在的固定值,因此,可通过优化似然函数等准则来确定参数值
842 | - 贝叶斯学派(Bayesian)则认为参数是未观察到的随机变量,其本身也可有分布,因此,可假定参数服从一个先验分布,然后 基千观测到的数据来计算参数的后验分布
843 |
844 | #### 似然函数定义
845 |
846 | 似然函数是 $ X_1=x_1,\dots,X_n=x_n $ 的联合概率密度:
847 |
848 | $$
849 | L(\theta)= L(x_1,\dots,x_n;\theta)=\prod_{i=1}^nf(x_i;\theta)
850 | $$
851 |
852 | #### 似然函数和概率密度函数有什么区别?
853 |
854 | 似然函数和概率密度函数都是描述概率的函数,形式相似,但有不同的含义和用途。
855 |
856 | 概率密度函数描述随机变量在已知参数的条件下的概率分布,而似然函数描述参数在已知数据的条件下的可能取值。在统计建模中,我们通常使用似然函数来推断参数的取值,而使用概率密度函数来计算随机变量的概率分布。
857 |
858 | #### 如何求解最大似然估计?
859 |
860 | 
861 |
862 | $ D_c $ 训练集中第 $ c $ 类样本的集合,假设独立同分布
863 |
864 | $$
865 | LL(\theta_c)=\log P(D_c|\theta_c)=\sum_{x\in D_c}\log P(x|\theta_c)\\
866 | \hat{\theta_c}=\arg\max_{\theta_c}LL(\theta_c)
867 | $$
868 |
869 | 例:连续属性,概率密度函数 $ p(x|c)\sim\mathcal N(\mu_c,\sigma_c^2) $ , $ \mu_c,\sigma^2_c $ 的极大似然估计:
870 |
871 | 
872 |
873 | #### 在机器学习中的应用?
874 |
875 | 训练线性回归、逻辑回归、朴素贝叶斯等模型。
876 |
877 | 具体训练步骤是:
878 |
879 | 1. 定义模型的假设空间:即模型的函数形式和参数的范围。
880 | 2. 定义似然函数
881 | 3. 求解最大似然估计
882 | 4. 评估模型:交叉验证等方法
883 |
884 | #### 缺点
885 |
886 | 缺点:概率分布假设需要准确,样本需要iid,要求数据量大。
887 |
888 | #### 什么是贝叶斯估计?与极大似然估计相比,它有什么优点和缺点?
889 |
890 | 贝叶斯估计是一种利用贝叶斯定理进行参数估计的方法。在贝叶斯估计中,我们先假设参数 $ \theta $ 服从一个先验分布 $ p(\theta) $ ,然后根据观测数据 $ X $ ,计算后验分布 $ p(\theta|X) $ ,再从中选择最优的参数值作为估计结果。
891 |
892 | $$
893 | p(\theta\vert X)=\frac{p(\theta)p(X\vert\theta)}{P(X)}=\frac{p(\theta)p(X\vert\theta)}{\int_{\theta}p(\theta)p(X\vert\theta)\text{d}\theta}
894 | $$
895 |
896 | 贝叶斯估计与极大似然估计的主要区别在于它引入了先验分布,使得估计结果更加准确和稳定。
897 |
898 | 优点:
899 |
900 | 1. 贝叶斯估计可以引入先验分布,使得估计结果更加准确和稳定,特别是当数据量较少时,先验分布可以在一定程度上抵消数据的不足,避免出现过拟合的问题。
901 | 2. 贝叶斯估计可以通过后验分布来描述参数的不确定性,这对于一些需要考虑风险和可靠性的应用场景非常重要。
902 | 3. 贝叶斯估计的方法比较灵活,可以根据具体情况灵活地选择不同的先验分布和后验计算方法。
903 |
904 | 缺点:
905 |
906 | 1. 贝叶斯估计需要先假设参数的先验分布,这需要对领域知识有一定的了解或者有一些实验结果来支持。如果先验分布假设不合理或者不准确,会导致估计结果的偏差。
907 | 2. 贝叶斯估计的计算复杂度比较高,需要进行积分计算,计算量通常比极大似然估计要大得多。在大规模数据集上,贝叶斯估计可能会面临计算复杂度的问题。
908 | 3. 贝叶斯估计的结果不是唯一的,因为先验分布的不同选择会导致不同的后验分布。这可能会给结果的解释和应用带来一定的不确定性。
909 |
910 | #### 在机器学习中,为什么使用对数似然函数进行优化比使用原始似然函数更好?
911 |
912 | 对数似然函数log-likelihood function
913 |
914 | - 可以将乘积转换为求和,简化计算
915 | - 避免数值下溢:由于似然函数通常是由很多个小概率相乘得到,这容易导致数值下溢问题。而对数似然函数可以避免这种情况,因为它将乘积转换为求和,将大量小概率相加。
916 |
917 | ### 估计量评价标准
918 |
919 | #### 无偏性
920 |
921 | 设 $ X_1,\dots,X_n $ 是来自总体 $ X $ 的样本,令 $ \hat{\theta}=\hat{\theta}(X_1,\dots,X_n) $ 是 $ \theta $ 的一个估计,若
922 |
923 | $$
924 | E_{X_1,\dots,X_n}[\hat{\theta}]=E_{X_1,\dots,X_n}[\hat{\theta}(X_1,\dots,X_n)]=\theta
925 | $$
926 |
927 | 则称 $ \hat\theta $ 是 $ \theta $ 的无偏估计
928 |
929 | #### 有效性
930 |
931 | $ \hat{\theta}_1=\hat{\theta}_1(X_1,\dots,X_n) $ 和 $ \hat{\theta}_2=\hat{\theta}_2(X_1,\dots,X_n) $ 是 $ \theta $ 的两个无偏估计,若 $ Var(\hat\theta_1)\leq Var(\hat\theta_2) $ ,则称 $ \hat{\theta}_1 $ 比 $ \hat{\theta}_2 $ 有效。
932 |
933 | [Rao-Crammer不等式] 令
934 |
935 | $$
936 | Var(\theta)=\frac{1}{nE\left[\left(\frac{\part\ln f(X;\theta)}{\part\theta}\right)^2\right]}或Var(\theta)=\frac{1}{nE\left[\left(\frac{\part\ln F(X;\theta)}{\part\theta}\right)^2\right]}
937 | $$
938 |
939 | 称 $ Var_{0}(\theta) $ 为估计量 $ \hat{\theta} $ 方差的下界,对任意无偏估计量有 $ Var(\hat\theta)\geq Var_0(\theta) $ 。
940 |
941 | **有效估计量**: $ Var(\hat{\theta})=Var_0(\theta) $
942 |
943 | #### 一致性
944 |
945 | 令 $ \hat{\theta}=\hat{\theta}(X_1,\dots,X_n) $ 是 $ \theta $ 的一个估计,若当 $ n\to\infty $ 时有 $ \hat{\theta}_n\overset{P}\to\theta $ 成立,即对任意 $ \epsilon>0 $ 有
946 |
947 | $$
948 | \lim_{n\to0}\left[\left\vert\hat\theta_n-\theta\right\vert>\epsilon\right]=0
949 | $$
950 |
951 | 则称 $ \hat\theta_n $ 为 $ \theta $ 的一致估计量
952 |
953 | - **[充分性条件]** 若 $ \displaystyle \lim_{n\to\infty}E\left[\hat\theta_n\right]=\theta $ 且 $ \displaystyle \lim_{n\to\infty}Var\left(\hat\theta_n\right)=0 $ ,则 $ \hat\theta_n $ 为 $ \theta $ 的一致估计量
954 |
955 | ### 区间估计
956 |
957 | #### 置信区间和置信度
958 |
959 | 对于总体 $ X $ 的分布函数的未知参数 $ \theta $ ,有
960 |
961 | $$
962 | \Pr\left[\hat{\theta}_1<\theta<\hat{\theta}_2\right]\geq1-\alpha
963 | $$
964 |
965 | 则 $ \alpha $ 为置信度; $ \left[\hat{\theta}_1,\hat{\theta}_2\right] $ 为 $ \theta $ 的置信度为 $ 1-\alpha $ 的置信区间。
966 |
967 | ## 假设检验
968 |
969 | Hypothesis Testing
970 |
971 | ### 假设检验定义
972 |
973 | 
974 |
975 | ### 假设检验的一般步骤
976 |
977 | 
978 |
979 | ### 参数假设检验
980 |
981 | #### Z检验
982 |
983 | 
984 |
985 | #### t检验
986 |
987 | 
988 |
989 | #### $ \chi^2 $ 检验
990 |
991 | 
992 |
993 | ### 非参数假设检验
994 |
--------------------------------------------------------------------------------
/深度学习.md:
--------------------------------------------------------------------------------
1 | # 深度学习
2 |
3 | ## Transformer
4 |
5 | ### Transformer简介
6 |
7 | 是一个有Encoder和Decoder的seq2seq模型。它基于attention机制,使得模型在处理长序列数据时能够更好地捕捉全局依赖关系。最初由Google的团队提出,用于解决机器翻译任务。
8 |
9 | ### Attention
10 |
11 | Attention可以用于处理序列数据的关联性和重要性。在文中使用的是Scaled Dot-Product Attention,是对Query和Key的内积缩放后过一个softmax,再乘以V。
12 | $$
13 | \text{Attention}(Q,K,V)=\text{softmax}\left(\frac{QK^\top}{\sqrt{d_k}}\right)V
14 | $$
15 |
16 | ### Self-attention
17 |
18 | $\displaystyle\text{Attention}(Q,K,V)=\text{softmax}(\frac{QK^\top}{\sqrt {d_k}})V$,这里Q和K分别是query和key,$\sqrt{d_k}$是缩放因子,让softmax里的内容方差为1。
19 |
20 | self attention:计算每个输入的词与其他词的关联性。做法:将input喂入三个fc,生成query, key, value(目的:提升模型的拟合能力,矩阵$W$都是可以训练的,起到一个缓冲的效果)
21 |
22 | ### Cross attention
23 |
24 | cross-attention的输入来自不同的序列,而self-attention的输入则是来自一个单一的嵌入序列。Cross-attention将两个相同维度的嵌入序列不对称地组合在一起,而其中一个序列用作查询Q输入,而另一个序列用作键K和值V输入。
25 |
26 | ### Multi-head attention
27 |
28 | 让$V, K, Q$通过不同的$h$组不同的、训练出的线性层,分别通过attention层,再concat在一起。
29 |
30 | #### 作用
31 |
32 | 通过多个注意力头并行计算,模型可以从不同的子空间中学习到更多的特征表示。每个注意力头都可以关注不同的相关性和信息,从而捕捉到输入序列的多个不同方面,增强了模型的表达能力和学习能力。
33 |
34 | #### 和CNN相关的地方
35 |
36 | 和CNN中通过多个卷积核学习多个不同的特征表示有些相似。
37 |
38 | ### 每一层做什么操作?
39 |
40 | 首先过一个attention,再通过一个MLP,再做Layer Normalization。
41 |
42 | #### 为什么要做层归一化Layer Normalization?
43 |
44 | 因为输入的seq不一定定长,导致训练的时候每个batch各样本的方差较大,不稳定;测试时使用全局均值和方差,如果遇到特别长的样本则无法处理。每个样本自己做layer normalization,则样本间相对独立。
45 |
46 | #### Layer Normalization & Batch Normalization
47 |
48 | Batch normalization是在每个特征维度上进行归一化,使得特征的均值接近于0,方差接近于1。训练时使用batch均值和方差,测试时使用全局均值和方差。批归一化适用于卷积层和全连接层等具有多维特征的层。
49 |
50 | Layer normalization是对每个样本在特定维度上进行归一化。层归一化适用于RNN等逐步处理序列的层。
51 |
52 | 归一化好处:减轻输入数据的分布偏移,加速模型收敛速度,提高模型的稳定性和泛化能力,可以缓解梯度问题。
53 |
54 | ### 如何记录词的位置信息?
55 |
56 | 将Positional Encoding的信息concat到词的embedding后,一起作为模型的输入信息。
57 |
58 | 使用sin和cos函数表示,共512维:
59 | $$
60 | PE(pos, 2i)=\sin\left(\frac{pos}{10000^{2i/d_{model}}}\right)\\
61 | PE(pos, 2i+1)=\cos\left(\frac{pos}{10000^{2i/d_{model}}}\right)
62 | $$
63 |
64 | ### Decoder为什么/怎么做masking?
65 |
66 | 因为decoder要执行的任务是:given $y_1,\dots,y_i$,预测$y_{i+1}$,为了保证训练任务和测试任务一致,所以要mask掉$y_{i+1},\dots,y_n$。
67 |
68 | 将这一位加上一个很大的负数,这样softmax以后就会变成0。
69 |
70 | ### RNN & Transformer?
71 |
72 | 都用于处理序列信息。
73 |
74 | RNN:将上一时刻的输出作为下一时刻的输入
75 |
76 | Transformer:通过Attention层获得全局序列信息。
77 |
78 | ## 什么是Transformer?
79 |
80 | 是一个有Encoder和Decoder的seq2seq模型,采用了一种基于注意力机制的结构,使得模型在处理长序列数据时能够更好地捕捉全局依赖关系。
81 |
82 |
83 |
84 | 
85 |
86 | [Illustrated Guide to Transformers Neural Network: A step by step explanation - YouTube](https://www.youtube.com/watch?v=4Bdc55j80l8)
87 |
88 | - encoder
89 |
90 | - input embedding:为每个词寻找一个向量表征
91 |
92 | - positional encoding:加入位置信息(使用sin和cos函数)
93 |
94 | - encoder layer:输入序列$\to$抽象连续表征
95 |
96 | - multi-head attention + norm:输入:序列,输出:每个单词与其他词的关联度
97 |
98 | - fully connected network + norm:residual connection
99 |
100 | - decoder:生成文本序列,autoregressive,masking(只能算和过去词语的attention score)
101 |
102 | - 和encoder相似
103 | - classifier
104 |
105 | Transformer模型的核心思想是通过自注意力机制(Self-Attention)来建立输入序列的表示。自注意力机制能够计算序列中各个位置之间的相关性,并根据相关性分配不同的权重,从而更好地捕捉上下文信息。通过多层堆叠的自注意力层和前馈神经网络层,Transformer能够对输入序列进行逐层的特征提取和组合,从而获得更丰富的表示。
106 |
107 | Transformer模型的另一个重要组成部分是位置编码(Positional Encoding),用于将序列中每个位置的信息嵌入到表示中,以考虑序列的顺序信息。位置编码可以告知模型每个输入在序列中的位置,从而在没有显式顺序信息的情况下仍能正确建模序列。
108 |
109 | 由于其出色的性能和可扩展性,Transformer模型不仅在机器翻译任务中表现出色,还被广泛应用于其他NLP任务,如文本生成、命名实体识别、情感分析等。此外,Transformer的思想也被拓展到其他领域,如计算机视觉(如图像生成和图像分类)和推荐系统等,取得了很好的效果。
110 |
111 |
112 |
113 | ## 什么是LSTM?
114 |
115 | [人人都能看懂的LSTM - 知乎 (zhihu.com)](https://zhuanlan.zhihu.com/p/32085405)
116 |
117 | LSTM就是long short-term memory,是一种循环神经网络的变体,通过引入“记忆单元”来解决长序列训练过程中的梯度消失和梯度爆炸问题。
118 |
119 | - 相比RNN只有一个传递状态$h^t$,LSTM有两个传输状态,一个$c^t$(cell state),和一个$h^t$(hidden state)。其中$c^t$通常是$c^{t-1}$加上一些值,改变得很慢;$h^t$在不同结点下往往有很大区别。
120 | - 加上了门控状态:
121 | - 忘记:$z^f$ (f for forget),来控制上一个状态的$c^{t-1}$哪些留哪些忘
122 | - 选择记忆:$z^i$ (i for information),对$x^t$进行选择性的记忆。$z$作为输入
123 | - 输出:决定哪些将会被当成状态的输出,用$z^o$来进行控制,并且还对上一阶段得到的$c^0$进行了放缩。
124 |
125 | 
126 |
127 | 
128 |
129 | 
130 |
131 | 
132 |
133 | ## 什么是CNN?
134 |
135 | CNN / convolutional neural networks / 卷积神经网络:用kernel对输入进行局部的特征提取
136 |
137 | 与传统的神经网络相比,CNN更加适合处理图像和语音等高维数据。
138 |
139 | CNN是一种前向反馈神经网络,主要由卷积层、池化层和全连接层等组成。在卷积层中,CNN通过卷积核对输入数据进行卷积运算,从而提取特征。卷积核可以在不同的位置进行卷积运算,这样可以检测出输入数据中的不同特征。在池化层中,CNN通过对卷积层输出进行下采样,从而降低数据维度,同时也可以减小数据量,提高模型的训练速度。在全连接层中,CNN将池化层输出的特征映射到输出层中,完成分类或回归任务。
140 |
141 | ## 什么是MLP?
142 |
143 | MLP / multi-layer perception / 多层感知器:除了输入输出层还有隐层
144 |
145 | ## 什么是GLU?
146 |
147 | GLU / Gated Linear Unit / 门控线性单元:$GLU(x,W,V,b,c)=\sigma(xW+b)\otimes (xV+c)$,其中$\sigma$是Sigmoid函数,$\otimes$是矩阵逐点相乘,总的来说效果比ReLU好。
--------------------------------------------------------------------------------
/线性代数.md:
--------------------------------------------------------------------------------
1 | # 线性代数
2 |
3 | ## 线性空间
4 |
5 | 线性空间:定义了合法加法和数乘(加法和数乘满足相应8条规则)的非空集合。
6 |
7 | 线性相关:存在一组不全为零的标量(系数),使得向量之间的线性组合等于零向量
8 |
9 | 线性无关:不线性相关,当且仅当系数均为0时,线性组合才等于零向量。说明每个向量均独立,没有冗余信息
10 |
11 | 线性空间的维度:线性空间中最大线性无关组的大小
12 |
13 | 基:1. 线性无关 2. 线性空间中任意向量都可以用它们线性表出
14 |
15 | 线性子空间:
16 |
17 | - 定义:1. 线性空间的非空子集 2. 对线性空间中的加法和数乘也构成数域上的线性空间
18 | - 性质:交也是,和也是
19 |
20 | ## 高斯空间
21 |
22 |
23 |
24 | ## 矩阵
25 |
26 | ### 秩
27 |
28 | 矩阵的秩定义为矩阵中线性无关的行或列的最大数量,记作 $\text{rank}(A)$。
29 |
30 | 1. 反应矩阵的线性相关性
31 | 2. 矩阵的逆:满秩$\iff$可逆,即有唯一逆向量
32 |
33 | ### 矩阵分解的意义?
34 |
35 | 加速计算
36 |
37 | ### 奇异值分解
38 |
39 | 可以作用与长方矩阵上,同时包含了旋转、缩放和投影三种作用。
40 |
41 | #### 什么是奇异值分解?
42 |
43 | $A=U\Sigma V^\top$,其中$U,V$均为正交矩阵,$\Sigma$为对角矩阵,对角线上的值按从大到小排列。
44 |
45 | #### 条件?
46 |
47 | $AA^\top,A^\top A$可以被特征值分解。
48 |
49 | #### 如何计算?
50 |
51 | 1. 对$A^\top A$进行特征值分解,得到特征值和特征向量。将特征值按照从大到小的顺序排列,特征向量也相应排序。$A^\top A$特征向量构成的正交矩阵,得到$V$。
52 | 2. 对$AA^\top$同理,得到$U$
53 | 3. 两次计算中的非零特征值从大到小排序,放在对角线,其他位置零。
54 |
55 | #### 应用?
56 |
57 | ### 特征值分解
58 |
59 | #### 什么是特征值和特征向量?
60 |
61 |  62 |
63 | #### 条件?
64 |
65 | $|\lambda E-A|$有非零解,只有可对角化矩阵才可以作特征分解。
66 |
67 | #### 如何进行特征值分解?
68 |
69 | 特征值分解:指将对$n\times n$,且有$N$个线性无关的特征向量$q_i$的方阵$A$,将其分解为$A=Q\Lambda Q^{-1}$。其中$Q$为$n\times n$,第$i$列为$A$的特征向量$q_i$,$\Lambda$为对角矩阵,对角线上的元素是对应的特征值。
70 |
71 | 1. 首先求解特征方程,得到矩阵$A$特征值$\lambda _i$(共$n$个)
72 |
73 | 2. 再由$(\lambda_i E-A)x=0$求基础解系,即矩阵$A$属于特征值$\lambda_i$的线性无关的特征向量。
74 | 3. 用求得的特征值和特征向量构造$Q,\Lambda$
75 |
76 | ## 正定矩阵
77 |
78 | ### 正定
79 |
80 | #### 正定二次型
81 |
82 | ##### 定义
83 |
84 | 实二次型 $f(x_1,x_2,\cdots,x_n)$ 若对任意一组不全为零的实数 $c_1,c_2,\cdots,c_n$ 都有
85 |
86 | $$
87 | f(c_1,c_2,\cdots,c_n)>0
88 | $$
89 |
90 | 则称 $f$ 为**正定二次型**.
91 |
92 | 如, $f(x_1,x_2,\cdots,x_n)=\displaystyle\sum_{i=1}^nx_i^2$ 是正定二次型.
93 |
94 | 但, $f(x_1,x_2,\cdots,x_n)=\displaystyle\sum_{i=1}^{n-1}x_i^2$ 不是正定二次型.
95 |
96 |
97 | ##### 判定
98 |
99 | 1. 实二次型 $\boldsymbol{x}^\top A\boldsymbol{x}$ 正定 $\Leftrightarrow$ $\forall \boldsymbol{x}\in\mathbb{R}^n$, 若 $\boldsymbol{x}\neq 0$, 则 $\boldsymbol{x}^\top A\boldsymbol{x}>0$
100 | 2. 设实二次型 $f(x_1,x_2,\cdots,x_n)=d_1x_1^2+d_2x_2^2+\cdots+d_nx_n^2$, $f$ 正定 $\Leftrightarrow$ $d_i>0,i=1,2,\cdots,n$
101 | 3. 非退化线性替换不改变二次型的正定性
102 | 4. 设实二次型 $f(x_1,x_2,\cdots,x_n)$, $f$ 正定 $\Leftrightarrow$ $rank(f)=n=p$ ($f$ 的正惯性指数)
103 |
104 | 其中判定二的充分性显然, 必要性只需带入所有的单位向量即可证.
105 |
106 | #### 正定矩阵
107 |
108 | ##### 定义
109 |
110 | 一个$n\times n$的实对称矩阵$A$被称为正定,如果对于任何非零向量$x\in\mathbb R^n$,都满足$x^\top A x>0$
111 |
112 | ##### 判定
113 |
114 | 1. 实对称矩阵 $A$ 正定 $\Leftrightarrow$ $A$ 与单位矩阵 $E$ 合同
115 | 2. 实对称矩阵 $A$ 正定 $\Leftrightarrow$ 存在可逆矩阵 $C$, 使 $A=C^\top C$
116 |
117 | ##### 性质
118 |
119 | 1. $A^{-1}$ 是正定矩阵
120 | 2. $kA,(k>0)$ 是正定矩阵
121 | 3. $A$ 的伴随矩阵 $A^*$ 是正定矩阵
122 | 4. $A^m$ 是正定矩阵 (m 为任意整数)
123 | 5. 若 $B$ 也是正定矩阵, 则 $A+B$ 也是正定矩阵
124 |
125 | ##### 必要条件
126 |
127 | 1. 实对称矩阵 $A=(a_{ij})_{n\times n}$ 正定 $\Rightarrow$ $a_{ii}>0,i=1,2,\cdots,n$
128 | 2. 实对称矩阵 $A$ 正定 $\Rightarrow$ $\det A=|A|>0$
129 |
130 | ##### 定理
131 |
132 | 二次型 $f(x_1,x_2,\cdots,x_n)=x^\top Ax$ 正定 (或 $A>0$) 的充分必要条件是 $A$ 的各阶顺序主子式都大于零.
133 |
134 | 证明:
135 |
136 | $\Rightarrow$:
137 |
138 | 分别取 $\boldsymbol{c}=(c_1,c_2,\cdots ,c_k,0,\cdots,0)$, 带入可知 $f(x_1,x_2,\cdots,x_k)$ 也是正定二次型
139 |
140 | $\therefore |A_k|>0$
141 |
142 | $\Leftrightarrow$:
143 |
144 | 使用数学归纳法.
145 |
146 | $E=G'A_{n-1}G$, 转化为对称矩阵
147 |
148 | ### 半正定
149 |
150 | 
151 |
152 | #### 协方差矩阵是半正定的
153 |
154 |
62 |
63 | #### 条件?
64 |
65 | $|\lambda E-A|$有非零解,只有可对角化矩阵才可以作特征分解。
66 |
67 | #### 如何进行特征值分解?
68 |
69 | 特征值分解:指将对$n\times n$,且有$N$个线性无关的特征向量$q_i$的方阵$A$,将其分解为$A=Q\Lambda Q^{-1}$。其中$Q$为$n\times n$,第$i$列为$A$的特征向量$q_i$,$\Lambda$为对角矩阵,对角线上的元素是对应的特征值。
70 |
71 | 1. 首先求解特征方程,得到矩阵$A$特征值$\lambda _i$(共$n$个)
72 |
73 | 2. 再由$(\lambda_i E-A)x=0$求基础解系,即矩阵$A$属于特征值$\lambda_i$的线性无关的特征向量。
74 | 3. 用求得的特征值和特征向量构造$Q,\Lambda$
75 |
76 | ## 正定矩阵
77 |
78 | ### 正定
79 |
80 | #### 正定二次型
81 |
82 | ##### 定义
83 |
84 | 实二次型 $f(x_1,x_2,\cdots,x_n)$ 若对任意一组不全为零的实数 $c_1,c_2,\cdots,c_n$ 都有
85 |
86 | $$
87 | f(c_1,c_2,\cdots,c_n)>0
88 | $$
89 |
90 | 则称 $f$ 为**正定二次型**.
91 |
92 | 如, $f(x_1,x_2,\cdots,x_n)=\displaystyle\sum_{i=1}^nx_i^2$ 是正定二次型.
93 |
94 | 但, $f(x_1,x_2,\cdots,x_n)=\displaystyle\sum_{i=1}^{n-1}x_i^2$ 不是正定二次型.
95 |
96 |
97 | ##### 判定
98 |
99 | 1. 实二次型 $\boldsymbol{x}^\top A\boldsymbol{x}$ 正定 $\Leftrightarrow$ $\forall \boldsymbol{x}\in\mathbb{R}^n$, 若 $\boldsymbol{x}\neq 0$, 则 $\boldsymbol{x}^\top A\boldsymbol{x}>0$
100 | 2. 设实二次型 $f(x_1,x_2,\cdots,x_n)=d_1x_1^2+d_2x_2^2+\cdots+d_nx_n^2$, $f$ 正定 $\Leftrightarrow$ $d_i>0,i=1,2,\cdots,n$
101 | 3. 非退化线性替换不改变二次型的正定性
102 | 4. 设实二次型 $f(x_1,x_2,\cdots,x_n)$, $f$ 正定 $\Leftrightarrow$ $rank(f)=n=p$ ($f$ 的正惯性指数)
103 |
104 | 其中判定二的充分性显然, 必要性只需带入所有的单位向量即可证.
105 |
106 | #### 正定矩阵
107 |
108 | ##### 定义
109 |
110 | 一个$n\times n$的实对称矩阵$A$被称为正定,如果对于任何非零向量$x\in\mathbb R^n$,都满足$x^\top A x>0$
111 |
112 | ##### 判定
113 |
114 | 1. 实对称矩阵 $A$ 正定 $\Leftrightarrow$ $A$ 与单位矩阵 $E$ 合同
115 | 2. 实对称矩阵 $A$ 正定 $\Leftrightarrow$ 存在可逆矩阵 $C$, 使 $A=C^\top C$
116 |
117 | ##### 性质
118 |
119 | 1. $A^{-1}$ 是正定矩阵
120 | 2. $kA,(k>0)$ 是正定矩阵
121 | 3. $A$ 的伴随矩阵 $A^*$ 是正定矩阵
122 | 4. $A^m$ 是正定矩阵 (m 为任意整数)
123 | 5. 若 $B$ 也是正定矩阵, 则 $A+B$ 也是正定矩阵
124 |
125 | ##### 必要条件
126 |
127 | 1. 实对称矩阵 $A=(a_{ij})_{n\times n}$ 正定 $\Rightarrow$ $a_{ii}>0,i=1,2,\cdots,n$
128 | 2. 实对称矩阵 $A$ 正定 $\Rightarrow$ $\det A=|A|>0$
129 |
130 | ##### 定理
131 |
132 | 二次型 $f(x_1,x_2,\cdots,x_n)=x^\top Ax$ 正定 (或 $A>0$) 的充分必要条件是 $A$ 的各阶顺序主子式都大于零.
133 |
134 | 证明:
135 |
136 | $\Rightarrow$:
137 |
138 | 分别取 $\boldsymbol{c}=(c_1,c_2,\cdots ,c_k,0,\cdots,0)$, 带入可知 $f(x_1,x_2,\cdots,x_k)$ 也是正定二次型
139 |
140 | $\therefore |A_k|>0$
141 |
142 | $\Leftrightarrow$:
143 |
144 | 使用数学归纳法.
145 |
146 | $E=G'A_{n-1}G$, 转化为对称矩阵
147 |
148 | ### 半正定
149 |
150 | 
151 |
152 | #### 协方差矩阵是半正定的
153 |
154 |  155 |
156 |
--------------------------------------------------------------------------------
/英文.md:
--------------------------------------------------------------------------------
1 | ### Self-Introduction
2 |
3 | ### Why do you choose to study at our school?
4 |
5 | ### What do you expect to achieve during your study if you are enrolled into this institute?
6 |
7 | ### What is your plan in the postgraduate study?
8 |
9 | ### Do you have a career plan in 5 years?
10 |
11 | ### Tell me something about your undergraduate life.
12 |
13 | ### What is your favorite subject and why?
14 |
15 | ### What has been your greatest success/ accomplishment in campus life?
16 |
17 | ### What book have you recently read?
18 |
19 | ### What professional paper have you read before? What's the main idea of this text.
20 |
21 | ### Tell me something about your hometown.
22 |
23 | ### Tell me something about Nanjing.
24 |
25 | ### Can you tell me something about your family?
26 |
27 | ### What's your favorite hobby?
28 |
29 | ### Who is your favorite basketball player?
30 |
31 | ### Strength
32 |
33 | ### Weaknesses
34 |
35 | ### What kind of character do you think you have?
36 |
--------------------------------------------------------------------------------
/面经.md:
--------------------------------------------------------------------------------
1 | # NJUAI面经
2 |
3 | # 2019
4 |
5 | ## [南大lamda实验室失败面经分享_彩虹糖梦的博客](https://blog.csdn.net/caozixuan98724/article/details/100975163)
6 |
7 | 接着看论文的老师问我朴素贝叶斯决策相关的内容,朴素贝叶斯我还是会的,说了一下思想和公式。然后他问我,朴素贝叶斯是独立分布还是独立条件分布?我当时不知道是怎么的鬼使神差,答了个独立分布...只能说脑子瓦特了,那天状态真的特别差。后来知道老师问我这个问题的原因是我在论文中用了大量条件分布的东西。
8 |
9 | 最后是我觉得最奇怪的一个问题,老师问quick sort,我一下就来劲了,quick sort我熟啊,刚复习的。然后老师问我,快排为什么叫快排啊?我“?????”我弱弱的回答“因为它快啊...”。老师又问我“它是最快的吗?”我“不是啊,快排是nlogn,基数排序能到O(n)呢”。老师问“那基数排序有什么代价呢?”我说“它需要大量的空间啊,空间换时间”。然后我就楞那里了。老师“你还是没回答我的问题啊,快排为啥叫快排啊?”我“...”。
10 |
11 | 之前对于算法,重点去掌握了它的流程,它的代码,忽略了一些特别关键和基础的点,比如什么大数定律,条件分布,决策树一些更加深入的东西,没有记忆在心中。对自己的项目也没有深挖,还是要不断反思,这个项目的核心是啥,遇到了什么困难,有什么收获。
12 |
13 | # 2020
14 |
15 | ## [南大人工智能AI学院夏令营面试经历_Alvassss的博客](https://blog.csdn.net/Alvassss/article/details/107244024)
16 |
17 | ### 1.LAMDA
18 |
19 | 一轮:自我介绍 概率题 算法题 项目简介
20 | 二轮:自我介绍 你大学最满意的项目是什么 详细问
21 | 听说有三轮 但我没过第二轮
22 |
23 | ### 2.南大MCG
24 |
25 | 自我介绍 老师完全按照简历询问
26 |
27 | ### 3.南大笔试
28 |
29 | 重点:
30 | 1.线代+概率 线代主要是概念 概率主要是网上那些脑筋急转弯
31 | 2.机器学习 建议西瓜书前十章要精通
32 | 3.数据结构 考的巨多 建议精通
33 | 4.算法 时间复杂度分析 渐进 背包问题 摊还
34 | 非重点:
35 | 博弈论 各种变换(傅里叶啥的 俺没学过)
36 |
37 | ### 4.南大面试
38 |
39 | 英语面试:是学院的一个越南老师面试 比较亲切 但我心态崩了
40 | 三个问题:
41 | 1min自我介绍(超时会直接截止 不要问我为什么知道)
42 | 最喜欢的课程 why
43 | 最喜欢的机器学习算法
44 | 中文面试:
45 | 快速排序和归并排序优缺点 排序为什么要稳定
46 | P问题 NP问题 NP完全问题的概念
47 | 全概率公式意义
48 | 项目问题
49 |
50 | ## [南大人工智能学院夏令营经历记录_TheRebel_的博客](https://blog.csdn.net/Anonymity_/article/details/105407815?spm=1001.2101.3001.6650.1&utm_medium=distribute.pc_relevant.none-task-blog-2~default~CTRLIST~Rate-1-105407815-blog-107244024.235^v31^pc_relevant_default_base3&depth_1-utm_source=distribute.pc_relevant.none-task-blog-2~default~CTRLIST~Rate-1-105407815-blog-107244024.235^v31^pc_relevant_default_base3&utm_relevant_index=2)
51 |
52 | 面试问了我大概五道题,一道问排序算法,及时间复杂度。第二道问我svd是什么。第三道是关于我最喜欢的深度学习模型。第四道和第五道是围绕我的项目经历问的。然后计算机营和ai营机试:面试比好像不一样。另外,ai院报周志华和lamda组的很多,但其实lamda在这之前已经招过一次了,所以夏令营他们再招的名额可能会比较小。
53 |
54 | ## [【计算机保研夏令营】2020年LAMDA保研面试经验](https://zhuanlan.zhihu.com/p/237472334)
55 |
56 | ### 面试 6.18
57 |
58 | 大概在报名结束后一周收到了第一次面谈的邀请邮件,LAMDA都是提前一天发邮件,第二天直接面试。这时候还在期末考试阶段,比较紧张,也没准备啥,就对着简历花了一小时思考了下。第一轮我们组是10个人,按姓名拼音排序进行面试的,面试官是组里的三个学长,先进行自我介绍,之后主要问了我以下三个问题:
59 |
60 | > 详细介绍了下比赛(我参加过一个数据挖掘的比赛)的特征工程,之后又问了模型部分(介绍了下Xgboost)
61 | > 对机器学习的理解(这个感觉自己答得不是很好,说的有点绕进去了)
62 | > 对开放动态环境下机器学习的挑战和瓶颈的认识(这个后来我查过,是那个学长的博士课题,听DJW学长说这个也是LAMDA组里的一个大坑,ps. 这里大坑指大方向,不是说坑,有学弟问了才发现有人会误解emmm)
63 |
64 | 总的来说,这一轮面试比较愉快,主要了解一些基本情况吧,感觉这一轮没有刷人。
65 |
66 | ### 3. 第二轮面试 6.20
67 |
68 | 第一轮面试结束第二天就发下一轮通知了,询问D学长了解去年的流程后,也大概猜到了这一轮可能是群面,面之前学长还说遇到ZDC老师坐等聊爆,结果8:50进入腾讯会议,我傻眼了,一奶即中。
69 |
70 | 首先还是少不了自我介绍,介绍完之后Z老师就问我对博士期间的规划,这个问题之前思考过很久,也是一个保研期间的必问问题,由于我把规划从大四说起(大四如果保研顺利结束想先强化学习数学基础,说了凸优化、随机过程、矩阵分析之类的),也给后续埋了个坑——下一个问题他问我最喜欢哪门课,我以为他想问上面三门,就问了句是不是本科阶段,被WW老师说难道你还有研究生阶段吗,有点尴尬。我作死的说了数据结构(但我确实真的很喜欢数据结构,其他课也没准备,想着数据结构学的还行就说了),但直接问我红黑树了,我有点傻眼了,老实说自己不会,只知道STL有些底层是红黑树实现的(有时间还是得看下红黑树,至少得了解思想)。
71 |
72 | 之后就是一连串的问题,先问了归并和快排的平均、最优、最坏复杂度,这个准备实习面试时都梳理过,都答出来了。然后接着这个问题问,既然归并的最坏也是O(nlogn),而快排最坏O(n^2),为啥现在大家都用的是快排。我只从空间复杂度进行了分析,后来面完查了下,其实实践证明,虽然二者时间复杂度相同,但快排还是要快一些,而且最坏情况遇到的可能性也比较低。之后问的应该是如何判断图中是否有环,我刚嘴里小声复述想思考下,老师就直接问下一个问题了,这里感觉这一轮应该就是压力面。
73 |
74 | 下一个问题问的是比赛,让我介绍Xgboost的优势,这个实习面试也复习过,答得还可以。接下来WW老师问我本科学校是985吗?是211吗?是双一流吗?一波三连搞得我有点尴尬,我校果然在南方知名度还是不行。
75 |
76 | 最后Z老师又问你本科北京的学校为啥想来南京,说以前很多北京的同学拿了offer又鸽了。这个问题就有的聊了,因为我本身是江苏人,高中物理竞赛又在南大两个校区住过一段时间,挺喜欢南大的,南大也算是高中dream school之一了,然后就是LAMDA很强哈哈哈哈。
77 |
78 | 总结一下,这一轮面试节奏很快,可能也是面试过程中比较兴奋,我整体回答问题几乎没有思考,没有用到10分钟应该。这一轮面试应该刷了一半人左右。
79 |
80 | ### 4. 第三轮面试 6.22
81 |
82 | 这一轮面试一直到6.21晚9点才通知,大部分人收到的邮件都写明了是哪个老师面试,根据这两轮小组面试人数的猜测,可能第二轮刷了有一半人,但不确定,也可能是分批。我的邮件没有写明老师,我第一志愿是JY老师,但听D学长说J老师学生有部分也都是Z老师带,所以猜测可能会使Z老师面。D学长给我看了他去年整理的面试经历,大概了解了一些情况以及基本问题。这时候由于已经期末考完了,但也没想到面试这么突然,也来不及准备太多,就稍微过了下线代和概率论的一些基本概念,理解了一下,然后准备了一下简历。
83 |
84 | 最终面我的还是J老师。第一个环节还是自我介绍,介绍完之后老师开始问“以后的规划”、“家庭背景”、“家人对自己的规划”等等,接下来又问了“简历中的数据挖掘比赛主要负责的内容以及收获”、“本科科研项目最大的收获”等问题,都很友好,聊了大概20多分钟。
85 |
86 | # 2021
87 |
88 | ## [2021年人工智能保研经历(xduee->njuai)](https://zhuanlan.zhihu.com/p/420184627)
89 |
90 | 人工智能学院的笔试主要考人工智能+计算机的基础知识。笔试用考试星机考的方式,考试时长2小时,大概我记得200道题目左右,应该是比2020年的笔试少了50道题目左右,题目难度适中,因为难题我全刚开始跳了,我差不多连猜带蒙在最后差10min的时候完成了所有题目。南大学院笔试的考核真的很重要很重要,属于超强committee,即使你提前被周老师录了,笔试没过也是没用的。
91 |
92 | 参营时间线的话,是2021.7.8举行笔试,然后7.11周日上午(当时正在看美洲杯决赛,印象深刻)出了笔试的结果,应该是进60%~70%左右的人。笔试结果出了后,就会让你选择学硕or直博。南大一般在这个时候才会让你选择学硕和直博,刚开始报名的选择只是预选择。下面就是面试,7.13一整天是学硕面试,7.14上午是直博生面试,直博面试应该有22人,录了多少我也不是很清楚,下面说说面试情况。
93 |
94 | 线上面试还是采用的腾讯会议,每人12min,4min英语问答+8min专业知识。我那组的面试官有4人,面试可以说是相当友好了,英语问答包含自我介绍,以及一些关于我科研的提问,还有一些闲聊,英语这部分总体来说不难,敢于去说就行。专业知识部分,主要还是在问机器学习+线性代数的相关知识,我感觉我个人准备的比较充分,所有问题都回答出来了,除了最后詹老师的一个关于编码的问题回答的不太行。
95 |
96 | 关于机器学习面试的问题可以参考我另一篇经验贴:**[计算机/人工智能方向保研高频面试题目整理](https://zhuanlan.zhihu.com/p/394374473)** ,这篇经验贴我应该概括的比较全面了。
97 |
98 | ### [计算机/人工智能方向保研高频面试题目整理](https://zhuanlan.zhihu.com/p/394374473)
99 |
100 | ### **1. 开放型问题**
101 |
102 | 开放型问题建议中英文都准备,大部分面试都有这个环节。
103 |
104 | - 自我介绍(1min/3min)
105 | - 研究生期间的规划
106 | - 参与的竞赛(数模等等),你做了哪儿些工作?
107 | - 简单介绍下你的科研工作
108 | - 对机器学习/深度学习的理解
109 | - 开放动态环境下机器学习的认识(来自南大某著名实验室)
110 |
111 | ### **2. 数学类**
112 |
113 | 数学类问题是ai方向保研面试问的最多的,主要是线代、概率论。
114 |
115 | - 线代:如何理解矩阵的秩?简述向量组线性无关的含义?解释正定矩阵以及半正定矩阵?特征值的含义以及矩阵分解的物理意义?
116 | - 概率论:简述大数定理,中心极限定理,全概率公式,最大似然估计,贝叶斯的含义
117 | - P问题 NP问题 NP完全问题的概念
118 |
119 | ### **3. 机器学习类**
120 |
121 | - 简述PCA的计算过程
122 | - 简述SVM,并解释SVM为什么要化对偶形?百万样本量可以用SVM吗?
123 | - 常用的机器学习算法的适用场景(例如KNN、朴素贝叶斯、决策树等)
124 | - 具体阐述残差神经网络的含义
125 | - 梯度消失和梯度爆炸是什么意思?有什么样的方法进行改善?
126 | - 简述几种集成学习方法Adaboost的计算过程以及Stacking Learning?
127 |
128 | ### **4. 数据结构与算法类**
129 |
130 | - 常用排序平均最优最坏时间复杂度以及空间复杂度,阐述快排和归并的优缺点以及回答为什么排序要稳定?
131 | - 归并排序的最坏时间复杂度优于快排,为什么我们还是选择快排?
132 | - TopK问题详解
133 | - 如何判断图里有环?
134 | - C++中new和malloc的区别
135 |
136 | ## [2021年一战南大AI上岸经验贴_Yuhan の Blog的博客](https://blog.csdn.net/qq_45228537/article/details/115448786)
137 |
138 | ### 复试笔试
139 |
140 | 南大AI的复试笔试是离散数学+机器学习;我是3月开学回学校才开始准备,这里建议早点准备离散,离散东西很多概念很杂而且考的也很难,所以我今年离散笔试应该基本没拿到分orz;今年的机器学习也不知道在搞什么,无语子,写着机器学习的label考了20道数据结构的选择题+一道不知道属于啥学科的问答,不过该准备的还是要准备的。
141 | 离散建议找一下南大本科的PPT,有重点地对着屈书进行复习;复试的机器学习建议细看一下,部分重点的数学推导要会(例如SVM的拉格朗日乘子法、KKT条件、PCA特征值分解),概念要十分清晰,即使复试没有考察到,面试老师也会问许多机器学习的相关知识。
142 |
143 | ### 复试机试
144 |
145 | 今年情况特殊,是线上复试,因此今年的机试是和笔试在一起考的,但我想,随着疫情逐渐得到有效控制+全民疫苗接种,今后应该会继续采用线下机试的方法。
146 | 个人本科练习过半年左右的OJ,因此有一点薄弱的基础,因此就是在考前临时复习了一下黄宇书上的4道DP例题+一些常见的DP题(01背包、完全背包、LCS、多重部分和问题、LIS、DP计数等等)+一些常用的数据结构和算法(例如并查集、kruskal、dijkstra、快速幂、素数筛、线段数、树状数组等等)。
147 | 对于南大的机试,我觉得重点是DP、搜索、图论。
148 |
149 | ### 复试面试
150 |
151 | 面试个人认为可以拆分成英语口语+线代+概率论+机器学习+项目经验+一些其它知识储备。
152 | 口语问了我这些问题:
153 |
154 | 1.本科所学专业
155 | 2.毕业后打算
156 | 3.兴趣爱好
157 | 4.介绍喜欢的电影
158 | 5.介绍最近读的一本书
159 |
160 | 面试:
161 |
162 | 1.你说你因为喜欢数据结构和算法才选择读AI,介绍一下它们的交集
163 | 2.本科有没有做过AI相关的项目
164 | 3.SVM为什么要采用对偶问题?(我答:虽然可以通过现成凸优化包求解,但是对偶问题求解更快)
165 | 4.为什么更快?(接4中我的回答内容
166 | 5.Boosting学习有什么特点?
167 | 6.为什么集成学习需要集成“好而不同”的学习器?(接5中我的回答内容
168 | 7.解释一下特征值的含义
169 | 8.简述一下特征值分解
170 | 9.为什么要选取前d大个特征值(接8中我的回答内容
171 | 10.你本科是软工的,问一下面向过程、面向对象、面向抽象的区别
172 | 11.具体介绍一下你学过的面向对象知识&应用
173 | 12.你觉得你本科所学的知识在将来读AI的时候会有哪些应用
174 |
175 | ### [南京大学LAMDA面经汇总_51CTO博客](https://blog.51cto.com/u_12312066/3695982)
176 |
177 | 面试吴建鑫老师的时候,问题如下:
178 |
179 | 方差的计算方法,他会提前写好一个方差表达式问你对不对,如果不对的话请写出正确的表达式;
180 | 方差中的n-1含义;
181 | 如果写一个程序计算方差,那么计算一次内存访问几次;
182 | 本科做过的项目,项目内容;
183 | 机器学习了解多少,看过什么;
184 | 了不了解本人是做什么研究的。
185 | 面试詹德川老师的时候,我不知道其他人是什么情况,但我是全程英文面试,问到的问题如下,注意:以下问题需要英文作答,实在英语回答不了,可以中文,不必有太大压力:
186 |
187 | 自我介绍一下;
188 | 介绍一下做过的项目;
189 | 介绍一下梯度下降法是什么;
190 | 介绍一下牛顿迭代是什么;
191 | 什么是特征值,特征值的含义;
192 | 唠嗑。
193 | 面试完当天晚上就会有邮件通知是否面试通过,最后我是被詹德川老师录取,但是通过LAMDA面试并不代表你就能100%能进入LAMDA读研了,最重要的一关是拿到南大夏令营的优秀营员,只有这样,通过两轮考核才能进入LAMDA。
194 |
195 | 下面说一下南大夏令营的流程,主要是三部分:各个实验室介绍、机试、面试,其中最最重要的是机试,只要机试通过,90%就能拿到优秀营员。
196 |
197 | 机试这次一共4道题,以前听说6道题,只要AC出其中的两道题就肯定没问题了,多做无用,有罚时,考核方式:OJ,题型:算法+数据结构,难度:ACM一般难度的题。这次的具体题目如下:
198 |
199 | 最大子串和;
200 | 无向图最长路径
201 | 表达式求值;
202 | 给一棵树求最长的路径。
203 | 面试问题如下(由于分组面试,每组没人问题不一样):
204 |
205 | 解释一下什么是时间复杂度;
206 | 快排的时间复杂度;
207 | 快排最坏时间复杂度为什么是$O(n^2)$,如何优化快排最坏时间复杂度;
208 | 看成绩单,问如何进行文献检索
209 | 英文回答:如何利用文献检索知识去检索一个机器学习的问题
210 |
211 | 就问了一个“ε-greedy”算法中ε取值的问题
212 |
213 | 然后问了离散的全序,偏序,操作系统,计算机组成原理内存啥的,还有居然问了软件工程的问题,真是醉了,那个时候软件工程都还没有学完。(黑人问号脸)然后,英文是让我介绍最喜欢的歌曲。
214 |
215 | 南大进行了一场霸面(不推荐,还是提早申请比较好)。
216 |
217 | 1.快排复杂度是多少,并且黑板上手写证明。
218 |
219 | 2.简述如何“快速选到第n个数”(快速选择,复杂度为O(n))。
220 |
221 | 3.讲简历上的项目,根据简历问
222 |
223 | 有无申请lamda都需要参加下面两场考试:
224 |
225 | 机试(两个小时,四选二,一般两道都做出来能入选):
226 |
227 | 1、连续最长子序列和(给了一堆正负的数字,任选其中一段连续的数字(可以全选),需要和最大)
228 |
229 | 2、无向图最长路径(单纯的Dijkstra)
230 |
231 | 3、给一个表达式,例如 (3*2+1/2)+1*2,计算结果
232 |
233 | 4、给了一棵树求最长的路径(根到叶节点)
234 |
235 | 面试:
236 |
237 | 1、英文自我介绍
238 |
239 | 2、按照不同专业方向问专业课程
240 |
241 | 3、大数定理、贝叶斯公式等
242 |
243 | 4、操作系统线程跟进程的区别等(操作系统的问题比较爱问)
244 |
245 | ## [2021年计算机保研(清深、南大AI、中科大、哈深、中山等)](https://zhuanlan.zhihu.com/p/416191365)
246 |
247 | ### 学院
248 |
249 | 考核方式:初审(985前5%) + 笔试 (机器学习、概率论、线性代数、数据结构等)+ 面试(机器学习、数学)
250 |
251 | 笔试:2小时做200多道填空和选择,其内容涵盖机器学习、概率论、线性代数、数据结构等。对于概率论和线性代数,建议耗时两三天刷完李永乐660,刷完就没问题。对于机器学习,建议把西瓜书前十章过一遍,主要是看概念即可。对于408,可以选择不看,考的不多。
252 |
253 | 面试:英语问答 + 专业知识考察。英语问答就准备好常见的英语问题,以及和你简历相关的英语问题即可。至于专业知识,就是考察机器学习和数学,建议把西瓜书或李航统计学细读并理解,数学建议把概率论和线代细读并理解。
254 |
255 | 总结:由于当时概率论和线代复习的不好,导致数学问题只答出一半,进入wl。要想过南大AI,没有别的秘诀!把线性代数、概率论、机器学习从头啃到位即可!
256 |
257 | # 2022
258 |
259 | ## [Kaslanarian/NJUAI-OpenDay-Interview: 南京大学人工智能学院本科生开放日面试经验分享 ](https://github.com/Kaslanarian/NJUAI-OpenDay-Interview)
260 |
261 | ### 同学A(同组)的面试问题
262 |
263 | 面试那天和我在一个房间,而且在我前面面,所以记录了所有的问题:
264 |
265 | - 英语面试:
266 | 1. 1分钟自我介绍;
267 | 2. 从事的研究细节(因为自我介绍中提及);
268 | 3. 你最感兴趣的课程;
269 | 4. 你以后是想留在学校做研究还是去公司工作。
270 | - 中文面试:
271 | 1. 大数定律是什么?
272 | 2. 中心极限定理是什么?
273 | 3. 讲一个你知道的聚类算法?
274 | 4. 你平时有什么放松方式?
275 | 5. Boosting的基本思想?
276 | 6. PCA的全称是什么?
277 | 7. PAC理论的全称是什么?
278 | 8. 欧拉图是什么?
279 | 9. 正定矩阵是什么?
280 | 10. 极大似然估计是什么?
281 | 11. SVM为什么叫支持向量机?
282 |
283 | 注意,上述问题只是前置问题,你说不会才会换问题,否则就会继续问。比如同学A说他不记得欧拉图了,然后对面就换下一个问题;面试到我的时候又问了这个问题,我答出了欧拉图定义,后面就问我判定方法了。
284 |
285 | ### 我的面试
286 |
287 | - 英语面试:
288 |
289 | - 1分钟自我介绍;
290 | - 介绍一下你参加的比赛(起因于我的腾讯会议背景是我上次参加的某比赛,然后忘了换😢,反过来想这也是一种思路,让面试官问出你想让他问的问题😄);
291 | - 以后的安排(类似于同学A的问题)。
292 |
293 | - 中文面试:
294 |
295 | - 大数定律是什么?(看我倒背如流就没问中心极限定理了)
296 |
297 | - 计算复杂度(P和NP),P=NP吗?
298 |
299 | - 遇到压力怎么放松?
300 |
301 | - 最喜欢的课程?
302 |
303 | - 介绍PCA;
304 |
305 | - 为什么机器学习中的基本假设是独立同分布,独立同分布全称是什么?(这个地方卡了,对面嫌我说多了)
306 |
307 | - 什么是欧拉图,如何判定欧拉图?(忘记了,只说记得存在一个充要条件)
308 |
309 | - 正定矩阵是什么,如何判定?
310 |
311 | > 跟面试官(王魏)怼了,他一直说我和书上的定义不一样,但我讲的是一个逻辑等价命题,他就说我不好好看书,弄得心态挺不好。幸好他是最后一个问问题的老师。
312 | >
313 | > 后来发现和我一组的同学都对他有意见的,比如同学B说他不会欧拉图,然后被他锐评:**你是不是没上过数学课?**
314 | >
315 | > 问同学C的时候,C回答不出来就咂嘴,问答少了就说”**这么不熟悉吗**“...
316 | >
317 | > 注:以上内容是节选,如果看的人多了就把老师名字给码了。感觉他是根据被面试者的态度进行反馈,比如我、B和C在面试的时候展现出自信,所以他很打压;A面试的时候很严肃,遇到不会的问题会说“对不起,我回去再看一下”,所以没咋刁难。反正看到的同学留个心眼吧。
318 |
319 | - 快速排序的平均时间复杂度,最坏时间复杂度,最坏情况是什么样?
320 |
321 | ### 本组其他同学的问题
322 |
323 | - 计算复杂度,但问的是:如果把时间换成空间,那么P=NP吗?
324 | - PAC理论了解多少?
325 | - TBD
326 |
327 | ### 其他组的问题
328 |
329 | 这里记录其他组同学那里听来的问题:
330 |
331 | - 喜欢的数学课?如果说了微积分这块,而不是AI相关,则会问:
332 | - 中值定理是什么?
333 | - 泰勒展开是什么?
334 | - 高阶无穷小是什么?
335 | - 傅里叶变换和拉普拉斯变换的关系?
336 | - 拉普拉斯变换的用处?
337 | - 双蛋问题,但是单蛋版,也就是你只有一个鸡蛋如何判定其不摔碎的最高楼层?
338 | - TBD
339 |
340 | ## [2022年/2023届预推免小记(科大6系&NJUAI)](https://zhuanlan.zhihu.com/p/570734028)
341 |
342 | NJUAI:
343 |
344 | 笔试:2h(记不太清了),题量很小,选择+问答
345 |
346 | 面试:英文自我介绍+英文专业问题+专业问题,南大是步步紧逼型面试,感觉问了不止十个问题。
347 |
348 | 比较迷惑的一点是面试是定死了12min/人,结果还剩20s的时候老师又问了一个问题,我刚说两句就直接结束了,这种情况主持人不应该提醒一下快到时间了吗(汗)
349 |
350 | ## [2022年(2023届)计算机保研——计算所vipl、南大lamda、北大计算机、人大高瓴等](https://zhuanlan.zhihu.com/p/570001872)
351 |
352 |
353 |
354 | 看了一些经验帖说,南大LAMDA比北大信科还难,有很多LAMDA面试没过的最后去了北大信科,所以我当初报名没报什么信心,找了一位和自己研究经历比较match的老师,就去参加了。
355 |
356 | 首先是初筛,985的5%应该都能过初筛,除此之外我觉得研究方向的match程度非常重要。
357 |
358 | 一面是学长面,先是一分钟自我介绍,然后就是基本的简历面,问了paper以及剩下几个科研项目做的是什么和创新点,差不多就结束了,没有问任何专业知识相关的问题。
359 |
360 | 二面是老师面,问题大概有:
361 |
362 | 1. 一分钟自我介绍
363 | 2. paper里我主要做的内容
364 | 3. AI for SE领域有什么地方还可以去尝试?
365 | 4. 最拿得出手的项目是什么
366 | 5. 遇到的挫折是什么
367 | 6. 你觉得图神经网络做代码生成目前的优点和缺点是什么?有什么改进的地方?
368 | 7. 有没有做过词法分析器和语法分析器
369 | 8. 智力问题,黑白帽子问题(可自行百度)
370 | 9. 剩下就是一些聊天性问题,比如如果离交稿ddl还剩两天,但是你的实验还有很大漏洞,论文也还没写完,这种情况怎么办;了解了我的家乡以及为什么想来南京等
371 |
372 | 最后获得了实验室的offer,我个人感觉成功的原因是 1. 由于方向match,所以了解比较深入,中间考察的一些对该领域科研的相关看法时回答的还不错;2. 正好问到了我之前思考过的比较有意思的idea,所以和老师聊的很愉快。
373 |
374 | 但是!只拿到实验室的offer还没结束,还需要通过南大AI学院的考核,于是就有了绿裙里通过实验室考核没通过学院考核的难兄难弟们(后来发现这些难兄难弟里有人去了贵系,只想说南大AI真牛)
375 |
376 | AI院笔试:题量很大,考察范围覆盖数据结构、机器学习(西瓜书)、概率论、线性代数、英语等,如果目标南大AI的建议提前好好复习一下。不要像我一样,“怎么还有过了LAMDA没过学院的” “小丑竟是我自己”
377 |
378 | 另:夏令营笔试寄了就彻底寄了,也没办法报名预推免了。
379 |
380 | ## [2022南京大学人工智能学院本科生开放日小记【保研向】](https://zhuanlan.zhihu.com/p/543677717)
381 |
382 | 夏令营笔试是双机位,考试星作答。去年是两百道选择题和填空题两个小时,今年则是66道选择题,20多道填空题,若干多选题,英文题以及简答题,一共一个半小时。考察的科目和去年倒是差不多,这点知乎上也是有人写的,机器学习、概率论、线性代数、数据结构与算法,都是需要复习的。因为是线上考试所以不会有太多复杂的计算,更多考察知识的广度与细节部分,也就是看书复习的时候各种细节都应该注意。我根据前面大佬的建议也用了几天刷了李永乐660的线代和概统部分,感觉还是有不少帮助的。经过我们的讨论,感觉AI营的重点是笔试而非面试。
383 |
384 | 面试也是双机位,腾讯会议面试。以往都是20分钟一个人,今年估计是报名人数比较多,所以改为了12分钟一个人。还是4个老师分别问不同学科的问题。我这里大概记了一下面试的问题(不同的组面试题差别还是挺大的)
385 |
386 | C:你研究生读完之后有什么打算?你有什么做研究的品质?(英文面试,有概率让你用英文自我介绍,也有可能没有)
387 |
388 | 詹:常微分方程f'(x) = cx的解的形式,如果c是常数,为什么形式,如果c为矩阵呢?霍夫曼编码的优势,霍夫曼编码的唯一性,香农编码是什么?
389 |
390 | 张:半正定矩阵的定义,性质(越多越好),PCA协方差矩阵的性质(半正定),以及为什么半正定(从原理上说明)?凸优化中梯度下降的学习率如何确定?(凸优化最后两课讲的)
391 |
392 | 姜:散列表的优势(相比其他查询方式),查询复杂度(分链表型和普通型)。研究生的“研究”二字是什么含义?研究生相比本科生有什么区别?
393 |
394 | 其他同学有问图灵机的,凸优化带约束的一阶条件的,中心极限定理,机器学习很多算法为什么要iid条件,SVM核函数的考察等等,比较广泛,只看西瓜书显然是不够的,还需要一些自己的思考和积累。
395 |
396 | 总体来说感觉面试是不断往深去问,老师会追问你问题的本质,直到不会为止。因此面试完成后问了一圈感觉都不是特别好,这也是正常现象。面试完之后就是漫长的几天等待时间。
397 |
398 | 7.11线上导师宣讲会,7.13开放日线上面试。
399 |
400 | ## [2023CS保研经验分享(清深、上交、南大LAMDA、同济、东南Palm等) - 知乎 (zhihu.com)](https://zhuanlan.zhihu.com/p/570722079)
401 |
402 | 第一轮面试主要是实验室的学长学姐进行,主要围绕就是一些理论知识和你自我介绍的项目中所涉及的一些问题。
403 |
404 | 项目的问题没啥共同性,我就列举一些印象中的常见问题:
405 |
406 | - 机器学习中FP、TP是什么?
407 | - 你为啥想要读直博?
408 | - 线代中的矩阵的秩和矩阵的关系?
409 | - 讲一讲线代中的矩阵的特征值?
410 | - ......
411 |
412 | 第二轮面试是意向导师单独面(我是这样的),L老师只是来聊了聊天,聊一下我想研究的方向和家是哪里的,为什么要来南大等等一些非学术问题,最后说因为直博已经确定了人选,只能给我学硕offer了。
413 |
414 | - 题量:应该是100道差不多,时长90分钟。
415 |
416 | - 题型:单选题、多选题、填空题、英文问答题。
417 |
418 | - 考察内容:
419 |
420 | - - 线性代数(有复杂计算,我遇到了张宇考研数学的原题)
421 | - 概率论(有奇怪的伤脑筋的题,得多练)
422 | - 数据结构(重点,有考察排序算法、链表)
423 | - 机器学习(把西瓜书看看就行,考的都是知识点,概念性的东西)
424 | - 印象中没有计组计网操作系统
425 |
426 |
--------------------------------------------------------------------------------
/面经(分类).md:
--------------------------------------------------------------------------------
1 | # 面经(分类整理)
2 |
3 | 笔试+上机(最关键,笔试过不掉救不了)
4 |
5 | - 100分笔试,机器学习,模式识别,数据结构与算法,知识推理(zyz,英文题,要看一下),人工智能,概率统计(简答题,其他是选择填空)
6 | - 50分编程题,什么方向不知道,应该和机器学习和算法相关。
7 | - 月底组内,积累点经验,问一下学长,口语是怎么样的。
8 | - 本校有一定的优势,尽可能做好,题量不少,做不对略过即可,不要纠结。
9 |
10 | ## 概率论
11 |
12 | - 大数定理
13 | - 中心极限定理
14 | - 全概率公式
15 | - 最大似然估计
16 | - 贝叶斯公式:接着看论文的老师问我朴素贝叶斯决策相关的内容,朴素贝叶斯我还是会的,说了一下思想和公式。然后他问我,朴素贝叶斯是独立分布还是独立条件分布?我当时不知道是怎么的鬼使神差,答了个独立分布...只能说脑子瓦特了,那天状态真的特别差。后来知道老师问我这个问题的原因是我在论文中用了大量条件分布的东西。
17 | - 网上那些脑筋急转弯
18 | - 独立同分布:为什么机器学习中的基本假设是独立同分布,独立同分布全称是什么?(这个地方卡了,对面嫌我说多了)
19 |
20 | ## 机器学习
21 |
22 | 西瓜书前十章精通
23 |
24 | - 对机器学习/深度学习的理解
25 | - 开放动态环境下机器学习的认识(来自南大某著名实验室)
26 | - PCA:简述PCA的计算过程,PCA的全称是什么
27 | - SVM:简述SVM,并解释SVM为什么要化对偶形?百万样本量可以用SVM吗?(我答:虽然可以通过现成凸优化包求解,但是对偶问题求解更快)为什么更快?
28 | - 讲一个你知道的聚类算法?
29 | - 集成学习:简述几种集成学习方法,Adaboost的计算过程,以及Stacking Learning?Boosting的基本思想?Boosting学习有什么特点?为什么集成学习需要集成“好而不同”的学习器?介绍Xgboost的优势
30 | - 常用的机器学习算法的适用场景(例如KNN、朴素贝叶斯、决策树等)
31 | - PAC理论:PAC理论的全称是什么?PAC理论了解多少?
32 | - 具体阐述残差神经网络的含义
33 | - 梯度消失和梯度爆炸是什么意思?有什么样的方法进行改善?
34 | - 介绍一下梯度下降法是什么
35 | - 介绍一下牛顿迭代是什么
36 | - 为什么机器学习中的基本假设是独立同分布,独立同分布全称是什么?(这个地方卡了,对面嫌我说多了)
37 | - $ \epsilon $ -greedy:就问了一个“ε-greedy”算法中ε取值的问题
38 | - 决策树一些更加深入的东西
39 | - 机器学习中FP、TP是什么?
40 |
41 | ## 数据结构与算法
42 |
43 | - 数据结构 考的巨多 建议精通
44 | - 时间复杂度分析
45 | - 渐进
46 | - 动态规划:背包问题
47 | - 摊还
48 | - 排序:
49 |
50 | - 排序:算法,平均最优最坏时间复杂度以及空间复杂度。黑板上手写证明。排序为什么要稳定。
51 | - 快排:平均、最优、最坏复杂度。最坏情况是什么样?优缺点。
52 | - 归并:平均最优最坏时间复杂度以及空间复杂度,优缺点。
53 | - 既然归并的最坏也是 $ O(n\log n) $ ,而快排最坏 $ O(n^2) $ ,为啥现在大家都用的是快排。(我只从空间复杂度进行了分析,后来面完查了下,其实实践证明,虽然二者时间复杂度相同,但快排还是要快一些,而且最坏情况遇到的可能性也比较低。)
54 | - P问题 NP问题 NP完全问题的概念
55 | - 直接问我红黑树了,我有点傻眼了,老实说自己不会,只知道STL有些底层是红黑树实现的(有时间还是得看下红黑树,至少得了解思想)
56 | - 图
57 |
58 | - 如何判断图中是否有环
59 | - 欧拉图是什么?判定方法?
60 | - TopK问题详解,“快速选到第n个数”(快速选择,复杂度为 $ O(n) $ )
61 | - C++中new和malloc的区别
62 | - 双蛋问题,但是单蛋版,也就是你只有一个鸡蛋如何判定其不摔碎的最高楼层?
63 | - 智力问题,黑白帽子问题(可自行百度)
64 | - 霍夫曼编码的优势,霍夫曼编码的唯一性,香农编码是什么?
65 | - 散列表的优势(相比其他查询方式),查询复杂度(分链表型和普通型)
66 |
67 | ## 线代
68 |
69 | - svd(奇异值分解)
70 | - 讲一讲线代中的矩阵的特征值?什么是特征值,特征值的含义,特征值分解
71 | - 正定矩阵是什么?
72 | - 如何理解矩阵的秩?线代中的矩阵的秩和矩阵的关系?
73 | - 简述向量组线性无关的含义?
74 | - 矩阵分解的物理意义?
75 | - 半正定矩阵的定义,性质(越多越好),PCA协方差矩阵的性质(半正定),以及为什么半正定(从原理上说明)?
76 |
77 | ## 凸优化
78 |
79 | - 凸优化带约束的一阶条件
80 | - 凸优化中梯度下降的学习率如何确定?(凸优化最后两课讲的)
81 |
82 | ## 操作系统
83 |
84 | - 操作系统线程跟进程的区别等(操作系统的问题比较爱问)
85 |
86 | ## 数学分析
87 |
88 | - 常微分方程f'(x) = cx的解的形式,如果c是常数,为什么形式,如果c为矩阵呢? $ \frac12x^\top Cx $
89 | - 傅里叶变换和拉普拉斯变换的关系?拉普拉斯变换的用处?
90 |
91 | ## 其他
92 |
93 | - 一分钟自我介绍,遇到的挫折是什么
94 | - 研究生的“研究”二字是什么含义?研究生相比本科生有什么区别?
95 | - 比如如果离交稿ddl还剩两天,但是你的实验还有很大漏洞,论文也还没写完,这种情况怎么办
96 | - 英文面试
97 | - 1分钟自我介绍
98 | - 从事的研究细节(因为自我介绍中提及)
99 | - 你最感兴趣的课程
100 | - 你以后是想留在学校做研究还是去公司工作。
101 | - 如何利用文献检索知识去检索一个机器学习的问题
102 | - 你研究生读完之后有什么打算?你有什么做研究的品质?
103 |
104 | ## 机试
105 |
106 | - 最大子串和(给了一堆正负的数字,任选其中一段连续的数字(可以全选),需要和最大);无向图最长路径(单纯的Dijkstra);表达式求值(例如 (3\*2+1/2)+1\*2,计算结果);给一棵树求最长的路径(根到叶节点)。
107 | - 南大的机试,我觉得重点是DP、搜索、图论
108 |
109 | ## 笔试
110 |
111 | - 题量:应该是100道差不多,时长90分钟。
112 | - 题型:单选题、多选题、填空题、英文问答题。
113 | - 考察内容:
114 | - 线性代数(有复杂计算,我遇到了张宇考研数学的原题)
115 |
116 | - 概率论(有奇怪的伤脑筋的题,得多练)
117 | - 数据结构(重点,有考察排序算法、链表)
118 | - 机器学习(把西瓜书看看就行,考的都是知识点,概念性的东西)
119 | - 印象中没有计组计网操作系统
120 |
121 | 1. 可靠性(Soundness):在命题逻辑中,可靠性是指逻辑系统的一个属性,表示该系统中的推理规则是正确的。如果一个逻辑系统是健全的,那么任何从该系统的有效前提推导出的结论都是真的。换句话说,如果一个论证是健全的,那么它不会导致从假前提推出真结论的情况。
122 | 2. 完备性(Completeness):在命题逻辑中,完备性是指逻辑系统的另一个属性,表示该系统中的每个真陈述都可以在该系统中被证明为真。换句话说,如果一个逻辑系统是完备的,那么对于任何为真的陈述,系统中存在一个证明或推理来证明它的真实性。
123 |
--------------------------------------------------------------------------------
/面试.md:
--------------------------------------------------------------------------------
1 | ### 机器学习
2 |
3 | - 机器学习:基于统计、数据驱动,不是基于演绎而是基于归纳的。可以解决规则难以解决的问题;深度学习:使用更深的网络结果增强表达能力,将特征提取和模式学习相结合
4 | - 梯度下降法:一种常用的优化算法,用于最小化目标函数。计算过程是迭代地向梯度下降最快的方向更新参数,新参数=旧参数-学习率$\times$梯度。
5 | - 条件:目标函数可导,凸;优点:应用范围广,简单;缺点:可能陷入局部最小值,需要人为确定学习率
6 | - 牛顿迭代法:求$f(x)=0$的解的方法。每次用切线与x轴的交点的x值更新参数,$\displaystyle x_{n+1}=x_n-\frac{f(x_n)}{f'(x_n)}$
7 | - 条件:目标函数二价可微,目标函数的海森矩阵必须正定或负定
8 | - 优点:更快地收敛到最优解,不用调参;缺点:计算成本高
9 | - 决策树:一种基于树结构进行决策的算法,其中每个内部节点表示一个属性或特征,每个叶子节点代表决策结果。该算法可以用于分类和回归问题。
10 | - 计算过程:基于分治思想,每次选择最优划分属性,将样本集合分成更小的子集。不断重复,直到所有的子集都属于同一个类别,或者已经达到了预先定义的最大深度。
11 | - SVM (Support Vector Machine): 支持向量机,一种可以用于解决分类和回归问题的机器学习算法,目标是在高维空间中找到最佳的超平面,使得间隔最大化。
12 | - 支持向量:离超平面最近的训练样本点。
13 | - SVM为什么要化对偶形?为了更高效地求解。当数据集的规模很大时,使用原始问题求解SVM会变得很慢,甚至变得不可行。化成对偶问题可以使用SMO这种近似算法更高效的求解。
14 | - 百万样本量可以用SVM吗?求解SVM的原问题计算复杂度过大,有些困难。
15 | - 朴素贝叶斯:一种采用了属性条件独立性假设的分类器,基于贝叶斯定理,选择概率最大的类作为结果。
16 | - 贝叶斯最优分类器:为最小化总体风险,在每个样本上选择那个能使条件风险最小的类别标记,此时判定准则称为贝叶斯最优分类器
17 | - EM算法:一种迭代地估计参数隐变量的方法。其中E步 (Expectation) 基于参数推断隐变量的分布;M步 (Maximization) 基于已观测变量X和Z对参数做极大似然估计。
18 | - PCA (Principal Component Analysis):无监督降维方法。
19 | - 适用于数据之间存在线性相关性的情况,对于非线性关系可以考虑使用Kernel PCA。
20 | - 计算过程:先将数据标准化,使得每个特征的均值为0;计算标准化后数据的协方差矩阵,对协方差矩阵做特征值分解,选择特征值最大的k个特征向量组成投影矩阵,最后将标准化后的数据乘以投影矩阵,将数据投影到新的特征空间上。
21 | - 计算后的主成分正交,即没有线性相关性。(正交$\Rightarrow$线性无关)
22 | - 集成学习 (ensemble learning,读“昂”):一种机器学习方法,核心思想是通过组合多个弱学习器,从而提高模型的预测能力和泛化性能。
23 | - Bagging (bootstrap aggregating):使用自助采样法得到不同的训练集,训练一系列基学习器,通过投票或者平均的方法得到预测结果。
24 | - Boosting:基本思想是通过迭代训练一系列弱分类器,每个弱分类器都针对前一轮训练中被错误分类的样本进行加权,以提高其分类准确性。
25 | - Stacking:一种叠加泛化的集成方法,通过训练一个元模型来结合多个基础模型的预测结果。元模型就是以不同基学习器的预测结果作为输入,结果作为输出。
26 | - “好而不同”:即基学习器的准确率高,多样性高。直观讲准确率越高越好是显然的,多样性高意味着不同的学习器可以互补,从而提高整体的学习性能。理论上有误差歧义分解证明了泛化误差=基学习器泛化误差的却权均值-基学习器的加权分歧值,可以说明基学习器的准确率高,多样性高,分类效果越好。
27 | - Adaboost计算过程:(二分类任务)在训练的每一轮中,使用当前的样本权重训练基学习器,计算分类误差率,如果误差大于0.5则break;根据错误率计算这个基学习器的权重;基于对分类正误情况更新数据分布,增加分错样本的影响,降低分对样本的影响;最后基于各个基学习器的加权,得到最终的分类器
28 | - K-means:一种原型聚类方法,目标是将数据集分成k个不重叠的簇。通过最小化数据点与所属簇的质心之间的距离来进行聚类。
29 | - 计算过程:用一种迭代近似的方法求解。初始化k个簇的质心,重复如下步骤:将每个数据点分到与其最近的质心所属的簇;对于每个簇,计算所有数据点的均值,得到新的质心。如此重复直到质心的位置不再发生显著变化或达到预定的迭代次数。
30 | - KNN:一种lazy learning的监督学习算法,基于与测试样本最近邻的k个邻居的信息预测结果。
31 | - lazy learning:训练阶段仅仅是把样本保存起来,训练时间开销为零,待 收到测试样本后再进行处理
32 | - PAC (Probably Approximately Correct):一种计算学习理论,核心思想是如果一个算法能够在有限的样本上以很高的概率产生一个"近似正确"的模型,那么该算法可以在未见过的数据上表现良好。
33 | - PAC可辨识:算法是否能以高概率产生一个近似正确的模型(泛化误差小于epsilon的概率大于等于1-delta,则称学习算法能从假设空间中PAC辨识概念类C)
34 | - PAC可学习:在有限样本下算法是否能够以高概率产生一个近似正确的模型
35 | - PAC学习算法:在有限的样本和时间限制下,学习算法是否能够以高概率产生一个近似正确的模型
36 |
37 | ### 线代
38 |
39 | - 秩:矩阵中线性无关的行或列的最大数量。矩阵的秩可以看作是矩阵所代表的线性变换值域的向量空间的维度,比如说PCA中的协方差矩阵如果秩是k,那么数据可以被无损压缩到k维。
40 | - 线性相关:存在一组不全为零的标量(系数),使得向量之间的线性组合等于零向量。
41 | - 特征值,特征向量:对于n阶矩阵$A$,常数$\lambda$,和非零的n维列向量$\alpha$,有$A \alpha=\lambda \alpha$成立,则称$\lambda$是矩阵A的一个特征值,$\alpha$为矩阵$A$属于特征值$\lambda$的特征向量。
42 | - 特征值分解:将一个有$n$个线性无关的特征向量的$n$阶方阵$A$分解为$A=Q \Lambda Q^{-1}$的过程。其中$Q$中的每一列都是特征向量,Lambda为对角矩阵,对角线上的元素是对应的特征值。
43 | - 首先求解特征方程$|\lambda E-A|=0$,得到矩阵$A$特征值$\lambda _i$(共$n$个)
44 | - 再由$(\lambda_i E-A)x=0$求基础解系,即矩阵$A$属于特征值$\lambda_i$的线性无关的特征向量。
45 | - 用求得的特征值和特征向量构造Q,Lambda
46 | - 奇异值分解:将矩阵A分解为$U \Sigma V^{-1}$,其中U V均为正交矩阵,Sigma为对角矩阵,对角线上的值按从大到小排列。
47 | - 计算:对$AA^\top$、$A^\top A$分别进行特征值分解,得到U和V。两次计算中的非零特征值从大到小排序,放在对角线,其他位置为零。
48 | - 矩阵分解的意义:将一个矩阵表示为多个矩阵的乘积的过程,有比如说奇异值分解,特征值分解。可以将复杂的矩阵问题简化为更易处理的子问题,提高计算效率。可以提取矩阵中的隐藏模式和结构,用于数据的降维、特征提取和模式识别等任务。
49 | - 正定:实对称矩阵$A$,对任何非零向量$x$,都满足$x^\top A x>0$
50 |
51 | - 充要条件:实对称矩阵 $A$ 正定 $\Leftrightarrow A$ 与单位矩阵 $E$ 合同;存在可逆矩阵 $C$,使 $A=C^\top C$;$A$的特征值均为正;正惯性指数$p=n$;$A$ 的各阶顺序主子式都大于零
52 | - 性质:$A^{-1}, kA,A^*,A^m, (A+B)$也是正定矩阵
53 | - 必要条件:实对称矩阵 $A$ 正定 $\Rightarrow a_{ii}>0$;$\det A=|A|>0$
54 | - 半正定:实对称矩阵$A$,对任何非零向量$x$,都满足$x^\top A x\geq0$
55 |
56 | - 等价命题:$f(x_1,x_2,\dots,x_n)$半正定
57 | - $A$半正定
58 | - $r(f)=r(A)=p$(正惯性指数)
59 | - $A$合同于非负对角阵,即存在可逆阵$C$,使得$C^\top AC=\text{diag} (d_1,\dots,d_n),d_i\geq 0$
60 | - 存在方阵$G\in R^{n\times n}$,使$A=G^\top G$
61 | - 所有主子式$\geq0$
62 | - 梯度消失和梯度爆炸是什么意思?有什么样的方法进行改善?梯度消失:残差连接(输出为输入和输出的求和),ReLU;梯度爆炸:归一化
63 |
64 |
65 | ### 概率论
66 |
67 | - 大数定律:随机变量的均值依概率收敛于期望的均值。
68 | - 中心极限定理:在适当的条件下,大量相互独立随机变量的均值依分布收敛于正态分布。
69 | - 局限:样本容量要求,可以用集中不等式解决。
70 | - 贝叶斯公式:用于计算在某个先验条件下事件的后验概率的公式。
71 | - 全概率公式:一个事件发生的概率等于它在与样本空间的一个划分中每个事件同时发生的概率之和。
72 | - 最大似然估计:是一种用于估计模型参数的统计方法。极大似然估计的基本思想是找到使观测数据的似然函数最大化的参数值。
73 |
74 | - 需要满足:样本独立同分布,参数化假设(参数可数且取值有限),模型合适
75 | - 独立同分布:independent and identically distributed,即独立同分布假设,假设数据集中的每个样本都是从同一个概率分布中独立地随机取出的。目的是简化建模。
76 | - 高维高斯分布:$\displaystyle p(x)=(2\pi)^{- D/2}|\Sigma|^{-1/2}\exp\{-\frac12(x-\mu)^{\top}\Sigma ^{-1}(x-\mu)\}$
77 |
78 | ### 数据结构与算法
79 |
80 | - P问题:可以在多项式时间内求解的决策问题。
81 | - NP问题:可以在多项式时间内验证答案是否正确的决策问题。
82 | - NP-complete :NP集合中最难的问题。是NP,且所有NP问题都可以在多项式时间内规约到它的问题。
83 | - NP-hard :所有NP问题都可以在多项式时间内规约到它的问题。
84 | - 排序稳定性:对于值相同的两个元素,排序后它们的先后顺序与原数组相同。比如在有些使用场景下需要保留原数据中元素的相对位置。
85 | - 快排:是一个基于分治的思想的排序算法,每次选择一个元素作为pivot,然后将给定的数组围绕这个基准进行划分,将小于基准的元素放到基准的左边,将大于基准的元素放到基准的右边,最终将基准放置在排序后的正确位置上。如此递归。优点:空间复杂度小,缺点:最坏复杂度无保证。选快排的原因:快排不需要进行分配和取消分配辅助数组等操作,其所需的常量时间小;空间复杂度低。
86 | - 归并排序:基于分治的思想的排序算法,每次将数组分为两个子数组,分别对子数组排序,再将两个子数组归并,形成最终的排序好的数组。优点:可并行;缺点:空间复杂度高。
87 | - topK:维护一个大小为k的小顶堆,时间复杂度$O(n\log k)$;类似快排,比如说找最大的数,pivot划分后左边80个,右边20个,只要对右边排序即可。最优$O(n)$,平均$O(n\log n)$
88 | - 判断图中有环:
89 | - 拓扑排序,最后如果还存在未被删除的顶点,则表示有环;否则没有环
90 | - DFS,如果在遍历的过程中,发现某个节点有一条边指向已经访问过的节点,并且这个已访问过的节点不是当前节点的父节点,则表示存在环(用黑白灰表示)
91 | - 对于有向图,若存在强连通分量(即存在$v_i \to v_j$的路径也存在$v_j\to v_i$的路径),图中有环。
92 | - 欧拉图:具有欧拉回路的图,欧拉回路是通过图中每条边恰好一次的回路
93 | - 有向图:非零度顶点是强连通的;每个顶点的入度和出度相等
94 | - 无向图是欧拉图当且仅当:非零度顶点是连通的;顶点的度数都是偶数
95 | - 霍夫曼编码:一种变长的数据压缩编码,通过让出现概率更小的字符长度更长,出现概率更大的字符长度更短进行数据压缩,是最优编码。基于霍夫曼树构造的。
96 | - 每次取出出现概率最小的两个结点,合并后结点权重为两个结点之和。直到所有结点构成一个二叉树。为二叉树的每个结点下的两个分支赋值为0、1,编码即从根节点到字符的叶节点的路径上01串。
97 | - 唯一可译码:因为霍夫曼编码是前缀编码,即没有一个编码是另一个编码的前缀。
98 | - 优点:最优编码。缺点:与计算机的数据结构不匹配;需要多次排序,耗费时间。
99 | - 香农编码:一种变长的数据压缩编码,效率略低于霍夫曼。
100 | - 编码方法:将符号按照其出现概率从大到小排序;把概率集合分成两个尽可能概率相等的子集,给前面一个子集合赋值为0,后面一个子集合赋值为1;如此重复直到各个子集合中只有一个元素为止;将每个元素所属的子集合的值依次串起来
101 | - 散列表的优势:查询高效,数据的存储和删除也高效。
102 | - 查询复杂度:链表型:每个哈希桶维护一个链表来存储冲突的键值对,最坏是O(n),平均接近O(1)
103 | - 普通型:当发生哈希冲突时,开放寻址再找到一个空的位置来存储冲突的值。最坏情况是O(n)(哈希表被填满),平均接近O(1)
104 | - 斐波那契:$O(2^n)$,存储结果$O(n)$;动态规划$O(n)$
105 |
106 | ### 其他
107 |
108 | - 操作系统线程跟进程的区别:进程是一个独立的程序运行的实例,线程是进程中的一个子任务。进程可以包含多个线程,进程之间是独立的,
109 | - 傅里叶变换:将信号从时域转换到频域的变换过程。
110 | - 拉普拉斯变换:傅里叶变换的一种扩展,可以将信号从时域转换到复频域。
111 | - 用处:在控制系统中,分析设计反馈控制系统;在信号处理中,用于滤波、信号重构、频谱估计和图像处理等
112 | - 两者关系:拉普拉斯变换是傅里叶变换的扩展形式;在频域分析中,拉普拉斯变换通常用于处理连续系统的输入-输出关系和系统响应,而傅里叶变换适用于连续信号和离散信号。
113 | - 凸优化带约束的一阶条件:定义域是凸集,$f(y)> f(x)+\nabla f(x)^\top (y-x)$
114 | - 二阶条件:对于开集内的任意一点,它的Hessian矩阵半正定。$\nabla^2 f(x)\geq 0$
115 | - KKT条件是非线性规划中最优解的一阶必要条件:拉格朗日函数的导数为0,原始可行性条件,对偶可行性条件,互补松弛条件。
116 | - 原始可行性条件:优化变量满足原问题的所有的约束条件,包括对于每个不等式约束和等式约束
117 | - 对偶可行性条件:对于每个不等式约束,对应的拉格朗日乘子大于等于0。
118 | - 互补松弛条件:约束的松弛变量与拉格朗日乘子的乘积为零
119 | - 凸优化中梯度下降的学习率:通过线搜索确定。线搜索是一种通过搜索确定每次迭代的合适学习率的方法。在每次迭代中,沿着梯度方向尝试不同的学习率值,通过一些准则来选择合适的学习率,使得目标函数在新的参数值上有足够的下降。精确,计算成本高。
120 | - 如果函数的定义域是凸集,且对于任意定义域上的$x,y$和任意$0\leq \theta\leq 1$,有$f(\theta x+(1-\theta)y)\leq \theta f(x)+(1-\theta)f(y)$,则函数是凸的。
121 |
122 | - 卷积和:将其中一个信号翻转再平移,再和另一个向量相乘,对乘积后的信号求和。
123 | - A*:树admissible则optimal,图consistent则optimal。admissible即到目标的估计成本<到目标的真实成本,consistent即结点与其后继的估计成本之差<这一步的真实成本
124 |
125 | - 原问题为什么要化成对偶问题:原问题线性可分就即凸,线性不可分则不凸
126 |
127 | - 对偶问题的求解可以用SMO等近似方法求解。可以引入核函数。(通过迭代地优化一对变量来求解SVM的优化问题。其主要思想是选择两个变量进行优化,将其他变量固定,并通过解析方法直接计算这两个变量的最优值。通过迭代地更新这对变量,SMO算法逐渐逼近全局最优解。)
128 |
129 | - 斐波那契数列求和:公式,DP,递归(拿字典存)
130 |
131 | - 双蛋问题:可以用动态规划求解,
132 |
133 | $W(n,h)$表示有n个鸡蛋h层楼所需的最少实验次数
134 | $$
135 | W(n,h)=1+\min(\max(W(n-1, i-1), W(n, h-i)))
136 | $$
137 | $n=2$:$W(h)=1+\min(\max(i-1, W(h-i)))$
138 |
139 | - 激活函数:引入非线性特性,Sigmoid,Tanh,ReLU,LeakyReLU。Sigmoid映射到(0,1),Tanh映射到(-1,1),这两个激活函数都存在梯度消失。ReLU可以一定缓解梯度消失问题,但是在负输入时不可导,可能存在神经元死亡的情况。LeakyReLU对ReLU改进,在负输入时保留一个小的梯度,有助于解决ReLU函数中的死亡神经元问题。
140 |
141 | - 特征值特征向量意义:特征值告诉我们特征向量在线性变换中的伸缩程度,PCA中特征值越大说明对应的特征向量相关性更大,取最大的k维。特征值可以用来判断矩阵的正定性等(特征值均>0)。
142 | - 数据规模大:对偶问题太复杂。
143 |
--------------------------------------------------------------------------------
155 |
156 |
--------------------------------------------------------------------------------
/英文.md:
--------------------------------------------------------------------------------
1 | ### Self-Introduction
2 |
3 | ### Why do you choose to study at our school?
4 |
5 | ### What do you expect to achieve during your study if you are enrolled into this institute?
6 |
7 | ### What is your plan in the postgraduate study?
8 |
9 | ### Do you have a career plan in 5 years?
10 |
11 | ### Tell me something about your undergraduate life.
12 |
13 | ### What is your favorite subject and why?
14 |
15 | ### What has been your greatest success/ accomplishment in campus life?
16 |
17 | ### What book have you recently read?
18 |
19 | ### What professional paper have you read before? What's the main idea of this text.
20 |
21 | ### Tell me something about your hometown.
22 |
23 | ### Tell me something about Nanjing.
24 |
25 | ### Can you tell me something about your family?
26 |
27 | ### What's your favorite hobby?
28 |
29 | ### Who is your favorite basketball player?
30 |
31 | ### Strength
32 |
33 | ### Weaknesses
34 |
35 | ### What kind of character do you think you have?
36 |
--------------------------------------------------------------------------------
/面经.md:
--------------------------------------------------------------------------------
1 | # NJUAI面经
2 |
3 | # 2019
4 |
5 | ## [南大lamda实验室失败面经分享_彩虹糖梦的博客](https://blog.csdn.net/caozixuan98724/article/details/100975163)
6 |
7 | 接着看论文的老师问我朴素贝叶斯决策相关的内容,朴素贝叶斯我还是会的,说了一下思想和公式。然后他问我,朴素贝叶斯是独立分布还是独立条件分布?我当时不知道是怎么的鬼使神差,答了个独立分布...只能说脑子瓦特了,那天状态真的特别差。后来知道老师问我这个问题的原因是我在论文中用了大量条件分布的东西。
8 |
9 | 最后是我觉得最奇怪的一个问题,老师问quick sort,我一下就来劲了,quick sort我熟啊,刚复习的。然后老师问我,快排为什么叫快排啊?我“?????”我弱弱的回答“因为它快啊...”。老师又问我“它是最快的吗?”我“不是啊,快排是nlogn,基数排序能到O(n)呢”。老师问“那基数排序有什么代价呢?”我说“它需要大量的空间啊,空间换时间”。然后我就楞那里了。老师“你还是没回答我的问题啊,快排为啥叫快排啊?”我“...”。
10 |
11 | 之前对于算法,重点去掌握了它的流程,它的代码,忽略了一些特别关键和基础的点,比如什么大数定律,条件分布,决策树一些更加深入的东西,没有记忆在心中。对自己的项目也没有深挖,还是要不断反思,这个项目的核心是啥,遇到了什么困难,有什么收获。
12 |
13 | # 2020
14 |
15 | ## [南大人工智能AI学院夏令营面试经历_Alvassss的博客](https://blog.csdn.net/Alvassss/article/details/107244024)
16 |
17 | ### 1.LAMDA
18 |
19 | 一轮:自我介绍 概率题 算法题 项目简介
20 | 二轮:自我介绍 你大学最满意的项目是什么 详细问
21 | 听说有三轮 但我没过第二轮
22 |
23 | ### 2.南大MCG
24 |
25 | 自我介绍 老师完全按照简历询问
26 |
27 | ### 3.南大笔试
28 |
29 | 重点:
30 | 1.线代+概率 线代主要是概念 概率主要是网上那些脑筋急转弯
31 | 2.机器学习 建议西瓜书前十章要精通
32 | 3.数据结构 考的巨多 建议精通
33 | 4.算法 时间复杂度分析 渐进 背包问题 摊还
34 | 非重点:
35 | 博弈论 各种变换(傅里叶啥的 俺没学过)
36 |
37 | ### 4.南大面试
38 |
39 | 英语面试:是学院的一个越南老师面试 比较亲切 但我心态崩了
40 | 三个问题:
41 | 1min自我介绍(超时会直接截止 不要问我为什么知道)
42 | 最喜欢的课程 why
43 | 最喜欢的机器学习算法
44 | 中文面试:
45 | 快速排序和归并排序优缺点 排序为什么要稳定
46 | P问题 NP问题 NP完全问题的概念
47 | 全概率公式意义
48 | 项目问题
49 |
50 | ## [南大人工智能学院夏令营经历记录_TheRebel_的博客](https://blog.csdn.net/Anonymity_/article/details/105407815?spm=1001.2101.3001.6650.1&utm_medium=distribute.pc_relevant.none-task-blog-2~default~CTRLIST~Rate-1-105407815-blog-107244024.235^v31^pc_relevant_default_base3&depth_1-utm_source=distribute.pc_relevant.none-task-blog-2~default~CTRLIST~Rate-1-105407815-blog-107244024.235^v31^pc_relevant_default_base3&utm_relevant_index=2)
51 |
52 | 面试问了我大概五道题,一道问排序算法,及时间复杂度。第二道问我svd是什么。第三道是关于我最喜欢的深度学习模型。第四道和第五道是围绕我的项目经历问的。然后计算机营和ai营机试:面试比好像不一样。另外,ai院报周志华和lamda组的很多,但其实lamda在这之前已经招过一次了,所以夏令营他们再招的名额可能会比较小。
53 |
54 | ## [【计算机保研夏令营】2020年LAMDA保研面试经验](https://zhuanlan.zhihu.com/p/237472334)
55 |
56 | ### 面试 6.18
57 |
58 | 大概在报名结束后一周收到了第一次面谈的邀请邮件,LAMDA都是提前一天发邮件,第二天直接面试。这时候还在期末考试阶段,比较紧张,也没准备啥,就对着简历花了一小时思考了下。第一轮我们组是10个人,按姓名拼音排序进行面试的,面试官是组里的三个学长,先进行自我介绍,之后主要问了我以下三个问题:
59 |
60 | > 详细介绍了下比赛(我参加过一个数据挖掘的比赛)的特征工程,之后又问了模型部分(介绍了下Xgboost)
61 | > 对机器学习的理解(这个感觉自己答得不是很好,说的有点绕进去了)
62 | > 对开放动态环境下机器学习的挑战和瓶颈的认识(这个后来我查过,是那个学长的博士课题,听DJW学长说这个也是LAMDA组里的一个大坑,ps. 这里大坑指大方向,不是说坑,有学弟问了才发现有人会误解emmm)
63 |
64 | 总的来说,这一轮面试比较愉快,主要了解一些基本情况吧,感觉这一轮没有刷人。
65 |
66 | ### 3. 第二轮面试 6.20
67 |
68 | 第一轮面试结束第二天就发下一轮通知了,询问D学长了解去年的流程后,也大概猜到了这一轮可能是群面,面之前学长还说遇到ZDC老师坐等聊爆,结果8:50进入腾讯会议,我傻眼了,一奶即中。
69 |
70 | 首先还是少不了自我介绍,介绍完之后Z老师就问我对博士期间的规划,这个问题之前思考过很久,也是一个保研期间的必问问题,由于我把规划从大四说起(大四如果保研顺利结束想先强化学习数学基础,说了凸优化、随机过程、矩阵分析之类的),也给后续埋了个坑——下一个问题他问我最喜欢哪门课,我以为他想问上面三门,就问了句是不是本科阶段,被WW老师说难道你还有研究生阶段吗,有点尴尬。我作死的说了数据结构(但我确实真的很喜欢数据结构,其他课也没准备,想着数据结构学的还行就说了),但直接问我红黑树了,我有点傻眼了,老实说自己不会,只知道STL有些底层是红黑树实现的(有时间还是得看下红黑树,至少得了解思想)。
71 |
72 | 之后就是一连串的问题,先问了归并和快排的平均、最优、最坏复杂度,这个准备实习面试时都梳理过,都答出来了。然后接着这个问题问,既然归并的最坏也是O(nlogn),而快排最坏O(n^2),为啥现在大家都用的是快排。我只从空间复杂度进行了分析,后来面完查了下,其实实践证明,虽然二者时间复杂度相同,但快排还是要快一些,而且最坏情况遇到的可能性也比较低。之后问的应该是如何判断图中是否有环,我刚嘴里小声复述想思考下,老师就直接问下一个问题了,这里感觉这一轮应该就是压力面。
73 |
74 | 下一个问题问的是比赛,让我介绍Xgboost的优势,这个实习面试也复习过,答得还可以。接下来WW老师问我本科学校是985吗?是211吗?是双一流吗?一波三连搞得我有点尴尬,我校果然在南方知名度还是不行。
75 |
76 | 最后Z老师又问你本科北京的学校为啥想来南京,说以前很多北京的同学拿了offer又鸽了。这个问题就有的聊了,因为我本身是江苏人,高中物理竞赛又在南大两个校区住过一段时间,挺喜欢南大的,南大也算是高中dream school之一了,然后就是LAMDA很强哈哈哈哈。
77 |
78 | 总结一下,这一轮面试节奏很快,可能也是面试过程中比较兴奋,我整体回答问题几乎没有思考,没有用到10分钟应该。这一轮面试应该刷了一半人左右。
79 |
80 | ### 4. 第三轮面试 6.22
81 |
82 | 这一轮面试一直到6.21晚9点才通知,大部分人收到的邮件都写明了是哪个老师面试,根据这两轮小组面试人数的猜测,可能第二轮刷了有一半人,但不确定,也可能是分批。我的邮件没有写明老师,我第一志愿是JY老师,但听D学长说J老师学生有部分也都是Z老师带,所以猜测可能会使Z老师面。D学长给我看了他去年整理的面试经历,大概了解了一些情况以及基本问题。这时候由于已经期末考完了,但也没想到面试这么突然,也来不及准备太多,就稍微过了下线代和概率论的一些基本概念,理解了一下,然后准备了一下简历。
83 |
84 | 最终面我的还是J老师。第一个环节还是自我介绍,介绍完之后老师开始问“以后的规划”、“家庭背景”、“家人对自己的规划”等等,接下来又问了“简历中的数据挖掘比赛主要负责的内容以及收获”、“本科科研项目最大的收获”等问题,都很友好,聊了大概20多分钟。
85 |
86 | # 2021
87 |
88 | ## [2021年人工智能保研经历(xduee->njuai)](https://zhuanlan.zhihu.com/p/420184627)
89 |
90 | 人工智能学院的笔试主要考人工智能+计算机的基础知识。笔试用考试星机考的方式,考试时长2小时,大概我记得200道题目左右,应该是比2020年的笔试少了50道题目左右,题目难度适中,因为难题我全刚开始跳了,我差不多连猜带蒙在最后差10min的时候完成了所有题目。南大学院笔试的考核真的很重要很重要,属于超强committee,即使你提前被周老师录了,笔试没过也是没用的。
91 |
92 | 参营时间线的话,是2021.7.8举行笔试,然后7.11周日上午(当时正在看美洲杯决赛,印象深刻)出了笔试的结果,应该是进60%~70%左右的人。笔试结果出了后,就会让你选择学硕or直博。南大一般在这个时候才会让你选择学硕和直博,刚开始报名的选择只是预选择。下面就是面试,7.13一整天是学硕面试,7.14上午是直博生面试,直博面试应该有22人,录了多少我也不是很清楚,下面说说面试情况。
93 |
94 | 线上面试还是采用的腾讯会议,每人12min,4min英语问答+8min专业知识。我那组的面试官有4人,面试可以说是相当友好了,英语问答包含自我介绍,以及一些关于我科研的提问,还有一些闲聊,英语这部分总体来说不难,敢于去说就行。专业知识部分,主要还是在问机器学习+线性代数的相关知识,我感觉我个人准备的比较充分,所有问题都回答出来了,除了最后詹老师的一个关于编码的问题回答的不太行。
95 |
96 | 关于机器学习面试的问题可以参考我另一篇经验贴:**[计算机/人工智能方向保研高频面试题目整理](https://zhuanlan.zhihu.com/p/394374473)** ,这篇经验贴我应该概括的比较全面了。
97 |
98 | ### [计算机/人工智能方向保研高频面试题目整理](https://zhuanlan.zhihu.com/p/394374473)
99 |
100 | ### **1. 开放型问题**
101 |
102 | 开放型问题建议中英文都准备,大部分面试都有这个环节。
103 |
104 | - 自我介绍(1min/3min)
105 | - 研究生期间的规划
106 | - 参与的竞赛(数模等等),你做了哪儿些工作?
107 | - 简单介绍下你的科研工作
108 | - 对机器学习/深度学习的理解
109 | - 开放动态环境下机器学习的认识(来自南大某著名实验室)
110 |
111 | ### **2. 数学类**
112 |
113 | 数学类问题是ai方向保研面试问的最多的,主要是线代、概率论。
114 |
115 | - 线代:如何理解矩阵的秩?简述向量组线性无关的含义?解释正定矩阵以及半正定矩阵?特征值的含义以及矩阵分解的物理意义?
116 | - 概率论:简述大数定理,中心极限定理,全概率公式,最大似然估计,贝叶斯的含义
117 | - P问题 NP问题 NP完全问题的概念
118 |
119 | ### **3. 机器学习类**
120 |
121 | - 简述PCA的计算过程
122 | - 简述SVM,并解释SVM为什么要化对偶形?百万样本量可以用SVM吗?
123 | - 常用的机器学习算法的适用场景(例如KNN、朴素贝叶斯、决策树等)
124 | - 具体阐述残差神经网络的含义
125 | - 梯度消失和梯度爆炸是什么意思?有什么样的方法进行改善?
126 | - 简述几种集成学习方法Adaboost的计算过程以及Stacking Learning?
127 |
128 | ### **4. 数据结构与算法类**
129 |
130 | - 常用排序平均最优最坏时间复杂度以及空间复杂度,阐述快排和归并的优缺点以及回答为什么排序要稳定?
131 | - 归并排序的最坏时间复杂度优于快排,为什么我们还是选择快排?
132 | - TopK问题详解
133 | - 如何判断图里有环?
134 | - C++中new和malloc的区别
135 |
136 | ## [2021年一战南大AI上岸经验贴_Yuhan の Blog的博客](https://blog.csdn.net/qq_45228537/article/details/115448786)
137 |
138 | ### 复试笔试
139 |
140 | 南大AI的复试笔试是离散数学+机器学习;我是3月开学回学校才开始准备,这里建议早点准备离散,离散东西很多概念很杂而且考的也很难,所以我今年离散笔试应该基本没拿到分orz;今年的机器学习也不知道在搞什么,无语子,写着机器学习的label考了20道数据结构的选择题+一道不知道属于啥学科的问答,不过该准备的还是要准备的。
141 | 离散建议找一下南大本科的PPT,有重点地对着屈书进行复习;复试的机器学习建议细看一下,部分重点的数学推导要会(例如SVM的拉格朗日乘子法、KKT条件、PCA特征值分解),概念要十分清晰,即使复试没有考察到,面试老师也会问许多机器学习的相关知识。
142 |
143 | ### 复试机试
144 |
145 | 今年情况特殊,是线上复试,因此今年的机试是和笔试在一起考的,但我想,随着疫情逐渐得到有效控制+全民疫苗接种,今后应该会继续采用线下机试的方法。
146 | 个人本科练习过半年左右的OJ,因此有一点薄弱的基础,因此就是在考前临时复习了一下黄宇书上的4道DP例题+一些常见的DP题(01背包、完全背包、LCS、多重部分和问题、LIS、DP计数等等)+一些常用的数据结构和算法(例如并查集、kruskal、dijkstra、快速幂、素数筛、线段数、树状数组等等)。
147 | 对于南大的机试,我觉得重点是DP、搜索、图论。
148 |
149 | ### 复试面试
150 |
151 | 面试个人认为可以拆分成英语口语+线代+概率论+机器学习+项目经验+一些其它知识储备。
152 | 口语问了我这些问题:
153 |
154 | 1.本科所学专业
155 | 2.毕业后打算
156 | 3.兴趣爱好
157 | 4.介绍喜欢的电影
158 | 5.介绍最近读的一本书
159 |
160 | 面试:
161 |
162 | 1.你说你因为喜欢数据结构和算法才选择读AI,介绍一下它们的交集
163 | 2.本科有没有做过AI相关的项目
164 | 3.SVM为什么要采用对偶问题?(我答:虽然可以通过现成凸优化包求解,但是对偶问题求解更快)
165 | 4.为什么更快?(接4中我的回答内容
166 | 5.Boosting学习有什么特点?
167 | 6.为什么集成学习需要集成“好而不同”的学习器?(接5中我的回答内容
168 | 7.解释一下特征值的含义
169 | 8.简述一下特征值分解
170 | 9.为什么要选取前d大个特征值(接8中我的回答内容
171 | 10.你本科是软工的,问一下面向过程、面向对象、面向抽象的区别
172 | 11.具体介绍一下你学过的面向对象知识&应用
173 | 12.你觉得你本科所学的知识在将来读AI的时候会有哪些应用
174 |
175 | ### [南京大学LAMDA面经汇总_51CTO博客](https://blog.51cto.com/u_12312066/3695982)
176 |
177 | 面试吴建鑫老师的时候,问题如下:
178 |
179 | 方差的计算方法,他会提前写好一个方差表达式问你对不对,如果不对的话请写出正确的表达式;
180 | 方差中的n-1含义;
181 | 如果写一个程序计算方差,那么计算一次内存访问几次;
182 | 本科做过的项目,项目内容;
183 | 机器学习了解多少,看过什么;
184 | 了不了解本人是做什么研究的。
185 | 面试詹德川老师的时候,我不知道其他人是什么情况,但我是全程英文面试,问到的问题如下,注意:以下问题需要英文作答,实在英语回答不了,可以中文,不必有太大压力:
186 |
187 | 自我介绍一下;
188 | 介绍一下做过的项目;
189 | 介绍一下梯度下降法是什么;
190 | 介绍一下牛顿迭代是什么;
191 | 什么是特征值,特征值的含义;
192 | 唠嗑。
193 | 面试完当天晚上就会有邮件通知是否面试通过,最后我是被詹德川老师录取,但是通过LAMDA面试并不代表你就能100%能进入LAMDA读研了,最重要的一关是拿到南大夏令营的优秀营员,只有这样,通过两轮考核才能进入LAMDA。
194 |
195 | 下面说一下南大夏令营的流程,主要是三部分:各个实验室介绍、机试、面试,其中最最重要的是机试,只要机试通过,90%就能拿到优秀营员。
196 |
197 | 机试这次一共4道题,以前听说6道题,只要AC出其中的两道题就肯定没问题了,多做无用,有罚时,考核方式:OJ,题型:算法+数据结构,难度:ACM一般难度的题。这次的具体题目如下:
198 |
199 | 最大子串和;
200 | 无向图最长路径
201 | 表达式求值;
202 | 给一棵树求最长的路径。
203 | 面试问题如下(由于分组面试,每组没人问题不一样):
204 |
205 | 解释一下什么是时间复杂度;
206 | 快排的时间复杂度;
207 | 快排最坏时间复杂度为什么是$O(n^2)$,如何优化快排最坏时间复杂度;
208 | 看成绩单,问如何进行文献检索
209 | 英文回答:如何利用文献检索知识去检索一个机器学习的问题
210 |
211 | 就问了一个“ε-greedy”算法中ε取值的问题
212 |
213 | 然后问了离散的全序,偏序,操作系统,计算机组成原理内存啥的,还有居然问了软件工程的问题,真是醉了,那个时候软件工程都还没有学完。(黑人问号脸)然后,英文是让我介绍最喜欢的歌曲。
214 |
215 | 南大进行了一场霸面(不推荐,还是提早申请比较好)。
216 |
217 | 1.快排复杂度是多少,并且黑板上手写证明。
218 |
219 | 2.简述如何“快速选到第n个数”(快速选择,复杂度为O(n))。
220 |
221 | 3.讲简历上的项目,根据简历问
222 |
223 | 有无申请lamda都需要参加下面两场考试:
224 |
225 | 机试(两个小时,四选二,一般两道都做出来能入选):
226 |
227 | 1、连续最长子序列和(给了一堆正负的数字,任选其中一段连续的数字(可以全选),需要和最大)
228 |
229 | 2、无向图最长路径(单纯的Dijkstra)
230 |
231 | 3、给一个表达式,例如 (3*2+1/2)+1*2,计算结果
232 |
233 | 4、给了一棵树求最长的路径(根到叶节点)
234 |
235 | 面试:
236 |
237 | 1、英文自我介绍
238 |
239 | 2、按照不同专业方向问专业课程
240 |
241 | 3、大数定理、贝叶斯公式等
242 |
243 | 4、操作系统线程跟进程的区别等(操作系统的问题比较爱问)
244 |
245 | ## [2021年计算机保研(清深、南大AI、中科大、哈深、中山等)](https://zhuanlan.zhihu.com/p/416191365)
246 |
247 | ### 学院
248 |
249 | 考核方式:初审(985前5%) + 笔试 (机器学习、概率论、线性代数、数据结构等)+ 面试(机器学习、数学)
250 |
251 | 笔试:2小时做200多道填空和选择,其内容涵盖机器学习、概率论、线性代数、数据结构等。对于概率论和线性代数,建议耗时两三天刷完李永乐660,刷完就没问题。对于机器学习,建议把西瓜书前十章过一遍,主要是看概念即可。对于408,可以选择不看,考的不多。
252 |
253 | 面试:英语问答 + 专业知识考察。英语问答就准备好常见的英语问题,以及和你简历相关的英语问题即可。至于专业知识,就是考察机器学习和数学,建议把西瓜书或李航统计学细读并理解,数学建议把概率论和线代细读并理解。
254 |
255 | 总结:由于当时概率论和线代复习的不好,导致数学问题只答出一半,进入wl。要想过南大AI,没有别的秘诀!把线性代数、概率论、机器学习从头啃到位即可!
256 |
257 | # 2022
258 |
259 | ## [Kaslanarian/NJUAI-OpenDay-Interview: 南京大学人工智能学院本科生开放日面试经验分享 ](https://github.com/Kaslanarian/NJUAI-OpenDay-Interview)
260 |
261 | ### 同学A(同组)的面试问题
262 |
263 | 面试那天和我在一个房间,而且在我前面面,所以记录了所有的问题:
264 |
265 | - 英语面试:
266 | 1. 1分钟自我介绍;
267 | 2. 从事的研究细节(因为自我介绍中提及);
268 | 3. 你最感兴趣的课程;
269 | 4. 你以后是想留在学校做研究还是去公司工作。
270 | - 中文面试:
271 | 1. 大数定律是什么?
272 | 2. 中心极限定理是什么?
273 | 3. 讲一个你知道的聚类算法?
274 | 4. 你平时有什么放松方式?
275 | 5. Boosting的基本思想?
276 | 6. PCA的全称是什么?
277 | 7. PAC理论的全称是什么?
278 | 8. 欧拉图是什么?
279 | 9. 正定矩阵是什么?
280 | 10. 极大似然估计是什么?
281 | 11. SVM为什么叫支持向量机?
282 |
283 | 注意,上述问题只是前置问题,你说不会才会换问题,否则就会继续问。比如同学A说他不记得欧拉图了,然后对面就换下一个问题;面试到我的时候又问了这个问题,我答出了欧拉图定义,后面就问我判定方法了。
284 |
285 | ### 我的面试
286 |
287 | - 英语面试:
288 |
289 | - 1分钟自我介绍;
290 | - 介绍一下你参加的比赛(起因于我的腾讯会议背景是我上次参加的某比赛,然后忘了换😢,反过来想这也是一种思路,让面试官问出你想让他问的问题😄);
291 | - 以后的安排(类似于同学A的问题)。
292 |
293 | - 中文面试:
294 |
295 | - 大数定律是什么?(看我倒背如流就没问中心极限定理了)
296 |
297 | - 计算复杂度(P和NP),P=NP吗?
298 |
299 | - 遇到压力怎么放松?
300 |
301 | - 最喜欢的课程?
302 |
303 | - 介绍PCA;
304 |
305 | - 为什么机器学习中的基本假设是独立同分布,独立同分布全称是什么?(这个地方卡了,对面嫌我说多了)
306 |
307 | - 什么是欧拉图,如何判定欧拉图?(忘记了,只说记得存在一个充要条件)
308 |
309 | - 正定矩阵是什么,如何判定?
310 |
311 | > 跟面试官(王魏)怼了,他一直说我和书上的定义不一样,但我讲的是一个逻辑等价命题,他就说我不好好看书,弄得心态挺不好。幸好他是最后一个问问题的老师。
312 | >
313 | > 后来发现和我一组的同学都对他有意见的,比如同学B说他不会欧拉图,然后被他锐评:**你是不是没上过数学课?**
314 | >
315 | > 问同学C的时候,C回答不出来就咂嘴,问答少了就说”**这么不熟悉吗**“...
316 | >
317 | > 注:以上内容是节选,如果看的人多了就把老师名字给码了。感觉他是根据被面试者的态度进行反馈,比如我、B和C在面试的时候展现出自信,所以他很打压;A面试的时候很严肃,遇到不会的问题会说“对不起,我回去再看一下”,所以没咋刁难。反正看到的同学留个心眼吧。
318 |
319 | - 快速排序的平均时间复杂度,最坏时间复杂度,最坏情况是什么样?
320 |
321 | ### 本组其他同学的问题
322 |
323 | - 计算复杂度,但问的是:如果把时间换成空间,那么P=NP吗?
324 | - PAC理论了解多少?
325 | - TBD
326 |
327 | ### 其他组的问题
328 |
329 | 这里记录其他组同学那里听来的问题:
330 |
331 | - 喜欢的数学课?如果说了微积分这块,而不是AI相关,则会问:
332 | - 中值定理是什么?
333 | - 泰勒展开是什么?
334 | - 高阶无穷小是什么?
335 | - 傅里叶变换和拉普拉斯变换的关系?
336 | - 拉普拉斯变换的用处?
337 | - 双蛋问题,但是单蛋版,也就是你只有一个鸡蛋如何判定其不摔碎的最高楼层?
338 | - TBD
339 |
340 | ## [2022年/2023届预推免小记(科大6系&NJUAI)](https://zhuanlan.zhihu.com/p/570734028)
341 |
342 | NJUAI:
343 |
344 | 笔试:2h(记不太清了),题量很小,选择+问答
345 |
346 | 面试:英文自我介绍+英文专业问题+专业问题,南大是步步紧逼型面试,感觉问了不止十个问题。
347 |
348 | 比较迷惑的一点是面试是定死了12min/人,结果还剩20s的时候老师又问了一个问题,我刚说两句就直接结束了,这种情况主持人不应该提醒一下快到时间了吗(汗)
349 |
350 | ## [2022年(2023届)计算机保研——计算所vipl、南大lamda、北大计算机、人大高瓴等](https://zhuanlan.zhihu.com/p/570001872)
351 |
352 |
353 |
354 | 看了一些经验帖说,南大LAMDA比北大信科还难,有很多LAMDA面试没过的最后去了北大信科,所以我当初报名没报什么信心,找了一位和自己研究经历比较match的老师,就去参加了。
355 |
356 | 首先是初筛,985的5%应该都能过初筛,除此之外我觉得研究方向的match程度非常重要。
357 |
358 | 一面是学长面,先是一分钟自我介绍,然后就是基本的简历面,问了paper以及剩下几个科研项目做的是什么和创新点,差不多就结束了,没有问任何专业知识相关的问题。
359 |
360 | 二面是老师面,问题大概有:
361 |
362 | 1. 一分钟自我介绍
363 | 2. paper里我主要做的内容
364 | 3. AI for SE领域有什么地方还可以去尝试?
365 | 4. 最拿得出手的项目是什么
366 | 5. 遇到的挫折是什么
367 | 6. 你觉得图神经网络做代码生成目前的优点和缺点是什么?有什么改进的地方?
368 | 7. 有没有做过词法分析器和语法分析器
369 | 8. 智力问题,黑白帽子问题(可自行百度)
370 | 9. 剩下就是一些聊天性问题,比如如果离交稿ddl还剩两天,但是你的实验还有很大漏洞,论文也还没写完,这种情况怎么办;了解了我的家乡以及为什么想来南京等
371 |
372 | 最后获得了实验室的offer,我个人感觉成功的原因是 1. 由于方向match,所以了解比较深入,中间考察的一些对该领域科研的相关看法时回答的还不错;2. 正好问到了我之前思考过的比较有意思的idea,所以和老师聊的很愉快。
373 |
374 | 但是!只拿到实验室的offer还没结束,还需要通过南大AI学院的考核,于是就有了绿裙里通过实验室考核没通过学院考核的难兄难弟们(后来发现这些难兄难弟里有人去了贵系,只想说南大AI真牛)
375 |
376 | AI院笔试:题量很大,考察范围覆盖数据结构、机器学习(西瓜书)、概率论、线性代数、英语等,如果目标南大AI的建议提前好好复习一下。不要像我一样,“怎么还有过了LAMDA没过学院的” “小丑竟是我自己”
377 |
378 | 另:夏令营笔试寄了就彻底寄了,也没办法报名预推免了。
379 |
380 | ## [2022南京大学人工智能学院本科生开放日小记【保研向】](https://zhuanlan.zhihu.com/p/543677717)
381 |
382 | 夏令营笔试是双机位,考试星作答。去年是两百道选择题和填空题两个小时,今年则是66道选择题,20多道填空题,若干多选题,英文题以及简答题,一共一个半小时。考察的科目和去年倒是差不多,这点知乎上也是有人写的,机器学习、概率论、线性代数、数据结构与算法,都是需要复习的。因为是线上考试所以不会有太多复杂的计算,更多考察知识的广度与细节部分,也就是看书复习的时候各种细节都应该注意。我根据前面大佬的建议也用了几天刷了李永乐660的线代和概统部分,感觉还是有不少帮助的。经过我们的讨论,感觉AI营的重点是笔试而非面试。
383 |
384 | 面试也是双机位,腾讯会议面试。以往都是20分钟一个人,今年估计是报名人数比较多,所以改为了12分钟一个人。还是4个老师分别问不同学科的问题。我这里大概记了一下面试的问题(不同的组面试题差别还是挺大的)
385 |
386 | C:你研究生读完之后有什么打算?你有什么做研究的品质?(英文面试,有概率让你用英文自我介绍,也有可能没有)
387 |
388 | 詹:常微分方程f'(x) = cx的解的形式,如果c是常数,为什么形式,如果c为矩阵呢?霍夫曼编码的优势,霍夫曼编码的唯一性,香农编码是什么?
389 |
390 | 张:半正定矩阵的定义,性质(越多越好),PCA协方差矩阵的性质(半正定),以及为什么半正定(从原理上说明)?凸优化中梯度下降的学习率如何确定?(凸优化最后两课讲的)
391 |
392 | 姜:散列表的优势(相比其他查询方式),查询复杂度(分链表型和普通型)。研究生的“研究”二字是什么含义?研究生相比本科生有什么区别?
393 |
394 | 其他同学有问图灵机的,凸优化带约束的一阶条件的,中心极限定理,机器学习很多算法为什么要iid条件,SVM核函数的考察等等,比较广泛,只看西瓜书显然是不够的,还需要一些自己的思考和积累。
395 |
396 | 总体来说感觉面试是不断往深去问,老师会追问你问题的本质,直到不会为止。因此面试完成后问了一圈感觉都不是特别好,这也是正常现象。面试完之后就是漫长的几天等待时间。
397 |
398 | 7.11线上导师宣讲会,7.13开放日线上面试。
399 |
400 | ## [2023CS保研经验分享(清深、上交、南大LAMDA、同济、东南Palm等) - 知乎 (zhihu.com)](https://zhuanlan.zhihu.com/p/570722079)
401 |
402 | 第一轮面试主要是实验室的学长学姐进行,主要围绕就是一些理论知识和你自我介绍的项目中所涉及的一些问题。
403 |
404 | 项目的问题没啥共同性,我就列举一些印象中的常见问题:
405 |
406 | - 机器学习中FP、TP是什么?
407 | - 你为啥想要读直博?
408 | - 线代中的矩阵的秩和矩阵的关系?
409 | - 讲一讲线代中的矩阵的特征值?
410 | - ......
411 |
412 | 第二轮面试是意向导师单独面(我是这样的),L老师只是来聊了聊天,聊一下我想研究的方向和家是哪里的,为什么要来南大等等一些非学术问题,最后说因为直博已经确定了人选,只能给我学硕offer了。
413 |
414 | - 题量:应该是100道差不多,时长90分钟。
415 |
416 | - 题型:单选题、多选题、填空题、英文问答题。
417 |
418 | - 考察内容:
419 |
420 | - - 线性代数(有复杂计算,我遇到了张宇考研数学的原题)
421 | - 概率论(有奇怪的伤脑筋的题,得多练)
422 | - 数据结构(重点,有考察排序算法、链表)
423 | - 机器学习(把西瓜书看看就行,考的都是知识点,概念性的东西)
424 | - 印象中没有计组计网操作系统
425 |
426 |
--------------------------------------------------------------------------------
/面经(分类).md:
--------------------------------------------------------------------------------
1 | # 面经(分类整理)
2 |
3 | 笔试+上机(最关键,笔试过不掉救不了)
4 |
5 | - 100分笔试,机器学习,模式识别,数据结构与算法,知识推理(zyz,英文题,要看一下),人工智能,概率统计(简答题,其他是选择填空)
6 | - 50分编程题,什么方向不知道,应该和机器学习和算法相关。
7 | - 月底组内,积累点经验,问一下学长,口语是怎么样的。
8 | - 本校有一定的优势,尽可能做好,题量不少,做不对略过即可,不要纠结。
9 |
10 | ## 概率论
11 |
12 | - 大数定理
13 | - 中心极限定理
14 | - 全概率公式
15 | - 最大似然估计
16 | - 贝叶斯公式:接着看论文的老师问我朴素贝叶斯决策相关的内容,朴素贝叶斯我还是会的,说了一下思想和公式。然后他问我,朴素贝叶斯是独立分布还是独立条件分布?我当时不知道是怎么的鬼使神差,答了个独立分布...只能说脑子瓦特了,那天状态真的特别差。后来知道老师问我这个问题的原因是我在论文中用了大量条件分布的东西。
17 | - 网上那些脑筋急转弯
18 | - 独立同分布:为什么机器学习中的基本假设是独立同分布,独立同分布全称是什么?(这个地方卡了,对面嫌我说多了)
19 |
20 | ## 机器学习
21 |
22 | 西瓜书前十章精通
23 |
24 | - 对机器学习/深度学习的理解
25 | - 开放动态环境下机器学习的认识(来自南大某著名实验室)
26 | - PCA:简述PCA的计算过程,PCA的全称是什么
27 | - SVM:简述SVM,并解释SVM为什么要化对偶形?百万样本量可以用SVM吗?(我答:虽然可以通过现成凸优化包求解,但是对偶问题求解更快)为什么更快?
28 | - 讲一个你知道的聚类算法?
29 | - 集成学习:简述几种集成学习方法,Adaboost的计算过程,以及Stacking Learning?Boosting的基本思想?Boosting学习有什么特点?为什么集成学习需要集成“好而不同”的学习器?介绍Xgboost的优势
30 | - 常用的机器学习算法的适用场景(例如KNN、朴素贝叶斯、决策树等)
31 | - PAC理论:PAC理论的全称是什么?PAC理论了解多少?
32 | - 具体阐述残差神经网络的含义
33 | - 梯度消失和梯度爆炸是什么意思?有什么样的方法进行改善?
34 | - 介绍一下梯度下降法是什么
35 | - 介绍一下牛顿迭代是什么
36 | - 为什么机器学习中的基本假设是独立同分布,独立同分布全称是什么?(这个地方卡了,对面嫌我说多了)
37 | - $ \epsilon $ -greedy:就问了一个“ε-greedy”算法中ε取值的问题
38 | - 决策树一些更加深入的东西
39 | - 机器学习中FP、TP是什么?
40 |
41 | ## 数据结构与算法
42 |
43 | - 数据结构 考的巨多 建议精通
44 | - 时间复杂度分析
45 | - 渐进
46 | - 动态规划:背包问题
47 | - 摊还
48 | - 排序:
49 |
50 | - 排序:算法,平均最优最坏时间复杂度以及空间复杂度。黑板上手写证明。排序为什么要稳定。
51 | - 快排:平均、最优、最坏复杂度。最坏情况是什么样?优缺点。
52 | - 归并:平均最优最坏时间复杂度以及空间复杂度,优缺点。
53 | - 既然归并的最坏也是 $ O(n\log n) $ ,而快排最坏 $ O(n^2) $ ,为啥现在大家都用的是快排。(我只从空间复杂度进行了分析,后来面完查了下,其实实践证明,虽然二者时间复杂度相同,但快排还是要快一些,而且最坏情况遇到的可能性也比较低。)
54 | - P问题 NP问题 NP完全问题的概念
55 | - 直接问我红黑树了,我有点傻眼了,老实说自己不会,只知道STL有些底层是红黑树实现的(有时间还是得看下红黑树,至少得了解思想)
56 | - 图
57 |
58 | - 如何判断图中是否有环
59 | - 欧拉图是什么?判定方法?
60 | - TopK问题详解,“快速选到第n个数”(快速选择,复杂度为 $ O(n) $ )
61 | - C++中new和malloc的区别
62 | - 双蛋问题,但是单蛋版,也就是你只有一个鸡蛋如何判定其不摔碎的最高楼层?
63 | - 智力问题,黑白帽子问题(可自行百度)
64 | - 霍夫曼编码的优势,霍夫曼编码的唯一性,香农编码是什么?
65 | - 散列表的优势(相比其他查询方式),查询复杂度(分链表型和普通型)
66 |
67 | ## 线代
68 |
69 | - svd(奇异值分解)
70 | - 讲一讲线代中的矩阵的特征值?什么是特征值,特征值的含义,特征值分解
71 | - 正定矩阵是什么?
72 | - 如何理解矩阵的秩?线代中的矩阵的秩和矩阵的关系?
73 | - 简述向量组线性无关的含义?
74 | - 矩阵分解的物理意义?
75 | - 半正定矩阵的定义,性质(越多越好),PCA协方差矩阵的性质(半正定),以及为什么半正定(从原理上说明)?
76 |
77 | ## 凸优化
78 |
79 | - 凸优化带约束的一阶条件
80 | - 凸优化中梯度下降的学习率如何确定?(凸优化最后两课讲的)
81 |
82 | ## 操作系统
83 |
84 | - 操作系统线程跟进程的区别等(操作系统的问题比较爱问)
85 |
86 | ## 数学分析
87 |
88 | - 常微分方程f'(x) = cx的解的形式,如果c是常数,为什么形式,如果c为矩阵呢? $ \frac12x^\top Cx $
89 | - 傅里叶变换和拉普拉斯变换的关系?拉普拉斯变换的用处?
90 |
91 | ## 其他
92 |
93 | - 一分钟自我介绍,遇到的挫折是什么
94 | - 研究生的“研究”二字是什么含义?研究生相比本科生有什么区别?
95 | - 比如如果离交稿ddl还剩两天,但是你的实验还有很大漏洞,论文也还没写完,这种情况怎么办
96 | - 英文面试
97 | - 1分钟自我介绍
98 | - 从事的研究细节(因为自我介绍中提及)
99 | - 你最感兴趣的课程
100 | - 你以后是想留在学校做研究还是去公司工作。
101 | - 如何利用文献检索知识去检索一个机器学习的问题
102 | - 你研究生读完之后有什么打算?你有什么做研究的品质?
103 |
104 | ## 机试
105 |
106 | - 最大子串和(给了一堆正负的数字,任选其中一段连续的数字(可以全选),需要和最大);无向图最长路径(单纯的Dijkstra);表达式求值(例如 (3\*2+1/2)+1\*2,计算结果);给一棵树求最长的路径(根到叶节点)。
107 | - 南大的机试,我觉得重点是DP、搜索、图论
108 |
109 | ## 笔试
110 |
111 | - 题量:应该是100道差不多,时长90分钟。
112 | - 题型:单选题、多选题、填空题、英文问答题。
113 | - 考察内容:
114 | - 线性代数(有复杂计算,我遇到了张宇考研数学的原题)
115 |
116 | - 概率论(有奇怪的伤脑筋的题,得多练)
117 | - 数据结构(重点,有考察排序算法、链表)
118 | - 机器学习(把西瓜书看看就行,考的都是知识点,概念性的东西)
119 | - 印象中没有计组计网操作系统
120 |
121 | 1. 可靠性(Soundness):在命题逻辑中,可靠性是指逻辑系统的一个属性,表示该系统中的推理规则是正确的。如果一个逻辑系统是健全的,那么任何从该系统的有效前提推导出的结论都是真的。换句话说,如果一个论证是健全的,那么它不会导致从假前提推出真结论的情况。
122 | 2. 完备性(Completeness):在命题逻辑中,完备性是指逻辑系统的另一个属性,表示该系统中的每个真陈述都可以在该系统中被证明为真。换句话说,如果一个逻辑系统是完备的,那么对于任何为真的陈述,系统中存在一个证明或推理来证明它的真实性。
123 |
--------------------------------------------------------------------------------
/面试.md:
--------------------------------------------------------------------------------
1 | ### 机器学习
2 |
3 | - 机器学习:基于统计、数据驱动,不是基于演绎而是基于归纳的。可以解决规则难以解决的问题;深度学习:使用更深的网络结果增强表达能力,将特征提取和模式学习相结合
4 | - 梯度下降法:一种常用的优化算法,用于最小化目标函数。计算过程是迭代地向梯度下降最快的方向更新参数,新参数=旧参数-学习率$\times$梯度。
5 | - 条件:目标函数可导,凸;优点:应用范围广,简单;缺点:可能陷入局部最小值,需要人为确定学习率
6 | - 牛顿迭代法:求$f(x)=0$的解的方法。每次用切线与x轴的交点的x值更新参数,$\displaystyle x_{n+1}=x_n-\frac{f(x_n)}{f'(x_n)}$
7 | - 条件:目标函数二价可微,目标函数的海森矩阵必须正定或负定
8 | - 优点:更快地收敛到最优解,不用调参;缺点:计算成本高
9 | - 决策树:一种基于树结构进行决策的算法,其中每个内部节点表示一个属性或特征,每个叶子节点代表决策结果。该算法可以用于分类和回归问题。
10 | - 计算过程:基于分治思想,每次选择最优划分属性,将样本集合分成更小的子集。不断重复,直到所有的子集都属于同一个类别,或者已经达到了预先定义的最大深度。
11 | - SVM (Support Vector Machine): 支持向量机,一种可以用于解决分类和回归问题的机器学习算法,目标是在高维空间中找到最佳的超平面,使得间隔最大化。
12 | - 支持向量:离超平面最近的训练样本点。
13 | - SVM为什么要化对偶形?为了更高效地求解。当数据集的规模很大时,使用原始问题求解SVM会变得很慢,甚至变得不可行。化成对偶问题可以使用SMO这种近似算法更高效的求解。
14 | - 百万样本量可以用SVM吗?求解SVM的原问题计算复杂度过大,有些困难。
15 | - 朴素贝叶斯:一种采用了属性条件独立性假设的分类器,基于贝叶斯定理,选择概率最大的类作为结果。
16 | - 贝叶斯最优分类器:为最小化总体风险,在每个样本上选择那个能使条件风险最小的类别标记,此时判定准则称为贝叶斯最优分类器
17 | - EM算法:一种迭代地估计参数隐变量的方法。其中E步 (Expectation) 基于参数推断隐变量的分布;M步 (Maximization) 基于已观测变量X和Z对参数做极大似然估计。
18 | - PCA (Principal Component Analysis):无监督降维方法。
19 | - 适用于数据之间存在线性相关性的情况,对于非线性关系可以考虑使用Kernel PCA。
20 | - 计算过程:先将数据标准化,使得每个特征的均值为0;计算标准化后数据的协方差矩阵,对协方差矩阵做特征值分解,选择特征值最大的k个特征向量组成投影矩阵,最后将标准化后的数据乘以投影矩阵,将数据投影到新的特征空间上。
21 | - 计算后的主成分正交,即没有线性相关性。(正交$\Rightarrow$线性无关)
22 | - 集成学习 (ensemble learning,读“昂”):一种机器学习方法,核心思想是通过组合多个弱学习器,从而提高模型的预测能力和泛化性能。
23 | - Bagging (bootstrap aggregating):使用自助采样法得到不同的训练集,训练一系列基学习器,通过投票或者平均的方法得到预测结果。
24 | - Boosting:基本思想是通过迭代训练一系列弱分类器,每个弱分类器都针对前一轮训练中被错误分类的样本进行加权,以提高其分类准确性。
25 | - Stacking:一种叠加泛化的集成方法,通过训练一个元模型来结合多个基础模型的预测结果。元模型就是以不同基学习器的预测结果作为输入,结果作为输出。
26 | - “好而不同”:即基学习器的准确率高,多样性高。直观讲准确率越高越好是显然的,多样性高意味着不同的学习器可以互补,从而提高整体的学习性能。理论上有误差歧义分解证明了泛化误差=基学习器泛化误差的却权均值-基学习器的加权分歧值,可以说明基学习器的准确率高,多样性高,分类效果越好。
27 | - Adaboost计算过程:(二分类任务)在训练的每一轮中,使用当前的样本权重训练基学习器,计算分类误差率,如果误差大于0.5则break;根据错误率计算这个基学习器的权重;基于对分类正误情况更新数据分布,增加分错样本的影响,降低分对样本的影响;最后基于各个基学习器的加权,得到最终的分类器
28 | - K-means:一种原型聚类方法,目标是将数据集分成k个不重叠的簇。通过最小化数据点与所属簇的质心之间的距离来进行聚类。
29 | - 计算过程:用一种迭代近似的方法求解。初始化k个簇的质心,重复如下步骤:将每个数据点分到与其最近的质心所属的簇;对于每个簇,计算所有数据点的均值,得到新的质心。如此重复直到质心的位置不再发生显著变化或达到预定的迭代次数。
30 | - KNN:一种lazy learning的监督学习算法,基于与测试样本最近邻的k个邻居的信息预测结果。
31 | - lazy learning:训练阶段仅仅是把样本保存起来,训练时间开销为零,待 收到测试样本后再进行处理
32 | - PAC (Probably Approximately Correct):一种计算学习理论,核心思想是如果一个算法能够在有限的样本上以很高的概率产生一个"近似正确"的模型,那么该算法可以在未见过的数据上表现良好。
33 | - PAC可辨识:算法是否能以高概率产生一个近似正确的模型(泛化误差小于epsilon的概率大于等于1-delta,则称学习算法能从假设空间中PAC辨识概念类C)
34 | - PAC可学习:在有限样本下算法是否能够以高概率产生一个近似正确的模型
35 | - PAC学习算法:在有限的样本和时间限制下,学习算法是否能够以高概率产生一个近似正确的模型
36 |
37 | ### 线代
38 |
39 | - 秩:矩阵中线性无关的行或列的最大数量。矩阵的秩可以看作是矩阵所代表的线性变换值域的向量空间的维度,比如说PCA中的协方差矩阵如果秩是k,那么数据可以被无损压缩到k维。
40 | - 线性相关:存在一组不全为零的标量(系数),使得向量之间的线性组合等于零向量。
41 | - 特征值,特征向量:对于n阶矩阵$A$,常数$\lambda$,和非零的n维列向量$\alpha$,有$A \alpha=\lambda \alpha$成立,则称$\lambda$是矩阵A的一个特征值,$\alpha$为矩阵$A$属于特征值$\lambda$的特征向量。
42 | - 特征值分解:将一个有$n$个线性无关的特征向量的$n$阶方阵$A$分解为$A=Q \Lambda Q^{-1}$的过程。其中$Q$中的每一列都是特征向量,Lambda为对角矩阵,对角线上的元素是对应的特征值。
43 | - 首先求解特征方程$|\lambda E-A|=0$,得到矩阵$A$特征值$\lambda _i$(共$n$个)
44 | - 再由$(\lambda_i E-A)x=0$求基础解系,即矩阵$A$属于特征值$\lambda_i$的线性无关的特征向量。
45 | - 用求得的特征值和特征向量构造Q,Lambda
46 | - 奇异值分解:将矩阵A分解为$U \Sigma V^{-1}$,其中U V均为正交矩阵,Sigma为对角矩阵,对角线上的值按从大到小排列。
47 | - 计算:对$AA^\top$、$A^\top A$分别进行特征值分解,得到U和V。两次计算中的非零特征值从大到小排序,放在对角线,其他位置为零。
48 | - 矩阵分解的意义:将一个矩阵表示为多个矩阵的乘积的过程,有比如说奇异值分解,特征值分解。可以将复杂的矩阵问题简化为更易处理的子问题,提高计算效率。可以提取矩阵中的隐藏模式和结构,用于数据的降维、特征提取和模式识别等任务。
49 | - 正定:实对称矩阵$A$,对任何非零向量$x$,都满足$x^\top A x>0$
50 |
51 | - 充要条件:实对称矩阵 $A$ 正定 $\Leftrightarrow A$ 与单位矩阵 $E$ 合同;存在可逆矩阵 $C$,使 $A=C^\top C$;$A$的特征值均为正;正惯性指数$p=n$;$A$ 的各阶顺序主子式都大于零
52 | - 性质:$A^{-1}, kA,A^*,A^m, (A+B)$也是正定矩阵
53 | - 必要条件:实对称矩阵 $A$ 正定 $\Rightarrow a_{ii}>0$;$\det A=|A|>0$
54 | - 半正定:实对称矩阵$A$,对任何非零向量$x$,都满足$x^\top A x\geq0$
55 |
56 | - 等价命题:$f(x_1,x_2,\dots,x_n)$半正定
57 | - $A$半正定
58 | - $r(f)=r(A)=p$(正惯性指数)
59 | - $A$合同于非负对角阵,即存在可逆阵$C$,使得$C^\top AC=\text{diag} (d_1,\dots,d_n),d_i\geq 0$
60 | - 存在方阵$G\in R^{n\times n}$,使$A=G^\top G$
61 | - 所有主子式$\geq0$
62 | - 梯度消失和梯度爆炸是什么意思?有什么样的方法进行改善?梯度消失:残差连接(输出为输入和输出的求和),ReLU;梯度爆炸:归一化
63 |
64 |
65 | ### 概率论
66 |
67 | - 大数定律:随机变量的均值依概率收敛于期望的均值。
68 | - 中心极限定理:在适当的条件下,大量相互独立随机变量的均值依分布收敛于正态分布。
69 | - 局限:样本容量要求,可以用集中不等式解决。
70 | - 贝叶斯公式:用于计算在某个先验条件下事件的后验概率的公式。
71 | - 全概率公式:一个事件发生的概率等于它在与样本空间的一个划分中每个事件同时发生的概率之和。
72 | - 最大似然估计:是一种用于估计模型参数的统计方法。极大似然估计的基本思想是找到使观测数据的似然函数最大化的参数值。
73 |
74 | - 需要满足:样本独立同分布,参数化假设(参数可数且取值有限),模型合适
75 | - 独立同分布:independent and identically distributed,即独立同分布假设,假设数据集中的每个样本都是从同一个概率分布中独立地随机取出的。目的是简化建模。
76 | - 高维高斯分布:$\displaystyle p(x)=(2\pi)^{- D/2}|\Sigma|^{-1/2}\exp\{-\frac12(x-\mu)^{\top}\Sigma ^{-1}(x-\mu)\}$
77 |
78 | ### 数据结构与算法
79 |
80 | - P问题:可以在多项式时间内求解的决策问题。
81 | - NP问题:可以在多项式时间内验证答案是否正确的决策问题。
82 | - NP-complete :NP集合中最难的问题。是NP,且所有NP问题都可以在多项式时间内规约到它的问题。
83 | - NP-hard :所有NP问题都可以在多项式时间内规约到它的问题。
84 | - 排序稳定性:对于值相同的两个元素,排序后它们的先后顺序与原数组相同。比如在有些使用场景下需要保留原数据中元素的相对位置。
85 | - 快排:是一个基于分治的思想的排序算法,每次选择一个元素作为pivot,然后将给定的数组围绕这个基准进行划分,将小于基准的元素放到基准的左边,将大于基准的元素放到基准的右边,最终将基准放置在排序后的正确位置上。如此递归。优点:空间复杂度小,缺点:最坏复杂度无保证。选快排的原因:快排不需要进行分配和取消分配辅助数组等操作,其所需的常量时间小;空间复杂度低。
86 | - 归并排序:基于分治的思想的排序算法,每次将数组分为两个子数组,分别对子数组排序,再将两个子数组归并,形成最终的排序好的数组。优点:可并行;缺点:空间复杂度高。
87 | - topK:维护一个大小为k的小顶堆,时间复杂度$O(n\log k)$;类似快排,比如说找最大的数,pivot划分后左边80个,右边20个,只要对右边排序即可。最优$O(n)$,平均$O(n\log n)$
88 | - 判断图中有环:
89 | - 拓扑排序,最后如果还存在未被删除的顶点,则表示有环;否则没有环
90 | - DFS,如果在遍历的过程中,发现某个节点有一条边指向已经访问过的节点,并且这个已访问过的节点不是当前节点的父节点,则表示存在环(用黑白灰表示)
91 | - 对于有向图,若存在强连通分量(即存在$v_i \to v_j$的路径也存在$v_j\to v_i$的路径),图中有环。
92 | - 欧拉图:具有欧拉回路的图,欧拉回路是通过图中每条边恰好一次的回路
93 | - 有向图:非零度顶点是强连通的;每个顶点的入度和出度相等
94 | - 无向图是欧拉图当且仅当:非零度顶点是连通的;顶点的度数都是偶数
95 | - 霍夫曼编码:一种变长的数据压缩编码,通过让出现概率更小的字符长度更长,出现概率更大的字符长度更短进行数据压缩,是最优编码。基于霍夫曼树构造的。
96 | - 每次取出出现概率最小的两个结点,合并后结点权重为两个结点之和。直到所有结点构成一个二叉树。为二叉树的每个结点下的两个分支赋值为0、1,编码即从根节点到字符的叶节点的路径上01串。
97 | - 唯一可译码:因为霍夫曼编码是前缀编码,即没有一个编码是另一个编码的前缀。
98 | - 优点:最优编码。缺点:与计算机的数据结构不匹配;需要多次排序,耗费时间。
99 | - 香农编码:一种变长的数据压缩编码,效率略低于霍夫曼。
100 | - 编码方法:将符号按照其出现概率从大到小排序;把概率集合分成两个尽可能概率相等的子集,给前面一个子集合赋值为0,后面一个子集合赋值为1;如此重复直到各个子集合中只有一个元素为止;将每个元素所属的子集合的值依次串起来
101 | - 散列表的优势:查询高效,数据的存储和删除也高效。
102 | - 查询复杂度:链表型:每个哈希桶维护一个链表来存储冲突的键值对,最坏是O(n),平均接近O(1)
103 | - 普通型:当发生哈希冲突时,开放寻址再找到一个空的位置来存储冲突的值。最坏情况是O(n)(哈希表被填满),平均接近O(1)
104 | - 斐波那契:$O(2^n)$,存储结果$O(n)$;动态规划$O(n)$
105 |
106 | ### 其他
107 |
108 | - 操作系统线程跟进程的区别:进程是一个独立的程序运行的实例,线程是进程中的一个子任务。进程可以包含多个线程,进程之间是独立的,
109 | - 傅里叶变换:将信号从时域转换到频域的变换过程。
110 | - 拉普拉斯变换:傅里叶变换的一种扩展,可以将信号从时域转换到复频域。
111 | - 用处:在控制系统中,分析设计反馈控制系统;在信号处理中,用于滤波、信号重构、频谱估计和图像处理等
112 | - 两者关系:拉普拉斯变换是傅里叶变换的扩展形式;在频域分析中,拉普拉斯变换通常用于处理连续系统的输入-输出关系和系统响应,而傅里叶变换适用于连续信号和离散信号。
113 | - 凸优化带约束的一阶条件:定义域是凸集,$f(y)> f(x)+\nabla f(x)^\top (y-x)$
114 | - 二阶条件:对于开集内的任意一点,它的Hessian矩阵半正定。$\nabla^2 f(x)\geq 0$
115 | - KKT条件是非线性规划中最优解的一阶必要条件:拉格朗日函数的导数为0,原始可行性条件,对偶可行性条件,互补松弛条件。
116 | - 原始可行性条件:优化变量满足原问题的所有的约束条件,包括对于每个不等式约束和等式约束
117 | - 对偶可行性条件:对于每个不等式约束,对应的拉格朗日乘子大于等于0。
118 | - 互补松弛条件:约束的松弛变量与拉格朗日乘子的乘积为零
119 | - 凸优化中梯度下降的学习率:通过线搜索确定。线搜索是一种通过搜索确定每次迭代的合适学习率的方法。在每次迭代中,沿着梯度方向尝试不同的学习率值,通过一些准则来选择合适的学习率,使得目标函数在新的参数值上有足够的下降。精确,计算成本高。
120 | - 如果函数的定义域是凸集,且对于任意定义域上的$x,y$和任意$0\leq \theta\leq 1$,有$f(\theta x+(1-\theta)y)\leq \theta f(x)+(1-\theta)f(y)$,则函数是凸的。
121 |
122 | - 卷积和:将其中一个信号翻转再平移,再和另一个向量相乘,对乘积后的信号求和。
123 | - A*:树admissible则optimal,图consistent则optimal。admissible即到目标的估计成本<到目标的真实成本,consistent即结点与其后继的估计成本之差<这一步的真实成本
124 |
125 | - 原问题为什么要化成对偶问题:原问题线性可分就即凸,线性不可分则不凸
126 |
127 | - 对偶问题的求解可以用SMO等近似方法求解。可以引入核函数。(通过迭代地优化一对变量来求解SVM的优化问题。其主要思想是选择两个变量进行优化,将其他变量固定,并通过解析方法直接计算这两个变量的最优值。通过迭代地更新这对变量,SMO算法逐渐逼近全局最优解。)
128 |
129 | - 斐波那契数列求和:公式,DP,递归(拿字典存)
130 |
131 | - 双蛋问题:可以用动态规划求解,
132 |
133 | $W(n,h)$表示有n个鸡蛋h层楼所需的最少实验次数
134 | $$
135 | W(n,h)=1+\min(\max(W(n-1, i-1), W(n, h-i)))
136 | $$
137 | $n=2$:$W(h)=1+\min(\max(i-1, W(h-i)))$
138 |
139 | - 激活函数:引入非线性特性,Sigmoid,Tanh,ReLU,LeakyReLU。Sigmoid映射到(0,1),Tanh映射到(-1,1),这两个激活函数都存在梯度消失。ReLU可以一定缓解梯度消失问题,但是在负输入时不可导,可能存在神经元死亡的情况。LeakyReLU对ReLU改进,在负输入时保留一个小的梯度,有助于解决ReLU函数中的死亡神经元问题。
140 |
141 | - 特征值特征向量意义:特征值告诉我们特征向量在线性变换中的伸缩程度,PCA中特征值越大说明对应的特征向量相关性更大,取最大的k维。特征值可以用来判断矩阵的正定性等(特征值均>0)。
142 | - 数据规模大:对偶问题太复杂。
143 |
--------------------------------------------------------------------------------
 349 |
350 | ## 线性模型
351 |
352 | ### 线性回归
353 |
354 | #### 线性回归的目标
355 |
356 | $$
357 | (w^*,b^*)=\arg \min_{(w,b)}\sum_{i=1}^m(f(x_i)-y_i)^2=\arg \min_{(w,b)}\sum_{i=1}^m(y_i-wx_i-b)^2
358 | $$
359 |
360 | #### 最小二乘
361 |
362 | 最小二乘“参数估计”:求解 $ w,b $ 使 $ \mathbb E_{(w,b)}=\sum_{i=1}^m(y_i-wx_i-b)^2 $ 最小化的过程。将 $ \mathbb E_{(w,b)} $ 对 $ w,b $ 求导,令之为零后得到 $ w,b $ 最优解的闭式解。
363 |
364 | #### 对数线性回归
365 |
366 | log-linear regression, $ \ln y=w^\top x+b $
367 |
368 | #### 广义线性模型
369 |
370 | generalized linear model, $ y=g^{-1}(w^\top x+b) $ ,其中 $ g(\cdot) $ 为联系函数link function
371 |
372 | ### 逻辑斯蒂回归
373 |
374 | #### 什么是逻辑斯蒂回归?
375 |
376 | 逻辑斯蒂回归为一个分类算法,通过对输入特征进行加权求和,并将结果通过一个值域为0-1的sigmoid函数(也称为逻辑函数)进行映射,从而得到输出概率值。
377 |
378 | #### Sigmoid函数是什么?为什么要用Sigmoid函数?
379 |
380 | Sigmoid函数即形似S的函数,目的是近似不连续不可导的单位阶跃函数(值域 $ \{0,1\} $ ),作为它的替代函数surrogate function。又称对数几率函数。公式为
381 |
382 | $$
383 | y=\frac1{1+e^{-z}}
384 | $$
385 |
386 | 值域为 $ [0,1] $
387 |
388 | #### 如何求解参数?
389 |
390 | 将后验概率估计代入对数几率的式子,用极大似然法找到Loss函数。然后用梯度下降法、牛顿法等数值优化方法找到使得Loss最小的 $ \beta $ ,即可得到参数。
391 |
392 | 具体见p59。
393 |
394 | #### 梯度下降
395 |
396 | > 什么是梯度下降法?
397 |
398 | 一阶迭代数值优化算法,用于寻找可微函数的局部最小值。
399 |
400 | 更新公式:
401 |
402 | $$
403 | x_{n+1}=x_{n}-\gamma\nabla f(x_n)
404 | $$
405 |
406 | 其中, $ \gamma $ 是学习率。 $ \nabla f $ 指向函数值增长最快的方向,则 $ -\nabla f $ 指向函数值增长最快的方向。理论上当 $ \gamma $ 足够小,则 $ f(x_n)\geq f(x_{n+1}) $
407 |
408 | > 需要满足什么条件?
409 |
410 | 前提:
411 |
412 | 1. 目标函数可导
413 | 2. 目标函数是凸函数(否则可能会陷入局部最优解)
414 |
415 | > 有什么优缺点?
416 |
417 | 优点:
418 |
419 | 1. 可以应用于许多不同的优化问题(线性回归,逻辑回归,神经网络)
420 | 2. 算法简单
421 | 3. 只需要计算一阶导数,计算成本相对较低。
422 | 4. 可以在大规模数据集上进行优化。
423 |
424 | 缺点:
425 |
426 | 1. 可能会陷入局部最小值,无法得到全局最小值。
427 | 2. 当函数存在平台、峡谷和其他复杂的非凸结构时,可能会出现震荡或缓慢收敛的情况。
428 | 3. 需要选择合适的学习率,过大或过小都会影响优化结果。
429 | 4. 对于某些问题,可能需要较多的迭代次数才能达到收敛。
430 |
431 | #### 什么是牛顿迭代法?需要满足什么条件?有什么优缺点?
432 |
433 | 目的:求 $ f(x)=0 $ 的解
434 |
435 | 初始化: $ x_0 $
436 |
437 | 重复:过 $ x_i $ 求 $ f(x) $ 的切线 $ L:y=f(x_{i})+f'(x_{i})(x-x_i) $ ,与x轴交点为 $ x_{i+1}=x_i-\frac{f(x_i)}{f'(x_i)} $
438 |
439 | 迭代公式:
440 |
441 | $$
442 | x_{n+1}=x_n-\frac{f(x_n)}{f'(x_n)}
443 | $$
444 |
445 | 对于 $ \beta^*=\arg\min_{\beta}\ell(\beta) $ 的优化问题,更新公式为:
446 |
447 | $$
448 | \beta^{t+1}=\beta^t-\left(\frac{\part^2\ell(\beta)}{\part \beta\part \beta^\top}\right)^{-1}\frac{\part\ell(\beta)}{\part \beta}
449 | $$
450 |
451 | 必要条件:
452 |
453 | 1. 目标函数二价可微
454 | 2. 目标函数的海森矩阵必须正定或负定
455 |
456 | 优点:
457 |
458 | 1. 可以更快地收敛到最优解,尤其是在函数存在二阶导数且二阶导数连续的情况下。
459 | 2. 可以解决梯度下降等一阶方法无法收敛的问题。
460 | 3. 可以自动调整学习率,减少手动调参的工作量。
461 |
462 | 缺点:
463 |
464 | 1. 对于高维问题,计算海森矩阵的代价非常昂贵。
465 | 2. 当海森矩阵不正定时,可能会导致算法发散。
466 | 3. 可能会陷入局部最小值,无法得到全局最小值。
467 | 4. 由于需要计算二阶导数,所以计算成本相对较高。
468 | 5. 当函数存在平台、峡谷和其他复杂的非凸结构时,可能会出现震荡或缓慢收敛的情况。
469 |
470 | ### 线性判别分析
471 |
472 | LDA, Linear Discriminant Analysis
473 |
474 | > 什么是LDA?
475 |
476 | LDA是一种常用的分类算法和数据降维方法。它可以将一个高维数据集降到一个更低的维度,同时保持样本类别信息,从而方便后续的分类任务。
477 |
478 | LDA 假设数据符合高斯分布,且各类别的协方差矩阵相等,基于此,它通过线性变换,将数据投影到一个低维空间中,使得同一类别的数据尽可能的接近,不同类别的数据尽可能的远离。这种投影方式保留了最大的类间差异性和最小的类内差异性,因此可以有效的提高分类准确率。
479 |
480 | 具体来说,LDA 算法主要包含两个步骤:(1)计算类内散度矩阵和类间散度矩阵;(2)通过求解广义瑞利商的特征向量,得到用于投影的变换矩阵。
481 |
482 | LDA 广泛应用于图像识别、人脸识别、语音识别等领域,并且在实际应用中表现良好。
483 |
484 | > 什么是类内散度矩阵,类间散度矩阵?
485 |
486 | $ X_i,\mu_i,\Sigma_i $ :第 $ i $ 类示例的集合、均值向量、协方差矩阵。
487 |
488 | $ w^\top \mu_i,w^\top \Sigma_i w $ :投影后的结果
489 |
490 | 目标:同类样例投影点的协方差尽可能小,即 $ w^\top \Sigma_0 w+w^\top \Sigma_1 w $ 尽可能小;类中心之间的距离尽可能大,即 $ ||w^\top \mu_0-w^\top\mu_1||_2^2 $ 尽可能大。即最大化
491 |
492 | $$
493 | J=\frac{||w^\top \mu_0-w^\top\mu_1||_2^2}{w^\top \Sigma_0 w+w^\top \Sigma_1 w}=\frac{w^\top (\mu_0-\mu_1)(\mu_0-\mu_1)^\top w}{w^\top(\Sigma_0+\Sigma_1)w}
494 | $$
495 |
496 | 其中**类内散度矩阵**within-class scatter matrix:
497 |
498 | $$
499 | S_w=\Sigma_0+\Sigma_1=\sum_{x\in X_0}(x-\mu_0)(x-\mu_0)^\top+\sum_{x\in X_1}(x-\mu_1)(x-\mu_1)^\top
500 | $$
501 |
502 | **类间散度矩阵**between-class scatter matrix:
503 |
504 | $$
505 | S_b=(\mu_0-\mu_1)(\mu_0-\mu_1)^\top
506 | $$
507 |
508 | 这就是LDA想要最大化的目标,即 $ S_b,S_w $ 的广义瑞利商generalized Rayleigh quotient:
509 |
510 | $$
511 | J=\frac{w^\top S_b w}{w^\top S_w w}
512 | $$
513 |
514 | > 如何求解LDA?
515 |
516 | 即确定能最大化 $ J $ 的 $ w $
517 |
518 | 令 $ w^\top S_ww=1 $ ,原式等价于
519 |
520 | $$
521 | \begin{aligned}
522 | &\min_w &&-w^\top S_b w\\
523 | &s.t. && w^\top S_w w=1
524 | \end{aligned}
525 | $$
526 |
527 | 由拉格朗日乘子法,等价于
528 |
529 | $$
530 | S_b w=\lambda S_ww
531 | $$
532 |
533 | $ S_b w $ 方向恒等于 $ \mu_0-\mu_1 $ ,令
534 |
535 | $$
536 | S_b w=\lambda(\mu_0-\mu_1)
537 | $$
538 |
539 | 有:
540 |
541 | $$
542 | w=S_w^{-1}(\mu_0-\mu_1)
543 | $$
544 |
545 | 考虑到数值解的稳定性,在实践中通常是对 $ S_w $ 进行奇异值分解,即 $ S_w= U\Sigma V^\top $ ,这里 $ \Sigma $ 是一个实对角矩阵,其对角线上的元素是 $ S_w $ 的奇异值,然后再由 $ S_w^{-1}=V\Sigma^{-1}U^\top $ 得到 $ S_w^{-1} $
546 |
547 | > 如何推广到多分类?[再看看!]
548 |
549 | 定义全局散度矩阵( $ \mu $ 是所有示例的均值之和)
550 |
551 | $$
552 | S_t=S_b+S_w=\sum_{i=1}^m(x_i-\mu)(x_i-\mu)^\top\\
553 | S_w=\sum_{i=1}^N S_{w_i}=\sum_{i=1}^N\sum_{x\in X_i}(x-\mu_i)(x-\mu_i)^\top\\
554 | S_b=S_t-S_w=\sum_{i=1}^N m_i(\mu_i-\mu)(\mu_i-\mu)^\top
555 | $$
556 |
557 | 优化目标:
558 |
559 | $$
560 | \max_W\frac{tr(W^\top S_bW)}{tr(W^\top S_wW)}
561 | $$
562 |
563 | 通过求解 $ S_b W=\lambda S_w W $ 可得, $ W $ 的闭式解为 $ S_w^{-1}S_b $ 的 $ N-1 $ 个最大广义特征值所对应的特征向量组成的矩阵。
564 |
565 | ### 多分类学习
566 |
567 | #### 有什么拆分策略?
568 |
569 | OvO(一对一,one vs one): $ \frac{N(N-1)}{2} $ 个分类器
570 |
571 | OvR(一对剩余,one vs rest): $ N $ 个分类器,选择置信度最大的类别标记
572 |
573 | MvM(多对多,many vs many):需要用ECOC编码特殊构造。
574 |
575 | ### 类别不平衡
576 |
577 | class-imbalance
578 |
579 | #### 有什么解决方法?
580 |
581 | “再缩放”,也是“代价敏感学习”cost-sensitive learning的基础
582 |
583 | 1. 对反例进行“欠采样”
584 | 2. 对正例进行“过采样”
585 | 3. 阈值移动
586 |
587 | ## 决策树
588 |
589 | ### 基本流程
590 |
591 | #### 什么是决策树?
592 |
593 | 决策树是一种基于树结构的分类算法,其中每个内部节点表示一个属性或特征,每个叶子节点代表一个类别。该算法可以用于分类和回归问题,它通过对样本集合进行递归分治来构建决策树。
594 |
595 | 在构建决策树时,算法会选择一个最好的属性或特征,将样本集合分成更小的子集。这个过程会不断重复,直到所有的子集都属于同一个类别,或者已经达到了预先定义的最大深度。
596 |
597 | 决策树算法具有可解释性和易于理解的优点,因为它可以清楚地显示分类决策的过程,还可以处理缺失值和噪声数据。不过,决策树算法在处理高维数据时可能会遇到困难,并且容易受到过拟合和欠拟合等问题的影响。
598 |
599 | #### 决策树算法的基本流程是什么?
600 |
601 | 决策树的生成是基于分治策略的递归过程。
602 |
603 | 首先生成结点,如果训练集中的样本均属于同一类别,则将该节点标记为该类叶子结点,返回。如果属性集为空或训练集在属性集上的取值相同,则将该节点标记为叶子结点,类别为数据集中样本数最多的类,返回。如果都不满足这两种情况的话,从属性集中选择最优划分 $ a^* $ 。对最优划分中的每一个值,为结点生成一个分支,构造相应取值的样本子集。如果样本子集为空,则将该节点标记为叶子结点,类别为数据集中样本数最多的类,返回。否则递归地对样本子集和最优划分的子集生成决策树。
604 |
605 | #### 什么情况会导致递归返回?
606 |
607 | 1. 当前结点包含的样本全属于同一类别,无需划分
608 | 2. 当前属性集为空,或是所有样本在所有属性上取值相同,无法划分
609 | 3. 当前结点包含的样本集合为空,不能划分。
610 |
611 | ### 划分选择
612 |
613 | #### 有什么划分的指标?它们的具体定义?
614 |
615 | 划分选择的目标是希望决策树的分支结点所包含的样本尽可能属于同一类别,即结点的“纯度” (purity) 越来越高。
616 |
617 | 划分的指标有:(ID3)信息增益、(C4.5)增益率、(CART)基尼指数。
618 |
619 | $ p_k $ :当前样本属于第 $ k $ 类的比例
620 |
621 | 假设离散属性 $ a $ 有 $ V $ 个可能的取值 $ \{a^1,\dots,a^V\} $ ,若使用 $ a $ 来对样本集 $ D $ 进行划分,则会产生 $ V $ 个分支结点,其中第 $ v $ 个分支结点包含了 $ D $ 中所有在属性 $ a $ 上取值为 $ a^v $ 的样本,记为 $ D^v $
622 |
623 | 信息熵:值越小,纯度越高
624 |
625 | $$
626 | Ent(D)=-\sum_{k=1}^{\mathcal Y}p_k\log_2 p_k
627 | $$
628 |
629 | 信息增益:值越大,说明使用属性 $ a $ 来划分所获得的纯度提升越大。
630 |
631 | $$
632 | Gain(D,a)=Ent(D)-\sum_{v=1}^V\frac{|D^v|}{|D|}Ent(D^v)
633 | $$
634 |
635 | 增益率:信息增益准则对可取值数目较多的属性有所偏好,为减少这种偏好可能带来的不利影响,引入增益率。其中 $ IV(a) $ 为属性 $ a $ 的固有值intrinsic value
636 |
637 | $$
638 | Gain_ratio(D,a)=\frac{Gain(D,a)}{IV(a)}\\
639 | IV(a)=-\sum_{v=1}^V\frac{|D|^v}{|D|}\log_2\frac{|D|^v}{|D|}
640 | $$
641 |
642 | 基尼指数Gini index:Gini反映从数据集 $ D $ 中随机抽取两个样本,其类别标记不一致的概率。越小纯度越高
643 |
644 | $$
645 | Gini(D)=\sum_{k=1}^{|\mathcal Y|}\sum_{k'\neq k}p_kp_{k'}=1-\sum_{k=1}^{|\mathcal Y|}p_k^2\\
646 | \text{Gini_Index}(D,a) =\sum_{v=1}^V\frac{|D^v|}{|D|}Gini(D^v)
647 | $$
648 |
649 | ### 剪枝
650 |
651 | #### 简述预剪枝和后剪枝的策略?
652 |
653 | 预剪枝:基于贪心思想,如果划分后验证集精度 $ \leq $ 原来的精度,则剪枝,禁止这些分支展开。
654 |
655 | 后剪枝:生成完整决策树后,从叶子结点开始遍历,如果划分后验证集精度 $ \leq $ 原来的精度,则剪枝,禁止这些分支展开。
656 |
657 | #### 两者的优缺点?
658 |
659 | | | 预剪枝 | 后剪枝 |
660 | | ------------- | ------------------------------ | ---------------------------------- |
661 | | 时间开销 | 测试时间降低,训练时间降低 | 测试时间降低,训练时间提高 |
662 | | 过/欠拟合风险 | 过拟合风险降低,欠拟合风险增加 | 过拟合风险降低,欠拟合风险基本不变 |
663 | | 泛化性能 | | 后剪枝通常优于预剪枝 |
664 |
665 | ### 连续值与缺失值
666 |
667 | #### 如何处理连续值?
668 |
669 | 基本思路是连续属性离散化
670 |
671 | 1. 二分法
672 | 2. 对于从大到小排序好的取值 $ \{a^1,\dots,a^n\} $ ,令划分点集合为 $ T_a=\left\{\frac{a^i+a^{i+1}}2|i\leq i\leq n-1\right\} $ ,然像离散属性值一样来考察这些划分点
673 |
674 | 需注意的是,与离散属性不同,若当前结点划分属性为连续属性,该属性还 可作为其后代结点的划分属性。
675 |
676 | #### 如何处理缺失值?
677 |
678 | 需要解决 1. 训练 2. 测试时的处理
679 |
680 | 令 $ \tilde D $ 为 $ D $ 在属性 $ a $ 上没有缺失值的样本子集,定义:
681 |
682 | 无缺失值比例: $ \displaystyle \rho=\frac{\sum_{x\in\tilde D} w_x}{\sum_{x\in D} w_x} $
683 |
684 | 无缺失值样本中第 $ k $ 类的比例: $ \displaystyle \tilde p_k=\frac{\sum_{x\in\tilde D_k} w_x}{\sum_{x\in \tilde D} w_x},1\leq k\leq|\mathcal Y| $
685 |
686 | 无缺失值样本中在属性 $ a $ 上取值为 $ a^v $ 的比例: $ \displaystyle \tilde r_v=\frac{\sum_{x\in\tilde D^v} w_x}{\sum_{x\in \tilde D} w_x},1\leq v\leq V $
687 |
688 | 推广:
689 |
690 | $$
691 | Ent(\tilde D)=-\sum_{k=1}^{\mathcal Y}\tilde p_k\log_2 \tilde p_k\\
692 | Gain(D,a)=\rho \times Gain(\tilde D,a)=\rho \times\left(Ent(D)-\sum_{v=1}^V \tilde r_v Ent(D^v)\right)
693 | $$
694 |
695 | ### 多变量决策树
696 |
697 | multivariate decision tree,在多变量决策树的学习过程中, 不是为每个非叶结点寻找一个最优划分属性,而是试图建立一个合适的线性分类器。
698 |
699 | ## 神经网络
700 |
701 | ## 支持向量机
702 |
703 | ### 基本概念
704 |
705 | #### 英文介绍
706 |
707 | Support Vector Machine (SVM) is a powerful machine learning algorithm used for classification and regression analysis. SVM finds the best hyperplane that separates different classes in a high-dimensional space. The hyperplane is chosen in such a way that it maximizes the margin or the distance between the two closest points of different classes. These closest points are called support vectors, and they play a crucial role in defining the hyperplane.
708 |
709 | SVM can handle both linearly separable and non-linearly separable data by using different types of kernel functions such as linear, polynomial, radial basis function (RBF), and sigmoid. The choice of kernel function depends on the data and the problem at hand. SVM can also handle multi-class classification problems using various techniques such as one-vs-one and one-vs-all.
710 |
711 | SVM has several advantages over other classification algorithms such as logistic regression and decision trees. It is less prone to overfitting, works well with high-dimensional data, and is computationally efficient. However, SVM has some limitations, such as the need for careful selection of kernel functions and hyperparameters, and the difficulty in handling large datasets.
712 |
713 | #### SVM是什么?
714 |
715 | 支持向量机是一种可以用于解决分类和回归问题的机器学习算法,目标是在高维空间中找到最佳的超平面,以最大化间隔,也就是margin。
716 |
717 | SVM问题的基本型(是一个凸二次优化问题):
718 |
719 | $$
720 | \begin{aligned}
721 | &\min_{w,b} \quad\frac12||w||^2\\
722 | &s.t. \quad y_i(w^\top x_i+b)\geq1,i=1,\dots,m
723 | \end{aligned}
724 | $$
725 |
726 | #### SVM中的“支持向量”指什么?在SVM中如何确定支持向量?
727 |
728 | “支持向量”是指离分隔超平面最近的训练样本点。这些样本点是最能影响分隔超平面位置和方向的点,如果它们的位置发生变化,会直接影响到分隔超平面的位置和方向。
729 |
730 | 我们在SVM的训练过程中确定支持向量。在SVM的训练过程中,我们首先随机初始化超平面参数,然后迭代地优化超平面参数,直到收敛为止。在每一次迭代中,我们根据当前的超平面参数计算每个训练样本点到超平面的距离,并根据这些距离来判断哪些样本点是支持向量。
731 |
732 | #### SVM在分类问题中如何定义“边界”(decision boundary)?
733 |
734 | 在SVM中,边界(decision boundary)是指将不同类别的数据点分开的超平面(hyperplane)。SVM的目标是寻找一个最优的超平面,将不同类别的数据点分开,并且使得该超平面与最近的数据点之间的距离(即margin)最大化。
735 |
736 | #### SVM有什么优点和缺点?
737 |
738 | 优点:
739 |
740 | 1. 能有效处理高维数据,例如图像和文本分类
741 | 2. 在小数据集处理时表现优异,因为它只需要少量的支持向量来定义边界
742 | 3. SVM对数据中的噪声具有鲁棒性,因为决策边界由支持向量确定,它们是距离边界最近的数据点。
743 | 4. 泛化性好
744 |
745 | 缺点:
746 |
747 | 1. 不适用于大数据集,因为计算开销过大
748 | 2. 对核函数选择和参数选择敏感
749 | 3. 只适用于二元问题
750 | 4. 缺乏概率解释
751 | 5. 不适用于有缺失值的数据
752 |
753 | ### 原问题和对偶问题
754 |
755 | #### 如何将SVM转化为对偶问题?
756 |
757 | 对偶问题(dual problem)是指将一个优化问题的原问题(primal problem)转化为一个新的优化问题,对偶问题和原问题有相同的最优解,但对于一些问题,通过求解对偶问题可以更方便或更有效地得到原问题的解。
758 |
759 | 对偶问题一定是凸优化问题。
760 |
761 | 可以使用拉格朗日乘子法得到SVM的对偶问题:
762 |
763 | 拉格朗日函数:
764 |
765 | $$
766 | L(w,b,\alpha)=\frac12||w||^2+\sum_{i=1}^m\alpha_i(1-y_i(\omega^\top x_i+b))
767 | $$
768 |
769 | 令 $ L(w,b,\alpha) $ 对 $ \omega,b $ 的偏导为零可得:
770 |
771 | $$
772 | w=\sum_{i=1}^m\alpha_i y_ix_i\quad(1)\\
773 | 0=\sum_{i=1}^m\alpha_i y_i\quad(2)
774 | $$
775 |
776 | 将(1)代入拉格朗日函数可消去 $ w,b $ ,考虑(2)的约束可以得到对偶问题:
777 |
778 | $$
779 | \begin{aligned}
780 | &\max_{\alpha}\quad \sum_{i=1}^m\alpha_i-\frac12\sum_{i=1}^m\sum_{i=1}^m\alpha_i\alpha_jy_iy_jx_i^\top x_j\\
781 | &s.t. \quad \sum_{i=1}^m\alpha_i y_i=0,\alpha_i\geq 0,i=1,\dots,m
782 | \end{aligned}
783 | $$
784 |
785 | 要满足KKT条件:
786 |
787 | $$
788 | \left\{\begin{aligned}
789 | &\alpha_i\geq0\\
790 | &y_if(x_i)-1\geq 0\\
791 | &\alpha_i(y_if(x_i)-1)=0
792 | \end{aligned}\right.
793 | $$
794 |
795 | ##### 什么是KKT条件?[x]
796 |
797 | Karush-Kuhn-Tucker (KKT)条件是非线性规划(nonlinear programming)最佳解的必要条件。
798 |
799 | 对于Lagrangian函数
800 |
801 | $$
802 | L(x,\lambda,\mu)=f(x)+\sum_{j=1}^m\lambda_jg_j(x)+\sum_{k=1}^n\mu_kh_k(x)
803 | $$
804 |
805 | KKT条件包括:**[术语怎么说?KKT只是必要条件,要到充分条件该如何做?内点]**
806 |
807 | $$
808 | \left\{\begin{aligned}
809 | &\nabla_xL=0\\
810 | &g_j(x)=0,j = 1,\dots,m\\
811 | &h_k(x)\leq 0,\\
812 | &\mu_k\geq 0,\\
813 | &\mu_kh_k(x)=0,k=1,\dots,p
814 | \end{aligned}\right.
815 | $$
816 |
817 | #### 为什么要将SVM转化为对偶问题?
818 |
819 | 虽然原问题本身就是一个凸二次规划(convex quadratic programming)问题,可以直接用现成的优化计算包求解,但是转化为对偶问题求解更高效。
820 |
821 | 原始的SVM问题是一个凸二次规划问题,通常使用二次规划算法求解。然而,当数据集的规模很大时,使用原始问题求解SVM会变得很慢,甚至变得不可行。此外,对于非线性SVM,计算的复杂度会随着特征空间的维度增加而急剧增加。
822 |
823 | 将SVM转化为对偶问题,就可以使用SMO算法等更高效的方法求解。
824 |
825 | 对偶问题和内积有关,可以引入核函数
826 |
827 | ##### 什么是SMO算法?
828 |
829 | ##### 为什么SMO算法不能用于求解原问题?
830 |
831 | ### 核函数
832 |
833 | kernel function
834 |
835 | #### SVM中的核函数是什么?
836 |
837 | 核函数是一种常用的技巧,用于将低维空间中线性不可分的数据映射到高维空间,从而使其在高维空间中变得线性可分。
838 |
839 | 如果原始空间是有限维(属性有限),那么一定存在一个高维特征空间使样本可分。
840 |
841 | 令 $ \phi(x) $ 为将 $ x $ 映射后的特征向量,于是,在特征空间中划分超平面所对应的模型可表示为
842 |
843 | $$
844 | f(x)=w^\top\phi(x)+b
845 | $$
846 |
847 | 原问题
848 |
849 | $$
850 | \begin{aligned}&\min_{w,b} \quad\frac12||w||^2\\&s.t. \quad y_i(w^\top \phi(x_i)+b)\geq1,i=1,\dots,m\end{aligned}
851 | $$
852 |
853 | 对偶问题
854 |
855 | $$
856 | \begin{aligned}
857 | &\max_{\alpha}\quad \sum_{i=1}^m\alpha_i-\frac12\sum_{i=1}^m\sum_{i=1}^m\alpha_i\alpha_jy_iy_j\phi(x_i)^\top\phi( x_j)\\
858 | &s.t. \quad \sum_{i=1}^m\alpha_i y_i=0,\alpha_i\geq 0,i=1,\dots,m
859 | \end{aligned}
860 | $$
861 |
862 | 核函数就是 $ \kappa(x_i,x_j)=<\phi(x_i),\phi(x_j)>=\phi(x_i)^\top\phi(x_j) $
863 |
864 | #### 核函数有什么性质?
865 |
866 | **[充要条件]** $ \kappa $ 是核函数当且仅当对于任意数据 $ D={x_1,\dots,x_m} $ ,核矩阵 $ K=[\kappa(x_i,x_i)]_{m\times m} $ 总是半正定的。
867 |
868 | 也就是说,对于一个半正定的核矩阵,总能找到一个与之对于的映射 $ \phi $ 。
869 |
870 | #### 有什么常用的核函数?
871 |
872 | | 名称 | 表达式 | 参数 | 适用场景 |
873 | | ----------- | ----------------------------------------------------------- | -------------------------- | ------------------------------------------------------------------------------------------------------------------------------------------------------------ |
874 | | 线性核 | $ \kappa(x_i,x_j)=x_i^\top x_j $ | | 输入特征维度较低,数据线性可分 |
875 | | 多项式核 | $ \kappa(x_i,x_j)=(x_i^\top x_j)^d $ | $ d\geq 1 $ ,多项式次数 | 数据中存在多项式关系 |
876 | | 高斯核(RBF) | $ \kappa(x_i,x_j)=\exp(-\frac{||x_i- x_j||^2}{2\sigma^2}) $ | $ \sigma>0 $ ,高斯核的带宽 | 输入特征维度较高 |
877 | | 拉普拉斯核 | $ \kappa(x_i,x_j)=\exp(-\frac{||x_i-x_j||}{\sigma}) $ | $ \sigma>0 $ | 采用 $ L_1 $ 范数来度量两个样本点之间的距离,而高斯核函数采用 $ L_2 $ 范数来度量。可以在一定程度上克服高斯核函数中存在的过拟合问题,适用于一些噪声较多的数据集。 |
878 | | Sigmoid核 | $ \kappa(x_i,x_j)=\tanh(\beta x_i^\top x_j+\theta) $ | $ \beta>0,\theta<0 $ | 数据集合线性不可分时,将数据映射到一个非线性空间中。表现不是很好,高斯核和拉普拉斯核更常用。 |
879 |
880 | 此外,若 $ \kappa_1,\kappa_2 $ 为核函数,则
881 |
882 | - $ \gamma_1\kappa_1+\gamma_2\kappa_2 $ 也是核函数
883 | - $ \kappa_1\otimes\kappa_2(x,z)=\kappa_1(x,z)\kappa_2(x,z) $ 也是核函数
884 | - 对于任意函数 $ g(x) $ , $ g(x)\kappa_1(x,z)g(z) $ 也是核函数
885 |
886 | #### 如何选择合适的核函数?[x]
887 |
888 | **[未完善]核函数需要满足什么性质?(很好地度量在希尔伯特空间里的距离,自反性,来回一样,对于自己为0...)**
889 |
890 | 根据根据具体的问题和数据选择。
891 |
892 | ### 软间隔与正则化
893 |
894 | #### 什么是软间隔SVM?
895 |
896 | 软间隔(soft margin)SVM通过设置松弛变量(slack variable),以允许某些样本不满足约束。传统硬间隔SVM要求数据完全线性可分,然而在实际情况下,由于数据可能存在一些噪声和异常点,很难找到完全线性可分的数据集。软间隔SVM通过允许一些样本出现在超平面的错误一侧,以此来解决线性不可分的问题。
897 |
898 | 优化目标可以写为
899 |
900 | 结构风险最小化+经验风险最小化
901 |
902 | $$
903 | \min_{w,b}\quad\frac12\vert\vert w\vert\vert^2+C\sum_{i=1}^{m}\ell_{0/1}\left(y_i(\omega^\top x_i+b)-1\right)
904 | $$
905 |
906 | 其中正则化常数 $ C>0 $ , $ \ell_{0/1} $ 为“0/1损失函数”, $ \ell_{0/1}=\left\{\begin{aligned}&1&z<0\\&0&otherwise\end{aligned}\right. $
907 |
908 | $ C\to\infty $ 时,会迫使所有样本均满足约束,等价于硬间隔; $ C $ 有限值时,允许一些样本不满足约束。
909 |
910 | #### 什么是替代损失?
911 |
912 | 由于 $ \ell_{0/1} $ 非凸、不连续,数学性质不好,使得优化目标难以直接求解,于是,使用其他一些函数替代 $ \ell_{0/1} $ ,称为替代损失(surrogate loss)
913 |
914 | - hinge损失(最常用): $ \ell_{hinge}(z)=\max(0,1-z) $
915 | - 指数损失exponential loss: $ \ell_{\exp}(z)=\exp(-z) $
916 | - 对率损失logistic loss: $ \ell_{\log}=\log(1+\exp(-z)) $
917 |
918 | 若采取hinge损失,优化目标可以改写为:
919 |
920 | $$
921 | \min_{w,b}\quad\frac12\vert\vert w\vert\vert^2+C\sum_{i=1}^{m}\max\left(0,1-y_i(\omega^\top x_i+b)\right)
922 | $$
923 |
924 | ##### 为什么使用Hinge Loss?[不知道!]
925 |
926 | Hinge Loss的优点在于它可以将最小化分类错误和最大化间隔相结合,即最小化损失的同时,最大化分类间隔。相比于其他损失函数,Hinge Loss对异常值的容忍度更高,可以更好地处理噪声和异常点的情况。同时,Hinge Loss的导数在0处不连续,使得模型更加稳定,不容易陷入局部最优解。(ChatGPT的回答)
927 |
928 | #### 什么是松弛变量?
929 |
930 | 引入松弛变量(slack variables),可将优化目标重写为
931 |
932 | $$
933 | \begin{aligned}
934 | &\min_{w,b}&\frac12\vert\vert w\vert\vert^2+C\sum_{i=1}^{m}\xi_{i}\\
935 | &s.t.&y_i(w^\top x_i+b)\geq1-\xi_{i}\\
936 | &&\xi_i\geq0,i=1,\dots,m
937 | \end{aligned}
938 | $$
939 |
940 | ##### 噪声和异常点的区别?
941 |
942 | | 噪声(noise) | 异常值(outliers) |
943 | | -------------------------------------------------------------- | ---------------------------------------------------------------------------------------------------- |
944 | | 数据中存在的错误或不准确的值 | 与其他数据点不同的、明显偏离正常情况的数据点 |
945 | | 可能是由于测量设备、传输问题或人为因素导致的 | 可能是由于记录或测量错误、系统故障或自然变异等原因导致的 |
946 | | 在整个数据集中分布较均匀 | |
947 | | 可能会对模型的性能产生一定影响,但它们不一定是非常明显的异常值 | 可能会对模型的训练和预测造成不良影响,因为它们可能会导致模型的偏差和方差增大,从而影响模型的泛化性能 |
948 | | 数据清洗和预处理噪声 | 使用特定的算法或技术来检测和处理异常点 |
949 |
950 | #### 与硬间隔SVM相比有何优势和劣势?
951 |
952 | hard margin
953 |
954 | 优势:
955 |
956 | 1. 对于存在噪声或异常点的数据,软间隔SVM可以允许一些样本不满足约束条件,从而更好地适应这些数据;
957 | 2. 更好地处理线性不可分数据集。
958 |
959 | 劣势:
960 |
961 | 1. 在使用松弛变量的情况下,软间隔SVM更容易出现过拟合现象,需要谨慎调参;
962 | 2. 计算复杂度增加,需要花费更多的计算资源和时间。
963 |
964 | #### 如何在SVM中使用正则化?
965 |
966 | 正则化(regularization)问题如下:
967 |
968 | $$
969 | \min_{f}\quad\Omega(f)+C\sum_{i=1}^{m}\ell(f(x_i),y_i)
970 | $$
971 |
972 | $ \Omega(f) $ :“结构风险”structural risk,正则化项用于描述模型 $ f $ 的某些性质
973 |
974 | $ \sum_{i=1}^{m}\ell(f(x_i),y_i) $ :“经验风险”empirical risk,用于描述模型与训练数据的契合程度
975 |
976 | $ C $ :正则化常数,折中两者,C越大,表示分类错误的惩罚越严厉,对于训练集的拟合效果更好,但是可能会过拟合;C越小,则表示更容忍分类错误,对于新数据的泛化性能更好,但是可能会欠拟合。
977 |
978 | #### $ L_1 $ 和 $ L_2 $ 正则化有何区别?
979 |
980 | $ L_p $ 范数是常用的正则化项, $ L_2 $ 倾向于 $ w $ 的分量取值尽量均衡,即非零分量个数尽量稠密; $ L_0 $ 范数(向量中非0的元素的个数)和 $ L_1 $ 范数倾向于 $ w $ 的分量尽量稀疏,即非零分量个数尽量少。
981 |
982 | ### 支持向量回归
983 |
984 | (Support Vector Regression,SVR)
985 |
986 | #### 什么是SVR?
987 |
988 | 有别于传统回归模型,SVR可以容忍 $ f(x) $ 和 $ y $ 之间最多有 $ \epsilon $ 的偏差,即仅当 $ f(x) $ 与 $ y $ 之间的差别绝对值大于 $ \epsilon $ 时才计算损失。这相当于构建了一个宽度为 $ 2\epsilon $ 的间隔带,若训练样本落入此间隔带,则认为预测正确。
989 |
990 | SVR可形式化为
991 |
992 | $$
993 | \min_{w,b}\quad\frac12\vert\vert w\vert\vert^2+C\sum_{i=1}^{m}\ell_{\epsilon}\left(f(x_i)-y_i\right)
994 | $$
995 |
996 | 其中正则化常数 $ C>0 $ , $ \ell_{\epsilon} $ 为 $ \epsilon $ -不敏感损失( $ \epsilon $ -insensitive loss)函数, $ \ell_{\epsilon}=\left\{\begin{aligned}&0&|z|\leq\epsilon\\&|z|-\epsilon&otherwise\end{aligned}\right. $
997 |
998 | #### 优化目标
999 |
1000 | ### 核方法
1001 |
1002 | #### KLDA[还没写]
1003 |
1004 | ### 具体任务
1005 |
1006 | #### 百万样本量可以用SVM吗?
1007 |
1008 | 对于百万级别的样本量,求解SVM的原问题计算复杂度过大,时空开销较大,可能存在着困难。不过,存在一些优化算法,使得可以在大规模数据集上使用SVM。
1009 |
1010 | 1. 一种方法是使用随机梯度下降(SGD)算法等在线学习算法,在每次迭代中随机选择一部分数据进行训练。这种方法的计算复杂度低,但可能会影响模型的收敛性和精度。
1011 | 2. 另一种方法是使用核函数的低秩近似,例如随机核近似(RKA)或核特征映射(KFM),以降低计算复杂度。这些方法将数据集投影到一个低维空间中,从而减少了计算量。不过,这些方法可能会对模型的精度产生一定的影响。
1012 | 3. 此外,还有一些并行化的方法,例如基于GPU的实现或者分布式计算框架的使用,可以加速SVM的训练过程。
1013 |
1014 | #### 在使用SVM时,如何处理不平衡的训练数据?
1015 |
1016 | - 改变类别权重:为少数样本增加权重
1017 | - 过采样少数样本
1018 | - 欠采样多数样本
1019 |
1020 | #### SVM中如何处理非线性可分数据?
1021 |
1022 | - 使用核函数:将原始数据映射到高维特征空间,从而使得原本线性不可分的数据在新的高维空间中成为线性可分的。
1023 | - 引入软间隔:允许某些样本不符合约束。
1024 |
1025 | #### 在SVM中如何处理多分类问题?
1026 |
1027 | - One-vs-All:对于 $ k $ 类问题,训练 $ k $ 个二元分类器,每个分类器的正例为第 $ i $ 类样本,负例为其他类别的所有样本。测试时,选择具有最高决策函数值的分类器。
1028 | - One-vs-One:对于 $ k $ 类问题,在任意两类样本之间设计一个SVM,因此 $ k $ 个类别的样本就需要设计 $ k(k-1)/2 $ 个SVM。当对一个未知样本进行分类时,最后得票最多的类别即为该未知样本的类别。Libsvm中的多类分类就是根据这个方法实现的。
1029 |
1030 | #### 在SVM中如何处理缺失数据?
1031 |
1032 | 1. 删除缺失值:直接删除包含缺失数据的样本,在剩余的完整数据上进行SVM训练。但是,这种方法会损失有用的信息,并且可能导致训练数据的减少。
1033 | 2. 插值:可以使用基于均值、中位数或其他统计量的简单插值方法,也可以使用更高级的插值方法,例如多重插值或KNN插值。然后使用填充后的数据进行SVM训练。
1034 |
1035 | 都会对SVM的性能造成负面影响。
1036 |
1037 | ### 训练细节
1038 |
1039 | #### 如何解决SVM模型过拟合(overfitting)的问题?
1040 |
1041 | 1. 减少特征数:使用特征选择技术,如主成分分析(PCA),来减少特征数量。
1042 | 2. 增加正则化:惩罚过于复杂的模型,防止过拟合。
1043 | 3. 增加数据量。
1044 | 4. 调整模型参数:如惩罚参数C、核函数类型等,来寻找最优模型。
1045 | 5. 使用交叉验证:可以使用交叉验证来评估模型性能和泛化能力,并进行模型选择。
1046 |
1047 | #### SVM中如何选择合适的超参数?如何通过网格搜索来选择超参数?
1048 |
1049 | 交叉验证。
1050 |
1051 | 正则化项 $ C $ :较大的值将使模型更加倾向于正确分类每个训练样本,但也可能导致过拟合。较小的值将允许更多的分类错误,但也可能导致欠拟合。
1052 |
1053 | (RBF核) $ \gamma $ :较大的值将导致决策边界更加复杂,可能会导致过拟合。较小的值将导致决策边界更加简单,可能会导致欠拟合。
1054 |
1055 | 需要避免使用测试集来选择,应该使用验证集来选择超参数,而将测试集保留到最后评估模型的性能。
1056 |
1057 | #### SVM模型的复杂度是如何计算的?如何通过交叉验证来选择合适的SVM模型?
1058 |
1059 | - 基于训练数据集大小(训练数据集大小 $ N $ ,特征维度 $ d $ , $ O(Nd^2) $ )
1060 | - 基于支持向量的复杂度(支持向量的数量为 $ m $ , $ O(md) $ )
1061 |
1062 | ### 模型对比
1063 |
1064 | #### SVM与逻辑回归相比有哪些优势和劣势?
1065 |
1066 | | | SVM | LR |
1067 | | ---------- | ------------------------------ | ---------------------------------------------- |
1068 | | 数据特征 | 对于线性可分的数据效果往往更好 | 能够处理非线性问题,可以使用多项式特征 |
1069 | | 数据规模 | 小数据集效果好 | 需要较多数据才能获得较好分类效果 |
1070 | | 噪声数据 | 容易受影响 | 容易受影响 |
1071 | | 参数选择 | 对参数的选择比较敏感 | 参数的选择比较简单 |
1072 | | 模型复杂度 | 复杂度较高 | 训练时间和内存开销相对较小,适合处理大规模数据 |
1073 |
1074 | #### SVM与神经网络有何异同点?
1075 |
1076 | (Answered by ChatGPT)
1077 |
1078 | 1. 工作原理不同:SVM是一种基于几何距离的分类器,它通过最大化分类间隔,寻找超平面将不同类别的数据分开;而神经网络则是通过模拟生物神经元的方式,使用一系列非线性变换来构建模型,实现分类和回归等任务。
1079 | 2. 模型结构不同:SVM的模型结构比较简单,只有一个决策边界;而神经网络的模型结构比较复杂,由多个神经元和层组成。
1080 | 3. 特征处理不同:SVM通常使用核函数将数据从低维空间映射到高维空间,以便找到更好的决策边界;而神经网络则通常使用输入层、隐藏层和输出层来提取和处理特征,不需要显式的特征转换过程。
1081 | 4. 训练方法不同:SVM使用凸优化算法来训练模型,而神经网络通常使用反向传播算法来训练模型。
1082 | 5. 适用场景不同:SVM适用于小规模、高维度的数据集,特别是在样本数目相对于特征数目较小的情况下表现更好,而神经网络适用于大规模、高维度的数据集,可以处理非线性问题和复杂的关系。
1083 |
1084 | 总之,SVM和神经网络都是有效的分类算法,但它们的实现方式和适用场景有所不同,需要根据具体的问题和数据情况选择适当的算法。
1085 |
1086 | ## 贝叶斯分类
1087 |
1088 | ### 贝叶斯决策论
1089 |
1090 | Bayes decision theory
1091 |
1092 | #### 贝叶斯判定准则,贝叶斯最优分类器,贝叶斯风险
1093 |
1094 | 贝叶斯判定准则Bayes decision rule:目标是找到最小化总体风险的判定准则 $ h:\mathcal X\to\mathcal Y $ ,只需在每个样本上选择那个能使条件风险 $ R(c|x) $ 最小的类别标记,即 $ h^*(x)=\arg\min_{c\in\mathcal Y} R(c|x) $ ,这里 $ h^* $ 是贝叶斯最优分类器 (Bayes optimal classifier) ,与之对应的总体风险 $ R(h^*) $ 称为贝叶斯风险 (Bayes risk),即通过机器学习所能产生的模型精度的理论上限。
1095 |
1096 | 定义:
1097 |
1098 | - 条件风险: $ \lambda_{ij} $ 为将 $ c_j $ 类别的样本误分类为 $ c_i $ 的损失
1099 |
1100 | $$
1101 | R(c_i|x)=\sum_{j=1}^N\lambda_{ij}P(c_j|x)
1102 | $$
1103 | - 总体风险
1104 |
1105 | $$
1106 | R(h)=\mathbb E_x[R(h(x)|x)]
1107 | $$
1108 |
1109 | #### 生成式模型,判别式模型
1110 |
1111 | 然而,后验概率 $ P(c|x) $ 难以直接获得,所以学习器要基于有限的训练样本集尽可能准确地估计出后验概率。
1112 |
1113 | - 判别式:直接建模 $ P(c|x) $
1114 | - 生成式:先建模联合概率分布 $ P(x,c) $ ,也就是 $ P(c) $ (先验)和 $ P(x|c) $ (似然)再得到 $ P(c|x) $
1115 |
1116 | ### 极大似然估计
1117 |
1118 | 见概率论
1119 |
1120 | ### 朴素贝叶斯分类器
1121 |
1122 | Naive Bayes classifier
1123 |
1124 | 朴素贝叶斯分类器 (naÏve Bayes classifier) 采用了**属性条件独立性假设**(attribute conditional independence assumption):假设每个属性独立地对分类结果发生影响。简化类条件概率 $ P(x|c) $ 的建模。
1125 |
1126 | 重写贝叶斯公式: $ x_i $ 为 $ x $ 在第 $ i $ 个属性上的取值.
1127 |
1128 | 
1129 |
1130 | 基于贝叶斯判定准则,朴素贝叶斯分类器表达式:
1131 |
1132 | $$
1133 | h_{nb}(x)=\arg\max_{c\in\mathcal Y}P(c)\prod_{i=1}^d P(x_i|c)
1134 | $$
1135 |
1136 | 离散:
1137 |
1138 | $$
1139 | P(c)=\frac{|D_c|}{|D|}\quad P(x_i|c)=\frac{|D_{c,x_i}|}{|D_c|}
1140 | $$
1141 |
1142 | 拉普拉斯修正(防止训练集中某个属性值没有与某个类同时出现过, $ |D_{c,x_i}|=0 $ 带来的误差。假设了属性值与类别的均匀分布,这是额外引入的 bias。 $ N $ 类别数, $ N_i $ 第 $ i $ 个属性可能的取值数)
1143 |
1144 | $$
1145 | \hat P(c)=\frac{|D_c|+1}{|D|+N}\quad P(x_i|c)=\frac{|D_{c,x_i}|+1}{|D_c|+N_i}
1146 | $$
1147 |
1148 | 连续:考虑概率密度函数
1149 |
1150 | ### 半朴素贝叶斯分类器
1151 |
1152 | 属性条件独立性假设在现实中很难成立,于是半朴素贝叶斯分类器(semi-naïve Bayes classifiers)对属性条件独立性假设进行一定程度的放松,适当考虑一部分属性问的相互依赖信息,从而既不需进行完全联合概率计算,又不至于彻底忽略了比较强的属性依赖关系。
1153 |
1154 | 采用独依赖估计(One-Dependent Estimator ,简称 ODE),新假设:每个属性在类别之外最多仅依赖于一个其他属性
1155 |
1156 | 
1157 |
1158 | 其中 $ pa_i $ 为属性 $ x_i $ 所依赖的属性,称为 $ x_i $ 的父属性,如何确定副属性引出不同算法
1159 |
1160 | 
1161 |
1162 | #### SPODE
1163 |
1164 | super-parent ODE,假设所有属性都依赖于同一个属性,通过交叉验证等模型选择方法来确定超父属性
1165 |
1166 | #### TAN
1167 |
1168 | 
1169 |
1170 | #### ADOE
1171 |
1172 | averaged one-dependent estimator,基于集成学习,尝试将每个属性作为超父来构建SPODE,然后将那些具有足够训练数据支撑的SPODE集成起来作为最终结果。
1173 |
1174 | #### kDE
1175 |
1176 | 将属性 $ pa_i $ 替换为包含 $ k $ 个属性的集合,随着 $ k $ 的增加,准确估计概率 $ P(x_i| y ,pai ) $ 所需的训练样本数量将以指数级增加。可能又会陷入求高阶联合概率的泥沼。
1177 |
1178 | ### 贝叶斯网
1179 |
1180 | 贝叶斯图(Bayesian network),也被称为信念网络(belief network)或概率有向无环图(probabilistic directed acyclic graph,PDAG),是一种图形化的概率模型,用于描述变量之间的概率依赖关系。变量(或节点)用圆圈表示,而变量之间的概率依赖关系则用有向箭头连接。箭头从一个变量指向依赖于它的变量,表示变量之间的因果关系或条件依赖关系。
1181 |
1182 | #### 贝叶斯网的条件独立性
1183 |
1184 | 
1185 |
1186 | $$
1187 | P(x_1,x_2,x_3,x_4,x_5)=P(x_1)P(x_2)P(x_3\vert x_1)P(x_4\vert x_1,x_2)P(x_5|x_2)
1188 | $$
1189 |
1190 | 
1191 |
1192 | 一个变量取值的确定与否,能对另两个变量间的独立性发生影响
1193 |
1194 | 同父:given $ x_1 $ , $ x_3,x_4 $ 独立
1195 |
1196 | V型:给定 $ x_4 $ ,必不独立; $ x_4 $ 未知,两者独立(边际独立性marginal independence, $ x_1\perp\!\!\!\perp x_2 $ ,两个随机变量在给定其他变量的边际分布下是独立的)
1197 |
1198 | 
1199 |
1200 | #### 边际分布
1201 |
1202 | #### Gibbs采样[没看]
1203 |
1204 | ### EM算法
1205 |
1206 | EM算法(Expectation-Maximization algorithm)是一种迭代优化算法,用于在存在隐变量(或缺失数据)的概率模型中进行参数估计。它是一种常用的无监督学习方法,通常用于处理含有不完整数据或观测数据中存在隐含变量的情况。非梯度
1207 |
1208 | EM算法的基本思想是通过迭代的方式,交替进行两个步骤:E步(Expectation step)和M步(Maximization step),以较好地逼近参数的最大似然估计。
1209 |
1210 | 已观测变量 $ X $ ,隐变量(未观测变量) $ Z $ ,模型参数 $ \Theta $ ,若对 $ \Theta $ 做极大似然估计,则应该最大化对数似然(对 $ Z $ 算期望)
1211 |
1212 | $$
1213 | LL(\Theta |X)=\ln P(X|\Theta)=\ln\sum_Z P(X,Z|\Theta)
1214 | $$
1215 |
1216 | EM算法步骤
1217 |
1218 | 1. 初始化模型参数。
1219 | 2.
349 |
350 | ## 线性模型
351 |
352 | ### 线性回归
353 |
354 | #### 线性回归的目标
355 |
356 | $$
357 | (w^*,b^*)=\arg \min_{(w,b)}\sum_{i=1}^m(f(x_i)-y_i)^2=\arg \min_{(w,b)}\sum_{i=1}^m(y_i-wx_i-b)^2
358 | $$
359 |
360 | #### 最小二乘
361 |
362 | 最小二乘“参数估计”:求解 $ w,b $ 使 $ \mathbb E_{(w,b)}=\sum_{i=1}^m(y_i-wx_i-b)^2 $ 最小化的过程。将 $ \mathbb E_{(w,b)} $ 对 $ w,b $ 求导,令之为零后得到 $ w,b $ 最优解的闭式解。
363 |
364 | #### 对数线性回归
365 |
366 | log-linear regression, $ \ln y=w^\top x+b $
367 |
368 | #### 广义线性模型
369 |
370 | generalized linear model, $ y=g^{-1}(w^\top x+b) $ ,其中 $ g(\cdot) $ 为联系函数link function
371 |
372 | ### 逻辑斯蒂回归
373 |
374 | #### 什么是逻辑斯蒂回归?
375 |
376 | 逻辑斯蒂回归为一个分类算法,通过对输入特征进行加权求和,并将结果通过一个值域为0-1的sigmoid函数(也称为逻辑函数)进行映射,从而得到输出概率值。
377 |
378 | #### Sigmoid函数是什么?为什么要用Sigmoid函数?
379 |
380 | Sigmoid函数即形似S的函数,目的是近似不连续不可导的单位阶跃函数(值域 $ \{0,1\} $ ),作为它的替代函数surrogate function。又称对数几率函数。公式为
381 |
382 | $$
383 | y=\frac1{1+e^{-z}}
384 | $$
385 |
386 | 值域为 $ [0,1] $
387 |
388 | #### 如何求解参数?
389 |
390 | 将后验概率估计代入对数几率的式子,用极大似然法找到Loss函数。然后用梯度下降法、牛顿法等数值优化方法找到使得Loss最小的 $ \beta $ ,即可得到参数。
391 |
392 | 具体见p59。
393 |
394 | #### 梯度下降
395 |
396 | > 什么是梯度下降法?
397 |
398 | 一阶迭代数值优化算法,用于寻找可微函数的局部最小值。
399 |
400 | 更新公式:
401 |
402 | $$
403 | x_{n+1}=x_{n}-\gamma\nabla f(x_n)
404 | $$
405 |
406 | 其中, $ \gamma $ 是学习率。 $ \nabla f $ 指向函数值增长最快的方向,则 $ -\nabla f $ 指向函数值增长最快的方向。理论上当 $ \gamma $ 足够小,则 $ f(x_n)\geq f(x_{n+1}) $
407 |
408 | > 需要满足什么条件?
409 |
410 | 前提:
411 |
412 | 1. 目标函数可导
413 | 2. 目标函数是凸函数(否则可能会陷入局部最优解)
414 |
415 | > 有什么优缺点?
416 |
417 | 优点:
418 |
419 | 1. 可以应用于许多不同的优化问题(线性回归,逻辑回归,神经网络)
420 | 2. 算法简单
421 | 3. 只需要计算一阶导数,计算成本相对较低。
422 | 4. 可以在大规模数据集上进行优化。
423 |
424 | 缺点:
425 |
426 | 1. 可能会陷入局部最小值,无法得到全局最小值。
427 | 2. 当函数存在平台、峡谷和其他复杂的非凸结构时,可能会出现震荡或缓慢收敛的情况。
428 | 3. 需要选择合适的学习率,过大或过小都会影响优化结果。
429 | 4. 对于某些问题,可能需要较多的迭代次数才能达到收敛。
430 |
431 | #### 什么是牛顿迭代法?需要满足什么条件?有什么优缺点?
432 |
433 | 目的:求 $ f(x)=0 $ 的解
434 |
435 | 初始化: $ x_0 $
436 |
437 | 重复:过 $ x_i $ 求 $ f(x) $ 的切线 $ L:y=f(x_{i})+f'(x_{i})(x-x_i) $ ,与x轴交点为 $ x_{i+1}=x_i-\frac{f(x_i)}{f'(x_i)} $
438 |
439 | 迭代公式:
440 |
441 | $$
442 | x_{n+1}=x_n-\frac{f(x_n)}{f'(x_n)}
443 | $$
444 |
445 | 对于 $ \beta^*=\arg\min_{\beta}\ell(\beta) $ 的优化问题,更新公式为:
446 |
447 | $$
448 | \beta^{t+1}=\beta^t-\left(\frac{\part^2\ell(\beta)}{\part \beta\part \beta^\top}\right)^{-1}\frac{\part\ell(\beta)}{\part \beta}
449 | $$
450 |
451 | 必要条件:
452 |
453 | 1. 目标函数二价可微
454 | 2. 目标函数的海森矩阵必须正定或负定
455 |
456 | 优点:
457 |
458 | 1. 可以更快地收敛到最优解,尤其是在函数存在二阶导数且二阶导数连续的情况下。
459 | 2. 可以解决梯度下降等一阶方法无法收敛的问题。
460 | 3. 可以自动调整学习率,减少手动调参的工作量。
461 |
462 | 缺点:
463 |
464 | 1. 对于高维问题,计算海森矩阵的代价非常昂贵。
465 | 2. 当海森矩阵不正定时,可能会导致算法发散。
466 | 3. 可能会陷入局部最小值,无法得到全局最小值。
467 | 4. 由于需要计算二阶导数,所以计算成本相对较高。
468 | 5. 当函数存在平台、峡谷和其他复杂的非凸结构时,可能会出现震荡或缓慢收敛的情况。
469 |
470 | ### 线性判别分析
471 |
472 | LDA, Linear Discriminant Analysis
473 |
474 | > 什么是LDA?
475 |
476 | LDA是一种常用的分类算法和数据降维方法。它可以将一个高维数据集降到一个更低的维度,同时保持样本类别信息,从而方便后续的分类任务。
477 |
478 | LDA 假设数据符合高斯分布,且各类别的协方差矩阵相等,基于此,它通过线性变换,将数据投影到一个低维空间中,使得同一类别的数据尽可能的接近,不同类别的数据尽可能的远离。这种投影方式保留了最大的类间差异性和最小的类内差异性,因此可以有效的提高分类准确率。
479 |
480 | 具体来说,LDA 算法主要包含两个步骤:(1)计算类内散度矩阵和类间散度矩阵;(2)通过求解广义瑞利商的特征向量,得到用于投影的变换矩阵。
481 |
482 | LDA 广泛应用于图像识别、人脸识别、语音识别等领域,并且在实际应用中表现良好。
483 |
484 | > 什么是类内散度矩阵,类间散度矩阵?
485 |
486 | $ X_i,\mu_i,\Sigma_i $ :第 $ i $ 类示例的集合、均值向量、协方差矩阵。
487 |
488 | $ w^\top \mu_i,w^\top \Sigma_i w $ :投影后的结果
489 |
490 | 目标:同类样例投影点的协方差尽可能小,即 $ w^\top \Sigma_0 w+w^\top \Sigma_1 w $ 尽可能小;类中心之间的距离尽可能大,即 $ ||w^\top \mu_0-w^\top\mu_1||_2^2 $ 尽可能大。即最大化
491 |
492 | $$
493 | J=\frac{||w^\top \mu_0-w^\top\mu_1||_2^2}{w^\top \Sigma_0 w+w^\top \Sigma_1 w}=\frac{w^\top (\mu_0-\mu_1)(\mu_0-\mu_1)^\top w}{w^\top(\Sigma_0+\Sigma_1)w}
494 | $$
495 |
496 | 其中**类内散度矩阵**within-class scatter matrix:
497 |
498 | $$
499 | S_w=\Sigma_0+\Sigma_1=\sum_{x\in X_0}(x-\mu_0)(x-\mu_0)^\top+\sum_{x\in X_1}(x-\mu_1)(x-\mu_1)^\top
500 | $$
501 |
502 | **类间散度矩阵**between-class scatter matrix:
503 |
504 | $$
505 | S_b=(\mu_0-\mu_1)(\mu_0-\mu_1)^\top
506 | $$
507 |
508 | 这就是LDA想要最大化的目标,即 $ S_b,S_w $ 的广义瑞利商generalized Rayleigh quotient:
509 |
510 | $$
511 | J=\frac{w^\top S_b w}{w^\top S_w w}
512 | $$
513 |
514 | > 如何求解LDA?
515 |
516 | 即确定能最大化 $ J $ 的 $ w $
517 |
518 | 令 $ w^\top S_ww=1 $ ,原式等价于
519 |
520 | $$
521 | \begin{aligned}
522 | &\min_w &&-w^\top S_b w\\
523 | &s.t. && w^\top S_w w=1
524 | \end{aligned}
525 | $$
526 |
527 | 由拉格朗日乘子法,等价于
528 |
529 | $$
530 | S_b w=\lambda S_ww
531 | $$
532 |
533 | $ S_b w $ 方向恒等于 $ \mu_0-\mu_1 $ ,令
534 |
535 | $$
536 | S_b w=\lambda(\mu_0-\mu_1)
537 | $$
538 |
539 | 有:
540 |
541 | $$
542 | w=S_w^{-1}(\mu_0-\mu_1)
543 | $$
544 |
545 | 考虑到数值解的稳定性,在实践中通常是对 $ S_w $ 进行奇异值分解,即 $ S_w= U\Sigma V^\top $ ,这里 $ \Sigma $ 是一个实对角矩阵,其对角线上的元素是 $ S_w $ 的奇异值,然后再由 $ S_w^{-1}=V\Sigma^{-1}U^\top $ 得到 $ S_w^{-1} $
546 |
547 | > 如何推广到多分类?[再看看!]
548 |
549 | 定义全局散度矩阵( $ \mu $ 是所有示例的均值之和)
550 |
551 | $$
552 | S_t=S_b+S_w=\sum_{i=1}^m(x_i-\mu)(x_i-\mu)^\top\\
553 | S_w=\sum_{i=1}^N S_{w_i}=\sum_{i=1}^N\sum_{x\in X_i}(x-\mu_i)(x-\mu_i)^\top\\
554 | S_b=S_t-S_w=\sum_{i=1}^N m_i(\mu_i-\mu)(\mu_i-\mu)^\top
555 | $$
556 |
557 | 优化目标:
558 |
559 | $$
560 | \max_W\frac{tr(W^\top S_bW)}{tr(W^\top S_wW)}
561 | $$
562 |
563 | 通过求解 $ S_b W=\lambda S_w W $ 可得, $ W $ 的闭式解为 $ S_w^{-1}S_b $ 的 $ N-1 $ 个最大广义特征值所对应的特征向量组成的矩阵。
564 |
565 | ### 多分类学习
566 |
567 | #### 有什么拆分策略?
568 |
569 | OvO(一对一,one vs one): $ \frac{N(N-1)}{2} $ 个分类器
570 |
571 | OvR(一对剩余,one vs rest): $ N $ 个分类器,选择置信度最大的类别标记
572 |
573 | MvM(多对多,many vs many):需要用ECOC编码特殊构造。
574 |
575 | ### 类别不平衡
576 |
577 | class-imbalance
578 |
579 | #### 有什么解决方法?
580 |
581 | “再缩放”,也是“代价敏感学习”cost-sensitive learning的基础
582 |
583 | 1. 对反例进行“欠采样”
584 | 2. 对正例进行“过采样”
585 | 3. 阈值移动
586 |
587 | ## 决策树
588 |
589 | ### 基本流程
590 |
591 | #### 什么是决策树?
592 |
593 | 决策树是一种基于树结构的分类算法,其中每个内部节点表示一个属性或特征,每个叶子节点代表一个类别。该算法可以用于分类和回归问题,它通过对样本集合进行递归分治来构建决策树。
594 |
595 | 在构建决策树时,算法会选择一个最好的属性或特征,将样本集合分成更小的子集。这个过程会不断重复,直到所有的子集都属于同一个类别,或者已经达到了预先定义的最大深度。
596 |
597 | 决策树算法具有可解释性和易于理解的优点,因为它可以清楚地显示分类决策的过程,还可以处理缺失值和噪声数据。不过,决策树算法在处理高维数据时可能会遇到困难,并且容易受到过拟合和欠拟合等问题的影响。
598 |
599 | #### 决策树算法的基本流程是什么?
600 |
601 | 决策树的生成是基于分治策略的递归过程。
602 |
603 | 首先生成结点,如果训练集中的样本均属于同一类别,则将该节点标记为该类叶子结点,返回。如果属性集为空或训练集在属性集上的取值相同,则将该节点标记为叶子结点,类别为数据集中样本数最多的类,返回。如果都不满足这两种情况的话,从属性集中选择最优划分 $ a^* $ 。对最优划分中的每一个值,为结点生成一个分支,构造相应取值的样本子集。如果样本子集为空,则将该节点标记为叶子结点,类别为数据集中样本数最多的类,返回。否则递归地对样本子集和最优划分的子集生成决策树。
604 |
605 | #### 什么情况会导致递归返回?
606 |
607 | 1. 当前结点包含的样本全属于同一类别,无需划分
608 | 2. 当前属性集为空,或是所有样本在所有属性上取值相同,无法划分
609 | 3. 当前结点包含的样本集合为空,不能划分。
610 |
611 | ### 划分选择
612 |
613 | #### 有什么划分的指标?它们的具体定义?
614 |
615 | 划分选择的目标是希望决策树的分支结点所包含的样本尽可能属于同一类别,即结点的“纯度” (purity) 越来越高。
616 |
617 | 划分的指标有:(ID3)信息增益、(C4.5)增益率、(CART)基尼指数。
618 |
619 | $ p_k $ :当前样本属于第 $ k $ 类的比例
620 |
621 | 假设离散属性 $ a $ 有 $ V $ 个可能的取值 $ \{a^1,\dots,a^V\} $ ,若使用 $ a $ 来对样本集 $ D $ 进行划分,则会产生 $ V $ 个分支结点,其中第 $ v $ 个分支结点包含了 $ D $ 中所有在属性 $ a $ 上取值为 $ a^v $ 的样本,记为 $ D^v $
622 |
623 | 信息熵:值越小,纯度越高
624 |
625 | $$
626 | Ent(D)=-\sum_{k=1}^{\mathcal Y}p_k\log_2 p_k
627 | $$
628 |
629 | 信息增益:值越大,说明使用属性 $ a $ 来划分所获得的纯度提升越大。
630 |
631 | $$
632 | Gain(D,a)=Ent(D)-\sum_{v=1}^V\frac{|D^v|}{|D|}Ent(D^v)
633 | $$
634 |
635 | 增益率:信息增益准则对可取值数目较多的属性有所偏好,为减少这种偏好可能带来的不利影响,引入增益率。其中 $ IV(a) $ 为属性 $ a $ 的固有值intrinsic value
636 |
637 | $$
638 | Gain_ratio(D,a)=\frac{Gain(D,a)}{IV(a)}\\
639 | IV(a)=-\sum_{v=1}^V\frac{|D|^v}{|D|}\log_2\frac{|D|^v}{|D|}
640 | $$
641 |
642 | 基尼指数Gini index:Gini反映从数据集 $ D $ 中随机抽取两个样本,其类别标记不一致的概率。越小纯度越高
643 |
644 | $$
645 | Gini(D)=\sum_{k=1}^{|\mathcal Y|}\sum_{k'\neq k}p_kp_{k'}=1-\sum_{k=1}^{|\mathcal Y|}p_k^2\\
646 | \text{Gini_Index}(D,a) =\sum_{v=1}^V\frac{|D^v|}{|D|}Gini(D^v)
647 | $$
648 |
649 | ### 剪枝
650 |
651 | #### 简述预剪枝和后剪枝的策略?
652 |
653 | 预剪枝:基于贪心思想,如果划分后验证集精度 $ \leq $ 原来的精度,则剪枝,禁止这些分支展开。
654 |
655 | 后剪枝:生成完整决策树后,从叶子结点开始遍历,如果划分后验证集精度 $ \leq $ 原来的精度,则剪枝,禁止这些分支展开。
656 |
657 | #### 两者的优缺点?
658 |
659 | | | 预剪枝 | 后剪枝 |
660 | | ------------- | ------------------------------ | ---------------------------------- |
661 | | 时间开销 | 测试时间降低,训练时间降低 | 测试时间降低,训练时间提高 |
662 | | 过/欠拟合风险 | 过拟合风险降低,欠拟合风险增加 | 过拟合风险降低,欠拟合风险基本不变 |
663 | | 泛化性能 | | 后剪枝通常优于预剪枝 |
664 |
665 | ### 连续值与缺失值
666 |
667 | #### 如何处理连续值?
668 |
669 | 基本思路是连续属性离散化
670 |
671 | 1. 二分法
672 | 2. 对于从大到小排序好的取值 $ \{a^1,\dots,a^n\} $ ,令划分点集合为 $ T_a=\left\{\frac{a^i+a^{i+1}}2|i\leq i\leq n-1\right\} $ ,然像离散属性值一样来考察这些划分点
673 |
674 | 需注意的是,与离散属性不同,若当前结点划分属性为连续属性,该属性还 可作为其后代结点的划分属性。
675 |
676 | #### 如何处理缺失值?
677 |
678 | 需要解决 1. 训练 2. 测试时的处理
679 |
680 | 令 $ \tilde D $ 为 $ D $ 在属性 $ a $ 上没有缺失值的样本子集,定义:
681 |
682 | 无缺失值比例: $ \displaystyle \rho=\frac{\sum_{x\in\tilde D} w_x}{\sum_{x\in D} w_x} $
683 |
684 | 无缺失值样本中第 $ k $ 类的比例: $ \displaystyle \tilde p_k=\frac{\sum_{x\in\tilde D_k} w_x}{\sum_{x\in \tilde D} w_x},1\leq k\leq|\mathcal Y| $
685 |
686 | 无缺失值样本中在属性 $ a $ 上取值为 $ a^v $ 的比例: $ \displaystyle \tilde r_v=\frac{\sum_{x\in\tilde D^v} w_x}{\sum_{x\in \tilde D} w_x},1\leq v\leq V $
687 |
688 | 推广:
689 |
690 | $$
691 | Ent(\tilde D)=-\sum_{k=1}^{\mathcal Y}\tilde p_k\log_2 \tilde p_k\\
692 | Gain(D,a)=\rho \times Gain(\tilde D,a)=\rho \times\left(Ent(D)-\sum_{v=1}^V \tilde r_v Ent(D^v)\right)
693 | $$
694 |
695 | ### 多变量决策树
696 |
697 | multivariate decision tree,在多变量决策树的学习过程中, 不是为每个非叶结点寻找一个最优划分属性,而是试图建立一个合适的线性分类器。
698 |
699 | ## 神经网络
700 |
701 | ## 支持向量机
702 |
703 | ### 基本概念
704 |
705 | #### 英文介绍
706 |
707 | Support Vector Machine (SVM) is a powerful machine learning algorithm used for classification and regression analysis. SVM finds the best hyperplane that separates different classes in a high-dimensional space. The hyperplane is chosen in such a way that it maximizes the margin or the distance between the two closest points of different classes. These closest points are called support vectors, and they play a crucial role in defining the hyperplane.
708 |
709 | SVM can handle both linearly separable and non-linearly separable data by using different types of kernel functions such as linear, polynomial, radial basis function (RBF), and sigmoid. The choice of kernel function depends on the data and the problem at hand. SVM can also handle multi-class classification problems using various techniques such as one-vs-one and one-vs-all.
710 |
711 | SVM has several advantages over other classification algorithms such as logistic regression and decision trees. It is less prone to overfitting, works well with high-dimensional data, and is computationally efficient. However, SVM has some limitations, such as the need for careful selection of kernel functions and hyperparameters, and the difficulty in handling large datasets.
712 |
713 | #### SVM是什么?
714 |
715 | 支持向量机是一种可以用于解决分类和回归问题的机器学习算法,目标是在高维空间中找到最佳的超平面,以最大化间隔,也就是margin。
716 |
717 | SVM问题的基本型(是一个凸二次优化问题):
718 |
719 | $$
720 | \begin{aligned}
721 | &\min_{w,b} \quad\frac12||w||^2\\
722 | &s.t. \quad y_i(w^\top x_i+b)\geq1,i=1,\dots,m
723 | \end{aligned}
724 | $$
725 |
726 | #### SVM中的“支持向量”指什么?在SVM中如何确定支持向量?
727 |
728 | “支持向量”是指离分隔超平面最近的训练样本点。这些样本点是最能影响分隔超平面位置和方向的点,如果它们的位置发生变化,会直接影响到分隔超平面的位置和方向。
729 |
730 | 我们在SVM的训练过程中确定支持向量。在SVM的训练过程中,我们首先随机初始化超平面参数,然后迭代地优化超平面参数,直到收敛为止。在每一次迭代中,我们根据当前的超平面参数计算每个训练样本点到超平面的距离,并根据这些距离来判断哪些样本点是支持向量。
731 |
732 | #### SVM在分类问题中如何定义“边界”(decision boundary)?
733 |
734 | 在SVM中,边界(decision boundary)是指将不同类别的数据点分开的超平面(hyperplane)。SVM的目标是寻找一个最优的超平面,将不同类别的数据点分开,并且使得该超平面与最近的数据点之间的距离(即margin)最大化。
735 |
736 | #### SVM有什么优点和缺点?
737 |
738 | 优点:
739 |
740 | 1. 能有效处理高维数据,例如图像和文本分类
741 | 2. 在小数据集处理时表现优异,因为它只需要少量的支持向量来定义边界
742 | 3. SVM对数据中的噪声具有鲁棒性,因为决策边界由支持向量确定,它们是距离边界最近的数据点。
743 | 4. 泛化性好
744 |
745 | 缺点:
746 |
747 | 1. 不适用于大数据集,因为计算开销过大
748 | 2. 对核函数选择和参数选择敏感
749 | 3. 只适用于二元问题
750 | 4. 缺乏概率解释
751 | 5. 不适用于有缺失值的数据
752 |
753 | ### 原问题和对偶问题
754 |
755 | #### 如何将SVM转化为对偶问题?
756 |
757 | 对偶问题(dual problem)是指将一个优化问题的原问题(primal problem)转化为一个新的优化问题,对偶问题和原问题有相同的最优解,但对于一些问题,通过求解对偶问题可以更方便或更有效地得到原问题的解。
758 |
759 | 对偶问题一定是凸优化问题。
760 |
761 | 可以使用拉格朗日乘子法得到SVM的对偶问题:
762 |
763 | 拉格朗日函数:
764 |
765 | $$
766 | L(w,b,\alpha)=\frac12||w||^2+\sum_{i=1}^m\alpha_i(1-y_i(\omega^\top x_i+b))
767 | $$
768 |
769 | 令 $ L(w,b,\alpha) $ 对 $ \omega,b $ 的偏导为零可得:
770 |
771 | $$
772 | w=\sum_{i=1}^m\alpha_i y_ix_i\quad(1)\\
773 | 0=\sum_{i=1}^m\alpha_i y_i\quad(2)
774 | $$
775 |
776 | 将(1)代入拉格朗日函数可消去 $ w,b $ ,考虑(2)的约束可以得到对偶问题:
777 |
778 | $$
779 | \begin{aligned}
780 | &\max_{\alpha}\quad \sum_{i=1}^m\alpha_i-\frac12\sum_{i=1}^m\sum_{i=1}^m\alpha_i\alpha_jy_iy_jx_i^\top x_j\\
781 | &s.t. \quad \sum_{i=1}^m\alpha_i y_i=0,\alpha_i\geq 0,i=1,\dots,m
782 | \end{aligned}
783 | $$
784 |
785 | 要满足KKT条件:
786 |
787 | $$
788 | \left\{\begin{aligned}
789 | &\alpha_i\geq0\\
790 | &y_if(x_i)-1\geq 0\\
791 | &\alpha_i(y_if(x_i)-1)=0
792 | \end{aligned}\right.
793 | $$
794 |
795 | ##### 什么是KKT条件?[x]
796 |
797 | Karush-Kuhn-Tucker (KKT)条件是非线性规划(nonlinear programming)最佳解的必要条件。
798 |
799 | 对于Lagrangian函数
800 |
801 | $$
802 | L(x,\lambda,\mu)=f(x)+\sum_{j=1}^m\lambda_jg_j(x)+\sum_{k=1}^n\mu_kh_k(x)
803 | $$
804 |
805 | KKT条件包括:**[术语怎么说?KKT只是必要条件,要到充分条件该如何做?内点]**
806 |
807 | $$
808 | \left\{\begin{aligned}
809 | &\nabla_xL=0\\
810 | &g_j(x)=0,j = 1,\dots,m\\
811 | &h_k(x)\leq 0,\\
812 | &\mu_k\geq 0,\\
813 | &\mu_kh_k(x)=0,k=1,\dots,p
814 | \end{aligned}\right.
815 | $$
816 |
817 | #### 为什么要将SVM转化为对偶问题?
818 |
819 | 虽然原问题本身就是一个凸二次规划(convex quadratic programming)问题,可以直接用现成的优化计算包求解,但是转化为对偶问题求解更高效。
820 |
821 | 原始的SVM问题是一个凸二次规划问题,通常使用二次规划算法求解。然而,当数据集的规模很大时,使用原始问题求解SVM会变得很慢,甚至变得不可行。此外,对于非线性SVM,计算的复杂度会随着特征空间的维度增加而急剧增加。
822 |
823 | 将SVM转化为对偶问题,就可以使用SMO算法等更高效的方法求解。
824 |
825 | 对偶问题和内积有关,可以引入核函数
826 |
827 | ##### 什么是SMO算法?
828 |
829 | ##### 为什么SMO算法不能用于求解原问题?
830 |
831 | ### 核函数
832 |
833 | kernel function
834 |
835 | #### SVM中的核函数是什么?
836 |
837 | 核函数是一种常用的技巧,用于将低维空间中线性不可分的数据映射到高维空间,从而使其在高维空间中变得线性可分。
838 |
839 | 如果原始空间是有限维(属性有限),那么一定存在一个高维特征空间使样本可分。
840 |
841 | 令 $ \phi(x) $ 为将 $ x $ 映射后的特征向量,于是,在特征空间中划分超平面所对应的模型可表示为
842 |
843 | $$
844 | f(x)=w^\top\phi(x)+b
845 | $$
846 |
847 | 原问题
848 |
849 | $$
850 | \begin{aligned}&\min_{w,b} \quad\frac12||w||^2\\&s.t. \quad y_i(w^\top \phi(x_i)+b)\geq1,i=1,\dots,m\end{aligned}
851 | $$
852 |
853 | 对偶问题
854 |
855 | $$
856 | \begin{aligned}
857 | &\max_{\alpha}\quad \sum_{i=1}^m\alpha_i-\frac12\sum_{i=1}^m\sum_{i=1}^m\alpha_i\alpha_jy_iy_j\phi(x_i)^\top\phi( x_j)\\
858 | &s.t. \quad \sum_{i=1}^m\alpha_i y_i=0,\alpha_i\geq 0,i=1,\dots,m
859 | \end{aligned}
860 | $$
861 |
862 | 核函数就是 $ \kappa(x_i,x_j)=<\phi(x_i),\phi(x_j)>=\phi(x_i)^\top\phi(x_j) $
863 |
864 | #### 核函数有什么性质?
865 |
866 | **[充要条件]** $ \kappa $ 是核函数当且仅当对于任意数据 $ D={x_1,\dots,x_m} $ ,核矩阵 $ K=[\kappa(x_i,x_i)]_{m\times m} $ 总是半正定的。
867 |
868 | 也就是说,对于一个半正定的核矩阵,总能找到一个与之对于的映射 $ \phi $ 。
869 |
870 | #### 有什么常用的核函数?
871 |
872 | | 名称 | 表达式 | 参数 | 适用场景 |
873 | | ----------- | ----------------------------------------------------------- | -------------------------- | ------------------------------------------------------------------------------------------------------------------------------------------------------------ |
874 | | 线性核 | $ \kappa(x_i,x_j)=x_i^\top x_j $ | | 输入特征维度较低,数据线性可分 |
875 | | 多项式核 | $ \kappa(x_i,x_j)=(x_i^\top x_j)^d $ | $ d\geq 1 $ ,多项式次数 | 数据中存在多项式关系 |
876 | | 高斯核(RBF) | $ \kappa(x_i,x_j)=\exp(-\frac{||x_i- x_j||^2}{2\sigma^2}) $ | $ \sigma>0 $ ,高斯核的带宽 | 输入特征维度较高 |
877 | | 拉普拉斯核 | $ \kappa(x_i,x_j)=\exp(-\frac{||x_i-x_j||}{\sigma}) $ | $ \sigma>0 $ | 采用 $ L_1 $ 范数来度量两个样本点之间的距离,而高斯核函数采用 $ L_2 $ 范数来度量。可以在一定程度上克服高斯核函数中存在的过拟合问题,适用于一些噪声较多的数据集。 |
878 | | Sigmoid核 | $ \kappa(x_i,x_j)=\tanh(\beta x_i^\top x_j+\theta) $ | $ \beta>0,\theta<0 $ | 数据集合线性不可分时,将数据映射到一个非线性空间中。表现不是很好,高斯核和拉普拉斯核更常用。 |
879 |
880 | 此外,若 $ \kappa_1,\kappa_2 $ 为核函数,则
881 |
882 | - $ \gamma_1\kappa_1+\gamma_2\kappa_2 $ 也是核函数
883 | - $ \kappa_1\otimes\kappa_2(x,z)=\kappa_1(x,z)\kappa_2(x,z) $ 也是核函数
884 | - 对于任意函数 $ g(x) $ , $ g(x)\kappa_1(x,z)g(z) $ 也是核函数
885 |
886 | #### 如何选择合适的核函数?[x]
887 |
888 | **[未完善]核函数需要满足什么性质?(很好地度量在希尔伯特空间里的距离,自反性,来回一样,对于自己为0...)**
889 |
890 | 根据根据具体的问题和数据选择。
891 |
892 | ### 软间隔与正则化
893 |
894 | #### 什么是软间隔SVM?
895 |
896 | 软间隔(soft margin)SVM通过设置松弛变量(slack variable),以允许某些样本不满足约束。传统硬间隔SVM要求数据完全线性可分,然而在实际情况下,由于数据可能存在一些噪声和异常点,很难找到完全线性可分的数据集。软间隔SVM通过允许一些样本出现在超平面的错误一侧,以此来解决线性不可分的问题。
897 |
898 | 优化目标可以写为
899 |
900 | 结构风险最小化+经验风险最小化
901 |
902 | $$
903 | \min_{w,b}\quad\frac12\vert\vert w\vert\vert^2+C\sum_{i=1}^{m}\ell_{0/1}\left(y_i(\omega^\top x_i+b)-1\right)
904 | $$
905 |
906 | 其中正则化常数 $ C>0 $ , $ \ell_{0/1} $ 为“0/1损失函数”, $ \ell_{0/1}=\left\{\begin{aligned}&1&z<0\\&0&otherwise\end{aligned}\right. $
907 |
908 | $ C\to\infty $ 时,会迫使所有样本均满足约束,等价于硬间隔; $ C $ 有限值时,允许一些样本不满足约束。
909 |
910 | #### 什么是替代损失?
911 |
912 | 由于 $ \ell_{0/1} $ 非凸、不连续,数学性质不好,使得优化目标难以直接求解,于是,使用其他一些函数替代 $ \ell_{0/1} $ ,称为替代损失(surrogate loss)
913 |
914 | - hinge损失(最常用): $ \ell_{hinge}(z)=\max(0,1-z) $
915 | - 指数损失exponential loss: $ \ell_{\exp}(z)=\exp(-z) $
916 | - 对率损失logistic loss: $ \ell_{\log}=\log(1+\exp(-z)) $
917 |
918 | 若采取hinge损失,优化目标可以改写为:
919 |
920 | $$
921 | \min_{w,b}\quad\frac12\vert\vert w\vert\vert^2+C\sum_{i=1}^{m}\max\left(0,1-y_i(\omega^\top x_i+b)\right)
922 | $$
923 |
924 | ##### 为什么使用Hinge Loss?[不知道!]
925 |
926 | Hinge Loss的优点在于它可以将最小化分类错误和最大化间隔相结合,即最小化损失的同时,最大化分类间隔。相比于其他损失函数,Hinge Loss对异常值的容忍度更高,可以更好地处理噪声和异常点的情况。同时,Hinge Loss的导数在0处不连续,使得模型更加稳定,不容易陷入局部最优解。(ChatGPT的回答)
927 |
928 | #### 什么是松弛变量?
929 |
930 | 引入松弛变量(slack variables),可将优化目标重写为
931 |
932 | $$
933 | \begin{aligned}
934 | &\min_{w,b}&\frac12\vert\vert w\vert\vert^2+C\sum_{i=1}^{m}\xi_{i}\\
935 | &s.t.&y_i(w^\top x_i+b)\geq1-\xi_{i}\\
936 | &&\xi_i\geq0,i=1,\dots,m
937 | \end{aligned}
938 | $$
939 |
940 | ##### 噪声和异常点的区别?
941 |
942 | | 噪声(noise) | 异常值(outliers) |
943 | | -------------------------------------------------------------- | ---------------------------------------------------------------------------------------------------- |
944 | | 数据中存在的错误或不准确的值 | 与其他数据点不同的、明显偏离正常情况的数据点 |
945 | | 可能是由于测量设备、传输问题或人为因素导致的 | 可能是由于记录或测量错误、系统故障或自然变异等原因导致的 |
946 | | 在整个数据集中分布较均匀 | |
947 | | 可能会对模型的性能产生一定影响,但它们不一定是非常明显的异常值 | 可能会对模型的训练和预测造成不良影响,因为它们可能会导致模型的偏差和方差增大,从而影响模型的泛化性能 |
948 | | 数据清洗和预处理噪声 | 使用特定的算法或技术来检测和处理异常点 |
949 |
950 | #### 与硬间隔SVM相比有何优势和劣势?
951 |
952 | hard margin
953 |
954 | 优势:
955 |
956 | 1. 对于存在噪声或异常点的数据,软间隔SVM可以允许一些样本不满足约束条件,从而更好地适应这些数据;
957 | 2. 更好地处理线性不可分数据集。
958 |
959 | 劣势:
960 |
961 | 1. 在使用松弛变量的情况下,软间隔SVM更容易出现过拟合现象,需要谨慎调参;
962 | 2. 计算复杂度增加,需要花费更多的计算资源和时间。
963 |
964 | #### 如何在SVM中使用正则化?
965 |
966 | 正则化(regularization)问题如下:
967 |
968 | $$
969 | \min_{f}\quad\Omega(f)+C\sum_{i=1}^{m}\ell(f(x_i),y_i)
970 | $$
971 |
972 | $ \Omega(f) $ :“结构风险”structural risk,正则化项用于描述模型 $ f $ 的某些性质
973 |
974 | $ \sum_{i=1}^{m}\ell(f(x_i),y_i) $ :“经验风险”empirical risk,用于描述模型与训练数据的契合程度
975 |
976 | $ C $ :正则化常数,折中两者,C越大,表示分类错误的惩罚越严厉,对于训练集的拟合效果更好,但是可能会过拟合;C越小,则表示更容忍分类错误,对于新数据的泛化性能更好,但是可能会欠拟合。
977 |
978 | #### $ L_1 $ 和 $ L_2 $ 正则化有何区别?
979 |
980 | $ L_p $ 范数是常用的正则化项, $ L_2 $ 倾向于 $ w $ 的分量取值尽量均衡,即非零分量个数尽量稠密; $ L_0 $ 范数(向量中非0的元素的个数)和 $ L_1 $ 范数倾向于 $ w $ 的分量尽量稀疏,即非零分量个数尽量少。
981 |
982 | ### 支持向量回归
983 |
984 | (Support Vector Regression,SVR)
985 |
986 | #### 什么是SVR?
987 |
988 | 有别于传统回归模型,SVR可以容忍 $ f(x) $ 和 $ y $ 之间最多有 $ \epsilon $ 的偏差,即仅当 $ f(x) $ 与 $ y $ 之间的差别绝对值大于 $ \epsilon $ 时才计算损失。这相当于构建了一个宽度为 $ 2\epsilon $ 的间隔带,若训练样本落入此间隔带,则认为预测正确。
989 |
990 | SVR可形式化为
991 |
992 | $$
993 | \min_{w,b}\quad\frac12\vert\vert w\vert\vert^2+C\sum_{i=1}^{m}\ell_{\epsilon}\left(f(x_i)-y_i\right)
994 | $$
995 |
996 | 其中正则化常数 $ C>0 $ , $ \ell_{\epsilon} $ 为 $ \epsilon $ -不敏感损失( $ \epsilon $ -insensitive loss)函数, $ \ell_{\epsilon}=\left\{\begin{aligned}&0&|z|\leq\epsilon\\&|z|-\epsilon&otherwise\end{aligned}\right. $
997 |
998 | #### 优化目标
999 |
1000 | ### 核方法
1001 |
1002 | #### KLDA[还没写]
1003 |
1004 | ### 具体任务
1005 |
1006 | #### 百万样本量可以用SVM吗?
1007 |
1008 | 对于百万级别的样本量,求解SVM的原问题计算复杂度过大,时空开销较大,可能存在着困难。不过,存在一些优化算法,使得可以在大规模数据集上使用SVM。
1009 |
1010 | 1. 一种方法是使用随机梯度下降(SGD)算法等在线学习算法,在每次迭代中随机选择一部分数据进行训练。这种方法的计算复杂度低,但可能会影响模型的收敛性和精度。
1011 | 2. 另一种方法是使用核函数的低秩近似,例如随机核近似(RKA)或核特征映射(KFM),以降低计算复杂度。这些方法将数据集投影到一个低维空间中,从而减少了计算量。不过,这些方法可能会对模型的精度产生一定的影响。
1012 | 3. 此外,还有一些并行化的方法,例如基于GPU的实现或者分布式计算框架的使用,可以加速SVM的训练过程。
1013 |
1014 | #### 在使用SVM时,如何处理不平衡的训练数据?
1015 |
1016 | - 改变类别权重:为少数样本增加权重
1017 | - 过采样少数样本
1018 | - 欠采样多数样本
1019 |
1020 | #### SVM中如何处理非线性可分数据?
1021 |
1022 | - 使用核函数:将原始数据映射到高维特征空间,从而使得原本线性不可分的数据在新的高维空间中成为线性可分的。
1023 | - 引入软间隔:允许某些样本不符合约束。
1024 |
1025 | #### 在SVM中如何处理多分类问题?
1026 |
1027 | - One-vs-All:对于 $ k $ 类问题,训练 $ k $ 个二元分类器,每个分类器的正例为第 $ i $ 类样本,负例为其他类别的所有样本。测试时,选择具有最高决策函数值的分类器。
1028 | - One-vs-One:对于 $ k $ 类问题,在任意两类样本之间设计一个SVM,因此 $ k $ 个类别的样本就需要设计 $ k(k-1)/2 $ 个SVM。当对一个未知样本进行分类时,最后得票最多的类别即为该未知样本的类别。Libsvm中的多类分类就是根据这个方法实现的。
1029 |
1030 | #### 在SVM中如何处理缺失数据?
1031 |
1032 | 1. 删除缺失值:直接删除包含缺失数据的样本,在剩余的完整数据上进行SVM训练。但是,这种方法会损失有用的信息,并且可能导致训练数据的减少。
1033 | 2. 插值:可以使用基于均值、中位数或其他统计量的简单插值方法,也可以使用更高级的插值方法,例如多重插值或KNN插值。然后使用填充后的数据进行SVM训练。
1034 |
1035 | 都会对SVM的性能造成负面影响。
1036 |
1037 | ### 训练细节
1038 |
1039 | #### 如何解决SVM模型过拟合(overfitting)的问题?
1040 |
1041 | 1. 减少特征数:使用特征选择技术,如主成分分析(PCA),来减少特征数量。
1042 | 2. 增加正则化:惩罚过于复杂的模型,防止过拟合。
1043 | 3. 增加数据量。
1044 | 4. 调整模型参数:如惩罚参数C、核函数类型等,来寻找最优模型。
1045 | 5. 使用交叉验证:可以使用交叉验证来评估模型性能和泛化能力,并进行模型选择。
1046 |
1047 | #### SVM中如何选择合适的超参数?如何通过网格搜索来选择超参数?
1048 |
1049 | 交叉验证。
1050 |
1051 | 正则化项 $ C $ :较大的值将使模型更加倾向于正确分类每个训练样本,但也可能导致过拟合。较小的值将允许更多的分类错误,但也可能导致欠拟合。
1052 |
1053 | (RBF核) $ \gamma $ :较大的值将导致决策边界更加复杂,可能会导致过拟合。较小的值将导致决策边界更加简单,可能会导致欠拟合。
1054 |
1055 | 需要避免使用测试集来选择,应该使用验证集来选择超参数,而将测试集保留到最后评估模型的性能。
1056 |
1057 | #### SVM模型的复杂度是如何计算的?如何通过交叉验证来选择合适的SVM模型?
1058 |
1059 | - 基于训练数据集大小(训练数据集大小 $ N $ ,特征维度 $ d $ , $ O(Nd^2) $ )
1060 | - 基于支持向量的复杂度(支持向量的数量为 $ m $ , $ O(md) $ )
1061 |
1062 | ### 模型对比
1063 |
1064 | #### SVM与逻辑回归相比有哪些优势和劣势?
1065 |
1066 | | | SVM | LR |
1067 | | ---------- | ------------------------------ | ---------------------------------------------- |
1068 | | 数据特征 | 对于线性可分的数据效果往往更好 | 能够处理非线性问题,可以使用多项式特征 |
1069 | | 数据规模 | 小数据集效果好 | 需要较多数据才能获得较好分类效果 |
1070 | | 噪声数据 | 容易受影响 | 容易受影响 |
1071 | | 参数选择 | 对参数的选择比较敏感 | 参数的选择比较简单 |
1072 | | 模型复杂度 | 复杂度较高 | 训练时间和内存开销相对较小,适合处理大规模数据 |
1073 |
1074 | #### SVM与神经网络有何异同点?
1075 |
1076 | (Answered by ChatGPT)
1077 |
1078 | 1. 工作原理不同:SVM是一种基于几何距离的分类器,它通过最大化分类间隔,寻找超平面将不同类别的数据分开;而神经网络则是通过模拟生物神经元的方式,使用一系列非线性变换来构建模型,实现分类和回归等任务。
1079 | 2. 模型结构不同:SVM的模型结构比较简单,只有一个决策边界;而神经网络的模型结构比较复杂,由多个神经元和层组成。
1080 | 3. 特征处理不同:SVM通常使用核函数将数据从低维空间映射到高维空间,以便找到更好的决策边界;而神经网络则通常使用输入层、隐藏层和输出层来提取和处理特征,不需要显式的特征转换过程。
1081 | 4. 训练方法不同:SVM使用凸优化算法来训练模型,而神经网络通常使用反向传播算法来训练模型。
1082 | 5. 适用场景不同:SVM适用于小规模、高维度的数据集,特别是在样本数目相对于特征数目较小的情况下表现更好,而神经网络适用于大规模、高维度的数据集,可以处理非线性问题和复杂的关系。
1083 |
1084 | 总之,SVM和神经网络都是有效的分类算法,但它们的实现方式和适用场景有所不同,需要根据具体的问题和数据情况选择适当的算法。
1085 |
1086 | ## 贝叶斯分类
1087 |
1088 | ### 贝叶斯决策论
1089 |
1090 | Bayes decision theory
1091 |
1092 | #### 贝叶斯判定准则,贝叶斯最优分类器,贝叶斯风险
1093 |
1094 | 贝叶斯判定准则Bayes decision rule:目标是找到最小化总体风险的判定准则 $ h:\mathcal X\to\mathcal Y $ ,只需在每个样本上选择那个能使条件风险 $ R(c|x) $ 最小的类别标记,即 $ h^*(x)=\arg\min_{c\in\mathcal Y} R(c|x) $ ,这里 $ h^* $ 是贝叶斯最优分类器 (Bayes optimal classifier) ,与之对应的总体风险 $ R(h^*) $ 称为贝叶斯风险 (Bayes risk),即通过机器学习所能产生的模型精度的理论上限。
1095 |
1096 | 定义:
1097 |
1098 | - 条件风险: $ \lambda_{ij} $ 为将 $ c_j $ 类别的样本误分类为 $ c_i $ 的损失
1099 |
1100 | $$
1101 | R(c_i|x)=\sum_{j=1}^N\lambda_{ij}P(c_j|x)
1102 | $$
1103 | - 总体风险
1104 |
1105 | $$
1106 | R(h)=\mathbb E_x[R(h(x)|x)]
1107 | $$
1108 |
1109 | #### 生成式模型,判别式模型
1110 |
1111 | 然而,后验概率 $ P(c|x) $ 难以直接获得,所以学习器要基于有限的训练样本集尽可能准确地估计出后验概率。
1112 |
1113 | - 判别式:直接建模 $ P(c|x) $
1114 | - 生成式:先建模联合概率分布 $ P(x,c) $ ,也就是 $ P(c) $ (先验)和 $ P(x|c) $ (似然)再得到 $ P(c|x) $
1115 |
1116 | ### 极大似然估计
1117 |
1118 | 见概率论
1119 |
1120 | ### 朴素贝叶斯分类器
1121 |
1122 | Naive Bayes classifier
1123 |
1124 | 朴素贝叶斯分类器 (naÏve Bayes classifier) 采用了**属性条件独立性假设**(attribute conditional independence assumption):假设每个属性独立地对分类结果发生影响。简化类条件概率 $ P(x|c) $ 的建模。
1125 |
1126 | 重写贝叶斯公式: $ x_i $ 为 $ x $ 在第 $ i $ 个属性上的取值.
1127 |
1128 | 
1129 |
1130 | 基于贝叶斯判定准则,朴素贝叶斯分类器表达式:
1131 |
1132 | $$
1133 | h_{nb}(x)=\arg\max_{c\in\mathcal Y}P(c)\prod_{i=1}^d P(x_i|c)
1134 | $$
1135 |
1136 | 离散:
1137 |
1138 | $$
1139 | P(c)=\frac{|D_c|}{|D|}\quad P(x_i|c)=\frac{|D_{c,x_i}|}{|D_c|}
1140 | $$
1141 |
1142 | 拉普拉斯修正(防止训练集中某个属性值没有与某个类同时出现过, $ |D_{c,x_i}|=0 $ 带来的误差。假设了属性值与类别的均匀分布,这是额外引入的 bias。 $ N $ 类别数, $ N_i $ 第 $ i $ 个属性可能的取值数)
1143 |
1144 | $$
1145 | \hat P(c)=\frac{|D_c|+1}{|D|+N}\quad P(x_i|c)=\frac{|D_{c,x_i}|+1}{|D_c|+N_i}
1146 | $$
1147 |
1148 | 连续:考虑概率密度函数
1149 |
1150 | ### 半朴素贝叶斯分类器
1151 |
1152 | 属性条件独立性假设在现实中很难成立,于是半朴素贝叶斯分类器(semi-naïve Bayes classifiers)对属性条件独立性假设进行一定程度的放松,适当考虑一部分属性问的相互依赖信息,从而既不需进行完全联合概率计算,又不至于彻底忽略了比较强的属性依赖关系。
1153 |
1154 | 采用独依赖估计(One-Dependent Estimator ,简称 ODE),新假设:每个属性在类别之外最多仅依赖于一个其他属性
1155 |
1156 | 
1157 |
1158 | 其中 $ pa_i $ 为属性 $ x_i $ 所依赖的属性,称为 $ x_i $ 的父属性,如何确定副属性引出不同算法
1159 |
1160 | 
1161 |
1162 | #### SPODE
1163 |
1164 | super-parent ODE,假设所有属性都依赖于同一个属性,通过交叉验证等模型选择方法来确定超父属性
1165 |
1166 | #### TAN
1167 |
1168 | 
1169 |
1170 | #### ADOE
1171 |
1172 | averaged one-dependent estimator,基于集成学习,尝试将每个属性作为超父来构建SPODE,然后将那些具有足够训练数据支撑的SPODE集成起来作为最终结果。
1173 |
1174 | #### kDE
1175 |
1176 | 将属性 $ pa_i $ 替换为包含 $ k $ 个属性的集合,随着 $ k $ 的增加,准确估计概率 $ P(x_i| y ,pai ) $ 所需的训练样本数量将以指数级增加。可能又会陷入求高阶联合概率的泥沼。
1177 |
1178 | ### 贝叶斯网
1179 |
1180 | 贝叶斯图(Bayesian network),也被称为信念网络(belief network)或概率有向无环图(probabilistic directed acyclic graph,PDAG),是一种图形化的概率模型,用于描述变量之间的概率依赖关系。变量(或节点)用圆圈表示,而变量之间的概率依赖关系则用有向箭头连接。箭头从一个变量指向依赖于它的变量,表示变量之间的因果关系或条件依赖关系。
1181 |
1182 | #### 贝叶斯网的条件独立性
1183 |
1184 | 
1185 |
1186 | $$
1187 | P(x_1,x_2,x_3,x_4,x_5)=P(x_1)P(x_2)P(x_3\vert x_1)P(x_4\vert x_1,x_2)P(x_5|x_2)
1188 | $$
1189 |
1190 | 
1191 |
1192 | 一个变量取值的确定与否,能对另两个变量间的独立性发生影响
1193 |
1194 | 同父:given $ x_1 $ , $ x_3,x_4 $ 独立
1195 |
1196 | V型:给定 $ x_4 $ ,必不独立; $ x_4 $ 未知,两者独立(边际独立性marginal independence, $ x_1\perp\!\!\!\perp x_2 $ ,两个随机变量在给定其他变量的边际分布下是独立的)
1197 |
1198 | 
1199 |
1200 | #### 边际分布
1201 |
1202 | #### Gibbs采样[没看]
1203 |
1204 | ### EM算法
1205 |
1206 | EM算法(Expectation-Maximization algorithm)是一种迭代优化算法,用于在存在隐变量(或缺失数据)的概率模型中进行参数估计。它是一种常用的无监督学习方法,通常用于处理含有不完整数据或观测数据中存在隐含变量的情况。非梯度
1207 |
1208 | EM算法的基本思想是通过迭代的方式,交替进行两个步骤:E步(Expectation step)和M步(Maximization step),以较好地逼近参数的最大似然估计。
1209 |
1210 | 已观测变量 $ X $ ,隐变量(未观测变量) $ Z $ ,模型参数 $ \Theta $ ,若对 $ \Theta $ 做极大似然估计,则应该最大化对数似然(对 $ Z $ 算期望)
1211 |
1212 | $$
1213 | LL(\Theta |X)=\ln P(X|\Theta)=\ln\sum_Z P(X,Z|\Theta)
1214 | $$
1215 |
1216 | EM算法步骤
1217 |
1218 | 1. 初始化模型参数。
1219 | 2.  1220 | 3. 重复执行E步和M步,直到收敛或达到预定的停止条件。
1221 |
1222 | ## 集成学习
1223 |
1224 | ### 基本概念
1225 |
1226 | #### 什么是集成学习?
1227 |
1228 | 集成学习ensemble learning(读“昂”)是一种机器学习方法,首先训练一组基学习器(也称为弱学习器),再将它们的预测结果通过某种策略结合,来完成学习任务。集成学习的核心思想是通过组合多个弱学习器,来达到比单个弱学习器更好的泛化性能,从而提高模型的预测能力。
1229 |
1230 | #### 为什么集成学习需要集成“好而不同”的学习器?
1231 |
1232 | 好指的是基学习器的准确性,不同指的是基学习器间的多样性。
1233 |
1234 | 直觉上,模型的准确性当然是越高越好,基学习器的准确率较低,集成学习的预测性能也会受到影响。基学习器具有多样性意味着不同的学习器可以捕捉到数据中的不同特征,因此可以相互补充、互相弥补,从而提高整体的学习性能。
1235 |
1236 | 数学上,可以用“误差-分歧分解”(error-ambiguity decomposition)证明:个体学习器准确性越高、多样性越大,则集成越好。
1237 |
1238 | 我们通过“分歧”来反应个体学习器的多样性,分歧的定义是各个学习器预测结果与集成的MSE的加权均值。
1239 |
1240 | 学习器 $ h_i $ 的分歧: $ A(h_i|x)=(h_i(x)-H(x))^2 $
1241 |
1242 | 集成 $ H $ 的分歧: $ \overline A(h|x)=\sum_{i=1}^T w_i(h_i(x)-H(x))^2 $
1243 |
1244 | 个体学习器的平方误差: $ E(h_i|x)=(f(x)-h_i(x))^2 $
1245 |
1246 | 集成的平方误差: $ E(H|x)=(f(x)-H(x))^2 $
1247 |
1248 | 个体学习器误差的加权均值: $ \overline E(h|x)=\sum_{i=1}^T w_i E(h_i|x) $
1249 |
1250 | 有:
1251 |
1252 | $$
1253 | \begin{aligned}
1254 | \overline A (h|x)&=\sum_{i=1}^Tw_i E(h_i|x)-E(H|x)\\
1255 | &=\overline E(h|x)-E(H|x)\\
1256 | \end{aligned}
1257 | $$
1258 |
1259 | 该式对所有样本 $ x $ 均成立,令 $ p(x) $ 表示样本的概率密度,则在全样本上有:
1260 |
1261 | $$
1262 | \sum_{i=1}^Tw_i\int A(h_i|x)p(x)\text{d}x=\sum_{i=1}^Tw_i\int E(h_i|x)p(x)\text{d}x-\int E(H|x)p(x)\text{d}x
1263 | $$
1264 |
1265 | 类似地,个体学习器 $ h_i $ 在全样本上的泛化误差和分歧项、集成的泛化误差分别为:
1266 |
1267 | $$
1268 | \begin{aligned}
1269 | E_i &= \int E(h_i|x)p(x)\text{d}x\\
1270 | A_i &= \int A(h_i|x)p(x)\text{d}x\\
1271 | E &= \int E(H|x)p(x)\text{d}x
1272 | \end{aligned}
1273 | $$
1274 |
1275 | 令 $ \overline E=\sum_{i=1}^Tw_i E_i $ 表示个体学习器的泛化误差的加权均值, $ \overline A=\sum_{i=1}^T w_iA_i $ 表示个体学习器的加权分歧值。有:
1276 |
1277 | $$
1278 | E = \overline E-\overline A
1279 | $$
1280 |
1281 | 这个漂亮的式子明确提示出:个体学习器准确性越高、多样性越大,则集成越好。
1282 |
1283 | [然而,个体学习器的"准确性"和"多样性"本身就存在冲突。一般的,准确性很高之后,要增加多样性就需牺牲准确性。因此我们需要达到两者的平衡。]
1284 |
1285 | [如何产生并结合“好而不同”的个体学习器,恰是集成学习研究的核心。]
1286 |
1287 | #### 有什么集成学习的方法?
1288 |
1289 | 1. 以Boosting为代表的,个体学习器问存在强依赖关系、必须串行生成的序列化方法
1290 | 2. 以Bagging, Random Forest为代表的,个体学习器间不存在强依赖关系、可同时生成的并行化方法
1291 | 3. 两者混合的方法
1292 |
1293 | #### 学习器结合的优点?
1294 |
1295 | 1. 减小泛化性能不佳的风险
1296 | 2. 降低陷入糟糕局部极小点的风险
1297 | 3. 扩大假设空间,可以学到更好的近似
1298 |
1299 | #### 各个算法的优缺点?
1300 |
1301 | Boosting:
1302 |
1303 | 优点:准确,鲁棒,泛化能力强。
1304 |
1305 | 缺点:因为是序列化训练,所以训练时间长;对噪声敏感,可能过拟合,可以增加正则化项、减少弱分类器数量;受初始值影响较大,需要用随机化的丰富减少影响。
1306 |
1307 | Bagging:
1308 |
1309 | 优点:可并行,准确,鲁棒,泛化能力强。
1310 |
1311 | 缺点:对高偏差模型效果不明显:Bagging主要的优势在于减少方差,对于高偏差的模型并不能很好地发挥作用。可解释性差。
1312 |
1313 | #### 学习器是越多越好吗?
1314 |
1315 | 不是,根据选择性集成,给定一组个体学习器,从中选择一部分来构建集成,经常会比使 用所有个体学习器更好 (更小的存储/时间开销,更强的泛化性能)。选择过程需考虑个体性能与多样性/互补性,仅选择“精度最高的”通常不好。
1316 |
1317 | ### Boosting
1318 |
1319 | #### 什么是Boosting?
1320 |
1321 | Boosting是一组可以将弱学习器提升为强学习器的算法。工作机制为:先从初始训练集中训练出一个基学习器,再根据基学习器的表现对训练样本分布进行调整,使得先前基学习器做错的训练样本在后续受到更多关注,然后基于调整后的样本分布来训练下一个基学习器。如此重复进行,直至基学习器数目达到事先指定的值 $ T $ 。最终将这 $ T $ 个基学习器进行加权结合。
1322 |
1323 | #### AdaBoost的计算过程是什么?
1324 |
1325 | 原始的AdaBoost算法只能处理二分类问题,计算过程如下:
1326 |
1327 |
1220 | 3. 重复执行E步和M步,直到收敛或达到预定的停止条件。
1221 |
1222 | ## 集成学习
1223 |
1224 | ### 基本概念
1225 |
1226 | #### 什么是集成学习?
1227 |
1228 | 集成学习ensemble learning(读“昂”)是一种机器学习方法,首先训练一组基学习器(也称为弱学习器),再将它们的预测结果通过某种策略结合,来完成学习任务。集成学习的核心思想是通过组合多个弱学习器,来达到比单个弱学习器更好的泛化性能,从而提高模型的预测能力。
1229 |
1230 | #### 为什么集成学习需要集成“好而不同”的学习器?
1231 |
1232 | 好指的是基学习器的准确性,不同指的是基学习器间的多样性。
1233 |
1234 | 直觉上,模型的准确性当然是越高越好,基学习器的准确率较低,集成学习的预测性能也会受到影响。基学习器具有多样性意味着不同的学习器可以捕捉到数据中的不同特征,因此可以相互补充、互相弥补,从而提高整体的学习性能。
1235 |
1236 | 数学上,可以用“误差-分歧分解”(error-ambiguity decomposition)证明:个体学习器准确性越高、多样性越大,则集成越好。
1237 |
1238 | 我们通过“分歧”来反应个体学习器的多样性,分歧的定义是各个学习器预测结果与集成的MSE的加权均值。
1239 |
1240 | 学习器 $ h_i $ 的分歧: $ A(h_i|x)=(h_i(x)-H(x))^2 $
1241 |
1242 | 集成 $ H $ 的分歧: $ \overline A(h|x)=\sum_{i=1}^T w_i(h_i(x)-H(x))^2 $
1243 |
1244 | 个体学习器的平方误差: $ E(h_i|x)=(f(x)-h_i(x))^2 $
1245 |
1246 | 集成的平方误差: $ E(H|x)=(f(x)-H(x))^2 $
1247 |
1248 | 个体学习器误差的加权均值: $ \overline E(h|x)=\sum_{i=1}^T w_i E(h_i|x) $
1249 |
1250 | 有:
1251 |
1252 | $$
1253 | \begin{aligned}
1254 | \overline A (h|x)&=\sum_{i=1}^Tw_i E(h_i|x)-E(H|x)\\
1255 | &=\overline E(h|x)-E(H|x)\\
1256 | \end{aligned}
1257 | $$
1258 |
1259 | 该式对所有样本 $ x $ 均成立,令 $ p(x) $ 表示样本的概率密度,则在全样本上有:
1260 |
1261 | $$
1262 | \sum_{i=1}^Tw_i\int A(h_i|x)p(x)\text{d}x=\sum_{i=1}^Tw_i\int E(h_i|x)p(x)\text{d}x-\int E(H|x)p(x)\text{d}x
1263 | $$
1264 |
1265 | 类似地,个体学习器 $ h_i $ 在全样本上的泛化误差和分歧项、集成的泛化误差分别为:
1266 |
1267 | $$
1268 | \begin{aligned}
1269 | E_i &= \int E(h_i|x)p(x)\text{d}x\\
1270 | A_i &= \int A(h_i|x)p(x)\text{d}x\\
1271 | E &= \int E(H|x)p(x)\text{d}x
1272 | \end{aligned}
1273 | $$
1274 |
1275 | 令 $ \overline E=\sum_{i=1}^Tw_i E_i $ 表示个体学习器的泛化误差的加权均值, $ \overline A=\sum_{i=1}^T w_iA_i $ 表示个体学习器的加权分歧值。有:
1276 |
1277 | $$
1278 | E = \overline E-\overline A
1279 | $$
1280 |
1281 | 这个漂亮的式子明确提示出:个体学习器准确性越高、多样性越大,则集成越好。
1282 |
1283 | [然而,个体学习器的"准确性"和"多样性"本身就存在冲突。一般的,准确性很高之后,要增加多样性就需牺牲准确性。因此我们需要达到两者的平衡。]
1284 |
1285 | [如何产生并结合“好而不同”的个体学习器,恰是集成学习研究的核心。]
1286 |
1287 | #### 有什么集成学习的方法?
1288 |
1289 | 1. 以Boosting为代表的,个体学习器问存在强依赖关系、必须串行生成的序列化方法
1290 | 2. 以Bagging, Random Forest为代表的,个体学习器间不存在强依赖关系、可同时生成的并行化方法
1291 | 3. 两者混合的方法
1292 |
1293 | #### 学习器结合的优点?
1294 |
1295 | 1. 减小泛化性能不佳的风险
1296 | 2. 降低陷入糟糕局部极小点的风险
1297 | 3. 扩大假设空间,可以学到更好的近似
1298 |
1299 | #### 各个算法的优缺点?
1300 |
1301 | Boosting:
1302 |
1303 | 优点:准确,鲁棒,泛化能力强。
1304 |
1305 | 缺点:因为是序列化训练,所以训练时间长;对噪声敏感,可能过拟合,可以增加正则化项、减少弱分类器数量;受初始值影响较大,需要用随机化的丰富减少影响。
1306 |
1307 | Bagging:
1308 |
1309 | 优点:可并行,准确,鲁棒,泛化能力强。
1310 |
1311 | 缺点:对高偏差模型效果不明显:Bagging主要的优势在于减少方差,对于高偏差的模型并不能很好地发挥作用。可解释性差。
1312 |
1313 | #### 学习器是越多越好吗?
1314 |
1315 | 不是,根据选择性集成,给定一组个体学习器,从中选择一部分来构建集成,经常会比使 用所有个体学习器更好 (更小的存储/时间开销,更强的泛化性能)。选择过程需考虑个体性能与多样性/互补性,仅选择“精度最高的”通常不好。
1316 |
1317 | ### Boosting
1318 |
1319 | #### 什么是Boosting?
1320 |
1321 | Boosting是一组可以将弱学习器提升为强学习器的算法。工作机制为:先从初始训练集中训练出一个基学习器,再根据基学习器的表现对训练样本分布进行调整,使得先前基学习器做错的训练样本在后续受到更多关注,然后基于调整后的样本分布来训练下一个基学习器。如此重复进行,直至基学习器数目达到事先指定的值 $ T $ 。最终将这 $ T $ 个基学习器进行加权结合。
1322 |
1323 | #### AdaBoost的计算过程是什么?
1324 |
1325 | 原始的AdaBoost算法只能处理二分类问题,计算过程如下:
1326 |
1327 |  1328 |
1329 | 1. 初始化数据分布
1330 | 2. 在训练的每一轮中:
1331 | 1. 使用当前的样本权重训练基学习器
1332 | 2. 计算分类误差率
1333 | 3. 如果分类误差率大于0.5,为了避免它进一步降低整个模型的准确率,算法会从循环中退出,停止训练
1334 | 4. 计算这个基学习器的权重
1335 | 5. 基于对分类正误情况更新数据分布,增加分错样本的影响,降低分对样本的影响
1336 | 3. 最后基于各个基学习器的权重,得到最终的分类器
1337 |
1338 | #### 为什么分布这样更新?[没回答]
1339 |
1340 | #### 在AdaBoost中,如何更新数据分布?
1341 |
1342 | 1. **重赋权法re-weighting**:在训练过程的每一轮中,根据样本分布为每个训练样本重新赋一个权重
1343 | 2. **重采样法re-sampling**:(对无法接受带权样本的基学习算法)在每一轮学习中,根据样本分布对训练 集重新进行采样,再用重采样而得的样本集对基学习器进行训练
1344 | 1. 可能获得**重启动**的机会以避免训练过程过早停止,即在抛弃不满足条件的当前基学习器之后,可根据当前分布重新对训练样本进行采样,再基于新的采样结果重新训练出基学习器,从而使得学习过程可以持 续到预设的 $ T $ 轮完成。
1345 |
1346 | 一般而言,这两种做法没有显著的优劣差别。
1347 |
1348 | ### Bagging,随机森林
1349 |
1350 | #### 什么是Bagging算法?
1351 |
1352 | bootstrap aggregating
1353 |
1354 | 基于自助采样法 (bootstrap sampling),得到含 $ m $ 个样本的采样集,基于每个采样集训练出一个基学习器,再将这些基学习器进行结合。对于分类任务,使用简单投票法;对于回归任务,使用简单平均法。
1355 |
1356 | 若分类预测时出现两个类收到同样票数的情形,则最简单的做法是随机选择一个,也可进一步考察学习器投票的置信度来确定最终胜者。
1357 |
1358 | 包外估计out-of-bag estimation: bootstrap使得每个基学习器值使用了初始训练集中约63.2%的样本,剩下的样本可以作为验证集来对泛化性能进行“包外估计“。
1359 |
1360 | #### Bagging的计算复杂度?
1361 |
1362 | 假定基学习器的计算复杂度为 $ O(m) $ ,则Bagging的复杂度大致为 $ T(O(m)+O(s)) $ ,采样与投票、平均过程的复杂度 $ O(s) $ 很小。
1363 |
1364 | #### 随机森林
1365 |
1366 | Random Forest
1367 |
1368 | 在以决策树为基学习器的Bagging集成的基础上,进一步在决策树的训练中引入了随机属性选择。(传统决策树:在当前结点的属性集合中选择一个最优属性;RF:对基决策树的每个接待您,先从结点的属性集合中随机选择一个包含 $ k $ 个属性的子集,然后再从一个子集中选择一个最优属性用于划分,推荐 $ k=\log_2 d $ )
1369 |
1370 | 在Bagging仅通过样本扰动增加多样性的基础上,引入了属性的扰动。
1371 |
1372 | ### Stacking
1373 |
1374 | Stacking 先从初始数据集训练出初级学习器,然后“生成”一个新数据集用于训练次级学习器。在这个新数据集中,初级学习器的输出被当作样例输入特征,而初始样本的标记仍被当作样例标记。这里我们假定初级学习器使用不同学习算法产生,即初级集成是异质的。若直接用初级学习器的训练集来产生次级训练集,则过拟合风险会比较大,因此一般是通过使用交叉验证或留一法这样的方式,用训练初级学习器未使用的样本来产生次级学习器的训练样本。
1375 |
1376 | ### 多样性
1377 |
1378 | #### 有什么多样性度量的方法?
1379 |
1380 | | | $ h_i=+1 $ | $ h_i=-1 $ |
1381 | | ---------- | ---------- | ---------- |
1382 | | $ h_j=+1 $ | a | c |
1383 | | $ h_j=-1 $ | b | d |
1384 |
1385 | - 不合度量disagreement measure:
1386 |
1387 | $$
1388 | dis_{ij}=\frac{b+c}m
1389 | $$
1390 |
1391 | $ dis_{ij} $ 值域为 $ [0,1] $ ,值越大则多样性越大。
1392 |
1393 | - 相关系数correlation coefficient
1394 |
1395 | $$
1396 | \rho_{ij}=\frac{ad-bc}{\sqrt{(a+b)(a+c)(c+d)(b+d)}}
1397 | $$
1398 |
1399 | $ \rho_{ij} $ 的值域为 $ [-1,1] $ 。若 $ h_i $ 与 $ h_j $ 无关,则值为0;若 $ h_i $ 与 $ h_j $ 正相关,则值为正,否则为负。
1400 |
1401 | - Q-统计量 Q-statistic
1402 |
1403 | $$
1404 | Q_{ij}=\frac{ad-bc}{ad+bc}
1405 | $$
1406 |
1407 | $ Q_{ij} $ 与相关系数 $ \rho_{ij} $ 的符号相同,且 $ |Q_{ij}|\leq |\rho_{ij}| $
1408 |
1409 | - $ \kappa $ -统计量 $ \kappa $ -statistic
1410 |
1411 | $$
1412 | \kappa=\frac{p_1-p_2}{1-p_2}
1413 | $$
1414 |
1415 | 其中 $ p_1 $ 是两个分类器取得一致的概率; $ p_2 $ 是两个分类器偶然达成一致的概率,它们可以由数据集 $ D $ 估算:
1416 |
1417 | $$
1418 | \begin{aligned}
1419 | p_1&=\frac{a+d}{m}\\
1420 | p_2&=\frac{(a+b)(a+c)+(c+d)(b+d)}{m^2}
1421 | \end{aligned}
1422 | $$
1423 |
1424 | 若分类器 $ h_i $ 与 $ h_j $ 在 $ D $ 上完全一致,则 $ \kappa = 1 $ ;若它们仅是偶然达成一致,则 $ \kappa = 0 $ 。188 $ \kappa $ 通常为非负值,仅在 $ h_i $ 与 $ h_j $ 达成一致的概率甚主低于偶然性的情况下取负值。
1425 |
1426 | #### 如何增强多样性?
1427 |
1428 | 对数据样本、输入属性、输出表示、算法参数进行扰动。
1429 |
1430 | ## 聚类
1431 |
1432 | ### 聚类任务
1433 |
1434 | #### 什么是聚类任务?
1435 |
1436 | 聚类试图将数据集中的样本划分为若干个通常是不相交的“簇”(cluster)。用于找寻数据内在的分布结构,也可作为分类等其他学习任务的前驱过程。
1437 |
1438 | ### 性能度量
1439 |
1440 | #### 直观上,什么样的聚类好?
1441 |
1442 | 直观上看,我们希望“物以类聚“,即同一簇的样本尽可能彼此相似,不同簇的样本尽可能不同。换言之,聚类结果的“簇内相似度 (intra-cluster similarity) 高且“簇间相似度” (inter-cluster similarity) 低。
1443 |
1444 | #### 什么是外部指标,内部指标?具体有什么指标?
1445 |
1446 | 外部指标external index,将聚类结果与某个“参考模型”reference model进行比较:
1447 |
1448 | $ a= |SS| $ ,属于同一簇且在参考模型中也属于同一簇的样本对数
1449 |
1450 | $ b= |SD| $ ,属于同一簇但在参考模型中不属于同一簇的样本对数
1451 |
1452 | $ c= |DS| $ ,不属于同一簇但在参考模型中属于同一簇的样本对数
1453 |
1454 | $ c= |DD| $ ,不属于同一簇且在参考模型中也不属于同一簇的样本对数
1455 |
1456 | - Jaccard系数,Jaccard Coefficient, JC
1457 | - FM指数
1458 | - Rand指数(p198)
1459 |
1460 | 内部指标internal index,直接考察聚类结果而不利用任何参考模型:
1461 |
1462 | - DBI,越小越好
1463 | - Dunn,越大越好
1464 |
1465 | ### 距离计算
1466 |
1467 | #### 距离度量需要满足什么基本性质?
1468 |
1469 | 非负性,同一性(距离为零当且仅当两点相等),对称性( $ \operatorname{dist}(a,b)=\operatorname{dist}(b,a) $ ),直递性( $ \operatorname{dist}(a,b)\leq\operatorname{dist}(a,c)+\operatorname{dist}(c,b) $ )
1470 |
1471 | #### 有什么常见的距离度量?
1472 |
1473 | - 对连续属性
1474 |
1475 | 闵可夫斯基距离Minkowski distance
1476 |
1477 | $$
1478 | \operatorname{dist}_{mk}(x_i,x_j)=\left(\sum_{u=1}^n |x_{iu}-x_{ju}|^p\right)^{\frac1p}
1479 | $$
1480 |
1481 | $ p=2 $ ,欧氏距离Euclidean distance
1482 |
1483 | $ p=1 $ ,曼哈顿距离Manhattan distance
1484 |
1485 | $ p=\infty $ ,切比雪夫距离 $ =\max(|x_2-x_1|,|y_2-y_1|) $
1486 |
1487 | - 对离散属性
1488 |
1489 | - 对有序属性:接近连续
1490 | - 对无序属性:VDM, value difference metric
1491 |
1492 | $ m_{u,a} $ 在属性 $ u $ 上取值为 $ a $ 的样本数, $ m_{u,a,i} $ 在第 $ i $ 个样本簇中在属性 $ u $ 上取值为 $ a $ 的样本数, $ k $ 样本簇数
1493 |
1494 | $$
1495 | VDM_p(a,b)=\sum_{i=1}^k\left\vert\frac{m_{u,a,i}}{m_{u,a}}-\frac{m_{u,b,i}}{m_{u,b}}\right\vert^p\\
1496 | $$
1497 | - 对混合属性
1498 |
1499 | 基于闵可夫斯基距离,括号里加上无序属性的VDM。
1500 |
1501 | #### 什么是距离度量学习?
1502 |
1503 | 在现实任务中基于数据样本来确定合适的距离计算式。
1504 |
1505 | ### 常见聚类方法
1506 |
1507 | - 原型聚类
1508 |
1509 | - 亦称“基于原型的聚类”(prototype-based clustering)
1510 | - 假设:聚类结构能通过一组原型刻画
1511 | - 过程:先对原型初始化,然后对原型进行迭代更新求解
1512 | - 代表:
1513 |
1514 | - k均值聚类:找到一组原型向量来刻画聚类结构,每个簇以该簇中所有样本点的“均值”表示
1515 | - 学习向量量化(LVQ):找到一组原型向量来刻画聚类结构,假设数据样本带有类别标记
1516 | - 高斯混合聚类Gaussian Mixture Clustering:生成式模型。采用概率模型来表达聚类原型,假设样本由高斯混合过程(先选成分,再根据其概率密度函数采样)生成相应的样本。用EM算法迭代优化求解其最大对数似然。
1517 | - 密度聚类
1518 |
1519 | - 亦称“基于密度的聚类”(density-based clustering)
1520 | - 假设:聚类结构能通过样本分布的紧密程度确定
1521 | - 过程:从样本密度的角度来考察样本之间的可连接性,并基于可连接样本不断扩展聚类簇
1522 | - 代表:DBSCAN, OPTICS, DENCLUE
1523 | - 层次聚类 (hierarchical clustering)
1524 |
1525 | - 假设:能够产生不同粒度的聚类结果
1526 | - 过程:在不同层次对数据集进行划分,从而形成树形的聚类结构
1527 | - 代表:AGNES (自底向上),DIANA (自顶向下)
1528 |
1529 | ## 降维与度量学习
1530 |
1531 | ### k近邻学习
1532 |
1533 | 给定测试样本,基于某种距离度量找出训练集中与其最靠近的k个训练样本,然后基于这k个"邻居"的信息来进行预测 .
1534 |
1535 | lazy learning,即在训练阶段仅仅是把样本保存起来,训练时间开销为零,待收到测试样本后再进行处理。
1536 |
1537 | ### 维数灾难
1538 |
1539 | #### 是什么
1540 |
1541 | curse of dimensionality,高维情形下出现的数据样本稀疏、 距离计算困难等问题
1542 |
1543 | #### 解决
1544 |
1545 | 降维dimension reduction,某种数学变换将原始高维属性空间转变为一个低维子空间,在这个子空间中样本密度大幅提高,距离计算也变得更为容易。
1546 |
1547 | #### 为什么可以降维
1548 |
1549 | 与学习任务密切相关的也许仅是某个低维分布,即高维空间中的一 个低维嵌入(embedding)
1550 |
1551 | #### MDS[没看]
1552 |
1553 | 经典降维方法,要求原始空间中样本之间的距离在低维空间中得以保持
1554 |
1555 | ### 主成分分析
1556 |
1557 | Principal Component Analysis,常用降维方法
1558 |
1559 | #### 推导[自己推一遍]
1560 |
1561 | 根据**最近重构性**(样本点到这个超平面的距离都足够近)和**最大可分性**(样本点在这个超平面上的投影能尽可能分开)的两个推导
1562 |
1563 | #### 计算过程
1564 |
1565 | 中心化:
1566 |
1567 | $ x_i=x_i-\overline {x_i} $
1568 |
1569 | 优化目标:
1570 |
1571 | $$
1572 | \min_W -\text{tr}(W^\top XX^\top W)\\
1573 | s.t. W^\top W=E
1574 | $$
1575 |
1576 | 拉格朗日乘子法:
1577 |
1578 | $$
1579 | XX^\top W=\lambda W
1580 | $$
1581 |
1582 | 对 $ XX^\top $ 特征值分解并将求得的特征值从大到小排序,选择前 $ d' $ 维特征值对应的特征向量构成 $ w_1,\dots,w_{d'} $
1583 |
1584 | #### 重构维度选择
1585 |
1586 | 一般事先指定,可以通过重构阈值设置。例如 $ t=95\% $
1587 |
1588 | 选择满足 $ \displaystyle \frac{\sum_{i=1}^{d'}\lambda_i}{\sum_{i=1}^{d}\lambda_i}\geq t $ 的最小 $ d' $
1589 |
1590 | #### 与LDA, FDA
1591 |
1592 | p231
1593 |
1594 | 借鉴LDA的方法,假设每个 样本自成一个类型,那么则 希望所有样本在超平面上的 投影尽可能分开。 LDA既要优化类间散度又要 优化类内散度,PCA相当于 通过固定类内散度来限制它
1595 |
1596 | PCA - FDA => LDA PCA是无监督学习方法,FDA是监督学习方法,考虑了标记的作用
1597 |
1598 | #### 应用[没看!]
1599 |
1600 | 特征脸(eigenface) robust PCA
1601 |
1602 | ### 度量学习
1603 |
1604 | 度量学习(Metric Learning)是机器学习领域的一个子领域,旨在通过学习适当的距离或度量函数,使得在特征空间中具有类似特性的样本之间的距离更小,而不同类别之间的距离更大。
1605 |
1606 | #### 马氏距离
1607 |
1608 | 
1609 |
1610 | #### 优化目标
1611 |
1612 | 
1613 |
1614 | ## 特征选择与稀疏学习
1615 |
1616 | #### L1正则化和
1617 |
1618 | ## 计算学习理论
1619 |
1620 | ### PAC学习
1621 |
1622 | #### PAC理论
1623 |
1624 | probably approximately correct。PAC理论是机器学习中的理论框架,通过控制样本复杂度和近似误差的方式,以一定的概率保证算法学得误差满足预设上限的模型。
1625 |
1626 | #### PAC辨识
1627 |
1628 | 
1629 |
1630 | #### PAC可学习
1631 |
1632 | 一个学习问题被称为PAC可学习,当且仅当存在一个学习算法,对于给定的样本数量和质量,以一定的概率保证在未见过的数据上产生近似正确的输出。
1633 |
1634 | 
1635 |
1636 | #### PAC学习算法
1637 |
1638 | (考虑时间复杂度)
1639 |
1640 | 
1641 |
1642 | #### 样本复杂度
1643 |
1644 | 
1645 |
1646 | ## 半监督学习
1647 |
1648 | ## 概率图模型
1649 |
1650 | 用图表示变量的相关关系的概率模型,点:变量,边:变量间的概率相关关系
1651 |
1652 | 有向无环图 - 贝叶斯网 - HMM
1653 |
1654 | 无向图 - 马尔科夫网
1655 |
1656 | ### HMM
1657 |
1658 | #### 静态过程/动态过程?
1659 |
1660 | $ P(X_{t+1}|X_t) $ 是否改变
1661 |
1662 | #### 马尔科夫链
1663 |
1664 | 具有马尔科夫性,系统下一时刻的状态仅由当前状态决定,不依赖于以往的任何状态。
1665 |
1666 | 
1667 |
1668 | 简化模型,避免了维度灾难的问题。
1669 |
1670 | #### 参数?
1671 |
1672 | 
1673 |
1674 | 
1675 |
1676 | #### 三个要解决的问题?
1677 |
1678 | 问题1:Evaluation估值,评估模型与观测序列 之间的匹配程度
1679 |
1680 |
1328 |
1329 | 1. 初始化数据分布
1330 | 2. 在训练的每一轮中:
1331 | 1. 使用当前的样本权重训练基学习器
1332 | 2. 计算分类误差率
1333 | 3. 如果分类误差率大于0.5,为了避免它进一步降低整个模型的准确率,算法会从循环中退出,停止训练
1334 | 4. 计算这个基学习器的权重
1335 | 5. 基于对分类正误情况更新数据分布,增加分错样本的影响,降低分对样本的影响
1336 | 3. 最后基于各个基学习器的权重,得到最终的分类器
1337 |
1338 | #### 为什么分布这样更新?[没回答]
1339 |
1340 | #### 在AdaBoost中,如何更新数据分布?
1341 |
1342 | 1. **重赋权法re-weighting**:在训练过程的每一轮中,根据样本分布为每个训练样本重新赋一个权重
1343 | 2. **重采样法re-sampling**:(对无法接受带权样本的基学习算法)在每一轮学习中,根据样本分布对训练 集重新进行采样,再用重采样而得的样本集对基学习器进行训练
1344 | 1. 可能获得**重启动**的机会以避免训练过程过早停止,即在抛弃不满足条件的当前基学习器之后,可根据当前分布重新对训练样本进行采样,再基于新的采样结果重新训练出基学习器,从而使得学习过程可以持 续到预设的 $ T $ 轮完成。
1345 |
1346 | 一般而言,这两种做法没有显著的优劣差别。
1347 |
1348 | ### Bagging,随机森林
1349 |
1350 | #### 什么是Bagging算法?
1351 |
1352 | bootstrap aggregating
1353 |
1354 | 基于自助采样法 (bootstrap sampling),得到含 $ m $ 个样本的采样集,基于每个采样集训练出一个基学习器,再将这些基学习器进行结合。对于分类任务,使用简单投票法;对于回归任务,使用简单平均法。
1355 |
1356 | 若分类预测时出现两个类收到同样票数的情形,则最简单的做法是随机选择一个,也可进一步考察学习器投票的置信度来确定最终胜者。
1357 |
1358 | 包外估计out-of-bag estimation: bootstrap使得每个基学习器值使用了初始训练集中约63.2%的样本,剩下的样本可以作为验证集来对泛化性能进行“包外估计“。
1359 |
1360 | #### Bagging的计算复杂度?
1361 |
1362 | 假定基学习器的计算复杂度为 $ O(m) $ ,则Bagging的复杂度大致为 $ T(O(m)+O(s)) $ ,采样与投票、平均过程的复杂度 $ O(s) $ 很小。
1363 |
1364 | #### 随机森林
1365 |
1366 | Random Forest
1367 |
1368 | 在以决策树为基学习器的Bagging集成的基础上,进一步在决策树的训练中引入了随机属性选择。(传统决策树:在当前结点的属性集合中选择一个最优属性;RF:对基决策树的每个接待您,先从结点的属性集合中随机选择一个包含 $ k $ 个属性的子集,然后再从一个子集中选择一个最优属性用于划分,推荐 $ k=\log_2 d $ )
1369 |
1370 | 在Bagging仅通过样本扰动增加多样性的基础上,引入了属性的扰动。
1371 |
1372 | ### Stacking
1373 |
1374 | Stacking 先从初始数据集训练出初级学习器,然后“生成”一个新数据集用于训练次级学习器。在这个新数据集中,初级学习器的输出被当作样例输入特征,而初始样本的标记仍被当作样例标记。这里我们假定初级学习器使用不同学习算法产生,即初级集成是异质的。若直接用初级学习器的训练集来产生次级训练集,则过拟合风险会比较大,因此一般是通过使用交叉验证或留一法这样的方式,用训练初级学习器未使用的样本来产生次级学习器的训练样本。
1375 |
1376 | ### 多样性
1377 |
1378 | #### 有什么多样性度量的方法?
1379 |
1380 | | | $ h_i=+1 $ | $ h_i=-1 $ |
1381 | | ---------- | ---------- | ---------- |
1382 | | $ h_j=+1 $ | a | c |
1383 | | $ h_j=-1 $ | b | d |
1384 |
1385 | - 不合度量disagreement measure:
1386 |
1387 | $$
1388 | dis_{ij}=\frac{b+c}m
1389 | $$
1390 |
1391 | $ dis_{ij} $ 值域为 $ [0,1] $ ,值越大则多样性越大。
1392 |
1393 | - 相关系数correlation coefficient
1394 |
1395 | $$
1396 | \rho_{ij}=\frac{ad-bc}{\sqrt{(a+b)(a+c)(c+d)(b+d)}}
1397 | $$
1398 |
1399 | $ \rho_{ij} $ 的值域为 $ [-1,1] $ 。若 $ h_i $ 与 $ h_j $ 无关,则值为0;若 $ h_i $ 与 $ h_j $ 正相关,则值为正,否则为负。
1400 |
1401 | - Q-统计量 Q-statistic
1402 |
1403 | $$
1404 | Q_{ij}=\frac{ad-bc}{ad+bc}
1405 | $$
1406 |
1407 | $ Q_{ij} $ 与相关系数 $ \rho_{ij} $ 的符号相同,且 $ |Q_{ij}|\leq |\rho_{ij}| $
1408 |
1409 | - $ \kappa $ -统计量 $ \kappa $ -statistic
1410 |
1411 | $$
1412 | \kappa=\frac{p_1-p_2}{1-p_2}
1413 | $$
1414 |
1415 | 其中 $ p_1 $ 是两个分类器取得一致的概率; $ p_2 $ 是两个分类器偶然达成一致的概率,它们可以由数据集 $ D $ 估算:
1416 |
1417 | $$
1418 | \begin{aligned}
1419 | p_1&=\frac{a+d}{m}\\
1420 | p_2&=\frac{(a+b)(a+c)+(c+d)(b+d)}{m^2}
1421 | \end{aligned}
1422 | $$
1423 |
1424 | 若分类器 $ h_i $ 与 $ h_j $ 在 $ D $ 上完全一致,则 $ \kappa = 1 $ ;若它们仅是偶然达成一致,则 $ \kappa = 0 $ 。188 $ \kappa $ 通常为非负值,仅在 $ h_i $ 与 $ h_j $ 达成一致的概率甚主低于偶然性的情况下取负值。
1425 |
1426 | #### 如何增强多样性?
1427 |
1428 | 对数据样本、输入属性、输出表示、算法参数进行扰动。
1429 |
1430 | ## 聚类
1431 |
1432 | ### 聚类任务
1433 |
1434 | #### 什么是聚类任务?
1435 |
1436 | 聚类试图将数据集中的样本划分为若干个通常是不相交的“簇”(cluster)。用于找寻数据内在的分布结构,也可作为分类等其他学习任务的前驱过程。
1437 |
1438 | ### 性能度量
1439 |
1440 | #### 直观上,什么样的聚类好?
1441 |
1442 | 直观上看,我们希望“物以类聚“,即同一簇的样本尽可能彼此相似,不同簇的样本尽可能不同。换言之,聚类结果的“簇内相似度 (intra-cluster similarity) 高且“簇间相似度” (inter-cluster similarity) 低。
1443 |
1444 | #### 什么是外部指标,内部指标?具体有什么指标?
1445 |
1446 | 外部指标external index,将聚类结果与某个“参考模型”reference model进行比较:
1447 |
1448 | $ a= |SS| $ ,属于同一簇且在参考模型中也属于同一簇的样本对数
1449 |
1450 | $ b= |SD| $ ,属于同一簇但在参考模型中不属于同一簇的样本对数
1451 |
1452 | $ c= |DS| $ ,不属于同一簇但在参考模型中属于同一簇的样本对数
1453 |
1454 | $ c= |DD| $ ,不属于同一簇且在参考模型中也不属于同一簇的样本对数
1455 |
1456 | - Jaccard系数,Jaccard Coefficient, JC
1457 | - FM指数
1458 | - Rand指数(p198)
1459 |
1460 | 内部指标internal index,直接考察聚类结果而不利用任何参考模型:
1461 |
1462 | - DBI,越小越好
1463 | - Dunn,越大越好
1464 |
1465 | ### 距离计算
1466 |
1467 | #### 距离度量需要满足什么基本性质?
1468 |
1469 | 非负性,同一性(距离为零当且仅当两点相等),对称性( $ \operatorname{dist}(a,b)=\operatorname{dist}(b,a) $ ),直递性( $ \operatorname{dist}(a,b)\leq\operatorname{dist}(a,c)+\operatorname{dist}(c,b) $ )
1470 |
1471 | #### 有什么常见的距离度量?
1472 |
1473 | - 对连续属性
1474 |
1475 | 闵可夫斯基距离Minkowski distance
1476 |
1477 | $$
1478 | \operatorname{dist}_{mk}(x_i,x_j)=\left(\sum_{u=1}^n |x_{iu}-x_{ju}|^p\right)^{\frac1p}
1479 | $$
1480 |
1481 | $ p=2 $ ,欧氏距离Euclidean distance
1482 |
1483 | $ p=1 $ ,曼哈顿距离Manhattan distance
1484 |
1485 | $ p=\infty $ ,切比雪夫距离 $ =\max(|x_2-x_1|,|y_2-y_1|) $
1486 |
1487 | - 对离散属性
1488 |
1489 | - 对有序属性:接近连续
1490 | - 对无序属性:VDM, value difference metric
1491 |
1492 | $ m_{u,a} $ 在属性 $ u $ 上取值为 $ a $ 的样本数, $ m_{u,a,i} $ 在第 $ i $ 个样本簇中在属性 $ u $ 上取值为 $ a $ 的样本数, $ k $ 样本簇数
1493 |
1494 | $$
1495 | VDM_p(a,b)=\sum_{i=1}^k\left\vert\frac{m_{u,a,i}}{m_{u,a}}-\frac{m_{u,b,i}}{m_{u,b}}\right\vert^p\\
1496 | $$
1497 | - 对混合属性
1498 |
1499 | 基于闵可夫斯基距离,括号里加上无序属性的VDM。
1500 |
1501 | #### 什么是距离度量学习?
1502 |
1503 | 在现实任务中基于数据样本来确定合适的距离计算式。
1504 |
1505 | ### 常见聚类方法
1506 |
1507 | - 原型聚类
1508 |
1509 | - 亦称“基于原型的聚类”(prototype-based clustering)
1510 | - 假设:聚类结构能通过一组原型刻画
1511 | - 过程:先对原型初始化,然后对原型进行迭代更新求解
1512 | - 代表:
1513 |
1514 | - k均值聚类:找到一组原型向量来刻画聚类结构,每个簇以该簇中所有样本点的“均值”表示
1515 | - 学习向量量化(LVQ):找到一组原型向量来刻画聚类结构,假设数据样本带有类别标记
1516 | - 高斯混合聚类Gaussian Mixture Clustering:生成式模型。采用概率模型来表达聚类原型,假设样本由高斯混合过程(先选成分,再根据其概率密度函数采样)生成相应的样本。用EM算法迭代优化求解其最大对数似然。
1517 | - 密度聚类
1518 |
1519 | - 亦称“基于密度的聚类”(density-based clustering)
1520 | - 假设:聚类结构能通过样本分布的紧密程度确定
1521 | - 过程:从样本密度的角度来考察样本之间的可连接性,并基于可连接样本不断扩展聚类簇
1522 | - 代表:DBSCAN, OPTICS, DENCLUE
1523 | - 层次聚类 (hierarchical clustering)
1524 |
1525 | - 假设:能够产生不同粒度的聚类结果
1526 | - 过程:在不同层次对数据集进行划分,从而形成树形的聚类结构
1527 | - 代表:AGNES (自底向上),DIANA (自顶向下)
1528 |
1529 | ## 降维与度量学习
1530 |
1531 | ### k近邻学习
1532 |
1533 | 给定测试样本,基于某种距离度量找出训练集中与其最靠近的k个训练样本,然后基于这k个"邻居"的信息来进行预测 .
1534 |
1535 | lazy learning,即在训练阶段仅仅是把样本保存起来,训练时间开销为零,待收到测试样本后再进行处理。
1536 |
1537 | ### 维数灾难
1538 |
1539 | #### 是什么
1540 |
1541 | curse of dimensionality,高维情形下出现的数据样本稀疏、 距离计算困难等问题
1542 |
1543 | #### 解决
1544 |
1545 | 降维dimension reduction,某种数学变换将原始高维属性空间转变为一个低维子空间,在这个子空间中样本密度大幅提高,距离计算也变得更为容易。
1546 |
1547 | #### 为什么可以降维
1548 |
1549 | 与学习任务密切相关的也许仅是某个低维分布,即高维空间中的一 个低维嵌入(embedding)
1550 |
1551 | #### MDS[没看]
1552 |
1553 | 经典降维方法,要求原始空间中样本之间的距离在低维空间中得以保持
1554 |
1555 | ### 主成分分析
1556 |
1557 | Principal Component Analysis,常用降维方法
1558 |
1559 | #### 推导[自己推一遍]
1560 |
1561 | 根据**最近重构性**(样本点到这个超平面的距离都足够近)和**最大可分性**(样本点在这个超平面上的投影能尽可能分开)的两个推导
1562 |
1563 | #### 计算过程
1564 |
1565 | 中心化:
1566 |
1567 | $ x_i=x_i-\overline {x_i} $
1568 |
1569 | 优化目标:
1570 |
1571 | $$
1572 | \min_W -\text{tr}(W^\top XX^\top W)\\
1573 | s.t. W^\top W=E
1574 | $$
1575 |
1576 | 拉格朗日乘子法:
1577 |
1578 | $$
1579 | XX^\top W=\lambda W
1580 | $$
1581 |
1582 | 对 $ XX^\top $ 特征值分解并将求得的特征值从大到小排序,选择前 $ d' $ 维特征值对应的特征向量构成 $ w_1,\dots,w_{d'} $
1583 |
1584 | #### 重构维度选择
1585 |
1586 | 一般事先指定,可以通过重构阈值设置。例如 $ t=95\% $
1587 |
1588 | 选择满足 $ \displaystyle \frac{\sum_{i=1}^{d'}\lambda_i}{\sum_{i=1}^{d}\lambda_i}\geq t $ 的最小 $ d' $
1589 |
1590 | #### 与LDA, FDA
1591 |
1592 | p231
1593 |
1594 | 借鉴LDA的方法,假设每个 样本自成一个类型,那么则 希望所有样本在超平面上的 投影尽可能分开。 LDA既要优化类间散度又要 优化类内散度,PCA相当于 通过固定类内散度来限制它
1595 |
1596 | PCA - FDA => LDA PCA是无监督学习方法,FDA是监督学习方法,考虑了标记的作用
1597 |
1598 | #### 应用[没看!]
1599 |
1600 | 特征脸(eigenface) robust PCA
1601 |
1602 | ### 度量学习
1603 |
1604 | 度量学习(Metric Learning)是机器学习领域的一个子领域,旨在通过学习适当的距离或度量函数,使得在特征空间中具有类似特性的样本之间的距离更小,而不同类别之间的距离更大。
1605 |
1606 | #### 马氏距离
1607 |
1608 | 
1609 |
1610 | #### 优化目标
1611 |
1612 | 
1613 |
1614 | ## 特征选择与稀疏学习
1615 |
1616 | #### L1正则化和
1617 |
1618 | ## 计算学习理论
1619 |
1620 | ### PAC学习
1621 |
1622 | #### PAC理论
1623 |
1624 | probably approximately correct。PAC理论是机器学习中的理论框架,通过控制样本复杂度和近似误差的方式,以一定的概率保证算法学得误差满足预设上限的模型。
1625 |
1626 | #### PAC辨识
1627 |
1628 | 
1629 |
1630 | #### PAC可学习
1631 |
1632 | 一个学习问题被称为PAC可学习,当且仅当存在一个学习算法,对于给定的样本数量和质量,以一定的概率保证在未见过的数据上产生近似正确的输出。
1633 |
1634 | 
1635 |
1636 | #### PAC学习算法
1637 |
1638 | (考虑时间复杂度)
1639 |
1640 | 
1641 |
1642 | #### 样本复杂度
1643 |
1644 | 
1645 |
1646 | ## 半监督学习
1647 |
1648 | ## 概率图模型
1649 |
1650 | 用图表示变量的相关关系的概率模型,点:变量,边:变量间的概率相关关系
1651 |
1652 | 有向无环图 - 贝叶斯网 - HMM
1653 |
1654 | 无向图 - 马尔科夫网
1655 |
1656 | ### HMM
1657 |
1658 | #### 静态过程/动态过程?
1659 |
1660 | $ P(X_{t+1}|X_t) $ 是否改变
1661 |
1662 | #### 马尔科夫链
1663 |
1664 | 具有马尔科夫性,系统下一时刻的状态仅由当前状态决定,不依赖于以往的任何状态。
1665 |
1666 | 
1667 |
1668 | 简化模型,避免了维度灾难的问题。
1669 |
1670 | #### 参数?
1671 |
1672 | 
1673 |
1674 | 
1675 |
1676 | #### 三个要解决的问题?
1677 |
1678 | 问题1:Evaluation估值,评估模型与观测序列 之间的匹配程度
1679 |
1680 |  1681 |
1682 | 问题2:Decoding解码,如何根据观测序列推断出隐藏的模型状态
1683 |
1684 | 维特比算法
1685 |
1686 |
1681 |
1682 | 问题2:Decoding解码,如何根据观测序列推断出隐藏的模型状态
1683 |
1684 | 维特比算法
1685 |
1686 |  1687 |
1688 | 问题3:Learning学习,如何训练模型使其能最好地描述观测数据
1689 |
1690 | Baum-Welch算法(EM的特例)
1691 |
1692 | 前两者都是DP,计算简单
1693 |
1694 |
1687 |
1688 | 问题3:Learning学习,如何训练模型使其能最好地描述观测数据
1689 |
1690 | Baum-Welch算法(EM的特例)
1691 |
1692 | 前两者都是DP,计算简单
1693 |
1694 |  1695 |
1696 | ### 1、什么是马尔科夫过程?
1697 |
1698 | 假设一个随机过程中,t_n 时刻的状态 x_n 的条件发布,只与其前一状态x_(n-1) 相关,即:
1699 |
1700 | 
1701 |
1702 | 则将其称为 马尔可夫过程。
1703 |
1704 | ### 2、马尔科夫过程的核心思想是什么?
1705 |
1706 | 对于马尔可夫过程的思想,用一句话去概括:当前时刻状态仅与上一时刻状态相关,与其他时刻不相关。
1707 |
1708 | 可以从 马尔可夫过程图去理解,由于每个状态间是以有向直线连接,也就是当前时刻状态仅与上一时刻状态相关。
1709 |
1710 | ### 3、隐马尔可夫算法中的两个假设是什么?
1711 |
1712 | 齐次马尔可夫性假设:即假设隐藏的马尔科夫链在任意时刻 t 的状态只依赖于其前一时刻的状态,与其他时刻的状态及观测无关,也与时刻 t 无关;
1713 |
1714 | 
1715 |
1716 | 观测独立性假设:即假设任意时刻的观测只依赖于该时刻的马尔科夫链的状态,与其他观测及状态无关。
1717 |
1718 | 
1719 |
1720 | ### 4、隐马尔可夫模型三个基本问题是什么?
1721 |
1722 | (1)概率计算问题:**给定模型(A,B, $ \pi $ )和观测序列**,计算在模型下观测序列出现的概率。(直接计算法理论可行,但计算复杂度太大(O(N^2T));用前向与后向计算法)
1723 |
1724 | (2)学习问题:**已知观测序列,估计模型参数**,使得在该模型下观测序列概率最大。(极大似然估计的方法来估计参数,Baum-Welch算法(EM算法))
1725 |
1726 | (3)预测问题,也称为解码问题:已知模型和观测序列,**求对给定观测序列条件概率最大的状态序列**。(维特比算法,动态规划,核心:**边计算边删掉不可能是答案的路径,在最后剩下的路径中挑选最优路径**)
1727 |
1728 | ### 5、隐马尔可夫模型三个基本问题的联系?
1729 |
1730 | 三个基本问题 存在 渐进关系。首先,要学会用前向算法和后向算法算观测序列出现的概率,然后用Baum-Welch算法求参数的时候,某些步骤是需要用到前向算法和后向算法的,计算得到参数后,我们就可以用来做预测了。因此可以看到,三个基本问题,它们是渐进的,解决NLP问题,应用HMM模型做解码任务应该是最终的目的。
1731 |
1732 | ### 6、隐马尔可夫算法存在哪些问题?
1733 |
1734 | 因为HMM模型其实它简化了很多问题,做了某些很强的假设,如齐次马尔可夫性假设和观测独立性假设,做了假设的好处是,简化求解的难度,坏处是对真实情况的建模能力变弱了。
1735 |
1736 | 在序列标注问题中,隐状态(标注)不仅和单个观测状态相关,还和观察序列的长度、上下文等信息相关。例如词性标注问题中,一个词被标注为动词还是名词,不仅与它本身以及它前一个词的标注有关,还依赖于上下文中的其他词。可以使用最大熵马尔科夫模型进行优化。
1737 |
1738 | ## 规则学习
1739 |
1740 | ## 强化学习
1741 |
--------------------------------------------------------------------------------
/概率论与数理统计.md:
--------------------------------------------------------------------------------
1 | # 概率论与数理统计
2 |
3 | ## 提纲
4 |
5 | ### 第一章 基本概念
6 |
7 | - 概率和统计的区别
8 | - 必然现象与随机现象
9 | - 随机试验:样本点,样本空间
10 | - 事件间的关系,事件与集合的对应关系,事件的运算规律
11 | - 概率的公理化定义,概率的性质
12 | - 古典概型,几何概型
13 | - 条件概率,全概率公式和贝叶斯公式
14 | - 独立性,独立与互斥的关系
15 | - Freivalds算法
16 |
17 | ### 第二章 随机变量及其分布
18 |
19 | - 分布函数定义,性质(单调性,规范性,右连续性);概率密度函数定义,性质(单调性,规范性,连续性)
20 | - 离散随机变量:均匀分布、二项分布、几何分布(无记忆性)、负二项分布(Pascal分布)、泊松分布(泊松定理)
21 | - 连续随机变量:均匀分布、指数分布(无记忆性)、正态分布
22 | - 德国坦克问题
23 |
24 | ### 第三章 多维随机变量
25 |
26 | - 联合分布函数定义、性质(对每个变量单调不减,非负性,规范性,右连续);边缘分布与独立性
27 | - 联合概率密度定义、性质(非负性,规范性);边缘概率密度,两变量独立的等价条件
28 | - 多维随机变量函数的分布(和、差、积、商、最大、最小)
29 |
30 | ### 第四章 随机变量的数学特征
31 |
32 | - 期望,方差,协方差,Pearson相关系数
33 |
34 | ### 第五章 大数定律与中心极限定理
35 |
36 | - 大数定律,依概率收敛
37 | - 中心极限定理,依分布收敛
38 | - 局限:独立同分布假设,有界方差要求,收敛速度未知
39 |
40 | ### 第六章 集中不等式
41 |
42 | - Markov不等式、Chebyshev不等式、Hölder不等式、 Cauchy-Schwartz不等式、单边Chebyshev不等式
43 | - Chernoff方法,Chernoff引理,0/1 Chernoff界,有界Chernoff界
44 |
45 | ### 第七章 统计的基本概念
46 |
47 | - 统计学的概念和三大研究内容(抽样,参数估计,假设检验)
48 | - Beta分布, $ \Gamma $ -分布、性质、独立可加性;标准正态分布的平方 $ \Gamma(\frac12,\frac12) $ ;Dirichlet分布、性质
49 | - $ \chi^2 $ 分布, $ t $ 分布(student分布), $ F $ 分布
50 | - 常见抽样分布定理
51 |
52 | ### 第八章 参数估计
53 |
54 | - 点估计:矩估计,极大似然估计
55 | - 估计量评估:无偏性,有效性,一致性
56 |
57 | ### 第九章 假设检验
58 |
59 | - 假设检验基本思想:小概率原理(小概率事件在一次实验中不应该发生),假设检验概念,两类错误,显著性检验 ,显著性检验基本步骤
60 |
61 | ## 随机事件与概率
62 |
63 | ### 对立事件和互斥事件的区别
64 |
65 | A的对立事件指所有不属于A的基本事件,有 $ \overline A\cap A=\varnothing,\overline A\cup A=\Omega $
66 |
67 | $ A,B $ 不能同时发生,则称他们互不相容(互斥),有 $ A\cap B=\varnothing $
68 |
69 | 区别是 $ A $ 与其对立事件的交为全集, $ A $ 与其互斥事件的交不一定是。
70 |
71 | ### 频率和概率的关系
72 |
73 | 概率是对事件发生的可能性度量,基于统计数据或主观判断。
74 |
75 | 频率是指在大量重复试验中,某一事件发生的实际次数。频率和概率之间有一定的关系,随着试验次数的增加,频率会趋近于概率。
76 |
77 | ### 概率和统计的区别
78 |
79 | - **概率**:**研究事件的不确定性**,在给定数据生成过程中观察,研究数据的性质,强调**公理体系**, **推理**。
80 | - **统计**:**收集与分析数据**,根据观察的数据反思其数据生成过程,强调**归纳**。
81 | - 概率和统计的重要的区别在于公理体系化。
82 |
83 | ### 概率公理化的三条公理
84 |
85 | - **非负性**:对于任何事件 $ A $ ,均有 $ P(A)\geq0 $
86 | - **规范性**:对样本空间 $ \Omega $ 有 $ P(\Omega)=1 $
87 | - **可列可加性**:若 $ A_1,A_2,\dots ,A_n,\dots $ 是可列无穷个互不相容的事件,即 $ A_iA_j=\varnothing(i\neq j) $ ,有
88 |
89 | $$
90 | P(A_1\cup A_2\cup \dots\cup A_n\cup \dots)=P(A_1)+P(A_2)+\dots+P(A_n)+\dots
91 | $$
92 |
93 | 满足这三个条件的实数 $ P(A) $ 为随机事件 $ A $ 的概率。
94 |
95 | ### 古典概型
96 |
97 | 试验E满足:有限种可能( $ \Omega=\{\omega_1,\omega_2,\dots,\omega_n\} $ ,其中 $ \omega_i $ 为基本事件);每种结果发生的可能性相同 $ P(\{\omega_i\})=P(\{\omega_j\}) $ ,即是古典概型。抛硬币即是古典概型问题。
98 |
99 | 古典概率的计算的本质是计数。常见的计数原理有**加法原理**和**乘法原理**。
100 |
101 | ### 排列和组合的概念与应用场景
102 |
103 | 排列:从 $ n $ 个不同的元素中无放回地取出 $ r $ 个元素进行排列,既要考虑取出的元素,也要顾及其排列顺序,则有 $ \displaystyle (n)_r=n(n-1)\dots(n-r+1) $ 种不同的排列。全排列: $ r=n $ ,有 $ n! $ 种。
104 |
105 | 组合:从 $ n $ 个不同的元素中无放回地取出 $ r $ 个元素,取出的元素之间无顺序关系,共有 $ (^n_r) $ 种不同的取法,其中
106 |
107 | $$
108 | \left(\begin{aligned}n\\r\end{aligned}\right)=\frac{n!}{r!(n-r)!}
109 | $$
110 |
111 | (不用考虑顺序,所有将排列数除以 $ r! $ )
112 |
113 | 这里 $ (^n_r) $ 称为组合数或二项系数,是二项展开式 $ (a+b)^n=\sum_{r=0}^{n}(^n_r)a^rb^{n-r} $ 中项 $ a^rb^{n-r} $ 的系数。
114 |
115 | ### 几何概型
116 |
117 | 几何概型:样本空间无限可测,基本事件等可能性。常常使用几何画图的解法求解。
118 |
119 | ## 条件概率和独立性
120 |
121 | ### 条件概率
122 |
123 | 条件概率是事件 $ A $ 发生的条件下事件 $ B $ 发生的概率。
124 |
125 | The conditional probability is the probability of event B occurring given that event A has occurred.
126 |
127 | $$
128 | P(B\vert A)=\frac{P(AB)}{P(A)}
129 | $$
130 |
131 | 这种概率的计算通常需要基于已知的信息和假设,具有一定的主观性。在人工智能领域,条件概率经常用于模型训练和推断过程中,例如朴素贝叶斯分类算法、隐马尔可夫模型等。
132 |
133 | 条件概率也满足非负性、规范性、可列可加性。也满足容斥原理。
134 |
135 | ### 乘法公式
136 |
137 | the multiplication rule
138 |
139 | 当两个事件 $ A $ 和 $ B $ 发生的概率都已知时,计算两个事件同时发生的概率的公式。其计算公式为:
140 |
141 | $$
142 | \begin{aligned}
143 | P(AB)&=P(A)P(B\vert A)=P(B)P(A\vert B)\\
144 | P(A_1A_2\dots A_n)&=P(A_1)P(A_2\vert A_1)P(A_3\vert A_1 A_2)\dots P(A_n\vert A_1A_2\dots A_{n-1})
145 | \end{aligned}
146 | $$
147 |
148 | 在自然语言处理领域中,我们可以用乘法公式来计算一个词在给定上下文条件下出现的概率;在机器学习领域中,我们可以用乘法公式来计算多个特征同时出现的概率,从而进行分类或回归任务。
149 |
150 | ### 全概率公式
151 |
152 | 全概率公式将一个事件的概率分解成多个事件的概率之和,再利用乘法公式求解各个事件的概率。具体来说,若事件 $ A_1,A_2,\dots,A_n $ 为样本空间 $ \Omega $ 的一个划分,对任意事件 $ B $ , $ B $ 的概率是每个 $ A_i $ 的概率与 $ B $ given $ A_i $ 概率的乘积的和。
153 |
154 | 若事件 $ A_1,A_2,\dots,A_n $ 为样本空间 $ \Omega $ 的一个划分,对任意事件 $ B $ 有:
155 |
156 | $$
157 | P(B)=\sum_{i=1}^{n}P(BA_i)=\sum_{i=1}^n P(A_i)P(B|A_i)
158 | $$
159 |
160 | 称之为全概率公式(law of total probability)
161 |
162 | 这里划分指: $ A_i\cap A_j=\varnothing \quad (i\neq j);\Omega=\bigcup_{i=1}^{n}A_i $
163 |
164 | 全概率公式在人工智能领域中的应用非常广泛。例如,在语音识别中,我们可以将不同的语音信号看作互不重叠的事件,应用全概率公式来计算每个语音信号被识别为不同单词的概率;在图像处理中,我们可以将不同的图像特征看作互不重叠的事件,应用全概率公式来计算每个特征对目标分类的贡献等。
165 |
166 | ### 贝叶斯公式
167 |
168 | 贝叶斯公式Baye's law用于计算在某个先验条件下事件的后验概率。
169 |
170 | $$
171 | \begin{aligned}
172 | P(A\vert B)&=\frac{P(B\vert A)P(A)}{P(B)}\\
173 | P(A_i\vert B)&=\frac{P(A_i B)}{P(B)}=\frac{P(A_i)P(B\vert A_i)}{\sum_{j=1}^n P(A_j)P(B\vert A_j)}
174 | \end{aligned}
175 | $$
176 |
177 | 先验概率prior: $ \Pr (A_i) $ ,因为不用考虑任何 $ B $ 的因素。
178 |
179 | 证据概率evidence: $ P(B)=\sum_{j=1}^n P(A_j)P(B\vert A_j) $
180 |
181 | 后验概率posterior: $ \Pr(A_i\vert B) $ 为事件 $ A_i $ 在事件 $ B $ (证据)发生的情况下的后验概率
182 |
183 | 似然度likelihood: $ P(B|A_i) $
184 |
185 | $$
186 | 后验概率=\frac{先验概率\times似然度}{证据概率}=常量\times似然度
187 | $$
188 |
189 | ### 独立性
190 |
191 | #### 定义
192 |
193 | 独立:指两个事件的发生不受彼此的影响,若事件 $ A,B $ 满足 $ P(AB)=P(A)P(B) $ ,则称事件 $ A $ 与 $ B $ 相互独立。
194 |
195 | 即 $ P(AB)=P(A)P(B)\iff P(B\vert A)=P(B)\iff P(A\vert B)=P(B) $
196 |
197 | #### 与互斥事件有何区别
198 |
199 | 互斥:指两个事件不能同时发生。 $ A\cap B=\varnothing $
200 |
201 | 互斥 $ \iff $ 不独立
202 |
203 | 多个事件的独立性: $ A,B,C $ 独立 $ \iff P(AB)=P(A)P(B),P(AC)=P(A)P(C),P(BC)=P(B)P(C),$$P(ABC)=P(A)P(B)P(C) $ 。
204 |
205 | ### iid
206 |
207 | #### 定义
208 |
209 | iid: independent and identically distributed,即独立同分布假设,假设数据集中的每个样本都是从同一个概率分布中独立地随机取出的。
210 |
211 | iid假设在概率统计领域中经常使用,因为它是许多统计方法的基础前提。例如,在机器学习中,训练数据通常被假定为iid,这意味着每个样本是相互独立且来自同一概率分布的,从而使得机器学习算法能够利用数据中的统计信息进行学习和预测。另外,许多假设检验和置信区间的推断方法也需要假定数据是iid的,以确保推断结果的有效性。
212 |
213 | #### 基于iid假设的机器学习算法
214 |
215 | 很多机器学习算法都基于iid假设,比如Linear regression, logistic regression, decision tree, SVM, neural network等等。
216 |
217 | #### 不基于iid假设的机器学习算法
218 |
219 | 1. 时间序列分析算法:时间序列分析算法通常用于分析和预测时间序列数据,这些数据之间存在时间上的相关性,因此不满足独立同分布假设。常见的时间序列分析算法包括自回归模型(AR)、滑动平均模型(MA)、自回归滑动平均模型(ARMA)、自回归积分滑动平均模型(ARIMA)等。
220 | 2. 隐马尔可夫模型(Hidden Markov Model,HMM):HMM 是一种用于建模序列数据的统计模型,通常用于自然语言处理和语音识别等领域。HMM 假设序列数据是由一个不可观测的马尔可夫链和一个可观测的输出过程组成,因此不满足独立同分布假设。
221 | 3. 图模型(Graphical Model):图模型是一类用图形化方式表示变量之间关系的统计模型。常见的图模型包括贝叶斯网络、马尔可夫随机场等,这些模型通常用于分析非独立同分布的数据。
222 |
223 | #### 为什么算法要基于iid假设
224 |
225 | 因为这个假设可以简化建模过程,减小计算复杂度,使得许多统计学理论和方法可以应用于机器学习中,让机器学习算法的性质和性能更加可靠和有效。
226 |
227 | 通过假设数据独立同分布,我们不必考虑数据样本之间的依赖关系,这种简化的假设可以使我们使用更简单的模型,减少模型参数数量,降低模型的计算复杂度,并更容易处理大规模数据。例如,许多基于iid假设的分类算法(如朴素贝叶斯、支持向量机等)只需要学习一个简单的概率模型或决策边界即可,而不需要学习整个数据分布的复杂性。
228 |
229 | 另外,iid假设使得机器学习算法可以使用统计学中的一些基本理论和方法,如中心极限定理、最大似然估计、假设检验等,这些方法可以提供对机器学习算法的性能进行分析和评估的工具。
230 |
231 | 然而,iid假设并不总是成立的,尤其是在处理时序数据、空间数据等场景下。在这些情况下,我们需要使用其他适当的建模方法来处理数据中的依赖关系和非独立同分布性质。
232 |
233 | #### 如果数据分布不符合iid假设,还可以用基于iid假设的算法求解吗?
234 |
235 | 如果数据分布不符合iid假设,使用基于iid假设的算法可能会导致模型偏差和预测结果不准确。因为这些算法的基本假设是样本之间是独立同分布的,如果这个假设不成立,就会导致样本之间的相关性被忽略,进而影响模型的泛化能力和性能。比如说,可以拿线性回归来处理时间序列数据,但是结构可能会偏差和不准确,因为忽略了时间序列数据中样本之间的相关性。
236 |
237 | 如果数据分布不符合iid假设,可以尝试使用其他适当的机器学习算法或方法。例如,可以使用时间序列模型或空间模型来处理序列数据或空间数据,使用聚类模型或关联规则模型来处理数据集中的非独立同分布问题,使用分层模型或多层模型来考虑样本之间的相关性等。
238 |
239 | 此外,对于一些基于iid假设的算法,也有针对性的改进方法,例如,在训练模型时引入权重,调整样本的权重,或者使用bootstrap方法来处理样本的相关性等。这些方法可以帮助我们更准确地建模和处理非独立同分布的数据。
240 |
241 | ### 小概率原理
242 |
243 | Law of small probabilities
244 |
245 | 若事件 $ A $ 在一次试验中发生的概率非常小,但是经过多次独立地重复试验,事件 $ A $ 的发生是必然的。
246 |
247 | ## 离散型/连续型随机变量
248 |
249 | ### 期望和方差
250 |
251 | #### 期望和方差的公式
252 |
253 | 期望反应随机变量 $ X $ 的平均值,离散变量: $ \displaystyle E(X)=\sum_{k=1}^{\infty}p_kx_k $ ;连续变量: $ \displaystyle E(X)=\int_{-\infty}^{+\infty}tf(t)\text{d}t $ (若积分 $ \displaystyle \int_{-\infty}^{+\infty} xf(x)\text{d}x $ 绝对收敛)
254 |
255 | 方差反应随机变量与期望的偏离程度: $ Var(X)=E(X-E(X))^2=E(X^2)-(E(X))^2 $
256 |
257 | 连续变量:(若 $ \displaystyle \int_{-\infty}^{+\infty}(t-E(X))^2f(t)\text{d}t $ )
258 |
259 | $$
260 | \begin{aligned}
261 | Var(X)&=E(X-E(X))^2=\int_{-\infty}^{+\infty}(t-E(X))^2f(t)\text{d}t\\
262 | &=E(X^2)-(E(X))^2=\int_{-\infty}^{+\infty} t^2f(t)\text{d}t-\left(\int_{-\infty}^{+\infty} tf(t)\text{d}t\right)^2
263 | \end{aligned}
264 | $$
265 |
266 | #### 为什么要使用方差公式的等价形式?
267 |
268 | 使用第一种定义,要遍历两遍;但使用第二种定义,则只需要遍历 $ x_1,\dots,x_n $ 一遍,可在线(online)计算方差。
269 |
270 | #### 为什么样本方差(sample variance)的无偏估计分母是n-1?
271 |
272 | 方差的estimator: $ \displaystyle S_1^2=\frac1n\sum_{i=1}^{n}(X_i-\overline X)^2 $
273 |
274 | 但这个estimator有bias,因为:
275 |
276 | $$
277 | \begin{aligned}
278 | E(S_1^2)&=\frac1n\sum_{i=1}^nE\left((X_i-\overline X)^2\right)\\
279 | &=\frac1n\sum_{i=1}^nE\left((X_i-\mu+\mu-\overline X)^2\right)\\
280 | &=\frac1n\sum_{i=1}^nE\left((X_i-\mu)^2+2(X_i-\mu)(\mu-\overline X)+(\mu-\overline X)^2\right)\\
281 | &=\frac1n \sum_{i=1}^nE\left((X_i-\mu)^2\right)+\frac2n\sum_{i=1}^n(X_i-\mu)(\mu-\overline X)+E\left((\mu-\overline X)^2\right)\\
282 | &=\frac1n \sum_{i=1}^nE\left((X_i-\mu)^2\right)+E\left((\overline X-\mu)^2\right)\\
283 | &=nVar(X)-Var(\overline X)=\sigma^2-\frac{\sigma^2}{n}=\frac{n-1}{n}\sigma^2
284 | \end{aligned}
285 | $$
286 |
287 | 所以使用修正值: $ \displaystyle S_1^2=\frac1n\sum_{i=1}^{n}(X_i-\overline X)^2 $
288 |
289 | 直观理解:因为均值已经用了n个数的平均来做估计,在求方差时,只有(n-1)个数和均值信息是不相关的。而第n个数已经可以由前(n-1)个数和均值来唯一确定,实际上没有信息量。所以在计算方差时,只除以(n-1)
290 |
291 | #### 性质
292 |
293 | - 线性: $ E(aX+b)=aE(X)+b,E(\sum_{i=1}^n c_ig_i(x))=\sum_{i=1}^n c_i E(g_i(x)) $
294 | - 对非负随机变量,有 $ E[X]=\int_{0}^{+\infty}P(X>t)\text{d}t $
295 | - 若 $ \int_{-\infty}^{+\infty}g(t)f(t)\text{d}t $ 绝对可积,则 $ E(g(X))=\int_{-\infty}^{+\infty}g(t)f(t)\text{d}t=\int_{0}^{+\infty} P(g(X)>t)\text{d}t $
296 | - Jenson不等式:对离散型随机变量 $ X\in[a,b] $ 和连续凸函数 $ g:[a,b]\to\mathbb R $ ,有 $ g(E(x))\leq E(g(X)) $
297 | - $ Var(aX+b)=a^2 Var(X) $
298 | - $ Var(X)=E(X-E(X))^2\leq E(X-a)^2 $
299 | - Bhatia-Davis不等式: $ Var[X]\leq (b-E(X))(E(X)-a)\leq \frac14(b-a)^2 $
300 |
301 | #### 在人工智能领域中的作用?
302 |
303 | 在人工智能领域中的常见应用场景:
304 |
305 | 1. 数据预处理:在机器学习中,经常需要对数据进行预处理,例如归一化、标准化等。这时候,期望和方差就非常有用。例如,在标准化时,可以先计算出每个特征的均值和方差,然后将特征值减去均值并除以方差,这样可以使得不同特征之间的取值范围相同,从而更容易进行模型训练和比较。
306 | 2. 概率模型:在概率模型中,期望和方差是重要的概念。例如,在高斯分布中,期望就是分布的中心,方差则决定了分布的形状。这些信息可以用来描述数据的统计特征,从而可以构建更加准确的概率模型。
307 | 3. 模型评估:在机器学习中,需要对不同的模型进行比较和评估。期望和方差可以作为评估指标之一,例如在回归问题中,可以计算预测值与真实值之间的平均方差,从而评估模型的拟合效果。
308 | 4. 异常检测:在人工智能中,经常需要进行异常检测,例如检测网络攻击、欺诈行为等。期望和方差可以用来判断数据是否偏离正常范围,例如可以计算数据与均值之间的距离,如果距离超过一定的阈值,则认为数据是异常的。
309 |
310 | #### 没有期望的情况
311 |
312 | 1. 无限的期望:如果随机变量的分布有“重尾”现象,即存在很小的概率,使得随机变量取到极大的值,此时随机变量的期望可能不存在。例如,柯西分布的期望就不存在。
313 | 2. 不收敛的期望:如果随机变量的绝对值的期望不收敛,也就是E(|X|)无限大,此时随机变量的期望也不存在。
314 |
315 | #### 没有方差的情况
316 |
317 | 1. 不存在期望:如果随机变量的期望不存在,则方差也不存在。因为方差的定义中包含了随机变量与其期望之间的差异。
318 | 2. 方差无穷大:如果随机变量的方差为无穷大,则方差不存在。例如,柯西分布的方差不存在。
319 | 3. 不连续的随机变量:如果随机变量的概率密度函数(或概率质量函数)在某些点上不连续,则方差可能不存在。因为方差的定义中包含了随机变量的平方,如果概率密度函数在某些点上不连续,随机变量的平方可能也不连续。
320 |
321 | ### 分布函数
322 |
323 | #### 定义
324 |
325 | Distribution function
326 |
327 | 分布函数是描述随机变量的概率分布的函数,用来描述随机变量 X 小于或等于某个值 x 的概率。公式为 $ F(x)=P(X\leq x) $ 。
328 |
329 | 可以用分布函数表示随机事件的概率,例如
330 |
331 | $ P(X\geq a)=1-F(a-0) $
332 |
333 | $ P(a\leq X\leq b)=F(b)-F(a-0) $
334 |
335 | #### 性质
336 |
337 | 单调性:若 $ x_1
1695 |
1696 | ### 1、什么是马尔科夫过程?
1697 |
1698 | 假设一个随机过程中,t_n 时刻的状态 x_n 的条件发布,只与其前一状态x_(n-1) 相关,即:
1699 |
1700 | 
1701 |
1702 | 则将其称为 马尔可夫过程。
1703 |
1704 | ### 2、马尔科夫过程的核心思想是什么?
1705 |
1706 | 对于马尔可夫过程的思想,用一句话去概括:当前时刻状态仅与上一时刻状态相关,与其他时刻不相关。
1707 |
1708 | 可以从 马尔可夫过程图去理解,由于每个状态间是以有向直线连接,也就是当前时刻状态仅与上一时刻状态相关。
1709 |
1710 | ### 3、隐马尔可夫算法中的两个假设是什么?
1711 |
1712 | 齐次马尔可夫性假设:即假设隐藏的马尔科夫链在任意时刻 t 的状态只依赖于其前一时刻的状态,与其他时刻的状态及观测无关,也与时刻 t 无关;
1713 |
1714 | 
1715 |
1716 | 观测独立性假设:即假设任意时刻的观测只依赖于该时刻的马尔科夫链的状态,与其他观测及状态无关。
1717 |
1718 | 
1719 |
1720 | ### 4、隐马尔可夫模型三个基本问题是什么?
1721 |
1722 | (1)概率计算问题:**给定模型(A,B, $ \pi $ )和观测序列**,计算在模型下观测序列出现的概率。(直接计算法理论可行,但计算复杂度太大(O(N^2T));用前向与后向计算法)
1723 |
1724 | (2)学习问题:**已知观测序列,估计模型参数**,使得在该模型下观测序列概率最大。(极大似然估计的方法来估计参数,Baum-Welch算法(EM算法))
1725 |
1726 | (3)预测问题,也称为解码问题:已知模型和观测序列,**求对给定观测序列条件概率最大的状态序列**。(维特比算法,动态规划,核心:**边计算边删掉不可能是答案的路径,在最后剩下的路径中挑选最优路径**)
1727 |
1728 | ### 5、隐马尔可夫模型三个基本问题的联系?
1729 |
1730 | 三个基本问题 存在 渐进关系。首先,要学会用前向算法和后向算法算观测序列出现的概率,然后用Baum-Welch算法求参数的时候,某些步骤是需要用到前向算法和后向算法的,计算得到参数后,我们就可以用来做预测了。因此可以看到,三个基本问题,它们是渐进的,解决NLP问题,应用HMM模型做解码任务应该是最终的目的。
1731 |
1732 | ### 6、隐马尔可夫算法存在哪些问题?
1733 |
1734 | 因为HMM模型其实它简化了很多问题,做了某些很强的假设,如齐次马尔可夫性假设和观测独立性假设,做了假设的好处是,简化求解的难度,坏处是对真实情况的建模能力变弱了。
1735 |
1736 | 在序列标注问题中,隐状态(标注)不仅和单个观测状态相关,还和观察序列的长度、上下文等信息相关。例如词性标注问题中,一个词被标注为动词还是名词,不仅与它本身以及它前一个词的标注有关,还依赖于上下文中的其他词。可以使用最大熵马尔科夫模型进行优化。
1737 |
1738 | ## 规则学习
1739 |
1740 | ## 强化学习
1741 |
--------------------------------------------------------------------------------
/概率论与数理统计.md:
--------------------------------------------------------------------------------
1 | # 概率论与数理统计
2 |
3 | ## 提纲
4 |
5 | ### 第一章 基本概念
6 |
7 | - 概率和统计的区别
8 | - 必然现象与随机现象
9 | - 随机试验:样本点,样本空间
10 | - 事件间的关系,事件与集合的对应关系,事件的运算规律
11 | - 概率的公理化定义,概率的性质
12 | - 古典概型,几何概型
13 | - 条件概率,全概率公式和贝叶斯公式
14 | - 独立性,独立与互斥的关系
15 | - Freivalds算法
16 |
17 | ### 第二章 随机变量及其分布
18 |
19 | - 分布函数定义,性质(单调性,规范性,右连续性);概率密度函数定义,性质(单调性,规范性,连续性)
20 | - 离散随机变量:均匀分布、二项分布、几何分布(无记忆性)、负二项分布(Pascal分布)、泊松分布(泊松定理)
21 | - 连续随机变量:均匀分布、指数分布(无记忆性)、正态分布
22 | - 德国坦克问题
23 |
24 | ### 第三章 多维随机变量
25 |
26 | - 联合分布函数定义、性质(对每个变量单调不减,非负性,规范性,右连续);边缘分布与独立性
27 | - 联合概率密度定义、性质(非负性,规范性);边缘概率密度,两变量独立的等价条件
28 | - 多维随机变量函数的分布(和、差、积、商、最大、最小)
29 |
30 | ### 第四章 随机变量的数学特征
31 |
32 | - 期望,方差,协方差,Pearson相关系数
33 |
34 | ### 第五章 大数定律与中心极限定理
35 |
36 | - 大数定律,依概率收敛
37 | - 中心极限定理,依分布收敛
38 | - 局限:独立同分布假设,有界方差要求,收敛速度未知
39 |
40 | ### 第六章 集中不等式
41 |
42 | - Markov不等式、Chebyshev不等式、Hölder不等式、 Cauchy-Schwartz不等式、单边Chebyshev不等式
43 | - Chernoff方法,Chernoff引理,0/1 Chernoff界,有界Chernoff界
44 |
45 | ### 第七章 统计的基本概念
46 |
47 | - 统计学的概念和三大研究内容(抽样,参数估计,假设检验)
48 | - Beta分布, $ \Gamma $ -分布、性质、独立可加性;标准正态分布的平方 $ \Gamma(\frac12,\frac12) $ ;Dirichlet分布、性质
49 | - $ \chi^2 $ 分布, $ t $ 分布(student分布), $ F $ 分布
50 | - 常见抽样分布定理
51 |
52 | ### 第八章 参数估计
53 |
54 | - 点估计:矩估计,极大似然估计
55 | - 估计量评估:无偏性,有效性,一致性
56 |
57 | ### 第九章 假设检验
58 |
59 | - 假设检验基本思想:小概率原理(小概率事件在一次实验中不应该发生),假设检验概念,两类错误,显著性检验 ,显著性检验基本步骤
60 |
61 | ## 随机事件与概率
62 |
63 | ### 对立事件和互斥事件的区别
64 |
65 | A的对立事件指所有不属于A的基本事件,有 $ \overline A\cap A=\varnothing,\overline A\cup A=\Omega $
66 |
67 | $ A,B $ 不能同时发生,则称他们互不相容(互斥),有 $ A\cap B=\varnothing $
68 |
69 | 区别是 $ A $ 与其对立事件的交为全集, $ A $ 与其互斥事件的交不一定是。
70 |
71 | ### 频率和概率的关系
72 |
73 | 概率是对事件发生的可能性度量,基于统计数据或主观判断。
74 |
75 | 频率是指在大量重复试验中,某一事件发生的实际次数。频率和概率之间有一定的关系,随着试验次数的增加,频率会趋近于概率。
76 |
77 | ### 概率和统计的区别
78 |
79 | - **概率**:**研究事件的不确定性**,在给定数据生成过程中观察,研究数据的性质,强调**公理体系**, **推理**。
80 | - **统计**:**收集与分析数据**,根据观察的数据反思其数据生成过程,强调**归纳**。
81 | - 概率和统计的重要的区别在于公理体系化。
82 |
83 | ### 概率公理化的三条公理
84 |
85 | - **非负性**:对于任何事件 $ A $ ,均有 $ P(A)\geq0 $
86 | - **规范性**:对样本空间 $ \Omega $ 有 $ P(\Omega)=1 $
87 | - **可列可加性**:若 $ A_1,A_2,\dots ,A_n,\dots $ 是可列无穷个互不相容的事件,即 $ A_iA_j=\varnothing(i\neq j) $ ,有
88 |
89 | $$
90 | P(A_1\cup A_2\cup \dots\cup A_n\cup \dots)=P(A_1)+P(A_2)+\dots+P(A_n)+\dots
91 | $$
92 |
93 | 满足这三个条件的实数 $ P(A) $ 为随机事件 $ A $ 的概率。
94 |
95 | ### 古典概型
96 |
97 | 试验E满足:有限种可能( $ \Omega=\{\omega_1,\omega_2,\dots,\omega_n\} $ ,其中 $ \omega_i $ 为基本事件);每种结果发生的可能性相同 $ P(\{\omega_i\})=P(\{\omega_j\}) $ ,即是古典概型。抛硬币即是古典概型问题。
98 |
99 | 古典概率的计算的本质是计数。常见的计数原理有**加法原理**和**乘法原理**。
100 |
101 | ### 排列和组合的概念与应用场景
102 |
103 | 排列:从 $ n $ 个不同的元素中无放回地取出 $ r $ 个元素进行排列,既要考虑取出的元素,也要顾及其排列顺序,则有 $ \displaystyle (n)_r=n(n-1)\dots(n-r+1) $ 种不同的排列。全排列: $ r=n $ ,有 $ n! $ 种。
104 |
105 | 组合:从 $ n $ 个不同的元素中无放回地取出 $ r $ 个元素,取出的元素之间无顺序关系,共有 $ (^n_r) $ 种不同的取法,其中
106 |
107 | $$
108 | \left(\begin{aligned}n\\r\end{aligned}\right)=\frac{n!}{r!(n-r)!}
109 | $$
110 |
111 | (不用考虑顺序,所有将排列数除以 $ r! $ )
112 |
113 | 这里 $ (^n_r) $ 称为组合数或二项系数,是二项展开式 $ (a+b)^n=\sum_{r=0}^{n}(^n_r)a^rb^{n-r} $ 中项 $ a^rb^{n-r} $ 的系数。
114 |
115 | ### 几何概型
116 |
117 | 几何概型:样本空间无限可测,基本事件等可能性。常常使用几何画图的解法求解。
118 |
119 | ## 条件概率和独立性
120 |
121 | ### 条件概率
122 |
123 | 条件概率是事件 $ A $ 发生的条件下事件 $ B $ 发生的概率。
124 |
125 | The conditional probability is the probability of event B occurring given that event A has occurred.
126 |
127 | $$
128 | P(B\vert A)=\frac{P(AB)}{P(A)}
129 | $$
130 |
131 | 这种概率的计算通常需要基于已知的信息和假设,具有一定的主观性。在人工智能领域,条件概率经常用于模型训练和推断过程中,例如朴素贝叶斯分类算法、隐马尔可夫模型等。
132 |
133 | 条件概率也满足非负性、规范性、可列可加性。也满足容斥原理。
134 |
135 | ### 乘法公式
136 |
137 | the multiplication rule
138 |
139 | 当两个事件 $ A $ 和 $ B $ 发生的概率都已知时,计算两个事件同时发生的概率的公式。其计算公式为:
140 |
141 | $$
142 | \begin{aligned}
143 | P(AB)&=P(A)P(B\vert A)=P(B)P(A\vert B)\\
144 | P(A_1A_2\dots A_n)&=P(A_1)P(A_2\vert A_1)P(A_3\vert A_1 A_2)\dots P(A_n\vert A_1A_2\dots A_{n-1})
145 | \end{aligned}
146 | $$
147 |
148 | 在自然语言处理领域中,我们可以用乘法公式来计算一个词在给定上下文条件下出现的概率;在机器学习领域中,我们可以用乘法公式来计算多个特征同时出现的概率,从而进行分类或回归任务。
149 |
150 | ### 全概率公式
151 |
152 | 全概率公式将一个事件的概率分解成多个事件的概率之和,再利用乘法公式求解各个事件的概率。具体来说,若事件 $ A_1,A_2,\dots,A_n $ 为样本空间 $ \Omega $ 的一个划分,对任意事件 $ B $ , $ B $ 的概率是每个 $ A_i $ 的概率与 $ B $ given $ A_i $ 概率的乘积的和。
153 |
154 | 若事件 $ A_1,A_2,\dots,A_n $ 为样本空间 $ \Omega $ 的一个划分,对任意事件 $ B $ 有:
155 |
156 | $$
157 | P(B)=\sum_{i=1}^{n}P(BA_i)=\sum_{i=1}^n P(A_i)P(B|A_i)
158 | $$
159 |
160 | 称之为全概率公式(law of total probability)
161 |
162 | 这里划分指: $ A_i\cap A_j=\varnothing \quad (i\neq j);\Omega=\bigcup_{i=1}^{n}A_i $
163 |
164 | 全概率公式在人工智能领域中的应用非常广泛。例如,在语音识别中,我们可以将不同的语音信号看作互不重叠的事件,应用全概率公式来计算每个语音信号被识别为不同单词的概率;在图像处理中,我们可以将不同的图像特征看作互不重叠的事件,应用全概率公式来计算每个特征对目标分类的贡献等。
165 |
166 | ### 贝叶斯公式
167 |
168 | 贝叶斯公式Baye's law用于计算在某个先验条件下事件的后验概率。
169 |
170 | $$
171 | \begin{aligned}
172 | P(A\vert B)&=\frac{P(B\vert A)P(A)}{P(B)}\\
173 | P(A_i\vert B)&=\frac{P(A_i B)}{P(B)}=\frac{P(A_i)P(B\vert A_i)}{\sum_{j=1}^n P(A_j)P(B\vert A_j)}
174 | \end{aligned}
175 | $$
176 |
177 | 先验概率prior: $ \Pr (A_i) $ ,因为不用考虑任何 $ B $ 的因素。
178 |
179 | 证据概率evidence: $ P(B)=\sum_{j=1}^n P(A_j)P(B\vert A_j) $
180 |
181 | 后验概率posterior: $ \Pr(A_i\vert B) $ 为事件 $ A_i $ 在事件 $ B $ (证据)发生的情况下的后验概率
182 |
183 | 似然度likelihood: $ P(B|A_i) $
184 |
185 | $$
186 | 后验概率=\frac{先验概率\times似然度}{证据概率}=常量\times似然度
187 | $$
188 |
189 | ### 独立性
190 |
191 | #### 定义
192 |
193 | 独立:指两个事件的发生不受彼此的影响,若事件 $ A,B $ 满足 $ P(AB)=P(A)P(B) $ ,则称事件 $ A $ 与 $ B $ 相互独立。
194 |
195 | 即 $ P(AB)=P(A)P(B)\iff P(B\vert A)=P(B)\iff P(A\vert B)=P(B) $
196 |
197 | #### 与互斥事件有何区别
198 |
199 | 互斥:指两个事件不能同时发生。 $ A\cap B=\varnothing $
200 |
201 | 互斥 $ \iff $ 不独立
202 |
203 | 多个事件的独立性: $ A,B,C $ 独立 $ \iff P(AB)=P(A)P(B),P(AC)=P(A)P(C),P(BC)=P(B)P(C),$$P(ABC)=P(A)P(B)P(C) $ 。
204 |
205 | ### iid
206 |
207 | #### 定义
208 |
209 | iid: independent and identically distributed,即独立同分布假设,假设数据集中的每个样本都是从同一个概率分布中独立地随机取出的。
210 |
211 | iid假设在概率统计领域中经常使用,因为它是许多统计方法的基础前提。例如,在机器学习中,训练数据通常被假定为iid,这意味着每个样本是相互独立且来自同一概率分布的,从而使得机器学习算法能够利用数据中的统计信息进行学习和预测。另外,许多假设检验和置信区间的推断方法也需要假定数据是iid的,以确保推断结果的有效性。
212 |
213 | #### 基于iid假设的机器学习算法
214 |
215 | 很多机器学习算法都基于iid假设,比如Linear regression, logistic regression, decision tree, SVM, neural network等等。
216 |
217 | #### 不基于iid假设的机器学习算法
218 |
219 | 1. 时间序列分析算法:时间序列分析算法通常用于分析和预测时间序列数据,这些数据之间存在时间上的相关性,因此不满足独立同分布假设。常见的时间序列分析算法包括自回归模型(AR)、滑动平均模型(MA)、自回归滑动平均模型(ARMA)、自回归积分滑动平均模型(ARIMA)等。
220 | 2. 隐马尔可夫模型(Hidden Markov Model,HMM):HMM 是一种用于建模序列数据的统计模型,通常用于自然语言处理和语音识别等领域。HMM 假设序列数据是由一个不可观测的马尔可夫链和一个可观测的输出过程组成,因此不满足独立同分布假设。
221 | 3. 图模型(Graphical Model):图模型是一类用图形化方式表示变量之间关系的统计模型。常见的图模型包括贝叶斯网络、马尔可夫随机场等,这些模型通常用于分析非独立同分布的数据。
222 |
223 | #### 为什么算法要基于iid假设
224 |
225 | 因为这个假设可以简化建模过程,减小计算复杂度,使得许多统计学理论和方法可以应用于机器学习中,让机器学习算法的性质和性能更加可靠和有效。
226 |
227 | 通过假设数据独立同分布,我们不必考虑数据样本之间的依赖关系,这种简化的假设可以使我们使用更简单的模型,减少模型参数数量,降低模型的计算复杂度,并更容易处理大规模数据。例如,许多基于iid假设的分类算法(如朴素贝叶斯、支持向量机等)只需要学习一个简单的概率模型或决策边界即可,而不需要学习整个数据分布的复杂性。
228 |
229 | 另外,iid假设使得机器学习算法可以使用统计学中的一些基本理论和方法,如中心极限定理、最大似然估计、假设检验等,这些方法可以提供对机器学习算法的性能进行分析和评估的工具。
230 |
231 | 然而,iid假设并不总是成立的,尤其是在处理时序数据、空间数据等场景下。在这些情况下,我们需要使用其他适当的建模方法来处理数据中的依赖关系和非独立同分布性质。
232 |
233 | #### 如果数据分布不符合iid假设,还可以用基于iid假设的算法求解吗?
234 |
235 | 如果数据分布不符合iid假设,使用基于iid假设的算法可能会导致模型偏差和预测结果不准确。因为这些算法的基本假设是样本之间是独立同分布的,如果这个假设不成立,就会导致样本之间的相关性被忽略,进而影响模型的泛化能力和性能。比如说,可以拿线性回归来处理时间序列数据,但是结构可能会偏差和不准确,因为忽略了时间序列数据中样本之间的相关性。
236 |
237 | 如果数据分布不符合iid假设,可以尝试使用其他适当的机器学习算法或方法。例如,可以使用时间序列模型或空间模型来处理序列数据或空间数据,使用聚类模型或关联规则模型来处理数据集中的非独立同分布问题,使用分层模型或多层模型来考虑样本之间的相关性等。
238 |
239 | 此外,对于一些基于iid假设的算法,也有针对性的改进方法,例如,在训练模型时引入权重,调整样本的权重,或者使用bootstrap方法来处理样本的相关性等。这些方法可以帮助我们更准确地建模和处理非独立同分布的数据。
240 |
241 | ### 小概率原理
242 |
243 | Law of small probabilities
244 |
245 | 若事件 $ A $ 在一次试验中发生的概率非常小,但是经过多次独立地重复试验,事件 $ A $ 的发生是必然的。
246 |
247 | ## 离散型/连续型随机变量
248 |
249 | ### 期望和方差
250 |
251 | #### 期望和方差的公式
252 |
253 | 期望反应随机变量 $ X $ 的平均值,离散变量: $ \displaystyle E(X)=\sum_{k=1}^{\infty}p_kx_k $ ;连续变量: $ \displaystyle E(X)=\int_{-\infty}^{+\infty}tf(t)\text{d}t $ (若积分 $ \displaystyle \int_{-\infty}^{+\infty} xf(x)\text{d}x $ 绝对收敛)
254 |
255 | 方差反应随机变量与期望的偏离程度: $ Var(X)=E(X-E(X))^2=E(X^2)-(E(X))^2 $
256 |
257 | 连续变量:(若 $ \displaystyle \int_{-\infty}^{+\infty}(t-E(X))^2f(t)\text{d}t $ )
258 |
259 | $$
260 | \begin{aligned}
261 | Var(X)&=E(X-E(X))^2=\int_{-\infty}^{+\infty}(t-E(X))^2f(t)\text{d}t\\
262 | &=E(X^2)-(E(X))^2=\int_{-\infty}^{+\infty} t^2f(t)\text{d}t-\left(\int_{-\infty}^{+\infty} tf(t)\text{d}t\right)^2
263 | \end{aligned}
264 | $$
265 |
266 | #### 为什么要使用方差公式的等价形式?
267 |
268 | 使用第一种定义,要遍历两遍;但使用第二种定义,则只需要遍历 $ x_1,\dots,x_n $ 一遍,可在线(online)计算方差。
269 |
270 | #### 为什么样本方差(sample variance)的无偏估计分母是n-1?
271 |
272 | 方差的estimator: $ \displaystyle S_1^2=\frac1n\sum_{i=1}^{n}(X_i-\overline X)^2 $
273 |
274 | 但这个estimator有bias,因为:
275 |
276 | $$
277 | \begin{aligned}
278 | E(S_1^2)&=\frac1n\sum_{i=1}^nE\left((X_i-\overline X)^2\right)\\
279 | &=\frac1n\sum_{i=1}^nE\left((X_i-\mu+\mu-\overline X)^2\right)\\
280 | &=\frac1n\sum_{i=1}^nE\left((X_i-\mu)^2+2(X_i-\mu)(\mu-\overline X)+(\mu-\overline X)^2\right)\\
281 | &=\frac1n \sum_{i=1}^nE\left((X_i-\mu)^2\right)+\frac2n\sum_{i=1}^n(X_i-\mu)(\mu-\overline X)+E\left((\mu-\overline X)^2\right)\\
282 | &=\frac1n \sum_{i=1}^nE\left((X_i-\mu)^2\right)+E\left((\overline X-\mu)^2\right)\\
283 | &=nVar(X)-Var(\overline X)=\sigma^2-\frac{\sigma^2}{n}=\frac{n-1}{n}\sigma^2
284 | \end{aligned}
285 | $$
286 |
287 | 所以使用修正值: $ \displaystyle S_1^2=\frac1n\sum_{i=1}^{n}(X_i-\overline X)^2 $
288 |
289 | 直观理解:因为均值已经用了n个数的平均来做估计,在求方差时,只有(n-1)个数和均值信息是不相关的。而第n个数已经可以由前(n-1)个数和均值来唯一确定,实际上没有信息量。所以在计算方差时,只除以(n-1)
290 |
291 | #### 性质
292 |
293 | - 线性: $ E(aX+b)=aE(X)+b,E(\sum_{i=1}^n c_ig_i(x))=\sum_{i=1}^n c_i E(g_i(x)) $
294 | - 对非负随机变量,有 $ E[X]=\int_{0}^{+\infty}P(X>t)\text{d}t $
295 | - 若 $ \int_{-\infty}^{+\infty}g(t)f(t)\text{d}t $ 绝对可积,则 $ E(g(X))=\int_{-\infty}^{+\infty}g(t)f(t)\text{d}t=\int_{0}^{+\infty} P(g(X)>t)\text{d}t $
296 | - Jenson不等式:对离散型随机变量 $ X\in[a,b] $ 和连续凸函数 $ g:[a,b]\to\mathbb R $ ,有 $ g(E(x))\leq E(g(X)) $
297 | - $ Var(aX+b)=a^2 Var(X) $
298 | - $ Var(X)=E(X-E(X))^2\leq E(X-a)^2 $
299 | - Bhatia-Davis不等式: $ Var[X]\leq (b-E(X))(E(X)-a)\leq \frac14(b-a)^2 $
300 |
301 | #### 在人工智能领域中的作用?
302 |
303 | 在人工智能领域中的常见应用场景:
304 |
305 | 1. 数据预处理:在机器学习中,经常需要对数据进行预处理,例如归一化、标准化等。这时候,期望和方差就非常有用。例如,在标准化时,可以先计算出每个特征的均值和方差,然后将特征值减去均值并除以方差,这样可以使得不同特征之间的取值范围相同,从而更容易进行模型训练和比较。
306 | 2. 概率模型:在概率模型中,期望和方差是重要的概念。例如,在高斯分布中,期望就是分布的中心,方差则决定了分布的形状。这些信息可以用来描述数据的统计特征,从而可以构建更加准确的概率模型。
307 | 3. 模型评估:在机器学习中,需要对不同的模型进行比较和评估。期望和方差可以作为评估指标之一,例如在回归问题中,可以计算预测值与真实值之间的平均方差,从而评估模型的拟合效果。
308 | 4. 异常检测:在人工智能中,经常需要进行异常检测,例如检测网络攻击、欺诈行为等。期望和方差可以用来判断数据是否偏离正常范围,例如可以计算数据与均值之间的距离,如果距离超过一定的阈值,则认为数据是异常的。
309 |
310 | #### 没有期望的情况
311 |
312 | 1. 无限的期望:如果随机变量的分布有“重尾”现象,即存在很小的概率,使得随机变量取到极大的值,此时随机变量的期望可能不存在。例如,柯西分布的期望就不存在。
313 | 2. 不收敛的期望:如果随机变量的绝对值的期望不收敛,也就是E(|X|)无限大,此时随机变量的期望也不存在。
314 |
315 | #### 没有方差的情况
316 |
317 | 1. 不存在期望:如果随机变量的期望不存在,则方差也不存在。因为方差的定义中包含了随机变量与其期望之间的差异。
318 | 2. 方差无穷大:如果随机变量的方差为无穷大,则方差不存在。例如,柯西分布的方差不存在。
319 | 3. 不连续的随机变量:如果随机变量的概率密度函数(或概率质量函数)在某些点上不连续,则方差可能不存在。因为方差的定义中包含了随机变量的平方,如果概率密度函数在某些点上不连续,随机变量的平方可能也不连续。
320 |
321 | ### 分布函数
322 |
323 | #### 定义
324 |
325 | Distribution function
326 |
327 | 分布函数是描述随机变量的概率分布的函数,用来描述随机变量 X 小于或等于某个值 x 的概率。公式为 $ F(x)=P(X\leq x) $ 。
328 |
329 | 可以用分布函数表示随机事件的概率,例如
330 |
331 | $ P(X\geq a)=1-F(a-0) $
332 |
333 | $ P(a\leq X\leq b)=F(b)-F(a-0) $
334 |
335 | #### 性质
336 |
337 | 单调性:若 $ x_1 62 |
63 | #### 条件?
64 |
65 | $|\lambda E-A|$有非零解,只有可对角化矩阵才可以作特征分解。
66 |
67 | #### 如何进行特征值分解?
68 |
69 | 特征值分解:指将对$n\times n$,且有$N$个线性无关的特征向量$q_i$的方阵$A$,将其分解为$A=Q\Lambda Q^{-1}$。其中$Q$为$n\times n$,第$i$列为$A$的特征向量$q_i$,$\Lambda$为对角矩阵,对角线上的元素是对应的特征值。
70 |
71 | 1. 首先求解特征方程,得到矩阵$A$特征值$\lambda _i$(共$n$个)
72 |
73 | 2. 再由$(\lambda_i E-A)x=0$求基础解系,即矩阵$A$属于特征值$\lambda_i$的线性无关的特征向量。
74 | 3. 用求得的特征值和特征向量构造$Q,\Lambda$
75 |
76 | ## 正定矩阵
77 |
78 | ### 正定
79 |
80 | #### 正定二次型
81 |
82 | ##### 定义
83 |
84 | 实二次型 $f(x_1,x_2,\cdots,x_n)$ 若对任意一组不全为零的实数 $c_1,c_2,\cdots,c_n$ 都有
85 |
86 | $$
87 | f(c_1,c_2,\cdots,c_n)>0
88 | $$
89 |
90 | 则称 $f$ 为**正定二次型**.
91 |
92 | 如, $f(x_1,x_2,\cdots,x_n)=\displaystyle\sum_{i=1}^nx_i^2$ 是正定二次型.
93 |
94 | 但, $f(x_1,x_2,\cdots,x_n)=\displaystyle\sum_{i=1}^{n-1}x_i^2$ 不是正定二次型.
95 |
96 |
97 | ##### 判定
98 |
99 | 1. 实二次型 $\boldsymbol{x}^\top A\boldsymbol{x}$ 正定 $\Leftrightarrow$ $\forall \boldsymbol{x}\in\mathbb{R}^n$, 若 $\boldsymbol{x}\neq 0$, 则 $\boldsymbol{x}^\top A\boldsymbol{x}>0$
100 | 2. 设实二次型 $f(x_1,x_2,\cdots,x_n)=d_1x_1^2+d_2x_2^2+\cdots+d_nx_n^2$, $f$ 正定 $\Leftrightarrow$ $d_i>0,i=1,2,\cdots,n$
101 | 3. 非退化线性替换不改变二次型的正定性
102 | 4. 设实二次型 $f(x_1,x_2,\cdots,x_n)$, $f$ 正定 $\Leftrightarrow$ $rank(f)=n=p$ ($f$ 的正惯性指数)
103 |
104 | 其中判定二的充分性显然, 必要性只需带入所有的单位向量即可证.
105 |
106 | #### 正定矩阵
107 |
108 | ##### 定义
109 |
110 | 一个$n\times n$的实对称矩阵$A$被称为正定,如果对于任何非零向量$x\in\mathbb R^n$,都满足$x^\top A x>0$
111 |
112 | ##### 判定
113 |
114 | 1. 实对称矩阵 $A$ 正定 $\Leftrightarrow$ $A$ 与单位矩阵 $E$ 合同
115 | 2. 实对称矩阵 $A$ 正定 $\Leftrightarrow$ 存在可逆矩阵 $C$, 使 $A=C^\top C$
116 |
117 | ##### 性质
118 |
119 | 1. $A^{-1}$ 是正定矩阵
120 | 2. $kA,(k>0)$ 是正定矩阵
121 | 3. $A$ 的伴随矩阵 $A^*$ 是正定矩阵
122 | 4. $A^m$ 是正定矩阵 (m 为任意整数)
123 | 5. 若 $B$ 也是正定矩阵, 则 $A+B$ 也是正定矩阵
124 |
125 | ##### 必要条件
126 |
127 | 1. 实对称矩阵 $A=(a_{ij})_{n\times n}$ 正定 $\Rightarrow$ $a_{ii}>0,i=1,2,\cdots,n$
128 | 2. 实对称矩阵 $A$ 正定 $\Rightarrow$ $\det A=|A|>0$
129 |
130 | ##### 定理
131 |
132 | 二次型 $f(x_1,x_2,\cdots,x_n)=x^\top Ax$ 正定 (或 $A>0$) 的充分必要条件是 $A$ 的各阶顺序主子式都大于零.
133 |
134 | 证明:
135 |
136 | $\Rightarrow$:
137 |
138 | 分别取 $\boldsymbol{c}=(c_1,c_2,\cdots ,c_k,0,\cdots,0)$, 带入可知 $f(x_1,x_2,\cdots,x_k)$ 也是正定二次型
139 |
140 | $\therefore |A_k|>0$
141 |
142 | $\Leftrightarrow$:
143 |
144 | 使用数学归纳法.
145 |
146 | $E=G'A_{n-1}G$, 转化为对称矩阵
147 |
148 | ### 半正定
149 |
150 | 
151 |
152 | #### 协方差矩阵是半正定的
153 |
154 |
62 |
63 | #### 条件?
64 |
65 | $|\lambda E-A|$有非零解,只有可对角化矩阵才可以作特征分解。
66 |
67 | #### 如何进行特征值分解?
68 |
69 | 特征值分解:指将对$n\times n$,且有$N$个线性无关的特征向量$q_i$的方阵$A$,将其分解为$A=Q\Lambda Q^{-1}$。其中$Q$为$n\times n$,第$i$列为$A$的特征向量$q_i$,$\Lambda$为对角矩阵,对角线上的元素是对应的特征值。
70 |
71 | 1. 首先求解特征方程,得到矩阵$A$特征值$\lambda _i$(共$n$个)
72 |
73 | 2. 再由$(\lambda_i E-A)x=0$求基础解系,即矩阵$A$属于特征值$\lambda_i$的线性无关的特征向量。
74 | 3. 用求得的特征值和特征向量构造$Q,\Lambda$
75 |
76 | ## 正定矩阵
77 |
78 | ### 正定
79 |
80 | #### 正定二次型
81 |
82 | ##### 定义
83 |
84 | 实二次型 $f(x_1,x_2,\cdots,x_n)$ 若对任意一组不全为零的实数 $c_1,c_2,\cdots,c_n$ 都有
85 |
86 | $$
87 | f(c_1,c_2,\cdots,c_n)>0
88 | $$
89 |
90 | 则称 $f$ 为**正定二次型**.
91 |
92 | 如, $f(x_1,x_2,\cdots,x_n)=\displaystyle\sum_{i=1}^nx_i^2$ 是正定二次型.
93 |
94 | 但, $f(x_1,x_2,\cdots,x_n)=\displaystyle\sum_{i=1}^{n-1}x_i^2$ 不是正定二次型.
95 |
96 |
97 | ##### 判定
98 |
99 | 1. 实二次型 $\boldsymbol{x}^\top A\boldsymbol{x}$ 正定 $\Leftrightarrow$ $\forall \boldsymbol{x}\in\mathbb{R}^n$, 若 $\boldsymbol{x}\neq 0$, 则 $\boldsymbol{x}^\top A\boldsymbol{x}>0$
100 | 2. 设实二次型 $f(x_1,x_2,\cdots,x_n)=d_1x_1^2+d_2x_2^2+\cdots+d_nx_n^2$, $f$ 正定 $\Leftrightarrow$ $d_i>0,i=1,2,\cdots,n$
101 | 3. 非退化线性替换不改变二次型的正定性
102 | 4. 设实二次型 $f(x_1,x_2,\cdots,x_n)$, $f$ 正定 $\Leftrightarrow$ $rank(f)=n=p$ ($f$ 的正惯性指数)
103 |
104 | 其中判定二的充分性显然, 必要性只需带入所有的单位向量即可证.
105 |
106 | #### 正定矩阵
107 |
108 | ##### 定义
109 |
110 | 一个$n\times n$的实对称矩阵$A$被称为正定,如果对于任何非零向量$x\in\mathbb R^n$,都满足$x^\top A x>0$
111 |
112 | ##### 判定
113 |
114 | 1. 实对称矩阵 $A$ 正定 $\Leftrightarrow$ $A$ 与单位矩阵 $E$ 合同
115 | 2. 实对称矩阵 $A$ 正定 $\Leftrightarrow$ 存在可逆矩阵 $C$, 使 $A=C^\top C$
116 |
117 | ##### 性质
118 |
119 | 1. $A^{-1}$ 是正定矩阵
120 | 2. $kA,(k>0)$ 是正定矩阵
121 | 3. $A$ 的伴随矩阵 $A^*$ 是正定矩阵
122 | 4. $A^m$ 是正定矩阵 (m 为任意整数)
123 | 5. 若 $B$ 也是正定矩阵, 则 $A+B$ 也是正定矩阵
124 |
125 | ##### 必要条件
126 |
127 | 1. 实对称矩阵 $A=(a_{ij})_{n\times n}$ 正定 $\Rightarrow$ $a_{ii}>0,i=1,2,\cdots,n$
128 | 2. 实对称矩阵 $A$ 正定 $\Rightarrow$ $\det A=|A|>0$
129 |
130 | ##### 定理
131 |
132 | 二次型 $f(x_1,x_2,\cdots,x_n)=x^\top Ax$ 正定 (或 $A>0$) 的充分必要条件是 $A$ 的各阶顺序主子式都大于零.
133 |
134 | 证明:
135 |
136 | $\Rightarrow$:
137 |
138 | 分别取 $\boldsymbol{c}=(c_1,c_2,\cdots ,c_k,0,\cdots,0)$, 带入可知 $f(x_1,x_2,\cdots,x_k)$ 也是正定二次型
139 |
140 | $\therefore |A_k|>0$
141 |
142 | $\Leftrightarrow$:
143 |
144 | 使用数学归纳法.
145 |
146 | $E=G'A_{n-1}G$, 转化为对称矩阵
147 |
148 | ### 半正定
149 |
150 | 
151 |
152 | #### 协方差矩阵是半正定的
153 |
154 |  155 |
156 |
--------------------------------------------------------------------------------
/英文.md:
--------------------------------------------------------------------------------
1 | ### Self-Introduction
2 |
3 | ### Why do you choose to study at our school?
4 |
5 | ### What do you expect to achieve during your study if you are enrolled into this institute?
6 |
7 | ### What is your plan in the postgraduate study?
8 |
9 | ### Do you have a career plan in 5 years?
10 |
11 | ### Tell me something about your undergraduate life.
12 |
13 | ### What is your favorite subject and why?
14 |
15 | ### What has been your greatest success/ accomplishment in campus life?
16 |
17 | ### What book have you recently read?
18 |
19 | ### What professional paper have you read before? What's the main idea of this text.
20 |
21 | ### Tell me something about your hometown.
22 |
23 | ### Tell me something about Nanjing.
24 |
25 | ### Can you tell me something about your family?
26 |
27 | ### What's your favorite hobby?
28 |
29 | ### Who is your favorite basketball player?
30 |
31 | ### Strength
32 |
33 | ### Weaknesses
34 |
35 | ### What kind of character do you think you have?
36 |
--------------------------------------------------------------------------------
/面经.md:
--------------------------------------------------------------------------------
1 | # NJUAI面经
2 |
3 | # 2019
4 |
5 | ## [南大lamda实验室失败面经分享_彩虹糖梦的博客](https://blog.csdn.net/caozixuan98724/article/details/100975163)
6 |
7 | 接着看论文的老师问我朴素贝叶斯决策相关的内容,朴素贝叶斯我还是会的,说了一下思想和公式。然后他问我,朴素贝叶斯是独立分布还是独立条件分布?我当时不知道是怎么的鬼使神差,答了个独立分布...只能说脑子瓦特了,那天状态真的特别差。后来知道老师问我这个问题的原因是我在论文中用了大量条件分布的东西。
8 |
9 | 最后是我觉得最奇怪的一个问题,老师问quick sort,我一下就来劲了,quick sort我熟啊,刚复习的。然后老师问我,快排为什么叫快排啊?我“?????”我弱弱的回答“因为它快啊...”。老师又问我“它是最快的吗?”我“不是啊,快排是nlogn,基数排序能到O(n)呢”。老师问“那基数排序有什么代价呢?”我说“它需要大量的空间啊,空间换时间”。然后我就楞那里了。老师“你还是没回答我的问题啊,快排为啥叫快排啊?”我“...”。
10 |
11 | 之前对于算法,重点去掌握了它的流程,它的代码,忽略了一些特别关键和基础的点,比如什么大数定律,条件分布,决策树一些更加深入的东西,没有记忆在心中。对自己的项目也没有深挖,还是要不断反思,这个项目的核心是啥,遇到了什么困难,有什么收获。
12 |
13 | # 2020
14 |
15 | ## [南大人工智能AI学院夏令营面试经历_Alvassss的博客](https://blog.csdn.net/Alvassss/article/details/107244024)
16 |
17 | ### 1.LAMDA
18 |
19 | 一轮:自我介绍 概率题 算法题 项目简介
20 | 二轮:自我介绍 你大学最满意的项目是什么 详细问
21 | 听说有三轮 但我没过第二轮
22 |
23 | ### 2.南大MCG
24 |
25 | 自我介绍 老师完全按照简历询问
26 |
27 | ### 3.南大笔试
28 |
29 | 重点:
30 | 1.线代+概率 线代主要是概念 概率主要是网上那些脑筋急转弯
31 | 2.机器学习 建议西瓜书前十章要精通
32 | 3.数据结构 考的巨多 建议精通
33 | 4.算法 时间复杂度分析 渐进 背包问题 摊还
34 | 非重点:
35 | 博弈论 各种变换(傅里叶啥的 俺没学过)
36 |
37 | ### 4.南大面试
38 |
39 | 英语面试:是学院的一个越南老师面试 比较亲切 但我心态崩了
40 | 三个问题:
41 | 1min自我介绍(超时会直接截止 不要问我为什么知道)
42 | 最喜欢的课程 why
43 | 最喜欢的机器学习算法
44 | 中文面试:
45 | 快速排序和归并排序优缺点 排序为什么要稳定
46 | P问题 NP问题 NP完全问题的概念
47 | 全概率公式意义
48 | 项目问题
49 |
50 | ## [南大人工智能学院夏令营经历记录_TheRebel_的博客](https://blog.csdn.net/Anonymity_/article/details/105407815?spm=1001.2101.3001.6650.1&utm_medium=distribute.pc_relevant.none-task-blog-2~default~CTRLIST~Rate-1-105407815-blog-107244024.235^v31^pc_relevant_default_base3&depth_1-utm_source=distribute.pc_relevant.none-task-blog-2~default~CTRLIST~Rate-1-105407815-blog-107244024.235^v31^pc_relevant_default_base3&utm_relevant_index=2)
51 |
52 | 面试问了我大概五道题,一道问排序算法,及时间复杂度。第二道问我svd是什么。第三道是关于我最喜欢的深度学习模型。第四道和第五道是围绕我的项目经历问的。然后计算机营和ai营机试:面试比好像不一样。另外,ai院报周志华和lamda组的很多,但其实lamda在这之前已经招过一次了,所以夏令营他们再招的名额可能会比较小。
53 |
54 | ## [【计算机保研夏令营】2020年LAMDA保研面试经验](https://zhuanlan.zhihu.com/p/237472334)
55 |
56 | ### 面试 6.18
57 |
58 | 大概在报名结束后一周收到了第一次面谈的邀请邮件,LAMDA都是提前一天发邮件,第二天直接面试。这时候还在期末考试阶段,比较紧张,也没准备啥,就对着简历花了一小时思考了下。第一轮我们组是10个人,按姓名拼音排序进行面试的,面试官是组里的三个学长,先进行自我介绍,之后主要问了我以下三个问题:
59 |
60 | > 详细介绍了下比赛(我参加过一个数据挖掘的比赛)的特征工程,之后又问了模型部分(介绍了下Xgboost)
61 | > 对机器学习的理解(这个感觉自己答得不是很好,说的有点绕进去了)
62 | > 对开放动态环境下机器学习的挑战和瓶颈的认识(这个后来我查过,是那个学长的博士课题,听DJW学长说这个也是LAMDA组里的一个大坑,ps. 这里大坑指大方向,不是说坑,有学弟问了才发现有人会误解emmm)
63 |
64 | 总的来说,这一轮面试比较愉快,主要了解一些基本情况吧,感觉这一轮没有刷人。
65 |
66 | ### 3. 第二轮面试 6.20
67 |
68 | 第一轮面试结束第二天就发下一轮通知了,询问D学长了解去年的流程后,也大概猜到了这一轮可能是群面,面之前学长还说遇到ZDC老师坐等聊爆,结果8:50进入腾讯会议,我傻眼了,一奶即中。
69 |
70 | 首先还是少不了自我介绍,介绍完之后Z老师就问我对博士期间的规划,这个问题之前思考过很久,也是一个保研期间的必问问题,由于我把规划从大四说起(大四如果保研顺利结束想先强化学习数学基础,说了凸优化、随机过程、矩阵分析之类的),也给后续埋了个坑——下一个问题他问我最喜欢哪门课,我以为他想问上面三门,就问了句是不是本科阶段,被WW老师说难道你还有研究生阶段吗,有点尴尬。我作死的说了数据结构(但我确实真的很喜欢数据结构,其他课也没准备,想着数据结构学的还行就说了),但直接问我红黑树了,我有点傻眼了,老实说自己不会,只知道STL有些底层是红黑树实现的(有时间还是得看下红黑树,至少得了解思想)。
71 |
72 | 之后就是一连串的问题,先问了归并和快排的平均、最优、最坏复杂度,这个准备实习面试时都梳理过,都答出来了。然后接着这个问题问,既然归并的最坏也是O(nlogn),而快排最坏O(n^2),为啥现在大家都用的是快排。我只从空间复杂度进行了分析,后来面完查了下,其实实践证明,虽然二者时间复杂度相同,但快排还是要快一些,而且最坏情况遇到的可能性也比较低。之后问的应该是如何判断图中是否有环,我刚嘴里小声复述想思考下,老师就直接问下一个问题了,这里感觉这一轮应该就是压力面。
73 |
74 | 下一个问题问的是比赛,让我介绍Xgboost的优势,这个实习面试也复习过,答得还可以。接下来WW老师问我本科学校是985吗?是211吗?是双一流吗?一波三连搞得我有点尴尬,我校果然在南方知名度还是不行。
75 |
76 | 最后Z老师又问你本科北京的学校为啥想来南京,说以前很多北京的同学拿了offer又鸽了。这个问题就有的聊了,因为我本身是江苏人,高中物理竞赛又在南大两个校区住过一段时间,挺喜欢南大的,南大也算是高中dream school之一了,然后就是LAMDA很强哈哈哈哈。
77 |
78 | 总结一下,这一轮面试节奏很快,可能也是面试过程中比较兴奋,我整体回答问题几乎没有思考,没有用到10分钟应该。这一轮面试应该刷了一半人左右。
79 |
80 | ### 4. 第三轮面试 6.22
81 |
82 | 这一轮面试一直到6.21晚9点才通知,大部分人收到的邮件都写明了是哪个老师面试,根据这两轮小组面试人数的猜测,可能第二轮刷了有一半人,但不确定,也可能是分批。我的邮件没有写明老师,我第一志愿是JY老师,但听D学长说J老师学生有部分也都是Z老师带,所以猜测可能会使Z老师面。D学长给我看了他去年整理的面试经历,大概了解了一些情况以及基本问题。这时候由于已经期末考完了,但也没想到面试这么突然,也来不及准备太多,就稍微过了下线代和概率论的一些基本概念,理解了一下,然后准备了一下简历。
83 |
84 | 最终面我的还是J老师。第一个环节还是自我介绍,介绍完之后老师开始问“以后的规划”、“家庭背景”、“家人对自己的规划”等等,接下来又问了“简历中的数据挖掘比赛主要负责的内容以及收获”、“本科科研项目最大的收获”等问题,都很友好,聊了大概20多分钟。
85 |
86 | # 2021
87 |
88 | ## [2021年人工智能保研经历(xduee->njuai)](https://zhuanlan.zhihu.com/p/420184627)
89 |
90 | 人工智能学院的笔试主要考人工智能+计算机的基础知识。笔试用考试星机考的方式,考试时长2小时,大概我记得200道题目左右,应该是比2020年的笔试少了50道题目左右,题目难度适中,因为难题我全刚开始跳了,我差不多连猜带蒙在最后差10min的时候完成了所有题目。南大学院笔试的考核真的很重要很重要,属于超强committee,即使你提前被周老师录了,笔试没过也是没用的。
91 |
92 | 参营时间线的话,是2021.7.8举行笔试,然后7.11周日上午(当时正在看美洲杯决赛,印象深刻)出了笔试的结果,应该是进60%~70%左右的人。笔试结果出了后,就会让你选择学硕or直博。南大一般在这个时候才会让你选择学硕和直博,刚开始报名的选择只是预选择。下面就是面试,7.13一整天是学硕面试,7.14上午是直博生面试,直博面试应该有22人,录了多少我也不是很清楚,下面说说面试情况。
93 |
94 | 线上面试还是采用的腾讯会议,每人12min,4min英语问答+8min专业知识。我那组的面试官有4人,面试可以说是相当友好了,英语问答包含自我介绍,以及一些关于我科研的提问,还有一些闲聊,英语这部分总体来说不难,敢于去说就行。专业知识部分,主要还是在问机器学习+线性代数的相关知识,我感觉我个人准备的比较充分,所有问题都回答出来了,除了最后詹老师的一个关于编码的问题回答的不太行。
95 |
96 | 关于机器学习面试的问题可以参考我另一篇经验贴:**[计算机/人工智能方向保研高频面试题目整理](https://zhuanlan.zhihu.com/p/394374473)** ,这篇经验贴我应该概括的比较全面了。
97 |
98 | ### [计算机/人工智能方向保研高频面试题目整理](https://zhuanlan.zhihu.com/p/394374473)
99 |
100 | ### **1. 开放型问题**
101 |
102 | 开放型问题建议中英文都准备,大部分面试都有这个环节。
103 |
104 | - 自我介绍(1min/3min)
105 | - 研究生期间的规划
106 | - 参与的竞赛(数模等等),你做了哪儿些工作?
107 | - 简单介绍下你的科研工作
108 | - 对机器学习/深度学习的理解
109 | - 开放动态环境下机器学习的认识(来自南大某著名实验室)
110 |
111 | ### **2. 数学类**
112 |
113 | 数学类问题是ai方向保研面试问的最多的,主要是线代、概率论。
114 |
115 | - 线代:如何理解矩阵的秩?简述向量组线性无关的含义?解释正定矩阵以及半正定矩阵?特征值的含义以及矩阵分解的物理意义?
116 | - 概率论:简述大数定理,中心极限定理,全概率公式,最大似然估计,贝叶斯的含义
117 | - P问题 NP问题 NP完全问题的概念
118 |
119 | ### **3. 机器学习类**
120 |
121 | - 简述PCA的计算过程
122 | - 简述SVM,并解释SVM为什么要化对偶形?百万样本量可以用SVM吗?
123 | - 常用的机器学习算法的适用场景(例如KNN、朴素贝叶斯、决策树等)
124 | - 具体阐述残差神经网络的含义
125 | - 梯度消失和梯度爆炸是什么意思?有什么样的方法进行改善?
126 | - 简述几种集成学习方法Adaboost的计算过程以及Stacking Learning?
127 |
128 | ### **4. 数据结构与算法类**
129 |
130 | - 常用排序平均最优最坏时间复杂度以及空间复杂度,阐述快排和归并的优缺点以及回答为什么排序要稳定?
131 | - 归并排序的最坏时间复杂度优于快排,为什么我们还是选择快排?
132 | - TopK问题详解
133 | - 如何判断图里有环?
134 | - C++中new和malloc的区别
135 |
136 | ## [2021年一战南大AI上岸经验贴_Yuhan の Blog的博客](https://blog.csdn.net/qq_45228537/article/details/115448786)
137 |
138 | ### 复试笔试
139 |
140 | 南大AI的复试笔试是离散数学+机器学习;我是3月开学回学校才开始准备,这里建议早点准备离散,离散东西很多概念很杂而且考的也很难,所以我今年离散笔试应该基本没拿到分orz;今年的机器学习也不知道在搞什么,无语子,写着机器学习的label考了20道数据结构的选择题+一道不知道属于啥学科的问答,不过该准备的还是要准备的。
141 | 离散建议找一下南大本科的PPT,有重点地对着屈书进行复习;复试的机器学习建议细看一下,部分重点的数学推导要会(例如SVM的拉格朗日乘子法、KKT条件、PCA特征值分解),概念要十分清晰,即使复试没有考察到,面试老师也会问许多机器学习的相关知识。
142 |
143 | ### 复试机试
144 |
145 | 今年情况特殊,是线上复试,因此今年的机试是和笔试在一起考的,但我想,随着疫情逐渐得到有效控制+全民疫苗接种,今后应该会继续采用线下机试的方法。
146 | 个人本科练习过半年左右的OJ,因此有一点薄弱的基础,因此就是在考前临时复习了一下黄宇书上的4道DP例题+一些常见的DP题(01背包、完全背包、LCS、多重部分和问题、LIS、DP计数等等)+一些常用的数据结构和算法(例如并查集、kruskal、dijkstra、快速幂、素数筛、线段数、树状数组等等)。
147 | 对于南大的机试,我觉得重点是DP、搜索、图论。
148 |
149 | ### 复试面试
150 |
151 | 面试个人认为可以拆分成英语口语+线代+概率论+机器学习+项目经验+一些其它知识储备。
152 | 口语问了我这些问题:
153 |
154 | 1.本科所学专业
155 | 2.毕业后打算
156 | 3.兴趣爱好
157 | 4.介绍喜欢的电影
158 | 5.介绍最近读的一本书
159 |
160 | 面试:
161 |
162 | 1.你说你因为喜欢数据结构和算法才选择读AI,介绍一下它们的交集
163 | 2.本科有没有做过AI相关的项目
164 | 3.SVM为什么要采用对偶问题?(我答:虽然可以通过现成凸优化包求解,但是对偶问题求解更快)
165 | 4.为什么更快?(接4中我的回答内容
166 | 5.Boosting学习有什么特点?
167 | 6.为什么集成学习需要集成“好而不同”的学习器?(接5中我的回答内容
168 | 7.解释一下特征值的含义
169 | 8.简述一下特征值分解
170 | 9.为什么要选取前d大个特征值(接8中我的回答内容
171 | 10.你本科是软工的,问一下面向过程、面向对象、面向抽象的区别
172 | 11.具体介绍一下你学过的面向对象知识&应用
173 | 12.你觉得你本科所学的知识在将来读AI的时候会有哪些应用
174 |
175 | ### [南京大学LAMDA面经汇总_51CTO博客](https://blog.51cto.com/u_12312066/3695982)
176 |
177 | 面试吴建鑫老师的时候,问题如下:
178 |
179 | 方差的计算方法,他会提前写好一个方差表达式问你对不对,如果不对的话请写出正确的表达式;
180 | 方差中的n-1含义;
181 | 如果写一个程序计算方差,那么计算一次内存访问几次;
182 | 本科做过的项目,项目内容;
183 | 机器学习了解多少,看过什么;
184 | 了不了解本人是做什么研究的。
185 | 面试詹德川老师的时候,我不知道其他人是什么情况,但我是全程英文面试,问到的问题如下,注意:以下问题需要英文作答,实在英语回答不了,可以中文,不必有太大压力:
186 |
187 | 自我介绍一下;
188 | 介绍一下做过的项目;
189 | 介绍一下梯度下降法是什么;
190 | 介绍一下牛顿迭代是什么;
191 | 什么是特征值,特征值的含义;
192 | 唠嗑。
193 | 面试完当天晚上就会有邮件通知是否面试通过,最后我是被詹德川老师录取,但是通过LAMDA面试并不代表你就能100%能进入LAMDA读研了,最重要的一关是拿到南大夏令营的优秀营员,只有这样,通过两轮考核才能进入LAMDA。
194 |
195 | 下面说一下南大夏令营的流程,主要是三部分:各个实验室介绍、机试、面试,其中最最重要的是机试,只要机试通过,90%就能拿到优秀营员。
196 |
197 | 机试这次一共4道题,以前听说6道题,只要AC出其中的两道题就肯定没问题了,多做无用,有罚时,考核方式:OJ,题型:算法+数据结构,难度:ACM一般难度的题。这次的具体题目如下:
198 |
199 | 最大子串和;
200 | 无向图最长路径
201 | 表达式求值;
202 | 给一棵树求最长的路径。
203 | 面试问题如下(由于分组面试,每组没人问题不一样):
204 |
205 | 解释一下什么是时间复杂度;
206 | 快排的时间复杂度;
207 | 快排最坏时间复杂度为什么是$O(n^2)$,如何优化快排最坏时间复杂度;
208 | 看成绩单,问如何进行文献检索
209 | 英文回答:如何利用文献检索知识去检索一个机器学习的问题
210 |
211 | 就问了一个“ε-greedy”算法中ε取值的问题
212 |
213 | 然后问了离散的全序,偏序,操作系统,计算机组成原理内存啥的,还有居然问了软件工程的问题,真是醉了,那个时候软件工程都还没有学完。(黑人问号脸)然后,英文是让我介绍最喜欢的歌曲。
214 |
215 | 南大进行了一场霸面(不推荐,还是提早申请比较好)。
216 |
217 | 1.快排复杂度是多少,并且黑板上手写证明。
218 |
219 | 2.简述如何“快速选到第n个数”(快速选择,复杂度为O(n))。
220 |
221 | 3.讲简历上的项目,根据简历问
222 |
223 | 有无申请lamda都需要参加下面两场考试:
224 |
225 | 机试(两个小时,四选二,一般两道都做出来能入选):
226 |
227 | 1、连续最长子序列和(给了一堆正负的数字,任选其中一段连续的数字(可以全选),需要和最大)
228 |
229 | 2、无向图最长路径(单纯的Dijkstra)
230 |
231 | 3、给一个表达式,例如 (3*2+1/2)+1*2,计算结果
232 |
233 | 4、给了一棵树求最长的路径(根到叶节点)
234 |
235 | 面试:
236 |
237 | 1、英文自我介绍
238 |
239 | 2、按照不同专业方向问专业课程
240 |
241 | 3、大数定理、贝叶斯公式等
242 |
243 | 4、操作系统线程跟进程的区别等(操作系统的问题比较爱问)
244 |
245 | ## [2021年计算机保研(清深、南大AI、中科大、哈深、中山等)](https://zhuanlan.zhihu.com/p/416191365)
246 |
247 | ### 学院
248 |
249 | 考核方式:初审(985前5%) + 笔试 (机器学习、概率论、线性代数、数据结构等)+ 面试(机器学习、数学)
250 |
251 | 笔试:2小时做200多道填空和选择,其内容涵盖机器学习、概率论、线性代数、数据结构等。对于概率论和线性代数,建议耗时两三天刷完李永乐660,刷完就没问题。对于机器学习,建议把西瓜书前十章过一遍,主要是看概念即可。对于408,可以选择不看,考的不多。
252 |
253 | 面试:英语问答 + 专业知识考察。英语问答就准备好常见的英语问题,以及和你简历相关的英语问题即可。至于专业知识,就是考察机器学习和数学,建议把西瓜书或李航统计学细读并理解,数学建议把概率论和线代细读并理解。
254 |
255 | 总结:由于当时概率论和线代复习的不好,导致数学问题只答出一半,进入wl。要想过南大AI,没有别的秘诀!把线性代数、概率论、机器学习从头啃到位即可!
256 |
257 | # 2022
258 |
259 | ## [Kaslanarian/NJUAI-OpenDay-Interview: 南京大学人工智能学院本科生开放日面试经验分享 ](https://github.com/Kaslanarian/NJUAI-OpenDay-Interview)
260 |
261 | ### 同学A(同组)的面试问题
262 |
263 | 面试那天和我在一个房间,而且在我前面面,所以记录了所有的问题:
264 |
265 | - 英语面试:
266 | 1. 1分钟自我介绍;
267 | 2. 从事的研究细节(因为自我介绍中提及);
268 | 3. 你最感兴趣的课程;
269 | 4. 你以后是想留在学校做研究还是去公司工作。
270 | - 中文面试:
271 | 1. 大数定律是什么?
272 | 2. 中心极限定理是什么?
273 | 3. 讲一个你知道的聚类算法?
274 | 4. 你平时有什么放松方式?
275 | 5. Boosting的基本思想?
276 | 6. PCA的全称是什么?
277 | 7. PAC理论的全称是什么?
278 | 8. 欧拉图是什么?
279 | 9. 正定矩阵是什么?
280 | 10. 极大似然估计是什么?
281 | 11. SVM为什么叫支持向量机?
282 |
283 | 注意,上述问题只是前置问题,你说不会才会换问题,否则就会继续问。比如同学A说他不记得欧拉图了,然后对面就换下一个问题;面试到我的时候又问了这个问题,我答出了欧拉图定义,后面就问我判定方法了。
284 |
285 | ### 我的面试
286 |
287 | - 英语面试:
288 |
289 | - 1分钟自我介绍;
290 | - 介绍一下你参加的比赛(起因于我的腾讯会议背景是我上次参加的某比赛,然后忘了换😢,反过来想这也是一种思路,让面试官问出你想让他问的问题😄);
291 | - 以后的安排(类似于同学A的问题)。
292 |
293 | - 中文面试:
294 |
295 | - 大数定律是什么?(看我倒背如流就没问中心极限定理了)
296 |
297 | - 计算复杂度(P和NP),P=NP吗?
298 |
299 | - 遇到压力怎么放松?
300 |
301 | - 最喜欢的课程?
302 |
303 | - 介绍PCA;
304 |
305 | - 为什么机器学习中的基本假设是独立同分布,独立同分布全称是什么?(这个地方卡了,对面嫌我说多了)
306 |
307 | - 什么是欧拉图,如何判定欧拉图?(忘记了,只说记得存在一个充要条件)
308 |
309 | - 正定矩阵是什么,如何判定?
310 |
311 | > 跟面试官(王魏)怼了,他一直说我和书上的定义不一样,但我讲的是一个逻辑等价命题,他就说我不好好看书,弄得心态挺不好。幸好他是最后一个问问题的老师。
312 | >
313 | > 后来发现和我一组的同学都对他有意见的,比如同学B说他不会欧拉图,然后被他锐评:**你是不是没上过数学课?**
314 | >
315 | > 问同学C的时候,C回答不出来就咂嘴,问答少了就说”**这么不熟悉吗**“...
316 | >
317 | > 注:以上内容是节选,如果看的人多了就把老师名字给码了。感觉他是根据被面试者的态度进行反馈,比如我、B和C在面试的时候展现出自信,所以他很打压;A面试的时候很严肃,遇到不会的问题会说“对不起,我回去再看一下”,所以没咋刁难。反正看到的同学留个心眼吧。
318 |
319 | - 快速排序的平均时间复杂度,最坏时间复杂度,最坏情况是什么样?
320 |
321 | ### 本组其他同学的问题
322 |
323 | - 计算复杂度,但问的是:如果把时间换成空间,那么P=NP吗?
324 | - PAC理论了解多少?
325 | - TBD
326 |
327 | ### 其他组的问题
328 |
329 | 这里记录其他组同学那里听来的问题:
330 |
331 | - 喜欢的数学课?如果说了微积分这块,而不是AI相关,则会问:
332 | - 中值定理是什么?
333 | - 泰勒展开是什么?
334 | - 高阶无穷小是什么?
335 | - 傅里叶变换和拉普拉斯变换的关系?
336 | - 拉普拉斯变换的用处?
337 | - 双蛋问题,但是单蛋版,也就是你只有一个鸡蛋如何判定其不摔碎的最高楼层?
338 | - TBD
339 |
340 | ## [2022年/2023届预推免小记(科大6系&NJUAI)](https://zhuanlan.zhihu.com/p/570734028)
341 |
342 | NJUAI:
343 |
344 | 笔试:2h(记不太清了),题量很小,选择+问答
345 |
346 | 面试:英文自我介绍+英文专业问题+专业问题,南大是步步紧逼型面试,感觉问了不止十个问题。
347 |
348 | 比较迷惑的一点是面试是定死了12min/人,结果还剩20s的时候老师又问了一个问题,我刚说两句就直接结束了,这种情况主持人不应该提醒一下快到时间了吗(汗)
349 |
350 | ## [2022年(2023届)计算机保研——计算所vipl、南大lamda、北大计算机、人大高瓴等](https://zhuanlan.zhihu.com/p/570001872)
351 |
352 |
353 |
354 | 看了一些经验帖说,南大LAMDA比北大信科还难,有很多LAMDA面试没过的最后去了北大信科,所以我当初报名没报什么信心,找了一位和自己研究经历比较match的老师,就去参加了。
355 |
356 | 首先是初筛,985的5%应该都能过初筛,除此之外我觉得研究方向的match程度非常重要。
357 |
358 | 一面是学长面,先是一分钟自我介绍,然后就是基本的简历面,问了paper以及剩下几个科研项目做的是什么和创新点,差不多就结束了,没有问任何专业知识相关的问题。
359 |
360 | 二面是老师面,问题大概有:
361 |
362 | 1. 一分钟自我介绍
363 | 2. paper里我主要做的内容
364 | 3. AI for SE领域有什么地方还可以去尝试?
365 | 4. 最拿得出手的项目是什么
366 | 5. 遇到的挫折是什么
367 | 6. 你觉得图神经网络做代码生成目前的优点和缺点是什么?有什么改进的地方?
368 | 7. 有没有做过词法分析器和语法分析器
369 | 8. 智力问题,黑白帽子问题(可自行百度)
370 | 9. 剩下就是一些聊天性问题,比如如果离交稿ddl还剩两天,但是你的实验还有很大漏洞,论文也还没写完,这种情况怎么办;了解了我的家乡以及为什么想来南京等
371 |
372 | 最后获得了实验室的offer,我个人感觉成功的原因是 1. 由于方向match,所以了解比较深入,中间考察的一些对该领域科研的相关看法时回答的还不错;2. 正好问到了我之前思考过的比较有意思的idea,所以和老师聊的很愉快。
373 |
374 | 但是!只拿到实验室的offer还没结束,还需要通过南大AI学院的考核,于是就有了绿裙里通过实验室考核没通过学院考核的难兄难弟们(后来发现这些难兄难弟里有人去了贵系,只想说南大AI真牛)
375 |
376 | AI院笔试:题量很大,考察范围覆盖数据结构、机器学习(西瓜书)、概率论、线性代数、英语等,如果目标南大AI的建议提前好好复习一下。不要像我一样,“怎么还有过了LAMDA没过学院的” “小丑竟是我自己”
377 |
378 | 另:夏令营笔试寄了就彻底寄了,也没办法报名预推免了。
379 |
380 | ## [2022南京大学人工智能学院本科生开放日小记【保研向】](https://zhuanlan.zhihu.com/p/543677717)
381 |
382 | 夏令营笔试是双机位,考试星作答。去年是两百道选择题和填空题两个小时,今年则是66道选择题,20多道填空题,若干多选题,英文题以及简答题,一共一个半小时。考察的科目和去年倒是差不多,这点知乎上也是有人写的,机器学习、概率论、线性代数、数据结构与算法,都是需要复习的。因为是线上考试所以不会有太多复杂的计算,更多考察知识的广度与细节部分,也就是看书复习的时候各种细节都应该注意。我根据前面大佬的建议也用了几天刷了李永乐660的线代和概统部分,感觉还是有不少帮助的。经过我们的讨论,感觉AI营的重点是笔试而非面试。
383 |
384 | 面试也是双机位,腾讯会议面试。以往都是20分钟一个人,今年估计是报名人数比较多,所以改为了12分钟一个人。还是4个老师分别问不同学科的问题。我这里大概记了一下面试的问题(不同的组面试题差别还是挺大的)
385 |
386 | C:你研究生读完之后有什么打算?你有什么做研究的品质?(英文面试,有概率让你用英文自我介绍,也有可能没有)
387 |
388 | 詹:常微分方程f'(x) = cx的解的形式,如果c是常数,为什么形式,如果c为矩阵呢?霍夫曼编码的优势,霍夫曼编码的唯一性,香农编码是什么?
389 |
390 | 张:半正定矩阵的定义,性质(越多越好),PCA协方差矩阵的性质(半正定),以及为什么半正定(从原理上说明)?凸优化中梯度下降的学习率如何确定?(凸优化最后两课讲的)
391 |
392 | 姜:散列表的优势(相比其他查询方式),查询复杂度(分链表型和普通型)。研究生的“研究”二字是什么含义?研究生相比本科生有什么区别?
393 |
394 | 其他同学有问图灵机的,凸优化带约束的一阶条件的,中心极限定理,机器学习很多算法为什么要iid条件,SVM核函数的考察等等,比较广泛,只看西瓜书显然是不够的,还需要一些自己的思考和积累。
395 |
396 | 总体来说感觉面试是不断往深去问,老师会追问你问题的本质,直到不会为止。因此面试完成后问了一圈感觉都不是特别好,这也是正常现象。面试完之后就是漫长的几天等待时间。
397 |
398 | 7.11线上导师宣讲会,7.13开放日线上面试。
399 |
400 | ## [2023CS保研经验分享(清深、上交、南大LAMDA、同济、东南Palm等) - 知乎 (zhihu.com)](https://zhuanlan.zhihu.com/p/570722079)
401 |
402 | 第一轮面试主要是实验室的学长学姐进行,主要围绕就是一些理论知识和你自我介绍的项目中所涉及的一些问题。
403 |
404 | 项目的问题没啥共同性,我就列举一些印象中的常见问题:
405 |
406 | - 机器学习中FP、TP是什么?
407 | - 你为啥想要读直博?
408 | - 线代中的矩阵的秩和矩阵的关系?
409 | - 讲一讲线代中的矩阵的特征值?
410 | - ......
411 |
412 | 第二轮面试是意向导师单独面(我是这样的),L老师只是来聊了聊天,聊一下我想研究的方向和家是哪里的,为什么要来南大等等一些非学术问题,最后说因为直博已经确定了人选,只能给我学硕offer了。
413 |
414 | - 题量:应该是100道差不多,时长90分钟。
415 |
416 | - 题型:单选题、多选题、填空题、英文问答题。
417 |
418 | - 考察内容:
419 |
420 | - - 线性代数(有复杂计算,我遇到了张宇考研数学的原题)
421 | - 概率论(有奇怪的伤脑筋的题,得多练)
422 | - 数据结构(重点,有考察排序算法、链表)
423 | - 机器学习(把西瓜书看看就行,考的都是知识点,概念性的东西)
424 | - 印象中没有计组计网操作系统
425 |
426 |
--------------------------------------------------------------------------------
/面经(分类).md:
--------------------------------------------------------------------------------
1 | # 面经(分类整理)
2 |
3 | 笔试+上机(最关键,笔试过不掉救不了)
4 |
5 | - 100分笔试,机器学习,模式识别,数据结构与算法,知识推理(zyz,英文题,要看一下),人工智能,概率统计(简答题,其他是选择填空)
6 | - 50分编程题,什么方向不知道,应该和机器学习和算法相关。
7 | - 月底组内,积累点经验,问一下学长,口语是怎么样的。
8 | - 本校有一定的优势,尽可能做好,题量不少,做不对略过即可,不要纠结。
9 |
10 | ## 概率论
11 |
12 | - 大数定理
13 | - 中心极限定理
14 | - 全概率公式
15 | - 最大似然估计
16 | - 贝叶斯公式:接着看论文的老师问我朴素贝叶斯决策相关的内容,朴素贝叶斯我还是会的,说了一下思想和公式。然后他问我,朴素贝叶斯是独立分布还是独立条件分布?我当时不知道是怎么的鬼使神差,答了个独立分布...只能说脑子瓦特了,那天状态真的特别差。后来知道老师问我这个问题的原因是我在论文中用了大量条件分布的东西。
17 | - 网上那些脑筋急转弯
18 | - 独立同分布:为什么机器学习中的基本假设是独立同分布,独立同分布全称是什么?(这个地方卡了,对面嫌我说多了)
19 |
20 | ## 机器学习
21 |
22 | 西瓜书前十章精通
23 |
24 | - 对机器学习/深度学习的理解
25 | - 开放动态环境下机器学习的认识(来自南大某著名实验室)
26 | - PCA:简述PCA的计算过程,PCA的全称是什么
27 | - SVM:简述SVM,并解释SVM为什么要化对偶形?百万样本量可以用SVM吗?(我答:虽然可以通过现成凸优化包求解,但是对偶问题求解更快)为什么更快?
28 | - 讲一个你知道的聚类算法?
29 | - 集成学习:简述几种集成学习方法,Adaboost的计算过程,以及Stacking Learning?Boosting的基本思想?Boosting学习有什么特点?为什么集成学习需要集成“好而不同”的学习器?介绍Xgboost的优势
30 | - 常用的机器学习算法的适用场景(例如KNN、朴素贝叶斯、决策树等)
31 | - PAC理论:PAC理论的全称是什么?PAC理论了解多少?
32 | - 具体阐述残差神经网络的含义
33 | - 梯度消失和梯度爆炸是什么意思?有什么样的方法进行改善?
34 | - 介绍一下梯度下降法是什么
35 | - 介绍一下牛顿迭代是什么
36 | - 为什么机器学习中的基本假设是独立同分布,独立同分布全称是什么?(这个地方卡了,对面嫌我说多了)
37 | - $ \epsilon $ -greedy:就问了一个“ε-greedy”算法中ε取值的问题
38 | - 决策树一些更加深入的东西
39 | - 机器学习中FP、TP是什么?
40 |
41 | ## 数据结构与算法
42 |
43 | - 数据结构 考的巨多 建议精通
44 | - 时间复杂度分析
45 | - 渐进
46 | - 动态规划:背包问题
47 | - 摊还
48 | - 排序:
49 |
50 | - 排序:算法,平均最优最坏时间复杂度以及空间复杂度。黑板上手写证明。排序为什么要稳定。
51 | - 快排:平均、最优、最坏复杂度。最坏情况是什么样?优缺点。
52 | - 归并:平均最优最坏时间复杂度以及空间复杂度,优缺点。
53 | - 既然归并的最坏也是 $ O(n\log n) $ ,而快排最坏 $ O(n^2) $ ,为啥现在大家都用的是快排。(我只从空间复杂度进行了分析,后来面完查了下,其实实践证明,虽然二者时间复杂度相同,但快排还是要快一些,而且最坏情况遇到的可能性也比较低。)
54 | - P问题 NP问题 NP完全问题的概念
55 | - 直接问我红黑树了,我有点傻眼了,老实说自己不会,只知道STL有些底层是红黑树实现的(有时间还是得看下红黑树,至少得了解思想)
56 | - 图
57 |
58 | - 如何判断图中是否有环
59 | - 欧拉图是什么?判定方法?
60 | - TopK问题详解,“快速选到第n个数”(快速选择,复杂度为 $ O(n) $ )
61 | - C++中new和malloc的区别
62 | - 双蛋问题,但是单蛋版,也就是你只有一个鸡蛋如何判定其不摔碎的最高楼层?
63 | - 智力问题,黑白帽子问题(可自行百度)
64 | - 霍夫曼编码的优势,霍夫曼编码的唯一性,香农编码是什么?
65 | - 散列表的优势(相比其他查询方式),查询复杂度(分链表型和普通型)
66 |
67 | ## 线代
68 |
69 | - svd(奇异值分解)
70 | - 讲一讲线代中的矩阵的特征值?什么是特征值,特征值的含义,特征值分解
71 | - 正定矩阵是什么?
72 | - 如何理解矩阵的秩?线代中的矩阵的秩和矩阵的关系?
73 | - 简述向量组线性无关的含义?
74 | - 矩阵分解的物理意义?
75 | - 半正定矩阵的定义,性质(越多越好),PCA协方差矩阵的性质(半正定),以及为什么半正定(从原理上说明)?
76 |
77 | ## 凸优化
78 |
79 | - 凸优化带约束的一阶条件
80 | - 凸优化中梯度下降的学习率如何确定?(凸优化最后两课讲的)
81 |
82 | ## 操作系统
83 |
84 | - 操作系统线程跟进程的区别等(操作系统的问题比较爱问)
85 |
86 | ## 数学分析
87 |
88 | - 常微分方程f'(x) = cx的解的形式,如果c是常数,为什么形式,如果c为矩阵呢? $ \frac12x^\top Cx $
89 | - 傅里叶变换和拉普拉斯变换的关系?拉普拉斯变换的用处?
90 |
91 | ## 其他
92 |
93 | - 一分钟自我介绍,遇到的挫折是什么
94 | - 研究生的“研究”二字是什么含义?研究生相比本科生有什么区别?
95 | - 比如如果离交稿ddl还剩两天,但是你的实验还有很大漏洞,论文也还没写完,这种情况怎么办
96 | - 英文面试
97 | - 1分钟自我介绍
98 | - 从事的研究细节(因为自我介绍中提及)
99 | - 你最感兴趣的课程
100 | - 你以后是想留在学校做研究还是去公司工作。
101 | - 如何利用文献检索知识去检索一个机器学习的问题
102 | - 你研究生读完之后有什么打算?你有什么做研究的品质?
103 |
104 | ## 机试
105 |
106 | - 最大子串和(给了一堆正负的数字,任选其中一段连续的数字(可以全选),需要和最大);无向图最长路径(单纯的Dijkstra);表达式求值(例如 (3\*2+1/2)+1\*2,计算结果);给一棵树求最长的路径(根到叶节点)。
107 | - 南大的机试,我觉得重点是DP、搜索、图论
108 |
109 | ## 笔试
110 |
111 | - 题量:应该是100道差不多,时长90分钟。
112 | - 题型:单选题、多选题、填空题、英文问答题。
113 | - 考察内容:
114 | - 线性代数(有复杂计算,我遇到了张宇考研数学的原题)
115 |
116 | - 概率论(有奇怪的伤脑筋的题,得多练)
117 | - 数据结构(重点,有考察排序算法、链表)
118 | - 机器学习(把西瓜书看看就行,考的都是知识点,概念性的东西)
119 | - 印象中没有计组计网操作系统
120 |
121 | 1. 可靠性(Soundness):在命题逻辑中,可靠性是指逻辑系统的一个属性,表示该系统中的推理规则是正确的。如果一个逻辑系统是健全的,那么任何从该系统的有效前提推导出的结论都是真的。换句话说,如果一个论证是健全的,那么它不会导致从假前提推出真结论的情况。
122 | 2. 完备性(Completeness):在命题逻辑中,完备性是指逻辑系统的另一个属性,表示该系统中的每个真陈述都可以在该系统中被证明为真。换句话说,如果一个逻辑系统是完备的,那么对于任何为真的陈述,系统中存在一个证明或推理来证明它的真实性。
123 |
--------------------------------------------------------------------------------
/面试.md:
--------------------------------------------------------------------------------
1 | ### 机器学习
2 |
3 | - 机器学习:基于统计、数据驱动,不是基于演绎而是基于归纳的。可以解决规则难以解决的问题;深度学习:使用更深的网络结果增强表达能力,将特征提取和模式学习相结合
4 | - 梯度下降法:一种常用的优化算法,用于最小化目标函数。计算过程是迭代地向梯度下降最快的方向更新参数,新参数=旧参数-学习率$\times$梯度。
5 | - 条件:目标函数可导,凸;优点:应用范围广,简单;缺点:可能陷入局部最小值,需要人为确定学习率
6 | - 牛顿迭代法:求$f(x)=0$的解的方法。每次用切线与x轴的交点的x值更新参数,$\displaystyle x_{n+1}=x_n-\frac{f(x_n)}{f'(x_n)}$
7 | - 条件:目标函数二价可微,目标函数的海森矩阵必须正定或负定
8 | - 优点:更快地收敛到最优解,不用调参;缺点:计算成本高
9 | - 决策树:一种基于树结构进行决策的算法,其中每个内部节点表示一个属性或特征,每个叶子节点代表决策结果。该算法可以用于分类和回归问题。
10 | - 计算过程:基于分治思想,每次选择最优划分属性,将样本集合分成更小的子集。不断重复,直到所有的子集都属于同一个类别,或者已经达到了预先定义的最大深度。
11 | - SVM (Support Vector Machine): 支持向量机,一种可以用于解决分类和回归问题的机器学习算法,目标是在高维空间中找到最佳的超平面,使得间隔最大化。
12 | - 支持向量:离超平面最近的训练样本点。
13 | - SVM为什么要化对偶形?为了更高效地求解。当数据集的规模很大时,使用原始问题求解SVM会变得很慢,甚至变得不可行。化成对偶问题可以使用SMO这种近似算法更高效的求解。
14 | - 百万样本量可以用SVM吗?求解SVM的原问题计算复杂度过大,有些困难。
15 | - 朴素贝叶斯:一种采用了属性条件独立性假设的分类器,基于贝叶斯定理,选择概率最大的类作为结果。
16 | - 贝叶斯最优分类器:为最小化总体风险,在每个样本上选择那个能使条件风险最小的类别标记,此时判定准则称为贝叶斯最优分类器
17 | - EM算法:一种迭代地估计参数隐变量的方法。其中E步 (Expectation) 基于参数推断隐变量的分布;M步 (Maximization) 基于已观测变量X和Z对参数做极大似然估计。
18 | - PCA (Principal Component Analysis):无监督降维方法。
19 | - 适用于数据之间存在线性相关性的情况,对于非线性关系可以考虑使用Kernel PCA。
20 | - 计算过程:先将数据标准化,使得每个特征的均值为0;计算标准化后数据的协方差矩阵,对协方差矩阵做特征值分解,选择特征值最大的k个特征向量组成投影矩阵,最后将标准化后的数据乘以投影矩阵,将数据投影到新的特征空间上。
21 | - 计算后的主成分正交,即没有线性相关性。(正交$\Rightarrow$线性无关)
22 | - 集成学习 (ensemble learning,读“昂”):一种机器学习方法,核心思想是通过组合多个弱学习器,从而提高模型的预测能力和泛化性能。
23 | - Bagging (bootstrap aggregating):使用自助采样法得到不同的训练集,训练一系列基学习器,通过投票或者平均的方法得到预测结果。
24 | - Boosting:基本思想是通过迭代训练一系列弱分类器,每个弱分类器都针对前一轮训练中被错误分类的样本进行加权,以提高其分类准确性。
25 | - Stacking:一种叠加泛化的集成方法,通过训练一个元模型来结合多个基础模型的预测结果。元模型就是以不同基学习器的预测结果作为输入,结果作为输出。
26 | - “好而不同”:即基学习器的准确率高,多样性高。直观讲准确率越高越好是显然的,多样性高意味着不同的学习器可以互补,从而提高整体的学习性能。理论上有误差歧义分解证明了泛化误差=基学习器泛化误差的却权均值-基学习器的加权分歧值,可以说明基学习器的准确率高,多样性高,分类效果越好。
27 | - Adaboost计算过程:(二分类任务)在训练的每一轮中,使用当前的样本权重训练基学习器,计算分类误差率,如果误差大于0.5则break;根据错误率计算这个基学习器的权重;基于对分类正误情况更新数据分布,增加分错样本的影响,降低分对样本的影响;最后基于各个基学习器的加权,得到最终的分类器
28 | - K-means:一种原型聚类方法,目标是将数据集分成k个不重叠的簇。通过最小化数据点与所属簇的质心之间的距离来进行聚类。
29 | - 计算过程:用一种迭代近似的方法求解。初始化k个簇的质心,重复如下步骤:将每个数据点分到与其最近的质心所属的簇;对于每个簇,计算所有数据点的均值,得到新的质心。如此重复直到质心的位置不再发生显著变化或达到预定的迭代次数。
30 | - KNN:一种lazy learning的监督学习算法,基于与测试样本最近邻的k个邻居的信息预测结果。
31 | - lazy learning:训练阶段仅仅是把样本保存起来,训练时间开销为零,待 收到测试样本后再进行处理
32 | - PAC (Probably Approximately Correct):一种计算学习理论,核心思想是如果一个算法能够在有限的样本上以很高的概率产生一个"近似正确"的模型,那么该算法可以在未见过的数据上表现良好。
33 | - PAC可辨识:算法是否能以高概率产生一个近似正确的模型(泛化误差小于epsilon的概率大于等于1-delta,则称学习算法能从假设空间中PAC辨识概念类C)
34 | - PAC可学习:在有限样本下算法是否能够以高概率产生一个近似正确的模型
35 | - PAC学习算法:在有限的样本和时间限制下,学习算法是否能够以高概率产生一个近似正确的模型
36 |
37 | ### 线代
38 |
39 | - 秩:矩阵中线性无关的行或列的最大数量。矩阵的秩可以看作是矩阵所代表的线性变换值域的向量空间的维度,比如说PCA中的协方差矩阵如果秩是k,那么数据可以被无损压缩到k维。
40 | - 线性相关:存在一组不全为零的标量(系数),使得向量之间的线性组合等于零向量。
41 | - 特征值,特征向量:对于n阶矩阵$A$,常数$\lambda$,和非零的n维列向量$\alpha$,有$A \alpha=\lambda \alpha$成立,则称$\lambda$是矩阵A的一个特征值,$\alpha$为矩阵$A$属于特征值$\lambda$的特征向量。
42 | - 特征值分解:将一个有$n$个线性无关的特征向量的$n$阶方阵$A$分解为$A=Q \Lambda Q^{-1}$的过程。其中$Q$中的每一列都是特征向量,Lambda为对角矩阵,对角线上的元素是对应的特征值。
43 | - 首先求解特征方程$|\lambda E-A|=0$,得到矩阵$A$特征值$\lambda _i$(共$n$个)
44 | - 再由$(\lambda_i E-A)x=0$求基础解系,即矩阵$A$属于特征值$\lambda_i$的线性无关的特征向量。
45 | - 用求得的特征值和特征向量构造Q,Lambda
46 | - 奇异值分解:将矩阵A分解为$U \Sigma V^{-1}$,其中U V均为正交矩阵,Sigma为对角矩阵,对角线上的值按从大到小排列。
47 | - 计算:对$AA^\top$、$A^\top A$分别进行特征值分解,得到U和V。两次计算中的非零特征值从大到小排序,放在对角线,其他位置为零。
48 | - 矩阵分解的意义:将一个矩阵表示为多个矩阵的乘积的过程,有比如说奇异值分解,特征值分解。可以将复杂的矩阵问题简化为更易处理的子问题,提高计算效率。可以提取矩阵中的隐藏模式和结构,用于数据的降维、特征提取和模式识别等任务。
49 | - 正定:实对称矩阵$A$,对任何非零向量$x$,都满足$x^\top A x>0$
50 |
51 | - 充要条件:实对称矩阵 $A$ 正定 $\Leftrightarrow A$ 与单位矩阵 $E$ 合同;存在可逆矩阵 $C$,使 $A=C^\top C$;$A$的特征值均为正;正惯性指数$p=n$;$A$ 的各阶顺序主子式都大于零
52 | - 性质:$A^{-1}, kA,A^*,A^m, (A+B)$也是正定矩阵
53 | - 必要条件:实对称矩阵 $A$ 正定 $\Rightarrow a_{ii}>0$;$\det A=|A|>0$
54 | - 半正定:实对称矩阵$A$,对任何非零向量$x$,都满足$x^\top A x\geq0$
55 |
56 | - 等价命题:$f(x_1,x_2,\dots,x_n)$半正定
57 | - $A$半正定
58 | - $r(f)=r(A)=p$(正惯性指数)
59 | - $A$合同于非负对角阵,即存在可逆阵$C$,使得$C^\top AC=\text{diag} (d_1,\dots,d_n),d_i\geq 0$
60 | - 存在方阵$G\in R^{n\times n}$,使$A=G^\top G$
61 | - 所有主子式$\geq0$
62 | - 梯度消失和梯度爆炸是什么意思?有什么样的方法进行改善?梯度消失:残差连接(输出为输入和输出的求和),ReLU;梯度爆炸:归一化
63 |
64 |
65 | ### 概率论
66 |
67 | - 大数定律:随机变量的均值依概率收敛于期望的均值。
68 | - 中心极限定理:在适当的条件下,大量相互独立随机变量的均值依分布收敛于正态分布。
69 | - 局限:样本容量要求,可以用集中不等式解决。
70 | - 贝叶斯公式:用于计算在某个先验条件下事件的后验概率的公式。
71 | - 全概率公式:一个事件发生的概率等于它在与样本空间的一个划分中每个事件同时发生的概率之和。
72 | - 最大似然估计:是一种用于估计模型参数的统计方法。极大似然估计的基本思想是找到使观测数据的似然函数最大化的参数值。
73 |
74 | - 需要满足:样本独立同分布,参数化假设(参数可数且取值有限),模型合适
75 | - 独立同分布:independent and identically distributed,即独立同分布假设,假设数据集中的每个样本都是从同一个概率分布中独立地随机取出的。目的是简化建模。
76 | - 高维高斯分布:$\displaystyle p(x)=(2\pi)^{- D/2}|\Sigma|^{-1/2}\exp\{-\frac12(x-\mu)^{\top}\Sigma ^{-1}(x-\mu)\}$
77 |
78 | ### 数据结构与算法
79 |
80 | - P问题:可以在多项式时间内求解的决策问题。
81 | - NP问题:可以在多项式时间内验证答案是否正确的决策问题。
82 | - NP-complete :NP集合中最难的问题。是NP,且所有NP问题都可以在多项式时间内规约到它的问题。
83 | - NP-hard :所有NP问题都可以在多项式时间内规约到它的问题。
84 | - 排序稳定性:对于值相同的两个元素,排序后它们的先后顺序与原数组相同。比如在有些使用场景下需要保留原数据中元素的相对位置。
85 | - 快排:是一个基于分治的思想的排序算法,每次选择一个元素作为pivot,然后将给定的数组围绕这个基准进行划分,将小于基准的元素放到基准的左边,将大于基准的元素放到基准的右边,最终将基准放置在排序后的正确位置上。如此递归。优点:空间复杂度小,缺点:最坏复杂度无保证。选快排的原因:快排不需要进行分配和取消分配辅助数组等操作,其所需的常量时间小;空间复杂度低。
86 | - 归并排序:基于分治的思想的排序算法,每次将数组分为两个子数组,分别对子数组排序,再将两个子数组归并,形成最终的排序好的数组。优点:可并行;缺点:空间复杂度高。
87 | - topK:维护一个大小为k的小顶堆,时间复杂度$O(n\log k)$;类似快排,比如说找最大的数,pivot划分后左边80个,右边20个,只要对右边排序即可。最优$O(n)$,平均$O(n\log n)$
88 | - 判断图中有环:
89 | - 拓扑排序,最后如果还存在未被删除的顶点,则表示有环;否则没有环
90 | - DFS,如果在遍历的过程中,发现某个节点有一条边指向已经访问过的节点,并且这个已访问过的节点不是当前节点的父节点,则表示存在环(用黑白灰表示)
91 | - 对于有向图,若存在强连通分量(即存在$v_i \to v_j$的路径也存在$v_j\to v_i$的路径),图中有环。
92 | - 欧拉图:具有欧拉回路的图,欧拉回路是通过图中每条边恰好一次的回路
93 | - 有向图:非零度顶点是强连通的;每个顶点的入度和出度相等
94 | - 无向图是欧拉图当且仅当:非零度顶点是连通的;顶点的度数都是偶数
95 | - 霍夫曼编码:一种变长的数据压缩编码,通过让出现概率更小的字符长度更长,出现概率更大的字符长度更短进行数据压缩,是最优编码。基于霍夫曼树构造的。
96 | - 每次取出出现概率最小的两个结点,合并后结点权重为两个结点之和。直到所有结点构成一个二叉树。为二叉树的每个结点下的两个分支赋值为0、1,编码即从根节点到字符的叶节点的路径上01串。
97 | - 唯一可译码:因为霍夫曼编码是前缀编码,即没有一个编码是另一个编码的前缀。
98 | - 优点:最优编码。缺点:与计算机的数据结构不匹配;需要多次排序,耗费时间。
99 | - 香农编码:一种变长的数据压缩编码,效率略低于霍夫曼。
100 | - 编码方法:将符号按照其出现概率从大到小排序;把概率集合分成两个尽可能概率相等的子集,给前面一个子集合赋值为0,后面一个子集合赋值为1;如此重复直到各个子集合中只有一个元素为止;将每个元素所属的子集合的值依次串起来
101 | - 散列表的优势:查询高效,数据的存储和删除也高效。
102 | - 查询复杂度:链表型:每个哈希桶维护一个链表来存储冲突的键值对,最坏是O(n),平均接近O(1)
103 | - 普通型:当发生哈希冲突时,开放寻址再找到一个空的位置来存储冲突的值。最坏情况是O(n)(哈希表被填满),平均接近O(1)
104 | - 斐波那契:$O(2^n)$,存储结果$O(n)$;动态规划$O(n)$
105 |
106 | ### 其他
107 |
108 | - 操作系统线程跟进程的区别:进程是一个独立的程序运行的实例,线程是进程中的一个子任务。进程可以包含多个线程,进程之间是独立的,
109 | - 傅里叶变换:将信号从时域转换到频域的变换过程。
110 | - 拉普拉斯变换:傅里叶变换的一种扩展,可以将信号从时域转换到复频域。
111 | - 用处:在控制系统中,分析设计反馈控制系统;在信号处理中,用于滤波、信号重构、频谱估计和图像处理等
112 | - 两者关系:拉普拉斯变换是傅里叶变换的扩展形式;在频域分析中,拉普拉斯变换通常用于处理连续系统的输入-输出关系和系统响应,而傅里叶变换适用于连续信号和离散信号。
113 | - 凸优化带约束的一阶条件:定义域是凸集,$f(y)> f(x)+\nabla f(x)^\top (y-x)$
114 | - 二阶条件:对于开集内的任意一点,它的Hessian矩阵半正定。$\nabla^2 f(x)\geq 0$
115 | - KKT条件是非线性规划中最优解的一阶必要条件:拉格朗日函数的导数为0,原始可行性条件,对偶可行性条件,互补松弛条件。
116 | - 原始可行性条件:优化变量满足原问题的所有的约束条件,包括对于每个不等式约束和等式约束
117 | - 对偶可行性条件:对于每个不等式约束,对应的拉格朗日乘子大于等于0。
118 | - 互补松弛条件:约束的松弛变量与拉格朗日乘子的乘积为零
119 | - 凸优化中梯度下降的学习率:通过线搜索确定。线搜索是一种通过搜索确定每次迭代的合适学习率的方法。在每次迭代中,沿着梯度方向尝试不同的学习率值,通过一些准则来选择合适的学习率,使得目标函数在新的参数值上有足够的下降。精确,计算成本高。
120 | - 如果函数的定义域是凸集,且对于任意定义域上的$x,y$和任意$0\leq \theta\leq 1$,有$f(\theta x+(1-\theta)y)\leq \theta f(x)+(1-\theta)f(y)$,则函数是凸的。
121 |
122 | - 卷积和:将其中一个信号翻转再平移,再和另一个向量相乘,对乘积后的信号求和。
123 | - A*:树admissible则optimal,图consistent则optimal。admissible即到目标的估计成本<到目标的真实成本,consistent即结点与其后继的估计成本之差<这一步的真实成本
124 |
125 | - 原问题为什么要化成对偶问题:原问题线性可分就即凸,线性不可分则不凸
126 |
127 | - 对偶问题的求解可以用SMO等近似方法求解。可以引入核函数。(通过迭代地优化一对变量来求解SVM的优化问题。其主要思想是选择两个变量进行优化,将其他变量固定,并通过解析方法直接计算这两个变量的最优值。通过迭代地更新这对变量,SMO算法逐渐逼近全局最优解。)
128 |
129 | - 斐波那契数列求和:公式,DP,递归(拿字典存)
130 |
131 | - 双蛋问题:可以用动态规划求解,
132 |
133 | $W(n,h)$表示有n个鸡蛋h层楼所需的最少实验次数
134 | $$
135 | W(n,h)=1+\min(\max(W(n-1, i-1), W(n, h-i)))
136 | $$
137 | $n=2$:$W(h)=1+\min(\max(i-1, W(h-i)))$
138 |
139 | - 激活函数:引入非线性特性,Sigmoid,Tanh,ReLU,LeakyReLU。Sigmoid映射到(0,1),Tanh映射到(-1,1),这两个激活函数都存在梯度消失。ReLU可以一定缓解梯度消失问题,但是在负输入时不可导,可能存在神经元死亡的情况。LeakyReLU对ReLU改进,在负输入时保留一个小的梯度,有助于解决ReLU函数中的死亡神经元问题。
140 |
141 | - 特征值特征向量意义:特征值告诉我们特征向量在线性变换中的伸缩程度,PCA中特征值越大说明对应的特征向量相关性更大,取最大的k维。特征值可以用来判断矩阵的正定性等(特征值均>0)。
142 | - 数据规模大:对偶问题太复杂。
143 |
--------------------------------------------------------------------------------
155 |
156 |
--------------------------------------------------------------------------------
/英文.md:
--------------------------------------------------------------------------------
1 | ### Self-Introduction
2 |
3 | ### Why do you choose to study at our school?
4 |
5 | ### What do you expect to achieve during your study if you are enrolled into this institute?
6 |
7 | ### What is your plan in the postgraduate study?
8 |
9 | ### Do you have a career plan in 5 years?
10 |
11 | ### Tell me something about your undergraduate life.
12 |
13 | ### What is your favorite subject and why?
14 |
15 | ### What has been your greatest success/ accomplishment in campus life?
16 |
17 | ### What book have you recently read?
18 |
19 | ### What professional paper have you read before? What's the main idea of this text.
20 |
21 | ### Tell me something about your hometown.
22 |
23 | ### Tell me something about Nanjing.
24 |
25 | ### Can you tell me something about your family?
26 |
27 | ### What's your favorite hobby?
28 |
29 | ### Who is your favorite basketball player?
30 |
31 | ### Strength
32 |
33 | ### Weaknesses
34 |
35 | ### What kind of character do you think you have?
36 |
--------------------------------------------------------------------------------
/面经.md:
--------------------------------------------------------------------------------
1 | # NJUAI面经
2 |
3 | # 2019
4 |
5 | ## [南大lamda实验室失败面经分享_彩虹糖梦的博客](https://blog.csdn.net/caozixuan98724/article/details/100975163)
6 |
7 | 接着看论文的老师问我朴素贝叶斯决策相关的内容,朴素贝叶斯我还是会的,说了一下思想和公式。然后他问我,朴素贝叶斯是独立分布还是独立条件分布?我当时不知道是怎么的鬼使神差,答了个独立分布...只能说脑子瓦特了,那天状态真的特别差。后来知道老师问我这个问题的原因是我在论文中用了大量条件分布的东西。
8 |
9 | 最后是我觉得最奇怪的一个问题,老师问quick sort,我一下就来劲了,quick sort我熟啊,刚复习的。然后老师问我,快排为什么叫快排啊?我“?????”我弱弱的回答“因为它快啊...”。老师又问我“它是最快的吗?”我“不是啊,快排是nlogn,基数排序能到O(n)呢”。老师问“那基数排序有什么代价呢?”我说“它需要大量的空间啊,空间换时间”。然后我就楞那里了。老师“你还是没回答我的问题啊,快排为啥叫快排啊?”我“...”。
10 |
11 | 之前对于算法,重点去掌握了它的流程,它的代码,忽略了一些特别关键和基础的点,比如什么大数定律,条件分布,决策树一些更加深入的东西,没有记忆在心中。对自己的项目也没有深挖,还是要不断反思,这个项目的核心是啥,遇到了什么困难,有什么收获。
12 |
13 | # 2020
14 |
15 | ## [南大人工智能AI学院夏令营面试经历_Alvassss的博客](https://blog.csdn.net/Alvassss/article/details/107244024)
16 |
17 | ### 1.LAMDA
18 |
19 | 一轮:自我介绍 概率题 算法题 项目简介
20 | 二轮:自我介绍 你大学最满意的项目是什么 详细问
21 | 听说有三轮 但我没过第二轮
22 |
23 | ### 2.南大MCG
24 |
25 | 自我介绍 老师完全按照简历询问
26 |
27 | ### 3.南大笔试
28 |
29 | 重点:
30 | 1.线代+概率 线代主要是概念 概率主要是网上那些脑筋急转弯
31 | 2.机器学习 建议西瓜书前十章要精通
32 | 3.数据结构 考的巨多 建议精通
33 | 4.算法 时间复杂度分析 渐进 背包问题 摊还
34 | 非重点:
35 | 博弈论 各种变换(傅里叶啥的 俺没学过)
36 |
37 | ### 4.南大面试
38 |
39 | 英语面试:是学院的一个越南老师面试 比较亲切 但我心态崩了
40 | 三个问题:
41 | 1min自我介绍(超时会直接截止 不要问我为什么知道)
42 | 最喜欢的课程 why
43 | 最喜欢的机器学习算法
44 | 中文面试:
45 | 快速排序和归并排序优缺点 排序为什么要稳定
46 | P问题 NP问题 NP完全问题的概念
47 | 全概率公式意义
48 | 项目问题
49 |
50 | ## [南大人工智能学院夏令营经历记录_TheRebel_的博客](https://blog.csdn.net/Anonymity_/article/details/105407815?spm=1001.2101.3001.6650.1&utm_medium=distribute.pc_relevant.none-task-blog-2~default~CTRLIST~Rate-1-105407815-blog-107244024.235^v31^pc_relevant_default_base3&depth_1-utm_source=distribute.pc_relevant.none-task-blog-2~default~CTRLIST~Rate-1-105407815-blog-107244024.235^v31^pc_relevant_default_base3&utm_relevant_index=2)
51 |
52 | 面试问了我大概五道题,一道问排序算法,及时间复杂度。第二道问我svd是什么。第三道是关于我最喜欢的深度学习模型。第四道和第五道是围绕我的项目经历问的。然后计算机营和ai营机试:面试比好像不一样。另外,ai院报周志华和lamda组的很多,但其实lamda在这之前已经招过一次了,所以夏令营他们再招的名额可能会比较小。
53 |
54 | ## [【计算机保研夏令营】2020年LAMDA保研面试经验](https://zhuanlan.zhihu.com/p/237472334)
55 |
56 | ### 面试 6.18
57 |
58 | 大概在报名结束后一周收到了第一次面谈的邀请邮件,LAMDA都是提前一天发邮件,第二天直接面试。这时候还在期末考试阶段,比较紧张,也没准备啥,就对着简历花了一小时思考了下。第一轮我们组是10个人,按姓名拼音排序进行面试的,面试官是组里的三个学长,先进行自我介绍,之后主要问了我以下三个问题:
59 |
60 | > 详细介绍了下比赛(我参加过一个数据挖掘的比赛)的特征工程,之后又问了模型部分(介绍了下Xgboost)
61 | > 对机器学习的理解(这个感觉自己答得不是很好,说的有点绕进去了)
62 | > 对开放动态环境下机器学习的挑战和瓶颈的认识(这个后来我查过,是那个学长的博士课题,听DJW学长说这个也是LAMDA组里的一个大坑,ps. 这里大坑指大方向,不是说坑,有学弟问了才发现有人会误解emmm)
63 |
64 | 总的来说,这一轮面试比较愉快,主要了解一些基本情况吧,感觉这一轮没有刷人。
65 |
66 | ### 3. 第二轮面试 6.20
67 |
68 | 第一轮面试结束第二天就发下一轮通知了,询问D学长了解去年的流程后,也大概猜到了这一轮可能是群面,面之前学长还说遇到ZDC老师坐等聊爆,结果8:50进入腾讯会议,我傻眼了,一奶即中。
69 |
70 | 首先还是少不了自我介绍,介绍完之后Z老师就问我对博士期间的规划,这个问题之前思考过很久,也是一个保研期间的必问问题,由于我把规划从大四说起(大四如果保研顺利结束想先强化学习数学基础,说了凸优化、随机过程、矩阵分析之类的),也给后续埋了个坑——下一个问题他问我最喜欢哪门课,我以为他想问上面三门,就问了句是不是本科阶段,被WW老师说难道你还有研究生阶段吗,有点尴尬。我作死的说了数据结构(但我确实真的很喜欢数据结构,其他课也没准备,想着数据结构学的还行就说了),但直接问我红黑树了,我有点傻眼了,老实说自己不会,只知道STL有些底层是红黑树实现的(有时间还是得看下红黑树,至少得了解思想)。
71 |
72 | 之后就是一连串的问题,先问了归并和快排的平均、最优、最坏复杂度,这个准备实习面试时都梳理过,都答出来了。然后接着这个问题问,既然归并的最坏也是O(nlogn),而快排最坏O(n^2),为啥现在大家都用的是快排。我只从空间复杂度进行了分析,后来面完查了下,其实实践证明,虽然二者时间复杂度相同,但快排还是要快一些,而且最坏情况遇到的可能性也比较低。之后问的应该是如何判断图中是否有环,我刚嘴里小声复述想思考下,老师就直接问下一个问题了,这里感觉这一轮应该就是压力面。
73 |
74 | 下一个问题问的是比赛,让我介绍Xgboost的优势,这个实习面试也复习过,答得还可以。接下来WW老师问我本科学校是985吗?是211吗?是双一流吗?一波三连搞得我有点尴尬,我校果然在南方知名度还是不行。
75 |
76 | 最后Z老师又问你本科北京的学校为啥想来南京,说以前很多北京的同学拿了offer又鸽了。这个问题就有的聊了,因为我本身是江苏人,高中物理竞赛又在南大两个校区住过一段时间,挺喜欢南大的,南大也算是高中dream school之一了,然后就是LAMDA很强哈哈哈哈。
77 |
78 | 总结一下,这一轮面试节奏很快,可能也是面试过程中比较兴奋,我整体回答问题几乎没有思考,没有用到10分钟应该。这一轮面试应该刷了一半人左右。
79 |
80 | ### 4. 第三轮面试 6.22
81 |
82 | 这一轮面试一直到6.21晚9点才通知,大部分人收到的邮件都写明了是哪个老师面试,根据这两轮小组面试人数的猜测,可能第二轮刷了有一半人,但不确定,也可能是分批。我的邮件没有写明老师,我第一志愿是JY老师,但听D学长说J老师学生有部分也都是Z老师带,所以猜测可能会使Z老师面。D学长给我看了他去年整理的面试经历,大概了解了一些情况以及基本问题。这时候由于已经期末考完了,但也没想到面试这么突然,也来不及准备太多,就稍微过了下线代和概率论的一些基本概念,理解了一下,然后准备了一下简历。
83 |
84 | 最终面我的还是J老师。第一个环节还是自我介绍,介绍完之后老师开始问“以后的规划”、“家庭背景”、“家人对自己的规划”等等,接下来又问了“简历中的数据挖掘比赛主要负责的内容以及收获”、“本科科研项目最大的收获”等问题,都很友好,聊了大概20多分钟。
85 |
86 | # 2021
87 |
88 | ## [2021年人工智能保研经历(xduee->njuai)](https://zhuanlan.zhihu.com/p/420184627)
89 |
90 | 人工智能学院的笔试主要考人工智能+计算机的基础知识。笔试用考试星机考的方式,考试时长2小时,大概我记得200道题目左右,应该是比2020年的笔试少了50道题目左右,题目难度适中,因为难题我全刚开始跳了,我差不多连猜带蒙在最后差10min的时候完成了所有题目。南大学院笔试的考核真的很重要很重要,属于超强committee,即使你提前被周老师录了,笔试没过也是没用的。
91 |
92 | 参营时间线的话,是2021.7.8举行笔试,然后7.11周日上午(当时正在看美洲杯决赛,印象深刻)出了笔试的结果,应该是进60%~70%左右的人。笔试结果出了后,就会让你选择学硕or直博。南大一般在这个时候才会让你选择学硕和直博,刚开始报名的选择只是预选择。下面就是面试,7.13一整天是学硕面试,7.14上午是直博生面试,直博面试应该有22人,录了多少我也不是很清楚,下面说说面试情况。
93 |
94 | 线上面试还是采用的腾讯会议,每人12min,4min英语问答+8min专业知识。我那组的面试官有4人,面试可以说是相当友好了,英语问答包含自我介绍,以及一些关于我科研的提问,还有一些闲聊,英语这部分总体来说不难,敢于去说就行。专业知识部分,主要还是在问机器学习+线性代数的相关知识,我感觉我个人准备的比较充分,所有问题都回答出来了,除了最后詹老师的一个关于编码的问题回答的不太行。
95 |
96 | 关于机器学习面试的问题可以参考我另一篇经验贴:**[计算机/人工智能方向保研高频面试题目整理](https://zhuanlan.zhihu.com/p/394374473)** ,这篇经验贴我应该概括的比较全面了。
97 |
98 | ### [计算机/人工智能方向保研高频面试题目整理](https://zhuanlan.zhihu.com/p/394374473)
99 |
100 | ### **1. 开放型问题**
101 |
102 | 开放型问题建议中英文都准备,大部分面试都有这个环节。
103 |
104 | - 自我介绍(1min/3min)
105 | - 研究生期间的规划
106 | - 参与的竞赛(数模等等),你做了哪儿些工作?
107 | - 简单介绍下你的科研工作
108 | - 对机器学习/深度学习的理解
109 | - 开放动态环境下机器学习的认识(来自南大某著名实验室)
110 |
111 | ### **2. 数学类**
112 |
113 | 数学类问题是ai方向保研面试问的最多的,主要是线代、概率论。
114 |
115 | - 线代:如何理解矩阵的秩?简述向量组线性无关的含义?解释正定矩阵以及半正定矩阵?特征值的含义以及矩阵分解的物理意义?
116 | - 概率论:简述大数定理,中心极限定理,全概率公式,最大似然估计,贝叶斯的含义
117 | - P问题 NP问题 NP完全问题的概念
118 |
119 | ### **3. 机器学习类**
120 |
121 | - 简述PCA的计算过程
122 | - 简述SVM,并解释SVM为什么要化对偶形?百万样本量可以用SVM吗?
123 | - 常用的机器学习算法的适用场景(例如KNN、朴素贝叶斯、决策树等)
124 | - 具体阐述残差神经网络的含义
125 | - 梯度消失和梯度爆炸是什么意思?有什么样的方法进行改善?
126 | - 简述几种集成学习方法Adaboost的计算过程以及Stacking Learning?
127 |
128 | ### **4. 数据结构与算法类**
129 |
130 | - 常用排序平均最优最坏时间复杂度以及空间复杂度,阐述快排和归并的优缺点以及回答为什么排序要稳定?
131 | - 归并排序的最坏时间复杂度优于快排,为什么我们还是选择快排?
132 | - TopK问题详解
133 | - 如何判断图里有环?
134 | - C++中new和malloc的区别
135 |
136 | ## [2021年一战南大AI上岸经验贴_Yuhan の Blog的博客](https://blog.csdn.net/qq_45228537/article/details/115448786)
137 |
138 | ### 复试笔试
139 |
140 | 南大AI的复试笔试是离散数学+机器学习;我是3月开学回学校才开始准备,这里建议早点准备离散,离散东西很多概念很杂而且考的也很难,所以我今年离散笔试应该基本没拿到分orz;今年的机器学习也不知道在搞什么,无语子,写着机器学习的label考了20道数据结构的选择题+一道不知道属于啥学科的问答,不过该准备的还是要准备的。
141 | 离散建议找一下南大本科的PPT,有重点地对着屈书进行复习;复试的机器学习建议细看一下,部分重点的数学推导要会(例如SVM的拉格朗日乘子法、KKT条件、PCA特征值分解),概念要十分清晰,即使复试没有考察到,面试老师也会问许多机器学习的相关知识。
142 |
143 | ### 复试机试
144 |
145 | 今年情况特殊,是线上复试,因此今年的机试是和笔试在一起考的,但我想,随着疫情逐渐得到有效控制+全民疫苗接种,今后应该会继续采用线下机试的方法。
146 | 个人本科练习过半年左右的OJ,因此有一点薄弱的基础,因此就是在考前临时复习了一下黄宇书上的4道DP例题+一些常见的DP题(01背包、完全背包、LCS、多重部分和问题、LIS、DP计数等等)+一些常用的数据结构和算法(例如并查集、kruskal、dijkstra、快速幂、素数筛、线段数、树状数组等等)。
147 | 对于南大的机试,我觉得重点是DP、搜索、图论。
148 |
149 | ### 复试面试
150 |
151 | 面试个人认为可以拆分成英语口语+线代+概率论+机器学习+项目经验+一些其它知识储备。
152 | 口语问了我这些问题:
153 |
154 | 1.本科所学专业
155 | 2.毕业后打算
156 | 3.兴趣爱好
157 | 4.介绍喜欢的电影
158 | 5.介绍最近读的一本书
159 |
160 | 面试:
161 |
162 | 1.你说你因为喜欢数据结构和算法才选择读AI,介绍一下它们的交集
163 | 2.本科有没有做过AI相关的项目
164 | 3.SVM为什么要采用对偶问题?(我答:虽然可以通过现成凸优化包求解,但是对偶问题求解更快)
165 | 4.为什么更快?(接4中我的回答内容
166 | 5.Boosting学习有什么特点?
167 | 6.为什么集成学习需要集成“好而不同”的学习器?(接5中我的回答内容
168 | 7.解释一下特征值的含义
169 | 8.简述一下特征值分解
170 | 9.为什么要选取前d大个特征值(接8中我的回答内容
171 | 10.你本科是软工的,问一下面向过程、面向对象、面向抽象的区别
172 | 11.具体介绍一下你学过的面向对象知识&应用
173 | 12.你觉得你本科所学的知识在将来读AI的时候会有哪些应用
174 |
175 | ### [南京大学LAMDA面经汇总_51CTO博客](https://blog.51cto.com/u_12312066/3695982)
176 |
177 | 面试吴建鑫老师的时候,问题如下:
178 |
179 | 方差的计算方法,他会提前写好一个方差表达式问你对不对,如果不对的话请写出正确的表达式;
180 | 方差中的n-1含义;
181 | 如果写一个程序计算方差,那么计算一次内存访问几次;
182 | 本科做过的项目,项目内容;
183 | 机器学习了解多少,看过什么;
184 | 了不了解本人是做什么研究的。
185 | 面试詹德川老师的时候,我不知道其他人是什么情况,但我是全程英文面试,问到的问题如下,注意:以下问题需要英文作答,实在英语回答不了,可以中文,不必有太大压力:
186 |
187 | 自我介绍一下;
188 | 介绍一下做过的项目;
189 | 介绍一下梯度下降法是什么;
190 | 介绍一下牛顿迭代是什么;
191 | 什么是特征值,特征值的含义;
192 | 唠嗑。
193 | 面试完当天晚上就会有邮件通知是否面试通过,最后我是被詹德川老师录取,但是通过LAMDA面试并不代表你就能100%能进入LAMDA读研了,最重要的一关是拿到南大夏令营的优秀营员,只有这样,通过两轮考核才能进入LAMDA。
194 |
195 | 下面说一下南大夏令营的流程,主要是三部分:各个实验室介绍、机试、面试,其中最最重要的是机试,只要机试通过,90%就能拿到优秀营员。
196 |
197 | 机试这次一共4道题,以前听说6道题,只要AC出其中的两道题就肯定没问题了,多做无用,有罚时,考核方式:OJ,题型:算法+数据结构,难度:ACM一般难度的题。这次的具体题目如下:
198 |
199 | 最大子串和;
200 | 无向图最长路径
201 | 表达式求值;
202 | 给一棵树求最长的路径。
203 | 面试问题如下(由于分组面试,每组没人问题不一样):
204 |
205 | 解释一下什么是时间复杂度;
206 | 快排的时间复杂度;
207 | 快排最坏时间复杂度为什么是$O(n^2)$,如何优化快排最坏时间复杂度;
208 | 看成绩单,问如何进行文献检索
209 | 英文回答:如何利用文献检索知识去检索一个机器学习的问题
210 |
211 | 就问了一个“ε-greedy”算法中ε取值的问题
212 |
213 | 然后问了离散的全序,偏序,操作系统,计算机组成原理内存啥的,还有居然问了软件工程的问题,真是醉了,那个时候软件工程都还没有学完。(黑人问号脸)然后,英文是让我介绍最喜欢的歌曲。
214 |
215 | 南大进行了一场霸面(不推荐,还是提早申请比较好)。
216 |
217 | 1.快排复杂度是多少,并且黑板上手写证明。
218 |
219 | 2.简述如何“快速选到第n个数”(快速选择,复杂度为O(n))。
220 |
221 | 3.讲简历上的项目,根据简历问
222 |
223 | 有无申请lamda都需要参加下面两场考试:
224 |
225 | 机试(两个小时,四选二,一般两道都做出来能入选):
226 |
227 | 1、连续最长子序列和(给了一堆正负的数字,任选其中一段连续的数字(可以全选),需要和最大)
228 |
229 | 2、无向图最长路径(单纯的Dijkstra)
230 |
231 | 3、给一个表达式,例如 (3*2+1/2)+1*2,计算结果
232 |
233 | 4、给了一棵树求最长的路径(根到叶节点)
234 |
235 | 面试:
236 |
237 | 1、英文自我介绍
238 |
239 | 2、按照不同专业方向问专业课程
240 |
241 | 3、大数定理、贝叶斯公式等
242 |
243 | 4、操作系统线程跟进程的区别等(操作系统的问题比较爱问)
244 |
245 | ## [2021年计算机保研(清深、南大AI、中科大、哈深、中山等)](https://zhuanlan.zhihu.com/p/416191365)
246 |
247 | ### 学院
248 |
249 | 考核方式:初审(985前5%) + 笔试 (机器学习、概率论、线性代数、数据结构等)+ 面试(机器学习、数学)
250 |
251 | 笔试:2小时做200多道填空和选择,其内容涵盖机器学习、概率论、线性代数、数据结构等。对于概率论和线性代数,建议耗时两三天刷完李永乐660,刷完就没问题。对于机器学习,建议把西瓜书前十章过一遍,主要是看概念即可。对于408,可以选择不看,考的不多。
252 |
253 | 面试:英语问答 + 专业知识考察。英语问答就准备好常见的英语问题,以及和你简历相关的英语问题即可。至于专业知识,就是考察机器学习和数学,建议把西瓜书或李航统计学细读并理解,数学建议把概率论和线代细读并理解。
254 |
255 | 总结:由于当时概率论和线代复习的不好,导致数学问题只答出一半,进入wl。要想过南大AI,没有别的秘诀!把线性代数、概率论、机器学习从头啃到位即可!
256 |
257 | # 2022
258 |
259 | ## [Kaslanarian/NJUAI-OpenDay-Interview: 南京大学人工智能学院本科生开放日面试经验分享 ](https://github.com/Kaslanarian/NJUAI-OpenDay-Interview)
260 |
261 | ### 同学A(同组)的面试问题
262 |
263 | 面试那天和我在一个房间,而且在我前面面,所以记录了所有的问题:
264 |
265 | - 英语面试:
266 | 1. 1分钟自我介绍;
267 | 2. 从事的研究细节(因为自我介绍中提及);
268 | 3. 你最感兴趣的课程;
269 | 4. 你以后是想留在学校做研究还是去公司工作。
270 | - 中文面试:
271 | 1. 大数定律是什么?
272 | 2. 中心极限定理是什么?
273 | 3. 讲一个你知道的聚类算法?
274 | 4. 你平时有什么放松方式?
275 | 5. Boosting的基本思想?
276 | 6. PCA的全称是什么?
277 | 7. PAC理论的全称是什么?
278 | 8. 欧拉图是什么?
279 | 9. 正定矩阵是什么?
280 | 10. 极大似然估计是什么?
281 | 11. SVM为什么叫支持向量机?
282 |
283 | 注意,上述问题只是前置问题,你说不会才会换问题,否则就会继续问。比如同学A说他不记得欧拉图了,然后对面就换下一个问题;面试到我的时候又问了这个问题,我答出了欧拉图定义,后面就问我判定方法了。
284 |
285 | ### 我的面试
286 |
287 | - 英语面试:
288 |
289 | - 1分钟自我介绍;
290 | - 介绍一下你参加的比赛(起因于我的腾讯会议背景是我上次参加的某比赛,然后忘了换😢,反过来想这也是一种思路,让面试官问出你想让他问的问题😄);
291 | - 以后的安排(类似于同学A的问题)。
292 |
293 | - 中文面试:
294 |
295 | - 大数定律是什么?(看我倒背如流就没问中心极限定理了)
296 |
297 | - 计算复杂度(P和NP),P=NP吗?
298 |
299 | - 遇到压力怎么放松?
300 |
301 | - 最喜欢的课程?
302 |
303 | - 介绍PCA;
304 |
305 | - 为什么机器学习中的基本假设是独立同分布,独立同分布全称是什么?(这个地方卡了,对面嫌我说多了)
306 |
307 | - 什么是欧拉图,如何判定欧拉图?(忘记了,只说记得存在一个充要条件)
308 |
309 | - 正定矩阵是什么,如何判定?
310 |
311 | > 跟面试官(王魏)怼了,他一直说我和书上的定义不一样,但我讲的是一个逻辑等价命题,他就说我不好好看书,弄得心态挺不好。幸好他是最后一个问问题的老师。
312 | >
313 | > 后来发现和我一组的同学都对他有意见的,比如同学B说他不会欧拉图,然后被他锐评:**你是不是没上过数学课?**
314 | >
315 | > 问同学C的时候,C回答不出来就咂嘴,问答少了就说”**这么不熟悉吗**“...
316 | >
317 | > 注:以上内容是节选,如果看的人多了就把老师名字给码了。感觉他是根据被面试者的态度进行反馈,比如我、B和C在面试的时候展现出自信,所以他很打压;A面试的时候很严肃,遇到不会的问题会说“对不起,我回去再看一下”,所以没咋刁难。反正看到的同学留个心眼吧。
318 |
319 | - 快速排序的平均时间复杂度,最坏时间复杂度,最坏情况是什么样?
320 |
321 | ### 本组其他同学的问题
322 |
323 | - 计算复杂度,但问的是:如果把时间换成空间,那么P=NP吗?
324 | - PAC理论了解多少?
325 | - TBD
326 |
327 | ### 其他组的问题
328 |
329 | 这里记录其他组同学那里听来的问题:
330 |
331 | - 喜欢的数学课?如果说了微积分这块,而不是AI相关,则会问:
332 | - 中值定理是什么?
333 | - 泰勒展开是什么?
334 | - 高阶无穷小是什么?
335 | - 傅里叶变换和拉普拉斯变换的关系?
336 | - 拉普拉斯变换的用处?
337 | - 双蛋问题,但是单蛋版,也就是你只有一个鸡蛋如何判定其不摔碎的最高楼层?
338 | - TBD
339 |
340 | ## [2022年/2023届预推免小记(科大6系&NJUAI)](https://zhuanlan.zhihu.com/p/570734028)
341 |
342 | NJUAI:
343 |
344 | 笔试:2h(记不太清了),题量很小,选择+问答
345 |
346 | 面试:英文自我介绍+英文专业问题+专业问题,南大是步步紧逼型面试,感觉问了不止十个问题。
347 |
348 | 比较迷惑的一点是面试是定死了12min/人,结果还剩20s的时候老师又问了一个问题,我刚说两句就直接结束了,这种情况主持人不应该提醒一下快到时间了吗(汗)
349 |
350 | ## [2022年(2023届)计算机保研——计算所vipl、南大lamda、北大计算机、人大高瓴等](https://zhuanlan.zhihu.com/p/570001872)
351 |
352 |
353 |
354 | 看了一些经验帖说,南大LAMDA比北大信科还难,有很多LAMDA面试没过的最后去了北大信科,所以我当初报名没报什么信心,找了一位和自己研究经历比较match的老师,就去参加了。
355 |
356 | 首先是初筛,985的5%应该都能过初筛,除此之外我觉得研究方向的match程度非常重要。
357 |
358 | 一面是学长面,先是一分钟自我介绍,然后就是基本的简历面,问了paper以及剩下几个科研项目做的是什么和创新点,差不多就结束了,没有问任何专业知识相关的问题。
359 |
360 | 二面是老师面,问题大概有:
361 |
362 | 1. 一分钟自我介绍
363 | 2. paper里我主要做的内容
364 | 3. AI for SE领域有什么地方还可以去尝试?
365 | 4. 最拿得出手的项目是什么
366 | 5. 遇到的挫折是什么
367 | 6. 你觉得图神经网络做代码生成目前的优点和缺点是什么?有什么改进的地方?
368 | 7. 有没有做过词法分析器和语法分析器
369 | 8. 智力问题,黑白帽子问题(可自行百度)
370 | 9. 剩下就是一些聊天性问题,比如如果离交稿ddl还剩两天,但是你的实验还有很大漏洞,论文也还没写完,这种情况怎么办;了解了我的家乡以及为什么想来南京等
371 |
372 | 最后获得了实验室的offer,我个人感觉成功的原因是 1. 由于方向match,所以了解比较深入,中间考察的一些对该领域科研的相关看法时回答的还不错;2. 正好问到了我之前思考过的比较有意思的idea,所以和老师聊的很愉快。
373 |
374 | 但是!只拿到实验室的offer还没结束,还需要通过南大AI学院的考核,于是就有了绿裙里通过实验室考核没通过学院考核的难兄难弟们(后来发现这些难兄难弟里有人去了贵系,只想说南大AI真牛)
375 |
376 | AI院笔试:题量很大,考察范围覆盖数据结构、机器学习(西瓜书)、概率论、线性代数、英语等,如果目标南大AI的建议提前好好复习一下。不要像我一样,“怎么还有过了LAMDA没过学院的” “小丑竟是我自己”
377 |
378 | 另:夏令营笔试寄了就彻底寄了,也没办法报名预推免了。
379 |
380 | ## [2022南京大学人工智能学院本科生开放日小记【保研向】](https://zhuanlan.zhihu.com/p/543677717)
381 |
382 | 夏令营笔试是双机位,考试星作答。去年是两百道选择题和填空题两个小时,今年则是66道选择题,20多道填空题,若干多选题,英文题以及简答题,一共一个半小时。考察的科目和去年倒是差不多,这点知乎上也是有人写的,机器学习、概率论、线性代数、数据结构与算法,都是需要复习的。因为是线上考试所以不会有太多复杂的计算,更多考察知识的广度与细节部分,也就是看书复习的时候各种细节都应该注意。我根据前面大佬的建议也用了几天刷了李永乐660的线代和概统部分,感觉还是有不少帮助的。经过我们的讨论,感觉AI营的重点是笔试而非面试。
383 |
384 | 面试也是双机位,腾讯会议面试。以往都是20分钟一个人,今年估计是报名人数比较多,所以改为了12分钟一个人。还是4个老师分别问不同学科的问题。我这里大概记了一下面试的问题(不同的组面试题差别还是挺大的)
385 |
386 | C:你研究生读完之后有什么打算?你有什么做研究的品质?(英文面试,有概率让你用英文自我介绍,也有可能没有)
387 |
388 | 詹:常微分方程f'(x) = cx的解的形式,如果c是常数,为什么形式,如果c为矩阵呢?霍夫曼编码的优势,霍夫曼编码的唯一性,香农编码是什么?
389 |
390 | 张:半正定矩阵的定义,性质(越多越好),PCA协方差矩阵的性质(半正定),以及为什么半正定(从原理上说明)?凸优化中梯度下降的学习率如何确定?(凸优化最后两课讲的)
391 |
392 | 姜:散列表的优势(相比其他查询方式),查询复杂度(分链表型和普通型)。研究生的“研究”二字是什么含义?研究生相比本科生有什么区别?
393 |
394 | 其他同学有问图灵机的,凸优化带约束的一阶条件的,中心极限定理,机器学习很多算法为什么要iid条件,SVM核函数的考察等等,比较广泛,只看西瓜书显然是不够的,还需要一些自己的思考和积累。
395 |
396 | 总体来说感觉面试是不断往深去问,老师会追问你问题的本质,直到不会为止。因此面试完成后问了一圈感觉都不是特别好,这也是正常现象。面试完之后就是漫长的几天等待时间。
397 |
398 | 7.11线上导师宣讲会,7.13开放日线上面试。
399 |
400 | ## [2023CS保研经验分享(清深、上交、南大LAMDA、同济、东南Palm等) - 知乎 (zhihu.com)](https://zhuanlan.zhihu.com/p/570722079)
401 |
402 | 第一轮面试主要是实验室的学长学姐进行,主要围绕就是一些理论知识和你自我介绍的项目中所涉及的一些问题。
403 |
404 | 项目的问题没啥共同性,我就列举一些印象中的常见问题:
405 |
406 | - 机器学习中FP、TP是什么?
407 | - 你为啥想要读直博?
408 | - 线代中的矩阵的秩和矩阵的关系?
409 | - 讲一讲线代中的矩阵的特征值?
410 | - ......
411 |
412 | 第二轮面试是意向导师单独面(我是这样的),L老师只是来聊了聊天,聊一下我想研究的方向和家是哪里的,为什么要来南大等等一些非学术问题,最后说因为直博已经确定了人选,只能给我学硕offer了。
413 |
414 | - 题量:应该是100道差不多,时长90分钟。
415 |
416 | - 题型:单选题、多选题、填空题、英文问答题。
417 |
418 | - 考察内容:
419 |
420 | - - 线性代数(有复杂计算,我遇到了张宇考研数学的原题)
421 | - 概率论(有奇怪的伤脑筋的题,得多练)
422 | - 数据结构(重点,有考察排序算法、链表)
423 | - 机器学习(把西瓜书看看就行,考的都是知识点,概念性的东西)
424 | - 印象中没有计组计网操作系统
425 |
426 |
--------------------------------------------------------------------------------
/面经(分类).md:
--------------------------------------------------------------------------------
1 | # 面经(分类整理)
2 |
3 | 笔试+上机(最关键,笔试过不掉救不了)
4 |
5 | - 100分笔试,机器学习,模式识别,数据结构与算法,知识推理(zyz,英文题,要看一下),人工智能,概率统计(简答题,其他是选择填空)
6 | - 50分编程题,什么方向不知道,应该和机器学习和算法相关。
7 | - 月底组内,积累点经验,问一下学长,口语是怎么样的。
8 | - 本校有一定的优势,尽可能做好,题量不少,做不对略过即可,不要纠结。
9 |
10 | ## 概率论
11 |
12 | - 大数定理
13 | - 中心极限定理
14 | - 全概率公式
15 | - 最大似然估计
16 | - 贝叶斯公式:接着看论文的老师问我朴素贝叶斯决策相关的内容,朴素贝叶斯我还是会的,说了一下思想和公式。然后他问我,朴素贝叶斯是独立分布还是独立条件分布?我当时不知道是怎么的鬼使神差,答了个独立分布...只能说脑子瓦特了,那天状态真的特别差。后来知道老师问我这个问题的原因是我在论文中用了大量条件分布的东西。
17 | - 网上那些脑筋急转弯
18 | - 独立同分布:为什么机器学习中的基本假设是独立同分布,独立同分布全称是什么?(这个地方卡了,对面嫌我说多了)
19 |
20 | ## 机器学习
21 |
22 | 西瓜书前十章精通
23 |
24 | - 对机器学习/深度学习的理解
25 | - 开放动态环境下机器学习的认识(来自南大某著名实验室)
26 | - PCA:简述PCA的计算过程,PCA的全称是什么
27 | - SVM:简述SVM,并解释SVM为什么要化对偶形?百万样本量可以用SVM吗?(我答:虽然可以通过现成凸优化包求解,但是对偶问题求解更快)为什么更快?
28 | - 讲一个你知道的聚类算法?
29 | - 集成学习:简述几种集成学习方法,Adaboost的计算过程,以及Stacking Learning?Boosting的基本思想?Boosting学习有什么特点?为什么集成学习需要集成“好而不同”的学习器?介绍Xgboost的优势
30 | - 常用的机器学习算法的适用场景(例如KNN、朴素贝叶斯、决策树等)
31 | - PAC理论:PAC理论的全称是什么?PAC理论了解多少?
32 | - 具体阐述残差神经网络的含义
33 | - 梯度消失和梯度爆炸是什么意思?有什么样的方法进行改善?
34 | - 介绍一下梯度下降法是什么
35 | - 介绍一下牛顿迭代是什么
36 | - 为什么机器学习中的基本假设是独立同分布,独立同分布全称是什么?(这个地方卡了,对面嫌我说多了)
37 | - $ \epsilon $ -greedy:就问了一个“ε-greedy”算法中ε取值的问题
38 | - 决策树一些更加深入的东西
39 | - 机器学习中FP、TP是什么?
40 |
41 | ## 数据结构与算法
42 |
43 | - 数据结构 考的巨多 建议精通
44 | - 时间复杂度分析
45 | - 渐进
46 | - 动态规划:背包问题
47 | - 摊还
48 | - 排序:
49 |
50 | - 排序:算法,平均最优最坏时间复杂度以及空间复杂度。黑板上手写证明。排序为什么要稳定。
51 | - 快排:平均、最优、最坏复杂度。最坏情况是什么样?优缺点。
52 | - 归并:平均最优最坏时间复杂度以及空间复杂度,优缺点。
53 | - 既然归并的最坏也是 $ O(n\log n) $ ,而快排最坏 $ O(n^2) $ ,为啥现在大家都用的是快排。(我只从空间复杂度进行了分析,后来面完查了下,其实实践证明,虽然二者时间复杂度相同,但快排还是要快一些,而且最坏情况遇到的可能性也比较低。)
54 | - P问题 NP问题 NP完全问题的概念
55 | - 直接问我红黑树了,我有点傻眼了,老实说自己不会,只知道STL有些底层是红黑树实现的(有时间还是得看下红黑树,至少得了解思想)
56 | - 图
57 |
58 | - 如何判断图中是否有环
59 | - 欧拉图是什么?判定方法?
60 | - TopK问题详解,“快速选到第n个数”(快速选择,复杂度为 $ O(n) $ )
61 | - C++中new和malloc的区别
62 | - 双蛋问题,但是单蛋版,也就是你只有一个鸡蛋如何判定其不摔碎的最高楼层?
63 | - 智力问题,黑白帽子问题(可自行百度)
64 | - 霍夫曼编码的优势,霍夫曼编码的唯一性,香农编码是什么?
65 | - 散列表的优势(相比其他查询方式),查询复杂度(分链表型和普通型)
66 |
67 | ## 线代
68 |
69 | - svd(奇异值分解)
70 | - 讲一讲线代中的矩阵的特征值?什么是特征值,特征值的含义,特征值分解
71 | - 正定矩阵是什么?
72 | - 如何理解矩阵的秩?线代中的矩阵的秩和矩阵的关系?
73 | - 简述向量组线性无关的含义?
74 | - 矩阵分解的物理意义?
75 | - 半正定矩阵的定义,性质(越多越好),PCA协方差矩阵的性质(半正定),以及为什么半正定(从原理上说明)?
76 |
77 | ## 凸优化
78 |
79 | - 凸优化带约束的一阶条件
80 | - 凸优化中梯度下降的学习率如何确定?(凸优化最后两课讲的)
81 |
82 | ## 操作系统
83 |
84 | - 操作系统线程跟进程的区别等(操作系统的问题比较爱问)
85 |
86 | ## 数学分析
87 |
88 | - 常微分方程f'(x) = cx的解的形式,如果c是常数,为什么形式,如果c为矩阵呢? $ \frac12x^\top Cx $
89 | - 傅里叶变换和拉普拉斯变换的关系?拉普拉斯变换的用处?
90 |
91 | ## 其他
92 |
93 | - 一分钟自我介绍,遇到的挫折是什么
94 | - 研究生的“研究”二字是什么含义?研究生相比本科生有什么区别?
95 | - 比如如果离交稿ddl还剩两天,但是你的实验还有很大漏洞,论文也还没写完,这种情况怎么办
96 | - 英文面试
97 | - 1分钟自我介绍
98 | - 从事的研究细节(因为自我介绍中提及)
99 | - 你最感兴趣的课程
100 | - 你以后是想留在学校做研究还是去公司工作。
101 | - 如何利用文献检索知识去检索一个机器学习的问题
102 | - 你研究生读完之后有什么打算?你有什么做研究的品质?
103 |
104 | ## 机试
105 |
106 | - 最大子串和(给了一堆正负的数字,任选其中一段连续的数字(可以全选),需要和最大);无向图最长路径(单纯的Dijkstra);表达式求值(例如 (3\*2+1/2)+1\*2,计算结果);给一棵树求最长的路径(根到叶节点)。
107 | - 南大的机试,我觉得重点是DP、搜索、图论
108 |
109 | ## 笔试
110 |
111 | - 题量:应该是100道差不多,时长90分钟。
112 | - 题型:单选题、多选题、填空题、英文问答题。
113 | - 考察内容:
114 | - 线性代数(有复杂计算,我遇到了张宇考研数学的原题)
115 |
116 | - 概率论(有奇怪的伤脑筋的题,得多练)
117 | - 数据结构(重点,有考察排序算法、链表)
118 | - 机器学习(把西瓜书看看就行,考的都是知识点,概念性的东西)
119 | - 印象中没有计组计网操作系统
120 |
121 | 1. 可靠性(Soundness):在命题逻辑中,可靠性是指逻辑系统的一个属性,表示该系统中的推理规则是正确的。如果一个逻辑系统是健全的,那么任何从该系统的有效前提推导出的结论都是真的。换句话说,如果一个论证是健全的,那么它不会导致从假前提推出真结论的情况。
122 | 2. 完备性(Completeness):在命题逻辑中,完备性是指逻辑系统的另一个属性,表示该系统中的每个真陈述都可以在该系统中被证明为真。换句话说,如果一个逻辑系统是完备的,那么对于任何为真的陈述,系统中存在一个证明或推理来证明它的真实性。
123 |
--------------------------------------------------------------------------------
/面试.md:
--------------------------------------------------------------------------------
1 | ### 机器学习
2 |
3 | - 机器学习:基于统计、数据驱动,不是基于演绎而是基于归纳的。可以解决规则难以解决的问题;深度学习:使用更深的网络结果增强表达能力,将特征提取和模式学习相结合
4 | - 梯度下降法:一种常用的优化算法,用于最小化目标函数。计算过程是迭代地向梯度下降最快的方向更新参数,新参数=旧参数-学习率$\times$梯度。
5 | - 条件:目标函数可导,凸;优点:应用范围广,简单;缺点:可能陷入局部最小值,需要人为确定学习率
6 | - 牛顿迭代法:求$f(x)=0$的解的方法。每次用切线与x轴的交点的x值更新参数,$\displaystyle x_{n+1}=x_n-\frac{f(x_n)}{f'(x_n)}$
7 | - 条件:目标函数二价可微,目标函数的海森矩阵必须正定或负定
8 | - 优点:更快地收敛到最优解,不用调参;缺点:计算成本高
9 | - 决策树:一种基于树结构进行决策的算法,其中每个内部节点表示一个属性或特征,每个叶子节点代表决策结果。该算法可以用于分类和回归问题。
10 | - 计算过程:基于分治思想,每次选择最优划分属性,将样本集合分成更小的子集。不断重复,直到所有的子集都属于同一个类别,或者已经达到了预先定义的最大深度。
11 | - SVM (Support Vector Machine): 支持向量机,一种可以用于解决分类和回归问题的机器学习算法,目标是在高维空间中找到最佳的超平面,使得间隔最大化。
12 | - 支持向量:离超平面最近的训练样本点。
13 | - SVM为什么要化对偶形?为了更高效地求解。当数据集的规模很大时,使用原始问题求解SVM会变得很慢,甚至变得不可行。化成对偶问题可以使用SMO这种近似算法更高效的求解。
14 | - 百万样本量可以用SVM吗?求解SVM的原问题计算复杂度过大,有些困难。
15 | - 朴素贝叶斯:一种采用了属性条件独立性假设的分类器,基于贝叶斯定理,选择概率最大的类作为结果。
16 | - 贝叶斯最优分类器:为最小化总体风险,在每个样本上选择那个能使条件风险最小的类别标记,此时判定准则称为贝叶斯最优分类器
17 | - EM算法:一种迭代地估计参数隐变量的方法。其中E步 (Expectation) 基于参数推断隐变量的分布;M步 (Maximization) 基于已观测变量X和Z对参数做极大似然估计。
18 | - PCA (Principal Component Analysis):无监督降维方法。
19 | - 适用于数据之间存在线性相关性的情况,对于非线性关系可以考虑使用Kernel PCA。
20 | - 计算过程:先将数据标准化,使得每个特征的均值为0;计算标准化后数据的协方差矩阵,对协方差矩阵做特征值分解,选择特征值最大的k个特征向量组成投影矩阵,最后将标准化后的数据乘以投影矩阵,将数据投影到新的特征空间上。
21 | - 计算后的主成分正交,即没有线性相关性。(正交$\Rightarrow$线性无关)
22 | - 集成学习 (ensemble learning,读“昂”):一种机器学习方法,核心思想是通过组合多个弱学习器,从而提高模型的预测能力和泛化性能。
23 | - Bagging (bootstrap aggregating):使用自助采样法得到不同的训练集,训练一系列基学习器,通过投票或者平均的方法得到预测结果。
24 | - Boosting:基本思想是通过迭代训练一系列弱分类器,每个弱分类器都针对前一轮训练中被错误分类的样本进行加权,以提高其分类准确性。
25 | - Stacking:一种叠加泛化的集成方法,通过训练一个元模型来结合多个基础模型的预测结果。元模型就是以不同基学习器的预测结果作为输入,结果作为输出。
26 | - “好而不同”:即基学习器的准确率高,多样性高。直观讲准确率越高越好是显然的,多样性高意味着不同的学习器可以互补,从而提高整体的学习性能。理论上有误差歧义分解证明了泛化误差=基学习器泛化误差的却权均值-基学习器的加权分歧值,可以说明基学习器的准确率高,多样性高,分类效果越好。
27 | - Adaboost计算过程:(二分类任务)在训练的每一轮中,使用当前的样本权重训练基学习器,计算分类误差率,如果误差大于0.5则break;根据错误率计算这个基学习器的权重;基于对分类正误情况更新数据分布,增加分错样本的影响,降低分对样本的影响;最后基于各个基学习器的加权,得到最终的分类器
28 | - K-means:一种原型聚类方法,目标是将数据集分成k个不重叠的簇。通过最小化数据点与所属簇的质心之间的距离来进行聚类。
29 | - 计算过程:用一种迭代近似的方法求解。初始化k个簇的质心,重复如下步骤:将每个数据点分到与其最近的质心所属的簇;对于每个簇,计算所有数据点的均值,得到新的质心。如此重复直到质心的位置不再发生显著变化或达到预定的迭代次数。
30 | - KNN:一种lazy learning的监督学习算法,基于与测试样本最近邻的k个邻居的信息预测结果。
31 | - lazy learning:训练阶段仅仅是把样本保存起来,训练时间开销为零,待 收到测试样本后再进行处理
32 | - PAC (Probably Approximately Correct):一种计算学习理论,核心思想是如果一个算法能够在有限的样本上以很高的概率产生一个"近似正确"的模型,那么该算法可以在未见过的数据上表现良好。
33 | - PAC可辨识:算法是否能以高概率产生一个近似正确的模型(泛化误差小于epsilon的概率大于等于1-delta,则称学习算法能从假设空间中PAC辨识概念类C)
34 | - PAC可学习:在有限样本下算法是否能够以高概率产生一个近似正确的模型
35 | - PAC学习算法:在有限的样本和时间限制下,学习算法是否能够以高概率产生一个近似正确的模型
36 |
37 | ### 线代
38 |
39 | - 秩:矩阵中线性无关的行或列的最大数量。矩阵的秩可以看作是矩阵所代表的线性变换值域的向量空间的维度,比如说PCA中的协方差矩阵如果秩是k,那么数据可以被无损压缩到k维。
40 | - 线性相关:存在一组不全为零的标量(系数),使得向量之间的线性组合等于零向量。
41 | - 特征值,特征向量:对于n阶矩阵$A$,常数$\lambda$,和非零的n维列向量$\alpha$,有$A \alpha=\lambda \alpha$成立,则称$\lambda$是矩阵A的一个特征值,$\alpha$为矩阵$A$属于特征值$\lambda$的特征向量。
42 | - 特征值分解:将一个有$n$个线性无关的特征向量的$n$阶方阵$A$分解为$A=Q \Lambda Q^{-1}$的过程。其中$Q$中的每一列都是特征向量,Lambda为对角矩阵,对角线上的元素是对应的特征值。
43 | - 首先求解特征方程$|\lambda E-A|=0$,得到矩阵$A$特征值$\lambda _i$(共$n$个)
44 | - 再由$(\lambda_i E-A)x=0$求基础解系,即矩阵$A$属于特征值$\lambda_i$的线性无关的特征向量。
45 | - 用求得的特征值和特征向量构造Q,Lambda
46 | - 奇异值分解:将矩阵A分解为$U \Sigma V^{-1}$,其中U V均为正交矩阵,Sigma为对角矩阵,对角线上的值按从大到小排列。
47 | - 计算:对$AA^\top$、$A^\top A$分别进行特征值分解,得到U和V。两次计算中的非零特征值从大到小排序,放在对角线,其他位置为零。
48 | - 矩阵分解的意义:将一个矩阵表示为多个矩阵的乘积的过程,有比如说奇异值分解,特征值分解。可以将复杂的矩阵问题简化为更易处理的子问题,提高计算效率。可以提取矩阵中的隐藏模式和结构,用于数据的降维、特征提取和模式识别等任务。
49 | - 正定:实对称矩阵$A$,对任何非零向量$x$,都满足$x^\top A x>0$
50 |
51 | - 充要条件:实对称矩阵 $A$ 正定 $\Leftrightarrow A$ 与单位矩阵 $E$ 合同;存在可逆矩阵 $C$,使 $A=C^\top C$;$A$的特征值均为正;正惯性指数$p=n$;$A$ 的各阶顺序主子式都大于零
52 | - 性质:$A^{-1}, kA,A^*,A^m, (A+B)$也是正定矩阵
53 | - 必要条件:实对称矩阵 $A$ 正定 $\Rightarrow a_{ii}>0$;$\det A=|A|>0$
54 | - 半正定:实对称矩阵$A$,对任何非零向量$x$,都满足$x^\top A x\geq0$
55 |
56 | - 等价命题:$f(x_1,x_2,\dots,x_n)$半正定
57 | - $A$半正定
58 | - $r(f)=r(A)=p$(正惯性指数)
59 | - $A$合同于非负对角阵,即存在可逆阵$C$,使得$C^\top AC=\text{diag} (d_1,\dots,d_n),d_i\geq 0$
60 | - 存在方阵$G\in R^{n\times n}$,使$A=G^\top G$
61 | - 所有主子式$\geq0$
62 | - 梯度消失和梯度爆炸是什么意思?有什么样的方法进行改善?梯度消失:残差连接(输出为输入和输出的求和),ReLU;梯度爆炸:归一化
63 |
64 |
65 | ### 概率论
66 |
67 | - 大数定律:随机变量的均值依概率收敛于期望的均值。
68 | - 中心极限定理:在适当的条件下,大量相互独立随机变量的均值依分布收敛于正态分布。
69 | - 局限:样本容量要求,可以用集中不等式解决。
70 | - 贝叶斯公式:用于计算在某个先验条件下事件的后验概率的公式。
71 | - 全概率公式:一个事件发生的概率等于它在与样本空间的一个划分中每个事件同时发生的概率之和。
72 | - 最大似然估计:是一种用于估计模型参数的统计方法。极大似然估计的基本思想是找到使观测数据的似然函数最大化的参数值。
73 |
74 | - 需要满足:样本独立同分布,参数化假设(参数可数且取值有限),模型合适
75 | - 独立同分布:independent and identically distributed,即独立同分布假设,假设数据集中的每个样本都是从同一个概率分布中独立地随机取出的。目的是简化建模。
76 | - 高维高斯分布:$\displaystyle p(x)=(2\pi)^{- D/2}|\Sigma|^{-1/2}\exp\{-\frac12(x-\mu)^{\top}\Sigma ^{-1}(x-\mu)\}$
77 |
78 | ### 数据结构与算法
79 |
80 | - P问题:可以在多项式时间内求解的决策问题。
81 | - NP问题:可以在多项式时间内验证答案是否正确的决策问题。
82 | - NP-complete :NP集合中最难的问题。是NP,且所有NP问题都可以在多项式时间内规约到它的问题。
83 | - NP-hard :所有NP问题都可以在多项式时间内规约到它的问题。
84 | - 排序稳定性:对于值相同的两个元素,排序后它们的先后顺序与原数组相同。比如在有些使用场景下需要保留原数据中元素的相对位置。
85 | - 快排:是一个基于分治的思想的排序算法,每次选择一个元素作为pivot,然后将给定的数组围绕这个基准进行划分,将小于基准的元素放到基准的左边,将大于基准的元素放到基准的右边,最终将基准放置在排序后的正确位置上。如此递归。优点:空间复杂度小,缺点:最坏复杂度无保证。选快排的原因:快排不需要进行分配和取消分配辅助数组等操作,其所需的常量时间小;空间复杂度低。
86 | - 归并排序:基于分治的思想的排序算法,每次将数组分为两个子数组,分别对子数组排序,再将两个子数组归并,形成最终的排序好的数组。优点:可并行;缺点:空间复杂度高。
87 | - topK:维护一个大小为k的小顶堆,时间复杂度$O(n\log k)$;类似快排,比如说找最大的数,pivot划分后左边80个,右边20个,只要对右边排序即可。最优$O(n)$,平均$O(n\log n)$
88 | - 判断图中有环:
89 | - 拓扑排序,最后如果还存在未被删除的顶点,则表示有环;否则没有环
90 | - DFS,如果在遍历的过程中,发现某个节点有一条边指向已经访问过的节点,并且这个已访问过的节点不是当前节点的父节点,则表示存在环(用黑白灰表示)
91 | - 对于有向图,若存在强连通分量(即存在$v_i \to v_j$的路径也存在$v_j\to v_i$的路径),图中有环。
92 | - 欧拉图:具有欧拉回路的图,欧拉回路是通过图中每条边恰好一次的回路
93 | - 有向图:非零度顶点是强连通的;每个顶点的入度和出度相等
94 | - 无向图是欧拉图当且仅当:非零度顶点是连通的;顶点的度数都是偶数
95 | - 霍夫曼编码:一种变长的数据压缩编码,通过让出现概率更小的字符长度更长,出现概率更大的字符长度更短进行数据压缩,是最优编码。基于霍夫曼树构造的。
96 | - 每次取出出现概率最小的两个结点,合并后结点权重为两个结点之和。直到所有结点构成一个二叉树。为二叉树的每个结点下的两个分支赋值为0、1,编码即从根节点到字符的叶节点的路径上01串。
97 | - 唯一可译码:因为霍夫曼编码是前缀编码,即没有一个编码是另一个编码的前缀。
98 | - 优点:最优编码。缺点:与计算机的数据结构不匹配;需要多次排序,耗费时间。
99 | - 香农编码:一种变长的数据压缩编码,效率略低于霍夫曼。
100 | - 编码方法:将符号按照其出现概率从大到小排序;把概率集合分成两个尽可能概率相等的子集,给前面一个子集合赋值为0,后面一个子集合赋值为1;如此重复直到各个子集合中只有一个元素为止;将每个元素所属的子集合的值依次串起来
101 | - 散列表的优势:查询高效,数据的存储和删除也高效。
102 | - 查询复杂度:链表型:每个哈希桶维护一个链表来存储冲突的键值对,最坏是O(n),平均接近O(1)
103 | - 普通型:当发生哈希冲突时,开放寻址再找到一个空的位置来存储冲突的值。最坏情况是O(n)(哈希表被填满),平均接近O(1)
104 | - 斐波那契:$O(2^n)$,存储结果$O(n)$;动态规划$O(n)$
105 |
106 | ### 其他
107 |
108 | - 操作系统线程跟进程的区别:进程是一个独立的程序运行的实例,线程是进程中的一个子任务。进程可以包含多个线程,进程之间是独立的,
109 | - 傅里叶变换:将信号从时域转换到频域的变换过程。
110 | - 拉普拉斯变换:傅里叶变换的一种扩展,可以将信号从时域转换到复频域。
111 | - 用处:在控制系统中,分析设计反馈控制系统;在信号处理中,用于滤波、信号重构、频谱估计和图像处理等
112 | - 两者关系:拉普拉斯变换是傅里叶变换的扩展形式;在频域分析中,拉普拉斯变换通常用于处理连续系统的输入-输出关系和系统响应,而傅里叶变换适用于连续信号和离散信号。
113 | - 凸优化带约束的一阶条件:定义域是凸集,$f(y)> f(x)+\nabla f(x)^\top (y-x)$
114 | - 二阶条件:对于开集内的任意一点,它的Hessian矩阵半正定。$\nabla^2 f(x)\geq 0$
115 | - KKT条件是非线性规划中最优解的一阶必要条件:拉格朗日函数的导数为0,原始可行性条件,对偶可行性条件,互补松弛条件。
116 | - 原始可行性条件:优化变量满足原问题的所有的约束条件,包括对于每个不等式约束和等式约束
117 | - 对偶可行性条件:对于每个不等式约束,对应的拉格朗日乘子大于等于0。
118 | - 互补松弛条件:约束的松弛变量与拉格朗日乘子的乘积为零
119 | - 凸优化中梯度下降的学习率:通过线搜索确定。线搜索是一种通过搜索确定每次迭代的合适学习率的方法。在每次迭代中,沿着梯度方向尝试不同的学习率值,通过一些准则来选择合适的学习率,使得目标函数在新的参数值上有足够的下降。精确,计算成本高。
120 | - 如果函数的定义域是凸集,且对于任意定义域上的$x,y$和任意$0\leq \theta\leq 1$,有$f(\theta x+(1-\theta)y)\leq \theta f(x)+(1-\theta)f(y)$,则函数是凸的。
121 |
122 | - 卷积和:将其中一个信号翻转再平移,再和另一个向量相乘,对乘积后的信号求和。
123 | - A*:树admissible则optimal,图consistent则optimal。admissible即到目标的估计成本<到目标的真实成本,consistent即结点与其后继的估计成本之差<这一步的真实成本
124 |
125 | - 原问题为什么要化成对偶问题:原问题线性可分就即凸,线性不可分则不凸
126 |
127 | - 对偶问题的求解可以用SMO等近似方法求解。可以引入核函数。(通过迭代地优化一对变量来求解SVM的优化问题。其主要思想是选择两个变量进行优化,将其他变量固定,并通过解析方法直接计算这两个变量的最优值。通过迭代地更新这对变量,SMO算法逐渐逼近全局最优解。)
128 |
129 | - 斐波那契数列求和:公式,DP,递归(拿字典存)
130 |
131 | - 双蛋问题:可以用动态规划求解,
132 |
133 | $W(n,h)$表示有n个鸡蛋h层楼所需的最少实验次数
134 | $$
135 | W(n,h)=1+\min(\max(W(n-1, i-1), W(n, h-i)))
136 | $$
137 | $n=2$:$W(h)=1+\min(\max(i-1, W(h-i)))$
138 |
139 | - 激活函数:引入非线性特性,Sigmoid,Tanh,ReLU,LeakyReLU。Sigmoid映射到(0,1),Tanh映射到(-1,1),这两个激活函数都存在梯度消失。ReLU可以一定缓解梯度消失问题,但是在负输入时不可导,可能存在神经元死亡的情况。LeakyReLU对ReLU改进,在负输入时保留一个小的梯度,有助于解决ReLU函数中的死亡神经元问题。
140 |
141 | - 特征值特征向量意义:特征值告诉我们特征向量在线性变换中的伸缩程度,PCA中特征值越大说明对应的特征向量相关性更大,取最大的k维。特征值可以用来判断矩阵的正定性等(特征值均>0)。
142 | - 数据规模大:对偶问题太复杂。
143 |
--------------------------------------------------------------------------------
 22 |
23 | - Breadth-first search
24 | - heap是FIFO queue
25 | - 完备性:如果$b$有限
26 | - Uniform-cost search
27 | - 解决边有权重的问题,Priority queue,权重最小先出栈
28 | - 当边权重为正时完备
29 | - 时空复杂度都是路径开销$\leq$最优解的节点个数
30 | - 最优性证明:
31 | - 它扩展最小成本的节点
32 | - 最优路径上的目标状态比任何次优路径上的目标状态具有更小的成本
33 | - 它永远不会在扩展最优路径上的目标状态之前,扩展次优路径上的目标状态
34 | - Depth-first search
35 | - heap是LIFO queue
36 | - 不完备:在无限深度空间、有环的空间中失败(如果有限、没有重复状态则完备)
37 |
38 | - Depth-limited search
39 |
40 | - Iterative deepening search
41 |
42 | - 对从0到$\infty$的depth,分别做Depth-limited search,直到找到结果
43 |
44 | - 时间复杂度(实际上重复搜索浪费的时间并不多):
45 | $$
46 | \begin{aligned}
47 | &b^0+(b^0+b^1)+\dots+(b^0+\dots+b^d)\\
48 | =&(d+1)b^0+db^1+\dots+b^d=O(b^d)
49 | \end{aligned}
50 | $$
51 |
52 | ### Informed Search
53 |
54 | - Greedy Search
55 |
56 | - heuristic function: $h(n)$ 为从$n$到最近目标的成本估计
57 | - 扩展**看起来**最接近目标的节点
58 | - 不完备(可以卡在环上),$T=O(b^m)$,$S=O(b^m)$,不最优
59 |
60 | - A\* Search
61 |
62 | - heuristic function: $f(n)=g(n)+h(n)$,其中$g(n)$为到目前为止达到$ n $的成本,$h(n)$为从$n$到最近目标的成本估计,$f(n)$为通过$ n $到达目标的路径的估计总成本
63 | - Admissible可接受:估值永远小于真实值,$0\leq h(n)\leq h^*(n)$
64 | - Consistent一致性:$h(n)\leq c(n,a',n')+h(n')$,其中$ n' $是由动作$ a' $生成的$ n $的后继,Consistent$\to$Admissible
65 | - 证明:对于树搜索,如果启发式函数是可接受的,则A\*最优**(重点理解)**
66 | - 假设$h$是admissible的,如果$A$是最优目标节点,$B $是次优目标节点,下证明:$A$会比$B$先扩展
67 | - 对于$A$的任意祖先$n$,证明:$n$会比$B$先扩展
68 | - 有$h(A)=h(B)=0$;$g(A)
22 |
23 | - Breadth-first search
24 | - heap是FIFO queue
25 | - 完备性:如果$b$有限
26 | - Uniform-cost search
27 | - 解决边有权重的问题,Priority queue,权重最小先出栈
28 | - 当边权重为正时完备
29 | - 时空复杂度都是路径开销$\leq$最优解的节点个数
30 | - 最优性证明:
31 | - 它扩展最小成本的节点
32 | - 最优路径上的目标状态比任何次优路径上的目标状态具有更小的成本
33 | - 它永远不会在扩展最优路径上的目标状态之前,扩展次优路径上的目标状态
34 | - Depth-first search
35 | - heap是LIFO queue
36 | - 不完备:在无限深度空间、有环的空间中失败(如果有限、没有重复状态则完备)
37 |
38 | - Depth-limited search
39 |
40 | - Iterative deepening search
41 |
42 | - 对从0到$\infty$的depth,分别做Depth-limited search,直到找到结果
43 |
44 | - 时间复杂度(实际上重复搜索浪费的时间并不多):
45 | $$
46 | \begin{aligned}
47 | &b^0+(b^0+b^1)+\dots+(b^0+\dots+b^d)\\
48 | =&(d+1)b^0+db^1+\dots+b^d=O(b^d)
49 | \end{aligned}
50 | $$
51 |
52 | ### Informed Search
53 |
54 | - Greedy Search
55 |
56 | - heuristic function: $h(n)$ 为从$n$到最近目标的成本估计
57 | - 扩展**看起来**最接近目标的节点
58 | - 不完备(可以卡在环上),$T=O(b^m)$,$S=O(b^m)$,不最优
59 |
60 | - A\* Search
61 |
62 | - heuristic function: $f(n)=g(n)+h(n)$,其中$g(n)$为到目前为止达到$ n $的成本,$h(n)$为从$n$到最近目标的成本估计,$f(n)$为通过$ n $到达目标的路径的估计总成本
63 | - Admissible可接受:估值永远小于真实值,$0\leq h(n)\leq h^*(n)$
64 | - Consistent一致性:$h(n)\leq c(n,a',n')+h(n')$,其中$ n' $是由动作$ a' $生成的$ n $的后继,Consistent$\to$Admissible
65 | - 证明:对于树搜索,如果启发式函数是可接受的,则A\*最优**(重点理解)**
66 | - 假设$h$是admissible的,如果$A$是最优目标节点,$B $是次优目标节点,下证明:$A$会比$B$先扩展
67 | - 对于$A$的任意祖先$n$,证明:$n$会比$B$先扩展
68 | - 有$h(A)=h(B)=0$;$g(A) 176 |
177 | #### 查准率P
178 |
179 | precision
180 |
181 | $$
182 | P=\frac{TP}{TP+FP}
183 | $$
184 |
185 | #### 查全率R
186 |
187 | Recall
188 |
189 | $$
190 | R=\frac{TP}{TP+FN}
191 | $$
192 |
193 | #### P-R曲线
194 |
195 |
176 |
177 | #### 查准率P
178 |
179 | precision
180 |
181 | $$
182 | P=\frac{TP}{TP+FP}
183 | $$
184 |
185 | #### 查全率R
186 |
187 | Recall
188 |
189 | $$
190 | R=\frac{TP}{TP+FN}
191 | $$
192 |
193 | #### P-R曲线
194 |
195 |  196 |
197 | 若一个学习器的P-R曲线被另一个学习器的曲线完全“包住”,则可断言后者的性能优于前者。如果两个学习器的P-R曲线发生了交叉,则难以一般性地断言两者孰优孰劣,只能在具体的查准率或查全率条件下进行比较。
198 |
199 | #### $ F_1 $ 度量
200 |
201 | $$
202 | F_1=\frac{2PR}{P+R}=\frac{2TP}{样例总数+TP-TN}
203 | $$
204 |
205 | (是P和R的调和平均 $ \frac1{F1}=\frac12(\frac1P+\frac1R) $ )
206 |
207 | #### $ F_\beta $ 度量
208 |
209 | 对查准率和查全率的重视程度有所不同的度量:
210 |
211 | $$
212 | F_\beta=\frac{1+\beta^2PR}{\beta^2P+R}
213 | $$
214 |
215 | $ \beta>1 $ 查全率更重要, $ \beta<1 $ 查准率更重要, $ \beta=1 $ 退化为 $ F_1 $ 。
216 |
217 | #### Macro
218 |
219 | $$
220 | \begin{aligned}
221 | \text{macro-}P&=\frac1n\sum_{i=1}^n P_i\\
222 | \text{macro-}R&=\frac1n\sum_{i=1}^n R_i\\
223 | \text{macro-}F_1&=\frac{2\times\text{macro-}P\times\text{macro-}R}{\text{macro-}P+\text{macro-}R}
224 | \end{aligned}
225 | $$
226 |
227 | #### Micro
228 |
229 | $$
230 | \begin{aligned}
231 | \text{micro-}P&=\frac{\overline {TP}}{\overline {TP}+\overline {FP}}\\
232 | \text{micro-}R&=\frac{\overline {TP}}{\overline {TP}+\overline {FN}}\\
233 | \text{micro-}F_1&=\frac{2\times\text{micro-}P\times\text{micro-}R}{\text{micro-}P+\text{micro-}R}
234 | \end{aligned}
235 | $$
236 |
237 | #### ROC & AUC
238 |
239 | 纵轴TPR,横轴FPR
240 |
241 | $$
242 | \begin{aligned}
243 | TPR&=\frac{TP}{TP+FN}\\
244 | FPR&=\frac{FP}{TN+FP}
245 | \end{aligned}
246 | $$
247 |
248 | 
249 |
250 | ROC曲线 (Receiver Operating Characteristic):若一个学习器的ROC曲线被另一个学习器的曲线完全“包住”,则可断言后者的性能优于前者;若两个学习器的ROC曲线发生交叉,则难以以般性地断言两者孰优孰劣。
251 |
252 | AUC (Area Under ROC Curve):
253 |
254 | $$
255 | \ell_{rank}=\frac1{m^+m^-}\sum_{x^+\in D^+}\sum_{x^-\in D^-}\left(\mathbb I\left((f(x^+)
196 |
197 | 若一个学习器的P-R曲线被另一个学习器的曲线完全“包住”,则可断言后者的性能优于前者。如果两个学习器的P-R曲线发生了交叉,则难以一般性地断言两者孰优孰劣,只能在具体的查准率或查全率条件下进行比较。
198 |
199 | #### $ F_1 $ 度量
200 |
201 | $$
202 | F_1=\frac{2PR}{P+R}=\frac{2TP}{样例总数+TP-TN}
203 | $$
204 |
205 | (是P和R的调和平均 $ \frac1{F1}=\frac12(\frac1P+\frac1R) $ )
206 |
207 | #### $ F_\beta $ 度量
208 |
209 | 对查准率和查全率的重视程度有所不同的度量:
210 |
211 | $$
212 | F_\beta=\frac{1+\beta^2PR}{\beta^2P+R}
213 | $$
214 |
215 | $ \beta>1 $ 查全率更重要, $ \beta<1 $ 查准率更重要, $ \beta=1 $ 退化为 $ F_1 $ 。
216 |
217 | #### Macro
218 |
219 | $$
220 | \begin{aligned}
221 | \text{macro-}P&=\frac1n\sum_{i=1}^n P_i\\
222 | \text{macro-}R&=\frac1n\sum_{i=1}^n R_i\\
223 | \text{macro-}F_1&=\frac{2\times\text{macro-}P\times\text{macro-}R}{\text{macro-}P+\text{macro-}R}
224 | \end{aligned}
225 | $$
226 |
227 | #### Micro
228 |
229 | $$
230 | \begin{aligned}
231 | \text{micro-}P&=\frac{\overline {TP}}{\overline {TP}+\overline {FP}}\\
232 | \text{micro-}R&=\frac{\overline {TP}}{\overline {TP}+\overline {FN}}\\
233 | \text{micro-}F_1&=\frac{2\times\text{micro-}P\times\text{micro-}R}{\text{micro-}P+\text{micro-}R}
234 | \end{aligned}
235 | $$
236 |
237 | #### ROC & AUC
238 |
239 | 纵轴TPR,横轴FPR
240 |
241 | $$
242 | \begin{aligned}
243 | TPR&=\frac{TP}{TP+FN}\\
244 | FPR&=\frac{FP}{TN+FP}
245 | \end{aligned}
246 | $$
247 |
248 | 
249 |
250 | ROC曲线 (Receiver Operating Characteristic):若一个学习器的ROC曲线被另一个学习器的曲线完全“包住”,则可断言后者的性能优于前者;若两个学习器的ROC曲线发生交叉,则难以以般性地断言两者孰优孰劣。
251 |
252 | AUC (Area Under ROC Curve):
253 |
254 | $$
255 | \ell_{rank}=\frac1{m^+m^-}\sum_{x^+\in D^+}\sum_{x^-\in D^-}\left(\mathbb I\left((f(x^+)