├── 1 深度学习介绍.md
├── 10 卷积神经网络.md
├── 11 深度卷积网络 实例探究.md
├── 12 目标检测.md
├── 13 特殊应用 人脸识别和神经风格转换.md
├── 14 序列模型.md
├── 15 自然语言处理与词嵌入.md
├── 2 神经网络基础.md
├── 3 浅层神经网络.md
├── 4 深层神经网络.md
├── 5 深度学习的实用层面.md
├── 6 优化算法.md
├── 7 超参数的调试,BN和程序框架.md
├── 8 机器学习(ML)策略(1).md
├── 9 机器学习(ML)策略(2).md
└── README.md
/1 深度学习介绍.md:
--------------------------------------------------------------------------------
1 | ## 深度学习基础介绍
2 |
3 | ### 1.简述深度学习
4 |
5 | 深度学习(DL, Deep Learning)是机器学习(ML, Machine Learning)领域中一个新的研究方向,它被引入机器学习使其更接近于最初的目标——人工智能(AI, Artificial Intelligence)。
6 |
7 | 深度学习就是模仿人脑的“神经网络“建立一个类似的学习策略(如下图),基于大量的数据进行训练和学习,在这个过程中不断修改模型的参数,得到的一个更好的模型,使得这个模型能类似于人一样,识别和处理一些问题,这就是其学习性,并且有些模型的能力甚至能够超越人类的水平。
8 |
9 | 深度学习的最终目标是让机器能够像人一样具有分析学习能力,能够识别文字、图像和声音等数据。
10 |
11 | 
12 |
13 | 深度学习最近几年才火起来,看似是比较新的技术,其实其早就在上个世纪被提出了,但当时由于硬件等因素,深度学习并没有引起很多人的关注和研究,如今随着各个领域的发展,深度学习有了其一定的发展前提和基础,就不断地有研究者和从业者投入其中进行研究和应用,在工业以及其他应用场景下,深度学习训练的模型为人们带来了更方便的生活,为企业带来更多的利润以及更多的剩余价值。
14 |
15 | ### 2.为什么深度学习会兴起
16 |
17 | 深度学习和神经网络之前的基础技术理念已经存在大概几十年了,为什么它们现在才突然流行起来呢?
18 |
19 | 
20 |
21 | 如上图,横轴为数据量,纵轴为模型的性能,可以看到,它的性能一开始在增加更多数据时会上升,但是一段变化后它的性能就会像一个高原一样。
22 |
23 | 而在过去的几十年里,训练模型的数据集是非常小的,当时的人们难以收集并且构建足够大,有效的数据集,从而导致模型没有充足地得到训练,而随着数字化社会的来临,现在的数据量都非常巨大,制作有效的数据集变得容易得多,模型也就能够得到充足的训练,这也是深度学习兴起的一大重要原因。
24 |
25 | 同时无论是在CPU还是GPU上面的,都在不断得发展,使得高计算量的深度学习模型能够更快的得到训练,以往需要训练两个月的数据量,现在只需要三天就能够完成。尤其是在最近这几年,我们也见证了算法方面的极大创新。许多算法方面的创新,一直是在尝试着使得神经网络运行的更快。
26 |
27 |
28 |
29 |
30 |
31 | ### 3.深度学习和机器学习以及人工智能之间的关系。
32 |
33 | 
34 |
35 | ### 3.学习深度学习需要什么前置知识
36 |
37 | 要有比较基础的高数和线性代数的知识
38 |
39 | 编程语言:python
40 |
41 | 最好有机器学习的基础,当然如果没有直接学习也没有什么影响(笔者建议可以有时间可以的看一下)
42 |
43 |
44 |
45 | ## 吴恩达深度学习课程介绍
46 |
47 | ### 1.简介:
48 |
49 | 吴恩达这门课可以说是非常适合新手,或者说对于零基础的人学习的,这几门课程的顺序也是由浅至深的进行,只要按照顺序学习,无需担心看不懂。
50 |
51 | 这些课程中可以学习到深度学习的基础,学会构建神经网络,也会有很多实操项目,帮助学生更好地应用自己学到的深度学习技术,解决真实世界问题。
52 |
53 |
54 |
55 | ### 2.具体结构:
56 |
57 | 吴恩达的课程主要分为五门课,具体内容如下:
58 |
59 | 第一门课程中,将学习如何建立神经网络(包含一个深度神经网络),以及如何在数据上面训练他们。
60 |
61 | 第二门课中,将进行深度学习方面的实践,学习严密地构建神经网络,如何真正让它表现良好,因此你将要学习超参数调整、正则化、诊断偏差和方差以及一些高级优化算法。以及神经网络的编程知识,了解神经网络的结构,逐步完善算法并思考如何使得神经网络高效地实现。
62 |
63 | 第三门课中,将学习如何结构化机器学习工程。
64 |
65 | 第四门课程中,将会学到如何搭建卷积神经网络(***\*CNN(s)\****)这样的模型。
66 |
67 | 第五门课中,将会学习到序列模型(循环神经网络(***\*RNN\****)、长短期记忆网络(***\*LSTM\****)),以及如何将它们应用于自然语言处理,以及其它问题。
68 |
69 |
70 |
71 |
72 |
73 | ## 深度学习学习资源
74 |
75 | 1.[吴恩达系列课](https://study.163.com/courses-search?keyword=%E5%90%B4%E6%81%A9%E8%BE%BE)
76 |
77 | 网易云课堂搜索 吴恩达(这个是免费的)
78 |
79 | 2.[吴恩达课后作业以及代码](https://blog.csdn.net/u013733326/article/details/79827273)
80 |
81 | 3.[吴恩达课程内容笔记](https://github.com/fengdu78/deeplearning_ai_books):(这个真的很全,主要有视频文字版,也有涉及的论文清单以及其他的相关的资料和)
82 |
83 | 4.[经典论文清单](https://github.com/terryum/awesome-deep-learning-papers)
84 |
85 | 5.[TensorFlow 2.0入门教程](https://github.com/snowkylin/tensorflow-handbook)(大家找TensorFlow的教程时一定要注意1.0和2.0的版本差别)
86 |
87 | 8.[Keras中文档案](https://keras.io/zh/why-use-keras/)
88 |
89 | 9.[CV进阶](http://cs231n.stanford.edu/):斯坦福的计算机视觉课CS231n(官网只有2017年的,b站有中文版)
90 |
91 | 11. [Deep Learning](https://link.zhihu.com/?target=http%3A//www.deeplearningbook.org/) by Yoshua Bengio, Ian Goodfellow and Aaron Courville
92 |
93 | 深度学习的一本教科书,知识面很全,书籍同时兼顾广度和深度,是很多深度学习系统化学习的参考教材。
94 |
95 | 12. [Neural networks and deep learning](https://link.zhihu.com/?target=http%3A//neuralnetworksanddeeplearning.com/) by Michael Nielsen
96 |
97 | 这是一本免费的在线书籍,主要介绍了神经网络和深度学习背后的核心概念。
98 |
99 | 13. [Deep Learning: Methods and Applications - Microsoft Research](https://link.zhihu.com/?target=https%3A//www.microsoft.com/en-us/research/publication/deep-learning-methods-and-applications/%3Ffrom%3Dhttp%3A%2F%2Fresearch.microsoft.com%2Fpubs%2F209355%2Fdeeplearning-nowpublishing-vol7-sig-039.pdf) Microsoft Research (2013)
100 |
101 | 本书旨在提供一般深度学习方法及其应用于各种信号和信息处理任务的概述,介绍了深度学习在语言、文字处理、信息检索、计算机视觉领域的具体运用。
102 |
103 | 14. [Deep Learning Tutorial](https://link.zhihu.com/?target=http%3A//deeplearning.net/tutorial/deeplearning.pdf) LISA lab, University of Montreal (Jan 6 2015)
104 |
105 | 蒙特利尔大学LISA实验室深度学习的教材,对卷积神经网络和LSTM、RNN等神经网络进行了具体的介绍,教材例子比较多,操作性比较强。
106 |
107 | 15. [An introduction to genetic algorithms](https://link.zhihu.com/?target=https%3A//svn-d1.mpi-inf.mpg.de/AG1/MultiCoreLab/papers/ebook-fuzzy-mitchell-99.pdf)
108 |
109 | 遗传算法简介
110 |
111 | 16. [Artificial Intelligence: A Modern Approach](https://link.zhihu.com/?target=http%3A//aima.cs.berkeley.edu/)
112 |
113 | 目前已经是第三版,是110多个国家超过1300所大学的教材,有免费的在线AI课程。主要是从数学的角度介绍人工智能、问题求解、知识与推理。
114 |
115 | 17. [Deep Learning in Neural Networks: An Overview](https://link.zhihu.com/?target=http%3A//arxiv.org/pdf/1404.7828v4.pdf)
116 |
117 | 本文详细地回顾了监督学习(包括反向传播)、无监督学习、强化学习和进化学习。
118 |
119 |
--------------------------------------------------------------------------------
/10 卷积神经网络.md:
--------------------------------------------------------------------------------
1 | ## 10 卷积神经网络
2 |
3 | ### 10.1 计算机视觉
4 |
5 | 计算机视觉(Computer Vision)是指用计算机实现人的视觉功能——对客观世界的三维场景的感知、识别和理解。它的任务包括:
6 |
7 | 1. 图片分类(图片识别):识别图像物体属于的类别。比如分辨图片中的猫咪。
8 |
9 | 2. 目标检测:用框去标出物体的位置,并给出物体的类别。比如无人驾驶项目中,识别图片中障碍物的位置,再将它们模拟成一个个盒子,并计算距离。
10 |
11 | 3. 风格迁移:如图1所示,两种不同的图片风格,可以利用神经网络将它们融合到一起,描绘出一张新的图片。它的整体轮廓来自于左边,却是右边的风格。
12 |
13 | 
14 |
15 | 图1
16 |
17 | 4. 图像语义分割:像素级分类,输出图像与输入图像大小一致,整体效果为图像的每一个区域都会分类。如图
18 |
19 | 
20 |
21 | 
22 |
23 | 为何难以使用全连接?
24 |
25 | 图片处理的数据量巨大。如果是1000x1000的彩色图片,因为每张图片都有3个颜色通道,那么输入就是300万,进入神经网络后假设第一层有1000个节点,那么$w_1$的参数个数就是30亿,如此大的参数量对内存和计算资源都是一种挑战,面对这个问题需要使用计算机视觉中常用的卷积操作。
26 |
27 |
28 |
29 |
30 | ### 10.2 边缘检测
31 |
32 | #### 10.2.1 卷积神经网络中的卷积运算
33 |
34 | 以一维灰度图像为例,输入是6×6×1的矩阵,构造一个3×3×1的矩阵,如图2所示。在卷积神经网络的术语中,它被称为过滤器(又称卷积核)。
35 |
36 | 对输入矩阵进行卷积,即输入矩阵与卷积核相乘,具体乘法方式为:从输入矩阵左上角开始找到与卷积核相同尺寸的小矩阵,并对应位置相乘求和,得到第一个卷积的结果,继续位移对整个矩阵进行该操作,得到新的矩阵,过程如下:
37 |
38 | 
39 |
40 | 图2
41 |
42 | 1. 计算输出矩阵第一个元素:对于4×4输出矩阵最左上角元素,使用3×3的过滤器,将其覆盖在输入图像,如图2所示。然后进行元素乘法运算,即:
43 |
44 | $$
45 | \left[\begin{array}{ccc}
46 | 3 \times 1 & 0 \times 0 & 1 \times(1) \\
47 | 1 \times 1 & 5 \times 0 & 8 \times(-1) \\
48 | 2 \times 1 & 7 \times 0 & 2 \times(-1)
49 | \end{array}\right]=\left[\begin{array}{ccc}
50 | 3 & 0 & -1 \\
51 | 1 & 0 & -8 \\
52 | 2 & 0 & -2
53 | \end{array}\right]
54 | $$
55 |
56 | 然后将该矩阵每个元素相加得到最左上角的元素,即3 + 1 + 2 + 0 + 0 + 0 + (-1) + (-8) + (-2) = -5。
57 |
58 | 2. 计算输出矩阵第二个元素:即图3标注的红框,先把蓝色的方块向右移动一步,再继续做同样的元素乘法,然后相加,所以是0×1 + 5×1 + 7×1 + 1×0 + 8×0 + 2×0 + 2×(-1) + 9×(-1) + 5×(-1) = -4。以此类推,可以计算输出矩阵第一行的值。
59 |
60 | 
61 |
62 | 图3
63 |
64 | 3. 得到下一行的元素:把蓝色块下移,到如图4所示位置,重复进行元素乘法,然后加起来。通过这样做得到-10。再将其右移得到-2,接着是2,3。以此类推,这样计算完矩阵中的其他元素。
65 |
66 | 
67 |
68 | 图3
69 |
70 | 左边矩阵容易被理解为一张图片,中间的这个被理解为过滤器,右边的图片可以理解为另一张图片。这就是垂直边缘检测器。结果如图所示:
71 |
72 | 
73 |
74 | 图4
75 |
76 | #### 10.2.2 垂直边缘检测
77 |
78 | 为了讲清楚,举一个简单的例子。这是一个简单的6×6图像,左边的一半是10,代表亮色,右边一半是0,代表暗色。在中间部分,就被视为一个垂直边缘。
79 |
80 | 使用一个3×3过滤器进行卷积运算,得到图5最右边4×4的输出矩阵,在中间有段亮一点的区域(30),即对应检查到6×6图像中间的垂直边缘。结果为正数(30),代表从左至右来看,原图左半部分较亮。
81 | 
82 |
83 | 图5
84 |
85 | #### 10.2.3 水平边缘检测
86 |
87 | 相似的,如图六所示,检测输入图片的水平边缘,左上方和右下方都相对较亮(10)。水平边缘过滤器则是一个3×3的矩阵,但是它的上边相对较亮(1),而下方相对较暗(-1)。
88 |
89 | 卷积后从输出矩阵看出一条水平边缘。其中左半部分为正数(30,10),代表从上至下来看,原图上面部分较亮。右半部分为负数(-10,-30),代表原图下面部分较亮。
90 |
91 | 
92 |
93 | 图6
94 |
95 | #### 10.2.4 区分正边和负边
96 |
97 | 假如把输入图片的颜色翻转,变成了左边比较暗,而右边比较亮,使用相同的过滤器进行卷积,最后得到的图中间会是-30,而不是30。表明是由暗向亮过渡,而不是由亮向暗过渡。因此,输出的正负即可代表边缘的过渡情况。
98 | 
99 |
100 | 图7
101 |
102 | #### 10.2.5 为什么是3*3的卷积核?
103 |
104 | 1. 3x3是最小的能够捕获像素八邻域信息的尺寸。
105 | 2. 两个3x3的卷积核有限感受野是5x5;三个3x3的卷积核的感受野是7x7,故可以通过小尺寸卷积层的堆叠替代大尺寸卷积层,并且感受野大小不变。
106 | 3. 多个3x3的卷积核比一个大尺寸卷积核有更多的非线性(更多层可以使用更多个非线性函数)。
107 | 4. 多个3x3的卷积层比一个大尺寸卷积核有更少的参数,如三个3x3的卷积层参数个数3x3x3=27;一个7x7的卷积层参数为49。唯一的不足是,在进行反向传播时,中间的卷积层可能会导致占用更多的内存。
108 |
109 |
110 | ### 10.3 更多的边缘检测
111 |
112 | 在历史上,在计算机视觉的文献中,对于这个3×3的过滤器来说,曾公平地争论过怎样的数字组合才是最好的。不同的过滤器可以起到不同的效果,如Sobel过滤器,Scharr过滤器。
113 |
114 | 1. Prewitt过滤器:是一种图像边缘检测的微分算子,其原理是利用特定区域内像素灰度值产生的差分实现边缘检测。实际上也是一种垂直边缘检测。将其翻转90度,就能得到对应水平边缘检测。
115 |
116 | $$
117 | \left[\begin{array}{lll}-1 & 0 & 1 \\-1 & 0 & 1 \\-1 & 0 & 1\end{array}\right]
118 | $$
119 |
120 |
121 | 2. Sobel的过滤器:它的优点在于增加了中间一行元素的权重,这使得结果的鲁棒性会更高一些。
122 |
123 | $$
124 | \left[\begin{array}{lll}
125 | 1 & 0 & -1 \\
126 | 2 & 0 & -2 \\
127 | 1 & 0 & -1
128 | \end{array}\right]
129 | $$
130 |
131 | 3. Scharr过滤器:它和sobel过滤器类似,但结果更为精确。
132 |
133 | $$
134 | \left[\begin{array}{lll}
135 | 3 & 0 & -3 \\
136 | 10 & 0 & -10 \\
137 | 3 & 0 & -3
138 | \end{array}\right]
139 | $$
140 |
141 | 4. 拉普拉斯(Laplacian) 过滤器:是 $n$ 维欧几里德空间中的一个二阶微分算子,常用于图像增强领域和边缘提取。它可以判断中心像素灰度与邻域内其他像素灰度的关系。Laplacian算子分为四邻域和八邻域,四邻域是对邻域中心像素的四个方向求梯度,八邻域是对八个方向求梯度。
142 | 其中,Laplacian算子四邻域模板如下所示:
143 |
144 | $$
145 | \begin{array}{l}
146 | \mathrm{H}=\left[\begin{array}{ccc}
147 | 0 & -1 & 0 \\
148 | -1 & 4 & -1 \\
149 | 0 & -1 & 0
150 | \end{array}\right] \\
151 | \end{array}
152 | $$
153 |
154 | 八邻域模板如下所示:
155 | $$
156 | \begin{array}{l}
157 | \mathrm{H}=\left[\begin{array}{ccc}
158 | -1 & -1 & -1 \\
159 | -1 & 8 & -1 \\
160 | -1 & -1 & -1
161 | \end{array}\right]
162 | \end{array}
163 | $$
164 |
165 | 5. Kirsch过滤器:类似于Sobel过滤器,Sobel过滤器计算出某点两个方向的梯度值$G_x$、$G_y$;但Kirsch过滤器利用8个卷积模板来确定梯度幅度值和梯度的方向,并以最大的卷积值作为该点的灰度值。
166 |
167 | 
168 |
169 | 图8
170 |
171 | 将过滤器的所有数字都设置为参数,可以通过反向传播学习,得到的滤波器没有特定的名称,但是可以检测不同的特征,如偏向45度的边缘检测,或者70度78度都可以检测。
172 | 这种将这9个数字当成参数的思想,已经成为计算机视觉中最为有效的思想之一。
173 |
174 | ### 10.4 Padding
175 |
176 | **为什么需要Padding?**
177 |
178 | 如果你用一个 3×3 的过滤器卷积一个 6×6 的图像,你最后会得到一个 4×4 的输出,也就是一个 4×4 矩阵。因为你的 3×3 过滤器在 6×6 矩阵中,只可能有 4×4 种可能的位置。这背后的数学解释是,如果我们有一个𝑛 × 𝑛的图像,用𝑓 × 𝑓的过滤器做卷积,那么输出的维度就是(𝑛 − 𝑓 + 1) × (𝑛 − 𝑓 + 1)。在这个例子里是6 − 3 + 1 = 4,因此得到了一个 4×4 的输出。
179 |
180 | 
181 |
182 | 这样的话会有两个缺点。
183 |
184 | 第一个缺点是**输出缩小**。每次做卷积操作,图像就会缩小,从 6×6 缩小到 4×4,你可能做了几次之后,你的图像就会变得很小了,可能会缩小到只有 1×1 的大小。但我们不想让图像在每次识别边缘或其他特征时都缩小。
185 |
186 | 第二个缺点是**丢失了图像边缘的大部分信息**。角落边缘的像素点只被一个输出所触碰或者使用,因为它位于这个 3×3 的区域的一角。但如果是在中间的像素点,就会有许多 3×3 的区域与之重叠。所以那些在角落或者边缘区域的像素点在输出中采用较少,意味着你丢掉了图像边缘位置的许多信息。
187 |
188 | 为了解决这些问题,我们可以进行Padding操作——在卷积操作之前填充这幅图像。
189 |
190 | **Padding**
191 |
192 | 
193 |
194 | 例如,我们沿着图像边缘再填充一层像素。那么 6×6 的图像就被你填充成了一个 8×8 的图像。如果你用 3×3 的图像对这个 8×8 的图像卷积,你得到的输出就不是 4×4 的,而是 6×6的图像,你就得到了一个尺寸和原始图像 6×6 的图像。习惯上,你可以用 0 去填充。
195 |
196 | **使用Padding后计算输出图像的大小**
197 |
198 | 如果𝑝是填充的数量,输出就变成(𝑛 + 2𝑝 − 𝑓 + 1) × (𝑛 + 2𝑝 − 𝑓 + 1)。
199 |
200 | 在这个案例中,𝑝 = 1,因为我们在周围都填充了一个像素点,所以就变成了(6 + 2 × 1 − 3 + 1) × (6 + 2 × 1 − 3 + 1) = 6 × 6。
201 |
202 | **Valid卷积**
203 |
204 | 意味着不填充。
205 | $$
206 | (n \times n) \text { * } (f \times f) \rightarrow (n-f+1) \times (n-f+1)
207 | $$
208 | **Same卷积**
209 |
210 | 意味着填充后输出大小和输入大小是一样的。
211 | $$
212 | (n+2 p) \times (n+2 p) \quad * \quad (f \times f) \rightarrow (n+2 p-f+1 ) \times (n+2 p-f+1)
213 | $$
214 | 根据这个公式𝑛 − 𝑓 + 1,当你填充𝑝个像素点,𝑛就变成了𝑛 + 2𝑝,最后公式变为𝑛 + 2𝑝 − 𝑓 + 1。因此如果你有一个𝑛 × 𝑛的图像,用𝑝个像素填充边缘,输出的大小就是这样的(𝑛 + 2𝑝 − 𝑓 + 1) × (𝑛 + 2𝑝 − 𝑓 + 1)。
215 |
216 | 如果你想让**𝑛 + 2𝑝 − 𝑓 + 1 = 𝑛**的话,使得输出和输入大小相等,如果你用这个等式求解𝑝,那么**𝑝 = (𝑓 − 1)/2**。所以当𝑓是一个奇数的时候,只要选择相应的填充尺寸,你就能确保得到和输入相同尺寸的输出。
217 |
218 | 习惯上,计算机视觉中,𝑓通常是奇数。如果𝑓是一个偶数,那么你只能使用一些不对称填充。只有𝑓是奇数的情况下,Same 卷积才会有自然的填充,我们可以以同样的数量填充四周,而不是左边填充多一点,右边填充少一点,这样不对称的填充。其次,当你有一个奇数维过滤器,比如 3×3 或者 5×5 的,它就有一个中心点。有时在计算机视觉里,如果有一个中心像素点会更方便,便于指出过滤器的位置。
219 |
220 | ### 10.5 卷积步长
221 |
222 | 卷积中的步幅是另一个构建卷积神经网络的基本操作,如下例。
223 |
224 | 
225 |
226 | 如果你想用 3×3 的过滤器卷积这个 7×7 的图像,和之前不同的是,我们把步幅设置成了2。你还和之前一样取左上方的 3×3 区域的元素的乘积,再加起来,最后结果为 91。
227 |
228 | 
229 |
230 | 只是之前我们移动蓝框的步长是 1,现在移动的步长是 2,我们让过滤器跳过 2 个步长,注意一下左上角,这个点移动到其后两格的点,跳过了一个位置。然后你还是将每个元素相乘并求和,你将会得到的结果是 100。
231 |
232 | 现在我们继续,将蓝色框移动两个步长,你将会得到 83 的结果。当你移动到下一行的时候,你也是使用步长 2 而不是步长 1,所以我们将蓝色框移动到这里:
233 |
234 | 
235 |
236 | 注意到我们跳过了一个位置,得到 69 的结果,现在你继续移动两个步长,会得到 91,127,最后一行分别是 44,72,74。
237 |
238 | 
239 |
240 | 在这个例子中,用 3×3 的矩阵卷积一个 7×7 的矩阵,得到一个 3×3 的输出。输入和输出的维度是由下面的公式决定的。
241 |
242 | 如果你用一个𝑓 × 𝑓的过滤器卷积一个𝑛 × 𝑛的图像,你的 padding为𝑝,步幅为𝑠,在这个例子中𝑠 = 2,你会得到一个输出,因为现在你不是一次移动一个步子,而是一次移动𝑠个步子,输出于是变为
243 | $$
244 | (\frac{n+2 p-f}{s}+1) \times (\frac{n+2 p-f}{s}+1)
245 | $$
246 | 如果商不是一个整数,则**向下取整**。
247 |
248 |  249 |
250 | ⌊ ⌋这是向下取整的符号,这也叫做对𝑧进行地板除(floor),这意味着𝑧向下取整到最近的整数。这个原则实现的方式是,你只在蓝框完全包括在图像或填充完的图像内部时,才对它进行运算。如果有任意一个蓝框移动到了外面,那你就不要进行相乘操作,这是一个惯例。
251 |
252 | 可以选择所有的数使结果是整数是挺不错的,尽管一些时候,你不必这样做,只要向下取整也就可以了。你也可以自己选择一些𝑛,𝑓,𝑝和𝑠的值来验证这个输出尺寸的公式是对的。
253 |
254 | **卷积(concolution)与互相关(cross-correlation)**
255 |
256 | 如果你看的是一本典型的数学教科书,那么卷积的定义是做元素乘积求和,实际上还有一个步骤是你首先要做的,也就是在把这个 6×6 的矩阵和 3×3 的过滤器卷积之前,首先你将 3×3 的过滤器沿水平和垂直轴翻转,所以
257 | $$
258 | \left[\begin{array}{ccc}
259 | 3 & 4 & 5 \\
260 | 1 & 0 & 2 \\
261 | -1 & 9 & 7
262 | \end{array}\right] \text { 变为 }\left[\begin{array}{ccc}
263 | 7 & 2 & 5 \\
264 | 9 & 0 & 4 \\
265 | -1 & 1 & 3
266 | \end{array}\right]
267 | $$
268 | 这相当于将 3×3 的过滤器做了个**镜像**,在水平和垂直轴上。然后再把这个翻转后的矩阵复制到这里(左边的图像矩阵),你要把这个翻转矩阵的元素相乘来计算输出的 4×4 矩阵左上角的元素,如图所示。然后取这 9 个数字,把它们平移一个位置,再平移一格,以此类推。
269 |
270 |
249 |
250 | ⌊ ⌋这是向下取整的符号,这也叫做对𝑧进行地板除(floor),这意味着𝑧向下取整到最近的整数。这个原则实现的方式是,你只在蓝框完全包括在图像或填充完的图像内部时,才对它进行运算。如果有任意一个蓝框移动到了外面,那你就不要进行相乘操作,这是一个惯例。
251 |
252 | 可以选择所有的数使结果是整数是挺不错的,尽管一些时候,你不必这样做,只要向下取整也就可以了。你也可以自己选择一些𝑛,𝑓,𝑝和𝑠的值来验证这个输出尺寸的公式是对的。
253 |
254 | **卷积(concolution)与互相关(cross-correlation)**
255 |
256 | 如果你看的是一本典型的数学教科书,那么卷积的定义是做元素乘积求和,实际上还有一个步骤是你首先要做的,也就是在把这个 6×6 的矩阵和 3×3 的过滤器卷积之前,首先你将 3×3 的过滤器沿水平和垂直轴翻转,所以
257 | $$
258 | \left[\begin{array}{ccc}
259 | 3 & 4 & 5 \\
260 | 1 & 0 & 2 \\
261 | -1 & 9 & 7
262 | \end{array}\right] \text { 变为 }\left[\begin{array}{ccc}
263 | 7 & 2 & 5 \\
264 | 9 & 0 & 4 \\
265 | -1 & 1 & 3
266 | \end{array}\right]
267 | $$
268 | 这相当于将 3×3 的过滤器做了个**镜像**,在水平和垂直轴上。然后再把这个翻转后的矩阵复制到这里(左边的图像矩阵),你要把这个翻转矩阵的元素相乘来计算输出的 4×4 矩阵左上角的元素,如图所示。然后取这 9 个数字,把它们平移一个位置,再平移一格,以此类推。
269 |
270 |  271 |
272 | 但在深度学习文献中,定义卷积运算时跳过了这个镜像操作。前面我们实际上做的,有时被称为互相关而不是卷积。
273 |
274 | 总结来说,按照机器学习的惯例,我们通常不进行翻转操作。从技术上说,这个操作可能叫做互相关更好。但在大部分的深度学习文献中都把它叫做卷积运算。
275 |
276 | ### 10.6 三维卷积
277 |
278 | **三维(RGB图像)上的卷积操作**
279 |
280 | 举例,假如你不仅想检测灰度图像的特征,也想检测 RGB 彩色图像的特征。彩色图像如果6×6×3,这里的第一个 6 代表图像高度,第二个 6 代表宽度,这个3 代表颜色通道的数目。你可以把它想象成三个 6×6图像的堆叠。为了检测图像的边缘或者其他的特征,不是把它跟原来的 3×3 的过滤器做卷积,而是跟一个三维的过滤器,它的维度是 3×3×3,这样这个过滤器也有三层,对应红、绿、蓝三个通道。得到的输出会是一个 4×4 的图像,注意是 4×4×1,最后一个数不是 3 了。
281 |
282 | 为了简化这个 3×3×3过滤器的图像,我们不把它画成 3 个矩阵的堆叠,而画成一个三维的立方体。
283 |
284 | 
285 |
286 | **计算过程**:
287 |
288 | 把这个 3×3×3 的过滤器先放到最左上角的位置,这个 3×3×3 的过滤器有 27 个数,27 个参数就是 3 的立方。依次取这 27 个数,然后乘以相应的红绿蓝通道中的数字。先取红色通道的前 9 个数字,然后是绿色通道,然后再是蓝色通道,乘以左边黄色立方体覆盖的对应的 27 个数,然后把这些数都加起来,就得到了输出的第一个数字。如果要计算下一个输出,你把这个立方体滑动一个单位,再与这 27 个数相乘,把它们都加起来,就得到了下一个输出,以此类推。
289 |
290 | 
291 |
292 |
293 |
294 | **作用**:
295 |
296 | 举例:
297 |
298 | - 如果你想检测图像红色通道的边缘,那么你可以将第一个过滤器设为$\left[\begin{array}{rrr}1 & 0 & -1 \\ 1 & 0 & -1 \\ 1 & 0 & -1\end{array}\right]$,和之前一样,而绿色通道全为 0,$\left[\begin{array}{lll}0 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0\end{array}\right]$,蓝色也全为 0。如果你把这三个堆叠在一起形成一个3×3×3的过滤器,那么这就是一个检测垂直边界的过滤器,但只对红色通道有用。
299 | - 或者如果你不关心垂直边界在哪个颜色通道里,那么你可以用一个这样的过滤器,$\left[\begin{array}{ccc}1 & 0 & -1 \\ 1 & 0 & -1 \\ 1 & 0 & -1\end{array}\right],\left[\begin{array}{ccc}1 & 0 & -1 \\ 1 & 0 & -1 \\ 1 & 0 & -1\end{array}\right],\left[\begin{array}{ccc}1 & 0 & -1 \\ 1 & 0 & -1 \\ 1 & 0 & -1\end{array}\right]$,所有三个通道都是这样。所以通过设置第二个过滤器参数,你就有了一个边界检测器,3×3×3 的边界检测器,用来检测任意颜色通道里的边界。参数的选择不同,可以得到不同的特征检测器,所有的都是 3×3×3 的过滤器。
300 |
301 | **同时用多个过滤器**
302 |
303 | 有时候我们会想要同时检测垂直边缘和水平边缘,还有 45°倾斜的边缘,还有 70°倾斜的边缘等等,这是就需要使用多个过滤器。
304 |
305 | 
306 |
307 | 例如我们让这个 6×6×3 的图像和这个 3×3×3 的过滤器卷积,得到 4×4 的输出。(第一个)这可能是一个垂直边界检测器或者是学习检测其他的特征。第二个过滤器可以用橘色来表示,它可以是一个水平边缘检测器。做完卷积,然后把这两个 4×4 的输出堆叠在一起,这样你就都得到了一个4×4×2 的输出立方体。这里的 2 的来源于我们用了两个不同的过滤器。
308 |
309 | **维度总结**
310 |
311 | 如果你有一个$n \times n \times n_{c}$(通道数)的输入图像,上例中就是 6×6×3,这里的$n_{c}$就是通道数目,然后卷积上一个$f \times f \times n_{c}$,这个例子中是 3×3×3,按照惯例,这个(前一个𝑛𝑐)和这个(后一个𝑛𝑐)必须数值相同。然后你就得到了,$(n-f+1)\times(n-f+1) \times n_{c^{\prime}}$这里$n_{c^{\prime}}$其实就是下一层的通道数,它就是你用的过滤器的个数,在我们的例子中,那就是 4×4×2。我写下这个假设时,用的步幅为 1,并且没有 padding。如果你用了不同的步幅或者 padding,那么这个$𝑛 − 𝑓 + 1$数值会变化。
312 | $$
313 | n \times n \times n_{c} \text { * } f \times f \times n_{c} \rightarrow (n-f+1)\times(n-f+1) \times n_{c^{\prime}}
314 | $$
315 | **思考**:为什么卷积核是3\*3channels而不是3\*3\*1在多个通道之间移动?
316 |
317 | 如果使用3\*3\*1的卷积核在多个通道中移动,那意味着每个通道都用同一个过滤器,而且每个过滤器(卷积核)都忽略了隐藏在通道之间的联系和信息,这无疑会降低卷积网络的效果。
318 |
319 | ### 10.7 单层卷积网络
320 |
321 | 
322 |
323 | 相比之前的卷积过程,CNN的单层结构多了激活函数ReLU和偏移量b,与神经网络的单层结构类似,即:
324 |
325 | $Z^{[l]}=W^{[l]} A^{[l-1]}+b$
326 | $A^{[l]}=g^{[l]}\left(Z^{[l]}\right)$
327 |
328 | 其中,卷积运算对应上式中的乘积运算,过滤器组数值对应着权重$W^{[l]}$,激活函数则为ReLU
329 |
330 | 上图中参数$W$的计算:每个过滤器组共有3x3x3=27个参数,两个过滤器组则共包含27x2=54个参数$W$
331 |
332 | 相关符号的总结(设层数为$l$)
333 |
334 | $f^{[l]}=$ filter size
335 | $p^{[l]}=$ padding
336 | $s^{[l]}=$ stride
337 | $n_{c}^{[l]}=$ number of filters
338 | $n_{H}^{[l]}=$ height of input
339 | $n_{W}^{[l]}=$ width of filters
340 |
341 | 输入维度为:
342 |
343 | $n_{H}^{[l-1]} \times n_{W}^{[l-1]} \times n_{c}^{[l-1]}$
344 | 每个滤波器组维度为:
345 |
346 | $f^{[l]} \times f^{[l]} \times n_{c}^{[l-1]}$
347 |
348 | 权重维度为:
349 |
350 | $f^{[l]} \times f^{[l]} \times n_{c}^{[l-1]} \times n_{c}^{[l]}$
351 |
352 | 偏置维度为:
353 |
354 | $ 1 \times 1 \times 1 \times n_{c}^{[l]}$
355 |
356 | 输出维度为 :
357 |
358 | $ n_{H}^{[l]} \times n_{W}^{[l]} \times n_{c}^{[l]}$
359 |
360 | 其中:
361 | $$
362 | \begin{aligned}
363 | n_{H}^{[l]} &=\left\lfloor\frac{n_{H}^{[l-1]}+2 p^{[l]}-f^{[l]}}{s^{[l]}}+1\right\rfloor \\
364 | n_{W}^{[l]} &=\left\lfloor\frac{n_{W}^{[l-1]}+2 p^{[l]}-f^{[l]}}{s^{[l]}}+1\right\rfloor
365 | \end{aligned}
366 | $$
367 | 若有$m$个样本进行向量化运算,则输出的维度为:
368 |
369 | $m \times n_{H}^{[l]} \times n_{W}^{[l]} \times n_{c}^{[l}$
370 |
371 | ### 10.8 简单卷积网络示例
372 |
373 | 
374 |
375 | 如上图,是一个简单的CNN模型,且$a^{[3]}$维度为7 x 7 x 40,若将$a^{[3]}$排成1列,则维度为1960 x 1,再与输出层连接,输出层若为1个神经元,则为二元分类;若为多个神经元,则为多元分类。由此得出预测输出$\hat{y}$。
376 |
377 | 当CNN层数增加时,一般$n_{H}^{[l]}$和$n_{W}^{[l]}$会逐渐减小,而$n_{c}^{[l]}$会逐渐增大。
378 |
379 | CNN有以下三种类型的layer:
380 |
381 | - Convolution(CONV)(最为常见)
382 | - Pooling(POOL)
383 | - Fully connected(FC)
384 |
385 | ### 10.9 池化层
386 |
387 | 池化是一种下采样(downsample)手段,是对信息进行抽象的过程。
388 |
389 | 池化并不只有最大池化Max Pooling一种,不过Max Pooling是最广泛使用的一种。
390 |
391 | #### 10.9.1 最大池化 Max Pooling
392 |
393 | 最大池化指的是在采样区间内用区间内的最大值代表这个区间。
394 |
395 | 
396 |
397 | 和卷积运算一样,池化也有自己的参数:池化大小、步长和Padding。只不过最常用的是2*2大小、步长为2和Valid Padding。下文如没有说明则都是采用这种最大池化。
398 |
399 | #### 10.9.2 其他池化
400 |
401 | * 平均池化:平均池化和最大池化相对应,用该区间的平均值来代表该区间。
402 | * 全局平均池化:和上述池化有点不同,是将一个通道的信息都用该通道的平均值代替。比如输入4\*4\*channels的特征图,输出一个长度为channels的特征向量。该向量每一个值都是对应通道(4*4=16个值)的平均值。通常用在最后一层卷积层后、softmax前。主要作用是代替全连接,降低参数个数。
403 | * ASPP(空洞卷积空间金字塔池化,Atrous Spatial Pyramid Pooling):和传统的池化操作不同,该池化并不降低分辨率(输出特征图的大小),但是同样可以起到对增加感受野的效果(下文介绍感受野)。
404 |
405 | #### 10.9.3 池化的作用
406 |
407 | 在介绍池化的作用前,先介绍一下感受野。
408 |
409 | **感受野 Receptive Field**
410 |
411 | 感受野表示了一个神经元(输出图的一个像素点)与多少个**原始图像**上的像素点有关联。浅层的感受野小,深层的感受野逐渐增大。对于单个神经元,其值只与其感受野有关,与感受野外无关。下图给出在经过两层3\*3的卷积后的神经元的感受野示例。
412 |
413 | 
414 |
415 | 上图还可以发现,两个3\*3的卷积核能够与单个5\*5的卷积核有相同的感受野。但是前者只有2\*3\*3=18个参数,后者有5\*5=25个参数。可见可以通过多层小的卷积核来获得和单个大卷积核的相同效果,同时参数更少。甚至可以在GoogleNet中看到将n\*n拆分为1\*n和n\*1两个卷积核的做法。
416 |
417 | 对于池化层有效的原因之一,在于池化操作可以只用少量的参数大大增加下一层的神经元的感受野。方便起见,下列感受野计算不计算到原始图像那层。如果卷积层之间没有加入池化层,那后一层的神经元的感受野只为3\*3=9(假设是3\*3的卷积核);如果加入了最大池化层,那后一层的神经元的感受野可以增大到3\*3\*4=36,用同样的参数数量直接扩大了4倍。当然,简单地增加卷积核的大小也可以增加感受野,但是这样做增加了计算成本、参数数量、以及过拟合的风险。
418 |
419 | **作用**
420 |
421 | 介绍完感受野,现在开始正式介绍池化的作用:
422 |
423 | * 降低分辨率、降维、压缩特征、可以减少后续的运算量等等。但是在某些需要保持分辨率的任务(图像语义分割)中会变成一种弊端。
424 | * 只用少量参数就可以大大增加后续神经元的感受野。
425 |
426 | ### 10.10 卷积神经网络示例
427 |
428 | #### 10.10.1 LeNet5
429 |
430 | LeNet的[论文连接](https://ieeexplore.ieee.org/document/726791?reload=true&arnumber=726791)。LeNet是一个很简单很小的网络,建立之初是为了手写字识别(0-9)。虽然简单,但是是第一个典型的CNN网络。麻雀虽小,五脏俱全,包含了卷积层、池化层和全连接层。
431 |
432 | 网络结构如下:
433 |
434 | 
435 |
436 |
437 |
438 | 该图没有说清楚,网络中所有卷积层的卷积核都是5*5的,以及步长为1,padding为0。图中的subsampling指的是池化,具体来说是最大池化。细心的话还会留意到最后一层用了Gaussian connections。我个人认为已经被淘汰了,感兴趣的可以自行了解。自己实现的时候当成全连接也可以。
439 |
440 | 该论文的典型之处主要在于:
441 |
442 | * 一层卷积一层池化交替出现。
443 | * 最后输出前若干层采用全连接层。
444 | * 全连接层的参数真的很多。卷积网络的参数主要集中在第一层全连接层(16\*5\*5\*120=48000)。
445 |
446 | #### 10.10.2 AlexNet
447 |
448 | AlexNet的[论文连接](http://papers.nips.cc/paper/4824-imagenet-classification-with-deep-convolutional-neural-networks.pdf)。这是第一个引起大家注意的卷积网络,该模型取得了2012年的ImageNet比赛冠军,而且也正是因为这次比赛而打响了名号。
449 |
450 | 网络结构如下:
451 |
452 | 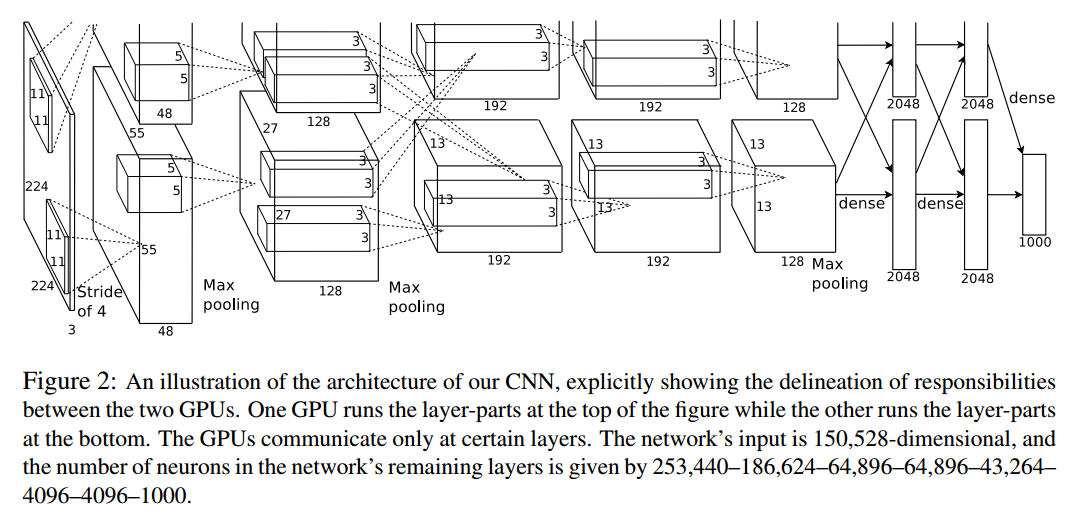
453 |
454 | 论文中该图片有误,第一个卷积层的输出应该是54\*54而不是55\*55,这个可以自己计算一下来验证。该网络在前两层就采用了相当大的卷积核,不过后面的层都只用3*3的了。该网络拿下冠军时,以比第二名少20%左右的误差率而取得优胜。
455 |
456 | 个人认为比较值得注意的点是:
457 |
458 | * 并不一定需要每层卷积层后都添加池化层。连续多层卷积层可以视为一层卷积核更大、能拟合更复杂函数的卷积层。
459 | * 对于更大的图片,感受野也需要对应增大。AlexNet的做法是前两层卷积层用了较大的卷积核。
460 |
461 | #### 10.10.3 VGG16
462 |
463 | VGG16的[论文连接](https://arxiv.org/abs/1409.1556)。该网络改进了AlexNet,改进的思路是:用更多层、更小的卷积核代替原来那些比较大的卷积核。最根本的一点是在不减小感受野的前提下增加层数和减少参数量。从结果上来看,这么做确实起到了不错的效果。
464 |
465 | 下图中,卷积层默认步长为1,padding为same。网络结构如下:
466 |
467 | 
468 |
469 | 该网络不止是本身很有价值,其来源(论文)也很有价值。该论文通过对比各种网络,来说明卷积网络越深效果越好这一点。VGG16中的16就是指除去池化层,该网络一个有16层。
470 |
471 | 对比AlexNet,该网络的改进如下:
472 |
473 | * 采用多层连续的3*3卷积层代替大卷积层。
474 | * 网络深度更深了。
475 | * 通道数全部用2的幂。更符合计算机的存储规则。
476 | * 两、三层卷积层 + 一层池化。
477 | * 池化后通道数翻倍。
478 | * 每层网络的步长都为1,padding都为same。
479 |
480 | 上述改进也是现在我所看到的大部分网络的构建习惯(趋势)。我想这足以说明这些“规律”有多好用。
481 |
482 | ### 10.11 为什么使用卷积
483 |
484 | #### 10.11.1 减少参数
485 |
486 | 1.10介绍的网络也基本可以看出,卷积网络中全连接层的参数占了绝大一部分。举例LeNet5,各层参数个数分别为:第一层卷积层 5\*5\*1\*6=150、第二层卷积层 5\*5\*6\*16=2400、第一层全连接层 5\*5\*16\*120=48000、第二层全连接层 120\*84=10080,若最后一层视为全连接层则有 84\*10=840。
487 |
488 | 不难发现,第一层全连接层的参数占据了$\frac{48000}{150+2400+48000+10080+840}=0.78=78%$的参数,这已经占据了一半以上的参数。很明显,卷积层对比全连接层来说可以大大减小参数的数量,一方面可以避免过拟合,另一方面减少了对设备的要求。
489 |
490 | 更进一步,卷积操作需要的参数很少的原因在于
491 |
492 | * **权值共享**。一个卷积核的权值可以适用到整个网络,而不是每个神经元独占一个权值。因为一个卷积核的工作可以理解为专门识别某一些特征。而且这个特征应该是通用的,与所处位置无关,即**平移不变性**。同时平移不变性也是网络学习的潜在目标之一。举例垂直边缘检测便可以检索对应区域是否有垂直边界,而不在乎这个边界的具体位置在哪。
493 | * **稀疏连接**。与全连接对应,在全连接中任意一个神经元都要与上一层的所有神经元连接;而卷积则只受感受野内的神经元影响,对于感受野外的并不关心。
494 |
495 | #### 10.11.2 训练卷积网络
496 |
497 | 假设要做一个猫咪检测网络,$x^{(i)}$表示第$i$张图片,$y^{(i)}$表示对应图片的标签。在选定一个网络后,设计好损失函数,对全部样本的损失求平均作为代价函数。随机初始化权重矩阵和偏置。在Python实现时还可以向量化$x^{(i)}$(当然,就我所知大部分架构也会这么做)。用梯度下降来训练网络,而且也可以采用优化器如$RMSProp$或$Adam$。
498 |
499 |
--------------------------------------------------------------------------------
/11 深度卷积网络 实例探究.md:
--------------------------------------------------------------------------------
1 | #第二周 深度卷积网络:实例探究
2 | ## 2.1为什么要实例探究
3 |
4 | 在计算机视觉的研究中,将卷积层、池化层及全连接层进行有有机结合,才能形成有效的卷积神经网络,而更好地去实现这种有机结合可以多多参考他人所构建的框架,而且在计算机视觉中,良好的神经网络框架往往也适用于其他的任务,所以多多参考其他案例有利于我们更好地应用卷积神经网络。在框架学习中,我们也可以多多研读计算机视觉领域相关的论文或相关的研讨内容。
5 |
6 |
7 |
8 | ## 2.2经典网络
9 |
10 | ### 2.2.1LeNet-5网络
11 |
12 | 
13 |
14 | 该网络是针对灰度图像训练的,该例用其对手写字体进行识别
15 |
16 | 在池化后选用$sigmoid$函数来进行非线性函数处理
17 |
18 | 其结构为卷积——池化——卷积——池化——全连接——全连接。
19 |
20 | 且采取了平均池化(当时年代的人们更倾向使用平均池化),然而现在会更多的使用最大池化。因没有使用padding或有效卷积,使得每完成一次卷积,图像的高度和宽度都缩小了。
21 |
22 | 最后输出层利用了$softmax$函数来分类输出十种结果。
23 |
24 | 相比于其他更复杂的神经网络,其参数较少,只有约六万个。
25 |
26 | 随着网络层次的加深,图像的高度和宽度都在缩小,信道数量则会增加。
27 |
28 | 其中的“一个或多个卷积层后跟着一个池化层,然后又是若干个卷积层,池化层,然后再是全连接层,最后输出。”这一模式仍被经常使用。
29 |
30 | ### 2.2.2AlexNet网络
31 |
32 | 
33 |
34 | 相比于LeNet-5,AlexNet网络要大得多,其有约六千万个参数,但优点在于在用于训练图像和数据集时,它能处理非常相似的基本构造模块,而往往这些模块有着隐藏单元或数据;同时采用了$Relu$函数。
35 |
36 | 在写这篇论文时,GPU的处理速度并不快,所以针对这个模型,采用了两个GPU进行训练,将不同的层拆分到两个GPU中进行训练,并用了一些专门的方法使这两个GPU得以交流。
37 |
38 | ### 2.2.3VGG-16
39 |
40 | 
41 |
42 | VGG-16中的“16”代表该网络结构包含16个卷积层和全连接层
43 |
44 | 这是一个极大的网络,约有1.38亿个参数,但其优点是其结构不复杂,一般为卷积层后跟着可压缩图像大小(高度和宽度)的池化层。其过滤器数量变化存在一定规律,变化为64→128→256→512,论文作者可能认为512的信道数量已经足够大了,故没有继续增加。除了VGG-16外,还有VGG-19模型,但VGG-19模型比VGG-16要大得多,但实现的效果并不比VGG-16要好多少,故较少使用VGG-19。
45 |
46 | 随着该网络的加深,图像的高度和宽度在不断缩小,每次池化后缩小一半,而信道数量在不断增加(每次卷积后增加1倍)。即图像缩小的比例和信道增加的比例是有规律的。
47 |
48 |
49 |
50 | ## 2.3残差网络
51 |
52 | 神经网络层数越多,网络越深,越容易受到梯度消失和梯度爆炸的影响。我们可以通过让神经网络某些层跳过下一层神经元的连接,隔层相连,弱化每层之间的强联系来解决该问题。而这样的神经网络即为残差网络(ResNets)
53 |
54 | ### 2.3.1残差块
55 |
56 | 残差网络由多个残差块组成,如下图为残差块组成
57 |
58 | 
59 |
60 | 图中红色箭头称为跳远连接,其建立了$a^{[l]}$与$a^{[l+2]}$的隔层联系。具体表达式为:
61 |
62 | $z^{[l+1]}=W^{[l+1]} a^{[l]}+b^{[l+1]}$
63 | $a^{[l+1]}=g\left(z^{[l+1]}\right)$
64 | $z^{[l+2]}=W^{[l+2]} a^{[l+1]}+b^{[l+2]}$
65 | $a^{[l+2]}=g\left(z^{[l+2]}+a^{[l]}\right)$
66 |
67 | 其中$a^{[l]}$与$z^{[l+2]}$共同作用,通过ReLU函数输出$a^{[l+2]}$
68 |
69 | 多个残差块构成了如下图所示的残差网络
70 |
71 | 
72 |
73 | ### 2.3.2与Plain Network对比
74 |
75 | 我们将非残差网络称为Plain Network,将其与ResNet对比可发现,残差网络可以有效解决梯度消失和梯度爆炸的问题,睡着网络层数的增加,Plain Network的training error甚至可能变大,而ResNet的training error则一直呈现下降趋势。如下图
76 |
77 | 详细可参考
78 |
79 | [Deep Residual Learning for Image Recognition](extension://ibllepbpahcoppkjjllbabhnigcbffpi/https://openaccess.thecvf.com/content_cvpr_2016/papers/He_Deep_Residual_Learning_CVPR_2016_paper.pdf)
80 |
81 |
82 |
83 |
84 | ### 2.4 网络中的网络/1*1卷积
85 |
86 | #### 2.4.1 定义
87 |
88 | 也被称为***\*Network in Network\****,对输入的个不同的位置都应用一个全连接层,全连接层的作用是便在输入层上实施一个非平凡(***\*non-trivial\****)计算。简单点说就是将输入数据的通道数进行压缩,压缩成所使用的过滤器的数量大小。
89 |
90 |
91 |
92 | #### 2.4.2例子一
93 |
94 | 假设这是一个28×28×192的输入层,可以使用池化层压缩它的高度和宽度,这个过程我们很清楚。但如果通道数量很大,该如何把它压缩为28×28×32维度的层呢?你可以用32个大小为1×1的过滤器,严格来讲每个过滤器大小都是1×1×192维,因为过滤器中通道数量必须与输入层中通道的数量保持一致。但是你使用了32个过滤器,输出层为28×28×32,这就是压缩通道数()的方法。
95 |
96 | 
97 |
98 |
99 |
100 | #### 2.4.3例子二
101 |
102 | 过滤器为1×1,输入一张6×6×32的图片,然后对它做卷积,遍历这36个单元格,计算左图中32个数字和过滤器中32个数字的元素积之和,然后应用***\*ReLU\****非线性函数。
103 |
104 | 我们以其中一个单元为例,它是这个输入层上的某个切片,用这36个数字乘以这个输入层上1×1切片,得到一个实数,像这样把它画在输出中。
105 |
106 | 
107 |
108 |
109 |
110 | 这个1×1×32过滤器中的32个数字可以这样理解,一个神经元的输入是32个数字(输入图片中左下角位置32个通道中的数字),即相同高度和宽度上某一切片上的32个数字,这32个数字具有不同通道,乘以32个权重(将过滤器中的32个数理解为权重),然后应用***\*ReLU\****非线性函数,在这里输出相应的结果。
111 |
112 | 
113 |
114 |
115 |
116 | 一般来说,如果过滤器不止一个,而是多个,就好像有多个输入单元,其输入内容为一个切片上所有数字,输出结果是6×6过滤器数量。
117 |
118 | 
119 |
120 |
121 |
122 |
123 |
124 |
125 |
126 | 所以1×1卷积可以从根本上理解为对这32个不同的位置都应用一个全连接层,全连接层的作用是输入32个数字(过滤器数量标记为,在这36个单元上重复此过程),输出结果是6×6×#filters(过滤器数量),以便在输入层上实施一个非平凡(***\*non-trivial\****)计算。此时,输入的结果的通道层数取决于过滤器的个数。
127 |
128 |
129 |
130 | #### 2.4.4深度可分离卷积
131 |
132 | **定义**:一个卷积核负责一个通道,一个通道只被一个卷积核卷积
133 |
134 | **引用博客**:https://blog.csdn.net/makefish/article/details/88716534
135 |
136 | 相较于一般卷积,深度可分离卷积有着不同的计算方法:
137 |
138 | 在卷积计算时,先用三个卷积对三个通道分别做卷积,这样在一次卷积后,输出3个数,然后这输出的三个数,再通过一个1x1x3的卷积核(pointwise核),得到一个数。下面进行分步解释;
139 |
140 | 第一步,对三个通道分别做卷积,输出三个通道的属性:
141 |
142 |
143 |
144 | 
145 |
146 |
147 |
148 |
149 |
150 | 第二步,用卷积核1x1x3对三个通道再次做卷积,这个时候的输出就和正常卷积一样,是8x8x1:
151 |
152 | 
153 |
154 |
155 |
156 | 如果要提取更多的属性,则需要设计更多的1x1x3卷积核心就可以(图片引用自原网站。感觉应该将8x8x256那个立方体绘制成256个8x8x1,因为他们不是一体的,代表了256个属性)::
157 |
158 | 
159 |
160 | **深度可分离卷积的优点缺点**:
161 |
162 | 对于需要提取大量属性或者特征的情景下,深度可分离卷积随着要提取的属性越来越多,就能够节省更多的参数。当然如果提取的特征属性不多,普通的卷积效果优于深度可分离卷积。
163 |
164 |
165 |
166 |
167 |
168 | ### 2.5 Inception网络
169 |
170 | #### 2.5.1作用
171 |
172 | 代替人工决定所使用的过滤器的大小,或者确定是否需要创建卷积层或池化层,
173 |
174 | #### 2.5.2 论文链接
175 |
176 | https://arxiv.org/pdf/1409.4842.pdf
177 |
178 | #### 2.5.3主要思想
179 |
180 | 不需要人为决定使用哪个过滤器或者是否需要池化,而是由网络自行确定这些参数,你可以给网络添加这些参数的所有可能值,然后把这些输出连接起来,让网络自己学习它需要什么样的参数,采用哪些过滤器组合。
181 |
182 | #### 2.5.4原理
183 |
184 | 利用多种维度的过滤器,分别使用不同的方法,产生大量长宽相等,通道可以不同的输出块,并将这些输出块堆积在一起,产生一个组合了各种类型的参数的输出,从而在后续的训练中,让网络自己学习它需要什么样的参数,采用哪些过滤器组合。
185 |
186 |
187 |
188 | 例如,这是你28×28×192维度的输入层,***\*Inception\****网络或***\*Inception\****层的作用就是代替人工来确定卷积层中的过滤器类型,或者确定是否需要创建卷积层或池化层,我们演示一下。
189 |
190 | 
191 |
192 |
193 |
194 | 如果使用1×1卷积,输出结果会是28×28×#(某个值),假设输出为28×28×64,并且这里只有一个层。
195 |
196 | 
197 |
198 |
199 |
200 | 如果使用3×3的过滤器,那么输出是28×28×128。然后我们把第二个值堆积到第一个值上,为了匹配维度,我们应用***\*same\****卷积,输出维度依然是28×28,和输入维度相同,即高度和宽度相同。
201 |
202 | 
203 |
204 |
205 |
206 | 或许你会说,我希望提升网络的表现,用5×5过滤器或许会更好,我们不妨试一下,输出变成28×28×32,我们再次使用***\*same\****卷积,保持维度不变。
207 |
208 | 
209 |
210 |
211 |
212 | 或许你不想要卷积层,那就用池化操作,得到一些不同的输出结果,我们把它也堆积起来,这里的池化输出是28×28×32。为了匹配所有维度,我们需要对最大池化使用***\*padding\****,它是一种特殊的池化形式,因为如果输入的高度和宽度为28×28,则输出的相应维度也是28×28。然后再进行池化,***\*padding\****不变,步幅为1。
213 |
214 | 
215 |
216 |
217 |
218 | 有了这样的***\*Inception\****模块,你就可以输入某个量,因为它累加了所有数字,这里的最终输出为32+32+128+64=256。***\*Inception\****模块的输入为28×28×192,输出为28×28×256。这就是Inception网络的核心内容。
219 |
220 |
221 |
222 | #### 2.5.5计算成本问题
223 |
224 | 由于进行了多种模型的计算,会造成计算成本会非常的大,如何缩小成本是一个非常重要的一环。
225 |
226 | 下面以5×5过滤器为例计算成本
227 |
228 | 
229 |
230 |
231 |
232 | 这是一个28×28×192的输入块,执行一个5×5卷积,它有32个过滤器,输出为28×28×32。我们来计算这个28×28×32输出的计算成本,它有32个过滤器,因为输出有32个通道,每个过滤器大小为5×5×192,输出大小为28×28×32,所以你要计算28×28×32个数字。对于输出中的每个数字来说,你都需要执行5×5×192次乘法运算,所以乘法运算的总次数为每个输出值所需要执行的乘法运算次数(5×5×192)乘以输出值个数(28×28×32),把这些数相乘结果等于1.2亿(120422400)。
233 |
234 | 
235 |
236 |
237 |
238 | 为了缩小成本,我们使用1*1卷积对输入进行通道缩小。对于输入层,使用1×1卷积把输入值从192个通道减少到16个通道。然后对这个较小层运行5×5卷积,得到最终输出。请注意,输入和输出的维度依然相同,输入是28×28×192,输出是28×28×32。
239 |
240 | 然后我们进行成本计算应用1×1卷积,过滤器个数为16,每个过滤器大小为1×1×192,这两个维度相匹配(输入通道数与过滤器通道数),28×28×16这个层的计算成本是,输出28×28×192中每个元素都做192次乘法,用1×1×192来表示,相乘结果约等于240万,这是第一个卷积层的计算成本。第二层的输出为28×28×32,对每个输出值应用一个5×5×16维度的过滤器,计算结果为1000万。
241 |
242 | 所以所需要乘法运算的总次数是这两层的计算成本之和,也就是1204万,与上一张幻灯片中的值做比较,计算成本从1.2亿下降到了原来的十分之一,即1204万。
243 |
244 |
245 |
246 | #### 2.5.6 瓶颈层
247 |
248 |
249 |
250 | 
251 |
252 |
253 |
254 | 这个被增加的1*1卷积层常被称为瓶颈层,即先缩小网络表示,然后再扩大它。
255 |
256 |
257 |
258 | 需要注意的是,只要合理构建瓶颈层,你既可以显著缩小表示层规模,又不会降低网络性能,从而节省了计算。
259 |
260 |
261 |
262 | #### 2.5.7 Inception Net
263 |
264 | 简述:由多个***\*Inception\*******\*模块所组成的神经网络。\****
265 |
266 | 原理:
267 |
268 | 首先如下图所示,建立前面所说的***\*Inception\****模块。
269 |
270 | 
271 |
272 |
273 |
274 | 为了能在最后将这些输出都连接起来,我们会使用***\*same\****类型的***\*padding\****来池化,使得输出的高和宽依然是28×28,这样才能将它与其他输出连接起来。
275 |
276 | 但注意,如果你进行了最大池化,即便用了***\*same padding\****,3×3的过滤器,***\*stride\****为1,其输出将会是28×28×192,其通道数或者说深度与这里的输入(通道数)相同。所以看起来它会有很多通道,我们实际要做的就是再加上一个1×1的卷积层,去进行我们在1×1卷积层的视频里所介绍的操作,将通道的数量缩小,缩小到28×28×32。
277 |
278 | 
279 |
280 |
281 |
282 | 最后,将这些方块全都连接起来。在这过程中,把得到的各个层的通道都加起来,最后得到一个28×28×256的输出。通道连接实际就是之前视频中看到过的,把所有方块连接在一起的操作。这就是一个***\*Inception\****模块,而***\*Inception\****网络所做的就是将这些模块都组合到一起。
283 |
284 | 
285 |
286 |
287 |
288 | ***\*上图为\*******\*Inception\****网络的图片,并且其由多个***\*Inception\*******\*模块所组成,需要注意的是有一些\*******\*Inception\*******\*模块中间还夹着一个最大池化层,如图中的6和7.\****
289 |
290 | 
291 |
292 |
293 |
294 | ***\*在论文原文中,网络里有着一些其他分支,如上图中的1、2、4,其中1是一个\*******\*softmax\****层,用于做出预测,编号2所做的就是通过隐藏层(编号3)来做出预测,所以这其实是一个***\*softmax\****输出(编号2),编号4也包含了一个隐藏层,通过一些全连接层,然后有一个***\*softmax\****来预测,输出结果的标签。 这些分支确保了即便是隐藏单元和中间层(编号5)也参与了特征计算,它们也能预测图片的分类。它在***\*Inception\****网络中,起到一种调整的效果,并且能防止网络发生过拟合。
295 |
296 |
297 |
298 | #### 2.5.8 Inception网络多种类型
299 |
300 | 参考博客:https://www.cnblogs.com/dengshunge/p/10808191.html
301 |
302 | ##### Inception v1
303 |
304 | v1其实就是我们前面所说的使用1*1卷积降低计算量后的Inception网络。
305 |
306 | 提升神经网络的性能是各种方法和算法的目的,当然提升网络的性能的方法有很多,例如增加网络的深度和宽度,但当深度和宽度不断增加时,需要训练的参数也会增加,过多的参数容易发生过拟合,并且会导致计算量增加。所以就有了v1结构来解决此问题,也就是利用1*1卷积降低计算量。
307 |
308 |
309 |
310 | ##### Inception v2
311 |
312 | 在训练时每层输入数据的分布会发生改变,所以需要较低的学习率和精心设置初始化参数。只要网络的前面几层发生微小的改变,那么后面几层就会被累积放大下去。一旦网络某一层的输入数据的分布发生改变,那么这一层网络就需要去适应学习这个新的数据分布,所以如果训练过程中,训练数据的分布一直在发生变化,那么将会影响网络的训练速度。为此,提出了v2版本的Inception网络。
313 |
314 | V2版本网络使用了BN算法,可以设置较大的初始学习率,并且减少对参数初始化的依赖,提高了训练速度,同时也可以能防止网络陷入饱和,即消除梯度弥散。
315 |
316 |
317 |
318 | ##### Inception v3
319 |
320 | Inception v3主要解决的是:inception结构过于复杂,使得我们很难对网络进行修改。
321 |
322 | V3主要思路为:利用小尺度的卷积来代替大尺度的卷积,在减少计算量的同时,保证能够学习到更多的信息。例如提出了使用两个级联的3*3的滤波器来代替一个5*5的滤波器,如下图所示:
323 |
324 | 
325 |
326 | 
327 |
328 |
329 |
330 | 同时又对3*3卷积进行分解为3*1+1*3,如下图所示,进而进一步降低计算量
331 |
332 | 
333 |
334 |
335 |
336 | V3主要遵循下列几条思想
337 |
338 | 1. 避免特征表示瓶颈,尤其是在网络的前面。要避免严重压缩导致的瓶颈。特征表示尺寸应该温和地减少,从输入端到输出端。特征表示的维度只是一个粗浅的信息量表示,它丢掉了一些重要的因素如相关性结构。
339 |
340 | 2. 高维信息更适合在网络的局部处理。在卷积网络中逐步增加非线性激活响应可以解耦合更多的特征,那么网络就会训练的更快。
341 |
342 | 3. 空间聚合可以通过低维嵌入,不会导致网络表示能力的降低。例如在进行大尺寸的卷积(如3*3)之前,我们可以在空间聚合前先对输入信息进行降维处理,如果这些信号是容易压缩的,那么降维甚至可以加快学习速度。
343 |
344 | 4. 平衡好网络的深度和宽度。通过平衡网络每层滤波器的个数和网络的层数可以是网络达到最佳性能。增加网络的宽度和深度都会提升网络的性能,但是两者并行增加获得的性能提升是最大的。所以计算资源应该被合理的分配到网络的宽度和深度。
345 |
346 |
347 |
348 | ##### Inception v4
349 |
350 | V4的提出主要是基于 ”当网络更深更宽时,inception网络能否一样高效”的问题提出的,v4具体的解决方法为,结合TensorFlow,简化训练,不需要将模型进行分割,并且将inception和resnet两者进行融合,进一步改善网络。
351 |
352 |
353 |
354 | 以上对Inception网络的4种模型进行概述,具体解释可参考下列博客 https://www.cnblogs.com/dengshunge/p/10808191.html
355 |
356 |
357 |
358 | ### 2.6使用开源实现方案
359 |
360 | 本节为介绍如何下载开源代码。
361 |
362 | 本节下载的代码网站为:
363 |
364 | ***\*ResNets\****实现的***\*GitHub\****地址:https://github.com/KaimingHe/deep-residual-networks
365 |
366 | 
367 |
368 |
369 |
370 |
371 |
372 | ***\*点击Code按钮,并且点击复制按钮复制代码的URL\****
373 |
374 | 
375 |
376 |
377 |
378 | 在需要保存代码的目录下打开cmd,使用下列指令进行代码的下载(复制)
379 |
380 | git clone your URL
381 |
382 | git clone https://github.com/KaimingHe/deep-residual-networks.git
383 |
384 | 
385 |
386 |
387 |
388 | 使用指令观察目录,说明此时代码已下载完毕。
389 |
390 | 接下来进行打开代码。
391 |
392 |
393 |
394 | 
395 |
396 |
397 |
398 | 代码储存在prototxt文件夹中
399 |
400 | 
401 |
402 |
403 |
404 | 使用指令打开其中一个文件。
405 |
406 | more 文件名
407 |
408 | 
409 |
410 | 当然也可以用ide直接打开来进行修改。
411 | ### 2.7 迁移学习
412 | #### 2.7.1 迁移学习的概念
413 | 迁移学习是从一个或多个源领域中通过训练该模型,得出有用的知识并将其用在新的目标任务上(未标记的同一类有相似特征的物品或者是未标记的不同类物品)本质是知识的迁移再利用。
414 | #### 2.7.2 ImageNet、MS COCO\Pascal数据集的获取
415 | ImageNet数据集的获取:
416 | 所有图像可通过url下载:不需要账号登录即可免费下载,下载链接:http://www.image-net.org/download-imageurls ,在SEARCH框中输入需要下载的synset,如tree,也可按类别下载即WordNet ID,下载链接:http://www.image-net.org/synset?wnid=n02084071 ,其中好像个别url已失效。
417 | MS COCO:
418 |
419 | 数据集官网首页:http://cocodataset.org/#home
420 |
421 | 数据集下载:
422 |
423 | 可用迅雷去下载官方链接,速度也挺快的。也可以去这个高中生搭建的下载站下载:http://bendfunction.f3322.net:666/share/。 他的首页是这样子的:http://bendfunction.f3322.net:666/
424 | https://pjreddie.com/projects/coco-mirror/
425 | #### 2.7.3 迁移学习的分类
426 | 按照迁移学习的定义,可以将迁移学习分为三种类型,分布差异迁移学习,特征差异迁移学习和标签差异迁移学习。分布差异迁移学习之源域和目标域数据的边缘分布或者条件概率分布不同,特征差异迁移学习之源域数据和目标数据特征空间不同,标签差异迁移学习指源域和目标域的数据标记空间不同。
427 | 用香蕉和苹果分类问题为例,源域数据是已有的带标签香蕉和苹果的文本数据,目标域是新来的不带标记的香蕉和苹果的文本数据,源域和目标域的数据来自不同的时间,不同地点,数据分布不同,但标记空间和特征空间是相同的,利用源域中的数据来进行目标域的学习问题就是属于分布差异迁移学习问题。源域数据是带有标记的苹果和香蕉的文本数据,而目标域是不带有 标记的苹果和香蕉的图片数据,源域和目标域一个是文本,一个是图像,属于特征差异迁移学习范围。源域数据是带有标记的香蕉和苹果的文本数据,属于二分类问题,目标域是不带标记的梨子,橘子和橙子的文本数据属于三分类问题,源域和目标域的数据标记空间不同,属于标记差异迁移学习的范围。
428 |
429 | 现已成熟的监督学习模式下,在大样本的已标记的数据量集中训练形成传统的监督学习,但是这种模式在运用到情况更为复杂,更多变的实际环境中往往会出现很大的误差,
430 | 所以迁移学习就是在样本量比较少的情况下,训练分类器,随之把这种模式可以运用到其他很多种情况下。
431 |
432 | ### 2.8 数据增强
433 | #### 2.8.1数据增强的基本操作
434 | 数据增强也叫数据扩增,意思是在不实质性的增加数据的情况下,让有限的数据产生等价于更多数据的价值。
435 | 数据增强的手段包括几何变换类,颜色变换类等。
436 |
437 | (1) 几何变换类
438 |
439 | 几何变换类即对图像进行几何变换,包括翻转,旋转,裁剪,变形,缩放等各类操作,下面展示以上操作。
440 | 图一2 3 4 5
441 | (2) 颜色变换类
442 | 颜色变换类时改变图片的R、G、B的值。
443 | #### 2.8.2数据增强的代码实现
444 | TensorFlow实现图片数据增强:
445 | 参见以下网址https://zhuanlan.zhihu.com/p/57284174
446 | #### 2.8.2数据增强的优缺点
447 | 优点:
448 | 增加训练的数据量,提高模型的泛化能力
449 | 增加噪声数据,提升模型的鲁棒性
450 | ### 2.9 计算机视觉现状
451 | #### 2.9.1计算机视觉现状
452 | 深度学习已经成功地应用于计算机视觉、自然语言处理、语音识别、在线广告、物流还有其他许多问题。
453 | 在计算机视觉的现状下,深度学习应用于计算机视觉应用有一些独特之处。
454 | ####2.9.2 banchmark
455 | Benchmark 基准测试,Benchmark是一个评价方式,在整个计算机领域有着长期的应用。
456 | Benchmark在计算机领域应用最成功的就是性能测试,主要测试负载的执行时间、传输速度、吞吐量、资源占用率等。基准测试同时也可以用来识别某段代码的CPU或者内存效率问题. 许多开发人员会用基准测试来测试不同的并发模式, 或者用基准测试来辅助配置工作池的数量, 以保证能最大化系统的吞吐量.
457 | 关于实战可参考:
458 | https://blog.csdn.net/woniu317/article/details/82560312
459 |
--------------------------------------------------------------------------------
/12 目标检测.md:
--------------------------------------------------------------------------------
1 | ## 12 目标检测
2 |
3 | ### 12.1 目标定位
4 |
5 | #### 12.1.1 定义
6 |
7 | 除了要识别出目标类(例如是否有汽车)以外,算法还需要能够给出目标的位置(例如用红框框出目标的位置),这是一种分类定位问题。分类定位问题可以是只有一个目标对象在图片中,也可以是多个目标对象在图片中的。先从单个目标对象的情况开始。
8 |
9 | #### 12.1.2 实现
10 |
11 | **1. 边界框参数定义**
12 |
13 | 图片分类我们已经比较熟悉了,知道最后通过 *softmax* 激活函数激活来表示该图片属于每一类的概率。相较于单纯的分类问题,目标定位还需要输出4个值:$b_x,b_y,b_h,b_w$。这四个值用于表示边框的位置和大小,具体为
14 | $$
15 | \begin{array}{l}
16 | b_x:边框的中心点的x轴坐标 \\
17 | b_y:边框的中心点的y轴坐标 \\
18 | b_h:边框的高度 \\
19 | b_w:边框的宽度 \\
20 | \end{array}
21 | $$
22 | 以上4个值的取值范围均为[0, 1],表示的是边界框与图片对应的**比例**。
23 |
24 | 关于坐标轴的选取,一般选图片的左上角为原点(0, 0),右下角为(1, 1)。且$x$轴为纵轴正方向向下,$y$轴为横轴正方向向右。
25 |
26 | **2. 标签的定义**
27 |
28 | 在确定需要增加的额外输出之后,也要重新定义目标标签 $y$:
29 | $$
30 | y=\left[\begin{array}{l}
31 | p_{c} \\
32 | b_{x} \\
33 | b_{y} \\
34 | b_{h} \\
35 | b_{w} \\
36 | c_{1} \\
37 | c_{2} \\
38 | c_{3}
39 | \end{array}\right]
40 | $$
41 | 其中额外增加了$p_c$,用于表示是否有对象属于类$c_1、c_2$或$c_3$,若为1则表示有目标类在图片中,为0表示只有背景。在只有背景(无目标类)时,其他输出均无效。
42 |
43 | 举一个具体的例子,如下图:
44 |
45 | 
46 |
47 | x 是输入,y 是标签,假设$c_2$表示为车,则最终标签应该如上图所示。当输入中不含任何目标类时,$p_c=0$,其他参数全用“?”表示,即不参与 loss 的计算。
48 |
49 | **3. 边界框参数取值范围**
50 |
51 | 关于边框的4个参数,吴恩达老师给出的取值范围都是[0, 1]的。虽然确实可以这么做,但是背后的原因却没有解释。个人猜测可能是以下原因:
52 |
53 | * 固定取值在[0, 1]之间更容易用激活函数表示,比如sigmoid可以将单个值映射到[0, 1];
54 | * 让标签的所有参数都在一个取值范围,这样在计算loss的时候就不会变相加权了;
55 | * 取值范围在[0, 1]内更容易训练、收敛。
56 |
57 | **4. 损失函数**
58 | $$
59 | L(\hat y,y)=
60 | \begin{cases}
61 | (\hat{y_1}-y_1)^2+(\hat{y_2}-y_2)^2+...+(\hat{y_n}-y_n)^2 & {y_1=1}\\
62 | (\hat{y_1}-y_1)^2 & {y_1=0}
63 | \end{cases}
64 | $$
65 |
66 | * 对于$p_c$可以采用 Logistic 回归的方法,甚至用均方误差$(p_c-\hat{p_c})^2$也可以;
67 | * 对于$b_x,b_y,b_w,b_h$,loss 可以用平方差或类似方法;
68 | * 对于$c_1,c_2,c_3$,是多分类问题,和之前一样用 softmax 即可。
69 |
70 | ### 12.2 特征点检测
71 |
72 | #### 12.2.1 定义
73 |
74 | 以下图为例,检测双眼的眼角位置
75 |
76 | 
77 |
78 | 这个就是特征点检测,主要任务是预测对应的特征点的位置,一般会同时预测多个点。
79 |
80 | #### 12.2.2 实现
81 |
82 | 对于单个点,其坐标为$(l_{ix},l_{iy}),i \in [1, m]$,$m$是特征点的个数,$l_{ix},l_{iy} \in [0,1]$。坐标轴的选取和目标定位时一致,以及需要保证每个样本的特征点的顺序是一致的,比如$l_1$都是左眼的左眼角,$l_2$都是左眼的右眼角等。
83 |
84 | 关于最后一层的激活函数,可以对每个坐标的值用 sigmoid 激活。
85 |
86 | ### 12.3 目标检测
87 |
88 | #### 12.3.1 滑动窗口目标检测算法
89 |
90 | 滑动窗口检测是分两步执行的:第一步是从原图中裁剪一部分并根据需求调整大小,第二步是检测裁剪部分有无目标对象。
91 |
92 | 对于第二步,是我们比较熟悉的分类算法,只是训练集需要人为调整到为几乎整张图都是目标对象,如下图:
93 |
94 | 
95 |
96 | $x$ 为一张无车的图片或者被车占满的图片,标签 $y$ 为1时有车,为0时无车。
97 |
98 | 对于第一步,滑动窗口用的方法是先选定一个裁剪大小,然后从图片的左上角开始,每隔一定像素(距离)裁剪一次,一直滑动到图片的右下角,然后下一个裁剪大小用相同的方法裁剪。如图,上图为3种裁剪大小,下图为一个滑动流程:
99 |
100 | 
101 |
102 | 
103 |
104 | #### 12.3.2 滑动窗口缺点——计算成本
105 |
106 | 看到这里不难发现,滑动窗口检测由于需要多个窗口且每个窗口滑动多次而导致运算量会相当巨大,运行时间过慢。而且如果滑动的步幅过大或者裁剪的大小不合适也会导致很难检测到目标。
107 |
108 | ### 12.4 卷积的滑动窗口实现
109 |
110 | #### 12.4.1 把神经网络的全连接层转化成卷积层
111 |
112 | 
113 |
114 | - 假设目标检测算法输入一个14×14×3的图像,过滤器大小为5×5,数量是16,14×14×3的图像在过滤器处理之后映射为10×10×16。
115 |
116 | - 然后通过参数为2×2的最大池化操作,图像减小到5×5×16。
117 |
118 | - 添加一个连接400个单元的全连接层,接着再添加一个全连接层。
119 |
120 | - 最后通过softmax单元输出,用4个数字来表示 ,它们分别对应softmax单元所输出的4个分类出现的概率。这4个分类可以是行人、汽车、摩托车和背景或其它对象。
121 |
122 | **全连接层转化为卷积层**
123 |
124 | 
125 |
126 | - 前几层和之前的一样。
127 |
128 | - 而对于全连接层,用5×5的过滤器来实现,数量是400个。输入图像大小为5×5×16,用5×5的过滤器对它进行卷积操作,过滤器实际上是5×5×16,因为在卷积过程中,过滤器会遍历这16个通道,所以这两处的通道数量必须保持一致,输出结果为1×1。假设应用400个这样的5×5×16过滤器,输出维度就是1×1×400。它不再是一个含有400个节点的集合,而是一个1×1×400的输出层。从数学角度看,它和全连接层是一样的,因为这400个节点中每个节点都有一个5×5×16维度的过滤器,所以每个值都是上一层这些5×5×16激活值经过某个任意线性函数的输出结果。
129 | - 再添加另外一个卷积层,这里用1×1卷积,假设有400个1×1的过滤器,在这400个过滤器的作用下,下一层的维度是1×1×400,它其实就是上个网络中的这一全连接层。最后经由1×1过滤器的处理,得到一个softmax激活值,通过卷积网络,我们最终得到这个1×1×4的输出层,而不是4个数字。
130 |
131 | 以上就是用卷积层代替全连接层的过程。
132 |
133 | #### 12.4.2 在卷积上应用滑动窗口对象检测算法
134 |
135 | 
136 |
137 | 假设向滑动窗口卷积网络输入14×14×3的图片。和前面一样,神经网络最后的输出层,即softmax单元的输出是1×1×4,这里画得比较简单,严格来说,14×14×3应该是一个长方体,第二个10×10×16也是一个长方体,为了方便,这里只画了正面,所以这里显示的都是平面图,而不是3D图像。
138 |
139 | 
140 |
141 | 假设输入给卷积网络的图片大小是14×14×3,测试集图片是16×16×3,现在给这个输入图片加上黄色条块,在最初的滑动窗口算法中,你会把这片蓝色区域输入卷积网络(红色笔标记)生成0或1分类。接着滑动窗口,步幅为2个像素,向右滑动2个像素,将这个绿框区域输入给卷积网络,运行整个卷积网络,得到另外一个标签0或1。继续将这个橘色区域输入给卷积网络,卷积后得到另一个标签,最后对右下方的紫色区域进行最后一次卷积操作。我们在这个16×16×3的小图像上滑动窗口,卷积网络运行了4次,于是输出了了4个标签。
142 |
143 | 
144 |
145 | 这4次卷积操作中很多计算都是重复的。所以执行滑动窗口的卷积时使得卷积网络在这4次前向传播过程中共享很多计算。
146 |
147 | - 卷积网络运行同样的参数,使得相同的5×5×16过滤器进行卷积操作,得到12×12×16的输出层。
148 |
149 | - 然后执行同样的最大池化,输出结果6×6×16。照旧应用400个5×5的过滤器,得到一个2×2×400的输出层,现在输出层为2×2×400,而不是1×1×400。
150 |
151 | - 应用1×1过滤器得到另一个2×2×400的输出层。
152 |
153 | - 再做一次全连接的操作,最终得到2×2×4的输出层,而不是1×1×4。
154 |
155 | - 最终,在输出层这4个子方块中,蓝色的是图像左上部分14×14的输出(红色箭头标识),右上角方块是图像右上部分(绿色箭头标识)的对应输出,左下角方块是输入层左下角(橘色箭头标识),也就是这个14×14区域经过卷积网络处理后的结果,同样,右下角这个方块是卷积网络处理输入层右下角14×14区域(紫色箭头标识)的结果。
156 |
157 | 该卷积操作的原理是我们不需要把输入图像分割成四个子集,分别执行前向传播,而是把它们作为一张图片输入给卷积网络进行计算,其中的公共区域可以共享很多计算,就像这里我们看到的这个4个14×14的方块一样。
158 |
159 | 
160 |
161 | 再看一个更大的图片样本,假如对一个28×28×3的图片应用滑动窗口操作,如果以同样的方式运行前向传播,最后得到8×8×4的结果。跟上一个范例一样,以14×14区域滑动窗口,首先在这个区域应用滑动窗口,其结果对应输出层的左上角部分。接着以大小为2的步幅不断地向右移动窗口,直到第8个单元格,得到输出层的第一行。然后向图片下方移动,最终输出这个8×8×4的结果。因为最大池化参数为2,相当于以大小为2的步幅在原始图片上应用神经网络。
162 |
163 | **滑动窗口的实现过程总结**
164 |
165 | 
166 |
167 | 在图片上剪切出一块区域,假设它的大小是14×14,把它输入到卷积网络。继续输入下一块区域,大小同样是14×14,重复操作,直到某个区域识别到汽车。
168 |
169 | 但是我们不用依靠连续的卷积操作来识别图片中的汽车,比如,我们可以对大小为28×28的整张图片进行卷积操作,一次得到所有预测值,如果足够幸运,神经网络便可以识别出汽车的位置。
170 |
171 | ### 12.5 Bounding Box预测
172 |
173 | 滑动窗口法的卷积实现的算法虽然效率更高,但仍然存在问题,不能输出最精准的边界框。
174 |
175 |
271 |
272 | 但在深度学习文献中,定义卷积运算时跳过了这个镜像操作。前面我们实际上做的,有时被称为互相关而不是卷积。
273 |
274 | 总结来说,按照机器学习的惯例,我们通常不进行翻转操作。从技术上说,这个操作可能叫做互相关更好。但在大部分的深度学习文献中都把它叫做卷积运算。
275 |
276 | ### 10.6 三维卷积
277 |
278 | **三维(RGB图像)上的卷积操作**
279 |
280 | 举例,假如你不仅想检测灰度图像的特征,也想检测 RGB 彩色图像的特征。彩色图像如果6×6×3,这里的第一个 6 代表图像高度,第二个 6 代表宽度,这个3 代表颜色通道的数目。你可以把它想象成三个 6×6图像的堆叠。为了检测图像的边缘或者其他的特征,不是把它跟原来的 3×3 的过滤器做卷积,而是跟一个三维的过滤器,它的维度是 3×3×3,这样这个过滤器也有三层,对应红、绿、蓝三个通道。得到的输出会是一个 4×4 的图像,注意是 4×4×1,最后一个数不是 3 了。
281 |
282 | 为了简化这个 3×3×3过滤器的图像,我们不把它画成 3 个矩阵的堆叠,而画成一个三维的立方体。
283 |
284 | 
285 |
286 | **计算过程**:
287 |
288 | 把这个 3×3×3 的过滤器先放到最左上角的位置,这个 3×3×3 的过滤器有 27 个数,27 个参数就是 3 的立方。依次取这 27 个数,然后乘以相应的红绿蓝通道中的数字。先取红色通道的前 9 个数字,然后是绿色通道,然后再是蓝色通道,乘以左边黄色立方体覆盖的对应的 27 个数,然后把这些数都加起来,就得到了输出的第一个数字。如果要计算下一个输出,你把这个立方体滑动一个单位,再与这 27 个数相乘,把它们都加起来,就得到了下一个输出,以此类推。
289 |
290 | 
291 |
292 |
293 |
294 | **作用**:
295 |
296 | 举例:
297 |
298 | - 如果你想检测图像红色通道的边缘,那么你可以将第一个过滤器设为$\left[\begin{array}{rrr}1 & 0 & -1 \\ 1 & 0 & -1 \\ 1 & 0 & -1\end{array}\right]$,和之前一样,而绿色通道全为 0,$\left[\begin{array}{lll}0 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0\end{array}\right]$,蓝色也全为 0。如果你把这三个堆叠在一起形成一个3×3×3的过滤器,那么这就是一个检测垂直边界的过滤器,但只对红色通道有用。
299 | - 或者如果你不关心垂直边界在哪个颜色通道里,那么你可以用一个这样的过滤器,$\left[\begin{array}{ccc}1 & 0 & -1 \\ 1 & 0 & -1 \\ 1 & 0 & -1\end{array}\right],\left[\begin{array}{ccc}1 & 0 & -1 \\ 1 & 0 & -1 \\ 1 & 0 & -1\end{array}\right],\left[\begin{array}{ccc}1 & 0 & -1 \\ 1 & 0 & -1 \\ 1 & 0 & -1\end{array}\right]$,所有三个通道都是这样。所以通过设置第二个过滤器参数,你就有了一个边界检测器,3×3×3 的边界检测器,用来检测任意颜色通道里的边界。参数的选择不同,可以得到不同的特征检测器,所有的都是 3×3×3 的过滤器。
300 |
301 | **同时用多个过滤器**
302 |
303 | 有时候我们会想要同时检测垂直边缘和水平边缘,还有 45°倾斜的边缘,还有 70°倾斜的边缘等等,这是就需要使用多个过滤器。
304 |
305 | 
306 |
307 | 例如我们让这个 6×6×3 的图像和这个 3×3×3 的过滤器卷积,得到 4×4 的输出。(第一个)这可能是一个垂直边界检测器或者是学习检测其他的特征。第二个过滤器可以用橘色来表示,它可以是一个水平边缘检测器。做完卷积,然后把这两个 4×4 的输出堆叠在一起,这样你就都得到了一个4×4×2 的输出立方体。这里的 2 的来源于我们用了两个不同的过滤器。
308 |
309 | **维度总结**
310 |
311 | 如果你有一个$n \times n \times n_{c}$(通道数)的输入图像,上例中就是 6×6×3,这里的$n_{c}$就是通道数目,然后卷积上一个$f \times f \times n_{c}$,这个例子中是 3×3×3,按照惯例,这个(前一个𝑛𝑐)和这个(后一个𝑛𝑐)必须数值相同。然后你就得到了,$(n-f+1)\times(n-f+1) \times n_{c^{\prime}}$这里$n_{c^{\prime}}$其实就是下一层的通道数,它就是你用的过滤器的个数,在我们的例子中,那就是 4×4×2。我写下这个假设时,用的步幅为 1,并且没有 padding。如果你用了不同的步幅或者 padding,那么这个$𝑛 − 𝑓 + 1$数值会变化。
312 | $$
313 | n \times n \times n_{c} \text { * } f \times f \times n_{c} \rightarrow (n-f+1)\times(n-f+1) \times n_{c^{\prime}}
314 | $$
315 | **思考**:为什么卷积核是3\*3channels而不是3\*3\*1在多个通道之间移动?
316 |
317 | 如果使用3\*3\*1的卷积核在多个通道中移动,那意味着每个通道都用同一个过滤器,而且每个过滤器(卷积核)都忽略了隐藏在通道之间的联系和信息,这无疑会降低卷积网络的效果。
318 |
319 | ### 10.7 单层卷积网络
320 |
321 | 
322 |
323 | 相比之前的卷积过程,CNN的单层结构多了激活函数ReLU和偏移量b,与神经网络的单层结构类似,即:
324 |
325 | $Z^{[l]}=W^{[l]} A^{[l-1]}+b$
326 | $A^{[l]}=g^{[l]}\left(Z^{[l]}\right)$
327 |
328 | 其中,卷积运算对应上式中的乘积运算,过滤器组数值对应着权重$W^{[l]}$,激活函数则为ReLU
329 |
330 | 上图中参数$W$的计算:每个过滤器组共有3x3x3=27个参数,两个过滤器组则共包含27x2=54个参数$W$
331 |
332 | 相关符号的总结(设层数为$l$)
333 |
334 | $f^{[l]}=$ filter size
335 | $p^{[l]}=$ padding
336 | $s^{[l]}=$ stride
337 | $n_{c}^{[l]}=$ number of filters
338 | $n_{H}^{[l]}=$ height of input
339 | $n_{W}^{[l]}=$ width of filters
340 |
341 | 输入维度为:
342 |
343 | $n_{H}^{[l-1]} \times n_{W}^{[l-1]} \times n_{c}^{[l-1]}$
344 | 每个滤波器组维度为:
345 |
346 | $f^{[l]} \times f^{[l]} \times n_{c}^{[l-1]}$
347 |
348 | 权重维度为:
349 |
350 | $f^{[l]} \times f^{[l]} \times n_{c}^{[l-1]} \times n_{c}^{[l]}$
351 |
352 | 偏置维度为:
353 |
354 | $ 1 \times 1 \times 1 \times n_{c}^{[l]}$
355 |
356 | 输出维度为 :
357 |
358 | $ n_{H}^{[l]} \times n_{W}^{[l]} \times n_{c}^{[l]}$
359 |
360 | 其中:
361 | $$
362 | \begin{aligned}
363 | n_{H}^{[l]} &=\left\lfloor\frac{n_{H}^{[l-1]}+2 p^{[l]}-f^{[l]}}{s^{[l]}}+1\right\rfloor \\
364 | n_{W}^{[l]} &=\left\lfloor\frac{n_{W}^{[l-1]}+2 p^{[l]}-f^{[l]}}{s^{[l]}}+1\right\rfloor
365 | \end{aligned}
366 | $$
367 | 若有$m$个样本进行向量化运算,则输出的维度为:
368 |
369 | $m \times n_{H}^{[l]} \times n_{W}^{[l]} \times n_{c}^{[l}$
370 |
371 | ### 10.8 简单卷积网络示例
372 |
373 | 
374 |
375 | 如上图,是一个简单的CNN模型,且$a^{[3]}$维度为7 x 7 x 40,若将$a^{[3]}$排成1列,则维度为1960 x 1,再与输出层连接,输出层若为1个神经元,则为二元分类;若为多个神经元,则为多元分类。由此得出预测输出$\hat{y}$。
376 |
377 | 当CNN层数增加时,一般$n_{H}^{[l]}$和$n_{W}^{[l]}$会逐渐减小,而$n_{c}^{[l]}$会逐渐增大。
378 |
379 | CNN有以下三种类型的layer:
380 |
381 | - Convolution(CONV)(最为常见)
382 | - Pooling(POOL)
383 | - Fully connected(FC)
384 |
385 | ### 10.9 池化层
386 |
387 | 池化是一种下采样(downsample)手段,是对信息进行抽象的过程。
388 |
389 | 池化并不只有最大池化Max Pooling一种,不过Max Pooling是最广泛使用的一种。
390 |
391 | #### 10.9.1 最大池化 Max Pooling
392 |
393 | 最大池化指的是在采样区间内用区间内的最大值代表这个区间。
394 |
395 | 
396 |
397 | 和卷积运算一样,池化也有自己的参数:池化大小、步长和Padding。只不过最常用的是2*2大小、步长为2和Valid Padding。下文如没有说明则都是采用这种最大池化。
398 |
399 | #### 10.9.2 其他池化
400 |
401 | * 平均池化:平均池化和最大池化相对应,用该区间的平均值来代表该区间。
402 | * 全局平均池化:和上述池化有点不同,是将一个通道的信息都用该通道的平均值代替。比如输入4\*4\*channels的特征图,输出一个长度为channels的特征向量。该向量每一个值都是对应通道(4*4=16个值)的平均值。通常用在最后一层卷积层后、softmax前。主要作用是代替全连接,降低参数个数。
403 | * ASPP(空洞卷积空间金字塔池化,Atrous Spatial Pyramid Pooling):和传统的池化操作不同,该池化并不降低分辨率(输出特征图的大小),但是同样可以起到对增加感受野的效果(下文介绍感受野)。
404 |
405 | #### 10.9.3 池化的作用
406 |
407 | 在介绍池化的作用前,先介绍一下感受野。
408 |
409 | **感受野 Receptive Field**
410 |
411 | 感受野表示了一个神经元(输出图的一个像素点)与多少个**原始图像**上的像素点有关联。浅层的感受野小,深层的感受野逐渐增大。对于单个神经元,其值只与其感受野有关,与感受野外无关。下图给出在经过两层3\*3的卷积后的神经元的感受野示例。
412 |
413 | 
414 |
415 | 上图还可以发现,两个3\*3的卷积核能够与单个5\*5的卷积核有相同的感受野。但是前者只有2\*3\*3=18个参数,后者有5\*5=25个参数。可见可以通过多层小的卷积核来获得和单个大卷积核的相同效果,同时参数更少。甚至可以在GoogleNet中看到将n\*n拆分为1\*n和n\*1两个卷积核的做法。
416 |
417 | 对于池化层有效的原因之一,在于池化操作可以只用少量的参数大大增加下一层的神经元的感受野。方便起见,下列感受野计算不计算到原始图像那层。如果卷积层之间没有加入池化层,那后一层的神经元的感受野只为3\*3=9(假设是3\*3的卷积核);如果加入了最大池化层,那后一层的神经元的感受野可以增大到3\*3\*4=36,用同样的参数数量直接扩大了4倍。当然,简单地增加卷积核的大小也可以增加感受野,但是这样做增加了计算成本、参数数量、以及过拟合的风险。
418 |
419 | **作用**
420 |
421 | 介绍完感受野,现在开始正式介绍池化的作用:
422 |
423 | * 降低分辨率、降维、压缩特征、可以减少后续的运算量等等。但是在某些需要保持分辨率的任务(图像语义分割)中会变成一种弊端。
424 | * 只用少量参数就可以大大增加后续神经元的感受野。
425 |
426 | ### 10.10 卷积神经网络示例
427 |
428 | #### 10.10.1 LeNet5
429 |
430 | LeNet的[论文连接](https://ieeexplore.ieee.org/document/726791?reload=true&arnumber=726791)。LeNet是一个很简单很小的网络,建立之初是为了手写字识别(0-9)。虽然简单,但是是第一个典型的CNN网络。麻雀虽小,五脏俱全,包含了卷积层、池化层和全连接层。
431 |
432 | 网络结构如下:
433 |
434 | 
435 |
436 |
437 |
438 | 该图没有说清楚,网络中所有卷积层的卷积核都是5*5的,以及步长为1,padding为0。图中的subsampling指的是池化,具体来说是最大池化。细心的话还会留意到最后一层用了Gaussian connections。我个人认为已经被淘汰了,感兴趣的可以自行了解。自己实现的时候当成全连接也可以。
439 |
440 | 该论文的典型之处主要在于:
441 |
442 | * 一层卷积一层池化交替出现。
443 | * 最后输出前若干层采用全连接层。
444 | * 全连接层的参数真的很多。卷积网络的参数主要集中在第一层全连接层(16\*5\*5\*120=48000)。
445 |
446 | #### 10.10.2 AlexNet
447 |
448 | AlexNet的[论文连接](http://papers.nips.cc/paper/4824-imagenet-classification-with-deep-convolutional-neural-networks.pdf)。这是第一个引起大家注意的卷积网络,该模型取得了2012年的ImageNet比赛冠军,而且也正是因为这次比赛而打响了名号。
449 |
450 | 网络结构如下:
451 |
452 | 
453 |
454 | 论文中该图片有误,第一个卷积层的输出应该是54\*54而不是55\*55,这个可以自己计算一下来验证。该网络在前两层就采用了相当大的卷积核,不过后面的层都只用3*3的了。该网络拿下冠军时,以比第二名少20%左右的误差率而取得优胜。
455 |
456 | 个人认为比较值得注意的点是:
457 |
458 | * 并不一定需要每层卷积层后都添加池化层。连续多层卷积层可以视为一层卷积核更大、能拟合更复杂函数的卷积层。
459 | * 对于更大的图片,感受野也需要对应增大。AlexNet的做法是前两层卷积层用了较大的卷积核。
460 |
461 | #### 10.10.3 VGG16
462 |
463 | VGG16的[论文连接](https://arxiv.org/abs/1409.1556)。该网络改进了AlexNet,改进的思路是:用更多层、更小的卷积核代替原来那些比较大的卷积核。最根本的一点是在不减小感受野的前提下增加层数和减少参数量。从结果上来看,这么做确实起到了不错的效果。
464 |
465 | 下图中,卷积层默认步长为1,padding为same。网络结构如下:
466 |
467 | 
468 |
469 | 该网络不止是本身很有价值,其来源(论文)也很有价值。该论文通过对比各种网络,来说明卷积网络越深效果越好这一点。VGG16中的16就是指除去池化层,该网络一个有16层。
470 |
471 | 对比AlexNet,该网络的改进如下:
472 |
473 | * 采用多层连续的3*3卷积层代替大卷积层。
474 | * 网络深度更深了。
475 | * 通道数全部用2的幂。更符合计算机的存储规则。
476 | * 两、三层卷积层 + 一层池化。
477 | * 池化后通道数翻倍。
478 | * 每层网络的步长都为1,padding都为same。
479 |
480 | 上述改进也是现在我所看到的大部分网络的构建习惯(趋势)。我想这足以说明这些“规律”有多好用。
481 |
482 | ### 10.11 为什么使用卷积
483 |
484 | #### 10.11.1 减少参数
485 |
486 | 1.10介绍的网络也基本可以看出,卷积网络中全连接层的参数占了绝大一部分。举例LeNet5,各层参数个数分别为:第一层卷积层 5\*5\*1\*6=150、第二层卷积层 5\*5\*6\*16=2400、第一层全连接层 5\*5\*16\*120=48000、第二层全连接层 120\*84=10080,若最后一层视为全连接层则有 84\*10=840。
487 |
488 | 不难发现,第一层全连接层的参数占据了$\frac{48000}{150+2400+48000+10080+840}=0.78=78%$的参数,这已经占据了一半以上的参数。很明显,卷积层对比全连接层来说可以大大减小参数的数量,一方面可以避免过拟合,另一方面减少了对设备的要求。
489 |
490 | 更进一步,卷积操作需要的参数很少的原因在于
491 |
492 | * **权值共享**。一个卷积核的权值可以适用到整个网络,而不是每个神经元独占一个权值。因为一个卷积核的工作可以理解为专门识别某一些特征。而且这个特征应该是通用的,与所处位置无关,即**平移不变性**。同时平移不变性也是网络学习的潜在目标之一。举例垂直边缘检测便可以检索对应区域是否有垂直边界,而不在乎这个边界的具体位置在哪。
493 | * **稀疏连接**。与全连接对应,在全连接中任意一个神经元都要与上一层的所有神经元连接;而卷积则只受感受野内的神经元影响,对于感受野外的并不关心。
494 |
495 | #### 10.11.2 训练卷积网络
496 |
497 | 假设要做一个猫咪检测网络,$x^{(i)}$表示第$i$张图片,$y^{(i)}$表示对应图片的标签。在选定一个网络后,设计好损失函数,对全部样本的损失求平均作为代价函数。随机初始化权重矩阵和偏置。在Python实现时还可以向量化$x^{(i)}$(当然,就我所知大部分架构也会这么做)。用梯度下降来训练网络,而且也可以采用优化器如$RMSProp$或$Adam$。
498 |
499 |
--------------------------------------------------------------------------------
/11 深度卷积网络 实例探究.md:
--------------------------------------------------------------------------------
1 | #第二周 深度卷积网络:实例探究
2 | ## 2.1为什么要实例探究
3 |
4 | 在计算机视觉的研究中,将卷积层、池化层及全连接层进行有有机结合,才能形成有效的卷积神经网络,而更好地去实现这种有机结合可以多多参考他人所构建的框架,而且在计算机视觉中,良好的神经网络框架往往也适用于其他的任务,所以多多参考其他案例有利于我们更好地应用卷积神经网络。在框架学习中,我们也可以多多研读计算机视觉领域相关的论文或相关的研讨内容。
5 |
6 |
7 |
8 | ## 2.2经典网络
9 |
10 | ### 2.2.1LeNet-5网络
11 |
12 | 
13 |
14 | 该网络是针对灰度图像训练的,该例用其对手写字体进行识别
15 |
16 | 在池化后选用$sigmoid$函数来进行非线性函数处理
17 |
18 | 其结构为卷积——池化——卷积——池化——全连接——全连接。
19 |
20 | 且采取了平均池化(当时年代的人们更倾向使用平均池化),然而现在会更多的使用最大池化。因没有使用padding或有效卷积,使得每完成一次卷积,图像的高度和宽度都缩小了。
21 |
22 | 最后输出层利用了$softmax$函数来分类输出十种结果。
23 |
24 | 相比于其他更复杂的神经网络,其参数较少,只有约六万个。
25 |
26 | 随着网络层次的加深,图像的高度和宽度都在缩小,信道数量则会增加。
27 |
28 | 其中的“一个或多个卷积层后跟着一个池化层,然后又是若干个卷积层,池化层,然后再是全连接层,最后输出。”这一模式仍被经常使用。
29 |
30 | ### 2.2.2AlexNet网络
31 |
32 | 
33 |
34 | 相比于LeNet-5,AlexNet网络要大得多,其有约六千万个参数,但优点在于在用于训练图像和数据集时,它能处理非常相似的基本构造模块,而往往这些模块有着隐藏单元或数据;同时采用了$Relu$函数。
35 |
36 | 在写这篇论文时,GPU的处理速度并不快,所以针对这个模型,采用了两个GPU进行训练,将不同的层拆分到两个GPU中进行训练,并用了一些专门的方法使这两个GPU得以交流。
37 |
38 | ### 2.2.3VGG-16
39 |
40 | 
41 |
42 | VGG-16中的“16”代表该网络结构包含16个卷积层和全连接层
43 |
44 | 这是一个极大的网络,约有1.38亿个参数,但其优点是其结构不复杂,一般为卷积层后跟着可压缩图像大小(高度和宽度)的池化层。其过滤器数量变化存在一定规律,变化为64→128→256→512,论文作者可能认为512的信道数量已经足够大了,故没有继续增加。除了VGG-16外,还有VGG-19模型,但VGG-19模型比VGG-16要大得多,但实现的效果并不比VGG-16要好多少,故较少使用VGG-19。
45 |
46 | 随着该网络的加深,图像的高度和宽度在不断缩小,每次池化后缩小一半,而信道数量在不断增加(每次卷积后增加1倍)。即图像缩小的比例和信道增加的比例是有规律的。
47 |
48 |
49 |
50 | ## 2.3残差网络
51 |
52 | 神经网络层数越多,网络越深,越容易受到梯度消失和梯度爆炸的影响。我们可以通过让神经网络某些层跳过下一层神经元的连接,隔层相连,弱化每层之间的强联系来解决该问题。而这样的神经网络即为残差网络(ResNets)
53 |
54 | ### 2.3.1残差块
55 |
56 | 残差网络由多个残差块组成,如下图为残差块组成
57 |
58 | 
59 |
60 | 图中红色箭头称为跳远连接,其建立了$a^{[l]}$与$a^{[l+2]}$的隔层联系。具体表达式为:
61 |
62 | $z^{[l+1]}=W^{[l+1]} a^{[l]}+b^{[l+1]}$
63 | $a^{[l+1]}=g\left(z^{[l+1]}\right)$
64 | $z^{[l+2]}=W^{[l+2]} a^{[l+1]}+b^{[l+2]}$
65 | $a^{[l+2]}=g\left(z^{[l+2]}+a^{[l]}\right)$
66 |
67 | 其中$a^{[l]}$与$z^{[l+2]}$共同作用,通过ReLU函数输出$a^{[l+2]}$
68 |
69 | 多个残差块构成了如下图所示的残差网络
70 |
71 | 
72 |
73 | ### 2.3.2与Plain Network对比
74 |
75 | 我们将非残差网络称为Plain Network,将其与ResNet对比可发现,残差网络可以有效解决梯度消失和梯度爆炸的问题,睡着网络层数的增加,Plain Network的training error甚至可能变大,而ResNet的training error则一直呈现下降趋势。如下图
76 |
77 | 详细可参考
78 |
79 | [Deep Residual Learning for Image Recognition](extension://ibllepbpahcoppkjjllbabhnigcbffpi/https://openaccess.thecvf.com/content_cvpr_2016/papers/He_Deep_Residual_Learning_CVPR_2016_paper.pdf)
80 |
81 |
82 |
83 |
84 | ### 2.4 网络中的网络/1*1卷积
85 |
86 | #### 2.4.1 定义
87 |
88 | 也被称为***\*Network in Network\****,对输入的个不同的位置都应用一个全连接层,全连接层的作用是便在输入层上实施一个非平凡(***\*non-trivial\****)计算。简单点说就是将输入数据的通道数进行压缩,压缩成所使用的过滤器的数量大小。
89 |
90 |
91 |
92 | #### 2.4.2例子一
93 |
94 | 假设这是一个28×28×192的输入层,可以使用池化层压缩它的高度和宽度,这个过程我们很清楚。但如果通道数量很大,该如何把它压缩为28×28×32维度的层呢?你可以用32个大小为1×1的过滤器,严格来讲每个过滤器大小都是1×1×192维,因为过滤器中通道数量必须与输入层中通道的数量保持一致。但是你使用了32个过滤器,输出层为28×28×32,这就是压缩通道数()的方法。
95 |
96 | 
97 |
98 |
99 |
100 | #### 2.4.3例子二
101 |
102 | 过滤器为1×1,输入一张6×6×32的图片,然后对它做卷积,遍历这36个单元格,计算左图中32个数字和过滤器中32个数字的元素积之和,然后应用***\*ReLU\****非线性函数。
103 |
104 | 我们以其中一个单元为例,它是这个输入层上的某个切片,用这36个数字乘以这个输入层上1×1切片,得到一个实数,像这样把它画在输出中。
105 |
106 | 
107 |
108 |
109 |
110 | 这个1×1×32过滤器中的32个数字可以这样理解,一个神经元的输入是32个数字(输入图片中左下角位置32个通道中的数字),即相同高度和宽度上某一切片上的32个数字,这32个数字具有不同通道,乘以32个权重(将过滤器中的32个数理解为权重),然后应用***\*ReLU\****非线性函数,在这里输出相应的结果。
111 |
112 | 
113 |
114 |
115 |
116 | 一般来说,如果过滤器不止一个,而是多个,就好像有多个输入单元,其输入内容为一个切片上所有数字,输出结果是6×6过滤器数量。
117 |
118 | 
119 |
120 |
121 |
122 |
123 |
124 |
125 |
126 | 所以1×1卷积可以从根本上理解为对这32个不同的位置都应用一个全连接层,全连接层的作用是输入32个数字(过滤器数量标记为,在这36个单元上重复此过程),输出结果是6×6×#filters(过滤器数量),以便在输入层上实施一个非平凡(***\*non-trivial\****)计算。此时,输入的结果的通道层数取决于过滤器的个数。
127 |
128 |
129 |
130 | #### 2.4.4深度可分离卷积
131 |
132 | **定义**:一个卷积核负责一个通道,一个通道只被一个卷积核卷积
133 |
134 | **引用博客**:https://blog.csdn.net/makefish/article/details/88716534
135 |
136 | 相较于一般卷积,深度可分离卷积有着不同的计算方法:
137 |
138 | 在卷积计算时,先用三个卷积对三个通道分别做卷积,这样在一次卷积后,输出3个数,然后这输出的三个数,再通过一个1x1x3的卷积核(pointwise核),得到一个数。下面进行分步解释;
139 |
140 | 第一步,对三个通道分别做卷积,输出三个通道的属性:
141 |
142 |
143 |
144 | 
145 |
146 |
147 |
148 |
149 |
150 | 第二步,用卷积核1x1x3对三个通道再次做卷积,这个时候的输出就和正常卷积一样,是8x8x1:
151 |
152 | 
153 |
154 |
155 |
156 | 如果要提取更多的属性,则需要设计更多的1x1x3卷积核心就可以(图片引用自原网站。感觉应该将8x8x256那个立方体绘制成256个8x8x1,因为他们不是一体的,代表了256个属性)::
157 |
158 | 
159 |
160 | **深度可分离卷积的优点缺点**:
161 |
162 | 对于需要提取大量属性或者特征的情景下,深度可分离卷积随着要提取的属性越来越多,就能够节省更多的参数。当然如果提取的特征属性不多,普通的卷积效果优于深度可分离卷积。
163 |
164 |
165 |
166 |
167 |
168 | ### 2.5 Inception网络
169 |
170 | #### 2.5.1作用
171 |
172 | 代替人工决定所使用的过滤器的大小,或者确定是否需要创建卷积层或池化层,
173 |
174 | #### 2.5.2 论文链接
175 |
176 | https://arxiv.org/pdf/1409.4842.pdf
177 |
178 | #### 2.5.3主要思想
179 |
180 | 不需要人为决定使用哪个过滤器或者是否需要池化,而是由网络自行确定这些参数,你可以给网络添加这些参数的所有可能值,然后把这些输出连接起来,让网络自己学习它需要什么样的参数,采用哪些过滤器组合。
181 |
182 | #### 2.5.4原理
183 |
184 | 利用多种维度的过滤器,分别使用不同的方法,产生大量长宽相等,通道可以不同的输出块,并将这些输出块堆积在一起,产生一个组合了各种类型的参数的输出,从而在后续的训练中,让网络自己学习它需要什么样的参数,采用哪些过滤器组合。
185 |
186 |
187 |
188 | 例如,这是你28×28×192维度的输入层,***\*Inception\****网络或***\*Inception\****层的作用就是代替人工来确定卷积层中的过滤器类型,或者确定是否需要创建卷积层或池化层,我们演示一下。
189 |
190 | 
191 |
192 |
193 |
194 | 如果使用1×1卷积,输出结果会是28×28×#(某个值),假设输出为28×28×64,并且这里只有一个层。
195 |
196 | 
197 |
198 |
199 |
200 | 如果使用3×3的过滤器,那么输出是28×28×128。然后我们把第二个值堆积到第一个值上,为了匹配维度,我们应用***\*same\****卷积,输出维度依然是28×28,和输入维度相同,即高度和宽度相同。
201 |
202 | 
203 |
204 |
205 |
206 | 或许你会说,我希望提升网络的表现,用5×5过滤器或许会更好,我们不妨试一下,输出变成28×28×32,我们再次使用***\*same\****卷积,保持维度不变。
207 |
208 | 
209 |
210 |
211 |
212 | 或许你不想要卷积层,那就用池化操作,得到一些不同的输出结果,我们把它也堆积起来,这里的池化输出是28×28×32。为了匹配所有维度,我们需要对最大池化使用***\*padding\****,它是一种特殊的池化形式,因为如果输入的高度和宽度为28×28,则输出的相应维度也是28×28。然后再进行池化,***\*padding\****不变,步幅为1。
213 |
214 | 
215 |
216 |
217 |
218 | 有了这样的***\*Inception\****模块,你就可以输入某个量,因为它累加了所有数字,这里的最终输出为32+32+128+64=256。***\*Inception\****模块的输入为28×28×192,输出为28×28×256。这就是Inception网络的核心内容。
219 |
220 |
221 |
222 | #### 2.5.5计算成本问题
223 |
224 | 由于进行了多种模型的计算,会造成计算成本会非常的大,如何缩小成本是一个非常重要的一环。
225 |
226 | 下面以5×5过滤器为例计算成本
227 |
228 | 
229 |
230 |
231 |
232 | 这是一个28×28×192的输入块,执行一个5×5卷积,它有32个过滤器,输出为28×28×32。我们来计算这个28×28×32输出的计算成本,它有32个过滤器,因为输出有32个通道,每个过滤器大小为5×5×192,输出大小为28×28×32,所以你要计算28×28×32个数字。对于输出中的每个数字来说,你都需要执行5×5×192次乘法运算,所以乘法运算的总次数为每个输出值所需要执行的乘法运算次数(5×5×192)乘以输出值个数(28×28×32),把这些数相乘结果等于1.2亿(120422400)。
233 |
234 | 
235 |
236 |
237 |
238 | 为了缩小成本,我们使用1*1卷积对输入进行通道缩小。对于输入层,使用1×1卷积把输入值从192个通道减少到16个通道。然后对这个较小层运行5×5卷积,得到最终输出。请注意,输入和输出的维度依然相同,输入是28×28×192,输出是28×28×32。
239 |
240 | 然后我们进行成本计算应用1×1卷积,过滤器个数为16,每个过滤器大小为1×1×192,这两个维度相匹配(输入通道数与过滤器通道数),28×28×16这个层的计算成本是,输出28×28×192中每个元素都做192次乘法,用1×1×192来表示,相乘结果约等于240万,这是第一个卷积层的计算成本。第二层的输出为28×28×32,对每个输出值应用一个5×5×16维度的过滤器,计算结果为1000万。
241 |
242 | 所以所需要乘法运算的总次数是这两层的计算成本之和,也就是1204万,与上一张幻灯片中的值做比较,计算成本从1.2亿下降到了原来的十分之一,即1204万。
243 |
244 |
245 |
246 | #### 2.5.6 瓶颈层
247 |
248 |
249 |
250 | 
251 |
252 |
253 |
254 | 这个被增加的1*1卷积层常被称为瓶颈层,即先缩小网络表示,然后再扩大它。
255 |
256 |
257 |
258 | 需要注意的是,只要合理构建瓶颈层,你既可以显著缩小表示层规模,又不会降低网络性能,从而节省了计算。
259 |
260 |
261 |
262 | #### 2.5.7 Inception Net
263 |
264 | 简述:由多个***\*Inception\*******\*模块所组成的神经网络。\****
265 |
266 | 原理:
267 |
268 | 首先如下图所示,建立前面所说的***\*Inception\****模块。
269 |
270 | 
271 |
272 |
273 |
274 | 为了能在最后将这些输出都连接起来,我们会使用***\*same\****类型的***\*padding\****来池化,使得输出的高和宽依然是28×28,这样才能将它与其他输出连接起来。
275 |
276 | 但注意,如果你进行了最大池化,即便用了***\*same padding\****,3×3的过滤器,***\*stride\****为1,其输出将会是28×28×192,其通道数或者说深度与这里的输入(通道数)相同。所以看起来它会有很多通道,我们实际要做的就是再加上一个1×1的卷积层,去进行我们在1×1卷积层的视频里所介绍的操作,将通道的数量缩小,缩小到28×28×32。
277 |
278 | 
279 |
280 |
281 |
282 | 最后,将这些方块全都连接起来。在这过程中,把得到的各个层的通道都加起来,最后得到一个28×28×256的输出。通道连接实际就是之前视频中看到过的,把所有方块连接在一起的操作。这就是一个***\*Inception\****模块,而***\*Inception\****网络所做的就是将这些模块都组合到一起。
283 |
284 | 
285 |
286 |
287 |
288 | ***\*上图为\*******\*Inception\****网络的图片,并且其由多个***\*Inception\*******\*模块所组成,需要注意的是有一些\*******\*Inception\*******\*模块中间还夹着一个最大池化层,如图中的6和7.\****
289 |
290 | 
291 |
292 |
293 |
294 | ***\*在论文原文中,网络里有着一些其他分支,如上图中的1、2、4,其中1是一个\*******\*softmax\****层,用于做出预测,编号2所做的就是通过隐藏层(编号3)来做出预测,所以这其实是一个***\*softmax\****输出(编号2),编号4也包含了一个隐藏层,通过一些全连接层,然后有一个***\*softmax\****来预测,输出结果的标签。 这些分支确保了即便是隐藏单元和中间层(编号5)也参与了特征计算,它们也能预测图片的分类。它在***\*Inception\****网络中,起到一种调整的效果,并且能防止网络发生过拟合。
295 |
296 |
297 |
298 | #### 2.5.8 Inception网络多种类型
299 |
300 | 参考博客:https://www.cnblogs.com/dengshunge/p/10808191.html
301 |
302 | ##### Inception v1
303 |
304 | v1其实就是我们前面所说的使用1*1卷积降低计算量后的Inception网络。
305 |
306 | 提升神经网络的性能是各种方法和算法的目的,当然提升网络的性能的方法有很多,例如增加网络的深度和宽度,但当深度和宽度不断增加时,需要训练的参数也会增加,过多的参数容易发生过拟合,并且会导致计算量增加。所以就有了v1结构来解决此问题,也就是利用1*1卷积降低计算量。
307 |
308 |
309 |
310 | ##### Inception v2
311 |
312 | 在训练时每层输入数据的分布会发生改变,所以需要较低的学习率和精心设置初始化参数。只要网络的前面几层发生微小的改变,那么后面几层就会被累积放大下去。一旦网络某一层的输入数据的分布发生改变,那么这一层网络就需要去适应学习这个新的数据分布,所以如果训练过程中,训练数据的分布一直在发生变化,那么将会影响网络的训练速度。为此,提出了v2版本的Inception网络。
313 |
314 | V2版本网络使用了BN算法,可以设置较大的初始学习率,并且减少对参数初始化的依赖,提高了训练速度,同时也可以能防止网络陷入饱和,即消除梯度弥散。
315 |
316 |
317 |
318 | ##### Inception v3
319 |
320 | Inception v3主要解决的是:inception结构过于复杂,使得我们很难对网络进行修改。
321 |
322 | V3主要思路为:利用小尺度的卷积来代替大尺度的卷积,在减少计算量的同时,保证能够学习到更多的信息。例如提出了使用两个级联的3*3的滤波器来代替一个5*5的滤波器,如下图所示:
323 |
324 | 
325 |
326 | 
327 |
328 |
329 |
330 | 同时又对3*3卷积进行分解为3*1+1*3,如下图所示,进而进一步降低计算量
331 |
332 | 
333 |
334 |
335 |
336 | V3主要遵循下列几条思想
337 |
338 | 1. 避免特征表示瓶颈,尤其是在网络的前面。要避免严重压缩导致的瓶颈。特征表示尺寸应该温和地减少,从输入端到输出端。特征表示的维度只是一个粗浅的信息量表示,它丢掉了一些重要的因素如相关性结构。
339 |
340 | 2. 高维信息更适合在网络的局部处理。在卷积网络中逐步增加非线性激活响应可以解耦合更多的特征,那么网络就会训练的更快。
341 |
342 | 3. 空间聚合可以通过低维嵌入,不会导致网络表示能力的降低。例如在进行大尺寸的卷积(如3*3)之前,我们可以在空间聚合前先对输入信息进行降维处理,如果这些信号是容易压缩的,那么降维甚至可以加快学习速度。
343 |
344 | 4. 平衡好网络的深度和宽度。通过平衡网络每层滤波器的个数和网络的层数可以是网络达到最佳性能。增加网络的宽度和深度都会提升网络的性能,但是两者并行增加获得的性能提升是最大的。所以计算资源应该被合理的分配到网络的宽度和深度。
345 |
346 |
347 |
348 | ##### Inception v4
349 |
350 | V4的提出主要是基于 ”当网络更深更宽时,inception网络能否一样高效”的问题提出的,v4具体的解决方法为,结合TensorFlow,简化训练,不需要将模型进行分割,并且将inception和resnet两者进行融合,进一步改善网络。
351 |
352 |
353 |
354 | 以上对Inception网络的4种模型进行概述,具体解释可参考下列博客 https://www.cnblogs.com/dengshunge/p/10808191.html
355 |
356 |
357 |
358 | ### 2.6使用开源实现方案
359 |
360 | 本节为介绍如何下载开源代码。
361 |
362 | 本节下载的代码网站为:
363 |
364 | ***\*ResNets\****实现的***\*GitHub\****地址:https://github.com/KaimingHe/deep-residual-networks
365 |
366 | 
367 |
368 |
369 |
370 |
371 |
372 | ***\*点击Code按钮,并且点击复制按钮复制代码的URL\****
373 |
374 | 
375 |
376 |
377 |
378 | 在需要保存代码的目录下打开cmd,使用下列指令进行代码的下载(复制)
379 |
380 | git clone your URL
381 |
382 | git clone https://github.com/KaimingHe/deep-residual-networks.git
383 |
384 | 
385 |
386 |
387 |
388 | 使用指令观察目录,说明此时代码已下载完毕。
389 |
390 | 接下来进行打开代码。
391 |
392 |
393 |
394 | 
395 |
396 |
397 |
398 | 代码储存在prototxt文件夹中
399 |
400 | 
401 |
402 |
403 |
404 | 使用指令打开其中一个文件。
405 |
406 | more 文件名
407 |
408 | 
409 |
410 | 当然也可以用ide直接打开来进行修改。
411 | ### 2.7 迁移学习
412 | #### 2.7.1 迁移学习的概念
413 | 迁移学习是从一个或多个源领域中通过训练该模型,得出有用的知识并将其用在新的目标任务上(未标记的同一类有相似特征的物品或者是未标记的不同类物品)本质是知识的迁移再利用。
414 | #### 2.7.2 ImageNet、MS COCO\Pascal数据集的获取
415 | ImageNet数据集的获取:
416 | 所有图像可通过url下载:不需要账号登录即可免费下载,下载链接:http://www.image-net.org/download-imageurls ,在SEARCH框中输入需要下载的synset,如tree,也可按类别下载即WordNet ID,下载链接:http://www.image-net.org/synset?wnid=n02084071 ,其中好像个别url已失效。
417 | MS COCO:
418 |
419 | 数据集官网首页:http://cocodataset.org/#home
420 |
421 | 数据集下载:
422 |
423 | 可用迅雷去下载官方链接,速度也挺快的。也可以去这个高中生搭建的下载站下载:http://bendfunction.f3322.net:666/share/。 他的首页是这样子的:http://bendfunction.f3322.net:666/
424 | https://pjreddie.com/projects/coco-mirror/
425 | #### 2.7.3 迁移学习的分类
426 | 按照迁移学习的定义,可以将迁移学习分为三种类型,分布差异迁移学习,特征差异迁移学习和标签差异迁移学习。分布差异迁移学习之源域和目标域数据的边缘分布或者条件概率分布不同,特征差异迁移学习之源域数据和目标数据特征空间不同,标签差异迁移学习指源域和目标域的数据标记空间不同。
427 | 用香蕉和苹果分类问题为例,源域数据是已有的带标签香蕉和苹果的文本数据,目标域是新来的不带标记的香蕉和苹果的文本数据,源域和目标域的数据来自不同的时间,不同地点,数据分布不同,但标记空间和特征空间是相同的,利用源域中的数据来进行目标域的学习问题就是属于分布差异迁移学习问题。源域数据是带有标记的苹果和香蕉的文本数据,而目标域是不带有 标记的苹果和香蕉的图片数据,源域和目标域一个是文本,一个是图像,属于特征差异迁移学习范围。源域数据是带有标记的香蕉和苹果的文本数据,属于二分类问题,目标域是不带标记的梨子,橘子和橙子的文本数据属于三分类问题,源域和目标域的数据标记空间不同,属于标记差异迁移学习的范围。
428 |
429 | 现已成熟的监督学习模式下,在大样本的已标记的数据量集中训练形成传统的监督学习,但是这种模式在运用到情况更为复杂,更多变的实际环境中往往会出现很大的误差,
430 | 所以迁移学习就是在样本量比较少的情况下,训练分类器,随之把这种模式可以运用到其他很多种情况下。
431 |
432 | ### 2.8 数据增强
433 | #### 2.8.1数据增强的基本操作
434 | 数据增强也叫数据扩增,意思是在不实质性的增加数据的情况下,让有限的数据产生等价于更多数据的价值。
435 | 数据增强的手段包括几何变换类,颜色变换类等。
436 |
437 | (1) 几何变换类
438 |
439 | 几何变换类即对图像进行几何变换,包括翻转,旋转,裁剪,变形,缩放等各类操作,下面展示以上操作。
440 | 图一2 3 4 5
441 | (2) 颜色变换类
442 | 颜色变换类时改变图片的R、G、B的值。
443 | #### 2.8.2数据增强的代码实现
444 | TensorFlow实现图片数据增强:
445 | 参见以下网址https://zhuanlan.zhihu.com/p/57284174
446 | #### 2.8.2数据增强的优缺点
447 | 优点:
448 | 增加训练的数据量,提高模型的泛化能力
449 | 增加噪声数据,提升模型的鲁棒性
450 | ### 2.9 计算机视觉现状
451 | #### 2.9.1计算机视觉现状
452 | 深度学习已经成功地应用于计算机视觉、自然语言处理、语音识别、在线广告、物流还有其他许多问题。
453 | 在计算机视觉的现状下,深度学习应用于计算机视觉应用有一些独特之处。
454 | ####2.9.2 banchmark
455 | Benchmark 基准测试,Benchmark是一个评价方式,在整个计算机领域有着长期的应用。
456 | Benchmark在计算机领域应用最成功的就是性能测试,主要测试负载的执行时间、传输速度、吞吐量、资源占用率等。基准测试同时也可以用来识别某段代码的CPU或者内存效率问题. 许多开发人员会用基准测试来测试不同的并发模式, 或者用基准测试来辅助配置工作池的数量, 以保证能最大化系统的吞吐量.
457 | 关于实战可参考:
458 | https://blog.csdn.net/woniu317/article/details/82560312
459 |
--------------------------------------------------------------------------------
/12 目标检测.md:
--------------------------------------------------------------------------------
1 | ## 12 目标检测
2 |
3 | ### 12.1 目标定位
4 |
5 | #### 12.1.1 定义
6 |
7 | 除了要识别出目标类(例如是否有汽车)以外,算法还需要能够给出目标的位置(例如用红框框出目标的位置),这是一种分类定位问题。分类定位问题可以是只有一个目标对象在图片中,也可以是多个目标对象在图片中的。先从单个目标对象的情况开始。
8 |
9 | #### 12.1.2 实现
10 |
11 | **1. 边界框参数定义**
12 |
13 | 图片分类我们已经比较熟悉了,知道最后通过 *softmax* 激活函数激活来表示该图片属于每一类的概率。相较于单纯的分类问题,目标定位还需要输出4个值:$b_x,b_y,b_h,b_w$。这四个值用于表示边框的位置和大小,具体为
14 | $$
15 | \begin{array}{l}
16 | b_x:边框的中心点的x轴坐标 \\
17 | b_y:边框的中心点的y轴坐标 \\
18 | b_h:边框的高度 \\
19 | b_w:边框的宽度 \\
20 | \end{array}
21 | $$
22 | 以上4个值的取值范围均为[0, 1],表示的是边界框与图片对应的**比例**。
23 |
24 | 关于坐标轴的选取,一般选图片的左上角为原点(0, 0),右下角为(1, 1)。且$x$轴为纵轴正方向向下,$y$轴为横轴正方向向右。
25 |
26 | **2. 标签的定义**
27 |
28 | 在确定需要增加的额外输出之后,也要重新定义目标标签 $y$:
29 | $$
30 | y=\left[\begin{array}{l}
31 | p_{c} \\
32 | b_{x} \\
33 | b_{y} \\
34 | b_{h} \\
35 | b_{w} \\
36 | c_{1} \\
37 | c_{2} \\
38 | c_{3}
39 | \end{array}\right]
40 | $$
41 | 其中额外增加了$p_c$,用于表示是否有对象属于类$c_1、c_2$或$c_3$,若为1则表示有目标类在图片中,为0表示只有背景。在只有背景(无目标类)时,其他输出均无效。
42 |
43 | 举一个具体的例子,如下图:
44 |
45 | 
46 |
47 | x 是输入,y 是标签,假设$c_2$表示为车,则最终标签应该如上图所示。当输入中不含任何目标类时,$p_c=0$,其他参数全用“?”表示,即不参与 loss 的计算。
48 |
49 | **3. 边界框参数取值范围**
50 |
51 | 关于边框的4个参数,吴恩达老师给出的取值范围都是[0, 1]的。虽然确实可以这么做,但是背后的原因却没有解释。个人猜测可能是以下原因:
52 |
53 | * 固定取值在[0, 1]之间更容易用激活函数表示,比如sigmoid可以将单个值映射到[0, 1];
54 | * 让标签的所有参数都在一个取值范围,这样在计算loss的时候就不会变相加权了;
55 | * 取值范围在[0, 1]内更容易训练、收敛。
56 |
57 | **4. 损失函数**
58 | $$
59 | L(\hat y,y)=
60 | \begin{cases}
61 | (\hat{y_1}-y_1)^2+(\hat{y_2}-y_2)^2+...+(\hat{y_n}-y_n)^2 & {y_1=1}\\
62 | (\hat{y_1}-y_1)^2 & {y_1=0}
63 | \end{cases}
64 | $$
65 |
66 | * 对于$p_c$可以采用 Logistic 回归的方法,甚至用均方误差$(p_c-\hat{p_c})^2$也可以;
67 | * 对于$b_x,b_y,b_w,b_h$,loss 可以用平方差或类似方法;
68 | * 对于$c_1,c_2,c_3$,是多分类问题,和之前一样用 softmax 即可。
69 |
70 | ### 12.2 特征点检测
71 |
72 | #### 12.2.1 定义
73 |
74 | 以下图为例,检测双眼的眼角位置
75 |
76 | 
77 |
78 | 这个就是特征点检测,主要任务是预测对应的特征点的位置,一般会同时预测多个点。
79 |
80 | #### 12.2.2 实现
81 |
82 | 对于单个点,其坐标为$(l_{ix},l_{iy}),i \in [1, m]$,$m$是特征点的个数,$l_{ix},l_{iy} \in [0,1]$。坐标轴的选取和目标定位时一致,以及需要保证每个样本的特征点的顺序是一致的,比如$l_1$都是左眼的左眼角,$l_2$都是左眼的右眼角等。
83 |
84 | 关于最后一层的激活函数,可以对每个坐标的值用 sigmoid 激活。
85 |
86 | ### 12.3 目标检测
87 |
88 | #### 12.3.1 滑动窗口目标检测算法
89 |
90 | 滑动窗口检测是分两步执行的:第一步是从原图中裁剪一部分并根据需求调整大小,第二步是检测裁剪部分有无目标对象。
91 |
92 | 对于第二步,是我们比较熟悉的分类算法,只是训练集需要人为调整到为几乎整张图都是目标对象,如下图:
93 |
94 | 
95 |
96 | $x$ 为一张无车的图片或者被车占满的图片,标签 $y$ 为1时有车,为0时无车。
97 |
98 | 对于第一步,滑动窗口用的方法是先选定一个裁剪大小,然后从图片的左上角开始,每隔一定像素(距离)裁剪一次,一直滑动到图片的右下角,然后下一个裁剪大小用相同的方法裁剪。如图,上图为3种裁剪大小,下图为一个滑动流程:
99 |
100 | 
101 |
102 | 
103 |
104 | #### 12.3.2 滑动窗口缺点——计算成本
105 |
106 | 看到这里不难发现,滑动窗口检测由于需要多个窗口且每个窗口滑动多次而导致运算量会相当巨大,运行时间过慢。而且如果滑动的步幅过大或者裁剪的大小不合适也会导致很难检测到目标。
107 |
108 | ### 12.4 卷积的滑动窗口实现
109 |
110 | #### 12.4.1 把神经网络的全连接层转化成卷积层
111 |
112 | 
113 |
114 | - 假设目标检测算法输入一个14×14×3的图像,过滤器大小为5×5,数量是16,14×14×3的图像在过滤器处理之后映射为10×10×16。
115 |
116 | - 然后通过参数为2×2的最大池化操作,图像减小到5×5×16。
117 |
118 | - 添加一个连接400个单元的全连接层,接着再添加一个全连接层。
119 |
120 | - 最后通过softmax单元输出,用4个数字来表示 ,它们分别对应softmax单元所输出的4个分类出现的概率。这4个分类可以是行人、汽车、摩托车和背景或其它对象。
121 |
122 | **全连接层转化为卷积层**
123 |
124 | 
125 |
126 | - 前几层和之前的一样。
127 |
128 | - 而对于全连接层,用5×5的过滤器来实现,数量是400个。输入图像大小为5×5×16,用5×5的过滤器对它进行卷积操作,过滤器实际上是5×5×16,因为在卷积过程中,过滤器会遍历这16个通道,所以这两处的通道数量必须保持一致,输出结果为1×1。假设应用400个这样的5×5×16过滤器,输出维度就是1×1×400。它不再是一个含有400个节点的集合,而是一个1×1×400的输出层。从数学角度看,它和全连接层是一样的,因为这400个节点中每个节点都有一个5×5×16维度的过滤器,所以每个值都是上一层这些5×5×16激活值经过某个任意线性函数的输出结果。
129 | - 再添加另外一个卷积层,这里用1×1卷积,假设有400个1×1的过滤器,在这400个过滤器的作用下,下一层的维度是1×1×400,它其实就是上个网络中的这一全连接层。最后经由1×1过滤器的处理,得到一个softmax激活值,通过卷积网络,我们最终得到这个1×1×4的输出层,而不是4个数字。
130 |
131 | 以上就是用卷积层代替全连接层的过程。
132 |
133 | #### 12.4.2 在卷积上应用滑动窗口对象检测算法
134 |
135 | 
136 |
137 | 假设向滑动窗口卷积网络输入14×14×3的图片。和前面一样,神经网络最后的输出层,即softmax单元的输出是1×1×4,这里画得比较简单,严格来说,14×14×3应该是一个长方体,第二个10×10×16也是一个长方体,为了方便,这里只画了正面,所以这里显示的都是平面图,而不是3D图像。
138 |
139 | 
140 |
141 | 假设输入给卷积网络的图片大小是14×14×3,测试集图片是16×16×3,现在给这个输入图片加上黄色条块,在最初的滑动窗口算法中,你会把这片蓝色区域输入卷积网络(红色笔标记)生成0或1分类。接着滑动窗口,步幅为2个像素,向右滑动2个像素,将这个绿框区域输入给卷积网络,运行整个卷积网络,得到另外一个标签0或1。继续将这个橘色区域输入给卷积网络,卷积后得到另一个标签,最后对右下方的紫色区域进行最后一次卷积操作。我们在这个16×16×3的小图像上滑动窗口,卷积网络运行了4次,于是输出了了4个标签。
142 |
143 | 
144 |
145 | 这4次卷积操作中很多计算都是重复的。所以执行滑动窗口的卷积时使得卷积网络在这4次前向传播过程中共享很多计算。
146 |
147 | - 卷积网络运行同样的参数,使得相同的5×5×16过滤器进行卷积操作,得到12×12×16的输出层。
148 |
149 | - 然后执行同样的最大池化,输出结果6×6×16。照旧应用400个5×5的过滤器,得到一个2×2×400的输出层,现在输出层为2×2×400,而不是1×1×400。
150 |
151 | - 应用1×1过滤器得到另一个2×2×400的输出层。
152 |
153 | - 再做一次全连接的操作,最终得到2×2×4的输出层,而不是1×1×4。
154 |
155 | - 最终,在输出层这4个子方块中,蓝色的是图像左上部分14×14的输出(红色箭头标识),右上角方块是图像右上部分(绿色箭头标识)的对应输出,左下角方块是输入层左下角(橘色箭头标识),也就是这个14×14区域经过卷积网络处理后的结果,同样,右下角这个方块是卷积网络处理输入层右下角14×14区域(紫色箭头标识)的结果。
156 |
157 | 该卷积操作的原理是我们不需要把输入图像分割成四个子集,分别执行前向传播,而是把它们作为一张图片输入给卷积网络进行计算,其中的公共区域可以共享很多计算,就像这里我们看到的这个4个14×14的方块一样。
158 |
159 | 
160 |
161 | 再看一个更大的图片样本,假如对一个28×28×3的图片应用滑动窗口操作,如果以同样的方式运行前向传播,最后得到8×8×4的结果。跟上一个范例一样,以14×14区域滑动窗口,首先在这个区域应用滑动窗口,其结果对应输出层的左上角部分。接着以大小为2的步幅不断地向右移动窗口,直到第8个单元格,得到输出层的第一行。然后向图片下方移动,最终输出这个8×8×4的结果。因为最大池化参数为2,相当于以大小为2的步幅在原始图片上应用神经网络。
162 |
163 | **滑动窗口的实现过程总结**
164 |
165 | 
166 |
167 | 在图片上剪切出一块区域,假设它的大小是14×14,把它输入到卷积网络。继续输入下一块区域,大小同样是14×14,重复操作,直到某个区域识别到汽车。
168 |
169 | 但是我们不用依靠连续的卷积操作来识别图片中的汽车,比如,我们可以对大小为28×28的整张图片进行卷积操作,一次得到所有预测值,如果足够幸运,神经网络便可以识别出汽车的位置。
170 |
171 | ### 12.5 Bounding Box预测
172 |
173 | 滑动窗口法的卷积实现的算法虽然效率更高,但仍然存在问题,不能输出最精准的边界框。
174 |
175 |  176 |
177 | 在滑动窗口法中,你取这些离散的位置集合,然后在它们上运行分类器,在这种情况下,这些边界框没有一个能完美匹配汽车位置,也许这个框(编号1)是最匹配的了。还有看起来这个真实值,最完美的边界框甚至不是方形,稍微有点长方形(红色方框所示),长宽比有点向水平方向延伸。
178 |
179 | 其中一个能得到更精准边界框的算法是**YOLO**算法,YOLO(You only look once)意思是你只看一次。
180 |
181 | #### 12.5.1 YOLO算法的具体实现
182 |
183 | 
184 |
185 | 比如你的输入图像是100×100的,然后在图像上放一个网格。为了介绍起来简单一些,这里用3×3网格,实际实现时会用更精细的网格,可能是19×19。
186 |
187 | 基本思路是使用图像分类和定位算法,将算法应用到9个格子上。
188 |
189 | 具体一点,需要定义训练标签,对于9个格子中的每一个指定一个标签$y$,$y$是8维的(上图蓝字):
190 |
191 | - $p_{c}$等于0或1取决于这个绿色格子中是否有图像。
192 |
193 | - $b_{x}$、$b_{y}$、$b_{h}$和$b_{w}$作用就是,如果那个格子里有对象,那么就给出边界框坐标。
194 |
195 | - $c_{1}$、$c_{2}$和$c_{3}$就是你想要识别的三个类别,背景类别不算,所以你尝试在背景类别中识别行人、汽车和摩托车,那么$c_{1}$、$c_{2}$和$c_{3}$可以是行人、汽车和摩托车类别。
196 |
197 | 这张图有两个对象,**YOLO算法**做的就是,**取两个对象的中点,然后将这个对象分配给包含其中点的格子**。
198 |
199 | 所以左边的汽车就分配到这个格子上(绿框),然后这辆中点在这里(绿点),标签为(上图绿字);右边的汽车分配给这个格子(黄色),中点在这里(黄点),标签为(上图黄字)。即使中心格子同时有两辆车的一部分,我们就假装中心格子没有任何我们感兴趣的对象。
200 |
201 | 没有检测对象的格子(除中间靠左、中间靠右外的其他格子)标签向量$y$都如上图紫字所示。
202 |
203 | 故对于这里9个格子中任何一个,你都会得到一个8维输出向量,因为这里是3×3的网格,所以有9个格子,总的输出尺寸是3×3×8,所以目标输出是3×3×8。
204 |
205 |
176 |
177 | 在滑动窗口法中,你取这些离散的位置集合,然后在它们上运行分类器,在这种情况下,这些边界框没有一个能完美匹配汽车位置,也许这个框(编号1)是最匹配的了。还有看起来这个真实值,最完美的边界框甚至不是方形,稍微有点长方形(红色方框所示),长宽比有点向水平方向延伸。
178 |
179 | 其中一个能得到更精准边界框的算法是**YOLO**算法,YOLO(You only look once)意思是你只看一次。
180 |
181 | #### 12.5.1 YOLO算法的具体实现
182 |
183 | 
184 |
185 | 比如你的输入图像是100×100的,然后在图像上放一个网格。为了介绍起来简单一些,这里用3×3网格,实际实现时会用更精细的网格,可能是19×19。
186 |
187 | 基本思路是使用图像分类和定位算法,将算法应用到9个格子上。
188 |
189 | 具体一点,需要定义训练标签,对于9个格子中的每一个指定一个标签$y$,$y$是8维的(上图蓝字):
190 |
191 | - $p_{c}$等于0或1取决于这个绿色格子中是否有图像。
192 |
193 | - $b_{x}$、$b_{y}$、$b_{h}$和$b_{w}$作用就是,如果那个格子里有对象,那么就给出边界框坐标。
194 |
195 | - $c_{1}$、$c_{2}$和$c_{3}$就是你想要识别的三个类别,背景类别不算,所以你尝试在背景类别中识别行人、汽车和摩托车,那么$c_{1}$、$c_{2}$和$c_{3}$可以是行人、汽车和摩托车类别。
196 |
197 | 这张图有两个对象,**YOLO算法**做的就是,**取两个对象的中点,然后将这个对象分配给包含其中点的格子**。
198 |
199 | 所以左边的汽车就分配到这个格子上(绿框),然后这辆中点在这里(绿点),标签为(上图绿字);右边的汽车分配给这个格子(黄色),中点在这里(黄点),标签为(上图黄字)。即使中心格子同时有两辆车的一部分,我们就假装中心格子没有任何我们感兴趣的对象。
200 |
201 | 没有检测对象的格子(除中间靠左、中间靠右外的其他格子)标签向量$y$都如上图紫字所示。
202 |
203 | 故对于这里9个格子中任何一个,你都会得到一个8维输出向量,因为这里是3×3的网格,所以有9个格子,总的输出尺寸是3×3×8,所以目标输出是3×3×8。
204 |
205 |  206 |
207 | 所以这个算法的优点在于神经网络可以输出精确的边界框,所以测试的时候,你做的是喂入输入图像$x$,然后跑正向传播,直到你得到这个输出$y$。然后对于这里3×3位置对应的9个输出,就可以读出1或0。如果那里有个对象,就可以读出那个对象是什么,还有格子中这个对象的边界框是什么。
208 |
209 | 只要每个格子中对象数目没有超过1个,这个算法应该是没问题的。一个格子中存在多个对象的问题,之后再讨论。这里用的是比较小的3×3网格,实践中你可能会使用更精细的19×19网格,所以输出就是19×19×8。这样的网格精细得多,那么多个对象分配到同一个格子的概率就小得多。
210 |
211 | 把对象分配到一个格子的过程是,你观察对象的中点,然后将这个对象分配到其中点所在的格子,所以即使对象可以横跨多个格子,也只会被分配到9个格子其中之一,就是3×3网络的其中一个格子,或者19×19网络的其中一个格子。在19×19网格中,两个对象的中点处于同一个格子的概率就会更低。
212 |
213 | YOLO算法有一个好处就是,它是一个卷积实现,共享了很多卷积计算,所以实际上它的运行速度非常快,可以达到实时识别。
214 |
215 | **编码边界框**
216 |
217 | 
218 |
219 | 对于这个方框(中右侧),我们约定左上这个点是(0,0),然后右下这个点是(1,1);
220 |
221 | 要指定橙色中点的位置,$b_{x}$大概是0.4,因为它的位置大概是水平长度的0.4,$b_{y}$大概是0.3;
222 |
223 | 边界框的高度用格子总体宽度的比例表示,所以这个红框的宽度可能是蓝线(图右下角蓝线)的90%,所以$b_h$是0.9,它的高度也许是格子总体高度的一半,这样的话$b_{w}$就是0.5。
224 |
225 | 换句话说,$b_{x}$、$b_{y}$、$b_{h}$和$b_{w}$单位是相对于格子尺寸的比例,所以$b_{x}$和$b_{y}$必须在0和1之间,因为从定义上看,橙色点位于对象分配到格子的范围内,如果它不在0和1之间,如果它在方块外,那么这个对象就应该分配到另一个格子上。但是$b_{h}$和$b_{w}$可能会大于1,特别是如果有一辆汽车的边界框是这样的(左下红框),那么边界框的宽度和高度有可能大于1。
226 |
227 | 指定边界框的方式有很多,但这种约定是比较合理的,还有其他更复杂的参数化方式,涉及到sigmoid函数,确保这个值($b_{x}$和$b_{y}$)介于0和1之间,然后使用指数参数化来确保$b_{h}$和$b_{w}$都是非负数。还有其他更高级的参数化方式,可能效果要更好一点,但这里讲的办法应该是管用的。
228 |
229 | #### 12.5.2 其他指定边界框的算法
230 |
231 | **1. SSD**:
232 |
233 | SSD(Single-Shot MultiBox Detector),使用 VGG19 网络作为特征提取器(和 Faster R-CNN 中使用的 CNN 一样)的单次检测器。我们在该网络之后添加自定义卷积层(蓝色),并使用卷积核(绿色)执行预测。
234 |
235 | 
236 |
237 | 然而,卷积层降低了空间维度和分辨率。因此上述模型仅可以检测较大的目标。为了解决该问题,我们从多个特征图上执行独立的目标检测。
238 |
239 | 
240 |
241 | 以下是特征图图示。
242 |
243 | 
244 |
245 | SSD 使用卷积网络中较深的层来检测目标。如果我们按接近真实的比例重绘上图,我们会发现图像的空间分辨率已经被显著降低,且可能已无法定位在低分辨率中难以检测的小目标。如果出现了这样的问题,我们需要增加输入图像的分辨率。
246 |
247 | 
248 |
249 |
250 |
251 |
252 | 参考博客:https://www.jianshu.com/p/468e08f739bd
253 |
254 | **2. FPN**:
255 |
256 | 使用不同尺寸特征图进行预测的网络称为特征金字塔网络(FPN),是一种旨在提高准确率和速度的特征提取器。数据流如下:
257 |
258 | 
259 |
260 | FPN 由自下而上和自上而下路径组成。其中自下而上的路径是用于特征提取的常用卷积网络。空间分辨率自下而上地下降。当检测到更高层的结构,每层的语义值增加。
261 |
262 | 
263 |
264 | SSD 通过多个特征图完成检测。但是,最底层不会被选择执行目标检测。它们的分辨率高但是语义值不够,导致速度显著下降而不能被使用。SSD 只使用较上层执行目标检测,因此对于小的物体的检测性能较差。
265 |
266 | 
267 |
268 | FPN 提供了一条自上而下的路径,从语义丰富的层利用上采样构建高分辨率的层。
269 |
270 | 
271 |
272 | 虽然该重建层的语义较强,但在经过所有的上采样和下采样之后,目标的位置不精确。在重建层和相应的特征图之间添加横向连接可以使位置侦测更加准确。
273 |
274 | 
275 |
276 | **3. RetianNet**:
277 |
278 | RetianNet是基于 ResNet、FPN以及利用 Focal loss 构建的 。
279 |
280 | 
281 |
282 | RetinaNet
283 |
284 | **4. Focal Loss**
285 |
286 | 类别不平衡会损害性能。SSD 在训练期间重新采样目标类和背景类的比率,这样它就不会被图像背景淹没。Focal loss(FL)采用另一种方法来减少训练良好的类的损失。因此,只要该模型能够很好地检测背景,就可以减少其损失并重新增强对目标类的训练。我们从交叉熵损失 (Cross Entroy Loss)开始,并添加一个权重来降低高可信度类的交叉熵。
287 |
288 | 
289 |
290 | 例如,令 γ = 0.5, 经良好分类的样本的 Focal Loss 趋近于 0。
291 |
292 | 
293 |
294 | ### 12.6 交并比
295 |
296 | #### 12.6.1 交并比函数的作用
297 |
298 | 交并比(IoU, Intersection over Union)函数衡量了两个边界框重叠的相对大小,用来评价对象检测算法是否运行良好,即检测对象定位是否准确。
299 |
300 | #### 12.6.2 交并比函数的实现
301 |
302 | 
303 |
304 | 假设识别的对象的实际边界框如上图中红框所示,用对象检测算法得到的边界框如紫框所示,这个结果是好是坏呢?
305 |
306 | 交并比函数做的是计算**两个边界框交集和并集之比**,交集部分如橙色阴影所示,并集部分如绿色阴影所示,如果预测边框和实际边框完美重叠,交集等于并集,$IoU = 1$,一般约定,在计算机检测任务中,若 $IoU \geq 0.5$,则说明预测的边界框是正确的,如果希望更严格,可以把IoU的阈值定得更高,IoU越高,边界框越精确。
307 |
308 | ### 12.7 非极大值抑制
309 |
310 | #### 12.7.1 非极大值抑制的作用
311 |
312 | 到目前为止我们学到的对象检测中的一个问题是,算法可能对同一个对象做出多次检测而不是一次,非极大值抑制法可以**确保算法对每个对象只检测一次**。
313 |
314 | #### 12.7.2 非极大值抑制的实现
315 |
316 | 非极大值抑制(Non-max suppression):只输出概率最大的分类结果,抑制很接近但不是最大的其他预测结果。
317 |
318 | 
319 |
320 | 假设要在这张图里检测行人和汽车,我们可能会在上面放个19×19的网格,理论上每辆汽车只有一个中点,应该只分配到中点所在的格子里,实践中在跑对象分类和定位算法时,对每个格子都跑一次,橙色和绿色方框的那些格子可能会想,这辆车的中点应该在其格子内部,觉得它们格子内有车的概率很高,而不是19×19=361个格子中仅有两个格子会报告它们检测出一个对象,所以最后可能会对同一个对象做出多次检测。
321 |
322 | 非极大值抑制做的就是清理这些检测结果,对每个对象只检测一次,而不是每个对象都触发多次检测。
323 |
324 | **非极大值抑制的实现步骤:**
325 |
326 | 
327 |
328 | 1. 去掉所有预测边界框中 $p_c \leq 0.6$ 的边界框(这里的0.6是阈值,可以自己设定),抛弃了所有概率比较低的输出边界框,则剩下的边界框中存在对象的概率至少有0.6。
329 | 2. 对于剩下的边界框,首先看看每次报告中每个检测结果相关的概率 $p_c$,找到**概率最大**的那个,这个例子中是0.9,认为这是最可靠的检测,用高亮标记,就说在这里找到了一辆车。
330 | 3. 接着,非极大值抑制就会逐一审视剩下的矩形,所有和这个最大的边界框有很高交并比、高度重叠的其他边界框的输出就会被抑制,所以这两个 $p_c$ 分别为0.6和0.7的矩形和最大边界框(淡蓝色矩形)重叠程度很高,会被抑制、变暗。
331 |
332 | 左边那辆车也同理,找到 $p_c$ 最大的一个是0.8,认为这里检测出一辆车,用高亮显示,而其他IoU值很高的矩形会被抑制而变暗。直接抛弃变暗的矩形,只剩下高亮显示的,就是最后得到的两个预测结果。
333 |
334 | 上面介绍的只是算法检测单个对象的情况,若想同时检测三种对象,比如行人、汽车和摩托,则需要独立进行三次非极大值抑制,对每个输出类别都做一次。
335 |
336 | ### 12.8 Anchor Boxes
337 |
338 | #### 12.8.1 为什么要用Anchor Boxes?
339 |
340 | 之前的算法只能在一个格子中检测出一个对象,Anchor Boxes可以**一个格子检测出多个对象**。如下图所示,使用3x3的网格,行人和汽车的中心几乎在同一个网格,这时就需要用到Anchor Boxes。
341 |
342 | 
343 |
344 | #### 12.8.2 思路
345 |
346 | 1. 预先定义几个不同形状的anchor box,把预测结果和这些anchor box关联起来。本例假设两个anchor box,对应行人和汽车。
347 |
348 | 
349 |
350 | 2. 定义类别标签,将原来的向量$$\left[\begin{array}{llllllll}
351 | p_{c} & b_{x} & b_{y} & b_{h} & b_{w} & c_{1} & c_{2} & c_{3}
352 | \end{array}\right]^{T}$$重复两次$$\left.\begin{array}{llllllllllllllll}
353 | y=\left[p_{c}\right. & b_{x} & b_{y} & b_{h} & b_{w} & c_{1} & c_{2} & c_{3} & p_{c} & b_{x} & b_{y} & b_{h} & b_{w} & c_{1} & c_{2} & c_{3}
354 | \end{array}\right]^{T}$$。其中,前面的8个参数和anchor box 1相关联,后面的8个参数和anchor box 2相关联。
355 |
356 | 
357 |
358 | 3. 行人一般符合anchor box1形状,所以用anchor box1来预测行人会达到很好的效果,这么编码 $p_c$ = 1,代表有个行人,用 $b_x, b_y ,b_h$ 和 $b_w$ 来编码包住行人的边界框,用$c_1, c_2 ,c_3$($c_1$ = 1,$c_2$ = 0,$c_3$ = 0)来说明这个对象是个行人。 汽车一般符合anchor box2形状,采用相同的编码方法,定义对象是汽车和边界框等,所有参数都和检测汽车相关( $p_c$ = 1, $b_x, b_y ,b_h$, $b_w$, $c_1$ = 0,$c_2$ = 1,$c_3$ = 0)。
359 |
360 | 4. 当两个anchor boxes对相同位置做出判别时,以交并比作为取舍指标。选择IoU最高的那个,用这个anchor box来进行预测。输出y的维度是$n \times n \times m \times c$(n为图片分成$n \times n$份,$m$为anchor box数量,$c$为class类别数)
361 |
362 | #### 12.8.3 怎么选择anchor box?
363 |
364 | 1. 一般手工指定anchor box形状,根据要检测的对象,指定有针对性的anchor box,可选择5-10个anchor box,使其尽可能覆盖到不同形状。
365 | 2. 使用K-means聚类算法获得anchor box,选择最具有代表性的一组anchor box。
366 |
367 | ### 12.9 YOLO 算法
368 |
369 | 目标检测架构分为两种,一种是two-stage,一种是one-stage。 two-stage 有region proposal (选取候选区域)过程,网络会根据候选区域生成位置和类别,而 one-stage 直接从图片生成位置和类别。
370 |
371 | YOLO 是一种 one-stage 方法,即 You Only Look Once 的缩写,意思是神经网络只需要看一次图片,就能输出结果。
372 |
373 |
374 | #### 12.9.1 YOLO算法的实现
375 |
376 | - 构造训练集:假设检测三种对象,行人,汽车和摩托。
377 | 输入图像,神经网络的输出尺寸是3x3x2x8(3x3的网格,2个anchor box,8个参数)。遍历9个格子,构造训练集,然后构成对应的目标向量y,判断和anchor box 有关的 $p_c$ 和边界框,指定正确类别。
378 |
379 | 
380 |
381 | - 如何预测:输入图像,神经网络的输出尺寸是3x3x2x8,对于9个格子,每个都有对应的向量,如上图所示。
382 | 对于1号蓝格,检测不到任何对象,所以2个anchor box的 $p_c$ = 0。剩下的是一些数字,多多少少都是噪音,但这些数字基本上会被忽略,因为神经网络告诉表示那里没有任何东西。(输出 y 如编号3所示)。
383 | 对于2号绿格,里面有汽车。对于边界框1(anchor box 1)来说 $p_c$ = 0,表示此格子中无行人。然后就是一组数字噪音,此格子中无行人。anchor box 2对应汽车,此格子中有车,因此希望数字可以对车子指定一个相当准确的边界框,即($$\left.p_{c}=1, b_{x}, b_{y}, b_{h}, b_{w}, c_{1}=0, c_{2}=1, c_{3}=0\right)$$,这就是神经网络做出预测的过程。
384 | - 运行非极大值抑制:看看一张新的测试图片,对于两个anchor box,那么对于9个格子中任何一个都会有两个预测的边界框。
385 | 针对每个框,抛弃概率低的预测,去掉那些连神经网络都说这里很可能什么都没有的边界框。如果希望检测行人、车子和摩托三个对象检测类别,那么需要对每个类别单独运行非极大值抑制,处理预测结果即此类别的边界框。
386 |
387 | 
388 |
389 | - 最后,输出位置和类别信息。
390 |
391 | #### 12.9.2 YOLO v1、v2、v3和v4
392 |
393 | YOLO 一共发布了四个版本,其中 YOLOv1 奠定了整个系列的基础,后面的系列就是在第一版基础上的改进,只为提升性能。
394 |
395 | - YOLOv2
396 | 提出了 ImageNet 和 COCO 数据集结合的联合训练方法,使算法可以在检测数据集和分类数据集上训练目标检测器。用检测数据集的数据学习物体的准确位置,用分类数据集的数据来增加分类的类别量、提升健壮性。
397 | - YOLOv3
398 | YOLOv3 的提出不是为了解决什么问题,将模型复杂了不少,可以通过改变模型结构的大小来权衡速度与精度。
399 | - YOLOv4
400 | YOLOv4的改进总结了几乎所有的检测技巧,又提出一点儿技巧,然后经过筛选,排列组合,挨个实验(ablation study)哪些方法有效,经过大量实验选出的性能最好的组合。
401 | 发展历程:
402 | 
403 |
404 | ### 12.10 RPN网络
405 |
406 | RPN:Region Proposal Network
407 |
408 | #### 12.10.1 Region with CNN(R-CNN)
409 |
410 | 意思基于候选区域(Region Proposal)的卷积网络,不再针对每个滑动窗口跑检测算法,而是使用某种算法求出候选区域,然后对每个候选区域跑一下分类器,每个区域会输出一个标签和一个边界框。这样就只是选择一些有意义的窗口,在少数窗口上运行卷积网络分类器,以节省时间。
411 |
412 | - 选出的候选区域方法:图像分割算法
413 |
414 | 
415 |
416 | 如上图所示。分割色块后,选择其对应的一个边界框,然后在色块上跑分类器,这样的处理比滑动窗口法处理的窗口少的多,可以减少卷积网络分类器运行时间,而不必在所有位置运行一遍分类器。
417 |
418 | 另外,说明一下,R-CNN算法不会直接信任输入的边界框,它也会输出一个边界框$$b_{x},\quad b_{y},\quad b_{h},\quad b_{w}$$,这样得到的边界框比较精确,比单纯使用图像分割算法给出的色块边界要好。
419 |
420 |
421 | #### 12.10.2 具体步骤
422 |
423 | 
424 |
425 | 1. 输入图像;运行图像分割算法,利用selective search对图像生成1K~2K的候选区域(region proposal);
426 | 2. 将每个候选区域缩放(warp)成227×227的大小并输入到CNN,将CNN的全连接层fc7的输出作为特征;
427 | 3. 对CNN的fc7层的输出特征输入到SVM进行分类;如果有十个类别,那么每个region proposal要经过10个SVM,得到预测的类别。
428 | 4. 修正:对于SVM分好类的Region Proposal做边框回归,用Bounding box回归值校正原来的候选窗口,生成预测窗口坐标。
429 |
430 | #### 12.10.3 缺点和改进
431 |
432 | R-CNN训练耗时,占用磁盘空间大,测试速度慢,每个候选区域需要运行整个前向CNN计算;因此提出了其它改进算法。
433 |
434 | 
435 |
436 | - Fast R-CNN:利用卷积实现了滑动窗口。相比于R-CNN,Fast R-CNN不再对每一个候选区域进行CNN特征提取,而是先将整张图片归一化后输入CNN网络进行特征提取,之后候选区域在特征图上进行截取,显著提升了R-CNN的速度。但是其缺点是得到候选区域的聚类步骤仍然非常缓慢。
437 |
438 | - Faster R-CNN:加入RPN网络,将特征提取、候选区域提取、bounding box regression、分类都整合在了一个网络中,使得综合性能有较大提高,在检测速度方面尤为明显。(仍比YOLO慢)
439 |
440 | - Gaussian Faster R-CNN主要有以下两个创新点:
441 | 1. 卷积的过程其实就是一个特征提取的过程,所以在预处理之后移除了全连接这个操作,简化了网络结构,以准确率换速度。
442 | 2. 假设在多次卷积之后,整个特征图是一个平稳的随机序列,符合高斯分布,则可以采用 $3\sigma$ 原理对树进行裁剪,因为四周的像素对分类任务来说无关紧要,但是完全压缩和分类这些无关紧要的像素会花费大量的CPU时间。最后用随机森林代替B-P神经网络,将时间复杂度由 $O(N)$ 降到 $O(log2N)$。
443 |
444 | ### 12.11 目标检测算法的评价指标
445 |
446 | #### 12.11.1 准确度指标——平均准确度均值mAP
447 |
448 | - **什么是TP、TN、FP、FN?**
449 |
450 | TP、TN、FP、FN即true positive, true negative, false positive, false negative的缩写,positive和negative表示的是预测得到的结果,预测为正类则为positive,预测为负类则为negative; true和false则表示预测的结果和真实结果是否相同,相同则是true,不同则为false,如下图:
451 |
452 | 
453 |
454 | 举个例子,假设现在有这样一个测试集,其中的图片只由大雁和飞机两种图片组成,如下图所示:
455 |
456 | 
457 |
458 | 假设分类系统最终的目的是取出测试集中所有飞机的图片,则 TP、TN、FP、FN的具体定义分别是:
459 |
460 | **True positives :** 飞机的图片被正确的识别成了飞机。
461 | **True negatives:** 大雁的图片没有被识别出来,系统正确地认为它们是大雁。
462 | **False positives:** 大雁的图片被错误地识别成了飞机。
463 | **False negatives:** 飞机的图片没有被识别出来,系统错误地认为它们是大雁。
464 |
465 | - **Precision 与 Recall**
466 |
467 | **Precision**(精确度、查准率)指的是模型判断该图片为正类且该图片也的确是正类的概率,即在模型判断为正类的图片中,True positives所占的比率,**衡量的是一个分类器分出来的正类的确是正类的概率**。
468 | $$
469 | Precision=\frac{TP}{TP+FP}
470 | $$
471 | 光是精确度还不能衡量分类器的好坏程度,比如50个正样本和50个负样本,如果分类器把49个正样本和50个负样本都分为负样本,剩下一个正样本分为正样本,这样精确度也是100%,所以还需要召回率来衡量。
472 |
473 | **Recall**(召回率、查全率)指的是测试集的所有正样本比例中,被模型正确识别为正样本的比例,即模型判断为正类且实际的确是正类的图像数量/真实类别是正类的图像数量,**衡量的是一个分类器能把所有的正类都找出来的能力**。
474 | $$
475 | Recall=\frac {TP}{TP+FN}
476 | $$
477 | 在上面所举的例子中,假设识别出了四个结果,如下图所示:
478 |
479 | 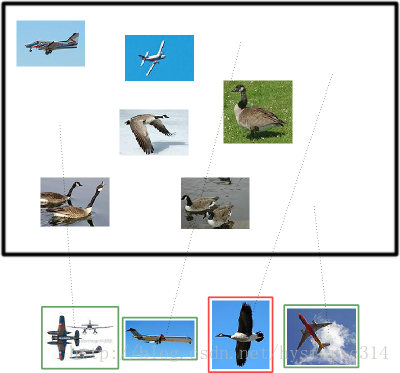
480 |
481 | 其中,在识别出来的四张照片中:
482 |
483 | **True positives :** 有三个,画绿色框的飞机,即 $TP=3$。
484 |
485 | **False positives:** 有一个,画红色框的大雁,即 $FP=1$。
486 |
487 | 没被识别出来的六张图片中:
488 | **True negatives :** 有四个,这四个大雁的图片,系统正确地没有把它们识别成飞机,即 $TN=4$。
489 | **False negatives:** 有两个,两个飞机没有被识别出来,系统错误地认为它们是大雁,即 $FN=2$。
490 |
491 | 故 $Precision=\frac {TP}{TP+FP}=\frac {3}{3+1}=0.75$ ,意味着在识别出来的结果中,飞机的图片占75%;$Recall=\frac {TP}{TP+FN}=\frac{3}{3+2}=0.6$,意味着在所有的飞机图片中,60%的飞机图片被正确识别为飞机。
492 |
493 | - **调整阈值**
494 |
495 | 可以通过调整阈值来选择让模型识别出多少图片,进而改变Precision或Recall的值。在某种阈值的前提下(蓝色虚线),模型识别出了四张图片,如下图所示:
496 | 
497 |
498 | 分类系统认为大于阈值(蓝色虚线之上)的四个图片更像飞机。
499 |
500 | 我们可以通过改变阈值(可以看作上下移动蓝色虚线)来选择让系统识别出多少张图片,从而改变Precision或Recall的值。比如,把蓝色虚线移到第一张图片下面,也就是说让系统只识别出最上面的那张飞机图片,那么Precision的值就是100%,而Recall的值是20%;如果把蓝色虚线放到第二张图片下面,也就是说让系统只识别出最上面的前两张图片,那么Precision的值还是100%,而Recall的值则增长到40%。下图为不同阈值条件下,Precision与Recall的变化情况:
501 | 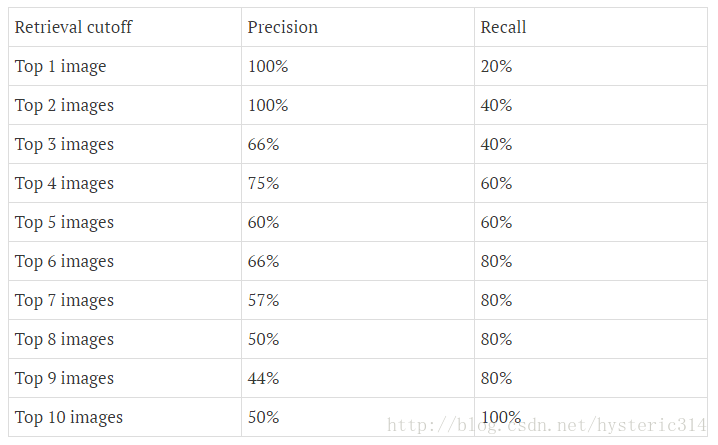
502 |
503 | - **Precision-Recall曲线**
504 |
505 | Precision-Recall曲线(P-R曲线)是以Precision和Recall作为纵、横轴坐标的二维曲线,通过选取不同阈值时对应的精确度和召回率画出,如下图所示。
506 |
507 | 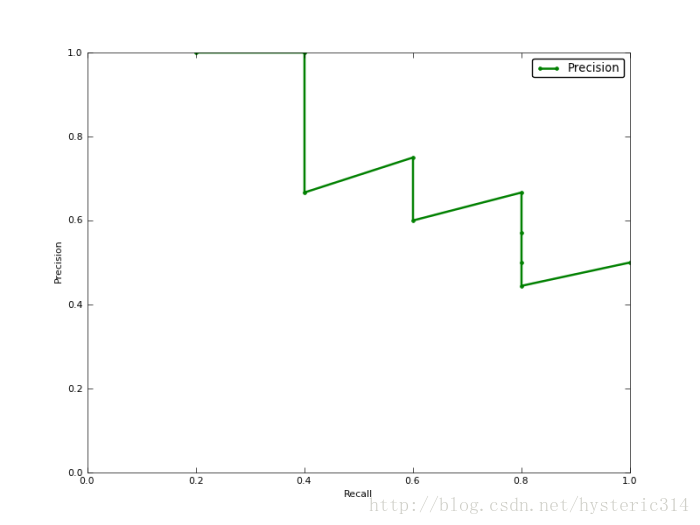
508 |
509 | 总体趋势是,精确度越高,召回率越低,当召回率达到1时,对应概率分数最低的正样本,这个时候正样本数量除以所有大于等于该阈值的样本数量就是最低的精确度。上图所示的分类器在不损失精度的条件下能达到40%的Recall,而当Recall达到100%时,Precision降到50%。
510 |
511 | Precision-Recall曲线可以用来显示分类器在Precision和Recall之间的权衡,从而评估分类器的性能。如果一个分类器的性能较好,那么它应该有如下的表现:被识别出的图片中飞机所占的比重比较大,并且在识别出大雁之间,尽可能多地正确识别出飞机,也就是让Recall值增长的同时保持Precision的值在一个很高的水平。而性能较差的分类器可能会损失很多Precision值才能换来Recall值的提高。
512 |
513 | - **平均准确度AP**
514 |
515 | AP:Average-Precision,平均准确度,综合考量了Precision和Recall的影响,反映了模型对某个类别识别的好坏。
516 |
517 | P-R曲线围起来的面积就是AP值,通常来说一个分类器越好,AP值越高。
518 |
519 | - **平均准确度均值mAP**
520 |
521 | mAP:mean Average-Precision,平均精确度均值,即所有类别AP的平均值,衡量的是在所有类别上的平均好坏程度。
522 |
523 | mAP的取值范围是[0,1],越大越好。
524 |
525 | - 为什么可以使用mAP来评价目标检测的效果?
526 |
527 | 目标检测的效果取决于预测框的位置和类别是否准确,从mAP的计算过程中可以看出通过计算预测框和真实框的IoU来判断预测框是否准确预测到了位置信息,同时精确度和召回率指标的引用可以评价预测框的类别是否准确,因此mAP是目前目标检测领域非常常用的评价指标。
528 |
529 | > 参考文献:
530 | >
531 | > 1. https://blog.csdn.net/syoung9029/article/details/56276567
532 | >
533 | > 2. https://www.cnblogs.com/wanghui-garcia/p/11084833.html
534 | > 3. https://blog.csdn.net/weixin_43423892/article/details/106643649
535 |
536 | #### 12.11.2 速度指标——FPS
537 |
538 | 目标检测技术的很多实际应用在准确度和速度上都有很高的要求,如果不计速度性能指标,只注重准确度表现的突破,其代价是更高的计算复杂度和更多内存需求。只有速度快,才能实现实时检测,这对一些应用场景极其重要。
539 |
540 | FPS:Frame Per Second,每秒帧率,即每秒内可以处理的图片数量。当然要对比FPS,需要在同一硬件上进行。
541 |
542 | 另外也可以使用处理一张图片所需时间来评估检测速度,时间越短,速度越快。
543 |
544 | > 参考:
545 | >
546 | > 1. https://zhuanlan.zhihu.com/p/70306015
547 | > 2. https://blog.csdn.net/qq_29893385/article/details/81213377
548 |
549 | #### 12.11.3 模型大小
550 |
551 | 自 2012 年 AlexNet 以来,卷积神经网络(简称 CNN)在图像分类、图像分割、目标检测等领域获得广泛应用。随着性能要求越来越高,AlexNet 已经无法满足大家的需求,于是乎各路大牛纷纷提出性能更优越的 CNN 网络,如 VGG、GoogLeNet、ResNet、DenseNet 等。由于神经网络的性质,为了获得更好的性能,网络层数不断增加,从 7 层 AlexNet 到 16 层 VGG,再从 16 层 VGG 到 GoogLeNet 的 22 层,再到 152 层 ResNet,更有上千层的 ResNet 和 DenseNet。虽然网络性能得到了提高,但随之而来的就是效率问题。
552 |
553 | 效率问题主要是**模型的存储问题和模型进行预测的速度问题**(以下简称速度问题)
554 |
555 | - 第一,存储问题。数百层网络有着大量的权值参数,保存大量权值参数对设备的内存要求很高;
556 | - 第二,速度问题。在实际应用中,往往是毫秒级别,为了达到实际应用标准,要么提高处理器性能(看英特尔的提高速度就知道了,这点暂时不指望),要么就减少计算量。
557 |
558 | 只有解决 CNN 效率问题,才能让 CNN 走出实验室,更广泛的应用于移动端。对于效率问题,通常的方法是进行**模型压缩**(Model Compression),即在已经训练好的模型上进行压缩,使得网络携带更少的网络参数,从而解决内存问题,同时可以解决速度问题。
559 |
560 | 相比于在已经训练好的模型上进行处理,轻量化模型设计则是另辟蹊径。**轻量化模型设计**主要思想在于设计更高效的网络计算方式(主要针对**卷积**方式),从而使网络参数减少的同时,不损失网络性能。近年提出的四个轻量化模型分别是:SqueezeNet、MobileNet、ShuffleNet、Xception,有兴趣的可以参考以下博客或查找论文以了解。
561 |
562 | > 参考:https://blog.csdn.net/u012426298/article/details/80817788
--------------------------------------------------------------------------------
/13 特殊应用 人脸识别和神经风格转换.md:
--------------------------------------------------------------------------------
1 | ## 13 特殊应用:人脸识别和神经风格转换
2 |
3 | ### 13.1 什么是人脸识别?
4 |
5 | #### 13.1.1 人脸验证 vs 人脸识别
6 |
7 | **人脸验证**(face verification):也被称为 “1对1” 问题。
8 |
9 | - 输入:一张图片以及某人的ID或名字
10 | - 输出:系统验证输入图片是否是这个人。
11 |
12 | **人脸识别**(face recognition):“1对K” 问题。
13 |
14 | - 拥有一个包含 $K$ 人信息的数据库
15 | - 输入:一张图片
16 | - 输出:若输入图片符合 $K$ 人中任意一个人的图像,输出这个人的ID,否则,输出"not recognized"。
17 |
18 | **人脸验证与人脸识别的关系:**
19 |
20 | 人脸识别比人脸验证要求更高。假设有一个验证系统准确率是99%,看起来这个验证系统性能不错,但如果应用到有100个人的数据库的人脸识别系统中,每个人的犯错概率是1%,整体犯错概率就放大了100倍,所以要想得到一个可接受的识别误差,就要构造一个准确率为99%甚至更高的验证系统才能得到很好的识别效果。也就是说,人脸验证系统的准确率要足够高才能应用到人脸识别系统中。
21 |
22 | #### 13.1.2 人脸识别的传统方法
23 |
24 | 主流的人脸识别技术基本上可以归结为三类,即:基于几何特征的方法、基于模板的方法和基于模型的方法。
25 |
26 | - 基于几何特征的方法是最早、最传统的方法,通常需要和其他算法结合才能有比较好的效果;
27 | - 基于模板的方法可以分为基于相关匹配的方法、特征脸方法、线性判别分析方法、奇异值分解方法、神经网络方法、动态连接匹配方法等。
28 | - 基于模型的方法则有基于隐马尔柯夫模型,主动形状模型和主动外观模型的方法等。
29 |
30 | 下文主要介绍三种传统的人脸识别方法:
31 |
32 | 1. 主成分分析法
33 |
34 | 主成分分析法(PAC,Principal Component Analysis)又称为特征脸法,是20世纪90年代初由Turk和Pentland提出的一种经典算法,根据图像的统计特征通过正交变换(即K-L变换)由高维向量转换为低维向量,并形成低维线性向量空间,利用人脸投影到这个低维空间所得到的投影系数作为识别的特征矢量,这样,就产生了一个由“特征脸”矢量形成的子空间,成为“人脸子空间”或“特征子空间”,每一幅人脸图像向其投影都可以获得一组坐标系数,这组坐标系数表明了人脸在子空间中的位置,因此利用特征脸方法可以重建和识别人脸。
35 |
36 | 2. 线性判别分析
37 |
38 | 线性判别分析是对费舍尔的线性鉴别方法的归纳,这种方法使用统计学、模式识别和机器学习方法,试图找到两类物体或事件的特征的一个线性组合,以能够特征化或区分它们。所得的组合可用来作为一个线性分类器,或者,更常见的是,为后续的分类做降维处理。
39 |
40 | 3. 支持向量机
41 |
42 | 支持向量机(SVM,Support Vector Machine)起源于统计学习理论,研究如何构造学籍及,实现模式分类问题。其基本思想是通过非线性变换将输入空间变换到一个高维空间,在高维空间求取最优线性分类面,以解决那些线性不可分的分类问题。而这种非线性变换是通过定义适当的内积函数(即核函数)来实现的,由于该方法是基于结构风险最小化原理,而不是传统统计学的经验风险最小化,因而表现出很多优于已有方法的性能,但该方法需要大量的存储空间,并且训练速度慢。
43 |
44 | > 参考:
45 | >
46 | > 1. https://www.jiqizhixin.com/articles/2019-02-10-4
47 | > 2. https://wenku.baidu.com/view/34c55025a100a6c30c22590102020740be1ecdb7.html
48 |
49 | ### 13.2 One-Shot学习
50 |
51 | #### 13.2.1 One-Shot学习的定义
52 |
53 | **One-Shot learning**:一次学习,只通过一个样本来进行学习以能够认出同一个人。
54 |
55 | 
56 |
57 | 如上图所示,假设人脸识别系统数据库里有4个人每人一张照片,需要仅仅通过每个人的一张照片来判断输入图片中是否含有这4个人的其中一个。
58 |
59 | #### 13.2.2 如何解决One-Shot学习问题
60 |
61 | 对于One-Shot学习问题,采用卷积神经网络进行识别分类的缺点:
62 |
63 | 1. 训练集太小,不足以训练一个稳健的神经网络;
64 | 2. 如果有新成员加入数据集,分类输出的标签数量要改变,神经网络得重新训练。
65 |
66 | 故要解决One-Shot学习问题,应该要**学习Similarity函数**(也称为d函数):
67 | $$
68 | \begin{equation}\begin{split}
69 | d(img1,&img2)=degree\ of\ difference\ between\ images\\[2ex]
70 | &If\ d(img1,img2)\ \le\ \tau\ \ \ \ "same"\\
71 | &If\ d(img1,img2)\ \ge\ \tau\ \ \ \ "different"\\
72 | \end{split}\end{equation}
73 | $$
74 | 以两张图片作为输入,然后输出这两张图片的差异值,差异值越小越相似。如果差异值小于某个阈值 $\tau$($\tau$ 是一个超参数),就预测输入的是同一个人的两张图片;如果差异值大于阈值,就预测输入的是两个不同的人的照片,从而实现人脸验证。
75 |
76 | 将其应用于人脸识别任务,分别将要预测的图片及数据库中的任一张图片输入,用d函数两两比较,如果有输出一个比阈值小的数字,则预测的图片就是那个人的照片,若没有,则要预测的人不是数据库中的任一个人。
77 |
78 | 
79 |
80 | 在上面这个例子中,首先输入要识别的图片和数据库中第一张图片,输出一个很大的值,说明不是同一个人;接着输入要识别的图片和数据库中第二张图片,输出一个很小的值,很可能是同一个人;再分别输入要识别的图片和数据库中第三、四张图片,输出的值都很大,不是同一个人。因此,要识别的图片是第二个人的。若输出的值都很大,则要识别的人不是数据库里的任一个人。
81 |
82 | 如果要加入新成员,只需将其照片加入数据库中,系统依然能照常工作。
83 |
84 | #### 13.2.3 Few-Shot learning
85 |
86 | **Few-Shot learning**:小样本学习,用很少的样本去做分类或者回归。
87 |
88 | Few-Shot learning与传统的监督学习算法不同,它的目标不是让机器识别训练集中图片并且泛化到测试集,而是**让机器自己学会学习**。可以理解为用一个小数据集训练神经网络,学习的目的不是让神经网络知道每个类别是什么,而是让模型理解事物的异同,学会区分不同的事物。
89 |
90 | 
91 |
92 | 比如上面这张图片,左边两张图是同一种动物,右边两张是同一种动物,Few-Shot learning要做的就是通过对上面这四张图的学习判断下面这张图是属于哪一种动物。
93 |
94 | 
95 |
96 | Few-Shot learning 问题的关键是解决过拟合 (overfitting) 的问题,因为训练的样本太少了,训练出的模型可能在训练集上效果还行,但是在测试集上面会遭遇灾难性的崩塌。
97 |
98 | **解决方法:**
99 |
100 | 1. 数据增强和正则化:这一类方法想法很直接简单,既然训练数据不够那就增加训练样本,既然过拟合那就使用正则化技术。
101 | - 数据加强:最常见的例子就是有时对 Omniglot 数据集的预处理,会将图片旋转 90 、180 、270 度,这样就可以使样本数量变为原来的 4 倍。
102 | - 正则化:在训练的时候加入一个正则项,这个正则项的构建选择是关键。比如 《Few-shot Classification on Graphs with Structural Regularized GCNs》。该论文讨论 Graph 中节点分类的 few-shot 问题,常见的节点分类是使用 GCN 从节点的特征向量 feature 学习一个 embedding 然后用 embedding 来做分类,如果是 few-shot 问题,性能会大大下降(准确率大约从 70% 到了 40%),作者在训练的时候给损失函数加了一个正则项。作者将 feature 到 embedding 的过程看成编码器 encoder,然后额外加了几层网络作为 decoder,将 embedding 重构为 feature ,然后重构误差作为正则项(准确率从 40% 提升了 50%,大约 10 个百分点)。
103 |
104 | 2. Meta-learning(元学习):核心想法是先学习一个先验知识(prior),这个先验知识对解决 few-shot learning 问题特别有帮助。也就是说,先学习很多很多 task,然后再来解决新的在之前的学习中没有见过的 task 。
105 |
106 | > 参考:
107 | >
108 | > 1. https://blog.csdn.net/weixin_37589575/article/details/92801610
109 | > 2. https://zhuanlan.zhihu.com/p/142381922
110 |
111 | ### 13.3 Siamese网络
112 |
113 | Siamese网络架构是实现Similarity函数的一种方式。
114 |
115 | #### 13.3.1 Siamese网络架构
116 |
117 | **Siamese网络架构**:对于两个不同的输入,运行相同的卷积神经网络,然后比较它们输出的特征向量从而判断是否是属于同一类。
118 |
119 | 
120 |
121 | 如上图所示,首先将第一张输入图像$x^{(1)}$送入卷积神经网络,经过一系列的卷积、池化、全连接后输出一个特征向量,将这个特征向量称为$f(x^{(1)})$,看作是输入图像$x^{(1)}$的编码;然后将第二张输入图像$x^{(2)}$送入同样的神经网络,也得到一个特征向量,称为$f(x^{(2)})$,代表输入图像$x^{(2)}$的编码。我们相信这两个编码可以很好地代表两张输入图像,故定义d函数为两张图片编码之差的范数:
122 | $$
123 | d(x^{(1)}, x^{(2)})=||f(x^{(1)})-f(x^{(2)})||_2^2
124 | $$
125 |
126 | #### 13.3.2 如何训练Siamese网络
127 |
128 | 由于Siamese网络中两个卷积神经网络是一样的,所以在训练Siamese网络时只需要训练一个就好。
129 |
130 | 
131 |
132 | 更准确地说,神经网络的参数定义了一个编码函数$f(x^{(i)})$,如果给定输入图像$x^{(i)}$,会输出$x^{(i)}$的一个编码(特征向量)。训练网络要做的就是学习参数,使得如果两个图片$x^{(i)}$和$x^{(j)}$是同一个人,得到的两个编码的距离就小;如果$x^{(i)}$和$x^{(j)}$是不同的人,则它们之间的编码距离会比较大。如果改变这个网络所有层的参数,会得到不同的编码结果,要用反向传播来改变这些所有的参数以确保满足上面的条件。
133 |
134 | ### 13.4 Triplet损失
135 |
136 | #### 13.4.1 Triplet损失的定义
137 |
138 | **Triplet loss**:三元组损失,通常需要同时看三张图片:Anchor图片(A)、Positive图片(P,即正类,跟Anchor是同一个人)和Negative图片(N,即负类,跟Anchor不是同一个人)。其中,A和P为一对,是同一个人,所以希望它们编码的距离很接近;A和N为一对,不是同一个人,所以希望它们编码的距离远一点。公式如下:
139 | $$
140 | ||f(A)-f(P)||^2 \le ||f(A)-f(N)||^2
141 | $$
142 | 即:$d(A,P) \le d(A,N)$
143 |
144 | 把方程右边项移到左边:
145 | $$
146 | ||f(A)-f(P)||^2-||f(A)-f(N)||^2 \le 0
147 | $$
148 |
149 | 有两种情况满足这个表达式但没有用处:
150 |
151 | 1. 所有的编码会总是输出0,即$f(img)=0$,则 $0-0=0$。
152 | 2. 把所有的编码都设成相等的,即如果每个图片的编码和其他图片一样,这种情况还是得到 $0-0=0$。
153 |
154 | 为了阻止网络出现这两种情况,应该把“小于等于0”这个目标改为“小于0”,故将目标改为“$0-\alpha$”($\alpha$是一个超参数),由于我们更习惯使用“$+\ \alpha$”,所以将“$-\ \alpha$”这项移到左边,得到:
155 | $$
156 | ||f(A)-f(P)||^2-||f(A)-f(N)||^2 \ +\ \alpha \le 0
157 | $$
158 |
159 | 故第一个式子也变为:
160 | $$
161 | ||f(A)-f(P)||^2\ +\ \alpha \le ||f(A)-f(N)||^2
162 | $$
163 |
164 | 其中,$\alpha$也叫做间隔(margin),假设间隔设为0.2,为了满足条件,可以把d(A, N)调大或者把d(A, P)调小让间隔至少是0.2,这样就拉大了anchor与positive图片对和anchor与negative图片对之间的差距。例如,假设d(A, P)等于0.5,如果d(A, N)只比d(A, P)大一点点,为0.51,就不能满足条件,因为我们想让d(A, N)比d(A, P)大很多,至少是0.7或者更高。
165 |
166 | #### 13.4.2 Triplet损失函数
167 |
168 | 对于**一个三元组定义的损失函数**:
169 | $$
170 | L(A,P,N)=max(||f(A)-f(P)||^2-||f(A)-f(N)||^2 \ +\ \alpha,0)
171 | $$
172 | 若$||f(A)-f(P)||^2-||f(A)-f(N)||^2 \ +\ \alpha$ 小于0,那么损失函数就是0;若大于0,则损失函数等于$||f(A)-f(P)||^2-||f(A)-f(N)||^2 \ +\ \alpha$ ,是一个正的损失值。通过最小化损失函数,只要这个损失函数等于0,达到的效果就是使$||f(A)-f(P)||^2-||f(A)-f(N)||^2 \ +\ \alpha$小于或等于0,网络不会关心它的负值有多大。
173 |
174 | **整个网络的代价函数**是训练集中这些单个三元组损失的总和:
175 | $$
176 | J=\sum_{i=1}^mL(A^{(i)},P^{(i)},N^{(i)})
177 | $$
178 | 假设有一个10000张图片的训练集,里面是1000个不同的人的照片,平均每人10张照片,要做的是取这10000张图片生成三元组,然后对代价函数用梯度下降从而训练学习算法,训练完成后就可以应用到一次学习问题中。
179 |
180 | 为了定义三元组的数据集,需要成对的A和P即同一个人的成对的图片,
181 |
182 | #### 13.4.3 如何选择三元组组成训练集
183 |
184 | 倘若从数据集中随机地选择A, P, N构成三元组,遵循A和P是同一个人而A和N是不同的人这一原则,则不是同一个人的概率比是同一个人的概率大很多,即d(A, N)比d(A, P)大$\alpha$ 的概率很大,目标很容易就达到,网络很轻松就能训练好,梯度算法不会有什么效果。
185 |
186 | 所以应该**尽可能选择难训练的三元组A P N即所有的三元组d(A, P)都很接近d(A, N)**,这样,学习算法就会竭尽全力使d(A, N)变大或者使d(A, P)变小使得二者之间至少间隔$\alpha$,并且选择这样的三元组训练难度大,梯度下降法才能发挥作用,从而增加学习算法的计算效率。
187 |
188 | 
189 |
190 | ### 13.5 面部验证与二分类
191 |
192 | #### 13.5.1 将人脸识别变成二分类问题
193 |
194 | Triplet loss是个学习人脸识别卷积网络参数的好方法,此外还有其他学习参数的方法,如将人脸识别当成一个二分类问题:
195 |
196 | 
197 |
198 | 选取一对神经网络,选用 Siamese 网络并使其同时计算这些特征向量,然后将其输入到逻辑回归单元进行预测,若是相同的人,那么输出是 1,若是不同的人,输出是 0。这就把人脸识别问题转换为一个二分类问题,训练这种系统时可以替换 Triplet loss的方法。
199 |
200 | #### 13.5.2 逻辑回归单元的处理
201 |
202 | 最后通过将sigmoid等函数应用到某些特征上来处理逻辑回归单元:
203 | $$
204 | \hat{y}=\sigma\left(\sum_{k=1}^{128} w_{i}\left|f\left(x^{(i)}\right)_{k}-f\left(x^{(j)}\right)_{k}\right|+b\right)
205 | $$
206 | 其中,符号$f\left(x^{(i)}\right)$代表图片$x^{(i)}$的编码,下标 $k$ 代表选择这个向量中的第$k$个元素,$\left|f\left(x^{(i)}\right)_{k}-f\left(x^{(j)}\right)_{k}\right|$对这两个编码取元素差的绝对值。就像普通的逻辑回归一样,把这128个元素当作特征,然后把他们放入逻辑回归中,最后的逻辑回归可以增加参数$w_{i}$和$b$。在这128个单元上训练合适的权重,用来预测两张图片是否是一个人。
207 |
208 | 还可以用$\chi^{2}$公式$\frac{\left(f\left(x^{(i)}\right)_{k}-f\left(x^{(j)}\right)_{k}\right)^{2}}{f\left(x^{(i)}\right)_{k}+f\left(x^{(j)}\right)_{k}}$,也被称作$\chi$平方相似度,来代替上式中$\left|f\left(x^{(i)}\right)_{k}-f\left(x^{(j)}\right)_{k}\right|$的计算。
209 |
210 | #### 13.5.3 预先计算思想
211 |
212 | 在上面的学习公式中,输入是一对图片($x^{(i)}$和$x^{(j)}$),输出$y$是0或者1取决于输入是相似图片还是非相似图片。与之前类似,训练一个Siamese网络,即两个神经网络拥有的参数是相同的,两组参数是绑定的。
213 |
214 | **预先计算好数据库中图片的编码可以节省大量的计算,显著提高部署效果。**
215 |
216 | 如你有一张新图片$x^{(i)}$,当员工走进门时,希望门可以自动为他打开,在数据库中的图片$x^{(j)}$,不需要每次都计算特征向量,可以提前计算好,那么当一个新员工走近时,可以使用上方的卷积网络来计算编码,然后将其和预先计算好的编码进行比较,输出预测值 $\hat{y}$。
217 |
218 | **总结**:把人脸验证当作一个监督学习,创建一个只有成对图片的训练集,不是三个一组,而是成对的图片,目标标签是1表示这对图片是一个人,目标标签是0表示图片中是不同的人。利用不同的成对图片,使用反向传播算法去训练神经网络,训练Siamese神经网络。
219 |
220 | ### 13.6 什么是神经风格迁移
221 |
222 | #### 13.6.1 神经风格迁移的定义
223 |
224 | 
225 |
226 | 比如这张照片,你想利用右边照片的风格来重新创造原本的照片,右边的是梵高的星空,神经风格迁移可以帮你生成下面这张照片。使用$C$来表示内容图像,$S$表示风格图像,$G$表示生成的图像。
227 |
228 | #### 13.6.2 神经风格迁移的常用方法
229 |
230 | 
231 |
232 | [参考博客]: https://www.jiqizhixin.com/articles/2018-05-15-5 "综述:图像风格化算法最全盘点 | 内附大量扩展应用"
233 |
234 | ### 13.7 深度卷积网络在学什么
235 |
236 | #### 13.7.1 可视化分析卷积神经网络的浅层
237 |
238 | 假如训练了一个卷积神经网络,是一个Alexnet,轻量级网络,希望将看到不同层之间隐藏单元的计算结果。
239 |
240 | 
241 |
242 | 你可以这样做,从第一层的隐藏单元开始,假设你遍历了训练集,然后找到那些使得单元激活最大化的一些图片或是图片块。换句话说,将你的训练集经过神经网络,然后弄明白哪一张图片最大限度地激活特定的单元。注意在第一层的隐藏单元,只能看到小部分卷积神经,如果要画出来哪些激活了激活单元,只有一小块图片块是有意义的,因为这就是特定单元所能看到的全部。你选择一个隐藏单元,发现有9个图片最大化了单元激活,你可能找到这样的9个图片块(左上九宫格),似乎是图片浅层区域显示了隐藏单元所看到的,找到了像这样的边缘或者线(上面的蓝格子),这就是那9个最大化地激活了隐藏单元激活项的图片块。
243 |
244 | 
245 |
246 | 然后你可以选一个另一个第一层的隐藏单元,重复刚才的步骤,这是另一个隐藏单元,似乎第二个由这9个图片块(上中九宫格)组成。看来这个隐藏单元在输入区域,寻找这样的线条(下面的蓝格子),我们也称之为接受域。
247 |
248 | 对其他隐藏单元也进行处理,会发现其他隐藏单元趋向于激活类似于这样的图片。右上九宫格似乎对垂直明亮边缘且左边是绿色的图片块感兴趣,左中九宫格的隐藏单元倾向于橘色图片块。
249 |
250 | 以此类推,这是9个不同的代表性神经元,每一个不同的图片块都最大化地激活了。你可以这样理解,第一层的隐藏单元通常会找一些简单的特征,比如说边缘或者颜色阴影。
251 |
252 | #### 13.7.2 可视化分析卷积神经网络的深层
253 |
254 | 在深层部分,一个隐藏单元会看到一张图片更大的部分,在极端的情况下,可以假设每一个像素都会影响到神经网络更深层的输出,靠后的隐藏单元可以看到更大的图片块。
255 |
256 | 
257 |
258 | 上图中Layer 1是之前第一层得到的,Layer 2是可视化的第2层中最大程度激活的9个隐藏单元。在更深的层上,可以重复这个过程。
259 |
260 | 放大第一层,这是第一个被高度激活的单元,你能在输入图片的区域看到所提取的这些边缘或颜色阴影。
261 |
262 | 
263 |
264 | 放大第二层的可视化图像。第二层似乎检测到更复杂的形状和模式,比如说中上九宫格这一隐藏单元会找到有很多垂线的垂直图案,右中九宫格的隐藏单元似乎在左侧有圆形图案时会被高度激活,左下九宫格所寻找的特征是很细的垂线,以此类推,第二层检测的特征变得更加复杂。
265 |
266 | 
267 |
268 | 放大第三层,这些东西激活了第三层。中心九宫格这一隐藏单元似乎对图像左下角的圆形很敏感,所以检测到很多车。右下九宫格似乎开始检测到人类,左上九宫格似乎检测特定的图案,比如蜂窝形状或者方形这样类似规律的图案。有些很难看出来,需要手动弄明白检测到什么,但是第三层明显,检测到更复杂的模式。
269 |
270 | 
271 |
272 |
273 |
274 | 这是第四层,检测到的模式和特征更加复杂,左上九宫格学习成了一个狗的检测器,但是这些狗看起来都很类似。右中九宫格似乎检测到鸟的脚等等。
275 |
276 |
206 |
207 | 所以这个算法的优点在于神经网络可以输出精确的边界框,所以测试的时候,你做的是喂入输入图像$x$,然后跑正向传播,直到你得到这个输出$y$。然后对于这里3×3位置对应的9个输出,就可以读出1或0。如果那里有个对象,就可以读出那个对象是什么,还有格子中这个对象的边界框是什么。
208 |
209 | 只要每个格子中对象数目没有超过1个,这个算法应该是没问题的。一个格子中存在多个对象的问题,之后再讨论。这里用的是比较小的3×3网格,实践中你可能会使用更精细的19×19网格,所以输出就是19×19×8。这样的网格精细得多,那么多个对象分配到同一个格子的概率就小得多。
210 |
211 | 把对象分配到一个格子的过程是,你观察对象的中点,然后将这个对象分配到其中点所在的格子,所以即使对象可以横跨多个格子,也只会被分配到9个格子其中之一,就是3×3网络的其中一个格子,或者19×19网络的其中一个格子。在19×19网格中,两个对象的中点处于同一个格子的概率就会更低。
212 |
213 | YOLO算法有一个好处就是,它是一个卷积实现,共享了很多卷积计算,所以实际上它的运行速度非常快,可以达到实时识别。
214 |
215 | **编码边界框**
216 |
217 | 
218 |
219 | 对于这个方框(中右侧),我们约定左上这个点是(0,0),然后右下这个点是(1,1);
220 |
221 | 要指定橙色中点的位置,$b_{x}$大概是0.4,因为它的位置大概是水平长度的0.4,$b_{y}$大概是0.3;
222 |
223 | 边界框的高度用格子总体宽度的比例表示,所以这个红框的宽度可能是蓝线(图右下角蓝线)的90%,所以$b_h$是0.9,它的高度也许是格子总体高度的一半,这样的话$b_{w}$就是0.5。
224 |
225 | 换句话说,$b_{x}$、$b_{y}$、$b_{h}$和$b_{w}$单位是相对于格子尺寸的比例,所以$b_{x}$和$b_{y}$必须在0和1之间,因为从定义上看,橙色点位于对象分配到格子的范围内,如果它不在0和1之间,如果它在方块外,那么这个对象就应该分配到另一个格子上。但是$b_{h}$和$b_{w}$可能会大于1,特别是如果有一辆汽车的边界框是这样的(左下红框),那么边界框的宽度和高度有可能大于1。
226 |
227 | 指定边界框的方式有很多,但这种约定是比较合理的,还有其他更复杂的参数化方式,涉及到sigmoid函数,确保这个值($b_{x}$和$b_{y}$)介于0和1之间,然后使用指数参数化来确保$b_{h}$和$b_{w}$都是非负数。还有其他更高级的参数化方式,可能效果要更好一点,但这里讲的办法应该是管用的。
228 |
229 | #### 12.5.2 其他指定边界框的算法
230 |
231 | **1. SSD**:
232 |
233 | SSD(Single-Shot MultiBox Detector),使用 VGG19 网络作为特征提取器(和 Faster R-CNN 中使用的 CNN 一样)的单次检测器。我们在该网络之后添加自定义卷积层(蓝色),并使用卷积核(绿色)执行预测。
234 |
235 | 
236 |
237 | 然而,卷积层降低了空间维度和分辨率。因此上述模型仅可以检测较大的目标。为了解决该问题,我们从多个特征图上执行独立的目标检测。
238 |
239 | 
240 |
241 | 以下是特征图图示。
242 |
243 | 
244 |
245 | SSD 使用卷积网络中较深的层来检测目标。如果我们按接近真实的比例重绘上图,我们会发现图像的空间分辨率已经被显著降低,且可能已无法定位在低分辨率中难以检测的小目标。如果出现了这样的问题,我们需要增加输入图像的分辨率。
246 |
247 | 
248 |
249 |
250 |
251 |
252 | 参考博客:https://www.jianshu.com/p/468e08f739bd
253 |
254 | **2. FPN**:
255 |
256 | 使用不同尺寸特征图进行预测的网络称为特征金字塔网络(FPN),是一种旨在提高准确率和速度的特征提取器。数据流如下:
257 |
258 | 
259 |
260 | FPN 由自下而上和自上而下路径组成。其中自下而上的路径是用于特征提取的常用卷积网络。空间分辨率自下而上地下降。当检测到更高层的结构,每层的语义值增加。
261 |
262 | 
263 |
264 | SSD 通过多个特征图完成检测。但是,最底层不会被选择执行目标检测。它们的分辨率高但是语义值不够,导致速度显著下降而不能被使用。SSD 只使用较上层执行目标检测,因此对于小的物体的检测性能较差。
265 |
266 | 
267 |
268 | FPN 提供了一条自上而下的路径,从语义丰富的层利用上采样构建高分辨率的层。
269 |
270 | 
271 |
272 | 虽然该重建层的语义较强,但在经过所有的上采样和下采样之后,目标的位置不精确。在重建层和相应的特征图之间添加横向连接可以使位置侦测更加准确。
273 |
274 | 
275 |
276 | **3. RetianNet**:
277 |
278 | RetianNet是基于 ResNet、FPN以及利用 Focal loss 构建的 。
279 |
280 | 
281 |
282 | RetinaNet
283 |
284 | **4. Focal Loss**
285 |
286 | 类别不平衡会损害性能。SSD 在训练期间重新采样目标类和背景类的比率,这样它就不会被图像背景淹没。Focal loss(FL)采用另一种方法来减少训练良好的类的损失。因此,只要该模型能够很好地检测背景,就可以减少其损失并重新增强对目标类的训练。我们从交叉熵损失 (Cross Entroy Loss)开始,并添加一个权重来降低高可信度类的交叉熵。
287 |
288 | 
289 |
290 | 例如,令 γ = 0.5, 经良好分类的样本的 Focal Loss 趋近于 0。
291 |
292 | 
293 |
294 | ### 12.6 交并比
295 |
296 | #### 12.6.1 交并比函数的作用
297 |
298 | 交并比(IoU, Intersection over Union)函数衡量了两个边界框重叠的相对大小,用来评价对象检测算法是否运行良好,即检测对象定位是否准确。
299 |
300 | #### 12.6.2 交并比函数的实现
301 |
302 | 
303 |
304 | 假设识别的对象的实际边界框如上图中红框所示,用对象检测算法得到的边界框如紫框所示,这个结果是好是坏呢?
305 |
306 | 交并比函数做的是计算**两个边界框交集和并集之比**,交集部分如橙色阴影所示,并集部分如绿色阴影所示,如果预测边框和实际边框完美重叠,交集等于并集,$IoU = 1$,一般约定,在计算机检测任务中,若 $IoU \geq 0.5$,则说明预测的边界框是正确的,如果希望更严格,可以把IoU的阈值定得更高,IoU越高,边界框越精确。
307 |
308 | ### 12.7 非极大值抑制
309 |
310 | #### 12.7.1 非极大值抑制的作用
311 |
312 | 到目前为止我们学到的对象检测中的一个问题是,算法可能对同一个对象做出多次检测而不是一次,非极大值抑制法可以**确保算法对每个对象只检测一次**。
313 |
314 | #### 12.7.2 非极大值抑制的实现
315 |
316 | 非极大值抑制(Non-max suppression):只输出概率最大的分类结果,抑制很接近但不是最大的其他预测结果。
317 |
318 | 
319 |
320 | 假设要在这张图里检测行人和汽车,我们可能会在上面放个19×19的网格,理论上每辆汽车只有一个中点,应该只分配到中点所在的格子里,实践中在跑对象分类和定位算法时,对每个格子都跑一次,橙色和绿色方框的那些格子可能会想,这辆车的中点应该在其格子内部,觉得它们格子内有车的概率很高,而不是19×19=361个格子中仅有两个格子会报告它们检测出一个对象,所以最后可能会对同一个对象做出多次检测。
321 |
322 | 非极大值抑制做的就是清理这些检测结果,对每个对象只检测一次,而不是每个对象都触发多次检测。
323 |
324 | **非极大值抑制的实现步骤:**
325 |
326 | 
327 |
328 | 1. 去掉所有预测边界框中 $p_c \leq 0.6$ 的边界框(这里的0.6是阈值,可以自己设定),抛弃了所有概率比较低的输出边界框,则剩下的边界框中存在对象的概率至少有0.6。
329 | 2. 对于剩下的边界框,首先看看每次报告中每个检测结果相关的概率 $p_c$,找到**概率最大**的那个,这个例子中是0.9,认为这是最可靠的检测,用高亮标记,就说在这里找到了一辆车。
330 | 3. 接着,非极大值抑制就会逐一审视剩下的矩形,所有和这个最大的边界框有很高交并比、高度重叠的其他边界框的输出就会被抑制,所以这两个 $p_c$ 分别为0.6和0.7的矩形和最大边界框(淡蓝色矩形)重叠程度很高,会被抑制、变暗。
331 |
332 | 左边那辆车也同理,找到 $p_c$ 最大的一个是0.8,认为这里检测出一辆车,用高亮显示,而其他IoU值很高的矩形会被抑制而变暗。直接抛弃变暗的矩形,只剩下高亮显示的,就是最后得到的两个预测结果。
333 |
334 | 上面介绍的只是算法检测单个对象的情况,若想同时检测三种对象,比如行人、汽车和摩托,则需要独立进行三次非极大值抑制,对每个输出类别都做一次。
335 |
336 | ### 12.8 Anchor Boxes
337 |
338 | #### 12.8.1 为什么要用Anchor Boxes?
339 |
340 | 之前的算法只能在一个格子中检测出一个对象,Anchor Boxes可以**一个格子检测出多个对象**。如下图所示,使用3x3的网格,行人和汽车的中心几乎在同一个网格,这时就需要用到Anchor Boxes。
341 |
342 | 
343 |
344 | #### 12.8.2 思路
345 |
346 | 1. 预先定义几个不同形状的anchor box,把预测结果和这些anchor box关联起来。本例假设两个anchor box,对应行人和汽车。
347 |
348 | 
349 |
350 | 2. 定义类别标签,将原来的向量$$\left[\begin{array}{llllllll}
351 | p_{c} & b_{x} & b_{y} & b_{h} & b_{w} & c_{1} & c_{2} & c_{3}
352 | \end{array}\right]^{T}$$重复两次$$\left.\begin{array}{llllllllllllllll}
353 | y=\left[p_{c}\right. & b_{x} & b_{y} & b_{h} & b_{w} & c_{1} & c_{2} & c_{3} & p_{c} & b_{x} & b_{y} & b_{h} & b_{w} & c_{1} & c_{2} & c_{3}
354 | \end{array}\right]^{T}$$。其中,前面的8个参数和anchor box 1相关联,后面的8个参数和anchor box 2相关联。
355 |
356 | 
357 |
358 | 3. 行人一般符合anchor box1形状,所以用anchor box1来预测行人会达到很好的效果,这么编码 $p_c$ = 1,代表有个行人,用 $b_x, b_y ,b_h$ 和 $b_w$ 来编码包住行人的边界框,用$c_1, c_2 ,c_3$($c_1$ = 1,$c_2$ = 0,$c_3$ = 0)来说明这个对象是个行人。 汽车一般符合anchor box2形状,采用相同的编码方法,定义对象是汽车和边界框等,所有参数都和检测汽车相关( $p_c$ = 1, $b_x, b_y ,b_h$, $b_w$, $c_1$ = 0,$c_2$ = 1,$c_3$ = 0)。
359 |
360 | 4. 当两个anchor boxes对相同位置做出判别时,以交并比作为取舍指标。选择IoU最高的那个,用这个anchor box来进行预测。输出y的维度是$n \times n \times m \times c$(n为图片分成$n \times n$份,$m$为anchor box数量,$c$为class类别数)
361 |
362 | #### 12.8.3 怎么选择anchor box?
363 |
364 | 1. 一般手工指定anchor box形状,根据要检测的对象,指定有针对性的anchor box,可选择5-10个anchor box,使其尽可能覆盖到不同形状。
365 | 2. 使用K-means聚类算法获得anchor box,选择最具有代表性的一组anchor box。
366 |
367 | ### 12.9 YOLO 算法
368 |
369 | 目标检测架构分为两种,一种是two-stage,一种是one-stage。 two-stage 有region proposal (选取候选区域)过程,网络会根据候选区域生成位置和类别,而 one-stage 直接从图片生成位置和类别。
370 |
371 | YOLO 是一种 one-stage 方法,即 You Only Look Once 的缩写,意思是神经网络只需要看一次图片,就能输出结果。
372 |
373 |
374 | #### 12.9.1 YOLO算法的实现
375 |
376 | - 构造训练集:假设检测三种对象,行人,汽车和摩托。
377 | 输入图像,神经网络的输出尺寸是3x3x2x8(3x3的网格,2个anchor box,8个参数)。遍历9个格子,构造训练集,然后构成对应的目标向量y,判断和anchor box 有关的 $p_c$ 和边界框,指定正确类别。
378 |
379 | 
380 |
381 | - 如何预测:输入图像,神经网络的输出尺寸是3x3x2x8,对于9个格子,每个都有对应的向量,如上图所示。
382 | 对于1号蓝格,检测不到任何对象,所以2个anchor box的 $p_c$ = 0。剩下的是一些数字,多多少少都是噪音,但这些数字基本上会被忽略,因为神经网络告诉表示那里没有任何东西。(输出 y 如编号3所示)。
383 | 对于2号绿格,里面有汽车。对于边界框1(anchor box 1)来说 $p_c$ = 0,表示此格子中无行人。然后就是一组数字噪音,此格子中无行人。anchor box 2对应汽车,此格子中有车,因此希望数字可以对车子指定一个相当准确的边界框,即($$\left.p_{c}=1, b_{x}, b_{y}, b_{h}, b_{w}, c_{1}=0, c_{2}=1, c_{3}=0\right)$$,这就是神经网络做出预测的过程。
384 | - 运行非极大值抑制:看看一张新的测试图片,对于两个anchor box,那么对于9个格子中任何一个都会有两个预测的边界框。
385 | 针对每个框,抛弃概率低的预测,去掉那些连神经网络都说这里很可能什么都没有的边界框。如果希望检测行人、车子和摩托三个对象检测类别,那么需要对每个类别单独运行非极大值抑制,处理预测结果即此类别的边界框。
386 |
387 | 
388 |
389 | - 最后,输出位置和类别信息。
390 |
391 | #### 12.9.2 YOLO v1、v2、v3和v4
392 |
393 | YOLO 一共发布了四个版本,其中 YOLOv1 奠定了整个系列的基础,后面的系列就是在第一版基础上的改进,只为提升性能。
394 |
395 | - YOLOv2
396 | 提出了 ImageNet 和 COCO 数据集结合的联合训练方法,使算法可以在检测数据集和分类数据集上训练目标检测器。用检测数据集的数据学习物体的准确位置,用分类数据集的数据来增加分类的类别量、提升健壮性。
397 | - YOLOv3
398 | YOLOv3 的提出不是为了解决什么问题,将模型复杂了不少,可以通过改变模型结构的大小来权衡速度与精度。
399 | - YOLOv4
400 | YOLOv4的改进总结了几乎所有的检测技巧,又提出一点儿技巧,然后经过筛选,排列组合,挨个实验(ablation study)哪些方法有效,经过大量实验选出的性能最好的组合。
401 | 发展历程:
402 | 
403 |
404 | ### 12.10 RPN网络
405 |
406 | RPN:Region Proposal Network
407 |
408 | #### 12.10.1 Region with CNN(R-CNN)
409 |
410 | 意思基于候选区域(Region Proposal)的卷积网络,不再针对每个滑动窗口跑检测算法,而是使用某种算法求出候选区域,然后对每个候选区域跑一下分类器,每个区域会输出一个标签和一个边界框。这样就只是选择一些有意义的窗口,在少数窗口上运行卷积网络分类器,以节省时间。
411 |
412 | - 选出的候选区域方法:图像分割算法
413 |
414 | 
415 |
416 | 如上图所示。分割色块后,选择其对应的一个边界框,然后在色块上跑分类器,这样的处理比滑动窗口法处理的窗口少的多,可以减少卷积网络分类器运行时间,而不必在所有位置运行一遍分类器。
417 |
418 | 另外,说明一下,R-CNN算法不会直接信任输入的边界框,它也会输出一个边界框$$b_{x},\quad b_{y},\quad b_{h},\quad b_{w}$$,这样得到的边界框比较精确,比单纯使用图像分割算法给出的色块边界要好。
419 |
420 |
421 | #### 12.10.2 具体步骤
422 |
423 | 
424 |
425 | 1. 输入图像;运行图像分割算法,利用selective search对图像生成1K~2K的候选区域(region proposal);
426 | 2. 将每个候选区域缩放(warp)成227×227的大小并输入到CNN,将CNN的全连接层fc7的输出作为特征;
427 | 3. 对CNN的fc7层的输出特征输入到SVM进行分类;如果有十个类别,那么每个region proposal要经过10个SVM,得到预测的类别。
428 | 4. 修正:对于SVM分好类的Region Proposal做边框回归,用Bounding box回归值校正原来的候选窗口,生成预测窗口坐标。
429 |
430 | #### 12.10.3 缺点和改进
431 |
432 | R-CNN训练耗时,占用磁盘空间大,测试速度慢,每个候选区域需要运行整个前向CNN计算;因此提出了其它改进算法。
433 |
434 | 
435 |
436 | - Fast R-CNN:利用卷积实现了滑动窗口。相比于R-CNN,Fast R-CNN不再对每一个候选区域进行CNN特征提取,而是先将整张图片归一化后输入CNN网络进行特征提取,之后候选区域在特征图上进行截取,显著提升了R-CNN的速度。但是其缺点是得到候选区域的聚类步骤仍然非常缓慢。
437 |
438 | - Faster R-CNN:加入RPN网络,将特征提取、候选区域提取、bounding box regression、分类都整合在了一个网络中,使得综合性能有较大提高,在检测速度方面尤为明显。(仍比YOLO慢)
439 |
440 | - Gaussian Faster R-CNN主要有以下两个创新点:
441 | 1. 卷积的过程其实就是一个特征提取的过程,所以在预处理之后移除了全连接这个操作,简化了网络结构,以准确率换速度。
442 | 2. 假设在多次卷积之后,整个特征图是一个平稳的随机序列,符合高斯分布,则可以采用 $3\sigma$ 原理对树进行裁剪,因为四周的像素对分类任务来说无关紧要,但是完全压缩和分类这些无关紧要的像素会花费大量的CPU时间。最后用随机森林代替B-P神经网络,将时间复杂度由 $O(N)$ 降到 $O(log2N)$。
443 |
444 | ### 12.11 目标检测算法的评价指标
445 |
446 | #### 12.11.1 准确度指标——平均准确度均值mAP
447 |
448 | - **什么是TP、TN、FP、FN?**
449 |
450 | TP、TN、FP、FN即true positive, true negative, false positive, false negative的缩写,positive和negative表示的是预测得到的结果,预测为正类则为positive,预测为负类则为negative; true和false则表示预测的结果和真实结果是否相同,相同则是true,不同则为false,如下图:
451 |
452 | 
453 |
454 | 举个例子,假设现在有这样一个测试集,其中的图片只由大雁和飞机两种图片组成,如下图所示:
455 |
456 | 
457 |
458 | 假设分类系统最终的目的是取出测试集中所有飞机的图片,则 TP、TN、FP、FN的具体定义分别是:
459 |
460 | **True positives :** 飞机的图片被正确的识别成了飞机。
461 | **True negatives:** 大雁的图片没有被识别出来,系统正确地认为它们是大雁。
462 | **False positives:** 大雁的图片被错误地识别成了飞机。
463 | **False negatives:** 飞机的图片没有被识别出来,系统错误地认为它们是大雁。
464 |
465 | - **Precision 与 Recall**
466 |
467 | **Precision**(精确度、查准率)指的是模型判断该图片为正类且该图片也的确是正类的概率,即在模型判断为正类的图片中,True positives所占的比率,**衡量的是一个分类器分出来的正类的确是正类的概率**。
468 | $$
469 | Precision=\frac{TP}{TP+FP}
470 | $$
471 | 光是精确度还不能衡量分类器的好坏程度,比如50个正样本和50个负样本,如果分类器把49个正样本和50个负样本都分为负样本,剩下一个正样本分为正样本,这样精确度也是100%,所以还需要召回率来衡量。
472 |
473 | **Recall**(召回率、查全率)指的是测试集的所有正样本比例中,被模型正确识别为正样本的比例,即模型判断为正类且实际的确是正类的图像数量/真实类别是正类的图像数量,**衡量的是一个分类器能把所有的正类都找出来的能力**。
474 | $$
475 | Recall=\frac {TP}{TP+FN}
476 | $$
477 | 在上面所举的例子中,假设识别出了四个结果,如下图所示:
478 |
479 | 
480 |
481 | 其中,在识别出来的四张照片中:
482 |
483 | **True positives :** 有三个,画绿色框的飞机,即 $TP=3$。
484 |
485 | **False positives:** 有一个,画红色框的大雁,即 $FP=1$。
486 |
487 | 没被识别出来的六张图片中:
488 | **True negatives :** 有四个,这四个大雁的图片,系统正确地没有把它们识别成飞机,即 $TN=4$。
489 | **False negatives:** 有两个,两个飞机没有被识别出来,系统错误地认为它们是大雁,即 $FN=2$。
490 |
491 | 故 $Precision=\frac {TP}{TP+FP}=\frac {3}{3+1}=0.75$ ,意味着在识别出来的结果中,飞机的图片占75%;$Recall=\frac {TP}{TP+FN}=\frac{3}{3+2}=0.6$,意味着在所有的飞机图片中,60%的飞机图片被正确识别为飞机。
492 |
493 | - **调整阈值**
494 |
495 | 可以通过调整阈值来选择让模型识别出多少图片,进而改变Precision或Recall的值。在某种阈值的前提下(蓝色虚线),模型识别出了四张图片,如下图所示:
496 | 
497 |
498 | 分类系统认为大于阈值(蓝色虚线之上)的四个图片更像飞机。
499 |
500 | 我们可以通过改变阈值(可以看作上下移动蓝色虚线)来选择让系统识别出多少张图片,从而改变Precision或Recall的值。比如,把蓝色虚线移到第一张图片下面,也就是说让系统只识别出最上面的那张飞机图片,那么Precision的值就是100%,而Recall的值是20%;如果把蓝色虚线放到第二张图片下面,也就是说让系统只识别出最上面的前两张图片,那么Precision的值还是100%,而Recall的值则增长到40%。下图为不同阈值条件下,Precision与Recall的变化情况:
501 | 
502 |
503 | - **Precision-Recall曲线**
504 |
505 | Precision-Recall曲线(P-R曲线)是以Precision和Recall作为纵、横轴坐标的二维曲线,通过选取不同阈值时对应的精确度和召回率画出,如下图所示。
506 |
507 | 
508 |
509 | 总体趋势是,精确度越高,召回率越低,当召回率达到1时,对应概率分数最低的正样本,这个时候正样本数量除以所有大于等于该阈值的样本数量就是最低的精确度。上图所示的分类器在不损失精度的条件下能达到40%的Recall,而当Recall达到100%时,Precision降到50%。
510 |
511 | Precision-Recall曲线可以用来显示分类器在Precision和Recall之间的权衡,从而评估分类器的性能。如果一个分类器的性能较好,那么它应该有如下的表现:被识别出的图片中飞机所占的比重比较大,并且在识别出大雁之间,尽可能多地正确识别出飞机,也就是让Recall值增长的同时保持Precision的值在一个很高的水平。而性能较差的分类器可能会损失很多Precision值才能换来Recall值的提高。
512 |
513 | - **平均准确度AP**
514 |
515 | AP:Average-Precision,平均准确度,综合考量了Precision和Recall的影响,反映了模型对某个类别识别的好坏。
516 |
517 | P-R曲线围起来的面积就是AP值,通常来说一个分类器越好,AP值越高。
518 |
519 | - **平均准确度均值mAP**
520 |
521 | mAP:mean Average-Precision,平均精确度均值,即所有类别AP的平均值,衡量的是在所有类别上的平均好坏程度。
522 |
523 | mAP的取值范围是[0,1],越大越好。
524 |
525 | - 为什么可以使用mAP来评价目标检测的效果?
526 |
527 | 目标检测的效果取决于预测框的位置和类别是否准确,从mAP的计算过程中可以看出通过计算预测框和真实框的IoU来判断预测框是否准确预测到了位置信息,同时精确度和召回率指标的引用可以评价预测框的类别是否准确,因此mAP是目前目标检测领域非常常用的评价指标。
528 |
529 | > 参考文献:
530 | >
531 | > 1. https://blog.csdn.net/syoung9029/article/details/56276567
532 | >
533 | > 2. https://www.cnblogs.com/wanghui-garcia/p/11084833.html
534 | > 3. https://blog.csdn.net/weixin_43423892/article/details/106643649
535 |
536 | #### 12.11.2 速度指标——FPS
537 |
538 | 目标检测技术的很多实际应用在准确度和速度上都有很高的要求,如果不计速度性能指标,只注重准确度表现的突破,其代价是更高的计算复杂度和更多内存需求。只有速度快,才能实现实时检测,这对一些应用场景极其重要。
539 |
540 | FPS:Frame Per Second,每秒帧率,即每秒内可以处理的图片数量。当然要对比FPS,需要在同一硬件上进行。
541 |
542 | 另外也可以使用处理一张图片所需时间来评估检测速度,时间越短,速度越快。
543 |
544 | > 参考:
545 | >
546 | > 1. https://zhuanlan.zhihu.com/p/70306015
547 | > 2. https://blog.csdn.net/qq_29893385/article/details/81213377
548 |
549 | #### 12.11.3 模型大小
550 |
551 | 自 2012 年 AlexNet 以来,卷积神经网络(简称 CNN)在图像分类、图像分割、目标检测等领域获得广泛应用。随着性能要求越来越高,AlexNet 已经无法满足大家的需求,于是乎各路大牛纷纷提出性能更优越的 CNN 网络,如 VGG、GoogLeNet、ResNet、DenseNet 等。由于神经网络的性质,为了获得更好的性能,网络层数不断增加,从 7 层 AlexNet 到 16 层 VGG,再从 16 层 VGG 到 GoogLeNet 的 22 层,再到 152 层 ResNet,更有上千层的 ResNet 和 DenseNet。虽然网络性能得到了提高,但随之而来的就是效率问题。
552 |
553 | 效率问题主要是**模型的存储问题和模型进行预测的速度问题**(以下简称速度问题)
554 |
555 | - 第一,存储问题。数百层网络有着大量的权值参数,保存大量权值参数对设备的内存要求很高;
556 | - 第二,速度问题。在实际应用中,往往是毫秒级别,为了达到实际应用标准,要么提高处理器性能(看英特尔的提高速度就知道了,这点暂时不指望),要么就减少计算量。
557 |
558 | 只有解决 CNN 效率问题,才能让 CNN 走出实验室,更广泛的应用于移动端。对于效率问题,通常的方法是进行**模型压缩**(Model Compression),即在已经训练好的模型上进行压缩,使得网络携带更少的网络参数,从而解决内存问题,同时可以解决速度问题。
559 |
560 | 相比于在已经训练好的模型上进行处理,轻量化模型设计则是另辟蹊径。**轻量化模型设计**主要思想在于设计更高效的网络计算方式(主要针对**卷积**方式),从而使网络参数减少的同时,不损失网络性能。近年提出的四个轻量化模型分别是:SqueezeNet、MobileNet、ShuffleNet、Xception,有兴趣的可以参考以下博客或查找论文以了解。
561 |
562 | > 参考:https://blog.csdn.net/u012426298/article/details/80817788
--------------------------------------------------------------------------------
/13 特殊应用 人脸识别和神经风格转换.md:
--------------------------------------------------------------------------------
1 | ## 13 特殊应用:人脸识别和神经风格转换
2 |
3 | ### 13.1 什么是人脸识别?
4 |
5 | #### 13.1.1 人脸验证 vs 人脸识别
6 |
7 | **人脸验证**(face verification):也被称为 “1对1” 问题。
8 |
9 | - 输入:一张图片以及某人的ID或名字
10 | - 输出:系统验证输入图片是否是这个人。
11 |
12 | **人脸识别**(face recognition):“1对K” 问题。
13 |
14 | - 拥有一个包含 $K$ 人信息的数据库
15 | - 输入:一张图片
16 | - 输出:若输入图片符合 $K$ 人中任意一个人的图像,输出这个人的ID,否则,输出"not recognized"。
17 |
18 | **人脸验证与人脸识别的关系:**
19 |
20 | 人脸识别比人脸验证要求更高。假设有一个验证系统准确率是99%,看起来这个验证系统性能不错,但如果应用到有100个人的数据库的人脸识别系统中,每个人的犯错概率是1%,整体犯错概率就放大了100倍,所以要想得到一个可接受的识别误差,就要构造一个准确率为99%甚至更高的验证系统才能得到很好的识别效果。也就是说,人脸验证系统的准确率要足够高才能应用到人脸识别系统中。
21 |
22 | #### 13.1.2 人脸识别的传统方法
23 |
24 | 主流的人脸识别技术基本上可以归结为三类,即:基于几何特征的方法、基于模板的方法和基于模型的方法。
25 |
26 | - 基于几何特征的方法是最早、最传统的方法,通常需要和其他算法结合才能有比较好的效果;
27 | - 基于模板的方法可以分为基于相关匹配的方法、特征脸方法、线性判别分析方法、奇异值分解方法、神经网络方法、动态连接匹配方法等。
28 | - 基于模型的方法则有基于隐马尔柯夫模型,主动形状模型和主动外观模型的方法等。
29 |
30 | 下文主要介绍三种传统的人脸识别方法:
31 |
32 | 1. 主成分分析法
33 |
34 | 主成分分析法(PAC,Principal Component Analysis)又称为特征脸法,是20世纪90年代初由Turk和Pentland提出的一种经典算法,根据图像的统计特征通过正交变换(即K-L变换)由高维向量转换为低维向量,并形成低维线性向量空间,利用人脸投影到这个低维空间所得到的投影系数作为识别的特征矢量,这样,就产生了一个由“特征脸”矢量形成的子空间,成为“人脸子空间”或“特征子空间”,每一幅人脸图像向其投影都可以获得一组坐标系数,这组坐标系数表明了人脸在子空间中的位置,因此利用特征脸方法可以重建和识别人脸。
35 |
36 | 2. 线性判别分析
37 |
38 | 线性判别分析是对费舍尔的线性鉴别方法的归纳,这种方法使用统计学、模式识别和机器学习方法,试图找到两类物体或事件的特征的一个线性组合,以能够特征化或区分它们。所得的组合可用来作为一个线性分类器,或者,更常见的是,为后续的分类做降维处理。
39 |
40 | 3. 支持向量机
41 |
42 | 支持向量机(SVM,Support Vector Machine)起源于统计学习理论,研究如何构造学籍及,实现模式分类问题。其基本思想是通过非线性变换将输入空间变换到一个高维空间,在高维空间求取最优线性分类面,以解决那些线性不可分的分类问题。而这种非线性变换是通过定义适当的内积函数(即核函数)来实现的,由于该方法是基于结构风险最小化原理,而不是传统统计学的经验风险最小化,因而表现出很多优于已有方法的性能,但该方法需要大量的存储空间,并且训练速度慢。
43 |
44 | > 参考:
45 | >
46 | > 1. https://www.jiqizhixin.com/articles/2019-02-10-4
47 | > 2. https://wenku.baidu.com/view/34c55025a100a6c30c22590102020740be1ecdb7.html
48 |
49 | ### 13.2 One-Shot学习
50 |
51 | #### 13.2.1 One-Shot学习的定义
52 |
53 | **One-Shot learning**:一次学习,只通过一个样本来进行学习以能够认出同一个人。
54 |
55 | 
56 |
57 | 如上图所示,假设人脸识别系统数据库里有4个人每人一张照片,需要仅仅通过每个人的一张照片来判断输入图片中是否含有这4个人的其中一个。
58 |
59 | #### 13.2.2 如何解决One-Shot学习问题
60 |
61 | 对于One-Shot学习问题,采用卷积神经网络进行识别分类的缺点:
62 |
63 | 1. 训练集太小,不足以训练一个稳健的神经网络;
64 | 2. 如果有新成员加入数据集,分类输出的标签数量要改变,神经网络得重新训练。
65 |
66 | 故要解决One-Shot学习问题,应该要**学习Similarity函数**(也称为d函数):
67 | $$
68 | \begin{equation}\begin{split}
69 | d(img1,&img2)=degree\ of\ difference\ between\ images\\[2ex]
70 | &If\ d(img1,img2)\ \le\ \tau\ \ \ \ "same"\\
71 | &If\ d(img1,img2)\ \ge\ \tau\ \ \ \ "different"\\
72 | \end{split}\end{equation}
73 | $$
74 | 以两张图片作为输入,然后输出这两张图片的差异值,差异值越小越相似。如果差异值小于某个阈值 $\tau$($\tau$ 是一个超参数),就预测输入的是同一个人的两张图片;如果差异值大于阈值,就预测输入的是两个不同的人的照片,从而实现人脸验证。
75 |
76 | 将其应用于人脸识别任务,分别将要预测的图片及数据库中的任一张图片输入,用d函数两两比较,如果有输出一个比阈值小的数字,则预测的图片就是那个人的照片,若没有,则要预测的人不是数据库中的任一个人。
77 |
78 | 
79 |
80 | 在上面这个例子中,首先输入要识别的图片和数据库中第一张图片,输出一个很大的值,说明不是同一个人;接着输入要识别的图片和数据库中第二张图片,输出一个很小的值,很可能是同一个人;再分别输入要识别的图片和数据库中第三、四张图片,输出的值都很大,不是同一个人。因此,要识别的图片是第二个人的。若输出的值都很大,则要识别的人不是数据库里的任一个人。
81 |
82 | 如果要加入新成员,只需将其照片加入数据库中,系统依然能照常工作。
83 |
84 | #### 13.2.3 Few-Shot learning
85 |
86 | **Few-Shot learning**:小样本学习,用很少的样本去做分类或者回归。
87 |
88 | Few-Shot learning与传统的监督学习算法不同,它的目标不是让机器识别训练集中图片并且泛化到测试集,而是**让机器自己学会学习**。可以理解为用一个小数据集训练神经网络,学习的目的不是让神经网络知道每个类别是什么,而是让模型理解事物的异同,学会区分不同的事物。
89 |
90 | 
91 |
92 | 比如上面这张图片,左边两张图是同一种动物,右边两张是同一种动物,Few-Shot learning要做的就是通过对上面这四张图的学习判断下面这张图是属于哪一种动物。
93 |
94 | 
95 |
96 | Few-Shot learning 问题的关键是解决过拟合 (overfitting) 的问题,因为训练的样本太少了,训练出的模型可能在训练集上效果还行,但是在测试集上面会遭遇灾难性的崩塌。
97 |
98 | **解决方法:**
99 |
100 | 1. 数据增强和正则化:这一类方法想法很直接简单,既然训练数据不够那就增加训练样本,既然过拟合那就使用正则化技术。
101 | - 数据加强:最常见的例子就是有时对 Omniglot 数据集的预处理,会将图片旋转 90 、180 、270 度,这样就可以使样本数量变为原来的 4 倍。
102 | - 正则化:在训练的时候加入一个正则项,这个正则项的构建选择是关键。比如 《Few-shot Classification on Graphs with Structural Regularized GCNs》。该论文讨论 Graph 中节点分类的 few-shot 问题,常见的节点分类是使用 GCN 从节点的特征向量 feature 学习一个 embedding 然后用 embedding 来做分类,如果是 few-shot 问题,性能会大大下降(准确率大约从 70% 到了 40%),作者在训练的时候给损失函数加了一个正则项。作者将 feature 到 embedding 的过程看成编码器 encoder,然后额外加了几层网络作为 decoder,将 embedding 重构为 feature ,然后重构误差作为正则项(准确率从 40% 提升了 50%,大约 10 个百分点)。
103 |
104 | 2. Meta-learning(元学习):核心想法是先学习一个先验知识(prior),这个先验知识对解决 few-shot learning 问题特别有帮助。也就是说,先学习很多很多 task,然后再来解决新的在之前的学习中没有见过的 task 。
105 |
106 | > 参考:
107 | >
108 | > 1. https://blog.csdn.net/weixin_37589575/article/details/92801610
109 | > 2. https://zhuanlan.zhihu.com/p/142381922
110 |
111 | ### 13.3 Siamese网络
112 |
113 | Siamese网络架构是实现Similarity函数的一种方式。
114 |
115 | #### 13.3.1 Siamese网络架构
116 |
117 | **Siamese网络架构**:对于两个不同的输入,运行相同的卷积神经网络,然后比较它们输出的特征向量从而判断是否是属于同一类。
118 |
119 | 
120 |
121 | 如上图所示,首先将第一张输入图像$x^{(1)}$送入卷积神经网络,经过一系列的卷积、池化、全连接后输出一个特征向量,将这个特征向量称为$f(x^{(1)})$,看作是输入图像$x^{(1)}$的编码;然后将第二张输入图像$x^{(2)}$送入同样的神经网络,也得到一个特征向量,称为$f(x^{(2)})$,代表输入图像$x^{(2)}$的编码。我们相信这两个编码可以很好地代表两张输入图像,故定义d函数为两张图片编码之差的范数:
122 | $$
123 | d(x^{(1)}, x^{(2)})=||f(x^{(1)})-f(x^{(2)})||_2^2
124 | $$
125 |
126 | #### 13.3.2 如何训练Siamese网络
127 |
128 | 由于Siamese网络中两个卷积神经网络是一样的,所以在训练Siamese网络时只需要训练一个就好。
129 |
130 | 
131 |
132 | 更准确地说,神经网络的参数定义了一个编码函数$f(x^{(i)})$,如果给定输入图像$x^{(i)}$,会输出$x^{(i)}$的一个编码(特征向量)。训练网络要做的就是学习参数,使得如果两个图片$x^{(i)}$和$x^{(j)}$是同一个人,得到的两个编码的距离就小;如果$x^{(i)}$和$x^{(j)}$是不同的人,则它们之间的编码距离会比较大。如果改变这个网络所有层的参数,会得到不同的编码结果,要用反向传播来改变这些所有的参数以确保满足上面的条件。
133 |
134 | ### 13.4 Triplet损失
135 |
136 | #### 13.4.1 Triplet损失的定义
137 |
138 | **Triplet loss**:三元组损失,通常需要同时看三张图片:Anchor图片(A)、Positive图片(P,即正类,跟Anchor是同一个人)和Negative图片(N,即负类,跟Anchor不是同一个人)。其中,A和P为一对,是同一个人,所以希望它们编码的距离很接近;A和N为一对,不是同一个人,所以希望它们编码的距离远一点。公式如下:
139 | $$
140 | ||f(A)-f(P)||^2 \le ||f(A)-f(N)||^2
141 | $$
142 | 即:$d(A,P) \le d(A,N)$
143 |
144 | 把方程右边项移到左边:
145 | $$
146 | ||f(A)-f(P)||^2-||f(A)-f(N)||^2 \le 0
147 | $$
148 |
149 | 有两种情况满足这个表达式但没有用处:
150 |
151 | 1. 所有的编码会总是输出0,即$f(img)=0$,则 $0-0=0$。
152 | 2. 把所有的编码都设成相等的,即如果每个图片的编码和其他图片一样,这种情况还是得到 $0-0=0$。
153 |
154 | 为了阻止网络出现这两种情况,应该把“小于等于0”这个目标改为“小于0”,故将目标改为“$0-\alpha$”($\alpha$是一个超参数),由于我们更习惯使用“$+\ \alpha$”,所以将“$-\ \alpha$”这项移到左边,得到:
155 | $$
156 | ||f(A)-f(P)||^2-||f(A)-f(N)||^2 \ +\ \alpha \le 0
157 | $$
158 |
159 | 故第一个式子也变为:
160 | $$
161 | ||f(A)-f(P)||^2\ +\ \alpha \le ||f(A)-f(N)||^2
162 | $$
163 |
164 | 其中,$\alpha$也叫做间隔(margin),假设间隔设为0.2,为了满足条件,可以把d(A, N)调大或者把d(A, P)调小让间隔至少是0.2,这样就拉大了anchor与positive图片对和anchor与negative图片对之间的差距。例如,假设d(A, P)等于0.5,如果d(A, N)只比d(A, P)大一点点,为0.51,就不能满足条件,因为我们想让d(A, N)比d(A, P)大很多,至少是0.7或者更高。
165 |
166 | #### 13.4.2 Triplet损失函数
167 |
168 | 对于**一个三元组定义的损失函数**:
169 | $$
170 | L(A,P,N)=max(||f(A)-f(P)||^2-||f(A)-f(N)||^2 \ +\ \alpha,0)
171 | $$
172 | 若$||f(A)-f(P)||^2-||f(A)-f(N)||^2 \ +\ \alpha$ 小于0,那么损失函数就是0;若大于0,则损失函数等于$||f(A)-f(P)||^2-||f(A)-f(N)||^2 \ +\ \alpha$ ,是一个正的损失值。通过最小化损失函数,只要这个损失函数等于0,达到的效果就是使$||f(A)-f(P)||^2-||f(A)-f(N)||^2 \ +\ \alpha$小于或等于0,网络不会关心它的负值有多大。
173 |
174 | **整个网络的代价函数**是训练集中这些单个三元组损失的总和:
175 | $$
176 | J=\sum_{i=1}^mL(A^{(i)},P^{(i)},N^{(i)})
177 | $$
178 | 假设有一个10000张图片的训练集,里面是1000个不同的人的照片,平均每人10张照片,要做的是取这10000张图片生成三元组,然后对代价函数用梯度下降从而训练学习算法,训练完成后就可以应用到一次学习问题中。
179 |
180 | 为了定义三元组的数据集,需要成对的A和P即同一个人的成对的图片,
181 |
182 | #### 13.4.3 如何选择三元组组成训练集
183 |
184 | 倘若从数据集中随机地选择A, P, N构成三元组,遵循A和P是同一个人而A和N是不同的人这一原则,则不是同一个人的概率比是同一个人的概率大很多,即d(A, N)比d(A, P)大$\alpha$ 的概率很大,目标很容易就达到,网络很轻松就能训练好,梯度算法不会有什么效果。
185 |
186 | 所以应该**尽可能选择难训练的三元组A P N即所有的三元组d(A, P)都很接近d(A, N)**,这样,学习算法就会竭尽全力使d(A, N)变大或者使d(A, P)变小使得二者之间至少间隔$\alpha$,并且选择这样的三元组训练难度大,梯度下降法才能发挥作用,从而增加学习算法的计算效率。
187 |
188 | 
189 |
190 | ### 13.5 面部验证与二分类
191 |
192 | #### 13.5.1 将人脸识别变成二分类问题
193 |
194 | Triplet loss是个学习人脸识别卷积网络参数的好方法,此外还有其他学习参数的方法,如将人脸识别当成一个二分类问题:
195 |
196 | 
197 |
198 | 选取一对神经网络,选用 Siamese 网络并使其同时计算这些特征向量,然后将其输入到逻辑回归单元进行预测,若是相同的人,那么输出是 1,若是不同的人,输出是 0。这就把人脸识别问题转换为一个二分类问题,训练这种系统时可以替换 Triplet loss的方法。
199 |
200 | #### 13.5.2 逻辑回归单元的处理
201 |
202 | 最后通过将sigmoid等函数应用到某些特征上来处理逻辑回归单元:
203 | $$
204 | \hat{y}=\sigma\left(\sum_{k=1}^{128} w_{i}\left|f\left(x^{(i)}\right)_{k}-f\left(x^{(j)}\right)_{k}\right|+b\right)
205 | $$
206 | 其中,符号$f\left(x^{(i)}\right)$代表图片$x^{(i)}$的编码,下标 $k$ 代表选择这个向量中的第$k$个元素,$\left|f\left(x^{(i)}\right)_{k}-f\left(x^{(j)}\right)_{k}\right|$对这两个编码取元素差的绝对值。就像普通的逻辑回归一样,把这128个元素当作特征,然后把他们放入逻辑回归中,最后的逻辑回归可以增加参数$w_{i}$和$b$。在这128个单元上训练合适的权重,用来预测两张图片是否是一个人。
207 |
208 | 还可以用$\chi^{2}$公式$\frac{\left(f\left(x^{(i)}\right)_{k}-f\left(x^{(j)}\right)_{k}\right)^{2}}{f\left(x^{(i)}\right)_{k}+f\left(x^{(j)}\right)_{k}}$,也被称作$\chi$平方相似度,来代替上式中$\left|f\left(x^{(i)}\right)_{k}-f\left(x^{(j)}\right)_{k}\right|$的计算。
209 |
210 | #### 13.5.3 预先计算思想
211 |
212 | 在上面的学习公式中,输入是一对图片($x^{(i)}$和$x^{(j)}$),输出$y$是0或者1取决于输入是相似图片还是非相似图片。与之前类似,训练一个Siamese网络,即两个神经网络拥有的参数是相同的,两组参数是绑定的。
213 |
214 | **预先计算好数据库中图片的编码可以节省大量的计算,显著提高部署效果。**
215 |
216 | 如你有一张新图片$x^{(i)}$,当员工走进门时,希望门可以自动为他打开,在数据库中的图片$x^{(j)}$,不需要每次都计算特征向量,可以提前计算好,那么当一个新员工走近时,可以使用上方的卷积网络来计算编码,然后将其和预先计算好的编码进行比较,输出预测值 $\hat{y}$。
217 |
218 | **总结**:把人脸验证当作一个监督学习,创建一个只有成对图片的训练集,不是三个一组,而是成对的图片,目标标签是1表示这对图片是一个人,目标标签是0表示图片中是不同的人。利用不同的成对图片,使用反向传播算法去训练神经网络,训练Siamese神经网络。
219 |
220 | ### 13.6 什么是神经风格迁移
221 |
222 | #### 13.6.1 神经风格迁移的定义
223 |
224 | 
225 |
226 | 比如这张照片,你想利用右边照片的风格来重新创造原本的照片,右边的是梵高的星空,神经风格迁移可以帮你生成下面这张照片。使用$C$来表示内容图像,$S$表示风格图像,$G$表示生成的图像。
227 |
228 | #### 13.6.2 神经风格迁移的常用方法
229 |
230 | 
231 |
232 | [参考博客]: https://www.jiqizhixin.com/articles/2018-05-15-5 "综述:图像风格化算法最全盘点 | 内附大量扩展应用"
233 |
234 | ### 13.7 深度卷积网络在学什么
235 |
236 | #### 13.7.1 可视化分析卷积神经网络的浅层
237 |
238 | 假如训练了一个卷积神经网络,是一个Alexnet,轻量级网络,希望将看到不同层之间隐藏单元的计算结果。
239 |
240 | 
241 |
242 | 你可以这样做,从第一层的隐藏单元开始,假设你遍历了训练集,然后找到那些使得单元激活最大化的一些图片或是图片块。换句话说,将你的训练集经过神经网络,然后弄明白哪一张图片最大限度地激活特定的单元。注意在第一层的隐藏单元,只能看到小部分卷积神经,如果要画出来哪些激活了激活单元,只有一小块图片块是有意义的,因为这就是特定单元所能看到的全部。你选择一个隐藏单元,发现有9个图片最大化了单元激活,你可能找到这样的9个图片块(左上九宫格),似乎是图片浅层区域显示了隐藏单元所看到的,找到了像这样的边缘或者线(上面的蓝格子),这就是那9个最大化地激活了隐藏单元激活项的图片块。
243 |
244 | 
245 |
246 | 然后你可以选一个另一个第一层的隐藏单元,重复刚才的步骤,这是另一个隐藏单元,似乎第二个由这9个图片块(上中九宫格)组成。看来这个隐藏单元在输入区域,寻找这样的线条(下面的蓝格子),我们也称之为接受域。
247 |
248 | 对其他隐藏单元也进行处理,会发现其他隐藏单元趋向于激活类似于这样的图片。右上九宫格似乎对垂直明亮边缘且左边是绿色的图片块感兴趣,左中九宫格的隐藏单元倾向于橘色图片块。
249 |
250 | 以此类推,这是9个不同的代表性神经元,每一个不同的图片块都最大化地激活了。你可以这样理解,第一层的隐藏单元通常会找一些简单的特征,比如说边缘或者颜色阴影。
251 |
252 | #### 13.7.2 可视化分析卷积神经网络的深层
253 |
254 | 在深层部分,一个隐藏单元会看到一张图片更大的部分,在极端的情况下,可以假设每一个像素都会影响到神经网络更深层的输出,靠后的隐藏单元可以看到更大的图片块。
255 |
256 | 
257 |
258 | 上图中Layer 1是之前第一层得到的,Layer 2是可视化的第2层中最大程度激活的9个隐藏单元。在更深的层上,可以重复这个过程。
259 |
260 | 放大第一层,这是第一个被高度激活的单元,你能在输入图片的区域看到所提取的这些边缘或颜色阴影。
261 |
262 | 
263 |
264 | 放大第二层的可视化图像。第二层似乎检测到更复杂的形状和模式,比如说中上九宫格这一隐藏单元会找到有很多垂线的垂直图案,右中九宫格的隐藏单元似乎在左侧有圆形图案时会被高度激活,左下九宫格所寻找的特征是很细的垂线,以此类推,第二层检测的特征变得更加复杂。
265 |
266 | 
267 |
268 | 放大第三层,这些东西激活了第三层。中心九宫格这一隐藏单元似乎对图像左下角的圆形很敏感,所以检测到很多车。右下九宫格似乎开始检测到人类,左上九宫格似乎检测特定的图案,比如蜂窝形状或者方形这样类似规律的图案。有些很难看出来,需要手动弄明白检测到什么,但是第三层明显,检测到更复杂的模式。
269 |
270 | 
271 |
272 |
273 |
274 | 这是第四层,检测到的模式和特征更加复杂,左上九宫格学习成了一个狗的检测器,但是这些狗看起来都很类似。右中九宫格似乎检测到鸟的脚等等。
275 |
276 |  277 |
278 |
279 |
280 | 第五层检测到更加复杂的事物,右下九宫格似乎是一个狗检测器,但是可以检测到的狗似乎更加多样性。左上九宫格可以检测到键盘或者是键盘质地的物体,可能是有很多点的物体。左中九宫格可能检测到文本,但是很难确定,左下九宫格检测到花。
281 |
282 |
277 |
278 |
279 |
280 | 第五层检测到更加复杂的事物,右下九宫格似乎是一个狗检测器,但是可以检测到的狗似乎更加多样性。左上九宫格可以检测到键盘或者是键盘质地的物体,可能是有很多点的物体。左中九宫格可能检测到文本,但是很难确定,左下九宫格检测到花。
281 |
282 |  283 |
284 | 由此,我们已经有了一些进展,**从检测简单的事物,比如说,第一层的边缘,第二层的质地,到深层的复杂物体**,更直观地了解卷积神经网络的浅层和深层是如何计算的。
285 |
286 | ### 13.8 代价函数
287 |
288 | #### 13.8.1 代价函数的作用
289 |
290 | 神经风格迁移系统用代价函数来评判某个生成图像的好坏。
291 |
292 | #### 13.8.2 代价函数的定义
293 |
294 | $$
295 | J(G)=αJ_{content}(C,G)+βJ_{style}(S,G)
296 | $$
297 |
298 | 其中,$J_{content}(C,G)$称为内容代价函数,用来衡量生成图片G的内容与图片C的内容有多相似;$J_{style}(S,G)$是风格代价函数,用来衡量图片G的风格与图片S的风格的相似度。超参数 $\alpha$ 和 $\beta$ 确定内容代价和风格代价两者之间的权重。
299 |
300 | #### 13.8.2 如何最小化代价函数
301 |
302 | 用梯度下降法来最小化代价函数:
303 | $$
304 | G=G-\frac{\partial}{\partial G}J(G)
305 | $$
306 | 实际上每次更新的是图像G的像素值。举个例子:
307 |
308 | 
309 |
310 | 要取上图中左边图片的内容和右边图片的风格生成图像G。随机初始化的生成图像如下图①所示,是一张随机选取像素的白噪声图;接下来运行梯度下降算法,最小化代价函数$J(G)$,逐步处理像素,逐步得到越来越像用风格图片的风格画出来的内容图片(下图中第②-④张图片)。
311 |
312 | 
313 |
314 | ### 13.9 内容代价函数
315 |
316 | #### 13.9.1 定义
317 |
318 | 内容代价函数:Content cost function,衡量内容图片和生成图片在内容上的相似度。
319 |
320 | 假如用隐含层 $l$ 来计算内容代价,$l$ 一般是选在网络的中间层,不会选的太浅或太深。然后用一个预训练的卷积模型,$a^{[l](C)}$和$a^{[l](G)}$分别代表内容图片C和生成图片G的 $l$ 层的激活函数值。如果这两个激活值相似,则这两张图片的内容相似。故将内容代价函数定义为两个激活值的不同或相似程度,即其差值的平方:
321 | $$
322 | J_{content}(C,G)=\frac{1}{2}||a^{[l](C)}-a^{[l](G)}||^2
323 | $$
324 | 其中,$\frac{1}{2}$ 是对其进行归一化,可以不加也可以是其他值,因为在整体代价函数中还可由超参数 $\alpha$ 调整内容代价函数的权重。
325 |
326 | ### 13.10 风格代价函数
327 |
328 | 风格代价函数:Style cost function,衡量风格图片和生成图片在风格上的相似度。
329 |
330 | #### 13.10.1 图像风格的定义
331 |
332 | 如下图所示,假如有这么一张图片输入卷积网络,对于某一隐藏层 $l$ ,图片的风格可以定义为 $l$ 层中各个通道之间激活项的相关系数。
333 |
334 | 
335 |
336 | 具体解释:
337 |
338 | 将 $l$ 层的激活项取出,是一个 $n_H \times n_W \times n_C$ 的三维激活项,将其不同通道渲染成不同的颜色,每个通道对应一个神经元,如下图所示,以前两个通道为例,红色通道对应的是第二个神经元(红色方框),能找出图片中的特定位置是否含有垂线纹理,黄色通道对应第四个神经元(黄色方框),可以粗略找出橙色区域,则这两个通道的相关系数指的就是图片中某处出现这种垂直纹理时该处又同时是橙色的可能性。若采用相关系数来描述通道的风格,则需测量生成图像中第一个通道是否与第二个通道相关,从而得知在生成图像中垂直纹理和橙色同时出现或不同时出现的概率,这样就能够测量生成图像的风格与输入的风格图像的相似程度。
339 |
340 | 
341 |
342 |
343 |
344 | #### 13.10.2 风格矩阵
345 |
346 | 对于风格图像与生成图像,需要计算其风格矩阵,说得更具体一点就是用 $l$ 层来测量风格。
347 |
348 | 假设 $a^{[l]}_{i,j,k}$ 为隐藏层 $l$ 中 $(i,j,k)$ 位置的激活项,i、j、k分别代表该位置的高度、宽度以及对应的通道数。现在要计算一个关于 $l$ 层和风格图像的矩阵 $G^{[l][S]}$ ( $l$ 表示层数,$S$ 表示风格图像),由于有 $n_c$ 个通道,故 $G^{[l][S]}$ 是一个 $n_c \times n_c$ 的矩阵,以便计算 $k$ 通道和 $k′$ 通道中每一对激活项的相关系数, $k$ 和 $k′$ 的取值范围则为$1,2,...,n_c$,
349 | 设这个关于 $l$ 层和风格图像的矩阵 $G^{[l][S]}$ 高度和宽度都是 $l$ 层的通道数,在这个矩阵中 $k$ 和 $k′$ 元素被用来描述 $k$ 通道和 $k′$ 通道之间的相关系数,则风格图像的风格矩阵是:
350 | $$
351 | G^{[l](S)}_{kk'}=\sum_i^{n^{[l]}_H} \sum_j^{n^{[l]}_W} a_{ijk}^{[l](S)}a_{ijk'}^{[l](S)}
352 | $$
353 | 其中,符号 $i$、$j$ 表示下界,对 $i$、$j$、$k$ 位置的激活项 $a_{ijk}^{[l](S)}$,乘以同样位置即 $i$、$j$、$k'$ 位置的激活项 $a_{ijk'}^{[l](S)}$,然后 $i$、$j$ 分别加到 $l$ 层的高度和宽度,即 $n^{[l]}_H$ 和 $n^{[l]}_W$,将这些不同位置的激活项都加起来即可得到风格矩阵。严格来说,这个公式是一种非标准的互相关函数,因为没有将其减去平均数,而是将它们直接相乘。
354 |
355 | 对生成图像做同样的操作即可得到生成图像的风格矩阵:
356 | $$
357 | G^{[l](G)}_{kk'}=\sum_i^{n^{[l]}_H} \sum_j^{n^{[l]}_W} a_{ijk}^{[l](G)}a_{ijk'}^{[l](G)}
358 | $$
359 |
360 | 之所以用大写字母 $G$ 来代表这些风格矩阵,是因为在线性代数中这种矩阵有时也叫 Gram 矩阵,但在这里只把它们叫做风格矩阵。
361 |
362 | 如果两个通道中的激活项数值都很大,那么 $G^{[l]}_{kk'}$ 也会很大,对应地,如果它们不相关那么 $G^{[l]}_{kk'}$ 就会很小。
363 |
364 | 下图形象地展示了风格矩阵的形成过程:
365 |
366 | 
367 |
368 | #### 13.10.3 风格代价函数
369 |
370 | 如果将 $S$ 和 $G$ 代入到风格代价函数中去计算将得到这两个矩阵之间的误差,实际上是计算两个矩阵对应元素相减的平方的和,由于 $G^{[l][S]}$ 和 $G^{[l][G]}$ 是矩阵,故加下标表 Frobenius 范数:
371 | $$
372 | J^{[l]}_{style}(S,G)=||G^{[l][S]}-G^{[l][G]}||^2_F
373 | $$
374 | 把这个式子展开,从 $k$ 和 $k′$ 开始作差,然后把得到的结果都加起来,即得到对 $l$ 层定义的风格代价函数:
375 | $$
376 | J^{[l]}_{style}(S,G)=\frac {1}{(2n_H^{[l]}n_W^{[l]}n_c^{[l]})^2} \sum_k \sum_{k'}(G^{[l](S)}_{kk'}-G^{[l](G)}_{kk'})^2
377 | $$
378 | 其中,使用了一个归一化常数$\frac {1}{(2n_H^{[l]}n_W^{[l]}n_c^{[l]})^2}$ ,但是一般情况下不用写这么多,只要将风格代价函数乘以一个超参数 $\beta$ 就行。
379 |
380 | 实际上,如果对各层都使用风格代价函数,会让结果变得更好。如果要对各层都使用风格代价函数,把各个层的结果(各层的风格代价函数)都加起来,就能定义它们全体了:
381 | $$
382 | J_{style}(S,G)=\sum_l \lambda^{[l]}J^{[l]}_{style}(S,G)
383 | $$
384 | 其中,需要对每个层定义权重,用 $\lambda^{[l]}$ 来表示,这样将能够在神经网络中使用不同的层,包括之前的一些可以测量类似边缘这样的低级特征的层以及之后的一些能测量高级特征的层,使得我们的神经网络在计算风格时能够同时考虑到这些低级和高级特征的相关系数。这样,在基础的训练中定义超参数时,可以尽可能地得到更合理的选择。
385 |
386 | 为了把这些东西封装起来,现在定义全体代价函数:
387 | $$
388 | J(G)=αJ_{content}(C,G)+βJ_{style}(S,G)
389 | $$
390 | 之后用梯度下降法,或者更复杂的优化算法来找到一个合适的图像 $G$,并计算 $J(G)$ 的最小值,从而将能够得到非常好看漂亮的结果。
391 |
392 | #### 13.10.4 用GAN做风格迁移
393 |
394 | GAN是解决风格迁移的深度学习方法。
395 |
396 | GAN由生成网络G和对抗网络D组成,G用于接收一个噪声z,从而生成图片G(z);D是一个判别网络,判别一张图片x是不是“真的”我们所需得到的目的图片或者是由G生成的(此时图片是“假的”),即D(x)。
397 | 生成网络G和对抗网络D在训练时候互为动态的博弈过程。
398 | 损失函数:
399 |
400 | 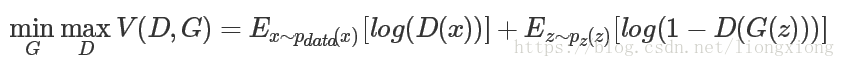
401 |
402 | 其中,x为真实图片,z表示输入G的随机噪声。
403 | GAN之所以能产生对抗博弈的训练过程和效果是因为GAN把训练过程分为了两个部分:
404 |
405 | 优化D:
406 | 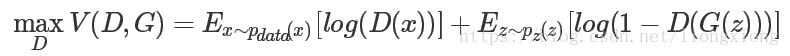
407 |
408 | 优化G:
409 |
410 | 
411 |
412 | 将D和G用CNN来表达就是适用于图像处理的DCGAN了。
413 | 更多方法详见“https://blog.csdn.net/liongxiong/article/details/80875885”。
414 |
415 | ### 13.11 一维到三维的推广
416 |
417 | #### 13.11.1 2D卷积
418 |
419 | 假设输入图像为14×14的2维图像,使用5×5的2维过滤器进行卷积,得到 10×10的二维图像,如下图所示:
420 | 
421 |
422 | #### 13.11.2 1D卷积
423 |
424 | 举个例子,下图左边是一个EKG信号(心电图),当在胸部放一个电极,电极透过胸部测量心脏带来的微弱电流,每个峰值对应一次心跳。如果想用EKG信号,就需要处理1维数据。因为EKG信号由时间序列对应的每个瞬间的电压组成,是一维的,输入的尺寸是14而不是14×14,就需要用一维过滤进行卷积如一个5的过滤器,而不是5×5。最终的输出尺寸是10。
425 | 
426 |
427 | #### 13.11.3 3D卷积
428 |
429 | 
430 | 如上图所示,假设现在输入是具有长度、宽度和高度的三维数据,例如14×14×14,使用5×5×5的过滤器进行卷积,输出将为10×10×10。某种程度上3D数据也可以使用3D confident学习。过滤器实现的功能是用输入的3D数据进行特征识别。
431 |
432 | 医疗检查是3D卷积的一个实例,如下图所示的CT扫描,用X光输出身体的3D模型:
433 |
434 | 
--------------------------------------------------------------------------------
/14 序列模型.md:
--------------------------------------------------------------------------------
1 | # 14序列模型
2 |
3 | ### 14.1 为什么选择序列模型
4 |
5 | #### 14.1.1 序列模型应用领域
6 |
7 | 序列模型广泛应用于语音识别,音乐生成,情感分析,DNA序列分析,机器翻译,视频行为识别,命名实体识别等众多领域。
8 |
9 | - 语音识别:将输入的语音信号直接输出相应的语音文本信息。无论是语音信号还是文本信息均是序列数据。
10 |
11 | - 音乐生成:生成音乐乐谱。只有输出的音乐乐谱是序列数据,输入可以是空或者一个整数。
12 |
13 | - 情感分类:将输入的评论句子转换为相应的等级或评分。输入是一个序列,输出则是一个单独的类别。
14 |
15 | - DNA序列分析:输入的DNA序列,找到匹配的蛋白质序列。
16 |
17 | - 机器翻译:两种不同语言之间的翻译。输入和输出均为序列数据。
18 |
19 | - 视频行为识别:识别输入的视频帧序列中的人物行为。
20 |
21 | - 命名实体识别:从输入的句子中识别实体的名字。
22 |
23 | 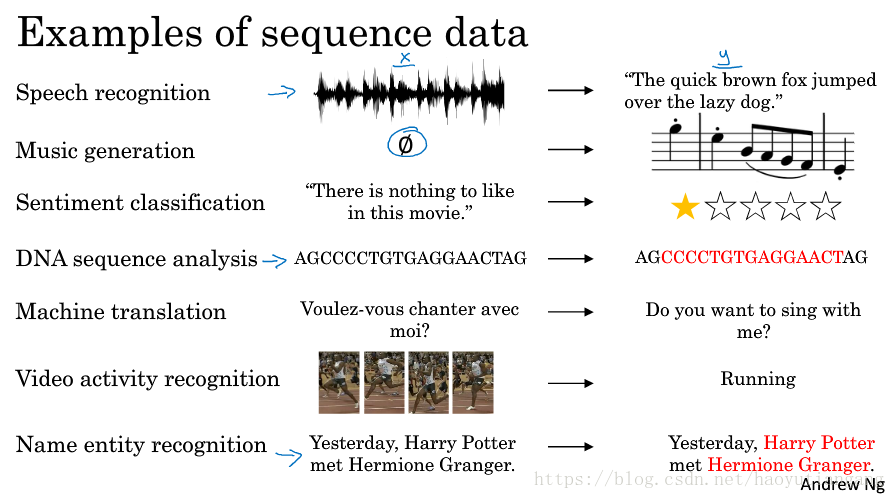
24 |
25 | #### 14.1.2 输入x和输出y的关系
26 |
27 | 上面那些问题可以看成使用标签数据$(x,y)$作为训练集的监督学习,但是输入与输出不一定都是序列,对应关系有非常多的组合,比如一对一,多对多,一对多,多对一,多对多(个数不同)等情况来针对不同的应用。
28 |
29 | ### 14.2 数学符号
30 |
31 | #### 14.2.1 符号含义
32 |
33 | - $x^{}$ 表示输入数据 x 中的第 t 个符号(eg:输入的英文句子中的单词)
34 | - $y^{}$ 表示输出 y 中的第 t 个符号(单词)
35 | - ${x^{(i)}}$ 表示第 i 个输入样本中的第 t 个符号(单词)
36 | - ${y^{(i)}}$ 表示第 i 个输出样本中的第 t 个符号(单词)
37 | - $T_x$ 表示输入 x 的长度
38 | - $T_y$ 表示输出 y 的长度
39 | - $T_x^{(i)}$ 表示第 i 个训练样本的输入序列长度
40 | - $T_y^{(i)}$ 表示第 i 个训练样本的输出序列长度
41 |
42 | #### 14.2.2 字典编码
43 |
44 | - 利用一个字(词)典向量,通常有3-5万个字(词),来表示$x^{}$的符号含义
45 |
46 | - 可以利用one-hot编码表示词典里的每个单词,构造一个输入的序列中每个单词$x^{}$的向量
47 |
48 | - 与字典向量大小一致(3-5万行)
49 | - $x^{}$代表的单词对应到字典里的单词,在对应索引位置(行数)是1,其余位置都是0。比如“and”在词典里排第367,所以相应的$x^{}$就是第367行是1,其余值都是0的向量。
50 | - 如果单词不在字典里,则创造一个新的“Unknow Word”伪单词,用<**UNK**>作为标记。
51 |
52 |
53 | ### 14.3 循环神经网络模型
54 |
55 | #### 14.3.1 为什么不用普通神经网络
56 |
57 | 试想如果将输入拆成每个字的 One-Hot 编码输入传统的深度神经网络中,经过一些隐藏层的计算得到输出 Y。
58 |
59 | 存在的问题:
60 |
61 | - 输入和输出数据在不同的例子中可以有不相等的长度
62 |
63 | - 不能共享从文本不同位置所学习到的特征:能学习到“and”在$x^{<1>}$位置的普通神经网络不能识别“and”在$x^{<4>}$时的情况。
64 |
65 | - 参数数量过多
66 |
67 | 循环神经网络可以解决以上问题
68 |
69 | #### 14.3.2 循环神经网络
70 |
71 | 循环神经网络,从左到右一个单词计算一步,每一步的计算不仅来自这一步的输入,也来自上一步的激活函数值。
72 |
73 | 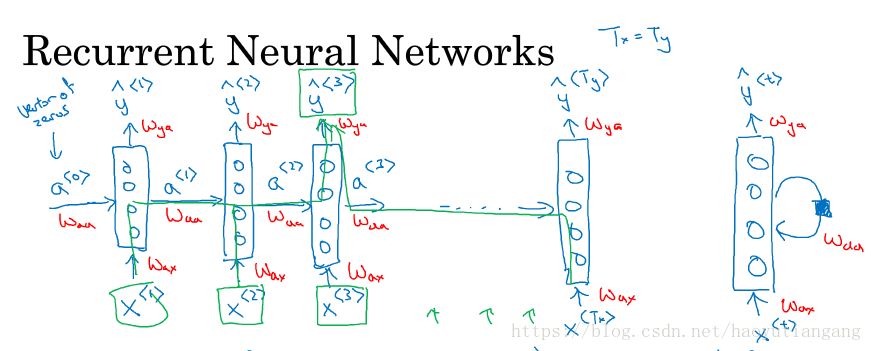
74 |
75 | - 最左侧第一层假设了一个来自第零层的激活值向量(通常设计为零向量或随机向量)
76 | - 有的研究论文上将循环神经网络的结构写成图片右边的形式,其和左边的形式是一致的。
77 |
78 | 循环神经网络从左到右扫描数据,同时共享每个时间步的参数。
79 |
80 | - $W_{ax}$ 管理从输入$x^{}$到隐藏层连接的一系列参数
81 | - $W_{aa}$ 管理激活值$a^{}$到隐藏层连接的一系列参数
82 | - $W_{ya}$ 管理隐藏层到输出结果 $y$ 连接的一系列参数
83 | - 每个时间步都使用相同的 $W_{ax}$ ,$W_{aa}$ ,$W_{ya}$
84 |
85 | #### 14.3.3 循环神经网络的前向传播
86 |
87 | 
88 |
89 | 如图,首先输入$a^{<0>}$,接着是前向传播过程,先计算$a^{<1>}$,再计算$y^{<1>}$
90 |
91 | $$
92 | \begin{array}{c}a^{<1>}=g_1\left(W_{a a} a^{<0>}+W_{a x} x^{<1>}+b_{a}\right) \\y^{<1>}=g_2\left(W_{y a} a^{<1>}+b_{y}\right)\end{array}
93 | $$
94 | 计算每步的激活函数 a 通常为**Tanh** ,也可由输出判断改用**ReLu**,**sigmoid**(二分类),**softmax**(k分类)
95 |
96 | 在 t 时刻:
97 |
98 | $$
99 | \begin{array}{c}
100 | a^{}=g\left(W_{a a} a^{}+W_{a x} x^{}+b_{a}\right) \\
101 | y^{}=g\left(W_{y a} a^{}+b_{y}\right)
102 | \end{array}
103 | $$
104 |
105 | > 1. 每一步都有一个激活函数 $a^t$ 和一个输出函数 $y^{}$
106 | > 2. 激活函数$a^t$来自于输入 $x^t$ 和上一步的激活函数 $a^{t−1}$, 输出函数 $y^{}$ 来自于激活函数 $a^t$ ,因此实现了利用这个序列中之前的所有序列信息来做出预测
107 | > 3. 激活函数或者输出函数都是 $g(WX+b)$ 这一点没有改变
108 | > 4. 参数W,b 的第一个下标表示是激活函数a 的参数还是输出函数 y 的参数, W的第二个下标表示这个参数是用来乘以哪个输入
109 |
110 | #### 14.3.4 前向传播参数的简化
111 |
112 | 下面参数可以精简合并为$WX+b$形式,以便建立更复杂的模型。
113 |
114 | $$
115 | \begin{array}{c}
116 | a^{}=g\left(W_{a}[ a^{}, x^{}]+b_{a}\right) \\
117 | y^{}=g\left(W_{y} a^{}+b_{y}\right)
118 | \end{array}
119 | $$
120 |
121 | 其中 $W_{a}=[W_{a a}:W_{a x}]$ ,表示两个矩阵并列放置,维度为[ len(a) , len(a) + len(x) ]。
122 |
123 | $[ a^{}, x^{}]=\left[\begin{array}{l}
124 | a^{}\\
125 | x^{} \\
126 | \end{array}\right]$,表示建立成一个列向量,维度为[ len(a) + len(x) , 1 ]。
127 |
128 | 这时 $[W_{a a}:W_{a x}]$ 乘以 $\left[\begin{array}{l}
129 | a^{}\\
130 | x^{} \\
131 | \end{array}\right]$ 正好等于 $W_{a a} a^{}+W_{a x} x^{}$。
132 |
133 | 而对$y^{}$简化为:
134 | $$
135 | W_{y}=W_{y a}
136 | $$
137 |
138 |
139 |
140 | ### 14.4 通过时间的反向传播
141 |
142 | #### 14.4.1 序列模型中的反向传播
143 |
144 | 在一些编程框架里实现RNN时,编程框架会自动为我们处理关于RNN的反向传播,但还是有必要粗略的了解一下反向传播在RNN中的实现。
145 |
146 | 如下图的前向传播
147 |
148 | 
149 |
150 | 对于$a^{}$的计算,需要参数$W_{aa}$ ;对于$y^{}$的计算,需要参数$W_{ya}$;与之前的对神经网络的训练相类似,在RNN中,进行反向传播的目的,是为了对这些参数进行更新,直到找到最为合适的参数。
151 |
152 |
153 |
154 | 
155 |
156 | 同样的,如上图,在RNN中实现反向传播仍然需要定义cost function。不同的在于,它需要对于每一个输出的$y^{}$进行概率值的计算,并最终将所有计算得出的$y^{}$进行求和,计算整体的cost function。
157 |
158 |
159 |
160 | 
161 |
162 | 计算出整体的cost function后,再进行求导、梯度下降的方法进行处理,将前向传播的箭头都反过来,最终更新出合适的参数。这就是大致的RNN中反向传播的过程。
163 |
164 |
165 |
166 | #### 14.4.2 反向传播中的损失函数
167 |
168 | 在反向传播中,定义的对于单个输出的cost function为
169 |
170 | $L^{}\left(\hat{y}^{}, y^{}\right)=-y^{} \log \hat{y}^{}-\left(1-y^{}\right) \log \left(1-\hat{y}^{}\right)$
171 |
172 | 称为交叉熵损失函数,用以计算序列中某一个特定的词为某一类别(如名字、地点等)的词的概率,如若计算该词为人名的概率为0.1,则输出0.1.
173 |
174 |
175 |
176 | 对于所有输出的预测值的求和,定义的cost function为
177 |
178 | $L(\hat{y}, y)=\sum_{t=1}^{T_{y}} L^{}\left(\hat{y}^{}, y^{}\right)$
179 |
180 | 即将每一个timestep的输出预测值进行求和。
181 |
182 | ### 14.5 不同类型的循环神经网络
183 |
184 | 以上介绍的,都是当$T_x$和$T_y$ 相同的情况下,RNN的实现。更多时候,$T_x$和$T_y$ 是不同的,面对两者不同时,我们要用不同的RNN模型。个人认为主要的调整在于,在不同的timestep进行输入和输出,以及将一些输出的信息作为输入,作用到下一个单元中。
185 |
186 | 大致如下图
187 |
188 | 
189 |
190 |
191 |
192 | ### 14.6 语言模型和序列生成
193 |
194 | 语言模型是NLP中比较重要的一个模块,它能够计算一句话被翻译成各种不同意思的概率,并选择最大概率的翻译作为正确翻译。
195 |
196 | #### 14.6.1 语言模型的构建
197 |
198 | 构建语言模型,首先需要建立一个足够大的training set,即一个包含很多句子的corpus,然后对corpus中的每句话进行tokenize操作,即将一整句话切分成每一个单词,利用one-hot,将单词转换成词向量。其中,句子结尾可以用符号表示;而对没有出现在corpus中的单词可以用表示。再利用RNN来计算一句话被翻译成具体意思的概率,如下图
199 |
200 | 
201 |
202 | $x^{<1>}$和$a^{<0>}$均为零向量,softmax层会根据$x^{<1>}$和$a^{<0>}$来预测输出$y^{<1>}$,它会计算第一个词分别为字典中的每一个词的概率具体为多少(如预测为“猫”、“狗”的概率分别为多少);而$y^{<2>}$则表示在出现第一个单词的基础上,出现第二个单词的概率,即为条件概率,以此类推,直到计算出出现的概率
203 |
204 | #### 14.6.2 概率计算
205 |
206 | 在softmax层中,计算单个元素的cost function为
207 |
208 | $L^{}\left(\hat{y}^{}, y^{}\right)=-\sum_{i} y_{i}^{} \log \hat{y}_{i}^{}$
209 |
210 | 计算所有元素的cost function为
211 |
212 | $L(\hat{y}, y)=\sum_{t} L^{}\left(\hat{y}^{}, y^{}\right)$
213 |
214 | 计算一句话被翻译正确的概率公式为
215 |
216 | $P\left(y^{<1>}, y^{<2>}, \cdots, y^{}\right)$
217 |
218 | 即对每个元素的cost function进行求和。
219 |
220 | 最后,整个语句出现的概率为语句中所有元素出现的条件概率的乘积,如,某个语句中包含$y^{<1>}$、$y^{<2>}$ 、 $y^{<3>}$,则整个语句出现的概率为
221 |
222 | $P\left(y^{<1>}, y^{<2>}, y^{<3>}\right)=P\left(y^{<1>}\right) \cdot P\left(y^{<2>} \mid y^{<1>}\right) \cdot P\left(y^{<3>} \mid y^{<1>}, y^{<2>}\right)$
223 |
224 |
225 |
226 | ### 14.7 新序列采样
227 |
228 | 在训练完一个序列模型之后,如果想了解这个模型学到了什么,那就可以选择进行一次新序列采样。不过这是非正式做法。
229 |
230 | 新序列采样可以理解为先给模型一个输入,然后从其预测结果中随机选取一个作为下一次的输入;直至满足不再采样的要求,这样就可以得到一连串的字符。这些字符构成一段文本,可以帮你了解你的模型学到了什么。接下来看具体怎么做。
231 |
232 | #### **14.7.1 生成随机语句**
233 |
234 | 首先要理解的是,你的模型会干什么:给定一个单词(也不一定是单词),预测下一个单词是词典中某个单词的概率。
235 |
236 | 1. 采样的第一个时间步,是输入$x^{<1>}=0,a^{<0>}=0$。然后得到输出向量,这个向量表示了词典中每个词出现的概率。然后根据给出的概率,随机选取一个词作为$\hat{y}^{<1>}$。具体实现可以用:
237 |
238 | ```python
239 | y_1 = np.random.choice(dictionary, p=y)
240 | ```
241 |
242 | 其中`y_1`表示$\hat{y}^{<1>}$,`dictionary`表示词典,`p=y`表示词典中的各值以对应`y`中的概率选取。`y`是模型输出的向量。
243 |
244 | 2. 第二个时间步,将$\hat{y}^{<1>}$作为这一步的输入$x^{<2>}$,然后得到预测$\hat{y}^{<2>}$。然后依次类推,重复若干次。
245 |
246 | 3. 当$\hat y$为结束符***EOS***或者已经获得足够的单词后,就可以停止采样了。
247 |
248 | 执行流程大概如图:
249 |
250 | 
251 |
252 | 这样下来,就可以得到由$\hat{y}^{}$组成的一句话或者一段文本了。
253 |
254 | #### **14.7.2 词典为字符与词典为单词的优缺点**
255 |
256 | **基于单词**的词典的优缺点
257 |
258 | * 优点:不会出现不存在的单词;序列很短就能构成句子、段落;
259 | * 缺点:可能出现未知标识***UNK***;字典会很大;
260 |
261 | **基于字符**的词典的优缺点
262 |
263 | * 优点:不会出现未知标识;字典小很多;
264 | * 缺点:可能出现不存在的单词;序列会太多太长,前面的单词会被遗忘;训练成本高昂;
265 |
266 | ### 14.8 带有神经网络的梯度消失
267 |
268 | #### 14.8.1 为什么会梯度消失
269 |
270 | 梯度消失并不只是存在于很深的卷积神经网络中,同样还存在于RNN中——因为RNN其实也可以看成是一个很深的网络,只不过深度由训练样本的长度决定。不过还要意识到,导致RNN能“有很多层”的原因是激活值$a^{}$的传递,所以如果要进行优化也是针对$a^{}$进行。
271 |
272 | 举个例子:对于样本“The **cat**, which already ate ……, **was** full.”,前面的单数**cat**决定了后面用的是**was**,而中间的字符可以任意长。如果想要 RNN 能发现这一点,就需要反向传播时能将**was**处的损失传播到**cat**处。但是实际情况下很可能由于已经传播了很多层(两者间单词过多)而导致梯度消失,最终对**cat**的影响微乎其微。
273 |
274 | 更普遍来说,对于长句子样本,句子前后的关联性会很难被发现、建立起来。
275 |
276 | #### 14.8.2 梯度修剪
277 |
278 | 其实RNN也存在梯度爆炸问题。但是相对于梯度爆炸,梯度消失更难发现。因为梯度消失只会让你的参数基本不变,而不像梯度爆炸会让你的参数出现很多的**NaN**,这意味着数值出现了溢出。
279 |
280 | 而且不同于梯度消失,梯度爆炸解决起来其实更容易一些。解决办法就是**梯度修剪**:
281 |
282 | 观察梯度向量,通过人为设定一个阈值(比较大的数),如果超过了阈值就缩放梯度向量,从而保证梯度不会过大。
283 |
284 | ### 14.9 GRU单元
285 |
286 | 为了解决梯度消失的问题,学者提出了GRU单元(门控循环单元网络)的概念。这个网络能有效解决梯度消失的问题,并且能够使你的神经网络捕获更长的长期依赖。
287 |
288 | #### 14.9.1 GRU单元实现
289 |
290 | 
291 |
292 | 回顾一下RNN单元的工作模式如上。记住公式
293 | $$
294 | a^{}=g\left(W_{a}\left[a^{}, x^{}\right]+b_{a}\right)
295 | $$
296 | 在处理一个句子的时候,如果想要记住一个以前出现过的单词,那就需要一个额外的变量保存:***c***(cell),代表了记忆细胞。记忆细胞负责记忆前面的**cat**是单数还是复数。记 $c^{}$ 为记忆细胞在时间 $t$ 时的取值。对于GRU来说,其实$c^{} = a^{}$。但还是会使用不同的标记,因为在**LSTM**中会有所不同。
297 |
298 | 记忆细胞在更新时,需要考虑是否忘记已经记住了的值并更新为需要记住的值。所以需要先计算候选值
299 | $$
300 | \tilde{c}^{}=\tanh \left(W_{c}\left[c^{}, x^{}\right]+b_{c}\right)
301 | $$
302 | 然后重点来了,GRU真正重要的思想是有一个**更新门**:
303 | $$
304 | \Gamma_{u}=\sigma\left(W_{u}\left[c^{}, x^{}\right]+b_{u}\right)
305 | $$
306 | 这个门的作用在于决定什么时候更新$c^{}$。但是在介绍怎么决定是否更新前,先明白$\Gamma_{u}$的含义:大写希腊字母$\Gamma$很像门,代表门的含义;下标$u$表示 updata 更新;然后计算用的是sigmoid函数,意味着取值处在 (0, 1) 间,并且大概率接近0或1。0/1的含义就很清楚了,可以用来表示更新/不更新。所以$c^{}$的更新公式可以写成:
307 | $$
308 | c^{}=\Gamma_{u} * \tilde{c}^{}+\left(1-\Gamma_{u}\right) * c^{}
309 | $$
310 | 其中的运算符$*$表示逐元素乘法。
311 |
312 | 这就是门的作用,可以决定是否更新记忆细胞。对于 cat 的例子,可以理解为判断是否已经过了要用到 was/were的地方。架构大致如下:
313 |
314 | 
315 |
316 |
317 |
318 | 理解了GRU的思想之后,还有一个完整的版本,会多一个**相关门**:
319 | $$
320 | \Gamma_{r}=\sigma\left(W_{r}\left[c^{}, x^{}\right]+b_{r}\right)
321 | $$
322 | $r$表示相关性(relevance),其作用在于计算候选值$\tilde{c}^{}$与$c^{}$的关联性。这需要更改$\tilde{c}^{}$的计算公式为:
323 | $$
324 | \tilde{c}^{}=\tanh \left(W_{c}\left[\Gamma_{r}*c^{}, x^{}\right]+b_{c}\right)
325 | $$
326 |
327 | #### 14.9.2 工作原理
328 |
329 | 上面只讲了GRU的实现,现在回到我们一开始想要解决的问题:梯度消失。
330 |
331 | $c^{}$的更新公式告诉我们,只有在需要用到这个记忆的时候才可能更新。因此$\Gamma_{u}$会长时间为接近0的数,近乎保证了$c^{}=c^{}$,也因此让梯度消失出现的可能性下降了。
332 |
333 | ### 14.10 长短期记忆(LSTM(long short term memory)unit)
334 |
335 | #### 14.10.1 LSTM用到的公式
336 |
337 | 在GRU的基础上做出如下修改
338 |
339 | $\tilde{c}^{\langle t\rangle}=\tanh \left(\omega_{i}\left[a^{(t-1\rangle}, x^{(t)}\right]+b_{c}\right)$
340 |
341 | $\Gamma_{u}=\sigma\left(\omega_{n}\left[a^{(t-1\rangle}, x^{(t\rangle}\right]+b_{u}\right)$
342 |
343 | $\Gamma_{f}=\sigma\left(\omega_{t}\left[a^{(t-1)}, x^{\langle t\rangle}\right]+b_{f}\right)$
344 |
345 | $\Gamma_{o}=-\left(\omega_{o}\left[a^{(t-1)}, x^{(t)}\right]+b_{o}\right)$
346 |
347 | $c^{(t\rangle}=\Gamma_{u} \times \tilde{c}^{\langle t\rangle}+\Gamma_{f} * c^{\langle t-1\rangle}$
348 |
349 | $a^{\langle t\rangle}=\Gamma_{o} * c^{\langle t\rangle}$
350 |
351 | LSTM中我们不再有和GRU相同的的情况,在GRU更新门控制公式中,我们将用不同的项来代替它们,要用$\Gamma_{f}$来取代GRU中的$1-\Gamma_{u}$,这个$\Gamma_{f}$也被称为遗忘门,也就是说,和GRU由两个门控制相比,LSTM的最大区别就在于其有三个门,分别为更新门和遗忘门以及输出门来进行控制。($\Gamma_{o}$是输出门)。
352 |
353 | #### 14.10.2LSTM单元图
354 |
355 | 
356 |
357 | 多个LSTM单元连接图:
358 |
359 | 
360 |
361 | 如上图所示,把多个多个LSTM单元连接起来,就是把它们按时间次序连起来,每一个单元的输出了上一个时间的a,会作为下一个时间步的输入,c也是同理。这条线显示了只要你正确地设置了遗忘门和更新门,LSTM是相当容易把的值$c^{\langle t\rangle}$(上图编号11所示)一直往下传递到右边。这就是为什么***\*LSTM\****和***\*GRU\****非常擅长于长时间记忆某个值,对于存在记忆细胞中的某个值,即使经过很长很长的时间步。
362 |
363 | 这里和一般使用的版本会有些不同,最常用的版本可能是门值不仅取决于$a^{\langle t\rangle-1}$和$x^{\langle t\rangle}$有时候也可以偷窥一下$c^{\langle t\rangle-1}$的值(上图编号13所示),这叫做"窥视孔连接”)。偷窥孔连接其实意思就是门值不仅取决于$a^{\langle t\rangle-1}$和$x^{\langle t\rangle}$,也取决于上一个记忆细胞的$c^{\langle t\rangle-1}$,然后“偷窥孔连接”就可以结合这三个门来计算了。
364 |
365 | 总的来说,GRU比LSTM少一个门,更加简单,而LSTM则由于有三个门而更加强大和灵活。
366 |
367 |
368 |
369 |
370 |
371 | ### 14.11 双向循环神经网络(Bidirectional RNN):
372 |
373 | #### 14.11.1 BRNN作用
374 |
375 | 这个模型可以让你在序列的某点处不仅可以获取之前的信息,还可以获取未来的信息
376 |
377 | #### 14.11.2 BRNN原理
378 |
379 | 如下图所示,我们需要对下列语句进行分析
380 |
381 | 
382 |
383 | 在判断第三个词Teddy是不是人名的一部分时,光看句子前面部分是不够的,为了判断$y^{\langle t\rangle}$是0还是1,除了前3个单词,你还需要更多的信息,因为根据前3个单词无法判断他们说的是Teddy,还是其他的词。
384 |
385 | 为了解决上述问题,需要使用双向RNN进行实现。
386 |
387 | 
388 |
389 | 如上图所示,我们用四个输入或者说一个只有4个单词的句子,这样输入只有4个,$x^{\langle 1\rangle}$到$x^{\langle 4\rangle}$。从这里开始的这个网络会有一个前向的循环单元叫做$a^{\langle 1\rangle}$到$a^{\langle 4\rangle}$,我在这上面加个向右的箭头来表示前向的循环单元,并且他们互相连接。这四个循环单元都有一个输入进去,得到预测的$y^{\langle 1\rangle}$到$y^{\langle 4\rangle}$。
390 |
391 | 
392 |
393 | 我们想要增加一个反向循环层,这里有个左箭头代表反向连接,如图中绿色的$a^{\langle 1\rangle}$到$a^{\langle 4\rangle}$,所以这里的左箭头代表反向连接。同样,我们把网络这样向上连接,这个a反向连接就依次反向向前连。这样,这个网络就构成了一个无环图。
394 |
395 | 给定一个输入序列,$x^{\langle 1\rangle}$到$x^{\langle 4\rangle}$,这个序列从左到由计算$a^{\langle 1\rangle}$到$a^{\langle 4\rangle}$。而反向序列从右到左反向进行。你计算的是网络激活值,这不是反向,而是前向的传播,而图中这个前向传播一部分计算是从左到右,一部分计算是从右到左。把所有这些激活值都计算完了就可以计算预测结果了。
396 |
397 | 
398 |
399 | 举个例子,为了预测结果,你的网络会有如$\hat{y}^{}, \hat{y}^{}=g\left(W_{g}\left[\vec{a}^{}, \bar{a}^{}\right]+b_{y}\right)$。在结合了左右两个方法的预测值带入到前面的式子当中,即可得到预测结果(即对$y^{\langle t\rangle}$的计算方式结合了左右两个方向运算而来的$a^{\langle t\rangle}$)。
400 |
401 | 这就是双向循环神经网络,并且这些基本单元不仅仅是标准***\*RNN\****单元,也可以是***\*GRU\****单元或者***\*LSTM\****单元。
402 |
403 |
404 |
405 | ### 14.12 深层循环神经网络(Deep RNNs)
406 |
407 | 我们首先对一个简单的单元进行分析。
408 |
409 | 一个标准的神经网络,首先是输入x,然后堆叠上隐含层,所以这里应该有激活值,比如说第一层是$a^{\langle 1\rangle}$,接着堆 叠上下一层,激活值$a^{\langle 2\rangle}$,可以再加一层,$a^{\langle 3\rangle}$然后得到预测值$\hat{y}$。
410 |
411 | 
412 |
413 | 深层神经网络也是同理,只是多个单元的连接来进行实现,具体如下图所示:
414 |
415 | 
416 |
417 | 这是我们一直见到的标准的RNN(上图边框中),这里的符号有点不同,不再用原来的$a^{\langle 0\rangle}$表示0时刻的激活值了,而是用$a^{\langle 1\rangle}$来表示第一层,所以我们现在用$a^{[l]\langle t\rangle}$,来表示第l层的激活值,这个表示第t个时间点,如上图所示,构建了三层隐层,并且堆叠在一起,进而得到了这个新的网络。
418 |
419 | 对于各个节点都有一个算法进行计算,我们看个具体的例子,看看$a^{[2]\langle 3\rangle}$这个值(上图编号5所示)是怎么算的,激活值$a^{[2]\langle 3\rangle}$有两个输入,一个是从下面过来的输入(上图编号6所示),还有一个是从左边过来的输入(上图编号7所示),$a^{[2]<3>}=g\left(\omega_{a}^{[2]}\left[a^{[2]<2>}, a^{[1]<3>}\right]+b_{a}^{[2]}\right)$这就是这个激活值的计算方法。参数w和b则是这一层的参数。
420 |
421 | 你可能见过很深的网络,甚至于100层深,而对于RNN来说,有三层就已经不少了。由于时间的维度,RNN网络会变得相当大,即使只有很少的几层,很少会看到这种网络堆叠到100层。但有一种会容易见到,就是在每一个上面堆叠循环层,把输出去掉,然后换成一些深的层,这些层并不水平连接,只是一个深层的网络,来分别预测各个y的值,这几个深层网络没有水平方向上的连接。
422 |
423 | 我们前面所说的单元,没必要非是标准的RNN,最简单的RNN模型,也可以是***\*GRU\****单元或者***\*LSTM\****单元,并且,你也可以构建深层的双向RNN网络。由于深层的RNN训练需要很多计算资源,需要很长的时间,尽管看起来没有多少循环层,这个也就是在时间上连接了三个深层的循环层,你看不到多少深层的循环层,不像卷积神经网络一样有大量的隐含层。
424 |
425 |
426 |
427 | 补充:
428 |
429 | seq 2 seq:https://www.jianshu.com/p/b2b95f945a98
430 |
431 | bert:https://zhuanlan.zhihu.com/p/48612853
432 |
433 | transformer:https://www.jianshu.com/p/923c8b489604
434 |
435 | code 2 seq:https://zhuanlan.zhihu.com/p/301058441?utm_source=wechat_session
436 |
437 | ALBERT(albert) :https://blog.csdn.net/u012526436/article/details/101924049
438 |
439 |
--------------------------------------------------------------------------------
/15 自然语言处理与词嵌入.md:
--------------------------------------------------------------------------------
1 | ### 15.1 词汇表征
2 |
3 | 在前面学习的内容中,我们表征词汇是直接使用英文单词来进行表征的,但是对于计算机来说,是无法直接认识单词的。为了让计算机能够能更好地理解我们的语言,建立更好的语言模型,我们需要将词汇进行表征。
4 |
5 | #### 15.1.1 词嵌入
6 |
7 | 词嵌入(Word Embedding)是一种将文本中的词转换成数字向量的方法,为了使用标准机器学习算法来对它们进行分析,就需要把这些被转换成数字的向量以数字形式作为输入。词嵌入过程就是把一个维数为所有词数量的高维空间嵌入到一个维数低得多的连续向量空间中,每个单词或词组被映射为实数域上的向量,词嵌入的结果就生成了词向量。
8 |
9 | 词向量是各种NLP任务中文本向量化的首选技术,如词性标注、命名实体识别、文本分类、文档聚类、情感分析、文档生成、问答系统等。引自[词嵌入 - 简书 ](https://www.jianshu.com/p/2fbd0dde8804)。
10 |
11 | #### 15.1.2 one-hot 表征
12 |
13 | 在前面的一节课程中,已经使用过了one-hot表征的方式对模型字典中的单词进行表征,对应单词的位置用1表示,其余位置用0表示,如下图所示:
14 |
15 |
283 |
284 | 由此,我们已经有了一些进展,**从检测简单的事物,比如说,第一层的边缘,第二层的质地,到深层的复杂物体**,更直观地了解卷积神经网络的浅层和深层是如何计算的。
285 |
286 | ### 13.8 代价函数
287 |
288 | #### 13.8.1 代价函数的作用
289 |
290 | 神经风格迁移系统用代价函数来评判某个生成图像的好坏。
291 |
292 | #### 13.8.2 代价函数的定义
293 |
294 | $$
295 | J(G)=αJ_{content}(C,G)+βJ_{style}(S,G)
296 | $$
297 |
298 | 其中,$J_{content}(C,G)$称为内容代价函数,用来衡量生成图片G的内容与图片C的内容有多相似;$J_{style}(S,G)$是风格代价函数,用来衡量图片G的风格与图片S的风格的相似度。超参数 $\alpha$ 和 $\beta$ 确定内容代价和风格代价两者之间的权重。
299 |
300 | #### 13.8.2 如何最小化代价函数
301 |
302 | 用梯度下降法来最小化代价函数:
303 | $$
304 | G=G-\frac{\partial}{\partial G}J(G)
305 | $$
306 | 实际上每次更新的是图像G的像素值。举个例子:
307 |
308 | 
309 |
310 | 要取上图中左边图片的内容和右边图片的风格生成图像G。随机初始化的生成图像如下图①所示,是一张随机选取像素的白噪声图;接下来运行梯度下降算法,最小化代价函数$J(G)$,逐步处理像素,逐步得到越来越像用风格图片的风格画出来的内容图片(下图中第②-④张图片)。
311 |
312 | 
313 |
314 | ### 13.9 内容代价函数
315 |
316 | #### 13.9.1 定义
317 |
318 | 内容代价函数:Content cost function,衡量内容图片和生成图片在内容上的相似度。
319 |
320 | 假如用隐含层 $l$ 来计算内容代价,$l$ 一般是选在网络的中间层,不会选的太浅或太深。然后用一个预训练的卷积模型,$a^{[l](C)}$和$a^{[l](G)}$分别代表内容图片C和生成图片G的 $l$ 层的激活函数值。如果这两个激活值相似,则这两张图片的内容相似。故将内容代价函数定义为两个激活值的不同或相似程度,即其差值的平方:
321 | $$
322 | J_{content}(C,G)=\frac{1}{2}||a^{[l](C)}-a^{[l](G)}||^2
323 | $$
324 | 其中,$\frac{1}{2}$ 是对其进行归一化,可以不加也可以是其他值,因为在整体代价函数中还可由超参数 $\alpha$ 调整内容代价函数的权重。
325 |
326 | ### 13.10 风格代价函数
327 |
328 | 风格代价函数:Style cost function,衡量风格图片和生成图片在风格上的相似度。
329 |
330 | #### 13.10.1 图像风格的定义
331 |
332 | 如下图所示,假如有这么一张图片输入卷积网络,对于某一隐藏层 $l$ ,图片的风格可以定义为 $l$ 层中各个通道之间激活项的相关系数。
333 |
334 | 
335 |
336 | 具体解释:
337 |
338 | 将 $l$ 层的激活项取出,是一个 $n_H \times n_W \times n_C$ 的三维激活项,将其不同通道渲染成不同的颜色,每个通道对应一个神经元,如下图所示,以前两个通道为例,红色通道对应的是第二个神经元(红色方框),能找出图片中的特定位置是否含有垂线纹理,黄色通道对应第四个神经元(黄色方框),可以粗略找出橙色区域,则这两个通道的相关系数指的就是图片中某处出现这种垂直纹理时该处又同时是橙色的可能性。若采用相关系数来描述通道的风格,则需测量生成图像中第一个通道是否与第二个通道相关,从而得知在生成图像中垂直纹理和橙色同时出现或不同时出现的概率,这样就能够测量生成图像的风格与输入的风格图像的相似程度。
339 |
340 | 
341 |
342 |
343 |
344 | #### 13.10.2 风格矩阵
345 |
346 | 对于风格图像与生成图像,需要计算其风格矩阵,说得更具体一点就是用 $l$ 层来测量风格。
347 |
348 | 假设 $a^{[l]}_{i,j,k}$ 为隐藏层 $l$ 中 $(i,j,k)$ 位置的激活项,i、j、k分别代表该位置的高度、宽度以及对应的通道数。现在要计算一个关于 $l$ 层和风格图像的矩阵 $G^{[l][S]}$ ( $l$ 表示层数,$S$ 表示风格图像),由于有 $n_c$ 个通道,故 $G^{[l][S]}$ 是一个 $n_c \times n_c$ 的矩阵,以便计算 $k$ 通道和 $k′$ 通道中每一对激活项的相关系数, $k$ 和 $k′$ 的取值范围则为$1,2,...,n_c$,
349 | 设这个关于 $l$ 层和风格图像的矩阵 $G^{[l][S]}$ 高度和宽度都是 $l$ 层的通道数,在这个矩阵中 $k$ 和 $k′$ 元素被用来描述 $k$ 通道和 $k′$ 通道之间的相关系数,则风格图像的风格矩阵是:
350 | $$
351 | G^{[l](S)}_{kk'}=\sum_i^{n^{[l]}_H} \sum_j^{n^{[l]}_W} a_{ijk}^{[l](S)}a_{ijk'}^{[l](S)}
352 | $$
353 | 其中,符号 $i$、$j$ 表示下界,对 $i$、$j$、$k$ 位置的激活项 $a_{ijk}^{[l](S)}$,乘以同样位置即 $i$、$j$、$k'$ 位置的激活项 $a_{ijk'}^{[l](S)}$,然后 $i$、$j$ 分别加到 $l$ 层的高度和宽度,即 $n^{[l]}_H$ 和 $n^{[l]}_W$,将这些不同位置的激活项都加起来即可得到风格矩阵。严格来说,这个公式是一种非标准的互相关函数,因为没有将其减去平均数,而是将它们直接相乘。
354 |
355 | 对生成图像做同样的操作即可得到生成图像的风格矩阵:
356 | $$
357 | G^{[l](G)}_{kk'}=\sum_i^{n^{[l]}_H} \sum_j^{n^{[l]}_W} a_{ijk}^{[l](G)}a_{ijk'}^{[l](G)}
358 | $$
359 |
360 | 之所以用大写字母 $G$ 来代表这些风格矩阵,是因为在线性代数中这种矩阵有时也叫 Gram 矩阵,但在这里只把它们叫做风格矩阵。
361 |
362 | 如果两个通道中的激活项数值都很大,那么 $G^{[l]}_{kk'}$ 也会很大,对应地,如果它们不相关那么 $G^{[l]}_{kk'}$ 就会很小。
363 |
364 | 下图形象地展示了风格矩阵的形成过程:
365 |
366 | 
367 |
368 | #### 13.10.3 风格代价函数
369 |
370 | 如果将 $S$ 和 $G$ 代入到风格代价函数中去计算将得到这两个矩阵之间的误差,实际上是计算两个矩阵对应元素相减的平方的和,由于 $G^{[l][S]}$ 和 $G^{[l][G]}$ 是矩阵,故加下标表 Frobenius 范数:
371 | $$
372 | J^{[l]}_{style}(S,G)=||G^{[l][S]}-G^{[l][G]}||^2_F
373 | $$
374 | 把这个式子展开,从 $k$ 和 $k′$ 开始作差,然后把得到的结果都加起来,即得到对 $l$ 层定义的风格代价函数:
375 | $$
376 | J^{[l]}_{style}(S,G)=\frac {1}{(2n_H^{[l]}n_W^{[l]}n_c^{[l]})^2} \sum_k \sum_{k'}(G^{[l](S)}_{kk'}-G^{[l](G)}_{kk'})^2
377 | $$
378 | 其中,使用了一个归一化常数$\frac {1}{(2n_H^{[l]}n_W^{[l]}n_c^{[l]})^2}$ ,但是一般情况下不用写这么多,只要将风格代价函数乘以一个超参数 $\beta$ 就行。
379 |
380 | 实际上,如果对各层都使用风格代价函数,会让结果变得更好。如果要对各层都使用风格代价函数,把各个层的结果(各层的风格代价函数)都加起来,就能定义它们全体了:
381 | $$
382 | J_{style}(S,G)=\sum_l \lambda^{[l]}J^{[l]}_{style}(S,G)
383 | $$
384 | 其中,需要对每个层定义权重,用 $\lambda^{[l]}$ 来表示,这样将能够在神经网络中使用不同的层,包括之前的一些可以测量类似边缘这样的低级特征的层以及之后的一些能测量高级特征的层,使得我们的神经网络在计算风格时能够同时考虑到这些低级和高级特征的相关系数。这样,在基础的训练中定义超参数时,可以尽可能地得到更合理的选择。
385 |
386 | 为了把这些东西封装起来,现在定义全体代价函数:
387 | $$
388 | J(G)=αJ_{content}(C,G)+βJ_{style}(S,G)
389 | $$
390 | 之后用梯度下降法,或者更复杂的优化算法来找到一个合适的图像 $G$,并计算 $J(G)$ 的最小值,从而将能够得到非常好看漂亮的结果。
391 |
392 | #### 13.10.4 用GAN做风格迁移
393 |
394 | GAN是解决风格迁移的深度学习方法。
395 |
396 | GAN由生成网络G和对抗网络D组成,G用于接收一个噪声z,从而生成图片G(z);D是一个判别网络,判别一张图片x是不是“真的”我们所需得到的目的图片或者是由G生成的(此时图片是“假的”),即D(x)。
397 | 生成网络G和对抗网络D在训练时候互为动态的博弈过程。
398 | 损失函数:
399 |
400 | 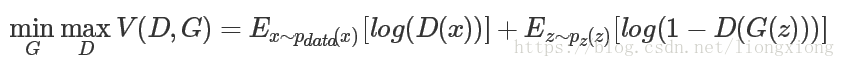
401 |
402 | 其中,x为真实图片,z表示输入G的随机噪声。
403 | GAN之所以能产生对抗博弈的训练过程和效果是因为GAN把训练过程分为了两个部分:
404 |
405 | 优化D:
406 | 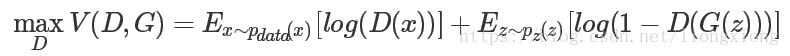
407 |
408 | 优化G:
409 |
410 | 
411 |
412 | 将D和G用CNN来表达就是适用于图像处理的DCGAN了。
413 | 更多方法详见“https://blog.csdn.net/liongxiong/article/details/80875885”。
414 |
415 | ### 13.11 一维到三维的推广
416 |
417 | #### 13.11.1 2D卷积
418 |
419 | 假设输入图像为14×14的2维图像,使用5×5的2维过滤器进行卷积,得到 10×10的二维图像,如下图所示:
420 | 
421 |
422 | #### 13.11.2 1D卷积
423 |
424 | 举个例子,下图左边是一个EKG信号(心电图),当在胸部放一个电极,电极透过胸部测量心脏带来的微弱电流,每个峰值对应一次心跳。如果想用EKG信号,就需要处理1维数据。因为EKG信号由时间序列对应的每个瞬间的电压组成,是一维的,输入的尺寸是14而不是14×14,就需要用一维过滤进行卷积如一个5的过滤器,而不是5×5。最终的输出尺寸是10。
425 | 
426 |
427 | #### 13.11.3 3D卷积
428 |
429 | 
430 | 如上图所示,假设现在输入是具有长度、宽度和高度的三维数据,例如14×14×14,使用5×5×5的过滤器进行卷积,输出将为10×10×10。某种程度上3D数据也可以使用3D confident学习。过滤器实现的功能是用输入的3D数据进行特征识别。
431 |
432 | 医疗检查是3D卷积的一个实例,如下图所示的CT扫描,用X光输出身体的3D模型:
433 |
434 | 
--------------------------------------------------------------------------------
/14 序列模型.md:
--------------------------------------------------------------------------------
1 | # 14序列模型
2 |
3 | ### 14.1 为什么选择序列模型
4 |
5 | #### 14.1.1 序列模型应用领域
6 |
7 | 序列模型广泛应用于语音识别,音乐生成,情感分析,DNA序列分析,机器翻译,视频行为识别,命名实体识别等众多领域。
8 |
9 | - 语音识别:将输入的语音信号直接输出相应的语音文本信息。无论是语音信号还是文本信息均是序列数据。
10 |
11 | - 音乐生成:生成音乐乐谱。只有输出的音乐乐谱是序列数据,输入可以是空或者一个整数。
12 |
13 | - 情感分类:将输入的评论句子转换为相应的等级或评分。输入是一个序列,输出则是一个单独的类别。
14 |
15 | - DNA序列分析:输入的DNA序列,找到匹配的蛋白质序列。
16 |
17 | - 机器翻译:两种不同语言之间的翻译。输入和输出均为序列数据。
18 |
19 | - 视频行为识别:识别输入的视频帧序列中的人物行为。
20 |
21 | - 命名实体识别:从输入的句子中识别实体的名字。
22 |
23 | 
24 |
25 | #### 14.1.2 输入x和输出y的关系
26 |
27 | 上面那些问题可以看成使用标签数据$(x,y)$作为训练集的监督学习,但是输入与输出不一定都是序列,对应关系有非常多的组合,比如一对一,多对多,一对多,多对一,多对多(个数不同)等情况来针对不同的应用。
28 |
29 | ### 14.2 数学符号
30 |
31 | #### 14.2.1 符号含义
32 |
33 | - $x^{}$ 表示输入数据 x 中的第 t 个符号(eg:输入的英文句子中的单词)
34 | - $y^{}$ 表示输出 y 中的第 t 个符号(单词)
35 | - ${x^{(i)}}$ 表示第 i 个输入样本中的第 t 个符号(单词)
36 | - ${y^{(i)}}$ 表示第 i 个输出样本中的第 t 个符号(单词)
37 | - $T_x$ 表示输入 x 的长度
38 | - $T_y$ 表示输出 y 的长度
39 | - $T_x^{(i)}$ 表示第 i 个训练样本的输入序列长度
40 | - $T_y^{(i)}$ 表示第 i 个训练样本的输出序列长度
41 |
42 | #### 14.2.2 字典编码
43 |
44 | - 利用一个字(词)典向量,通常有3-5万个字(词),来表示$x^{}$的符号含义
45 |
46 | - 可以利用one-hot编码表示词典里的每个单词,构造一个输入的序列中每个单词$x^{}$的向量
47 |
48 | - 与字典向量大小一致(3-5万行)
49 | - $x^{}$代表的单词对应到字典里的单词,在对应索引位置(行数)是1,其余位置都是0。比如“and”在词典里排第367,所以相应的$x^{}$就是第367行是1,其余值都是0的向量。
50 | - 如果单词不在字典里,则创造一个新的“Unknow Word”伪单词,用<**UNK**>作为标记。
51 |
52 |
53 | ### 14.3 循环神经网络模型
54 |
55 | #### 14.3.1 为什么不用普通神经网络
56 |
57 | 试想如果将输入拆成每个字的 One-Hot 编码输入传统的深度神经网络中,经过一些隐藏层的计算得到输出 Y。
58 |
59 | 存在的问题:
60 |
61 | - 输入和输出数据在不同的例子中可以有不相等的长度
62 |
63 | - 不能共享从文本不同位置所学习到的特征:能学习到“and”在$x^{<1>}$位置的普通神经网络不能识别“and”在$x^{<4>}$时的情况。
64 |
65 | - 参数数量过多
66 |
67 | 循环神经网络可以解决以上问题
68 |
69 | #### 14.3.2 循环神经网络
70 |
71 | 循环神经网络,从左到右一个单词计算一步,每一步的计算不仅来自这一步的输入,也来自上一步的激活函数值。
72 |
73 | 
74 |
75 | - 最左侧第一层假设了一个来自第零层的激活值向量(通常设计为零向量或随机向量)
76 | - 有的研究论文上将循环神经网络的结构写成图片右边的形式,其和左边的形式是一致的。
77 |
78 | 循环神经网络从左到右扫描数据,同时共享每个时间步的参数。
79 |
80 | - $W_{ax}$ 管理从输入$x^{}$到隐藏层连接的一系列参数
81 | - $W_{aa}$ 管理激活值$a^{}$到隐藏层连接的一系列参数
82 | - $W_{ya}$ 管理隐藏层到输出结果 $y$ 连接的一系列参数
83 | - 每个时间步都使用相同的 $W_{ax}$ ,$W_{aa}$ ,$W_{ya}$
84 |
85 | #### 14.3.3 循环神经网络的前向传播
86 |
87 | 
88 |
89 | 如图,首先输入$a^{<0>}$,接着是前向传播过程,先计算$a^{<1>}$,再计算$y^{<1>}$
90 |
91 | $$
92 | \begin{array}{c}a^{<1>}=g_1\left(W_{a a} a^{<0>}+W_{a x} x^{<1>}+b_{a}\right) \\y^{<1>}=g_2\left(W_{y a} a^{<1>}+b_{y}\right)\end{array}
93 | $$
94 | 计算每步的激活函数 a 通常为**Tanh** ,也可由输出判断改用**ReLu**,**sigmoid**(二分类),**softmax**(k分类)
95 |
96 | 在 t 时刻:
97 |
98 | $$
99 | \begin{array}{c}
100 | a^{}=g\left(W_{a a} a^{}+W_{a x} x^{}+b_{a}\right) \\
101 | y^{}=g\left(W_{y a} a^{}+b_{y}\right)
102 | \end{array}
103 | $$
104 |
105 | > 1. 每一步都有一个激活函数 $a^t$ 和一个输出函数 $y^{}$
106 | > 2. 激活函数$a^t$来自于输入 $x^t$ 和上一步的激活函数 $a^{t−1}$, 输出函数 $y^{}$ 来自于激活函数 $a^t$ ,因此实现了利用这个序列中之前的所有序列信息来做出预测
107 | > 3. 激活函数或者输出函数都是 $g(WX+b)$ 这一点没有改变
108 | > 4. 参数W,b 的第一个下标表示是激活函数a 的参数还是输出函数 y 的参数, W的第二个下标表示这个参数是用来乘以哪个输入
109 |
110 | #### 14.3.4 前向传播参数的简化
111 |
112 | 下面参数可以精简合并为$WX+b$形式,以便建立更复杂的模型。
113 |
114 | $$
115 | \begin{array}{c}
116 | a^{}=g\left(W_{a}[ a^{}, x^{}]+b_{a}\right) \\
117 | y^{}=g\left(W_{y} a^{}+b_{y}\right)
118 | \end{array}
119 | $$
120 |
121 | 其中 $W_{a}=[W_{a a}:W_{a x}]$ ,表示两个矩阵并列放置,维度为[ len(a) , len(a) + len(x) ]。
122 |
123 | $[ a^{}, x^{}]=\left[\begin{array}{l}
124 | a^{}\\
125 | x^{} \\
126 | \end{array}\right]$,表示建立成一个列向量,维度为[ len(a) + len(x) , 1 ]。
127 |
128 | 这时 $[W_{a a}:W_{a x}]$ 乘以 $\left[\begin{array}{l}
129 | a^{}\\
130 | x^{} \\
131 | \end{array}\right]$ 正好等于 $W_{a a} a^{}+W_{a x} x^{}$。
132 |
133 | 而对$y^{}$简化为:
134 | $$
135 | W_{y}=W_{y a}
136 | $$
137 |
138 |
139 |
140 | ### 14.4 通过时间的反向传播
141 |
142 | #### 14.4.1 序列模型中的反向传播
143 |
144 | 在一些编程框架里实现RNN时,编程框架会自动为我们处理关于RNN的反向传播,但还是有必要粗略的了解一下反向传播在RNN中的实现。
145 |
146 | 如下图的前向传播
147 |
148 | 
149 |
150 | 对于$a^{}$的计算,需要参数$W_{aa}$ ;对于$y^{}$的计算,需要参数$W_{ya}$;与之前的对神经网络的训练相类似,在RNN中,进行反向传播的目的,是为了对这些参数进行更新,直到找到最为合适的参数。
151 |
152 |
153 |
154 | 
155 |
156 | 同样的,如上图,在RNN中实现反向传播仍然需要定义cost function。不同的在于,它需要对于每一个输出的$y^{}$进行概率值的计算,并最终将所有计算得出的$y^{}$进行求和,计算整体的cost function。
157 |
158 |
159 |
160 | 
161 |
162 | 计算出整体的cost function后,再进行求导、梯度下降的方法进行处理,将前向传播的箭头都反过来,最终更新出合适的参数。这就是大致的RNN中反向传播的过程。
163 |
164 |
165 |
166 | #### 14.4.2 反向传播中的损失函数
167 |
168 | 在反向传播中,定义的对于单个输出的cost function为
169 |
170 | $L^{}\left(\hat{y}^{}, y^{}\right)=-y^{} \log \hat{y}^{}-\left(1-y^{}\right) \log \left(1-\hat{y}^{}\right)$
171 |
172 | 称为交叉熵损失函数,用以计算序列中某一个特定的词为某一类别(如名字、地点等)的词的概率,如若计算该词为人名的概率为0.1,则输出0.1.
173 |
174 |
175 |
176 | 对于所有输出的预测值的求和,定义的cost function为
177 |
178 | $L(\hat{y}, y)=\sum_{t=1}^{T_{y}} L^{}\left(\hat{y}^{}, y^{}\right)$
179 |
180 | 即将每一个timestep的输出预测值进行求和。
181 |
182 | ### 14.5 不同类型的循环神经网络
183 |
184 | 以上介绍的,都是当$T_x$和$T_y$ 相同的情况下,RNN的实现。更多时候,$T_x$和$T_y$ 是不同的,面对两者不同时,我们要用不同的RNN模型。个人认为主要的调整在于,在不同的timestep进行输入和输出,以及将一些输出的信息作为输入,作用到下一个单元中。
185 |
186 | 大致如下图
187 |
188 | 
189 |
190 |
191 |
192 | ### 14.6 语言模型和序列生成
193 |
194 | 语言模型是NLP中比较重要的一个模块,它能够计算一句话被翻译成各种不同意思的概率,并选择最大概率的翻译作为正确翻译。
195 |
196 | #### 14.6.1 语言模型的构建
197 |
198 | 构建语言模型,首先需要建立一个足够大的training set,即一个包含很多句子的corpus,然后对corpus中的每句话进行tokenize操作,即将一整句话切分成每一个单词,利用one-hot,将单词转换成词向量。其中,句子结尾可以用符号表示;而对没有出现在corpus中的单词可以用表示。再利用RNN来计算一句话被翻译成具体意思的概率,如下图
199 |
200 | 
201 |
202 | $x^{<1>}$和$a^{<0>}$均为零向量,softmax层会根据$x^{<1>}$和$a^{<0>}$来预测输出$y^{<1>}$,它会计算第一个词分别为字典中的每一个词的概率具体为多少(如预测为“猫”、“狗”的概率分别为多少);而$y^{<2>}$则表示在出现第一个单词的基础上,出现第二个单词的概率,即为条件概率,以此类推,直到计算出出现的概率
203 |
204 | #### 14.6.2 概率计算
205 |
206 | 在softmax层中,计算单个元素的cost function为
207 |
208 | $L^{}\left(\hat{y}^{}, y^{}\right)=-\sum_{i} y_{i}^{} \log \hat{y}_{i}^{}$
209 |
210 | 计算所有元素的cost function为
211 |
212 | $L(\hat{y}, y)=\sum_{t} L^{}\left(\hat{y}^{}, y^{}\right)$
213 |
214 | 计算一句话被翻译正确的概率公式为
215 |
216 | $P\left(y^{<1>}, y^{<2>}, \cdots, y^{}\right)$
217 |
218 | 即对每个元素的cost function进行求和。
219 |
220 | 最后,整个语句出现的概率为语句中所有元素出现的条件概率的乘积,如,某个语句中包含$y^{<1>}$、$y^{<2>}$ 、 $y^{<3>}$,则整个语句出现的概率为
221 |
222 | $P\left(y^{<1>}, y^{<2>}, y^{<3>}\right)=P\left(y^{<1>}\right) \cdot P\left(y^{<2>} \mid y^{<1>}\right) \cdot P\left(y^{<3>} \mid y^{<1>}, y^{<2>}\right)$
223 |
224 |
225 |
226 | ### 14.7 新序列采样
227 |
228 | 在训练完一个序列模型之后,如果想了解这个模型学到了什么,那就可以选择进行一次新序列采样。不过这是非正式做法。
229 |
230 | 新序列采样可以理解为先给模型一个输入,然后从其预测结果中随机选取一个作为下一次的输入;直至满足不再采样的要求,这样就可以得到一连串的字符。这些字符构成一段文本,可以帮你了解你的模型学到了什么。接下来看具体怎么做。
231 |
232 | #### **14.7.1 生成随机语句**
233 |
234 | 首先要理解的是,你的模型会干什么:给定一个单词(也不一定是单词),预测下一个单词是词典中某个单词的概率。
235 |
236 | 1. 采样的第一个时间步,是输入$x^{<1>}=0,a^{<0>}=0$。然后得到输出向量,这个向量表示了词典中每个词出现的概率。然后根据给出的概率,随机选取一个词作为$\hat{y}^{<1>}$。具体实现可以用:
237 |
238 | ```python
239 | y_1 = np.random.choice(dictionary, p=y)
240 | ```
241 |
242 | 其中`y_1`表示$\hat{y}^{<1>}$,`dictionary`表示词典,`p=y`表示词典中的各值以对应`y`中的概率选取。`y`是模型输出的向量。
243 |
244 | 2. 第二个时间步,将$\hat{y}^{<1>}$作为这一步的输入$x^{<2>}$,然后得到预测$\hat{y}^{<2>}$。然后依次类推,重复若干次。
245 |
246 | 3. 当$\hat y$为结束符***EOS***或者已经获得足够的单词后,就可以停止采样了。
247 |
248 | 执行流程大概如图:
249 |
250 | 
251 |
252 | 这样下来,就可以得到由$\hat{y}^{}$组成的一句话或者一段文本了。
253 |
254 | #### **14.7.2 词典为字符与词典为单词的优缺点**
255 |
256 | **基于单词**的词典的优缺点
257 |
258 | * 优点:不会出现不存在的单词;序列很短就能构成句子、段落;
259 | * 缺点:可能出现未知标识***UNK***;字典会很大;
260 |
261 | **基于字符**的词典的优缺点
262 |
263 | * 优点:不会出现未知标识;字典小很多;
264 | * 缺点:可能出现不存在的单词;序列会太多太长,前面的单词会被遗忘;训练成本高昂;
265 |
266 | ### 14.8 带有神经网络的梯度消失
267 |
268 | #### 14.8.1 为什么会梯度消失
269 |
270 | 梯度消失并不只是存在于很深的卷积神经网络中,同样还存在于RNN中——因为RNN其实也可以看成是一个很深的网络,只不过深度由训练样本的长度决定。不过还要意识到,导致RNN能“有很多层”的原因是激活值$a^{}$的传递,所以如果要进行优化也是针对$a^{}$进行。
271 |
272 | 举个例子:对于样本“The **cat**, which already ate ……, **was** full.”,前面的单数**cat**决定了后面用的是**was**,而中间的字符可以任意长。如果想要 RNN 能发现这一点,就需要反向传播时能将**was**处的损失传播到**cat**处。但是实际情况下很可能由于已经传播了很多层(两者间单词过多)而导致梯度消失,最终对**cat**的影响微乎其微。
273 |
274 | 更普遍来说,对于长句子样本,句子前后的关联性会很难被发现、建立起来。
275 |
276 | #### 14.8.2 梯度修剪
277 |
278 | 其实RNN也存在梯度爆炸问题。但是相对于梯度爆炸,梯度消失更难发现。因为梯度消失只会让你的参数基本不变,而不像梯度爆炸会让你的参数出现很多的**NaN**,这意味着数值出现了溢出。
279 |
280 | 而且不同于梯度消失,梯度爆炸解决起来其实更容易一些。解决办法就是**梯度修剪**:
281 |
282 | 观察梯度向量,通过人为设定一个阈值(比较大的数),如果超过了阈值就缩放梯度向量,从而保证梯度不会过大。
283 |
284 | ### 14.9 GRU单元
285 |
286 | 为了解决梯度消失的问题,学者提出了GRU单元(门控循环单元网络)的概念。这个网络能有效解决梯度消失的问题,并且能够使你的神经网络捕获更长的长期依赖。
287 |
288 | #### 14.9.1 GRU单元实现
289 |
290 | 
291 |
292 | 回顾一下RNN单元的工作模式如上。记住公式
293 | $$
294 | a^{}=g\left(W_{a}\left[a^{}, x^{}\right]+b_{a}\right)
295 | $$
296 | 在处理一个句子的时候,如果想要记住一个以前出现过的单词,那就需要一个额外的变量保存:***c***(cell),代表了记忆细胞。记忆细胞负责记忆前面的**cat**是单数还是复数。记 $c^{}$ 为记忆细胞在时间 $t$ 时的取值。对于GRU来说,其实$c^{} = a^{}$。但还是会使用不同的标记,因为在**LSTM**中会有所不同。
297 |
298 | 记忆细胞在更新时,需要考虑是否忘记已经记住了的值并更新为需要记住的值。所以需要先计算候选值
299 | $$
300 | \tilde{c}^{}=\tanh \left(W_{c}\left[c^{}, x^{}\right]+b_{c}\right)
301 | $$
302 | 然后重点来了,GRU真正重要的思想是有一个**更新门**:
303 | $$
304 | \Gamma_{u}=\sigma\left(W_{u}\left[c^{}, x^{}\right]+b_{u}\right)
305 | $$
306 | 这个门的作用在于决定什么时候更新$c^{}$。但是在介绍怎么决定是否更新前,先明白$\Gamma_{u}$的含义:大写希腊字母$\Gamma$很像门,代表门的含义;下标$u$表示 updata 更新;然后计算用的是sigmoid函数,意味着取值处在 (0, 1) 间,并且大概率接近0或1。0/1的含义就很清楚了,可以用来表示更新/不更新。所以$c^{}$的更新公式可以写成:
307 | $$
308 | c^{}=\Gamma_{u} * \tilde{c}^{}+\left(1-\Gamma_{u}\right) * c^{}
309 | $$
310 | 其中的运算符$*$表示逐元素乘法。
311 |
312 | 这就是门的作用,可以决定是否更新记忆细胞。对于 cat 的例子,可以理解为判断是否已经过了要用到 was/were的地方。架构大致如下:
313 |
314 | 
315 |
316 |
317 |
318 | 理解了GRU的思想之后,还有一个完整的版本,会多一个**相关门**:
319 | $$
320 | \Gamma_{r}=\sigma\left(W_{r}\left[c^{}, x^{}\right]+b_{r}\right)
321 | $$
322 | $r$表示相关性(relevance),其作用在于计算候选值$\tilde{c}^{}$与$c^{}$的关联性。这需要更改$\tilde{c}^{}$的计算公式为:
323 | $$
324 | \tilde{c}^{}=\tanh \left(W_{c}\left[\Gamma_{r}*c^{}, x^{}\right]+b_{c}\right)
325 | $$
326 |
327 | #### 14.9.2 工作原理
328 |
329 | 上面只讲了GRU的实现,现在回到我们一开始想要解决的问题:梯度消失。
330 |
331 | $c^{}$的更新公式告诉我们,只有在需要用到这个记忆的时候才可能更新。因此$\Gamma_{u}$会长时间为接近0的数,近乎保证了$c^{}=c^{}$,也因此让梯度消失出现的可能性下降了。
332 |
333 | ### 14.10 长短期记忆(LSTM(long short term memory)unit)
334 |
335 | #### 14.10.1 LSTM用到的公式
336 |
337 | 在GRU的基础上做出如下修改
338 |
339 | $\tilde{c}^{\langle t\rangle}=\tanh \left(\omega_{i}\left[a^{(t-1\rangle}, x^{(t)}\right]+b_{c}\right)$
340 |
341 | $\Gamma_{u}=\sigma\left(\omega_{n}\left[a^{(t-1\rangle}, x^{(t\rangle}\right]+b_{u}\right)$
342 |
343 | $\Gamma_{f}=\sigma\left(\omega_{t}\left[a^{(t-1)}, x^{\langle t\rangle}\right]+b_{f}\right)$
344 |
345 | $\Gamma_{o}=-\left(\omega_{o}\left[a^{(t-1)}, x^{(t)}\right]+b_{o}\right)$
346 |
347 | $c^{(t\rangle}=\Gamma_{u} \times \tilde{c}^{\langle t\rangle}+\Gamma_{f} * c^{\langle t-1\rangle}$
348 |
349 | $a^{\langle t\rangle}=\Gamma_{o} * c^{\langle t\rangle}$
350 |
351 | LSTM中我们不再有和GRU相同的的情况,在GRU更新门控制公式中,我们将用不同的项来代替它们,要用$\Gamma_{f}$来取代GRU中的$1-\Gamma_{u}$,这个$\Gamma_{f}$也被称为遗忘门,也就是说,和GRU由两个门控制相比,LSTM的最大区别就在于其有三个门,分别为更新门和遗忘门以及输出门来进行控制。($\Gamma_{o}$是输出门)。
352 |
353 | #### 14.10.2LSTM单元图
354 |
355 | 
356 |
357 | 多个LSTM单元连接图:
358 |
359 | 
360 |
361 | 如上图所示,把多个多个LSTM单元连接起来,就是把它们按时间次序连起来,每一个单元的输出了上一个时间的a,会作为下一个时间步的输入,c也是同理。这条线显示了只要你正确地设置了遗忘门和更新门,LSTM是相当容易把的值$c^{\langle t\rangle}$(上图编号11所示)一直往下传递到右边。这就是为什么***\*LSTM\****和***\*GRU\****非常擅长于长时间记忆某个值,对于存在记忆细胞中的某个值,即使经过很长很长的时间步。
362 |
363 | 这里和一般使用的版本会有些不同,最常用的版本可能是门值不仅取决于$a^{\langle t\rangle-1}$和$x^{\langle t\rangle}$有时候也可以偷窥一下$c^{\langle t\rangle-1}$的值(上图编号13所示),这叫做"窥视孔连接”)。偷窥孔连接其实意思就是门值不仅取决于$a^{\langle t\rangle-1}$和$x^{\langle t\rangle}$,也取决于上一个记忆细胞的$c^{\langle t\rangle-1}$,然后“偷窥孔连接”就可以结合这三个门来计算了。
364 |
365 | 总的来说,GRU比LSTM少一个门,更加简单,而LSTM则由于有三个门而更加强大和灵活。
366 |
367 |
368 |
369 |
370 |
371 | ### 14.11 双向循环神经网络(Bidirectional RNN):
372 |
373 | #### 14.11.1 BRNN作用
374 |
375 | 这个模型可以让你在序列的某点处不仅可以获取之前的信息,还可以获取未来的信息
376 |
377 | #### 14.11.2 BRNN原理
378 |
379 | 如下图所示,我们需要对下列语句进行分析
380 |
381 | 
382 |
383 | 在判断第三个词Teddy是不是人名的一部分时,光看句子前面部分是不够的,为了判断$y^{\langle t\rangle}$是0还是1,除了前3个单词,你还需要更多的信息,因为根据前3个单词无法判断他们说的是Teddy,还是其他的词。
384 |
385 | 为了解决上述问题,需要使用双向RNN进行实现。
386 |
387 | 
388 |
389 | 如上图所示,我们用四个输入或者说一个只有4个单词的句子,这样输入只有4个,$x^{\langle 1\rangle}$到$x^{\langle 4\rangle}$。从这里开始的这个网络会有一个前向的循环单元叫做$a^{\langle 1\rangle}$到$a^{\langle 4\rangle}$,我在这上面加个向右的箭头来表示前向的循环单元,并且他们互相连接。这四个循环单元都有一个输入进去,得到预测的$y^{\langle 1\rangle}$到$y^{\langle 4\rangle}$。
390 |
391 | 
392 |
393 | 我们想要增加一个反向循环层,这里有个左箭头代表反向连接,如图中绿色的$a^{\langle 1\rangle}$到$a^{\langle 4\rangle}$,所以这里的左箭头代表反向连接。同样,我们把网络这样向上连接,这个a反向连接就依次反向向前连。这样,这个网络就构成了一个无环图。
394 |
395 | 给定一个输入序列,$x^{\langle 1\rangle}$到$x^{\langle 4\rangle}$,这个序列从左到由计算$a^{\langle 1\rangle}$到$a^{\langle 4\rangle}$。而反向序列从右到左反向进行。你计算的是网络激活值,这不是反向,而是前向的传播,而图中这个前向传播一部分计算是从左到右,一部分计算是从右到左。把所有这些激活值都计算完了就可以计算预测结果了。
396 |
397 | 
398 |
399 | 举个例子,为了预测结果,你的网络会有如$\hat{y}^{}, \hat{y}^{}=g\left(W_{g}\left[\vec{a}^{}, \bar{a}^{}\right]+b_{y}\right)$。在结合了左右两个方法的预测值带入到前面的式子当中,即可得到预测结果(即对$y^{\langle t\rangle}$的计算方式结合了左右两个方向运算而来的$a^{\langle t\rangle}$)。
400 |
401 | 这就是双向循环神经网络,并且这些基本单元不仅仅是标准***\*RNN\****单元,也可以是***\*GRU\****单元或者***\*LSTM\****单元。
402 |
403 |
404 |
405 | ### 14.12 深层循环神经网络(Deep RNNs)
406 |
407 | 我们首先对一个简单的单元进行分析。
408 |
409 | 一个标准的神经网络,首先是输入x,然后堆叠上隐含层,所以这里应该有激活值,比如说第一层是$a^{\langle 1\rangle}$,接着堆 叠上下一层,激活值$a^{\langle 2\rangle}$,可以再加一层,$a^{\langle 3\rangle}$然后得到预测值$\hat{y}$。
410 |
411 | 
412 |
413 | 深层神经网络也是同理,只是多个单元的连接来进行实现,具体如下图所示:
414 |
415 | 
416 |
417 | 这是我们一直见到的标准的RNN(上图边框中),这里的符号有点不同,不再用原来的$a^{\langle 0\rangle}$表示0时刻的激活值了,而是用$a^{\langle 1\rangle}$来表示第一层,所以我们现在用$a^{[l]\langle t\rangle}$,来表示第l层的激活值,这个表示第t个时间点,如上图所示,构建了三层隐层,并且堆叠在一起,进而得到了这个新的网络。
418 |
419 | 对于各个节点都有一个算法进行计算,我们看个具体的例子,看看$a^{[2]\langle 3\rangle}$这个值(上图编号5所示)是怎么算的,激活值$a^{[2]\langle 3\rangle}$有两个输入,一个是从下面过来的输入(上图编号6所示),还有一个是从左边过来的输入(上图编号7所示),$a^{[2]<3>}=g\left(\omega_{a}^{[2]}\left[a^{[2]<2>}, a^{[1]<3>}\right]+b_{a}^{[2]}\right)$这就是这个激活值的计算方法。参数w和b则是这一层的参数。
420 |
421 | 你可能见过很深的网络,甚至于100层深,而对于RNN来说,有三层就已经不少了。由于时间的维度,RNN网络会变得相当大,即使只有很少的几层,很少会看到这种网络堆叠到100层。但有一种会容易见到,就是在每一个上面堆叠循环层,把输出去掉,然后换成一些深的层,这些层并不水平连接,只是一个深层的网络,来分别预测各个y的值,这几个深层网络没有水平方向上的连接。
422 |
423 | 我们前面所说的单元,没必要非是标准的RNN,最简单的RNN模型,也可以是***\*GRU\****单元或者***\*LSTM\****单元,并且,你也可以构建深层的双向RNN网络。由于深层的RNN训练需要很多计算资源,需要很长的时间,尽管看起来没有多少循环层,这个也就是在时间上连接了三个深层的循环层,你看不到多少深层的循环层,不像卷积神经网络一样有大量的隐含层。
424 |
425 |
426 |
427 | 补充:
428 |
429 | seq 2 seq:https://www.jianshu.com/p/b2b95f945a98
430 |
431 | bert:https://zhuanlan.zhihu.com/p/48612853
432 |
433 | transformer:https://www.jianshu.com/p/923c8b489604
434 |
435 | code 2 seq:https://zhuanlan.zhihu.com/p/301058441?utm_source=wechat_session
436 |
437 | ALBERT(albert) :https://blog.csdn.net/u012526436/article/details/101924049
438 |
439 |
--------------------------------------------------------------------------------
/15 自然语言处理与词嵌入.md:
--------------------------------------------------------------------------------
1 | ### 15.1 词汇表征
2 |
3 | 在前面学习的内容中,我们表征词汇是直接使用英文单词来进行表征的,但是对于计算机来说,是无法直接认识单词的。为了让计算机能够能更好地理解我们的语言,建立更好的语言模型,我们需要将词汇进行表征。
4 |
5 | #### 15.1.1 词嵌入
6 |
7 | 词嵌入(Word Embedding)是一种将文本中的词转换成数字向量的方法,为了使用标准机器学习算法来对它们进行分析,就需要把这些被转换成数字的向量以数字形式作为输入。词嵌入过程就是把一个维数为所有词数量的高维空间嵌入到一个维数低得多的连续向量空间中,每个单词或词组被映射为实数域上的向量,词嵌入的结果就生成了词向量。
8 |
9 | 词向量是各种NLP任务中文本向量化的首选技术,如词性标注、命名实体识别、文本分类、文档聚类、情感分析、文档生成、问答系统等。引自[词嵌入 - 简书 ](https://www.jianshu.com/p/2fbd0dde8804)。
10 |
11 | #### 15.1.2 one-hot 表征
12 |
13 | 在前面的一节课程中,已经使用过了one-hot表征的方式对模型字典中的单词进行表征,对应单词的位置用1表示,其余位置用0表示,如下图所示:
14 |
15 |  16 |
17 | one-hot表征的缺点:这种方法将每个词孤立起来,使得模型对相关词的泛化能力不强。每个词向量之间的距离都一样,乘积均为0,所以无法获取词与词之间的相似性和关联性。
18 |
19 | #### 15.1.3 特征表征:词嵌入
20 |
21 | 用不同的特征来对各个词汇进行表征,相对与不同的特征,不同的单词均有不同的值。如下例所示:
22 |
23 |
16 |
17 | one-hot表征的缺点:这种方法将每个词孤立起来,使得模型对相关词的泛化能力不强。每个词向量之间的距离都一样,乘积均为0,所以无法获取词与词之间的相似性和关联性。
18 |
19 | #### 15.1.3 特征表征:词嵌入
20 |
21 | 用不同的特征来对各个词汇进行表征,相对与不同的特征,不同的单词均有不同的值。如下例所示:
22 |
23 |  24 |
25 | 这种表征方式使得词与词之间的相似性很容易地表征出来,这样对于不同的单词,模型的泛化性能会好很多。下面是使用t-SNE算法将高维的词向量映射到2维空间,进而对词向量进行可视化,很明显我们可以看出对于相似的词总是聚集在一块儿:
26 |
27 |
24 |
25 | 这种表征方式使得词与词之间的相似性很容易地表征出来,这样对于不同的单词,模型的泛化性能会好很多。下面是使用t-SNE算法将高维的词向量映射到2维空间,进而对词向量进行可视化,很明显我们可以看出对于相似的词总是聚集在一块儿:
26 |
27 |  28 |
29 | #### 15.1.4 编码原则
30 |
31 | 词嵌入本质就是对自然语言的一种编码方式,那自然也需要考虑一些编码原则。下列给出一些常见的编码原则:
32 |
33 | * **最佳编码**:平均编码长度最小,用最少的内存表达相同的内容,尽可能逼近香农极限。比如让出现频率高的编码更短,出现频率低的编码更长。
34 | * **正交**:用多维向量进行编码,且各维相互正交。比如PCA。
35 | * **无偏见**:在词嵌入中,有时候会学到一些带有偏见的知识。因此如何消除这个偏见也是很重要的。
36 |
37 | ### 15.2 使用词嵌入
38 |
39 | Word Embeddings对不同单词进行了实现了特征化的表示,那么如何将这种表示方法应用到自然语言处理的应用中呢?
40 |
41 | #### **15.2.1 名字实体识别的例子:**
42 |
43 | 如下面的一个句子中名字实体的定位识别问题,假如我们有一个比较小的数据集,可能不包含durain(榴莲)和cultivator(培育家)这样的词汇,那么我们就很难从包含这两个词汇的句子中识别名字实体。但是如果我们从网上的其他地方获取了一个学习好的word Embedding,它将告诉我们榴莲是一种水果,并且培育家和农民相似,那么我们就有可能从我们少量的训练集中,归纳出没有见过的词汇中的名字实体。
44 |
45 |
28 |
29 | #### 15.1.4 编码原则
30 |
31 | 词嵌入本质就是对自然语言的一种编码方式,那自然也需要考虑一些编码原则。下列给出一些常见的编码原则:
32 |
33 | * **最佳编码**:平均编码长度最小,用最少的内存表达相同的内容,尽可能逼近香农极限。比如让出现频率高的编码更短,出现频率低的编码更长。
34 | * **正交**:用多维向量进行编码,且各维相互正交。比如PCA。
35 | * **无偏见**:在词嵌入中,有时候会学到一些带有偏见的知识。因此如何消除这个偏见也是很重要的。
36 |
37 | ### 15.2 使用词嵌入
38 |
39 | Word Embeddings对不同单词进行了实现了特征化的表示,那么如何将这种表示方法应用到自然语言处理的应用中呢?
40 |
41 | #### **15.2.1 名字实体识别的例子:**
42 |
43 | 如下面的一个句子中名字实体的定位识别问题,假如我们有一个比较小的数据集,可能不包含durain(榴莲)和cultivator(培育家)这样的词汇,那么我们就很难从包含这两个词汇的句子中识别名字实体。但是如果我们从网上的其他地方获取了一个学习好的word Embedding,它将告诉我们榴莲是一种水果,并且培育家和农民相似,那么我们就有可能从我们少量的训练集中,归纳出没有见过的词汇中的名字实体。
44 |
45 |  46 |
47 | #### **15.2.2 词嵌入的迁移学习:**
48 |
49 | 有了词嵌入,就可以让我们能够使用迁移学习,通过网上大量的无标签的文本中学习到的知识,应用到我们少量文本训练集的任务中。下面是做词嵌入迁移学习的步骤:
50 |
51 | - 第一步:从大量的文本集合中学习word Embeddings(1-100B words),或者从网上下载预训练好的词嵌入模型;
52 | - 第二步:将词嵌入模型迁移到我们小训练集的新任务上;
53 | - 第三步:可选,使用我们新的标记数据对词嵌入模型继续进行微调。
54 |
55 | #### **15.2.3 词嵌入和人脸编码:**
56 |
57 | 词嵌入和人脸编码之间有很奇妙的联系。在人脸识别领域,我们会将人脸图片预编码成不同的编码向量,以表示不同的人脸,进而在识别的过程中使用编码来进行比对识别。词嵌入则和人脸编码有一定的相似性。
58 |
59 |
46 |
47 | #### **15.2.2 词嵌入的迁移学习:**
48 |
49 | 有了词嵌入,就可以让我们能够使用迁移学习,通过网上大量的无标签的文本中学习到的知识,应用到我们少量文本训练集的任务中。下面是做词嵌入迁移学习的步骤:
50 |
51 | - 第一步:从大量的文本集合中学习word Embeddings(1-100B words),或者从网上下载预训练好的词嵌入模型;
52 | - 第二步:将词嵌入模型迁移到我们小训练集的新任务上;
53 | - 第三步:可选,使用我们新的标记数据对词嵌入模型继续进行微调。
54 |
55 | #### **15.2.3 词嵌入和人脸编码:**
56 |
57 | 词嵌入和人脸编码之间有很奇妙的联系。在人脸识别领域,我们会将人脸图片预编码成不同的编码向量,以表示不同的人脸,进而在识别的过程中使用编码来进行比对识别。词嵌入则和人脸编码有一定的相似性。
58 |
59 |  60 |
61 | 但是不同的是,对于人脸识别,我们可以将任意一个没有见过的人脸照片输入到我们构建的网络中,则可输出一个对应的人脸编码。而在词嵌入模型中,所有词汇的编码是在一个固定的词汇表中进行学习单词的编码以及其之间的关系的。
62 |
63 | ### 15.3 词嵌入的特性
64 |
65 | #### **15.3.1 类比推理特性:**
66 |
67 | 词嵌入还有一个重要的特性,它还能够帮助实现类比推理。如下面的例子中,通过不同词向量之间的相减计算,可以发现不同词之间的类比关系,man——woman、king——queen,如下图所示:
68 |
69 |
60 |
61 | 但是不同的是,对于人脸识别,我们可以将任意一个没有见过的人脸照片输入到我们构建的网络中,则可输出一个对应的人脸编码。而在词嵌入模型中,所有词汇的编码是在一个固定的词汇表中进行学习单词的编码以及其之间的关系的。
62 |
63 | ### 15.3 词嵌入的特性
64 |
65 | #### **15.3.1 类比推理特性:**
66 |
67 | 词嵌入还有一个重要的特性,它还能够帮助实现类比推理。如下面的例子中,通过不同词向量之间的相减计算,可以发现不同词之间的类比关系,man——woman、king——queen,如下图所示:
68 |
69 |  70 |
71 | 这种思想帮助研究者们对词嵌入建立了更加深刻的理解和认识。
72 |
73 | 计算词与词之间的相似度,实际上是在多维空间中,寻找词向量之间各个维度的距离相似度。
74 |
75 |
70 |
71 | 这种思想帮助研究者们对词嵌入建立了更加深刻的理解和认识。
72 |
73 | 计算词与词之间的相似度,实际上是在多维空间中,寻找词向量之间各个维度的距离相似度。
74 |
75 |  76 |
77 | #### **15.3.2 相似度函数:**
78 |
79 | - 曼哈顿距离(Manhattan Distance)
80 |
81 | 顾名思义,在曼哈顿街区要从一个十字路口开车到另一个十字路口,驾驶距离显然不是两点间的直线距离。这个实际驾驶距离就是“曼哈顿距离”。曼哈顿距离也称为“城市街区距离”(City Block distance)。
82 |
83 | 
84 |
85 | * 二维平面两点a(x1,y1)与b(x2,y2)间的曼哈顿距离:
86 |
87 | $$
88 | d_{12}=\left|x_{1}-x_{2}\right|+\left|y_{1}-y_{2}\right|
89 | $$
90 |
91 | - n维空间点a(x11,x12,…,x1n)与b(x21,x22,…,x2n)的曼哈顿距离:
92 | $$
93 | \mathrm{d}_{12}=\sum_{k=1}^{n}\left|\mathrm{x}_{1 k}-x_{2 k}\right|
94 | $$
95 |
96 |
97 | - 切比雪夫距离 (Chebyshev Distance)
98 |
99 | 国际象棋中,国王可以直行、横行、斜行,所以国王走一步可以移动到相邻8个方格中的任意一个。国王从格子(x1,y1)走到格子(x2,y2)最少需要多少步?这个距离就叫切比雪夫距离。
100 |
101 | 
102 |
103 | * 二维平面两点a(x1,y1)与b(x2,y2)间的切比雪夫距离:
104 | $$
105 | d_{12}=\max \left(\left|x_{1}-x_{2}\right|,\left|y_{1}-y_{2}\right|\right)
106 | $$
107 |
108 |
109 | - n维空间点a(x11,x12,…,x1n)与b(x21,x22,…,x2n)的切比雪夫距离:
110 | $$
111 | d_{12}=\max _{i}\left(\left|x_{1 i}-x_{2 i}\right|\right)
112 | $$
113 |
114 |
115 | - 欧氏距离
116 |
117 | * 二维平面上两点a(x1,y1)与b(x2,y2)间的欧氏距离(拓展到n维同理)
118 | $$
119 | d_{a b}=\sqrt{\left(x_{1}-x_{2}\right)^{2}}
120 | $$
121 |
122 |
123 | 两个n维向量a(x11,x12,…,x1n)与 b(x21,x22,…,x2n)间的欧氏距离
124 | $$
125 | d_{a b}=\sqrt{\sum_{k=1}^{n}\left(x_{1 k}-x_{2 k}\right)^{2}}
126 | $$
127 |
128 | * 向量运算的形式:
129 |
130 | $$
131 | d_{a b}=\sqrt{(a-b)(a-b)^{T}}
132 | $$
133 |
134 | - 余弦相似度函数(Cosine similarity)
135 |
136 | 余弦相似度,又称为余弦相似性,是通过计算两个向量的夹角余弦值来评估他们的相似度。余弦相似度将向量根据坐标值,绘制到向量空间中,如最常见的二维空间。
137 |
138 | 余弦相似度衡量的是2个向量间的夹角大小,通过夹角的余弦值表示结果,因此2个向量的余弦相似度为:
139 | $$
140 | \cos \theta=\frac{A \cdot B}{\|A\| *\|B\|}
141 | $$
142 | 分子为向量A与向量B的点乘,分母为二者各自的L2相乘,即将所有维度值的平方相加后开方。 余弦相似度的取值为[-1,1],值越大表示越相似。
143 |
144 |
76 |
77 | #### **15.3.2 相似度函数:**
78 |
79 | - 曼哈顿距离(Manhattan Distance)
80 |
81 | 顾名思义,在曼哈顿街区要从一个十字路口开车到另一个十字路口,驾驶距离显然不是两点间的直线距离。这个实际驾驶距离就是“曼哈顿距离”。曼哈顿距离也称为“城市街区距离”(City Block distance)。
82 |
83 | 
84 |
85 | * 二维平面两点a(x1,y1)与b(x2,y2)间的曼哈顿距离:
86 |
87 | $$
88 | d_{12}=\left|x_{1}-x_{2}\right|+\left|y_{1}-y_{2}\right|
89 | $$
90 |
91 | - n维空间点a(x11,x12,…,x1n)与b(x21,x22,…,x2n)的曼哈顿距离:
92 | $$
93 | \mathrm{d}_{12}=\sum_{k=1}^{n}\left|\mathrm{x}_{1 k}-x_{2 k}\right|
94 | $$
95 |
96 |
97 | - 切比雪夫距离 (Chebyshev Distance)
98 |
99 | 国际象棋中,国王可以直行、横行、斜行,所以国王走一步可以移动到相邻8个方格中的任意一个。国王从格子(x1,y1)走到格子(x2,y2)最少需要多少步?这个距离就叫切比雪夫距离。
100 |
101 | 
102 |
103 | * 二维平面两点a(x1,y1)与b(x2,y2)间的切比雪夫距离:
104 | $$
105 | d_{12}=\max \left(\left|x_{1}-x_{2}\right|,\left|y_{1}-y_{2}\right|\right)
106 | $$
107 |
108 |
109 | - n维空间点a(x11,x12,…,x1n)与b(x21,x22,…,x2n)的切比雪夫距离:
110 | $$
111 | d_{12}=\max _{i}\left(\left|x_{1 i}-x_{2 i}\right|\right)
112 | $$
113 |
114 |
115 | - 欧氏距离
116 |
117 | * 二维平面上两点a(x1,y1)与b(x2,y2)间的欧氏距离(拓展到n维同理)
118 | $$
119 | d_{a b}=\sqrt{\left(x_{1}-x_{2}\right)^{2}}
120 | $$
121 |
122 |
123 | 两个n维向量a(x11,x12,…,x1n)与 b(x21,x22,…,x2n)间的欧氏距离
124 | $$
125 | d_{a b}=\sqrt{\sum_{k=1}^{n}\left(x_{1 k}-x_{2 k}\right)^{2}}
126 | $$
127 |
128 | * 向量运算的形式:
129 |
130 | $$
131 | d_{a b}=\sqrt{(a-b)(a-b)^{T}}
132 | $$
133 |
134 | - 余弦相似度函数(Cosine similarity)
135 |
136 | 余弦相似度,又称为余弦相似性,是通过计算两个向量的夹角余弦值来评估他们的相似度。余弦相似度将向量根据坐标值,绘制到向量空间中,如最常见的二维空间。
137 |
138 | 余弦相似度衡量的是2个向量间的夹角大小,通过夹角的余弦值表示结果,因此2个向量的余弦相似度为:
139 | $$
140 | \cos \theta=\frac{A \cdot B}{\|A\| *\|B\|}
141 | $$
142 | 分子为向量A与向量B的点乘,分母为二者各自的L2相乘,即将所有维度值的平方相加后开方。 余弦相似度的取值为[-1,1],值越大表示越相似。
143 |
144 | 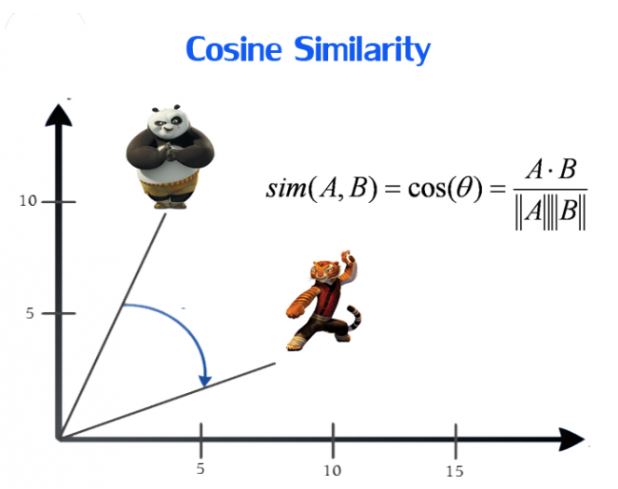 145 |
146 | python代码实现:
147 |
148 | ```python
149 | import numpy as np
150 | def cosine_dis(x,y):
151 | num = sum(map(float,x*y))
152 | denom = np.linalg.norm(x)*np.linalg.norm(y)
153 | return round(num/float(denom),3)
154 | print(cosine_dis(np.array([3,45,7,2]),np.array([2,54,13,15])))
155 | ```
156 |
157 | PS: 函数参数: linalg=linear(线性)+algebra(代数),norm则表示范数。
158 |
159 | ```python
160 | x_norm=np.linalg.norm(x, ord=None, axis=None, keepdims=False)
161 | ```
162 |
163 | - x: 表示矩阵(也可以是一维)
164 | - ord:范数类型
165 |
166 | | 参数 | 说明 | 计算方法 |
167 | | ---------- | ------------------------------------------------------------ | ------------------------------------------------------------ |
168 | | 默认 | 二范数: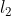 | 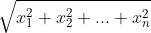 |
169 | | ord=2 | 二范数: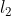 | 同上 |
170 | | ord=1 | 一范数: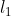 | 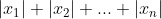 |
171 | | ord=np.inf | 无穷范数: | 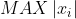 |
172 |
173 | 结果:
174 |
175 |
145 |
146 | python代码实现:
147 |
148 | ```python
149 | import numpy as np
150 | def cosine_dis(x,y):
151 | num = sum(map(float,x*y))
152 | denom = np.linalg.norm(x)*np.linalg.norm(y)
153 | return round(num/float(denom),3)
154 | print(cosine_dis(np.array([3,45,7,2]),np.array([2,54,13,15])))
155 | ```
156 |
157 | PS: 函数参数: linalg=linear(线性)+algebra(代数),norm则表示范数。
158 |
159 | ```python
160 | x_norm=np.linalg.norm(x, ord=None, axis=None, keepdims=False)
161 | ```
162 |
163 | - x: 表示矩阵(也可以是一维)
164 | - ord:范数类型
165 |
166 | | 参数 | 说明 | 计算方法 |
167 | | ---------- | ------------------------------------------------------------ | ------------------------------------------------------------ |
168 | | 默认 | 二范数: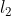 | 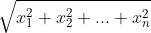 |
169 | | ord=2 | 二范数: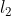 | 同上 |
170 | | ord=1 | 一范数: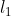 | 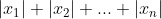 |
171 | | ord=np.inf | 无穷范数: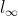 | 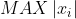 |
172 |
173 | 结果:
174 |
175 |  176 |
177 | ### 15.4 嵌入矩阵
178 |
179 | 在学习词嵌入时,实际上学习的是一个嵌入矩阵,这个矩阵用于将原来的one-hot编码转化为用特征表示的向量。
180 |
181 | #### 15.4.1 定义
182 |
183 | 假设词典共有10,000个单词,嵌入特征为300维。
184 |
185 | $o_i$:表示一个one-hot向量(10000$\times$1),且第$i$位为1,其余位为0。比如orange在词典中的编号为6257,则对应$o_{6257}$。
186 |
187 | $e_i$:表示一个嵌入向量(300$\times$1),对应由one-hot向量$o_i$得到的嵌入向量。
188 |
189 | $E$:表示嵌入矩阵,shape为300$\times$10000。
190 |
191 | 有如下关系:
192 | $$
193 | e_i = E \cdot o_i
194 | $$
195 | 由(3)式可知,嵌入矩阵$E$的作用在于将one-hot向量映射为嵌入向量。因此,学习词嵌入的本质是学习嵌入矩阵。
196 |
197 | #### 15.4.3 实现技巧
198 |
199 | 观察下图,可以发现由于one-hot向量的特殊性,对于$o_i$,嵌入矩阵实际上会用影响到$e_i$的值的只有第$i$列。
200 |
201 | 
202 |
203 | 所以在使用代码实现的时候,我们只需要抽取出对应的列即可,无需真的将如此大的矩阵与向量做矩阵乘法。
204 |
205 | 下面是代码示例:
206 |
207 | ```
208 | # 定义one-hot向量o_2, shape为(4, 1)
209 | o = np.array([[0, 0, 1, 0]]).T
210 |
211 | # 定义嵌入矩阵, shape为(2, 4)
212 | E = np.array([
213 | [10, 11, 12, 13],
214 | [20, 21, 22, 23]
215 | ])
216 |
217 | # 获得编号i
218 | i = np.where(o==1)[0]
219 |
220 | # 计算e_i, shape为(2, 1), 结果为 [ [12], [22] ]
221 | e = E[:, i]
222 | ```
223 |
224 | ### 15.5 学习词嵌入
225 |
226 | #### 15.5.1 简单的语言模型
227 |
228 | 假设搭建了一个用神经网络来实现的语言模型,用于预测“I want a glass of orange \_\_\_\_”。
229 |
230 | 
231 |
232 | 预测的具体方法如上图:
233 |
234 | 1. 对每个单词进行one-hot编码,得到一系列$o_i$
235 | 2. 映射为嵌入向量$e_i$
236 | 3. 将这些嵌入向量都放到神经网络中,该神经网络有自己的参数$W^{[1]}$和$b^{[1]}$,输入为 (6$\times$300)=1800维
237 | 4. 最后通过softmax层激活得到预测词的one-hot向量,也有自己的参数$W^{[2]}$和$b^{[2]}$。
238 |
239 | 实际应用上,会选择每次预测只向前看4个单词(一个超参数,可以修改),则神经网络的输入会变为(4$\times$300)=1200维。
240 |
241 | #### 15.5.2 反向传播
242 |
243 | 在搭建模型后,我们明确了这个模型的参数有$E,W^{[1]},W^{[2]},b^{[1]},b^{[2]}$,因此可以开始用反向传播进行训练。这样这个网络会发现要想最好地拟合训练集,就要使apple(苹果)、orange(橘子)、grape(葡萄)和pear(梨)等等,还有像durian(榴莲)这种很稀有的水果都拥有相似的特征向量。
244 |
245 | #### 15.5.3 采用不同的上下文
246 |
247 | 除了刚刚提到的每次预测只使用前4个单词,还可以选择目标词左右各4个词作为上下文;也可以仅使用目标词的前一个单词进行预测。
248 |
249 | 不同的上下文会得到不同的效果,但是学习的嵌入矩阵仍会是相似的。
250 |
251 | #### 15.5.4 相关的重要人物
252 |
253 | Yoshua Bengio,Rejean Ducharme,Pascal Vincent,Rejean Ducharme,Pascal Vincent还有Christian Jauvin。
254 |
255 | ### 15.6 Word2Vec
256 |
257 | Word2Vec有两个版本,其中Skip-Gram是更常用的那个,另一个是CBOW。下面先介绍Skip-Gram。
258 |
259 | #### 15.6.1 Skip-Gram模型
260 |
261 | Skip-Gram模型的思想是,学习给定嵌入向量$e_c$预测对应的$e_t$。但是由于一个$e_c$是可以对应多个$e_t$的(因为一个词附近出现的词有很多个,不可能一直只有一个),所以最后学习的结果会将$e_c$附近的词都认为拥有相似的特征。
262 |
263 | 
264 |
265 | 在该模型中,上下文不一定总是目标单词之前离得最近的四个单词,或最近的n个单词。在给定一个训练样本(如“I want a glass of orange juice to go along with my cereal.”)该模型的算法如下:
266 |
267 | 1. **随机**选一个词作为上下文 $c$(比如orange)
268 |
269 | 2. 然后基于 $c$,随机在一定词距内选另一个词作为目标词 $t$(比如juice,也可能是后方的my或者前方的glass)
270 |
271 | 3. 根据$c,t$分别得到one-hot向量$o_c,o_t$以及嵌入向量$e_c$。那一个训练样本就是($e_c$,$o_t$)
272 |
273 | 4. 然后将$e_c$喂给softmax单元,该单元用于预测不同目标词的概率,公式如下:
274 | $$
275 | \operatorname{Softmax}: p(t \mid c)=\frac{e^{\theta_{t}^{T} e_{c}}}{\sum_{j=1}^{10,000} e^{\theta_{j}^{T} e_{c}}}
276 | $$
277 | 其中$\theta_t$是与输出$t$相关的参数(可训练),即某个词$t$与标签相符的概率。$\theta_{t}^{T} e_{c}$描述了两者的关联性。
278 |
279 | 5. 用$y$表示目标词(one-hot向量),$\hat y$表预测词(可能目标词的概率),均为10,000维的向量。损失函数如下:
280 | $$
281 | L(\hat{y}, y)=-\sum_{i=1}^{10,000} y_{i} \log \hat{y}_{i}
282 | $$
283 |
284 | 最后,通过优化这个损失函数就可以得到一个不错的词嵌入。
285 |
286 | #### 15.6.2 分级的Softmax
287 |
288 | 其实上述的Skip-Gram模型有一个很明显的问题:计算速度。在计算softmax单元时,需要对10,000个词做求和运算,甚至更多的词。这会导致速度会变得相当慢,扩大词汇表(词典)更是几乎不可能的。
289 |
290 | 所以提出了分级的(hierarchical)的softmax,结构如下图:
291 |
292 | 
293 |
294 | 这样每个结点都是一个二分类器,给定一个词,第一个分类器判断这个词是前5000个词中还是后5000个词中;第二个分类器判断是前2500中还是后2500个至前5000个词中……以此类推,最后到达的叶子结点就是目标类别,并给出对应的概率。
295 |
296 | 实际应用时,常用词会更接近树的根部,罕见词会在很深的地方;因此这个树并非一颗平衡树。
297 |
298 | #### 15.6.3 Skip-Gram与CBOW
299 |
300 | ***CBOW***,即连续词袋模型(Continuous Bag-Of-Words Model),它获得中间词两边的的上下文,然后用周围的词去预测中间的词。在训练时相当于是用缺省的词(预测词)来影响周围的词。
301 |
302 | 这个模型也很有效,也有一些优点和缺点。结构如下图。
303 |
304 | 
305 |
306 | 对应的,Skip-Gram是用中间词去预测周围的词,训练时则相当于用一个词周围的词来影响中间词。结构如下图:
307 |
308 | 
309 |
310 | CBOW对小型数据库比较合适,而Skip-Gram在大型语料中表现更好;CBOW是从原始语句推测目标字词,而Skip-Gram正好相反,是从目标字词推测出原始语句。
311 |
312 | cbow是 1个老师 VS K个学生,K个学生(周围词)都会从老师(中心词)那里学习知识,但是老师(中心词)是一视同仁的,教给大家的一样的知识。至于你学到了多少,还要看下一轮(假如还在窗口内),或者以后的某一轮,你还有机会加入老师的课堂当中(再次出现作为周围词),跟着大家一起学习,然后进步一点。所以对于罕见词来说,学习效果比较差。CBOW总的预测次数是O(V),只与训练样本的词汇数有关。
313 |
314 | 相对的,skip-gram是 1个学生 VS K个老师,1个学生(中心词)会从K个老师(K个周围词)那里学习知识。skip-gram总的预测次数是O(V*K),与训练样本的词汇数以及窗口的大小有关。因此数据集较大时K不宜太大。
315 |
316 | #### 15.6.4 相关的重要论文
317 |
318 | 1. Mikolov T, Chen K, Corrado G, et al. Efficient Estimation of Word Representations in Vector Space[J]. Computer Science, 2013.
319 |
320 | #### 15.6.5 Doc2Vec
321 |
322 | 与Word2Vec对应,既然有词向量,那也可以考虑文本向量。Doc2Vec 的目的就是获得文本的一个固定长度的向量表达。
323 |
324 | word2vec只是基于词的维度进行“语义分析”的,并不具有上下文的“语义分析”能力。因此在word2vec的基础上增加一个段落向量,该方法是doc2vec。该模型也有两个方法:Distributed Memory(DM) 和 Distributed Bag of Words(DBOW)。 DM试图给定上下文和段落向量的情况下预测单词的概率。在一个句子或者段落文档训练过程中,段落ID保存不变,共享同一个段落向量。DBOW则在只给定段落向量的情况下预测段落中一组随机单词的概率。引自[word2vec和doc2vec](https://www.jianshu.com/p/048bff9b0f65)。
325 |
326 | ### 15.7 负采样
327 |
328 | #### 15.7.1 什么是负采样
329 |
330 | skip-gram模型可以构造一个监督学习任务,把上下文映射到目标词上,以学习一个实用的词嵌入,但缺点是softmax计算起来很慢。负采样能够做到和 skip-gram相似的功能但是使用起来更加高效,理论上就是将10000分类的softmax转化为10000个二分类任务,来简化训练过程。
331 |
332 | 简单来说,构造一个新的监督学习问题,比如给定一对单词,比如orange和juice,判断上下文词(context)与目标词(target)是否为匹配的一对,如果是一对,则是正样本,如果不是一对,则是负样本.
333 | 在这个例子中orange和juice称作个正样本,用1作为标记,orange和king就是个负样本,标为0。要做的就是采样得到一个上下文词和一个目标词,中间列叫做词(word)。然后:
334 |
335 | - 正样本的生成是采样得到一个上下文词和一个目标词。先抽取一个context,在一定词距内(比如说正负10个词距内)随机选择一个单词作为target,生成这个表的第一行,即orange– juice -1的过程
336 | - 生成一个负样本,用相同的context,再在字典中随机选一个词,如king、book、the、of,标记为0。因为如果随机选一个词,它很可能跟orange没关联。其中同一 上下文词生成 *K个* 负样本
337 |
338 | - 注意:正负样本的区别仅取决于单词对的来源,比如of正好出现在了orange正负10个词之内标为1,但是of又被作为随机从字典中选取的单词, of - orange单词对仍然会被标记为负样本。
339 |
340 | K值的选取:
341 |
342 | - 小数据集的话,K设置为从5到20,数据集越小K被设定的越大。
343 | - 如果数据集很大,K就选的小一点。对于更大的数据集K设置为从2到5。
344 |
345 | #### 15.7.2 模型学习原理
346 |
347 | - 算法定义 :输入Context 为 c, Word为 t , 定义输出Target为 y
348 |
349 | | context | word | target |
350 | | ------- | ----- | ------ |
351 | | c | t | y |
352 | | $x_1$ | $x_2$ | y |
353 | | orange | juice | 1 |
354 | | orange | king | 0 |
355 | | orange | book | 0 |
356 | | orange | the | 0 |
357 | | orange | of | 0 |
358 |
359 | - 损失函数定义为给定样本单词对的情况下,y = 1的概率:
360 | - 使用$e_c$表示context的词嵌入向量,其中$\theta_{t}$表示每个样本对应的参数.
361 | - $P(y=1 \mid c, t)=\sigma\left(\theta_{t}^{T} e_{c}\right)$
362 | - 对于每个正样本都有 *K* 个负样本来训练一个类似logisitic回归的模型。
363 |
364 | #### 15.7.3 算法流程
365 |
366 | 1. 如果输入词是orange ,即词典中的第6257个词,将其使用one-hot向量表示 $ o_{6257}$,和 E (词嵌入向量矩阵)相乘得到 orange的嵌入向量$ e_{6357}$。
367 |
368 | 2. $e_{6357}$是一个10,000维(字典中总单词数量)的向量,可以看成是1W个可能的logistic回归分类问题,其中一个(编号4)将会是用来判断目标词是否是juice的分类器,其他的词比如下面的某个分类器(编号5)是用来预测king是否是目标词。
369 |
370 | 每次迭代不都是训练所有的样本, 只会训练一个正样本和随机选取的 K 个负样本,即模型总共包含了k+1个binary classification。对比之前10000个输出单元的softmax分类,negative sampling转化为k+1个二分类问题,每次迭代并不是训练10000个,而仅训练其中k+1个,计算量要小很多,大大提高了模型运算速度。
371 |
372 | 这种方法就叫做负采样(Negative Sampling):*选择一个正样本,随机采样k个负样本。
373 |
374 | #### 15.7.4 如何选取负样本
375 |
376 | - 仅仅通过单词在语料库中出现的频率进行采样:导致负样本中一些类似a、the、of等词的频率较高。
377 |
378 | - 均匀随机地抽取负样本,分母是词汇表中总词数,没有很好的代表性。
379 | - 推荐采样公式:
380 |
381 | $$
382 | P\left(w_{i}\right)=\frac{f\left(w_{i}\right)^{\frac{3}{4}}}{\sum_{j=1}^{10,000} f\left(w_{j}\right)^{\frac{3}{4}}}
383 | $$
384 |
385 | 这种方法处于上面两种极端采样方法之间,即不用频率分布,也不用均匀分布,而采用的是对词频的$\frac{3}{4}$除以词频$\frac{3}{4}$整体的和进行采样的。其中,$f(w_j)$是语料库中观察到的某个词的词频。
386 |
387 |
388 | #### 15.7.5 相关的重要论文
389 |
390 | Mikolov T, Sutskever I, Chen K, et al. Distributed representations of words and phrases and their compositionality[C]// International Conference on Neural Information Processing Systems. Curran Associates Inc. 2013:3111-3119.[地址](https://papers.nips.cc/paper/2013/file/9aa42b31882ec039965f3c4923ce901b-Paper.pdf)
391 |
392 | 讲解 skip-gram 模型以及优化和扩展,包括层次 Softmax,负采样等内容。
393 |
394 | ### 15.8 GloVe词向量
395 |
396 | 该算法虽然不如Word2Vec热门,但也是简单且不错的模型,在NLP社区有一定的势头。
397 |
398 | #### 15.8.1 什么是GloVe算法
399 |
400 | 全称Global vectors for word representation(基于全局统计的词表征)。在此之前,我们曾通过挑选语料库中位置相近的两个词,列举出词对,即上下文和目标词,GloVe算法做的就是使其关系开始明确化。假定 $X_{ij}$是单词 $i$在单词 $j$上下文中出现的次数,那么这里 $i$与 $j$就和 $t$与 $c$的功能一样,所以你可以认为 $X_{ij}$等同于 $X_{tc}$。
401 |
402 | 如果上下文定义为目标词左右各10个词左右,还会得到$X_{ij}=X_{ji}$的结论。相反,如果上下文总是目标词的前一个则没有这种对称性。这个其实很容易理解,当目标词的上下文包括左右两部分时,则意味着对于上下文 $c$来说,目标词 $t$也是 $c$的上下文。
403 |
404 | **共现矩阵**:其实$X_{ij}$就是共现矩阵的其中一个元素。共现矩阵的横、纵轴均为词汇表的大小,行对应目标词的编号,列对应上下文的编号。计算方法就是遍历一个句子,比如“I love you”,则目标词为“I”时上下文有“love”和“you”,执行$X_{I,love}+1$和$X_{I,you}+1$。最后遍历语料库后即完成共现矩阵的计算。
405 |
406 | **目标**:GloVe的目标是最小化函数:
407 | $$
408 | \operatorname{minimize} \sum_{i=1}^{10,000} \sum_{j=1}^{10,000} f\left(X_{i j}\right)\left(\theta_{i}^{T} e_{j}+b_{i}+b_{j}^{\prime}-\log X_{i j}\right)^{2}
409 | $$
410 | 这个函数表示的是两者间的差距。$\theta_{i}^{T} e_{j}$同$\theta_{t}^{T} e_{c}$一样描述了两者同时出现的频率是多少。如果想要最小化这个函数,毫无疑问需要让$\theta_{i}^{T} e_{j}+b_{i}+b_{j}^{\prime}$逼近$\log X_{ij}$。
411 |
412 | 通过梯度下降算法即可学习嵌入矩阵$E$,并且学会预测两个单词同时出现的频率。
413 |
414 | **细节**:如果$X_{ij}=0$,则$\log X_{ij}$为无穷大,因此要添加一个额外的加权项$f(X_{ij})$,约定$f(0)(\ldots-\log 0)=0$。即当$X_{ij}=0$时不计入求和项;同时对于常见词如a、the、of等词,给与一个较小的权重;对于罕见词如durion则给予一个较大的权重。
415 |
416 | 还有一个细节就是现在的$\theta$和$e$现在是完全对称的,即$\theta_i$和$e_j$是对称的。只看公式的话两者功能相似。
417 |
418 | **对比**:首先,两种算法学习词嵌入都用到了一个信息:词汇共现(co-occurrence),即利用两个词一起出现这个信息来学习词嵌入、隐含的语义等。不同之处在于,word2vec学习了这个共现,本质上做的是预测任务(Predictive),要么根据中心词预测上下文,要么根据上下文预测中心词;而GloVe做的是对已经得到的共现信息(共现矩阵)进行降维、编码(Count-based)。
419 |
420 | **优缺点**:相对来说word2vec没有很好地利用共现信息,而GloVe则因为共现矩阵需要花费相当大的内存;但是不采用负采样的word2vec非常快,GloVe则更容易优化准确率也比没有用负采样的word2vec高。
421 |
422 | #### 15.8.2 为什么不能保证嵌入向量的独立组成部分是能够理解的
423 |
424 | 首先,我们可以将词嵌入理解为“特征提取”,比如提取出Gender、Royal等属性来进行描述,这些特征对于我们来说是可以理解的。但是,我们刚刚提到的算法都是自己学自己的,并不一定会学出Gender等属性。
425 |
426 | 更具体一点,可以当成是进行了降维,用更少的轴来描述原来的单词;如果这些轴分别表示Gender、Royal等属性则是可理解的,并且相互正交;但是我们提到的算法都没有去保证“这两个特征之间是相互正交的”,也就是说他学到的特征很可能是多个正交特征的混合,比如第一个轴是Gender和Royal的混合,第二个轴是Royal和Age的混合等等。
427 |
428 | 所以,才说不能保证嵌入向量的独立组成部分是能够理解的。
429 |
430 | #### 15.8.3 相关重要论文
431 |
432 | 1. Pennington J, Socher R, Manning C. Glove: Global Vectors for Word Representation[C]// Conference on Empirical Methods in Natural Language Processing. 2014:1532-1543.
433 |
434 | ### 15.9 情感分类
435 |
436 | 情感分类:Sentiment classification
437 |
438 | 词嵌入:word embeddings,将一个词语(word)转换为一个向量 (vector)表示, 所以词嵌入有时又被叫作“**word2vec**"。
439 |
440 | 情感分类是一个很难但很有趣的方向,相对来说也很容易出项目,应用到各种场合。
441 |
442 | #### 15.9.1 什么是情感分类
443 |
444 | 情感分类:对带有感情色彩的主观性文本进行分析,分析说话人的态度是倾向正面还是反面,是NLP中最重要的模块之一。
445 |
446 | 
447 |
448 | 举个例子,如上图所示,输入 $x$ 是一段文本,输出 $y$ 是要预测的相应情感,比如是对一个餐馆评价的星级。现在很多人会把用餐的情况与感受分享在一些社交平台上,如果基于像上面这样标记的数据集可以训练一个从 $x$ 到 $y$ 的映射也就是一个情感分类器,就可以用来搜集大家对这个餐馆的评价,从文本中分析出顾客对餐馆评论的情感是正面的还是负面的,可以让餐馆发现自身的问题所在也能让其他顾客了解到这个餐馆是否值得光顾。
449 |
450 | 情感分类最大的挑战是**标记的训练集不够多**,对于情感分类任务来说,训练集大小从10000到100000个单词都很常见,甚至有时会小于10000个单词,但采用**词嵌入**效果可以好很多,即使只有中等大小的标记的训练集,也能构建一个不错的情感分类器。
451 |
452 | #### 15.9.2 一个简单的情感分类模型
453 |
454 | 
455 |
456 | 如上图所示,假设有一个句子“The dessert is excellent(甜点很棒)”,要构建一个分类器把它映射成输出四个星。首先,我们从词典里找到这些词相应的一位编码表示,如“the”的**一位编码**是 $o_{8928}$,乘以**嵌入矩阵 $E$**($E$ 可以从一个很大的文本集里学习到,比如从一亿个词或者一百亿个词里学习嵌入表达,从中获取很多知识甚至从有些不常用的词中获取然后应用到要解决的问题中,即使你的标记数据集里没有这些词),得到单词“the”的**嵌入向量 $e_{8928}$**,对其他三个单词做同样的步骤。将这些嵌入向量求和或者求平均(把所有单词的意思加起来或取平均),假设这里用的是一个平均值计算单元Avg,这个单元会输出一个相同维度的特征向量,把这个特征向量送进softmax分类器,输出5个可能结果(从一星到五星)的概率值,进而输出预测结果 $\hat y$。
457 |
458 | 这个算法有一个问题就是**没考虑词序**,像“Completely lacking in good taste, good service, and good ambience(完全没有好的味道、好的服务、好的氛围)”虽然是负面评价,但”good“这个词出现了很多次,如果还用上面的算法,忽略词序而仅仅把所有单词的词嵌入加起来或者取平均,则最后的特征向量会有很多good的表示,分类器就可能误认为这是一个好评。
459 |
460 | #### 15.9.3 用RNN实现情感分类
461 |
462 | 
463 |
464 | 首先找到这条评论中每一个单词的一位编码表示,乘以词嵌入矩阵 $E$ 得到词嵌入表达 $e$,然后把它们送进我们之前学过的多对一的RNN网络结构里,RNN的工作就是在最后一步计算一个特征向量来预测 $\hat y$。这种算法考虑了词的顺序,效果更好,能够意识到“Completely lacking in good taste, good service, and good ambience(完全没有好的味道、好的服务、好的氛围)”是个负面评价。由于词嵌入 $E$ 是在一个更大的数据集里训练的,可以更好地泛化一些没有见过的新单词,比如其他人可能会说“Completely absent of good taste...”,即使"absent"这个词不在标记的训练集里,但它仍然可以判断对并且泛化得很好。
465 |
466 | ### 15.10 词嵌入除偏
467 |
468 | 算法安全性;偏见原因:**数据集**不完整(cv:黑人数据不够多)、打**标签**有偏见、**算法**本身的偏见(推荐算法的导向性,推之前没有的,试探性,引导往其他方向走);解决方法:采样更丰富和比例更合理(数据增强)、***设计算法创新处理有偏数据集得到无偏结果***;老人无健康码上不了车,考虑少数人、边缘化等;
469 |
470 | 词嵌入除偏:Debiasing word embeddings
471 |
472 | #### 15.10.1 为什么需要除偏
473 |
474 | 这里的“偏(bias)"不是指偏见,而是指性别、种族、性取向方面的偏见。
475 |
476 | “Man is to computer programmer as woman is to homemaker? debiasing word embeddings.”这篇论文提出,如果说Man对应Computer programmer则Woman会对应什么呢?一个已经完成学习的词嵌入可能会输出Homemaker,这个结果就反映了一个十分不良的性别歧视,如果输出的是Computer programmer则会更合理。再比如说Father对应Doctor那么Mother应该对应什么?有些完成学习的词嵌入会输出nurse,这也是不对的。
477 |
478 | 也就是说,根据训练模型所使用的文本,**词嵌入可能会反映出性别、种族、年龄、性取向等其他方面的偏见**,这些偏见都和社会经济状态相关。因为机器学习算法正用来制定十分重要的决策,影响着世间万物,所以尽量修改学习算法来尽可能**减少或是理想化消除这些非预期形式的偏见**是十分重要的,因此需要对词嵌入进行除偏。
479 |
480 | **偏见产生的原因**:
481 |
482 | * **数据集**不完整。比如在做图像处理的时候由于黑人的数据不够多而导致效果不好。
483 |
484 | * **标签**有偏见。由于标签都是人打上去的,因此如果打标签的人带有偏见,则最后标签也会带有偏见并产生实际影响。
485 |
486 | * **算法**本身的偏见。常见于推荐算法,有的推荐算法具有导向性,会通过试探性地推荐之前没有的物品,引导用户养成新的兴趣,有时候甚至会带有“恶意”将用户引导到不好的方向。
487 |
488 | #### 15.10.2 什么是词嵌入除偏
489 |
490 | 假设我们已经完成一个词嵌入的学习,babysister、doctor、grandmother、grandfather、girl、boy、she、he这些词的嵌入位置如下图所示,
491 |
492 |
176 |
177 | ### 15.4 嵌入矩阵
178 |
179 | 在学习词嵌入时,实际上学习的是一个嵌入矩阵,这个矩阵用于将原来的one-hot编码转化为用特征表示的向量。
180 |
181 | #### 15.4.1 定义
182 |
183 | 假设词典共有10,000个单词,嵌入特征为300维。
184 |
185 | $o_i$:表示一个one-hot向量(10000$\times$1),且第$i$位为1,其余位为0。比如orange在词典中的编号为6257,则对应$o_{6257}$。
186 |
187 | $e_i$:表示一个嵌入向量(300$\times$1),对应由one-hot向量$o_i$得到的嵌入向量。
188 |
189 | $E$:表示嵌入矩阵,shape为300$\times$10000。
190 |
191 | 有如下关系:
192 | $$
193 | e_i = E \cdot o_i
194 | $$
195 | 由(3)式可知,嵌入矩阵$E$的作用在于将one-hot向量映射为嵌入向量。因此,学习词嵌入的本质是学习嵌入矩阵。
196 |
197 | #### 15.4.3 实现技巧
198 |
199 | 观察下图,可以发现由于one-hot向量的特殊性,对于$o_i$,嵌入矩阵实际上会用影响到$e_i$的值的只有第$i$列。
200 |
201 | 
202 |
203 | 所以在使用代码实现的时候,我们只需要抽取出对应的列即可,无需真的将如此大的矩阵与向量做矩阵乘法。
204 |
205 | 下面是代码示例:
206 |
207 | ```
208 | # 定义one-hot向量o_2, shape为(4, 1)
209 | o = np.array([[0, 0, 1, 0]]).T
210 |
211 | # 定义嵌入矩阵, shape为(2, 4)
212 | E = np.array([
213 | [10, 11, 12, 13],
214 | [20, 21, 22, 23]
215 | ])
216 |
217 | # 获得编号i
218 | i = np.where(o==1)[0]
219 |
220 | # 计算e_i, shape为(2, 1), 结果为 [ [12], [22] ]
221 | e = E[:, i]
222 | ```
223 |
224 | ### 15.5 学习词嵌入
225 |
226 | #### 15.5.1 简单的语言模型
227 |
228 | 假设搭建了一个用神经网络来实现的语言模型,用于预测“I want a glass of orange \_\_\_\_”。
229 |
230 | 
231 |
232 | 预测的具体方法如上图:
233 |
234 | 1. 对每个单词进行one-hot编码,得到一系列$o_i$
235 | 2. 映射为嵌入向量$e_i$
236 | 3. 将这些嵌入向量都放到神经网络中,该神经网络有自己的参数$W^{[1]}$和$b^{[1]}$,输入为 (6$\times$300)=1800维
237 | 4. 最后通过softmax层激活得到预测词的one-hot向量,也有自己的参数$W^{[2]}$和$b^{[2]}$。
238 |
239 | 实际应用上,会选择每次预测只向前看4个单词(一个超参数,可以修改),则神经网络的输入会变为(4$\times$300)=1200维。
240 |
241 | #### 15.5.2 反向传播
242 |
243 | 在搭建模型后,我们明确了这个模型的参数有$E,W^{[1]},W^{[2]},b^{[1]},b^{[2]}$,因此可以开始用反向传播进行训练。这样这个网络会发现要想最好地拟合训练集,就要使apple(苹果)、orange(橘子)、grape(葡萄)和pear(梨)等等,还有像durian(榴莲)这种很稀有的水果都拥有相似的特征向量。
244 |
245 | #### 15.5.3 采用不同的上下文
246 |
247 | 除了刚刚提到的每次预测只使用前4个单词,还可以选择目标词左右各4个词作为上下文;也可以仅使用目标词的前一个单词进行预测。
248 |
249 | 不同的上下文会得到不同的效果,但是学习的嵌入矩阵仍会是相似的。
250 |
251 | #### 15.5.4 相关的重要人物
252 |
253 | Yoshua Bengio,Rejean Ducharme,Pascal Vincent,Rejean Ducharme,Pascal Vincent还有Christian Jauvin。
254 |
255 | ### 15.6 Word2Vec
256 |
257 | Word2Vec有两个版本,其中Skip-Gram是更常用的那个,另一个是CBOW。下面先介绍Skip-Gram。
258 |
259 | #### 15.6.1 Skip-Gram模型
260 |
261 | Skip-Gram模型的思想是,学习给定嵌入向量$e_c$预测对应的$e_t$。但是由于一个$e_c$是可以对应多个$e_t$的(因为一个词附近出现的词有很多个,不可能一直只有一个),所以最后学习的结果会将$e_c$附近的词都认为拥有相似的特征。
262 |
263 | 
264 |
265 | 在该模型中,上下文不一定总是目标单词之前离得最近的四个单词,或最近的n个单词。在给定一个训练样本(如“I want a glass of orange juice to go along with my cereal.”)该模型的算法如下:
266 |
267 | 1. **随机**选一个词作为上下文 $c$(比如orange)
268 |
269 | 2. 然后基于 $c$,随机在一定词距内选另一个词作为目标词 $t$(比如juice,也可能是后方的my或者前方的glass)
270 |
271 | 3. 根据$c,t$分别得到one-hot向量$o_c,o_t$以及嵌入向量$e_c$。那一个训练样本就是($e_c$,$o_t$)
272 |
273 | 4. 然后将$e_c$喂给softmax单元,该单元用于预测不同目标词的概率,公式如下:
274 | $$
275 | \operatorname{Softmax}: p(t \mid c)=\frac{e^{\theta_{t}^{T} e_{c}}}{\sum_{j=1}^{10,000} e^{\theta_{j}^{T} e_{c}}}
276 | $$
277 | 其中$\theta_t$是与输出$t$相关的参数(可训练),即某个词$t$与标签相符的概率。$\theta_{t}^{T} e_{c}$描述了两者的关联性。
278 |
279 | 5. 用$y$表示目标词(one-hot向量),$\hat y$表预测词(可能目标词的概率),均为10,000维的向量。损失函数如下:
280 | $$
281 | L(\hat{y}, y)=-\sum_{i=1}^{10,000} y_{i} \log \hat{y}_{i}
282 | $$
283 |
284 | 最后,通过优化这个损失函数就可以得到一个不错的词嵌入。
285 |
286 | #### 15.6.2 分级的Softmax
287 |
288 | 其实上述的Skip-Gram模型有一个很明显的问题:计算速度。在计算softmax单元时,需要对10,000个词做求和运算,甚至更多的词。这会导致速度会变得相当慢,扩大词汇表(词典)更是几乎不可能的。
289 |
290 | 所以提出了分级的(hierarchical)的softmax,结构如下图:
291 |
292 | 
293 |
294 | 这样每个结点都是一个二分类器,给定一个词,第一个分类器判断这个词是前5000个词中还是后5000个词中;第二个分类器判断是前2500中还是后2500个至前5000个词中……以此类推,最后到达的叶子结点就是目标类别,并给出对应的概率。
295 |
296 | 实际应用时,常用词会更接近树的根部,罕见词会在很深的地方;因此这个树并非一颗平衡树。
297 |
298 | #### 15.6.3 Skip-Gram与CBOW
299 |
300 | ***CBOW***,即连续词袋模型(Continuous Bag-Of-Words Model),它获得中间词两边的的上下文,然后用周围的词去预测中间的词。在训练时相当于是用缺省的词(预测词)来影响周围的词。
301 |
302 | 这个模型也很有效,也有一些优点和缺点。结构如下图。
303 |
304 | 
305 |
306 | 对应的,Skip-Gram是用中间词去预测周围的词,训练时则相当于用一个词周围的词来影响中间词。结构如下图:
307 |
308 | 
309 |
310 | CBOW对小型数据库比较合适,而Skip-Gram在大型语料中表现更好;CBOW是从原始语句推测目标字词,而Skip-Gram正好相反,是从目标字词推测出原始语句。
311 |
312 | cbow是 1个老师 VS K个学生,K个学生(周围词)都会从老师(中心词)那里学习知识,但是老师(中心词)是一视同仁的,教给大家的一样的知识。至于你学到了多少,还要看下一轮(假如还在窗口内),或者以后的某一轮,你还有机会加入老师的课堂当中(再次出现作为周围词),跟着大家一起学习,然后进步一点。所以对于罕见词来说,学习效果比较差。CBOW总的预测次数是O(V),只与训练样本的词汇数有关。
313 |
314 | 相对的,skip-gram是 1个学生 VS K个老师,1个学生(中心词)会从K个老师(K个周围词)那里学习知识。skip-gram总的预测次数是O(V*K),与训练样本的词汇数以及窗口的大小有关。因此数据集较大时K不宜太大。
315 |
316 | #### 15.6.4 相关的重要论文
317 |
318 | 1. Mikolov T, Chen K, Corrado G, et al. Efficient Estimation of Word Representations in Vector Space[J]. Computer Science, 2013.
319 |
320 | #### 15.6.5 Doc2Vec
321 |
322 | 与Word2Vec对应,既然有词向量,那也可以考虑文本向量。Doc2Vec 的目的就是获得文本的一个固定长度的向量表达。
323 |
324 | word2vec只是基于词的维度进行“语义分析”的,并不具有上下文的“语义分析”能力。因此在word2vec的基础上增加一个段落向量,该方法是doc2vec。该模型也有两个方法:Distributed Memory(DM) 和 Distributed Bag of Words(DBOW)。 DM试图给定上下文和段落向量的情况下预测单词的概率。在一个句子或者段落文档训练过程中,段落ID保存不变,共享同一个段落向量。DBOW则在只给定段落向量的情况下预测段落中一组随机单词的概率。引自[word2vec和doc2vec](https://www.jianshu.com/p/048bff9b0f65)。
325 |
326 | ### 15.7 负采样
327 |
328 | #### 15.7.1 什么是负采样
329 |
330 | skip-gram模型可以构造一个监督学习任务,把上下文映射到目标词上,以学习一个实用的词嵌入,但缺点是softmax计算起来很慢。负采样能够做到和 skip-gram相似的功能但是使用起来更加高效,理论上就是将10000分类的softmax转化为10000个二分类任务,来简化训练过程。
331 |
332 | 简单来说,构造一个新的监督学习问题,比如给定一对单词,比如orange和juice,判断上下文词(context)与目标词(target)是否为匹配的一对,如果是一对,则是正样本,如果不是一对,则是负样本.
333 | 在这个例子中orange和juice称作个正样本,用1作为标记,orange和king就是个负样本,标为0。要做的就是采样得到一个上下文词和一个目标词,中间列叫做词(word)。然后:
334 |
335 | - 正样本的生成是采样得到一个上下文词和一个目标词。先抽取一个context,在一定词距内(比如说正负10个词距内)随机选择一个单词作为target,生成这个表的第一行,即orange– juice -1的过程
336 | - 生成一个负样本,用相同的context,再在字典中随机选一个词,如king、book、the、of,标记为0。因为如果随机选一个词,它很可能跟orange没关联。其中同一 上下文词生成 *K个* 负样本
337 |
338 | - 注意:正负样本的区别仅取决于单词对的来源,比如of正好出现在了orange正负10个词之内标为1,但是of又被作为随机从字典中选取的单词, of - orange单词对仍然会被标记为负样本。
339 |
340 | K值的选取:
341 |
342 | - 小数据集的话,K设置为从5到20,数据集越小K被设定的越大。
343 | - 如果数据集很大,K就选的小一点。对于更大的数据集K设置为从2到5。
344 |
345 | #### 15.7.2 模型学习原理
346 |
347 | - 算法定义 :输入Context 为 c, Word为 t , 定义输出Target为 y
348 |
349 | | context | word | target |
350 | | ------- | ----- | ------ |
351 | | c | t | y |
352 | | $x_1$ | $x_2$ | y |
353 | | orange | juice | 1 |
354 | | orange | king | 0 |
355 | | orange | book | 0 |
356 | | orange | the | 0 |
357 | | orange | of | 0 |
358 |
359 | - 损失函数定义为给定样本单词对的情况下,y = 1的概率:
360 | - 使用$e_c$表示context的词嵌入向量,其中$\theta_{t}$表示每个样本对应的参数.
361 | - $P(y=1 \mid c, t)=\sigma\left(\theta_{t}^{T} e_{c}\right)$
362 | - 对于每个正样本都有 *K* 个负样本来训练一个类似logisitic回归的模型。
363 |
364 | #### 15.7.3 算法流程
365 |
366 | 1. 如果输入词是orange ,即词典中的第6257个词,将其使用one-hot向量表示 $ o_{6257}$,和 E (词嵌入向量矩阵)相乘得到 orange的嵌入向量$ e_{6357}$。
367 |
368 | 2. $e_{6357}$是一个10,000维(字典中总单词数量)的向量,可以看成是1W个可能的logistic回归分类问题,其中一个(编号4)将会是用来判断目标词是否是juice的分类器,其他的词比如下面的某个分类器(编号5)是用来预测king是否是目标词。
369 |
370 | 每次迭代不都是训练所有的样本, 只会训练一个正样本和随机选取的 K 个负样本,即模型总共包含了k+1个binary classification。对比之前10000个输出单元的softmax分类,negative sampling转化为k+1个二分类问题,每次迭代并不是训练10000个,而仅训练其中k+1个,计算量要小很多,大大提高了模型运算速度。
371 |
372 | 这种方法就叫做负采样(Negative Sampling):*选择一个正样本,随机采样k个负样本。
373 |
374 | #### 15.7.4 如何选取负样本
375 |
376 | - 仅仅通过单词在语料库中出现的频率进行采样:导致负样本中一些类似a、the、of等词的频率较高。
377 |
378 | - 均匀随机地抽取负样本,分母是词汇表中总词数,没有很好的代表性。
379 | - 推荐采样公式:
380 |
381 | $$
382 | P\left(w_{i}\right)=\frac{f\left(w_{i}\right)^{\frac{3}{4}}}{\sum_{j=1}^{10,000} f\left(w_{j}\right)^{\frac{3}{4}}}
383 | $$
384 |
385 | 这种方法处于上面两种极端采样方法之间,即不用频率分布,也不用均匀分布,而采用的是对词频的$\frac{3}{4}$除以词频$\frac{3}{4}$整体的和进行采样的。其中,$f(w_j)$是语料库中观察到的某个词的词频。
386 |
387 |
388 | #### 15.7.5 相关的重要论文
389 |
390 | Mikolov T, Sutskever I, Chen K, et al. Distributed representations of words and phrases and their compositionality[C]// International Conference on Neural Information Processing Systems. Curran Associates Inc. 2013:3111-3119.[地址](https://papers.nips.cc/paper/2013/file/9aa42b31882ec039965f3c4923ce901b-Paper.pdf)
391 |
392 | 讲解 skip-gram 模型以及优化和扩展,包括层次 Softmax,负采样等内容。
393 |
394 | ### 15.8 GloVe词向量
395 |
396 | 该算法虽然不如Word2Vec热门,但也是简单且不错的模型,在NLP社区有一定的势头。
397 |
398 | #### 15.8.1 什么是GloVe算法
399 |
400 | 全称Global vectors for word representation(基于全局统计的词表征)。在此之前,我们曾通过挑选语料库中位置相近的两个词,列举出词对,即上下文和目标词,GloVe算法做的就是使其关系开始明确化。假定 $X_{ij}$是单词 $i$在单词 $j$上下文中出现的次数,那么这里 $i$与 $j$就和 $t$与 $c$的功能一样,所以你可以认为 $X_{ij}$等同于 $X_{tc}$。
401 |
402 | 如果上下文定义为目标词左右各10个词左右,还会得到$X_{ij}=X_{ji}$的结论。相反,如果上下文总是目标词的前一个则没有这种对称性。这个其实很容易理解,当目标词的上下文包括左右两部分时,则意味着对于上下文 $c$来说,目标词 $t$也是 $c$的上下文。
403 |
404 | **共现矩阵**:其实$X_{ij}$就是共现矩阵的其中一个元素。共现矩阵的横、纵轴均为词汇表的大小,行对应目标词的编号,列对应上下文的编号。计算方法就是遍历一个句子,比如“I love you”,则目标词为“I”时上下文有“love”和“you”,执行$X_{I,love}+1$和$X_{I,you}+1$。最后遍历语料库后即完成共现矩阵的计算。
405 |
406 | **目标**:GloVe的目标是最小化函数:
407 | $$
408 | \operatorname{minimize} \sum_{i=1}^{10,000} \sum_{j=1}^{10,000} f\left(X_{i j}\right)\left(\theta_{i}^{T} e_{j}+b_{i}+b_{j}^{\prime}-\log X_{i j}\right)^{2}
409 | $$
410 | 这个函数表示的是两者间的差距。$\theta_{i}^{T} e_{j}$同$\theta_{t}^{T} e_{c}$一样描述了两者同时出现的频率是多少。如果想要最小化这个函数,毫无疑问需要让$\theta_{i}^{T} e_{j}+b_{i}+b_{j}^{\prime}$逼近$\log X_{ij}$。
411 |
412 | 通过梯度下降算法即可学习嵌入矩阵$E$,并且学会预测两个单词同时出现的频率。
413 |
414 | **细节**:如果$X_{ij}=0$,则$\log X_{ij}$为无穷大,因此要添加一个额外的加权项$f(X_{ij})$,约定$f(0)(\ldots-\log 0)=0$。即当$X_{ij}=0$时不计入求和项;同时对于常见词如a、the、of等词,给与一个较小的权重;对于罕见词如durion则给予一个较大的权重。
415 |
416 | 还有一个细节就是现在的$\theta$和$e$现在是完全对称的,即$\theta_i$和$e_j$是对称的。只看公式的话两者功能相似。
417 |
418 | **对比**:首先,两种算法学习词嵌入都用到了一个信息:词汇共现(co-occurrence),即利用两个词一起出现这个信息来学习词嵌入、隐含的语义等。不同之处在于,word2vec学习了这个共现,本质上做的是预测任务(Predictive),要么根据中心词预测上下文,要么根据上下文预测中心词;而GloVe做的是对已经得到的共现信息(共现矩阵)进行降维、编码(Count-based)。
419 |
420 | **优缺点**:相对来说word2vec没有很好地利用共现信息,而GloVe则因为共现矩阵需要花费相当大的内存;但是不采用负采样的word2vec非常快,GloVe则更容易优化准确率也比没有用负采样的word2vec高。
421 |
422 | #### 15.8.2 为什么不能保证嵌入向量的独立组成部分是能够理解的
423 |
424 | 首先,我们可以将词嵌入理解为“特征提取”,比如提取出Gender、Royal等属性来进行描述,这些特征对于我们来说是可以理解的。但是,我们刚刚提到的算法都是自己学自己的,并不一定会学出Gender等属性。
425 |
426 | 更具体一点,可以当成是进行了降维,用更少的轴来描述原来的单词;如果这些轴分别表示Gender、Royal等属性则是可理解的,并且相互正交;但是我们提到的算法都没有去保证“这两个特征之间是相互正交的”,也就是说他学到的特征很可能是多个正交特征的混合,比如第一个轴是Gender和Royal的混合,第二个轴是Royal和Age的混合等等。
427 |
428 | 所以,才说不能保证嵌入向量的独立组成部分是能够理解的。
429 |
430 | #### 15.8.3 相关重要论文
431 |
432 | 1. Pennington J, Socher R, Manning C. Glove: Global Vectors for Word Representation[C]// Conference on Empirical Methods in Natural Language Processing. 2014:1532-1543.
433 |
434 | ### 15.9 情感分类
435 |
436 | 情感分类:Sentiment classification
437 |
438 | 词嵌入:word embeddings,将一个词语(word)转换为一个向量 (vector)表示, 所以词嵌入有时又被叫作“**word2vec**"。
439 |
440 | 情感分类是一个很难但很有趣的方向,相对来说也很容易出项目,应用到各种场合。
441 |
442 | #### 15.9.1 什么是情感分类
443 |
444 | 情感分类:对带有感情色彩的主观性文本进行分析,分析说话人的态度是倾向正面还是反面,是NLP中最重要的模块之一。
445 |
446 | 
447 |
448 | 举个例子,如上图所示,输入 $x$ 是一段文本,输出 $y$ 是要预测的相应情感,比如是对一个餐馆评价的星级。现在很多人会把用餐的情况与感受分享在一些社交平台上,如果基于像上面这样标记的数据集可以训练一个从 $x$ 到 $y$ 的映射也就是一个情感分类器,就可以用来搜集大家对这个餐馆的评价,从文本中分析出顾客对餐馆评论的情感是正面的还是负面的,可以让餐馆发现自身的问题所在也能让其他顾客了解到这个餐馆是否值得光顾。
449 |
450 | 情感分类最大的挑战是**标记的训练集不够多**,对于情感分类任务来说,训练集大小从10000到100000个单词都很常见,甚至有时会小于10000个单词,但采用**词嵌入**效果可以好很多,即使只有中等大小的标记的训练集,也能构建一个不错的情感分类器。
451 |
452 | #### 15.9.2 一个简单的情感分类模型
453 |
454 | 
455 |
456 | 如上图所示,假设有一个句子“The dessert is excellent(甜点很棒)”,要构建一个分类器把它映射成输出四个星。首先,我们从词典里找到这些词相应的一位编码表示,如“the”的**一位编码**是 $o_{8928}$,乘以**嵌入矩阵 $E$**($E$ 可以从一个很大的文本集里学习到,比如从一亿个词或者一百亿个词里学习嵌入表达,从中获取很多知识甚至从有些不常用的词中获取然后应用到要解决的问题中,即使你的标记数据集里没有这些词),得到单词“the”的**嵌入向量 $e_{8928}$**,对其他三个单词做同样的步骤。将这些嵌入向量求和或者求平均(把所有单词的意思加起来或取平均),假设这里用的是一个平均值计算单元Avg,这个单元会输出一个相同维度的特征向量,把这个特征向量送进softmax分类器,输出5个可能结果(从一星到五星)的概率值,进而输出预测结果 $\hat y$。
457 |
458 | 这个算法有一个问题就是**没考虑词序**,像“Completely lacking in good taste, good service, and good ambience(完全没有好的味道、好的服务、好的氛围)”虽然是负面评价,但”good“这个词出现了很多次,如果还用上面的算法,忽略词序而仅仅把所有单词的词嵌入加起来或者取平均,则最后的特征向量会有很多good的表示,分类器就可能误认为这是一个好评。
459 |
460 | #### 15.9.3 用RNN实现情感分类
461 |
462 | 
463 |
464 | 首先找到这条评论中每一个单词的一位编码表示,乘以词嵌入矩阵 $E$ 得到词嵌入表达 $e$,然后把它们送进我们之前学过的多对一的RNN网络结构里,RNN的工作就是在最后一步计算一个特征向量来预测 $\hat y$。这种算法考虑了词的顺序,效果更好,能够意识到“Completely lacking in good taste, good service, and good ambience(完全没有好的味道、好的服务、好的氛围)”是个负面评价。由于词嵌入 $E$ 是在一个更大的数据集里训练的,可以更好地泛化一些没有见过的新单词,比如其他人可能会说“Completely absent of good taste...”,即使"absent"这个词不在标记的训练集里,但它仍然可以判断对并且泛化得很好。
465 |
466 | ### 15.10 词嵌入除偏
467 |
468 | 算法安全性;偏见原因:**数据集**不完整(cv:黑人数据不够多)、打**标签**有偏见、**算法**本身的偏见(推荐算法的导向性,推之前没有的,试探性,引导往其他方向走);解决方法:采样更丰富和比例更合理(数据增强)、***设计算法创新处理有偏数据集得到无偏结果***;老人无健康码上不了车,考虑少数人、边缘化等;
469 |
470 | 词嵌入除偏:Debiasing word embeddings
471 |
472 | #### 15.10.1 为什么需要除偏
473 |
474 | 这里的“偏(bias)"不是指偏见,而是指性别、种族、性取向方面的偏见。
475 |
476 | “Man is to computer programmer as woman is to homemaker? debiasing word embeddings.”这篇论文提出,如果说Man对应Computer programmer则Woman会对应什么呢?一个已经完成学习的词嵌入可能会输出Homemaker,这个结果就反映了一个十分不良的性别歧视,如果输出的是Computer programmer则会更合理。再比如说Father对应Doctor那么Mother应该对应什么?有些完成学习的词嵌入会输出nurse,这也是不对的。
477 |
478 | 也就是说,根据训练模型所使用的文本,**词嵌入可能会反映出性别、种族、年龄、性取向等其他方面的偏见**,这些偏见都和社会经济状态相关。因为机器学习算法正用来制定十分重要的决策,影响着世间万物,所以尽量修改学习算法来尽可能**减少或是理想化消除这些非预期形式的偏见**是十分重要的,因此需要对词嵌入进行除偏。
479 |
480 | **偏见产生的原因**:
481 |
482 | * **数据集**不完整。比如在做图像处理的时候由于黑人的数据不够多而导致效果不好。
483 |
484 | * **标签**有偏见。由于标签都是人打上去的,因此如果打标签的人带有偏见,则最后标签也会带有偏见并产生实际影响。
485 |
486 | * **算法**本身的偏见。常见于推荐算法,有的推荐算法具有导向性,会通过试探性地推荐之前没有的物品,引导用户养成新的兴趣,有时候甚至会带有“恶意”将用户引导到不好的方向。
487 |
488 | #### 15.10.2 什么是词嵌入除偏
489 |
490 | 假设我们已经完成一个词嵌入的学习,babysister、doctor、grandmother、grandfather、girl、boy、she、he这些词的嵌入位置如下图所示,
491 |
492 |  493 |
494 | 词嵌入除偏有以下三步:
495 |
496 | 1. **辨别出我们想要减少或想要消除的特定偏见的趋势**。假设这里要讨论的是性别歧视,则可以是将向量 $e_{he}$ 减去向量 $e_{she}$ ,将 $e_{male}$ 减去向量 $e_{female}$ ,因为它们的性别不同,然后将这些差取平均,就能够发现像上图这种情况下横向趋势看起来就是性别趋势或说是偏见趋势(bias),纵向趋与我们想要尝试处理的特定偏见并不相关,因此是无偏见趋势(non-bias),如下图所示。在这种情况下,偏见趋势可以将它看做1维子空间,所以这个无偏见趋势就会是299维的子空间。偏见趋势可以比1维更高,同时相比于取平均值,实际上它会用一个更加复杂的算法叫做SVD(Singular value decomposition,奇值分解,与主成分分析很类似)。
497 |
498 |
493 |
494 | 词嵌入除偏有以下三步:
495 |
496 | 1. **辨别出我们想要减少或想要消除的特定偏见的趋势**。假设这里要讨论的是性别歧视,则可以是将向量 $e_{he}$ 减去向量 $e_{she}$ ,将 $e_{male}$ 减去向量 $e_{female}$ ,因为它们的性别不同,然后将这些差取平均,就能够发现像上图这种情况下横向趋势看起来就是性别趋势或说是偏见趋势(bias),纵向趋与我们想要尝试处理的特定偏见并不相关,因此是无偏见趋势(non-bias),如下图所示。在这种情况下,偏见趋势可以将它看做1维子空间,所以这个无偏见趋势就会是299维的子空间。偏见趋势可以比1维更高,同时相比于取平均值,实际上它会用一个更加复杂的算法叫做SVD(Singular value decomposition,奇值分解,与主成分分析很类似)。
497 |
498 |  499 |
500 | 2. **中和(neutralize)**:对于那些**定义不确切的词**可以将其处理一下避免偏见。有些词本质上就和性别有关,像grandmother、grandfather、girl、boy、she、he,他们的定义中本就含有性别的内容,不过也有一些词,像doctor、babysister,我们想使之在性别方面是中立的,同时,在更通常的情况下,可能会更希望像doctor或babysister这些词成为种族中立的或是性取向中立的等等,不过这里仍然只用性别来举例说明。对于这些定义不明确的词即基本意思不像grandmother和grandfather这种定义里有着十分合理的性别含义的,可以将它们在横轴上进行处理,来减少或是消除它们的性别歧视趋势的成分,也就是说**减少它们在水平方向上的距离**,如下图所示。
501 |
502 |
499 |
500 | 2. **中和(neutralize)**:对于那些**定义不确切的词**可以将其处理一下避免偏见。有些词本质上就和性别有关,像grandmother、grandfather、girl、boy、she、he,他们的定义中本就含有性别的内容,不过也有一些词,像doctor、babysister,我们想使之在性别方面是中立的,同时,在更通常的情况下,可能会更希望像doctor或babysister这些词成为种族中立的或是性取向中立的等等,不过这里仍然只用性别来举例说明。对于这些定义不明确的词即基本意思不像grandmother和grandfather这种定义里有着十分合理的性别含义的,可以将它们在横轴上进行处理,来减少或是消除它们的性别歧视趋势的成分,也就是说**减少它们在水平方向上的距离**,如下图所示。
501 |
502 |  503 |
504 | 3. **均衡(Equalize pairs)**:可能会有grandmother和grandfather、gir和boy这样的词对,对于这些词嵌入,**只希望性别是其区别**。在这个例子中,babysister和grandmother之间的距离或者说是相似度小于babysister和grandfather之间,如下图所示($d1 < d2$),可能会加重不良状态或者可能是非预期的偏见,也就是说grandmother相比于grandfather最终更有可能输出babysister,所以在最后的均衡步中,我们想要确保的是像grandmother和grandfather这样的词都能够有**一致的相似度或者说是相等的距离**,这其中会有一些线性代数的步骤,主要做的就是将grandmother和grandfather**移至与中间轴线等距的一对点上**,如下图所示,现在性别歧视的影响也就是这两个词与babysister的距离就完全相同了。还有许多对象比如grandmother和grandfather、gir和boy、sorority和fraternity、girlhood和boyhood、sister和brother、niece和nephew、daughter和son这样的词对都可以通过均衡步来解决。
505 |
506 |
503 |
504 | 3. **均衡(Equalize pairs)**:可能会有grandmother和grandfather、gir和boy这样的词对,对于这些词嵌入,**只希望性别是其区别**。在这个例子中,babysister和grandmother之间的距离或者说是相似度小于babysister和grandfather之间,如下图所示($d1 < d2$),可能会加重不良状态或者可能是非预期的偏见,也就是说grandmother相比于grandfather最终更有可能输出babysister,所以在最后的均衡步中,我们想要确保的是像grandmother和grandfather这样的词都能够有**一致的相似度或者说是相等的距离**,这其中会有一些线性代数的步骤,主要做的就是将grandmother和grandfather**移至与中间轴线等距的一对点上**,如下图所示,现在性别歧视的影响也就是这两个词与babysister的距离就完全相同了。还有许多对象比如grandmother和grandfather、gir和boy、sorority和fraternity、girlhood和boyhood、sister和brother、niece和nephew、daughter和son这样的词对都可以通过均衡步来解决。
505 |
506 |  507 |
508 | 最后一个细节是怎样才能够决定哪个词是中立的呢?对于这个例子来说,doctor看起来像是一个应该是中立的单词来使之性别不确定或是种族不确定,相反地,grandmother和grandfather就不应是性别不确定的词,也会有些词像是beard,一个统计学上的事实是男性相比于女性更可能拥有胡子,因此相比于female,beard应该更靠近male一些。论文“Man is to computer programmer as woman is to homemaker? debiasing word embeddings. ”的作者做的就是训练一个分类器来尝试解决哪些词是有明确定义的,哪些词是性别确定的哪些词不是,结果表明英语里大部分词在性别方面上是没有明确定义的,即性别并不是其定义的一部分,只有一部分词像grandmother和grandfather、gir和boy、sorority和fraternity等不是性别中立的。一个线性分类器能够告诉你哪些词能够通过中和来预测这个偏见趋势或将其与这个本质是299维的子空间进行处理。最后,你需要平衡的词对的数量实际上是很小的,至少对于性别歧视这个例子来说,用手都能够数出来你需要平衡的大部分词对。完整的算法会比这里展示的更复杂一些,可以去看一下这篇论文了解详细内容。
509 |
510 | #### 15.10.3 相关的重要论文
511 |
512 | 1. Yoshua Bengio , et al. “A neural probabilistic language model.”*Journal of machine learning research*3.Feb (2003): 1137-1155.
513 |
514 | 证明使用神经网络训练的语言模型可以生成比One-hot更好的词向量。
515 |
516 | 2. Mikolov, T., Chen, K., Corrado, G., & Dean, J. Efficient estimation of word representations in vector space. *arXiv preprint arXiv:1301.3781*. (2013).
517 |
518 | 提出词嵌入领域最经典的两个模型:连续词袋模型(Continuous Bag Of Words, CBOW) 和跨词序列模型(Skip-gram)。
519 |
520 | 3. Tolga Bolukbasi, Kai-Wei Chang, James Zou, Venkatesh Saligrama, and Adam Kalai. 2016. Man is to computer programmer as woman is to homemaker? debiasing word embeddings. In Proceedings of the 30th International Conference on Neural Information Processing Systems (NIPS'16).
521 |
522 | 发现并消除了词嵌入中的社会性别偏见问题。
523 |
524 | 4. Zhao Jieyu, Wang Tianlu, Yatskar Mark, Ordonez Vicente and Chang Kai-Wei "Men Also Like Shopping: Reducing Gender Bias Amplification using Corpus-level Constraints."(2017)
525 |
526 | 发现并消除了视觉相关任务中使用结构预测模型偏见放大的问题。
527 |
528 | 5. Chengyue Gong, Di He, Xu Tan, Tao Qin, Liwei Wang, and Tie-Yan Liu. Frage: Frequency-agnostic word representation. In NeurIPS, 2018.
529 |
530 | 针对高频词和低频词在传统词嵌入模型中的表现,把它们身上“高频/低频词''这个标签拿掉后再来看训练效果。
531 |
532 | 6. Tianlu Wang, Xi Victoria Lin, Nazeen Fatema Rajani, Bryan McCann, Vicente Ordonez and Caiming Xiong. Double-Hard Debias: Tailoring Word Embeddings for Gender Bias Mitigation. ACL 2020.
533 |
534 | 提出运用“双硬去偏”法来消除词频对性别方向的负面影响。
535 |
536 | > 参考:https://www.sohu.com/a/406401979_651893?_f=index_pagefocus_7
537 |
538 |
539 |
540 |
541 |
542 |
--------------------------------------------------------------------------------
/2 神经网络基础.md:
--------------------------------------------------------------------------------
1 | ## 2 神经网络基础(Nerual network basic)
2 |
3 | ### 2.1 二分分类
4 |
5 | #### **2.1.1 定义**
6 |
7 | 对某个事件或者事物进行“是”或者“否”的判断,即可表示为如“0”和“1”两种数据形式。
8 |
9 | #### **2.1.2 数学定义**
10 |
11 | 对某个事件的结果y进行判断
12 |
13 | $y∈{0,1}.$
14 | 需要有一个期望值$h_{\theta}\left(x\right)$,使得:
15 |
16 | $0⩽h_{\theta}\left(x\right)⩽1.$
17 |
18 | 最后根据期望值hθ(x)与0.5的大小,输出结果
19 |
20 | $ y_{0}=\left\{\begin{array}{ll}0, & h_{\theta}\left(x_{0}\right)<0.5 \\ 1, & h_{\theta}\left(x_{0}\right) \geq 0.5\end{array}\right.$
21 |
22 | 当然,也不一定是将期望值与0.5去进行比较,因为最终得到的期望值其实并不完全等同于我们判断的概率,现实当中可以根据实际需要及时调整。
23 |
24 | 引用文献:https://blog.csdn.net/mathlxj/article/details/81490288
25 |
26 | **例子**:对一张图片中的动物是否是猫。
27 |
28 | 具体的判断方法为:利用图片中的各个像素点的三原色(红、绿、蓝)的亮度值来表示图片的特征,并且将这些亮度值转换为n维特征向量作为算法的输入值,最后利用逻辑回归(logistic回归)算法等各种算法判断出图片中的动物是否是猫,最后给出对应的结果。
29 |
30 | 简单点说,***分析图片三原色亮度值 → 获取特征向量作为输入 → logistic回归算法进行运算 → 输出判断结果***
31 |
32 | #### **2.1.3 常用符号**
33 |
34 | | 符号 | 含义 | 作用 |
35 | | :-----------: |:-------------:| :----:|
36 | | x | x维特征向量 | 常用于表示图片的特征 |
37 | | $n_{x}$或$n$ | 输入特征向量维度 | |
38 | | y | 预测结果 | 二分类中用0或1表示结果 |
39 | | (x,y) | 一个单独的样本 | 训练集的一个成员 |
40 | | $\left(x^{(i)}, y^{(i)}\right)$ | 一个训练集中的第i个样本 | 区分训练集中的每个样本 |
41 | | m或者m_train | 训练集样本个数 | |
42 | | $X=\left[\begin{array}{ccc}\cdots & \cdots & \cdots \\ x^{1} & x^{2} & \cdots \\ \cdots & \cdots & \cdots\end{array}\right]$ | 大写X表示训练集中所有样本的输入特征向量的矩阵集合 | m列x行,作为输入矩阵 |
43 | | $Y=\left[y^{(1)} y^{(2)} \cdots \cdot y^{(m)}\right]$ | 训练集样本预期值矩阵 | 1*m矩阵 |
44 | | $z^{(i)}$ | sigmoid()函数对于样本i计算值 | 常用于表示样本i的计算值 |
45 | | $$W^{(i)}$$ |表示第i层卷积层的参数W的特征向量 | 常用于sigmoid()函数的计算 |
46 | | $\hat{y}$ | 对样本输入的预测向量 | |
47 | | $J(x,W,b,y)$ | 损失函数 | |
48 |
49 | 需要注意,**矩阵X不能用特征向量横向集合而成**,即不能写成如下形式:
50 |
51 | $X=\left[\begin{array}{ccc}\cdots & x^{1} & \cdots \\ \cdots & x^{2} & \cdots \\ \cdots & \cdots & \cdots\end{array}\right]$(错误)
52 |
53 | #### 2.1.4 多分类
54 |
55 | 本质上是在二分分类上的拓展,讲判断结果分成了更多的部分。例如,识别水果的种类是苹果还是西瓜,或者是香蕉。
56 |
57 |
58 |
59 | ### 2.2 logistic回归
60 |
61 | #### **2.2.1 定义**
62 |
63 | 利于一定的参数,对特征向量进行一定的计算,从而得出判断结果。
64 |
65 | #### **2.2.2 相关函数**
66 |
67 | 1.**线性回归**:
68 |
69 | **a.** 函数形式: y = $\omega^{\top} x+b$;
70 |
71 | T为转置符,交换特征向量的行和列。
72 |
73 | **b.** 参数:w,b
74 |
75 | w和b参数常相互独立的进行分开分析(在后面的求导中也是分开求导以及分别改变和优化自身的值)
76 |
77 | **c.** y范围 :(0,1)
78 |
79 | 由于这个范围大于(0,1),并不符合当前判断正误的场景(即0或者1的场景)。所以为了保证y的值在0和1的范围内,需要使用$sigmoid()$函数将 y转化到0到1的范围内。
80 |
81 | 为了容易区分,将线性函数的输出值y改为z,即 $z = wx + b$,并且将z作为sigmoid(z)函数的输入。
82 |
83 | 2.**sigmoid函数**:
84 |
85 | **a.** 表达式:$y = sigmoid(z)=\frac{1}{1+e^{-z}}$
86 |
87 | **b.**函数图像:
88 |
89 | 
90 |
91 | 当z越大,y的值越接近于1,当z越小,y的值越接近于0。
92 |
93 | #### 2.2.3 python实现
94 |
95 | ```python
96 | #-*- coding: utf-8 -*-
97 | from __future__ import print_function
98 | import numpy as np
99 | import matplotlib.pyplot as plt
100 | from scipy import optimize
101 | from matplotlib.font_manager import FontProperties
102 | font = FontProperties(fname=r"c:\windows\fonts\simsun.ttc", size=14) # 解决windows环境下画图汉字乱码问题
103 |
104 |
105 | def LogisticRegression():
106 | data = loadtxtAndcsv_data("data2.txt", ",", np.float64)
107 | X = data[:,0:-1]
108 | y = data[:,-1]
109 |
110 | plot_data(X,y) # 作图
111 |
112 | X = mapFeature(X[:,0],X[:,1]) #映射为多项式
113 | initial_theta = np.zeros((X.shape[1],1))#初始化theta
114 | initial_lambda = 0.1 #初始化正则化系数,一般取0.01,0.1,1.....
115 |
116 | J = costFunction(initial_theta,X,y,initial_lambda) #计算一下给定初始化的theta和lambda求出的代价J
117 |
118 | print(J) #输出一下计算的值,应该为0.693147
119 | #result = optimize.fmin(costFunction, initial_theta, args=(X,y,initial_lambda)) #直接使用最小化的方法,效果不好
120 | '''调用scipy中的优化算法fmin_bfgs(拟牛顿法Broyden-Fletcher-Goldfarb-Shanno)
121 | - costFunction是自己实现的一个求代价的函数,
122 | - initial_theta表示初始化的值,
123 | - fprime指定costFunction的梯度
124 | - args是其余测参数,以元组的形式传入,最后会将最小化costFunction的theta返回
125 | '''
126 | result = optimize.fmin_bfgs(costFunction, initial_theta, fprime=gradient, args=(X,y,initial_lambda))
127 | p = predict(X, result) #预测
128 | print(u'在训练集上的准确度为%f%%'%np.mean(np.float64(p==y)*100)) # 与真实值比较,p==y返回True,转化为float
129 |
130 | X = data[:,0:-1]
131 | y = data[:,-1]
132 | plotDecisionBoundary(result,X,y) #画决策边界
133 |
134 |
135 |
136 | # 加载txt和csv文件
137 | def loadtxtAndcsv_data(fileName,split,dataType):
138 | return np.loadtxt(fileName,delimiter=split,dtype=dataType)
139 |
140 | # 加载npy文件
141 | def loadnpy_data(fileName):
142 | return np.load(fileName)
143 |
144 | # 显示二维图形
145 | def plot_data(X,y):
146 | pos = np.where(y==1) #找到y==1的坐标位置
147 | neg = np.where(y==0) #找到y==0的坐标位置
148 | #作图
149 | plt.figure(figsize=(15,12))
150 | plt.plot(X[pos,0],X[pos,1],'ro') # red o
151 | plt.plot(X[neg,0],X[neg,1],'bo') # blue o
152 | plt.title(u"两个类别散点图",fontproperties=font)
153 | plt.show()
154 |
155 | # 映射为多项式
156 | def mapFeature(X1,X2):
157 | degree = 2; # 映射的最高次方
158 | out = np.ones((X1.shape[0],1)) # 映射后的结果数组(取代X)
159 | '''
160 | 这里以degree=2为例,映射为1,x1,x2,x1^2,x1,x2,x2^2
161 | '''
162 | for i in np.arange(1,degree+1):
163 | for j in range(i+1):
164 | temp = X1**(i-j)*(X2**j) #矩阵直接乘相当于matlab中的点乘.*
165 | out = np.hstack((out, temp.reshape(-1,1)))
166 | return out
167 |
168 | # 代价函数
169 | def costFunction(initial_theta,X,y,inital_lambda):
170 | m = len(y)
171 | J = 0
172 |
173 | h = sigmoid(np.dot(X,initial_theta)) # 计算h(z)
174 | theta1 = initial_theta.copy() # 因为正则化j=1从1开始,不包含0,所以复制一份,前theta(0)值为0
175 | theta1[0] = 0
176 |
177 | temp = np.dot(np.transpose(theta1),theta1)
178 | J = (-np.dot(np.transpose(y),np.log(h))-np.dot(np.transpose(1-y),np.log(1-h))+temp*inital_lambda/2)/m # 正则化的代价方程
179 | return J
180 |
181 | # 计算梯度
182 | def gradient(initial_theta,X,y,inital_lambda):
183 | m = len(y)
184 | grad = np.zeros((initial_theta.shape[0]))
185 |
186 | h = sigmoid(np.dot(X,initial_theta))# 计算h(z)
187 | theta1 = initial_theta.copy()
188 | theta1[0] = 0
189 |
190 | grad = np.dot(np.transpose(X),h-y)/m+inital_lambda/m*theta1 #正则化的梯度
191 | return grad
192 |
193 | # S型函数
194 | def sigmoid(z):
195 | h = np.zeros((len(z),1)) # 初始化,与z的长度一置
196 |
197 | h = 1.0/(1.0+np.exp(-z))
198 | return h
199 |
200 |
201 | #画决策边界
202 | def plotDecisionBoundary(theta,X,y):
203 | pos = np.where(y==1) #找到y==1的坐标位置
204 | neg = np.where(y==0) #找到y==0的坐标位置
205 | #作图
206 | plt.figure(figsize=(15,12))
207 | plt.plot(X[pos,0],X[pos,1],'ro') # red o
208 | plt.plot(X[neg,0],X[neg,1],'bo') # blue o
209 | plt.title(u"决策边界",fontproperties=font)
210 |
211 | #u = np.linspace(30,100,100)
212 | #v = np.linspace(30,100,100)
213 |
214 | u = np.linspace(-1,1.5,50) #根据具体的数据,这里需要调整
215 | v = np.linspace(-1,1.5,50)
216 |
217 | z = np.zeros((len(u),len(v)))
218 | for i in range(len(u)):
219 | for j in range(len(v)):
220 | z[i,j] = np.dot(mapFeature(u[i].reshape(1,-1),v[j].reshape(1,-1)),theta) # 计算对应的值,需要map
221 |
222 | z = np.transpose(z)
223 | plt.contour(u,v,z,[0,0.01],linewidth=2.0) # 画等高线,范围在[0,0.01],即近似为决策边界
224 | #plt.legend()
225 | plt.show()
226 |
227 | # 预测
228 | def predict(X,theta):
229 | m = X.shape[0]
230 | p = np.zeros((m,1))
231 | p = sigmoid(np.dot(X,theta)) # 预测的结果,是个概率值
232 |
233 | for i in range(m):
234 | if p[i] > 0.5: #概率大于0.5预测为1,否则预测为0
235 | p[i] = 1
236 | else:
237 | p[i] = 0
238 | return p
239 |
240 |
241 | # 测试逻辑回归函数
242 | def testLogisticRegression():
243 | LogisticRegression()
244 |
245 |
246 | if __name__ == "__main__":
247 | testLogisticRegression()
248 | ```
249 |
250 | ### 2.3 **损失函数**
251 |
252 | #### **2.3.1** 定义
253 |
254 | 对当前输出y和训练样本的预期值之间的误差的计算,进而用于修正函数的各种参数(如前面线性回归中的w和z)。
255 | 损失函数也常被称为误差函数。
256 |
257 | 损失函数的计算结果越小说明参数越准确。
258 |
259 | #### **2.3.2 **常见的损失函数
260 |
261 | **L1 Loss:**
262 |
263 | * 基本形式:计算预测值与目标值的绝对差值
264 | $$
265 | L=\sum_{i=1}^{n}\left|y_{i}-\hat{y}_{i}\right|
266 | $$
267 |
268 | * pytorch实现:
269 |
270 | ```python
271 | torch.nn.L1Loss(reduction='mean')
272 | ```
273 |
274 | 关于参数
275 |
276 | reduction: none(不使用约简)、mean(返回loss和的平均值)、sum(返回loss的总和)。默认mean。
277 |
278 | * 适用场景:
279 |
280 | L1 Loss能处理数据中的异常值。这或许在那些异常值可能被安全地和有效地忽略的研究中很有用。如果**需要考虑任一或全部的异常值**,那么最小绝对值偏差是更好的选择(对比L2 Loss)。
281 |
282 | * 优缺点:
283 |
284 | 优点:鲁棒
285 |
286 | 缺点:不稳定解、可能多个解
287 |
288 | **MSE Loss:**
289 |
290 | * 基本形式:计算预测值和目标值的差值的平方
291 | $$
292 | L=\frac{1}{N} \sum_{i=1}^{N}\left(y_{i}-\hat{y}_{i}\right)^{2}
293 | $$
294 |
295 | * pytorch实现:
296 |
297 | ```python
298 | torch.nn.MSELoss(reduction='mean')
299 | ```
300 |
301 | 关于参数
302 |
303 | reduction: none(不使用约简)、mean(返回loss和的平均值)、sum(返回loss的总和)。默认mean。
304 |
305 | * 适用场景:
306 |
307 | 适合作为回归问题的损失函数,比如房价预测,销量预测,流量预测等。
308 |
309 | * 优缺点:
310 |
311 | 优点:各点都连续光滑,方便求导,具有较为稳定的解
312 |
313 | 缺点:不是特别稳健,当差值过大时梯度会非常大,可能导致梯度爆炸
314 |
315 | **Cross Entropy Loss:**
316 |
317 | * 基本形式:二分类问题与多分类问题的形式略有区别,但是本质是一样的(二分类是多分类的一个特例)
318 | $$
319 | L=-[y \log \hat{y}+(1-y) \log (1-\hat{y})]
320 | $$
321 |
322 | $$
323 | L=-\sum_{i=1}^N y_i \log \hat{y}
324 | $$
325 |
326 | 首先理解二分类时如何工作:标签$y\in\{0,1\}$,因此$y=1 \space\text{or}\space (1-y)=1$,则该损失函数变为$L=-\log \hat y $(标签为1时)或者$L=-\log(1-\hat y)$(标签为0时)。$\hat y \in[0,1]$,因此$-\log \hat y \in[0,+\infty]$,所以最终结果是$\hat y$离$y$误差越大,损失函数越大。
327 |
328 | 多分类同样分析。
329 |
330 | * pytorch实现:
331 |
332 | ```python
333 | torch.nn.CrossEntropyLoss(weight=None,ignore_index=-100, reduction='mean')
334 | ```
335 |
336 | 关于参数
337 |
338 | weight: weight(Tensor, optional),自定义的每个类别的权重。必须是长为C的Tensor。
339 |
340 | ignore_index(int, optional),设置一个目标值, 该目标值会被忽略, 从而不会影响到输入的梯度。
341 |
342 | reduction: none(不使用约简)、mean(返回loss和的平均值)、sum(返回loss的总和)。默认mean。
343 |
344 | * 适用场景:
345 |
346 | 适合分类任务,无论是二分类还是多分类。比如逻辑回归和神经网络。常与softmax激活函数一起使用。
347 |
348 | * 优缺点:
349 |
350 | 优点:求导简单,导数之与输出值和真实值的差距有关,收敛更快
351 |
352 | 缺点:在类别过多时计算量过大(比如语言模型中,一个词典包含成千上万个类别)
353 |
354 | **KL散度Loss:**
355 |
356 | KL散度又叫相对熵,与交叉熵的关系有$KLD(p\|q)=CE(p,q)-H(p)$,其中$p$是真实分布,$CE$是交叉熵,信息熵$H(p)=p\log(p)$。
357 |
358 | * 基本形式:
359 | $$
360 | L=-\sum y \log (\hat y)-\left(-\sum y \log (y)\right)
361 | $$
362 |
363 | * pytorch实现:
364 |
365 | ```python
366 | torch.nn.KLDivLoss(reduction='mean')
367 | ```
368 |
369 | 关于参数
370 |
371 | reduction: none(不使用约简)、mean(返回loss和的平均值)、sum(返回loss的总和)。默认mean。
372 |
373 | * 适用场景:
374 |
375 | KL 散度可用于衡量不同的连续分布之间的距离,在连续的输出分布的空间上(离散采样)上进行直接回归时很有效。
376 |
377 | * 优缺点:
378 |
379 | **Huber Loss:**
380 |
381 | 又叫平滑L1损失(Smooth L1 Loss)。
382 |
383 | * 基本形式:
384 | $$
385 | L=\frac{1}{n} \sum_{i} z_{i}
386 | $$
387 | 其中
388 | $$
389 | z_{i}=\left\{\begin{array}{ll}
390 | 0.5\left(y_{i}-\hat y_{i}\right)^{2}, & \text { if }\left|y_{i}-\hat y_{i}\right|<1 \\
391 | \left|y_{i}-\hat y_{i}\right|-0.5, & \text { otherwise }
392 | \end{array}\right.
393 | $$
394 | 如下图,看了就能明白为什么叫平滑L1了:
395 |
396 | 
397 |
398 | * pytorch实现:
399 |
400 | ```python
401 | torch.nn.SmoothL1Loss(reduction='mean')
402 | ```
403 |
404 | 关于参数
405 |
406 | reduction: none(不使用约简)、mean(返回loss和的平均值)、sum(返回loss的总和)。默认mean。
407 |
408 | * 适用场景:
409 |
410 | 适合处理回归问题。
411 |
412 | * 优缺点:
413 |
414 | 优点:在零点也可微,并且在误差很小时梯度也会减小,方便收敛
415 |
416 | 缺点:对于数据中异常值的敏感性要差一些
417 |
418 | #### 2.3.3 **成本函数**
419 |
420 | **a.**定义:即一个训练集中所有样本的损失函数输出值$σ$的平均值,用于衡量当前模型的参数的准确性。平均值越小,参数越准确。
421 |
422 | **b.**公式:
423 | $$
424 | J(\omega, b)=\frac{1}{m} \sum_{i=1}^{m} σ\left(\hat{y}^{(i)}, y^{(i)}\right)=-\frac{1}{m} \sum_{i=1}^{n}\left[y^{(j)} \log \hat{y}^{(i)}+\left(1-y\right) \log \left(1-\hat{y}^{(j)}\right) \right]
425 | $$
426 |
427 | 损失函数与成本函数的区别:
428 |
429 | 损失函数(Loss function)是定义在单个训练样本上的,也就是就算一个样本的误差,比如我们想要分类,就是预测的类别和实际类别的区别,是一个样本的哦,用L表示
430 |
431 | 代价函数(Cost function)是定义在整个训练集上面的,也就是所有样本的误差的总和的平均,也就是损失函数的总和的平均,有没有这个平均其实不会影响最后的参数的求解结果。
432 |
433 | ### 2.4 梯度下降法
434 |
435 | #### **2.4.1 **定义
436 |
437 | 通过对参数(如w,b)进行求导,用于训练模型中的各种参数(如线性回归的w和b参数),从而达到成本函数值的最低点(也就是函数图像的最低点)。
438 |
439 | #### **2.4.2 **函数图像
440 |
441 | 
442 |
443 | 在图中,x和y轴分别为需要训练的参数w和b(参数越多时维数越高),z轴为J(w,b)的值
444 |
445 | #### **2.4.3 **具体操作方式
446 |
447 | 在logistic回归当中参数进行任意初始化后,进行一次logistic回归计算,并且计算出当前J(w,b)的公式和值,并且分别对公式进行关于不同参数的导数,进而求出斜率最低的方向,即再图像中为当前点最陡的方向,再向这个方向移动一定的距离(这个距离按照学习率,也就是步长决定),具体的移动方法就是使用变化函数改变参数的值,也就是对参数进行优化,并且不断重复上述过程,从而达到最优点(损失函数最低点)。
448 |
449 | 
450 |
451 | #### **2.4.4 **变化函数:(以参数w为例)
452 |
453 | $w:=w-\alpha \frac{d J(w)}{d w}$
454 |
455 | $w:=$ 为更新w的值
456 |
457 | $\alpha$ 为学习率,代表着步长,控制着每次迭代的移动长度,学习率越大,步长越大
458 |
459 | $\frac{d J(w)}{d w}$ :为J进行关于w的导数,后面常用$d(w)$直接表示
460 |
461 | #### **2.4.5 **过程图示
462 |
463 | 
464 |
465 | ### 2.5 导数 ###
466 |
467 | #### 2.5.1 导数定义
468 |
469 | 1. 导数第一种定义
470 |
471 | 设函数$ y = f(x)$ 在点 $x0 $的某个邻域内有定义,当自变量$x$ 在 $x0$ 处有增量$\Delta x$($x0 + \Delta x $也在该邻域内 ) 时相应地函数取得增量 $\Delta y =f(x0 + \Delta x) - f(x0)$ 如果 $\Delta y$与$ \Delta x$ 之比当 $\Delta x→0$ 时极限存在则称函数$ y = f(x) $在点 $x0 $处可导,并称这个极限值为函数$ y = f(x)$ 在点$ x0$ 处的导数记为$ f'(x0)$ ,即导数第一定义。
472 | $$
473 | f'(x)=\lim_{\Delta x\to 0}\frac{f(x+\Delta x)-f(x) }{\Delta x}
474 | $$
475 |
476 | 2. 导数第二种定义
477 | 设函数$ y = f(x)$ 在点$ x0$ 的某个邻域内有定义,当自变量$x$ 在$ x0$ 处有增量$-\Delta x$($x0 - \Delta x $也在该邻域内 ) 时相应地函数取得增量 $\Delta y=f(x0)-f(x0 - \Delta x)$ 如果 $\Delta y $与$ \Delta x$ 之比当 $\Delta x→0$ 时极限存在则称函数$ y = f(x) $在点 $x0$ 处可导,并称这个极限值为函数$ y = f(x)$ 在点 $x0$ 处的导数记为$ f'(x0)$ ,即导数第二定义。
478 | $$
479 | f'(x)=\lim_{\Delta x\to 0}\frac{f(x)-f(x-\Delta x)}{\Delta x}
480 | $$
481 |
482 |
483 | 3. 几何意义
484 | 函数$y=f(x)$在$x0$点的导数$f'(x0)$的几何意义表示函数曲线在P0 点的切线斜率。
485 |
486 | 
487 |
488 | #### 2.5.2 导数计算公式
489 |
490 | 这里将列举六类基本初等函数的导数:
491 |
492 | **1.常函数** 即常数$y=c(c为常数) y'=0$
493 |
494 | **2.幂函数** $y=x^n,y'=n*x^(n-1)(n∈R)$
495 |
496 | **3.基本导数公式** 指数函数$y=a^x,y'=a^x * lna $
497 |
498 | **4对数函数** $y=logaX,y'=1/(xlna) (a>0且a≠1,x>0)$
499 |
500 | **5.三角函数**
501 |
502 | (1)正弦函数:$y=(sinx) y'=cosx$
503 |
504 | (2)余弦函数:$y=cosx y'=-sinx$
505 |
506 | (3)正切函数:$y=(tanx y'=1/(cosx)^2$
507 |
508 | (4)余切函数:$y=cotx y'=-1/(sinx)^2$
509 |
510 | **6.反三角函数**
511 |
512 | (1)反正弦函数$y=arcsinx y'=1/\sqrt{1-x^2}$
513 |
514 | (2)反余弦函数$y=arccosx y'=-1/\sqrt{1-x^2}$
515 |
516 | (3)反正切函数$y=arctanx y'=1/(1+x^2)$
517 |
518 | (4)反余切函数$y=arccotx y'=-1/(1+x^2)$
519 |
520 | #### 2.5.3 偏导数
521 |
522 | 在数学中,一个多变量的函数的偏导数,就是它关于其中一个变量的导数,同时保持其他变量恒定。
523 |
524 | #### 2.5.4 偏导数几何意义
525 |
526 | 表示固定面上一点的切线斜率。
527 |
528 | 偏导数 f'x(x0,y0) 表示固定面上一点对 x 轴的切线斜率;偏导数$ f'y(x0,y0) $表示固定面上一点对 y 轴的切线斜率。
529 |
530 | 高阶偏导数:如果二元函数 z=f(x,y) 的偏导数 $f'x(x,y) $与$ f'y(x,y)$ 仍然可导,那么这两个偏导函数的偏导数称为 $z=f(x,y)$ 的二阶偏导数。二元函数的二阶偏导数有四个: $f"xx,f"xy,f"yx,f"yy$。
531 |
532 | **注意:**
533 |
534 | $f"xy$与$f"yx$的区别在于:前者是先对 x 求偏导,然后将所得的偏导函数再对 y 求偏导;后者是先对 y 求偏导再对 x 求偏导。**当$ f"xy $与 $f"yx$ 都连续时,求导的结果与先后次序无关。**
535 | #### 2.5.5 链式法则 ####
536 | 复合函数对自变量的导数等于已知函数对中间变量的导数乘以中间变量对自变量的导数--称为链式法则。
537 |
538 | 链式法则(chain rule)是微积分中的求导法则,用以求一个复合函数的导数。所谓的复合函数,是指以一个函数作为另一个函数的自变量。如设$f(x)=3x,g(x)=x+3,g(f(x))$就是一个复合函数,并且$g′(f(x))=3$。若$h(x)=f(g(x))$,则$h'(x)=f'(g(x))g'(x)$。
539 |
540 | 链式法则用文字描述,就是“由两个函数凑起来的复合函数,其导数等于里边函数代入外边函数的值之导数,乘以里边函数的导数。
541 |
542 |
543 |
544 | ### 2.6 计算图 ###
545 |
546 | #### 2.6.1 计算图的定义
547 |
548 | 计算图是用箭头画出来的,从左到右的计算。以下以函数$J=3(a+bc)$为例。
549 | 如图所示,先计算出bc的数值,并将其存在变量u中,之后计算a+u,并将其存在变量v中,之后计算3*v,计算结果即为变量J 的数值。从左到右,箭头表示出了计算的顺序。
550 | 
551 |
552 | #### 2.6.2 计算图的导数运算 ####
553 | 那么如何计算J的导数呢?如图中所示:
554 | 
555 | 结合链式法则,从最右侧算起,$dJ/dv=3,故dJ=3dv。dJ/da=dJ/dv*dv/da=3*1=3$;这个过程其实就是反向传播。那dJ/du是多少呢?根据链式法则,从图中右侧向左计算,$dJ/du=dJ/dv*dv/du=3*1=3$。
556 |
557 | 同理可知$dJ/db=dJ/dv*dv/du*du/db=3*1*c=6;dJ/dc=dJ/dv*dv/du*du/dc=3*1*3=9$。
558 |
559 |
560 |
561 | ### 2.7 logistic回归中的梯度下降法 ###
562 | logistic回归的公式如下图所示,
563 |
564 |
507 |
508 | 最后一个细节是怎样才能够决定哪个词是中立的呢?对于这个例子来说,doctor看起来像是一个应该是中立的单词来使之性别不确定或是种族不确定,相反地,grandmother和grandfather就不应是性别不确定的词,也会有些词像是beard,一个统计学上的事实是男性相比于女性更可能拥有胡子,因此相比于female,beard应该更靠近male一些。论文“Man is to computer programmer as woman is to homemaker? debiasing word embeddings. ”的作者做的就是训练一个分类器来尝试解决哪些词是有明确定义的,哪些词是性别确定的哪些词不是,结果表明英语里大部分词在性别方面上是没有明确定义的,即性别并不是其定义的一部分,只有一部分词像grandmother和grandfather、gir和boy、sorority和fraternity等不是性别中立的。一个线性分类器能够告诉你哪些词能够通过中和来预测这个偏见趋势或将其与这个本质是299维的子空间进行处理。最后,你需要平衡的词对的数量实际上是很小的,至少对于性别歧视这个例子来说,用手都能够数出来你需要平衡的大部分词对。完整的算法会比这里展示的更复杂一些,可以去看一下这篇论文了解详细内容。
509 |
510 | #### 15.10.3 相关的重要论文
511 |
512 | 1. Yoshua Bengio , et al. “A neural probabilistic language model.”*Journal of machine learning research*3.Feb (2003): 1137-1155.
513 |
514 | 证明使用神经网络训练的语言模型可以生成比One-hot更好的词向量。
515 |
516 | 2. Mikolov, T., Chen, K., Corrado, G., & Dean, J. Efficient estimation of word representations in vector space. *arXiv preprint arXiv:1301.3781*. (2013).
517 |
518 | 提出词嵌入领域最经典的两个模型:连续词袋模型(Continuous Bag Of Words, CBOW) 和跨词序列模型(Skip-gram)。
519 |
520 | 3. Tolga Bolukbasi, Kai-Wei Chang, James Zou, Venkatesh Saligrama, and Adam Kalai. 2016. Man is to computer programmer as woman is to homemaker? debiasing word embeddings. In Proceedings of the 30th International Conference on Neural Information Processing Systems (NIPS'16).
521 |
522 | 发现并消除了词嵌入中的社会性别偏见问题。
523 |
524 | 4. Zhao Jieyu, Wang Tianlu, Yatskar Mark, Ordonez Vicente and Chang Kai-Wei "Men Also Like Shopping: Reducing Gender Bias Amplification using Corpus-level Constraints."(2017)
525 |
526 | 发现并消除了视觉相关任务中使用结构预测模型偏见放大的问题。
527 |
528 | 5. Chengyue Gong, Di He, Xu Tan, Tao Qin, Liwei Wang, and Tie-Yan Liu. Frage: Frequency-agnostic word representation. In NeurIPS, 2018.
529 |
530 | 针对高频词和低频词在传统词嵌入模型中的表现,把它们身上“高频/低频词''这个标签拿掉后再来看训练效果。
531 |
532 | 6. Tianlu Wang, Xi Victoria Lin, Nazeen Fatema Rajani, Bryan McCann, Vicente Ordonez and Caiming Xiong. Double-Hard Debias: Tailoring Word Embeddings for Gender Bias Mitigation. ACL 2020.
533 |
534 | 提出运用“双硬去偏”法来消除词频对性别方向的负面影响。
535 |
536 | > 参考:https://www.sohu.com/a/406401979_651893?_f=index_pagefocus_7
537 |
538 |
539 |
540 |
541 |
542 |
--------------------------------------------------------------------------------
/2 神经网络基础.md:
--------------------------------------------------------------------------------
1 | ## 2 神经网络基础(Nerual network basic)
2 |
3 | ### 2.1 二分分类
4 |
5 | #### **2.1.1 定义**
6 |
7 | 对某个事件或者事物进行“是”或者“否”的判断,即可表示为如“0”和“1”两种数据形式。
8 |
9 | #### **2.1.2 数学定义**
10 |
11 | 对某个事件的结果y进行判断
12 |
13 | $y∈{0,1}.$
14 | 需要有一个期望值$h_{\theta}\left(x\right)$,使得:
15 |
16 | $0⩽h_{\theta}\left(x\right)⩽1.$
17 |
18 | 最后根据期望值hθ(x)与0.5的大小,输出结果
19 |
20 | $ y_{0}=\left\{\begin{array}{ll}0, & h_{\theta}\left(x_{0}\right)<0.5 \\ 1, & h_{\theta}\left(x_{0}\right) \geq 0.5\end{array}\right.$
21 |
22 | 当然,也不一定是将期望值与0.5去进行比较,因为最终得到的期望值其实并不完全等同于我们判断的概率,现实当中可以根据实际需要及时调整。
23 |
24 | 引用文献:https://blog.csdn.net/mathlxj/article/details/81490288
25 |
26 | **例子**:对一张图片中的动物是否是猫。
27 |
28 | 具体的判断方法为:利用图片中的各个像素点的三原色(红、绿、蓝)的亮度值来表示图片的特征,并且将这些亮度值转换为n维特征向量作为算法的输入值,最后利用逻辑回归(logistic回归)算法等各种算法判断出图片中的动物是否是猫,最后给出对应的结果。
29 |
30 | 简单点说,***分析图片三原色亮度值 → 获取特征向量作为输入 → logistic回归算法进行运算 → 输出判断结果***
31 |
32 | #### **2.1.3 常用符号**
33 |
34 | | 符号 | 含义 | 作用 |
35 | | :-----------: |:-------------:| :----:|
36 | | x | x维特征向量 | 常用于表示图片的特征 |
37 | | $n_{x}$或$n$ | 输入特征向量维度 | |
38 | | y | 预测结果 | 二分类中用0或1表示结果 |
39 | | (x,y) | 一个单独的样本 | 训练集的一个成员 |
40 | | $\left(x^{(i)}, y^{(i)}\right)$ | 一个训练集中的第i个样本 | 区分训练集中的每个样本 |
41 | | m或者m_train | 训练集样本个数 | |
42 | | $X=\left[\begin{array}{ccc}\cdots & \cdots & \cdots \\ x^{1} & x^{2} & \cdots \\ \cdots & \cdots & \cdots\end{array}\right]$ | 大写X表示训练集中所有样本的输入特征向量的矩阵集合 | m列x行,作为输入矩阵 |
43 | | $Y=\left[y^{(1)} y^{(2)} \cdots \cdot y^{(m)}\right]$ | 训练集样本预期值矩阵 | 1*m矩阵 |
44 | | $z^{(i)}$ | sigmoid()函数对于样本i计算值 | 常用于表示样本i的计算值 |
45 | | $$W^{(i)}$$ |表示第i层卷积层的参数W的特征向量 | 常用于sigmoid()函数的计算 |
46 | | $\hat{y}$ | 对样本输入的预测向量 | |
47 | | $J(x,W,b,y)$ | 损失函数 | |
48 |
49 | 需要注意,**矩阵X不能用特征向量横向集合而成**,即不能写成如下形式:
50 |
51 | $X=\left[\begin{array}{ccc}\cdots & x^{1} & \cdots \\ \cdots & x^{2} & \cdots \\ \cdots & \cdots & \cdots\end{array}\right]$(错误)
52 |
53 | #### 2.1.4 多分类
54 |
55 | 本质上是在二分分类上的拓展,讲判断结果分成了更多的部分。例如,识别水果的种类是苹果还是西瓜,或者是香蕉。
56 |
57 |
58 |
59 | ### 2.2 logistic回归
60 |
61 | #### **2.2.1 定义**
62 |
63 | 利于一定的参数,对特征向量进行一定的计算,从而得出判断结果。
64 |
65 | #### **2.2.2 相关函数**
66 |
67 | 1.**线性回归**:
68 |
69 | **a.** 函数形式: y = $\omega^{\top} x+b$;
70 |
71 | T为转置符,交换特征向量的行和列。
72 |
73 | **b.** 参数:w,b
74 |
75 | w和b参数常相互独立的进行分开分析(在后面的求导中也是分开求导以及分别改变和优化自身的值)
76 |
77 | **c.** y范围 :(0,1)
78 |
79 | 由于这个范围大于(0,1),并不符合当前判断正误的场景(即0或者1的场景)。所以为了保证y的值在0和1的范围内,需要使用$sigmoid()$函数将 y转化到0到1的范围内。
80 |
81 | 为了容易区分,将线性函数的输出值y改为z,即 $z = wx + b$,并且将z作为sigmoid(z)函数的输入。
82 |
83 | 2.**sigmoid函数**:
84 |
85 | **a.** 表达式:$y = sigmoid(z)=\frac{1}{1+e^{-z}}$
86 |
87 | **b.**函数图像:
88 |
89 | 
90 |
91 | 当z越大,y的值越接近于1,当z越小,y的值越接近于0。
92 |
93 | #### 2.2.3 python实现
94 |
95 | ```python
96 | #-*- coding: utf-8 -*-
97 | from __future__ import print_function
98 | import numpy as np
99 | import matplotlib.pyplot as plt
100 | from scipy import optimize
101 | from matplotlib.font_manager import FontProperties
102 | font = FontProperties(fname=r"c:\windows\fonts\simsun.ttc", size=14) # 解决windows环境下画图汉字乱码问题
103 |
104 |
105 | def LogisticRegression():
106 | data = loadtxtAndcsv_data("data2.txt", ",", np.float64)
107 | X = data[:,0:-1]
108 | y = data[:,-1]
109 |
110 | plot_data(X,y) # 作图
111 |
112 | X = mapFeature(X[:,0],X[:,1]) #映射为多项式
113 | initial_theta = np.zeros((X.shape[1],1))#初始化theta
114 | initial_lambda = 0.1 #初始化正则化系数,一般取0.01,0.1,1.....
115 |
116 | J = costFunction(initial_theta,X,y,initial_lambda) #计算一下给定初始化的theta和lambda求出的代价J
117 |
118 | print(J) #输出一下计算的值,应该为0.693147
119 | #result = optimize.fmin(costFunction, initial_theta, args=(X,y,initial_lambda)) #直接使用最小化的方法,效果不好
120 | '''调用scipy中的优化算法fmin_bfgs(拟牛顿法Broyden-Fletcher-Goldfarb-Shanno)
121 | - costFunction是自己实现的一个求代价的函数,
122 | - initial_theta表示初始化的值,
123 | - fprime指定costFunction的梯度
124 | - args是其余测参数,以元组的形式传入,最后会将最小化costFunction的theta返回
125 | '''
126 | result = optimize.fmin_bfgs(costFunction, initial_theta, fprime=gradient, args=(X,y,initial_lambda))
127 | p = predict(X, result) #预测
128 | print(u'在训练集上的准确度为%f%%'%np.mean(np.float64(p==y)*100)) # 与真实值比较,p==y返回True,转化为float
129 |
130 | X = data[:,0:-1]
131 | y = data[:,-1]
132 | plotDecisionBoundary(result,X,y) #画决策边界
133 |
134 |
135 |
136 | # 加载txt和csv文件
137 | def loadtxtAndcsv_data(fileName,split,dataType):
138 | return np.loadtxt(fileName,delimiter=split,dtype=dataType)
139 |
140 | # 加载npy文件
141 | def loadnpy_data(fileName):
142 | return np.load(fileName)
143 |
144 | # 显示二维图形
145 | def plot_data(X,y):
146 | pos = np.where(y==1) #找到y==1的坐标位置
147 | neg = np.where(y==0) #找到y==0的坐标位置
148 | #作图
149 | plt.figure(figsize=(15,12))
150 | plt.plot(X[pos,0],X[pos,1],'ro') # red o
151 | plt.plot(X[neg,0],X[neg,1],'bo') # blue o
152 | plt.title(u"两个类别散点图",fontproperties=font)
153 | plt.show()
154 |
155 | # 映射为多项式
156 | def mapFeature(X1,X2):
157 | degree = 2; # 映射的最高次方
158 | out = np.ones((X1.shape[0],1)) # 映射后的结果数组(取代X)
159 | '''
160 | 这里以degree=2为例,映射为1,x1,x2,x1^2,x1,x2,x2^2
161 | '''
162 | for i in np.arange(1,degree+1):
163 | for j in range(i+1):
164 | temp = X1**(i-j)*(X2**j) #矩阵直接乘相当于matlab中的点乘.*
165 | out = np.hstack((out, temp.reshape(-1,1)))
166 | return out
167 |
168 | # 代价函数
169 | def costFunction(initial_theta,X,y,inital_lambda):
170 | m = len(y)
171 | J = 0
172 |
173 | h = sigmoid(np.dot(X,initial_theta)) # 计算h(z)
174 | theta1 = initial_theta.copy() # 因为正则化j=1从1开始,不包含0,所以复制一份,前theta(0)值为0
175 | theta1[0] = 0
176 |
177 | temp = np.dot(np.transpose(theta1),theta1)
178 | J = (-np.dot(np.transpose(y),np.log(h))-np.dot(np.transpose(1-y),np.log(1-h))+temp*inital_lambda/2)/m # 正则化的代价方程
179 | return J
180 |
181 | # 计算梯度
182 | def gradient(initial_theta,X,y,inital_lambda):
183 | m = len(y)
184 | grad = np.zeros((initial_theta.shape[0]))
185 |
186 | h = sigmoid(np.dot(X,initial_theta))# 计算h(z)
187 | theta1 = initial_theta.copy()
188 | theta1[0] = 0
189 |
190 | grad = np.dot(np.transpose(X),h-y)/m+inital_lambda/m*theta1 #正则化的梯度
191 | return grad
192 |
193 | # S型函数
194 | def sigmoid(z):
195 | h = np.zeros((len(z),1)) # 初始化,与z的长度一置
196 |
197 | h = 1.0/(1.0+np.exp(-z))
198 | return h
199 |
200 |
201 | #画决策边界
202 | def plotDecisionBoundary(theta,X,y):
203 | pos = np.where(y==1) #找到y==1的坐标位置
204 | neg = np.where(y==0) #找到y==0的坐标位置
205 | #作图
206 | plt.figure(figsize=(15,12))
207 | plt.plot(X[pos,0],X[pos,1],'ro') # red o
208 | plt.plot(X[neg,0],X[neg,1],'bo') # blue o
209 | plt.title(u"决策边界",fontproperties=font)
210 |
211 | #u = np.linspace(30,100,100)
212 | #v = np.linspace(30,100,100)
213 |
214 | u = np.linspace(-1,1.5,50) #根据具体的数据,这里需要调整
215 | v = np.linspace(-1,1.5,50)
216 |
217 | z = np.zeros((len(u),len(v)))
218 | for i in range(len(u)):
219 | for j in range(len(v)):
220 | z[i,j] = np.dot(mapFeature(u[i].reshape(1,-1),v[j].reshape(1,-1)),theta) # 计算对应的值,需要map
221 |
222 | z = np.transpose(z)
223 | plt.contour(u,v,z,[0,0.01],linewidth=2.0) # 画等高线,范围在[0,0.01],即近似为决策边界
224 | #plt.legend()
225 | plt.show()
226 |
227 | # 预测
228 | def predict(X,theta):
229 | m = X.shape[0]
230 | p = np.zeros((m,1))
231 | p = sigmoid(np.dot(X,theta)) # 预测的结果,是个概率值
232 |
233 | for i in range(m):
234 | if p[i] > 0.5: #概率大于0.5预测为1,否则预测为0
235 | p[i] = 1
236 | else:
237 | p[i] = 0
238 | return p
239 |
240 |
241 | # 测试逻辑回归函数
242 | def testLogisticRegression():
243 | LogisticRegression()
244 |
245 |
246 | if __name__ == "__main__":
247 | testLogisticRegression()
248 | ```
249 |
250 | ### 2.3 **损失函数**
251 |
252 | #### **2.3.1** 定义
253 |
254 | 对当前输出y和训练样本的预期值之间的误差的计算,进而用于修正函数的各种参数(如前面线性回归中的w和z)。
255 | 损失函数也常被称为误差函数。
256 |
257 | 损失函数的计算结果越小说明参数越准确。
258 |
259 | #### **2.3.2 **常见的损失函数
260 |
261 | **L1 Loss:**
262 |
263 | * 基本形式:计算预测值与目标值的绝对差值
264 | $$
265 | L=\sum_{i=1}^{n}\left|y_{i}-\hat{y}_{i}\right|
266 | $$
267 |
268 | * pytorch实现:
269 |
270 | ```python
271 | torch.nn.L1Loss(reduction='mean')
272 | ```
273 |
274 | 关于参数
275 |
276 | reduction: none(不使用约简)、mean(返回loss和的平均值)、sum(返回loss的总和)。默认mean。
277 |
278 | * 适用场景:
279 |
280 | L1 Loss能处理数据中的异常值。这或许在那些异常值可能被安全地和有效地忽略的研究中很有用。如果**需要考虑任一或全部的异常值**,那么最小绝对值偏差是更好的选择(对比L2 Loss)。
281 |
282 | * 优缺点:
283 |
284 | 优点:鲁棒
285 |
286 | 缺点:不稳定解、可能多个解
287 |
288 | **MSE Loss:**
289 |
290 | * 基本形式:计算预测值和目标值的差值的平方
291 | $$
292 | L=\frac{1}{N} \sum_{i=1}^{N}\left(y_{i}-\hat{y}_{i}\right)^{2}
293 | $$
294 |
295 | * pytorch实现:
296 |
297 | ```python
298 | torch.nn.MSELoss(reduction='mean')
299 | ```
300 |
301 | 关于参数
302 |
303 | reduction: none(不使用约简)、mean(返回loss和的平均值)、sum(返回loss的总和)。默认mean。
304 |
305 | * 适用场景:
306 |
307 | 适合作为回归问题的损失函数,比如房价预测,销量预测,流量预测等。
308 |
309 | * 优缺点:
310 |
311 | 优点:各点都连续光滑,方便求导,具有较为稳定的解
312 |
313 | 缺点:不是特别稳健,当差值过大时梯度会非常大,可能导致梯度爆炸
314 |
315 | **Cross Entropy Loss:**
316 |
317 | * 基本形式:二分类问题与多分类问题的形式略有区别,但是本质是一样的(二分类是多分类的一个特例)
318 | $$
319 | L=-[y \log \hat{y}+(1-y) \log (1-\hat{y})]
320 | $$
321 |
322 | $$
323 | L=-\sum_{i=1}^N y_i \log \hat{y}
324 | $$
325 |
326 | 首先理解二分类时如何工作:标签$y\in\{0,1\}$,因此$y=1 \space\text{or}\space (1-y)=1$,则该损失函数变为$L=-\log \hat y $(标签为1时)或者$L=-\log(1-\hat y)$(标签为0时)。$\hat y \in[0,1]$,因此$-\log \hat y \in[0,+\infty]$,所以最终结果是$\hat y$离$y$误差越大,损失函数越大。
327 |
328 | 多分类同样分析。
329 |
330 | * pytorch实现:
331 |
332 | ```python
333 | torch.nn.CrossEntropyLoss(weight=None,ignore_index=-100, reduction='mean')
334 | ```
335 |
336 | 关于参数
337 |
338 | weight: weight(Tensor, optional),自定义的每个类别的权重。必须是长为C的Tensor。
339 |
340 | ignore_index(int, optional),设置一个目标值, 该目标值会被忽略, 从而不会影响到输入的梯度。
341 |
342 | reduction: none(不使用约简)、mean(返回loss和的平均值)、sum(返回loss的总和)。默认mean。
343 |
344 | * 适用场景:
345 |
346 | 适合分类任务,无论是二分类还是多分类。比如逻辑回归和神经网络。常与softmax激活函数一起使用。
347 |
348 | * 优缺点:
349 |
350 | 优点:求导简单,导数之与输出值和真实值的差距有关,收敛更快
351 |
352 | 缺点:在类别过多时计算量过大(比如语言模型中,一个词典包含成千上万个类别)
353 |
354 | **KL散度Loss:**
355 |
356 | KL散度又叫相对熵,与交叉熵的关系有$KLD(p\|q)=CE(p,q)-H(p)$,其中$p$是真实分布,$CE$是交叉熵,信息熵$H(p)=p\log(p)$。
357 |
358 | * 基本形式:
359 | $$
360 | L=-\sum y \log (\hat y)-\left(-\sum y \log (y)\right)
361 | $$
362 |
363 | * pytorch实现:
364 |
365 | ```python
366 | torch.nn.KLDivLoss(reduction='mean')
367 | ```
368 |
369 | 关于参数
370 |
371 | reduction: none(不使用约简)、mean(返回loss和的平均值)、sum(返回loss的总和)。默认mean。
372 |
373 | * 适用场景:
374 |
375 | KL 散度可用于衡量不同的连续分布之间的距离,在连续的输出分布的空间上(离散采样)上进行直接回归时很有效。
376 |
377 | * 优缺点:
378 |
379 | **Huber Loss:**
380 |
381 | 又叫平滑L1损失(Smooth L1 Loss)。
382 |
383 | * 基本形式:
384 | $$
385 | L=\frac{1}{n} \sum_{i} z_{i}
386 | $$
387 | 其中
388 | $$
389 | z_{i}=\left\{\begin{array}{ll}
390 | 0.5\left(y_{i}-\hat y_{i}\right)^{2}, & \text { if }\left|y_{i}-\hat y_{i}\right|<1 \\
391 | \left|y_{i}-\hat y_{i}\right|-0.5, & \text { otherwise }
392 | \end{array}\right.
393 | $$
394 | 如下图,看了就能明白为什么叫平滑L1了:
395 |
396 | 
397 |
398 | * pytorch实现:
399 |
400 | ```python
401 | torch.nn.SmoothL1Loss(reduction='mean')
402 | ```
403 |
404 | 关于参数
405 |
406 | reduction: none(不使用约简)、mean(返回loss和的平均值)、sum(返回loss的总和)。默认mean。
407 |
408 | * 适用场景:
409 |
410 | 适合处理回归问题。
411 |
412 | * 优缺点:
413 |
414 | 优点:在零点也可微,并且在误差很小时梯度也会减小,方便收敛
415 |
416 | 缺点:对于数据中异常值的敏感性要差一些
417 |
418 | #### 2.3.3 **成本函数**
419 |
420 | **a.**定义:即一个训练集中所有样本的损失函数输出值$σ$的平均值,用于衡量当前模型的参数的准确性。平均值越小,参数越准确。
421 |
422 | **b.**公式:
423 | $$
424 | J(\omega, b)=\frac{1}{m} \sum_{i=1}^{m} σ\left(\hat{y}^{(i)}, y^{(i)}\right)=-\frac{1}{m} \sum_{i=1}^{n}\left[y^{(j)} \log \hat{y}^{(i)}+\left(1-y\right) \log \left(1-\hat{y}^{(j)}\right) \right]
425 | $$
426 |
427 | 损失函数与成本函数的区别:
428 |
429 | 损失函数(Loss function)是定义在单个训练样本上的,也就是就算一个样本的误差,比如我们想要分类,就是预测的类别和实际类别的区别,是一个样本的哦,用L表示
430 |
431 | 代价函数(Cost function)是定义在整个训练集上面的,也就是所有样本的误差的总和的平均,也就是损失函数的总和的平均,有没有这个平均其实不会影响最后的参数的求解结果。
432 |
433 | ### 2.4 梯度下降法
434 |
435 | #### **2.4.1 **定义
436 |
437 | 通过对参数(如w,b)进行求导,用于训练模型中的各种参数(如线性回归的w和b参数),从而达到成本函数值的最低点(也就是函数图像的最低点)。
438 |
439 | #### **2.4.2 **函数图像
440 |
441 | 
442 |
443 | 在图中,x和y轴分别为需要训练的参数w和b(参数越多时维数越高),z轴为J(w,b)的值
444 |
445 | #### **2.4.3 **具体操作方式
446 |
447 | 在logistic回归当中参数进行任意初始化后,进行一次logistic回归计算,并且计算出当前J(w,b)的公式和值,并且分别对公式进行关于不同参数的导数,进而求出斜率最低的方向,即再图像中为当前点最陡的方向,再向这个方向移动一定的距离(这个距离按照学习率,也就是步长决定),具体的移动方法就是使用变化函数改变参数的值,也就是对参数进行优化,并且不断重复上述过程,从而达到最优点(损失函数最低点)。
448 |
449 | 
450 |
451 | #### **2.4.4 **变化函数:(以参数w为例)
452 |
453 | $w:=w-\alpha \frac{d J(w)}{d w}$
454 |
455 | $w:=$ 为更新w的值
456 |
457 | $\alpha$ 为学习率,代表着步长,控制着每次迭代的移动长度,学习率越大,步长越大
458 |
459 | $\frac{d J(w)}{d w}$ :为J进行关于w的导数,后面常用$d(w)$直接表示
460 |
461 | #### **2.4.5 **过程图示
462 |
463 | 
464 |
465 | ### 2.5 导数 ###
466 |
467 | #### 2.5.1 导数定义
468 |
469 | 1. 导数第一种定义
470 |
471 | 设函数$ y = f(x)$ 在点 $x0 $的某个邻域内有定义,当自变量$x$ 在 $x0$ 处有增量$\Delta x$($x0 + \Delta x $也在该邻域内 ) 时相应地函数取得增量 $\Delta y =f(x0 + \Delta x) - f(x0)$ 如果 $\Delta y$与$ \Delta x$ 之比当 $\Delta x→0$ 时极限存在则称函数$ y = f(x) $在点 $x0 $处可导,并称这个极限值为函数$ y = f(x)$ 在点$ x0$ 处的导数记为$ f'(x0)$ ,即导数第一定义。
472 | $$
473 | f'(x)=\lim_{\Delta x\to 0}\frac{f(x+\Delta x)-f(x) }{\Delta x}
474 | $$
475 |
476 | 2. 导数第二种定义
477 | 设函数$ y = f(x)$ 在点$ x0$ 的某个邻域内有定义,当自变量$x$ 在$ x0$ 处有增量$-\Delta x$($x0 - \Delta x $也在该邻域内 ) 时相应地函数取得增量 $\Delta y=f(x0)-f(x0 - \Delta x)$ 如果 $\Delta y $与$ \Delta x$ 之比当 $\Delta x→0$ 时极限存在则称函数$ y = f(x) $在点 $x0$ 处可导,并称这个极限值为函数$ y = f(x)$ 在点 $x0$ 处的导数记为$ f'(x0)$ ,即导数第二定义。
478 | $$
479 | f'(x)=\lim_{\Delta x\to 0}\frac{f(x)-f(x-\Delta x)}{\Delta x}
480 | $$
481 |
482 |
483 | 3. 几何意义
484 | 函数$y=f(x)$在$x0$点的导数$f'(x0)$的几何意义表示函数曲线在P0 点的切线斜率。
485 |
486 | 
487 |
488 | #### 2.5.2 导数计算公式
489 |
490 | 这里将列举六类基本初等函数的导数:
491 |
492 | **1.常函数** 即常数$y=c(c为常数) y'=0$
493 |
494 | **2.幂函数** $y=x^n,y'=n*x^(n-1)(n∈R)$
495 |
496 | **3.基本导数公式** 指数函数$y=a^x,y'=a^x * lna $
497 |
498 | **4对数函数** $y=logaX,y'=1/(xlna) (a>0且a≠1,x>0)$
499 |
500 | **5.三角函数**
501 |
502 | (1)正弦函数:$y=(sinx) y'=cosx$
503 |
504 | (2)余弦函数:$y=cosx y'=-sinx$
505 |
506 | (3)正切函数:$y=(tanx y'=1/(cosx)^2$
507 |
508 | (4)余切函数:$y=cotx y'=-1/(sinx)^2$
509 |
510 | **6.反三角函数**
511 |
512 | (1)反正弦函数$y=arcsinx y'=1/\sqrt{1-x^2}$
513 |
514 | (2)反余弦函数$y=arccosx y'=-1/\sqrt{1-x^2}$
515 |
516 | (3)反正切函数$y=arctanx y'=1/(1+x^2)$
517 |
518 | (4)反余切函数$y=arccotx y'=-1/(1+x^2)$
519 |
520 | #### 2.5.3 偏导数
521 |
522 | 在数学中,一个多变量的函数的偏导数,就是它关于其中一个变量的导数,同时保持其他变量恒定。
523 |
524 | #### 2.5.4 偏导数几何意义
525 |
526 | 表示固定面上一点的切线斜率。
527 |
528 | 偏导数 f'x(x0,y0) 表示固定面上一点对 x 轴的切线斜率;偏导数$ f'y(x0,y0) $表示固定面上一点对 y 轴的切线斜率。
529 |
530 | 高阶偏导数:如果二元函数 z=f(x,y) 的偏导数 $f'x(x,y) $与$ f'y(x,y)$ 仍然可导,那么这两个偏导函数的偏导数称为 $z=f(x,y)$ 的二阶偏导数。二元函数的二阶偏导数有四个: $f"xx,f"xy,f"yx,f"yy$。
531 |
532 | **注意:**
533 |
534 | $f"xy$与$f"yx$的区别在于:前者是先对 x 求偏导,然后将所得的偏导函数再对 y 求偏导;后者是先对 y 求偏导再对 x 求偏导。**当$ f"xy $与 $f"yx$ 都连续时,求导的结果与先后次序无关。**
535 | #### 2.5.5 链式法则 ####
536 | 复合函数对自变量的导数等于已知函数对中间变量的导数乘以中间变量对自变量的导数--称为链式法则。
537 |
538 | 链式法则(chain rule)是微积分中的求导法则,用以求一个复合函数的导数。所谓的复合函数,是指以一个函数作为另一个函数的自变量。如设$f(x)=3x,g(x)=x+3,g(f(x))$就是一个复合函数,并且$g′(f(x))=3$。若$h(x)=f(g(x))$,则$h'(x)=f'(g(x))g'(x)$。
539 |
540 | 链式法则用文字描述,就是“由两个函数凑起来的复合函数,其导数等于里边函数代入外边函数的值之导数,乘以里边函数的导数。
541 |
542 |
543 |
544 | ### 2.6 计算图 ###
545 |
546 | #### 2.6.1 计算图的定义
547 |
548 | 计算图是用箭头画出来的,从左到右的计算。以下以函数$J=3(a+bc)$为例。
549 | 如图所示,先计算出bc的数值,并将其存在变量u中,之后计算a+u,并将其存在变量v中,之后计算3*v,计算结果即为变量J 的数值。从左到右,箭头表示出了计算的顺序。
550 | 
551 |
552 | #### 2.6.2 计算图的导数运算 ####
553 | 那么如何计算J的导数呢?如图中所示:
554 | 
555 | 结合链式法则,从最右侧算起,$dJ/dv=3,故dJ=3dv。dJ/da=dJ/dv*dv/da=3*1=3$;这个过程其实就是反向传播。那dJ/du是多少呢?根据链式法则,从图中右侧向左计算,$dJ/du=dJ/dv*dv/du=3*1=3$。
556 |
557 | 同理可知$dJ/db=dJ/dv*dv/du*du/db=3*1*c=6;dJ/dc=dJ/dv*dv/du*du/dc=3*1*3=9$。
558 |
559 |
560 |
561 | ### 2.7 logistic回归中的梯度下降法 ###
562 | logistic回归的公式如下图所示,
563 |
564 |  565 | 只考虑单个样本的情况,损失函数为$L(a,y)$,a是logistic回归的输出,y为样本的基本真值标签值,该样本的偏导数流程图如下图所示。
566 | 
567 |
568 | 假设样本只有两个特征值x1和x2,为了计算Z,我们需要输入参数w1和w2和b,在logistic回归中,我们要做的就是变换参数w和b的值,来最小化损失函数。首先,我们需要向前一步,先计算损失函数的导数,计算函数L关于a的导数,在代码中,只需要使用da来表示这个变量;之后,再向后一步,计算$dz$,$dz$是损失函数关于z的导数,向后传播的最后一步,w和b需要如何变化,关于b的求导:$db=dz=a-y$。因此,关于单个样本的梯度下降法,所需要做的就是使用这个计算公式计算dz,然后计算dw1、dw2、db,然后更新w1为w1减去学习率乘以dw1;更新w2为w2减去学习率乘以$dw2$;更新b为b减去学习率乘以db,这就是单个样本实例的一次梯度更新步骤。
569 |
570 |
571 |
572 | ### 2.8 向量化
573 |
574 | #### 2.8.1 向量化代码示例
575 |
576 | **向量化作用**
577 |
578 | 相比于显式的for循环,向量化可以大大缩短数据的运算时间,得到同样的结果,使用for循环所花费时间是将代码向量化后运行时间的近300倍。示例代码如下:
579 |
580 | ```python
581 | import numpy as np
582 | import time
583 |
584 | a=np.array([1,2,3,4])
585 | a=np.random.rand(1000000)
586 | b=np.random.rand(1000000)
587 |
588 | tic=time.time()
589 | c=np.dot(a,b)
590 | toc=time.time()
591 |
592 | print("Vectorized version:"+str(1000*(toc-tic))+"ms")
593 |
594 | c=0
595 | tic=time.time()
596 | for i in range(1000000):
597 | c += a[i] * b[i]
598 | toc=time.time()
599 | print("for loop:"+str(1000*(toc-tic))+"ms")
600 |
601 | # 结果
602 | # Vectorized version:6.882190704345703ms
603 | # for loop:559.5316886901855ms
604 | ```
605 |
606 | **GPU和CPU的对比**
607 |
608 | GPU为图像处理单元,CPU为中央处理器。两者都有并行化指令,有时称为SIMD指令(单指令多数据流),这能够让python使用其中的内置函数(可以去掉显式for循环的函数,如:numpy),GPU更为擅长运用SIMD指令,但CPU也同样可以实现。
609 |
610 | pytorch在GPU中配置方法:博客https://blog.csdn.net/qq_44420246/article/details/107249283
611 |
612 | #### 2.8.2 初步向量化logistic函数
613 |
614 | 若用如下程序计算logistic回归导数
615 |
616 | $$\begin{array}{l}
617 | J=0, \quad d w 1=0, \quad d w 2=0, \quad d b=0 \\
618 | \text { for } i=1 \text { to m: } \\
619 | \qquad \begin{array}{l}
620 | z^{(i)}=w^{T} x^{(i)}+b \\
621 | a^{(i)}=\sigma\left(z^{(i)}\right) \\
622 | J+=-\left[y^{(i)} \log \hat{y}^{(i)}+\left(1-y^{(i)}\right) \log \left(1-\hat{y}^{(i)}\right)\right] \\
623 | d z^{(i)}=a^{(i)}\left(1-a^{(i)}\right) \\
624 | d w_{1}+=x_{1}^{(i)} d z^{(i)} \\
625 | d w_{2}+=x_{2}^{(i)} d z^{(i)} \\
626 | d b^ {}+=d z^{(i)}
627 | \end{array} \\
628 | J=J / m, \quad d w_{1}=d w_{1} / m, \quad d w_{2}=d w_{2} / m, \quad d b=d b / m
629 | \end{array}$$
630 |
631 | 该程序实际包含两个for循环,第一个for循环即第二行的“for”,第二个for循环。在程序中,为以下的这一部分
632 |
633 | $d w_{1}+=x_{1}^{(i)} d z^{(i)}$
634 | $d w_{2}+=x_{2}^{(i)} d z^{(i)}$
635 |
636 | 即如果特征不止2个,有n个的话,则需重复执行该步骤n次
637 | 现用向量化的方法去掉第二个for循环,将dw通过$$\mathrm{dw}=\text { np.zeros }(\mathrm{n}, 1)$$转化为初始值为0的n*1维的向量
638 | 则原程序中的$$d w 1=0, \quad d w 2=0$$部分可取缔。
639 |
640 | 原程序的
641 |
642 |
643 |
644 | $$d w_{1}+=x_{1}^{(i)} d z^{(i)}$$ $$d w_{2}+=x_{2}^{(i)} d z^{(i)}$$
645 |
646 |
647 |
648 | 可以用$$d w+=x^{(i)} d z^{(i)}$$代替。
649 |
650 | 原程序的$$d w_{1}=d w_{1} / m, \quad d w_{2}=d w_{2} / m$$
651 | 可以用$$d w /=m$$代替。
652 |
653 | 以此去掉了第二个for循环,通过向量化的方法,使程序得到了初步的简化。
654 |
655 |
656 |
657 | **高效计算激活函数**
658 |
659 | 已知函数$z=\omega^{\top} x+b$和$a^{}=\sigma\left(z^{}\right)$,可以利用向量的方法对数据进行高效计算
660 | 首先,将所有训练样本(m个n维的向量)横向堆叠得到一个n\*m的矩阵X,以此作为训练输入
661 | 其中,X矩阵如下
662 |
663 | $X=\left[x^{(1)}, x^{(2)}, \cdots, x^{(m)}\right] $
664 |
665 | $x^{(1)}$为第一个训练样本的向量,依此类推
666 | 再定义一个1\*m的矩阵Z,如下
667 |
668 | $z=\left[z^{(1)}, z^{(2)} \cdots, z^{(m)}\right]$
669 |
670 | 定义1*m矩阵如下*
671 |
672 |
673 | $[b, b, b, \cdots b]$
674 |
675 | 定义矩阵A如下
676 |
677 | $A=\left[a^{(1)}, a^{(2)}, \cdots, a^{(m)}\right]$
678 |
679 | 则高效计算得出:
680 |
681 | $z=\left[z^{(1)}, z^{(2)} \ldots, z^{(m)}\right]=\omega^{\top} x+[b, b, \cdots, b)=\left[\omega^{\top} x^{(1)}+b, \cdots, \omega^{(m)}+b\right]$
682 | $A=\sigma(z)$
683 |
684 | **在python中的操作**
685 |
686 | 调用numpy库,定义向量和矩阵后,使用z=np.dot(w.T,x+b)语句进行计算,其中python自动将b扩展为1*m的向量(python的“广播”)
687 | 调用sigmoid函数,由$A=\sigma(z)$计算$a^{(1)},a^{(2)}$.....$a^{(m)}$
688 |
689 | $v=\left[\begin{array}{c}v_{1} \\ \vdots \\ v_{n}\end{array}\right] \rightarrow u=\left[\begin{array}{c}e^{v_{1}} \\ e^{v_{c}} \\ e^{j_{n}}\end{array}\right]$
690 |
691 | #### 2.8.3 高度向量化logistic
692 |
693 | 定义矩阵X如下
694 | $X=\left[x^{(1)}, x^{(2)}, \cdots, x^{(m)}\right]$
695 | 定义矩阵Y如下
696 | $Y=\left[\begin{array}{lll}y^{(1)} & ,\cdots & ,y^{(m)}\end{array}\right]$
697 | 定义矩阵A如下
698 | $A=\left[a^{(1)}, a^{(2)}, \cdots, a^{(m)}\right]$
699 | 定义矩阵dz如下
700 | $d z=\left[d z^{(1)} ,d z^{(2)}, \cdots ,d z^{(m)}\right]$
701 | 有$d z^{(1)}=a^{(1)}-y^{(1)} \quad ,$.....$,d z^{(m)}=a^{(m)}-y^{(m)}$
702 |
703 |
704 |
705 | **则高度向量化后,程序如下**
706 |
707 | $z=w^{T} X+b$
708 | $A=\sigma(z)$
709 | $d z=A-Y$
710 | $d w=\frac{1}{m} xd z^{T}$
711 | $db=\frac{1}{m} \sum_{i=1}^{n} d z^{(i)}$
712 |
713 | 在python中,调用numpy库(np),则矩阵Z可下方代码计算得出:
714 | Z$=n p \cdot \log (w . T, x)+b$
715 | db可用下方代码计算得出:
716 | $d b=\frac{1}{m} n p \cdot \operatorname{sum}(d z)$
717 |
718 | ### 2.9 关于python / numpy向量的说明 ###
719 | 默认以下的向量指的是np.array,直译是数组,但是在神经网络的项目中称为向量是更符合的。以下将对其的一些概念做介绍。
720 |
721 | #### 2.9.1 相关定义
722 |
723 | **轴(axis)**
724 |
725 | 对于array.shape形如 (a, b, c, ...) 的数组,a是其第0轴,b是第1轴,以此类推。数轴简单,但这些轴有什么意思?
726 | 对于shape为 (x, y) 的array,0轴就是行的轴,遍历该轴可以遍历所有行;1轴是列的轴,遍历该列可以遍历所有列。但是为什么是这样?
727 |
728 | a[x][y]我们都懂,是访问数组a的第x行,第y列。那么轴的概念就在于,搭建一个坐标系(二维的是xOy坐标系),可以用坐标轴上的数表示数组的任意一个数。在这里,x就是a[x][y]在0轴的位置,y是在1轴的位置。那么自然而然0轴对应的是行号的轴,1轴对应的是列号的轴。对于有更多轴(秩更高)的数组来说这样解释同样是合适的。
729 |
730 | 了解了轴的概念之后,那就应该也了解函数np.sum中参数axis的含义了:沿着(遍历)某一个轴进行求和。对于其他含义该参数的函数来说,也是遍历该轴的意思。
731 |
732 | **维数(dimension / dim)**
733 |
734 | 我曾经在入门的时候遇到了这样一个难题:
735 |
736 | 一个博主说 np.zeros((1000,))是获得一个1000维的向量。
737 |
738 | 我当时就懵了,1000维?一张图片才3维,就算所有图片叠在一起也才4维,为什么要1000维?后来才知道此维非彼维:“维”指的是一个轴的“大小”(取值范围),而不是接下来要讲的秩的含义。对“维”的误解主要出自我们一般称a[][] 为二维数组,b[][][]为三维数组之类的说法。不过在真正了解维数/dim的定义之后就基本不会再有误解了。
739 |
740 | **秩(rank)**
741 |
742 | 在一些论文中,可能会出现这个**单词**。而且如果用的是翻译软件进行阅读,很有可能被翻译为其他东西而影响阅读,故特地标明了对应的英文rank。
743 |
744 | 秩指的是一个向量的轴的数量。秩0是单个数字,秩1是[]向量,秩2是[][]向量,以此类推。
745 |
746 | 或许有的同学在学线性代数时学过秩这个概念,不过又是此秩非彼秩。
747 |
748 | **示例代码**
749 |
750 | ```python
751 | a = np.array([[1, 2],
752 | [3, 4],
753 | [5, 6]]
754 | )
755 | b = np.sum(a, axis=0)
756 | # b is [9, 12]
757 | c = np.sum(a, axis=1)
758 | # c is [3, 7, 11]
759 | ```
760 |
761 | 你可能也发现了一个细节:sum之后降秩了。如果不想这么做,可以传多一个参数keepdims
762 |
763 | b = np.sum(a, axis=0, keepdims=True)
764 | # b shape (1, 2)
765 |
766 | 这样就可以避免可能由于降秩而带来的bug。
767 |
768 |
769 | #### 2.9.2 Python中的广播 ####
770 | Python中的广播(broadcasting),是一种自动将“低秩”向量拓展到高秩向量,以便与高秩向量进行逐元素运算(+-*/)的机制。
771 |
772 | a = 3
773 | b = np.array([[1, 2],
774 | [3, 4],
775 | [5, 6]]
776 | )
777 | c = b + a
778 | # c = a + b 结果也一致
779 | print(c)
780 | # c is [[4, 5], [6, 7], [8, 9]]
781 | 值得注意的是,这个“低秩”并不一定是真正的低秩。
782 |
783 | **广播机制的规则**
784 |
785 | * 假设低秩向量shape为(a, b),高秩向量shape为(a, b, c, d, ...)或(..., c, d, a, b)。即高秩向量shape的最前面或者最后面“包含”低秩向量的shape,则可以进行广播。
786 | * 两个同秩向量,若对应的**部分轴(不要求连续)**的维数相等,且维数不同的轴,其中一个向量(不一定总是同一个向量)的维数为1,则可以进行广播。
787 | * 单个实数x(秩0),可以和任意向量广播。
788 |
789 | 广播可以理解为通过复制操作,将**低维的轴**的维数增加到和高秩向量一致。
790 |
791 |
792 |
793 | **示例代码**
794 |
795 | a = np.zeros((3, 4))
796 | b = np.zeros((1, 2, 3, 4))
797 | t = a + b # 可以广播
798 |
799 | c = np.zeros((3, 4, 5, 6, 7))
800 | t = a - c # 可以广播
801 |
802 | d = np.zeros((1, 2, 3, 4, 5, 6))
803 | t = a * d # 不可以广播
804 |
805 | e = np.random.randn(1, 1, 2, 1, 4, 1)
806 | f = np.random.randn(7, 6, 2, 3, 4, 8)
807 | t = e / f # 可以广播
808 |
809 | g = np.random.randn(5, 6, 1, 3, 1, 8)
810 | t = e + g # 可以广播
811 |
812 |
813 | #### 2.9.3 Jupyter / Ipython笔记本快速指南 ####
814 | 本文参考了[Jupyter Notebook介绍、安装及使用教程](https:https://www.jianshu.com/p/91365f343585),提取了其中的一部分,适用于只是想快速运行python代码、验证自己的想法的同学。如果想了解过多细节,可以参考原文。
815 |
816 | **安装**
817 |
818 | 介绍两种安装方式,分别对应到安装了anaconda和万能的场合
819 |
820 | **方法一**
821 |
822 | 安装了anaconda的话,常规来说自带Jupyter。如果没有,尝试如下指令:
823 |
824 | conda install jupyter notebook
825 |
826 |
827 |
828 | **方法二**
829 |
830 | 只要你安装了python(版本支持前提下)就能安装的方法(win10):
831 |
832 | 打开cmd(不知道如何打开可以搜索),输入
833 |
834 | pip install jupyter
835 |
836 | 一般来说,会自动安装到目录:...\Python\Python36\Scripts\ 。
837 | 具体安装到了哪,要看你的python安装到了哪。然后此时你可以按照下一步运行jupyter;如果提示没有这个命令,则是环境变量的问题,解决办法:
838 |
839 | 1. 右键我的电脑->属性->高级系统设置->环境变量
840 |
841 | 2. 双击第一个窗口 用户变量 下的Path->新建
842 |
843 | 3. 将jupyter安装的目录 “...\Python\Python36\Scripts” 复制到此处。连点ok。完成。
844 |
845 |
846 |
847 | **打开运行**
848 |
849 | 打开cmd,输入 jupyter notebook,回车。然后顺利的话会弹出一个游览器,先别急着关掉cmd,关掉的话你的jupyter也会一起“关掉”的。
850 |
851 | 点击右边的new->python3 ,然后会打开/跳转一个新页面,于是就可以愉快滴快速验证代码啦!
852 |
853 |
854 |
855 | **简单的使用教程**
856 |
857 | 一开始只有一个 **In[]** ,你可以输入代码,回车键输入下一行,并且一个In可以视为一个“块”,在执行时是一个块一个块执行的。
858 |
859 | 输入代码之后如果想要运行,用 **shift+enter**(回车)即可。然后回到刚刚提到的块问题,如果你后面的块依赖前面的块的代码,那么在修改前面的块的代码之后,需要将“受到牵连”的所有块重新执行,才能将结果更新到后面的块,否则输出是不会自动改变的。
860 |
861 | 在运行之后,有时候会有输出块 **Out[]** ,有时候没有。这个取决于该块中**最后一句**代码是否有返回值,有则显示返回值内容,否则不显示任何东西。对于print显示的内容,将在块正下方的空白处显示,而不是在 Out[] 中显示。
862 |
863 | #### 2.9.4 logistic损失函数的解释 ####
864 | 首先,要知道我们的logistic回归在做什么:“拟合”一个函数,该函数对于输入图形x,给出概率p(y|x),其中p(y|x)是图中有猫的概率。
865 | 那这个函数可以写成:
866 |
867 | > a, y=1
868 | >
869 | > 1-a, y=0
870 |
871 | 其中a是logistic回归的输出,也即y-hat(y帽),y的预测值。
872 | 更进一步,可以写成:
873 |
874 |
565 | 只考虑单个样本的情况,损失函数为$L(a,y)$,a是logistic回归的输出,y为样本的基本真值标签值,该样本的偏导数流程图如下图所示。
566 | 
567 |
568 | 假设样本只有两个特征值x1和x2,为了计算Z,我们需要输入参数w1和w2和b,在logistic回归中,我们要做的就是变换参数w和b的值,来最小化损失函数。首先,我们需要向前一步,先计算损失函数的导数,计算函数L关于a的导数,在代码中,只需要使用da来表示这个变量;之后,再向后一步,计算$dz$,$dz$是损失函数关于z的导数,向后传播的最后一步,w和b需要如何变化,关于b的求导:$db=dz=a-y$。因此,关于单个样本的梯度下降法,所需要做的就是使用这个计算公式计算dz,然后计算dw1、dw2、db,然后更新w1为w1减去学习率乘以dw1;更新w2为w2减去学习率乘以$dw2$;更新b为b减去学习率乘以db,这就是单个样本实例的一次梯度更新步骤。
569 |
570 |
571 |
572 | ### 2.8 向量化
573 |
574 | #### 2.8.1 向量化代码示例
575 |
576 | **向量化作用**
577 |
578 | 相比于显式的for循环,向量化可以大大缩短数据的运算时间,得到同样的结果,使用for循环所花费时间是将代码向量化后运行时间的近300倍。示例代码如下:
579 |
580 | ```python
581 | import numpy as np
582 | import time
583 |
584 | a=np.array([1,2,3,4])
585 | a=np.random.rand(1000000)
586 | b=np.random.rand(1000000)
587 |
588 | tic=time.time()
589 | c=np.dot(a,b)
590 | toc=time.time()
591 |
592 | print("Vectorized version:"+str(1000*(toc-tic))+"ms")
593 |
594 | c=0
595 | tic=time.time()
596 | for i in range(1000000):
597 | c += a[i] * b[i]
598 | toc=time.time()
599 | print("for loop:"+str(1000*(toc-tic))+"ms")
600 |
601 | # 结果
602 | # Vectorized version:6.882190704345703ms
603 | # for loop:559.5316886901855ms
604 | ```
605 |
606 | **GPU和CPU的对比**
607 |
608 | GPU为图像处理单元,CPU为中央处理器。两者都有并行化指令,有时称为SIMD指令(单指令多数据流),这能够让python使用其中的内置函数(可以去掉显式for循环的函数,如:numpy),GPU更为擅长运用SIMD指令,但CPU也同样可以实现。
609 |
610 | pytorch在GPU中配置方法:博客https://blog.csdn.net/qq_44420246/article/details/107249283
611 |
612 | #### 2.8.2 初步向量化logistic函数
613 |
614 | 若用如下程序计算logistic回归导数
615 |
616 | $$\begin{array}{l}
617 | J=0, \quad d w 1=0, \quad d w 2=0, \quad d b=0 \\
618 | \text { for } i=1 \text { to m: } \\
619 | \qquad \begin{array}{l}
620 | z^{(i)}=w^{T} x^{(i)}+b \\
621 | a^{(i)}=\sigma\left(z^{(i)}\right) \\
622 | J+=-\left[y^{(i)} \log \hat{y}^{(i)}+\left(1-y^{(i)}\right) \log \left(1-\hat{y}^{(i)}\right)\right] \\
623 | d z^{(i)}=a^{(i)}\left(1-a^{(i)}\right) \\
624 | d w_{1}+=x_{1}^{(i)} d z^{(i)} \\
625 | d w_{2}+=x_{2}^{(i)} d z^{(i)} \\
626 | d b^ {}+=d z^{(i)}
627 | \end{array} \\
628 | J=J / m, \quad d w_{1}=d w_{1} / m, \quad d w_{2}=d w_{2} / m, \quad d b=d b / m
629 | \end{array}$$
630 |
631 | 该程序实际包含两个for循环,第一个for循环即第二行的“for”,第二个for循环。在程序中,为以下的这一部分
632 |
633 | $d w_{1}+=x_{1}^{(i)} d z^{(i)}$
634 | $d w_{2}+=x_{2}^{(i)} d z^{(i)}$
635 |
636 | 即如果特征不止2个,有n个的话,则需重复执行该步骤n次
637 | 现用向量化的方法去掉第二个for循环,将dw通过$$\mathrm{dw}=\text { np.zeros }(\mathrm{n}, 1)$$转化为初始值为0的n*1维的向量
638 | 则原程序中的$$d w 1=0, \quad d w 2=0$$部分可取缔。
639 |
640 | 原程序的
641 |
642 |
643 |
644 | $$d w_{1}+=x_{1}^{(i)} d z^{(i)}$$ $$d w_{2}+=x_{2}^{(i)} d z^{(i)}$$
645 |
646 |
647 |
648 | 可以用$$d w+=x^{(i)} d z^{(i)}$$代替。
649 |
650 | 原程序的$$d w_{1}=d w_{1} / m, \quad d w_{2}=d w_{2} / m$$
651 | 可以用$$d w /=m$$代替。
652 |
653 | 以此去掉了第二个for循环,通过向量化的方法,使程序得到了初步的简化。
654 |
655 |
656 |
657 | **高效计算激活函数**
658 |
659 | 已知函数$z=\omega^{\top} x+b$和$a^{}=\sigma\left(z^{}\right)$,可以利用向量的方法对数据进行高效计算
660 | 首先,将所有训练样本(m个n维的向量)横向堆叠得到一个n\*m的矩阵X,以此作为训练输入
661 | 其中,X矩阵如下
662 |
663 | $X=\left[x^{(1)}, x^{(2)}, \cdots, x^{(m)}\right] $
664 |
665 | $x^{(1)}$为第一个训练样本的向量,依此类推
666 | 再定义一个1\*m的矩阵Z,如下
667 |
668 | $z=\left[z^{(1)}, z^{(2)} \cdots, z^{(m)}\right]$
669 |
670 | 定义1*m矩阵如下*
671 |
672 |
673 | $[b, b, b, \cdots b]$
674 |
675 | 定义矩阵A如下
676 |
677 | $A=\left[a^{(1)}, a^{(2)}, \cdots, a^{(m)}\right]$
678 |
679 | 则高效计算得出:
680 |
681 | $z=\left[z^{(1)}, z^{(2)} \ldots, z^{(m)}\right]=\omega^{\top} x+[b, b, \cdots, b)=\left[\omega^{\top} x^{(1)}+b, \cdots, \omega^{(m)}+b\right]$
682 | $A=\sigma(z)$
683 |
684 | **在python中的操作**
685 |
686 | 调用numpy库,定义向量和矩阵后,使用z=np.dot(w.T,x+b)语句进行计算,其中python自动将b扩展为1*m的向量(python的“广播”)
687 | 调用sigmoid函数,由$A=\sigma(z)$计算$a^{(1)},a^{(2)}$.....$a^{(m)}$
688 |
689 | $v=\left[\begin{array}{c}v_{1} \\ \vdots \\ v_{n}\end{array}\right] \rightarrow u=\left[\begin{array}{c}e^{v_{1}} \\ e^{v_{c}} \\ e^{j_{n}}\end{array}\right]$
690 |
691 | #### 2.8.3 高度向量化logistic
692 |
693 | 定义矩阵X如下
694 | $X=\left[x^{(1)}, x^{(2)}, \cdots, x^{(m)}\right]$
695 | 定义矩阵Y如下
696 | $Y=\left[\begin{array}{lll}y^{(1)} & ,\cdots & ,y^{(m)}\end{array}\right]$
697 | 定义矩阵A如下
698 | $A=\left[a^{(1)}, a^{(2)}, \cdots, a^{(m)}\right]$
699 | 定义矩阵dz如下
700 | $d z=\left[d z^{(1)} ,d z^{(2)}, \cdots ,d z^{(m)}\right]$
701 | 有$d z^{(1)}=a^{(1)}-y^{(1)} \quad ,$.....$,d z^{(m)}=a^{(m)}-y^{(m)}$
702 |
703 |
704 |
705 | **则高度向量化后,程序如下**
706 |
707 | $z=w^{T} X+b$
708 | $A=\sigma(z)$
709 | $d z=A-Y$
710 | $d w=\frac{1}{m} xd z^{T}$
711 | $db=\frac{1}{m} \sum_{i=1}^{n} d z^{(i)}$
712 |
713 | 在python中,调用numpy库(np),则矩阵Z可下方代码计算得出:
714 | Z$=n p \cdot \log (w . T, x)+b$
715 | db可用下方代码计算得出:
716 | $d b=\frac{1}{m} n p \cdot \operatorname{sum}(d z)$
717 |
718 | ### 2.9 关于python / numpy向量的说明 ###
719 | 默认以下的向量指的是np.array,直译是数组,但是在神经网络的项目中称为向量是更符合的。以下将对其的一些概念做介绍。
720 |
721 | #### 2.9.1 相关定义
722 |
723 | **轴(axis)**
724 |
725 | 对于array.shape形如 (a, b, c, ...) 的数组,a是其第0轴,b是第1轴,以此类推。数轴简单,但这些轴有什么意思?
726 | 对于shape为 (x, y) 的array,0轴就是行的轴,遍历该轴可以遍历所有行;1轴是列的轴,遍历该列可以遍历所有列。但是为什么是这样?
727 |
728 | a[x][y]我们都懂,是访问数组a的第x行,第y列。那么轴的概念就在于,搭建一个坐标系(二维的是xOy坐标系),可以用坐标轴上的数表示数组的任意一个数。在这里,x就是a[x][y]在0轴的位置,y是在1轴的位置。那么自然而然0轴对应的是行号的轴,1轴对应的是列号的轴。对于有更多轴(秩更高)的数组来说这样解释同样是合适的。
729 |
730 | 了解了轴的概念之后,那就应该也了解函数np.sum中参数axis的含义了:沿着(遍历)某一个轴进行求和。对于其他含义该参数的函数来说,也是遍历该轴的意思。
731 |
732 | **维数(dimension / dim)**
733 |
734 | 我曾经在入门的时候遇到了这样一个难题:
735 |
736 | 一个博主说 np.zeros((1000,))是获得一个1000维的向量。
737 |
738 | 我当时就懵了,1000维?一张图片才3维,就算所有图片叠在一起也才4维,为什么要1000维?后来才知道此维非彼维:“维”指的是一个轴的“大小”(取值范围),而不是接下来要讲的秩的含义。对“维”的误解主要出自我们一般称a[][] 为二维数组,b[][][]为三维数组之类的说法。不过在真正了解维数/dim的定义之后就基本不会再有误解了。
739 |
740 | **秩(rank)**
741 |
742 | 在一些论文中,可能会出现这个**单词**。而且如果用的是翻译软件进行阅读,很有可能被翻译为其他东西而影响阅读,故特地标明了对应的英文rank。
743 |
744 | 秩指的是一个向量的轴的数量。秩0是单个数字,秩1是[]向量,秩2是[][]向量,以此类推。
745 |
746 | 或许有的同学在学线性代数时学过秩这个概念,不过又是此秩非彼秩。
747 |
748 | **示例代码**
749 |
750 | ```python
751 | a = np.array([[1, 2],
752 | [3, 4],
753 | [5, 6]]
754 | )
755 | b = np.sum(a, axis=0)
756 | # b is [9, 12]
757 | c = np.sum(a, axis=1)
758 | # c is [3, 7, 11]
759 | ```
760 |
761 | 你可能也发现了一个细节:sum之后降秩了。如果不想这么做,可以传多一个参数keepdims
762 |
763 | b = np.sum(a, axis=0, keepdims=True)
764 | # b shape (1, 2)
765 |
766 | 这样就可以避免可能由于降秩而带来的bug。
767 |
768 |
769 | #### 2.9.2 Python中的广播 ####
770 | Python中的广播(broadcasting),是一种自动将“低秩”向量拓展到高秩向量,以便与高秩向量进行逐元素运算(+-*/)的机制。
771 |
772 | a = 3
773 | b = np.array([[1, 2],
774 | [3, 4],
775 | [5, 6]]
776 | )
777 | c = b + a
778 | # c = a + b 结果也一致
779 | print(c)
780 | # c is [[4, 5], [6, 7], [8, 9]]
781 | 值得注意的是,这个“低秩”并不一定是真正的低秩。
782 |
783 | **广播机制的规则**
784 |
785 | * 假设低秩向量shape为(a, b),高秩向量shape为(a, b, c, d, ...)或(..., c, d, a, b)。即高秩向量shape的最前面或者最后面“包含”低秩向量的shape,则可以进行广播。
786 | * 两个同秩向量,若对应的**部分轴(不要求连续)**的维数相等,且维数不同的轴,其中一个向量(不一定总是同一个向量)的维数为1,则可以进行广播。
787 | * 单个实数x(秩0),可以和任意向量广播。
788 |
789 | 广播可以理解为通过复制操作,将**低维的轴**的维数增加到和高秩向量一致。
790 |
791 |
792 |
793 | **示例代码**
794 |
795 | a = np.zeros((3, 4))
796 | b = np.zeros((1, 2, 3, 4))
797 | t = a + b # 可以广播
798 |
799 | c = np.zeros((3, 4, 5, 6, 7))
800 | t = a - c # 可以广播
801 |
802 | d = np.zeros((1, 2, 3, 4, 5, 6))
803 | t = a * d # 不可以广播
804 |
805 | e = np.random.randn(1, 1, 2, 1, 4, 1)
806 | f = np.random.randn(7, 6, 2, 3, 4, 8)
807 | t = e / f # 可以广播
808 |
809 | g = np.random.randn(5, 6, 1, 3, 1, 8)
810 | t = e + g # 可以广播
811 |
812 |
813 | #### 2.9.3 Jupyter / Ipython笔记本快速指南 ####
814 | 本文参考了[Jupyter Notebook介绍、安装及使用教程](https:https://www.jianshu.com/p/91365f343585),提取了其中的一部分,适用于只是想快速运行python代码、验证自己的想法的同学。如果想了解过多细节,可以参考原文。
815 |
816 | **安装**
817 |
818 | 介绍两种安装方式,分别对应到安装了anaconda和万能的场合
819 |
820 | **方法一**
821 |
822 | 安装了anaconda的话,常规来说自带Jupyter。如果没有,尝试如下指令:
823 |
824 | conda install jupyter notebook
825 |
826 |
827 |
828 | **方法二**
829 |
830 | 只要你安装了python(版本支持前提下)就能安装的方法(win10):
831 |
832 | 打开cmd(不知道如何打开可以搜索),输入
833 |
834 | pip install jupyter
835 |
836 | 一般来说,会自动安装到目录:...\Python\Python36\Scripts\ 。
837 | 具体安装到了哪,要看你的python安装到了哪。然后此时你可以按照下一步运行jupyter;如果提示没有这个命令,则是环境变量的问题,解决办法:
838 |
839 | 1. 右键我的电脑->属性->高级系统设置->环境变量
840 |
841 | 2. 双击第一个窗口 用户变量 下的Path->新建
842 |
843 | 3. 将jupyter安装的目录 “...\Python\Python36\Scripts” 复制到此处。连点ok。完成。
844 |
845 |
846 |
847 | **打开运行**
848 |
849 | 打开cmd,输入 jupyter notebook,回车。然后顺利的话会弹出一个游览器,先别急着关掉cmd,关掉的话你的jupyter也会一起“关掉”的。
850 |
851 | 点击右边的new->python3 ,然后会打开/跳转一个新页面,于是就可以愉快滴快速验证代码啦!
852 |
853 |
854 |
855 | **简单的使用教程**
856 |
857 | 一开始只有一个 **In[]** ,你可以输入代码,回车键输入下一行,并且一个In可以视为一个“块”,在执行时是一个块一个块执行的。
858 |
859 | 输入代码之后如果想要运行,用 **shift+enter**(回车)即可。然后回到刚刚提到的块问题,如果你后面的块依赖前面的块的代码,那么在修改前面的块的代码之后,需要将“受到牵连”的所有块重新执行,才能将结果更新到后面的块,否则输出是不会自动改变的。
860 |
861 | 在运行之后,有时候会有输出块 **Out[]** ,有时候没有。这个取决于该块中**最后一句**代码是否有返回值,有则显示返回值内容,否则不显示任何东西。对于print显示的内容,将在块正下方的空白处显示,而不是在 Out[] 中显示。
862 |
863 | #### 2.9.4 logistic损失函数的解释 ####
864 | 首先,要知道我们的logistic回归在做什么:“拟合”一个函数,该函数对于输入图形x,给出概率p(y|x),其中p(y|x)是图中有猫的概率。
865 | 那这个函数可以写成:
866 |
867 | > a, y=1
868 | >
869 | > 1-a, y=0
870 |
871 | 其中a是logistic回归的输出,也即y-hat(y帽),y的预测值。
872 | 更进一步,可以写成:
873 |
874 |  875 |
876 |
877 | 那么我们的任务就成了找出一组权值w和偏置b,使得p(y|x)最大。有没有让你想起来**最大似然估计**?没错,就是差不多的任务。那么对数似然函数可以写作:
878 |
879 |
875 |
876 |
877 | 那么我们的任务就成了找出一组权值w和偏置b,使得p(y|x)最大。有没有让你想起来**最大似然估计**?没错,就是差不多的任务。那么对数似然函数可以写作:
878 |
879 |  880 | 我们目标就是让上面的那个函数取最大值。再加个负号,改为取最小值:
881 |
882 |
880 | 我们目标就是让上面的那个函数取最大值。再加个负号,改为取最小值:
881 |
882 |  883 |
884 |
885 | 于是,我们的损失函数(loss)就定义为了上式。
886 |
887 | #### 2.9.5 似然和概率 ####
888 | 既然提到了最大似然估计,那就提提似然和概率的区别:
889 |
890 | > 简单来讲,似然与概率分别是针对不同内容的估计和近似。概率(密度)表达给定θ下样本**X**=x的可能性,而似然表达了给定样本X=x下参数θ=θ1(相对于另外的参数取值θ2而言)为真实值的可能性
891 |
892 | 引自[似然(likelihood)和概率(probability)的区别与联系](https://blog.csdn.net/songyu0120/article/details/85059149)
893 |
894 |
895 |
896 |
897 |
--------------------------------------------------------------------------------
/5 深度学习的实用层面.md:
--------------------------------------------------------------------------------
1 | ## 5 深度学习的实用层面
2 |
3 | ### 5.1 训练集(Train sets)
4 |
5 | 在机器学习中,通常将训练数据分为**训练集**(train sets)、简单交叉验证集(简称**验证集**,dev sets)和**测试集**(test sets)。对训练集执行训练算法,通过验证集选择最好的模型,经过充分验证选定最终模型后,在测试集上进行评估。
6 | 
7 |
8 | **数据集划分比例:**
9 |
10 | - **对数据集规模较小的:**
11 | 如果没有明确设置验证集,常见做法是将所有数据**三七分**(70%训练集和30%测试集);或者划分为60%训练集、20%验证集和20%测试集。
12 | - **对数据集规模较大的:**
13 | **验证集和测试集占数据总量的比例会趋向于变得更小(低于数据总量的20%甚至10%)**。因为验证集的目的是验证不同的算法中哪一种更有效,故验证集要足够大才能评估,比如现有100万条数据,则取1万条便足以评估算法性能。同样地,根据最终选择的分类器,测试集的主要目的是正确评估分类器的性能,若拥有百万数据,只需1万条数据便足以评估单个分类器。所以倘若有100万条数据,可以将其中1万条作为验证集1万条作为测试集,即98%训练集、1%验证集和1%测试集。对于数据量过百万的应用,训练集可以达到99.5%,验证集和测试集各占0.25%或者验证集占0.4%测试集占0.1%。
14 |
15 | **对验证集和测试集的要求:**
16 | 1. 确保**验证集和测试集的数据来自同一分布**。因为要用验证集评估不同的模型以尽可能地优化性能,如果验证集和测试集来自同一分布会更好,机器学习算法会训练得更快。
17 | 2. **可以没有测试集**。测试集的目的是对最终选定的神经网络系统做出无偏评估,若不需要无偏评估,就可以不设置测试集。在只有训练集和验证集的情况下,需要在训练集上训练、尝试不同的模型框架,在验证集上评估这些模型,迭代并选出最适合的模型,训练集仍称为训练集,而验证集被称为测试集。
18 |
19 | 搭建训练测试集和验证集能够加速神经网络的集成,更有效地衡量算法的偏差和方差,从而更高效地选择合适的方法优化算法。
20 |
21 |
22 |
23 | ### 5.2 偏差和方差(Bias/Variance)
24 |
25 | 我们先定义好我们要用到的公式中变量的含义:
26 |
27 | 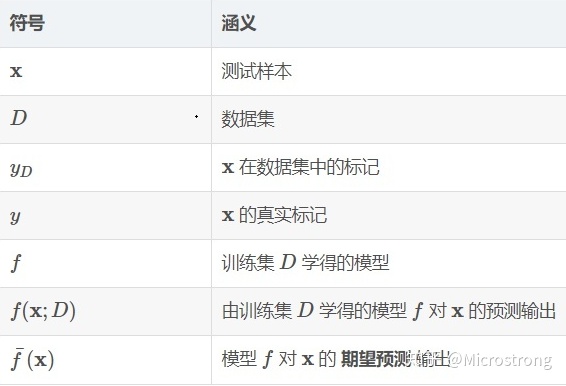
28 |
29 | #### **5.2.1 偏差**
30 |
31 | 描述的是预测值的期望与真实值之间的差距。偏差越大,越偏离真实数据,拟合度越低,如下图第二行所示。故偏差度量的是学习算法的期望预测与真实结果的偏离程度,即**拟合能力**。
32 |
33 | 期望输出与真实标记的差别称为偏差,即:
34 | $$
35 | \operatorname{bias}^{2}(\boldsymbol{x})=(\bar{f}(\boldsymbol{x})-y)^{2}
36 | $$
37 |
38 | #### **5.2.2 方差**
39 |
40 | 描述的是预测值的变化范围,即离散程度。方差越大,数据的分布越分散,如下图右列所示。故方差度量的是同样大小的训练集的变动所导致的学习性能的变化,即刻画了**数据扰动**造成的影响。
41 |
42 | 使用样本数相同的不同训练集产生的**方差**为:
43 | $$
44 | \operatorname{var}(\boldsymbol{x})=\mathbb{E}_{D}\left[(f(\boldsymbol{x} ; D)-\bar{f}(\boldsymbol{x}))^{2}\right]
45 | $$
46 |
47 |
48 | 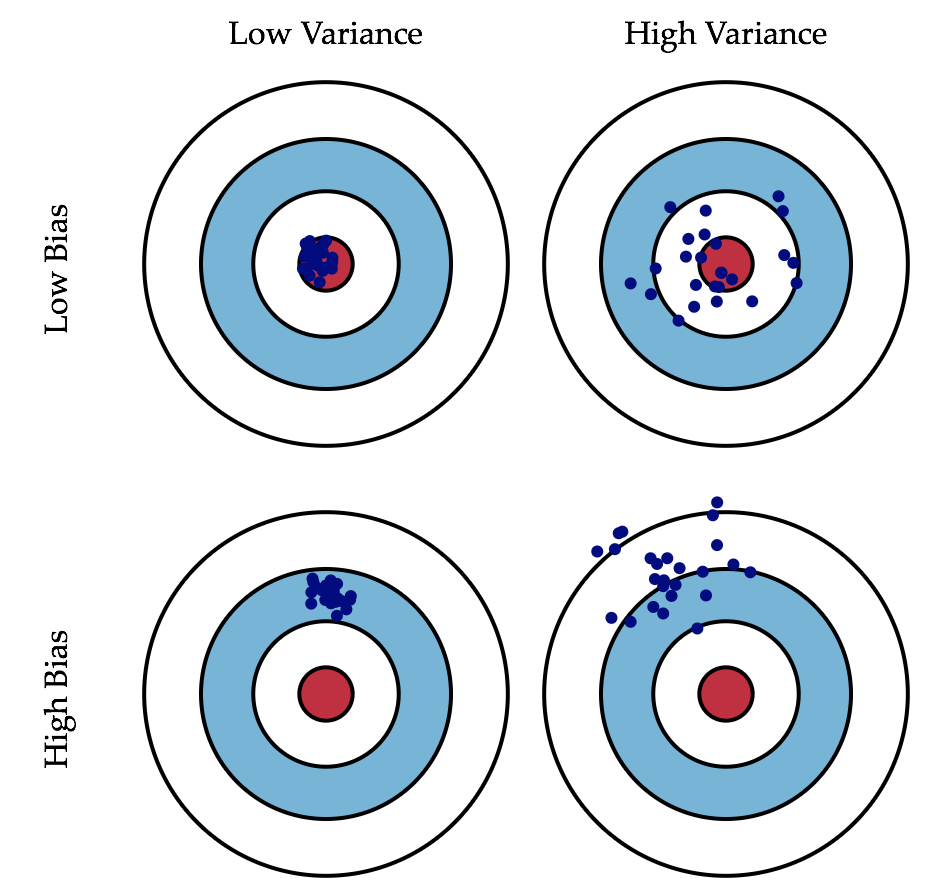
49 |
50 | #### **5.2.3 泛化**
51 |
52 | 学习后的模型对未知数据的预测能力。在实际情况中,通常通过测试误差来评价学习方法的泛化能力,泛化误差(generalization error)是新输入的误差期望,为偏差、方差与噪声之和,给定学习任务,为了取得好的泛化性能,则需使偏差较小,即能够充分拟合数据,并且使方差较小,即使得数据扰动产生的影响小。
53 |
54 | 泛化误差 $=$ 错误率 $($ error $)=\operatorname{bias}^{2}(x)+\operatorname{var}(x)+\varepsilon^{2}$
55 |
56 | 也就是说,泛化误差可以通过一系列公式分解运算证明:泛化误差为偏差、方差与噪声之和。**证明过程如下:**为了便于讨论,我们假定噪声期望为零,即$E_{D}\left[y_{D}-y\right]=0$。通过简单的多项式展开合并,可对算法的期望泛化误差进行分解:
57 | $$
58 | \begin{aligned}
59 | E(f ; D)=& \mathbb{E}_{D}\left[\left(f(\boldsymbol{x} ; D)-y_{D}\right)^{2}\right] \\
60 | =& \mathbb{E}_{D}\left[\left(f(\boldsymbol{x} ; D)-\bar{f}(\boldsymbol{x})+\bar{f}(\boldsymbol{x})-y_{D}\right)^{2}\right] \\
61 | =& \mathbb{E}_{D}\left[(f(\boldsymbol{x} ; D)-\bar{f}(\boldsymbol{x}))^{2}\right]+\mathbb{E}_{D}\left[\left(\bar{f}(\boldsymbol{x})-y_{D}\right)^{2}\right] \\
62 | &+\mathbb{E}_{D}\left[2(f(\boldsymbol{x} ; D)-\bar{f}(\boldsymbol{x}))\left(\bar{f}(\boldsymbol{x})-y_{D}\right)\right] \\
63 | =& \mathbb{E}_{D}\left[(f(\boldsymbol{x} ; D)-\bar{f}(\boldsymbol{x}))^{2}\right]+\mathbb{E}_{D}\left[\left(\bar{f}(\boldsymbol{x})-y_{D}\right)^{2}\right] \\
64 | =& \mathbb{E}_{D}\left[(f(\boldsymbol{x} ; D)-\bar{f}(\boldsymbol{x}))^{2}\right]+\mathbb{E}_{D}\left[\left(\bar{f}(\boldsymbol{x})-y+y-y_{D}\right)^{2}\right] \\
65 | =& \mathbb{E}_{D}\left[(f(\boldsymbol{x} ; D)-\bar{f}(\boldsymbol{x}))^{2}\right]+\mathbb{E}_{D}\left[(\bar{f}(\boldsymbol{x})-y)^{2}\right]+\mathbb{E}_{D}\left[\left(y-y_{D}\right)^{2}\right] \\
66 | &+2 \mathbb{E}_{D}\left[(\bar{f}(\boldsymbol{x})-y)\left(y-y_{D}\right)\right] \\
67 | =& \mathbb{E}_{D}\left[(f(\boldsymbol{x} ; D)-\bar{f}(\boldsymbol{x}))^{2}\right]+(\bar{f}(\boldsymbol{x})-y)^{2}+\mathbb{E}_{\bar{D}}\left[\begin{array}{ll}
68 | \boldsymbol({y}_{D}-y)^2 &
69 | \end{array}\right] \\
70 | \end{aligned}
71 | $$
72 | 于是, 最终得到:
73 | $$
74 | E(f ; D)=\operatorname{bias}^{2}(\boldsymbol{x})+\operatorname{var}(\boldsymbol{x})+\varepsilon^{2}
75 | $$
76 | "偏差-方差分解" 说明, 泛化性能是由学习算法的能力、数据的充分性以及学习任务本身的难度 所共同决定的。给定学习任务, 为了取得好的泛化性能, 则需使偏差较小, 即能够充分拟合数据 并且使方差较小, 即使得数据扰动产生的影响小
77 |
78 | #### 5.2.4 拟合
79 |
80 | - **欠拟合**(Underfitting):常在模型学习能力较弱而数据复杂度较高的情况下出现。由于模型的学习能力不足,无法学习到数据集中的“一般规律”,因而导致模型的泛化能力较弱。
81 | - **过拟合**(Overfitting):常在模型学习能力较强而数据复杂度较弱的情况下出现。此时由于模型的学习能力太强,以至于将训练集中单个样本自身的特点都能捕捉到,并将其认为是“一般规律”,这种情况同样会导致模型的泛化能力下降。
82 | - **适度拟合**(just right):介于欠拟合和过拟合之间,数据拟合适度,复杂程度适中,泛化能力强。
83 |
84 | 
85 |
86 | #### 5.2.5 偏差和方差与训练集和验证集误差的关系
87 |
88 | 理解偏差和方差的两个关键数据是**训练集误差**(Train set error)和**验证集误差**(Dev set error)。假设人眼辨别错误率接近0(即最优误差或称为贝叶斯误差接近0),训练集和验证集数据来自相同分布,则可通过查看训练集误差判断数据拟合情况,从而判断是否有偏差问题(训练集误差越大,拟合度越低,偏差越高);然后查看错误率(验证集误差-训练集误差)有多高,判断方差是否过高(错误率越大,方差越高)。
89 | 下表是在不同的训练集和验证集的误差组合情况下对偏差和方差的分析:
90 | 
91 |
92 |
93 |
94 |
95 | 
96 |
97 | #### 5.2.6 **偏差、方差与bagging、boosting的关系**
98 |
99 | Bagging算法是对训练样本进行采样,产生出若干不同的子集,再从每个数据子集中训练出一个分类器,**取这些分类器的平均,所以是降低模型的方差(variance)**。Bagging算法和Random Forest这种并行算法都有这个效果。
100 |
101 | Boosting则是迭代算法,每一次迭代都根据上一次迭代的预测结果对样本进行权重调整,**所以随着迭代不断进行,误差会越来越小**,所以模型的偏差(bias)会不断降低。
102 |
103 | #### 5.2.7 **偏差、方差和K折交叉验证的关系**
104 |
105 | K-fold Cross Validation的思想:将原始数据分成K组 $($ 一般是均分 $)$, 将每个子集数据分别做一次 验证集, 其余的K-1组子集数据作为训练集, 这样会得到K个模型, 用这K个模型最终的验证集的分 类准确率的平均数作为此K-CV下分类器的性能指标。
106 | 对于一系列模型 $F(\hat{f}, \theta)$, 我们使用Cross Validation的目的是获得预测误差的无偏估计量CV, 从而可以用来选择一个最优的Theta*,使得CV最小。假设K-folds cross validation, CV统计量定 义为每个子集中误差的平均值, 而K的大小和CV平均值的bias和variance是有关的:
107 | $C V=\frac{1}{K} \sum_{k=1}^{K} \frac{1}{m} \sum_{i=1}^{m}\left(\hat{f}^{k}-y_{i}\right)^{2}$
108 | 其中, $\mathrm{m}=\mathrm{N} / \mathrm{K}$ 代表每个子集的大小, $\quad$N是总的训练样本量, K是子集的数目。当K较大时, $\mathrm{m}$ 较小,模型建立在较大的N-m上, 经过更多次数的平均可以学习得到更符合真实数 据分布的模型, Bias就小了,**但是这样一来模型就更加拟合训练数据集, 再去测试集上预测的时候 预测误差的期望值就变大了,从而Variance就大了**; $\mathrm{k}$ 较小的时候, 模型不会过度拟合训练数据, 从而Bias较大,**但是正因为没有过度拟合训练数据, Variance也较小**。
109 |
110 | ### 5.3 处理偏差和方差
111 |
112 | #### 5.3.1 针对不同偏差的不同处理
113 |
114 | 评估训练集或训练数据的性能,若偏差较高,可以选择以下几种方法:
115 | - 选择更大的网络,比如含有更多隐藏层或隐藏单元的网络
116 | - 花费更多时间训练网络(不一定有用,但没坏处)
117 | - 尝试更先进的优化算法
118 | - 选择更适合解决此问题的神经网络架构(可能有用,可能没用)
119 |
120 | 训练学习算法时,不断尝试这些方法,直到可以拟合数据,解决掉偏差问题为止,至少能够拟合训练集。
121 | #### 5.3.2 针对不同方差的不同处理
122 | 偏差降低到可以接受的数值,查看验证集性能来评估方差,如果方差高,可以选择下列方法:
123 | - 采用更多数据(最好的解决办法)
124 | - 正则化
125 | - 尝试更适合的神经网络框架(有时可以同时减少偏差和方差)
126 |
127 | 解决高方差最优方法是准备更多的数据,但可能无法实时准备足够多的数据或数据成本很高时,**正则化**可帮助避免过拟合,减少网络误差。
128 |
129 | 通过不断重复尝试,找到一个低偏差、低方差的框架。
130 | > 高偏差和高方差尝试的方法可能完全不同,明确这点来选择最有效的方法。
131 | 只要正则适度,通常构建更大网络便可以在不影响方差的同时减少偏差。采用更多数据通常可以在不过多影响偏差的同时减少方差。我们有很多的选择可以减少偏差或方差而不影响另一方。
132 |
133 |
134 | ### 5.4 正则化
135 |
136 | **定义**:一种为了减小方差(测试误差)的行为
137 | **作用**:使用比较复杂的模型比如神经网络,去拟合数据时,容易出现过拟合现象,导致模型的泛化能力下降,这时我们使用正则化,降低模型的复杂度,让模型在面对新数据的时候,可以有很好的表现。
138 |
139 | #### 5.4.1 logistic 回归的正则化
140 | - **L2 正则化**
141 | $J(w, b)=\frac{1}{m} \sum_{i=1}^{m} L\left(\hat{y}^{(i)}, y^{(i)}\right)+\frac{\lambda}{2 m}\|w\|_{2}^{2}$
142 | 每次更新w时:
143 |
144 | $$w:=w-\alpha d w=\left(1-\frac{\alpha \lambda}{m}\right) w-\frac{\partial J}{\partial w}$$
145 |
146 | 从上式看出,每次更新对特征系数做一个**比例的缩放**而不是像L1正则化减去一个固定值。这使得系数趋向变小而不会变为0,因此L2正则化**让模型变得更简单,防止过拟合**。
147 | - **L1 正则化**
148 | $$J(w, b)=\frac{1}{m} \sum_{i=1}^{m} L\left(\hat{y}^{(i)}, y^{(i)}\right)+\frac{\lambda}{2 m}\|w\|_{1}$$
149 |
150 | 每次更新w时:
151 | $$\begin{array}{c}
152 | w:=w-\alpha d w\\
153 | =w-\frac{\alpha \lambda}{2 m} \operatorname{sign}\left(w\right)-\frac{\partial J}{\partial w}
154 | \end{array}$$
155 | 若 w 为正数,则每次更新减去一个常数;若 w 为负数,则每次更新加上一个常数,故容易产生特征的系数为0的情况,特征系数为 0 表示该特征不会对结果有任何影响,因此L1正则化让w变得稀疏,起到**特征选择**的作用。
156 | > - 参数 w 向量的L2 范数:$\|w\|_{2}^{2}=\sum_{j=1}^{n_{x}} w_{j}^{2}=w^{T} w$
157 | 参数 w 向量的L1 范数:$\|w\|_{1}=\sum_{j=1}^{n_{x}}\left|w_{j}\right|$
158 | > - $w\in \mathbb{R}^{n_{x}}, b \in \mathbb{R}$,习惯只正则化w,省略参数b。因为w通常是一个高维参数矢量,b只是单个数字,即w几乎涵盖所有参数,b只是众多参数中的一个,b通常省略不计,加上也没问题。
159 | >- $\lambda$是正则化参数,是一个需要调整的超参数,Python 编程语言中,lambda 是一个保留字段,编写代码时,删掉a,写成lambd,以免冲突。
160 |
161 | **总结**
162 | 两者都通过加上一个和项来限制参数大小,效果却不同:L1正则化适用于**特征选择**,L2正则化适用于**防止模型过拟合**。
163 | 在训练网络时,倾向于使用**L2正则化**。
164 |
165 |
166 |
167 | #### 5.4.2 神经网络中实现L2正则化
168 |
169 | $$J\left(w^{[1]}, b^{[1]}, \ldots, w^{[L]}, b^{[L]}\right)=\frac{1}{m} \sum_{i=1}^{m} L\left(\hat{y}^{(i)}, y^{(i)}\right)+\frac{\lambda}{2 m} \sum_{l=1}^{L}\|w\|_{F}^{2}$$
170 | **Frobenius 范数**:
171 | 下标F标注,表示一个矩阵中所有元素的平方和。
172 | $$\|w\|_{F}^{2}=\sum_{i=1}^{n^{[l-1]}} \sum_{j=1}^{n^{[l]}}\left(w_{i j}^{[l]}\right)^{2}$$
173 |
174 | 其中,$w:\left(n^{[l-1]}, n^{[l]}\right)$ $n^{[l]}$表示第$l$层单元数量,$n^{[l-1]}$表示第$l-1$层单元数量
175 |
176 | 实现梯度下降:
177 | $$\begin{aligned} w^{[l]}: &=w^{[l]}-\alpha\left[(\text { from backprop })+\frac{\lambda}{m} w^{[l]}\right] \\ &=\left(1-\frac{\alpha \lambda}{m}\right) w^{[l]}-\alpha(\text { from backprop }) \end{aligned}$$
178 | 实际上,相当于给矩阵$w^{[l]}$乘上$1-\frac{\alpha \lambda}{m}$倍的权重,而该系数小于1,因此L2正则化也被称为**权重衰减**
179 |
180 |
181 |
182 | ### 5.5 正则化有效的原理
183 | - 正则化参数$\lambda$增加到足够大,权重矩阵$w^{[l]}$会接近于0,大量隐藏单元的影响变得更小了,神经网络越来越简单,接近逻辑回归,这样更不容易发生过拟合。
184 |
185 | 举例:
186 | 假设使用$\tanh (z)$激活函数,如果$z$的值始终在接近原点的小范围内,激活函数大致呈线性,每层几乎都是线性的,和线性回归一样。
187 |
188 | 
189 | 当正则化参数$\lambda$足够大,参数$w$很小,$z$也会相对变小,激活函数$\tanh (z)$会相对呈线性,整个神经网络会计算接近线性函数的值,即一个很简单的函数,而不是极复杂的高度非线性函数,不会发生过拟合。
190 |
191 | 参考文章:[机器学习中的正则化](https://www.jianshu.com/p/569efedf6985)
192 |
193 |
194 |
195 |
196 |
197 | ### 5.6 Dropout正则化 ###
198 | Dropout正则化是较常用的避免过拟合的方法之一。
199 |
200 | **Dropout**
201 |
202 | 首先介绍一下Dropout正则化:在**训练**神经网络时,对于每一层神经网络中的所有节点,每个结点都有keep_prob的概率保留,1 - keep_prob的概率丢弃。这里的丢弃指的是**每一次**前向传播的时候随机丢弃部分结点,每次前向传播都重新计算要丢弃的结点。要注意在更新权值和真正应用已经训练好的网络时,是不会随机丢弃的。
203 | 
204 |
205 | **原理**
206 |
207 | 有没有觉得很神奇,竟然随机丢掉一些结点反而能“更好”地训练神经网络,也太“玄乎”了。当然,能生效的正则化肯定有它成功的理由,下面给出解释:
208 | 1. 随机删除一些结点,本质上相当于缩小网络。而过拟合的原因之一是网络太大而导致的拟合效果“好过头”了,那缩小网络自然能一定程度上避免过拟合。
209 | 2. 由于所有节点都可能被丢弃,所以训练时不会过渡依赖任何一个结点(特征),表现为尽可能缩小所有权值。那就有点接近L2正则化那种收缩权值的效果了。
210 |
211 | **代码实现**
212 |
213 | # 操作 < keep_prob 可使本来的随机向量变为True、False组成的向量
214 | d3 = np.random.randn(a3.shape[0], a3.shape[1]) < keep_prob
215 | # 实际运算时,True、False会变为1和0
216 | a3 *= d3
217 | # 修正a3的均值,保持和Dropout前不变
218 | a3 /= keep_prob
219 |
220 | 技术细节上,用了一个小于运算符自动将随机值转换为0、1;在将部分值归0后,a3的均值也会变为原来的keep_prob倍,所以最后对所有数除以keep_prob以保证a3的均值不变,保证$z3=wa3+b$的均值不变
221 |
222 |
223 |
224 |
225 | ### 5.7 其他正则化方法 ###
226 | #### 5.7.1 数据增强/Data Augmentation ####
227 | 前文提到解决high variance(高方差)/ 过拟合的解决办法之一是收集更多的数据,更大的训练集。但有时候并不是那么容易就能短时间内收集的。所以提出了一个基于已有数据的增加数据量的方法:数据增强。
228 | 具体方法:
229 |
230 | 1. 翻转(水平、上下等)
231 | 2. 随机裁剪。指放大后旋转、裁剪
232 | 3. 扭曲变形,有很多更具体的成熟的方法。
233 |
234 | 但是数据增强并不是万用的方法,有时候可能会对网络的训练造成负面影响:比如从图片中提取文字的网络不适应翻转等等。甚至识别人脸的网络也不适合翻转,原因是“视觉手性”,感兴趣的可以阅读[Visual Chirality](https://arxiv.org/abs/2006.09512
235 | )。
236 |
237 | #### 5.7.2 Early Stopping ####
238 | Early stopping顾名思义,提早结束(训练)。具体操作是:
239 |
240 | 1. 训练足够多的次数,并且记录train set和dev set的error曲线。如图
241 | 
242 |
243 | 2. 找到dev error曲线的最低点,该点的迭代次数(附近)作为最佳迭代次数。
244 |
245 | 原理也很简单,在网络过拟合之前停止训练,不就能阻止网络过拟合了嘛。操作起来也很简单,训练一次就知道下次要训练多久了。不过简单的做法自然带来偷懒的弊端。过早停止训练,意味着网络可能还没得到充分的训练,过早停止优化cost函数,虽然低方差但是可能高偏差。
246 |
247 |
248 | ### 5.8 正则化输入 ###
249 | **命名问题**
250 |
251 | 首先提一下有关归一化和标准化的命名问题。如果你去百度一下很容易就发现吴恩达老师教的归一化(Normalizing)和百度的不一样,倒是和百度的标准化(Standardization)差不多。大名鼎鼎的吴恩达老师竟然会犯这种低级错误?笔者一开始也这么认为,但是想了想我只是刚入门的怎么可以那么轻易怀疑大师。于是在多百度了几次(无果)、查几篇国内外论文、最后一次百度(知乎)后,得出了结果:
252 | 归一化和标准化都是一种特征放缩(Feature scaling)。特征放缩有很多种方法,这里只讲涉及到的这两种。
253 |
254 | 1. min-max normalizing(Rescaling),也就是百度的归一化normalizing:
255 | $$
256 | x^{\prime}=\frac{x-\min (x)}{\max (x)-\min (x)}
257 | $$
258 |
259 | 2. Z-score normalization(Standardization),也就是百度的标准化:
260 | $$
261 | x^{\prime}=\frac{\left(x-\mu\right)}{\sigma}
262 | $$
263 |
264 | 猜测吴恩达老师是简称Z-score normalization为normalization了?也可能是其他原因吧。彻底帮我解决问题的[回答](https://www.zhihu.com/question/20467170)。
265 |
266 | **为什么要Z-score normalization**
267 |
268 | 有时候我们的数据的分布并不是“很好看”(图1、2),不是很利于网络的训练。这时候我们就可以考虑处理一下数据,使得数据的分布“更好看”(图3、4)。**注意**:图片中的名称用的是吴恩达老师课程中的名称。
269 | 
270 | 
271 | 
272 | 
273 | 什么时候数据会不好看?当输入的特征$x_{1}$和$x_{2}$取值范围有很大差别时就会,比如:$x_{1}$在[0,1]内,$x_{2}$在[1, 100]内。这样就会导致数据的分布为椭圆形,那在梯度下降时如果学习率不够小很容易就会一直震荡而艰难收敛;而更对称的分布,学习率就算大一点也很容易就能收敛。
274 | 所以一般当输入特征的取值范围差距较大时就考虑Z-score normalization,不过无脑使用也没什么坏事,所以是比较推荐的方法。
275 |
276 | **实现**
277 |
278 | 首先要注意的一点是,尽量别分多次计算均值$\mu$和方差$\sigma$,比如这两个值都由训练集得出就不更改了。
279 | Python代码:
280 |
281 | # 计算均值
282 | x_mean = np.mean(x)
283 | # 计算标准差;计算方差用np.var
284 | x_std = np.std(x)
285 | # 标准化
286 | x = (x - x_mean) / x_std
287 |
288 | 多提一句,对于图片,如果想实现min-max normalizing,一般只需要默认0为最小值,255为最大值即可:
289 |
290 | # x = (x-0) / (255-0)
291 | x = x / 255
292 |
293 |
294 |
295 |
296 | ### 5.9 梯度消失和梯度爆炸 ###
297 | #### 5.9.1 介绍 ####
298 | 英文称:vanishing and exploding gradients。
299 | 首先简单“展示”一下梯度爆炸是怎么样的:
300 | 假设有$L$层,$\text W^{[l]}=\left[\begin{array}{cc}
301 | 1.5 & 0 \\
302 | 0 & 1.5
303 | \end{array}\right],
304 | b^{[l]}=0$($l∈[1, L]$),且激活函数全部采用线性激活(恒等函数),则
305 |
306 | $$\begin{array}{l}
307 | \hat{y}=W^{[L]}W^{[L-1]} \ldots W^{[1]}x \\
308 | =\left[\begin{array}{cc}
309 | 1.5 & 0 \\
310 | 0 & 1.5
311 | \end{array}\right]^{L}x \\
312 | =\left[\begin{array}{cc}
313 | 1.5^{L} & 0 \\
314 | 0 & 1.5^{L}
315 | \end{array}\right]x
316 | \end{array}$$
317 |
318 | 可见,$W^{[l]}$中大于1的元素,将会因指数级增长而“爆炸”;同理,小于1的元素,则会以指数级递减而“消失”(真实情况会更复杂一些,但上述例子足以说明这种可能性)。
319 | 这不仅仅适用于$\hat{y}$的计算,还适用于梯度$dW、db$的计算——过深的网络在梯度下降时计算的梯度很有可能接近0或过大。这会直接导致网络的学习停滞不前或者发散,严重影响学习效果。
320 |
321 | #### 5.9.2 权重初始化 ####
322 | 既然梯度消失和爆炸都是由于$L$过大而形成的指数级缩小/放大,那在不减少$L$的前提下比较有限的方法就是让每次输出尽可能接近1了。$z$的计算可写成:
323 | $$z=w_{1}a_{1}+w_{2}a_{2}+\ldots+w_{n}a_{n}$$那么当$n$增大时,想让$z$减小则可以通过减小$w_{i}$做到;而$w_{i}$是符合高斯分布(标准正态分布,np.random.randn())的,所以$z$可**看似**服从分布$N(0, n)$,那$w_{i}$除以$n$就可以让$z$近似服从分布$N(0, 1)$,已达到。
324 | 具体做法是初始化时,用以下语句:
325 |
326 | w[l] = np.random.randn(n[l], n[l-1])*np.sqrt(2 / (n[l-1]))
327 |
328 | 其中*sqrt*中的表达式和使用的激活函数有关。ReLU采用上式($\frac{2}{n^{l-1}}$),tanh则采用$\frac{1}{n^{[l-1]}}$,其他形式的有$\frac{2}{n^{[l+1]}+n^{[l]}}$。
329 | 这么做的目的主要是修改$W^{[l]}$的分布,将方差除以输入
330 |
331 | #### 5.9.3 梯度逼近 ####
332 | 我们在计算梯度时用的是“手写”的公式(自己推导的公式),可能有时候会犯一点小错误。那我们就需要对梯度的计算进行验算,看看有没有错。但是不可能用同样的式子进行验算,因为计算机不会产生“计算失误”。所以我们需要不同的,计算结果很接近的方法来重新计算一次,那就是梯度逼近。
333 | 回顾高数/高中知识,梯度(导数)是切线斜率。近似地我们可以通过计算一个点附近的割线的斜率来代替该点的切线斜率。如图,可以用$\frac{ f(\theta+\varepsilon)-f(\theta-\varepsilon)}{2\varepsilon}$代替$f^{\prime}(\theta)$。当然,$\varepsilon$越小越接近。图来自吴恩达课程的1.12梯度的数值逼近。
334 | 
335 | 可能会有人疑惑为什么不采用单边,比如$\frac{ f(\theta+\varepsilon) - f(\theta)}{\varepsilon}$,而是要这样两边都取。抽象地你可以理解为单边计算出来的斜率更接近$\theta$的左右偏移一点点的$\theta^{\prime}$的值;而双边计算$\theta$正好位于割线的“正中间”,计算出来的斜率也自然要更接近一些。
336 |
337 | #### 5.9.4 梯度检验 ####
338 | 进入正题,介绍如何进行检验。首先对于所有参数$W^{[l]}$和$b^{[l]}$,按顺序链接成一个参数集$\theta$。对于$dW^{[l]}$和$db^{[l]}$也同样链接成$d\theta$。这里分别对应前向传播和反向传播。$\theta$和$d\theta$有一样的shape,$\theta[i]$表示第$i$个参数。然后计算$d\theta$的近似值$d\theta_{approx}$:
339 | 1. 遍历参数集$\theta$中的$\theta[i]$。
340 | 2. 计算$$d\theta_{approx}[i] = \frac{J(\theta[1], \theta[2], \ldots, \theta[i]+\varepsilon, \ldots)-J(\theta[1], \theta[2], \ldots, \theta[i] - \varepsilon, \ldots )} { 2\varepsilon} $$
341 | 3. 计算$\Delta = \frac{\|d\theta_{approx}-d\theta\|} {\|d\theta_{approx}\|+\|d\theta\|}$欧几里得范数,实际上就是根号下误差平方之和。
342 | 4. 如果$\Delta > \varepsilon$(如$\varepsilon=10^{-7}$),则视为误差超出阈值,否则为正常。
343 |
344 | #### 5.9.5 其他解决办法
345 |
346 | - relu、leakrelu等激活函数
347 |
348 | Relu:思想也很简单,如果激活函数的导数为1,那么就不存在梯度消失爆炸的问题了,每层的网络都可以得到相同的更新速度。
349 |
350 | relu的优点: 解决了梯度消失、爆炸的问题;计算方便,计算速度快,加速了网络的训练
351 |
352 | relu的缺点:由于负数部分恒为0,会导致一些神经元无法激活(可通过设置小学习率部分解决);输出不是以0为中心的
353 |
354 | **尽管relu也有缺点,但是仍然是目前使用最多的激活函数。**
355 |
356 | leakrelu激活函数在前面介绍激活函数时已经讲过了,这里就不再赘述了。
357 |
358 | - 梯度裁剪
359 |
360 | - batch normalization
361 |
362 | - 残差结构
363 |
364 | 上面的方法在下面的内容里面我们还会讲,这里就不再赘述了。
365 |
366 | #### 5.9.6 注意细节 ####
367 |
368 | 讲一下代码实现有几个细节:
369 | 1. 要实现cost function,并且接受参数$\theta$。
370 | 2. 欧几里得范数可以用 np.linalg.norm(array) 计算。
371 | 3. 不要和Dropout一起使用。
372 | 4. 只在debug时开启,正常训练无需启动,否则会花费大量的时间。
373 | 5. 应用了L2正则化的cost function和一般的不一样,梯度计算也会不一样。
374 |
375 |
376 |
377 | ### 5.10 参考文献
378 |
379 | https://zhuanlan.zhihu.com/p/38853908
380 |
381 |
382 |
383 |
384 |
385 |
386 |
387 |
388 |
--------------------------------------------------------------------------------
/7 超参数的调试,BN和程序框架.md:
--------------------------------------------------------------------------------
1 | ## 7 超参数调试,Batch Norm和程序框架
2 |
3 | ### 7.1 调试处理
4 |
5 | #### 7.1.1 超参数的重要性比较
6 |
7 | **深度学习中,用到的超参数有**
8 |
9 | $α $:学习率
10 |
11 | $β$:动量梯度下降因子
12 |
13 | $β1,β2,ε$:Adam算法参数
14 |
15 | layers:神经网络层数
16 |
17 | hidden units:各隐藏层神经元个数
18 |
19 | learning rate decay:学习因子下降参数
20 |
21 | mini-batch size:批量训练样本包含的样本个数
22 |
23 |
24 |
25 | 学习率$α$为最重要的超参数;
26 |
27 | 动量梯度下降因子$β$、各隐藏层神经元个数hidden units、批量训练样本包含的样本个数mini-batch size,三者重要性仅次于学习因子$α$;
28 |
29 | 接下来为神经网络层数layers和学习因子下降参数learning rate decay;最后,由于Adam算法参数$β1,β2,ε$三个参数一般设置为0.9,0.999和$10^{-8}$,不需要反复调试,所以重要性较弱。
30 |
31 | 但超参数的重要性排名不是一成不变的,可能会根据情况的不同而发生一定的变化
32 |
33 |
34 |
35 | #### 7.1.2 超参数的调试过程
36 |
37 | 在传统的机器学习中,我们对每个参数等距离选取任意个数的点,然后,分别使用不同点对应的参数组合进行训练,最后根据验证集上的表现,来选定最佳的参数。例如有两个待调试的参数,分别在每个参数上选取5个点,这样构成了5x5=25的参数组合,如图:
38 |
39 | 
40 |
41 | 此做法在参数较少的时候效果较好。但在深度学习的神经网络中,比较好的做法是使用随机选择。即:对于上面这个例子,我们随机选择25个点,作为待调试的超参数,如图:
42 |
43 | 
44 |
45 |
46 | 随机选择参数的目的是为了尽可能地得到更多种参数组合。如上面的例子,如果使用均匀采样的话,每个参数只有5种情况;而使用随机采样的话,每个参数有25种可能的情况,因此更有可能得到最佳的参数组合。
47 |
48 | 这种做法的另一个好处是能够对重要性不同的参数之间的选择效果更好。假设hyperparameter1为$α$,hyperparameter2为$ε$,二者的重要性是不一样的。如果使用第一种均匀采样的方法,$ε$的影响很小,相当于只选择了5个$α$值。而如果使用第二种随机采样的方法,$ε$和$α$都有可能选择25种不同值。这大大增加了$α$调试的个数,选择到最优值的可能更大了。在完全不知道哪个参数更加重要的情况下,随机采样的方式可以有效解决这一问题,但是均匀采样不能够解决该问题。
49 |
50 | 在随机采样后,可以得到某些区域模型的表现较好。为了得到更精确的最佳参数,我们应该继续对选定的区域进行由粗到细的采样(coarse to fine sampling scheme)。即放大表现较好的区域,再对此区域做更密集的随机采样。例如,对下图中右下角的方形区域再做25点的随机采样,以获得最佳参数。
51 | 
52 |
53 | ### 7.2 为超参数选择合适的范围
54 |
55 | #### 7.2.1 不同超参数合适的标尺
56 |
57 | 例如:神经网络层数layers和各隐藏层神经元个数hidden units,因为两者都为正整数,所以可以直接进行随机均匀采样(即每次变化的幅度是一样的);而对于学习率$α$和动量梯度下降因子$β$,则需要使用非均匀随机采样。
58 |
59 | #### 7.2.2 对数轴的取值过程
60 |
61 | 通过将linear scale转换为log scale来实现均匀尺度转化为非均匀尺度,然后再在log scale下进行均匀采样。如,[0.0001, 0.001],[0.001, 0.01],[0.01, 0.1],[0.1, 1]各个区间内随机采样的超参数个数基本一致,也就扩大了之前[0.0001, 0.1]区间内采样值个数。假设线性区间为[a, b],令$m=log(a),n=log(b)$,则对应的log区间为[m,n]。对log区间的[m,n]进行随机均匀采样,得到的采样值$r$,再反推到线性区间,即10的r次方。则10的r次方为最终采样的超参数。
62 |
63 | #### 7.2.3 为什么$β$不用linear scale进行取值
64 |
65 | 假设β从0.9000变化为0.9005,则$1/1−β$基本没有变化。但如果$β$从0.9990变为0.9995,那么$1/1−β$前后差别1000。即:$β$越接近1,指数加权平均的个数越多,变化越大。因此在$β$接近1的区间,应采集得更密集一些。
66 |
67 | ### 7.3 超参数训练的实践: Pandas VS Caviar
68 |
69 | #### 7.3.1 熊猫方式Panda approach
70 |
71 | 只能够对一个模型进行训练,调试不同的超参数,使得这个模型有最佳的表现。
72 |
73 | #### 7.3.2 鱼子酱方式Caviar approach
74 |
75 | 可以对多个模型同时进行训练,每个模型上调试不同的超参数,根据模型的表现,选择最优的模型
76 |
77 | 一般对于非常复杂或者数据量很大的模型,更多使用Panda approach。
78 |
79 |
80 |
81 | ### 7.4 归一化网络的激活函数
82 |
83 | #### 7.4.1 logistic 回归中归一化输入特征
84 |
85 | 
86 | $$
87 | \begin{array}{l}
88 | \mu=\frac{1}{m} \sum_{i} x^{(i)} \\
89 | X=X-\mu \\
90 | \sigma^{2}=\frac{1}{m} \sum_{i} x^{(i) 2} \\
91 | X=X / \sigma^{2}
92 | \end{array}
93 | $$
94 | 计算平均值,从训练集中减去平均值;计算方差,根据方差归一化数据集。变化学习问题的轮廓,易于算法优化。即归一化$x_{1}$,$x_{2}$,$x_{3}$有助于更有效的训练$w$和$b$。
95 |
96 |
883 |
884 |
885 | 于是,我们的损失函数(loss)就定义为了上式。
886 |
887 | #### 2.9.5 似然和概率 ####
888 | 既然提到了最大似然估计,那就提提似然和概率的区别:
889 |
890 | > 简单来讲,似然与概率分别是针对不同内容的估计和近似。概率(密度)表达给定θ下样本**X**=x的可能性,而似然表达了给定样本X=x下参数θ=θ1(相对于另外的参数取值θ2而言)为真实值的可能性
891 |
892 | 引自[似然(likelihood)和概率(probability)的区别与联系](https://blog.csdn.net/songyu0120/article/details/85059149)
893 |
894 |
895 |
896 |
897 |
--------------------------------------------------------------------------------
/5 深度学习的实用层面.md:
--------------------------------------------------------------------------------
1 | ## 5 深度学习的实用层面
2 |
3 | ### 5.1 训练集(Train sets)
4 |
5 | 在机器学习中,通常将训练数据分为**训练集**(train sets)、简单交叉验证集(简称**验证集**,dev sets)和**测试集**(test sets)。对训练集执行训练算法,通过验证集选择最好的模型,经过充分验证选定最终模型后,在测试集上进行评估。
6 | 
7 |
8 | **数据集划分比例:**
9 |
10 | - **对数据集规模较小的:**
11 | 如果没有明确设置验证集,常见做法是将所有数据**三七分**(70%训练集和30%测试集);或者划分为60%训练集、20%验证集和20%测试集。
12 | - **对数据集规模较大的:**
13 | **验证集和测试集占数据总量的比例会趋向于变得更小(低于数据总量的20%甚至10%)**。因为验证集的目的是验证不同的算法中哪一种更有效,故验证集要足够大才能评估,比如现有100万条数据,则取1万条便足以评估算法性能。同样地,根据最终选择的分类器,测试集的主要目的是正确评估分类器的性能,若拥有百万数据,只需1万条数据便足以评估单个分类器。所以倘若有100万条数据,可以将其中1万条作为验证集1万条作为测试集,即98%训练集、1%验证集和1%测试集。对于数据量过百万的应用,训练集可以达到99.5%,验证集和测试集各占0.25%或者验证集占0.4%测试集占0.1%。
14 |
15 | **对验证集和测试集的要求:**
16 | 1. 确保**验证集和测试集的数据来自同一分布**。因为要用验证集评估不同的模型以尽可能地优化性能,如果验证集和测试集来自同一分布会更好,机器学习算法会训练得更快。
17 | 2. **可以没有测试集**。测试集的目的是对最终选定的神经网络系统做出无偏评估,若不需要无偏评估,就可以不设置测试集。在只有训练集和验证集的情况下,需要在训练集上训练、尝试不同的模型框架,在验证集上评估这些模型,迭代并选出最适合的模型,训练集仍称为训练集,而验证集被称为测试集。
18 |
19 | 搭建训练测试集和验证集能够加速神经网络的集成,更有效地衡量算法的偏差和方差,从而更高效地选择合适的方法优化算法。
20 |
21 |
22 |
23 | ### 5.2 偏差和方差(Bias/Variance)
24 |
25 | 我们先定义好我们要用到的公式中变量的含义:
26 |
27 | 
28 |
29 | #### **5.2.1 偏差**
30 |
31 | 描述的是预测值的期望与真实值之间的差距。偏差越大,越偏离真实数据,拟合度越低,如下图第二行所示。故偏差度量的是学习算法的期望预测与真实结果的偏离程度,即**拟合能力**。
32 |
33 | 期望输出与真实标记的差别称为偏差,即:
34 | $$
35 | \operatorname{bias}^{2}(\boldsymbol{x})=(\bar{f}(\boldsymbol{x})-y)^{2}
36 | $$
37 |
38 | #### **5.2.2 方差**
39 |
40 | 描述的是预测值的变化范围,即离散程度。方差越大,数据的分布越分散,如下图右列所示。故方差度量的是同样大小的训练集的变动所导致的学习性能的变化,即刻画了**数据扰动**造成的影响。
41 |
42 | 使用样本数相同的不同训练集产生的**方差**为:
43 | $$
44 | \operatorname{var}(\boldsymbol{x})=\mathbb{E}_{D}\left[(f(\boldsymbol{x} ; D)-\bar{f}(\boldsymbol{x}))^{2}\right]
45 | $$
46 |
47 |
48 | 
49 |
50 | #### **5.2.3 泛化**
51 |
52 | 学习后的模型对未知数据的预测能力。在实际情况中,通常通过测试误差来评价学习方法的泛化能力,泛化误差(generalization error)是新输入的误差期望,为偏差、方差与噪声之和,给定学习任务,为了取得好的泛化性能,则需使偏差较小,即能够充分拟合数据,并且使方差较小,即使得数据扰动产生的影响小。
53 |
54 | 泛化误差 $=$ 错误率 $($ error $)=\operatorname{bias}^{2}(x)+\operatorname{var}(x)+\varepsilon^{2}$
55 |
56 | 也就是说,泛化误差可以通过一系列公式分解运算证明:泛化误差为偏差、方差与噪声之和。**证明过程如下:**为了便于讨论,我们假定噪声期望为零,即$E_{D}\left[y_{D}-y\right]=0$。通过简单的多项式展开合并,可对算法的期望泛化误差进行分解:
57 | $$
58 | \begin{aligned}
59 | E(f ; D)=& \mathbb{E}_{D}\left[\left(f(\boldsymbol{x} ; D)-y_{D}\right)^{2}\right] \\
60 | =& \mathbb{E}_{D}\left[\left(f(\boldsymbol{x} ; D)-\bar{f}(\boldsymbol{x})+\bar{f}(\boldsymbol{x})-y_{D}\right)^{2}\right] \\
61 | =& \mathbb{E}_{D}\left[(f(\boldsymbol{x} ; D)-\bar{f}(\boldsymbol{x}))^{2}\right]+\mathbb{E}_{D}\left[\left(\bar{f}(\boldsymbol{x})-y_{D}\right)^{2}\right] \\
62 | &+\mathbb{E}_{D}\left[2(f(\boldsymbol{x} ; D)-\bar{f}(\boldsymbol{x}))\left(\bar{f}(\boldsymbol{x})-y_{D}\right)\right] \\
63 | =& \mathbb{E}_{D}\left[(f(\boldsymbol{x} ; D)-\bar{f}(\boldsymbol{x}))^{2}\right]+\mathbb{E}_{D}\left[\left(\bar{f}(\boldsymbol{x})-y_{D}\right)^{2}\right] \\
64 | =& \mathbb{E}_{D}\left[(f(\boldsymbol{x} ; D)-\bar{f}(\boldsymbol{x}))^{2}\right]+\mathbb{E}_{D}\left[\left(\bar{f}(\boldsymbol{x})-y+y-y_{D}\right)^{2}\right] \\
65 | =& \mathbb{E}_{D}\left[(f(\boldsymbol{x} ; D)-\bar{f}(\boldsymbol{x}))^{2}\right]+\mathbb{E}_{D}\left[(\bar{f}(\boldsymbol{x})-y)^{2}\right]+\mathbb{E}_{D}\left[\left(y-y_{D}\right)^{2}\right] \\
66 | &+2 \mathbb{E}_{D}\left[(\bar{f}(\boldsymbol{x})-y)\left(y-y_{D}\right)\right] \\
67 | =& \mathbb{E}_{D}\left[(f(\boldsymbol{x} ; D)-\bar{f}(\boldsymbol{x}))^{2}\right]+(\bar{f}(\boldsymbol{x})-y)^{2}+\mathbb{E}_{\bar{D}}\left[\begin{array}{ll}
68 | \boldsymbol({y}_{D}-y)^2 &
69 | \end{array}\right] \\
70 | \end{aligned}
71 | $$
72 | 于是, 最终得到:
73 | $$
74 | E(f ; D)=\operatorname{bias}^{2}(\boldsymbol{x})+\operatorname{var}(\boldsymbol{x})+\varepsilon^{2}
75 | $$
76 | "偏差-方差分解" 说明, 泛化性能是由学习算法的能力、数据的充分性以及学习任务本身的难度 所共同决定的。给定学习任务, 为了取得好的泛化性能, 则需使偏差较小, 即能够充分拟合数据 并且使方差较小, 即使得数据扰动产生的影响小
77 |
78 | #### 5.2.4 拟合
79 |
80 | - **欠拟合**(Underfitting):常在模型学习能力较弱而数据复杂度较高的情况下出现。由于模型的学习能力不足,无法学习到数据集中的“一般规律”,因而导致模型的泛化能力较弱。
81 | - **过拟合**(Overfitting):常在模型学习能力较强而数据复杂度较弱的情况下出现。此时由于模型的学习能力太强,以至于将训练集中单个样本自身的特点都能捕捉到,并将其认为是“一般规律”,这种情况同样会导致模型的泛化能力下降。
82 | - **适度拟合**(just right):介于欠拟合和过拟合之间,数据拟合适度,复杂程度适中,泛化能力强。
83 |
84 | 
85 |
86 | #### 5.2.5 偏差和方差与训练集和验证集误差的关系
87 |
88 | 理解偏差和方差的两个关键数据是**训练集误差**(Train set error)和**验证集误差**(Dev set error)。假设人眼辨别错误率接近0(即最优误差或称为贝叶斯误差接近0),训练集和验证集数据来自相同分布,则可通过查看训练集误差判断数据拟合情况,从而判断是否有偏差问题(训练集误差越大,拟合度越低,偏差越高);然后查看错误率(验证集误差-训练集误差)有多高,判断方差是否过高(错误率越大,方差越高)。
89 | 下表是在不同的训练集和验证集的误差组合情况下对偏差和方差的分析:
90 | 
91 |
92 |
93 |
94 |
95 | 
96 |
97 | #### 5.2.6 **偏差、方差与bagging、boosting的关系**
98 |
99 | Bagging算法是对训练样本进行采样,产生出若干不同的子集,再从每个数据子集中训练出一个分类器,**取这些分类器的平均,所以是降低模型的方差(variance)**。Bagging算法和Random Forest这种并行算法都有这个效果。
100 |
101 | Boosting则是迭代算法,每一次迭代都根据上一次迭代的预测结果对样本进行权重调整,**所以随着迭代不断进行,误差会越来越小**,所以模型的偏差(bias)会不断降低。
102 |
103 | #### 5.2.7 **偏差、方差和K折交叉验证的关系**
104 |
105 | K-fold Cross Validation的思想:将原始数据分成K组 $($ 一般是均分 $)$, 将每个子集数据分别做一次 验证集, 其余的K-1组子集数据作为训练集, 这样会得到K个模型, 用这K个模型最终的验证集的分 类准确率的平均数作为此K-CV下分类器的性能指标。
106 | 对于一系列模型 $F(\hat{f}, \theta)$, 我们使用Cross Validation的目的是获得预测误差的无偏估计量CV, 从而可以用来选择一个最优的Theta*,使得CV最小。假设K-folds cross validation, CV统计量定 义为每个子集中误差的平均值, 而K的大小和CV平均值的bias和variance是有关的:
107 | $C V=\frac{1}{K} \sum_{k=1}^{K} \frac{1}{m} \sum_{i=1}^{m}\left(\hat{f}^{k}-y_{i}\right)^{2}$
108 | 其中, $\mathrm{m}=\mathrm{N} / \mathrm{K}$ 代表每个子集的大小, $\quad$N是总的训练样本量, K是子集的数目。当K较大时, $\mathrm{m}$ 较小,模型建立在较大的N-m上, 经过更多次数的平均可以学习得到更符合真实数 据分布的模型, Bias就小了,**但是这样一来模型就更加拟合训练数据集, 再去测试集上预测的时候 预测误差的期望值就变大了,从而Variance就大了**; $\mathrm{k}$ 较小的时候, 模型不会过度拟合训练数据, 从而Bias较大,**但是正因为没有过度拟合训练数据, Variance也较小**。
109 |
110 | ### 5.3 处理偏差和方差
111 |
112 | #### 5.3.1 针对不同偏差的不同处理
113 |
114 | 评估训练集或训练数据的性能,若偏差较高,可以选择以下几种方法:
115 | - 选择更大的网络,比如含有更多隐藏层或隐藏单元的网络
116 | - 花费更多时间训练网络(不一定有用,但没坏处)
117 | - 尝试更先进的优化算法
118 | - 选择更适合解决此问题的神经网络架构(可能有用,可能没用)
119 |
120 | 训练学习算法时,不断尝试这些方法,直到可以拟合数据,解决掉偏差问题为止,至少能够拟合训练集。
121 | #### 5.3.2 针对不同方差的不同处理
122 | 偏差降低到可以接受的数值,查看验证集性能来评估方差,如果方差高,可以选择下列方法:
123 | - 采用更多数据(最好的解决办法)
124 | - 正则化
125 | - 尝试更适合的神经网络框架(有时可以同时减少偏差和方差)
126 |
127 | 解决高方差最优方法是准备更多的数据,但可能无法实时准备足够多的数据或数据成本很高时,**正则化**可帮助避免过拟合,减少网络误差。
128 |
129 | 通过不断重复尝试,找到一个低偏差、低方差的框架。
130 | > 高偏差和高方差尝试的方法可能完全不同,明确这点来选择最有效的方法。
131 | 只要正则适度,通常构建更大网络便可以在不影响方差的同时减少偏差。采用更多数据通常可以在不过多影响偏差的同时减少方差。我们有很多的选择可以减少偏差或方差而不影响另一方。
132 |
133 |
134 | ### 5.4 正则化
135 |
136 | **定义**:一种为了减小方差(测试误差)的行为
137 | **作用**:使用比较复杂的模型比如神经网络,去拟合数据时,容易出现过拟合现象,导致模型的泛化能力下降,这时我们使用正则化,降低模型的复杂度,让模型在面对新数据的时候,可以有很好的表现。
138 |
139 | #### 5.4.1 logistic 回归的正则化
140 | - **L2 正则化**
141 | $J(w, b)=\frac{1}{m} \sum_{i=1}^{m} L\left(\hat{y}^{(i)}, y^{(i)}\right)+\frac{\lambda}{2 m}\|w\|_{2}^{2}$
142 | 每次更新w时:
143 |
144 | $$w:=w-\alpha d w=\left(1-\frac{\alpha \lambda}{m}\right) w-\frac{\partial J}{\partial w}$$
145 |
146 | 从上式看出,每次更新对特征系数做一个**比例的缩放**而不是像L1正则化减去一个固定值。这使得系数趋向变小而不会变为0,因此L2正则化**让模型变得更简单,防止过拟合**。
147 | - **L1 正则化**
148 | $$J(w, b)=\frac{1}{m} \sum_{i=1}^{m} L\left(\hat{y}^{(i)}, y^{(i)}\right)+\frac{\lambda}{2 m}\|w\|_{1}$$
149 |
150 | 每次更新w时:
151 | $$\begin{array}{c}
152 | w:=w-\alpha d w\\
153 | =w-\frac{\alpha \lambda}{2 m} \operatorname{sign}\left(w\right)-\frac{\partial J}{\partial w}
154 | \end{array}$$
155 | 若 w 为正数,则每次更新减去一个常数;若 w 为负数,则每次更新加上一个常数,故容易产生特征的系数为0的情况,特征系数为 0 表示该特征不会对结果有任何影响,因此L1正则化让w变得稀疏,起到**特征选择**的作用。
156 | > - 参数 w 向量的L2 范数:$\|w\|_{2}^{2}=\sum_{j=1}^{n_{x}} w_{j}^{2}=w^{T} w$
157 | 参数 w 向量的L1 范数:$\|w\|_{1}=\sum_{j=1}^{n_{x}}\left|w_{j}\right|$
158 | > - $w\in \mathbb{R}^{n_{x}}, b \in \mathbb{R}$,习惯只正则化w,省略参数b。因为w通常是一个高维参数矢量,b只是单个数字,即w几乎涵盖所有参数,b只是众多参数中的一个,b通常省略不计,加上也没问题。
159 | >- $\lambda$是正则化参数,是一个需要调整的超参数,Python 编程语言中,lambda 是一个保留字段,编写代码时,删掉a,写成lambd,以免冲突。
160 |
161 | **总结**
162 | 两者都通过加上一个和项来限制参数大小,效果却不同:L1正则化适用于**特征选择**,L2正则化适用于**防止模型过拟合**。
163 | 在训练网络时,倾向于使用**L2正则化**。
164 |
165 |
166 |
167 | #### 5.4.2 神经网络中实现L2正则化
168 |
169 | $$J\left(w^{[1]}, b^{[1]}, \ldots, w^{[L]}, b^{[L]}\right)=\frac{1}{m} \sum_{i=1}^{m} L\left(\hat{y}^{(i)}, y^{(i)}\right)+\frac{\lambda}{2 m} \sum_{l=1}^{L}\|w\|_{F}^{2}$$
170 | **Frobenius 范数**:
171 | 下标F标注,表示一个矩阵中所有元素的平方和。
172 | $$\|w\|_{F}^{2}=\sum_{i=1}^{n^{[l-1]}} \sum_{j=1}^{n^{[l]}}\left(w_{i j}^{[l]}\right)^{2}$$
173 |
174 | 其中,$w:\left(n^{[l-1]}, n^{[l]}\right)$ $n^{[l]}$表示第$l$层单元数量,$n^{[l-1]}$表示第$l-1$层单元数量
175 |
176 | 实现梯度下降:
177 | $$\begin{aligned} w^{[l]}: &=w^{[l]}-\alpha\left[(\text { from backprop })+\frac{\lambda}{m} w^{[l]}\right] \\ &=\left(1-\frac{\alpha \lambda}{m}\right) w^{[l]}-\alpha(\text { from backprop }) \end{aligned}$$
178 | 实际上,相当于给矩阵$w^{[l]}$乘上$1-\frac{\alpha \lambda}{m}$倍的权重,而该系数小于1,因此L2正则化也被称为**权重衰减**
179 |
180 |
181 |
182 | ### 5.5 正则化有效的原理
183 | - 正则化参数$\lambda$增加到足够大,权重矩阵$w^{[l]}$会接近于0,大量隐藏单元的影响变得更小了,神经网络越来越简单,接近逻辑回归,这样更不容易发生过拟合。
184 |
185 | 举例:
186 | 假设使用$\tanh (z)$激活函数,如果$z$的值始终在接近原点的小范围内,激活函数大致呈线性,每层几乎都是线性的,和线性回归一样。
187 |
188 | 
189 | 当正则化参数$\lambda$足够大,参数$w$很小,$z$也会相对变小,激活函数$\tanh (z)$会相对呈线性,整个神经网络会计算接近线性函数的值,即一个很简单的函数,而不是极复杂的高度非线性函数,不会发生过拟合。
190 |
191 | 参考文章:[机器学习中的正则化](https://www.jianshu.com/p/569efedf6985)
192 |
193 |
194 |
195 |
196 |
197 | ### 5.6 Dropout正则化 ###
198 | Dropout正则化是较常用的避免过拟合的方法之一。
199 |
200 | **Dropout**
201 |
202 | 首先介绍一下Dropout正则化:在**训练**神经网络时,对于每一层神经网络中的所有节点,每个结点都有keep_prob的概率保留,1 - keep_prob的概率丢弃。这里的丢弃指的是**每一次**前向传播的时候随机丢弃部分结点,每次前向传播都重新计算要丢弃的结点。要注意在更新权值和真正应用已经训练好的网络时,是不会随机丢弃的。
203 | 
204 |
205 | **原理**
206 |
207 | 有没有觉得很神奇,竟然随机丢掉一些结点反而能“更好”地训练神经网络,也太“玄乎”了。当然,能生效的正则化肯定有它成功的理由,下面给出解释:
208 | 1. 随机删除一些结点,本质上相当于缩小网络。而过拟合的原因之一是网络太大而导致的拟合效果“好过头”了,那缩小网络自然能一定程度上避免过拟合。
209 | 2. 由于所有节点都可能被丢弃,所以训练时不会过渡依赖任何一个结点(特征),表现为尽可能缩小所有权值。那就有点接近L2正则化那种收缩权值的效果了。
210 |
211 | **代码实现**
212 |
213 | # 操作 < keep_prob 可使本来的随机向量变为True、False组成的向量
214 | d3 = np.random.randn(a3.shape[0], a3.shape[1]) < keep_prob
215 | # 实际运算时,True、False会变为1和0
216 | a3 *= d3
217 | # 修正a3的均值,保持和Dropout前不变
218 | a3 /= keep_prob
219 |
220 | 技术细节上,用了一个小于运算符自动将随机值转换为0、1;在将部分值归0后,a3的均值也会变为原来的keep_prob倍,所以最后对所有数除以keep_prob以保证a3的均值不变,保证$z3=wa3+b$的均值不变
221 |
222 |
223 |
224 |
225 | ### 5.7 其他正则化方法 ###
226 | #### 5.7.1 数据增强/Data Augmentation ####
227 | 前文提到解决high variance(高方差)/ 过拟合的解决办法之一是收集更多的数据,更大的训练集。但有时候并不是那么容易就能短时间内收集的。所以提出了一个基于已有数据的增加数据量的方法:数据增强。
228 | 具体方法:
229 |
230 | 1. 翻转(水平、上下等)
231 | 2. 随机裁剪。指放大后旋转、裁剪
232 | 3. 扭曲变形,有很多更具体的成熟的方法。
233 |
234 | 但是数据增强并不是万用的方法,有时候可能会对网络的训练造成负面影响:比如从图片中提取文字的网络不适应翻转等等。甚至识别人脸的网络也不适合翻转,原因是“视觉手性”,感兴趣的可以阅读[Visual Chirality](https://arxiv.org/abs/2006.09512
235 | )。
236 |
237 | #### 5.7.2 Early Stopping ####
238 | Early stopping顾名思义,提早结束(训练)。具体操作是:
239 |
240 | 1. 训练足够多的次数,并且记录train set和dev set的error曲线。如图
241 | 
242 |
243 | 2. 找到dev error曲线的最低点,该点的迭代次数(附近)作为最佳迭代次数。
244 |
245 | 原理也很简单,在网络过拟合之前停止训练,不就能阻止网络过拟合了嘛。操作起来也很简单,训练一次就知道下次要训练多久了。不过简单的做法自然带来偷懒的弊端。过早停止训练,意味着网络可能还没得到充分的训练,过早停止优化cost函数,虽然低方差但是可能高偏差。
246 |
247 |
248 | ### 5.8 正则化输入 ###
249 | **命名问题**
250 |
251 | 首先提一下有关归一化和标准化的命名问题。如果你去百度一下很容易就发现吴恩达老师教的归一化(Normalizing)和百度的不一样,倒是和百度的标准化(Standardization)差不多。大名鼎鼎的吴恩达老师竟然会犯这种低级错误?笔者一开始也这么认为,但是想了想我只是刚入门的怎么可以那么轻易怀疑大师。于是在多百度了几次(无果)、查几篇国内外论文、最后一次百度(知乎)后,得出了结果:
252 | 归一化和标准化都是一种特征放缩(Feature scaling)。特征放缩有很多种方法,这里只讲涉及到的这两种。
253 |
254 | 1. min-max normalizing(Rescaling),也就是百度的归一化normalizing:
255 | $$
256 | x^{\prime}=\frac{x-\min (x)}{\max (x)-\min (x)}
257 | $$
258 |
259 | 2. Z-score normalization(Standardization),也就是百度的标准化:
260 | $$
261 | x^{\prime}=\frac{\left(x-\mu\right)}{\sigma}
262 | $$
263 |
264 | 猜测吴恩达老师是简称Z-score normalization为normalization了?也可能是其他原因吧。彻底帮我解决问题的[回答](https://www.zhihu.com/question/20467170)。
265 |
266 | **为什么要Z-score normalization**
267 |
268 | 有时候我们的数据的分布并不是“很好看”(图1、2),不是很利于网络的训练。这时候我们就可以考虑处理一下数据,使得数据的分布“更好看”(图3、4)。**注意**:图片中的名称用的是吴恩达老师课程中的名称。
269 | 
270 | 
271 | 
272 | 
273 | 什么时候数据会不好看?当输入的特征$x_{1}$和$x_{2}$取值范围有很大差别时就会,比如:$x_{1}$在[0,1]内,$x_{2}$在[1, 100]内。这样就会导致数据的分布为椭圆形,那在梯度下降时如果学习率不够小很容易就会一直震荡而艰难收敛;而更对称的分布,学习率就算大一点也很容易就能收敛。
274 | 所以一般当输入特征的取值范围差距较大时就考虑Z-score normalization,不过无脑使用也没什么坏事,所以是比较推荐的方法。
275 |
276 | **实现**
277 |
278 | 首先要注意的一点是,尽量别分多次计算均值$\mu$和方差$\sigma$,比如这两个值都由训练集得出就不更改了。
279 | Python代码:
280 |
281 | # 计算均值
282 | x_mean = np.mean(x)
283 | # 计算标准差;计算方差用np.var
284 | x_std = np.std(x)
285 | # 标准化
286 | x = (x - x_mean) / x_std
287 |
288 | 多提一句,对于图片,如果想实现min-max normalizing,一般只需要默认0为最小值,255为最大值即可:
289 |
290 | # x = (x-0) / (255-0)
291 | x = x / 255
292 |
293 |
294 |
295 |
296 | ### 5.9 梯度消失和梯度爆炸 ###
297 | #### 5.9.1 介绍 ####
298 | 英文称:vanishing and exploding gradients。
299 | 首先简单“展示”一下梯度爆炸是怎么样的:
300 | 假设有$L$层,$\text W^{[l]}=\left[\begin{array}{cc}
301 | 1.5 & 0 \\
302 | 0 & 1.5
303 | \end{array}\right],
304 | b^{[l]}=0$($l∈[1, L]$),且激活函数全部采用线性激活(恒等函数),则
305 |
306 | $$\begin{array}{l}
307 | \hat{y}=W^{[L]}W^{[L-1]} \ldots W^{[1]}x \\
308 | =\left[\begin{array}{cc}
309 | 1.5 & 0 \\
310 | 0 & 1.5
311 | \end{array}\right]^{L}x \\
312 | =\left[\begin{array}{cc}
313 | 1.5^{L} & 0 \\
314 | 0 & 1.5^{L}
315 | \end{array}\right]x
316 | \end{array}$$
317 |
318 | 可见,$W^{[l]}$中大于1的元素,将会因指数级增长而“爆炸”;同理,小于1的元素,则会以指数级递减而“消失”(真实情况会更复杂一些,但上述例子足以说明这种可能性)。
319 | 这不仅仅适用于$\hat{y}$的计算,还适用于梯度$dW、db$的计算——过深的网络在梯度下降时计算的梯度很有可能接近0或过大。这会直接导致网络的学习停滞不前或者发散,严重影响学习效果。
320 |
321 | #### 5.9.2 权重初始化 ####
322 | 既然梯度消失和爆炸都是由于$L$过大而形成的指数级缩小/放大,那在不减少$L$的前提下比较有限的方法就是让每次输出尽可能接近1了。$z$的计算可写成:
323 | $$z=w_{1}a_{1}+w_{2}a_{2}+\ldots+w_{n}a_{n}$$那么当$n$增大时,想让$z$减小则可以通过减小$w_{i}$做到;而$w_{i}$是符合高斯分布(标准正态分布,np.random.randn())的,所以$z$可**看似**服从分布$N(0, n)$,那$w_{i}$除以$n$就可以让$z$近似服从分布$N(0, 1)$,已达到。
324 | 具体做法是初始化时,用以下语句:
325 |
326 | w[l] = np.random.randn(n[l], n[l-1])*np.sqrt(2 / (n[l-1]))
327 |
328 | 其中*sqrt*中的表达式和使用的激活函数有关。ReLU采用上式($\frac{2}{n^{l-1}}$),tanh则采用$\frac{1}{n^{[l-1]}}$,其他形式的有$\frac{2}{n^{[l+1]}+n^{[l]}}$。
329 | 这么做的目的主要是修改$W^{[l]}$的分布,将方差除以输入
330 |
331 | #### 5.9.3 梯度逼近 ####
332 | 我们在计算梯度时用的是“手写”的公式(自己推导的公式),可能有时候会犯一点小错误。那我们就需要对梯度的计算进行验算,看看有没有错。但是不可能用同样的式子进行验算,因为计算机不会产生“计算失误”。所以我们需要不同的,计算结果很接近的方法来重新计算一次,那就是梯度逼近。
333 | 回顾高数/高中知识,梯度(导数)是切线斜率。近似地我们可以通过计算一个点附近的割线的斜率来代替该点的切线斜率。如图,可以用$\frac{ f(\theta+\varepsilon)-f(\theta-\varepsilon)}{2\varepsilon}$代替$f^{\prime}(\theta)$。当然,$\varepsilon$越小越接近。图来自吴恩达课程的1.12梯度的数值逼近。
334 | 
335 | 可能会有人疑惑为什么不采用单边,比如$\frac{ f(\theta+\varepsilon) - f(\theta)}{\varepsilon}$,而是要这样两边都取。抽象地你可以理解为单边计算出来的斜率更接近$\theta$的左右偏移一点点的$\theta^{\prime}$的值;而双边计算$\theta$正好位于割线的“正中间”,计算出来的斜率也自然要更接近一些。
336 |
337 | #### 5.9.4 梯度检验 ####
338 | 进入正题,介绍如何进行检验。首先对于所有参数$W^{[l]}$和$b^{[l]}$,按顺序链接成一个参数集$\theta$。对于$dW^{[l]}$和$db^{[l]}$也同样链接成$d\theta$。这里分别对应前向传播和反向传播。$\theta$和$d\theta$有一样的shape,$\theta[i]$表示第$i$个参数。然后计算$d\theta$的近似值$d\theta_{approx}$:
339 | 1. 遍历参数集$\theta$中的$\theta[i]$。
340 | 2. 计算$$d\theta_{approx}[i] = \frac{J(\theta[1], \theta[2], \ldots, \theta[i]+\varepsilon, \ldots)-J(\theta[1], \theta[2], \ldots, \theta[i] - \varepsilon, \ldots )} { 2\varepsilon} $$
341 | 3. 计算$\Delta = \frac{\|d\theta_{approx}-d\theta\|} {\|d\theta_{approx}\|+\|d\theta\|}$欧几里得范数,实际上就是根号下误差平方之和。
342 | 4. 如果$\Delta > \varepsilon$(如$\varepsilon=10^{-7}$),则视为误差超出阈值,否则为正常。
343 |
344 | #### 5.9.5 其他解决办法
345 |
346 | - relu、leakrelu等激活函数
347 |
348 | Relu:思想也很简单,如果激活函数的导数为1,那么就不存在梯度消失爆炸的问题了,每层的网络都可以得到相同的更新速度。
349 |
350 | relu的优点: 解决了梯度消失、爆炸的问题;计算方便,计算速度快,加速了网络的训练
351 |
352 | relu的缺点:由于负数部分恒为0,会导致一些神经元无法激活(可通过设置小学习率部分解决);输出不是以0为中心的
353 |
354 | **尽管relu也有缺点,但是仍然是目前使用最多的激活函数。**
355 |
356 | leakrelu激活函数在前面介绍激活函数时已经讲过了,这里就不再赘述了。
357 |
358 | - 梯度裁剪
359 |
360 | - batch normalization
361 |
362 | - 残差结构
363 |
364 | 上面的方法在下面的内容里面我们还会讲,这里就不再赘述了。
365 |
366 | #### 5.9.6 注意细节 ####
367 |
368 | 讲一下代码实现有几个细节:
369 | 1. 要实现cost function,并且接受参数$\theta$。
370 | 2. 欧几里得范数可以用 np.linalg.norm(array) 计算。
371 | 3. 不要和Dropout一起使用。
372 | 4. 只在debug时开启,正常训练无需启动,否则会花费大量的时间。
373 | 5. 应用了L2正则化的cost function和一般的不一样,梯度计算也会不一样。
374 |
375 |
376 |
377 | ### 5.10 参考文献
378 |
379 | https://zhuanlan.zhihu.com/p/38853908
380 |
381 |
382 |
383 |
384 |
385 |
386 |
387 |
388 |
--------------------------------------------------------------------------------
/7 超参数的调试,BN和程序框架.md:
--------------------------------------------------------------------------------
1 | ## 7 超参数调试,Batch Norm和程序框架
2 |
3 | ### 7.1 调试处理
4 |
5 | #### 7.1.1 超参数的重要性比较
6 |
7 | **深度学习中,用到的超参数有**
8 |
9 | $α $:学习率
10 |
11 | $β$:动量梯度下降因子
12 |
13 | $β1,β2,ε$:Adam算法参数
14 |
15 | layers:神经网络层数
16 |
17 | hidden units:各隐藏层神经元个数
18 |
19 | learning rate decay:学习因子下降参数
20 |
21 | mini-batch size:批量训练样本包含的样本个数
22 |
23 |
24 |
25 | 学习率$α$为最重要的超参数;
26 |
27 | 动量梯度下降因子$β$、各隐藏层神经元个数hidden units、批量训练样本包含的样本个数mini-batch size,三者重要性仅次于学习因子$α$;
28 |
29 | 接下来为神经网络层数layers和学习因子下降参数learning rate decay;最后,由于Adam算法参数$β1,β2,ε$三个参数一般设置为0.9,0.999和$10^{-8}$,不需要反复调试,所以重要性较弱。
30 |
31 | 但超参数的重要性排名不是一成不变的,可能会根据情况的不同而发生一定的变化
32 |
33 |
34 |
35 | #### 7.1.2 超参数的调试过程
36 |
37 | 在传统的机器学习中,我们对每个参数等距离选取任意个数的点,然后,分别使用不同点对应的参数组合进行训练,最后根据验证集上的表现,来选定最佳的参数。例如有两个待调试的参数,分别在每个参数上选取5个点,这样构成了5x5=25的参数组合,如图:
38 |
39 | 
40 |
41 | 此做法在参数较少的时候效果较好。但在深度学习的神经网络中,比较好的做法是使用随机选择。即:对于上面这个例子,我们随机选择25个点,作为待调试的超参数,如图:
42 |
43 | 
44 |
45 |
46 | 随机选择参数的目的是为了尽可能地得到更多种参数组合。如上面的例子,如果使用均匀采样的话,每个参数只有5种情况;而使用随机采样的话,每个参数有25种可能的情况,因此更有可能得到最佳的参数组合。
47 |
48 | 这种做法的另一个好处是能够对重要性不同的参数之间的选择效果更好。假设hyperparameter1为$α$,hyperparameter2为$ε$,二者的重要性是不一样的。如果使用第一种均匀采样的方法,$ε$的影响很小,相当于只选择了5个$α$值。而如果使用第二种随机采样的方法,$ε$和$α$都有可能选择25种不同值。这大大增加了$α$调试的个数,选择到最优值的可能更大了。在完全不知道哪个参数更加重要的情况下,随机采样的方式可以有效解决这一问题,但是均匀采样不能够解决该问题。
49 |
50 | 在随机采样后,可以得到某些区域模型的表现较好。为了得到更精确的最佳参数,我们应该继续对选定的区域进行由粗到细的采样(coarse to fine sampling scheme)。即放大表现较好的区域,再对此区域做更密集的随机采样。例如,对下图中右下角的方形区域再做25点的随机采样,以获得最佳参数。
51 | 
52 |
53 | ### 7.2 为超参数选择合适的范围
54 |
55 | #### 7.2.1 不同超参数合适的标尺
56 |
57 | 例如:神经网络层数layers和各隐藏层神经元个数hidden units,因为两者都为正整数,所以可以直接进行随机均匀采样(即每次变化的幅度是一样的);而对于学习率$α$和动量梯度下降因子$β$,则需要使用非均匀随机采样。
58 |
59 | #### 7.2.2 对数轴的取值过程
60 |
61 | 通过将linear scale转换为log scale来实现均匀尺度转化为非均匀尺度,然后再在log scale下进行均匀采样。如,[0.0001, 0.001],[0.001, 0.01],[0.01, 0.1],[0.1, 1]各个区间内随机采样的超参数个数基本一致,也就扩大了之前[0.0001, 0.1]区间内采样值个数。假设线性区间为[a, b],令$m=log(a),n=log(b)$,则对应的log区间为[m,n]。对log区间的[m,n]进行随机均匀采样,得到的采样值$r$,再反推到线性区间,即10的r次方。则10的r次方为最终采样的超参数。
62 |
63 | #### 7.2.3 为什么$β$不用linear scale进行取值
64 |
65 | 假设β从0.9000变化为0.9005,则$1/1−β$基本没有变化。但如果$β$从0.9990变为0.9995,那么$1/1−β$前后差别1000。即:$β$越接近1,指数加权平均的个数越多,变化越大。因此在$β$接近1的区间,应采集得更密集一些。
66 |
67 | ### 7.3 超参数训练的实践: Pandas VS Caviar
68 |
69 | #### 7.3.1 熊猫方式Panda approach
70 |
71 | 只能够对一个模型进行训练,调试不同的超参数,使得这个模型有最佳的表现。
72 |
73 | #### 7.3.2 鱼子酱方式Caviar approach
74 |
75 | 可以对多个模型同时进行训练,每个模型上调试不同的超参数,根据模型的表现,选择最优的模型
76 |
77 | 一般对于非常复杂或者数据量很大的模型,更多使用Panda approach。
78 |
79 |
80 |
81 | ### 7.4 归一化网络的激活函数
82 |
83 | #### 7.4.1 logistic 回归中归一化输入特征
84 |
85 | 
86 | $$
87 | \begin{array}{l}
88 | \mu=\frac{1}{m} \sum_{i} x^{(i)} \\
89 | X=X-\mu \\
90 | \sigma^{2}=\frac{1}{m} \sum_{i} x^{(i) 2} \\
91 | X=X / \sigma^{2}
92 | \end{array}
93 | $$
94 | 计算平均值,从训练集中减去平均值;计算方差,根据方差归一化数据集。变化学习问题的轮廓,易于算法优化。即归一化$x_{1}$,$x_{2}$,$x_{3}$有助于更有效的训练$w$和$b$。
95 |
96 |  97 |
98 |
99 |
100 | #### 7.4.2 更深层的模型的归一化
101 |
102 | 
103 |
104 | **分析**:此例中,与上例同理,归一化$a^{[2]}$的平均值和方差以便使$w^{[3]}$,$b^{[3]}$的训练更有效率,严格来说我们真正归一化的不是$a^{[2]}$而是$z^{[2]}$。关于归一化$a^{[2]}$还是$z^{[2]}$,深度学习文献中有一些争论,实践中,常做的是**归一化$z^{[2]}$**,吴恩达推荐其为默认选择。
105 |
106 | **实施BN**:
107 |
108 | 在神经网络中,给定一些中间值,假设你有一些隐藏单元值,从$z^{(1)}$到$z^{(m)}$,这些来源于隐藏层,写为$z^{[l](i)}$会更准确,我们省略$𝑙$及方括号,以便简化这一行的符号。
109 |
110 | 已知这些值,计算平均值,所有这些都是针对𝑙层,但省略$𝑙$及方括号,接着,取每个$z^{(i)}$值,使其归一化,如下,减去均值再除以标准偏差,为了使数值稳定,通常分母加上$𝜀$,以防$𝜎 = 0$的情况。
111 |
112 |
113 | $$
114 | \begin{array}{l}
115 | \mu=\frac{1}{m} \sum_{i} z^{(i)} \\
116 | \sigma^{2}=\frac{1}{m} \sum_{i}\left(z^{(i)}-\mu\right)^{2} \\
117 | z_{\text {norm}}^{(i)}=\frac{z^{(i)}-\mu}{\sqrt{\sigma^{2}+\varepsilon}}
118 | \end{array}
119 | $$
120 | 这时,已把这些$z$值归一化,化为平均值0和标准单位方差,所以每个分量都含有平均值0和方差1,但我们不想让隐藏单元总是含有平均值0和方差1,隐藏单元有了不同的分布才会有意义。于是做如下计算:
121 | $$
122 | \tilde{z}^{(i)}=\gamma z_{\text {norm}}^{(i)}+\beta
123 | $$
124 | 这里,$\gamma$和$\beta$是模型的**学习参数**,使用梯度下降或一些其他类似梯度下降的算法,如Momentum,或Nesterov,Adam更新$\gamma$和$\beta$,正如神经网络的权重。
125 |
126 | $\gamma$和$\beta$的作用是可以随意设置$\tilde{z}^{(i)}$的平均值。当$\gamma=\sqrt{\sigma^{2}+\varepsilon}$, $\beta=\mu$时,$\tilde{z}^{(i)}=z^{(i)}$。此时,该归一化过程,即这四个等式,只是计算恒等函数。但通过对$\gamma$和$\beta$合理设定,可以构造含其他平均值和方差的隐藏单元值。在网络中,用$\tilde{z}^{(i)}$取代$z^{(i)}$,方便神经网络中的后续计算。
127 |
128 | **归纳**:$Batch Norm$归一化的不只是输入层,同样应用于深度隐藏层。但训练输入和隐藏单元值的一个区别是,我们不希望隐藏单元值总是均值0和方差1。
129 |
130 |
97 |
98 |
99 |
100 | #### 7.4.2 更深层的模型的归一化
101 |
102 | 
103 |
104 | **分析**:此例中,与上例同理,归一化$a^{[2]}$的平均值和方差以便使$w^{[3]}$,$b^{[3]}$的训练更有效率,严格来说我们真正归一化的不是$a^{[2]}$而是$z^{[2]}$。关于归一化$a^{[2]}$还是$z^{[2]}$,深度学习文献中有一些争论,实践中,常做的是**归一化$z^{[2]}$**,吴恩达推荐其为默认选择。
105 |
106 | **实施BN**:
107 |
108 | 在神经网络中,给定一些中间值,假设你有一些隐藏单元值,从$z^{(1)}$到$z^{(m)}$,这些来源于隐藏层,写为$z^{[l](i)}$会更准确,我们省略$𝑙$及方括号,以便简化这一行的符号。
109 |
110 | 已知这些值,计算平均值,所有这些都是针对𝑙层,但省略$𝑙$及方括号,接着,取每个$z^{(i)}$值,使其归一化,如下,减去均值再除以标准偏差,为了使数值稳定,通常分母加上$𝜀$,以防$𝜎 = 0$的情况。
111 |
112 |
113 | $$
114 | \begin{array}{l}
115 | \mu=\frac{1}{m} \sum_{i} z^{(i)} \\
116 | \sigma^{2}=\frac{1}{m} \sum_{i}\left(z^{(i)}-\mu\right)^{2} \\
117 | z_{\text {norm}}^{(i)}=\frac{z^{(i)}-\mu}{\sqrt{\sigma^{2}+\varepsilon}}
118 | \end{array}
119 | $$
120 | 这时,已把这些$z$值归一化,化为平均值0和标准单位方差,所以每个分量都含有平均值0和方差1,但我们不想让隐藏单元总是含有平均值0和方差1,隐藏单元有了不同的分布才会有意义。于是做如下计算:
121 | $$
122 | \tilde{z}^{(i)}=\gamma z_{\text {norm}}^{(i)}+\beta
123 | $$
124 | 这里,$\gamma$和$\beta$是模型的**学习参数**,使用梯度下降或一些其他类似梯度下降的算法,如Momentum,或Nesterov,Adam更新$\gamma$和$\beta$,正如神经网络的权重。
125 |
126 | $\gamma$和$\beta$的作用是可以随意设置$\tilde{z}^{(i)}$的平均值。当$\gamma=\sqrt{\sigma^{2}+\varepsilon}$, $\beta=\mu$时,$\tilde{z}^{(i)}=z^{(i)}$。此时,该归一化过程,即这四个等式,只是计算恒等函数。但通过对$\gamma$和$\beta$合理设定,可以构造含其他平均值和方差的隐藏单元值。在网络中,用$\tilde{z}^{(i)}$取代$z^{(i)}$,方便神经网络中的后续计算。
127 |
128 | **归纳**:$Batch Norm$归一化的不只是输入层,同样应用于深度隐藏层。但训练输入和隐藏单元值的一个区别是,我们不希望隐藏单元值总是均值0和方差1。
129 |
130 |  131 |
132 | 比如我们使用sigmoid激活函数,想使它们有更大的方差或非0的均值,以便更好的利用非线性的sigmoid函数,而不是所有值都集中在线性区域中。
133 |
134 | 有了$\gamma$和$\beta$两个参数,均值和方差由其控制,使隐藏单元值的均值和方差归一化,即$z^{(i)}$有固定的均值和方差。其均值和方差可以是0和1,也可以是其他值。
135 |
136 | ### 7.5 将 Batch Norm 拟合进神经网络
137 |
138 | #### 7.5.1 在网络中加入 Batch Norm
139 |
140 |
131 |
132 | 比如我们使用sigmoid激活函数,想使它们有更大的方差或非0的均值,以便更好的利用非线性的sigmoid函数,而不是所有值都集中在线性区域中。
133 |
134 | 有了$\gamma$和$\beta$两个参数,均值和方差由其控制,使隐藏单元值的均值和方差归一化,即$z^{(i)}$有固定的均值和方差。其均值和方差可以是0和1,也可以是其他值。
135 |
136 | ### 7.5 将 Batch Norm 拟合进神经网络
137 |
138 | #### 7.5.1 在网络中加入 Batch Norm
139 |
140 |  141 |
142 | BN发生在计算 $z$ 的计算和 $a$ 之间。与其应用没有归一化的 $z$ 值,不如用归一过的 𝑧̃ 。
143 |
144 | 得到算法的新参数:
145 | $$
146 | \begin{array}{l}
147 | w^{[1]}, b^{[1]}, w^{[2]}, b^{[2]}, \ldots w^{[L]}, b^{[L]} \\
148 | \beta^{[1]}, \gamma^{[1]}, \beta^{[2]}, \gamma^{[2]}, \ldots \beta^{[L]}, \gamma^{[L]}
149 | \end{array}
150 | $$
151 | 接下来可以用想用的任何一种优化算法来更新它们。比如使用梯度下降法,对给定层计算$d \beta^{[l]}$接着更新参数$\beta$为$\beta^{[l]}=\beta^{[l]}-\alpha d \beta^{[l]}$。也可以使用Adam或RMSprop或Momentum等更新$\gamma$和$\beta$。
152 |
153 | 如果使用深度学习编程框架,通常不需要自己将Batch Norm步骤应用于Batch Norm层,比如说,在Tensorflow框架中,可以用函数(tf.nn.batch_normalization)来实现Batch Normalization。
154 |
155 | #### 7.5.2 Batch Norm与mini-batch一起使用
156 |
157 | 实践中,Batch Norm通常和训练集的mini-batch一同使用。
158 |
159 | 
160 |
161 | 过程:
162 |
163 | - 用第一个 mini-batch($X^{\{1\}}$)应用参数$w^{[1]}$,$b^{[1]}$计算$z^{[1]}$,接着BN会减去均值,除以标准差,由$\beta^{[1]}$和$\gamma^{[1]}$重新缩放,得到$\tilde{z}^{[1]}$,再应用激活函数得到$a^{[1]}$,然后用$w^{[2]}$,$b^{[2]}$计算$z^{[2]}$等等。
164 | - 在第二、三...个mini-batch上同样这样做,继续训练。
165 |
166 | 由于计算$z$的方式:$z^{[l]}=w^{[l]} a^{[l-1]}+b^{[l]}$,而BN先将$z^{[l]}$归一化,结果为均值0和标准方差,再由$\gamma$和$\beta$缩放。这意味着,无论$b^{[l]}$的值是多少,都会被减去,因为在BN过程中,要计算$z^{[l]}$的均值再减去平均值,在此例中的mini-batch中增加任何常数,都将会被均值减去所抵消,数值不会改变。
167 |
168 | 故在使用BN时,消除参数$b^{[l]}$,或者将其设置为0,参数计算变为:
169 | $$
170 | z^{[l]}=w^{[l]} a^{[l-1]}\\
171 | z_{\text {norm}}^{[l]}\\
172 | \tilde{z}^{[l]}=\gamma^{[l]} z_{\text {norm}}^{[l]}+\beta^{[l]}
173 | $$
174 | 最后用$\beta^{[l]}$影响转置或偏置条件。
175 |
176 | 此例中,$z^{[l]}$,$\beta^{[l]}$,$\gamma^{[l]}$维度都是$\left(n^{[l]}, 1\right)$。
177 |
178 | #### 7.5.3 用BN来应用梯度下降法
179 |
180 | for t = 1......num Mini Batches
181 |
182 | compute forward prop on $X^{\{t\}}$
183 |
184 | in each hidden layer,use BN to replace $z^{[l]}$with $\tilde{z}^{[l]}$
185 |
186 | Use backprop to compute $d w^{[l]}$,$d \beta^{[l]}$,$d \gamma^{[l]}$
187 |
188 | Update parameters $w^{[l]}=w^{[l]}-\alpha d w^{[l]}$, $\beta^{[l]}=\beta^{[l]}-\alpha d \beta^{[l]}$ ,$\gamma^{[l]}=\gamma^{[l]}-\alpha d \gamma^{[l]}$
189 |
190 | Works with momentum rmsprop,adam
191 |
192 | ------
193 |
194 |
195 |
196 | - 假设使用 mini-batch梯度下降法,运行𝑡 = 1到 batch 数量的 for 循环,
197 |
198 | - 在 mini-batch $X^{\{t\}}$上应用正向传播,每个隐藏层都应用正向传播,使用 BN代替$z^{[l]}$为$\tilde{z}^{[l]}$。确保在这个 mini-batch 中,$𝑧$值有归一化的均值和方差,归一化均值和方差后是$\tilde{z}^{[l]}$
199 | - 然后,反向传播计算$d w^{[l]}$,及所有 $l$ 层所有的参数,$d \beta^{[l]}$和$d \gamma^{[l]}$。
200 | - 最后,更新这些参数$w^{[l]}=w^{[l]}-\alpha d w^{[l]}$, $\beta^{[l]}=\beta^{[l]}-\alpha d \beta^{[l]}$ ,$\gamma^{[l]}=\gamma^{[l]}-\alpha d \gamma^{[l]}$
201 |
202 | 也适用于有 Momentum、RMSprop、Adam 的梯度下降法及其它的一些优化算法来更新由 Batch 归一化添加到算法中的$\beta$和$\gamma$ 参数。
203 |
204 | ### 7.6 Batch Norm 为什么奏效
205 |
206 | #### 7.6.1 什么是Internal Covariate Shift
207 |
208 | Batch Normalization的原论文作者给了Internal Covariate Shift一个较规范的定义:在深层网络训练的过程中,由于网络中**参数变化**而引起内部结点**数据分布发生变化**的这一过程被称作Internal Covariate Shift。
209 |
210 | 深度神经网络之所以如此难训练,其中一个重要原因就是网络中层与层之间存在高度的关联性与耦合性。下图是一个多层的神经网络,层与层之间采用全连接的方式进行连接。
211 |
212 | 我们规定左侧为神经网络的底层,右侧为神经网络的上层。那么网络中层与层之间的关联性会导致如下的状况:随着训练的进行,网络中的参数也随着梯度下降在不停更新。一方面,当底层网络中参数发生微弱变化时,由于每一层中的线性变换与非线性激活映射,这些微弱变化随着网络层数的加深而被放大(类似蝴蝶效应);另一方面,参数的变化导致每一层的输入分布会发生改变,进而上层的网络需要不停地去适应这些分布变化,使得我们的模型训练变得困难。上述这一现象叫做Internal Covariate Shift。
213 |
214 |
141 |
142 | BN发生在计算 $z$ 的计算和 $a$ 之间。与其应用没有归一化的 $z$ 值,不如用归一过的 𝑧̃ 。
143 |
144 | 得到算法的新参数:
145 | $$
146 | \begin{array}{l}
147 | w^{[1]}, b^{[1]}, w^{[2]}, b^{[2]}, \ldots w^{[L]}, b^{[L]} \\
148 | \beta^{[1]}, \gamma^{[1]}, \beta^{[2]}, \gamma^{[2]}, \ldots \beta^{[L]}, \gamma^{[L]}
149 | \end{array}
150 | $$
151 | 接下来可以用想用的任何一种优化算法来更新它们。比如使用梯度下降法,对给定层计算$d \beta^{[l]}$接着更新参数$\beta$为$\beta^{[l]}=\beta^{[l]}-\alpha d \beta^{[l]}$。也可以使用Adam或RMSprop或Momentum等更新$\gamma$和$\beta$。
152 |
153 | 如果使用深度学习编程框架,通常不需要自己将Batch Norm步骤应用于Batch Norm层,比如说,在Tensorflow框架中,可以用函数(tf.nn.batch_normalization)来实现Batch Normalization。
154 |
155 | #### 7.5.2 Batch Norm与mini-batch一起使用
156 |
157 | 实践中,Batch Norm通常和训练集的mini-batch一同使用。
158 |
159 | 
160 |
161 | 过程:
162 |
163 | - 用第一个 mini-batch($X^{\{1\}}$)应用参数$w^{[1]}$,$b^{[1]}$计算$z^{[1]}$,接着BN会减去均值,除以标准差,由$\beta^{[1]}$和$\gamma^{[1]}$重新缩放,得到$\tilde{z}^{[1]}$,再应用激活函数得到$a^{[1]}$,然后用$w^{[2]}$,$b^{[2]}$计算$z^{[2]}$等等。
164 | - 在第二、三...个mini-batch上同样这样做,继续训练。
165 |
166 | 由于计算$z$的方式:$z^{[l]}=w^{[l]} a^{[l-1]}+b^{[l]}$,而BN先将$z^{[l]}$归一化,结果为均值0和标准方差,再由$\gamma$和$\beta$缩放。这意味着,无论$b^{[l]}$的值是多少,都会被减去,因为在BN过程中,要计算$z^{[l]}$的均值再减去平均值,在此例中的mini-batch中增加任何常数,都将会被均值减去所抵消,数值不会改变。
167 |
168 | 故在使用BN时,消除参数$b^{[l]}$,或者将其设置为0,参数计算变为:
169 | $$
170 | z^{[l]}=w^{[l]} a^{[l-1]}\\
171 | z_{\text {norm}}^{[l]}\\
172 | \tilde{z}^{[l]}=\gamma^{[l]} z_{\text {norm}}^{[l]}+\beta^{[l]}
173 | $$
174 | 最后用$\beta^{[l]}$影响转置或偏置条件。
175 |
176 | 此例中,$z^{[l]}$,$\beta^{[l]}$,$\gamma^{[l]}$维度都是$\left(n^{[l]}, 1\right)$。
177 |
178 | #### 7.5.3 用BN来应用梯度下降法
179 |
180 | for t = 1......num Mini Batches
181 |
182 | compute forward prop on $X^{\{t\}}$
183 |
184 | in each hidden layer,use BN to replace $z^{[l]}$with $\tilde{z}^{[l]}$
185 |
186 | Use backprop to compute $d w^{[l]}$,$d \beta^{[l]}$,$d \gamma^{[l]}$
187 |
188 | Update parameters $w^{[l]}=w^{[l]}-\alpha d w^{[l]}$, $\beta^{[l]}=\beta^{[l]}-\alpha d \beta^{[l]}$ ,$\gamma^{[l]}=\gamma^{[l]}-\alpha d \gamma^{[l]}$
189 |
190 | Works with momentum rmsprop,adam
191 |
192 | ------
193 |
194 |
195 |
196 | - 假设使用 mini-batch梯度下降法,运行𝑡 = 1到 batch 数量的 for 循环,
197 |
198 | - 在 mini-batch $X^{\{t\}}$上应用正向传播,每个隐藏层都应用正向传播,使用 BN代替$z^{[l]}$为$\tilde{z}^{[l]}$。确保在这个 mini-batch 中,$𝑧$值有归一化的均值和方差,归一化均值和方差后是$\tilde{z}^{[l]}$
199 | - 然后,反向传播计算$d w^{[l]}$,及所有 $l$ 层所有的参数,$d \beta^{[l]}$和$d \gamma^{[l]}$。
200 | - 最后,更新这些参数$w^{[l]}=w^{[l]}-\alpha d w^{[l]}$, $\beta^{[l]}=\beta^{[l]}-\alpha d \beta^{[l]}$ ,$\gamma^{[l]}=\gamma^{[l]}-\alpha d \gamma^{[l]}$
201 |
202 | 也适用于有 Momentum、RMSprop、Adam 的梯度下降法及其它的一些优化算法来更新由 Batch 归一化添加到算法中的$\beta$和$\gamma$ 参数。
203 |
204 | ### 7.6 Batch Norm 为什么奏效
205 |
206 | #### 7.6.1 什么是Internal Covariate Shift
207 |
208 | Batch Normalization的原论文作者给了Internal Covariate Shift一个较规范的定义:在深层网络训练的过程中,由于网络中**参数变化**而引起内部结点**数据分布发生变化**的这一过程被称作Internal Covariate Shift。
209 |
210 | 深度神经网络之所以如此难训练,其中一个重要原因就是网络中层与层之间存在高度的关联性与耦合性。下图是一个多层的神经网络,层与层之间采用全连接的方式进行连接。
211 |
212 | 我们规定左侧为神经网络的底层,右侧为神经网络的上层。那么网络中层与层之间的关联性会导致如下的状况:随着训练的进行,网络中的参数也随着梯度下降在不停更新。一方面,当底层网络中参数发生微弱变化时,由于每一层中的线性变换与非线性激活映射,这些微弱变化随着网络层数的加深而被放大(类似蝴蝶效应);另一方面,参数的变化导致每一层的输入分布会发生改变,进而上层的网络需要不停地去适应这些分布变化,使得我们的模型训练变得困难。上述这一现象叫做Internal Covariate Shift。
213 |
214 |  215 |
216 | #### 7.6.2 如何减缓Internal Covariate Shift
217 |
218 | **(1)白化(Whitening)**
219 |
220 | 白化(Whitening)是机器学习里面常用的一种规范化数据分布的方法,主要是PCA白化与ZCA白化。白化是对输入数据分布进行变换,进而达到以下两个目的:
221 |
222 | - **使得输入特征分布具有相同的均值与方差。**其中PCA白化保证了所有特征分布均值为0,方差为1;而ZCA白化则保证了所有特征分布均值为0,方差相同;
223 | - **去除特征之间的相关性。**
224 |
225 | 通过白化操作,可以减缓ICS的问题,进而固定每一层网络输入分布,加速网络训练过程的收敛。
226 |
227 | 然而,白化的方法具有一定缺陷,主要有以下两个问题:
228 |
229 | - **白化过程计算成本太高,**并且在每一轮训练中的每一层我们都需要做如此高成本计算的白化操作;
230 | - **白化过程由于改变了网络每一层的分布**,因而改变了网络层中本身数据的表达能力。底层网络学习到的参数信息会被白化操作丢失掉。
231 |
232 | **(2)Batch Normalization**
233 |
234 | 为解决上面两个问题,提出BN方法简化计算过程同时让归一化处理后的数据尽可能保留原始表达能力。
235 | $$
236 | \begin{array}{l}
237 | \mu=\frac{1}{m} \sum_{i} z^{(i)} \\
238 | \sigma^{2}=\frac{1}{m} \sum_{i}\left(z^{(i)}-\mu\right)^{2} \\
239 | z_{\text {norm}}^{(i)}=\frac{z^{(i)}-\mu}{\sqrt{\sigma^{2}+\varepsilon}}
240 | \end{array}
241 | $$
242 | 通过上面的变换,**解决了第一个问题,即用更加简化的方式来对数据进行规范化,使得第 $l$层的输入每个特征的分布均值为0,方差为1。**
243 |
244 | 如同上面提到的,Normalization操作我们虽然缓解了ICS问题,让每一层网络的输入数据分布都变得稳定,但却导致了数据表达能力的缺失。也就是我们通过变换操作改变了原有数据的信息表达(representation ability of the network),使得底层网络学习到的参数信息丢失。另一方面,通过让每一层的输入分布均值为0,方差为1,会使得输入在经过sigmoid或tanh激活函数时,容易陷入非线性激活函数的线性区域。
245 |
246 | 因此,BN引入的两个可学习(learnable)的参数$\gamma$和$\beta$,恢复数据本身的表达能力,对归一化后端数据进行线性变换,即:
247 | $$
248 | \tilde{z}^{[l]}=\gamma^{[l]} z_{\text {norm}}^{[l]}+\beta^{[l]}
249 | $$
250 | 特别地,当$\gamma^{2}=\sigma^{2}, \beta=\mu$时,可以实现等价变换(identity transform)并且保留了原始输入特征的分布信息。
251 |
252 | **通过上面的步骤,我们就在一定程度上保证了输入数据的表达能力。**
253 |
254 | 简单来说,BN减弱了前层参数的作用与后层参数的作用之间的联系,它使得网络每层都可以自己学习,稍稍独立于其它层,这让我们可以使用**更大的学习率**,初值可以更随意,有助于加速整个网络的学习。
255 |
256 | #### 7.6.3 BN的效果总结:
257 |
258 | **(1)BN使得网络中每层输入数据的分布相对稳定,加速模型学习速度**
259 |
260 | BN通过规范化与线性变换使得每一层网络的输入数据的均值与方差都在一定范围内,使得后一层网络不必不断去适应底层网络中输入的变化,从而实现了网络中层与层之间的解耦,允许每一层进行独立学习,有利于提高整个神经网络的学习速度。
261 |
262 | **(2)BN使得模型对网络中的参数不那么敏感,简化调参过程,使得网络学习更加稳定**
263 |
264 | 在神经网络中,我们经常会谨慎地采用一些权重初始化方法(例如Xavier)或者合适的学习率来保证网络稳定训练。
265 |
266 | 当学习率设置太高时,会使得参数更新步伐过大,容易出现震荡和不收敛。但是使用BN的网络将不会受到参数数值大小的影响。
267 |
268 | 例如,我们对参数$W$进行缩放得到$aW$。对于缩放前的值$Wu$($u$表示当前层输入,前一层的输出),设其均值为$\mu_{1}$,方差为$\sigma_{1}^{2}$;对于缩放值$aWu$,设其均值为$\mu_{2}$,方差为$\sigma_{2}^{2}$,则有:
269 | $$
270 | \mu_{2}=a \mu_{1}, \quad \sigma_{2}^{2}=a^{2} \sigma_{1}^{2}
271 | $$
272 | 我们忽略$\epsilon$,则有:
273 | $$
274 | \begin{array}{l}
275 | B N(a W u)=\gamma \cdot \frac{a W u-\mu_{2}}{\sqrt{\sigma_{2}^{2}}}+\beta=\gamma \cdot \frac{a W u-a \mu_{1}}{\sqrt{a^{2} \sigma_{1}^{2}}}+\beta=\gamma \cdot \frac{W u-\mu_{1}}{\sqrt{\sigma_{1}^{2}}}+\beta=B N(W u) \\
276 | \frac{\partial B N((a W) u)}{\partial u}=\gamma \cdot \frac{a W}{\sqrt{\sigma_{2}^{2}}}=\gamma \cdot \frac{a W}{\sqrt{a^{2} \sigma_{1}^{2}}}=\frac{\partial B N(W u)}{\partial u} \\
277 | \frac{\partial B N((a W) u)}{\partial(a W)}=\gamma \cdot \frac{u}{\sqrt{\sigma_{2}^{2}}}=\gamma \cdot \frac{u}{a \sqrt{\sigma_{1}^{2}}}=\frac{1}{a} \cdot \frac{\partial B N(W u)}{\partial W}
278 | \end{array}
279 | $$
280 | 可以看到,经过BN操作以后,权重的缩放值会被“抹去”,因此保证了输入数据分布稳定在一定范围内。另外,权重的缩放并不会影响到对$u$的梯度计算;并且当权重越大时,即$a$越大,$\frac{1}{a}$越小,意味着权重$W$的梯度反而越小,这样BN就保证了梯度不会依赖于参数的scale,使得参数的更新处在更加稳定的状态。
281 |
282 | 因此,在使用Batch Normalization之后,抑制了参数微小变化随着网络层数加深被放大的问题,使得网络对参数大小的适应能力更强,此时我们可以设置较大的学习率而不用过于担心模型divergence的风险。
283 |
284 | **(3)BN允许网络使用饱和性激活函数(例如sigmoid,tanh等),缓解梯度消失问题**
285 |
286 | 在不使用BN层的时候,由于网络的深度与复杂性,很容易使得底层网络变化累积到上层网络中,导致模型的训练很容易进入到激活函数的梯度饱和区;通过normalize操作可以让激活函数的输入数据落在梯度非饱和区,缓解梯度消失的问题;另外通过自适应学习$\gamma$和$\beta$又让数据保留更多的原始信息。
287 |
288 | **(4)BN具有一定的正则化效果**
289 |
290 | - BN只在每个mini-batch上计算均值和方差,而不是在整个数据集上
291 | - 均值和方差只是由一小部分数据估计得出的,有一些小的噪声,缩放过程从$z^{[l]}$到$\tilde{z}^{[l]}$也有一些噪声,因为它是用有些噪声的均值和方差计算得出的。
292 | - 故和dropout相似,它在每个隐藏层的激活值上增加了噪音。dropout 使一个隐藏的单元以一定的概率乘以 0,以一定的概率乘以 1,所以 dropout含一些噪音,因为它乘以 0 或 1。
293 |
294 | 因此,类似于dropout,BN有轻微的正则化效果,因为给隐藏单元添加了噪音,使得后部单元不过分依赖任何一个隐藏单元。如果想得到更强大的正则化效果,可以将BN和dropout一起使用。
295 |
296 | 如果应用较大的mini-batch可以减少噪音,减少正则化效果。
297 |
298 | **参考文章**:
299 |
300 | [1]: https://zhuanlan.zhihu.com/p/34879333 "Batch Normalization原理与实战"
301 | [2]: BatchNormalizationAcceleratingDeepNetworkTrainingbyReducingInternalCovariateShift
302 |
303 |
304 |
305 | ### 7.7 测试时的 Batch Norm
306 |
307 | 我们知道BN在每一层计算的 ![[公式]](https://www.zhihu.com/equation?tex=%5Cmu) 与 ![[公式]](https://www.zhihu.com/equation?tex=%5Csigma%5E2) 都是基于当前batch中的训练数据,但是这就带来了一个问题:我们在预测阶段,有可能只需要预测一个样本或很少的样本,没有像训练样本中那么多的数据,此时 ![[公式]](https://www.zhihu.com/equation?tex=%5Cmu) 与 ![[公式]](https://www.zhihu.com/equation?tex=%5Csigma%5E2) 的计算一定是有偏估计,这个时候我们该如何进行计算呢?
308 |
309 | **论文中的方法**:
310 |
311 | 利用BN训练好模型后,我们保留了每组mini-batch训练数据在网络中每一层的 ![[公式]](https://www.zhihu.com/equation?tex=%5Cmu_%7Bbatch%7D) 与 ![[公式]](https://www.zhihu.com/equation?tex=%5Csigma%5E2_%7Bbatch%7D) 。此时我们使用整个样本的统计量来对Test数据进行归一化,具体来说使用均值与方差的无偏估计:
312 |
313 | ![[公式]](https://www.zhihu.com/equation?tex=%5Cmu_%7Btest%7D%3D%5Cmathbb%7BE%7D+%28%5Cmu_%7Bbatch%7D%29)
314 |
315 | ![[公式]](https://www.zhihu.com/equation?tex=%5Csigma%5E2_%7Btest%7D%3D%5Cfrac%7Bm%7D%7Bm-1%7D%5Cmathbb%7BE%7D%28%5Csigma%5E2_%7Bbatch%7D%29)
316 |
317 | 得到每个特征的均值与方差的无偏估计后,我们对test数据采用同样的normalization方法:
318 |
319 | ![[公式]](https://www.zhihu.com/equation?tex=BN%28X_%7Btest%7D%29%3D%5Cgamma%5Ccdot+%5Cfrac%7BX_%7Btest%7D-%5Cmu_%7Btest%7D%7D%7B%5Csqrt%7B%5Csigma%5E2_%7Btest%7D%2B%5Cepsilon%7D%7D%2B%5Cbeta)
320 |
321 | **吴恩达老师讲的方法**
322 |
323 | 对训练阶段每个batch计算的$\mu$和$\sigma^{2}$采用指数加权平均来得到测试阶段$\mu$和$\sigma^{2}$的估计。
324 |
325 | 我们选择 𝑙层,假设我们有 mini-batch,$X^{\{1\}}$,$X^{\{2\}}$,$X^{\{3\}}$......以及对应的$y$值等等,那么在训练$X^{\{1\}}$时,就得到了$\mu^{\{1\}[l]}$,训练第二个mini-batch时,就会得到$\mu^{\{2\}[l]}$值。然后在这一隐藏层的第三个 mini-batch,得到第三个$\mu$($\mu^{\{3\}[l]}$)值。使用指数加权平均来追踪这个均值向量的最新平均值,于是该指数加权平均成了你对这一隐藏层的$z$均值的估值。
326 |
327 | 同样的,可以用指数加权平均来追踪这一层每个mini-batch的$\sigma^{2}$的值。因此在用不同mini-batch训练神经网络的同时,能够得到你所查看每一层$\mu$和$\sigma^{2}$的平均数的实时数值。
328 |
329 | 最后在测试时对test数据采用同样的normalization方法(同上)。
330 |
331 | ### 7.8 BN与其他Normalization的方法比较
332 |
333 | 参考文章:https://zhuanlan.zhihu.com/p/33173246
334 |
335 | https://www.cnblogs.com/LXP-Never/p/11566064.html
336 |
337 | https://blog.csdn.net/shwan_ma/article/details/85292024
338 |
339 | https://bbs.cvmart.net/topics/1569
340 |
341 |
342 |
343 | 常用的Normalization方法主要有:Batch Normalization(BN,2015年)、Layer Normalization(LN,2016年)、Instance Normalization(IN,2017年)、Group Normalization(GN,2018年)。它们都是从激活函数的输入来考虑、做文章的,以不同的方式**对激活函数的输入进行 Norm** 的。
344 |
345 | 将输入的图像shape记为[**N**, **C**hannel, **H**eight, **W**idth],这几个方法主要的区别就是在,
346 |
347 | - **batch Norm**:在batch上,对NHW做归一化,对小batchsize效果不好;
348 | - **layer Norm**:在通道方向上,对CHW归一化,主要对RNN作用明显;
349 | - **instance Norm**:在图像像素上,对HW做归一化,用在风格化迁移;
350 | - **Group Norm**:将channel分组,然后再做归一化;
351 | - **Switchable Norm**:将BN、LN、IN结合,赋予权重,让网络自己去学习归一化层应该使用什么方法。
352 |
353 | 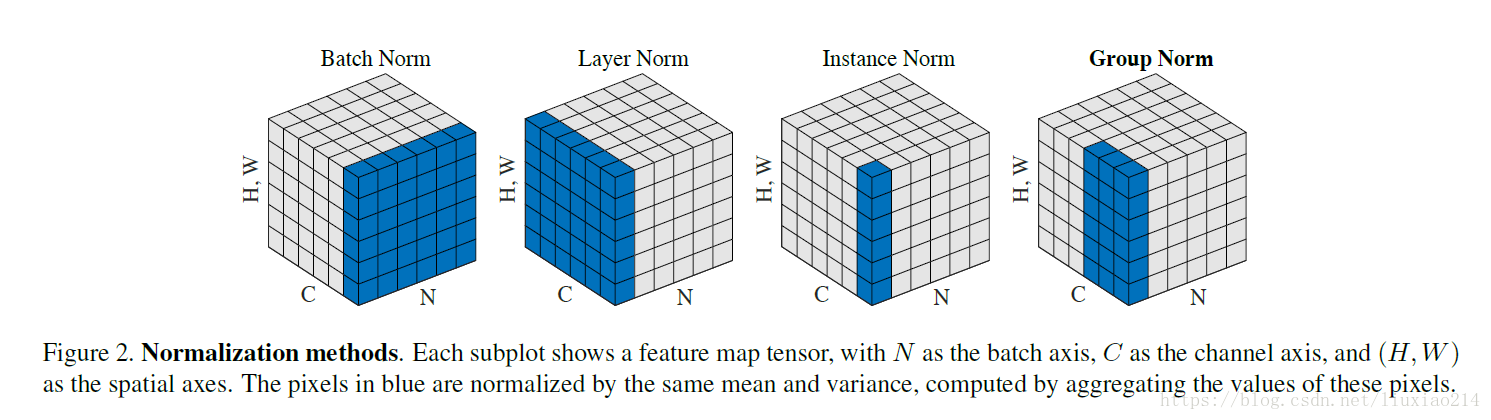
354 |
355 | 如果把特征图![[公式]](https://www.zhihu.com/equation?tex=x%5Cin%5Cmathbb%7BR%7D%5E%7BN%5Ctimes+C+%5Ctimes+H+%5Ctimes+W%7D)比喻成一摞书,这摞书总共有 N 本,每本有 C 页,每页有 H 行,每行 有W 个字符。
356 |
357 | #### 7.8.1 Batch Normalization
358 |
359 | $$
360 | \begin{array}{c}
361 | \mu=\frac{1}{m} \sum_{i=1}^{m} x_{i} \\
362 | \sigma=\sqrt{\left.\frac{1}{m} \sum_{i=1}^{m}\left(x_{i}-\mu\right)^{2}\right)} \\
363 | y=\frac{(x-\mu)}{\sqrt{\sigma^{2}+\epsilon}}+\beta=B N(x)
364 | \end{array}
365 | $$
366 |
367 | tf.nn.batch_normalization(x, mean, variance, offset, scale, variance_epsilon, name=None`)`
368 |
369 | 参数
370 |
371 | - x:输入数据
372 | - mean:均值
373 | - variance:方差
374 |
375 | 返回
376 |
377 | - 标准化后的数据
378 |
379 | **BN缺点:**
380 |
381 | - 对batch size的大小比较敏感,由于每次计算均值和方差是在一个batch上,所以如果batch size太小,则计算的均值、方差不足以代表整个数据分布;
382 | - BN实际使用时需要计算并且保存某一层神经网络batch的均值和方差等统计信息,对于对一个固定深度的前向神经网络(DNN,CNN)使用BN,很方便;但对于RNN来说,sequence的长度是不一致的,换句话说RNN的深度不是固定的,不同的time-step需要保存不同的statics特征,可能存在一个特殊sequence比其他sequence长很多,这样training时,计算很麻烦。
383 |
384 | #### 7.8.2 Layer Normalization
385 |
386 | LN是针对深度网络的某一层的所有神经元的输入按以下公式进行normalize操作。计算该层的平均输入值和输入方差,然后用同一个规范化操作来转换各个维度的输入。
387 | $$
388 | \begin{array}{c}
389 | \mu^{l}=\frac{1}{H} \sum_{i=1}^{H} a_{i}^{l} \\
390 | \sigma^{l}=\sqrt{\frac{1}{H} \sum_{i=1}^{H}\left(a_{i}^{l}-\mu^{l}\right)^{2}}
391 | \end{array}
392 | $$
393 | **BN与LN的区别在于**:
394 |
395 | - LN中同层神经元输入拥有相同的均值和方差,不同的输入样本有不同的均值和方差;
396 | - BN中则针对不同神经元输入计算均值和方差,同一个batch中的输入拥有相同的均值和方差。
397 |
398 | 所以,LN不依赖于batch的大小和输入sequence的深度,因此可以用于batchsize为1和RNN中对边长的输入sequence的normalize操作。
399 |
400 | BN 的转换是针对单个神经元可训练的——不同神经元的输入经过再平移和再缩放后分布在不同的区间,而 LN 对于一整层的神经元训练得到同一个转换——所有的输入都在同一个区间范围内。如果不同输入特征不属于相似的类别(比如颜色和大小),那么 LN 的处理可能会降低模型的表达能力。LN用于RNN效果比较明显,但是在CNN上,不如BN。
401 |
402 | tf.keras.layers.LayerNormalization(axis=-1, epsilon=0.001, center=True, scale=True)
403 |
404 | 参数
405 |
406 | - axis:想要规范化的轴(通常是特征轴)
407 | - epsilon:将较小的浮点数添加到方差以避免被零除。
408 | - center:如果为True,则将的偏移`beta`量添加到标准化张量。
409 | - `scale`:如果为True,则乘以`gamma`
410 |
411 | 返回
412 |
413 | - shape与输入形状相同的值
414 |
415 | #### 7.8.3 Instace Normalization
416 |
417 | BN注重对每个batch进行归一化,保证数据分布一致,因为判别模型中结果取决于数据整体分布。
418 |
419 | 但是图像风格转换中,生成结果主要依赖于某个图像实例,所以对整个batch归一化不适合图像风格化中,因而对HW做归一化。可以加速模型收敛,并且保持每个图像实例之间的独立。
420 | $$
421 | \begin{array}{c}
422 | \mu_{t i}=\frac{1}{H W} \sum_{l=1}^{W} \sum_{m=1}^{H} x_{t i l m} \\
423 | \sigma=\sqrt{\frac{1}{H W}} \sum_{l=1}^{W} \sum_{m=1}^{H}\left(x_{t i l m}-\mu_{y i}\right)^{2} \\
424 | y_{t i j k}=\frac{x_{P t i j k}-\mu_{y i}}{\sqrt{\sigma_{t i}^{2}}-\epsilon}
425 | \end{array}
426 | $$
427 | [`tfa.layers.normalizations.InstanceNormalization`](https://www.tensorflow.org/addons/api_docs/python/tfa/layers/InstanceNormalization)
428 |
429 | 输入:仅在该层只有一个输入(即,它连接到一个传入层)时适用。
430 |
431 | 返回:输入张量或输入张量列表。
432 |
433 | #### 7.8.4 Group Normalization
434 |
435 | 主要是针对Batch Normalization对小batchsize效果差,GN将channel方向分group,然后每个group内做归一化,算(C//G)*H*W的均值,这样与batchsize无关,不受其约束。
436 | $$
437 | S_{i}=\left\{k \mid k_{N}=i_{N},\left[\frac{k_{C}}{C / G}\right]=\left[\frac{i_{C}}{C / G}\right]\right\}
438 | $$
439 | Group Normalization 在要求 Batch Size 比较小的场景下或者物体检测/视频分类等应用场景下效果是优于 BN 的。
440 |
441 | #### 7.8.5 Switchable Normalization
442 |
443 | 本篇论文作者认为,
444 |
445 | - 第一,归一化虽然提高模型泛化能力,然而归一化层的操作是人工设计的。在实际应用中,解决不同的问题原则上需要设计不同的归一化操作,并没有一个通用的归一化方法能够解决所有应用问题;
446 | - 第二,一个深度神经网络往往包含几十个归一化层,通常这些归一化层都使用同样的归一化操作,因为手工为每一个归一化层设计操作需要进行大量的实验。
447 |
448 | 因此作者提出自适配归一化方法——Switchable Normalization(SN)来解决上述问题。与强化学习不同,SN使用可微分学习,为一个深度网络中的每一个归一化层确定合适的归一化操作。
449 | $$
450 | \begin{array}{c}
451 | \hat{h}_{h c i j}=\gamma \frac{h_{h c i j}-\sum_{k \in \Omega W_{k} \mu_{k}}}{\sqrt{\sum_{k \in \Omega} w_{k}^{\prime} \sigma_{k}^{2}+\epsilon}}+\beta \\
452 | w_{k}=\frac{e^{\lambda_{k}}}{\sum_{z \in\{i n, l n, b n\} e t}}, \quad k \in\{i n, l n, b n\} \\
453 | \mu_{i n}=\frac{1}{H W} \sum_{i, j}^{H, W} h_{n c i j}, \quad \sigma^{2}=\frac{1}{H W} \sum_{i, j}^{H, W}\left(h_{n c i j}-\mu_{i n}\right)^{2} \\
454 | \mu_{l n}=\frac{1}{C} \sum_{c=1}^{C} \mu_{i n}, \quad \sigma_{l n}^{2}=\frac{1}{C} \sum_{c=1}^{C}\left(\sigma_{i n}^{2}+\mu_{i n}^{2}\right)-\mu_{l n}^{2} \\
455 | \mu_{b n}=\frac{1}{N} \sum_{n=1}^{N} \mu_{i n}, \quad \sigma^{2}=\frac{1}{N} \sum_{n=1}^{N}\left(\sigma_{i n}^{2}+\mu_{i n}^{2}\right)-\mu_{b n}^{2}
456 | \end{array}
457 | $$
458 |
459 |
460 | #### 7.8.6 weight Normalization
461 |
462 | BN 和 LN 均将规范化应用于输入的特征数据 $X$ ,而 WN 则另辟蹊径,将规范化应用于线性变换函数的权重 $W$ ,这就是 WN 名称的来源。
463 |
464 | 对于人工神经网络中的一个神经元来说,其输出$y$表示为:
465 | $$
466 | y=\phi(\boldsymbol{w} \boldsymbol{x}+b)
467 | $$
468 | 其中$w$是$k$维权重向量,$b$是标量偏差,$x$是$k$维输入特征,$\phi(.)$是激活函数。
469 |
470 | 对权重$w$用参数向量$v$和标量$g$进行表示,则新参数表示为:
471 | $$
472 | \boldsymbol{w}=\frac{g}{\|\boldsymbol{v}\|} \boldsymbol{v}
473 | $$
474 | 其中$v$是$k$维向量,$g$是标量,$\|\boldsymbol{v}\|$为$v$的欧式范数。
475 | 通过上述参数表示,我们可以发现,$\|\boldsymbol{w}\|=g$与参数$v$独立,而权重$w$的方向也变更为$\frac{v}{\|\boldsymbol{v}\|}$。因此重参数将权重向量$w$用了两个独立的参数表示其幅度和方向。实验证明,在利用SGD优化算法时,重参数加速了网络的收敛速度。
476 |
477 | **Gradients:**
478 |
479 | 则对于$v$,$g$
480 | $$
481 | \begin{array}{c}
482 | \nabla_{g} L=\frac{\nabla_{w} L \cdot \boldsymbol{v}}{\|v\|} \\
483 | \nabla_{v} L=\frac{\boldsymbol{g} \cdot \nabla_{w} L}{\|v\|}-\frac{\boldsymbol{g} \cdot \nabla_{g} L}{\|v\|} \cdot \boldsymbol{v}
484 | \end{array}
485 | $$
486 | 其中$\nabla_{w} L$为目标函数对未进行WN的权重为$w$的偏导。
487 |
488 | 相比与BN,WN带有如下优点:WN的计算量非常低,并且其不会因为mini-batch的随机性而引入噪声统计。在RNN,LSTM,或者Reinforcement Learning上,WN能够表现出比BN更好的性能。
489 |
490 |
491 |
492 | ### 7.9 Softmax 回归
493 |
494 | Softmax回归:logistic回归的一般形式,将logistic回归推广到 C 类而不仅仅是两类,能在试图识别某一分类时做出预测且任何两个分类之间的决策边界都是线性的。
495 |
496 | 符号定义:
497 |
498 | $C$ :类别总数(类别编号分别为 $0, 2, ..., C-1$),故输出层L的神经元个数为 $C$,每个神经元分别输出该输入属于该类别的概率,$C$ 个神经元输出的概率总和应等于 1 。当 $C=2$ 时,Softmax回归即logistic回归。
499 |
500 | #### 7.9.1 Softmax层
501 |
502 | 在分类问题中,神经网络的**输出层**通常选用Softmax激活函数,使得最后输出的是归一化后的实数向量,每一元素代表该样本属于某一类的概率,则该层称为Softmax层。
503 |
504 | #### 7.9.2 Softmax激活函数
505 |
506 | - 定义:Softmax激活函数只用于多于一个神经元的输出层,它保证所有的输出神经元之和为1,所以一般输出的是小于1的概率值,可以很直观地比较各输出值。
507 |
508 | - 作用:为了得到属于每个类别的概率,先通过$e^{z^{[L]}}$将$z^{[L]}$的各元素值映射到 $(0, + \infty)$,然后再归一化到(0, 1)。
509 |
510 | - 具体实现:
511 |
512 | 在神经网络的最后一层,依然先计算线性部分:
513 | $$
514 | z^{[L]}=W^{[L]}a^{[L-1]}+b^{[L]}
515 | $$
516 |
517 |
518 | 然后应用**Softmax激活函数**:$a^{[L]}=g^{[L]}(z^{[L]})$,该函数的具体计算如下:
519 |
520 | (1)计算临时变量 $t=e^{z^{[L]}}$,对 $z^{[L]}$ 中的所有元素求幂,故 $t$ 的维度与 $z^{[L]}$ 相同。
521 |
522 | (2)对 $t$ **归一化**,得到输出 $a^{[L]}$ 即 $\hat{y}$ :$a^{[L]}=\frac{e^{z^{[L]}}}{\sum_{j=1}^{n^{[L]}} t_{i}}$,$a^{[L]}$的维度与 $t$ 相同,即也与 $z^{[L]}$ 相同,都为$(n^{[L]},1)$。其中,对$a^{[L]}$的每一个元素,$a_i^{[L]}=\frac{t_i}{\sum_{j=1}^{n^{[L]}} t_{i}}$。
523 |
524 | **tips:**之前所学的激活函数如sigmod和ReLU激活函数,都是输入一个实数,输出一个实数,而Softmax激活函数由于需要将所有可能的输出归一化,需要**输入一个向量,输出一个向量**。
525 |
526 | #### 7.9.3 softmax配合log似然代价函数训练ANN
527 |
528 | 在人工神经网络(ANN)中,Softmax通常被用作输出层的激活函数。这不仅是因为它的效果好,而且因为它使得ANN的输出值更易于理解。同时,softmax配合log似然代价函数,其训练效果也要比采用二次代价函数的方式好。
529 |
530 | log似然代价函数的公式为:
531 | $$
532 | C=-\sum_{k} y_{k} \log a_{k}
533 | $$
534 |
535 |
536 | 其中,$a_{k}$表示第k个神经元的输出值,$y_{k}$表示第k个神经元对应的真实值,取值为0或1。
537 |
538 | 该代价函数的简单理解为:在ANN中输入一个样本,那么只有一个神经元对应了该样本的正确类别;若这个神经元输出的概率值越高,则按照以上的代价函数公式,其产生的代价就越小;反之,则产生的代价就越高。
539 |
540 | 为了检验softmax和这个代价函数也可以解决训练ANN时训练速度变慢的问题,接下来的重点就是推导ANN的权重W和偏置b的梯度公式。以偏置b为例:
541 |
542 | 
543 |
544 | 同理可得:
545 | $$
546 | \frac{\partial C}{\partial w_{j k}}=a_{k}^{L-1}\left(a_{j}^{L}-y_{j}\right)
547 | $$
548 | 从上述梯度公式可知,softmax函数配合log似然代价函数可以很好地训练ANN,不存在学习速度变慢的问题。
549 |
550 | 参考文献:https://blog.csdn.net/orangefly0214/article/details/80406584
551 |
552 | ### 7.10 训练一个 Softmax 分类器
553 |
554 | #### 7.10.1 定义损失函数
555 |
556 | - 单样本:$$L(\hat{y}, y)=-\sum_{j=1}^C y_{j} \log \hat{y}_{j}$$
557 | - 整个训练集:$J\left(W^{[L]},b^{[L]} \ldots\right)=\frac{1}{m} \sum_{i=1}^{m} L\left(\hat{y}^{(i)}, y^{(i)}\right)$
558 | - 作用:找到样本所属的真实类别,并试图使该类别相应的概率尽可能地高。
559 |
560 | #### 7.10.2 正向传播
561 |
562 | 依次计算出:$z^{[L]} → a^{[L]} = \hat y → L\left(\hat{y}^{(i)}, y^{(i)}\right)$
563 |
564 | #### 7.10.3.反向传播(实现梯度下降法)
565 |
566 | (1)初始化反向传播:$dz^{[L]}=\frac{\partial J}{\partial z^{[L]}}=\hat y-y$
567 |
568 | (2)用深度学习编程框架自动实现反向传播的其余导数计算。
569 |
570 | ### 7.11 深度学习框架
571 |
572 | 深度学习框架可以使神经网络的实现变得更简单。每个框架都是针对某一个用户或开发者群体的
573 |
574 | #### 7.11.1 现有deep learning框架
575 |
576 | - **Caffe/Caffe2**:第一个主流的工业级深度学习工具。开始于2013年底,由UC Berkely的Yangqing Jia老师编写和维护的具有出色的卷积神经网络实现。在计算机视觉领域依然是最流行的工具包,有很多扩展,但是由于一些遗留的架构问题,不够灵活且对递归网络和语言建模的支持很差。
577 | - **CNTK**:是微软研究院开源的深度学习框架。最早由 start the deep learning craze 的演讲人创建,目前已经发展成一个通用的、跨平台的深度学习系统,在语音识别领域的使用尤其广泛。
578 | - **DL4J**:是一个基于 Java 和 Scala 的开源的分布式深度学习库,由 Skymind 于 2014 年 6 月发布,其核心目标是创建一个即插即用的解决方案原型。
579 | - **Keras**:是一个崇尚极简、高度模块化的神经网络库,使用 Python 实现,并可以同时运行在 TensorFlow 和 Theano 上。它旨在让用户进行最快速的原型实验,让想法变为结果的这个过程最短。Theano 和 TensorFlow 的计算图支持更通用的计算,而 Keras 则专精于深度学习。提供了目前为止最方便的 API,用户只需要将高级的模块拼在一起,就可以设计神经网络,它大大降低了编程开销和阅读别人代码时的理解开销。
580 | - **Lasagne**:是一个基于 Theano 的轻量级的神经网络库。Lasagne是 Theano 的上层封装,但又不像 Keras 那样进行了重度的封装,Keras 隐藏了 Theano 中所有的方法和对象,而 Lasagne 则是借用了 Theano 中很多的类,算是介于基础的 Theano 和高度抽象的 Keras 之间的一个轻度封装,简化了操作同时支持比较底层的操作。Lasagne 设计的六个原则是简洁、透明、模块化、实用、聚焦和专注。
581 | - **MXNet**:是李沐和陈天奇等各路英雄豪杰打造的开源深度学习框架,是分布式机器学习通用工具包DMLC的重要组成部分。注重灵活性和效率,文档也非常的详细,同时强调提高内存使用的效率,甚至能在智能手机上运行诸如图像识别等任务。
582 | - **PaddlePaddle**:是百度自主研发的集深度学习核心框架、工具组件和服务平台为一体的技术领先、功能完备的开源深度学习平台,有全面的官方支持的工业级应用模型,涵盖自然语言处理、计算机视觉、推荐引擎等多个领域,并开放多个预训练中文模型。目前已经被中国企业广泛使用,并拥有活跃的开发者社区生态。
583 | - **TensorFlow**:Google开源的其第二代深度学习技术——被使用在Google搜索、图像识别以及邮箱的深度学习框架。是一个理想的RNN(递归神经网络)API和实现,使用了向量运算的符号图方法,使得新网络的指定变得相当容易,支持快速开发。缺点是速度慢,内存占用较大(比如相对于Torch)。
584 | - **Theano**:2008年诞生于蒙特利尔理工学院,主要开发语言是Python。派生出了大量深度学习Python软件包,最著名的包括Blocks和Keras。Theano的最大特点是非常的灵活,适合做学术研究的实验,且对递归网络和语言建模有较好的支持,缺点是速度较慢。
585 | - **Torch**:Facebook力推的深度学习框架,主要开发语言是C和Lua。有较好的灵活性和速度。实现并且优化了基本的计算单元,使用者可以很简单地在此基础上实现自己的算法,不用浪费精力在计算优化上面。核心的计算单元使用C或者cuda做了很好的优化。在此基础之上,使用lua构建了常见的模型。缺点是接口为lua语言,需要一点时间来学习。
586 |
587 | 参考文献:
588 |
589 | - https://blog.csdn.net/dlaicxf/article/details/52846651
590 | - https://www.leiphone.com/news/201702/T5e31Y2ZpeG1ZtaN.html
591 |
592 | #### 7.11.2 几种主流dl框架的比较
593 |
594 | | **库名称** | **开发语言** | **速度** | **灵活性** | **文档** | **适合模型** | **平台** | **上手难易** |
595 | | :--------: | :-------------: | :------: | :--------: | -------: | :----------: | :--------: | :----------: |
596 | | Caffe | c++/cuda | 快 | 一般 | 全面 | CNN | 所有系统 | 中等 |
597 | | TensorFlow | c++/cuda/Python | 中等 | 好 | 中等 | CNN/RNN | Linux, OSX | 难 |
598 | | Keras | Python | 快 | 好 | 中等 | CNN/RNN | Linux, OSX | 易 |
599 | | MXNet | c++/cuda | 快 | 好 | 全面 | CNN | 所有系统 | 中等 |
600 | | Torch | c++/lua/cuda | 快 | 好 | 全面 | CNN/RNN | Linux, OSX | 中等 |
601 | | Theano | Python/c++/cuda | 中等 | 好 | 中等 | CNN/RNN | Linux, OSX | 易 |
602 |
603 | #### 7.11.3 选择框架的标准
604 |
605 | - **便于编程**:包括神经网络的开发和迭代、为产品进行配置等。
606 | - **运行速度**:特别是训练大数据集时,一些框架可以更高效地运行和训练神经网络。
607 | - **框架是否真的开放**:一个真的开放的框架,不仅需要开源,还需要良好的管理。
608 |
609 | PyTorch常用代码段合集 https://mp.weixin.qq.com/s/JnIO_HjTrC0DCWtKrkYC8A
610 |
611 |
612 |
613 |
614 |
615 |
616 |
617 |
--------------------------------------------------------------------------------
/8 机器学习(ML)策略(1).md:
--------------------------------------------------------------------------------
1 | # 1.1 为什么是ML策略
2 |
3 | 如果你训练了一段时间自己的神经网络,准确率到达了一定水平(比如90%)但却还不能满足你的要求,那这个时候必然需要对网络做出一些调整。你可能想到了几个解决思路,比如收集更多的数据、用不同的优化算法、训练得更久一些、加入正则化甚至修改网络架构等等。
4 |
5 | 但是这些办法并不是总是有效的,可能收集了6个月的数据却发现对网络的性能没有任何帮助。就是说如果你作出了错误的选择,那很可能浪费大量的时间和精力而得不到任何有效进展。
6 |
7 | 于是接下来希望教学一些策略:ML策略,以帮助我们向着有希望的方向前进。
8 |
9 | # 1.2 正交化
10 |
11 | 这里的正交化可以简单地理解为,每个自变量的改变只会引起一个因变量发生改变。举个反例,假设有$y_1=x_1+0.9x_2$,$y_2=0.1x_2$,则自变量$x_2$的改变会同时引起因变量$y_1,y_2$的改变,同时若想要通过$x_2$调整$y_1$时会不可避免的也调整了$y_2$。
12 |
13 | 在ML策略中,正交化是一种设计方法,以保证你在修改超参的时候不会引起两个以上的参数的变化。
14 |
15 | ## 四个参数
16 |
17 | 假设你需要正交化而确保不同时改变的四个参数是:
18 |
19 | * 收敛后的训练集的代价(cost)
20 | * 交叉验证集的代价
21 | * 测试集的代价
22 | * 真实应用的效果
23 |
24 | 当然,以上的参数是“按顺序”得到的。即只有在当前参数算优的情况下你才会做下一步而得到下一个参数的值。
25 |
26 | 对于第一点,如果训练集上的效果不好甚至无法收敛,可以考虑更大的神经网络或其他优化算法比如$Adam$。
27 |
28 | 对于第二点,可能原因是过拟合了,那可以尝试加入正则化或采用更大的训练集。
29 |
30 | 对于第三点,可以考虑采用更大的交叉验证集。
31 |
32 | 对于第四点,则考虑改变交叉验证集的图源或改变损失函数。
33 |
34 | 举个不正交的例子是 early stopping。因为 early stopping 会基于开发集的效果而提早停止训练,所以带来的影响是两方面的:训练集的代价还没收敛至最优的同时降低了在开发集上的代价。
35 |
36 | # 1.3 单一数字评估指标
37 |
38 | 对于一个网络的性能评估,我们有时候会采用多个指标以便更了解自己搭建的网络的效果。但是当你需要从多个网络中选出最好的一个时,多评估指标可能会导致你无法轻易选出优胜者——有的网络某一些指标最好,另一些指标则比不上其他网络。这个时候,单一数字评估指标就能很方便地帮你评价出最优的网络。
39 |
40 | ## 1.3.1常用指标
41 |
42 | 参考文章[在这](https://zhuanlan.zhihu.com/p/73569538)。
43 |
44 | ## 1.3.2混淆矩阵:
45 |
46 | 为了方便表达各指标如何计算,先介绍混淆矩阵:
47 |
48 | 
49 |
50 | 阴阳可理解为真假、1/0。a是预测为真真实也为真的样本数,其余类比。
51 |
52 | ## 1.3.3指标
53 |
54 | 1. Precision查准率/精度:评价网络做出的预测的准确率。对于二分类来说(比如猫/非猫分类器), $$P= \frac{预测为1且正确的样本数}{所有预测为1的样本数} = \frac{a}{a+b}$$。
55 |
56 | 2. 对于进行one-hot热值编码的多分类来说同样适用。
57 |
58 | 3. Recall查全率/True Positive真阳率/Sensitivity敏感性:评价网络对于目标类的识别率。对于二分类来说,
59 |
60 | $$R= \frac {所有预测为1且正确的样本数}{所有真实值为1的样本数} \frac{a}{a+c}$$。
61 |
62 | 对于进行了one-hot热值编码的多分类来说同样适用。
63 |
64 | 4. Accuracy准确率:评价网络所有类预测的准确率。对于二分类来说,$Acc= \frac{所有预测正确的样本数}{总的样本数}= \frac{a+d}{a+b+c+d}$。
65 |
66 | 5. 对于进行了one-hot热值编码的多分类同样适用。
67 |
68 | 6. False Positive误检率/假阳率:评价网络对阴性预测的错误率,为
69 |
70 | $$\frac{预测为1且错误的样本数}{真实值为0的样本数}=\frac{b}{b+d}$$。
71 |
72 | 7. F1分数:$$\frac{2}{\frac{1}{P}+\frac{1}{R}}$$
73 |
74 | P 和 R 分别代指 Precision 和 Recall。是 Precision 和 Recall 的调和平均数。
75 |
76 | # 1.4满足和优化指标
77 |
78 | 如果你想考虑的多个指标取值范围是相同的,那取平均值就可以简单地将多个指标“整合”成单一评估指标。但是如果其中一个是准确率P(%),另一个是单张图的预测时间T(ms),那取平均值的做法是几乎不合理的。线性组合$$aP+bT$$这样的做法或许可行,但是参数a、b的值却又可能难以设计。
79 |
80 | 所以,可以从另一个角度考虑:其中一个(甚至多个)指标只用于淘汰、筛选模型;另一个指标作为评估指标,是判断哪一个更优的指标。这分别对应满足指标和优化指标。
81 |
82 | ## 1.4.1满足指标
83 |
84 | 该指标是你关心的指标之一,但是又并不那么重要:该指标只需要到达一定范围即可,不是你**最想优化**的指标。比方说你很关心模型的准确率,同时也希望运行速度足够快,那将 T 视为满足指标是合适的。
85 |
86 | 满足指标的用意在于如果你有多个指标想要兼顾,但是大部分指标又并不是那么重要,那作为用于筛选模型的指标是很不错的选择。比如唤醒 Siri 你最关注的是 Recall,这能确保有人真的想唤醒 Siri 时能及时做出反应;但你也关注在没人想唤醒 Siri 时,Siri 被错误唤醒的概率。那将误检率/假阳率作为满足指标是可行的,比如设置为每24小时只有一次错误唤醒。
87 |
88 | ## 1.4.2优化指标
89 |
90 | 优化指标应该是你最关心的指标,是你最想优化的指标,比如唤醒 Siri 时的Recall。
91 |
92 | 由于单一数字评估指标的原因,优化指标应该只有一个,而其余你关心的指标都应该设为满足指标,或者和优化指标合理地整合为一个指标。
93 |
94 | # 1.5测试集、交叉验证集、测试集的划分
95 |
96 | ## 1.5.1 训练集、交叉验证集、测试集的作用
97 |
98 | - **训练集**:用以训练模型;
99 |
100 | - **交叉验证集** (也叫dev 集、开发集):衡量训练效果的同时进行超参数调优;
101 |
102 | - **测试集**:评测模型训练效果(测定泛化误差)。
103 |
104 | 以课后作业、期末考试、高考三者间的关系类比训练、开发、测试集的作用:
105 |
106 | - 课后作业(训练集):让你学会知识;
107 | - 期末考试(交叉验证集):让你检验自己是否真的学会了知识,发现了问题后,你会调整学习方法(调整超参数);
108 | - 高考(测试集):最终的测试,测试你在**没见过的**题上究竟能做到什么程度(泛化能力),且不再给你调整的机会。
109 |
110 | ## 1.5.2 如何设立交叉验证集和测试集
111 |
112 | 建议在设立交叉验证集和测试集时,要选择能够反映未来你希望得到的并认为做好很重要的数据作为交叉验证集和测试集。
113 |
114 | > Choose a dev set and test set to reflect data you expect to get in the future and consider important to do well on.
115 |
116 | 交叉验证集和测试集最好来自**同一分布**:不管未来会得到什么样的数据,一旦你的算法效果不错,要尝试收集类似的数据且不管那些数据是什么,都要**随机分配**到开发集和测试集中,这样才能瞄准想要的目标,让团队高速迭代来逼近同一个目标。
117 |
118 | ## 1.5.3 如此设立交叉验证集和测试集的原因
119 |
120 | 设立交叉验证集以及一个单实数评估指标就像是定下目标,告诉你的团队那就是你要瞄准的靶心,一旦建立了这样的开发集和指标,团队就可以快速迭代,可以很快地使用交叉验证集和指标去评估不同分类器,然后尝试选出最好的那个,针对开发集上的指标优化。
121 |
122 | 如果交叉验证集和测试集来自不同的分布,就像设定了一个目标,结果在团队逼近这个目标工作几个月后,想要把成果应用到另一个目标。为了避免这种情况,建议将所有数据随机洗牌放入开发集和测试集,所以交叉集和测试集都有来自所有不同分类的数据并且开发集和测试集都来自同一分布,这个分布就是所有的数据混在一起。
123 |
124 | # 1.6 交叉验证集和测试集的大小
125 |
126 | ## 1.6.1 交叉验证集和测试集大小设置的原则
127 |
128 | 1、经验法则:把取得的所有数据划分为 **70%训练集+30%测试集** 或 **60%训练集+20%交叉验证集+20%测试集**。
129 |
130 | 这种经验法则使用于机器学习的早期,即数据集规模较小的情况下。
131 |
132 | 2、在现代机器学习中,数据集规模很大,可分为**98%训练集+1%交叉验证集+1%测试集**。
133 |
134 | 训练集的大小:深度学习算法对数据的胃口很大,故要把占更高比例的数据划分到训练集中;
135 |
136 | 测试集的大小:测试集的目的是完成系统开发后用测试集评估系统性能,故要令测试集足够大,能够以高置信度评估系统整体性能。所以除非需要对最终系统有一个很精确的指标,一般来说,测试集不需要上百万个例子,有10000或100000个大概就足够了,当数据量很大时,测试集就会远远小于数据集的30%或20%。
137 |
138 | ## 1.6.2 什么情况下可以没有测试集
139 |
140 | 对于不需要对系统性能有置信度很高的评估的应用,可以不用划分测试集,只需要训练集和交叉验证集,只要有数据去训练、有数据去调试就够了,但是并不建议在系统搭建时省略测试集,有个单独的测试集会更好,因为可以用这组不带偏差的数据来测量系统的性能,但如果交叉验证集非常大,就不会对交叉验证集过拟合得太厉害,在这种情况下只有训练集和交叉验证集也不是完全不合理。
141 |
142 | 在实际实践中,有时只把数据集划分为训练集和测试集,实际上这是在测试集上迭代,所以这里的测试集其实是交叉验证集,即只把数据分为训练集和交叉验证集,没有测试集。
143 |
144 | # 1.7 什么时候该改变交叉验证/测试集和指标
145 |
146 | ## 1.7.1 如何定义一个指标去评估分类器
147 |
148 | 评估指标的意义在于,准确告诉你已知的两个分类器哪一个更适合你的应用。
149 |
150 | 当已设定的评估指标无法正确衡量算法之间的优劣排序时,就应该改变评估指标或者改变交叉验证集或测试集。
151 |
152 | 例如,若对旧的误差指标 $Error = \frac{1}{m_{dev}} \sum_{i=1}^{m_{dev}}I[y_{pred}^{(i)}≠y^{(i)}]$ 不满意,可以尝试定义一个新的能够更加符合你的偏好的指标,从而定义出更适合的算法,如在 $I$ 项前加一个权重项 $\omega^{(i)}$,即
153 |
154 | $Error = \frac{1}{m_{dev}} \sum_{i=1}^{m_{dev}} \omega^{(i)} I[y_{pred}^{(i)}≠y^{(i)}]$
155 |
156 | 其中,
157 |
158 | $\omega^{(i)}=\left\{\begin{array}{ll}1 & \text { if } x^{(i)}... \\ 10 & \text { if } x^{(i)}...\end{array}\right.$,
159 |
160 | 当 $x^{(i)}$ 是预期分类中的数据时,赋予较小的权重1,当 $x^{(i)}$ 不是预期分类中的数据时,赋予较大的权重10,误差项迅速变大,即把非预期分类数据分类成某一类的惩罚权重加大10倍。
161 |
162 | ## 1.7.2 机器学习的两个独立步骤(正交化)
163 |
164 | 1. 设定目标:弄清楚如何定义一个指标来衡量你想做的事情的表现(**定义指标**);
165 | 2. 瞄准/射击目标:分开考虑如何改善系统在这个指标上的表现(**调整指标**以优化系统)。
166 |
167 | ## 1.7.3 需改变评价标准的情况
168 |
169 | 如果系统在当前指标、当前交叉验证集或者交叉验证集和测试集分布中表现很好,但在实际应用程序即你真正关注的地方表现不好(当前的指标和当前用来评估的数据和你真正关心必须做好的事情关系不大),就需要修改指标或交叉验证/测试集,让它们能够更好地反映算法需要处理好的数据。
170 |
171 | 举例:假设有两个猫分类器A和B,用开发集评估分别得到3%和5%的误差,做评估时用的是高质量图片的交叉验证集和测试集但在实际应用时上传的图片取景不专业,没有把猫完整拍下来或猫的表情很古怪,或者图像很模糊,在实际测试算法时可能会发现算法B比算法A更好,此时就应该修改指标或交叉验证/测试集。
172 |
173 | # 1.8为什么是人的表现
174 |
175 | 机器学习模型的准确性有两个层级,分别为
176 |
177 | 1.human-level performance(人的表现)
178 |
179 | 2.Bayes optimal error(贝叶斯最优误差)
180 |
181 | 机器学习模型表现常与人的学习表现相比较
182 |
183 | 如图,随着训练时间的不断增长,模型的准确性会不断接近“人的表现”并最终超过。当超过“人的表现”后,准确性的上升会比较缓慢,并不断靠近理想的最优情况,即贝叶斯最优误差。而实际上,“人的表现”,在许多如语音识别、图像识别的部分是非常具有优势的,让机器学习模型的准确性不断接近“人的表现”非常有必要。
184 |
185 | 1.Get labeled data from humans.
186 |
187 | 2.Gain insight from manual error analysis: Why did a person get this right?
188 |
189 | 3.Better analysis of bias/variance.
190 |
191 | 以上方法可以让模型不断接近人的表现。
192 |
193 | # 1.9可避免偏差
194 |
195 | 在实际应用中,要看human-level error,training error和dev error的相对值。例如猫类识别的例子中,
196 |
197 | 
198 |
199 |
200 |
201 | 对于物体识别这类CV问题,human-level error是很低的,很接近理想情况下的贝叶斯最优误差。因此,上面例子中的1%和7.5%都可以近似看成是两种情况下对应的bayes optimal error。实际应用中,我们一般会用human-level error代表bayes optimal error。
202 |
203 |
204 |
205 | 通常,我们把training error与human-level error之间的差值称作avoidable bias(可避免偏差);把dev error与training error之间的差值称为方差(variance)。根据bias和variance值的相对大小,可以知道算法模型是否发生了欠拟合或者过拟合。
206 |
207 | 若相比于方差(variance),bias较大,则我们对模型的调整主要在于减小偏差
208 |
209 | 若相比于方差(variance),bias较小,则可采用正则化、采集更多数据等方法减小方差
210 |
211 | # 1.10理解人的表现
212 |
213 | human-level performance有时能够代表bayes optimal error。但是,human-level performance如何定义呢?举个医学图像识别的例子,不同人群的error有所不同:
214 |
215 | 
216 |
217 | 由于bayes optimal error是最优的理想情况,一般来说,我们将表现最好的那一组,即Team of experienced doctors作为human-level performance,以此来代替bayes optimal error。
218 |
219 |
220 |
221 | 但在实际应用时,human-level performance的选择也会因人而异,不同取值的human-level performance会在一定程度上影响bias和variance的相对大小。如下图
222 |
223 |
224 |
225 | 
226 |
227 | 在方案C中,由于Training error和Development error数值差只为0.1,即variance只有0.1,此时不同取值的human-level performance会影响到bias和variance的相对大小,影响到了后续对模型的调整与改善。
228 |
229 | 而这种情况一般只在模型表现很好,接近bayes optimal error 时才会出现,此时,由于human-level performance较模糊难以定义,而影响到了模型的优化。
230 |
231 | # 1.11超过人的表现
232 |
233 | 
234 |
235 | 对于自然感知类问题,例如视觉、听觉等,机器学习的表现还不及人类。但是在很多其它方面,如
236 |
237 |
238 |
239 | - Online advertising(在线广告)
240 | - Product recommendations(产品推荐)
241 | - Logistics(predicting transit time)(预测交通时间)
242 | - Loan approvals(贷款批准)
243 |
244 | 这些方面,机器的表现优于人类。
245 |
246 | 机器学习模型超过human-level performance是比较困难的。但是如果有足够多的样本,训练更加复杂的神经网络,模型预测准确性会不断得到提高,最终接近并超过human-level performance。然而当机器模型的表现超过human-level performance时,难以直觉来继续提高算法模型性能。
247 |
248 | # 1.12改善模型表现
249 |
250 | 提高机器学习模型性能主要要解决两个问题:avoidable bias和variance。
251 |
252 | 解决avoidable bias的常用方法包括:
253 |
254 | - Train bigger model(训练更大的模型)
255 |
256 | - Train longer/better optimization algorithms: momentum, RMSprop, Adam
257 |
258 | (使用更好的算法:momentum、RMSprop、Adam)
259 |
260 | - NN architecture/hyperparameters search(选用不同的神经网络结构)
261 |
262 | 解决variance的常用方法包括:
263 |
264 | - More data(使用更多数据)
265 | - Regularization: L2, dropout, data augmentation(使用正则化方法)
266 | - NN architecture/hyperparameters search(选用不同的神经网络结构)
267 |
268 |
--------------------------------------------------------------------------------
/9 机器学习(ML)策略(2).md:
--------------------------------------------------------------------------------
1 | ## 9 机器学习(ML)策略(2)
2 |
3 | ### 9.1误差分析
4 |
5 | #### 9.1.1 定义
6 |
7 | 你希望让学习算法能够胜任人类能做的任务,但你的学习算法还没有达到人类的表现,那么人工检查一下你的算法犯的错误也许可以让你了解接下来应该做什么。**这个过程称为错误分误差**。
8 |
9 | 通过对一组错误样本进行逐一检查后,分析错误样本的类型的比例,来决定朝着哪个方向来进行优化,或者给你构思新优化方向的灵感。
10 |
11 |
12 |
13 | #### 9.1.2 举例
14 |
15 | 假设你正在调试猫分类器,注意到一些算法分类出错的例子中,算法将一些狗分类为猫,为了解决的这个问题,我们不需要,去设计一些只处理狗的算法功能之类的,为了让你的猫分类器在狗图上做的更好,让算法不再将狗分类成猫,因为这花费的时间太长了。而是需要进行误差分析,以便于决定哪一个方向值得努力。
16 |
17 | 首先,比如收集100个错误标记的开发集样本,然后手动检查,一次只看一个,看看你的开发集里有多少错误标记的样本是狗。假设100个错误标记样本中只有5%是狗这意味着100个样本,在典型的100个出错样本中,即使你完全解决了狗的问题,你也只能修正这100个错误中的5个,也就是最多只能将错误率从10%下降到9.5%,效果并不明显。但假设100个错误标记的开发集样本,你发现实际有50张图都是狗,也就是有50%都是狗的照片,现在花时间去解决狗的问题可能效果就很好,错误率可能就从10%下降到5%。
18 |
19 |
20 |
21 | #### 9.1.3 利用表格进行误差分析
22 |
23 | 当然在进行误差分析时,也可以对多个情况或者想法进行评估(比如对狗的照片错认为猫和对狮子的照片错认为猫)。有效且清晰的做法是设计一个表格来对各种错误样本进行填表式的分类,最后统计错误类型的百分比,再针对各种错误类型百分比的大小,进而决定优化的方向,同时最好在每个样本的后面增加备注,以方便进行分析。
24 |
25 | 
26 |
27 | 当然,在分类的过程中,如果发现了新的错误类型,也可以直接创建一个新的错误类型
28 |
29 |
30 |
31 |
32 |
33 | ### 9.2 清除标注错误的数据
34 |
35 | 错误的数据:结果的标签是错的。比如猫的图片被标注为不是猫。
36 |
37 | #### 9.2.1 处理标签错误的数据
38 |
39 | 1.对于总数据集总足够大,实际错误率不高的情况下:有时候放着不管也可以,并不会对训练出来的结果有太大的影响
40 |
41 | 2.对于系统性的错误:需要进行修改
42 |
43 | (实际错误率高,比如一直把白色的狗标记成猫,分类器学习之后,会把所有白色的狗都分类为猫)
44 |
45 |
46 |
47 | 总的来说,在进行误差分析后如果这些标记错误严重影响了你在开发集上评估算法的能力,那么就应该去花时间修正错误的标签。但是,如果它们没有严重影响到你用开发集评估成本偏差的能力,那么可能就不应该花宝贵的时间去处理。
48 |
49 |
50 |
51 | #### 9.2.2 分析错误数据的指标
52 |
53 | 关注整体的开发集错误率、错误标记引起的错误的数量或者百分比,最后根据标记错误引发的错误占总体总体错误率的比例来决定。(简单点说就是标记错误占所有错误的百分比的大小,该百分比越大,说明越值得修改错误标签)
54 |
55 | 比如,系统达到了90%整体准确度,所以有10%错误率,那么你应该看看错误标记引起的错误的数量或者百分比。所以在这种情况下,6%的错误来自标记出错,所以10%的6%就是0.6%。也许你应该看看其他原因导致的错误,如果你的开发集上有10%错误,其中0.6%是因为标记出错,剩下的占9.4%,是其他原因导致的。这个时候更应该考虑对9.4%进行优化或者修正。
56 |
57 | 假设你把错误率降到了2%,但总体错误中的0.6%还是标记出错导致的,此时错误标签导致的错误占总体错误的30%,那么这种情况就值得进行错误标签的修正。
58 |
59 |
60 |
61 | #### 9.2.3 修正标签的原则
62 |
63 | 1.修正标签时,都要同时作用到验证集和测试集上,也就是必须同时检查验证集和测试集,因为验证和测试集必须来自相同的分布。
64 |
65 | 2.要考虑同时检验算法判断正确和判断错误的样本,因为如果你只修正算法出错的样本,你对算法的偏差估计可能会变大,这会让你的算法有一点不公平的优势。
66 |
67 | 3.修正训练集中的标签其实相对没那么重要。
68 |
69 |
70 |
71 | 第二点不常遵循,因为一般判断正确的样本所占的比重要大得多。
72 |
73 |
74 |
75 | ### 9.3 快速搭建你的第一个系统
76 |
77 | 一般来说,对于几乎所有的机器学习程序可能会有50个不同的方向可以前进,并且每个方向都是相对合理的可以改善你的系统。所以快速设立开发集和测试集还有指标,能够确定系统迭代的方向,并且及时利用训练集对机器学习系统进行训练,再根据结果进行分析来确定下一步优先做什么。
78 |
79 |
80 |
81 | 下面以建立一个语音识别系统为例子介绍:
82 |
83 | 你可以选择很多不同的技术,让你听写下来的文本可读性更强,所以你可以做很多事情来改进语音识别系统。但对于多种方法你会感到非常迷茫,但当你建立第一个系统后,就能够进行误差分析让你了解到大部分的错误的来源是什么,比如说话人远离麦克风,那么你就有很好的理由去集中精力研究这些技术,也就是确定了你努力的方向
84 |
85 |
86 |
87 |
88 |
89 | ### 9.4 在不同的划分下进行训练并测试
90 |
91 | #### 9.4.1 划分的定义
92 |
93 | 划分即在选择数据进行训练时,将不是来自同一分布的数据进行分开,并分别作为数据集的训练集,以及数据集中的验证集和测试集(验证集和测试集得保证来自同分布)。
94 |
95 | 注:在视频中,字幕将dev set翻译为开发集,而以往的笔记中使用的命名为验证集,这里我使用验证集
96 |
97 | #### 9.4.2 为什么需要进行划分
98 |
99 | 进行划分的目的在于设定模型的优化方向,也就是“靶心”,通过将需要应用时的数据作为测试集和验证集来进行训练,保证在该模型投入应用时能够有较高的识别率。
100 |
101 | eg.在识别猫的图片的模型当中,可能会出现拥有充足且清晰的猫的图片进行模型的训练,而对于用户使用这个模型时,可能会使用模糊的照片,而专注于识别清晰照片的模型就较大的概率出现错误。并且这些模糊的照片在刚投入使用的时相较于训练模型时的清晰照片的数量少的多,如训练时清晰的照片可能有20w张,而用户的照片可能只有1w张,并不足以进行训练。
102 |
103 | 如果将清晰的照片和模糊的照片随机分布于数据集当中进行训练,则在期望上清晰的照片在测试集和验证集中的占比就会远大于模糊照片的比例,这就会导致在多次训练中,模型更加偏向于朝着清晰图片的识别的方向进行优化,而不是对用户上传的模糊照片的识别进行优化。
104 |
105 | 如果将模糊和清晰的照片进行划分,将清晰的图片作为训练集,并且将用户模糊的照片作为测试集和验证集,即把模型的优化方向设定为对用户上传的照片的识别,进而不断的提高对用户上传的照片的识别准确率。
106 |
107 |
108 |
109 | ### 9.5 不匹配数据划分上的偏差和方差
110 |
111 | 方差和偏差定义:第二门课第一周笔记
112 |
113 | #### 9.5.1 不匹配数据划分对方差和偏差的影响
114 |
115 | 以猫的识别为例,对猫的识别的最优误差几乎为0%,而如果训练集和验证集的数据并不是来自同一分布,如训练集是清晰的照片而测试集是模糊的照片,则训练集的照片容易识别,训练误差小,而验证集的照片难以识别,验证误差大,此时我们不能通过这两个误差值来判断该神经网络的方差是否真的偏大或者偏小,也就是两者的大小区别到底是训练集的数据造成的(也就是方差的问题),还是由于数据来自不同的分布而导致的(也就是数据不匹配问题)(或者两者哪个的影响更大)
116 |
117 | #### 9.5.2 训练-验证集(Training-dev set)
118 |
119 | 定义:为了解决在不匹配数据的情况下(也就是上述情况)对方差的判断,我们随机从训练集中抽取一组数据来作为新的子集,也就是训练-验证集。(此时数据集就被分为了四个部分:训练集、训练-验证集、验证集和测试集)
120 |
121 |
215 |
216 | #### 7.6.2 如何减缓Internal Covariate Shift
217 |
218 | **(1)白化(Whitening)**
219 |
220 | 白化(Whitening)是机器学习里面常用的一种规范化数据分布的方法,主要是PCA白化与ZCA白化。白化是对输入数据分布进行变换,进而达到以下两个目的:
221 |
222 | - **使得输入特征分布具有相同的均值与方差。**其中PCA白化保证了所有特征分布均值为0,方差为1;而ZCA白化则保证了所有特征分布均值为0,方差相同;
223 | - **去除特征之间的相关性。**
224 |
225 | 通过白化操作,可以减缓ICS的问题,进而固定每一层网络输入分布,加速网络训练过程的收敛。
226 |
227 | 然而,白化的方法具有一定缺陷,主要有以下两个问题:
228 |
229 | - **白化过程计算成本太高,**并且在每一轮训练中的每一层我们都需要做如此高成本计算的白化操作;
230 | - **白化过程由于改变了网络每一层的分布**,因而改变了网络层中本身数据的表达能力。底层网络学习到的参数信息会被白化操作丢失掉。
231 |
232 | **(2)Batch Normalization**
233 |
234 | 为解决上面两个问题,提出BN方法简化计算过程同时让归一化处理后的数据尽可能保留原始表达能力。
235 | $$
236 | \begin{array}{l}
237 | \mu=\frac{1}{m} \sum_{i} z^{(i)} \\
238 | \sigma^{2}=\frac{1}{m} \sum_{i}\left(z^{(i)}-\mu\right)^{2} \\
239 | z_{\text {norm}}^{(i)}=\frac{z^{(i)}-\mu}{\sqrt{\sigma^{2}+\varepsilon}}
240 | \end{array}
241 | $$
242 | 通过上面的变换,**解决了第一个问题,即用更加简化的方式来对数据进行规范化,使得第 $l$层的输入每个特征的分布均值为0,方差为1。**
243 |
244 | 如同上面提到的,Normalization操作我们虽然缓解了ICS问题,让每一层网络的输入数据分布都变得稳定,但却导致了数据表达能力的缺失。也就是我们通过变换操作改变了原有数据的信息表达(representation ability of the network),使得底层网络学习到的参数信息丢失。另一方面,通过让每一层的输入分布均值为0,方差为1,会使得输入在经过sigmoid或tanh激活函数时,容易陷入非线性激活函数的线性区域。
245 |
246 | 因此,BN引入的两个可学习(learnable)的参数$\gamma$和$\beta$,恢复数据本身的表达能力,对归一化后端数据进行线性变换,即:
247 | $$
248 | \tilde{z}^{[l]}=\gamma^{[l]} z_{\text {norm}}^{[l]}+\beta^{[l]}
249 | $$
250 | 特别地,当$\gamma^{2}=\sigma^{2}, \beta=\mu$时,可以实现等价变换(identity transform)并且保留了原始输入特征的分布信息。
251 |
252 | **通过上面的步骤,我们就在一定程度上保证了输入数据的表达能力。**
253 |
254 | 简单来说,BN减弱了前层参数的作用与后层参数的作用之间的联系,它使得网络每层都可以自己学习,稍稍独立于其它层,这让我们可以使用**更大的学习率**,初值可以更随意,有助于加速整个网络的学习。
255 |
256 | #### 7.6.3 BN的效果总结:
257 |
258 | **(1)BN使得网络中每层输入数据的分布相对稳定,加速模型学习速度**
259 |
260 | BN通过规范化与线性变换使得每一层网络的输入数据的均值与方差都在一定范围内,使得后一层网络不必不断去适应底层网络中输入的变化,从而实现了网络中层与层之间的解耦,允许每一层进行独立学习,有利于提高整个神经网络的学习速度。
261 |
262 | **(2)BN使得模型对网络中的参数不那么敏感,简化调参过程,使得网络学习更加稳定**
263 |
264 | 在神经网络中,我们经常会谨慎地采用一些权重初始化方法(例如Xavier)或者合适的学习率来保证网络稳定训练。
265 |
266 | 当学习率设置太高时,会使得参数更新步伐过大,容易出现震荡和不收敛。但是使用BN的网络将不会受到参数数值大小的影响。
267 |
268 | 例如,我们对参数$W$进行缩放得到$aW$。对于缩放前的值$Wu$($u$表示当前层输入,前一层的输出),设其均值为$\mu_{1}$,方差为$\sigma_{1}^{2}$;对于缩放值$aWu$,设其均值为$\mu_{2}$,方差为$\sigma_{2}^{2}$,则有:
269 | $$
270 | \mu_{2}=a \mu_{1}, \quad \sigma_{2}^{2}=a^{2} \sigma_{1}^{2}
271 | $$
272 | 我们忽略$\epsilon$,则有:
273 | $$
274 | \begin{array}{l}
275 | B N(a W u)=\gamma \cdot \frac{a W u-\mu_{2}}{\sqrt{\sigma_{2}^{2}}}+\beta=\gamma \cdot \frac{a W u-a \mu_{1}}{\sqrt{a^{2} \sigma_{1}^{2}}}+\beta=\gamma \cdot \frac{W u-\mu_{1}}{\sqrt{\sigma_{1}^{2}}}+\beta=B N(W u) \\
276 | \frac{\partial B N((a W) u)}{\partial u}=\gamma \cdot \frac{a W}{\sqrt{\sigma_{2}^{2}}}=\gamma \cdot \frac{a W}{\sqrt{a^{2} \sigma_{1}^{2}}}=\frac{\partial B N(W u)}{\partial u} \\
277 | \frac{\partial B N((a W) u)}{\partial(a W)}=\gamma \cdot \frac{u}{\sqrt{\sigma_{2}^{2}}}=\gamma \cdot \frac{u}{a \sqrt{\sigma_{1}^{2}}}=\frac{1}{a} \cdot \frac{\partial B N(W u)}{\partial W}
278 | \end{array}
279 | $$
280 | 可以看到,经过BN操作以后,权重的缩放值会被“抹去”,因此保证了输入数据分布稳定在一定范围内。另外,权重的缩放并不会影响到对$u$的梯度计算;并且当权重越大时,即$a$越大,$\frac{1}{a}$越小,意味着权重$W$的梯度反而越小,这样BN就保证了梯度不会依赖于参数的scale,使得参数的更新处在更加稳定的状态。
281 |
282 | 因此,在使用Batch Normalization之后,抑制了参数微小变化随着网络层数加深被放大的问题,使得网络对参数大小的适应能力更强,此时我们可以设置较大的学习率而不用过于担心模型divergence的风险。
283 |
284 | **(3)BN允许网络使用饱和性激活函数(例如sigmoid,tanh等),缓解梯度消失问题**
285 |
286 | 在不使用BN层的时候,由于网络的深度与复杂性,很容易使得底层网络变化累积到上层网络中,导致模型的训练很容易进入到激活函数的梯度饱和区;通过normalize操作可以让激活函数的输入数据落在梯度非饱和区,缓解梯度消失的问题;另外通过自适应学习$\gamma$和$\beta$又让数据保留更多的原始信息。
287 |
288 | **(4)BN具有一定的正则化效果**
289 |
290 | - BN只在每个mini-batch上计算均值和方差,而不是在整个数据集上
291 | - 均值和方差只是由一小部分数据估计得出的,有一些小的噪声,缩放过程从$z^{[l]}$到$\tilde{z}^{[l]}$也有一些噪声,因为它是用有些噪声的均值和方差计算得出的。
292 | - 故和dropout相似,它在每个隐藏层的激活值上增加了噪音。dropout 使一个隐藏的单元以一定的概率乘以 0,以一定的概率乘以 1,所以 dropout含一些噪音,因为它乘以 0 或 1。
293 |
294 | 因此,类似于dropout,BN有轻微的正则化效果,因为给隐藏单元添加了噪音,使得后部单元不过分依赖任何一个隐藏单元。如果想得到更强大的正则化效果,可以将BN和dropout一起使用。
295 |
296 | 如果应用较大的mini-batch可以减少噪音,减少正则化效果。
297 |
298 | **参考文章**:
299 |
300 | [1]: https://zhuanlan.zhihu.com/p/34879333 "Batch Normalization原理与实战"
301 | [2]: BatchNormalizationAcceleratingDeepNetworkTrainingbyReducingInternalCovariateShift
302 |
303 |
304 |
305 | ### 7.7 测试时的 Batch Norm
306 |
307 | 我们知道BN在每一层计算的 ![[公式]](https://www.zhihu.com/equation?tex=%5Cmu) 与 ![[公式]](https://www.zhihu.com/equation?tex=%5Csigma%5E2) 都是基于当前batch中的训练数据,但是这就带来了一个问题:我们在预测阶段,有可能只需要预测一个样本或很少的样本,没有像训练样本中那么多的数据,此时 ![[公式]](https://www.zhihu.com/equation?tex=%5Cmu) 与 ![[公式]](https://www.zhihu.com/equation?tex=%5Csigma%5E2) 的计算一定是有偏估计,这个时候我们该如何进行计算呢?
308 |
309 | **论文中的方法**:
310 |
311 | 利用BN训练好模型后,我们保留了每组mini-batch训练数据在网络中每一层的 ![[公式]](https://www.zhihu.com/equation?tex=%5Cmu_%7Bbatch%7D) 与 ![[公式]](https://www.zhihu.com/equation?tex=%5Csigma%5E2_%7Bbatch%7D) 。此时我们使用整个样本的统计量来对Test数据进行归一化,具体来说使用均值与方差的无偏估计:
312 |
313 | ![[公式]](https://www.zhihu.com/equation?tex=%5Cmu_%7Btest%7D%3D%5Cmathbb%7BE%7D+%28%5Cmu_%7Bbatch%7D%29)
314 |
315 | ![[公式]](https://www.zhihu.com/equation?tex=%5Csigma%5E2_%7Btest%7D%3D%5Cfrac%7Bm%7D%7Bm-1%7D%5Cmathbb%7BE%7D%28%5Csigma%5E2_%7Bbatch%7D%29)
316 |
317 | 得到每个特征的均值与方差的无偏估计后,我们对test数据采用同样的normalization方法:
318 |
319 | ![[公式]](https://www.zhihu.com/equation?tex=BN%28X_%7Btest%7D%29%3D%5Cgamma%5Ccdot+%5Cfrac%7BX_%7Btest%7D-%5Cmu_%7Btest%7D%7D%7B%5Csqrt%7B%5Csigma%5E2_%7Btest%7D%2B%5Cepsilon%7D%7D%2B%5Cbeta)
320 |
321 | **吴恩达老师讲的方法**
322 |
323 | 对训练阶段每个batch计算的$\mu$和$\sigma^{2}$采用指数加权平均来得到测试阶段$\mu$和$\sigma^{2}$的估计。
324 |
325 | 我们选择 𝑙层,假设我们有 mini-batch,$X^{\{1\}}$,$X^{\{2\}}$,$X^{\{3\}}$......以及对应的$y$值等等,那么在训练$X^{\{1\}}$时,就得到了$\mu^{\{1\}[l]}$,训练第二个mini-batch时,就会得到$\mu^{\{2\}[l]}$值。然后在这一隐藏层的第三个 mini-batch,得到第三个$\mu$($\mu^{\{3\}[l]}$)值。使用指数加权平均来追踪这个均值向量的最新平均值,于是该指数加权平均成了你对这一隐藏层的$z$均值的估值。
326 |
327 | 同样的,可以用指数加权平均来追踪这一层每个mini-batch的$\sigma^{2}$的值。因此在用不同mini-batch训练神经网络的同时,能够得到你所查看每一层$\mu$和$\sigma^{2}$的平均数的实时数值。
328 |
329 | 最后在测试时对test数据采用同样的normalization方法(同上)。
330 |
331 | ### 7.8 BN与其他Normalization的方法比较
332 |
333 | 参考文章:https://zhuanlan.zhihu.com/p/33173246
334 |
335 | https://www.cnblogs.com/LXP-Never/p/11566064.html
336 |
337 | https://blog.csdn.net/shwan_ma/article/details/85292024
338 |
339 | https://bbs.cvmart.net/topics/1569
340 |
341 |
342 |
343 | 常用的Normalization方法主要有:Batch Normalization(BN,2015年)、Layer Normalization(LN,2016年)、Instance Normalization(IN,2017年)、Group Normalization(GN,2018年)。它们都是从激活函数的输入来考虑、做文章的,以不同的方式**对激活函数的输入进行 Norm** 的。
344 |
345 | 将输入的图像shape记为[**N**, **C**hannel, **H**eight, **W**idth],这几个方法主要的区别就是在,
346 |
347 | - **batch Norm**:在batch上,对NHW做归一化,对小batchsize效果不好;
348 | - **layer Norm**:在通道方向上,对CHW归一化,主要对RNN作用明显;
349 | - **instance Norm**:在图像像素上,对HW做归一化,用在风格化迁移;
350 | - **Group Norm**:将channel分组,然后再做归一化;
351 | - **Switchable Norm**:将BN、LN、IN结合,赋予权重,让网络自己去学习归一化层应该使用什么方法。
352 |
353 | 
354 |
355 | 如果把特征图![[公式]](https://www.zhihu.com/equation?tex=x%5Cin%5Cmathbb%7BR%7D%5E%7BN%5Ctimes+C+%5Ctimes+H+%5Ctimes+W%7D)比喻成一摞书,这摞书总共有 N 本,每本有 C 页,每页有 H 行,每行 有W 个字符。
356 |
357 | #### 7.8.1 Batch Normalization
358 |
359 | $$
360 | \begin{array}{c}
361 | \mu=\frac{1}{m} \sum_{i=1}^{m} x_{i} \\
362 | \sigma=\sqrt{\left.\frac{1}{m} \sum_{i=1}^{m}\left(x_{i}-\mu\right)^{2}\right)} \\
363 | y=\frac{(x-\mu)}{\sqrt{\sigma^{2}+\epsilon}}+\beta=B N(x)
364 | \end{array}
365 | $$
366 |
367 | tf.nn.batch_normalization(x, mean, variance, offset, scale, variance_epsilon, name=None`)`
368 |
369 | 参数
370 |
371 | - x:输入数据
372 | - mean:均值
373 | - variance:方差
374 |
375 | 返回
376 |
377 | - 标准化后的数据
378 |
379 | **BN缺点:**
380 |
381 | - 对batch size的大小比较敏感,由于每次计算均值和方差是在一个batch上,所以如果batch size太小,则计算的均值、方差不足以代表整个数据分布;
382 | - BN实际使用时需要计算并且保存某一层神经网络batch的均值和方差等统计信息,对于对一个固定深度的前向神经网络(DNN,CNN)使用BN,很方便;但对于RNN来说,sequence的长度是不一致的,换句话说RNN的深度不是固定的,不同的time-step需要保存不同的statics特征,可能存在一个特殊sequence比其他sequence长很多,这样training时,计算很麻烦。
383 |
384 | #### 7.8.2 Layer Normalization
385 |
386 | LN是针对深度网络的某一层的所有神经元的输入按以下公式进行normalize操作。计算该层的平均输入值和输入方差,然后用同一个规范化操作来转换各个维度的输入。
387 | $$
388 | \begin{array}{c}
389 | \mu^{l}=\frac{1}{H} \sum_{i=1}^{H} a_{i}^{l} \\
390 | \sigma^{l}=\sqrt{\frac{1}{H} \sum_{i=1}^{H}\left(a_{i}^{l}-\mu^{l}\right)^{2}}
391 | \end{array}
392 | $$
393 | **BN与LN的区别在于**:
394 |
395 | - LN中同层神经元输入拥有相同的均值和方差,不同的输入样本有不同的均值和方差;
396 | - BN中则针对不同神经元输入计算均值和方差,同一个batch中的输入拥有相同的均值和方差。
397 |
398 | 所以,LN不依赖于batch的大小和输入sequence的深度,因此可以用于batchsize为1和RNN中对边长的输入sequence的normalize操作。
399 |
400 | BN 的转换是针对单个神经元可训练的——不同神经元的输入经过再平移和再缩放后分布在不同的区间,而 LN 对于一整层的神经元训练得到同一个转换——所有的输入都在同一个区间范围内。如果不同输入特征不属于相似的类别(比如颜色和大小),那么 LN 的处理可能会降低模型的表达能力。LN用于RNN效果比较明显,但是在CNN上,不如BN。
401 |
402 | tf.keras.layers.LayerNormalization(axis=-1, epsilon=0.001, center=True, scale=True)
403 |
404 | 参数
405 |
406 | - axis:想要规范化的轴(通常是特征轴)
407 | - epsilon:将较小的浮点数添加到方差以避免被零除。
408 | - center:如果为True,则将的偏移`beta`量添加到标准化张量。
409 | - `scale`:如果为True,则乘以`gamma`
410 |
411 | 返回
412 |
413 | - shape与输入形状相同的值
414 |
415 | #### 7.8.3 Instace Normalization
416 |
417 | BN注重对每个batch进行归一化,保证数据分布一致,因为判别模型中结果取决于数据整体分布。
418 |
419 | 但是图像风格转换中,生成结果主要依赖于某个图像实例,所以对整个batch归一化不适合图像风格化中,因而对HW做归一化。可以加速模型收敛,并且保持每个图像实例之间的独立。
420 | $$
421 | \begin{array}{c}
422 | \mu_{t i}=\frac{1}{H W} \sum_{l=1}^{W} \sum_{m=1}^{H} x_{t i l m} \\
423 | \sigma=\sqrt{\frac{1}{H W}} \sum_{l=1}^{W} \sum_{m=1}^{H}\left(x_{t i l m}-\mu_{y i}\right)^{2} \\
424 | y_{t i j k}=\frac{x_{P t i j k}-\mu_{y i}}{\sqrt{\sigma_{t i}^{2}}-\epsilon}
425 | \end{array}
426 | $$
427 | [`tfa.layers.normalizations.InstanceNormalization`](https://www.tensorflow.org/addons/api_docs/python/tfa/layers/InstanceNormalization)
428 |
429 | 输入:仅在该层只有一个输入(即,它连接到一个传入层)时适用。
430 |
431 | 返回:输入张量或输入张量列表。
432 |
433 | #### 7.8.4 Group Normalization
434 |
435 | 主要是针对Batch Normalization对小batchsize效果差,GN将channel方向分group,然后每个group内做归一化,算(C//G)*H*W的均值,这样与batchsize无关,不受其约束。
436 | $$
437 | S_{i}=\left\{k \mid k_{N}=i_{N},\left[\frac{k_{C}}{C / G}\right]=\left[\frac{i_{C}}{C / G}\right]\right\}
438 | $$
439 | Group Normalization 在要求 Batch Size 比较小的场景下或者物体检测/视频分类等应用场景下效果是优于 BN 的。
440 |
441 | #### 7.8.5 Switchable Normalization
442 |
443 | 本篇论文作者认为,
444 |
445 | - 第一,归一化虽然提高模型泛化能力,然而归一化层的操作是人工设计的。在实际应用中,解决不同的问题原则上需要设计不同的归一化操作,并没有一个通用的归一化方法能够解决所有应用问题;
446 | - 第二,一个深度神经网络往往包含几十个归一化层,通常这些归一化层都使用同样的归一化操作,因为手工为每一个归一化层设计操作需要进行大量的实验。
447 |
448 | 因此作者提出自适配归一化方法——Switchable Normalization(SN)来解决上述问题。与强化学习不同,SN使用可微分学习,为一个深度网络中的每一个归一化层确定合适的归一化操作。
449 | $$
450 | \begin{array}{c}
451 | \hat{h}_{h c i j}=\gamma \frac{h_{h c i j}-\sum_{k \in \Omega W_{k} \mu_{k}}}{\sqrt{\sum_{k \in \Omega} w_{k}^{\prime} \sigma_{k}^{2}+\epsilon}}+\beta \\
452 | w_{k}=\frac{e^{\lambda_{k}}}{\sum_{z \in\{i n, l n, b n\} e t}}, \quad k \in\{i n, l n, b n\} \\
453 | \mu_{i n}=\frac{1}{H W} \sum_{i, j}^{H, W} h_{n c i j}, \quad \sigma^{2}=\frac{1}{H W} \sum_{i, j}^{H, W}\left(h_{n c i j}-\mu_{i n}\right)^{2} \\
454 | \mu_{l n}=\frac{1}{C} \sum_{c=1}^{C} \mu_{i n}, \quad \sigma_{l n}^{2}=\frac{1}{C} \sum_{c=1}^{C}\left(\sigma_{i n}^{2}+\mu_{i n}^{2}\right)-\mu_{l n}^{2} \\
455 | \mu_{b n}=\frac{1}{N} \sum_{n=1}^{N} \mu_{i n}, \quad \sigma^{2}=\frac{1}{N} \sum_{n=1}^{N}\left(\sigma_{i n}^{2}+\mu_{i n}^{2}\right)-\mu_{b n}^{2}
456 | \end{array}
457 | $$
458 |
459 |
460 | #### 7.8.6 weight Normalization
461 |
462 | BN 和 LN 均将规范化应用于输入的特征数据 $X$ ,而 WN 则另辟蹊径,将规范化应用于线性变换函数的权重 $W$ ,这就是 WN 名称的来源。
463 |
464 | 对于人工神经网络中的一个神经元来说,其输出$y$表示为:
465 | $$
466 | y=\phi(\boldsymbol{w} \boldsymbol{x}+b)
467 | $$
468 | 其中$w$是$k$维权重向量,$b$是标量偏差,$x$是$k$维输入特征,$\phi(.)$是激活函数。
469 |
470 | 对权重$w$用参数向量$v$和标量$g$进行表示,则新参数表示为:
471 | $$
472 | \boldsymbol{w}=\frac{g}{\|\boldsymbol{v}\|} \boldsymbol{v}
473 | $$
474 | 其中$v$是$k$维向量,$g$是标量,$\|\boldsymbol{v}\|$为$v$的欧式范数。
475 | 通过上述参数表示,我们可以发现,$\|\boldsymbol{w}\|=g$与参数$v$独立,而权重$w$的方向也变更为$\frac{v}{\|\boldsymbol{v}\|}$。因此重参数将权重向量$w$用了两个独立的参数表示其幅度和方向。实验证明,在利用SGD优化算法时,重参数加速了网络的收敛速度。
476 |
477 | **Gradients:**
478 |
479 | 则对于$v$,$g$
480 | $$
481 | \begin{array}{c}
482 | \nabla_{g} L=\frac{\nabla_{w} L \cdot \boldsymbol{v}}{\|v\|} \\
483 | \nabla_{v} L=\frac{\boldsymbol{g} \cdot \nabla_{w} L}{\|v\|}-\frac{\boldsymbol{g} \cdot \nabla_{g} L}{\|v\|} \cdot \boldsymbol{v}
484 | \end{array}
485 | $$
486 | 其中$\nabla_{w} L$为目标函数对未进行WN的权重为$w$的偏导。
487 |
488 | 相比与BN,WN带有如下优点:WN的计算量非常低,并且其不会因为mini-batch的随机性而引入噪声统计。在RNN,LSTM,或者Reinforcement Learning上,WN能够表现出比BN更好的性能。
489 |
490 |
491 |
492 | ### 7.9 Softmax 回归
493 |
494 | Softmax回归:logistic回归的一般形式,将logistic回归推广到 C 类而不仅仅是两类,能在试图识别某一分类时做出预测且任何两个分类之间的决策边界都是线性的。
495 |
496 | 符号定义:
497 |
498 | $C$ :类别总数(类别编号分别为 $0, 2, ..., C-1$),故输出层L的神经元个数为 $C$,每个神经元分别输出该输入属于该类别的概率,$C$ 个神经元输出的概率总和应等于 1 。当 $C=2$ 时,Softmax回归即logistic回归。
499 |
500 | #### 7.9.1 Softmax层
501 |
502 | 在分类问题中,神经网络的**输出层**通常选用Softmax激活函数,使得最后输出的是归一化后的实数向量,每一元素代表该样本属于某一类的概率,则该层称为Softmax层。
503 |
504 | #### 7.9.2 Softmax激活函数
505 |
506 | - 定义:Softmax激活函数只用于多于一个神经元的输出层,它保证所有的输出神经元之和为1,所以一般输出的是小于1的概率值,可以很直观地比较各输出值。
507 |
508 | - 作用:为了得到属于每个类别的概率,先通过$e^{z^{[L]}}$将$z^{[L]}$的各元素值映射到 $(0, + \infty)$,然后再归一化到(0, 1)。
509 |
510 | - 具体实现:
511 |
512 | 在神经网络的最后一层,依然先计算线性部分:
513 | $$
514 | z^{[L]}=W^{[L]}a^{[L-1]}+b^{[L]}
515 | $$
516 |
517 |
518 | 然后应用**Softmax激活函数**:$a^{[L]}=g^{[L]}(z^{[L]})$,该函数的具体计算如下:
519 |
520 | (1)计算临时变量 $t=e^{z^{[L]}}$,对 $z^{[L]}$ 中的所有元素求幂,故 $t$ 的维度与 $z^{[L]}$ 相同。
521 |
522 | (2)对 $t$ **归一化**,得到输出 $a^{[L]}$ 即 $\hat{y}$ :$a^{[L]}=\frac{e^{z^{[L]}}}{\sum_{j=1}^{n^{[L]}} t_{i}}$,$a^{[L]}$的维度与 $t$ 相同,即也与 $z^{[L]}$ 相同,都为$(n^{[L]},1)$。其中,对$a^{[L]}$的每一个元素,$a_i^{[L]}=\frac{t_i}{\sum_{j=1}^{n^{[L]}} t_{i}}$。
523 |
524 | **tips:**之前所学的激活函数如sigmod和ReLU激活函数,都是输入一个实数,输出一个实数,而Softmax激活函数由于需要将所有可能的输出归一化,需要**输入一个向量,输出一个向量**。
525 |
526 | #### 7.9.3 softmax配合log似然代价函数训练ANN
527 |
528 | 在人工神经网络(ANN)中,Softmax通常被用作输出层的激活函数。这不仅是因为它的效果好,而且因为它使得ANN的输出值更易于理解。同时,softmax配合log似然代价函数,其训练效果也要比采用二次代价函数的方式好。
529 |
530 | log似然代价函数的公式为:
531 | $$
532 | C=-\sum_{k} y_{k} \log a_{k}
533 | $$
534 |
535 |
536 | 其中,$a_{k}$表示第k个神经元的输出值,$y_{k}$表示第k个神经元对应的真实值,取值为0或1。
537 |
538 | 该代价函数的简单理解为:在ANN中输入一个样本,那么只有一个神经元对应了该样本的正确类别;若这个神经元输出的概率值越高,则按照以上的代价函数公式,其产生的代价就越小;反之,则产生的代价就越高。
539 |
540 | 为了检验softmax和这个代价函数也可以解决训练ANN时训练速度变慢的问题,接下来的重点就是推导ANN的权重W和偏置b的梯度公式。以偏置b为例:
541 |
542 | 
543 |
544 | 同理可得:
545 | $$
546 | \frac{\partial C}{\partial w_{j k}}=a_{k}^{L-1}\left(a_{j}^{L}-y_{j}\right)
547 | $$
548 | 从上述梯度公式可知,softmax函数配合log似然代价函数可以很好地训练ANN,不存在学习速度变慢的问题。
549 |
550 | 参考文献:https://blog.csdn.net/orangefly0214/article/details/80406584
551 |
552 | ### 7.10 训练一个 Softmax 分类器
553 |
554 | #### 7.10.1 定义损失函数
555 |
556 | - 单样本:$$L(\hat{y}, y)=-\sum_{j=1}^C y_{j} \log \hat{y}_{j}$$
557 | - 整个训练集:$J\left(W^{[L]},b^{[L]} \ldots\right)=\frac{1}{m} \sum_{i=1}^{m} L\left(\hat{y}^{(i)}, y^{(i)}\right)$
558 | - 作用:找到样本所属的真实类别,并试图使该类别相应的概率尽可能地高。
559 |
560 | #### 7.10.2 正向传播
561 |
562 | 依次计算出:$z^{[L]} → a^{[L]} = \hat y → L\left(\hat{y}^{(i)}, y^{(i)}\right)$
563 |
564 | #### 7.10.3.反向传播(实现梯度下降法)
565 |
566 | (1)初始化反向传播:$dz^{[L]}=\frac{\partial J}{\partial z^{[L]}}=\hat y-y$
567 |
568 | (2)用深度学习编程框架自动实现反向传播的其余导数计算。
569 |
570 | ### 7.11 深度学习框架
571 |
572 | 深度学习框架可以使神经网络的实现变得更简单。每个框架都是针对某一个用户或开发者群体的
573 |
574 | #### 7.11.1 现有deep learning框架
575 |
576 | - **Caffe/Caffe2**:第一个主流的工业级深度学习工具。开始于2013年底,由UC Berkely的Yangqing Jia老师编写和维护的具有出色的卷积神经网络实现。在计算机视觉领域依然是最流行的工具包,有很多扩展,但是由于一些遗留的架构问题,不够灵活且对递归网络和语言建模的支持很差。
577 | - **CNTK**:是微软研究院开源的深度学习框架。最早由 start the deep learning craze 的演讲人创建,目前已经发展成一个通用的、跨平台的深度学习系统,在语音识别领域的使用尤其广泛。
578 | - **DL4J**:是一个基于 Java 和 Scala 的开源的分布式深度学习库,由 Skymind 于 2014 年 6 月发布,其核心目标是创建一个即插即用的解决方案原型。
579 | - **Keras**:是一个崇尚极简、高度模块化的神经网络库,使用 Python 实现,并可以同时运行在 TensorFlow 和 Theano 上。它旨在让用户进行最快速的原型实验,让想法变为结果的这个过程最短。Theano 和 TensorFlow 的计算图支持更通用的计算,而 Keras 则专精于深度学习。提供了目前为止最方便的 API,用户只需要将高级的模块拼在一起,就可以设计神经网络,它大大降低了编程开销和阅读别人代码时的理解开销。
580 | - **Lasagne**:是一个基于 Theano 的轻量级的神经网络库。Lasagne是 Theano 的上层封装,但又不像 Keras 那样进行了重度的封装,Keras 隐藏了 Theano 中所有的方法和对象,而 Lasagne 则是借用了 Theano 中很多的类,算是介于基础的 Theano 和高度抽象的 Keras 之间的一个轻度封装,简化了操作同时支持比较底层的操作。Lasagne 设计的六个原则是简洁、透明、模块化、实用、聚焦和专注。
581 | - **MXNet**:是李沐和陈天奇等各路英雄豪杰打造的开源深度学习框架,是分布式机器学习通用工具包DMLC的重要组成部分。注重灵活性和效率,文档也非常的详细,同时强调提高内存使用的效率,甚至能在智能手机上运行诸如图像识别等任务。
582 | - **PaddlePaddle**:是百度自主研发的集深度学习核心框架、工具组件和服务平台为一体的技术领先、功能完备的开源深度学习平台,有全面的官方支持的工业级应用模型,涵盖自然语言处理、计算机视觉、推荐引擎等多个领域,并开放多个预训练中文模型。目前已经被中国企业广泛使用,并拥有活跃的开发者社区生态。
583 | - **TensorFlow**:Google开源的其第二代深度学习技术——被使用在Google搜索、图像识别以及邮箱的深度学习框架。是一个理想的RNN(递归神经网络)API和实现,使用了向量运算的符号图方法,使得新网络的指定变得相当容易,支持快速开发。缺点是速度慢,内存占用较大(比如相对于Torch)。
584 | - **Theano**:2008年诞生于蒙特利尔理工学院,主要开发语言是Python。派生出了大量深度学习Python软件包,最著名的包括Blocks和Keras。Theano的最大特点是非常的灵活,适合做学术研究的实验,且对递归网络和语言建模有较好的支持,缺点是速度较慢。
585 | - **Torch**:Facebook力推的深度学习框架,主要开发语言是C和Lua。有较好的灵活性和速度。实现并且优化了基本的计算单元,使用者可以很简单地在此基础上实现自己的算法,不用浪费精力在计算优化上面。核心的计算单元使用C或者cuda做了很好的优化。在此基础之上,使用lua构建了常见的模型。缺点是接口为lua语言,需要一点时间来学习。
586 |
587 | 参考文献:
588 |
589 | - https://blog.csdn.net/dlaicxf/article/details/52846651
590 | - https://www.leiphone.com/news/201702/T5e31Y2ZpeG1ZtaN.html
591 |
592 | #### 7.11.2 几种主流dl框架的比较
593 |
594 | | **库名称** | **开发语言** | **速度** | **灵活性** | **文档** | **适合模型** | **平台** | **上手难易** |
595 | | :--------: | :-------------: | :------: | :--------: | -------: | :----------: | :--------: | :----------: |
596 | | Caffe | c++/cuda | 快 | 一般 | 全面 | CNN | 所有系统 | 中等 |
597 | | TensorFlow | c++/cuda/Python | 中等 | 好 | 中等 | CNN/RNN | Linux, OSX | 难 |
598 | | Keras | Python | 快 | 好 | 中等 | CNN/RNN | Linux, OSX | 易 |
599 | | MXNet | c++/cuda | 快 | 好 | 全面 | CNN | 所有系统 | 中等 |
600 | | Torch | c++/lua/cuda | 快 | 好 | 全面 | CNN/RNN | Linux, OSX | 中等 |
601 | | Theano | Python/c++/cuda | 中等 | 好 | 中等 | CNN/RNN | Linux, OSX | 易 |
602 |
603 | #### 7.11.3 选择框架的标准
604 |
605 | - **便于编程**:包括神经网络的开发和迭代、为产品进行配置等。
606 | - **运行速度**:特别是训练大数据集时,一些框架可以更高效地运行和训练神经网络。
607 | - **框架是否真的开放**:一个真的开放的框架,不仅需要开源,还需要良好的管理。
608 |
609 | PyTorch常用代码段合集 https://mp.weixin.qq.com/s/JnIO_HjTrC0DCWtKrkYC8A
610 |
611 |
612 |
613 |
614 |
615 |
616 |
617 |
--------------------------------------------------------------------------------
/8 机器学习(ML)策略(1).md:
--------------------------------------------------------------------------------
1 | # 1.1 为什么是ML策略
2 |
3 | 如果你训练了一段时间自己的神经网络,准确率到达了一定水平(比如90%)但却还不能满足你的要求,那这个时候必然需要对网络做出一些调整。你可能想到了几个解决思路,比如收集更多的数据、用不同的优化算法、训练得更久一些、加入正则化甚至修改网络架构等等。
4 |
5 | 但是这些办法并不是总是有效的,可能收集了6个月的数据却发现对网络的性能没有任何帮助。就是说如果你作出了错误的选择,那很可能浪费大量的时间和精力而得不到任何有效进展。
6 |
7 | 于是接下来希望教学一些策略:ML策略,以帮助我们向着有希望的方向前进。
8 |
9 | # 1.2 正交化
10 |
11 | 这里的正交化可以简单地理解为,每个自变量的改变只会引起一个因变量发生改变。举个反例,假设有$y_1=x_1+0.9x_2$,$y_2=0.1x_2$,则自变量$x_2$的改变会同时引起因变量$y_1,y_2$的改变,同时若想要通过$x_2$调整$y_1$时会不可避免的也调整了$y_2$。
12 |
13 | 在ML策略中,正交化是一种设计方法,以保证你在修改超参的时候不会引起两个以上的参数的变化。
14 |
15 | ## 四个参数
16 |
17 | 假设你需要正交化而确保不同时改变的四个参数是:
18 |
19 | * 收敛后的训练集的代价(cost)
20 | * 交叉验证集的代价
21 | * 测试集的代价
22 | * 真实应用的效果
23 |
24 | 当然,以上的参数是“按顺序”得到的。即只有在当前参数算优的情况下你才会做下一步而得到下一个参数的值。
25 |
26 | 对于第一点,如果训练集上的效果不好甚至无法收敛,可以考虑更大的神经网络或其他优化算法比如$Adam$。
27 |
28 | 对于第二点,可能原因是过拟合了,那可以尝试加入正则化或采用更大的训练集。
29 |
30 | 对于第三点,可以考虑采用更大的交叉验证集。
31 |
32 | 对于第四点,则考虑改变交叉验证集的图源或改变损失函数。
33 |
34 | 举个不正交的例子是 early stopping。因为 early stopping 会基于开发集的效果而提早停止训练,所以带来的影响是两方面的:训练集的代价还没收敛至最优的同时降低了在开发集上的代价。
35 |
36 | # 1.3 单一数字评估指标
37 |
38 | 对于一个网络的性能评估,我们有时候会采用多个指标以便更了解自己搭建的网络的效果。但是当你需要从多个网络中选出最好的一个时,多评估指标可能会导致你无法轻易选出优胜者——有的网络某一些指标最好,另一些指标则比不上其他网络。这个时候,单一数字评估指标就能很方便地帮你评价出最优的网络。
39 |
40 | ## 1.3.1常用指标
41 |
42 | 参考文章[在这](https://zhuanlan.zhihu.com/p/73569538)。
43 |
44 | ## 1.3.2混淆矩阵:
45 |
46 | 为了方便表达各指标如何计算,先介绍混淆矩阵:
47 |
48 | 
49 |
50 | 阴阳可理解为真假、1/0。a是预测为真真实也为真的样本数,其余类比。
51 |
52 | ## 1.3.3指标
53 |
54 | 1. Precision查准率/精度:评价网络做出的预测的准确率。对于二分类来说(比如猫/非猫分类器), $$P= \frac{预测为1且正确的样本数}{所有预测为1的样本数} = \frac{a}{a+b}$$。
55 |
56 | 2. 对于进行one-hot热值编码的多分类来说同样适用。
57 |
58 | 3. Recall查全率/True Positive真阳率/Sensitivity敏感性:评价网络对于目标类的识别率。对于二分类来说,
59 |
60 | $$R= \frac {所有预测为1且正确的样本数}{所有真实值为1的样本数} \frac{a}{a+c}$$。
61 |
62 | 对于进行了one-hot热值编码的多分类来说同样适用。
63 |
64 | 4. Accuracy准确率:评价网络所有类预测的准确率。对于二分类来说,$Acc= \frac{所有预测正确的样本数}{总的样本数}= \frac{a+d}{a+b+c+d}$。
65 |
66 | 5. 对于进行了one-hot热值编码的多分类同样适用。
67 |
68 | 6. False Positive误检率/假阳率:评价网络对阴性预测的错误率,为
69 |
70 | $$\frac{预测为1且错误的样本数}{真实值为0的样本数}=\frac{b}{b+d}$$。
71 |
72 | 7. F1分数:$$\frac{2}{\frac{1}{P}+\frac{1}{R}}$$
73 |
74 | P 和 R 分别代指 Precision 和 Recall。是 Precision 和 Recall 的调和平均数。
75 |
76 | # 1.4满足和优化指标
77 |
78 | 如果你想考虑的多个指标取值范围是相同的,那取平均值就可以简单地将多个指标“整合”成单一评估指标。但是如果其中一个是准确率P(%),另一个是单张图的预测时间T(ms),那取平均值的做法是几乎不合理的。线性组合$$aP+bT$$这样的做法或许可行,但是参数a、b的值却又可能难以设计。
79 |
80 | 所以,可以从另一个角度考虑:其中一个(甚至多个)指标只用于淘汰、筛选模型;另一个指标作为评估指标,是判断哪一个更优的指标。这分别对应满足指标和优化指标。
81 |
82 | ## 1.4.1满足指标
83 |
84 | 该指标是你关心的指标之一,但是又并不那么重要:该指标只需要到达一定范围即可,不是你**最想优化**的指标。比方说你很关心模型的准确率,同时也希望运行速度足够快,那将 T 视为满足指标是合适的。
85 |
86 | 满足指标的用意在于如果你有多个指标想要兼顾,但是大部分指标又并不是那么重要,那作为用于筛选模型的指标是很不错的选择。比如唤醒 Siri 你最关注的是 Recall,这能确保有人真的想唤醒 Siri 时能及时做出反应;但你也关注在没人想唤醒 Siri 时,Siri 被错误唤醒的概率。那将误检率/假阳率作为满足指标是可行的,比如设置为每24小时只有一次错误唤醒。
87 |
88 | ## 1.4.2优化指标
89 |
90 | 优化指标应该是你最关心的指标,是你最想优化的指标,比如唤醒 Siri 时的Recall。
91 |
92 | 由于单一数字评估指标的原因,优化指标应该只有一个,而其余你关心的指标都应该设为满足指标,或者和优化指标合理地整合为一个指标。
93 |
94 | # 1.5测试集、交叉验证集、测试集的划分
95 |
96 | ## 1.5.1 训练集、交叉验证集、测试集的作用
97 |
98 | - **训练集**:用以训练模型;
99 |
100 | - **交叉验证集** (也叫dev 集、开发集):衡量训练效果的同时进行超参数调优;
101 |
102 | - **测试集**:评测模型训练效果(测定泛化误差)。
103 |
104 | 以课后作业、期末考试、高考三者间的关系类比训练、开发、测试集的作用:
105 |
106 | - 课后作业(训练集):让你学会知识;
107 | - 期末考试(交叉验证集):让你检验自己是否真的学会了知识,发现了问题后,你会调整学习方法(调整超参数);
108 | - 高考(测试集):最终的测试,测试你在**没见过的**题上究竟能做到什么程度(泛化能力),且不再给你调整的机会。
109 |
110 | ## 1.5.2 如何设立交叉验证集和测试集
111 |
112 | 建议在设立交叉验证集和测试集时,要选择能够反映未来你希望得到的并认为做好很重要的数据作为交叉验证集和测试集。
113 |
114 | > Choose a dev set and test set to reflect data you expect to get in the future and consider important to do well on.
115 |
116 | 交叉验证集和测试集最好来自**同一分布**:不管未来会得到什么样的数据,一旦你的算法效果不错,要尝试收集类似的数据且不管那些数据是什么,都要**随机分配**到开发集和测试集中,这样才能瞄准想要的目标,让团队高速迭代来逼近同一个目标。
117 |
118 | ## 1.5.3 如此设立交叉验证集和测试集的原因
119 |
120 | 设立交叉验证集以及一个单实数评估指标就像是定下目标,告诉你的团队那就是你要瞄准的靶心,一旦建立了这样的开发集和指标,团队就可以快速迭代,可以很快地使用交叉验证集和指标去评估不同分类器,然后尝试选出最好的那个,针对开发集上的指标优化。
121 |
122 | 如果交叉验证集和测试集来自不同的分布,就像设定了一个目标,结果在团队逼近这个目标工作几个月后,想要把成果应用到另一个目标。为了避免这种情况,建议将所有数据随机洗牌放入开发集和测试集,所以交叉集和测试集都有来自所有不同分类的数据并且开发集和测试集都来自同一分布,这个分布就是所有的数据混在一起。
123 |
124 | # 1.6 交叉验证集和测试集的大小
125 |
126 | ## 1.6.1 交叉验证集和测试集大小设置的原则
127 |
128 | 1、经验法则:把取得的所有数据划分为 **70%训练集+30%测试集** 或 **60%训练集+20%交叉验证集+20%测试集**。
129 |
130 | 这种经验法则使用于机器学习的早期,即数据集规模较小的情况下。
131 |
132 | 2、在现代机器学习中,数据集规模很大,可分为**98%训练集+1%交叉验证集+1%测试集**。
133 |
134 | 训练集的大小:深度学习算法对数据的胃口很大,故要把占更高比例的数据划分到训练集中;
135 |
136 | 测试集的大小:测试集的目的是完成系统开发后用测试集评估系统性能,故要令测试集足够大,能够以高置信度评估系统整体性能。所以除非需要对最终系统有一个很精确的指标,一般来说,测试集不需要上百万个例子,有10000或100000个大概就足够了,当数据量很大时,测试集就会远远小于数据集的30%或20%。
137 |
138 | ## 1.6.2 什么情况下可以没有测试集
139 |
140 | 对于不需要对系统性能有置信度很高的评估的应用,可以不用划分测试集,只需要训练集和交叉验证集,只要有数据去训练、有数据去调试就够了,但是并不建议在系统搭建时省略测试集,有个单独的测试集会更好,因为可以用这组不带偏差的数据来测量系统的性能,但如果交叉验证集非常大,就不会对交叉验证集过拟合得太厉害,在这种情况下只有训练集和交叉验证集也不是完全不合理。
141 |
142 | 在实际实践中,有时只把数据集划分为训练集和测试集,实际上这是在测试集上迭代,所以这里的测试集其实是交叉验证集,即只把数据分为训练集和交叉验证集,没有测试集。
143 |
144 | # 1.7 什么时候该改变交叉验证/测试集和指标
145 |
146 | ## 1.7.1 如何定义一个指标去评估分类器
147 |
148 | 评估指标的意义在于,准确告诉你已知的两个分类器哪一个更适合你的应用。
149 |
150 | 当已设定的评估指标无法正确衡量算法之间的优劣排序时,就应该改变评估指标或者改变交叉验证集或测试集。
151 |
152 | 例如,若对旧的误差指标 $Error = \frac{1}{m_{dev}} \sum_{i=1}^{m_{dev}}I[y_{pred}^{(i)}≠y^{(i)}]$ 不满意,可以尝试定义一个新的能够更加符合你的偏好的指标,从而定义出更适合的算法,如在 $I$ 项前加一个权重项 $\omega^{(i)}$,即
153 |
154 | $Error = \frac{1}{m_{dev}} \sum_{i=1}^{m_{dev}} \omega^{(i)} I[y_{pred}^{(i)}≠y^{(i)}]$
155 |
156 | 其中,
157 |
158 | $\omega^{(i)}=\left\{\begin{array}{ll}1 & \text { if } x^{(i)}... \\ 10 & \text { if } x^{(i)}...\end{array}\right.$,
159 |
160 | 当 $x^{(i)}$ 是预期分类中的数据时,赋予较小的权重1,当 $x^{(i)}$ 不是预期分类中的数据时,赋予较大的权重10,误差项迅速变大,即把非预期分类数据分类成某一类的惩罚权重加大10倍。
161 |
162 | ## 1.7.2 机器学习的两个独立步骤(正交化)
163 |
164 | 1. 设定目标:弄清楚如何定义一个指标来衡量你想做的事情的表现(**定义指标**);
165 | 2. 瞄准/射击目标:分开考虑如何改善系统在这个指标上的表现(**调整指标**以优化系统)。
166 |
167 | ## 1.7.3 需改变评价标准的情况
168 |
169 | 如果系统在当前指标、当前交叉验证集或者交叉验证集和测试集分布中表现很好,但在实际应用程序即你真正关注的地方表现不好(当前的指标和当前用来评估的数据和你真正关心必须做好的事情关系不大),就需要修改指标或交叉验证/测试集,让它们能够更好地反映算法需要处理好的数据。
170 |
171 | 举例:假设有两个猫分类器A和B,用开发集评估分别得到3%和5%的误差,做评估时用的是高质量图片的交叉验证集和测试集但在实际应用时上传的图片取景不专业,没有把猫完整拍下来或猫的表情很古怪,或者图像很模糊,在实际测试算法时可能会发现算法B比算法A更好,此时就应该修改指标或交叉验证/测试集。
172 |
173 | # 1.8为什么是人的表现
174 |
175 | 机器学习模型的准确性有两个层级,分别为
176 |
177 | 1.human-level performance(人的表现)
178 |
179 | 2.Bayes optimal error(贝叶斯最优误差)
180 |
181 | 机器学习模型表现常与人的学习表现相比较
182 |
183 | 如图,随着训练时间的不断增长,模型的准确性会不断接近“人的表现”并最终超过。当超过“人的表现”后,准确性的上升会比较缓慢,并不断靠近理想的最优情况,即贝叶斯最优误差。而实际上,“人的表现”,在许多如语音识别、图像识别的部分是非常具有优势的,让机器学习模型的准确性不断接近“人的表现”非常有必要。
184 |
185 | 1.Get labeled data from humans.
186 |
187 | 2.Gain insight from manual error analysis: Why did a person get this right?
188 |
189 | 3.Better analysis of bias/variance.
190 |
191 | 以上方法可以让模型不断接近人的表现。
192 |
193 | # 1.9可避免偏差
194 |
195 | 在实际应用中,要看human-level error,training error和dev error的相对值。例如猫类识别的例子中,
196 |
197 | 
198 |
199 |
200 |
201 | 对于物体识别这类CV问题,human-level error是很低的,很接近理想情况下的贝叶斯最优误差。因此,上面例子中的1%和7.5%都可以近似看成是两种情况下对应的bayes optimal error。实际应用中,我们一般会用human-level error代表bayes optimal error。
202 |
203 |
204 |
205 | 通常,我们把training error与human-level error之间的差值称作avoidable bias(可避免偏差);把dev error与training error之间的差值称为方差(variance)。根据bias和variance值的相对大小,可以知道算法模型是否发生了欠拟合或者过拟合。
206 |
207 | 若相比于方差(variance),bias较大,则我们对模型的调整主要在于减小偏差
208 |
209 | 若相比于方差(variance),bias较小,则可采用正则化、采集更多数据等方法减小方差
210 |
211 | # 1.10理解人的表现
212 |
213 | human-level performance有时能够代表bayes optimal error。但是,human-level performance如何定义呢?举个医学图像识别的例子,不同人群的error有所不同:
214 |
215 | 
216 |
217 | 由于bayes optimal error是最优的理想情况,一般来说,我们将表现最好的那一组,即Team of experienced doctors作为human-level performance,以此来代替bayes optimal error。
218 |
219 |
220 |
221 | 但在实际应用时,human-level performance的选择也会因人而异,不同取值的human-level performance会在一定程度上影响bias和variance的相对大小。如下图
222 |
223 |
224 |
225 | 
226 |
227 | 在方案C中,由于Training error和Development error数值差只为0.1,即variance只有0.1,此时不同取值的human-level performance会影响到bias和variance的相对大小,影响到了后续对模型的调整与改善。
228 |
229 | 而这种情况一般只在模型表现很好,接近bayes optimal error 时才会出现,此时,由于human-level performance较模糊难以定义,而影响到了模型的优化。
230 |
231 | # 1.11超过人的表现
232 |
233 | 
234 |
235 | 对于自然感知类问题,例如视觉、听觉等,机器学习的表现还不及人类。但是在很多其它方面,如
236 |
237 |
238 |
239 | - Online advertising(在线广告)
240 | - Product recommendations(产品推荐)
241 | - Logistics(predicting transit time)(预测交通时间)
242 | - Loan approvals(贷款批准)
243 |
244 | 这些方面,机器的表现优于人类。
245 |
246 | 机器学习模型超过human-level performance是比较困难的。但是如果有足够多的样本,训练更加复杂的神经网络,模型预测准确性会不断得到提高,最终接近并超过human-level performance。然而当机器模型的表现超过human-level performance时,难以直觉来继续提高算法模型性能。
247 |
248 | # 1.12改善模型表现
249 |
250 | 提高机器学习模型性能主要要解决两个问题:avoidable bias和variance。
251 |
252 | 解决avoidable bias的常用方法包括:
253 |
254 | - Train bigger model(训练更大的模型)
255 |
256 | - Train longer/better optimization algorithms: momentum, RMSprop, Adam
257 |
258 | (使用更好的算法:momentum、RMSprop、Adam)
259 |
260 | - NN architecture/hyperparameters search(选用不同的神经网络结构)
261 |
262 | 解决variance的常用方法包括:
263 |
264 | - More data(使用更多数据)
265 | - Regularization: L2, dropout, data augmentation(使用正则化方法)
266 | - NN architecture/hyperparameters search(选用不同的神经网络结构)
267 |
268 |
--------------------------------------------------------------------------------
/9 机器学习(ML)策略(2).md:
--------------------------------------------------------------------------------
1 | ## 9 机器学习(ML)策略(2)
2 |
3 | ### 9.1误差分析
4 |
5 | #### 9.1.1 定义
6 |
7 | 你希望让学习算法能够胜任人类能做的任务,但你的学习算法还没有达到人类的表现,那么人工检查一下你的算法犯的错误也许可以让你了解接下来应该做什么。**这个过程称为错误分误差**。
8 |
9 | 通过对一组错误样本进行逐一检查后,分析错误样本的类型的比例,来决定朝着哪个方向来进行优化,或者给你构思新优化方向的灵感。
10 |
11 |
12 |
13 | #### 9.1.2 举例
14 |
15 | 假设你正在调试猫分类器,注意到一些算法分类出错的例子中,算法将一些狗分类为猫,为了解决的这个问题,我们不需要,去设计一些只处理狗的算法功能之类的,为了让你的猫分类器在狗图上做的更好,让算法不再将狗分类成猫,因为这花费的时间太长了。而是需要进行误差分析,以便于决定哪一个方向值得努力。
16 |
17 | 首先,比如收集100个错误标记的开发集样本,然后手动检查,一次只看一个,看看你的开发集里有多少错误标记的样本是狗。假设100个错误标记样本中只有5%是狗这意味着100个样本,在典型的100个出错样本中,即使你完全解决了狗的问题,你也只能修正这100个错误中的5个,也就是最多只能将错误率从10%下降到9.5%,效果并不明显。但假设100个错误标记的开发集样本,你发现实际有50张图都是狗,也就是有50%都是狗的照片,现在花时间去解决狗的问题可能效果就很好,错误率可能就从10%下降到5%。
18 |
19 |
20 |
21 | #### 9.1.3 利用表格进行误差分析
22 |
23 | 当然在进行误差分析时,也可以对多个情况或者想法进行评估(比如对狗的照片错认为猫和对狮子的照片错认为猫)。有效且清晰的做法是设计一个表格来对各种错误样本进行填表式的分类,最后统计错误类型的百分比,再针对各种错误类型百分比的大小,进而决定优化的方向,同时最好在每个样本的后面增加备注,以方便进行分析。
24 |
25 | 
26 |
27 | 当然,在分类的过程中,如果发现了新的错误类型,也可以直接创建一个新的错误类型
28 |
29 |
30 |
31 |
32 |
33 | ### 9.2 清除标注错误的数据
34 |
35 | 错误的数据:结果的标签是错的。比如猫的图片被标注为不是猫。
36 |
37 | #### 9.2.1 处理标签错误的数据
38 |
39 | 1.对于总数据集总足够大,实际错误率不高的情况下:有时候放着不管也可以,并不会对训练出来的结果有太大的影响
40 |
41 | 2.对于系统性的错误:需要进行修改
42 |
43 | (实际错误率高,比如一直把白色的狗标记成猫,分类器学习之后,会把所有白色的狗都分类为猫)
44 |
45 |
46 |
47 | 总的来说,在进行误差分析后如果这些标记错误严重影响了你在开发集上评估算法的能力,那么就应该去花时间修正错误的标签。但是,如果它们没有严重影响到你用开发集评估成本偏差的能力,那么可能就不应该花宝贵的时间去处理。
48 |
49 |
50 |
51 | #### 9.2.2 分析错误数据的指标
52 |
53 | 关注整体的开发集错误率、错误标记引起的错误的数量或者百分比,最后根据标记错误引发的错误占总体总体错误率的比例来决定。(简单点说就是标记错误占所有错误的百分比的大小,该百分比越大,说明越值得修改错误标签)
54 |
55 | 比如,系统达到了90%整体准确度,所以有10%错误率,那么你应该看看错误标记引起的错误的数量或者百分比。所以在这种情况下,6%的错误来自标记出错,所以10%的6%就是0.6%。也许你应该看看其他原因导致的错误,如果你的开发集上有10%错误,其中0.6%是因为标记出错,剩下的占9.4%,是其他原因导致的。这个时候更应该考虑对9.4%进行优化或者修正。
56 |
57 | 假设你把错误率降到了2%,但总体错误中的0.6%还是标记出错导致的,此时错误标签导致的错误占总体错误的30%,那么这种情况就值得进行错误标签的修正。
58 |
59 |
60 |
61 | #### 9.2.3 修正标签的原则
62 |
63 | 1.修正标签时,都要同时作用到验证集和测试集上,也就是必须同时检查验证集和测试集,因为验证和测试集必须来自相同的分布。
64 |
65 | 2.要考虑同时检验算法判断正确和判断错误的样本,因为如果你只修正算法出错的样本,你对算法的偏差估计可能会变大,这会让你的算法有一点不公平的优势。
66 |
67 | 3.修正训练集中的标签其实相对没那么重要。
68 |
69 |
70 |
71 | 第二点不常遵循,因为一般判断正确的样本所占的比重要大得多。
72 |
73 |
74 |
75 | ### 9.3 快速搭建你的第一个系统
76 |
77 | 一般来说,对于几乎所有的机器学习程序可能会有50个不同的方向可以前进,并且每个方向都是相对合理的可以改善你的系统。所以快速设立开发集和测试集还有指标,能够确定系统迭代的方向,并且及时利用训练集对机器学习系统进行训练,再根据结果进行分析来确定下一步优先做什么。
78 |
79 |
80 |
81 | 下面以建立一个语音识别系统为例子介绍:
82 |
83 | 你可以选择很多不同的技术,让你听写下来的文本可读性更强,所以你可以做很多事情来改进语音识别系统。但对于多种方法你会感到非常迷茫,但当你建立第一个系统后,就能够进行误差分析让你了解到大部分的错误的来源是什么,比如说话人远离麦克风,那么你就有很好的理由去集中精力研究这些技术,也就是确定了你努力的方向
84 |
85 |
86 |
87 |
88 |
89 | ### 9.4 在不同的划分下进行训练并测试
90 |
91 | #### 9.4.1 划分的定义
92 |
93 | 划分即在选择数据进行训练时,将不是来自同一分布的数据进行分开,并分别作为数据集的训练集,以及数据集中的验证集和测试集(验证集和测试集得保证来自同分布)。
94 |
95 | 注:在视频中,字幕将dev set翻译为开发集,而以往的笔记中使用的命名为验证集,这里我使用验证集
96 |
97 | #### 9.4.2 为什么需要进行划分
98 |
99 | 进行划分的目的在于设定模型的优化方向,也就是“靶心”,通过将需要应用时的数据作为测试集和验证集来进行训练,保证在该模型投入应用时能够有较高的识别率。
100 |
101 | eg.在识别猫的图片的模型当中,可能会出现拥有充足且清晰的猫的图片进行模型的训练,而对于用户使用这个模型时,可能会使用模糊的照片,而专注于识别清晰照片的模型就较大的概率出现错误。并且这些模糊的照片在刚投入使用的时相较于训练模型时的清晰照片的数量少的多,如训练时清晰的照片可能有20w张,而用户的照片可能只有1w张,并不足以进行训练。
102 |
103 | 如果将清晰的照片和模糊的照片随机分布于数据集当中进行训练,则在期望上清晰的照片在测试集和验证集中的占比就会远大于模糊照片的比例,这就会导致在多次训练中,模型更加偏向于朝着清晰图片的识别的方向进行优化,而不是对用户上传的模糊照片的识别进行优化。
104 |
105 | 如果将模糊和清晰的照片进行划分,将清晰的图片作为训练集,并且将用户模糊的照片作为测试集和验证集,即把模型的优化方向设定为对用户上传的照片的识别,进而不断的提高对用户上传的照片的识别准确率。
106 |
107 |
108 |
109 | ### 9.5 不匹配数据划分上的偏差和方差
110 |
111 | 方差和偏差定义:第二门课第一周笔记
112 |
113 | #### 9.5.1 不匹配数据划分对方差和偏差的影响
114 |
115 | 以猫的识别为例,对猫的识别的最优误差几乎为0%,而如果训练集和验证集的数据并不是来自同一分布,如训练集是清晰的照片而测试集是模糊的照片,则训练集的照片容易识别,训练误差小,而验证集的照片难以识别,验证误差大,此时我们不能通过这两个误差值来判断该神经网络的方差是否真的偏大或者偏小,也就是两者的大小区别到底是训练集的数据造成的(也就是方差的问题),还是由于数据来自不同的分布而导致的(也就是数据不匹配问题)(或者两者哪个的影响更大)
116 |
117 | #### 9.5.2 训练-验证集(Training-dev set)
118 |
119 | 定义:为了解决在不匹配数据的情况下(也就是上述情况)对方差的判断,我们随机从训练集中抽取一组数据来作为新的子集,也就是训练-验证集。(此时数据集就被分为了四个部分:训练集、训练-验证集、验证集和测试集)
120 |
121 |  122 |
123 | 特点:训练-验证集和训练集来自同一分布,验证集和测试集来自同一分布。
124 |
125 | 训练-验证集并不参加训练集对模型的训练,而是和验证集参加反向传播。
126 |
127 | 训练-验证集同时也会进行误差计算,叫做训练-验证集上的误差。
128 |
129 | #### 9.5.3 不匹配数据划分下偏差、方差的判断
130 |
131 | 在引入训练-验证集之后,我们通过对训练-验证集的误差值和训练误差以及验证误差三者相结合进行判断,进而得出方差大小或者不同分布对结果影响的结论,当训练误差和训练-验证集误差相差较大时,说明方差较大,当训练-验证集误差和验证误差相差较大时,说明不同分布对结果影响较大,下面将用例子的形式进行判断。
132 |
133 | 对于偏差问题,仍然可以按照以前的方法进行判断。
134 |
135 | 不同分布对结果影响和方差较大问题是可以同时存在的。
136 |
137 | (1)训练误差:1% 训练-验证集误差:9% 验证误差:10%
138 |
139 | 训练误差和训练-验证集误差相差较大,方差较大,训练-验证集误差和验证误差相差较小,不同分布对结果影响较小。
140 |
141 | (2)训练误差:1% 训练-验证集误差:1.5% 验证误差:10%
142 |
143 | 训练误差和训练-验证集误差相差较小,方差较小,训练-验证集误差和验证误差相差较大,不同分布对结果影响较大。
144 |
145 | (3)训练误差:10% 训练-验证集误差:11% 验证误差:20%
146 |
147 | 训练误差和训练-验证集误差相差较大,方差较大,训练-验证集误差和验证误差相差较大,不同分布对结果影响较大。
148 |
149 | (4)训练误差:7% 训练-验证集误差:10% 验证误差:6%
150 |
151 | 出现这种和前三种都不同的情况说明,验证集的识别比训练集和训练-验证集这同一分布的数据的识别更加容易。
152 |
153 |
154 |
155 | **对方差,偏差,数据不匹配和过拟合的判断的总结:**
156 |
157 | (1)偏差:通过比较最优误差(人类判断误差)和训练误差大小来判断,两者相差越大,偏差越大。
158 |
159 | (2)方差:通过比较训练-验证集误差和训练误差大小来判断,两者相差越大,方差越大。
160 |
161 | (3)数据不匹配:通过比较训练-验证集误差和验证误差大小来判断,两者相差越大,数据越不匹配。
162 |
163 | (4)过拟合:通过比较验证误差和测试误差大小来判断,两者相差越大,模型就越过拟合。
164 |
165 |
166 |
167 | 对于降低方差和偏差的方法在第二门课第一周笔记有具体的讲解。
168 |
169 |
170 |
171 |
172 |
173 |
174 |
175 |
176 |
177 | ### 9.6 处理数据不匹配问题
178 |
179 | **数据不匹配问题**:训练集和开发/测试集来自不同的分布。
180 |
181 | #### 9.6.1 处理方法
182 |
183 | - 做错误分析,尝试了解训练集和开发/测试集的具体差异(比如有无噪音)。为避免对测试集过拟合,应该人工看开发集而不是测试集。
184 | - 把训练数据变得更像开发集(如人工数据合成),或收集更多类似你的开发集和测试集的数据。
185 |
186 | **人工数据合成**:
187 |
188 | 通过对不同类型的数据进行合成,产生需要使用的目的数据。
189 |
190 | 同时人工数据合成也存在问题,在合成数据时,如果选择某类数据时只使用了一小部分进行合成,也就是这类数据类型的子集,从整体的角度来看,这个子集的数据作为样本会导致过拟合的情况出现,也就是过于拟合这个子集数据的特点。而对于这个子集外的同类数据识别效果差。
191 |
192 | - 举例一:
193 |
194 | 
195 |
196 | 建立**语音识别系统**时,在需要解决汽车噪音问题情况,没有那么多实际再汽车背景噪音下录得的音频。这是可以人工合成数据。假设录制了大量清晰的音频,不带车辆背景噪音的音频后,你可以收集一段这样的汽车噪音。然后将两个音频片段放到一起,就可以合成出带有汽车噪声的语音音频。这是一个相对简单的音频合成例子。在实践中,你可能会合成其他音频效果,比如混响,就是声音从汽车内壁上反弹叠加的效果。
197 |
198 | 通过人工数据合成,你可以快速制造更多的训练数据,就像真的在车里录的那样,那就不需要花时间实际出去收集数据,比如说在实际行驶中的车子,录下上万小时的音频。所以,如果错误分析显示你应该尝试让你的数据听起来更像在车里录的,那么人工合成那种音频,然后喂给你的机器学习算法。
199 |
200 | **潜在问题**:
201 |
202 | 比如说,你在安静的背景里录得10,000 小时音频数据,然后,比如说,你只录了一小时车辆背景噪音,那么,你可以这么做,将这 1 小时汽车噪音回放 10,000 次,并叠加到在安静的背景下录得的 10,000 小时数据。如果你这么做了,人听起来这个音频没什么问题。但是有可能你的学习算法对这1 小时汽车噪音过拟合。
203 |
204 | - 举例二:
205 |
206 | 
207 |
208 | 假设你在研发无人驾驶汽车,你可能希望检测出这样的车,然后用框包住它,可以用计算机合成图像来模拟成千上万的车辆。
209 |
210 | **潜在问题:**
211 |
212 | 如果你只合成这些车中很小的子集,对于人眼来说也许这样合成图像没什么问题,但你的学习算法可能会对合成的这一个小子集过拟合。特别是很多人都独立提出了一个想法,一旦你找到一个电脑游戏,里面车辆渲染的画面很逼真,那么就可以截图,得到数量巨大的汽车图片数据集。事实证明,如果你仔细观察一个视频游戏,如果这个游戏只有 20 辆独立的车。因为你是在游戏里开车,你只看到这 20 辆车,这个模拟看起来相当逼真。但现实世界里车辆的设计可不只 20 种,如果你用着 20 量独特的车合成的照片去训练系统,那么你的神经网络很可能对这 20 辆车过拟合,但人类很难分辨出来。即使这些图像看起来很逼真,你可能真的只用了所有可能出现的车辆的很小的子集。
213 |
214 | - 故使用人工数据合成时,一定要谨慎,要记住你有可能从所有可能性的空间只选了很小一部分去模拟数据。
215 |
216 |
217 |
218 | ### 9.7 迁移学习
219 |
220 | #### **9.7.1 定义**
221 |
222 | 将一个问题上训练好的模型通过简单的调整使其适用于一个新的问题。
223 |
224 | #### **9.7.2 举例一**
225 |
226 | 假设你已经训练好一个图像识别神经网络,所以你首先用一个神经网络,并在$(𝑥, 𝑦)$对上训练,其中$𝑥$是图像,$𝑦$是某些对象的判断,图像是猫、狗、鸟或其他东西。如果你把这个神经网络拿来,然后让它适应或者说迁移,在不同任务中学到的知识,比如放射科诊断,就是说阅读𝑋射线扫描图。你可以做的是把神经网络最后的输出层拿走,就把它删掉,还有进入到最后一层的权重删掉,然后为最后一层重新赋予随机权重,然后让它在放射诊断数据上训练。
227 |
228 | 
229 |
230 | 具体来说,在第一阶段训练过程中,当你进行图像识别任务时时,你可以训练神经网络的所有常用参数,所有的权重,所有的层,然后你就得到了一个能够做图像识别预测的网络。在训练了这个神经网络后,要实现迁移学习,你现在要做的是,把数据集换成新的$(𝑥, 𝑦)$对,现在这些变成放射科图像,而$𝑦$是你想要预测的诊断,你要做的是初始化最后一层的权重,让我们称之为$w^{[L]}$和$b^{[L]}$随机初始化。
231 |
232 | 如果你重新训练神经网络中的所有参数,那么这个在图像识别数据的初期训练阶段,有时称为**预训练**(pre -training),因为你在用图像识别数据去预先初始化,或者预训练神经网络的权重。然后,如果你以后更新所有权重,然后在放射科数据上训练,有时这个过程叫**微调**(fine tuning)
233 |
234 | #### **9.7.3 举例二**
235 |
236 | 
237 |
238 | 假设你已经训练出一个语音识别系统,现在$𝑥$是音频或音频片段输入,而$𝑦$是听写文本,所以你已经训练了语音识别系统,让它输出听写文本。现在我们说你想搭建一个“唤醒词”或“触发词”检测系统,所谓唤醒词或触发词就是我们说的一句话,可以唤醒家里的语音控制设备,比如你说“Alexa”可以唤醒一个亚马逊 Echo设备,或用“OK Google”来唤醒 Google 设备,用"Hey Siri"来唤醒苹果设备,用"你好百度"唤醒一个百度设备。要做到这点,你可能需要去掉神经网络的最后一层,然后加入新的输出节点,但有时你可以不只加入一个新节点,或者甚至往你的神经网络加入几个新层,然后把唤醒词检测问题的标签$𝑦$喂进去训练。再次,这取决于你有多少数据,你可能只需要重新训练网络的新层,也许你需要重新训练神经网络中更多的层。
239 |
240 | #### **9.7.4 迁移学习有效的原因**
241 |
242 | 在例一中我们把图像识别中学到的知识应用或迁移到放射科诊断上来。有很多低层次特征,比如说边缘检测、曲线检测、阳性对象检测,**从非常大的图像识别数据库中习得这些能力可能有助于你的学习算法在放射科诊断中做得更好**,算法学到了很多结构信息,图像形状的信息,其中一些知识可能会很用,所以学会了图像识别,它就可能学到足够多的信息,可以了解不同图像的组成部分是怎样的,学到线条、点、曲线这些知识,也许对象的一小部分,这些知识有可能帮助你的放射科诊断网络学习更快一些,或者需要更少的学习数据。
243 |
244 | 对于第二个例子语音识别,也许你已经用 10,000 小时数据训练过你的语言识别系统,所以你从这10,000 小时数据学到了很多人类声音的特征,这数据量其实很多了。但对于触发字检测,也许你只有 1 小时数据,所以这数据太小,不能用来拟合很多参数。所以在这种情况下,预先学到很多人类声音的特征人类语言的组成部分等等知识,可以帮你建立一个很好的唤醒字检测器,即使你的数据集相对较小。
245 |
246 | #### **9.7.5 迁移学习起作用的场合**
247 |
248 | 1.以任务A迁移到任务B为例,任务A和任务B都有同样的输入x时,如输入都是图片
249 |
250 | 2.任务A的数据比任务B的多得多,任务A的数据才会对B有帮助。
251 |
252 | 3.任务A的低层次特征可以帮助B的学习
253 |
254 | 如果你尝试优化任务𝐵的性能,通常这个任务数据相对较少,例如,在放射科中你知道很难收集很多𝑋射线扫描图来搭建一个性能良好的放射科诊断系统,所以在这种情况下,你可能会找一个相关但不同的任务,如图像识别,其中你可能用 1 百万张图片训练过了,并从中学到很多低层次特征,所以那也许能帮助网络在任务𝐵在放射科任务上做得更好,尽管任务𝐵没有这么多数据。
255 |
256 |
257 |
258 | ### 9.8 多任务学习
259 |
260 | #### **9.8.1 定义**
261 |
262 | 让单个神经网络同时做几个任务,并且这里每个任务都能帮到其他所有任务。
263 |
264 | #### **9.8.2 举例**
265 |
266 | 假设你在研发无人驾驶车辆,那么你的无人驾驶车可能需要同时检测不同的物体,比如检测行人、车辆、停车标志,还有交通灯各种其他东西。
267 |
268 | 如果这是输入图像$𝑥^{(𝑖)}$,那么这里不再是一个标签 $y^{(𝑖)}$,而是有 4 个标签。在这个例子中,没有行人,有一辆车,有一个停车标志,没有交通灯。然后如果你尝试检测其他物体,也许 $y^{(𝑖)}$的维数会更高,现在我们就先用 4 个,所以 $y^{(𝑖)}$是个 4×1 向量。如果你从整体来看这个训练集标签和以前类似,我们将训练集的标签水平堆叠起来,像这样$y^{(1)}$一直到$y^{(m)}$:
269 | $$
270 | Y=\left[\begin{array}{ccccc}| & | & | & \ldots & | \\ y^{(1)} & y^{(2)} & y^{(3)} & \ldots & y^{(m)} \\ | & | & | & \ldots & |\end{array}\right]
271 | $$
272 | 不过现在$y^{(𝑖)}$是 4×1 向量,所以这些都是竖向的列向量,所以这个矩阵$𝑌$现在变成4 × 𝑚矩阵。而之前,当$𝑦$是单实数时,这就是1 × 𝑚矩阵。
273 |
274 | 
275 |
276 | 训练一个神经网络,来预测这些𝑦值,你就得到这样的神经网络,输入$𝑥$,现在输出是一个四维向量$𝑦$。请注意,这里输出我画了四个节点,所以第一个节点就是我们想预测图中有没有行人,然后第二个输出节点预测的是有没有车,第三个节点预测有没有停车标志,第四个节点预测有没有交通灯,所以这里$\hat{y}$是四维的。
277 |
278 | 要训练这个神经网络,你现在需要定义神经网络的损失函数,对于一个输出$\hat{y}$,是个4维向量,对于整个训练集的平均损失:
279 | $$
280 | \frac{1}{m} \sum_{i=1}^{m} \sum_{j=1}^{4} L\left(\hat{y}_{j}^{(i)}, y_{j}^{(i)}\right)
281 | $$
282 |
283 |
284 | $\sum_{j=1}^{4} L\left(\hat{y}_{j}^{(i)}, y_{j}^{(i)}\right)$是单个预测的损失,即对四个分量的求和,行人、车、停车标志、交通灯。$L$指的是logistic损失:
285 | $$
286 | L\left(\hat{y}_{j}^{(i)}, y_{j}^{(i)}\right)=-y_{j}^{(i)} \log \hat{y}_{j}^{(i)}-\left(1-y_{j}^{(i)}\right) \log \left(1-\hat{y}_{j}^{(i)}\right)
287 | $$
288 | 整个训练集的平均损失和之前分类猫的例子主要区别在于,现在你要对$𝑗 = 1$到$4$求和,这与 **softmax** 回归的主要区别在于,**softmax** 将单个标签分配给单个样本。
289 |
290 | 在这个场合,一张图可以有多个标签。如果你训练了一个神经网络,试图最小化这个成本函数,你做的就是多任务学习。因为你现在做的是建立单个神经网络,观察每张图,然后解决四个问题,系统试图告诉你,每张图里面有没有这四个物体。另外你也可以训练四个不同的神经网络,而不是训练一个网络做四件事情。但**神经网络一些早期特征,在识别不同物体时都会用到**,然后你发现,训练一个神经网络做四件事情会比训练四个完全独立的神经网络分别做四件事性能要更好,这就是多任务学习的力量。
291 |
292 |
122 |
123 | 特点:训练-验证集和训练集来自同一分布,验证集和测试集来自同一分布。
124 |
125 | 训练-验证集并不参加训练集对模型的训练,而是和验证集参加反向传播。
126 |
127 | 训练-验证集同时也会进行误差计算,叫做训练-验证集上的误差。
128 |
129 | #### 9.5.3 不匹配数据划分下偏差、方差的判断
130 |
131 | 在引入训练-验证集之后,我们通过对训练-验证集的误差值和训练误差以及验证误差三者相结合进行判断,进而得出方差大小或者不同分布对结果影响的结论,当训练误差和训练-验证集误差相差较大时,说明方差较大,当训练-验证集误差和验证误差相差较大时,说明不同分布对结果影响较大,下面将用例子的形式进行判断。
132 |
133 | 对于偏差问题,仍然可以按照以前的方法进行判断。
134 |
135 | 不同分布对结果影响和方差较大问题是可以同时存在的。
136 |
137 | (1)训练误差:1% 训练-验证集误差:9% 验证误差:10%
138 |
139 | 训练误差和训练-验证集误差相差较大,方差较大,训练-验证集误差和验证误差相差较小,不同分布对结果影响较小。
140 |
141 | (2)训练误差:1% 训练-验证集误差:1.5% 验证误差:10%
142 |
143 | 训练误差和训练-验证集误差相差较小,方差较小,训练-验证集误差和验证误差相差较大,不同分布对结果影响较大。
144 |
145 | (3)训练误差:10% 训练-验证集误差:11% 验证误差:20%
146 |
147 | 训练误差和训练-验证集误差相差较大,方差较大,训练-验证集误差和验证误差相差较大,不同分布对结果影响较大。
148 |
149 | (4)训练误差:7% 训练-验证集误差:10% 验证误差:6%
150 |
151 | 出现这种和前三种都不同的情况说明,验证集的识别比训练集和训练-验证集这同一分布的数据的识别更加容易。
152 |
153 |
154 |
155 | **对方差,偏差,数据不匹配和过拟合的判断的总结:**
156 |
157 | (1)偏差:通过比较最优误差(人类判断误差)和训练误差大小来判断,两者相差越大,偏差越大。
158 |
159 | (2)方差:通过比较训练-验证集误差和训练误差大小来判断,两者相差越大,方差越大。
160 |
161 | (3)数据不匹配:通过比较训练-验证集误差和验证误差大小来判断,两者相差越大,数据越不匹配。
162 |
163 | (4)过拟合:通过比较验证误差和测试误差大小来判断,两者相差越大,模型就越过拟合。
164 |
165 |
166 |
167 | 对于降低方差和偏差的方法在第二门课第一周笔记有具体的讲解。
168 |
169 |
170 |
171 |
172 |
173 |
174 |
175 |
176 |
177 | ### 9.6 处理数据不匹配问题
178 |
179 | **数据不匹配问题**:训练集和开发/测试集来自不同的分布。
180 |
181 | #### 9.6.1 处理方法
182 |
183 | - 做错误分析,尝试了解训练集和开发/测试集的具体差异(比如有无噪音)。为避免对测试集过拟合,应该人工看开发集而不是测试集。
184 | - 把训练数据变得更像开发集(如人工数据合成),或收集更多类似你的开发集和测试集的数据。
185 |
186 | **人工数据合成**:
187 |
188 | 通过对不同类型的数据进行合成,产生需要使用的目的数据。
189 |
190 | 同时人工数据合成也存在问题,在合成数据时,如果选择某类数据时只使用了一小部分进行合成,也就是这类数据类型的子集,从整体的角度来看,这个子集的数据作为样本会导致过拟合的情况出现,也就是过于拟合这个子集数据的特点。而对于这个子集外的同类数据识别效果差。
191 |
192 | - 举例一:
193 |
194 | 
195 |
196 | 建立**语音识别系统**时,在需要解决汽车噪音问题情况,没有那么多实际再汽车背景噪音下录得的音频。这是可以人工合成数据。假设录制了大量清晰的音频,不带车辆背景噪音的音频后,你可以收集一段这样的汽车噪音。然后将两个音频片段放到一起,就可以合成出带有汽车噪声的语音音频。这是一个相对简单的音频合成例子。在实践中,你可能会合成其他音频效果,比如混响,就是声音从汽车内壁上反弹叠加的效果。
197 |
198 | 通过人工数据合成,你可以快速制造更多的训练数据,就像真的在车里录的那样,那就不需要花时间实际出去收集数据,比如说在实际行驶中的车子,录下上万小时的音频。所以,如果错误分析显示你应该尝试让你的数据听起来更像在车里录的,那么人工合成那种音频,然后喂给你的机器学习算法。
199 |
200 | **潜在问题**:
201 |
202 | 比如说,你在安静的背景里录得10,000 小时音频数据,然后,比如说,你只录了一小时车辆背景噪音,那么,你可以这么做,将这 1 小时汽车噪音回放 10,000 次,并叠加到在安静的背景下录得的 10,000 小时数据。如果你这么做了,人听起来这个音频没什么问题。但是有可能你的学习算法对这1 小时汽车噪音过拟合。
203 |
204 | - 举例二:
205 |
206 | 
207 |
208 | 假设你在研发无人驾驶汽车,你可能希望检测出这样的车,然后用框包住它,可以用计算机合成图像来模拟成千上万的车辆。
209 |
210 | **潜在问题:**
211 |
212 | 如果你只合成这些车中很小的子集,对于人眼来说也许这样合成图像没什么问题,但你的学习算法可能会对合成的这一个小子集过拟合。特别是很多人都独立提出了一个想法,一旦你找到一个电脑游戏,里面车辆渲染的画面很逼真,那么就可以截图,得到数量巨大的汽车图片数据集。事实证明,如果你仔细观察一个视频游戏,如果这个游戏只有 20 辆独立的车。因为你是在游戏里开车,你只看到这 20 辆车,这个模拟看起来相当逼真。但现实世界里车辆的设计可不只 20 种,如果你用着 20 量独特的车合成的照片去训练系统,那么你的神经网络很可能对这 20 辆车过拟合,但人类很难分辨出来。即使这些图像看起来很逼真,你可能真的只用了所有可能出现的车辆的很小的子集。
213 |
214 | - 故使用人工数据合成时,一定要谨慎,要记住你有可能从所有可能性的空间只选了很小一部分去模拟数据。
215 |
216 |
217 |
218 | ### 9.7 迁移学习
219 |
220 | #### **9.7.1 定义**
221 |
222 | 将一个问题上训练好的模型通过简单的调整使其适用于一个新的问题。
223 |
224 | #### **9.7.2 举例一**
225 |
226 | 假设你已经训练好一个图像识别神经网络,所以你首先用一个神经网络,并在$(𝑥, 𝑦)$对上训练,其中$𝑥$是图像,$𝑦$是某些对象的判断,图像是猫、狗、鸟或其他东西。如果你把这个神经网络拿来,然后让它适应或者说迁移,在不同任务中学到的知识,比如放射科诊断,就是说阅读𝑋射线扫描图。你可以做的是把神经网络最后的输出层拿走,就把它删掉,还有进入到最后一层的权重删掉,然后为最后一层重新赋予随机权重,然后让它在放射诊断数据上训练。
227 |
228 | 
229 |
230 | 具体来说,在第一阶段训练过程中,当你进行图像识别任务时时,你可以训练神经网络的所有常用参数,所有的权重,所有的层,然后你就得到了一个能够做图像识别预测的网络。在训练了这个神经网络后,要实现迁移学习,你现在要做的是,把数据集换成新的$(𝑥, 𝑦)$对,现在这些变成放射科图像,而$𝑦$是你想要预测的诊断,你要做的是初始化最后一层的权重,让我们称之为$w^{[L]}$和$b^{[L]}$随机初始化。
231 |
232 | 如果你重新训练神经网络中的所有参数,那么这个在图像识别数据的初期训练阶段,有时称为**预训练**(pre -training),因为你在用图像识别数据去预先初始化,或者预训练神经网络的权重。然后,如果你以后更新所有权重,然后在放射科数据上训练,有时这个过程叫**微调**(fine tuning)
233 |
234 | #### **9.7.3 举例二**
235 |
236 | 
237 |
238 | 假设你已经训练出一个语音识别系统,现在$𝑥$是音频或音频片段输入,而$𝑦$是听写文本,所以你已经训练了语音识别系统,让它输出听写文本。现在我们说你想搭建一个“唤醒词”或“触发词”检测系统,所谓唤醒词或触发词就是我们说的一句话,可以唤醒家里的语音控制设备,比如你说“Alexa”可以唤醒一个亚马逊 Echo设备,或用“OK Google”来唤醒 Google 设备,用"Hey Siri"来唤醒苹果设备,用"你好百度"唤醒一个百度设备。要做到这点,你可能需要去掉神经网络的最后一层,然后加入新的输出节点,但有时你可以不只加入一个新节点,或者甚至往你的神经网络加入几个新层,然后把唤醒词检测问题的标签$𝑦$喂进去训练。再次,这取决于你有多少数据,你可能只需要重新训练网络的新层,也许你需要重新训练神经网络中更多的层。
239 |
240 | #### **9.7.4 迁移学习有效的原因**
241 |
242 | 在例一中我们把图像识别中学到的知识应用或迁移到放射科诊断上来。有很多低层次特征,比如说边缘检测、曲线检测、阳性对象检测,**从非常大的图像识别数据库中习得这些能力可能有助于你的学习算法在放射科诊断中做得更好**,算法学到了很多结构信息,图像形状的信息,其中一些知识可能会很用,所以学会了图像识别,它就可能学到足够多的信息,可以了解不同图像的组成部分是怎样的,学到线条、点、曲线这些知识,也许对象的一小部分,这些知识有可能帮助你的放射科诊断网络学习更快一些,或者需要更少的学习数据。
243 |
244 | 对于第二个例子语音识别,也许你已经用 10,000 小时数据训练过你的语言识别系统,所以你从这10,000 小时数据学到了很多人类声音的特征,这数据量其实很多了。但对于触发字检测,也许你只有 1 小时数据,所以这数据太小,不能用来拟合很多参数。所以在这种情况下,预先学到很多人类声音的特征人类语言的组成部分等等知识,可以帮你建立一个很好的唤醒字检测器,即使你的数据集相对较小。
245 |
246 | #### **9.7.5 迁移学习起作用的场合**
247 |
248 | 1.以任务A迁移到任务B为例,任务A和任务B都有同样的输入x时,如输入都是图片
249 |
250 | 2.任务A的数据比任务B的多得多,任务A的数据才会对B有帮助。
251 |
252 | 3.任务A的低层次特征可以帮助B的学习
253 |
254 | 如果你尝试优化任务𝐵的性能,通常这个任务数据相对较少,例如,在放射科中你知道很难收集很多𝑋射线扫描图来搭建一个性能良好的放射科诊断系统,所以在这种情况下,你可能会找一个相关但不同的任务,如图像识别,其中你可能用 1 百万张图片训练过了,并从中学到很多低层次特征,所以那也许能帮助网络在任务𝐵在放射科任务上做得更好,尽管任务𝐵没有这么多数据。
255 |
256 |
257 |
258 | ### 9.8 多任务学习
259 |
260 | #### **9.8.1 定义**
261 |
262 | 让单个神经网络同时做几个任务,并且这里每个任务都能帮到其他所有任务。
263 |
264 | #### **9.8.2 举例**
265 |
266 | 假设你在研发无人驾驶车辆,那么你的无人驾驶车可能需要同时检测不同的物体,比如检测行人、车辆、停车标志,还有交通灯各种其他东西。
267 |
268 | 如果这是输入图像$𝑥^{(𝑖)}$,那么这里不再是一个标签 $y^{(𝑖)}$,而是有 4 个标签。在这个例子中,没有行人,有一辆车,有一个停车标志,没有交通灯。然后如果你尝试检测其他物体,也许 $y^{(𝑖)}$的维数会更高,现在我们就先用 4 个,所以 $y^{(𝑖)}$是个 4×1 向量。如果你从整体来看这个训练集标签和以前类似,我们将训练集的标签水平堆叠起来,像这样$y^{(1)}$一直到$y^{(m)}$:
269 | $$
270 | Y=\left[\begin{array}{ccccc}| & | & | & \ldots & | \\ y^{(1)} & y^{(2)} & y^{(3)} & \ldots & y^{(m)} \\ | & | & | & \ldots & |\end{array}\right]
271 | $$
272 | 不过现在$y^{(𝑖)}$是 4×1 向量,所以这些都是竖向的列向量,所以这个矩阵$𝑌$现在变成4 × 𝑚矩阵。而之前,当$𝑦$是单实数时,这就是1 × 𝑚矩阵。
273 |
274 | 
275 |
276 | 训练一个神经网络,来预测这些𝑦值,你就得到这样的神经网络,输入$𝑥$,现在输出是一个四维向量$𝑦$。请注意,这里输出我画了四个节点,所以第一个节点就是我们想预测图中有没有行人,然后第二个输出节点预测的是有没有车,第三个节点预测有没有停车标志,第四个节点预测有没有交通灯,所以这里$\hat{y}$是四维的。
277 |
278 | 要训练这个神经网络,你现在需要定义神经网络的损失函数,对于一个输出$\hat{y}$,是个4维向量,对于整个训练集的平均损失:
279 | $$
280 | \frac{1}{m} \sum_{i=1}^{m} \sum_{j=1}^{4} L\left(\hat{y}_{j}^{(i)}, y_{j}^{(i)}\right)
281 | $$
282 |
283 |
284 | $\sum_{j=1}^{4} L\left(\hat{y}_{j}^{(i)}, y_{j}^{(i)}\right)$是单个预测的损失,即对四个分量的求和,行人、车、停车标志、交通灯。$L$指的是logistic损失:
285 | $$
286 | L\left(\hat{y}_{j}^{(i)}, y_{j}^{(i)}\right)=-y_{j}^{(i)} \log \hat{y}_{j}^{(i)}-\left(1-y_{j}^{(i)}\right) \log \left(1-\hat{y}_{j}^{(i)}\right)
287 | $$
288 | 整个训练集的平均损失和之前分类猫的例子主要区别在于,现在你要对$𝑗 = 1$到$4$求和,这与 **softmax** 回归的主要区别在于,**softmax** 将单个标签分配给单个样本。
289 |
290 | 在这个场合,一张图可以有多个标签。如果你训练了一个神经网络,试图最小化这个成本函数,你做的就是多任务学习。因为你现在做的是建立单个神经网络,观察每张图,然后解决四个问题,系统试图告诉你,每张图里面有没有这四个物体。另外你也可以训练四个不同的神经网络,而不是训练一个网络做四件事情。但**神经网络一些早期特征,在识别不同物体时都会用到**,然后你发现,训练一个神经网络做四件事情会比训练四个完全独立的神经网络分别做四件事性能要更好,这就是多任务学习的力量。
291 |
292 |  293 |
294 | 多任务学习也**可以处理图像只有部分物体被标记的情况**。所以第一个训练样本,我们说有人,给数据贴标签的人告诉你里面有一个行人,没有车,但他们没有标记是否有停车标志,或者是否有交通灯。也许第二个例子中,有行人,有车。但是,当标记人看着那张图片时,他们没有加标签,没有标记是否有停车标志,是否有交通灯等等。也许有些样本都有标记,但也许有些样本他们只标记了有没有车,然后还有一些是问号。
295 |
296 | 即使是这样的数据集,你也可以在上面训练算法,同时做四个任务,即使一些图像只有一小部分标签,其他是问号或者不管是什么。然后你训练算法的方式,即使这里有些标签是问号,或者没有标记,这就是对𝑗从 1 到 4 求和,你就只对带 0 和 1 标签的$𝑗$值求和,所以当有问号的时候,你就在求和时忽略那个项,这样只对有标签的值求和,于是你就能利用这样的数据集。
297 |
298 | #### **9.8.3 和迁移学习的不同**
299 |
300 | 多任务学习是一种迁移学习的方法,但不同于其他种类的迁移学习,多任务学习并不注重源领域和未知领域的知识迁移,它主要利用域之间相似的知识信息,提升特定任务的学习效果,注重领域知识的共享性。两者特点的不同决定了学习过程的差别,迁移学习的目的是通过从源任务中转移知识来提升目标任务中的性能,而多任务学习则试图同时学习目标任务和源任务。
301 |
302 | 参考文章:张钰,刘建伟,左信.多任务学习[J].计算机学报,2020,43(07):1340-1378.
303 |
304 | #### **9.8.4 多任务学习使用场合**
305 |
306 | - **你训练的一组任务,可以共用低层次的特征。**
307 |
308 | 对于无人驾驶的例子,同时识别交通灯、汽车和行人是有道理的,这些物体有相似的特征,也许能帮你识别停车标志,因为这些都是道路上的特征。
309 |
310 | - **每个任务的数据量很接近。**
311 |
312 | 这个准则不一定对。
313 |
314 | 在多任务学习中,你通常有更多任务而不仅仅是两个,所以也许你有,以前我们有 4个任务,但比如说你要完成 100 个任务,而你要做多任务学习,尝试同时识别 100 种不同类型的物体。你可能会发现,每个任务大概有 1000 个样本。所以如果你专注加强单个任务的性能,比如我们专注加强第 100 个任务的表现,我们用𝐴100表示,如果你试图单独去做这个最后的任务,你只有 1000 个样本去训练这个任务,这是 100 项任务之一,而通过在其他99 项任务的训练,这些加起来可以一共有 99000 个样本,这可能大幅提升算法性能,可以提供很多知识来增强这个任务的性能。不然对于任务𝐴100,只有 1000 个样本的训练集,效果可能会很差。如果有对称性,这其他 99 个任务,也许能提供一些数据或提供一些知识来帮到这 100 个任务中的每一个任务。
315 |
316 | 所以第二点不是绝对正确的准则,但我通常会看的是如果你专注于单项任务,如果想要从多任务学习得到很大性能提升,那么其他任务加起来必须要有比单个任务大得多的数据量。要满足这个条件,其中一种方法是,比如右边这个例子这样,或者如果每个任务中的数据量很相近,但关键在于,如果对于单个任务你已经有 1000个样本了,那么对于所有其他任务,你最好有超过 1000 个样本,这样其他任务的知识才能帮你改善这个任务的性能。
317 |
318 | - **当你可以训练一个足够大的神经网络,同时做好所有工作。**
319 |
320 | 多任务学习的替代方法是为每个任务训练一个单独的神经网络。所以不是训练单个神经网络同时处理行人、汽车、停车标志和交通灯检测。你可以训练一个用于行人检测的神经网络,一个用于汽车检测的神经网络,一个用于停车标志检测的神经网络和一个用于交通信号灯检测的神经网络。
321 |
322 | 多任务学习会降低性能的唯一情况,和训练单个神经网络相比性能更低的情况就是你的神经网络还不够大。但如果你可以训练一个足够大的神经网络,那么多任务学习肯定不会或者很少会降低性能,我们都希望它可以提升性能,比单独训练神经网络来单独完成各个任务性能要更好。
323 |
324 |
325 |
326 | (Life long learning)
327 |
328 |
329 |
330 | ### 9.9 什么是端到端的深入学习
331 |
332 | #### 9.9.1 端到端学习定义
333 |
334 | 以往对于一次任务可能需要分解成多个阶段的学习(流水线),端到端的深度学习用单个神经网络替换多个学习过程,只需要把训练集拿过来,直接学到$x$和$y$之间的函数映射,绕过了其中很多步骤。
335 | 下图以语音识别为例,进行两者间的对比。
336 |
337 | 
338 |
339 | 端到端的深入学习需要大量数据,如果数据量较小,以往的流水线可能会好于端到端的深度学习。
340 |
341 | #### 9.9.2 端到端学习应用场景
342 |
343 | - 例子一:在人脸识别任务中,端到端的深度学习并不能很好的完成任务,而以往的分步识别效果更佳,先识别人脸位置,随后和数据库进行人脸比对,因为分解到两个任务后可以对每个任务进行有效处理。
344 |
345 | - 例子二:机器翻译,端到端深度学习在机器翻译领域非常好用,可以收集大量成对的大数据集,如原文句子和对应的翻译。
346 |
347 | - 例子三:从手部X射线图估计孩子年龄,拆分任务效果更好,分析知道不同骨骼的长度后,可以查表查到儿童手中骨头的平均长度。而端到端的深度学习并未取得很好的效果,因为没有足够的数据来用端到端的方式来训练这个任务。
348 |
349 |
350 |
351 |
352 | ### 9.10 是否要使用端到端学习
353 |
354 | 当决定是否使用端对端方法时,可以参考端到端深度学习的一些优缺点来进行判断。
355 |
356 | #### 9.10.1 端对端方法的优点
357 |
358 | 1. 可以让数据说话,挖掘客观信息,不用引入人类的成见。
359 |
360 | 例如,在语音识别领域,人类学习的音位概念更像是是人类语言学家生造出来的。而学习算法不会强迫以音位为单位思考,它能够学习的任意的表示方式。
361 |
362 | 2. 需要手工设计的组件很少,也许能够简化设计工作流程。我们只需要把训练集拿过来,直接学到$x$和$y$之间的函数映射,绕过了其中很多步骤。
363 |
364 | #### 9.10.2 端对端方法的缺点
365 |
366 | 1. 需要大量的数据。
367 |
368 | 比如人脸识别,需要收集很多数据用来分辨图像中的人脸。但是对于整个端到端任务,可能只有更少的数据可用。
369 |
370 | 2. 排除了一些可能有用的人工组件。因为直接从系统的一端学习到系统的另一端,舍弃了人类对这个问题的很多认识。
371 |
372 | 比如,把手的X射线照片直接映射到孩子的年龄,可能需要很复杂的函数,如果用纯端到端方法,也需要大量数据去学习。
373 |
374 | **可以看出,决定是否要使用端到端深度学习的主要因素是是否有足够的数据来训练。**复杂问题有时候并不适合端到端,人类的意见还是很有必要的,手工设计的组件往往在训练集更小的时候帮助更大。
--------------------------------------------------------------------------------
/README.md:
--------------------------------------------------------------------------------
1 | # Deep-Learning-Tutorial
2 | 介绍一些有关深度学习的基础知识点,主要内容来自吴恩达老师的机器学习课程
3 | 后面会不定期更新
4 |
5 |
--------------------------------------------------------------------------------
293 |
294 | 多任务学习也**可以处理图像只有部分物体被标记的情况**。所以第一个训练样本,我们说有人,给数据贴标签的人告诉你里面有一个行人,没有车,但他们没有标记是否有停车标志,或者是否有交通灯。也许第二个例子中,有行人,有车。但是,当标记人看着那张图片时,他们没有加标签,没有标记是否有停车标志,是否有交通灯等等。也许有些样本都有标记,但也许有些样本他们只标记了有没有车,然后还有一些是问号。
295 |
296 | 即使是这样的数据集,你也可以在上面训练算法,同时做四个任务,即使一些图像只有一小部分标签,其他是问号或者不管是什么。然后你训练算法的方式,即使这里有些标签是问号,或者没有标记,这就是对𝑗从 1 到 4 求和,你就只对带 0 和 1 标签的$𝑗$值求和,所以当有问号的时候,你就在求和时忽略那个项,这样只对有标签的值求和,于是你就能利用这样的数据集。
297 |
298 | #### **9.8.3 和迁移学习的不同**
299 |
300 | 多任务学习是一种迁移学习的方法,但不同于其他种类的迁移学习,多任务学习并不注重源领域和未知领域的知识迁移,它主要利用域之间相似的知识信息,提升特定任务的学习效果,注重领域知识的共享性。两者特点的不同决定了学习过程的差别,迁移学习的目的是通过从源任务中转移知识来提升目标任务中的性能,而多任务学习则试图同时学习目标任务和源任务。
301 |
302 | 参考文章:张钰,刘建伟,左信.多任务学习[J].计算机学报,2020,43(07):1340-1378.
303 |
304 | #### **9.8.4 多任务学习使用场合**
305 |
306 | - **你训练的一组任务,可以共用低层次的特征。**
307 |
308 | 对于无人驾驶的例子,同时识别交通灯、汽车和行人是有道理的,这些物体有相似的特征,也许能帮你识别停车标志,因为这些都是道路上的特征。
309 |
310 | - **每个任务的数据量很接近。**
311 |
312 | 这个准则不一定对。
313 |
314 | 在多任务学习中,你通常有更多任务而不仅仅是两个,所以也许你有,以前我们有 4个任务,但比如说你要完成 100 个任务,而你要做多任务学习,尝试同时识别 100 种不同类型的物体。你可能会发现,每个任务大概有 1000 个样本。所以如果你专注加强单个任务的性能,比如我们专注加强第 100 个任务的表现,我们用𝐴100表示,如果你试图单独去做这个最后的任务,你只有 1000 个样本去训练这个任务,这是 100 项任务之一,而通过在其他99 项任务的训练,这些加起来可以一共有 99000 个样本,这可能大幅提升算法性能,可以提供很多知识来增强这个任务的性能。不然对于任务𝐴100,只有 1000 个样本的训练集,效果可能会很差。如果有对称性,这其他 99 个任务,也许能提供一些数据或提供一些知识来帮到这 100 个任务中的每一个任务。
315 |
316 | 所以第二点不是绝对正确的准则,但我通常会看的是如果你专注于单项任务,如果想要从多任务学习得到很大性能提升,那么其他任务加起来必须要有比单个任务大得多的数据量。要满足这个条件,其中一种方法是,比如右边这个例子这样,或者如果每个任务中的数据量很相近,但关键在于,如果对于单个任务你已经有 1000个样本了,那么对于所有其他任务,你最好有超过 1000 个样本,这样其他任务的知识才能帮你改善这个任务的性能。
317 |
318 | - **当你可以训练一个足够大的神经网络,同时做好所有工作。**
319 |
320 | 多任务学习的替代方法是为每个任务训练一个单独的神经网络。所以不是训练单个神经网络同时处理行人、汽车、停车标志和交通灯检测。你可以训练一个用于行人检测的神经网络,一个用于汽车检测的神经网络,一个用于停车标志检测的神经网络和一个用于交通信号灯检测的神经网络。
321 |
322 | 多任务学习会降低性能的唯一情况,和训练单个神经网络相比性能更低的情况就是你的神经网络还不够大。但如果你可以训练一个足够大的神经网络,那么多任务学习肯定不会或者很少会降低性能,我们都希望它可以提升性能,比单独训练神经网络来单独完成各个任务性能要更好。
323 |
324 |
325 |
326 | (Life long learning)
327 |
328 |
329 |
330 | ### 9.9 什么是端到端的深入学习
331 |
332 | #### 9.9.1 端到端学习定义
333 |
334 | 以往对于一次任务可能需要分解成多个阶段的学习(流水线),端到端的深度学习用单个神经网络替换多个学习过程,只需要把训练集拿过来,直接学到$x$和$y$之间的函数映射,绕过了其中很多步骤。
335 | 下图以语音识别为例,进行两者间的对比。
336 |
337 | 
338 |
339 | 端到端的深入学习需要大量数据,如果数据量较小,以往的流水线可能会好于端到端的深度学习。
340 |
341 | #### 9.9.2 端到端学习应用场景
342 |
343 | - 例子一:在人脸识别任务中,端到端的深度学习并不能很好的完成任务,而以往的分步识别效果更佳,先识别人脸位置,随后和数据库进行人脸比对,因为分解到两个任务后可以对每个任务进行有效处理。
344 |
345 | - 例子二:机器翻译,端到端深度学习在机器翻译领域非常好用,可以收集大量成对的大数据集,如原文句子和对应的翻译。
346 |
347 | - 例子三:从手部X射线图估计孩子年龄,拆分任务效果更好,分析知道不同骨骼的长度后,可以查表查到儿童手中骨头的平均长度。而端到端的深度学习并未取得很好的效果,因为没有足够的数据来用端到端的方式来训练这个任务。
348 |
349 |
350 |
351 |
352 | ### 9.10 是否要使用端到端学习
353 |
354 | 当决定是否使用端对端方法时,可以参考端到端深度学习的一些优缺点来进行判断。
355 |
356 | #### 9.10.1 端对端方法的优点
357 |
358 | 1. 可以让数据说话,挖掘客观信息,不用引入人类的成见。
359 |
360 | 例如,在语音识别领域,人类学习的音位概念更像是是人类语言学家生造出来的。而学习算法不会强迫以音位为单位思考,它能够学习的任意的表示方式。
361 |
362 | 2. 需要手工设计的组件很少,也许能够简化设计工作流程。我们只需要把训练集拿过来,直接学到$x$和$y$之间的函数映射,绕过了其中很多步骤。
363 |
364 | #### 9.10.2 端对端方法的缺点
365 |
366 | 1. 需要大量的数据。
367 |
368 | 比如人脸识别,需要收集很多数据用来分辨图像中的人脸。但是对于整个端到端任务,可能只有更少的数据可用。
369 |
370 | 2. 排除了一些可能有用的人工组件。因为直接从系统的一端学习到系统的另一端,舍弃了人类对这个问题的很多认识。
371 |
372 | 比如,把手的X射线照片直接映射到孩子的年龄,可能需要很复杂的函数,如果用纯端到端方法,也需要大量数据去学习。
373 |
374 | **可以看出,决定是否要使用端到端深度学习的主要因素是是否有足够的数据来训练。**复杂问题有时候并不适合端到端,人类的意见还是很有必要的,手工设计的组件往往在训练集更小的时候帮助更大。
--------------------------------------------------------------------------------
/README.md:
--------------------------------------------------------------------------------
1 | # Deep-Learning-Tutorial
2 | 介绍一些有关深度学习的基础知识点,主要内容来自吴恩达老师的机器学习课程
3 | 后面会不定期更新
4 |
5 |
--------------------------------------------------------------------------------
 16 |
17 | one-hot表征的缺点:这种方法将每个词孤立起来,使得模型对相关词的泛化能力不强。每个词向量之间的距离都一样,乘积均为0,所以无法获取词与词之间的相似性和关联性。
18 |
19 | #### 15.1.3 特征表征:词嵌入
20 |
21 | 用不同的特征来对各个词汇进行表征,相对与不同的特征,不同的单词均有不同的值。如下例所示:
22 |
23 |
16 |
17 | one-hot表征的缺点:这种方法将每个词孤立起来,使得模型对相关词的泛化能力不强。每个词向量之间的距离都一样,乘积均为0,所以无法获取词与词之间的相似性和关联性。
18 |
19 | #### 15.1.3 特征表征:词嵌入
20 |
21 | 用不同的特征来对各个词汇进行表征,相对与不同的特征,不同的单词均有不同的值。如下例所示:
22 |
23 |  24 |
25 | 这种表征方式使得词与词之间的相似性很容易地表征出来,这样对于不同的单词,模型的泛化性能会好很多。下面是使用t-SNE算法将高维的词向量映射到2维空间,进而对词向量进行可视化,很明显我们可以看出对于相似的词总是聚集在一块儿:
26 |
27 |
24 |
25 | 这种表征方式使得词与词之间的相似性很容易地表征出来,这样对于不同的单词,模型的泛化性能会好很多。下面是使用t-SNE算法将高维的词向量映射到2维空间,进而对词向量进行可视化,很明显我们可以看出对于相似的词总是聚集在一块儿:
26 |
27 |  28 |
29 | #### 15.1.4 编码原则
30 |
31 | 词嵌入本质就是对自然语言的一种编码方式,那自然也需要考虑一些编码原则。下列给出一些常见的编码原则:
32 |
33 | * **最佳编码**:平均编码长度最小,用最少的内存表达相同的内容,尽可能逼近香农极限。比如让出现频率高的编码更短,出现频率低的编码更长。
34 | * **正交**:用多维向量进行编码,且各维相互正交。比如PCA。
35 | * **无偏见**:在词嵌入中,有时候会学到一些带有偏见的知识。因此如何消除这个偏见也是很重要的。
36 |
37 | ### 15.2 使用词嵌入
38 |
39 | Word Embeddings对不同单词进行了实现了特征化的表示,那么如何将这种表示方法应用到自然语言处理的应用中呢?
40 |
41 | #### **15.2.1 名字实体识别的例子:**
42 |
43 | 如下面的一个句子中名字实体的定位识别问题,假如我们有一个比较小的数据集,可能不包含durain(榴莲)和cultivator(培育家)这样的词汇,那么我们就很难从包含这两个词汇的句子中识别名字实体。但是如果我们从网上的其他地方获取了一个学习好的word Embedding,它将告诉我们榴莲是一种水果,并且培育家和农民相似,那么我们就有可能从我们少量的训练集中,归纳出没有见过的词汇中的名字实体。
44 |
45 |
28 |
29 | #### 15.1.4 编码原则
30 |
31 | 词嵌入本质就是对自然语言的一种编码方式,那自然也需要考虑一些编码原则。下列给出一些常见的编码原则:
32 |
33 | * **最佳编码**:平均编码长度最小,用最少的内存表达相同的内容,尽可能逼近香农极限。比如让出现频率高的编码更短,出现频率低的编码更长。
34 | * **正交**:用多维向量进行编码,且各维相互正交。比如PCA。
35 | * **无偏见**:在词嵌入中,有时候会学到一些带有偏见的知识。因此如何消除这个偏见也是很重要的。
36 |
37 | ### 15.2 使用词嵌入
38 |
39 | Word Embeddings对不同单词进行了实现了特征化的表示,那么如何将这种表示方法应用到自然语言处理的应用中呢?
40 |
41 | #### **15.2.1 名字实体识别的例子:**
42 |
43 | 如下面的一个句子中名字实体的定位识别问题,假如我们有一个比较小的数据集,可能不包含durain(榴莲)和cultivator(培育家)这样的词汇,那么我们就很难从包含这两个词汇的句子中识别名字实体。但是如果我们从网上的其他地方获取了一个学习好的word Embedding,它将告诉我们榴莲是一种水果,并且培育家和农民相似,那么我们就有可能从我们少量的训练集中,归纳出没有见过的词汇中的名字实体。
44 |
45 |  46 |
47 | #### **15.2.2 词嵌入的迁移学习:**
48 |
49 | 有了词嵌入,就可以让我们能够使用迁移学习,通过网上大量的无标签的文本中学习到的知识,应用到我们少量文本训练集的任务中。下面是做词嵌入迁移学习的步骤:
50 |
51 | - 第一步:从大量的文本集合中学习word Embeddings(1-100B words),或者从网上下载预训练好的词嵌入模型;
52 | - 第二步:将词嵌入模型迁移到我们小训练集的新任务上;
53 | - 第三步:可选,使用我们新的标记数据对词嵌入模型继续进行微调。
54 |
55 | #### **15.2.3 词嵌入和人脸编码:**
56 |
57 | 词嵌入和人脸编码之间有很奇妙的联系。在人脸识别领域,我们会将人脸图片预编码成不同的编码向量,以表示不同的人脸,进而在识别的过程中使用编码来进行比对识别。词嵌入则和人脸编码有一定的相似性。
58 |
59 |
46 |
47 | #### **15.2.2 词嵌入的迁移学习:**
48 |
49 | 有了词嵌入,就可以让我们能够使用迁移学习,通过网上大量的无标签的文本中学习到的知识,应用到我们少量文本训练集的任务中。下面是做词嵌入迁移学习的步骤:
50 |
51 | - 第一步:从大量的文本集合中学习word Embeddings(1-100B words),或者从网上下载预训练好的词嵌入模型;
52 | - 第二步:将词嵌入模型迁移到我们小训练集的新任务上;
53 | - 第三步:可选,使用我们新的标记数据对词嵌入模型继续进行微调。
54 |
55 | #### **15.2.3 词嵌入和人脸编码:**
56 |
57 | 词嵌入和人脸编码之间有很奇妙的联系。在人脸识别领域,我们会将人脸图片预编码成不同的编码向量,以表示不同的人脸,进而在识别的过程中使用编码来进行比对识别。词嵌入则和人脸编码有一定的相似性。
58 |
59 |  60 |
61 | 但是不同的是,对于人脸识别,我们可以将任意一个没有见过的人脸照片输入到我们构建的网络中,则可输出一个对应的人脸编码。而在词嵌入模型中,所有词汇的编码是在一个固定的词汇表中进行学习单词的编码以及其之间的关系的。
62 |
63 | ### 15.3 词嵌入的特性
64 |
65 | #### **15.3.1 类比推理特性:**
66 |
67 | 词嵌入还有一个重要的特性,它还能够帮助实现类比推理。如下面的例子中,通过不同词向量之间的相减计算,可以发现不同词之间的类比关系,man——woman、king——queen,如下图所示:
68 |
69 |
60 |
61 | 但是不同的是,对于人脸识别,我们可以将任意一个没有见过的人脸照片输入到我们构建的网络中,则可输出一个对应的人脸编码。而在词嵌入模型中,所有词汇的编码是在一个固定的词汇表中进行学习单词的编码以及其之间的关系的。
62 |
63 | ### 15.3 词嵌入的特性
64 |
65 | #### **15.3.1 类比推理特性:**
66 |
67 | 词嵌入还有一个重要的特性,它还能够帮助实现类比推理。如下面的例子中,通过不同词向量之间的相减计算,可以发现不同词之间的类比关系,man——woman、king——queen,如下图所示:
68 |
69 |  70 |
71 | 这种思想帮助研究者们对词嵌入建立了更加深刻的理解和认识。
72 |
73 | 计算词与词之间的相似度,实际上是在多维空间中,寻找词向量之间各个维度的距离相似度。
74 |
75 |
70 |
71 | 这种思想帮助研究者们对词嵌入建立了更加深刻的理解和认识。
72 |
73 | 计算词与词之间的相似度,实际上是在多维空间中,寻找词向量之间各个维度的距离相似度。
74 |
75 |  76 |
77 | #### **15.3.2 相似度函数:**
78 |
79 | - 曼哈顿距离(Manhattan Distance)
80 |
81 | 顾名思义,在曼哈顿街区要从一个十字路口开车到另一个十字路口,驾驶距离显然不是两点间的直线距离。这个实际驾驶距离就是“曼哈顿距离”。曼哈顿距离也称为“城市街区距离”(City Block distance)。
82 |
83 | 
84 |
85 | * 二维平面两点a(x1,y1)与b(x2,y2)间的曼哈顿距离:
86 |
87 | $$
88 | d_{12}=\left|x_{1}-x_{2}\right|+\left|y_{1}-y_{2}\right|
89 | $$
90 |
91 | - n维空间点a(x11,x12,…,x1n)与b(x21,x22,…,x2n)的曼哈顿距离:
92 | $$
93 | \mathrm{d}_{12}=\sum_{k=1}^{n}\left|\mathrm{x}_{1 k}-x_{2 k}\right|
94 | $$
95 |
96 |
97 | - 切比雪夫距离 (Chebyshev Distance)
98 |
99 | 国际象棋中,国王可以直行、横行、斜行,所以国王走一步可以移动到相邻8个方格中的任意一个。国王从格子(x1,y1)走到格子(x2,y2)最少需要多少步?这个距离就叫切比雪夫距离。
100 |
101 | 
102 |
103 | * 二维平面两点a(x1,y1)与b(x2,y2)间的切比雪夫距离:
104 | $$
105 | d_{12}=\max \left(\left|x_{1}-x_{2}\right|,\left|y_{1}-y_{2}\right|\right)
106 | $$
107 |
108 |
109 | - n维空间点a(x11,x12,…,x1n)与b(x21,x22,…,x2n)的切比雪夫距离:
110 | $$
111 | d_{12}=\max _{i}\left(\left|x_{1 i}-x_{2 i}\right|\right)
112 | $$
113 |
114 |
115 | - 欧氏距离
116 |
117 | * 二维平面上两点a(x1,y1)与b(x2,y2)间的欧氏距离(拓展到n维同理)
118 | $$
119 | d_{a b}=\sqrt{\left(x_{1}-x_{2}\right)^{2}}
120 | $$
121 |
122 |
123 | 两个n维向量a(x11,x12,…,x1n)与 b(x21,x22,…,x2n)间的欧氏距离
124 | $$
125 | d_{a b}=\sqrt{\sum_{k=1}^{n}\left(x_{1 k}-x_{2 k}\right)^{2}}
126 | $$
127 |
128 | * 向量运算的形式:
129 |
130 | $$
131 | d_{a b}=\sqrt{(a-b)(a-b)^{T}}
132 | $$
133 |
134 | - 余弦相似度函数(Cosine similarity)
135 |
136 | 余弦相似度,又称为余弦相似性,是通过计算两个向量的夹角余弦值来评估他们的相似度。余弦相似度将向量根据坐标值,绘制到向量空间中,如最常见的二维空间。
137 |
138 | 余弦相似度衡量的是2个向量间的夹角大小,通过夹角的余弦值表示结果,因此2个向量的余弦相似度为:
139 | $$
140 | \cos \theta=\frac{A \cdot B}{\|A\| *\|B\|}
141 | $$
142 | 分子为向量A与向量B的点乘,分母为二者各自的L2相乘,即将所有维度值的平方相加后开方。 余弦相似度的取值为[-1,1],值越大表示越相似。
143 |
144 |
76 |
77 | #### **15.3.2 相似度函数:**
78 |
79 | - 曼哈顿距离(Manhattan Distance)
80 |
81 | 顾名思义,在曼哈顿街区要从一个十字路口开车到另一个十字路口,驾驶距离显然不是两点间的直线距离。这个实际驾驶距离就是“曼哈顿距离”。曼哈顿距离也称为“城市街区距离”(City Block distance)。
82 |
83 | 
84 |
85 | * 二维平面两点a(x1,y1)与b(x2,y2)间的曼哈顿距离:
86 |
87 | $$
88 | d_{12}=\left|x_{1}-x_{2}\right|+\left|y_{1}-y_{2}\right|
89 | $$
90 |
91 | - n维空间点a(x11,x12,…,x1n)与b(x21,x22,…,x2n)的曼哈顿距离:
92 | $$
93 | \mathrm{d}_{12}=\sum_{k=1}^{n}\left|\mathrm{x}_{1 k}-x_{2 k}\right|
94 | $$
95 |
96 |
97 | - 切比雪夫距离 (Chebyshev Distance)
98 |
99 | 国际象棋中,国王可以直行、横行、斜行,所以国王走一步可以移动到相邻8个方格中的任意一个。国王从格子(x1,y1)走到格子(x2,y2)最少需要多少步?这个距离就叫切比雪夫距离。
100 |
101 | 
102 |
103 | * 二维平面两点a(x1,y1)与b(x2,y2)间的切比雪夫距离:
104 | $$
105 | d_{12}=\max \left(\left|x_{1}-x_{2}\right|,\left|y_{1}-y_{2}\right|\right)
106 | $$
107 |
108 |
109 | - n维空间点a(x11,x12,…,x1n)与b(x21,x22,…,x2n)的切比雪夫距离:
110 | $$
111 | d_{12}=\max _{i}\left(\left|x_{1 i}-x_{2 i}\right|\right)
112 | $$
113 |
114 |
115 | - 欧氏距离
116 |
117 | * 二维平面上两点a(x1,y1)与b(x2,y2)间的欧氏距离(拓展到n维同理)
118 | $$
119 | d_{a b}=\sqrt{\left(x_{1}-x_{2}\right)^{2}}
120 | $$
121 |
122 |
123 | 两个n维向量a(x11,x12,…,x1n)与 b(x21,x22,…,x2n)间的欧氏距离
124 | $$
125 | d_{a b}=\sqrt{\sum_{k=1}^{n}\left(x_{1 k}-x_{2 k}\right)^{2}}
126 | $$
127 |
128 | * 向量运算的形式:
129 |
130 | $$
131 | d_{a b}=\sqrt{(a-b)(a-b)^{T}}
132 | $$
133 |
134 | - 余弦相似度函数(Cosine similarity)
135 |
136 | 余弦相似度,又称为余弦相似性,是通过计算两个向量的夹角余弦值来评估他们的相似度。余弦相似度将向量根据坐标值,绘制到向量空间中,如最常见的二维空间。
137 |
138 | 余弦相似度衡量的是2个向量间的夹角大小,通过夹角的余弦值表示结果,因此2个向量的余弦相似度为:
139 | $$
140 | \cos \theta=\frac{A \cdot B}{\|A\| *\|B\|}
141 | $$
142 | 分子为向量A与向量B的点乘,分母为二者各自的L2相乘,即将所有维度值的平方相加后开方。 余弦相似度的取值为[-1,1],值越大表示越相似。
143 |
144 |  145 |
146 | python代码实现:
147 |
148 | ```python
149 | import numpy as np
150 | def cosine_dis(x,y):
151 | num = sum(map(float,x*y))
152 | denom = np.linalg.norm(x)*np.linalg.norm(y)
153 | return round(num/float(denom),3)
154 | print(cosine_dis(np.array([3,45,7,2]),np.array([2,54,13,15])))
155 | ```
156 |
157 | PS: 函数参数: linalg=linear(线性)+algebra(代数),norm则表示范数。
158 |
159 | ```python
160 | x_norm=np.linalg.norm(x, ord=None, axis=None, keepdims=False)
161 | ```
162 |
163 | - x: 表示矩阵(也可以是一维)
164 | - ord:范数类型
165 |
166 | | 参数 | 说明 | 计算方法 |
167 | | ---------- | ------------------------------------------------------------ | ------------------------------------------------------------ |
168 | | 默认 | 二范数: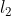 | 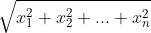 |
169 | | ord=2 | 二范数: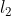 | 同上 |
170 | | ord=1 | 一范数: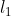 | 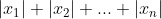 |
171 | | ord=np.inf | 无穷范数: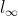 | 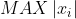 |
172 |
173 | 结果:
174 |
175 |
145 |
146 | python代码实现:
147 |
148 | ```python
149 | import numpy as np
150 | def cosine_dis(x,y):
151 | num = sum(map(float,x*y))
152 | denom = np.linalg.norm(x)*np.linalg.norm(y)
153 | return round(num/float(denom),3)
154 | print(cosine_dis(np.array([3,45,7,2]),np.array([2,54,13,15])))
155 | ```
156 |
157 | PS: 函数参数: linalg=linear(线性)+algebra(代数),norm则表示范数。
158 |
159 | ```python
160 | x_norm=np.linalg.norm(x, ord=None, axis=None, keepdims=False)
161 | ```
162 |
163 | - x: 表示矩阵(也可以是一维)
164 | - ord:范数类型
165 |
166 | | 参数 | 说明 | 计算方法 |
167 | | ---------- | ------------------------------------------------------------ | ------------------------------------------------------------ |
168 | | 默认 | 二范数: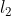 | 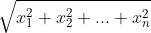 |
169 | | ord=2 | 二范数: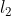 | 同上 |
170 | | ord=1 | 一范数: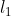 | 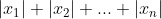 |
171 | | ord=np.inf | 无穷范数: | 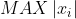 |
172 |
173 | 结果:
174 |
175 |  176 |
177 | ### 15.4 嵌入矩阵
178 |
179 | 在学习词嵌入时,实际上学习的是一个嵌入矩阵,这个矩阵用于将原来的one-hot编码转化为用特征表示的向量。
180 |
181 | #### 15.4.1 定义
182 |
183 | 假设词典共有10,000个单词,嵌入特征为300维。
184 |
185 | $o_i$:表示一个one-hot向量(10000$\times$1),且第$i$位为1,其余位为0。比如orange在词典中的编号为6257,则对应$o_{6257}$。
186 |
187 | $e_i$:表示一个嵌入向量(300$\times$1),对应由one-hot向量$o_i$得到的嵌入向量。
188 |
189 | $E$:表示嵌入矩阵,shape为300$\times$10000。
190 |
191 | 有如下关系:
192 | $$
193 | e_i = E \cdot o_i
194 | $$
195 | 由(3)式可知,嵌入矩阵$E$的作用在于将one-hot向量映射为嵌入向量。因此,学习词嵌入的本质是学习嵌入矩阵。
196 |
197 | #### 15.4.3 实现技巧
198 |
199 | 观察下图,可以发现由于one-hot向量的特殊性,对于$o_i$,嵌入矩阵实际上会用影响到$e_i$的值的只有第$i$列。
200 |
201 | 
202 |
203 | 所以在使用代码实现的时候,我们只需要抽取出对应的列即可,无需真的将如此大的矩阵与向量做矩阵乘法。
204 |
205 | 下面是代码示例:
206 |
207 | ```
208 | # 定义one-hot向量o_2, shape为(4, 1)
209 | o = np.array([[0, 0, 1, 0]]).T
210 |
211 | # 定义嵌入矩阵, shape为(2, 4)
212 | E = np.array([
213 | [10, 11, 12, 13],
214 | [20, 21, 22, 23]
215 | ])
216 |
217 | # 获得编号i
218 | i = np.where(o==1)[0]
219 |
220 | # 计算e_i, shape为(2, 1), 结果为 [ [12], [22] ]
221 | e = E[:, i]
222 | ```
223 |
224 | ### 15.5 学习词嵌入
225 |
226 | #### 15.5.1 简单的语言模型
227 |
228 | 假设搭建了一个用神经网络来实现的语言模型,用于预测“I want a glass of orange \_\_\_\_”。
229 |
230 | 
231 |
232 | 预测的具体方法如上图:
233 |
234 | 1. 对每个单词进行one-hot编码,得到一系列$o_i$
235 | 2. 映射为嵌入向量$e_i$
236 | 3. 将这些嵌入向量都放到神经网络中,该神经网络有自己的参数$W^{[1]}$和$b^{[1]}$,输入为 (6$\times$300)=1800维
237 | 4. 最后通过softmax层激活得到预测词的one-hot向量,也有自己的参数$W^{[2]}$和$b^{[2]}$。
238 |
239 | 实际应用上,会选择每次预测只向前看4个单词(一个超参数,可以修改),则神经网络的输入会变为(4$\times$300)=1200维。
240 |
241 | #### 15.5.2 反向传播
242 |
243 | 在搭建模型后,我们明确了这个模型的参数有$E,W^{[1]},W^{[2]},b^{[1]},b^{[2]}$,因此可以开始用反向传播进行训练。这样这个网络会发现要想最好地拟合训练集,就要使apple(苹果)、orange(橘子)、grape(葡萄)和pear(梨)等等,还有像durian(榴莲)这种很稀有的水果都拥有相似的特征向量。
244 |
245 | #### 15.5.3 采用不同的上下文
246 |
247 | 除了刚刚提到的每次预测只使用前4个单词,还可以选择目标词左右各4个词作为上下文;也可以仅使用目标词的前一个单词进行预测。
248 |
249 | 不同的上下文会得到不同的效果,但是学习的嵌入矩阵仍会是相似的。
250 |
251 | #### 15.5.4 相关的重要人物
252 |
253 | Yoshua Bengio,Rejean Ducharme,Pascal Vincent,Rejean Ducharme,Pascal Vincent还有Christian Jauvin。
254 |
255 | ### 15.6 Word2Vec
256 |
257 | Word2Vec有两个版本,其中Skip-Gram是更常用的那个,另一个是CBOW。下面先介绍Skip-Gram。
258 |
259 | #### 15.6.1 Skip-Gram模型
260 |
261 | Skip-Gram模型的思想是,学习给定嵌入向量$e_c$预测对应的$e_t$。但是由于一个$e_c$是可以对应多个$e_t$的(因为一个词附近出现的词有很多个,不可能一直只有一个),所以最后学习的结果会将$e_c$附近的词都认为拥有相似的特征。
262 |
263 | 
264 |
265 | 在该模型中,上下文不一定总是目标单词之前离得最近的四个单词,或最近的n个单词。在给定一个训练样本(如“I want a glass of orange juice to go along with my cereal.”)该模型的算法如下:
266 |
267 | 1. **随机**选一个词作为上下文 $c$(比如orange)
268 |
269 | 2. 然后基于 $c$,随机在一定词距内选另一个词作为目标词 $t$(比如juice,也可能是后方的my或者前方的glass)
270 |
271 | 3. 根据$c,t$分别得到one-hot向量$o_c,o_t$以及嵌入向量$e_c$。那一个训练样本就是($e_c$,$o_t$)
272 |
273 | 4. 然后将$e_c$喂给softmax单元,该单元用于预测不同目标词的概率,公式如下:
274 | $$
275 | \operatorname{Softmax}: p(t \mid c)=\frac{e^{\theta_{t}^{T} e_{c}}}{\sum_{j=1}^{10,000} e^{\theta_{j}^{T} e_{c}}}
276 | $$
277 | 其中$\theta_t$是与输出$t$相关的参数(可训练),即某个词$t$与标签相符的概率。$\theta_{t}^{T} e_{c}$描述了两者的关联性。
278 |
279 | 5. 用$y$表示目标词(one-hot向量),$\hat y$表预测词(可能目标词的概率),均为10,000维的向量。损失函数如下:
280 | $$
281 | L(\hat{y}, y)=-\sum_{i=1}^{10,000} y_{i} \log \hat{y}_{i}
282 | $$
283 |
284 | 最后,通过优化这个损失函数就可以得到一个不错的词嵌入。
285 |
286 | #### 15.6.2 分级的Softmax
287 |
288 | 其实上述的Skip-Gram模型有一个很明显的问题:计算速度。在计算softmax单元时,需要对10,000个词做求和运算,甚至更多的词。这会导致速度会变得相当慢,扩大词汇表(词典)更是几乎不可能的。
289 |
290 | 所以提出了分级的(hierarchical)的softmax,结构如下图:
291 |
292 | 
293 |
294 | 这样每个结点都是一个二分类器,给定一个词,第一个分类器判断这个词是前5000个词中还是后5000个词中;第二个分类器判断是前2500中还是后2500个至前5000个词中……以此类推,最后到达的叶子结点就是目标类别,并给出对应的概率。
295 |
296 | 实际应用时,常用词会更接近树的根部,罕见词会在很深的地方;因此这个树并非一颗平衡树。
297 |
298 | #### 15.6.3 Skip-Gram与CBOW
299 |
300 | ***CBOW***,即连续词袋模型(Continuous Bag-Of-Words Model),它获得中间词两边的的上下文,然后用周围的词去预测中间的词。在训练时相当于是用缺省的词(预测词)来影响周围的词。
301 |
302 | 这个模型也很有效,也有一些优点和缺点。结构如下图。
303 |
304 | 
305 |
306 | 对应的,Skip-Gram是用中间词去预测周围的词,训练时则相当于用一个词周围的词来影响中间词。结构如下图:
307 |
308 | 
309 |
310 | CBOW对小型数据库比较合适,而Skip-Gram在大型语料中表现更好;CBOW是从原始语句推测目标字词,而Skip-Gram正好相反,是从目标字词推测出原始语句。
311 |
312 | cbow是 1个老师 VS K个学生,K个学生(周围词)都会从老师(中心词)那里学习知识,但是老师(中心词)是一视同仁的,教给大家的一样的知识。至于你学到了多少,还要看下一轮(假如还在窗口内),或者以后的某一轮,你还有机会加入老师的课堂当中(再次出现作为周围词),跟着大家一起学习,然后进步一点。所以对于罕见词来说,学习效果比较差。CBOW总的预测次数是O(V),只与训练样本的词汇数有关。
313 |
314 | 相对的,skip-gram是 1个学生 VS K个老师,1个学生(中心词)会从K个老师(K个周围词)那里学习知识。skip-gram总的预测次数是O(V*K),与训练样本的词汇数以及窗口的大小有关。因此数据集较大时K不宜太大。
315 |
316 | #### 15.6.4 相关的重要论文
317 |
318 | 1. Mikolov T, Chen K, Corrado G, et al. Efficient Estimation of Word Representations in Vector Space[J]. Computer Science, 2013.
319 |
320 | #### 15.6.5 Doc2Vec
321 |
322 | 与Word2Vec对应,既然有词向量,那也可以考虑文本向量。Doc2Vec 的目的就是获得文本的一个固定长度的向量表达。
323 |
324 | word2vec只是基于词的维度进行“语义分析”的,并不具有上下文的“语义分析”能力。因此在word2vec的基础上增加一个段落向量,该方法是doc2vec。该模型也有两个方法:Distributed Memory(DM) 和 Distributed Bag of Words(DBOW)。 DM试图给定上下文和段落向量的情况下预测单词的概率。在一个句子或者段落文档训练过程中,段落ID保存不变,共享同一个段落向量。DBOW则在只给定段落向量的情况下预测段落中一组随机单词的概率。引自[word2vec和doc2vec](https://www.jianshu.com/p/048bff9b0f65)。
325 |
326 | ### 15.7 负采样
327 |
328 | #### 15.7.1 什么是负采样
329 |
330 | skip-gram模型可以构造一个监督学习任务,把上下文映射到目标词上,以学习一个实用的词嵌入,但缺点是softmax计算起来很慢。负采样能够做到和 skip-gram相似的功能但是使用起来更加高效,理论上就是将10000分类的softmax转化为10000个二分类任务,来简化训练过程。
331 |
332 | 简单来说,构造一个新的监督学习问题,比如给定一对单词,比如orange和juice,判断上下文词(context)与目标词(target)是否为匹配的一对,如果是一对,则是正样本,如果不是一对,则是负样本.
333 | 在这个例子中orange和juice称作个正样本,用1作为标记,orange和king就是个负样本,标为0。要做的就是采样得到一个上下文词和一个目标词,中间列叫做词(word)。然后:
334 |
335 | - 正样本的生成是采样得到一个上下文词和一个目标词。先抽取一个context,在一定词距内(比如说正负10个词距内)随机选择一个单词作为target,生成这个表的第一行,即orange– juice -1的过程
336 | - 生成一个负样本,用相同的context,再在字典中随机选一个词,如king、book、the、of,标记为0。因为如果随机选一个词,它很可能跟orange没关联。其中同一 上下文词生成 *K个* 负样本
337 |
338 | - 注意:正负样本的区别仅取决于单词对的来源,比如of正好出现在了orange正负10个词之内标为1,但是of又被作为随机从字典中选取的单词, of - orange单词对仍然会被标记为负样本。
339 |
340 | K值的选取:
341 |
342 | - 小数据集的话,K设置为从5到20,数据集越小K被设定的越大。
343 | - 如果数据集很大,K就选的小一点。对于更大的数据集K设置为从2到5。
344 |
345 | #### 15.7.2 模型学习原理
346 |
347 | - 算法定义 :输入Context 为 c, Word为 t , 定义输出Target为 y
348 |
349 | | context | word | target |
350 | | ------- | ----- | ------ |
351 | | c | t | y |
352 | | $x_1$ | $x_2$ | y |
353 | | orange | juice | 1 |
354 | | orange | king | 0 |
355 | | orange | book | 0 |
356 | | orange | the | 0 |
357 | | orange | of | 0 |
358 |
359 | - 损失函数定义为给定样本单词对的情况下,y = 1的概率:
360 | - 使用$e_c$表示context的词嵌入向量,其中$\theta_{t}$表示每个样本对应的参数.
361 | - $P(y=1 \mid c, t)=\sigma\left(\theta_{t}^{T} e_{c}\right)$
362 | - 对于每个正样本都有 *K* 个负样本来训练一个类似logisitic回归的模型。
363 |
364 | #### 15.7.3 算法流程
365 |
366 | 1. 如果输入词是orange ,即词典中的第6257个词,将其使用one-hot向量表示 $ o_{6257}$,和 E (词嵌入向量矩阵)相乘得到 orange的嵌入向量$ e_{6357}$。
367 |
368 | 2. $e_{6357}$是一个10,000维(字典中总单词数量)的向量,可以看成是1W个可能的logistic回归分类问题,其中一个(编号4)将会是用来判断目标词是否是juice的分类器,其他的词比如下面的某个分类器(编号5)是用来预测king是否是目标词。
369 |
370 | 每次迭代不都是训练所有的样本, 只会训练一个正样本和随机选取的 K 个负样本,即模型总共包含了k+1个binary classification。对比之前10000个输出单元的softmax分类,negative sampling转化为k+1个二分类问题,每次迭代并不是训练10000个,而仅训练其中k+1个,计算量要小很多,大大提高了模型运算速度。
371 |
372 | 这种方法就叫做负采样(Negative Sampling):*选择一个正样本,随机采样k个负样本。
373 |
374 | #### 15.7.4 如何选取负样本
375 |
376 | - 仅仅通过单词在语料库中出现的频率进行采样:导致负样本中一些类似a、the、of等词的频率较高。
377 |
378 | - 均匀随机地抽取负样本,分母是词汇表中总词数,没有很好的代表性。
379 | - 推荐采样公式:
380 |
381 | $$
382 | P\left(w_{i}\right)=\frac{f\left(w_{i}\right)^{\frac{3}{4}}}{\sum_{j=1}^{10,000} f\left(w_{j}\right)^{\frac{3}{4}}}
383 | $$
384 |
385 | 这种方法处于上面两种极端采样方法之间,即不用频率分布,也不用均匀分布,而采用的是对词频的$\frac{3}{4}$除以词频$\frac{3}{4}$整体的和进行采样的。其中,$f(w_j)$是语料库中观察到的某个词的词频。
386 |
387 |
388 | #### 15.7.5 相关的重要论文
389 |
390 | Mikolov T, Sutskever I, Chen K, et al. Distributed representations of words and phrases and their compositionality[C]// International Conference on Neural Information Processing Systems. Curran Associates Inc. 2013:3111-3119.[地址](https://papers.nips.cc/paper/2013/file/9aa42b31882ec039965f3c4923ce901b-Paper.pdf)
391 |
392 | 讲解 skip-gram 模型以及优化和扩展,包括层次 Softmax,负采样等内容。
393 |
394 | ### 15.8 GloVe词向量
395 |
396 | 该算法虽然不如Word2Vec热门,但也是简单且不错的模型,在NLP社区有一定的势头。
397 |
398 | #### 15.8.1 什么是GloVe算法
399 |
400 | 全称Global vectors for word representation(基于全局统计的词表征)。在此之前,我们曾通过挑选语料库中位置相近的两个词,列举出词对,即上下文和目标词,GloVe算法做的就是使其关系开始明确化。假定 $X_{ij}$是单词 $i$在单词 $j$上下文中出现的次数,那么这里 $i$与 $j$就和 $t$与 $c$的功能一样,所以你可以认为 $X_{ij}$等同于 $X_{tc}$。
401 |
402 | 如果上下文定义为目标词左右各10个词左右,还会得到$X_{ij}=X_{ji}$的结论。相反,如果上下文总是目标词的前一个则没有这种对称性。这个其实很容易理解,当目标词的上下文包括左右两部分时,则意味着对于上下文 $c$来说,目标词 $t$也是 $c$的上下文。
403 |
404 | **共现矩阵**:其实$X_{ij}$就是共现矩阵的其中一个元素。共现矩阵的横、纵轴均为词汇表的大小,行对应目标词的编号,列对应上下文的编号。计算方法就是遍历一个句子,比如“I love you”,则目标词为“I”时上下文有“love”和“you”,执行$X_{I,love}+1$和$X_{I,you}+1$。最后遍历语料库后即完成共现矩阵的计算。
405 |
406 | **目标**:GloVe的目标是最小化函数:
407 | $$
408 | \operatorname{minimize} \sum_{i=1}^{10,000} \sum_{j=1}^{10,000} f\left(X_{i j}\right)\left(\theta_{i}^{T} e_{j}+b_{i}+b_{j}^{\prime}-\log X_{i j}\right)^{2}
409 | $$
410 | 这个函数表示的是两者间的差距。$\theta_{i}^{T} e_{j}$同$\theta_{t}^{T} e_{c}$一样描述了两者同时出现的频率是多少。如果想要最小化这个函数,毫无疑问需要让$\theta_{i}^{T} e_{j}+b_{i}+b_{j}^{\prime}$逼近$\log X_{ij}$。
411 |
412 | 通过梯度下降算法即可学习嵌入矩阵$E$,并且学会预测两个单词同时出现的频率。
413 |
414 | **细节**:如果$X_{ij}=0$,则$\log X_{ij}$为无穷大,因此要添加一个额外的加权项$f(X_{ij})$,约定$f(0)(\ldots-\log 0)=0$。即当$X_{ij}=0$时不计入求和项;同时对于常见词如a、the、of等词,给与一个较小的权重;对于罕见词如durion则给予一个较大的权重。
415 |
416 | 还有一个细节就是现在的$\theta$和$e$现在是完全对称的,即$\theta_i$和$e_j$是对称的。只看公式的话两者功能相似。
417 |
418 | **对比**:首先,两种算法学习词嵌入都用到了一个信息:词汇共现(co-occurrence),即利用两个词一起出现这个信息来学习词嵌入、隐含的语义等。不同之处在于,word2vec学习了这个共现,本质上做的是预测任务(Predictive),要么根据中心词预测上下文,要么根据上下文预测中心词;而GloVe做的是对已经得到的共现信息(共现矩阵)进行降维、编码(Count-based)。
419 |
420 | **优缺点**:相对来说word2vec没有很好地利用共现信息,而GloVe则因为共现矩阵需要花费相当大的内存;但是不采用负采样的word2vec非常快,GloVe则更容易优化准确率也比没有用负采样的word2vec高。
421 |
422 | #### 15.8.2 为什么不能保证嵌入向量的独立组成部分是能够理解的
423 |
424 | 首先,我们可以将词嵌入理解为“特征提取”,比如提取出Gender、Royal等属性来进行描述,这些特征对于我们来说是可以理解的。但是,我们刚刚提到的算法都是自己学自己的,并不一定会学出Gender等属性。
425 |
426 | 更具体一点,可以当成是进行了降维,用更少的轴来描述原来的单词;如果这些轴分别表示Gender、Royal等属性则是可理解的,并且相互正交;但是我们提到的算法都没有去保证“这两个特征之间是相互正交的”,也就是说他学到的特征很可能是多个正交特征的混合,比如第一个轴是Gender和Royal的混合,第二个轴是Royal和Age的混合等等。
427 |
428 | 所以,才说不能保证嵌入向量的独立组成部分是能够理解的。
429 |
430 | #### 15.8.3 相关重要论文
431 |
432 | 1. Pennington J, Socher R, Manning C. Glove: Global Vectors for Word Representation[C]// Conference on Empirical Methods in Natural Language Processing. 2014:1532-1543.
433 |
434 | ### 15.9 情感分类
435 |
436 | 情感分类:Sentiment classification
437 |
438 | 词嵌入:word embeddings,将一个词语(word)转换为一个向量 (vector)表示, 所以词嵌入有时又被叫作“**word2vec**"。
439 |
440 | 情感分类是一个很难但很有趣的方向,相对来说也很容易出项目,应用到各种场合。
441 |
442 | #### 15.9.1 什么是情感分类
443 |
444 | 情感分类:对带有感情色彩的主观性文本进行分析,分析说话人的态度是倾向正面还是反面,是NLP中最重要的模块之一。
445 |
446 | 
447 |
448 | 举个例子,如上图所示,输入 $x$ 是一段文本,输出 $y$ 是要预测的相应情感,比如是对一个餐馆评价的星级。现在很多人会把用餐的情况与感受分享在一些社交平台上,如果基于像上面这样标记的数据集可以训练一个从 $x$ 到 $y$ 的映射也就是一个情感分类器,就可以用来搜集大家对这个餐馆的评价,从文本中分析出顾客对餐馆评论的情感是正面的还是负面的,可以让餐馆发现自身的问题所在也能让其他顾客了解到这个餐馆是否值得光顾。
449 |
450 | 情感分类最大的挑战是**标记的训练集不够多**,对于情感分类任务来说,训练集大小从10000到100000个单词都很常见,甚至有时会小于10000个单词,但采用**词嵌入**效果可以好很多,即使只有中等大小的标记的训练集,也能构建一个不错的情感分类器。
451 |
452 | #### 15.9.2 一个简单的情感分类模型
453 |
454 | 
455 |
456 | 如上图所示,假设有一个句子“The dessert is excellent(甜点很棒)”,要构建一个分类器把它映射成输出四个星。首先,我们从词典里找到这些词相应的一位编码表示,如“the”的**一位编码**是 $o_{8928}$,乘以**嵌入矩阵 $E$**($E$ 可以从一个很大的文本集里学习到,比如从一亿个词或者一百亿个词里学习嵌入表达,从中获取很多知识甚至从有些不常用的词中获取然后应用到要解决的问题中,即使你的标记数据集里没有这些词),得到单词“the”的**嵌入向量 $e_{8928}$**,对其他三个单词做同样的步骤。将这些嵌入向量求和或者求平均(把所有单词的意思加起来或取平均),假设这里用的是一个平均值计算单元Avg,这个单元会输出一个相同维度的特征向量,把这个特征向量送进softmax分类器,输出5个可能结果(从一星到五星)的概率值,进而输出预测结果 $\hat y$。
457 |
458 | 这个算法有一个问题就是**没考虑词序**,像“Completely lacking in good taste, good service, and good ambience(完全没有好的味道、好的服务、好的氛围)”虽然是负面评价,但”good“这个词出现了很多次,如果还用上面的算法,忽略词序而仅仅把所有单词的词嵌入加起来或者取平均,则最后的特征向量会有很多good的表示,分类器就可能误认为这是一个好评。
459 |
460 | #### 15.9.3 用RNN实现情感分类
461 |
462 | 
463 |
464 | 首先找到这条评论中每一个单词的一位编码表示,乘以词嵌入矩阵 $E$ 得到词嵌入表达 $e$,然后把它们送进我们之前学过的多对一的RNN网络结构里,RNN的工作就是在最后一步计算一个特征向量来预测 $\hat y$。这种算法考虑了词的顺序,效果更好,能够意识到“Completely lacking in good taste, good service, and good ambience(完全没有好的味道、好的服务、好的氛围)”是个负面评价。由于词嵌入 $E$ 是在一个更大的数据集里训练的,可以更好地泛化一些没有见过的新单词,比如其他人可能会说“Completely absent of good taste...”,即使"absent"这个词不在标记的训练集里,但它仍然可以判断对并且泛化得很好。
465 |
466 | ### 15.10 词嵌入除偏
467 |
468 | 算法安全性;偏见原因:**数据集**不完整(cv:黑人数据不够多)、打**标签**有偏见、**算法**本身的偏见(推荐算法的导向性,推之前没有的,试探性,引导往其他方向走);解决方法:采样更丰富和比例更合理(数据增强)、***设计算法创新处理有偏数据集得到无偏结果***;老人无健康码上不了车,考虑少数人、边缘化等;
469 |
470 | 词嵌入除偏:Debiasing word embeddings
471 |
472 | #### 15.10.1 为什么需要除偏
473 |
474 | 这里的“偏(bias)"不是指偏见,而是指性别、种族、性取向方面的偏见。
475 |
476 | “Man is to computer programmer as woman is to homemaker? debiasing word embeddings.”这篇论文提出,如果说Man对应Computer programmer则Woman会对应什么呢?一个已经完成学习的词嵌入可能会输出Homemaker,这个结果就反映了一个十分不良的性别歧视,如果输出的是Computer programmer则会更合理。再比如说Father对应Doctor那么Mother应该对应什么?有些完成学习的词嵌入会输出nurse,这也是不对的。
477 |
478 | 也就是说,根据训练模型所使用的文本,**词嵌入可能会反映出性别、种族、年龄、性取向等其他方面的偏见**,这些偏见都和社会经济状态相关。因为机器学习算法正用来制定十分重要的决策,影响着世间万物,所以尽量修改学习算法来尽可能**减少或是理想化消除这些非预期形式的偏见**是十分重要的,因此需要对词嵌入进行除偏。
479 |
480 | **偏见产生的原因**:
481 |
482 | * **数据集**不完整。比如在做图像处理的时候由于黑人的数据不够多而导致效果不好。
483 |
484 | * **标签**有偏见。由于标签都是人打上去的,因此如果打标签的人带有偏见,则最后标签也会带有偏见并产生实际影响。
485 |
486 | * **算法**本身的偏见。常见于推荐算法,有的推荐算法具有导向性,会通过试探性地推荐之前没有的物品,引导用户养成新的兴趣,有时候甚至会带有“恶意”将用户引导到不好的方向。
487 |
488 | #### 15.10.2 什么是词嵌入除偏
489 |
490 | 假设我们已经完成一个词嵌入的学习,babysister、doctor、grandmother、grandfather、girl、boy、she、he这些词的嵌入位置如下图所示,
491 |
492 |
176 |
177 | ### 15.4 嵌入矩阵
178 |
179 | 在学习词嵌入时,实际上学习的是一个嵌入矩阵,这个矩阵用于将原来的one-hot编码转化为用特征表示的向量。
180 |
181 | #### 15.4.1 定义
182 |
183 | 假设词典共有10,000个单词,嵌入特征为300维。
184 |
185 | $o_i$:表示一个one-hot向量(10000$\times$1),且第$i$位为1,其余位为0。比如orange在词典中的编号为6257,则对应$o_{6257}$。
186 |
187 | $e_i$:表示一个嵌入向量(300$\times$1),对应由one-hot向量$o_i$得到的嵌入向量。
188 |
189 | $E$:表示嵌入矩阵,shape为300$\times$10000。
190 |
191 | 有如下关系:
192 | $$
193 | e_i = E \cdot o_i
194 | $$
195 | 由(3)式可知,嵌入矩阵$E$的作用在于将one-hot向量映射为嵌入向量。因此,学习词嵌入的本质是学习嵌入矩阵。
196 |
197 | #### 15.4.3 实现技巧
198 |
199 | 观察下图,可以发现由于one-hot向量的特殊性,对于$o_i$,嵌入矩阵实际上会用影响到$e_i$的值的只有第$i$列。
200 |
201 | 
202 |
203 | 所以在使用代码实现的时候,我们只需要抽取出对应的列即可,无需真的将如此大的矩阵与向量做矩阵乘法。
204 |
205 | 下面是代码示例:
206 |
207 | ```
208 | # 定义one-hot向量o_2, shape为(4, 1)
209 | o = np.array([[0, 0, 1, 0]]).T
210 |
211 | # 定义嵌入矩阵, shape为(2, 4)
212 | E = np.array([
213 | [10, 11, 12, 13],
214 | [20, 21, 22, 23]
215 | ])
216 |
217 | # 获得编号i
218 | i = np.where(o==1)[0]
219 |
220 | # 计算e_i, shape为(2, 1), 结果为 [ [12], [22] ]
221 | e = E[:, i]
222 | ```
223 |
224 | ### 15.5 学习词嵌入
225 |
226 | #### 15.5.1 简单的语言模型
227 |
228 | 假设搭建了一个用神经网络来实现的语言模型,用于预测“I want a glass of orange \_\_\_\_”。
229 |
230 | 
231 |
232 | 预测的具体方法如上图:
233 |
234 | 1. 对每个单词进行one-hot编码,得到一系列$o_i$
235 | 2. 映射为嵌入向量$e_i$
236 | 3. 将这些嵌入向量都放到神经网络中,该神经网络有自己的参数$W^{[1]}$和$b^{[1]}$,输入为 (6$\times$300)=1800维
237 | 4. 最后通过softmax层激活得到预测词的one-hot向量,也有自己的参数$W^{[2]}$和$b^{[2]}$。
238 |
239 | 实际应用上,会选择每次预测只向前看4个单词(一个超参数,可以修改),则神经网络的输入会变为(4$\times$300)=1200维。
240 |
241 | #### 15.5.2 反向传播
242 |
243 | 在搭建模型后,我们明确了这个模型的参数有$E,W^{[1]},W^{[2]},b^{[1]},b^{[2]}$,因此可以开始用反向传播进行训练。这样这个网络会发现要想最好地拟合训练集,就要使apple(苹果)、orange(橘子)、grape(葡萄)和pear(梨)等等,还有像durian(榴莲)这种很稀有的水果都拥有相似的特征向量。
244 |
245 | #### 15.5.3 采用不同的上下文
246 |
247 | 除了刚刚提到的每次预测只使用前4个单词,还可以选择目标词左右各4个词作为上下文;也可以仅使用目标词的前一个单词进行预测。
248 |
249 | 不同的上下文会得到不同的效果,但是学习的嵌入矩阵仍会是相似的。
250 |
251 | #### 15.5.4 相关的重要人物
252 |
253 | Yoshua Bengio,Rejean Ducharme,Pascal Vincent,Rejean Ducharme,Pascal Vincent还有Christian Jauvin。
254 |
255 | ### 15.6 Word2Vec
256 |
257 | Word2Vec有两个版本,其中Skip-Gram是更常用的那个,另一个是CBOW。下面先介绍Skip-Gram。
258 |
259 | #### 15.6.1 Skip-Gram模型
260 |
261 | Skip-Gram模型的思想是,学习给定嵌入向量$e_c$预测对应的$e_t$。但是由于一个$e_c$是可以对应多个$e_t$的(因为一个词附近出现的词有很多个,不可能一直只有一个),所以最后学习的结果会将$e_c$附近的词都认为拥有相似的特征。
262 |
263 | 
264 |
265 | 在该模型中,上下文不一定总是目标单词之前离得最近的四个单词,或最近的n个单词。在给定一个训练样本(如“I want a glass of orange juice to go along with my cereal.”)该模型的算法如下:
266 |
267 | 1. **随机**选一个词作为上下文 $c$(比如orange)
268 |
269 | 2. 然后基于 $c$,随机在一定词距内选另一个词作为目标词 $t$(比如juice,也可能是后方的my或者前方的glass)
270 |
271 | 3. 根据$c,t$分别得到one-hot向量$o_c,o_t$以及嵌入向量$e_c$。那一个训练样本就是($e_c$,$o_t$)
272 |
273 | 4. 然后将$e_c$喂给softmax单元,该单元用于预测不同目标词的概率,公式如下:
274 | $$
275 | \operatorname{Softmax}: p(t \mid c)=\frac{e^{\theta_{t}^{T} e_{c}}}{\sum_{j=1}^{10,000} e^{\theta_{j}^{T} e_{c}}}
276 | $$
277 | 其中$\theta_t$是与输出$t$相关的参数(可训练),即某个词$t$与标签相符的概率。$\theta_{t}^{T} e_{c}$描述了两者的关联性。
278 |
279 | 5. 用$y$表示目标词(one-hot向量),$\hat y$表预测词(可能目标词的概率),均为10,000维的向量。损失函数如下:
280 | $$
281 | L(\hat{y}, y)=-\sum_{i=1}^{10,000} y_{i} \log \hat{y}_{i}
282 | $$
283 |
284 | 最后,通过优化这个损失函数就可以得到一个不错的词嵌入。
285 |
286 | #### 15.6.2 分级的Softmax
287 |
288 | 其实上述的Skip-Gram模型有一个很明显的问题:计算速度。在计算softmax单元时,需要对10,000个词做求和运算,甚至更多的词。这会导致速度会变得相当慢,扩大词汇表(词典)更是几乎不可能的。
289 |
290 | 所以提出了分级的(hierarchical)的softmax,结构如下图:
291 |
292 | 
293 |
294 | 这样每个结点都是一个二分类器,给定一个词,第一个分类器判断这个词是前5000个词中还是后5000个词中;第二个分类器判断是前2500中还是后2500个至前5000个词中……以此类推,最后到达的叶子结点就是目标类别,并给出对应的概率。
295 |
296 | 实际应用时,常用词会更接近树的根部,罕见词会在很深的地方;因此这个树并非一颗平衡树。
297 |
298 | #### 15.6.3 Skip-Gram与CBOW
299 |
300 | ***CBOW***,即连续词袋模型(Continuous Bag-Of-Words Model),它获得中间词两边的的上下文,然后用周围的词去预测中间的词。在训练时相当于是用缺省的词(预测词)来影响周围的词。
301 |
302 | 这个模型也很有效,也有一些优点和缺点。结构如下图。
303 |
304 | 
305 |
306 | 对应的,Skip-Gram是用中间词去预测周围的词,训练时则相当于用一个词周围的词来影响中间词。结构如下图:
307 |
308 | 
309 |
310 | CBOW对小型数据库比较合适,而Skip-Gram在大型语料中表现更好;CBOW是从原始语句推测目标字词,而Skip-Gram正好相反,是从目标字词推测出原始语句。
311 |
312 | cbow是 1个老师 VS K个学生,K个学生(周围词)都会从老师(中心词)那里学习知识,但是老师(中心词)是一视同仁的,教给大家的一样的知识。至于你学到了多少,还要看下一轮(假如还在窗口内),或者以后的某一轮,你还有机会加入老师的课堂当中(再次出现作为周围词),跟着大家一起学习,然后进步一点。所以对于罕见词来说,学习效果比较差。CBOW总的预测次数是O(V),只与训练样本的词汇数有关。
313 |
314 | 相对的,skip-gram是 1个学生 VS K个老师,1个学生(中心词)会从K个老师(K个周围词)那里学习知识。skip-gram总的预测次数是O(V*K),与训练样本的词汇数以及窗口的大小有关。因此数据集较大时K不宜太大。
315 |
316 | #### 15.6.4 相关的重要论文
317 |
318 | 1. Mikolov T, Chen K, Corrado G, et al. Efficient Estimation of Word Representations in Vector Space[J]. Computer Science, 2013.
319 |
320 | #### 15.6.5 Doc2Vec
321 |
322 | 与Word2Vec对应,既然有词向量,那也可以考虑文本向量。Doc2Vec 的目的就是获得文本的一个固定长度的向量表达。
323 |
324 | word2vec只是基于词的维度进行“语义分析”的,并不具有上下文的“语义分析”能力。因此在word2vec的基础上增加一个段落向量,该方法是doc2vec。该模型也有两个方法:Distributed Memory(DM) 和 Distributed Bag of Words(DBOW)。 DM试图给定上下文和段落向量的情况下预测单词的概率。在一个句子或者段落文档训练过程中,段落ID保存不变,共享同一个段落向量。DBOW则在只给定段落向量的情况下预测段落中一组随机单词的概率。引自[word2vec和doc2vec](https://www.jianshu.com/p/048bff9b0f65)。
325 |
326 | ### 15.7 负采样
327 |
328 | #### 15.7.1 什么是负采样
329 |
330 | skip-gram模型可以构造一个监督学习任务,把上下文映射到目标词上,以学习一个实用的词嵌入,但缺点是softmax计算起来很慢。负采样能够做到和 skip-gram相似的功能但是使用起来更加高效,理论上就是将10000分类的softmax转化为10000个二分类任务,来简化训练过程。
331 |
332 | 简单来说,构造一个新的监督学习问题,比如给定一对单词,比如orange和juice,判断上下文词(context)与目标词(target)是否为匹配的一对,如果是一对,则是正样本,如果不是一对,则是负样本.
333 | 在这个例子中orange和juice称作个正样本,用1作为标记,orange和king就是个负样本,标为0。要做的就是采样得到一个上下文词和一个目标词,中间列叫做词(word)。然后:
334 |
335 | - 正样本的生成是采样得到一个上下文词和一个目标词。先抽取一个context,在一定词距内(比如说正负10个词距内)随机选择一个单词作为target,生成这个表的第一行,即orange– juice -1的过程
336 | - 生成一个负样本,用相同的context,再在字典中随机选一个词,如king、book、the、of,标记为0。因为如果随机选一个词,它很可能跟orange没关联。其中同一 上下文词生成 *K个* 负样本
337 |
338 | - 注意:正负样本的区别仅取决于单词对的来源,比如of正好出现在了orange正负10个词之内标为1,但是of又被作为随机从字典中选取的单词, of - orange单词对仍然会被标记为负样本。
339 |
340 | K值的选取:
341 |
342 | - 小数据集的话,K设置为从5到20,数据集越小K被设定的越大。
343 | - 如果数据集很大,K就选的小一点。对于更大的数据集K设置为从2到5。
344 |
345 | #### 15.7.2 模型学习原理
346 |
347 | - 算法定义 :输入Context 为 c, Word为 t , 定义输出Target为 y
348 |
349 | | context | word | target |
350 | | ------- | ----- | ------ |
351 | | c | t | y |
352 | | $x_1$ | $x_2$ | y |
353 | | orange | juice | 1 |
354 | | orange | king | 0 |
355 | | orange | book | 0 |
356 | | orange | the | 0 |
357 | | orange | of | 0 |
358 |
359 | - 损失函数定义为给定样本单词对的情况下,y = 1的概率:
360 | - 使用$e_c$表示context的词嵌入向量,其中$\theta_{t}$表示每个样本对应的参数.
361 | - $P(y=1 \mid c, t)=\sigma\left(\theta_{t}^{T} e_{c}\right)$
362 | - 对于每个正样本都有 *K* 个负样本来训练一个类似logisitic回归的模型。
363 |
364 | #### 15.7.3 算法流程
365 |
366 | 1. 如果输入词是orange ,即词典中的第6257个词,将其使用one-hot向量表示 $ o_{6257}$,和 E (词嵌入向量矩阵)相乘得到 orange的嵌入向量$ e_{6357}$。
367 |
368 | 2. $e_{6357}$是一个10,000维(字典中总单词数量)的向量,可以看成是1W个可能的logistic回归分类问题,其中一个(编号4)将会是用来判断目标词是否是juice的分类器,其他的词比如下面的某个分类器(编号5)是用来预测king是否是目标词。
369 |
370 | 每次迭代不都是训练所有的样本, 只会训练一个正样本和随机选取的 K 个负样本,即模型总共包含了k+1个binary classification。对比之前10000个输出单元的softmax分类,negative sampling转化为k+1个二分类问题,每次迭代并不是训练10000个,而仅训练其中k+1个,计算量要小很多,大大提高了模型运算速度。
371 |
372 | 这种方法就叫做负采样(Negative Sampling):*选择一个正样本,随机采样k个负样本。
373 |
374 | #### 15.7.4 如何选取负样本
375 |
376 | - 仅仅通过单词在语料库中出现的频率进行采样:导致负样本中一些类似a、the、of等词的频率较高。
377 |
378 | - 均匀随机地抽取负样本,分母是词汇表中总词数,没有很好的代表性。
379 | - 推荐采样公式:
380 |
381 | $$
382 | P\left(w_{i}\right)=\frac{f\left(w_{i}\right)^{\frac{3}{4}}}{\sum_{j=1}^{10,000} f\left(w_{j}\right)^{\frac{3}{4}}}
383 | $$
384 |
385 | 这种方法处于上面两种极端采样方法之间,即不用频率分布,也不用均匀分布,而采用的是对词频的$\frac{3}{4}$除以词频$\frac{3}{4}$整体的和进行采样的。其中,$f(w_j)$是语料库中观察到的某个词的词频。
386 |
387 |
388 | #### 15.7.5 相关的重要论文
389 |
390 | Mikolov T, Sutskever I, Chen K, et al. Distributed representations of words and phrases and their compositionality[C]// International Conference on Neural Information Processing Systems. Curran Associates Inc. 2013:3111-3119.[地址](https://papers.nips.cc/paper/2013/file/9aa42b31882ec039965f3c4923ce901b-Paper.pdf)
391 |
392 | 讲解 skip-gram 模型以及优化和扩展,包括层次 Softmax,负采样等内容。
393 |
394 | ### 15.8 GloVe词向量
395 |
396 | 该算法虽然不如Word2Vec热门,但也是简单且不错的模型,在NLP社区有一定的势头。
397 |
398 | #### 15.8.1 什么是GloVe算法
399 |
400 | 全称Global vectors for word representation(基于全局统计的词表征)。在此之前,我们曾通过挑选语料库中位置相近的两个词,列举出词对,即上下文和目标词,GloVe算法做的就是使其关系开始明确化。假定 $X_{ij}$是单词 $i$在单词 $j$上下文中出现的次数,那么这里 $i$与 $j$就和 $t$与 $c$的功能一样,所以你可以认为 $X_{ij}$等同于 $X_{tc}$。
401 |
402 | 如果上下文定义为目标词左右各10个词左右,还会得到$X_{ij}=X_{ji}$的结论。相反,如果上下文总是目标词的前一个则没有这种对称性。这个其实很容易理解,当目标词的上下文包括左右两部分时,则意味着对于上下文 $c$来说,目标词 $t$也是 $c$的上下文。
403 |
404 | **共现矩阵**:其实$X_{ij}$就是共现矩阵的其中一个元素。共现矩阵的横、纵轴均为词汇表的大小,行对应目标词的编号,列对应上下文的编号。计算方法就是遍历一个句子,比如“I love you”,则目标词为“I”时上下文有“love”和“you”,执行$X_{I,love}+1$和$X_{I,you}+1$。最后遍历语料库后即完成共现矩阵的计算。
405 |
406 | **目标**:GloVe的目标是最小化函数:
407 | $$
408 | \operatorname{minimize} \sum_{i=1}^{10,000} \sum_{j=1}^{10,000} f\left(X_{i j}\right)\left(\theta_{i}^{T} e_{j}+b_{i}+b_{j}^{\prime}-\log X_{i j}\right)^{2}
409 | $$
410 | 这个函数表示的是两者间的差距。$\theta_{i}^{T} e_{j}$同$\theta_{t}^{T} e_{c}$一样描述了两者同时出现的频率是多少。如果想要最小化这个函数,毫无疑问需要让$\theta_{i}^{T} e_{j}+b_{i}+b_{j}^{\prime}$逼近$\log X_{ij}$。
411 |
412 | 通过梯度下降算法即可学习嵌入矩阵$E$,并且学会预测两个单词同时出现的频率。
413 |
414 | **细节**:如果$X_{ij}=0$,则$\log X_{ij}$为无穷大,因此要添加一个额外的加权项$f(X_{ij})$,约定$f(0)(\ldots-\log 0)=0$。即当$X_{ij}=0$时不计入求和项;同时对于常见词如a、the、of等词,给与一个较小的权重;对于罕见词如durion则给予一个较大的权重。
415 |
416 | 还有一个细节就是现在的$\theta$和$e$现在是完全对称的,即$\theta_i$和$e_j$是对称的。只看公式的话两者功能相似。
417 |
418 | **对比**:首先,两种算法学习词嵌入都用到了一个信息:词汇共现(co-occurrence),即利用两个词一起出现这个信息来学习词嵌入、隐含的语义等。不同之处在于,word2vec学习了这个共现,本质上做的是预测任务(Predictive),要么根据中心词预测上下文,要么根据上下文预测中心词;而GloVe做的是对已经得到的共现信息(共现矩阵)进行降维、编码(Count-based)。
419 |
420 | **优缺点**:相对来说word2vec没有很好地利用共现信息,而GloVe则因为共现矩阵需要花费相当大的内存;但是不采用负采样的word2vec非常快,GloVe则更容易优化准确率也比没有用负采样的word2vec高。
421 |
422 | #### 15.8.2 为什么不能保证嵌入向量的独立组成部分是能够理解的
423 |
424 | 首先,我们可以将词嵌入理解为“特征提取”,比如提取出Gender、Royal等属性来进行描述,这些特征对于我们来说是可以理解的。但是,我们刚刚提到的算法都是自己学自己的,并不一定会学出Gender等属性。
425 |
426 | 更具体一点,可以当成是进行了降维,用更少的轴来描述原来的单词;如果这些轴分别表示Gender、Royal等属性则是可理解的,并且相互正交;但是我们提到的算法都没有去保证“这两个特征之间是相互正交的”,也就是说他学到的特征很可能是多个正交特征的混合,比如第一个轴是Gender和Royal的混合,第二个轴是Royal和Age的混合等等。
427 |
428 | 所以,才说不能保证嵌入向量的独立组成部分是能够理解的。
429 |
430 | #### 15.8.3 相关重要论文
431 |
432 | 1. Pennington J, Socher R, Manning C. Glove: Global Vectors for Word Representation[C]// Conference on Empirical Methods in Natural Language Processing. 2014:1532-1543.
433 |
434 | ### 15.9 情感分类
435 |
436 | 情感分类:Sentiment classification
437 |
438 | 词嵌入:word embeddings,将一个词语(word)转换为一个向量 (vector)表示, 所以词嵌入有时又被叫作“**word2vec**"。
439 |
440 | 情感分类是一个很难但很有趣的方向,相对来说也很容易出项目,应用到各种场合。
441 |
442 | #### 15.9.1 什么是情感分类
443 |
444 | 情感分类:对带有感情色彩的主观性文本进行分析,分析说话人的态度是倾向正面还是反面,是NLP中最重要的模块之一。
445 |
446 | 
447 |
448 | 举个例子,如上图所示,输入 $x$ 是一段文本,输出 $y$ 是要预测的相应情感,比如是对一个餐馆评价的星级。现在很多人会把用餐的情况与感受分享在一些社交平台上,如果基于像上面这样标记的数据集可以训练一个从 $x$ 到 $y$ 的映射也就是一个情感分类器,就可以用来搜集大家对这个餐馆的评价,从文本中分析出顾客对餐馆评论的情感是正面的还是负面的,可以让餐馆发现自身的问题所在也能让其他顾客了解到这个餐馆是否值得光顾。
449 |
450 | 情感分类最大的挑战是**标记的训练集不够多**,对于情感分类任务来说,训练集大小从10000到100000个单词都很常见,甚至有时会小于10000个单词,但采用**词嵌入**效果可以好很多,即使只有中等大小的标记的训练集,也能构建一个不错的情感分类器。
451 |
452 | #### 15.9.2 一个简单的情感分类模型
453 |
454 | 
455 |
456 | 如上图所示,假设有一个句子“The dessert is excellent(甜点很棒)”,要构建一个分类器把它映射成输出四个星。首先,我们从词典里找到这些词相应的一位编码表示,如“the”的**一位编码**是 $o_{8928}$,乘以**嵌入矩阵 $E$**($E$ 可以从一个很大的文本集里学习到,比如从一亿个词或者一百亿个词里学习嵌入表达,从中获取很多知识甚至从有些不常用的词中获取然后应用到要解决的问题中,即使你的标记数据集里没有这些词),得到单词“the”的**嵌入向量 $e_{8928}$**,对其他三个单词做同样的步骤。将这些嵌入向量求和或者求平均(把所有单词的意思加起来或取平均),假设这里用的是一个平均值计算单元Avg,这个单元会输出一个相同维度的特征向量,把这个特征向量送进softmax分类器,输出5个可能结果(从一星到五星)的概率值,进而输出预测结果 $\hat y$。
457 |
458 | 这个算法有一个问题就是**没考虑词序**,像“Completely lacking in good taste, good service, and good ambience(完全没有好的味道、好的服务、好的氛围)”虽然是负面评价,但”good“这个词出现了很多次,如果还用上面的算法,忽略词序而仅仅把所有单词的词嵌入加起来或者取平均,则最后的特征向量会有很多good的表示,分类器就可能误认为这是一个好评。
459 |
460 | #### 15.9.3 用RNN实现情感分类
461 |
462 | 
463 |
464 | 首先找到这条评论中每一个单词的一位编码表示,乘以词嵌入矩阵 $E$ 得到词嵌入表达 $e$,然后把它们送进我们之前学过的多对一的RNN网络结构里,RNN的工作就是在最后一步计算一个特征向量来预测 $\hat y$。这种算法考虑了词的顺序,效果更好,能够意识到“Completely lacking in good taste, good service, and good ambience(完全没有好的味道、好的服务、好的氛围)”是个负面评价。由于词嵌入 $E$ 是在一个更大的数据集里训练的,可以更好地泛化一些没有见过的新单词,比如其他人可能会说“Completely absent of good taste...”,即使"absent"这个词不在标记的训练集里,但它仍然可以判断对并且泛化得很好。
465 |
466 | ### 15.10 词嵌入除偏
467 |
468 | 算法安全性;偏见原因:**数据集**不完整(cv:黑人数据不够多)、打**标签**有偏见、**算法**本身的偏见(推荐算法的导向性,推之前没有的,试探性,引导往其他方向走);解决方法:采样更丰富和比例更合理(数据增强)、***设计算法创新处理有偏数据集得到无偏结果***;老人无健康码上不了车,考虑少数人、边缘化等;
469 |
470 | 词嵌入除偏:Debiasing word embeddings
471 |
472 | #### 15.10.1 为什么需要除偏
473 |
474 | 这里的“偏(bias)"不是指偏见,而是指性别、种族、性取向方面的偏见。
475 |
476 | “Man is to computer programmer as woman is to homemaker? debiasing word embeddings.”这篇论文提出,如果说Man对应Computer programmer则Woman会对应什么呢?一个已经完成学习的词嵌入可能会输出Homemaker,这个结果就反映了一个十分不良的性别歧视,如果输出的是Computer programmer则会更合理。再比如说Father对应Doctor那么Mother应该对应什么?有些完成学习的词嵌入会输出nurse,这也是不对的。
477 |
478 | 也就是说,根据训练模型所使用的文本,**词嵌入可能会反映出性别、种族、年龄、性取向等其他方面的偏见**,这些偏见都和社会经济状态相关。因为机器学习算法正用来制定十分重要的决策,影响着世间万物,所以尽量修改学习算法来尽可能**减少或是理想化消除这些非预期形式的偏见**是十分重要的,因此需要对词嵌入进行除偏。
479 |
480 | **偏见产生的原因**:
481 |
482 | * **数据集**不完整。比如在做图像处理的时候由于黑人的数据不够多而导致效果不好。
483 |
484 | * **标签**有偏见。由于标签都是人打上去的,因此如果打标签的人带有偏见,则最后标签也会带有偏见并产生实际影响。
485 |
486 | * **算法**本身的偏见。常见于推荐算法,有的推荐算法具有导向性,会通过试探性地推荐之前没有的物品,引导用户养成新的兴趣,有时候甚至会带有“恶意”将用户引导到不好的方向。
487 |
488 | #### 15.10.2 什么是词嵌入除偏
489 |
490 | 假设我们已经完成一个词嵌入的学习,babysister、doctor、grandmother、grandfather、girl、boy、she、he这些词的嵌入位置如下图所示,
491 |
492 |  565 | 只考虑单个样本的情况,损失函数为$L(a,y)$,a是logistic回归的输出,y为样本的基本真值标签值,该样本的偏导数流程图如下图所示。
566 | 
567 |
568 | 假设样本只有两个特征值x1和x2,为了计算Z,我们需要输入参数w1和w2和b,在logistic回归中,我们要做的就是变换参数w和b的值,来最小化损失函数。首先,我们需要向前一步,先计算损失函数的导数,计算函数L关于a的导数,在代码中,只需要使用da来表示这个变量;之后,再向后一步,计算$dz$,$dz$是损失函数关于z的导数,向后传播的最后一步,w和b需要如何变化,关于b的求导:$db=dz=a-y$。因此,关于单个样本的梯度下降法,所需要做的就是使用这个计算公式计算dz,然后计算dw1、dw2、db,然后更新w1为w1减去学习率乘以dw1;更新w2为w2减去学习率乘以$dw2$;更新b为b减去学习率乘以db,这就是单个样本实例的一次梯度更新步骤。
569 |
570 |
571 |
572 | ### 2.8 向量化
573 |
574 | #### 2.8.1 向量化代码示例
575 |
576 | **向量化作用**
577 |
578 | 相比于显式的for循环,向量化可以大大缩短数据的运算时间,得到同样的结果,使用for循环所花费时间是将代码向量化后运行时间的近300倍。示例代码如下:
579 |
580 | ```python
581 | import numpy as np
582 | import time
583 |
584 | a=np.array([1,2,3,4])
585 | a=np.random.rand(1000000)
586 | b=np.random.rand(1000000)
587 |
588 | tic=time.time()
589 | c=np.dot(a,b)
590 | toc=time.time()
591 |
592 | print("Vectorized version:"+str(1000*(toc-tic))+"ms")
593 |
594 | c=0
595 | tic=time.time()
596 | for i in range(1000000):
597 | c += a[i] * b[i]
598 | toc=time.time()
599 | print("for loop:"+str(1000*(toc-tic))+"ms")
600 |
601 | # 结果
602 | # Vectorized version:6.882190704345703ms
603 | # for loop:559.5316886901855ms
604 | ```
605 |
606 | **GPU和CPU的对比**
607 |
608 | GPU为图像处理单元,CPU为中央处理器。两者都有并行化指令,有时称为SIMD指令(单指令多数据流),这能够让python使用其中的内置函数(可以去掉显式for循环的函数,如:numpy),GPU更为擅长运用SIMD指令,但CPU也同样可以实现。
609 |
610 | pytorch在GPU中配置方法:博客https://blog.csdn.net/qq_44420246/article/details/107249283
611 |
612 | #### 2.8.2 初步向量化logistic函数
613 |
614 | 若用如下程序计算logistic回归导数
615 |
616 | $$\begin{array}{l}
617 | J=0, \quad d w 1=0, \quad d w 2=0, \quad d b=0 \\
618 | \text { for } i=1 \text { to m: } \\
619 | \qquad \begin{array}{l}
620 | z^{(i)}=w^{T} x^{(i)}+b \\
621 | a^{(i)}=\sigma\left(z^{(i)}\right) \\
622 | J+=-\left[y^{(i)} \log \hat{y}^{(i)}+\left(1-y^{(i)}\right) \log \left(1-\hat{y}^{(i)}\right)\right] \\
623 | d z^{(i)}=a^{(i)}\left(1-a^{(i)}\right) \\
624 | d w_{1}+=x_{1}^{(i)} d z^{(i)} \\
625 | d w_{2}+=x_{2}^{(i)} d z^{(i)} \\
626 | d b^ {}+=d z^{(i)}
627 | \end{array} \\
628 | J=J / m, \quad d w_{1}=d w_{1} / m, \quad d w_{2}=d w_{2} / m, \quad d b=d b / m
629 | \end{array}$$
630 |
631 | 该程序实际包含两个for循环,第一个for循环即第二行的“for”,第二个for循环。在程序中,为以下的这一部分
632 |
633 | $d w_{1}+=x_{1}^{(i)} d z^{(i)}$
634 | $d w_{2}+=x_{2}^{(i)} d z^{(i)}$
635 |
636 | 即如果特征不止2个,有n个的话,则需重复执行该步骤n次
637 | 现用向量化的方法去掉第二个for循环,将dw通过$$\mathrm{dw}=\text { np.zeros }(\mathrm{n}, 1)$$转化为初始值为0的n*1维的向量
638 | 则原程序中的$$d w 1=0, \quad d w 2=0$$部分可取缔。
639 |
640 | 原程序的
641 |
642 |
643 |
644 | $$d w_{1}+=x_{1}^{(i)} d z^{(i)}$$ $$d w_{2}+=x_{2}^{(i)} d z^{(i)}$$
645 |
646 |
647 |
648 | 可以用$$d w+=x^{(i)} d z^{(i)}$$代替。
649 |
650 | 原程序的$$d w_{1}=d w_{1} / m, \quad d w_{2}=d w_{2} / m$$
651 | 可以用$$d w /=m$$代替。
652 |
653 | 以此去掉了第二个for循环,通过向量化的方法,使程序得到了初步的简化。
654 |
655 |
656 |
657 | **高效计算激活函数**
658 |
659 | 已知函数$z=\omega^{\top} x+b$和$a^{}=\sigma\left(z^{}\right)$,可以利用向量的方法对数据进行高效计算
660 | 首先,将所有训练样本(m个n维的向量)横向堆叠得到一个n\*m的矩阵X,以此作为训练输入
661 | 其中,X矩阵如下
662 |
663 | $X=\left[x^{(1)}, x^{(2)}, \cdots, x^{(m)}\right] $
664 |
665 | $x^{(1)}$为第一个训练样本的向量,依此类推
666 | 再定义一个1\*m的矩阵Z,如下
667 |
668 | $z=\left[z^{(1)}, z^{(2)} \cdots, z^{(m)}\right]$
669 |
670 | 定义1*m矩阵如下*
671 |
672 |
673 | $[b, b, b, \cdots b]$
674 |
675 | 定义矩阵A如下
676 |
677 | $A=\left[a^{(1)}, a^{(2)}, \cdots, a^{(m)}\right]$
678 |
679 | 则高效计算得出:
680 |
681 | $z=\left[z^{(1)}, z^{(2)} \ldots, z^{(m)}\right]=\omega^{\top} x+[b, b, \cdots, b)=\left[\omega^{\top} x^{(1)}+b, \cdots, \omega^{(m)}+b\right]$
682 | $A=\sigma(z)$
683 |
684 | **在python中的操作**
685 |
686 | 调用numpy库,定义向量和矩阵后,使用z=np.dot(w.T,x+b)语句进行计算,其中python自动将b扩展为1*m的向量(python的“广播”)
687 | 调用sigmoid函数,由$A=\sigma(z)$计算$a^{(1)},a^{(2)}$.....$a^{(m)}$
688 |
689 | $v=\left[\begin{array}{c}v_{1} \\ \vdots \\ v_{n}\end{array}\right] \rightarrow u=\left[\begin{array}{c}e^{v_{1}} \\ e^{v_{c}} \\ e^{j_{n}}\end{array}\right]$
690 |
691 | #### 2.8.3 高度向量化logistic
692 |
693 | 定义矩阵X如下
694 | $X=\left[x^{(1)}, x^{(2)}, \cdots, x^{(m)}\right]$
695 | 定义矩阵Y如下
696 | $Y=\left[\begin{array}{lll}y^{(1)} & ,\cdots & ,y^{(m)}\end{array}\right]$
697 | 定义矩阵A如下
698 | $A=\left[a^{(1)}, a^{(2)}, \cdots, a^{(m)}\right]$
699 | 定义矩阵dz如下
700 | $d z=\left[d z^{(1)} ,d z^{(2)}, \cdots ,d z^{(m)}\right]$
701 | 有$d z^{(1)}=a^{(1)}-y^{(1)} \quad ,$.....$,d z^{(m)}=a^{(m)}-y^{(m)}$
702 |
703 |
704 |
705 | **则高度向量化后,程序如下**
706 |
707 | $z=w^{T} X+b$
708 | $A=\sigma(z)$
709 | $d z=A-Y$
710 | $d w=\frac{1}{m} xd z^{T}$
711 | $db=\frac{1}{m} \sum_{i=1}^{n} d z^{(i)}$
712 |
713 | 在python中,调用numpy库(np),则矩阵Z可下方代码计算得出:
714 | Z$=n p \cdot \log (w . T, x)+b$
715 | db可用下方代码计算得出:
716 | $d b=\frac{1}{m} n p \cdot \operatorname{sum}(d z)$
717 |
718 | ### 2.9 关于python / numpy向量的说明 ###
719 | 默认以下的向量指的是np.array,直译是数组,但是在神经网络的项目中称为向量是更符合的。以下将对其的一些概念做介绍。
720 |
721 | #### 2.9.1 相关定义
722 |
723 | **轴(axis)**
724 |
725 | 对于array.shape形如 (a, b, c, ...) 的数组,a是其第0轴,b是第1轴,以此类推。数轴简单,但这些轴有什么意思?
726 | 对于shape为 (x, y) 的array,0轴就是行的轴,遍历该轴可以遍历所有行;1轴是列的轴,遍历该列可以遍历所有列。但是为什么是这样?
727 |
728 | a[x][y]我们都懂,是访问数组a的第x行,第y列。那么轴的概念就在于,搭建一个坐标系(二维的是xOy坐标系),可以用坐标轴上的数表示数组的任意一个数。在这里,x就是a[x][y]在0轴的位置,y是在1轴的位置。那么自然而然0轴对应的是行号的轴,1轴对应的是列号的轴。对于有更多轴(秩更高)的数组来说这样解释同样是合适的。
729 |
730 | 了解了轴的概念之后,那就应该也了解函数np.sum中参数axis的含义了:沿着(遍历)某一个轴进行求和。对于其他含义该参数的函数来说,也是遍历该轴的意思。
731 |
732 | **维数(dimension / dim)**
733 |
734 | 我曾经在入门的时候遇到了这样一个难题:
735 |
736 | 一个博主说 np.zeros((1000,))是获得一个1000维的向量。
737 |
738 | 我当时就懵了,1000维?一张图片才3维,就算所有图片叠在一起也才4维,为什么要1000维?后来才知道此维非彼维:“维”指的是一个轴的“大小”(取值范围),而不是接下来要讲的秩的含义。对“维”的误解主要出自我们一般称a[][] 为二维数组,b[][][]为三维数组之类的说法。不过在真正了解维数/dim的定义之后就基本不会再有误解了。
739 |
740 | **秩(rank)**
741 |
742 | 在一些论文中,可能会出现这个**单词**。而且如果用的是翻译软件进行阅读,很有可能被翻译为其他东西而影响阅读,故特地标明了对应的英文rank。
743 |
744 | 秩指的是一个向量的轴的数量。秩0是单个数字,秩1是[]向量,秩2是[][]向量,以此类推。
745 |
746 | 或许有的同学在学线性代数时学过秩这个概念,不过又是此秩非彼秩。
747 |
748 | **示例代码**
749 |
750 | ```python
751 | a = np.array([[1, 2],
752 | [3, 4],
753 | [5, 6]]
754 | )
755 | b = np.sum(a, axis=0)
756 | # b is [9, 12]
757 | c = np.sum(a, axis=1)
758 | # c is [3, 7, 11]
759 | ```
760 |
761 | 你可能也发现了一个细节:sum之后降秩了。如果不想这么做,可以传多一个参数keepdims
762 |
763 | b = np.sum(a, axis=0, keepdims=True)
764 | # b shape (1, 2)
765 |
766 | 这样就可以避免可能由于降秩而带来的bug。
767 |
768 |
769 | #### 2.9.2 Python中的广播 ####
770 | Python中的广播(broadcasting),是一种自动将“低秩”向量拓展到高秩向量,以便与高秩向量进行逐元素运算(+-*/)的机制。
771 |
772 | a = 3
773 | b = np.array([[1, 2],
774 | [3, 4],
775 | [5, 6]]
776 | )
777 | c = b + a
778 | # c = a + b 结果也一致
779 | print(c)
780 | # c is [[4, 5], [6, 7], [8, 9]]
781 | 值得注意的是,这个“低秩”并不一定是真正的低秩。
782 |
783 | **广播机制的规则**
784 |
785 | * 假设低秩向量shape为(a, b),高秩向量shape为(a, b, c, d, ...)或(..., c, d, a, b)。即高秩向量shape的最前面或者最后面“包含”低秩向量的shape,则可以进行广播。
786 | * 两个同秩向量,若对应的**部分轴(不要求连续)**的维数相等,且维数不同的轴,其中一个向量(不一定总是同一个向量)的维数为1,则可以进行广播。
787 | * 单个实数x(秩0),可以和任意向量广播。
788 |
789 | 广播可以理解为通过复制操作,将**低维的轴**的维数增加到和高秩向量一致。
790 |
791 |
792 |
793 | **示例代码**
794 |
795 | a = np.zeros((3, 4))
796 | b = np.zeros((1, 2, 3, 4))
797 | t = a + b # 可以广播
798 |
799 | c = np.zeros((3, 4, 5, 6, 7))
800 | t = a - c # 可以广播
801 |
802 | d = np.zeros((1, 2, 3, 4, 5, 6))
803 | t = a * d # 不可以广播
804 |
805 | e = np.random.randn(1, 1, 2, 1, 4, 1)
806 | f = np.random.randn(7, 6, 2, 3, 4, 8)
807 | t = e / f # 可以广播
808 |
809 | g = np.random.randn(5, 6, 1, 3, 1, 8)
810 | t = e + g # 可以广播
811 |
812 |
813 | #### 2.9.3 Jupyter / Ipython笔记本快速指南 ####
814 | 本文参考了[Jupyter Notebook介绍、安装及使用教程](https:https://www.jianshu.com/p/91365f343585),提取了其中的一部分,适用于只是想快速运行python代码、验证自己的想法的同学。如果想了解过多细节,可以参考原文。
815 |
816 | **安装**
817 |
818 | 介绍两种安装方式,分别对应到安装了anaconda和万能的场合
819 |
820 | **方法一**
821 |
822 | 安装了anaconda的话,常规来说自带Jupyter。如果没有,尝试如下指令:
823 |
824 | conda install jupyter notebook
825 |
826 |
827 |
828 | **方法二**
829 |
830 | 只要你安装了python(版本支持前提下)就能安装的方法(win10):
831 |
832 | 打开cmd(不知道如何打开可以搜索),输入
833 |
834 | pip install jupyter
835 |
836 | 一般来说,会自动安装到目录:...\Python\Python36\Scripts\ 。
837 | 具体安装到了哪,要看你的python安装到了哪。然后此时你可以按照下一步运行jupyter;如果提示没有这个命令,则是环境变量的问题,解决办法:
838 |
839 | 1. 右键我的电脑->属性->高级系统设置->环境变量
840 |
841 | 2. 双击第一个窗口 用户变量 下的Path->新建
842 |
843 | 3. 将jupyter安装的目录 “...\Python\Python36\Scripts” 复制到此处。连点ok。完成。
844 |
845 |
846 |
847 | **打开运行**
848 |
849 | 打开cmd,输入 jupyter notebook,回车。然后顺利的话会弹出一个游览器,先别急着关掉cmd,关掉的话你的jupyter也会一起“关掉”的。
850 |
851 | 点击右边的new->python3 ,然后会打开/跳转一个新页面,于是就可以愉快滴快速验证代码啦!
852 |
853 |
854 |
855 | **简单的使用教程**
856 |
857 | 一开始只有一个 **In[]** ,你可以输入代码,回车键输入下一行,并且一个In可以视为一个“块”,在执行时是一个块一个块执行的。
858 |
859 | 输入代码之后如果想要运行,用 **shift+enter**(回车)即可。然后回到刚刚提到的块问题,如果你后面的块依赖前面的块的代码,那么在修改前面的块的代码之后,需要将“受到牵连”的所有块重新执行,才能将结果更新到后面的块,否则输出是不会自动改变的。
860 |
861 | 在运行之后,有时候会有输出块 **Out[]** ,有时候没有。这个取决于该块中**最后一句**代码是否有返回值,有则显示返回值内容,否则不显示任何东西。对于print显示的内容,将在块正下方的空白处显示,而不是在 Out[] 中显示。
862 |
863 | #### 2.9.4 logistic损失函数的解释 ####
864 | 首先,要知道我们的logistic回归在做什么:“拟合”一个函数,该函数对于输入图形x,给出概率p(y|x),其中p(y|x)是图中有猫的概率。
865 | 那这个函数可以写成:
866 |
867 | > a, y=1
868 | >
869 | > 1-a, y=0
870 |
871 | 其中a是logistic回归的输出,也即y-hat(y帽),y的预测值。
872 | 更进一步,可以写成:
873 |
874 |
565 | 只考虑单个样本的情况,损失函数为$L(a,y)$,a是logistic回归的输出,y为样本的基本真值标签值,该样本的偏导数流程图如下图所示。
566 | 
567 |
568 | 假设样本只有两个特征值x1和x2,为了计算Z,我们需要输入参数w1和w2和b,在logistic回归中,我们要做的就是变换参数w和b的值,来最小化损失函数。首先,我们需要向前一步,先计算损失函数的导数,计算函数L关于a的导数,在代码中,只需要使用da来表示这个变量;之后,再向后一步,计算$dz$,$dz$是损失函数关于z的导数,向后传播的最后一步,w和b需要如何变化,关于b的求导:$db=dz=a-y$。因此,关于单个样本的梯度下降法,所需要做的就是使用这个计算公式计算dz,然后计算dw1、dw2、db,然后更新w1为w1减去学习率乘以dw1;更新w2为w2减去学习率乘以$dw2$;更新b为b减去学习率乘以db,这就是单个样本实例的一次梯度更新步骤。
569 |
570 |
571 |
572 | ### 2.8 向量化
573 |
574 | #### 2.8.1 向量化代码示例
575 |
576 | **向量化作用**
577 |
578 | 相比于显式的for循环,向量化可以大大缩短数据的运算时间,得到同样的结果,使用for循环所花费时间是将代码向量化后运行时间的近300倍。示例代码如下:
579 |
580 | ```python
581 | import numpy as np
582 | import time
583 |
584 | a=np.array([1,2,3,4])
585 | a=np.random.rand(1000000)
586 | b=np.random.rand(1000000)
587 |
588 | tic=time.time()
589 | c=np.dot(a,b)
590 | toc=time.time()
591 |
592 | print("Vectorized version:"+str(1000*(toc-tic))+"ms")
593 |
594 | c=0
595 | tic=time.time()
596 | for i in range(1000000):
597 | c += a[i] * b[i]
598 | toc=time.time()
599 | print("for loop:"+str(1000*(toc-tic))+"ms")
600 |
601 | # 结果
602 | # Vectorized version:6.882190704345703ms
603 | # for loop:559.5316886901855ms
604 | ```
605 |
606 | **GPU和CPU的对比**
607 |
608 | GPU为图像处理单元,CPU为中央处理器。两者都有并行化指令,有时称为SIMD指令(单指令多数据流),这能够让python使用其中的内置函数(可以去掉显式for循环的函数,如:numpy),GPU更为擅长运用SIMD指令,但CPU也同样可以实现。
609 |
610 | pytorch在GPU中配置方法:博客https://blog.csdn.net/qq_44420246/article/details/107249283
611 |
612 | #### 2.8.2 初步向量化logistic函数
613 |
614 | 若用如下程序计算logistic回归导数
615 |
616 | $$\begin{array}{l}
617 | J=0, \quad d w 1=0, \quad d w 2=0, \quad d b=0 \\
618 | \text { for } i=1 \text { to m: } \\
619 | \qquad \begin{array}{l}
620 | z^{(i)}=w^{T} x^{(i)}+b \\
621 | a^{(i)}=\sigma\left(z^{(i)}\right) \\
622 | J+=-\left[y^{(i)} \log \hat{y}^{(i)}+\left(1-y^{(i)}\right) \log \left(1-\hat{y}^{(i)}\right)\right] \\
623 | d z^{(i)}=a^{(i)}\left(1-a^{(i)}\right) \\
624 | d w_{1}+=x_{1}^{(i)} d z^{(i)} \\
625 | d w_{2}+=x_{2}^{(i)} d z^{(i)} \\
626 | d b^ {}+=d z^{(i)}
627 | \end{array} \\
628 | J=J / m, \quad d w_{1}=d w_{1} / m, \quad d w_{2}=d w_{2} / m, \quad d b=d b / m
629 | \end{array}$$
630 |
631 | 该程序实际包含两个for循环,第一个for循环即第二行的“for”,第二个for循环。在程序中,为以下的这一部分
632 |
633 | $d w_{1}+=x_{1}^{(i)} d z^{(i)}$
634 | $d w_{2}+=x_{2}^{(i)} d z^{(i)}$
635 |
636 | 即如果特征不止2个,有n个的话,则需重复执行该步骤n次
637 | 现用向量化的方法去掉第二个for循环,将dw通过$$\mathrm{dw}=\text { np.zeros }(\mathrm{n}, 1)$$转化为初始值为0的n*1维的向量
638 | 则原程序中的$$d w 1=0, \quad d w 2=0$$部分可取缔。
639 |
640 | 原程序的
641 |
642 |
643 |
644 | $$d w_{1}+=x_{1}^{(i)} d z^{(i)}$$ $$d w_{2}+=x_{2}^{(i)} d z^{(i)}$$
645 |
646 |
647 |
648 | 可以用$$d w+=x^{(i)} d z^{(i)}$$代替。
649 |
650 | 原程序的$$d w_{1}=d w_{1} / m, \quad d w_{2}=d w_{2} / m$$
651 | 可以用$$d w /=m$$代替。
652 |
653 | 以此去掉了第二个for循环,通过向量化的方法,使程序得到了初步的简化。
654 |
655 |
656 |
657 | **高效计算激活函数**
658 |
659 | 已知函数$z=\omega^{\top} x+b$和$a^{}=\sigma\left(z^{}\right)$,可以利用向量的方法对数据进行高效计算
660 | 首先,将所有训练样本(m个n维的向量)横向堆叠得到一个n\*m的矩阵X,以此作为训练输入
661 | 其中,X矩阵如下
662 |
663 | $X=\left[x^{(1)}, x^{(2)}, \cdots, x^{(m)}\right] $
664 |
665 | $x^{(1)}$为第一个训练样本的向量,依此类推
666 | 再定义一个1\*m的矩阵Z,如下
667 |
668 | $z=\left[z^{(1)}, z^{(2)} \cdots, z^{(m)}\right]$
669 |
670 | 定义1*m矩阵如下*
671 |
672 |
673 | $[b, b, b, \cdots b]$
674 |
675 | 定义矩阵A如下
676 |
677 | $A=\left[a^{(1)}, a^{(2)}, \cdots, a^{(m)}\right]$
678 |
679 | 则高效计算得出:
680 |
681 | $z=\left[z^{(1)}, z^{(2)} \ldots, z^{(m)}\right]=\omega^{\top} x+[b, b, \cdots, b)=\left[\omega^{\top} x^{(1)}+b, \cdots, \omega^{(m)}+b\right]$
682 | $A=\sigma(z)$
683 |
684 | **在python中的操作**
685 |
686 | 调用numpy库,定义向量和矩阵后,使用z=np.dot(w.T,x+b)语句进行计算,其中python自动将b扩展为1*m的向量(python的“广播”)
687 | 调用sigmoid函数,由$A=\sigma(z)$计算$a^{(1)},a^{(2)}$.....$a^{(m)}$
688 |
689 | $v=\left[\begin{array}{c}v_{1} \\ \vdots \\ v_{n}\end{array}\right] \rightarrow u=\left[\begin{array}{c}e^{v_{1}} \\ e^{v_{c}} \\ e^{j_{n}}\end{array}\right]$
690 |
691 | #### 2.8.3 高度向量化logistic
692 |
693 | 定义矩阵X如下
694 | $X=\left[x^{(1)}, x^{(2)}, \cdots, x^{(m)}\right]$
695 | 定义矩阵Y如下
696 | $Y=\left[\begin{array}{lll}y^{(1)} & ,\cdots & ,y^{(m)}\end{array}\right]$
697 | 定义矩阵A如下
698 | $A=\left[a^{(1)}, a^{(2)}, \cdots, a^{(m)}\right]$
699 | 定义矩阵dz如下
700 | $d z=\left[d z^{(1)} ,d z^{(2)}, \cdots ,d z^{(m)}\right]$
701 | 有$d z^{(1)}=a^{(1)}-y^{(1)} \quad ,$.....$,d z^{(m)}=a^{(m)}-y^{(m)}$
702 |
703 |
704 |
705 | **则高度向量化后,程序如下**
706 |
707 | $z=w^{T} X+b$
708 | $A=\sigma(z)$
709 | $d z=A-Y$
710 | $d w=\frac{1}{m} xd z^{T}$
711 | $db=\frac{1}{m} \sum_{i=1}^{n} d z^{(i)}$
712 |
713 | 在python中,调用numpy库(np),则矩阵Z可下方代码计算得出:
714 | Z$=n p \cdot \log (w . T, x)+b$
715 | db可用下方代码计算得出:
716 | $d b=\frac{1}{m} n p \cdot \operatorname{sum}(d z)$
717 |
718 | ### 2.9 关于python / numpy向量的说明 ###
719 | 默认以下的向量指的是np.array,直译是数组,但是在神经网络的项目中称为向量是更符合的。以下将对其的一些概念做介绍。
720 |
721 | #### 2.9.1 相关定义
722 |
723 | **轴(axis)**
724 |
725 | 对于array.shape形如 (a, b, c, ...) 的数组,a是其第0轴,b是第1轴,以此类推。数轴简单,但这些轴有什么意思?
726 | 对于shape为 (x, y) 的array,0轴就是行的轴,遍历该轴可以遍历所有行;1轴是列的轴,遍历该列可以遍历所有列。但是为什么是这样?
727 |
728 | a[x][y]我们都懂,是访问数组a的第x行,第y列。那么轴的概念就在于,搭建一个坐标系(二维的是xOy坐标系),可以用坐标轴上的数表示数组的任意一个数。在这里,x就是a[x][y]在0轴的位置,y是在1轴的位置。那么自然而然0轴对应的是行号的轴,1轴对应的是列号的轴。对于有更多轴(秩更高)的数组来说这样解释同样是合适的。
729 |
730 | 了解了轴的概念之后,那就应该也了解函数np.sum中参数axis的含义了:沿着(遍历)某一个轴进行求和。对于其他含义该参数的函数来说,也是遍历该轴的意思。
731 |
732 | **维数(dimension / dim)**
733 |
734 | 我曾经在入门的时候遇到了这样一个难题:
735 |
736 | 一个博主说 np.zeros((1000,))是获得一个1000维的向量。
737 |
738 | 我当时就懵了,1000维?一张图片才3维,就算所有图片叠在一起也才4维,为什么要1000维?后来才知道此维非彼维:“维”指的是一个轴的“大小”(取值范围),而不是接下来要讲的秩的含义。对“维”的误解主要出自我们一般称a[][] 为二维数组,b[][][]为三维数组之类的说法。不过在真正了解维数/dim的定义之后就基本不会再有误解了。
739 |
740 | **秩(rank)**
741 |
742 | 在一些论文中,可能会出现这个**单词**。而且如果用的是翻译软件进行阅读,很有可能被翻译为其他东西而影响阅读,故特地标明了对应的英文rank。
743 |
744 | 秩指的是一个向量的轴的数量。秩0是单个数字,秩1是[]向量,秩2是[][]向量,以此类推。
745 |
746 | 或许有的同学在学线性代数时学过秩这个概念,不过又是此秩非彼秩。
747 |
748 | **示例代码**
749 |
750 | ```python
751 | a = np.array([[1, 2],
752 | [3, 4],
753 | [5, 6]]
754 | )
755 | b = np.sum(a, axis=0)
756 | # b is [9, 12]
757 | c = np.sum(a, axis=1)
758 | # c is [3, 7, 11]
759 | ```
760 |
761 | 你可能也发现了一个细节:sum之后降秩了。如果不想这么做,可以传多一个参数keepdims
762 |
763 | b = np.sum(a, axis=0, keepdims=True)
764 | # b shape (1, 2)
765 |
766 | 这样就可以避免可能由于降秩而带来的bug。
767 |
768 |
769 | #### 2.9.2 Python中的广播 ####
770 | Python中的广播(broadcasting),是一种自动将“低秩”向量拓展到高秩向量,以便与高秩向量进行逐元素运算(+-*/)的机制。
771 |
772 | a = 3
773 | b = np.array([[1, 2],
774 | [3, 4],
775 | [5, 6]]
776 | )
777 | c = b + a
778 | # c = a + b 结果也一致
779 | print(c)
780 | # c is [[4, 5], [6, 7], [8, 9]]
781 | 值得注意的是,这个“低秩”并不一定是真正的低秩。
782 |
783 | **广播机制的规则**
784 |
785 | * 假设低秩向量shape为(a, b),高秩向量shape为(a, b, c, d, ...)或(..., c, d, a, b)。即高秩向量shape的最前面或者最后面“包含”低秩向量的shape,则可以进行广播。
786 | * 两个同秩向量,若对应的**部分轴(不要求连续)**的维数相等,且维数不同的轴,其中一个向量(不一定总是同一个向量)的维数为1,则可以进行广播。
787 | * 单个实数x(秩0),可以和任意向量广播。
788 |
789 | 广播可以理解为通过复制操作,将**低维的轴**的维数增加到和高秩向量一致。
790 |
791 |
792 |
793 | **示例代码**
794 |
795 | a = np.zeros((3, 4))
796 | b = np.zeros((1, 2, 3, 4))
797 | t = a + b # 可以广播
798 |
799 | c = np.zeros((3, 4, 5, 6, 7))
800 | t = a - c # 可以广播
801 |
802 | d = np.zeros((1, 2, 3, 4, 5, 6))
803 | t = a * d # 不可以广播
804 |
805 | e = np.random.randn(1, 1, 2, 1, 4, 1)
806 | f = np.random.randn(7, 6, 2, 3, 4, 8)
807 | t = e / f # 可以广播
808 |
809 | g = np.random.randn(5, 6, 1, 3, 1, 8)
810 | t = e + g # 可以广播
811 |
812 |
813 | #### 2.9.3 Jupyter / Ipython笔记本快速指南 ####
814 | 本文参考了[Jupyter Notebook介绍、安装及使用教程](https:https://www.jianshu.com/p/91365f343585),提取了其中的一部分,适用于只是想快速运行python代码、验证自己的想法的同学。如果想了解过多细节,可以参考原文。
815 |
816 | **安装**
817 |
818 | 介绍两种安装方式,分别对应到安装了anaconda和万能的场合
819 |
820 | **方法一**
821 |
822 | 安装了anaconda的话,常规来说自带Jupyter。如果没有,尝试如下指令:
823 |
824 | conda install jupyter notebook
825 |
826 |
827 |
828 | **方法二**
829 |
830 | 只要你安装了python(版本支持前提下)就能安装的方法(win10):
831 |
832 | 打开cmd(不知道如何打开可以搜索),输入
833 |
834 | pip install jupyter
835 |
836 | 一般来说,会自动安装到目录:...\Python\Python36\Scripts\ 。
837 | 具体安装到了哪,要看你的python安装到了哪。然后此时你可以按照下一步运行jupyter;如果提示没有这个命令,则是环境变量的问题,解决办法:
838 |
839 | 1. 右键我的电脑->属性->高级系统设置->环境变量
840 |
841 | 2. 双击第一个窗口 用户变量 下的Path->新建
842 |
843 | 3. 将jupyter安装的目录 “...\Python\Python36\Scripts” 复制到此处。连点ok。完成。
844 |
845 |
846 |
847 | **打开运行**
848 |
849 | 打开cmd,输入 jupyter notebook,回车。然后顺利的话会弹出一个游览器,先别急着关掉cmd,关掉的话你的jupyter也会一起“关掉”的。
850 |
851 | 点击右边的new->python3 ,然后会打开/跳转一个新页面,于是就可以愉快滴快速验证代码啦!
852 |
853 |
854 |
855 | **简单的使用教程**
856 |
857 | 一开始只有一个 **In[]** ,你可以输入代码,回车键输入下一行,并且一个In可以视为一个“块”,在执行时是一个块一个块执行的。
858 |
859 | 输入代码之后如果想要运行,用 **shift+enter**(回车)即可。然后回到刚刚提到的块问题,如果你后面的块依赖前面的块的代码,那么在修改前面的块的代码之后,需要将“受到牵连”的所有块重新执行,才能将结果更新到后面的块,否则输出是不会自动改变的。
860 |
861 | 在运行之后,有时候会有输出块 **Out[]** ,有时候没有。这个取决于该块中**最后一句**代码是否有返回值,有则显示返回值内容,否则不显示任何东西。对于print显示的内容,将在块正下方的空白处显示,而不是在 Out[] 中显示。
862 |
863 | #### 2.9.4 logistic损失函数的解释 ####
864 | 首先,要知道我们的logistic回归在做什么:“拟合”一个函数,该函数对于输入图形x,给出概率p(y|x),其中p(y|x)是图中有猫的概率。
865 | 那这个函数可以写成:
866 |
867 | > a, y=1
868 | >
869 | > 1-a, y=0
870 |
871 | 其中a是logistic回归的输出,也即y-hat(y帽),y的预测值。
872 | 更进一步,可以写成:
873 |
874 |  875 |
876 |
877 | 那么我们的任务就成了找出一组权值w和偏置b,使得p(y|x)最大。有没有让你想起来**最大似然估计**?没错,就是差不多的任务。那么对数似然函数可以写作:
878 |
879 |
875 |
876 |
877 | 那么我们的任务就成了找出一组权值w和偏置b,使得p(y|x)最大。有没有让你想起来**最大似然估计**?没错,就是差不多的任务。那么对数似然函数可以写作:
878 |
879 |  880 | 我们目标就是让上面的那个函数取最大值。再加个负号,改为取最小值:
881 |
882 |
880 | 我们目标就是让上面的那个函数取最大值。再加个负号,改为取最小值:
881 |
882 |  883 |
884 |
885 | 于是,我们的损失函数(loss)就定义为了上式。
886 |
887 | #### 2.9.5 似然和概率 ####
888 | 既然提到了最大似然估计,那就提提似然和概率的区别:
889 |
890 | > 简单来讲,似然与概率分别是针对不同内容的估计和近似。概率(密度)表达给定θ下样本**X**=x的可能性,而似然表达了给定样本X=x下参数θ=θ1(相对于另外的参数取值θ2而言)为真实值的可能性
891 |
892 | 引自[似然(likelihood)和概率(probability)的区别与联系](https://blog.csdn.net/songyu0120/article/details/85059149)
893 |
894 |
895 |
896 |
897 |
--------------------------------------------------------------------------------
/5 深度学习的实用层面.md:
--------------------------------------------------------------------------------
1 | ## 5 深度学习的实用层面
2 |
3 | ### 5.1 训练集(Train sets)
4 |
5 | 在机器学习中,通常将训练数据分为**训练集**(train sets)、简单交叉验证集(简称**验证集**,dev sets)和**测试集**(test sets)。对训练集执行训练算法,通过验证集选择最好的模型,经过充分验证选定最终模型后,在测试集上进行评估。
6 | 
7 |
8 | **数据集划分比例:**
9 |
10 | - **对数据集规模较小的:**
11 | 如果没有明确设置验证集,常见做法是将所有数据**三七分**(70%训练集和30%测试集);或者划分为60%训练集、20%验证集和20%测试集。
12 | - **对数据集规模较大的:**
13 | **验证集和测试集占数据总量的比例会趋向于变得更小(低于数据总量的20%甚至10%)**。因为验证集的目的是验证不同的算法中哪一种更有效,故验证集要足够大才能评估,比如现有100万条数据,则取1万条便足以评估算法性能。同样地,根据最终选择的分类器,测试集的主要目的是正确评估分类器的性能,若拥有百万数据,只需1万条数据便足以评估单个分类器。所以倘若有100万条数据,可以将其中1万条作为验证集1万条作为测试集,即98%训练集、1%验证集和1%测试集。对于数据量过百万的应用,训练集可以达到99.5%,验证集和测试集各占0.25%或者验证集占0.4%测试集占0.1%。
14 |
15 | **对验证集和测试集的要求:**
16 | 1. 确保**验证集和测试集的数据来自同一分布**。因为要用验证集评估不同的模型以尽可能地优化性能,如果验证集和测试集来自同一分布会更好,机器学习算法会训练得更快。
17 | 2. **可以没有测试集**。测试集的目的是对最终选定的神经网络系统做出无偏评估,若不需要无偏评估,就可以不设置测试集。在只有训练集和验证集的情况下,需要在训练集上训练、尝试不同的模型框架,在验证集上评估这些模型,迭代并选出最适合的模型,训练集仍称为训练集,而验证集被称为测试集。
18 |
19 | 搭建训练测试集和验证集能够加速神经网络的集成,更有效地衡量算法的偏差和方差,从而更高效地选择合适的方法优化算法。
20 |
21 |
22 |
23 | ### 5.2 偏差和方差(Bias/Variance)
24 |
25 | 我们先定义好我们要用到的公式中变量的含义:
26 |
27 | 
28 |
29 | #### **5.2.1 偏差**
30 |
31 | 描述的是预测值的期望与真实值之间的差距。偏差越大,越偏离真实数据,拟合度越低,如下图第二行所示。故偏差度量的是学习算法的期望预测与真实结果的偏离程度,即**拟合能力**。
32 |
33 | 期望输出与真实标记的差别称为偏差,即:
34 | $$
35 | \operatorname{bias}^{2}(\boldsymbol{x})=(\bar{f}(\boldsymbol{x})-y)^{2}
36 | $$
37 |
38 | #### **5.2.2 方差**
39 |
40 | 描述的是预测值的变化范围,即离散程度。方差越大,数据的分布越分散,如下图右列所示。故方差度量的是同样大小的训练集的变动所导致的学习性能的变化,即刻画了**数据扰动**造成的影响。
41 |
42 | 使用样本数相同的不同训练集产生的**方差**为:
43 | $$
44 | \operatorname{var}(\boldsymbol{x})=\mathbb{E}_{D}\left[(f(\boldsymbol{x} ; D)-\bar{f}(\boldsymbol{x}))^{2}\right]
45 | $$
46 |
47 |
48 | 
49 |
50 | #### **5.2.3 泛化**
51 |
52 | 学习后的模型对未知数据的预测能力。在实际情况中,通常通过测试误差来评价学习方法的泛化能力,泛化误差(generalization error)是新输入的误差期望,为偏差、方差与噪声之和,给定学习任务,为了取得好的泛化性能,则需使偏差较小,即能够充分拟合数据,并且使方差较小,即使得数据扰动产生的影响小。
53 |
54 | 泛化误差 $=$ 错误率 $($ error $)=\operatorname{bias}^{2}(x)+\operatorname{var}(x)+\varepsilon^{2}$
55 |
56 | 也就是说,泛化误差可以通过一系列公式分解运算证明:泛化误差为偏差、方差与噪声之和。**证明过程如下:**为了便于讨论,我们假定噪声期望为零,即$E_{D}\left[y_{D}-y\right]=0$。通过简单的多项式展开合并,可对算法的期望泛化误差进行分解:
57 | $$
58 | \begin{aligned}
59 | E(f ; D)=& \mathbb{E}_{D}\left[\left(f(\boldsymbol{x} ; D)-y_{D}\right)^{2}\right] \\
60 | =& \mathbb{E}_{D}\left[\left(f(\boldsymbol{x} ; D)-\bar{f}(\boldsymbol{x})+\bar{f}(\boldsymbol{x})-y_{D}\right)^{2}\right] \\
61 | =& \mathbb{E}_{D}\left[(f(\boldsymbol{x} ; D)-\bar{f}(\boldsymbol{x}))^{2}\right]+\mathbb{E}_{D}\left[\left(\bar{f}(\boldsymbol{x})-y_{D}\right)^{2}\right] \\
62 | &+\mathbb{E}_{D}\left[2(f(\boldsymbol{x} ; D)-\bar{f}(\boldsymbol{x}))\left(\bar{f}(\boldsymbol{x})-y_{D}\right)\right] \\
63 | =& \mathbb{E}_{D}\left[(f(\boldsymbol{x} ; D)-\bar{f}(\boldsymbol{x}))^{2}\right]+\mathbb{E}_{D}\left[\left(\bar{f}(\boldsymbol{x})-y_{D}\right)^{2}\right] \\
64 | =& \mathbb{E}_{D}\left[(f(\boldsymbol{x} ; D)-\bar{f}(\boldsymbol{x}))^{2}\right]+\mathbb{E}_{D}\left[\left(\bar{f}(\boldsymbol{x})-y+y-y_{D}\right)^{2}\right] \\
65 | =& \mathbb{E}_{D}\left[(f(\boldsymbol{x} ; D)-\bar{f}(\boldsymbol{x}))^{2}\right]+\mathbb{E}_{D}\left[(\bar{f}(\boldsymbol{x})-y)^{2}\right]+\mathbb{E}_{D}\left[\left(y-y_{D}\right)^{2}\right] \\
66 | &+2 \mathbb{E}_{D}\left[(\bar{f}(\boldsymbol{x})-y)\left(y-y_{D}\right)\right] \\
67 | =& \mathbb{E}_{D}\left[(f(\boldsymbol{x} ; D)-\bar{f}(\boldsymbol{x}))^{2}\right]+(\bar{f}(\boldsymbol{x})-y)^{2}+\mathbb{E}_{\bar{D}}\left[\begin{array}{ll}
68 | \boldsymbol({y}_{D}-y)^2 &
69 | \end{array}\right] \\
70 | \end{aligned}
71 | $$
72 | 于是, 最终得到:
73 | $$
74 | E(f ; D)=\operatorname{bias}^{2}(\boldsymbol{x})+\operatorname{var}(\boldsymbol{x})+\varepsilon^{2}
75 | $$
76 | "偏差-方差分解" 说明, 泛化性能是由学习算法的能力、数据的充分性以及学习任务本身的难度 所共同决定的。给定学习任务, 为了取得好的泛化性能, 则需使偏差较小, 即能够充分拟合数据 并且使方差较小, 即使得数据扰动产生的影响小
77 |
78 | #### 5.2.4 拟合
79 |
80 | - **欠拟合**(Underfitting):常在模型学习能力较弱而数据复杂度较高的情况下出现。由于模型的学习能力不足,无法学习到数据集中的“一般规律”,因而导致模型的泛化能力较弱。
81 | - **过拟合**(Overfitting):常在模型学习能力较强而数据复杂度较弱的情况下出现。此时由于模型的学习能力太强,以至于将训练集中单个样本自身的特点都能捕捉到,并将其认为是“一般规律”,这种情况同样会导致模型的泛化能力下降。
82 | - **适度拟合**(just right):介于欠拟合和过拟合之间,数据拟合适度,复杂程度适中,泛化能力强。
83 |
84 | 
85 |
86 | #### 5.2.5 偏差和方差与训练集和验证集误差的关系
87 |
88 | 理解偏差和方差的两个关键数据是**训练集误差**(Train set error)和**验证集误差**(Dev set error)。假设人眼辨别错误率接近0(即最优误差或称为贝叶斯误差接近0),训练集和验证集数据来自相同分布,则可通过查看训练集误差判断数据拟合情况,从而判断是否有偏差问题(训练集误差越大,拟合度越低,偏差越高);然后查看错误率(验证集误差-训练集误差)有多高,判断方差是否过高(错误率越大,方差越高)。
89 | 下表是在不同的训练集和验证集的误差组合情况下对偏差和方差的分析:
90 | 
91 |
92 |
93 |
94 |
95 | 
96 |
97 | #### 5.2.6 **偏差、方差与bagging、boosting的关系**
98 |
99 | Bagging算法是对训练样本进行采样,产生出若干不同的子集,再从每个数据子集中训练出一个分类器,**取这些分类器的平均,所以是降低模型的方差(variance)**。Bagging算法和Random Forest这种并行算法都有这个效果。
100 |
101 | Boosting则是迭代算法,每一次迭代都根据上一次迭代的预测结果对样本进行权重调整,**所以随着迭代不断进行,误差会越来越小**,所以模型的偏差(bias)会不断降低。
102 |
103 | #### 5.2.7 **偏差、方差和K折交叉验证的关系**
104 |
105 | K-fold Cross Validation的思想:将原始数据分成K组 $($ 一般是均分 $)$, 将每个子集数据分别做一次 验证集, 其余的K-1组子集数据作为训练集, 这样会得到K个模型, 用这K个模型最终的验证集的分 类准确率的平均数作为此K-CV下分类器的性能指标。
106 | 对于一系列模型 $F(\hat{f}, \theta)$, 我们使用Cross Validation的目的是获得预测误差的无偏估计量CV, 从而可以用来选择一个最优的Theta*,使得CV最小。假设K-folds cross validation, CV统计量定 义为每个子集中误差的平均值, 而K的大小和CV平均值的bias和variance是有关的:
107 | $C V=\frac{1}{K} \sum_{k=1}^{K} \frac{1}{m} \sum_{i=1}^{m}\left(\hat{f}^{k}-y_{i}\right)^{2}$
108 | 其中, $\mathrm{m}=\mathrm{N} / \mathrm{K}$ 代表每个子集的大小, $\quad$N是总的训练样本量, K是子集的数目。当K较大时, $\mathrm{m}$ 较小,模型建立在较大的N-m上, 经过更多次数的平均可以学习得到更符合真实数 据分布的模型, Bias就小了,**但是这样一来模型就更加拟合训练数据集, 再去测试集上预测的时候 预测误差的期望值就变大了,从而Variance就大了**; $\mathrm{k}$ 较小的时候, 模型不会过度拟合训练数据, 从而Bias较大,**但是正因为没有过度拟合训练数据, Variance也较小**。
109 |
110 | ### 5.3 处理偏差和方差
111 |
112 | #### 5.3.1 针对不同偏差的不同处理
113 |
114 | 评估训练集或训练数据的性能,若偏差较高,可以选择以下几种方法:
115 | - 选择更大的网络,比如含有更多隐藏层或隐藏单元的网络
116 | - 花费更多时间训练网络(不一定有用,但没坏处)
117 | - 尝试更先进的优化算法
118 | - 选择更适合解决此问题的神经网络架构(可能有用,可能没用)
119 |
120 | 训练学习算法时,不断尝试这些方法,直到可以拟合数据,解决掉偏差问题为止,至少能够拟合训练集。
121 | #### 5.3.2 针对不同方差的不同处理
122 | 偏差降低到可以接受的数值,查看验证集性能来评估方差,如果方差高,可以选择下列方法:
123 | - 采用更多数据(最好的解决办法)
124 | - 正则化
125 | - 尝试更适合的神经网络框架(有时可以同时减少偏差和方差)
126 |
127 | 解决高方差最优方法是准备更多的数据,但可能无法实时准备足够多的数据或数据成本很高时,**正则化**可帮助避免过拟合,减少网络误差。
128 |
129 | 通过不断重复尝试,找到一个低偏差、低方差的框架。
130 | > 高偏差和高方差尝试的方法可能完全不同,明确这点来选择最有效的方法。
131 | 只要正则适度,通常构建更大网络便可以在不影响方差的同时减少偏差。采用更多数据通常可以在不过多影响偏差的同时减少方差。我们有很多的选择可以减少偏差或方差而不影响另一方。
132 |
133 |
134 | ### 5.4 正则化
135 |
136 | **定义**:一种为了减小方差(测试误差)的行为
137 | **作用**:使用比较复杂的模型比如神经网络,去拟合数据时,容易出现过拟合现象,导致模型的泛化能力下降,这时我们使用正则化,降低模型的复杂度,让模型在面对新数据的时候,可以有很好的表现。
138 |
139 | #### 5.4.1 logistic 回归的正则化
140 | - **L2 正则化**
141 | $J(w, b)=\frac{1}{m} \sum_{i=1}^{m} L\left(\hat{y}^{(i)}, y^{(i)}\right)+\frac{\lambda}{2 m}\|w\|_{2}^{2}$
142 | 每次更新w时:
143 |
144 | $$w:=w-\alpha d w=\left(1-\frac{\alpha \lambda}{m}\right) w-\frac{\partial J}{\partial w}$$
145 |
146 | 从上式看出,每次更新对特征系数做一个**比例的缩放**而不是像L1正则化减去一个固定值。这使得系数趋向变小而不会变为0,因此L2正则化**让模型变得更简单,防止过拟合**。
147 | - **L1 正则化**
148 | $$J(w, b)=\frac{1}{m} \sum_{i=1}^{m} L\left(\hat{y}^{(i)}, y^{(i)}\right)+\frac{\lambda}{2 m}\|w\|_{1}$$
149 |
150 | 每次更新w时:
151 | $$\begin{array}{c}
152 | w:=w-\alpha d w\\
153 | =w-\frac{\alpha \lambda}{2 m} \operatorname{sign}\left(w\right)-\frac{\partial J}{\partial w}
154 | \end{array}$$
155 | 若 w 为正数,则每次更新减去一个常数;若 w 为负数,则每次更新加上一个常数,故容易产生特征的系数为0的情况,特征系数为 0 表示该特征不会对结果有任何影响,因此L1正则化让w变得稀疏,起到**特征选择**的作用。
156 | > - 参数 w 向量的L2 范数:$\|w\|_{2}^{2}=\sum_{j=1}^{n_{x}} w_{j}^{2}=w^{T} w$
157 | 参数 w 向量的L1 范数:$\|w\|_{1}=\sum_{j=1}^{n_{x}}\left|w_{j}\right|$
158 | > - $w\in \mathbb{R}^{n_{x}}, b \in \mathbb{R}$,习惯只正则化w,省略参数b。因为w通常是一个高维参数矢量,b只是单个数字,即w几乎涵盖所有参数,b只是众多参数中的一个,b通常省略不计,加上也没问题。
159 | >- $\lambda$是正则化参数,是一个需要调整的超参数,Python 编程语言中,lambda 是一个保留字段,编写代码时,删掉a,写成lambd,以免冲突。
160 |
161 | **总结**
162 | 两者都通过加上一个和项来限制参数大小,效果却不同:L1正则化适用于**特征选择**,L2正则化适用于**防止模型过拟合**。
163 | 在训练网络时,倾向于使用**L2正则化**。
164 |
165 |
166 |
167 | #### 5.4.2 神经网络中实现L2正则化
168 |
169 | $$J\left(w^{[1]}, b^{[1]}, \ldots, w^{[L]}, b^{[L]}\right)=\frac{1}{m} \sum_{i=1}^{m} L\left(\hat{y}^{(i)}, y^{(i)}\right)+\frac{\lambda}{2 m} \sum_{l=1}^{L}\|w\|_{F}^{2}$$
170 | **Frobenius 范数**:
171 | 下标F标注,表示一个矩阵中所有元素的平方和。
172 | $$\|w\|_{F}^{2}=\sum_{i=1}^{n^{[l-1]}} \sum_{j=1}^{n^{[l]}}\left(w_{i j}^{[l]}\right)^{2}$$
173 |
174 | 其中,$w:\left(n^{[l-1]}, n^{[l]}\right)$ $n^{[l]}$表示第$l$层单元数量,$n^{[l-1]}$表示第$l-1$层单元数量
175 |
176 | 实现梯度下降:
177 | $$\begin{aligned} w^{[l]}: &=w^{[l]}-\alpha\left[(\text { from backprop })+\frac{\lambda}{m} w^{[l]}\right] \\ &=\left(1-\frac{\alpha \lambda}{m}\right) w^{[l]}-\alpha(\text { from backprop }) \end{aligned}$$
178 | 实际上,相当于给矩阵$w^{[l]}$乘上$1-\frac{\alpha \lambda}{m}$倍的权重,而该系数小于1,因此L2正则化也被称为**权重衰减**
179 |
180 |
181 |
182 | ### 5.5 正则化有效的原理
183 | - 正则化参数$\lambda$增加到足够大,权重矩阵$w^{[l]}$会接近于0,大量隐藏单元的影响变得更小了,神经网络越来越简单,接近逻辑回归,这样更不容易发生过拟合。
184 |
185 | 举例:
186 | 假设使用$\tanh (z)$激活函数,如果$z$的值始终在接近原点的小范围内,激活函数大致呈线性,每层几乎都是线性的,和线性回归一样。
187 |
188 | 
189 | 当正则化参数$\lambda$足够大,参数$w$很小,$z$也会相对变小,激活函数$\tanh (z)$会相对呈线性,整个神经网络会计算接近线性函数的值,即一个很简单的函数,而不是极复杂的高度非线性函数,不会发生过拟合。
190 |
191 | 参考文章:[机器学习中的正则化](https://www.jianshu.com/p/569efedf6985)
192 |
193 |
194 |
195 |
196 |
197 | ### 5.6 Dropout正则化 ###
198 | Dropout正则化是较常用的避免过拟合的方法之一。
199 |
200 | **Dropout**
201 |
202 | 首先介绍一下Dropout正则化:在**训练**神经网络时,对于每一层神经网络中的所有节点,每个结点都有keep_prob的概率保留,1 - keep_prob的概率丢弃。这里的丢弃指的是**每一次**前向传播的时候随机丢弃部分结点,每次前向传播都重新计算要丢弃的结点。要注意在更新权值和真正应用已经训练好的网络时,是不会随机丢弃的。
203 | 
204 |
205 | **原理**
206 |
207 | 有没有觉得很神奇,竟然随机丢掉一些结点反而能“更好”地训练神经网络,也太“玄乎”了。当然,能生效的正则化肯定有它成功的理由,下面给出解释:
208 | 1. 随机删除一些结点,本质上相当于缩小网络。而过拟合的原因之一是网络太大而导致的拟合效果“好过头”了,那缩小网络自然能一定程度上避免过拟合。
209 | 2. 由于所有节点都可能被丢弃,所以训练时不会过渡依赖任何一个结点(特征),表现为尽可能缩小所有权值。那就有点接近L2正则化那种收缩权值的效果了。
210 |
211 | **代码实现**
212 |
213 | # 操作 < keep_prob 可使本来的随机向量变为True、False组成的向量
214 | d3 = np.random.randn(a3.shape[0], a3.shape[1]) < keep_prob
215 | # 实际运算时,True、False会变为1和0
216 | a3 *= d3
217 | # 修正a3的均值,保持和Dropout前不变
218 | a3 /= keep_prob
219 |
220 | 技术细节上,用了一个小于运算符自动将随机值转换为0、1;在将部分值归0后,a3的均值也会变为原来的keep_prob倍,所以最后对所有数除以keep_prob以保证a3的均值不变,保证$z3=wa3+b$的均值不变
221 |
222 |
223 |
224 |
225 | ### 5.7 其他正则化方法 ###
226 | #### 5.7.1 数据增强/Data Augmentation ####
227 | 前文提到解决high variance(高方差)/ 过拟合的解决办法之一是收集更多的数据,更大的训练集。但有时候并不是那么容易就能短时间内收集的。所以提出了一个基于已有数据的增加数据量的方法:数据增强。
228 | 具体方法:
229 |
230 | 1. 翻转(水平、上下等)
231 | 2. 随机裁剪。指放大后旋转、裁剪
232 | 3. 扭曲变形,有很多更具体的成熟的方法。
233 |
234 | 但是数据增强并不是万用的方法,有时候可能会对网络的训练造成负面影响:比如从图片中提取文字的网络不适应翻转等等。甚至识别人脸的网络也不适合翻转,原因是“视觉手性”,感兴趣的可以阅读[Visual Chirality](https://arxiv.org/abs/2006.09512
235 | )。
236 |
237 | #### 5.7.2 Early Stopping ####
238 | Early stopping顾名思义,提早结束(训练)。具体操作是:
239 |
240 | 1. 训练足够多的次数,并且记录train set和dev set的error曲线。如图
241 | 
242 |
243 | 2. 找到dev error曲线的最低点,该点的迭代次数(附近)作为最佳迭代次数。
244 |
245 | 原理也很简单,在网络过拟合之前停止训练,不就能阻止网络过拟合了嘛。操作起来也很简单,训练一次就知道下次要训练多久了。不过简单的做法自然带来偷懒的弊端。过早停止训练,意味着网络可能还没得到充分的训练,过早停止优化cost函数,虽然低方差但是可能高偏差。
246 |
247 |
248 | ### 5.8 正则化输入 ###
249 | **命名问题**
250 |
251 | 首先提一下有关归一化和标准化的命名问题。如果你去百度一下很容易就发现吴恩达老师教的归一化(Normalizing)和百度的不一样,倒是和百度的标准化(Standardization)差不多。大名鼎鼎的吴恩达老师竟然会犯这种低级错误?笔者一开始也这么认为,但是想了想我只是刚入门的怎么可以那么轻易怀疑大师。于是在多百度了几次(无果)、查几篇国内外论文、最后一次百度(知乎)后,得出了结果:
252 | 归一化和标准化都是一种特征放缩(Feature scaling)。特征放缩有很多种方法,这里只讲涉及到的这两种。
253 |
254 | 1. min-max normalizing(Rescaling),也就是百度的归一化normalizing:
255 | $$
256 | x^{\prime}=\frac{x-\min (x)}{\max (x)-\min (x)}
257 | $$
258 |
259 | 2. Z-score normalization(Standardization),也就是百度的标准化:
260 | $$
261 | x^{\prime}=\frac{\left(x-\mu\right)}{\sigma}
262 | $$
263 |
264 | 猜测吴恩达老师是简称Z-score normalization为normalization了?也可能是其他原因吧。彻底帮我解决问题的[回答](https://www.zhihu.com/question/20467170)。
265 |
266 | **为什么要Z-score normalization**
267 |
268 | 有时候我们的数据的分布并不是“很好看”(图1、2),不是很利于网络的训练。这时候我们就可以考虑处理一下数据,使得数据的分布“更好看”(图3、4)。**注意**:图片中的名称用的是吴恩达老师课程中的名称。
269 | 
270 | 
271 | 
272 | 
273 | 什么时候数据会不好看?当输入的特征$x_{1}$和$x_{2}$取值范围有很大差别时就会,比如:$x_{1}$在[0,1]内,$x_{2}$在[1, 100]内。这样就会导致数据的分布为椭圆形,那在梯度下降时如果学习率不够小很容易就会一直震荡而艰难收敛;而更对称的分布,学习率就算大一点也很容易就能收敛。
274 | 所以一般当输入特征的取值范围差距较大时就考虑Z-score normalization,不过无脑使用也没什么坏事,所以是比较推荐的方法。
275 |
276 | **实现**
277 |
278 | 首先要注意的一点是,尽量别分多次计算均值$\mu$和方差$\sigma$,比如这两个值都由训练集得出就不更改了。
279 | Python代码:
280 |
281 | # 计算均值
282 | x_mean = np.mean(x)
283 | # 计算标准差;计算方差用np.var
284 | x_std = np.std(x)
285 | # 标准化
286 | x = (x - x_mean) / x_std
287 |
288 | 多提一句,对于图片,如果想实现min-max normalizing,一般只需要默认0为最小值,255为最大值即可:
289 |
290 | # x = (x-0) / (255-0)
291 | x = x / 255
292 |
293 |
294 |
295 |
296 | ### 5.9 梯度消失和梯度爆炸 ###
297 | #### 5.9.1 介绍 ####
298 | 英文称:vanishing and exploding gradients。
299 | 首先简单“展示”一下梯度爆炸是怎么样的:
300 | 假设有$L$层,$\text W^{[l]}=\left[\begin{array}{cc}
301 | 1.5 & 0 \\
302 | 0 & 1.5
303 | \end{array}\right],
304 | b^{[l]}=0$($l∈[1, L]$),且激活函数全部采用线性激活(恒等函数),则
305 |
306 | $$\begin{array}{l}
307 | \hat{y}=W^{[L]}W^{[L-1]} \ldots W^{[1]}x \\
308 | =\left[\begin{array}{cc}
309 | 1.5 & 0 \\
310 | 0 & 1.5
311 | \end{array}\right]^{L}x \\
312 | =\left[\begin{array}{cc}
313 | 1.5^{L} & 0 \\
314 | 0 & 1.5^{L}
315 | \end{array}\right]x
316 | \end{array}$$
317 |
318 | 可见,$W^{[l]}$中大于1的元素,将会因指数级增长而“爆炸”;同理,小于1的元素,则会以指数级递减而“消失”(真实情况会更复杂一些,但上述例子足以说明这种可能性)。
319 | 这不仅仅适用于$\hat{y}$的计算,还适用于梯度$dW、db$的计算——过深的网络在梯度下降时计算的梯度很有可能接近0或过大。这会直接导致网络的学习停滞不前或者发散,严重影响学习效果。
320 |
321 | #### 5.9.2 权重初始化 ####
322 | 既然梯度消失和爆炸都是由于$L$过大而形成的指数级缩小/放大,那在不减少$L$的前提下比较有限的方法就是让每次输出尽可能接近1了。$z$的计算可写成:
323 | $$z=w_{1}a_{1}+w_{2}a_{2}+\ldots+w_{n}a_{n}$$那么当$n$增大时,想让$z$减小则可以通过减小$w_{i}$做到;而$w_{i}$是符合高斯分布(标准正态分布,np.random.randn())的,所以$z$可**看似**服从分布$N(0, n)$,那$w_{i}$除以$n$就可以让$z$近似服从分布$N(0, 1)$,已达到。
324 | 具体做法是初始化时,用以下语句:
325 |
326 | w[l] = np.random.randn(n[l], n[l-1])*np.sqrt(2 / (n[l-1]))
327 |
328 | 其中*sqrt*中的表达式和使用的激活函数有关。ReLU采用上式($\frac{2}{n^{l-1}}$),tanh则采用$\frac{1}{n^{[l-1]}}$,其他形式的有$\frac{2}{n^{[l+1]}+n^{[l]}}$。
329 | 这么做的目的主要是修改$W^{[l]}$的分布,将方差除以输入
330 |
331 | #### 5.9.3 梯度逼近 ####
332 | 我们在计算梯度时用的是“手写”的公式(自己推导的公式),可能有时候会犯一点小错误。那我们就需要对梯度的计算进行验算,看看有没有错。但是不可能用同样的式子进行验算,因为计算机不会产生“计算失误”。所以我们需要不同的,计算结果很接近的方法来重新计算一次,那就是梯度逼近。
333 | 回顾高数/高中知识,梯度(导数)是切线斜率。近似地我们可以通过计算一个点附近的割线的斜率来代替该点的切线斜率。如图,可以用$\frac{ f(\theta+\varepsilon)-f(\theta-\varepsilon)}{2\varepsilon}$代替$f^{\prime}(\theta)$。当然,$\varepsilon$越小越接近。图来自吴恩达课程的1.12梯度的数值逼近。
334 | 
335 | 可能会有人疑惑为什么不采用单边,比如$\frac{ f(\theta+\varepsilon) - f(\theta)}{\varepsilon}$,而是要这样两边都取。抽象地你可以理解为单边计算出来的斜率更接近$\theta$的左右偏移一点点的$\theta^{\prime}$的值;而双边计算$\theta$正好位于割线的“正中间”,计算出来的斜率也自然要更接近一些。
336 |
337 | #### 5.9.4 梯度检验 ####
338 | 进入正题,介绍如何进行检验。首先对于所有参数$W^{[l]}$和$b^{[l]}$,按顺序链接成一个参数集$\theta$。对于$dW^{[l]}$和$db^{[l]}$也同样链接成$d\theta$。这里分别对应前向传播和反向传播。$\theta$和$d\theta$有一样的shape,$\theta[i]$表示第$i$个参数。然后计算$d\theta$的近似值$d\theta_{approx}$:
339 | 1. 遍历参数集$\theta$中的$\theta[i]$。
340 | 2. 计算$$d\theta_{approx}[i] = \frac{J(\theta[1], \theta[2], \ldots, \theta[i]+\varepsilon, \ldots)-J(\theta[1], \theta[2], \ldots, \theta[i] - \varepsilon, \ldots )} { 2\varepsilon} $$
341 | 3. 计算$\Delta = \frac{\|d\theta_{approx}-d\theta\|} {\|d\theta_{approx}\|+\|d\theta\|}$欧几里得范数,实际上就是根号下误差平方之和。
342 | 4. 如果$\Delta > \varepsilon$(如$\varepsilon=10^{-7}$),则视为误差超出阈值,否则为正常。
343 |
344 | #### 5.9.5 其他解决办法
345 |
346 | - relu、leakrelu等激活函数
347 |
348 | Relu:思想也很简单,如果激活函数的导数为1,那么就不存在梯度消失爆炸的问题了,每层的网络都可以得到相同的更新速度。
349 |
350 | relu的优点: 解决了梯度消失、爆炸的问题;计算方便,计算速度快,加速了网络的训练
351 |
352 | relu的缺点:由于负数部分恒为0,会导致一些神经元无法激活(可通过设置小学习率部分解决);输出不是以0为中心的
353 |
354 | **尽管relu也有缺点,但是仍然是目前使用最多的激活函数。**
355 |
356 | leakrelu激活函数在前面介绍激活函数时已经讲过了,这里就不再赘述了。
357 |
358 | - 梯度裁剪
359 |
360 | - batch normalization
361 |
362 | - 残差结构
363 |
364 | 上面的方法在下面的内容里面我们还会讲,这里就不再赘述了。
365 |
366 | #### 5.9.6 注意细节 ####
367 |
368 | 讲一下代码实现有几个细节:
369 | 1. 要实现cost function,并且接受参数$\theta$。
370 | 2. 欧几里得范数可以用 np.linalg.norm(array) 计算。
371 | 3. 不要和Dropout一起使用。
372 | 4. 只在debug时开启,正常训练无需启动,否则会花费大量的时间。
373 | 5. 应用了L2正则化的cost function和一般的不一样,梯度计算也会不一样。
374 |
375 |
376 |
377 | ### 5.10 参考文献
378 |
379 | https://zhuanlan.zhihu.com/p/38853908
380 |
381 |
382 |
383 |
384 |
385 |
386 |
387 |
388 |
--------------------------------------------------------------------------------
/7 超参数的调试,BN和程序框架.md:
--------------------------------------------------------------------------------
1 | ## 7 超参数调试,Batch Norm和程序框架
2 |
3 | ### 7.1 调试处理
4 |
5 | #### 7.1.1 超参数的重要性比较
6 |
7 | **深度学习中,用到的超参数有**
8 |
9 | $α $:学习率
10 |
11 | $β$:动量梯度下降因子
12 |
13 | $β1,β2,ε$:Adam算法参数
14 |
15 | layers:神经网络层数
16 |
17 | hidden units:各隐藏层神经元个数
18 |
19 | learning rate decay:学习因子下降参数
20 |
21 | mini-batch size:批量训练样本包含的样本个数
22 |
23 |
24 |
25 | 学习率$α$为最重要的超参数;
26 |
27 | 动量梯度下降因子$β$、各隐藏层神经元个数hidden units、批量训练样本包含的样本个数mini-batch size,三者重要性仅次于学习因子$α$;
28 |
29 | 接下来为神经网络层数layers和学习因子下降参数learning rate decay;最后,由于Adam算法参数$β1,β2,ε$三个参数一般设置为0.9,0.999和$10^{-8}$,不需要反复调试,所以重要性较弱。
30 |
31 | 但超参数的重要性排名不是一成不变的,可能会根据情况的不同而发生一定的变化
32 |
33 |
34 |
35 | #### 7.1.2 超参数的调试过程
36 |
37 | 在传统的机器学习中,我们对每个参数等距离选取任意个数的点,然后,分别使用不同点对应的参数组合进行训练,最后根据验证集上的表现,来选定最佳的参数。例如有两个待调试的参数,分别在每个参数上选取5个点,这样构成了5x5=25的参数组合,如图:
38 |
39 | 
40 |
41 | 此做法在参数较少的时候效果较好。但在深度学习的神经网络中,比较好的做法是使用随机选择。即:对于上面这个例子,我们随机选择25个点,作为待调试的超参数,如图:
42 |
43 | 
44 |
45 |
46 | 随机选择参数的目的是为了尽可能地得到更多种参数组合。如上面的例子,如果使用均匀采样的话,每个参数只有5种情况;而使用随机采样的话,每个参数有25种可能的情况,因此更有可能得到最佳的参数组合。
47 |
48 | 这种做法的另一个好处是能够对重要性不同的参数之间的选择效果更好。假设hyperparameter1为$α$,hyperparameter2为$ε$,二者的重要性是不一样的。如果使用第一种均匀采样的方法,$ε$的影响很小,相当于只选择了5个$α$值。而如果使用第二种随机采样的方法,$ε$和$α$都有可能选择25种不同值。这大大增加了$α$调试的个数,选择到最优值的可能更大了。在完全不知道哪个参数更加重要的情况下,随机采样的方式可以有效解决这一问题,但是均匀采样不能够解决该问题。
49 |
50 | 在随机采样后,可以得到某些区域模型的表现较好。为了得到更精确的最佳参数,我们应该继续对选定的区域进行由粗到细的采样(coarse to fine sampling scheme)。即放大表现较好的区域,再对此区域做更密集的随机采样。例如,对下图中右下角的方形区域再做25点的随机采样,以获得最佳参数。
51 | 
52 |
53 | ### 7.2 为超参数选择合适的范围
54 |
55 | #### 7.2.1 不同超参数合适的标尺
56 |
57 | 例如:神经网络层数layers和各隐藏层神经元个数hidden units,因为两者都为正整数,所以可以直接进行随机均匀采样(即每次变化的幅度是一样的);而对于学习率$α$和动量梯度下降因子$β$,则需要使用非均匀随机采样。
58 |
59 | #### 7.2.2 对数轴的取值过程
60 |
61 | 通过将linear scale转换为log scale来实现均匀尺度转化为非均匀尺度,然后再在log scale下进行均匀采样。如,[0.0001, 0.001],[0.001, 0.01],[0.01, 0.1],[0.1, 1]各个区间内随机采样的超参数个数基本一致,也就扩大了之前[0.0001, 0.1]区间内采样值个数。假设线性区间为[a, b],令$m=log(a),n=log(b)$,则对应的log区间为[m,n]。对log区间的[m,n]进行随机均匀采样,得到的采样值$r$,再反推到线性区间,即10的r次方。则10的r次方为最终采样的超参数。
62 |
63 | #### 7.2.3 为什么$β$不用linear scale进行取值
64 |
65 | 假设β从0.9000变化为0.9005,则$1/1−β$基本没有变化。但如果$β$从0.9990变为0.9995,那么$1/1−β$前后差别1000。即:$β$越接近1,指数加权平均的个数越多,变化越大。因此在$β$接近1的区间,应采集得更密集一些。
66 |
67 | ### 7.3 超参数训练的实践: Pandas VS Caviar
68 |
69 | #### 7.3.1 熊猫方式Panda approach
70 |
71 | 只能够对一个模型进行训练,调试不同的超参数,使得这个模型有最佳的表现。
72 |
73 | #### 7.3.2 鱼子酱方式Caviar approach
74 |
75 | 可以对多个模型同时进行训练,每个模型上调试不同的超参数,根据模型的表现,选择最优的模型
76 |
77 | 一般对于非常复杂或者数据量很大的模型,更多使用Panda approach。
78 |
79 |
80 |
81 | ### 7.4 归一化网络的激活函数
82 |
83 | #### 7.4.1 logistic 回归中归一化输入特征
84 |
85 | 
86 | $$
87 | \begin{array}{l}
88 | \mu=\frac{1}{m} \sum_{i} x^{(i)} \\
89 | X=X-\mu \\
90 | \sigma^{2}=\frac{1}{m} \sum_{i} x^{(i) 2} \\
91 | X=X / \sigma^{2}
92 | \end{array}
93 | $$
94 | 计算平均值,从训练集中减去平均值;计算方差,根据方差归一化数据集。变化学习问题的轮廓,易于算法优化。即归一化$x_{1}$,$x_{2}$,$x_{3}$有助于更有效的训练$w$和$b$。
95 |
96 |
883 |
884 |
885 | 于是,我们的损失函数(loss)就定义为了上式。
886 |
887 | #### 2.9.5 似然和概率 ####
888 | 既然提到了最大似然估计,那就提提似然和概率的区别:
889 |
890 | > 简单来讲,似然与概率分别是针对不同内容的估计和近似。概率(密度)表达给定θ下样本**X**=x的可能性,而似然表达了给定样本X=x下参数θ=θ1(相对于另外的参数取值θ2而言)为真实值的可能性
891 |
892 | 引自[似然(likelihood)和概率(probability)的区别与联系](https://blog.csdn.net/songyu0120/article/details/85059149)
893 |
894 |
895 |
896 |
897 |
--------------------------------------------------------------------------------
/5 深度学习的实用层面.md:
--------------------------------------------------------------------------------
1 | ## 5 深度学习的实用层面
2 |
3 | ### 5.1 训练集(Train sets)
4 |
5 | 在机器学习中,通常将训练数据分为**训练集**(train sets)、简单交叉验证集(简称**验证集**,dev sets)和**测试集**(test sets)。对训练集执行训练算法,通过验证集选择最好的模型,经过充分验证选定最终模型后,在测试集上进行评估。
6 | 
7 |
8 | **数据集划分比例:**
9 |
10 | - **对数据集规模较小的:**
11 | 如果没有明确设置验证集,常见做法是将所有数据**三七分**(70%训练集和30%测试集);或者划分为60%训练集、20%验证集和20%测试集。
12 | - **对数据集规模较大的:**
13 | **验证集和测试集占数据总量的比例会趋向于变得更小(低于数据总量的20%甚至10%)**。因为验证集的目的是验证不同的算法中哪一种更有效,故验证集要足够大才能评估,比如现有100万条数据,则取1万条便足以评估算法性能。同样地,根据最终选择的分类器,测试集的主要目的是正确评估分类器的性能,若拥有百万数据,只需1万条数据便足以评估单个分类器。所以倘若有100万条数据,可以将其中1万条作为验证集1万条作为测试集,即98%训练集、1%验证集和1%测试集。对于数据量过百万的应用,训练集可以达到99.5%,验证集和测试集各占0.25%或者验证集占0.4%测试集占0.1%。
14 |
15 | **对验证集和测试集的要求:**
16 | 1. 确保**验证集和测试集的数据来自同一分布**。因为要用验证集评估不同的模型以尽可能地优化性能,如果验证集和测试集来自同一分布会更好,机器学习算法会训练得更快。
17 | 2. **可以没有测试集**。测试集的目的是对最终选定的神经网络系统做出无偏评估,若不需要无偏评估,就可以不设置测试集。在只有训练集和验证集的情况下,需要在训练集上训练、尝试不同的模型框架,在验证集上评估这些模型,迭代并选出最适合的模型,训练集仍称为训练集,而验证集被称为测试集。
18 |
19 | 搭建训练测试集和验证集能够加速神经网络的集成,更有效地衡量算法的偏差和方差,从而更高效地选择合适的方法优化算法。
20 |
21 |
22 |
23 | ### 5.2 偏差和方差(Bias/Variance)
24 |
25 | 我们先定义好我们要用到的公式中变量的含义:
26 |
27 | 
28 |
29 | #### **5.2.1 偏差**
30 |
31 | 描述的是预测值的期望与真实值之间的差距。偏差越大,越偏离真实数据,拟合度越低,如下图第二行所示。故偏差度量的是学习算法的期望预测与真实结果的偏离程度,即**拟合能力**。
32 |
33 | 期望输出与真实标记的差别称为偏差,即:
34 | $$
35 | \operatorname{bias}^{2}(\boldsymbol{x})=(\bar{f}(\boldsymbol{x})-y)^{2}
36 | $$
37 |
38 | #### **5.2.2 方差**
39 |
40 | 描述的是预测值的变化范围,即离散程度。方差越大,数据的分布越分散,如下图右列所示。故方差度量的是同样大小的训练集的变动所导致的学习性能的变化,即刻画了**数据扰动**造成的影响。
41 |
42 | 使用样本数相同的不同训练集产生的**方差**为:
43 | $$
44 | \operatorname{var}(\boldsymbol{x})=\mathbb{E}_{D}\left[(f(\boldsymbol{x} ; D)-\bar{f}(\boldsymbol{x}))^{2}\right]
45 | $$
46 |
47 |
48 | 
49 |
50 | #### **5.2.3 泛化**
51 |
52 | 学习后的模型对未知数据的预测能力。在实际情况中,通常通过测试误差来评价学习方法的泛化能力,泛化误差(generalization error)是新输入的误差期望,为偏差、方差与噪声之和,给定学习任务,为了取得好的泛化性能,则需使偏差较小,即能够充分拟合数据,并且使方差较小,即使得数据扰动产生的影响小。
53 |
54 | 泛化误差 $=$ 错误率 $($ error $)=\operatorname{bias}^{2}(x)+\operatorname{var}(x)+\varepsilon^{2}$
55 |
56 | 也就是说,泛化误差可以通过一系列公式分解运算证明:泛化误差为偏差、方差与噪声之和。**证明过程如下:**为了便于讨论,我们假定噪声期望为零,即$E_{D}\left[y_{D}-y\right]=0$。通过简单的多项式展开合并,可对算法的期望泛化误差进行分解:
57 | $$
58 | \begin{aligned}
59 | E(f ; D)=& \mathbb{E}_{D}\left[\left(f(\boldsymbol{x} ; D)-y_{D}\right)^{2}\right] \\
60 | =& \mathbb{E}_{D}\left[\left(f(\boldsymbol{x} ; D)-\bar{f}(\boldsymbol{x})+\bar{f}(\boldsymbol{x})-y_{D}\right)^{2}\right] \\
61 | =& \mathbb{E}_{D}\left[(f(\boldsymbol{x} ; D)-\bar{f}(\boldsymbol{x}))^{2}\right]+\mathbb{E}_{D}\left[\left(\bar{f}(\boldsymbol{x})-y_{D}\right)^{2}\right] \\
62 | &+\mathbb{E}_{D}\left[2(f(\boldsymbol{x} ; D)-\bar{f}(\boldsymbol{x}))\left(\bar{f}(\boldsymbol{x})-y_{D}\right)\right] \\
63 | =& \mathbb{E}_{D}\left[(f(\boldsymbol{x} ; D)-\bar{f}(\boldsymbol{x}))^{2}\right]+\mathbb{E}_{D}\left[\left(\bar{f}(\boldsymbol{x})-y_{D}\right)^{2}\right] \\
64 | =& \mathbb{E}_{D}\left[(f(\boldsymbol{x} ; D)-\bar{f}(\boldsymbol{x}))^{2}\right]+\mathbb{E}_{D}\left[\left(\bar{f}(\boldsymbol{x})-y+y-y_{D}\right)^{2}\right] \\
65 | =& \mathbb{E}_{D}\left[(f(\boldsymbol{x} ; D)-\bar{f}(\boldsymbol{x}))^{2}\right]+\mathbb{E}_{D}\left[(\bar{f}(\boldsymbol{x})-y)^{2}\right]+\mathbb{E}_{D}\left[\left(y-y_{D}\right)^{2}\right] \\
66 | &+2 \mathbb{E}_{D}\left[(\bar{f}(\boldsymbol{x})-y)\left(y-y_{D}\right)\right] \\
67 | =& \mathbb{E}_{D}\left[(f(\boldsymbol{x} ; D)-\bar{f}(\boldsymbol{x}))^{2}\right]+(\bar{f}(\boldsymbol{x})-y)^{2}+\mathbb{E}_{\bar{D}}\left[\begin{array}{ll}
68 | \boldsymbol({y}_{D}-y)^2 &
69 | \end{array}\right] \\
70 | \end{aligned}
71 | $$
72 | 于是, 最终得到:
73 | $$
74 | E(f ; D)=\operatorname{bias}^{2}(\boldsymbol{x})+\operatorname{var}(\boldsymbol{x})+\varepsilon^{2}
75 | $$
76 | "偏差-方差分解" 说明, 泛化性能是由学习算法的能力、数据的充分性以及学习任务本身的难度 所共同决定的。给定学习任务, 为了取得好的泛化性能, 则需使偏差较小, 即能够充分拟合数据 并且使方差较小, 即使得数据扰动产生的影响小
77 |
78 | #### 5.2.4 拟合
79 |
80 | - **欠拟合**(Underfitting):常在模型学习能力较弱而数据复杂度较高的情况下出现。由于模型的学习能力不足,无法学习到数据集中的“一般规律”,因而导致模型的泛化能力较弱。
81 | - **过拟合**(Overfitting):常在模型学习能力较强而数据复杂度较弱的情况下出现。此时由于模型的学习能力太强,以至于将训练集中单个样本自身的特点都能捕捉到,并将其认为是“一般规律”,这种情况同样会导致模型的泛化能力下降。
82 | - **适度拟合**(just right):介于欠拟合和过拟合之间,数据拟合适度,复杂程度适中,泛化能力强。
83 |
84 | 
85 |
86 | #### 5.2.5 偏差和方差与训练集和验证集误差的关系
87 |
88 | 理解偏差和方差的两个关键数据是**训练集误差**(Train set error)和**验证集误差**(Dev set error)。假设人眼辨别错误率接近0(即最优误差或称为贝叶斯误差接近0),训练集和验证集数据来自相同分布,则可通过查看训练集误差判断数据拟合情况,从而判断是否有偏差问题(训练集误差越大,拟合度越低,偏差越高);然后查看错误率(验证集误差-训练集误差)有多高,判断方差是否过高(错误率越大,方差越高)。
89 | 下表是在不同的训练集和验证集的误差组合情况下对偏差和方差的分析:
90 | 
91 |
92 |
93 |
94 |
95 | 
96 |
97 | #### 5.2.6 **偏差、方差与bagging、boosting的关系**
98 |
99 | Bagging算法是对训练样本进行采样,产生出若干不同的子集,再从每个数据子集中训练出一个分类器,**取这些分类器的平均,所以是降低模型的方差(variance)**。Bagging算法和Random Forest这种并行算法都有这个效果。
100 |
101 | Boosting则是迭代算法,每一次迭代都根据上一次迭代的预测结果对样本进行权重调整,**所以随着迭代不断进行,误差会越来越小**,所以模型的偏差(bias)会不断降低。
102 |
103 | #### 5.2.7 **偏差、方差和K折交叉验证的关系**
104 |
105 | K-fold Cross Validation的思想:将原始数据分成K组 $($ 一般是均分 $)$, 将每个子集数据分别做一次 验证集, 其余的K-1组子集数据作为训练集, 这样会得到K个模型, 用这K个模型最终的验证集的分 类准确率的平均数作为此K-CV下分类器的性能指标。
106 | 对于一系列模型 $F(\hat{f}, \theta)$, 我们使用Cross Validation的目的是获得预测误差的无偏估计量CV, 从而可以用来选择一个最优的Theta*,使得CV最小。假设K-folds cross validation, CV统计量定 义为每个子集中误差的平均值, 而K的大小和CV平均值的bias和variance是有关的:
107 | $C V=\frac{1}{K} \sum_{k=1}^{K} \frac{1}{m} \sum_{i=1}^{m}\left(\hat{f}^{k}-y_{i}\right)^{2}$
108 | 其中, $\mathrm{m}=\mathrm{N} / \mathrm{K}$ 代表每个子集的大小, $\quad$N是总的训练样本量, K是子集的数目。当K较大时, $\mathrm{m}$ 较小,模型建立在较大的N-m上, 经过更多次数的平均可以学习得到更符合真实数 据分布的模型, Bias就小了,**但是这样一来模型就更加拟合训练数据集, 再去测试集上预测的时候 预测误差的期望值就变大了,从而Variance就大了**; $\mathrm{k}$ 较小的时候, 模型不会过度拟合训练数据, 从而Bias较大,**但是正因为没有过度拟合训练数据, Variance也较小**。
109 |
110 | ### 5.3 处理偏差和方差
111 |
112 | #### 5.3.1 针对不同偏差的不同处理
113 |
114 | 评估训练集或训练数据的性能,若偏差较高,可以选择以下几种方法:
115 | - 选择更大的网络,比如含有更多隐藏层或隐藏单元的网络
116 | - 花费更多时间训练网络(不一定有用,但没坏处)
117 | - 尝试更先进的优化算法
118 | - 选择更适合解决此问题的神经网络架构(可能有用,可能没用)
119 |
120 | 训练学习算法时,不断尝试这些方法,直到可以拟合数据,解决掉偏差问题为止,至少能够拟合训练集。
121 | #### 5.3.2 针对不同方差的不同处理
122 | 偏差降低到可以接受的数值,查看验证集性能来评估方差,如果方差高,可以选择下列方法:
123 | - 采用更多数据(最好的解决办法)
124 | - 正则化
125 | - 尝试更适合的神经网络框架(有时可以同时减少偏差和方差)
126 |
127 | 解决高方差最优方法是准备更多的数据,但可能无法实时准备足够多的数据或数据成本很高时,**正则化**可帮助避免过拟合,减少网络误差。
128 |
129 | 通过不断重复尝试,找到一个低偏差、低方差的框架。
130 | > 高偏差和高方差尝试的方法可能完全不同,明确这点来选择最有效的方法。
131 | 只要正则适度,通常构建更大网络便可以在不影响方差的同时减少偏差。采用更多数据通常可以在不过多影响偏差的同时减少方差。我们有很多的选择可以减少偏差或方差而不影响另一方。
132 |
133 |
134 | ### 5.4 正则化
135 |
136 | **定义**:一种为了减小方差(测试误差)的行为
137 | **作用**:使用比较复杂的模型比如神经网络,去拟合数据时,容易出现过拟合现象,导致模型的泛化能力下降,这时我们使用正则化,降低模型的复杂度,让模型在面对新数据的时候,可以有很好的表现。
138 |
139 | #### 5.4.1 logistic 回归的正则化
140 | - **L2 正则化**
141 | $J(w, b)=\frac{1}{m} \sum_{i=1}^{m} L\left(\hat{y}^{(i)}, y^{(i)}\right)+\frac{\lambda}{2 m}\|w\|_{2}^{2}$
142 | 每次更新w时:
143 |
144 | $$w:=w-\alpha d w=\left(1-\frac{\alpha \lambda}{m}\right) w-\frac{\partial J}{\partial w}$$
145 |
146 | 从上式看出,每次更新对特征系数做一个**比例的缩放**而不是像L1正则化减去一个固定值。这使得系数趋向变小而不会变为0,因此L2正则化**让模型变得更简单,防止过拟合**。
147 | - **L1 正则化**
148 | $$J(w, b)=\frac{1}{m} \sum_{i=1}^{m} L\left(\hat{y}^{(i)}, y^{(i)}\right)+\frac{\lambda}{2 m}\|w\|_{1}$$
149 |
150 | 每次更新w时:
151 | $$\begin{array}{c}
152 | w:=w-\alpha d w\\
153 | =w-\frac{\alpha \lambda}{2 m} \operatorname{sign}\left(w\right)-\frac{\partial J}{\partial w}
154 | \end{array}$$
155 | 若 w 为正数,则每次更新减去一个常数;若 w 为负数,则每次更新加上一个常数,故容易产生特征的系数为0的情况,特征系数为 0 表示该特征不会对结果有任何影响,因此L1正则化让w变得稀疏,起到**特征选择**的作用。
156 | > - 参数 w 向量的L2 范数:$\|w\|_{2}^{2}=\sum_{j=1}^{n_{x}} w_{j}^{2}=w^{T} w$
157 | 参数 w 向量的L1 范数:$\|w\|_{1}=\sum_{j=1}^{n_{x}}\left|w_{j}\right|$
158 | > - $w\in \mathbb{R}^{n_{x}}, b \in \mathbb{R}$,习惯只正则化w,省略参数b。因为w通常是一个高维参数矢量,b只是单个数字,即w几乎涵盖所有参数,b只是众多参数中的一个,b通常省略不计,加上也没问题。
159 | >- $\lambda$是正则化参数,是一个需要调整的超参数,Python 编程语言中,lambda 是一个保留字段,编写代码时,删掉a,写成lambd,以免冲突。
160 |
161 | **总结**
162 | 两者都通过加上一个和项来限制参数大小,效果却不同:L1正则化适用于**特征选择**,L2正则化适用于**防止模型过拟合**。
163 | 在训练网络时,倾向于使用**L2正则化**。
164 |
165 |
166 |
167 | #### 5.4.2 神经网络中实现L2正则化
168 |
169 | $$J\left(w^{[1]}, b^{[1]}, \ldots, w^{[L]}, b^{[L]}\right)=\frac{1}{m} \sum_{i=1}^{m} L\left(\hat{y}^{(i)}, y^{(i)}\right)+\frac{\lambda}{2 m} \sum_{l=1}^{L}\|w\|_{F}^{2}$$
170 | **Frobenius 范数**:
171 | 下标F标注,表示一个矩阵中所有元素的平方和。
172 | $$\|w\|_{F}^{2}=\sum_{i=1}^{n^{[l-1]}} \sum_{j=1}^{n^{[l]}}\left(w_{i j}^{[l]}\right)^{2}$$
173 |
174 | 其中,$w:\left(n^{[l-1]}, n^{[l]}\right)$ $n^{[l]}$表示第$l$层单元数量,$n^{[l-1]}$表示第$l-1$层单元数量
175 |
176 | 实现梯度下降:
177 | $$\begin{aligned} w^{[l]}: &=w^{[l]}-\alpha\left[(\text { from backprop })+\frac{\lambda}{m} w^{[l]}\right] \\ &=\left(1-\frac{\alpha \lambda}{m}\right) w^{[l]}-\alpha(\text { from backprop }) \end{aligned}$$
178 | 实际上,相当于给矩阵$w^{[l]}$乘上$1-\frac{\alpha \lambda}{m}$倍的权重,而该系数小于1,因此L2正则化也被称为**权重衰减**
179 |
180 |
181 |
182 | ### 5.5 正则化有效的原理
183 | - 正则化参数$\lambda$增加到足够大,权重矩阵$w^{[l]}$会接近于0,大量隐藏单元的影响变得更小了,神经网络越来越简单,接近逻辑回归,这样更不容易发生过拟合。
184 |
185 | 举例:
186 | 假设使用$\tanh (z)$激活函数,如果$z$的值始终在接近原点的小范围内,激活函数大致呈线性,每层几乎都是线性的,和线性回归一样。
187 |
188 | 
189 | 当正则化参数$\lambda$足够大,参数$w$很小,$z$也会相对变小,激活函数$\tanh (z)$会相对呈线性,整个神经网络会计算接近线性函数的值,即一个很简单的函数,而不是极复杂的高度非线性函数,不会发生过拟合。
190 |
191 | 参考文章:[机器学习中的正则化](https://www.jianshu.com/p/569efedf6985)
192 |
193 |
194 |
195 |
196 |
197 | ### 5.6 Dropout正则化 ###
198 | Dropout正则化是较常用的避免过拟合的方法之一。
199 |
200 | **Dropout**
201 |
202 | 首先介绍一下Dropout正则化:在**训练**神经网络时,对于每一层神经网络中的所有节点,每个结点都有keep_prob的概率保留,1 - keep_prob的概率丢弃。这里的丢弃指的是**每一次**前向传播的时候随机丢弃部分结点,每次前向传播都重新计算要丢弃的结点。要注意在更新权值和真正应用已经训练好的网络时,是不会随机丢弃的。
203 | 
204 |
205 | **原理**
206 |
207 | 有没有觉得很神奇,竟然随机丢掉一些结点反而能“更好”地训练神经网络,也太“玄乎”了。当然,能生效的正则化肯定有它成功的理由,下面给出解释:
208 | 1. 随机删除一些结点,本质上相当于缩小网络。而过拟合的原因之一是网络太大而导致的拟合效果“好过头”了,那缩小网络自然能一定程度上避免过拟合。
209 | 2. 由于所有节点都可能被丢弃,所以训练时不会过渡依赖任何一个结点(特征),表现为尽可能缩小所有权值。那就有点接近L2正则化那种收缩权值的效果了。
210 |
211 | **代码实现**
212 |
213 | # 操作 < keep_prob 可使本来的随机向量变为True、False组成的向量
214 | d3 = np.random.randn(a3.shape[0], a3.shape[1]) < keep_prob
215 | # 实际运算时,True、False会变为1和0
216 | a3 *= d3
217 | # 修正a3的均值,保持和Dropout前不变
218 | a3 /= keep_prob
219 |
220 | 技术细节上,用了一个小于运算符自动将随机值转换为0、1;在将部分值归0后,a3的均值也会变为原来的keep_prob倍,所以最后对所有数除以keep_prob以保证a3的均值不变,保证$z3=wa3+b$的均值不变
221 |
222 |
223 |
224 |
225 | ### 5.7 其他正则化方法 ###
226 | #### 5.7.1 数据增强/Data Augmentation ####
227 | 前文提到解决high variance(高方差)/ 过拟合的解决办法之一是收集更多的数据,更大的训练集。但有时候并不是那么容易就能短时间内收集的。所以提出了一个基于已有数据的增加数据量的方法:数据增强。
228 | 具体方法:
229 |
230 | 1. 翻转(水平、上下等)
231 | 2. 随机裁剪。指放大后旋转、裁剪
232 | 3. 扭曲变形,有很多更具体的成熟的方法。
233 |
234 | 但是数据增强并不是万用的方法,有时候可能会对网络的训练造成负面影响:比如从图片中提取文字的网络不适应翻转等等。甚至识别人脸的网络也不适合翻转,原因是“视觉手性”,感兴趣的可以阅读[Visual Chirality](https://arxiv.org/abs/2006.09512
235 | )。
236 |
237 | #### 5.7.2 Early Stopping ####
238 | Early stopping顾名思义,提早结束(训练)。具体操作是:
239 |
240 | 1. 训练足够多的次数,并且记录train set和dev set的error曲线。如图
241 | 
242 |
243 | 2. 找到dev error曲线的最低点,该点的迭代次数(附近)作为最佳迭代次数。
244 |
245 | 原理也很简单,在网络过拟合之前停止训练,不就能阻止网络过拟合了嘛。操作起来也很简单,训练一次就知道下次要训练多久了。不过简单的做法自然带来偷懒的弊端。过早停止训练,意味着网络可能还没得到充分的训练,过早停止优化cost函数,虽然低方差但是可能高偏差。
246 |
247 |
248 | ### 5.8 正则化输入 ###
249 | **命名问题**
250 |
251 | 首先提一下有关归一化和标准化的命名问题。如果你去百度一下很容易就发现吴恩达老师教的归一化(Normalizing)和百度的不一样,倒是和百度的标准化(Standardization)差不多。大名鼎鼎的吴恩达老师竟然会犯这种低级错误?笔者一开始也这么认为,但是想了想我只是刚入门的怎么可以那么轻易怀疑大师。于是在多百度了几次(无果)、查几篇国内外论文、最后一次百度(知乎)后,得出了结果:
252 | 归一化和标准化都是一种特征放缩(Feature scaling)。特征放缩有很多种方法,这里只讲涉及到的这两种。
253 |
254 | 1. min-max normalizing(Rescaling),也就是百度的归一化normalizing:
255 | $$
256 | x^{\prime}=\frac{x-\min (x)}{\max (x)-\min (x)}
257 | $$
258 |
259 | 2. Z-score normalization(Standardization),也就是百度的标准化:
260 | $$
261 | x^{\prime}=\frac{\left(x-\mu\right)}{\sigma}
262 | $$
263 |
264 | 猜测吴恩达老师是简称Z-score normalization为normalization了?也可能是其他原因吧。彻底帮我解决问题的[回答](https://www.zhihu.com/question/20467170)。
265 |
266 | **为什么要Z-score normalization**
267 |
268 | 有时候我们的数据的分布并不是“很好看”(图1、2),不是很利于网络的训练。这时候我们就可以考虑处理一下数据,使得数据的分布“更好看”(图3、4)。**注意**:图片中的名称用的是吴恩达老师课程中的名称。
269 | 
270 | 
271 | 
272 | 
273 | 什么时候数据会不好看?当输入的特征$x_{1}$和$x_{2}$取值范围有很大差别时就会,比如:$x_{1}$在[0,1]内,$x_{2}$在[1, 100]内。这样就会导致数据的分布为椭圆形,那在梯度下降时如果学习率不够小很容易就会一直震荡而艰难收敛;而更对称的分布,学习率就算大一点也很容易就能收敛。
274 | 所以一般当输入特征的取值范围差距较大时就考虑Z-score normalization,不过无脑使用也没什么坏事,所以是比较推荐的方法。
275 |
276 | **实现**
277 |
278 | 首先要注意的一点是,尽量别分多次计算均值$\mu$和方差$\sigma$,比如这两个值都由训练集得出就不更改了。
279 | Python代码:
280 |
281 | # 计算均值
282 | x_mean = np.mean(x)
283 | # 计算标准差;计算方差用np.var
284 | x_std = np.std(x)
285 | # 标准化
286 | x = (x - x_mean) / x_std
287 |
288 | 多提一句,对于图片,如果想实现min-max normalizing,一般只需要默认0为最小值,255为最大值即可:
289 |
290 | # x = (x-0) / (255-0)
291 | x = x / 255
292 |
293 |
294 |
295 |
296 | ### 5.9 梯度消失和梯度爆炸 ###
297 | #### 5.9.1 介绍 ####
298 | 英文称:vanishing and exploding gradients。
299 | 首先简单“展示”一下梯度爆炸是怎么样的:
300 | 假设有$L$层,$\text W^{[l]}=\left[\begin{array}{cc}
301 | 1.5 & 0 \\
302 | 0 & 1.5
303 | \end{array}\right],
304 | b^{[l]}=0$($l∈[1, L]$),且激活函数全部采用线性激活(恒等函数),则
305 |
306 | $$\begin{array}{l}
307 | \hat{y}=W^{[L]}W^{[L-1]} \ldots W^{[1]}x \\
308 | =\left[\begin{array}{cc}
309 | 1.5 & 0 \\
310 | 0 & 1.5
311 | \end{array}\right]^{L}x \\
312 | =\left[\begin{array}{cc}
313 | 1.5^{L} & 0 \\
314 | 0 & 1.5^{L}
315 | \end{array}\right]x
316 | \end{array}$$
317 |
318 | 可见,$W^{[l]}$中大于1的元素,将会因指数级增长而“爆炸”;同理,小于1的元素,则会以指数级递减而“消失”(真实情况会更复杂一些,但上述例子足以说明这种可能性)。
319 | 这不仅仅适用于$\hat{y}$的计算,还适用于梯度$dW、db$的计算——过深的网络在梯度下降时计算的梯度很有可能接近0或过大。这会直接导致网络的学习停滞不前或者发散,严重影响学习效果。
320 |
321 | #### 5.9.2 权重初始化 ####
322 | 既然梯度消失和爆炸都是由于$L$过大而形成的指数级缩小/放大,那在不减少$L$的前提下比较有限的方法就是让每次输出尽可能接近1了。$z$的计算可写成:
323 | $$z=w_{1}a_{1}+w_{2}a_{2}+\ldots+w_{n}a_{n}$$那么当$n$增大时,想让$z$减小则可以通过减小$w_{i}$做到;而$w_{i}$是符合高斯分布(标准正态分布,np.random.randn())的,所以$z$可**看似**服从分布$N(0, n)$,那$w_{i}$除以$n$就可以让$z$近似服从分布$N(0, 1)$,已达到。
324 | 具体做法是初始化时,用以下语句:
325 |
326 | w[l] = np.random.randn(n[l], n[l-1])*np.sqrt(2 / (n[l-1]))
327 |
328 | 其中*sqrt*中的表达式和使用的激活函数有关。ReLU采用上式($\frac{2}{n^{l-1}}$),tanh则采用$\frac{1}{n^{[l-1]}}$,其他形式的有$\frac{2}{n^{[l+1]}+n^{[l]}}$。
329 | 这么做的目的主要是修改$W^{[l]}$的分布,将方差除以输入
330 |
331 | #### 5.9.3 梯度逼近 ####
332 | 我们在计算梯度时用的是“手写”的公式(自己推导的公式),可能有时候会犯一点小错误。那我们就需要对梯度的计算进行验算,看看有没有错。但是不可能用同样的式子进行验算,因为计算机不会产生“计算失误”。所以我们需要不同的,计算结果很接近的方法来重新计算一次,那就是梯度逼近。
333 | 回顾高数/高中知识,梯度(导数)是切线斜率。近似地我们可以通过计算一个点附近的割线的斜率来代替该点的切线斜率。如图,可以用$\frac{ f(\theta+\varepsilon)-f(\theta-\varepsilon)}{2\varepsilon}$代替$f^{\prime}(\theta)$。当然,$\varepsilon$越小越接近。图来自吴恩达课程的1.12梯度的数值逼近。
334 | 
335 | 可能会有人疑惑为什么不采用单边,比如$\frac{ f(\theta+\varepsilon) - f(\theta)}{\varepsilon}$,而是要这样两边都取。抽象地你可以理解为单边计算出来的斜率更接近$\theta$的左右偏移一点点的$\theta^{\prime}$的值;而双边计算$\theta$正好位于割线的“正中间”,计算出来的斜率也自然要更接近一些。
336 |
337 | #### 5.9.4 梯度检验 ####
338 | 进入正题,介绍如何进行检验。首先对于所有参数$W^{[l]}$和$b^{[l]}$,按顺序链接成一个参数集$\theta$。对于$dW^{[l]}$和$db^{[l]}$也同样链接成$d\theta$。这里分别对应前向传播和反向传播。$\theta$和$d\theta$有一样的shape,$\theta[i]$表示第$i$个参数。然后计算$d\theta$的近似值$d\theta_{approx}$:
339 | 1. 遍历参数集$\theta$中的$\theta[i]$。
340 | 2. 计算$$d\theta_{approx}[i] = \frac{J(\theta[1], \theta[2], \ldots, \theta[i]+\varepsilon, \ldots)-J(\theta[1], \theta[2], \ldots, \theta[i] - \varepsilon, \ldots )} { 2\varepsilon} $$
341 | 3. 计算$\Delta = \frac{\|d\theta_{approx}-d\theta\|} {\|d\theta_{approx}\|+\|d\theta\|}$欧几里得范数,实际上就是根号下误差平方之和。
342 | 4. 如果$\Delta > \varepsilon$(如$\varepsilon=10^{-7}$),则视为误差超出阈值,否则为正常。
343 |
344 | #### 5.9.5 其他解决办法
345 |
346 | - relu、leakrelu等激活函数
347 |
348 | Relu:思想也很简单,如果激活函数的导数为1,那么就不存在梯度消失爆炸的问题了,每层的网络都可以得到相同的更新速度。
349 |
350 | relu的优点: 解决了梯度消失、爆炸的问题;计算方便,计算速度快,加速了网络的训练
351 |
352 | relu的缺点:由于负数部分恒为0,会导致一些神经元无法激活(可通过设置小学习率部分解决);输出不是以0为中心的
353 |
354 | **尽管relu也有缺点,但是仍然是目前使用最多的激活函数。**
355 |
356 | leakrelu激活函数在前面介绍激活函数时已经讲过了,这里就不再赘述了。
357 |
358 | - 梯度裁剪
359 |
360 | - batch normalization
361 |
362 | - 残差结构
363 |
364 | 上面的方法在下面的内容里面我们还会讲,这里就不再赘述了。
365 |
366 | #### 5.9.6 注意细节 ####
367 |
368 | 讲一下代码实现有几个细节:
369 | 1. 要实现cost function,并且接受参数$\theta$。
370 | 2. 欧几里得范数可以用 np.linalg.norm(array) 计算。
371 | 3. 不要和Dropout一起使用。
372 | 4. 只在debug时开启,正常训练无需启动,否则会花费大量的时间。
373 | 5. 应用了L2正则化的cost function和一般的不一样,梯度计算也会不一样。
374 |
375 |
376 |
377 | ### 5.10 参考文献
378 |
379 | https://zhuanlan.zhihu.com/p/38853908
380 |
381 |
382 |
383 |
384 |
385 |
386 |
387 |
388 |
--------------------------------------------------------------------------------
/7 超参数的调试,BN和程序框架.md:
--------------------------------------------------------------------------------
1 | ## 7 超参数调试,Batch Norm和程序框架
2 |
3 | ### 7.1 调试处理
4 |
5 | #### 7.1.1 超参数的重要性比较
6 |
7 | **深度学习中,用到的超参数有**
8 |
9 | $α $:学习率
10 |
11 | $β$:动量梯度下降因子
12 |
13 | $β1,β2,ε$:Adam算法参数
14 |
15 | layers:神经网络层数
16 |
17 | hidden units:各隐藏层神经元个数
18 |
19 | learning rate decay:学习因子下降参数
20 |
21 | mini-batch size:批量训练样本包含的样本个数
22 |
23 |
24 |
25 | 学习率$α$为最重要的超参数;
26 |
27 | 动量梯度下降因子$β$、各隐藏层神经元个数hidden units、批量训练样本包含的样本个数mini-batch size,三者重要性仅次于学习因子$α$;
28 |
29 | 接下来为神经网络层数layers和学习因子下降参数learning rate decay;最后,由于Adam算法参数$β1,β2,ε$三个参数一般设置为0.9,0.999和$10^{-8}$,不需要反复调试,所以重要性较弱。
30 |
31 | 但超参数的重要性排名不是一成不变的,可能会根据情况的不同而发生一定的变化
32 |
33 |
34 |
35 | #### 7.1.2 超参数的调试过程
36 |
37 | 在传统的机器学习中,我们对每个参数等距离选取任意个数的点,然后,分别使用不同点对应的参数组合进行训练,最后根据验证集上的表现,来选定最佳的参数。例如有两个待调试的参数,分别在每个参数上选取5个点,这样构成了5x5=25的参数组合,如图:
38 |
39 | 
40 |
41 | 此做法在参数较少的时候效果较好。但在深度学习的神经网络中,比较好的做法是使用随机选择。即:对于上面这个例子,我们随机选择25个点,作为待调试的超参数,如图:
42 |
43 | 
44 |
45 |
46 | 随机选择参数的目的是为了尽可能地得到更多种参数组合。如上面的例子,如果使用均匀采样的话,每个参数只有5种情况;而使用随机采样的话,每个参数有25种可能的情况,因此更有可能得到最佳的参数组合。
47 |
48 | 这种做法的另一个好处是能够对重要性不同的参数之间的选择效果更好。假设hyperparameter1为$α$,hyperparameter2为$ε$,二者的重要性是不一样的。如果使用第一种均匀采样的方法,$ε$的影响很小,相当于只选择了5个$α$值。而如果使用第二种随机采样的方法,$ε$和$α$都有可能选择25种不同值。这大大增加了$α$调试的个数,选择到最优值的可能更大了。在完全不知道哪个参数更加重要的情况下,随机采样的方式可以有效解决这一问题,但是均匀采样不能够解决该问题。
49 |
50 | 在随机采样后,可以得到某些区域模型的表现较好。为了得到更精确的最佳参数,我们应该继续对选定的区域进行由粗到细的采样(coarse to fine sampling scheme)。即放大表现较好的区域,再对此区域做更密集的随机采样。例如,对下图中右下角的方形区域再做25点的随机采样,以获得最佳参数。
51 | 
52 |
53 | ### 7.2 为超参数选择合适的范围
54 |
55 | #### 7.2.1 不同超参数合适的标尺
56 |
57 | 例如:神经网络层数layers和各隐藏层神经元个数hidden units,因为两者都为正整数,所以可以直接进行随机均匀采样(即每次变化的幅度是一样的);而对于学习率$α$和动量梯度下降因子$β$,则需要使用非均匀随机采样。
58 |
59 | #### 7.2.2 对数轴的取值过程
60 |
61 | 通过将linear scale转换为log scale来实现均匀尺度转化为非均匀尺度,然后再在log scale下进行均匀采样。如,[0.0001, 0.001],[0.001, 0.01],[0.01, 0.1],[0.1, 1]各个区间内随机采样的超参数个数基本一致,也就扩大了之前[0.0001, 0.1]区间内采样值个数。假设线性区间为[a, b],令$m=log(a),n=log(b)$,则对应的log区间为[m,n]。对log区间的[m,n]进行随机均匀采样,得到的采样值$r$,再反推到线性区间,即10的r次方。则10的r次方为最终采样的超参数。
62 |
63 | #### 7.2.3 为什么$β$不用linear scale进行取值
64 |
65 | 假设β从0.9000变化为0.9005,则$1/1−β$基本没有变化。但如果$β$从0.9990变为0.9995,那么$1/1−β$前后差别1000。即:$β$越接近1,指数加权平均的个数越多,变化越大。因此在$β$接近1的区间,应采集得更密集一些。
66 |
67 | ### 7.3 超参数训练的实践: Pandas VS Caviar
68 |
69 | #### 7.3.1 熊猫方式Panda approach
70 |
71 | 只能够对一个模型进行训练,调试不同的超参数,使得这个模型有最佳的表现。
72 |
73 | #### 7.3.2 鱼子酱方式Caviar approach
74 |
75 | 可以对多个模型同时进行训练,每个模型上调试不同的超参数,根据模型的表现,选择最优的模型
76 |
77 | 一般对于非常复杂或者数据量很大的模型,更多使用Panda approach。
78 |
79 |
80 |
81 | ### 7.4 归一化网络的激活函数
82 |
83 | #### 7.4.1 logistic 回归中归一化输入特征
84 |
85 | 
86 | $$
87 | \begin{array}{l}
88 | \mu=\frac{1}{m} \sum_{i} x^{(i)} \\
89 | X=X-\mu \\
90 | \sigma^{2}=\frac{1}{m} \sum_{i} x^{(i) 2} \\
91 | X=X / \sigma^{2}
92 | \end{array}
93 | $$
94 | 计算平均值,从训练集中减去平均值;计算方差,根据方差归一化数据集。变化学习问题的轮廓,易于算法优化。即归一化$x_{1}$,$x_{2}$,$x_{3}$有助于更有效的训练$w$和$b$。
95 |
96 |  97 |
98 |
99 |
100 | #### 7.4.2 更深层的模型的归一化
101 |
102 | 
103 |
104 | **分析**:此例中,与上例同理,归一化$a^{[2]}$的平均值和方差以便使$w^{[3]}$,$b^{[3]}$的训练更有效率,严格来说我们真正归一化的不是$a^{[2]}$而是$z^{[2]}$。关于归一化$a^{[2]}$还是$z^{[2]}$,深度学习文献中有一些争论,实践中,常做的是**归一化$z^{[2]}$**,吴恩达推荐其为默认选择。
105 |
106 | **实施BN**:
107 |
108 | 在神经网络中,给定一些中间值,假设你有一些隐藏单元值,从$z^{(1)}$到$z^{(m)}$,这些来源于隐藏层,写为$z^{[l](i)}$会更准确,我们省略$𝑙$及方括号,以便简化这一行的符号。
109 |
110 | 已知这些值,计算平均值,所有这些都是针对𝑙层,但省略$𝑙$及方括号,接着,取每个$z^{(i)}$值,使其归一化,如下,减去均值再除以标准偏差,为了使数值稳定,通常分母加上$𝜀$,以防$𝜎 = 0$的情况。
111 |
112 |
113 | $$
114 | \begin{array}{l}
115 | \mu=\frac{1}{m} \sum_{i} z^{(i)} \\
116 | \sigma^{2}=\frac{1}{m} \sum_{i}\left(z^{(i)}-\mu\right)^{2} \\
117 | z_{\text {norm}}^{(i)}=\frac{z^{(i)}-\mu}{\sqrt{\sigma^{2}+\varepsilon}}
118 | \end{array}
119 | $$
120 | 这时,已把这些$z$值归一化,化为平均值0和标准单位方差,所以每个分量都含有平均值0和方差1,但我们不想让隐藏单元总是含有平均值0和方差1,隐藏单元有了不同的分布才会有意义。于是做如下计算:
121 | $$
122 | \tilde{z}^{(i)}=\gamma z_{\text {norm}}^{(i)}+\beta
123 | $$
124 | 这里,$\gamma$和$\beta$是模型的**学习参数**,使用梯度下降或一些其他类似梯度下降的算法,如Momentum,或Nesterov,Adam更新$\gamma$和$\beta$,正如神经网络的权重。
125 |
126 | $\gamma$和$\beta$的作用是可以随意设置$\tilde{z}^{(i)}$的平均值。当$\gamma=\sqrt{\sigma^{2}+\varepsilon}$, $\beta=\mu$时,$\tilde{z}^{(i)}=z^{(i)}$。此时,该归一化过程,即这四个等式,只是计算恒等函数。但通过对$\gamma$和$\beta$合理设定,可以构造含其他平均值和方差的隐藏单元值。在网络中,用$\tilde{z}^{(i)}$取代$z^{(i)}$,方便神经网络中的后续计算。
127 |
128 | **归纳**:$Batch Norm$归一化的不只是输入层,同样应用于深度隐藏层。但训练输入和隐藏单元值的一个区别是,我们不希望隐藏单元值总是均值0和方差1。
129 |
130 |
97 |
98 |
99 |
100 | #### 7.4.2 更深层的模型的归一化
101 |
102 | 
103 |
104 | **分析**:此例中,与上例同理,归一化$a^{[2]}$的平均值和方差以便使$w^{[3]}$,$b^{[3]}$的训练更有效率,严格来说我们真正归一化的不是$a^{[2]}$而是$z^{[2]}$。关于归一化$a^{[2]}$还是$z^{[2]}$,深度学习文献中有一些争论,实践中,常做的是**归一化$z^{[2]}$**,吴恩达推荐其为默认选择。
105 |
106 | **实施BN**:
107 |
108 | 在神经网络中,给定一些中间值,假设你有一些隐藏单元值,从$z^{(1)}$到$z^{(m)}$,这些来源于隐藏层,写为$z^{[l](i)}$会更准确,我们省略$𝑙$及方括号,以便简化这一行的符号。
109 |
110 | 已知这些值,计算平均值,所有这些都是针对𝑙层,但省略$𝑙$及方括号,接着,取每个$z^{(i)}$值,使其归一化,如下,减去均值再除以标准偏差,为了使数值稳定,通常分母加上$𝜀$,以防$𝜎 = 0$的情况。
111 |
112 |
113 | $$
114 | \begin{array}{l}
115 | \mu=\frac{1}{m} \sum_{i} z^{(i)} \\
116 | \sigma^{2}=\frac{1}{m} \sum_{i}\left(z^{(i)}-\mu\right)^{2} \\
117 | z_{\text {norm}}^{(i)}=\frac{z^{(i)}-\mu}{\sqrt{\sigma^{2}+\varepsilon}}
118 | \end{array}
119 | $$
120 | 这时,已把这些$z$值归一化,化为平均值0和标准单位方差,所以每个分量都含有平均值0和方差1,但我们不想让隐藏单元总是含有平均值0和方差1,隐藏单元有了不同的分布才会有意义。于是做如下计算:
121 | $$
122 | \tilde{z}^{(i)}=\gamma z_{\text {norm}}^{(i)}+\beta
123 | $$
124 | 这里,$\gamma$和$\beta$是模型的**学习参数**,使用梯度下降或一些其他类似梯度下降的算法,如Momentum,或Nesterov,Adam更新$\gamma$和$\beta$,正如神经网络的权重。
125 |
126 | $\gamma$和$\beta$的作用是可以随意设置$\tilde{z}^{(i)}$的平均值。当$\gamma=\sqrt{\sigma^{2}+\varepsilon}$, $\beta=\mu$时,$\tilde{z}^{(i)}=z^{(i)}$。此时,该归一化过程,即这四个等式,只是计算恒等函数。但通过对$\gamma$和$\beta$合理设定,可以构造含其他平均值和方差的隐藏单元值。在网络中,用$\tilde{z}^{(i)}$取代$z^{(i)}$,方便神经网络中的后续计算。
127 |
128 | **归纳**:$Batch Norm$归一化的不只是输入层,同样应用于深度隐藏层。但训练输入和隐藏单元值的一个区别是,我们不希望隐藏单元值总是均值0和方差1。
129 |
130 |  131 |
132 | 比如我们使用sigmoid激活函数,想使它们有更大的方差或非0的均值,以便更好的利用非线性的sigmoid函数,而不是所有值都集中在线性区域中。
133 |
134 | 有了$\gamma$和$\beta$两个参数,均值和方差由其控制,使隐藏单元值的均值和方差归一化,即$z^{(i)}$有固定的均值和方差。其均值和方差可以是0和1,也可以是其他值。
135 |
136 | ### 7.5 将 Batch Norm 拟合进神经网络
137 |
138 | #### 7.5.1 在网络中加入 Batch Norm
139 |
140 |
131 |
132 | 比如我们使用sigmoid激活函数,想使它们有更大的方差或非0的均值,以便更好的利用非线性的sigmoid函数,而不是所有值都集中在线性区域中。
133 |
134 | 有了$\gamma$和$\beta$两个参数,均值和方差由其控制,使隐藏单元值的均值和方差归一化,即$z^{(i)}$有固定的均值和方差。其均值和方差可以是0和1,也可以是其他值。
135 |
136 | ### 7.5 将 Batch Norm 拟合进神经网络
137 |
138 | #### 7.5.1 在网络中加入 Batch Norm
139 |
140 |  141 |
142 | BN发生在计算 $z$ 的计算和 $a$ 之间。与其应用没有归一化的 $z$ 值,不如用归一过的 𝑧̃ 。
143 |
144 | 得到算法的新参数:
145 | $$
146 | \begin{array}{l}
147 | w^{[1]}, b^{[1]}, w^{[2]}, b^{[2]}, \ldots w^{[L]}, b^{[L]} \\
148 | \beta^{[1]}, \gamma^{[1]}, \beta^{[2]}, \gamma^{[2]}, \ldots \beta^{[L]}, \gamma^{[L]}
149 | \end{array}
150 | $$
151 | 接下来可以用想用的任何一种优化算法来更新它们。比如使用梯度下降法,对给定层计算$d \beta^{[l]}$接着更新参数$\beta$为$\beta^{[l]}=\beta^{[l]}-\alpha d \beta^{[l]}$。也可以使用Adam或RMSprop或Momentum等更新$\gamma$和$\beta$。
152 |
153 | 如果使用深度学习编程框架,通常不需要自己将Batch Norm步骤应用于Batch Norm层,比如说,在Tensorflow框架中,可以用函数(tf.nn.batch_normalization)来实现Batch Normalization。
154 |
155 | #### 7.5.2 Batch Norm与mini-batch一起使用
156 |
157 | 实践中,Batch Norm通常和训练集的mini-batch一同使用。
158 |
159 | 
160 |
161 | 过程:
162 |
163 | - 用第一个 mini-batch($X^{\{1\}}$)应用参数$w^{[1]}$,$b^{[1]}$计算$z^{[1]}$,接着BN会减去均值,除以标准差,由$\beta^{[1]}$和$\gamma^{[1]}$重新缩放,得到$\tilde{z}^{[1]}$,再应用激活函数得到$a^{[1]}$,然后用$w^{[2]}$,$b^{[2]}$计算$z^{[2]}$等等。
164 | - 在第二、三...个mini-batch上同样这样做,继续训练。
165 |
166 | 由于计算$z$的方式:$z^{[l]}=w^{[l]} a^{[l-1]}+b^{[l]}$,而BN先将$z^{[l]}$归一化,结果为均值0和标准方差,再由$\gamma$和$\beta$缩放。这意味着,无论$b^{[l]}$的值是多少,都会被减去,因为在BN过程中,要计算$z^{[l]}$的均值再减去平均值,在此例中的mini-batch中增加任何常数,都将会被均值减去所抵消,数值不会改变。
167 |
168 | 故在使用BN时,消除参数$b^{[l]}$,或者将其设置为0,参数计算变为:
169 | $$
170 | z^{[l]}=w^{[l]} a^{[l-1]}\\
171 | z_{\text {norm}}^{[l]}\\
172 | \tilde{z}^{[l]}=\gamma^{[l]} z_{\text {norm}}^{[l]}+\beta^{[l]}
173 | $$
174 | 最后用$\beta^{[l]}$影响转置或偏置条件。
175 |
176 | 此例中,$z^{[l]}$,$\beta^{[l]}$,$\gamma^{[l]}$维度都是$\left(n^{[l]}, 1\right)$。
177 |
178 | #### 7.5.3 用BN来应用梯度下降法
179 |
180 | for t = 1......num Mini Batches
181 |
182 | compute forward prop on $X^{\{t\}}$
183 |
184 | in each hidden layer,use BN to replace $z^{[l]}$with $\tilde{z}^{[l]}$
185 |
186 | Use backprop to compute $d w^{[l]}$,$d \beta^{[l]}$,$d \gamma^{[l]}$
187 |
188 | Update parameters $w^{[l]}=w^{[l]}-\alpha d w^{[l]}$, $\beta^{[l]}=\beta^{[l]}-\alpha d \beta^{[l]}$ ,$\gamma^{[l]}=\gamma^{[l]}-\alpha d \gamma^{[l]}$
189 |
190 | Works with momentum rmsprop,adam
191 |
192 | ------
193 |
194 |
195 |
196 | - 假设使用 mini-batch梯度下降法,运行𝑡 = 1到 batch 数量的 for 循环,
197 |
198 | - 在 mini-batch $X^{\{t\}}$上应用正向传播,每个隐藏层都应用正向传播,使用 BN代替$z^{[l]}$为$\tilde{z}^{[l]}$。确保在这个 mini-batch 中,$𝑧$值有归一化的均值和方差,归一化均值和方差后是$\tilde{z}^{[l]}$
199 | - 然后,反向传播计算$d w^{[l]}$,及所有 $l$ 层所有的参数,$d \beta^{[l]}$和$d \gamma^{[l]}$。
200 | - 最后,更新这些参数$w^{[l]}=w^{[l]}-\alpha d w^{[l]}$, $\beta^{[l]}=\beta^{[l]}-\alpha d \beta^{[l]}$ ,$\gamma^{[l]}=\gamma^{[l]}-\alpha d \gamma^{[l]}$
201 |
202 | 也适用于有 Momentum、RMSprop、Adam 的梯度下降法及其它的一些优化算法来更新由 Batch 归一化添加到算法中的$\beta$和$\gamma$ 参数。
203 |
204 | ### 7.6 Batch Norm 为什么奏效
205 |
206 | #### 7.6.1 什么是Internal Covariate Shift
207 |
208 | Batch Normalization的原论文作者给了Internal Covariate Shift一个较规范的定义:在深层网络训练的过程中,由于网络中**参数变化**而引起内部结点**数据分布发生变化**的这一过程被称作Internal Covariate Shift。
209 |
210 | 深度神经网络之所以如此难训练,其中一个重要原因就是网络中层与层之间存在高度的关联性与耦合性。下图是一个多层的神经网络,层与层之间采用全连接的方式进行连接。
211 |
212 | 我们规定左侧为神经网络的底层,右侧为神经网络的上层。那么网络中层与层之间的关联性会导致如下的状况:随着训练的进行,网络中的参数也随着梯度下降在不停更新。一方面,当底层网络中参数发生微弱变化时,由于每一层中的线性变换与非线性激活映射,这些微弱变化随着网络层数的加深而被放大(类似蝴蝶效应);另一方面,参数的变化导致每一层的输入分布会发生改变,进而上层的网络需要不停地去适应这些分布变化,使得我们的模型训练变得困难。上述这一现象叫做Internal Covariate Shift。
213 |
214 |
141 |
142 | BN发生在计算 $z$ 的计算和 $a$ 之间。与其应用没有归一化的 $z$ 值,不如用归一过的 𝑧̃ 。
143 |
144 | 得到算法的新参数:
145 | $$
146 | \begin{array}{l}
147 | w^{[1]}, b^{[1]}, w^{[2]}, b^{[2]}, \ldots w^{[L]}, b^{[L]} \\
148 | \beta^{[1]}, \gamma^{[1]}, \beta^{[2]}, \gamma^{[2]}, \ldots \beta^{[L]}, \gamma^{[L]}
149 | \end{array}
150 | $$
151 | 接下来可以用想用的任何一种优化算法来更新它们。比如使用梯度下降法,对给定层计算$d \beta^{[l]}$接着更新参数$\beta$为$\beta^{[l]}=\beta^{[l]}-\alpha d \beta^{[l]}$。也可以使用Adam或RMSprop或Momentum等更新$\gamma$和$\beta$。
152 |
153 | 如果使用深度学习编程框架,通常不需要自己将Batch Norm步骤应用于Batch Norm层,比如说,在Tensorflow框架中,可以用函数(tf.nn.batch_normalization)来实现Batch Normalization。
154 |
155 | #### 7.5.2 Batch Norm与mini-batch一起使用
156 |
157 | 实践中,Batch Norm通常和训练集的mini-batch一同使用。
158 |
159 | 
160 |
161 | 过程:
162 |
163 | - 用第一个 mini-batch($X^{\{1\}}$)应用参数$w^{[1]}$,$b^{[1]}$计算$z^{[1]}$,接着BN会减去均值,除以标准差,由$\beta^{[1]}$和$\gamma^{[1]}$重新缩放,得到$\tilde{z}^{[1]}$,再应用激活函数得到$a^{[1]}$,然后用$w^{[2]}$,$b^{[2]}$计算$z^{[2]}$等等。
164 | - 在第二、三...个mini-batch上同样这样做,继续训练。
165 |
166 | 由于计算$z$的方式:$z^{[l]}=w^{[l]} a^{[l-1]}+b^{[l]}$,而BN先将$z^{[l]}$归一化,结果为均值0和标准方差,再由$\gamma$和$\beta$缩放。这意味着,无论$b^{[l]}$的值是多少,都会被减去,因为在BN过程中,要计算$z^{[l]}$的均值再减去平均值,在此例中的mini-batch中增加任何常数,都将会被均值减去所抵消,数值不会改变。
167 |
168 | 故在使用BN时,消除参数$b^{[l]}$,或者将其设置为0,参数计算变为:
169 | $$
170 | z^{[l]}=w^{[l]} a^{[l-1]}\\
171 | z_{\text {norm}}^{[l]}\\
172 | \tilde{z}^{[l]}=\gamma^{[l]} z_{\text {norm}}^{[l]}+\beta^{[l]}
173 | $$
174 | 最后用$\beta^{[l]}$影响转置或偏置条件。
175 |
176 | 此例中,$z^{[l]}$,$\beta^{[l]}$,$\gamma^{[l]}$维度都是$\left(n^{[l]}, 1\right)$。
177 |
178 | #### 7.5.3 用BN来应用梯度下降法
179 |
180 | for t = 1......num Mini Batches
181 |
182 | compute forward prop on $X^{\{t\}}$
183 |
184 | in each hidden layer,use BN to replace $z^{[l]}$with $\tilde{z}^{[l]}$
185 |
186 | Use backprop to compute $d w^{[l]}$,$d \beta^{[l]}$,$d \gamma^{[l]}$
187 |
188 | Update parameters $w^{[l]}=w^{[l]}-\alpha d w^{[l]}$, $\beta^{[l]}=\beta^{[l]}-\alpha d \beta^{[l]}$ ,$\gamma^{[l]}=\gamma^{[l]}-\alpha d \gamma^{[l]}$
189 |
190 | Works with momentum rmsprop,adam
191 |
192 | ------
193 |
194 |
195 |
196 | - 假设使用 mini-batch梯度下降法,运行𝑡 = 1到 batch 数量的 for 循环,
197 |
198 | - 在 mini-batch $X^{\{t\}}$上应用正向传播,每个隐藏层都应用正向传播,使用 BN代替$z^{[l]}$为$\tilde{z}^{[l]}$。确保在这个 mini-batch 中,$𝑧$值有归一化的均值和方差,归一化均值和方差后是$\tilde{z}^{[l]}$
199 | - 然后,反向传播计算$d w^{[l]}$,及所有 $l$ 层所有的参数,$d \beta^{[l]}$和$d \gamma^{[l]}$。
200 | - 最后,更新这些参数$w^{[l]}=w^{[l]}-\alpha d w^{[l]}$, $\beta^{[l]}=\beta^{[l]}-\alpha d \beta^{[l]}$ ,$\gamma^{[l]}=\gamma^{[l]}-\alpha d \gamma^{[l]}$
201 |
202 | 也适用于有 Momentum、RMSprop、Adam 的梯度下降法及其它的一些优化算法来更新由 Batch 归一化添加到算法中的$\beta$和$\gamma$ 参数。
203 |
204 | ### 7.6 Batch Norm 为什么奏效
205 |
206 | #### 7.6.1 什么是Internal Covariate Shift
207 |
208 | Batch Normalization的原论文作者给了Internal Covariate Shift一个较规范的定义:在深层网络训练的过程中,由于网络中**参数变化**而引起内部结点**数据分布发生变化**的这一过程被称作Internal Covariate Shift。
209 |
210 | 深度神经网络之所以如此难训练,其中一个重要原因就是网络中层与层之间存在高度的关联性与耦合性。下图是一个多层的神经网络,层与层之间采用全连接的方式进行连接。
211 |
212 | 我们规定左侧为神经网络的底层,右侧为神经网络的上层。那么网络中层与层之间的关联性会导致如下的状况:随着训练的进行,网络中的参数也随着梯度下降在不停更新。一方面,当底层网络中参数发生微弱变化时,由于每一层中的线性变换与非线性激活映射,这些微弱变化随着网络层数的加深而被放大(类似蝴蝶效应);另一方面,参数的变化导致每一层的输入分布会发生改变,进而上层的网络需要不停地去适应这些分布变化,使得我们的模型训练变得困难。上述这一现象叫做Internal Covariate Shift。
213 |
214 |  215 |
216 | #### 7.6.2 如何减缓Internal Covariate Shift
217 |
218 | **(1)白化(Whitening)**
219 |
220 | 白化(Whitening)是机器学习里面常用的一种规范化数据分布的方法,主要是PCA白化与ZCA白化。白化是对输入数据分布进行变换,进而达到以下两个目的:
221 |
222 | - **使得输入特征分布具有相同的均值与方差。**其中PCA白化保证了所有特征分布均值为0,方差为1;而ZCA白化则保证了所有特征分布均值为0,方差相同;
223 | - **去除特征之间的相关性。**
224 |
225 | 通过白化操作,可以减缓ICS的问题,进而固定每一层网络输入分布,加速网络训练过程的收敛。
226 |
227 | 然而,白化的方法具有一定缺陷,主要有以下两个问题:
228 |
229 | - **白化过程计算成本太高,**并且在每一轮训练中的每一层我们都需要做如此高成本计算的白化操作;
230 | - **白化过程由于改变了网络每一层的分布**,因而改变了网络层中本身数据的表达能力。底层网络学习到的参数信息会被白化操作丢失掉。
231 |
232 | **(2)Batch Normalization**
233 |
234 | 为解决上面两个问题,提出BN方法简化计算过程同时让归一化处理后的数据尽可能保留原始表达能力。
235 | $$
236 | \begin{array}{l}
237 | \mu=\frac{1}{m} \sum_{i} z^{(i)} \\
238 | \sigma^{2}=\frac{1}{m} \sum_{i}\left(z^{(i)}-\mu\right)^{2} \\
239 | z_{\text {norm}}^{(i)}=\frac{z^{(i)}-\mu}{\sqrt{\sigma^{2}+\varepsilon}}
240 | \end{array}
241 | $$
242 | 通过上面的变换,**解决了第一个问题,即用更加简化的方式来对数据进行规范化,使得第 $l$层的输入每个特征的分布均值为0,方差为1。**
243 |
244 | 如同上面提到的,Normalization操作我们虽然缓解了ICS问题,让每一层网络的输入数据分布都变得稳定,但却导致了数据表达能力的缺失。也就是我们通过变换操作改变了原有数据的信息表达(representation ability of the network),使得底层网络学习到的参数信息丢失。另一方面,通过让每一层的输入分布均值为0,方差为1,会使得输入在经过sigmoid或tanh激活函数时,容易陷入非线性激活函数的线性区域。
245 |
246 | 因此,BN引入的两个可学习(learnable)的参数$\gamma$和$\beta$,恢复数据本身的表达能力,对归一化后端数据进行线性变换,即:
247 | $$
248 | \tilde{z}^{[l]}=\gamma^{[l]} z_{\text {norm}}^{[l]}+\beta^{[l]}
249 | $$
250 | 特别地,当$\gamma^{2}=\sigma^{2}, \beta=\mu$时,可以实现等价变换(identity transform)并且保留了原始输入特征的分布信息。
251 |
252 | **通过上面的步骤,我们就在一定程度上保证了输入数据的表达能力。**
253 |
254 | 简单来说,BN减弱了前层参数的作用与后层参数的作用之间的联系,它使得网络每层都可以自己学习,稍稍独立于其它层,这让我们可以使用**更大的学习率**,初值可以更随意,有助于加速整个网络的学习。
255 |
256 | #### 7.6.3 BN的效果总结:
257 |
258 | **(1)BN使得网络中每层输入数据的分布相对稳定,加速模型学习速度**
259 |
260 | BN通过规范化与线性变换使得每一层网络的输入数据的均值与方差都在一定范围内,使得后一层网络不必不断去适应底层网络中输入的变化,从而实现了网络中层与层之间的解耦,允许每一层进行独立学习,有利于提高整个神经网络的学习速度。
261 |
262 | **(2)BN使得模型对网络中的参数不那么敏感,简化调参过程,使得网络学习更加稳定**
263 |
264 | 在神经网络中,我们经常会谨慎地采用一些权重初始化方法(例如Xavier)或者合适的学习率来保证网络稳定训练。
265 |
266 | 当学习率设置太高时,会使得参数更新步伐过大,容易出现震荡和不收敛。但是使用BN的网络将不会受到参数数值大小的影响。
267 |
268 | 例如,我们对参数$W$进行缩放得到$aW$。对于缩放前的值$Wu$($u$表示当前层输入,前一层的输出),设其均值为$\mu_{1}$,方差为$\sigma_{1}^{2}$;对于缩放值$aWu$,设其均值为$\mu_{2}$,方差为$\sigma_{2}^{2}$,则有:
269 | $$
270 | \mu_{2}=a \mu_{1}, \quad \sigma_{2}^{2}=a^{2} \sigma_{1}^{2}
271 | $$
272 | 我们忽略$\epsilon$,则有:
273 | $$
274 | \begin{array}{l}
275 | B N(a W u)=\gamma \cdot \frac{a W u-\mu_{2}}{\sqrt{\sigma_{2}^{2}}}+\beta=\gamma \cdot \frac{a W u-a \mu_{1}}{\sqrt{a^{2} \sigma_{1}^{2}}}+\beta=\gamma \cdot \frac{W u-\mu_{1}}{\sqrt{\sigma_{1}^{2}}}+\beta=B N(W u) \\
276 | \frac{\partial B N((a W) u)}{\partial u}=\gamma \cdot \frac{a W}{\sqrt{\sigma_{2}^{2}}}=\gamma \cdot \frac{a W}{\sqrt{a^{2} \sigma_{1}^{2}}}=\frac{\partial B N(W u)}{\partial u} \\
277 | \frac{\partial B N((a W) u)}{\partial(a W)}=\gamma \cdot \frac{u}{\sqrt{\sigma_{2}^{2}}}=\gamma \cdot \frac{u}{a \sqrt{\sigma_{1}^{2}}}=\frac{1}{a} \cdot \frac{\partial B N(W u)}{\partial W}
278 | \end{array}
279 | $$
280 | 可以看到,经过BN操作以后,权重的缩放值会被“抹去”,因此保证了输入数据分布稳定在一定范围内。另外,权重的缩放并不会影响到对$u$的梯度计算;并且当权重越大时,即$a$越大,$\frac{1}{a}$越小,意味着权重$W$的梯度反而越小,这样BN就保证了梯度不会依赖于参数的scale,使得参数的更新处在更加稳定的状态。
281 |
282 | 因此,在使用Batch Normalization之后,抑制了参数微小变化随着网络层数加深被放大的问题,使得网络对参数大小的适应能力更强,此时我们可以设置较大的学习率而不用过于担心模型divergence的风险。
283 |
284 | **(3)BN允许网络使用饱和性激活函数(例如sigmoid,tanh等),缓解梯度消失问题**
285 |
286 | 在不使用BN层的时候,由于网络的深度与复杂性,很容易使得底层网络变化累积到上层网络中,导致模型的训练很容易进入到激活函数的梯度饱和区;通过normalize操作可以让激活函数的输入数据落在梯度非饱和区,缓解梯度消失的问题;另外通过自适应学习$\gamma$和$\beta$又让数据保留更多的原始信息。
287 |
288 | **(4)BN具有一定的正则化效果**
289 |
290 | - BN只在每个mini-batch上计算均值和方差,而不是在整个数据集上
291 | - 均值和方差只是由一小部分数据估计得出的,有一些小的噪声,缩放过程从$z^{[l]}$到$\tilde{z}^{[l]}$也有一些噪声,因为它是用有些噪声的均值和方差计算得出的。
292 | - 故和dropout相似,它在每个隐藏层的激活值上增加了噪音。dropout 使一个隐藏的单元以一定的概率乘以 0,以一定的概率乘以 1,所以 dropout含一些噪音,因为它乘以 0 或 1。
293 |
294 | 因此,类似于dropout,BN有轻微的正则化效果,因为给隐藏单元添加了噪音,使得后部单元不过分依赖任何一个隐藏单元。如果想得到更强大的正则化效果,可以将BN和dropout一起使用。
295 |
296 | 如果应用较大的mini-batch可以减少噪音,减少正则化效果。
297 |
298 | **参考文章**:
299 |
300 | [1]: https://zhuanlan.zhihu.com/p/34879333 "Batch Normalization原理与实战"
301 | [2]: BatchNormalizationAcceleratingDeepNetworkTrainingbyReducingInternalCovariateShift
302 |
303 |
304 |
305 | ### 7.7 测试时的 Batch Norm
306 |
307 | 我们知道BN在每一层计算的 ![[公式]](https://www.zhihu.com/equation?tex=%5Cmu) 与 ![[公式]](https://www.zhihu.com/equation?tex=%5Csigma%5E2) 都是基于当前batch中的训练数据,但是这就带来了一个问题:我们在预测阶段,有可能只需要预测一个样本或很少的样本,没有像训练样本中那么多的数据,此时 ![[公式]](https://www.zhihu.com/equation?tex=%5Cmu) 与 ![[公式]](https://www.zhihu.com/equation?tex=%5Csigma%5E2) 的计算一定是有偏估计,这个时候我们该如何进行计算呢?
308 |
309 | **论文中的方法**:
310 |
311 | 利用BN训练好模型后,我们保留了每组mini-batch训练数据在网络中每一层的 ![[公式]](https://www.zhihu.com/equation?tex=%5Cmu_%7Bbatch%7D) 与 ![[公式]](https://www.zhihu.com/equation?tex=%5Csigma%5E2_%7Bbatch%7D) 。此时我们使用整个样本的统计量来对Test数据进行归一化,具体来说使用均值与方差的无偏估计:
312 |
313 | ![[公式]](https://www.zhihu.com/equation?tex=%5Cmu_%7Btest%7D%3D%5Cmathbb%7BE%7D+%28%5Cmu_%7Bbatch%7D%29)
314 |
315 | ![[公式]](https://www.zhihu.com/equation?tex=%5Csigma%5E2_%7Btest%7D%3D%5Cfrac%7Bm%7D%7Bm-1%7D%5Cmathbb%7BE%7D%28%5Csigma%5E2_%7Bbatch%7D%29)
316 |
317 | 得到每个特征的均值与方差的无偏估计后,我们对test数据采用同样的normalization方法:
318 |
319 | ![[公式]](https://www.zhihu.com/equation?tex=BN%28X_%7Btest%7D%29%3D%5Cgamma%5Ccdot+%5Cfrac%7BX_%7Btest%7D-%5Cmu_%7Btest%7D%7D%7B%5Csqrt%7B%5Csigma%5E2_%7Btest%7D%2B%5Cepsilon%7D%7D%2B%5Cbeta)
320 |
321 | **吴恩达老师讲的方法**
322 |
323 | 对训练阶段每个batch计算的$\mu$和$\sigma^{2}$采用指数加权平均来得到测试阶段$\mu$和$\sigma^{2}$的估计。
324 |
325 | 我们选择 𝑙层,假设我们有 mini-batch,$X^{\{1\}}$,$X^{\{2\}}$,$X^{\{3\}}$......以及对应的$y$值等等,那么在训练$X^{\{1\}}$时,就得到了$\mu^{\{1\}[l]}$,训练第二个mini-batch时,就会得到$\mu^{\{2\}[l]}$值。然后在这一隐藏层的第三个 mini-batch,得到第三个$\mu$($\mu^{\{3\}[l]}$)值。使用指数加权平均来追踪这个均值向量的最新平均值,于是该指数加权平均成了你对这一隐藏层的$z$均值的估值。
326 |
327 | 同样的,可以用指数加权平均来追踪这一层每个mini-batch的$\sigma^{2}$的值。因此在用不同mini-batch训练神经网络的同时,能够得到你所查看每一层$\mu$和$\sigma^{2}$的平均数的实时数值。
328 |
329 | 最后在测试时对test数据采用同样的normalization方法(同上)。
330 |
331 | ### 7.8 BN与其他Normalization的方法比较
332 |
333 | 参考文章:https://zhuanlan.zhihu.com/p/33173246
334 |
335 | https://www.cnblogs.com/LXP-Never/p/11566064.html
336 |
337 | https://blog.csdn.net/shwan_ma/article/details/85292024
338 |
339 | https://bbs.cvmart.net/topics/1569
340 |
341 |
342 |
343 | 常用的Normalization方法主要有:Batch Normalization(BN,2015年)、Layer Normalization(LN,2016年)、Instance Normalization(IN,2017年)、Group Normalization(GN,2018年)。它们都是从激活函数的输入来考虑、做文章的,以不同的方式**对激活函数的输入进行 Norm** 的。
344 |
345 | 将输入的图像shape记为[**N**, **C**hannel, **H**eight, **W**idth],这几个方法主要的区别就是在,
346 |
347 | - **batch Norm**:在batch上,对NHW做归一化,对小batchsize效果不好;
348 | - **layer Norm**:在通道方向上,对CHW归一化,主要对RNN作用明显;
349 | - **instance Norm**:在图像像素上,对HW做归一化,用在风格化迁移;
350 | - **Group Norm**:将channel分组,然后再做归一化;
351 | - **Switchable Norm**:将BN、LN、IN结合,赋予权重,让网络自己去学习归一化层应该使用什么方法。
352 |
353 | 
354 |
355 | 如果把特征图![[公式]](https://www.zhihu.com/equation?tex=x%5Cin%5Cmathbb%7BR%7D%5E%7BN%5Ctimes+C+%5Ctimes+H+%5Ctimes+W%7D)比喻成一摞书,这摞书总共有 N 本,每本有 C 页,每页有 H 行,每行 有W 个字符。
356 |
357 | #### 7.8.1 Batch Normalization
358 |
359 | $$
360 | \begin{array}{c}
361 | \mu=\frac{1}{m} \sum_{i=1}^{m} x_{i} \\
362 | \sigma=\sqrt{\left.\frac{1}{m} \sum_{i=1}^{m}\left(x_{i}-\mu\right)^{2}\right)} \\
363 | y=\frac{(x-\mu)}{\sqrt{\sigma^{2}+\epsilon}}+\beta=B N(x)
364 | \end{array}
365 | $$
366 |
367 | tf.nn.batch_normalization(x, mean, variance, offset, scale, variance_epsilon, name=None`)`
368 |
369 | 参数
370 |
371 | - x:输入数据
372 | - mean:均值
373 | - variance:方差
374 |
375 | 返回
376 |
377 | - 标准化后的数据
378 |
379 | **BN缺点:**
380 |
381 | - 对batch size的大小比较敏感,由于每次计算均值和方差是在一个batch上,所以如果batch size太小,则计算的均值、方差不足以代表整个数据分布;
382 | - BN实际使用时需要计算并且保存某一层神经网络batch的均值和方差等统计信息,对于对一个固定深度的前向神经网络(DNN,CNN)使用BN,很方便;但对于RNN来说,sequence的长度是不一致的,换句话说RNN的深度不是固定的,不同的time-step需要保存不同的statics特征,可能存在一个特殊sequence比其他sequence长很多,这样training时,计算很麻烦。
383 |
384 | #### 7.8.2 Layer Normalization
385 |
386 | LN是针对深度网络的某一层的所有神经元的输入按以下公式进行normalize操作。计算该层的平均输入值和输入方差,然后用同一个规范化操作来转换各个维度的输入。
387 | $$
388 | \begin{array}{c}
389 | \mu^{l}=\frac{1}{H} \sum_{i=1}^{H} a_{i}^{l} \\
390 | \sigma^{l}=\sqrt{\frac{1}{H} \sum_{i=1}^{H}\left(a_{i}^{l}-\mu^{l}\right)^{2}}
391 | \end{array}
392 | $$
393 | **BN与LN的区别在于**:
394 |
395 | - LN中同层神经元输入拥有相同的均值和方差,不同的输入样本有不同的均值和方差;
396 | - BN中则针对不同神经元输入计算均值和方差,同一个batch中的输入拥有相同的均值和方差。
397 |
398 | 所以,LN不依赖于batch的大小和输入sequence的深度,因此可以用于batchsize为1和RNN中对边长的输入sequence的normalize操作。
399 |
400 | BN 的转换是针对单个神经元可训练的——不同神经元的输入经过再平移和再缩放后分布在不同的区间,而 LN 对于一整层的神经元训练得到同一个转换——所有的输入都在同一个区间范围内。如果不同输入特征不属于相似的类别(比如颜色和大小),那么 LN 的处理可能会降低模型的表达能力。LN用于RNN效果比较明显,但是在CNN上,不如BN。
401 |
402 | tf.keras.layers.LayerNormalization(axis=-1, epsilon=0.001, center=True, scale=True)
403 |
404 | 参数
405 |
406 | - axis:想要规范化的轴(通常是特征轴)
407 | - epsilon:将较小的浮点数添加到方差以避免被零除。
408 | - center:如果为True,则将的偏移`beta`量添加到标准化张量。
409 | - `scale`:如果为True,则乘以`gamma`
410 |
411 | 返回
412 |
413 | - shape与输入形状相同的值
414 |
415 | #### 7.8.3 Instace Normalization
416 |
417 | BN注重对每个batch进行归一化,保证数据分布一致,因为判别模型中结果取决于数据整体分布。
418 |
419 | 但是图像风格转换中,生成结果主要依赖于某个图像实例,所以对整个batch归一化不适合图像风格化中,因而对HW做归一化。可以加速模型收敛,并且保持每个图像实例之间的独立。
420 | $$
421 | \begin{array}{c}
422 | \mu_{t i}=\frac{1}{H W} \sum_{l=1}^{W} \sum_{m=1}^{H} x_{t i l m} \\
423 | \sigma=\sqrt{\frac{1}{H W}} \sum_{l=1}^{W} \sum_{m=1}^{H}\left(x_{t i l m}-\mu_{y i}\right)^{2} \\
424 | y_{t i j k}=\frac{x_{P t i j k}-\mu_{y i}}{\sqrt{\sigma_{t i}^{2}}-\epsilon}
425 | \end{array}
426 | $$
427 | [`tfa.layers.normalizations.InstanceNormalization`](https://www.tensorflow.org/addons/api_docs/python/tfa/layers/InstanceNormalization)
428 |
429 | 输入:仅在该层只有一个输入(即,它连接到一个传入层)时适用。
430 |
431 | 返回:输入张量或输入张量列表。
432 |
433 | #### 7.8.4 Group Normalization
434 |
435 | 主要是针对Batch Normalization对小batchsize效果差,GN将channel方向分group,然后每个group内做归一化,算(C//G)*H*W的均值,这样与batchsize无关,不受其约束。
436 | $$
437 | S_{i}=\left\{k \mid k_{N}=i_{N},\left[\frac{k_{C}}{C / G}\right]=\left[\frac{i_{C}}{C / G}\right]\right\}
438 | $$
439 | Group Normalization 在要求 Batch Size 比较小的场景下或者物体检测/视频分类等应用场景下效果是优于 BN 的。
440 |
441 | #### 7.8.5 Switchable Normalization
442 |
443 | 本篇论文作者认为,
444 |
445 | - 第一,归一化虽然提高模型泛化能力,然而归一化层的操作是人工设计的。在实际应用中,解决不同的问题原则上需要设计不同的归一化操作,并没有一个通用的归一化方法能够解决所有应用问题;
446 | - 第二,一个深度神经网络往往包含几十个归一化层,通常这些归一化层都使用同样的归一化操作,因为手工为每一个归一化层设计操作需要进行大量的实验。
447 |
448 | 因此作者提出自适配归一化方法——Switchable Normalization(SN)来解决上述问题。与强化学习不同,SN使用可微分学习,为一个深度网络中的每一个归一化层确定合适的归一化操作。
449 | $$
450 | \begin{array}{c}
451 | \hat{h}_{h c i j}=\gamma \frac{h_{h c i j}-\sum_{k \in \Omega W_{k} \mu_{k}}}{\sqrt{\sum_{k \in \Omega} w_{k}^{\prime} \sigma_{k}^{2}+\epsilon}}+\beta \\
452 | w_{k}=\frac{e^{\lambda_{k}}}{\sum_{z \in\{i n, l n, b n\} e t}}, \quad k \in\{i n, l n, b n\} \\
453 | \mu_{i n}=\frac{1}{H W} \sum_{i, j}^{H, W} h_{n c i j}, \quad \sigma^{2}=\frac{1}{H W} \sum_{i, j}^{H, W}\left(h_{n c i j}-\mu_{i n}\right)^{2} \\
454 | \mu_{l n}=\frac{1}{C} \sum_{c=1}^{C} \mu_{i n}, \quad \sigma_{l n}^{2}=\frac{1}{C} \sum_{c=1}^{C}\left(\sigma_{i n}^{2}+\mu_{i n}^{2}\right)-\mu_{l n}^{2} \\
455 | \mu_{b n}=\frac{1}{N} \sum_{n=1}^{N} \mu_{i n}, \quad \sigma^{2}=\frac{1}{N} \sum_{n=1}^{N}\left(\sigma_{i n}^{2}+\mu_{i n}^{2}\right)-\mu_{b n}^{2}
456 | \end{array}
457 | $$
458 |
459 |
460 | #### 7.8.6 weight Normalization
461 |
462 | BN 和 LN 均将规范化应用于输入的特征数据 $X$ ,而 WN 则另辟蹊径,将规范化应用于线性变换函数的权重 $W$ ,这就是 WN 名称的来源。
463 |
464 | 对于人工神经网络中的一个神经元来说,其输出$y$表示为:
465 | $$
466 | y=\phi(\boldsymbol{w} \boldsymbol{x}+b)
467 | $$
468 | 其中$w$是$k$维权重向量,$b$是标量偏差,$x$是$k$维输入特征,$\phi(.)$是激活函数。
469 |
470 | 对权重$w$用参数向量$v$和标量$g$进行表示,则新参数表示为:
471 | $$
472 | \boldsymbol{w}=\frac{g}{\|\boldsymbol{v}\|} \boldsymbol{v}
473 | $$
474 | 其中$v$是$k$维向量,$g$是标量,$\|\boldsymbol{v}\|$为$v$的欧式范数。
475 | 通过上述参数表示,我们可以发现,$\|\boldsymbol{w}\|=g$与参数$v$独立,而权重$w$的方向也变更为$\frac{v}{\|\boldsymbol{v}\|}$。因此重参数将权重向量$w$用了两个独立的参数表示其幅度和方向。实验证明,在利用SGD优化算法时,重参数加速了网络的收敛速度。
476 |
477 | **Gradients:**
478 |
479 | 则对于$v$,$g$
480 | $$
481 | \begin{array}{c}
482 | \nabla_{g} L=\frac{\nabla_{w} L \cdot \boldsymbol{v}}{\|v\|} \\
483 | \nabla_{v} L=\frac{\boldsymbol{g} \cdot \nabla_{w} L}{\|v\|}-\frac{\boldsymbol{g} \cdot \nabla_{g} L}{\|v\|} \cdot \boldsymbol{v}
484 | \end{array}
485 | $$
486 | 其中$\nabla_{w} L$为目标函数对未进行WN的权重为$w$的偏导。
487 |
488 | 相比与BN,WN带有如下优点:WN的计算量非常低,并且其不会因为mini-batch的随机性而引入噪声统计。在RNN,LSTM,或者Reinforcement Learning上,WN能够表现出比BN更好的性能。
489 |
490 |
491 |
492 | ### 7.9 Softmax 回归
493 |
494 | Softmax回归:logistic回归的一般形式,将logistic回归推广到 C 类而不仅仅是两类,能在试图识别某一分类时做出预测且任何两个分类之间的决策边界都是线性的。
495 |
496 | 符号定义:
497 |
498 | $C$ :类别总数(类别编号分别为 $0, 2, ..., C-1$),故输出层L的神经元个数为 $C$,每个神经元分别输出该输入属于该类别的概率,$C$ 个神经元输出的概率总和应等于 1 。当 $C=2$ 时,Softmax回归即logistic回归。
499 |
500 | #### 7.9.1 Softmax层
501 |
502 | 在分类问题中,神经网络的**输出层**通常选用Softmax激活函数,使得最后输出的是归一化后的实数向量,每一元素代表该样本属于某一类的概率,则该层称为Softmax层。
503 |
504 | #### 7.9.2 Softmax激活函数
505 |
506 | - 定义:Softmax激活函数只用于多于一个神经元的输出层,它保证所有的输出神经元之和为1,所以一般输出的是小于1的概率值,可以很直观地比较各输出值。
507 |
508 | - 作用:为了得到属于每个类别的概率,先通过$e^{z^{[L]}}$将$z^{[L]}$的各元素值映射到 $(0, + \infty)$,然后再归一化到(0, 1)。
509 |
510 | - 具体实现:
511 |
512 | 在神经网络的最后一层,依然先计算线性部分:
513 | $$
514 | z^{[L]}=W^{[L]}a^{[L-1]}+b^{[L]}
515 | $$
516 |
517 |
518 | 然后应用**Softmax激活函数**:$a^{[L]}=g^{[L]}(z^{[L]})$,该函数的具体计算如下:
519 |
520 | (1)计算临时变量 $t=e^{z^{[L]}}$,对 $z^{[L]}$ 中的所有元素求幂,故 $t$ 的维度与 $z^{[L]}$ 相同。
521 |
522 | (2)对 $t$ **归一化**,得到输出 $a^{[L]}$ 即 $\hat{y}$ :$a^{[L]}=\frac{e^{z^{[L]}}}{\sum_{j=1}^{n^{[L]}} t_{i}}$,$a^{[L]}$的维度与 $t$ 相同,即也与 $z^{[L]}$ 相同,都为$(n^{[L]},1)$。其中,对$a^{[L]}$的每一个元素,$a_i^{[L]}=\frac{t_i}{\sum_{j=1}^{n^{[L]}} t_{i}}$。
523 |
524 | **tips:**之前所学的激活函数如sigmod和ReLU激活函数,都是输入一个实数,输出一个实数,而Softmax激活函数由于需要将所有可能的输出归一化,需要**输入一个向量,输出一个向量**。
525 |
526 | #### 7.9.3 softmax配合log似然代价函数训练ANN
527 |
528 | 在人工神经网络(ANN)中,Softmax通常被用作输出层的激活函数。这不仅是因为它的效果好,而且因为它使得ANN的输出值更易于理解。同时,softmax配合log似然代价函数,其训练效果也要比采用二次代价函数的方式好。
529 |
530 | log似然代价函数的公式为:
531 | $$
532 | C=-\sum_{k} y_{k} \log a_{k}
533 | $$
534 |
535 |
536 | 其中,$a_{k}$表示第k个神经元的输出值,$y_{k}$表示第k个神经元对应的真实值,取值为0或1。
537 |
538 | 该代价函数的简单理解为:在ANN中输入一个样本,那么只有一个神经元对应了该样本的正确类别;若这个神经元输出的概率值越高,则按照以上的代价函数公式,其产生的代价就越小;反之,则产生的代价就越高。
539 |
540 | 为了检验softmax和这个代价函数也可以解决训练ANN时训练速度变慢的问题,接下来的重点就是推导ANN的权重W和偏置b的梯度公式。以偏置b为例:
541 |
542 | 
543 |
544 | 同理可得:
545 | $$
546 | \frac{\partial C}{\partial w_{j k}}=a_{k}^{L-1}\left(a_{j}^{L}-y_{j}\right)
547 | $$
548 | 从上述梯度公式可知,softmax函数配合log似然代价函数可以很好地训练ANN,不存在学习速度变慢的问题。
549 |
550 | 参考文献:https://blog.csdn.net/orangefly0214/article/details/80406584
551 |
552 | ### 7.10 训练一个 Softmax 分类器
553 |
554 | #### 7.10.1 定义损失函数
555 |
556 | - 单样本:$$L(\hat{y}, y)=-\sum_{j=1}^C y_{j} \log \hat{y}_{j}$$
557 | - 整个训练集:$J\left(W^{[L]},b^{[L]} \ldots\right)=\frac{1}{m} \sum_{i=1}^{m} L\left(\hat{y}^{(i)}, y^{(i)}\right)$
558 | - 作用:找到样本所属的真实类别,并试图使该类别相应的概率尽可能地高。
559 |
560 | #### 7.10.2 正向传播
561 |
562 | 依次计算出:$z^{[L]} → a^{[L]} = \hat y → L\left(\hat{y}^{(i)}, y^{(i)}\right)$
563 |
564 | #### 7.10.3.反向传播(实现梯度下降法)
565 |
566 | (1)初始化反向传播:$dz^{[L]}=\frac{\partial J}{\partial z^{[L]}}=\hat y-y$
567 |
568 | (2)用深度学习编程框架自动实现反向传播的其余导数计算。
569 |
570 | ### 7.11 深度学习框架
571 |
572 | 深度学习框架可以使神经网络的实现变得更简单。每个框架都是针对某一个用户或开发者群体的
573 |
574 | #### 7.11.1 现有deep learning框架
575 |
576 | - **Caffe/Caffe2**:第一个主流的工业级深度学习工具。开始于2013年底,由UC Berkely的Yangqing Jia老师编写和维护的具有出色的卷积神经网络实现。在计算机视觉领域依然是最流行的工具包,有很多扩展,但是由于一些遗留的架构问题,不够灵活且对递归网络和语言建模的支持很差。
577 | - **CNTK**:是微软研究院开源的深度学习框架。最早由 start the deep learning craze 的演讲人创建,目前已经发展成一个通用的、跨平台的深度学习系统,在语音识别领域的使用尤其广泛。
578 | - **DL4J**:是一个基于 Java 和 Scala 的开源的分布式深度学习库,由 Skymind 于 2014 年 6 月发布,其核心目标是创建一个即插即用的解决方案原型。
579 | - **Keras**:是一个崇尚极简、高度模块化的神经网络库,使用 Python 实现,并可以同时运行在 TensorFlow 和 Theano 上。它旨在让用户进行最快速的原型实验,让想法变为结果的这个过程最短。Theano 和 TensorFlow 的计算图支持更通用的计算,而 Keras 则专精于深度学习。提供了目前为止最方便的 API,用户只需要将高级的模块拼在一起,就可以设计神经网络,它大大降低了编程开销和阅读别人代码时的理解开销。
580 | - **Lasagne**:是一个基于 Theano 的轻量级的神经网络库。Lasagne是 Theano 的上层封装,但又不像 Keras 那样进行了重度的封装,Keras 隐藏了 Theano 中所有的方法和对象,而 Lasagne 则是借用了 Theano 中很多的类,算是介于基础的 Theano 和高度抽象的 Keras 之间的一个轻度封装,简化了操作同时支持比较底层的操作。Lasagne 设计的六个原则是简洁、透明、模块化、实用、聚焦和专注。
581 | - **MXNet**:是李沐和陈天奇等各路英雄豪杰打造的开源深度学习框架,是分布式机器学习通用工具包DMLC的重要组成部分。注重灵活性和效率,文档也非常的详细,同时强调提高内存使用的效率,甚至能在智能手机上运行诸如图像识别等任务。
582 | - **PaddlePaddle**:是百度自主研发的集深度学习核心框架、工具组件和服务平台为一体的技术领先、功能完备的开源深度学习平台,有全面的官方支持的工业级应用模型,涵盖自然语言处理、计算机视觉、推荐引擎等多个领域,并开放多个预训练中文模型。目前已经被中国企业广泛使用,并拥有活跃的开发者社区生态。
583 | - **TensorFlow**:Google开源的其第二代深度学习技术——被使用在Google搜索、图像识别以及邮箱的深度学习框架。是一个理想的RNN(递归神经网络)API和实现,使用了向量运算的符号图方法,使得新网络的指定变得相当容易,支持快速开发。缺点是速度慢,内存占用较大(比如相对于Torch)。
584 | - **Theano**:2008年诞生于蒙特利尔理工学院,主要开发语言是Python。派生出了大量深度学习Python软件包,最著名的包括Blocks和Keras。Theano的最大特点是非常的灵活,适合做学术研究的实验,且对递归网络和语言建模有较好的支持,缺点是速度较慢。
585 | - **Torch**:Facebook力推的深度学习框架,主要开发语言是C和Lua。有较好的灵活性和速度。实现并且优化了基本的计算单元,使用者可以很简单地在此基础上实现自己的算法,不用浪费精力在计算优化上面。核心的计算单元使用C或者cuda做了很好的优化。在此基础之上,使用lua构建了常见的模型。缺点是接口为lua语言,需要一点时间来学习。
586 |
587 | 参考文献:
588 |
589 | - https://blog.csdn.net/dlaicxf/article/details/52846651
590 | - https://www.leiphone.com/news/201702/T5e31Y2ZpeG1ZtaN.html
591 |
592 | #### 7.11.2 几种主流dl框架的比较
593 |
594 | | **库名称** | **开发语言** | **速度** | **灵活性** | **文档** | **适合模型** | **平台** | **上手难易** |
595 | | :--------: | :-------------: | :------: | :--------: | -------: | :----------: | :--------: | :----------: |
596 | | Caffe | c++/cuda | 快 | 一般 | 全面 | CNN | 所有系统 | 中等 |
597 | | TensorFlow | c++/cuda/Python | 中等 | 好 | 中等 | CNN/RNN | Linux, OSX | 难 |
598 | | Keras | Python | 快 | 好 | 中等 | CNN/RNN | Linux, OSX | 易 |
599 | | MXNet | c++/cuda | 快 | 好 | 全面 | CNN | 所有系统 | 中等 |
600 | | Torch | c++/lua/cuda | 快 | 好 | 全面 | CNN/RNN | Linux, OSX | 中等 |
601 | | Theano | Python/c++/cuda | 中等 | 好 | 中等 | CNN/RNN | Linux, OSX | 易 |
602 |
603 | #### 7.11.3 选择框架的标准
604 |
605 | - **便于编程**:包括神经网络的开发和迭代、为产品进行配置等。
606 | - **运行速度**:特别是训练大数据集时,一些框架可以更高效地运行和训练神经网络。
607 | - **框架是否真的开放**:一个真的开放的框架,不仅需要开源,还需要良好的管理。
608 |
609 | PyTorch常用代码段合集 https://mp.weixin.qq.com/s/JnIO_HjTrC0DCWtKrkYC8A
610 |
611 |
612 |
613 |
614 |
615 |
616 |
617 |
--------------------------------------------------------------------------------
/8 机器学习(ML)策略(1).md:
--------------------------------------------------------------------------------
1 | # 1.1 为什么是ML策略
2 |
3 | 如果你训练了一段时间自己的神经网络,准确率到达了一定水平(比如90%)但却还不能满足你的要求,那这个时候必然需要对网络做出一些调整。你可能想到了几个解决思路,比如收集更多的数据、用不同的优化算法、训练得更久一些、加入正则化甚至修改网络架构等等。
4 |
5 | 但是这些办法并不是总是有效的,可能收集了6个月的数据却发现对网络的性能没有任何帮助。就是说如果你作出了错误的选择,那很可能浪费大量的时间和精力而得不到任何有效进展。
6 |
7 | 于是接下来希望教学一些策略:ML策略,以帮助我们向着有希望的方向前进。
8 |
9 | # 1.2 正交化
10 |
11 | 这里的正交化可以简单地理解为,每个自变量的改变只会引起一个因变量发生改变。举个反例,假设有$y_1=x_1+0.9x_2$,$y_2=0.1x_2$,则自变量$x_2$的改变会同时引起因变量$y_1,y_2$的改变,同时若想要通过$x_2$调整$y_1$时会不可避免的也调整了$y_2$。
12 |
13 | 在ML策略中,正交化是一种设计方法,以保证你在修改超参的时候不会引起两个以上的参数的变化。
14 |
15 | ## 四个参数
16 |
17 | 假设你需要正交化而确保不同时改变的四个参数是:
18 |
19 | * 收敛后的训练集的代价(cost)
20 | * 交叉验证集的代价
21 | * 测试集的代价
22 | * 真实应用的效果
23 |
24 | 当然,以上的参数是“按顺序”得到的。即只有在当前参数算优的情况下你才会做下一步而得到下一个参数的值。
25 |
26 | 对于第一点,如果训练集上的效果不好甚至无法收敛,可以考虑更大的神经网络或其他优化算法比如$Adam$。
27 |
28 | 对于第二点,可能原因是过拟合了,那可以尝试加入正则化或采用更大的训练集。
29 |
30 | 对于第三点,可以考虑采用更大的交叉验证集。
31 |
32 | 对于第四点,则考虑改变交叉验证集的图源或改变损失函数。
33 |
34 | 举个不正交的例子是 early stopping。因为 early stopping 会基于开发集的效果而提早停止训练,所以带来的影响是两方面的:训练集的代价还没收敛至最优的同时降低了在开发集上的代价。
35 |
36 | # 1.3 单一数字评估指标
37 |
38 | 对于一个网络的性能评估,我们有时候会采用多个指标以便更了解自己搭建的网络的效果。但是当你需要从多个网络中选出最好的一个时,多评估指标可能会导致你无法轻易选出优胜者——有的网络某一些指标最好,另一些指标则比不上其他网络。这个时候,单一数字评估指标就能很方便地帮你评价出最优的网络。
39 |
40 | ## 1.3.1常用指标
41 |
42 | 参考文章[在这](https://zhuanlan.zhihu.com/p/73569538)。
43 |
44 | ## 1.3.2混淆矩阵:
45 |
46 | 为了方便表达各指标如何计算,先介绍混淆矩阵:
47 |
48 | 
49 |
50 | 阴阳可理解为真假、1/0。a是预测为真真实也为真的样本数,其余类比。
51 |
52 | ## 1.3.3指标
53 |
54 | 1. Precision查准率/精度:评价网络做出的预测的准确率。对于二分类来说(比如猫/非猫分类器), $$P= \frac{预测为1且正确的样本数}{所有预测为1的样本数} = \frac{a}{a+b}$$。
55 |
56 | 2. 对于进行one-hot热值编码的多分类来说同样适用。
57 |
58 | 3. Recall查全率/True Positive真阳率/Sensitivity敏感性:评价网络对于目标类的识别率。对于二分类来说,
59 |
60 | $$R= \frac {所有预测为1且正确的样本数}{所有真实值为1的样本数} \frac{a}{a+c}$$。
61 |
62 | 对于进行了one-hot热值编码的多分类来说同样适用。
63 |
64 | 4. Accuracy准确率:评价网络所有类预测的准确率。对于二分类来说,$Acc= \frac{所有预测正确的样本数}{总的样本数}= \frac{a+d}{a+b+c+d}$。
65 |
66 | 5. 对于进行了one-hot热值编码的多分类同样适用。
67 |
68 | 6. False Positive误检率/假阳率:评价网络对阴性预测的错误率,为
69 |
70 | $$\frac{预测为1且错误的样本数}{真实值为0的样本数}=\frac{b}{b+d}$$。
71 |
72 | 7. F1分数:$$\frac{2}{\frac{1}{P}+\frac{1}{R}}$$
73 |
74 | P 和 R 分别代指 Precision 和 Recall。是 Precision 和 Recall 的调和平均数。
75 |
76 | # 1.4满足和优化指标
77 |
78 | 如果你想考虑的多个指标取值范围是相同的,那取平均值就可以简单地将多个指标“整合”成单一评估指标。但是如果其中一个是准确率P(%),另一个是单张图的预测时间T(ms),那取平均值的做法是几乎不合理的。线性组合$$aP+bT$$这样的做法或许可行,但是参数a、b的值却又可能难以设计。
79 |
80 | 所以,可以从另一个角度考虑:其中一个(甚至多个)指标只用于淘汰、筛选模型;另一个指标作为评估指标,是判断哪一个更优的指标。这分别对应满足指标和优化指标。
81 |
82 | ## 1.4.1满足指标
83 |
84 | 该指标是你关心的指标之一,但是又并不那么重要:该指标只需要到达一定范围即可,不是你**最想优化**的指标。比方说你很关心模型的准确率,同时也希望运行速度足够快,那将 T 视为满足指标是合适的。
85 |
86 | 满足指标的用意在于如果你有多个指标想要兼顾,但是大部分指标又并不是那么重要,那作为用于筛选模型的指标是很不错的选择。比如唤醒 Siri 你最关注的是 Recall,这能确保有人真的想唤醒 Siri 时能及时做出反应;但你也关注在没人想唤醒 Siri 时,Siri 被错误唤醒的概率。那将误检率/假阳率作为满足指标是可行的,比如设置为每24小时只有一次错误唤醒。
87 |
88 | ## 1.4.2优化指标
89 |
90 | 优化指标应该是你最关心的指标,是你最想优化的指标,比如唤醒 Siri 时的Recall。
91 |
92 | 由于单一数字评估指标的原因,优化指标应该只有一个,而其余你关心的指标都应该设为满足指标,或者和优化指标合理地整合为一个指标。
93 |
94 | # 1.5测试集、交叉验证集、测试集的划分
95 |
96 | ## 1.5.1 训练集、交叉验证集、测试集的作用
97 |
98 | - **训练集**:用以训练模型;
99 |
100 | - **交叉验证集** (也叫dev 集、开发集):衡量训练效果的同时进行超参数调优;
101 |
102 | - **测试集**:评测模型训练效果(测定泛化误差)。
103 |
104 | 以课后作业、期末考试、高考三者间的关系类比训练、开发、测试集的作用:
105 |
106 | - 课后作业(训练集):让你学会知识;
107 | - 期末考试(交叉验证集):让你检验自己是否真的学会了知识,发现了问题后,你会调整学习方法(调整超参数);
108 | - 高考(测试集):最终的测试,测试你在**没见过的**题上究竟能做到什么程度(泛化能力),且不再给你调整的机会。
109 |
110 | ## 1.5.2 如何设立交叉验证集和测试集
111 |
112 | 建议在设立交叉验证集和测试集时,要选择能够反映未来你希望得到的并认为做好很重要的数据作为交叉验证集和测试集。
113 |
114 | > Choose a dev set and test set to reflect data you expect to get in the future and consider important to do well on.
115 |
116 | 交叉验证集和测试集最好来自**同一分布**:不管未来会得到什么样的数据,一旦你的算法效果不错,要尝试收集类似的数据且不管那些数据是什么,都要**随机分配**到开发集和测试集中,这样才能瞄准想要的目标,让团队高速迭代来逼近同一个目标。
117 |
118 | ## 1.5.3 如此设立交叉验证集和测试集的原因
119 |
120 | 设立交叉验证集以及一个单实数评估指标就像是定下目标,告诉你的团队那就是你要瞄准的靶心,一旦建立了这样的开发集和指标,团队就可以快速迭代,可以很快地使用交叉验证集和指标去评估不同分类器,然后尝试选出最好的那个,针对开发集上的指标优化。
121 |
122 | 如果交叉验证集和测试集来自不同的分布,就像设定了一个目标,结果在团队逼近这个目标工作几个月后,想要把成果应用到另一个目标。为了避免这种情况,建议将所有数据随机洗牌放入开发集和测试集,所以交叉集和测试集都有来自所有不同分类的数据并且开发集和测试集都来自同一分布,这个分布就是所有的数据混在一起。
123 |
124 | # 1.6 交叉验证集和测试集的大小
125 |
126 | ## 1.6.1 交叉验证集和测试集大小设置的原则
127 |
128 | 1、经验法则:把取得的所有数据划分为 **70%训练集+30%测试集** 或 **60%训练集+20%交叉验证集+20%测试集**。
129 |
130 | 这种经验法则使用于机器学习的早期,即数据集规模较小的情况下。
131 |
132 | 2、在现代机器学习中,数据集规模很大,可分为**98%训练集+1%交叉验证集+1%测试集**。
133 |
134 | 训练集的大小:深度学习算法对数据的胃口很大,故要把占更高比例的数据划分到训练集中;
135 |
136 | 测试集的大小:测试集的目的是完成系统开发后用测试集评估系统性能,故要令测试集足够大,能够以高置信度评估系统整体性能。所以除非需要对最终系统有一个很精确的指标,一般来说,测试集不需要上百万个例子,有10000或100000个大概就足够了,当数据量很大时,测试集就会远远小于数据集的30%或20%。
137 |
138 | ## 1.6.2 什么情况下可以没有测试集
139 |
140 | 对于不需要对系统性能有置信度很高的评估的应用,可以不用划分测试集,只需要训练集和交叉验证集,只要有数据去训练、有数据去调试就够了,但是并不建议在系统搭建时省略测试集,有个单独的测试集会更好,因为可以用这组不带偏差的数据来测量系统的性能,但如果交叉验证集非常大,就不会对交叉验证集过拟合得太厉害,在这种情况下只有训练集和交叉验证集也不是完全不合理。
141 |
142 | 在实际实践中,有时只把数据集划分为训练集和测试集,实际上这是在测试集上迭代,所以这里的测试集其实是交叉验证集,即只把数据分为训练集和交叉验证集,没有测试集。
143 |
144 | # 1.7 什么时候该改变交叉验证/测试集和指标
145 |
146 | ## 1.7.1 如何定义一个指标去评估分类器
147 |
148 | 评估指标的意义在于,准确告诉你已知的两个分类器哪一个更适合你的应用。
149 |
150 | 当已设定的评估指标无法正确衡量算法之间的优劣排序时,就应该改变评估指标或者改变交叉验证集或测试集。
151 |
152 | 例如,若对旧的误差指标 $Error = \frac{1}{m_{dev}} \sum_{i=1}^{m_{dev}}I[y_{pred}^{(i)}≠y^{(i)}]$ 不满意,可以尝试定义一个新的能够更加符合你的偏好的指标,从而定义出更适合的算法,如在 $I$ 项前加一个权重项 $\omega^{(i)}$,即
153 |
154 | $Error = \frac{1}{m_{dev}} \sum_{i=1}^{m_{dev}} \omega^{(i)} I[y_{pred}^{(i)}≠y^{(i)}]$
155 |
156 | 其中,
157 |
158 | $\omega^{(i)}=\left\{\begin{array}{ll}1 & \text { if } x^{(i)}... \\ 10 & \text { if } x^{(i)}...\end{array}\right.$,
159 |
160 | 当 $x^{(i)}$ 是预期分类中的数据时,赋予较小的权重1,当 $x^{(i)}$ 不是预期分类中的数据时,赋予较大的权重10,误差项迅速变大,即把非预期分类数据分类成某一类的惩罚权重加大10倍。
161 |
162 | ## 1.7.2 机器学习的两个独立步骤(正交化)
163 |
164 | 1. 设定目标:弄清楚如何定义一个指标来衡量你想做的事情的表现(**定义指标**);
165 | 2. 瞄准/射击目标:分开考虑如何改善系统在这个指标上的表现(**调整指标**以优化系统)。
166 |
167 | ## 1.7.3 需改变评价标准的情况
168 |
169 | 如果系统在当前指标、当前交叉验证集或者交叉验证集和测试集分布中表现很好,但在实际应用程序即你真正关注的地方表现不好(当前的指标和当前用来评估的数据和你真正关心必须做好的事情关系不大),就需要修改指标或交叉验证/测试集,让它们能够更好地反映算法需要处理好的数据。
170 |
171 | 举例:假设有两个猫分类器A和B,用开发集评估分别得到3%和5%的误差,做评估时用的是高质量图片的交叉验证集和测试集但在实际应用时上传的图片取景不专业,没有把猫完整拍下来或猫的表情很古怪,或者图像很模糊,在实际测试算法时可能会发现算法B比算法A更好,此时就应该修改指标或交叉验证/测试集。
172 |
173 | # 1.8为什么是人的表现
174 |
175 | 机器学习模型的准确性有两个层级,分别为
176 |
177 | 1.human-level performance(人的表现)
178 |
179 | 2.Bayes optimal error(贝叶斯最优误差)
180 |
181 | 机器学习模型表现常与人的学习表现相比较
182 |
183 | 如图,随着训练时间的不断增长,模型的准确性会不断接近“人的表现”并最终超过。当超过“人的表现”后,准确性的上升会比较缓慢,并不断靠近理想的最优情况,即贝叶斯最优误差。而实际上,“人的表现”,在许多如语音识别、图像识别的部分是非常具有优势的,让机器学习模型的准确性不断接近“人的表现”非常有必要。
184 |
185 | 1.Get labeled data from humans.
186 |
187 | 2.Gain insight from manual error analysis: Why did a person get this right?
188 |
189 | 3.Better analysis of bias/variance.
190 |
191 | 以上方法可以让模型不断接近人的表现。
192 |
193 | # 1.9可避免偏差
194 |
195 | 在实际应用中,要看human-level error,training error和dev error的相对值。例如猫类识别的例子中,
196 |
197 | 
198 |
199 |
200 |
201 | 对于物体识别这类CV问题,human-level error是很低的,很接近理想情况下的贝叶斯最优误差。因此,上面例子中的1%和7.5%都可以近似看成是两种情况下对应的bayes optimal error。实际应用中,我们一般会用human-level error代表bayes optimal error。
202 |
203 |
204 |
205 | 通常,我们把training error与human-level error之间的差值称作avoidable bias(可避免偏差);把dev error与training error之间的差值称为方差(variance)。根据bias和variance值的相对大小,可以知道算法模型是否发生了欠拟合或者过拟合。
206 |
207 | 若相比于方差(variance),bias较大,则我们对模型的调整主要在于减小偏差
208 |
209 | 若相比于方差(variance),bias较小,则可采用正则化、采集更多数据等方法减小方差
210 |
211 | # 1.10理解人的表现
212 |
213 | human-level performance有时能够代表bayes optimal error。但是,human-level performance如何定义呢?举个医学图像识别的例子,不同人群的error有所不同:
214 |
215 | 
216 |
217 | 由于bayes optimal error是最优的理想情况,一般来说,我们将表现最好的那一组,即Team of experienced doctors作为human-level performance,以此来代替bayes optimal error。
218 |
219 |
220 |
221 | 但在实际应用时,human-level performance的选择也会因人而异,不同取值的human-level performance会在一定程度上影响bias和variance的相对大小。如下图
222 |
223 |
224 |
225 | 
226 |
227 | 在方案C中,由于Training error和Development error数值差只为0.1,即variance只有0.1,此时不同取值的human-level performance会影响到bias和variance的相对大小,影响到了后续对模型的调整与改善。
228 |
229 | 而这种情况一般只在模型表现很好,接近bayes optimal error 时才会出现,此时,由于human-level performance较模糊难以定义,而影响到了模型的优化。
230 |
231 | # 1.11超过人的表现
232 |
233 | 
234 |
235 | 对于自然感知类问题,例如视觉、听觉等,机器学习的表现还不及人类。但是在很多其它方面,如
236 |
237 |
238 |
239 | - Online advertising(在线广告)
240 | - Product recommendations(产品推荐)
241 | - Logistics(predicting transit time)(预测交通时间)
242 | - Loan approvals(贷款批准)
243 |
244 | 这些方面,机器的表现优于人类。
245 |
246 | 机器学习模型超过human-level performance是比较困难的。但是如果有足够多的样本,训练更加复杂的神经网络,模型预测准确性会不断得到提高,最终接近并超过human-level performance。然而当机器模型的表现超过human-level performance时,难以直觉来继续提高算法模型性能。
247 |
248 | # 1.12改善模型表现
249 |
250 | 提高机器学习模型性能主要要解决两个问题:avoidable bias和variance。
251 |
252 | 解决avoidable bias的常用方法包括:
253 |
254 | - Train bigger model(训练更大的模型)
255 |
256 | - Train longer/better optimization algorithms: momentum, RMSprop, Adam
257 |
258 | (使用更好的算法:momentum、RMSprop、Adam)
259 |
260 | - NN architecture/hyperparameters search(选用不同的神经网络结构)
261 |
262 | 解决variance的常用方法包括:
263 |
264 | - More data(使用更多数据)
265 | - Regularization: L2, dropout, data augmentation(使用正则化方法)
266 | - NN architecture/hyperparameters search(选用不同的神经网络结构)
267 |
268 |
--------------------------------------------------------------------------------
/9 机器学习(ML)策略(2).md:
--------------------------------------------------------------------------------
1 | ## 9 机器学习(ML)策略(2)
2 |
3 | ### 9.1误差分析
4 |
5 | #### 9.1.1 定义
6 |
7 | 你希望让学习算法能够胜任人类能做的任务,但你的学习算法还没有达到人类的表现,那么人工检查一下你的算法犯的错误也许可以让你了解接下来应该做什么。**这个过程称为错误分误差**。
8 |
9 | 通过对一组错误样本进行逐一检查后,分析错误样本的类型的比例,来决定朝着哪个方向来进行优化,或者给你构思新优化方向的灵感。
10 |
11 |
12 |
13 | #### 9.1.2 举例
14 |
15 | 假设你正在调试猫分类器,注意到一些算法分类出错的例子中,算法将一些狗分类为猫,为了解决的这个问题,我们不需要,去设计一些只处理狗的算法功能之类的,为了让你的猫分类器在狗图上做的更好,让算法不再将狗分类成猫,因为这花费的时间太长了。而是需要进行误差分析,以便于决定哪一个方向值得努力。
16 |
17 | 首先,比如收集100个错误标记的开发集样本,然后手动检查,一次只看一个,看看你的开发集里有多少错误标记的样本是狗。假设100个错误标记样本中只有5%是狗这意味着100个样本,在典型的100个出错样本中,即使你完全解决了狗的问题,你也只能修正这100个错误中的5个,也就是最多只能将错误率从10%下降到9.5%,效果并不明显。但假设100个错误标记的开发集样本,你发现实际有50张图都是狗,也就是有50%都是狗的照片,现在花时间去解决狗的问题可能效果就很好,错误率可能就从10%下降到5%。
18 |
19 |
20 |
21 | #### 9.1.3 利用表格进行误差分析
22 |
23 | 当然在进行误差分析时,也可以对多个情况或者想法进行评估(比如对狗的照片错认为猫和对狮子的照片错认为猫)。有效且清晰的做法是设计一个表格来对各种错误样本进行填表式的分类,最后统计错误类型的百分比,再针对各种错误类型百分比的大小,进而决定优化的方向,同时最好在每个样本的后面增加备注,以方便进行分析。
24 |
25 | 
26 |
27 | 当然,在分类的过程中,如果发现了新的错误类型,也可以直接创建一个新的错误类型
28 |
29 |
30 |
31 |
32 |
33 | ### 9.2 清除标注错误的数据
34 |
35 | 错误的数据:结果的标签是错的。比如猫的图片被标注为不是猫。
36 |
37 | #### 9.2.1 处理标签错误的数据
38 |
39 | 1.对于总数据集总足够大,实际错误率不高的情况下:有时候放着不管也可以,并不会对训练出来的结果有太大的影响
40 |
41 | 2.对于系统性的错误:需要进行修改
42 |
43 | (实际错误率高,比如一直把白色的狗标记成猫,分类器学习之后,会把所有白色的狗都分类为猫)
44 |
45 |
46 |
47 | 总的来说,在进行误差分析后如果这些标记错误严重影响了你在开发集上评估算法的能力,那么就应该去花时间修正错误的标签。但是,如果它们没有严重影响到你用开发集评估成本偏差的能力,那么可能就不应该花宝贵的时间去处理。
48 |
49 |
50 |
51 | #### 9.2.2 分析错误数据的指标
52 |
53 | 关注整体的开发集错误率、错误标记引起的错误的数量或者百分比,最后根据标记错误引发的错误占总体总体错误率的比例来决定。(简单点说就是标记错误占所有错误的百分比的大小,该百分比越大,说明越值得修改错误标签)
54 |
55 | 比如,系统达到了90%整体准确度,所以有10%错误率,那么你应该看看错误标记引起的错误的数量或者百分比。所以在这种情况下,6%的错误来自标记出错,所以10%的6%就是0.6%。也许你应该看看其他原因导致的错误,如果你的开发集上有10%错误,其中0.6%是因为标记出错,剩下的占9.4%,是其他原因导致的。这个时候更应该考虑对9.4%进行优化或者修正。
56 |
57 | 假设你把错误率降到了2%,但总体错误中的0.6%还是标记出错导致的,此时错误标签导致的错误占总体错误的30%,那么这种情况就值得进行错误标签的修正。
58 |
59 |
60 |
61 | #### 9.2.3 修正标签的原则
62 |
63 | 1.修正标签时,都要同时作用到验证集和测试集上,也就是必须同时检查验证集和测试集,因为验证和测试集必须来自相同的分布。
64 |
65 | 2.要考虑同时检验算法判断正确和判断错误的样本,因为如果你只修正算法出错的样本,你对算法的偏差估计可能会变大,这会让你的算法有一点不公平的优势。
66 |
67 | 3.修正训练集中的标签其实相对没那么重要。
68 |
69 |
70 |
71 | 第二点不常遵循,因为一般判断正确的样本所占的比重要大得多。
72 |
73 |
74 |
75 | ### 9.3 快速搭建你的第一个系统
76 |
77 | 一般来说,对于几乎所有的机器学习程序可能会有50个不同的方向可以前进,并且每个方向都是相对合理的可以改善你的系统。所以快速设立开发集和测试集还有指标,能够确定系统迭代的方向,并且及时利用训练集对机器学习系统进行训练,再根据结果进行分析来确定下一步优先做什么。
78 |
79 |
80 |
81 | 下面以建立一个语音识别系统为例子介绍:
82 |
83 | 你可以选择很多不同的技术,让你听写下来的文本可读性更强,所以你可以做很多事情来改进语音识别系统。但对于多种方法你会感到非常迷茫,但当你建立第一个系统后,就能够进行误差分析让你了解到大部分的错误的来源是什么,比如说话人远离麦克风,那么你就有很好的理由去集中精力研究这些技术,也就是确定了你努力的方向
84 |
85 |
86 |
87 |
88 |
89 | ### 9.4 在不同的划分下进行训练并测试
90 |
91 | #### 9.4.1 划分的定义
92 |
93 | 划分即在选择数据进行训练时,将不是来自同一分布的数据进行分开,并分别作为数据集的训练集,以及数据集中的验证集和测试集(验证集和测试集得保证来自同分布)。
94 |
95 | 注:在视频中,字幕将dev set翻译为开发集,而以往的笔记中使用的命名为验证集,这里我使用验证集
96 |
97 | #### 9.4.2 为什么需要进行划分
98 |
99 | 进行划分的目的在于设定模型的优化方向,也就是“靶心”,通过将需要应用时的数据作为测试集和验证集来进行训练,保证在该模型投入应用时能够有较高的识别率。
100 |
101 | eg.在识别猫的图片的模型当中,可能会出现拥有充足且清晰的猫的图片进行模型的训练,而对于用户使用这个模型时,可能会使用模糊的照片,而专注于识别清晰照片的模型就较大的概率出现错误。并且这些模糊的照片在刚投入使用的时相较于训练模型时的清晰照片的数量少的多,如训练时清晰的照片可能有20w张,而用户的照片可能只有1w张,并不足以进行训练。
102 |
103 | 如果将清晰的照片和模糊的照片随机分布于数据集当中进行训练,则在期望上清晰的照片在测试集和验证集中的占比就会远大于模糊照片的比例,这就会导致在多次训练中,模型更加偏向于朝着清晰图片的识别的方向进行优化,而不是对用户上传的模糊照片的识别进行优化。
104 |
105 | 如果将模糊和清晰的照片进行划分,将清晰的图片作为训练集,并且将用户模糊的照片作为测试集和验证集,即把模型的优化方向设定为对用户上传的照片的识别,进而不断的提高对用户上传的照片的识别准确率。
106 |
107 |
108 |
109 | ### 9.5 不匹配数据划分上的偏差和方差
110 |
111 | 方差和偏差定义:第二门课第一周笔记
112 |
113 | #### 9.5.1 不匹配数据划分对方差和偏差的影响
114 |
115 | 以猫的识别为例,对猫的识别的最优误差几乎为0%,而如果训练集和验证集的数据并不是来自同一分布,如训练集是清晰的照片而测试集是模糊的照片,则训练集的照片容易识别,训练误差小,而验证集的照片难以识别,验证误差大,此时我们不能通过这两个误差值来判断该神经网络的方差是否真的偏大或者偏小,也就是两者的大小区别到底是训练集的数据造成的(也就是方差的问题),还是由于数据来自不同的分布而导致的(也就是数据不匹配问题)(或者两者哪个的影响更大)
116 |
117 | #### 9.5.2 训练-验证集(Training-dev set)
118 |
119 | 定义:为了解决在不匹配数据的情况下(也就是上述情况)对方差的判断,我们随机从训练集中抽取一组数据来作为新的子集,也就是训练-验证集。(此时数据集就被分为了四个部分:训练集、训练-验证集、验证集和测试集)
120 |
121 |
215 |
216 | #### 7.6.2 如何减缓Internal Covariate Shift
217 |
218 | **(1)白化(Whitening)**
219 |
220 | 白化(Whitening)是机器学习里面常用的一种规范化数据分布的方法,主要是PCA白化与ZCA白化。白化是对输入数据分布进行变换,进而达到以下两个目的:
221 |
222 | - **使得输入特征分布具有相同的均值与方差。**其中PCA白化保证了所有特征分布均值为0,方差为1;而ZCA白化则保证了所有特征分布均值为0,方差相同;
223 | - **去除特征之间的相关性。**
224 |
225 | 通过白化操作,可以减缓ICS的问题,进而固定每一层网络输入分布,加速网络训练过程的收敛。
226 |
227 | 然而,白化的方法具有一定缺陷,主要有以下两个问题:
228 |
229 | - **白化过程计算成本太高,**并且在每一轮训练中的每一层我们都需要做如此高成本计算的白化操作;
230 | - **白化过程由于改变了网络每一层的分布**,因而改变了网络层中本身数据的表达能力。底层网络学习到的参数信息会被白化操作丢失掉。
231 |
232 | **(2)Batch Normalization**
233 |
234 | 为解决上面两个问题,提出BN方法简化计算过程同时让归一化处理后的数据尽可能保留原始表达能力。
235 | $$
236 | \begin{array}{l}
237 | \mu=\frac{1}{m} \sum_{i} z^{(i)} \\
238 | \sigma^{2}=\frac{1}{m} \sum_{i}\left(z^{(i)}-\mu\right)^{2} \\
239 | z_{\text {norm}}^{(i)}=\frac{z^{(i)}-\mu}{\sqrt{\sigma^{2}+\varepsilon}}
240 | \end{array}
241 | $$
242 | 通过上面的变换,**解决了第一个问题,即用更加简化的方式来对数据进行规范化,使得第 $l$层的输入每个特征的分布均值为0,方差为1。**
243 |
244 | 如同上面提到的,Normalization操作我们虽然缓解了ICS问题,让每一层网络的输入数据分布都变得稳定,但却导致了数据表达能力的缺失。也就是我们通过变换操作改变了原有数据的信息表达(representation ability of the network),使得底层网络学习到的参数信息丢失。另一方面,通过让每一层的输入分布均值为0,方差为1,会使得输入在经过sigmoid或tanh激活函数时,容易陷入非线性激活函数的线性区域。
245 |
246 | 因此,BN引入的两个可学习(learnable)的参数$\gamma$和$\beta$,恢复数据本身的表达能力,对归一化后端数据进行线性变换,即:
247 | $$
248 | \tilde{z}^{[l]}=\gamma^{[l]} z_{\text {norm}}^{[l]}+\beta^{[l]}
249 | $$
250 | 特别地,当$\gamma^{2}=\sigma^{2}, \beta=\mu$时,可以实现等价变换(identity transform)并且保留了原始输入特征的分布信息。
251 |
252 | **通过上面的步骤,我们就在一定程度上保证了输入数据的表达能力。**
253 |
254 | 简单来说,BN减弱了前层参数的作用与后层参数的作用之间的联系,它使得网络每层都可以自己学习,稍稍独立于其它层,这让我们可以使用**更大的学习率**,初值可以更随意,有助于加速整个网络的学习。
255 |
256 | #### 7.6.3 BN的效果总结:
257 |
258 | **(1)BN使得网络中每层输入数据的分布相对稳定,加速模型学习速度**
259 |
260 | BN通过规范化与线性变换使得每一层网络的输入数据的均值与方差都在一定范围内,使得后一层网络不必不断去适应底层网络中输入的变化,从而实现了网络中层与层之间的解耦,允许每一层进行独立学习,有利于提高整个神经网络的学习速度。
261 |
262 | **(2)BN使得模型对网络中的参数不那么敏感,简化调参过程,使得网络学习更加稳定**
263 |
264 | 在神经网络中,我们经常会谨慎地采用一些权重初始化方法(例如Xavier)或者合适的学习率来保证网络稳定训练。
265 |
266 | 当学习率设置太高时,会使得参数更新步伐过大,容易出现震荡和不收敛。但是使用BN的网络将不会受到参数数值大小的影响。
267 |
268 | 例如,我们对参数$W$进行缩放得到$aW$。对于缩放前的值$Wu$($u$表示当前层输入,前一层的输出),设其均值为$\mu_{1}$,方差为$\sigma_{1}^{2}$;对于缩放值$aWu$,设其均值为$\mu_{2}$,方差为$\sigma_{2}^{2}$,则有:
269 | $$
270 | \mu_{2}=a \mu_{1}, \quad \sigma_{2}^{2}=a^{2} \sigma_{1}^{2}
271 | $$
272 | 我们忽略$\epsilon$,则有:
273 | $$
274 | \begin{array}{l}
275 | B N(a W u)=\gamma \cdot \frac{a W u-\mu_{2}}{\sqrt{\sigma_{2}^{2}}}+\beta=\gamma \cdot \frac{a W u-a \mu_{1}}{\sqrt{a^{2} \sigma_{1}^{2}}}+\beta=\gamma \cdot \frac{W u-\mu_{1}}{\sqrt{\sigma_{1}^{2}}}+\beta=B N(W u) \\
276 | \frac{\partial B N((a W) u)}{\partial u}=\gamma \cdot \frac{a W}{\sqrt{\sigma_{2}^{2}}}=\gamma \cdot \frac{a W}{\sqrt{a^{2} \sigma_{1}^{2}}}=\frac{\partial B N(W u)}{\partial u} \\
277 | \frac{\partial B N((a W) u)}{\partial(a W)}=\gamma \cdot \frac{u}{\sqrt{\sigma_{2}^{2}}}=\gamma \cdot \frac{u}{a \sqrt{\sigma_{1}^{2}}}=\frac{1}{a} \cdot \frac{\partial B N(W u)}{\partial W}
278 | \end{array}
279 | $$
280 | 可以看到,经过BN操作以后,权重的缩放值会被“抹去”,因此保证了输入数据分布稳定在一定范围内。另外,权重的缩放并不会影响到对$u$的梯度计算;并且当权重越大时,即$a$越大,$\frac{1}{a}$越小,意味着权重$W$的梯度反而越小,这样BN就保证了梯度不会依赖于参数的scale,使得参数的更新处在更加稳定的状态。
281 |
282 | 因此,在使用Batch Normalization之后,抑制了参数微小变化随着网络层数加深被放大的问题,使得网络对参数大小的适应能力更强,此时我们可以设置较大的学习率而不用过于担心模型divergence的风险。
283 |
284 | **(3)BN允许网络使用饱和性激活函数(例如sigmoid,tanh等),缓解梯度消失问题**
285 |
286 | 在不使用BN层的时候,由于网络的深度与复杂性,很容易使得底层网络变化累积到上层网络中,导致模型的训练很容易进入到激活函数的梯度饱和区;通过normalize操作可以让激活函数的输入数据落在梯度非饱和区,缓解梯度消失的问题;另外通过自适应学习$\gamma$和$\beta$又让数据保留更多的原始信息。
287 |
288 | **(4)BN具有一定的正则化效果**
289 |
290 | - BN只在每个mini-batch上计算均值和方差,而不是在整个数据集上
291 | - 均值和方差只是由一小部分数据估计得出的,有一些小的噪声,缩放过程从$z^{[l]}$到$\tilde{z}^{[l]}$也有一些噪声,因为它是用有些噪声的均值和方差计算得出的。
292 | - 故和dropout相似,它在每个隐藏层的激活值上增加了噪音。dropout 使一个隐藏的单元以一定的概率乘以 0,以一定的概率乘以 1,所以 dropout含一些噪音,因为它乘以 0 或 1。
293 |
294 | 因此,类似于dropout,BN有轻微的正则化效果,因为给隐藏单元添加了噪音,使得后部单元不过分依赖任何一个隐藏单元。如果想得到更强大的正则化效果,可以将BN和dropout一起使用。
295 |
296 | 如果应用较大的mini-batch可以减少噪音,减少正则化效果。
297 |
298 | **参考文章**:
299 |
300 | [1]: https://zhuanlan.zhihu.com/p/34879333 "Batch Normalization原理与实战"
301 | [2]: BatchNormalizationAcceleratingDeepNetworkTrainingbyReducingInternalCovariateShift
302 |
303 |
304 |
305 | ### 7.7 测试时的 Batch Norm
306 |
307 | 我们知道BN在每一层计算的 ![[公式]](https://www.zhihu.com/equation?tex=%5Cmu) 与 ![[公式]](https://www.zhihu.com/equation?tex=%5Csigma%5E2) 都是基于当前batch中的训练数据,但是这就带来了一个问题:我们在预测阶段,有可能只需要预测一个样本或很少的样本,没有像训练样本中那么多的数据,此时 ![[公式]](https://www.zhihu.com/equation?tex=%5Cmu) 与 ![[公式]](https://www.zhihu.com/equation?tex=%5Csigma%5E2) 的计算一定是有偏估计,这个时候我们该如何进行计算呢?
308 |
309 | **论文中的方法**:
310 |
311 | 利用BN训练好模型后,我们保留了每组mini-batch训练数据在网络中每一层的 ![[公式]](https://www.zhihu.com/equation?tex=%5Cmu_%7Bbatch%7D) 与 ![[公式]](https://www.zhihu.com/equation?tex=%5Csigma%5E2_%7Bbatch%7D) 。此时我们使用整个样本的统计量来对Test数据进行归一化,具体来说使用均值与方差的无偏估计:
312 |
313 | ![[公式]](https://www.zhihu.com/equation?tex=%5Cmu_%7Btest%7D%3D%5Cmathbb%7BE%7D+%28%5Cmu_%7Bbatch%7D%29)
314 |
315 | ![[公式]](https://www.zhihu.com/equation?tex=%5Csigma%5E2_%7Btest%7D%3D%5Cfrac%7Bm%7D%7Bm-1%7D%5Cmathbb%7BE%7D%28%5Csigma%5E2_%7Bbatch%7D%29)
316 |
317 | 得到每个特征的均值与方差的无偏估计后,我们对test数据采用同样的normalization方法:
318 |
319 | ![[公式]](https://www.zhihu.com/equation?tex=BN%28X_%7Btest%7D%29%3D%5Cgamma%5Ccdot+%5Cfrac%7BX_%7Btest%7D-%5Cmu_%7Btest%7D%7D%7B%5Csqrt%7B%5Csigma%5E2_%7Btest%7D%2B%5Cepsilon%7D%7D%2B%5Cbeta)
320 |
321 | **吴恩达老师讲的方法**
322 |
323 | 对训练阶段每个batch计算的$\mu$和$\sigma^{2}$采用指数加权平均来得到测试阶段$\mu$和$\sigma^{2}$的估计。
324 |
325 | 我们选择 𝑙层,假设我们有 mini-batch,$X^{\{1\}}$,$X^{\{2\}}$,$X^{\{3\}}$......以及对应的$y$值等等,那么在训练$X^{\{1\}}$时,就得到了$\mu^{\{1\}[l]}$,训练第二个mini-batch时,就会得到$\mu^{\{2\}[l]}$值。然后在这一隐藏层的第三个 mini-batch,得到第三个$\mu$($\mu^{\{3\}[l]}$)值。使用指数加权平均来追踪这个均值向量的最新平均值,于是该指数加权平均成了你对这一隐藏层的$z$均值的估值。
326 |
327 | 同样的,可以用指数加权平均来追踪这一层每个mini-batch的$\sigma^{2}$的值。因此在用不同mini-batch训练神经网络的同时,能够得到你所查看每一层$\mu$和$\sigma^{2}$的平均数的实时数值。
328 |
329 | 最后在测试时对test数据采用同样的normalization方法(同上)。
330 |
331 | ### 7.8 BN与其他Normalization的方法比较
332 |
333 | 参考文章:https://zhuanlan.zhihu.com/p/33173246
334 |
335 | https://www.cnblogs.com/LXP-Never/p/11566064.html
336 |
337 | https://blog.csdn.net/shwan_ma/article/details/85292024
338 |
339 | https://bbs.cvmart.net/topics/1569
340 |
341 |
342 |
343 | 常用的Normalization方法主要有:Batch Normalization(BN,2015年)、Layer Normalization(LN,2016年)、Instance Normalization(IN,2017年)、Group Normalization(GN,2018年)。它们都是从激活函数的输入来考虑、做文章的,以不同的方式**对激活函数的输入进行 Norm** 的。
344 |
345 | 将输入的图像shape记为[**N**, **C**hannel, **H**eight, **W**idth],这几个方法主要的区别就是在,
346 |
347 | - **batch Norm**:在batch上,对NHW做归一化,对小batchsize效果不好;
348 | - **layer Norm**:在通道方向上,对CHW归一化,主要对RNN作用明显;
349 | - **instance Norm**:在图像像素上,对HW做归一化,用在风格化迁移;
350 | - **Group Norm**:将channel分组,然后再做归一化;
351 | - **Switchable Norm**:将BN、LN、IN结合,赋予权重,让网络自己去学习归一化层应该使用什么方法。
352 |
353 | 
354 |
355 | 如果把特征图![[公式]](https://www.zhihu.com/equation?tex=x%5Cin%5Cmathbb%7BR%7D%5E%7BN%5Ctimes+C+%5Ctimes+H+%5Ctimes+W%7D)比喻成一摞书,这摞书总共有 N 本,每本有 C 页,每页有 H 行,每行 有W 个字符。
356 |
357 | #### 7.8.1 Batch Normalization
358 |
359 | $$
360 | \begin{array}{c}
361 | \mu=\frac{1}{m} \sum_{i=1}^{m} x_{i} \\
362 | \sigma=\sqrt{\left.\frac{1}{m} \sum_{i=1}^{m}\left(x_{i}-\mu\right)^{2}\right)} \\
363 | y=\frac{(x-\mu)}{\sqrt{\sigma^{2}+\epsilon}}+\beta=B N(x)
364 | \end{array}
365 | $$
366 |
367 | tf.nn.batch_normalization(x, mean, variance, offset, scale, variance_epsilon, name=None`)`
368 |
369 | 参数
370 |
371 | - x:输入数据
372 | - mean:均值
373 | - variance:方差
374 |
375 | 返回
376 |
377 | - 标准化后的数据
378 |
379 | **BN缺点:**
380 |
381 | - 对batch size的大小比较敏感,由于每次计算均值和方差是在一个batch上,所以如果batch size太小,则计算的均值、方差不足以代表整个数据分布;
382 | - BN实际使用时需要计算并且保存某一层神经网络batch的均值和方差等统计信息,对于对一个固定深度的前向神经网络(DNN,CNN)使用BN,很方便;但对于RNN来说,sequence的长度是不一致的,换句话说RNN的深度不是固定的,不同的time-step需要保存不同的statics特征,可能存在一个特殊sequence比其他sequence长很多,这样training时,计算很麻烦。
383 |
384 | #### 7.8.2 Layer Normalization
385 |
386 | LN是针对深度网络的某一层的所有神经元的输入按以下公式进行normalize操作。计算该层的平均输入值和输入方差,然后用同一个规范化操作来转换各个维度的输入。
387 | $$
388 | \begin{array}{c}
389 | \mu^{l}=\frac{1}{H} \sum_{i=1}^{H} a_{i}^{l} \\
390 | \sigma^{l}=\sqrt{\frac{1}{H} \sum_{i=1}^{H}\left(a_{i}^{l}-\mu^{l}\right)^{2}}
391 | \end{array}
392 | $$
393 | **BN与LN的区别在于**:
394 |
395 | - LN中同层神经元输入拥有相同的均值和方差,不同的输入样本有不同的均值和方差;
396 | - BN中则针对不同神经元输入计算均值和方差,同一个batch中的输入拥有相同的均值和方差。
397 |
398 | 所以,LN不依赖于batch的大小和输入sequence的深度,因此可以用于batchsize为1和RNN中对边长的输入sequence的normalize操作。
399 |
400 | BN 的转换是针对单个神经元可训练的——不同神经元的输入经过再平移和再缩放后分布在不同的区间,而 LN 对于一整层的神经元训练得到同一个转换——所有的输入都在同一个区间范围内。如果不同输入特征不属于相似的类别(比如颜色和大小),那么 LN 的处理可能会降低模型的表达能力。LN用于RNN效果比较明显,但是在CNN上,不如BN。
401 |
402 | tf.keras.layers.LayerNormalization(axis=-1, epsilon=0.001, center=True, scale=True)
403 |
404 | 参数
405 |
406 | - axis:想要规范化的轴(通常是特征轴)
407 | - epsilon:将较小的浮点数添加到方差以避免被零除。
408 | - center:如果为True,则将的偏移`beta`量添加到标准化张量。
409 | - `scale`:如果为True,则乘以`gamma`
410 |
411 | 返回
412 |
413 | - shape与输入形状相同的值
414 |
415 | #### 7.8.3 Instace Normalization
416 |
417 | BN注重对每个batch进行归一化,保证数据分布一致,因为判别模型中结果取决于数据整体分布。
418 |
419 | 但是图像风格转换中,生成结果主要依赖于某个图像实例,所以对整个batch归一化不适合图像风格化中,因而对HW做归一化。可以加速模型收敛,并且保持每个图像实例之间的独立。
420 | $$
421 | \begin{array}{c}
422 | \mu_{t i}=\frac{1}{H W} \sum_{l=1}^{W} \sum_{m=1}^{H} x_{t i l m} \\
423 | \sigma=\sqrt{\frac{1}{H W}} \sum_{l=1}^{W} \sum_{m=1}^{H}\left(x_{t i l m}-\mu_{y i}\right)^{2} \\
424 | y_{t i j k}=\frac{x_{P t i j k}-\mu_{y i}}{\sqrt{\sigma_{t i}^{2}}-\epsilon}
425 | \end{array}
426 | $$
427 | [`tfa.layers.normalizations.InstanceNormalization`](https://www.tensorflow.org/addons/api_docs/python/tfa/layers/InstanceNormalization)
428 |
429 | 输入:仅在该层只有一个输入(即,它连接到一个传入层)时适用。
430 |
431 | 返回:输入张量或输入张量列表。
432 |
433 | #### 7.8.4 Group Normalization
434 |
435 | 主要是针对Batch Normalization对小batchsize效果差,GN将channel方向分group,然后每个group内做归一化,算(C//G)*H*W的均值,这样与batchsize无关,不受其约束。
436 | $$
437 | S_{i}=\left\{k \mid k_{N}=i_{N},\left[\frac{k_{C}}{C / G}\right]=\left[\frac{i_{C}}{C / G}\right]\right\}
438 | $$
439 | Group Normalization 在要求 Batch Size 比较小的场景下或者物体检测/视频分类等应用场景下效果是优于 BN 的。
440 |
441 | #### 7.8.5 Switchable Normalization
442 |
443 | 本篇论文作者认为,
444 |
445 | - 第一,归一化虽然提高模型泛化能力,然而归一化层的操作是人工设计的。在实际应用中,解决不同的问题原则上需要设计不同的归一化操作,并没有一个通用的归一化方法能够解决所有应用问题;
446 | - 第二,一个深度神经网络往往包含几十个归一化层,通常这些归一化层都使用同样的归一化操作,因为手工为每一个归一化层设计操作需要进行大量的实验。
447 |
448 | 因此作者提出自适配归一化方法——Switchable Normalization(SN)来解决上述问题。与强化学习不同,SN使用可微分学习,为一个深度网络中的每一个归一化层确定合适的归一化操作。
449 | $$
450 | \begin{array}{c}
451 | \hat{h}_{h c i j}=\gamma \frac{h_{h c i j}-\sum_{k \in \Omega W_{k} \mu_{k}}}{\sqrt{\sum_{k \in \Omega} w_{k}^{\prime} \sigma_{k}^{2}+\epsilon}}+\beta \\
452 | w_{k}=\frac{e^{\lambda_{k}}}{\sum_{z \in\{i n, l n, b n\} e t}}, \quad k \in\{i n, l n, b n\} \\
453 | \mu_{i n}=\frac{1}{H W} \sum_{i, j}^{H, W} h_{n c i j}, \quad \sigma^{2}=\frac{1}{H W} \sum_{i, j}^{H, W}\left(h_{n c i j}-\mu_{i n}\right)^{2} \\
454 | \mu_{l n}=\frac{1}{C} \sum_{c=1}^{C} \mu_{i n}, \quad \sigma_{l n}^{2}=\frac{1}{C} \sum_{c=1}^{C}\left(\sigma_{i n}^{2}+\mu_{i n}^{2}\right)-\mu_{l n}^{2} \\
455 | \mu_{b n}=\frac{1}{N} \sum_{n=1}^{N} \mu_{i n}, \quad \sigma^{2}=\frac{1}{N} \sum_{n=1}^{N}\left(\sigma_{i n}^{2}+\mu_{i n}^{2}\right)-\mu_{b n}^{2}
456 | \end{array}
457 | $$
458 |
459 |
460 | #### 7.8.6 weight Normalization
461 |
462 | BN 和 LN 均将规范化应用于输入的特征数据 $X$ ,而 WN 则另辟蹊径,将规范化应用于线性变换函数的权重 $W$ ,这就是 WN 名称的来源。
463 |
464 | 对于人工神经网络中的一个神经元来说,其输出$y$表示为:
465 | $$
466 | y=\phi(\boldsymbol{w} \boldsymbol{x}+b)
467 | $$
468 | 其中$w$是$k$维权重向量,$b$是标量偏差,$x$是$k$维输入特征,$\phi(.)$是激活函数。
469 |
470 | 对权重$w$用参数向量$v$和标量$g$进行表示,则新参数表示为:
471 | $$
472 | \boldsymbol{w}=\frac{g}{\|\boldsymbol{v}\|} \boldsymbol{v}
473 | $$
474 | 其中$v$是$k$维向量,$g$是标量,$\|\boldsymbol{v}\|$为$v$的欧式范数。
475 | 通过上述参数表示,我们可以发现,$\|\boldsymbol{w}\|=g$与参数$v$独立,而权重$w$的方向也变更为$\frac{v}{\|\boldsymbol{v}\|}$。因此重参数将权重向量$w$用了两个独立的参数表示其幅度和方向。实验证明,在利用SGD优化算法时,重参数加速了网络的收敛速度。
476 |
477 | **Gradients:**
478 |
479 | 则对于$v$,$g$
480 | $$
481 | \begin{array}{c}
482 | \nabla_{g} L=\frac{\nabla_{w} L \cdot \boldsymbol{v}}{\|v\|} \\
483 | \nabla_{v} L=\frac{\boldsymbol{g} \cdot \nabla_{w} L}{\|v\|}-\frac{\boldsymbol{g} \cdot \nabla_{g} L}{\|v\|} \cdot \boldsymbol{v}
484 | \end{array}
485 | $$
486 | 其中$\nabla_{w} L$为目标函数对未进行WN的权重为$w$的偏导。
487 |
488 | 相比与BN,WN带有如下优点:WN的计算量非常低,并且其不会因为mini-batch的随机性而引入噪声统计。在RNN,LSTM,或者Reinforcement Learning上,WN能够表现出比BN更好的性能。
489 |
490 |
491 |
492 | ### 7.9 Softmax 回归
493 |
494 | Softmax回归:logistic回归的一般形式,将logistic回归推广到 C 类而不仅仅是两类,能在试图识别某一分类时做出预测且任何两个分类之间的决策边界都是线性的。
495 |
496 | 符号定义:
497 |
498 | $C$ :类别总数(类别编号分别为 $0, 2, ..., C-1$),故输出层L的神经元个数为 $C$,每个神经元分别输出该输入属于该类别的概率,$C$ 个神经元输出的概率总和应等于 1 。当 $C=2$ 时,Softmax回归即logistic回归。
499 |
500 | #### 7.9.1 Softmax层
501 |
502 | 在分类问题中,神经网络的**输出层**通常选用Softmax激活函数,使得最后输出的是归一化后的实数向量,每一元素代表该样本属于某一类的概率,则该层称为Softmax层。
503 |
504 | #### 7.9.2 Softmax激活函数
505 |
506 | - 定义:Softmax激活函数只用于多于一个神经元的输出层,它保证所有的输出神经元之和为1,所以一般输出的是小于1的概率值,可以很直观地比较各输出值。
507 |
508 | - 作用:为了得到属于每个类别的概率,先通过$e^{z^{[L]}}$将$z^{[L]}$的各元素值映射到 $(0, + \infty)$,然后再归一化到(0, 1)。
509 |
510 | - 具体实现:
511 |
512 | 在神经网络的最后一层,依然先计算线性部分:
513 | $$
514 | z^{[L]}=W^{[L]}a^{[L-1]}+b^{[L]}
515 | $$
516 |
517 |
518 | 然后应用**Softmax激活函数**:$a^{[L]}=g^{[L]}(z^{[L]})$,该函数的具体计算如下:
519 |
520 | (1)计算临时变量 $t=e^{z^{[L]}}$,对 $z^{[L]}$ 中的所有元素求幂,故 $t$ 的维度与 $z^{[L]}$ 相同。
521 |
522 | (2)对 $t$ **归一化**,得到输出 $a^{[L]}$ 即 $\hat{y}$ :$a^{[L]}=\frac{e^{z^{[L]}}}{\sum_{j=1}^{n^{[L]}} t_{i}}$,$a^{[L]}$的维度与 $t$ 相同,即也与 $z^{[L]}$ 相同,都为$(n^{[L]},1)$。其中,对$a^{[L]}$的每一个元素,$a_i^{[L]}=\frac{t_i}{\sum_{j=1}^{n^{[L]}} t_{i}}$。
523 |
524 | **tips:**之前所学的激活函数如sigmod和ReLU激活函数,都是输入一个实数,输出一个实数,而Softmax激活函数由于需要将所有可能的输出归一化,需要**输入一个向量,输出一个向量**。
525 |
526 | #### 7.9.3 softmax配合log似然代价函数训练ANN
527 |
528 | 在人工神经网络(ANN)中,Softmax通常被用作输出层的激活函数。这不仅是因为它的效果好,而且因为它使得ANN的输出值更易于理解。同时,softmax配合log似然代价函数,其训练效果也要比采用二次代价函数的方式好。
529 |
530 | log似然代价函数的公式为:
531 | $$
532 | C=-\sum_{k} y_{k} \log a_{k}
533 | $$
534 |
535 |
536 | 其中,$a_{k}$表示第k个神经元的输出值,$y_{k}$表示第k个神经元对应的真实值,取值为0或1。
537 |
538 | 该代价函数的简单理解为:在ANN中输入一个样本,那么只有一个神经元对应了该样本的正确类别;若这个神经元输出的概率值越高,则按照以上的代价函数公式,其产生的代价就越小;反之,则产生的代价就越高。
539 |
540 | 为了检验softmax和这个代价函数也可以解决训练ANN时训练速度变慢的问题,接下来的重点就是推导ANN的权重W和偏置b的梯度公式。以偏置b为例:
541 |
542 | 
543 |
544 | 同理可得:
545 | $$
546 | \frac{\partial C}{\partial w_{j k}}=a_{k}^{L-1}\left(a_{j}^{L}-y_{j}\right)
547 | $$
548 | 从上述梯度公式可知,softmax函数配合log似然代价函数可以很好地训练ANN,不存在学习速度变慢的问题。
549 |
550 | 参考文献:https://blog.csdn.net/orangefly0214/article/details/80406584
551 |
552 | ### 7.10 训练一个 Softmax 分类器
553 |
554 | #### 7.10.1 定义损失函数
555 |
556 | - 单样本:$$L(\hat{y}, y)=-\sum_{j=1}^C y_{j} \log \hat{y}_{j}$$
557 | - 整个训练集:$J\left(W^{[L]},b^{[L]} \ldots\right)=\frac{1}{m} \sum_{i=1}^{m} L\left(\hat{y}^{(i)}, y^{(i)}\right)$
558 | - 作用:找到样本所属的真实类别,并试图使该类别相应的概率尽可能地高。
559 |
560 | #### 7.10.2 正向传播
561 |
562 | 依次计算出:$z^{[L]} → a^{[L]} = \hat y → L\left(\hat{y}^{(i)}, y^{(i)}\right)$
563 |
564 | #### 7.10.3.反向传播(实现梯度下降法)
565 |
566 | (1)初始化反向传播:$dz^{[L]}=\frac{\partial J}{\partial z^{[L]}}=\hat y-y$
567 |
568 | (2)用深度学习编程框架自动实现反向传播的其余导数计算。
569 |
570 | ### 7.11 深度学习框架
571 |
572 | 深度学习框架可以使神经网络的实现变得更简单。每个框架都是针对某一个用户或开发者群体的
573 |
574 | #### 7.11.1 现有deep learning框架
575 |
576 | - **Caffe/Caffe2**:第一个主流的工业级深度学习工具。开始于2013年底,由UC Berkely的Yangqing Jia老师编写和维护的具有出色的卷积神经网络实现。在计算机视觉领域依然是最流行的工具包,有很多扩展,但是由于一些遗留的架构问题,不够灵活且对递归网络和语言建模的支持很差。
577 | - **CNTK**:是微软研究院开源的深度学习框架。最早由 start the deep learning craze 的演讲人创建,目前已经发展成一个通用的、跨平台的深度学习系统,在语音识别领域的使用尤其广泛。
578 | - **DL4J**:是一个基于 Java 和 Scala 的开源的分布式深度学习库,由 Skymind 于 2014 年 6 月发布,其核心目标是创建一个即插即用的解决方案原型。
579 | - **Keras**:是一个崇尚极简、高度模块化的神经网络库,使用 Python 实现,并可以同时运行在 TensorFlow 和 Theano 上。它旨在让用户进行最快速的原型实验,让想法变为结果的这个过程最短。Theano 和 TensorFlow 的计算图支持更通用的计算,而 Keras 则专精于深度学习。提供了目前为止最方便的 API,用户只需要将高级的模块拼在一起,就可以设计神经网络,它大大降低了编程开销和阅读别人代码时的理解开销。
580 | - **Lasagne**:是一个基于 Theano 的轻量级的神经网络库。Lasagne是 Theano 的上层封装,但又不像 Keras 那样进行了重度的封装,Keras 隐藏了 Theano 中所有的方法和对象,而 Lasagne 则是借用了 Theano 中很多的类,算是介于基础的 Theano 和高度抽象的 Keras 之间的一个轻度封装,简化了操作同时支持比较底层的操作。Lasagne 设计的六个原则是简洁、透明、模块化、实用、聚焦和专注。
581 | - **MXNet**:是李沐和陈天奇等各路英雄豪杰打造的开源深度学习框架,是分布式机器学习通用工具包DMLC的重要组成部分。注重灵活性和效率,文档也非常的详细,同时强调提高内存使用的效率,甚至能在智能手机上运行诸如图像识别等任务。
582 | - **PaddlePaddle**:是百度自主研发的集深度学习核心框架、工具组件和服务平台为一体的技术领先、功能完备的开源深度学习平台,有全面的官方支持的工业级应用模型,涵盖自然语言处理、计算机视觉、推荐引擎等多个领域,并开放多个预训练中文模型。目前已经被中国企业广泛使用,并拥有活跃的开发者社区生态。
583 | - **TensorFlow**:Google开源的其第二代深度学习技术——被使用在Google搜索、图像识别以及邮箱的深度学习框架。是一个理想的RNN(递归神经网络)API和实现,使用了向量运算的符号图方法,使得新网络的指定变得相当容易,支持快速开发。缺点是速度慢,内存占用较大(比如相对于Torch)。
584 | - **Theano**:2008年诞生于蒙特利尔理工学院,主要开发语言是Python。派生出了大量深度学习Python软件包,最著名的包括Blocks和Keras。Theano的最大特点是非常的灵活,适合做学术研究的实验,且对递归网络和语言建模有较好的支持,缺点是速度较慢。
585 | - **Torch**:Facebook力推的深度学习框架,主要开发语言是C和Lua。有较好的灵活性和速度。实现并且优化了基本的计算单元,使用者可以很简单地在此基础上实现自己的算法,不用浪费精力在计算优化上面。核心的计算单元使用C或者cuda做了很好的优化。在此基础之上,使用lua构建了常见的模型。缺点是接口为lua语言,需要一点时间来学习。
586 |
587 | 参考文献:
588 |
589 | - https://blog.csdn.net/dlaicxf/article/details/52846651
590 | - https://www.leiphone.com/news/201702/T5e31Y2ZpeG1ZtaN.html
591 |
592 | #### 7.11.2 几种主流dl框架的比较
593 |
594 | | **库名称** | **开发语言** | **速度** | **灵活性** | **文档** | **适合模型** | **平台** | **上手难易** |
595 | | :--------: | :-------------: | :------: | :--------: | -------: | :----------: | :--------: | :----------: |
596 | | Caffe | c++/cuda | 快 | 一般 | 全面 | CNN | 所有系统 | 中等 |
597 | | TensorFlow | c++/cuda/Python | 中等 | 好 | 中等 | CNN/RNN | Linux, OSX | 难 |
598 | | Keras | Python | 快 | 好 | 中等 | CNN/RNN | Linux, OSX | 易 |
599 | | MXNet | c++/cuda | 快 | 好 | 全面 | CNN | 所有系统 | 中等 |
600 | | Torch | c++/lua/cuda | 快 | 好 | 全面 | CNN/RNN | Linux, OSX | 中等 |
601 | | Theano | Python/c++/cuda | 中等 | 好 | 中等 | CNN/RNN | Linux, OSX | 易 |
602 |
603 | #### 7.11.3 选择框架的标准
604 |
605 | - **便于编程**:包括神经网络的开发和迭代、为产品进行配置等。
606 | - **运行速度**:特别是训练大数据集时,一些框架可以更高效地运行和训练神经网络。
607 | - **框架是否真的开放**:一个真的开放的框架,不仅需要开源,还需要良好的管理。
608 |
609 | PyTorch常用代码段合集 https://mp.weixin.qq.com/s/JnIO_HjTrC0DCWtKrkYC8A
610 |
611 |
612 |
613 |
614 |
615 |
616 |
617 |
--------------------------------------------------------------------------------
/8 机器学习(ML)策略(1).md:
--------------------------------------------------------------------------------
1 | # 1.1 为什么是ML策略
2 |
3 | 如果你训练了一段时间自己的神经网络,准确率到达了一定水平(比如90%)但却还不能满足你的要求,那这个时候必然需要对网络做出一些调整。你可能想到了几个解决思路,比如收集更多的数据、用不同的优化算法、训练得更久一些、加入正则化甚至修改网络架构等等。
4 |
5 | 但是这些办法并不是总是有效的,可能收集了6个月的数据却发现对网络的性能没有任何帮助。就是说如果你作出了错误的选择,那很可能浪费大量的时间和精力而得不到任何有效进展。
6 |
7 | 于是接下来希望教学一些策略:ML策略,以帮助我们向着有希望的方向前进。
8 |
9 | # 1.2 正交化
10 |
11 | 这里的正交化可以简单地理解为,每个自变量的改变只会引起一个因变量发生改变。举个反例,假设有$y_1=x_1+0.9x_2$,$y_2=0.1x_2$,则自变量$x_2$的改变会同时引起因变量$y_1,y_2$的改变,同时若想要通过$x_2$调整$y_1$时会不可避免的也调整了$y_2$。
12 |
13 | 在ML策略中,正交化是一种设计方法,以保证你在修改超参的时候不会引起两个以上的参数的变化。
14 |
15 | ## 四个参数
16 |
17 | 假设你需要正交化而确保不同时改变的四个参数是:
18 |
19 | * 收敛后的训练集的代价(cost)
20 | * 交叉验证集的代价
21 | * 测试集的代价
22 | * 真实应用的效果
23 |
24 | 当然,以上的参数是“按顺序”得到的。即只有在当前参数算优的情况下你才会做下一步而得到下一个参数的值。
25 |
26 | 对于第一点,如果训练集上的效果不好甚至无法收敛,可以考虑更大的神经网络或其他优化算法比如$Adam$。
27 |
28 | 对于第二点,可能原因是过拟合了,那可以尝试加入正则化或采用更大的训练集。
29 |
30 | 对于第三点,可以考虑采用更大的交叉验证集。
31 |
32 | 对于第四点,则考虑改变交叉验证集的图源或改变损失函数。
33 |
34 | 举个不正交的例子是 early stopping。因为 early stopping 会基于开发集的效果而提早停止训练,所以带来的影响是两方面的:训练集的代价还没收敛至最优的同时降低了在开发集上的代价。
35 |
36 | # 1.3 单一数字评估指标
37 |
38 | 对于一个网络的性能评估,我们有时候会采用多个指标以便更了解自己搭建的网络的效果。但是当你需要从多个网络中选出最好的一个时,多评估指标可能会导致你无法轻易选出优胜者——有的网络某一些指标最好,另一些指标则比不上其他网络。这个时候,单一数字评估指标就能很方便地帮你评价出最优的网络。
39 |
40 | ## 1.3.1常用指标
41 |
42 | 参考文章[在这](https://zhuanlan.zhihu.com/p/73569538)。
43 |
44 | ## 1.3.2混淆矩阵:
45 |
46 | 为了方便表达各指标如何计算,先介绍混淆矩阵:
47 |
48 | 
49 |
50 | 阴阳可理解为真假、1/0。a是预测为真真实也为真的样本数,其余类比。
51 |
52 | ## 1.3.3指标
53 |
54 | 1. Precision查准率/精度:评价网络做出的预测的准确率。对于二分类来说(比如猫/非猫分类器), $$P= \frac{预测为1且正确的样本数}{所有预测为1的样本数} = \frac{a}{a+b}$$。
55 |
56 | 2. 对于进行one-hot热值编码的多分类来说同样适用。
57 |
58 | 3. Recall查全率/True Positive真阳率/Sensitivity敏感性:评价网络对于目标类的识别率。对于二分类来说,
59 |
60 | $$R= \frac {所有预测为1且正确的样本数}{所有真实值为1的样本数} \frac{a}{a+c}$$。
61 |
62 | 对于进行了one-hot热值编码的多分类来说同样适用。
63 |
64 | 4. Accuracy准确率:评价网络所有类预测的准确率。对于二分类来说,$Acc= \frac{所有预测正确的样本数}{总的样本数}= \frac{a+d}{a+b+c+d}$。
65 |
66 | 5. 对于进行了one-hot热值编码的多分类同样适用。
67 |
68 | 6. False Positive误检率/假阳率:评价网络对阴性预测的错误率,为
69 |
70 | $$\frac{预测为1且错误的样本数}{真实值为0的样本数}=\frac{b}{b+d}$$。
71 |
72 | 7. F1分数:$$\frac{2}{\frac{1}{P}+\frac{1}{R}}$$
73 |
74 | P 和 R 分别代指 Precision 和 Recall。是 Precision 和 Recall 的调和平均数。
75 |
76 | # 1.4满足和优化指标
77 |
78 | 如果你想考虑的多个指标取值范围是相同的,那取平均值就可以简单地将多个指标“整合”成单一评估指标。但是如果其中一个是准确率P(%),另一个是单张图的预测时间T(ms),那取平均值的做法是几乎不合理的。线性组合$$aP+bT$$这样的做法或许可行,但是参数a、b的值却又可能难以设计。
79 |
80 | 所以,可以从另一个角度考虑:其中一个(甚至多个)指标只用于淘汰、筛选模型;另一个指标作为评估指标,是判断哪一个更优的指标。这分别对应满足指标和优化指标。
81 |
82 | ## 1.4.1满足指标
83 |
84 | 该指标是你关心的指标之一,但是又并不那么重要:该指标只需要到达一定范围即可,不是你**最想优化**的指标。比方说你很关心模型的准确率,同时也希望运行速度足够快,那将 T 视为满足指标是合适的。
85 |
86 | 满足指标的用意在于如果你有多个指标想要兼顾,但是大部分指标又并不是那么重要,那作为用于筛选模型的指标是很不错的选择。比如唤醒 Siri 你最关注的是 Recall,这能确保有人真的想唤醒 Siri 时能及时做出反应;但你也关注在没人想唤醒 Siri 时,Siri 被错误唤醒的概率。那将误检率/假阳率作为满足指标是可行的,比如设置为每24小时只有一次错误唤醒。
87 |
88 | ## 1.4.2优化指标
89 |
90 | 优化指标应该是你最关心的指标,是你最想优化的指标,比如唤醒 Siri 时的Recall。
91 |
92 | 由于单一数字评估指标的原因,优化指标应该只有一个,而其余你关心的指标都应该设为满足指标,或者和优化指标合理地整合为一个指标。
93 |
94 | # 1.5测试集、交叉验证集、测试集的划分
95 |
96 | ## 1.5.1 训练集、交叉验证集、测试集的作用
97 |
98 | - **训练集**:用以训练模型;
99 |
100 | - **交叉验证集** (也叫dev 集、开发集):衡量训练效果的同时进行超参数调优;
101 |
102 | - **测试集**:评测模型训练效果(测定泛化误差)。
103 |
104 | 以课后作业、期末考试、高考三者间的关系类比训练、开发、测试集的作用:
105 |
106 | - 课后作业(训练集):让你学会知识;
107 | - 期末考试(交叉验证集):让你检验自己是否真的学会了知识,发现了问题后,你会调整学习方法(调整超参数);
108 | - 高考(测试集):最终的测试,测试你在**没见过的**题上究竟能做到什么程度(泛化能力),且不再给你调整的机会。
109 |
110 | ## 1.5.2 如何设立交叉验证集和测试集
111 |
112 | 建议在设立交叉验证集和测试集时,要选择能够反映未来你希望得到的并认为做好很重要的数据作为交叉验证集和测试集。
113 |
114 | > Choose a dev set and test set to reflect data you expect to get in the future and consider important to do well on.
115 |
116 | 交叉验证集和测试集最好来自**同一分布**:不管未来会得到什么样的数据,一旦你的算法效果不错,要尝试收集类似的数据且不管那些数据是什么,都要**随机分配**到开发集和测试集中,这样才能瞄准想要的目标,让团队高速迭代来逼近同一个目标。
117 |
118 | ## 1.5.3 如此设立交叉验证集和测试集的原因
119 |
120 | 设立交叉验证集以及一个单实数评估指标就像是定下目标,告诉你的团队那就是你要瞄准的靶心,一旦建立了这样的开发集和指标,团队就可以快速迭代,可以很快地使用交叉验证集和指标去评估不同分类器,然后尝试选出最好的那个,针对开发集上的指标优化。
121 |
122 | 如果交叉验证集和测试集来自不同的分布,就像设定了一个目标,结果在团队逼近这个目标工作几个月后,想要把成果应用到另一个目标。为了避免这种情况,建议将所有数据随机洗牌放入开发集和测试集,所以交叉集和测试集都有来自所有不同分类的数据并且开发集和测试集都来自同一分布,这个分布就是所有的数据混在一起。
123 |
124 | # 1.6 交叉验证集和测试集的大小
125 |
126 | ## 1.6.1 交叉验证集和测试集大小设置的原则
127 |
128 | 1、经验法则:把取得的所有数据划分为 **70%训练集+30%测试集** 或 **60%训练集+20%交叉验证集+20%测试集**。
129 |
130 | 这种经验法则使用于机器学习的早期,即数据集规模较小的情况下。
131 |
132 | 2、在现代机器学习中,数据集规模很大,可分为**98%训练集+1%交叉验证集+1%测试集**。
133 |
134 | 训练集的大小:深度学习算法对数据的胃口很大,故要把占更高比例的数据划分到训练集中;
135 |
136 | 测试集的大小:测试集的目的是完成系统开发后用测试集评估系统性能,故要令测试集足够大,能够以高置信度评估系统整体性能。所以除非需要对最终系统有一个很精确的指标,一般来说,测试集不需要上百万个例子,有10000或100000个大概就足够了,当数据量很大时,测试集就会远远小于数据集的30%或20%。
137 |
138 | ## 1.6.2 什么情况下可以没有测试集
139 |
140 | 对于不需要对系统性能有置信度很高的评估的应用,可以不用划分测试集,只需要训练集和交叉验证集,只要有数据去训练、有数据去调试就够了,但是并不建议在系统搭建时省略测试集,有个单独的测试集会更好,因为可以用这组不带偏差的数据来测量系统的性能,但如果交叉验证集非常大,就不会对交叉验证集过拟合得太厉害,在这种情况下只有训练集和交叉验证集也不是完全不合理。
141 |
142 | 在实际实践中,有时只把数据集划分为训练集和测试集,实际上这是在测试集上迭代,所以这里的测试集其实是交叉验证集,即只把数据分为训练集和交叉验证集,没有测试集。
143 |
144 | # 1.7 什么时候该改变交叉验证/测试集和指标
145 |
146 | ## 1.7.1 如何定义一个指标去评估分类器
147 |
148 | 评估指标的意义在于,准确告诉你已知的两个分类器哪一个更适合你的应用。
149 |
150 | 当已设定的评估指标无法正确衡量算法之间的优劣排序时,就应该改变评估指标或者改变交叉验证集或测试集。
151 |
152 | 例如,若对旧的误差指标 $Error = \frac{1}{m_{dev}} \sum_{i=1}^{m_{dev}}I[y_{pred}^{(i)}≠y^{(i)}]$ 不满意,可以尝试定义一个新的能够更加符合你的偏好的指标,从而定义出更适合的算法,如在 $I$ 项前加一个权重项 $\omega^{(i)}$,即
153 |
154 | $Error = \frac{1}{m_{dev}} \sum_{i=1}^{m_{dev}} \omega^{(i)} I[y_{pred}^{(i)}≠y^{(i)}]$
155 |
156 | 其中,
157 |
158 | $\omega^{(i)}=\left\{\begin{array}{ll}1 & \text { if } x^{(i)}... \\ 10 & \text { if } x^{(i)}...\end{array}\right.$,
159 |
160 | 当 $x^{(i)}$ 是预期分类中的数据时,赋予较小的权重1,当 $x^{(i)}$ 不是预期分类中的数据时,赋予较大的权重10,误差项迅速变大,即把非预期分类数据分类成某一类的惩罚权重加大10倍。
161 |
162 | ## 1.7.2 机器学习的两个独立步骤(正交化)
163 |
164 | 1. 设定目标:弄清楚如何定义一个指标来衡量你想做的事情的表现(**定义指标**);
165 | 2. 瞄准/射击目标:分开考虑如何改善系统在这个指标上的表现(**调整指标**以优化系统)。
166 |
167 | ## 1.7.3 需改变评价标准的情况
168 |
169 | 如果系统在当前指标、当前交叉验证集或者交叉验证集和测试集分布中表现很好,但在实际应用程序即你真正关注的地方表现不好(当前的指标和当前用来评估的数据和你真正关心必须做好的事情关系不大),就需要修改指标或交叉验证/测试集,让它们能够更好地反映算法需要处理好的数据。
170 |
171 | 举例:假设有两个猫分类器A和B,用开发集评估分别得到3%和5%的误差,做评估时用的是高质量图片的交叉验证集和测试集但在实际应用时上传的图片取景不专业,没有把猫完整拍下来或猫的表情很古怪,或者图像很模糊,在实际测试算法时可能会发现算法B比算法A更好,此时就应该修改指标或交叉验证/测试集。
172 |
173 | # 1.8为什么是人的表现
174 |
175 | 机器学习模型的准确性有两个层级,分别为
176 |
177 | 1.human-level performance(人的表现)
178 |
179 | 2.Bayes optimal error(贝叶斯最优误差)
180 |
181 | 机器学习模型表现常与人的学习表现相比较
182 |
183 | 如图,随着训练时间的不断增长,模型的准确性会不断接近“人的表现”并最终超过。当超过“人的表现”后,准确性的上升会比较缓慢,并不断靠近理想的最优情况,即贝叶斯最优误差。而实际上,“人的表现”,在许多如语音识别、图像识别的部分是非常具有优势的,让机器学习模型的准确性不断接近“人的表现”非常有必要。
184 |
185 | 1.Get labeled data from humans.
186 |
187 | 2.Gain insight from manual error analysis: Why did a person get this right?
188 |
189 | 3.Better analysis of bias/variance.
190 |
191 | 以上方法可以让模型不断接近人的表现。
192 |
193 | # 1.9可避免偏差
194 |
195 | 在实际应用中,要看human-level error,training error和dev error的相对值。例如猫类识别的例子中,
196 |
197 | 
198 |
199 |
200 |
201 | 对于物体识别这类CV问题,human-level error是很低的,很接近理想情况下的贝叶斯最优误差。因此,上面例子中的1%和7.5%都可以近似看成是两种情况下对应的bayes optimal error。实际应用中,我们一般会用human-level error代表bayes optimal error。
202 |
203 |
204 |
205 | 通常,我们把training error与human-level error之间的差值称作avoidable bias(可避免偏差);把dev error与training error之间的差值称为方差(variance)。根据bias和variance值的相对大小,可以知道算法模型是否发生了欠拟合或者过拟合。
206 |
207 | 若相比于方差(variance),bias较大,则我们对模型的调整主要在于减小偏差
208 |
209 | 若相比于方差(variance),bias较小,则可采用正则化、采集更多数据等方法减小方差
210 |
211 | # 1.10理解人的表现
212 |
213 | human-level performance有时能够代表bayes optimal error。但是,human-level performance如何定义呢?举个医学图像识别的例子,不同人群的error有所不同:
214 |
215 | 
216 |
217 | 由于bayes optimal error是最优的理想情况,一般来说,我们将表现最好的那一组,即Team of experienced doctors作为human-level performance,以此来代替bayes optimal error。
218 |
219 |
220 |
221 | 但在实际应用时,human-level performance的选择也会因人而异,不同取值的human-level performance会在一定程度上影响bias和variance的相对大小。如下图
222 |
223 |
224 |
225 | 
226 |
227 | 在方案C中,由于Training error和Development error数值差只为0.1,即variance只有0.1,此时不同取值的human-level performance会影响到bias和variance的相对大小,影响到了后续对模型的调整与改善。
228 |
229 | 而这种情况一般只在模型表现很好,接近bayes optimal error 时才会出现,此时,由于human-level performance较模糊难以定义,而影响到了模型的优化。
230 |
231 | # 1.11超过人的表现
232 |
233 | 
234 |
235 | 对于自然感知类问题,例如视觉、听觉等,机器学习的表现还不及人类。但是在很多其它方面,如
236 |
237 |
238 |
239 | - Online advertising(在线广告)
240 | - Product recommendations(产品推荐)
241 | - Logistics(predicting transit time)(预测交通时间)
242 | - Loan approvals(贷款批准)
243 |
244 | 这些方面,机器的表现优于人类。
245 |
246 | 机器学习模型超过human-level performance是比较困难的。但是如果有足够多的样本,训练更加复杂的神经网络,模型预测准确性会不断得到提高,最终接近并超过human-level performance。然而当机器模型的表现超过human-level performance时,难以直觉来继续提高算法模型性能。
247 |
248 | # 1.12改善模型表现
249 |
250 | 提高机器学习模型性能主要要解决两个问题:avoidable bias和variance。
251 |
252 | 解决avoidable bias的常用方法包括:
253 |
254 | - Train bigger model(训练更大的模型)
255 |
256 | - Train longer/better optimization algorithms: momentum, RMSprop, Adam
257 |
258 | (使用更好的算法:momentum、RMSprop、Adam)
259 |
260 | - NN architecture/hyperparameters search(选用不同的神经网络结构)
261 |
262 | 解决variance的常用方法包括:
263 |
264 | - More data(使用更多数据)
265 | - Regularization: L2, dropout, data augmentation(使用正则化方法)
266 | - NN architecture/hyperparameters search(选用不同的神经网络结构)
267 |
268 |
--------------------------------------------------------------------------------
/9 机器学习(ML)策略(2).md:
--------------------------------------------------------------------------------
1 | ## 9 机器学习(ML)策略(2)
2 |
3 | ### 9.1误差分析
4 |
5 | #### 9.1.1 定义
6 |
7 | 你希望让学习算法能够胜任人类能做的任务,但你的学习算法还没有达到人类的表现,那么人工检查一下你的算法犯的错误也许可以让你了解接下来应该做什么。**这个过程称为错误分误差**。
8 |
9 | 通过对一组错误样本进行逐一检查后,分析错误样本的类型的比例,来决定朝着哪个方向来进行优化,或者给你构思新优化方向的灵感。
10 |
11 |
12 |
13 | #### 9.1.2 举例
14 |
15 | 假设你正在调试猫分类器,注意到一些算法分类出错的例子中,算法将一些狗分类为猫,为了解决的这个问题,我们不需要,去设计一些只处理狗的算法功能之类的,为了让你的猫分类器在狗图上做的更好,让算法不再将狗分类成猫,因为这花费的时间太长了。而是需要进行误差分析,以便于决定哪一个方向值得努力。
16 |
17 | 首先,比如收集100个错误标记的开发集样本,然后手动检查,一次只看一个,看看你的开发集里有多少错误标记的样本是狗。假设100个错误标记样本中只有5%是狗这意味着100个样本,在典型的100个出错样本中,即使你完全解决了狗的问题,你也只能修正这100个错误中的5个,也就是最多只能将错误率从10%下降到9.5%,效果并不明显。但假设100个错误标记的开发集样本,你发现实际有50张图都是狗,也就是有50%都是狗的照片,现在花时间去解决狗的问题可能效果就很好,错误率可能就从10%下降到5%。
18 |
19 |
20 |
21 | #### 9.1.3 利用表格进行误差分析
22 |
23 | 当然在进行误差分析时,也可以对多个情况或者想法进行评估(比如对狗的照片错认为猫和对狮子的照片错认为猫)。有效且清晰的做法是设计一个表格来对各种错误样本进行填表式的分类,最后统计错误类型的百分比,再针对各种错误类型百分比的大小,进而决定优化的方向,同时最好在每个样本的后面增加备注,以方便进行分析。
24 |
25 | 
26 |
27 | 当然,在分类的过程中,如果发现了新的错误类型,也可以直接创建一个新的错误类型
28 |
29 |
30 |
31 |
32 |
33 | ### 9.2 清除标注错误的数据
34 |
35 | 错误的数据:结果的标签是错的。比如猫的图片被标注为不是猫。
36 |
37 | #### 9.2.1 处理标签错误的数据
38 |
39 | 1.对于总数据集总足够大,实际错误率不高的情况下:有时候放着不管也可以,并不会对训练出来的结果有太大的影响
40 |
41 | 2.对于系统性的错误:需要进行修改
42 |
43 | (实际错误率高,比如一直把白色的狗标记成猫,分类器学习之后,会把所有白色的狗都分类为猫)
44 |
45 |
46 |
47 | 总的来说,在进行误差分析后如果这些标记错误严重影响了你在开发集上评估算法的能力,那么就应该去花时间修正错误的标签。但是,如果它们没有严重影响到你用开发集评估成本偏差的能力,那么可能就不应该花宝贵的时间去处理。
48 |
49 |
50 |
51 | #### 9.2.2 分析错误数据的指标
52 |
53 | 关注整体的开发集错误率、错误标记引起的错误的数量或者百分比,最后根据标记错误引发的错误占总体总体错误率的比例来决定。(简单点说就是标记错误占所有错误的百分比的大小,该百分比越大,说明越值得修改错误标签)
54 |
55 | 比如,系统达到了90%整体准确度,所以有10%错误率,那么你应该看看错误标记引起的错误的数量或者百分比。所以在这种情况下,6%的错误来自标记出错,所以10%的6%就是0.6%。也许你应该看看其他原因导致的错误,如果你的开发集上有10%错误,其中0.6%是因为标记出错,剩下的占9.4%,是其他原因导致的。这个时候更应该考虑对9.4%进行优化或者修正。
56 |
57 | 假设你把错误率降到了2%,但总体错误中的0.6%还是标记出错导致的,此时错误标签导致的错误占总体错误的30%,那么这种情况就值得进行错误标签的修正。
58 |
59 |
60 |
61 | #### 9.2.3 修正标签的原则
62 |
63 | 1.修正标签时,都要同时作用到验证集和测试集上,也就是必须同时检查验证集和测试集,因为验证和测试集必须来自相同的分布。
64 |
65 | 2.要考虑同时检验算法判断正确和判断错误的样本,因为如果你只修正算法出错的样本,你对算法的偏差估计可能会变大,这会让你的算法有一点不公平的优势。
66 |
67 | 3.修正训练集中的标签其实相对没那么重要。
68 |
69 |
70 |
71 | 第二点不常遵循,因为一般判断正确的样本所占的比重要大得多。
72 |
73 |
74 |
75 | ### 9.3 快速搭建你的第一个系统
76 |
77 | 一般来说,对于几乎所有的机器学习程序可能会有50个不同的方向可以前进,并且每个方向都是相对合理的可以改善你的系统。所以快速设立开发集和测试集还有指标,能够确定系统迭代的方向,并且及时利用训练集对机器学习系统进行训练,再根据结果进行分析来确定下一步优先做什么。
78 |
79 |
80 |
81 | 下面以建立一个语音识别系统为例子介绍:
82 |
83 | 你可以选择很多不同的技术,让你听写下来的文本可读性更强,所以你可以做很多事情来改进语音识别系统。但对于多种方法你会感到非常迷茫,但当你建立第一个系统后,就能够进行误差分析让你了解到大部分的错误的来源是什么,比如说话人远离麦克风,那么你就有很好的理由去集中精力研究这些技术,也就是确定了你努力的方向
84 |
85 |
86 |
87 |
88 |
89 | ### 9.4 在不同的划分下进行训练并测试
90 |
91 | #### 9.4.1 划分的定义
92 |
93 | 划分即在选择数据进行训练时,将不是来自同一分布的数据进行分开,并分别作为数据集的训练集,以及数据集中的验证集和测试集(验证集和测试集得保证来自同分布)。
94 |
95 | 注:在视频中,字幕将dev set翻译为开发集,而以往的笔记中使用的命名为验证集,这里我使用验证集
96 |
97 | #### 9.4.2 为什么需要进行划分
98 |
99 | 进行划分的目的在于设定模型的优化方向,也就是“靶心”,通过将需要应用时的数据作为测试集和验证集来进行训练,保证在该模型投入应用时能够有较高的识别率。
100 |
101 | eg.在识别猫的图片的模型当中,可能会出现拥有充足且清晰的猫的图片进行模型的训练,而对于用户使用这个模型时,可能会使用模糊的照片,而专注于识别清晰照片的模型就较大的概率出现错误。并且这些模糊的照片在刚投入使用的时相较于训练模型时的清晰照片的数量少的多,如训练时清晰的照片可能有20w张,而用户的照片可能只有1w张,并不足以进行训练。
102 |
103 | 如果将清晰的照片和模糊的照片随机分布于数据集当中进行训练,则在期望上清晰的照片在测试集和验证集中的占比就会远大于模糊照片的比例,这就会导致在多次训练中,模型更加偏向于朝着清晰图片的识别的方向进行优化,而不是对用户上传的模糊照片的识别进行优化。
104 |
105 | 如果将模糊和清晰的照片进行划分,将清晰的图片作为训练集,并且将用户模糊的照片作为测试集和验证集,即把模型的优化方向设定为对用户上传的照片的识别,进而不断的提高对用户上传的照片的识别准确率。
106 |
107 |
108 |
109 | ### 9.5 不匹配数据划分上的偏差和方差
110 |
111 | 方差和偏差定义:第二门课第一周笔记
112 |
113 | #### 9.5.1 不匹配数据划分对方差和偏差的影响
114 |
115 | 以猫的识别为例,对猫的识别的最优误差几乎为0%,而如果训练集和验证集的数据并不是来自同一分布,如训练集是清晰的照片而测试集是模糊的照片,则训练集的照片容易识别,训练误差小,而验证集的照片难以识别,验证误差大,此时我们不能通过这两个误差值来判断该神经网络的方差是否真的偏大或者偏小,也就是两者的大小区别到底是训练集的数据造成的(也就是方差的问题),还是由于数据来自不同的分布而导致的(也就是数据不匹配问题)(或者两者哪个的影响更大)
116 |
117 | #### 9.5.2 训练-验证集(Training-dev set)
118 |
119 | 定义:为了解决在不匹配数据的情况下(也就是上述情况)对方差的判断,我们随机从训练集中抽取一组数据来作为新的子集,也就是训练-验证集。(此时数据集就被分为了四个部分:训练集、训练-验证集、验证集和测试集)
120 |
121 |  122 |
123 | 特点:训练-验证集和训练集来自同一分布,验证集和测试集来自同一分布。
124 |
125 | 训练-验证集并不参加训练集对模型的训练,而是和验证集参加反向传播。
126 |
127 | 训练-验证集同时也会进行误差计算,叫做训练-验证集上的误差。
128 |
129 | #### 9.5.3 不匹配数据划分下偏差、方差的判断
130 |
131 | 在引入训练-验证集之后,我们通过对训练-验证集的误差值和训练误差以及验证误差三者相结合进行判断,进而得出方差大小或者不同分布对结果影响的结论,当训练误差和训练-验证集误差相差较大时,说明方差较大,当训练-验证集误差和验证误差相差较大时,说明不同分布对结果影响较大,下面将用例子的形式进行判断。
132 |
133 | 对于偏差问题,仍然可以按照以前的方法进行判断。
134 |
135 | 不同分布对结果影响和方差较大问题是可以同时存在的。
136 |
137 | (1)训练误差:1% 训练-验证集误差:9% 验证误差:10%
138 |
139 | 训练误差和训练-验证集误差相差较大,方差较大,训练-验证集误差和验证误差相差较小,不同分布对结果影响较小。
140 |
141 | (2)训练误差:1% 训练-验证集误差:1.5% 验证误差:10%
142 |
143 | 训练误差和训练-验证集误差相差较小,方差较小,训练-验证集误差和验证误差相差较大,不同分布对结果影响较大。
144 |
145 | (3)训练误差:10% 训练-验证集误差:11% 验证误差:20%
146 |
147 | 训练误差和训练-验证集误差相差较大,方差较大,训练-验证集误差和验证误差相差较大,不同分布对结果影响较大。
148 |
149 | (4)训练误差:7% 训练-验证集误差:10% 验证误差:6%
150 |
151 | 出现这种和前三种都不同的情况说明,验证集的识别比训练集和训练-验证集这同一分布的数据的识别更加容易。
152 |
153 |
154 |
155 | **对方差,偏差,数据不匹配和过拟合的判断的总结:**
156 |
157 | (1)偏差:通过比较最优误差(人类判断误差)和训练误差大小来判断,两者相差越大,偏差越大。
158 |
159 | (2)方差:通过比较训练-验证集误差和训练误差大小来判断,两者相差越大,方差越大。
160 |
161 | (3)数据不匹配:通过比较训练-验证集误差和验证误差大小来判断,两者相差越大,数据越不匹配。
162 |
163 | (4)过拟合:通过比较验证误差和测试误差大小来判断,两者相差越大,模型就越过拟合。
164 |
165 |
166 |
167 | 对于降低方差和偏差的方法在第二门课第一周笔记有具体的讲解。
168 |
169 |
170 |
171 |
172 |
173 |
174 |
175 |
176 |
177 | ### 9.6 处理数据不匹配问题
178 |
179 | **数据不匹配问题**:训练集和开发/测试集来自不同的分布。
180 |
181 | #### 9.6.1 处理方法
182 |
183 | - 做错误分析,尝试了解训练集和开发/测试集的具体差异(比如有无噪音)。为避免对测试集过拟合,应该人工看开发集而不是测试集。
184 | - 把训练数据变得更像开发集(如人工数据合成),或收集更多类似你的开发集和测试集的数据。
185 |
186 | **人工数据合成**:
187 |
188 | 通过对不同类型的数据进行合成,产生需要使用的目的数据。
189 |
190 | 同时人工数据合成也存在问题,在合成数据时,如果选择某类数据时只使用了一小部分进行合成,也就是这类数据类型的子集,从整体的角度来看,这个子集的数据作为样本会导致过拟合的情况出现,也就是过于拟合这个子集数据的特点。而对于这个子集外的同类数据识别效果差。
191 |
192 | - 举例一:
193 |
194 | 
195 |
196 | 建立**语音识别系统**时,在需要解决汽车噪音问题情况,没有那么多实际再汽车背景噪音下录得的音频。这是可以人工合成数据。假设录制了大量清晰的音频,不带车辆背景噪音的音频后,你可以收集一段这样的汽车噪音。然后将两个音频片段放到一起,就可以合成出带有汽车噪声的语音音频。这是一个相对简单的音频合成例子。在实践中,你可能会合成其他音频效果,比如混响,就是声音从汽车内壁上反弹叠加的效果。
197 |
198 | 通过人工数据合成,你可以快速制造更多的训练数据,就像真的在车里录的那样,那就不需要花时间实际出去收集数据,比如说在实际行驶中的车子,录下上万小时的音频。所以,如果错误分析显示你应该尝试让你的数据听起来更像在车里录的,那么人工合成那种音频,然后喂给你的机器学习算法。
199 |
200 | **潜在问题**:
201 |
202 | 比如说,你在安静的背景里录得10,000 小时音频数据,然后,比如说,你只录了一小时车辆背景噪音,那么,你可以这么做,将这 1 小时汽车噪音回放 10,000 次,并叠加到在安静的背景下录得的 10,000 小时数据。如果你这么做了,人听起来这个音频没什么问题。但是有可能你的学习算法对这1 小时汽车噪音过拟合。
203 |
204 | - 举例二:
205 |
206 | 
207 |
208 | 假设你在研发无人驾驶汽车,你可能希望检测出这样的车,然后用框包住它,可以用计算机合成图像来模拟成千上万的车辆。
209 |
210 | **潜在问题:**
211 |
212 | 如果你只合成这些车中很小的子集,对于人眼来说也许这样合成图像没什么问题,但你的学习算法可能会对合成的这一个小子集过拟合。特别是很多人都独立提出了一个想法,一旦你找到一个电脑游戏,里面车辆渲染的画面很逼真,那么就可以截图,得到数量巨大的汽车图片数据集。事实证明,如果你仔细观察一个视频游戏,如果这个游戏只有 20 辆独立的车。因为你是在游戏里开车,你只看到这 20 辆车,这个模拟看起来相当逼真。但现实世界里车辆的设计可不只 20 种,如果你用着 20 量独特的车合成的照片去训练系统,那么你的神经网络很可能对这 20 辆车过拟合,但人类很难分辨出来。即使这些图像看起来很逼真,你可能真的只用了所有可能出现的车辆的很小的子集。
213 |
214 | - 故使用人工数据合成时,一定要谨慎,要记住你有可能从所有可能性的空间只选了很小一部分去模拟数据。
215 |
216 |
217 |
218 | ### 9.7 迁移学习
219 |
220 | #### **9.7.1 定义**
221 |
222 | 将一个问题上训练好的模型通过简单的调整使其适用于一个新的问题。
223 |
224 | #### **9.7.2 举例一**
225 |
226 | 假设你已经训练好一个图像识别神经网络,所以你首先用一个神经网络,并在$(𝑥, 𝑦)$对上训练,其中$𝑥$是图像,$𝑦$是某些对象的判断,图像是猫、狗、鸟或其他东西。如果你把这个神经网络拿来,然后让它适应或者说迁移,在不同任务中学到的知识,比如放射科诊断,就是说阅读𝑋射线扫描图。你可以做的是把神经网络最后的输出层拿走,就把它删掉,还有进入到最后一层的权重删掉,然后为最后一层重新赋予随机权重,然后让它在放射诊断数据上训练。
227 |
228 | 
229 |
230 | 具体来说,在第一阶段训练过程中,当你进行图像识别任务时时,你可以训练神经网络的所有常用参数,所有的权重,所有的层,然后你就得到了一个能够做图像识别预测的网络。在训练了这个神经网络后,要实现迁移学习,你现在要做的是,把数据集换成新的$(𝑥, 𝑦)$对,现在这些变成放射科图像,而$𝑦$是你想要预测的诊断,你要做的是初始化最后一层的权重,让我们称之为$w^{[L]}$和$b^{[L]}$随机初始化。
231 |
232 | 如果你重新训练神经网络中的所有参数,那么这个在图像识别数据的初期训练阶段,有时称为**预训练**(pre -training),因为你在用图像识别数据去预先初始化,或者预训练神经网络的权重。然后,如果你以后更新所有权重,然后在放射科数据上训练,有时这个过程叫**微调**(fine tuning)
233 |
234 | #### **9.7.3 举例二**
235 |
236 | 
237 |
238 | 假设你已经训练出一个语音识别系统,现在$𝑥$是音频或音频片段输入,而$𝑦$是听写文本,所以你已经训练了语音识别系统,让它输出听写文本。现在我们说你想搭建一个“唤醒词”或“触发词”检测系统,所谓唤醒词或触发词就是我们说的一句话,可以唤醒家里的语音控制设备,比如你说“Alexa”可以唤醒一个亚马逊 Echo设备,或用“OK Google”来唤醒 Google 设备,用"Hey Siri"来唤醒苹果设备,用"你好百度"唤醒一个百度设备。要做到这点,你可能需要去掉神经网络的最后一层,然后加入新的输出节点,但有时你可以不只加入一个新节点,或者甚至往你的神经网络加入几个新层,然后把唤醒词检测问题的标签$𝑦$喂进去训练。再次,这取决于你有多少数据,你可能只需要重新训练网络的新层,也许你需要重新训练神经网络中更多的层。
239 |
240 | #### **9.7.4 迁移学习有效的原因**
241 |
242 | 在例一中我们把图像识别中学到的知识应用或迁移到放射科诊断上来。有很多低层次特征,比如说边缘检测、曲线检测、阳性对象检测,**从非常大的图像识别数据库中习得这些能力可能有助于你的学习算法在放射科诊断中做得更好**,算法学到了很多结构信息,图像形状的信息,其中一些知识可能会很用,所以学会了图像识别,它就可能学到足够多的信息,可以了解不同图像的组成部分是怎样的,学到线条、点、曲线这些知识,也许对象的一小部分,这些知识有可能帮助你的放射科诊断网络学习更快一些,或者需要更少的学习数据。
243 |
244 | 对于第二个例子语音识别,也许你已经用 10,000 小时数据训练过你的语言识别系统,所以你从这10,000 小时数据学到了很多人类声音的特征,这数据量其实很多了。但对于触发字检测,也许你只有 1 小时数据,所以这数据太小,不能用来拟合很多参数。所以在这种情况下,预先学到很多人类声音的特征人类语言的组成部分等等知识,可以帮你建立一个很好的唤醒字检测器,即使你的数据集相对较小。
245 |
246 | #### **9.7.5 迁移学习起作用的场合**
247 |
248 | 1.以任务A迁移到任务B为例,任务A和任务B都有同样的输入x时,如输入都是图片
249 |
250 | 2.任务A的数据比任务B的多得多,任务A的数据才会对B有帮助。
251 |
252 | 3.任务A的低层次特征可以帮助B的学习
253 |
254 | 如果你尝试优化任务𝐵的性能,通常这个任务数据相对较少,例如,在放射科中你知道很难收集很多𝑋射线扫描图来搭建一个性能良好的放射科诊断系统,所以在这种情况下,你可能会找一个相关但不同的任务,如图像识别,其中你可能用 1 百万张图片训练过了,并从中学到很多低层次特征,所以那也许能帮助网络在任务𝐵在放射科任务上做得更好,尽管任务𝐵没有这么多数据。
255 |
256 |
257 |
258 | ### 9.8 多任务学习
259 |
260 | #### **9.8.1 定义**
261 |
262 | 让单个神经网络同时做几个任务,并且这里每个任务都能帮到其他所有任务。
263 |
264 | #### **9.8.2 举例**
265 |
266 | 假设你在研发无人驾驶车辆,那么你的无人驾驶车可能需要同时检测不同的物体,比如检测行人、车辆、停车标志,还有交通灯各种其他东西。
267 |
268 | 如果这是输入图像$𝑥^{(𝑖)}$,那么这里不再是一个标签 $y^{(𝑖)}$,而是有 4 个标签。在这个例子中,没有行人,有一辆车,有一个停车标志,没有交通灯。然后如果你尝试检测其他物体,也许 $y^{(𝑖)}$的维数会更高,现在我们就先用 4 个,所以 $y^{(𝑖)}$是个 4×1 向量。如果你从整体来看这个训练集标签和以前类似,我们将训练集的标签水平堆叠起来,像这样$y^{(1)}$一直到$y^{(m)}$:
269 | $$
270 | Y=\left[\begin{array}{ccccc}| & | & | & \ldots & | \\ y^{(1)} & y^{(2)} & y^{(3)} & \ldots & y^{(m)} \\ | & | & | & \ldots & |\end{array}\right]
271 | $$
272 | 不过现在$y^{(𝑖)}$是 4×1 向量,所以这些都是竖向的列向量,所以这个矩阵$𝑌$现在变成4 × 𝑚矩阵。而之前,当$𝑦$是单实数时,这就是1 × 𝑚矩阵。
273 |
274 | 
275 |
276 | 训练一个神经网络,来预测这些𝑦值,你就得到这样的神经网络,输入$𝑥$,现在输出是一个四维向量$𝑦$。请注意,这里输出我画了四个节点,所以第一个节点就是我们想预测图中有没有行人,然后第二个输出节点预测的是有没有车,第三个节点预测有没有停车标志,第四个节点预测有没有交通灯,所以这里$\hat{y}$是四维的。
277 |
278 | 要训练这个神经网络,你现在需要定义神经网络的损失函数,对于一个输出$\hat{y}$,是个4维向量,对于整个训练集的平均损失:
279 | $$
280 | \frac{1}{m} \sum_{i=1}^{m} \sum_{j=1}^{4} L\left(\hat{y}_{j}^{(i)}, y_{j}^{(i)}\right)
281 | $$
282 |
283 |
284 | $\sum_{j=1}^{4} L\left(\hat{y}_{j}^{(i)}, y_{j}^{(i)}\right)$是单个预测的损失,即对四个分量的求和,行人、车、停车标志、交通灯。$L$指的是logistic损失:
285 | $$
286 | L\left(\hat{y}_{j}^{(i)}, y_{j}^{(i)}\right)=-y_{j}^{(i)} \log \hat{y}_{j}^{(i)}-\left(1-y_{j}^{(i)}\right) \log \left(1-\hat{y}_{j}^{(i)}\right)
287 | $$
288 | 整个训练集的平均损失和之前分类猫的例子主要区别在于,现在你要对$𝑗 = 1$到$4$求和,这与 **softmax** 回归的主要区别在于,**softmax** 将单个标签分配给单个样本。
289 |
290 | 在这个场合,一张图可以有多个标签。如果你训练了一个神经网络,试图最小化这个成本函数,你做的就是多任务学习。因为你现在做的是建立单个神经网络,观察每张图,然后解决四个问题,系统试图告诉你,每张图里面有没有这四个物体。另外你也可以训练四个不同的神经网络,而不是训练一个网络做四件事情。但**神经网络一些早期特征,在识别不同物体时都会用到**,然后你发现,训练一个神经网络做四件事情会比训练四个完全独立的神经网络分别做四件事性能要更好,这就是多任务学习的力量。
291 |
292 |
122 |
123 | 特点:训练-验证集和训练集来自同一分布,验证集和测试集来自同一分布。
124 |
125 | 训练-验证集并不参加训练集对模型的训练,而是和验证集参加反向传播。
126 |
127 | 训练-验证集同时也会进行误差计算,叫做训练-验证集上的误差。
128 |
129 | #### 9.5.3 不匹配数据划分下偏差、方差的判断
130 |
131 | 在引入训练-验证集之后,我们通过对训练-验证集的误差值和训练误差以及验证误差三者相结合进行判断,进而得出方差大小或者不同分布对结果影响的结论,当训练误差和训练-验证集误差相差较大时,说明方差较大,当训练-验证集误差和验证误差相差较大时,说明不同分布对结果影响较大,下面将用例子的形式进行判断。
132 |
133 | 对于偏差问题,仍然可以按照以前的方法进行判断。
134 |
135 | 不同分布对结果影响和方差较大问题是可以同时存在的。
136 |
137 | (1)训练误差:1% 训练-验证集误差:9% 验证误差:10%
138 |
139 | 训练误差和训练-验证集误差相差较大,方差较大,训练-验证集误差和验证误差相差较小,不同分布对结果影响较小。
140 |
141 | (2)训练误差:1% 训练-验证集误差:1.5% 验证误差:10%
142 |
143 | 训练误差和训练-验证集误差相差较小,方差较小,训练-验证集误差和验证误差相差较大,不同分布对结果影响较大。
144 |
145 | (3)训练误差:10% 训练-验证集误差:11% 验证误差:20%
146 |
147 | 训练误差和训练-验证集误差相差较大,方差较大,训练-验证集误差和验证误差相差较大,不同分布对结果影响较大。
148 |
149 | (4)训练误差:7% 训练-验证集误差:10% 验证误差:6%
150 |
151 | 出现这种和前三种都不同的情况说明,验证集的识别比训练集和训练-验证集这同一分布的数据的识别更加容易。
152 |
153 |
154 |
155 | **对方差,偏差,数据不匹配和过拟合的判断的总结:**
156 |
157 | (1)偏差:通过比较最优误差(人类判断误差)和训练误差大小来判断,两者相差越大,偏差越大。
158 |
159 | (2)方差:通过比较训练-验证集误差和训练误差大小来判断,两者相差越大,方差越大。
160 |
161 | (3)数据不匹配:通过比较训练-验证集误差和验证误差大小来判断,两者相差越大,数据越不匹配。
162 |
163 | (4)过拟合:通过比较验证误差和测试误差大小来判断,两者相差越大,模型就越过拟合。
164 |
165 |
166 |
167 | 对于降低方差和偏差的方法在第二门课第一周笔记有具体的讲解。
168 |
169 |
170 |
171 |
172 |
173 |
174 |
175 |
176 |
177 | ### 9.6 处理数据不匹配问题
178 |
179 | **数据不匹配问题**:训练集和开发/测试集来自不同的分布。
180 |
181 | #### 9.6.1 处理方法
182 |
183 | - 做错误分析,尝试了解训练集和开发/测试集的具体差异(比如有无噪音)。为避免对测试集过拟合,应该人工看开发集而不是测试集。
184 | - 把训练数据变得更像开发集(如人工数据合成),或收集更多类似你的开发集和测试集的数据。
185 |
186 | **人工数据合成**:
187 |
188 | 通过对不同类型的数据进行合成,产生需要使用的目的数据。
189 |
190 | 同时人工数据合成也存在问题,在合成数据时,如果选择某类数据时只使用了一小部分进行合成,也就是这类数据类型的子集,从整体的角度来看,这个子集的数据作为样本会导致过拟合的情况出现,也就是过于拟合这个子集数据的特点。而对于这个子集外的同类数据识别效果差。
191 |
192 | - 举例一:
193 |
194 | 
195 |
196 | 建立**语音识别系统**时,在需要解决汽车噪音问题情况,没有那么多实际再汽车背景噪音下录得的音频。这是可以人工合成数据。假设录制了大量清晰的音频,不带车辆背景噪音的音频后,你可以收集一段这样的汽车噪音。然后将两个音频片段放到一起,就可以合成出带有汽车噪声的语音音频。这是一个相对简单的音频合成例子。在实践中,你可能会合成其他音频效果,比如混响,就是声音从汽车内壁上反弹叠加的效果。
197 |
198 | 通过人工数据合成,你可以快速制造更多的训练数据,就像真的在车里录的那样,那就不需要花时间实际出去收集数据,比如说在实际行驶中的车子,录下上万小时的音频。所以,如果错误分析显示你应该尝试让你的数据听起来更像在车里录的,那么人工合成那种音频,然后喂给你的机器学习算法。
199 |
200 | **潜在问题**:
201 |
202 | 比如说,你在安静的背景里录得10,000 小时音频数据,然后,比如说,你只录了一小时车辆背景噪音,那么,你可以这么做,将这 1 小时汽车噪音回放 10,000 次,并叠加到在安静的背景下录得的 10,000 小时数据。如果你这么做了,人听起来这个音频没什么问题。但是有可能你的学习算法对这1 小时汽车噪音过拟合。
203 |
204 | - 举例二:
205 |
206 | 
207 |
208 | 假设你在研发无人驾驶汽车,你可能希望检测出这样的车,然后用框包住它,可以用计算机合成图像来模拟成千上万的车辆。
209 |
210 | **潜在问题:**
211 |
212 | 如果你只合成这些车中很小的子集,对于人眼来说也许这样合成图像没什么问题,但你的学习算法可能会对合成的这一个小子集过拟合。特别是很多人都独立提出了一个想法,一旦你找到一个电脑游戏,里面车辆渲染的画面很逼真,那么就可以截图,得到数量巨大的汽车图片数据集。事实证明,如果你仔细观察一个视频游戏,如果这个游戏只有 20 辆独立的车。因为你是在游戏里开车,你只看到这 20 辆车,这个模拟看起来相当逼真。但现实世界里车辆的设计可不只 20 种,如果你用着 20 量独特的车合成的照片去训练系统,那么你的神经网络很可能对这 20 辆车过拟合,但人类很难分辨出来。即使这些图像看起来很逼真,你可能真的只用了所有可能出现的车辆的很小的子集。
213 |
214 | - 故使用人工数据合成时,一定要谨慎,要记住你有可能从所有可能性的空间只选了很小一部分去模拟数据。
215 |
216 |
217 |
218 | ### 9.7 迁移学习
219 |
220 | #### **9.7.1 定义**
221 |
222 | 将一个问题上训练好的模型通过简单的调整使其适用于一个新的问题。
223 |
224 | #### **9.7.2 举例一**
225 |
226 | 假设你已经训练好一个图像识别神经网络,所以你首先用一个神经网络,并在$(𝑥, 𝑦)$对上训练,其中$𝑥$是图像,$𝑦$是某些对象的判断,图像是猫、狗、鸟或其他东西。如果你把这个神经网络拿来,然后让它适应或者说迁移,在不同任务中学到的知识,比如放射科诊断,就是说阅读𝑋射线扫描图。你可以做的是把神经网络最后的输出层拿走,就把它删掉,还有进入到最后一层的权重删掉,然后为最后一层重新赋予随机权重,然后让它在放射诊断数据上训练。
227 |
228 | 
229 |
230 | 具体来说,在第一阶段训练过程中,当你进行图像识别任务时时,你可以训练神经网络的所有常用参数,所有的权重,所有的层,然后你就得到了一个能够做图像识别预测的网络。在训练了这个神经网络后,要实现迁移学习,你现在要做的是,把数据集换成新的$(𝑥, 𝑦)$对,现在这些变成放射科图像,而$𝑦$是你想要预测的诊断,你要做的是初始化最后一层的权重,让我们称之为$w^{[L]}$和$b^{[L]}$随机初始化。
231 |
232 | 如果你重新训练神经网络中的所有参数,那么这个在图像识别数据的初期训练阶段,有时称为**预训练**(pre -training),因为你在用图像识别数据去预先初始化,或者预训练神经网络的权重。然后,如果你以后更新所有权重,然后在放射科数据上训练,有时这个过程叫**微调**(fine tuning)
233 |
234 | #### **9.7.3 举例二**
235 |
236 | 
237 |
238 | 假设你已经训练出一个语音识别系统,现在$𝑥$是音频或音频片段输入,而$𝑦$是听写文本,所以你已经训练了语音识别系统,让它输出听写文本。现在我们说你想搭建一个“唤醒词”或“触发词”检测系统,所谓唤醒词或触发词就是我们说的一句话,可以唤醒家里的语音控制设备,比如你说“Alexa”可以唤醒一个亚马逊 Echo设备,或用“OK Google”来唤醒 Google 设备,用"Hey Siri"来唤醒苹果设备,用"你好百度"唤醒一个百度设备。要做到这点,你可能需要去掉神经网络的最后一层,然后加入新的输出节点,但有时你可以不只加入一个新节点,或者甚至往你的神经网络加入几个新层,然后把唤醒词检测问题的标签$𝑦$喂进去训练。再次,这取决于你有多少数据,你可能只需要重新训练网络的新层,也许你需要重新训练神经网络中更多的层。
239 |
240 | #### **9.7.4 迁移学习有效的原因**
241 |
242 | 在例一中我们把图像识别中学到的知识应用或迁移到放射科诊断上来。有很多低层次特征,比如说边缘检测、曲线检测、阳性对象检测,**从非常大的图像识别数据库中习得这些能力可能有助于你的学习算法在放射科诊断中做得更好**,算法学到了很多结构信息,图像形状的信息,其中一些知识可能会很用,所以学会了图像识别,它就可能学到足够多的信息,可以了解不同图像的组成部分是怎样的,学到线条、点、曲线这些知识,也许对象的一小部分,这些知识有可能帮助你的放射科诊断网络学习更快一些,或者需要更少的学习数据。
243 |
244 | 对于第二个例子语音识别,也许你已经用 10,000 小时数据训练过你的语言识别系统,所以你从这10,000 小时数据学到了很多人类声音的特征,这数据量其实很多了。但对于触发字检测,也许你只有 1 小时数据,所以这数据太小,不能用来拟合很多参数。所以在这种情况下,预先学到很多人类声音的特征人类语言的组成部分等等知识,可以帮你建立一个很好的唤醒字检测器,即使你的数据集相对较小。
245 |
246 | #### **9.7.5 迁移学习起作用的场合**
247 |
248 | 1.以任务A迁移到任务B为例,任务A和任务B都有同样的输入x时,如输入都是图片
249 |
250 | 2.任务A的数据比任务B的多得多,任务A的数据才会对B有帮助。
251 |
252 | 3.任务A的低层次特征可以帮助B的学习
253 |
254 | 如果你尝试优化任务𝐵的性能,通常这个任务数据相对较少,例如,在放射科中你知道很难收集很多𝑋射线扫描图来搭建一个性能良好的放射科诊断系统,所以在这种情况下,你可能会找一个相关但不同的任务,如图像识别,其中你可能用 1 百万张图片训练过了,并从中学到很多低层次特征,所以那也许能帮助网络在任务𝐵在放射科任务上做得更好,尽管任务𝐵没有这么多数据。
255 |
256 |
257 |
258 | ### 9.8 多任务学习
259 |
260 | #### **9.8.1 定义**
261 |
262 | 让单个神经网络同时做几个任务,并且这里每个任务都能帮到其他所有任务。
263 |
264 | #### **9.8.2 举例**
265 |
266 | 假设你在研发无人驾驶车辆,那么你的无人驾驶车可能需要同时检测不同的物体,比如检测行人、车辆、停车标志,还有交通灯各种其他东西。
267 |
268 | 如果这是输入图像$𝑥^{(𝑖)}$,那么这里不再是一个标签 $y^{(𝑖)}$,而是有 4 个标签。在这个例子中,没有行人,有一辆车,有一个停车标志,没有交通灯。然后如果你尝试检测其他物体,也许 $y^{(𝑖)}$的维数会更高,现在我们就先用 4 个,所以 $y^{(𝑖)}$是个 4×1 向量。如果你从整体来看这个训练集标签和以前类似,我们将训练集的标签水平堆叠起来,像这样$y^{(1)}$一直到$y^{(m)}$:
269 | $$
270 | Y=\left[\begin{array}{ccccc}| & | & | & \ldots & | \\ y^{(1)} & y^{(2)} & y^{(3)} & \ldots & y^{(m)} \\ | & | & | & \ldots & |\end{array}\right]
271 | $$
272 | 不过现在$y^{(𝑖)}$是 4×1 向量,所以这些都是竖向的列向量,所以这个矩阵$𝑌$现在变成4 × 𝑚矩阵。而之前,当$𝑦$是单实数时,这就是1 × 𝑚矩阵。
273 |
274 | 
275 |
276 | 训练一个神经网络,来预测这些𝑦值,你就得到这样的神经网络,输入$𝑥$,现在输出是一个四维向量$𝑦$。请注意,这里输出我画了四个节点,所以第一个节点就是我们想预测图中有没有行人,然后第二个输出节点预测的是有没有车,第三个节点预测有没有停车标志,第四个节点预测有没有交通灯,所以这里$\hat{y}$是四维的。
277 |
278 | 要训练这个神经网络,你现在需要定义神经网络的损失函数,对于一个输出$\hat{y}$,是个4维向量,对于整个训练集的平均损失:
279 | $$
280 | \frac{1}{m} \sum_{i=1}^{m} \sum_{j=1}^{4} L\left(\hat{y}_{j}^{(i)}, y_{j}^{(i)}\right)
281 | $$
282 |
283 |
284 | $\sum_{j=1}^{4} L\left(\hat{y}_{j}^{(i)}, y_{j}^{(i)}\right)$是单个预测的损失,即对四个分量的求和,行人、车、停车标志、交通灯。$L$指的是logistic损失:
285 | $$
286 | L\left(\hat{y}_{j}^{(i)}, y_{j}^{(i)}\right)=-y_{j}^{(i)} \log \hat{y}_{j}^{(i)}-\left(1-y_{j}^{(i)}\right) \log \left(1-\hat{y}_{j}^{(i)}\right)
287 | $$
288 | 整个训练集的平均损失和之前分类猫的例子主要区别在于,现在你要对$𝑗 = 1$到$4$求和,这与 **softmax** 回归的主要区别在于,**softmax** 将单个标签分配给单个样本。
289 |
290 | 在这个场合,一张图可以有多个标签。如果你训练了一个神经网络,试图最小化这个成本函数,你做的就是多任务学习。因为你现在做的是建立单个神经网络,观察每张图,然后解决四个问题,系统试图告诉你,每张图里面有没有这四个物体。另外你也可以训练四个不同的神经网络,而不是训练一个网络做四件事情。但**神经网络一些早期特征,在识别不同物体时都会用到**,然后你发现,训练一个神经网络做四件事情会比训练四个完全独立的神经网络分别做四件事性能要更好,这就是多任务学习的力量。
291 |
292 |  293 |
294 | 多任务学习也**可以处理图像只有部分物体被标记的情况**。所以第一个训练样本,我们说有人,给数据贴标签的人告诉你里面有一个行人,没有车,但他们没有标记是否有停车标志,或者是否有交通灯。也许第二个例子中,有行人,有车。但是,当标记人看着那张图片时,他们没有加标签,没有标记是否有停车标志,是否有交通灯等等。也许有些样本都有标记,但也许有些样本他们只标记了有没有车,然后还有一些是问号。
295 |
296 | 即使是这样的数据集,你也可以在上面训练算法,同时做四个任务,即使一些图像只有一小部分标签,其他是问号或者不管是什么。然后你训练算法的方式,即使这里有些标签是问号,或者没有标记,这就是对𝑗从 1 到 4 求和,你就只对带 0 和 1 标签的$𝑗$值求和,所以当有问号的时候,你就在求和时忽略那个项,这样只对有标签的值求和,于是你就能利用这样的数据集。
297 |
298 | #### **9.8.3 和迁移学习的不同**
299 |
300 | 多任务学习是一种迁移学习的方法,但不同于其他种类的迁移学习,多任务学习并不注重源领域和未知领域的知识迁移,它主要利用域之间相似的知识信息,提升特定任务的学习效果,注重领域知识的共享性。两者特点的不同决定了学习过程的差别,迁移学习的目的是通过从源任务中转移知识来提升目标任务中的性能,而多任务学习则试图同时学习目标任务和源任务。
301 |
302 | 参考文章:张钰,刘建伟,左信.多任务学习[J].计算机学报,2020,43(07):1340-1378.
303 |
304 | #### **9.8.4 多任务学习使用场合**
305 |
306 | - **你训练的一组任务,可以共用低层次的特征。**
307 |
308 | 对于无人驾驶的例子,同时识别交通灯、汽车和行人是有道理的,这些物体有相似的特征,也许能帮你识别停车标志,因为这些都是道路上的特征。
309 |
310 | - **每个任务的数据量很接近。**
311 |
312 | 这个准则不一定对。
313 |
314 | 在多任务学习中,你通常有更多任务而不仅仅是两个,所以也许你有,以前我们有 4个任务,但比如说你要完成 100 个任务,而你要做多任务学习,尝试同时识别 100 种不同类型的物体。你可能会发现,每个任务大概有 1000 个样本。所以如果你专注加强单个任务的性能,比如我们专注加强第 100 个任务的表现,我们用𝐴100表示,如果你试图单独去做这个最后的任务,你只有 1000 个样本去训练这个任务,这是 100 项任务之一,而通过在其他99 项任务的训练,这些加起来可以一共有 99000 个样本,这可能大幅提升算法性能,可以提供很多知识来增强这个任务的性能。不然对于任务𝐴100,只有 1000 个样本的训练集,效果可能会很差。如果有对称性,这其他 99 个任务,也许能提供一些数据或提供一些知识来帮到这 100 个任务中的每一个任务。
315 |
316 | 所以第二点不是绝对正确的准则,但我通常会看的是如果你专注于单项任务,如果想要从多任务学习得到很大性能提升,那么其他任务加起来必须要有比单个任务大得多的数据量。要满足这个条件,其中一种方法是,比如右边这个例子这样,或者如果每个任务中的数据量很相近,但关键在于,如果对于单个任务你已经有 1000个样本了,那么对于所有其他任务,你最好有超过 1000 个样本,这样其他任务的知识才能帮你改善这个任务的性能。
317 |
318 | - **当你可以训练一个足够大的神经网络,同时做好所有工作。**
319 |
320 | 多任务学习的替代方法是为每个任务训练一个单独的神经网络。所以不是训练单个神经网络同时处理行人、汽车、停车标志和交通灯检测。你可以训练一个用于行人检测的神经网络,一个用于汽车检测的神经网络,一个用于停车标志检测的神经网络和一个用于交通信号灯检测的神经网络。
321 |
322 | 多任务学习会降低性能的唯一情况,和训练单个神经网络相比性能更低的情况就是你的神经网络还不够大。但如果你可以训练一个足够大的神经网络,那么多任务学习肯定不会或者很少会降低性能,我们都希望它可以提升性能,比单独训练神经网络来单独完成各个任务性能要更好。
323 |
324 |
325 |
326 | (Life long learning)
327 |
328 |
329 |
330 | ### 9.9 什么是端到端的深入学习
331 |
332 | #### 9.9.1 端到端学习定义
333 |
334 | 以往对于一次任务可能需要分解成多个阶段的学习(流水线),端到端的深度学习用单个神经网络替换多个学习过程,只需要把训练集拿过来,直接学到$x$和$y$之间的函数映射,绕过了其中很多步骤。
335 | 下图以语音识别为例,进行两者间的对比。
336 |
337 | 
338 |
339 | 端到端的深入学习需要大量数据,如果数据量较小,以往的流水线可能会好于端到端的深度学习。
340 |
341 | #### 9.9.2 端到端学习应用场景
342 |
343 | - 例子一:在人脸识别任务中,端到端的深度学习并不能很好的完成任务,而以往的分步识别效果更佳,先识别人脸位置,随后和数据库进行人脸比对,因为分解到两个任务后可以对每个任务进行有效处理。
344 |
345 | - 例子二:机器翻译,端到端深度学习在机器翻译领域非常好用,可以收集大量成对的大数据集,如原文句子和对应的翻译。
346 |
347 | - 例子三:从手部X射线图估计孩子年龄,拆分任务效果更好,分析知道不同骨骼的长度后,可以查表查到儿童手中骨头的平均长度。而端到端的深度学习并未取得很好的效果,因为没有足够的数据来用端到端的方式来训练这个任务。
348 |
349 |
350 |
351 |
352 | ### 9.10 是否要使用端到端学习
353 |
354 | 当决定是否使用端对端方法时,可以参考端到端深度学习的一些优缺点来进行判断。
355 |
356 | #### 9.10.1 端对端方法的优点
357 |
358 | 1. 可以让数据说话,挖掘客观信息,不用引入人类的成见。
359 |
360 | 例如,在语音识别领域,人类学习的音位概念更像是是人类语言学家生造出来的。而学习算法不会强迫以音位为单位思考,它能够学习的任意的表示方式。
361 |
362 | 2. 需要手工设计的组件很少,也许能够简化设计工作流程。我们只需要把训练集拿过来,直接学到$x$和$y$之间的函数映射,绕过了其中很多步骤。
363 |
364 | #### 9.10.2 端对端方法的缺点
365 |
366 | 1. 需要大量的数据。
367 |
368 | 比如人脸识别,需要收集很多数据用来分辨图像中的人脸。但是对于整个端到端任务,可能只有更少的数据可用。
369 |
370 | 2. 排除了一些可能有用的人工组件。因为直接从系统的一端学习到系统的另一端,舍弃了人类对这个问题的很多认识。
371 |
372 | 比如,把手的X射线照片直接映射到孩子的年龄,可能需要很复杂的函数,如果用纯端到端方法,也需要大量数据去学习。
373 |
374 | **可以看出,决定是否要使用端到端深度学习的主要因素是是否有足够的数据来训练。**复杂问题有时候并不适合端到端,人类的意见还是很有必要的,手工设计的组件往往在训练集更小的时候帮助更大。
--------------------------------------------------------------------------------
/README.md:
--------------------------------------------------------------------------------
1 | # Deep-Learning-Tutorial
2 | 介绍一些有关深度学习的基础知识点,主要内容来自吴恩达老师的机器学习课程
3 | 后面会不定期更新
4 |
5 |
--------------------------------------------------------------------------------
293 |
294 | 多任务学习也**可以处理图像只有部分物体被标记的情况**。所以第一个训练样本,我们说有人,给数据贴标签的人告诉你里面有一个行人,没有车,但他们没有标记是否有停车标志,或者是否有交通灯。也许第二个例子中,有行人,有车。但是,当标记人看着那张图片时,他们没有加标签,没有标记是否有停车标志,是否有交通灯等等。也许有些样本都有标记,但也许有些样本他们只标记了有没有车,然后还有一些是问号。
295 |
296 | 即使是这样的数据集,你也可以在上面训练算法,同时做四个任务,即使一些图像只有一小部分标签,其他是问号或者不管是什么。然后你训练算法的方式,即使这里有些标签是问号,或者没有标记,这就是对𝑗从 1 到 4 求和,你就只对带 0 和 1 标签的$𝑗$值求和,所以当有问号的时候,你就在求和时忽略那个项,这样只对有标签的值求和,于是你就能利用这样的数据集。
297 |
298 | #### **9.8.3 和迁移学习的不同**
299 |
300 | 多任务学习是一种迁移学习的方法,但不同于其他种类的迁移学习,多任务学习并不注重源领域和未知领域的知识迁移,它主要利用域之间相似的知识信息,提升特定任务的学习效果,注重领域知识的共享性。两者特点的不同决定了学习过程的差别,迁移学习的目的是通过从源任务中转移知识来提升目标任务中的性能,而多任务学习则试图同时学习目标任务和源任务。
301 |
302 | 参考文章:张钰,刘建伟,左信.多任务学习[J].计算机学报,2020,43(07):1340-1378.
303 |
304 | #### **9.8.4 多任务学习使用场合**
305 |
306 | - **你训练的一组任务,可以共用低层次的特征。**
307 |
308 | 对于无人驾驶的例子,同时识别交通灯、汽车和行人是有道理的,这些物体有相似的特征,也许能帮你识别停车标志,因为这些都是道路上的特征。
309 |
310 | - **每个任务的数据量很接近。**
311 |
312 | 这个准则不一定对。
313 |
314 | 在多任务学习中,你通常有更多任务而不仅仅是两个,所以也许你有,以前我们有 4个任务,但比如说你要完成 100 个任务,而你要做多任务学习,尝试同时识别 100 种不同类型的物体。你可能会发现,每个任务大概有 1000 个样本。所以如果你专注加强单个任务的性能,比如我们专注加强第 100 个任务的表现,我们用𝐴100表示,如果你试图单独去做这个最后的任务,你只有 1000 个样本去训练这个任务,这是 100 项任务之一,而通过在其他99 项任务的训练,这些加起来可以一共有 99000 个样本,这可能大幅提升算法性能,可以提供很多知识来增强这个任务的性能。不然对于任务𝐴100,只有 1000 个样本的训练集,效果可能会很差。如果有对称性,这其他 99 个任务,也许能提供一些数据或提供一些知识来帮到这 100 个任务中的每一个任务。
315 |
316 | 所以第二点不是绝对正确的准则,但我通常会看的是如果你专注于单项任务,如果想要从多任务学习得到很大性能提升,那么其他任务加起来必须要有比单个任务大得多的数据量。要满足这个条件,其中一种方法是,比如右边这个例子这样,或者如果每个任务中的数据量很相近,但关键在于,如果对于单个任务你已经有 1000个样本了,那么对于所有其他任务,你最好有超过 1000 个样本,这样其他任务的知识才能帮你改善这个任务的性能。
317 |
318 | - **当你可以训练一个足够大的神经网络,同时做好所有工作。**
319 |
320 | 多任务学习的替代方法是为每个任务训练一个单独的神经网络。所以不是训练单个神经网络同时处理行人、汽车、停车标志和交通灯检测。你可以训练一个用于行人检测的神经网络,一个用于汽车检测的神经网络,一个用于停车标志检测的神经网络和一个用于交通信号灯检测的神经网络。
321 |
322 | 多任务学习会降低性能的唯一情况,和训练单个神经网络相比性能更低的情况就是你的神经网络还不够大。但如果你可以训练一个足够大的神经网络,那么多任务学习肯定不会或者很少会降低性能,我们都希望它可以提升性能,比单独训练神经网络来单独完成各个任务性能要更好。
323 |
324 |
325 |
326 | (Life long learning)
327 |
328 |
329 |
330 | ### 9.9 什么是端到端的深入学习
331 |
332 | #### 9.9.1 端到端学习定义
333 |
334 | 以往对于一次任务可能需要分解成多个阶段的学习(流水线),端到端的深度学习用单个神经网络替换多个学习过程,只需要把训练集拿过来,直接学到$x$和$y$之间的函数映射,绕过了其中很多步骤。
335 | 下图以语音识别为例,进行两者间的对比。
336 |
337 | 
338 |
339 | 端到端的深入学习需要大量数据,如果数据量较小,以往的流水线可能会好于端到端的深度学习。
340 |
341 | #### 9.9.2 端到端学习应用场景
342 |
343 | - 例子一:在人脸识别任务中,端到端的深度学习并不能很好的完成任务,而以往的分步识别效果更佳,先识别人脸位置,随后和数据库进行人脸比对,因为分解到两个任务后可以对每个任务进行有效处理。
344 |
345 | - 例子二:机器翻译,端到端深度学习在机器翻译领域非常好用,可以收集大量成对的大数据集,如原文句子和对应的翻译。
346 |
347 | - 例子三:从手部X射线图估计孩子年龄,拆分任务效果更好,分析知道不同骨骼的长度后,可以查表查到儿童手中骨头的平均长度。而端到端的深度学习并未取得很好的效果,因为没有足够的数据来用端到端的方式来训练这个任务。
348 |
349 |
350 |
351 |
352 | ### 9.10 是否要使用端到端学习
353 |
354 | 当决定是否使用端对端方法时,可以参考端到端深度学习的一些优缺点来进行判断。
355 |
356 | #### 9.10.1 端对端方法的优点
357 |
358 | 1. 可以让数据说话,挖掘客观信息,不用引入人类的成见。
359 |
360 | 例如,在语音识别领域,人类学习的音位概念更像是是人类语言学家生造出来的。而学习算法不会强迫以音位为单位思考,它能够学习的任意的表示方式。
361 |
362 | 2. 需要手工设计的组件很少,也许能够简化设计工作流程。我们只需要把训练集拿过来,直接学到$x$和$y$之间的函数映射,绕过了其中很多步骤。
363 |
364 | #### 9.10.2 端对端方法的缺点
365 |
366 | 1. 需要大量的数据。
367 |
368 | 比如人脸识别,需要收集很多数据用来分辨图像中的人脸。但是对于整个端到端任务,可能只有更少的数据可用。
369 |
370 | 2. 排除了一些可能有用的人工组件。因为直接从系统的一端学习到系统的另一端,舍弃了人类对这个问题的很多认识。
371 |
372 | 比如,把手的X射线照片直接映射到孩子的年龄,可能需要很复杂的函数,如果用纯端到端方法,也需要大量数据去学习。
373 |
374 | **可以看出,决定是否要使用端到端深度学习的主要因素是是否有足够的数据来训练。**复杂问题有时候并不适合端到端,人类的意见还是很有必要的,手工设计的组件往往在训练集更小的时候帮助更大。
--------------------------------------------------------------------------------
/README.md:
--------------------------------------------------------------------------------
1 | # Deep-Learning-Tutorial
2 | 介绍一些有关深度学习的基础知识点,主要内容来自吴恩达老师的机器学习课程
3 | 后面会不定期更新
4 |
5 |
--------------------------------------------------------------------------------
 249 |
250 | ⌊ ⌋这是向下取整的符号,这也叫做对𝑧进行地板除(floor),这意味着𝑧向下取整到最近的整数。这个原则实现的方式是,你只在蓝框完全包括在图像或填充完的图像内部时,才对它进行运算。如果有任意一个蓝框移动到了外面,那你就不要进行相乘操作,这是一个惯例。
251 |
252 | 可以选择所有的数使结果是整数是挺不错的,尽管一些时候,你不必这样做,只要向下取整也就可以了。你也可以自己选择一些𝑛,𝑓,𝑝和𝑠的值来验证这个输出尺寸的公式是对的。
253 |
254 | **卷积(concolution)与互相关(cross-correlation)**
255 |
256 | 如果你看的是一本典型的数学教科书,那么卷积的定义是做元素乘积求和,实际上还有一个步骤是你首先要做的,也就是在把这个 6×6 的矩阵和 3×3 的过滤器卷积之前,首先你将 3×3 的过滤器沿水平和垂直轴翻转,所以
257 | $$
258 | \left[\begin{array}{ccc}
259 | 3 & 4 & 5 \\
260 | 1 & 0 & 2 \\
261 | -1 & 9 & 7
262 | \end{array}\right] \text { 变为 }\left[\begin{array}{ccc}
263 | 7 & 2 & 5 \\
264 | 9 & 0 & 4 \\
265 | -1 & 1 & 3
266 | \end{array}\right]
267 | $$
268 | 这相当于将 3×3 的过滤器做了个**镜像**,在水平和垂直轴上。然后再把这个翻转后的矩阵复制到这里(左边的图像矩阵),你要把这个翻转矩阵的元素相乘来计算输出的 4×4 矩阵左上角的元素,如图所示。然后取这 9 个数字,把它们平移一个位置,再平移一格,以此类推。
269 |
270 |
249 |
250 | ⌊ ⌋这是向下取整的符号,这也叫做对𝑧进行地板除(floor),这意味着𝑧向下取整到最近的整数。这个原则实现的方式是,你只在蓝框完全包括在图像或填充完的图像内部时,才对它进行运算。如果有任意一个蓝框移动到了外面,那你就不要进行相乘操作,这是一个惯例。
251 |
252 | 可以选择所有的数使结果是整数是挺不错的,尽管一些时候,你不必这样做,只要向下取整也就可以了。你也可以自己选择一些𝑛,𝑓,𝑝和𝑠的值来验证这个输出尺寸的公式是对的。
253 |
254 | **卷积(concolution)与互相关(cross-correlation)**
255 |
256 | 如果你看的是一本典型的数学教科书,那么卷积的定义是做元素乘积求和,实际上还有一个步骤是你首先要做的,也就是在把这个 6×6 的矩阵和 3×3 的过滤器卷积之前,首先你将 3×3 的过滤器沿水平和垂直轴翻转,所以
257 | $$
258 | \left[\begin{array}{ccc}
259 | 3 & 4 & 5 \\
260 | 1 & 0 & 2 \\
261 | -1 & 9 & 7
262 | \end{array}\right] \text { 变为 }\left[\begin{array}{ccc}
263 | 7 & 2 & 5 \\
264 | 9 & 0 & 4 \\
265 | -1 & 1 & 3
266 | \end{array}\right]
267 | $$
268 | 这相当于将 3×3 的过滤器做了个**镜像**,在水平和垂直轴上。然后再把这个翻转后的矩阵复制到这里(左边的图像矩阵),你要把这个翻转矩阵的元素相乘来计算输出的 4×4 矩阵左上角的元素,如图所示。然后取这 9 个数字,把它们平移一个位置,再平移一格,以此类推。
269 |
270 |  271 |
272 | 但在深度学习文献中,定义卷积运算时跳过了这个镜像操作。前面我们实际上做的,有时被称为互相关而不是卷积。
273 |
274 | 总结来说,按照机器学习的惯例,我们通常不进行翻转操作。从技术上说,这个操作可能叫做互相关更好。但在大部分的深度学习文献中都把它叫做卷积运算。
275 |
276 | ### 10.6 三维卷积
277 |
278 | **三维(RGB图像)上的卷积操作**
279 |
280 | 举例,假如你不仅想检测灰度图像的特征,也想检测 RGB 彩色图像的特征。彩色图像如果6×6×3,这里的第一个 6 代表图像高度,第二个 6 代表宽度,这个3 代表颜色通道的数目。你可以把它想象成三个 6×6图像的堆叠。为了检测图像的边缘或者其他的特征,不是把它跟原来的 3×3 的过滤器做卷积,而是跟一个三维的过滤器,它的维度是 3×3×3,这样这个过滤器也有三层,对应红、绿、蓝三个通道。得到的输出会是一个 4×4 的图像,注意是 4×4×1,最后一个数不是 3 了。
281 |
282 | 为了简化这个 3×3×3过滤器的图像,我们不把它画成 3 个矩阵的堆叠,而画成一个三维的立方体。
283 |
284 | 
285 |
286 | **计算过程**:
287 |
288 | 把这个 3×3×3 的过滤器先放到最左上角的位置,这个 3×3×3 的过滤器有 27 个数,27 个参数就是 3 的立方。依次取这 27 个数,然后乘以相应的红绿蓝通道中的数字。先取红色通道的前 9 个数字,然后是绿色通道,然后再是蓝色通道,乘以左边黄色立方体覆盖的对应的 27 个数,然后把这些数都加起来,就得到了输出的第一个数字。如果要计算下一个输出,你把这个立方体滑动一个单位,再与这 27 个数相乘,把它们都加起来,就得到了下一个输出,以此类推。
289 |
290 | 
291 |
292 |
293 |
294 | **作用**:
295 |
296 | 举例:
297 |
298 | - 如果你想检测图像红色通道的边缘,那么你可以将第一个过滤器设为$\left[\begin{array}{rrr}1 & 0 & -1 \\ 1 & 0 & -1 \\ 1 & 0 & -1\end{array}\right]$,和之前一样,而绿色通道全为 0,$\left[\begin{array}{lll}0 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0\end{array}\right]$,蓝色也全为 0。如果你把这三个堆叠在一起形成一个3×3×3的过滤器,那么这就是一个检测垂直边界的过滤器,但只对红色通道有用。
299 | - 或者如果你不关心垂直边界在哪个颜色通道里,那么你可以用一个这样的过滤器,$\left[\begin{array}{ccc}1 & 0 & -1 \\ 1 & 0 & -1 \\ 1 & 0 & -1\end{array}\right],\left[\begin{array}{ccc}1 & 0 & -1 \\ 1 & 0 & -1 \\ 1 & 0 & -1\end{array}\right],\left[\begin{array}{ccc}1 & 0 & -1 \\ 1 & 0 & -1 \\ 1 & 0 & -1\end{array}\right]$,所有三个通道都是这样。所以通过设置第二个过滤器参数,你就有了一个边界检测器,3×3×3 的边界检测器,用来检测任意颜色通道里的边界。参数的选择不同,可以得到不同的特征检测器,所有的都是 3×3×3 的过滤器。
300 |
301 | **同时用多个过滤器**
302 |
303 | 有时候我们会想要同时检测垂直边缘和水平边缘,还有 45°倾斜的边缘,还有 70°倾斜的边缘等等,这是就需要使用多个过滤器。
304 |
305 | 
306 |
307 | 例如我们让这个 6×6×3 的图像和这个 3×3×3 的过滤器卷积,得到 4×4 的输出。(第一个)这可能是一个垂直边界检测器或者是学习检测其他的特征。第二个过滤器可以用橘色来表示,它可以是一个水平边缘检测器。做完卷积,然后把这两个 4×4 的输出堆叠在一起,这样你就都得到了一个4×4×2 的输出立方体。这里的 2 的来源于我们用了两个不同的过滤器。
308 |
309 | **维度总结**
310 |
311 | 如果你有一个$n \times n \times n_{c}$(通道数)的输入图像,上例中就是 6×6×3,这里的$n_{c}$就是通道数目,然后卷积上一个$f \times f \times n_{c}$,这个例子中是 3×3×3,按照惯例,这个(前一个𝑛𝑐)和这个(后一个𝑛𝑐)必须数值相同。然后你就得到了,$(n-f+1)\times(n-f+1) \times n_{c^{\prime}}$这里$n_{c^{\prime}}$其实就是下一层的通道数,它就是你用的过滤器的个数,在我们的例子中,那就是 4×4×2。我写下这个假设时,用的步幅为 1,并且没有 padding。如果你用了不同的步幅或者 padding,那么这个$𝑛 − 𝑓 + 1$数值会变化。
312 | $$
313 | n \times n \times n_{c} \text { * } f \times f \times n_{c} \rightarrow (n-f+1)\times(n-f+1) \times n_{c^{\prime}}
314 | $$
315 | **思考**:为什么卷积核是3\*3channels而不是3\*3\*1在多个通道之间移动?
316 |
317 | 如果使用3\*3\*1的卷积核在多个通道中移动,那意味着每个通道都用同一个过滤器,而且每个过滤器(卷积核)都忽略了隐藏在通道之间的联系和信息,这无疑会降低卷积网络的效果。
318 |
319 | ### 10.7 单层卷积网络
320 |
321 | 
322 |
323 | 相比之前的卷积过程,CNN的单层结构多了激活函数ReLU和偏移量b,与神经网络的单层结构类似,即:
324 |
325 | $Z^{[l]}=W^{[l]} A^{[l-1]}+b$
326 | $A^{[l]}=g^{[l]}\left(Z^{[l]}\right)$
327 |
328 | 其中,卷积运算对应上式中的乘积运算,过滤器组数值对应着权重$W^{[l]}$,激活函数则为ReLU
329 |
330 | 上图中参数$W$的计算:每个过滤器组共有3x3x3=27个参数,两个过滤器组则共包含27x2=54个参数$W$
331 |
332 | 相关符号的总结(设层数为$l$)
333 |
334 | $f^{[l]}=$ filter size
335 | $p^{[l]}=$ padding
336 | $s^{[l]}=$ stride
337 | $n_{c}^{[l]}=$ number of filters
338 | $n_{H}^{[l]}=$ height of input
339 | $n_{W}^{[l]}=$ width of filters
340 |
341 | 输入维度为:
342 |
343 | $n_{H}^{[l-1]} \times n_{W}^{[l-1]} \times n_{c}^{[l-1]}$
344 | 每个滤波器组维度为:
345 |
346 | $f^{[l]} \times f^{[l]} \times n_{c}^{[l-1]}$
347 |
348 | 权重维度为:
349 |
350 | $f^{[l]} \times f^{[l]} \times n_{c}^{[l-1]} \times n_{c}^{[l]}$
351 |
352 | 偏置维度为:
353 |
354 | $ 1 \times 1 \times 1 \times n_{c}^{[l]}$
355 |
356 | 输出维度为 :
357 |
358 | $ n_{H}^{[l]} \times n_{W}^{[l]} \times n_{c}^{[l]}$
359 |
360 | 其中:
361 | $$
362 | \begin{aligned}
363 | n_{H}^{[l]} &=\left\lfloor\frac{n_{H}^{[l-1]}+2 p^{[l]}-f^{[l]}}{s^{[l]}}+1\right\rfloor \\
364 | n_{W}^{[l]} &=\left\lfloor\frac{n_{W}^{[l-1]}+2 p^{[l]}-f^{[l]}}{s^{[l]}}+1\right\rfloor
365 | \end{aligned}
366 | $$
367 | 若有$m$个样本进行向量化运算,则输出的维度为:
368 |
369 | $m \times n_{H}^{[l]} \times n_{W}^{[l]} \times n_{c}^{[l}$
370 |
371 | ### 10.8 简单卷积网络示例
372 |
373 | 
374 |
375 | 如上图,是一个简单的CNN模型,且$a^{[3]}$维度为7 x 7 x 40,若将$a^{[3]}$排成1列,则维度为1960 x 1,再与输出层连接,输出层若为1个神经元,则为二元分类;若为多个神经元,则为多元分类。由此得出预测输出$\hat{y}$。
376 |
377 | 当CNN层数增加时,一般$n_{H}^{[l]}$和$n_{W}^{[l]}$会逐渐减小,而$n_{c}^{[l]}$会逐渐增大。
378 |
379 | CNN有以下三种类型的layer:
380 |
381 | - Convolution(CONV)(最为常见)
382 | - Pooling(POOL)
383 | - Fully connected(FC)
384 |
385 | ### 10.9 池化层
386 |
387 | 池化是一种下采样(downsample)手段,是对信息进行抽象的过程。
388 |
389 | 池化并不只有最大池化Max Pooling一种,不过Max Pooling是最广泛使用的一种。
390 |
391 | #### 10.9.1 最大池化 Max Pooling
392 |
393 | 最大池化指的是在采样区间内用区间内的最大值代表这个区间。
394 |
395 | 
396 |
397 | 和卷积运算一样,池化也有自己的参数:池化大小、步长和Padding。只不过最常用的是2*2大小、步长为2和Valid Padding。下文如没有说明则都是采用这种最大池化。
398 |
399 | #### 10.9.2 其他池化
400 |
401 | * 平均池化:平均池化和最大池化相对应,用该区间的平均值来代表该区间。
402 | * 全局平均池化:和上述池化有点不同,是将一个通道的信息都用该通道的平均值代替。比如输入4\*4\*channels的特征图,输出一个长度为channels的特征向量。该向量每一个值都是对应通道(4*4=16个值)的平均值。通常用在最后一层卷积层后、softmax前。主要作用是代替全连接,降低参数个数。
403 | * ASPP(空洞卷积空间金字塔池化,Atrous Spatial Pyramid Pooling):和传统的池化操作不同,该池化并不降低分辨率(输出特征图的大小),但是同样可以起到对增加感受野的效果(下文介绍感受野)。
404 |
405 | #### 10.9.3 池化的作用
406 |
407 | 在介绍池化的作用前,先介绍一下感受野。
408 |
409 | **感受野 Receptive Field**
410 |
411 | 感受野表示了一个神经元(输出图的一个像素点)与多少个**原始图像**上的像素点有关联。浅层的感受野小,深层的感受野逐渐增大。对于单个神经元,其值只与其感受野有关,与感受野外无关。下图给出在经过两层3\*3的卷积后的神经元的感受野示例。
412 |
413 | 
414 |
415 | 上图还可以发现,两个3\*3的卷积核能够与单个5\*5的卷积核有相同的感受野。但是前者只有2\*3\*3=18个参数,后者有5\*5=25个参数。可见可以通过多层小的卷积核来获得和单个大卷积核的相同效果,同时参数更少。甚至可以在GoogleNet中看到将n\*n拆分为1\*n和n\*1两个卷积核的做法。
416 |
417 | 对于池化层有效的原因之一,在于池化操作可以只用少量的参数大大增加下一层的神经元的感受野。方便起见,下列感受野计算不计算到原始图像那层。如果卷积层之间没有加入池化层,那后一层的神经元的感受野只为3\*3=9(假设是3\*3的卷积核);如果加入了最大池化层,那后一层的神经元的感受野可以增大到3\*3\*4=36,用同样的参数数量直接扩大了4倍。当然,简单地增加卷积核的大小也可以增加感受野,但是这样做增加了计算成本、参数数量、以及过拟合的风险。
418 |
419 | **作用**
420 |
421 | 介绍完感受野,现在开始正式介绍池化的作用:
422 |
423 | * 降低分辨率、降维、压缩特征、可以减少后续的运算量等等。但是在某些需要保持分辨率的任务(图像语义分割)中会变成一种弊端。
424 | * 只用少量参数就可以大大增加后续神经元的感受野。
425 |
426 | ### 10.10 卷积神经网络示例
427 |
428 | #### 10.10.1 LeNet5
429 |
430 | LeNet的[论文连接](https://ieeexplore.ieee.org/document/726791?reload=true&arnumber=726791)。LeNet是一个很简单很小的网络,建立之初是为了手写字识别(0-9)。虽然简单,但是是第一个典型的CNN网络。麻雀虽小,五脏俱全,包含了卷积层、池化层和全连接层。
431 |
432 | 网络结构如下:
433 |
434 | 
435 |
436 |
437 |
438 | 该图没有说清楚,网络中所有卷积层的卷积核都是5*5的,以及步长为1,padding为0。图中的subsampling指的是池化,具体来说是最大池化。细心的话还会留意到最后一层用了Gaussian connections。我个人认为已经被淘汰了,感兴趣的可以自行了解。自己实现的时候当成全连接也可以。
439 |
440 | 该论文的典型之处主要在于:
441 |
442 | * 一层卷积一层池化交替出现。
443 | * 最后输出前若干层采用全连接层。
444 | * 全连接层的参数真的很多。卷积网络的参数主要集中在第一层全连接层(16\*5\*5\*120=48000)。
445 |
446 | #### 10.10.2 AlexNet
447 |
448 | AlexNet的[论文连接](http://papers.nips.cc/paper/4824-imagenet-classification-with-deep-convolutional-neural-networks.pdf)。这是第一个引起大家注意的卷积网络,该模型取得了2012年的ImageNet比赛冠军,而且也正是因为这次比赛而打响了名号。
449 |
450 | 网络结构如下:
451 |
452 | 
453 |
454 | 论文中该图片有误,第一个卷积层的输出应该是54\*54而不是55\*55,这个可以自己计算一下来验证。该网络在前两层就采用了相当大的卷积核,不过后面的层都只用3*3的了。该网络拿下冠军时,以比第二名少20%左右的误差率而取得优胜。
455 |
456 | 个人认为比较值得注意的点是:
457 |
458 | * 并不一定需要每层卷积层后都添加池化层。连续多层卷积层可以视为一层卷积核更大、能拟合更复杂函数的卷积层。
459 | * 对于更大的图片,感受野也需要对应增大。AlexNet的做法是前两层卷积层用了较大的卷积核。
460 |
461 | #### 10.10.3 VGG16
462 |
463 | VGG16的[论文连接](https://arxiv.org/abs/1409.1556)。该网络改进了AlexNet,改进的思路是:用更多层、更小的卷积核代替原来那些比较大的卷积核。最根本的一点是在不减小感受野的前提下增加层数和减少参数量。从结果上来看,这么做确实起到了不错的效果。
464 |
465 | 下图中,卷积层默认步长为1,padding为same。网络结构如下:
466 |
467 | 
468 |
469 | 该网络不止是本身很有价值,其来源(论文)也很有价值。该论文通过对比各种网络,来说明卷积网络越深效果越好这一点。VGG16中的16就是指除去池化层,该网络一个有16层。
470 |
471 | 对比AlexNet,该网络的改进如下:
472 |
473 | * 采用多层连续的3*3卷积层代替大卷积层。
474 | * 网络深度更深了。
475 | * 通道数全部用2的幂。更符合计算机的存储规则。
476 | * 两、三层卷积层 + 一层池化。
477 | * 池化后通道数翻倍。
478 | * 每层网络的步长都为1,padding都为same。
479 |
480 | 上述改进也是现在我所看到的大部分网络的构建习惯(趋势)。我想这足以说明这些“规律”有多好用。
481 |
482 | ### 10.11 为什么使用卷积
483 |
484 | #### 10.11.1 减少参数
485 |
486 | 1.10介绍的网络也基本可以看出,卷积网络中全连接层的参数占了绝大一部分。举例LeNet5,各层参数个数分别为:第一层卷积层 5\*5\*1\*6=150、第二层卷积层 5\*5\*6\*16=2400、第一层全连接层 5\*5\*16\*120=48000、第二层全连接层 120\*84=10080,若最后一层视为全连接层则有 84\*10=840。
487 |
488 | 不难发现,第一层全连接层的参数占据了$\frac{48000}{150+2400+48000+10080+840}=0.78=78%$的参数,这已经占据了一半以上的参数。很明显,卷积层对比全连接层来说可以大大减小参数的数量,一方面可以避免过拟合,另一方面减少了对设备的要求。
489 |
490 | 更进一步,卷积操作需要的参数很少的原因在于
491 |
492 | * **权值共享**。一个卷积核的权值可以适用到整个网络,而不是每个神经元独占一个权值。因为一个卷积核的工作可以理解为专门识别某一些特征。而且这个特征应该是通用的,与所处位置无关,即**平移不变性**。同时平移不变性也是网络学习的潜在目标之一。举例垂直边缘检测便可以检索对应区域是否有垂直边界,而不在乎这个边界的具体位置在哪。
493 | * **稀疏连接**。与全连接对应,在全连接中任意一个神经元都要与上一层的所有神经元连接;而卷积则只受感受野内的神经元影响,对于感受野外的并不关心。
494 |
495 | #### 10.11.2 训练卷积网络
496 |
497 | 假设要做一个猫咪检测网络,$x^{(i)}$表示第$i$张图片,$y^{(i)}$表示对应图片的标签。在选定一个网络后,设计好损失函数,对全部样本的损失求平均作为代价函数。随机初始化权重矩阵和偏置。在Python实现时还可以向量化$x^{(i)}$(当然,就我所知大部分架构也会这么做)。用梯度下降来训练网络,而且也可以采用优化器如$RMSProp$或$Adam$。
498 |
499 |
--------------------------------------------------------------------------------
/11 深度卷积网络 实例探究.md:
--------------------------------------------------------------------------------
1 | #第二周 深度卷积网络:实例探究
2 | ## 2.1为什么要实例探究
3 |
4 | 在计算机视觉的研究中,将卷积层、池化层及全连接层进行有有机结合,才能形成有效的卷积神经网络,而更好地去实现这种有机结合可以多多参考他人所构建的框架,而且在计算机视觉中,良好的神经网络框架往往也适用于其他的任务,所以多多参考其他案例有利于我们更好地应用卷积神经网络。在框架学习中,我们也可以多多研读计算机视觉领域相关的论文或相关的研讨内容。
5 |
6 |
7 |
8 | ## 2.2经典网络
9 |
10 | ### 2.2.1LeNet-5网络
11 |
12 | 
13 |
14 | 该网络是针对灰度图像训练的,该例用其对手写字体进行识别
15 |
16 | 在池化后选用$sigmoid$函数来进行非线性函数处理
17 |
18 | 其结构为卷积——池化——卷积——池化——全连接——全连接。
19 |
20 | 且采取了平均池化(当时年代的人们更倾向使用平均池化),然而现在会更多的使用最大池化。因没有使用padding或有效卷积,使得每完成一次卷积,图像的高度和宽度都缩小了。
21 |
22 | 最后输出层利用了$softmax$函数来分类输出十种结果。
23 |
24 | 相比于其他更复杂的神经网络,其参数较少,只有约六万个。
25 |
26 | 随着网络层次的加深,图像的高度和宽度都在缩小,信道数量则会增加。
27 |
28 | 其中的“一个或多个卷积层后跟着一个池化层,然后又是若干个卷积层,池化层,然后再是全连接层,最后输出。”这一模式仍被经常使用。
29 |
30 | ### 2.2.2AlexNet网络
31 |
32 | 
33 |
34 | 相比于LeNet-5,AlexNet网络要大得多,其有约六千万个参数,但优点在于在用于训练图像和数据集时,它能处理非常相似的基本构造模块,而往往这些模块有着隐藏单元或数据;同时采用了$Relu$函数。
35 |
36 | 在写这篇论文时,GPU的处理速度并不快,所以针对这个模型,采用了两个GPU进行训练,将不同的层拆分到两个GPU中进行训练,并用了一些专门的方法使这两个GPU得以交流。
37 |
38 | ### 2.2.3VGG-16
39 |
40 | 
41 |
42 | VGG-16中的“16”代表该网络结构包含16个卷积层和全连接层
43 |
44 | 这是一个极大的网络,约有1.38亿个参数,但其优点是其结构不复杂,一般为卷积层后跟着可压缩图像大小(高度和宽度)的池化层。其过滤器数量变化存在一定规律,变化为64→128→256→512,论文作者可能认为512的信道数量已经足够大了,故没有继续增加。除了VGG-16外,还有VGG-19模型,但VGG-19模型比VGG-16要大得多,但实现的效果并不比VGG-16要好多少,故较少使用VGG-19。
45 |
46 | 随着该网络的加深,图像的高度和宽度在不断缩小,每次池化后缩小一半,而信道数量在不断增加(每次卷积后增加1倍)。即图像缩小的比例和信道增加的比例是有规律的。
47 |
48 |
49 |
50 | ## 2.3残差网络
51 |
52 | 神经网络层数越多,网络越深,越容易受到梯度消失和梯度爆炸的影响。我们可以通过让神经网络某些层跳过下一层神经元的连接,隔层相连,弱化每层之间的强联系来解决该问题。而这样的神经网络即为残差网络(ResNets)
53 |
54 | ### 2.3.1残差块
55 |
56 | 残差网络由多个残差块组成,如下图为残差块组成
57 |
58 | 
59 |
60 | 图中红色箭头称为跳远连接,其建立了$a^{[l]}$与$a^{[l+2]}$的隔层联系。具体表达式为:
61 |
62 | $z^{[l+1]}=W^{[l+1]} a^{[l]}+b^{[l+1]}$
63 | $a^{[l+1]}=g\left(z^{[l+1]}\right)$
64 | $z^{[l+2]}=W^{[l+2]} a^{[l+1]}+b^{[l+2]}$
65 | $a^{[l+2]}=g\left(z^{[l+2]}+a^{[l]}\right)$
66 |
67 | 其中$a^{[l]}$与$z^{[l+2]}$共同作用,通过ReLU函数输出$a^{[l+2]}$
68 |
69 | 多个残差块构成了如下图所示的残差网络
70 |
71 | 
72 |
73 | ### 2.3.2与Plain Network对比
74 |
75 | 我们将非残差网络称为Plain Network,将其与ResNet对比可发现,残差网络可以有效解决梯度消失和梯度爆炸的问题,睡着网络层数的增加,Plain Network的training error甚至可能变大,而ResNet的training error则一直呈现下降趋势。如下图
76 |
77 | 详细可参考
78 |
79 | [Deep Residual Learning for Image Recognition](extension://ibllepbpahcoppkjjllbabhnigcbffpi/https://openaccess.thecvf.com/content_cvpr_2016/papers/He_Deep_Residual_Learning_CVPR_2016_paper.pdf)
80 |
81 |
82 |
83 |
84 | ### 2.4 网络中的网络/1*1卷积
85 |
86 | #### 2.4.1 定义
87 |
88 | 也被称为***\*Network in Network\****,对输入的个不同的位置都应用一个全连接层,全连接层的作用是便在输入层上实施一个非平凡(***\*non-trivial\****)计算。简单点说就是将输入数据的通道数进行压缩,压缩成所使用的过滤器的数量大小。
89 |
90 |
91 |
92 | #### 2.4.2例子一
93 |
94 | 假设这是一个28×28×192的输入层,可以使用池化层压缩它的高度和宽度,这个过程我们很清楚。但如果通道数量很大,该如何把它压缩为28×28×32维度的层呢?你可以用32个大小为1×1的过滤器,严格来讲每个过滤器大小都是1×1×192维,因为过滤器中通道数量必须与输入层中通道的数量保持一致。但是你使用了32个过滤器,输出层为28×28×32,这就是压缩通道数()的方法。
95 |
96 | 
97 |
98 |
99 |
100 | #### 2.4.3例子二
101 |
102 | 过滤器为1×1,输入一张6×6×32的图片,然后对它做卷积,遍历这36个单元格,计算左图中32个数字和过滤器中32个数字的元素积之和,然后应用***\*ReLU\****非线性函数。
103 |
104 | 我们以其中一个单元为例,它是这个输入层上的某个切片,用这36个数字乘以这个输入层上1×1切片,得到一个实数,像这样把它画在输出中。
105 |
106 | 
107 |
108 |
109 |
110 | 这个1×1×32过滤器中的32个数字可以这样理解,一个神经元的输入是32个数字(输入图片中左下角位置32个通道中的数字),即相同高度和宽度上某一切片上的32个数字,这32个数字具有不同通道,乘以32个权重(将过滤器中的32个数理解为权重),然后应用***\*ReLU\****非线性函数,在这里输出相应的结果。
111 |
112 | 
113 |
114 |
115 |
116 | 一般来说,如果过滤器不止一个,而是多个,就好像有多个输入单元,其输入内容为一个切片上所有数字,输出结果是6×6过滤器数量。
117 |
118 | 
119 |
120 |
121 |
122 |
123 |
124 |
125 |
126 | 所以1×1卷积可以从根本上理解为对这32个不同的位置都应用一个全连接层,全连接层的作用是输入32个数字(过滤器数量标记为,在这36个单元上重复此过程),输出结果是6×6×#filters(过滤器数量),以便在输入层上实施一个非平凡(***\*non-trivial\****)计算。此时,输入的结果的通道层数取决于过滤器的个数。
127 |
128 |
129 |
130 | #### 2.4.4深度可分离卷积
131 |
132 | **定义**:一个卷积核负责一个通道,一个通道只被一个卷积核卷积
133 |
134 | **引用博客**:https://blog.csdn.net/makefish/article/details/88716534
135 |
136 | 相较于一般卷积,深度可分离卷积有着不同的计算方法:
137 |
138 | 在卷积计算时,先用三个卷积对三个通道分别做卷积,这样在一次卷积后,输出3个数,然后这输出的三个数,再通过一个1x1x3的卷积核(pointwise核),得到一个数。下面进行分步解释;
139 |
140 | 第一步,对三个通道分别做卷积,输出三个通道的属性:
141 |
142 |
143 |
144 | 
145 |
146 |
147 |
148 |
149 |
150 | 第二步,用卷积核1x1x3对三个通道再次做卷积,这个时候的输出就和正常卷积一样,是8x8x1:
151 |
152 | 
153 |
154 |
155 |
156 | 如果要提取更多的属性,则需要设计更多的1x1x3卷积核心就可以(图片引用自原网站。感觉应该将8x8x256那个立方体绘制成256个8x8x1,因为他们不是一体的,代表了256个属性)::
157 |
158 | 
159 |
160 | **深度可分离卷积的优点缺点**:
161 |
162 | 对于需要提取大量属性或者特征的情景下,深度可分离卷积随着要提取的属性越来越多,就能够节省更多的参数。当然如果提取的特征属性不多,普通的卷积效果优于深度可分离卷积。
163 |
164 |
165 |
166 |
167 |
168 | ### 2.5 Inception网络
169 |
170 | #### 2.5.1作用
171 |
172 | 代替人工决定所使用的过滤器的大小,或者确定是否需要创建卷积层或池化层,
173 |
174 | #### 2.5.2 论文链接
175 |
176 | https://arxiv.org/pdf/1409.4842.pdf
177 |
178 | #### 2.5.3主要思想
179 |
180 | 不需要人为决定使用哪个过滤器或者是否需要池化,而是由网络自行确定这些参数,你可以给网络添加这些参数的所有可能值,然后把这些输出连接起来,让网络自己学习它需要什么样的参数,采用哪些过滤器组合。
181 |
182 | #### 2.5.4原理
183 |
184 | 利用多种维度的过滤器,分别使用不同的方法,产生大量长宽相等,通道可以不同的输出块,并将这些输出块堆积在一起,产生一个组合了各种类型的参数的输出,从而在后续的训练中,让网络自己学习它需要什么样的参数,采用哪些过滤器组合。
185 |
186 |
187 |
188 | 例如,这是你28×28×192维度的输入层,***\*Inception\****网络或***\*Inception\****层的作用就是代替人工来确定卷积层中的过滤器类型,或者确定是否需要创建卷积层或池化层,我们演示一下。
189 |
190 | 
191 |
192 |
193 |
194 | 如果使用1×1卷积,输出结果会是28×28×#(某个值),假设输出为28×28×64,并且这里只有一个层。
195 |
196 | 
197 |
198 |
199 |
200 | 如果使用3×3的过滤器,那么输出是28×28×128。然后我们把第二个值堆积到第一个值上,为了匹配维度,我们应用***\*same\****卷积,输出维度依然是28×28,和输入维度相同,即高度和宽度相同。
201 |
202 | 
203 |
204 |
205 |
206 | 或许你会说,我希望提升网络的表现,用5×5过滤器或许会更好,我们不妨试一下,输出变成28×28×32,我们再次使用***\*same\****卷积,保持维度不变。
207 |
208 | 
209 |
210 |
211 |
212 | 或许你不想要卷积层,那就用池化操作,得到一些不同的输出结果,我们把它也堆积起来,这里的池化输出是28×28×32。为了匹配所有维度,我们需要对最大池化使用***\*padding\****,它是一种特殊的池化形式,因为如果输入的高度和宽度为28×28,则输出的相应维度也是28×28。然后再进行池化,***\*padding\****不变,步幅为1。
213 |
214 | 
215 |
216 |
217 |
218 | 有了这样的***\*Inception\****模块,你就可以输入某个量,因为它累加了所有数字,这里的最终输出为32+32+128+64=256。***\*Inception\****模块的输入为28×28×192,输出为28×28×256。这就是Inception网络的核心内容。
219 |
220 |
221 |
222 | #### 2.5.5计算成本问题
223 |
224 | 由于进行了多种模型的计算,会造成计算成本会非常的大,如何缩小成本是一个非常重要的一环。
225 |
226 | 下面以5×5过滤器为例计算成本
227 |
228 | 
229 |
230 |
231 |
232 | 这是一个28×28×192的输入块,执行一个5×5卷积,它有32个过滤器,输出为28×28×32。我们来计算这个28×28×32输出的计算成本,它有32个过滤器,因为输出有32个通道,每个过滤器大小为5×5×192,输出大小为28×28×32,所以你要计算28×28×32个数字。对于输出中的每个数字来说,你都需要执行5×5×192次乘法运算,所以乘法运算的总次数为每个输出值所需要执行的乘法运算次数(5×5×192)乘以输出值个数(28×28×32),把这些数相乘结果等于1.2亿(120422400)。
233 |
234 | 
235 |
236 |
237 |
238 | 为了缩小成本,我们使用1*1卷积对输入进行通道缩小。对于输入层,使用1×1卷积把输入值从192个通道减少到16个通道。然后对这个较小层运行5×5卷积,得到最终输出。请注意,输入和输出的维度依然相同,输入是28×28×192,输出是28×28×32。
239 |
240 | 然后我们进行成本计算应用1×1卷积,过滤器个数为16,每个过滤器大小为1×1×192,这两个维度相匹配(输入通道数与过滤器通道数),28×28×16这个层的计算成本是,输出28×28×192中每个元素都做192次乘法,用1×1×192来表示,相乘结果约等于240万,这是第一个卷积层的计算成本。第二层的输出为28×28×32,对每个输出值应用一个5×5×16维度的过滤器,计算结果为1000万。
241 |
242 | 所以所需要乘法运算的总次数是这两层的计算成本之和,也就是1204万,与上一张幻灯片中的值做比较,计算成本从1.2亿下降到了原来的十分之一,即1204万。
243 |
244 |
245 |
246 | #### 2.5.6 瓶颈层
247 |
248 |
249 |
250 | 
251 |
252 |
253 |
254 | 这个被增加的1*1卷积层常被称为瓶颈层,即先缩小网络表示,然后再扩大它。
255 |
256 |
257 |
258 | 需要注意的是,只要合理构建瓶颈层,你既可以显著缩小表示层规模,又不会降低网络性能,从而节省了计算。
259 |
260 |
261 |
262 | #### 2.5.7 Inception Net
263 |
264 | 简述:由多个***\*Inception\*******\*模块所组成的神经网络。\****
265 |
266 | 原理:
267 |
268 | 首先如下图所示,建立前面所说的***\*Inception\****模块。
269 |
270 | 
271 |
272 |
273 |
274 | 为了能在最后将这些输出都连接起来,我们会使用***\*same\****类型的***\*padding\****来池化,使得输出的高和宽依然是28×28,这样才能将它与其他输出连接起来。
275 |
276 | 但注意,如果你进行了最大池化,即便用了***\*same padding\****,3×3的过滤器,***\*stride\****为1,其输出将会是28×28×192,其通道数或者说深度与这里的输入(通道数)相同。所以看起来它会有很多通道,我们实际要做的就是再加上一个1×1的卷积层,去进行我们在1×1卷积层的视频里所介绍的操作,将通道的数量缩小,缩小到28×28×32。
277 |
278 | 
279 |
280 |
281 |
282 | 最后,将这些方块全都连接起来。在这过程中,把得到的各个层的通道都加起来,最后得到一个28×28×256的输出。通道连接实际就是之前视频中看到过的,把所有方块连接在一起的操作。这就是一个***\*Inception\****模块,而***\*Inception\****网络所做的就是将这些模块都组合到一起。
283 |
284 | 
285 |
286 |
287 |
288 | ***\*上图为\*******\*Inception\****网络的图片,并且其由多个***\*Inception\*******\*模块所组成,需要注意的是有一些\*******\*Inception\*******\*模块中间还夹着一个最大池化层,如图中的6和7.\****
289 |
290 | 
291 |
292 |
293 |
294 | ***\*在论文原文中,网络里有着一些其他分支,如上图中的1、2、4,其中1是一个\*******\*softmax\****层,用于做出预测,编号2所做的就是通过隐藏层(编号3)来做出预测,所以这其实是一个***\*softmax\****输出(编号2),编号4也包含了一个隐藏层,通过一些全连接层,然后有一个***\*softmax\****来预测,输出结果的标签。 这些分支确保了即便是隐藏单元和中间层(编号5)也参与了特征计算,它们也能预测图片的分类。它在***\*Inception\****网络中,起到一种调整的效果,并且能防止网络发生过拟合。
295 |
296 |
297 |
298 | #### 2.5.8 Inception网络多种类型
299 |
300 | 参考博客:https://www.cnblogs.com/dengshunge/p/10808191.html
301 |
302 | ##### Inception v1
303 |
304 | v1其实就是我们前面所说的使用1*1卷积降低计算量后的Inception网络。
305 |
306 | 提升神经网络的性能是各种方法和算法的目的,当然提升网络的性能的方法有很多,例如增加网络的深度和宽度,但当深度和宽度不断增加时,需要训练的参数也会增加,过多的参数容易发生过拟合,并且会导致计算量增加。所以就有了v1结构来解决此问题,也就是利用1*1卷积降低计算量。
307 |
308 |
309 |
310 | ##### Inception v2
311 |
312 | 在训练时每层输入数据的分布会发生改变,所以需要较低的学习率和精心设置初始化参数。只要网络的前面几层发生微小的改变,那么后面几层就会被累积放大下去。一旦网络某一层的输入数据的分布发生改变,那么这一层网络就需要去适应学习这个新的数据分布,所以如果训练过程中,训练数据的分布一直在发生变化,那么将会影响网络的训练速度。为此,提出了v2版本的Inception网络。
313 |
314 | V2版本网络使用了BN算法,可以设置较大的初始学习率,并且减少对参数初始化的依赖,提高了训练速度,同时也可以能防止网络陷入饱和,即消除梯度弥散。
315 |
316 |
317 |
318 | ##### Inception v3
319 |
320 | Inception v3主要解决的是:inception结构过于复杂,使得我们很难对网络进行修改。
321 |
322 | V3主要思路为:利用小尺度的卷积来代替大尺度的卷积,在减少计算量的同时,保证能够学习到更多的信息。例如提出了使用两个级联的3*3的滤波器来代替一个5*5的滤波器,如下图所示:
323 |
324 | 
325 |
326 | 
327 |
328 |
329 |
330 | 同时又对3*3卷积进行分解为3*1+1*3,如下图所示,进而进一步降低计算量
331 |
332 | 
333 |
334 |
335 |
336 | V3主要遵循下列几条思想
337 |
338 | 1. 避免特征表示瓶颈,尤其是在网络的前面。要避免严重压缩导致的瓶颈。特征表示尺寸应该温和地减少,从输入端到输出端。特征表示的维度只是一个粗浅的信息量表示,它丢掉了一些重要的因素如相关性结构。
339 |
340 | 2. 高维信息更适合在网络的局部处理。在卷积网络中逐步增加非线性激活响应可以解耦合更多的特征,那么网络就会训练的更快。
341 |
342 | 3. 空间聚合可以通过低维嵌入,不会导致网络表示能力的降低。例如在进行大尺寸的卷积(如3*3)之前,我们可以在空间聚合前先对输入信息进行降维处理,如果这些信号是容易压缩的,那么降维甚至可以加快学习速度。
343 |
344 | 4. 平衡好网络的深度和宽度。通过平衡网络每层滤波器的个数和网络的层数可以是网络达到最佳性能。增加网络的宽度和深度都会提升网络的性能,但是两者并行增加获得的性能提升是最大的。所以计算资源应该被合理的分配到网络的宽度和深度。
345 |
346 |
347 |
348 | ##### Inception v4
349 |
350 | V4的提出主要是基于 ”当网络更深更宽时,inception网络能否一样高效”的问题提出的,v4具体的解决方法为,结合TensorFlow,简化训练,不需要将模型进行分割,并且将inception和resnet两者进行融合,进一步改善网络。
351 |
352 |
353 |
354 | 以上对Inception网络的4种模型进行概述,具体解释可参考下列博客 https://www.cnblogs.com/dengshunge/p/10808191.html
355 |
356 |
357 |
358 | ### 2.6使用开源实现方案
359 |
360 | 本节为介绍如何下载开源代码。
361 |
362 | 本节下载的代码网站为:
363 |
364 | ***\*ResNets\****实现的***\*GitHub\****地址:https://github.com/KaimingHe/deep-residual-networks
365 |
366 | 
367 |
368 |
369 |
370 |
371 |
372 | ***\*点击Code按钮,并且点击复制按钮复制代码的URL\****
373 |
374 | 
375 |
376 |
377 |
378 | 在需要保存代码的目录下打开cmd,使用下列指令进行代码的下载(复制)
379 |
380 | git clone your URL
381 |
382 | git clone https://github.com/KaimingHe/deep-residual-networks.git
383 |
384 | 
385 |
386 |
387 |
388 | 使用指令观察目录,说明此时代码已下载完毕。
389 |
390 | 接下来进行打开代码。
391 |
392 |
393 |
394 | 
395 |
396 |
397 |
398 | 代码储存在prototxt文件夹中
399 |
400 | 
401 |
402 |
403 |
404 | 使用指令打开其中一个文件。
405 |
406 | more 文件名
407 |
408 | 
409 |
410 | 当然也可以用ide直接打开来进行修改。
411 | ### 2.7 迁移学习
412 | #### 2.7.1 迁移学习的概念
413 | 迁移学习是从一个或多个源领域中通过训练该模型,得出有用的知识并将其用在新的目标任务上(未标记的同一类有相似特征的物品或者是未标记的不同类物品)本质是知识的迁移再利用。
414 | #### 2.7.2 ImageNet、MS COCO\Pascal数据集的获取
415 | ImageNet数据集的获取:
416 | 所有图像可通过url下载:不需要账号登录即可免费下载,下载链接:http://www.image-net.org/download-imageurls ,在SEARCH框中输入需要下载的synset,如tree,也可按类别下载即WordNet ID,下载链接:http://www.image-net.org/synset?wnid=n02084071 ,其中好像个别url已失效。
417 | MS COCO:
418 |
419 | 数据集官网首页:http://cocodataset.org/#home
420 |
421 | 数据集下载:
422 |
423 | 可用迅雷去下载官方链接,速度也挺快的。也可以去这个高中生搭建的下载站下载:http://bendfunction.f3322.net:666/share/。 他的首页是这样子的:http://bendfunction.f3322.net:666/
424 | https://pjreddie.com/projects/coco-mirror/
425 | #### 2.7.3 迁移学习的分类
426 | 按照迁移学习的定义,可以将迁移学习分为三种类型,分布差异迁移学习,特征差异迁移学习和标签差异迁移学习。分布差异迁移学习之源域和目标域数据的边缘分布或者条件概率分布不同,特征差异迁移学习之源域数据和目标数据特征空间不同,标签差异迁移学习指源域和目标域的数据标记空间不同。
427 | 用香蕉和苹果分类问题为例,源域数据是已有的带标签香蕉和苹果的文本数据,目标域是新来的不带标记的香蕉和苹果的文本数据,源域和目标域的数据来自不同的时间,不同地点,数据分布不同,但标记空间和特征空间是相同的,利用源域中的数据来进行目标域的学习问题就是属于分布差异迁移学习问题。源域数据是带有标记的苹果和香蕉的文本数据,而目标域是不带有 标记的苹果和香蕉的图片数据,源域和目标域一个是文本,一个是图像,属于特征差异迁移学习范围。源域数据是带有标记的香蕉和苹果的文本数据,属于二分类问题,目标域是不带标记的梨子,橘子和橙子的文本数据属于三分类问题,源域和目标域的数据标记空间不同,属于标记差异迁移学习的范围。
428 |
429 | 现已成熟的监督学习模式下,在大样本的已标记的数据量集中训练形成传统的监督学习,但是这种模式在运用到情况更为复杂,更多变的实际环境中往往会出现很大的误差,
430 | 所以迁移学习就是在样本量比较少的情况下,训练分类器,随之把这种模式可以运用到其他很多种情况下。
431 |
432 | ### 2.8 数据增强
433 | #### 2.8.1数据增强的基本操作
434 | 数据增强也叫数据扩增,意思是在不实质性的增加数据的情况下,让有限的数据产生等价于更多数据的价值。
435 | 数据增强的手段包括几何变换类,颜色变换类等。
436 |
437 | (1) 几何变换类
438 |
439 | 几何变换类即对图像进行几何变换,包括翻转,旋转,裁剪,变形,缩放等各类操作,下面展示以上操作。
440 | 图一2 3 4 5
441 | (2) 颜色变换类
442 | 颜色变换类时改变图片的R、G、B的值。
443 | #### 2.8.2数据增强的代码实现
444 | TensorFlow实现图片数据增强:
445 | 参见以下网址https://zhuanlan.zhihu.com/p/57284174
446 | #### 2.8.2数据增强的优缺点
447 | 优点:
448 | 增加训练的数据量,提高模型的泛化能力
449 | 增加噪声数据,提升模型的鲁棒性
450 | ### 2.9 计算机视觉现状
451 | #### 2.9.1计算机视觉现状
452 | 深度学习已经成功地应用于计算机视觉、自然语言处理、语音识别、在线广告、物流还有其他许多问题。
453 | 在计算机视觉的现状下,深度学习应用于计算机视觉应用有一些独特之处。
454 | ####2.9.2 banchmark
455 | Benchmark 基准测试,Benchmark是一个评价方式,在整个计算机领域有着长期的应用。
456 | Benchmark在计算机领域应用最成功的就是性能测试,主要测试负载的执行时间、传输速度、吞吐量、资源占用率等。基准测试同时也可以用来识别某段代码的CPU或者内存效率问题. 许多开发人员会用基准测试来测试不同的并发模式, 或者用基准测试来辅助配置工作池的数量, 以保证能最大化系统的吞吐量.
457 | 关于实战可参考:
458 | https://blog.csdn.net/woniu317/article/details/82560312
459 |
--------------------------------------------------------------------------------
/12 目标检测.md:
--------------------------------------------------------------------------------
1 | ## 12 目标检测
2 |
3 | ### 12.1 目标定位
4 |
5 | #### 12.1.1 定义
6 |
7 | 除了要识别出目标类(例如是否有汽车)以外,算法还需要能够给出目标的位置(例如用红框框出目标的位置),这是一种分类定位问题。分类定位问题可以是只有一个目标对象在图片中,也可以是多个目标对象在图片中的。先从单个目标对象的情况开始。
8 |
9 | #### 12.1.2 实现
10 |
11 | **1. 边界框参数定义**
12 |
13 | 图片分类我们已经比较熟悉了,知道最后通过 *softmax* 激活函数激活来表示该图片属于每一类的概率。相较于单纯的分类问题,目标定位还需要输出4个值:$b_x,b_y,b_h,b_w$。这四个值用于表示边框的位置和大小,具体为
14 | $$
15 | \begin{array}{l}
16 | b_x:边框的中心点的x轴坐标 \\
17 | b_y:边框的中心点的y轴坐标 \\
18 | b_h:边框的高度 \\
19 | b_w:边框的宽度 \\
20 | \end{array}
21 | $$
22 | 以上4个值的取值范围均为[0, 1],表示的是边界框与图片对应的**比例**。
23 |
24 | 关于坐标轴的选取,一般选图片的左上角为原点(0, 0),右下角为(1, 1)。且$x$轴为纵轴正方向向下,$y$轴为横轴正方向向右。
25 |
26 | **2. 标签的定义**
27 |
28 | 在确定需要增加的额外输出之后,也要重新定义目标标签 $y$:
29 | $$
30 | y=\left[\begin{array}{l}
31 | p_{c} \\
32 | b_{x} \\
33 | b_{y} \\
34 | b_{h} \\
35 | b_{w} \\
36 | c_{1} \\
37 | c_{2} \\
38 | c_{3}
39 | \end{array}\right]
40 | $$
41 | 其中额外增加了$p_c$,用于表示是否有对象属于类$c_1、c_2$或$c_3$,若为1则表示有目标类在图片中,为0表示只有背景。在只有背景(无目标类)时,其他输出均无效。
42 |
43 | 举一个具体的例子,如下图:
44 |
45 | 
46 |
47 | x 是输入,y 是标签,假设$c_2$表示为车,则最终标签应该如上图所示。当输入中不含任何目标类时,$p_c=0$,其他参数全用“?”表示,即不参与 loss 的计算。
48 |
49 | **3. 边界框参数取值范围**
50 |
51 | 关于边框的4个参数,吴恩达老师给出的取值范围都是[0, 1]的。虽然确实可以这么做,但是背后的原因却没有解释。个人猜测可能是以下原因:
52 |
53 | * 固定取值在[0, 1]之间更容易用激活函数表示,比如sigmoid可以将单个值映射到[0, 1];
54 | * 让标签的所有参数都在一个取值范围,这样在计算loss的时候就不会变相加权了;
55 | * 取值范围在[0, 1]内更容易训练、收敛。
56 |
57 | **4. 损失函数**
58 | $$
59 | L(\hat y,y)=
60 | \begin{cases}
61 | (\hat{y_1}-y_1)^2+(\hat{y_2}-y_2)^2+...+(\hat{y_n}-y_n)^2 & {y_1=1}\\
62 | (\hat{y_1}-y_1)^2 & {y_1=0}
63 | \end{cases}
64 | $$
65 |
66 | * 对于$p_c$可以采用 Logistic 回归的方法,甚至用均方误差$(p_c-\hat{p_c})^2$也可以;
67 | * 对于$b_x,b_y,b_w,b_h$,loss 可以用平方差或类似方法;
68 | * 对于$c_1,c_2,c_3$,是多分类问题,和之前一样用 softmax 即可。
69 |
70 | ### 12.2 特征点检测
71 |
72 | #### 12.2.1 定义
73 |
74 | 以下图为例,检测双眼的眼角位置
75 |
76 | 
77 |
78 | 这个就是特征点检测,主要任务是预测对应的特征点的位置,一般会同时预测多个点。
79 |
80 | #### 12.2.2 实现
81 |
82 | 对于单个点,其坐标为$(l_{ix},l_{iy}),i \in [1, m]$,$m$是特征点的个数,$l_{ix},l_{iy} \in [0,1]$。坐标轴的选取和目标定位时一致,以及需要保证每个样本的特征点的顺序是一致的,比如$l_1$都是左眼的左眼角,$l_2$都是左眼的右眼角等。
83 |
84 | 关于最后一层的激活函数,可以对每个坐标的值用 sigmoid 激活。
85 |
86 | ### 12.3 目标检测
87 |
88 | #### 12.3.1 滑动窗口目标检测算法
89 |
90 | 滑动窗口检测是分两步执行的:第一步是从原图中裁剪一部分并根据需求调整大小,第二步是检测裁剪部分有无目标对象。
91 |
92 | 对于第二步,是我们比较熟悉的分类算法,只是训练集需要人为调整到为几乎整张图都是目标对象,如下图:
93 |
94 | 
95 |
96 | $x$ 为一张无车的图片或者被车占满的图片,标签 $y$ 为1时有车,为0时无车。
97 |
98 | 对于第一步,滑动窗口用的方法是先选定一个裁剪大小,然后从图片的左上角开始,每隔一定像素(距离)裁剪一次,一直滑动到图片的右下角,然后下一个裁剪大小用相同的方法裁剪。如图,上图为3种裁剪大小,下图为一个滑动流程:
99 |
100 | 
101 |
102 | 
103 |
104 | #### 12.3.2 滑动窗口缺点——计算成本
105 |
106 | 看到这里不难发现,滑动窗口检测由于需要多个窗口且每个窗口滑动多次而导致运算量会相当巨大,运行时间过慢。而且如果滑动的步幅过大或者裁剪的大小不合适也会导致很难检测到目标。
107 |
108 | ### 12.4 卷积的滑动窗口实现
109 |
110 | #### 12.4.1 把神经网络的全连接层转化成卷积层
111 |
112 | 
113 |
114 | - 假设目标检测算法输入一个14×14×3的图像,过滤器大小为5×5,数量是16,14×14×3的图像在过滤器处理之后映射为10×10×16。
115 |
116 | - 然后通过参数为2×2的最大池化操作,图像减小到5×5×16。
117 |
118 | - 添加一个连接400个单元的全连接层,接着再添加一个全连接层。
119 |
120 | - 最后通过softmax单元输出,用4个数字来表示 ,它们分别对应softmax单元所输出的4个分类出现的概率。这4个分类可以是行人、汽车、摩托车和背景或其它对象。
121 |
122 | **全连接层转化为卷积层**
123 |
124 | 
125 |
126 | - 前几层和之前的一样。
127 |
128 | - 而对于全连接层,用5×5的过滤器来实现,数量是400个。输入图像大小为5×5×16,用5×5的过滤器对它进行卷积操作,过滤器实际上是5×5×16,因为在卷积过程中,过滤器会遍历这16个通道,所以这两处的通道数量必须保持一致,输出结果为1×1。假设应用400个这样的5×5×16过滤器,输出维度就是1×1×400。它不再是一个含有400个节点的集合,而是一个1×1×400的输出层。从数学角度看,它和全连接层是一样的,因为这400个节点中每个节点都有一个5×5×16维度的过滤器,所以每个值都是上一层这些5×5×16激活值经过某个任意线性函数的输出结果。
129 | - 再添加另外一个卷积层,这里用1×1卷积,假设有400个1×1的过滤器,在这400个过滤器的作用下,下一层的维度是1×1×400,它其实就是上个网络中的这一全连接层。最后经由1×1过滤器的处理,得到一个softmax激活值,通过卷积网络,我们最终得到这个1×1×4的输出层,而不是4个数字。
130 |
131 | 以上就是用卷积层代替全连接层的过程。
132 |
133 | #### 12.4.2 在卷积上应用滑动窗口对象检测算法
134 |
135 | 
136 |
137 | 假设向滑动窗口卷积网络输入14×14×3的图片。和前面一样,神经网络最后的输出层,即softmax单元的输出是1×1×4,这里画得比较简单,严格来说,14×14×3应该是一个长方体,第二个10×10×16也是一个长方体,为了方便,这里只画了正面,所以这里显示的都是平面图,而不是3D图像。
138 |
139 | 
140 |
141 | 假设输入给卷积网络的图片大小是14×14×3,测试集图片是16×16×3,现在给这个输入图片加上黄色条块,在最初的滑动窗口算法中,你会把这片蓝色区域输入卷积网络(红色笔标记)生成0或1分类。接着滑动窗口,步幅为2个像素,向右滑动2个像素,将这个绿框区域输入给卷积网络,运行整个卷积网络,得到另外一个标签0或1。继续将这个橘色区域输入给卷积网络,卷积后得到另一个标签,最后对右下方的紫色区域进行最后一次卷积操作。我们在这个16×16×3的小图像上滑动窗口,卷积网络运行了4次,于是输出了了4个标签。
142 |
143 | 
144 |
145 | 这4次卷积操作中很多计算都是重复的。所以执行滑动窗口的卷积时使得卷积网络在这4次前向传播过程中共享很多计算。
146 |
147 | - 卷积网络运行同样的参数,使得相同的5×5×16过滤器进行卷积操作,得到12×12×16的输出层。
148 |
149 | - 然后执行同样的最大池化,输出结果6×6×16。照旧应用400个5×5的过滤器,得到一个2×2×400的输出层,现在输出层为2×2×400,而不是1×1×400。
150 |
151 | - 应用1×1过滤器得到另一个2×2×400的输出层。
152 |
153 | - 再做一次全连接的操作,最终得到2×2×4的输出层,而不是1×1×4。
154 |
155 | - 最终,在输出层这4个子方块中,蓝色的是图像左上部分14×14的输出(红色箭头标识),右上角方块是图像右上部分(绿色箭头标识)的对应输出,左下角方块是输入层左下角(橘色箭头标识),也就是这个14×14区域经过卷积网络处理后的结果,同样,右下角这个方块是卷积网络处理输入层右下角14×14区域(紫色箭头标识)的结果。
156 |
157 | 该卷积操作的原理是我们不需要把输入图像分割成四个子集,分别执行前向传播,而是把它们作为一张图片输入给卷积网络进行计算,其中的公共区域可以共享很多计算,就像这里我们看到的这个4个14×14的方块一样。
158 |
159 | 
160 |
161 | 再看一个更大的图片样本,假如对一个28×28×3的图片应用滑动窗口操作,如果以同样的方式运行前向传播,最后得到8×8×4的结果。跟上一个范例一样,以14×14区域滑动窗口,首先在这个区域应用滑动窗口,其结果对应输出层的左上角部分。接着以大小为2的步幅不断地向右移动窗口,直到第8个单元格,得到输出层的第一行。然后向图片下方移动,最终输出这个8×8×4的结果。因为最大池化参数为2,相当于以大小为2的步幅在原始图片上应用神经网络。
162 |
163 | **滑动窗口的实现过程总结**
164 |
165 | 
166 |
167 | 在图片上剪切出一块区域,假设它的大小是14×14,把它输入到卷积网络。继续输入下一块区域,大小同样是14×14,重复操作,直到某个区域识别到汽车。
168 |
169 | 但是我们不用依靠连续的卷积操作来识别图片中的汽车,比如,我们可以对大小为28×28的整张图片进行卷积操作,一次得到所有预测值,如果足够幸运,神经网络便可以识别出汽车的位置。
170 |
171 | ### 12.5 Bounding Box预测
172 |
173 | 滑动窗口法的卷积实现的算法虽然效率更高,但仍然存在问题,不能输出最精准的边界框。
174 |
175 |
271 |
272 | 但在深度学习文献中,定义卷积运算时跳过了这个镜像操作。前面我们实际上做的,有时被称为互相关而不是卷积。
273 |
274 | 总结来说,按照机器学习的惯例,我们通常不进行翻转操作。从技术上说,这个操作可能叫做互相关更好。但在大部分的深度学习文献中都把它叫做卷积运算。
275 |
276 | ### 10.6 三维卷积
277 |
278 | **三维(RGB图像)上的卷积操作**
279 |
280 | 举例,假如你不仅想检测灰度图像的特征,也想检测 RGB 彩色图像的特征。彩色图像如果6×6×3,这里的第一个 6 代表图像高度,第二个 6 代表宽度,这个3 代表颜色通道的数目。你可以把它想象成三个 6×6图像的堆叠。为了检测图像的边缘或者其他的特征,不是把它跟原来的 3×3 的过滤器做卷积,而是跟一个三维的过滤器,它的维度是 3×3×3,这样这个过滤器也有三层,对应红、绿、蓝三个通道。得到的输出会是一个 4×4 的图像,注意是 4×4×1,最后一个数不是 3 了。
281 |
282 | 为了简化这个 3×3×3过滤器的图像,我们不把它画成 3 个矩阵的堆叠,而画成一个三维的立方体。
283 |
284 | 
285 |
286 | **计算过程**:
287 |
288 | 把这个 3×3×3 的过滤器先放到最左上角的位置,这个 3×3×3 的过滤器有 27 个数,27 个参数就是 3 的立方。依次取这 27 个数,然后乘以相应的红绿蓝通道中的数字。先取红色通道的前 9 个数字,然后是绿色通道,然后再是蓝色通道,乘以左边黄色立方体覆盖的对应的 27 个数,然后把这些数都加起来,就得到了输出的第一个数字。如果要计算下一个输出,你把这个立方体滑动一个单位,再与这 27 个数相乘,把它们都加起来,就得到了下一个输出,以此类推。
289 |
290 | 
291 |
292 |
293 |
294 | **作用**:
295 |
296 | 举例:
297 |
298 | - 如果你想检测图像红色通道的边缘,那么你可以将第一个过滤器设为$\left[\begin{array}{rrr}1 & 0 & -1 \\ 1 & 0 & -1 \\ 1 & 0 & -1\end{array}\right]$,和之前一样,而绿色通道全为 0,$\left[\begin{array}{lll}0 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0\end{array}\right]$,蓝色也全为 0。如果你把这三个堆叠在一起形成一个3×3×3的过滤器,那么这就是一个检测垂直边界的过滤器,但只对红色通道有用。
299 | - 或者如果你不关心垂直边界在哪个颜色通道里,那么你可以用一个这样的过滤器,$\left[\begin{array}{ccc}1 & 0 & -1 \\ 1 & 0 & -1 \\ 1 & 0 & -1\end{array}\right],\left[\begin{array}{ccc}1 & 0 & -1 \\ 1 & 0 & -1 \\ 1 & 0 & -1\end{array}\right],\left[\begin{array}{ccc}1 & 0 & -1 \\ 1 & 0 & -1 \\ 1 & 0 & -1\end{array}\right]$,所有三个通道都是这样。所以通过设置第二个过滤器参数,你就有了一个边界检测器,3×3×3 的边界检测器,用来检测任意颜色通道里的边界。参数的选择不同,可以得到不同的特征检测器,所有的都是 3×3×3 的过滤器。
300 |
301 | **同时用多个过滤器**
302 |
303 | 有时候我们会想要同时检测垂直边缘和水平边缘,还有 45°倾斜的边缘,还有 70°倾斜的边缘等等,这是就需要使用多个过滤器。
304 |
305 | 
306 |
307 | 例如我们让这个 6×6×3 的图像和这个 3×3×3 的过滤器卷积,得到 4×4 的输出。(第一个)这可能是一个垂直边界检测器或者是学习检测其他的特征。第二个过滤器可以用橘色来表示,它可以是一个水平边缘检测器。做完卷积,然后把这两个 4×4 的输出堆叠在一起,这样你就都得到了一个4×4×2 的输出立方体。这里的 2 的来源于我们用了两个不同的过滤器。
308 |
309 | **维度总结**
310 |
311 | 如果你有一个$n \times n \times n_{c}$(通道数)的输入图像,上例中就是 6×6×3,这里的$n_{c}$就是通道数目,然后卷积上一个$f \times f \times n_{c}$,这个例子中是 3×3×3,按照惯例,这个(前一个𝑛𝑐)和这个(后一个𝑛𝑐)必须数值相同。然后你就得到了,$(n-f+1)\times(n-f+1) \times n_{c^{\prime}}$这里$n_{c^{\prime}}$其实就是下一层的通道数,它就是你用的过滤器的个数,在我们的例子中,那就是 4×4×2。我写下这个假设时,用的步幅为 1,并且没有 padding。如果你用了不同的步幅或者 padding,那么这个$𝑛 − 𝑓 + 1$数值会变化。
312 | $$
313 | n \times n \times n_{c} \text { * } f \times f \times n_{c} \rightarrow (n-f+1)\times(n-f+1) \times n_{c^{\prime}}
314 | $$
315 | **思考**:为什么卷积核是3\*3channels而不是3\*3\*1在多个通道之间移动?
316 |
317 | 如果使用3\*3\*1的卷积核在多个通道中移动,那意味着每个通道都用同一个过滤器,而且每个过滤器(卷积核)都忽略了隐藏在通道之间的联系和信息,这无疑会降低卷积网络的效果。
318 |
319 | ### 10.7 单层卷积网络
320 |
321 | 
322 |
323 | 相比之前的卷积过程,CNN的单层结构多了激活函数ReLU和偏移量b,与神经网络的单层结构类似,即:
324 |
325 | $Z^{[l]}=W^{[l]} A^{[l-1]}+b$
326 | $A^{[l]}=g^{[l]}\left(Z^{[l]}\right)$
327 |
328 | 其中,卷积运算对应上式中的乘积运算,过滤器组数值对应着权重$W^{[l]}$,激活函数则为ReLU
329 |
330 | 上图中参数$W$的计算:每个过滤器组共有3x3x3=27个参数,两个过滤器组则共包含27x2=54个参数$W$
331 |
332 | 相关符号的总结(设层数为$l$)
333 |
334 | $f^{[l]}=$ filter size
335 | $p^{[l]}=$ padding
336 | $s^{[l]}=$ stride
337 | $n_{c}^{[l]}=$ number of filters
338 | $n_{H}^{[l]}=$ height of input
339 | $n_{W}^{[l]}=$ width of filters
340 |
341 | 输入维度为:
342 |
343 | $n_{H}^{[l-1]} \times n_{W}^{[l-1]} \times n_{c}^{[l-1]}$
344 | 每个滤波器组维度为:
345 |
346 | $f^{[l]} \times f^{[l]} \times n_{c}^{[l-1]}$
347 |
348 | 权重维度为:
349 |
350 | $f^{[l]} \times f^{[l]} \times n_{c}^{[l-1]} \times n_{c}^{[l]}$
351 |
352 | 偏置维度为:
353 |
354 | $ 1 \times 1 \times 1 \times n_{c}^{[l]}$
355 |
356 | 输出维度为 :
357 |
358 | $ n_{H}^{[l]} \times n_{W}^{[l]} \times n_{c}^{[l]}$
359 |
360 | 其中:
361 | $$
362 | \begin{aligned}
363 | n_{H}^{[l]} &=\left\lfloor\frac{n_{H}^{[l-1]}+2 p^{[l]}-f^{[l]}}{s^{[l]}}+1\right\rfloor \\
364 | n_{W}^{[l]} &=\left\lfloor\frac{n_{W}^{[l-1]}+2 p^{[l]}-f^{[l]}}{s^{[l]}}+1\right\rfloor
365 | \end{aligned}
366 | $$
367 | 若有$m$个样本进行向量化运算,则输出的维度为:
368 |
369 | $m \times n_{H}^{[l]} \times n_{W}^{[l]} \times n_{c}^{[l}$
370 |
371 | ### 10.8 简单卷积网络示例
372 |
373 | 
374 |
375 | 如上图,是一个简单的CNN模型,且$a^{[3]}$维度为7 x 7 x 40,若将$a^{[3]}$排成1列,则维度为1960 x 1,再与输出层连接,输出层若为1个神经元,则为二元分类;若为多个神经元,则为多元分类。由此得出预测输出$\hat{y}$。
376 |
377 | 当CNN层数增加时,一般$n_{H}^{[l]}$和$n_{W}^{[l]}$会逐渐减小,而$n_{c}^{[l]}$会逐渐增大。
378 |
379 | CNN有以下三种类型的layer:
380 |
381 | - Convolution(CONV)(最为常见)
382 | - Pooling(POOL)
383 | - Fully connected(FC)
384 |
385 | ### 10.9 池化层
386 |
387 | 池化是一种下采样(downsample)手段,是对信息进行抽象的过程。
388 |
389 | 池化并不只有最大池化Max Pooling一种,不过Max Pooling是最广泛使用的一种。
390 |
391 | #### 10.9.1 最大池化 Max Pooling
392 |
393 | 最大池化指的是在采样区间内用区间内的最大值代表这个区间。
394 |
395 | 
396 |
397 | 和卷积运算一样,池化也有自己的参数:池化大小、步长和Padding。只不过最常用的是2*2大小、步长为2和Valid Padding。下文如没有说明则都是采用这种最大池化。
398 |
399 | #### 10.9.2 其他池化
400 |
401 | * 平均池化:平均池化和最大池化相对应,用该区间的平均值来代表该区间。
402 | * 全局平均池化:和上述池化有点不同,是将一个通道的信息都用该通道的平均值代替。比如输入4\*4\*channels的特征图,输出一个长度为channels的特征向量。该向量每一个值都是对应通道(4*4=16个值)的平均值。通常用在最后一层卷积层后、softmax前。主要作用是代替全连接,降低参数个数。
403 | * ASPP(空洞卷积空间金字塔池化,Atrous Spatial Pyramid Pooling):和传统的池化操作不同,该池化并不降低分辨率(输出特征图的大小),但是同样可以起到对增加感受野的效果(下文介绍感受野)。
404 |
405 | #### 10.9.3 池化的作用
406 |
407 | 在介绍池化的作用前,先介绍一下感受野。
408 |
409 | **感受野 Receptive Field**
410 |
411 | 感受野表示了一个神经元(输出图的一个像素点)与多少个**原始图像**上的像素点有关联。浅层的感受野小,深层的感受野逐渐增大。对于单个神经元,其值只与其感受野有关,与感受野外无关。下图给出在经过两层3\*3的卷积后的神经元的感受野示例。
412 |
413 | 
414 |
415 | 上图还可以发现,两个3\*3的卷积核能够与单个5\*5的卷积核有相同的感受野。但是前者只有2\*3\*3=18个参数,后者有5\*5=25个参数。可见可以通过多层小的卷积核来获得和单个大卷积核的相同效果,同时参数更少。甚至可以在GoogleNet中看到将n\*n拆分为1\*n和n\*1两个卷积核的做法。
416 |
417 | 对于池化层有效的原因之一,在于池化操作可以只用少量的参数大大增加下一层的神经元的感受野。方便起见,下列感受野计算不计算到原始图像那层。如果卷积层之间没有加入池化层,那后一层的神经元的感受野只为3\*3=9(假设是3\*3的卷积核);如果加入了最大池化层,那后一层的神经元的感受野可以增大到3\*3\*4=36,用同样的参数数量直接扩大了4倍。当然,简单地增加卷积核的大小也可以增加感受野,但是这样做增加了计算成本、参数数量、以及过拟合的风险。
418 |
419 | **作用**
420 |
421 | 介绍完感受野,现在开始正式介绍池化的作用:
422 |
423 | * 降低分辨率、降维、压缩特征、可以减少后续的运算量等等。但是在某些需要保持分辨率的任务(图像语义分割)中会变成一种弊端。
424 | * 只用少量参数就可以大大增加后续神经元的感受野。
425 |
426 | ### 10.10 卷积神经网络示例
427 |
428 | #### 10.10.1 LeNet5
429 |
430 | LeNet的[论文连接](https://ieeexplore.ieee.org/document/726791?reload=true&arnumber=726791)。LeNet是一个很简单很小的网络,建立之初是为了手写字识别(0-9)。虽然简单,但是是第一个典型的CNN网络。麻雀虽小,五脏俱全,包含了卷积层、池化层和全连接层。
431 |
432 | 网络结构如下:
433 |
434 | 
435 |
436 |
437 |
438 | 该图没有说清楚,网络中所有卷积层的卷积核都是5*5的,以及步长为1,padding为0。图中的subsampling指的是池化,具体来说是最大池化。细心的话还会留意到最后一层用了Gaussian connections。我个人认为已经被淘汰了,感兴趣的可以自行了解。自己实现的时候当成全连接也可以。
439 |
440 | 该论文的典型之处主要在于:
441 |
442 | * 一层卷积一层池化交替出现。
443 | * 最后输出前若干层采用全连接层。
444 | * 全连接层的参数真的很多。卷积网络的参数主要集中在第一层全连接层(16\*5\*5\*120=48000)。
445 |
446 | #### 10.10.2 AlexNet
447 |
448 | AlexNet的[论文连接](http://papers.nips.cc/paper/4824-imagenet-classification-with-deep-convolutional-neural-networks.pdf)。这是第一个引起大家注意的卷积网络,该模型取得了2012年的ImageNet比赛冠军,而且也正是因为这次比赛而打响了名号。
449 |
450 | 网络结构如下:
451 |
452 | 
453 |
454 | 论文中该图片有误,第一个卷积层的输出应该是54\*54而不是55\*55,这个可以自己计算一下来验证。该网络在前两层就采用了相当大的卷积核,不过后面的层都只用3*3的了。该网络拿下冠军时,以比第二名少20%左右的误差率而取得优胜。
455 |
456 | 个人认为比较值得注意的点是:
457 |
458 | * 并不一定需要每层卷积层后都添加池化层。连续多层卷积层可以视为一层卷积核更大、能拟合更复杂函数的卷积层。
459 | * 对于更大的图片,感受野也需要对应增大。AlexNet的做法是前两层卷积层用了较大的卷积核。
460 |
461 | #### 10.10.3 VGG16
462 |
463 | VGG16的[论文连接](https://arxiv.org/abs/1409.1556)。该网络改进了AlexNet,改进的思路是:用更多层、更小的卷积核代替原来那些比较大的卷积核。最根本的一点是在不减小感受野的前提下增加层数和减少参数量。从结果上来看,这么做确实起到了不错的效果。
464 |
465 | 下图中,卷积层默认步长为1,padding为same。网络结构如下:
466 |
467 | 
468 |
469 | 该网络不止是本身很有价值,其来源(论文)也很有价值。该论文通过对比各种网络,来说明卷积网络越深效果越好这一点。VGG16中的16就是指除去池化层,该网络一个有16层。
470 |
471 | 对比AlexNet,该网络的改进如下:
472 |
473 | * 采用多层连续的3*3卷积层代替大卷积层。
474 | * 网络深度更深了。
475 | * 通道数全部用2的幂。更符合计算机的存储规则。
476 | * 两、三层卷积层 + 一层池化。
477 | * 池化后通道数翻倍。
478 | * 每层网络的步长都为1,padding都为same。
479 |
480 | 上述改进也是现在我所看到的大部分网络的构建习惯(趋势)。我想这足以说明这些“规律”有多好用。
481 |
482 | ### 10.11 为什么使用卷积
483 |
484 | #### 10.11.1 减少参数
485 |
486 | 1.10介绍的网络也基本可以看出,卷积网络中全连接层的参数占了绝大一部分。举例LeNet5,各层参数个数分别为:第一层卷积层 5\*5\*1\*6=150、第二层卷积层 5\*5\*6\*16=2400、第一层全连接层 5\*5\*16\*120=48000、第二层全连接层 120\*84=10080,若最后一层视为全连接层则有 84\*10=840。
487 |
488 | 不难发现,第一层全连接层的参数占据了$\frac{48000}{150+2400+48000+10080+840}=0.78=78%$的参数,这已经占据了一半以上的参数。很明显,卷积层对比全连接层来说可以大大减小参数的数量,一方面可以避免过拟合,另一方面减少了对设备的要求。
489 |
490 | 更进一步,卷积操作需要的参数很少的原因在于
491 |
492 | * **权值共享**。一个卷积核的权值可以适用到整个网络,而不是每个神经元独占一个权值。因为一个卷积核的工作可以理解为专门识别某一些特征。而且这个特征应该是通用的,与所处位置无关,即**平移不变性**。同时平移不变性也是网络学习的潜在目标之一。举例垂直边缘检测便可以检索对应区域是否有垂直边界,而不在乎这个边界的具体位置在哪。
493 | * **稀疏连接**。与全连接对应,在全连接中任意一个神经元都要与上一层的所有神经元连接;而卷积则只受感受野内的神经元影响,对于感受野外的并不关心。
494 |
495 | #### 10.11.2 训练卷积网络
496 |
497 | 假设要做一个猫咪检测网络,$x^{(i)}$表示第$i$张图片,$y^{(i)}$表示对应图片的标签。在选定一个网络后,设计好损失函数,对全部样本的损失求平均作为代价函数。随机初始化权重矩阵和偏置。在Python实现时还可以向量化$x^{(i)}$(当然,就我所知大部分架构也会这么做)。用梯度下降来训练网络,而且也可以采用优化器如$RMSProp$或$Adam$。
498 |
499 |
--------------------------------------------------------------------------------
/11 深度卷积网络 实例探究.md:
--------------------------------------------------------------------------------
1 | #第二周 深度卷积网络:实例探究
2 | ## 2.1为什么要实例探究
3 |
4 | 在计算机视觉的研究中,将卷积层、池化层及全连接层进行有有机结合,才能形成有效的卷积神经网络,而更好地去实现这种有机结合可以多多参考他人所构建的框架,而且在计算机视觉中,良好的神经网络框架往往也适用于其他的任务,所以多多参考其他案例有利于我们更好地应用卷积神经网络。在框架学习中,我们也可以多多研读计算机视觉领域相关的论文或相关的研讨内容。
5 |
6 |
7 |
8 | ## 2.2经典网络
9 |
10 | ### 2.2.1LeNet-5网络
11 |
12 | 
13 |
14 | 该网络是针对灰度图像训练的,该例用其对手写字体进行识别
15 |
16 | 在池化后选用$sigmoid$函数来进行非线性函数处理
17 |
18 | 其结构为卷积——池化——卷积——池化——全连接——全连接。
19 |
20 | 且采取了平均池化(当时年代的人们更倾向使用平均池化),然而现在会更多的使用最大池化。因没有使用padding或有效卷积,使得每完成一次卷积,图像的高度和宽度都缩小了。
21 |
22 | 最后输出层利用了$softmax$函数来分类输出十种结果。
23 |
24 | 相比于其他更复杂的神经网络,其参数较少,只有约六万个。
25 |
26 | 随着网络层次的加深,图像的高度和宽度都在缩小,信道数量则会增加。
27 |
28 | 其中的“一个或多个卷积层后跟着一个池化层,然后又是若干个卷积层,池化层,然后再是全连接层,最后输出。”这一模式仍被经常使用。
29 |
30 | ### 2.2.2AlexNet网络
31 |
32 | 
33 |
34 | 相比于LeNet-5,AlexNet网络要大得多,其有约六千万个参数,但优点在于在用于训练图像和数据集时,它能处理非常相似的基本构造模块,而往往这些模块有着隐藏单元或数据;同时采用了$Relu$函数。
35 |
36 | 在写这篇论文时,GPU的处理速度并不快,所以针对这个模型,采用了两个GPU进行训练,将不同的层拆分到两个GPU中进行训练,并用了一些专门的方法使这两个GPU得以交流。
37 |
38 | ### 2.2.3VGG-16
39 |
40 | 
41 |
42 | VGG-16中的“16”代表该网络结构包含16个卷积层和全连接层
43 |
44 | 这是一个极大的网络,约有1.38亿个参数,但其优点是其结构不复杂,一般为卷积层后跟着可压缩图像大小(高度和宽度)的池化层。其过滤器数量变化存在一定规律,变化为64→128→256→512,论文作者可能认为512的信道数量已经足够大了,故没有继续增加。除了VGG-16外,还有VGG-19模型,但VGG-19模型比VGG-16要大得多,但实现的效果并不比VGG-16要好多少,故较少使用VGG-19。
45 |
46 | 随着该网络的加深,图像的高度和宽度在不断缩小,每次池化后缩小一半,而信道数量在不断增加(每次卷积后增加1倍)。即图像缩小的比例和信道增加的比例是有规律的。
47 |
48 |
49 |
50 | ## 2.3残差网络
51 |
52 | 神经网络层数越多,网络越深,越容易受到梯度消失和梯度爆炸的影响。我们可以通过让神经网络某些层跳过下一层神经元的连接,隔层相连,弱化每层之间的强联系来解决该问题。而这样的神经网络即为残差网络(ResNets)
53 |
54 | ### 2.3.1残差块
55 |
56 | 残差网络由多个残差块组成,如下图为残差块组成
57 |
58 | 
59 |
60 | 图中红色箭头称为跳远连接,其建立了$a^{[l]}$与$a^{[l+2]}$的隔层联系。具体表达式为:
61 |
62 | $z^{[l+1]}=W^{[l+1]} a^{[l]}+b^{[l+1]}$
63 | $a^{[l+1]}=g\left(z^{[l+1]}\right)$
64 | $z^{[l+2]}=W^{[l+2]} a^{[l+1]}+b^{[l+2]}$
65 | $a^{[l+2]}=g\left(z^{[l+2]}+a^{[l]}\right)$
66 |
67 | 其中$a^{[l]}$与$z^{[l+2]}$共同作用,通过ReLU函数输出$a^{[l+2]}$
68 |
69 | 多个残差块构成了如下图所示的残差网络
70 |
71 | 
72 |
73 | ### 2.3.2与Plain Network对比
74 |
75 | 我们将非残差网络称为Plain Network,将其与ResNet对比可发现,残差网络可以有效解决梯度消失和梯度爆炸的问题,睡着网络层数的增加,Plain Network的training error甚至可能变大,而ResNet的training error则一直呈现下降趋势。如下图
76 |
77 | 详细可参考
78 |
79 | [Deep Residual Learning for Image Recognition](extension://ibllepbpahcoppkjjllbabhnigcbffpi/https://openaccess.thecvf.com/content_cvpr_2016/papers/He_Deep_Residual_Learning_CVPR_2016_paper.pdf)
80 |
81 |
82 |
83 |
84 | ### 2.4 网络中的网络/1*1卷积
85 |
86 | #### 2.4.1 定义
87 |
88 | 也被称为***\*Network in Network\****,对输入的个不同的位置都应用一个全连接层,全连接层的作用是便在输入层上实施一个非平凡(***\*non-trivial\****)计算。简单点说就是将输入数据的通道数进行压缩,压缩成所使用的过滤器的数量大小。
89 |
90 |
91 |
92 | #### 2.4.2例子一
93 |
94 | 假设这是一个28×28×192的输入层,可以使用池化层压缩它的高度和宽度,这个过程我们很清楚。但如果通道数量很大,该如何把它压缩为28×28×32维度的层呢?你可以用32个大小为1×1的过滤器,严格来讲每个过滤器大小都是1×1×192维,因为过滤器中通道数量必须与输入层中通道的数量保持一致。但是你使用了32个过滤器,输出层为28×28×32,这就是压缩通道数()的方法。
95 |
96 | 
97 |
98 |
99 |
100 | #### 2.4.3例子二
101 |
102 | 过滤器为1×1,输入一张6×6×32的图片,然后对它做卷积,遍历这36个单元格,计算左图中32个数字和过滤器中32个数字的元素积之和,然后应用***\*ReLU\****非线性函数。
103 |
104 | 我们以其中一个单元为例,它是这个输入层上的某个切片,用这36个数字乘以这个输入层上1×1切片,得到一个实数,像这样把它画在输出中。
105 |
106 | 
107 |
108 |
109 |
110 | 这个1×1×32过滤器中的32个数字可以这样理解,一个神经元的输入是32个数字(输入图片中左下角位置32个通道中的数字),即相同高度和宽度上某一切片上的32个数字,这32个数字具有不同通道,乘以32个权重(将过滤器中的32个数理解为权重),然后应用***\*ReLU\****非线性函数,在这里输出相应的结果。
111 |
112 | 
113 |
114 |
115 |
116 | 一般来说,如果过滤器不止一个,而是多个,就好像有多个输入单元,其输入内容为一个切片上所有数字,输出结果是6×6过滤器数量。
117 |
118 | 
119 |
120 |
121 |
122 |
123 |
124 |
125 |
126 | 所以1×1卷积可以从根本上理解为对这32个不同的位置都应用一个全连接层,全连接层的作用是输入32个数字(过滤器数量标记为,在这36个单元上重复此过程),输出结果是6×6×#filters(过滤器数量),以便在输入层上实施一个非平凡(***\*non-trivial\****)计算。此时,输入的结果的通道层数取决于过滤器的个数。
127 |
128 |
129 |
130 | #### 2.4.4深度可分离卷积
131 |
132 | **定义**:一个卷积核负责一个通道,一个通道只被一个卷积核卷积
133 |
134 | **引用博客**:https://blog.csdn.net/makefish/article/details/88716534
135 |
136 | 相较于一般卷积,深度可分离卷积有着不同的计算方法:
137 |
138 | 在卷积计算时,先用三个卷积对三个通道分别做卷积,这样在一次卷积后,输出3个数,然后这输出的三个数,再通过一个1x1x3的卷积核(pointwise核),得到一个数。下面进行分步解释;
139 |
140 | 第一步,对三个通道分别做卷积,输出三个通道的属性:
141 |
142 |
143 |
144 | 
145 |
146 |
147 |
148 |
149 |
150 | 第二步,用卷积核1x1x3对三个通道再次做卷积,这个时候的输出就和正常卷积一样,是8x8x1:
151 |
152 | 
153 |
154 |
155 |
156 | 如果要提取更多的属性,则需要设计更多的1x1x3卷积核心就可以(图片引用自原网站。感觉应该将8x8x256那个立方体绘制成256个8x8x1,因为他们不是一体的,代表了256个属性)::
157 |
158 | 
159 |
160 | **深度可分离卷积的优点缺点**:
161 |
162 | 对于需要提取大量属性或者特征的情景下,深度可分离卷积随着要提取的属性越来越多,就能够节省更多的参数。当然如果提取的特征属性不多,普通的卷积效果优于深度可分离卷积。
163 |
164 |
165 |
166 |
167 |
168 | ### 2.5 Inception网络
169 |
170 | #### 2.5.1作用
171 |
172 | 代替人工决定所使用的过滤器的大小,或者确定是否需要创建卷积层或池化层,
173 |
174 | #### 2.5.2 论文链接
175 |
176 | https://arxiv.org/pdf/1409.4842.pdf
177 |
178 | #### 2.5.3主要思想
179 |
180 | 不需要人为决定使用哪个过滤器或者是否需要池化,而是由网络自行确定这些参数,你可以给网络添加这些参数的所有可能值,然后把这些输出连接起来,让网络自己学习它需要什么样的参数,采用哪些过滤器组合。
181 |
182 | #### 2.5.4原理
183 |
184 | 利用多种维度的过滤器,分别使用不同的方法,产生大量长宽相等,通道可以不同的输出块,并将这些输出块堆积在一起,产生一个组合了各种类型的参数的输出,从而在后续的训练中,让网络自己学习它需要什么样的参数,采用哪些过滤器组合。
185 |
186 |
187 |
188 | 例如,这是你28×28×192维度的输入层,***\*Inception\****网络或***\*Inception\****层的作用就是代替人工来确定卷积层中的过滤器类型,或者确定是否需要创建卷积层或池化层,我们演示一下。
189 |
190 | 
191 |
192 |
193 |
194 | 如果使用1×1卷积,输出结果会是28×28×#(某个值),假设输出为28×28×64,并且这里只有一个层。
195 |
196 | 
197 |
198 |
199 |
200 | 如果使用3×3的过滤器,那么输出是28×28×128。然后我们把第二个值堆积到第一个值上,为了匹配维度,我们应用***\*same\****卷积,输出维度依然是28×28,和输入维度相同,即高度和宽度相同。
201 |
202 | 
203 |
204 |
205 |
206 | 或许你会说,我希望提升网络的表现,用5×5过滤器或许会更好,我们不妨试一下,输出变成28×28×32,我们再次使用***\*same\****卷积,保持维度不变。
207 |
208 | 
209 |
210 |
211 |
212 | 或许你不想要卷积层,那就用池化操作,得到一些不同的输出结果,我们把它也堆积起来,这里的池化输出是28×28×32。为了匹配所有维度,我们需要对最大池化使用***\*padding\****,它是一种特殊的池化形式,因为如果输入的高度和宽度为28×28,则输出的相应维度也是28×28。然后再进行池化,***\*padding\****不变,步幅为1。
213 |
214 | 
215 |
216 |
217 |
218 | 有了这样的***\*Inception\****模块,你就可以输入某个量,因为它累加了所有数字,这里的最终输出为32+32+128+64=256。***\*Inception\****模块的输入为28×28×192,输出为28×28×256。这就是Inception网络的核心内容。
219 |
220 |
221 |
222 | #### 2.5.5计算成本问题
223 |
224 | 由于进行了多种模型的计算,会造成计算成本会非常的大,如何缩小成本是一个非常重要的一环。
225 |
226 | 下面以5×5过滤器为例计算成本
227 |
228 | 
229 |
230 |
231 |
232 | 这是一个28×28×192的输入块,执行一个5×5卷积,它有32个过滤器,输出为28×28×32。我们来计算这个28×28×32输出的计算成本,它有32个过滤器,因为输出有32个通道,每个过滤器大小为5×5×192,输出大小为28×28×32,所以你要计算28×28×32个数字。对于输出中的每个数字来说,你都需要执行5×5×192次乘法运算,所以乘法运算的总次数为每个输出值所需要执行的乘法运算次数(5×5×192)乘以输出值个数(28×28×32),把这些数相乘结果等于1.2亿(120422400)。
233 |
234 | 
235 |
236 |
237 |
238 | 为了缩小成本,我们使用1*1卷积对输入进行通道缩小。对于输入层,使用1×1卷积把输入值从192个通道减少到16个通道。然后对这个较小层运行5×5卷积,得到最终输出。请注意,输入和输出的维度依然相同,输入是28×28×192,输出是28×28×32。
239 |
240 | 然后我们进行成本计算应用1×1卷积,过滤器个数为16,每个过滤器大小为1×1×192,这两个维度相匹配(输入通道数与过滤器通道数),28×28×16这个层的计算成本是,输出28×28×192中每个元素都做192次乘法,用1×1×192来表示,相乘结果约等于240万,这是第一个卷积层的计算成本。第二层的输出为28×28×32,对每个输出值应用一个5×5×16维度的过滤器,计算结果为1000万。
241 |
242 | 所以所需要乘法运算的总次数是这两层的计算成本之和,也就是1204万,与上一张幻灯片中的值做比较,计算成本从1.2亿下降到了原来的十分之一,即1204万。
243 |
244 |
245 |
246 | #### 2.5.6 瓶颈层
247 |
248 |
249 |
250 | 
251 |
252 |
253 |
254 | 这个被增加的1*1卷积层常被称为瓶颈层,即先缩小网络表示,然后再扩大它。
255 |
256 |
257 |
258 | 需要注意的是,只要合理构建瓶颈层,你既可以显著缩小表示层规模,又不会降低网络性能,从而节省了计算。
259 |
260 |
261 |
262 | #### 2.5.7 Inception Net
263 |
264 | 简述:由多个***\*Inception\*******\*模块所组成的神经网络。\****
265 |
266 | 原理:
267 |
268 | 首先如下图所示,建立前面所说的***\*Inception\****模块。
269 |
270 | 
271 |
272 |
273 |
274 | 为了能在最后将这些输出都连接起来,我们会使用***\*same\****类型的***\*padding\****来池化,使得输出的高和宽依然是28×28,这样才能将它与其他输出连接起来。
275 |
276 | 但注意,如果你进行了最大池化,即便用了***\*same padding\****,3×3的过滤器,***\*stride\****为1,其输出将会是28×28×192,其通道数或者说深度与这里的输入(通道数)相同。所以看起来它会有很多通道,我们实际要做的就是再加上一个1×1的卷积层,去进行我们在1×1卷积层的视频里所介绍的操作,将通道的数量缩小,缩小到28×28×32。
277 |
278 | 
279 |
280 |
281 |
282 | 最后,将这些方块全都连接起来。在这过程中,把得到的各个层的通道都加起来,最后得到一个28×28×256的输出。通道连接实际就是之前视频中看到过的,把所有方块连接在一起的操作。这就是一个***\*Inception\****模块,而***\*Inception\****网络所做的就是将这些模块都组合到一起。
283 |
284 | 
285 |
286 |
287 |
288 | ***\*上图为\*******\*Inception\****网络的图片,并且其由多个***\*Inception\*******\*模块所组成,需要注意的是有一些\*******\*Inception\*******\*模块中间还夹着一个最大池化层,如图中的6和7.\****
289 |
290 | 
291 |
292 |
293 |
294 | ***\*在论文原文中,网络里有着一些其他分支,如上图中的1、2、4,其中1是一个\*******\*softmax\****层,用于做出预测,编号2所做的就是通过隐藏层(编号3)来做出预测,所以这其实是一个***\*softmax\****输出(编号2),编号4也包含了一个隐藏层,通过一些全连接层,然后有一个***\*softmax\****来预测,输出结果的标签。 这些分支确保了即便是隐藏单元和中间层(编号5)也参与了特征计算,它们也能预测图片的分类。它在***\*Inception\****网络中,起到一种调整的效果,并且能防止网络发生过拟合。
295 |
296 |
297 |
298 | #### 2.5.8 Inception网络多种类型
299 |
300 | 参考博客:https://www.cnblogs.com/dengshunge/p/10808191.html
301 |
302 | ##### Inception v1
303 |
304 | v1其实就是我们前面所说的使用1*1卷积降低计算量后的Inception网络。
305 |
306 | 提升神经网络的性能是各种方法和算法的目的,当然提升网络的性能的方法有很多,例如增加网络的深度和宽度,但当深度和宽度不断增加时,需要训练的参数也会增加,过多的参数容易发生过拟合,并且会导致计算量增加。所以就有了v1结构来解决此问题,也就是利用1*1卷积降低计算量。
307 |
308 |
309 |
310 | ##### Inception v2
311 |
312 | 在训练时每层输入数据的分布会发生改变,所以需要较低的学习率和精心设置初始化参数。只要网络的前面几层发生微小的改变,那么后面几层就会被累积放大下去。一旦网络某一层的输入数据的分布发生改变,那么这一层网络就需要去适应学习这个新的数据分布,所以如果训练过程中,训练数据的分布一直在发生变化,那么将会影响网络的训练速度。为此,提出了v2版本的Inception网络。
313 |
314 | V2版本网络使用了BN算法,可以设置较大的初始学习率,并且减少对参数初始化的依赖,提高了训练速度,同时也可以能防止网络陷入饱和,即消除梯度弥散。
315 |
316 |
317 |
318 | ##### Inception v3
319 |
320 | Inception v3主要解决的是:inception结构过于复杂,使得我们很难对网络进行修改。
321 |
322 | V3主要思路为:利用小尺度的卷积来代替大尺度的卷积,在减少计算量的同时,保证能够学习到更多的信息。例如提出了使用两个级联的3*3的滤波器来代替一个5*5的滤波器,如下图所示:
323 |
324 | 
325 |
326 | 
327 |
328 |
329 |
330 | 同时又对3*3卷积进行分解为3*1+1*3,如下图所示,进而进一步降低计算量
331 |
332 | 
333 |
334 |
335 |
336 | V3主要遵循下列几条思想
337 |
338 | 1. 避免特征表示瓶颈,尤其是在网络的前面。要避免严重压缩导致的瓶颈。特征表示尺寸应该温和地减少,从输入端到输出端。特征表示的维度只是一个粗浅的信息量表示,它丢掉了一些重要的因素如相关性结构。
339 |
340 | 2. 高维信息更适合在网络的局部处理。在卷积网络中逐步增加非线性激活响应可以解耦合更多的特征,那么网络就会训练的更快。
341 |
342 | 3. 空间聚合可以通过低维嵌入,不会导致网络表示能力的降低。例如在进行大尺寸的卷积(如3*3)之前,我们可以在空间聚合前先对输入信息进行降维处理,如果这些信号是容易压缩的,那么降维甚至可以加快学习速度。
343 |
344 | 4. 平衡好网络的深度和宽度。通过平衡网络每层滤波器的个数和网络的层数可以是网络达到最佳性能。增加网络的宽度和深度都会提升网络的性能,但是两者并行增加获得的性能提升是最大的。所以计算资源应该被合理的分配到网络的宽度和深度。
345 |
346 |
347 |
348 | ##### Inception v4
349 |
350 | V4的提出主要是基于 ”当网络更深更宽时,inception网络能否一样高效”的问题提出的,v4具体的解决方法为,结合TensorFlow,简化训练,不需要将模型进行分割,并且将inception和resnet两者进行融合,进一步改善网络。
351 |
352 |
353 |
354 | 以上对Inception网络的4种模型进行概述,具体解释可参考下列博客 https://www.cnblogs.com/dengshunge/p/10808191.html
355 |
356 |
357 |
358 | ### 2.6使用开源实现方案
359 |
360 | 本节为介绍如何下载开源代码。
361 |
362 | 本节下载的代码网站为:
363 |
364 | ***\*ResNets\****实现的***\*GitHub\****地址:https://github.com/KaimingHe/deep-residual-networks
365 |
366 | 
367 |
368 |
369 |
370 |
371 |
372 | ***\*点击Code按钮,并且点击复制按钮复制代码的URL\****
373 |
374 | 
375 |
376 |
377 |
378 | 在需要保存代码的目录下打开cmd,使用下列指令进行代码的下载(复制)
379 |
380 | git clone your URL
381 |
382 | git clone https://github.com/KaimingHe/deep-residual-networks.git
383 |
384 | 
385 |
386 |
387 |
388 | 使用指令观察目录,说明此时代码已下载完毕。
389 |
390 | 接下来进行打开代码。
391 |
392 |
393 |
394 | 
395 |
396 |
397 |
398 | 代码储存在prototxt文件夹中
399 |
400 | 
401 |
402 |
403 |
404 | 使用指令打开其中一个文件。
405 |
406 | more 文件名
407 |
408 | 
409 |
410 | 当然也可以用ide直接打开来进行修改。
411 | ### 2.7 迁移学习
412 | #### 2.7.1 迁移学习的概念
413 | 迁移学习是从一个或多个源领域中通过训练该模型,得出有用的知识并将其用在新的目标任务上(未标记的同一类有相似特征的物品或者是未标记的不同类物品)本质是知识的迁移再利用。
414 | #### 2.7.2 ImageNet、MS COCO\Pascal数据集的获取
415 | ImageNet数据集的获取:
416 | 所有图像可通过url下载:不需要账号登录即可免费下载,下载链接:http://www.image-net.org/download-imageurls ,在SEARCH框中输入需要下载的synset,如tree,也可按类别下载即WordNet ID,下载链接:http://www.image-net.org/synset?wnid=n02084071 ,其中好像个别url已失效。
417 | MS COCO:
418 |
419 | 数据集官网首页:http://cocodataset.org/#home
420 |
421 | 数据集下载:
422 |
423 | 可用迅雷去下载官方链接,速度也挺快的。也可以去这个高中生搭建的下载站下载:http://bendfunction.f3322.net:666/share/。 他的首页是这样子的:http://bendfunction.f3322.net:666/
424 | https://pjreddie.com/projects/coco-mirror/
425 | #### 2.7.3 迁移学习的分类
426 | 按照迁移学习的定义,可以将迁移学习分为三种类型,分布差异迁移学习,特征差异迁移学习和标签差异迁移学习。分布差异迁移学习之源域和目标域数据的边缘分布或者条件概率分布不同,特征差异迁移学习之源域数据和目标数据特征空间不同,标签差异迁移学习指源域和目标域的数据标记空间不同。
427 | 用香蕉和苹果分类问题为例,源域数据是已有的带标签香蕉和苹果的文本数据,目标域是新来的不带标记的香蕉和苹果的文本数据,源域和目标域的数据来自不同的时间,不同地点,数据分布不同,但标记空间和特征空间是相同的,利用源域中的数据来进行目标域的学习问题就是属于分布差异迁移学习问题。源域数据是带有标记的苹果和香蕉的文本数据,而目标域是不带有 标记的苹果和香蕉的图片数据,源域和目标域一个是文本,一个是图像,属于特征差异迁移学习范围。源域数据是带有标记的香蕉和苹果的文本数据,属于二分类问题,目标域是不带标记的梨子,橘子和橙子的文本数据属于三分类问题,源域和目标域的数据标记空间不同,属于标记差异迁移学习的范围。
428 |
429 | 现已成熟的监督学习模式下,在大样本的已标记的数据量集中训练形成传统的监督学习,但是这种模式在运用到情况更为复杂,更多变的实际环境中往往会出现很大的误差,
430 | 所以迁移学习就是在样本量比较少的情况下,训练分类器,随之把这种模式可以运用到其他很多种情况下。
431 |
432 | ### 2.8 数据增强
433 | #### 2.8.1数据增强的基本操作
434 | 数据增强也叫数据扩增,意思是在不实质性的增加数据的情况下,让有限的数据产生等价于更多数据的价值。
435 | 数据增强的手段包括几何变换类,颜色变换类等。
436 |
437 | (1) 几何变换类
438 |
439 | 几何变换类即对图像进行几何变换,包括翻转,旋转,裁剪,变形,缩放等各类操作,下面展示以上操作。
440 | 图一2 3 4 5
441 | (2) 颜色变换类
442 | 颜色变换类时改变图片的R、G、B的值。
443 | #### 2.8.2数据增强的代码实现
444 | TensorFlow实现图片数据增强:
445 | 参见以下网址https://zhuanlan.zhihu.com/p/57284174
446 | #### 2.8.2数据增强的优缺点
447 | 优点:
448 | 增加训练的数据量,提高模型的泛化能力
449 | 增加噪声数据,提升模型的鲁棒性
450 | ### 2.9 计算机视觉现状
451 | #### 2.9.1计算机视觉现状
452 | 深度学习已经成功地应用于计算机视觉、自然语言处理、语音识别、在线广告、物流还有其他许多问题。
453 | 在计算机视觉的现状下,深度学习应用于计算机视觉应用有一些独特之处。
454 | ####2.9.2 banchmark
455 | Benchmark 基准测试,Benchmark是一个评价方式,在整个计算机领域有着长期的应用。
456 | Benchmark在计算机领域应用最成功的就是性能测试,主要测试负载的执行时间、传输速度、吞吐量、资源占用率等。基准测试同时也可以用来识别某段代码的CPU或者内存效率问题. 许多开发人员会用基准测试来测试不同的并发模式, 或者用基准测试来辅助配置工作池的数量, 以保证能最大化系统的吞吐量.
457 | 关于实战可参考:
458 | https://blog.csdn.net/woniu317/article/details/82560312
459 |
--------------------------------------------------------------------------------
/12 目标检测.md:
--------------------------------------------------------------------------------
1 | ## 12 目标检测
2 |
3 | ### 12.1 目标定位
4 |
5 | #### 12.1.1 定义
6 |
7 | 除了要识别出目标类(例如是否有汽车)以外,算法还需要能够给出目标的位置(例如用红框框出目标的位置),这是一种分类定位问题。分类定位问题可以是只有一个目标对象在图片中,也可以是多个目标对象在图片中的。先从单个目标对象的情况开始。
8 |
9 | #### 12.1.2 实现
10 |
11 | **1. 边界框参数定义**
12 |
13 | 图片分类我们已经比较熟悉了,知道最后通过 *softmax* 激活函数激活来表示该图片属于每一类的概率。相较于单纯的分类问题,目标定位还需要输出4个值:$b_x,b_y,b_h,b_w$。这四个值用于表示边框的位置和大小,具体为
14 | $$
15 | \begin{array}{l}
16 | b_x:边框的中心点的x轴坐标 \\
17 | b_y:边框的中心点的y轴坐标 \\
18 | b_h:边框的高度 \\
19 | b_w:边框的宽度 \\
20 | \end{array}
21 | $$
22 | 以上4个值的取值范围均为[0, 1],表示的是边界框与图片对应的**比例**。
23 |
24 | 关于坐标轴的选取,一般选图片的左上角为原点(0, 0),右下角为(1, 1)。且$x$轴为纵轴正方向向下,$y$轴为横轴正方向向右。
25 |
26 | **2. 标签的定义**
27 |
28 | 在确定需要增加的额外输出之后,也要重新定义目标标签 $y$:
29 | $$
30 | y=\left[\begin{array}{l}
31 | p_{c} \\
32 | b_{x} \\
33 | b_{y} \\
34 | b_{h} \\
35 | b_{w} \\
36 | c_{1} \\
37 | c_{2} \\
38 | c_{3}
39 | \end{array}\right]
40 | $$
41 | 其中额外增加了$p_c$,用于表示是否有对象属于类$c_1、c_2$或$c_3$,若为1则表示有目标类在图片中,为0表示只有背景。在只有背景(无目标类)时,其他输出均无效。
42 |
43 | 举一个具体的例子,如下图:
44 |
45 | 
46 |
47 | x 是输入,y 是标签,假设$c_2$表示为车,则最终标签应该如上图所示。当输入中不含任何目标类时,$p_c=0$,其他参数全用“?”表示,即不参与 loss 的计算。
48 |
49 | **3. 边界框参数取值范围**
50 |
51 | 关于边框的4个参数,吴恩达老师给出的取值范围都是[0, 1]的。虽然确实可以这么做,但是背后的原因却没有解释。个人猜测可能是以下原因:
52 |
53 | * 固定取值在[0, 1]之间更容易用激活函数表示,比如sigmoid可以将单个值映射到[0, 1];
54 | * 让标签的所有参数都在一个取值范围,这样在计算loss的时候就不会变相加权了;
55 | * 取值范围在[0, 1]内更容易训练、收敛。
56 |
57 | **4. 损失函数**
58 | $$
59 | L(\hat y,y)=
60 | \begin{cases}
61 | (\hat{y_1}-y_1)^2+(\hat{y_2}-y_2)^2+...+(\hat{y_n}-y_n)^2 & {y_1=1}\\
62 | (\hat{y_1}-y_1)^2 & {y_1=0}
63 | \end{cases}
64 | $$
65 |
66 | * 对于$p_c$可以采用 Logistic 回归的方法,甚至用均方误差$(p_c-\hat{p_c})^2$也可以;
67 | * 对于$b_x,b_y,b_w,b_h$,loss 可以用平方差或类似方法;
68 | * 对于$c_1,c_2,c_3$,是多分类问题,和之前一样用 softmax 即可。
69 |
70 | ### 12.2 特征点检测
71 |
72 | #### 12.2.1 定义
73 |
74 | 以下图为例,检测双眼的眼角位置
75 |
76 | 
77 |
78 | 这个就是特征点检测,主要任务是预测对应的特征点的位置,一般会同时预测多个点。
79 |
80 | #### 12.2.2 实现
81 |
82 | 对于单个点,其坐标为$(l_{ix},l_{iy}),i \in [1, m]$,$m$是特征点的个数,$l_{ix},l_{iy} \in [0,1]$。坐标轴的选取和目标定位时一致,以及需要保证每个样本的特征点的顺序是一致的,比如$l_1$都是左眼的左眼角,$l_2$都是左眼的右眼角等。
83 |
84 | 关于最后一层的激活函数,可以对每个坐标的值用 sigmoid 激活。
85 |
86 | ### 12.3 目标检测
87 |
88 | #### 12.3.1 滑动窗口目标检测算法
89 |
90 | 滑动窗口检测是分两步执行的:第一步是从原图中裁剪一部分并根据需求调整大小,第二步是检测裁剪部分有无目标对象。
91 |
92 | 对于第二步,是我们比较熟悉的分类算法,只是训练集需要人为调整到为几乎整张图都是目标对象,如下图:
93 |
94 | 
95 |
96 | $x$ 为一张无车的图片或者被车占满的图片,标签 $y$ 为1时有车,为0时无车。
97 |
98 | 对于第一步,滑动窗口用的方法是先选定一个裁剪大小,然后从图片的左上角开始,每隔一定像素(距离)裁剪一次,一直滑动到图片的右下角,然后下一个裁剪大小用相同的方法裁剪。如图,上图为3种裁剪大小,下图为一个滑动流程:
99 |
100 | 
101 |
102 | 
103 |
104 | #### 12.3.2 滑动窗口缺点——计算成本
105 |
106 | 看到这里不难发现,滑动窗口检测由于需要多个窗口且每个窗口滑动多次而导致运算量会相当巨大,运行时间过慢。而且如果滑动的步幅过大或者裁剪的大小不合适也会导致很难检测到目标。
107 |
108 | ### 12.4 卷积的滑动窗口实现
109 |
110 | #### 12.4.1 把神经网络的全连接层转化成卷积层
111 |
112 | 
113 |
114 | - 假设目标检测算法输入一个14×14×3的图像,过滤器大小为5×5,数量是16,14×14×3的图像在过滤器处理之后映射为10×10×16。
115 |
116 | - 然后通过参数为2×2的最大池化操作,图像减小到5×5×16。
117 |
118 | - 添加一个连接400个单元的全连接层,接着再添加一个全连接层。
119 |
120 | - 最后通过softmax单元输出,用4个数字来表示 ,它们分别对应softmax单元所输出的4个分类出现的概率。这4个分类可以是行人、汽车、摩托车和背景或其它对象。
121 |
122 | **全连接层转化为卷积层**
123 |
124 | 
125 |
126 | - 前几层和之前的一样。
127 |
128 | - 而对于全连接层,用5×5的过滤器来实现,数量是400个。输入图像大小为5×5×16,用5×5的过滤器对它进行卷积操作,过滤器实际上是5×5×16,因为在卷积过程中,过滤器会遍历这16个通道,所以这两处的通道数量必须保持一致,输出结果为1×1。假设应用400个这样的5×5×16过滤器,输出维度就是1×1×400。它不再是一个含有400个节点的集合,而是一个1×1×400的输出层。从数学角度看,它和全连接层是一样的,因为这400个节点中每个节点都有一个5×5×16维度的过滤器,所以每个值都是上一层这些5×5×16激活值经过某个任意线性函数的输出结果。
129 | - 再添加另外一个卷积层,这里用1×1卷积,假设有400个1×1的过滤器,在这400个过滤器的作用下,下一层的维度是1×1×400,它其实就是上个网络中的这一全连接层。最后经由1×1过滤器的处理,得到一个softmax激活值,通过卷积网络,我们最终得到这个1×1×4的输出层,而不是4个数字。
130 |
131 | 以上就是用卷积层代替全连接层的过程。
132 |
133 | #### 12.4.2 在卷积上应用滑动窗口对象检测算法
134 |
135 | 
136 |
137 | 假设向滑动窗口卷积网络输入14×14×3的图片。和前面一样,神经网络最后的输出层,即softmax单元的输出是1×1×4,这里画得比较简单,严格来说,14×14×3应该是一个长方体,第二个10×10×16也是一个长方体,为了方便,这里只画了正面,所以这里显示的都是平面图,而不是3D图像。
138 |
139 | 
140 |
141 | 假设输入给卷积网络的图片大小是14×14×3,测试集图片是16×16×3,现在给这个输入图片加上黄色条块,在最初的滑动窗口算法中,你会把这片蓝色区域输入卷积网络(红色笔标记)生成0或1分类。接着滑动窗口,步幅为2个像素,向右滑动2个像素,将这个绿框区域输入给卷积网络,运行整个卷积网络,得到另外一个标签0或1。继续将这个橘色区域输入给卷积网络,卷积后得到另一个标签,最后对右下方的紫色区域进行最后一次卷积操作。我们在这个16×16×3的小图像上滑动窗口,卷积网络运行了4次,于是输出了了4个标签。
142 |
143 | 
144 |
145 | 这4次卷积操作中很多计算都是重复的。所以执行滑动窗口的卷积时使得卷积网络在这4次前向传播过程中共享很多计算。
146 |
147 | - 卷积网络运行同样的参数,使得相同的5×5×16过滤器进行卷积操作,得到12×12×16的输出层。
148 |
149 | - 然后执行同样的最大池化,输出结果6×6×16。照旧应用400个5×5的过滤器,得到一个2×2×400的输出层,现在输出层为2×2×400,而不是1×1×400。
150 |
151 | - 应用1×1过滤器得到另一个2×2×400的输出层。
152 |
153 | - 再做一次全连接的操作,最终得到2×2×4的输出层,而不是1×1×4。
154 |
155 | - 最终,在输出层这4个子方块中,蓝色的是图像左上部分14×14的输出(红色箭头标识),右上角方块是图像右上部分(绿色箭头标识)的对应输出,左下角方块是输入层左下角(橘色箭头标识),也就是这个14×14区域经过卷积网络处理后的结果,同样,右下角这个方块是卷积网络处理输入层右下角14×14区域(紫色箭头标识)的结果。
156 |
157 | 该卷积操作的原理是我们不需要把输入图像分割成四个子集,分别执行前向传播,而是把它们作为一张图片输入给卷积网络进行计算,其中的公共区域可以共享很多计算,就像这里我们看到的这个4个14×14的方块一样。
158 |
159 | 
160 |
161 | 再看一个更大的图片样本,假如对一个28×28×3的图片应用滑动窗口操作,如果以同样的方式运行前向传播,最后得到8×8×4的结果。跟上一个范例一样,以14×14区域滑动窗口,首先在这个区域应用滑动窗口,其结果对应输出层的左上角部分。接着以大小为2的步幅不断地向右移动窗口,直到第8个单元格,得到输出层的第一行。然后向图片下方移动,最终输出这个8×8×4的结果。因为最大池化参数为2,相当于以大小为2的步幅在原始图片上应用神经网络。
162 |
163 | **滑动窗口的实现过程总结**
164 |
165 | 
166 |
167 | 在图片上剪切出一块区域,假设它的大小是14×14,把它输入到卷积网络。继续输入下一块区域,大小同样是14×14,重复操作,直到某个区域识别到汽车。
168 |
169 | 但是我们不用依靠连续的卷积操作来识别图片中的汽车,比如,我们可以对大小为28×28的整张图片进行卷积操作,一次得到所有预测值,如果足够幸运,神经网络便可以识别出汽车的位置。
170 |
171 | ### 12.5 Bounding Box预测
172 |
173 | 滑动窗口法的卷积实现的算法虽然效率更高,但仍然存在问题,不能输出最精准的边界框。
174 |
175 |  176 |
177 | 在滑动窗口法中,你取这些离散的位置集合,然后在它们上运行分类器,在这种情况下,这些边界框没有一个能完美匹配汽车位置,也许这个框(编号1)是最匹配的了。还有看起来这个真实值,最完美的边界框甚至不是方形,稍微有点长方形(红色方框所示),长宽比有点向水平方向延伸。
178 |
179 | 其中一个能得到更精准边界框的算法是**YOLO**算法,YOLO(You only look once)意思是你只看一次。
180 |
181 | #### 12.5.1 YOLO算法的具体实现
182 |
183 | 
184 |
185 | 比如你的输入图像是100×100的,然后在图像上放一个网格。为了介绍起来简单一些,这里用3×3网格,实际实现时会用更精细的网格,可能是19×19。
186 |
187 | 基本思路是使用图像分类和定位算法,将算法应用到9个格子上。
188 |
189 | 具体一点,需要定义训练标签,对于9个格子中的每一个指定一个标签$y$,$y$是8维的(上图蓝字):
190 |
191 | - $p_{c}$等于0或1取决于这个绿色格子中是否有图像。
192 |
193 | - $b_{x}$、$b_{y}$、$b_{h}$和$b_{w}$作用就是,如果那个格子里有对象,那么就给出边界框坐标。
194 |
195 | - $c_{1}$、$c_{2}$和$c_{3}$就是你想要识别的三个类别,背景类别不算,所以你尝试在背景类别中识别行人、汽车和摩托车,那么$c_{1}$、$c_{2}$和$c_{3}$可以是行人、汽车和摩托车类别。
196 |
197 | 这张图有两个对象,**YOLO算法**做的就是,**取两个对象的中点,然后将这个对象分配给包含其中点的格子**。
198 |
199 | 所以左边的汽车就分配到这个格子上(绿框),然后这辆中点在这里(绿点),标签为(上图绿字);右边的汽车分配给这个格子(黄色),中点在这里(黄点),标签为(上图黄字)。即使中心格子同时有两辆车的一部分,我们就假装中心格子没有任何我们感兴趣的对象。
200 |
201 | 没有检测对象的格子(除中间靠左、中间靠右外的其他格子)标签向量$y$都如上图紫字所示。
202 |
203 | 故对于这里9个格子中任何一个,你都会得到一个8维输出向量,因为这里是3×3的网格,所以有9个格子,总的输出尺寸是3×3×8,所以目标输出是3×3×8。
204 |
205 |
176 |
177 | 在滑动窗口法中,你取这些离散的位置集合,然后在它们上运行分类器,在这种情况下,这些边界框没有一个能完美匹配汽车位置,也许这个框(编号1)是最匹配的了。还有看起来这个真实值,最完美的边界框甚至不是方形,稍微有点长方形(红色方框所示),长宽比有点向水平方向延伸。
178 |
179 | 其中一个能得到更精准边界框的算法是**YOLO**算法,YOLO(You only look once)意思是你只看一次。
180 |
181 | #### 12.5.1 YOLO算法的具体实现
182 |
183 | 
184 |
185 | 比如你的输入图像是100×100的,然后在图像上放一个网格。为了介绍起来简单一些,这里用3×3网格,实际实现时会用更精细的网格,可能是19×19。
186 |
187 | 基本思路是使用图像分类和定位算法,将算法应用到9个格子上。
188 |
189 | 具体一点,需要定义训练标签,对于9个格子中的每一个指定一个标签$y$,$y$是8维的(上图蓝字):
190 |
191 | - $p_{c}$等于0或1取决于这个绿色格子中是否有图像。
192 |
193 | - $b_{x}$、$b_{y}$、$b_{h}$和$b_{w}$作用就是,如果那个格子里有对象,那么就给出边界框坐标。
194 |
195 | - $c_{1}$、$c_{2}$和$c_{3}$就是你想要识别的三个类别,背景类别不算,所以你尝试在背景类别中识别行人、汽车和摩托车,那么$c_{1}$、$c_{2}$和$c_{3}$可以是行人、汽车和摩托车类别。
196 |
197 | 这张图有两个对象,**YOLO算法**做的就是,**取两个对象的中点,然后将这个对象分配给包含其中点的格子**。
198 |
199 | 所以左边的汽车就分配到这个格子上(绿框),然后这辆中点在这里(绿点),标签为(上图绿字);右边的汽车分配给这个格子(黄色),中点在这里(黄点),标签为(上图黄字)。即使中心格子同时有两辆车的一部分,我们就假装中心格子没有任何我们感兴趣的对象。
200 |
201 | 没有检测对象的格子(除中间靠左、中间靠右外的其他格子)标签向量$y$都如上图紫字所示。
202 |
203 | 故对于这里9个格子中任何一个,你都会得到一个8维输出向量,因为这里是3×3的网格,所以有9个格子,总的输出尺寸是3×3×8,所以目标输出是3×3×8。
204 |
205 |  206 |
207 | 所以这个算法的优点在于神经网络可以输出精确的边界框,所以测试的时候,你做的是喂入输入图像$x$,然后跑正向传播,直到你得到这个输出$y$。然后对于这里3×3位置对应的9个输出,就可以读出1或0。如果那里有个对象,就可以读出那个对象是什么,还有格子中这个对象的边界框是什么。
208 |
209 | 只要每个格子中对象数目没有超过1个,这个算法应该是没问题的。一个格子中存在多个对象的问题,之后再讨论。这里用的是比较小的3×3网格,实践中你可能会使用更精细的19×19网格,所以输出就是19×19×8。这样的网格精细得多,那么多个对象分配到同一个格子的概率就小得多。
210 |
211 | 把对象分配到一个格子的过程是,你观察对象的中点,然后将这个对象分配到其中点所在的格子,所以即使对象可以横跨多个格子,也只会被分配到9个格子其中之一,就是3×3网络的其中一个格子,或者19×19网络的其中一个格子。在19×19网格中,两个对象的中点处于同一个格子的概率就会更低。
212 |
213 | YOLO算法有一个好处就是,它是一个卷积实现,共享了很多卷积计算,所以实际上它的运行速度非常快,可以达到实时识别。
214 |
215 | **编码边界框**
216 |
217 | 
218 |
219 | 对于这个方框(中右侧),我们约定左上这个点是(0,0),然后右下这个点是(1,1);
220 |
221 | 要指定橙色中点的位置,$b_{x}$大概是0.4,因为它的位置大概是水平长度的0.4,$b_{y}$大概是0.3;
222 |
223 | 边界框的高度用格子总体宽度的比例表示,所以这个红框的宽度可能是蓝线(图右下角蓝线)的90%,所以$b_h$是0.9,它的高度也许是格子总体高度的一半,这样的话$b_{w}$就是0.5。
224 |
225 | 换句话说,$b_{x}$、$b_{y}$、$b_{h}$和$b_{w}$单位是相对于格子尺寸的比例,所以$b_{x}$和$b_{y}$必须在0和1之间,因为从定义上看,橙色点位于对象分配到格子的范围内,如果它不在0和1之间,如果它在方块外,那么这个对象就应该分配到另一个格子上。但是$b_{h}$和$b_{w}$可能会大于1,特别是如果有一辆汽车的边界框是这样的(左下红框),那么边界框的宽度和高度有可能大于1。
226 |
227 | 指定边界框的方式有很多,但这种约定是比较合理的,还有其他更复杂的参数化方式,涉及到sigmoid函数,确保这个值($b_{x}$和$b_{y}$)介于0和1之间,然后使用指数参数化来确保$b_{h}$和$b_{w}$都是非负数。还有其他更高级的参数化方式,可能效果要更好一点,但这里讲的办法应该是管用的。
228 |
229 | #### 12.5.2 其他指定边界框的算法
230 |
231 | **1. SSD**:
232 |
233 | SSD(Single-Shot MultiBox Detector),使用 VGG19 网络作为特征提取器(和 Faster R-CNN 中使用的 CNN 一样)的单次检测器。我们在该网络之后添加自定义卷积层(蓝色),并使用卷积核(绿色)执行预测。
234 |
235 | 
236 |
237 | 然而,卷积层降低了空间维度和分辨率。因此上述模型仅可以检测较大的目标。为了解决该问题,我们从多个特征图上执行独立的目标检测。
238 |
239 | 
240 |
241 | 以下是特征图图示。
242 |
243 | 
244 |
245 | SSD 使用卷积网络中较深的层来检测目标。如果我们按接近真实的比例重绘上图,我们会发现图像的空间分辨率已经被显著降低,且可能已无法定位在低分辨率中难以检测的小目标。如果出现了这样的问题,我们需要增加输入图像的分辨率。
246 |
247 | 
248 |
249 |
250 |
251 |
252 | 参考博客:https://www.jianshu.com/p/468e08f739bd
253 |
254 | **2. FPN**:
255 |
256 | 使用不同尺寸特征图进行预测的网络称为特征金字塔网络(FPN),是一种旨在提高准确率和速度的特征提取器。数据流如下:
257 |
258 | 
259 |
260 | FPN 由自下而上和自上而下路径组成。其中自下而上的路径是用于特征提取的常用卷积网络。空间分辨率自下而上地下降。当检测到更高层的结构,每层的语义值增加。
261 |
262 | 
263 |
264 | SSD 通过多个特征图完成检测。但是,最底层不会被选择执行目标检测。它们的分辨率高但是语义值不够,导致速度显著下降而不能被使用。SSD 只使用较上层执行目标检测,因此对于小的物体的检测性能较差。
265 |
266 | 
267 |
268 | FPN 提供了一条自上而下的路径,从语义丰富的层利用上采样构建高分辨率的层。
269 |
270 | 
271 |
272 | 虽然该重建层的语义较强,但在经过所有的上采样和下采样之后,目标的位置不精确。在重建层和相应的特征图之间添加横向连接可以使位置侦测更加准确。
273 |
274 | 
275 |
276 | **3. RetianNet**:
277 |
278 | RetianNet是基于 ResNet、FPN以及利用 Focal loss 构建的 。
279 |
280 | 
281 |
282 | RetinaNet
283 |
284 | **4. Focal Loss**
285 |
286 | 类别不平衡会损害性能。SSD 在训练期间重新采样目标类和背景类的比率,这样它就不会被图像背景淹没。Focal loss(FL)采用另一种方法来减少训练良好的类的损失。因此,只要该模型能够很好地检测背景,就可以减少其损失并重新增强对目标类的训练。我们从交叉熵损失 (Cross Entroy Loss)开始,并添加一个权重来降低高可信度类的交叉熵。
287 |
288 | 
289 |
290 | 例如,令 γ = 0.5, 经良好分类的样本的 Focal Loss 趋近于 0。
291 |
292 | 
293 |
294 | ### 12.6 交并比
295 |
296 | #### 12.6.1 交并比函数的作用
297 |
298 | 交并比(IoU, Intersection over Union)函数衡量了两个边界框重叠的相对大小,用来评价对象检测算法是否运行良好,即检测对象定位是否准确。
299 |
300 | #### 12.6.2 交并比函数的实现
301 |
302 | 
303 |
304 | 假设识别的对象的实际边界框如上图中红框所示,用对象检测算法得到的边界框如紫框所示,这个结果是好是坏呢?
305 |
306 | 交并比函数做的是计算**两个边界框交集和并集之比**,交集部分如橙色阴影所示,并集部分如绿色阴影所示,如果预测边框和实际边框完美重叠,交集等于并集,$IoU = 1$,一般约定,在计算机检测任务中,若 $IoU \geq 0.5$,则说明预测的边界框是正确的,如果希望更严格,可以把IoU的阈值定得更高,IoU越高,边界框越精确。
307 |
308 | ### 12.7 非极大值抑制
309 |
310 | #### 12.7.1 非极大值抑制的作用
311 |
312 | 到目前为止我们学到的对象检测中的一个问题是,算法可能对同一个对象做出多次检测而不是一次,非极大值抑制法可以**确保算法对每个对象只检测一次**。
313 |
314 | #### 12.7.2 非极大值抑制的实现
315 |
316 | 非极大值抑制(Non-max suppression):只输出概率最大的分类结果,抑制很接近但不是最大的其他预测结果。
317 |
318 | 
319 |
320 | 假设要在这张图里检测行人和汽车,我们可能会在上面放个19×19的网格,理论上每辆汽车只有一个中点,应该只分配到中点所在的格子里,实践中在跑对象分类和定位算法时,对每个格子都跑一次,橙色和绿色方框的那些格子可能会想,这辆车的中点应该在其格子内部,觉得它们格子内有车的概率很高,而不是19×19=361个格子中仅有两个格子会报告它们检测出一个对象,所以最后可能会对同一个对象做出多次检测。
321 |
322 | 非极大值抑制做的就是清理这些检测结果,对每个对象只检测一次,而不是每个对象都触发多次检测。
323 |
324 | **非极大值抑制的实现步骤:**
325 |
326 | 
327 |
328 | 1. 去掉所有预测边界框中 $p_c \leq 0.6$ 的边界框(这里的0.6是阈值,可以自己设定),抛弃了所有概率比较低的输出边界框,则剩下的边界框中存在对象的概率至少有0.6。
329 | 2. 对于剩下的边界框,首先看看每次报告中每个检测结果相关的概率 $p_c$,找到**概率最大**的那个,这个例子中是0.9,认为这是最可靠的检测,用高亮标记,就说在这里找到了一辆车。
330 | 3. 接着,非极大值抑制就会逐一审视剩下的矩形,所有和这个最大的边界框有很高交并比、高度重叠的其他边界框的输出就会被抑制,所以这两个 $p_c$ 分别为0.6和0.7的矩形和最大边界框(淡蓝色矩形)重叠程度很高,会被抑制、变暗。
331 |
332 | 左边那辆车也同理,找到 $p_c$ 最大的一个是0.8,认为这里检测出一辆车,用高亮显示,而其他IoU值很高的矩形会被抑制而变暗。直接抛弃变暗的矩形,只剩下高亮显示的,就是最后得到的两个预测结果。
333 |
334 | 上面介绍的只是算法检测单个对象的情况,若想同时检测三种对象,比如行人、汽车和摩托,则需要独立进行三次非极大值抑制,对每个输出类别都做一次。
335 |
336 | ### 12.8 Anchor Boxes
337 |
338 | #### 12.8.1 为什么要用Anchor Boxes?
339 |
340 | 之前的算法只能在一个格子中检测出一个对象,Anchor Boxes可以**一个格子检测出多个对象**。如下图所示,使用3x3的网格,行人和汽车的中心几乎在同一个网格,这时就需要用到Anchor Boxes。
341 |
342 | 
343 |
344 | #### 12.8.2 思路
345 |
346 | 1. 预先定义几个不同形状的anchor box,把预测结果和这些anchor box关联起来。本例假设两个anchor box,对应行人和汽车。
347 |
348 | 
349 |
350 | 2. 定义类别标签,将原来的向量$$\left[\begin{array}{llllllll}
351 | p_{c} & b_{x} & b_{y} & b_{h} & b_{w} & c_{1} & c_{2} & c_{3}
352 | \end{array}\right]^{T}$$重复两次$$\left.\begin{array}{llllllllllllllll}
353 | y=\left[p_{c}\right. & b_{x} & b_{y} & b_{h} & b_{w} & c_{1} & c_{2} & c_{3} & p_{c} & b_{x} & b_{y} & b_{h} & b_{w} & c_{1} & c_{2} & c_{3}
354 | \end{array}\right]^{T}$$。其中,前面的8个参数和anchor box 1相关联,后面的8个参数和anchor box 2相关联。
355 |
356 | 
357 |
358 | 3. 行人一般符合anchor box1形状,所以用anchor box1来预测行人会达到很好的效果,这么编码 $p_c$ = 1,代表有个行人,用 $b_x, b_y ,b_h$ 和 $b_w$ 来编码包住行人的边界框,用$c_1, c_2 ,c_3$($c_1$ = 1,$c_2$ = 0,$c_3$ = 0)来说明这个对象是个行人。 汽车一般符合anchor box2形状,采用相同的编码方法,定义对象是汽车和边界框等,所有参数都和检测汽车相关( $p_c$ = 1, $b_x, b_y ,b_h$, $b_w$, $c_1$ = 0,$c_2$ = 1,$c_3$ = 0)。
359 |
360 | 4. 当两个anchor boxes对相同位置做出判别时,以交并比作为取舍指标。选择IoU最高的那个,用这个anchor box来进行预测。输出y的维度是$n \times n \times m \times c$(n为图片分成$n \times n$份,$m$为anchor box数量,$c$为class类别数)
361 |
362 | #### 12.8.3 怎么选择anchor box?
363 |
364 | 1. 一般手工指定anchor box形状,根据要检测的对象,指定有针对性的anchor box,可选择5-10个anchor box,使其尽可能覆盖到不同形状。
365 | 2. 使用K-means聚类算法获得anchor box,选择最具有代表性的一组anchor box。
366 |
367 | ### 12.9 YOLO 算法
368 |
369 | 目标检测架构分为两种,一种是two-stage,一种是one-stage。 two-stage 有region proposal (选取候选区域)过程,网络会根据候选区域生成位置和类别,而 one-stage 直接从图片生成位置和类别。
370 |
371 | YOLO 是一种 one-stage 方法,即 You Only Look Once 的缩写,意思是神经网络只需要看一次图片,就能输出结果。
372 |
373 |
374 | #### 12.9.1 YOLO算法的实现
375 |
376 | - 构造训练集:假设检测三种对象,行人,汽车和摩托。
377 | 输入图像,神经网络的输出尺寸是3x3x2x8(3x3的网格,2个anchor box,8个参数)。遍历9个格子,构造训练集,然后构成对应的目标向量y,判断和anchor box 有关的 $p_c$ 和边界框,指定正确类别。
378 |
379 | 
380 |
381 | - 如何预测:输入图像,神经网络的输出尺寸是3x3x2x8,对于9个格子,每个都有对应的向量,如上图所示。
382 | 对于1号蓝格,检测不到任何对象,所以2个anchor box的 $p_c$ = 0。剩下的是一些数字,多多少少都是噪音,但这些数字基本上会被忽略,因为神经网络告诉表示那里没有任何东西。(输出 y 如编号3所示)。
383 | 对于2号绿格,里面有汽车。对于边界框1(anchor box 1)来说 $p_c$ = 0,表示此格子中无行人。然后就是一组数字噪音,此格子中无行人。anchor box 2对应汽车,此格子中有车,因此希望数字可以对车子指定一个相当准确的边界框,即($$\left.p_{c}=1, b_{x}, b_{y}, b_{h}, b_{w}, c_{1}=0, c_{2}=1, c_{3}=0\right)$$,这就是神经网络做出预测的过程。
384 | - 运行非极大值抑制:看看一张新的测试图片,对于两个anchor box,那么对于9个格子中任何一个都会有两个预测的边界框。
385 | 针对每个框,抛弃概率低的预测,去掉那些连神经网络都说这里很可能什么都没有的边界框。如果希望检测行人、车子和摩托三个对象检测类别,那么需要对每个类别单独运行非极大值抑制,处理预测结果即此类别的边界框。
386 |
387 | 
388 |
389 | - 最后,输出位置和类别信息。
390 |
391 | #### 12.9.2 YOLO v1、v2、v3和v4
392 |
393 | YOLO 一共发布了四个版本,其中 YOLOv1 奠定了整个系列的基础,后面的系列就是在第一版基础上的改进,只为提升性能。
394 |
395 | - YOLOv2
396 | 提出了 ImageNet 和 COCO 数据集结合的联合训练方法,使算法可以在检测数据集和分类数据集上训练目标检测器。用检测数据集的数据学习物体的准确位置,用分类数据集的数据来增加分类的类别量、提升健壮性。
397 | - YOLOv3
398 | YOLOv3 的提出不是为了解决什么问题,将模型复杂了不少,可以通过改变模型结构的大小来权衡速度与精度。
399 | - YOLOv4
400 | YOLOv4的改进总结了几乎所有的检测技巧,又提出一点儿技巧,然后经过筛选,排列组合,挨个实验(ablation study)哪些方法有效,经过大量实验选出的性能最好的组合。
401 | 发展历程:
402 | 
403 |
404 | ### 12.10 RPN网络
405 |
406 | RPN:Region Proposal Network
407 |
408 | #### 12.10.1 Region with CNN(R-CNN)
409 |
410 | 意思基于候选区域(Region Proposal)的卷积网络,不再针对每个滑动窗口跑检测算法,而是使用某种算法求出候选区域,然后对每个候选区域跑一下分类器,每个区域会输出一个标签和一个边界框。这样就只是选择一些有意义的窗口,在少数窗口上运行卷积网络分类器,以节省时间。
411 |
412 | - 选出的候选区域方法:图像分割算法
413 |
414 | 
415 |
416 | 如上图所示。分割色块后,选择其对应的一个边界框,然后在色块上跑分类器,这样的处理比滑动窗口法处理的窗口少的多,可以减少卷积网络分类器运行时间,而不必在所有位置运行一遍分类器。
417 |
418 | 另外,说明一下,R-CNN算法不会直接信任输入的边界框,它也会输出一个边界框$$b_{x},\quad b_{y},\quad b_{h},\quad b_{w}$$,这样得到的边界框比较精确,比单纯使用图像分割算法给出的色块边界要好。
419 |
420 |
421 | #### 12.10.2 具体步骤
422 |
423 | 
424 |
425 | 1. 输入图像;运行图像分割算法,利用selective search对图像生成1K~2K的候选区域(region proposal);
426 | 2. 将每个候选区域缩放(warp)成227×227的大小并输入到CNN,将CNN的全连接层fc7的输出作为特征;
427 | 3. 对CNN的fc7层的输出特征输入到SVM进行分类;如果有十个类别,那么每个region proposal要经过10个SVM,得到预测的类别。
428 | 4. 修正:对于SVM分好类的Region Proposal做边框回归,用Bounding box回归值校正原来的候选窗口,生成预测窗口坐标。
429 |
430 | #### 12.10.3 缺点和改进
431 |
432 | R-CNN训练耗时,占用磁盘空间大,测试速度慢,每个候选区域需要运行整个前向CNN计算;因此提出了其它改进算法。
433 |
434 | 
435 |
436 | - Fast R-CNN:利用卷积实现了滑动窗口。相比于R-CNN,Fast R-CNN不再对每一个候选区域进行CNN特征提取,而是先将整张图片归一化后输入CNN网络进行特征提取,之后候选区域在特征图上进行截取,显著提升了R-CNN的速度。但是其缺点是得到候选区域的聚类步骤仍然非常缓慢。
437 |
438 | - Faster R-CNN:加入RPN网络,将特征提取、候选区域提取、bounding box regression、分类都整合在了一个网络中,使得综合性能有较大提高,在检测速度方面尤为明显。(仍比YOLO慢)
439 |
440 | - Gaussian Faster R-CNN主要有以下两个创新点:
441 | 1. 卷积的过程其实就是一个特征提取的过程,所以在预处理之后移除了全连接这个操作,简化了网络结构,以准确率换速度。
442 | 2. 假设在多次卷积之后,整个特征图是一个平稳的随机序列,符合高斯分布,则可以采用 $3\sigma$ 原理对树进行裁剪,因为四周的像素对分类任务来说无关紧要,但是完全压缩和分类这些无关紧要的像素会花费大量的CPU时间。最后用随机森林代替B-P神经网络,将时间复杂度由 $O(N)$ 降到 $O(log2N)$。
443 |
444 | ### 12.11 目标检测算法的评价指标
445 |
446 | #### 12.11.1 准确度指标——平均准确度均值mAP
447 |
448 | - **什么是TP、TN、FP、FN?**
449 |
450 | TP、TN、FP、FN即true positive, true negative, false positive, false negative的缩写,positive和negative表示的是预测得到的结果,预测为正类则为positive,预测为负类则为negative; true和false则表示预测的结果和真实结果是否相同,相同则是true,不同则为false,如下图:
451 |
452 | 
453 |
454 | 举个例子,假设现在有这样一个测试集,其中的图片只由大雁和飞机两种图片组成,如下图所示:
455 |
456 | 
457 |
458 | 假设分类系统最终的目的是取出测试集中所有飞机的图片,则 TP、TN、FP、FN的具体定义分别是:
459 |
460 | **True positives :** 飞机的图片被正确的识别成了飞机。
461 | **True negatives:** 大雁的图片没有被识别出来,系统正确地认为它们是大雁。
462 | **False positives:** 大雁的图片被错误地识别成了飞机。
463 | **False negatives:** 飞机的图片没有被识别出来,系统错误地认为它们是大雁。
464 |
465 | - **Precision 与 Recall**
466 |
467 | **Precision**(精确度、查准率)指的是模型判断该图片为正类且该图片也的确是正类的概率,即在模型判断为正类的图片中,True positives所占的比率,**衡量的是一个分类器分出来的正类的确是正类的概率**。
468 | $$
469 | Precision=\frac{TP}{TP+FP}
470 | $$
471 | 光是精确度还不能衡量分类器的好坏程度,比如50个正样本和50个负样本,如果分类器把49个正样本和50个负样本都分为负样本,剩下一个正样本分为正样本,这样精确度也是100%,所以还需要召回率来衡量。
472 |
473 | **Recall**(召回率、查全率)指的是测试集的所有正样本比例中,被模型正确识别为正样本的比例,即模型判断为正类且实际的确是正类的图像数量/真实类别是正类的图像数量,**衡量的是一个分类器能把所有的正类都找出来的能力**。
474 | $$
475 | Recall=\frac {TP}{TP+FN}
476 | $$
477 | 在上面所举的例子中,假设识别出了四个结果,如下图所示:
478 |
479 | 
480 |
481 | 其中,在识别出来的四张照片中:
482 |
483 | **True positives :** 有三个,画绿色框的飞机,即 $TP=3$。
484 |
485 | **False positives:** 有一个,画红色框的大雁,即 $FP=1$。
486 |
487 | 没被识别出来的六张图片中:
488 | **True negatives :** 有四个,这四个大雁的图片,系统正确地没有把它们识别成飞机,即 $TN=4$。
489 | **False negatives:** 有两个,两个飞机没有被识别出来,系统错误地认为它们是大雁,即 $FN=2$。
490 |
491 | 故 $Precision=\frac {TP}{TP+FP}=\frac {3}{3+1}=0.75$ ,意味着在识别出来的结果中,飞机的图片占75%;$Recall=\frac {TP}{TP+FN}=\frac{3}{3+2}=0.6$,意味着在所有的飞机图片中,60%的飞机图片被正确识别为飞机。
492 |
493 | - **调整阈值**
494 |
495 | 可以通过调整阈值来选择让模型识别出多少图片,进而改变Precision或Recall的值。在某种阈值的前提下(蓝色虚线),模型识别出了四张图片,如下图所示:
496 | 
497 |
498 | 分类系统认为大于阈值(蓝色虚线之上)的四个图片更像飞机。
499 |
500 | 我们可以通过改变阈值(可以看作上下移动蓝色虚线)来选择让系统识别出多少张图片,从而改变Precision或Recall的值。比如,把蓝色虚线移到第一张图片下面,也就是说让系统只识别出最上面的那张飞机图片,那么Precision的值就是100%,而Recall的值是20%;如果把蓝色虚线放到第二张图片下面,也就是说让系统只识别出最上面的前两张图片,那么Precision的值还是100%,而Recall的值则增长到40%。下图为不同阈值条件下,Precision与Recall的变化情况:
501 | 
502 |
503 | - **Precision-Recall曲线**
504 |
505 | Precision-Recall曲线(P-R曲线)是以Precision和Recall作为纵、横轴坐标的二维曲线,通过选取不同阈值时对应的精确度和召回率画出,如下图所示。
506 |
507 | 
508 |
509 | 总体趋势是,精确度越高,召回率越低,当召回率达到1时,对应概率分数最低的正样本,这个时候正样本数量除以所有大于等于该阈值的样本数量就是最低的精确度。上图所示的分类器在不损失精度的条件下能达到40%的Recall,而当Recall达到100%时,Precision降到50%。
510 |
511 | Precision-Recall曲线可以用来显示分类器在Precision和Recall之间的权衡,从而评估分类器的性能。如果一个分类器的性能较好,那么它应该有如下的表现:被识别出的图片中飞机所占的比重比较大,并且在识别出大雁之间,尽可能多地正确识别出飞机,也就是让Recall值增长的同时保持Precision的值在一个很高的水平。而性能较差的分类器可能会损失很多Precision值才能换来Recall值的提高。
512 |
513 | - **平均准确度AP**
514 |
515 | AP:Average-Precision,平均准确度,综合考量了Precision和Recall的影响,反映了模型对某个类别识别的好坏。
516 |
517 | P-R曲线围起来的面积就是AP值,通常来说一个分类器越好,AP值越高。
518 |
519 | - **平均准确度均值mAP**
520 |
521 | mAP:mean Average-Precision,平均精确度均值,即所有类别AP的平均值,衡量的是在所有类别上的平均好坏程度。
522 |
523 | mAP的取值范围是[0,1],越大越好。
524 |
525 | - 为什么可以使用mAP来评价目标检测的效果?
526 |
527 | 目标检测的效果取决于预测框的位置和类别是否准确,从mAP的计算过程中可以看出通过计算预测框和真实框的IoU来判断预测框是否准确预测到了位置信息,同时精确度和召回率指标的引用可以评价预测框的类别是否准确,因此mAP是目前目标检测领域非常常用的评价指标。
528 |
529 | > 参考文献:
530 | >
531 | > 1. https://blog.csdn.net/syoung9029/article/details/56276567
532 | >
533 | > 2. https://www.cnblogs.com/wanghui-garcia/p/11084833.html
534 | > 3. https://blog.csdn.net/weixin_43423892/article/details/106643649
535 |
536 | #### 12.11.2 速度指标——FPS
537 |
538 | 目标检测技术的很多实际应用在准确度和速度上都有很高的要求,如果不计速度性能指标,只注重准确度表现的突破,其代价是更高的计算复杂度和更多内存需求。只有速度快,才能实现实时检测,这对一些应用场景极其重要。
539 |
540 | FPS:Frame Per Second,每秒帧率,即每秒内可以处理的图片数量。当然要对比FPS,需要在同一硬件上进行。
541 |
542 | 另外也可以使用处理一张图片所需时间来评估检测速度,时间越短,速度越快。
543 |
544 | > 参考:
545 | >
546 | > 1. https://zhuanlan.zhihu.com/p/70306015
547 | > 2. https://blog.csdn.net/qq_29893385/article/details/81213377
548 |
549 | #### 12.11.3 模型大小
550 |
551 | 自 2012 年 AlexNet 以来,卷积神经网络(简称 CNN)在图像分类、图像分割、目标检测等领域获得广泛应用。随着性能要求越来越高,AlexNet 已经无法满足大家的需求,于是乎各路大牛纷纷提出性能更优越的 CNN 网络,如 VGG、GoogLeNet、ResNet、DenseNet 等。由于神经网络的性质,为了获得更好的性能,网络层数不断增加,从 7 层 AlexNet 到 16 层 VGG,再从 16 层 VGG 到 GoogLeNet 的 22 层,再到 152 层 ResNet,更有上千层的 ResNet 和 DenseNet。虽然网络性能得到了提高,但随之而来的就是效率问题。
552 |
553 | 效率问题主要是**模型的存储问题和模型进行预测的速度问题**(以下简称速度问题)
554 |
555 | - 第一,存储问题。数百层网络有着大量的权值参数,保存大量权值参数对设备的内存要求很高;
556 | - 第二,速度问题。在实际应用中,往往是毫秒级别,为了达到实际应用标准,要么提高处理器性能(看英特尔的提高速度就知道了,这点暂时不指望),要么就减少计算量。
557 |
558 | 只有解决 CNN 效率问题,才能让 CNN 走出实验室,更广泛的应用于移动端。对于效率问题,通常的方法是进行**模型压缩**(Model Compression),即在已经训练好的模型上进行压缩,使得网络携带更少的网络参数,从而解决内存问题,同时可以解决速度问题。
559 |
560 | 相比于在已经训练好的模型上进行处理,轻量化模型设计则是另辟蹊径。**轻量化模型设计**主要思想在于设计更高效的网络计算方式(主要针对**卷积**方式),从而使网络参数减少的同时,不损失网络性能。近年提出的四个轻量化模型分别是:SqueezeNet、MobileNet、ShuffleNet、Xception,有兴趣的可以参考以下博客或查找论文以了解。
561 |
562 | > 参考:https://blog.csdn.net/u012426298/article/details/80817788
--------------------------------------------------------------------------------
/13 特殊应用 人脸识别和神经风格转换.md:
--------------------------------------------------------------------------------
1 | ## 13 特殊应用:人脸识别和神经风格转换
2 |
3 | ### 13.1 什么是人脸识别?
4 |
5 | #### 13.1.1 人脸验证 vs 人脸识别
6 |
7 | **人脸验证**(face verification):也被称为 “1对1” 问题。
8 |
9 | - 输入:一张图片以及某人的ID或名字
10 | - 输出:系统验证输入图片是否是这个人。
11 |
12 | **人脸识别**(face recognition):“1对K” 问题。
13 |
14 | - 拥有一个包含 $K$ 人信息的数据库
15 | - 输入:一张图片
16 | - 输出:若输入图片符合 $K$ 人中任意一个人的图像,输出这个人的ID,否则,输出"not recognized"。
17 |
18 | **人脸验证与人脸识别的关系:**
19 |
20 | 人脸识别比人脸验证要求更高。假设有一个验证系统准确率是99%,看起来这个验证系统性能不错,但如果应用到有100个人的数据库的人脸识别系统中,每个人的犯错概率是1%,整体犯错概率就放大了100倍,所以要想得到一个可接受的识别误差,就要构造一个准确率为99%甚至更高的验证系统才能得到很好的识别效果。也就是说,人脸验证系统的准确率要足够高才能应用到人脸识别系统中。
21 |
22 | #### 13.1.2 人脸识别的传统方法
23 |
24 | 主流的人脸识别技术基本上可以归结为三类,即:基于几何特征的方法、基于模板的方法和基于模型的方法。
25 |
26 | - 基于几何特征的方法是最早、最传统的方法,通常需要和其他算法结合才能有比较好的效果;
27 | - 基于模板的方法可以分为基于相关匹配的方法、特征脸方法、线性判别分析方法、奇异值分解方法、神经网络方法、动态连接匹配方法等。
28 | - 基于模型的方法则有基于隐马尔柯夫模型,主动形状模型和主动外观模型的方法等。
29 |
30 | 下文主要介绍三种传统的人脸识别方法:
31 |
32 | 1. 主成分分析法
33 |
34 | 主成分分析法(PAC,Principal Component Analysis)又称为特征脸法,是20世纪90年代初由Turk和Pentland提出的一种经典算法,根据图像的统计特征通过正交变换(即K-L变换)由高维向量转换为低维向量,并形成低维线性向量空间,利用人脸投影到这个低维空间所得到的投影系数作为识别的特征矢量,这样,就产生了一个由“特征脸”矢量形成的子空间,成为“人脸子空间”或“特征子空间”,每一幅人脸图像向其投影都可以获得一组坐标系数,这组坐标系数表明了人脸在子空间中的位置,因此利用特征脸方法可以重建和识别人脸。
35 |
36 | 2. 线性判别分析
37 |
38 | 线性判别分析是对费舍尔的线性鉴别方法的归纳,这种方法使用统计学、模式识别和机器学习方法,试图找到两类物体或事件的特征的一个线性组合,以能够特征化或区分它们。所得的组合可用来作为一个线性分类器,或者,更常见的是,为后续的分类做降维处理。
39 |
40 | 3. 支持向量机
41 |
42 | 支持向量机(SVM,Support Vector Machine)起源于统计学习理论,研究如何构造学籍及,实现模式分类问题。其基本思想是通过非线性变换将输入空间变换到一个高维空间,在高维空间求取最优线性分类面,以解决那些线性不可分的分类问题。而这种非线性变换是通过定义适当的内积函数(即核函数)来实现的,由于该方法是基于结构风险最小化原理,而不是传统统计学的经验风险最小化,因而表现出很多优于已有方法的性能,但该方法需要大量的存储空间,并且训练速度慢。
43 |
44 | > 参考:
45 | >
46 | > 1. https://www.jiqizhixin.com/articles/2019-02-10-4
47 | > 2. https://wenku.baidu.com/view/34c55025a100a6c30c22590102020740be1ecdb7.html
48 |
49 | ### 13.2 One-Shot学习
50 |
51 | #### 13.2.1 One-Shot学习的定义
52 |
53 | **One-Shot learning**:一次学习,只通过一个样本来进行学习以能够认出同一个人。
54 |
55 | 
56 |
57 | 如上图所示,假设人脸识别系统数据库里有4个人每人一张照片,需要仅仅通过每个人的一张照片来判断输入图片中是否含有这4个人的其中一个。
58 |
59 | #### 13.2.2 如何解决One-Shot学习问题
60 |
61 | 对于One-Shot学习问题,采用卷积神经网络进行识别分类的缺点:
62 |
63 | 1. 训练集太小,不足以训练一个稳健的神经网络;
64 | 2. 如果有新成员加入数据集,分类输出的标签数量要改变,神经网络得重新训练。
65 |
66 | 故要解决One-Shot学习问题,应该要**学习Similarity函数**(也称为d函数):
67 | $$
68 | \begin{equation}\begin{split}
69 | d(img1,&img2)=degree\ of\ difference\ between\ images\\[2ex]
70 | &If\ d(img1,img2)\ \le\ \tau\ \ \ \ "same"\\
71 | &If\ d(img1,img2)\ \ge\ \tau\ \ \ \ "different"\\
72 | \end{split}\end{equation}
73 | $$
74 | 以两张图片作为输入,然后输出这两张图片的差异值,差异值越小越相似。如果差异值小于某个阈值 $\tau$($\tau$ 是一个超参数),就预测输入的是同一个人的两张图片;如果差异值大于阈值,就预测输入的是两个不同的人的照片,从而实现人脸验证。
75 |
76 | 将其应用于人脸识别任务,分别将要预测的图片及数据库中的任一张图片输入,用d函数两两比较,如果有输出一个比阈值小的数字,则预测的图片就是那个人的照片,若没有,则要预测的人不是数据库中的任一个人。
77 |
78 | 
79 |
80 | 在上面这个例子中,首先输入要识别的图片和数据库中第一张图片,输出一个很大的值,说明不是同一个人;接着输入要识别的图片和数据库中第二张图片,输出一个很小的值,很可能是同一个人;再分别输入要识别的图片和数据库中第三、四张图片,输出的值都很大,不是同一个人。因此,要识别的图片是第二个人的。若输出的值都很大,则要识别的人不是数据库里的任一个人。
81 |
82 | 如果要加入新成员,只需将其照片加入数据库中,系统依然能照常工作。
83 |
84 | #### 13.2.3 Few-Shot learning
85 |
86 | **Few-Shot learning**:小样本学习,用很少的样本去做分类或者回归。
87 |
88 | Few-Shot learning与传统的监督学习算法不同,它的目标不是让机器识别训练集中图片并且泛化到测试集,而是**让机器自己学会学习**。可以理解为用一个小数据集训练神经网络,学习的目的不是让神经网络知道每个类别是什么,而是让模型理解事物的异同,学会区分不同的事物。
89 |
90 | 
91 |
92 | 比如上面这张图片,左边两张图是同一种动物,右边两张是同一种动物,Few-Shot learning要做的就是通过对上面这四张图的学习判断下面这张图是属于哪一种动物。
93 |
94 | 
95 |
96 | Few-Shot learning 问题的关键是解决过拟合 (overfitting) 的问题,因为训练的样本太少了,训练出的模型可能在训练集上效果还行,但是在测试集上面会遭遇灾难性的崩塌。
97 |
98 | **解决方法:**
99 |
100 | 1. 数据增强和正则化:这一类方法想法很直接简单,既然训练数据不够那就增加训练样本,既然过拟合那就使用正则化技术。
101 | - 数据加强:最常见的例子就是有时对 Omniglot 数据集的预处理,会将图片旋转 90 、180 、270 度,这样就可以使样本数量变为原来的 4 倍。
102 | - 正则化:在训练的时候加入一个正则项,这个正则项的构建选择是关键。比如 《Few-shot Classification on Graphs with Structural Regularized GCNs》。该论文讨论 Graph 中节点分类的 few-shot 问题,常见的节点分类是使用 GCN 从节点的特征向量 feature 学习一个 embedding 然后用 embedding 来做分类,如果是 few-shot 问题,性能会大大下降(准确率大约从 70% 到了 40%),作者在训练的时候给损失函数加了一个正则项。作者将 feature 到 embedding 的过程看成编码器 encoder,然后额外加了几层网络作为 decoder,将 embedding 重构为 feature ,然后重构误差作为正则项(准确率从 40% 提升了 50%,大约 10 个百分点)。
103 |
104 | 2. Meta-learning(元学习):核心想法是先学习一个先验知识(prior),这个先验知识对解决 few-shot learning 问题特别有帮助。也就是说,先学习很多很多 task,然后再来解决新的在之前的学习中没有见过的 task 。
105 |
106 | > 参考:
107 | >
108 | > 1. https://blog.csdn.net/weixin_37589575/article/details/92801610
109 | > 2. https://zhuanlan.zhihu.com/p/142381922
110 |
111 | ### 13.3 Siamese网络
112 |
113 | Siamese网络架构是实现Similarity函数的一种方式。
114 |
115 | #### 13.3.1 Siamese网络架构
116 |
117 | **Siamese网络架构**:对于两个不同的输入,运行相同的卷积神经网络,然后比较它们输出的特征向量从而判断是否是属于同一类。
118 |
119 | 
120 |
121 | 如上图所示,首先将第一张输入图像$x^{(1)}$送入卷积神经网络,经过一系列的卷积、池化、全连接后输出一个特征向量,将这个特征向量称为$f(x^{(1)})$,看作是输入图像$x^{(1)}$的编码;然后将第二张输入图像$x^{(2)}$送入同样的神经网络,也得到一个特征向量,称为$f(x^{(2)})$,代表输入图像$x^{(2)}$的编码。我们相信这两个编码可以很好地代表两张输入图像,故定义d函数为两张图片编码之差的范数:
122 | $$
123 | d(x^{(1)}, x^{(2)})=||f(x^{(1)})-f(x^{(2)})||_2^2
124 | $$
125 |
126 | #### 13.3.2 如何训练Siamese网络
127 |
128 | 由于Siamese网络中两个卷积神经网络是一样的,所以在训练Siamese网络时只需要训练一个就好。
129 |
130 | 
131 |
132 | 更准确地说,神经网络的参数定义了一个编码函数$f(x^{(i)})$,如果给定输入图像$x^{(i)}$,会输出$x^{(i)}$的一个编码(特征向量)。训练网络要做的就是学习参数,使得如果两个图片$x^{(i)}$和$x^{(j)}$是同一个人,得到的两个编码的距离就小;如果$x^{(i)}$和$x^{(j)}$是不同的人,则它们之间的编码距离会比较大。如果改变这个网络所有层的参数,会得到不同的编码结果,要用反向传播来改变这些所有的参数以确保满足上面的条件。
133 |
134 | ### 13.4 Triplet损失
135 |
136 | #### 13.4.1 Triplet损失的定义
137 |
138 | **Triplet loss**:三元组损失,通常需要同时看三张图片:Anchor图片(A)、Positive图片(P,即正类,跟Anchor是同一个人)和Negative图片(N,即负类,跟Anchor不是同一个人)。其中,A和P为一对,是同一个人,所以希望它们编码的距离很接近;A和N为一对,不是同一个人,所以希望它们编码的距离远一点。公式如下:
139 | $$
140 | ||f(A)-f(P)||^2 \le ||f(A)-f(N)||^2
141 | $$
142 | 即:$d(A,P) \le d(A,N)$
143 |
144 | 把方程右边项移到左边:
145 | $$
146 | ||f(A)-f(P)||^2-||f(A)-f(N)||^2 \le 0
147 | $$
148 |
149 | 有两种情况满足这个表达式但没有用处:
150 |
151 | 1. 所有的编码会总是输出0,即$f(img)=0$,则 $0-0=0$。
152 | 2. 把所有的编码都设成相等的,即如果每个图片的编码和其他图片一样,这种情况还是得到 $0-0=0$。
153 |
154 | 为了阻止网络出现这两种情况,应该把“小于等于0”这个目标改为“小于0”,故将目标改为“$0-\alpha$”($\alpha$是一个超参数),由于我们更习惯使用“$+\ \alpha$”,所以将“$-\ \alpha$”这项移到左边,得到:
155 | $$
156 | ||f(A)-f(P)||^2-||f(A)-f(N)||^2 \ +\ \alpha \le 0
157 | $$
158 |
159 | 故第一个式子也变为:
160 | $$
161 | ||f(A)-f(P)||^2\ +\ \alpha \le ||f(A)-f(N)||^2
162 | $$
163 |
164 | 其中,$\alpha$也叫做间隔(margin),假设间隔设为0.2,为了满足条件,可以把d(A, N)调大或者把d(A, P)调小让间隔至少是0.2,这样就拉大了anchor与positive图片对和anchor与negative图片对之间的差距。例如,假设d(A, P)等于0.5,如果d(A, N)只比d(A, P)大一点点,为0.51,就不能满足条件,因为我们想让d(A, N)比d(A, P)大很多,至少是0.7或者更高。
165 |
166 | #### 13.4.2 Triplet损失函数
167 |
168 | 对于**一个三元组定义的损失函数**:
169 | $$
170 | L(A,P,N)=max(||f(A)-f(P)||^2-||f(A)-f(N)||^2 \ +\ \alpha,0)
171 | $$
172 | 若$||f(A)-f(P)||^2-||f(A)-f(N)||^2 \ +\ \alpha$ 小于0,那么损失函数就是0;若大于0,则损失函数等于$||f(A)-f(P)||^2-||f(A)-f(N)||^2 \ +\ \alpha$ ,是一个正的损失值。通过最小化损失函数,只要这个损失函数等于0,达到的效果就是使$||f(A)-f(P)||^2-||f(A)-f(N)||^2 \ +\ \alpha$小于或等于0,网络不会关心它的负值有多大。
173 |
174 | **整个网络的代价函数**是训练集中这些单个三元组损失的总和:
175 | $$
176 | J=\sum_{i=1}^mL(A^{(i)},P^{(i)},N^{(i)})
177 | $$
178 | 假设有一个10000张图片的训练集,里面是1000个不同的人的照片,平均每人10张照片,要做的是取这10000张图片生成三元组,然后对代价函数用梯度下降从而训练学习算法,训练完成后就可以应用到一次学习问题中。
179 |
180 | 为了定义三元组的数据集,需要成对的A和P即同一个人的成对的图片,
181 |
182 | #### 13.4.3 如何选择三元组组成训练集
183 |
184 | 倘若从数据集中随机地选择A, P, N构成三元组,遵循A和P是同一个人而A和N是不同的人这一原则,则不是同一个人的概率比是同一个人的概率大很多,即d(A, N)比d(A, P)大$\alpha$ 的概率很大,目标很容易就达到,网络很轻松就能训练好,梯度算法不会有什么效果。
185 |
186 | 所以应该**尽可能选择难训练的三元组A P N即所有的三元组d(A, P)都很接近d(A, N)**,这样,学习算法就会竭尽全力使d(A, N)变大或者使d(A, P)变小使得二者之间至少间隔$\alpha$,并且选择这样的三元组训练难度大,梯度下降法才能发挥作用,从而增加学习算法的计算效率。
187 |
188 | 
189 |
190 | ### 13.5 面部验证与二分类
191 |
192 | #### 13.5.1 将人脸识别变成二分类问题
193 |
194 | Triplet loss是个学习人脸识别卷积网络参数的好方法,此外还有其他学习参数的方法,如将人脸识别当成一个二分类问题:
195 |
196 | 
197 |
198 | 选取一对神经网络,选用 Siamese 网络并使其同时计算这些特征向量,然后将其输入到逻辑回归单元进行预测,若是相同的人,那么输出是 1,若是不同的人,输出是 0。这就把人脸识别问题转换为一个二分类问题,训练这种系统时可以替换 Triplet loss的方法。
199 |
200 | #### 13.5.2 逻辑回归单元的处理
201 |
202 | 最后通过将sigmoid等函数应用到某些特征上来处理逻辑回归单元:
203 | $$
204 | \hat{y}=\sigma\left(\sum_{k=1}^{128} w_{i}\left|f\left(x^{(i)}\right)_{k}-f\left(x^{(j)}\right)_{k}\right|+b\right)
205 | $$
206 | 其中,符号$f\left(x^{(i)}\right)$代表图片$x^{(i)}$的编码,下标 $k$ 代表选择这个向量中的第$k$个元素,$\left|f\left(x^{(i)}\right)_{k}-f\left(x^{(j)}\right)_{k}\right|$对这两个编码取元素差的绝对值。就像普通的逻辑回归一样,把这128个元素当作特征,然后把他们放入逻辑回归中,最后的逻辑回归可以增加参数$w_{i}$和$b$。在这128个单元上训练合适的权重,用来预测两张图片是否是一个人。
207 |
208 | 还可以用$\chi^{2}$公式$\frac{\left(f\left(x^{(i)}\right)_{k}-f\left(x^{(j)}\right)_{k}\right)^{2}}{f\left(x^{(i)}\right)_{k}+f\left(x^{(j)}\right)_{k}}$,也被称作$\chi$平方相似度,来代替上式中$\left|f\left(x^{(i)}\right)_{k}-f\left(x^{(j)}\right)_{k}\right|$的计算。
209 |
210 | #### 13.5.3 预先计算思想
211 |
212 | 在上面的学习公式中,输入是一对图片($x^{(i)}$和$x^{(j)}$),输出$y$是0或者1取决于输入是相似图片还是非相似图片。与之前类似,训练一个Siamese网络,即两个神经网络拥有的参数是相同的,两组参数是绑定的。
213 |
214 | **预先计算好数据库中图片的编码可以节省大量的计算,显著提高部署效果。**
215 |
216 | 如你有一张新图片$x^{(i)}$,当员工走进门时,希望门可以自动为他打开,在数据库中的图片$x^{(j)}$,不需要每次都计算特征向量,可以提前计算好,那么当一个新员工走近时,可以使用上方的卷积网络来计算编码,然后将其和预先计算好的编码进行比较,输出预测值 $\hat{y}$。
217 |
218 | **总结**:把人脸验证当作一个监督学习,创建一个只有成对图片的训练集,不是三个一组,而是成对的图片,目标标签是1表示这对图片是一个人,目标标签是0表示图片中是不同的人。利用不同的成对图片,使用反向传播算法去训练神经网络,训练Siamese神经网络。
219 |
220 | ### 13.6 什么是神经风格迁移
221 |
222 | #### 13.6.1 神经风格迁移的定义
223 |
224 | 
225 |
226 | 比如这张照片,你想利用右边照片的风格来重新创造原本的照片,右边的是梵高的星空,神经风格迁移可以帮你生成下面这张照片。使用$C$来表示内容图像,$S$表示风格图像,$G$表示生成的图像。
227 |
228 | #### 13.6.2 神经风格迁移的常用方法
229 |
230 | 
231 |
232 | [参考博客]: https://www.jiqizhixin.com/articles/2018-05-15-5 "综述:图像风格化算法最全盘点 | 内附大量扩展应用"
233 |
234 | ### 13.7 深度卷积网络在学什么
235 |
236 | #### 13.7.1 可视化分析卷积神经网络的浅层
237 |
238 | 假如训练了一个卷积神经网络,是一个Alexnet,轻量级网络,希望将看到不同层之间隐藏单元的计算结果。
239 |
240 | 
241 |
242 | 你可以这样做,从第一层的隐藏单元开始,假设你遍历了训练集,然后找到那些使得单元激活最大化的一些图片或是图片块。换句话说,将你的训练集经过神经网络,然后弄明白哪一张图片最大限度地激活特定的单元。注意在第一层的隐藏单元,只能看到小部分卷积神经,如果要画出来哪些激活了激活单元,只有一小块图片块是有意义的,因为这就是特定单元所能看到的全部。你选择一个隐藏单元,发现有9个图片最大化了单元激活,你可能找到这样的9个图片块(左上九宫格),似乎是图片浅层区域显示了隐藏单元所看到的,找到了像这样的边缘或者线(上面的蓝格子),这就是那9个最大化地激活了隐藏单元激活项的图片块。
243 |
244 | 
245 |
246 | 然后你可以选一个另一个第一层的隐藏单元,重复刚才的步骤,这是另一个隐藏单元,似乎第二个由这9个图片块(上中九宫格)组成。看来这个隐藏单元在输入区域,寻找这样的线条(下面的蓝格子),我们也称之为接受域。
247 |
248 | 对其他隐藏单元也进行处理,会发现其他隐藏单元趋向于激活类似于这样的图片。右上九宫格似乎对垂直明亮边缘且左边是绿色的图片块感兴趣,左中九宫格的隐藏单元倾向于橘色图片块。
249 |
250 | 以此类推,这是9个不同的代表性神经元,每一个不同的图片块都最大化地激活了。你可以这样理解,第一层的隐藏单元通常会找一些简单的特征,比如说边缘或者颜色阴影。
251 |
252 | #### 13.7.2 可视化分析卷积神经网络的深层
253 |
254 | 在深层部分,一个隐藏单元会看到一张图片更大的部分,在极端的情况下,可以假设每一个像素都会影响到神经网络更深层的输出,靠后的隐藏单元可以看到更大的图片块。
255 |
256 | 
257 |
258 | 上图中Layer 1是之前第一层得到的,Layer 2是可视化的第2层中最大程度激活的9个隐藏单元。在更深的层上,可以重复这个过程。
259 |
260 | 放大第一层,这是第一个被高度激活的单元,你能在输入图片的区域看到所提取的这些边缘或颜色阴影。
261 |
262 | 
263 |
264 | 放大第二层的可视化图像。第二层似乎检测到更复杂的形状和模式,比如说中上九宫格这一隐藏单元会找到有很多垂线的垂直图案,右中九宫格的隐藏单元似乎在左侧有圆形图案时会被高度激活,左下九宫格所寻找的特征是很细的垂线,以此类推,第二层检测的特征变得更加复杂。
265 |
266 | 
267 |
268 | 放大第三层,这些东西激活了第三层。中心九宫格这一隐藏单元似乎对图像左下角的圆形很敏感,所以检测到很多车。右下九宫格似乎开始检测到人类,左上九宫格似乎检测特定的图案,比如蜂窝形状或者方形这样类似规律的图案。有些很难看出来,需要手动弄明白检测到什么,但是第三层明显,检测到更复杂的模式。
269 |
270 | 
271 |
272 |
273 |
274 | 这是第四层,检测到的模式和特征更加复杂,左上九宫格学习成了一个狗的检测器,但是这些狗看起来都很类似。右中九宫格似乎检测到鸟的脚等等。
275 |
276 |
206 |
207 | 所以这个算法的优点在于神经网络可以输出精确的边界框,所以测试的时候,你做的是喂入输入图像$x$,然后跑正向传播,直到你得到这个输出$y$。然后对于这里3×3位置对应的9个输出,就可以读出1或0。如果那里有个对象,就可以读出那个对象是什么,还有格子中这个对象的边界框是什么。
208 |
209 | 只要每个格子中对象数目没有超过1个,这个算法应该是没问题的。一个格子中存在多个对象的问题,之后再讨论。这里用的是比较小的3×3网格,实践中你可能会使用更精细的19×19网格,所以输出就是19×19×8。这样的网格精细得多,那么多个对象分配到同一个格子的概率就小得多。
210 |
211 | 把对象分配到一个格子的过程是,你观察对象的中点,然后将这个对象分配到其中点所在的格子,所以即使对象可以横跨多个格子,也只会被分配到9个格子其中之一,就是3×3网络的其中一个格子,或者19×19网络的其中一个格子。在19×19网格中,两个对象的中点处于同一个格子的概率就会更低。
212 |
213 | YOLO算法有一个好处就是,它是一个卷积实现,共享了很多卷积计算,所以实际上它的运行速度非常快,可以达到实时识别。
214 |
215 | **编码边界框**
216 |
217 | 
218 |
219 | 对于这个方框(中右侧),我们约定左上这个点是(0,0),然后右下这个点是(1,1);
220 |
221 | 要指定橙色中点的位置,$b_{x}$大概是0.4,因为它的位置大概是水平长度的0.4,$b_{y}$大概是0.3;
222 |
223 | 边界框的高度用格子总体宽度的比例表示,所以这个红框的宽度可能是蓝线(图右下角蓝线)的90%,所以$b_h$是0.9,它的高度也许是格子总体高度的一半,这样的话$b_{w}$就是0.5。
224 |
225 | 换句话说,$b_{x}$、$b_{y}$、$b_{h}$和$b_{w}$单位是相对于格子尺寸的比例,所以$b_{x}$和$b_{y}$必须在0和1之间,因为从定义上看,橙色点位于对象分配到格子的范围内,如果它不在0和1之间,如果它在方块外,那么这个对象就应该分配到另一个格子上。但是$b_{h}$和$b_{w}$可能会大于1,特别是如果有一辆汽车的边界框是这样的(左下红框),那么边界框的宽度和高度有可能大于1。
226 |
227 | 指定边界框的方式有很多,但这种约定是比较合理的,还有其他更复杂的参数化方式,涉及到sigmoid函数,确保这个值($b_{x}$和$b_{y}$)介于0和1之间,然后使用指数参数化来确保$b_{h}$和$b_{w}$都是非负数。还有其他更高级的参数化方式,可能效果要更好一点,但这里讲的办法应该是管用的。
228 |
229 | #### 12.5.2 其他指定边界框的算法
230 |
231 | **1. SSD**:
232 |
233 | SSD(Single-Shot MultiBox Detector),使用 VGG19 网络作为特征提取器(和 Faster R-CNN 中使用的 CNN 一样)的单次检测器。我们在该网络之后添加自定义卷积层(蓝色),并使用卷积核(绿色)执行预测。
234 |
235 | 
236 |
237 | 然而,卷积层降低了空间维度和分辨率。因此上述模型仅可以检测较大的目标。为了解决该问题,我们从多个特征图上执行独立的目标检测。
238 |
239 | 
240 |
241 | 以下是特征图图示。
242 |
243 | 
244 |
245 | SSD 使用卷积网络中较深的层来检测目标。如果我们按接近真实的比例重绘上图,我们会发现图像的空间分辨率已经被显著降低,且可能已无法定位在低分辨率中难以检测的小目标。如果出现了这样的问题,我们需要增加输入图像的分辨率。
246 |
247 | 
248 |
249 |
250 |
251 |
252 | 参考博客:https://www.jianshu.com/p/468e08f739bd
253 |
254 | **2. FPN**:
255 |
256 | 使用不同尺寸特征图进行预测的网络称为特征金字塔网络(FPN),是一种旨在提高准确率和速度的特征提取器。数据流如下:
257 |
258 | 
259 |
260 | FPN 由自下而上和自上而下路径组成。其中自下而上的路径是用于特征提取的常用卷积网络。空间分辨率自下而上地下降。当检测到更高层的结构,每层的语义值增加。
261 |
262 | 
263 |
264 | SSD 通过多个特征图完成检测。但是,最底层不会被选择执行目标检测。它们的分辨率高但是语义值不够,导致速度显著下降而不能被使用。SSD 只使用较上层执行目标检测,因此对于小的物体的检测性能较差。
265 |
266 | 
267 |
268 | FPN 提供了一条自上而下的路径,从语义丰富的层利用上采样构建高分辨率的层。
269 |
270 | 
271 |
272 | 虽然该重建层的语义较强,但在经过所有的上采样和下采样之后,目标的位置不精确。在重建层和相应的特征图之间添加横向连接可以使位置侦测更加准确。
273 |
274 | 
275 |
276 | **3. RetianNet**:
277 |
278 | RetianNet是基于 ResNet、FPN以及利用 Focal loss 构建的 。
279 |
280 | 
281 |
282 | RetinaNet
283 |
284 | **4. Focal Loss**
285 |
286 | 类别不平衡会损害性能。SSD 在训练期间重新采样目标类和背景类的比率,这样它就不会被图像背景淹没。Focal loss(FL)采用另一种方法来减少训练良好的类的损失。因此,只要该模型能够很好地检测背景,就可以减少其损失并重新增强对目标类的训练。我们从交叉熵损失 (Cross Entroy Loss)开始,并添加一个权重来降低高可信度类的交叉熵。
287 |
288 | 
289 |
290 | 例如,令 γ = 0.5, 经良好分类的样本的 Focal Loss 趋近于 0。
291 |
292 | 
293 |
294 | ### 12.6 交并比
295 |
296 | #### 12.6.1 交并比函数的作用
297 |
298 | 交并比(IoU, Intersection over Union)函数衡量了两个边界框重叠的相对大小,用来评价对象检测算法是否运行良好,即检测对象定位是否准确。
299 |
300 | #### 12.6.2 交并比函数的实现
301 |
302 | 
303 |
304 | 假设识别的对象的实际边界框如上图中红框所示,用对象检测算法得到的边界框如紫框所示,这个结果是好是坏呢?
305 |
306 | 交并比函数做的是计算**两个边界框交集和并集之比**,交集部分如橙色阴影所示,并集部分如绿色阴影所示,如果预测边框和实际边框完美重叠,交集等于并集,$IoU = 1$,一般约定,在计算机检测任务中,若 $IoU \geq 0.5$,则说明预测的边界框是正确的,如果希望更严格,可以把IoU的阈值定得更高,IoU越高,边界框越精确。
307 |
308 | ### 12.7 非极大值抑制
309 |
310 | #### 12.7.1 非极大值抑制的作用
311 |
312 | 到目前为止我们学到的对象检测中的一个问题是,算法可能对同一个对象做出多次检测而不是一次,非极大值抑制法可以**确保算法对每个对象只检测一次**。
313 |
314 | #### 12.7.2 非极大值抑制的实现
315 |
316 | 非极大值抑制(Non-max suppression):只输出概率最大的分类结果,抑制很接近但不是最大的其他预测结果。
317 |
318 | 
319 |
320 | 假设要在这张图里检测行人和汽车,我们可能会在上面放个19×19的网格,理论上每辆汽车只有一个中点,应该只分配到中点所在的格子里,实践中在跑对象分类和定位算法时,对每个格子都跑一次,橙色和绿色方框的那些格子可能会想,这辆车的中点应该在其格子内部,觉得它们格子内有车的概率很高,而不是19×19=361个格子中仅有两个格子会报告它们检测出一个对象,所以最后可能会对同一个对象做出多次检测。
321 |
322 | 非极大值抑制做的就是清理这些检测结果,对每个对象只检测一次,而不是每个对象都触发多次检测。
323 |
324 | **非极大值抑制的实现步骤:**
325 |
326 | 
327 |
328 | 1. 去掉所有预测边界框中 $p_c \leq 0.6$ 的边界框(这里的0.6是阈值,可以自己设定),抛弃了所有概率比较低的输出边界框,则剩下的边界框中存在对象的概率至少有0.6。
329 | 2. 对于剩下的边界框,首先看看每次报告中每个检测结果相关的概率 $p_c$,找到**概率最大**的那个,这个例子中是0.9,认为这是最可靠的检测,用高亮标记,就说在这里找到了一辆车。
330 | 3. 接着,非极大值抑制就会逐一审视剩下的矩形,所有和这个最大的边界框有很高交并比、高度重叠的其他边界框的输出就会被抑制,所以这两个 $p_c$ 分别为0.6和0.7的矩形和最大边界框(淡蓝色矩形)重叠程度很高,会被抑制、变暗。
331 |
332 | 左边那辆车也同理,找到 $p_c$ 最大的一个是0.8,认为这里检测出一辆车,用高亮显示,而其他IoU值很高的矩形会被抑制而变暗。直接抛弃变暗的矩形,只剩下高亮显示的,就是最后得到的两个预测结果。
333 |
334 | 上面介绍的只是算法检测单个对象的情况,若想同时检测三种对象,比如行人、汽车和摩托,则需要独立进行三次非极大值抑制,对每个输出类别都做一次。
335 |
336 | ### 12.8 Anchor Boxes
337 |
338 | #### 12.8.1 为什么要用Anchor Boxes?
339 |
340 | 之前的算法只能在一个格子中检测出一个对象,Anchor Boxes可以**一个格子检测出多个对象**。如下图所示,使用3x3的网格,行人和汽车的中心几乎在同一个网格,这时就需要用到Anchor Boxes。
341 |
342 | 
343 |
344 | #### 12.8.2 思路
345 |
346 | 1. 预先定义几个不同形状的anchor box,把预测结果和这些anchor box关联起来。本例假设两个anchor box,对应行人和汽车。
347 |
348 | 
349 |
350 | 2. 定义类别标签,将原来的向量$$\left[\begin{array}{llllllll}
351 | p_{c} & b_{x} & b_{y} & b_{h} & b_{w} & c_{1} & c_{2} & c_{3}
352 | \end{array}\right]^{T}$$重复两次$$\left.\begin{array}{llllllllllllllll}
353 | y=\left[p_{c}\right. & b_{x} & b_{y} & b_{h} & b_{w} & c_{1} & c_{2} & c_{3} & p_{c} & b_{x} & b_{y} & b_{h} & b_{w} & c_{1} & c_{2} & c_{3}
354 | \end{array}\right]^{T}$$。其中,前面的8个参数和anchor box 1相关联,后面的8个参数和anchor box 2相关联。
355 |
356 | 
357 |
358 | 3. 行人一般符合anchor box1形状,所以用anchor box1来预测行人会达到很好的效果,这么编码 $p_c$ = 1,代表有个行人,用 $b_x, b_y ,b_h$ 和 $b_w$ 来编码包住行人的边界框,用$c_1, c_2 ,c_3$($c_1$ = 1,$c_2$ = 0,$c_3$ = 0)来说明这个对象是个行人。 汽车一般符合anchor box2形状,采用相同的编码方法,定义对象是汽车和边界框等,所有参数都和检测汽车相关( $p_c$ = 1, $b_x, b_y ,b_h$, $b_w$, $c_1$ = 0,$c_2$ = 1,$c_3$ = 0)。
359 |
360 | 4. 当两个anchor boxes对相同位置做出判别时,以交并比作为取舍指标。选择IoU最高的那个,用这个anchor box来进行预测。输出y的维度是$n \times n \times m \times c$(n为图片分成$n \times n$份,$m$为anchor box数量,$c$为class类别数)
361 |
362 | #### 12.8.3 怎么选择anchor box?
363 |
364 | 1. 一般手工指定anchor box形状,根据要检测的对象,指定有针对性的anchor box,可选择5-10个anchor box,使其尽可能覆盖到不同形状。
365 | 2. 使用K-means聚类算法获得anchor box,选择最具有代表性的一组anchor box。
366 |
367 | ### 12.9 YOLO 算法
368 |
369 | 目标检测架构分为两种,一种是two-stage,一种是one-stage。 two-stage 有region proposal (选取候选区域)过程,网络会根据候选区域生成位置和类别,而 one-stage 直接从图片生成位置和类别。
370 |
371 | YOLO 是一种 one-stage 方法,即 You Only Look Once 的缩写,意思是神经网络只需要看一次图片,就能输出结果。
372 |
373 |
374 | #### 12.9.1 YOLO算法的实现
375 |
376 | - 构造训练集:假设检测三种对象,行人,汽车和摩托。
377 | 输入图像,神经网络的输出尺寸是3x3x2x8(3x3的网格,2个anchor box,8个参数)。遍历9个格子,构造训练集,然后构成对应的目标向量y,判断和anchor box 有关的 $p_c$ 和边界框,指定正确类别。
378 |
379 | 
380 |
381 | - 如何预测:输入图像,神经网络的输出尺寸是3x3x2x8,对于9个格子,每个都有对应的向量,如上图所示。
382 | 对于1号蓝格,检测不到任何对象,所以2个anchor box的 $p_c$ = 0。剩下的是一些数字,多多少少都是噪音,但这些数字基本上会被忽略,因为神经网络告诉表示那里没有任何东西。(输出 y 如编号3所示)。
383 | 对于2号绿格,里面有汽车。对于边界框1(anchor box 1)来说 $p_c$ = 0,表示此格子中无行人。然后就是一组数字噪音,此格子中无行人。anchor box 2对应汽车,此格子中有车,因此希望数字可以对车子指定一个相当准确的边界框,即($$\left.p_{c}=1, b_{x}, b_{y}, b_{h}, b_{w}, c_{1}=0, c_{2}=1, c_{3}=0\right)$$,这就是神经网络做出预测的过程。
384 | - 运行非极大值抑制:看看一张新的测试图片,对于两个anchor box,那么对于9个格子中任何一个都会有两个预测的边界框。
385 | 针对每个框,抛弃概率低的预测,去掉那些连神经网络都说这里很可能什么都没有的边界框。如果希望检测行人、车子和摩托三个对象检测类别,那么需要对每个类别单独运行非极大值抑制,处理预测结果即此类别的边界框。
386 |
387 | 
388 |
389 | - 最后,输出位置和类别信息。
390 |
391 | #### 12.9.2 YOLO v1、v2、v3和v4
392 |
393 | YOLO 一共发布了四个版本,其中 YOLOv1 奠定了整个系列的基础,后面的系列就是在第一版基础上的改进,只为提升性能。
394 |
395 | - YOLOv2
396 | 提出了 ImageNet 和 COCO 数据集结合的联合训练方法,使算法可以在检测数据集和分类数据集上训练目标检测器。用检测数据集的数据学习物体的准确位置,用分类数据集的数据来增加分类的类别量、提升健壮性。
397 | - YOLOv3
398 | YOLOv3 的提出不是为了解决什么问题,将模型复杂了不少,可以通过改变模型结构的大小来权衡速度与精度。
399 | - YOLOv4
400 | YOLOv4的改进总结了几乎所有的检测技巧,又提出一点儿技巧,然后经过筛选,排列组合,挨个实验(ablation study)哪些方法有效,经过大量实验选出的性能最好的组合。
401 | 发展历程:
402 | 
403 |
404 | ### 12.10 RPN网络
405 |
406 | RPN:Region Proposal Network
407 |
408 | #### 12.10.1 Region with CNN(R-CNN)
409 |
410 | 意思基于候选区域(Region Proposal)的卷积网络,不再针对每个滑动窗口跑检测算法,而是使用某种算法求出候选区域,然后对每个候选区域跑一下分类器,每个区域会输出一个标签和一个边界框。这样就只是选择一些有意义的窗口,在少数窗口上运行卷积网络分类器,以节省时间。
411 |
412 | - 选出的候选区域方法:图像分割算法
413 |
414 | 
415 |
416 | 如上图所示。分割色块后,选择其对应的一个边界框,然后在色块上跑分类器,这样的处理比滑动窗口法处理的窗口少的多,可以减少卷积网络分类器运行时间,而不必在所有位置运行一遍分类器。
417 |
418 | 另外,说明一下,R-CNN算法不会直接信任输入的边界框,它也会输出一个边界框$$b_{x},\quad b_{y},\quad b_{h},\quad b_{w}$$,这样得到的边界框比较精确,比单纯使用图像分割算法给出的色块边界要好。
419 |
420 |
421 | #### 12.10.2 具体步骤
422 |
423 | 
424 |
425 | 1. 输入图像;运行图像分割算法,利用selective search对图像生成1K~2K的候选区域(region proposal);
426 | 2. 将每个候选区域缩放(warp)成227×227的大小并输入到CNN,将CNN的全连接层fc7的输出作为特征;
427 | 3. 对CNN的fc7层的输出特征输入到SVM进行分类;如果有十个类别,那么每个region proposal要经过10个SVM,得到预测的类别。
428 | 4. 修正:对于SVM分好类的Region Proposal做边框回归,用Bounding box回归值校正原来的候选窗口,生成预测窗口坐标。
429 |
430 | #### 12.10.3 缺点和改进
431 |
432 | R-CNN训练耗时,占用磁盘空间大,测试速度慢,每个候选区域需要运行整个前向CNN计算;因此提出了其它改进算法。
433 |
434 | 
435 |
436 | - Fast R-CNN:利用卷积实现了滑动窗口。相比于R-CNN,Fast R-CNN不再对每一个候选区域进行CNN特征提取,而是先将整张图片归一化后输入CNN网络进行特征提取,之后候选区域在特征图上进行截取,显著提升了R-CNN的速度。但是其缺点是得到候选区域的聚类步骤仍然非常缓慢。
437 |
438 | - Faster R-CNN:加入RPN网络,将特征提取、候选区域提取、bounding box regression、分类都整合在了一个网络中,使得综合性能有较大提高,在检测速度方面尤为明显。(仍比YOLO慢)
439 |
440 | - Gaussian Faster R-CNN主要有以下两个创新点:
441 | 1. 卷积的过程其实就是一个特征提取的过程,所以在预处理之后移除了全连接这个操作,简化了网络结构,以准确率换速度。
442 | 2. 假设在多次卷积之后,整个特征图是一个平稳的随机序列,符合高斯分布,则可以采用 $3\sigma$ 原理对树进行裁剪,因为四周的像素对分类任务来说无关紧要,但是完全压缩和分类这些无关紧要的像素会花费大量的CPU时间。最后用随机森林代替B-P神经网络,将时间复杂度由 $O(N)$ 降到 $O(log2N)$。
443 |
444 | ### 12.11 目标检测算法的评价指标
445 |
446 | #### 12.11.1 准确度指标——平均准确度均值mAP
447 |
448 | - **什么是TP、TN、FP、FN?**
449 |
450 | TP、TN、FP、FN即true positive, true negative, false positive, false negative的缩写,positive和negative表示的是预测得到的结果,预测为正类则为positive,预测为负类则为negative; true和false则表示预测的结果和真实结果是否相同,相同则是true,不同则为false,如下图:
451 |
452 | 
453 |
454 | 举个例子,假设现在有这样一个测试集,其中的图片只由大雁和飞机两种图片组成,如下图所示:
455 |
456 | 
457 |
458 | 假设分类系统最终的目的是取出测试集中所有飞机的图片,则 TP、TN、FP、FN的具体定义分别是:
459 |
460 | **True positives :** 飞机的图片被正确的识别成了飞机。
461 | **True negatives:** 大雁的图片没有被识别出来,系统正确地认为它们是大雁。
462 | **False positives:** 大雁的图片被错误地识别成了飞机。
463 | **False negatives:** 飞机的图片没有被识别出来,系统错误地认为它们是大雁。
464 |
465 | - **Precision 与 Recall**
466 |
467 | **Precision**(精确度、查准率)指的是模型判断该图片为正类且该图片也的确是正类的概率,即在模型判断为正类的图片中,True positives所占的比率,**衡量的是一个分类器分出来的正类的确是正类的概率**。
468 | $$
469 | Precision=\frac{TP}{TP+FP}
470 | $$
471 | 光是精确度还不能衡量分类器的好坏程度,比如50个正样本和50个负样本,如果分类器把49个正样本和50个负样本都分为负样本,剩下一个正样本分为正样本,这样精确度也是100%,所以还需要召回率来衡量。
472 |
473 | **Recall**(召回率、查全率)指的是测试集的所有正样本比例中,被模型正确识别为正样本的比例,即模型判断为正类且实际的确是正类的图像数量/真实类别是正类的图像数量,**衡量的是一个分类器能把所有的正类都找出来的能力**。
474 | $$
475 | Recall=\frac {TP}{TP+FN}
476 | $$
477 | 在上面所举的例子中,假设识别出了四个结果,如下图所示:
478 |
479 | 
480 |
481 | 其中,在识别出来的四张照片中:
482 |
483 | **True positives :** 有三个,画绿色框的飞机,即 $TP=3$。
484 |
485 | **False positives:** 有一个,画红色框的大雁,即 $FP=1$。
486 |
487 | 没被识别出来的六张图片中:
488 | **True negatives :** 有四个,这四个大雁的图片,系统正确地没有把它们识别成飞机,即 $TN=4$。
489 | **False negatives:** 有两个,两个飞机没有被识别出来,系统错误地认为它们是大雁,即 $FN=2$。
490 |
491 | 故 $Precision=\frac {TP}{TP+FP}=\frac {3}{3+1}=0.75$ ,意味着在识别出来的结果中,飞机的图片占75%;$Recall=\frac {TP}{TP+FN}=\frac{3}{3+2}=0.6$,意味着在所有的飞机图片中,60%的飞机图片被正确识别为飞机。
492 |
493 | - **调整阈值**
494 |
495 | 可以通过调整阈值来选择让模型识别出多少图片,进而改变Precision或Recall的值。在某种阈值的前提下(蓝色虚线),模型识别出了四张图片,如下图所示:
496 | 
497 |
498 | 分类系统认为大于阈值(蓝色虚线之上)的四个图片更像飞机。
499 |
500 | 我们可以通过改变阈值(可以看作上下移动蓝色虚线)来选择让系统识别出多少张图片,从而改变Precision或Recall的值。比如,把蓝色虚线移到第一张图片下面,也就是说让系统只识别出最上面的那张飞机图片,那么Precision的值就是100%,而Recall的值是20%;如果把蓝色虚线放到第二张图片下面,也就是说让系统只识别出最上面的前两张图片,那么Precision的值还是100%,而Recall的值则增长到40%。下图为不同阈值条件下,Precision与Recall的变化情况:
501 | 
502 |
503 | - **Precision-Recall曲线**
504 |
505 | Precision-Recall曲线(P-R曲线)是以Precision和Recall作为纵、横轴坐标的二维曲线,通过选取不同阈值时对应的精确度和召回率画出,如下图所示。
506 |
507 | 
508 |
509 | 总体趋势是,精确度越高,召回率越低,当召回率达到1时,对应概率分数最低的正样本,这个时候正样本数量除以所有大于等于该阈值的样本数量就是最低的精确度。上图所示的分类器在不损失精度的条件下能达到40%的Recall,而当Recall达到100%时,Precision降到50%。
510 |
511 | Precision-Recall曲线可以用来显示分类器在Precision和Recall之间的权衡,从而评估分类器的性能。如果一个分类器的性能较好,那么它应该有如下的表现:被识别出的图片中飞机所占的比重比较大,并且在识别出大雁之间,尽可能多地正确识别出飞机,也就是让Recall值增长的同时保持Precision的值在一个很高的水平。而性能较差的分类器可能会损失很多Precision值才能换来Recall值的提高。
512 |
513 | - **平均准确度AP**
514 |
515 | AP:Average-Precision,平均准确度,综合考量了Precision和Recall的影响,反映了模型对某个类别识别的好坏。
516 |
517 | P-R曲线围起来的面积就是AP值,通常来说一个分类器越好,AP值越高。
518 |
519 | - **平均准确度均值mAP**
520 |
521 | mAP:mean Average-Precision,平均精确度均值,即所有类别AP的平均值,衡量的是在所有类别上的平均好坏程度。
522 |
523 | mAP的取值范围是[0,1],越大越好。
524 |
525 | - 为什么可以使用mAP来评价目标检测的效果?
526 |
527 | 目标检测的效果取决于预测框的位置和类别是否准确,从mAP的计算过程中可以看出通过计算预测框和真实框的IoU来判断预测框是否准确预测到了位置信息,同时精确度和召回率指标的引用可以评价预测框的类别是否准确,因此mAP是目前目标检测领域非常常用的评价指标。
528 |
529 | > 参考文献:
530 | >
531 | > 1. https://blog.csdn.net/syoung9029/article/details/56276567
532 | >
533 | > 2. https://www.cnblogs.com/wanghui-garcia/p/11084833.html
534 | > 3. https://blog.csdn.net/weixin_43423892/article/details/106643649
535 |
536 | #### 12.11.2 速度指标——FPS
537 |
538 | 目标检测技术的很多实际应用在准确度和速度上都有很高的要求,如果不计速度性能指标,只注重准确度表现的突破,其代价是更高的计算复杂度和更多内存需求。只有速度快,才能实现实时检测,这对一些应用场景极其重要。
539 |
540 | FPS:Frame Per Second,每秒帧率,即每秒内可以处理的图片数量。当然要对比FPS,需要在同一硬件上进行。
541 |
542 | 另外也可以使用处理一张图片所需时间来评估检测速度,时间越短,速度越快。
543 |
544 | > 参考:
545 | >
546 | > 1. https://zhuanlan.zhihu.com/p/70306015
547 | > 2. https://blog.csdn.net/qq_29893385/article/details/81213377
548 |
549 | #### 12.11.3 模型大小
550 |
551 | 自 2012 年 AlexNet 以来,卷积神经网络(简称 CNN)在图像分类、图像分割、目标检测等领域获得广泛应用。随着性能要求越来越高,AlexNet 已经无法满足大家的需求,于是乎各路大牛纷纷提出性能更优越的 CNN 网络,如 VGG、GoogLeNet、ResNet、DenseNet 等。由于神经网络的性质,为了获得更好的性能,网络层数不断增加,从 7 层 AlexNet 到 16 层 VGG,再从 16 层 VGG 到 GoogLeNet 的 22 层,再到 152 层 ResNet,更有上千层的 ResNet 和 DenseNet。虽然网络性能得到了提高,但随之而来的就是效率问题。
552 |
553 | 效率问题主要是**模型的存储问题和模型进行预测的速度问题**(以下简称速度问题)
554 |
555 | - 第一,存储问题。数百层网络有着大量的权值参数,保存大量权值参数对设备的内存要求很高;
556 | - 第二,速度问题。在实际应用中,往往是毫秒级别,为了达到实际应用标准,要么提高处理器性能(看英特尔的提高速度就知道了,这点暂时不指望),要么就减少计算量。
557 |
558 | 只有解决 CNN 效率问题,才能让 CNN 走出实验室,更广泛的应用于移动端。对于效率问题,通常的方法是进行**模型压缩**(Model Compression),即在已经训练好的模型上进行压缩,使得网络携带更少的网络参数,从而解决内存问题,同时可以解决速度问题。
559 |
560 | 相比于在已经训练好的模型上进行处理,轻量化模型设计则是另辟蹊径。**轻量化模型设计**主要思想在于设计更高效的网络计算方式(主要针对**卷积**方式),从而使网络参数减少的同时,不损失网络性能。近年提出的四个轻量化模型分别是:SqueezeNet、MobileNet、ShuffleNet、Xception,有兴趣的可以参考以下博客或查找论文以了解。
561 |
562 | > 参考:https://blog.csdn.net/u012426298/article/details/80817788
--------------------------------------------------------------------------------
/13 特殊应用 人脸识别和神经风格转换.md:
--------------------------------------------------------------------------------
1 | ## 13 特殊应用:人脸识别和神经风格转换
2 |
3 | ### 13.1 什么是人脸识别?
4 |
5 | #### 13.1.1 人脸验证 vs 人脸识别
6 |
7 | **人脸验证**(face verification):也被称为 “1对1” 问题。
8 |
9 | - 输入:一张图片以及某人的ID或名字
10 | - 输出:系统验证输入图片是否是这个人。
11 |
12 | **人脸识别**(face recognition):“1对K” 问题。
13 |
14 | - 拥有一个包含 $K$ 人信息的数据库
15 | - 输入:一张图片
16 | - 输出:若输入图片符合 $K$ 人中任意一个人的图像,输出这个人的ID,否则,输出"not recognized"。
17 |
18 | **人脸验证与人脸识别的关系:**
19 |
20 | 人脸识别比人脸验证要求更高。假设有一个验证系统准确率是99%,看起来这个验证系统性能不错,但如果应用到有100个人的数据库的人脸识别系统中,每个人的犯错概率是1%,整体犯错概率就放大了100倍,所以要想得到一个可接受的识别误差,就要构造一个准确率为99%甚至更高的验证系统才能得到很好的识别效果。也就是说,人脸验证系统的准确率要足够高才能应用到人脸识别系统中。
21 |
22 | #### 13.1.2 人脸识别的传统方法
23 |
24 | 主流的人脸识别技术基本上可以归结为三类,即:基于几何特征的方法、基于模板的方法和基于模型的方法。
25 |
26 | - 基于几何特征的方法是最早、最传统的方法,通常需要和其他算法结合才能有比较好的效果;
27 | - 基于模板的方法可以分为基于相关匹配的方法、特征脸方法、线性判别分析方法、奇异值分解方法、神经网络方法、动态连接匹配方法等。
28 | - 基于模型的方法则有基于隐马尔柯夫模型,主动形状模型和主动外观模型的方法等。
29 |
30 | 下文主要介绍三种传统的人脸识别方法:
31 |
32 | 1. 主成分分析法
33 |
34 | 主成分分析法(PAC,Principal Component Analysis)又称为特征脸法,是20世纪90年代初由Turk和Pentland提出的一种经典算法,根据图像的统计特征通过正交变换(即K-L变换)由高维向量转换为低维向量,并形成低维线性向量空间,利用人脸投影到这个低维空间所得到的投影系数作为识别的特征矢量,这样,就产生了一个由“特征脸”矢量形成的子空间,成为“人脸子空间”或“特征子空间”,每一幅人脸图像向其投影都可以获得一组坐标系数,这组坐标系数表明了人脸在子空间中的位置,因此利用特征脸方法可以重建和识别人脸。
35 |
36 | 2. 线性判别分析
37 |
38 | 线性判别分析是对费舍尔的线性鉴别方法的归纳,这种方法使用统计学、模式识别和机器学习方法,试图找到两类物体或事件的特征的一个线性组合,以能够特征化或区分它们。所得的组合可用来作为一个线性分类器,或者,更常见的是,为后续的分类做降维处理。
39 |
40 | 3. 支持向量机
41 |
42 | 支持向量机(SVM,Support Vector Machine)起源于统计学习理论,研究如何构造学籍及,实现模式分类问题。其基本思想是通过非线性变换将输入空间变换到一个高维空间,在高维空间求取最优线性分类面,以解决那些线性不可分的分类问题。而这种非线性变换是通过定义适当的内积函数(即核函数)来实现的,由于该方法是基于结构风险最小化原理,而不是传统统计学的经验风险最小化,因而表现出很多优于已有方法的性能,但该方法需要大量的存储空间,并且训练速度慢。
43 |
44 | > 参考:
45 | >
46 | > 1. https://www.jiqizhixin.com/articles/2019-02-10-4
47 | > 2. https://wenku.baidu.com/view/34c55025a100a6c30c22590102020740be1ecdb7.html
48 |
49 | ### 13.2 One-Shot学习
50 |
51 | #### 13.2.1 One-Shot学习的定义
52 |
53 | **One-Shot learning**:一次学习,只通过一个样本来进行学习以能够认出同一个人。
54 |
55 | 
56 |
57 | 如上图所示,假设人脸识别系统数据库里有4个人每人一张照片,需要仅仅通过每个人的一张照片来判断输入图片中是否含有这4个人的其中一个。
58 |
59 | #### 13.2.2 如何解决One-Shot学习问题
60 |
61 | 对于One-Shot学习问题,采用卷积神经网络进行识别分类的缺点:
62 |
63 | 1. 训练集太小,不足以训练一个稳健的神经网络;
64 | 2. 如果有新成员加入数据集,分类输出的标签数量要改变,神经网络得重新训练。
65 |
66 | 故要解决One-Shot学习问题,应该要**学习Similarity函数**(也称为d函数):
67 | $$
68 | \begin{equation}\begin{split}
69 | d(img1,&img2)=degree\ of\ difference\ between\ images\\[2ex]
70 | &If\ d(img1,img2)\ \le\ \tau\ \ \ \ "same"\\
71 | &If\ d(img1,img2)\ \ge\ \tau\ \ \ \ "different"\\
72 | \end{split}\end{equation}
73 | $$
74 | 以两张图片作为输入,然后输出这两张图片的差异值,差异值越小越相似。如果差异值小于某个阈值 $\tau$($\tau$ 是一个超参数),就预测输入的是同一个人的两张图片;如果差异值大于阈值,就预测输入的是两个不同的人的照片,从而实现人脸验证。
75 |
76 | 将其应用于人脸识别任务,分别将要预测的图片及数据库中的任一张图片输入,用d函数两两比较,如果有输出一个比阈值小的数字,则预测的图片就是那个人的照片,若没有,则要预测的人不是数据库中的任一个人。
77 |
78 | 
79 |
80 | 在上面这个例子中,首先输入要识别的图片和数据库中第一张图片,输出一个很大的值,说明不是同一个人;接着输入要识别的图片和数据库中第二张图片,输出一个很小的值,很可能是同一个人;再分别输入要识别的图片和数据库中第三、四张图片,输出的值都很大,不是同一个人。因此,要识别的图片是第二个人的。若输出的值都很大,则要识别的人不是数据库里的任一个人。
81 |
82 | 如果要加入新成员,只需将其照片加入数据库中,系统依然能照常工作。
83 |
84 | #### 13.2.3 Few-Shot learning
85 |
86 | **Few-Shot learning**:小样本学习,用很少的样本去做分类或者回归。
87 |
88 | Few-Shot learning与传统的监督学习算法不同,它的目标不是让机器识别训练集中图片并且泛化到测试集,而是**让机器自己学会学习**。可以理解为用一个小数据集训练神经网络,学习的目的不是让神经网络知道每个类别是什么,而是让模型理解事物的异同,学会区分不同的事物。
89 |
90 | 
91 |
92 | 比如上面这张图片,左边两张图是同一种动物,右边两张是同一种动物,Few-Shot learning要做的就是通过对上面这四张图的学习判断下面这张图是属于哪一种动物。
93 |
94 | 
95 |
96 | Few-Shot learning 问题的关键是解决过拟合 (overfitting) 的问题,因为训练的样本太少了,训练出的模型可能在训练集上效果还行,但是在测试集上面会遭遇灾难性的崩塌。
97 |
98 | **解决方法:**
99 |
100 | 1. 数据增强和正则化:这一类方法想法很直接简单,既然训练数据不够那就增加训练样本,既然过拟合那就使用正则化技术。
101 | - 数据加强:最常见的例子就是有时对 Omniglot 数据集的预处理,会将图片旋转 90 、180 、270 度,这样就可以使样本数量变为原来的 4 倍。
102 | - 正则化:在训练的时候加入一个正则项,这个正则项的构建选择是关键。比如 《Few-shot Classification on Graphs with Structural Regularized GCNs》。该论文讨论 Graph 中节点分类的 few-shot 问题,常见的节点分类是使用 GCN 从节点的特征向量 feature 学习一个 embedding 然后用 embedding 来做分类,如果是 few-shot 问题,性能会大大下降(准确率大约从 70% 到了 40%),作者在训练的时候给损失函数加了一个正则项。作者将 feature 到 embedding 的过程看成编码器 encoder,然后额外加了几层网络作为 decoder,将 embedding 重构为 feature ,然后重构误差作为正则项(准确率从 40% 提升了 50%,大约 10 个百分点)。
103 |
104 | 2. Meta-learning(元学习):核心想法是先学习一个先验知识(prior),这个先验知识对解决 few-shot learning 问题特别有帮助。也就是说,先学习很多很多 task,然后再来解决新的在之前的学习中没有见过的 task 。
105 |
106 | > 参考:
107 | >
108 | > 1. https://blog.csdn.net/weixin_37589575/article/details/92801610
109 | > 2. https://zhuanlan.zhihu.com/p/142381922
110 |
111 | ### 13.3 Siamese网络
112 |
113 | Siamese网络架构是实现Similarity函数的一种方式。
114 |
115 | #### 13.3.1 Siamese网络架构
116 |
117 | **Siamese网络架构**:对于两个不同的输入,运行相同的卷积神经网络,然后比较它们输出的特征向量从而判断是否是属于同一类。
118 |
119 | 
120 |
121 | 如上图所示,首先将第一张输入图像$x^{(1)}$送入卷积神经网络,经过一系列的卷积、池化、全连接后输出一个特征向量,将这个特征向量称为$f(x^{(1)})$,看作是输入图像$x^{(1)}$的编码;然后将第二张输入图像$x^{(2)}$送入同样的神经网络,也得到一个特征向量,称为$f(x^{(2)})$,代表输入图像$x^{(2)}$的编码。我们相信这两个编码可以很好地代表两张输入图像,故定义d函数为两张图片编码之差的范数:
122 | $$
123 | d(x^{(1)}, x^{(2)})=||f(x^{(1)})-f(x^{(2)})||_2^2
124 | $$
125 |
126 | #### 13.3.2 如何训练Siamese网络
127 |
128 | 由于Siamese网络中两个卷积神经网络是一样的,所以在训练Siamese网络时只需要训练一个就好。
129 |
130 | 
131 |
132 | 更准确地说,神经网络的参数定义了一个编码函数$f(x^{(i)})$,如果给定输入图像$x^{(i)}$,会输出$x^{(i)}$的一个编码(特征向量)。训练网络要做的就是学习参数,使得如果两个图片$x^{(i)}$和$x^{(j)}$是同一个人,得到的两个编码的距离就小;如果$x^{(i)}$和$x^{(j)}$是不同的人,则它们之间的编码距离会比较大。如果改变这个网络所有层的参数,会得到不同的编码结果,要用反向传播来改变这些所有的参数以确保满足上面的条件。
133 |
134 | ### 13.4 Triplet损失
135 |
136 | #### 13.4.1 Triplet损失的定义
137 |
138 | **Triplet loss**:三元组损失,通常需要同时看三张图片:Anchor图片(A)、Positive图片(P,即正类,跟Anchor是同一个人)和Negative图片(N,即负类,跟Anchor不是同一个人)。其中,A和P为一对,是同一个人,所以希望它们编码的距离很接近;A和N为一对,不是同一个人,所以希望它们编码的距离远一点。公式如下:
139 | $$
140 | ||f(A)-f(P)||^2 \le ||f(A)-f(N)||^2
141 | $$
142 | 即:$d(A,P) \le d(A,N)$
143 |
144 | 把方程右边项移到左边:
145 | $$
146 | ||f(A)-f(P)||^2-||f(A)-f(N)||^2 \le 0
147 | $$
148 |
149 | 有两种情况满足这个表达式但没有用处:
150 |
151 | 1. 所有的编码会总是输出0,即$f(img)=0$,则 $0-0=0$。
152 | 2. 把所有的编码都设成相等的,即如果每个图片的编码和其他图片一样,这种情况还是得到 $0-0=0$。
153 |
154 | 为了阻止网络出现这两种情况,应该把“小于等于0”这个目标改为“小于0”,故将目标改为“$0-\alpha$”($\alpha$是一个超参数),由于我们更习惯使用“$+\ \alpha$”,所以将“$-\ \alpha$”这项移到左边,得到:
155 | $$
156 | ||f(A)-f(P)||^2-||f(A)-f(N)||^2 \ +\ \alpha \le 0
157 | $$
158 |
159 | 故第一个式子也变为:
160 | $$
161 | ||f(A)-f(P)||^2\ +\ \alpha \le ||f(A)-f(N)||^2
162 | $$
163 |
164 | 其中,$\alpha$也叫做间隔(margin),假设间隔设为0.2,为了满足条件,可以把d(A, N)调大或者把d(A, P)调小让间隔至少是0.2,这样就拉大了anchor与positive图片对和anchor与negative图片对之间的差距。例如,假设d(A, P)等于0.5,如果d(A, N)只比d(A, P)大一点点,为0.51,就不能满足条件,因为我们想让d(A, N)比d(A, P)大很多,至少是0.7或者更高。
165 |
166 | #### 13.4.2 Triplet损失函数
167 |
168 | 对于**一个三元组定义的损失函数**:
169 | $$
170 | L(A,P,N)=max(||f(A)-f(P)||^2-||f(A)-f(N)||^2 \ +\ \alpha,0)
171 | $$
172 | 若$||f(A)-f(P)||^2-||f(A)-f(N)||^2 \ +\ \alpha$ 小于0,那么损失函数就是0;若大于0,则损失函数等于$||f(A)-f(P)||^2-||f(A)-f(N)||^2 \ +\ \alpha$ ,是一个正的损失值。通过最小化损失函数,只要这个损失函数等于0,达到的效果就是使$||f(A)-f(P)||^2-||f(A)-f(N)||^2 \ +\ \alpha$小于或等于0,网络不会关心它的负值有多大。
173 |
174 | **整个网络的代价函数**是训练集中这些单个三元组损失的总和:
175 | $$
176 | J=\sum_{i=1}^mL(A^{(i)},P^{(i)},N^{(i)})
177 | $$
178 | 假设有一个10000张图片的训练集,里面是1000个不同的人的照片,平均每人10张照片,要做的是取这10000张图片生成三元组,然后对代价函数用梯度下降从而训练学习算法,训练完成后就可以应用到一次学习问题中。
179 |
180 | 为了定义三元组的数据集,需要成对的A和P即同一个人的成对的图片,
181 |
182 | #### 13.4.3 如何选择三元组组成训练集
183 |
184 | 倘若从数据集中随机地选择A, P, N构成三元组,遵循A和P是同一个人而A和N是不同的人这一原则,则不是同一个人的概率比是同一个人的概率大很多,即d(A, N)比d(A, P)大$\alpha$ 的概率很大,目标很容易就达到,网络很轻松就能训练好,梯度算法不会有什么效果。
185 |
186 | 所以应该**尽可能选择难训练的三元组A P N即所有的三元组d(A, P)都很接近d(A, N)**,这样,学习算法就会竭尽全力使d(A, N)变大或者使d(A, P)变小使得二者之间至少间隔$\alpha$,并且选择这样的三元组训练难度大,梯度下降法才能发挥作用,从而增加学习算法的计算效率。
187 |
188 | 
189 |
190 | ### 13.5 面部验证与二分类
191 |
192 | #### 13.5.1 将人脸识别变成二分类问题
193 |
194 | Triplet loss是个学习人脸识别卷积网络参数的好方法,此外还有其他学习参数的方法,如将人脸识别当成一个二分类问题:
195 |
196 | 
197 |
198 | 选取一对神经网络,选用 Siamese 网络并使其同时计算这些特征向量,然后将其输入到逻辑回归单元进行预测,若是相同的人,那么输出是 1,若是不同的人,输出是 0。这就把人脸识别问题转换为一个二分类问题,训练这种系统时可以替换 Triplet loss的方法。
199 |
200 | #### 13.5.2 逻辑回归单元的处理
201 |
202 | 最后通过将sigmoid等函数应用到某些特征上来处理逻辑回归单元:
203 | $$
204 | \hat{y}=\sigma\left(\sum_{k=1}^{128} w_{i}\left|f\left(x^{(i)}\right)_{k}-f\left(x^{(j)}\right)_{k}\right|+b\right)
205 | $$
206 | 其中,符号$f\left(x^{(i)}\right)$代表图片$x^{(i)}$的编码,下标 $k$ 代表选择这个向量中的第$k$个元素,$\left|f\left(x^{(i)}\right)_{k}-f\left(x^{(j)}\right)_{k}\right|$对这两个编码取元素差的绝对值。就像普通的逻辑回归一样,把这128个元素当作特征,然后把他们放入逻辑回归中,最后的逻辑回归可以增加参数$w_{i}$和$b$。在这128个单元上训练合适的权重,用来预测两张图片是否是一个人。
207 |
208 | 还可以用$\chi^{2}$公式$\frac{\left(f\left(x^{(i)}\right)_{k}-f\left(x^{(j)}\right)_{k}\right)^{2}}{f\left(x^{(i)}\right)_{k}+f\left(x^{(j)}\right)_{k}}$,也被称作$\chi$平方相似度,来代替上式中$\left|f\left(x^{(i)}\right)_{k}-f\left(x^{(j)}\right)_{k}\right|$的计算。
209 |
210 | #### 13.5.3 预先计算思想
211 |
212 | 在上面的学习公式中,输入是一对图片($x^{(i)}$和$x^{(j)}$),输出$y$是0或者1取决于输入是相似图片还是非相似图片。与之前类似,训练一个Siamese网络,即两个神经网络拥有的参数是相同的,两组参数是绑定的。
213 |
214 | **预先计算好数据库中图片的编码可以节省大量的计算,显著提高部署效果。**
215 |
216 | 如你有一张新图片$x^{(i)}$,当员工走进门时,希望门可以自动为他打开,在数据库中的图片$x^{(j)}$,不需要每次都计算特征向量,可以提前计算好,那么当一个新员工走近时,可以使用上方的卷积网络来计算编码,然后将其和预先计算好的编码进行比较,输出预测值 $\hat{y}$。
217 |
218 | **总结**:把人脸验证当作一个监督学习,创建一个只有成对图片的训练集,不是三个一组,而是成对的图片,目标标签是1表示这对图片是一个人,目标标签是0表示图片中是不同的人。利用不同的成对图片,使用反向传播算法去训练神经网络,训练Siamese神经网络。
219 |
220 | ### 13.6 什么是神经风格迁移
221 |
222 | #### 13.6.1 神经风格迁移的定义
223 |
224 | 
225 |
226 | 比如这张照片,你想利用右边照片的风格来重新创造原本的照片,右边的是梵高的星空,神经风格迁移可以帮你生成下面这张照片。使用$C$来表示内容图像,$S$表示风格图像,$G$表示生成的图像。
227 |
228 | #### 13.6.2 神经风格迁移的常用方法
229 |
230 | 
231 |
232 | [参考博客]: https://www.jiqizhixin.com/articles/2018-05-15-5 "综述:图像风格化算法最全盘点 | 内附大量扩展应用"
233 |
234 | ### 13.7 深度卷积网络在学什么
235 |
236 | #### 13.7.1 可视化分析卷积神经网络的浅层
237 |
238 | 假如训练了一个卷积神经网络,是一个Alexnet,轻量级网络,希望将看到不同层之间隐藏单元的计算结果。
239 |
240 | 
241 |
242 | 你可以这样做,从第一层的隐藏单元开始,假设你遍历了训练集,然后找到那些使得单元激活最大化的一些图片或是图片块。换句话说,将你的训练集经过神经网络,然后弄明白哪一张图片最大限度地激活特定的单元。注意在第一层的隐藏单元,只能看到小部分卷积神经,如果要画出来哪些激活了激活单元,只有一小块图片块是有意义的,因为这就是特定单元所能看到的全部。你选择一个隐藏单元,发现有9个图片最大化了单元激活,你可能找到这样的9个图片块(左上九宫格),似乎是图片浅层区域显示了隐藏单元所看到的,找到了像这样的边缘或者线(上面的蓝格子),这就是那9个最大化地激活了隐藏单元激活项的图片块。
243 |
244 | 
245 |
246 | 然后你可以选一个另一个第一层的隐藏单元,重复刚才的步骤,这是另一个隐藏单元,似乎第二个由这9个图片块(上中九宫格)组成。看来这个隐藏单元在输入区域,寻找这样的线条(下面的蓝格子),我们也称之为接受域。
247 |
248 | 对其他隐藏单元也进行处理,会发现其他隐藏单元趋向于激活类似于这样的图片。右上九宫格似乎对垂直明亮边缘且左边是绿色的图片块感兴趣,左中九宫格的隐藏单元倾向于橘色图片块。
249 |
250 | 以此类推,这是9个不同的代表性神经元,每一个不同的图片块都最大化地激活了。你可以这样理解,第一层的隐藏单元通常会找一些简单的特征,比如说边缘或者颜色阴影。
251 |
252 | #### 13.7.2 可视化分析卷积神经网络的深层
253 |
254 | 在深层部分,一个隐藏单元会看到一张图片更大的部分,在极端的情况下,可以假设每一个像素都会影响到神经网络更深层的输出,靠后的隐藏单元可以看到更大的图片块。
255 |
256 | 
257 |
258 | 上图中Layer 1是之前第一层得到的,Layer 2是可视化的第2层中最大程度激活的9个隐藏单元。在更深的层上,可以重复这个过程。
259 |
260 | 放大第一层,这是第一个被高度激活的单元,你能在输入图片的区域看到所提取的这些边缘或颜色阴影。
261 |
262 | 
263 |
264 | 放大第二层的可视化图像。第二层似乎检测到更复杂的形状和模式,比如说中上九宫格这一隐藏单元会找到有很多垂线的垂直图案,右中九宫格的隐藏单元似乎在左侧有圆形图案时会被高度激活,左下九宫格所寻找的特征是很细的垂线,以此类推,第二层检测的特征变得更加复杂。
265 |
266 | 
267 |
268 | 放大第三层,这些东西激活了第三层。中心九宫格这一隐藏单元似乎对图像左下角的圆形很敏感,所以检测到很多车。右下九宫格似乎开始检测到人类,左上九宫格似乎检测特定的图案,比如蜂窝形状或者方形这样类似规律的图案。有些很难看出来,需要手动弄明白检测到什么,但是第三层明显,检测到更复杂的模式。
269 |
270 | 
271 |
272 |
273 |
274 | 这是第四层,检测到的模式和特征更加复杂,左上九宫格学习成了一个狗的检测器,但是这些狗看起来都很类似。右中九宫格似乎检测到鸟的脚等等。
275 |
276 |  277 |
278 |
279 |
280 | 第五层检测到更加复杂的事物,右下九宫格似乎是一个狗检测器,但是可以检测到的狗似乎更加多样性。左上九宫格可以检测到键盘或者是键盘质地的物体,可能是有很多点的物体。左中九宫格可能检测到文本,但是很难确定,左下九宫格检测到花。
281 |
282 |
277 |
278 |
279 |
280 | 第五层检测到更加复杂的事物,右下九宫格似乎是一个狗检测器,但是可以检测到的狗似乎更加多样性。左上九宫格可以检测到键盘或者是键盘质地的物体,可能是有很多点的物体。左中九宫格可能检测到文本,但是很难确定,左下九宫格检测到花。
281 |
282 |  283 |
284 | 由此,我们已经有了一些进展,**从检测简单的事物,比如说,第一层的边缘,第二层的质地,到深层的复杂物体**,更直观地了解卷积神经网络的浅层和深层是如何计算的。
285 |
286 | ### 13.8 代价函数
287 |
288 | #### 13.8.1 代价函数的作用
289 |
290 | 神经风格迁移系统用代价函数来评判某个生成图像的好坏。
291 |
292 | #### 13.8.2 代价函数的定义
293 |
294 | $$
295 | J(G)=αJ_{content}(C,G)+βJ_{style}(S,G)
296 | $$
297 |
298 | 其中,$J_{content}(C,G)$称为内容代价函数,用来衡量生成图片G的内容与图片C的内容有多相似;$J_{style}(S,G)$是风格代价函数,用来衡量图片G的风格与图片S的风格的相似度。超参数 $\alpha$ 和 $\beta$ 确定内容代价和风格代价两者之间的权重。
299 |
300 | #### 13.8.2 如何最小化代价函数
301 |
302 | 用梯度下降法来最小化代价函数:
303 | $$
304 | G=G-\frac{\partial}{\partial G}J(G)
305 | $$
306 | 实际上每次更新的是图像G的像素值。举个例子:
307 |
308 | 
309 |
310 | 要取上图中左边图片的内容和右边图片的风格生成图像G。随机初始化的生成图像如下图①所示,是一张随机选取像素的白噪声图;接下来运行梯度下降算法,最小化代价函数$J(G)$,逐步处理像素,逐步得到越来越像用风格图片的风格画出来的内容图片(下图中第②-④张图片)。
311 |
312 | 
313 |
314 | ### 13.9 内容代价函数
315 |
316 | #### 13.9.1 定义
317 |
318 | 内容代价函数:Content cost function,衡量内容图片和生成图片在内容上的相似度。
319 |
320 | 假如用隐含层 $l$ 来计算内容代价,$l$ 一般是选在网络的中间层,不会选的太浅或太深。然后用一个预训练的卷积模型,$a^{[l](C)}$和$a^{[l](G)}$分别代表内容图片C和生成图片G的 $l$ 层的激活函数值。如果这两个激活值相似,则这两张图片的内容相似。故将内容代价函数定义为两个激活值的不同或相似程度,即其差值的平方:
321 | $$
322 | J_{content}(C,G)=\frac{1}{2}||a^{[l](C)}-a^{[l](G)}||^2
323 | $$
324 | 其中,$\frac{1}{2}$ 是对其进行归一化,可以不加也可以是其他值,因为在整体代价函数中还可由超参数 $\alpha$ 调整内容代价函数的权重。
325 |
326 | ### 13.10 风格代价函数
327 |
328 | 风格代价函数:Style cost function,衡量风格图片和生成图片在风格上的相似度。
329 |
330 | #### 13.10.1 图像风格的定义
331 |
332 | 如下图所示,假如有这么一张图片输入卷积网络,对于某一隐藏层 $l$ ,图片的风格可以定义为 $l$ 层中各个通道之间激活项的相关系数。
333 |
334 | 
335 |
336 | 具体解释:
337 |
338 | 将 $l$ 层的激活项取出,是一个 $n_H \times n_W \times n_C$ 的三维激活项,将其不同通道渲染成不同的颜色,每个通道对应一个神经元,如下图所示,以前两个通道为例,红色通道对应的是第二个神经元(红色方框),能找出图片中的特定位置是否含有垂线纹理,黄色通道对应第四个神经元(黄色方框),可以粗略找出橙色区域,则这两个通道的相关系数指的就是图片中某处出现这种垂直纹理时该处又同时是橙色的可能性。若采用相关系数来描述通道的风格,则需测量生成图像中第一个通道是否与第二个通道相关,从而得知在生成图像中垂直纹理和橙色同时出现或不同时出现的概率,这样就能够测量生成图像的风格与输入的风格图像的相似程度。
339 |
340 | 
341 |
342 |
343 |
344 | #### 13.10.2 风格矩阵
345 |
346 | 对于风格图像与生成图像,需要计算其风格矩阵,说得更具体一点就是用 $l$ 层来测量风格。
347 |
348 | 假设 $a^{[l]}_{i,j,k}$ 为隐藏层 $l$ 中 $(i,j,k)$ 位置的激活项,i、j、k分别代表该位置的高度、宽度以及对应的通道数。现在要计算一个关于 $l$ 层和风格图像的矩阵 $G^{[l][S]}$ ( $l$ 表示层数,$S$ 表示风格图像),由于有 $n_c$ 个通道,故 $G^{[l][S]}$ 是一个 $n_c \times n_c$ 的矩阵,以便计算 $k$ 通道和 $k′$ 通道中每一对激活项的相关系数, $k$ 和 $k′$ 的取值范围则为$1,2,...,n_c$,
349 | 设这个关于 $l$ 层和风格图像的矩阵 $G^{[l][S]}$ 高度和宽度都是 $l$ 层的通道数,在这个矩阵中 $k$ 和 $k′$ 元素被用来描述 $k$ 通道和 $k′$ 通道之间的相关系数,则风格图像的风格矩阵是:
350 | $$
351 | G^{[l](S)}_{kk'}=\sum_i^{n^{[l]}_H} \sum_j^{n^{[l]}_W} a_{ijk}^{[l](S)}a_{ijk'}^{[l](S)}
352 | $$
353 | 其中,符号 $i$、$j$ 表示下界,对 $i$、$j$、$k$ 位置的激活项 $a_{ijk}^{[l](S)}$,乘以同样位置即 $i$、$j$、$k'$ 位置的激活项 $a_{ijk'}^{[l](S)}$,然后 $i$、$j$ 分别加到 $l$ 层的高度和宽度,即 $n^{[l]}_H$ 和 $n^{[l]}_W$,将这些不同位置的激活项都加起来即可得到风格矩阵。严格来说,这个公式是一种非标准的互相关函数,因为没有将其减去平均数,而是将它们直接相乘。
354 |
355 | 对生成图像做同样的操作即可得到生成图像的风格矩阵:
356 | $$
357 | G^{[l](G)}_{kk'}=\sum_i^{n^{[l]}_H} \sum_j^{n^{[l]}_W} a_{ijk}^{[l](G)}a_{ijk'}^{[l](G)}
358 | $$
359 |
360 | 之所以用大写字母 $G$ 来代表这些风格矩阵,是因为在线性代数中这种矩阵有时也叫 Gram 矩阵,但在这里只把它们叫做风格矩阵。
361 |
362 | 如果两个通道中的激活项数值都很大,那么 $G^{[l]}_{kk'}$ 也会很大,对应地,如果它们不相关那么 $G^{[l]}_{kk'}$ 就会很小。
363 |
364 | 下图形象地展示了风格矩阵的形成过程:
365 |
366 | 
367 |
368 | #### 13.10.3 风格代价函数
369 |
370 | 如果将 $S$ 和 $G$ 代入到风格代价函数中去计算将得到这两个矩阵之间的误差,实际上是计算两个矩阵对应元素相减的平方的和,由于 $G^{[l][S]}$ 和 $G^{[l][G]}$ 是矩阵,故加下标表 Frobenius 范数:
371 | $$
372 | J^{[l]}_{style}(S,G)=||G^{[l][S]}-G^{[l][G]}||^2_F
373 | $$
374 | 把这个式子展开,从 $k$ 和 $k′$ 开始作差,然后把得到的结果都加起来,即得到对 $l$ 层定义的风格代价函数:
375 | $$
376 | J^{[l]}_{style}(S,G)=\frac {1}{(2n_H^{[l]}n_W^{[l]}n_c^{[l]})^2} \sum_k \sum_{k'}(G^{[l](S)}_{kk'}-G^{[l](G)}_{kk'})^2
377 | $$
378 | 其中,使用了一个归一化常数$\frac {1}{(2n_H^{[l]}n_W^{[l]}n_c^{[l]})^2}$ ,但是一般情况下不用写这么多,只要将风格代价函数乘以一个超参数 $\beta$ 就行。
379 |
380 | 实际上,如果对各层都使用风格代价函数,会让结果变得更好。如果要对各层都使用风格代价函数,把各个层的结果(各层的风格代价函数)都加起来,就能定义它们全体了:
381 | $$
382 | J_{style}(S,G)=\sum_l \lambda^{[l]}J^{[l]}_{style}(S,G)
383 | $$
384 | 其中,需要对每个层定义权重,用 $\lambda^{[l]}$ 来表示,这样将能够在神经网络中使用不同的层,包括之前的一些可以测量类似边缘这样的低级特征的层以及之后的一些能测量高级特征的层,使得我们的神经网络在计算风格时能够同时考虑到这些低级和高级特征的相关系数。这样,在基础的训练中定义超参数时,可以尽可能地得到更合理的选择。
385 |
386 | 为了把这些东西封装起来,现在定义全体代价函数:
387 | $$
388 | J(G)=αJ_{content}(C,G)+βJ_{style}(S,G)
389 | $$
390 | 之后用梯度下降法,或者更复杂的优化算法来找到一个合适的图像 $G$,并计算 $J(G)$ 的最小值,从而将能够得到非常好看漂亮的结果。
391 |
392 | #### 13.10.4 用GAN做风格迁移
393 |
394 | GAN是解决风格迁移的深度学习方法。
395 |
396 | GAN由生成网络G和对抗网络D组成,G用于接收一个噪声z,从而生成图片G(z);D是一个判别网络,判别一张图片x是不是“真的”我们所需得到的目的图片或者是由G生成的(此时图片是“假的”),即D(x)。
397 | 生成网络G和对抗网络D在训练时候互为动态的博弈过程。
398 | 损失函数:
399 |
400 | 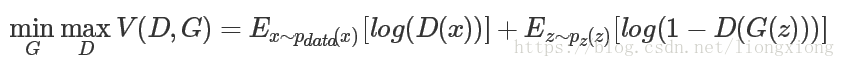
401 |
402 | 其中,x为真实图片,z表示输入G的随机噪声。
403 | GAN之所以能产生对抗博弈的训练过程和效果是因为GAN把训练过程分为了两个部分:
404 |
405 | 优化D:
406 | 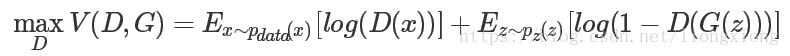
407 |
408 | 优化G:
409 |
410 | 
411 |
412 | 将D和G用CNN来表达就是适用于图像处理的DCGAN了。
413 | 更多方法详见“https://blog.csdn.net/liongxiong/article/details/80875885”。
414 |
415 | ### 13.11 一维到三维的推广
416 |
417 | #### 13.11.1 2D卷积
418 |
419 | 假设输入图像为14×14的2维图像,使用5×5的2维过滤器进行卷积,得到 10×10的二维图像,如下图所示:
420 | 
421 |
422 | #### 13.11.2 1D卷积
423 |
424 | 举个例子,下图左边是一个EKG信号(心电图),当在胸部放一个电极,电极透过胸部测量心脏带来的微弱电流,每个峰值对应一次心跳。如果想用EKG信号,就需要处理1维数据。因为EKG信号由时间序列对应的每个瞬间的电压组成,是一维的,输入的尺寸是14而不是14×14,就需要用一维过滤进行卷积如一个5的过滤器,而不是5×5。最终的输出尺寸是10。
425 | 
426 |
427 | #### 13.11.3 3D卷积
428 |
429 | 
430 | 如上图所示,假设现在输入是具有长度、宽度和高度的三维数据,例如14×14×14,使用5×5×5的过滤器进行卷积,输出将为10×10×10。某种程度上3D数据也可以使用3D confident学习。过滤器实现的功能是用输入的3D数据进行特征识别。
431 |
432 | 医疗检查是3D卷积的一个实例,如下图所示的CT扫描,用X光输出身体的3D模型:
433 |
434 | 
--------------------------------------------------------------------------------
/14 序列模型.md:
--------------------------------------------------------------------------------
1 | # 14序列模型
2 |
3 | ### 14.1 为什么选择序列模型
4 |
5 | #### 14.1.1 序列模型应用领域
6 |
7 | 序列模型广泛应用于语音识别,音乐生成,情感分析,DNA序列分析,机器翻译,视频行为识别,命名实体识别等众多领域。
8 |
9 | - 语音识别:将输入的语音信号直接输出相应的语音文本信息。无论是语音信号还是文本信息均是序列数据。
10 |
11 | - 音乐生成:生成音乐乐谱。只有输出的音乐乐谱是序列数据,输入可以是空或者一个整数。
12 |
13 | - 情感分类:将输入的评论句子转换为相应的等级或评分。输入是一个序列,输出则是一个单独的类别。
14 |
15 | - DNA序列分析:输入的DNA序列,找到匹配的蛋白质序列。
16 |
17 | - 机器翻译:两种不同语言之间的翻译。输入和输出均为序列数据。
18 |
19 | - 视频行为识别:识别输入的视频帧序列中的人物行为。
20 |
21 | - 命名实体识别:从输入的句子中识别实体的名字。
22 |
23 | 
24 |
25 | #### 14.1.2 输入x和输出y的关系
26 |
27 | 上面那些问题可以看成使用标签数据$(x,y)$作为训练集的监督学习,但是输入与输出不一定都是序列,对应关系有非常多的组合,比如一对一,多对多,一对多,多对一,多对多(个数不同)等情况来针对不同的应用。
28 |
29 | ### 14.2 数学符号
30 |
31 | #### 14.2.1 符号含义
32 |
33 | - $x^{
283 |
284 | 由此,我们已经有了一些进展,**从检测简单的事物,比如说,第一层的边缘,第二层的质地,到深层的复杂物体**,更直观地了解卷积神经网络的浅层和深层是如何计算的。
285 |
286 | ### 13.8 代价函数
287 |
288 | #### 13.8.1 代价函数的作用
289 |
290 | 神经风格迁移系统用代价函数来评判某个生成图像的好坏。
291 |
292 | #### 13.8.2 代价函数的定义
293 |
294 | $$
295 | J(G)=αJ_{content}(C,G)+βJ_{style}(S,G)
296 | $$
297 |
298 | 其中,$J_{content}(C,G)$称为内容代价函数,用来衡量生成图片G的内容与图片C的内容有多相似;$J_{style}(S,G)$是风格代价函数,用来衡量图片G的风格与图片S的风格的相似度。超参数 $\alpha$ 和 $\beta$ 确定内容代价和风格代价两者之间的权重。
299 |
300 | #### 13.8.2 如何最小化代价函数
301 |
302 | 用梯度下降法来最小化代价函数:
303 | $$
304 | G=G-\frac{\partial}{\partial G}J(G)
305 | $$
306 | 实际上每次更新的是图像G的像素值。举个例子:
307 |
308 | 
309 |
310 | 要取上图中左边图片的内容和右边图片的风格生成图像G。随机初始化的生成图像如下图①所示,是一张随机选取像素的白噪声图;接下来运行梯度下降算法,最小化代价函数$J(G)$,逐步处理像素,逐步得到越来越像用风格图片的风格画出来的内容图片(下图中第②-④张图片)。
311 |
312 | 
313 |
314 | ### 13.9 内容代价函数
315 |
316 | #### 13.9.1 定义
317 |
318 | 内容代价函数:Content cost function,衡量内容图片和生成图片在内容上的相似度。
319 |
320 | 假如用隐含层 $l$ 来计算内容代价,$l$ 一般是选在网络的中间层,不会选的太浅或太深。然后用一个预训练的卷积模型,$a^{[l](C)}$和$a^{[l](G)}$分别代表内容图片C和生成图片G的 $l$ 层的激活函数值。如果这两个激活值相似,则这两张图片的内容相似。故将内容代价函数定义为两个激活值的不同或相似程度,即其差值的平方:
321 | $$
322 | J_{content}(C,G)=\frac{1}{2}||a^{[l](C)}-a^{[l](G)}||^2
323 | $$
324 | 其中,$\frac{1}{2}$ 是对其进行归一化,可以不加也可以是其他值,因为在整体代价函数中还可由超参数 $\alpha$ 调整内容代价函数的权重。
325 |
326 | ### 13.10 风格代价函数
327 |
328 | 风格代价函数:Style cost function,衡量风格图片和生成图片在风格上的相似度。
329 |
330 | #### 13.10.1 图像风格的定义
331 |
332 | 如下图所示,假如有这么一张图片输入卷积网络,对于某一隐藏层 $l$ ,图片的风格可以定义为 $l$ 层中各个通道之间激活项的相关系数。
333 |
334 | 
335 |
336 | 具体解释:
337 |
338 | 将 $l$ 层的激活项取出,是一个 $n_H \times n_W \times n_C$ 的三维激活项,将其不同通道渲染成不同的颜色,每个通道对应一个神经元,如下图所示,以前两个通道为例,红色通道对应的是第二个神经元(红色方框),能找出图片中的特定位置是否含有垂线纹理,黄色通道对应第四个神经元(黄色方框),可以粗略找出橙色区域,则这两个通道的相关系数指的就是图片中某处出现这种垂直纹理时该处又同时是橙色的可能性。若采用相关系数来描述通道的风格,则需测量生成图像中第一个通道是否与第二个通道相关,从而得知在生成图像中垂直纹理和橙色同时出现或不同时出现的概率,这样就能够测量生成图像的风格与输入的风格图像的相似程度。
339 |
340 | 
341 |
342 |
343 |
344 | #### 13.10.2 风格矩阵
345 |
346 | 对于风格图像与生成图像,需要计算其风格矩阵,说得更具体一点就是用 $l$ 层来测量风格。
347 |
348 | 假设 $a^{[l]}_{i,j,k}$ 为隐藏层 $l$ 中 $(i,j,k)$ 位置的激活项,i、j、k分别代表该位置的高度、宽度以及对应的通道数。现在要计算一个关于 $l$ 层和风格图像的矩阵 $G^{[l][S]}$ ( $l$ 表示层数,$S$ 表示风格图像),由于有 $n_c$ 个通道,故 $G^{[l][S]}$ 是一个 $n_c \times n_c$ 的矩阵,以便计算 $k$ 通道和 $k′$ 通道中每一对激活项的相关系数, $k$ 和 $k′$ 的取值范围则为$1,2,...,n_c$,
349 | 设这个关于 $l$ 层和风格图像的矩阵 $G^{[l][S]}$ 高度和宽度都是 $l$ 层的通道数,在这个矩阵中 $k$ 和 $k′$ 元素被用来描述 $k$ 通道和 $k′$ 通道之间的相关系数,则风格图像的风格矩阵是:
350 | $$
351 | G^{[l](S)}_{kk'}=\sum_i^{n^{[l]}_H} \sum_j^{n^{[l]}_W} a_{ijk}^{[l](S)}a_{ijk'}^{[l](S)}
352 | $$
353 | 其中,符号 $i$、$j$ 表示下界,对 $i$、$j$、$k$ 位置的激活项 $a_{ijk}^{[l](S)}$,乘以同样位置即 $i$、$j$、$k'$ 位置的激活项 $a_{ijk'}^{[l](S)}$,然后 $i$、$j$ 分别加到 $l$ 层的高度和宽度,即 $n^{[l]}_H$ 和 $n^{[l]}_W$,将这些不同位置的激活项都加起来即可得到风格矩阵。严格来说,这个公式是一种非标准的互相关函数,因为没有将其减去平均数,而是将它们直接相乘。
354 |
355 | 对生成图像做同样的操作即可得到生成图像的风格矩阵:
356 | $$
357 | G^{[l](G)}_{kk'}=\sum_i^{n^{[l]}_H} \sum_j^{n^{[l]}_W} a_{ijk}^{[l](G)}a_{ijk'}^{[l](G)}
358 | $$
359 |
360 | 之所以用大写字母 $G$ 来代表这些风格矩阵,是因为在线性代数中这种矩阵有时也叫 Gram 矩阵,但在这里只把它们叫做风格矩阵。
361 |
362 | 如果两个通道中的激活项数值都很大,那么 $G^{[l]}_{kk'}$ 也会很大,对应地,如果它们不相关那么 $G^{[l]}_{kk'}$ 就会很小。
363 |
364 | 下图形象地展示了风格矩阵的形成过程:
365 |
366 | 
367 |
368 | #### 13.10.3 风格代价函数
369 |
370 | 如果将 $S$ 和 $G$ 代入到风格代价函数中去计算将得到这两个矩阵之间的误差,实际上是计算两个矩阵对应元素相减的平方的和,由于 $G^{[l][S]}$ 和 $G^{[l][G]}$ 是矩阵,故加下标表 Frobenius 范数:
371 | $$
372 | J^{[l]}_{style}(S,G)=||G^{[l][S]}-G^{[l][G]}||^2_F
373 | $$
374 | 把这个式子展开,从 $k$ 和 $k′$ 开始作差,然后把得到的结果都加起来,即得到对 $l$ 层定义的风格代价函数:
375 | $$
376 | J^{[l]}_{style}(S,G)=\frac {1}{(2n_H^{[l]}n_W^{[l]}n_c^{[l]})^2} \sum_k \sum_{k'}(G^{[l](S)}_{kk'}-G^{[l](G)}_{kk'})^2
377 | $$
378 | 其中,使用了一个归一化常数$\frac {1}{(2n_H^{[l]}n_W^{[l]}n_c^{[l]})^2}$ ,但是一般情况下不用写这么多,只要将风格代价函数乘以一个超参数 $\beta$ 就行。
379 |
380 | 实际上,如果对各层都使用风格代价函数,会让结果变得更好。如果要对各层都使用风格代价函数,把各个层的结果(各层的风格代价函数)都加起来,就能定义它们全体了:
381 | $$
382 | J_{style}(S,G)=\sum_l \lambda^{[l]}J^{[l]}_{style}(S,G)
383 | $$
384 | 其中,需要对每个层定义权重,用 $\lambda^{[l]}$ 来表示,这样将能够在神经网络中使用不同的层,包括之前的一些可以测量类似边缘这样的低级特征的层以及之后的一些能测量高级特征的层,使得我们的神经网络在计算风格时能够同时考虑到这些低级和高级特征的相关系数。这样,在基础的训练中定义超参数时,可以尽可能地得到更合理的选择。
385 |
386 | 为了把这些东西封装起来,现在定义全体代价函数:
387 | $$
388 | J(G)=αJ_{content}(C,G)+βJ_{style}(S,G)
389 | $$
390 | 之后用梯度下降法,或者更复杂的优化算法来找到一个合适的图像 $G$,并计算 $J(G)$ 的最小值,从而将能够得到非常好看漂亮的结果。
391 |
392 | #### 13.10.4 用GAN做风格迁移
393 |
394 | GAN是解决风格迁移的深度学习方法。
395 |
396 | GAN由生成网络G和对抗网络D组成,G用于接收一个噪声z,从而生成图片G(z);D是一个判别网络,判别一张图片x是不是“真的”我们所需得到的目的图片或者是由G生成的(此时图片是“假的”),即D(x)。
397 | 生成网络G和对抗网络D在训练时候互为动态的博弈过程。
398 | 损失函数:
399 |
400 | 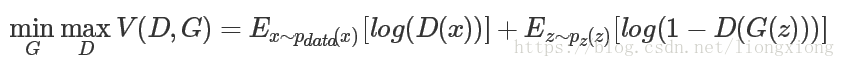
401 |
402 | 其中,x为真实图片,z表示输入G的随机噪声。
403 | GAN之所以能产生对抗博弈的训练过程和效果是因为GAN把训练过程分为了两个部分:
404 |
405 | 优化D:
406 | 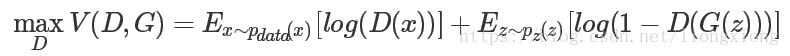
407 |
408 | 优化G:
409 |
410 | 
411 |
412 | 将D和G用CNN来表达就是适用于图像处理的DCGAN了。
413 | 更多方法详见“https://blog.csdn.net/liongxiong/article/details/80875885”。
414 |
415 | ### 13.11 一维到三维的推广
416 |
417 | #### 13.11.1 2D卷积
418 |
419 | 假设输入图像为14×14的2维图像,使用5×5的2维过滤器进行卷积,得到 10×10的二维图像,如下图所示:
420 | 
421 |
422 | #### 13.11.2 1D卷积
423 |
424 | 举个例子,下图左边是一个EKG信号(心电图),当在胸部放一个电极,电极透过胸部测量心脏带来的微弱电流,每个峰值对应一次心跳。如果想用EKG信号,就需要处理1维数据。因为EKG信号由时间序列对应的每个瞬间的电压组成,是一维的,输入的尺寸是14而不是14×14,就需要用一维过滤进行卷积如一个5的过滤器,而不是5×5。最终的输出尺寸是10。
425 | 
426 |
427 | #### 13.11.3 3D卷积
428 |
429 | 
430 | 如上图所示,假设现在输入是具有长度、宽度和高度的三维数据,例如14×14×14,使用5×5×5的过滤器进行卷积,输出将为10×10×10。某种程度上3D数据也可以使用3D confident学习。过滤器实现的功能是用输入的3D数据进行特征识别。
431 |
432 | 医疗检查是3D卷积的一个实例,如下图所示的CT扫描,用X光输出身体的3D模型:
433 |
434 | 
--------------------------------------------------------------------------------
/14 序列模型.md:
--------------------------------------------------------------------------------
1 | # 14序列模型
2 |
3 | ### 14.1 为什么选择序列模型
4 |
5 | #### 14.1.1 序列模型应用领域
6 |
7 | 序列模型广泛应用于语音识别,音乐生成,情感分析,DNA序列分析,机器翻译,视频行为识别,命名实体识别等众多领域。
8 |
9 | - 语音识别:将输入的语音信号直接输出相应的语音文本信息。无论是语音信号还是文本信息均是序列数据。
10 |
11 | - 音乐生成:生成音乐乐谱。只有输出的音乐乐谱是序列数据,输入可以是空或者一个整数。
12 |
13 | - 情感分类:将输入的评论句子转换为相应的等级或评分。输入是一个序列,输出则是一个单独的类别。
14 |
15 | - DNA序列分析:输入的DNA序列,找到匹配的蛋白质序列。
16 |
17 | - 机器翻译:两种不同语言之间的翻译。输入和输出均为序列数据。
18 |
19 | - 视频行为识别:识别输入的视频帧序列中的人物行为。
20 |
21 | - 命名实体识别:从输入的句子中识别实体的名字。
22 |
23 | 
24 |
25 | #### 14.1.2 输入x和输出y的关系
26 |
27 | 上面那些问题可以看成使用标签数据$(x,y)$作为训练集的监督学习,但是输入与输出不一定都是序列,对应关系有非常多的组合,比如一对一,多对多,一对多,多对一,多对多(个数不同)等情况来针对不同的应用。
28 |
29 | ### 14.2 数学符号
30 |
31 | #### 14.2.1 符号含义
32 |
33 | - $x^{