├── version.txt
├── docs
├── assets
│ ├── js
│ │ ├── mathjax-config.js
│ │ └── mathjax-script-type.js
│ └── images
│ │ ├── logo.png
│ │ ├── deformation.png
│ │ ├── logo.svg
│ │ └── deformation.svg
├── api
│ ├── functions
│ │ ├── index.md
│ │ ├── asabqarray.md
│ │ ├── trace.md
│ │ ├── determinant.md
│ │ ├── norm.md
│ │ ├── deviator.md
│ │ ├── transpose.md
│ │ ├── inverse.md
│ │ ├── permute.md
│ │ ├── unimodular.md
│ │ ├── voigtstrain.md
│ │ ├── squareroot.md
│ │ ├── power.md
│ │ ├── rotation.md
│ │ ├── asarray.md
│ │ ├── identity.md
│ │ ├── astensor.md
│ │ ├── asvoigt.md
│ │ └── piola.md
│ ├── assignments.md
│ ├── operators.md
│ ├── tensordatatypes.md
│ └── index.md
├── _includes
│ ├── head_custom.html
│ └── mathjax.html
├── _layouts
│ └── mathjax.html
├── Gemfile
├── _config.yml
├── examples
│ ├── index.md
│ ├── Marc
│ │ ├── hypela2_nh_ttb_simple.f
│ │ ├── hypela2_stvenantkirchhoff.f
│ │ ├── hypela2_nh_ttb.f
│ │ └── hypela2_nonlinear_viscoelasticity.f
│ ├── Abaqus
│ │ ├── umat_nh_ttb_simple.f
│ │ └── umat_nh_ttb.f
│ ├── script_umat.f
│ ├── ex02_neohooke.md
│ └── ex01_stvenantkirchhoff.md
├── installation
│ ├── index.md
│ └── quickstartguide.md
├── Gemfile.lock
└── index.md
├── .github
├── dependabot.yml
└── workflows
│ ├── ci.yml
│ └── pages.yml
├── ttb
├── libtools.f
├── libtrace.f
├── libdev.f
├── libreducedim.f
├── libnorm.f
├── librotation.f
├── libdet.f
├── libdyadic.f
├── libassignten2sym.f
├── libasabqarray.f
├── libtransp.f
├── libidentity.f
├── libstrainstore.f
├── libpower.f
├── libcrossdyadic.f
├── libunimodular.f
├── libasarray.f
├── libtenstore.f
├── libpermute.f
├── libsub.f
├── libadd.f
├── libpiola.f
├── libsymstore.f
├── libassignarray.f
├── libsqrt.f
├── libassignscalar.f
├── libdiv.f
├── libinv.f
├── libddot.f
├── libdot.f
└── ttb_library.f
├── CITATION.cff
├── .gitignore
├── LICENSE
├── CHANGELOG.md
└── README.md
/version.txt:
--------------------------------------------------------------------------------
1 | 2.2.0-dev
2 |
--------------------------------------------------------------------------------
/docs/assets/js/mathjax-config.js:
--------------------------------------------------------------------------------
1 | window.MathJax = {
2 | tex: {
3 | tags: 'all'
4 | }
5 | };
--------------------------------------------------------------------------------
/docs/assets/images/logo.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/adtzlr/ttb/HEAD/docs/assets/images/logo.png
--------------------------------------------------------------------------------
/docs/assets/images/deformation.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/adtzlr/ttb/HEAD/docs/assets/images/deformation.png
--------------------------------------------------------------------------------
/docs/api/functions/index.md:
--------------------------------------------------------------------------------
1 | ---
2 | title: Functions
3 | layout: page
4 | nav_order: 3
5 | parent: API Reference
6 | has_children: true
7 | ---
8 |
9 | # Functions
--------------------------------------------------------------------------------
/.github/dependabot.yml:
--------------------------------------------------------------------------------
1 | version: 2
2 | updates:
3 | - package-ecosystem: bundler
4 | directory: /
5 | schedule:
6 | interval: daily
7 | allow:
8 | - dependency-type: direct
9 |
--------------------------------------------------------------------------------
/docs/_includes/head_custom.html:
--------------------------------------------------------------------------------
1 | {% assign math = page.math | default: layout.math | default: site.math %}
2 |
3 | {% case math %}
4 | {% when "mathjax" %}
5 | {% include mathjax.html %}
6 | {% endcase %}
--------------------------------------------------------------------------------
/docs/_layouts/mathjax.html:
--------------------------------------------------------------------------------
1 | ---
2 | layout: default
3 | math: mathjax
4 | ---
5 |
6 | \(
7 |
9 | \)
10 |
11 |
12 | {{ content }}
--------------------------------------------------------------------------------
/ttb/libtools.f:
--------------------------------------------------------------------------------
1 | function fact_i(n)
2 |
3 | integer, intent(in) :: n
4 | real(kind=8) :: fact_i
5 | integer :: i
6 |
7 | fact_i = 1.d0
8 | do i = 2, n
9 | fact_i = fact_i * i
10 | enddo
11 |
12 | end function fact_i
--------------------------------------------------------------------------------
/docs/Gemfile:
--------------------------------------------------------------------------------
1 | source 'https://rubygems.org'
2 |
3 | gem "jekyll", "~> 4.3.3" # installed by `gem jekyll`
4 | # gem "webrick" # required when using Ruby >= 3 and Jekyll <= 4.2.2
5 |
6 | gem "just-the-docs", "0.8.2" # pinned to the current release
7 | # gem "just-the-docs" # always download the latest release
8 |
--------------------------------------------------------------------------------
/docs/api/functions/asabqarray.md:
--------------------------------------------------------------------------------
1 | ---
2 | title: As Abaqus Array
3 | layout: page
4 | nav_order: 3
5 | parent: Functions
6 | grand_parent: API Reference
7 | ---
8 |
9 | ## As Abaqus Array
10 |
11 | Same function as [`asarray`]({% link api/functions/asarray.md %}) but with `11,22,33,12,13,23` output ordering for Abaqus. For details see [`asarray`]({% link api/functions/asarray.md %}).
--------------------------------------------------------------------------------
/CITATION.cff:
--------------------------------------------------------------------------------
1 | authors:
2 | - family-names: "Dutzler"
3 | given-names: "Andreas"
4 | orcid: "https://orcid.org/0000-0002-9383-9686"
5 | cff-version: 1.2.0
6 | message: "If you use this software, please cite it using these metadata."
7 | title: "Tensor Toolbox for Modern Fortran - High-Level Tensor Manipulation in Fortran"
8 | type: software
9 | doi: 10.5281/zenodo.4077378
10 | url: https://github.com/adtzlr/ttb
11 | license: GPL-3.0
--------------------------------------------------------------------------------
/ttb/libtrace.f:
--------------------------------------------------------------------------------
1 | function tr_2(T)
2 | implicit none
3 |
4 | type(Tensor2) :: T
5 | real(kind=8) :: tr_2
6 |
7 | tr_2 = T%ab(1,1)+T%ab(2,2)+T%ab(3,3)
8 |
9 | end function tr_2
10 |
11 | function tr_2s(T)
12 | implicit none
13 |
14 | type(Tensor2s) :: T
15 | real(kind=8) :: tr_2s
16 |
17 | tr_2s = T%a6(1)+T%a6(2)+T%a6(3)
18 |
19 | end function tr_2s
--------------------------------------------------------------------------------
/.gitignore:
--------------------------------------------------------------------------------
1 | # Not sure what a .gitignore is?
2 | # See: https://git-scm.com/docs/gitignore
3 |
4 | # These are directly copied from Jekyll's first-party docs on `.gitignore` files:
5 | # https://jekyllrb.com/tutorials/using-jekyll-with-bundler/#commit-to-source-control
6 |
7 | # Ignore the default location of the built site, and caches and metadata generated by Jekyll
8 | _site/
9 | .sass-cache/
10 | .jekyll-cache/
11 | .jekyll-metadata
12 |
13 | # Ignore folders generated by Bundler
14 | .bundle/
15 | vendor/
16 |
--------------------------------------------------------------------------------
/docs/api/functions/trace.md:
--------------------------------------------------------------------------------
1 | ---
2 | title: Trace
3 | layout: page
4 | nav_order: 3
5 | parent: Functions
6 | grand_parent: API Reference
7 | ---
8 |
9 | ## Trace
10 |
11 | Sum of diagonal terms of a rank 2 Tensor.
12 |
13 | | Property | Value |
14 | | --- | --- |
15 | | Result | Scalar-valued function |
16 | | Data Types | `Tensor2`, `Tensor2s` |
17 |
18 | ### Example
19 |
20 | ```fortran
21 | type(Tensor2) :: T
22 | real(kind=8) :: trace
23 |
24 | trace = tr(T)
25 | ```
26 |
--------------------------------------------------------------------------------
/docs/api/functions/determinant.md:
--------------------------------------------------------------------------------
1 | ---
2 | title: Determinant
3 | layout: page
4 | nav_order: 3
5 | parent: Functions
6 | grand_parent: API Reference
7 | ---
8 |
9 | ## Determinant
10 |
11 | Determinant of a rank 2 Tensor.
12 |
13 | | Property | Value |
14 | | --- | --- |
15 | | Result | Scalar-valued function |
16 | | Data Types | `Tensor2`, `Tensor2s` |
17 |
18 | ### Example
19 |
20 | ```fortran
21 | type(Tensor2) :: T
22 | real(kind=8) :: det_T
23 |
24 | det_T = det(T)
25 | ```
26 |
--------------------------------------------------------------------------------
/docs/_includes/mathjax.html:
--------------------------------------------------------------------------------
1 |
2 |
5 |
6 |
7 |
10 |
11 |
--------------------------------------------------------------------------------
/docs/api/functions/norm.md:
--------------------------------------------------------------------------------
1 | ---
2 | title: Norm
3 | layout: page
4 | nav_order: 3
5 | parent: Functions
6 | grand_parent: API Reference
7 | ---
8 |
9 | ## Norm
10 |
11 | Euclidean norm of a rank 1 Tensor (Vector). Square root of the sum of the squared components `sqrt( sum( T%a**2 ))`.
12 |
13 | | Property | Value |
14 | | --- | --- |
15 | | Result | Scalar-valued function |
16 | | Data Types | `Tensor1` |
17 |
18 | ### Example
19 |
20 | ```fortran
21 | type(Tensor1) :: v
22 | real(kind=8) :: norm_v
23 |
24 | norm_v = norm(v)
25 | ```
26 |
--------------------------------------------------------------------------------
/ttb/libdev.f:
--------------------------------------------------------------------------------
1 | function dev_2(T)
2 | implicit none
3 |
4 | type(Tensor2), intent(in) :: T
5 | type(Tensor2) :: dev_2,Eye
6 |
7 | Eye = identity2(Eye)
8 | dev_2%ab = T%ab - tr(T)/3.d0*Eye%ab
9 |
10 | end function dev_2
11 |
12 | function dev_2s(T)
13 | implicit none
14 |
15 | type(Tensor2s), intent(in) :: T
16 | type(Tensor2s) :: dev_2s,Eye
17 |
18 | Eye = identity2(Eye)
19 | dev_2s%a6 = T%a6 - tr(T)/3.d0*Eye%a6
20 |
21 | end function dev_2s
22 |
--------------------------------------------------------------------------------
/ttb/libreducedim.f:
--------------------------------------------------------------------------------
1 | function reduce_dim_2s(T,i)
2 | implicit none
3 |
4 | type(Tensor2s), intent(in) :: T
5 | integer, intent(in) :: i
6 | real(kind=8), dimension(i) :: reduce_dim_2s
7 |
8 | reduce_dim_2s = T%a6(1:i)
9 |
10 | end function reduce_dim_2s
11 |
12 | function reduce_dim_4s(T,i,j)
13 | implicit none
14 |
15 | type(Tensor4s), intent(in) :: T
16 | integer, intent(in) :: i,j
17 | real(kind=8), dimension(i,j) :: reduce_dim_4s
18 |
19 | reduce_dim_4s = T%a6b6(1:i,1:j)
20 |
21 | end function reduce_dim_4s
--------------------------------------------------------------------------------
/docs/_config.yml:
--------------------------------------------------------------------------------
1 | title: Tensor Toolbox
2 | description: Tensor Toolbox for Modern Fortran
3 | theme: just-the-docs
4 |
5 | url: https://adtzlr.github.io/ttb
6 | logo: "assets/images/logo.png"
7 |
8 | math: mathjax
9 |
10 | callouts:
11 | warning:
12 | title: Warning
13 | color: red
14 | important:
15 | title: Important
16 | color: blue
17 | note:
18 | title: Note
19 | color: purple
20 | seealso:
21 | title: See Also
22 | color: green
23 |
24 | last_edit_timestamp: true # requires `last_modified_date` in frontmatter
25 | last_edit_time_format: "%Y-%m-%d"
26 |
27 | aux_links:
28 | Tensor Toolbox on GitHub: https://github.com/adtzlr/ttb
--------------------------------------------------------------------------------
/docs/api/functions/deviator.md:
--------------------------------------------------------------------------------
1 | ---
2 | title: Deviator
3 | layout: page
4 | nav_order: 3
5 | parent: Functions
6 | grand_parent: API Reference
7 | ---
8 |
9 | ## Deviator
10 |
11 | Deviator of a rank 2 Tensor.
12 |
13 | $$
14 | \begin{equation}
15 | \text{dev}(\mathbf{C}) = \mathbf{C} - \frac{\text{tr}(\mathbf{C})}{3} \mathbf{1}
16 | \end{equation}
17 | $$
18 |
19 | | Property | Value |
20 | | --- | --- |
21 | | Result | Tensor-valued function |
22 | | Data Types | `Tensor2`, `Tensor2s` |
23 |
24 | ### Example
25 |
26 | ```fortran
27 | type(Tensor2) :: C, devC
28 | ! type(Tensor2s) :: C, devC
29 |
30 | devC = dev(C)
31 | ```
32 |
--------------------------------------------------------------------------------
/docs/examples/index.md:
--------------------------------------------------------------------------------
1 | ---
2 | title: Examples
3 | layout: page
4 | nav_order: 4
5 | has_children: true
6 | ---
7 |
8 | # Examples
9 |
10 | This section contains examples for user subroutines for Marc and Abaqus, including
11 |
12 | * the implementation of the [St.Venant Kirchhoff material]({% link examples/ex01_stvenantkirchhoff.md %}),
13 | * the implementation of the [Neo-Hookean material]({% link examples/ex02_neohooke.md %}),
14 | * a [basic understandig of the tensor toolbox](script_umat.f),
15 | * a [full featured Marc Neo-Hookean material HYPELA2 user subroutine](Marc/hypela2_nh_ttb.f) and
16 | * an [easy-to-extend Abaqus Neo-Hookean material UMAT user subroutine](Abaqus/umat_nh_ttb.f).
--------------------------------------------------------------------------------
/ttb/libnorm.f:
--------------------------------------------------------------------------------
1 | function norm_1(T)
2 | implicit none
3 |
4 | type(Tensor1) :: T
5 | real(kind=8) :: norm_1
6 |
7 | norm_1 = sqrt(sum((T%a)**2))
8 |
9 | end function norm_1
10 |
11 | function norm_2(T)
12 | implicit none
13 |
14 | type(Tensor2) :: T
15 | real(kind=8) :: norm_2
16 |
17 | norm_2 = sqrt(T**T)
18 |
19 | end function norm_2
20 |
21 | function norm_2s(T)
22 | implicit none
23 |
24 | type(Tensor2s) :: T
25 | real(kind=8) :: norm_2s
26 |
27 | norm_2s = sqrt(T**T)
28 |
29 | end function norm_2s
--------------------------------------------------------------------------------
/docs/installation/index.md:
--------------------------------------------------------------------------------
1 | ---
2 | title: Installation
3 | layout: page
4 | nav_order: 2
5 | has_children: true
6 | ---
7 |
8 | # Installation
9 |
10 | This Toolbox is a fortran module which can be used inside modern Fortran compilers. For compatibility reasons to commercial FEM Software packages it is written in _Fixed Format_.
11 |
12 | ## Installation Requirements
13 | This Toolbox is tested on Linux and Windows with both Intel Fortran >2015 and GFortran >6.3. It has been succesfully used with Marc, Abaqus and LS Dyna.
14 |
15 | ## Download
16 | [Download the module](https://github.com/adtzlr/ttb/archive/main.zip), put the `ttb`-Folder in your working directory and you are ready to dive into comfortable tensor manipulations in Fortran.
--------------------------------------------------------------------------------
/docs/api/functions/transpose.md:
--------------------------------------------------------------------------------
1 | ---
2 | title: Transpose
3 | layout: page
4 | nav_order: 3
5 | parent: Functions
6 | grand_parent: API Reference
7 | ---
8 |
9 | ## Transpose
10 |
11 | Transpose of a rank 2 Tensor or major transpose of a rank 4 Tensor.
12 |
13 | | Property | Value |
14 | | --- | --- |
15 | | Result | Tensor-valued function |
16 | | Data Types | `Tensor2`, `Tensor2s`, `Tensor4`, `Tensor4s` |
17 |
18 | ### Example
19 |
20 | ```fortran
21 | type(Tensor2) :: C, C_T
22 | ! type(Tensor2s) :: C, C_T
23 |
24 | type(Tensor4) :: C4, C4_T
25 | ! type(Tensor4s) :: C4, C4_T
26 |
27 | C_T = transpose(C)
28 | C4_T = transpose(C4)
29 | ```
30 |
--------------------------------------------------------------------------------
/docs/assets/js/mathjax-script-type.js:
--------------------------------------------------------------------------------
1 | // Copied from https://docs.mathjax.org/en/latest/upgrading/v2.html#changes-in-the-mathjax-api
2 | MathJax = {
3 | options: {
4 | renderActions: {
5 | findScript: [10, function (doc) {
6 | for (const node of document.querySelectorAll('script[type^="math/tex"]')) {
7 | const display = !!node.type.match(/; *mode=display/);
8 | const math = new doc.options.MathItem(node.textContent, doc.inputJax[0], display);
9 | const text = document.createTextNode('');
10 | node.parentNode.replaceChild(text, node);
11 | math.start = {node: text, delim: '', n: 0};
12 | math.end = {node: text, delim: '', n: 0};
13 | doc.math.push(math);
14 | }
15 | }, '']
16 | }
17 | }
18 | };
--------------------------------------------------------------------------------
/docs/api/functions/inverse.md:
--------------------------------------------------------------------------------
1 | ---
2 | title: Inverse
3 | layout: page
4 | nav_order: 3
5 | parent: Functions
6 | grand_parent: API Reference
7 | ---
8 |
9 | ## Inverse
10 |
11 | Inverse of a positive definite rank 2 Tensor (Determinant > 0).
12 |
13 | Optional Argument
14 | - Determinant
15 |
16 | | Property | Value |
17 | | --- | --- |
18 | | Result | Tensor-valued function |
19 | | Data Types | `Tensor2`, `Tensor2s` |
20 |
21 | $$
22 | \begin{equation}
23 | \boldsymbol{C} \boldsymbol{C}^{-1} = \boldsymbol{1}
24 | \end{equation}
25 | $$
26 |
27 | ### Example
28 |
29 | ```fortran
30 | type(Tensor2) :: C, invC
31 | ! type(Tensor2s) :: C, invC
32 | real(kind=8) :: detC
33 |
34 | invC = inv(C)
35 |
36 | detC = det(C)
37 | invC = inv(C, detC)
38 | ```
39 |
--------------------------------------------------------------------------------
/docs/api/functions/permute.md:
--------------------------------------------------------------------------------
1 | ---
2 | title: Permute
3 | layout: page
4 | nav_order: 3
5 | parent: Functions
6 | grand_parent: API Reference
7 | ---
8 |
9 | ## Permute
10 |
11 | Index permutation of a rank 2 or a rank 4 Tensor. For rank 2 Tensors this is equal to the transpose function.
12 |
13 | | Property | Value |
14 | | --- | --- |
15 | | Result | Tensor-valued function |
16 | | Data Types | `Tensor2`, `Tensor2s`, `Tensor4`, `Tensor4s` |
17 |
18 | ### Example
19 |
20 | ```fortran
21 | type(Tensor2) :: C, C_p
22 | ! type(Tensor2s) :: C, C_p
23 |
24 | type(Tensor4) :: C4, C4_p
25 | ! type(Tensor4s) :: C4, C4_p
26 |
27 | C_p = permute(C, 2,1)
28 | C4_p = permute(C4,1,3,2,4)
29 | ```
30 |
--------------------------------------------------------------------------------
/docs/api/functions/unimodular.md:
--------------------------------------------------------------------------------
1 | ---
2 | title: Unimodular
3 | layout: page
4 | nav_order: 3
5 | parent: Functions
6 | grand_parent: API Reference
7 | ---
8 |
9 | ## Unimodular Part of Tensor
10 |
11 | Unimodular Part of a rank 2 Tensor.
12 |
13 | $$
14 | \begin{align}
15 | \hat{\boldsymbol{C}} &= \det(\boldsymbol{C})^{-1/3} \ \boldsymbol{C} \\
16 | (\det(\hat{\boldsymbol{C}}) &= 1) \nonumber
17 | \end{align}
18 | $$
19 |
20 | | Property | Value |
21 | | --- | --- |
22 | | Result | Tensor-valued function |
23 | | Data Types | `Tensor2`, `Tensor2s` |
24 |
25 | ### Example
26 |
27 | ```fortran
28 | type(Tensor2) :: C, hatC
29 | ! type(Tensor2s) :: C, hatC
30 |
31 | hatC = unimodular(C)
32 |
33 | print *, "proof:"
34 | print *, (hatC - (det(C)**(-1./3.)*C))
35 | ```
36 |
--------------------------------------------------------------------------------
/.github/workflows/ci.yml:
--------------------------------------------------------------------------------
1 | name: CI
2 |
3 | on:
4 | push:
5 | branches: ["main"]
6 | pull_request:
7 |
8 | jobs:
9 | # Build job
10 | build:
11 | runs-on: ubuntu-latest
12 | defaults:
13 | run:
14 | working-directory: docs
15 | steps:
16 | - name: Checkout
17 | uses: actions/checkout@v3
18 | - name: Setup Ruby
19 | uses: ruby/setup-ruby@v1
20 | with:
21 | ruby-version: '3.1' # Not needed with a .ruby-version file
22 | bundler-cache: true # runs 'bundle install' and caches installed gems automatically
23 | cache-version: 0 # Increment this number if you need to re-download cached gems
24 | working-directory: '${{ github.workspace }}/docs'
25 | - name: Build with Jekyll
26 | run: bundle exec jekyll build
27 |
--------------------------------------------------------------------------------
/docs/api/assignments.md:
--------------------------------------------------------------------------------
1 | ---
2 | title: Assignments
3 | layout: page
4 | nav_order: 3
5 | parent: API Reference
6 | ---
7 |
8 | ## Assignments
9 |
10 | If there is a symmetric rank 2 tensor `type(Tensor2s) :: T2` on the left and a rank 2 tensor `type(Tensor2) :: T1` on the right hand side of the assignment `=` operator then the function `T2 = asvoigt(T1)` is automatically called. So it is possible to write the following examples:
11 |
12 | ```fortran
13 | type(Tensor2) :: F
14 | type(Tensor2) :: C ! full 3x3 tensor
15 |
16 | C = transpose(F)*F
17 | ```
18 |
19 | Now it is super simple to switch between full tensor and Voigt matrix storage with only one litte change:
20 |
21 | ```fortran
22 | type(Tensor2) :: F
23 | type(Tensor2s) :: C ! now stored as 6x1 matrix
24 |
25 | C = transpose(F)*F
26 | ```
27 |
28 | The same assignments are also possible for rank 4 Tensor data types.
--------------------------------------------------------------------------------
/ttb/librotation.f:
--------------------------------------------------------------------------------
1 | function rotation_2(phi,i)
2 | implicit none
3 |
4 | real(kind=8), intent(in) :: phi
5 | integer, intent(in) :: i
6 | real(kind=8), dimension(2,2) :: R
7 | type(Tensor2) :: rotation_2
8 |
9 | R = reshape( (/cos(phi), sin(phi),
10 | * -sin(phi), cos(phi)/), (/2,2/) )
11 |
12 | rotation_2 = identity2(rotation_2)
13 |
14 | if (i == 1) then
15 | rotation_2%ab(2:3,2:3) = R
16 | else if (i == 3) then
17 | rotation_2%ab(1:2,1:2) = R
18 | else !i == 2
19 | rotation_2%ab(1,1) = R(1,1)
20 | rotation_2%ab(3,3) = R(2,2)
21 | rotation_2%ab(1,3) = R(2,1)
22 | rotation_2%ab(3,1) = R(1,2)
23 | end if
24 |
25 | end function rotation_2
--------------------------------------------------------------------------------
/ttb/libdet.f:
--------------------------------------------------------------------------------
1 | function det_2(T)
2 | implicit none
3 |
4 | type(Tensor2) :: T
5 | real(kind=8) :: det_2
6 |
7 | det_2 = T%ab(1,1)*(T%ab(2,2)*T%ab(3,3)-T%ab(2,3)*T%ab(3,2))
8 | * + T%ab(1,2)*(T%ab(2,3)*T%ab(3,1)-T%ab(2,1)*T%ab(3,3))
9 | * + T%ab(1,3)*(T%ab(2,1)*T%ab(3,2)-T%ab(2,2)*T%ab(3,1))
10 |
11 | end function det_2
12 |
13 | function det_2s(T)
14 | implicit none
15 |
16 | type(Tensor2s), intent(in) :: T
17 | real(kind=8) :: det_2s
18 |
19 | det_2s = T%a6(1)*T%a6(2)*T%a6(3)
20 | * + T%a6(4)*T%a6(5)*T%a6(6)
21 | * + T%a6(6)*T%a6(4)*T%a6(5)
22 | * - T%a6(6)*T%a6(2)*T%a6(6)
23 | * - T%a6(5)*T%a6(5)*T%a6(1)
24 | * - T%a6(3)*T%a6(4)*T%a6(4)
25 |
26 | end function det_2s
27 |
--------------------------------------------------------------------------------
/docs/installation/quickstartguide.md:
--------------------------------------------------------------------------------
1 | ---
2 | title: Quick Start Guide
3 | layout: page
4 | nav_order: 2
5 | parent: Installation
6 | ---
7 |
8 | ## Quick Start Guide
9 | The most basic example on how to use this module is to [download the module](https://github.com/adtzlr/ttb/archive/main.zip), put the 'ttb'-Folder in your working directory and add two lines of code:
10 |
11 | ```fortran
12 | include 'ttb/ttb_library.f'
13 |
14 | program script101_ttb
15 | use Tensor
16 | implicit none
17 |
18 | ! user code
19 |
20 | end program script101_ttb
21 | ```
22 | The `include 'ttb/ttb_library.f'` statement replaces the line with the content of the ttb-module. The first line in a program or subroutine is now a `use Tensor` statement. That's it - now you're ready to go.
23 |
24 | Continue to the [Example]({% link examples/index.md %}) section. For a list and detailed information of available functions go [here]({% link api/index.md %}).
--------------------------------------------------------------------------------
/docs/api/functions/voigtstrain.md:
--------------------------------------------------------------------------------
1 | ---
2 | title: Voigtstrain
3 | layout: page
4 | nav_order: 3
5 | parent: Functions
6 | grand_parent: API Reference
7 | ---
8 |
9 | ## Voigtstrain
10 |
11 | Import a strain array in voigt storage. As this Module does not use doubled shear items for the symmetric voigt-like storage a strain-like array has to be imported rather than assigned to a Tensor.
12 | - `ndi` number of direct compononets
13 | - `nshear` number of shear components
14 | - `ngens` dimension of strain array
15 |
16 | | Property | Value |
17 | | --- | --- |
18 | | Result | Tensor-valued function |
19 | | Input | `E(ngens)`, ndi, nshear, ngens |
20 | | Output | `Tensor2s` |
21 |
22 | ### Example
23 |
24 | ```fortran
25 |
26 | integer :: ndi,nshear,ngens
27 | real(kind=8), dimension(ngens) :: e
28 |
29 | type(Tensor2s) :: C, Eye
30 |
31 | Eye = identity2(Eye)
32 | C = Eye + 2.*voigtstrain(e,ndi,nshear,ngens)
33 | ```
--------------------------------------------------------------------------------
/docs/api/functions/squareroot.md:
--------------------------------------------------------------------------------
1 | ---
2 | title: Matrix Square Root
3 | layout: page
4 | nav_order: 3
5 | parent: Functions
6 | grand_parent: API Reference
7 | ---
8 |
9 | ## Square Root
10 |
11 | Tensorial (matrix) square root of a positive definite rank 2 Tensor. For algorithmic details see [Franka, L.P. (1988)](https://inis.iaea.org/search/search.aspx?orig_q=RN:20064555). This function can be used to obtain the stretch tensor. For a rank 1 Tensor (vector), the element-wise square root is returned.
12 |
13 | $$
14 | \begin{align}
15 | \mathbf{C} &= \mathbf{U}^2 \\
16 | \mathbf{U} &= \sqrt{\mathbf{C}}
17 | \end{align}
18 | $$
19 |
20 | | Property | Value |
21 | | --- | --- |
22 | | Result | Tensor-valued function |
23 | | Data Types | `Tensor2`, `Tensor2s` |
24 |
25 | ### Example
26 |
27 | ```fortran
28 | type(Tensor2) :: F, R
29 |
30 | type(Tensor2) :: U, C
31 | ! type(Tensor2s) :: U, C
32 |
33 | C = transpose(F)*F
34 | U = sqrt(C)
35 |
36 | ! polar decomposition F = R*U
37 | R = F*inv(U)
38 | ```
39 |
40 |
--------------------------------------------------------------------------------
/ttb/libdyadic.f:
--------------------------------------------------------------------------------
1 | function dyadic_11(T1, T2)
2 | implicit none
3 |
4 | type(Tensor1), intent(in) :: T1, T2
5 | type(Tensor2) :: dyadic_11
6 | integer i, j
7 |
8 | forall(i=1:3,j=1:3) dyadic_11%ab(i,j) = T1%a(i) * T2%a(j)
9 |
10 | end function dyadic_11
11 |
12 | function dyadic_22(T1, T2)
13 | implicit none
14 |
15 | type(Tensor2), intent(in) :: T1, T2
16 | type(Tensor4) :: dyadic_22
17 | integer i, j, k, l
18 |
19 | forall(i=1:3,j=1:3,k=1:3,l=1:3) dyadic_22%abcd(i,j,k,l)
20 | * = T1%ab(i,j) * T2%ab(k,l)
21 |
22 | end function dyadic_22
23 |
24 | function dyadic_2s2s(T1, T2)
25 | implicit none
26 |
27 | type(Tensor2s), intent(in) :: T1, T2
28 | type(Tensor4s) :: dyadic_2s2s
29 | integer i, j
30 |
31 | forall(i=1:6,j=1:6) dyadic_2s2s%a6b6(i,j) = T1%a6(i) * T2%a6(j)
32 |
33 | end function dyadic_2s2s
--------------------------------------------------------------------------------
/ttb/libassignten2sym.f:
--------------------------------------------------------------------------------
1 | subroutine assignten2sym_2(T,A)
2 | implicit none
3 |
4 | type(Tensor2s), intent(inout) :: T
5 | type(Tensor2), intent(in) :: A
6 |
7 | T = voigt(A)
8 |
9 | end subroutine assignten2sym_2
10 |
11 | subroutine assignten2sym_4(T,A)
12 | implicit none
13 |
14 | type(Tensor4s), intent(inout) :: T
15 | type(Tensor4), intent(in) :: A
16 |
17 | T = voigt(A)
18 |
19 | end subroutine assignten2sym_4
20 |
21 | subroutine assignsym2ten_2(T,A)
22 | implicit none
23 |
24 | type(Tensor2), intent(inout) :: T
25 | type(Tensor2s), intent(in) :: A
26 |
27 | T = astensor(A)
28 |
29 | end subroutine assignsym2ten_2
30 |
31 | subroutine assignsym2ten_4(T,A)
32 | implicit none
33 |
34 | type(Tensor4), intent(inout) :: T
35 | type(Tensor4s), intent(in) :: A
36 |
37 | T = astensor(A)
38 |
39 | end subroutine assignsym2ten_4
--------------------------------------------------------------------------------
/LICENSE:
--------------------------------------------------------------------------------
1 | MIT License
2 |
3 | Copyright (c) 2024 Andreas Dutzler
4 |
5 | Permission is hereby granted, free of charge, to any person obtaining a copy
6 | of this software and associated documentation files (the "Software"), to deal
7 | in the Software without restriction, including without limitation the rights
8 | to use, copy, modify, merge, publish, distribute, sublicense, and/or sell
9 | copies of the Software, and to permit persons to whom the Software is
10 | furnished to do so, subject to the following conditions:
11 |
12 | The above copyright notice and this permission notice shall be included in all
13 | copies or substantial portions of the Software.
14 |
15 | THE SOFTWARE IS PROVIDED "AS IS", WITHOUT WARRANTY OF ANY KIND, EXPRESS OR
16 | IMPLIED, INCLUDING BUT NOT LIMITED TO THE WARRANTIES OF MERCHANTABILITY,
17 | FITNESS FOR A PARTICULAR PURPOSE AND NONINFRINGEMENT. IN NO EVENT SHALL THE
18 | AUTHORS OR COPYRIGHT HOLDERS BE LIABLE FOR ANY CLAIM, DAMAGES OR OTHER
19 | LIABILITY, WHETHER IN AN ACTION OF CONTRACT, TORT OR OTHERWISE, ARISING FROM,
20 | OUT OF OR IN CONNECTION WITH THE SOFTWARE OR THE USE OR OTHER DEALINGS IN THE
21 | SOFTWARE.
22 |
--------------------------------------------------------------------------------
/docs/api/operators.md:
--------------------------------------------------------------------------------
1 | ---
2 | title: Operators
3 | layout: page
4 | nav_order: 3
5 | parent: API Reference
6 | ---
7 |
8 | ## Operators Overview
9 |
10 | This module uses derived data types where the default operators are overloaded with custom functions. Currently there are the following operators available:
11 |
12 | - Addition `A+B`
13 | - Subtraction `A-B`
14 | - Divison by scalar `A/5.`
15 | - Multiplication by scalar `A*5.`
16 | - Dot-Product (single contraction) `A*B`
17 | - Double-Dot-Product (double contraction) `A**B`
18 |
19 | {: .seealso }
20 | > There are also functions available for the dyadic product `A.dya.B` and the symmetric crossed-dyadic product `A.cdya.B` to perform `C(i,j,k,l) = (A(i,k)*B(j,l) + A(i,l)*B(j,k) + B(i,k)*A(j,l) + B(i,l)*A(j,k)) / 4.`.
21 |
22 | {: .warning }
23 | > Be sure to use brackets around functions which should be evaluated first because the double contraction has the highest priority as it is replaced by the conventional power function. This leads to wrong results in combination with crossed-dyadic products as they must be evaluated first. Always use brackets like `A**(B.cdya.B)`. Unfortunately this is a limitation of Fortran.
24 |
--------------------------------------------------------------------------------
/docs/api/functions/power.md:
--------------------------------------------------------------------------------
1 | ---
2 | title: Power
3 | layout: page
4 | nav_order: 3
5 | parent: Functions
6 | grand_parent: API Reference
7 | ---
8 |
9 | ## Power
10 |
11 | Multiply a Tensor i-times by itself. Note that for a given Tensor C:
12 | - `i < 0` calculate the i-th power of inv(C)
13 | - `i == 0` calculate the identity tensor
14 | - `i > 0` calculate the i-th power of C
15 |
16 | | Property | Value |
17 | | --- | --- |
18 | | Result | Tensor-valued function |
19 | | Data Types | `Tensor2`, `Tensor2s` |
20 |
21 | ### Example
22 |
23 | ```fortran
24 |
25 | type(Tensor2) :: C, C3, invC, Eye
26 | ! type(Tensor2s) :: C, C3, invC, Eye
27 |
28 | ! i-th power of C
29 | C3 = C**3
30 |
31 | ! i-th power of inverse of C
32 | invC3 = C**(-3)
33 |
34 | ! identity tensor
35 | Eye = C**0
36 | ```
37 |
38 | {: .warning }
39 | > Don't use `C**(1/2)` because in Fortran an integer division, e.g. `1/2`, gives an integer `0` and this function will return the identity tensor instead of the square root.
40 |
41 | {: .important }
42 | > For the evaluation of the tensorial square root, use [sqrt]({% link api/functions/squareroot.md %}) instead.
--------------------------------------------------------------------------------
/ttb/libasabqarray.f:
--------------------------------------------------------------------------------
1 | ! ------AS ABAQUS ARRAY SECTION-------------------
2 | function asabqarray_2s(T,i,j)
3 | implicit none
4 |
5 | type(Tensor2s), intent(in) :: T
6 | integer, intent(in) :: i
7 | integer, intent(in), optional :: j
8 | real(kind=8), dimension(i) :: asabqarray_2s
9 | integer :: i1
10 |
11 | asabqarray_2s(1:min(i,4)) = T%a6(1:min(i,4))
12 |
13 | if (i.ge.5) then
14 | asabqarray_2s(5) = T%a6(6)
15 | end if
16 |
17 | if (i.ge.6) then
18 | asabqarray_2s(6) = T%a6(5)
19 | endif
20 |
21 | end function asabqarray_2s
22 |
23 | function asabqarray_4s(T,i,j)
24 | implicit none
25 |
26 | type(Tensor4s), intent(in) :: T
27 | integer, intent(in) :: i,j
28 | real(kind=8), dimension(i,j) :: asabqarray_4s
29 | integer, dimension(6) :: imap
30 | integer :: i1,j1
31 |
32 | imap = (/1,2,3,4,6,5/)
33 |
34 | forall (i1=1:i,j1=1:j) asabqarray_4s(i1,j1) =
35 | * T%a6b6(imap(i1),imap(j1))
36 |
37 | end function asabqarray_4s
--------------------------------------------------------------------------------
/ttb/libtransp.f:
--------------------------------------------------------------------------------
1 | function transp2(T)
2 | implicit none
3 |
4 | type(Tensor2), intent(in) :: T
5 | type(Tensor2) :: transp2
6 |
7 | transp2%ab = transpose(T%ab)
8 |
9 | end function transp2
10 |
11 | function transp2s(T)
12 | implicit none
13 |
14 | type(Tensor2s), intent(in) :: T
15 | type(Tensor2s) :: transp2s
16 |
17 | transp2s%a6 = T%a6
18 |
19 | end function transp2s
20 |
21 | function transp4(T)
22 | implicit none
23 |
24 | type(Tensor4), intent(in) :: T
25 | type(Tensor4) :: transp4
26 | integer :: i,j,k,l
27 |
28 | transp4%abcd = 0.d0
29 | forall (i=1:3,j=1:3,k=1:3,l=1:3) transp4%abcd(i,j,k,l)
30 | * = T%abcd(k,l,i,j)
31 |
32 | end function transp4
33 |
34 | function transp4s(T)
35 | implicit none
36 |
37 | type(Tensor4s), intent(in) :: T
38 | type(Tensor4s) :: transp4s
39 |
40 | transp4s%a6b6 = transpose(T%a6b6)
41 |
42 | end function transp4s
43 |
--------------------------------------------------------------------------------
/ttb/libidentity.f:
--------------------------------------------------------------------------------
1 | function ident_2(T)
2 | implicit none
3 |
4 | type(Tensor2), intent(in) :: T
5 | type(Tensor2) :: ident_2
6 | integer :: i
7 |
8 | ident_2%ab = 0.d0
9 | do i = 1,3
10 | ident_2%ab(i,i) = 1.d0
11 | enddo
12 |
13 | end function ident_2
14 |
15 | function ident_2s(T)
16 | implicit none
17 |
18 | type(Tensor2s), intent(in) :: T
19 | type(Tensor2s) :: ident_2s
20 | integer :: i
21 |
22 | ident_2s%a6 = 0.d0
23 | do i = 1,3
24 | ident_2s%a6(i) = 1.d0
25 | enddo
26 |
27 | end function ident_2s
28 |
29 | function ident_4(T)
30 | implicit none
31 |
32 | type(Tensor2), intent(in) :: T
33 | type(Tensor4) :: ident_4
34 |
35 | ident_4 = T.cdya.T
36 |
37 | end function ident_4
38 |
39 | function ident_4s(T)
40 | implicit none
41 |
42 | type(Tensor2s), intent(in) :: T
43 | type(Tensor4s) :: ident_4s
44 |
45 | ident_4s = T.cdya.T
46 |
47 | end function ident_4s
48 |
--------------------------------------------------------------------------------
/ttb/libstrainstore.f:
--------------------------------------------------------------------------------
1 | C function str2ten_2(E,ndi,nshear,ngens)
2 | C implicit none
3 | C
4 | C integer :: ndi,nshear,ngens
5 | C real(kind=8), dimension(ngens) :: E
6 | C type(Tensor2) :: str2ten_2
7 | C integer, dimension(3) :: ii, jj
8 | C integer :: i
9 | C
10 | C str2ten_2 = Identity2(str2ten_2)
11 | C
12 | C do i=1,ndi
13 | C str2ten_2%ab(i,i) = E(i)
14 | C enddo
15 | C
16 | C ii = (/1,2,3/)
17 | C jj = (/2,3,1/)
18 | C
19 | C do i=1,nshear
20 | C str2ten_2%ab(ii(i),jj(i)) = E(i+ndi)/2.
21 | C end do
22 |
23 | C end function str2ten_2
24 |
25 | function str2ten_2s(E,ndi,nshear,ngens)
26 | implicit none
27 |
28 | integer :: ndi, nshear, ngens
29 | real(kind=8), dimension(ngens) :: E
30 | type(Tensor2s) :: str2ten_2s
31 | integer :: i
32 |
33 | str2ten_2s = Identity2(str2ten_2s)
34 |
35 | do i=1,ndi
36 | str2ten_2s%a6(i) = E(i)
37 | enddo
38 |
39 | do i=1,nshear
40 | str2ten_2s%a6(i+3) = E(i+ndi)/2.
41 | end do
42 |
43 | end function str2ten_2s
--------------------------------------------------------------------------------
/docs/api/functions/rotation.md:
--------------------------------------------------------------------------------
1 | ---
2 | title: Rotation Matrix
3 | layout: page
4 | nav_order: 3
5 | parent: Functions
6 | grand_parent: API Reference
7 | ---
8 |
9 | ## Rotation Matrix
10 |
11 | Rotation Matrix with inputs angle in rad and rotation axis.
12 |
13 | | Property | Value |
14 | | --- | --- |
15 | | Result | Tensor-valued function |
16 | | Data Types | `Tensor2` |
17 |
18 | There are 3 possible cases:
19 |
20 | ### `rotation_matrix(phi,3)`
21 | $$
22 | \begin{equation}
23 | \mathbf{R} = \begin{bmatrix} \cos \varphi & -\sin \varphi & 0 \\ \sin \varphi & \cos \varphi & 0 \\ 0 & 0 & 1 \end{bmatrix}
24 | \end{equation}
25 | $$
26 |
27 | ### `rotation_matrix(phi,2)`
28 | $$
29 | \begin{equation}
30 | \mathbf{R} = \begin{bmatrix} \cos \varphi & 0 & \sin \varphi\\ 0 & 1 & 0 \\ -\sin \varphi & 0 & \cos \varphi\\ \end{bmatrix}
31 | \end{equation}
32 | $$
33 |
34 | ### `rotation_matrix(phi,1)`
35 | $$
36 | \begin{equation}
37 | \mathbf{R} = \begin{bmatrix} 1 & 0 & 0 \\ 0 &\cos \varphi & -\sin \varphi\\ 0 & \sin \varphi & \cos \varphi\\ \end{bmatrix}
38 | \end{equation}
39 | $$
40 |
41 | ### Example
42 |
43 | ```fortran
44 | real(kind=8) :: phi
45 | type(Tensor2) :: R
46 |
47 | R = rotation_matrix(phi,1)
48 |
49 | ```
50 |
--------------------------------------------------------------------------------
/ttb/libpower.f:
--------------------------------------------------------------------------------
1 | function pow_2(T,i)
2 | implicit none
3 |
4 | type(Tensor2), intent(in) :: T
5 | integer, intent(in) :: i
6 |
7 | type(Tensor2) :: pow_2, invT
8 | integer :: j
9 |
10 | if (i > 0) then
11 | pow_2 = T
12 | do j=1,i-1
13 | pow_2 = pow_2*T
14 | end do
15 | else if (i == 0) then
16 | pow_2 = identity2(T)
17 | else
18 | invT = inv(T)
19 | pow_2 = invT
20 | do j=1,abs(i)-1
21 | pow_2 = pow_2*invT
22 | end do
23 | end if
24 |
25 | end function pow_2
26 |
27 | function pow_2s(T,i)
28 | implicit none
29 |
30 | type(Tensor2s), intent(in) :: T
31 | integer, intent(in) :: i
32 |
33 | type(Tensor2s) :: pow_2s, invT
34 | integer :: j
35 |
36 | if (i > 0) then
37 | pow_2s = T
38 | do j=1,i-1
39 | pow_2s = pow_2s*T
40 | end do
41 | else if (i == 0) then
42 | pow_2s = identity2(T)
43 | else
44 | invT = inv(T)
45 | pow_2s = invT
46 | do j=1,abs(i)-1
47 | pow_2s = pow_2s*invT
48 | end do
49 | end if
50 |
51 | end function pow_2s
52 |
53 |
--------------------------------------------------------------------------------
/docs/api/tensordatatypes.md:
--------------------------------------------------------------------------------
1 | ---
2 | title: Tensor Types
3 | layout: page
4 | nav_order: 3
5 | parent: API Reference
6 | ---
7 |
8 | # Tensor Data Types
9 |
10 | There are several Tensor Data Types available inside this module:
11 | - `Tensor 1` rank 1 Tensor (Vector)
12 | - `Tensor 2` rank 2 Tensor
13 | - `Tensor 4` rank 4 Tensor
14 | - `Tensor 2s` rank 2 Tensor (symmetric)
15 | - `Tensor 4s` rank 4 Tensor (symmetric)
16 |
17 | ## Data Type `Tensor1`
18 | This is a rank 1 tensor which represents a vector in 3D cartesian coordinates with length 3.
19 | Access to i-th component: `T%a(i)`
20 |
21 | ## Data Type `Tensor2`
22 | This is a rank 2 tensor in 3D cartesian coordinates with dimension 3x3.
23 | Access to i,j-component: `T%ab(i,j)`
24 |
25 | ## Data Type `Tensor4`
26 | This is a rank 4 tensor in 3D cartesian coordinates with dimension 3x3x3x3.
27 | Access to i,j,k,l-component: `T%abcd(i,j,k,l)`
28 |
29 | ## Data Type `Tensor2s`
30 | This is a symmetric rank 2 tensor in 3D cartesian coordinates which is stored as a vector with length 6. The storage order is `11,22,33,12,23,31`.
31 | Access to i-th component: `T%a6(i)`
32 |
33 | ## Data Type `Tensor4s`
34 | This is a symmetric rank 4 tensor in 3D cartesian coordinates which is stored as a matrix with dimension 6x6. The storage order for both axis components is `11,22,33,12,23,31`.
35 | Access to i,j-component: `T%a6b6(i,j)`
36 |
--------------------------------------------------------------------------------
/docs/api/functions/asarray.md:
--------------------------------------------------------------------------------
1 | ---
2 | title: As Array
3 | layout: page
4 | nav_order: 3
5 | parent: Functions
6 | grand_parent: API Reference
7 | ---
8 |
9 | ## As Array
10 |
11 | Convert Tensor to Array. This is useful to export results back to the code which is not using the tensor toolbox.
12 |
13 | {: .note }
14 | > This function is very useful because Fortran does not allow access to Tensor components of a function result `s = (dev(S*C)*inv(C))%ab`. Instead this function can be used.
15 |
16 | {: .warning }
17 | > If you use Abaqus please use [`asabqarray`]({% link api/functions/asabqarray.md %}) to export Tensor components.
18 |
19 | `asarray` is called with one (rank 2) or two (rank 4) integers to slice dimensions. This is useful if an axisymmetric analysis is evaluated (3 direct and 1 shear components = 4x4 tangent matrix instead of full 6x6 storage).
20 |
21 | | Property | Value |
22 | | --- | --- |
23 | | Result | array |
24 | | Data Types | `Tensor2`, `Tensor2s`, `Tensor4`, `Tensor4s` |
25 |
26 | ### Example
27 |
28 | ```fortran
29 | type(Tensor2) :: S1
30 | type(Tensor4) :: C4
31 | ! type(Tensor2s) :: S1
32 | ! type(Tensor4s) :: C4
33 |
34 | integer :: ndim
35 |
36 | real(kind=8), dimension(ndim) :: s
37 | real(kind=8), dimension(ndim,ndim) :: d
38 |
39 | s(1:ndim) = asarray( voigt(S1), ndim )
40 | d(1:ndim, 1:ndim) = asarray( voigt(C4), ndim, ndim )
41 | ```
42 |
--------------------------------------------------------------------------------
/ttb/libcrossdyadic.f:
--------------------------------------------------------------------------------
1 | function crossdyadic_22(T1, T2)
2 | implicit none
3 |
4 | type(Tensor2), intent(in) :: T1, T2
5 | type(Tensor4) :: crossdyadic_22
6 | integer i, j, k, l
7 |
8 | forall(i=1:3,j=1:3,k=1:3,l=1:3) crossdyadic_22%abcd(i,j,k,l)
9 | * = (T1%ab(i,k) * T2%ab(j,l) + T1%ab(i,l) * T2%ab(j,k) +
10 | * T2%ab(i,k) * T1%ab(j,l) + T2%ab(i,l) * T1%ab(j,k))/4.d0
11 |
12 | end function crossdyadic_22
13 |
14 | function crossdyadic_2s2s(T1, T2)
15 | implicit none
16 |
17 | type(Tensor2s), intent(in) :: T1, T2
18 | type(Tensor4s) :: crossdyadic_2s2s
19 | integer :: i,j,k,l
20 | integer, dimension(3,3) :: i6
21 |
22 | i6 = reshape( (/1,4,6, 4,2,5, 6,5,3/), (/3, 3/) )
23 |
24 | crossdyadic_2s2s%a6b6 = 0.d0
25 |
26 | do i=1,3
27 | do j=1,3
28 | if (i.le.j) then
29 | do k=1,3
30 | do l=1,3
31 | if (k.le.l) then
32 | crossdyadic_2s2s%a6b6(i6(i,j),i6(k,l))
33 | * = ( T1%a6(i6(i,k)) * T2%a6(i6(j,l))
34 | * +T1%a6(i6(i,l)) * T2%a6(i6(j,k))
35 | * +T2%a6(i6(i,k)) * T1%a6(i6(j,l))
36 | * +T2%a6(i6(i,l)) * T1%a6(i6(j,k)) )/4.d0
37 | end if
38 | end do
39 | end do
40 | end if
41 | end do
42 | end do
43 |
44 | end function crossdyadic_2s2s
45 |
--------------------------------------------------------------------------------
/ttb/libunimodular.f:
--------------------------------------------------------------------------------
1 | function unimod_2(T)
2 | implicit none
3 |
4 | type(Tensor2), intent(in) :: T
5 | type(Tensor2) :: unimod_2, Eye
6 | real(kind=8) :: detT
7 |
8 | detT = det(T)
9 | Eye = identity2(Eye)
10 |
11 | unimod_2 = detT**(-1./3.) * T
12 |
13 | end function unimod_2
14 |
15 | function unimod_2s(T)
16 | implicit none
17 |
18 | type(Tensor2s), intent(in) :: T
19 | type(Tensor2s) :: unimod_2s, Eye
20 | real(kind=8) :: detT
21 |
22 | detT = det(T)
23 | Eye = identity2(Eye)
24 |
25 | unimod_2s = detT**(-1./3.) * T
26 |
27 | end function unimod_2s
28 |
29 | function unimod_2d(T,detT)
30 | implicit none
31 |
32 | type(Tensor2), intent(in) :: T
33 | type(Tensor2) :: unimod_2d, Eye
34 | real(kind=8), intent(in) :: detT
35 |
36 | Eye = identity2(Eye)
37 |
38 | unimod_2d = detT**(-1./3.) * T
39 |
40 | end function unimod_2d
41 |
42 | function unimod_2sd(T,detT)
43 | implicit none
44 |
45 | type(Tensor2s), intent(in) :: T
46 | type(Tensor2s) :: unimod_2sd, Eye
47 | real(kind=8), intent(in) :: detT
48 |
49 | Eye = identity2(Eye)
50 |
51 | unimod_2sd = detT**(-1./3.) * T
52 |
53 | end function unimod_2sd
--------------------------------------------------------------------------------
/docs/api/functions/identity.md:
--------------------------------------------------------------------------------
1 | ---
2 | title: Identity
3 | layout: page
4 | nav_order: 3
5 | parent: Functions
6 | grand_parent: API Reference
7 | ---
8 |
9 | ## Identity
10 |
11 | Calculate the identity tensor. Two functions for generating identities are implemented:
12 |
13 | - `Eye = identity2(C)` calculate Eye with the same tensor data type as C. The components of C are ignored.
14 | - `I4 = identity4(Eye)` calculate the symmetric fourth order identity tensor with the property `C = I4 : C`
15 |
16 | For the fourth order variant the function argument is not only used for defining the data type. For example the fourth order "inverse-identity" tensor may be obtained with `I4invC = identity4(inv(C))` with the property `invC = I4invC : C`
17 |
18 |
19 |
20 | | Property | Value |
21 | | --- | --- |
22 | | Result | Tensor-valued function |
23 | | Data Types | `Tensor2`, `Tensor2s` |
24 |
25 | ### Example
26 |
27 | ```fortran
28 |
29 | type(Tensor2) :: C, invC, Eye
30 | ! type(Tensor2s) :: C, invC, Eye
31 |
32 | type(Tensor4) :: I4, I4invC
33 | ! type(Tensor4s) :: I4, I4invC
34 |
35 | ! the argument is only used for setting the data type
36 | Eye = identity2(Eye)
37 | Eye = identity2(C)
38 |
39 | I4 = identity4(Eye)
40 | C = I4**C
41 | I4invC = identity4(inv(C))
42 | invC = I4invC**C
43 | ```
44 |
45 | **Note**: the operator `**` for two tensor data types represents a double contraction. See double contraction for details. `Eye.cdya.Eye` is equivalent to `identity4(Eye)`. See crossed-dyadic product for details.
46 |
47 |
--------------------------------------------------------------------------------
/docs/api/functions/astensor.md:
--------------------------------------------------------------------------------
1 | ---
2 | title: As Tensor
3 | layout: page
4 | nav_order: 3
5 | parent: Functions
6 | grand_parent: API Reference
7 | ---
8 |
9 | ## As Tensor
10 |
11 | Converts a `Tensor2s` or `Tensor4s` data type to a full tensor storage `Tensor2` or `Tensor4`.
12 |
13 | $$
14 | \begin{align}
15 | \boldsymbol{C} = \begin{bmatrix}
16 | C_{11} \\ C_{22} \\ C_{33} \\ C_{12} \\ C_{23} \\ C_{13}
17 | \end{bmatrix} \longrightarrow
18 | \begin{bmatrix}
19 | C_{11} & C_{12} & C_{13} \\
20 | C_{12} & C_{22} & C_{23} \\
21 | C_{13} & C_{23} & C_{33}
22 | \end{bmatrix}
23 | \end{align}
24 | $$
25 |
26 | $$
27 | \begin{align}
28 | \mathbb{A} &= \begin{bmatrix}
29 | A_{1111} & A_{1122} & A_{1133} & A_{1112} & A_{1123} & A_{1113} \\
30 | A_{2211} & A_{2222} & A_{2233} & A_{2212} & A_{2223} & A_{2213} \\
31 | \dots & \dots & \dots & \dots & \dots & \dots \\
32 | A_{1311} & A_{1322} & A_{1333} & A_{1312} & A_{1323} & A_{1313}
33 | \end{bmatrix} \nonumber \\
34 | &\longrightarrow \begin{bmatrix}
35 | A_{1111} & A_{1112} & A_{1113} &
36 | A_{1121} & A_{1122} & A_{1123} &
37 | A_{1131} & A_{1132} & A_{1133} \\
38 | A_{1211} & A_{1212} & A_{1213} &
39 | A_{1221} & A_{1222} & A_{1223} &
40 | A_{1231} & A_{1232} & A_{1233} \\
41 | \dots & \dots & \dots & \dots & \dots & \dots & \dots & \dots & \dots \\
42 | A_{3111} & A_{3112} & A_{3113} &
43 | A_{3121} & A_{3122} & A_{3123} &
44 | A_{3131} & A_{3132} & A_{3133}
45 | \end{bmatrix}
46 | \end{align}
47 | $$
48 |
49 | Alias:
50 | - `tensorstore(T)`
51 |
52 | ### Example
53 |
54 | ```fortran
55 | type(Tensor2s) :: T
56 | type(Tensor2) :: U
57 |
58 | U = astensor(T)
59 | ```
60 |
--------------------------------------------------------------------------------
/docs/api/functions/asvoigt.md:
--------------------------------------------------------------------------------
1 | ---
2 | title: As Voigt
3 | layout: page
4 | nav_order: 3
5 | parent: Functions
6 | grand_parent: API Reference
7 | ---
8 |
9 | ## As Voigt
10 |
11 | Converts a `Tensor2` or `Tensor4` data type to a reduced Voigt-storage `Tensor2s` or `Tensor4s`.
12 |
13 | Aliases:
14 | - `voigt(T)`
15 | - `symstore(T)`
16 |
17 | $$
18 | \begin{align}
19 | \boldsymbol{C} = \begin{bmatrix}
20 | C_{11} & C_{12} & C_{13} \\
21 | C_{12} & C_{22} & C_{23} \\
22 | C_{13} & C_{23} & C_{33}
23 | \end{bmatrix} \longrightarrow
24 | \begin{bmatrix}
25 | C_{11} \\ C_{22} \\ C_{33} \\ C_{12} \\ C_{23} \\ C_{13}
26 | \end{bmatrix}
27 | \end{align}
28 | $$
29 |
30 | $$
31 | \begin{align}
32 | \mathbb{A} &= \begin{bmatrix}
33 | A_{1111} & A_{1112} & A_{1113} &
34 | A_{1121} & A_{1122} & A_{1123} &
35 | A_{1131} & A_{1132} & A_{1133} \\
36 | A_{1211} & A_{1212} & A_{1213} &
37 | A_{1221} & A_{1222} & A_{1223} &
38 | A_{1231} & A_{1232} & A_{1233} \\
39 | \dots & \dots & \dots & \dots & \dots & \dots & \dots & \dots & \dots \\
40 | A_{3111} & A_{3112} & A_{3113} &
41 | A_{3121} & A_{3122} & A_{3123} &
42 | A_{3131} & A_{3132} & A_{3133}
43 | \end{bmatrix} \nonumber \\
44 | &\longrightarrow
45 | \begin{bmatrix}
46 | A_{1111} & A_{1122} & A_{1133} & A_{1112} & A_{1123} & A_{1113} \\
47 | A_{2211} & A_{2222} & A_{2233} & A_{2212} & A_{2223} & A_{2213} \\
48 | \dots & \dots & \dots & \dots & \dots & \dots \\
49 | A_{1311} & A_{1322} & A_{1333} & A_{1312} & A_{1323} & A_{1313}
50 | \end{bmatrix}
51 | \end{align}
52 | $$
53 |
54 | ### Example
55 |
56 | ```fortran
57 | type(Tensor2) :: T
58 | type(Tensor2s) :: U
59 |
60 | U = asvoigt(T)
61 | ```
62 |
--------------------------------------------------------------------------------
/ttb/libasarray.f:
--------------------------------------------------------------------------------
1 | ! ------AS ARRAY SECTION------------------------------------
2 | function asarray_1(T,i,j,k,l)
3 | implicit none
4 |
5 | type(Tensor1), intent(in) :: T
6 | integer, intent(in) :: i
7 | integer, intent(in), optional :: j,k,l
8 | real(kind=8), dimension(i) :: asarray_1
9 |
10 | asarray_1 = T%a(1:i)
11 |
12 | end function asarray_1
13 |
14 | function asarray_2(T,i,j,k,l)
15 | implicit none
16 |
17 | type(Tensor2), intent(in) :: T
18 | integer, intent(in) :: i,j
19 | integer, intent(in), optional :: k,l
20 | real(kind=8), dimension(i,j) :: asarray_2
21 |
22 | asarray_2 = T%ab(1:i,1:j)
23 |
24 | end function asarray_2
25 |
26 | function asarray_2s(T,i,j,k,l)
27 | implicit none
28 |
29 | type(Tensor2s), intent(in) :: T
30 | integer, intent(in) :: i
31 | integer, intent(in), optional :: j,k,l
32 | real(kind=8), dimension(i) :: asarray_2s
33 |
34 | asarray_2s = T%a6(1:i)
35 |
36 | end function asarray_2s
37 |
38 | function asarray_4(T,i,j,k,l)
39 | implicit none
40 |
41 | type(Tensor4), intent(in) :: T
42 | integer, intent(in) :: i,j,k,l
43 | real(kind=8), dimension(i,j,k,l) :: asarray_4
44 |
45 | asarray_4 = T%abcd(1:i,1:j,1:k,1:l)
46 |
47 | end function asarray_4
48 |
49 | function asarray_4s(T,i,j,k,l)
50 | implicit none
51 |
52 | type(Tensor4s), intent(in) :: T
53 | integer, intent(in) :: i,j
54 | integer, intent(in), optional :: k,l
55 | real(kind=8), dimension(i,j) :: asarray_4s
56 |
57 | asarray_4s = T%a6b6(1:i,1:j)
58 |
59 | end function asarray_4s
--------------------------------------------------------------------------------
/docs/api/functions/piola.md:
--------------------------------------------------------------------------------
1 | ---
2 | title: Piola Transformation
3 | layout: page
4 | nav_order: 3
5 | parent: Functions
6 | grand_parent: API Reference
7 | ---
8 |
9 | ## Piola Transformation
10 |
11 | Perform a Piola transformation. It is assumed that the tensor's components are all either co- or contravariant as this toolbox has no information about co- and contravariant tensor components. All indices are transformed with the same mixed-variant argument tensor. This means it is not possible to perform a push forward of a mixed variant fourth order tensor. To perform a push forward of the contra-variant indices of the tangent matrix from material components in the reference configuration to spatial components in the current configuration write `piola(F,C4)`. When using symmetric variants of tensor data types (Voigt-notation) a faster contraction with less calculations due to symmetric properties is performed.
12 |
13 | - `piola(F,S)` where `S` is a stress tensor is equal to `F*S*transpose(F)`
14 | - `piola(F,C4)` where `C4` is a fourth order elasticity tensor means `c4(i,j,k,l) = F(i,I) F(j,J) F(k,K) F(l,L) C4(I,J,K,L)`
15 |
16 | | Property | Value |
17 | | --- | --- |
18 | | Result | Tensor-valued function |
19 | | Data Types | `Tensor2`, `Tensor2s`, `Tensor4`, `Tensor4s` |
20 |
21 | ### Example
22 |
23 | ```fortran
24 |
25 | real(kind=8) :: J
26 |
27 | type(Tensor2) :: F, S
28 | ! type(Tensor2s) :: S
29 |
30 | type(Tensor4) :: C4
31 | ! type(Tensor4s) :: C4
32 |
33 | J = det(F)
34 |
35 | ! push forward of (contra-variant) PK2 stress tensor
36 | tau = 1./J * piola(F,S)
37 |
38 | ! is equal to
39 | Sigma = 1./J * F*S*transpose(F)
40 |
41 | ! push forward of (contra-variant) fourth order material elasticity tensor
42 | c4 = 1./J * piola(F,C4)
43 | ```
44 |
45 |
--------------------------------------------------------------------------------
/ttb/libtenstore.f:
--------------------------------------------------------------------------------
1 | function tenstore_2s(T)
2 | implicit none
3 |
4 | type(Tensor2s), intent(in) :: T
5 | type(Tensor2) :: tenstore_2s
6 | integer :: i
7 |
8 | tenstore_2s%ab = 0.d0
9 | do i=1,3
10 | tenstore_2s%ab(i,i) = T%a6(i)
11 | enddo
12 | tenstore_2s%ab(1,2) = T%a6(4)
13 | tenstore_2s%ab(2,3) = T%a6(5)
14 | tenstore_2s%ab(3,1) = T%a6(6)
15 | tenstore_2s%ab(2,1) = tenstore_2s%ab(1,2)
16 | tenstore_2s%ab(3,2) = tenstore_2s%ab(2,3)
17 | tenstore_2s%ab(1,3) = tenstore_2s%ab(3,1)
18 |
19 | end function tenstore_2s
20 |
21 | function tenstore_2(T)
22 | implicit none
23 |
24 | type(Tensor2), intent(in) :: T
25 | type(Tensor2) :: tenstore_2
26 |
27 | tenstore_2%ab = T%ab
28 |
29 | end function tenstore_2
30 |
31 | function tenstore_2a(T)
32 | implicit none
33 |
34 | real(kind=8), dimension(3,3), intent(in) :: T
35 | type(Tensor2) :: tenstore_2a
36 |
37 | tenstore_2a%ab = T
38 |
39 | end function tenstore_2a
40 |
41 | function tenstore_4(T)
42 | implicit none
43 |
44 | type(Tensor4), intent(in) :: T
45 | type(Tensor4) :: tenstore_4
46 |
47 | tenstore_4%abcd = T%abcd
48 |
49 | end function tenstore_4
50 |
51 | function tenstore_4a(T)
52 | implicit none
53 |
54 | real(kind=8), dimension(3,3,3,3), intent(in) :: T
55 | type(Tensor4) :: tenstore_4a
56 |
57 | tenstore_4a%abcd = T
58 |
59 | end function tenstore_4a
60 |
61 | function tenstore_4s(T)
62 | implicit none
63 |
64 | type(Tensor4s), intent(in) :: T
65 | type(Tensor4) :: tenstore_4s
66 | integer :: i,j,k,l
67 | integer, dimension(3,3) :: i6j6
68 |
69 | i6j6 = reshape( (/1,4,6, 4,2,5, 6,5,3/), (/3, 3/) )
70 |
71 | forall (i=1:3,j=1:3,k=1:3,l=1:3) tenstore_4s%abcd(i,j,k,l)
72 | * = T%a6b6(i6j6(i,j),i6j6(k,l))
73 |
74 | end function tenstore_4s
--------------------------------------------------------------------------------
/.github/workflows/pages.yml:
--------------------------------------------------------------------------------
1 | # This workflow uses actions that are not certified by GitHub.
2 | # They are provided by a third-party and are governed by
3 | # separate terms of service, privacy policy, and support
4 | # documentation.
5 |
6 | # Sample workflow for building and deploying a Jekyll site to GitHub Pages
7 | name: Deploy Jekyll site to Pages
8 |
9 | on:
10 | push:
11 | branches:
12 | - "main"
13 | paths:
14 | - "docs/**"
15 |
16 | # Allows you to run this workflow manually from the Actions tab
17 | workflow_dispatch:
18 |
19 | # Sets permissions of the GITHUB_TOKEN to allow deployment to GitHub Pages
20 | permissions:
21 | contents: read
22 | pages: write
23 | id-token: write
24 |
25 | # Allow one concurrent deployment
26 | concurrency:
27 | group: "pages"
28 | cancel-in-progress: true
29 |
30 | jobs:
31 | # Build job
32 | build:
33 | runs-on: ubuntu-latest
34 | defaults:
35 | run:
36 | working-directory: docs
37 | steps:
38 | - name: Checkout
39 | uses: actions/checkout@v3
40 | - name: Setup Ruby
41 | uses: ruby/setup-ruby@v1
42 | with:
43 | ruby-version: '3.1' # Not needed with a .ruby-version file
44 | bundler-cache: true # runs 'bundle install' and caches installed gems automatically
45 | cache-version: 0 # Increment this number if you need to re-download cached gems
46 | working-directory: '${{ github.workspace }}/docs'
47 | - name: Setup Pages
48 | id: pages
49 | uses: actions/configure-pages@v3
50 | - name: Build with Jekyll
51 | # Outputs to the './_site' directory by default
52 | run: bundle exec jekyll build --baseurl "${{ steps.pages.outputs.base_path }}"
53 | env:
54 | JEKYLL_ENV: production
55 | - name: Upload artifact
56 | # Automatically uploads an artifact from the './_site' directory by default
57 | uses: actions/upload-pages-artifact@v1
58 | with:
59 | path: "docs/_site/"
60 |
61 | # Deployment job
62 | deploy:
63 | environment:
64 | name: github-pages
65 | url: ${{ steps.deployment.outputs.page_url }}
66 | runs-on: ubuntu-latest
67 | needs: build
68 | steps:
69 | - name: Deploy to GitHub Pages
70 | id: deployment
71 | uses: actions/deploy-pages@v2
72 |
--------------------------------------------------------------------------------
/CHANGELOG.md:
--------------------------------------------------------------------------------
1 | # Changelog
2 | All notable changes to this project will be documented in this file. The format is based on [Keep a Changelog](https://keepachangelog.com/en/1.0.0/), and this project adheres to [Semantic Versioning](https://semver.org/spec/v2.0.0.html).
3 |
4 | ## [Unreleased]
5 |
6 | ## [2.1.1] - 2024-01-03
7 |
8 | ### Changed
9 | - Rename internal matrix square-root from `stretch_2` and `stretch_2s` to `sqrt_2` and `sqrt_2s`. This does not affect the public API which remains unchanged as (matrix) square root `sqrt(T)`.
10 | - Remove an unused print statement in `sqrt_2()`.
11 |
12 | ### Fixed
13 | - Fix the orientation of `rotation_matrix(phi,2)` for a rotation matrix around axis 2. Also fix the docs for `rotation_matrix(phi,1)` and `rotation_matrix(phi,3)`.
14 |
15 | ## [2.1.0] - 2023-09-25
16 |
17 | ### Added
18 | - Add a new example for an easy-to-extend Neo-Hookean Abaqus Umat.
19 |
20 | ### Fixed
21 | - Fix a typo in the basic Neo-Hooke example for Abaqus Umat.
22 | - Disable `implicit none` for the basic Neo-Hooke example for Abaqus Umat (not supported in combination with `INCLUDE 'ABA_PARAM.INC'`).
23 |
24 | ## [2.0.0] - 2023-07-23
25 |
26 | ### Added
27 | - Add a warning in the docs that `C**(1/2)` equals to `C**0`. The square root operator must be used instead.
28 |
29 | ### Changed
30 | - Evaluate the i-th power of the inverse of a tensor for negative exponents in `C**-3`.
31 | - Initialize all tensor components to zero.
32 |
33 | ### Fixed
34 | - Fix assignments of scalars to tensors.
35 | - Ensure major- and minor-symmetric result in `cdya()`: `C(i,j,k,l) = (A(i,k) B(j,l) + A(i,l) B(j,k) + B(i,k) A(j,l) + B(i,l) A(j,k))/4`.
36 |
37 | ### Removed
38 | - Remove `ln`, `exp`, `dexp` functions which were based on isotropic tensor function-approximations. This could be misleading if one assumes these are analytic (exact) functions.
39 | - Remove unused internal variables and comments.
40 | - Remove unused `archive_functions.md` from the docs.
41 | - Remove incorrect implementation of `libinnercrossdyadic.f`.
42 |
43 | ## [1.1.2] - 2023-05-13
44 |
45 | ### Added
46 | - Add more badges in `README.md` (documentation, latest release).
47 |
48 | ### Changed
49 | - Better readability of text logo on white background.
50 |
51 | ## [1.1.1] - 2023-05-13
52 |
53 | ### Added
54 | - Start keeping a Changelog.
55 | - Add `CITATION.cff` file and remove *How To Cite* section in README.
56 | - Add a text logo and add badges to `README.md`.
57 |
--------------------------------------------------------------------------------
/ttb/libpermute.f:
--------------------------------------------------------------------------------
1 | function permute_2(T,i1,j1)
2 | ! permute tensor of rank 2 for orders 2,1 = transpose(T)
3 | implicit none
4 |
5 | type(Tensor2), intent(in) :: T
6 | integer, intent(in) :: i1,j1
7 |
8 | type(Tensor2) :: permute_2
9 |
10 | permute_2%ab = transpose(T%ab)
11 |
12 | end function permute_2
13 |
14 | function permute_2s(T,i1,j1)
15 | ! permute tensor of rank 2 for orders 2,1 = transpose(T)
16 | implicit none
17 |
18 | type(Tensor2s), intent(in) :: T
19 | integer, intent(in) :: i1,j1
20 |
21 | type(Tensor2s) :: permute_2s
22 |
23 | permute_2s%a6 = T%a6
24 |
25 | end function permute_2s
26 |
27 | function permute_4(T,i1,j1,k1,l1)
28 | ! permute tensor of rank 4
29 | implicit none
30 |
31 | type(Tensor4), intent(in) :: T
32 | integer, intent(in) :: i1,j1,k1,l1
33 |
34 | type(Tensor4) :: permute_4
35 | integer i,j,k,l
36 |
37 | c hard-coded permutation
38 | c if (i1==1 .and. j1==3 .and. k1==2 .and. l1==4) then
39 | c forall(i=1:3,j=1:3,k=1:3,l=1:3) permute_4%abcd(i,j,k,l)
40 | c * = T%abcd(i,k,j,l)
41 | c else if (i1==1 .and. j1==4 .and. k1==2 .and. l1==3) then
42 | c forall(i=1:3,j=1:3,k=1:3,l=1:3) permute_4%abcd(i,j,k,l)
43 | c * = T%abcd(i,l,j,k)
44 | c else
45 | c permute_4%abcd = T%abcd
46 | c end if
47 |
48 | permute_4%abcd = reshape(T%abcd,(/3,3,3,3/),
49 | * (/0.d0/),(/i1,j1,k1,l1/))
50 |
51 | end function permute_4
52 |
53 | function permute_4s(T,i1,j1,k1,l1)
54 | ! permute tensor of rank 4s
55 | implicit none
56 |
57 | type(Tensor4s), intent(in) :: T
58 | type(Tensor4) :: Tp
59 | integer, intent(in) :: i1,j1,k1,l1
60 | type(Tensor4) :: permute_4
61 | type(Tensor4s) :: permute_4s
62 |
63 | integer i,j,k,l
64 |
65 | Tp = tensorstore(T)
66 |
67 | permute_4%abcd = reshape(Tp%abcd,(/3,3,3,3/),
68 | * (/0.d0/),(/i1,j1,k1,l1/))
69 | permute_4s = symstore(permute_4)
70 |
71 | end function permute_4s
--------------------------------------------------------------------------------
/ttb/libsub.f:
--------------------------------------------------------------------------------
1 | function sub_11(T1, T2)
2 | implicit none
3 |
4 | type(Tensor1), intent(in) :: T1, T2
5 | type(Tensor1) :: sub_11
6 |
7 | sub_11%a = T1%a - T2%a
8 |
9 | end function sub_11
10 |
11 | function sub_22(T1, T2)
12 | implicit none
13 |
14 | type(Tensor2), intent(in) :: T1, T2
15 | type(Tensor2) :: sub_22
16 |
17 | sub_22%ab = T1%ab - T2%ab
18 |
19 | end function sub_22
20 |
21 | function sub_2s2s(T1, T2)
22 | implicit none
23 |
24 | type(Tensor2s), intent(in) :: T1, T2
25 | type(Tensor2s) :: sub_2s2s
26 |
27 | sub_2s2s%a6 = T1%a6 - T2%a6
28 |
29 | end function sub_2s2s
30 |
31 | function sub_22s(T1, T2)
32 | implicit none
33 |
34 | type(Tensor2), intent(in) :: T1
35 | type(Tensor2s), intent(in) :: T2
36 | type(Tensor2) :: sub_22s
37 |
38 | sub_22s = T1 - astensor(T2)
39 |
40 | end function sub_22s
41 |
42 | function sub_2s2(T1, T2)
43 | implicit none
44 |
45 | type(Tensor2s), intent(in) :: T1
46 | type(Tensor2), intent(in) :: T2
47 | type(Tensor2) :: sub_2s2
48 |
49 | sub_2s2 = astensor(T1) - T2
50 |
51 | end function sub_2s2
52 |
53 | function sub_44(T1, T2)
54 | implicit none
55 |
56 | type(Tensor4), intent(in) :: T1, T2
57 | type(Tensor4) :: sub_44
58 |
59 | sub_44%abcd = T1%abcd - T2%abcd
60 |
61 | end function sub_44
62 |
63 | function sub_4s4s(T1, T2)
64 | implicit none
65 |
66 | type(Tensor4s), intent(in) :: T1, T2
67 | type(Tensor4s) :: sub_4s4s
68 |
69 | sub_4s4s%a6b6 = T1%a6b6 - T2%a6b6
70 |
71 | end function sub_4s4s
72 |
73 | function sub_44s(T1, T2)
74 | implicit none
75 |
76 | type(Tensor4), intent(in) :: T1
77 | type(Tensor4s), intent(in) :: T2
78 | type(Tensor4) :: sub_44s
79 |
80 | sub_44s = T1 - astensor(T2)
81 |
82 | end function sub_44s
83 |
84 | function sub_4s4(T1, T2)
85 | implicit none
86 |
87 | type(Tensor4s), intent(in) :: T1
88 | type(Tensor4), intent(in) :: T2
89 | type(Tensor4) :: sub_4s4
90 |
91 | sub_4s4 = astensor(T1) - T2
92 |
93 | end function sub_4s4
--------------------------------------------------------------------------------
/ttb/libadd.f:
--------------------------------------------------------------------------------
1 | function add_11(T1, T2)
2 | implicit none
3 |
4 | type(Tensor1), intent(in) :: T1, T2
5 | type(Tensor1) :: add_11
6 |
7 | add_11%a = T1%a + T2%a
8 |
9 | end function add_11
10 |
11 | function add_22(T1, T2)
12 | implicit none
13 |
14 | type(Tensor2), intent(in) :: T1, T2
15 | type(Tensor2) :: add_22
16 |
17 | add_22%ab = T1%ab + T2%ab
18 |
19 | end function add_22
20 |
21 | function add_2s2s(T1, T2)
22 | implicit none
23 |
24 | type(Tensor2s), intent(in) :: T1, T2
25 | type(Tensor2s) :: add_2s2s
26 |
27 | add_2s2s%a6 = T1%a6 + T2%a6
28 |
29 | end function add_2s2s
30 |
31 | function add_22s(T1, T2)
32 | implicit none
33 |
34 | type(Tensor2), intent(in) :: T1
35 | type(Tensor2s), intent(in) :: T2
36 | type(Tensor2) :: add_22s
37 |
38 | add_22s = T1 + astensor(T2)
39 |
40 | end function add_22s
41 |
42 | function add_2s2(T1, T2)
43 | implicit none
44 |
45 | type(Tensor2s), intent(in) :: T1
46 | type(Tensor2), intent(in) :: T2
47 | type(Tensor2) :: add_2s2
48 |
49 | add_2s2 = astensor(T1) + T2
50 |
51 | end function add_2s2
52 |
53 | function add_44(T1, T2)
54 | implicit none
55 |
56 | type(Tensor4), intent(in) :: T1, T2
57 | type(Tensor4) :: add_44
58 |
59 | add_44%abcd = T1%abcd + T2%abcd
60 |
61 | end function add_44
62 |
63 | function add_4s4s(T1, T2)
64 | implicit none
65 |
66 | type(Tensor4s), intent(in) :: T1, T2
67 | type(Tensor4s) :: add_4s4s
68 |
69 | add_4s4s%a6b6 = T1%a6b6 + T2%a6b6
70 |
71 | end function add_4s4s
72 |
73 | function add_44s(T1, T2)
74 | implicit none
75 |
76 | type(Tensor4), intent(in) :: T1
77 | type(Tensor4s), intent(in) :: T2
78 | type(Tensor4) :: add_44s
79 |
80 | add_44s = T1 + astensor(T2)
81 |
82 | end function add_44s
83 |
84 | function add_4s4(T1, T2)
85 | implicit none
86 |
87 | type(Tensor4s), intent(in) :: T1
88 | type(Tensor4), intent(in) :: T2
89 | type(Tensor4) :: add_4s4
90 |
91 | add_4s4 = astensor(T1) + T2
92 |
93 | end function add_4s4
94 |
--------------------------------------------------------------------------------
/docs/examples/Marc/hypela2_nh_ttb_simple.f:
--------------------------------------------------------------------------------
1 | include 'ttb/ttb_library.f'
2 |
3 | subroutine hypela2(d,g,e,de,s,t,dt,ngens,m,nn,kcus,matus,ndi,
4 | 2 nshear,disp,dispt,coord,ffn,frotn,strechn,eigvn,ffn1,
5 | 3 frotn1,strechn1,eigvn1,ncrd,itel,ndeg,ndm,
6 | 4 nnode,jtype,lclass,ifr,ifu)
7 |
8 | ! UMAT: Nearly-Incompressible Neo-Hookean Material
9 | ! Example for usage of Tensor Toolbox
10 | ! capability: 3D, Axisymmetric
11 | ! Formulation: Total Lagrange
12 | ! Voigt Notation: Change commented Tensor Datatypes
13 | ! Andreas Dutzler, 2018-01-02, Graz University of Technology
14 |
15 | use Tensor
16 | implicit none
17 |
18 | integer :: ifr,ifu,itel,jtype,ncrd,ndeg,ndi,ndm,ngens,
19 | * nn,nnode,nshear
20 | integer, dimension(2) :: m,matus,kcus,lclass
21 | real(kind=8), dimension(*) :: e,de,t,dt,g,s
22 | real(kind=8), dimension(itel) :: strechn,strechn1
23 | real(kind=8), dimension(ngens,*) :: d
24 | real(kind=8), dimension(ncrd,*) :: coord
25 | real(kind=8), dimension(ndeg,*) :: disp, dispt
26 | real(kind=8), dimension(itel,3) :: ffn,ffn1,frotn,frotn1
27 | real(kind=8), dimension(itel,*) :: eigvn,eigvn1
28 |
29 | type(Tensor2) :: F1
30 | real(kind=8) :: J,kappa,C10
31 |
32 | ! to use voigt notation change to type Tensor2s, Tensor4s
33 | type(Tensor2) :: C1,invC1,S1,Eye
34 | type(Tensor4) :: C4
35 |
36 | ! material parameters
37 | C10 = 0.5
38 | kappa = 5.0
39 |
40 | Eye = identity2(Eye)
41 | F1 = ffn1(1:3,1:3) ! use slices (ffn1 is an assumed size array)
42 | J = det(F1)
43 |
44 | ! right cauchy-green deformation tensor and it's inverse
45 | C1 = transpose(F1)*F1
46 | invC1 = inv(C1) ! faster method: invC1 = inv(C1,J**2)
47 |
48 | ! pk2 stress
49 | S1 = 2.*C10*J**(-2./3.)*dev(C1)*invC1 + kappa*(J-1)*J*invC1
50 |
51 | ! material elasticity tensor
52 | C4 = 2.*C10 * J**(-2./3.) * 2./3. *
53 | * ( tr(C1) * (invC1.cdya.invC1)
54 | * - (Eye.dya.invC1) - (invC1.dya.Eye)
55 | * + tr(C1)/3. * (invC1.dya.invC1) )
56 | * + (kappa*(J-1)*J+kappa*J**2) * (invC1.dya.invC1)
57 | * - 2.*kappa*(J-1)*J* (invC1.cdya.invC1)
58 |
59 | ! output as array
60 | s(1:ngens) = asarray( voigt(S1), ngens )
61 | d(1:ngens,1:ngens) = asarray( voigt(C4), ngens, ngens )
62 |
63 | return
64 | end
--------------------------------------------------------------------------------
/docs/Gemfile.lock:
--------------------------------------------------------------------------------
1 | GEM
2 | remote: https://rubygems.org/
3 | specs:
4 | addressable (2.8.6)
5 | public_suffix (>= 2.0.2, < 6.0)
6 | bigdecimal (3.1.8)
7 | colorator (1.1.0)
8 | concurrent-ruby (1.2.3)
9 | em-websocket (0.5.3)
10 | eventmachine (>= 0.12.9)
11 | http_parser.rb (~> 0)
12 | eventmachine (1.2.7)
13 | ffi (1.16.3)
14 | forwardable-extended (2.6.0)
15 | google-protobuf (4.27.5-arm64-darwin)
16 | bigdecimal
17 | rake (>= 13)
18 | google-protobuf (4.27.5-x86_64-linux)
19 | bigdecimal
20 | rake (>= 13)
21 | http_parser.rb (0.8.0)
22 | i18n (1.14.4)
23 | concurrent-ruby (~> 1.0)
24 | jekyll (4.3.3)
25 | addressable (~> 2.4)
26 | colorator (~> 1.0)
27 | em-websocket (~> 0.5)
28 | i18n (~> 1.0)
29 | jekyll-sass-converter (>= 2.0, < 4.0)
30 | jekyll-watch (~> 2.0)
31 | kramdown (~> 2.3, >= 2.3.1)
32 | kramdown-parser-gfm (~> 1.0)
33 | liquid (~> 4.0)
34 | mercenary (>= 0.3.6, < 0.5)
35 | pathutil (~> 0.9)
36 | rouge (>= 3.0, < 5.0)
37 | safe_yaml (~> 1.0)
38 | terminal-table (>= 1.8, < 4.0)
39 | webrick (~> 1.7)
40 | jekyll-include-cache (0.2.1)
41 | jekyll (>= 3.7, < 5.0)
42 | jekyll-sass-converter (3.0.0)
43 | sass-embedded (~> 1.54)
44 | jekyll-seo-tag (2.8.0)
45 | jekyll (>= 3.8, < 5.0)
46 | jekyll-watch (2.2.1)
47 | listen (~> 3.0)
48 | just-the-docs (0.8.2)
49 | jekyll (>= 3.8.5)
50 | jekyll-include-cache
51 | jekyll-seo-tag (>= 2.0)
52 | rake (>= 12.3.1)
53 | kramdown (2.4.0)
54 | rexml
55 | kramdown-parser-gfm (1.1.0)
56 | kramdown (~> 2.0)
57 | liquid (4.0.4)
58 | listen (3.9.0)
59 | rb-fsevent (~> 0.10, >= 0.10.3)
60 | rb-inotify (~> 0.9, >= 0.9.10)
61 | mercenary (0.4.0)
62 | pathutil (0.16.2)
63 | forwardable-extended (~> 2.6)
64 | public_suffix (5.0.5)
65 | rake (13.2.1)
66 | rb-fsevent (0.11.2)
67 | rb-inotify (0.10.1)
68 | ffi (~> 1.0)
69 | rexml (3.4.2)
70 | rouge (4.2.1)
71 | safe_yaml (1.0.5)
72 | sass-embedded (1.75.0-arm64-darwin)
73 | google-protobuf (>= 3.25, < 5.0)
74 | sass-embedded (1.75.0-x86_64-linux-gnu)
75 | google-protobuf (>= 3.25, < 5.0)
76 | terminal-table (3.0.2)
77 | unicode-display_width (>= 1.1.1, < 3)
78 | unicode-display_width (2.5.0)
79 | webrick (1.8.2)
80 |
81 | PLATFORMS
82 | arm64-darwin
83 | x86_64-linux-gnu
84 |
85 | DEPENDENCIES
86 | jekyll (~> 4.3.3)
87 | just-the-docs (= 0.8.2)
88 |
89 | BUNDLED WITH
90 | 2.5.9
91 |
--------------------------------------------------------------------------------
/docs/examples/Marc/hypela2_stvenantkirchhoff.f:
--------------------------------------------------------------------------------
1 | include 'ttb/ttb_library.f'
2 |
3 | subroutine hypela2(d,g,e,de,s,t,dt,ngens,m,nn,kcus,matus,ndi,
4 | 2 nshear,disp,dispt,coord,ffn,frotn,strechn,eigvn,ffn1,
5 | 3 frotn1,strechn1,eigvn1,ncrd,itel,ndeg,ndm,
6 | 4 nnode,jtype,lclass,ifr,ifu)
7 |
8 | ! HYPELA2 St. Venant - Kirchhoff Material
9 | ! Formulation: Total Lagrange, Large Strain
10 | ! (Updated Lagrange with Push Forward
11 | ! and Jaumann Correction)
12 | !
13 | ! Andreas Dutzler, Graz University of Technology
14 | ! 2018-02-11
15 |
16 | use Tensor
17 | implicit none
18 |
19 | real*8 coord, d, de, disp, dispt, dt, e, eigvn, eigvn1, ffn, ffn1
20 | real*8 frotn, frotn1, g
21 | integer ifr, ifu, itel, jtype, kcus, lclass, matus, m, ncrd, ndeg
22 | integer ndi, ndm, ngens, nn, nnode, nshear
23 | real*8 s, strechn, strechn1, t
24 |
25 | dimension e(*),de(*),t(*),dt(*),g(*),d(ngens,*),s(*)
26 | dimension m(2),coord(ncrd,*),disp(ndeg,*),matus(2),
27 | * dispt(ndeg,*),ffn(itel,3),frotn(itel,3),
28 | * strechn(itel),eigvn(itel,*),ffn1(itel,3),
29 | * frotn1(itel,3),strechn1(itel),eigvn1(itel,*),
30 | * kcus(2),lclass(2)
31 |
32 | include 'concom'
33 |
34 | type(Tensor2) :: F1
35 |
36 | type(Tensor2s) :: E1,S1,Eye
37 | type(Tensor4s) :: C4
38 |
39 | real(kind=8) :: J,young,nu,lambda,mu
40 |
41 | ! material parameters
42 | young = 210000.0
43 | nu = 0.3
44 |
45 | ! lame parameter
46 | mu = young / ( 2.*(1.+nu) )
47 | lambda = nu*young / ((1.+nu)*(1.-2.*nu))
48 |
49 | ! large strain formulation
50 | Eye = Eye**0
51 | F1 = Eye
52 | F1%ab(1:itel,1:3) = ffn1(1:itel,1:3)
53 | E1 = 0.5*(transpose(F1)*F1-Eye)
54 |
55 | ! material elasticity tensor
56 | C4 = lambda*(Eye.dya.Eye) + 2.*mu*(Eye.cdya.Eye)
57 |
58 | ! pk2 stress
59 | S1 = lambda*tr(E1)*Eye + 2.*mu*E1
60 |
61 | if (iupdat.eq.1) then ! updated lagrange
62 | J = det(F1)
63 | ! cauchy stress
64 | S1 = piola(F1,S1)/J
65 | ! tangent matrix (jaumann)
66 | C4 = piola(F1,C4)/J
67 | * + (S1.cdya.Eye) + (Eye.cdya.S1)
68 | endif
69 |
70 | ! output as array
71 | s(1:ngens) = asarray( asvoigt(S1), ngens )
72 | d(1:ngens,1:ngens) = asarray( asvoigt(C4), ngens,ngens )
73 |
74 | return
75 | end
--------------------------------------------------------------------------------
/ttb/libpiola.f:
--------------------------------------------------------------------------------
1 | function piola2(F, T)
2 | implicit none
3 |
4 | type(Tensor2), intent(in) :: T, F
5 | type(Tensor2) :: piola2
6 |
7 | piola2 = F*T*transpose(F)
8 |
9 | end function piola2
10 |
11 | function piola2s(F, T)
12 | implicit none
13 |
14 | type(Tensor2s), intent(in) :: T
15 | type(Tensor2), intent(in) :: F
16 | type(Tensor2s) :: piola2s
17 |
18 | piola2s = symstore(F*tensorstore(T)*transpose(F))
19 |
20 | end function piola2s
21 |
22 | function piola4(F, T)
23 | implicit none
24 |
25 | type(Tensor2), intent(in) :: F
26 | type(Tensor4), intent(in) :: T
27 | type(Tensor4) :: piola4
28 | integer :: i,j,k,l,ii,jj,kk,ll
29 |
30 | piola4%abcd = 0.d0
31 | do i=1,3
32 | do j=1,3
33 | do k=1,3
34 | do l=1,3
35 | do ii=1,3
36 | do jj=1,3
37 | do kk=1,3
38 | do ll=1,3
39 | piola4%abcd(i,j,k,l) = piola4%abcd(i,j,k,l) +
40 | * F%ab(i,ii)*F%ab(j,jj)*F%ab(k,kk)*F%ab(l,ll)
41 | * *T%abcd(ii,jj,kk,ll)
42 | end do
43 | end do
44 | end do
45 | end do
46 | end do
47 | end do
48 | end do
49 | end do
50 |
51 | end function piola4
52 |
53 | function piola4s(F, T)
54 | implicit none
55 |
56 | type(Tensor2), intent(in) :: F
57 | type(Tensor4s), intent(in) :: T
58 | ! type(Tensor4) :: T2, piola4
59 | type(Tensor4s) :: piola4s,FF
60 | ! integer :: i,j,k,l,ii,jj,kk,ll
61 |
62 | ! piola4%abcd = 0.d0
63 | ! T2 = tensorstore(T)
64 |
65 | ! do i=1,3
66 | ! do j=1,3
67 | ! do k=1,3
68 | ! do l=1,3
69 | ! do ii=1,3
70 | ! do jj=1,3
71 | ! do kk=1,3
72 | ! do ll=1,3
73 | ! piola4%abcd(i,j,k,l) = piola4%abcd(i,j,k,l) +
74 | C ! * F%ab(i,ii)*F%ab(j,jj)*F%ab(k,kk)*F%ab(l,ll)
75 | C ! * *T2%abcd(ii,jj,kk,ll)
76 | ! end do
77 | ! end do
78 | ! end do
79 | ! end do
80 | ! end do
81 | ! end do
82 | ! end do
83 | ! end do
84 | ! piola4s = symstore(piola4)
85 |
86 | FF = symstore(F.cdya.F)
87 | piola4s = FF**T**transpose(FF)
88 |
89 | end function piola4s
--------------------------------------------------------------------------------
/docs/examples/Abaqus/umat_nh_ttb_simple.f:
--------------------------------------------------------------------------------
1 | include 'ttb/ttb_library.f'
2 |
3 | SUBROUTINE UMAT(STRESS,STATEV,DDSDDE,SSE,SPD,SCD,
4 | 1 RPL,DDSDDT,DRPLDE,DRPLDT,
5 | 2 STRAN,DSTRAN,TIME,DTIME,TEMP,DTEMP,PREDEF,DPRED,CMNAME,
6 | 3 NDI,NSHR,NTENS,NSTATV,PROPS,NPROPS,COORDS,DROT,PNEWDT,
7 | 4 CELENT,DFGRD0,DFGRD1,NOEL,NPT,LAYER,KSPT,JSTEP,KINC)
8 |
9 | ! ABAQUS UMAT: Nearly-Incompressible Neo-Hookean Material
10 | ! Example for usage of Tensor Toolbox
11 | ! capability: 3D, Axisymmetric
12 | ! Formulation: Total Lagrange with push forward for Abaqus
13 | ! Andreas Dutzler, 2018-07-22, Graz University of Technology
14 |
15 | use Tensor
16 |
17 | ! `implicit none` is not supported if 'ABA_PARAM.INC' is included.
18 | ! declare all double-variables which start with `i,j,k,l,m,n`
19 | ! - otherwise they will be integers
20 |
21 | ! implicit none
22 | INCLUDE 'ABA_PARAM.INC'
23 |
24 | CHARACTER*80 CMNAME
25 | DIMENSION STRESS(NTENS),STATEV(NSTATV),
26 | 1 DDSDDE(NTENS,NTENS),DDSDDT(NTENS),DRPLDE(NTENS),
27 | 2 STRAN(NTENS),DSTRAN(NTENS),TIME(2),PREDEF(1),DPRED(1),
28 | 3 PROPS(NPROPS),COORDS(3),DROT(3,3),DFGRD0(3,3),DFGRD1(3,3),
29 | 4 JSTEP(4)
30 |
31 | type(Tensor2) :: F1
32 | real(kind=8) :: J,kappa,C10
33 |
34 | type(Tensor2s) :: C1,invC1,S1,Eye
35 | type(Tensor4s) :: C4
36 |
37 | ! material parameters
38 | C10 = 0.5
39 | kappa = 5.0
40 |
41 | Eye = identity2(Eye)
42 | F1 = dfgrd1(1:3,1:3)
43 | J = det(F1)
44 |
45 | ! right cauchy-green deformation tensor and its inverse
46 | C1 = transpose(F1)*F1
47 | invC1 = inv(C1)
48 |
49 | ! pk2 stress
50 | S1 = 2.*C10*J**(-2./3.)*dev(C1)*invC1 + kappa*(J-1)*J*invC1
51 |
52 | ! push forward to cauchy stress
53 | S1 = piola(F1,S1)/J
54 |
55 | ! material elasticity tensor
56 | C4 = 2.*C10 * J**(-2./3.) * 2./3. *
57 | * ( tr(C1) * (invC1.cdya.invC1)
58 | * - (Eye.dya.invC1) - (invC1.dya.Eye)
59 | * + tr(C1)/3. * (invC1.dya.invC1) )
60 | * + (kappa*(J-1)*J+kappa*J**2) * (invC1.dya.invC1)
61 | * - 2.*kappa*(J-1)*J* (invC1.cdya.invC1)
62 |
63 | ! push forward to jaumann tangent of cauchy stress for abaqus
64 | C4 = piola(F1,C4)/J + (S1.cdya.Eye)+(Eye.cdya.S1)
65 |
66 | ! output as array
67 | STRESS(1:ntens) = asabqarray(voigt(S1),ntens)
68 | DDSDDE(1:ntens,1:ntens) = asabqarray(voigt(C4),ntens,ntens)
69 |
70 | return
71 | end
72 |
--------------------------------------------------------------------------------
/ttb/libsymstore.f:
--------------------------------------------------------------------------------
1 | function symstore_2s(T)
2 | implicit none
3 |
4 | type(Tensor2s), intent(in) :: T
5 | type(Tensor2s) :: symstore_2s
6 |
7 | symstore_2s%a6 = T%a6
8 | end function symstore_2s
9 |
10 | function symstore_2sa(T)
11 | implicit none
12 |
13 | real(kind=8), dimension(6), intent(in) :: T
14 | type(Tensor2s) :: symstore_2sa
15 |
16 | symstore_2sa%a6 = T
17 |
18 | end function symstore_2sa
19 |
20 | function symstore_4s(T)
21 | implicit none
22 |
23 | type(Tensor4s), intent(in) :: T
24 | type(Tensor4s) :: symstore_4s
25 |
26 | symstore_4s%a6b6 = T%a6b6
27 |
28 | end function symstore_4s
29 |
30 | function symstore_4sa(T)
31 | implicit none
32 |
33 | real(kind=8), dimension(6,6), intent(in) :: T
34 | type(Tensor4s) :: symstore_4sa
35 |
36 | symstore_4sa%a6b6 = T
37 |
38 | end function symstore_4sa
39 |
40 | function symstore_2(T)
41 | implicit none
42 |
43 | type(Tensor2), intent(in) :: T
44 | type(Tensor2s) :: symstore_2
45 | integer :: i
46 |
47 | symstore_2%a6 = 0.d0
48 | do i=1,3
49 | symstore_2%a6(i) = T%ab(i,i)
50 | enddo
51 | symstore_2%a6(4) = T%ab(1,2)
52 | symstore_2%a6(5) = T%ab(2,3)
53 | symstore_2%a6(6) = T%ab(3,1)
54 |
55 | end function symstore_2
56 |
57 | function symstore_4(T)
58 | implicit none
59 |
60 | type(Tensor4), intent(in) :: T
61 | type(Tensor4s) :: symstore_4
62 | integer :: i,j
63 |
64 | symstore_4%a6b6 = 0.d0
65 | do i=1,3
66 | do j=1,3
67 | symstore_4%a6b6(i,j) = T%abcd(i,i,j,j)
68 | enddo
69 | enddo
70 |
71 | symstore_4%a6b6(4,4) = T%abcd(1,2,1,2)
72 | symstore_4%a6b6(5,5) = T%abcd(2,3,2,3)
73 | symstore_4%a6b6(6,6) = T%abcd(3,1,3,1)
74 |
75 | do i=1,3
76 | symstore_4%a6b6(i,4) = T%abcd(i,i,1,2)
77 | symstore_4%a6b6(i,5) = T%abcd(i,i,2,3)
78 | symstore_4%a6b6(i,6) = T%abcd(i,i,3,1)
79 | symstore_4%a6b6(4,i) = T%abcd(1,2,i,i)
80 | symstore_4%a6b6(5,i) = T%abcd(2,3,i,i)
81 | symstore_4%a6b6(6,i) = T%abcd(3,1,i,i)
82 | enddo
83 |
84 | symstore_4%a6b6(4,5) = T%abcd(1,2,2,3)
85 | symstore_4%a6b6(4,6) = T%abcd(1,2,3,1)
86 |
87 | symstore_4%a6b6(5,4) = T%abcd(2,3,1,2)
88 | symstore_4%a6b6(5,6) = T%abcd(2,3,3,1)
89 |
90 | symstore_4%a6b6(6,4) = T%abcd(3,1,1,2)
91 | symstore_4%a6b6(6,5) = T%abcd(3,1,2,3)
92 |
93 | end function symstore_4
--------------------------------------------------------------------------------
/ttb/libassignarray.f:
--------------------------------------------------------------------------------
1 | subroutine assignarr_2s(T,A)
2 | implicit none
3 |
4 | type(Tensor2s), intent(inout) :: T
5 | real(kind=8), dimension(6), intent(in) :: A
6 |
7 | T%a6 = A
8 |
9 | end subroutine assignarr_2s
10 |
11 | subroutine assignarr_2sr4(T,A)
12 | implicit none
13 |
14 | type(Tensor2s), intent(inout) :: T
15 | real(kind=4), dimension(6), intent(in) :: A
16 |
17 | T%a6 = dble(A)
18 |
19 | end subroutine assignarr_2sr4
20 |
21 | subroutine assignarr_4s(T,A)
22 | implicit none
23 |
24 | type(Tensor4s), intent(inout) :: T
25 | real(kind=8), dimension(6,6), intent(in) :: A
26 |
27 | T%a6b6 = A
28 |
29 | end subroutine assignarr_4s
30 |
31 | subroutine assignarr_4sr4(T,A)
32 | implicit none
33 |
34 | type(Tensor4s), intent(inout) :: T
35 | real(kind=4), dimension(6,6), intent(in) :: A
36 |
37 | T%a6b6 = dble(A)
38 |
39 | end subroutine assignarr_4sr4
40 |
41 | subroutine assignarr_1(T,A)
42 | implicit none
43 |
44 | type(Tensor1), intent(inout) :: T
45 | real(kind=8), dimension(3), intent(in) :: A
46 |
47 | T%a = A
48 |
49 | end subroutine assignarr_1
50 |
51 | subroutine assignarr_1r4(T,A)
52 | implicit none
53 |
54 | type(Tensor1), intent(inout) :: T
55 | real(kind=4), dimension(3), intent(in) :: A
56 |
57 | T%a = dble(A)
58 |
59 | end subroutine assignarr_1r4
60 |
61 | subroutine assignarr_2(T,A)
62 | implicit none
63 |
64 | type(Tensor2), intent(inout) :: T
65 | real(kind=8), dimension(3,3), intent(in) :: A
66 |
67 | T%ab = A
68 |
69 | end subroutine assignarr_2
70 |
71 | subroutine assignarr_2r4(T,A)
72 | implicit none
73 |
74 | type(Tensor2), intent(inout) :: T
75 | real(kind=4), dimension(3,3), intent(in) :: A
76 |
77 | T%ab = dble(A)
78 |
79 | end subroutine assignarr_2r4
80 |
81 | subroutine assignarr_4(T,A)
82 | implicit none
83 |
84 | type(Tensor4), intent(inout) :: T
85 | real(kind=8), dimension(3,3,3,3), intent(in) :: A
86 |
87 | T%abcd = A
88 |
89 | end subroutine assignarr_4
90 |
91 | subroutine assignarr_4r4(T,A)
92 | implicit none
93 |
94 | type(Tensor4), intent(inout) :: T
95 | real(kind=4), dimension(3,3,3,3), intent(in) :: A
96 |
97 | T%abcd = dble(A)
98 |
99 | end subroutine assignarr_4r4
--------------------------------------------------------------------------------
/ttb/libsqrt.f:
--------------------------------------------------------------------------------
1 | function sqrt_1(T)
2 | implicit none
3 |
4 | type(Tensor1), intent(in) :: T
5 | type(Tensor1) :: sqrt_1
6 |
7 | sqrt_1%a = dsqrt(T%a)
8 |
9 | end function sqrt_1
10 |
11 | function sqrt_2(T)
12 | ! Source:
13 | !
14 | ! Franca, L.P. (1989): AN ALGORITHM TO COMPUTE
15 | ! THE SQUARE ROOT OF A POSITIVE DEFINITE MATRIX
16 | !
17 | implicit none
18 |
19 | type(Tensor2), intent(in) :: T
20 | type(Tensor2) :: sqrt_2
21 |
22 | real(kind=8) :: I_T,II_T,III_T,I_U,II_U,III_U,k,l,lam,phi
23 |
24 | ! Invariants of T
25 | I_T = tr(T)
26 | II_T = 0.5*(I_T**2-T**T)
27 | III_T = det(T)
28 | k = I_T**2-3.*II_T
29 |
30 | ! Isotropy check
31 | if (dabs(k).le.1.0d-8) then
32 | lam = (I_T/3.)**(1./2.)
33 | sqrt_2 = lam * identity2(T)
34 | return
35 | end if
36 |
37 | ! Calculate largest eigenvalues
38 | l = I_T**3 - 9./2. * I_T*II_T + 27./2. * III_T
39 | phi = dacos(l/k**(3./2.))
40 | lam = dsqrt(1./3.*(I_T+2*k**(1./2.)*dcos(phi/3.)))
41 |
42 | ! Invariants of U
43 | III_U = (III_T)**(1./2.)
44 | I_U = lam + dsqrt(-lam**2+I_T+2.*III_U/lam)
45 | II_U = (I_U**2-I_T)/2.
46 |
47 | sqrt_2 = 1./(I_U*II_U-III_U)
48 | * *(I_U*III_U*identity2(T) + (I_U**2-II_U)*T-T**2)
49 |
50 | end function sqrt_2
51 |
52 | function sqrt_2s(T)
53 | ! Source:
54 | !
55 | ! Franca, L.P. (1989): AN ALGORITHM TO COMPUTE
56 | ! THE SQUARE ROOT OF A POSITIVE DEFINITE MATRIX
57 | !
58 | implicit none
59 |
60 | type(Tensor2s), intent(in) :: T
61 | type(Tensor2s) :: sqrt_2s
62 |
63 | real(kind=8) :: I_T,II_T,III_T,I_U,II_U,III_U,k,l,lam,phi
64 |
65 | ! Invariants of T
66 | I_T = tr(T)
67 | II_T = 0.5*(I_T**2-tr(T*T))
68 | III_T = det(T)
69 | k = I_T**2-3.*II_T
70 |
71 | ! Isotropy check
72 | if (k.le.1.0d-8) then
73 | lam = (I_T/3.)**(1./2.)
74 | sqrt_2s = lam * identity2(T)
75 | return
76 | end if
77 |
78 | ! Calculate largest eigenvalues
79 | l = I_T**3 - 9./2. * I_T*II_T + 27./2. * III_T
80 | phi = dacos(l/k**(3./2.))
81 | lam = dsqrt(1./3.*(I_T+2*k**(1./2.)*dcos(phi/3.)))
82 |
83 | ! Invariants of U
84 | III_U = (III_T)**(1./2.)
85 | I_U = lam + dsqrt(-lam**2+I_T+2.*III_U/lam)
86 | II_U = (I_U**2-I_T)/2.
87 |
88 | sqrt_2s = 1./(I_U*II_U-III_U)
89 | * *(I_U*III_U*identity2(T) + (I_U**2-II_U)*T-T*T)
90 |
91 | end function sqrt_2s
--------------------------------------------------------------------------------
/ttb/libassignscalar.f:
--------------------------------------------------------------------------------
1 | subroutine assignscalar_2s(T,w)
2 | implicit none
3 |
4 | type(Tensor2s), intent(inout) :: T
5 | real(kind=8), intent(in) :: w
6 |
7 | T%a6 = w
8 |
9 | end subroutine assignscalar_2s
10 |
11 | subroutine assignscalar_2sr4(T,w)
12 | implicit none
13 |
14 | type(Tensor2s), intent(inout) :: T
15 | real(kind=4), intent(in) :: w
16 |
17 | T%a6 = dble(w)
18 |
19 | end subroutine assignscalar_2sr4
20 |
21 | subroutine assignscalar_4s(T,w)
22 | implicit none
23 |
24 | type(Tensor4s), intent(inout) :: T
25 | real(kind=8), intent(in) :: w
26 |
27 | T%a6b6 = w
28 |
29 | end subroutine assignscalar_4s
30 |
31 | subroutine assignscalar_4sr4(T,w)
32 | implicit none
33 |
34 | type(Tensor4s), intent(inout) :: T
35 | real(kind=4), intent(in) :: w
36 |
37 | T%a6b6 = dble(w)
38 |
39 | end subroutine assignscalar_4sr4
40 |
41 | subroutine assignscalar_1(T,w)
42 | implicit none
43 |
44 | type(Tensor1), intent(inout) :: T
45 | real(kind=8), intent(in) :: w
46 |
47 | T%a = w
48 |
49 | end subroutine assignscalar_1
50 |
51 | subroutine assignscalar_1r4(T,w)
52 | implicit none
53 |
54 | type(Tensor1), intent(inout) :: T
55 | real(kind=4), intent(in) :: w
56 |
57 | T%a = dble(w)
58 |
59 | end subroutine assignscalar_1r4
60 |
61 | subroutine assignscalar_2(T,w)
62 | implicit none
63 |
64 | type(Tensor2), intent(inout) :: T
65 | real(kind=8), intent(in) :: w
66 |
67 | T%ab = w
68 |
69 | end subroutine assignscalar_2
70 |
71 | subroutine assignscalar_2r4(T,w)
72 | implicit none
73 |
74 | type(Tensor2), intent(inout) :: T
75 | real(kind=4), intent(in) :: w
76 |
77 | T%ab = dble(w)
78 |
79 | end subroutine assignscalar_2r4
80 |
81 | subroutine assignscalar_4(T,w)
82 | implicit none
83 |
84 | type(Tensor4), intent(inout) :: T
85 | real(kind=8), intent(in) :: w
86 |
87 | T%abcd = w
88 |
89 | end subroutine assignscalar_4
90 |
91 | subroutine assignscalar_4r4(T,w)
92 | implicit none
93 |
94 | type(Tensor4), intent(inout) :: T
95 | real(kind=4), intent(in) :: w
96 |
97 | T%abcd = dble(w)
98 |
99 | end subroutine assignscalar_4r4
100 |
--------------------------------------------------------------------------------
/docs/index.md:
--------------------------------------------------------------------------------
1 | ---
2 | title: Home
3 | layout: home
4 | nav_order: 1
5 | last_modified_date: 2023-07-07
6 | ---
7 |
8 | # Tensor Toolbox for Modern Fortran
9 |
10 | 
11 |
12 | ## What is this toolbox about?
13 |
14 | Commercial FEM software packages offer interfaces (user subroutines written in Fortran) for custom defined user materials like UMAT in [Abaqus](https://www.3ds.com/products-services/simulia/products/abaqus/) or HYPELA2 in [Marc](https://hexagon.com/products/marc). In comparison to other scientific programming languages like MATLAB or Python Fortran is not as comfortable to use when dealing with high level programming features of tensor manipulations. On the other hand it's super fast - so why not combine the handy features from MATLAB or Python's NumPy/Scipy with the speed of Fortran? That's the reason why I started working on a simple but effective module called **Tensor Toolbox for Modern Fortran**. The idea is adopted from [1].
15 |
16 | ## How to cite
17 |
18 | [](https://doi.org/10.5281/zenodo.4077378)
19 |
20 | If you use *Tensor Toolbox for Modern Fortran (ttb)* in your work, please cite this toolbox in your publications and let us know. Thanks!
21 |
22 | {: .note }
23 | >The DOI-badge always resolves to the latest version of this toolbox - if you prefer a version-specific DOI, hit the DOI-badge and pick a version on Zenodo.
24 |
25 | Andreas Dutzler. *Tensor Toolbox for Modern Fortran - High-Level Tensor Manipulation in Fortran*. DOI: 10.5281/zenodo.4077378.
26 |
27 | ```
28 | @software{dutzler2021,
29 | author = {Andreas Dutzler},
30 | title = {Tensor Toolbox for Modern Fortran - High-Level Tensor Manipulation in Fortran},
31 | doi = {10.5281/zenodo.4077378},
32 | url = {https://doi.org/10.5281/zenodo.4077378}
33 | }
34 | ```
35 |
36 | ## Overview
37 | - [Installation]({% link installation/index.md %})
38 | - [Quick Start Guide]({% link installation/quickstartguide.md %})
39 | - [Tensor Data Types]({% link api/tensordatatypes.md %})
40 | - [API Reference]({% link api/index.md %})
41 | - Example 1: [St.Venant-Kirchhoff Material]({% link examples/ex01_stvenantkirchhoff.md %})
42 | - Example 2: [Nearly-Incompressible Neo-Hookean Material]({% link examples/ex02_neohooke.md %})
43 | - Example 3: [Neo-Hookean Hyperelasticity with Maxwell-Viscoelasticity](examples/Marc/hypela2_nonlinear_viscoelasticity.f)
44 |
45 | ## Author
46 | Andreas Dutzler, Graz University of Technology, Austria.
47 |
48 | ## Changelog
49 | All notable changes to this project will be documented in [this file](https://github.com/adtzlr/ttb/blob/main/CHANGELOG.md). The format is based on [Keep a Changelog](https://keepachangelog.com/en/1.0.0/), and this project adheres to [Semantic Versioning](https://semver.org/spec/v2.0.0.html).
50 |
51 | ## References
52 | [1] Naumann, C.: [Chemisch-mechanisch gekoppelte Modellierung und Simulation oxidativer Alterungsvorgänge in Gummibauteilen (German)](http://nbn-resolving.de/urn:nbn:de:bsz:ch1-qucosa-222075). PhD thesis. Fakultät für Maschinenbau der Technischen Universität Chemnitz, 2016.
53 |
--------------------------------------------------------------------------------
/docs/examples/script_umat.f:
--------------------------------------------------------------------------------
1 | include 'ttb/ttb_library.f'
2 |
3 | program script_tensortoolbox
4 |
5 | ! Example program for ttb-usage
6 | ! ttb is only active inside user subroutine
7 |
8 | implicit none
9 |
10 | real(kind=8), dimension(3,3) :: F, E, Eye
11 |
12 | real(kind=8), dimension(3,3) :: Siso
13 | real(kind=8), dimension(3,3,3,3) :: C4iso
14 |
15 | ! Deformation Gradient
16 | F = 0.0
17 | F(1,1) = 1.1
18 | F(2,2) = 1.0
19 | F(3,3) = 1.0
20 | F(1,2) = 0.1
21 | F(1,3) = 0.0
22 |
23 | Eye = 0.0
24 | Eye(1,1) = 1.0
25 | Eye(2,2) = 1.0
26 | Eye(3,3) = 1.0
27 |
28 | ! Green-Lagrange Strain
29 | E = 0.5*(matmul(transpose(F),F) - Eye)
30 |
31 | ! User Material Subroutine
32 | call umat(Siso,C4iso,F,E)
33 |
34 | ! Outputs
35 | print *, ''
36 | print *, '2nd Piola Kirchhoff Stress Tensor'
37 | write (*,993) Siso
38 | print *, ''
39 | print *, 'Material Elasticity Tensor'
40 | write (*,999) C4iso
41 | print *, ''
42 |
43 | 993 format('| ',f8.2,' ',f8.2,' ',f8.2,' |')
44 | 996 format('| ',f8.2,' ',f8.2,' ',f8.2,' ',
45 | * f8.2,' ',f8.2,' ',f8.2,' |')
46 | 999 format('| ',f8.2,' ',f8.2,' ',f8.2,' ',
47 | * f8.2,' ',f8.2,' ',f8.2,' ',
48 | * f8.2,' ',f8.2,' ',f8.2,' |')
49 |
50 | end program script_tensortoolbox
51 |
52 | subroutine umat(Siso_arr,C4iso_arr,F_arr,E_arr)
53 | ! A very basic Example of a User Material Subroutine
54 | ! Isochoric part of nearly-incompressible Neo-Hookean material
55 |
56 | use Tensor
57 |
58 | implicit none
59 |
60 | real(kind=8) :: J
61 |
62 | real(kind=8), dimension(3,3), intent(in) :: F_arr, E_arr
63 | real(kind=8), dimension(3,3), intent(inout) :: Siso_arr
64 | real(kind=8), dimension(3,3,3,3), intent(inout) :: C4iso_arr
65 |
66 | type(Tensor2) :: F, E
67 | type(Tensor2) :: Siso
68 | type(Tensor4) :: C4iso
69 |
70 | type(Tensor2) :: Shat, Eye, C, invC
71 | type(Tensor4) :: C4hat, P4
72 |
73 | F = F_arr
74 | E = E_arr
75 |
76 | J = det(F)
77 | Eye = identity2(Eye)
78 |
79 | C = transpose(F)*F
80 | invC = inv(C)
81 |
82 | Shat = J**(-2./3.)*Eye
83 |
84 | ! Isochoric part of 2nd Piola Kirchhoff stress tensor
85 | Siso = dev(Shat*C)*invC
86 |
87 | ! Deviatoric projection tensor
88 | P4 = identity4(Eye)-1./3.*(invC.dya.C)
89 | C4hat = J**(-4./3.)*0.d0
90 |
91 | ! Isochoric part of Material Elasticity tensor
92 | C4iso = P4**C4hat**transpose(P4)
93 | * + 2./3.*tr(Shat*C)*identity4(invC)
94 | * - 2./3.*((Shat.dya.invC)+(invC.dya.Shat))
95 | * + 2./9.*tr(Shat*C)*(invC.dya.invC)
96 |
97 | ! Ouput Tensor as Array with given dimensions
98 | Siso_arr(1:3,1:3) = Siso%ab(1:3,1:3)
99 | C4iso_arr(1:3,1:3,1:3,1:3) = C4iso%abcd(1:3,1:3,1:3,1:3)
100 |
101 | end
102 |
--------------------------------------------------------------------------------
/ttb/libdiv.f:
--------------------------------------------------------------------------------
1 | ! ------REAL(KIND=8)--------------------------------------
2 | function div_10(T, w)
3 | implicit none
4 |
5 | real(kind=8), intent(in) :: w
6 | type(Tensor1), intent(in) :: T
7 | type(Tensor1) :: div_10
8 |
9 | div_10%a = T%a / w
10 |
11 | end function div_10
12 |
13 | function div_20(T, w)
14 | implicit none
15 |
16 | real(kind=8), intent(in) :: w
17 | type(Tensor2), intent(in) :: T
18 | type(Tensor2) :: div_20
19 |
20 | div_20%ab = T%ab / w
21 |
22 | end function div_20
23 |
24 | function div_20s(T, w)
25 | implicit none
26 |
27 | real(kind=8), intent(in) :: w
28 | type(Tensor2s), intent(in) :: T
29 | type(Tensor2s) :: div_20s
30 |
31 | div_20s%a6 = T%a6 / w
32 |
33 | end function div_20s
34 |
35 | function div_40(T, w)
36 | implicit none
37 |
38 | real(kind=8), intent(in) :: w
39 | type(Tensor4), intent(in) :: T
40 | type(Tensor4) :: div_40
41 |
42 | div_40%abcd = T%abcd / w
43 |
44 | end function div_40
45 |
46 | function div_40s(T, w)
47 | implicit none
48 |
49 | real(kind=8), intent(in) :: w
50 | type(Tensor4s), intent(in) :: T
51 | type(Tensor4s) :: div_40s
52 |
53 | div_40s%a6b6 = T%a6b6 / w
54 |
55 | end function div_40s
56 | ! ------REAL(KIND=4)----------------------------------------
57 | function div_10_r4(T, w)
58 | implicit none
59 |
60 | real(kind=4), intent(in) :: w
61 | type(Tensor1), intent(in) :: T
62 | type(Tensor1) :: div_10_r4
63 |
64 | div_10_r4%a = T%a / dble(w)
65 |
66 | end function div_10_r4
67 |
68 | function div_20_r4(T, w)
69 | implicit none
70 |
71 | real(kind=4), intent(in) :: w
72 | type(Tensor2), intent(in) :: T
73 | type(Tensor2) :: div_20_r4
74 |
75 | div_20_r4%ab = T%ab / dble(w)
76 |
77 | end function div_20_r4
78 |
79 | function div_20s_r4(T, w)
80 | implicit none
81 |
82 | real(kind=4), intent(in) :: w
83 | type(Tensor2s), intent(in) :: T
84 | type(Tensor2s) :: div_20s_r4
85 |
86 | div_20s_r4%a6 = T%a6 / dble(w)
87 |
88 | end function div_20s_r4
89 |
90 | function div_40_r4(T, w)
91 | implicit none
92 |
93 | real(kind=4), intent(in) :: w
94 | type(Tensor4), intent(in) :: T
95 | type(Tensor4) :: div_40_r4
96 |
97 | div_40_r4%abcd = T%abcd / dble(w)
98 |
99 | end function div_40_r4
100 |
101 | function div_40s_r4(T, w)
102 | implicit none
103 |
104 | real(kind=4), intent(in) :: w
105 | type(Tensor4s), intent(in) :: T
106 | type(Tensor4s) :: div_40s_r4
107 |
108 | div_40s_r4%a6b6 = T%a6b6 / dble(w)
109 |
110 | end function div_40s_r4
--------------------------------------------------------------------------------
/ttb/libinv.f:
--------------------------------------------------------------------------------
1 | function inv_2(T)
2 | implicit none
3 |
4 | type(Tensor2), intent(in) :: T
5 | type(Tensor2) :: inv_2
6 | real(kind=8) :: idetT
7 |
8 | idetT = 1.d0/det(T)
9 |
10 | inv_2%ab(1,1)=+idetT*(T%ab(2,2)*T%ab(3,3)-T%ab(2,3)*T%ab(3,2))
11 | inv_2%ab(2,1)=-idetT*(T%ab(2,1)*T%ab(3,3)-T%ab(2,3)*T%ab(3,1))
12 | inv_2%ab(3,1)=+idetT*(T%ab(2,1)*T%ab(3,2)-T%ab(2,2)*T%ab(3,1))
13 | inv_2%ab(1,2)=-idetT*(T%ab(1,2)*T%ab(3,3)-T%ab(1,3)*T%ab(3,2))
14 | inv_2%ab(2,2)=+idetT*(T%ab(1,1)*T%ab(3,3)-T%ab(1,3)*T%ab(3,1))
15 | inv_2%ab(3,2)=-idetT*(T%ab(1,1)*T%ab(3,2)-T%ab(1,2)*T%ab(3,1))
16 | inv_2%ab(1,3)=+idetT*(T%ab(1,2)*T%ab(2,3)-T%ab(1,3)*T%ab(2,2))
17 | inv_2%ab(2,3)=-idetT*(T%ab(1,1)*T%ab(2,3)-T%ab(1,3)*T%ab(2,1))
18 | inv_2%ab(3,3)=+idetT*(T%ab(1,1)*T%ab(2,2)-T%ab(1,2)*T%ab(2,1))
19 |
20 | end function inv_2
21 |
22 | function inv_2s(T)
23 | implicit none
24 |
25 | type(Tensor2s), intent(in) :: T
26 | type(Tensor2s) :: inv_2s
27 | real(kind=8) :: idetT
28 |
29 | idetT = 1.d0/det(T)
30 |
31 | inv_2s%a6(1)=+idetT*(T%a6(2)*T%a6(3) -T%a6(5)*T%a6(5))
32 | inv_2s%a6(4)=-idetT*(T%a6(4)*T%a6(3) -T%a6(5)*T%a6(6))
33 | inv_2s%a6(6)=+idetT*(T%a6(4)*T%a6(5) -T%a6(2)*T%a6(6))
34 | inv_2s%a6(2)=+idetT*(T%a6(1)*T%a6(3) -T%a6(6)*T%a6(6))
35 | inv_2s%a6(5)=-idetT*(T%a6(1)*T%a6(5) -T%a6(4)*T%a6(6))
36 | inv_2s%a6(3)=+idetT*(T%a6(1)*T%a6(2) -T%a6(4)*T%a6(4))
37 |
38 | end function inv_2s
39 |
40 | function inv2d(T,detT)
41 | implicit none
42 |
43 | type(Tensor2), intent(in) :: T
44 | type(Tensor2) :: inv2d
45 | real(kind=8) :: detT, idetT
46 |
47 | idetT = 1.d0/detT
48 |
49 | inv2d%ab(1,1)=+idetT*(T%ab(2,2)*T%ab(3,3)-T%ab(2,3)*T%ab(3,2))
50 | inv2d%ab(2,1)=-idetT*(T%ab(2,1)*T%ab(3,3)-T%ab(2,3)*T%ab(3,1))
51 | inv2d%ab(3,1)=+idetT*(T%ab(2,1)*T%ab(3,2)-T%ab(2,2)*T%ab(3,1))
52 | inv2d%ab(1,2)=-idetT*(T%ab(1,2)*T%ab(3,3)-T%ab(1,3)*T%ab(3,2))
53 | inv2d%ab(2,2)=+idetT*(T%ab(1,1)*T%ab(3,3)-T%ab(1,3)*T%ab(3,1))
54 | inv2d%ab(3,2)=-idetT*(T%ab(1,1)*T%ab(3,2)-T%ab(1,2)*T%ab(3,1))
55 | inv2d%ab(1,3)=+idetT*(T%ab(1,2)*T%ab(2,3)-T%ab(1,3)*T%ab(2,2))
56 | inv2d%ab(2,3)=-idetT*(T%ab(1,1)*T%ab(2,3)-T%ab(1,3)*T%ab(2,1))
57 | inv2d%ab(3,3)=+idetT*(T%ab(1,1)*T%ab(2,2)-T%ab(1,2)*T%ab(2,1))
58 |
59 | end function inv2d
60 |
61 | function inv2sd(T,detT)
62 | implicit none
63 |
64 | type(Tensor2s), intent(in) :: T
65 | type(Tensor2s) :: inv2sd
66 | real(kind=8):: detT, idetT
67 |
68 | idetT = 1.d0/detT
69 |
70 | inv2sd%a6(1)=+idetT*(T%a6(2)*T%a6(3) -T%a6(5)*T%a6(5))
71 | inv2sd%a6(4)=-idetT*(T%a6(4)*T%a6(3) -T%a6(5)*T%a6(6))
72 | inv2sd%a6(6)=+idetT*(T%a6(4)*T%a6(5) -T%a6(2)*T%a6(6))
73 | inv2sd%a6(2)=+idetT*(T%a6(1)*T%a6(3) -T%a6(6)*T%a6(6))
74 | inv2sd%a6(5)=-idetT*(T%a6(1)*T%a6(5) -T%a6(4)*T%a6(6))
75 | inv2sd%a6(3)=+idetT*(T%a6(1)*T%a6(2) -T%a6(4)*T%a6(4))
76 |
77 | end function inv2sd
--------------------------------------------------------------------------------
/docs/api/index.md:
--------------------------------------------------------------------------------
1 | ---
2 | title: API Reference
3 | layout: page
4 | nav_order: 3
5 | has_children: true
6 | ---
7 |
8 | # Module Function Overview
9 | This module provides several useful assignments, operators and functions for the derived Tensor Data Types.
10 |
11 | ## A word on Voigt notation
12 | Symmetric 3x3 Tensors may be stored as 6x1 column vectors with the help of the well known [Voigt notation](https://en.wikipedia.org/wiki/Voigt_notation). In an analogous way a transformation may be obtained for at least minor symmetric fourth order tensors (3x3x3x3) which may be stored as a 6x6 matrix. If the fourth order tensor is also major symmetric the reduced 6x6 matrix is also symmetric.
13 |
14 | There is no unique method for the storage ordering of tensor components - this toolbox uses the following approach:
15 | `11,22,33,12,23,31`. If you use Abaqus please use `asabqarray` to export tensor components.
16 |
17 | To ensure consistency in calculating the virtual work shear terms are treated differently in Voigt notation: "stress"-like tensors or, to be more precisely, contra-variant tensor components are stored "as they are" whereas "strain"-like tensors or, again, co-variant tensor components are stored with **doubled** shear components. As this method is quite complicate for mixed-variant tensors and not really straight-forward to implement inside a whole toolbox this module uses a different "Voigt"-like approach:
18 |
19 | All tensors, whether they are "stress"- or "strain"-like are stored with original (**no doubled**) shear components. Instead all dot- and double-dot-products are modified to take virtual work consistency into account. To be more precise, the function `asvoigt` is not really a Voigt storage - it is more a synonym for storing symmetric tensors as vectors and matrices. The user does have to take care of that storage if the strain in a user subroutine is used as an input for a `Tensor2s` data type and divide all shear components by a factor of `2`.
20 |
21 | ## Assignments
22 | - [General behaviour of data type conversion]({% link api/assignments.md %})
23 |
24 | ## Operators
25 | - [Dot Product]({% link api/operators.md %})
26 | - [Double Dot Product]({% link api/operators.md %})
27 | - [Dyadic Product]({% link api/operators.md %})
28 | - [Crossed-dyadic Product]({% link api/operators.md %})
29 | - [Division]({% link api/operators.md %})
30 | - [Addition]({% link api/operators.md %})
31 | - [Subtraction]({% link api/operators.md %})
32 |
33 | ## Scalar-valued functions
34 | - [Trace]({% link api/functions/trace.md %})
35 | - [Determinant]({% link api/functions/determinant.md %})
36 | - [Norm]({% link api/functions/norm.md %})
37 |
38 | ## Tensor-valued functions
39 | - [Deviator]({% link api/functions/deviator.md %})
40 | - [Unimodular]({% link api/functions/unimodular.md %})
41 | - [Inverse]({% link api/functions/inverse.md %})
42 | - [Transpose]({% link api/functions/transpose.md %})
43 | - [Permute]({% link api/functions/permute.md %})
44 | - [Square root]({% link api/functions/squareroot.md %})
45 | - [Power]({% link api/functions/power.md %})
46 | - [Identity]({% link api/functions/identity.md %})
47 | - [Piola Operation]({% link api/functions/piola.md %})
48 | - [Rotation Matrix]({% link api/functions/rotation.md %})
49 |
50 | ## Helper Functions
51 | - [As Array]({% link api/functions/asarray.md %})
52 | - [As Abaqus Array]({% link api/functions/asabqarray.md %})
53 | - [As Voigt]({% link api/functions/asvoigt.md %})
54 | - [As Tensor]({% link api/functions/astensor.md %})
55 | - [Import Strain]({% link api/functions/voigtstrain.md %})
56 |
--------------------------------------------------------------------------------
/docs/examples/Marc/hypela2_nh_ttb.f:
--------------------------------------------------------------------------------
1 | include 'ttb/ttb_library.f'
2 |
3 | subroutine hypela2(d,g,e,de,s,t,dt,ngens,m,nn,kcus,matus,ndi,
4 | 2 nshear,disp,dispt,coord,ffn,frotn,strechn,eigvn,ffn1,
5 | 3 frotn1,strechn1,eigvn1,ncrd,itel,ndeg,ndm,
6 | 4 nnode,jtype,lclass,ifr,ifu)
7 |
8 | ! HYPELA2 Nearly-Incompressible Neo-Hookean Material
9 | ! Formulation: Total Lagrange, Displacement and Herrmann Elements
10 | ! Updated Lagrange: Push Forward and transform to Jaumann Tangent
11 | ! Example for usage of Tensor Toolbox
12 | !
13 | ! Switch to Voigt Notation:
14 | ! - change commented Tensor Datatypes
15 | !
16 | ! Andreas Dutzler
17 | ! 2017-12-21
18 | ! Graz University of Technology
19 |
20 | use Tensor
21 | implicit none
22 |
23 | real*8 coord, d, de, disp, dispt, dt, e, eigvn, eigvn1, ffn, ffn1
24 | real*8 frotn, frotn1, g
25 | integer ifr, ifu, itel, jtype, kcus, lclass, matus, m, ncrd, ndeg
26 | integer ndi, ndm, ngens, nn, nnode, nshear
27 | real*8 s, strechn, strechn1, t
28 |
29 | dimension e(*),de(*),t(*),dt(*),g(*),d(ngens,*),s(*)
30 | dimension m(2),coord(ncrd,*),disp(ndeg,*),matus(2),
31 | * dispt(ndeg,*),ffn(itel,3),frotn(itel,3),
32 | * strechn(itel),eigvn(itel,*),ffn1(itel,3),
33 | * frotn1(itel,3),strechn1(itel),eigvn1(itel,*),
34 | * kcus(2),lclass(2)
35 | include 'concom'
36 | include 'creeps'
37 |
38 | type(Tensor2) :: F1
39 | type(Tensor2s) :: E1
40 |
41 | ! voigt notation: change to type Tensor2s, Tensor4s
42 | type(Tensor2s) :: C1,S1,invC1,Eye
43 | type(Tensor4s) :: C4, I4, SdyaI
44 |
45 | real(kind=8) :: J,J_th,p,dpdJ,kappa,C10,alpha
46 |
47 | integer ndim
48 |
49 | ! dimension
50 | ndim = ndi+nshear
51 |
52 | ! material parameters
53 | C10 = 0.5
54 | kappa = 500.0
55 | alpha = 1.5d-4
56 |
57 | Eye = identity2(Eye)
58 | F1 = tensorstore(Eye)
59 | F1%ab(1:itel,1:3) = ffn1(1:itel,1:3)
60 | J = det(F1)
61 | J_th = (1+alpha*(t(1)+dt(1)))**3
62 |
63 | C1 = transpose(F1)*F1
64 | J = det(C1)**(1./2.)
65 | invC1 = inv(C1)
66 |
67 | ! u or u/p formulation
68 | if (ngens > ndim) then
69 | p = e(ngens)+de(ngens)
70 | dpdJ = 0.d0
71 | else
72 | p = kappa*(J/J_th-1)
73 | dpdJ = kappa/J_th
74 | end if
75 |
76 | ! pk2 stress
77 | S1 = 2.*C10 * J**(-2./3.) * dev(C1)*invC1 + p*J*invC1
78 |
79 | if (iupdat.eq.1) then
80 | S1 = piola(F1,S1)/J ! S1 = 1/J * F1*S1*transpose(F1)
81 | endif
82 |
83 | ! output as array
84 | s(1:ndim) = asarray( voigt(S1), ndim )
85 |
86 | ! material elasticity tensor
87 | I4 = invC1.cdya.invC1
88 | C4 = 2.*C10*J**(-2./3.)*2./3. * (tr(C1)*I4
89 | * -(Eye.dya.invC1)-(invC1.dya.Eye)
90 | * +tr(C1)/3.*(invC1.dya.invC1))
91 | * +(p*J+dpdJ*J**2)*(invC1.dya.invC1)
92 | * -2.*p*J*I4
93 | if (iupdat.eq.1) then
94 | C4 = piola(F1,C4)/detF1 + (S1.cdya.Eye)+(Eye.cdya.S1)
95 | endif
96 |
97 | ! output as array
98 | d(1:ndim,1:ndim) = asarray( voigt(C4), ndim, ndim )
99 |
100 | ! herrmann formulation
101 | if (iupdat.eq.1) then
102 | invC1 = Eye/J
103 | endif
104 | if (ngens > ndim) then
105 | s(ngens) = (J-J_th) - p*J_th**2/kappa
106 | d(ngens,1:ndim) = asarray( J*voigt(invC1), ndim)
107 | d(1:ndim,ngens) = d(ngens,1:ndim)
108 | d(ngens,ngens) = -J_th**2/kappa
109 | g(1:ndim) = 0.d0
110 | g(ngens) = -(1+2*p/kappa*J_th) * 3.*alpha*J_th**(2./3.)*dt(1)
111 | else
112 | g(1:ndim) = -kappa*J/J_th**2 * 3.*alpha*J_th**(2./3.)
113 | * * J * asarray(voigt(invC1), ndim)*dt(1)
114 | endif
115 |
116 | return
117 | end
--------------------------------------------------------------------------------
/docs/examples/Abaqus/umat_nh_ttb.f:
--------------------------------------------------------------------------------
1 | include 'ttb/ttb_library.f'
2 |
3 | SUBROUTINE UMAT(STRESS,STATEV,DDSDDE,SSE,SPD,SCD,
4 | 1 RPL,DDSDDT,DRPLDE,DRPLDT,
5 | 2 STRAN,DSTRAN,TIME,DTIME,TEMP,DTEMP,PREDEF,DPRED,CMNAME,
6 | 3 NDI,NSHR,NTENS,NSTATV,PROPS,NPROPS,COORDS,DROT,PNEWDT,
7 | 4 CELENT,DFGRD0,DFGRD1,NOEL,NPT,LAYER,KSPT,JSTEP,KINC)
8 |
9 | ! ABAQUS UMAT: Easy-to-extend Nearly-Incompressible Neo-Hookean
10 | ! Material Formulation
11 | ! Example for usage of Tensor Toolbox
12 | ! capability: 3D, Axisymmetric
13 | ! Formulation: Total Lagrange with push forward for Abaqus
14 | ! Reference: Holzapfel, G. (2001). NONLINEAR SOLID MECHANICS.
15 | ! A Continuum Approach for Engineering.
16 | !
17 | ! Jamal Bhatti, 2023-09-23, Leibniz University Hannover
18 |
19 | use Tensor
20 |
21 | ! `implicit none` is not supported if 'ABA_PARAM.INC' is included.
22 | ! declare all double-variables which start with `i,j,k,l,m,n`
23 | ! - otherwise they will be integers
24 |
25 | ! implicit none
26 | INCLUDE 'ABA_PARAM.INC'
27 |
28 | CHARACTER*80 CMNAME
29 | DIMENSION STRESS(NTENS),STATEV(NSTATV),
30 | 1 DDSDDE(NTENS,NTENS),DDSDDT(NTENS),DRPLDE(NTENS),
31 | 2 STRAN(NTENS),DSTRAN(NTENS),TIME(2),PREDEF(1),DPRED(1),
32 | 3 PROPS(NPROPS),COORDS(3),DROT(3,3),DFGRD0(3,3),DFGRD1(3,3),
33 | 4 JSTEP(4)
34 |
35 | PARAMETER(ZERO=0.D0, ONE=1.D0, TWO=2.D0, THREE=3.D0, FOUR=4.D0)
36 |
37 | type(Tensor2) :: F1
38 | type(Tensor4) :: P4
39 | real(kind=8) :: J,kappa,C10,D1,dUdI1bar,dUdI2bar,dUdJ,ddUdJdJ
40 | real(kind=8) :: ddUdI1bardI1bar,ddUdI2bardI2bar,ddUdI1bardI2bar
41 | real(kind=8) :: p,ptilde,gama1bar,gama2bar,I1bar
42 | real(kind=8) :: delta1bar,delta2bar,delta3bar,delta4bar
43 |
44 | ! also possible as types Tensor2s and Tensor4s
45 | type(Tensor2) :: C1,invC1,S1,Eye,Cbar,Sbar,Siso
46 | type(Tensor4) :: C4,C4bar,P4tilde,C4iso,C4vol
47 |
48 | ! material parameters
49 | C10 = PROPS(2)
50 | D1 = PROPS(1)
51 | kappa = TWO/D1
52 |
53 | Eye = identity2(Eye)
54 | F1 = dfgrd1(1:3,1:3)
55 | J = det(F1)
56 |
57 | ! right cauchy-green deformation tensor and its inverse
58 | C1 = transpose(F1) * F1
59 | invC1 = inv(C1)
60 |
61 | dUdJ = kappa * (J - 1)
62 | ddUdJdJ = kappa
63 |
64 | dUdI1bar = C10
65 | dUdI2bar = ZERO
66 |
67 | ! double derivatives
68 | ddUdI1bardI1bar = ZERO
69 | ddUdI1bardI2bar = ZERO
70 | ddUdI2bardI2bar = ZERO
71 |
72 | Cbar = J**(-2./3.) * C1
73 | I1bar = tr(Cbar)
74 | gama1bar = TWO * (dUdI1bar + I1bar * dUdI2bar)
75 | gama2bar = -TWO * dUdI2bar
76 | Sbar = gama1bar * Eye + gama2bar * Cbar
77 |
78 | p = dUdJ
79 | ptilde = p + J * ddUdJdJ
80 | P4 = identity4(Eye) - 1./3. * (invC1.dya.C1)
81 | Siso = J**(-2./3.) * (P4**Sbar)
82 |
83 | ! push forward of pk2 stress to cauchy stress
84 | S1 = piola(F1, J * p * invC1 + Siso) / J
85 |
86 | ! coefficients for the elasticity tensor
87 | delta1bar = FOUR * (ddUdI1bardI1bar +
88 | * TWO * I1bar * ddUdI1bardI2bar + dUdI2bar +
89 | * I1bar**2 * ddUdI2bardI2bar)
90 | delta2bar = -FOUR * (ddUdI1bardI2bar + I1bar * ddUdI2bardI2bar)
91 | delta3bar = FOUR * ddUdI2bardI2bar
92 | delta4bar = -FOUR * dUdI2bar
93 |
94 | C4bar = J**(-4./3.) * (delta1bar * (Eye.dya.Eye)
95 | * + delta2bar * ((Eye.dya.Cbar) + (Cbar.dya.Eye))
96 | * + delta3bar * (Cbar.dya.Cbar)
97 | * + delta4bar * identity4(Eye))
98 |
99 | P4tilde = identity4(invC1) - 1./3. * (invC1.dya.invC1)
100 |
101 | C4iso = P4**C4bar**transpose(P4)
102 | * + 2./3. * tr(Sbar*Cbar) * P4tilde
103 | * - 2./3. * ((invC1.dya.Siso) + (Siso.dya.invC1))
104 | C4vol = (J * ptilde) * ((invC1.dya.invC1)) - (2. * J * p)
105 | * * (identity4(invC1))
106 |
107 | ! push forward to jaumann tangent of cauchy stress for abaqus
108 | C4 = piola(F1, C4iso + C4vol) / J + (S1.cdya.Eye) + (Eye.cdya.S1)
109 |
110 | ! output as array
111 | STRESS(1:ntens) = asabqarray(voigt(S1),ntens)
112 | DDSDDE(1:ntens,1:ntens) = asabqarray(voigt(C4),ntens,ntens)
113 |
114 | return
115 | end
116 |
--------------------------------------------------------------------------------
/ttb/libddot.f:
--------------------------------------------------------------------------------
1 | function ddot_22(T1, T2)
2 | implicit none
3 |
4 | type(Tensor2), intent(in) :: T1
5 | type(Tensor2), intent(in) :: T2
6 | real(kind=8) :: ddot_22
7 | integer :: i,j
8 |
9 | ddot_22 = 0.d0
10 | do i = 1,3
11 | do j = 1,3
12 | ddot_22 = ddot_22 + T1%ab(i,j)*T2%ab(i,j)
13 | enddo
14 | enddo
15 |
16 | end function ddot_22
17 |
18 | function ddot_2s2s(T1, T2)
19 | implicit none
20 |
21 | type(Tensor2s), intent(in) :: T1
22 | type(Tensor2s), intent(in) :: T2
23 | real(kind=8) :: ddot_2s2s
24 | integer :: i
25 |
26 | ddot_2s2s = 0.d0
27 | do i=1,3
28 | ddot_2s2s = ddot_2s2s + T1%a6(i)*T2%a6(i)
29 | enddo
30 | do i=4,6
31 | ddot_2s2s = ddot_2s2s + T1%a6(i)*T2%a6(i)*2.d0
32 | enddo
33 |
34 | end function ddot_2s2s
35 |
36 | function ddot_24(T1, T2)
37 | implicit none
38 |
39 | type(Tensor2), intent(in) :: T1
40 | type(Tensor4), intent(in) :: T2
41 | type(Tensor2) :: ddot_24
42 | integer :: i,j,k,l
43 |
44 | ddot_24%ab = 0.d0
45 | do i = 1,3
46 | do j = 1,3
47 | do k = 1,3
48 | do l = 1,3
49 | ddot_24%ab(k,l) = ddot_24%ab(k,l)
50 | * + T1%ab(i,j)*T2%abcd(i,j,k,l)
51 | enddo
52 | enddo
53 | enddo
54 | enddo
55 |
56 | end function ddot_24
57 |
58 | function ddot_2s4s(T1, T2)
59 | implicit none
60 |
61 | type(Tensor2s), intent(in) :: T1
62 | type(Tensor4s), intent(in) :: T2
63 | type(Tensor2s) :: ddot_2s4s
64 | real(kind=8) :: w
65 | integer :: i,j
66 |
67 | ddot_2s4s%a6 = 0.d0
68 | do i = 1,6
69 | do j = 1,6
70 | if (i > 3) then
71 | w = 2.d0
72 | else
73 | w = 1.d0
74 | endif
75 | ddot_2s4s%a6(j) = ddot_2s4s%a6(j)
76 | * + T1%a6(i)*T2%a6b6(i,j)*w
77 | enddo
78 | enddo
79 |
80 | end function ddot_2s4s
81 |
82 | function ddot_42(T1, T2)
83 | implicit none
84 |
85 | type(Tensor4), intent(in) :: T1
86 | type(Tensor2), intent(in) :: T2
87 | type(Tensor2) :: ddot_42
88 | integer :: i,j,k,l
89 |
90 | ddot_42%ab = 0.d0
91 | do i = 1,3
92 | do j = 1,3
93 | do k = 1,3
94 | do l = 1,3
95 | ddot_42%ab(i,j) = ddot_42%ab(i,j)
96 | * + T1%abcd(i,j,k,l)*T2%ab(k,l)
97 | enddo
98 | enddo
99 | enddo
100 | enddo
101 |
102 | end function ddot_42
103 |
104 | function ddot_4s2s(T1, T2)
105 | implicit none
106 |
107 | type(Tensor4s), intent(in) :: T1
108 | type(Tensor2s), intent(in) :: T2
109 | type(Tensor2s) :: ddot_4s2s
110 | real(kind=8) :: w
111 | integer :: i,j
112 |
113 | ddot_4s2s%a6 = 0.d0
114 | do i = 1,6
115 | do j = 1,6
116 | if (j > 3) then
117 | w = 2.d0
118 | else
119 | w = 1.d0
120 | endif
121 | ddot_4s2s%a6(i) = ddot_4s2s%a6(i)
122 | * + T1%a6b6(i,j)*T2%a6(j)*w
123 | enddo
124 | enddo
125 |
126 | end function ddot_4s2s
127 |
128 | function ddot_44(T1, T2)
129 | implicit none
130 |
131 | type(Tensor4), intent(in) :: T1
132 | type(Tensor4), intent(in) :: T2
133 | type(Tensor4) :: ddot_44
134 | integer :: i,j,k,l,m,n
135 |
136 | ddot_44%abcd = 0.d0
137 | do i = 1,3
138 | do j = 1,3
139 | do m = 1,3
140 | do n = 1,3
141 | do k = 1,3
142 | do l = 1,3
143 | ddot_44%abcd(i,j,k,l) = ddot_44%abcd(i,j,k,l)
144 | * + T1%abcd(i,j,m,n)*T2%abcd(m,n,k,l)
145 | enddo
146 | enddo
147 | enddo
148 | enddo
149 | enddo
150 | enddo
151 | end function ddot_44
152 |
153 | function ddot_4s4s(T1, T2)
154 | implicit none
155 |
156 | type(Tensor4s), intent(in) :: T1
157 | type(Tensor4s), intent(in) :: T2
158 | type(Tensor4s) :: ddot_4s4s
159 | real(kind=8) :: w
160 | integer :: i,j,k
161 |
162 | ddot_4s4s%a6b6 = 0.d0
163 | do i = 1,6
164 | do k = 1,6
165 | do j = 1,6
166 | if (k > 3) then
167 | w = 2.d0
168 | else
169 | w = 1.d0
170 | endif
171 | ddot_4s4s%a6b6(i,j) = ddot_4s4s%a6b6(i,j)
172 | * + T1%a6b6(i,k)*T2%a6b6(k,j)*w
173 | enddo
174 | enddo
175 | enddo
176 |
177 | end function ddot_4s4s
--------------------------------------------------------------------------------
/docs/examples/Marc/hypela2_nonlinear_viscoelasticity.f:
--------------------------------------------------------------------------------
1 | include 'ttb/ttb_library.f'
2 |
3 | subroutine hypela2(d,g,e,de,s,t,dt,ngens,m,nn,kcus,matus,ndi,
4 | 2 nshear,disp,dispt,coord,ffn,frotn,strechn,eigvn,ffn1,
5 | 3 frotn1,strechn1,eigvn1,ncrd,itel,ndeg,ndm,
6 | 4 nnode,jtype,lclass,ifr,ifu)
7 |
8 | ! HYPELA2 Nonlinear Viscoelasticity with
9 | ! Neo-Hookean Hyperelasticity
10 | ! ----------------------------------------------------------------
11 | ! Source: Shutov et.al. (2013): An explicit solution for
12 | ! implicit time stepping in multiplicative
13 | ! finite strain viscoelasticity.
14 | ! DOI: http://dx.doi.org/10.1016/j.cma.2013.07.004
15 | ! --> Lagrangian formulation, EBMSC-method (eq.41f)
16 | !
17 | ! Formulation: Total Lagrange, Large Strain
18 | ! (with option for Updated Lagrange with Push Forward
19 | ! and Jaumann-like Tangent Correction included)
20 | !
21 | ! ----------------------------------------------------------------
22 | ! Andreas Dutzler, Graz University of Technology
23 | ! 2018-04-05
24 |
25 | use Tensor
26 | implicit none
27 |
28 | integer :: ifr,ifu,itel,jtype,ncrd,ndeg,ndi,ndm,ngens,
29 | * nn,nnode,nshear
30 | integer, dimension(2) :: m,matus,kcus,lclass
31 | real(kind=8), dimension(*) :: e,de,t,dt,g,s
32 | real(kind=8), dimension(itel) :: strechn,strechn1
33 | real(kind=8), dimension(ngens,*) :: d
34 | real(kind=8), dimension(ncrd,*) :: coord
35 | real(kind=8), dimension(ndeg,*) :: disp, dispt
36 | real(kind=8), dimension(itel,3) :: ffn,ffn1,frotn,frotn1
37 | real(kind=8), dimension(itel,*) :: eigvn,eigvn1
38 |
39 | include 'concom'
40 | include 'creeps'
41 |
42 | ! begin user code
43 | type(Tensor2) :: F1
44 | type(Tensor2s) :: C1,invC1,C0_i,invC1_i,S1,S1_hat,S1_bar,Eye,
45 | * Phi,Phi_hat,invPhi
46 | type(Tensor4s) :: C4,C4_hat,C4_bar,I4,P4,Eye4
47 | real(kind=8) :: J,J_th,C10,mu,eta,kappa,tr_SC,
48 | * p,dpdJ,detPhi,dtime
49 |
50 | ! material parameters
51 | C10 = 0.5
52 | mu = 2.0
53 | eta = 10.0
54 | kappa = 50.0
55 |
56 | ! time increment
57 | dtime = timinc
58 |
59 | ! deformation gradient
60 | Eye = identity2(Eye)
61 | F1 = Eye
62 | F1%ab(1:itel,1:3) = ffn1(1:itel,1:3)
63 |
64 | ! volumetric ratio
65 | J = det(F1)
66 |
67 | ! hydrostatic stress and derivative
68 | p = kappa*(J-1)
69 | dpdJ = kappa
70 |
71 | ! right cauchy-green deformation tensor and inverse
72 | C1 = transpose(F1)*F1
73 | invC1 = inv(C1,J**2)
74 |
75 | ! PK2-stress elastic ground network
76 | S1_hat = 2.*C10*Eye
77 | C4_hat = 0.0
78 |
79 | ! inelastic deformation at beginning of the inc.
80 | C0_i = t(2:7)
81 | if (t(2) == 0.0) then
82 | ! if start of analysis is detected
83 | ! --> no inelastic deformation
84 | C0_i = Eye
85 | end if
86 |
87 | ! inelastic part of rCG (= Phi_hat)
88 | Phi = C0_i + mu*dtime/eta * J**(-2./3.)*C1
89 | Phi_hat = unimodular(Phi)
90 | invC1_i = inv(Phi_hat,1.d0)
91 |
92 | ! PK2-stress viscous overstress
93 | S1_hat = S1_hat + mu*(invC1_i)
94 | Eye4 = Eye.cdya.Eye
95 | detPhi = det(Phi)
96 | invPhi = inv(Phi,detPhi)
97 | C4_hat = C4_hat + (mu*(invC1_i.cdya.invC1_i))**
98 | * (detPhi**(-1./3.) * 2.*mu*dtime/eta*
99 | * (Eye4 - 1./3.*(Phi.dya.invPhi)))
100 |
101 | S1_bar = J**(-2./3.) * S1_hat
102 | C4_bar = J**(-4./3.) * C4_hat
103 |
104 | ! distortional + hydrostatic component of PK2-stress
105 | tr_SC = S1_bar**C1
106 | S1 = (S1_bar - 1./3.*tr_SC*invC1) + p*J*invC1
107 |
108 | ! material elasticity tensor
109 | I4 = invC1.cdya.invC1
110 | P4 = (Eye.cdya.Eye) - 1./3.*(invC1.dya.C1)
111 | C4 = P4**C4_bar**transpose(P4)
112 | * + 2./3. * (tr_SC*I4
113 | * -(S1_bar.dya.invC1)-(invC1.dya.S1_bar)
114 | * +tr_SC/3.*(invC1.dya.invC1))
115 | * +(p*J+dpdJ*J**2)*(invC1.dya.invC1)
116 | * -2.*p*J*I4
117 |
118 | ! (lovl==6) --> solution converged, save state variables
119 | if (lovl.eq.6) then
120 | t(2:7) = asarray( asvoigt(Phi_hat), 6)
121 | end if
122 |
123 | ! updated lagrange
124 | if (iupdat.eq.1) then
125 | ! cauchy stress
126 | S1 = piola(F1,S1)/J
127 | ! tangent matrix (jaumann-like co-rotated)
128 | C4 = piola(F1,C4)/J
129 | * + (S1.cdya.Eye) + (Eye.cdya.S1)
130 | endif
131 |
132 | ! output as array
133 | s(1:ngens) = asarray( asvoigt(S1), ngens )
134 | d(1:ngens,1:ngens) = asarray( asvoigt(C4), ngens,ngens )
135 |
136 | return
137 | end
--------------------------------------------------------------------------------
/docs/assets/images/logo.svg:
--------------------------------------------------------------------------------
1 |
2 |
3 |
4 |
101 |
--------------------------------------------------------------------------------
/docs/examples/ex02_neohooke.md:
--------------------------------------------------------------------------------
1 | ---
2 | title: Ex. 02 - Neo-Hooke
3 | layout: page
4 | nav_order: 4
5 | parent: Examples
6 | ---
7 |
8 | # Neo-Hooke
9 | This is a very basic example on how to implement a nearly-incompressible version of the Neo-Hookean material model in a commercial FEM package (HYPELA2 for Marc or UMAT for Abaqus).
10 |
11 | ## Hyperelasticity
12 | The strain energy density function per unit reference volume is additively splitted into an isochoric and volumetric contribution, see Eq. $$\eqref{eq:psi}$$. The first one is assumed to be proportional to the first invariant of the isochoric part of the right Cauchy-Green deformation tensor whereas the volumetric part is only a function of the volumetric ratio (the determinant of the deformation gradient), see Eq. $$\eqref{eq:psi-nh}$$.
13 |
14 | $$
15 | \begin{align}
16 | \psi(\mathbf{C}) &= \psi(\mathbf{\hat C}) + U(J) \label{eq:psi} \\
17 | \psi(\mathbf{C}) &= \text{C}_{10} (\text{I}_\mathbf{\hat C}-3) + \frac{\kappa}{2} (J-1)^2 \label{eq:psi-nh}
18 | \end{align}
19 | $$
20 |
21 | We get the second Piola-Kirchhoff stress with the derivative of the strain energy density function per unit reference volume with respect to one half of the right Cauchy-Green deformation tensor as shown in Eq. $$\eqref{eq:pk2-nh}$$.
22 |
23 | $$
24 | \begin{align}
25 | \mathbf{S} &= \frac{\partial \psi(\mathbf{C})}{\partial \frac{1}{2}\mathbf{C}} \nonumber \\
26 | \mathbf{S} &= 2\text{C}_{10} \ \text{dev}(\hat{\mathbf{C}}) \mathbf{C}^{-1} + \kappa (J-1) J \mathbf{C}^{-1}
27 | \label{eq:pk2-nh}
28 | \end{align}
29 | $$
30 |
31 | By evaluating the derivative of the stress with respect to one half of the right Cauchy-Green deformation tensor we get the material elasticity tensor, see Eq. $$\eqref{eq:c4-nh}$$,
32 |
33 | $$
34 | \begin{align}
35 | \mathbb{C} &= \frac{\partial \mathbf{S}}{\partial\frac{1}{2}\mathbf{C}} \nonumber \\
36 | \mathbb{C} &= 2\text{C}_{10} J^{-2/3} \frac{2}{3} \ (\text{tr}(\mathbf{C}) \ \mathbb{I} - \mathbf{1} \otimes \mathbf{C}^{-1} - \mathbf{C}^{-1} \otimes \mathbf{1} + \frac{1}{3} \text{tr}(\mathbf{C}) \ \mathbf{C}^{-1} \otimes \mathbf{C}^{-1}) \nonumber \\
37 | &+ \left(\kappa (J-1) J + \kappa J^2\right) \ \mathbf{C}^{-1} \otimes \mathbf{C}^{-1} - 2 \kappa (J-1) J \ \mathbb{I}
38 | \label{eq:c4-nh}
39 | \end{align}
40 | $$
41 |
42 | with the fourth order identity tensor in Eq. $$\eqref{eq:i4}$$.
43 |
44 | $$
45 | \begin{align}
46 | \mathbb{I} &= \mathbf{C}^{-1} \odot \mathbf{C}^{-1} \nonumber \\
47 | \mathbf{C}^{-1} &= \mathbb{I} : \mathbf{C} \label{eq:i4}
48 | \end{align}
49 | $$
50 |
51 |
52 | Implementation for Marc
53 |
54 | ## HYPELA2 User Subroutine for Marc
55 | Eq. $$\eqref{eq:pk2-nh}$$ and Eq. $$\eqref{eq:c4-nh}$$ are implemented in a Total Lagrange [user subroutine](Marc/hypela2_nh_ttb_simple.f) with the help of this Tensor module.
56 |
57 | {: .warning }
58 | > As no special two- or three-field variational principle is used in this example, it is not suitable for nearly-incompressible material behaviour. Otherwise the elements tend to show excessive volumetric locking during deformation and hence, wrong results are calculated.
59 |
60 | ```fortran
61 | include 'ttb/ttb_library.f'
62 |
63 | subroutine hypela2(d,g,e,de,s,t,dt,ngens,m,nn,kcus,matus,ndi,
64 | 2 nshear,disp,dispt,coord,ffn,frotn,strechn,eigvn,ffn1,
65 | 3 frotn1,strechn1,eigvn1,ncrd,itel,ndeg,ndm,
66 | 4 nnode,jtype,lclass,ifr,ifu)
67 |
68 | ! HYPELA2: Nearly-Incompressible Neo-Hookean Material
69 | ! Example for usage of Tensor Toolbox
70 | ! capability: 3D, Axisymmetric
71 | ! Formulation: Total Lagrange
72 | ! Voigt Notation: Change commented Tensor Datatypes
73 | ! Andreas Dutzler, 2018-01-02, Graz University of Technology
74 |
75 | use Tensor
76 | implicit none
77 |
78 | integer :: ifr,ifu,itel,jtype,ncrd,ndeg,ndi,ndm,ngens,
79 | * nn,nnode,nshear
80 | integer, dimension(2) :: m,matus,kcus,lclass
81 | real(kind=8), dimension(*) :: e,de,t,dt,g,s
82 | real(kind=8), dimension(itel) :: strechn,strechn1
83 | real(kind=8), dimension(ngens,*) :: d
84 | real(kind=8), dimension(ncrd,*) :: coord
85 | real(kind=8), dimension(ndeg,*) :: disp, dispt
86 | real(kind=8), dimension(itel,3) :: ffn,ffn1,frotn,frotn1
87 | real(kind=8), dimension(itel,*) :: eigvn,eigvn1
88 |
89 | type(Tensor2) :: F1
90 | real(kind=8) :: J,kappa,C10
91 |
92 | ! to use voigt notation change to type Tensor2s, Tensor4s
93 | type(Tensor2) :: C1,invC1,S1,Eye
94 | type(Tensor4) :: C4
95 |
96 | ! material parameters
97 | C10 = 0.5
98 | kappa = 5.0
99 |
100 | Eye = identity2(Eye)
101 | F1 = ffn1(1:3,1:3) ! use slices (ffn1 is an assumed size array)
102 | J = det(F1)
103 |
104 | ! right cauchy-green deformation tensor and it's inverse
105 | C1 = transpose(F1)*F1
106 | invC1 = inv(C1) ! faster method: invC1 = inv(C1,J**2)
107 |
108 | ! pk2 stress
109 | S1 = 2.*C10*J**(-2./3.)*dev(C1)*invC1 + kappa*(J-1)*J*invC1
110 |
111 | ! material elasticity tensor
112 | C4 = 2.*C10 * J**(-2./3.) * 2./3. *
113 | * ( tr(C1) * (invC1.cdya.invC1)
114 | * - (Eye.dya.invC1) - (invC1.dya.Eye)
115 | * + tr(C1)/3. * (invC1.dya.invC1) )
116 | * + (kappa*(J-1)*J+kappa*J**2) * (invC1.dya.invC1)
117 | * - 2.*kappa*(J-1)*J* (invC1.cdya.invC1)
118 |
119 | ! output as array
120 | s(1:ngens) = asarray( voigt(S1), ngens )
121 | d(1:ngens,1:ngens) = asarray( voigt(C4), ngens, ngens )
122 |
123 | return
124 | end
125 | ```
126 |
127 |
128 |
129 |
130 | Implementation for Abaqus
131 |
132 | ## UMAT User Subroutine for Abaqus
133 | Abaqus uses an Updated-Lagrange approach and hence, Eq. $$\eqref{eq:pk2-nh}$$ and Eq. $$\eqref{eq:c4-nh}$$ are transformed and implemented in a [user subroutine](Abaqus/umat_nh_ttb_simple.f) with the help of this Tensor module.
134 |
135 | ```fortran
136 | include 'ttb/ttb_library.f'
137 |
138 | SUBROUTINE UMAT(STRESS,STATEV,DDSDDE,SSE,SPD,SCD,
139 | 1 RPL,DDSDDT,DRPLDE,DRPLDT,
140 | 2 STRAN,DSTRAN,TIME,DTIME,TEMP,DTEMP,PREDEF,DPRED,CMNAME,
141 | 3 NDI,NSHR,NTENS,NSTATV,PROPS,NPROPS,COORDS,DROT,PNEWDT,
142 | 4 CELENT,DFGRD0,DFGRD1,NOEL,NPT,LAYER,KSPT,JSTEP,KINC)
143 |
144 | ! ABAQUS UMAT: Nearly-Incompressible Neo-Hookean Material
145 | ! Example for usage of Tensor Toolbox
146 | ! capability: 3D, Axisymmetric
147 | ! Formulation: Total Lagrange with push forward for Abaqus
148 | ! Andreas Dutzler, 2018-07-22, Graz University of Technology
149 |
150 | use Tensor
151 |
152 | ! `implicit none` is not supported if 'ABA_PARAM.INC' is included.
153 | ! declare all double-variables which start with `i,j,k,l,m,n`
154 | ! - otherwise they will be integers
155 |
156 | ! implicit none
157 | INCLUDE 'ABA_PARAM.INC'
158 |
159 | CHARACTER*80 CMNAME
160 | DIMENSION STRESS(NTENS),STATEV(NSTATV),
161 | 1 DDSDDE(NTENS,NTENS),DDSDDT(NTENS),DRPLDE(NTENS),
162 | 2 STRAN(NTENS),DSTRAN(NTENS),TIME(2),PREDEF(1),DPRED(1),
163 | 3 PROPS(NPROPS),COORDS(3),DROT(3,3),DFGRD0(3,3),DFGRD1(3,3),
164 | 4 JSTEP(4)
165 |
166 | type(Tensor2) :: F1
167 | real(kind=8) :: J,kappa,C10
168 |
169 | type(Tensor2s) :: C1,invC1,S1,Eye
170 | type(Tensor4s) :: C4
171 |
172 | ! material parameters
173 | C10 = 0.5
174 | kappa = 5.0
175 |
176 | Eye = identity2(Eye)
177 | F1 = dfgrd1(1:3,1:3)
178 | J = det(F1)
179 |
180 | ! right cauchy-green deformation tensor and its inverse
181 | C1 = transpose(F1)*F1
182 | invC1 = inv(C1)
183 |
184 | ! pk2 stress
185 | S1 = 2.*C10*J**(-2./3.)*dev(C1)*invC1 + kappa*(J-1)*J*invC1
186 |
187 | ! push forward to cauchy stress
188 | S1 = piola(F1,S1)/J
189 |
190 | ! material elasticity tensor
191 | C4 = 2.*C10 * J**(-2./3.) * 2./3. *
192 | * ( tr(C1) * (invC1.cdya.invC1)
193 | * - (Eye.dya.invC1) - (invC1.dya.Eye)
194 | * + tr(C1)/3. * (invC1.dya.invC1) )
195 | * + (kappa*(J-1)*J+kappa*J**2) * (invC1.dya.invC1)
196 | * - 2.*kappa*(J-1)*J* (invC1.cdya.invC1)
197 |
198 | ! push forward to jaumann tangent of cauchy stress for abaqus
199 | C4 = piola(F1,C4)/J + (S1.cdya.Eye)+(Eye.cdya.S1)
200 |
201 | ! output as array
202 | STRESS(1:ntens) = asabqarray(voigt(S1),ntens)
203 | DDSDDE(1:ntens,1:ntens) = asabqarray(voigt(C4),ntens,ntens)
204 |
205 | return
206 | end
207 | ```
208 |
209 |
210 |
--------------------------------------------------------------------------------
/README.md:
--------------------------------------------------------------------------------
1 |
2 |  3 |
3 |
Tensor Toolbox for Modern Fortran.
4 |
5 |
6 | 
7 | 
8 | 
9 | [](https://adtzlr.github.io/ttb)
10 | [](https://doi.org/10.5281/zenodo.4077378)
11 |
12 | Commercial FEM software packages offer interfaces (user subroutines written in Fortran) for custom defined user materials like UMAT in [Abaqus](https://www.3ds.com/products-services/simulia/products/abaqus/) or HYPELA2 in [MSC.Marc](http://www.mscsoftware.com/product/marc). In comparison to other scientific programming languages like MATLAB or Python Fortran is not as comfortable to use when dealing with high level programming features of tensor manipulation. On the other hand it's super fast - so why not combine the handy features from MATLAB or Python's NumPy/Scipy with the speed of Fortran? That's the reason why I started working on a simple but effective module called **Tensor Toolbox for Modern Fortran**. I adopted the idea to my needs from [Naumann, C. (2016)](http://nbn-resolving.de/urn:nbn:de:bsz:ch1-qucosa-222075).
13 |
14 | The full documentation is available at [https://adtzlr.github.io/ttb](https://adtzlr.github.io/ttb). This project is licensed under the terms of the [MIT license](LICENSE).
15 |
16 | ## Overview
17 |
18 | 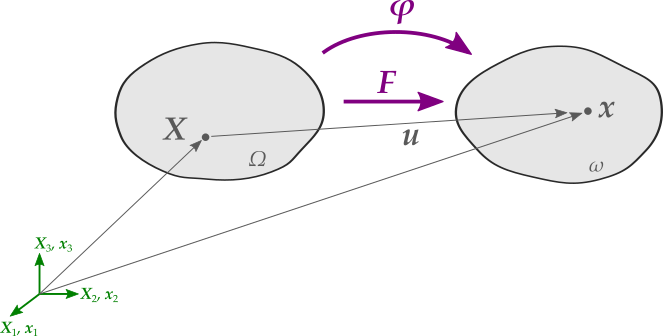
19 |
20 | This tensor toolbox provides the following [basic operations for tensor calculus](docs/api/index.md) (all written in double precision `real(kind=8)`):
21 | - Dot Product `C(i,j) = A(i,k) B(k,j)` written as `C = A*B`
22 | - Double Dot Product `C = A(i,j) B(i,j)` written as `C = A**B`
23 | - Dyadic Product `C(i,j,k,l) = A(i,j) B(k,l)` written as `C = A.dya.B`
24 | - Crossed Dyadic Product `C(i,j,k,l) = (A(i,k) B(j,l) + A(i,l) B(j,k) + B(i,k) A(j,l) + B(i,l) A(j,k))/4` written as `C = A.cdya.B`
25 | - Addition `C(i,j) = A(i,j) + B(i,j)` written as `C = A+B`
26 | - Subtraction `C(i,j) = A(i,j) - B(i,j)` written as `C = A-B`
27 | - Multiplication and Division by a Scalar
28 | - Deviatoric Part of Tensor `dev(C) = C - tr(C)/3 * Eye` written as `dev(C)`
29 | - Transpose and Permutation of indices written as `B = permute(A,1,3,2,4)`
30 | - Rank 2 Identity tensor of input type `Eye = identity2(Eye)` with `C = Eye*C`
31 | - Rank 4 Identity tensor (symmetric variant) of input type `I4 = identity4(Eye)` or `I4 = Eye.cdya.Eye` with `C = I4**C` or `inv(C) = identity4(inv(C))**C`
32 | - Square Root of a positive definite rank 2 tensor `U = sqrt(C)`
33 | - Assigment of a real-valued Scalar to all components of a Tensor `A = 0.0` or `A = 0.d0`
34 | - Assigment of a real-valued Array to a Tensor with matching dimensions `A = B` where B is an Array and A a Tensor
35 | - Assigment of a Tensor in Voigt notation to a Tensor in tensorial notation and vice versa
36 |
37 | The idea is to create derived data types for rank 1, rank 2 and rank 4 tensors (and it's symmetric variants). In a next step the operators are defined in a way that Fortran calls different functions based on the input types of the operator: performing a dot product between a vector and a rank 2 tensor or a rank 2 and a rank 2 tensor is a different function. Best of it: you don't have to take care of that.
38 |
39 | ## Basic Usage
40 | The most basic example on how to use this module is to [download the module](https://github.com/adtzlr/ttb/archive/main.zip), put the 'ttb'-Folder in your working directory and add two lines of code:
41 |
42 | ```fortran
43 | include 'ttb/ttb_library.f'
44 |
45 | program script101_ttb
46 | use Tensor
47 | implicit none
48 |
49 | ! user code
50 |
51 | end program script101_ttb
52 | ```
53 | The `include 'ttb/ttb_library.f'` statement replaces the line with the content of the ttb-module. The first line in a program or subroutine is now a `use Tensor` statement. That's it - now you're ready to go.
54 |
55 | ## Tensor or Voigt Notation
56 | It depends on your preferences: either you store all tensors in full tensor `dimension(3,3)` or in [voigt](https://en.wikipedia.org/wiki/Voigt_notation) `dimension(6)` notation. The equations remain (nearly) the same. Dot Product, Double Dot Product - every function is implemented in both full tensor and voigt notation. Look for the voigt-comments in an [example](docs/examples/Marc/hypela2_nh_ttb.f) of a user subroutine for MSC.Marc.
57 |
58 | ## Access Tensor components by Array
59 | Tensor components may be accessed by a conventional array with the name of the tensor variable `T` followed by a percent operator `%` and a type-specific keyword as follows:
60 |
61 | - Tensor of rank 1 components as array: `T%a`. i-th component of T: `T%a(i)`
62 | - Tensor of rank 2 components as array: `T%ab`. i,j component of T: `T%ab(i,j)`
63 | - Tensor of rank 4 components as array: `T%abcd`. i,j,k,l component of T: `T%abcd(i,j,k,l)`
64 |
65 | - Symmetric Tensor of rank 2 (Voigt) components as array: `T%a6`. i-th component of T: `T%a6(i)`
66 | - Symmetric Tensor of rank 4 (Voigt) components as array: `T%a6b6`. i,j component of T: `T%a6b6(i,j)` (at least minor symmetric)
67 |
68 | ### Warning: Output as array
69 | It is not possible to access tensor components of a tensor valued function in a direct way `s = symstore(S1)%a6` - unfortunately this is a limitation of Fortran. To avoid the creation of an extra variable it is possible to use the `asarray(T,i_max[,j_max,k_max,l_max])` function to access tensor components. `i_max,j_max,k_max,l_max` is **not** the single component, instead a slice `T%abcd(1:i_max,1:j_max,1:k_max,1:l_max)` is returned. This can be useful when dealing with mixed formulation or variation principles where the last entry/entries of stress and strain voigt vectors are used for the pressure boundary. To export a full stress tensor `S1` to voigt notation use:
70 |
71 | ```fortran
72 | s(1:ndim) = asarray( voigt(S1), ndim )
73 | d(1:ndim,1:ndim) = asarray( voigt(C4), ndim, ndim )
74 | ```
75 |
76 | #### Abaqus Users: Output as abqarray
77 | To export a stress tensor to Abaqus Voigt notation use `asabqarray` which reorders the storage indices to `11,22,33,12,13,23`. This function is available for `Tensor2s` and `Tensor4s` data types.
78 |
79 | ```fortran
80 | s(1:ndim) = asabqarray( symstore(S1), ndim )
81 | ddsdde(1:ndim,1:ndim) = asabqarray( symstore(C4), ndim, ndim )
82 | ```
83 |
84 | ## A note on the Permutation of Indices
85 | The permutation function reorders indices in the given order for a fourth order tensor of data type `Tensor4`. Example: `(i,j,k,l) --> (i,k,j,l)` with `permute(C4,1,3,2,4)`.
86 |
87 | ## Neo-Hookean Material
88 | With the help of the Tensor module the Second Piola-Kirchhoff stress tensor `S` of a nearly-incompressible Neo-Hookean material model is basically a one-liner:
89 |
90 | ### Second Piola Kirchhoff Stress Tensor
91 | ```fortran
92 | S = mu*det(C)**(-1./3.)*dev(C)*inv(C)+p*det(C)**(1./2.)*inv(C)
93 | ```
94 |
95 | While this is of course not the fastest way of calculating the stress tensor it is extremely short and readable. Also the second order tensor variables `S, C` and scalar quantities `mu, p` have to be created at the beginning of the program. A minimal working example for a very simple umat user subroutine can be found in [script_umat.f](docs/examples/script_umat.f). The program is just an example where a subroutine `umat` is called and an output information is printed. It is shown that the tensor toolbox is only used inside the material user subroutine `umat`.
96 |
97 | ### Material Elasticity Tensor
98 | The isochoric part of the material elasticity tensor `C4_iso` of a nearly-incompressible Neo-Hookean material model is defined and coded as:
99 |
100 | ```fortran
101 | C4_iso = det(F)**(-2./3.) * 2./3.* (
102 | * tr(C) * identity4(inv(C))
103 | * - (Eye.dya.inv(C)) - (inv(C).dya.Eye)
104 | * + tr(C)/3. * (inv(C).dya.inv(C)) )
105 | ```
106 |
107 | ### Example of Marc HYPELA2
108 | [Here](docs/examples/Marc/hypela2_nh_ttb.f) you can find an example of a nearly-incompressible version of a Neo-Hookean material for Marc. Updated Lagrange is implemented by a push forward operator of both the stress and the fourth-order elasticity tensor. Herrmann Elements are automatically detected. As HYPELA2 is called twice per iteration the stiffness calculation is only active during stage `lovl == 4`. One of the best things is the super-simple switch from tensor to voigt notation: Change data types of all symmetric tensors and save the right Cauchy-Green deformation tensor in voigt notation. See commented lines for details.
109 |
110 | [Download HYPELA2](docs/examples/Marc/hypela2_nh_ttb.f): *Neo-Hooke, Marc, Total Lagrange, Tensor Toolbox*
111 |
112 | ## Credits
113 | Naumann, C.: [Chemisch-mechanisch gekoppelte Modellierung und Simulation oxidativer Alterungsvorgänge in Gummibauteilen (German)](http://nbn-resolving.de/urn:nbn:de:bsz:ch1-qucosa-222075). PhD thesis. Fakultät für Maschinenbau der Technischen Universität Chemnitz, 2016.
114 |
115 | # Changelog
116 | All notable changes to this project will be documented in [this file](CHANGELOG.md). The format is based on [Keep a Changelog](https://keepachangelog.com/en/1.0.0/), and this project adheres to [Semantic Versioning](https://semver.org/spec/v2.0.0.html).
117 |
--------------------------------------------------------------------------------
/docs/examples/ex01_stvenantkirchhoff.md:
--------------------------------------------------------------------------------
1 | ---
2 | title: Ex. 01 - Saint Venant-Kirchhoff
3 | layout: page
4 | nav_order: 4
5 | parent: Examples
6 | ---
7 |
8 | # Saint Venant-Kirchhoff
9 |
10 | The following example discusses the implementation of a Saint Venant-Kirchhoff material in a very simple and readable user subroutine. The Saint Venant-Kirchhoff material is possibly the simplest example for a hyperelastic material but suffers from practical relevance beyond the small strain range [1]. Anyway, it's a good starting point because stress tensor and elasticity matrix are of the same form as the linear elasticity formulation, except that Green-Lagrange strains are used.
11 |
12 | ## Kinematics
13 | Starting from the Deformation Gradient, we calculate the Green-Lagrange strain tensor in Eq. $$\eqref{eq:gl-strain}$$ with the right Cauchy-Green deformation tensor, see Eq. $$\eqref{eq:cauchy-green}$$.
14 |
15 | $$
16 | \begin{equation}
17 | \boldsymbol{E} = \frac{1}{2} (\boldsymbol{C} - \boldsymbol{1}) \label{eq:gl-strain}
18 | \end{equation}
19 | $$
20 |
21 | and
22 |
23 | $$
24 | \begin{equation}
25 | \boldsymbol{C} = \boldsymbol{F}^T \boldsymbol{F} \label{eq:cauchy-green}
26 | \end{equation}
27 | $$
28 |
29 | ## Subroutine Header for user materials
30 | Before we are able to add our own user code, we have to start with an empty fortran subroutine header. Headers are provided e.g. for Marc, Abaqus, Dyna, ANSYS in their corresponding manuals.
31 |
32 |
33 | Header for Marc
34 |
35 | ### HYPELA2 for Marc
36 |
37 | ```fortran
38 | include 'ttb/ttb_library.f'
39 |
40 | subroutine hypela2(d,g,e,de,s,t,dt,ngens,m,nn,kcus,matus,ndi,
41 | 2 nshear,disp,dispt,coord,ffn,frotn,strechn,eigvn,ffn1,
42 | 3 frotn1,strechn1,eigvn1,ncrd,itel,ndeg,ndm,
43 | 4 nnode,jtype,lclass,ifr,ifu)
44 |
45 | use Tensor
46 | implicit none
47 |
48 | integer :: ifr,ifu,itel,jtype,ncrd,ndeg,ndi,ndm,ngens,
49 | * nn,nnode,nshear
50 | integer, dimension(2) :: m,matus,kcus,lclass
51 | real(kind=8), dimension(*) :: e,de,t,dt,g,s
52 | real(kind=8), dimension(itel) :: strechn,strechn1
53 | real(kind=8), dimension(ngens,*) :: d
54 | real(kind=8), dimension(ncrd,*) :: coord
55 | real(kind=8), dimension(ndeg,*) :: disp, dispt
56 | real(kind=8), dimension(itel,3) :: ffn,ffn1,frotn,frotn1
57 | real(kind=8), dimension(itel,*) :: eigvn,eigvn1
58 |
59 | ! ...user code...
60 |
61 | return
62 | end
63 | ```
64 |
65 |
66 |
67 |
68 | Header for Abaqus
69 |
70 | ### UMAT for Abaqus
71 |
72 | ```fortran
73 | include 'ttb/ttb_library.f'
74 |
75 | SUBROUTINE UMAT(STRESS,STATEV,DDSDDE,SSE,SPD,SCD,
76 | 1 RPL,DDSDDT,DRPLDE,DRPLDT,
77 | 2 STRAN,DSTRAN,TIME,DTIME,TEMP,DTEMP,PREDEF,DPRED,CMNAME,
78 | 3 NDI,NSHR,NTENS,NSTATV,PROPS,NPROPS,COORDS,DROT,PNEWDT,
79 | 4 CELENT,DFGRD0,DFGRD1,NOEL,NPT,LAYER,KSPT,JSTEP,KINC)
80 |
81 | use Tensor
82 | implicit none
83 |
84 | CHARACTER*80 CMNAME
85 | DIMENSION STRESS(NTENS),STATEV(NSTATV),
86 | 1 DDSDDE(NTENS,NTENS),DDSDDT(NTENS),DRPLDE(NTENS),
87 | 2 STRAN(NTENS),DSTRAN(NTENS),TIME(2),PREDEF(1),DPRED(1),
88 | 3 PROPS(NPROPS),COORDS(3),DROT(3,3),DFGRD0(3,3),DFGRD1(3,3),
89 | 4 JSTEP(4)
90 |
91 | ! ...user code...
92 |
93 | return
94 | end
95 | ```
96 |
97 |
98 |
99 | First we need to define our material parameters, which will be entered as young's modulus and poisson ratio.
100 |
101 | ```fortran
102 | real(kind=8) :: young,nu,lambda,mu
103 |
104 | ! material parameters
105 | young = 210000.0
106 | nu = 0.3
107 |
108 | ! lame parameter
109 | mu = young / ( 2.*(1.+nu) )
110 | lambda = nu*young / ((1.+nu)*(1.-2.*nu))
111 | ```
112 |
113 | In our code implementation the strain tensor looks like:
114 |
115 | ```fortran
116 | type(Tensor2) :: F1
117 | type(Tensor2s) :: E1,Eye
118 |
119 | Eye = Eye**0
120 |
121 | F1 = Eye
122 | F1%ab(1:3,1:3) = ffn1(1:3,1:3)
123 |
124 | E1 = 0.5*(transpose(F1)*F1-Eye)
125 | ```
126 |
127 | We first initialize a rank 2 Identity Tensor `Eye`. Then the Deformation Gradient Tensor at the end of the increment `F1` is initialized with no deformation and overwritten by `ffn1` with dimension `(itel,3)` where `itel` being an integer `2` or `3` based on the analysis type. This is necessary because this module is hardcoded to three dimensions whereas MSC.Marc has reduced storage options for the Deformation Gradient in plane or axisymmetric analysis types. Finally we calculate the Green-Lagrange Strain Tensor.
128 |
129 | ## Strain Energy Potential
130 | We'll derive both stress and elasticity tensor in the material (reference) configuration. At first we need the definition for the strain energy density function per unit reference volume which depends on the Green-Lagrange strain tensor, see Eq. $$\eqref{eq:psi-svk}$$.
131 |
132 | $$
133 | \begin{equation}
134 | \psi(\boldsymbol{E}) = \frac{1}{2} \lambda(\text{tr}\boldsymbol{E})^2+\mu \boldsymbol{E} : \boldsymbol{E}
135 | \label{eq:psi-svk}
136 | \end{equation}
137 | $$
138 |
139 | ## Material Stress Tensor
140 | In the next step, we get the 2nd Piola-Kirchhoff stress tensor as a partial derivative of the strain energy potential with respect to the Green-Lagrange strain tensor, see Eq. $$\eqref{eq:pk2-svk}$$.
141 |
142 | $$
143 | \begin{equation}
144 | \boldsymbol{S} = \frac{\partial \psi(\boldsymbol{E})}{\partial \boldsymbol{E}} = \lambda(\text{tr}\boldsymbol{E}) \boldsymbol{1} + 2 \mu \boldsymbol{E}
145 | \label{eq:pk2-svk}
146 | \end{equation}
147 | $$
148 |
149 | Inside our subroutine the stress tensor is
150 |
151 | ```fortran
152 | type(Tensor2s) :: S1
153 |
154 | S1 = lambda*tr(E1)*Eye + 2.*mu*E1
155 | ```
156 |
157 | ## Material Elasticity Tensor
158 | With the second derivative of the strain energy potential we get the corresponding elasticity tensor, see Eq. $$\eqref{eq:c4-svk}$$.
159 |
160 | $$
161 | \begin{equation}
162 | \mathbb{C} = \frac{\partial^2 \psi(\boldsymbol{E})}{\partial \boldsymbol{E} \partial \boldsymbol{E}} = \lambda \boldsymbol{1} \otimes \boldsymbol{1} + 2 \mu \boldsymbol{1} \odot \boldsymbol{1}
163 | \label{eq:c4-svk}
164 | \end{equation}
165 | $$
166 |
167 | Again, in our fortran subroutine the code for this elasticity tensor is as follows:
168 |
169 | ```fortran
170 | type(Tensor4s) :: C4
171 |
172 | C4 = lambda*(Eye.dya.Eye) + 2.*mu*(Eye.cdya.Eye)
173 | ```
174 |
175 | The crossed dyadic product is implemented as the symmetric variant in this module, so writing `Eye.cdya.Eye` is enough for the symmetric version of the rank 4 Identity Tensor.
176 |
177 | ## Export as Array
178 | Finally we have to export our Tensor data back to conventional fortran arrays.
179 |
180 |
181 | Export for Marc
182 |
183 | {: .important }
184 | > If we would like to use the Updated Lagrange framework in Marc, we'll have to check whether the updated or the total lagrange framework is active. Please note that for the updated lagrange framework it is common to use the jaumann rate of kirchhoff stress in commercial FE codes. First, the tangent matrix is pushed forward to spatial components `(i,j,k,l)`, divided by the volumetric ratio `J` and then transformed to the jaumann rate of kirchhoff stress. For the elasticity tensor conversion have a look at Maria Holland's Hitchhiker's Guide to Abaqus [2].
185 |
186 | ```fortran
187 | real(kind=8) :: J
188 |
189 | ! ...some code...
190 |
191 | if (iupdat.eq.1) then ! updated lagrange
192 | J = det(F1)
193 | ! cauchy stress
194 | S1 = piola(F1,S1)/J
195 | ! tangent matrix (jaumann)
196 | C4 = piola(F1,C4)/J
197 | * + (S1.cdya.Eye) + (Eye.cdya.S1)
198 | endif
199 | ```
200 |
201 | In this code `iupdat` is an integer with
202 |
203 | * `0` for total lagrange and
204 | * `1` for updated lagrange.
205 |
206 | ```fortran
207 | ! output as array
208 | s(1:ngens) = asarray( asvoigt(S1), ngens )
209 | d(1:ngens,1:ngens) = asarray( asvoigt(C4), ngens, ngens )
210 | ```
211 |
212 | You may download the example as a [HYPELA2 user subroutine](Marc/hypela2_stvenantkirchhoff.f) for Marc.
213 |
214 |
215 |
216 |
217 | Export for Abaqus
218 |
219 | {: .important }
220 | > Abaqus uses the Updated Lagrange framework. Please note that for the updated lagrange framework it is common to use the jaumann rate of kirchhoff stress in commercial FE codes. First, the tangent matrix is pushed forward to spatial components `(i,j,k,l)`, divided by the volumetric ratio `J` and then transformed to the jaumann rate of kirchhoff stress. For the elasticity tensor conversion have a look at Maria Holland's Hitchhiker's Guide to Abaqus [2].
221 |
222 | ```fortran
223 | ! push forward to cauchy stress
224 | J = det(F1)
225 | S1 = piola(F1,S1)/J
226 |
227 | ! push forward to jaumann tangent of cauchy stress for abaqus
228 | C4 = piola(F1,C4)/J + (S1.cdya.Eye)+(Eye.cdya.S1)
229 |
230 | ! output as abaqus array
231 | STRESS(1:ntens) = asabqarray( voigt(S1), ntens )
232 | DDSDDE(1:ntens,1:ntens) = asabqarray( voigt(C4), ntens, ntens )
233 | ```
234 |
235 |
236 |
237 | ## References
238 | [1] Bonet, J., Gil, A. J., & Wood, R. D. (2016). Nonlinear Solid Mechanics for Finite Element Analysis: Statics. Cambridge University Press. [](https://doi.org/10.1017/cbo9781316336144)
239 |
240 | [2] Holland, M. (2018, May 7). Mholla/Hitchhikers-Guide-To-Abaqus: Initial Release (Version v1.0). Zenodo. [](https://doi.org/10.5281/zenodo.1243270)
241 |
--------------------------------------------------------------------------------
/ttb/libdot.f:
--------------------------------------------------------------------------------
1 | ! ------DOT SECTION-----------------------------------------
2 | ! ------SIMPLE DOT SECTION----------------------------------
3 | ! ------REAL(KIND=8)----------------------------------------
4 | function dot_01(w, T)
5 | implicit none
6 |
7 | real(kind=8), intent(in) :: w
8 | type(Tensor1), intent(in) :: T
9 | type(Tensor1) :: dot_01
10 |
11 | dot_01%a = w * T%a
12 |
13 | end function dot_01
14 |
15 | function dot_10(T, w)
16 | implicit none
17 |
18 | real(kind=8), intent(in) :: w
19 | type(Tensor1), intent(in) :: T
20 | type(Tensor1) :: dot_10
21 |
22 | dot_10%a = w * T%a
23 |
24 | end function dot_10
25 |
26 | function dot_02(w, T)
27 | implicit none
28 |
29 | real(kind=8), intent(in) :: w
30 | type(Tensor2), intent(in) :: T
31 | type(Tensor2) :: dot_02
32 |
33 | dot_02%ab = w * T%ab
34 |
35 | end function dot_02
36 |
37 | function dot_02s(w, T)
38 | implicit none
39 |
40 | real(kind=8), intent(in) :: w
41 | type(Tensor2s), intent(in) :: T
42 | type(Tensor2s) :: dot_02s
43 |
44 | dot_02s%a6 = w * T%a6
45 |
46 | end function dot_02s
47 |
48 | function dot_20(T, w)
49 | implicit none
50 |
51 | real(kind=8), intent(in) :: w
52 | type(Tensor2), intent(in) :: T
53 | type(Tensor2) :: dot_20
54 |
55 | dot_20%ab = w * T%ab
56 |
57 | end function dot_20
58 |
59 | function dot_20s(T, w)
60 | implicit none
61 |
62 | real(kind=8), intent(in) :: w
63 | type(Tensor2s), intent(in) :: T
64 | type(Tensor2s) :: dot_20s
65 |
66 | dot_20s%a6 = w * T%a6
67 |
68 | end function dot_20s
69 |
70 | function dot_04(w, T)
71 | implicit none
72 |
73 | real(kind=8), intent(in) :: w
74 | type(Tensor4), intent(in) :: T
75 | type(Tensor4) :: dot_04
76 |
77 | dot_04%abcd = w * T%abcd
78 |
79 | end function dot_04
80 |
81 | function dot_04s(w, T)
82 | implicit none
83 |
84 | real(kind=8), intent(in) :: w
85 | type(Tensor4s), intent(in) :: T
86 | type(Tensor4s) :: dot_04s
87 |
88 | dot_04s%a6b6 = w * T%a6b6
89 |
90 | end function dot_04s
91 |
92 | function dot_40(T, w)
93 | implicit none
94 |
95 | real(kind=8), intent(in) :: w
96 | type(Tensor4), intent(in) :: T
97 | type(Tensor4) :: dot_40
98 |
99 | dot_40%abcd = w * T%abcd
100 |
101 | end function dot_40
102 |
103 | function dot_40s(T, w)
104 | implicit none
105 |
106 | real(kind=8), intent(in) :: w
107 | type(Tensor4s), intent(in) :: T
108 | type(Tensor4s) :: dot_40s
109 |
110 | dot_40s%a6b6 = w * T%a6b6
111 |
112 | end function dot_40s
113 | ! ------REAL(KIND=4)----------------------------------------
114 | function dot_01_r4(w, T)
115 | implicit none
116 |
117 | real(kind=4), intent(in) :: w
118 | type(Tensor1), intent(in) :: T
119 | type(Tensor1) :: dot_01_r4
120 |
121 | dot_01_r4%a = dble(w) * T%a
122 |
123 | end function dot_01_r4
124 |
125 | function dot_10_r4(T, w)
126 | implicit none
127 |
128 | real(kind=4), intent(in) :: w
129 | type(Tensor1), intent(in) :: T
130 | type(Tensor1) :: dot_10_r4
131 |
132 | dot_10_r4%a = dble(w) * T%a
133 |
134 | end function dot_10_r4
135 |
136 | function dot_02_r4(w, T)
137 | implicit none
138 |
139 | real(kind=4), intent(in) :: w
140 | type(Tensor2), intent(in) :: T
141 | type(Tensor2) :: dot_02_r4
142 |
143 | dot_02_r4%ab = dble(w) * T%ab
144 |
145 | end function dot_02_r4
146 |
147 | function dot_02s_r4(w, T)
148 | implicit none
149 |
150 | real(kind=4), intent(in) :: w
151 | type(Tensor2s), intent(in) :: T
152 | type(Tensor2s) :: dot_02s_r4
153 |
154 | dot_02s_r4%a6 = dble(w) * T%a6
155 |
156 | end function dot_02s_r4
157 |
158 | function dot_20_r4(T, w)
159 | implicit none
160 |
161 | real(kind=4), intent(in) :: w
162 | type(Tensor2), intent(in) :: T
163 | type(Tensor2) :: dot_20_r4
164 |
165 | dot_20_r4%ab = dble(w) * T%ab
166 |
167 | end function dot_20_r4
168 |
169 | function dot_20s_r4(T, w)
170 | implicit none
171 |
172 | real(kind=4), intent(in) :: w
173 | type(Tensor2s), intent(in) :: T
174 | type(Tensor2s) :: dot_20s_r4
175 |
176 | dot_20s_r4%a6 = dble(w) * T%a6
177 |
178 | end function dot_20s_r4
179 |
180 | function dot_04_r4(w, T)
181 | implicit none
182 |
183 | real(kind=4), intent(in) :: w
184 | type(Tensor4), intent(in) :: T
185 | type(Tensor4) :: dot_04_r4
186 |
187 | dot_04_r4%abcd = dble(w) * T%abcd
188 |
189 | end function dot_04_r4
190 |
191 | function dot_04s_r4(w, T)
192 | implicit none
193 |
194 | real(kind=4), intent(in) :: w
195 | type(Tensor4s), intent(in) :: T
196 | type(Tensor4s) :: dot_04s_r4
197 |
198 | dot_04s_r4%a6b6 = dble(w) * T%a6b6
199 |
200 | end function dot_04s_r4
201 |
202 | function dot_40_r4(T, w)
203 | implicit none
204 |
205 | real(kind=4), intent(in) :: w
206 | type(Tensor4), intent(in) :: T
207 | type(Tensor4) :: dot_40_r4
208 |
209 | dot_40_r4%abcd = dble(w) * T%abcd
210 |
211 | end function dot_40_r4
212 |
213 | function dot_40s_r4(T, w)
214 | implicit none
215 |
216 | real(kind=4), intent(in) :: w
217 | type(Tensor4s), intent(in) :: T
218 | type(Tensor4s) :: dot_40s_r4
219 |
220 | dot_40s_r4%a6b6 = dble(w) * T%a6b6
221 |
222 | end function dot_40s_r4
223 |
224 | ! ------REAL(KIND=8)----------------------------------------
225 | function dot_21(T1, T2)
226 | implicit none
227 |
228 | type(Tensor2), intent(in) :: T1
229 | type(Tensor1), intent(in) :: T2
230 | type(Tensor1) :: dot_21
231 | integer :: i, j
232 |
233 | do i = 1,3
234 | dot_21%a(i) = 0.d0
235 | do j = 1,3
236 | dot_21%a(i) = dot_21%a(i) + T1%ab(i,j)*T2%a(j)
237 | enddo
238 | enddo
239 |
240 | end function dot_21
241 |
242 | function dot_2s1(T1, T2)
243 | implicit none
244 |
245 | type(Tensor2s), intent(in) :: T1
246 | type(Tensor1), intent(in) :: T2
247 | type(Tensor1) :: dot_2s1
248 |
249 | dot_2s1%a(1)=T1%a6(1)*T2%a(1)+T1%a6(4)*T2%a(2)+T1%a6(6)*T2%a(3)
250 | dot_2s1%a(2)=T1%a6(4)*T2%a(1)+T1%a6(2)*T2%a(2)+T1%a6(5)*T2%a(3)
251 | dot_2s1%a(3)=T1%a6(6)*T2%a(1)+T1%a6(5)*T2%a(2)+T1%a6(3)*T2%a(3)
252 |
253 | end function dot_2s1
254 |
255 | function dot_12(T1, T2)
256 | implicit none
257 |
258 | type(Tensor1), intent(in) :: T1
259 | type(Tensor2), intent(in) :: T2
260 | type(Tensor1) :: dot_12
261 | integer :: i, j
262 |
263 | do i = 1,3
264 | dot_12%a(i) = 0.d0
265 | do j = 1,3
266 | dot_12%a(i) = dot_12%a(i) + T1%a(j)*T2%ab(j,i)
267 | enddo
268 | enddo
269 |
270 | end function dot_12
271 |
272 | function dot_12s(T1, T2)
273 | implicit none
274 |
275 | type(Tensor2s), intent(in) :: T2
276 | type(Tensor1), intent(in) :: T1
277 | type(Tensor1) :: dot_12s
278 |
279 | dot_12s%a(1)=T1%a(1)*T2%a6(1)+T1%a(2)*T2%a6(4)+T1%a(3)*T2%a6(6)
280 | dot_12s%a(2)=T1%a(1)*T2%a6(4)+T1%a(2)*T2%a6(2)+T1%a(3)*T2%a6(5)
281 | dot_12s%a(3)=T1%a(1)*T2%a6(6)+T1%a(2)*T2%a6(5)+T1%a(3)*T2%a6(3)
282 |
283 | end function dot_12s
284 |
285 | function dot_11(T1, T2)
286 | implicit none
287 |
288 | type(Tensor1), intent(in) :: T1
289 | type(Tensor1), intent(in) :: T2
290 | real(kind=8) :: dot_11
291 | integer :: i
292 |
293 | dot_11 = 0.d0
294 | do i = 1,3
295 | dot_11 = dot_11 + T1%a(i)*T2%a(i)
296 | enddo
297 | end function dot_11
298 |
299 | function dot_22(T1, T2)
300 | implicit none
301 |
302 | type(Tensor2), intent(in) :: T1
303 | type(Tensor2), intent(in) :: T2
304 | type(Tensor2) :: dot_22
305 | integer :: i,j,k
306 |
307 | dot_22%ab = 0.d0
308 | do i = 1,3
309 | do j = 1,3
310 | do k = 1,3
311 | dot_22%ab(i,j) = dot_22%ab(i,j) + T1%ab(i,k)*T2%ab(k,j)
312 | enddo
313 | enddo
314 | enddo
315 | end function dot_22
316 |
317 | function dot_2s2s(T1, T2)
318 | implicit none
319 |
320 | type(Tensor2s), intent(in) :: T1, T2
321 | type(Tensor2) :: dot_2s2s
322 |
323 | dot_2s2s%ab(1,1) = T1%a6(1)*T2%a6(1)+T1%a6(4)*T2%a6(4)
324 | * +T1%a6(6)*T2%a6(6)
325 | dot_2s2s%ab(2,2) = T1%a6(4)*T2%a6(4)+T1%a6(2)*T2%a6(2)
326 | * +T1%a6(5)*T2%a6(5)
327 | dot_2s2s%ab(3,3) = T1%a6(6)*T2%a6(6)+T1%a6(5)*T2%a6(5)
328 | * +T1%a6(3)*T2%a6(3)
329 | dot_2s2s%ab(1,2) = T1%a6(1)*T2%a6(4)+T1%a6(4)*T2%a6(2)
330 | * +T1%a6(6)*T2%a6(5)
331 | dot_2s2s%ab(2,1) = T1%a6(4)*T2%a6(1)+T1%a6(2)*T2%a6(4)
332 | * +T1%a6(5)*T2%a6(6)
333 | dot_2s2s%ab(2,3) = T1%a6(4)*T2%a6(6)+T1%a6(2)*T2%a6(5)
334 | * +T1%a6(5)*T2%a6(3)
335 | dot_2s2s%ab(3,2) = T1%a6(6)*T2%a6(4)+T1%a6(5)*T2%a6(2)
336 | * +T1%a6(3)*T2%a6(5)
337 | dot_2s2s%ab(1,3) = T1%a6(1)*T2%a6(6)+T1%a6(4)*T2%a6(5)
338 | * +T1%a6(6)*T2%a6(3)
339 | dot_2s2s%ab(3,1) = T1%a6(6)*T2%a6(1)+T1%a6(5)*T2%a6(4)
340 | * +T1%a6(3)*T2%a6(6)
341 | end function dot_2s2s
342 |
--------------------------------------------------------------------------------
/ttb/ttb_library.f:
--------------------------------------------------------------------------------
1 | ! -----------MODULE TENSOR---------------------------------------
2 | module Tensor
3 | ! ---------------------------------------
4 | ! Tensor Toolbox Module for Fortran
5 | ! Andreas Dutzler
6 | ! Graz University of Technology
7 | ! Institute of Structural Durability
8 | ! and Railway Technology
9 | ! ---------------------------------------
10 | ! tested on: Windows 10 (64bit)
11 | ! - Intel Fortran >2015
12 | ! - MinGW gfortran >6.3
13 | ! ---------------------------------------
14 | ! use this module in the following form:
15 | ! ---------------------------------------
16 | ! include 'ttb/ttb_library.f'
17 | ! program sample
18 | ! use Tensor
19 | ! ...
20 | ! end program sample
21 | ! ---------------------------------------
22 |
23 | type Tensor1
24 | ! tensor of rank 1
25 | real(kind=8), dimension(3) :: a = 0.d0
26 | end type Tensor1
27 |
28 | type Tensor2
29 | ! tensor of rank 2
30 | real(kind=8), dimension(3,3) :: ab = 0.d0
31 | end type Tensor2
32 |
33 | type Tensor2S
34 | ! symmetric tensor of rank 2 stored as vector
35 | real(kind=8), dimension(6) :: a6 = 0.d0
36 | end type Tensor2S
37 |
38 | type Tensor4
39 | ! tensor of rank 4
40 | real(kind=8), dimension(3,3,3,3) :: abcd = 0.d0
41 | end type Tensor4
42 |
43 | type Tensor4S
44 | ! symmetric tensor of rank 4 stored as 6x6 matrix
45 | real(kind=8), dimension(6, 6) :: a6b6 = 0.d0
46 | end type Tensor4S
47 |
48 | ! ------BEGIN INTERFACE-------------------------------------
49 | interface operator (/)
50 | module procedure div_10
51 | module procedure div_20
52 | module procedure div_20s
53 | module procedure div_40
54 | module procedure div_40s
55 | module procedure div_10_r4
56 | module procedure div_20_r4
57 | module procedure div_20s_r4
58 | module procedure div_40_r4
59 | module procedure div_40s_r4
60 | end interface
61 | interface operator (.div.)
62 | module procedure div_10
63 | module procedure div_20
64 | module procedure div_20s
65 | module procedure div_40
66 | module procedure div_40s
67 | module procedure div_10_r4
68 | module procedure div_20_r4
69 | module procedure div_20s_r4
70 | module procedure div_40_r4
71 | module procedure div_40s_r4
72 | end interface
73 |
74 | interface operator (*)
75 | ! simple dot-product of rank 1 and rank 2 tensor combinations
76 | module procedure dot_01
77 | module procedure dot_10
78 | module procedure dot_02
79 | module procedure dot_02s
80 | module procedure dot_20
81 | module procedure dot_20s
82 | module procedure dot_04
83 | module procedure dot_04s
84 | module procedure dot_40
85 | module procedure dot_40s
86 | module procedure dot_11
87 | module procedure dot_12
88 | module procedure dot_21
89 | module procedure dot_2s1
90 | module procedure dot_12s
91 | module procedure dot_22
92 | module procedure dot_2s2s
93 | module procedure dot_01_r4
94 | module procedure dot_10_r4
95 | module procedure dot_02_r4
96 | module procedure dot_02s_r4
97 | module procedure dot_20_r4
98 | module procedure dot_20s_r4
99 | module procedure dot_04_r4
100 | module procedure dot_04s_r4
101 | module procedure dot_40_r4
102 | module procedure dot_40s_r4
103 | end interface
104 | interface operator (.dot.)
105 | ! simple dot-product of rank 1 and rank 2 tensor combinations
106 | module procedure dot_01
107 | module procedure dot_10
108 | module procedure dot_02
109 | module procedure dot_02s
110 | module procedure dot_20
111 | module procedure dot_20s
112 | module procedure dot_04
113 | module procedure dot_04s
114 | module procedure dot_40
115 | module procedure dot_40s
116 | module procedure dot_11
117 | module procedure dot_12
118 | module procedure dot_21
119 | module procedure dot_2s1
120 | module procedure dot_12s
121 | module procedure dot_22
122 | module procedure dot_2s2s
123 | module procedure dot_01_r4
124 | module procedure dot_10_r4
125 | module procedure dot_02_r4
126 | module procedure dot_02s_r4
127 | module procedure dot_20_r4
128 | module procedure dot_20s_r4
129 | module procedure dot_04_r4
130 | module procedure dot_04s_r4
131 | module procedure dot_40_r4
132 | module procedure dot_40s_r4
133 | end interface
134 |
135 | interface operator (**)
136 | ! double dot-product of rank 1 and rank 2 tensor combinations
137 | module procedure ddot_22
138 | module procedure ddot_2s2s
139 | module procedure ddot_24
140 | module procedure ddot_2s4s
141 | module procedure ddot_42
142 | module procedure ddot_4s2s
143 | module procedure ddot_44
144 | module procedure ddot_4s4s
145 | module procedure pow_2
146 | module procedure pow_2s
147 | end interface
148 |
149 | interface operator (.ddot.)
150 | ! double dot-product of rank 1 and rank 2 tensor combinations
151 | module procedure ddot_22
152 | module procedure ddot_2s2s
153 | module procedure ddot_24
154 | module procedure ddot_2s4s
155 | module procedure ddot_42
156 | module procedure ddot_4s2s
157 | module procedure ddot_44
158 | module procedure ddot_4s4s
159 | end interface
160 |
161 | interface operator (.pow.)
162 | module procedure pow_2
163 | module procedure pow_2s
164 | end interface
165 |
166 | interface operator (+)
167 | ! addition of rank 1 and rank 2 tensors
168 | module procedure add_11
169 | module procedure add_22
170 | module procedure add_44
171 | module procedure add_2s2s
172 | module procedure add_22s
173 | module procedure add_2s2
174 | module procedure add_4s4s
175 | module procedure add_44s
176 | module procedure add_4s4
177 | end interface
178 | interface operator (.add.)
179 | ! addition of rank 1 and rank 2 tensors
180 | module procedure add_11
181 | module procedure add_22
182 | module procedure add_44
183 | module procedure add_2s2s
184 | module procedure add_22s
185 | module procedure add_2s2
186 | module procedure add_4s4s
187 | module procedure add_44s
188 | module procedure add_4s4
189 | end interface
190 |
191 | interface operator (-)
192 | ! subtraction of rank 1 and rank 2 tensors
193 | module procedure sub_11
194 | module procedure sub_22
195 | module procedure sub_44
196 | module procedure sub_2s2s
197 | module procedure sub_22s
198 | module procedure sub_2s2
199 | module procedure sub_4s4s
200 | module procedure sub_44s
201 | module procedure sub_4s4
202 | end interface
203 | interface operator (.sub.)
204 | ! subtraction of rank 1 and rank 2 tensors
205 | module procedure sub_11
206 | module procedure sub_22
207 | module procedure sub_44
208 | module procedure sub_2s2s
209 | module procedure sub_22s
210 | module procedure sub_2s2
211 | module procedure sub_4s4s
212 | module procedure sub_44s
213 | module procedure sub_4s4
214 | end interface
215 |
216 | interface operator (.dya.)
217 | ! dyadic product of rank 2 and rank 4 tensor combinations
218 | module procedure dyadic_11
219 | module procedure dyadic_22
220 | module procedure dyadic_2s2s
221 | end interface
222 |
223 | interface operator (.cdya.)
224 | ! symmetric crossed dyadic product of rank 2 tensor combinations
225 | ! (i,j,k,l) = 1/2 * (i,k,j,l)*(i,l,j,k)
226 | module procedure crossdyadic_22
227 | module procedure crossdyadic_2s2s
228 | end interface
229 |
230 | interface fact
231 | module procedure fact_i
232 | end interface
233 |
234 | interface tr
235 | module procedure tr_2
236 | module procedure tr_2s
237 | end interface
238 |
239 | interface det
240 | module procedure det_2
241 | module procedure det_2s
242 | end interface
243 |
244 | interface dev
245 | module procedure dev_2
246 | module procedure dev_2s
247 | end interface
248 |
249 | interface unimodular
250 | module procedure unimod_2
251 | module procedure unimod_2s
252 | module procedure unimod_2d
253 | module procedure unimod_2sd
254 | end interface
255 |
256 | interface inv
257 | module procedure inv_2
258 | module procedure inv_2s
259 | module procedure inv2d
260 | module procedure inv2sd
261 | end interface
262 |
263 | interface norm
264 | module procedure norm_1
265 | module procedure norm_2
266 | module procedure norm_2s
267 | end interface
268 |
269 | interface sqrt
270 | module procedure sqrt_1
271 | module procedure sqrt_2
272 | module procedure sqrt_2s
273 | end interface
274 |
275 | interface dsqrt
276 | module procedure sqrt_1
277 | module procedure sqrt_2
278 | module procedure sqrt_2s
279 | end interface
280 |
281 | interface rotation_matrix
282 | module procedure rotation_2
283 | end interface
284 |
285 | interface identity2
286 | module procedure ident_2
287 | module procedure ident_2s
288 | end interface
289 |
290 | interface identity4
291 | module procedure ident_4
292 | module procedure ident_4s
293 | end interface
294 |
295 | interface tensorstore
296 | module procedure tenstore_2
297 | module procedure tenstore_2a
298 | module procedure tenstore_2s
299 | module procedure tenstore_4
300 | module procedure tenstore_4a
301 | module procedure tenstore_4s
302 | end interface
303 |
304 | interface astensor
305 | module procedure tenstore_2
306 | module procedure tenstore_2a
307 | module procedure tenstore_2s
308 | module procedure tenstore_4
309 | module procedure tenstore_4a
310 | module procedure tenstore_4s
311 | end interface
312 |
313 | interface symstore
314 | module procedure symstore_2
315 | module procedure symstore_4
316 | module procedure symstore_2s
317 | module procedure symstore_4s
318 | module procedure symstore_2sa
319 | module procedure symstore_4sa
320 | end interface
321 |
322 | interface strain
323 | ! module procedure str2ten_2
324 | module procedure str2ten_2s
325 | end interface
326 |
327 | interface asvoigt
328 | module procedure symstore_2
329 | module procedure symstore_4
330 | module procedure symstore_2s
331 | module procedure symstore_4s
332 | module procedure symstore_2sa
333 | module procedure symstore_4sa
334 | end interface
335 |
336 | interface voigt
337 | module procedure symstore_2
338 | module procedure symstore_4
339 | module procedure symstore_2s
340 | module procedure symstore_4s
341 | module procedure symstore_2sa
342 | module procedure symstore_4sa
343 | end interface
344 |
345 | interface reduce_dim
346 | module procedure reduce_dim_2s
347 | module procedure reduce_dim_4s
348 | end interface
349 |
350 | interface permute
351 | ! double dot-product of rank 1 and rank 2 tensor combinations
352 | module procedure permute_2
353 | module procedure permute_2s
354 | module procedure permute_4
355 | module procedure permute_4s
356 | end interface
357 |
358 | interface transpose
359 | module procedure transp2
360 | module procedure transp2s
361 | module procedure transp4
362 | module procedure transp4s
363 | end interface
364 |
365 | interface piola
366 | module procedure piola2
367 | module procedure piola2s
368 | module procedure piola4
369 | module procedure piola4s
370 | end interface
371 |
372 | interface asarray
373 | module procedure asarray_1
374 | module procedure asarray_2
375 | module procedure asarray_4
376 | module procedure asarray_2s
377 | module procedure asarray_4s
378 | end interface
379 |
380 | interface asabqarray
381 | module procedure asabqarray_2s
382 | module procedure asabqarray_4s
383 | end interface
384 |
385 | interface assignment (=)
386 | module procedure assignscalar_1
387 | module procedure assignscalar_2
388 | module procedure assignscalar_2s
389 | module procedure assignscalar_4
390 | module procedure assignscalar_4s
391 | module procedure assignarr_1
392 | module procedure assignarr_2
393 | module procedure assignarr_2s
394 | module procedure assignarr_4
395 | module procedure assignarr_4s
396 | module procedure assignten2sym_2
397 | module procedure assignten2sym_4
398 | module procedure assignsym2ten_2
399 | module procedure assignsym2ten_4
400 | module procedure assignscalar_1r4
401 | module procedure assignscalar_2r4
402 | module procedure assignscalar_2sr4
403 | module procedure assignscalar_4r4
404 | module procedure assignscalar_4sr4
405 | module procedure assignarr_2r4
406 | module procedure assignarr_2sr4
407 | module procedure assignarr_4r4
408 | module procedure assignarr_4sr4
409 | end interface
410 | ! ------END INTERFACE---------------------------------------
411 |
412 | contains
413 |
414 | ! ------BEGIN FUNCTIONS-------------------------------------
415 | ! ------MATH TOOLS SECTION----------------------------------
416 | include 'ttb/libtools.f'
417 | ! ------+/- SECTION-----------------------------------------
418 | include 'ttb/libadd.f'
419 | include 'ttb/libsub.f'
420 | ! ------DIVISION SECTION------------------------------------
421 | include 'ttb/libdiv.f'
422 | ! ------DOT SECTION-----------------------------------------
423 | include 'ttb/libdot.f'
424 | ! ------DOUBLE DOT SECTION----------------------------------
425 | include 'ttb/libddot.f'
426 | ! ------POWER SECTION---------------------------------------
427 | include 'ttb/libpower.f'
428 | ! ------DYADIC SECTION--------------------------------------
429 | include 'ttb/libdyadic.f'
430 | ! ------CROSS-DYADIC SECTION--------------------------------
431 | include 'ttb/libcrossdyadic.f'
432 | ! ------PERMUTE SECTION-------------------------------------
433 | include 'ttb/libpermute.f'
434 | ! ------TENSOR FUNCTION SECTION-----------------------------
435 | include 'ttb/libtransp.f'
436 | include 'ttb/libtrace.f'
437 | include 'ttb/libdet.f'
438 | include 'ttb/libdev.f'
439 | include 'ttb/libunimodular.f'
440 | include 'ttb/libinv.f'
441 | include 'ttb/libnorm.f'
442 | include 'ttb/libsqrt.f'
443 | include 'ttb/librotation.f'
444 | ! ------TENSOR INITIALIZATION SECTION-----------------------
445 | include 'ttb/libidentity.f'
446 | ! ------SYMSTORE SECTION------------------------------------
447 | include 'ttb/libsymstore.f'
448 | ! ------USYMSTORE SECTION-----------------------------------
449 | include 'ttb/libtenstore.f'
450 | ! ------STRAINSTORE SECTION---------------------------------
451 | include 'ttb/libstrainstore.f'
452 | ! ------REDUCE DIM. SECTION---------------------------------
453 | include 'ttb/libreducedim.f'
454 | ! ------AS ARRAY SECTION------------------------------------
455 | include 'ttb/libasarray.f'
456 | include 'ttb/libasabqarray.f'
457 | ! ------PIOLA SECTION---------------------------------------
458 | include 'ttb/libpiola.f'
459 | ! ------END FUNCTIONS---------------------------------------
460 | ! ------BEGIN SUBROUTINES-----------------------------------
461 | include 'ttb/libassignscalar.f'
462 | include 'ttb/libassignarray.f'
463 | include 'ttb/libassignten2sym.f'
464 |
465 | end module Tensor
466 |
--------------------------------------------------------------------------------
/docs/assets/images/deformation.svg:
--------------------------------------------------------------------------------
1 |
2 |
3 |
4 |
378 |
--------------------------------------------------------------------------------
3 |