├── src
├── data-structures
│ ├── trie
│ │ ├── index.js
│ │ └── README.md
│ ├── avl-tree
│ │ ├── index.js
│ │ └── README.md
│ ├── b-tree
│ │ └── index.js
│ ├── max-heap
│ │ ├── index.js
│ │ └── README.md
│ ├── min-heap
│ │ ├── index.js
│ │ └── README.md
│ ├── skip-list
│ │ ├── index.js
│ │ └── README.md
│ ├── binomial-heap
│ │ └── index.js
│ ├── bloom-filter
│ │ └── index.js
│ ├── fibonacci-heap
│ │ └── index.js
│ ├── red-black-tree
│ │ └── index.js
│ ├── splay-tree
│ │ └── index.js
│ ├── tree
│ │ ├── node.js
│ │ ├── index.js
│ │ └── README.md
│ ├── doubly-linked-list
│ │ ├── node.js
│ │ └── README.md
│ ├── linked-list
│ │ ├── node.js
│ │ └── README.md
│ ├── binary-search-tree
│ │ └── node.js
│ ├── array
│ │ ├── README.md
│ │ └── index.js
│ ├── priority-queue
│ │ ├── README.md
│ │ └── index.js
│ ├── set
│ │ ├── README.md
│ │ └── index.js
│ ├── stack
│ │ ├── README.md
│ │ └── index.js
│ ├── queue
│ │ ├── README.md
│ │ └── index.js
│ ├── disjoint-set
│ │ ├── README.md
│ │ ├── item.js
│ │ └── index.js
│ ├── README.md
│ └── graph
│ │ └── index.js
├── utils
│ ├── index.js
│ └── isArraySorted.js
└── algorithms
│ ├── searching
│ ├── linear-search
│ │ ├── index.js
│ │ └── README.md
│ ├── binary-search
│ │ ├── README.md
│ │ └── index.js
│ ├── jump-search
│ │ └── README.md
│ └── interpolation-search
│ │ └── README.md
│ ├── math
│ ├── factorial
│ │ ├── index.js
│ │ └── README.md
│ ├── fibonacci
│ │ ├── index.js
│ │ └── README.md
│ ├── integer-partition
│ │ └── README.md
│ ├── prime-number
│ │ └── README.md
│ ├── is-power-of-two
│ │ └── README.md
│ ├── sieve-of-eratosthenes
│ │ └── README.md
│ ├── lcm
│ │ └── README.md
│ ├── pascals-triangle
│ │ └── README.md
│ └── euclidean-algorithm
│ │ └── README.md
│ ├── tree
│ ├── breadth-first-search
│ │ ├── index.js
│ │ └── README.md
│ └── depth-first-search
│ │ ├── README.md
│ │ └── index.js
│ ├── set
│ ├── shortest-common-supersequence
│ │ └── README.md
│ ├── maximum-subarray
│ │ └── README.md
│ ├── longest-common-subsequence
│ │ └── README.md
│ ├── longest-increasing-subsequence
│ │ └── README.md
│ ├── combination-sum
│ │ └── README.md
│ ├── permutations
│ │ └── README.md
│ └── combinations
│ │ └── README.md
│ ├── graph
│ ├── depth-first-search
│ │ ├── README.md
│ │ └── index.js
│ ├── breadth-first-search
│ │ ├── README.md
│ │ └── index.js
│ ├── dijkstra-algorithm
│ │ └── README.md
│ ├── travelling-salesman
│ │ └── README.md
│ ├── prims-algorithm
│ │ └── README.md
│ └── kruskals-algorithm
│ │ └── README.md
│ ├── sorting
│ ├── shell-sort
│ │ ├── index.js
│ │ └── README.md
│ ├── insertion-sort
│ │ ├── README.md
│ │ └── index.js
│ ├── bubble-sort
│ │ ├── README.md
│ │ └── index.js
│ ├── heap-sort
│ │ └── README.md
│ ├── selection-sort
│ │ ├── README.md
│ │ └── index.js
│ ├── merge-sort
│ │ ├── README.md
│ │ └── index.js
│ ├── quick-sort
│ │ ├── README.md
│ │ └── index.js
│ ├── radix-sort
│ │ └── README.md
│ └── counting-sort
│ │ └── README.md
│ └── others
│ └── tower-of-hanoi
│ └── README.md
├── __tests__
├── integration
│ └── index.spec.js
├── .eslintrc
└── unit
│ ├── index.spec.js
│ └── src
│ ├── algorithms
│ ├── tree-dfs.spec.js
│ ├── tree-bfs.spec.js
│ ├── graph-dfs.spec.js
│ ├── graph-bfs.spec.js
│ ├── factorial.spec.js
│ ├── shell-sort.spec.js
│ ├── bubble-sort.spec.js
│ ├── insertion-sort.spec.js
│ ├── selection-sort.spec.js
│ ├── fibonacci.spec.js
│ ├── linear-search.spec.js
│ ├── merge-sort.spec.js
│ ├── quick-sort.spec.js
│ └── binary-search.spec.js
│ └── data-structures
│ ├── tree.spec.js
│ ├── array.spec.js
│ ├── stack.spec.js
│ ├── hash-table.spec.js
│ ├── graph.spec.js
│ ├── queue.spec.js
│ └── priority-queue.spec.js
├── index.js
├── assets
├── stack.png
├── union.gif
├── delete-1.gif
├── delete-2.gif
├── decrease-key.gif
├── fib-heap-union.gif
├── big-o-comparison.png
├── extract-minimum.gif
├── ds-operations-big-o.png
├── fib-heap-decrease-key.gif
├── fib-heap-extract-minimum-1.gif
├── fib-heap-extract-minimum-2.gif
├── insert.svg
├── find-minimum.svg
├── mu.svg
└── constant-time.svg
├── .babelrc
├── .travis.yml
├── .github
├── ISSUE_TEMPLATE.md
├── PULL_REQUEST_TEMPLATE.md
└── CODE_OF_CONDUCT.md
├── LICENSE
├── .eslintrc
├── .gitignore
├── .cz-config.js
└── package.json
/src/data-structures/trie/index.js:
--------------------------------------------------------------------------------
1 |
--------------------------------------------------------------------------------
/__tests__/integration/index.spec.js:
--------------------------------------------------------------------------------
1 |
--------------------------------------------------------------------------------
/src/data-structures/avl-tree/index.js:
--------------------------------------------------------------------------------
1 |
--------------------------------------------------------------------------------
/src/data-structures/b-tree/index.js:
--------------------------------------------------------------------------------
1 |
--------------------------------------------------------------------------------
/src/data-structures/max-heap/index.js:
--------------------------------------------------------------------------------
1 |
--------------------------------------------------------------------------------
/src/data-structures/min-heap/index.js:
--------------------------------------------------------------------------------
1 |
--------------------------------------------------------------------------------
/src/data-structures/skip-list/index.js:
--------------------------------------------------------------------------------
1 |
--------------------------------------------------------------------------------
/src/data-structures/binomial-heap/index.js:
--------------------------------------------------------------------------------
1 |
--------------------------------------------------------------------------------
/src/data-structures/bloom-filter/index.js:
--------------------------------------------------------------------------------
1 |
--------------------------------------------------------------------------------
/src/data-structures/fibonacci-heap/index.js:
--------------------------------------------------------------------------------
1 |
--------------------------------------------------------------------------------
/src/data-structures/red-black-tree/index.js:
--------------------------------------------------------------------------------
1 |
--------------------------------------------------------------------------------
/src/data-structures/splay-tree/index.js:
--------------------------------------------------------------------------------
1 |
--------------------------------------------------------------------------------
/index.js:
--------------------------------------------------------------------------------
1 | const helloWorld = to => `Hello ${to}!`;
2 |
3 | export default helloWorld;
4 |
--------------------------------------------------------------------------------
/__tests__/.eslintrc:
--------------------------------------------------------------------------------
1 | {
2 | "extends": "../.eslintrc",
3 | "env": {
4 | "mocha": true
5 | },
6 | }
7 |
--------------------------------------------------------------------------------
/assets/stack.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/akhenda/es6-data-structures-and-algorithms/HEAD/assets/stack.png
--------------------------------------------------------------------------------
/assets/union.gif:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/akhenda/es6-data-structures-and-algorithms/HEAD/assets/union.gif
--------------------------------------------------------------------------------
/src/utils/index.js:
--------------------------------------------------------------------------------
1 | import isArraySorted from './isArraySorted';
2 |
3 | export {
4 | isArraySorted,
5 | };
6 |
--------------------------------------------------------------------------------
/assets/delete-1.gif:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/akhenda/es6-data-structures-and-algorithms/HEAD/assets/delete-1.gif
--------------------------------------------------------------------------------
/assets/delete-2.gif:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/akhenda/es6-data-structures-and-algorithms/HEAD/assets/delete-2.gif
--------------------------------------------------------------------------------
/assets/decrease-key.gif:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/akhenda/es6-data-structures-and-algorithms/HEAD/assets/decrease-key.gif
--------------------------------------------------------------------------------
/assets/fib-heap-union.gif:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/akhenda/es6-data-structures-and-algorithms/HEAD/assets/fib-heap-union.gif
--------------------------------------------------------------------------------
/assets/big-o-comparison.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/akhenda/es6-data-structures-and-algorithms/HEAD/assets/big-o-comparison.png
--------------------------------------------------------------------------------
/assets/extract-minimum.gif:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/akhenda/es6-data-structures-and-algorithms/HEAD/assets/extract-minimum.gif
--------------------------------------------------------------------------------
/assets/ds-operations-big-o.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/akhenda/es6-data-structures-and-algorithms/HEAD/assets/ds-operations-big-o.png
--------------------------------------------------------------------------------
/assets/fib-heap-decrease-key.gif:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/akhenda/es6-data-structures-and-algorithms/HEAD/assets/fib-heap-decrease-key.gif
--------------------------------------------------------------------------------
/assets/fib-heap-extract-minimum-1.gif:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/akhenda/es6-data-structures-and-algorithms/HEAD/assets/fib-heap-extract-minimum-1.gif
--------------------------------------------------------------------------------
/assets/fib-heap-extract-minimum-2.gif:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/akhenda/es6-data-structures-and-algorithms/HEAD/assets/fib-heap-extract-minimum-2.gif
--------------------------------------------------------------------------------
/src/data-structures/tree/node.js:
--------------------------------------------------------------------------------
1 | export default class Node {
2 | /**
3 | * initialize the Node
4 | * @param {number|string} data
5 | */
6 | constructor(data) {
7 | this.data = data;
8 | this.children = [];
9 | }
10 | }
11 |
--------------------------------------------------------------------------------
/src/data-structures/doubly-linked-list/node.js:
--------------------------------------------------------------------------------
1 | export default class Node {
2 | /**
3 | * initializes the node
4 | */
5 | constructor(data, next = null, prev = null) {
6 | this.data = data;
7 | this.prev = prev;
8 | this.next = next;
9 | }
10 | }
11 |
--------------------------------------------------------------------------------
/src/data-structures/linked-list/node.js:
--------------------------------------------------------------------------------
1 | export default class Node {
2 | /**
3 | * initializes the node
4 | * @param {any} data - the value of the node
5 | */
6 | constructor(data, next = null) {
7 | this.data = data;
8 | this.next = next;
9 | }
10 | }
11 |
--------------------------------------------------------------------------------
/src/data-structures/binary-search-tree/node.js:
--------------------------------------------------------------------------------
1 | export default class Node {
2 | /**
3 | * initialize the Node
4 | * @param {number|string} data
5 | */
6 | constructor(data) {
7 | this.data = data;
8 | this.left = null;
9 | this.right = null;
10 | }
11 | }
12 |
--------------------------------------------------------------------------------
/src/utils/isArraySorted.js:
--------------------------------------------------------------------------------
1 | /**
2 | * utility function to check if an array is sorted
3 | * @param {array} array the array to be checked
4 | * @return {Boolean}
5 | */
6 | const isArraySorted = (array) => {
7 | return array.every((val, i, arr) => !i || (val >= arr[i - 1]));
8 | };
9 |
10 | export default isArraySorted;
11 |
--------------------------------------------------------------------------------
/__tests__/unit/index.spec.js:
--------------------------------------------------------------------------------
1 | import chai from 'chai';
2 | import hello from '../../index';
3 |
4 |
5 | const { expect } = chai;
6 |
7 | describe('Hello 😃', () => {
8 | it('should return a greeting to the parameter', () => {
9 | const greeting = hello('world');
10 | expect(greeting).to.be.equal('Hello world!');
11 | });
12 | });
13 |
--------------------------------------------------------------------------------
/.babelrc:
--------------------------------------------------------------------------------
1 | {
2 | "presets": ["es2015", "stage-0"],
3 | "plugins": [
4 | ["module-resolver", {
5 | "root": ["./src"],
6 | "alias": {
7 | "src": "./src",
8 | "tests": "./_tests_"
9 | },
10 | "cwd": "babelrc"
11 | }],
12 | ["transform-runtime", {
13 | "polyfill": false,
14 | "regenerator": true
15 | }]
16 | ]
17 | }
18 |
--------------------------------------------------------------------------------
/.travis.yml:
--------------------------------------------------------------------------------
1 | language: node_js
2 | node_js:
3 | - stable
4 | cache:
5 | yarn: true
6 | directories:
7 | - node_modules
8 | install:
9 | - npm install -g codecov
10 | - yarn
11 |
12 | jobs:
13 | include:
14 | - stage: Run Tests
15 | script:
16 | - yarn run test-with-coverage
17 | - codecov
18 | - stage: Run Semantic Release
19 | script:
20 | - npx semantic-release
21 |
--------------------------------------------------------------------------------
/src/algorithms/searching/linear-search/index.js:
--------------------------------------------------------------------------------
1 | /**
2 | * Linear Search implementation
3 | * @param {array} array
4 | * @param {string|number} target
5 | * @return {number} the index of the found element
6 | */
7 | const linearSearch = (array, target) => {
8 | let result = -1;
9 |
10 | array.forEach((item, index) => {
11 | if (target === item) result = index;
12 | });
13 |
14 | return result;
15 | };
16 |
17 | export default linearSearch;
18 |
--------------------------------------------------------------------------------
/.github/ISSUE_TEMPLATE.md:
--------------------------------------------------------------------------------
1 | _(Thanks for reporting an issue to es6-data-structures-and-algorithms! If you haven't already read the [contributor guidelines](../docs/CONTRIBUTING.md), Please do that now, then proceed to fill out the details below.)_
2 |
3 | ## What are the minimum necessary steps to reproduce this issue?
4 |
5 | 1. …
6 | 2. …
7 | 3. …
8 |
9 | ## What happens?
10 |
11 | …
12 |
13 | ## What were you expecting to happen?
14 |
15 | …
16 |
17 | ## Please paste any error or log messages here
18 |
19 | (if long, you can [link to a gist](https://gist.github.com/))
20 |
21 | ## Any other details
22 |
23 | …
24 |
--------------------------------------------------------------------------------
/src/algorithms/math/factorial/index.js:
--------------------------------------------------------------------------------
1 | /**
2 | * Factorial implementation using iteration
3 | * @param {number} number
4 | * @return {number}
5 | */
6 | const factorial = (number) => {
7 | let result = 1;
8 |
9 | for (let i = 2; i <= number; i += 1) {
10 | result *= i;
11 | }
12 |
13 | return result;
14 | };
15 |
16 | /**
17 | * Factorial implementation using recursion
18 | * @param {number} number
19 | * @return {number}
20 | */
21 | export const recursiveFactorial = (number) => {
22 | return number > 1 ? number * recursiveFactorial(number - 1) : 1;
23 | };
24 |
25 | export default factorial;
26 |
--------------------------------------------------------------------------------
/src/algorithms/tree/breadth-first-search/index.js:
--------------------------------------------------------------------------------
1 | import Queue from 'src/data-structures/queue';
2 |
3 | /**
4 | * tree breadth first search implementation
5 | * @param {Tree} tree
6 | * @param {Function} cb
7 | * @return {string}
8 | */
9 | const breadthFirstSearch = (tree, cb) => {
10 | let result = '';
11 | const queue = new Queue();
12 |
13 | queue.enqueue(tree.root);
14 |
15 | while (queue.size()) {
16 | const node = queue.dequeue();
17 |
18 | if (cb) result += `${cb(node)} `;
19 |
20 | for (let i = 0; i < node.children.length; i++) {
21 | queue.enqueue(node.children[i]);
22 | }
23 | }
24 |
25 | return result.trim();
26 | };
27 |
28 | export default breadthFirstSearch;
29 |
--------------------------------------------------------------------------------
/src/algorithms/set/shortest-common-supersequence/README.md:
--------------------------------------------------------------------------------
1 | # Shortest Common Supersequence
2 |
3 | The shortest common supersequence (SCS) of two sequences `X` and `Y` is the shortest sequence which has `X` and `Y` as subsequences.
4 |
5 | In other words assume we're given two strings str1 and str2, find the shortest string that has both str1 and str2 as subsequences.
6 |
7 | This is a problem closely related to the longest common subsequence problem.
8 |
9 | ## Example
10 |
11 | ```
12 | Input: str1 = "geek", str2 = "eke"
13 | Output: "geeke"
14 |
15 | Input: str1 = "AGGTAB", str2 = "GXTXAYB"
16 | Output: "AGXGTXAYB"
17 | ```
18 |
19 | ## References
20 |
21 | - [GeeksForGeeks](https://www.geeksforgeeks.org/shortest-common-supersequence/)
22 |
--------------------------------------------------------------------------------
/src/data-structures/array/README.md:
--------------------------------------------------------------------------------
1 | ## Array
2 |
3 | According to Wikipedia:
4 |
5 | > An Array data structure, or simply an Array, is a data structure consisting of a collection of elements (values or variables), each identified by at least one array index or key. The simplest type of data structure is a linear array, also called one-dimensional array.
6 |
7 | Arrays are among the oldest and most important data structures and are used by every program. They are also used to implement many other data structures.
8 |
9 | ### Complexity
10 |
11 | #### Average
12 |
13 | | Operation | Complexity |
14 | | :-------: | :--------: |
15 | | Access | O(1) |
16 | | Search | O(n) |
17 | | Insertion | O(n) |
18 | | Deletion | O(n) |
19 |
--------------------------------------------------------------------------------
/src/algorithms/graph/depth-first-search/README.md:
--------------------------------------------------------------------------------
1 | # Depth-First Search (DFS)
2 |
3 | Depth-first search (DFS) is an algorithm for traversing or searching tree or graph data structures. One starts at the root (selecting some arbitrary node as the root in the case of a graph) and explores as far as possible along each branch before backtracking.
4 |
5 | 
6 |
7 | ## References
8 |
9 | - [Wikipedia](https://en.wikipedia.org/wiki/Depth-first_search)
10 | - [Tree Traversals (Inorder, Preorder and Postorder)](https://www.geeksforgeeks.org/tree-traversals-inorder-preorder-and-postorder/)
11 | - [BFS vs DFS](https://www.geeksforgeeks.org/bfs-vs-dfs-binary-tree/)
12 |
--------------------------------------------------------------------------------
/src/algorithms/tree/depth-first-search/README.md:
--------------------------------------------------------------------------------
1 | # Depth-First Search (DFS)
2 |
3 | Depth-first search (DFS) is an algorithm for traversing or
4 | searching tree or graph data structures. One starts at
5 | the root (selecting some arbitrary node as the root in
6 | the case of a graph) and explores as far as possible
7 | along each branch before backtracking.
8 |
9 | 
10 |
11 | ## References
12 |
13 | - [Wikipedia](https://en.wikipedia.org/wiki/Depth-first_search)
14 | - [Tree Traversals (Inorder, Preorder and Postorder)](https://www.geeksforgeeks.org/tree-traversals-inorder-preorder-and-postorder/)
15 | - [BFS vs DFS](https://www.geeksforgeeks.org/bfs-vs-dfs-binary-tree/)
16 |
--------------------------------------------------------------------------------
/src/algorithms/graph/breadth-first-search/README.md:
--------------------------------------------------------------------------------
1 | # Breadth-First Search (BFS)
2 |
3 | Breadth-first search (BFS) is an algorithm for traversing or searching tree or graph data structures. It starts at the tree root (or some arbitrary node of a graph, sometimes referred to as a 'search key') and explores the neighbor nodes first, before moving to the next level neighbors.
4 |
5 | 
6 |
7 | ## References
8 |
9 | - [Wikipedia](https://en.wikipedia.org/wiki/Breadth-first_search)
10 | - [Tree Traversals (Inorder, Preorder and Postorder)](https://www.geeksforgeeks.org/tree-traversals-inorder-preorder-and-postorder/)
11 | - [BFS vs DFS](https://www.geeksforgeeks.org/bfs-vs-dfs-binary-tree/)
12 |
--------------------------------------------------------------------------------
/src/algorithms/math/fibonacci/index.js:
--------------------------------------------------------------------------------
1 | /**
2 | * fibonacci implementation
3 | * @param {number} number
4 | * @return {number}
5 | */
6 | const fibonacci = (number) => {
7 | if (number === 0 || number === 1) return number;
8 |
9 | return fibonacci(number - 1) + fibonacci(number - 2);
10 | };
11 |
12 | /**
13 | * fibonacci implementation using Dynamic Programming
14 | * @param {number} number
15 | * @return {number}
16 | */
17 | export const fibonacciDP = (number) => {
18 | const cache = {
19 | 0: 0,
20 | 1: 1,
21 | };
22 |
23 | function recurse(num) {
24 | if (cache[num] === undefined) {
25 | cache[num] = recurse(num - 1) + recurse(num - 2);
26 | }
27 |
28 | return cache[num];
29 | }
30 |
31 | return recurse(number);
32 | };
33 |
34 | export default fibonacci;
35 |
--------------------------------------------------------------------------------
/src/algorithms/tree/breadth-first-search/README.md:
--------------------------------------------------------------------------------
1 | # Breadth-First Search (BFS)
2 |
3 | Breadth-first search (BFS) is an algorithm for traversing
4 | or searching tree or graph data structures. It starts at
5 | the tree root (or some arbitrary node of a graph, sometimes
6 | referred to as a 'search key') and explores the neighbor
7 | nodes first, before moving to the next level neighbors.
8 |
9 | 
10 |
11 | ## References
12 |
13 | - [Wikipedia](https://en.wikipedia.org/wiki/Breadth-first_search)
14 | - [Tree Traversals (Inorder, Preorder and Postorder)](https://www.geeksforgeeks.org/tree-traversals-inorder-preorder-and-postorder/)
15 | - [BFS vs DFS](https://www.geeksforgeeks.org/bfs-vs-dfs-binary-tree/)
16 |
--------------------------------------------------------------------------------
/src/algorithms/searching/linear-search/README.md:
--------------------------------------------------------------------------------
1 | # Linear Search
2 | In computer science, linear search or sequential search is a method for finding a target value within a list. It sequentially checks each element of the list for the target value until a match is found or until all the elements have been searched. Linear search runs in at worst linear time and makes at most `n` comparisons, where `n` is the length of the list.
3 |
4 | 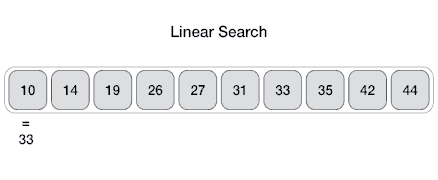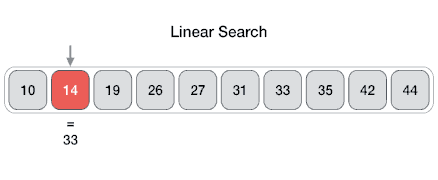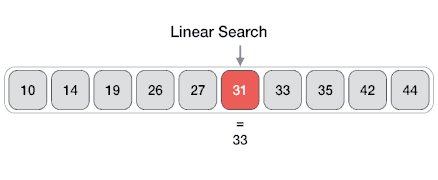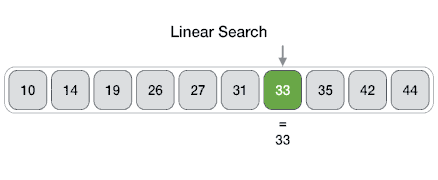
5 |
6 | ## Complexity
7 |
8 | **Time Complexity**: `O(n)` - since in worst case we're checking each element exactly once.
9 |
10 | ## References
11 | - [Wikipedia](https://en.wikipedia.org/wiki/Linear_search)
12 | - [TutorialsPoint](https://www.tutorialspoint.com/data_structures_algorithms/linear_search_algorithm.htm)
13 | - [Youtube](https://www.youtube.com/watch?v=SGU9duLE30w)
14 |
--------------------------------------------------------------------------------
/src/algorithms/math/fibonacci/README.md:
--------------------------------------------------------------------------------
1 | # Fibonacci
2 |
3 | In mathematics, the Fibonacci numbers are the numbers in the following integer sequence, called the Fibonacci sequence, and characterized by the fact that every number after the first two is the sum of the two preceding ones:
4 |
5 | `0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, ...`
6 |
7 | A tiling with squares whose side lengths are successive Fibonacci numbers
8 |
9 | 
10 |
11 | The Fibonacci spiral: an approximation of the golden spiral created by drawing circular arcs connecting the opposite corners of squares in the Fibonacci tiling; this one uses squares of sizes 1, 1, 2, 3, 5, 8, 13 and 21.
12 |
13 | 
14 |
15 | ## References
16 |
17 | - [Wikipedia](https://en.wikipedia.org/wiki/Fibonacci_number)
18 |
--------------------------------------------------------------------------------
/__tests__/unit/src/algorithms/tree-dfs.spec.js:
--------------------------------------------------------------------------------
1 | import chai from 'chai';
2 | import Tree from 'src/data-structures/tree';
3 | import depthFirstSearch from 'src/algorithms/tree/depth-first-search';
4 |
5 |
6 | const { expect } = chai;
7 |
8 | describe('Tree Depth First Search', () => {
9 | it('traverses the tree using DFS', () => {
10 | const tree = new Tree();
11 |
12 | tree.addNode('ceo');
13 | tree.addNode('cto', 'ceo');
14 | tree.addNode('dev1', 'cto');
15 | tree.addNode('dev2', 'cto');
16 | tree.addNode('dev3', 'cto');
17 | tree.addNode('cfo', 'ceo');
18 | tree.addNode('accountant', 'cfo');
19 | tree.addNode('cmo', 'ceo');
20 |
21 | const callbackFn = (node) => {
22 | console.log(node.data);
23 | return node.data;
24 | };
25 |
26 | const expectedResult = 'ceo cto dev1 dev2 dev3 cfo accountant cmo';
27 |
28 | expect(depthFirstSearch(tree, callbackFn)).to.equal(expectedResult);
29 | });
30 | });
31 |
--------------------------------------------------------------------------------
/__tests__/unit/src/algorithms/tree-bfs.spec.js:
--------------------------------------------------------------------------------
1 | import chai from 'chai';
2 | import Tree from 'src/data-structures/tree';
3 | import breadthFirstSearch from 'src/algorithms/tree/breadth-first-search';
4 |
5 |
6 | const { expect } = chai;
7 |
8 | describe('Tree Breadth First Search', () => {
9 | it('traverses the tree using BFS', () => {
10 | const tree = new Tree();
11 |
12 | tree.addNode('ceo');
13 | tree.addNode('cto', 'ceo');
14 | tree.addNode('dev1', 'cto');
15 | tree.addNode('dev2', 'cto');
16 | tree.addNode('dev3', 'cto');
17 | tree.addNode('cfo', 'ceo');
18 | tree.addNode('accountant', 'cfo');
19 | tree.addNode('cmo', 'ceo');
20 |
21 | const callbackFn = (node) => {
22 | console.log(node.data);
23 | return node.data;
24 | };
25 |
26 | const expectedResult = 'ceo cto cfo cmo dev1 dev2 dev3 accountant';
27 |
28 | expect(breadthFirstSearch(tree, callbackFn)).to.equal(expectedResult);
29 | });
30 | });
31 |
--------------------------------------------------------------------------------
/src/algorithms/sorting/shell-sort/index.js:
--------------------------------------------------------------------------------
1 | // our intervals
2 | const GAPS = [500, 240, 128, 54, 26, 9, 4, 1];
3 |
4 | /**
5 | * shell sort implementation
6 | *
7 | * can be seen as either a generalization of sorting
8 | * by exchange (bubble sort) or sorting by insertion (insertion sort)
9 | * the method starts by sorting pairs of elements far apart from each
10 | * other, then progressively reducing the gap between elements to be compared
11 | *
12 | * @param {array} array
13 | * @return {array} sorted array
14 | */
15 | const shellSort = (array) => {
16 | GAPS.forEach((gap) => {
17 | for (let index = gap; index < array.length; index++) {
18 | let j = index;
19 | const temp = array[index];
20 |
21 | for (j; j >= gap && array[j - gap] > temp; j -= gap) {
22 | array[j] = array[j - gap];
23 | }
24 |
25 | array[j] = temp;
26 | }
27 | });
28 |
29 | return array;
30 | };
31 |
32 | export default shellSort;
33 |
--------------------------------------------------------------------------------
/src/algorithms/searching/binary-search/README.md:
--------------------------------------------------------------------------------
1 | # Binary Search
2 |
3 | In computer science, binary search, also known as half-interval search, logarithmic search, or binary chop, is a search algorithm that finds the position of a target value within a sorted array. Binary search compares the target value to the middle element of the array; if they are unequal, the half in which the target cannot lie is eliminated and the search continues on the remaining half until it is successful. If the search ends with the remaining half being empty, the target is not in the array.
4 |
5 | 
6 |
7 | ## Complexity
8 |
9 | **Time Complexity**: `O(log(n))` - since we split search area by two for every next iteration.
10 |
11 | ## References
12 |
13 | - [Wikipedia](https://en.wikipedia.org/wiki/Binary_search_algorithm)
14 | - [YouTube](https://www.youtube.com/watch?v=P3YID7liBug&index=29&list=PLLXdhg_r2hKA7DPDsunoDZ-Z769jWn4R8)
15 |
--------------------------------------------------------------------------------
/assets/insert.svg:
--------------------------------------------------------------------------------
1 |
--------------------------------------------------------------------------------
/src/algorithms/set/maximum-subarray/README.md:
--------------------------------------------------------------------------------
1 | # Maximum Subarray Problem
2 |
3 | The maximum subarray problem is the task of finding the contiguous subarray within a one-dimensional array, `a[1...n]`, of numbers which has the largest sum, where,
4 |
5 | 
6 |
7 | 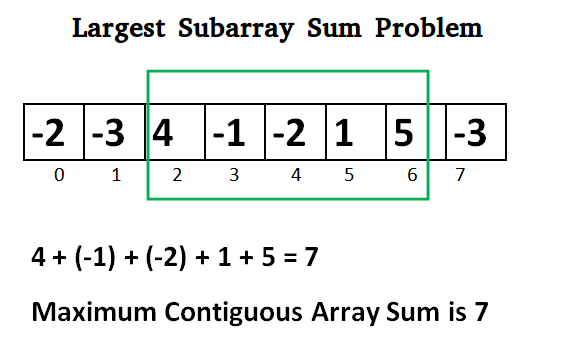
8 |
9 | ## Example
10 |
11 | The list usually contains both positive and negative numbers along
12 | with `0`. For example, for the array of
13 | values `−2, 1, −3, 4, −1, 2, 1, −5, 4` the contiguous subarray
14 | with the largest sum is `4, −1, 2, 1`, with sum `6`.
15 |
16 | ## References
17 |
18 | - [Wikipedia](https://en.wikipedia.org/wiki/Maximum_subarray_problem)
19 | - [YouTube](https://www.youtube.com/watch?v=ohHWQf1HDfU&list=PLLXdhg_r2hKA7DPDsunoDZ-Z769jWn4R8)
20 | - [GeeksForGeeks](https://www.geeksforgeeks.org/largest-sum-contiguous-subarray/)
21 |
--------------------------------------------------------------------------------
/src/algorithms/sorting/insertion-sort/README.md:
--------------------------------------------------------------------------------
1 | # Insertion Sort
2 |
3 | Insertion sort is a simple sorting algorithm that builds the final sorted array (or list) one item at a time. It is much less efficient on large lists than more advanced algorithms such as quicksort, heapsort, or merge sort.
4 |
5 | 
6 |
7 | 
8 |
9 | ## Complexity
10 |
11 | | Name | Best | Average | Worst | Memory | Stable | Comments |
12 | | --------------------- | :-------------: | :-----------------: | :-----------------: | :-------: | :-------: | :-------- |
13 | | **Insertion sort** | n | n2 | n2 | 1 | Yes | |
14 |
15 | ## References
16 |
17 | - [Wikipedia](https://en.wikipedia.org/wiki/Insertion_sort)
18 |
--------------------------------------------------------------------------------
/src/data-structures/priority-queue/README.md:
--------------------------------------------------------------------------------
1 | ## Priority Queue
2 |
3 | According to Wikipedia:
4 |
5 | > In computer science, a priority queue is an abstract data type which is like a regular queue or stack data structure, but where additionally each element has a "priority" associated with it. In a priority queue, an element with high priority is served before an element with low priority. If two elements have the same priority, they are served according to their order in the queue.
6 |
7 | ### Complexity
8 |
9 | #### Average
10 |
11 | | Operation | Complexity |
12 | | :-------: | :--------: |
13 | | Access | O(n) |
14 | | Search | O(n) |
15 | | Insertion | O(1) |
16 | | Deletion | O(n) |
17 |
18 | Simple representation of a priority queue
19 |
20 | 
21 |
22 | ## References
23 |
24 | - [Wikipedia](https://en.wikipedia.org/wiki/Priority_queue)
25 | - [YouTube](https://www.youtube.com/watch?v=wptevk0bshY&list=PLLXdhg_r2hKA7DPDsunoDZ-Z769jWn4R8&index=6)
26 |
--------------------------------------------------------------------------------
/src/algorithms/sorting/insertion-sort/index.js:
--------------------------------------------------------------------------------
1 | /**
2 | * insertion sort implementation
3 | * @param {array} array an unsorted array
4 | * @return {array} sorted array
5 | */
6 | const insertionSort = (array) => {
7 | array.forEach((number, index) => {
8 | // to begin, this algorithm considers the leftmost number fully sorted
9 | let previousIndex = index - 1;
10 | const temp = array[index];
11 |
12 | // next, from the remaining numbers the leftmost number is taken out
13 | // and compared to the already sorted number to its left
14 | while (previousIndex >= 0 && array[previousIndex] > temp) {
15 | // if the already sorted number is larger, the two numbers swap
16 | array[previousIndex + 1] = array[previousIndex];
17 | previousIndex--;
18 | }
19 |
20 | // the above operation repeats until either a number smaller
21 | // appears, or the number reaches the left edge
22 |
23 | array[previousIndex + 1] = temp;
24 | });
25 |
26 | return array;
27 | };
28 |
29 | export default insertionSort;
30 |
--------------------------------------------------------------------------------
/__tests__/unit/src/algorithms/graph-dfs.spec.js:
--------------------------------------------------------------------------------
1 | import chai from 'chai';
2 | import Graph from 'src/data-structures/graph';
3 | import depthFirstSearch from 'src/algorithms/graph/depth-first-search';
4 |
5 |
6 | const { expect } = chai;
7 |
8 | describe('Graph Depth First Search', () => {
9 | it('traverses the graph using DFS', () => {
10 | const graph = new Graph();
11 |
12 | graph.addVertex(1);
13 | graph.addVertex(2);
14 | graph.addVertex(3);
15 | graph.addVertex(4);
16 | graph.addVertex(5);
17 | graph.addVertex(6);
18 |
19 | graph.addEdge(1, 2);
20 | graph.addEdge(1, 5);
21 | graph.addEdge(2, 3);
22 | graph.addEdge(2, 5);
23 | graph.addEdge(3, 4);
24 | graph.addEdge(4, 5);
25 | graph.addEdge(4, 6);
26 |
27 | const callbackFn = (vertex) => {
28 | console.log(vertex);
29 | return vertex;
30 | };
31 |
32 | expect(depthFirstSearch(graph, 1, callbackFn)).to.equal('1 -> 2 -> 3 -> 4 -> 5 -> 6');
33 | expect(depthFirstSearch(graph, 0, callbackFn)).to.equal('Vertex not found');
34 | });
35 | });
36 |
--------------------------------------------------------------------------------
/__tests__/unit/src/algorithms/graph-bfs.spec.js:
--------------------------------------------------------------------------------
1 | import chai from 'chai';
2 | import Graph from 'src/data-structures/graph';
3 | import breadthFirstSearch from 'src/algorithms/graph/breadth-first-search';
4 |
5 |
6 | const { expect } = chai;
7 |
8 | describe('Graph Breadth First Search', () => {
9 | it('traverses the graph using BFS', () => {
10 | const graph = new Graph();
11 |
12 | graph.addVertex(1);
13 | graph.addVertex(2);
14 | graph.addVertex(3);
15 | graph.addVertex(4);
16 | graph.addVertex(5);
17 | graph.addVertex(6);
18 |
19 | graph.addEdge(1, 2);
20 | graph.addEdge(1, 5);
21 | graph.addEdge(2, 3);
22 | graph.addEdge(2, 5);
23 | graph.addEdge(3, 4);
24 | graph.addEdge(4, 5);
25 | graph.addEdge(4, 6);
26 |
27 | const callbackFn = (vertex) => {
28 | console.log(vertex);
29 | return vertex;
30 | };
31 |
32 | expect(breadthFirstSearch(graph, 1, callbackFn)).to.equal('1 -> 2 -> 5 -> 3 -> 4 -> 6');
33 | expect(breadthFirstSearch(graph, 0, callbackFn)).to.equal('Vertex not found');
34 | });
35 | });
36 |
--------------------------------------------------------------------------------
/src/algorithms/graph/breadth-first-search/index.js:
--------------------------------------------------------------------------------
1 | import Queue from 'src/data-structures/queue';
2 |
3 | /**
4 | * graph breadth first search implementation
5 | * @param {Graph} graph
6 | * @param {number} startVertex
7 | * @param {Function} cb
8 | * @return {string}
9 | */
10 | const breadthFirstSearch = (graph, startVertex, cb) => {
11 | if (graph.vertices.indexOf(startVertex) === -1) return 'Vertex not found';
12 |
13 | let result = '';
14 | const queue = new Queue();
15 | const visited = [];
16 |
17 | queue.enqueue(startVertex);
18 | visited[startVertex] = true;
19 |
20 | while (queue.size()) {
21 | startVertex = queue.dequeue();
22 |
23 | result += `${cb(startVertex)} -> `;
24 |
25 | for (let i = 0; i < graph.edges[startVertex].length; i++) {
26 | if (!visited[graph.edges[startVertex][i]]) {
27 | visited[graph.edges[startVertex][i]] = true;
28 | queue.enqueue(graph.edges[startVertex][i]);
29 | }
30 | }
31 | }
32 |
33 | return result.slice(0, -4);
34 | };
35 |
36 | export default breadthFirstSearch;
37 |
--------------------------------------------------------------------------------
/__tests__/unit/src/algorithms/factorial.spec.js:
--------------------------------------------------------------------------------
1 | import chai from 'chai';
2 | import factorial, { recursiveFactorial } from 'src/algorithms/math/factorial';
3 |
4 |
5 | const { expect } = chai;
6 |
7 | describe('Factorial', () => {
8 | describe('using iteration', () => {
9 | it('should compute factorial', () => {
10 | expect(factorial(0)).to.be.equal(1);
11 | expect(factorial(1)).to.be.equal(1);
12 | expect(factorial(3)).to.be.equal(6);
13 | expect(factorial(7)).to.be.equal(5040);
14 | expect(factorial(9)).to.be.equal(362880);
15 | expect(factorial(10)).to.be.equal(3628800);
16 | });
17 | });
18 |
19 | describe('using recursion', () => {
20 | it('should compute factorial', () => {
21 | expect(recursiveFactorial(0)).to.be.equal(1);
22 | expect(recursiveFactorial(1)).to.be.equal(1);
23 | expect(recursiveFactorial(3)).to.be.equal(6);
24 | expect(recursiveFactorial(7)).to.be.equal(5040);
25 | expect(recursiveFactorial(9)).to.be.equal(362880);
26 | expect(recursiveFactorial(10)).to.be.equal(3628800);
27 | });
28 | });
29 | });
30 |
--------------------------------------------------------------------------------
/src/algorithms/sorting/bubble-sort/README.md:
--------------------------------------------------------------------------------
1 | # Bubble Sort
2 |
3 | Bubble sort, sometimes referred to as sinking sort, is a simple sorting algorithm that repeatedly steps through the list to be sorted, compares each pair of adjacent items and swaps them if they are in the wrong order. The pass through the list is repeated until no swaps are needed, which indicates that the list is sorted.
4 |
5 | 
6 |
7 | ## Complexity
8 |
9 | | Name | Best | Average | Worst | Memory | Stable | Comments |
10 | | --------------------- | :-------------: | :-----------------: | :-----------------: | :-------: | :-------: | :-------- |
11 | | **Bubble sort** | n | n2 | n2 | 1 | Yes | |
12 |
13 | ## References
14 |
15 | - [Wikipedia](https://en.wikipedia.org/wiki/Bubble_sort)
16 | - [YouTube](https://www.youtube.com/watch?v=6Gv8vg0kcHc&index=27&t=0s&list=PLLXdhg_r2hKA7DPDsunoDZ-Z769jWn4R8)
17 |
--------------------------------------------------------------------------------
/__tests__/unit/src/algorithms/shell-sort.spec.js:
--------------------------------------------------------------------------------
1 | import chai from 'chai';
2 | import shellSort from 'src/algorithms/sorting/shell-sort';
3 |
4 |
5 | const { expect } = chai;
6 |
7 | describe('Shell Sort', () => {
8 | it('should return empty array', () => {
9 | expect(shellSort([])).to.deep.equal([]);
10 | });
11 |
12 | it('should return the passed array', () => {
13 | expect(shellSort([1])).to.deep.equal([1]);
14 | expect(shellSort([2])).to.deep.equal([2]);
15 | expect(shellSort([5])).to.deep.equal([5]);
16 | expect(shellSort([356])).to.deep.equal([356]);
17 | });
18 |
19 | it('should sort a random array', () => {
20 | const array = [2, 8, 10, 11, 12, 13, 14, 18, 19, 20];
21 | const sortedArray = [2, 8, 10, 11, 12, 13, 14, 18, 19, 20];
22 |
23 | expect(shellSort(array)).to.deep.equal(sortedArray);
24 | });
25 |
26 | it('should sort a reversed sorted array', () => {
27 | const reversedArray = [12, 10, 8, 7, 6, 5, 4, 3, 2, 1];
28 | const sortedArray = [1, 2, 3, 4, 5, 6, 7, 8, 10, 12];
29 |
30 | expect(shellSort(reversedArray)).to.deep.equal(sortedArray);
31 | });
32 | });
33 |
--------------------------------------------------------------------------------
/__tests__/unit/src/algorithms/bubble-sort.spec.js:
--------------------------------------------------------------------------------
1 | import chai from 'chai';
2 | import bubbleSort from 'src/algorithms/sorting/bubble-sort';
3 |
4 |
5 | const { expect } = chai;
6 |
7 | describe('Bubble Sort', () => {
8 | it('should return empty array', () => {
9 | expect(bubbleSort([])).to.deep.equal([]);
10 | });
11 |
12 | it('should return the passed array', () => {
13 | expect(bubbleSort([1])).to.deep.equal([1]);
14 | expect(bubbleSort([2])).to.deep.equal([2]);
15 | expect(bubbleSort([5])).to.deep.equal([5]);
16 | expect(bubbleSort([356])).to.deep.equal([356]);
17 | });
18 |
19 | it('should sort a random array', () => {
20 | const array = [2, 8, 10, 11, 12, 13, 14, 18, 19, 20];
21 | const sortedArray = [2, 8, 10, 11, 12, 13, 14, 18, 19, 20];
22 |
23 | expect(bubbleSort(array)).to.deep.equal(sortedArray);
24 | });
25 |
26 | it('should sort a reversed sorted array', () => {
27 | const reversedArray = [12, 10, 8, 7, 6, 5, 4, 3, 2, 1];
28 | const sortedArray = [1, 2, 3, 4, 5, 6, 7, 8, 10, 12];
29 |
30 | expect(bubbleSort(reversedArray)).to.deep.equal(sortedArray);
31 | });
32 | });
33 |
--------------------------------------------------------------------------------
/src/algorithms/math/factorial/README.md:
--------------------------------------------------------------------------------
1 | # Factorial
2 |
3 | In mathematics, the factorial of a non-negative integer `n`, denoted by `n!`, is the product of all positive integers less than or equal to `n`. For example:
4 |
5 | ```
6 | 5! = 5 * 4 * 3 * 2 * 1 = 120
7 | ```
8 |
9 | | n | n! |
10 | | ----- | --------------------------: |
11 | | 0 | 1 |
12 | | 1 | 1 |
13 | | 2 | 2 |
14 | | 3 | 6 |
15 | | 4 | 24 |
16 | | 5 | 120 |
17 | | 6 | 720 |
18 | | 7 | 5 040 |
19 | | 8 | 40 320 |
20 | | 9 | 362 880 |
21 | | 10 | 3 628 800 |
22 | | 11 | 39 916 800 |
23 | | 12 | 479 001 600 |
24 | | 13 | 6 227 020 800 |
25 | | 14 | 87 178 291 200 |
26 | | 15 | 1 307 674 368 000 |
27 |
28 | ## References
29 |
30 | - [Wikipedia](https://en.wikipedia.org/wiki/Factorial)
31 |
--------------------------------------------------------------------------------
/LICENSE:
--------------------------------------------------------------------------------
1 | The MIT License (MIT)
2 |
3 | Copyright (c) 2018 Joseph Akhenda
4 |
5 | Permission is hereby granted, free of charge, to any person obtaining a copy
6 | of this software and associated documentation files (the "Software"), to deal
7 | in the Software without restriction, including without limitation the rights
8 | to use, copy, modify, merge, publish, distribute, sublicense, and/or sell
9 | copies of the Software, and to permit persons to whom the Software is
10 | furnished to do so, subject to the following conditions:
11 |
12 | The above copyright notice and this permission notice shall be included in all
13 | copies or substantial portions of the Software.
14 |
15 | THE SOFTWARE IS PROVIDED "AS IS", WITHOUT WARRANTY OF ANY KIND, EXPRESS OR
16 | IMPLIED, INCLUDING BUT NOT LIMITED TO THE WARRANTIES OF MERCHANTABILITY,
17 | FITNESS FOR A PARTICULAR PURPOSE AND NONINFRINGEMENT. IN NO EVENT SHALL THE
18 | AUTHORS OR COPYRIGHT HOLDERS BE LIABLE FOR ANY CLAIM, DAMAGES OR OTHER
19 | LIABILITY, WHETHER IN AN ACTION OF CONTRACT, TORT OR OTHERWISE, ARISING FROM,
20 | OUT OF OR IN CONNECTION WITH THE SOFTWARE OR THE USE OR OTHER DEALINGS IN THE
21 | SOFTWARE.
22 |
--------------------------------------------------------------------------------
/src/algorithms/graph/depth-first-search/index.js:
--------------------------------------------------------------------------------
1 | /**
2 | * dfs recursive traversal utility function
3 | * @param {Graph} graph
4 | * @param {number} vertex
5 | * @param {array} visited
6 | * @param {string} result
7 | * @param {Function} fn
8 | * @return {string}
9 | */
10 | const traverse = (graph, vertex, visited, result, fn) => {
11 | visited[vertex] = true;
12 |
13 | if (graph.edges[vertex] !== undefined) result += `${fn(vertex)} -> `;
14 |
15 | graph.edges[vertex].forEach((item) => {
16 | if (!visited[item]) result = traverse(graph, item, visited, result, fn);
17 | });
18 |
19 | return result;
20 | };
21 |
22 | /**
23 | * graph depth first search implementation
24 | * @param {Graph} graph
25 | * @param {number} startVertex
26 | * @param {Function} cb
27 | * @return {string}
28 | */
29 | const depthFirstSearch = (graph, startVertex, cb) => {
30 | if (graph.vertices.indexOf(startVertex) === -1) return 'Vertex not found';
31 |
32 | const result = '';
33 | const visited = [];
34 | return traverse(graph, startVertex, visited, result, cb).slice(0, -3).trim();
35 | };
36 |
37 | export default depthFirstSearch;
38 |
--------------------------------------------------------------------------------
/src/algorithms/set/longest-common-subsequence/README.md:
--------------------------------------------------------------------------------
1 | # Longest Common Subsequence
2 |
3 | The longest common subsequence (LCS) problem is the problem of finding the longest subsequence common to all sequences in a set of sequences (often just two sequences). It differs from the longest common substring problem: unlike substrings, subsequences are not required to occupy consecutive positions within the original sequences.
4 |
5 | ## Application
6 |
7 | The longest common subsequence problem is a classic computer science problem, the basis of data comparison programs such as the diff utility, and has applications in bioinformatics. It is also widely used by revision control systems such as Git for reconciling multiple changes made to a revision-controlled collection of files.
8 |
9 | ## Example
10 |
11 | - LCS for input Sequences `ABCDGH` and `AEDFHR` is `ADH` of length 3.
12 | - LCS for input Sequences `AGGTAB` and `GXTXAYB` is `GTAB` of length 4.
13 |
14 | ## References
15 |
16 | - [Wikipedia](https://en.wikipedia.org/wiki/Longest_common_subsequence_problem)
17 | - [YouTube](https://www.youtube.com/watch?v=NnD96abizww&list=PLLXdhg_r2hKA7DPDsunoDZ-Z769jWn4R8)
18 |
--------------------------------------------------------------------------------
/__tests__/unit/src/algorithms/insertion-sort.spec.js:
--------------------------------------------------------------------------------
1 | import chai from 'chai';
2 | import insertionSort from 'src/algorithms/sorting/insertion-sort';
3 |
4 |
5 | const { expect } = chai;
6 |
7 | describe('Insertion Sort', () => {
8 | it('should return empty array', () => {
9 | expect(insertionSort([])).to.deep.equal([]);
10 | });
11 |
12 | it('should return the passed array', () => {
13 | expect(insertionSort([1])).to.deep.equal([1]);
14 | expect(insertionSort([2])).to.deep.equal([2]);
15 | expect(insertionSort([5])).to.deep.equal([5]);
16 | expect(insertionSort([356])).to.deep.equal([356]);
17 | });
18 |
19 | it('should sort a random array', () => {
20 | const array = [2, 8, 10, 11, 12, 13, 14, 18, 19, 20];
21 | const sortedArray = [2, 8, 10, 11, 12, 13, 14, 18, 19, 20];
22 |
23 | expect(insertionSort(array)).to.deep.equal(sortedArray);
24 | });
25 |
26 | it('should sort a reversed sorted array', () => {
27 | const reversedArray = [12, 10, 8, 7, 6, 5, 4, 3, 2, 1];
28 | const sortedArray = [1, 2, 3, 4, 5, 6, 7, 8, 10, 12];
29 |
30 | expect(insertionSort(reversedArray)).to.deep.equal(sortedArray);
31 | });
32 | });
33 |
--------------------------------------------------------------------------------
/__tests__/unit/src/algorithms/selection-sort.spec.js:
--------------------------------------------------------------------------------
1 | import chai from 'chai';
2 | import selectionSort from 'src/algorithms/sorting/selection-sort';
3 |
4 |
5 | const { expect } = chai;
6 |
7 | describe('Selection Sort', () => {
8 | it('should return empty array', () => {
9 | expect(selectionSort([])).to.deep.equal([]);
10 | });
11 |
12 | it('should return the passed array', () => {
13 | expect(selectionSort([1])).to.deep.equal([1]);
14 | expect(selectionSort([2])).to.deep.equal([2]);
15 | expect(selectionSort([5])).to.deep.equal([5]);
16 | expect(selectionSort([356])).to.deep.equal([356]);
17 | });
18 |
19 | it('should sort a random array', () => {
20 | const array = [2, 8, 10, 11, 12, 13, 14, 18, 19, 20];
21 | const sortedArray = [2, 8, 10, 11, 12, 13, 14, 18, 19, 20];
22 |
23 | expect(selectionSort(array)).to.deep.equal(sortedArray);
24 | });
25 |
26 | it('should sort a reversed sorted array', () => {
27 | const reversedArray = [12, 10, 8, 7, 6, 5, 4, 3, 2, 1];
28 | const sortedArray = [1, 2, 3, 4, 5, 6, 7, 8, 10, 12];
29 |
30 | expect(selectionSort(reversedArray)).to.deep.equal(sortedArray);
31 | });
32 | });
33 |
--------------------------------------------------------------------------------
/src/algorithms/sorting/heap-sort/README.md:
--------------------------------------------------------------------------------
1 | # Heap Sort
2 |
3 | Heapsort is a comparison-based sorting algorithm. Heapsort can be thought of as an improved selection sort: like that algorithm, it divides its input into a sorted and an unsorted region, and it iteratively shrinks the unsorted region by extracting the largest element and moving that to the sorted region. The improvement consists of the use of a heap data structure rather than a linear-time search to find the maximum.
4 |
5 | 
6 |
7 | 
8 |
9 | ## Complexity
10 |
11 | | Name | Best | Average | Worst | Memory | Stable | Comments |
12 | | --------------------- | :-------------: | :-----------------: | :-----------------: | :-------: | :-------: | :-------- |
13 | | **Heap sort** | n log(n) | n log(n) | n log(n) | 1 | No | |
14 |
15 | ## References
16 |
17 | - [Wikipedia](https://en.wikipedia.org/wiki/Heapsort)
18 |
--------------------------------------------------------------------------------
/src/algorithms/sorting/selection-sort/README.md:
--------------------------------------------------------------------------------
1 | # Selection Sort
2 |
3 | Selection sort is a sorting algorithm, specifically an in-place comparison sort. It has O(n2) time complexity, making it inefficient on large lists, and generally performs worse than the similar insertion sort. Selection sort is noted for its simplicity, and it has performance advantages over more complicated algorithms in certain situations, particularly where auxiliary memory is limited.
4 |
5 | 
6 |
7 | 
8 |
9 | ## Complexity
10 |
11 | | Name | Best | Average | Worst | Memory | Stable | Comments |
12 | | --------------------- | :-------------: | :-----------------: | :-----------------: | :-------: | :-------: | :-------- |
13 | | **Selection sort** | n2 | n2 | n2 | 1 | No | |
14 |
15 | ## References
16 |
17 | - [Wikipedia](https://en.wikipedia.org/wiki/Selection_sort)
18 |
--------------------------------------------------------------------------------
/src/algorithms/math/integer-partition/README.md:
--------------------------------------------------------------------------------
1 | # Integer Partition
2 |
3 | In number theory and combinatorics, a partition of a positive integer `n`, also called an **integer partition**, is a way of writing `n` as a sum of positive integers.
4 |
5 | Two sums that differ only in the order of their summands are considered the same partition. For example, `4` can be partitioned in five distinct ways:
6 |
7 | ```
8 | 4
9 | 3 + 1
10 | 2 + 2
11 | 2 + 1 + 1
12 | 1 + 1 + 1 + 1
13 | ```
14 |
15 | The order-dependent composition `1 + 3` is the same partition as `3 + 1`, while the two distinct compositions `1 + 2 + 1` and `1 + 1 + 2` represent the same partition `2 + 1 + 1`.
16 |
17 | Young diagrams associated to the partitions of the positive integers `1` through `8`. They are arranged so that images under the reflection about the main diagonal of the square are conjugate partitions.
18 |
19 | 
20 |
21 | ## References
22 |
23 | - [Wikipedia](https://en.wikipedia.org/wiki/Partition_(number_theory))
24 | - [YouTube](https://www.youtube.com/watch?v=ZaVM057DuzE&list=PLLXdhg_r2hKA7DPDsunoDZ-Z769jWn4R8)
25 |
--------------------------------------------------------------------------------
/.eslintrc:
--------------------------------------------------------------------------------
1 | {
2 | "parser": "babel-eslint",
3 | "env": {
4 | "es6": true,
5 | "node": true
6 | },
7 | "extends": [
8 | "eslint:recommended",
9 | "airbnb-base"
10 | ],
11 | "rules": {
12 | "arrow-body-style": 0,
13 | "class-methods-use-this": 0,
14 | "consistent-return": 0,
15 | "func-names": 0,
16 | "global-require": 0,
17 | "import/no-extraneous-dependencies": 0,
18 | "import/extensions": 0,
19 | "import/prefer-default-export": 0,
20 | "jsx-a11y/label-has-for": 0,
21 | "no-trailing-spaces": 0,
22 | "no-console": 0,
23 | "no-confusing-arrow": 0,
24 | "no-unused-vars": 1,
25 | "no-param-reassign": 0,
26 | "no-use-before-define": 0,
27 | "no-constant-condition": 0,
28 | "space-infix-ops": 0,
29 | "react/prefer-default-export": 0,
30 | "react/require-default-props": 0,
31 | "react/jsx-filename-extension": 0,
32 | "react/prefer-stateless-function": 0,
33 | "react/forbid-prop-types": 0,
34 | "react/jsx-indent": 0,
35 | "import/named": 2,
36 | "no-plusplus": 0,
37 | "no-underscore-dangle": 0
38 | },
39 | "settings": {
40 | "import/resolver": {
41 | "babel-module": {}
42 | }
43 | }
44 | }
45 |
--------------------------------------------------------------------------------
/assets/find-minimum.svg:
--------------------------------------------------------------------------------
1 |
--------------------------------------------------------------------------------
/src/algorithms/graph/dijkstra-algorithm/README.md:
--------------------------------------------------------------------------------
1 | # Dijkstra's Algorithm
2 |
3 | Dijkstra's algorithm is an algorithm for finding the shortest paths between nodes in a graph, which may represent, for example, road networks.
4 |
5 | The algorithm exists in many variants; Dijkstra's original variant found the shortest path between two nodes, but a more common variant fixes a single node as the "source" node and finds shortest paths from the source to all other nodes in the graph, producing a shortest-path tree.
6 |
7 | 
8 |
9 | Dijkstra's algorithm to find the shortest path between `a` and `b`. It picks the unvisited vertex with the lowest distance, calculates the distance through it to each unvisited neighbor, and updates the neighbor's distance if smaller. Mark visited (set to red) when done with neighbors.
10 |
11 | ## References
12 |
13 | - [Wikipedia](https://en.wikipedia.org/wiki/Dijkstra%27s_algorithm)
14 | - [On YouTube by Nathaniel Fan](https://www.youtube.com/watch?v=gdmfOwyQlcI&list=PLLXdhg_r2hKA7DPDsunoDZ-Z769jWn4R8)
15 | - [On YouTube by Tushar Roy](https://www.youtube.com/watch?v=lAXZGERcDf4&list=PLLXdhg_r2hKA7DPDsunoDZ-Z769jWn4R8)
16 |
--------------------------------------------------------------------------------
/src/algorithms/math/prime-number/README.md:
--------------------------------------------------------------------------------
1 | # Primality Test
2 |
3 | A **prime number** (or a **prime**) is a natural number greater than `1` that cannot be formed by multiplying two smaller natural numbers. A natural number greater than `1` that is not prime is called a composite number. For example, `5` is prime because the only ways of writing it as a product, `1 × 5` or `5 × 1`, involve `5` itself. However, `6` is composite because it is the product of two numbers `(2 × 3)` that are both smaller than `6`.
4 |
5 | 
6 |
7 | A **primality test** is an algorithm for determining whether an input number is prime. Among other fields of mathematics, it is used for cryptography. Unlike integer factorization, primality tests do not generally give prime factors, only stating whether the input number is prime or not. Factorization is thought to be a computationally difficult problem, whereas primality testing is comparatively easy (its running time is polynomial in the size of the input).
8 |
9 | ## References
10 |
11 | - [Prime Numbers on Wikipedia](https://en.wikipedia.org/wiki/Prime_number)
12 | - [Primality Test on Wikipedia](https://en.wikipedia.org/wiki/Primality_test)
13 |
--------------------------------------------------------------------------------
/src/data-structures/max-heap/README.md:
--------------------------------------------------------------------------------
1 | ## Max Heap
2 |
3 | According to Tutorialspoint:
4 |
5 | > **Heap** is a special case of balanced binary tree data structure where the root-node key is compared with its children and arranged accordingly. If **α** has child node **β** then −
6 | >
7 | > **key(α) ≥ key(β)**
8 | >
9 | > As the value of parent is greater than that of child, this property generates **Max Heap**
10 |
11 | ```
12 | For Input → 35 33 42 10 14 19 27 44 26 31
13 | ```
14 | **Min-Heap** − Where the value of the root node is less than or equal to either of its children.
15 |
16 | 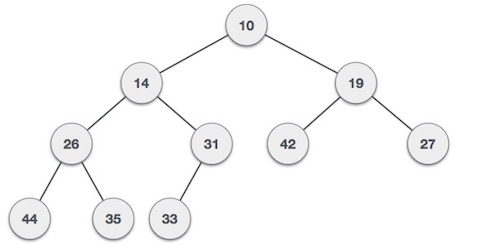
17 |
18 | **Max-Heap** − Where the value of the root node is greater than or equal to either of its children.
19 |
20 | 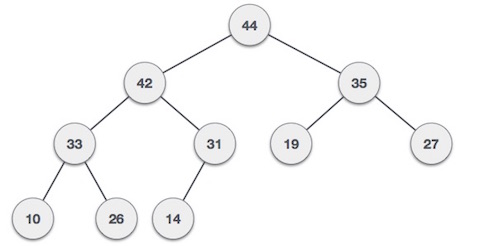
21 |
22 | Both trees are constructed using the same input and order of arrival.
23 |
24 | ## References
25 |
26 | - [Tutorialspoint](https://www.tutorialspoint.com/data_structures_algorithms/heap_data_structure.htm)
27 | - [YouTube - Yusuf Shakeel](https://www.youtube.com/watch?v=ixdWTKWSz7s)
28 | - [YouTube - Hackerank](https://www.youtube.com/watch?v=t0Cq6tVNRBA&t=34s)
29 |
--------------------------------------------------------------------------------
/src/algorithms/graph/travelling-salesman/README.md:
--------------------------------------------------------------------------------
1 | # Travelling Salesman Problem
2 |
3 | The travelling salesman problem (TSP) asks the following question:
4 | "Given a list of cities and the distances between each pair of cities, what is the shortest possible route that visits each city and returns to the origin city?"
5 |
6 | 
7 |
8 | Solution of a travelling salesman problem: the black line shows the shortest possible loop that connects every red dot.
9 |
10 | 
11 |
12 | TSP can be modelled as an undirected weighted graph, such that cities are the graph's vertices, paths are the graph's edges, and a path's distance is the edge's weight. It is a minimization problem starting and finishing at a specified vertex after having visited each other vertex exactly once. Often, the model is a complete graph (i.e. each pair of vertices is connected by an edge). If no path exists between two cities, adding an arbitrarily long edge will complete the graph without affecting the optimal tour.
13 |
14 | ## References
15 |
16 | - [Wikipedia](https://en.wikipedia.org/wiki/Travelling_salesman_problem)
17 |
--------------------------------------------------------------------------------
/src/algorithms/tree/depth-first-search/index.js:
--------------------------------------------------------------------------------
1 | /**
2 | * dfs pre-order traversal utility function
3 | * @param {Node} node
4 | * @param {string} result
5 | * @param {Function} fn
6 | * @return {void}
7 | */
8 | const preOrderTraversal = (node, result, fn) => {
9 | if (node) {
10 | if (fn) result += `${fn(node)} `;
11 |
12 | node.children.forEach((child) => {
13 | result = preOrderTraversal(child, result, fn);
14 | });
15 | }
16 |
17 | return result;
18 | };
19 |
20 | /**
21 | * dfs post-order traversal utility function
22 | * @param {Node} node
23 | * @param {string} result
24 | * @param {Function} fn
25 | * @return {void}
26 | */
27 | const postOrderTraversal = (node, result, fn) => {
28 | if (node) {
29 | node.children.forEach((child) => {
30 | result = postOrderTraversal(child, result, fn);
31 | });
32 |
33 | if (fn) result += `${fn(node)} `;
34 | }
35 | };
36 |
37 | /**
38 | * tree depth first search implementation
39 | * @param {Tree} tree
40 | * @param {Function} cb
41 | * @return {string}
42 | */
43 | const depthFirstSearch = (tree, cb) => {
44 | const result = '';
45 | const current = tree.root;
46 |
47 | return preOrderTraversal(current, result, cb).trim();
48 | };
49 |
50 | export default depthFirstSearch;
51 |
--------------------------------------------------------------------------------
/src/algorithms/sorting/selection-sort/index.js:
--------------------------------------------------------------------------------
1 | /**
2 | * selection sort implementation
3 | * @param {array} array an unsorted array
4 | * @return {array} sorted array
5 | */
6 | const selectionSort = (array) => {
7 | array.forEach((number, index) => {
8 | let indexOfMin = index;
9 |
10 | // using linear search, the smallest value's index
11 | // in the sequesnce is located. we can replace this
12 | // for loop block with the linear search algorithm
13 | // written elsewhere in this repo
14 | for (let j = index + 1; j < array.length; j++) {
15 | if (array[j] < array[indexOfMin]) indexOfMin = j;
16 | }
17 |
18 | // if the smallest value happens to already be in the
19 | // leftmost position, no operation is carried out
20 | if (indexOfMin !== index) {
21 | const lesser = array[indexOfMin];
22 |
23 | // the smallest value swaps with the leftmost
24 | // number and is considered fully sorted
25 | array[indexOfMin] = array[index];
26 | array[index] = lesser;
27 | }
28 |
29 | // the same above operation is repeated until all
30 | // the numbers are fully sorted as evidence by
31 | // our forEach array helper
32 | });
33 |
34 | // sorting is complete
35 | // return the array
36 | return array;
37 | };
38 |
39 | export default selectionSort;
40 |
--------------------------------------------------------------------------------
/src/algorithms/searching/jump-search/README.md:
--------------------------------------------------------------------------------
1 | # Jump Search
2 |
3 | Like Binary Search, **Jump Search** (or **Block Search**) is a searching algorithm for sorted arrays. The basic idea is to check fewer elements (than linear search) by jumping ahead by fixed steps or skipping some elements in place of searching all elements.
4 |
5 | For example, suppose we have an array `arr[]` of size `n` and block (to be jumped) of size `m`. Then we search at the indexes `arr[0]`, `arr[m]`, `arr[2 * m]`, ..., `arr[k * m]` and so on. Once we find the interval `arr[k * m] < x < arr[(k+1) * m]`, we perform a linear search operation from the index `k * m` to find the element `x`.
6 |
7 | **What is the optimal block size to be skipped?**
8 | In the worst case, we have to do `n/m` jumps and if the last checked value is greater than the element to be searched for, we perform `m - 1` comparisons more for linear search. Therefore the total number of comparisons in the worst case will be `((n/m) + m - 1)`. The value of the function `((n/m) + m - 1)` will be minimum when `m = √n`. Therefore, the best step size is `m = √n`.
9 |
10 | ## Complexity
11 |
12 | **Time complexity**: `O(√n)` - because we do search by blocks of size `√n`.
13 |
14 | ## References
15 |
16 | - [GeeksForGeeks](https://www.geeksforgeeks.org/jump-search/)
17 | - [Wikipedia](https://en.wikipedia.org/wiki/Jump_search)
18 |
--------------------------------------------------------------------------------
/.github/PULL_REQUEST_TEMPLATE.md:
--------------------------------------------------------------------------------
1 | ## Prerequisites
2 |
3 | - [ ] Have you searched for existing issues (open and close) to see if the bug or feature request has already been reported?
4 | - [ ] If this is a bug report, are you running the latest version of ES6 Data Structures and Algorithms? If not, please update to the latest version and verify that the issue still occurs before proceeding.
5 | - [ ] Have you read the [Contributing Guide](../docs/CONTRIBUTING.md)?
6 | - [ ] Have you reviewed the project readme (you might find advice about creating new issues)?
7 | - [ ] Are you creating an issue in the correct repository? (if this related to a dependency, please create the issue on that repository)
8 |
9 | Ready? Great! Please provide the following details:
10 |
11 | ## Version
12 |
13 | [version]
14 |
15 | ## Description
16 |
17 | Please describe the bug or feature, and:
18 |
19 | - [ ] Expected behavior and actual behavior.
20 | - [ ] Steps to reproduce the problem.
21 |
22 | [description]
23 |
24 | ## Error Message
25 |
26 | ```sh
27 | # please paste any error messages here
28 | ```
29 |
30 | ## ES6 Data Structures and Algorithms config file
31 |
32 | ```js
33 | // Please paste contents of your ES6 Data Structures and Algorithms config file here, or in a gist.
34 | // Be sure to include any additional comments that might help
35 | // us resolve the issue.
36 | ```
37 |
--------------------------------------------------------------------------------
/src/algorithms/others/tower-of-hanoi/README.md:
--------------------------------------------------------------------------------
1 | # Tower of Hanoi
2 |
3 | The Tower of Hanoi (also called the Tower of Brahma or Lucas' Tower and sometimes pluralized) is a mathematical game or puzzle. It consists of three rods and a number of disks of different sizes, which can slide onto any rod. The puzzle starts with the disks in a neat stack in ascending order of size on one rod, the smallest at the top, thus making a conical shape.
4 |
5 | The objective of the puzzle is to move the entire stack to another rod, obeying the following simple rules:
6 |
7 | - Only one disk can be moved at a time.
8 | - Each move consists of taking the upper disk from one of the stacks and placing it on top of another stack or on an empty rod.
9 | - No disk may be placed on top of a smaller disk.
10 |
11 | 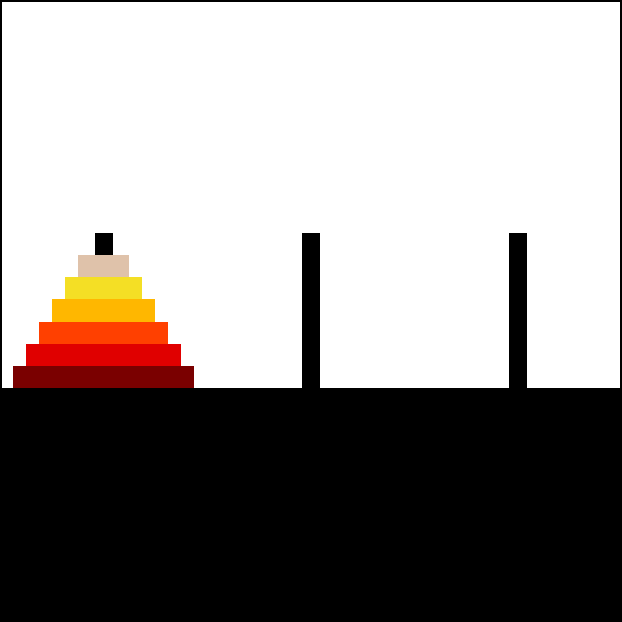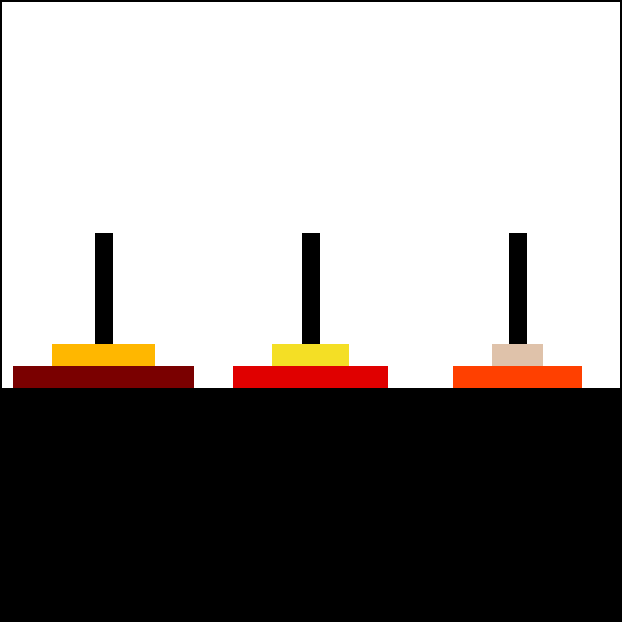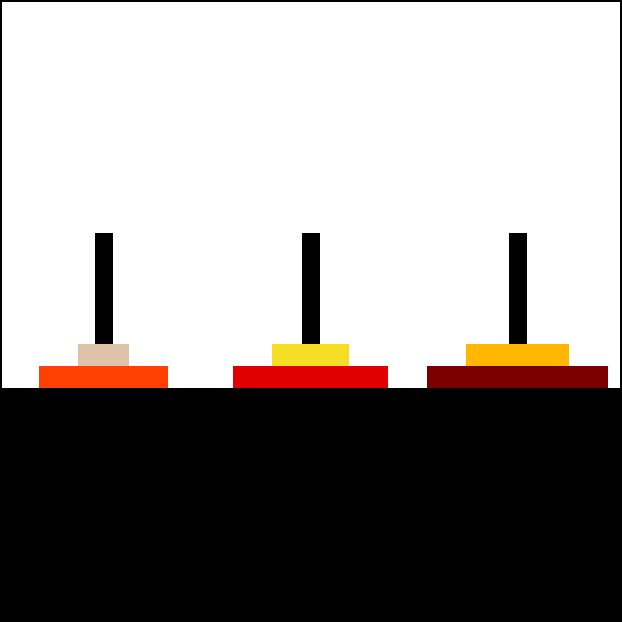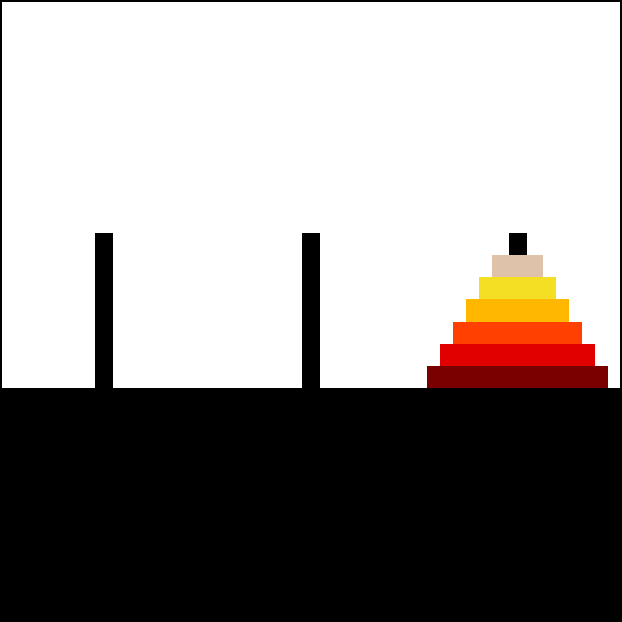
12 |
13 | Animation of an iterative algorithm solving 6-disk problem
14 |
15 | With `3` disks, the puzzle can be solved in `7` moves. The minimal number of moves required to solve a Tower of Hanoi puzzle is `2^n − 1`, where `n` is the number of disks.
16 |
17 | ## References
18 |
19 | - [Wikipedia](https://en.wikipedia.org/wiki/Tower_of_Hanoi)
20 | - [HackerEarth](https://www.hackerearth.com/blog/algorithms/tower-hanoi-recursion-game-algorithm-explained/)
21 |
--------------------------------------------------------------------------------
/src/algorithms/sorting/bubble-sort/index.js:
--------------------------------------------------------------------------------
1 | /**
2 | * bubble sort implementation
3 | * @param {array} array an unsorted array
4 | * @return {array} sorted array
5 | */
6 | const bubbleSort = (array) => {
7 | array.forEach((item, index) => {
8 | for (let i = 0; i < (array.length - index - 1); i++) {
9 | // we can either start at the beggining or finish of the arrays
10 | // starting at the beggining, we compare the first two numbers
11 | // together
12 | if (array[i] > array[i + 1]) {
13 | // after comparing them, if the number on the right is found
14 | // to be smaller, the numbers will be swapped
15 | const smaller = array[i + 1];
16 | array[i + 1] = array[i];
17 | array[i] = smaller;
18 | }
19 | // after the comparison is finished, the scales (our comparator,
20 | // comparing two numbers at a time), move one position to the
21 | // right i.e. we advance to the next index and the numbers are
22 | // compared once again and this operation is repeated until the
23 | // scales reach the end of the sequence/array
24 | }
25 |
26 | // The same above operations are repeated until all the numbers
27 | // are fully sorted as evidenced by the use of our forEach
28 | // array helper here.
29 | });
30 |
31 | // return the array as it is sorted by now
32 | return array;
33 | };
34 |
35 | export default bubbleSort;
36 |
--------------------------------------------------------------------------------
/src/algorithms/math/is-power-of-two/README.md:
--------------------------------------------------------------------------------
1 | # Is a power of two
2 |
3 | Given a positive integer, write a function to find if it is a power of two or not.
4 |
5 | **Naive solution**
6 |
7 | In naive solution we just keep dividing the number by two unless the number becomes `1` and every time we do so we check that remainder after division is always `0`. Otherwise the number can't be a power of two.
8 |
9 | **Bitwise solution**
10 |
11 | Powers of two in binary form always have just one bit. The only exception is with a signed integer (e.g. an 8-bit signed integer with a value of -128 looks like: `10000000`)
12 |
13 | ```
14 | 1: 0001
15 | 2: 0010
16 | 4: 0100
17 | 8: 1000
18 | ```
19 |
20 | So after checking that the number is greater than zero, we can use a bitwise hack to test that one and only one bit is set.
21 |
22 | ```
23 | number & (number - 1)
24 | ```
25 |
26 | For example for number `8` that operations will look like:
27 |
28 | ```
29 | 1000
30 | - 0001
31 | ----
32 | 0111
33 |
34 | 1000
35 | & 0111
36 | ----
37 | 0000
38 | ```
39 |
40 | ## References
41 |
42 | - [GeeksForGeeks](https://www.geeksforgeeks.org/program-to-find-whether-a-no-is-power-of-two/)
43 | - [Bitwise Solution on Stanford](http://www.graphics.stanford.edu/~seander/bithacks.html#DetermineIfPowerOf2)
44 | - [Binary number subtraction on YouTube](https://www.youtube.com/watch?v=S9LJknZTyos&t=0s&list=PLLXdhg_r2hKA7DPDsunoDZ-Z769jWn4R8&index=66)
45 |
--------------------------------------------------------------------------------
/src/data-structures/set/README.md:
--------------------------------------------------------------------------------
1 | ## Set
2 |
3 | According to Wikipedia:
4 |
5 | > In computer science, a set is an abstract data type that can store unique values, without any particular order. It is a computer implementation of the mathematical concept of a finite set. Unlike most other collection types, rather than retrieving a specific element from a set, one typically tests a value for membership in a set.
6 |
7 | Some set data structures are designed for static or frozen sets that do not change after they are constructed. Static sets allow only query operations on their elements — such as checking whether a given value is in the set, or enumerating the values in some arbitrary order. Other variants, called dynamic or mutable sets, allow also the insertion and deletion of elements from the set.
8 |
9 | ### Complexity
10 |
11 | #### Average
12 |
13 | | Operation | Complexity |
14 | | :-------: | :--------: |
15 | | Access | --- |
16 | | Search | O(n) |
17 | | Insertion | O(n) |
18 | | Deletion | O(n) |
19 |
20 | Simple representation of a Set
21 |
22 | #### Input
23 | 
24 |
25 | #### Output
26 | 
27 |
28 | ## References
29 |
30 | - [Wikipedia](https://en.wikipedia.org/wiki/Set_(abstract_data_type))
31 | - [Prof. Steven Skiena](http://algorist.com/problems/Set_Data_Structures.html)
32 |
--------------------------------------------------------------------------------
/src/algorithms/set/longest-increasing-subsequence/README.md:
--------------------------------------------------------------------------------
1 | # Longest Increasing Subsequence
2 |
3 | The longest increasing subsequence problem is to find a subsequence of a given sequence in which the subsequence's elements are in sorted order, lowest to highest, and in which the subsequence is as long as possible. This subsequence is not necessarily contiguous, or unique.
4 |
5 | ## Complexity
6 |
7 | The longest increasing subsequence problem is solvable in time `O(n log n)`, where `n` denotes the length of the input sequence.
8 |
9 | Dynamic programming approach has complexity `O(n * n)`.
10 |
11 | ## Example
12 |
13 | In the first 16 terms of the binary Van der Corput sequence
14 |
15 | ```
16 | 0, 8, 4, 12, 2, 10, 6, 14, 1, 9, 5, 13, 3, 11, 7, 15
17 | ```
18 |
19 | a longest increasing subsequence is
20 |
21 | ```
22 | 0, 2, 6, 9, 11, 15.
23 | ```
24 |
25 | This subsequence has length six;
26 | the input sequence has no seven-member increasing subsequences. The longest increasing subsequence in this example is not unique: for instance,
27 |
28 | ```
29 | 0, 4, 6, 9, 11, 15 or
30 | 0, 2, 6, 9, 13, 15 or
31 | 0, 4, 6, 9, 13, 15
32 | ```
33 |
34 | are other increasing subsequences of equal length in the same input sequence.
35 |
36 | ## References
37 |
38 | - [Wikipedia](https://en.wikipedia.org/wiki/Longest_increasing_subsequence)
39 | - [Dynamic Programming Approach on YouTube](https://www.youtube.com/watch?v=CE2b_-XfVDk&list=PLLXdhg_r2hKA7DPDsunoDZ-Z769jWn4R8)
40 |
--------------------------------------------------------------------------------
/src/data-structures/stack/README.md:
--------------------------------------------------------------------------------
1 | ## Stack
2 |
3 | According to Wikipedia:
4 |
5 | > A Stack is an abstract data type that serves as a collection of elements, with two principal operations: push, which adds an element to the collection, and pop, which removes the most recently added element that was not yet removed. The order in which elements come off a Stack gives rise to its alternative name, LIFO (for last in, first out).
6 |
7 | A Stack often has a third method peek which allows to check the last pushed element without popping it.
8 |
9 | It is a list of elements that are accessible only from one end of the list, which is called the top.
10 |
11 | Stacks implement a LIFO (Last-In First-Out) structure which means that the last element added to the structure must be the first one to be removed
12 |
13 | In this implementation, an object is used to build the stack.
14 |
15 | ### Complexity
16 |
17 | #### Average
18 |
19 | | Operation | Complexity |
20 | | :-------: | :--------: |
21 | | Access | O(n) |
22 | | Search | O(n) |
23 | | Insertion | O(1) |
24 | | Deletion | O(1) |
25 |
26 | Simple representation of a stack runtime with push and pop operations.
27 |
28 | 
29 |
30 | ## References
31 |
32 | - [Wikipedia](https://en.wikipedia.org/wiki/Stack_(abstract_data_type))
33 | - [YouTube](https://www.youtube.com/watch?v=wjI1WNcIntg&list=PLLXdhg_r2hKA7DPDsunoDZ-Z769jWn4R8&index=3&)
34 |
--------------------------------------------------------------------------------
/src/algorithms/math/sieve-of-eratosthenes/README.md:
--------------------------------------------------------------------------------
1 | # Sieve of Eratosthenes
2 |
3 | The Sieve of Eratosthenes is an algorithm for finding all prime numbers up to some limit `n`.
4 |
5 | It is attributed to Eratosthenes of Cyrene, an ancient Greek mathematician.
6 |
7 | ## How it works
8 |
9 | 1. Create a boolean array of `n + 1` positions (to represent the numbers `0` through `n`)
10 | 2. Set positions `0` and `1` to `false`, and the rest to `true`
11 | 3. Start at position `p = 2` (the first prime number)
12 | 4. Mark as `false` all the multiples of `p` (that is, positions `2 * p`, `3 * p`, `4 * p`... until you reach the end of the array)
13 | 5. Find the first position greater than `p` that is `true` in the array. If there is no such position, stop. Otherwise, let `p` equal this new number (which is the next prime), and repeat from step 4
14 |
15 | When the algorithm terminates, the numbers remaining `true` in the array are all the primes below `n`.
16 |
17 | An improvement of this algorithm is, in step 4, start marking multiples of `p` from `p * p`, and not from `2 * p`. The reason why this works is because, at that point, smaller multiples of `p` will have already been marked `false`.
18 |
19 | ## Example
20 |
21 | 
22 |
23 | ## Complexity
24 |
25 | The algorithm has a complexity of `O(n log(log n))`.
26 |
27 | ## References
28 |
29 | - [Wikipedia](https://en.wikipedia.org/wiki/Sieve_of_Eratosthenes)
30 |
--------------------------------------------------------------------------------
/src/algorithms/set/combination-sum/README.md:
--------------------------------------------------------------------------------
1 | # Combination Sum
2 |
3 | Given a **set** of candidate numbers (`candidates`) **(without duplicates)** and a target number (`target`), find all unique combinations in `candidates` where the candidate numbers sums to `target`.
4 |
5 | The **same** repeated number may be chosen from `candidates` unlimited number of times.
6 |
7 | **Note:**
8 |
9 | - All numbers (including `target`) will be positive integers.
10 | - The solution set must not contain duplicate combinations.
11 |
12 | ## Examples
13 |
14 | ```
15 | Input: candidates = [2,3,6,7], target = 7,
16 |
17 | A solution set is:
18 | [
19 | [7],
20 | [2,2,3]
21 | ]
22 | ```
23 |
24 | ```
25 | Input: candidates = [2,3,5], target = 8,
26 |
27 | A solution set is:
28 | [
29 | [2,2,2,2],
30 | [2,3,3],
31 | [3,5]
32 | ]
33 | ```
34 |
35 | ## Explanations
36 |
37 | Since the problem is to get all the possible results, not the best or the number of result, thus we don’t need to consider DP (dynamic programming), backtracking approach using recursion is needed to handle it.
38 |
39 | Here is an example of decision tree for the situation when `candidates = [2, 3]` and `target = 6`:
40 |
41 | ```
42 | 0
43 | / \
44 | +2 +3
45 | / \ \
46 | +2 +3 +3
47 | / \ / \ \
48 | +2 ✘ ✘ ✘ ✓
49 | / \
50 | ✓ ✘
51 | ```
52 |
53 | ## References
54 |
55 | - [LeetCode](https://leetcode.com/problems/combination-sum/description/)
56 |
--------------------------------------------------------------------------------
/.gitignore:
--------------------------------------------------------------------------------
1 | # Created by https://www.gitignore.io/api/node
2 |
3 | ### Node ###
4 | # Logs
5 | logs
6 | *.log
7 | npm-debug.log*
8 | yarn-debug.log*
9 | yarn-error.log*
10 |
11 | # Runtime data
12 | pids
13 | *.pid
14 | *.seed
15 | *.pid.lock
16 |
17 | # Directory for instrumented libs generated by jscoverage/JSCover
18 | lib-cov
19 |
20 | # Coverage directory used by tools like istanbul
21 | coverage
22 |
23 | # nyc test coverage
24 | .nyc_output
25 |
26 | # Grunt intermediate storage (http://gruntjs.com/creating-plugins#storing-task-files)
27 | .grunt
28 |
29 | # Bower dependency directory (https://bower.io/)
30 | bower_components
31 |
32 | # node-waf configuration
33 | .lock-wscript
34 |
35 | # Compiled binary addons (https://nodejs.org/api/addons.html)
36 | build/Release
37 |
38 | # Dependency directories
39 | node_modules/
40 | jspm_packages/
41 |
42 | # TypeScript v1 declaration files
43 | typings/
44 |
45 | # Optional npm cache directory
46 | .npm
47 |
48 | # Optional eslint cache
49 | .eslintcache
50 |
51 | # Optional REPL history
52 | .node_repl_history
53 |
54 | # Output of 'npm pack'
55 | *.tgz
56 |
57 | # Yarn Integrity file
58 | .yarn-integrity
59 |
60 | # dotenv environment variables file
61 | .env
62 |
63 | # parcel-bundler cache (https://parceljs.org/)
64 | .cache
65 |
66 | # next.js build output
67 | .next
68 |
69 | # nuxt.js build output
70 | .nuxt
71 |
72 | # vuepress build output
73 | .vuepress/dist
74 |
75 | # Serverless directories
76 | .serverless
77 |
78 |
79 | # End of https://www.gitignore.io/api/node
80 |
81 | .DS_Store
82 |
--------------------------------------------------------------------------------
/__tests__/unit/src/algorithms/fibonacci.spec.js:
--------------------------------------------------------------------------------
1 | import chai from 'chai';
2 | import fibonacci, { fibonacciDP } from 'src/algorithms/math/fibonacci';
3 |
4 |
5 | const { expect } = chai;
6 |
7 | describe('Factorial', () => {
8 | describe('using recursion', () => {
9 | it('should compute fibonacci number at the given position', () => {
10 | expect(fibonacci(0)).to.be.equal(0);
11 | expect(fibonacci(1)).to.be.equal(1);
12 | expect(fibonacci(2)).to.be.equal(1);
13 | expect(fibonacci(3)).to.be.equal(2);
14 | expect(fibonacci(4)).to.be.equal(3);
15 | expect(fibonacci(5)).to.be.equal(5);
16 | expect(fibonacci(6)).to.be.equal(8);
17 | expect(fibonacci(7)).to.be.equal(13);
18 | expect(fibonacci(8)).to.be.equal(21);
19 | expect(fibonacci(9)).to.be.equal(34);
20 | expect(fibonacci(10)).to.be.equal(55);
21 | });
22 | });
23 |
24 | describe('using dynamic programming', () => {
25 | it('should compute fibonacci number at the given position', () => {
26 | expect(fibonacciDP(0)).to.be.equal(0);
27 | expect(fibonacciDP(1)).to.be.equal(1);
28 | expect(fibonacciDP(2)).to.be.equal(1);
29 | expect(fibonacciDP(3)).to.be.equal(2);
30 | expect(fibonacciDP(4)).to.be.equal(3);
31 | expect(fibonacciDP(5)).to.be.equal(5);
32 | expect(fibonacciDP(6)).to.be.equal(8);
33 | expect(fibonacciDP(7)).to.be.equal(13);
34 | expect(fibonacciDP(8)).to.be.equal(21);
35 | expect(fibonacciDP(9)).to.be.equal(34);
36 | expect(fibonacciDP(10)).to.be.equal(55);
37 | });
38 | });
39 | });
40 |
--------------------------------------------------------------------------------
/src/data-structures/array/index.js:
--------------------------------------------------------------------------------
1 | export default class MyArray {
2 | /**
3 | * initialize MyArray
4 | *
5 | * in this case we'll use JavaScript built-in array 😄
6 | * we should probably try using an object next time
7 | */
8 | constructor() {
9 | this.array = [];
10 | }
11 |
12 | /**
13 | * adds an item onto the array
14 | * @param {any} item
15 | */
16 | add(item) {
17 | this.array.push(item);
18 | }
19 |
20 | /**
21 | * removes an item from the array
22 | * @param {any} item
23 | */
24 | remove(item) {
25 | this.array = this.array.filter(data => data !== item);
26 | }
27 |
28 | /**
29 | * look for the given item in the array
30 | * @param {any} item
31 | * @return {number} the array index position of the item found
32 | */
33 | search(item) {
34 | const foundIndex = this.array.indexOf(item);
35 |
36 | return foundIndex || null;
37 | }
38 |
39 | /**
40 | * get an item given its index on the array
41 | * @param {number} index index of the item to get
42 | * @return {any} the item found at the given index
43 | */
44 | getAtIndex(index) {
45 | return this.array[index];
46 | }
47 |
48 | /**
49 | * returns the size/length of the array
50 | * @return {number} the size of the array
51 | */
52 | length() {
53 | return this.array.length;
54 | }
55 |
56 | /**
57 | * prints the contents of the array
58 | * @return {any}
59 | */
60 | print() {
61 | // console.log(this.array.join(' '));
62 |
63 | return this.array.join(' ');
64 | }
65 | }
66 |
--------------------------------------------------------------------------------
/src/algorithms/sorting/merge-sort/README.md:
--------------------------------------------------------------------------------
1 | # Merge Sort
2 |
3 | In computer science, merge sort (also commonly spelled mergesort) is an efficient, general-purpose, comparison-based sorting algorithm. Most implementations produce a stable sort, which means that the implementation preserves the input order of equal elements in the sorted output. Mergesort is a divide and conquer algorithm that was invented by John von Neumann in 1945.
4 |
5 | An example of merge sort. First divide the list into the smallest unit (1 element), then compare each element with the adjacent list to sort and merge the two adjacent lists. Finally all the elements are sorted and merged.
6 |
7 | 
8 |
9 | A recursive merge sort algorithm used to sort an array of 7 integer values. These are the steps a human would take to emulate merge sort (top-down).
10 |
11 | 
12 |
13 | ## Complexity
14 |
15 | | Name | Best | Average | Worst | Memory | Stable | Comments |
16 | | --------------------- | :-------------: | :-----------------: | :-----------------: | :-------: | :-------: | :-------- |
17 | | **Merge sort** | n log(n) | n log(n) | n log(n) | n | Yes | |
18 |
19 | ## References
20 |
21 | - [Wikipedia](https://en.wikipedia.org/wiki/Merge_sort)
22 | - [YouTube](https://www.youtube.com/watch?v=KF2j-9iSf4Q&index=27&list=PLLXdhg_r2hKA7DPDsunoDZ-Z769jWn4R8)
23 |
--------------------------------------------------------------------------------
/src/algorithms/sorting/merge-sort/index.js:
--------------------------------------------------------------------------------
1 | /**
2 | * utility function that merges and sorts two arrays
3 | * @param {array} left
4 | * @param {array} right
5 | * @return {array} the merged sorted array
6 | */
7 | export const merge = (left, right) => {
8 | const results = [];
9 |
10 | // when being combined, each group's numbers are arranged so that
11 | // they are ordered from smallest to largest after combination
12 | // when groups with multiple numbers are combined, the first
13 | // numbers are compared
14 | while (left.length && right.length) {
15 | if (left[0] < right[0]) {
16 | results.push(left.shift());
17 | } else {
18 | results.push(right.shift());
19 | }
20 | }
21 |
22 | return [...results, ...left, ...right];
23 | };
24 |
25 | /**
26 | * merge sort implementation
27 | * @param {array} array an unsorted array
28 | * @return {array} sorted array
29 | */
30 | const mergeSort = (array) => {
31 | if (array.length <= 1) return array;
32 |
33 | // first, the sequence/array is divided further and further into halves
34 | // in our algorithm, the divisions are done via recursion i.e. calling
35 | // this function over and over again until the divisions are complete
36 | const middle = Math.floor(array.length / 2);
37 | const left = array.slice(0, middle);
38 | const right = array.slice(middle);
39 |
40 | // next, the divided groups are combined using our helper merge function
41 | // also, the combining of groups is repeated recursively until all numbers
42 | // form one group
43 | return merge(mergeSort(left), mergeSort(right));
44 | };
45 |
46 | export default mergeSort;
47 |
--------------------------------------------------------------------------------
/src/algorithms/sorting/quick-sort/README.md:
--------------------------------------------------------------------------------
1 | # Quicksort
2 |
3 | Quicksort is a divide and conquer algorithm. It first divides a large array into two smaller sub-arrays: the low elements and the high elements. Quicksort can then recursively sort the sub-arrays
4 |
5 | The steps are:
6 |
7 | 1. Pick an element, called a pivot, from the array.
8 | 2. Partitioning: reorder the array so that all elements with values less than the pivot come before the pivot, while all elements with values greater than the pivot come after it (equal values can go either way). After this partitioning, the pivot is in its final position. This is called the partition operation.
9 | 3. Recursively apply the above steps to the sub-array of elements with smaller values and separately to the sub-array of elements with greater values.
10 |
11 | Animated visualization of the quicksort algorithm.
12 | The horizontal lines are pivot values.
13 |
14 | 
15 |
16 | ## Complexity
17 |
18 | | Name | Best | Average | Worst | Memory | Stable | Comments |
19 | | --------------------- | :-------------: | :-----------------: | :-----------------: | :-------: | :-------: | :-------- |
20 | | **Quick sort** | n log(n) | n log(n) | n2 | log(n) | No | Quicksort is usually done in-place with O(log(n)) stack space |
21 |
22 | ## References
23 |
24 | - [Wikipedia](https://en.wikipedia.org/wiki/Quicksort)
25 | - [YouTube](https://www.youtube.com/watch?v=SLauY6PpjW4&index=28&list=PLLXdhg_r2hKA7DPDsunoDZ-Z769jWn4R8)
26 |
--------------------------------------------------------------------------------
/__tests__/unit/src/algorithms/linear-search.spec.js:
--------------------------------------------------------------------------------
1 | import chai from 'chai';
2 | import linearSearch from 'src/algorithms/searching/linear-search';
3 |
4 |
5 | const { expect } = chai;
6 |
7 | describe('Linear Search', () => {
8 | describe('using array helper "forEach"', () => {
9 | it('should return the correct index of a given number', () => {
10 | const array = [0, 1, 2, 3, 4, 5, 6, 10, 26, 35, 45, 50];
11 |
12 | expect(linearSearch(array, 0)).to.be.equal(0);
13 | expect(linearSearch(array, 2)).to.be.equal(2);
14 | expect(linearSearch(array, 4)).to.be.equal(4);
15 | expect(linearSearch(array, 5)).to.be.equal(5);
16 | expect(linearSearch(array, 10)).to.be.equal(7);
17 | expect(linearSearch(array, 35)).to.be.equal(9);
18 | });
19 |
20 | it('should return the correct index of a given string', () => {
21 | const array = ['a', 'b', 'd', 'f', 'c', 'e'];
22 |
23 | expect(linearSearch(array, 'a')).to.be.equal(0);
24 | expect(linearSearch(array, 'b')).to.be.equal(1);
25 | expect(linearSearch(array, 'c')).to.be.equal(4);
26 | expect(linearSearch(array, 'd')).to.be.equal(2);
27 | expect(linearSearch(array, 'e')).to.be.equal(5);
28 | expect(linearSearch(array, 'f')).to.be.equal(3);
29 | });
30 |
31 | it('should return -1 for an item not found in the array', () => {
32 | const array = [0, 1, 2, 3, 4, 5, 6, 10, 26, 35, 45, 50];
33 |
34 | expect(linearSearch(array, 17)).to.be.equal(-1);
35 | expect(linearSearch(array, 73)).to.be.equal(-1);
36 | expect(linearSearch(array, 'a')).to.be.equal(-1);
37 | expect(linearSearch(array, 'h')).to.be.equal(-1);
38 | });
39 | });
40 | });
41 |
--------------------------------------------------------------------------------
/__tests__/unit/src/algorithms/merge-sort.spec.js:
--------------------------------------------------------------------------------
1 | import chai from 'chai';
2 | import mergeSort, { merge } from 'src/algorithms/sorting/merge-sort';
3 |
4 |
5 | const { expect } = chai;
6 |
7 | describe('Merge Sort', () => {
8 | describe('merge helper function', () => {
9 | it('should merge two arrays', () => {
10 | const array1 = [2, 1, 4];
11 | const array2 = [5, 3, 6, 7];
12 | const mergedArray = [2, 1, 4, 5, 3, 6, 7];
13 |
14 | expect(merge([], [])).to.deep.equal([]);
15 | expect(merge([1], [])).to.deep.equal([1]);
16 | expect(merge([1], [2])).to.deep.equal([1, 2]);
17 | expect(merge(array1, array2)).to.deep.equal(mergedArray);
18 | });
19 | });
20 |
21 | describe('sorting operation', () => {
22 | it('should return empty array', () => {
23 | expect(mergeSort([])).to.deep.equal([]);
24 | });
25 |
26 | it('should return the passed array', () => {
27 | expect(mergeSort([1])).to.deep.equal([1]);
28 | expect(mergeSort([2])).to.deep.equal([2]);
29 | expect(mergeSort([5])).to.deep.equal([5]);
30 | expect(mergeSort([356])).to.deep.equal([356]);
31 | });
32 |
33 | it('should sort a random array', () => {
34 | const array = [2, 8, 10, 11, 12, 13, 14, 18, 19, 20];
35 | const sortedArray = [2, 8, 10, 11, 12, 13, 14, 18, 19, 20];
36 |
37 | expect(mergeSort(array)).to.deep.equal(sortedArray);
38 | });
39 |
40 | it('should sort a reversed sorted array', () => {
41 | const reversedArray = [12, 10, 8, 7, 6, 5, 4, 3, 2, 1];
42 | const sortedArray = [1, 2, 3, 4, 5, 6, 7, 8, 10, 12];
43 |
44 | expect(mergeSort(reversedArray)).to.deep.equal(sortedArray);
45 | });
46 | });
47 | });
48 |
--------------------------------------------------------------------------------
/src/algorithms/searching/interpolation-search/README.md:
--------------------------------------------------------------------------------
1 | # Interpolation Search
2 |
3 | **Interpolation search** is an algorithm for searching for a key in an array that has been ordered by numerical values assigned to the keys (key values).
4 |
5 | For example we have a sorted array of `n` uniformly distributed values `arr[]`, and we need to write a function to search for a particular element `x` in the array.
6 |
7 | **Linear Search** finds the element in `O(n)` time, **Jump Search** takes `O(√ n)` time and **Binary Search** take `O(Log n)` time.
8 |
9 | The **Interpolation Search** is an improvement over Binary Search for instances, where the values in a sorted array are _uniformly_ distributed. Binary Search always goes to the middle element to check. On the other hand, interpolation search may go to different locations according to the value of the key being searched. For example, if the value of the key is closer to the last element, interpolation search is likely to start search toward the end side.
10 |
11 | To find the position to be searched, it uses following formula:
12 |
13 | ```
14 | // The idea of formula is to return higher value of pos
15 | // when element to be searched is closer to arr[hi]. And
16 | // smaller value when closer to arr[lo]
17 | pos = lo + ((x - arr[lo]) * (hi - lo) / (arr[hi] - arr[Lo]))
18 |
19 | arr[] - Array where elements need to be searched
20 | x - Element to be searched
21 | lo - Starting index in arr[]
22 | hi - Ending index in arr[]
23 | ```
24 |
25 | ## Complexity
26 |
27 | **Time complexity**: `O(log(log(n))`
28 |
29 | ## References
30 |
31 | - [GeeksForGeeks](https://www.geeksforgeeks.org/interpolation-search/)
32 | - [Wikipedia](https://en.wikipedia.org/wiki/Interpolation_search)
33 |
--------------------------------------------------------------------------------
/src/algorithms/searching/binary-search/index.js:
--------------------------------------------------------------------------------
1 | import { isArraySorted } from 'src/utils';
2 |
3 | /**
4 | * Binary Search implementation using iteration
5 | * @param {array} sortedArray
6 | * @param {string|number} target
7 | * @return {number} the index of the found element
8 | */
9 | const binarySearch = (sortedArray, target) => {
10 | if (!isArraySorted(sortedArray)) throw new Error('The provided array is not sorted');
11 |
12 | let start = 0;
13 | let end = sortedArray.length - 1;
14 |
15 | while (start <= end) {
16 | const mid = Math.floor((end - start) / 2) + start;
17 |
18 | if (target < sortedArray[mid]) {
19 | end = mid - 1;
20 | } else if (target > sortedArray[mid]) {
21 | start = mid + 1;
22 | } else {
23 | return mid;
24 | }
25 | }
26 |
27 | return -1;
28 | };
29 |
30 | /**
31 | * Binary Search implementation using recursion
32 | * @param {array} sortedArray
33 | * @param {string|number} target
34 | * @return {number} the index of the found element
35 | */
36 | export const recursiveBinarySearch = (sortedArray, target) => {
37 | if (!isArraySorted(sortedArray)) throw new Error('The provided array is not sorted');
38 |
39 | return ((function recurse(start, end) {
40 | let result = -1;
41 |
42 | if (start > end) return result;
43 |
44 | const mid = Math.floor((end - start) / 2) + start;
45 |
46 | if (target === sortedArray[mid]) {
47 | result = mid;
48 | } else if (target < sortedArray[mid]) {
49 | result = recurse(start, mid - 1);
50 | } else {
51 | result = recurse(mid + 1, end);
52 | }
53 |
54 | return result;
55 | })(0, sortedArray.length - 1));
56 | };
57 |
58 | export default binarySearch;
59 |
--------------------------------------------------------------------------------
/src/data-structures/queue/README.md:
--------------------------------------------------------------------------------
1 | ## Queue
2 |
3 | According to Wikipedia:
4 |
5 | > In computer science, a queue is a particular kind of abstract data type or collection in which the entities in the collection are kept in order and the principal (or only) operations on the collection are the addition of entities to the rear terminal position, known as enqueue, and removal of entities from the front terminal position, known as dequeue. This makes the queue a First-In-First-Out (FIFO) data structure. In a FIFO data structure, the first element added to the queue will be the first one to be removed. This is equivalent to the requirement that once a new element is added, all elements that were added before have to be removed before the new element can be removed. Often a peek or front operation is also entered, returning the value of the front element without dequeuing it. A queue is an example of a linear data structure, or more abstractly a sequential collection.
6 |
7 | As with the Stack data structure, a peek operation is often added to the Queue data structure. It returns the value of the front element without dequeuing it.
8 |
9 | In this implementation, an array is used to build the queue.
10 |
11 | ### Complexity
12 |
13 | #### Average
14 |
15 | | Operation | Complexity |
16 | | :-------: | :--------: |
17 | | Access | O(n) |
18 | | Search | O(n) |
19 | | Insertion | O(1) |
20 | | Deletion | O(n) |
21 |
22 | Simple representation of a queue runtime with enqueue and dequeue operations.
23 |
24 | 
25 |
26 | ## References
27 |
28 | - [Wikipedia](https://en.wikipedia.org/wiki/Queue_(abstract_data_type))
29 | - [YouTube](https://www.youtube.com/watch?v=wjI1WNcIntg&list=PLLXdhg_r2hKA7DPDsunoDZ-Z769jWn4R8&index=3&)
30 |
--------------------------------------------------------------------------------
/src/data-structures/doubly-linked-list/README.md:
--------------------------------------------------------------------------------
1 | ## Doubly Linked List
2 |
3 | According to Wikipedia:
4 |
5 | > In computer science, a doubly linked list is a linked data structure that consists of a set of sequentially linked records called nodes. Each node contains two fields, called links, that are references to the previous and to the next node in the sequence of nodes. The beginning and ending nodes' previous and next links, respectively, point to some kind of terminator, typically a sentinel node or null, to facilitate traversal of the list. If there is only one sentinel node, then the list is circularly linked via the sentinel node. It can be conceptualized as two singly linked lists formed from the same data items, but in opposite sequential orders.
6 |
7 | The two node links allow traversal of the list in either direction. While adding or removing a node in a doubly linked list requires changing more links than the same operations on a singly linked list, the operations are simpler and potentially more efficient (for nodes other than first nodes) because there is no need to keep track of the previous node during traversal or no need to traverse the list to find the previous node, so that its link can be modified.
8 |
9 | ### Complexity
10 |
11 | #### Average
12 |
13 | | Operation | Complexity |
14 | | :-------: | :--------: |
15 | | Access | O(n) |
16 | | Search | O(n) |
17 | | Insertion | O(1) |
18 | | Deletion | O(1) |
19 |
20 | Simple representation of a doubly linked list.
21 |
22 | 
23 |
24 | ## References
25 |
26 | - [Wikipedia](https://en.wikipedia.org/wiki/Doubly_linked_list)
27 | - [YouTube](https://www.youtube.com/watch?v=JdQeNxWCguQ&t=7s&index=72&list=PLLXdhg_r2hKA7DPDsunoDZ-Z769jWn4R8)
28 |
--------------------------------------------------------------------------------
/__tests__/unit/src/data-structures/tree.spec.js:
--------------------------------------------------------------------------------
1 | import chai from 'chai';
2 | import Tree from 'src/data-structures/tree';
3 |
4 |
5 | const { expect } = chai;
6 |
7 | describe('Tree', () => {
8 | const tree = new Tree();
9 |
10 | it('is a class', () => {
11 | expect(typeof Tree.prototype.constructor).to.equal('function');
12 | });
13 |
14 | describe('.addNode()', () => {
15 | it('adds nodes to the tree', () => {
16 | tree.addNode('ceo');
17 | tree.addNode('cto', 'ceo');
18 | tree.addNode('dev1', 'cto');
19 | tree.addNode('dev2', 'cto');
20 | tree.addNode('dev3', 'cto');
21 | tree.addNode('cfo', 'ceo');
22 | tree.addNode('accountant', 'cfo');
23 | tree.addNode('cmo', 'ceo');
24 |
25 | const treeStr = 'ceo | cto cfo cmo | dev1 dev2 dev3 accountant';
26 | const treeByLevel = 'ceo \ncto cfo cmo \ndev1 dev2 dev3 accountant';
27 |
28 | expect(tree.print()).to.equal(treeStr);
29 | expect(tree.printByLevel()).to.equal(treeByLevel);
30 | expect(tree.addNode('ceo')).to.equal('Root node is already assigned');
31 | });
32 | });
33 |
34 | describe('.remove()', () => {
35 | it('removes nodes from the tree', () => {
36 | tree.remove('cmo');
37 |
38 | const treeStr = 'ceo | cto cfo | dev1 dev2 dev3 accountant';
39 |
40 | expect(tree.print()).to.equal(treeStr);
41 | });
42 | });
43 |
44 | describe('.contains()', () => {
45 | it('checks whether the tree has the provided node data', () => {
46 | expect(tree.contains('dev1')).to.equal(true);
47 | expect(tree.contains('dev4')).to.equal(false);
48 |
49 | tree.remove('ceo');
50 |
51 | expect(tree.contains('ceo')).to.equal(false);
52 | expect(tree.print()).to.equal('No root node found');
53 | expect(tree.printByLevel()).to.equal('No root node found');
54 | });
55 | });
56 | });
57 |
--------------------------------------------------------------------------------
/.cz-config.js:
--------------------------------------------------------------------------------
1 | module.exports = {
2 | types: [
3 | { value: 'feat', name: 'feat: A new feature' },
4 | { value: 'fix', name: 'fix: A bug fix' },
5 | { value: 'docs', name: 'docs: Documentation only changes' },
6 | { value: 'style', name: 'style: Changes that do not affect the meaning of the code\n (white-space, formatting, missing semi-colons, etc)' },
7 | { value: 'refactor', name: 'refactor: A code change that neither fixes a bug nor adds a feature' },
8 | { value: 'perf', name: 'perf: A code change that improves performance' },
9 | { value: 'test', name: 'test: Adding missing tests' },
10 | { value: 'chore', name: 'chore: Changes to the build process or auxiliary tools\n and libraries such as documentation generation' },
11 | { value: 'revert', name: 'revert: Revert to a commit' },
12 | { value: 'WIP', name: 'WIP: Work in progress' },
13 | ],
14 |
15 | scopes: [
16 | { name: 'repo' },
17 | { name: 'config' },
18 | { name: 'ds' },
19 | { name: 'algorithm' },
20 | { name: 'util' },
21 | ],
22 |
23 | // override the messages, defaults are as follows
24 | messages: {
25 | type: 'Select the type of change that you\'re committing:',
26 | scope: '\nDenote the SCOPE of this change (optional):',
27 | // used if allowCustomScopes is true
28 | customScope: 'Denote the SCOPE of this change:',
29 | subject: 'Write a SHORT, IMPERATIVE tense description of the change:\n',
30 | body: 'Provide a LONGER description of the change (optional). Use "|" to break new line:\n',
31 | breaking: 'List any BREAKING CHANGES (optional):\n',
32 | footer: 'List any ISSUES CLOSED by this change (optional). E.g.: #31, #34:\n',
33 | confirmCommit: 'Are you sure you want to proceed with the commit above?',
34 | },
35 |
36 | allowCustomScopes: true,
37 | allowBreakingChanges: ['feat', 'fix'],
38 | };
39 |
--------------------------------------------------------------------------------
/src/algorithms/set/permutations/README.md:
--------------------------------------------------------------------------------
1 | # Permutations
2 |
3 | When the order doesn't matter, it is a **Combination**.
4 |
5 | When the order **does** matter it is a **Permutation**.
6 |
7 | **"The combination to the safe is 472"**. We do care about the order. `724` won't work, nor will `247`. It has to be exactly `4-7-2`.
8 |
9 | ## Permutations without repetitions
10 |
11 | A permutation, also called an “arrangement number” or “order”, is a rearrangement of the elements of an ordered list `S` into a one-to-one correspondence with `S` itself.
12 |
13 | Below are the permutations of string `ABC`.
14 |
15 | `ABC ACB BAC BCA CBA CAB`
16 |
17 | Or for example the first three people in a running race: you can't be first and second.
18 |
19 | **Number of combinations**
20 |
21 | ```
22 | n * (n-1) * (n -2) * ... * 1 = n!
23 | ```
24 |
25 | ## Permutations with repetitions
26 |
27 | When repetition is allowed we have permutations with repetitions.
28 | For example the the lock below: it could be `333`.
29 |
30 | 
31 |
32 | **Number of combinations**
33 |
34 | ```
35 | n * n * n ... (r times) = n^r
36 | ```
37 |
38 | ## Cheat Sheets
39 |
40 | Permutations cheat sheet
41 |
42 | 
43 |
44 | Combinations cheat sheet
45 |
46 | 
47 |
48 | Permutations/combinations algorithm ideas.
49 |
50 | 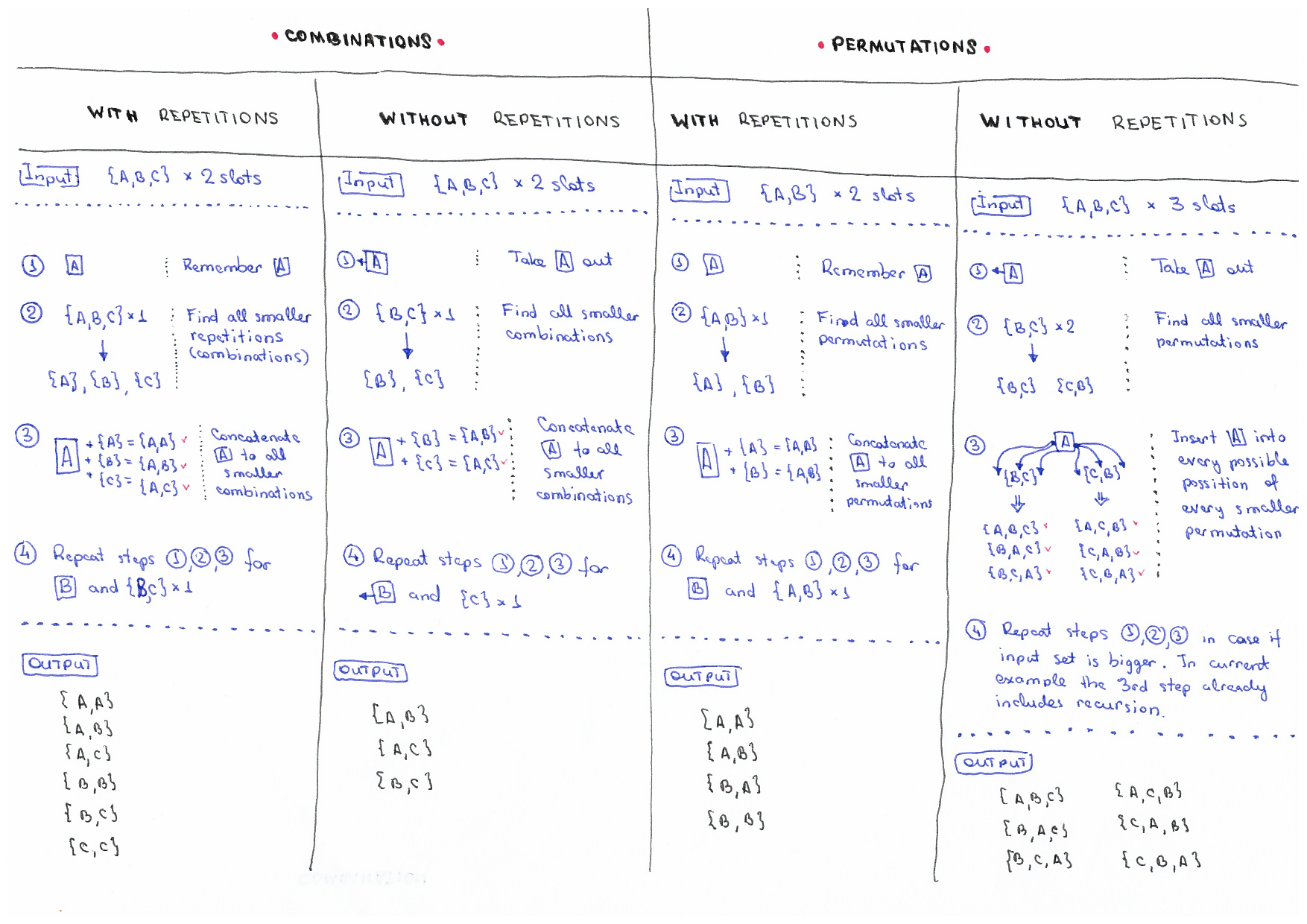
51 |
52 | ## References
53 |
54 | - [Math Is Fun](https://www.mathsisfun.com/combinatorics/combinations-permutations.html)
55 | - [Permutations/combinations cheat sheets](https://medium.com/@trekhleb/permutations-combinations-algorithms-cheat-sheet-68c14879aba5)
56 |
--------------------------------------------------------------------------------
/src/data-structures/disjoint-set/README.md:
--------------------------------------------------------------------------------
1 | ## Disjoint Set
2 |
3 | According to Wikipedia:
4 |
5 | > In computer science, a disjoint-set data structure (also called a union–find data structure or merge–find set) is a data structure that tracks a set of elements partitioned into a number of disjoint (non-overlapping) subsets. It provides near-constant-time operations (bounded by the inverse Ackermann function) to add new sets, to merge existing sets, and to determine whether elements are in the same set. In addition to many other uses (see the Applications section), disjoint-sets play a key role in Kruskal's algorithm for finding the minimum spanning tree of a graph.
6 |
7 | 
8 |
9 | *MakeSet* creates 8 singletons.
10 |
11 | 
12 |
13 | After some operations of *Union*, some sets are grouped together.
14 |
15 | The idea of Disjoint Sets can be perfectly applied in finding the minimal spanning tree. The Disjoint Sets consist of two basic operations: finding the group (parent) of any element, unioning two or more sets.
16 |
17 | ### Complexity
18 |
19 | #### Average
20 |
21 | | Operation | Complexity |
22 | | :-------: | :--------: |
23 | | Access | --- |
24 | | Search | O(1) |
25 | | Space | O(n) |
26 | | Merge | O(1) |
27 |
28 | Simple representation of a Disjoint Set
29 |
30 | 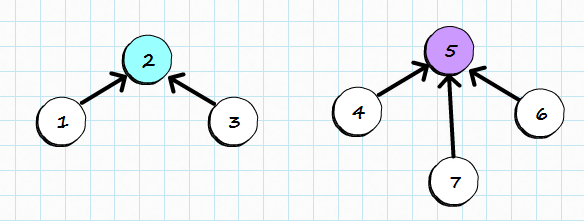
31 |
32 | Two sets, one with 3 the other with 4 items
33 |
34 | **Merging:**
35 |
36 | 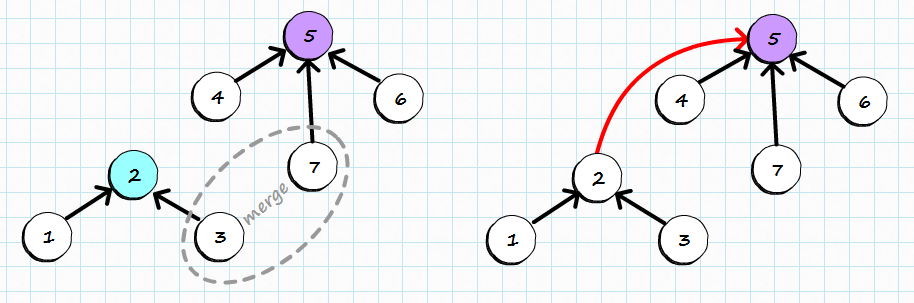
37 |
38 | Merging sets
39 |
40 | ## References
41 |
42 | - [Wikipedia](https://en.wikipedia.org/wiki/Disjoint-set_data_structure)
43 | - [YouTube - Abdul Bari](https://www.youtube.com/watch?v=wU6udHRIkcc&index=14&t=0s&list=PLLXdhg_r2hKA7DPDsunoDZ-Z769jWn4R8)
44 |
--------------------------------------------------------------------------------
/src/algorithms/math/lcm/README.md:
--------------------------------------------------------------------------------
1 | # Least Common Multiple
2 |
3 | In arithmetic and number theory, the least common multiple, lowest common multiple, or smallest common multiple of two integers `a` and `b`, usually denoted by `LCM(a, b)`, is the smallest positive integer that is divisible by both `a` and `b`. Since division of integers by zero is undefined, this definition has meaning only if `a` and `b` are both different from zero. However, some authors define `lcm(a,0)` as `0` for all `a`, which is the result of taking the `lcm` to be the least upper bound in the lattice of divisibility.
4 |
5 | ## Example
6 |
7 | What is the LCM of 4 and 6?
8 |
9 | Multiples of `4` are:
10 |
11 | ```
12 | 4, 8, 12, 16, 20, 24, 28, 32, 36, 40, 44, 48, 52, 56, 60, 64, 68, 72, 76, ...
13 | ```
14 |
15 | and the multiples of `6` are:
16 |
17 | ```
18 | 6, 12, 18, 24, 30, 36, 42, 48, 54, 60, 66, 72, ...
19 | ```
20 |
21 | Common multiples of `4` and `6` are simply the numbers that are in both lists:
22 |
23 | ```
24 | 12, 24, 36, 48, 60, 72, ....
25 | ```
26 |
27 | So, from this list of the first few common multiples of the numbers `4` and `6`, their least common multiple is `12`.
28 |
29 | ## Computing the least common multiple
30 |
31 | The following formula reduces the problem of computing the least common multiple to the problem of computing the greatest common divisor (GCD), also known as the greatest common factor:
32 |
33 | ```
34 | lcm(a, b) = |a * b| / gcd(a, b)
35 | ```
36 |
37 | 
38 |
39 | A Venn diagram showing the least common multiples of combinations of `2`, `3`, `4`, `5` and `7` (`6` is skipped as it is `2 × 3`, both of which are already represented).
40 |
41 | For example, a card game which requires its cards to be divided equally among up to `5` players requires at least `60` cards, the number at the intersection of the `2`, `3`, `4` and `5` sets, but not the `7` set.
42 |
43 | ## References
44 |
45 | - [Wikipedia](https://en.wikipedia.org/wiki/Least_common_multiple)
46 |
--------------------------------------------------------------------------------
/src/data-structures/stack/index.js:
--------------------------------------------------------------------------------
1 | export default class Stack {
2 | /**
3 | * initializes the stack
4 | * @param {number} capacity - the capacity of the stack
5 | */
6 | constructor(capacity = Infinity) {
7 | this._capacity = capacity;
8 | this._data = {};
9 | this._top = 0;
10 | }
11 |
12 | /**
13 | * adds a new element onto the stack
14 | * @param {any} element
15 | * @return {number|string} the index of the added element or stack overflow message
16 | */
17 | push(element) {
18 | if (this._top < this._capacity) {
19 | this._data[this._top++] = element;
20 |
21 | return this._top;
22 | }
23 |
24 | return 'Max capacity already reached. Remove element before adding a new one.';
25 | }
26 |
27 | /**
28 | * does the reverse of the push() and then decrements the top pointer variable
29 | * @return {any} the element in the top position of the stack or an error message
30 | */
31 | pop() {
32 | if (this._top === 0) {
33 | return 'No element inside the stack. Add element before poping.';
34 | }
35 |
36 | const element = this._data[--this._top];
37 | delete this._data[this._top];
38 |
39 | if (this._top < 0) {
40 | this._top = 0;
41 | }
42 |
43 | return element;
44 | }
45 |
46 | /**
47 | * returns the most recent element added onto the stack
48 | * @return {any} returns the top element of the stack
49 | */
50 | peek() {
51 | return this._data[this._top - 1];
52 | }
53 |
54 | /**
55 | * returns the size/length of the stack
56 | * @return {number} the value of top
57 | */
58 | size() {
59 | return this._top;
60 | }
61 |
62 | /**
63 | * check whether the stack is empty
64 | * @return {boolean}
65 | */
66 | isEmpty() {
67 | return this._top === 0;
68 | }
69 |
70 | /**
71 | * clears the stack and sets the top pointer variable back to 0
72 | */
73 | clear() {
74 | this._data = {};
75 | this._top = 0;
76 | }
77 |
78 | /**
79 | * displays the stack
80 | */
81 | print() {
82 | return Object.values(this._data).join(' ');
83 | }
84 | }
85 |
--------------------------------------------------------------------------------
/src/data-structures/disjoint-set/item.js:
--------------------------------------------------------------------------------
1 | export default class Item {
2 | /**
3 | * initializes the Disjoint Set Item
4 | * @param {number|string} value
5 | */
6 | constructor(value) {
7 | this.value = value;
8 | this.parent = null;
9 | this.children = {};
10 | }
11 |
12 | /**
13 | * get Disjoint Set item's key which is the value by default here
14 | * @return {string|number} [description]
15 | */
16 | getKey() {
17 | return this.value;
18 | }
19 |
20 | /**
21 | * return a Disjoint Set Item
22 | * @return {DisjointSetItem}
23 | */
24 | getRoot() {
25 | return this.isRoot() ? this : this.parent.getRoot();
26 | }
27 |
28 | /**
29 | * check whether the item is the root
30 | * @return {boolean}
31 | */
32 | isRoot() {
33 | return this.parent === null;
34 | }
35 |
36 | /**
37 | * get the number of all ancestors an item has
38 | * @return {number}
39 | */
40 | getRank() {
41 | if (this.getChildren().length === 0) {
42 | return 0;
43 | }
44 |
45 | let rank = 0;
46 |
47 | this.getChildren().forEach((child) => {
48 | rank += 1;
49 | rank += child.getRank();
50 | });
51 |
52 | return rank;
53 | }
54 |
55 | /**
56 | * get this item's children
57 | * @return {array} arrray of Disjoint Set Items
58 | */
59 | getChildren() {
60 | return Object.values(this.children);
61 | }
62 |
63 | /**
64 | * set a parent for the current DisjointSetItem
65 | * @param {DisjointSetItem} parentItem
66 | * @return {DisjointSetItem} the current DisjointSetItem
67 | */
68 | setParent(parentItem, forceSettingParentChild = true) {
69 | this.parent = parentItem;
70 | if (forceSettingParentChild) parentItem.addChild(this);
71 |
72 | return this;
73 | }
74 |
75 | /**
76 | * add a child DisjointSetItem to the current DisjointSetItem
77 | * @param {DisjointSetItem} childItem
78 | * @return {DisjointSetItem} the current DisjointSetItem
79 | */
80 | addChild(childItem) {
81 | this.children[childItem.getKey()] = childItem;
82 | childItem.setParent(this, false);
83 |
84 | return this;
85 | }
86 | }
87 |
--------------------------------------------------------------------------------
/__tests__/unit/src/data-structures/array.spec.js:
--------------------------------------------------------------------------------
1 | import chai from 'chai';
2 | import MyArray from 'src/data-structures/array';
3 |
4 |
5 | const { expect } = chai;
6 |
7 | describe('Array', () => {
8 | const array = new MyArray();
9 |
10 | beforeEach(() => {});
11 |
12 | it('creates an array successfully', () => {
13 | expect(array).to.be.an('object');
14 | expect(array).to.be.an.instanceof(MyArray);
15 | });
16 |
17 | describe('when we add to the array', () => {
18 | it('it adds "1" to the array', () => {
19 | array.add(1);
20 | expect(array.length()).to.equal(1);
21 | });
22 |
23 | it('it adds "2" to the array', () => {
24 | array.add(2);
25 | expect(array.length()).to.equal(2);
26 | });
27 |
28 | it('it adds "3" to the array', () => {
29 | array.add(3);
30 | expect(array.length()).to.equal(3);
31 | });
32 |
33 | it('it adds "4" to the array', () => {
34 | array.add(4);
35 | expect(array.length()).to.equal(4);
36 | });
37 |
38 | it('it has a length of 4', () => {
39 | expect(array.length()).to.equal(4);
40 | });
41 |
42 | it('it prints all the elements we have just added to the array', () => {
43 | expect(array.print()).to.equal('1 2 3 4');
44 | });
45 | });
46 |
47 | describe('when we search or get', () => {
48 | it('it searches for the element "3"', () => {
49 | expect(array.search(3)).to.equal(2);
50 | });
51 |
52 | it('it gets element at index "2"', () => {
53 | expect(array.getAtIndex(2)).to.equal(3);
54 | });
55 | });
56 |
57 | describe('when we remove, add and print elements', () => {
58 | it('it removes the element "3"', () => {
59 | array.remove(3);
60 | expect(array.print()).to.equal('1 2 4');
61 | });
62 |
63 | it('it adds "5" to the array', () => {
64 | array.add(5);
65 | expect(array.length()).to.equal(4);
66 | });
67 |
68 | it('it adds another "5" to the array', () => {
69 | array.add(5);
70 | expect(array.length()).to.equal(5);
71 | });
72 |
73 | it('it prints out the array again', () => {
74 | expect(array.print()).to.equal('1 2 4 5 5');
75 | });
76 |
77 | it('it removes the element "5"', () => {
78 | array.remove(5);
79 | expect(array.print()).to.equal('1 2 4');
80 | });
81 | });
82 | });
83 |
--------------------------------------------------------------------------------
/src/algorithms/graph/prims-algorithm/README.md:
--------------------------------------------------------------------------------
1 | # Prim's Algorithm
2 |
3 | In computer science, **Prim's algorithm** is a greedy algorithm that finds a minimum spanning tree for a weighted undirected graph.
4 |
5 | The algorithm operates by building this tree one vertex at a time, from an arbitrary starting vertex, at each step adding the cheapest possible connection from the tree to another vertex.
6 |
7 | 
8 |
9 | Prim's algorithm starting at vertex `A`. In the third step, edges `BD` and `AB` both have weight `2`, so `BD` is chosen arbitrarily. After that step, `AB` is no longer a candidate for addition to the tree because it links two nodes that are already in the tree.
10 |
11 | ## Minimum Spanning Tree
12 |
13 | A **minimum spanning tree** (MST) or minimum weight spanning tree is a subset of the edges of a connected, edge-weighted (un)directed graph that connects all the vertices together, without any cycles and with the minimum possible total edge weight. That is, it is a spanning tree whose sum of edge weights is as small as possible. More generally, any edge-weighted undirected graph (not necessarily connected) has a minimum spanning forest, which is a union of the minimum spanning trees for its connected components.
14 |
15 | 
16 |
17 | A planar graph and its minimum spanning tree. Each edge is labeled with its weight, which here is roughly proportional to its length.
18 |
19 | 
20 |
21 | This figure shows there may be more than one minimum spanning tree in a graph. In the figure, the two trees below the graph are two possibilities of minimum spanning tree of the given graph.
22 |
23 | ## References
24 |
25 | - [Minimum Spanning Tree on Wikipedia](https://en.wikipedia.org/wiki/Minimum_spanning_tree)
26 | - [Prim's Algorithm on Wikipedia](https://en.wikipedia.org/wiki/Prim%27s_algorithm)
27 | - [Prim's Algorithm on YouTube by Tushar Roy](https://www.youtube.com/watch?v=oP2-8ysT3QQ&list=PLLXdhg_r2hKA7DPDsunoDZ-Z769jWn4R8)
28 | - [Prim's Algorithm on YouTube by Michael Sambol](https://www.youtube.com/watch?v=cplfcGZmX7I&list=PLLXdhg_r2hKA7DPDsunoDZ-Z769jWn4R8)
29 |
--------------------------------------------------------------------------------
/src/algorithms/sorting/radix-sort/README.md:
--------------------------------------------------------------------------------
1 | # Radix Sort
2 |
3 | In computer science, **radix sort** is a non-comparative integer sorting algorithm that sorts data with integer keys by grouping keys by the individual digits which share the same significant position and value. A positional notation is required, but because integers can represent strings of characters (e.g., names or dates) and specially formatted floating point numbers, radix sort is not limited to integers.
4 |
5 | ## Efficiency
6 |
7 | The topic of the efficiency of radix sort compared to other sorting algorithms is somewhat tricky and subject to quite a lot of misunderstandings. Whether radix sort is equally efficient, less efficient or more efficient than the best comparison-based algorithms depends on the details of the assumptions made.
8 | Radix sort complexity is `O(wn)` for `n` keys which are integers of word size `w`. Sometimes `w` is presented as a constant, which would make radix sort better (for sufficiently large `n`) than the best comparison-based sorting algorithms, which all perform `O(n log n)` comparisons to sort `n` keys. However, in general `w` cannot be considered a constant: if all `n` keys are distinct, then `w` has to be at least `log n` for a random-access machine to be able to store them in memory, which gives at best a time complexity `O(n log n)`. That would seem to make radix sort at most equally efficient as the best comparison-based sorts (and worse if keys are much longer than `log n`).
9 |
10 | 
11 |
12 | ## Complexity
13 |
14 | | Name | Best | Average | Worst | Memory | Stable | Comments |
15 | | --------------------- | :-------------: | :-----------------: | :-----------------: | :-------: | :-------: | :-------- |
16 | | **Radix sort** | n * k | n * k | n * k | n + k | Yes | k - length of longest key |
17 |
18 | ## References
19 |
20 | - [Wikipedia](https://en.wikipedia.org/wiki/Radix_sort)
21 | - [YouTube](https://www.youtube.com/watch?v=XiuSW_mEn7g&index=62&t=0s&list=PLLXdhg_r2hKA7DPDsunoDZ-Z769jWn4R8)
22 | - [ResearchGate](https://www.researchgate.net/figure/Simplistic-illustration-of-the-steps-performed-in-a-radix-sort-In-this-example-the_fig1_291086231)
23 |
--------------------------------------------------------------------------------
/src/algorithms/graph/kruskals-algorithm/README.md:
--------------------------------------------------------------------------------
1 | # Kruskal's Algorithm
2 |
3 | Kruskal's algorithm is a minimum-spanning-tree algorithm which finds an edge of the least possible weight that connects any two trees in the forest. It is a greedy algorithm in graph theory as it finds a minimum spanning tree for a connected weighted graph adding increasing cost arcs at each step. This means it finds a subset of the edges that forms a tree that includes every vertex, where the total weight of all the edges in the tree is minimized. If the graph is not connected, then it finds a minimum spanning forest (a minimum spanning tree for each connected component).
4 |
5 | 
6 |
7 | 
8 |
9 | A demo for Kruskal's algorithm based on Euclidean distance.
10 |
11 | ## Minimum Spanning Tree
12 |
13 | A **minimum spanning tree** (MST) or minimum weight spanning tree is a subset of the edges of a connected, edge-weighted (un)directed graph that connects all the vertices together, without any cycles and with the minimum possible total edge weight. That is, it is a spanning tree whose sum of edge weights is as small as possible. More generally, any edge-weighted undirected graph (not necessarily connected) has a minimum spanning forest, which is a union of the minimum spanning trees for its connected components.
14 |
15 | 
16 |
17 | A planar graph and its minimum spanning tree. Each edge is labeled with its weight, which here is roughly proportional to its length.
18 |
19 | 
20 |
21 | This figure shows there may be more than one minimum spanning tree in a graph. In the figure, the two trees below the graph are two possibilities of minimum spanning tree of the given graph.
22 |
23 | ## References
24 |
25 | - [Minimum Spanning Tree on Wikipedia](https://en.wikipedia.org/wiki/Minimum_spanning_tree)
26 | - [Kruskal's Algorithm on Wikipedia](https://en.wikipedia.org/wiki/Kruskal%27s_algorithm)
27 | - [Kruskal's Algorithm on YouTube by Tushar Roy](https://www.youtube.com/watch?v=fAuF0EuZVCk&list=PLLXdhg_r2hKA7DPDsunoDZ-Z769jWn4R8)
28 | - [Kruskal's Algorithm on YouTube by Michael Sambol](https://www.youtube.com/watch?v=71UQH7Pr9kU&list=PLLXdhg_r2hKA7DPDsunoDZ-Z769jWn4R8)
29 |
--------------------------------------------------------------------------------
/src/algorithms/set/combinations/README.md:
--------------------------------------------------------------------------------
1 | # Combinations
2 |
3 | When the order doesn't matter, it is a **Combination**.
4 |
5 | When the order **does** matter it is a **Permutation**.
6 |
7 | **"My fruit salad is a combination of apples, grapes and bananas"**
8 | We don't care what order the fruits are in, they could also be "bananas, grapes and apples" or "grapes, apples and bananas", its the same fruit salad.
9 |
10 | ## Combinations without repetitions
11 |
12 | This is how lotteries work. The numbers are drawn one at a time, and if we have the lucky numbers (no matter what order) we win!
13 |
14 | No Repetition: such as lottery numbers `(2,14,15,27,30,33)`
15 |
16 | **Number of combinations**
17 |
18 | 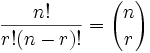
19 |
20 | where `n` is the number of things to choose from, and we choose `r` of them, no repetition, order doesn't matter.
21 |
22 | It is often called "n choose r" (such as "16 choose 3"). And is also known as the Binomial Coefficient.
23 |
24 | ## Combinations with repetitions
25 |
26 | Repetition is Allowed: such as coins in your pocket `(5,5,5,10,10)`
27 |
28 | Or let us say there are five flavours of ice cream: `banana`, `chocolate`, `lemon`, `strawberry` and `vanilla`.
29 |
30 | We can have three scoops. How many variations will there be?
31 |
32 | Let's use letters for the flavours: `{b, c, l, s, v}`.
33 | Example selections include:
34 |
35 | - `{c, c, c}` (3 scoops of chocolate)
36 | - `{b, l, v}` (one each of banana, lemon and vanilla)
37 | - `{b, v, v}` (one of banana, two of vanilla)
38 |
39 | **Number of combinations**
40 |
41 | 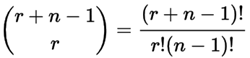
42 |
43 | Where `n` is the number of things to choose from, and we choose `r` of them. Repetition allowed, order doesn't matter.
44 |
45 | ## Cheat Sheets
46 |
47 | Permutations cheat sheet
48 |
49 | 
50 |
51 | Combinations cheat sheet
52 |
53 | 
54 |
55 | Permutations/combinations algorithm ideas.
56 |
57 | 
58 |
59 | ## References
60 |
61 | - [Math Is Fun](https://www.mathsisfun.com/combinatorics/combinations-permutations.html)
62 | - [Permutations/combinations cheat sheets](https://medium.com/@trekhleb/permutations-combinations-algorithms-cheat-sheet-68c14879aba5)
63 |
--------------------------------------------------------------------------------
/src/algorithms/sorting/shell-sort/README.md:
--------------------------------------------------------------------------------
1 | # Shell Sort
2 |
3 | Shellsort, also known as Shell sort or Shell's method, is an in-place comparison sort. It can be seen as either a generalization of sorting by exchange (bubble sort) or sorting by insertion (insertion sort). The method starts by sorting pairs of elements far apart from each other, then progressively reducing the gap between elements to be compared. Starting with far apart elements, it can move some out-of-place elements into position faster than a simple nearest neighbor exchange
4 |
5 | 
6 |
7 | ## How Shell Sort Works
8 |
9 | For our example and ease of understanding, we take the interval of `4`. Make a virtual sub-list of all values located at the interval of 4 positions. Here these values are `{35, 14}`, `{33, 19}`, `{42, 27}` and `{10, 44}`
10 |
11 | 
12 |
13 | We compare values in each sub-list and swap them (if necessary) in the original array. After this step, the new array should look like this
14 |
15 | 
16 |
17 | Then, we take interval of 2 and this gap generates two sub-lists - `{14, 27, 35, 42}`, `{19, 10, 33, 44}`
18 |
19 | 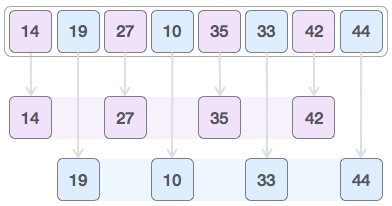
20 |
21 | We compare and swap the values, if required, in the original array.
22 | After this step, the array should look like this
23 |
24 | 
25 |
26 | Finally, we sort the rest of the array using interval of value 1.
27 | Shell sort uses insertion sort to sort the array.
28 |
29 | 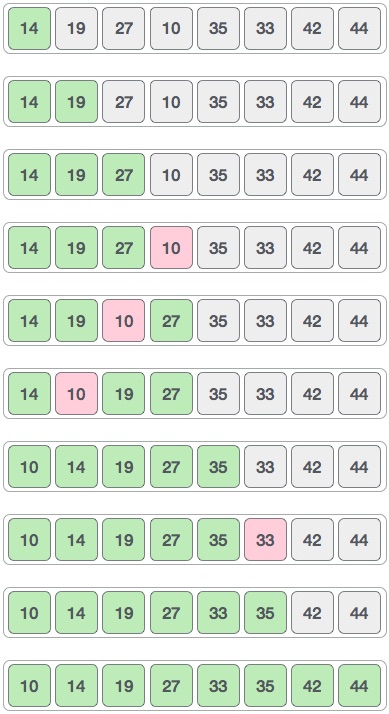
30 |
31 | ## Complexity
32 |
33 | | Name | Best | Average | Worst | Memory | Stable | Comments |
34 | | --------------------- | :-------------: | :-----------------: | :-----------------: | :-------: | :-------: | :-------- |
35 | | **Shell sort** | n log(n) | depends on gap sequence | n (log(n))2 | 1 | No | |
36 |
37 | ## References
38 |
39 | * [Tutorials Point](https://www.tutorialspoint.com/data_structures_algorithms/shell_sort_algorithm.htm)
40 | * [Wikipedia](https://en.wikipedia.org/wiki/Shellsort)
41 |
--------------------------------------------------------------------------------
/src/data-structures/README.md:
--------------------------------------------------------------------------------
1 | ## Data Structures
2 |
3 | According to Wikipedia:
4 |
5 | > In computer science, a data structure is a particular way of storing and organizing data in a computer so that it can be used efficiently.
6 |
7 | The following terms are the foundation terms of a data structure.
8 |
9 | * **Interface** - This represents the set of operation supported by a data structure
10 | * **Implementation** - This provides the definition of algorithms used in the operations of the data structure i.e. it provides the internal representation of the data structure
11 |
12 | ### Characteristics of a Data Structure
13 | 1. **Correctness** - a data structure should implement its interface correctly
14 | 2. **Time Complexity** - execution time of operations of a data structure should be as small as possible
15 | 3. **Space Complexity** - memory usage of a data structure operation should be as little as possible
16 |
17 | ### Data Structure Operations Complexity
18 |
19 | | Data Structure | Access | Search | Insertion | Deletion |
20 | | ----------------------- | :-------: | :-------: | :-------: | :-------: |
21 | | **Array** | 1 | n | n | n |
22 | | **Stack** | n | n | 1 | 1 |
23 | | **Queue** | n | n | 1 | 1 |
24 | | **Linked List** | n | n | 1 | 1 |
25 | | **Hash Table** | - | n | n | n |
26 | | **Binary Search Tree** | n | n | n | n |
27 | | **B-Tree** | log(n) | log(n) | log(n) | log(n) |
28 | | **AVL Tree** | log(n) | log(n) | log(n) | log(n) |
29 |
30 |
31 | 
32 |
33 | The following are the data structures covered here:
34 |
35 | - [Array](array)
36 | - [Linked List](linked-list)
37 | - [Doubly Linked List](doubly-linked-list)
38 | - [Stack](stack)
39 | - [Queue](queue)
40 | - [Priority Queue](priority-queue)
41 | - [Set](set)
42 | - [Disjoint Set](disjoint-set)
43 | - [Bloom Filter](bloom-filter)
44 | - [Skip List](skip-list)
45 | - [Hash Table](hash-table)
46 | - [Graph](graph)
47 | - [Tree](tree)
48 | - [Binary Search Tree](binary-search-tree)
49 | - [AVL Tree](avl-tree)
50 | - [Red Black Tree](red-black-tree)
51 | - [Splay Tree](splay-tree)
52 | - [B-Tree](b-tree)
53 | - [Trie](trie)
54 | - [Min Heap](min-heap)
55 | - [Max Heap](max-heap)
56 | - [Binomial Heap](binomial-heap)
57 | - [Fibonacci Heap](fibonacci-heap)
58 |
--------------------------------------------------------------------------------
/__tests__/unit/src/algorithms/quick-sort.spec.js:
--------------------------------------------------------------------------------
1 | import chai from 'chai';
2 | import quickSort, { simpleQuickSort, partitionLomuto } from 'src/algorithms/sorting/quick-sort';
3 |
4 |
5 | const { expect } = chai;
6 |
7 | describe('Quick Sort', () => {
8 | describe('partitionLomuto helper function', () => {
9 | it('should partion an array and return the pivot element', () => {
10 | const array = [2, 8, 10, 11, 12, 13, 14, 18, 19, 20];
11 |
12 | expect(partitionLomuto(array, 0, 9)).to.equal(9);
13 | });
14 | });
15 |
16 | describe('classic quick sort using Hoare partitioning', () => {
17 | it('should return empty array', () => {
18 | expect(quickSort([])).to.deep.equal([]);
19 | });
20 |
21 | it('should return the passed array', () => {
22 | expect(quickSort([1])).to.deep.equal([1]);
23 | expect(quickSort([2])).to.deep.equal([2]);
24 | expect(quickSort([5])).to.deep.equal([5]);
25 | expect(quickSort([356])).to.deep.equal([356]);
26 | });
27 |
28 | it('should sort a random array', () => {
29 | const array = [2, 8, 10, 11, 12, 13, 14, 18, 19, 20];
30 | const sortedArray = [2, 8, 10, 11, 12, 13, 14, 18, 19, 20];
31 |
32 | expect(quickSort(array)).to.deep.equal(sortedArray);
33 | });
34 |
35 | it('should sort a reversed sorted array', () => {
36 | const reversedArray = [12, 10, 8, 7, 6, 5, 4, 3, 2, 1];
37 | const sortedArray = [1, 2, 3, 4, 5, 6, 7, 8, 10, 12];
38 |
39 | expect(quickSort(reversedArray)).to.deep.equal(sortedArray);
40 | });
41 | });
42 |
43 | describe('my simple version of the quick sort', () => {
44 | it('should return empty array', () => {
45 | expect(simpleQuickSort([])).to.deep.equal([]);
46 | });
47 |
48 | it('should return the passed array', () => {
49 | expect(simpleQuickSort([1])).to.deep.equal([1]);
50 | expect(simpleQuickSort([2])).to.deep.equal([2]);
51 | expect(simpleQuickSort([5])).to.deep.equal([5]);
52 | expect(simpleQuickSort([356])).to.deep.equal([356]);
53 | });
54 |
55 | it('should sort a random array', () => {
56 | const array = [2, 8, 10, 11, 12, 13, 14, 18, 19, 20];
57 | const sortedArray = [2, 8, 10, 11, 12, 13, 14, 18, 19, 20];
58 |
59 | expect(simpleQuickSort(array)).to.deep.equal(sortedArray);
60 | });
61 |
62 | it('should sort a reversed sorted array', () => {
63 | const reversedArray = [12, 10, 8, 7, 6, 5, 4, 3, 2, 1];
64 | const sortedArray = [1, 2, 3, 4, 5, 6, 7, 8, 10, 12];
65 |
66 | expect(simpleQuickSort(reversedArray)).to.deep.equal(sortedArray);
67 | });
68 | });
69 | });
70 |
--------------------------------------------------------------------------------
/src/data-structures/min-heap/README.md:
--------------------------------------------------------------------------------
1 | ## Min Heap
2 |
3 | According to Wikipedia:
4 |
5 | > In computer science, a heap is a specialized tree-based data structure that satisfies the heap property: if P is a parent node of C, then the key (the value) of P is either greater than or equal to (in a max heap) or less than or equal to (in a min heap) the key of C. The node at the "top" of the heap (with no parents) is called the root node.
6 | >
7 | > The heap is one maximally efficient implementation of an abstract data type called a priority queue, and in fact priority queues are often referred to as "heaps", regardless of how they may be implemented. A common implementation of a heap is the binary heap, in which the tree is a binary tree. The heap data structure, specifically the binary heap, was introduced by J. W. J. Williams in 1964, as a data structure for the heapsort sorting algorithm. Heaps are also crucial in several efficient graph algorithms such as Dijkstra's algorithm. In a heap, the highest (or lowest) priority element is always stored at the root. A heap is not a sorted structure and can be regarded as partially ordered. As visible from the heap-diagram, there is no particular relationship among nodes on any given level, even among the siblings. When a heap is a complete binary tree, it has a smallest possible height—a heap with N nodes and for each node a branches always has loga N height. A heap is a useful data structure when you need to remove the object with the highest (or lowest) priority.
8 | >
9 | > Note that, as shown in the graphic, there is no implied ordering between siblings or cousins and no implied sequence for an in-order traversal (as there would be in, e.g., a binary search tree). The heap relation mentioned above applies only between nodes and their parents, grandparents, etc. The maximum number of children each node can have depends on the type of heap, but in many types it is at most two, which is known as a binary heap.
10 |
11 | A **heap** is a specialized tree-based data structure that satisfies the heap property described below.
12 |
13 | In a *min heap*, if `P` is a parent node of `C`, then the key (the value) of `P` is less than or equal to the key of `C`.
14 |
15 | 
16 |
17 | In a *max heap*, the key of `P` is greater than or equal to the key of `C`
18 |
19 | 
20 |
21 | The node at the "top" of the heap with no parents is called the root node.
22 |
23 |
24 | ## References
25 |
26 | - [Wikipedia](https://en.wikipedia.org/wiki/Heap_(data_structure))
27 | - [YouTube](https://www.youtube.com/watch?v=t0Cq6tVNRBA&index=5&t=0s&list=PLLXdhg_r2hKA7DPDsunoDZ-Z769jWn4R8)
28 |
--------------------------------------------------------------------------------
/__tests__/unit/src/algorithms/binary-search.spec.js:
--------------------------------------------------------------------------------
1 | import chai from 'chai';
2 | import binarySearch, { recursiveBinarySearch } from 'src/algorithms/searching/binary-search';
3 |
4 |
5 | const { expect } = chai;
6 |
7 | describe('Binary Search', () => {
8 | describe('using iteration', () => {
9 | it('should throw an error if given an unsorted array', () => {
10 | const array = [0, 1, 2, 3, 4, 5, 8, 6];
11 |
12 | function unsortedArraySearch1() {
13 | binarySearch(array, 4);
14 | }
15 |
16 | function unsortedArraySearch2() {
17 | recursiveBinarySearch(array, 4);
18 | }
19 |
20 | expect(unsortedArraySearch1).to.throw(/not sorted/);
21 | expect(unsortedArraySearch2).to.throw(/not sorted/);
22 | });
23 |
24 | it('should return the correct index of a search item', () => {
25 | const array = [0, 1, 2, 3, 4, 5, 6, 10, 26, 35, 45, 50];
26 |
27 | expect(binarySearch(array, 0)).to.be.equal(0);
28 | expect(binarySearch(array, 2)).to.be.equal(2);
29 | expect(binarySearch(array, 4)).to.be.equal(4);
30 | expect(binarySearch(array, 5)).to.be.equal(5);
31 | expect(binarySearch(array, 10)).to.be.equal(7);
32 | expect(binarySearch(array, 35)).to.be.equal(9);
33 | });
34 |
35 | it('should return -1 for an item not found in the array', () => {
36 | const array = [0, 1, 2, 3, 4, 5, 6, 10, 26, 35, 45, 50];
37 |
38 | expect(binarySearch(array, 17)).to.be.equal(-1);
39 | expect(binarySearch(array, 73)).to.be.equal(-1);
40 | });
41 | });
42 |
43 | describe('using recursion', () => {
44 | it('should throw an error if given an unsorted array', () => {
45 | function unsortedArraySearch() {
46 | const array = [0, 1, 2, 3, 4, 5, 8, 6];
47 |
48 | binarySearch(array, 4);
49 | }
50 |
51 | expect(unsortedArraySearch).to.throw(/not sorted/);
52 | });
53 |
54 | it('should return the correct index of a search item', () => {
55 | const array = [0, 1, 2, 3, 4, 5, 6, 10, 26, 35, 45, 50];
56 |
57 | expect(recursiveBinarySearch(array, 0)).to.be.equal(0);
58 | expect(recursiveBinarySearch(array, 2)).to.be.equal(2);
59 | expect(recursiveBinarySearch(array, 4)).to.be.equal(4);
60 | expect(recursiveBinarySearch(array, 5)).to.be.equal(5);
61 | expect(recursiveBinarySearch(array, 10)).to.be.equal(7);
62 | expect(recursiveBinarySearch(array, 35)).to.be.equal(9);
63 | });
64 |
65 | it('should return -1 for an item not found in the array', () => {
66 | const array = [0, 1, 2, 3, 4, 5, 6, 10, 26, 35, 45, 50];
67 |
68 | expect(recursiveBinarySearch(array, 17)).to.be.equal(-1);
69 | expect(recursiveBinarySearch(array, 73)).to.be.equal(-1);
70 | });
71 | });
72 | });
73 |
--------------------------------------------------------------------------------
/src/algorithms/math/pascals-triangle/README.md:
--------------------------------------------------------------------------------
1 | # Pascal's Triangle
2 |
3 | In mathematics, **Pascal's triangle** is a triangular array of the [binomial coefficients](https://en.wikipedia.org/wiki/Binomial_coefficient).
4 |
5 | The rows of Pascal's triangle are conventionally enumerated starting with row `n = 0` at the top (the `0th` row). The entries in each row are numbered from the left beginning with `k = 0` and are usually staggered relative to the numbers in the adjacent rows. The triangle may be constructed in the following manner: In row `0` (the topmost row), there is a unique nonzero entry `1`. Each entry of each subsequent row is constructed by adding the number above and to the left with the number above and to the right, treating blank entries as `0`. For example, the initial number in the first (or any other) row is `1` (the sum of `0` and `1`), whereas the numbers `1` and `3` in the third row are added to produce the number `4` in the fourth row.
6 |
7 | 
8 |
9 | ## Formula
10 |
11 | The entry in the `nth` row and `kth` column of Pascal's triangle is denoted .
12 | For example, the unique nonzero entry in the topmost
13 | row is .
14 |
15 | With this notation, the construction of the previous paragraph may be written as follows:
16 |
17 | 
18 |
19 | for any non-negative integer `n` and any integer `k` between `0` and `n`, inclusive.
20 |
21 | 
22 |
23 | ## Calculating triangle entries in O(n) time
24 |
25 | We know that `i`-th entry in a line number `lineNumber` is Binomial Coefficient `C(lineNumber, i)` and all lines start with value `1`. The idea is to calculate `C(lineNumber, i)` using `C(lineNumber, i-1)`. It can be calculated in `O(1)` time using the following:
26 |
27 | ```
28 | C(lineNumber, i) = lineNumber! / ((lineNumber - i)! * i!)
29 | C(lineNumber, i - 1) = lineNumber! / ((lineNumber - i + 1)! * (i - 1)!)
30 | ```
31 |
32 | We can derive following expression from above two expressions:
33 |
34 | ```
35 | C(lineNumber, i) = C(lineNumber, i - 1) * (lineNumber - i + 1) / i
36 | ```
37 |
38 | So `C(lineNumber, i)` can be calculated
39 | from `C(lineNumber, i - 1)` in `O(1)` time.
40 |
41 | ## References
42 |
43 | - [Wikipedia](https://en.wikipedia.org/wiki/Pascal%27s_triangle)
44 | - [GeeksForGeeks](https://www.geeksforgeeks.org/pascal-triangle/)
45 |
--------------------------------------------------------------------------------
/src/algorithms/math/euclidean-algorithm/README.md:
--------------------------------------------------------------------------------
1 | # Euclidean algorithm
2 |
3 | In mathematics, the Euclidean algorithm, or Euclid's algorithm, is an efficient method for computing the greatest common divisor (GCD) of two numbers, the largest number that divides both of them without leaving a remainder.
4 |
5 | The Euclidean algorithm is based on the principle that the greatest common divisor of two numbers does not change if the larger number is replaced by its difference with the smaller number. For example, `21` is the GCD of `252` and `105` (as `252 = 21 × 12` and `105 = 21 × 5`), and the same number `21` is also the GCD of `105` and `252 − 105 = 147`.
6 |
7 | Since this replacement reduces the larger of the two numbers, repeating this process gives successively smaller pairs of numbers until the two numbers become equal. When that occurs, they are the GCD of the original two numbers.
8 |
9 | By reversing the steps, the GCD can be expressed as a sum of the two original numbers each multiplied by a positive or negative integer, e.g., `21 = 5 × 105 + (−2) × 252`. The fact that the GCD can always be expressed in this way is known as Bézout's identity.
10 |
11 | 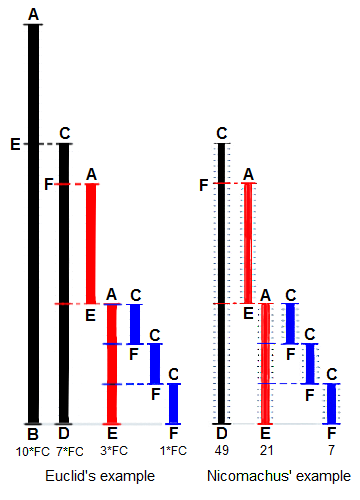
12 |
13 | Euclid's method for finding the greatest common divisor (GCD) of two starting lengths `BA` and `DC`, both defined to be multiples of a common "unit" length. The length `DC` being shorter, it is used to "measure" `BA`, but only once because remainder `EA` is less than `DC`. EA now measures (twice) the shorter length `DC`, with remainder `FC` shorter than `EA`. Then `FC` measures (three times) length `EA`. Because there is no remainder, the process ends with `FC` being the `GCD`. On the right Nicomachus' example with numbers `49` and `21` resulting in their GCD of `7` (derived from Heath 1908:300).
14 |
15 | 
16 |
17 | A `24-by-60` rectangle is covered with ten `12-by-12` square tiles, where `12` is the GCD of `24` and `60`. More generally, an `a-by-b` rectangle can be covered with square tiles of side-length `c` only if `c` is a common divisor of `a` and `b`.
18 |
19 | 
20 |
21 | Subtraction-based animation of the Euclidean algorithm.
22 | The initial rectangle has dimensions `a = 1071` and `b = 462`.
23 | Squares of size `462×462` are placed within it leaving a `462×147` rectangle. This rectangle is tiled with `147×147` squares until a `21×147` rectangle is left, which in turn is tiled with `21×21` squares, leaving no uncovered area.
24 | The smallest square size, `21`, is the GCD of `1071` and `462`.
25 |
26 | ## References
27 |
28 | - [Wikipedia](https://en.wikipedia.org/wiki/Euclidean_algorithm)
29 |
--------------------------------------------------------------------------------
/src/data-structures/disjoint-set/index.js:
--------------------------------------------------------------------------------
1 | import DisjointSetItem from './item';
2 |
3 | export default class DisjointSet {
4 | /**
5 | * initializes the DisjointSet
6 | */
7 | constructor() {
8 | this.items = {};
9 | }
10 |
11 | /**
12 | * checks if the two provided keys are valid
13 | * @param {string|number} key1
14 | * @param {string|number} key2
15 | * @return {void} throw an error or return nothing
16 | */
17 | _checkKeys(key1, key2) {
18 | const areKeysValid = !(key1 === null || key2 === null);
19 |
20 | if (!areKeysValid) throw new Error('One or all of the values provided are not in sets');
21 | }
22 |
23 | /**
24 | * make a set out of the item value provided
25 | * @param {string|number} value
26 | * @return {DisjointSet}
27 | */
28 | makeSet(value) {
29 | const disjointSetItem = new DisjointSetItem(value);
30 |
31 | if (!this.items[disjointSetItem.getKey()]) {
32 | this.items[disjointSetItem.getKey()] = disjointSetItem;
33 | }
34 |
35 | return this;
36 | }
37 |
38 | /**
39 | * find set representation node
40 | * @param {string|number} value [description]
41 | * @return {string|number} the key of the value provided
42 | */
43 | find(value) {
44 | const disjointSetItem = new DisjointSetItem(value);
45 |
46 | if (!this.items[disjointSetItem.getKey()]) return null;
47 |
48 | return this.items[disjointSetItem.getKey()].getRoot().getKey();
49 | }
50 |
51 | /**
52 | * do a union on the values provided by rank
53 | * @param {DisjointSetItem} valueA
54 | * @param {DisjointSetItem} valueB
55 | * @return {DisjointSet}
56 | */
57 | union(valueA, valueB) {
58 | const rootKeyA = this.find(valueA);
59 | const rootKeyB = this.find(valueB);
60 | this._checkKeys(rootKeyA, rootKeyB);
61 |
62 | if (rootKeyA === rootKeyB) {
63 | // if both keys are already in the same set just return the caller object's key
64 | return this;
65 | }
66 |
67 | const rootA = this.items[rootKeyA];
68 | const rootB = this.items[rootKeyB];
69 |
70 | if (rootA.getRank() < rootB.getRank()) {
71 | // if rootB's tree is bigger then make rootB to be a new root.
72 | rootB.addChild(rootA);
73 | } else {
74 | // if rootA's tree is bigger then make rootA to be a new root.
75 | rootA.addChild(rootB);
76 | }
77 |
78 | return this;
79 | }
80 |
81 | /**
82 | * checks whether the provided items are in the same set
83 | * @param {DisjointSetItem} valueA
84 | * @param {DisjointSetItem} valueB
85 | * @return {boolean}
86 | */
87 | inSameSet(valueA, valueB) {
88 | const rootKeyA = this.find(valueA);
89 | const rootKeyB = this.find(valueB);
90 | this._checkKeys(rootKeyA, rootKeyB);
91 |
92 | return rootKeyA === rootKeyB;
93 | }
94 | }
95 |
--------------------------------------------------------------------------------
/__tests__/unit/src/data-structures/stack.spec.js:
--------------------------------------------------------------------------------
1 | import chai from 'chai';
2 | import Stack from 'src/data-structures/stack';
3 |
4 |
5 | const { expect } = chai;
6 |
7 | describe('Stack', () => {
8 | const stack = new Stack(4);
9 |
10 | beforeEach(() => {});
11 |
12 | it('creates an stack successfully', () => {
13 | expect(stack).to.be.an('object');
14 | expect(stack).to.be.an.instanceof(Stack);
15 | });
16 |
17 | describe('when we push to the stack', () => {
18 | it('it pushes "1" onto the stack', () => {
19 | stack.push(1);
20 | expect(stack.size()).to.equal(1);
21 | });
22 |
23 | it('it pushes "2" onto the stack', () => {
24 | stack.push(2);
25 | expect(stack.size()).to.equal(2);
26 | });
27 |
28 | it('it pushes "3" onto the stack', () => {
29 | stack.push(3);
30 | expect(stack.size()).to.equal(3);
31 | });
32 |
33 | it('it pushes "4" onto the stack', () => {
34 | stack.push(4);
35 | expect(stack.size()).to.equal(4);
36 | });
37 |
38 | it('it has a size of 4', () => {
39 | expect(stack.size()).to.equal(4);
40 | });
41 |
42 | it('it prints all the elements we have just pushed onto the stack', () => {
43 | expect(stack.print()).to.equal('1 2 3 4');
44 | });
45 |
46 | it('it does not add "5" onto the Stack', () => {
47 | const msg = 'Max capacity already reached. Remove element before adding a new one.';
48 | expect(stack.push(5)).to.equal(msg);
49 | });
50 | });
51 |
52 | describe('when we peek, pop, push and print elements', () => {
53 | it('it peeks at the stack', () => {
54 | expect(stack.peek()).to.equal(4);
55 | });
56 |
57 | it('it pops the stack', () => {
58 | expect(stack.pop()).to.equal(4);
59 | });
60 |
61 | it('it prints elements in the stack', () => {
62 | expect(stack.print()).to.equal('1 2 3');
63 | });
64 |
65 | it('it pops the stack again', () => {
66 | expect(stack.pop()).to.equal(3);
67 | });
68 |
69 | it('it has a size of 2 now', () => {
70 | expect(stack.size()).to.equal(2);
71 | });
72 |
73 | it('it pops the stack again', () => {
74 | expect(stack.pop()).to.equal(2);
75 | });
76 |
77 | it('it has a size of 1 now', () => {
78 | expect(stack.size()).to.equal(1);
79 | });
80 |
81 | it('it pops the stack again', () => {
82 | expect(stack.pop()).to.equal(1);
83 | });
84 |
85 | it('it prints again elements in the stack', () => {
86 | expect(stack.print()).to.equal('');
87 | });
88 |
89 | it('it peeks at the stack again', () => {
90 | expect(stack.peek()).to.equal(undefined);
91 | });
92 |
93 | it('it pops the stack again', () => {
94 | const msg = 'No element inside the stack. Add element before poping.';
95 | expect(stack.pop()).to.equal(msg);
96 | });
97 | });
98 | });
99 |
--------------------------------------------------------------------------------
/assets/mu.svg:
--------------------------------------------------------------------------------
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
--------------------------------------------------------------------------------
/src/data-structures/skip-list/README.md:
--------------------------------------------------------------------------------
1 | ## Skip List
2 |
3 | According to Wikipedia:
4 |
5 | > In computer science, a skip list is a data structure that allows fast search within an ordered sequence of elements. Fast search is made possible by maintaining a linked hierarchy of subsequences, with each successive subsequence skipping over fewer elements than the previous one (see the picture below on the right). Searching starts in the sparsest subsequence until two consecutive elements have been found, one smaller and one larger than or equal to the element searched for. Via the linked hierarchy, these two elements link to elements of the next sparsest subsequence, where searching is continued until finally we are searching in the full sequence. The elements that are skipped over may be chosen probabilistically or deterministically, with the former being more common.
6 |
7 | Skip lists are a linked-list-like structure which allows for fast search. It consists of a base list holding the elements, together with a tower of lists maintaining a linked hierarchy of subsequences, each skipping over fewer elements.
8 |
9 | 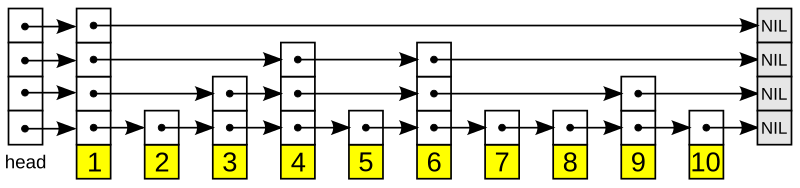
10 |
11 | A schematic picture of the skip list data structure. Each box with an arrow represents a pointer and a row is a linked list giving a sparse subsequence; the numbered boxes (in yellow) at the bottom represent the ordered data sequence. Searching proceeds downwards from the sparsest subsequence at the top until consecutive elements bracketing the search element are found.
12 |
13 | 
14 |
15 | Inserting elements to skip list
16 |
17 |
18 | ### Advantages
19 |
20 | - Skip lists perform very well on rapid insertions because there are no rotations or reallocations.
21 | - They’re simpler to implement than both self-balancing binary search trees and hash tables.
22 | - You can retrieve the next element in constant time (compare to logarithmic time for inorder traversal for BSTs and linear time in hash tables).
23 | - The algorithms can easily be modified to a more specialized structure (like segment or range “trees”, indexable skip lists, or keyed priority queues).
24 | - Making it lockless is simple.
25 | - It does well in persistent (slow) storage (often even better than AVL and EH).
26 |
27 | ### Complexity
28 |
29 | #### Average
30 |
31 | | Operation | Complexity |
32 | | :-------: | :--------: |
33 | | Space | O(n) |
34 | | Search | O(log n) |
35 | | Insertion | O(log n) |
36 | | Deletion | O(log n) |
37 |
38 | A simple representation of a Skip List
39 |
40 | 
41 |
42 | ## References
43 |
44 | - [Wikipedia](https://en.wikipedia.org/wiki/Skip_list)
45 | - [Tiki Blog](http://ticki.github.io/blog/skip-lists-done-right/)
46 | - [YouTube - GeeksforGeeks](https://www.youtube.com/watch?v=ypod5jeYzAU)
47 | - [YouTube](https://www.youtube.com/watch?v=7GWXfL6T3fM)
48 |
--------------------------------------------------------------------------------
/src/data-structures/queue/index.js:
--------------------------------------------------------------------------------
1 | export default class Queue {
2 | /**
3 | * initializes the queue
4 | * @param {number} capacity - the capacity of the queue
5 | */
6 | constructor(capacity = Infinity) {
7 | this._capacity = capacity;
8 | this._data = [];
9 | this._front = 0;
10 | this._rear = 0;
11 | }
12 |
13 | /**
14 | * adds a new element onto the queue
15 | * @param {any} element
16 | * @return {number|string} the index of the added element or queue overflow message
17 | */
18 | enqueue(element) {
19 | if (this.size() < this._capacity) {
20 | this._rear++;
21 | this._data.push(element);
22 |
23 | return this._rear;
24 | }
25 |
26 | return 'Max capacity reached. Remove element before adding a new one.';
27 | }
28 |
29 | /**
30 | * does the reverse of the enqueue() i.e. removes an element
31 | * from the queue and then increments the front pointer variable
32 | * @return {any} the element in the front position of the queue or an error message
33 | */
34 | dequeue() {
35 | if (this._front === this._rear) {
36 | return 'No element inside the queue. Add element before dequeuing.';
37 | }
38 |
39 | const element = this._data.shift();
40 |
41 | if (this._front < this._rear) this._front++;
42 |
43 | return element;
44 | }
45 |
46 | /**
47 | * returns the oldest element added onto the queue. similar to dequeue but
48 | * does not remove element from queue
49 | * @return {any} returns the oldest element in the queue
50 | */
51 | peek() {
52 | return this._data[this._front];
53 | }
54 |
55 | /**
56 | * examine the front element of the queue
57 | * @return {any} the element in the front position of the queue
58 | */
59 | front() {
60 | return this._data[this._front];
61 | }
62 |
63 | /**
64 | * examine the back element of the queue
65 | * @return {any} the element in the rear position of the queue
66 | */
67 | back() {
68 | return this._data[this._rear - 1];
69 | }
70 |
71 | /**
72 | * returns the size/length of the queue
73 | * @return {number} the difference of the front and rear values
74 | */
75 | size() {
76 | return this._rear - this._front;
77 | }
78 |
79 | /**
80 | * check whether the queue is empty
81 | * @return {boolean}
82 | */
83 | isEmpty() {
84 | return this._rear - 1 - this._front === 0;
85 | }
86 |
87 | /**
88 | * clears the queue and sets the top pointer variable back to 0
89 | */
90 | clear() {
91 | this._rear = 0;
92 | this._front = 0;
93 | this._data = [];
94 | }
95 |
96 | /**
97 | * displays the queue
98 | */
99 | print() {
100 | return this._data.join(' ');
101 | }
102 |
103 | /**
104 | * returns the set capacity of the stack
105 | * @return {number}
106 | */
107 | capacity() {
108 | return this._capacity;
109 | }
110 |
111 | /**
112 | * check wheteher an element exists in the queue
113 | * @param {any} element the element to search
114 | * @return {boolean}
115 | */
116 | contains(element) {
117 | return this._data.includes(element);
118 | }
119 | }
120 |
--------------------------------------------------------------------------------
/src/algorithms/sorting/counting-sort/README.md:
--------------------------------------------------------------------------------
1 | # Counting Sort
2 |
3 | In computer science, **counting sort** is an algorithm for sorting a collection of objects according to keys that are small integers; that is, it is an integer sorting algorithm. It operates by counting the number of objects that have each distinct key value, and using arithmetic on those counts to determine the positions of each key value in the output sequence. Its running time is linear in the number of items and the difference between the maximum and minimum key values, so it is only suitable for direct use in situations where the variation in keys is not significantly greater than the number of items. However, it is often used as a subroutine in another sorting algorithm, radix sort, that can handle larger keys more efficiently.
4 |
5 | Because counting sort uses key values as indexes into an array, it is not a comparison sort, and the `Ω(n log n)` lower bound for comparison sorting does not apply to it. Bucket sort may be used for many of the same tasks as counting sort, with a similar time analysis; however, compared to counting sort, bucket sort requires linked lists, dynamic arrays or a large amount of preallocated memory to hold the sets of items within each bucket, whereas counting sort instead stores a single number (the count of items) per bucket.
6 |
7 | Counting sorting works best when the range of numbers for each array element is very small.
8 |
9 | ## Algorithm
10 |
11 | **Step I**
12 |
13 | In first step we calculate the count of all the elements of the input array `A`. Then Store the result in the count array `C`. The way we count is depicted below.
14 |
15 | 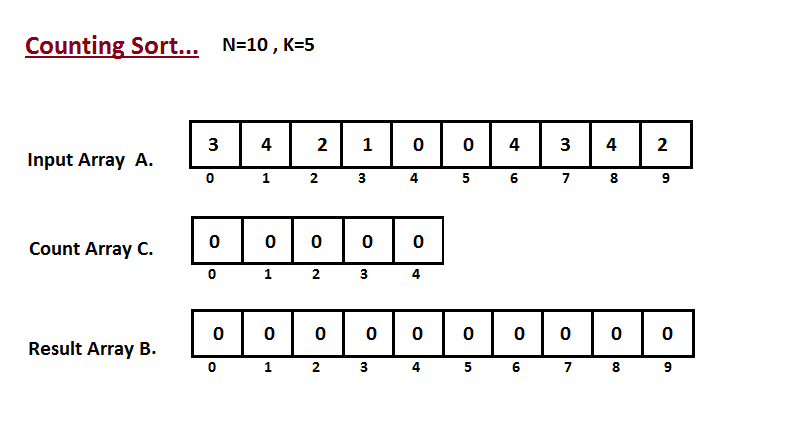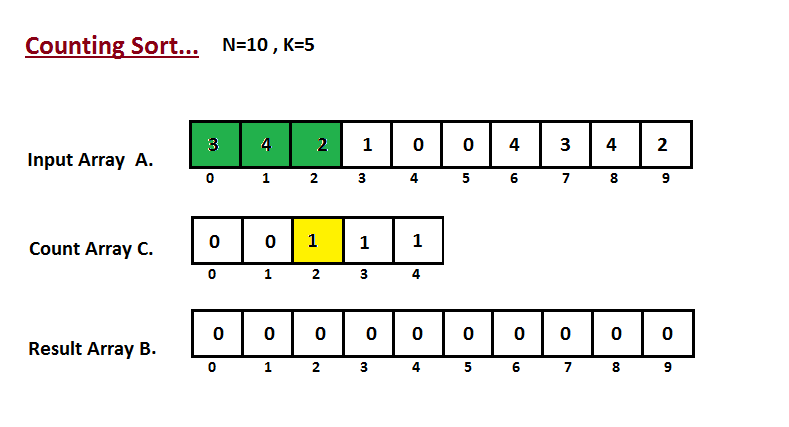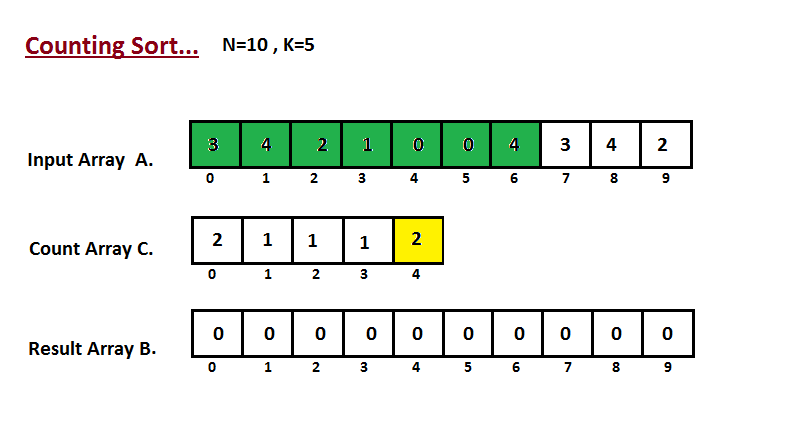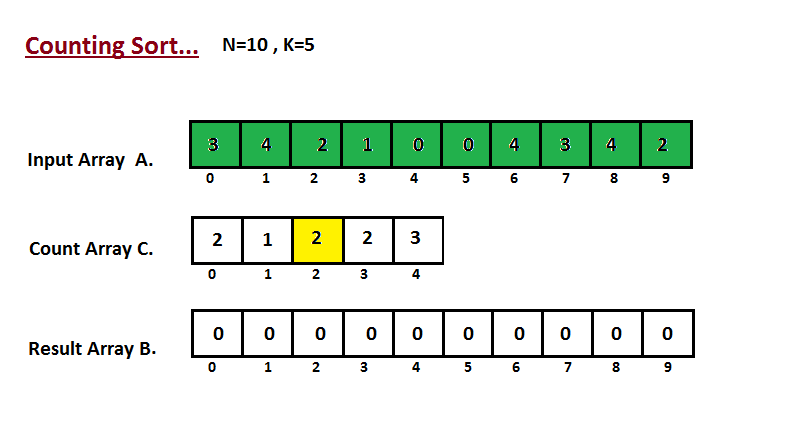
16 |
17 | **Step II**
18 |
19 | In second step we calculate how many elements exist in the input array `A` which are less than or equals for the given index. `Ci` = numbers of elements less than or equals to `i` in input array.
20 |
21 | 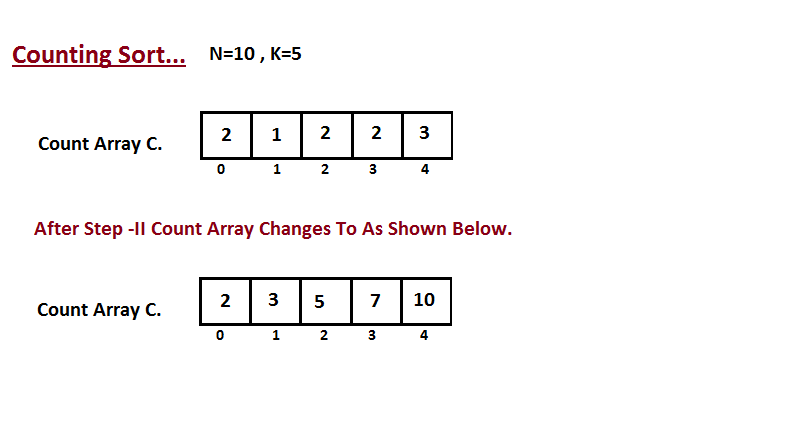
22 |
23 | **Step III**
24 |
25 | In this step we place the input array `A` element at sorted
26 | position by taking help of constructed count array `C` ,i.e what
27 | we constructed in step two. We used the result array `B` to store
28 | the sorted elements. Here we handled the index of `B` start from
29 | zero.
30 |
31 | 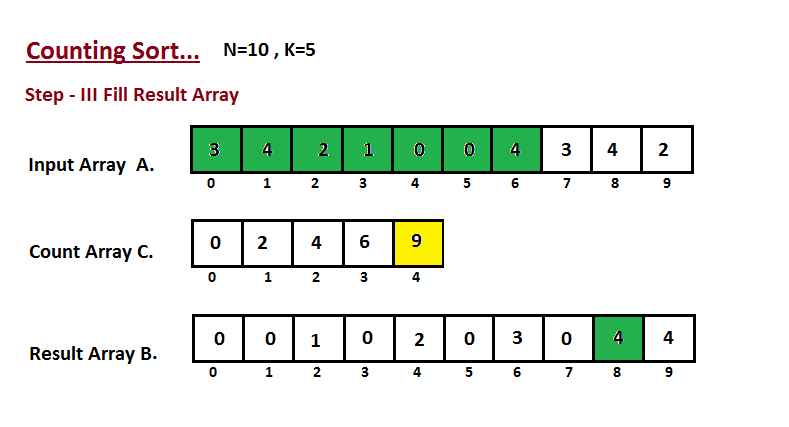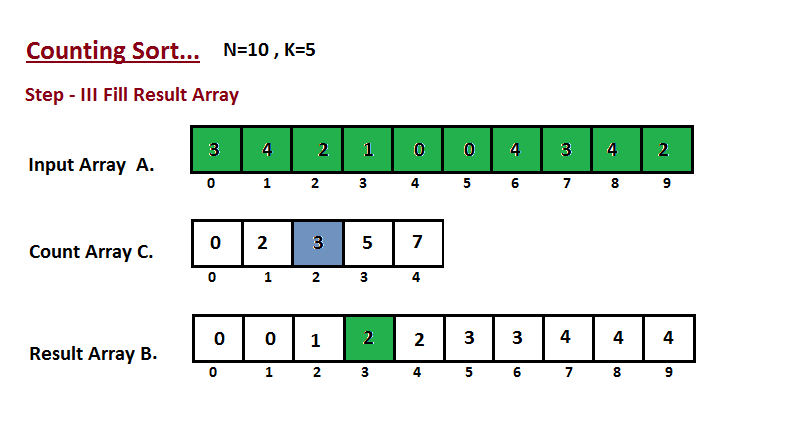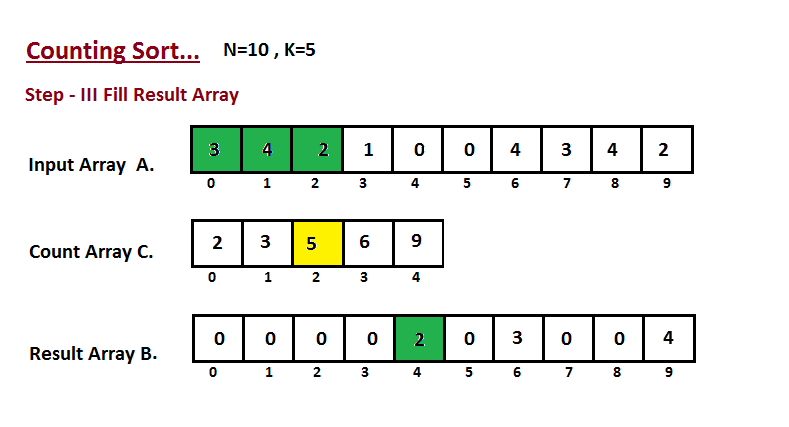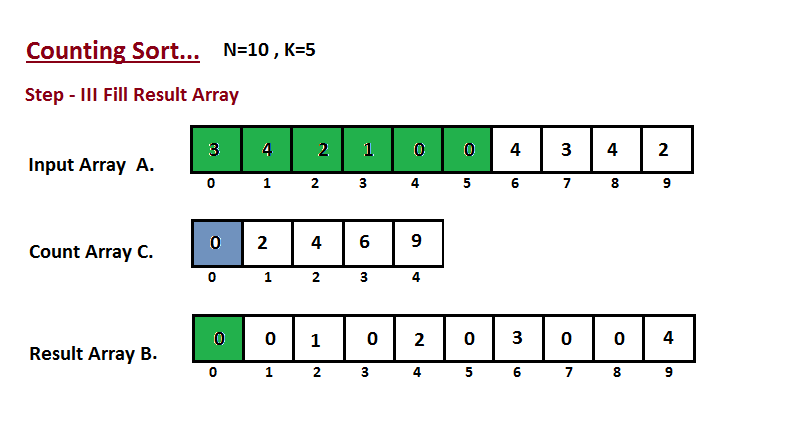
32 |
33 | ## Complexity
34 |
35 | | Name | Best | Average | Worst | Memory | Stable | Comments |
36 | | --------------------- | :-------------: | :-----------------: | :-----------------: | :-------: | :-------: | :-------- |
37 | | **Counting sort** | n + r | n + r | n + r | n + r | Yes | r - biggest number in array |
38 |
39 | ## References
40 |
41 | - [Wikipedia](https://en.wikipedia.org/wiki/Counting_sort)
42 | - [YouTube](https://www.youtube.com/watch?v=OKd534EWcdk&index=61&t=0s&list=PLLXdhg_r2hKA7DPDsunoDZ-Z769jWn4R8)
43 | - [EfficientAlgorithms](https://efficientalgorithms.blogspot.com/2016/09/lenear-sorting-counting-sort.html)
44 |
--------------------------------------------------------------------------------
/.github/CODE_OF_CONDUCT.md:
--------------------------------------------------------------------------------
1 | # Contributor Covenant Code of Conduct
2 |
3 | ## Our Pledge
4 |
5 | In the interest of fostering an open and welcoming environment, we as contributors and maintainers pledge to making participation in our project and our community a harassment-free experience for everyone, regardless of age, body size, disability, ethnicity, gender identity and expression, level of experience, nationality, personal appearance, race, religion, or sexual identity and orientation.
6 |
7 | ## Our Standards
8 |
9 | Examples of behavior that contributes to creating a positive environment include:
10 |
11 | * Using welcoming and inclusive language
12 | * Being respectful of differing viewpoints and experiences
13 | * Gracefully accepting constructive criticism
14 | * Focusing on what is best for the community
15 | * Showing empathy towards other community members
16 |
17 | Examples of unacceptable behavior by participants include:
18 |
19 | * The use of sexualized language or imagery and unwelcome sexual attention or advances
20 | * Trolling, insulting/derogatory comments, and personal or political attacks
21 | * Public or private harassment
22 | * Publishing others' private information, such as a physical or electronic address, without explicit permission
23 | * Other conduct which could reasonably be considered inappropriate in a professional setting
24 |
25 | ## Our Responsibilities
26 |
27 | Project maintainers are responsible for clarifying the standards of acceptable behavior and are expected to take appropriate and fair corrective action in response to any instances of unacceptable behavior.
28 |
29 | Project maintainers have the right and responsibility to remove, edit, or reject comments, commits, code, wiki edits, issues, and other contributions that are not aligned to this Code of Conduct, or to ban temporarily or permanently any contributor for other behaviors that they deem inappropriate, threatening, offensive, or harmful.
30 |
31 | ## Scope
32 |
33 | This Code of Conduct applies both within project spaces and in public spaces when an individual is representing the project or its community. Examples of representing a project or community include using an official project e-mail address, posting via an official social media account, or acting as an appointed representative at an online or offline event. Representation of a project may be further defined and clarified by project maintainers.
34 |
35 | ## Enforcement
36 |
37 | Instances of abusive, harassing, or otherwise unacceptable behavior may be reported by contacting the project team at akhenda@gmail.com. The project team will review and investigate all complaints, and will respond in a way that it deems appropriate to the circumstances. The project team is obligated to maintain confidentiality with regard to the reporter of an incident. Further details of specific enforcement policies may be posted separately.
38 |
39 | Project maintainers who do not follow or enforce the Code of Conduct in good faith may face temporary or permanent repercussions as determined by other members of the project's leadership.
40 |
41 | ## Attribution
42 |
43 | This Code of Conduct is adapted from the [Contributor Covenant][homepage], version 1.4, available at [http://contributor-covenant.org/version/1/4][version]
44 |
45 | [homepage]: http://contributor-covenant.org
46 | [version]: http://contributor-covenant.org/version/1/4/
47 |
--------------------------------------------------------------------------------
/src/data-structures/tree/index.js:
--------------------------------------------------------------------------------
1 | import Node from './node';
2 |
3 | export default class Tree {
4 | /**
5 | * initialize the Tree
6 | */
7 | constructor() {
8 | this.root = null;
9 | }
10 |
11 | /**
12 | * adds a Node to the Tree
13 | * @param {string|number} data
14 | * @param {string|number} toNodeData
15 | */
16 | addNode(data, toNodeData) {
17 | const node = new Node(data);
18 | const parent = toNodeData ? this.findBFS(toNodeData) : null;
19 |
20 | if (!parent && !this.root) {
21 | this.root = node;
22 | } else if (!parent && this.root) {
23 | return 'Root node is already assigned';
24 | } else {
25 | parent.children.push(node);
26 | }
27 | }
28 |
29 | /**
30 | * remove a Node from the Tree
31 | * @param {number|string} data
32 | * @return {void}
33 | */
34 | remove(data) {
35 | if (this.root.data === data) this.root = null;
36 |
37 | const queue = [this.root];
38 |
39 | while (queue.length && this.root) {
40 | const node = queue.shift();
41 |
42 | node.children.forEach((childNode, i) => {
43 | if (childNode.data === data) {
44 | node.children.splice(i, 1);
45 | } else {
46 | queue.push(childNode);
47 | }
48 | });
49 | }
50 | }
51 |
52 | /**
53 | * check whether the tree contains the given data
54 | * @param {number|string} data
55 | * @return {Boolean}
56 | */
57 | contains(data) {
58 | return this.root ? !!this.findBFS(data) : false;
59 | }
60 |
61 | /**
62 | * find data in the tree using BFS
63 | * @param {number|string} data
64 | * @return {Node}
65 | */
66 | findBFS(data) {
67 | const queue = [this.root];
68 |
69 | while (queue.length && this.root) {
70 | const node = queue.shift();
71 |
72 | if (node.data === data) return node;
73 |
74 | node.children.forEach(childNode => (queue.push(childNode)));
75 | }
76 |
77 | return null;
78 | }
79 |
80 | /**
81 | * prints a representation of the tree on a single line
82 | * @return {string} tree representation
83 | */
84 | print() {
85 | if (!this.root) return 'No root node found';
86 |
87 | let string = '';
88 | const newline = new Node('|');
89 | const queue = [this.root, newline];
90 |
91 | while (queue.length) {
92 | const node = queue.shift();
93 |
94 | string += `${node.data.toString()} `;
95 |
96 | if (node === newline && queue.length) queue.push(newline);
97 |
98 | node.children.forEach(childNode => (queue.push(childNode)));
99 | }
100 |
101 | console.log(string.slice(0, -2).trim());
102 | return string.slice(0, -2).trim();
103 | }
104 |
105 | /**
106 | * prints a representation of the tree level by level
107 | * on multiple lines
108 | * @return {string} tree representation
109 | */
110 | printByLevel() {
111 | if (!this.root) return 'No root node found';
112 |
113 | let string = '';
114 | const newline = new Node('\n');
115 | const queue = [this.root, newline];
116 |
117 | while (queue.length) {
118 | const node = queue.shift();
119 |
120 | string += `${node.data.toString()}${(node.data !== '\n' ? ' ' : '')}`;
121 |
122 | if (node === newline && queue.length) queue.push(newline);
123 |
124 | node.children.forEach(childNode => (queue.push(childNode)));
125 | }
126 |
127 | console.log(string.trim());
128 | return string.trim();
129 | }
130 | }
131 |
--------------------------------------------------------------------------------
/src/data-structures/linked-list/README.md:
--------------------------------------------------------------------------------
1 | ## Linked List
2 |
3 | According to Wikipedia:
4 |
5 | > In computer science, a linked list is a linear collection of data elements, whose order is not given by their physical placement in memory. Instead, each element points to the next. It is a data structure consisting of a collection of nodes which together represent a sequence. In its most basic form, each node contains: data, and a reference (in other words, a link) to the next node in the sequence. This structure allows for efficient insertion or removal of elements from any position in the sequence during iteration. More complex variants add additional links, allowing more efficient insertion or removal of nodes at arbitrary positions. A drawback of linked lists is that access time is linear (and difficult to pipeline). Faster access, such as random access, is not feasible. Arrays have better cache locality compared to linked lists.
6 |
7 | Linked Lists are among the simplest and most common data structures because they allow for efficient insertion or removal of elements from any position in the sequence.
8 |
9 | They are made of groups of nodes which together represent a sequence. You will notice that both the Queue and the Stack where made using the basic idea of a linked list. However, they have special rule which makes them different in functionality.
10 |
11 | Like arrays, they store data elements in sequential order. Instead of keeping indexes, linked lists hold pointers to other elements. The first node is called the head while the last node is called the tail. In a singly-linked list, each node has only one pointer to the next node. Here, the head is where we begin our walk down the rest of the list. In a doubly-linked list, a pointer to the previous node is also kept. Therefore, we can also start from the tail and walk “backwards” toward the head.
12 |
13 | Linked lists have constant-time insertions and deletions because we can just change the pointers. To do the same operations in arrays requires linear time because subsequent items need to be shifted over. Also, linked lists can grow as long as there is space.
14 |
15 | Like arrays, linked lists can operate as stacks. It’s as simple as having the head be the only place for insertion and removal. Linked lists can also operate as queues. This can be achieved with a doubly-linked list, where insertion occurs at the tail and removal occurs at the head, or vice versa.
16 |
17 | Linked lists are useful on both the client and server. On the client, state management libraries like Redux structure its middleware logic in a linked-list fashion. When actions are dispatched, they are piped from one middleware to the next until all is visited before reaching the reducers. On the server, web frameworks like Express also structure its middleware logic in a similar fashion. When a request is received, it is piped from one middleware to the next until a response is issued.
18 |
19 | ### Complexity
20 |
21 | #### Average
22 |
23 | | Operation | Complexity |
24 | | :-------: | :--------: |
25 | | Access | O(n) |
26 | | Search | O(n) |
27 | | Insertion | O(1) |
28 | | Deletion | O(1) |
29 |
30 | Simple representation of a linked list.
31 |
32 | 
33 |
34 | ## References
35 |
36 | - [Wikipedia](https://en.wikipedia.org/wiki/Linked_list)
37 | - [Silicon Wat(Medium)](https://medium.com/siliconwat/data-structures-in-javascript-1b9aed0ea17c)
38 | - [YouTube](https://www.youtube.com/watch?v=njTh_OwMljA&index=2&t=1s&list=PLLXdhg_r2hKA7DPDsunoDZ-Z769jWn4R8)
39 |
--------------------------------------------------------------------------------
/src/data-structures/set/index.js:
--------------------------------------------------------------------------------
1 | export default class Set {
2 | /**
3 | * initializes the set
4 | */
5 | constructor() {
6 | this._data = [];
7 | this._count = 0;
8 | }
9 |
10 | /**
11 | * returns data in the set
12 | * @return {array} set data
13 | */
14 | data() {
15 | return this._data;
16 | }
17 |
18 | /**
19 | * adds an element into the set
20 | * @param {string|number} element
21 | */
22 | add(element) {
23 | if (this._data.indexOf(element) < 0) {
24 | this._data.push(element);
25 | this._count++;
26 | }
27 | }
28 |
29 | /**
30 | * removes an element from the set
31 | * @param {string|number} element - the element to be removed
32 | * @return {void}
33 | */
34 | remove(element) {
35 | const index = this._data.indexOf(element);
36 | if (index >= 0) {
37 | this._data.splice(index, 1);
38 | this._count--;
39 | }
40 | }
41 |
42 | /**
43 | * checks whether an element exists in the set
44 | * @param {number|string} element - the element to be searched
45 | * @return {boolean}
46 | */
47 | contains(element) {
48 | return this._data.indexOf(element) !== -1;
49 | }
50 |
51 | /**
52 | * check the union between this set and the provided set
53 | * i.e. return elements in Set1 and Set2 without the duplicates
54 | * @param {array} set - the set to union with
55 | * @return {array} the new set that is a union of the 2 sets
56 | */
57 | union(set) {
58 | const newSet = new Set();
59 |
60 | set.data().forEach((element) => {
61 | newSet.add(element);
62 | });
63 |
64 | this._data.forEach((element) => {
65 | newSet.add(element);
66 | });
67 |
68 | return newSet;
69 | }
70 |
71 | /**
72 | * check the intersect between this set and the provided set
73 | * i.e. return elements in Set1 that are also in Set2
74 | * @param {array} set - the set to union with
75 | * @return {array} the new set that is a intersect of the 2 sets
76 | */
77 | intersect(set) {
78 | const newSet = new Set();
79 |
80 | this._data.forEach((element) => {
81 | if (set.contains(element)) {
82 | newSet.add(element);
83 | }
84 | });
85 |
86 | return newSet;
87 | }
88 |
89 | /**
90 | * performs difference operation between called set and otherSet
91 | * i.e. a Set is said to be a difference of Set A and B if it contains
92 | * set of element e which are present in Set A but not in Set B.
93 | * @param {array} set - the set to difference with
94 | * @return {array} the new set that is the difference between this set and provided set
95 | */
96 | difference(set) {
97 | const newSet = new Set();
98 |
99 | this._data.forEach((element) => {
100 | if (!set.contains(element)) {
101 | newSet.add(element);
102 | }
103 | });
104 |
105 | return newSet;
106 | }
107 |
108 | /**
109 | * check whether the set on which the method is invoked is the
110 | * subset of otherset or not
111 | * @param {array} set - the set to check if this is a subset of
112 | * @return {boolean}
113 | */
114 | isSubset(set) {
115 | return set.data().every((element) => {
116 | return this.contains(element);
117 | }, this);
118 | }
119 |
120 | /**
121 | * returns the size/length of the set
122 | * @return {number}
123 | */
124 | length() {
125 | return this._count;
126 | }
127 |
128 | /**
129 | * displays the set
130 | */
131 | print() {
132 | return this._data.join(' ');
133 | }
134 | }
135 |
--------------------------------------------------------------------------------
/src/data-structures/priority-queue/index.js:
--------------------------------------------------------------------------------
1 | export default class PriorityQueue {
2 | /**
3 | * initializes the queue
4 | * @param {number} capacity - the capacity of the queue
5 | */
6 | constructor(capacity = Infinity) {
7 | this._capacity = capacity;
8 | this._data = [];
9 | this._front = 0;
10 | this._rear = 0;
11 | this._priorities = {};
12 | }
13 |
14 | /**
15 | * adds a new element onto the queue
16 | * @param {any} element
17 | * @param {number} priority
18 | * @return {number|string} the index of the added element or queue overflow message
19 | */
20 | enqueue(element, priority) {
21 | let enqueued = false;
22 |
23 | if (this.size() < this._capacity) {
24 | this._rear++;
25 | this._data.forEach((item, index) => {
26 | if (this._priorities[item] > priority) {
27 | this._data.splice(index, 0, element);
28 | enqueued = true;
29 | }
30 | });
31 |
32 | if (!enqueued) {
33 | this._data.push(element);
34 | }
35 |
36 | this._priorities[element] = priority;
37 |
38 | return this._rear;
39 | }
40 |
41 | return 'Max capacity reached. Remove element before adding a new one.';
42 | }
43 |
44 | /**
45 | * does the reverse of the enqueue() i.e. removes an element
46 | * from the queue and then increments the front pointer variable
47 | * @return {any} the element in the front position of the queue or an error message
48 | */
49 | dequeue() {
50 | if (this._front === this._rear) {
51 | return 'No element inside the queue. Add element before dequeuing.';
52 | }
53 |
54 | const element = this._data.shift();
55 |
56 | delete this._priorities[element];
57 |
58 | if (this._front < this._rear) this._front++;
59 |
60 | return element;
61 | }
62 |
63 | /**
64 | * returns the oldest element added onto the queue. similar to dequeue but
65 | * does not remove element from queue
66 | * @return {any} returns the oldest element in the queue
67 | */
68 | peek() {
69 | return this._data[this._front];
70 | }
71 |
72 | /**
73 | * examine the front element of the queue
74 | * @return {any} the element in the front position of the queue
75 | */
76 | front() {
77 | return this._data[this._front];
78 | }
79 |
80 | /**
81 | * examine the back element of the queue
82 | * @return {any} the element in the rear position of the queue
83 | */
84 | back() {
85 | return this._data[this._rear - 1];
86 | }
87 |
88 | /**
89 | * returns the size/length of the queue
90 | * @return {number} the difference of the front and rear values
91 | */
92 | size() {
93 | return this._rear - this._front;
94 | }
95 |
96 | /**
97 | * check whether the queue is empty
98 | * @return {boolean}
99 | */
100 | isEmpty() {
101 | return this._rear - 1 - this._front === 0;
102 | }
103 |
104 | /**
105 | * clears the queue and sets the top pointer variable back to 0
106 | */
107 | clear() {
108 | this._rear = 0;
109 | this._front = 0;
110 | this._data = [];
111 | }
112 |
113 | /**
114 | * displays the queue
115 | */
116 | print() {
117 | return this._data.join(' ');
118 | }
119 |
120 | /**
121 | * returns the set capacity of the stack
122 | * @return {number}
123 | */
124 | capacity() {
125 | return this._capacity;
126 | }
127 |
128 | /**
129 | * check wheteher an element exists in the queue
130 | * @param {any} element the element to search
131 | * @return {boolean}
132 | */
133 | contains(element) {
134 | return this._data.includes(element);
135 | }
136 | }
137 |
--------------------------------------------------------------------------------
/src/data-structures/tree/README.md:
--------------------------------------------------------------------------------
1 | ## Tree
2 |
3 | According to Wikipedia:
4 |
5 | > In computer science, a tree is a widely used abstract data type (ADT)—or data structure implementing this ADT—that simulates a hierarchical tree structure, with a root value and subtrees of children with a parent node, represented as a set of linked nodes.
6 | >
7 | > A tree data structure can be defined recursively (locally) as a collection of nodes (starting at a root node), where each node is a data structure consisting of a value, together with a list of references to nodes (the "children"), with the constraints that no reference is duplicated, and none points to the root.
8 | >
9 | > Alternatively, a tree can be defined abstractly as a whole (globally) as an ordered tree, with a value assigned to each node. Both these perspectives are useful: while a tree can be analyzed mathematically as a whole, when actually represented as a data structure it is usually represented and worked with separately by node (rather than as a set of nodes and an adjacency list of edges between nodes, as one may represent a digraph, for instance). For example, looking at a tree as a whole, one can talk about "the parent node" of a given node, but in general as a data structure a given node only contains the list of its children, but does not contain a reference to its parent (if any).
10 |
11 | A tree is a *nonlinear* data structure that is used to store data in a **hierarchical** manner. Tree data structures are used to store *hierarchical* data, such as the *files* in a **file system**.
12 |
13 | A tree is made up of a set of nodes connected by *edges*. Special types of trees, called **binary trees** or **binary search trees**, restrict the number of child nodes to no more than two.
14 |
15 | A tree can be broken down into *levels*. The root node is at **level 0**, its children are at **level 1**, those nodes' children are at **level 2**, and so on.
16 |
17 | A `Tree` is like a linked list, except it keeps references to many **child nodes** in a hierarchical structure i.e, each node can have no more than one parent. The **Document Object Model (DOM)** is such a structure, with a root `html` node that branches into the `head` and `body` nodes, which further subdivide into all the familiar html tags. As an in-memory representation of the DOM, React’s **Virtual DOM** is also a tree structure.
18 |
19 | Take a look at the following tree:-
20 |
21 | 
22 |
23 | A simple unordered tree; in this diagram, the node labeled 7 has two children, labeled 2 and 6, and one parent, labeled 2. The root node, at the top, has no parent.
24 |
25 | ### Complexity
26 |
27 | #### Average
28 |
29 | | Operation | Complexity |
30 | | :-------: | :--------: |
31 | | Access | |
32 | | Search | |
33 | | Insertion | |
34 | | Deletion | |
35 |
36 | ## References
37 |
38 | - [Wikipedia](https://en.wikipedia.org/wiki/Tree_(data_structure))
39 | - [Java2s](http://www.java2s.com/Tutorials/Javascript/Javascript_Data_Structure/0420__Javascript_Binary_Tree.htm)
40 | - [YouTube](https://www.youtube.com/watch?v=qH6yxkw0u78)
41 | - [YouTube](https://www.youtube.com/watch?v=oSWTXtMglKE)
42 |
--------------------------------------------------------------------------------
/src/algorithms/sorting/quick-sort/index.js:
--------------------------------------------------------------------------------
1 | /**
2 | * simple quick sort implementation (pivot is the first element of the array)
3 | * @param {array} array an unsorted array
4 | * @return {array} sorted array
5 | */
6 | export const simpleQuickSort = (array) => {
7 | // one characteristics of quicksort is that it involves fewer
8 | // comparisons and swaps than other algorithms, so it's able
9 | // to sort quickly in many cases
10 |
11 | // let's start. the first operation targets the entire
12 | // array/sequence of numbers.
13 |
14 | // if array has less than or equal to one elements
15 | // then it is already sorted.
16 | if (array.length < 2) return array;
17 |
18 | // initialize left and right arrays
19 | const left = [];
20 | const right = [];
21 |
22 | // a number is chosen as a reference for sorting
23 | // this number is called the "pivot"
24 | // the pivot is normally a number chosen at random but, this time,
25 | // for convinience, the leftmost number will be chosen as the pivot
26 | // take the first element of the array as the pivot
27 | const pivot = array.shift();
28 |
29 | array.forEach((number, index) => {
30 | if (array[index] < pivot) {
31 | left.push(array[index]);
32 | } else {
33 | right.push(array[index]);
34 | }
35 | });
36 |
37 | // return [...simpleQuickSort(left), pivot, ...simpleQuickSort(right)];
38 | return simpleQuickSort(left).concat(pivot, simpleQuickSort(right));
39 | };
40 |
41 | /**
42 | * swap helper function
43 | * @param {array} array
44 | * @param {number} i
45 | * @param {number} j
46 | * @return {void}
47 | */
48 | const swap = (array, i, j) => {
49 | const temp = array[i];
50 |
51 | array[i] = array[j];
52 | array[j] = temp;
53 | };
54 |
55 | /**
56 | * lomuto partition scheme, it is less efficient than the Hoare partition scheme
57 | * @param {array} array array to partion
58 | * @param {number} left leftmost index
59 | * @param {number} right rightmost index
60 | * @return {number} the pivot element
61 | */
62 | export const partitionLomuto = (array, left, right) => {
63 | let i = left;
64 | let j = left;
65 | const pivot = right;
66 |
67 | for (j; j < right; j++) {
68 | if (array[j] <= array[pivot]) {
69 | swap(array, i, j);
70 | i += 1;
71 | }
72 | }
73 |
74 | swap(array, i, j);
75 |
76 | return i;
77 | };
78 |
79 | /**
80 | * hoare partition scheme, it is more efficient than the
81 | * lomuto partition scheme because it does three times
82 | * fewer swaps on average
83 | * @param {array} array array to partion
84 | * @param {number} left leftmost index
85 | * @param {number} right rightmost index
86 | * @return {number} the pivot element
87 | */
88 | export const partitionHoare = (array, left, right) => {
89 | const pivot = Math.floor((left + right) / 2);
90 |
91 | while (left <= right) {
92 | while (array[left] < array[pivot]) left++;
93 |
94 | while (array[right] > array[pivot]) right--;
95 |
96 | if (left <= right) {
97 | swap(array, left, right);
98 | left++;
99 | right--;
100 | }
101 | }
102 |
103 | return left;
104 | };
105 |
106 | /**
107 | * classic implementation (with hoare or lomuto partition scheme)
108 | * @param {array} array array to be sorted
109 | * @param {number} left leftmost index
110 | * @param {number} right rightmost index
111 | * @return {array} sorted array
112 | */
113 | const quickSort = (array, left = 0, right = array.length - 1) => {
114 | const pivot = partitionHoare(array, left, right);
115 |
116 | if (left < pivot - 1) quickSort(array, left, pivot - 1);
117 |
118 | if (right > pivot) quickSort(array, pivot, right);
119 |
120 | return array;
121 | };
122 |
123 | export default quickSort;
124 |
--------------------------------------------------------------------------------
/package.json:
--------------------------------------------------------------------------------
1 | {
2 | "name": "es6-data-structures-and-algorithms",
3 | "version": "1.9.1",
4 | "description": "Popular Data Structures and Algorithms done in JavaScript ES6",
5 | "main": "index.js",
6 | "directories": {
7 | "doc": "docs"
8 | },
9 | "scripts": {
10 | "gc": "git add . && git-cz",
11 | "start": "babel-node -- index",
12 | "test": "export NODE_PATH=./ && nyc --reporter=lcov mocha --compilers js:babel-register --recursive ./__tests__ --timeout 120000 --exit",
13 | "test-with-coverage": "export NODE_PATH=./ && nyc --reporter=lcov mocha --compilers js:babel-register --recursive ./__tests__ --timeout 120000 --exit && cat ./coverage/lcov.info | codacy-coverage",
14 | "lint": "eslint index.js src/**/*.js __tests__/**/*.js",
15 | "validate": "npm run lint && npm run test",
16 | "commitmsg": "commitlint -e $GIT_PARAMS",
17 | "precommit": "npm run validate",
18 | "prepush": "npm run validate"
19 | },
20 | "repository": {
21 | "type": "git",
22 | "url": "git+https://github.com/akhenda/es6-data-structures-and-algorithms.git"
23 | },
24 | "keywords": [
25 | "data-structures",
26 | "algorithms",
27 | "data-structures-and-algorithms",
28 | "es6",
29 | "es2015"
30 | ],
31 | "author": "Joseph Akhenda",
32 | "license": "MIT",
33 | "bugs": {
34 | "url": "https://github.com/akhenda/es6-data-structures-and-algorithms/issues"
35 | },
36 | "homepage": "https://github.com/akhenda/es6-data-structures-and-algorithms#readme",
37 | "contributors": {},
38 | "dependencies": {
39 | "babel-runtime": "^6.26.0"
40 | },
41 | "devDependencies": {
42 | "@commitlint/cli": "^7.0.0",
43 | "@commitlint/config-conventional": "^7.0.1",
44 | "@semantic-release/changelog": "^3.0.0",
45 | "@semantic-release/git": "^7.0.1",
46 | "babel-cli": "^6.26.0",
47 | "babel-eslint": "^8.2.6",
48 | "babel-plugin-module-resolver": "^3.1.1",
49 | "babel-plugin-transform-runtime": "^6.23.0",
50 | "babel-preset-es2015": "^6.24.1",
51 | "babel-preset-stage-0": "^6.24.1",
52 | "chai": "^4.1.2",
53 | "codacy-coverage": "^3.0.0",
54 | "commitizen": "^2.10.1",
55 | "cz-customizable": "^5.2.0",
56 | "eslint": "^5.2.0",
57 | "eslint-config-airbnb-base": "^13.0.0",
58 | "eslint-import-resolver-babel-module": "^4.0.0",
59 | "eslint-plugin-import": "^2.13.0",
60 | "husky": "^0.14.3",
61 | "istanbul": "^0.4.5",
62 | "mocha": "^5.2.0",
63 | "nyc": "^12.0.2",
64 | "semantic-release": "^15.8.1"
65 | },
66 | "config": {
67 | "commitizen": {
68 | "path": "node_modules/cz-customizable"
69 | },
70 | "cz-customizable": {
71 | "config": ".cz-config.js"
72 | }
73 | },
74 | "commitlint": {
75 | "extends": [
76 | "@commitlint/config-conventional"
77 | ]
78 | },
79 | "release": {
80 | "branch": "develop",
81 | "verifyConditions": [
82 | "@semantic-release/changelog",
83 | "@semantic-release/git",
84 | "@semantic-release/github"
85 | ],
86 | "getLastRelease": "@semantic-release/git",
87 | "prepare": [
88 | {
89 | "path": "@semantic-release/changelog",
90 | "changelogFile": "docs/CHANGELOG.md"
91 | },
92 | {
93 | "path": "@semantic-release/npm",
94 | "npmPublish": false
95 | },
96 | {
97 | "path": "@semantic-release/git",
98 | "assets": [
99 | "package.json",
100 | "docs"
101 | ],
102 | "message": "chore(release): v${nextRelease.version} - <%= new Date().toLocaleDateString('en-US', {year: 'numeric', month: 'short', day: 'numeric', hour: 'numeric', minute: 'numeric'}) %> [skip ci]\n\n${nextRelease.notes}"
103 | }
104 | ],
105 | "publish": [
106 | "@semantic-release/github"
107 | ]
108 | }
109 | }
110 |
--------------------------------------------------------------------------------
/assets/constant-time.svg:
--------------------------------------------------------------------------------
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
--------------------------------------------------------------------------------
/src/data-structures/trie/README.md:
--------------------------------------------------------------------------------
1 | ## Trie
2 |
3 | According to Wikipedia:
4 |
5 | > In computer science, a trie, also called digital tree, radix tree or prefix tree is a kind of search tree—an ordered tree data structure used to store a dynamic set or associative array where the keys are usually strings. Unlike a binary search tree, no node in the tree stores the key associated with that node; instead, its position in the tree defines the key with which it is associated. All the descendants of a node have a common prefix of the string associated with that node, and the root is associated with the empty string. Keys tend to be associated with leaves, though some inner nodes may correspond to keys of interest. Hence, keys are not necessarily associated with every node. For the space-optimized presentation of prefix tree, see compact prefix tree.
6 | >
7 | > In the example shown, keys are listed in the nodes and values below them. Each complete English word has an arbitrary integer value associated with it. A trie can be seen as a tree-shaped deterministic finite automaton. Each finite language is generated by a trie automaton, and each trie can be compressed into a deterministic acyclic finite state automaton.
8 |
9 | Take a look at the following trie:-
10 |
11 | 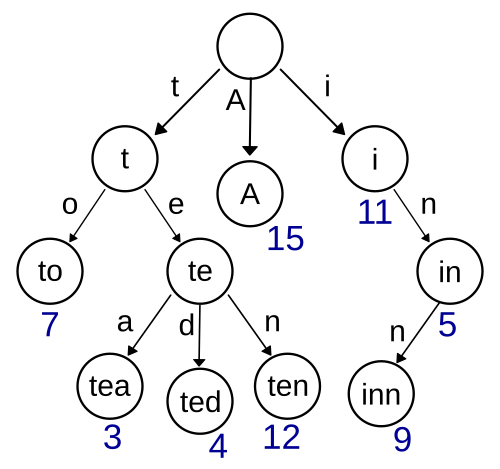
12 |
13 | > A trie for keys "A","to", "tea", "ted", "ten", "i", "in", and "inn".
14 |
15 | A **trie** is a `tree-like` data structure whose nodes store the letters of an alphabet. By structuring the nodes in a particular way, words and strings can be retrieved from the structure by traversing down a branch path of the tree.
16 |
17 | Tries in the context of computer science are a relatively new thing. The first time that they were considered in computing was back in *1959*, when a Frenchman named **René de la Briandais** suggested using them. According to Donald Knuth’s research in *The Art of Computer Programming*:
18 |
19 | > Trie memory for computer searching was first recommended by René de la Briandais. He pointed out that we can save memory space at the expense of running time if we use a linked list for each node vector, since most of the entries in the vectors tend to be empty.
20 |
21 | **Trie** is an efficient information re**Trie**val data structure. Using Trie, search complexities can be brought to optimal limit (key length). If we store keys in binary search tree, a well balanced BST will need time proportional to , where **M** is maximum string length and **N** is number of keys in tree. Using Trie, we can search the key in time. However the penalty is on Trie storage requirements.
22 |
23 | ### Complexity
24 |
25 | #### Average
26 |
27 | | Operation | Complexity |
28 | | :-------: | :--------: |
29 | | Access | |
30 | | Search | |
31 | | Insertion | |
32 | | Deletion | |
33 |
34 | where **k** is the word length.
35 |
36 | ## References
37 |
38 | - [Wikipedia](https://en.wikipedia.org/wiki/Trie)
39 | - [Vaidehi Joshi](https://medium.com/basecs/trying-to-understand-tries-3ec6bede0014)
40 | - [GeeksforGeeks](https://www.geeksforgeeks.org/trie-insert-and-search/)
41 | - [YouTube](https://www.youtube.com/watch?v=zIjfhVPRZCg&list=PLLXdhg_r2hKA7DPDsunoDZ-Z769jWn4R8&index=7&t=0s)
42 | - [YouTube](https://www.youtube.com/watch?v=dUBkaqrcYT8)
43 |
--------------------------------------------------------------------------------
/src/data-structures/avl-tree/README.md:
--------------------------------------------------------------------------------
1 | ## AVL Tree
2 |
3 | According to Wikipedia:
4 |
5 | > In computer science, an **AVL** tree (named after inventors **A**delson-**V**elsky and **L**andis) is a self-balancing binary search tree. It was the first such data structure to be invented. In an AVL tree, the heights of the two child subtrees of any node differ by at most one; if at any time they differ by more than one, rebalancing is done to restore this property. Lookup, insertion, and deletion all take time in both the average and worst cases, where *n* is the number of nodes in the tree prior to the operation. Insertions and deletions may require the tree to be rebalanced by one or more tree rotations.
6 | >
7 | > The AVL tree is named after its two Soviet inventors, Georgy Adelson-Velsky and Evgenii Landis, who published it in their 1962 paper "An algorithm for the organization of information".
8 | >
9 | > AVL trees are often compared with red–black trees because both support the same set of operations and take time for the basic operations. For lookup-intensive applications, AVL trees are faster than red–black trees because they are more strictly balanced. Similar to red–black trees, AVL trees are height-balanced. Both are, in general, neither weight-balanced nor -balanced for any that is, sibling nodes can have hugely differing numbers of descendants.
10 |
11 | Take a look at the following AVL-Tree :-
12 |
13 | 
14 |
15 | Animation showing the insertion of several elements into an AVL tree. It includes left, right, left-right and right-left rotations.
16 |
17 | Shown below is an AVL tree with balance factors (green)
18 |
19 | 
20 |
21 | ### Complexity
22 |
23 | #### Average
24 |
25 | | Operation | Complexity |
26 | | :-------: | :---------: |
27 | | Space | |
28 | | Search | |
29 | | Insertion | |
30 | | Deletion | |
31 |
32 |
33 | ### AVL Tree Rotations
34 |
35 | **Left-Left Rotation**
36 |
37 | 
38 |
39 | **Right-Right Rotation**
40 |
41 | 
42 |
43 | **Left-Right Rotation**
44 |
45 | 
46 |
47 | **Right-Left Rotation**
48 |
49 | 
50 |
51 | ## References
52 |
53 | - [Wikipedia](https://en.wikipedia.org/wiki/AVL_tree)
54 | - [Tutorials Point](https://www.tutorialspoint.com/data_structures_algorithms/avl_tree_algorithm.htm)
55 | - [BTech](http://btechsmartclass.com/DS/U5_T2.html)
56 | - [AVL Tree Insertion on YouTube](https://www.youtube.com/watch?v=rbg7Qf8GkQ4&list=PLLXdhg_r2hKA7DPDsunoDZ-Z769jWn4R8&index=12&)
57 | - [AVL Tree Interactive Visualisations](https://www.cs.usfca.edu/~galles/visualization/AVLtree.html)
58 |
--------------------------------------------------------------------------------
/src/data-structures/graph/index.js:
--------------------------------------------------------------------------------
1 | export default class Graph {
2 | /**
3 | * initialize the Graph
4 | */
5 | constructor() {
6 | this.edges = [];
7 | this.vertices = [];
8 | this.numberOfEdges = 0;
9 | this.numberOfVertices = 0;
10 | }
11 |
12 | /**
13 | * add a vertex to the graph
14 | * @param {number} vertex
15 | */
16 | addVertex(vertex) {
17 | this.vertices.push(vertex);
18 | this.edges[vertex] = [];
19 | this.numberOfVertices += 1;
20 | }
21 |
22 | /**
23 | * removes a vertex from the graph
24 | * @param {number} vertex
25 | */
26 | removeVertex(vertex) {
27 | const index = this.vertices.indexOf(vertex);
28 |
29 | if (index >= 0) this.vertices.splice(index, 1);
30 |
31 | while (this.edges[vertex].length) {
32 | const adjacentVertex = this.edges[vertex].pop();
33 | this.removeEdge(adjacentVertex, vertex);
34 | }
35 |
36 | this.numberOfVertices -= 1;
37 | }
38 |
39 | /**
40 | * checks if the graph has a vertex
41 | * @param {number} vertex
42 | * @return {Boolean}
43 | */
44 | hasVertex(vertex) {
45 | return this.vertices.includes(vertex);
46 | }
47 |
48 | /**
49 | * adds an edge between two existing vertices
50 | * @param {number} vertex1
51 | * @param {number} vertex2
52 | */
53 | addEdge(vertex1, vertex2) {
54 | this.edges[vertex1].push(vertex2);
55 | this.edges[vertex2].push(vertex1);
56 | this.numberOfEdges++;
57 | }
58 |
59 | /**
60 | * removes an existing edge between two vertices
61 | * @param {number} vertex1
62 | * @param {number} vertex2
63 | */
64 | removeEdge(vertex1, vertex2) {
65 | const index1 = this.edges[vertex1] ? this.edges[vertex1].indexOf(vertex2) : -1;
66 | const index2 = this.edges[vertex2] ? this.edges[vertex2].indexOf(vertex1) : -1;
67 |
68 | if (index1 >= 0) {
69 | this.edges[vertex1].splice(index1, 1);
70 | this.numberOfEdges--;
71 | }
72 |
73 | if (index2 >= 0) this.edges[vertex2].splice(index2, 1);
74 | }
75 |
76 | /**
77 | * checks if the graph has an edge between two existing vertices
78 | * @param {number} vertex1
79 | * @param {number} vertex2
80 | * @return {Boolean}
81 | */
82 | hasEdge(vertex1, vertex2) {
83 | if (this.hasVertex(vertex1) && this.hasVertex(vertex2)) {
84 | if (this.edges[vertex1].includes(vertex2) && this.edges[vertex2].includes(vertex1)) {
85 | return true;
86 | }
87 | }
88 |
89 | return false;
90 | }
91 |
92 | /**
93 | * returns the size of the graph
94 | * @return {number}
95 | */
96 | size() {
97 | return this.vertices.length;
98 | }
99 |
100 | /**
101 | * returns the number of edges in the graph
102 | * @return {[type]} [description]
103 | */
104 | relations() {
105 | return this.numberOfEdges;
106 | }
107 |
108 | /**
109 | * traverse the graph using using a traversal algorithm
110 | * @param {[type]} vertex starting vertex number
111 | * @param {Function} cb function that is called with each vertex value
112 | * @param {[type]} type traversal type, default is breadth-first
113 | * @return {void}
114 | */
115 | traverse(vertex, cb, type) {
116 | switch (type) {
117 | case 'dfs':
118 | // call DFS Graph traversal algorithm here
119 | break;
120 | default:
121 | // call BFS Graph traversal algorithm here
122 | break;
123 | }
124 | }
125 |
126 | /**
127 | * prints a representation of the graph
128 | * @return {string} graph representation as a string
129 | */
130 | print() {
131 | const output = this.vertices.map((vertex) => {
132 | return (`${vertex} -> ${this.edges[vertex].join(', ')}`).trim();
133 | }, this).join(' | ');
134 |
135 | console.log(output);
136 | return output;
137 | }
138 |
139 | /**
140 | * clears the graph
141 | * @return {void}
142 | */
143 | clear() {
144 | this.edges = [];
145 | this.vertices = [];
146 | this.numberOfEdges = 0;
147 | this.numberOfVertices = 0;
148 | }
149 | }
150 |
--------------------------------------------------------------------------------
/__tests__/unit/src/data-structures/hash-table.spec.js:
--------------------------------------------------------------------------------
1 | import chai from 'chai';
2 | import HashTable from 'src/data-structures/hash-table';
3 |
4 |
5 | const { expect } = chai;
6 |
7 | describe('HashTable', () => {
8 | it('should create hash table of certain capacity', () => {
9 | const hashTable = new HashTable();
10 | expect(hashTable.cells.length).to.equal(32);
11 |
12 | const biggerHashTable = new HashTable(128);
13 | expect(biggerHashTable.cells.length).to.equal(128);
14 | });
15 |
16 | it('should generate proper hash for specified keys', () => {
17 | const hashTable = new HashTable();
18 |
19 | expect(hashTable.hash('a')).to.equal(1);
20 | expect(hashTable.hash('b')).to.equal(2);
21 | expect(hashTable.hash('abc')).to.equal(6);
22 | });
23 |
24 | it('should insert, retrieve and remove data with collisions', () => {
25 | const hashTable = new HashTable(3, true);
26 |
27 | expect(hashTable.hash('a')).to.equal(1);
28 | expect(hashTable.hash('b')).to.equal(2);
29 | expect(hashTable.hash('c')).to.equal(0);
30 | expect(hashTable.hash('d')).to.equal(1);
31 |
32 | hashTable.insert('a', 'stargate-0');
33 | hashTable.insert('a', 'stargate-1');
34 | hashTable.insert('b', 'SG1');
35 | hashTable.insert('c', 'Atlantis');
36 | hashTable.insert('d', 'Universe');
37 |
38 | expect(hashTable.has('x')).to.equal(false);
39 | expect(hashTable.has('b')).to.equal(true);
40 | expect(hashTable.has('c')).to.equal(true);
41 |
42 | expect(hashTable.cells[0]).to.deep.equal({ c: 'Atlantis' });
43 | expect(hashTable.cells[1]).to.deep.equal({ a: 'stargate-1', d: 'Universe' });
44 | expect(hashTable.cells[2]).to.deep.equal({ b: 'SG1' });
45 |
46 | expect(hashTable.retrieve('a')).to.equal('stargate-1');
47 | expect(hashTable.retrieve('d')).to.equal('Universe');
48 | expect(hashTable.retrieve('x')).to.be.a('null');
49 | expect(hashTable.length()).to.be.equal(3);
50 |
51 | hashTable.remove('a');
52 |
53 | expect(hashTable.remove('not-existing')).to.be.a('null');
54 |
55 | expect(hashTable.retrieve('a')).to.be.a('null');
56 | expect(hashTable.retrieve('d')).to.equal('Universe');
57 | expect(hashTable.length()).to.be.equal(3);
58 |
59 | hashTable.insert('d', 'Universe-new');
60 | expect(hashTable.retrieve('d')).to.equal('Universe-new');
61 | });
62 |
63 | it('should be possible to add objects to hash table', () => {
64 | const hashTable = new HashTable();
65 |
66 | hashTable.insert('objectKey', { prop1: 'a', prop2: 'b' });
67 |
68 | const object = hashTable.retrieve('objectKey');
69 | expect(object).to.not.be.an('undefined');
70 | expect(object.prop1).to.equal('a');
71 | expect(object.prop2).to.equal('b');
72 | });
73 |
74 | it('should track actual keys', () => {
75 | const hashTable = new HashTable(3);
76 |
77 | hashTable.insert('a', 'stargate-0');
78 | hashTable.insert('a', 'stargate-1');
79 | hashTable.insert('b', 'SG1');
80 | hashTable.insert('c', 'Atlantis');
81 | hashTable.insert('d', 'Universe');
82 |
83 | expect(hashTable.getKeys()).to.deep.equal(['a', 'b', 'c', 'd']);
84 | expect(hashTable.has('a')).to.equal(true);
85 | expect(hashTable.has('x')).to.equal(false);
86 |
87 | hashTable.remove('a');
88 |
89 | expect(hashTable.has('a')).to.equal(false);
90 | expect(hashTable.has('b')).to.equal(true);
91 | expect(hashTable.has('x')).to.equal(false);
92 | });
93 |
94 | it('should print the hash table', () => {
95 | const hashTable = new HashTable(3, false);
96 |
97 | hashTable.insert('a', 'stargate-0');
98 | hashTable.insert('a', 'stargate-1');
99 | hashTable.insert('b', 'SG1');
100 | hashTable.insert('c', 'Atlantis');
101 | hashTable.insert('d', 'Universe');
102 |
103 | const result = '[{"c":"Atlantis"},{"a":"stargate-1","d":"Universe"},{"b":"SG1"}]';
104 |
105 | expect(hashTable.print()).to.equal(result);
106 |
107 | hashTable.remove('a');
108 |
109 | expect(hashTable.print()).to.equal('[{"c":"Atlantis"},{"d":"Universe"},{"b":"SG1"}]');
110 | });
111 | });
112 |
--------------------------------------------------------------------------------
/__tests__/unit/src/data-structures/graph.spec.js:
--------------------------------------------------------------------------------
1 | import chai from 'chai';
2 | import Graph from 'src/data-structures/graph';
3 |
4 |
5 | const { expect } = chai;
6 |
7 | describe('Graph', () => {
8 | const graph = new Graph();
9 |
10 | it('is a class', () => {
11 | expect(typeof Graph.prototype.constructor).to.equal('function');
12 | });
13 |
14 | describe('.addVertex()', () => {
15 | it('adds vertices to the graph', () => {
16 | graph.addVertex(1);
17 | graph.addVertex(2);
18 | graph.addVertex(3);
19 | graph.addVertex(4);
20 | graph.addVertex(5);
21 | graph.addVertex(6);
22 |
23 | const graphString = '1 -> | 2 -> | 3 -> | 4 -> | 5 -> | 6 ->';
24 |
25 | expect(graph.size()).to.equal(6);
26 | expect(graph.print()).to.equal(graphString);
27 | });
28 | });
29 |
30 | describe('.removeVertex()', () => {
31 | it('removes vertices from the graph', () => {
32 | graph.removeVertex(2);
33 | graph.removeVertex(5);
34 |
35 | const graphString = '1 -> | 3 -> | 4 -> | 6 ->';
36 |
37 | expect(graph.size()).to.equal(4);
38 | expect(graph.print()).to.equal(graphString);
39 | });
40 | });
41 |
42 | describe('.hasVertex()', () => {
43 | it('checks whether the graph has the provided vertex', () => {
44 | expect(graph.hasVertex(6)).to.equal(true);
45 | expect(graph.hasVertex(2)).to.equal(false);
46 | });
47 | });
48 |
49 | describe('.addEdge()', () => {
50 | it('adds edges to the graph', () => {
51 | expect(graph.size()).to.equal(4);
52 |
53 | graph.addVertex(2);
54 | graph.addVertex(5);
55 |
56 | expect(graph.size()).to.equal(6);
57 |
58 | graph.addEdge(1, 2);
59 | graph.addEdge(1, 5);
60 | graph.addEdge(2, 3);
61 | graph.addEdge(2, 5);
62 | graph.addEdge(3, 4);
63 | graph.addEdge(4, 5);
64 | graph.addEdge(4, 6);
65 |
66 | const graphString = '1 -> 2, 5 | 3 -> 2, 4 | 4 -> 3, 5, 6 | 6 -> 4 | 2 -> 1, 3, 5 | 5 -> 1, 2, 4';
67 |
68 | expect(graph.size()).to.equal(6);
69 | expect(graph.print()).to.equal(graphString);
70 | });
71 | });
72 |
73 | describe('.removeEdge()', () => {
74 | it('removes edges from the graph', () => {
75 | graph.removeEdge(1, 2);
76 | graph.removeEdge(4, 5);
77 | graph.removeEdge(10, 11);
78 |
79 | const graphString = '1 -> 5 | 3 -> 2, 4 | 4 -> 3, 6 | 6 -> 4 | 2 -> 3, 5 | 5 -> 1, 2';
80 |
81 | expect(graph.size()).to.equal(6);
82 | expect(graph.print()).to.equal(graphString);
83 | });
84 | });
85 |
86 | describe('.hasEdge()', () => {
87 | it('checks whether the graph has the provided edge', () => {
88 | expect(graph.hasEdge(1, 2)).to.equal(false);
89 | expect(graph.hasEdge(3, 2)).to.equal(true);
90 | });
91 | });
92 |
93 | describe('.size()', () => {
94 | it('returns the size of the graph', () => {
95 | expect(graph.size()).to.equal(6);
96 | });
97 | });
98 |
99 | describe('.relations()', () => {
100 | it('returns the number of edges in the graph', () => {
101 | graph.removeVertex(6);
102 |
103 | expect(graph.relations()).to.equal(4);
104 | });
105 | });
106 |
107 | describe('.traverse()', () => {
108 | it('traverses the graph using the provided algorithm', () => {
109 | // we'll write this tests later
110 | expect(graph.traverse(1, () => null, 'bfs')).to.be.an('undefined');
111 | expect(graph.traverse(1, () => null, 'dfs')).to.be.an('undefined');
112 | });
113 | });
114 |
115 | describe('.print()', () => {
116 | it('prints a representation of the graph', () => {
117 | const graphString = '1 -> 5 | 3 -> 2, 4 | 4 -> 3 | 2 -> 3, 5 | 5 -> 1, 2';
118 |
119 | expect(graph.print()).to.equal(graphString);
120 | });
121 | });
122 |
123 | describe('.clear()', () => {
124 | it('clears the graph', () => {
125 | graph.clear();
126 |
127 | expect(graph.size()).to.equal(0);
128 | expect(graph.print()).to.equal('');
129 | expect(graph.relations()).to.equal(0);
130 | });
131 | });
132 | });
133 |
--------------------------------------------------------------------------------
/__tests__/unit/src/data-structures/queue.spec.js:
--------------------------------------------------------------------------------
1 | import chai from 'chai';
2 | import Queue from 'src/data-structures/queue';
3 |
4 |
5 | const { expect } = chai;
6 |
7 | describe('Queue', () => {
8 | const queue = new Queue(4);
9 |
10 | beforeEach(() => {});
11 |
12 | it('creates a queue successfully', () => {
13 | expect(queue).to.be.an('object');
14 | expect(queue).to.be.an.instanceof(Queue);
15 | });
16 |
17 | it('the queue has a capacity of 4', () => {
18 | expect(queue.capacity()).to.equal(4);
19 | });
20 |
21 | describe('when we enqueue the queue', () => {
22 | it('it enqueues "a" onto the queue', () => {
23 | queue.enqueue('a');
24 | expect(queue.isEmpty()).to.equal(true);
25 | expect(queue.size()).to.equal(1);
26 | });
27 |
28 | it('it enqueues "b" onto the queue', () => {
29 | queue.enqueue('b');
30 | expect(queue.size()).to.equal(2);
31 | });
32 |
33 | it('it enqueues "c" onto the queue', () => {
34 | queue.enqueue('c');
35 | expect(queue.size()).to.equal(3);
36 | });
37 |
38 | it('it enqueues "d" onto the queue', () => {
39 | queue.enqueue('d');
40 | expect(queue.size()).to.equal(4);
41 | });
42 |
43 | it('it has a size of 4', () => {
44 | expect(queue.size()).to.equal(4);
45 | expect(queue.isEmpty()).to.equal(false);
46 | });
47 |
48 | it('it prints all the elements we have just enqueued', () => {
49 | expect(queue.print()).to.equal('a b c d');
50 | });
51 |
52 | it('it has "a" in front of others', () => {
53 | expect(queue.front()).to.equal('a');
54 | });
55 |
56 | it('it has "d" at the back of the queue', () => {
57 | expect(queue.back()).to.equal('d');
58 | });
59 |
60 | it('it does not enqueue "e" onto the queue', () => {
61 | const msg = 'Max capacity reached. Remove element before adding a new one.';
62 | expect(queue.enqueue('e')).to.equal(msg);
63 | });
64 | });
65 |
66 | describe('when we peek, dequeue, enqueue and print elements', () => {
67 | it('it peeks at the queue', () => {
68 | expect(queue.peek()).to.equal('a');
69 | });
70 |
71 | it('it dequeues the queue', () => {
72 | expect(queue.dequeue()).to.equal('a');
73 | });
74 |
75 | it('it prints elements in the queue', () => {
76 | expect(queue.print()).to.equal('b c d');
77 | });
78 |
79 | it('it dequeues the queue again', () => {
80 | expect(queue.dequeue()).to.equal('b');
81 | });
82 |
83 | it('it has a size of 2 now', () => {
84 | expect(queue.size()).to.equal(2);
85 | });
86 |
87 | it('it dequeues the queue again', () => {
88 | expect(queue.dequeue()).to.equal('c');
89 | });
90 |
91 | it('it has a size of 1 now', () => {
92 | expect(queue.size()).to.equal(1);
93 | });
94 |
95 | it('it dequeues the queue again', () => {
96 | expect(queue.dequeue()).to.equal('d');
97 | });
98 |
99 | it('it prints again elements in the queue', () => {
100 | expect(queue.print()).to.equal('');
101 | });
102 |
103 | it('it peeks at the queue again', () => {
104 | expect(queue.peek()).to.equal(undefined);
105 | });
106 |
107 | it('it dequeues the queue again', () => {
108 | const msg = 'No element inside the queue. Add element before dequeuing.';
109 | expect(queue.dequeue()).to.equal(msg);
110 | });
111 | });
112 |
113 | describe('when we search for an element', () => {
114 | it('it enqueues "f" onto the queue', () => {
115 | queue.enqueue('f');
116 | expect(queue.size()).to.equal(1);
117 | });
118 |
119 | it('it does not contain "a"', () => {
120 | expect(queue.contains('a')).to.equal(false);
121 | });
122 |
123 | it('it does not contain "c"', () => {
124 | expect(queue.contains('c')).to.equal(false);
125 | });
126 |
127 | it('it contains "f"', () => {
128 | expect(queue.contains('f')).to.equal(true);
129 | });
130 |
131 | it('it now does not contain "f"', () => {
132 | queue.clear();
133 | expect(queue.contains('f')).to.equal(false);
134 | });
135 | });
136 | });
137 |
--------------------------------------------------------------------------------
/__tests__/unit/src/data-structures/priority-queue.spec.js:
--------------------------------------------------------------------------------
1 | import chai from 'chai';
2 | import PriorityQueue from 'src/data-structures/priority-queue';
3 |
4 |
5 | const { expect } = chai;
6 |
7 | describe('PriorityQueue', () => {
8 | const queue = new PriorityQueue(4);
9 |
10 | beforeEach(() => {});
11 |
12 | it('creates a queue successfully', () => {
13 | expect(queue).to.be.an('object');
14 | expect(queue).to.be.an.instanceof(PriorityQueue);
15 | });
16 |
17 | it('the queue has a capacity of 4', () => {
18 | expect(queue.capacity()).to.equal(4);
19 | });
20 |
21 | describe('when we enqueue the queue', () => {
22 | it('it enqueues "a" onto the queue', () => {
23 | queue.enqueue('a', 2);
24 | expect(queue.isEmpty()).to.equal(true);
25 | expect(queue.size()).to.equal(1);
26 | });
27 |
28 | it('it enqueues "b" onto the queue', () => {
29 | queue.enqueue('b', 1);
30 | expect(queue.size()).to.equal(2);
31 | });
32 |
33 | it('it enqueues "c" onto the queue', () => {
34 | queue.enqueue('c', 1);
35 | expect(queue.size()).to.equal(3);
36 | });
37 |
38 | it('it enqueues "d" onto the queue', () => {
39 | queue.enqueue('d', 5);
40 | expect(queue.size()).to.equal(4);
41 | });
42 |
43 | it('it has a size of 4', () => {
44 | expect(queue.size()).to.equal(4);
45 | expect(queue.isEmpty()).to.equal(false);
46 | });
47 |
48 | it('it prints all the elements we have just enqueued', () => {
49 | expect(queue.print()).to.equal('b c a d');
50 | });
51 |
52 | it('it has "b" in front of others', () => {
53 | expect(queue.front()).to.equal('b');
54 | });
55 |
56 | it('it has "d" at the back of the queue', () => {
57 | expect(queue.back()).to.equal('d');
58 | });
59 |
60 | it('it does not enqueue "e" onto the queue', () => {
61 | const msg = 'Max capacity reached. Remove element before adding a new one.';
62 | expect(queue.enqueue('e', 3)).to.equal(msg);
63 | });
64 | });
65 |
66 | describe('when we peek, dequeue, enqueue and print elements', () => {
67 | it('it peeks at the queue', () => {
68 | expect(queue.peek()).to.equal('b');
69 | });
70 |
71 | it('it dequeues the queue', () => {
72 | expect(queue.dequeue()).to.equal('b');
73 | });
74 |
75 | it('it prints elements in the queue', () => {
76 | expect(queue.print()).to.equal('c a d');
77 | });
78 |
79 | it('it dequeues the queue again', () => {
80 | expect(queue.dequeue()).to.equal('c');
81 | });
82 |
83 | it('it has a size of 2 now', () => {
84 | expect(queue.size()).to.equal(2);
85 | });
86 |
87 | it('it dequeues the queue again', () => {
88 | expect(queue.dequeue()).to.equal('a');
89 | });
90 |
91 | it('it has a size of 1 now', () => {
92 | expect(queue.size()).to.equal(1);
93 | });
94 |
95 | it('it dequeues the queue again', () => {
96 | expect(queue.dequeue()).to.equal('d');
97 | });
98 |
99 | it('it prints again elements in the queue', () => {
100 | expect(queue.print()).to.equal('');
101 | });
102 |
103 | it('it peeks at the queue again', () => {
104 | expect(queue.peek()).to.equal(undefined);
105 | });
106 |
107 | it('it dequeues the queue again', () => {
108 | const msg = 'No element inside the queue. Add element before dequeuing.';
109 | expect(queue.dequeue()).to.equal(msg);
110 | });
111 | });
112 |
113 | describe('when we search for an element', () => {
114 | it('it enqueues "f" onto the queue', () => {
115 | queue.enqueue('f');
116 | expect(queue.size()).to.equal(1);
117 | });
118 |
119 | it('it does not contain "a"', () => {
120 | expect(queue.contains('a')).to.equal(false);
121 | });
122 |
123 | it('it does not contain "c"', () => {
124 | expect(queue.contains('c')).to.equal(false);
125 | });
126 |
127 | it('it contains "f"', () => {
128 | expect(queue.contains('f')).to.equal(true);
129 | });
130 |
131 | it('it now does not contain "f"', () => {
132 | queue.clear();
133 | expect(queue.contains('f')).to.equal(false);
134 | });
135 | });
136 | });
137 |
--------------------------------------------------------------------------------