├── .gitignore
├── LICENSE
├── README.md
├── interface.c
├── interface.h
├── main.c
├── makefile
├── solver.c
└── solver.h
/.gitignore:
--------------------------------------------------------------------------------
1 | .vscode/
2 | main
3 | *.o
4 | .DS_Store
--------------------------------------------------------------------------------
/LICENSE:
--------------------------------------------------------------------------------
1 | MIT License
2 |
3 | Copyright (c) 2024 begilbert-sys
4 |
5 | Permission is hereby granted, free of charge, to any person obtaining a copy
6 | of this software and associated documentation files (the "Software"), to deal
7 | in the Software without restriction, including without limitation the rights
8 | to use, copy, modify, merge, publish, distribute, sublicense, and/or sell
9 | copies of the Software, and to permit persons to whom the Software is
10 | furnished to do so, subject to the following conditions:
11 |
12 | The above copyright notice and this permission notice shall be included in all
13 | copies or substantial portions of the Software.
14 |
15 | THE SOFTWARE IS PROVIDED "AS IS", WITHOUT WARRANTY OF ANY KIND, EXPRESS OR
16 | IMPLIED, INCLUDING BUT NOT LIMITED TO THE WARRANTIES OF MERCHANTABILITY,
17 | FITNESS FOR A PARTICULAR PURPOSE AND NONINFRINGEMENT. IN NO EVENT SHALL THE
18 | AUTHORS OR COPYRIGHT HOLDERS BE LIABLE FOR ANY CLAIM, DAMAGES OR OTHER
19 | LIABILITY, WHETHER IN AN ACTION OF CONTRACT, TORT OR OTHERWISE, ARISING FROM,
20 | OUT OF OR IN CONNECTION WITH THE SOFTWARE OR THE USE OR OTHER DEALINGS IN THE
21 | SOFTWARE.
22 |
--------------------------------------------------------------------------------
/README.md:
--------------------------------------------------------------------------------
1 | # Sudoku Solver
2 | Written entirely in C. Most boards are solved in milliseconds, the most difficult boards can be solved in under 2 seconds.
3 |
4 |  5 |
6 | ## How to Run
7 | Put all the files in the same directory and run the following commands in that directory:
8 | ```
9 | make
10 | ./main
11 | ```
12 | For cleanup you can run `make clean`.
13 | ## Algorithm Explanation
14 |
15 | This algorithm uses backtracking (brute-force) combined with bit masking. All of the relevant code can be found in `solver.c`.
16 | ### Bit Masking
17 |
18 | As far as sudoku solvers go, this algorithm is not too crazy. But it does require that you know what bitmasking is, and how binary numbers and bitwise operators work.
19 |
20 | Start off by initializing three `int` arrays of length 9: `rows`, `cols`, and `squares`. Each `int` element in these arrays will represent the filled numbers in an entire row, column or square.
21 |
22 | Let's examine our `squares` array. Each `int` in the array can be represented as 9 bits, and each bit represents a number in that square.
23 | ```
24 | Number: 9 8 7 6 5 4 3 2 1
25 | Bit Digit: 0 0 0 0 0 0 0 0 0
26 | ```
27 | A value of `000000000` would mean that the square is completely empty, and a value of `111111111` (512) would mean that the square has been filled. To elaborate, let's say we have the following square, which is the **center-left** square on a board. Squares are numbered from left-to-right, top-to-bottom. So this square would be index 3 in the `squares` array.
28 | ```
29 | 5 3 •
30 |
31 | 6 • •
32 |
33 | • 9 8
34 | ```
35 | Representing the square as bits would look like this:
36 | ```
37 | Number: 9 8 7 6 5 4 3 2 1
38 | Bit Value: 1 1 0 1 1 0 1 0 0
39 | ```
40 | Thus, index 3 in the `squares` array is `110110100` (or 436). The `0`s in this bit represent the remaining candidates for this square.
41 |
42 | To add a number to our board, we can pick a tile, and use the three arrays to triangulate the candidates for that specific tile. Let's fill one of the blank tiles in our square (denoted by `?`)
43 | ```
44 | 5 3 ?
45 |
46 | 6 • •
47 |
48 | • 9 8
49 | ```
50 |
51 |
52 | The tile selected is in the 4th row, 3rd column and 4th square. In our 0-indexed arrays this corresponds to `rows[3]`, `cols[2]`, and `squares[3]`. We already know the value of `squares[3]`. So let's make up some integer values for `rows[3]` and `cols[2]`:
53 | ```
54 | int binary numbers filled
55 | rows[3] -> 151 010010111 1, 2, 3, 5, 8
56 | cols[2] -> 297 100101001 1, 4, 6, 9
57 | squares[3] -> 436 110110100 3, 5, 6, 8, 9
58 | ```
59 | There's only one remaining candidate for this tile: **7**. The computer can figure this out by bitwise `OR`-ing all three integers together:
60 |
61 | ```
62 | rows[3] | cols[2] | squares[3] -> 110111111 (447)
63 | ```
64 | The binary result reveals that 7 is the only available slot. So let's fill our tile with a 7. All we have to do is update the board, and then update the three integers in our arrays by setting the 7th bit in each one to a `1`.
65 |
66 | ```
67 | rows[3] |= (i << 7)
68 | cols[2] |= (i << 7)
69 | squares[3] |= (i << 7)
70 | ```
71 | There we go! Although this is kind of a pain to do manually, it's efficient for the computer.
72 |
73 | Now imagine we find that our **7** was misplaced. To reset those bits back to zero, we do the following:
74 | ```
75 | rows[4] &= ~(i << 7)
76 | cols[2] &= ~(i << 7)
77 | squares[3] &= ~(i << 7)
78 | ```
79 |
80 | Now we have to do this for every empty tile on the board.
81 |
82 |
83 | ### Backtracking
84 | This is the simpler part. The algorithm uses brute force.
85 |
86 | We start by making one pass through the entire board to update our `rows`, `cols`, and `squares` arrays with the values that are already present.
87 |
88 | After that, we can recursively iterate through the board tile-by-tile. Each call to the `solveRecur` function examines exactly one tile. Tiles that already contain numbers are skipped. Tiles that are empty can use our three arrays to deduce the candidates. For each candidate, we set the tile to that candidate and make a recursive call to the next tile.
89 |
90 | If a tile has no valid candidates, we know that we've screwed up somewhere, and the function returns `false`. This backtracks to the previous tile and allows it to try a different candidate. If the previous tile runs out of candidates, then it can backtrack one tile further, and so on.
91 |
92 | Here's a great visual representation of what's happening:
93 |
94 |
5 |
6 | ## How to Run
7 | Put all the files in the same directory and run the following commands in that directory:
8 | ```
9 | make
10 | ./main
11 | ```
12 | For cleanup you can run `make clean`.
13 | ## Algorithm Explanation
14 |
15 | This algorithm uses backtracking (brute-force) combined with bit masking. All of the relevant code can be found in `solver.c`.
16 | ### Bit Masking
17 |
18 | As far as sudoku solvers go, this algorithm is not too crazy. But it does require that you know what bitmasking is, and how binary numbers and bitwise operators work.
19 |
20 | Start off by initializing three `int` arrays of length 9: `rows`, `cols`, and `squares`. Each `int` element in these arrays will represent the filled numbers in an entire row, column or square.
21 |
22 | Let's examine our `squares` array. Each `int` in the array can be represented as 9 bits, and each bit represents a number in that square.
23 | ```
24 | Number: 9 8 7 6 5 4 3 2 1
25 | Bit Digit: 0 0 0 0 0 0 0 0 0
26 | ```
27 | A value of `000000000` would mean that the square is completely empty, and a value of `111111111` (512) would mean that the square has been filled. To elaborate, let's say we have the following square, which is the **center-left** square on a board. Squares are numbered from left-to-right, top-to-bottom. So this square would be index 3 in the `squares` array.
28 | ```
29 | 5 3 •
30 |
31 | 6 • •
32 |
33 | • 9 8
34 | ```
35 | Representing the square as bits would look like this:
36 | ```
37 | Number: 9 8 7 6 5 4 3 2 1
38 | Bit Value: 1 1 0 1 1 0 1 0 0
39 | ```
40 | Thus, index 3 in the `squares` array is `110110100` (or 436). The `0`s in this bit represent the remaining candidates for this square.
41 |
42 | To add a number to our board, we can pick a tile, and use the three arrays to triangulate the candidates for that specific tile. Let's fill one of the blank tiles in our square (denoted by `?`)
43 | ```
44 | 5 3 ?
45 |
46 | 6 • •
47 |
48 | • 9 8
49 | ```
50 |
51 |
52 | The tile selected is in the 4th row, 3rd column and 4th square. In our 0-indexed arrays this corresponds to `rows[3]`, `cols[2]`, and `squares[3]`. We already know the value of `squares[3]`. So let's make up some integer values for `rows[3]` and `cols[2]`:
53 | ```
54 | int binary numbers filled
55 | rows[3] -> 151 010010111 1, 2, 3, 5, 8
56 | cols[2] -> 297 100101001 1, 4, 6, 9
57 | squares[3] -> 436 110110100 3, 5, 6, 8, 9
58 | ```
59 | There's only one remaining candidate for this tile: **7**. The computer can figure this out by bitwise `OR`-ing all three integers together:
60 |
61 | ```
62 | rows[3] | cols[2] | squares[3] -> 110111111 (447)
63 | ```
64 | The binary result reveals that 7 is the only available slot. So let's fill our tile with a 7. All we have to do is update the board, and then update the three integers in our arrays by setting the 7th bit in each one to a `1`.
65 |
66 | ```
67 | rows[3] |= (i << 7)
68 | cols[2] |= (i << 7)
69 | squares[3] |= (i << 7)
70 | ```
71 | There we go! Although this is kind of a pain to do manually, it's efficient for the computer.
72 |
73 | Now imagine we find that our **7** was misplaced. To reset those bits back to zero, we do the following:
74 | ```
75 | rows[4] &= ~(i << 7)
76 | cols[2] &= ~(i << 7)
77 | squares[3] &= ~(i << 7)
78 | ```
79 |
80 | Now we have to do this for every empty tile on the board.
81 |
82 |
83 | ### Backtracking
84 | This is the simpler part. The algorithm uses brute force.
85 |
86 | We start by making one pass through the entire board to update our `rows`, `cols`, and `squares` arrays with the values that are already present.
87 |
88 | After that, we can recursively iterate through the board tile-by-tile. Each call to the `solveRecur` function examines exactly one tile. Tiles that already contain numbers are skipped. Tiles that are empty can use our three arrays to deduce the candidates. For each candidate, we set the tile to that candidate and make a recursive call to the next tile.
89 |
90 | If a tile has no valid candidates, we know that we've screwed up somewhere, and the function returns `false`. This backtracks to the previous tile and allows it to try a different candidate. If the previous tile runs out of candidates, then it can backtrack one tile further, and so on.
91 |
92 | Here's a great visual representation of what's happening:
93 |
94 | 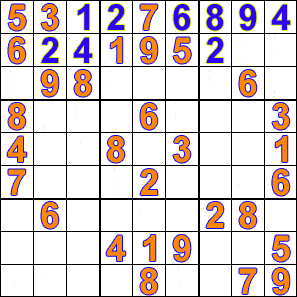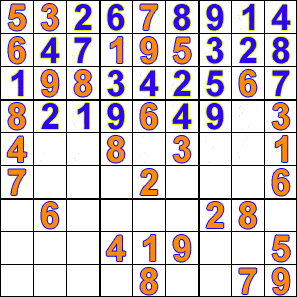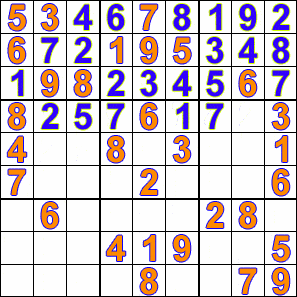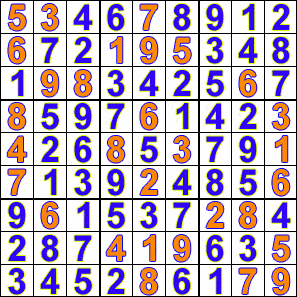 95 |
96 |
97 | If our function manages to make it past the last tile on the board, then we know the board is solved, because there would be no way to reach the end without every tile being valid. The function returns a `true` which propogates upward until all recursive function calls are off the stack.
--------------------------------------------------------------------------------
/interface.c:
--------------------------------------------------------------------------------
1 | #include "interface.h"
2 |
3 | #define BLANK_TILE ACS_BULLET
4 |
5 | void printRow(int leftPiece, int betweenPiece, int dividingPiece, int rightPiece) {
6 | /*
7 | draw one row of the board
8 | the args represent the symbols used to draw the row
9 | */
10 | addch(leftPiece);
11 | for (int i = 0; i < 23; i++) {
12 | if (i == 7 || i == 15) {
13 | addch(dividingPiece);
14 | } else {
15 | addch(betweenPiece);
16 | }
17 | }
18 | addch(rightPiece);
19 | }
20 |
21 | void printBoard(char board[9][9]) {
22 | /*
23 | print the sudoku board
24 | the ACS variables are just constants representing the symbols used to draw
25 | */
26 | refresh();
27 | move(0, 0);
28 | // top row
29 | printRow(ACS_ULCORNER, ACS_HLINE, ACS_TTEE, ACS_URCORNER);
30 | int row = 0;
31 | for (int y = 1; y < 12; y++) {
32 | move(y, 0);
33 | if (y == 4 || y == 8) {
34 | // dividing row
35 | printRow(ACS_LTEE, ACS_HLINE, ACS_PLUS, ACS_RTEE);
36 | } else {
37 | // row with numbers
38 | printRow(ACS_VLINE, ' ', ACS_VLINE, ACS_VLINE);
39 | int col = 0;
40 | for (int x = 2; x < 24; x += 2) {
41 | if (x % 8 != 0) { // skip the dividing columns
42 | move(y, x);
43 | if (board[row][col] == '.') {
44 | addch(BLANK_TILE);
45 | } else {
46 | addch(board[row][col]);
47 | }
48 | col++;
49 | }
50 | }
51 | row++;
52 | }
53 | }
54 | // bottom row
55 | move(12, 0);
56 | printRow(ACS_LLCORNER, ACS_HLINE, ACS_BTEE, ACS_LRCORNER);
57 | }
58 |
59 | void inputBoard(char board[9][9]) {
60 | /*
61 | initialize ncurses, and wait for the user to enter their sudoku board
62 | */
63 | initscr();
64 | keypad(stdscr, TRUE);
65 | printBoard(board);
66 | int cursorY = 1;
67 | int cursorX = 2;
68 | int row = 0;
69 | int col = 0;
70 | bool done = false;
71 | while (!done) {
72 | move(0, 0);
73 | move(cursorY, cursorX);
74 | int ch = getch();
75 | switch (ch) {
76 | case KEY_DOWN:
77 | if (cursorY < 11) {
78 | // skip over dividng rows
79 | (cursorY + 1) % 4 == 0 ? (cursorY += 2) : (cursorY++);
80 | row++;
81 | }
82 | break;
83 | case KEY_UP:
84 | if (cursorY > 1) {
85 | (cursorY - 1) % 4 == 0 ? (cursorY -= 2) : (cursorY--);
86 | row--;
87 | }
88 | break;
89 | case KEY_RIGHT:
90 | if (cursorX < 22) {
91 | (cursorX + 2) % 8 == 0 ? (cursorX += 4) : (cursorX += 2);
92 | col++;
93 | }
94 | break;
95 | case KEY_LEFT:
96 | if (cursorX > 2) {
97 | (cursorX - 2) % 8 == 0 ? (cursorX -= 4) : (cursorX -= 2);
98 | col--;
99 | }
100 | break;
101 |
102 | case KEY_BACKSPACE:
103 | case KEY_DC:
104 | case 127: // 127 is the backspace key on my computer
105 | board[row][col] = '.';
106 | printBoard(board);
107 | break;
108 |
109 | case KEY_ENTER:
110 | case 10: // 10 is the enter key on my computer
111 | done = true;
112 | break;
113 |
114 | default:
115 | if ('0' < ch && ch <= '9') {
116 | board[row][col] = ch;
117 | printBoard(board);
118 | }
119 | printBoard(board);
120 | break;
121 | }
122 | }
123 | }
124 |
125 | void waitForExit() {
126 | /*
127 | wait for the user to press "enter"
128 | */
129 | move(13, 0);
130 | printw("Press [ENTER] key to exit");
131 | bool done = false;
132 | while (!done) {
133 | int ch = getch();
134 | switch (ch) {
135 | case KEY_ENTER:
136 | case 10:
137 | done = true;
138 | }
139 | }
140 | }
--------------------------------------------------------------------------------
/interface.h:
--------------------------------------------------------------------------------
1 | #ifndef INTERFACE_H
2 | #define INTERFACE_H
3 | #include
4 | #include
5 | void printBoard(char board[9][9]);
6 | void inputBoard(char board[9][9]);
7 | void waitForExit();
8 | #endif
--------------------------------------------------------------------------------
/main.c:
--------------------------------------------------------------------------------
1 | #include "interface.h"
2 | #include "solver.h"
3 |
4 | void initBlankBoard(char board[9][9]) {
5 | /* set every tile in the board to "blank" */
6 | for (int row = 0; row < 9; row++) {
7 | for (int col = 0; col < 9; col++) {
8 | board[row][col] = '.';
9 | }
10 | }
11 | }
12 | int main() {
13 | char board[9][9];
14 | initBlankBoard(board);
15 | inputBoard(board);
16 |
17 | if (solve(board)) {
18 | printBoard(board);
19 | waitForExit();
20 | } else {
21 | printf("ERROR: This board is not solvable!");
22 | }
23 | return 1;
24 | }
--------------------------------------------------------------------------------
/makefile:
--------------------------------------------------------------------------------
1 | CC = gcc
2 | DEPS = solver.h interface.h
3 | OBJ = main.o solver.o interface.o
4 | %.o: %.c $(DEPS)
5 | $(CC) -c -o $@ $<
6 | main: $(OBJ)
7 | $(CC) -lcurses -o $@ $^
8 | clean:
9 | rm -f *.o
10 | rm -f main
--------------------------------------------------------------------------------
/solver.c:
--------------------------------------------------------------------------------
1 | #include "solver.h"
2 | #include
3 |
4 | int tileValue(char board[9][9], int row, int col) {
5 | /* get the integer value of a tile
6 | return -1 if the tile is empty */
7 | if (board[row][col] == '.') {
8 | return -1;
9 | } else {
10 | return board[row][col] - '1';
11 | }
12 | }
13 |
14 | char intToChar(int value) {
15 | /* convert an integer into a sudoku number (0 -> '1', 1 -> '2', etc.)*/
16 | return '1' + value;
17 | }
18 |
19 | int getSquare(int row, int col) {
20 | /* calculate a tile's sqaure based on its row and column */
21 | return ((row / 3) * 3) + (col / 3);
22 | }
23 |
24 | bool prepare(char board[9][9], int rows[9], int cols[9], int squares[9]) {
25 | /* prepopulate the rows, cols, and squares arrays with every value that's
26 | already on the board
27 | return false if the board is invalid */
28 | for (int row = 0; row < 9; row++) {
29 | for (int col = 0; col < 9; col++) {
30 | int square = getSquare(row, col);
31 | int intValue = tileValue(board, row, col);
32 | int candidateBits = rows[row] | cols[col] | squares[square];
33 | if (intValue != -1 &&(candidateBits >> intValue & 1) == 1) {
34 | return false;
35 | }
36 | if (intValue != -1) {
37 | rows[row] |= (1 << intValue);
38 | cols[col] |= (1 << intValue);
39 | squares[square] |= (1 << intValue);
40 | }
41 | }
42 | }
43 | return true;
44 | }
45 |
46 | bool solveRecur(char board[9][9], int rows[9], int cols[9], int squares[9], int row, int col) {
47 | /* recursively solve the entire board */
48 | if (row == 9) {
49 | return true;
50 | }
51 | int nextrow = (col == 8 ? row + 1 : row);
52 | int nextcol = (col == 8 ? 0 : col + 1);
53 |
54 | int square = getSquare(row, col);
55 |
56 | int intValue = tileValue(board, row, col);
57 |
58 | if (intValue != -1) { // skip tiles that already have numbers
59 | return solveRecur(board, rows, cols, squares, nextrow, nextcol);
60 | }
61 | // get the possible values for the tile's row, column and square
62 | int rowBits = rows[row];
63 | int colBits = cols[col];
64 |
65 | int squareBits = squares[square];
66 |
67 | // OR them all together to get the final candidates
68 | int candidateBits = rowBits | colBits | squareBits;
69 |
70 | for (int i = 0; i < 9; i++) {
71 | // iterate through each bit and only attempt the 0 bits
72 | if ((candidateBits >> i & 1) == 0) {
73 | // set the bit to 1
74 | rows[row] |= (1 << i);
75 | cols[col] |= (1 << i);
76 | squares[square] |= (1 << i);
77 | board[row][col] = intToChar(i);
78 | if (solveRecur(board, rows, cols, squares, nextrow, nextcol)) {
79 | return true;
80 | }
81 | // if the bit didn't work out, reset it to 0
82 | rows[row] &= ~(1 << i);
83 | cols[col] &= ~(1 << i);
84 | squares[square] &= ~(1 << i);
85 | }
86 | }
87 |
88 | board[row][col] = '.';
89 | return false;
90 | }
91 |
92 | bool solve(char board[9][9]) {
93 | /* set up the recursion function and run it
94 | return false if the board is unsolvable */
95 | int rows[9] = {0};
96 | int cols[9] = {0};
97 | int squares[9] = {0};
98 | if (!prepare(board, rows, cols, squares)) {
99 | return false;
100 | }
101 | return solveRecur(board, rows, cols, squares, 0, 0);
102 | }
103 |
--------------------------------------------------------------------------------
/solver.h:
--------------------------------------------------------------------------------
1 | #ifndef SOLVER_H
2 | #define SOLVER_H
3 | #include
4 | bool solve(char board[9][9]);
5 | #endif
--------------------------------------------------------------------------------
95 |
96 |
97 | If our function manages to make it past the last tile on the board, then we know the board is solved, because there would be no way to reach the end without every tile being valid. The function returns a `true` which propogates upward until all recursive function calls are off the stack.
--------------------------------------------------------------------------------
/interface.c:
--------------------------------------------------------------------------------
1 | #include "interface.h"
2 |
3 | #define BLANK_TILE ACS_BULLET
4 |
5 | void printRow(int leftPiece, int betweenPiece, int dividingPiece, int rightPiece) {
6 | /*
7 | draw one row of the board
8 | the args represent the symbols used to draw the row
9 | */
10 | addch(leftPiece);
11 | for (int i = 0; i < 23; i++) {
12 | if (i == 7 || i == 15) {
13 | addch(dividingPiece);
14 | } else {
15 | addch(betweenPiece);
16 | }
17 | }
18 | addch(rightPiece);
19 | }
20 |
21 | void printBoard(char board[9][9]) {
22 | /*
23 | print the sudoku board
24 | the ACS variables are just constants representing the symbols used to draw
25 | */
26 | refresh();
27 | move(0, 0);
28 | // top row
29 | printRow(ACS_ULCORNER, ACS_HLINE, ACS_TTEE, ACS_URCORNER);
30 | int row = 0;
31 | for (int y = 1; y < 12; y++) {
32 | move(y, 0);
33 | if (y == 4 || y == 8) {
34 | // dividing row
35 | printRow(ACS_LTEE, ACS_HLINE, ACS_PLUS, ACS_RTEE);
36 | } else {
37 | // row with numbers
38 | printRow(ACS_VLINE, ' ', ACS_VLINE, ACS_VLINE);
39 | int col = 0;
40 | for (int x = 2; x < 24; x += 2) {
41 | if (x % 8 != 0) { // skip the dividing columns
42 | move(y, x);
43 | if (board[row][col] == '.') {
44 | addch(BLANK_TILE);
45 | } else {
46 | addch(board[row][col]);
47 | }
48 | col++;
49 | }
50 | }
51 | row++;
52 | }
53 | }
54 | // bottom row
55 | move(12, 0);
56 | printRow(ACS_LLCORNER, ACS_HLINE, ACS_BTEE, ACS_LRCORNER);
57 | }
58 |
59 | void inputBoard(char board[9][9]) {
60 | /*
61 | initialize ncurses, and wait for the user to enter their sudoku board
62 | */
63 | initscr();
64 | keypad(stdscr, TRUE);
65 | printBoard(board);
66 | int cursorY = 1;
67 | int cursorX = 2;
68 | int row = 0;
69 | int col = 0;
70 | bool done = false;
71 | while (!done) {
72 | move(0, 0);
73 | move(cursorY, cursorX);
74 | int ch = getch();
75 | switch (ch) {
76 | case KEY_DOWN:
77 | if (cursorY < 11) {
78 | // skip over dividng rows
79 | (cursorY + 1) % 4 == 0 ? (cursorY += 2) : (cursorY++);
80 | row++;
81 | }
82 | break;
83 | case KEY_UP:
84 | if (cursorY > 1) {
85 | (cursorY - 1) % 4 == 0 ? (cursorY -= 2) : (cursorY--);
86 | row--;
87 | }
88 | break;
89 | case KEY_RIGHT:
90 | if (cursorX < 22) {
91 | (cursorX + 2) % 8 == 0 ? (cursorX += 4) : (cursorX += 2);
92 | col++;
93 | }
94 | break;
95 | case KEY_LEFT:
96 | if (cursorX > 2) {
97 | (cursorX - 2) % 8 == 0 ? (cursorX -= 4) : (cursorX -= 2);
98 | col--;
99 | }
100 | break;
101 |
102 | case KEY_BACKSPACE:
103 | case KEY_DC:
104 | case 127: // 127 is the backspace key on my computer
105 | board[row][col] = '.';
106 | printBoard(board);
107 | break;
108 |
109 | case KEY_ENTER:
110 | case 10: // 10 is the enter key on my computer
111 | done = true;
112 | break;
113 |
114 | default:
115 | if ('0' < ch && ch <= '9') {
116 | board[row][col] = ch;
117 | printBoard(board);
118 | }
119 | printBoard(board);
120 | break;
121 | }
122 | }
123 | }
124 |
125 | void waitForExit() {
126 | /*
127 | wait for the user to press "enter"
128 | */
129 | move(13, 0);
130 | printw("Press [ENTER] key to exit");
131 | bool done = false;
132 | while (!done) {
133 | int ch = getch();
134 | switch (ch) {
135 | case KEY_ENTER:
136 | case 10:
137 | done = true;
138 | }
139 | }
140 | }
--------------------------------------------------------------------------------
/interface.h:
--------------------------------------------------------------------------------
1 | #ifndef INTERFACE_H
2 | #define INTERFACE_H
3 | #include
4 | #include
5 | void printBoard(char board[9][9]);
6 | void inputBoard(char board[9][9]);
7 | void waitForExit();
8 | #endif
--------------------------------------------------------------------------------
/main.c:
--------------------------------------------------------------------------------
1 | #include "interface.h"
2 | #include "solver.h"
3 |
4 | void initBlankBoard(char board[9][9]) {
5 | /* set every tile in the board to "blank" */
6 | for (int row = 0; row < 9; row++) {
7 | for (int col = 0; col < 9; col++) {
8 | board[row][col] = '.';
9 | }
10 | }
11 | }
12 | int main() {
13 | char board[9][9];
14 | initBlankBoard(board);
15 | inputBoard(board);
16 |
17 | if (solve(board)) {
18 | printBoard(board);
19 | waitForExit();
20 | } else {
21 | printf("ERROR: This board is not solvable!");
22 | }
23 | return 1;
24 | }
--------------------------------------------------------------------------------
/makefile:
--------------------------------------------------------------------------------
1 | CC = gcc
2 | DEPS = solver.h interface.h
3 | OBJ = main.o solver.o interface.o
4 | %.o: %.c $(DEPS)
5 | $(CC) -c -o $@ $<
6 | main: $(OBJ)
7 | $(CC) -lcurses -o $@ $^
8 | clean:
9 | rm -f *.o
10 | rm -f main
--------------------------------------------------------------------------------
/solver.c:
--------------------------------------------------------------------------------
1 | #include "solver.h"
2 | #include
3 |
4 | int tileValue(char board[9][9], int row, int col) {
5 | /* get the integer value of a tile
6 | return -1 if the tile is empty */
7 | if (board[row][col] == '.') {
8 | return -1;
9 | } else {
10 | return board[row][col] - '1';
11 | }
12 | }
13 |
14 | char intToChar(int value) {
15 | /* convert an integer into a sudoku number (0 -> '1', 1 -> '2', etc.)*/
16 | return '1' + value;
17 | }
18 |
19 | int getSquare(int row, int col) {
20 | /* calculate a tile's sqaure based on its row and column */
21 | return ((row / 3) * 3) + (col / 3);
22 | }
23 |
24 | bool prepare(char board[9][9], int rows[9], int cols[9], int squares[9]) {
25 | /* prepopulate the rows, cols, and squares arrays with every value that's
26 | already on the board
27 | return false if the board is invalid */
28 | for (int row = 0; row < 9; row++) {
29 | for (int col = 0; col < 9; col++) {
30 | int square = getSquare(row, col);
31 | int intValue = tileValue(board, row, col);
32 | int candidateBits = rows[row] | cols[col] | squares[square];
33 | if (intValue != -1 &&(candidateBits >> intValue & 1) == 1) {
34 | return false;
35 | }
36 | if (intValue != -1) {
37 | rows[row] |= (1 << intValue);
38 | cols[col] |= (1 << intValue);
39 | squares[square] |= (1 << intValue);
40 | }
41 | }
42 | }
43 | return true;
44 | }
45 |
46 | bool solveRecur(char board[9][9], int rows[9], int cols[9], int squares[9], int row, int col) {
47 | /* recursively solve the entire board */
48 | if (row == 9) {
49 | return true;
50 | }
51 | int nextrow = (col == 8 ? row + 1 : row);
52 | int nextcol = (col == 8 ? 0 : col + 1);
53 |
54 | int square = getSquare(row, col);
55 |
56 | int intValue = tileValue(board, row, col);
57 |
58 | if (intValue != -1) { // skip tiles that already have numbers
59 | return solveRecur(board, rows, cols, squares, nextrow, nextcol);
60 | }
61 | // get the possible values for the tile's row, column and square
62 | int rowBits = rows[row];
63 | int colBits = cols[col];
64 |
65 | int squareBits = squares[square];
66 |
67 | // OR them all together to get the final candidates
68 | int candidateBits = rowBits | colBits | squareBits;
69 |
70 | for (int i = 0; i < 9; i++) {
71 | // iterate through each bit and only attempt the 0 bits
72 | if ((candidateBits >> i & 1) == 0) {
73 | // set the bit to 1
74 | rows[row] |= (1 << i);
75 | cols[col] |= (1 << i);
76 | squares[square] |= (1 << i);
77 | board[row][col] = intToChar(i);
78 | if (solveRecur(board, rows, cols, squares, nextrow, nextcol)) {
79 | return true;
80 | }
81 | // if the bit didn't work out, reset it to 0
82 | rows[row] &= ~(1 << i);
83 | cols[col] &= ~(1 << i);
84 | squares[square] &= ~(1 << i);
85 | }
86 | }
87 |
88 | board[row][col] = '.';
89 | return false;
90 | }
91 |
92 | bool solve(char board[9][9]) {
93 | /* set up the recursion function and run it
94 | return false if the board is unsolvable */
95 | int rows[9] = {0};
96 | int cols[9] = {0};
97 | int squares[9] = {0};
98 | if (!prepare(board, rows, cols, squares)) {
99 | return false;
100 | }
101 | return solveRecur(board, rows, cols, squares, 0, 0);
102 | }
103 |
--------------------------------------------------------------------------------
/solver.h:
--------------------------------------------------------------------------------
1 | #ifndef SOLVER_H
2 | #define SOLVER_H
3 | #include
4 | bool solve(char board[9][9]);
5 | #endif
--------------------------------------------------------------------------------
 5 |
6 | ## How to Run
7 | Put all the files in the same directory and run the following commands in that directory:
8 | ```
9 | make
10 | ./main
11 | ```
12 | For cleanup you can run `make clean`.
13 | ## Algorithm Explanation
14 |
15 | This algorithm uses backtracking (brute-force) combined with bit masking. All of the relevant code can be found in `solver.c`.
16 | ### Bit Masking
17 |
18 | As far as sudoku solvers go, this algorithm is not too crazy. But it does require that you know what bitmasking is, and how binary numbers and bitwise operators work.
19 |
20 | Start off by initializing three `int` arrays of length 9: `rows`, `cols`, and `squares`. Each `int` element in these arrays will represent the filled numbers in an entire row, column or square.
21 |
22 | Let's examine our `squares` array. Each `int` in the array can be represented as 9 bits, and each bit represents a number in that square.
23 | ```
24 | Number: 9 8 7 6 5 4 3 2 1
25 | Bit Digit: 0 0 0 0 0 0 0 0 0
26 | ```
27 | A value of `000000000` would mean that the square is completely empty, and a value of `111111111` (512) would mean that the square has been filled. To elaborate, let's say we have the following square, which is the **center-left** square on a board. Squares are numbered from left-to-right, top-to-bottom. So this square would be index 3 in the `squares` array.
28 | ```
29 | 5 3 •
30 |
31 | 6 • •
32 |
33 | • 9 8
34 | ```
35 | Representing the square as bits would look like this:
36 | ```
37 | Number: 9 8 7 6 5 4 3 2 1
38 | Bit Value: 1 1 0 1 1 0 1 0 0
39 | ```
40 | Thus, index 3 in the `squares` array is `110110100` (or 436). The `0`s in this bit represent the remaining candidates for this square.
41 |
42 | To add a number to our board, we can pick a tile, and use the three arrays to triangulate the candidates for that specific tile. Let's fill one of the blank tiles in our square (denoted by `?`)
43 | ```
44 | 5 3 ?
45 |
46 | 6 • •
47 |
48 | • 9 8
49 | ```
50 |
51 |
52 | The tile selected is in the 4th row, 3rd column and 4th square. In our 0-indexed arrays this corresponds to `rows[3]`, `cols[2]`, and `squares[3]`. We already know the value of `squares[3]`. So let's make up some integer values for `rows[3]` and `cols[2]`:
53 | ```
54 | int binary numbers filled
55 | rows[3] -> 151 010010111 1, 2, 3, 5, 8
56 | cols[2] -> 297 100101001 1, 4, 6, 9
57 | squares[3] -> 436 110110100 3, 5, 6, 8, 9
58 | ```
59 | There's only one remaining candidate for this tile: **7**. The computer can figure this out by bitwise `OR`-ing all three integers together:
60 |
61 | ```
62 | rows[3] | cols[2] | squares[3] -> 110111111 (447)
63 | ```
64 | The binary result reveals that 7 is the only available slot. So let's fill our tile with a 7. All we have to do is update the board, and then update the three integers in our arrays by setting the 7th bit in each one to a `1`.
65 |
66 | ```
67 | rows[3] |= (i << 7)
68 | cols[2] |= (i << 7)
69 | squares[3] |= (i << 7)
70 | ```
71 | There we go! Although this is kind of a pain to do manually, it's efficient for the computer.
72 |
73 | Now imagine we find that our **7** was misplaced. To reset those bits back to zero, we do the following:
74 | ```
75 | rows[4] &= ~(i << 7)
76 | cols[2] &= ~(i << 7)
77 | squares[3] &= ~(i << 7)
78 | ```
79 |
80 | Now we have to do this for every empty tile on the board.
81 |
82 |
83 | ### Backtracking
84 | This is the simpler part. The algorithm uses brute force.
85 |
86 | We start by making one pass through the entire board to update our `rows`, `cols`, and `squares` arrays with the values that are already present.
87 |
88 | After that, we can recursively iterate through the board tile-by-tile. Each call to the `solveRecur` function examines exactly one tile. Tiles that already contain numbers are skipped. Tiles that are empty can use our three arrays to deduce the candidates. For each candidate, we set the tile to that candidate and make a recursive call to the next tile.
89 |
90 | If a tile has no valid candidates, we know that we've screwed up somewhere, and the function returns `false`. This backtracks to the previous tile and allows it to try a different candidate. If the previous tile runs out of candidates, then it can backtrack one tile further, and so on.
91 |
92 | Here's a great visual representation of what's happening:
93 |
94 |
5 |
6 | ## How to Run
7 | Put all the files in the same directory and run the following commands in that directory:
8 | ```
9 | make
10 | ./main
11 | ```
12 | For cleanup you can run `make clean`.
13 | ## Algorithm Explanation
14 |
15 | This algorithm uses backtracking (brute-force) combined with bit masking. All of the relevant code can be found in `solver.c`.
16 | ### Bit Masking
17 |
18 | As far as sudoku solvers go, this algorithm is not too crazy. But it does require that you know what bitmasking is, and how binary numbers and bitwise operators work.
19 |
20 | Start off by initializing three `int` arrays of length 9: `rows`, `cols`, and `squares`. Each `int` element in these arrays will represent the filled numbers in an entire row, column or square.
21 |
22 | Let's examine our `squares` array. Each `int` in the array can be represented as 9 bits, and each bit represents a number in that square.
23 | ```
24 | Number: 9 8 7 6 5 4 3 2 1
25 | Bit Digit: 0 0 0 0 0 0 0 0 0
26 | ```
27 | A value of `000000000` would mean that the square is completely empty, and a value of `111111111` (512) would mean that the square has been filled. To elaborate, let's say we have the following square, which is the **center-left** square on a board. Squares are numbered from left-to-right, top-to-bottom. So this square would be index 3 in the `squares` array.
28 | ```
29 | 5 3 •
30 |
31 | 6 • •
32 |
33 | • 9 8
34 | ```
35 | Representing the square as bits would look like this:
36 | ```
37 | Number: 9 8 7 6 5 4 3 2 1
38 | Bit Value: 1 1 0 1 1 0 1 0 0
39 | ```
40 | Thus, index 3 in the `squares` array is `110110100` (or 436). The `0`s in this bit represent the remaining candidates for this square.
41 |
42 | To add a number to our board, we can pick a tile, and use the three arrays to triangulate the candidates for that specific tile. Let's fill one of the blank tiles in our square (denoted by `?`)
43 | ```
44 | 5 3 ?
45 |
46 | 6 • •
47 |
48 | • 9 8
49 | ```
50 |
51 |
52 | The tile selected is in the 4th row, 3rd column and 4th square. In our 0-indexed arrays this corresponds to `rows[3]`, `cols[2]`, and `squares[3]`. We already know the value of `squares[3]`. So let's make up some integer values for `rows[3]` and `cols[2]`:
53 | ```
54 | int binary numbers filled
55 | rows[3] -> 151 010010111 1, 2, 3, 5, 8
56 | cols[2] -> 297 100101001 1, 4, 6, 9
57 | squares[3] -> 436 110110100 3, 5, 6, 8, 9
58 | ```
59 | There's only one remaining candidate for this tile: **7**. The computer can figure this out by bitwise `OR`-ing all three integers together:
60 |
61 | ```
62 | rows[3] | cols[2] | squares[3] -> 110111111 (447)
63 | ```
64 | The binary result reveals that 7 is the only available slot. So let's fill our tile with a 7. All we have to do is update the board, and then update the three integers in our arrays by setting the 7th bit in each one to a `1`.
65 |
66 | ```
67 | rows[3] |= (i << 7)
68 | cols[2] |= (i << 7)
69 | squares[3] |= (i << 7)
70 | ```
71 | There we go! Although this is kind of a pain to do manually, it's efficient for the computer.
72 |
73 | Now imagine we find that our **7** was misplaced. To reset those bits back to zero, we do the following:
74 | ```
75 | rows[4] &= ~(i << 7)
76 | cols[2] &= ~(i << 7)
77 | squares[3] &= ~(i << 7)
78 | ```
79 |
80 | Now we have to do this for every empty tile on the board.
81 |
82 |
83 | ### Backtracking
84 | This is the simpler part. The algorithm uses brute force.
85 |
86 | We start by making one pass through the entire board to update our `rows`, `cols`, and `squares` arrays with the values that are already present.
87 |
88 | After that, we can recursively iterate through the board tile-by-tile. Each call to the `solveRecur` function examines exactly one tile. Tiles that already contain numbers are skipped. Tiles that are empty can use our three arrays to deduce the candidates. For each candidate, we set the tile to that candidate and make a recursive call to the next tile.
89 |
90 | If a tile has no valid candidates, we know that we've screwed up somewhere, and the function returns `false`. This backtracks to the previous tile and allows it to try a different candidate. If the previous tile runs out of candidates, then it can backtrack one tile further, and so on.
91 |
92 | Here's a great visual representation of what's happening:
93 |
94 |