9 |
10 | Graph Attention Networks는 spatial 하게 인접한 노드들에 attention weight를 부과하여 이를 통해 각 노드를 표현한다.
11 |
12 | 위 그림에서, 가장 먼저 shared linear transformation, parameterized weight matrix W 를 구해야 합니다.
13 |
14 | 서로 다른 노드와 자신과의 self-attention을 통해 우리는 다음과 같은 식을 얻습니다.
15 |
16 |
17 |
18 | 코드 상에서 이 식은 다음과 같습니다.
19 |
20 | ```bash
21 | h = torch.mm(input, self.W)
22 |
23 | # a1, a2 = (out_features x 1)
24 | f_1 = torch.matmul(h, self.a1)
25 | f_2 = torch.matmul(h, self.a2)
26 | e = f_1 + f_2.transpose(0,1)
27 | ```
28 |
29 | 여기에 negative input slope 가 0.2 인 LeakyReLU non-linearity를 적용하고, normalize를 시켜줍니다.
30 |
31 | (normalize 방법으론 일반적으로 softmax를 이용합니다.)
32 |
33 |
34 |
35 | 코드 상에서 이 식은 다음과 같습니다.
36 |
37 | ```bash
38 | e = self.leakyrelu(e)
39 | attention = torch.where(adj > 0, e, zero_vec)
40 | attention = F.softmax(attention, dim=1)
41 | ```
42 |
43 | 학습의 안정성을 위하여, 본 논문에서는 multi-head attention을 진행합니다.
44 |
45 | 마지막 layer 이전 모든 layer에서는 이 작업을 head 의 개수만큼 반복하여 concat 하여 주고,
46 |
47 | 마지막 layer에서는 head의 개수만큼 발생한 output의 average를 취해줍니다.
48 |
49 |
50 |
51 | 코드 상에서 이 식은 다음과 같습니다.
52 |
53 | ```bash
54 | self.attentions = [GraphAttention(nfeat, nhid, dropout=dropout, alpha=alpha, concat=True) for _ in range(nheads)] # concat
55 | self.out_att = [GraphAttention(nhid * nheads, nclass, dropout=dropout, alpha=alpha, concat=False) for _ in range(nouts)]
56 |
57 | # Output layer 가 아닌 layer의 경우
58 | x = torch.cat([att(x, adj) for att in self.attentions], dim=1) # concat
59 |
60 | # Output layer 의 경우
61 | x = torch.mean(torch.stack([att(x, adj) for att in self.out_att], dim=1), dim=1) # avg (for pubmed)
62 | ```
63 |
64 | Normalize 는 Xavier Initialization 의 다른 이름인 'Glorot Initialization'을 사용했으며,
65 |
66 | Transductive task의 경우
67 | ```bash
68 | # cora, citeseer
69 | nvidia-docker run -it bumsoo python 4_Spatial_Graph_Convolution/train.py --dataset [:dataset] --weight_decay 5e-4 --dropout 0.6 --nb_heads 8 --nb_outs 1
70 |
71 | # pubmed (용량을 매우 많이 차지하므로 느리더라도 CPU 학습을 추천합니다.)
72 | docker run -it bumsoo python 4_Spatial_Graph_Convolution/train.py --dataset pubmed --weight_decay 1e-3 --dropout 0.6 --nb_heads 8 --nb_outs 8
73 | ```
74 |
75 | ## Train Planetoid Network
76 |
77 | | dataset | classes | nodes | # of edge |
78 | |:-------:|:-------:|:-----:|:-----------:|
79 | | citeseer| 6 | 3,327 | 4,676 |
80 | | cora | 7 | 2,708 | 5,278 |
81 | | pubmed | 3 | 19,717| 44,327 |
82 |
83 |
84 | 이전 튜토리얼과 마찬가지로, [2_Understanding_Graphs](../2_Understanding_Graphs) 에서 다루었던 Planetoid의 데이터셋에 대해 학습을 해보겠습니다.
85 |
86 | 아래의 script를 실행시키면, 원하시는 데이터셋에 GCN 을 학습시키실 수 있습니다.
87 |
88 | [2_Understanding_Graphs](../2_Understanding_Graphs) 에서 설명한 것과 같이 Planetoid 데이터셋을 다운로드 받으신 후, [:dir to dataset] 에 대입하여 실행하시면 됩니다. (Dockerfile 에서 자동적으로 데이터를 받아 필요한 경로로 이동시켜줍니다)
89 |
90 | 기본 default 설정은 2_Understanding_Graphs 의 /home/[:user]/Data/Planetoid 디렉토리로 설정되어 있습니다.
91 |
92 | 이전 2번 튜토리얼 레포에서 보셨던 데이터의 전처리에 관한 사항은, [utils.py](utils.py) 에서 확인해보실 수 있습니다.
93 |
94 | ```bash
95 | # nvidia docker run -it bumsoo-graph-tutorial /bin/bash 실행 이후
96 | > python train.py --dataroot [:dir to dataset] --datset [:cora | citeseer | pubmed]
97 |
98 | # 바로 실행하는 경우
99 | $ nvidia-docker run -it bumsoo python 4_Spatial_Graph_Convolution/train.py --dataset pubmed --lr 0.01 --weight_decay 1e-3 --nb_heads 8
100 | $ nvidia-docker run -it bumsoo python 4_Spatial_Graph_Convolution/train.py --dataset [:else] --lr 5e-3
101 | ```
102 |
103 | 위 코드를 실행하면, 아래와 같은 결과화면을 얻으실 수 있습니다.
104 |
105 | 
106 |
107 | ## Test (Inference) Planetoid networks
108 |
109 | Training 과정을 모두 마치신 이후, 다음과 같은 코드를 통해 학습된 weight를 테스트셋에 적용해보실 수 있습니다.
110 |
111 | ```bash
112 | # nvidia docker run -it bumsoo-graph-tutorial /bin/bash 실행 이후
113 | > python test.py --dataroot [:dir to dataset] --dataset [:cora | citeseer | pubmed]
114 |
115 | # 바로 실행하는 경우
116 | $ nvidia-docker run -it bumsoo python 4_Spatial_Graph_Convolution/test.py --dataset [:dataset]
117 | ```
118 |
119 | 위 코드를 실행하면, 아래와 같은 결과화면을 얻으실 수 있습니다.
120 |
121 | 
122 |
123 | ## Result
124 |
125 | 800 epoch 후 학습된 최종 성능은 다음과 같습니다.
126 |
127 | GAT (recon) 이 본 repository의 코드로 학습 후, test data 에 적용한 결과입니다.
128 |
129 | | Method | Citeseer | Cora | Pubmed |
130 | |:------------|:---------|:-----|:-------|
131 | | GCN (rand) | 67.9 | 80.1 | 78.9 |
132 | | GCN (paper) | 70.3 | 81.5 | 79.0 |
133 | | GAT (paper) | 72.5 | 83.0 | 79.0 |
134 | | **GAT (recon)** | **72.2** | **82.2** | **78.6** |
135 |
--------------------------------------------------------------------------------
/3_Spectral_Graph_Convolution/molecule_utils.py:
--------------------------------------------------------------------------------
1 | import sys
2 | import numpy as np
3 | import networkx as nx
4 | import scipy.sparse as sp
5 | import torch.nn.functional as F
6 | import torch
7 | from scipy import sparse
8 | from rdkit import Chem
9 | from scipy.sparse import csgraph
10 |
11 | class ContrastiveLoss(torch.nn.Module):
12 | """
13 | Contrastive loss function.
14 | Based on: http://yann.lecun.com/exdb/publis/pdf/hadsell-chopra-lecun-06.pdf
15 | """
16 |
17 | def __init__(self, margin=2.0):
18 | super(ContrastiveLoss, self).__init__()
19 | self.margin = margin
20 |
21 | def forward(self, output1, output2, label):
22 | euclidean_distance = F.pairwise_distance(output1, output2)
23 | loss_contrastive = torch.mean((1-label) * torch.pow(euclidean_distance, 2) +
24 | (label) * torch.pow(torch.clamp(self.margin - euclidean_distance, min=0.0), 2))
25 |
26 | return loss_contrastive
27 |
28 | def parse_index_file(filename):
29 | index = []
30 |
31 | for line in open(filename):
32 | index.append(int(line.strip()))
33 |
34 | return index
35 |
36 | def normalize(mx):
37 | """Row-normalize sparse matrix"""
38 | rowsum = np.array(mx.sum(1), dtype=float)
39 | r_inv = np.power(rowsum, -1).flatten()
40 | r_inv[np.isinf(r_inv)] = 0.
41 | r_mat_inv = sp.diags(r_inv)
42 | mx = r_mat_inv.dot(mx)
43 |
44 | return mx
45 |
46 | def normalize_adj(mx):
47 | """Row-normalize sparse matrix"""
48 | rowsum = np.array(mx.sum(1))
49 | r_inv_sqrt = np.power(rowsum, -0.5).flatten()
50 | r_inv_sqrt[np.isinf(r_inv_sqrt)] = 0.
51 | r_mat_inv_sqrt = sp.diags(r_inv_sqrt)
52 |
53 | return mx.dot(r_mat_inv_sqrt).transpose().dot(r_mat_inv_sqrt).tocoo()
54 |
55 | def one_of_k_encoding(x, allowable_set):
56 | if x not in allowable_set:
57 | raise Exception("input {0} not in allowable set{1}:".format(x, allowable_set))
58 | return list(map(lambda s: x==s, allowable_set))
59 |
60 | def one_of_k_encoding_unk(x, allowable_set):
61 | if x not in allowable_set:
62 | x = allowable_set[-1]
63 |
64 | return list(map(lambda s: x==s, allowable_set))
65 |
66 | def atom_features(atom):
67 | # atom (vertex) will have 62 dimensions
68 | return np.array(one_of_k_encoding_unk(atom.GetSymbol(),
69 | ['C', 'N', 'O', 'S', 'F', 'Si', 'P', 'Cl', 'Br', 'Mg', 'Na',
70 | 'Ca', 'Fe', 'As', 'Al', 'I', 'B', 'V', 'K', 'Tl', 'Yb',
71 | 'Sb', 'Sn', 'Ag', 'Pd', 'Co', 'Se', 'Ti', 'Zn', 'H',
72 | 'Li', 'Ge', 'Cu', 'Au', 'Ni', 'Cd', 'In', 'Mn', 'Zr',
73 | 'Cr', 'Pt', 'Hg', 'Pb', 'Unknown']) +
74 | one_of_k_encoding(atom.GetDegree(), [0, 1, 2, 3, 4, 5]) +
75 | one_of_k_encoding_unk(atom.GetTotalNumHs(), [0, 1, 2, 3, 4]) +
76 | one_of_k_encoding_unk(atom.GetImplicitValence(), [0, 1, 2, 3, 4, 5]) +
77 | [atom.GetIsAromatic()])
78 |
79 | def bond_features(bond):
80 | bt = bond.GetBondType()
81 |
82 | # bond (edge) will have 6 dimensions
83 | return np.array([bt == Chem.rdchem.BondType.SINGLE,
84 | bt == Chem.rdchem.BondType.DOUBLE,
85 | bt == Chem.rdchem.BondType.TRIPLE,
86 | bt == Chem.rdchem.BondType.AROMATIC,
87 | bond.GetIsConjugated(),
88 | bond.IsInRing()])
89 |
90 | # Obtain dim(atom features) through a toy chemical compound 'CC'
91 | def num_atom_features():
92 | m = Chem.MolFromSmiles('CC')
93 | alist = m.GetAtoms()
94 | a = alist[0]
95 | return len(atom_features(a))
96 |
97 | # Obtain dim(bond features) through a toy chemical compound 'CC'
98 | def num_bond_features():
99 | simple_mol = Chem.MolFromSmiles('CC')
100 | Chem.SanitizeMol(simple_mol)
101 | return len(bond_features(simple_mol.GetBonds()[0]))
102 |
103 | # Create (feature, adj) from a mol
104 | def create_graph(mol):
105 | num_atom = max([atom.GetIdx() for atom in mol.GetAtoms()]) + 1
106 | adj = np.zeros((num_atom, num_atom, num_bond_features()))
107 |
108 | features = [atom_features(atom) * 1 for atom in mol.GetAtoms()]
109 | feature = np.stack(features, axis=0)
110 |
111 | edge_list = [(bond.GetBeginAtomIdx(), bond.GetEndAtomIdx(), bond_features(bond))
112 | for bond in mol.GetBonds()]
113 |
114 | for edge in edge_list:
115 | v1, v2, f = edge
116 | f = f * 1 # Convert boolean to int
117 | adj[v1][v2] = f
118 | adj[v2][v1] = f
119 |
120 | # normalize feature
121 | sparse_features = sparse.csr_matrix(features)
122 | normed_features = normalize(sparse_features)
123 | features = np.array(normed_features.todense())
124 |
125 | # normalize adj
126 | for layer in range(num_bond_features()):
127 | sparse_adj = sparse.csr_matrix(adj[:,:,layer])
128 | normed_adj = normalize_adj(sparse_adj + sparse.eye(sparse_adj.shape[0]))
129 | adj[:,:,layer] = np.array(normed_adj.todense())
130 |
131 | return adj, feature
132 |
--------------------------------------------------------------------------------
/2_Understanding_Graphs/README.md:
--------------------------------------------------------------------------------
1 | ## Graph Structure
2 | 참고자료 : [slides](https://www.cl.cam.ac.uk/~pv273/slides/UCLGraph.pdf)
3 |
4 | ## Planetoid Dataset
5 | Planetoid 데이터셋은 graph 형식의 데이터를 다루는 테스크 중 일반적인 성능의 지표로 많이 사용되는 데이터셋입니다.
6 | Planetoid를 통해 evaluation을 한 논문은 다음과 같은 예시가 대표적입니다.
7 |
8 | - [Semi-Supervised Classification with Graph Convolutional Networks](https://arxiv.org/pdf/1609.02907.pdf)
9 | - [Graph Attention Networks](https://mila.quebec/wp-content/uploads/2018/07/d1ac95b60310f43bb5a0b8024522fbe08fb2a482.pdf)
10 | - [Topology Adaptive Graph Convolutional Networks](https://arxiv.org/pdf/1710.10370.pdf)
11 | - [Deeper Insights into Graph Convolutional Networks for Semi-Supervised Learning](https://arxiv.org/pdf/1801.07606.pdf)
12 |
13 | 튜토리얼에서 사용된 Planetoid는 아래 논문의 데이터셋을 참조하였습니다:
14 | [Revisiting Semi-Supervised Learning with Graph Embeddings](https://arxiv.org/abs/1603.08861).
15 |
16 | Planetoid 데이터셋은 3개의 데이터로 구성이 되어있습니다. ('pubmed', 'cora', 'citeseer')
17 |
18 | Each node in the dataset represents a document, and the edge represents the 'reference' relationship between the documents.
19 |
20 | Planetoid 데이터셋에서, 각 노드는 'document'를 의미하며, 각 edge는 'document'간 reference 관계를 나타냅니다.
21 | 예를 들어, 아래 그림과 같이 paper A 에서 paper B 를 reference 했다면, edge(A, B) = 1 입니다.
22 |
23 | [:예시 그림]
24 |
25 | ## Planetoid Dataset Download
26 | [Github planetoid repo](https://github.com/kimiyoung/planetoid) 를 다운로드 받은 후, 내부에 있는 data 폴더를 ~/Data/Planetoid 로 이동시켜줍니다. (이후 튜토리얼에서 환경설정은 모두 동일합니다.)
27 |
28 | ```bash
29 | $ git clone https://github.com/kimiyoung/planetoid.git
30 | $ mkdir ~/Data
31 | $ mv ./data ~/Data/Planetoid/
32 | ```
33 |
34 | ## [STEP 1] : Planetoid data 읽어보기
35 |
36 | 첫번째 단계로, Planetoid 의 세 개의 데이터셋(cora, pubmed, citeseer)을 읽어보겠습니다.
37 | docker 환경을 실행한 상태에서, 아래 코드를 돌리면 Planetoid 데이터를 읽을 수 있습니다.
38 |
39 | ```bash
40 | $ python load_planetoid.py --dataset cora
41 | $ python load_planetoid.py --dataset citeseer
42 | $ python load_planetoid.py --dataset pubmed
43 | ```
44 |
45 | 데이터는 다음과 같은 두 가지 방식으로 학습할 수 있습니다.
46 |
47 | ### 전이학습 (Transductive learning)
48 | - x : 각 training 데이터 중, 레이블이 존재하는 instance에 대한 feature vector
49 | - y : 각 training 데이터에 대한 label 이 one-hot 방식으로 표현되어 있습니다.
50 | - graph : dict{index: [index of neighber nodes]}, 각 노드의 인접 노드는 list 형식으로 표현되어 있습니다.
51 |
52 | ### 추론 학습 (Inductive learning)
53 | - x : 각 training 데이터의 feature vector
54 | - y : 각 training 데이터에 대한 label 이 one-hot 방식으로 표현되어 있습니다.
55 | - allx : training 데이터 중, 레이블의 유무와 관련 없이 모든 instance에 대한 feature vector.
56 | - graph : dict{index: [index of neighber nodes]}, 각 노드의 인접 노드는 list 형식으로 표현되어 있습니다.
57 |
58 | ## [STEP 2] : Pre-processing
59 |
60 | Pre-processing 은 총 세 단계로 이루어진다.
61 |
62 | - train / test split
63 | - isolated node 검사
64 | - normalize
65 |
66 | ### train / val / test split
67 |
68 | Pre-processing 의 첫 번째 단게로, train / val / test split 을 해야합니다.
69 |
70 | validation set 은 따로 지정되있지 않으므로, 500개로 설정하여 실험을 진행합니다.
71 |
72 | ```bash
73 | $ python preprocess_planetoid.py --dataset [:dataset] --step split
74 |
75 | # Citeseer example
76 | $ python preprocess_planetoid.py --dataset citeseer --step split
77 | > [STEP 1]: Upload citeseer dataset.
78 | > | # of train set : 120
79 | > | # of validation set : 500
80 | > | # of test set : 1000
81 | ```
82 |
83 | Pre-processing 의 두 번째 단계로, graph에 존재하는 isolated node를 검사해야 합니다.
84 |
85 | ```bash
86 | $ python preprocess_planetoid.py --dataset pubmed --step isolate
87 | > Isolated Nodes : []
88 |
89 | $ python preprocess_planetoid.py --dataset cora --step isolate
90 | > Isolated Nodes : []
91 |
92 | $ python preprocess_planetoid.py --dataset citeseer --step isolate
93 | > Isolated Nodes : [2407, 2489, 2553, 2682, 2781, 2953, 3042, 3063, 3212, 3214, 3250, 3292, 3305, 3306, 3309]
94 | ```
95 |
96 | 세 개의 dataset 중, citeseer 데이터셋의 test 데이터에 다음과 같은 isolated node를 발견할 수 있습니다.
97 |
98 | ### Normalize
99 |
100 | Normalize 는 feature와 adjacency matrix 에 대해서 모두 Row normalize를 진행합니다.
101 |
102 | Feature vector에는, degree를 normalize 하기 위하여 row-wise normalization을 진행합니다.
103 |
104 | Adjacency Matrix에서는, 인접 노드의 개수에 따른 degree의 차이를 normalize 해주기 위하여 Symmetric Laplacian을 이용합니다. 이를 통해서, 한 노드와 인접 노드 간의 spectrum을 표현할 수 있습니다.
105 |
106 | Adjacency Matrix의 normalize는원 저자의 [paper](https://arxiv.org/pdf/1609.02907.pdf)에서 확인이 가능합니다.
107 |
108 | 
109 |
110 | normalize 를 실행하고 결과를 확인하기 위해서는 아래의 코드를 실행하시면 됩니다.
111 |
112 | ```bash
113 | $ python preprocess_planetoid.py --dataset [:dataset] --step normalize
114 | ```
115 |
116 | ## Pitfall
117 |
118 | 기존 논문 저자의 [repository](https://github.com/kimiyoung/planetoid) 에 공개된 데이터에는, 몇 가지 문제가 있습니다.
119 |
120 | - 중복된 edge 의 존재 (한 노드가 다른 노드를 두 번 이상 reference)
121 | - self citation의 존재 (self citation을 고려할지 그렇지 않을지에 대한 정의를 명확히 해야할 것 같습니다. 본 논문에서 제시된 edge 개수를 맞추려면 self citation을 고려해야하므로, 본 튜토리얼에서도 똑같이 적용하였습니다.)
122 |
123 | ```bash
124 | $ python preprocess_planetoid.py --dataset [:dataset] --step normalize --mode pitfall
125 | ```
126 |
127 | | dataset | classes | nodes | # of redundant | # of self citation | reported edge | actual edge |
128 | |:-------:|:-------:|:-----:|:--------------:|:------------------:|:-------------:|:-----------:|
129 | | citeseer| 6 | 3,327 | 232 | 124 | 4,732 | 4,676 |
130 | | cora | 7 | 2,708 | 302 | 0 | 5,429 | 5,278 |
131 | | pubmed | 3 | 19,717| 25 | 3 | 44,338 | 44,327 |
132 |
133 | 기존의 구현은 [링크](https://github.com/kimiyoung/planetoid)의 repository에서 볼 수 있습니다.
134 |
--------------------------------------------------------------------------------
/3_Spectral_Graph_Convolution/utils.py:
--------------------------------------------------------------------------------
1 | # ************************************************************
2 | # Author : Bumsoo Kim, 2018
3 | # Github : https://github.com/meliketoy/graph-tutorial.pytorch
4 | #
5 | # Korea University, Data-Mining Lab
6 | # Basic Tutorial for Non-Euclidean Graph Representation Learning
7 | #
8 | # Description : utils.py
9 | # Code for uploading planetoid dataset
10 | # ***********************************************************
11 |
12 | import sys
13 | import numpy as np
14 | import pickle as pkl
15 | import networkx as nx
16 | import scipy.sparse as sp
17 | import torch
18 | from scipy.sparse import csgraph
19 |
20 | def parse_index_file(filename):
21 | index = []
22 |
23 | for line in open(filename):
24 | index.append(int(line.strip()))
25 |
26 | return index
27 |
28 | def missing_elements(L):
29 | start, end = L[0], L[-1]
30 | return sorted(set(range(start, end+1)).difference(L))
31 |
32 | def normalize_sparse_features(mx):
33 | """Row-normalize sparse matrix"""
34 | rowsum = np.array(mx.sum(1))
35 | r_inv = np.power(rowsum, -1).flatten()
36 | r_inv[np.isinf(r_inv)] = 0.
37 | r_mat_inv = sp.diags(r_inv)
38 | mx = r_mat_inv.dot(mx)
39 |
40 | return mx
41 |
42 | def normalize_sparse_adj(mx):
43 | """Laplacian Normalization"""
44 | rowsum = np.array(mx.sum(1))
45 | r_inv_sqrt = np.power(rowsum, -0.5).flatten()
46 | r_inv_sqrt[np.isinf(r_inv_sqrt)] = 0.
47 | r_mat_inv_sqrt = sp.diags(r_inv_sqrt)
48 |
49 | return mx.dot(r_mat_inv_sqrt).transpose().dot(r_mat_inv_sqrt).tocoo()
50 |
51 | def accuracy(output, labels):
52 | preds = output.max(1)[1].type_as(labels)
53 | correct = preds.eq(labels).double()
54 | correct = correct.sum()
55 | return correct / len(labels)
56 |
57 | def load_data(path="/home/bumsoo/Data/Planetoid", dataset="cora"):
58 | """
59 | ind.[:dataset].x => the feature vectors of the training instances (scipy.sparse.csr.csr_matrix)
60 | ind.[:dataset].y => the one-hot labels of the labeled training instances (numpy.ndarray)
61 | ind.[:dataset].allx => the feature vectors of both labeled and unlabeled training instances (csr_matrix)
62 | ind.[:dataset].ally => the labels for instances in ind.dataset_str.allx (numpy.ndarray)
63 | ind.[:dataset].graph => the dict in the format {index: [index of neighbor nodes]} (collections.defaultdict)
64 |
65 | ind.[:dataset].tx => the feature vectors of the test instances (scipy.sparse.csr.csr_matrix)
66 | ind.[:dataset].ty => the one-hot labels of the test instances (numpy.ndarray)
67 |
68 | ind.[:dataset].test.index => indices of test instances in graph, for the inductive setting
69 | """
70 | print("\n[STEP 1]: Upload {} dataset.".format(dataset))
71 |
72 | names = ['x', 'y', 'tx', 'ty', 'allx', 'ally', 'graph']
73 | objects = []
74 |
75 | for i in range(len(names)):
76 | with open("{}/ind.{}.{}".format(path, dataset, names[i]), 'rb') as f:
77 | if (sys.version_info > (3,0)):
78 | objects.append(pkl.load(f, encoding='latin1')) # python3 compatibility
79 | else:
80 | objects.append(pkl.load(f)) # python2
81 |
82 | x, y, tx, ty, allx, ally, graph = tuple(objects)
83 |
84 | test_idx = parse_index_file("{}/ind.{}.test.index".format(path, dataset))
85 | test_idx_range = np.sort(test_idx)
86 |
87 | if dataset == 'citeseer':
88 | #Citeseer dataset contains some isolated nodes in the graph
89 | test_idx_range_full = range(min(test_idx), max(test_idx)+1)
90 | tx_extended = sp.lil_matrix((len(test_idx_range_full), x.shape[1]))
91 | tx_extended[test_idx_range-min(test_idx_range), :] = tx
92 | tx = tx_extended
93 |
94 | ty_extended = np.zeros((len(test_idx_range_full), y.shape[1]))
95 | ty_extended[test_idx_range-min(test_idx_range), :] = ty
96 | ty = ty_extended
97 |
98 | # Feature & Adjacency Matrix
99 | features = sp.vstack((allx, tx)).tolil()
100 | features[test_idx, :] = features[test_idx_range, :]
101 | adj = nx.adjacency_matrix(nx.from_dict_of_lists(graph))
102 | print("| # of nodes : {}".format(adj.shape[0]))
103 | print("| # of edges : {}".format(int(adj.sum().sum()/2 + adj.diagonal().sum()/2)))
104 |
105 | # Normalization
106 | features = normalize_sparse_features(features)
107 | adj = normalize_sparse_adj(adj + sp.eye(adj.shape[0])) # Input is A_hat
108 | print("| # of features : {}".format(features.shape[1]))
109 | print("| # of clases : {}".format(ally.shape[1]))
110 |
111 | features = torch.FloatTensor(np.array(features.todense()))
112 | sparse_mx = adj.tocoo().astype(np.float32)
113 | adj = torch.FloatTensor(np.array(adj.todense()))
114 |
115 | labels = np.vstack((ally, ty))
116 | labels[test_idx, :] = labels[test_idx_range, :]
117 |
118 | if dataset == 'citeseer':
119 | save_label = np.where(labels)[1]
120 | labels = torch.LongTensor(np.where(labels)[1])
121 |
122 | idx_train = range(len(y))
123 | idx_val = range(len(y), len(y)+500)
124 | idx_test = test_idx_range.tolist()
125 |
126 | print("| # of train set : {}".format(len(idx_train)))
127 | print("| # of val set : {}".format(len(idx_val)))
128 | print("| # of test set : {}".format(len(idx_test)))
129 |
130 | idx_train, idx_val, idx_test = list(map(lambda x: torch.LongTensor(x), [idx_train, idx_val, idx_test]))
131 |
132 | if dataset == 'citeseer':
133 | L = np.sort(idx_test)
134 | missing = missing_elements(L)
135 |
136 | for element in missing:
137 | save_label = np.insert(save_label, element, 0)
138 |
139 | labels = torch.LongTensor(save_label)
140 |
141 | return adj, features, labels, idx_train, idx_val, idx_test
142 |
--------------------------------------------------------------------------------
/4_Spatial_Graph_Convolution/utils.py:
--------------------------------------------------------------------------------
1 | # ************************************************************
2 | # Author : Bumsoo Kim, 2018
3 | # Github : https://github.com/meliketoy/graph-tutorial.pytorch
4 | #
5 | # Korea University, Data-Mining Lab
6 | # Basic Tutorial for Non-Euclidean Graph Representation Learning
7 | #
8 | # Description : utils.py
9 | # Code for uploading planetoid dataset
10 | # ***********************************************************
11 |
12 | import sys
13 | import numpy as np
14 | import pickle as pkl
15 | import networkx as nx
16 | import scipy.sparse as sp
17 | import torch
18 | from scipy.sparse import csgraph
19 |
20 | def parse_index_file(filename):
21 | index = []
22 |
23 | for line in open(filename):
24 | index.append(int(line.strip()))
25 |
26 | return index
27 |
28 | def missing_elements(L):
29 | start, end = L[0], L[-1]
30 | return sorted(set(range(start, end+1)).difference(L))
31 |
32 | def normalize_sparse_features(mx):
33 | """Row-normalize sparse matrix"""
34 | rowsum = np.array(mx.sum(1))
35 | rowsum[rowsum == 0] = -9e15
36 | r_inv = np.power(rowsum, -1).flatten()
37 | r_inv[np.isinf(r_inv)] = 0.
38 | r_mat_inv = sp.diags(r_inv)
39 | mx = r_mat_inv.dot(mx)
40 |
41 | return mx
42 |
43 | def normalize_sparse_adj(mx):
44 | """Laplacian Normalization"""
45 | rowsum = np.array(mx.sum(1))
46 | r_inv_sqrt = np.power(rowsum, -0.5).flatten()
47 | r_inv_sqrt[np.isinf(r_inv_sqrt)] = 0.
48 | r_mat_inv_sqrt = sp.diags(r_inv_sqrt)
49 |
50 | return mx.dot(r_mat_inv_sqrt).transpose().dot(r_mat_inv_sqrt).tocoo()
51 |
52 | def accuracy(output, labels):
53 | preds = output.max(1)[1].type_as(labels)
54 | correct = preds.eq(labels).double()
55 | correct = correct.sum()
56 | return correct / len(labels)
57 |
58 | def load_data(path="/home/bumsoo/Data/Planetoid", dataset="cora"):
59 | """
60 | ind.[:dataset].x => the feature vectors of the training instances (scipy.sparse.csr.csr_matrix)
61 | ind.[:dataset].y => the one-hot labels of the labeled training instances (numpy.ndarray)
62 | ind.[:dataset].allx => the feature vectors of both labeled and unlabeled training instances (csr_matrix)
63 | ind.[:dataset].ally => the labels for instances in ind.dataset_str.allx (numpy.ndarray)
64 | ind.[:dataset].graph => the dict in the format {index: [index of neighbor nodes]} (collections.defaultdict)
65 |
66 | ind.[:dataset].tx => the feature vectors of the test instances (scipy.sparse.csr.csr_matrix)
67 | ind.[:dataset].ty => the one-hot labels of the test instances (numpy.ndarray)
68 |
69 | ind.[:dataset].test.index => indices of test instances in graph, for the inductive setting
70 | """
71 | print("\n[STEP 1]: Upload {} dataset.".format(dataset))
72 |
73 | names = ['x', 'y', 'tx', 'ty', 'allx', 'ally', 'graph']
74 | objects = []
75 |
76 | for i in range(len(names)):
77 | with open("{}/ind.{}.{}".format(path, dataset, names[i]), 'rb') as f:
78 | if (sys.version_info > (3,0)):
79 | objects.append(pkl.load(f, encoding='latin1')) # python3 compatibility
80 | else:
81 | objects.append(pkl.load(f)) # python2
82 |
83 | x, y, tx, ty, allx, ally, graph = tuple(objects)
84 |
85 | test_idx = parse_index_file("{}/ind.{}.test.index".format(path, dataset))
86 | test_idx_range = np.sort(test_idx)
87 |
88 | if dataset == 'citeseer':
89 | #Citeseer dataset contains some isolated nodes in the graph
90 | test_idx_range_full = range(min(test_idx), max(test_idx)+1)
91 | tx_extended = sp.lil_matrix((len(test_idx_range_full), x.shape[1]))
92 | tx_extended[test_idx_range-min(test_idx_range), :] = tx
93 | tx = tx_extended
94 |
95 | ty_extended = np.zeros((len(test_idx_range_full), y.shape[1]))
96 | ty_extended[test_idx_range-min(test_idx_range), :] = ty
97 | ty = ty_extended
98 |
99 | # Feature & Adjacency Matrix
100 | features = sp.vstack((allx, tx)).tolil()
101 | features[test_idx, :] = features[test_idx_range, :]
102 | adj = nx.adjacency_matrix(nx.from_dict_of_lists(graph))
103 | print("| # of nodes : {}".format(adj.shape[0]))
104 | print("| # of edges : {}".format(int(adj.sum().sum()/2 + adj.diagonal().sum()/2)))
105 |
106 | # Normalization
107 | features = normalize_sparse_features(features)
108 | adj = normalize_sparse_adj(adj + sp.eye(adj.shape[0])) # Input is A_hat
109 | print("| # of features : {}".format(features.shape[1]))
110 | print("| # of clases : {}".format(ally.shape[1]))
111 |
112 | features = torch.FloatTensor(np.array(features.todense()))
113 | sparse_mx = adj.tocoo().astype(np.float32)
114 | adj = torch.FloatTensor(np.array(adj.todense()))
115 |
116 | labels = np.vstack((ally, ty))
117 | labels[test_idx, :] = labels[test_idx_range, :]
118 |
119 | if dataset == 'citeseer':
120 | save_label = np.where(labels)[1]
121 | labels = torch.LongTensor(np.where(labels)[1])
122 |
123 | idx_train = range(len(y))
124 | idx_val = range(len(y), len(y)+500)
125 | idx_test = test_idx_range.tolist()
126 |
127 | print("| # of train set : {}".format(len(idx_train)))
128 | print("| # of val set : {}".format(len(idx_val)))
129 | print("| # of test set : {}".format(len(idx_test)))
130 |
131 | idx_train, idx_val, idx_test = list(map(lambda x: torch.LongTensor(x), [idx_train, idx_val, idx_test]))
132 |
133 | if dataset == 'citeseer':
134 | L = np.sort(idx_test)
135 | missing = missing_elements(L)
136 |
137 | for element in missing:
138 | save_label = np.insert(save_label, element, 0)
139 |
140 | labels = torch.LongTensor(save_label)
141 |
142 | return adj, features, labels, idx_train, idx_val, idx_test
143 |
--------------------------------------------------------------------------------
/3_Spectral_Graph_Convolution/forward_mol.py:
--------------------------------------------------------------------------------
1 | import math
2 | import numpy as np
3 | from rdkit import Chem
4 | import torch
5 | import torch.nn as nn
6 | import torch.nn.functional as F
7 | from torch.nn.parameter import Parameter
8 | from torch.nn.modules.module import Module
9 | from molecule_utils import atom_features, bond_features, num_atom_features, num_bond_features
10 |
11 | # Graph Convolution Layer
12 | class GraphConvolution(Module):
13 | def __init__(self, in_features, out_features, edge_features, bias=True, init='xavier'):
14 | super(GraphConvolution, self).__init__()
15 | self.in_features = in_features
16 | self.out_features = out_features
17 | self.weight = Parameter(nn.init.xavier_normal_(torch.Tensor(in_features, out_features).type(torch.cuda.FloatTensor if torch.cuda.is_available() else torch.FloatTensor), gain=np.sqrt(2.0)), requires_grad=True)
18 |
19 | if bias:
20 | self.bias = Parameter(torch.Tensor(out_features).type(torch.cuda.FloatTensor if torch.cuda.is_available() else torch.FloatTensor))
21 | else:
22 | self.register_parameter('bias', None)
23 |
24 | if init=='uniform':
25 | #print("| Uniform Initialization")
26 | self.reset_parameters_uniform()
27 | elif init=='xavier':
28 | #print("| Xavier Initialization")
29 | self.reset_parameters_xavier()
30 | elif init=='kaiminig':
31 | #print("| Kaiming Initialization")
32 | self.reset_parameters_kaiming()
33 | else:
34 | raise NotImplementedError
35 |
36 | # Initializations
37 | def reset_parameters_uniform(self):
38 | stdv = 1. / math.sqrt(self.weight.size(1))
39 | self.weight.data.uniform_(-stdv, stdv)
40 | if self.bias is not None:
41 | self.bias.data.uniform_(-stdv, stdv)
42 |
43 | def reset_parameters_xavier(self):
44 | nn.init.xavier_normal_(self.weight.data, gain=0.02) # Implement Xavier Uniform
45 | if self.bias is not None:
46 | nn.init.constant_(self.bias.data, 0.0)
47 |
48 | def reset_parameters_kaiming(self):
49 | nn.init.kaiming_normal_(self.weight.data, a=0, mode='fan_in')
50 | if self.bias is not None:
51 | nn.init.constant_(self.bias.data, 0.0)
52 |
53 | # Forward
54 | def forward(self, input, adj):
55 | support = torch.mm(input, self.weight)
56 | output = torch.mm(adj, support)
57 | if self.bias is not None:
58 | return output + self.bias
59 | else:
60 | return output
61 |
62 | # Graph Convolution Network Model
63 | class GCN(nn.Module):
64 | def __init__(self, nfeat, nhid, nclass, nedges, dropout, init):
65 | super(GCN, self).__init__()
66 |
67 | self.weight = Parameter(nn.init.xavier_normal_(torch.Tensor(nfeat, nhid).type(torch.cuda.FloatTensor if torch.cuda.is_available() else torch.FloatTensor), gain=np.sqrt(2.0)), requires_grad=True)
68 |
69 | self.gc1 = [GraphConvolution(nhid, nhid, nedges, init=init) for _ in range(nedges)]
70 | for idx, gc1 in enumerate(self.gc1):
71 | self.add_module('GCN_1_%d' %idx, gc1)
72 | self.gc2 = [GraphConvolution(nhid, nclass, nedges, init=init) for _ in range(nedges)]
73 | for idx, gc2 in enumerate(self.gc2):
74 | self.add_module('GCN_2_%d' %idx, gc2)
75 |
76 | self.dropout = dropout
77 | self.adj_dropout = dropout
78 |
79 | def AGG(self, x1, x2, method='add'):
80 | res = None
81 |
82 | if method == 'add':
83 | res = x1 + x2
84 | elif method == 'max':
85 | res = max(x1, x2)
86 | elif method == 'min':
87 | res = min(x1, x2)
88 | else:
89 | raise NotImplementedError
90 |
91 | return res
92 |
93 | def forward(self, x, adj):
94 | # iterate through the edges
95 | prev = None
96 | in_x = torch.matmul(x,self.weight)
97 |
98 | for i in range(adj.shape[2]):
99 | x = F.leaky_relu(self.gc1[i](F.dropout(in_x,self.dropout,self.training), F.dropout(adj[:,:,i], self.adj_dropout, self.training)), negative_slope = 0.2, inplace = False)
100 | x = F.leaky_relu(self.gc2[i](F.dropout(x,self.dropout,self.training), F.dropout(adj[:,:,i], self.adj_dropout, self.training)), 0.2)
101 |
102 | if i == 0:
103 | prev = x
104 | else:
105 | prev = self.AGG(prev, x)
106 |
107 | return prev
108 |
109 | if __name__ == "__main__":
110 | print("Forward path for molecule GCN processing")
111 |
112 | # name = 1-benzylimidazole
113 | # pid = BRD-K32795028
114 | smiles = 'c1ccc(Cn2ccnc2)cc1'
115 | mol = Chem.MolFromSmiles(smiles)
116 |
117 | num_atom = max([atom.GetIdx() for atom in mol.GetAtoms()]) + 1
118 | adj = np.zeros((num_atom, num_atom, num_bond_features()))
119 |
120 | features = [atom_features(atom) * 1 for atom in mol.GetAtoms()]
121 | feature = np.stack(features, axis=0)
122 |
123 | edge_list = [(bond.GetBeginAtomIdx(), bond.GetEndAtomIdx(), bond_features(bond)) for bond in mol.GetBonds()]
124 |
125 | for edge in edge_list:
126 | v1, v2, f = edge
127 | f = f * 1
128 | adj[v1][v2] = f
129 | adj[v2][v1] = f
130 |
131 | adj, feature = list(map(lambda x : torch.FloatTensor(x), [adj, feature]))
132 | if torch.cuda.is_available():
133 | adj, feature = list(map(lambda x : x.cuda(), [adj, feature]))
134 |
135 | print("Input Feature (# nodes x 62): " + str(feature.shape)) # node x 62
136 | print("Input adjacency (# nodes x # nodes x 6): " + str(adj.shape)) # node x node x 6
137 |
138 | model = GCN(
139 | nfeat = num_atom_features(),
140 | nhid = 100,
141 | nclass = 500,
142 | nedges = num_bond_features(),
143 | dropout = 0.5,
144 | init = 'xavier'
145 | )
146 |
147 | output = model(feature, adj)
148 | print("Output (# of nodes x 500): " + str(output.shape))
149 |
150 | max_lst, idx = ((torch.max(output, dim=0)))
151 | print("Max pool to a 500 dimensional vector : "+ str(max_lst.shape))
152 |
--------------------------------------------------------------------------------
/2_Understanding_Graphs/preprocess_planetoid.py:
--------------------------------------------------------------------------------
1 | # ************************************************************
2 | # Author : Bumsoo Kim, 2018
3 | # Github : https://github.com/meliketoy/graph-tutorial.pytorch
4 | #
5 | # Korea University, Data-Mining Lab
6 | # Basic Tutorial for Non-Euclidean Graph Representation Learning
7 | #
8 | # Description : preprocess.py
9 | # Code for preprocessing planetoid dataset
10 | # ***********************************************************
11 |
12 | import torch
13 | import pickle as pkl
14 | import argparse
15 | import os
16 | import numpy as np
17 | import scipy.sparse as sp
18 | import networkx as nx
19 | from pathlib import Path
20 | from load_planetoid import read_data
21 |
22 | def parse_index_file(filename):
23 | index = []
24 |
25 | for line in open(filename):
26 | index.append(int(line.strip()))
27 |
28 | return index
29 |
30 | def missing_elements(L):
31 | start, end = L[0], L[-1]
32 | return sorted(set(range(start, end+1)).difference(L))
33 |
34 | def preprocess_citeseer(tx, ty, test_idx):
35 | #Citeseer dataset contains some isolated nodes in the graph
36 | bef_tx = (tx.todense())
37 | test_idx_range = np.asarray(test_idx, dtype=np.int64)
38 | test_idx_range_full = range(min(test_idx), max(test_idx)+1)
39 | tx_extended = sp.lil_matrix((len(test_idx_range_full), tx.shape[1]))
40 | tx_extended[test_idx_range-min(test_idx_range), :] = tx
41 | tx = tx_extended
42 |
43 | if (args.step == 'isolate'):
44 | print("Citeseer 전처리 이전 test shape : %s" %str(bef_tx.shape))
45 | print("Citeseer 전처리 이후 test shape : %s" %str(tx.todense().shape))
46 |
47 | ty_extended = np.zeros((len(test_idx_range_full), ty.shape[1]))
48 | ty_extended[test_idx_range-min(test_idx_range), :] = ty
49 | ty = ty_extended
50 |
51 | return tx, ty
52 |
53 | def normalize_sparse_feature(mx):
54 | """Row-normalize sparse matrix"""
55 | rowsum = np.array(mx.sum(1))
56 | r_inv = np.power(rowsum, -1).flatten()
57 | r_inv[np.isinf(r_inv)] = 0.
58 | r_mat_inv = sp.diags(r_inv)
59 | mx = r_mat_inv.dot(mx)
60 |
61 | return mx
62 |
63 | def normalize_sparse_adj(mx):
64 | """Row-normalize sparse matrix"""
65 | rowsum = np.array(mx.sum(1)) # D_hat (Diagonal Matrix for Degrees)
66 | r_inv_sqrt = np.power(rowsum, -0.5).flatten() # D_hat^(-1/2)
67 | r_inv_sqrt[np.isinf(r_inv_sqrt)] = 0.
68 | r_mat_inv_sqrt = sp.diags(r_inv_sqrt) # list of diagonal of D_hat^(-1/2)
69 |
70 | return mx.dot(r_mat_inv_sqrt).transpose().dot(r_mat_inv_sqrt).tocoo() # D_hat^(-1/2) . A_hat . D_hat^(-1/2)
71 |
72 | def check_symmetric(a, tol=1e-8):
73 | return not False in (np.abs(a-a.T) < tol)
74 |
75 | def pitfall(path, dataset):
76 | x, y, tx, ty, allx, ally, graph = read_data(path=args.data_path, dataset=args.dataset)
77 |
78 | print("Redundant edges in the Graph!")
79 | # 데이터 그래프 내의 redundant한 edge가 존재합니다. 따라서 원 논문과 node 개수는 동일하나,
80 | # 엣지 개수는 다른 adjacency matrix가 출력됩니다.
81 | edges = 0
82 | idx = 0
83 | for key in graph:
84 | orig_lst = (graph[key])
85 | set_lst = set(graph[key])
86 | edges += len(orig_lst)
87 |
88 | if len(orig_lst) != len(set_lst):
89 | print(orig_lst)
90 | idx += (len(orig_lst) - len(set_lst))
91 |
92 | print("Number of Redundant Edges : %d" %idx)
93 | print("Reported Edges : %d" %(edges/2))
94 |
95 | # adj
96 | adj = nx.adjacency_matrix(nx.from_dict_of_lists(graph))
97 |
98 | # edge from adj
99 | print("There also exists {} self inferences!!".format(adj.diagonal().sum()))
100 | # Self inference도 존재하므로 (원래 adjacency matrix의 diagonal의 합은 0이어야 합니다)
101 | act_edges = adj.sum().sum() + adj.diagonal().sum() # diagonal 은 한 번만 계산되므로 /2 이전 한 번 더 더해줍니다.
102 | print("Actual Edges in the Adjacency Matrix : %d" %(act_edges/2))
103 |
104 | def preprocess_data(path, dataset):
105 | x, y, tx, ty, allx, ally, graph = read_data(path=args.data_path, dataset=args.dataset)
106 |
107 | test_idx = parse_index_file("{}/ind.{}.test.index".format(path, dataset))
108 | test_idx_range = np.sort(test_idx) # test idx 를 오름차순으로 정리한다.
109 |
110 | idx_train = range(len(y))
111 | idx_val = range(len(y), len(y)+500)
112 | idx_test = test_idx_range.tolist()
113 |
114 | # train / val / test split
115 | if (args.step == 'split'):
116 | print("| # of train set : {}".format(len(idx_train)))
117 | print("| # of validation set : {}".format(len(idx_val)))
118 | print("| # of test set : {}".format(len(idx_test)))
119 |
120 | L = np.sort(idx_test)
121 | missing = missing_elements(L)
122 |
123 | if (args.step == 'isolate'):
124 | print("Isolated Nodes : %s" %str(missing))
125 |
126 | # citeseer 데이터 전처리
127 | if dataset == 'citeseer':
128 | tx, ty = preprocess_citeseer(tx, ty, test_idx)
129 |
130 | # feature, adj
131 | features = sp.vstack((allx, tx)).tolil()
132 | features[test_idx, :] = features[test_idx_range, :]
133 | adj = nx.adjacency_matrix(nx.from_dict_of_lists(graph))
134 |
135 | print("| # of nodes : {}".format(adj.shape[0]))
136 | print("| # of edges : {}".format((adj.sum().sum() + adj.diagonal().sum())/2))
137 | print("| # of features : {}".format(features.shape[1]))
138 | print("| # of clases : {}".format(ally.shape[1]))
139 |
140 | if args.step == 'normalize':
141 | bef_features = features
142 | bef_adj = adj
143 |
144 | features = normalize_sparse_feature(features)
145 | adj = normalize_sparse_adj(adj+sp.eye(adj.shape[0])) # input is A_hat
146 |
147 | print("Features example before normalization : ")
148 | print(bef_features[:2])
149 | print("Features example after normalization : ")
150 | print(features[:2])
151 | print("Adjacency matrix before normalization : ")
152 | print(bef_adj)
153 | print("Adjacency matrix after normalization : ")
154 | print(adj)
155 |
156 | features = torch.FloatTensor(np.array(features.todense()))
157 | sparse_mx = adj.tocoo().astype(np.float32)
158 | adj = torch.FloatTensor(np.array(adj.todense()))
159 |
160 | labels = np.vstack((ally, ty))
161 | labels[test_idx, :] = labels[test_idx_range, :]
162 |
163 | if dataset == 'citeseer':
164 | save_label = np.where(labels)[1]
165 | for element in missing:
166 | save_label = np.insert(save_label, element, 0) # Missing (Isolated) Nodes 자리에 0 을 채운다.
167 | labels = torch.LongTensor(save_label)
168 | else:
169 | labels = torch.LongTensor(np.where(labels)[1])
170 |
171 | idx_train, idx_val, idx_test = list(map(lambda x: torch.LongTensor(x), [idx_train, idx_val, idx_test]))
172 |
173 | return adj, features, labels, idx_train, idx_val, idx_test
174 |
175 | if __name__ == '__main__':
176 | # Argument
177 | parser = argparse.ArgumentParser(description='PyTorch KR Tutorial')
178 | parser.add_argument('--dataset', required=True, type=str, help='dataset')
179 | parser.add_argument('--data_path',
180 | default=os.path.join(Path.home(), "Data", "Planetoid"), type=str, help='data path')
181 | parser.add_argument('--step', required=True, type=str, help='[split | isolate | normalize]')
182 | parser.add_argument('--mode', default='process', type=str, help='[process | pitfall]')
183 | args = parser.parse_args()
184 |
185 | # Main
186 | if args.mode == 'process':
187 | adj, features, labels, idx_train, idx_val, idx_test = preprocess_data(path=args.data_path, dataset=args.dataset)
188 | elif args.mode == 'pitfall':
189 | pitfall(path=args.data_path, dataset=args.dataset)
190 |
--------------------------------------------------------------------------------
/1_Going_Beyond_Euclidean_Data/README.md:
--------------------------------------------------------------------------------
1 | Geometric Deep Learning: Going Beyond Euclidean Data
2 | -------------------------------------------------------
3 | 저자 논문 : [here](https://arxiv.org/pdf/1611.08097.pdf).
4 |
5 | # Euclidean vs Non-Euclidean
6 |
7 | ## 1.1 Euclidean 공간이란?
8 |
9 | Euclidean 공간(혹은 Euclidean Geometry)란, 수학적으로 유클리드가 연구했던 평면과 공간의 일반화된 표현입니다.
10 |
11 | 좁은 의미에서 유클리드 공간은, [피타고라스의 정의](https://ko.wikipedia.org/wiki/%ED%94%BC%ED%83%80%EA%B3%A0%EB%9D%BC%EC%8A%A4%EC%9D%98_%EC%A0%95%EB%A6%AC)에 의한 길이소의 제곱의 계수가 모두 양수인 공간을 이야기합니다.
12 | 넓은 의미에서 유클리드 공간은, **그리드(Grid)**로 표현이 가능한 모든 공간을 일컫습니다.
13 | 이 때 그리드(Grid)는, 시간과 공간적 개념을 모두 포함하며, 대표적인 예시로는 '2D 이미지', '3D Voxel', '음성' 데이터 등을 들 수 있습니다.
14 |
15 | | | | |
16 | |:---:|:---:|:---:|
17 | | **2D 이미지** | **3D Voxel** | **음성** |
18 |
19 | ## 1.2 Non Euclidean 공간이란?
20 |
21 | 문자 그대로 'Euclidean 공간이 아닌 공간'을 지칭하며, 대표적으로 두 가지를 들 수 있습니다.
22 |
23 | ### [1.2.1 Manifold](https://ko.wikipedia.org/wiki/%EB%8B%A4%EC%96%91%EC%B2%B4)
24 |
25 | Manifold란, 두 점 사이의 거리 혹은 유사도가 근거리에서는 유클리디안(Euclidean metric, 직선거리)를 따르지만 원거리에서는 그렇지 않은 공간을 일컫습니다.
26 |
27 | 이해가 쉬운 가장 간단한 예로는, 구의 표면(2차원 매니폴드)를 들 수 있습니다.
28 | 3차원 공간에서 A점과 B점 사이의 유클리디안 거리(얇은 실선)와 실제의 거리(geodesic distance, 굵은 실선)는 일치하지 않는 것을 볼 수 있습니다.
29 |
30 |
31 |
32 | 이러한 Manifold 형태를 가지는 데이터의 대표적인 예시로는 3D mesh 혹은 point cloud 형태를 들 수 있습니다.
33 |
34 | - 3D Mesh
35 |
36 | [Wikipedia] Material made of a network of wire or thread.
37 |
38 | 3D Mesh란, 다각형의 조합을 통해 3D 모델을 구성한 것을 의미한다.
39 |
40 | 매우 많은 개수의 다각형으로 실제에 가깝게 사물을 표현할 수 있으면서도, 적은 개수의 간단한 모양의 조합으로도 사물을 빠르게 표현할 수 있는 것이 가장 큰 장점이다.
41 |
42 | - Point cloud
43 |
44 | 점구름(point cloud)란, 3차원 좌표계에서 X, Y, Z 좌표로 정의되며 사물의 표면을 나타내는 데에 주로 사용된다.
45 | 3D scanner에서 주로 이용하는 3차원 표현 방식이다.
46 |
47 | 이런 point cloud는, surface reconstruction을 위해 앞서 소개한 mesh 로 변형하여 처리하기도 한다.
48 |
49 | |
|
|
50 | |:---:|:---:|
51 | | **3D Mesh** | **Point cloud** |
52 |
53 | ### [1.2.2 Graph](https://en.wikipedia.org/wiki/Graph_\(discrete_mathematics\))
54 |
55 | Graph란, 일련의 노드의 집합 **V**와 연결(변)의 집합 **E**로 구성된 자료 구조의 일종입니다.
56 | 일반적으로 노드에는 데이터가, 엣지엔 노드와 노드 사이의 관계 정보가 포함되어 있습니다.
57 |
58 | 일상적으로 볼 수 있는 Graph형 데이터의 예시로는 Social network 혹은 Brain functional connectivity network등이 있습니다.
59 |
60 | |
|
|
61 | |:---:|:---:|
62 | | **Social Networks** | **Brain Functional Networks** |
63 |
64 | 용어 설명 : [출처](https://ratsgo.github.io/data%20structure&algorithm/2017/11/18/graph/)
65 |
66 | | 용어 | 설명 |
67 | |:------------:|:--------------------|
68 | | sparse graph | node의 개수 `>` edge의 개수 |
69 | | dense graph | node의 개수 `<` edge의 개수 |
70 | | adjacent | 임의의 두 node가 하나의 edge로 연결되어 있을 경우, 두 node는 서로 adjacent 하다 |
71 | | incident | 임의의 두 node가 하나의 edge로 연결되어 있을 경우, edge는 두 node에 incident 하다 |
72 | | degree | node에 연결된 edge의 개수 |
73 |
74 | - 20190107 Issue
75 |
76 | Sparse Graph와 Dense Graph는 위와 같은 정의 외에도,
77 |
78 | a)
79 | Sparse Graph : A sparse graph is a graph G = (V, E) in which |E| = O(|V|).
80 | Dense Graph : A dense graph is a graph G = (V, E) in which |E| = Θ(|V|2).
81 |
82 | b)
83 | A dense graph is a graph in which the number of edges is close to the maximal number of edges.
84 | A sparse graph is a graph in which the number of edges is close to the minimal number of edges.
85 |
86 | 와 같은 정의도 존재합니다.
87 |
88 | ------------------------------------------------------------------------------------------------------------
89 |
90 | # Spatial vs Spectral
91 |
92 | 딥러닝, 특히 CNN(Convolutional Neural Networks)는 일정한 grid 로 정의할 수 있는 (길이, 시간 등) spatial한 성격의 데이터에 대해 뛰어난 성능을 드러내며 발전해왔습니다.
93 |
94 | 이러한 기존의 Euclidean data (이미지, 음향 등)에서는 두 가지 특징이 성립했습니다.
95 |
96 | - Grid structure
97 | - Translational Equivariance/Invariance
98 |
99 | 그렇다면, 각각 Grid structure 와 Translational Equivariance/Invariance는 어떤 성질이길래 CNN과 같은 알고리즘이 성공적으로 적용될 수 있었을까요?
100 |
101 | ## 2.1 Grid structure
102 |
103 | Grid based metric은 input 크기와 무관하게 적은 parameter의 개수로 이를 학습하는 것을 가능하게 합니다.
104 |
105 | 즉, 이미지의 grid structure는 CNN이 사용하는 아주 작은 크기의 filter만으로도 방대한 이미지의 특징을 빠르게 파악할 수 있도록 해줍니다.
106 |
107 | ## 2.2 'Translational Equivariance/Invariance'란?
108 |
109 | Translational Equivariance/Invariance를 알아보기 위해, 먼저 이미지 처리의 경우를 살펴봅시다.
110 |
111 | 이미지 I 가 (x,y) 에서 가장 중요한 classifier feature인 최대값 m 을 가진다고 가정합시다. 이 때, classifier의 가장 흥미로운 특징 중 하나는, 이미지를 왜곡한 distorted image I' 에서도 m에 의해 마찬가지로 classification이 된다는 점입니다.
112 |
113 | 이러한 특징을 데이터의 Translational한 구조라고 하는데, Translational한 구조의 데이터는 모델의 weight sharing을 가능하게 만들어, 학습 시 매우 큰 이점을 줄 수 있습니다.
114 |
115 | Translational 구조에는 대표적으로 Equivariance와 Invariance를 들 수 있습니다.
116 |
117 | Translational Equivariance/Invariance란, 모든 벡터에 대해 translation (u,v)를 적용한다고 했을 때, translation된 새로운 이미지 I'의 최대값 m' 는 m과 동일하며(Equivariance), 최대값이 나타나는 자리 (x', y')는 (x-u, y-v)로 distortion에 대해 "equally" 변화한다는 것을 의미합니다(Invariance).
118 |
119 | | 용어 | 공식 | 설명 |
120 | |:---|:-----------------------|:---|
121 | | Translational Invariance | (x',y') = (x-u, y-v) | 변형에도 불구하고 같은 feature로 mapping 된다. |
122 | | Translational Equivariance | m' = m | 이미지에서의 변형식은 feature에서의 변형식과 대응된다. |
123 |
124 | 우리가 흔히 사용하는 2D convnet의 input인 image는, translation에 대해서는 equivariant하나, rotation에 대해서는 equivariant하지 않습니다.
125 |
126 | 따라서, 이것이 흔히 이미지 인식 학습 코드에 나타나있는 augmentation코드에 'rotation'이 자주 등장하는 이유라고 생각할 수 있습니다.
127 |
128 | 참고자료 : [참고자료1](https://www.slideshare.net/ssuser06e0c5/brief-intro-invariance-and-equivariance),
129 | [참고자료2](https://www.quora.com/What-is-the-difference-between-equivariance-and-invariance-in-Convolution-neural-networks)
130 |
131 | Invariance와 Equivariance한 성질을 부각하여 학습을 조금 더 효과적으로 하기 위하여 다음과 같은 방법이 활용됩니다.
132 |
133 | ### 2.2.1 Invariance
134 |
135 | CNN을 transformation-invariant하게 만들기 위해, training sample에 대한 data-augmentation을 수행합니다.
136 |
137 |
138 |
139 | 위에 나타난 일련의 augmentation을 통해서, 우리는 이미지가 변형됨에도 불구하고 같은 feature vector로 맵핑되도록 학습할 수 있게 됩니다.
140 |
141 | 이는 generalization 단계에서 기존의 이미지 인식 방식보다 월등히 높은 성능을 거둘 수 있도록 하는 데에 큰 역할을 차지하였습니다.
142 |
143 | ### 2.2.2 Equivariance
144 |
145 | - [Group Convnet](https://arxiv.org/pdf/1602.07576.pdf)
146 | - [Capsule Net](https://arxiv.org/pdf/1710.09829.pdf), [CNN의 한계와 CapsNet에 관한 설명](https://jayhey.github.io/deep%20learning/2017/11/28/CapsNet_1/)
147 |
148 | ----------------------------------------------------------------------------------------------------------------
149 |
150 | ## 2.3 Non Euclidean Data : Geometric Deep Learning
151 |
152 | 그렇다면, 위의 두 조건이 충족되지 않는 ***Non-Euclidean data*** 에 대해서는 어떻게 학습을 할 수 있을까요?
153 |
154 | 대표적으로 두 가지의 접근법이 있어왔는데, 한가지는 Spatial한 접근법이고, 한 가지는 Spectral한 접근법입니다.
155 |
156 | ## 2.3.1 Spatial Domain
157 |
158 | 기존에 알고 있던 그리드로 표현할 수 있는 데이터들은 대부분 Spatial Domain 에서 처리가 가능합니다.
159 | 대표적인 Spatial Domain에서의 처리는 이미지 인식에 이미 널리 알려진 Convolutional Neural Network가 존재합니다.
160 |
161 | 또한, 그리드로 정의되어 있지 않는 데이터 역시 spatial domain에서 처리하고자 하는 시도들이 존재한다.
162 | 대표적인 것으로 [Graph Attention Network](https://arxiv.org/pdf/1710.10903.pdf) 를 들 수 있습니다.
163 |
164 | - Spatial 접근 예시 : [Spectral Networks and Deep Locally Connected Networks on Graphs](https://arxiv.org/pdf/1312.6203.pdf)
165 |
166 | 더 자세한 내용은 [4_Spatial_Graph_Convolution](../4_Spatial_Graph_Convolution)에서 다루겠습니다.
167 |
168 | ## 2.3.2 Spectral Domain
169 |
170 | Spatial Domain 내에서 일정한 grid 를 가지지 않아 처리하기가 복잡한 데이터를 다루는 방법 중의 하나는 이를 spectral domain으로 사영시키는 것이다.
171 |
172 | 이는 Fourier Transformation 을 통해 이루어진다.
173 |
174 | 그래프 구조에서는, Laplacian 변환을 통해 spectral space의 basis를 구하며, normalization과 결합하여 아래와 같은 형태로 표현되게 됩니다.
175 |
176 |
177 |
178 | - Spectral 접근 예시 : [Spectral CNN](http://www.cs.yale.edu/homes/spielman/561/)
179 |
180 | 더 자세한 내용은 [3_Spectral_Graph_Convolution](../3_Spectral_Graph_Convolution) 에서 다루겠습니다.
181 |
--------------------------------------------------------------------------------
/3_Spectral_Graph_Convolution/README.md:
--------------------------------------------------------------------------------
1 | # Spectral Graph Convolutional Networks
2 |
3 | 기존의 Euclidean data 에서, Spatial CNN은 다음과 같은 조건 아래에서 뛰어난 성능을 보였습니다.
4 |
5 | - Grid structure
6 | - Translational Equivalance/Invariance
7 |
8 | 그러나, Spatial CNN은 위의 두 조건이 충족되지 않는 Non-Euclidean data에 대해서 학습이 어렵다는 한계점을 지니고 있습니다.
9 | 이를 해결하기 위한 첫 번째 방법은, Spatial domain에서 Spectral domain 으로 옮기는 접근법입니다. [Spectral CNN](http://www.cs.yale.edu/homes/spielman/561/), [Semi-Supervised Classification with Graph Convolutional Networks](https://arxiv.org/pdf/1609.02907.pdf)
10 |
11 | ## Graph Convolutional Networks
12 |
13 | Social Networks, Knowledge Graphs, Protein interaction networks, World Wide Web 등, 우리 주변의 많은 데이터들은 그래 프 구조를 지니고 있습니다.
14 | 대부분의 Graph Neural Network 모델들은 공통된 구조를 가지고 있고, 그래프의 모든 위치에 대해 공유된 필터를 사용한다는 점에 착안하여 CNN(Convolutional Neural Network)와 마찬가지로 이를 GCN(Graph Convolutional Networks)라고 합니다.
15 |
16 |
17 |
18 | Graph Convolutional Networks의 목표는, G=(V, E) (여기서, V는 Vertex, 즉 노드의 표현형이며, E는 Edge, 각 변 혹은 엣지의 표현형입니다.)로 표현되는 그래프 데이터에서 특정 시그널이나 feature를 잡는 함수를 학습하는 것입니다.
19 |
20 | **Input**
21 | - N x D 차원의 feature vector (N : Number of nodes, D : number of input features)
22 | - Graph의 구조를 반영할 수 있는 매트릭스 형태의 표현식; 일반적으로 adjacency matrix A 를 사용합니다.
23 |
24 | **Output**
25 | - N x F 차원의 feature 매트릭스 (N : Number of nodes, F : number of output features)
26 |
27 | 각 뉴럴 네트워크의 계층은 이런 input을 ReLU 혹은 pooling 등의 non-linear function ***f*** 를 적용합니다.
28 |
29 |
30 |
31 | ***f*** 함수를 어떻게 결정하고 parameter화 시키냐에 따라  와 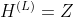, 로부터 원하는 특정 모델을 구상할 수 있게 됩니다.
32 |
33 | 이번 튜토리얼에서 사용할 GCN 구조는 아래와 같습니다.
34 |
35 |
36 |
37 | Non-linear activation function 으로는 ReLU (Rectified Linear Unit)를 사용하며, 이를 통해 아래의 식을 도출할 수 있습니다.
38 |
39 |
40 |
41 | ***A*** 와의 곱은 각 노드에 대해 자기 자신을 제외한(self connection이 존재하지 않는다는 가정 하에) 모든 인접 노드의 feature vector를 합하는 것을 의미합니다.
42 |
43 | 이와 같은 방식에선, 스스로의 feature 값을 참조할 수 없으므로, 이를 해결하기 위하여 ***A*** 를 사용하는 대신 ***A+I*** (A_hat) 을 사용하여 계산합니다.
44 |
45 | ***A*** 는 일반적으로 normalize가 되어있지 않은 상태이므로, ***A*** 와의 곱은 각 feature vector의 scale을 완전히 바꿔놓을 수 있게 됩니다.
46 |
47 | 따라서, 우리는 이전에 기술한 것과 마찬가지로 ***A*** 의 모든 열의 합이 1 이 될 수 있도록 row-wise normalize를 feature와 adjacency matrix에 각각 진행합니다.
48 |
49 | 이는 random walk 방식으로는 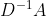이 되며, 원 논문에서 사용한 방식으로는
50 |
51 |
52 |
53 | 가 됩니다.
54 |
55 | 이를 [코드](utils.py)에서 살펴보면
56 |
57 | ```bash
58 | # line 107
59 | adj = normalize_sparse_adj(adj + sp.eye(adj.shape[0])) # pass (A+I) (or A_hat)
60 |
61 | # line 42
62 | def normalize_sparse_adj(mx):
63 | """Laplacian Normalization"""
64 | rowsum = np.array(mx.sum(1)) # D_hat
65 | r_inv_sqrt = np.power(rowsum, -0.5).flatten() # D_hat^(-1/2)
66 | r_inv_sqrt[np.isinf(r_inv_sqrt)] = 0.
67 | r_mat_inv_sqrt = sp.diags(r_inv_sqrt)
68 |
69 | return mx.dot(r_mat_inv_sqrt).transpose().dot(r_mat_inv_sqrt).tocoo() # D_hat^(-1/2) x A_hat x D_hat^(-1/2)
70 | ```
71 |
72 | 각 단계의 계산과정이 코드 상에 어디에 해당하는지는 [gcn.py](./gcn.py) 코드 내에 주석으로 삽입하였습니다.
73 |
74 | **최종 구현 :**
75 |
76 | 위의 모든 구현 이론을 종합하여 [Kipf & Welling](http://arxiv.org/abs/1609.02907) (ICLR 2017) 논문에서 소개한 Graph Convolutional Neural Network 를 구현하였습니다.
77 |
78 | 더 많은 세부 정보를 위해서는, [여기](https://tkipf.github.io/graph-convolutional-networks/)를 참조하시면 좋을 것 같습니다.
79 |
80 | ## Molecule Structure Processing
81 |
82 |
83 |
84 | Graph Structure 데이터의 가장 대표적인 예로는, 분자 구조가 존재할 수 있습니다.
85 |
86 | 이전 neural network 구조에서는, 분자 구조를 사용할 때는 ECFP (Extended Connectivity FingerPrint)를 사용하여 고정된 형식의 벡터 표현식을 이용해왔습니다. [예시자료](https://arxiv.org/pdf/1811.09714.pdf)
87 |
88 |
89 |
90 | 그러나, 이는 Graph 단위에서 특정 요소가 존재하는지의 여부에 대한 표현식이므로, 분명한 한계가 존재할 수 밖에 없습니다.
91 |
92 | 이와 같은 그래프 형태의, non-Euclidean graph 데이터의 구조를 Graph Convolution network를 통하여 학습할 수 있습니다.
93 |
94 | 본 튜토리얼에서는 이를 처리하여 고정된 형식의 벡터를 만드는 forward path를 소개하며, 이후 이를 활용하는 것은
95 |
96 | 마지막 layer의 vector를 연결하여 [classification](https://arxiv.org/pdf/1805.10988.pdf)을 하거나, [fingerprint](https://arxiv.org/pdf/1509.09292.pdf)를 만들거나, siamese network를 구상하여 [유사도를 측정](https://arxiv.org/pdf/1703.02161.pdf)할 수 있습니다.
97 |
98 | 그러나, 분자 구조에는 edge가 위처럼 2차원의 단순한 adjacency matrix에서 표현되지 못합니다.
99 | Edge에도 여러가지 type이 존재하기 때문입니다.
100 |
101 | ## Graphs with Mulitple Type Edges
102 |
103 | 분자 구조의 경우에는, Edge (Bond라고 표현합니다)가 여러가지 type을 가질 수 있습니다. 가장 대표적인 것으로는 single, double, triple, aromatic 등의 bond type이 있습니다.
104 |
105 |
106 |
107 | 이런 경우에는, 일반적으로 Aggregation 이라는 방법을 통해 데이터를 처리합니다. [reference](https://arxiv.org/pdf/1806.02473.pdf)
108 |
109 | 아래의 코드는, 튜토리얼 내에서 지정한 임의의 pid를 가진 molecule vector를 [RDkit](https://www.rdkit.org/)을 통해 graph 형태로 표현한 뒤, 이를 GCN forward path 에 대입하여 100차원의 feature vector를 생성하는 과정입니다.
110 |
111 | 사용된 화합물은 아래와 같이 생긴 1-benzylimidazole 입니다.
112 |
113 |
114 |
115 |
116 | ```bash
117 | # docker run -it bumsoo /bin/bash 실행된 환경
118 | $ python forward_mol.py
119 |
120 | # docker 외부 실행환경
121 | $ docker run -it bumsoo python 3_Spectral_Graph_Convolution/forward_mol.py
122 | ```
123 |
124 | 위 코드를 실행시키면, 아래와 같은 결과를 얻을 수 있습니다.
125 |
126 | 
127 |
128 | 결과 화면을 통해, adj = (12 x 12 x 6), feat = (12 x 62) 짜리 그래프로부터 고정된 500 크기의 vector 로 forward가 됐음을 확인할 수 있습니다.
129 |
130 | ## Train Planetoid Network
131 |
132 | | dataset | classes | nodes | # of edge |
133 | |:-------:|:-------:|:-----:|:-----------:|
134 | | citeseer| 6 | 3,327 | 4,676 |
135 | | cora | 7 | 2,708 | 5,278 |
136 | | pubmed | 3 | 19,717| 44,327 |
137 |
138 |
139 | 이번에는, [2_Understanding_Graphs](../2_Understanding_Graphs) 에서 다루었던 Planetoid의 데이터셋에 대해 학습을 해보겠습니다.
140 |
141 | Planetoid는 node classification task 이며, document에 해당하는 각 노드가 주어진
142 |
143 | k 개의 class 중 어느 class 에 해당하는지 classification을 하면 되는 문제입니다.
144 |
145 | 아래의 script를 실행시키면, 원하시는 데이터셋에 GCN 을 학습시키실 수 있습니다.
146 |
147 | [2_Understanding_Graphs](../2_Understanding_Graphs) 에서 설명한 것과 같이 Planetoid 데이터셋을 다운로드 받으신 후, [:dir to dataset] 에 대입하여 실행하시면 됩니다.
148 |
149 | 기본 default 설정은 2_Understanding_Graphs 의 /home/[:user]/Data/Planetoid 디렉토리로 설정되어 있습니다.
150 |
151 | 이전 2번 튜토리얼 레포에서 보셨던 데이터의 전처리에 관한 사항은, [utils.py](utils.py) 에서 확인해보실 수 있습니다.
152 |
153 | ```bash
154 | # nvidia docker run -it bumsoo-graph-tutorial /bin/bash 실행 이후
155 | > python train.py --dataroot [:dir to dataset] --datset [:cora | citeseer | pubmed]
156 |
157 | # 바로 실행하는 경우
158 | $ nvidia-docker run -it bumsoo python 3_Spatial_Graph_Convolution/train.py --dataset [:dataset]
159 | ```
160 |
161 | 위 코드를 실행하면 다음과 같은 결과 화면을 보실 수 있습니다.
162 |
163 | 
164 |
165 | ## Test (Inference) Planetoid networks
166 |
167 | Training 과정을 모두 마치신 이후, 다음과 같은 코드를 통해 학습된 weight를 테스트셋에 적용해보실 수 있습니다.
168 |
169 | ```bash
170 | # nvidia docker run -it bumsoo-graph-tutorial /bin/bash 실행 이후
171 | > python test.py --dataroot [:dir to dataset] --dataset [:cora | citeseer | pubmed]
172 |
173 | # 바로 실행하는 경우
174 | $ nvidia-docker run -it bumsoo python 3_Spatial_Graph_Convolution/test.py --dataset [:dataset]
175 | ```
176 |
177 | 위 코드를 실행하면 다음과 같은 결과 화면을 보실 수 있습니다.
178 |
179 | 
180 |
181 | ## Result
182 |
183 | 최종 성능은 다음과 같습니다. GCN (recon) 이 본 repository의 코드로 학습 후, test data 에 적용한 결과입니다.
184 |
185 | | Method | Citeseer | Cora | Pubmed |
186 | |:------------|:---------|:-----|:-------|
187 | | GCN (rand) | 67.9 | 80.1 | 78.9 |
188 | | GCN (paper) | 70.3 | 81.5 | 79.0 |
189 | | **GCN (recon)** | **70.6** | **80.9** | **80.8** |
190 |
--------------------------------------------------------------------------------