├── .gitignore
├── README.md
├── README_files
    ├── README_11_1.png
    ├── README_13_0.png
    ├── README_26_0.png
    ├── README_28_0.png
    ├── README_30_0.png
    ├── README_32_0.png
    ├── README_37_0.png
    ├── README_39_0.png
    ├── README_4_1.png
    └── README_6_0.png
├── build.sh
├── images
    └── uncertainty.png
├── main.ipynb
├── main.notebook.py
├── main.py
├── main.streambook.py
├── poetry.lock
├── presentation.md
├── pyproject.toml
├── requirements.txt
└── update_readme.py


/.gitignore:
--------------------------------------------------------------------------------
  1 | # Byte-compiled / optimized / DLL files
  2 | __pycache__/
  3 | *.py[cod]
  4 | *$py.class
  5 | 
  6 | # C extensions
  7 | *.so
  8 | 
  9 | # Distribution / packaging
 10 | .Python
 11 | build/
 12 | develop-eggs/
 13 | dist/
 14 | downloads/
 15 | eggs/
 16 | .eggs/
 17 | lib/
 18 | lib64/
 19 | parts/
 20 | sdist/
 21 | var/
 22 | wheels/
 23 | share/python-wheels/
 24 | *.egg-info/
 25 | .installed.cfg
 26 | *.egg
 27 | MANIFEST
 28 | 
 29 | # PyInstaller
 30 | #  Usually these files are written by a python script from a template
 31 | #  before PyInstaller builds the exe, so as to inject date/other infos into it.
 32 | *.manifest
 33 | *.spec
 34 | 
 35 | # Installer logs
 36 | pip-log.txt
 37 | pip-delete-this-directory.txt
 38 | 
 39 | # Unit test / coverage reports
 40 | htmlcov/
 41 | .tox/
 42 | .nox/
 43 | .coverage
 44 | .coverage.*
 45 | .cache
 46 | nosetests.xml
 47 | coverage.xml
 48 | *.cover
 49 | *.py,cover
 50 | .hypothesis/
 51 | .pytest_cache/
 52 | cover/
 53 | 
 54 | # Translations
 55 | *.mo
 56 | *.pot
 57 | 
 58 | # Django stuff:
 59 | *.log
 60 | local_settings.py
 61 | db.sqlite3
 62 | db.sqlite3-journal
 63 | 
 64 | # Flask stuff:
 65 | instance/
 66 | .webassets-cache
 67 | 
 68 | # Scrapy stuff:
 69 | .scrapy
 70 | 
 71 | # Sphinx documentation
 72 | docs/_build/
 73 | 
 74 | # PyBuilder
 75 | .pybuilder/
 76 | target/
 77 | 
 78 | # Jupyter Notebook
 79 | .ipynb_checkpoints
 80 | 
 81 | # IPython
 82 | profile_default/
 83 | ipython_config.py
 84 | 
 85 | # pyenv
 86 | #   For a library or package, you might want to ignore these files since the code is
 87 | #   intended to run in multiple environments; otherwise, check them in:
 88 | # .python-version
 89 | 
 90 | # pipenv
 91 | #   According to pypa/pipenv#598, it is recommended to include Pipfile.lock in version control.
 92 | #   However, in case of collaboration, if having platform-specific dependencies or dependencies
 93 | #   having no cross-platform support, pipenv may install dependencies that don't work, or not
 94 | #   install all needed dependencies.
 95 | #Pipfile.lock
 96 | 
 97 | # PEP 582; used by e.g. github.com/David-OConnor/pyflow
 98 | __pypackages__/
 99 | 
100 | # Celery stuff
101 | celerybeat-schedule
102 | celerybeat.pid
103 | 
104 | # SageMath parsed files
105 | *.sage.py
106 | 
107 | # Environments
108 | .env
109 | .venv
110 | env/
111 | venv/
112 | ENV/
113 | env.bak/
114 | venv.bak/
115 | 
116 | # Spyder project settings
117 | .spyderproject
118 | .spyproject
119 | 
120 | # Rope project settings
121 | .ropeproject
122 | 
123 | # mkdocs documentation
124 | /site
125 | 
126 | # mypy
127 | .mypy_cache/
128 | .dmypy.json
129 | dmypy.json
130 | 
131 | # Pyre type checker
132 | .pyre/
133 | 
134 | # pytype static type analyzer
135 | .pytype/
136 | 
137 | # Cython debug symbols
138 | cython_debug/
139 | 
140 | # custom
141 | .vscode
142 | 


--------------------------------------------------------------------------------
/README.md:
--------------------------------------------------------------------------------
  1 | # Quantile Regression
  2 | _A simple method to estimate uncertainty in Machine Learning_
  3 | 
  4 | <a href="https://github.com/cgarciae/quantile-regression" target="_parent">
  5 |     <img src="https://img.shields.io/badge/R-Open%20Repo-blue"/>
  6 | </a>
  7 | <a href="https://hackmd.io/@cgarciae/quantile-regression" target="_parent">
  8 |     <img src="https://img.shields.io/badge/B-Open%20Blog-blue"/>
  9 | </a>
 10 | <a href="https://hackmd.io/@cgarciae/quantile-regression-presentation#/" target="_parent">
 11 |     <img src="https://img.shields.io/badge/S-Open%20Slides-blue"/>
 12 | </a>
 13 | <a href="https://colab.research.google.com/github/cgarciae/quantile-regression/blob/master/main.ipynb" target="_parent">
 14 |     <img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open in Colab"/>
 15 | </a>
 16 | 
 17 | 
 18 | 
 19 | ## Motivation
 20 | When generating predictions about an output, it is sometimes useful to get a confidence score or, similarly, a range of values around this expected value in which the actual value might be found. Practical examples include estimating an upper and lower bound when predicting an ETA or stock price since you not only care about the average outcome but are also very interested in the best-case and worst-case scenarios in when trying to minimize risk e.g. avoid getting late or not loosing money.
 21 | 
 22 | While most Machine Learning techniques do not provide a natural way of doing this, in this article, we will be exploring **Quantile Regression** as a means of doing so. This technique will allow us to learn some critical statistical properties of our data: the quantiles.
 23 | 
 24 | <details>
 25 | <summary markdown="span">Install Dependencies</summary>
 26 | 
 27 | 
 28 | ```python
 29 | # uncomment to install dependencies
 30 | # ! curl -Ls https://raw.githubusercontent.com/cgarciae/quantile-regression/master/requirements.txt > requirements.txt
 31 | # ! pip install -qr requirements.txt
 32 | # ! pip install -U matplotlib
 33 | ```
 34 | 
 35 | </details>
 36 | 
 37 | To begin our journey into quantile regression, we will first get a hold on some data:
 38 | 
 39 | <details>
 40 | <summary markdown="span">Show Code</summary>
 41 | 
 42 | 
 43 | ```python
 44 | import numpy as np
 45 | import matplotlib.pyplot as plt
 46 | import os
 47 | 
 48 | plt.rcParams["figure.dpi"] = int(os.environ.get("FIGURE_DPI", 150))
 49 | plt.rcParams["figure.facecolor"] = os.environ.get("FIGURE_FACECOLOR", "white")
 50 | np.random.seed(69)
 51 | 
 52 | 
 53 | def create_data(multimodal: bool):
 54 |     x = np.random.uniform(0.3, 10, 1000)
 55 |     y = np.log(x) + np.random.exponential(0.1 + x / 20.0)
 56 | 
 57 |     if multimodal:
 58 |         x = np.concatenate([x, np.random.uniform(5, 10, 500)])
 59 |         y = np.concatenate([y, np.random.normal(6.0, 0.3, 500)])
 60 | 
 61 |     return x[..., None], y[..., None]
 62 | 
 63 | 
 64 | multimodal: bool = False
 65 | 
 66 | x, y = create_data(multimodal)
 67 | 
 68 | fig = plt.figure()
 69 | plt.scatter(x[..., 0], y[..., 0], s=20, facecolors="none", edgecolors="k")
 70 | plt.close()
 71 | ```
 72 | 
 73 | </details>
 74 | 
 75 | 
 76 | ```python
 77 | fig
 78 | ```
 79 | 
 80 | 
 81 | 
 82 | 
 83 |     
 84 | 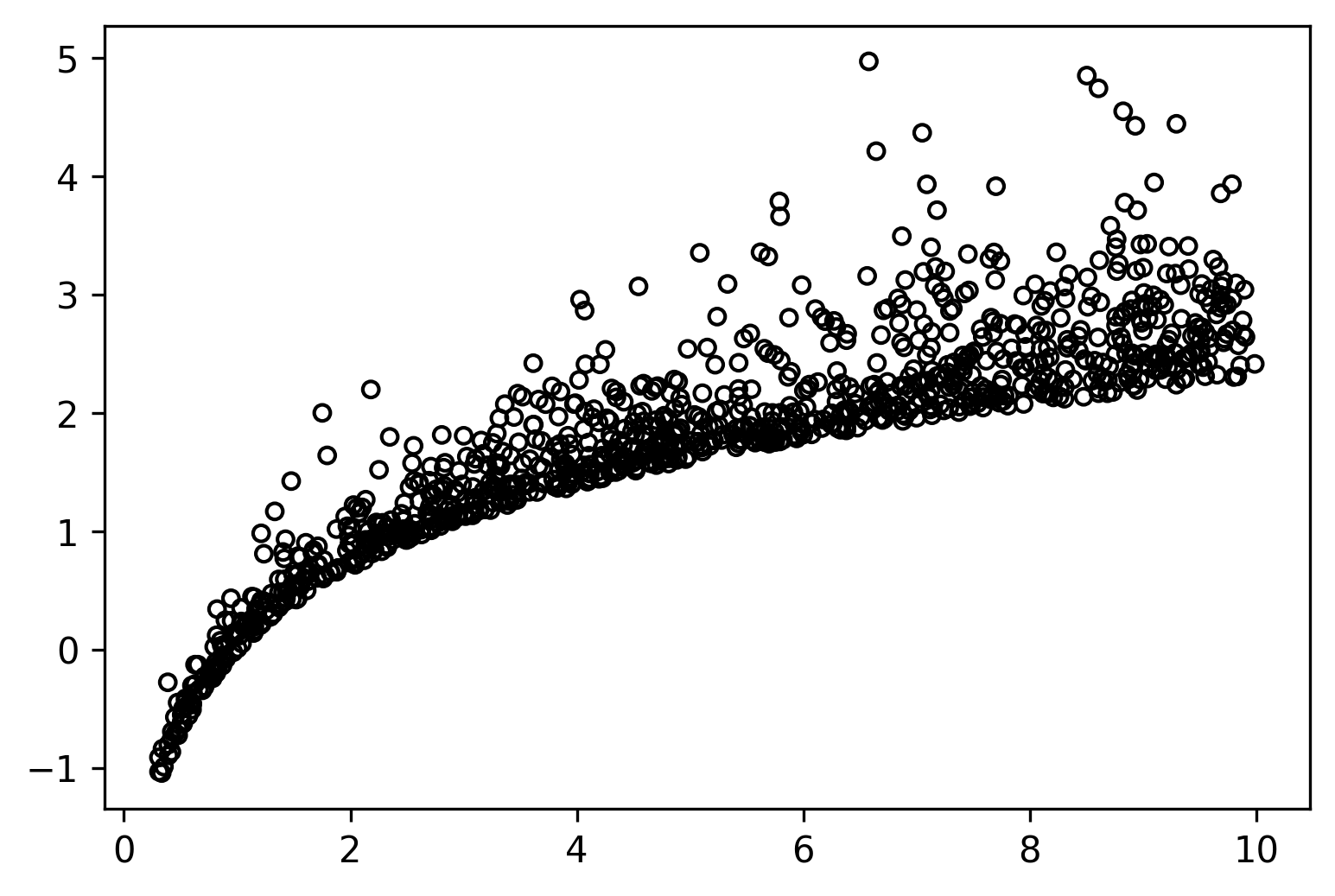![png](https://raw.githubusercontent.com/cgarciae/quantile-regression/master/README_files/README_6_0.png)
 85 |     
 86 | 
 87 | 
 88 | 
 89 | Here we have a simple 2D dataset; however, notice that `y` has some very peculiar statistical properties:
 90 | 
 91 | 1. The data does not have the property of being normally distributed. The data is exponentially distributed.
 92 | 2. The previous also means its noise is not symmetric.
 93 | 3. Its variance is not constant. It increases as x increases.
 94 | 
 95 | When making predictions for this kind of data, we might be very interested in knowing what range of values our data revolves around such that we can judge if a specific outcome is expected or not, what are the best and worst-case scenarios, and so on.
 96 | 
 97 | ## Quantile Loss
 98 | The only thing special about quantile regression is its loss function. Instead of the usual MAE or MSE losses for quantile regression, we use the following function:
 99 | 
100 | $$
101 | \begin{aligned}
102 |     E &= y - f(x) \\
103 |     L_q &= \begin{cases}
104 |         q  E,     &    E \gt 0  \\
105 |         (1 - q) (-E), &    E \lt 0
106 |     \end{cases}
107 | \end{aligned}
108 | $$
109 | 
110 | Here $E$ is the error term, and $L_q$ is the loss function for the quantile $q$. So what do we mean by this? Concretely it means that $L_q$ will bias $f(x)$ to output the value of the $q$'th quantile instead of the usual mean or median statistic. The big question is: how does it do it?
111 | 
112 | First lets notice that this formula can be rewritten as follows:
113 | 
114 | $$
115 | \begin{aligned}
116 |     E &= y - f(x) \\
117 |     L_q &= \max \begin{cases}
118 |         q  E   \\
119 |         (q - 1) E
120 |     \end{cases}
121 | \end{aligned}
122 | $$
123 | 
124 | Using $\max$ instead of a conditional statement will make it more straightforward to implement on tensor/array libraries. We will do this next in jax.
125 | 
126 | 
127 | ```python
128 | import jax
129 | import jax.numpy as jnp
130 | 
131 | 
132 | def quantile_loss(q, y_true, y_pred):
133 |     e = y_true - y_pred
134 |     return jnp.maximum(q * e, (q - 1.0) * e)
135 | ```
136 | 
137 | ## Loss Landscape
138 | Now that we have this function let us explore the error landscape for a particular set of predictions. Here we will generate values for `y_true` in the range $[10, 20]$, and for a particular value of $q$ (0.8 by default), we will compute the total error you would get for each value `y_pred` could take. Ideally, we want to find the value of `y_pred` where the error is the smallest.
139 | 
140 | <details>
141 | <summary markdown="span">Show code</summary>
142 | 
143 | 
144 | ```python
145 | def calculate_error(q):
146 |     y_true = np.linspace(10, 20, 100)
147 |     y_pred = np.linspace(10, 20, 200)
148 | 
149 |     loss = jax.vmap(quantile_loss, in_axes=(None, None, 0))(q, y_true, y_pred)
150 |     loss = loss.mean(axis=1)
151 | 
152 |     return y_true, y_pred, loss
153 | 
154 | 
155 | q = 0.8
156 | y_true, y_pred, loss = calculate_error(q)
157 | q_true = np.quantile(y_true, q)
158 | 
159 | 
160 | fig = plt.figure()
161 | plt.plot(y_pred, loss)
162 | plt.vlines(q_true, 0, loss.max(), linestyles="dashed", colors="k")
163 | plt.gca().set_xlabel("y_pred")
164 | plt.gca().set_ylabel("loss")
165 | plt.title(f"Q({q:.2f}) = {q_true:.1f}")
166 | plt.close()
167 | ```
168 | 
169 |     WARNING:absl:No GPU/TPU found, falling back to CPU. (Set TF_CPP_MIN_LOG_LEVEL=0 and rerun for more info.)
170 | 
171 | 
172 | </details>
173 | 
174 | 
175 | ```python
176 | fig
177 | ```
178 | 
179 | 
180 | 
181 | 
182 |     
183 | 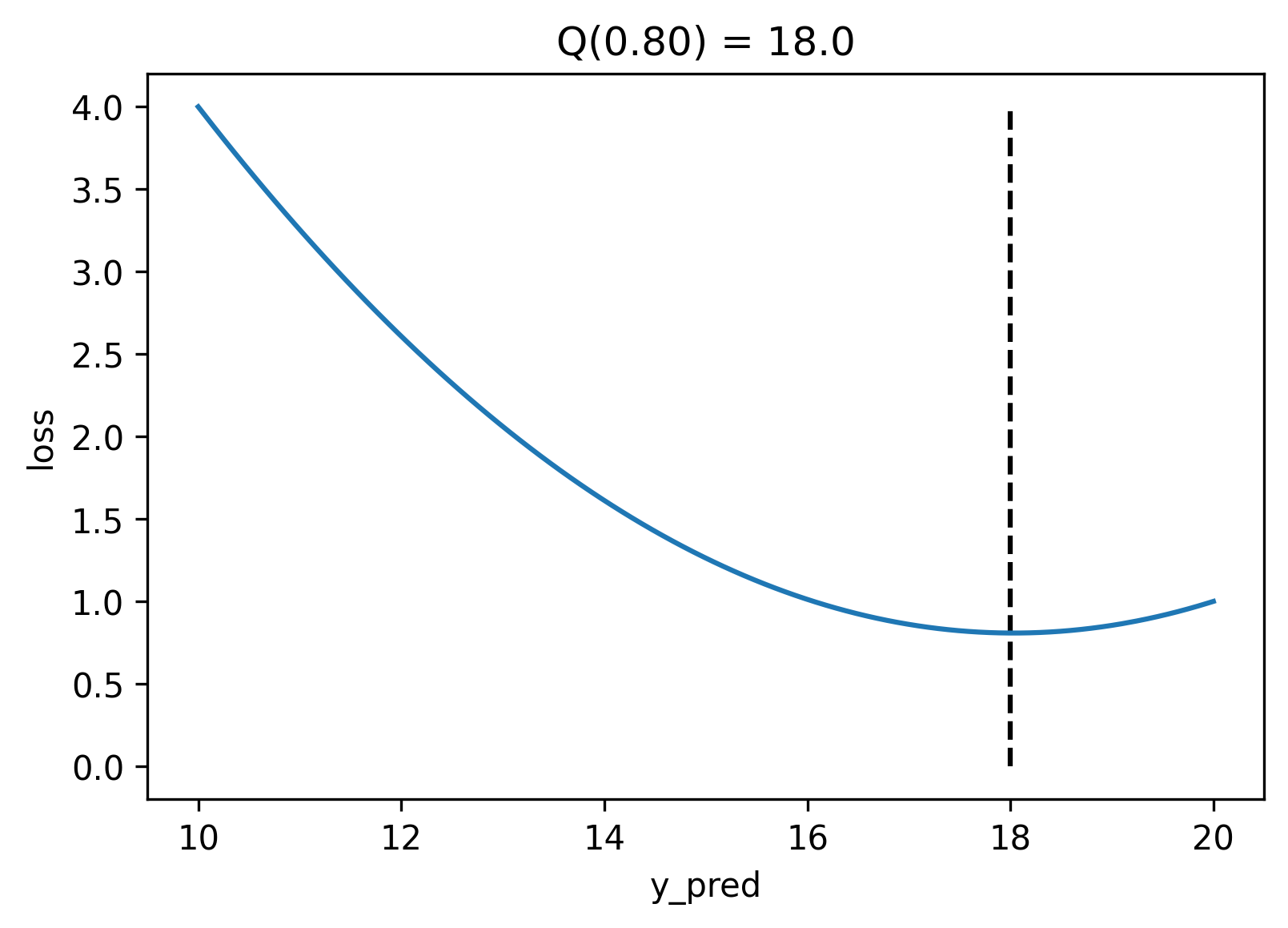![png](https://raw.githubusercontent.com/cgarciae/quantile-regression/master/README_files/README_13_0.png)
184 |     
185 | 
186 | 
187 | 
188 | If we plot the error, the quantile loss's minimum value is strictly at the value of the $q$th quantile. It achieves this because the quantile loss is not symmetrical; for quantiles above `0.5` it penalizes positive  errors stronger than negative errors, and the opposite is true for quantiles below `0.5`. In particular, quantile `0.5` is the median, and its formula is equivalent to the MAE.
189 | 
190 | ## Deep Quantile Regression
191 | 
192 | Generally, we would need to create to create a model per quantile. However, if we use a neural network, we can output the predictions for all the quantiles simultaneously. Here will use `elegy` to create a neural network with two hidden layers with `relu` activations and linear layers with `n_quantiles` output units.
193 | 
194 | 
195 | ```python
196 | import elegy
197 | 
198 | 
199 | class QuantileRegression(elegy.Module):
200 |     def __init__(self, n_quantiles: int):
201 |         super().__init__()
202 |         self.n_quantiles = n_quantiles
203 | 
204 |     def call(self, x):
205 |         x = elegy.nn.Linear(128)(x)
206 |         x = jax.nn.relu(x)
207 |         x = elegy.nn.Linear(64)(x)
208 |         x = jax.nn.relu(x)
209 |         x = elegy.nn.Linear(self.n_quantiles)(x)
210 | 
211 |         return x
212 | ```
213 | 
214 | Now we will adequately define a `QuantileLoss` class that is parameterized by
215 | a set of user-defined `quantiles`.
216 | 
217 | <details>
218 | <summary markdown="span">Show code</summary>
219 | 
220 | 
221 | ```python
222 | class QuantileLoss(elegy.Loss):
223 |     def __init__(self, quantiles):
224 |         super().__init__()
225 |         self.quantiles = np.array(quantiles)
226 | 
227 |     def call(self, y_true, y_pred):
228 |         loss = jax.vmap(quantile_loss, in_axes=(0, None, -1), out_axes=1)(
229 |             self.quantiles, y_true[:, 0], y_pred
230 |         )
231 |         return jnp.sum(loss, axis=-1)
232 | ```
233 | 
234 | </details>
235 | 
236 | Notice that we use the same `quantile_loss` that we created previously, along with some `jax.vmap` magic to properly vectorize the function. Finally, we will create a simple function that creates and trains our model for a set of quantiles using `elegy`.
237 | 
238 | <details>
239 | <summary markdown="span">Show code</summary>
240 | 
241 | 
242 | ```python
243 | import optax
244 | 
245 | 
246 | def train_model(quantiles, epochs: int, lr: float, eager: bool):
247 |     model = elegy.Model(
248 |         QuantileRegression(n_quantiles=len(quantiles)),
249 |         loss=QuantileLoss(quantiles),
250 |         optimizer=optax.adamw(lr),
251 |         run_eagerly=eager,
252 |     )
253 | 
254 |     model.fit(x, y, epochs=epochs, batch_size=64, verbose=0)
255 | 
256 |     return model
257 | 
258 | 
259 | if not multimodal:
260 |     quantiles = (0.05, 0.1, 0.3, 0.5, 0.7, 0.9, 0.95)
261 | else:
262 |     quantiles = np.linspace(0.05, 0.95, 9)
263 | 
264 | model = train_model(quantiles=quantiles, epochs=3001, lr=1e-4, eager=False)
265 | ```
266 | 
267 | </details>
268 | 
269 | 
270 | ```python
271 | model.summary(x)
272 | ```
273 | 
274 | 
275 | <pre style="white-space:pre;overflow-x:auto;line-height:normal;font-family:Menlo,'DejaVu Sans Mono',consolas,'Courier New',monospace">┏━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━┓
276 | ┃<span style="font-weight: bold"> Layer                        </span>┃<span style="font-weight: bold"> Outputs Shape        </span>┃<span style="font-weight: bold"> Trainable        </span>┃<span style="font-weight: bold"> Non-trainable </span>┃
277 | ┃                              ┃                      ┃<span style="font-weight: bold"> Parameters       </span>┃<span style="font-weight: bold"> Parameters    </span>┃
278 | ┡━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━┩
279 | │ Inputs                       │ (1000, 1)    <span style="color: #7f7f7f; text-decoration-color: #7f7f7f">float64</span> │                  │               │
280 | ├──────────────────────────────┼──────────────────────┼──────────────────┼───────────────┤
281 | │ linear    <span style="color: #7f7f7f; text-decoration-color: #7f7f7f">Linear</span>             │ (1000, 128)  <span style="color: #7f7f7f; text-decoration-color: #7f7f7f">float32</span> │ <span style="color: #008000; text-decoration-color: #008000">256</span>      <span style="color: #7f7f7f; text-decoration-color: #7f7f7f">1.0 KB</span>  │               │
282 | ├──────────────────────────────┼──────────────────────┼──────────────────┼───────────────┤
283 | │ linear_1  <span style="color: #7f7f7f; text-decoration-color: #7f7f7f">Linear</span>             │ (1000, 64)   <span style="color: #7f7f7f; text-decoration-color: #7f7f7f">float32</span> │ <span style="color: #008000; text-decoration-color: #008000">8,256</span>    <span style="color: #7f7f7f; text-decoration-color: #7f7f7f">33.0 KB</span> │               │
284 | ├──────────────────────────────┼──────────────────────┼──────────────────┼───────────────┤
285 | │ linear_2  <span style="color: #7f7f7f; text-decoration-color: #7f7f7f">Linear</span>             │ (1000, 7)    <span style="color: #7f7f7f; text-decoration-color: #7f7f7f">float32</span> │ <span style="color: #008000; text-decoration-color: #008000">455</span>      <span style="color: #7f7f7f; text-decoration-color: #7f7f7f">1.8 KB</span>  │               │
286 | ├──────────────────────────────┼──────────────────────┼──────────────────┼───────────────┤
287 | │ *         <span style="color: #7f7f7f; text-decoration-color: #7f7f7f">QuantileRegression</span> │ (1000, 7)    <span style="color: #7f7f7f; text-decoration-color: #7f7f7f">float32</span> │                  │               │
288 | ├──────────────────────────────┼──────────────────────┼──────────────────┼───────────────┤
289 | │<span style="font-weight: bold">                              </span>│<span style="font-weight: bold">                Total </span>│<span style="font-weight: bold"> </span><span style="color: #008000; text-decoration-color: #008000; font-weight: bold">8,967</span><span style="font-weight: bold">    </span><span style="color: #7f7f7f; text-decoration-color: #7f7f7f; font-weight: bold">35.9 KB</span><span style="font-weight: bold"> </span>│<span style="font-weight: bold">               </span>│
290 | └──────────────────────────────┴──────────────────────┴──────────────────┴───────────────┘
291 | <span style="font-weight: bold">                                                                                          </span>
292 | <span style="font-weight: bold">                            Total Parameters: </span><span style="color: #008000; text-decoration-color: #008000; font-weight: bold">8,967</span><span style="font-weight: bold">   </span><span style="color: #7f7f7f; text-decoration-color: #7f7f7f; font-weight: bold">35.9 KB</span><span style="font-weight: bold">                             </span>
293 | </pre>
294 | 
295 | 
296 | 
297 |     
298 |     
299 | 
300 | 
301 | Now that we have a model let us generate some test data that spans the entire domain and compute the predicted quantiles.
302 | 
303 | <details>
304 | <summary markdown="span">Show code</summary>
305 | 
306 | 
307 | ```python
308 | x_test = np.linspace(x.min(), x.max(), 100)
309 | y_pred = model.predict(x_test[..., None])
310 | 
311 | fig = plt.figure()
312 | plt.scatter(x, y, s=20, facecolors="none", edgecolors="k")
313 | 
314 | for i, q_values in enumerate(np.split(y_pred, len(quantiles), axis=-1)):
315 |     plt.plot(x_test, q_values[:, 0], linewidth=2, label=f"Q({quantiles[i]:.2f})")
316 | 
317 | plt.legend()
318 | plt.close()
319 | ```
320 | 
321 | </details>
322 | 
323 | 
324 | ```python
325 | fig
326 | ```
327 | 
328 | 
329 | 
330 | 
331 |     
332 | 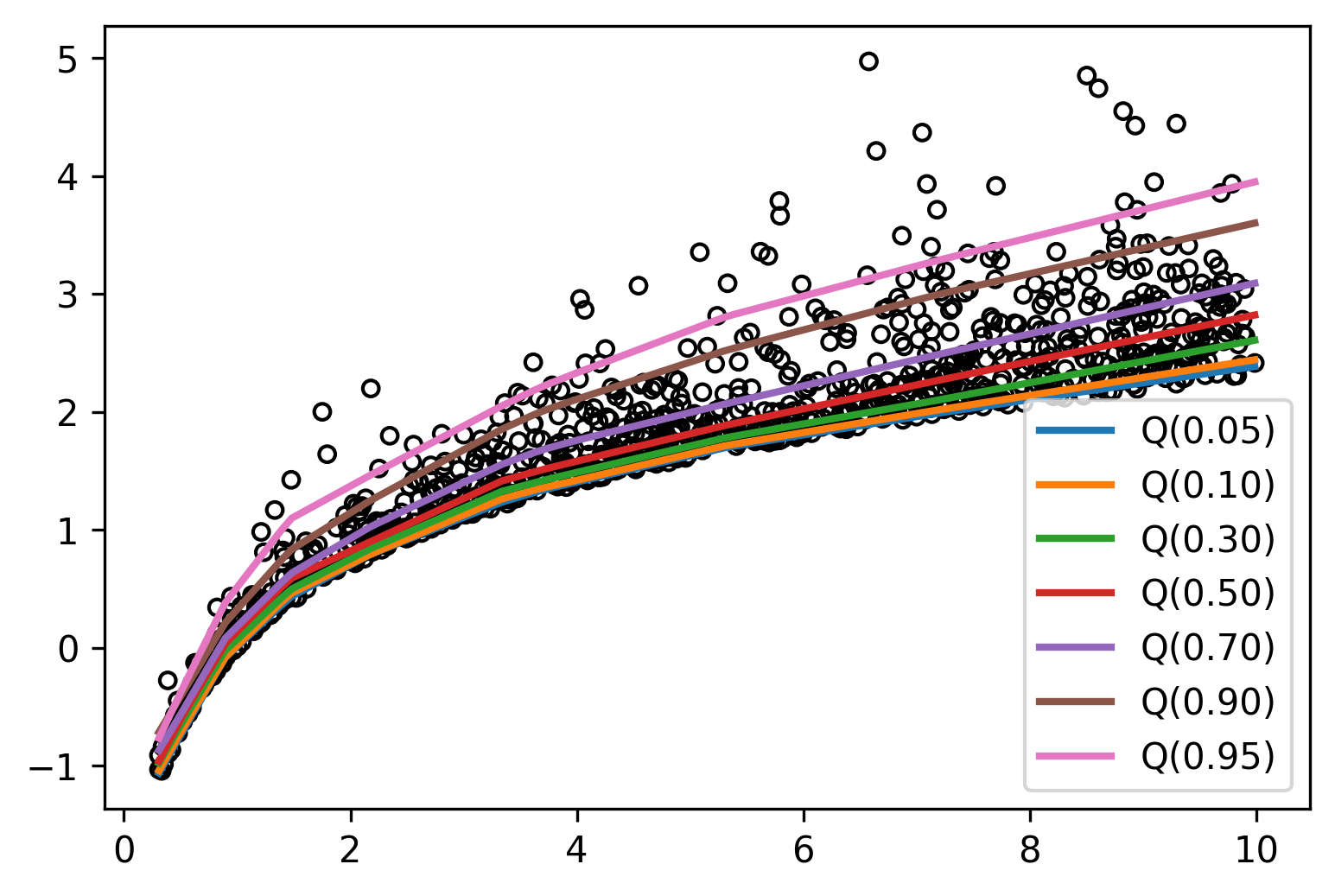![png](https://raw.githubusercontent.com/cgarciae/quantile-regression/master/README_files/README_28_0.png)
333 |     
334 | 
335 | 
336 | 
337 | Amazing! Notice how the first few quantiles are tightly packed together while the last ones spread out, capturing the behavior of the exponential distribution. We can also visualize the region between the highest and lowest quantiles, and this gives us some bounds on our predictions.
338 | 
339 | <details>
340 | <summary markdown="span">Show code</summary>
341 | 
342 | 
343 | ```python
344 | median_idx = np.where(np.isclose(quantiles, 0.5))[0]
345 | 
346 | fig = plt.figure()
347 | plt.fill_between(x_test, y_pred[:, -1], y_pred[:, 0], alpha=0.5, color="b")
348 | plt.scatter(x, y, s=20, facecolors="none", edgecolors="k")
349 | plt.plot(
350 |     x_test,
351 |     y_pred[:, median_idx],
352 |     color="r",
353 |     linestyle="dashed",
354 |     label="Q(0.5)",
355 | )
356 | plt.legend()
357 | plt.close()
358 | ```
359 | 
360 | </details>
361 | 
362 | 
363 | ```python
364 | fig
365 | ```
366 | 
367 | 
368 | 
369 | 
370 |     
371 | 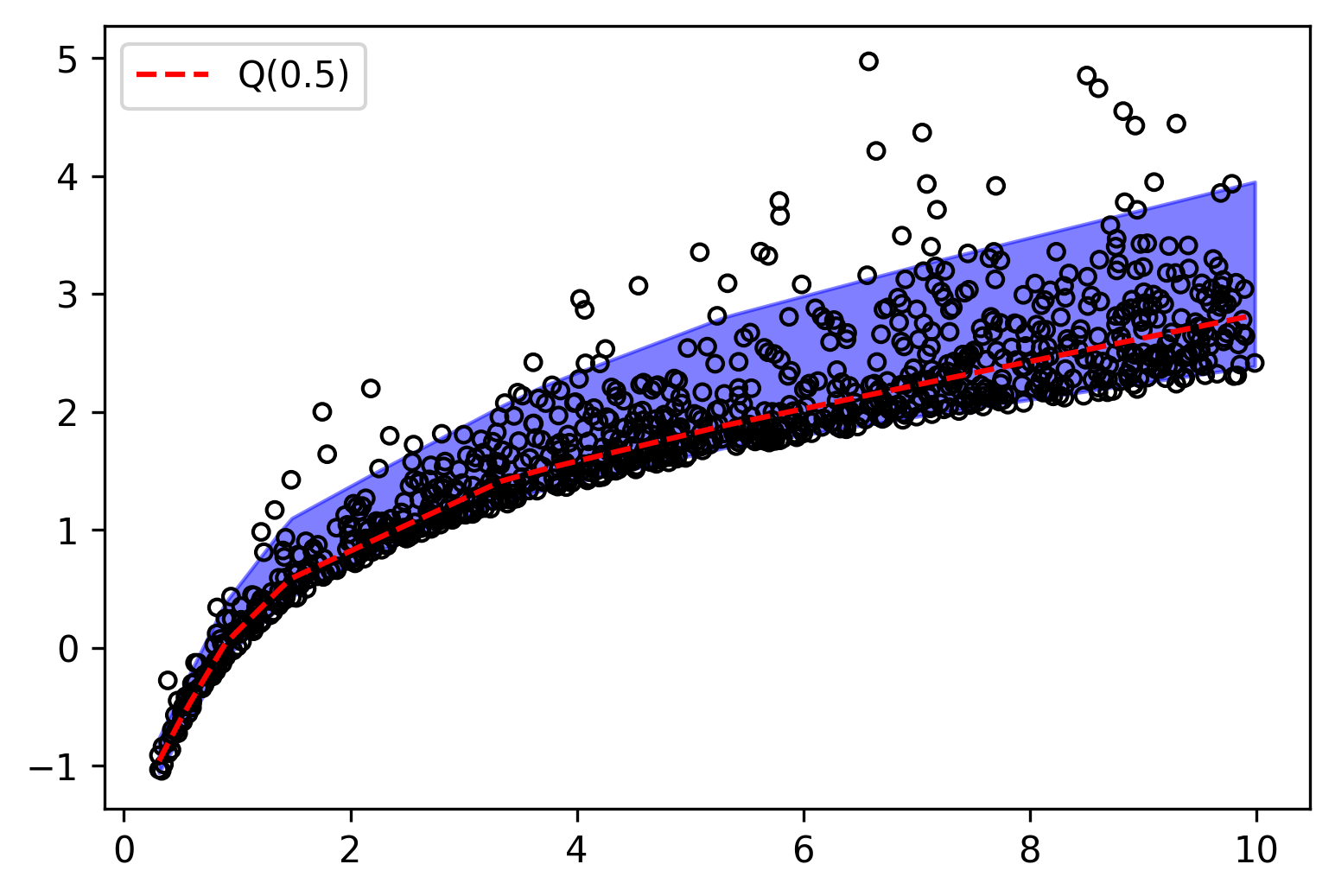![png](https://raw.githubusercontent.com/cgarciae/quantile-regression/master/README_files/README_32_0.png)
372 |     
373 | 
374 | 
375 | 
376 | On the other hand, having multiple quantile values allows us to estimate the density of the data. Since the difference between two adjacent quantiles represent the probability that a point lies between them, we can construct a piecewise function that approximates the density of the data.
377 | 
378 | <details>
379 | <summary markdown="span">Show code</summary>
380 | 
381 | 
382 | ```python
383 | def get_pdf(quantiles, q_values):
384 |     densities = []
385 | 
386 |     for i in range(len(quantiles) - 1):
387 |         area = quantiles[i + 1] - quantiles[i]
388 |         b = q_values[i + 1] - q_values[i]
389 |         a = area / b
390 | 
391 |         densities.append(a)
392 | 
393 |     return densities
394 | 
395 | 
396 | def piecewise(xs):
397 |     return [xs[i + j] for i in range(len(xs) - 1) for j in range(2)]
398 | 
399 | 
400 | def doubled(xs):
401 |     return [np.clip(xs[i], 0, 3) for i in range(len(xs)) for _ in range(2)]
402 | ```
403 | 
404 | </details>
405 | 
406 | For a given `x`, we can compute the quantile values and then use these to compute the conditional piecewise density function of `y` given `x`.
407 | 
408 | <details>
409 | <summary markdown="span">Show code</summary>
410 | 
411 | 
412 | ```python
413 | xi = 7.0
414 | 
415 | q_values = model.predict(np.array([[xi]]))[0].tolist()
416 | 
417 | densities = get_pdf(quantiles, q_values)
418 | 
419 | fig = plt.figure()
420 | plt.title(f"x = {xi}")
421 | plt.fill_between(piecewise(q_values), 0, doubled(densities))
422 | # plt.fill_between(q_values, 0, densities + [0])
423 | # plt.plot(q_values, densities + [0], color="k")
424 | plt.xlim(0, y.max())
425 | plt.gca().set_xlabel("y")
426 | plt.gca().set_ylabel("p(y)")
427 | plt.close()
428 | ```
429 | 
430 | </details>
431 | 
432 | 
433 | ```python
434 | fig
435 | ```
436 | 
437 | 
438 | 
439 | 
440 |     
441 | 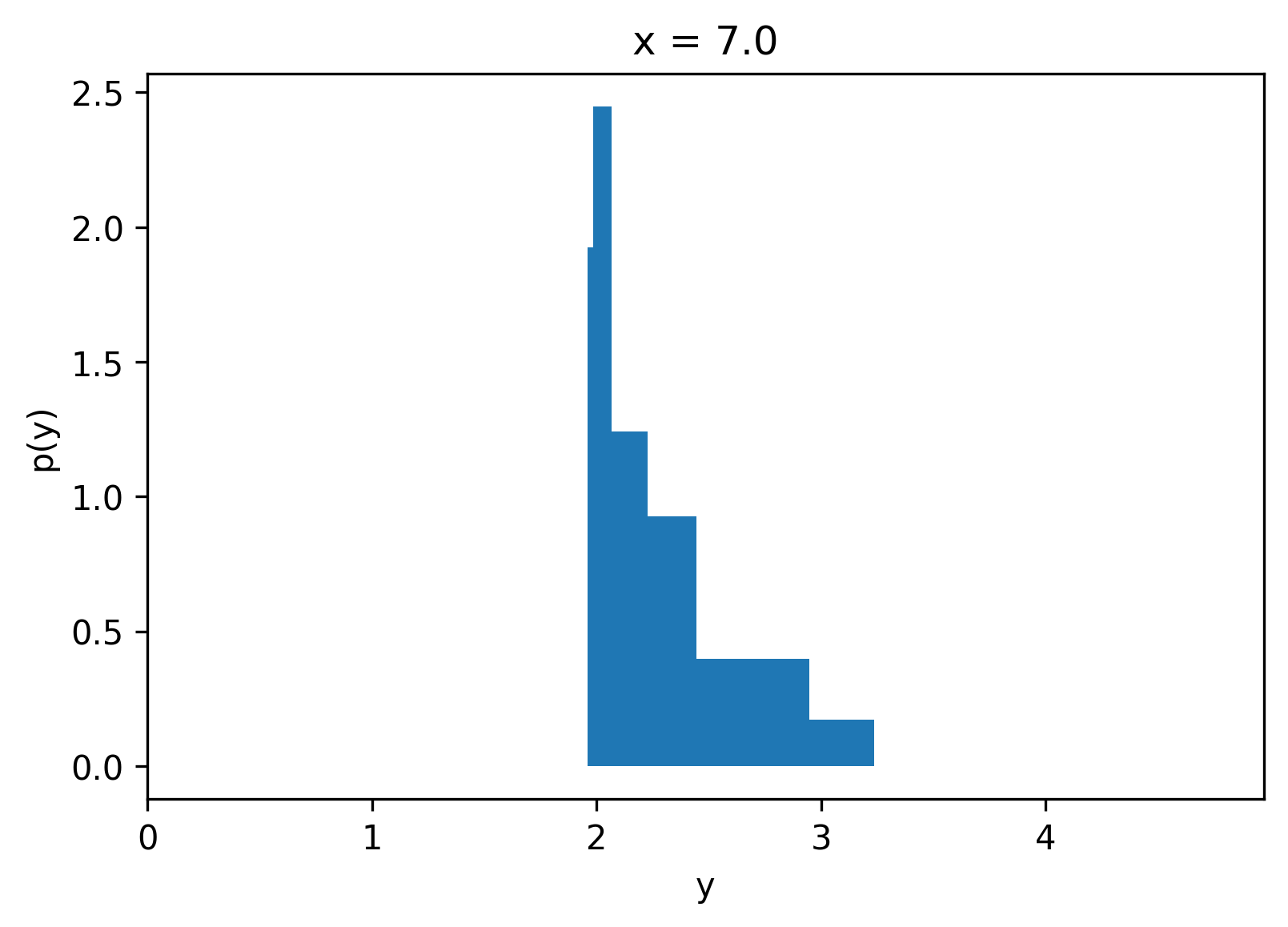![png](https://raw.githubusercontent.com/cgarciae/quantile-regression/master/README_files/README_39_0.png)
442 |     
443 | 
444 | 
445 | 
446 | One of the exciting properties of Quantile Regression is that we did not need to know a priori the output distribution, and training is easy compared to other methods.
447 | 
448 | ## Recap
449 | * Quantile Regression is a simple and effective method for learning some statistics
450 | about the output distribution.
451 | * It is advantageous to establish bounds on the predictions of a model when risk management is desired.
452 | * The Quantile Loss function is simple and easy to implement.
453 | * Quantile Regression can be efficiently implemented using Neural Networks since a single model can predict all the quantiles.
454 | * The quantiles can be used to estimate the conditional density of the data.
455 | 
456 | ## Next Steps
457 | * Try running this notebook with `multimodal = True`.
458 | * Take a look at Mixture Density Networks.
459 | * Learn more about [jax](https://github.com/google/jax) and [elegy](https://github.com/poets-ai/elegy).
460 | 
461 | ## Acknowledgments
462 | Many thanks to [David Cardozo](https://github.com/davidnet) for his proofreading and getting the notebook to run in colab.
463 | 


--------------------------------------------------------------------------------
/README_files/README_11_1.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/cgarciae/quantile-regression/b79ef700c1c45e858caa095db08d2f1eb272f0d3/README_files/README_11_1.png


--------------------------------------------------------------------------------
/README_files/README_13_0.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/cgarciae/quantile-regression/b79ef700c1c45e858caa095db08d2f1eb272f0d3/README_files/README_13_0.png


--------------------------------------------------------------------------------
/README_files/README_26_0.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/cgarciae/quantile-regression/b79ef700c1c45e858caa095db08d2f1eb272f0d3/README_files/README_26_0.png


--------------------------------------------------------------------------------
/README_files/README_28_0.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/cgarciae/quantile-regression/b79ef700c1c45e858caa095db08d2f1eb272f0d3/README_files/README_28_0.png


--------------------------------------------------------------------------------
/README_files/README_30_0.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/cgarciae/quantile-regression/b79ef700c1c45e858caa095db08d2f1eb272f0d3/README_files/README_30_0.png


--------------------------------------------------------------------------------
/README_files/README_32_0.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/cgarciae/quantile-regression/b79ef700c1c45e858caa095db08d2f1eb272f0d3/README_files/README_32_0.png


--------------------------------------------------------------------------------
/README_files/README_37_0.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/cgarciae/quantile-regression/b79ef700c1c45e858caa095db08d2f1eb272f0d3/README_files/README_37_0.png


--------------------------------------------------------------------------------
/README_files/README_39_0.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/cgarciae/quantile-regression/b79ef700c1c45e858caa095db08d2f1eb272f0d3/README_files/README_39_0.png


--------------------------------------------------------------------------------
/README_files/README_4_1.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/cgarciae/quantile-regression/b79ef700c1c45e858caa095db08d2f1eb272f0d3/README_files/README_4_1.png


--------------------------------------------------------------------------------
/README_files/README_6_0.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/cgarciae/quantile-regression/b79ef700c1c45e858caa095db08d2f1eb272f0d3/README_files/README_6_0.png


--------------------------------------------------------------------------------
/build.sh:
--------------------------------------------------------------------------------
 1 | #!/bin/env bash
 2 | 
 3 | export FIGURE_DPI=300
 4 | 
 5 | streambook export main.py
 6 | jupytext --to notebook --execute main.notebook.py --output main.ipynb
 7 | rm -fr main_files
 8 | jupyter nbconvert --to markdown --output README.md main.ipynb
 9 | python update_readme.py
10 | poetry export --without-hashes -f requirements.txt --output requirements.txt


--------------------------------------------------------------------------------
/images/uncertainty.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/cgarciae/quantile-regression/b79ef700c1c45e858caa095db08d2f1eb272f0d3/images/uncertainty.png


--------------------------------------------------------------------------------
/main.notebook.py:
--------------------------------------------------------------------------------
  1 | # %% [markdown]
  2 | """
  3 | # Quantile Regression
  4 | _A simple method to estimate uncertainty in Machine Learning_
  5 | 
  6 | <a href="https://github.com/cgarciae/quantile-regression" target="_parent">
  7 |     <img src="https://img.shields.io/badge/R-Open%20Repo-blue"/>
  8 | </a>
  9 | <a href="https://hackmd.io/@cgarciae/quantile-regression" target="_parent">
 10 |     <img src="https://img.shields.io/badge/B-Open%20Blog-blue"/>
 11 | </a>
 12 | <a href="https://hackmd.io/@cgarciae/quantile-regression-presentation#/" target="_parent">
 13 |     <img src="https://img.shields.io/badge/S-Open%20Slides-blue"/>
 14 | </a>
 15 | <a href="https://colab.research.google.com/github/cgarciae/quantile-regression/blob/master/main.ipynb" target="_parent">
 16 |     <img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open in Colab"/>
 17 | </a>
 18 | 
 19 | 
 20 | 
 21 | ## Motivation
 22 | When generating predictions about an output, it is sometimes useful to get a confidence score or, similarly, a range of values around this expected value in which the actual value might be found. Practical examples include estimating an upper and lower bound when predicting an ETA or stock price since you not only care about the average outcome but are also very interested in the best-case and worst-case scenarios in when trying to minimize risk e.g. avoid getting late or not loosing money.
 23 | 
 24 | While most Machine Learning techniques do not provide a natural way of doing this, in this article, we will be exploring **Quantile Regression** as a means of doing so. This technique will allow us to learn some critical statistical properties of our data: the quantiles.
 25 | 
 26 | <details>
 27 | <summary markdown="span">Install Dependencies</summary>
 28 | """
 29 | # %%
 30 | # uncomment to install dependencies
 31 | ## ! curl -Ls https://raw.githubusercontent.com/cgarciae/quantile-regression/master/requirements.txt > requirements.txt
 32 | ## ! pip install -qr requirements.txt
 33 | ## ! pip install -U matplotlib
 34 | 
 35 | # %% [markdown]
 36 | """
 37 | </details>
 38 | """
 39 | # %% [markdown]
 40 | """
 41 | To begin our journey into quantile regression, we will first get a hold on some data:
 42 | 
 43 | <details>
 44 | <summary markdown="span">Show Code</summary>
 45 | """
 46 | # %%
 47 | import numpy as np
 48 | import matplotlib.pyplot as plt
 49 | import os
 50 | 
 51 | plt.rcParams["figure.dpi"] = int(os.environ.get("FIGURE_DPI", 150))
 52 | plt.rcParams["figure.facecolor"] = os.environ.get("FIGURE_FACECOLOR", "white")
 53 | np.random.seed(69)
 54 | 
 55 | 
 56 | def create_data(multimodal: bool):
 57 |     x = np.random.uniform(0.3, 10, 1000)
 58 |     y = np.log(x) + np.random.exponential(0.1 + x / 20.0)
 59 | 
 60 |     if multimodal:
 61 |         x = np.concatenate([x, np.random.uniform(5, 10, 500)])
 62 |         y = np.concatenate([y, np.random.normal(6.0, 0.3, 500)])
 63 | 
 64 |     return x[..., None], y[..., None]
 65 | 
 66 | 
 67 | multimodal: bool = False
 68 | 
 69 | x, y = create_data(multimodal)
 70 | 
 71 | fig = plt.figure()
 72 | plt.scatter(x[..., 0], y[..., 0], s=20, facecolors="none", edgecolors="k")
 73 | plt.close()
 74 | 
 75 | 
 76 | # %% [markdown]
 77 | """
 78 | </details>
 79 | """
 80 | # %%
 81 | fig
 82 | 
 83 | # %% [markdown]
 84 | """
 85 | Here we have a simple 2D dataset; however, notice that `y` has some very peculiar statistical properties:
 86 | 
 87 | 1. The data does not have the property of being normally distributed. The data is exponentially distributed.
 88 | 2. The previous also means its noise is not symmetric.
 89 | 3. Its variance is not constant. It increases as x increases.
 90 | 
 91 | When making predictions for this kind of data, we might be very interested in knowing what range of values our data revolves around such that we can judge if a specific outcome is expected or not, what are the best and worst-case scenarios, and so on.
 92 | 
 93 | ## Quantile Loss
 94 | The only thing special about quantile regression is its loss function. Instead of the usual MAE or MSE losses for quantile regression, we use the following function:
 95 | 
 96 | $$
 97 | \begin{aligned}
 98 |     E &= y - f(x) \\
 99 |     L_q &= \begin{cases}
100 |         q  E,     &    E \gt 0  \\
101 |         (1 - q) (-E), &    E \lt 0
102 |     \end{cases}
103 | \end{aligned}
104 | $$
105 | 
106 | Here $E$ is the error term, and $L_q$ is the loss function for the quantile $q$. So what do we mean by this? Concretely it means that $L_q$ will bias $f(x)$ to output the value of the $q$'th quantile instead of the usual mean or median statistic. The big question is: how does it do it?
107 | 
108 | First lets notice that this formula can be rewritten as follows:
109 | 
110 | $$
111 | \begin{aligned}
112 |     E &= y - f(x) \\
113 |     L_q &= \max \begin{cases}
114 |         q  E   \\
115 |         (q - 1) E
116 |     \end{cases}
117 | \end{aligned}
118 | $$
119 | 
120 | Using $\max$ instead of a conditional statement will make it more straightforward to implement on tensor/array libraries. We will do this next in jax.
121 | """
122 | # %%
123 | import jax
124 | import jax.numpy as jnp
125 | 
126 | 
127 | def quantile_loss(q, y_true, y_pred):
128 |     e = y_true - y_pred
129 |     return jnp.maximum(q * e, (q - 1.0) * e)
130 | 
131 | 
132 | # %% [markdown]
133 | """
134 | ## Loss Landscape
135 | Now that we have this function let us explore the error landscape for a particular set of predictions. Here we will generate values for `y_true` in the range $[10, 20]$, and for a particular value of $q$ (0.8 by default), we will compute the total error you would get for each value `y_pred` could take. Ideally, we want to find the value of `y_pred` where the error is the smallest.
136 | """
137 | # %% [markdown]
138 | """
139 | <details>
140 | <summary markdown="span">Show code</summary>
141 | """
142 | # %%
143 | def calculate_error(q):
144 |     y_true = np.linspace(10, 20, 100)
145 |     y_pred = np.linspace(10, 20, 200)
146 | 
147 |     loss = jax.vmap(quantile_loss, in_axes=(None, None, 0))(q, y_true, y_pred)
148 |     loss = loss.mean(axis=1)
149 | 
150 |     return y_true, y_pred, loss
151 | 
152 | 
153 | q = 0.8
154 | y_true, y_pred, loss = calculate_error(q)
155 | q_true = np.quantile(y_true, q)
156 | 
157 | 
158 | fig = plt.figure()
159 | plt.plot(y_pred, loss)
160 | plt.vlines(q_true, 0, loss.max(), linestyles="dashed", colors="k")
161 | plt.gca().set_xlabel("y_pred")
162 | plt.gca().set_ylabel("loss")
163 | plt.title(f"Q({q:.2f}) = {q_true:.1f}")
164 | plt.close()
165 | 
166 | 
167 | # %% [markdown]
168 | """
169 | </details>
170 | """
171 | # %%
172 | fig
173 | 
174 | # %% [markdown]
175 | """
176 | If we plot the error, the quantile loss's minimum value is strictly at the value of the $q$th quantile. It achieves this because the quantile loss is not symmetrical; for quantiles above `0.5` it penalizes positive  errors stronger than negative errors, and the opposite is true for quantiles below `0.5`. In particular, quantile `0.5` is the median, and its formula is equivalent to the MAE.
177 | 
178 | ## Deep Quantile Regression
179 | 
180 | Generally, we would need to create to create a model per quantile. However, if we use a neural network, we can output the predictions for all the quantiles simultaneously. Here will use `elegy` to create a neural network with two hidden layers with `relu` activations and linear layers with `n_quantiles` output units.
181 | """
182 | 
183 | # %%
184 | import elegy
185 | 
186 | 
187 | class QuantileRegression(elegy.Module):
188 |     def __init__(self, n_quantiles: int):
189 |         super().__init__()
190 |         self.n_quantiles = n_quantiles
191 | 
192 |     def call(self, x):
193 |         x = elegy.nn.Linear(128)(x)
194 |         x = jax.nn.relu(x)
195 |         x = elegy.nn.Linear(64)(x)
196 |         x = jax.nn.relu(x)
197 |         x = elegy.nn.Linear(self.n_quantiles)(x)
198 | 
199 |         return x
200 | 
201 | 
202 | # %% [markdown]
203 | """
204 | Now we will adequately define a `QuantileLoss` class that is parameterized by
205 | a set of user-defined `quantiles`.
206 | 
207 | <details>
208 | <summary markdown="span">Show code</summary>
209 | """
210 | # %%
211 | class QuantileLoss(elegy.Loss):
212 |     def __init__(self, quantiles):
213 |         super().__init__()
214 |         self.quantiles = np.array(quantiles)
215 | 
216 |     def call(self, y_true, y_pred):
217 |         loss = jax.vmap(quantile_loss, in_axes=(0, None, -1), out_axes=1)(
218 |             self.quantiles, y_true[:, 0], y_pred
219 |         )
220 |         return jnp.sum(loss, axis=-1)
221 | 
222 | 
223 | # %% [markdown]
224 | """
225 | </details>
226 | """
227 | # %% [markdown]
228 | """
229 | Notice that we use the same `quantile_loss` that we created previously, along with some `jax.vmap` magic to properly vectorize the function. Finally, we will create a simple function that creates and trains our model for a set of quantiles using `elegy`.
230 | """
231 | 
232 | # %% [markdown]
233 | """
234 | <details>
235 | <summary markdown="span">Show code</summary>
236 | """
237 | # %%
238 | import optax
239 | 
240 | 
241 | def train_model(quantiles, epochs: int, lr: float, eager: bool):
242 |     model = elegy.Model(
243 |         QuantileRegression(n_quantiles=len(quantiles)),
244 |         loss=QuantileLoss(quantiles),
245 |         optimizer=optax.adamw(lr),
246 |         run_eagerly=eager,
247 |     )
248 | 
249 |     model.fit(x, y, epochs=epochs, batch_size=64, verbose=0)
250 | 
251 |     return model
252 | 
253 | 
254 | if not multimodal:
255 |     quantiles = (0.05, 0.1, 0.3, 0.5, 0.7, 0.9, 0.95)
256 | else:
257 |     quantiles = np.linspace(0.05, 0.95, 9)
258 | 
259 | model = train_model(quantiles=quantiles, epochs=3001, lr=1e-4, eager=False)
260 | # %% [markdown]
261 | """
262 | </details>
263 | """
264 | # %%
265 | model.summary(x)
266 | 
267 | # %% [markdown]
268 | """
269 | Now that we have a model let us generate some test data that spans the entire domain and compute the predicted quantiles.
270 | """
271 | # %% [markdown]
272 | """
273 | <details>
274 | <summary markdown="span">Show code</summary>
275 | """
276 | # %% tags=["hide_input"]
277 | x_test = np.linspace(x.min(), x.max(), 100)
278 | y_pred = model.predict(x_test[..., None])
279 | 
280 | fig = plt.figure()
281 | plt.scatter(x, y, s=20, facecolors="none", edgecolors="k")
282 | 
283 | for i, q_values in enumerate(np.split(y_pred, len(quantiles), axis=-1)):
284 |     plt.plot(x_test, q_values[:, 0], linewidth=2, label=f"Q({quantiles[i]:.2f})")
285 | 
286 | plt.legend()
287 | plt.close()
288 | 
289 | # %% [markdown]
290 | """
291 | </details>
292 | """
293 | # %%
294 | fig
295 | # %% [markdown]
296 | """
297 | Amazing! Notice how the first few quantiles are tightly packed together while the last ones spread out, capturing the behavior of the exponential distribution. We can also visualize the region between the highest and lowest quantiles, and this gives us some bounds on our predictions.
298 | 
299 | <details>
300 | <summary markdown="span">Show code</summary>
301 | """
302 | # %%
303 | median_idx = np.where(np.isclose(quantiles, 0.5))[0]
304 | 
305 | fig = plt.figure()
306 | plt.fill_between(x_test, y_pred[:, -1], y_pred[:, 0], alpha=0.5, color="b")
307 | plt.scatter(x, y, s=20, facecolors="none", edgecolors="k")
308 | plt.plot(
309 |     x_test,
310 |     y_pred[:, median_idx],
311 |     color="r",
312 |     linestyle="dashed",
313 |     label="Q(0.5)",
314 | )
315 | plt.legend()
316 | plt.close()
317 | 
318 | # %% [markdown]
319 | """
320 | </details>
321 | """
322 | # %%
323 | fig
324 | # %% [markdown]
325 | """
326 | On the other hand, having multiple quantile values allows us to estimate the density of the data. Since the difference between two adjacent quantiles represent the probability that a point lies between them, we can construct a piecewise function that approximates the density of the data.
327 | 
328 | <details>
329 | <summary markdown="span">Show code</summary>
330 | """
331 | # %%
332 | def get_pdf(quantiles, q_values):
333 |     densities = []
334 | 
335 |     for i in range(len(quantiles) - 1):
336 |         area = quantiles[i + 1] - quantiles[i]
337 |         b = q_values[i + 1] - q_values[i]
338 |         a = area / b
339 | 
340 |         densities.append(a)
341 | 
342 |     return densities
343 | 
344 | 
345 | def piecewise(xs):
346 |     return [xs[i + j] for i in range(len(xs) - 1) for j in range(2)]
347 | 
348 | 
349 | def doubled(xs):
350 |     return [np.clip(xs[i], 0, 3) for i in range(len(xs)) for _ in range(2)]
351 | 
352 | 
353 | # %% [markdown]
354 | """
355 | </details>
356 | """
357 | # %% [markdown]
358 | """
359 | For a given `x`, we can compute the quantile values and then use these to compute the conditional piecewise density function of `y` given `x`.
360 | 
361 | <details>
362 | <summary markdown="span">Show code</summary>
363 | """
364 | # %%
365 | xi = 7.0
366 | 
367 | q_values = model.predict(np.array([[xi]]))[0].tolist()
368 | 
369 | densities = get_pdf(quantiles, q_values)
370 | 
371 | fig = plt.figure()
372 | plt.title(f"x = {xi}")
373 | plt.fill_between(piecewise(q_values), 0, doubled(densities))
374 | # plt.fill_between(q_values, 0, densities + [0])
375 | # plt.plot(q_values, densities + [0], color="k")
376 | plt.xlim(0, y.max())
377 | plt.gca().set_xlabel("y")
378 | plt.gca().set_ylabel("p(y)")
379 | plt.close()
380 | 
381 | # %% [markdown]
382 | """
383 | </details>
384 | """
385 | # %%
386 | fig
387 | # %% [markdown]
388 | """
389 | One of the exciting properties of Quantile Regression is that we did not need to know a priori the output distribution, and training is easy compared to other methods.
390 | 
391 | ## Recap
392 | * Quantile Regression is a simple and effective method for learning some statistics
393 | about the output distribution.
394 | * It is advantageous to establish bounds on the predictions of a model when risk management is desired.
395 | * The Quantile Loss function is simple and easy to implement.
396 | * Quantile Regression can be efficiently implemented using Neural Networks since a single model can predict all the quantiles.
397 | * The quantiles can be used to estimate the conditional density of the data.
398 | 
399 | ## Next Steps
400 | * Try running this notebook with `multimodal = True`.
401 | * Take a look at Mixture Density Networks.
402 | * Learn more about [jax](https://github.com/google/jax) and [elegy](https://github.com/poets-ai/elegy).
403 | 
404 | ## Acknowledgments
405 | Many thanks to [David Cardozo](https://github.com/davidnet) for his proofreading and getting the notebook to run in colab.
406 | """
407 | 


--------------------------------------------------------------------------------
/main.py:
--------------------------------------------------------------------------------
  1 | # %% [markdown]
  2 | """
  3 | # Quantile Regression
  4 | _A simple method to estimate uncertainty in Machine Learning_
  5 | 
  6 | <a href="https://github.com/cgarciae/quantile-regression" target="_parent">
  7 |     <img src="https://img.shields.io/badge/R-Open%20Repo-blue"/>
  8 | </a>
  9 | <a href="https://hackmd.io/@cgarciae/quantile-regression" target="_parent">
 10 |     <img src="https://img.shields.io/badge/B-Open%20Blog-blue"/>
 11 | </a>
 12 | <a href="https://hackmd.io/@cgarciae/quantile-regression-presentation#/" target="_parent">
 13 |     <img src="https://img.shields.io/badge/S-Open%20Slides-blue"/>
 14 | </a>
 15 | <a href="https://colab.research.google.com/github/cgarciae/quantile-regression/blob/master/main.ipynb" target="_parent">
 16 |     <img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open in Colab"/>
 17 | </a>
 18 | 
 19 | 
 20 | 
 21 | ## Motivation
 22 | When generating predictions about an output, it is sometimes useful to get a confidence score or, similarly, a range of values around this expected value in which the actual value might be found. Practical examples include estimating an upper and lower bound when predicting an ETA or stock price since you not only care about the average outcome but are also very interested in the best-case and worst-case scenarios in when trying to minimize risk e.g. avoid getting late or not loosing money.
 23 | 
 24 | While most Machine Learning techniques do not provide a natural way of doing this, in this article, we will be exploring **Quantile Regression** as a means of doing so. This technique will allow us to learn some critical statistical properties of our data: the quantiles.
 25 | 
 26 | <details>
 27 | <summary markdown="span">Install Dependencies</summary>
 28 | """
 29 | # %%
 30 | _ = __st
 31 | # uncomment to install dependencies
 32 | ## ! curl -Ls https://raw.githubusercontent.com/cgarciae/quantile-regression/master/requirements.txt > requirements.txt
 33 | ## ! pip install -qr requirements.txt
 34 | ## ! pip install -U matplotlib
 35 | 
 36 | # %% [markdown]
 37 | """
 38 | </details>
 39 | """
 40 | # %% [markdown]
 41 | """
 42 | To begin our journey into quantile regression, we will first get a hold on some data:
 43 | 
 44 | <details>
 45 | <summary markdown="span">Show Code</summary>
 46 | """
 47 | # %%
 48 | import numpy as np
 49 | import matplotlib.pyplot as plt
 50 | import os
 51 | 
 52 | plt.rcParams["figure.dpi"] = int(os.environ.get("FIGURE_DPI", 150))
 53 | plt.rcParams["figure.facecolor"] = os.environ.get("FIGURE_FACECOLOR", "white")
 54 | np.random.seed(69)
 55 | 
 56 | 
 57 | @__st.cache
 58 | def create_data(multimodal: bool):
 59 |     x = np.random.uniform(0.3, 10, 1000)
 60 |     y = np.log(x) + np.random.exponential(0.1 + x / 20.0)
 61 | 
 62 |     if multimodal:
 63 |         x = np.concatenate([x, np.random.uniform(5, 10, 500)])
 64 |         y = np.concatenate([y, np.random.normal(6.0, 0.3, 500)])
 65 | 
 66 |     return x[..., None], y[..., None]
 67 | 
 68 | 
 69 | multimodal: bool = False
 70 | multimodal = __st.checkbox("Use multimodal data", False)
 71 | 
 72 | x, y = create_data(multimodal)
 73 | 
 74 | fig = plt.figure()
 75 | plt.scatter(x[..., 0], y[..., 0], s=20, facecolors="none", edgecolors="k")
 76 | plt.close()
 77 | 
 78 | 
 79 | # %% [markdown]
 80 | """
 81 | </details>
 82 | """
 83 | # %%
 84 | fig
 85 | 
 86 | # %% [markdown]
 87 | """
 88 | Here we have a simple 2D dataset; however, notice that `y` has some very peculiar statistical properties:
 89 | 
 90 | 1. The data does not have the property of being normally distributed. The data is exponentially distributed.
 91 | 2. The previous also means its noise is not symmetric.
 92 | 3. Its variance is not constant. It increases as x increases.
 93 | 
 94 | When making predictions for this kind of data, we might be very interested in knowing what range of values our data revolves around such that we can judge if a specific outcome is expected or not, what are the best and worst-case scenarios, and so on.
 95 | 
 96 | ## Quantile Loss
 97 | The only thing special about quantile regression is its loss function. Instead of the usual MAE or MSE losses for quantile regression, we use the following function:
 98 | 
 99 | $$
100 | \begin{aligned}
101 |     E &= y - f(x) \\
102 |     L_q &= \begin{cases}
103 |         q  E,     &    E \gt 0  \\
104 |         (1 - q) (-E), &    E \lt 0
105 |     \end{cases}
106 | \end{aligned}
107 | $$
108 | 
109 | Here $E$ is the error term, and $L_q$ is the loss function for the quantile $q$. So what do we mean by this? Concretely it means that $L_q$ will bias $f(x)$ to output the value of the $q$'th quantile instead of the usual mean or median statistic. The big question is: how does it do it?
110 | 
111 | First lets notice that this formula can be rewritten as follows:
112 | 
113 | $$
114 | \begin{aligned}
115 |     E &= y - f(x) \\
116 |     L_q &= \max \begin{cases}
117 |         q  E   \\
118 |         (q - 1) E
119 |     \end{cases}
120 | \end{aligned}
121 | $$
122 | 
123 | Using $\max$ instead of a conditional statement will make it more straightforward to implement on tensor/array libraries. We will do this next in jax.
124 | """
125 | # %%
126 | import jax
127 | import jax.numpy as jnp
128 | 
129 | 
130 | def quantile_loss(q, y_true, y_pred):
131 |     e = y_true - y_pred
132 |     return jnp.maximum(q * e, (q - 1.0) * e)
133 | 
134 | 
135 | # %% [markdown]
136 | """
137 | ## Loss Landscape
138 | Now that we have this function let us explore the error landscape for a particular set of predictions. Here we will generate values for `y_true` in the range $[10, 20]$, and for a particular value of $q$ (0.8 by default), we will compute the total error you would get for each value `y_pred` could take. Ideally, we want to find the value of `y_pred` where the error is the smallest.
139 | """
140 | # %% [markdown]
141 | """
142 | <details>
143 | <summary markdown="span">Show code</summary>
144 | """
145 | # %%
146 | @__st.cache
147 | def calculate_error(q):
148 |     y_true = np.linspace(10, 20, 100)
149 |     y_pred = np.linspace(10, 20, 200)
150 | 
151 |     loss = jax.vmap(quantile_loss, in_axes=(None, None, 0))(q, y_true, y_pred)
152 |     loss = loss.mean(axis=1)
153 | 
154 |     return y_true, y_pred, loss
155 | 
156 | 
157 | q = 0.8
158 | q = __st.slider("q", 0.001, 0.999, q)
159 | y_true, y_pred, loss = calculate_error(q)
160 | q_true = np.quantile(y_true, q)
161 | 
162 | 
163 | fig = plt.figure()
164 | plt.plot(y_pred, loss)
165 | plt.vlines(q_true, 0, loss.max(), linestyles="dashed", colors="k")
166 | plt.gca().set_xlabel("y_pred")
167 | plt.gca().set_ylabel("loss")
168 | plt.title(f"Q({q:.2f}) = {q_true:.1f}")
169 | plt.close()
170 | 
171 | 
172 | # %% [markdown]
173 | """
174 | </details>
175 | """
176 | # %%
177 | fig
178 | 
179 | # %% [markdown]
180 | """
181 | If we plot the error, the quantile loss's minimum value is strictly at the value of the $q$th quantile. It achieves this because the quantile loss is not symmetrical; for quantiles above `0.5` it penalizes positive  errors stronger than negative errors, and the opposite is true for quantiles below `0.5`. In particular, quantile `0.5` is the median, and its formula is equivalent to the MAE.
182 | 
183 | ## Deep Quantile Regression
184 | 
185 | Generally, we would need to create to create a model per quantile. However, if we use a neural network, we can output the predictions for all the quantiles simultaneously. Here will use `elegy` to create a neural network with two hidden layers with `relu` activations and linear layers with `n_quantiles` output units.
186 | """
187 | 
188 | # %%
189 | import elegy
190 | 
191 | 
192 | class QuantileRegression(elegy.Module):
193 |     def __init__(self, n_quantiles: int):
194 |         super().__init__()
195 |         self.n_quantiles = n_quantiles
196 | 
197 |     def call(self, x):
198 |         x = elegy.nn.Linear(128)(x)
199 |         x = jax.nn.relu(x)
200 |         x = elegy.nn.Linear(64)(x)
201 |         x = jax.nn.relu(x)
202 |         x = elegy.nn.Linear(self.n_quantiles)(x)
203 | 
204 |         return x
205 | 
206 | 
207 | # %% [markdown]
208 | """
209 | Now we will adequately define a `QuantileLoss` class that is parameterized by
210 | a set of user-defined `quantiles`.
211 | 
212 | <details>
213 | <summary markdown="span">Show code</summary>
214 | """
215 | # %%
216 | class QuantileLoss(elegy.Loss):
217 |     def __init__(self, quantiles):
218 |         super().__init__()
219 |         self.quantiles = np.array(quantiles)
220 | 
221 |     def call(self, y_true, y_pred):
222 |         loss = jax.vmap(quantile_loss, in_axes=(0, None, -1), out_axes=1)(
223 |             self.quantiles, y_true[:, 0], y_pred
224 |         )
225 |         return jnp.sum(loss, axis=-1)
226 | 
227 | 
228 | # %% [markdown]
229 | """
230 | </details>
231 | """
232 | # %% [markdown]
233 | """
234 | Notice that we use the same `quantile_loss` that we created previously, along with some `jax.vmap` magic to properly vectorize the function. Finally, we will create a simple function that creates and trains our model for a set of quantiles using `elegy`.
235 | """
236 | 
237 | # %% [markdown]
238 | """
239 | <details>
240 | <summary markdown="span">Show code</summary>
241 | """
242 | # %%
243 | import optax
244 | 
245 | 
246 | @__st.cache(allow_output_mutation=True)
247 | def train_model(quantiles, epochs: int, lr: float, eager: bool):
248 |     model = elegy.Model(
249 |         QuantileRegression(n_quantiles=len(quantiles)),
250 |         loss=QuantileLoss(quantiles),
251 |         optimizer=optax.adamw(lr),
252 |         run_eagerly=eager,
253 |     )
254 | 
255 |     model.fit(x, y, epochs=epochs, batch_size=64, verbose=0)
256 | 
257 |     return model
258 | 
259 | 
260 | if not multimodal:
261 |     quantiles = (0.05, 0.1, 0.3, 0.5, 0.7, 0.9, 0.95)
262 | else:
263 |     quantiles = np.linspace(0.05, 0.95, 9)
264 | 
265 | model = train_model(quantiles=quantiles, epochs=3001, lr=1e-4, eager=False)
266 | # %% [markdown]
267 | """
268 | </details>
269 | """
270 | # %%
271 | model.summary(x)
272 | 
273 | # %% [markdown]
274 | """
275 | Now that we have a model let us generate some test data that spans the entire domain and compute the predicted quantiles.
276 | """
277 | # %% [markdown]
278 | """
279 | <details>
280 | <summary markdown="span">Show code</summary>
281 | """
282 | # %% tags=["hide_input"]
283 | x_test = np.linspace(x.min(), x.max(), 100)
284 | y_pred = model.predict(x_test[..., None])
285 | 
286 | fig = plt.figure()
287 | plt.scatter(x, y, s=20, facecolors="none", edgecolors="k")
288 | 
289 | for i, q_values in enumerate(np.split(y_pred, len(quantiles), axis=-1)):
290 |     plt.plot(x_test, q_values[:, 0], linewidth=2, label=f"Q({quantiles[i]:.2f})")
291 | 
292 | plt.legend()
293 | plt.close()
294 | 
295 | # %% [markdown]
296 | """
297 | </details>
298 | """
299 | # %%
300 | fig
301 | # %% [markdown]
302 | """
303 | Amazing! Notice how the first few quantiles are tightly packed together while the last ones spread out, capturing the behavior of the exponential distribution. We can also visualize the region between the highest and lowest quantiles, and this gives us some bounds on our predictions.
304 | 
305 | <details>
306 | <summary markdown="span">Show code</summary>
307 | """
308 | # %%
309 | median_idx = np.where(np.isclose(quantiles, 0.5))[0]
310 | 
311 | fig = plt.figure()
312 | plt.fill_between(x_test, y_pred[:, -1], y_pred[:, 0], alpha=0.5, color="b")
313 | plt.scatter(x, y, s=20, facecolors="none", edgecolors="k")
314 | plt.plot(
315 |     x_test,
316 |     y_pred[:, median_idx],
317 |     color="r",
318 |     linestyle="dashed",
319 |     label="Q(0.5)",
320 | )
321 | plt.legend()
322 | plt.close()
323 | 
324 | # %% [markdown]
325 | """
326 | </details>
327 | """
328 | # %%
329 | fig
330 | # %% [markdown]
331 | """
332 | On the other hand, having multiple quantile values allows us to estimate the density of the data. Since the difference between two adjacent quantiles represent the probability that a point lies between them, we can construct a piecewise function that approximates the density of the data.
333 | 
334 | <details>
335 | <summary markdown="span">Show code</summary>
336 | """
337 | # %%
338 | def get_pdf(quantiles, q_values):
339 |     densities = []
340 | 
341 |     for i in range(len(quantiles) - 1):
342 |         area = quantiles[i + 1] - quantiles[i]
343 |         b = q_values[i + 1] - q_values[i]
344 |         a = area / b
345 | 
346 |         densities.append(a)
347 | 
348 |     return densities
349 | 
350 | 
351 | def piecewise(xs):
352 |     return [xs[i + j] for i in range(len(xs) - 1) for j in range(2)]
353 | 
354 | 
355 | def doubled(xs):
356 |     return [np.clip(xs[i], 0, 3) for i in range(len(xs)) for _ in range(2)]
357 | 
358 | 
359 | # %% [markdown]
360 | """
361 | </details>
362 | """
363 | # %% [markdown]
364 | """
365 | For a given `x`, we can compute the quantile values and then use these to compute the conditional piecewise density function of `y` given `x`.
366 | 
367 | <details>
368 | <summary markdown="span">Show code</summary>
369 | """
370 | # %%
371 | xi = 7.0
372 | xi = __st.slider("xi", 0.0001, 11.0, xi)
373 | 
374 | q_values = model.predict(np.array([[xi]]))[0].tolist()
375 | 
376 | densities = get_pdf(quantiles, q_values)
377 | 
378 | fig = plt.figure()
379 | plt.title(f"x = {xi}")
380 | plt.fill_between(piecewise(q_values), 0, doubled(densities))
381 | # plt.fill_between(q_values, 0, densities + [0])
382 | # plt.plot(q_values, densities + [0], color="k")
383 | plt.xlim(0, y.max())
384 | plt.gca().set_xlabel("y")
385 | plt.gca().set_ylabel("p(y)")
386 | plt.close()
387 | 
388 | # %% [markdown]
389 | """
390 | </details>
391 | """
392 | # %%
393 | fig
394 | # %% [markdown]
395 | """
396 | One of the exciting properties of Quantile Regression is that we did not need to know a priori the output distribution, and training is easy compared to other methods.
397 | 
398 | ## Recap
399 | * Quantile Regression is a simple and effective method for learning some statistics
400 | about the output distribution.
401 | * It is advantageous to establish bounds on the predictions of a model when risk management is desired.
402 | * The Quantile Loss function is simple and easy to implement.
403 | * Quantile Regression can be efficiently implemented using Neural Networks since a single model can predict all the quantiles.
404 | * The quantiles can be used to estimate the conditional density of the data.
405 | 
406 | ## Next Steps
407 | * Try running this notebook with `multimodal = True`.
408 | * Take a look at Mixture Density Networks.
409 | * Learn more about [jax](https://github.com/google/jax) and [elegy](https://github.com/poets-ai/elegy).
410 | 
411 | ## Acknowledgments
412 | Many thanks to [David Cardozo](https://github.com/davidnet) for his proofreading and getting the notebook to run in colab.
413 | """
414 | 


--------------------------------------------------------------------------------
/main.streambook.py:
--------------------------------------------------------------------------------
  1 | 
  2 | import streamlit as __st
  3 | import streambook
  4 | __toc = streambook.TOCSidebar()
  5 | __toc._add(streambook.H1('Quantile Regression'))
  6 | __toc._add(streambook.H2('Motivation'))
  7 | __toc._add(streambook.H2('Quantile Loss'))
  8 | __toc._add(streambook.H2('Loss Landscape'))
  9 | __toc._add(streambook.H2('Deep Quantile Regression'))
 10 | __toc._add(streambook.H2('Recap'))
 11 | __toc._add(streambook.H2('Next Steps'))
 12 | __toc._add(streambook.H2('Acknowledgments'))
 13 | 
 14 | __toc.generate()
 15 | __st.markdown(r"""<span id='Quantile Regression'> </span><span id='Motivation'> </span>
 16 | # Quantile Regression
 17 | _A simple method to estimate uncertainty in Machine Learning_
 18 | 
 19 | <a href="https://github.com/cgarciae/quantile-regression" target="_parent">
 20 |     <img src="https://img.shields.io/badge/R-Open%20Repo-blue"/>
 21 | </a>
 22 | <a href="https://hackmd.io/@cgarciae/quantile-regression" target="_parent">
 23 |     <img src="https://img.shields.io/badge/B-Open%20Blog-blue"/>
 24 | </a>
 25 | <a href="https://hackmd.io/@cgarciae/quantile-regression-presentation#/" target="_parent">
 26 |     <img src="https://img.shields.io/badge/S-Open%20Slides-blue"/>
 27 | </a>
 28 | <a href="https://colab.research.google.com/github/cgarciae/quantile-regression/blob/master/main.ipynb" target="_parent">
 29 |     <img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open in Colab"/>
 30 | </a>
 31 | 
 32 | 
 33 | 
 34 | ## Motivation
 35 | When generating predictions about an output, it is sometimes useful to get a confidence score or, similarly, a range of values around this expected value in which the actual value might be found. Practical examples include estimating an upper and lower bound when predicting an ETA or stock price since you not only care about the average outcome but are also very interested in the best-case and worst-case scenarios in when trying to minimize risk e.g. avoid getting late or not loosing money.
 36 | 
 37 | While most Machine Learning techniques do not provide a natural way of doing this, in this article, we will be exploring **Quantile Regression** as a means of doing so. This technique will allow us to learn some critical statistical properties of our data: the quantiles.
 38 | 
 39 | <details>
 40 | <summary markdown="span">Install Dependencies</summary>""", unsafe_allow_html=True)
 41 | with __st.echo(), streambook.st_stdout('info'):
 42 |     _ = __st
 43 |     # uncomment to install dependencies
 44 |     # ! curl -Ls https://raw.githubusercontent.com/cgarciae/quantile-regression/master/requirements.txt > requirements.txt
 45 |     # ! pip install -qr requirements.txt
 46 |     # ! pip install -U matplotlib
 47 | __st.markdown(r"""</details>""", unsafe_allow_html=True)
 48 | __st.markdown(r"""To begin our journey into quantile regression, we will first get a hold on some data:
 49 | 
 50 | <details>
 51 | <summary markdown="span">Show Code</summary>""", unsafe_allow_html=True)
 52 | with __st.echo(), streambook.st_stdout('info'):
 53 |     import numpy as np
 54 |     import matplotlib.pyplot as plt
 55 |     import os
 56 | 
 57 |     plt.rcParams["figure.dpi"] = int(os.environ.get("FIGURE_DPI", 150))
 58 |     plt.rcParams["figure.facecolor"] = os.environ.get("FIGURE_FACECOLOR", "white")
 59 |     np.random.seed(69)
 60 | 
 61 | 
 62 |     @__st.cache
 63 |     def create_data(multimodal: bool):
 64 |         x = np.random.uniform(0.3, 10, 1000)
 65 |         y = np.log(x) + np.random.exponential(0.1 + x / 20.0)
 66 | 
 67 |         if multimodal:
 68 |             x = np.concatenate([x, np.random.uniform(5, 10, 500)])
 69 |             y = np.concatenate([y, np.random.normal(6.0, 0.3, 500)])
 70 | 
 71 |         return x[..., None], y[..., None]
 72 | 
 73 | 
 74 |     multimodal: bool = False
 75 |     multimodal = __st.checkbox("Use multimodal data", False)
 76 | 
 77 |     x, y = create_data(multimodal)
 78 | 
 79 |     fig = plt.figure()
 80 |     plt.scatter(x[..., 0], y[..., 0], s=20, facecolors="none", edgecolors="k")
 81 |     plt.close()
 82 | __st.markdown(r"""</details>""", unsafe_allow_html=True)
 83 | with __st.echo(), streambook.st_stdout('info'):
 84 |     fig
 85 | __st.markdown(r"""<span id='Quantile Loss'> </span>
 86 | Here we have a simple 2D dataset; however, notice that `y` has some very peculiar statistical properties:
 87 | 
 88 | 1. The data does not have the property of being normally distributed. The data is exponentially distributed.
 89 | 2. The previous also means its noise is not symmetric.
 90 | 3. Its variance is not constant. It increases as x increases.
 91 | 
 92 | When making predictions for this kind of data, we might be very interested in knowing what range of values our data revolves around such that we can judge if a specific outcome is expected or not, what are the best and worst-case scenarios, and so on.
 93 | 
 94 | ## Quantile Loss
 95 | The only thing special about quantile regression is its loss function. Instead of the usual MAE or MSE losses for quantile regression, we use the following function:
 96 | 
 97 | $$
 98 | \begin{aligned}
 99 |     E &= y - f(x) \\
100 |     L_q &= \begin{cases}
101 |         q  E,     &    E \gt 0  \\
102 |         (1 - q) (-E), &    E \lt 0
103 |     \end{cases}
104 | \end{aligned}
105 | $$
106 | 
107 | Here $E$ is the error term, and $L_q$ is the loss function for the quantile $q$. So what do we mean by this? Concretely it means that $L_q$ will bias $f(x)$ to output the value of the $q$'th quantile instead of the usual mean or median statistic. The big question is: how does it do it?
108 | 
109 | First lets notice that this formula can be rewritten as follows:
110 | 
111 | $$
112 | \begin{aligned}
113 |     E &= y - f(x) \\
114 |     L_q &= \max \begin{cases}
115 |         q  E   \\
116 |         (q - 1) E
117 |     \end{cases}
118 | \end{aligned}
119 | $$
120 | 
121 | Using $\max$ instead of a conditional statement will make it more straightforward to implement on tensor/array libraries. We will do this next in jax.""", unsafe_allow_html=True)
122 | with __st.echo(), streambook.st_stdout('info'):
123 |     import jax
124 |     import jax.numpy as jnp
125 | 
126 | 
127 |     def quantile_loss(q, y_true, y_pred):
128 |         e = y_true - y_pred
129 |         return jnp.maximum(q * e, (q - 1.0) * e)
130 | __st.markdown(r"""<span id='Loss Landscape'> </span>
131 | ## Loss Landscape
132 | Now that we have this function let us explore the error landscape for a particular set of predictions. Here we will generate values for `y_true` in the range $[10, 20]$, and for a particular value of $q$ (0.8 by default), we will compute the total error you would get for each value `y_pred` could take. Ideally, we want to find the value of `y_pred` where the error is the smallest.""", unsafe_allow_html=True)
133 | __st.markdown(r"""<details>
134 | <summary markdown="span">Show code</summary>""", unsafe_allow_html=True)
135 | with __st.echo(), streambook.st_stdout('info'):
136 |     @__st.cache
137 |     def calculate_error(q):
138 |         y_true = np.linspace(10, 20, 100)
139 |         y_pred = np.linspace(10, 20, 200)
140 | 
141 |         loss = jax.vmap(quantile_loss, in_axes=(None, None, 0))(q, y_true, y_pred)
142 |         loss = loss.mean(axis=1)
143 | 
144 |         return y_true, y_pred, loss
145 | 
146 | 
147 |     q = 0.8
148 |     q = __st.slider("q", 0.001, 0.999, q)
149 |     y_true, y_pred, loss = calculate_error(q)
150 |     q_true = np.quantile(y_true, q)
151 | 
152 | 
153 |     fig = plt.figure()
154 |     plt.plot(y_pred, loss)
155 |     plt.vlines(q_true, 0, loss.max(), linestyles="dashed", colors="k")
156 |     plt.gca().set_xlabel("y_pred")
157 |     plt.gca().set_ylabel("loss")
158 |     plt.title(f"Q({q:.2f}) = {q_true:.1f}")
159 |     plt.close()
160 | __st.markdown(r"""</details>""", unsafe_allow_html=True)
161 | with __st.echo(), streambook.st_stdout('info'):
162 |     fig
163 | __st.markdown(r"""<span id='Deep Quantile Regression'> </span>
164 | If we plot the error, the quantile loss's minimum value is strictly at the value of the $q$th quantile. It achieves this because the quantile loss is not symmetrical; for quantiles above `0.5` it penalizes positive  errors stronger than negative errors, and the opposite is true for quantiles below `0.5`. In particular, quantile `0.5` is the median, and its formula is equivalent to the MAE.
165 | 
166 | ## Deep Quantile Regression
167 | 
168 | Generally, we would need to create to create a model per quantile. However, if we use a neural network, we can output the predictions for all the quantiles simultaneously. Here will use `elegy` to create a neural network with two hidden layers with `relu` activations and linear layers with `n_quantiles` output units.""", unsafe_allow_html=True)
169 | with __st.echo(), streambook.st_stdout('info'):
170 |     import elegy
171 | 
172 | 
173 |     class QuantileRegression(elegy.Module):
174 |         def __init__(self, n_quantiles: int):
175 |             super().__init__()
176 |             self.n_quantiles = n_quantiles
177 | 
178 |         def call(self, x):
179 |             x = elegy.nn.Linear(128)(x)
180 |             x = jax.nn.relu(x)
181 |             x = elegy.nn.Linear(64)(x)
182 |             x = jax.nn.relu(x)
183 |             x = elegy.nn.Linear(self.n_quantiles)(x)
184 | 
185 |             return x
186 | __st.markdown(r"""Now we will adequately define a `QuantileLoss` class that is parameterized by
187 | a set of user-defined `quantiles`.
188 | 
189 | <details>
190 | <summary markdown="span">Show code</summary>""", unsafe_allow_html=True)
191 | with __st.echo(), streambook.st_stdout('info'):
192 |     class QuantileLoss(elegy.Loss):
193 |         def __init__(self, quantiles):
194 |             super().__init__()
195 |             self.quantiles = np.array(quantiles)
196 | 
197 |         def call(self, y_true, y_pred):
198 |             loss = jax.vmap(quantile_loss, in_axes=(0, None, -1), out_axes=1)(
199 |                 self.quantiles, y_true[:, 0], y_pred
200 |             )
201 |             return jnp.sum(loss, axis=-1)
202 | __st.markdown(r"""</details>""", unsafe_allow_html=True)
203 | __st.markdown(r"""Notice that we use the same `quantile_loss` that we created previously, along with some `jax.vmap` magic to properly vectorize the function. Finally, we will create a simple function that creates and trains our model for a set of quantiles using `elegy`.""", unsafe_allow_html=True)
204 | __st.markdown(r"""<details>
205 | <summary markdown="span">Show code</summary>""", unsafe_allow_html=True)
206 | with __st.echo(), streambook.st_stdout('info'):
207 |     import optax
208 | 
209 | 
210 |     @__st.cache(allow_output_mutation=True)
211 |     def train_model(quantiles, epochs: int, lr: float, eager: bool):
212 |         model = elegy.Model(
213 |             QuantileRegression(n_quantiles=len(quantiles)),
214 |             loss=QuantileLoss(quantiles),
215 |             optimizer=optax.adamw(lr),
216 |             run_eagerly=eager,
217 |         )
218 | 
219 |         model.fit(x, y, epochs=epochs, batch_size=64, verbose=0)
220 | 
221 |         return model
222 | 
223 | 
224 |     if not multimodal:
225 |         quantiles = (0.05, 0.1, 0.3, 0.5, 0.7, 0.9, 0.95)
226 |     else:
227 |         quantiles = np.linspace(0.05, 0.95, 9)
228 | 
229 |     model = train_model(quantiles=quantiles, epochs=3001, lr=1e-4, eager=False)
230 | __st.markdown(r"""</details>""", unsafe_allow_html=True)
231 | with __st.echo(), streambook.st_stdout('info'):
232 |     model.summary(x)
233 | __st.markdown(r"""Now that we have a model let us generate some test data that spans the entire domain and compute the predicted quantiles.""", unsafe_allow_html=True)
234 | __st.markdown(r"""<details>
235 | <summary markdown="span">Show code</summary>""", unsafe_allow_html=True)
236 | with __st.echo(), streambook.st_stdout('info'):
237 |     x_test = np.linspace(x.min(), x.max(), 100)
238 |     y_pred = model.predict(x_test[..., None])
239 | 
240 |     fig = plt.figure()
241 |     plt.scatter(x, y, s=20, facecolors="none", edgecolors="k")
242 | 
243 |     for i, q_values in enumerate(np.split(y_pred, len(quantiles), axis=-1)):
244 |         plt.plot(x_test, q_values[:, 0], linewidth=2, label=f"Q({quantiles[i]:.2f})")
245 | 
246 |     plt.legend()
247 |     plt.close()
248 | __st.markdown(r"""</details>""", unsafe_allow_html=True)
249 | with __st.echo(), streambook.st_stdout('info'):
250 |     fig
251 | __st.markdown(r"""Amazing! Notice how the first few quantiles are tightly packed together while the last ones spread out, capturing the behavior of the exponential distribution. We can also visualize the region between the highest and lowest quantiles, and this gives us some bounds on our predictions.
252 | 
253 | <details>
254 | <summary markdown="span">Show code</summary>""", unsafe_allow_html=True)
255 | with __st.echo(), streambook.st_stdout('info'):
256 |     median_idx = np.where(np.isclose(quantiles, 0.5))[0]
257 | 
258 |     fig = plt.figure()
259 |     plt.fill_between(x_test, y_pred[:, -1], y_pred[:, 0], alpha=0.5, color="b")
260 |     plt.scatter(x, y, s=20, facecolors="none", edgecolors="k")
261 |     plt.plot(
262 |         x_test,
263 |         y_pred[:, median_idx],
264 |         color="r",
265 |         linestyle="dashed",
266 |         label="Q(0.5)",
267 |     )
268 |     plt.legend()
269 |     plt.close()
270 | __st.markdown(r"""</details>""", unsafe_allow_html=True)
271 | with __st.echo(), streambook.st_stdout('info'):
272 |     fig
273 | __st.markdown(r"""On the other hand, having multiple quantile values allows us to estimate the density of the data. Since the difference between two adjacent quantiles represent the probability that a point lies between them, we can construct a piecewise function that approximates the density of the data.
274 | 
275 | <details>
276 | <summary markdown="span">Show code</summary>""", unsafe_allow_html=True)
277 | with __st.echo(), streambook.st_stdout('info'):
278 |     def get_pdf(quantiles, q_values):
279 |         densities = []
280 | 
281 |         for i in range(len(quantiles) - 1):
282 |             area = quantiles[i + 1] - quantiles[i]
283 |             b = q_values[i + 1] - q_values[i]
284 |             a = area / b
285 | 
286 |             densities.append(a)
287 | 
288 |         return densities
289 | 
290 | 
291 |     def piecewise(xs):
292 |         return [xs[i + j] for i in range(len(xs) - 1) for j in range(2)]
293 | 
294 | 
295 |     def doubled(xs):
296 |         return [np.clip(xs[i], 0, 3) for i in range(len(xs)) for _ in range(2)]
297 | __st.markdown(r"""</details>""", unsafe_allow_html=True)
298 | __st.markdown(r"""For a given `x`, we can compute the quantile values and then use these to compute the conditional piecewise density function of `y` given `x`.
299 | 
300 | <details>
301 | <summary markdown="span">Show code</summary>""", unsafe_allow_html=True)
302 | with __st.echo(), streambook.st_stdout('info'):
303 |     xi = 7.0
304 |     xi = __st.slider("xi", 0.0001, 11.0, xi)
305 | 
306 |     q_values = model.predict(np.array([[xi]]))[0].tolist()
307 | 
308 |     densities = get_pdf(quantiles, q_values)
309 | 
310 |     fig = plt.figure()
311 |     plt.title(f"x = {xi}")
312 |     plt.fill_between(piecewise(q_values), 0, doubled(densities))
313 |     # plt.fill_between(q_values, 0, densities + [0])
314 |     # plt.plot(q_values, densities + [0], color="k")
315 |     plt.xlim(0, y.max())
316 |     plt.gca().set_xlabel("y")
317 |     plt.gca().set_ylabel("p(y)")
318 |     plt.close()
319 | __st.markdown(r"""</details>""", unsafe_allow_html=True)
320 | with __st.echo(), streambook.st_stdout('info'):
321 |     fig
322 | __st.markdown(r"""<span id='Recap'> </span><span id='Next Steps'> </span><span id='Acknowledgments'> </span>
323 | One of the exciting properties of Quantile Regression is that we did not need to know a priori the output distribution, and training is easy compared to other methods.
324 | 
325 | ## Recap
326 | * Quantile Regression is a simple and effective method for learning some statistics
327 | about the output distribution.
328 | * It is advantageous to establish bounds on the predictions of a model when risk management is desired.
329 | * The Quantile Loss function is simple and easy to implement.
330 | * Quantile Regression can be efficiently implemented using Neural Networks since a single model can predict all the quantiles.
331 | * The quantiles can be used to estimate the conditional density of the data.
332 | 
333 | ## Next Steps
334 | * Try running this notebook with `multimodal = True`.
335 | * Take a look at Mixture Density Networks.
336 | * Learn more about [jax](https://github.com/google/jax) and [elegy](https://github.com/poets-ai/elegy).
337 | 
338 | ## Acknowledgments
339 | Many thanks to [David Cardozo](https://github.com/davidnet) for his proofreading and getting the notebook to run in colab.""", unsafe_allow_html=True)
340 | 
341 | 


--------------------------------------------------------------------------------
/presentation.md:
--------------------------------------------------------------------------------
  1 | ---
  2 | title: Quantile Regression Presentation
  3 | tags: presentation
  4 | slideOptions:
  5 |   theme: white
  6 |   transition: 'fade'
  7 | ---
  8 | <style>
  9 | .reveal section img { background:none; border:none; box-shadow:none; }
 10 | </style>
 11 | 
 12 | # Quantile Regression
 13 | A simple method to estimate uncertainty in Machine Learning
 14 | 
 15 | ---
 16 | 
 17 | ## Why estimate uncertainty?
 18 | 
 19 | * Get bounds for the data.
 20 | * Estimate the distribution of the output.
 21 | <span>
 22 | * **Reduce Risk**.<!-- .element: class="fragment" data-fragment-index="1" -->
 23 | </span>
 24 | 
 25 | ---
 26 | 
 27 | ## Problem
 28 | 
 29 | <img src="https://raw.githubusercontent.com/cgarciae/quantile-regression/master/main_files/main_1_0.png" height="500" />
 30 | 
 31 | ---
 32 | 
 33 | ## Problem
 34 | 1. It is not normally distributed.
 35 | 2. Noise it not symetric. 
 36 | 3. Its variance is not constant.
 37 | 
 38 | ---
 39 | 
 40 | ## Solution
 41 | Estimate uncertainty by predicting the <br> quantiles of $y$ given $x$.
 42 | 
 43 | 
 44 | ---
 45 | 
 46 | ## Quantile Loss
 47 | 
 48 | $$
 49 | \begin{aligned}
 50 |     E &= y - f(x) \\
 51 |     L_q &= \begin{cases}
 52 |         q  E,     &    E \gt 0  \\
 53 |         (1 - q) (-E), &    E \lt 0
 54 |     \end{cases}
 55 | \end{aligned}
 56 | $$
 57 | 
 58 | ---
 59 | 
 60 | ## Quantile Loss
 61 | 
 62 | $$
 63 | \begin{aligned}
 64 |     E &= y - f(x) \\
 65 |     L_q &= \max \begin{cases}
 66 |         q  E   \\
 67 |         (q - 1) E
 68 |     \end{cases}
 69 | \end{aligned}
 70 | $$
 71 | 
 72 | ---
 73 | 
 74 | ## JAX Implementation
 75 | ```python
 76 | 
 77 |     def quantile_loss(q, y_true, y_pred):
 78 |         e = y_true - y_pred
 79 |         return jnp.maximum(q * e, (q - 1.0) * e)
 80 | 
 81 | ```
 82 | 
 83 | ---
 84 | 
 85 | <img src="https://raw.githubusercontent.com/cgarciae/quantile-regression/master/main_files/main_5_1.png" height="550">
 86 |     
 87 | **Loss landscape** for a continous sequence of `y_true` values  between `[10, 20]`.
 88 | <!-- .element: style="font-size: 20px;" -->
 89 | 
 90 | ---
 91 | 
 92 | <!-- ## Deep Quantile Regression -->
 93 | ```python
 94 | 
 95 |     class QuantileRegression(elegy.Module):
 96 |         def __init__(self, n_quantiles: int):
 97 |             super().__init__()
 98 |             self.n_quantiles = n_quantiles
 99 | 
100 |         def call(self, x):
101 |             x = elegy.nn.Linear(128)(x)
102 |             x = jax.nn.relu(x)
103 |             x = elegy.nn.Linear(64)(x)
104 |             x = jax.nn.relu(x)
105 |             x = elegy.nn.Linear(self.n_quantiles)(x)
106 |             
107 |             return x
108 | ```
109 | 
110 | ---
111 | 
112 | <img src="https://raw.githubusercontent.com/cgarciae/quantile-regression/master/main_files/main_13_0.png">
113 | 
114 | ---
115 | 
116 | <img src="https://raw.githubusercontent.com/cgarciae/quantile-regression/master/main_files/main_15_0.png">
117 | 
118 | ---
119 | 
120 | <img src="https://raw.githubusercontent.com/cgarciae/quantile-regression/master/main_files/main_19_0.png">
121 |     
122 | 
123 | ---
124 | 
125 | ## Recap
126 | * Quantile Regression: simple and effective.
127 | * Use when risk management is needed.
128 | * Neural Networks are an efficient way to predict multiple quantiles.
129 | * With sufficient quantiles you can approximate the density function.
130 | <!-- .element: style="font-size: 36px;" -->
131 | 
132 | ---
133 | 
134 | ## Next Steps
135 | * Check out the blog and repo
136 |     * Blog: BLOG_URL
137 |     * Repo: [cgarciae/quantile-regression](https://github.com/cgarciae/quantile-regression)
138 | * Take a look at Mixture Density Networks.
139 | * Learn more about [jax]("https://github.com/google/jax) and [elegy]("https://github.com/poets-ai/elegy).
140 | 


--------------------------------------------------------------------------------
/pyproject.toml:
--------------------------------------------------------------------------------
 1 | [tool.poetry]
 2 | name = "quantile-regression"
 3 | version = "0.1.0"
 4 | description = ""
 5 | authors = ["Cristian Garcia <cgarcia.e88@gmail.com>"]
 6 | license = "MIT"
 7 | 
 8 | [tool.poetry.dependencies]
 9 | python = ">=3.8,<3.9"
10 | numpy = "^1.21.0"
11 | elegy = "^0.7.4"
12 | matplotlib = "^3.4.2"
13 | pandas = "<1.3"
14 | 
15 | [tool.poetry.dev-dependencies]
16 | streambook = "^0.2"
17 | debugpy = "^1.4.1"
18 | jupyterlab = "<3.1.0"
19 | black = {version = "^21.7b0", allow-prereleases = true}
20 | 
21 | [build-system]
22 | requires = ["poetry-core>=1.0.0"]
23 | build-backend = "poetry.core.masonry.api"
24 | 


--------------------------------------------------------------------------------
/requirements.txt:
--------------------------------------------------------------------------------
 1 | absl-py==0.13.0; python_full_version >= "3.6.1" and python_version < "3.9" and python_version >= "3.7"
 2 | chex==0.0.8; python_full_version >= "3.6.1" and python_version < "3.9" and python_version >= "3.6"
 3 | cloudpickle==1.6.0; python_full_version >= "3.6.1" and python_version < "3.9" and python_version >= "3.5"
 4 | colorama==0.4.4; python_version >= "3.6" and python_version < "3.9" and python_full_version >= "3.6.1"
 5 | commonmark==0.9.1; python_version >= "3.6" and python_version < "3.9" and python_full_version >= "3.6.1"
 6 | cycler==0.10.0; python_version >= "3.7"
 7 | dm-haiku==0.0.2; python_full_version >= "3.6.1" and python_version < "3.9"
 8 | dm-tree==0.1.6; python_full_version >= "3.6.1" and python_version < "3.9" and python_version >= "3.6"
 9 | elegy==0.7.4; python_full_version >= "3.6.1" and python_version < "3.9"
10 | flatbuffers==2.0; python_full_version >= "3.6.1" and python_version < "3.9" and python_version >= "3.7"
11 | jax==0.2.18; python_full_version >= "3.6.1" and python_version < "3.9" and python_version >= "3.7"
12 | jaxlib==0.1.70; python_full_version >= "3.6.1" and python_version < "3.9" and python_version >= "3.7"
13 | kiwisolver==1.3.1; python_version >= "3.7"
14 | matplotlib==3.4.2; python_version >= "3.7"
15 | numpy==1.21.1; python_version >= "3.7"
16 | opt-einsum==3.3.0; python_full_version >= "3.6.1" and python_version < "3.9" and python_version >= "3.7"
17 | optax==0.0.6; python_full_version >= "3.6.1" and python_version < "3.9" and python_version >= "3.6"
18 | pandas==1.2.5; python_full_version >= "3.7.1"
19 | pillow==8.3.1; python_version >= "3.7"
20 | protobuf==3.17.3; python_full_version >= "3.6.1" and python_version < "3.9"
21 | pygments==2.9.0; python_version >= "3.6" and python_version < "3.9" and python_full_version >= "3.6.1"
22 | pyparsing==2.4.7; python_version >= "3.7" and python_full_version < "3.0.0" or python_full_version >= "3.3.0" and python_version >= "3.7"
23 | python-dateutil==2.8.2; python_full_version >= "3.7.1" and python_version >= "3.7"
24 | pytz==2021.1; python_full_version >= "3.7.1"
25 | pyyaml==5.4.1; python_full_version >= "3.6.1" and python_version < "3.9"
26 | rich==9.13.0; python_version >= "3.6" and python_version < "3.9" and python_full_version >= "3.6.1"
27 | scipy==1.7.1; python_version >= "3.7" and python_version < "3.9" and python_full_version >= "3.6.1"
28 | six==1.16.0; python_full_version >= "3.6.1" and python_version >= "3.7" and python_version < "3.9"
29 | tabulate==0.8.9; python_full_version >= "3.6.1" and python_version < "3.9"
30 | tensorboardx==2.4; python_full_version >= "3.6.1" and python_version < "3.9"
31 | toolz==0.10.0; python_full_version >= "3.6.1" and python_version < "3.9" and python_version >= "3.6"
32 | typing-extensions==3.10.0.0; python_version >= "3.6" and python_version < "3.9" and python_full_version >= "3.6.1"
33 | 


--------------------------------------------------------------------------------
/update_readme.py:
--------------------------------------------------------------------------------
1 | from pathlib import Path
2 | 
3 | path = Path("README.md")
4 | text = path.read_text()
5 | 
6 | text = text.replace("![png](", "![png](https://raw.githubusercontent.com/cgarciae/quantile-regression/master/")
7 | 
8 | path.write_text(text)


--------------------------------------------------------------------------------