├── .husky ├── .gitignore └── pre-commit ├── .npmrc ├── .babelrc ├── src ├── playground │ ├── playground.js │ ├── __test__ │ │ └── playground.test.js │ └── README.md ├── algorithms │ ├── math │ │ ├── bits │ │ │ ├── divideByTwo.js │ │ │ ├── isEven.js │ │ │ ├── multiplyByTwo.js │ │ │ ├── isPowerOfTwo.js │ │ │ ├── getBit.js │ │ │ ├── setBit.js │ │ │ ├── switchSign.js │ │ │ ├── clearBit.js │ │ │ ├── bitLength.js │ │ │ ├── bitsDiff.js │ │ │ ├── isPositive.js │ │ │ ├── __test__ │ │ │ │ ├── divideByTwo.test.js │ │ │ │ ├── setBit.test.js │ │ │ │ ├── bitsDiff.test.js │ │ │ │ ├── clearBit.test.js │ │ │ │ ├── multiplyByTwo.test.js │ │ │ │ ├── switchSign.test.js │ │ │ │ ├── bitLength.test.js │ │ │ │ ├── multiplyUnsigned.test.js │ │ │ │ ├── getBit.test.js │ │ │ │ ├── multiply.test.js │ │ │ │ ├── fullAdder.test.js │ │ │ │ ├── isEven.test.js │ │ │ │ ├── updateBit.test.js │ │ │ │ ├── isPositive.test.js │ │ │ │ ├── countSetBits.test.js │ │ │ │ └── isPowerOfTwo.test.js │ │ │ ├── countSetBits.js │ │ │ ├── updateBit.js │ │ │ └── multiplyUnsigned.js │ │ ├── radian │ │ │ ├── degreeToRadian.js │ │ │ ├── radianToDegree.js │ │ │ ├── __test__ │ │ │ │ ├── degreeToRadian.test.js │ │ │ │ └── radianToDegree.test.js │ │ │ └── README.md │ │ ├── factorial │ │ │ ├── factorialRecursive.js │ │ │ ├── factorial.js │ │ │ ├── __test__ │ │ │ │ ├── factorial.test.js │ │ │ │ └── factorialRecursive.test.js │ │ │ ├── README.zh-CN.md │ │ │ ├── README.md │ │ │ └── README.fr-FR.md │ │ ├── fourier-transform │ │ │ └── __test__ │ │ │ │ ├── discreteFourierTransform.test.js │ │ │ │ └── inverseDiscreteFourierTransform.test.js │ │ ├── least-common-multiple │ │ │ ├── leastCommonMultiple.js │ │ │ └── __test__ │ │ │ │ └── leastCommonMultiple.test.js │ │ ├── horner-method │ │ │ ├── hornerMethod.js │ │ │ ├── classicPolynome.js │ │ │ └── __test__ │ │ │ │ ├── classicPolynome.test.js │ │ │ │ └── hornerMethod.test.js │ │ ├── pascal-triangle │ │ │ ├── pascalTriangle.js │ │ │ ├── __test__ │ │ │ │ ├── pascalTriangle.test.js │ │ │ │ └── pascalTriangleRecursive.test.js │ │ │ └── pascalTriangleRecursive.js │ │ ├── sieve-of-eratosthenes │ │ │ ├── __test__ │ │ │ │ └── sieveOfEratosthenes.test.js │ │ │ └── sieveOfEratosthenes.js │ │ ├── integer-partition │ │ │ ├── __test__ │ │ │ │ └── integerPartition.test.js │ │ │ └── README.md │ │ ├── liu-hui │ │ │ └── __test__ │ │ │ │ └── liuHui.test.js │ │ ├── fibonacci │ │ │ ├── fibonacciNth.js │ │ │ ├── fibonacci.js │ │ │ ├── README.zh-CN.md │ │ │ ├── __test__ │ │ │ │ ├── fibonacci.test.js │ │ │ │ ├── fibonacciNth.test.js │ │ │ │ └── fibonacciNthClosedForm.test.js │ │ │ ├── fibonacciNthClosedForm.js │ │ │ ├── README.fr-FR.md │ │ │ └── README.md │ │ ├── euclidean-algorithm │ │ │ ├── euclideanAlgorithm.js │ │ │ ├── euclideanAlgorithmIterative.js │ │ │ └── __test__ │ │ │ │ └── euclideanAlgorithm.test.js │ │ ├── is-power-of-two │ │ │ ├── isPowerOfTwo.js │ │ │ ├── isPowerOfTwoBitwise.js │ │ │ └── __test__ │ │ │ │ ├── isPowerOfTwo.test.js │ │ │ │ └── isPowerOfTwoBitwise.test.js │ │ ├── euclidean-distance │ │ │ ├── euclideanDistance.js │ │ │ └── __tests__ │ │ │ │ └── euclideanDistance.test.js │ │ ├── primality-test │ │ │ ├── trialDivision.js │ │ │ ├── README.md │ │ │ └── __test__ │ │ │ │ └── trialDivision.test.js │ │ ├── fast-powering │ │ │ ├── fastPowering.js │ │ │ └── __test__ │ │ │ │ └── fastPowering.test.js │ │ └── prime-factors │ │ │ └── primeFactors.js │ ├── image-processing │ │ └── seam-carving │ │ │ └── __tests__ │ │ │ ├── test-image-after.jpg │ │ │ └── test-image-before.jpg │ ├── sorting │ │ ├── __test__ │ │ │ └── Sort.test.js │ │ ├── heap-sort │ │ │ ├── HeapSort.js │ │ │ └── README.md │ │ ├── radix-sort │ │ │ └── __test__ │ │ │ │ └── RadixSort.test.js │ │ ├── insertion-sort │ │ │ ├── README.md │ │ │ └── InsertionSort.js │ │ ├── selection-sort │ │ │ ├── SelectionSort.js │ │ │ └── README.md │ │ ├── bubble-sort │ │ │ ├── README.pt-BR.md │ │ │ ├── BubbleSort.js │ │ │ └── README.md │ │ ├── Sort.js │ │ └── shell-sort │ │ │ └── ShellSort.js │ ├── uncategorized │ │ ├── unique-paths │ │ │ ├── uniquePaths.js │ │ │ └── __test__ │ │ │ │ ├── uniquePaths.test.js │ │ │ │ ├── btUniquePaths.test.js │ │ │ │ └── dpUniquePaths.test.js │ │ ├── n-queens │ │ │ ├── __test__ │ │ │ │ ├── nQueensBitwise.test.js │ │ │ │ └── QueensPosition.test.js │ │ │ └── QueenPosition.js │ │ ├── jump-game │ │ │ └── __test__ │ │ │ │ ├── greedyJumpGame.test.js │ │ │ │ ├── dpTopDownJumpGame.test.js │ │ │ │ ├── dpBottomUpJumpGame.test.js │ │ │ │ └── backtrackingJumpGame.test.js │ │ ├── best-time-to-buy-sell-stocks │ │ │ ├── accumulatorBestTimeToBuySellStocks.js │ │ │ ├── dpBestTimeToBuySellStocks.js │ │ │ └── peakvalleyBestTimeToBuySellStocks.js │ │ ├── recursive-staircase │ │ │ ├── __test__ │ │ │ │ ├── recursiveStaircaseIT.test.js │ │ │ │ ├── recursiveStaircaseBF.test.js │ │ │ │ ├── recursiveStaircaseDP.test.js │ │ │ │ └── recursiveStaircaseMEM.test.js │ │ │ ├── recursiveStaircaseBF.js │ │ │ ├── README.md │ │ │ ├── recursiveStaircaseDP.js │ │ │ └── recursiveStaircaseIT.js │ │ ├── knight-tour │ │ │ └── __test__ │ │ │ │ └── knightTour.test.js │ │ ├── rain-terraces │ │ │ ├── __test__ │ │ │ │ ├── bfRainTerraces.test.js │ │ │ │ └── dpRainTerraces.test.js │ │ │ └── bfRainTerraces.js │ │ ├── square-matrix-rotation │ │ │ └── squareMatrixRotation.js │ │ └── hanoi-tower │ │ │ └── README.md │ ├── linked-list │ │ ├── traversal │ │ │ ├── traversal.js │ │ │ ├── README.md │ │ │ ├── README.ru-RU.md │ │ │ └── __test__ │ │ │ │ └── traversal.test.js │ │ └── reverse-traversal │ │ │ ├── README.md │ │ │ ├── reverseTraversal.js │ │ │ └── __test__ │ │ │ └── reverseTraversal.test.js │ ├── string │ │ ├── hamming-distance │ │ │ ├── hammingDistance.js │ │ │ ├── README.md │ │ │ └── __test__ │ │ │ │ └── hammingDistance.test.js │ │ ├── longest-common-substring │ │ │ ├── README.md │ │ │ └── __test__ │ │ │ │ └── longestCommonSubstring.test.js │ │ ├── knuth-morris-pratt │ │ │ ├── README.md │ │ │ └── __test__ │ │ │ │ └── knuthMorrisPratt.test.js │ │ ├── z-algorithm │ │ │ └── __test__ │ │ │ │ └── zAlgorithm.test.js │ │ └── levenshtein-distance │ │ │ └── __test__ │ │ │ └── levenshteinDistance.test.js │ ├── sets │ │ ├── power-set │ │ │ └── __test__ │ │ │ │ ├── bwPowerSet.test.js │ │ │ │ └── btPowerSet.test.js │ │ ├── fisher-yates │ │ │ ├── fisherYates.js │ │ │ ├── README.md │ │ │ └── __test__ │ │ │ │ └── fisherYates.test.js │ │ ├── cartesian-product │ │ │ ├── README.md │ │ │ ├── __test__ │ │ │ │ └── cartesianProduct.test.js │ │ │ └── cartesianProduct.js │ │ ├── combination-sum │ │ │ └── __test__ │ │ │ │ └── combinationSum.test.js │ │ ├── shortest-common-supersequence │ │ │ └── README.md │ │ ├── maximum-subarray │ │ │ ├── bfMaximumSubarray.js │ │ │ ├── __test__ │ │ │ │ ├── bfMaximumSubarray.test.js │ │ │ │ └── dpMaximumSubarray.test.js │ │ │ └── README.md │ │ ├── permutations │ │ │ ├── permutateWithRepetitions.js │ │ │ └── permutateWithoutRepetitions.js │ │ ├── knapsack-problem │ │ │ └── KnapsackItem.js │ │ ├── longest-increasing-subsequence │ │ │ └── __test__ │ │ │ │ └── dpLongestIncreasingSubsequence.test.js │ │ ├── longest-common-subsequence │ │ │ ├── __test__ │ │ │ │ └── longestCommonSubsequence.test.js │ │ │ └── README.md │ │ └── combinations │ │ │ ├── combineWithRepetitions.js │ │ │ └── combineWithoutRepetitions.js │ ├── search │ │ ├── linear-search │ │ │ ├── linearSearch.js │ │ │ ├── README.md │ │ │ └── __test__ │ │ │ │ └── linearSearch.test.js │ │ ├── binary-search │ │ │ └── README.md │ │ └── jump-search │ │ │ └── README.md │ ├── tree │ │ ├── depth-first-search │ │ │ └── README.md │ │ └── breadth-first-search │ │ │ └── README.md │ ├── graph │ │ ├── strongly-connected-components │ │ │ └── README.md │ │ ├── depth-first-search │ │ │ └── README.md │ │ ├── breadth-first-search │ │ │ └── README.md │ │ ├── bellman-ford │ │ │ └── README.md │ │ ├── articulation-points │ │ │ └── README.md │ │ ├── dijkstra │ │ │ └── README.md │ │ ├── bridges │ │ │ └── README.md │ │ ├── travelling-salesman │ │ │ └── README.md │ │ └── detect-cycle │ │ │ └── detectUndirectedCycleUsingDisjointSet.js │ └── ml │ │ └── k-means │ │ └── __test__ │ │ └── kMeans.test.js └── data-structures │ ├── linked-list │ └── LinkedListNode.js │ ├── heap │ ├── __test__ │ │ └── Heap.test.js │ ├── MaxHeap.js │ ├── MinHeap.js │ ├── README.ja-JP.md │ ├── README.zh-CN.md │ ├── README.pt-BR.md │ ├── README.fr-FR.md │ ├── README.md │ └── README.ru-RU.md │ ├── doubly-linked-list │ └── DoublyLinkedListNode.js │ ├── queue │ ├── README.zh-CN.md │ ├── README.ja-JP.md │ └── README.ru-RU.md │ ├── priority-queue │ ├── README.zh-CN.md │ ├── README.ja-JP.md │ ├── README.fr-FR.md │ ├── README.md │ ├── README.pt-BR.md │ └── README.ru-RU.md │ ├── stack │ ├── README.zh-CN.md │ ├── README.ja-JP.md │ ├── README.ru-RU.md │ ├── README.pt-BR.md │ └── README.fr-FR.md │ ├── trie │ ├── README.zh-CN.md │ └── README.md │ ├── graph │ ├── README.zh-CN.md │ ├── GraphEdge.js │ ├── README.pt-BR.md │ └── README.md │ ├── hash-table │ ├── README.ja-JP.md │ ├── README.zh-CN.md │ ├── README.pt-BR.md │ ├── README.md │ └── README.fr-FR.md │ ├── tree │ ├── README.zh-CN.md │ └── binary-search-tree │ │ └── BinarySearchTree.js │ └── disjoint-set │ ├── README.md │ ├── README.ru-RU.md │ └── README.pt-BR.md ├── .gitignore ├── assets └── big-o-graph.png ├── .github ├── FUNDING.yml └── workflows │ └── CI.yml ├── .editorconfig ├── .eslintrc ├── BACKERS.md ├── LICENSE ├── CONTRIBUTING.md └── jest.config.js /.husky/.gitignore: -------------------------------------------------------------------------------- 1 | _ 2 | -------------------------------------------------------------------------------- /.npmrc: -------------------------------------------------------------------------------- 1 | engine-strict=false 2 | -------------------------------------------------------------------------------- /.babelrc: -------------------------------------------------------------------------------- 1 | { 2 | "presets": ["@babel/preset-env"] 3 | } 4 | -------------------------------------------------------------------------------- /src/playground/playground.js: -------------------------------------------------------------------------------- 1 | // Place your playground code here. 2 | -------------------------------------------------------------------------------- /.gitignore: -------------------------------------------------------------------------------- 1 | node_modules 2 | .idea 3 | coverage 4 | .vscode 5 | .DS_Store 6 | -------------------------------------------------------------------------------- /.husky/pre-commit: -------------------------------------------------------------------------------- 1 | #!/bin/sh 2 | . "$(dirname "$0")/_/husky.sh" 3 | 4 | npm run lint 5 | # npm run test 6 | -------------------------------------------------------------------------------- /assets/big-o-graph.png: -------------------------------------------------------------------------------- https://raw.githubusercontent.com/codewithsadee/javascript-algorithms/HEAD/assets/big-o-graph.png -------------------------------------------------------------------------------- /.github/FUNDING.yml: -------------------------------------------------------------------------------- 1 | # @see: https://docs.github.com/en/github/administering-a-repository/displaying-a-sponsor-button-in-your-repository 2 | github: trekhleb 3 | patreon: trekhleb 4 | -------------------------------------------------------------------------------- /src/algorithms/math/bits/divideByTwo.js: -------------------------------------------------------------------------------- 1 | /** 2 | * @param {number} number 3 | * @return {number} 4 | */ 5 | export default function divideByTwo(number) { 6 | return number >> 1; 7 | } 8 | -------------------------------------------------------------------------------- /src/algorithms/math/bits/isEven.js: -------------------------------------------------------------------------------- 1 | /** 2 | * @param {number} number 3 | * @return {boolean} 4 | */ 5 | export default function isEven(number) { 6 | return (number & 1) === 0; 7 | } 8 | -------------------------------------------------------------------------------- /src/playground/__test__/playground.test.js: -------------------------------------------------------------------------------- 1 | describe('playground', () => { 2 | it('should perform playground tasks', () => { 3 | // Place your playground tests here. 4 | }); 5 | }); 6 | -------------------------------------------------------------------------------- /src/algorithms/math/bits/multiplyByTwo.js: -------------------------------------------------------------------------------- 1 | /** 2 | * @param {number} number 3 | * @return {number} 4 | */ 5 | export default function multiplyByTwo(number) { 6 | return number << 1; 7 | } 8 | -------------------------------------------------------------------------------- /src/algorithms/math/bits/isPowerOfTwo.js: -------------------------------------------------------------------------------- 1 | /** 2 | * @param {number} number 3 | * @return bool 4 | */ 5 | export default function isPowerOfTwo(number) { 6 | return (number & (number - 1)) === 0; 7 | } 8 | -------------------------------------------------------------------------------- /src/algorithms/math/radian/degreeToRadian.js: -------------------------------------------------------------------------------- 1 | /** 2 | * @param {number} degree 3 | * @return {number} 4 | */ 5 | export default function degreeToRadian(degree) { 6 | return degree * (Math.PI / 180); 7 | } 8 | -------------------------------------------------------------------------------- /src/algorithms/math/radian/radianToDegree.js: -------------------------------------------------------------------------------- 1 | /** 2 | * @param {number} radian 3 | * @return {number} 4 | */ 5 | export default function radianToDegree(radian) { 6 | return radian * (180 / Math.PI); 7 | } 8 | -------------------------------------------------------------------------------- /src/algorithms/image-processing/seam-carving/__tests__/test-image-after.jpg: -------------------------------------------------------------------------------- https://raw.githubusercontent.com/codewithsadee/javascript-algorithms/HEAD/src/algorithms/image-processing/seam-carving/__tests__/test-image-after.jpg -------------------------------------------------------------------------------- /src/algorithms/image-processing/seam-carving/__tests__/test-image-before.jpg: -------------------------------------------------------------------------------- https://raw.githubusercontent.com/codewithsadee/javascript-algorithms/HEAD/src/algorithms/image-processing/seam-carving/__tests__/test-image-before.jpg -------------------------------------------------------------------------------- /.editorconfig: -------------------------------------------------------------------------------- 1 | # @see: https://editorconfig.org/ 2 | root = true 3 | 4 | [*] 5 | end_of_line = lf 6 | insert_final_newline = true 7 | charset = utf-8 8 | indent_style = space 9 | indent_size = 2 10 | trim_trailing_whitespace = true 11 | -------------------------------------------------------------------------------- /src/algorithms/math/factorial/factorialRecursive.js: -------------------------------------------------------------------------------- 1 | /** 2 | * @param {number} number 3 | * @return {number} 4 | */ 5 | export default function factorialRecursive(number) { 6 | return number > 1 ? number * factorialRecursive(number - 1) : 1; 7 | } 8 | -------------------------------------------------------------------------------- /src/algorithms/math/bits/getBit.js: -------------------------------------------------------------------------------- 1 | /** 2 | * @param {number} number 3 | * @param {number} bitPosition - zero based. 4 | * @return {number} 5 | */ 6 | export default function getBit(number, bitPosition) { 7 | return (number >> bitPosition) & 1; 8 | } 9 | -------------------------------------------------------------------------------- /src/algorithms/math/bits/setBit.js: -------------------------------------------------------------------------------- 1 | /** 2 | * @param {number} number 3 | * @param {number} bitPosition - zero based. 4 | * @return {number} 5 | */ 6 | export default function setBit(number, bitPosition) { 7 | return number | (1 << bitPosition); 8 | } 9 | -------------------------------------------------------------------------------- /src/algorithms/math/bits/switchSign.js: -------------------------------------------------------------------------------- 1 | /** 2 | * Switch the sign of the number using "Twos Complement" approach. 3 | * @param {number} number 4 | * @return {number} 5 | */ 6 | export default function switchSign(number) { 7 | return ~number + 1; 8 | } 9 | -------------------------------------------------------------------------------- /src/algorithms/math/bits/clearBit.js: -------------------------------------------------------------------------------- 1 | /** 2 | * @param {number} number 3 | * @param {number} bitPosition - zero based. 4 | * @return {number} 5 | */ 6 | export default function clearBit(number, bitPosition) { 7 | const mask = ~(1 << bitPosition); 8 | 9 | return number & mask; 10 | } 11 | -------------------------------------------------------------------------------- /src/algorithms/math/factorial/factorial.js: -------------------------------------------------------------------------------- 1 | /** 2 | * @param {number} number 3 | * @return {number} 4 | */ 5 | export default function factorial(number) { 6 | let result = 1; 7 | 8 | for (let i = 2; i <= number; i += 1) { 9 | result *= i; 10 | } 11 | 12 | return result; 13 | } 14 | -------------------------------------------------------------------------------- /src/data-structures/linked-list/LinkedListNode.js: -------------------------------------------------------------------------------- 1 | export default class LinkedListNode { 2 | constructor(value, next = null) { 3 | this.value = value; 4 | this.next = next; 5 | } 6 | 7 | toString(callback) { 8 | return callback ? callback(this.value) : `${this.value}`; 9 | } 10 | } 11 | -------------------------------------------------------------------------------- /src/playground/README.md: -------------------------------------------------------------------------------- 1 | # Playground 2 | 3 | You may use `playground.js` file to play with data 4 | structures and algorithms. The code from `playground.js` may 5 | be tested in `./__test__/playground.test.js` file. 6 | 7 | To run tests simply run: 8 | 9 | ``` 10 | npm test -- -t 'playground' 11 | ``` 12 | -------------------------------------------------------------------------------- /src/data-structures/heap/__test__/Heap.test.js: -------------------------------------------------------------------------------- 1 | import Heap from '../Heap'; 2 | 3 | describe('Heap', () => { 4 | it('should not allow to create instance of the Heap directly', () => { 5 | const instantiateHeap = () => { 6 | const heap = new Heap(); 7 | heap.add(5); 8 | }; 9 | 10 | expect(instantiateHeap).toThrow(); 11 | }); 12 | }); 13 | -------------------------------------------------------------------------------- /src/algorithms/sorting/__test__/Sort.test.js: -------------------------------------------------------------------------------- 1 | import Sort from '../Sort'; 2 | 3 | describe('Sort', () => { 4 | it('should throw an error when trying to call Sort.sort() method directly', () => { 5 | function doForbiddenSort() { 6 | const sorter = new Sort(); 7 | sorter.sort(); 8 | } 9 | 10 | expect(doForbiddenSort).toThrow(); 11 | }); 12 | }); 13 | -------------------------------------------------------------------------------- /src/data-structures/doubly-linked-list/DoublyLinkedListNode.js: -------------------------------------------------------------------------------- 1 | export default class DoublyLinkedListNode { 2 | constructor(value, next = null, previous = null) { 3 | this.value = value; 4 | this.next = next; 5 | this.previous = previous; 6 | } 7 | 8 | toString(callback) { 9 | return callback ? callback(this.value) : `${this.value}`; 10 | } 11 | } 12 | -------------------------------------------------------------------------------- /src/algorithms/math/bits/bitLength.js: -------------------------------------------------------------------------------- 1 | /** 2 | * Return the number of bits used in the binary representation of the number. 3 | * 4 | * @param {number} number 5 | * @return {number} 6 | */ 7 | export default function bitLength(number) { 8 | let bitsCounter = 0; 9 | 10 | while ((1 << bitsCounter) <= number) { 11 | bitsCounter += 1; 12 | } 13 | 14 | return bitsCounter; 15 | } 16 | -------------------------------------------------------------------------------- /src/algorithms/math/fourier-transform/__test__/discreteFourierTransform.test.js: -------------------------------------------------------------------------------- 1 | import discreteFourierTransform from '../discreteFourierTransform'; 2 | import FourierTester from './FourierTester'; 3 | 4 | describe('discreteFourierTransform', () => { 5 | it('should split signal into frequencies', () => { 6 | FourierTester.testDirectFourierTransform(discreteFourierTransform); 7 | }); 8 | }); 9 | -------------------------------------------------------------------------------- /src/algorithms/math/least-common-multiple/leastCommonMultiple.js: -------------------------------------------------------------------------------- 1 | import euclideanAlgorithm from '../euclidean-algorithm/euclideanAlgorithm'; 2 | 3 | /** 4 | * @param {number} a 5 | * @param {number} b 6 | * @return {number} 7 | */ 8 | 9 | export default function leastCommonMultiple(a, b) { 10 | return ((a === 0) || (b === 0)) ? 0 : Math.abs(a * b) / euclideanAlgorithm(a, b); 11 | } 12 | -------------------------------------------------------------------------------- /src/algorithms/math/factorial/__test__/factorial.test.js: -------------------------------------------------------------------------------- 1 | import factorial from '../factorial'; 2 | 3 | describe('factorial', () => { 4 | it('should calculate factorial', () => { 5 | expect(factorial(0)).toBe(1); 6 | expect(factorial(1)).toBe(1); 7 | expect(factorial(5)).toBe(120); 8 | expect(factorial(8)).toBe(40320); 9 | expect(factorial(10)).toBe(3628800); 10 | }); 11 | }); 12 | -------------------------------------------------------------------------------- /src/algorithms/math/bits/bitsDiff.js: -------------------------------------------------------------------------------- 1 | import countSetBits from './countSetBits'; 2 | 3 | /** 4 | * Counts the number of bits that need to be change in order 5 | * to convert numberA to numberB. 6 | * 7 | * @param {number} numberA 8 | * @param {number} numberB 9 | * @return {number} 10 | */ 11 | export default function bitsDiff(numberA, numberB) { 12 | return countSetBits(numberA ^ numberB); 13 | } 14 | -------------------------------------------------------------------------------- /.eslintrc: -------------------------------------------------------------------------------- 1 | { 2 | "root": true, 3 | "extends": "airbnb", 4 | "plugins": ["jest"], 5 | "env": { 6 | "jest/globals": true 7 | }, 8 | "rules": { 9 | "no-bitwise": "off", 10 | "no-lonely-if": "off", 11 | "class-methods-use-this": "off", 12 | "arrow-body-style": "off", 13 | "no-loop-func": "off" 14 | }, 15 | "settings": { 16 | "react": { 17 | "version": "latest" 18 | } 19 | } 20 | } 21 | -------------------------------------------------------------------------------- /src/algorithms/math/bits/isPositive.js: -------------------------------------------------------------------------------- 1 | /** 2 | * @param {number} number - 32-bit integer. 3 | * @return {boolean} 4 | */ 5 | export default function isPositive(number) { 6 | // Zero is neither a positive nor a negative number. 7 | if (number === 0) { 8 | return false; 9 | } 10 | 11 | // The most significant 32nd bit can be used to determine whether the number is positive. 12 | return ((number >> 31) & 1) === 0; 13 | } 14 | -------------------------------------------------------------------------------- /src/algorithms/math/fourier-transform/__test__/inverseDiscreteFourierTransform.test.js: -------------------------------------------------------------------------------- 1 | import inverseDiscreteFourierTransform from '../inverseDiscreteFourierTransform'; 2 | import FourierTester from './FourierTester'; 3 | 4 | describe('inverseDiscreteFourierTransform', () => { 5 | it('should calculate output signal out of input frequencies', () => { 6 | FourierTester.testInverseFourierTransform(inverseDiscreteFourierTransform); 7 | }); 8 | }); 9 | -------------------------------------------------------------------------------- /src/algorithms/uncategorized/unique-paths/uniquePaths.js: -------------------------------------------------------------------------------- 1 | import pascalTriangle from '../../math/pascal-triangle/pascalTriangle'; 2 | 3 | /** 4 | * @param {number} width 5 | * @param {number} height 6 | * @return {number} 7 | */ 8 | export default function uniquePaths(width, height) { 9 | const pascalLine = width + height - 2; 10 | const pascalLinePosition = Math.min(width, height) - 1; 11 | 12 | return pascalTriangle(pascalLine)[pascalLinePosition]; 13 | } 14 | -------------------------------------------------------------------------------- /src/algorithms/math/bits/__test__/divideByTwo.test.js: -------------------------------------------------------------------------------- 1 | import divideByTwo from '../divideByTwo'; 2 | 3 | describe('divideByTwo', () => { 4 | it('should divide numbers by two using bitwise operations', () => { 5 | expect(divideByTwo(0)).toBe(0); 6 | expect(divideByTwo(1)).toBe(0); 7 | expect(divideByTwo(3)).toBe(1); 8 | expect(divideByTwo(10)).toBe(5); 9 | expect(divideByTwo(17)).toBe(8); 10 | expect(divideByTwo(125)).toBe(62); 11 | }); 12 | }); 13 | -------------------------------------------------------------------------------- /src/algorithms/math/bits/__test__/setBit.test.js: -------------------------------------------------------------------------------- 1 | import setBit from '../setBit'; 2 | 3 | describe('setBit', () => { 4 | it('should set bit at specific position', () => { 5 | // 1 = 0b0001 6 | expect(setBit(1, 0)).toBe(1); 7 | expect(setBit(1, 1)).toBe(3); 8 | expect(setBit(1, 2)).toBe(5); 9 | 10 | // 10 = 0b1010 11 | expect(setBit(10, 0)).toBe(11); 12 | expect(setBit(10, 1)).toBe(10); 13 | expect(setBit(10, 2)).toBe(14); 14 | }); 15 | }); 16 | -------------------------------------------------------------------------------- /src/algorithms/math/factorial/__test__/factorialRecursive.test.js: -------------------------------------------------------------------------------- 1 | import factorialRecursive from '../factorialRecursive'; 2 | 3 | describe('factorialRecursive', () => { 4 | it('should calculate factorial', () => { 5 | expect(factorialRecursive(0)).toBe(1); 6 | expect(factorialRecursive(1)).toBe(1); 7 | expect(factorialRecursive(5)).toBe(120); 8 | expect(factorialRecursive(8)).toBe(40320); 9 | expect(factorialRecursive(10)).toBe(3628800); 10 | }); 11 | }); 12 | -------------------------------------------------------------------------------- /src/algorithms/linked-list/traversal/traversal.js: -------------------------------------------------------------------------------- 1 | /** 2 | * Traversal callback function. 3 | * @callback traversalCallback 4 | * @param {*} nodeValue 5 | */ 6 | 7 | /** 8 | * @param {LinkedList} linkedList 9 | * @param {traversalCallback} callback 10 | */ 11 | export default function traversal(linkedList, callback) { 12 | let currentNode = linkedList.head; 13 | 14 | while (currentNode) { 15 | callback(currentNode.value); 16 | currentNode = currentNode.next; 17 | } 18 | } 19 | -------------------------------------------------------------------------------- /src/algorithms/string/hamming-distance/hammingDistance.js: -------------------------------------------------------------------------------- 1 | /** 2 | * @param {string} a 3 | * @param {string} b 4 | * @return {number} 5 | */ 6 | export default function hammingDistance(a, b) { 7 | if (a.length !== b.length) { 8 | throw new Error('Strings must be of the same length'); 9 | } 10 | 11 | let distance = 0; 12 | 13 | for (let i = 0; i < a.length; i += 1) { 14 | if (a[i] !== b[i]) { 15 | distance += 1; 16 | } 17 | } 18 | 19 | return distance; 20 | } 21 | -------------------------------------------------------------------------------- /src/algorithms/math/bits/__test__/bitsDiff.test.js: -------------------------------------------------------------------------------- 1 | import bitsDiff from '../bitsDiff'; 2 | 3 | describe('bitsDiff', () => { 4 | it('should calculate bits difference between two numbers', () => { 5 | expect(bitsDiff(0, 0)).toBe(0); 6 | expect(bitsDiff(1, 1)).toBe(0); 7 | expect(bitsDiff(124, 124)).toBe(0); 8 | expect(bitsDiff(0, 1)).toBe(1); 9 | expect(bitsDiff(1, 0)).toBe(1); 10 | expect(bitsDiff(1, 2)).toBe(2); 11 | expect(bitsDiff(1, 3)).toBe(1); 12 | }); 13 | }); 14 | -------------------------------------------------------------------------------- /src/algorithms/math/bits/__test__/clearBit.test.js: -------------------------------------------------------------------------------- 1 | import clearBit from '../clearBit'; 2 | 3 | describe('clearBit', () => { 4 | it('should clear bit at specific position', () => { 5 | // 1 = 0b0001 6 | expect(clearBit(1, 0)).toBe(0); 7 | expect(clearBit(1, 1)).toBe(1); 8 | expect(clearBit(1, 2)).toBe(1); 9 | 10 | // 10 = 0b1010 11 | expect(clearBit(10, 0)).toBe(10); 12 | expect(clearBit(10, 1)).toBe(8); 13 | expect(clearBit(10, 3)).toBe(2); 14 | }); 15 | }); 16 | -------------------------------------------------------------------------------- /src/algorithms/math/bits/__test__/multiplyByTwo.test.js: -------------------------------------------------------------------------------- 1 | import multiplyByTwo from '../multiplyByTwo'; 2 | 3 | describe('multiplyByTwo', () => { 4 | it('should multiply numbers by two using bitwise operations', () => { 5 | expect(multiplyByTwo(0)).toBe(0); 6 | expect(multiplyByTwo(1)).toBe(2); 7 | expect(multiplyByTwo(3)).toBe(6); 8 | expect(multiplyByTwo(10)).toBe(20); 9 | expect(multiplyByTwo(17)).toBe(34); 10 | expect(multiplyByTwo(125)).toBe(250); 11 | }); 12 | }); 13 | -------------------------------------------------------------------------------- /src/algorithms/math/bits/countSetBits.js: -------------------------------------------------------------------------------- 1 | /** 2 | * @param {number} originalNumber 3 | * @return {number} 4 | */ 5 | export default function countSetBits(originalNumber) { 6 | let setBitsCount = 0; 7 | let number = originalNumber; 8 | 9 | while (number) { 10 | // Add last bit of the number to the sum of set bits. 11 | setBitsCount += number & 1; 12 | 13 | // Shift number right by one bit to investigate other bits. 14 | number >>>= 1; 15 | } 16 | 17 | return setBitsCount; 18 | } 19 | -------------------------------------------------------------------------------- /src/algorithms/uncategorized/unique-paths/__test__/uniquePaths.test.js: -------------------------------------------------------------------------------- 1 | import uniquePaths from '../uniquePaths'; 2 | 3 | describe('uniquePaths', () => { 4 | it('should find the number of unique paths on board', () => { 5 | expect(uniquePaths(3, 2)).toBe(3); 6 | expect(uniquePaths(7, 3)).toBe(28); 7 | expect(uniquePaths(3, 7)).toBe(28); 8 | expect(uniquePaths(10, 10)).toBe(48620); 9 | expect(uniquePaths(100, 1)).toBe(1); 10 | expect(uniquePaths(1, 100)).toBe(1); 11 | }); 12 | }); 13 | -------------------------------------------------------------------------------- /src/algorithms/math/bits/__test__/switchSign.test.js: -------------------------------------------------------------------------------- 1 | import switchSign from '../switchSign'; 2 | 3 | describe('switchSign', () => { 4 | it('should switch the sign of the number using twos complement approach', () => { 5 | expect(switchSign(0)).toBe(0); 6 | expect(switchSign(1)).toBe(-1); 7 | expect(switchSign(-1)).toBe(1); 8 | expect(switchSign(32)).toBe(-32); 9 | expect(switchSign(-32)).toBe(32); 10 | expect(switchSign(23)).toBe(-23); 11 | expect(switchSign(-23)).toBe(23); 12 | }); 13 | }); 14 | -------------------------------------------------------------------------------- /src/data-structures/queue/README.zh-CN.md: -------------------------------------------------------------------------------- 1 | # 队列 2 | 3 | 在计算机科学中, 一个 **队列(queue)** 是一种特殊类型的抽象数据类型或集合。集合中的实体按顺序保存。 4 | 5 | 队列基本操作有两种：入队和出队。从队列的后端位置添加实体，称为入队；从队列的前端位置移除实体，称为出队。 6 | 7 | 8 | 队列中元素先进先出 FIFO (first in, first out)的示意 9 | 10 | ![Queue](https://upload.wikimedia.org/wikipedia/commons/5/52/Data_Queue.svg) 11 | 12 | ## 参考 13 | 14 | - [Wikipedia](https://en.wikipedia.org/wiki/Queue_(abstract_data_type)) 15 | - [YouTube](https://www.youtube.com/watch?v=wjI1WNcIntg&list=PLLXdhg_r2hKA7DPDsunoDZ-Z769jWn4R8&index=3&) 16 | -------------------------------------------------------------------------------- /src/algorithms/sets/power-set/__test__/bwPowerSet.test.js: -------------------------------------------------------------------------------- 1 | import bwPowerSet from '../bwPowerSet'; 2 | 3 | describe('bwPowerSet', () => { 4 | it('should calculate power set of given set using bitwise approach', () => { 5 | expect(bwPowerSet([1])).toEqual([ 6 | [], 7 | [1], 8 | ]); 9 | 10 | expect(bwPowerSet([1, 2, 3])).toEqual([ 11 | [], 12 | [1], 13 | [2], 14 | [1, 2], 15 | [3], 16 | [1, 3], 17 | [2, 3], 18 | [1, 2, 3], 19 | ]); 20 | }); 21 | }); 22 | -------------------------------------------------------------------------------- /src/algorithms/uncategorized/unique-paths/__test__/btUniquePaths.test.js: -------------------------------------------------------------------------------- 1 | import btUniquePaths from '../btUniquePaths'; 2 | 3 | describe('btUniquePaths', () => { 4 | it('should find the number of unique paths on board', () => { 5 | expect(btUniquePaths(3, 2)).toBe(3); 6 | expect(btUniquePaths(7, 3)).toBe(28); 7 | expect(btUniquePaths(3, 7)).toBe(28); 8 | expect(btUniquePaths(10, 10)).toBe(48620); 9 | expect(btUniquePaths(100, 1)).toBe(1); 10 | expect(btUniquePaths(1, 100)).toBe(1); 11 | }); 12 | }); 13 | -------------------------------------------------------------------------------- /src/algorithms/uncategorized/unique-paths/__test__/dpUniquePaths.test.js: -------------------------------------------------------------------------------- 1 | import dpUniquePaths from '../dpUniquePaths'; 2 | 3 | describe('dpUniquePaths', () => { 4 | it('should find the number of unique paths on board', () => { 5 | expect(dpUniquePaths(3, 2)).toBe(3); 6 | expect(dpUniquePaths(7, 3)).toBe(28); 7 | expect(dpUniquePaths(3, 7)).toBe(28); 8 | expect(dpUniquePaths(10, 10)).toBe(48620); 9 | expect(dpUniquePaths(100, 1)).toBe(1); 10 | expect(dpUniquePaths(1, 100)).toBe(1); 11 | }); 12 | }); 13 | -------------------------------------------------------------------------------- /src/algorithms/sets/power-set/__test__/btPowerSet.test.js: -------------------------------------------------------------------------------- 1 | import btPowerSet from '../btPowerSet'; 2 | 3 | describe('btPowerSet', () => { 4 | it('should calculate power set of given set using backtracking approach', () => { 5 | expect(btPowerSet([1])).toEqual([ 6 | [], 7 | [1], 8 | ]); 9 | 10 | expect(btPowerSet([1, 2, 3])).toEqual([ 11 | [], 12 | [1], 13 | [1, 2], 14 | [1, 2, 3], 15 | [1, 3], 16 | [2], 17 | [2, 3], 18 | [3], 19 | ]); 20 | }); 21 | }); 22 | -------------------------------------------------------------------------------- /src/algorithms/math/radian/__test__/degreeToRadian.test.js: -------------------------------------------------------------------------------- 1 | import degreeToRadian from '../degreeToRadian'; 2 | 3 | describe('degreeToRadian', () => { 4 | it('should convert degree to radian', () => { 5 | expect(degreeToRadian(0)).toBe(0); 6 | expect(degreeToRadian(45)).toBe(Math.PI / 4); 7 | expect(degreeToRadian(90)).toBe(Math.PI / 2); 8 | expect(degreeToRadian(180)).toBe(Math.PI); 9 | expect(degreeToRadian(270)).toBe((3 * Math.PI) / 2); 10 | expect(degreeToRadian(360)).toBe(2 * Math.PI); 11 | }); 12 | }); 13 | -------------------------------------------------------------------------------- /src/algorithms/math/radian/__test__/radianToDegree.test.js: -------------------------------------------------------------------------------- 1 | import radianToDegree from '../radianToDegree'; 2 | 3 | describe('radianToDegree', () => { 4 | it('should convert radian to degree', () => { 5 | expect(radianToDegree(0)).toBe(0); 6 | expect(radianToDegree(Math.PI / 4)).toBe(45); 7 | expect(radianToDegree(Math.PI / 2)).toBe(90); 8 | expect(radianToDegree(Math.PI)).toBe(180); 9 | expect(radianToDegree((3 * Math.PI) / 2)).toBe(270); 10 | expect(radianToDegree(2 * Math.PI)).toBe(360); 11 | }); 12 | }); 13 | -------------------------------------------------------------------------------- /src/algorithms/math/horner-method/hornerMethod.js: -------------------------------------------------------------------------------- 1 | /** 2 | * Returns the evaluation of a polynomial function at a certain point. 3 | * Uses Horner's rule. 4 | * 5 | * @param {number[]} coefficients - i.e. [4, 3, 2] for (4 * x^2 + 3 * x + 2) 6 | * @param {number} xVal 7 | * @return {number} 8 | */ 9 | export default function hornerMethod(coefficients, xVal) { 10 | return coefficients.reduce( 11 | (accumulator, currentCoefficient) => { 12 | return accumulator * xVal + currentCoefficient; 13 | }, 14 | 0, 15 | ); 16 | } 17 | -------------------------------------------------------------------------------- /src/data-structures/priority-queue/README.zh-CN.md: -------------------------------------------------------------------------------- 1 | # 优先队列 2 | 3 | 在计算机科学中, **优先级队列(priority queue)** 是一种抽象数据类型, 它类似于常规的队列或栈, 但每个元素都有与之关联的“优先级”。 4 | 5 | 在优先队列中, 低优先级的元素之前前面应该是高优先级的元素。 如果两个元素具有相同的优先级, 则根据它们在队列中的顺序是它们的出现顺序即可。 6 | 7 | 优先队列虽通常用堆来实现,但它在概念上与堆不同。优先队列是一个抽象概念，就像“列表”或“图”这样的抽象概念一样; 8 | 9 | 正如列表可以用链表或数组实现一样，优先队列可以用堆或各种其他方法实现,例如无序数组。 10 | 11 | 12 | ## 参考 13 | 14 | - [Wikipedia](https://en.wikipedia.org/wiki/Priority_queue) 15 | - [YouTube](https://www.youtube.com/watch?v=wptevk0bshY&list=PLLXdhg_r2hKA7DPDsunoDZ-Z769jWn4R8&index=6) 16 | -------------------------------------------------------------------------------- /src/algorithms/sets/fisher-yates/fisherYates.js: -------------------------------------------------------------------------------- 1 | /** 2 | * @param {*[]} originalArray 3 | * @return {*[]} 4 | */ 5 | export default function fisherYates(originalArray) { 6 | // Clone array from preventing original array from modification (for testing purpose). 7 | const array = originalArray.slice(0); 8 | 9 | for (let i = (array.length - 1); i > 0; i -= 1) { 10 | const randomIndex = Math.floor(Math.random() * (i + 1)); 11 | [array[i], array[randomIndex]] = [array[randomIndex], array[i]]; 12 | } 13 | 14 | return array; 15 | } 16 | -------------------------------------------------------------------------------- /src/algorithms/linked-list/reverse-traversal/README.md: -------------------------------------------------------------------------------- 1 | # Reversed Linked List Traversal 2 | 3 | The task is to traverse the given linked list in reversed order. 4 | 5 | For example for the following linked list: 6 | 7 | ![](https://upload.wikimedia.org/wikipedia/commons/6/6d/Singly-linked-list.svg) 8 | 9 | The order of traversal should be: 10 | 11 | ```text 12 | 37 → 99 → 12 13 | ``` 14 | 15 | The time complexity is `O(n)` because we visit every node only once. 16 | 17 | ## Reference 18 | 19 | - [Wikipedia](https://en.wikipedia.org/wiki/Linked_list) 20 | -------------------------------------------------------------------------------- /src/algorithms/math/pascal-triangle/pascalTriangle.js: -------------------------------------------------------------------------------- 1 | /** 2 | * @param {number} lineNumber - zero based. 3 | * @return {number[]} 4 | */ 5 | export default function pascalTriangle(lineNumber) { 6 | const currentLine = [1]; 7 | 8 | const currentLineSize = lineNumber + 1; 9 | 10 | for (let numIndex = 1; numIndex < currentLineSize; numIndex += 1) { 11 | // See explanation of this formula in README. 12 | currentLine[numIndex] = (currentLine[numIndex - 1] * (lineNumber - numIndex + 1)) / numIndex; 13 | } 14 | 15 | return currentLine; 16 | } 17 | -------------------------------------------------------------------------------- /src/algorithms/math/sieve-of-eratosthenes/__test__/sieveOfEratosthenes.test.js: -------------------------------------------------------------------------------- 1 | import sieveOfEratosthenes from '../sieveOfEratosthenes'; 2 | 3 | describe('sieveOfEratosthenes', () => { 4 | it('should find all primes less than or equal to n', () => { 5 | expect(sieveOfEratosthenes(5)).toEqual([2, 3, 5]); 6 | expect(sieveOfEratosthenes(10)).toEqual([2, 3, 5, 7]); 7 | expect(sieveOfEratosthenes(100)).toEqual([ 8 | 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 9 | 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97, 10 | ]); 11 | }); 12 | }); 13 | -------------------------------------------------------------------------------- /src/algorithms/math/bits/updateBit.js: -------------------------------------------------------------------------------- 1 | /** 2 | * @param {number} number 3 | * @param {number} bitPosition - zero based. 4 | * @param {number} bitValue - 0 or 1. 5 | * @return {number} 6 | */ 7 | export default function updateBit(number, bitPosition, bitValue) { 8 | // Normalized bit value. 9 | const bitValueNormalized = bitValue ? 1 : 0; 10 | 11 | // Init clear mask. 12 | const clearMask = ~(1 << bitPosition); 13 | 14 | // Clear bit value and then set it up to required value. 15 | return (number & clearMask) | (bitValueNormalized << bitPosition); 16 | } 17 | -------------------------------------------------------------------------------- /src/algorithms/math/bits/__test__/bitLength.test.js: -------------------------------------------------------------------------------- 1 | import bitLength from '../bitLength'; 2 | 3 | describe('bitLength', () => { 4 | it('should calculate number of bits that the number is consists of', () => { 5 | expect(bitLength(0b0)).toBe(0); 6 | expect(bitLength(0b1)).toBe(1); 7 | expect(bitLength(0b01)).toBe(1); 8 | expect(bitLength(0b101)).toBe(3); 9 | expect(bitLength(0b0101)).toBe(3); 10 | expect(bitLength(0b10101)).toBe(5); 11 | expect(bitLength(0b11110101)).toBe(8); 12 | expect(bitLength(0b00011110101)).toBe(8); 13 | }); 14 | }); 15 | -------------------------------------------------------------------------------- /src/data-structures/priority-queue/README.ja-JP.md: -------------------------------------------------------------------------------- 1 | # 優先度付きキュー 2 | 3 | コンピュータサイエンスにおいて、**優先度付きキュー**は通常のキューやスタックのデータ構造と似た抽象データ型ですが、各要素に「優先度」が関連づけられています。優先度付きキューでは優先度の高い要素が優先度の低い要素よりも先に処理されます。もし2つの要素が同じ優先度だった場合、それらはキュー内の順序に従って処理されます。 4 | 5 | 優先度付きキューは多くの場合ヒープによって実装されていますが、概念的にはヒープとは異なります。優先度付きキューは「リスト」や「マップ」のような抽象的な概念です。リストがリンクリストや配列で実装できるのと同様に、優先度付きキューはヒープや未ソート配列のような様々な方法で実装することができます。 6 | 7 | ## 参考 8 | 9 | - [Wikipedia](https://en.wikipedia.org/wiki/Priority_queue) 10 | - [YouTube](https://www.youtube.com/watch?v=wptevk0bshY&list=PLLXdhg_r2hKA7DPDsunoDZ-Z769jWn4R8&index=6) 11 | -------------------------------------------------------------------------------- /src/data-structures/heap/MaxHeap.js: -------------------------------------------------------------------------------- 1 | import Heap from './Heap'; 2 | 3 | export default class MaxHeap extends Heap { 4 | /** 5 | * Checks if pair of heap elements is in correct order. 6 | * For MinHeap the first element must be always smaller or equal. 7 | * For MaxHeap the first element must be always bigger or equal. 8 | * 9 | * @param {*} firstElement 10 | * @param {*} secondElement 11 | * @return {boolean} 12 | */ 13 | pairIsInCorrectOrder(firstElement, secondElement) { 14 | return this.compare.greaterThanOrEqual(firstElement, secondElement); 15 | } 16 | } 17 | -------------------------------------------------------------------------------- /src/data-structures/heap/MinHeap.js: -------------------------------------------------------------------------------- 1 | import Heap from './Heap'; 2 | 3 | export default class MinHeap extends Heap { 4 | /** 5 | * Checks if pair of heap elements is in correct order. 6 | * For MinHeap the first element must be always smaller or equal. 7 | * For MaxHeap the first element must be always bigger or equal. 8 | * 9 | * @param {*} firstElement 10 | * @param {*} secondElement 11 | * @return {boolean} 12 | */ 13 | pairIsInCorrectOrder(firstElement, secondElement) { 14 | return this.compare.lessThanOrEqual(firstElement, secondElement); 15 | } 16 | } 17 | -------------------------------------------------------------------------------- /src/algorithms/math/integer-partition/__test__/integerPartition.test.js: -------------------------------------------------------------------------------- 1 | import integerPartition from '../integerPartition'; 2 | 3 | describe('integerPartition', () => { 4 | it('should partition the number', () => { 5 | expect(integerPartition(1)).toBe(1); 6 | expect(integerPartition(2)).toBe(2); 7 | expect(integerPartition(3)).toBe(3); 8 | expect(integerPartition(4)).toBe(5); 9 | expect(integerPartition(5)).toBe(7); 10 | expect(integerPartition(6)).toBe(11); 11 | expect(integerPartition(7)).toBe(15); 12 | expect(integerPartition(8)).toBe(22); 13 | }); 14 | }); 15 | -------------------------------------------------------------------------------- /src/algorithms/uncategorized/n-queens/__test__/nQueensBitwise.test.js: -------------------------------------------------------------------------------- 1 | import nQueensBitwise from '../nQueensBitwise'; 2 | 3 | describe('nQueensBitwise', () => { 4 | it('should have solutions for 4 to N queens', () => { 5 | expect(nQueensBitwise(4)).toBe(2); 6 | expect(nQueensBitwise(5)).toBe(10); 7 | expect(nQueensBitwise(6)).toBe(4); 8 | expect(nQueensBitwise(7)).toBe(40); 9 | expect(nQueensBitwise(8)).toBe(92); 10 | expect(nQueensBitwise(9)).toBe(352); 11 | expect(nQueensBitwise(10)).toBe(724); 12 | expect(nQueensBitwise(11)).toBe(2680); 13 | }); 14 | }); 15 | -------------------------------------------------------------------------------- /src/algorithms/math/horner-method/classicPolynome.js: -------------------------------------------------------------------------------- 1 | /** 2 | * Returns the evaluation of a polynomial function at a certain point. 3 | * Uses straightforward approach with powers. 4 | * 5 | * @param {number[]} coefficients - i.e. [4, 3, 2] for (4 * x^2 + 3 * x + 2) 6 | * @param {number} xVal 7 | * @return {number} 8 | */ 9 | export default function classicPolynome(coefficients, xVal) { 10 | return coefficients.reverse().reduce( 11 | (accumulator, currentCoefficient, index) => { 12 | return accumulator + currentCoefficient * (xVal ** index); 13 | }, 14 | 0, 15 | ); 16 | } 17 | -------------------------------------------------------------------------------- /BACKERS.md: -------------------------------------------------------------------------------- 1 | # Project Backers 2 | 3 | > You may support this project via ❤️️ [GitHub](https://github.com/sponsors/trekhleb) or ❤️️ [Patreon](https://www.patreon.com/trekhleb). 4 | 5 | ## `O(2ⁿ)` Backers 6 | 7 | `null` 8 | 9 | ## `O(n²)` Backers 10 | 11 | `null` 12 | 13 | ## `O(n×log(n))` Backers 14 | 15 | `null` 16 | 17 | 31 | -------------------------------------------------------------------------------- /src/algorithms/math/liu-hui/__test__/liuHui.test.js: -------------------------------------------------------------------------------- 1 | import liuHui from '../liuHui'; 2 | 3 | describe('liuHui', () => { 4 | it('should calculate π based on 12-gon', () => { 5 | expect(liuHui(1)).toBe(3); 6 | }); 7 | 8 | it('should calculate π based on 24-gon', () => { 9 | expect(liuHui(2)).toBe(3.105828541230249); 10 | }); 11 | 12 | it('should calculate π based on 6144-gon', () => { 13 | expect(liuHui(10)).toBe(3.1415921059992717); 14 | }); 15 | 16 | it('should calculate π based on 201326592-gon', () => { 17 | expect(liuHui(25)).toBe(3.141592653589793); 18 | }); 19 | }); 20 | -------------------------------------------------------------------------------- /src/algorithms/math/fibonacci/fibonacciNth.js: -------------------------------------------------------------------------------- 1 | /** 2 | * Calculate fibonacci number at specific position using Dynamic Programming approach. 3 | * 4 | * @param n 5 | * @return {number} 6 | */ 7 | export default function fibonacciNth(n) { 8 | let currentValue = 1; 9 | let previousValue = 0; 10 | 11 | if (n === 1) { 12 | return 1; 13 | } 14 | 15 | let iterationsCounter = n - 1; 16 | 17 | while (iterationsCounter) { 18 | currentValue += previousValue; 19 | previousValue = currentValue - previousValue; 20 | 21 | iterationsCounter -= 1; 22 | } 23 | 24 | return currentValue; 25 | } 26 | -------------------------------------------------------------------------------- /src/algorithms/math/euclidean-algorithm/euclideanAlgorithm.js: -------------------------------------------------------------------------------- 1 | /** 2 | * Recursive version of Euclidean Algorithm of finding greatest common divisor (GCD). 3 | * @param {number} originalA 4 | * @param {number} originalB 5 | * @return {number} 6 | */ 7 | export default function euclideanAlgorithm(originalA, originalB) { 8 | // Make input numbers positive. 9 | const a = Math.abs(originalA); 10 | const b = Math.abs(originalB); 11 | 12 | // To make algorithm work faster instead of subtracting one number from the other 13 | // we may use modulo operation. 14 | return (b === 0) ? a : euclideanAlgorithm(b, a % b); 15 | } 16 | -------------------------------------------------------------------------------- /src/algorithms/sets/cartesian-product/README.md: -------------------------------------------------------------------------------- 1 | # Cartesian Product 2 | 3 | In set theory a Cartesian product is a mathematical operation that returns a set 4 | (or product set or simply product) from multiple sets. That is, for sets A and B, 5 | the Cartesian product A × B is the set of all ordered pairs (a, b) 6 | where a ∈ A and b ∈ B. 7 | 8 | Cartesian product `AxB` of two sets `A={x,y,z}` and `B={1,2,3}` 9 | 10 | ![Cartesian Product of Two Sets](https://upload.wikimedia.org/wikipedia/commons/4/4e/Cartesian_Product_qtl1.svg) 11 | 12 | ## References 13 | 14 | [Wikipedia](https://en.wikipedia.org/wiki/Cartesian_product) 15 | -------------------------------------------------------------------------------- /src/algorithms/linked-list/traversal/README.md: -------------------------------------------------------------------------------- 1 | # Linked List Traversal 2 | 3 | _Read this in other languages:_ 4 | [_Русский_](README.ru-RU.md) 5 | 6 | The task is to traverse the given linked list in straight order. 7 | 8 | For example for the following linked list: 9 | 10 | ![Singly linked list](https://upload.wikimedia.org/wikipedia/commons/6/6d/Singly-linked-list.svg) 11 | 12 | The order of traversal should be: 13 | 14 | ```text 15 | 12 → 99 → 37 16 | ``` 17 | 18 | The time complexity is `O(n)` because we visit every node only once. 19 | 20 | ## Reference 21 | 22 | - [Wikipedia](https://en.wikipedia.org/wiki/Linked_list) 23 | -------------------------------------------------------------------------------- /src/algorithms/linked-list/traversal/README.ru-RU.md: -------------------------------------------------------------------------------- 1 | # Обход связного списка 2 | 3 | Задача состоит в том, чтобы обойти связный список в прямом порядке. 4 | 5 | Например, для следующего связного списка: 6 | 7 | ![Singly linked list](https://upload.wikimedia.org/wikipedia/commons/6/6d/Singly-linked-list.svg) 8 | 9 | Порядок обхода будет такой: 10 | 11 | ```text 12 | 12 → 99 → 37 13 | ``` 14 | 15 | Временная сложность - `O(n)`, потому что мы посещаем каждый узел только один раз. 16 | 17 | ## Ссылки 18 | 19 | - [Wikipedia](https://ru.wikipedia.org/wiki/%D0%A1%D0%B2%D1%8F%D0%B7%D0%BD%D1%8B%D0%B9_%D1%81%D0%BF%D0%B8%D1%81%D0%BE%D0%BA) 20 | -------------------------------------------------------------------------------- /src/data-structures/stack/README.zh-CN.md: -------------------------------------------------------------------------------- 1 | # 栈 2 | 3 | 在计算机科学中, 一个 **栈(stack)** 是一种抽象数据类型,用作表示元素的集合,具有两种主要操作: 4 | 5 | * **push**, 添加元素到栈的顶端(末尾); 6 | * **pop**, 移除栈最顶端(末尾)的元素. 7 | 8 | 以上两种操作可以简单概括为“后进先出(LIFO = last in, first out)”。 9 | 10 | 此外,应有一个 `peek` 操作用于访问栈当前顶端(末尾)的元素。 11 | 12 | "栈"这个名称,可类比于一组物体的堆叠(一摞书,一摞盘子之类的)。 13 | 14 | 栈的 push 和 pop 操作的示意 15 | 16 | ![Stack](https://upload.wikimedia.org/wikipedia/commons/b/b4/Lifo_stack.png) 17 | 18 | ## 参考 19 | 20 | - [Wikipedia](https://en.wikipedia.org/wiki/Stack_(abstract_data_type)) 21 | - [YouTube](https://www.youtube.com/watch?v=wjI1WNcIntg&list=PLLXdhg_r2hKA7DPDsunoDZ-Z769jWn4R8&index=3&) 22 | -------------------------------------------------------------------------------- /src/data-structures/trie/README.zh-CN.md: -------------------------------------------------------------------------------- 1 | # 字典树 2 | 3 | 在计算机科学中, **字典树(trie,中文又被称为”单词查找树“或 ”键树“)**, 也称为数字树,有时候也被称为基数树或前缀树（因为它们可以通过前缀搜索）,它是一种搜索树--一种已排序的数据结构,通常用于存储动态集或键为字符串的关联数组。 4 | 5 | 与二叉搜索树不同, 树上没有节点存储与该节点关联的键; 相反,节点在树上的位置定义了与之关联的键。一个节点的全部后代节点都有一个与该节点关联的通用的字符串前缀, 与根节点关联的是空字符串。 6 | 7 | 值对于字典树中关联的节点来说,不是必需的,相反,值往往和相关的叶子相关,以及与一些键相关的内部节点相关。 8 | 9 | 有关字典树的空间优化示意,请参阅紧凑前缀树 10 | 11 | ![Trie](https://upload.wikimedia.org/wikipedia/commons/b/be/Trie_example.svg) 12 | 13 | ## 参考 14 | 15 | - [Wikipedia](https://en.wikipedia.org/wiki/Trie) 16 | - [YouTube](https://www.youtube.com/watch?v=zIjfhVPRZCg&list=PLLXdhg_r2hKA7DPDsunoDZ-Z769jWn4R8&index=7&t=0s) 17 | -------------------------------------------------------------------------------- /src/algorithms/math/fibonacci/fibonacci.js: -------------------------------------------------------------------------------- 1 | /** 2 | * Return a fibonacci sequence as an array. 3 | * 4 | * @param n 5 | * @return {number[]} 6 | */ 7 | export default function fibonacci(n) { 8 | const fibSequence = [1]; 9 | 10 | let currentValue = 1; 11 | let previousValue = 0; 12 | 13 | if (n === 1) { 14 | return fibSequence; 15 | } 16 | 17 | let iterationsCounter = n - 1; 18 | 19 | while (iterationsCounter) { 20 | currentValue += previousValue; 21 | previousValue = currentValue - previousValue; 22 | 23 | fibSequence.push(currentValue); 24 | 25 | iterationsCounter -= 1; 26 | } 27 | 28 | return fibSequence; 29 | } 30 | -------------------------------------------------------------------------------- /src/data-structures/heap/README.ja-JP.md: -------------------------------------------------------------------------------- 1 | # ヒープ (データ構造) 2 | 3 | コンピュータサイエンスにおいて、*ヒープ*は特殊な木構造のデータ構造で、後述するヒープの特性を持っています。 4 | 5 | *最小ヒープ*では、もし`P`が`C`の親ノードの場合、`P`のキー(値)は`C`のキーより小さい、または等しくなります。 6 | 7 | ![MinHeap](https://upload.wikimedia.org/wikipedia/commons/6/69/Min-heap.png) 8 | 9 | *最大ヒープ*では、`P`のキーは`C`のキーより大きい、もしくは等しくなります。 10 | 11 | ![Heap](https://upload.wikimedia.org/wikipedia/commons/3/38/Max-Heap.svg) 12 | 13 | ヒープの「トップ」のノードには親ノードが存在せず、ルートノードと呼ばれます。 14 | 15 | ## 参考 16 | 17 | - [Wikipedia](https://en.wikipedia.org/wiki/Heap_(data_structure)) 18 | - [YouTube](https://www.youtube.com/watch?v=t0Cq6tVNRBA&index=5&t=0s&list=PLLXdhg_r2hKA7DPDsunoDZ-Z769jWn4R8) 19 | -------------------------------------------------------------------------------- /src/algorithms/math/bits/__test__/multiplyUnsigned.test.js: -------------------------------------------------------------------------------- 1 | import multiplyUnsigned from '../multiplyUnsigned'; 2 | 3 | describe('multiplyUnsigned', () => { 4 | it('should multiply two unsigned numbers', () => { 5 | expect(multiplyUnsigned(0, 2)).toBe(0); 6 | expect(multiplyUnsigned(2, 0)).toBe(0); 7 | expect(multiplyUnsigned(1, 1)).toBe(1); 8 | expect(multiplyUnsigned(1, 2)).toBe(2); 9 | expect(multiplyUnsigned(2, 7)).toBe(14); 10 | expect(multiplyUnsigned(7, 2)).toBe(14); 11 | expect(multiplyUnsigned(30, 2)).toBe(60); 12 | expect(multiplyUnsigned(17, 34)).toBe(578); 13 | expect(multiplyUnsigned(170, 2340)).toBe(397800); 14 | }); 15 | }); 16 | -------------------------------------------------------------------------------- /src/algorithms/uncategorized/n-queens/__test__/QueensPosition.test.js: -------------------------------------------------------------------------------- 1 | import QueenPosition from '../QueenPosition'; 2 | 3 | describe('QueenPosition', () => { 4 | it('should store queen position on chessboard', () => { 5 | const position1 = new QueenPosition(0, 0); 6 | const position2 = new QueenPosition(2, 1); 7 | 8 | expect(position2.columnIndex).toBe(1); 9 | expect(position2.rowIndex).toBe(2); 10 | expect(position1.leftDiagonal).toBe(0); 11 | expect(position1.rightDiagonal).toBe(0); 12 | expect(position2.leftDiagonal).toBe(1); 13 | expect(position2.rightDiagonal).toBe(3); 14 | expect(position2.toString()).toBe('2,1'); 15 | }); 16 | }); 17 | -------------------------------------------------------------------------------- /src/algorithms/math/bits/__test__/getBit.test.js: -------------------------------------------------------------------------------- 1 | import getBit from '../getBit'; 2 | 3 | describe('getBit', () => { 4 | it('should get bit at specific position', () => { 5 | // 1 = 0b0001 6 | expect(getBit(1, 0)).toBe(1); 7 | expect(getBit(1, 1)).toBe(0); 8 | 9 | // 2 = 0b0010 10 | expect(getBit(2, 0)).toBe(0); 11 | expect(getBit(2, 1)).toBe(1); 12 | 13 | // 3 = 0b0011 14 | expect(getBit(3, 0)).toBe(1); 15 | expect(getBit(3, 1)).toBe(1); 16 | 17 | // 10 = 0b1010 18 | expect(getBit(10, 0)).toBe(0); 19 | expect(getBit(10, 1)).toBe(1); 20 | expect(getBit(10, 2)).toBe(0); 21 | expect(getBit(10, 3)).toBe(1); 22 | }); 23 | }); 24 | -------------------------------------------------------------------------------- /src/algorithms/math/bits/__test__/multiply.test.js: -------------------------------------------------------------------------------- 1 | import multiply from '../multiply'; 2 | 3 | describe('multiply', () => { 4 | it('should multiply two numbers', () => { 5 | expect(multiply(0, 0)).toBe(0); 6 | expect(multiply(2, 0)).toBe(0); 7 | expect(multiply(0, 2)).toBe(0); 8 | expect(multiply(1, 2)).toBe(2); 9 | expect(multiply(2, 1)).toBe(2); 10 | expect(multiply(6, 6)).toBe(36); 11 | expect(multiply(-2, 4)).toBe(-8); 12 | expect(multiply(4, -2)).toBe(-8); 13 | expect(multiply(-4, -4)).toBe(16); 14 | expect(multiply(4, -5)).toBe(-20); 15 | expect(multiply(2, 121)).toBe(242); 16 | expect(multiply(121, 2)).toBe(242); 17 | }); 18 | }); 19 | -------------------------------------------------------------------------------- /src/algorithms/search/linear-search/linearSearch.js: -------------------------------------------------------------------------------- 1 | import Comparator from '../../../utils/comparator/Comparator'; 2 | 3 | /** 4 | * Linear search implementation. 5 | * 6 | * @param {*[]} array 7 | * @param {*} seekElement 8 | * @param {function(a, b)} [comparatorCallback] 9 | * @return {number[]} 10 | */ 11 | export default function linearSearch(array, seekElement, comparatorCallback) { 12 | const comparator = new Comparator(comparatorCallback); 13 | const foundIndices = []; 14 | 15 | array.forEach((element, index) => { 16 | if (comparator.equal(element, seekElement)) { 17 | foundIndices.push(index); 18 | } 19 | }); 20 | 21 | return foundIndices; 22 | } 23 | -------------------------------------------------------------------------------- /src/algorithms/linked-list/reverse-traversal/reverseTraversal.js: -------------------------------------------------------------------------------- 1 | /** 2 | * Traversal callback function. 3 | * @callback traversalCallback 4 | * @param {*} nodeValue 5 | */ 6 | 7 | /** 8 | * @param {LinkedListNode} node 9 | * @param {traversalCallback} callback 10 | */ 11 | function reverseTraversalRecursive(node, callback) { 12 | if (node) { 13 | reverseTraversalRecursive(node.next, callback); 14 | callback(node.value); 15 | } 16 | } 17 | 18 | /** 19 | * @param {LinkedList} linkedList 20 | * @param {traversalCallback} callback 21 | */ 22 | export default function reverseTraversal(linkedList, callback) { 23 | reverseTraversalRecursive(linkedList.head, callback); 24 | } 25 | -------------------------------------------------------------------------------- /src/algorithms/linked-list/traversal/__test__/traversal.test.js: -------------------------------------------------------------------------------- 1 | import LinkedList from '../../../../data-structures/linked-list/LinkedList'; 2 | import traversal from '../traversal'; 3 | 4 | describe('traversal', () => { 5 | it('should traverse linked list', () => { 6 | const linkedList = new LinkedList(); 7 | 8 | linkedList 9 | .append(1) 10 | .append(2) 11 | .append(3); 12 | 13 | const traversedNodeValues = []; 14 | const traversalCallback = (nodeValue) => { 15 | traversedNodeValues.push(nodeValue); 16 | }; 17 | 18 | traversal(linkedList, traversalCallback); 19 | 20 | expect(traversedNodeValues).toEqual([1, 2, 3]); 21 | }); 22 | }); 23 | -------------------------------------------------------------------------------- /src/data-structures/heap/README.zh-CN.md: -------------------------------------------------------------------------------- 1 | # 堆 (数据结构) 2 | 3 | 在计算机科学中, 一个 **堆(heap)** 是一种特殊的基于树的数据结构，它满足下面描述的堆属性。 4 | 5 | 在一个 *最小堆(min heap)* 中, 如果 `P` 是 `C` 的一个父级节点, 那么 `P` 的key(或value)应小于或等于 `C` 的对应值. 6 | 7 | ![最小堆](https://upload.wikimedia.org/wikipedia/commons/6/69/Min-heap.png) 8 | 9 | 在一个 *最大堆(max heap)* 中, `P` 的key(或value)大于 `C` 的对应值。 10 | 11 | ![堆](https://upload.wikimedia.org/wikipedia/commons/3/38/Max-Heap.svg) 12 | 13 | 14 | 在堆“顶部”的没有父级节点的节点,被称之为根节点。 15 | 16 | ## 参考 17 | 18 | - [Wikipedia](https://en.wikipedia.org/wiki/Heap_(data_structure)) 19 | - [YouTube](https://www.youtube.com/watch?v=t0Cq6tVNRBA&index=5&t=0s&list=PLLXdhg_r2hKA7DPDsunoDZ-Z769jWn4R8) 20 | -------------------------------------------------------------------------------- /src/algorithms/math/bits/__test__/fullAdder.test.js: -------------------------------------------------------------------------------- 1 | import fullAdder from '../fullAdder'; 2 | 3 | describe('fullAdder', () => { 4 | it('should add up two numbers', () => { 5 | expect(fullAdder(0, 0)).toBe(0); 6 | expect(fullAdder(2, 0)).toBe(2); 7 | expect(fullAdder(0, 2)).toBe(2); 8 | expect(fullAdder(1, 2)).toBe(3); 9 | expect(fullAdder(2, 1)).toBe(3); 10 | expect(fullAdder(6, 6)).toBe(12); 11 | expect(fullAdder(-2, 4)).toBe(2); 12 | expect(fullAdder(4, -2)).toBe(2); 13 | expect(fullAdder(-4, -4)).toBe(-8); 14 | expect(fullAdder(4, -5)).toBe(-1); 15 | expect(fullAdder(2, 121)).toBe(123); 16 | expect(fullAdder(121, 2)).toBe(123); 17 | }); 18 | }); 19 | -------------------------------------------------------------------------------- /src/algorithms/sets/combination-sum/__test__/combinationSum.test.js: -------------------------------------------------------------------------------- 1 | import combinationSum from '../combinationSum'; 2 | 3 | describe('combinationSum', () => { 4 | it('should find all combinations with specific sum', () => { 5 | expect(combinationSum([1], 4)).toEqual([ 6 | [1, 1, 1, 1], 7 | ]); 8 | 9 | expect(combinationSum([2, 3, 6, 7], 7)).toEqual([ 10 | [2, 2, 3], 11 | [7], 12 | ]); 13 | 14 | expect(combinationSum([2, 3, 5], 8)).toEqual([ 15 | [2, 2, 2, 2], 16 | [2, 3, 3], 17 | [3, 5], 18 | ]); 19 | 20 | expect(combinationSum([2, 5], 3)).toEqual([]); 21 | 22 | expect(combinationSum([], 3)).toEqual([]); 23 | }); 24 | }); 25 | -------------------------------------------------------------------------------- /src/data-structures/stack/README.ja-JP.md: -------------------------------------------------------------------------------- 1 | # スタック 2 | 3 | コンピュータサイエンスにおいて、**スタック**は抽象データ型で、2つの主要な操作ができる要素のコレクションです。 4 | 5 | * **プッシュ**はコレクションに要素を追加します。 6 | * **ポップ**は最近追加された要素でまだ削除されていないものを削除します。 7 | 8 | 要素がスタックから外れる順番から、LIFO(後入れ先出し)とも呼ばれます。スタックに変更を加えることなく、先頭の要素を検査するピーク操作を備えることもあります。「スタック」という名前は、物理的な物を上に積み重ねていく様子との類似性に由来しています。一番上の物を取ることは簡単ですが、スタックの下の方にあるものを取るときは先に上にある複数の物を取り除く必要があります。 9 | 10 | プッシュとポップの例 11 | 12 | ![Stack](https://upload.wikimedia.org/wikipedia/commons/b/b4/Lifo_stack.png) 13 | 14 | ## 参考 15 | 16 | - [Wikipedia](https://en.wikipedia.org/wiki/Stack_(abstract_data_type)) 17 | - [YouTube](https://www.youtube.com/watch?v=wjI1WNcIntg&list=PLLXdhg_r2hKA7DPDsunoDZ-Z769jWn4R8&index=3&) 18 | -------------------------------------------------------------------------------- /src/algorithms/math/bits/__test__/isEven.test.js: -------------------------------------------------------------------------------- 1 | import isEven from '../isEven'; 2 | 3 | describe('isEven', () => { 4 | it('should detect if a number is even', () => { 5 | expect(isEven(0)).toBe(true); 6 | expect(isEven(2)).toBe(true); 7 | expect(isEven(-2)).toBe(true); 8 | expect(isEven(1)).toBe(false); 9 | expect(isEven(-1)).toBe(false); 10 | expect(isEven(-3)).toBe(false); 11 | expect(isEven(3)).toBe(false); 12 | expect(isEven(8)).toBe(true); 13 | expect(isEven(9)).toBe(false); 14 | expect(isEven(121)).toBe(false); 15 | expect(isEven(122)).toBe(true); 16 | expect(isEven(1201)).toBe(false); 17 | expect(isEven(1202)).toBe(true); 18 | }); 19 | }); 20 | -------------------------------------------------------------------------------- /src/algorithms/math/fibonacci/README.zh-CN.md: -------------------------------------------------------------------------------- 1 | # 斐波那契数 2 | 3 | _Read this in other languages:_ 4 | [français](README.fr-FR.md), 5 | [english](README.md). 6 | 7 | 在数学中，斐波那契数是以下整数序列（称为斐波那契数列）中的数字，其特征在于前两个数字之后的每个数字都是前两个数字的和： 8 | 9 | `0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, ...` 10 | 11 | 边长为连续斐波纳契数的正方形平铺 12 | 13 | ![Fibonacci](https://upload.wikimedia.org/wikipedia/commons/d/db/34%2A21-FibonacciBlocks.png) 14 | 15 | 16 | 斐波那契螺旋：通过绘制连接斐波那契平铺中正方形的相对角的圆弧而创建的金色螺旋的近似值； [4]该三角形使用大小为1、1、2、3、5、8、13和21的正方形。 17 | 18 | ![Fibonacci Spiral](https://upload.wikimedia.org/wikipedia/commons/2/2e/FibonacciSpiral.svg) 19 | 20 | ## References 21 | 22 | - [Wikipedia](https://en.wikipedia.org/wiki/Fibonacci_number) 23 | -------------------------------------------------------------------------------- /src/algorithms/math/bits/__test__/updateBit.test.js: -------------------------------------------------------------------------------- 1 | import updateBit from '../updateBit'; 2 | 3 | describe('updateBit', () => { 4 | it('should update bit at specific position', () => { 5 | // 1 = 0b0001 6 | expect(updateBit(1, 0, 1)).toBe(1); 7 | expect(updateBit(1, 0, 0)).toBe(0); 8 | expect(updateBit(1, 1, 1)).toBe(3); 9 | expect(updateBit(1, 2, 1)).toBe(5); 10 | 11 | // 10 = 0b1010 12 | expect(updateBit(10, 0, 1)).toBe(11); 13 | expect(updateBit(10, 0, 0)).toBe(10); 14 | expect(updateBit(10, 1, 1)).toBe(10); 15 | expect(updateBit(10, 1, 0)).toBe(8); 16 | expect(updateBit(10, 2, 1)).toBe(14); 17 | expect(updateBit(10, 2, 0)).toBe(10); 18 | }); 19 | }); 20 | -------------------------------------------------------------------------------- /src/algorithms/math/is-power-of-two/isPowerOfTwo.js: -------------------------------------------------------------------------------- 1 | /** 2 | * @param {number} number 3 | * @return {boolean} 4 | */ 5 | export default function isPowerOfTwo(number) { 6 | // 1 (2^0) is the smallest power of two. 7 | if (number < 1) { 8 | return false; 9 | } 10 | 11 | // Let's find out if we can divide the number by two 12 | // many times without remainder. 13 | let dividedNumber = number; 14 | while (dividedNumber !== 1) { 15 | if (dividedNumber % 2 !== 0) { 16 | // For every case when remainder isn't zero we can say that this number 17 | // couldn't be a result of power of two. 18 | return false; 19 | } 20 | 21 | dividedNumber /= 2; 22 | } 23 | 24 | return true; 25 | } 26 | -------------------------------------------------------------------------------- /src/algorithms/math/pascal-triangle/__test__/pascalTriangle.test.js: -------------------------------------------------------------------------------- 1 | import pascalTriangle from '../pascalTriangle'; 2 | 3 | describe('pascalTriangle', () => { 4 | it('should calculate Pascal Triangle coefficients for specific line number', () => { 5 | expect(pascalTriangle(0)).toEqual([1]); 6 | expect(pascalTriangle(1)).toEqual([1, 1]); 7 | expect(pascalTriangle(2)).toEqual([1, 2, 1]); 8 | expect(pascalTriangle(3)).toEqual([1, 3, 3, 1]); 9 | expect(pascalTriangle(4)).toEqual([1, 4, 6, 4, 1]); 10 | expect(pascalTriangle(5)).toEqual([1, 5, 10, 10, 5, 1]); 11 | expect(pascalTriangle(6)).toEqual([1, 6, 15, 20, 15, 6, 1]); 12 | expect(pascalTriangle(7)).toEqual([1, 7, 21, 35, 35, 21, 7, 1]); 13 | }); 14 | }); 15 | -------------------------------------------------------------------------------- /src/algorithms/string/longest-common-substring/README.md: -------------------------------------------------------------------------------- 1 | # Longest Common Substring Problem 2 | 3 | The longest common substring problem is to find the longest string 4 | (or strings) that is a substring (or are substrings) of two or more 5 | strings. 6 | 7 | ## Example 8 | 9 | The longest common substring of the strings `ABABC`, `BABCA` and 10 | `ABCBA` is string `ABC` of length 3. Other common substrings are 11 | `A`, `AB`, `B`, `BA`, `BC` and `C`. 12 | 13 | ``` 14 | ABABC 15 | ||| 16 | BABCA 17 | ||| 18 | ABCBA 19 | ``` 20 | 21 | ## References 22 | 23 | - [Wikipedia](https://en.wikipedia.org/wiki/Longest_common_substring_problem) 24 | - [YouTube](https://www.youtube.com/watch?v=BysNXJHzCEs&list=PLLXdhg_r2hKA7DPDsunoDZ-Z769jWn4R8) 25 | -------------------------------------------------------------------------------- /src/data-structures/queue/README.ja-JP.md: -------------------------------------------------------------------------------- 1 | # キュー 2 | 3 | コンピュータサイエンスにおいて、**キュー**は特定の種類の抽象データ型またはコレクションです。コレクションの中のエンティティは順番に並べられており、コレクションに対する基本的な（または唯一の)操作は末尾にエンティティを追加するエンキューと、先頭からエンティティを削除するデキューがあります。これにより、キューは先入れ先出し(FIFO)のデータ構造となります。FIFOのデータ構造では、キューに追加された最初の要素が最初に削除されます。これは、新しい要素が追加されたら、その要素を削除するにはそれまでに追加された全ての要素が削除されなければならないという要件と同じです。多くの場合、ピークのような先頭の要素を検査する操作も備えていて、これはデキューせずに先頭の要素の値を返します。キューは線形のデータ構造や、より抽象的なシーケンシャルなコレクションの一例です。 4 | 5 | FIFO(先入れ先出し)のキュー 6 | 7 | ![Queue](https://upload.wikimedia.org/wikipedia/commons/5/52/Data_Queue.svg) 8 | 9 | ## 参考 10 | 11 | - [Wikipedia](https://en.wikipedia.org/wiki/Queue_(abstract_data_type)) 12 | - [YouTube](https://www.youtube.com/watch?v=wjI1WNcIntg&list=PLLXdhg_r2hKA7DPDsunoDZ-Z769jWn4R8&index=3&) 13 | -------------------------------------------------------------------------------- /src/algorithms/math/bits/__test__/isPositive.test.js: -------------------------------------------------------------------------------- 1 | import isPositive from '../isPositive'; 2 | 3 | describe('isPositive', () => { 4 | it('should detect if a number is positive', () => { 5 | expect(isPositive(1)).toBe(true); 6 | expect(isPositive(2)).toBe(true); 7 | expect(isPositive(3)).toBe(true); 8 | expect(isPositive(5665)).toBe(true); 9 | expect(isPositive(56644325)).toBe(true); 10 | 11 | expect(isPositive(0)).toBe(false); 12 | expect(isPositive(-0)).toBe(false); 13 | expect(isPositive(-1)).toBe(false); 14 | expect(isPositive(-2)).toBe(false); 15 | expect(isPositive(-126)).toBe(false); 16 | expect(isPositive(-5665)).toBe(false); 17 | expect(isPositive(-56644325)).toBe(false); 18 | }); 19 | }); 20 | -------------------------------------------------------------------------------- /src/data-structures/graph/README.zh-CN.md: -------------------------------------------------------------------------------- 1 | # 图 2 | 3 | 在计算机科学中, **图(graph)** 是一种抽象数据类型, 4 | 旨在实现数学中的无向图和有向图概念，特别是图论领域。 5 | 6 | 一个图数据结构是一个(由有限个或者可变数量的)顶点/节点/点和边构成的有限集。 7 | 8 | 如果顶点对之间是无序的,称为无序图,否则称为有序图; 9 | 10 | 如果顶点对之间的边是没有方向的,称为无向图,否则称为有向图; 11 | 12 | 如果顶点对之间的边是有权重的,该图可称为加权图。 13 | 14 | 15 | 16 | ![Graph](https://www.tutorialspoint.com/data_structures_algorithms/images/graph.jpg) 17 | 18 | ## 参考 19 | 20 | - [Wikipedia](https://en.wikipedia.org/wiki/Graph_(abstract_data_type)) 21 | - [Introduction to Graphs on YouTube](https://www.youtube.com/watch?v=gXgEDyodOJU&index=9&list=PLLXdhg_r2hKA7DPDsunoDZ-Z769jWn4R8) 22 | - [Graphs representation on YouTube](https://www.youtube.com/watch?v=k1wraWzqtvQ&index=10&list=PLLXdhg_r2hKA7DPDsunoDZ-Z769jWn4R8) 23 | -------------------------------------------------------------------------------- /src/algorithms/sets/cartesian-product/__test__/cartesianProduct.test.js: -------------------------------------------------------------------------------- 1 | import cartesianProduct from '../cartesianProduct'; 2 | 3 | describe('cartesianProduct', () => { 4 | it('should return null if there is not enough info for calculation', () => { 5 | const product1 = cartesianProduct([1], null); 6 | const product2 = cartesianProduct([], null); 7 | 8 | expect(product1).toBeNull(); 9 | expect(product2).toBeNull(); 10 | }); 11 | 12 | it('should calculate the product of two sets', () => { 13 | const product1 = cartesianProduct([1], [1]); 14 | const product2 = cartesianProduct([1, 2], [3, 5]); 15 | 16 | expect(product1).toEqual([[1, 1]]); 17 | expect(product2).toEqual([[1, 3], [1, 5], [2, 3], [2, 5]]); 18 | }); 19 | }); 20 | -------------------------------------------------------------------------------- /src/algorithms/sets/fisher-yates/README.md: -------------------------------------------------------------------------------- 1 | # Fisher–Yates shuffle 2 | 3 | The Fisher–Yates shuffle is an algorithm for generating a random 4 | permutation of a finite sequence—in plain terms, the algorithm 5 | shuffles the sequence. The algorithm effectively puts all the 6 | elements into a hat; it continually determines the next element 7 | by randomly drawing an element from the hat until no elements 8 | remain. The algorithm produces an unbiased permutation: every 9 | permutation is equally likely. The modern version of the 10 | algorithm is efficient: it takes time proportional to the 11 | number of items being shuffled and shuffles them in place. 12 | 13 | ## References 14 | 15 | [Wikipedia](https://en.wikipedia.org/wiki/Fisher%E2%80%93Yates_shuffle) 16 | -------------------------------------------------------------------------------- /src/algorithms/sets/fisher-yates/__test__/fisherYates.test.js: -------------------------------------------------------------------------------- 1 | import fisherYates from '../fisherYates'; 2 | import { sortedArr } from '../../../sorting/SortTester'; 3 | import QuickSort from '../../../sorting/quick-sort/QuickSort'; 4 | 5 | describe('fisherYates', () => { 6 | it('should shuffle small arrays', () => { 7 | expect(fisherYates([])).toEqual([]); 8 | expect(fisherYates([1])).toEqual([1]); 9 | }); 10 | 11 | it('should shuffle array randomly', () => { 12 | const shuffledArray = fisherYates(sortedArr); 13 | const sorter = new QuickSort(); 14 | 15 | expect(shuffledArray.length).toBe(sortedArr.length); 16 | expect(shuffledArray).not.toEqual(sortedArr); 17 | expect(sorter.sort(shuffledArray)).toEqual(sortedArr); 18 | }); 19 | }); 20 | -------------------------------------------------------------------------------- /src/algorithms/sets/shortest-common-supersequence/README.md: -------------------------------------------------------------------------------- 1 | # Shortest Common Supersequence 2 | 3 | The shortest common supersequence (SCS) of two sequences `X` and `Y` 4 | is the shortest sequence which has `X` and `Y` as subsequences. 5 | 6 | In other words assume we're given two strings str1 and str2, find 7 | the shortest string that has both str1 and str2 as subsequences. 8 | 9 | This is a problem closely related to the longest common 10 | subsequence problem. 11 | 12 | ## Example 13 | 14 | ``` 15 | Input: str1 = "geek", str2 = "eke" 16 | Output: "geeke" 17 | 18 | Input: str1 = "AGGTAB", str2 = "GXTXAYB" 19 | Output: "AGXGTXAYB" 20 | ``` 21 | 22 | ## References 23 | 24 | - [GeeksForGeeks](https://www.geeksforgeeks.org/shortest-common-supersequence/) 25 | -------------------------------------------------------------------------------- /src/algorithms/math/euclidean-distance/euclideanDistance.js: -------------------------------------------------------------------------------- 1 | /** 2 | * @typedef {import('../matrix/Matrix.js').Matrix} Matrix 3 | */ 4 | 5 | import * as mtrx from '../matrix/Matrix'; 6 | 7 | /** 8 | * Calculates the euclidean distance between 2 matrices. 9 | * 10 | * @param {Matrix} a 11 | * @param {Matrix} b 12 | * @returns {number} 13 | * @trows {Error} 14 | */ 15 | const euclideanDistance = (a, b) => { 16 | mtrx.validateSameShape(a, b); 17 | 18 | let squaresTotal = 0; 19 | 20 | mtrx.walk(a, (indices, aCellValue) => { 21 | const bCellValue = mtrx.getCellAtIndex(b, indices); 22 | squaresTotal += (aCellValue - bCellValue) ** 2; 23 | }); 24 | 25 | return Number(Math.sqrt(squaresTotal).toFixed(2)); 26 | }; 27 | 28 | export default euclideanDistance; 29 | -------------------------------------------------------------------------------- /src/algorithms/math/fibonacci/__test__/fibonacci.test.js: -------------------------------------------------------------------------------- 1 | import fibonacci from '../fibonacci'; 2 | 3 | describe('fibonacci', () => { 4 | it('should calculate fibonacci correctly', () => { 5 | expect(fibonacci(1)).toEqual([1]); 6 | expect(fibonacci(2)).toEqual([1, 1]); 7 | expect(fibonacci(3)).toEqual([1, 1, 2]); 8 | expect(fibonacci(4)).toEqual([1, 1, 2, 3]); 9 | expect(fibonacci(5)).toEqual([1, 1, 2, 3, 5]); 10 | expect(fibonacci(6)).toEqual([1, 1, 2, 3, 5, 8]); 11 | expect(fibonacci(7)).toEqual([1, 1, 2, 3, 5, 8, 13]); 12 | expect(fibonacci(8)).toEqual([1, 1, 2, 3, 5, 8, 13, 21]); 13 | expect(fibonacci(9)).toEqual([1, 1, 2, 3, 5, 8, 13, 21, 34]); 14 | expect(fibonacci(10)).toEqual([1, 1, 2, 3, 5, 8, 13, 21, 34, 55]); 15 | }); 16 | }); 17 | -------------------------------------------------------------------------------- /src/algorithms/tree/depth-first-search/README.md: -------------------------------------------------------------------------------- 1 | # Depth-First Search (DFS) 2 | 3 | Depth-first search (DFS) is an algorithm for traversing or 4 | searching tree or graph data structures. One starts at 5 | the root (selecting some arbitrary node as the root in 6 | the case of a graph) and explores as far as possible 7 | along each branch before backtracking. 8 | 9 | ![Algorithm Visualization](https://upload.wikimedia.org/wikipedia/commons/7/7f/Depth-First-Search.gif) 10 | 11 | ## References 12 | 13 | - [Wikipedia](https://en.wikipedia.org/wiki/Depth-first_search) 14 | - [Tree Traversals (Inorder, Preorder and Postorder)](https://www.geeksforgeeks.org/tree-traversals-inorder-preorder-and-postorder/) 15 | - [BFS vs DFS](https://www.geeksforgeeks.org/bfs-vs-dfs-binary-tree/) 16 | -------------------------------------------------------------------------------- /src/data-structures/hash-table/README.ja-JP.md: -------------------------------------------------------------------------------- 1 | # ハッシュテーブル 2 | 3 | コンピュータサイエンスにおいて、**ハッシュテーブル**（ハッシュマップ)は*キーを値にマッピング*できる*連想配列*の機能を持ったデータ構造です。ハッシュテーブルは*ハッシュ関数*を使ってバケットやスロットの配列へのインデックスを計算し、そこから目的の値を見つけることができます。 4 | 5 | 理想的には、ハッシュ関数は各キーを一意のバケットに割り当てますが、ほとんどのハッシュテーブルは不完全なハッシュ関数を採用しているため、複数のキーに対して同じインデックスを生成した時にハッシュの衝突が起こります。このような衝突は何らかの方法で対処する必要があります。 6 | 7 | ![Hash Table](https://upload.wikimedia.org/wikipedia/commons/7/7d/Hash_table_3_1_1_0_1_0_0_SP.svg) 8 | 9 | チェイン法によるハッシュの衝突の解決例 10 | 11 | ![Hash Collision](https://upload.wikimedia.org/wikipedia/commons/d/d0/Hash_table_5_0_1_1_1_1_1_LL.svg) 12 | 13 | ## 参考 14 | 15 | - [Wikipedia](https://en.wikipedia.org/wiki/Hash_table) 16 | - [YouTube](https://www.youtube.com/watch?v=shs0KM3wKv8&index=4&list=PLLXdhg_r2hKA7DPDsunoDZ-Z769jWn4R8) 17 | -------------------------------------------------------------------------------- /src/algorithms/graph/strongly-connected-components/README.md: -------------------------------------------------------------------------------- 1 | # Strongly Connected Component 2 | 3 | A directed graph is called **strongly connected** if there is a path 4 | in each direction between each pair of vertices of the graph. 5 | In a directed graph G that may not itself be strongly connected, 6 | a pair of vertices `u` and `v` are said to be strongly connected 7 | to each other if there is a path in each direction between them. 8 | 9 | 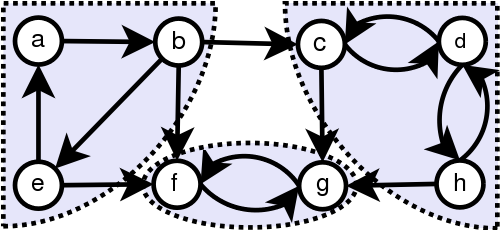![Strongly Connected](https://upload.wikimedia.org/wikipedia/commons/5/5c/Scc.png) 10 | 11 | Graph with strongly connected components marked 12 | 13 | ## References 14 | 15 | - [Wikipedia](https://en.wikipedia.org/wiki/Strongly_connected_component) 16 | - [YouTube](https://www.youtube.com/watch?v=RpgcYiky7uw&list=PLLXdhg_r2hKA7DPDsunoDZ-Z769jWn4R8) 17 | -------------------------------------------------------------------------------- /src/algorithms/math/bits/__test__/countSetBits.test.js: -------------------------------------------------------------------------------- 1 | import countSetBits from '../countSetBits'; 2 | 3 | describe('countSetBits', () => { 4 | it('should return number of set bits', () => { 5 | expect(countSetBits(0)).toBe(0); 6 | expect(countSetBits(1)).toBe(1); 7 | expect(countSetBits(2)).toBe(1); 8 | expect(countSetBits(3)).toBe(2); 9 | expect(countSetBits(4)).toBe(1); 10 | expect(countSetBits(5)).toBe(2); 11 | expect(countSetBits(21)).toBe(3); 12 | expect(countSetBits(255)).toBe(8); 13 | expect(countSetBits(1023)).toBe(10); 14 | expect(countSetBits(-1)).toBe(32); 15 | expect(countSetBits(-21)).toBe(30); 16 | expect(countSetBits(-255)).toBe(25); 17 | expect(countSetBits(-1023)).toBe(23); 18 | expect(countSetBits(-4294967296)).toBe(0); 19 | }); 20 | }); 21 | -------------------------------------------------------------------------------- /src/data-structures/hash-table/README.zh-CN.md: -------------------------------------------------------------------------------- 1 | # 哈希表 2 | 3 | 在计算中, 一个 **哈希表(hash table 或hash map)** 是一种实现 *关联数组(associative array)* 4 | 的抽象数据；类型, 该结构可以将 *键映射到值*。 5 | 6 | 哈希表使用 *哈希函数/散列函数* 来计算一个值在数组或桶(buckets)中或槽(slots)中对应的索引,可使用该索引找到所需的值。 7 | 8 | 理想情况下,散列函数将为每个键分配给一个唯一的桶(bucket),但是大多数哈希表设计采用不完美的散列函数,这可能会导致"哈希冲突(hash collisions)",也就是散列函数为多个键(key)生成了相同的索引,这种碰撞必须 9 | 以某种方式进行处理。 10 | 11 | 12 | ![Hash Table](https://upload.wikimedia.org/wikipedia/commons/7/7d/Hash_table_3_1_1_0_1_0_0_SP.svg) 13 | 14 | 通过单独的链接解决哈希冲突 15 | 16 | ![Hash Collision](https://upload.wikimedia.org/wikipedia/commons/d/d0/Hash_table_5_0_1_1_1_1_1_LL.svg) 17 | 18 | ## 参考 19 | 20 | - [Wikipedia](https://en.wikipedia.org/wiki/Hash_table) 21 | - [YouTube](https://www.youtube.com/watch?v=shs0KM3wKv8&index=4&list=PLLXdhg_r2hKA7DPDsunoDZ-Z769jWn4R8) 22 | -------------------------------------------------------------------------------- /src/algorithms/string/knuth-morris-pratt/README.md: -------------------------------------------------------------------------------- 1 | # Knuth–Morris–Pratt Algorithm 2 | 3 | The Knuth–Morris–Pratt string searching algorithm (or 4 | KMP algorithm) searches for occurrences of a "word" `W` 5 | within a main "text string" `T` by employing the 6 | observation that when a mismatch occurs, the word itself 7 | embodies sufficient information to determine where the 8 | next match could begin, thus bypassing re-examination 9 | of previously matched characters. 10 | 11 | ## Complexity 12 | 13 | - **Time:** `O(|W| + |T|)` (much faster comparing to trivial `O(|W| * |T|)`) 14 | - **Space:** `O(|W|)` 15 | 16 | ## References 17 | 18 | - [Wikipedia](https://en.wikipedia.org/wiki/Knuth%E2%80%93Morris%E2%80%93Pratt_algorithm) 19 | - [YouTube](https://www.youtube.com/watch?v=GTJr8OvyEVQ&list=PLLXdhg_r2hKA7DPDsunoDZ-Z769jWn4R8) 20 | -------------------------------------------------------------------------------- /src/algorithms/math/is-power-of-two/isPowerOfTwoBitwise.js: -------------------------------------------------------------------------------- 1 | /** 2 | * @param {number} number 3 | * @return {boolean} 4 | */ 5 | export default function isPowerOfTwoBitwise(number) { 6 | // 1 (2^0) is the smallest power of two. 7 | if (number < 1) { 8 | return false; 9 | } 10 | 11 | /* 12 | * Powers of two in binary look like this: 13 | * 1: 0001 14 | * 2: 0010 15 | * 4: 0100 16 | * 8: 1000 17 | * 18 | * Note that there is always exactly 1 bit set. The only exception is with a signed integer. 19 | * e.g. An 8-bit signed integer with a value of -128 looks like: 20 | * 10000000 21 | * 22 | * So after checking that the number is greater than zero, we can use a clever little bit 23 | * hack to test that one and only one bit is set. 24 | */ 25 | return (number & (number - 1)) === 0; 26 | } 27 | -------------------------------------------------------------------------------- /.github/workflows/CI.yml: -------------------------------------------------------------------------------- 1 | name: CI 2 | 3 | on: 4 | push: 5 | branches: [ master ] 6 | pull_request: 7 | branches: [ master ] 8 | 9 | jobs: 10 | test: 11 | runs-on: ubuntu-latest 12 | strategy: 13 | matrix: 14 | node-version: [ 14.x ] 15 | 16 | steps: 17 | - name: Checkout repository 18 | uses: actions/checkout@v2 19 | 20 | - name: Setup Node.js ${{ matrix.node-version }} 21 | uses: actions/setup-node@v1 22 | with: 23 | node-version: ${{ matrix.node-version }} 24 | 25 | - name: Install dependencies 26 | run: npm i 27 | 28 | - name: Run linting 29 | run: npm run lint 30 | 31 | - name: Run tests 32 | run: npm run coverage 33 | 34 | - name: Upload coverage to Codecov 35 | uses: codecov/codecov-action@v1 36 | -------------------------------------------------------------------------------- /src/algorithms/math/euclidean-algorithm/euclideanAlgorithmIterative.js: -------------------------------------------------------------------------------- 1 | /** 2 | * Iterative version of Euclidean Algorithm of finding greatest common divisor (GCD). 3 | * @param {number} originalA 4 | * @param {number} originalB 5 | * @return {number} 6 | */ 7 | export default function euclideanAlgorithmIterative(originalA, originalB) { 8 | // Make input numbers positive. 9 | let a = Math.abs(originalA); 10 | let b = Math.abs(originalB); 11 | 12 | // Subtract one number from another until both numbers would become the same. 13 | // This will be out GCD. Also quit the loop if one of the numbers is zero. 14 | while (a && b && a !== b) { 15 | [a, b] = a > b ? [a - b, b] : [a, b - a]; 16 | } 17 | 18 | // Return the number that is not equal to zero since the last subtraction (it will be a GCD). 19 | return a || b; 20 | } 21 | -------------------------------------------------------------------------------- /src/algorithms/math/pascal-triangle/__test__/pascalTriangleRecursive.test.js: -------------------------------------------------------------------------------- 1 | import pascalTriangleRecursive from '../pascalTriangleRecursive'; 2 | 3 | describe('pascalTriangleRecursive', () => { 4 | it('should calculate Pascal Triangle coefficients for specific line number', () => { 5 | expect(pascalTriangleRecursive(0)).toEqual([1]); 6 | expect(pascalTriangleRecursive(1)).toEqual([1, 1]); 7 | expect(pascalTriangleRecursive(2)).toEqual([1, 2, 1]); 8 | expect(pascalTriangleRecursive(3)).toEqual([1, 3, 3, 1]); 9 | expect(pascalTriangleRecursive(4)).toEqual([1, 4, 6, 4, 1]); 10 | expect(pascalTriangleRecursive(5)).toEqual([1, 5, 10, 10, 5, 1]); 11 | expect(pascalTriangleRecursive(6)).toEqual([1, 6, 15, 20, 15, 6, 1]); 12 | expect(pascalTriangleRecursive(7)).toEqual([1, 7, 21, 35, 35, 21, 7, 1]); 13 | }); 14 | }); 15 | -------------------------------------------------------------------------------- /src/algorithms/uncategorized/jump-game/__test__/greedyJumpGame.test.js: -------------------------------------------------------------------------------- 1 | import greedyJumpGame from '../greedyJumpGame'; 2 | 3 | describe('greedyJumpGame', () => { 4 | it('should solve Jump Game problem in greedy manner', () => { 5 | expect(greedyJumpGame([1, 0])).toBe(true); 6 | expect(greedyJumpGame([100, 0])).toBe(true); 7 | expect(greedyJumpGame([2, 3, 1, 1, 4])).toBe(true); 8 | expect(greedyJumpGame([1, 1, 1, 1, 1])).toBe(true); 9 | expect(greedyJumpGame([1, 1, 1, 10, 1])).toBe(true); 10 | expect(greedyJumpGame([1, 5, 2, 1, 0, 2, 0])).toBe(true); 11 | 12 | expect(greedyJumpGame([1, 0, 1])).toBe(false); 13 | expect(greedyJumpGame([3, 2, 1, 0, 4])).toBe(false); 14 | expect(greedyJumpGame([0, 0, 0, 0, 0])).toBe(false); 15 | expect(greedyJumpGame([5, 4, 3, 2, 1, 0, 0])).toBe(false); 16 | }); 17 | }); 18 | -------------------------------------------------------------------------------- /src/algorithms/math/bits/__test__/isPowerOfTwo.test.js: -------------------------------------------------------------------------------- 1 | import isPowerOfTwo from '../isPowerOfTwo'; 2 | 3 | describe('isPowerOfTwo', () => { 4 | it('should detect if the number is power of two', () => { 5 | expect(isPowerOfTwo(1)).toBe(true); 6 | expect(isPowerOfTwo(2)).toBe(true); 7 | expect(isPowerOfTwo(3)).toBe(false); 8 | expect(isPowerOfTwo(4)).toBe(true); 9 | expect(isPowerOfTwo(5)).toBe(false); 10 | expect(isPowerOfTwo(6)).toBe(false); 11 | expect(isPowerOfTwo(7)).toBe(false); 12 | expect(isPowerOfTwo(8)).toBe(true); 13 | expect(isPowerOfTwo(9)).toBe(false); 14 | expect(isPowerOfTwo(16)).toBe(true); 15 | expect(isPowerOfTwo(23)).toBe(false); 16 | expect(isPowerOfTwo(32)).toBe(true); 17 | expect(isPowerOfTwo(127)).toBe(false); 18 | expect(isPowerOfTwo(128)).toBe(true); 19 | }); 20 | }); 21 | -------------------------------------------------------------------------------- /src/data-structures/tree/README.zh-CN.md: -------------------------------------------------------------------------------- 1 | # 树 2 | 3 | * [二叉搜索树](binary-search-tree) 4 | * [AVL树](avl-tree) 5 | * [红黑树](red-black-tree) 6 | * [线段树](segment-tree) - with min/max/sum range queries examples 7 | * [芬威克树/Fenwick Tree](fenwick-tree) (Binary Indexed Tree) 8 | 9 | 在计算机科学中, **树(tree)** 是一种广泛使用的抽象数据类型(ADT)— 或实现此ADT的数据结构 — 模拟分层树结构, 具有根节点和有父节点的子树,表示为一组链接节点。 10 | 11 | 树可以被(本地地)递归定义为一个(始于一个根节点的)节点集, 每个节点都是一个包含了值的数据结构, 除了值,还有该节点的节点引用列表(子节点)一起。 12 | 树的节点之间没有引用重复的约束。 13 | 14 | 一棵简单的无序树; 在下图中: 15 | 16 | 标记为7的节点具有两个子节点, 标记为2和6; 17 | 一个父节点,标记为2,作为根节点, 在顶部,没有父节点。 18 | 19 | ![Tree](https://upload.wikimedia.org/wikipedia/commons/f/f7/Binary_tree.svg) 20 | 21 | ## 参考 22 | 23 | - [Wikipedia](https://en.wikipedia.org/wiki/Tree_(data_structure)) 24 | - [YouTube](https://www.youtube.com/watch?v=oSWTXtMglKE&list=PLLXdhg_r2hKA7DPDsunoDZ-Z769jWn4R8&index=8) 25 | -------------------------------------------------------------------------------- /src/algorithms/graph/depth-first-search/README.md: -------------------------------------------------------------------------------- 1 | # Depth-First Search (DFS) 2 | 3 | Depth-first search (DFS) is an algorithm for traversing or 4 | searching tree or graph data structures. One starts at 5 | the root (selecting some arbitrary node as the root in 6 | the case of a graph) and explores as far as possible 7 | along each branch before backtracking. 8 | 9 | ![Algorithm Visualization](https://upload.wikimedia.org/wikipedia/commons/7/7f/Depth-First-Search.gif) 10 | 11 | ## References 12 | 13 | - [Wikipedia](https://en.wikipedia.org/wiki/Depth-first_search) 14 | - [Tree Traversals (Inorder, Preorder and Postorder)](https://www.geeksforgeeks.org/tree-traversals-inorder-preorder-and-postorder/) 15 | - [BFS vs DFS](https://www.geeksforgeeks.org/bfs-vs-dfs-binary-tree/) 16 | - [DFS Visualization](https://www.cs.usfca.edu/~galles/visualization/DFS.html) 17 | -------------------------------------------------------------------------------- /src/algorithms/string/knuth-morris-pratt/__test__/knuthMorrisPratt.test.js: -------------------------------------------------------------------------------- 1 | import knuthMorrisPratt from '../knuthMorrisPratt'; 2 | 3 | describe('knuthMorrisPratt', () => { 4 | it('should find word position in given text', () => { 5 | expect(knuthMorrisPratt('', '')).toBe(0); 6 | expect(knuthMorrisPratt('a', '')).toBe(0); 7 | expect(knuthMorrisPratt('a', 'a')).toBe(0); 8 | expect(knuthMorrisPratt('abcbcglx', 'abca')).toBe(-1); 9 | expect(knuthMorrisPratt('abcbcglx', 'bcgl')).toBe(3); 10 | expect(knuthMorrisPratt('abcxabcdabxabcdabcdabcy', 'abcdabcy')).toBe(15); 11 | expect(knuthMorrisPratt('abcxabcdabxabcdabcdabcy', 'abcdabca')).toBe(-1); 12 | expect(knuthMorrisPratt('abcxabcdabxaabcdabcabcdabcdabcy', 'abcdabca')).toBe(12); 13 | expect(knuthMorrisPratt('abcxabcdabxaabaabaaaabcdabcdabcy', 'aabaabaaa')).toBe(11); 14 | }); 15 | }); 16 | -------------------------------------------------------------------------------- /src/algorithms/uncategorized/best-time-to-buy-sell-stocks/accumulatorBestTimeToBuySellStocks.js: -------------------------------------------------------------------------------- 1 | /** 2 | * Finds the maximum profit from selling and buying the stocks. 3 | * ACCUMULATOR APPROACH. 4 | * 5 | * @param {number[]} prices - Array of stock prices, i.e. [7, 6, 4, 3, 1] 6 | * @param {function(): void} visit - Visiting callback to calculate the number of iterations. 7 | * @return {number} - The maximum profit 8 | */ 9 | const accumulatorBestTimeToBuySellStocks = (prices, visit = () => {}) => { 10 | visit(); 11 | let profit = 0; 12 | for (let day = 1; day < prices.length; day += 1) { 13 | visit(); 14 | // Add the increase of the price from yesterday till today (if there was any) to the profit. 15 | profit += Math.max(prices[day] - prices[day - 1], 0); 16 | } 17 | return profit; 18 | }; 19 | 20 | export default accumulatorBestTimeToBuySellStocks; 21 | -------------------------------------------------------------------------------- /src/algorithms/uncategorized/recursive-staircase/__test__/recursiveStaircaseIT.test.js: -------------------------------------------------------------------------------- 1 | import recursiveStaircaseIT from '../recursiveStaircaseIT'; 2 | 3 | describe('recursiveStaircaseIT', () => { 4 | it('should calculate number of variants using Iterative solution', () => { 5 | expect(recursiveStaircaseIT(-1)).toBe(0); 6 | expect(recursiveStaircaseIT(0)).toBe(0); 7 | expect(recursiveStaircaseIT(1)).toBe(1); 8 | expect(recursiveStaircaseIT(2)).toBe(2); 9 | expect(recursiveStaircaseIT(3)).toBe(3); 10 | expect(recursiveStaircaseIT(4)).toBe(5); 11 | expect(recursiveStaircaseIT(5)).toBe(8); 12 | expect(recursiveStaircaseIT(6)).toBe(13); 13 | expect(recursiveStaircaseIT(7)).toBe(21); 14 | expect(recursiveStaircaseIT(8)).toBe(34); 15 | expect(recursiveStaircaseIT(9)).toBe(55); 16 | expect(recursiveStaircaseIT(10)).toBe(89); 17 | }); 18 | }); 19 | -------------------------------------------------------------------------------- /src/algorithms/uncategorized/recursive-staircase/__test__/recursiveStaircaseBF.test.js: -------------------------------------------------------------------------------- 1 | import recursiveStaircaseBF from '../recursiveStaircaseBF'; 2 | 3 | describe('recursiveStaircaseBF', () => { 4 | it('should calculate number of variants using Brute Force solution', () => { 5 | expect(recursiveStaircaseBF(-1)).toBe(0); 6 | expect(recursiveStaircaseBF(0)).toBe(0); 7 | expect(recursiveStaircaseBF(1)).toBe(1); 8 | expect(recursiveStaircaseBF(2)).toBe(2); 9 | expect(recursiveStaircaseBF(3)).toBe(3); 10 | expect(recursiveStaircaseBF(4)).toBe(5); 11 | expect(recursiveStaircaseBF(5)).toBe(8); 12 | expect(recursiveStaircaseBF(6)).toBe(13); 13 | expect(recursiveStaircaseBF(7)).toBe(21); 14 | expect(recursiveStaircaseBF(8)).toBe(34); 15 | expect(recursiveStaircaseBF(9)).toBe(55); 16 | expect(recursiveStaircaseBF(10)).toBe(89); 17 | }); 18 | }); 19 | -------------------------------------------------------------------------------- /src/algorithms/math/least-common-multiple/__test__/leastCommonMultiple.test.js: -------------------------------------------------------------------------------- 1 | import leastCommonMultiple from '../leastCommonMultiple'; 2 | 3 | describe('leastCommonMultiple', () => { 4 | it('should find least common multiple', () => { 5 | expect(leastCommonMultiple(0, 0)).toBe(0); 6 | expect(leastCommonMultiple(1, 0)).toBe(0); 7 | expect(leastCommonMultiple(0, 1)).toBe(0); 8 | expect(leastCommonMultiple(4, 6)).toBe(12); 9 | expect(leastCommonMultiple(6, 21)).toBe(42); 10 | expect(leastCommonMultiple(7, 2)).toBe(14); 11 | expect(leastCommonMultiple(3, 5)).toBe(15); 12 | expect(leastCommonMultiple(7, 3)).toBe(21); 13 | expect(leastCommonMultiple(1000000, 2)).toBe(1000000); 14 | expect(leastCommonMultiple(-9, -18)).toBe(18); 15 | expect(leastCommonMultiple(-7, -9)).toBe(63); 16 | expect(leastCommonMultiple(-7, 9)).toBe(63); 17 | }); 18 | }); 19 | -------------------------------------------------------------------------------- /src/algorithms/uncategorized/recursive-staircase/__test__/recursiveStaircaseDP.test.js: -------------------------------------------------------------------------------- 1 | import recursiveStaircaseDP from '../recursiveStaircaseDP'; 2 | 3 | describe('recursiveStaircaseDP', () => { 4 | it('should calculate number of variants using Dynamic Programming solution', () => { 5 | expect(recursiveStaircaseDP(-1)).toBe(0); 6 | expect(recursiveStaircaseDP(0)).toBe(0); 7 | expect(recursiveStaircaseDP(1)).toBe(1); 8 | expect(recursiveStaircaseDP(2)).toBe(2); 9 | expect(recursiveStaircaseDP(3)).toBe(3); 10 | expect(recursiveStaircaseDP(4)).toBe(5); 11 | expect(recursiveStaircaseDP(5)).toBe(8); 12 | expect(recursiveStaircaseDP(6)).toBe(13); 13 | expect(recursiveStaircaseDP(7)).toBe(21); 14 | expect(recursiveStaircaseDP(8)).toBe(34); 15 | expect(recursiveStaircaseDP(9)).toBe(55); 16 | expect(recursiveStaircaseDP(10)).toBe(89); 17 | }); 18 | }); 19 | -------------------------------------------------------------------------------- /src/algorithms/math/horner-method/__test__/classicPolynome.test.js: -------------------------------------------------------------------------------- 1 | import classicPolynome from '../classicPolynome'; 2 | 3 | describe('classicPolynome', () => { 4 | it('should evaluate the polynomial for the specified value of x correctly', () => { 5 | expect(classicPolynome([8], 0.1)).toBe(8); 6 | expect(classicPolynome([2, 4, 2, 5], 0.555)).toBe(7.68400775); 7 | expect(classicPolynome([2, 4, 2, 5], 0.75)).toBe(9.59375); 8 | expect(classicPolynome([1, 1, 1, 1, 1], 1.75)).toBe(20.55078125); 9 | expect(classicPolynome([15, 3.5, 0, 2, 1.42, 0.41], 0.315)).toBe(1.1367300651406251); 10 | expect(classicPolynome([0, 0, 2.77, 1.42, 0.41], 1.35)).toBe(7.375325000000001); 11 | expect(classicPolynome([0, 0, 2.77, 1.42, 2.3311], 1.35)).toBe(9.296425000000001); 12 | expect(classicPolynome([2, 0, 0, 5.757, 5.31412, 12.3213], 3.141)).toBe(697.2731167035034); 13 | }); 14 | }); 15 | -------------------------------------------------------------------------------- /src/algorithms/graph/breadth-first-search/README.md: -------------------------------------------------------------------------------- 1 | # Breadth-First Search (BFS) 2 | 3 | Breadth-first search (BFS) is an algorithm for traversing 4 | or searching tree or graph data structures. It starts at 5 | the tree root (or some arbitrary node of a graph, sometimes 6 | referred to as a 'search key') and explores the neighbor 7 | nodes first, before moving to the next level neighbors. 8 | 9 | ![Algorithm Visualization](https://upload.wikimedia.org/wikipedia/commons/5/5d/Breadth-First-Search-Algorithm.gif) 10 | 11 | ## References 12 | 13 | - [Wikipedia](https://en.wikipedia.org/wiki/Breadth-first_search) 14 | - [Tree Traversals (Inorder, Preorder and Postorder)](https://www.geeksforgeeks.org/tree-traversals-inorder-preorder-and-postorder/) 15 | - [BFS vs DFS](https://www.geeksforgeeks.org/bfs-vs-dfs-binary-tree/) 16 | - [BFS Visualization](https://www.cs.usfca.edu/~galles/visualization/BFS.html) 17 | -------------------------------------------------------------------------------- /src/algorithms/uncategorized/jump-game/__test__/dpTopDownJumpGame.test.js: -------------------------------------------------------------------------------- 1 | import dpTopDownJumpGame from '../dpTopDownJumpGame'; 2 | 3 | describe('dpTopDownJumpGame', () => { 4 | it('should solve Jump Game problem in top-down dynamic programming manner', () => { 5 | expect(dpTopDownJumpGame([1, 0])).toBe(true); 6 | expect(dpTopDownJumpGame([100, 0])).toBe(true); 7 | expect(dpTopDownJumpGame([2, 3, 1, 1, 4])).toBe(true); 8 | expect(dpTopDownJumpGame([1, 1, 1, 1, 1])).toBe(true); 9 | expect(dpTopDownJumpGame([1, 1, 1, 10, 1])).toBe(true); 10 | expect(dpTopDownJumpGame([1, 5, 2, 1, 0, 2, 0])).toBe(true); 11 | 12 | expect(dpTopDownJumpGame([1, 0, 1])).toBe(false); 13 | expect(dpTopDownJumpGame([3, 2, 1, 0, 4])).toBe(false); 14 | expect(dpTopDownJumpGame([0, 0, 0, 0, 0])).toBe(false); 15 | expect(dpTopDownJumpGame([5, 4, 3, 2, 1, 0, 0])).toBe(false); 16 | }); 17 | }); 18 | -------------------------------------------------------------------------------- /src/algorithms/uncategorized/recursive-staircase/__test__/recursiveStaircaseMEM.test.js: -------------------------------------------------------------------------------- 1 | import recursiveStaircaseMEM from '../recursiveStaircaseMEM'; 2 | 3 | describe('recursiveStaircaseMEM', () => { 4 | it('should calculate number of variants using Brute Force with Memoization', () => { 5 | expect(recursiveStaircaseMEM(-1)).toBe(0); 6 | expect(recursiveStaircaseMEM(0)).toBe(0); 7 | expect(recursiveStaircaseMEM(1)).toBe(1); 8 | expect(recursiveStaircaseMEM(2)).toBe(2); 9 | expect(recursiveStaircaseMEM(3)).toBe(3); 10 | expect(recursiveStaircaseMEM(4)).toBe(5); 11 | expect(recursiveStaircaseMEM(5)).toBe(8); 12 | expect(recursiveStaircaseMEM(6)).toBe(13); 13 | expect(recursiveStaircaseMEM(7)).toBe(21); 14 | expect(recursiveStaircaseMEM(8)).toBe(34); 15 | expect(recursiveStaircaseMEM(9)).toBe(55); 16 | expect(recursiveStaircaseMEM(10)).toBe(89); 17 | }); 18 | }); 19 | -------------------------------------------------------------------------------- /src/algorithms/graph/bellman-ford/README.md: -------------------------------------------------------------------------------- 1 | # Bellman–Ford Algorithm 2 | 3 | The Bellman–Ford algorithm is an algorithm that computes shortest 4 | paths from a single source vertex to all of the other vertices 5 | in a weighted digraph. It is slower than Dijkstra's algorithm 6 | for the same problem, but more versatile, as it is capable of 7 | handling graphs in which some of the edge weights are negative 8 | numbers. 9 | 10 | ![Bellman-Ford](https://upload.wikimedia.org/wikipedia/commons/2/2e/Shortest_path_Dijkstra_vs_BellmanFord.gif) 11 | 12 | ## Complexity 13 | 14 | Worst-case performance `O(|V||E|)` 15 | Best-case performance `O(|E|)` 16 | Worst-case space complexity `O(|V|)` 17 | 18 | ## References 19 | 20 | - [Wikipedia](https://en.wikipedia.org/wiki/Bellman%E2%80%93Ford_algorithm) 21 | - [On YouTube by Michael Sambol](https://www.youtube.com/watch?v=obWXjtg0L64&list=PLLXdhg_r2hKA7DPDsunoDZ-Z769jWn4R8) 22 | -------------------------------------------------------------------------------- /src/algorithms/string/z-algorithm/__test__/zAlgorithm.test.js: -------------------------------------------------------------------------------- 1 | import zAlgorithm from '../zAlgorithm'; 2 | 3 | describe('zAlgorithm', () => { 4 | it('should find word positions in given text', () => { 5 | expect(zAlgorithm('abcbcglx', 'abca')).toEqual([]); 6 | expect(zAlgorithm('abca', 'abca')).toEqual([0]); 7 | expect(zAlgorithm('abca', 'abcadfd')).toEqual([]); 8 | expect(zAlgorithm('abcbcglabcx', 'abc')).toEqual([0, 7]); 9 | expect(zAlgorithm('abcbcglx', 'bcgl')).toEqual([3]); 10 | expect(zAlgorithm('abcbcglx', 'cglx')).toEqual([4]); 11 | expect(zAlgorithm('abcxabcdabxabcdabcdabcy', 'abcdabcy')).toEqual([15]); 12 | expect(zAlgorithm('abcxabcdabxabcdabcdabcy', 'abcdabca')).toEqual([]); 13 | expect(zAlgorithm('abcxabcdabxaabcdabcabcdabcdabcy', 'abcdabca')).toEqual([12]); 14 | expect(zAlgorithm('abcxabcdabxaabaabaaaabcdabcdabcy', 'aabaabaaa')).toEqual([11]); 15 | }); 16 | }); 17 | -------------------------------------------------------------------------------- /src/algorithms/uncategorized/jump-game/__test__/dpBottomUpJumpGame.test.js: -------------------------------------------------------------------------------- 1 | import dpBottomUpJumpGame from '../dpBottomUpJumpGame'; 2 | 3 | describe('dpBottomUpJumpGame', () => { 4 | it('should solve Jump Game problem in bottom-up dynamic programming manner', () => { 5 | expect(dpBottomUpJumpGame([1, 0])).toBe(true); 6 | expect(dpBottomUpJumpGame([100, 0])).toBe(true); 7 | expect(dpBottomUpJumpGame([2, 3, 1, 1, 4])).toBe(true); 8 | expect(dpBottomUpJumpGame([1, 1, 1, 1, 1])).toBe(true); 9 | expect(dpBottomUpJumpGame([1, 1, 1, 10, 1])).toBe(true); 10 | expect(dpBottomUpJumpGame([1, 5, 2, 1, 0, 2, 0])).toBe(true); 11 | 12 | expect(dpBottomUpJumpGame([1, 0, 1])).toBe(false); 13 | expect(dpBottomUpJumpGame([3, 2, 1, 0, 4])).toBe(false); 14 | expect(dpBottomUpJumpGame([0, 0, 0, 0, 0])).toBe(false); 15 | expect(dpBottomUpJumpGame([5, 4, 3, 2, 1, 0, 0])).toBe(false); 16 | }); 17 | }); 18 | -------------------------------------------------------------------------------- /src/data-structures/heap/README.pt-BR.md: -------------------------------------------------------------------------------- 1 | # Heap (estrutura de dados) 2 | 3 | Na ciência da computação, um **heap** é uma estrutura de dados 4 | baseada em uma árvore especializada que satisfaz a propriedade _heap_ descrita abaixo. 5 | 6 | Em um *heap mínimo* (min heap), caso `P` é um nó pai de `C`, então a chave 7 | (o valor) de `P` é menor ou igual a chave de `C`. 8 | 9 | ![MinHeap](https://upload.wikimedia.org/wikipedia/commons/6/69/Min-heap.png) 10 | 11 | Em uma *heap máximo* (max heap), a chave de `P` é maior ou igual 12 | a chave de `C`. 13 | 14 | ![Heap](https://upload.wikimedia.org/wikipedia/commons/3/38/Max-Heap.svg) 15 | 16 | O nó no "topo" do _heap_, cujo não possui pais, é chamado de nó raiz. 17 | 18 | ## References 19 | 20 | - [Wikipedia](https://en.wikipedia.org/wiki/Heap_(data_structure)) 21 | - [YouTube](https://www.youtube.com/watch?v=t0Cq6tVNRBA&index=5&t=0s&list=PLLXdhg_r2hKA7DPDsunoDZ-Z769jWn4R8) 22 | -------------------------------------------------------------------------------- /src/data-structures/stack/README.ru-RU.md: -------------------------------------------------------------------------------- 1 | # Стек 2 | 3 | Стек (англ. stack — стопка) — абстрактный тип данных, представляющий собой 4 | список элементов, организованных по принципу LIFO (последним пришёл — первым вышел). 5 | 6 | Стек имеет две ключевые операции: 7 | * **добавление (push)** элемента в конец стека, и 8 | * **удаление (pop)**, последнего добавленного элемента. 9 | 10 | Дополнительная операция чтения головного элемента (peek) даёт доступ 11 | к последнему элементу стека без изменения самого стека. 12 | 13 | Чаще всего принцип работы стека сравнивают со стопкой тарелок: чтобы взять вторую 14 | сверху, нужно снять верхнюю. 15 | 16 | Иллюстрация работы со стеком. 17 | 18 | ![Стек](https://upload.wikimedia.org/wikipedia/commons/b/b4/Lifo_stack.png) 19 | 20 | ## Ссылки 21 | 22 | - [Wikipedia](https://ru.wikipedia.org/wiki/%D0%A1%D1%82%D0%B5%D0%BA) 23 | - [YouTube](https://www.youtube.com/watch?v=tH8qi7lej5U) 24 | -------------------------------------------------------------------------------- /src/algorithms/uncategorized/best-time-to-buy-sell-stocks/dpBestTimeToBuySellStocks.js: -------------------------------------------------------------------------------- 1 | /** 2 | * Finds the maximum profit from selling and buying the stocks. 3 | * DYNAMIC PROGRAMMING APPROACH. 4 | * 5 | * @param {number[]} prices - Array of stock prices, i.e. [7, 6, 4, 3, 1] 6 | * @param {function(): void} visit - Visiting callback to calculate the number of iterations. 7 | * @return {number} - The maximum profit 8 | */ 9 | const dpBestTimeToBuySellStocks = (prices, visit = () => {}) => { 10 | visit(); 11 | let lastBuy = -prices[0]; 12 | let lastSold = 0; 13 | 14 | for (let day = 1; day < prices.length; day += 1) { 15 | visit(); 16 | const curBuy = Math.max(lastBuy, lastSold - prices[day]); 17 | const curSold = Math.max(lastSold, lastBuy + prices[day]); 18 | lastBuy = curBuy; 19 | lastSold = curSold; 20 | } 21 | 22 | return lastSold; 23 | }; 24 | 25 | export default dpBestTimeToBuySellStocks; 26 | -------------------------------------------------------------------------------- /src/algorithms/uncategorized/jump-game/__test__/backtrackingJumpGame.test.js: -------------------------------------------------------------------------------- 1 | import backtrackingJumpGame from '../backtrackingJumpGame'; 2 | 3 | describe('backtrackingJumpGame', () => { 4 | it('should solve Jump Game problem in backtracking manner', () => { 5 | expect(backtrackingJumpGame([1, 0])).toBe(true); 6 | expect(backtrackingJumpGame([100, 0])).toBe(true); 7 | expect(backtrackingJumpGame([2, 3, 1, 1, 4])).toBe(true); 8 | expect(backtrackingJumpGame([1, 1, 1, 1, 1])).toBe(true); 9 | expect(backtrackingJumpGame([1, 1, 1, 10, 1])).toBe(true); 10 | expect(backtrackingJumpGame([1, 5, 2, 1, 0, 2, 0])).toBe(true); 11 | 12 | expect(backtrackingJumpGame([1, 0, 1])).toBe(false); 13 | expect(backtrackingJumpGame([3, 2, 1, 0, 4])).toBe(false); 14 | expect(backtrackingJumpGame([0, 0, 0, 0, 0])).toBe(false); 15 | expect(backtrackingJumpGame([5, 4, 3, 2, 1, 0, 0])).toBe(false); 16 | }); 17 | }); 18 | -------------------------------------------------------------------------------- /src/data-structures/heap/README.fr-FR.md: -------------------------------------------------------------------------------- 1 | # Tas (structure de données) 2 | 3 | En informatique, un **tas** est une structure de données arborescente spécialisée qui satisfait la propriété de tas décrite ci-dessous. 4 | 5 | Dans un *tas minimal* (en anglais *min heap*), si `P` est un nœud parent de `C`, alors la clé (la valeur) de `P` est inférieure ou égale à la clé de `C`. 6 | 7 | ![MinHeap](https://upload.wikimedia.org/wikipedia/commons/6/69/Min-heap.png) 8 | 9 | Dans un *tas maximal* (en anglais *max heap*), la clé de `P` est supérieure ou égale à la clé de `C`. 10 | 11 | ![Heap](https://upload.wikimedia.org/wikipedia/commons/3/38/Max-Heap.svg) 12 | 13 | Le nœud au «sommet» du tas sans parents est appelé le nœud racine. 14 | 15 | ## Références 16 | 17 | - [Wikipedia](https://fr.wikipedia.org/wiki/Tas_(informatique)) 18 | - [YouTube](https://www.youtube.com/watch?v=t0Cq6tVNRBA&index=5&t=0s&list=PLLXdhg_r2hKA7DPDsunoDZ-Z769jWn4R8) 19 | -------------------------------------------------------------------------------- /src/algorithms/search/linear-search/README.md: -------------------------------------------------------------------------------- 1 | # Linear Search 2 | In computer science, linear search or sequential search is a 3 | method for finding a target value within a list. It sequentially 4 | checks each element of the list for the target value until a 5 | match is found or until all the elements have been searched. 6 | Linear search runs in at worst linear time and makes at most `n` 7 | comparisons, where `n` is the length of the list. 8 | 9 | 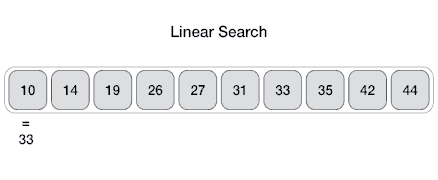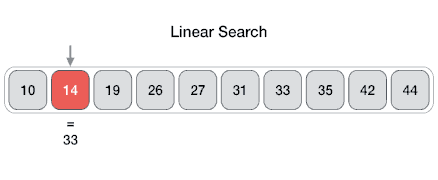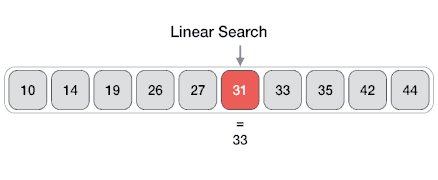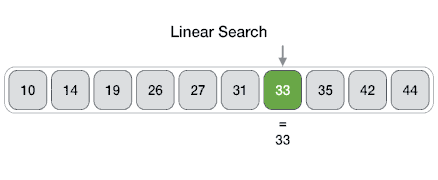![Linear Search](https://www.tutorialspoint.com/data_structures_algorithms/images/linear_search.gif) 10 | 11 | ## Complexity 12 | 13 | **Time Complexity**: `O(n)` - since in worst case we're checking each element 14 | exactly once. 15 | 16 | ## References 17 | - [Wikipedia](https://en.wikipedia.org/wiki/Linear_search) 18 | - [TutorialsPoint](https://www.tutorialspoint.com/data_structures_algorithms/linear_search_algorithm.htm) 19 | - [Youtube](https://www.youtube.com/watch?v=SGU9duLE30w) 20 | -------------------------------------------------------------------------------- /src/algorithms/string/hamming-distance/README.md: -------------------------------------------------------------------------------- 1 | # Hamming Distance 2 | 3 | the Hamming distance between two strings of equal length is the 4 | number of positions at which the corresponding symbols are 5 | different. In other words, it measures the minimum number of 6 | substitutions required to change one string into the other, or 7 | the minimum number of errors that could have transformed one 8 | string into the other. In a more general context, the Hamming 9 | distance is one of several string metrics for measuring the 10 | edit distance between two sequences. 11 | 12 | ## Examples 13 | 14 | The Hamming distance between: 15 | 16 | - "ka**rol**in" and "ka**thr**in" is **3**. 17 | - "k**a**r**ol**in" and "k**e**r**st**in" is **3**. 18 | - 10**1**1**1**01 and 10**0**1**0**01 is **2**. 19 | - 2**17**3**8**96 and 2**23**3**7**96 is **3**. 20 | 21 | ## References 22 | 23 | [Wikipedia](https://en.wikipedia.org/wiki/Hamming_distance) 24 | -------------------------------------------------------------------------------- /src/algorithms/string/hamming-distance/__test__/hammingDistance.test.js: -------------------------------------------------------------------------------- 1 | import hammingDistance from '../hammingDistance'; 2 | 3 | describe('hammingDistance', () => { 4 | it('should throw an error when trying to compare the strings of different lengths', () => { 5 | const compareStringsOfDifferentLength = () => { 6 | hammingDistance('a', 'aa'); 7 | }; 8 | 9 | expect(compareStringsOfDifferentLength).toThrowError(); 10 | }); 11 | 12 | it('should calculate difference between two strings', () => { 13 | expect(hammingDistance('a', 'a')).toBe(0); 14 | expect(hammingDistance('a', 'b')).toBe(1); 15 | expect(hammingDistance('abc', 'add')).toBe(2); 16 | expect(hammingDistance('karolin', 'kathrin')).toBe(3); 17 | expect(hammingDistance('karolin', 'kerstin')).toBe(3); 18 | expect(hammingDistance('1011101', '1001001')).toBe(2); 19 | expect(hammingDistance('2173896', '2233796')).toBe(3); 20 | }); 21 | }); 22 | -------------------------------------------------------------------------------- /src/algorithms/sets/cartesian-product/cartesianProduct.js: -------------------------------------------------------------------------------- 1 | /** 2 | * Generates Cartesian Product of two sets. 3 | * @param {*[]} setA 4 | * @param {*[]} setB 5 | * @return {*[]} 6 | */ 7 | export default function cartesianProduct(setA, setB) { 8 | // Check if input sets are not empty. 9 | // Otherwise return null since we can't generate Cartesian Product out of them. 10 | if (!setA || !setB || !setA.length || !setB.length) { 11 | return null; 12 | } 13 | 14 | // Init product set. 15 | const product = []; 16 | 17 | // Now, let's go through all elements of a first and second set and form all possible pairs. 18 | for (let indexA = 0; indexA < setA.length; indexA += 1) { 19 | for (let indexB = 0; indexB < setB.length; indexB += 1) { 20 | // Add current product pair to the product set. 21 | product.push([setA[indexA], setB[indexB]]); 22 | } 23 | } 24 | 25 | // Return cartesian product set. 26 | return product; 27 | } 28 | -------------------------------------------------------------------------------- /src/data-structures/graph/GraphEdge.js: -------------------------------------------------------------------------------- 1 | export default class GraphEdge { 2 | /** 3 | * @param {GraphVertex} startVertex 4 | * @param {GraphVertex} endVertex 5 | * @param {number} [weight=1] 6 | */ 7 | constructor(startVertex, endVertex, weight = 0) { 8 | this.startVertex = startVertex; 9 | this.endVertex = endVertex; 10 | this.weight = weight; 11 | } 12 | 13 | /** 14 | * @return {string} 15 | */ 16 | getKey() { 17 | const startVertexKey = this.startVertex.getKey(); 18 | const endVertexKey = this.endVertex.getKey(); 19 | 20 | return `${startVertexKey}_${endVertexKey}`; 21 | } 22 | 23 | /** 24 | * @return {GraphEdge} 25 | */ 26 | reverse() { 27 | const tmp = this.startVertex; 28 | this.startVertex = this.endVertex; 29 | this.endVertex = tmp; 30 | 31 | return this; 32 | } 33 | 34 | /** 35 | * @return {string} 36 | */ 37 | toString() { 38 | return this.getKey(); 39 | } 40 | } 41 | -------------------------------------------------------------------------------- /src/algorithms/math/factorial/README.zh-CN.md: -------------------------------------------------------------------------------- 1 | # 阶乘 2 | 3 | 在数学上, 一个正整数 `n` 的阶乘 (写作 `n!`), 就是所有小于等于 `n` 的正整数的乘积. 比如: 4 | 5 | ``` 6 | 5! = 5 * 4 * 3 * 2 * 1 = 120 7 | ``` 8 | 9 | | n | n! | 10 | | ----- | --------------------------: | 11 | | 0 | 1 | 12 | | 1 | 1 | 13 | | 2 | 2 | 14 | | 3 | 6 | 15 | | 4 | 24 | 16 | | 5 | 120 | 17 | | 6 | 720 | 18 | | 7 | 5 040 | 19 | | 8 | 40 320 | 20 | | 9 | 362 880 | 21 | | 10 | 3 628 800 | 22 | | 11 | 39 916 800 | 23 | | 12 | 479 001 600 | 24 | | 13 | 6 227 020 800 | 25 | | 14 | 87 178 291 200 | 26 | | 15 | 1 307 674 368 000 | 27 | 28 | -------------------------------------------------------------------------------- /src/algorithms/sets/maximum-subarray/bfMaximumSubarray.js: -------------------------------------------------------------------------------- 1 | /** 2 | * Brute Force solution. 3 | * Complexity: O(n^2) 4 | * 5 | * @param {Number[]} inputArray 6 | * @return {Number[]} 7 | */ 8 | export default function bfMaximumSubarray(inputArray) { 9 | let maxSubarrayStartIndex = 0; 10 | let maxSubarrayLength = 0; 11 | let maxSubarraySum = null; 12 | 13 | for (let startIndex = 0; startIndex < inputArray.length; startIndex += 1) { 14 | let subarraySum = 0; 15 | for (let arrLength = 1; arrLength <= (inputArray.length - startIndex); arrLength += 1) { 16 | subarraySum += inputArray[startIndex + (arrLength - 1)]; 17 | if (maxSubarraySum === null || subarraySum > maxSubarraySum) { 18 | maxSubarraySum = subarraySum; 19 | maxSubarrayStartIndex = startIndex; 20 | maxSubarrayLength = arrLength; 21 | } 22 | } 23 | } 24 | 25 | return inputArray.slice(maxSubarrayStartIndex, maxSubarrayStartIndex + maxSubarrayLength); 26 | } 27 | -------------------------------------------------------------------------------- /src/algorithms/uncategorized/knight-tour/__test__/knightTour.test.js: -------------------------------------------------------------------------------- 1 | import knightTour from '../knightTour'; 2 | 3 | describe('knightTour', () => { 4 | it('should not find solution on 3x3 board', () => { 5 | const moves = knightTour(3); 6 | 7 | expect(moves.length).toBe(0); 8 | }); 9 | 10 | it('should find one solution to do knight tour on 5x5 board', () => { 11 | const moves = knightTour(5); 12 | 13 | expect(moves.length).toBe(25); 14 | 15 | expect(moves).toEqual([ 16 | [0, 0], 17 | [1, 2], 18 | [2, 0], 19 | [0, 1], 20 | [1, 3], 21 | [3, 4], 22 | [2, 2], 23 | [4, 1], 24 | [3, 3], 25 | [1, 4], 26 | [0, 2], 27 | [1, 0], 28 | [3, 1], 29 | [4, 3], 30 | [2, 4], 31 | [0, 3], 32 | [1, 1], 33 | [3, 0], 34 | [4, 2], 35 | [2, 1], 36 | [4, 0], 37 | [3, 2], 38 | [4, 4], 39 | [2, 3], 40 | [0, 4], 41 | ]); 42 | }); 43 | }); 44 | -------------------------------------------------------------------------------- /src/algorithms/math/fibonacci/fibonacciNthClosedForm.js: -------------------------------------------------------------------------------- 1 | /** 2 | * Calculate fibonacci number at specific position using closed form function (Binet's formula). 3 | * @see: https://en.wikipedia.org/wiki/Fibonacci_number#Closed-form_expression 4 | * 5 | * @param {number} position - Position number of fibonacci sequence (must be number from 1 to 75). 6 | * @return {number} 7 | */ 8 | export default function fibonacciClosedForm(position) { 9 | const topMaxValidPosition = 70; 10 | 11 | // Check that position is valid. 12 | if (position < 1 || position > topMaxValidPosition) { 13 | throw new Error(`Can't handle position smaller than 1 or greater than ${topMaxValidPosition}`); 14 | } 15 | 16 | // Calculate √5 to re-use it in further formulas. 17 | const sqrt5 = Math.sqrt(5); 18 | // Calculate φ constant (≈ 1.61803). 19 | const phi = (1 + sqrt5) / 2; 20 | 21 | // Calculate fibonacci number using Binet's formula. 22 | return Math.floor((phi ** position) / sqrt5 + 0.5); 23 | } 24 | -------------------------------------------------------------------------------- /src/algorithms/math/primality-test/trialDivision.js: -------------------------------------------------------------------------------- 1 | /** 2 | * @param {number} number 3 | * @return {boolean} 4 | */ 5 | export default function trialDivision(number) { 6 | // Check if number is integer. 7 | if (number % 1 !== 0) { 8 | return false; 9 | } 10 | 11 | if (number <= 1) { 12 | // If number is less than one then it isn't prime by definition. 13 | return false; 14 | } 15 | 16 | if (number <= 3) { 17 | // All numbers from 2 to 3 are prime. 18 | return true; 19 | } 20 | 21 | // If the number is not divided by 2 then we may eliminate all further even dividers. 22 | if (number % 2 === 0) { 23 | return false; 24 | } 25 | 26 | // If there is no dividers up to square root of n then there is no higher dividers as well. 27 | const dividerLimit = Math.sqrt(number); 28 | for (let divider = 3; divider <= dividerLimit; divider += 2) { 29 | if (number % divider === 0) { 30 | return false; 31 | } 32 | } 33 | 34 | return true; 35 | } 36 | -------------------------------------------------------------------------------- /src/algorithms/sets/maximum-subarray/__test__/bfMaximumSubarray.test.js: -------------------------------------------------------------------------------- 1 | import bfMaximumSubarray from '../bfMaximumSubarray'; 2 | 3 | describe('bfMaximumSubarray', () => { 4 | it('should find maximum subarray using brute force algorithm', () => { 5 | expect(bfMaximumSubarray([])).toEqual([]); 6 | expect(bfMaximumSubarray([0, 0])).toEqual([0]); 7 | expect(bfMaximumSubarray([0, 0, 1])).toEqual([0, 0, 1]); 8 | expect(bfMaximumSubarray([0, 0, 1, 2])).toEqual([0, 0, 1, 2]); 9 | expect(bfMaximumSubarray([0, 0, -1, 2])).toEqual([2]); 10 | expect(bfMaximumSubarray([-1, -2, -3, -4, -5])).toEqual([-1]); 11 | expect(bfMaximumSubarray([1, 2, 3, 2, 3, 4, 5])).toEqual([1, 2, 3, 2, 3, 4, 5]); 12 | expect(bfMaximumSubarray([-2, 1, -3, 4, -1, 2, 1, -5, 4])).toEqual([4, -1, 2, 1]); 13 | expect(bfMaximumSubarray([-2, -3, 4, -1, -2, 1, 5, -3])).toEqual([4, -1, -2, 1, 5]); 14 | expect(bfMaximumSubarray([1, -3, 2, -5, 7, 6, -1, 4, 11, -23])).toEqual([7, 6, -1, 4, 11]); 15 | }); 16 | }); 17 | -------------------------------------------------------------------------------- /src/algorithms/math/is-power-of-two/__test__/isPowerOfTwo.test.js: -------------------------------------------------------------------------------- 1 | import isPowerOfTwo from '../isPowerOfTwo'; 2 | 3 | describe('isPowerOfTwo', () => { 4 | it('should check if the number is made by multiplying twos', () => { 5 | expect(isPowerOfTwo(-1)).toBe(false); 6 | expect(isPowerOfTwo(0)).toBe(false); 7 | expect(isPowerOfTwo(1)).toBe(true); 8 | expect(isPowerOfTwo(2)).toBe(true); 9 | expect(isPowerOfTwo(3)).toBe(false); 10 | expect(isPowerOfTwo(4)).toBe(true); 11 | expect(isPowerOfTwo(5)).toBe(false); 12 | expect(isPowerOfTwo(6)).toBe(false); 13 | expect(isPowerOfTwo(7)).toBe(false); 14 | expect(isPowerOfTwo(8)).toBe(true); 15 | expect(isPowerOfTwo(10)).toBe(false); 16 | expect(isPowerOfTwo(12)).toBe(false); 17 | expect(isPowerOfTwo(16)).toBe(true); 18 | expect(isPowerOfTwo(31)).toBe(false); 19 | expect(isPowerOfTwo(64)).toBe(true); 20 | expect(isPowerOfTwo(1024)).toBe(true); 21 | expect(isPowerOfTwo(1023)).toBe(false); 22 | }); 23 | }); 24 | -------------------------------------------------------------------------------- /src/algorithms/sets/permutations/permutateWithRepetitions.js: -------------------------------------------------------------------------------- 1 | /** 2 | * @param {*[]} permutationOptions 3 | * @param {number} permutationLength 4 | * @return {*[]} 5 | */ 6 | export default function permutateWithRepetitions( 7 | permutationOptions, 8 | permutationLength = permutationOptions.length, 9 | ) { 10 | if (permutationLength === 1) { 11 | return permutationOptions.map((permutationOption) => [permutationOption]); 12 | } 13 | 14 | // Init permutations array. 15 | const permutations = []; 16 | 17 | // Get smaller permutations. 18 | const smallerPermutations = permutateWithRepetitions( 19 | permutationOptions, 20 | permutationLength - 1, 21 | ); 22 | 23 | // Go through all options and join it to the smaller permutations. 24 | permutationOptions.forEach((currentOption) => { 25 | smallerPermutations.forEach((smallerPermutation) => { 26 | permutations.push([currentOption].concat(smallerPermutation)); 27 | }); 28 | }); 29 | 30 | return permutations; 31 | } 32 | -------------------------------------------------------------------------------- /src/algorithms/sets/maximum-subarray/__test__/dpMaximumSubarray.test.js: -------------------------------------------------------------------------------- 1 | import dpMaximumSubarray from '../dpMaximumSubarray'; 2 | 3 | describe('dpMaximumSubarray', () => { 4 | it('should find maximum subarray using dynamic programming algorithm', () => { 5 | expect(dpMaximumSubarray([])).toEqual([]); 6 | expect(dpMaximumSubarray([0, 0])).toEqual([0]); 7 | expect(dpMaximumSubarray([0, 0, 1])).toEqual([0, 0, 1]); 8 | expect(dpMaximumSubarray([0, 0, 1, 2])).toEqual([0, 0, 1, 2]); 9 | expect(dpMaximumSubarray([0, 0, -1, 2])).toEqual([2]); 10 | expect(dpMaximumSubarray([-1, -2, -3, -4, -5])).toEqual([-1]); 11 | expect(dpMaximumSubarray([1, 2, 3, 2, 3, 4, 5])).toEqual([1, 2, 3, 2, 3, 4, 5]); 12 | expect(dpMaximumSubarray([-2, 1, -3, 4, -1, 2, 1, -5, 4])).toEqual([4, -1, 2, 1]); 13 | expect(dpMaximumSubarray([-2, -3, 4, -1, -2, 1, 5, -3])).toEqual([4, -1, -2, 1, 5]); 14 | expect(dpMaximumSubarray([1, -3, 2, -5, 7, 6, -1, 4, 11, -23])).toEqual([7, 6, -1, 4, 11]); 15 | }); 16 | }); 17 | -------------------------------------------------------------------------------- /src/algorithms/sorting/heap-sort/HeapSort.js: -------------------------------------------------------------------------------- 1 | import Sort from '../Sort'; 2 | import MinHeap from '../../../data-structures/heap/MinHeap'; 3 | 4 | export default class HeapSort extends Sort { 5 | sort(originalArray) { 6 | const sortedArray = []; 7 | const minHeap = new MinHeap(this.callbacks.compareCallback); 8 | 9 | // Insert all array elements to the heap. 10 | originalArray.forEach((element) => { 11 | // Call visiting callback. 12 | this.callbacks.visitingCallback(element); 13 | 14 | minHeap.add(element); 15 | }); 16 | 17 | // Now we have min heap with minimal element always on top. 18 | // Let's poll that minimal element one by one and thus form the sorted array. 19 | while (!minHeap.isEmpty()) { 20 | const nextMinElement = minHeap.poll(); 21 | 22 | // Call visiting callback. 23 | this.callbacks.visitingCallback(nextMinElement); 24 | 25 | sortedArray.push(nextMinElement); 26 | } 27 | 28 | return sortedArray; 29 | } 30 | } 31 | -------------------------------------------------------------------------------- /src/algorithms/sorting/radix-sort/__test__/RadixSort.test.js: -------------------------------------------------------------------------------- 1 | import RadixSort from '../RadixSort'; 2 | import { SortTester } from '../../SortTester'; 3 | 4 | // Complexity constants. 5 | const ARRAY_OF_STRINGS_VISIT_COUNT = 24; 6 | const ARRAY_OF_INTEGERS_VISIT_COUNT = 77; 7 | describe('RadixSort', () => { 8 | it('should sort array', () => { 9 | SortTester.testSort(RadixSort); 10 | }); 11 | 12 | it('should visit array of strings n (number of strings) x m (length of longest element) times', () => { 13 | SortTester.testAlgorithmTimeComplexity( 14 | RadixSort, 15 | ['zzz', 'bb', 'a', 'rr', 'rrb', 'rrba'], 16 | ARRAY_OF_STRINGS_VISIT_COUNT, 17 | ); 18 | }); 19 | 20 | it('should visit array of integers n (number of elements) x m (length of longest integer) times', () => { 21 | SortTester.testAlgorithmTimeComplexity( 22 | RadixSort, 23 | [3, 1, 75, 32, 884, 523, 4343456, 232, 123, 656, 343], 24 | ARRAY_OF_INTEGERS_VISIT_COUNT, 25 | ); 26 | }); 27 | }); 28 | -------------------------------------------------------------------------------- /src/data-structures/queue/README.ru-RU.md: -------------------------------------------------------------------------------- 1 | # Очередь 2 | 3 | Очередь (англ. queue) - структура данных в информатике, в которой элементы 4 | хранятся в порядке их добавления. Добавление новых элементов(enqueue) 5 | осуществляется в начало списка. А удаление элементов (dequeue) 6 | осуществляется с конца. Таким образом очередь реализует принцип 7 | "первым вошёл - первым вышел" (FIFO). Часто реализуется операция чтения 8 | головного элемента (peek), которая возвращает первый в очереди элемент, 9 | при этом не удаляя его. Очередь является примером линейной структуры 10 | данных или последовательной коллекции. 11 | 12 | Иллюстрация работы с очередью. 13 | 14 | ![Очередь](https://upload.wikimedia.org/wikipedia/commons/5/52/Data_Queue.svg) 15 | 16 | ## References 17 | 18 | - [Wikipedia](https://ru.wikipedia.org/wiki/%D0%9E%D1%87%D0%B5%D1%80%D0%B5%D0%B4%D1%8C_(%D0%BF%D1%80%D0%BE%D0%B3%D1%80%D0%B0%D0%BC%D0%BC%D0%B8%D1%80%D0%BE%D0%B2%D0%B0%D0%BD%D0%B8%D0%B5)) 19 | - [YouTube](https://www.youtube.com/watch?v=GRsVMTlBIoE) 20 | -------------------------------------------------------------------------------- /src/algorithms/sets/maximum-subarray/README.md: -------------------------------------------------------------------------------- 1 | # Maximum subarray problem 2 | 3 | The maximum subarray problem is the task of finding the contiguous 4 | subarray within a one-dimensional array, `a[1...n]`, of numbers 5 | which has the largest sum, where, 6 | 7 | ![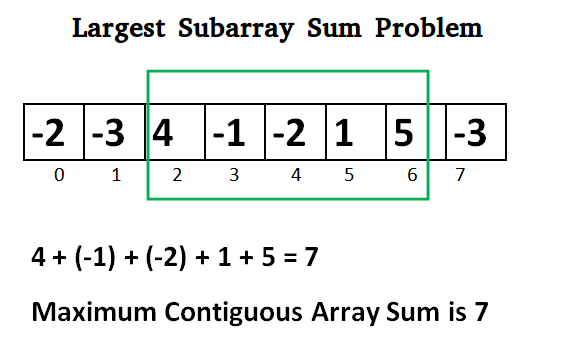Maximum subarray](https://wikimedia.org/api/rest_v1/media/math/render/svg/e8960f093107b71b21827e726e2bad8b023779b2) 8 | 9 | ![Maximum subarray](https://www.geeksforgeeks.org/wp-content/uploads/kadane-Algorithm.png) 10 | 11 | ## Example 12 | 13 | The list usually contains both positive and negative numbers along 14 | with `0`. For example, for the array of 15 | values `−2, 1, −3, 4, −1, 2, 1, −5, 4` the contiguous subarray 16 | with the largest sum is `4, −1, 2, 1`, with sum `6`. 17 | 18 | ## References 19 | 20 | - [Wikipedia](https://en.wikipedia.org/wiki/Maximum_subarray_problem) 21 | - [YouTube](https://www.youtube.com/watch?v=ohHWQf1HDfU&list=PLLXdhg_r2hKA7DPDsunoDZ-Z769jWn4R8) 22 | - [GeeksForGeeks](https://www.geeksforgeeks.org/largest-sum-contiguous-subarray/) 23 | -------------------------------------------------------------------------------- /src/algorithms/sorting/insertion-sort/README.md: -------------------------------------------------------------------------------- 1 | # Insertion Sort 2 | 3 | Insertion sort is a simple sorting algorithm that builds 4 | the final sorted array (or list) one item at a time. 5 | It is much less efficient on large lists than more 6 | advanced algorithms such as quicksort, heapsort, or merge 7 | sort. 8 | 9 | ![Algorithm Visualization](https://upload.wikimedia.org/wikipedia/commons/4/42/Insertion_sort.gif) 10 | 11 | ![Algorithm Visualization](https://upload.wikimedia.org/wikipedia/commons/0/0f/Insertion-sort-example-300px.gif) 12 | 13 | ## Complexity 14 | 15 | | Name | Best | Average | Worst | Memory | Stable | Comments | 16 | | --------------------- | :-------------: | :-----------------: | :-----------------: | :-------: | :-------: | :-------- | 17 | | **Insertion sort** | n | n2 | n2 | 1 | Yes | | 18 | 19 | ## References 20 | 21 | [Wikipedia](https://en.wikipedia.org/wiki/Insertion_sort) 22 | -------------------------------------------------------------------------------- /src/algorithms/math/factorial/README.md: -------------------------------------------------------------------------------- 1 | # Factorial 2 | 3 | _Read this in other languages:_ 4 | [_简体中文_](README.zh-CN.md), [français](README.fr-FR.md). 5 | 6 | In mathematics, the factorial of a non-negative integer `n`, 7 | denoted by `n!`, is the product of all positive integers less 8 | than or equal to `n`. For example: 9 | 10 | ``` 11 | 5! = 5 * 4 * 3 * 2 * 1 = 120 12 | ``` 13 | 14 | | n | n! | 15 | | --- | ----------------: | 16 | | 0 | 1 | 17 | | 1 | 1 | 18 | | 2 | 2 | 19 | | 3 | 6 | 20 | | 4 | 24 | 21 | | 5 | 120 | 22 | | 6 | 720 | 23 | | 7 | 5 040 | 24 | | 8 | 40 320 | 25 | | 9 | 362 880 | 26 | | 10 | 3 628 800 | 27 | | 11 | 39 916 800 | 28 | | 12 | 479 001 600 | 29 | | 13 | 6 227 020 800 | 30 | | 14 | 87 178 291 200 | 31 | | 15 | 1 307 674 368 000 | 32 | 33 | ## References 34 | 35 | [Wikipedia](https://en.wikipedia.org/wiki/Factorial) 36 | -------------------------------------------------------------------------------- /src/algorithms/math/fast-powering/fastPowering.js: -------------------------------------------------------------------------------- 1 | /** 2 | * Fast Powering Algorithm. 3 | * Recursive implementation to compute power. 4 | * 5 | * Complexity: log(n) 6 | * 7 | * @param {number} base - Number that will be raised to the power. 8 | * @param {number} power - The power that number will be raised to. 9 | * @return {number} 10 | */ 11 | export default function fastPowering(base, power) { 12 | if (power === 0) { 13 | // Anything that is raised to the power of zero is 1. 14 | return 1; 15 | } 16 | 17 | if (power % 2 === 0) { 18 | // If the power is even... 19 | // we may recursively redefine the result via twice smaller powers: 20 | // x^8 = x^4 * x^4. 21 | const multiplier = fastPowering(base, power / 2); 22 | return multiplier * multiplier; 23 | } 24 | 25 | // If the power is odd... 26 | // we may recursively redefine the result via twice smaller powers: 27 | // x^9 = x^4 * x^4 * x. 28 | const multiplier = fastPowering(base, Math.floor(power / 2)); 29 | return multiplier * multiplier * base; 30 | } 31 | -------------------------------------------------------------------------------- /src/algorithms/search/binary-search/README.md: -------------------------------------------------------------------------------- 1 | # Binary Search 2 | 3 | In computer science, binary search, also known as half-interval 4 | search, logarithmic search, or binary chop, is a search algorithm 5 | that finds the position of a target value within a sorted 6 | array. Binary search compares the target value to the middle 7 | element of the array; if they are unequal, the half in which 8 | the target cannot lie is eliminated and the search continues 9 | on the remaining half until it is successful. If the search 10 | ends with the remaining half being empty, the target is not 11 | in the array. 12 | 13 | ![Binary Search](https://upload.wikimedia.org/wikipedia/commons/8/83/Binary_Search_Depiction.svg) 14 | 15 | ## Complexity 16 | 17 | **Time Complexity**: `O(log(n))` - since we split search area by two for every 18 | next iteration. 19 | 20 | ## References 21 | 22 | - [Wikipedia](https://en.wikipedia.org/wiki/Binary_search_algorithm) 23 | - [YouTube](https://www.youtube.com/watch?v=P3YID7liBug&index=29&list=PLLXdhg_r2hKA7DPDsunoDZ-Z769jWn4R8) 24 | -------------------------------------------------------------------------------- /src/algorithms/sorting/selection-sort/SelectionSort.js: -------------------------------------------------------------------------------- 1 | import Sort from '../Sort'; 2 | 3 | export default class SelectionSort extends Sort { 4 | sort(originalArray) { 5 | // Clone original array to prevent its modification. 6 | const array = [...originalArray]; 7 | 8 | for (let i = 0; i < array.length - 1; i += 1) { 9 | let minIndex = i; 10 | 11 | // Call visiting callback. 12 | this.callbacks.visitingCallback(array[i]); 13 | 14 | // Find minimum element in the rest of array. 15 | for (let j = i + 1; j < array.length; j += 1) { 16 | // Call visiting callback. 17 | this.callbacks.visitingCallback(array[j]); 18 | 19 | if (this.comparator.lessThan(array[j], array[minIndex])) { 20 | minIndex = j; 21 | } 22 | } 23 | 24 | // If new minimum element has been found then swap it with current i-th element. 25 | if (minIndex !== i) { 26 | [array[i], array[minIndex]] = [array[minIndex], array[i]]; 27 | } 28 | } 29 | 30 | return array; 31 | } 32 | } 33 | -------------------------------------------------------------------------------- /src/algorithms/uncategorized/recursive-staircase/recursiveStaircaseBF.js: -------------------------------------------------------------------------------- 1 | /** 2 | * Recursive Staircase Problem (Brute Force Solution). 3 | * 4 | * @param {number} stairsNum - Number of stairs to climb on. 5 | * @return {number} - Number of ways to climb a staircase. 6 | */ 7 | export default function recursiveStaircaseBF(stairsNum) { 8 | if (stairsNum <= 0) { 9 | // There is no way to go down - you climb the stairs only upwards. 10 | // Also if you're standing on the ground floor that you don't need to do any further steps. 11 | return 0; 12 | } 13 | 14 | if (stairsNum === 1) { 15 | // There is only one way to go to the first step. 16 | return 1; 17 | } 18 | 19 | if (stairsNum === 2) { 20 | // There are two ways to get to the second steps: (1 + 1) or (2). 21 | return 2; 22 | } 23 | 24 | // Sum up how many steps we need to take after doing one step up with the number of 25 | // steps we need to take after doing two steps up. 26 | return recursiveStaircaseBF(stairsNum - 1) + recursiveStaircaseBF(stairsNum - 2); 27 | } 28 | -------------------------------------------------------------------------------- /src/algorithms/math/fast-powering/__test__/fastPowering.test.js: -------------------------------------------------------------------------------- 1 | import fastPowering from '../fastPowering'; 2 | 3 | describe('fastPowering', () => { 4 | it('should compute power in log(n) time', () => { 5 | expect(fastPowering(1, 1)).toBe(1); 6 | expect(fastPowering(2, 0)).toBe(1); 7 | expect(fastPowering(2, 2)).toBe(4); 8 | expect(fastPowering(2, 3)).toBe(8); 9 | expect(fastPowering(2, 4)).toBe(16); 10 | expect(fastPowering(2, 5)).toBe(32); 11 | expect(fastPowering(2, 6)).toBe(64); 12 | expect(fastPowering(2, 7)).toBe(128); 13 | expect(fastPowering(2, 8)).toBe(256); 14 | expect(fastPowering(3, 4)).toBe(81); 15 | expect(fastPowering(190, 2)).toBe(36100); 16 | expect(fastPowering(11, 5)).toBe(161051); 17 | expect(fastPowering(13, 11)).toBe(1792160394037); 18 | expect(fastPowering(9, 16)).toBe(1853020188851841); 19 | expect(fastPowering(16, 16)).toBe(18446744073709552000); 20 | expect(fastPowering(7, 21)).toBe(558545864083284000); 21 | expect(fastPowering(100, 9)).toBe(1000000000000000000); 22 | }); 23 | }); 24 | -------------------------------------------------------------------------------- /src/algorithms/math/fibonacci/README.fr-FR.md: -------------------------------------------------------------------------------- 1 | # Nombre de Fibonacci 2 | 3 | _Read this in other languages:_ 4 | [english](README.md). 5 | 6 | En mathématiques, la suite de Fibonacci est une suite d'entiers 7 | dans laquelle chaque terme (après les deux premiers) 8 | est la somme des deux termes qui le précèdent. 9 | Les termes de cette suite sont appelés nombres de Fibonacci: 10 | 11 | `0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, ...` 12 | 13 | Les carrés de Fibonacci en spirale s'ajustent ensemble pour former une spirale d'or. 14 | 15 | ![Fibonacci](https://upload.wikimedia.org/wikipedia/commons/d/db/34%2A21-FibonacciBlocks.png) 16 | 17 | La spirale de Fibonacci: approximation d'une spirale d'or créée en dessinant des arcs de cercle reliant les coins opposés de carrés dans un pavage Fibonacci[4] . Celui-ci utilise des carrés de tailles 1, 1, 2, 3, 5, 8, 13, 21, et 34. 18 | 19 | ![Fibonacci Spiral](https://upload.wikimedia.org/wikipedia/commons/2/2e/FibonacciSpiral.svg) 20 | 21 | ## References 22 | 23 | - [Wikipedia](https://fr.wikipedia.org/wiki/Suite_de_Fibonacci) 24 | -------------------------------------------------------------------------------- /src/algorithms/math/fibonacci/README.md: -------------------------------------------------------------------------------- 1 | # Fibonacci Number 2 | 3 | _Read this in other languages:_ 4 | [français](README.fr-FR.md), 5 | [简体中文](README.zh-CN.md). 6 | 7 | In mathematics, the Fibonacci numbers are the numbers in the following 8 | integer sequence, called the Fibonacci sequence, and characterized by 9 | the fact that every number after the first two is the sum of the two 10 | preceding ones: 11 | 12 | `0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, ...` 13 | 14 | A tiling with squares whose side lengths are successive Fibonacci numbers 15 | 16 | ![Fibonacci](https://upload.wikimedia.org/wikipedia/commons/d/db/34%2A21-FibonacciBlocks.png) 17 | 18 | The Fibonacci spiral: an approximation of the golden spiral created by drawing circular arcs connecting the opposite corners of squares in the Fibonacci tiling;[4] this one uses squares of sizes 1, 1, 2, 3, 5, 8, 13 and 21. 19 | 20 | ![Fibonacci Spiral](https://upload.wikimedia.org/wikipedia/commons/2/2e/FibonacciSpiral.svg) 21 | 22 | ## References 23 | 24 | - [Wikipedia](https://en.wikipedia.org/wiki/Fibonacci_number) 25 | -------------------------------------------------------------------------------- /src/data-structures/tree/binary-search-tree/BinarySearchTree.js: -------------------------------------------------------------------------------- 1 | import BinarySearchTreeNode from './BinarySearchTreeNode'; 2 | 3 | export default class BinarySearchTree { 4 | /** 5 | * @param {function} [nodeValueCompareFunction] 6 | */ 7 | constructor(nodeValueCompareFunction) { 8 | this.root = new BinarySearchTreeNode(null, nodeValueCompareFunction); 9 | 10 | // Steal node comparator from the root. 11 | this.nodeComparator = this.root.nodeComparator; 12 | } 13 | 14 | /** 15 | * @param {*} value 16 | * @return {BinarySearchTreeNode} 17 | */ 18 | insert(value) { 19 | return this.root.insert(value); 20 | } 21 | 22 | /** 23 | * @param {*} value 24 | * @return {boolean} 25 | */ 26 | contains(value) { 27 | return this.root.contains(value); 28 | } 29 | 30 | /** 31 | * @param {*} value 32 | * @return {boolean} 33 | */ 34 | remove(value) { 35 | return this.root.remove(value); 36 | } 37 | 38 | /** 39 | * @return {string} 40 | */ 41 | toString() { 42 | return this.root.toString(); 43 | } 44 | } 45 | -------------------------------------------------------------------------------- /src/algorithms/math/factorial/README.fr-FR.md: -------------------------------------------------------------------------------- 1 | # Factorielle 2 | 3 | _Lisez ceci dans d'autres langues:_ 4 | [english](README.md), [_简体中文_](README.zh-CN.md). 5 | 6 | En mathématiques, la factorielle d'un entier naturel `n`, 7 | notée avec un point d'exclamation `n!`, est le produit des nombres entiers 8 | strictement positifs inférieurs ou égaux à n. Par exemple: 9 | 10 | ``` 11 | 5! = 5 * 4 * 3 * 2 * 1 = 120 12 | ``` 13 | 14 | | n | n! | 15 | | --- | ----------------: | 16 | | 0 | 1 | 17 | | 1 | 1 | 18 | | 2 | 2 | 19 | | 3 | 6 | 20 | | 4 | 24 | 21 | | 5 | 120 | 22 | | 6 | 720 | 23 | | 7 | 5 040 | 24 | | 8 | 40 320 | 25 | | 9 | 362 880 | 26 | | 10 | 3 628 800 | 27 | | 11 | 39 916 800 | 28 | | 12 | 479 001 600 | 29 | | 13 | 6 227 020 800 | 30 | | 14 | 87 178 291 200 | 31 | | 15 | 1 307 674 368 000 | 32 | 33 | ## References 34 | 35 | [Wikipedia](https://fr.wikipedia.org/wiki/Factorielle) 36 | -------------------------------------------------------------------------------- /src/data-structures/heap/README.md: -------------------------------------------------------------------------------- 1 | # Heap (data-structure) 2 | 3 | _Read this in other languages:_ 4 | [_简体中文_](README.zh-CN.md), 5 | [_Русский_](README.ru-RU.md), 6 | [_日本語_](README.ja-JP.md), 7 | [_Français_](README.fr-FR.md), 8 | [_Português_](README.pt-BR.md) 9 | 10 | In computer science, a **heap** is a specialized tree-based 11 | data structure that satisfies the heap property described 12 | below. 13 | 14 | In a *min heap*, if `P` is a parent node of `C`, then the 15 | key (the value) of `P` is less than or equal to the 16 | key of `C`. 17 | 18 | ![MinHeap](https://upload.wikimedia.org/wikipedia/commons/6/69/Min-heap.png) 19 | 20 | In a *max heap*, the key of `P` is greater than or equal 21 | to the key of `C` 22 | 23 | ![Heap](https://upload.wikimedia.org/wikipedia/commons/3/38/Max-Heap.svg) 24 | 25 | The node at the "top" of the heap with no parents is 26 | called the root node. 27 | 28 | ## References 29 | 30 | - [Wikipedia](https://en.wikipedia.org/wiki/Heap_(data_structure)) 31 | - [YouTube](https://www.youtube.com/watch?v=t0Cq6tVNRBA&index=5&t=0s&list=PLLXdhg_r2hKA7DPDsunoDZ-Z769jWn4R8) 32 | -------------------------------------------------------------------------------- /src/algorithms/uncategorized/rain-terraces/__test__/bfRainTerraces.test.js: -------------------------------------------------------------------------------- 1 | import bfRainTerraces from '../bfRainTerraces'; 2 | 3 | describe('bfRainTerraces', () => { 4 | it('should find the amount of water collected after raining', () => { 5 | expect(bfRainTerraces([1])).toBe(0); 6 | expect(bfRainTerraces([1, 0])).toBe(0); 7 | expect(bfRainTerraces([0, 1])).toBe(0); 8 | expect(bfRainTerraces([0, 1, 0])).toBe(0); 9 | expect(bfRainTerraces([0, 1, 0, 0])).toBe(0); 10 | expect(bfRainTerraces([0, 1, 0, 0, 1, 0])).toBe(2); 11 | expect(bfRainTerraces([0, 2, 0, 0, 1, 0])).toBe(2); 12 | expect(bfRainTerraces([2, 0, 2])).toBe(2); 13 | expect(bfRainTerraces([2, 0, 5])).toBe(2); 14 | expect(bfRainTerraces([3, 0, 0, 2, 0, 4])).toBe(10); 15 | expect(bfRainTerraces([0, 1, 0, 2, 1, 0, 1, 3, 2, 1, 2, 1])).toBe(6); 16 | expect(bfRainTerraces([1, 1, 1, 1, 1])).toBe(0); 17 | expect(bfRainTerraces([1, 2, 3, 4, 5])).toBe(0); 18 | expect(bfRainTerraces([4, 1, 3, 1, 2, 1, 2, 1])).toBe(4); 19 | expect(bfRainTerraces([0, 2, 4, 3, 4, 2, 4, 0, 8, 7, 0])).toBe(7); 20 | }); 21 | }); 22 | -------------------------------------------------------------------------------- /src/algorithms/uncategorized/rain-terraces/__test__/dpRainTerraces.test.js: -------------------------------------------------------------------------------- 1 | import dpRainTerraces from '../dpRainTerraces'; 2 | 3 | describe('dpRainTerraces', () => { 4 | it('should find the amount of water collected after raining', () => { 5 | expect(dpRainTerraces([1])).toBe(0); 6 | expect(dpRainTerraces([1, 0])).toBe(0); 7 | expect(dpRainTerraces([0, 1])).toBe(0); 8 | expect(dpRainTerraces([0, 1, 0])).toBe(0); 9 | expect(dpRainTerraces([0, 1, 0, 0])).toBe(0); 10 | expect(dpRainTerraces([0, 1, 0, 0, 1, 0])).toBe(2); 11 | expect(dpRainTerraces([0, 2, 0, 0, 1, 0])).toBe(2); 12 | expect(dpRainTerraces([2, 0, 2])).toBe(2); 13 | expect(dpRainTerraces([2, 0, 5])).toBe(2); 14 | expect(dpRainTerraces([3, 0, 0, 2, 0, 4])).toBe(10); 15 | expect(dpRainTerraces([0, 1, 0, 2, 1, 0, 1, 3, 2, 1, 2, 1])).toBe(6); 16 | expect(dpRainTerraces([1, 1, 1, 1, 1])).toBe(0); 17 | expect(dpRainTerraces([1, 2, 3, 4, 5])).toBe(0); 18 | expect(dpRainTerraces([4, 1, 3, 1, 2, 1, 2, 1])).toBe(4); 19 | expect(dpRainTerraces([0, 2, 4, 3, 4, 2, 4, 0, 8, 7, 0])).toBe(7); 20 | }); 21 | }); 22 | -------------------------------------------------------------------------------- /src/algorithms/sets/knapsack-problem/KnapsackItem.js: -------------------------------------------------------------------------------- 1 | export default class KnapsackItem { 2 | /** 3 | * @param {Object} itemSettings - knapsack item settings, 4 | * @param {number} itemSettings.value - value of the item. 5 | * @param {number} itemSettings.weight - weight of the item. 6 | * @param {number} itemSettings.itemsInStock - how many items are available to be added. 7 | */ 8 | constructor({ value, weight, itemsInStock = 1 }) { 9 | this.value = value; 10 | this.weight = weight; 11 | this.itemsInStock = itemsInStock; 12 | // Actual number of items that is going to be added to knapsack. 13 | this.quantity = 1; 14 | } 15 | 16 | get totalValue() { 17 | return this.value * this.quantity; 18 | } 19 | 20 | get totalWeight() { 21 | return this.weight * this.quantity; 22 | } 23 | 24 | // This coefficient shows how valuable the 1 unit of weight is 25 | // for current item. 26 | get valuePerWeightRatio() { 27 | return this.value / this.weight; 28 | } 29 | 30 | toString() { 31 | return `v${this.value} w${this.weight} x ${this.quantity}`; 32 | } 33 | } 34 | -------------------------------------------------------------------------------- /src/algorithms/math/euclidean-distance/__tests__/euclideanDistance.test.js: -------------------------------------------------------------------------------- 1 | import euclideanDistance from '../euclideanDistance'; 2 | 3 | describe('euclideanDistance', () => { 4 | it('should calculate euclidean distance between vectors', () => { 5 | expect(euclideanDistance([[1]], [[2]])).toEqual(1); 6 | expect(euclideanDistance([[2]], [[1]])).toEqual(1); 7 | expect(euclideanDistance([[5, 8]], [[7, 3]])).toEqual(5.39); 8 | expect(euclideanDistance([[5], [8]], [[7], [3]])).toEqual(5.39); 9 | expect(euclideanDistance([[8, 2, 6]], [[3, 5, 7]])).toEqual(5.92); 10 | expect(euclideanDistance([[8], [2], [6]], [[3], [5], [7]])).toEqual(5.92); 11 | expect(euclideanDistance([[[8]], [[2]], [[6]]], [[[3]], [[5]], [[7]]])).toEqual(5.92); 12 | }); 13 | 14 | it('should throw an error in case if two matrices are of different shapes', () => { 15 | expect(() => euclideanDistance([[1]], [[[2]]])).toThrowError( 16 | 'Matrices have different dimensions', 17 | ); 18 | 19 | expect(() => euclideanDistance([[1]], [[2, 3]])).toThrowError( 20 | 'Matrices have different shapes', 21 | ); 22 | }); 23 | }); 24 | -------------------------------------------------------------------------------- /src/algorithms/math/fibonacci/__test__/fibonacciNth.test.js: -------------------------------------------------------------------------------- 1 | import fibonacciNth from '../fibonacciNth'; 2 | 3 | describe('fibonacciNth', () => { 4 | it('should calculate fibonacci correctly', () => { 5 | expect(fibonacciNth(1)).toBe(1); 6 | expect(fibonacciNth(2)).toBe(1); 7 | expect(fibonacciNth(3)).toBe(2); 8 | expect(fibonacciNth(4)).toBe(3); 9 | expect(fibonacciNth(5)).toBe(5); 10 | expect(fibonacciNth(6)).toBe(8); 11 | expect(fibonacciNth(7)).toBe(13); 12 | expect(fibonacciNth(8)).toBe(21); 13 | expect(fibonacciNth(20)).toBe(6765); 14 | expect(fibonacciNth(30)).toBe(832040); 15 | expect(fibonacciNth(50)).toBe(12586269025); 16 | expect(fibonacciNth(70)).toBe(190392490709135); 17 | expect(fibonacciNth(71)).toBe(308061521170129); 18 | expect(fibonacciNth(72)).toBe(498454011879264); 19 | expect(fibonacciNth(73)).toBe(806515533049393); 20 | expect(fibonacciNth(74)).toBe(1304969544928657); 21 | expect(fibonacciNth(75)).toBe(2111485077978050); 22 | expect(fibonacciNth(80)).toBe(23416728348467685); 23 | expect(fibonacciNth(90)).toBe(2880067194370816120); 24 | }); 25 | }); 26 | -------------------------------------------------------------------------------- /src/algorithms/math/is-power-of-two/__test__/isPowerOfTwoBitwise.test.js: -------------------------------------------------------------------------------- 1 | import isPowerOfTwoBitwise from '../isPowerOfTwoBitwise'; 2 | 3 | describe('isPowerOfTwoBitwise', () => { 4 | it('should check if the number is made by multiplying twos', () => { 5 | expect(isPowerOfTwoBitwise(-1)).toBe(false); 6 | expect(isPowerOfTwoBitwise(0)).toBe(false); 7 | expect(isPowerOfTwoBitwise(1)).toBe(true); 8 | expect(isPowerOfTwoBitwise(2)).toBe(true); 9 | expect(isPowerOfTwoBitwise(3)).toBe(false); 10 | expect(isPowerOfTwoBitwise(4)).toBe(true); 11 | expect(isPowerOfTwoBitwise(5)).toBe(false); 12 | expect(isPowerOfTwoBitwise(6)).toBe(false); 13 | expect(isPowerOfTwoBitwise(7)).toBe(false); 14 | expect(isPowerOfTwoBitwise(8)).toBe(true); 15 | expect(isPowerOfTwoBitwise(10)).toBe(false); 16 | expect(isPowerOfTwoBitwise(12)).toBe(false); 17 | expect(isPowerOfTwoBitwise(16)).toBe(true); 18 | expect(isPowerOfTwoBitwise(31)).toBe(false); 19 | expect(isPowerOfTwoBitwise(64)).toBe(true); 20 | expect(isPowerOfTwoBitwise(1024)).toBe(true); 21 | expect(isPowerOfTwoBitwise(1023)).toBe(false); 22 | }); 23 | }); 24 | -------------------------------------------------------------------------------- /LICENSE: -------------------------------------------------------------------------------- 1 | The MIT License (MIT) 2 | 3 | Copyright (c) 2018 Oleksii Trekhleb 4 | 5 | Permission is hereby granted, free of charge, to any person obtaining a copy 6 | of this software and associated documentation files (the "Software"), to deal 7 | in the Software without restriction, including without limitation the rights 8 | to use, copy, modify, merge, publish, distribute, sublicense, and/or sell 9 | copies of the Software, and to permit persons to whom the Software is 10 | furnished to do so, subject to the following conditions: 11 | 12 | The above copyright notice and this permission notice shall be included in all 13 | copies or substantial portions of the Software. 14 | 15 | THE SOFTWARE IS PROVIDED "AS IS", WITHOUT WARRANTY OF ANY KIND, EXPRESS OR 16 | IMPLIED, INCLUDING BUT NOT LIMITED TO THE WARRANTIES OF MERCHANTABILITY, 17 | FITNESS FOR A PARTICULAR PURPOSE AND NONINFRINGEMENT. IN NO EVENT SHALL THE 18 | AUTHORS OR COPYRIGHT HOLDERS BE LIABLE FOR ANY CLAIM, DAMAGES OR OTHER 19 | LIABILITY, WHETHER IN AN ACTION OF CONTRACT, TORT OR OTHERWISE, ARISING FROM, 20 | OUT OF OR IN CONNECTION WITH THE SOFTWARE OR THE USE OR OTHER DEALINGS IN THE 21 | SOFTWARE. 22 | -------------------------------------------------------------------------------- /src/algorithms/graph/articulation-points/README.md: -------------------------------------------------------------------------------- 1 | # Articulation Points (or Cut Vertices) 2 | 3 | A vertex in an undirected connected graph is an articulation point 4 | (or cut vertex) if removing it (and edges through it) disconnects 5 | the graph. Articulation points represent vulnerabilities in a 6 | connected network – single points whose failure would split the 7 | network into 2 or more disconnected components. They are useful for 8 | designing reliable networks. 9 | 10 | For a disconnected undirected graph, an articulation point is a 11 | vertex removing which increases number of connected components. 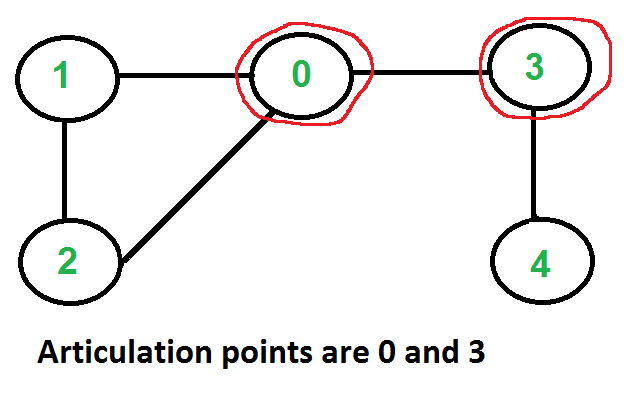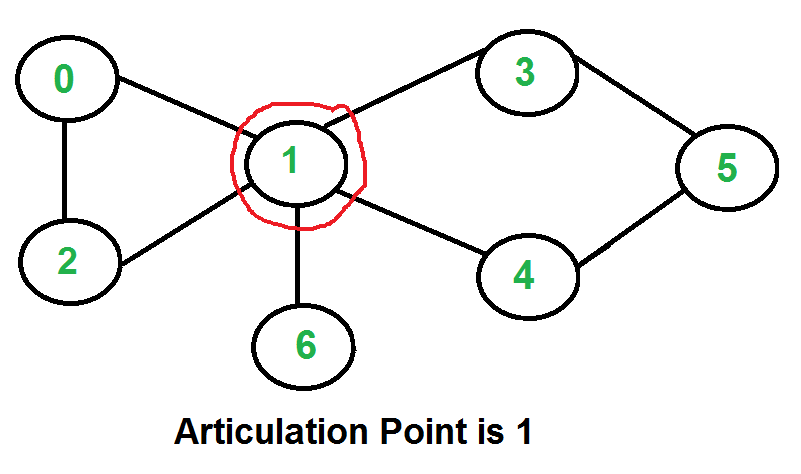12 | 13 | ![Articulation Points](https://www.geeksforgeeks.org/wp-content/uploads/ArticulationPoints.png) 14 | 15 | ![Articulation Points](https://www.geeksforgeeks.org/wp-content/uploads/ArticulationPoints1.png) 16 | 17 | ![Articulation Points](https://www.geeksforgeeks.org/wp-content/uploads/ArticulationPoints21.png) 18 | 19 | ## References 20 | 21 | - [GeeksForGeeks](https://www.geeksforgeeks.org/articulation-points-or-cut-vertices-in-a-graph/) 22 | - [YouTube](https://www.youtube.com/watch?v=2kREIkF9UAs&list=PLLXdhg_r2hKA7DPDsunoDZ-Z769jWn4R8) 23 | -------------------------------------------------------------------------------- /src/algorithms/sets/longest-increasing-subsequence/__test__/dpLongestIncreasingSubsequence.test.js: -------------------------------------------------------------------------------- 1 | import dpLongestIncreasingSubsequence from '../dpLongestIncreasingSubsequence'; 2 | 3 | describe('dpLongestIncreasingSubsequence', () => { 4 | it('should find longest increasing subsequence length', () => { 5 | // Should be: 6 | // 9 or 7 | // 8 or 8 | // 7 or 9 | // 6 or 10 | // ... 11 | expect(dpLongestIncreasingSubsequence([ 12 | 9, 8, 7, 6, 5, 4, 3, 2, 1, 0, 13 | ])).toBe(1); 14 | 15 | // Should be: 16 | // 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 17 | expect(dpLongestIncreasingSubsequence([ 18 | 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 19 | ])).toBe(10); 20 | 21 | // Should be: 22 | // -1, 0, 2, 3 23 | expect(dpLongestIncreasingSubsequence([ 24 | 3, 4, -1, 0, 6, 2, 3, 25 | ])).toBe(4); 26 | 27 | // Should be: 28 | // 0, 2, 6, 9, 11, 15 or 29 | // 0, 4, 6, 9, 11, 15 or 30 | // 0, 2, 6, 9, 13, 15 or 31 | // 0, 4, 6, 9, 13, 15 32 | expect(dpLongestIncreasingSubsequence([ 33 | 0, 8, 4, 12, 2, 10, 6, 14, 1, 9, 5, 13, 3, 11, 7, 15, 34 | ])).toBe(6); 35 | }); 36 | }); 37 | -------------------------------------------------------------------------------- /src/data-structures/priority-queue/README.fr-FR.md: -------------------------------------------------------------------------------- 1 | # File de priorité 2 | 3 | En informatique, une **file de priorité** est un type 4 | de données abstrait qui s'apparente à une file d'attente normale 5 | ou une structure de données empilées, mais où chaque élément est 6 | en plus associé à une "priorité". 7 | Dans une file de priorité, un élément avec une priorité élevée 8 | est servi avant un élément à faible priorité. Si deux éléments ont 9 | la même priorité, ils sont servis selon leur ordre dans la file 10 | d'attente. 11 | 12 | Alors que les files de priorité sont souvent implémentées avec des tas, 13 | elles sont conceptuellement distinctes des tas. Une file de priorité 14 | est un concept abstrait comme "une liste" ou "une carte"; tout comme 15 | une liste peut être implémentée avec une liste chaînée ou un tableau, 16 | une file de priorité peut être implémentée avec un tas ou une variété 17 | d'autres méthodes telles qu'un tableau non ordonné. 18 | 19 | ## Références 20 | 21 | - [Wikipedia](https://fr.wikipedia.org/wiki/File_de_priorit%C3%A9) 22 | - [YouTube](https://www.youtube.com/watch?v=wptevk0bshY&list=PLLXdhg_r2hKA7DPDsunoDZ-Z769jWn4R8&index=6) 23 | -------------------------------------------------------------------------------- /src/algorithms/sorting/bubble-sort/README.pt-BR.md: -------------------------------------------------------------------------------- 1 | # Bubble Sort 2 | 3 | O bubble sort, ou ordenação por flutuação (literalmente "por bolha"), é um algoritmo de ordenação dos mais simples. A ideia é percorrer o vetor diversas vezes, e a cada passagem fazer flutuar para o topo o maior elemento da sequência. Essa movimentação lembra a forma como as bolhas em um tanque de água procuram seu próprio nível, e disso vem o nome do algoritmo. 4 | 5 | ![Algorithm Visualization](https://upload.wikimedia.org/wikipedia/commons/c/c8/Bubble-sort-example-300px.gif) 6 | 7 | ## Complexity 8 | 9 | | Name | Best | Average | Worst | Memory | Stable | Comments | 10 | | --------------------- | :-------------: | :-----------------: | :-----------------: | :-------: | :-------: | :-------- | 11 | | **Bubble sort** | n | n2 | n2 | 1 | Yes | | 12 | 13 | ## References 14 | 15 | - [Wikipedia](https://pt.wikipedia.org/wiki/Bubble_sort) 16 | - [YouTube](https://www.youtube.com/watch?v=6Gv8vg0kcHc&index=27&t=0s&list=PLLXdhg_r2hKA7DPDsunoDZ-Z769jWn4R8) 17 | 18 | -------------------------------------------------------------------------------- /src/algorithms/math/pascal-triangle/pascalTriangleRecursive.js: -------------------------------------------------------------------------------- 1 | /** 2 | * @param {number} lineNumber - zero based. 3 | * @return {number[]} 4 | */ 5 | export default function pascalTriangleRecursive(lineNumber) { 6 | if (lineNumber === 0) { 7 | return [1]; 8 | } 9 | 10 | const currentLineSize = lineNumber + 1; 11 | const previousLineSize = currentLineSize - 1; 12 | 13 | // Create container for current line values. 14 | const currentLine = []; 15 | 16 | // We'll calculate current line based on previous one. 17 | const previousLine = pascalTriangleRecursive(lineNumber - 1); 18 | 19 | // Let's go through all elements of current line except the first and 20 | // last one (since they were and will be filled with 1's) and calculate 21 | // current coefficient based on previous line. 22 | for (let numIndex = 0; numIndex < currentLineSize; numIndex += 1) { 23 | const leftCoefficient = (numIndex - 1) >= 0 ? previousLine[numIndex - 1] : 0; 24 | const rightCoefficient = numIndex < previousLineSize ? previousLine[numIndex] : 0; 25 | 26 | currentLine[numIndex] = leftCoefficient + rightCoefficient; 27 | } 28 | 29 | return currentLine; 30 | } 31 | -------------------------------------------------------------------------------- /src/algorithms/sets/longest-common-subsequence/__test__/longestCommonSubsequence.test.js: -------------------------------------------------------------------------------- 1 | import longestCommonSubsequence from '../longestCommonSubsequence'; 2 | 3 | describe('longestCommonSubsequence', () => { 4 | it('should find longest common subsequence for two strings', () => { 5 | expect(longestCommonSubsequence([''], [''])).toEqual(['']); 6 | 7 | expect(longestCommonSubsequence([''], ['A', 'B', 'C'])).toEqual(['']); 8 | 9 | expect(longestCommonSubsequence(['A', 'B', 'C'], [''])).toEqual(['']); 10 | 11 | expect(longestCommonSubsequence( 12 | ['A', 'B', 'C'], 13 | ['D', 'E', 'F', 'G'], 14 | )).toEqual(['']); 15 | 16 | expect(longestCommonSubsequence( 17 | ['A', 'B', 'C', 'D', 'G', 'H'], 18 | ['A', 'E', 'D', 'F', 'H', 'R'], 19 | )).toEqual(['A', 'D', 'H']); 20 | 21 | expect(longestCommonSubsequence( 22 | ['A', 'G', 'G', 'T', 'A', 'B'], 23 | ['G', 'X', 'T', 'X', 'A', 'Y', 'B'], 24 | )).toEqual(['G', 'T', 'A', 'B']); 25 | 26 | expect(longestCommonSubsequence( 27 | ['A', 'B', 'C', 'D', 'A', 'F'], 28 | ['A', 'C', 'B', 'C', 'F'], 29 | )).toEqual(['A', 'B', 'C', 'F']); 30 | }); 31 | }); 32 | -------------------------------------------------------------------------------- /src/algorithms/math/sieve-of-eratosthenes/sieveOfEratosthenes.js: -------------------------------------------------------------------------------- 1 | /** 2 | * @param {number} maxNumber 3 | * @return {number[]} 4 | */ 5 | export default function sieveOfEratosthenes(maxNumber) { 6 | const isPrime = new Array(maxNumber + 1).fill(true); 7 | isPrime[0] = false; 8 | isPrime[1] = false; 9 | 10 | const primes = []; 11 | 12 | for (let number = 2; number <= maxNumber; number += 1) { 13 | if (isPrime[number] === true) { 14 | primes.push(number); 15 | 16 | /* 17 | * Optimisation. 18 | * Start marking multiples of `p` from `p * p`, and not from `2 * p`. 19 | * The reason why this works is because, at that point, smaller multiples 20 | * of `p` will have already been marked `false`. 21 | * 22 | * Warning: When working with really big numbers, the following line may cause overflow 23 | * In that case, it can be changed to: 24 | * let nextNumber = 2 * number; 25 | */ 26 | let nextNumber = number * number; 27 | 28 | while (nextNumber <= maxNumber) { 29 | isPrime[nextNumber] = false; 30 | nextNumber += number; 31 | } 32 | } 33 | } 34 | 35 | return primes; 36 | } 37 | -------------------------------------------------------------------------------- /src/algorithms/sets/combinations/combineWithRepetitions.js: -------------------------------------------------------------------------------- 1 | /** 2 | * @param {*[]} comboOptions 3 | * @param {number} comboLength 4 | * @return {*[]} 5 | */ 6 | export default function combineWithRepetitions(comboOptions, comboLength) { 7 | // If the length of the combination is 1 then each element of the original array 8 | // is a combination itself. 9 | if (comboLength === 1) { 10 | return comboOptions.map((comboOption) => [comboOption]); 11 | } 12 | 13 | // Init combinations array. 14 | const combos = []; 15 | 16 | // Remember characters one by one and concatenate them to combinations of smaller lengths. 17 | // We don't extract elements here because the repetitions are allowed. 18 | comboOptions.forEach((currentOption, optionIndex) => { 19 | // Generate combinations of smaller size. 20 | const smallerCombos = combineWithRepetitions( 21 | comboOptions.slice(optionIndex), 22 | comboLength - 1, 23 | ); 24 | 25 | // Concatenate currentOption with all combinations of smaller size. 26 | smallerCombos.forEach((smallerCombo) => { 27 | combos.push([currentOption].concat(smallerCombo)); 28 | }); 29 | }); 30 | 31 | return combos; 32 | } 33 | -------------------------------------------------------------------------------- /src/algorithms/uncategorized/recursive-staircase/README.md: -------------------------------------------------------------------------------- 1 | # Recursive Staircase Problem 2 | 3 | ## The Problem 4 | 5 | There are `n` stairs, a person standing at the bottom wants to reach the top. The person can climb either `1` or `2` stairs at a time. _Count the number of ways, the person can reach the top._ 6 | 7 | ![](https://cdncontribute.geeksforgeeks.org/wp-content/uploads/nth-stair.png) 8 | 9 | ## The Solution 10 | 11 | This is an interesting problem because there are several ways of how it may be solved that illustrate different programming paradigms. 12 | 13 | - [Brute Force Recursive Solution](./recursiveStaircaseBF.js) - Time: `O(2^n)`; Space: `O(1)` 14 | - [Recursive Solution With Memoization](./recursiveStaircaseMEM.js) - Time: `O(n)`; Space: `O(n)` 15 | - [Dynamic Programming Solution](./recursiveStaircaseDP.js) - Time: `O(n)`; Space: `O(n)` 16 | - [Iterative Solution](./recursiveStaircaseIT.js) - Time: `O(n)`; Space: `O(1)` 17 | 18 | ## References 19 | 20 | - [On YouTube by Gayle Laakmann McDowell](https://www.youtube.com/watch?v=eREiwuvzaUM&list=PLLXdhg_r2hKA7DPDsunoDZ-Z769jWn4R8&index=81&t=0s) 21 | - [GeeksForGeeks](https://www.geeksforgeeks.org/count-ways-reach-nth-stair/) 22 | -------------------------------------------------------------------------------- /src/algorithms/math/fibonacci/__test__/fibonacciNthClosedForm.test.js: -------------------------------------------------------------------------------- 1 | import fibonacciNthClosedForm from '../fibonacciNthClosedForm'; 2 | 3 | describe('fibonacciClosedForm', () => { 4 | it('should throw an error when trying to calculate fibonacci for not allowed positions', () => { 5 | const calculateFibonacciForNotAllowedPosition = () => { 6 | fibonacciNthClosedForm(76); 7 | }; 8 | 9 | expect(calculateFibonacciForNotAllowedPosition).toThrow(); 10 | }); 11 | 12 | it('should calculate fibonacci correctly', () => { 13 | expect(fibonacciNthClosedForm(1)).toBe(1); 14 | expect(fibonacciNthClosedForm(2)).toBe(1); 15 | expect(fibonacciNthClosedForm(3)).toBe(2); 16 | expect(fibonacciNthClosedForm(4)).toBe(3); 17 | expect(fibonacciNthClosedForm(5)).toBe(5); 18 | expect(fibonacciNthClosedForm(6)).toBe(8); 19 | expect(fibonacciNthClosedForm(7)).toBe(13); 20 | expect(fibonacciNthClosedForm(8)).toBe(21); 21 | expect(fibonacciNthClosedForm(20)).toBe(6765); 22 | expect(fibonacciNthClosedForm(30)).toBe(832040); 23 | expect(fibonacciNthClosedForm(50)).toBe(12586269025); 24 | expect(fibonacciNthClosedForm(70)).toBe(190392490709135); 25 | }); 26 | }); 27 | -------------------------------------------------------------------------------- /src/data-structures/heap/README.ru-RU.md: -------------------------------------------------------------------------------- 1 | # Куча (структура данных) 2 | 3 | В компьютерных науках куча — это специализированная структура данных типа дерево, которая удовлетворяет свойству кучи: 4 | если B является узлом-потомком узла A, то ключ(A) ≥ ключ(B). Из этого следует, что элемент с наибольшим ключом всегда 5 | является корневым узлом кучи, поэтому иногда такие кучи называют max-кучами. 6 | 7 | ![Max-куча](https://upload.wikimedia.org/wikipedia/commons/3/38/Max-Heap.svg) 8 | 9 | Если сравнение перевернуть, то наименьший элемент будет всегда корневым узлом, такие кучи называют min-кучами. 10 | 11 | ![Min-куча](https://upload.wikimedia.org/wikipedia/commons/6/69/Min-heap.png) 12 | 13 | Не существует никаких ограничений относительно того, сколько узлов-потомков имеет каждый узел кучи. На практике их 14 | число обычно не более двух. Куча является максимально эффективной реализацией абстрактного типа данных, который 15 | называется очередью с приоритетом. 16 | 17 | Узел на вершине кучи, у которого нет родителей, называется корневым узлом. 18 | 19 | ## Ссылки 20 | 21 | - [Wikipedia](https://ru.wikipedia.org/wiki/Куча_(структура_данных)) 22 | - [YouTube](https://www.youtube.com/watch?v=noQ4SUoqrQA) 23 | -------------------------------------------------------------------------------- /CONTRIBUTING.md: -------------------------------------------------------------------------------- 1 | ## Contributing 2 | 3 | **General Rules** 4 | 5 | - As much as possible, try to follow the existing format of markdown and code. 6 | - Don't forget to run `npm run lint` and `npm test` before submitting pull requests. 7 | - Make sure that **100%** of your code is covered by tests. 8 | 9 | **Contributing New Translation** 10 | 11 | - Create new `README.xx-XX.md` file with translation alongside with 12 | main `README.md` file where `xx-XX` is [locale and country/region codes](http://www.lingoes.net/en/translator/langcode.htm). 13 | For example `en-US`, `zh-CN`, `zh-TW`, `ko-KR` etc. 14 | - You may also translate all other sub-folders by creating 15 | related `README.xx-XX.md` files in each of them. 16 | 17 | **Contributing New Algorithms** 18 | 19 | - Make your pull requests to be **specific** and **focused**. Instead of 20 | contributing "several sorting algorithms" all at once contribute them all 21 | one by one separately (i.e. one pull request for "Quick Sort", another one 22 | for "Heap Sort" and so on). 23 | - Provide **README.md** for each of the algorithms **with explanations** of 24 | the algorithm and **with links** to further readings. 25 | - Describe what you do in code using **comments**. 26 | -------------------------------------------------------------------------------- /src/algorithms/sets/longest-common-subsequence/README.md: -------------------------------------------------------------------------------- 1 | # Longest common subsequence problem 2 | 3 | The longest common subsequence (LCS) problem is the problem of finding 4 | the longest subsequence common to all sequences in a set of sequences 5 | (often just two sequences). It differs from the longest common substring 6 | problem: unlike substrings, subsequences are not required to occupy 7 | consecutive positions within the original sequences. 8 | 9 | ## Application 10 | 11 | The longest common subsequence problem is a classic computer science 12 | problem, the basis of data comparison programs such as the diff utility, 13 | and has applications in bioinformatics. It is also widely used by 14 | revision control systems such as Git for reconciling multiple changes 15 | made to a revision-controlled collection of files. 16 | 17 | ## Example 18 | 19 | - LCS for input Sequences `ABCDGH` and `AEDFHR` is `ADH` of length 3. 20 | - LCS for input Sequences `AGGTAB` and `GXTXAYB` is `GTAB` of length 4. 21 | 22 | ## References 23 | 24 | - [Wikipedia](https://en.wikipedia.org/wiki/Longest_common_subsequence_problem) 25 | - [YouTube](https://www.youtube.com/watch?v=NnD96abizww&list=PLLXdhg_r2hKA7DPDsunoDZ-Z769jWn4R8) 26 | -------------------------------------------------------------------------------- /src/algorithms/sorting/insertion-sort/InsertionSort.js: -------------------------------------------------------------------------------- 1 | import Sort from '../Sort'; 2 | 3 | export default class InsertionSort extends Sort { 4 | sort(originalArray) { 5 | const array = [...originalArray]; 6 | 7 | // Go through all array elements... 8 | for (let i = 1; i < array.length; i += 1) { 9 | let currentIndex = i; 10 | 11 | // Call visiting callback. 12 | this.callbacks.visitingCallback(array[i]); 13 | 14 | // Check if previous element is greater than current element. 15 | // If so, swap the two elements. 16 | while ( 17 | array[currentIndex - 1] !== undefined 18 | && this.comparator.lessThan(array[currentIndex], array[currentIndex - 1]) 19 | ) { 20 | // Call visiting callback. 21 | this.callbacks.visitingCallback(array[currentIndex - 1]); 22 | 23 | // Swap the elements. 24 | [ 25 | array[currentIndex - 1], 26 | array[currentIndex], 27 | ] = [ 28 | array[currentIndex], 29 | array[currentIndex - 1], 30 | ]; 31 | 32 | // Shift current index left. 33 | currentIndex -= 1; 34 | } 35 | } 36 | 37 | return array; 38 | } 39 | } 40 | -------------------------------------------------------------------------------- /src/algorithms/linked-list/reverse-traversal/__test__/reverseTraversal.test.js: -------------------------------------------------------------------------------- 1 | import LinkedList from '../../../../data-structures/linked-list/LinkedList'; 2 | import reverseTraversal from '../reverseTraversal'; 3 | 4 | describe('reverseTraversal', () => { 5 | it('should traverse linked list in reverse order', () => { 6 | const linkedList = new LinkedList(); 7 | 8 | linkedList 9 | .append(1) 10 | .append(2) 11 | .append(3); 12 | 13 | const traversedNodeValues = []; 14 | const traversalCallback = (nodeValue) => { 15 | traversedNodeValues.push(nodeValue); 16 | }; 17 | 18 | reverseTraversal(linkedList, traversalCallback); 19 | 20 | expect(traversedNodeValues).toEqual([3, 2, 1]); 21 | }); 22 | }); 23 | 24 | // it('should reverse traversal the linked list with callback', () => { 25 | // const linkedList = new LinkedList(); 26 | // 27 | // linkedList 28 | // .append(1) 29 | // .append(2) 30 | // .append(3); 31 | // 32 | // expect(linkedList.toString()).toBe('1,2,3'); 33 | // expect(linkedList.reverseTraversal(linkedList.head, value => value * 2)).toEqual([6, 4, 2]); 34 | // expect(() => linkedList.reverseTraversal(linkedList.head)).toThrow(); 35 | // }); 36 | -------------------------------------------------------------------------------- /src/algorithms/sets/combinations/combineWithoutRepetitions.js: -------------------------------------------------------------------------------- 1 | /** 2 | * @param {*[]} comboOptions 3 | * @param {number} comboLength 4 | * @return {*[]} 5 | */ 6 | export default function combineWithoutRepetitions(comboOptions, comboLength) { 7 | // If the length of the combination is 1 then each element of the original array 8 | // is a combination itself. 9 | if (comboLength === 1) { 10 | return comboOptions.map((comboOption) => [comboOption]); 11 | } 12 | 13 | // Init combinations array. 14 | const combos = []; 15 | 16 | // Extract characters one by one and concatenate them to combinations of smaller lengths. 17 | // We need to extract them because we don't want to have repetitions after concatenation. 18 | comboOptions.forEach((currentOption, optionIndex) => { 19 | // Generate combinations of smaller size. 20 | const smallerCombos = combineWithoutRepetitions( 21 | comboOptions.slice(optionIndex + 1), 22 | comboLength - 1, 23 | ); 24 | 25 | // Concatenate currentOption with all combinations of smaller size. 26 | smallerCombos.forEach((smallerCombo) => { 27 | combos.push([currentOption].concat(smallerCombo)); 28 | }); 29 | }); 30 | 31 | return combos; 32 | } 33 | -------------------------------------------------------------------------------- /src/algorithms/sorting/heap-sort/README.md: -------------------------------------------------------------------------------- 1 | # Heap Sort 2 | 3 | Heapsort is a comparison-based sorting algorithm. 4 | Heapsort can be thought of as an improved selection 5 | sort: like that algorithm, it divides its input into 6 | a sorted and an unsorted region, and it iteratively 7 | shrinks the unsorted region by extracting the largest 8 | element and moving that to the sorted region. The 9 | improvement consists of the use of a heap data structure 10 | rather than a linear-time search to find the maximum. 11 | 12 | ![Algorithm Visualization](https://upload.wikimedia.org/wikipedia/commons/1/1b/Sorting_heapsort_anim.gif) 13 | 14 | ![Algorithm Visualization](https://upload.wikimedia.org/wikipedia/commons/4/4d/Heapsort-example.gif) 15 | 16 | ## Complexity 17 | 18 | | Name | Best | Average | Worst | Memory | Stable | Comments | 19 | | --------------------- | :-------------: | :-----------------: | :-----------------: | :-------: | :-------: | :-------- | 20 | | **Heap sort** | n log(n) | n log(n) | n log(n) | 1 | No | | 21 | 22 | ## References 23 | 24 | [Wikipedia](https://en.wikipedia.org/wiki/Heapsort) 25 | -------------------------------------------------------------------------------- /src/algorithms/sorting/selection-sort/README.md: -------------------------------------------------------------------------------- 1 | # Selection Sort 2 | 3 | Selection sort is a sorting algorithm, specifically an 4 | in-place comparison sort. It has O(n2) time complexity, 5 | making it inefficient on large lists, and generally 6 | performs worse than the similar insertion sort. 7 | Selection sort is noted for its simplicity, and it has 8 | performance advantages over more complicated algorithms 9 | in certain situations, particularly where auxiliary 10 | memory is limited. 11 | 12 | ![Algorithm Visualization](https://upload.wikimedia.org/wikipedia/commons/b/b0/Selection_sort_animation.gif) 13 | 14 | ![Algorithm Visualization](https://upload.wikimedia.org/wikipedia/commons/9/94/Selection-Sort-Animation.gif) 15 | 16 | ## Complexity 17 | 18 | | Name | Best | Average | Worst | Memory | Stable | Comments | 19 | | --------------------- | :-------------: | :-----------------: | :-----------------: | :-------: | :-------: | :-------- | 20 | | **Selection sort** | n2 | n2 | n2 | 1 | No | | 21 | 22 | ## References 23 | 24 | [Wikipedia](https://en.wikipedia.org/wiki/Selection_sort) 25 | -------------------------------------------------------------------------------- /src/algorithms/sorting/Sort.js: -------------------------------------------------------------------------------- 1 | import Comparator from '../../utils/comparator/Comparator'; 2 | 3 | /** 4 | * @typedef {Object} SorterCallbacks 5 | * @property {function(a: *, b: *)} compareCallback - If provided then all elements comparisons 6 | * will be done through this callback. 7 | * @property {function(a: *)} visitingCallback - If provided it will be called each time the sorting 8 | * function is visiting the next element. 9 | */ 10 | 11 | export default class Sort { 12 | constructor(originalCallbacks) { 13 | this.callbacks = Sort.initSortingCallbacks(originalCallbacks); 14 | this.comparator = new Comparator(this.callbacks.compareCallback); 15 | } 16 | 17 | /** 18 | * @param {SorterCallbacks} originalCallbacks 19 | * @returns {SorterCallbacks} 20 | */ 21 | static initSortingCallbacks(originalCallbacks) { 22 | const callbacks = originalCallbacks || {}; 23 | const stubCallback = () => {}; 24 | 25 | callbacks.compareCallback = callbacks.compareCallback || undefined; 26 | callbacks.visitingCallback = callbacks.visitingCallback || stubCallback; 27 | 28 | return callbacks; 29 | } 30 | 31 | sort() { 32 | throw new Error('sort method must be implemented'); 33 | } 34 | } 35 | -------------------------------------------------------------------------------- /src/algorithms/sorting/bubble-sort/BubbleSort.js: -------------------------------------------------------------------------------- 1 | import Sort from '../Sort'; 2 | 3 | export default class BubbleSort extends Sort { 4 | sort(originalArray) { 5 | // Flag that holds info about whether the swap has occur or not. 6 | let swapped = false; 7 | // Clone original array to prevent its modification. 8 | const array = [...originalArray]; 9 | 10 | for (let i = 1; i < array.length; i += 1) { 11 | swapped = false; 12 | 13 | // Call visiting callback. 14 | this.callbacks.visitingCallback(array[i]); 15 | 16 | for (let j = 0; j < array.length - i; j += 1) { 17 | // Call visiting callback. 18 | this.callbacks.visitingCallback(array[j]); 19 | 20 | // Swap elements if they are in wrong order. 21 | if (this.comparator.lessThan(array[j + 1], array[j])) { 22 | [array[j], array[j + 1]] = [array[j + 1], array[j]]; 23 | 24 | // Register the swap. 25 | swapped = true; 26 | } 27 | } 28 | 29 | // If there were no swaps then array is already sorted and there is 30 | // no need to proceed. 31 | if (!swapped) { 32 | return array; 33 | } 34 | } 35 | 36 | return array; 37 | } 38 | } 39 | -------------------------------------------------------------------------------- /src/data-structures/stack/README.pt-BR.md: -------------------------------------------------------------------------------- 1 | # Stack 2 | 3 | Na ciência da computação, um **stack** é uma estrutura de dados abstrata 4 | que serve como uma coleção de elementos com duas operações principais: 5 | 6 | * **push**, pela qual adiciona um elemento à coleção, e 7 | * **pop**, pela qual remove o último elemento adicionado. 8 | 9 | A ordem em que os elementos saem de um _stack_ dá origem ao seu 10 | nome alternativo, LIFO (last in, first out). Adicionalmente, uma 11 | espiar a operação pode dar acesso ao topo sem modificar o _stack_. 12 | O nome "stack" para este tipo de estrutura vem da analogia de 13 | um conjunto de itens físicos empilhados uns sobre os outros, 14 | o que facilita retirar um item do topo da pilha, enquanto para chegar a 15 | um item mais profundo na pilha pode exigir a retirada de 16 | vários outros itens primeiro. 17 | 18 | Representação simples de um tempo de execução de pilha com operações 19 | _push_ e _pop_. 20 | 21 | ![Stack](https://upload.wikimedia.org/wikipedia/commons/b/b4/Lifo_stack.png) 22 | 23 | ## Referências 24 | 25 | - [Wikipedia](https://en.wikipedia.org/wiki/Stack_(abstract_data_type)) 26 | - [YouTube](https://www.youtube.com/watch?v=wjI1WNcIntg&list=PLLXdhg_r2hKA7DPDsunoDZ-Z769jWn4R8&index=3&) 27 | -------------------------------------------------------------------------------- /src/algorithms/string/longest-common-substring/__test__/longestCommonSubstring.test.js: -------------------------------------------------------------------------------- 1 | import longestCommonSubstring from '../longestCommonSubstring'; 2 | 3 | describe('longestCommonSubstring', () => { 4 | it('should find longest common substring between two strings', () => { 5 | expect(longestCommonSubstring('', '')).toBe(''); 6 | expect(longestCommonSubstring('ABC', '')).toBe(''); 7 | expect(longestCommonSubstring('', 'ABC')).toBe(''); 8 | expect(longestCommonSubstring('ABABC', 'BABCA')).toBe('BABC'); 9 | expect(longestCommonSubstring('BABCA', 'ABCBA')).toBe('ABC'); 10 | expect(longestCommonSubstring( 11 | 'Algorithms and data structures implemented in JavaScript', 12 | 'Here you may find Algorithms and data structures that are implemented in JavaScript', 13 | )).toBe('Algorithms and data structures '); 14 | }); 15 | 16 | it('should handle unicode correctly', () => { 17 | expect(longestCommonSubstring('𐌵𐌵**ABC', '𐌵𐌵--ABC')).toBe('ABC'); 18 | expect(longestCommonSubstring('𐌵𐌵**A', '𐌵𐌵--A')).toBe('𐌵𐌵'); 19 | expect(longestCommonSubstring('A买B时', '买B时GD')).toBe('买B时'); 20 | expect(longestCommonSubstring('After test买时 case', 'another_test买时')).toBe('test买时'); 21 | }); 22 | }); 23 | -------------------------------------------------------------------------------- /src/algorithms/math/integer-partition/README.md: -------------------------------------------------------------------------------- 1 | # Integer Partition 2 | 3 | In number theory and combinatorics, a partition of a positive 4 | integer `n`, also called an **integer partition**, is a way of 5 | writing `n` as a sum of positive integers. 6 | 7 | Two sums that differ only in the order of their summands are 8 | considered the same partition. For example, `4` can be partitioned 9 | in five distinct ways: 10 | 11 | ``` 12 | 4 13 | 3 + 1 14 | 2 + 2 15 | 2 + 1 + 1 16 | 1 + 1 + 1 + 1 17 | ``` 18 | 19 | The order-dependent composition `1 + 3` is the same partition 20 | as `3 + 1`, while the two distinct 21 | compositions `1 + 2 + 1` and `1 + 1 + 2` represent the same 22 | partition `2 + 1 + 1`. 23 | 24 | Young diagrams associated to the partitions of the positive 25 | integers `1` through `8`. They are arranged so that images 26 | under the reflection about the main diagonal of the square 27 | are conjugate partitions. 28 | 29 | ![Integer Partition](https://upload.wikimedia.org/wikipedia/commons/d/d8/Ferrer_partitioning_diagrams.svg) 30 | 31 | ## References 32 | 33 | - [Wikipedia](https://en.wikipedia.org/wiki/Partition_(number_theory)) 34 | - [YouTube](https://www.youtube.com/watch?v=ZaVM057DuzE&list=PLLXdhg_r2hKA7DPDsunoDZ-Z769jWn4R8) 35 | -------------------------------------------------------------------------------- /src/algorithms/uncategorized/recursive-staircase/recursiveStaircaseDP.js: -------------------------------------------------------------------------------- 1 | /** 2 | * Recursive Staircase Problem (Dynamic Programming Solution). 3 | * 4 | * @param {number} stairsNum - Number of stairs to climb on. 5 | * @return {number} - Number of ways to climb a staircase. 6 | */ 7 | export default function recursiveStaircaseDP(stairsNum) { 8 | if (stairsNum < 0) { 9 | // There is no way to go down - you climb the stairs only upwards. 10 | return 0; 11 | } 12 | 13 | // Init the steps vector that will hold all possible ways to get to the corresponding step. 14 | const steps = new Array(stairsNum + 1).fill(0); 15 | 16 | // Init the number of ways to get to the 0th, 1st and 2nd steps. 17 | steps[0] = 0; 18 | steps[1] = 1; 19 | steps[2] = 2; 20 | 21 | if (stairsNum <= 2) { 22 | // Return the number of ways to get to the 0th or 1st or 2nd steps. 23 | return steps[stairsNum]; 24 | } 25 | 26 | // Calculate every next step based on two previous ones. 27 | for (let currentStep = 3; currentStep <= stairsNum; currentStep += 1) { 28 | steps[currentStep] = steps[currentStep - 1] + steps[currentStep - 2]; 29 | } 30 | 31 | // Return possible ways to get to the requested step. 32 | return steps[stairsNum]; 33 | } 34 | -------------------------------------------------------------------------------- /src/data-structures/priority-queue/README.md: -------------------------------------------------------------------------------- 1 | # Priority Queue 2 | 3 | _Read this in other languages:_ 4 | [_简体中文_](README.zh-CN.md), 5 | [_Русский_](README.ru-RU.md), 6 | [_日本語_](README.ja-JP.md), 7 | [_Français_](README.fr-FR.md), 8 | [_Português_](README.pt-BR.md) 9 | 10 | In computer science, a **priority queue** is an abstract data type 11 | which is like a regular queue or stack data structure, but where 12 | additionally each element has a "priority" associated with it. 13 | In a priority queue, an element with high priority is served before 14 | an element with low priority. If two elements have the same 15 | priority, they are served according to their order in the queue. 16 | 17 | While priority queues are often implemented with heaps, they are 18 | conceptually distinct from heaps. A priority queue is an abstract 19 | concept like "a list" or "a map"; just as a list can be implemented 20 | with a linked list or an array, a priority queue can be implemented 21 | with a heap or a variety of other methods such as an unordered 22 | array. 23 | 24 | ## References 25 | 26 | - [Wikipedia](https://en.wikipedia.org/wiki/Priority_queue) 27 | - [YouTube](https://www.youtube.com/watch?v=wptevk0bshY&list=PLLXdhg_r2hKA7DPDsunoDZ-Z769jWn4R8&index=6) 28 | -------------------------------------------------------------------------------- /src/algorithms/sorting/bubble-sort/README.md: -------------------------------------------------------------------------------- 1 | # Bubble Sort 2 | 3 | _Read this in other languages:_ 4 | [_Português_](README.pt-BR.md) 5 | 6 | Bubble sort, sometimes referred to as sinking sort, is a 7 | simple sorting algorithm that repeatedly steps through 8 | the list to be sorted, compares each pair of adjacent 9 | items and swaps them if they are in the wrong order 10 | (ascending or descending arrangement). The pass through 11 | the list is repeated until no swaps are needed, which 12 | indicates that the list is sorted. 13 | 14 | ![Algorithm Visualization](https://upload.wikimedia.org/wikipedia/commons/c/c8/Bubble-sort-example-300px.gif) 15 | 16 | ## Complexity 17 | 18 | | Name | Best | Average | Worst | Memory | Stable | Comments | 19 | | --------------------- | :-------------: | :-----------------: | :-----------------: | :-------: | :-------: | :-------- | 20 | | **Bubble sort** | n | n2 | n2 | 1 | Yes | | 21 | 22 | ## References 23 | 24 | - [Wikipedia](https://en.wikipedia.org/wiki/Bubble_sort) 25 | - [YouTube](https://www.youtube.com/watch?v=6Gv8vg0kcHc&index=27&t=0s&list=PLLXdhg_r2hKA7DPDsunoDZ-Z769jWn4R8) 26 | -------------------------------------------------------------------------------- /src/algorithms/uncategorized/best-time-to-buy-sell-stocks/peakvalleyBestTimeToBuySellStocks.js: -------------------------------------------------------------------------------- 1 | /** 2 | * Finds the maximum profit from selling and buying the stocks. 3 | * PEAK VALLEY APPROACH. 4 | * 5 | * @param {number[]} prices - Array of stock prices, i.e. [7, 6, 4, 3, 1] 6 | * @param {function(): void} visit - Visiting callback to calculate the number of iterations. 7 | * @return {number} - The maximum profit 8 | */ 9 | const peakvalleyBestTimeToBuySellStocks = (prices, visit = () => {}) => { 10 | visit(); 11 | let profit = 0; 12 | let low = prices[0]; 13 | let high = prices[0]; 14 | 15 | prices.slice(1).forEach((currentPrice) => { 16 | visit(); 17 | if (currentPrice < high) { 18 | // If price went down, we need to sell. 19 | profit += high - low; 20 | low = currentPrice; 21 | high = currentPrice; 22 | } else { 23 | // If price went up, we don't need to do anything but increase a high record. 24 | high = currentPrice; 25 | } 26 | }); 27 | 28 | // In case if price went up during the last day 29 | // and we didn't have chance to sell inside the forEach loop. 30 | profit += high - low; 31 | 32 | return profit; 33 | }; 34 | 35 | export default peakvalleyBestTimeToBuySellStocks; 36 | -------------------------------------------------------------------------------- /src/algorithms/math/radian/README.md: -------------------------------------------------------------------------------- 1 | # Radian 2 | 3 | The **radian** (symbol **rad**) is the unit for measuring angles, and is the 4 | standard unit of angular measure used in many areas of mathematics. 5 | 6 | The length of an arc of a unit circle is numerically equal to the measurement 7 | in radians of the angle that it subtends; one radian is just under `57.3` degrees. 8 | 9 | An arc of a circle with the same length as the radius of that circle subtends an 10 | angle of `1 radian`. The circumference subtends an angle of `2π radians`. 11 | 12 | ![Radian](https://upload.wikimedia.org/wikipedia/commons/4/4e/Circle_radians.gif) 13 | 14 | A complete revolution is 2π radians (shown here with a circle of radius one and 15 | thus circumference `2π`). 16 | 17 | ![2 pi Radian](https://upload.wikimedia.org/wikipedia/commons/6/67/2pi-unrolled.gif) 18 | 19 | **Conversions** 20 | 21 | | Radians | Degrees | 22 | | :-----: | :-----: | 23 | | 0 | 0° | 24 | | π/12 | 15° | 25 | | π/6 | 30° | 26 | | π/4 | 45° | 27 | | 1 | 57.3° | 28 | | π/3 | 60° | 29 | | π/2 | 90° | 30 | | π | 180° | 31 | | 2π | 360° | 32 | 33 | 34 | ## References 35 | 36 | - [Wikipedia](https://en.wikipedia.org/wiki/Radian) 37 | -------------------------------------------------------------------------------- /src/algorithms/math/horner-method/__test__/hornerMethod.test.js: -------------------------------------------------------------------------------- 1 | import hornerMethod from '../hornerMethod'; 2 | import classicPolynome from '../classicPolynome'; 3 | 4 | describe('hornerMethod', () => { 5 | it('should evaluate the polynomial for the specified value of x correctly', () => { 6 | expect(hornerMethod([8], 0.1)).toBe(8); 7 | expect(hornerMethod([2, 4, 2, 5], 0.555)).toBe(7.68400775); 8 | expect(hornerMethod([2, 4, 2, 5], 0.75)).toBe(9.59375); 9 | expect(hornerMethod([1, 1, 1, 1, 1], 1.75)).toBe(20.55078125); 10 | expect(hornerMethod([15, 3.5, 0, 2, 1.42, 0.41], 0.315)).toBe(1.136730065140625); 11 | expect(hornerMethod([0, 0, 2.77, 1.42, 0.41], 1.35)).toBe(7.375325000000001); 12 | expect(hornerMethod([0, 0, 2.77, 1.42, 2.3311], 1.35)).toBe(9.296425000000001); 13 | expect(hornerMethod([2, 0, 0, 5.757, 5.31412, 12.3213], 3.141)).toBe(697.2731167035034); 14 | }); 15 | 16 | it('should evaluate the same polynomial value as classical approach', () => { 17 | expect(hornerMethod([8], 0.1)).toBe(classicPolynome([8], 0.1)); 18 | expect(hornerMethod([2, 4, 2, 5], 0.555)).toBe(classicPolynome([2, 4, 2, 5], 0.555)); 19 | expect(hornerMethod([2, 4, 2, 5], 0.75)).toBe(classicPolynome([2, 4, 2, 5], 0.75)); 20 | }); 21 | }); 22 | -------------------------------------------------------------------------------- /src/algorithms/uncategorized/recursive-staircase/recursiveStaircaseIT.js: -------------------------------------------------------------------------------- 1 | /** 2 | * Recursive Staircase Problem (Iterative Solution). 3 | * 4 | * @param {number} stairsNum - Number of stairs to climb on. 5 | * @return {number} - Number of ways to climb a staircase. 6 | */ 7 | export default function recursiveStaircaseIT(stairsNum) { 8 | if (stairsNum <= 0) { 9 | // There is no way to go down - you climb the stairs only upwards. 10 | // Also you don't need to do anything to stay on the 0th step. 11 | return 0; 12 | } 13 | 14 | // Init the number of ways to get to the 0th, 1st and 2nd steps. 15 | const steps = [1, 2]; 16 | 17 | if (stairsNum <= 2) { 18 | // Return the number of possible ways of how to get to the 1st or 2nd steps. 19 | return steps[stairsNum - 1]; 20 | } 21 | 22 | // Calculate the number of ways to get to the n'th step based on previous ones. 23 | // Comparing to Dynamic Programming solution we don't store info for all the steps but 24 | // rather for two previous ones only. 25 | for (let currentStep = 3; currentStep <= stairsNum; currentStep += 1) { 26 | [steps[0], steps[1]] = [steps[1], steps[0] + steps[1]]; 27 | } 28 | 29 | // Return possible ways to get to the requested step. 30 | return steps[1]; 31 | } 32 | -------------------------------------------------------------------------------- /src/data-structures/priority-queue/README.pt-BR.md: -------------------------------------------------------------------------------- 1 | # Fila de Prioridade (Priority Queue) 2 | 3 | Na ciência da computação, uma **fila de prioridade** é um tipo de dados 4 | abastrato que é como uma fila regular (regular queue) ou estrutura de 5 | dados de pilha (stack), mas adicionalmente cada elemento possui uma 6 | "prioridade" associada. 7 | 8 | Em uma fila de prioridade, um elemento com uma prioridade alta é servido 9 | antes de um elemento com baixa prioridade. Caso dois elementos posusam a 10 | mesma prioridade, eles serão servidos de acordo com sua ordem na fila. 11 | 12 | Enquanto as filas de prioridade são frequentemente implementadas com 13 | pilhas (heaps), elas são conceitualmente distintas das pilhas (heaps). 14 | A fila de prioridade é um conceito abstrato como uma "lista" (list) ou 15 | um "mapa" (map); assim como uma lista pode ser implementada com uma 16 | lista encadeada (liked list) ou um array, a fila de prioridade pode ser 17 | implementada com uma pilha (heap) ou com uima variedade de outros métodos, 18 | como um array não ordenado (unordered array). 19 | 20 | ## Referências 21 | 22 | - [Wikipedia](https://en.wikipedia.org/wiki/Priority_queue) 23 | - [YouTube](https://www.youtube.com/watch?v=wptevk0bshY&list=PLLXdhg_r2hKA7DPDsunoDZ-Z769jWn4R8&index=6) 24 | -------------------------------------------------------------------------------- /src/algorithms/graph/dijkstra/README.md: -------------------------------------------------------------------------------- 1 | # Dijkstra's Algorithm 2 | 3 | Dijkstra's algorithm is an algorithm for finding the shortest 4 | paths between nodes in a graph, which may represent, for example, 5 | road networks. 6 | 7 | The algorithm exists in many variants; Dijkstra's original variant 8 | found the shortest path between two nodes, but a more common 9 | variant fixes a single node as the "source" node and finds 10 | shortest paths from the source to all other nodes in the graph, 11 | producing a shortest-path tree. 12 | 13 | ![Dijkstra](https://upload.wikimedia.org/wikipedia/commons/5/57/Dijkstra_Animation.gif) 14 | 15 | Dijkstra's algorithm to find the shortest path between `a` and `b`. 16 | It picks the unvisited vertex with the lowest distance, 17 | calculates the distance through it to each unvisited neighbor, 18 | and updates the neighbor's distance if smaller. Mark visited 19 | (set to red) when done with neighbors. 20 | 21 | ## References 22 | 23 | - [Wikipedia](https://en.wikipedia.org/wiki/Dijkstra%27s_algorithm) 24 | - [On YouTube by Nathaniel Fan](https://www.youtube.com/watch?v=gdmfOwyQlcI&list=PLLXdhg_r2hKA7DPDsunoDZ-Z769jWn4R8) 25 | - [On YouTube by Tushar Roy](https://www.youtube.com/watch?v=lAXZGERcDf4&list=PLLXdhg_r2hKA7DPDsunoDZ-Z769jWn4R8) 26 | -------------------------------------------------------------------------------- /src/data-structures/hash-table/README.pt-BR.md: -------------------------------------------------------------------------------- 1 | # Tabela de Hash (Hash Table) 2 | 3 | Na ciência da computação, uma **tabela de hash** (hash map) é uma 4 | estrutura de dados pela qual implementa um tipo de dado abstrado de 5 | *array associativo*, uma estrutura que pode *mapear chaves para valores*. 6 | Uma tabela de hash utiliza uma *função de hash* para calcular um índice 7 | em um _array_ de buckets ou slots, a partir do qual o valor desejado 8 | pode ser encontrado. 9 | 10 | Idealmente, a função de hash irá atribuir a cada chave a um bucket único, 11 | mas a maioria dos designs de tabela de hash emprega uma função de hash 12 | imperfeita, pela qual poderá causar colisões de hashes onde a função de hash 13 | gera o mesmo índice para mais de uma chave.Tais colisões devem ser 14 | acomodados de alguma forma. 15 | 16 | ![Hash Table](https://upload.wikimedia.org/wikipedia/commons/7/7d/Hash_table_3_1_1_0_1_0_0_SP.svg) 17 | 18 | Colisão de hash resolvida por encadeamento separado. 19 | 20 | ![Hash Collision](https://upload.wikimedia.org/wikipedia/commons/d/d0/Hash_table_5_0_1_1_1_1_1_LL.svg) 21 | 22 | ## Referências 23 | 24 | - [Wikipedia](https://en.wikipedia.org/wiki/Hash_table) 25 | - [YouTube](https://www.youtube.com/watch?v=shs0KM3wKv8&index=4&list=PLLXdhg_r2hKA7DPDsunoDZ-Z769jWn4R8) 26 | -------------------------------------------------------------------------------- /src/algorithms/math/euclidean-algorithm/__test__/euclideanAlgorithm.test.js: -------------------------------------------------------------------------------- 1 | import euclideanAlgorithm from '../euclideanAlgorithm'; 2 | 3 | describe('euclideanAlgorithm', () => { 4 | it('should calculate GCD recursively', () => { 5 | expect(euclideanAlgorithm(0, 0)).toBe(0); 6 | expect(euclideanAlgorithm(2, 0)).toBe(2); 7 | expect(euclideanAlgorithm(0, 2)).toBe(2); 8 | expect(euclideanAlgorithm(1, 2)).toBe(1); 9 | expect(euclideanAlgorithm(2, 1)).toBe(1); 10 | expect(euclideanAlgorithm(6, 6)).toBe(6); 11 | expect(euclideanAlgorithm(2, 4)).toBe(2); 12 | expect(euclideanAlgorithm(4, 2)).toBe(2); 13 | expect(euclideanAlgorithm(12, 4)).toBe(4); 14 | expect(euclideanAlgorithm(4, 12)).toBe(4); 15 | expect(euclideanAlgorithm(5, 13)).toBe(1); 16 | expect(euclideanAlgorithm(27, 13)).toBe(1); 17 | expect(euclideanAlgorithm(24, 60)).toBe(12); 18 | expect(euclideanAlgorithm(60, 24)).toBe(12); 19 | expect(euclideanAlgorithm(252, 105)).toBe(21); 20 | expect(euclideanAlgorithm(105, 252)).toBe(21); 21 | expect(euclideanAlgorithm(1071, 462)).toBe(21); 22 | expect(euclideanAlgorithm(462, 1071)).toBe(21); 23 | expect(euclideanAlgorithm(462, -1071)).toBe(21); 24 | expect(euclideanAlgorithm(-462, -1071)).toBe(21); 25 | }); 26 | }); 27 | -------------------------------------------------------------------------------- /src/algorithms/graph/bridges/README.md: -------------------------------------------------------------------------------- 1 | # Bridges in Graph 2 | 3 | In graph theory, a **bridge**, **isthmus**, **cut-edge**, or **cut arc** is an edge 4 | of a graph whose deletion increases its number of connected components. Equivalently, 5 | an edge is a bridge if and only if it is not contained in any cycle. A graph is said 6 | to be bridgeless or isthmus-free if it contains no bridges. 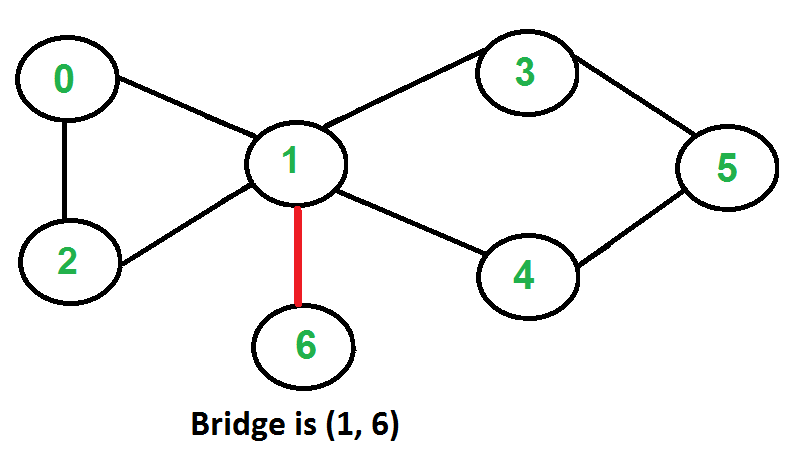7 | 8 | ![Bridges in graph](https://upload.wikimedia.org/wikipedia/commons/d/df/Graph_cut_edges.svg) 9 | 10 | A graph with 16 vertices and 6 bridges (highlighted in red) 11 | 12 | ![Bridgeless](https://upload.wikimedia.org/wikipedia/commons/b/bf/Undirected.svg) 13 | 14 | An undirected connected graph with no cut edges 15 | 16 | ![Bridges in graph](https://www.geeksforgeeks.org/wp-content/uploads/Bridge1.png) 17 | 18 | ![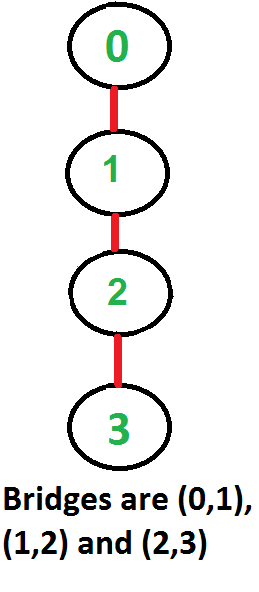Bridges in graph](https://www.geeksforgeeks.org/wp-content/uploads/Bridge2.png) 19 | 20 | ![Bridges in graph](https://www.geeksforgeeks.org/wp-content/uploads/Bridge3.png) 21 | 22 | ## References 23 | 24 | - [GeeksForGeeks on YouTube](https://www.youtube.com/watch?v=thLQYBlz2DM&list=PLLXdhg_r2hKA7DPDsunoDZ-Z769jWn4R8) 25 | - [Wikipedia](https://en.wikipedia.org/wiki/Bridge_%28graph_theory%29#Tarjan.27s_Bridge-finding_algorithm) 26 | - [GeeksForGeeks](https://www.geeksforgeeks.org/bridge-in-a-graph/) 27 | -------------------------------------------------------------------------------- /src/algorithms/uncategorized/n-queens/QueenPosition.js: -------------------------------------------------------------------------------- 1 | /** 2 | * Class that represents queen position on the chessboard. 3 | */ 4 | export default class QueenPosition { 5 | /** 6 | * @param {number} rowIndex 7 | * @param {number} columnIndex 8 | */ 9 | constructor(rowIndex, columnIndex) { 10 | this.rowIndex = rowIndex; 11 | this.columnIndex = columnIndex; 12 | } 13 | 14 | /** 15 | * @return {number} 16 | */ 17 | get leftDiagonal() { 18 | // Each position on the same left (\) diagonal has the same difference of 19 | // rowIndex and columnIndex. This fact may be used to quickly check if two 20 | // positions (queens) are on the same left diagonal. 21 | // @see https://youtu.be/xouin83ebxE?t=1m59s 22 | return this.rowIndex - this.columnIndex; 23 | } 24 | 25 | /** 26 | * @return {number} 27 | */ 28 | get rightDiagonal() { 29 | // Each position on the same right diagonal (/) has the same 30 | // sum of rowIndex and columnIndex. This fact may be used to quickly 31 | // check if two positions (queens) are on the same right diagonal. 32 | // @see https://youtu.be/xouin83ebxE?t=1m59s 33 | return this.rowIndex + this.columnIndex; 34 | } 35 | 36 | toString() { 37 | return `${this.rowIndex},${this.columnIndex}`; 38 | } 39 | } 40 | -------------------------------------------------------------------------------- /src/algorithms/uncategorized/square-matrix-rotation/squareMatrixRotation.js: -------------------------------------------------------------------------------- 1 | /** 2 | * @param {*[][]} originalMatrix 3 | * @return {*[][]} 4 | */ 5 | export default function squareMatrixRotation(originalMatrix) { 6 | const matrix = originalMatrix.slice(); 7 | 8 | // Do top-right/bottom-left diagonal reflection of the matrix. 9 | for (let rowIndex = 0; rowIndex < matrix.length; rowIndex += 1) { 10 | for (let columnIndex = rowIndex + 1; columnIndex < matrix.length; columnIndex += 1) { 11 | // Swap elements. 12 | [ 13 | matrix[columnIndex][rowIndex], 14 | matrix[rowIndex][columnIndex], 15 | ] = [ 16 | matrix[rowIndex][columnIndex], 17 | matrix[columnIndex][rowIndex], 18 | ]; 19 | } 20 | } 21 | 22 | // Do horizontal reflection of the matrix. 23 | for (let rowIndex = 0; rowIndex < matrix.length; rowIndex += 1) { 24 | for (let columnIndex = 0; columnIndex < matrix.length / 2; columnIndex += 1) { 25 | // Swap elements. 26 | [ 27 | matrix[rowIndex][matrix.length - columnIndex - 1], 28 | matrix[rowIndex][columnIndex], 29 | ] = [ 30 | matrix[rowIndex][columnIndex], 31 | matrix[rowIndex][matrix.length - columnIndex - 1], 32 | ]; 33 | } 34 | } 35 | 36 | return matrix; 37 | } 38 | -------------------------------------------------------------------------------- /src/data-structures/disjoint-set/README.md: -------------------------------------------------------------------------------- 1 | # Disjoint Set 2 | 3 | _Read this in other languages:_ 4 | [_Русский_](README.ru-RU.md), 5 | [_Português_](README.pt-BR.md) 6 | 7 | 8 | **Disjoint-set** data structure (also called a union–find data structure or merge–find set) is a data 9 | structure that tracks a set of elements partitioned into a number of disjoint (non-overlapping) subsets. 10 | It provides near-constant-time operations (bounded by the inverse Ackermann function) to *add new sets*, 11 | to *merge existing sets*, and to *determine whether elements are in the same set*. 12 | In addition to many other uses (see the Applications section), disjoint-sets play a key role in Kruskal's algorithm for finding the minimum spanning tree of a graph. 13 | 14 | ![disjoint set](https://upload.wikimedia.org/wikipedia/commons/6/67/Dsu_disjoint_sets_init.svg) 15 | 16 | *MakeSet* creates 8 singletons. 17 | 18 | ![disjoint set](https://upload.wikimedia.org/wikipedia/commons/a/ac/Dsu_disjoint_sets_final.svg) 19 | 20 | After some operations of *Union*, some sets are grouped together. 21 | 22 | ## References 23 | 24 | - [Wikipedia](https://en.wikipedia.org/wiki/Disjoint-set_data_structure) 25 | - [By Abdul Bari on YouTube](https://www.youtube.com/watch?v=wU6udHRIkcc&index=14&t=0s&list=PLLXdhg_r2hKA7DPDsunoDZ-Z769jWn4R8) 26 | -------------------------------------------------------------------------------- /src/algorithms/string/levenshtein-distance/__test__/levenshteinDistance.test.js: -------------------------------------------------------------------------------- 1 | import levenshteinDistance from '../levenshteinDistance'; 2 | 3 | describe('levenshteinDistance', () => { 4 | it('should calculate edit distance between two strings', () => { 5 | expect(levenshteinDistance('', '')).toBe(0); 6 | expect(levenshteinDistance('a', '')).toBe(1); 7 | expect(levenshteinDistance('', 'a')).toBe(1); 8 | expect(levenshteinDistance('abc', '')).toBe(3); 9 | expect(levenshteinDistance('', 'abc')).toBe(3); 10 | 11 | // Should just add I to the beginning. 12 | expect(levenshteinDistance('islander', 'slander')).toBe(1); 13 | 14 | // Needs to substitute M by K, T by M and add an A to the end 15 | expect(levenshteinDistance('mart', 'karma')).toBe(3); 16 | 17 | // Substitute K by S, E by I and insert G at the end. 18 | expect(levenshteinDistance('kitten', 'sitting')).toBe(3); 19 | 20 | // Should add 4 letters FOOT at the beginning. 21 | expect(levenshteinDistance('ball', 'football')).toBe(4); 22 | 23 | // Should delete 4 letters FOOT at the beginning. 24 | expect(levenshteinDistance('football', 'foot')).toBe(4); 25 | 26 | // Needs to substitute the first 5 chars: INTEN by EXECU 27 | expect(levenshteinDistance('intention', 'execution')).toBe(5); 28 | }); 29 | }); 30 | -------------------------------------------------------------------------------- /src/data-structures/priority-queue/README.ru-RU.md: -------------------------------------------------------------------------------- 1 | # Очередь с приоритетом 2 | 3 | Очередь с приоритетом (англ. priority queue) — абстрактный тип данных в информатике, 4 | для каждого элемента которого можно вычислить его приоритет. 5 | 6 | В очереди с приоритетами элемент с высоким приоритетом обслуживается раньше 7 | элемента с низким приоритетом. Если два элемента имеют одинаковый приоритет, они 8 | обслуживаются в соответствии с их порядком в очереди. 9 | 10 | Очередь с приоритетом поддерживает две обязательные операции — добавить элемент и 11 | извлечь максимум(минимум). 12 | 13 | Хотя приоритетные очереди часто реализуются в виде куч(heaps), они 14 | концептуально отличаются от куч. Очередь приоритетов является абстрактной 15 | концепцией вроде «списка» или «карты»; так же, как список может быть реализован 16 | в виде связного списка или массива, так и очередь с приоритетом может быть реализована 17 | в виде кучи или множеством других методов, например в виде неупорядоченного массива. 18 | 19 | ## Ссылки 20 | 21 | - [Wikipedia](https://ru.wikipedia.org/wiki/%D0%9E%D1%87%D0%B5%D1%80%D0%B5%D0%B4%D1%8C_%D1%81_%D0%BF%D1%80%D0%B8%D0%BE%D1%80%D0%B8%D1%82%D0%B5%D1%82%D0%BE%D0%BC_(%D0%BF%D1%80%D0%BE%D0%B3%D1%80%D0%B0%D0%BC%D0%BC%D0%B8%D1%80%D0%BE%D0%B2%D0%B0%D0%BD%D0%B8%D0%B5)) 22 | - [YouTube](https://www.youtube.com/watch?v=y_2toG5-j_M) 23 | -------------------------------------------------------------------------------- /src/algorithms/math/primality-test/README.md: -------------------------------------------------------------------------------- 1 | # Primality Test 2 | 3 | A **prime number** (or a **prime**) is a natural number greater than `1` that 4 | cannot be formed by multiplying two smaller natural numbers. A natural number 5 | greater than `1` that is not prime is called a composite number. For 6 | example, `5` is prime because the only ways of writing it as a 7 | product, `1 × 5` or `5 × 1`, involve `5` itself. However, `6` is 8 | composite because it is the product of two numbers `(2 × 3)` that are 9 | both smaller than `6`. 10 | 11 | ![Prime Numbers](https://upload.wikimedia.org/wikipedia/commons/f/f0/Primes-vs-composites.svg) 12 | 13 | A **primality test** is an algorithm for determining whether an input 14 | number is prime. Among other fields of mathematics, it is used 15 | for cryptography. Unlike integer factorization, primality tests 16 | do not generally give prime factors, only stating whether the 17 | input number is prime or not. Factorization is thought to be 18 | a computationally difficult problem, whereas primality testing 19 | is comparatively easy (its running time is polynomial in the 20 | size of the input). 21 | 22 | ## References 23 | 24 | - [Prime Numbers on Wikipedia](https://en.wikipedia.org/wiki/Prime_number) 25 | - [Primality Test on Wikipedia](https://en.wikipedia.org/wiki/Primality_test) 26 | -------------------------------------------------------------------------------- /src/algorithms/math/prime-factors/primeFactors.js: -------------------------------------------------------------------------------- 1 | /** 2 | * Finds prime factors of a number. 3 | * 4 | * @param {number} n - the number that is going to be split into prime factors. 5 | * @returns {number[]} - array of prime factors. 6 | */ 7 | export function primeFactors(n) { 8 | // Clone n to avoid function arguments override. 9 | let nn = n; 10 | 11 | // Array that stores the all the prime factors. 12 | const factors = []; 13 | 14 | // Running the loop till sqrt(n) instead of n to optimise time complexity from O(n) to O(sqrt(n)). 15 | for (let factor = 2; factor <= Math.sqrt(nn); factor += 1) { 16 | // Check that factor divides n without a reminder. 17 | while (nn % factor === 0) { 18 | // Overriding the value of n. 19 | nn /= factor; 20 | // Saving the factor. 21 | factors.push(factor); 22 | } 23 | } 24 | 25 | // The ultimate reminder should be a last prime factor, 26 | // unless it is not 1 (since 1 is not a prime number). 27 | if (nn !== 1) { 28 | factors.push(nn); 29 | } 30 | 31 | return factors; 32 | } 33 | 34 | /** 35 | * Hardy-Ramanujan approximation of prime factors count. 36 | * 37 | * @param {number} n 38 | * @returns {number} - approximate number of prime factors. 39 | */ 40 | export function hardyRamanujan(n) { 41 | return Math.log(Math.log(n)); 42 | } 43 | -------------------------------------------------------------------------------- /src/algorithms/search/linear-search/__test__/linearSearch.test.js: -------------------------------------------------------------------------------- 1 | import linearSearch from '../linearSearch'; 2 | 3 | describe('linearSearch', () => { 4 | it('should search all numbers in array', () => { 5 | const array = [1, 2, 4, 6, 2]; 6 | 7 | expect(linearSearch(array, 10)).toEqual([]); 8 | expect(linearSearch(array, 1)).toEqual([0]); 9 | expect(linearSearch(array, 2)).toEqual([1, 4]); 10 | }); 11 | 12 | it('should search all strings in array', () => { 13 | const array = ['a', 'b', 'a']; 14 | 15 | expect(linearSearch(array, 'c')).toEqual([]); 16 | expect(linearSearch(array, 'b')).toEqual([1]); 17 | expect(linearSearch(array, 'a')).toEqual([0, 2]); 18 | }); 19 | 20 | it('should search through objects as well', () => { 21 | const comparatorCallback = (a, b) => { 22 | if (a.key === b.key) { 23 | return 0; 24 | } 25 | 26 | return a.key <= b.key ? -1 : 1; 27 | }; 28 | 29 | const array = [ 30 | { key: 5 }, 31 | { key: 6 }, 32 | { key: 7 }, 33 | { key: 6 }, 34 | ]; 35 | 36 | expect(linearSearch(array, { key: 10 }, comparatorCallback)).toEqual([]); 37 | expect(linearSearch(array, { key: 5 }, comparatorCallback)).toEqual([0]); 38 | expect(linearSearch(array, { key: 6 }, comparatorCallback)).toEqual([1, 3]); 39 | }); 40 | }); 41 | -------------------------------------------------------------------------------- /src/algorithms/sets/permutations/permutateWithoutRepetitions.js: -------------------------------------------------------------------------------- 1 | /** 2 | * @param {*[]} permutationOptions 3 | * @return {*[]} 4 | */ 5 | export default function permutateWithoutRepetitions(permutationOptions) { 6 | if (permutationOptions.length === 1) { 7 | return [permutationOptions]; 8 | } 9 | 10 | // Init permutations array. 11 | const permutations = []; 12 | 13 | // Get all permutations for permutationOptions excluding the first element. 14 | const smallerPermutations = permutateWithoutRepetitions(permutationOptions.slice(1)); 15 | 16 | // Insert first option into every possible position of every smaller permutation. 17 | const firstOption = permutationOptions[0]; 18 | 19 | for (let permIndex = 0; permIndex < smallerPermutations.length; permIndex += 1) { 20 | const smallerPermutation = smallerPermutations[permIndex]; 21 | 22 | // Insert first option into every possible position of smallerPermutation. 23 | for (let positionIndex = 0; positionIndex <= smallerPermutation.length; positionIndex += 1) { 24 | const permutationPrefix = smallerPermutation.slice(0, positionIndex); 25 | const permutationSuffix = smallerPermutation.slice(positionIndex); 26 | permutations.push(permutationPrefix.concat([firstOption], permutationSuffix)); 27 | } 28 | } 29 | 30 | return permutations; 31 | } 32 | -------------------------------------------------------------------------------- /src/algorithms/tree/breadth-first-search/README.md: -------------------------------------------------------------------------------- 1 | # Breadth-First Search (BFS) 2 | 3 | Breadth-first search (BFS) is an algorithm for traversing 4 | or searching tree or graph data structures. It starts at 5 | the tree root (or some arbitrary node of a graph, sometimes 6 | referred to as a 'search key') and explores the neighbor 7 | nodes first, before moving to the next level neighbors. 8 | 9 | ![Algorithm Visualization](https://upload.wikimedia.org/wikipedia/commons/5/5d/Breadth-First-Search-Algorithm.gif) 10 | 11 | ## Pseudocode 12 | 13 | ```text 14 | BFS(root) 15 | Pre: root is the node of the BST 16 | Post: the nodes in the BST have been visited in breadth first order 17 | q ← queue 18 | while root = ø 19 | yield root.value 20 | if root.left = ø 21 | q.enqueue(root.left) 22 | end if 23 | if root.right = ø 24 | q.enqueue(root.right) 25 | end if 26 | if !q.isEmpty() 27 | root ← q.dequeue() 28 | else 29 | root ← ø 30 | end if 31 | end while 32 | end BFS 33 | ``` 34 | 35 | ## References 36 | 37 | - [Wikipedia](https://en.wikipedia.org/wiki/Breadth-first_search) 38 | - [Tree Traversals (Inorder, Preorder and Postorder)](https://www.geeksforgeeks.org/tree-traversals-inorder-preorder-and-postorder/) 39 | - [BFS vs DFS](https://www.geeksforgeeks.org/bfs-vs-dfs-binary-tree/) 40 | -------------------------------------------------------------------------------- /src/algorithms/math/primality-test/__test__/trialDivision.test.js: -------------------------------------------------------------------------------- 1 | import trialDivision from '../trialDivision'; 2 | 3 | /** 4 | * @param {function(n: number)} testFunction 5 | */ 6 | function primalityTest(testFunction) { 7 | expect(testFunction(1)).toBe(false); 8 | expect(testFunction(2)).toBe(true); 9 | expect(testFunction(3)).toBe(true); 10 | expect(testFunction(5)).toBe(true); 11 | expect(testFunction(11)).toBe(true); 12 | expect(testFunction(191)).toBe(true); 13 | expect(testFunction(191)).toBe(true); 14 | expect(testFunction(199)).toBe(true); 15 | 16 | expect(testFunction(-1)).toBe(false); 17 | expect(testFunction(0)).toBe(false); 18 | expect(testFunction(4)).toBe(false); 19 | expect(testFunction(6)).toBe(false); 20 | expect(testFunction(12)).toBe(false); 21 | expect(testFunction(14)).toBe(false); 22 | expect(testFunction(25)).toBe(false); 23 | expect(testFunction(192)).toBe(false); 24 | expect(testFunction(200)).toBe(false); 25 | expect(testFunction(400)).toBe(false); 26 | 27 | // It should also deal with floats. 28 | expect(testFunction(0.5)).toBe(false); 29 | expect(testFunction(1.3)).toBe(false); 30 | expect(testFunction(10.5)).toBe(false); 31 | } 32 | 33 | describe('trialDivision', () => { 34 | it('should detect prime numbers', () => { 35 | primalityTest(trialDivision); 36 | }); 37 | }); 38 | -------------------------------------------------------------------------------- /src/algorithms/graph/travelling-salesman/README.md: -------------------------------------------------------------------------------- 1 | # Travelling Salesman Problem 2 | 3 | The travelling salesman problem (TSP) asks the following question: 4 | "Given a list of cities and the distances between each pair of 5 | cities, what is the shortest possible route that visits each city 6 | and returns to the origin city?" 7 | 8 | ![Travelling Salesman](https://upload.wikimedia.org/wikipedia/commons/1/11/GLPK_solution_of_a_travelling_salesman_problem.svg) 9 | 10 | Solution of a travelling salesman problem: the black line shows 11 | the shortest possible loop that connects every red dot. 12 | 13 | ![Travelling Salesman Graph](https://upload.wikimedia.org/wikipedia/commons/3/30/Weighted_K4.svg) 14 | 15 | TSP can be modelled as an undirected weighted graph, such that 16 | cities are the graph's vertices, paths are the graph's edges, 17 | and a path's distance is the edge's weight. It is a minimization 18 | problem starting and finishing at a specified vertex after having 19 | visited each other vertex exactly once. Often, the model is a 20 | complete graph (i.e. each pair of vertices is connected by an 21 | edge). If no path exists between two cities, adding an arbitrarily 22 | long edge will complete the graph without affecting the optimal tour. 23 | 24 | ## References 25 | 26 | - [Wikipedia](https://en.wikipedia.org/wiki/Travelling_salesman_problem) 27 | -------------------------------------------------------------------------------- /src/algorithms/uncategorized/rain-terraces/bfRainTerraces.js: -------------------------------------------------------------------------------- 1 | /** 2 | * BRUTE FORCE approach of solving Trapping Rain Water problem. 3 | * 4 | * @param {number[]} terraces 5 | * @return {number} 6 | */ 7 | export default function bfRainTerraces(terraces) { 8 | let waterAmount = 0; 9 | 10 | for (let terraceIndex = 0; terraceIndex < terraces.length; terraceIndex += 1) { 11 | // Get left most high terrace. 12 | let leftHighestLevel = 0; 13 | for (let leftIndex = terraceIndex - 1; leftIndex >= 0; leftIndex -= 1) { 14 | leftHighestLevel = Math.max(leftHighestLevel, terraces[leftIndex]); 15 | } 16 | 17 | // Get right most high terrace. 18 | let rightHighestLevel = 0; 19 | for (let rightIndex = terraceIndex + 1; rightIndex < terraces.length; rightIndex += 1) { 20 | rightHighestLevel = Math.max(rightHighestLevel, terraces[rightIndex]); 21 | } 22 | 23 | // Add current terrace water amount. 24 | const terraceBoundaryLevel = Math.min(leftHighestLevel, rightHighestLevel); 25 | if (terraceBoundaryLevel > terraces[terraceIndex]) { 26 | // Terrace will be able to store the water if the lowest of two left and right highest 27 | // terraces are still higher than the current one. 28 | waterAmount += terraceBoundaryLevel - terraces[terraceIndex]; 29 | } 30 | } 31 | 32 | return waterAmount; 33 | } 34 | -------------------------------------------------------------------------------- /src/algorithms/graph/detect-cycle/detectUndirectedCycleUsingDisjointSet.js: -------------------------------------------------------------------------------- 1 | import DisjointSet from '../../../data-structures/disjoint-set/DisjointSet'; 2 | 3 | /** 4 | * Detect cycle in undirected graph using disjoint sets. 5 | * 6 | * @param {Graph} graph 7 | */ 8 | export default function detectUndirectedCycleUsingDisjointSet(graph) { 9 | // Create initial singleton disjoint sets for each graph vertex. 10 | /** @param {GraphVertex} graphVertex */ 11 | const keyExtractor = (graphVertex) => graphVertex.getKey(); 12 | const disjointSet = new DisjointSet(keyExtractor); 13 | graph.getAllVertices().forEach((graphVertex) => disjointSet.makeSet(graphVertex)); 14 | 15 | // Go trough all graph edges one by one and check if edge vertices are from the 16 | // different sets. In this case joint those sets together. Do this until you find 17 | // an edge where to edge vertices are already in one set. This means that current 18 | // edge will create a cycle. 19 | let cycleFound = false; 20 | /** @param {GraphEdge} graphEdge */ 21 | graph.getAllEdges().forEach((graphEdge) => { 22 | if (disjointSet.inSameSet(graphEdge.startVertex, graphEdge.endVertex)) { 23 | // Cycle found. 24 | cycleFound = true; 25 | } else { 26 | disjointSet.union(graphEdge.startVertex, graphEdge.endVertex); 27 | } 28 | }); 29 | 30 | return cycleFound; 31 | } 32 | -------------------------------------------------------------------------------- /src/algorithms/math/bits/multiplyUnsigned.js: -------------------------------------------------------------------------------- 1 | /** 2 | * Multiply to unsigned numbers using bitwise operator. 3 | * 4 | * The main idea of bitwise multiplication is that every number may be split 5 | * to the sum of powers of two: 6 | * 7 | * I.e. 19 = 2^4 + 2^1 + 2^0 8 | * 9 | * Then multiplying number x by 19 is equivalent of: 10 | * 11 | * x * 19 = x * 2^4 + x * 2^1 + x * 2^0 12 | * 13 | * Now we need to remember that (x * 2^4) is equivalent of shifting x left by 4 bits (x << 4). 14 | * 15 | * @param {number} number1 16 | * @param {number} number2 17 | * @return {number} 18 | */ 19 | export default function multiplyUnsigned(number1, number2) { 20 | let result = 0; 21 | 22 | // Let's treat number2 as a multiplier for the number1. 23 | let multiplier = number2; 24 | 25 | // Multiplier current bit index. 26 | let bitIndex = 0; 27 | 28 | // Go through all bits of number2. 29 | while (multiplier !== 0) { 30 | // Check if current multiplier bit is set. 31 | if (multiplier & 1) { 32 | // In case if multiplier's bit at position bitIndex is set 33 | // it would mean that we need to multiply number1 by the power 34 | // of bit with index bitIndex and then add it to the result. 35 | result += (number1 << bitIndex); 36 | } 37 | 38 | bitIndex += 1; 39 | multiplier >>= 1; 40 | } 41 | 42 | return result; 43 | } 44 | -------------------------------------------------------------------------------- /src/data-structures/disjoint-set/README.ru-RU.md: -------------------------------------------------------------------------------- 1 | # Система непересекающихся множеств 2 | 3 | **Система непересекающихся множеств** это структура данных (также называемая структурой данной поиска пересечения или 4 | множеством поиска слияния), которая управляет множеством элементов, разбитых на несколько непересекающихся подмножеств. 5 | Она предоставляет около-константное время выполнения операций (ограниченное обратной функцией Акерманна) по *добавлению 6 | новых множеств*, *слиянию существующих множеств* и *опеределению, относятся ли элементы к одному и тому же множеству*. 7 | 8 | Применяется для хранения компонент связности в графах, в частности, алгоритму Краскала необходима подобная структура 9 | данных для эффективной реализации. 10 | 11 | Основные операции: 12 | 13 | - *MakeSet(x)* - создаёт одноэлементное множество {x}, 14 | - *Find(x)* - возвращает идентификатор множества, содержащего элемент x, 15 | - *Union(x,y)* - объединение множеств, содержащих x и y. 16 | 17 | После некоторых операций *объединения*, некоторые множества собраны вместе 18 | 19 | ## Ссылки 20 | - [СНМ на Wikipedia](https://ru.wikipedia.org/wiki/%D0%A1%D0%B8%D1%81%D1%82%D0%B5%D0%BC%D0%B0_%D0%BD%D0%B5%D0%BF%D0%B5%D1%80%D0%B5%D1%81%D0%B5%D0%BA%D0%B0%D1%8E%D1%89%D0%B8%D1%85%D1%81%D1%8F_%D0%BC%D0%BD%D0%BE%D0%B6%D0%B5%D1%81%D1%82%D0%B2) 21 | - [СНМ на YouTube](https://www.youtube.com/watch?v=bXBHYqNeBLo) 22 | -------------------------------------------------------------------------------- /src/data-structures/hash-table/README.md: -------------------------------------------------------------------------------- 1 | # Hash Table 2 | 3 | _Read this in other languages:_ 4 | [_简体中文_](README.zh-CN.md), 5 | [_Русский_](README.ru-RU.md), 6 | [_日本語_](README.ja-JP.md), 7 | [_Français_](README.fr-FR.md), 8 | [_Português_](README.pt-BR.md) 9 | 10 | In computing, a **hash table** (hash map) is a data 11 | structure which implements an *associative array* 12 | abstract data type, a structure that can *map keys 13 | to values*. A hash table uses a *hash function* to 14 | compute an index into an array of buckets or slots, 15 | from which the desired value can be found 16 | 17 | Ideally, the hash function will assign each key to a 18 | unique bucket, but most hash table designs employ an 19 | imperfect hash function, which might cause hash 20 | collisions where the hash function generates the same 21 | index for more than one key. Such collisions must be 22 | accommodated in some way. 23 | 24 | ![Hash Table](https://upload.wikimedia.org/wikipedia/commons/7/7d/Hash_table_3_1_1_0_1_0_0_SP.svg) 25 | 26 | Hash collision resolved by separate chaining. 27 | 28 | ![Hash Collision](https://upload.wikimedia.org/wikipedia/commons/d/d0/Hash_table_5_0_1_1_1_1_1_LL.svg) 29 | 30 | ## References 31 | 32 | - [Wikipedia](https://en.wikipedia.org/wiki/Hash_table) 33 | - [YouTube](https://www.youtube.com/watch?v=shs0KM3wKv8&index=4&list=PLLXdhg_r2hKA7DPDsunoDZ-Z769jWn4R8) 34 | -------------------------------------------------------------------------------- /src/data-structures/trie/README.md: -------------------------------------------------------------------------------- 1 | # Trie 2 | 3 | _Read this in other languages:_ 4 | [_简体中文_](README.zh-CN.md), 5 | [_Русский_](README.ru-RU.md), 6 | [_Português_](README.pt-BR.md) 7 | 8 | In computer science, a **trie**, also called digital tree and sometimes 9 | radix tree or prefix tree (as they can be searched by prefixes), 10 | is a kind of search tree—an ordered tree data structure that is 11 | used to store a dynamic set or associative array where the keys 12 | are usually strings. Unlike a binary search tree, no node in the 13 | tree stores the key associated with that node; instead, its 14 | position in the tree defines the key with which it is associated. 15 | All the descendants of a node have a common prefix of the string 16 | associated with that node, and the root is associated with the 17 | empty string. Values are not necessarily associated with every 18 | node. Rather, values tend only to be associated with leaves, 19 | and with some inner nodes that correspond to keys of interest. 20 | For the space-optimized presentation of prefix tree, see compact 21 | prefix tree. 22 | 23 | ![Trie](https://upload.wikimedia.org/wikipedia/commons/b/be/Trie_example.svg) 24 | 25 | ## References 26 | 27 | - [Wikipedia](https://en.wikipedia.org/wiki/Trie) 28 | - [YouTube](https://www.youtube.com/watch?v=zIjfhVPRZCg&list=PLLXdhg_r2hKA7DPDsunoDZ-Z769jWn4R8&index=7&t=0s) 29 | -------------------------------------------------------------------------------- /src/algorithms/ml/k-means/__test__/kMeans.test.js: -------------------------------------------------------------------------------- 1 | import KMeans from '../kMeans'; 2 | 3 | describe('kMeans', () => { 4 | it('should throw an error on invalid data', () => { 5 | expect(() => { 6 | KMeans(); 7 | }).toThrowError('The data is empty'); 8 | }); 9 | 10 | it('should throw an error on inconsistent data', () => { 11 | expect(() => { 12 | KMeans([[1, 2], [1]], 2); 13 | }).toThrowError('Matrices have different shapes'); 14 | }); 15 | 16 | it('should find the nearest neighbour', () => { 17 | const data = [[1, 1], [6, 2], [3, 3], [4, 5], [9, 2], [2, 4], [8, 7]]; 18 | const k = 2; 19 | const expectedClusters = [0, 1, 0, 1, 1, 0, 1]; 20 | expect(KMeans(data, k)).toEqual(expectedClusters); 21 | 22 | expect(KMeans([[0, 0], [0, 1], [10, 10]], 2)).toEqual( 23 | [0, 0, 1], 24 | ); 25 | }); 26 | 27 | it('should find the clusters with equal distances', () => { 28 | const dataSet = [[0, 0], [1, 1], [2, 2]]; 29 | const k = 3; 30 | const expectedCluster = [0, 1, 2]; 31 | expect(KMeans(dataSet, k)).toEqual(expectedCluster); 32 | }); 33 | 34 | it('should find the nearest neighbour in 3D space', () => { 35 | const dataSet = [[0, 0, 0], [0, 1, 0], [2, 0, 2]]; 36 | const k = 2; 37 | const expectedCluster = [1, 1, 0]; 38 | expect(KMeans(dataSet, k)).toEqual(expectedCluster); 39 | }); 40 | }); 41 | -------------------------------------------------------------------------------- /src/data-structures/hash-table/README.fr-FR.md: -------------------------------------------------------------------------------- 1 | # Table de hachage 2 | 3 | En informatique, une **table de hachage** (carte de 4 | hachage) est une structure de données qui implémente 5 | un type de données abstrait *tableau nassociatif*, 6 | une structure qui permet de *mapper des clés sur des 7 | valeurs*. Une table de hachage utilise une *fonction 8 | de hachage* pour calculer un index dans un tableau 9 | d'alvéoles (en anglais, buckets ou slots), à partir 10 | duquel la valeur souhaitée peut être trouvée. 11 | 12 | Idéalement, la fonction de hachage affectera chaque clé 13 | à une alvéole unique, mais la plupart des tables de 14 | hachage conçues emploient une fonction de hachage 15 | imparfaite, ce qui peut provoquer des collisions de 16 | hachage où la fonction de hachage génère le même index 17 | pour plusieurs clés. De telles collisions doivent être 18 | accommodées d'une manière ou d'une autre. 19 | 20 | ![Hash Table](https://upload.wikimedia.org/wikipedia/commons/7/7d/Hash_table_3_1_1_0_1_0_0_SP.svg) 21 | 22 | Collision de hachage résolue par chaînage séparé. 23 | 24 | ![Hash Collision](https://upload.wikimedia.org/wikipedia/commons/d/d0/Hash_table_5_0_1_1_1_1_1_LL.svg) 25 | 26 | ## Références 27 | 28 | - [Wikipedia](https://fr.wikipedia.org/wiki/Table_de_hachage) 29 | - [YouTube](https://www.youtube.com/watch?v=shs0KM3wKv8&index=4&list=PLLXdhg_r2hKA7DPDsunoDZ-Z769jWn4R8) 30 | -------------------------------------------------------------------------------- /src/algorithms/sorting/shell-sort/ShellSort.js: -------------------------------------------------------------------------------- 1 | import Sort from '../Sort'; 2 | 3 | export default class ShellSort extends Sort { 4 | sort(originalArray) { 5 | // Prevent original array from mutations. 6 | const array = [...originalArray]; 7 | 8 | // Define a gap distance. 9 | let gap = Math.floor(array.length / 2); 10 | 11 | // Until gap is bigger then zero do elements comparisons and swaps. 12 | while (gap > 0) { 13 | // Go and compare all distant element pairs. 14 | for (let i = 0; i < (array.length - gap); i += 1) { 15 | let currentIndex = i; 16 | let gapShiftedIndex = i + gap; 17 | 18 | while (currentIndex >= 0) { 19 | // Call visiting callback. 20 | this.callbacks.visitingCallback(array[currentIndex]); 21 | 22 | // Compare and swap array elements if needed. 23 | if (this.comparator.lessThan(array[gapShiftedIndex], array[currentIndex])) { 24 | const tmp = array[currentIndex]; 25 | array[currentIndex] = array[gapShiftedIndex]; 26 | array[gapShiftedIndex] = tmp; 27 | } 28 | 29 | gapShiftedIndex = currentIndex; 30 | currentIndex -= gap; 31 | } 32 | } 33 | 34 | // Shrink the gap. 35 | gap = Math.floor(gap / 2); 36 | } 37 | 38 | // Return sorted copy of an original array. 39 | return array; 40 | } 41 | } 42 | -------------------------------------------------------------------------------- /src/data-structures/disjoint-set/README.pt-BR.md: -------------------------------------------------------------------------------- 1 | # Conjunto Disjuntor (Disjoint Set) 2 | 3 | **Conjunto Disjuntor** 4 | 5 | **Conjunto Disjuntor** é uma estrutura de dados (também chamado de 6 | estrutura de dados de union–find ou merge–find) é uma estrutura de dados 7 | que rastreia um conjunto de elementos particionados em um número de 8 | subconjuntos separados (sem sobreposição). 9 | Ele fornece operações de tempo quase constante (limitadas pela função 10 | inversa de Ackermann) para *adicionar novos conjuntos*, para 11 | *mesclar/fundir conjuntos existentes* e para *determinar se os elementos 12 | estão no mesmo conjunto*. 13 | Além de muitos outros usos (veja a seção Applications), conjunto disjuntor 14 | desempenham um papel fundamental no algoritmo de Kruskal para encontrar a 15 | árvore geradora mínima de um gráfico (graph). 16 | 17 | ![disjoint set](https://upload.wikimedia.org/wikipedia/commons/6/67/Dsu_disjoint_sets_init.svg) 18 | 19 | *MakeSet* cria 8 singletons. 20 | 21 | ![disjoint set](https://upload.wikimedia.org/wikipedia/commons/a/ac/Dsu_disjoint_sets_final.svg) 22 | 23 | Depois de algumas operações de *Uniões*, alguns conjuntos são agrupados juntos. 24 | 25 | ## Referências 26 | 27 | - [Wikipedia](https://en.wikipedia.org/wiki/Disjoint-set_data_structure) 28 | - [By Abdul Bari on YouTube](https://www.youtube.com/watch?v=wU6udHRIkcc&index=14&t=0s&list=PLLXdhg_r2hKA7DPDsunoDZ-Z769jWn4R8) 29 | -------------------------------------------------------------------------------- /src/data-structures/stack/README.fr-FR.md: -------------------------------------------------------------------------------- 1 | # Pile 2 | 3 | En informatique, une **pile** est un type de données abstrait 4 | qui sert de collection d'éléments, avec deux opérations principales: 5 | 6 | * **empiler** (en anglais *push*), qui ajoute un élément à la collection, et 7 | * **dépiler** (en anglais *pop*), qui supprime l'élément le plus récemment 8 | ajouté qui n'a pas encore été supprimé. 9 | 10 | L'ordre dans lequel les éléments sortent d'une pile donne 11 | lieu à son nom alternatif, LIFO ("last in, first out", 12 | littéralement "dernier arrivé, premier sorti"). En outre, 13 | une opération d'aperçu peut donner accès au sommet sans 14 | modifier la pile. Le nom "pile" pour ce type de structure 15 | vient de l'analogie avec un ensemble d'éléments physiques empilés 16 | les uns sur les autres, ce qui permet de retirer facilement un 17 | élément du haut de la pile, tout comme accéder à un élément plus 18 | profond dans le la pile peut nécessiter de retirer plusieurs 19 | autres articles en premier. 20 | 21 | Représentation simple de l'éxecution d'une pile avec des opérations empiler (push) et dépiler (pop). 22 | 23 | ![Stack](https://upload.wikimedia.org/wikipedia/commons/b/b4/Lifo_stack.png) 24 | 25 | ## Références 26 | 27 | - [Wikipedia](https://fr.wikipedia.org/wiki/Pile_(informatique)) 28 | - [YouTube](https://www.youtube.com/watch?v=wjI1WNcIntg&list=PLLXdhg_r2hKA7DPDsunoDZ-Z769jWn4R8&index=3&) 29 | -------------------------------------------------------------------------------- /src/data-structures/graph/README.pt-BR.md: -------------------------------------------------------------------------------- 1 | # Grafo (Graph) 2 | 3 | Na ciência da computação, um **grafo** é uma abstração de estrutura 4 | de dados que se destina a implementar os conceitos da matemática de 5 | grafos direcionados e não direcionados, especificamente o campo da 6 | teoria dos grafos. 7 | 8 | Uma estrutura de dados grafos consiste em um finito (e possivelmente 9 | mutável) conjunto de vértices, nós ou pontos, juntos com um 10 | conjunto de pares não ordenados desses vértices para um grafo não 11 | direcionado ou para um conjunto de pares ordenados para um grafo 12 | direcionado. Esses pares são conhecidos como arestas, arcos 13 | ou linhas diretas para um grafo não direcionado e como setas, 14 | arestas direcionadas, arcos direcionados ou linhas direcionadas 15 | para um grafo direcionado. 16 | 17 | Os vértices podem fazer parte a estrutura do grafo, ou podem 18 | ser entidades externas representadas por índices inteiros ou referências. 19 | 20 | ![Graph](https://www.tutorialspoint.com/data_structures_algorithms/images/graph.jpg) 21 | 22 | ## Referências 23 | 24 | - [Wikipedia](https://en.wikipedia.org/wiki/Graph_(abstract_data_type)) 25 | - [Introduction to Graphs on YouTube](https://www.youtube.com/watch?v=gXgEDyodOJU&index=9&list=PLLXdhg_r2hKA7DPDsunoDZ-Z769jWn4R8) 26 | - [Graphs representation on YouTube](https://www.youtube.com/watch?v=k1wraWzqtvQ&index=10&list=PLLXdhg_r2hKA7DPDsunoDZ-Z769jWn4R8) 27 | -------------------------------------------------------------------------------- /src/algorithms/search/jump-search/README.md: -------------------------------------------------------------------------------- 1 | # Jump Search 2 | 3 | Like Binary Search, **Jump Search** (or **Block Search**) is a searching algorithm 4 | for sorted arrays. The basic idea is to check fewer elements (than linear search) 5 | by jumping ahead by fixed steps or skipping some elements in place of searching all 6 | elements. 7 | 8 | For example, suppose we have an array `arr[]` of size `n` and block (to be jumped) 9 | of size `m`. Then we search at the indexes `arr[0]`, `arr[m]`, `arr[2 * m]`, ..., `arr[k * m]` and 10 | so on. Once we find the interval `arr[k * m] < x < arr[(k+1) * m]`, we perform a 11 | linear search operation from the index `k * m` to find the element `x`. 12 | 13 | **What is the optimal block size to be skipped?** 14 | In the worst case, we have to do `n/m` jumps and if the last checked value is 15 | greater than the element to be searched for, we perform `m - 1` comparisons more 16 | for linear search. Therefore the total number of comparisons in the worst case 17 | will be `((n/m) + m - 1)`. The value of the function `((n/m) + m - 1)` will be 18 | minimum when `m = √n`. Therefore, the best step size is `m = √n`. 19 | 20 | ## Complexity 21 | 22 | **Time complexity**: `O(√n)` - because we do search by blocks of size `√n`. 23 | 24 | ## References 25 | 26 | - [GeeksForGeeks](https://www.geeksforgeeks.org/jump-search/) 27 | - [Wikipedia](https://en.wikipedia.org/wiki/Jump_search) 28 | -------------------------------------------------------------------------------- /src/algorithms/uncategorized/hanoi-tower/README.md: -------------------------------------------------------------------------------- 1 | # Tower of Hanoi 2 | 3 | The Tower of Hanoi (also called the Tower of Brahma or Lucas' 4 | Tower and sometimes pluralized) is a mathematical game or puzzle. 5 | It consists of three rods and a number of disks of different sizes, 6 | which can slide onto any rod. The puzzle starts with the disks in 7 | a neat stack in ascending order of size on one rod, the smallest 8 | at the top, thus making a conical shape. 9 | 10 | The objective of the puzzle is to move the entire stack to another 11 | rod, obeying the following simple rules: 12 | 13 | - Only one disk can be moved at a time. 14 | - Each move consists of taking the upper disk from one of the 15 | stacks and placing it on top of another stack or on an empty rod. 16 | - No disk may be placed on top of a smaller disk. 17 | 18 | ![Hanoi Tower](https://upload.wikimedia.org/wikipedia/commons/8/8d/Iterative_algorithm_solving_a_6_disks_Tower_of_Hanoi.gif) 19 | 20 | Animation of an iterative algorithm solving 6-disk problem 21 | 22 | With `3` disks, the puzzle can be solved in `7` moves. The minimal 23 | number of moves required to solve a Tower of Hanoi puzzle 24 | is `2^n − 1`, where `n` is the number of disks. 25 | 26 | ## References 27 | 28 | - [Wikipedia](https://en.wikipedia.org/wiki/Tower_of_Hanoi) 29 | - [HackerEarth](https://www.hackerearth.com/blog/algorithms/tower-hanoi-recursion-game-algorithm-explained/) 30 | -------------------------------------------------------------------------------- /jest.config.js: -------------------------------------------------------------------------------- 1 | module.exports = { 2 | // The bail config option can be used here to have Jest stop running tests after 3 | // the first failure. 4 | bail: false, 5 | 6 | // Indicates whether each individual test should be reported during the run. 7 | verbose: false, 8 | 9 | // Indicates whether the coverage information should be collected while executing the test 10 | collectCoverage: false, 11 | 12 | // The directory where Jest should output its coverage files. 13 | coverageDirectory: './coverage/', 14 | 15 | // If the test path matches any of the patterns, it will be skipped. 16 | testPathIgnorePatterns: ['/node_modules/'], 17 | 18 | // If the file path matches any of the patterns, coverage information will be skipped. 19 | coveragePathIgnorePatterns: ['/node_modules/'], 20 | 21 | // The pattern Jest uses to detect test files. 22 | testRegex: '(/__tests__/.*|(\\.|/)(test|spec))\\.jsx?$', 23 | 24 | // This option sets the URL for the jsdom environment. 25 | // It is reflected in properties such as location.href. 26 | // @see: https://github.com/facebook/jest/issues/6769 27 | testURL: 'http://localhost/', 28 | 29 | // @see: https://jestjs.io/docs/en/configuration#coveragethreshold-object 30 | coverageThreshold: { 31 | global: { 32 | statements: 100, 33 | branches: 95, 34 | functions: 100, 35 | lines: 100, 36 | }, 37 | }, 38 | }; 39 | -------------------------------------------------------------------------------- /src/data-structures/graph/README.md: -------------------------------------------------------------------------------- 1 | # Graph 2 | 3 | _Read this in other languages:_ 4 | [_简体中文_](README.zh-CN.md), 5 | [_Русский_](README.ru-RU.md), 6 | [_Português_](README.pt-BR.md) 7 | 8 | In computer science, a **graph** is an abstract data type 9 | that is meant to implement the undirected graph and 10 | directed graph concepts from mathematics, specifically 11 | the field of graph theory 12 | 13 | A graph data structure consists of a finite (and possibly 14 | mutable) set of vertices or nodes or points, together 15 | with a set of unordered pairs of these vertices for an 16 | undirected graph or a set of ordered pairs for a 17 | directed graph. These pairs are known as edges, arcs, 18 | or lines for an undirected graph and as arrows, 19 | directed edges, directed arcs, or directed lines 20 | for a directed graph. The vertices may be part of 21 | the graph structure, or may be external entities 22 | represented by integer indices or references. 23 | 24 | ![Graph](https://www.tutorialspoint.com/data_structures_algorithms/images/graph.jpg) 25 | 26 | ## References 27 | 28 | - [Wikipedia](https://en.wikipedia.org/wiki/Graph_(abstract_data_type)) 29 | - [Introduction to Graphs on YouTube](https://www.youtube.com/watch?v=gXgEDyodOJU&index=9&list=PLLXdhg_r2hKA7DPDsunoDZ-Z769jWn4R8) 30 | - [Graphs representation on YouTube](https://www.youtube.com/watch?v=k1wraWzqtvQ&index=10&list=PLLXdhg_r2hKA7DPDsunoDZ-Z769jWn4R8) 31 | --------------------------------------------------------------------------------