countS, countT;
28 | for (int i = 0; i < s.size(); i++) {
29 | countS[s[i]]++;
30 | countT[t[i]]++;
31 | }
32 | return countS == countT;
33 | }
34 | };
35 |
--------------------------------------------------------------------------------
/Level 1/Week 04/Trees/110. Balanced Binary Tree/README.md:
--------------------------------------------------------------------------------
1 | Easy
Given a binary tree, determine if it is height-balanced.
2 |
3 |
4 | Example 1:
5 |  6 |
6 |
7 | Input: root = [3,9,20,null,null,15,7]
8 | Output: true
9 |
10 |
11 | Example 2:
12 |  13 |
13 |
14 | Input: root = [1,2,2,3,3,null,null,4,4]
15 | Output: false
16 |
17 |
18 | Example 3:
19 |
20 |
21 | Input: root = []
22 | Output: true
23 |
24 |
25 |
26 | Constraints:
27 |
28 |
29 | - The number of nodes in the tree is in the range
[0, 5000].
30 | -104 <= Node.val <= 104
32 |
--------------------------------------------------------------------------------
/Level 1/Week 06/Stack/739. Daily Temperatures/README.md:
--------------------------------------------------------------------------------
1 | Medium
Given an array of integers temperatures represents the daily temperatures, return an array answer such that answer[i] is the number of days you have to wait after the ith day to get a warmer temperature. If there is no future day for which this is possible, keep answer[i] == 0 instead.
2 |
3 |
4 | Example 1:
5 | Input: temperatures = [73,74,75,71,69,72,76,73]
6 | Output: [1,1,4,2,1,1,0,0]
7 |
Example 2:
8 | Input: temperatures = [30,40,50,60]
9 | Output: [1,1,1,0]
10 |
Example 3:
11 | Input: temperatures = [30,60,90]
12 | Output: [1,1,0]
13 |
14 |
15 | Constraints:
16 |
17 |
18 | 1 <= temperatures.length <= 10530 <= temperatures[i] <= 100
21 |
--------------------------------------------------------------------------------
/Level 0/7 Sliding Window/03. 0219-contains-duplicate-ii/README.md:
--------------------------------------------------------------------------------
1 | Easy
Given an integer array nums and an integer k, return true if there are two distinct indices i and j in the array such that nums[i] == nums[j] and abs(i - j) <= k.
2 |
3 |
4 | Example 1:
5 |
6 |
7 | Input: nums = [1,2,3,1], k = 3
8 | Output: true
9 |
10 |
11 | Example 2:
12 |
13 |
14 | Input: nums = [1,0,1,1], k = 1
15 | Output: true
16 |
17 |
18 | Example 3:
19 |
20 |
21 | Input: nums = [1,2,3,1,2,3], k = 2
22 | Output: false
23 |
24 |
25 |
26 | Constraints:
27 |
28 |
29 | 1 <= nums.length <= 105-109 <= nums[i] <= 1090 <= k <= 105
33 |
--------------------------------------------------------------------------------
/Level 1/Week 11/Dynamic Programming/322. Coin Change/README.md:
--------------------------------------------------------------------------------
1 | # Coin Change
2 |
3 | **Difficulty:** Medium
4 |
5 | ## Problem Description
6 |
7 | You are given an integer array `coins` representing coins of different denominations and an integer `amount` representing a total amount of money.
8 |
9 | Return the fewest number of coins that you need to make up that amount. If that amount of money cannot be made up by any combination of the coins, return `-1`.
10 |
11 | You may assume that you have an infinite number of each kind of coin.
12 |
13 | ---
14 |
15 | ## Examples
16 |
17 | ### Example 1
18 | Input: coins = [1,3,4], amount = 6
19 | Output: 2
20 | Explanation: 6 = 3 + 3
21 |
22 | ### Example 2
23 | Input: coins = [2], amount = 3
24 | Output: -1
25 |
26 | ### Example 3
27 | Input: coins = [1], amount = 0
28 | Output: 0
29 |
30 | ---
31 |
32 | ## Constraints
33 |
34 | - `1 <= coins.length <= 12`
35 | - `1 <= coins[i] <= 2^31 - 1`
36 | - `0 <= amount <= 10^4`
37 |
38 | ---
39 |
40 | ## Approaches
41 |
42 | This problem can be solved using 4 different dynamic programming approaches:
43 |
44 | 1. **Recursion** - Direct recursive implementation
45 | 2. **Memoization** - Top-down DP with caching
46 | 3. **Tabulation** - Bottom-up DP with array
47 | 4. **Space Optimization** - Optimized space complexity
48 |
49 | ---
50 |
--------------------------------------------------------------------------------
/Level 1/Week 02/Sliding windows/219. Contains Duplicate II/README.md:
--------------------------------------------------------------------------------
1 | Easy
Given an integer array nums and an integer k, return true if there are two distinct indices i and j in the array such that nums[i] == nums[j] and abs(i - j) <= k.
2 |
3 |
4 | Example 1:
5 |
6 |
7 | Input: nums = [1,2,3,1], k = 3
8 | Output: true
9 |
10 |
11 | Example 2:
12 |
13 |
14 | Input: nums = [1,0,1,1], k = 1
15 | Output: true
16 |
17 |
18 | Example 3:
19 |
20 |
21 | Input: nums = [1,2,3,1,2,3], k = 2
22 | Output: false
23 |
24 |
25 |
26 | Constraints:
27 |
28 |
29 | 1 <= nums.length <= 105-109 <= nums[i] <= 1090 <= k <= 105
33 |
--------------------------------------------------------------------------------
/Level 1/Week 12/Graph/130. Surrounded Regions/README.md:
--------------------------------------------------------------------------------
1 | # Surrounded Regions
2 |
3 | **Difficulty:** Medium
4 |
5 | ## Problem Description
6 |
7 | Given an `m x n` matrix `board` containing `'X'` and `'O'`, *capture all regions that are 4-directionally surrounded by* `'X'`.
8 |
9 | A region is **captured** by flipping all `'O'`'s into `'X'`'s in that surrounded region.
10 |
11 | ---
12 |
13 | ## Examples
14 |
15 | ### Example 1
16 | Input: board = [["X","X","X","X"],["X","O","O","X"],["X","X","O","X"],["X","O","X","X"]]
17 | Output: [["X","X","X","X"],["X","X","X","X"],["X","X","X","X"],["X","O","X","X"]]
18 |
19 | ### Example 2
20 | Input: board = [["X"]]
21 | Output: [["X"]]
22 |
23 | ---
24 |
25 | ## Constraints
26 |
27 | - `m == board.length`
28 | - `n == board[i].length`
29 | - `1 <= m, n <= 200`
30 | - `board[i][j]` is `'X'` or `'O'`.
31 |
32 | ---
33 |
34 | ## Approach
35 |
36 | This problem can be solved using DFS from the boundaries:
37 | 1. Start DFS from all 'O' cells on the boundaries
38 | 2. Mark all 'O' cells that are connected to boundaries as safe
39 | 3. Flip all remaining 'O' cells to 'X'
40 | 4. The key insight is to work backwards from the boundaries
41 |
42 | The key insight is that only 'O' cells connected to boundaries cannot be surrounded, so we mark them as safe and flip the rest.
43 |
44 | ---
45 |
--------------------------------------------------------------------------------
/Level 0/8 Trees/09. 0105-construct-binary-tree-from-preorder-and-inorder-traversal/README.md:
--------------------------------------------------------------------------------
1 | # 105. Construct Binary Tree from Preorder and Inorder Traversal
2 |
3 | ## Problem Description
4 |
5 | Given two integer arrays `preorder` and `inorder` where `preorder` is the preorder traversal of a binary tree and `inorder` is the inorder traversal of the same tree, construct and return *the binary tree*.
6 |
7 | ## Examples
8 |
9 | ### Example 1:
10 | 
11 |
12 | **Input:** `preorder = [3,9,20,15,7], inorder = [9,3,15,20,7]`
13 |
14 | **Output:** `[3,9,20,null,null,15,7]`
15 |
16 | ### Example 2:
17 |
18 | **Input:** `preorder = [-1], inorder = [-1]`
19 |
20 | **Output:** `[-1]`
21 |
22 | ## Constraints
23 |
24 | - `1 <= preorder.length <= 3000`
25 | - `inorder.length == preorder.length`
26 | - `-3000 <= preorder[i], inorder[i] <= 3000`
27 | - `preorder` and `inorder` consist of **unique** values.
28 | - Each value of `inorder` also appears in `preorder`.
29 | - `preorder` is **guaranteed** to be the preorder traversal of the tree.
30 | - `inorder` is **guaranteed** to be the inorder traversal of the tree.
31 |
32 | ## Related Topics
33 |
34 | - Array
35 | - Hash Table
36 | - Divide and Conquer
37 | - Tree
38 | - Binary Tree
39 |
40 | ## Difficulty
41 |
42 | Medium
43 |
--------------------------------------------------------------------------------
/Level 1/Week 02/2 pointers/2824. Count Pairs Whose Sum is Less than Target/code.cpp:
--------------------------------------------------------------------------------
1 | // ✅ Approach: Two Pointer Technique
2 | //
3 | // 1. Sort the array to make it easier to apply the two-pointer strategy.
4 | // 2. Use two pointers:
5 | // - l = 0 (left/start of array)
6 | // - r = nums.size() - 1 (right/end of array)
7 | // 3. While l < r:
8 | // - If nums[l] + nums[r] < target, it means all elements from l to r-1
9 | // will also form valid pairs with nums[l] (since the array is sorted).
10 | // So we add (r - l) to the count and move l++.
11 | // - If the sum is greater than or equal to target, we move r-- to try smaller values.
12 | // 4. This avoids checking all pairs explicitly and improves efficiency.
13 | //
14 | // ✅ Time Complexity: O(n log n) due to sorting
15 | // ✅ Space Complexity: O(1) — constant extra space
16 |
17 | class Solution {
18 | public:
19 | int countPairs(vector& nums, int target) {
20 | sort(nums.begin(), nums.end());
21 | int l = 0;
22 | int r = nums.size() - 1;
23 | int cnt = 0;
24 | while (l < r) {
25 | if (nums[l] + nums[r] < target) {
26 | cnt += r - l;
27 | l++;
28 | } else {
29 | r--;
30 | }
31 | }
32 | return cnt;
33 | }
34 | };
35 |
--------------------------------------------------------------------------------
/Level 1/Week 03/LinkedList/21. Merge Two Sorted Lists/code.cpp:
--------------------------------------------------------------------------------
1 | /**
2 | * Approach:
3 | * We use an **iterative two-pointer technique** to merge two sorted linked lists.
4 | * - Create a dummy node to serve as the start of the merged list.
5 | * - Use a pointer `cur` to build the new list by comparing the current nodes of `list1` and `list2`.
6 | * - At each step, attach the node with the smaller value to `cur->next`, then move the corresponding list forward.
7 | * - Continue this process until one of the lists becomes null.
8 | * - Finally, append the remaining part of the non-null list (if any) to `cur->next`.
9 | * - Return `dummy.next` which points to the head of the merged sorted list.
10 | */
11 |
12 | class Solution {
13 | public:
14 | ListNode* mergeTwoLists(ListNode* list1, ListNode* list2) {
15 | ListNode dummy(0);
16 | ListNode* cur = &dummy;
17 |
18 | while (list1 && list2) {
19 | if (list1->val < list2->val) {
20 | cur->next = list1;
21 | list1 = list1->next;
22 | } else {
23 | cur->next = list2;
24 | list2 = list2->next;
25 | }
26 | cur = cur->next;
27 | }
28 |
29 | cur->next = (list1 != nullptr) ? list1 : list2;
30 | return dummy.next;
31 | }
32 | };
33 |
--------------------------------------------------------------------------------
/Common/Math/Odd/README.md:
--------------------------------------------------------------------------------
1 | # 🔢 Check if a Number is Odd – C++ Solutions
2 |
3 | ### 💡 What is an Odd Number?
4 |
5 | An **odd number** is any number that **cannot be divided evenly by 2**.
6 | This means there will always be a **remainder of 1** when you divide it by 2.
7 |
8 | 🧠 Examples:
9 | - 3 → 3 % 2 = 1 ✅ Odd
10 | - 6 → 6 % 2 = 0 ❌ Not Odd
11 |
12 | ---
13 |
14 | ## 📘 What’s Inside This File?
15 |
16 | This program explores **four different ways** to check if a number is odd in C++.
17 |
18 | | Approach | Description |
19 | |---------|-------------|
20 | | 1 | Using modulo `%` operator |
21 | | 2 | Using bitwise AND `&` to inspect binary form |
22 | | 3 | Using integer division and reverse calculation |
23 | | 4 | Recursive subtraction down to 0 or 1 |
24 |
25 | ---
26 |
27 | ## 🗂 File Structure
28 |
29 | Odd/
30 | │
31 | ├── odd_number.cpp # All approaches with full comments
32 | ├── README.md # This file
33 |
34 | └── Makefile # Build and run commands
35 | ---
36 |
37 | ## 🔍 Sample Usage
38 |
39 | ```cpp
40 | #include
41 | using namespace std;
42 |
43 | int main() {
44 | int n = 7;
45 |
46 | if (odd(n)) {
47 | cout << n << " is odd\n";
48 | } else {
49 | cout << n << " is even\n";
50 | }
51 |
52 | // Try others:
53 | // odd_bitwise(n), odd_division(n), odd_recursive(n)
54 | }
--------------------------------------------------------------------------------
/Level 0/1 Simulation - Strings/README.md:
--------------------------------------------------------------------------------
1 | ## 📚 List of Problems
2 |
3 | 1. [Jewels and Stones](https://leetcode.com/problems/jewels-and-stones/description/)
4 | 2. [Reverse String](https://leetcode.com/problems/reverse-string/description/)
5 | 3. [Merge Strings Alternately](https://leetcode.com/problems/merge-strings-alternately/description/)
6 | 4. [Fizz Buzz](https://leetcode.com/problems/fizz-buzz/description/)
7 | 5. [Valid Anagram](https://leetcode.com/problems/valid-anagram/description/)
8 | 6. [Reverse Vowels of a String](https://leetcode.com/problems/reverse-vowels-of-a-string/)
9 | 7. [Valid Palindrome](https://leetcode.com/problems/valid-palindrome/description/)
10 | 8. [Repeated Substring Pattern](https://leetcode.com/problems/repeated-substring-pattern/description/)
11 | 9. [Isomorphic Strings](https://leetcode.com/problems/isomorphic-strings/description/)
12 | 10. [Is Subsequence](https://leetcode.com/problems/is-subsequence/description/)
13 | 11. [Rotate String](https://leetcode.com/problems/rotate-string)
14 | ---
15 |
16 | ## 💡 Suggestions
17 |
18 | - Make sure to prepare your notes alongside solving each problem.
19 | - Don’t spend more than 30–40 minutes on a single problem.
20 | - If you’re stuck on a problem, search on YouTube using the problem number.
21 | - Try to solve a problem in multiple ways.
22 |
--------------------------------------------------------------------------------
/Level 0/8 Trees/02. 0572-subtree-of-another-tree/README.md:
--------------------------------------------------------------------------------
1 | # 572. Subtree of Another Tree
2 |
3 | ## Problem Description
4 |
5 | Given the roots of two binary trees `root` and `subRoot`, return `true` if there is a subtree of `root` with the same structure and node values of `subRoot` and `false` otherwise.
6 |
7 | A subtree of a binary tree `tree` is a tree that consists of a node in `tree` and all of this node's descendants. The tree `tree` could also be considered as a subtree of itself.
8 |
9 | ## Examples
10 |
11 | ### Example 1:
12 | 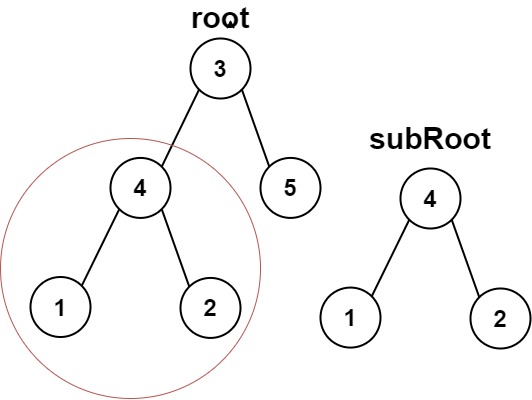
13 |
14 | **Input:** `root = [3,4,5,1,2], subRoot = [4,1,2]`
15 |
16 | **Output:** `true`
17 |
18 | ### Example 2:
19 | 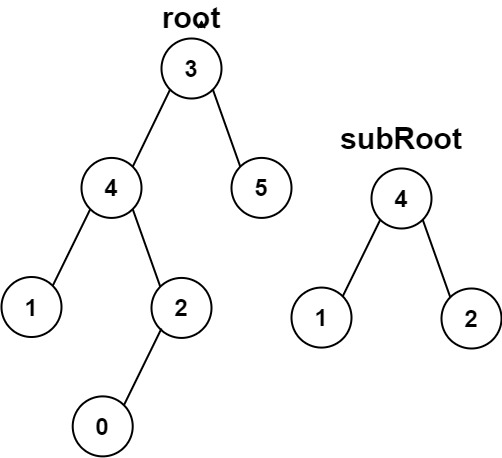
20 |
21 | **Input:** `root = [3,4,5,1,2,null,null,null,null,0], subRoot = [4,1,2]`
22 |
23 | **Output:** `false`
24 |
25 | ## Constraints
26 |
27 | - The number of nodes in the `root` tree is in the range `[1, 2000]`.
28 | - The number of nodes in the `subRoot` tree is in the range `[1, 1000]`.
29 | - `-10^4 <= root.val <= 10^4`
30 | - `-10^4 <= subRoot.val <= 10^4`
31 |
32 | ## Related Topics
33 |
34 | - Tree
35 | - Depth-First Search
36 | - String Matching
37 | - Binary Tree
38 | - Hash Function
39 |
40 | ## Difficulty
41 |
42 | Easy
43 |
--------------------------------------------------------------------------------
/Level 1/Week 04/Trees/104. Maximum Depth of Binary Tree/code.cpp:
--------------------------------------------------------------------------------
1 | /**
2 | * Approach:
3 | * The goal is to find the maximum depth (or height) of a binary tree.
4 | *
5 | * This is done using recursion (Depth-First Search):
6 | * 1. If the current node is NULL, return 0 (base case).
7 | * 2. Recursively find the maximum depth of the left and right subtrees.
8 | * 3. Return the greater of the two depths plus 1 (for the current node).
9 | *
10 | * Time Complexity: O(n), where n is the number of nodes in the tree (each node is visited once).
11 | * Space Complexity: O(h), where h is the height of the tree due to the recursion stack.
12 | */
13 |
14 | /**
15 | * Definition for a binary tree node.
16 | * struct TreeNode {
17 | * int val;
18 | * TreeNode *left;
19 | * TreeNode *right;
20 | * TreeNode() : val(0), left(nullptr), right(nullptr) {}
21 | * TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
22 | * TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
23 | * };
24 | */
25 | class Solution {
26 | public:
27 | int maxDepth(TreeNode* root) {
28 | if (root == NULL) {
29 | return 0;
30 | }
31 | int lefth = maxDepth(root->left);
32 | int righth = maxDepth(root->right);
33 | return max(lefth, righth) + 1;
34 | }
35 | };
36 |
--------------------------------------------------------------------------------
/Level 1/Week 06/Queue/862. Shortest Subarray with Sum at Least K/README.md:
--------------------------------------------------------------------------------
1 | Hard
Given an integer array nums and an integer k, return the length of the shortest non-empty subarray whose sum is at least k. If there is no such subarray, return -1.
2 |
3 | A subarray is a contiguous part of an array.
4 |
5 |
6 | Example 1:
7 |
8 |
9 | Input: nums = [1], k = 1
10 | Output: 1
11 |
12 |
13 | Example 2:
14 |
15 |
16 | Input: nums = [1,2], k = 4
17 | Output: -1
18 |
19 |
20 | Example 3:
21 |
22 |
23 | Input: nums = [2,-1,2], k = 3
24 | Output: 3
25 |
26 |
27 |
28 | Constraints:
29 |
30 |
31 | 1 <= nums.length <= 105-105 <= nums[i] <= 1051 <= k <= 109
--------------------------------------------------------------------------------
/Level 1/Week 10/Recursion/23. Merge k Sorted Lists/README.md:
--------------------------------------------------------------------------------
1 | # Merge k Sorted Lists
2 |
3 | **Difficulty:** Hard
4 |
5 | ## Problem Description
6 |
7 | You are given an array of `k` linked-lists `lists`, each linked-list is sorted in ascending order.
8 |
9 | *Merge all the linked-lists into one sorted linked-list and return it.*
10 |
11 | ---
12 |
13 | ## Examples
14 |
15 | ### Example 1
16 | Input: lists = [[1,4,5],[1,3,4],[2,6]]
17 | Output: [1,1,2,3,4,4,5,6]
18 |
19 | ### Example 2
20 | Input: lists = []
21 | Output: []
22 |
23 | ### Example 3
24 | Input: lists = [[]]
25 | Output: []
26 |
27 | ---
28 |
29 | ## Constraints
30 |
31 | - `k == lists.length`
32 | - `0 <= k <= 10^4`
33 | - `0 <= lists[i].length <= 500`
34 | - `-10^4 <= lists[i][j] <= 10^4`
35 | - `lists[i]` is sorted in **ascending order**.
36 | - The sum of `lists[i].length` will not exceed `10^4`.
37 |
38 | ---
39 |
40 | ## Approach
41 |
42 | This problem can be solved using divide and conquer with recursion:
43 | 1. Base case: if there are 0 or 1 lists, return the list or empty
44 | 2. Recursive case: divide the lists into two halves
45 | 3. Recursively merge each half
46 | 4. Merge the two merged halves using the two-list merge approach
47 | 5. Return the final merged list
48 |
49 | The recursive approach naturally breaks down the problem into smaller subproblems.
50 |
51 | ---
52 |
--------------------------------------------------------------------------------
/Level 1/Week 07/K way merge [Heaps]/Find Median from Data Stream/code.cpp:
--------------------------------------------------------------------------------
1 | /*
2 | Approach:
3 |
4 | Use two heaps:
5 | - Max heap for lower half
6 | - Min heap for upper half
7 |
8 | Balance the heaps so their sizes differ by at most one. Median is either the top of one heap or the average of the tops.
9 |
10 | Time Complexity: O(log n) per insertion, O(1) for median
11 | Space Complexity: O(n)
12 | */
13 |
14 | #include
15 | using namespace std;
16 |
17 | class MedianFinder {
18 | priority_queue maxHeap; // lower half
19 | priority_queue, greater> minHeap; // upper half
20 | public:
21 | MedianFinder() {}
22 | void addNum(int num) {
23 | if (maxHeap.empty() || num <= maxHeap.top()) {
24 | maxHeap.push(num);
25 | } else {
26 | minHeap.push(num);
27 | }
28 | // Balance
29 | if (maxHeap.size() > minHeap.size() + 1) {
30 | minHeap.push(maxHeap.top()); maxHeap.pop();
31 | } else if (minHeap.size() > maxHeap.size()) {
32 | maxHeap.push(minHeap.top()); minHeap.pop();
33 | }
34 | }
35 | double findMedian() {
36 | if (maxHeap.size() == minHeap.size()) {
37 | return (maxHeap.top() + minHeap.top()) / 2.0;
38 | } else {
39 | return maxHeap.top();
40 | }
41 | }
42 | };
--------------------------------------------------------------------------------
/Level 1/Week 09/Greedy/53. Maximum Subarray/code.cpp:
--------------------------------------------------------------------------------
1 | /*
2 | Approach: Kadane's Algorithm (Greedy)
3 |
4 | This is the classic maximum subarray problem that can be solved using Kadane's algorithm.
5 | The greedy approach is to keep a running sum and reset it to the current element
6 | when it becomes negative, as a negative prefix would only decrease the sum.
7 |
8 | Algorithm:
9 | 1. Initialize maxSum to the first element and currentMax to 0
10 | 2. For each element:
11 | - If currentMax is negative, start a new subarray from current element
12 | - Otherwise, extend the current subarray by adding current element
13 | - Update maxSum if currentMax is greater
14 |
15 | Time Complexity: O(n)
16 | Space Complexity: O(1)
17 | */
18 |
19 | #include
20 | #include
21 | using namespace std;
22 |
23 | class Solution {
24 | public:
25 | int maxSubArray(vector& nums) {
26 | int maxSum = nums[0];
27 | int currentMax = 0;
28 |
29 | for (int i = 0; i < nums.size(); i++){
30 | if (currentMax < 0){
31 | currentMax = nums[i];
32 | } else {
33 | currentMax = nums[i] + currentMax;
34 | }
35 |
36 | if (currentMax > maxSum){
37 | maxSum = currentMax;
38 | }
39 | }
40 | return maxSum;
41 | }
42 | };
43 |
--------------------------------------------------------------------------------
/Common/Math/Even/README.md:
--------------------------------------------------------------------------------
1 | # 🔢 Check if a Number is Even – C++ Solutions
2 |
3 | ### 💡 What is an Even Number?
4 |
5 | An **even number** is a number that can be **divided by 2 without any remainder**.
6 | In other words, if you divide it by 2 and there's nothing left over, it’s even.
7 |
8 | 🧠 Examples:
9 | - 4 → 4 % 2 = 0 ✅ Even
10 | - 9 → 9 % 2 = 1 ❌ Not Even
11 |
12 | ---
13 |
14 | ## 📘 What’s Inside This File?
15 |
16 | This program demonstrates **four different approaches** to check if a number is even in C++.
17 |
18 | | Approach | Description |
19 | |---------|-------------|
20 | | 1 | Using modulo (`%`) operator |
21 | | 2 | Using bitwise AND (`&`) to check the least significant bit |
22 | | 3 | Using integer division logic |
23 | | 4 | Recursive subtraction method |
24 |
25 | ---
26 |
27 | ## 🗂 File Structure
28 |
29 | Even/
30 | │
31 | ├── even_number.cpp # All approaches with comments
32 | ├── README.md # This file
33 |
34 | └── Makefile # Build and run the program
35 | ---
36 |
37 | ## 🔍 Sample Usage
38 |
39 | ```cpp
40 | #include
41 | using namespace std;
42 |
43 | int main() {
44 | int n = 10;
45 |
46 | if (even(n)) {
47 | cout << n << " is even\n";
48 | } else {
49 | cout << n << " is odd\n";
50 | }
51 |
52 | // Try others:
53 | // even_bitwise(n), even_division(n), even_recursive(n)
54 | }
--------------------------------------------------------------------------------
/Level 1/Week 02/2 pointers/26. Remove Duplicates from Sorted Array/code.cpp:
--------------------------------------------------------------------------------
1 | /*
2 | ✅ Approach: Two Pointer Technique
3 |
4 | We're given a **sorted array**, and we need to **remove duplicates in-place**, returning the length of the new array with unique elements at the beginning.
5 |
6 | 💡 Why Two Pointers?
7 | Since the array is sorted, all duplicates will be **next to each other**.
8 | We can use two pointers:
9 | - `i` → Points to the **last unique element** found
10 | - `j` → Goes through the array to find **new unique elements**
11 |
12 | 🔄 How it works:
13 | 1. Start with `i = 0` (first element is always unique)
14 | 2. Move `j` from index 1 to end:
15 | - If `nums[j] != nums[i]`, it means a new unique element is found
16 | - So, place it at `i+1`, and move `i` forward
17 | 3. Finally, return `i + 1` as the count of unique elements
18 |
19 | ✅ This modifies the input array to have all unique elements at the start.
20 | 📦 Time: O(n), Space: O(1) — done in-place without extra space.
21 | */
22 | class Solution {
23 | public:
24 | int removeDuplicates(vector& nums) {
25 | int n = nums.size();
26 | int i =0;
27 | for(int j = i+1 ; j
20 | using namespace std;
21 |
22 | class Solution {
23 | public:
24 | int canCompleteCircuit(vector& gas, vector& cost) {
25 | int n = gas.size();
26 | int totalTank = 0;
27 | int currentTank = 0;
28 | int startingStation = 0;
29 |
30 | for (int i = 0; i < n; i++) {
31 | totalTank += gas[i] - cost[i];
32 | currentTank += gas[i] - cost[i];
33 |
34 | if (currentTank < 0) {
35 | startingStation = i + 1;
36 | currentTank = 0;
37 | }
38 | }
39 |
40 | return totalTank >= 0 ? startingStation : -1;
41 | }
42 | };
43 |
--------------------------------------------------------------------------------
/Level 0/0 Simulation - Arrays/README.md:
--------------------------------------------------------------------------------
1 | ## 📚 List of Problems
2 |
3 | 1. [Running Sum of 1d Array](https://leetcode.com/problems/running-sum-of-1d-array/description/)
4 | 2. [Find the Highest Altitude](https://leetcode.com/problems/find-the-highest-altitude/)
5 | 3. [Final Value of Variable After Performing Operations](https://leetcode.com/problems/final-value-of-variable-after-performing-operations/description/)
6 | 4. [Squares of a Sorted Array](https://leetcode.com/problems/squares-of-a-sorted-array/description/)
7 | 5. [Concatenation of Array](https://leetcode.com/problems/concatenation-of-array/)
8 | 6. [Number of Good Pairs](https://leetcode.com/problems/number-of-good-pairs/description/)
9 | 7. [Shuffle the Array](https://leetcode.com/problems/shuffle-the-array/description/)
10 | 8. [Move Zeroes](https://leetcode.com/problems/move-zeroes/description/)
11 | 9. [Maximum Consecutive Ones](https://leetcode.com/problems/max-consecutive-ones/)
12 | 10. [Left Rotate an array by one place](https://leetcode.com/problems/rotate-array/)
13 |
14 | ---
15 |
16 | ## 💡 Suggestions
17 |
18 | - Make sure to prepare your notes alongside solving each problem.
19 | - Don’t spend more than 30–40 minutes on a single problem.
20 | - If you’re stuck on a problem, search on YouTube using the problem number.
21 | - Try to solve a problem in multiple ways.
22 |
--------------------------------------------------------------------------------
/Level 0/10 Backtracking/05. 090-subsets-ii/code.cpp:
--------------------------------------------------------------------------------
1 | class Solution {
2 | private:
3 | vector> result;
4 |
5 | void backtrack(vector& nums, vector& current, int start) {
6 | // Add current subset to result
7 | result.push_back(current);
8 |
9 | // Try all possible elements starting from 'start'
10 | for (int i = start; i < nums.size(); i++) {
11 | // Skip duplicates at the same level to avoid duplicate subsets
12 | if (i > start && nums[i] == nums[i-1]) {
13 | continue;
14 | }
15 |
16 | // Make choice: include nums[i]
17 | current.push_back(nums[i]);
18 |
19 | // Recurse with next element
20 | backtrack(nums, current, i + 1);
21 |
22 | // Backtrack: remove nums[i]
23 | current.pop_back();
24 | }
25 | }
26 |
27 | public:
28 | vector> subsetsWithDup(vector& nums) {
29 | // Sort nums to handle duplicates efficiently
30 | sort(nums.begin(), nums.end());
31 |
32 | vector current;
33 | backtrack(nums, current, 0);
34 | return result;
35 | }
36 | };
37 |
38 | /*
39 | Time Complexity: O(2^n) where n is the length of nums
40 | Space Complexity: O(n) for recursion stack
41 | */
--------------------------------------------------------------------------------
/Level 1/Week 02/Sliding windows/3. Longest Substring Without Repeating Characters/code.cpp:
--------------------------------------------------------------------------------
1 | /*
2 | Approach (Sliding Window + HashSet):
3 |
4 | We aim to find the length of the longest substring without repeating characters.
5 |
6 | ⚙️ Logic:
7 | 1. Use a sliding window with two pointers: `left` and `right`.
8 | 2. Maintain a hash set to track characters in the current window.
9 | 3. As you expand `right`, check if `s[right]` is already in the window:
10 | - If it is, shrink the window from the left by removing `s[left]` until it's unique again.
11 | 4. Update `maxLen` with the size of the current valid window.
12 |
13 | ✅ Time Complexity: O(n)
14 | ✅ Space Complexity: O(min(n, charset)) – where charset is the size of the character set (e.g., 26 for lowercase, 128 for ASCII)
15 | */
16 |
17 | class Solution {
18 | public:
19 | int lengthOfLongestSubstring(string s) {
20 | unordered_set window;
21 | int left = 0;
22 | int maxLen = 0;
23 | for (int right = 0; right < s.size(); right++) {
24 | while (window.find(s[right]) != window.end()) {
25 | window.erase(s[left]);
26 | left++;
27 | }
28 | window.insert(s[right]);
29 | int windowSize = right - left + 1;
30 | maxLen = max(maxLen, windowSize);
31 | }
32 | return maxLen;
33 | }
34 | };
35 |
--------------------------------------------------------------------------------
/Level 1/Week 06/Stack/84. Largest Rectangle in Histogram/README.md:
--------------------------------------------------------------------------------
1 | Hard
Given an array of integers heights representing the histogram's bar height where the width of each bar is 1, return the area of the largest rectangle in the histogram.
2 |
3 |
4 | Example 1:
5 |  6 |
6 |
7 | Input: heights = [2,1,5,6,2,3]
8 | Output: 10
9 | Explanation: The above is a histogram where width of each bar is 1.
10 | The largest rectangle is shown in the red area, which has an area = 10 units.
11 |
12 |
13 | Example 2:
14 |  15 |
15 |
16 | Input: heights = [2,4]
17 | Output: 4
18 |
19 |
20 |
21 | Constraints:
22 |
23 |
24 | 1 <= heights.length <= 1050 <= heights[i] <= 104
27 |
--------------------------------------------------------------------------------
/Level 1/Week 10/Recursion/21. Merge Two Sorted Lists/README.md:
--------------------------------------------------------------------------------
1 | # Merge Two Sorted Lists
2 |
3 | **Difficulty:** Easy
4 |
5 | ## Problem Description
6 |
7 | You are given the heads of two sorted linked lists `list1` and `list2`.
8 |
9 | Merge the two lists into one **sorted** list. The list should be made by splicing together the nodes of the first two lists.
10 |
11 | Return *the head of the merged linked list*.
12 |
13 | ---
14 |
15 | ## Examples
16 |
17 | ### Example 1
18 | Input: list1 = [1,2,4], list2 = [1,3,4]
19 | Output: [1,1,2,3,4,4]
20 |
21 | ### Example 2
22 | Input: list1 = [], list2 = []
23 | Output: []
24 |
25 | ### Example 3
26 | Input: list1 = [], list2 = [0]
27 | Output: [0]
28 |
29 | ---
30 |
31 | ## Constraints
32 |
33 | - The number of nodes in both lists is in the range `[0, 50]`.
34 | - `-100 <= Node.val <= 100`
35 | - Both `list1` and `list2` are sorted in **non-decreasing** order.
36 |
37 | ---
38 |
39 | ## Approach
40 |
41 | This problem can be solved elegantly using recursion:
42 | 1. Base case: if one list is empty, return the other list
43 | 2. Recursive case: compare the heads of both lists
44 | 3. Choose the smaller head and recursively merge the rest
45 | 4. Connect the chosen head with the result of recursive merge
46 | 5. Return the merged list
47 |
48 | The recursive approach naturally handles the comparison and merging process.
49 |
50 | ---
51 |
--------------------------------------------------------------------------------
/Level 1/Week 10/Recursion/25. Reverse Nodes in k-Group/README.md:
--------------------------------------------------------------------------------
1 | # Reverse Nodes in k-Group
2 |
3 | **Difficulty:** Hard
4 |
5 | ## Problem Description
6 |
7 | Given the `head` of a linked list, reverse the nodes of the list `k` at a time, and return the modified list.
8 |
9 | `k` is a positive integer and is less than or equal to the length of the linked list. If the number of nodes is not a multiple of `k` then left-out nodes, in the end, should remain as it is.
10 |
11 | You may not alter the values in the list's nodes, only nodes themselves may be changed.
12 |
13 | ---
14 |
15 | ## Examples
16 |
17 | ### Example 1
18 | Input: head = [1,2,3,4,5], k = 2
19 | Output: [2,1,4,3,5]
20 |
21 | ### Example 2
22 | Input: head = [1,2,3,4,5], k = 3
23 | Output: [3,2,1,4,5]
24 |
25 | ---
26 |
27 | ## Constraints
28 |
29 | - The number of nodes in the list is `n`.
30 | - `1 <= k <= n <= 5000`
31 | - `0 <= Node.val <= 1000`
32 |
33 | ---
34 |
35 | ## Approach
36 |
37 | This problem uses recursion with multiple steps:
38 | 1. Check if there are k nodes remaining to reverse
39 | 2. If yes, reverse the first k nodes
40 | 3. Recursively process the remaining nodes
41 | 4. Connect the reversed group with the result of recursive call
42 | 5. Handle the case where remaining nodes are less than k
43 |
44 | The key is to reverse nodes in groups and maintain the connections between groups.
45 |
46 | ---
47 |
--------------------------------------------------------------------------------
/Level 1/Week 03/LinkedList/19. Remove Nth Node From End of List/README.md:
--------------------------------------------------------------------------------
1 | Medium
Given the head of a linked list, remove the nth node from the end of the list and return its head.
2 |
3 |
4 | Example 1:
5 | 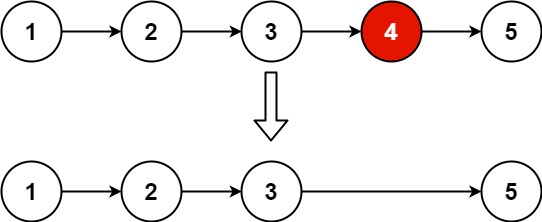 6 |
6 |
7 | Input: head = [1,2,3,4,5], n = 2
8 | Output: [1,2,3,5]
9 |
10 |
11 | Example 2:
12 |
13 |
14 | Input: head = [1], n = 1
15 | Output: []
16 |
17 |
18 | Example 3:
19 |
20 |
21 | Input: head = [1,2], n = 1
22 | Output: [1]
23 |
24 |
25 |
26 | Constraints:
27 |
28 |
29 | - The number of nodes in the list is
sz.
30 | 1 <= sz <= 300 <= Node.val <= 1001 <= n <= sz
34 |
35 |
36 | Follow up: Could you do this in one pass?
37 |
--------------------------------------------------------------------------------
/Level 0/10 Backtracking/02. 039-combination-sum/README.md:
--------------------------------------------------------------------------------
1 | # 39. Combination Sum
2 |
3 | ## Problem Description
4 |
5 | Given an array of **distinct** integers `candidates` and a target integer `target`, return *a list of all **unique combinations** of `candidates` where the chosen numbers sum to `target`*. You may return the combinations in **any order**.
6 |
7 | The **same** number may be chosen from `candidates` an **unlimited number of times**. Two combinations are unique if the frequency of at least one of the chosen numbers is different.
8 |
9 | ## Examples
10 |
11 | ### Example 1:
12 |
13 | **Input:** `candidates = [2,3,6,7]`, `target = 7`
14 |
15 | **Output:** `[[2,2,3],[7]]`
16 |
17 | **Explanation:**
18 | - 2 and 3 are candidates, and 2 + 2 + 3 = 7. Note that 2 can be used multiple times.
19 | - 7 is a candidate, and 7 = 7.
20 | - These are the only two combinations.
21 |
22 | ### Example 2:
23 |
24 | **Input:** `candidates = [2,3,5]`, `target = 8`
25 |
26 | **Output:** `[[2,2,2,2],[2,3,3],[3,5]]`
27 |
28 | ### Example 3:
29 |
30 | **Input:** `candidates = [2]`, `target = 1`
31 |
32 | **Output:** `[]`
33 |
34 | ## Constraints
35 |
36 | - `1 <= candidates.length <= 30`
37 | - `2 <= candidates[i] <= 40`
38 | - All elements of `candidates` are **distinct**.
39 | - `1 <= target <= 40`
40 |
41 | ## Related Topics
42 |
43 | - Array
44 | - Backtracking
45 |
46 | ## Difficulty
47 |
48 | Medium
--------------------------------------------------------------------------------
/Level 0/9 Modified Binary Search/07. 0074-search-a-2d-matrix/0074-search-a-2d-matrix.cpp:
--------------------------------------------------------------------------------
1 | class Solution {
2 | public:
3 | bool searchMatrix(vector>& matrix, int target) {
4 | int n = matrix.size(); // number of rows
5 | int m = matrix[0].size(); // number of columns
6 |
7 | int low = 0;
8 | int high = n * m - 1;
9 |
10 | while (low <= high) {
11 | int mid = (low + high) / 2;
12 | int row = mid / m;
13 | int col = mid % m;
14 |
15 | if (matrix[row][col] == target) {
16 | return true;
17 | } else if (matrix[row][col] < target) {
18 | low = mid + 1;
19 | } else {
20 | high = mid - 1;
21 | }
22 | }
23 |
24 | return false;
25 | }
26 | };
27 |
28 |
29 | // Approach 1
30 |
31 | // bool searchMatrix(vector>& matrix, int target) {
32 | // int n = matrix.size(); // number of rows
33 | // int m = matrix[0].size(); // number of columns
34 |
35 | // int i = 0;
36 | // int j = m - 1;
37 | // while (i < n && j >= 0) {
38 | // if (matrix[i][j] == target) {
39 | // return true;
40 | // } else if (matrix[i][j] > target) {
41 | // j--; // move left
42 | // } else {
43 | // i++; // move down
44 | // }
45 | // }
46 | // return false;
47 | // }
48 |
--------------------------------------------------------------------------------
/Level 0/9 Modified Binary Search/02. 0034-find-first-and-last-position-of-element-in-sorted-array/0034-find-first-and-last-position-of-element-in-sorted-array.cpp:
--------------------------------------------------------------------------------
1 | class Solution {
2 | public:
3 | vector searchRange(vector& nums, int target) {
4 | vector res;
5 |
6 | int left = 0;
7 | int right = nums.size() - 1;
8 |
9 | int position = -1;
10 |
11 | while(left <= right){
12 | int mid = left + (right - left) / 2;
13 |
14 | if(nums[mid] == target){
15 | position = mid;
16 | right = mid - 1;
17 | }else if(nums[mid] > target){
18 | right = mid - 1;
19 | }else{
20 | left = mid + 1;
21 | }
22 | }
23 |
24 | res.push_back(position);
25 |
26 | position = -1;
27 |
28 | left = 0;
29 | right = nums.size() - 1;
30 |
31 | while(left <= right){
32 | int mid = left + (right - left) / 2;
33 |
34 | if(nums[mid] == target){
35 | position = mid;
36 | left = mid + 1;
37 | }else if(nums[mid] > target){
38 | right = mid - 1;
39 | }else{
40 | left = mid + 1;
41 | }
42 | }
43 |
44 | res.push_back(position);
45 |
46 | return res;
47 | }
48 | };
--------------------------------------------------------------------------------
/Level 0/8 Trees/10. 0124-binary-tree-maximum-path-sum/README.md:
--------------------------------------------------------------------------------
1 | # 124. Binary Tree Maximum Path Sum
2 |
3 | ## Problem Description
4 |
5 | A **path** in a binary tree is a sequence of nodes where each pair of adjacent nodes in the sequence has an edge connecting them. A node can only appear in the sequence **at most once**. Note that the path does not need to pass through the root.
6 |
7 | The **path sum** of a path is the sum of the node's values in the path.
8 |
9 | Given the `root` of a binary tree, return *the maximum **path sum** of any **non-empty** path*.
10 |
11 | ## Examples
12 |
13 | ### Example 1:
14 | 
15 |
16 | **Input:** `root = [1,2,3]`
17 |
18 | **Output:** `6`
19 |
20 | **Explanation:** The optimal path is 2 -> 1 -> 3 with a path sum of 2 + 1 + 3 = 6.
21 |
22 | ### Example 2:
23 | 
24 |
25 | **Input:** `root = [-10,9,20,null,null,15,7]`
26 |
27 | **Output:** `42`
28 |
29 | **Explanation:** The optimal path is 15 -> 20 -> 7 with a path sum of 15 + 20 + 7 = 42.
30 |
31 | ## Constraints
32 |
33 | - The number of nodes in the tree is in the range `[1, 3 * 10^4]`.
34 | - `-1000 <= Node.val <= 1000`
35 |
36 | ## Related Topics
37 |
38 | - Dynamic Programming
39 | - Tree
40 | - Depth-First Search
41 | - Binary Tree
42 |
43 | ## Difficulty
44 |
45 | Hard
46 |
--------------------------------------------------------------------------------
/Level 1/Week 03/LinkedList/206. Reverse Linked List/README.md:
--------------------------------------------------------------------------------
1 | Easy
Given the head of a singly linked list, reverse the list, and return the reversed list.
2 |
3 |
4 | Example 1:
5 |  6 |
6 |
7 | Input: head = [1,2,3,4,5]
8 | Output: [5,4,3,2,1]
9 |
10 |
11 | Example 2:
12 |  13 |
13 |
14 | Input: head = [1,2]
15 | Output: [2,1]
16 |
17 |
18 | Example 3:
19 |
20 |
21 | Input: head = []
22 | Output: []
23 |
24 |
25 |
26 | Constraints:
27 |
28 |
29 | - The number of nodes in the list is the range
[0, 5000].
30 | -5000 <= Node.val <= 5000
32 |
33 |
34 | Follow up: A linked list can be reversed either iteratively or recursively. Could you implement both?
35 |
--------------------------------------------------------------------------------
/Level 1/Week 03/LinkedList/25. Reverse Nodes in k-Group/code.cpp:
--------------------------------------------------------------------------------
1 | /**
2 | * Definition for singly-linked list.
3 | * struct ListNode {
4 | * int val;
5 | * ListNode *next;
6 | * ListNode() : val(0), next(nullptr) {}
7 | * ListNode(int x) : val(x), next(nullptr) {}
8 | * ListNode(int x, ListNode *next) : val(x), next(next) {}
9 | * };
10 | */
11 | class Solution {
12 | public:
13 | ListNode* reverseKGroup(ListNode* head, int k) {
14 | if (!head || k == 1) return head;
15 |
16 | ListNode* dummy = new ListNode(0);
17 | dummy->next = head;
18 | ListNode* group1 = dummy;
19 |
20 | while (true) {
21 | ListNode* kth = group1;
22 | for (int i = 0; i < k && kth; i++) {
23 | kth = kth->next;
24 | }
25 | if (!kth) break;
26 |
27 | ListNode* group2 = kth->next;
28 | ListNode* group3 = group1->next;
29 |
30 | // Reverse group
31 | ListNode* prev = group2;
32 | ListNode* curr = group3;
33 | while (curr != group2) {
34 | ListNode* temp = curr->next;
35 | curr->next = prev;
36 | prev = curr;
37 | curr = temp;
38 | }
39 |
40 | group1->next = kth;
41 | group1 = group3;
42 | }
43 |
44 | return dummy->next;
45 | }
46 | };
--------------------------------------------------------------------------------
/Level 1/Week 05/Modified Binary Search/4. Median of Two Sorted Arrays/README.md:
--------------------------------------------------------------------------------
1 | Hard
Given two sorted arrays nums1 and nums2 of size m and n respectively, return the median of the two sorted arrays.
2 |
3 | The overall run time complexity should be O(log (m+n)).
4 |
5 |
6 | Example 1:
7 |
8 |
9 | Input: nums1 = [1,3], nums2 = [2]
10 | Output: 2.00000
11 | Explanation: merged array = [1,2,3] and median is 2.
12 |
13 |
14 | Example 2:
15 |
16 |
17 | Input: nums1 = [1,2], nums2 = [3,4]
18 | Output: 2.50000
19 | Explanation: merged array = [1,2,3,4] and median is (2 + 3) / 2 = 2.5.
20 |
21 |
22 |
23 | Constraints:
24 |
25 |
26 | nums1.length == mnums2.length == n0 <= m <= 10000 <= n <= 10001 <= m + n <= 2000-106 <= nums1[i], nums2[i] <= 106
33 |
--------------------------------------------------------------------------------
/Level 0/9 Modified Binary Search/01. 0792-binary-search/README.md:
--------------------------------------------------------------------------------
1 | Easy
Given an array of integers nums which is sorted in ascending order, and an integer target, write a function to search target in nums. If target exists, then return its index. Otherwise, return -1.
2 |
3 | You must write an algorithm with O(log n) runtime complexity.
4 |
5 |
6 | Example 1:
7 |
8 |
9 | Input: nums = [-1,0,3,5,9,12], target = 9
10 | Output: 4
11 | Explanation: 9 exists in nums and its index is 4
12 |
13 |
14 | Example 2:
15 |
16 |
17 | Input: nums = [-1,0,3,5,9,12], target = 2
18 | Output: -1
19 | Explanation: 2 does not exist in nums so return -1
20 |
21 |
22 |
23 | Constraints:
24 |
25 |
26 | 1 <= nums.length <= 104-104 < nums[i], target < 104- All the integers in
nums are unique.
29 | nums is sorted in ascending order.
31 |
--------------------------------------------------------------------------------
/Level 1/Week 05/Modified Binary Search/704. Binary Search/README.md:
--------------------------------------------------------------------------------
1 | Easy
Given an array of integers nums which is sorted in ascending order, and an integer target, write a function to search target in nums. If target exists, then return its index. Otherwise, return -1.
2 |
3 | You must write an algorithm with O(log n) runtime complexity.
4 |
5 |
6 | Example 1:
7 |
8 |
9 | Input: nums = [-1,0,3,5,9,12], target = 9
10 | Output: 4
11 | Explanation: 9 exists in nums and its index is 4
12 |
13 |
14 | Example 2:
15 |
16 |
17 | Input: nums = [-1,0,3,5,9,12], target = 2
18 | Output: -1
19 | Explanation: 2 does not exist in nums so return -1
20 |
21 |
22 |
23 | Constraints:
24 |
25 |
26 | 1 <= nums.length <= 104-104 < nums[i], target < 104- All the integers in
nums are unique.
29 | nums is sorted in ascending order.
31 |
--------------------------------------------------------------------------------
/Level 1/Week 07/K way merge [Heaps]/1046. Last Stone Weight/README.md:
--------------------------------------------------------------------------------
1 | # Last Stone Weight
2 |
3 | **Difficulty:** Easy
4 |
5 | ## Problem Description
6 |
7 | You are given an array of integers `stones` where `stones[i]` is the weight of the `ith` stone.
8 |
9 | We are playing a game with the stones. On each turn, we choose the **heaviest two stones** and smash them together. Suppose the heaviest two stones have weights `x` and `y` with `x <= y`. The result of this smash is:
10 |
11 | - If `x == y`, both stones are destroyed, and
12 | - If `x != y`, the stone of weight `x` is destroyed, and the stone of weight `y` has new weight `y - x`.
13 |
14 | At the end of the game, there is **at most one stone** left.
15 |
16 | Return the weight of the last remaining stone. If there are no stones left, return `0`.
17 |
18 | ---
19 |
20 | ## Examples
21 |
22 | ### Example 1
23 | Input: stones = [2,7,4,1,8,1]
24 | Output: 1
25 | Explanation:
26 | We combine 7 and 8 to get 1 so the array converts to [2,4,1,1,1] then,
27 | we combine 2 and 4 to get 2 so the array converts to [2,1,1,1] then,
28 | we combine 2 and 1 to get 1 so the array converts to [1,1,1] then,
29 | we combine 1 and 1 to get 0 so the array converts to [1] then that's the value of the last stone.
30 |
31 | ### Example 2
32 | Input: stones = [1]
33 | Output: 1
34 |
35 | ---
36 |
37 | ## Constraints
38 |
39 | - `1 <= stones.length <= 30`
40 | - `1 <= stones[i] <= 1000`
41 |
42 | ---
--------------------------------------------------------------------------------
/Level 1/Week 11/Dynamic Programming/62. Unique Paths/README.md:
--------------------------------------------------------------------------------
1 | # Unique Paths
2 |
3 | **Difficulty:** Medium
4 |
5 | ## Problem Description
6 |
7 | There is a robot on an `m x n` grid. The robot is initially located at the **top-left corner** (i.e., `grid[0][0]`). The robot tries to move to the **bottom-right corner** (i.e., `grid[m - 1][n - 1]`). The robot can only move either down or right at any point in time.
8 |
9 | Given the two integers `m` and `n`, return the number of possible unique paths that the robot can take to reach the bottom-right corner.
10 |
11 | The test cases are generated so that the answer will be less than or equal to `2 * 10^9`.
12 |
13 | ---
14 |
15 | ## Examples
16 |
17 | ### Example 1
18 | Input: m = 3, n = 7
19 | Output: 28
20 |
21 | ### Example 2
22 | Input: m = 3, n = 2
23 | Output: 3
24 | Explanation: From the top-left corner, there are a total of 3 ways to reach the bottom-right corner:
25 | 1. Right -> Down -> Down
26 | 2. Down -> Down -> Right
27 | 3. Down -> Right -> Down
28 |
29 | ---
30 |
31 | ## Constraints
32 |
33 | - `1 <= m, n <= 100`
34 |
35 | ---
36 |
37 | ## Approaches
38 |
39 | This problem can be solved using 4 different dynamic programming approaches:
40 |
41 | 1. **Recursion** - Direct recursive implementation
42 | 2. **Memoization** - Top-down DP with caching
43 | 3. **Tabulation** - Bottom-up DP with 2D array
44 | 4. **Space Optimization** - Optimized to 1D array
45 |
46 | ---
47 |
--------------------------------------------------------------------------------
/Level 1/Week 05/Modified Binary Search/704. Binary Search/code.cpp:
--------------------------------------------------------------------------------
1 | /*
2 | Approach: Binary Search
3 |
4 | 1. **Initialize Pointers**:
5 | - Set `low = 0` and `high = nums.size() - 1` to define the search range.
6 |
7 | 2. **Iterative Loop**:
8 | - While `low <= high`, calculate the middle index: `mid = low + (high - low) / 2`.
9 | - Compare `nums[mid]` with the `target`.
10 |
11 | 3. **Comparison Cases**:
12 | - If `nums[mid] == target`: return `mid` (target found).
13 | - If `nums[mid] < target`: move to the right half → set `low = mid + 1`.
14 | - If `nums[mid] > target`: move to the left half → set `high = mid - 1`.
15 |
16 | 4. **Not Found**:
17 | - If the loop ends without returning, the target does not exist → return `-1`.
18 |
19 | Time Complexity: O(log n)
20 | Space Complexity: O(1)
21 | (Because the search space is halved each iteration and only a few variables are used)
22 | */
23 |
24 | class Solution {
25 | public:
26 | int search(vector& nums, int target) {
27 | int low = 0;
28 | int high = nums.size() -1;
29 | while(low<=high){
30 | int mid = low + (high - low)/2;
31 | if(nums[mid] == target){
32 | return mid;
33 | } else if (nums[mid] < target){
34 | low = mid +1;
35 | } else {
36 | high = mid - 1;
37 | }
38 | }
39 | return -1;
40 | }
41 | };
42 |
--------------------------------------------------------------------------------
/Level 1/Week 02/2 pointers/287. Find the Duplicate Number/code.cpp:
--------------------------------------------------------------------------------
1 | // ✅ Approach:
2 | // We treat the array like a linked list where:
3 | // - Each index represents a node.
4 | // - The value at each index points to the next node (like a pointer).
5 | // Since one number is repeated, it causes a cycle in this "linked list".
6 | // To detect the cycle, we use Floyd’s Tortoise and Hare algorithm:
7 | // 1. Initialize two pointers: slow and fast, both starting from index 0.
8 | // 2. Move slow one step at a time (slow = nums[slow]).
9 | // Move fast two steps at a time (fast = nums[nums[fast]]).
10 | // 3. When they meet, it confirms a cycle exists.
11 | // 4. Reset slow to start, move both one step at a time until they meet again.
12 | // 5. The point where they meet is the duplicate number (entry point of the cycle).
13 |
14 | class Solution {
15 | public:
16 | int findDuplicate(vector& nums) {
17 | int slow = nums[0];
18 | int fast = nums[0];
19 |
20 | // Phase 1: Detect intersection point in cycle
21 | do {
22 | slow = nums[slow];
23 | fast = nums[nums[fast]];
24 | } while (slow != fast);
25 |
26 | // Phase 2: Find the start of the cycle (duplicate number)
27 | slow = nums[0];
28 | while (slow != fast) {
29 | slow = nums[slow];
30 | fast = nums[fast];
31 | }
32 |
33 | return fast;
34 | }
35 | };
36 |
--------------------------------------------------------------------------------
/Level 1/Week 10/Backtracking/78. Subsets/code.cpp:
--------------------------------------------------------------------------------
1 | /*
2 | Problem: 78. Subsets
3 |
4 | This is a classic backtracking problem where we need to generate all possible subsets.
5 | For each element, we have two choices: include it or exclude it.
6 | We use backtracking to explore all combinations systematically.
7 |
8 | Time Complexity: O(2^n) - we generate 2^n subsets
9 | Space Complexity: O(n) - recursion stack depth
10 | */
11 |
12 | #include
13 | using namespace std;
14 |
15 | class Solution {
16 | public:
17 | vector> subsets(vector& nums) {
18 | vector> result;
19 | vector current;
20 | backtrack(nums, 0, current, result);
21 | return result;
22 | }
23 |
24 | private:
25 | void backtrack(vector& nums, int index, vector& current, vector>& result) {
26 | // Base case: when we've processed all elements
27 | if (index == nums.size()) {
28 | result.push_back(current); // Add current subset to result
29 | return;
30 | }
31 |
32 | // Choice 1: Include the current element
33 | current.push_back(nums[index]);
34 | backtrack(nums, index + 1, current, result);
35 | current.pop_back(); // Backtrack: remove the element
36 |
37 | // Choice 2: Exclude the current element
38 | backtrack(nums, index + 1, current, result);
39 | }
40 | };
41 |
--------------------------------------------------------------------------------
/Common/Math/Count Digits/count.cpp:
--------------------------------------------------------------------------------
1 | #include
2 | using namespace std;
3 |
4 | /*
5 | ---------------------------------------------------
6 | 🔸 Approach 1: Brute Force using Modulo
7 | - Loop through each digit using modulo
8 | - Check if digit != 0 and divides original number
9 | ---------------------------------------------------
10 | */
11 | int evenDigits(int n) {
12 | int cnt = 0;
13 | int N = n; // Store original number
14 |
15 | while (n > 0) {
16 | int digit = n % 10;
17 | n /= 10;
18 |
19 | if (digit != 0 && N % digit == 0) {
20 | cnt++;
21 | }
22 | }
23 | return cnt;
24 | }
25 |
26 | /*
27 | ---------------------------------------------------
28 | 🔸 Approach 2: Count Total Digits Using log10
29 | - Just counts total digits, not the ones that divide
30 | - Use: log10(num) + 1
31 | - Not relevant to "divisible digits" but useful
32 | ---------------------------------------------------
33 | */
34 | int totalDigits(int num) {
35 | if (num == 0) return 1;
36 | return (int)(log10(num) + 1);
37 | }
38 |
39 | int main() {
40 | int number;
41 | cout << "Enter a number: ";
42 | cin >> number;
43 |
44 | cout << "Number of digits in " << number << " that divide it evenly: "
45 | << evenDigits(number) << endl;
46 |
47 | cout << "Total number of digits in " << number << ": "
48 | << totalDigits(number) << endl;
49 |
50 | return 0;
51 | }
52 |
--------------------------------------------------------------------------------
/Level 1/Week 07/K way merge [Heaps]/703. Kth Largest Element in a Stream/README.md:
--------------------------------------------------------------------------------
1 | # Kth Largest Element in a Stream
2 |
3 | **Difficulty:** Easy
4 |
5 | ## Problem Description
6 |
7 | Design a class to find the **kth largest** element in a stream. Note that it is the kth largest element in the **sorted order**, not the kth distinct element.
8 |
9 | Implement the `KthLargest` class:
10 |
11 | - `KthLargest(int k, int[] nums)` Initializes the object with the integer `k` and the stream of integers `nums`.
12 | - `int add(int val)` Appends the integer `val` to the stream and returns the element representing the kth largest element in the stream.
13 |
14 | ---
15 |
16 | ## Examples
17 |
18 | ### Example 1
19 | Input:
20 | ["KthLargest", "add", "add", "add", "add", "add"]
21 | [[3, [4, 5, 8, 2]], [3], [5], [10], [9], [4]]
22 | Output: [null, 4, 5, 5, 8, 8]
23 |
24 | Explanation:
25 | KthLargest kthLargest = new KthLargest(3, [4, 5, 8, 2]);
26 | kthLargest.add(3); // return 4
27 | kthLargest.add(5); // return 5
28 | kthLargest.add(10); // return 5
29 | kthLargest.add(9); // return 8
30 | kthLargest.add(4); // return 8
31 |
32 | ---
33 |
34 | ## Constraints
35 |
36 | - `1 <= k <= 10^4`
37 | - `0 <= nums.length <= 10^4`
38 | - `-10^4 <= nums[i] <= 10^4`
39 | - `-10^4 <= val <= 10^4`
40 | - At most `10^4` calls will be made to `add`.
41 | - It is guaranteed that there will be at least `k` elements in the array when you search for the kth element.
42 |
43 | ---
--------------------------------------------------------------------------------
/Level 0/10 Backtracking/04. 046-permutations/code.cpp:
--------------------------------------------------------------------------------
1 | class Solution {
2 | private:
3 | vector> result;
4 |
5 | void backtrack(vector& nums, vector& current, vector& used) {
6 | // Base case: if current permutation has all elements
7 | if (current.size() == nums.size()) {
8 | result.push_back(current);
9 | return;
10 | }
11 |
12 | // Try all elements for current position
13 | for (int i = 0; i < nums.size(); i++) {
14 | // Skip if element is already used
15 | if (used[i]) {
16 | continue;
17 | }
18 |
19 | // Make choice: use nums[i] at current position
20 | used[i] = true;
21 | current.push_back(nums[i]);
22 |
23 | // Recurse to fill next position
24 | backtrack(nums, current, used);
25 |
26 | // Backtrack: undo the choice
27 | current.pop_back();
28 | used[i] = false;
29 | }
30 | }
31 |
32 | public:
33 | vector> permute(vector& nums) {
34 | vector current;
35 | vector used(nums.size(), false);
36 | backtrack(nums, current, used);
37 | return result;
38 | }
39 | };
40 |
41 | /*
42 | Time Complexity: O(n!) where n is the length of nums
43 | Space Complexity: O(n) for recursion stack and used array
44 | */
--------------------------------------------------------------------------------
/Level 0/10 Backtracking/02. 039-combination-sum/code.cpp:
--------------------------------------------------------------------------------
1 | class Solution {
2 | private:
3 | vector> result;
4 |
5 | void backtrack(vector& candidates, vector& current, int target, int start) {
6 | // Base case: if target becomes 0, we found a valid combination
7 | if (target == 0) {
8 | result.push_back(current);
9 | return;
10 | }
11 |
12 | // Base case: if target becomes negative, this path is invalid
13 | if (target < 0) {
14 | return;
15 | }
16 |
17 | // Try all candidates starting from 'start' index
18 | for (int i = start; i < candidates.size(); i++) {
19 | // Make choice: include candidates[i]
20 | current.push_back(candidates[i]);
21 |
22 | // Recurse with updated target (can reuse same element)
23 | backtrack(candidates, current, target - candidates[i], i);
24 |
25 | // Backtrack: remove candidates[i]
26 | current.pop_back();
27 | }
28 | }
29 |
30 | public:
31 | vector> combinationSum(vector& candidates, int target) {
32 | vector current;
33 | backtrack(candidates, current, target, 0);
34 | return result;
35 | }
36 | };
37 |
38 | /*
39 | Time Complexity: O(k * 2^target) where k is the average length of combinations
40 | Space Complexity: O(target) for recursion stack
41 | */
--------------------------------------------------------------------------------
/Level 1/Week 06/Stack/20. Valid Parentheses/README.md:
--------------------------------------------------------------------------------
1 | Easy
Given a string s containing just the characters '(', ')', '{', '}', '[' and ']', determine if the input string is valid.
2 |
3 | An input string is valid if:
4 |
5 |
6 | - Open brackets must be closed by the same type of brackets.
7 | - Open brackets must be closed in the correct order.
8 | - Every close bracket has a corresponding open bracket of the same type.
9 |
10 |
11 |
12 | Example 1:
13 |
14 |
15 | Input: s = "()"
16 | Output: true
17 |
18 |
19 | Example 2:
20 |
21 |
22 | Input: s = "()[]{}"
23 | Output: true
24 |
25 |
26 | Example 3:
27 |
28 |
29 | Input: s = "(]"
30 | Output: false
31 |
32 |
33 |
34 | Constraints:
35 |
36 |
37 | 1 <= s.length <= 104s consists of parentheses only '()[]{}'.
40 |
--------------------------------------------------------------------------------
/Level 1/Week 12/Graph/200. Number of Islands/README.md:
--------------------------------------------------------------------------------
1 | # Number of Islands
2 |
3 | **Difficulty:** Medium
4 |
5 | ## Problem Description
6 |
7 | Given an `m x n` 2D binary grid `grid` which represents a map of `'1'`s (land) and `'0'`s (water), return *the number of islands*.
8 |
9 | An **island** is surrounded by water and is formed by connecting adjacent lands horizontally or vertically. You may assume all four edges of the grid are all surrounded by water.
10 |
11 | ---
12 |
13 | ## Examples
14 |
15 | ### Example 1
16 | Input: grid = [
17 | ["1","1","1","1","0"],
18 | ["1","1","0","1","0"],
19 | ["1","1","0","0","0"],
20 | ["0","0","0","0","0"]
21 | ]
22 | Output: 1
23 |
24 | ### Example 2
25 | Input: grid = [
26 | ["1","1","0","0","0"],
27 | ["1","1","0","0","0"],
28 | ["0","0","1","0","0"],
29 | ["0","0","0","1","1"]
30 | ]
31 | Output: 3
32 |
33 | ---
34 |
35 | ## Constraints
36 |
37 | - `m == grid.length`
38 | - `n == grid[i].length`
39 | - `1 <= m, n <= 300`
40 | - `grid[i][j]` is `'0'` or `'1'`.
41 |
42 | ---
43 |
44 | ## Approach
45 |
46 | This problem can be solved using DFS or BFS:
47 | 1. Iterate through each cell in the grid
48 | 2. When we find a land cell ('1'), start a DFS/BFS to explore the entire island
49 | 3. Mark visited cells to avoid counting them again
50 | 4. Count the number of times we start a new exploration (number of islands)
51 |
52 | The key insight is to use a flood-fill approach to mark all connected land cells as visited.
53 |
54 | ---
55 |
--------------------------------------------------------------------------------
/Common/Math/Odd/odd_number.cpp:
--------------------------------------------------------------------------------
1 | #include
2 | using namespace std;
3 |
4 | /*
5 | ------------------------------------------
6 | 🔹 Approach 1: Modulo Operator (%)
7 | - If a number divided by 2 leaves remainder 1,
8 | it's odd.
9 | - Straightforward and easy to understand.
10 | ------------------------------------------
11 | */
12 | bool odd(int n) {
13 | return n % 2 == 1;
14 | }
15 |
16 | /*
17 | ------------------------------------------
18 | 🔹 Approach 2: Bitwise AND Operator (&)
19 | - Odd numbers have 1 as the last binary digit.
20 | - So, if (n & 1) == 1, it's odd.
21 | - Fast and efficient.
22 | ------------------------------------------
23 | */
24 | bool odd_bitwise(int n) {
25 | return (n & 1) != 0;
26 | }
27 |
28 | /*
29 | ------------------------------------------
30 | 🔹 Approach 3: Integer Division
31 | - Divide the number by 2 and multiply it back.
32 | - If the result is not equal to original,
33 | it's odd.
34 | ------------------------------------------
35 | */
36 | bool odd_division(int n) {
37 | return (n / 2) * 2 != n;
38 | }
39 |
40 | /*
41 | ------------------------------------------
42 | 🔹 Approach 4: Recursive Method
43 | - Base case: 0 → false (even), 1 → true (odd)
44 | - Reduce n by 1 each time to reach the base case.
45 | - Helps understand recursion.
46 | ------------------------------------------
47 | */
48 | bool odd_recursive(int n) {
49 | if (n == 0) return false;
50 | if (n == 1) return true;
51 | return odd_recursive(n - 2);
52 | }
53 |
--------------------------------------------------------------------------------
/Level 1/Week 03/LinkedList/21. Merge Two Sorted Lists/README.md:
--------------------------------------------------------------------------------
1 | Easy
You are given the heads of two sorted linked lists list1 and list2.
2 |
3 | Merge the two lists into one sorted list. The list should be made by splicing together the nodes of the first two lists.
4 |
5 | Return the head of the merged linked list.
6 |
7 |
8 | Example 1:
9 |  10 |
10 |
11 | Input: list1 = [1,2,4], list2 = [1,3,4]
12 | Output: [1,1,2,3,4,4]
13 |
14 |
15 | Example 2:
16 |
17 |
18 | Input: list1 = [], list2 = []
19 | Output: []
20 |
21 |
22 | Example 3:
23 |
24 |
25 | Input: list1 = [], list2 = [0]
26 | Output: [0]
27 |
28 |
29 |
30 | Constraints:
31 |
32 |
33 | - The number of nodes in both lists is in the range
[0, 50].
34 | -100 <= Node.val <= 100- Both
list1 and list2 are sorted in non-decreasing order.
36 |
37 |
--------------------------------------------------------------------------------
/Level 1/Week 10/Recursion/445. Add Two Numbers II/README.md:
--------------------------------------------------------------------------------
1 | # Add Two Numbers II
2 |
3 | **Difficulty:** Medium
4 |
5 | ## Problem Description
6 |
7 | You are given two **non-empty** linked lists representing two non-negative integers. The most significant digit comes first and each of their nodes contains a single digit. Add the two numbers and return the sum as a linked list.
8 |
9 | You may assume the two numbers do not contain any leading zero, except the number 0 itself.
10 |
11 | ---
12 |
13 | ## Examples
14 |
15 | ### Example 1
16 | Input: l1 = [7,2,4,3], l2 = [5,6,4]
17 | Output: [7,8,0,7]
18 |
19 | ### Example 2
20 | Input: l1 = [2,4,3], l2 = [5,6,4]
21 | Output: [8,0,7]
22 |
23 | ### Example 3
24 | Input: l1 = [0], l2 = [0]
25 | Output: [0]
26 |
27 | ---
28 |
29 | ## Constraints
30 |
31 | - The number of nodes in each linked list is in the range `[1, 100]`.
32 | - `0 <= Node.val <= 9`
33 | - It is guaranteed that the list represents a number that does not have leading zeros.
34 |
35 | ---
36 |
37 | ## Approach
38 |
39 | This problem is more complex than Add Two Numbers I because digits are in forward order:
40 | 1. First, we need to reverse both lists to work with least significant digits first
41 | 2. Use the recursive approach from Add Two Numbers I
42 | 3. Reverse the result back to get the correct order
43 | 4. Handle the carry propagation from least to most significant digits
44 |
45 | The recursive approach handles the addition, while list reversal handles the digit order.
46 |
47 | ---
48 |
--------------------------------------------------------------------------------
/Level 1/Week 01/Arrays & Hashing/49. Group Anagrams/code.cpp:
--------------------------------------------------------------------------------
1 | /*
2 | Approach:
3 |
4 | To group anagrams from a list of strings, we leverage the property that anagrams share the same characters in a different order.
5 |
6 | 1. We use a hash map (`unordered_map`) where:
7 | - The key is the sorted version of the string.
8 | - The value is a vector of strings that are anagrams of each other.
9 |
10 | 2. For each string in the input:
11 | - We create a copy and sort it alphabetically.
12 | - This sorted string acts as a key to group all its anagrams together in the map.
13 |
14 | 3. After processing all strings, we extract the grouped anagrams from the map and return them as a vector of vectors.
15 |
16 | Time Complexity:
17 | - O(n * k log k), where `n` is the number of strings and `k` is the average length of each string (due to sorting).
18 |
19 | Space Complexity:
20 | - O(n * k), for storing the grouped anagrams.
21 |
22 | */
23 |
24 | class Solution {
25 | public:
26 | vector> groupAnagrams(vector& strs) {
27 | unordered_map> Groups;
28 |
29 | for (string s : strs) {
30 | string sortedStr = s;
31 | sort(sortedStr.begin(), sortedStr.end());
32 | Groups[sortedStr].push_back(s);
33 | }
34 |
35 | vector> result;
36 | for (auto& pair : Groups) {
37 | result.push_back(pair.second);
38 | }
39 |
40 | return result;
41 | }
42 | };
43 |
--------------------------------------------------------------------------------
/Level 1/Week 10/Recursion/2. Add Two Numbers/README.md:
--------------------------------------------------------------------------------
1 | # Add Two Numbers
2 |
3 | **Difficulty:** Medium
4 |
5 | ## Problem Description
6 |
7 | You are given two **non-empty** linked lists representing two non-negative integers. The digits are stored in **reverse order**, and each of their nodes contains a single digit. Add the two numbers and return the sum as a linked list.
8 |
9 | You may assume the two numbers do not contain any leading zero, except the number 0 itself.
10 |
11 | ---
12 |
13 | ## Examples
14 |
15 | ### Example 1
16 | Input: l1 = [2,4,3], l2 = [5,6,4]
17 | Output: [7,0,8]
18 | Explanation: 342 + 465 = 807.
19 |
20 | ### Example 2
21 | Input: l1 = [0], l2 = [0]
22 | Output: [0]
23 |
24 | ### Example 3
25 | Input: l1 = [9,9,9,9,9,9,9], l2 = [9,9,9,9]
26 | Output: [8,9,9,9,0,0,0,1]
27 |
28 | ---
29 |
30 | ## Constraints
31 |
32 | - The number of nodes in each linked list is in the range `[1, 100]`.
33 | - `0 <= Node.val <= 9`
34 | - It is guaranteed that the list represents a number that does not have leading zeros.
35 |
36 | ---
37 |
38 | ## Approach
39 |
40 | This problem can be solved using recursion:
41 | 1. Base case: if both lists are null and no carry remains
42 | 2. Recursive case: add current digits and carry
43 | 3. Create a new node with the sum modulo 10
44 | 4. Recursively add the remaining digits with the carry
45 | 5. Connect the current node with the recursive result
46 |
47 | The recursive approach naturally handles the digit-by-digit addition and carry propagation.
48 |
49 | ---
50 |
--------------------------------------------------------------------------------
/Level 1/Week 06/Queue/239. Sliding Window Maximum/README.md:
--------------------------------------------------------------------------------
1 | Hard
You are given an array of integers nums, there is a sliding window of size k which is moving from the very left of the array to the very right. You can only see the k numbers in the window. Each time the sliding window moves right by one position.
2 |
3 | Return the max sliding window.
4 |
5 |
6 | Example 1:
7 |
8 |
9 | Input: nums = [1,3,-1,-3,5,3,6,7], k = 3
10 | Output: [3,3,5,5,6,7]
11 | Explanation:
12 | Window position Max
13 | --------------- -----
14 | [1 3 -1] -3 5 3 6 7 3
15 | 1 [3 -1 -3] 5 3 6 7 3
16 | 1 3 [-1 -3 5] 3 6 7 5
17 | 1 3 -1 [-3 5 3] 6 7 5
18 | 1 3 -1 -3 [5 3 6] 7 6
19 | 1 3 -1 -3 5 [3 6 7] 7
20 |
21 |
22 | Example 2:
23 |
24 |
25 | Input: nums = [1], k = 1
26 | Output: [1]
27 |
28 |
29 |
30 | Constraints:
31 |
32 |
33 | 1 <= nums.length <= 105-104 <= nums[i] <= 1041 <= k <= nums.length
--------------------------------------------------------------------------------
/Level 1/Week 12/Graph/994. Rotting Oranges/README.md:
--------------------------------------------------------------------------------
1 | # Rotting Oranges
2 |
3 | **Difficulty:** Medium
4 |
5 | ## Problem Description
6 |
7 | You are given an `m x n` `grid` where each cell can have one of three values:
8 |
9 | - `0` representing an empty cell,
10 | - `1` representing a fresh orange, or
11 | - `2` representing a rotten orange.
12 |
13 | Every minute, any fresh orange that is **4-directionally adjacent** to a rotten orange becomes rotten.
14 |
15 | Return *the minimum number of minutes that must elapse until no cell has a fresh orange*. If *this is impossible, return* `-1`.
16 |
17 | ---
18 |
19 | ## Examples
20 |
21 | ### Example 1
22 | Input: grid = [[2,1,1],[1,1,0],[0,1,1]]
23 | Output: 4
24 |
25 | ### Example 2
26 | Input: grid = [[2,1,1],[0,1,1],[1,0,1]]
27 | Output: -1
28 |
29 | ### Example 3
30 | Input: grid = [[0,2]]
31 | Output: 0
32 |
33 | ---
34 |
35 | ## Constraints
36 |
37 | - `m == grid.length`
38 | - `n == grid[i].length`
39 | - `1 <= m, n <= 10`
40 | - `grid[i][j]` is only `0`, `1`, or `2`.
41 |
42 | ---
43 |
44 | ## Approach
45 |
46 | This problem can be solved using BFS:
47 | 1. Find all rotten oranges and add them to a queue
48 | 2. Use BFS to simulate the rotting process minute by minute
49 | 3. Track the number of minutes elapsed
50 | 4. Check if all fresh oranges become rotten
51 | 5. Return -1 if some fresh oranges remain unreachable
52 |
53 | The key insight is to use BFS to simulate the spreading process level by level, where each level represents one minute.
54 |
55 | ---
56 |
--------------------------------------------------------------------------------
/Level 0/9 Modified Binary Search/02. 0034-find-first-and-last-position-of-element-in-sorted-array/README.md:
--------------------------------------------------------------------------------
1 | Medium
Given an array of integers nums sorted in non-decreasing order, find the starting and ending position of a given target value.
2 |
3 | If target is not found in the array, return [-1, -1].
4 |
5 | You must write an algorithm with O(log n) runtime complexity.
6 |
7 |
8 | Example 1:
9 | Input: nums = [5,7,7,8,8,10], target = 8
10 | Output: [3,4]
11 |
Example 2:
12 | Input: nums = [5,7,7,8,8,10], target = 6
13 | Output: [-1,-1]
14 |
Example 3:
15 | Input: nums = [], target = 0
16 | Output: [-1,-1]
17 |
18 |
19 | Constraints:
20 |
21 |
22 | 0 <= nums.length <= 105-109 <= nums[i] <= 109nums is a non-decreasing array.-109 <= target <= 109
27 |
--------------------------------------------------------------------------------
/Level 1/Week 04/Trees/226. Invert Binary Tree/code.cpp:
--------------------------------------------------------------------------------
1 | /**
2 | * Approach:
3 | * The goal is to invert a binary tree, meaning swap every left and right subtree recursively.
4 | * This is done using a Depth-First Search (DFS) approach:
5 | *
6 | * 1. Traverse the tree recursively.
7 | * 2. At each node, recursively invert the left and right subtrees.
8 | * 3. Swap the left and right pointers of the current node.
9 | * 4. Return the root after the entire tree has been inverted.
10 | *
11 | * Time Complexity: O(n), where n is the number of nodes in the tree.
12 | * Space Complexity: O(h), where h is the height of the tree due to the recursion stack.
13 | */
14 |
15 | /**
16 | * Definition for a binary tree node.
17 | * struct TreeNode {
18 | * int val;
19 | * TreeNode *left;
20 | * TreeNode *right;
21 | * TreeNode() : val(0), left(nullptr), right(nullptr) {}
22 | * TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
23 | * TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
24 | * };
25 | */
26 | class Solution {
27 | public:
28 | TreeNode* invert(TreeNode* root) {
29 | if (root == NULL) {
30 | return NULL;
31 | }
32 | TreeNode* left = invert(root->left);
33 | TreeNode* right = invert(root->right);
34 | root->left = right;
35 | root->right = left;
36 | return root;
37 | }
38 |
39 | TreeNode* invertTree(TreeNode* root) {
40 | return invert(root);
41 | }
42 | };
43 |
--------------------------------------------------------------------------------
/Level 1/Week 04/Trees/230. Kth Smallest Element in a BST/README.md:
--------------------------------------------------------------------------------
1 | Medium
Given the root of a binary search tree, and an integer k, return the kth smallest value (1-indexed) of all the values of the nodes in the tree.
2 |
3 |
4 | Example 1:
5 |  6 |
6 |
7 | Input: root = [3,1,4,null,2], k = 1
8 | Output: 1
9 |
10 |
11 | Example 2:
12 |  13 |
13 |
14 | Input: root = [5,3,6,2,4,null,null,1], k = 3
15 | Output: 3
16 |
17 |
18 |
19 | Constraints:
20 |
21 |
22 | - The number of nodes in the tree is
n.
23 | 1 <= k <= n <= 1040 <= Node.val <= 104
26 |
27 |
28 | Follow up: If the BST is modified often (i.e., we can do insert and delete operations) and you need to find the kth smallest frequently, how would you optimize?
29 |
--------------------------------------------------------------------------------
/Level 1/Week 06/Stack/20. Valid Parentheses/code.cpp:
--------------------------------------------------------------------------------
1 | // 🧠 Approach:
2 | // This problem checks for valid matching parentheses using a **stack**.
3 | // 1. Traverse the string character by character.
4 | // 2. If the character is an opening bracket `(`, `{`, or `[`, push it onto the stack.
5 | // 3. If the character is a closing bracket `)`, `}`, or `]`:
6 | // - Check if the stack is empty → if yes, return false (no matching opening).
7 | // - Otherwise, check if the top of the stack has the matching opening bracket.
8 | // If it doesn't match, return false.
9 | // - If it matches, pop the top from the stack.
10 | // 4. After the loop, the stack must be empty for the string to be valid (all opened brackets closed).
11 |
12 | // ✅ Time Complexity: O(n), where n = length of the string.
13 | // ✅ Space Complexity: O(n), for the stack usage in the worst case (all characters are opening brackets).
14 |
15 | class Solution {
16 | public:
17 | bool isValid(string s) {
18 | stack st;
19 | for (char c : s) {
20 | if (c == '(' || c == '{' || c == '[') {
21 | st.push(c);
22 | } else {
23 | if (st.empty() ||
24 | (c == ')' && st.top() != '(') ||
25 | (c == '}' && st.top() != '{') ||
26 | (c == ']' && st.top() != '[')) {
27 | return false;
28 | }
29 | st.pop();
30 | }
31 | }
32 | return st.empty();
33 | }
34 | };
35 |
--------------------------------------------------------------------------------
/Common/Math/GCD_HCF_Calculation/README.md:
--------------------------------------------------------------------------------
1 | # 🔗 GCD / HCF of Two Numbers — C++ Implementation
2 |
3 | ---
4 |
5 | ## 📘 Problem Statement
6 |
7 | You are given two integers `a` and `b`.
8 | Your task is to compute their **GCD (Greatest Common Divisor)**, which is also called **HCF (Highest Common Factor)**.
9 |
10 | > ✅ GCD is the largest number that divides both `a` and `b` without leaving a remainder.
11 |
12 | ---
13 |
14 | ## ✳️ Example
15 |
16 | Input: 20, 15
17 | Divisors of 20 → 1, 2, 4, 5, 10, 20
18 | Divisors of 15 → 1, 3, 5, 15
19 | Common Divisors → 1, 5
20 | GCD = 5
21 |
22 |
23 | ---
24 |
25 | ## 🚀 Approaches
26 |
27 | ### 🔸 1. Brute Force
28 |
29 | - Loop from 1 to `min(a, b)`
30 | - Check if the number divides both `a` and `b`
31 | - Keep updating the largest such number
32 |
33 | #### ⏱️ Time Complexity:
34 | - O(min(a, b))
35 |
36 | #### ✅ Usage:
37 | Good for small values or when learning the basics.
38 |
39 | ---
40 |
41 | ### 🔸 2. Euclidean Algorithm
42 |
43 | Uses the fact that:
44 | gcd(a, b) = gcd(b, a % b)
45 |
46 |
47 |
48 | - Repeat until one of the numbers becomes 0
49 | - The other number is the result
50 |
51 | #### ⏱️ Time Complexity:
52 | - O(log(min(a, b)))
53 |
54 | #### ✅ Usage:
55 | Efficient and used in real-world applications, competitive coding, cryptography, etc.
56 |
57 | ---
58 |
59 | ## 📂 File Structure
60 |
61 | GCD_HCF_Calculations/
62 | ├── gcd.cpp # Full C++ source with both methods
63 | ├── README.md # Explanation and documentation
64 | ├── Makefile # Build and run commands
--------------------------------------------------------------------------------
/Common/Math/Even/even_number.cpp:
--------------------------------------------------------------------------------
1 | #include
2 | using namespace std;
3 |
4 | /*
5 | ------------------------------------------
6 | 🔹 Approach 1: Modulo Operator (%)
7 | - If a number divided by 2 has no remainder,
8 | it is even.
9 | - Classic and most readable method.
10 | ------------------------------------------
11 | */
12 | bool even(int n) {
13 | return n % 2 == 0;
14 | }
15 |
16 | /*
17 | ------------------------------------------
18 | 🔹 Approach 2: Bitwise AND Operator (&)
19 | - Binary trick: even numbers have 0 as the last bit.
20 | - Checking (n & 1) gives 0 if it's even.
21 | - Very efficient.
22 | ------------------------------------------
23 | */
24 | bool even_bitwise(int n) {
25 | return (n & 1) == 0;
26 | }
27 |
28 | /*
29 | ------------------------------------------
30 | 🔹 Approach 3: Integer Division Trick
31 | - Divide the number by 2 and multiply it back.
32 | - If the result equals original number, it's even.
33 | - Uncommon but clever.
34 | ------------------------------------------
35 | */
36 | bool even_division(int n) {
37 | return (n / 2) * 2 == n;
38 | }
39 |
40 | /*
41 | ------------------------------------------
42 | 🔹 Approach 4: Recursive Method
43 | - Subtract 2 recursively until 0 or 1.
44 | - Base Case: 0 = even, 1 = odd.
45 | - Great for learning recursion but not optimal.
46 | ------------------------------------------
47 | */
48 | bool even_recursive(int n) {
49 | if (n == 0) return true;
50 | if (n == 1) return false;
51 | return even_recursive(n - 2);
52 | }
53 |
--------------------------------------------------------------------------------
/Level 1/Week 09/Greedy/45. Jump Game II/code.cpp:
--------------------------------------------------------------------------------
1 | /*
2 | Approach: Greedy Algorithm
3 |
4 | The greedy approach is to always jump to the position that allows us to reach the farthest.
5 | We keep track of the current jump's range and the farthest position we can reach.
6 | When we reach the end of the current jump's range, we make another jump.
7 |
8 | Algorithm:
9 | 1. Track the farthest position reachable and current jump boundary
10 | 2. For each position, update the farthest reachable position
11 | 3. When we reach the current jump boundary, increment jumps and update boundary
12 | 4. Continue until we can reach the last index
13 |
14 | Time Complexity: O(n)
15 | Space Complexity: O(1)
16 | */
17 |
18 | #include
19 | #include
20 | using namespace std;
21 |
22 | class Solution {
23 | public:
24 | int jump(vector& nums)
25 | {
26 | int n = nums.size();
27 |
28 | if (n <= 1)
29 | {
30 | return 0;
31 | }
32 |
33 | int jumps = 0;
34 | int farthest = 0;
35 | int currentEnd = 0;
36 |
37 | for (int i = 0; i < n - 1; i++)
38 | {
39 | farthest = max(farthest, i + nums[i]);
40 |
41 | if (i == currentEnd)
42 | {
43 | ++jumps;
44 | currentEnd = farthest;
45 |
46 | if (currentEnd >= n - 1)
47 | {
48 | break;
49 | }
50 | }
51 | }
52 |
53 | return jumps;
54 | }
55 | };
56 |
--------------------------------------------------------------------------------
/Level 1/Week 10/Backtracking/51. N-Queens/README.md:
--------------------------------------------------------------------------------
1 | # N-Queens
2 |
3 | **Difficulty:** Hard
4 |
5 | ## Problem Description
6 |
7 | The **n-queens puzzle** is the problem of placing `n` queens on an `n x n` chessboard such that no two queens attack each other.
8 |
9 | Given an integer `n`, return *all distinct solutions to the **n-queens puzzle***. You may return the answer in **any order**.
10 |
11 | Each solution contains a distinct board configuration of the n-queens' placement, where `'Q'` and `'.'` both indicate a queen and an empty space, respectively.
12 |
13 | ---
14 |
15 | ## Examples
16 |
17 | ### Example 1
18 | Input: n = 4
19 | Output: [[".Q..","...Q","Q...","..Q."],["..Q.","Q...","...Q",".Q.."]]
20 | Explanation: There exist two distinct solutions to the 4-queens puzzle as shown above.
21 |
22 | ### Example 2
23 | Input: n = 1
24 | Output: [["Q"]]
25 |
26 | ---
27 |
28 | ## Constraints
29 |
30 | - `1 <= n <= 9`
31 |
32 | ---
33 |
34 | ## Approach
35 |
36 | This is a classic backtracking problem:
37 | 1. We place queens one by one in each row
38 | 2. For each row, we try placing a queen in each column
39 | 3. Before placing a queen, we check if it's safe (no conflicts with existing queens)
40 | 4. We check for conflicts in the same column, same diagonal, and same anti-diagonal
41 | 5. If safe, we place the queen and recursively try to place queens in the next row
42 | 6. We backtrack by removing the queen to try different positions
43 | 7. When we've placed all n queens, we add the board configuration to our result
44 |
45 | ---
46 |
--------------------------------------------------------------------------------
/Level 1/Week 11/Dynamic Programming/198. House Robber/README.md:
--------------------------------------------------------------------------------
1 | # House Robber
2 |
3 | **Difficulty:** Medium
4 |
5 | ## Problem Description
6 |
7 | You are a professional robber planning to rob houses along a street. Each house has a certain amount of money stashed, the only constraint stopping you from robbing each of them is that adjacent houses have security systems connected and **it will automatically contact the police if two adjacent houses were broken into on the same night**.
8 |
9 | Given an integer array `nums` representing the amount of money of each house, return the maximum amount of money you can rob tonight **without alerting the police**.
10 |
11 | ---
12 |
13 | ## Examples
14 |
15 | ### Example 1
16 | Input: nums = [1,2,3,1]
17 | Output: 4
18 | Explanation: Rob house 1 (money = 1) and then rob house 3 (money = 3).
19 | Total amount you can rob = 1 + 3 = 4.
20 |
21 | ### Example 2
22 | Input: nums = [2,7,9,3,1]
23 | Output: 12
24 | Explanation: Rob house 1 (money = 2), rob house 3 (money = 9) and rob house 5 (money = 1).
25 | Total amount you can rob = 2 + 9 + 1 = 12.
26 |
27 | ---
28 |
29 | ## Constraints
30 |
31 | - `1 <= nums.length <= 100`
32 | - `0 <= nums[i] <= 400`
33 |
34 | ---
35 |
36 | ## Approaches
37 |
38 | This problem can be solved using 4 different dynamic programming approaches:
39 |
40 | 1. **Recursion** - Direct recursive implementation
41 | 2. **Memoization** - Top-down DP with caching
42 | 3. **Tabulation** - Bottom-up DP with array
43 | 4. **Space Optimization** - Optimized space complexity
44 |
45 | ---
46 |
--------------------------------------------------------------------------------
/Common/Math/Extract Digits/README.md:
--------------------------------------------------------------------------------
1 | # 🔢 Extract Digits & Count Total – C++ Implementation
2 |
3 | ---
4 |
5 | ## 📘 Problem Statement
6 |
7 | You are given a number `n`. The goal is to **extract its digits** and **count how many digits** the number has.
8 |
9 | This is a basic math operation used in problems such as:
10 | - Reverse a number
11 | - Palindrome checks
12 | - Sum of digits
13 | - Armstrong number logic
14 |
15 | ---
16 |
17 | ## ✳️ Example:
18 |
19 | ### Input:
20 | 1234
21 | ### Steps:
22 | 1234 % 10 = 4 → count = 1
23 | 123 % 10 = 3 → count = 2
24 | 12 % 10 = 2 → count = 3
25 | 1 % 10 = 1 → count = 4
26 | 0 → loop stops
27 |
28 | ### Output:
29 | 4
30 |
31 | ---
32 |
33 | ## 🚀 Approach
34 |
35 | ### 🔸 Using `%` and `/`
36 |
37 | | Operation | Meaning |
38 | |----------:|-------------------------|
39 | | `n % 10` | Extract the last digit |
40 | | `n / 10` | Remove the last digit |
41 |
42 | Repeat these steps until the number becomes `0`. For every iteration, increase the digit count.
43 |
44 | ---
45 |
46 | ## 🧠 Why This Works?
47 |
48 | Every number in base-10 can be broken down into its digits using:
49 | - `% 10` → gets the last digit
50 | - `/ 10` → removes the last digit
51 |
52 | This is the foundation for many number-based algorithms.
53 |
54 | ---
55 |
56 | ## 📂 File Structure
57 |
58 | ExtractDigit/
59 | ├── extract_digit.cpp # Full working code
60 | ├── README.md # Explanation and approach
61 |
62 | └── Makefile # Build and run the code
63 |
64 |
65 |
66 |
67 |
68 |
69 |
70 |
71 |
72 |
--------------------------------------------------------------------------------
/Level 1/Week 11/Dynamic Programming/518. Coin Change II/README.md:
--------------------------------------------------------------------------------
1 | # Coin Change II
2 |
3 | **Difficulty:** Medium
4 |
5 | ## Problem Description
6 |
7 | You are given an integer array `coins` representing coins of different denominations and an integer `amount` representing a total amount of money.
8 |
9 | Return the number of combinations that make up that amount. If that amount of money cannot be made up by any combination of the coins, return `0`.
10 |
11 | You may assume that you have an infinite number of each kind of coin.
12 |
13 | The answer is **guaranteed** to fit into a signed **32-bit** integer.
14 |
15 | ---
16 |
17 | ## Examples
18 |
19 | ### Example 1
20 | Input: amount = 5, coins = [1,2,5]
21 | Output: 4
22 | Explanation: there are four ways to make up the amount:
23 | 5=5
24 | 5=2+2+1
25 | 5=2+1+1+1
26 | 5=1+1+1+1+1
27 |
28 | ### Example 2
29 | Input: amount = 3, coins = [2]
30 | Output: 0
31 | Explanation: the amount of 3 cannot be made up just with coins of 2.
32 |
33 | ### Example 3
34 | Input: amount = 10, coins = [10]
35 | Output: 1
36 |
37 | ---
38 |
39 | ## Constraints
40 |
41 | - `1 <= coins.length <= 300`
42 | - `1 <= coins[i] <= 5000`
43 | - `0 <= amount <= 5000`
44 |
45 | ---
46 |
47 | ## Approaches
48 |
49 | This problem can be solved using 4 different dynamic programming approaches:
50 |
51 | 1. **Recursion** - Direct recursive implementation
52 | 2. **Memoization** - Top-down DP with caching
53 | 3. **Tabulation** - Bottom-up DP with array
54 | 4. **Space Optimization** - Optimized space complexity
55 |
56 | ---
57 |
--------------------------------------------------------------------------------
/Level 0/7 Sliding Window/08. 0003-longest-substring-without-repeating-characters/README.md:
--------------------------------------------------------------------------------
1 | Medium
Given a string s, find the length of the longest substring without duplicate characters.
2 |
3 |
4 | Example 1:
5 |
6 |
7 | Input: s = "abcabcbb"
8 | Output: 3
9 | Explanation: The answer is "abc", with the length of 3.
10 |
11 |
12 | Example 2:
13 |
14 |
15 | Input: s = "bbbbb"
16 | Output: 1
17 | Explanation: The answer is "b", with the length of 1.
18 |
19 |
20 | Example 3:
21 |
22 |
23 | Input: s = "pwwkew"
24 | Output: 3
25 | Explanation: The answer is "wke", with the length of 3.
26 | Notice that the answer must be a substring, "pwke" is a subsequence and not a substring.
27 |
28 |
29 |
30 | Constraints:
31 |
32 |
33 | 0 <= s.length <= 5 * 104s consists of English letters, digits, symbols and spaces.
36 |
--------------------------------------------------------------------------------
/Level 0/8 Trees/06. 1448-count-good-nodes-in-binary-tree/README.md:
--------------------------------------------------------------------------------
1 | # 1448. Count Good Nodes in Binary Tree
2 |
3 | ## Problem Description
4 |
5 | Given a binary tree `root`, a node *X* in the tree is named **good** if in the path from root to *X* there are no nodes with a value *greater than* X.
6 |
7 | Return the number of **good** nodes in the binary tree.
8 |
9 | ## Examples
10 |
11 | ### Example 1:
12 | 
13 |
14 | **Input:** `root = [3,1,4,3,null,1,5]`
15 |
16 | **Output:** `4`
17 |
18 | **Explanation:** Nodes in blue are **good**.
19 | Root Node (3) is always a good node.
20 | Node 4 -> (3,4) is the maximum value in the path starting from the root.
21 | Node 5 -> (3,4,5) is the maximum value in the path
22 | Node 3 -> (3,1,3) is the maximum value in the path.
23 |
24 | ### Example 2:
25 | 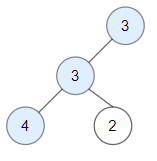
26 |
27 | **Input:** `root = [3,3,null,4,2]`
28 |
29 | **Output:** `3`
30 |
31 | **Explanation:** Node 2 -> (3, 3, 2) is not good, because "3" is higher than it.
32 |
33 | ### Example 3:
34 |
35 | **Input:** `root = [1]`
36 |
37 | **Output:** `1`
38 |
39 | **Explanation:** Root is considered as good.
40 |
41 | ## Constraints
42 |
43 | - The number of nodes in the binary tree is in the range `[1, 10^5]`.
44 | - Each node's value is between `[-10^4, 10^4]`.
45 |
46 | ## Related Topics
47 |
48 | - Tree
49 | - Depth-First Search
50 | - Breadth-First Search
51 | - Binary Tree
52 |
53 | ## Difficulty
54 |
55 | Medium
56 |
--------------------------------------------------------------------------------
/Level 1/Week 02/Sliding windows/3. Longest Substring Without Repeating Characters/README.md:
--------------------------------------------------------------------------------
1 | Medium
Given a string s, find the length of the longest substring without repeating characters.
2 |
3 |
4 | Example 1:
5 |
6 |
7 | Input: s = "abcabcbb"
8 | Output: 3
9 | Explanation: The answer is "abc", with the length of 3.
10 |
11 |
12 | Example 2:
13 |
14 |
15 | Input: s = "bbbbb"
16 | Output: 1
17 | Explanation: The answer is "b", with the length of 1.
18 |
19 |
20 | Example 3:
21 |
22 |
23 | Input: s = "pwwkew"
24 | Output: 3
25 | Explanation: The answer is "wke", with the length of 3.
26 | Notice that the answer must be a substring, "pwke" is a subsequence and not a substring.
27 |
28 |
29 |
30 | Constraints:
31 |
32 |
33 | 0 <= s.length <= 5 * 104s consists of English letters, digits, symbols and spaces.
36 |
--------------------------------------------------------------------------------
/Level 0/10 Backtracking/07. 0017-letter-combinations-of-a-phone-number/code.cpp:
--------------------------------------------------------------------------------
1 | class Solution {
2 | private:
3 | vector result;
4 | vector digitMap = {
5 | "", "", "abc", "def", "ghi", "jkl", "mno", "pqrs", "tuv", "wxyz"
6 | };
7 |
8 | void backtrack(const string& digits, string& current, int index) {
9 | // Base case: if we've processed all digits
10 | if (index >= digits.length()) {
11 | if (!current.empty()) {
12 | result.push_back(current);
13 | }
14 | return;
15 | }
16 |
17 | // Get the letters for current digit
18 | int digit = digits[index] - '0';
19 | string letters = digitMap[digit];
20 |
21 | // Try each letter for current digit
22 | for (char letter : letters) {
23 | // Make choice: add letter
24 | current += letter;
25 |
26 | // Recurse to next digit
27 | backtrack(digits, current, index + 1);
28 |
29 | // Backtrack: remove letter
30 | current.pop_back();
31 | }
32 | }
33 |
34 | public:
35 | vector letterCombinations(string digits) {
36 | if (digits.empty()) {
37 | return result;
38 | }
39 |
40 | string current;
41 | backtrack(digits, current, 0);
42 | return result;
43 | }
44 | };
45 |
46 | /*
47 | Time Complexity: O(4^n) where n is the length of digits
48 | Space Complexity: O(n) for recursion stack
49 | */
--------------------------------------------------------------------------------
/Common/Math/Reverse Number/README.md:
--------------------------------------------------------------------------------
1 | # 🔁 Reverse a Number – C++ Techniques
2 |
3 | ---
4 |
5 | ## 📘 Problem Statement
6 |
7 | Given an integer `n`, return the number formed by reversing its digits.
8 |
9 | ---
10 |
11 | ## ✳️ Example
12 |
13 | Input: 1234
14 | Output: 4321
15 |
16 | Input: 900
17 | Output: 9
18 |
19 |
20 | ---
21 |
22 | ## 🚀 Approaches
23 |
24 | ### ✅ 1. Using While Loop (Mathematical)
25 | - Extract last digit using `% 10`
26 | - Build the reversed number using: `reversed = reversed * 10 + digit`
27 | - Remove last digit using `/= 10`
28 |
29 | 🕒 **Time Complexity**: O(d) where d = number of digits
30 | 🧠 **Space Complexity**: O(1)
31 |
32 | ---
33 |
34 | ### ✅ 2. Recursive Approach
35 | - Base case: if num == 0 → return reversed
36 | - Recursive step: reverse `num/10` while building reversed number
37 |
38 | 🕒 **Time Complexity**: O(d)
39 | 🧠 **Space Complexity**: O(d) (recursive call stack)
40 |
41 | ---
42 |
43 | ### ✅ 3. Using String Conversion
44 | - Convert number to string
45 | - Reverse the string
46 | - Convert back to integer
47 |
48 | 🕒 **Time Complexity**: O(d)
49 | 🧠 **Space Complexity**: O(d)
50 |
51 | ---
52 |
53 | ### ✅ 4. For Loop (Math Variant)
54 | - More compact math version using `for` loop
55 | - Equivalent logic to the while loop approach
56 |
57 | 🕒 **Time Complexity**: O(d)
58 |
59 | ---
60 |
61 | ## 📂 Folder Structure
62 | ReverseNumberTechniques/
63 | ├── reverse_number.cpp # Full code with all 4 approaches
64 | ├── README.md # Detailed explanation and usage
65 | ├── Makefile # Build and run commands
66 |
--------------------------------------------------------------------------------
/Level 1/Week 03/LinkedList/143. Reorder List/README.md:
--------------------------------------------------------------------------------
1 | Medium
You are given the head of a singly linked-list. The list can be represented as:
2 |
3 |
4 | L0 → L1 → … → Ln - 1 → Ln
5 |
6 |
7 | Reorder the list to be on the following form:
8 |
9 |
10 | L0 → Ln → L1 → Ln - 1 → L2 → Ln - 2 → …
11 |
12 |
13 | You may not modify the values in the list's nodes. Only nodes themselves may be changed.
14 |
15 |
16 | Example 1:
17 |  18 |
18 |
19 | Input: head = [1,2,3,4]
20 | Output: [1,4,2,3]
21 |
22 |
23 | Example 2:
24 |  25 |
25 |
26 | Input: head = [1,2,3,4,5]
27 | Output: [1,5,2,4,3]
28 |
29 |
30 |
31 | Constraints:
32 |
33 |
34 | - The number of nodes in the list is in the range
[1, 5 * 104].
35 | 1 <= Node.val <= 1000
37 |
--------------------------------------------------------------------------------
/Level 1/Week 12/Graph/133. Clone Graph/README.md:
--------------------------------------------------------------------------------
1 | # Clone Graph
2 |
3 | **Difficulty:** Medium
4 |
5 | ## Problem Description
6 |
7 | Given a reference of a node in a **[connected](https://en.wikipedia.org/wiki/Connectivity_(graph_theory)#Connected_graph)** undirected graph.
8 |
9 | Return a [**deep copy**](https://en.wikipedia.org/wiki/Object_copying#Deep_copy) (clone) of the graph.
10 |
11 | Each node in the graph contains a val (`int`) and a list (`List[Node]`) of its neighbors.
12 |
13 | ---
14 |
15 | ## Examples
16 |
17 | ### Example 1
18 | Input: adjList = [[2,4],[1,3],[2,4],[1,3]]
19 | Output: [[2,4],[1,3],[2,4],[1,3]]
20 |
21 | ### Example 2
22 | Input: adjList = [[]]
23 | Output: [[]]
24 |
25 | ### Example 3
26 | Input: adjList = []
27 | Output: []
28 |
29 | ---
30 |
31 | ## Constraints
32 |
33 | - The number of nodes in the graph is in the range `[0, 100]`.
34 | - `1 <= Node.val <= 100`
35 | - `Node.val` is unique for each node.
36 | - There are no repeated edges and no self-loops in the graph.
37 | - The Graph is connected and all nodes can be visited starting from the given node.
38 |
39 | ---
40 |
41 | ## Approach
42 |
43 | This problem requires a deep copy of a graph:
44 | 1. Use DFS or BFS to traverse the original graph
45 | 2. Create a new node for each node we visit
46 | 3. Use a hash map to track which nodes have been cloned
47 | 4. Copy the neighbors recursively
48 | 5. Handle the case where a node has already been cloned
49 |
50 | The key insight is to use a hash map to avoid infinite recursion and ensure each node is cloned only once.
51 |
52 | ---
53 |
--------------------------------------------------------------------------------
/Level 1/Week 10/Backtracking/17. Letter Combinations of a Phone Number/README.md:
--------------------------------------------------------------------------------
1 | # Letter Combinations of a Phone Number
2 |
3 | **Difficulty:** Medium
4 |
5 | ## Problem Description
6 |
7 | Given a string containing digits from `2-9` inclusive, return all possible letter combinations that the number could represent. Return the answer in **any order**.
8 |
9 | A mapping of digits to letters (just like on the telephone buttons) is given below. Note that 1 does not map to any letters.
10 |
11 | ```
12 | 2: abc
13 | 3: def
14 | 4: ghi
15 | 5: jkl
16 | 6: mno
17 | 7: pqrs
18 | 8: tuv
19 | 9: wxyz
20 | ```
21 |
22 | ---
23 |
24 | ## Examples
25 |
26 | ### Example 1
27 | Input: digits = "23"
28 | Output: ["ad","ae","af","bd","be","bf","cd","ce","cf"]
29 |
30 | ### Example 2
31 | Input: digits = ""
32 | Output: []
33 |
34 | ### Example 3
35 | Input: digits = "2"
36 | Output: ["a","b","c"]
37 |
38 | ---
39 |
40 | ## Constraints
41 |
42 | - `0 <= digits.length <= 4`
43 | - `digits[i]` is a digit in the range `['2', '9']`.
44 |
45 | ---
46 |
47 | ## Approach
48 |
49 | This problem uses backtracking to generate all possible letter combinations:
50 | 1. We build the combination incrementally by choosing one letter at a time
51 | 2. For each digit, we try all possible letters that it can represent
52 | 3. We use a mapping array to convert digits to letters
53 | 4. We backtrack by removing the last added letter to try different combinations
54 | 5. When we've processed all digits, we add the complete combination to our result
55 | 6. We handle the empty string case separately
56 |
57 | ---
58 |
--------------------------------------------------------------------------------
/Level 1/Week 12/Graph/207. Course Schedule/README.md:
--------------------------------------------------------------------------------
1 | # Course Schedule
2 |
3 | **Difficulty:** Medium
4 |
5 | ## Problem Description
6 |
7 | There are a total of `numCourses` courses you have to take, labeled from `0` to `numCourses - 1`. You are given an array `prerequisites` where `prerequisites[i] = [ai, bi]` indicates that you **must** take course `bi` first if you want to take course `ai`.
8 |
9 | - For example, the pair `[0, 1]`, indicates that to take course `0` you have to first take course `1`.
10 |
11 | Return `true` if you can finish all courses. Otherwise, return `false`.
12 |
13 | ---
14 |
15 | ## Examples
16 |
17 | ### Example 1
18 | Input: numCourses = 2, prerequisites = [[1,0]]
19 | Output: true
20 |
21 | ### Example 2
22 | Input: numCourses = 2, prerequisites = [[1,0],[0,1]]
23 | Output: false
24 |
25 | ---
26 |
27 | ## Constraints
28 |
29 | - `1 <= numCourses <= 2000`
30 | - `0 <= prerequisites.length <= 5000`
31 | - `prerequisites[i].length == 2`
32 | - `0 <= ai, bi < numCourses`
33 | - All the pairs `prerequisites[i]` are **unique**.
34 |
35 | ---
36 |
37 | ## Approach
38 |
39 | This problem can be solved using topological sort or cycle detection:
40 | 1. Build an adjacency list representation of the graph
41 | 2. Use DFS to detect cycles in the graph
42 | 3. If there's a cycle, it's impossible to complete all courses
43 | 4. Use a visited array to track visited nodes and detect cycles
44 | 5. Return true if no cycles are found
45 |
46 | The key insight is that if there's a cycle in the dependency graph, it's impossible to complete all courses.
47 |
48 | ---
49 |
--------------------------------------------------------------------------------
/Level 1/Week 03/LinkedList/2. Add Two Numbers/README.md:
--------------------------------------------------------------------------------
1 | Medium
You are given two non-empty linked lists representing two non-negative integers. The digits are stored in reverse order, and each of their nodes contains a single digit. Add the two numbers and return the sum as a linked list.
2 |
3 | You may assume the two numbers do not contain any leading zero, except the number 0 itself.
4 |
5 |
6 | Example 1:
7 | 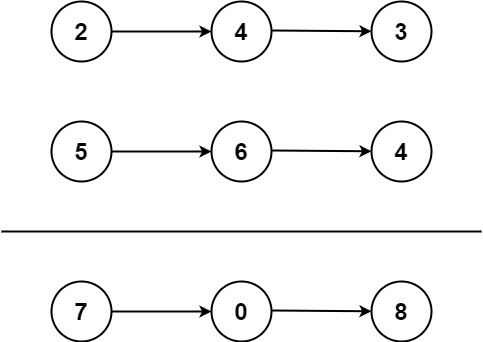 8 |
8 |
9 | Input: l1 = [2,4,3], l2 = [5,6,4]
10 | Output: [7,0,8]
11 | Explanation: 342 + 465 = 807.
12 |
13 |
14 | Example 2:
15 |
16 |
17 | Input: l1 = [0], l2 = [0]
18 | Output: [0]
19 |
20 |
21 | Example 3:
22 |
23 |
24 | Input: l1 = [9,9,9,9,9,9,9], l2 = [9,9,9,9]
25 | Output: [8,9,9,9,0,0,0,1]
26 |
27 |
28 |
29 | Constraints:
30 |
31 |
32 | - The number of nodes in each linked list is in the range
[1, 100].
33 | 0 <= Node.val <= 9- It is guaranteed that the list represents a number that does not have leading zeros.
35 |
36 |
--------------------------------------------------------------------------------
/Level 0/8 Trees/11. 0297-serialize-and-deserialize-binary-tree/README.md:
--------------------------------------------------------------------------------
1 | # 297. Serialize and Deserialize Binary Tree
2 |
3 | ## Problem Description
4 |
5 | Serialization is the process of converting a data structure or object into a sequence of bits so that it can be stored in a file or memory buffer, or transmitted across a network connection link to be reconstructed later in the same or another computer environment.
6 |
7 | Design an algorithm to serialize and deserialize a binary tree. There is no restriction on how your serialization/deserialization algorithm should work. You just need to ensure that a binary tree can be serialized to a string and this string can be deserialized to the original tree structure.
8 |
9 | **Clarification:** The input/output format is the same as [how LeetCode serializes a binary tree](https://support.leetcode.com/hc/en-us/articles/360011883654-What-does-`1,null,2,3,4`-mean-in-binary-tree-representation-). You do not necessarily need to follow this format, so please be creative and come up with different approaches yourself.
10 |
11 | ## Examples
12 |
13 | ### Example 1:
14 |
15 | **Input:** `root = [1,2,3,null,null,4,5]`
16 |
17 | **Output:** `[1,2,3,null,null,4,5]`
18 |
19 | ### Example 2:
20 |
21 | **Input:** `root = []`
22 |
23 | **Output:** `[]`
24 |
25 | ## Constraints
26 |
27 | - The number of nodes in the tree is in the range `[0, 10^4]`.
28 | - `-1000 <= Node.val <= 1000`
29 |
30 | ## Related Topics
31 |
32 | - String
33 | - Tree
34 | - Depth-First Search
35 | - Breadth-First Search
36 | - Design
37 | - Binary Tree
38 |
39 | ## Difficulty
40 |
41 | Hard
42 |
--------------------------------------------------------------------------------
/Level 1/Week 02/Sliding windows/424. Longest Repeating Character Replacement/code.cpp:
--------------------------------------------------------------------------------
1 | /*
2 | Approach (Sliding Window with Frequency Count):
3 |
4 | We aim to find the length of the longest substring that can be made of the same character after replacing at most `k` characters.
5 |
6 | ⚙️ Logic:
7 | 1. Use a sliding window defined by two pointers: `left` and `right`.
8 | 2. Maintain a frequency array `hash[26]` to count letters in the current window.
9 | 3. Track the most frequent character count in the window as `maxfre`.
10 | 4. If the number of characters to be replaced → `(right - left + 1) - maxfre` > `k`, then shrink the window from the left.
11 | 5. At every step, update the maximum window length.
12 |
13 | ✅ Time Complexity: O(n)
14 | ✅ Space Complexity: O(1) – only 26 alphabet characters
15 |
16 | 📌 Note:
17 | We don't shrink the window on every invalid step — only when needed. This helps us maintain a valid window efficiently.
18 | */
19 |
20 | class Solution {
21 | public:
22 | int characterReplacement(string s, int k) {
23 | int left = 0;
24 | int maxLen = 0;
25 | int maxfre = 0;
26 | vector hash(26, 0);
27 |
28 | for (int right = 0; right < s.size(); right++) {
29 | hash[s[right] - 'A']++;
30 | maxfre = max(maxfre, hash[s[right] - 'A']);
31 |
32 | if ((right - left + 1) - maxfre > k) {
33 | hash[s[left] - 'A']--;
34 | left++;
35 | }
36 |
37 | maxLen = max(maxLen, right - left + 1);
38 | }
39 |
40 | return maxLen;
41 | }
42 | };
43 |
--------------------------------------------------------------------------------
/Level 1/Week 09/Greedy/1899. Merge Triplets to Form Target Triplet/code.cpp:
--------------------------------------------------------------------------------
1 | /*
2 | Approach: Greedy Algorithm
3 |
4 | The key insight is that we can only use triplets that don't exceed the target in any dimension.
5 | If any element of a triplet is greater than the corresponding target element,
6 | that triplet can never be part of the solution.
7 |
8 | Algorithm:
9 | 1. Filter triplets: only consider triplets where all elements <= corresponding target elements
10 | 2. For valid triplets, track the maximum value we can achieve in each position
11 | 3. Check if we can exactly match the target in all three positions
12 |
13 | Time Complexity: O(n) where n is the number of triplets
14 | Space Complexity: O(1)
15 | */
16 |
17 | #include
18 | #include
19 | using namespace std;
20 |
21 | class Solution {
22 | public:
23 | bool mergeTriplets(vector>& triplets, vector& target) {
24 | vector maxTriplet(3, 0);
25 |
26 | for (const auto& triplet : triplets) {
27 | // Only consider triplets that don't exceed target in any dimension
28 | if (triplet[0] <= target[0] && triplet[1] <= target[1] && triplet[2] <= target[2]) {
29 | maxTriplet[0] = max(maxTriplet[0], triplet[0]);
30 | maxTriplet[1] = max(maxTriplet[1], triplet[1]);
31 | maxTriplet[2] = max(maxTriplet[2], triplet[2]);
32 | }
33 | }
34 |
35 | return (maxTriplet[0] == target[0] &&
36 | maxTriplet[1] == target[1] &&
37 | maxTriplet[2] == target[2]);
38 | }
39 | };
40 |
--------------------------------------------------------------------------------
/Level 1/Week 10/Recursion/24. Swap Nodes in Pairs/code.cpp:
--------------------------------------------------------------------------------
1 | /*
2 | Problem: 24. Swap Nodes in Pairs
3 |
4 | This is a classic linked list problem that can be solved elegantly using recursion.
5 | Key insights:
6 | 1. We swap the first two nodes at each recursive call
7 | 2. We recursively process the remaining nodes
8 | 3. We need to handle edge cases (empty list, single node)
9 | 4. The recursive approach naturally handles the list structure
10 |
11 | Time Complexity: O(n) - we visit each node once
12 | Space Complexity: O(n) - recursion stack depth
13 | */
14 |
15 | /**
16 | * Definition for singly-linked list.
17 | * struct ListNode {
18 | * int val;
19 | * ListNode *next;
20 | * ListNode() : val(0), next(nullptr) {}
21 | * ListNode(int x) : val(x), next(nullptr) {}
22 | * ListNode(int x, ListNode *next) : val(x), next(next) {}
23 | * };
24 | */
25 |
26 | class Solution {
27 | public:
28 | ListNode* swapPairs(ListNode* head) {
29 | // Base case: if head is null or only one node remains
30 | if (head == nullptr || head->next == nullptr) {
31 | return head;
32 | }
33 |
34 | // Store the second node as it will become the new head
35 | ListNode* second = head->next;
36 |
37 | // Recursively swap the remaining nodes
38 | ListNode* remaining = swapPairs(second->next);
39 |
40 | // Swap the first two nodes
41 | second->next = head;
42 | head->next = remaining;
43 |
44 | // Return the new head (second node)
45 | return second;
46 | }
47 | };
48 |
--------------------------------------------------------------------------------
/Level 0/7 Sliding Window/09. 0424-longest-repeating-character-replacement/README.md:
--------------------------------------------------------------------------------
1 | Medium
You are given a string s and an integer k. You can choose any character of the string and change it to any other uppercase English character. You can perform this operation at most k times.
2 |
3 | Return the length of the longest substring containing the same letter you can get after performing the above operations.
4 |
5 |
6 | Example 1:
7 |
8 |
9 | Input: s = "ABAB", k = 2
10 | Output: 4
11 | Explanation: Replace the two 'A's with two 'B's or vice versa.
12 |
13 |
14 | Example 2:
15 |
16 |
17 | Input: s = "AABABBA", k = 1
18 | Output: 4
19 | Explanation: Replace the one 'A' in the middle with 'B' and form "AABBBBA".
20 | The substring "BBBB" has the longest repeating letters, which is 4.
21 | There may exists other ways to achieve this answer too.
22 |
23 |
24 | Constraints:
25 |
26 |
27 | 1 <= s.length <= 105s consists of only uppercase English letters.0 <= k <= s.length
31 |
--------------------------------------------------------------------------------
/Level 1/Week 10/Backtracking/79. Word Search/README.md:
--------------------------------------------------------------------------------
1 | # Word Search
2 |
3 | **Difficulty:** Medium
4 |
5 | ## Problem Description
6 |
7 | Given an `m x n` grid of characters `board` and a string `word`, return `true` *if* `word` *exists in the grid*.
8 |
9 | The word can be constructed from letters of sequentially adjacent cells, where adjacent cells are horizontally or vertically neighboring. The same letter cell may not be used more than once.
10 |
11 | ---
12 |
13 | ## Examples
14 |
15 | ### Example 1
16 | Input: board = [["A","B","C","E"],["S","F","C","S"],["A","D","E","E"]], word = "ABCCED"
17 | Output: true
18 |
19 | ### Example 2
20 | Input: board = [["A","B","C","E"],["S","F","C","S"],["A","D","E","E"]], word = "SEE"
21 | Output: true
22 |
23 | ### Example 3
24 | Input: board = [["A","B","C","E"],["S","F","C","S"],["A","D","E","E"]], word = "ABCB"
25 | Output: false
26 |
27 | ---
28 |
29 | ## Constraints
30 |
31 | - `m == board.length`
32 | - `n == board[i].length`
33 | - `1 <= m, n <= 6`
34 | - `1 <= word.length <= 15`
35 | - `board` and `word` consists of only lowercase and uppercase English letters.
36 |
37 | ---
38 |
39 | ## Approach
40 |
41 | This problem uses backtracking with DFS:
42 | 1. We start from each cell in the grid
43 | 2. For each cell, we try to match the first character of the word
44 | 3. If matched, we recursively search in all four directions (up, down, left, right)
45 | 4. We mark visited cells to avoid reusing them
46 | 5. We backtrack by unmarking cells when the current path doesn't lead to a solution
47 | 6. We return true if we can match the entire word
48 |
49 | ---
50 |
--------------------------------------------------------------------------------
/Common/Math/Prime/README.md:
--------------------------------------------------------------------------------
1 | # 🔢 Prime Number Checker – C++ Implementations
2 |
3 | ---
4 |
5 | ## 🧠 What is a Prime Number?
6 |
7 | A **prime number** is a natural number greater than 1 that:
8 | - Has exactly **two distinct** positive divisors: **1 and itself**
9 | - Cannot be formed by multiplying two smaller natural numbers
10 |
11 | ### ✅ Examples:
12 | - 2 → Prime (only 1 and 2)
13 | - 3 → Prime (only 1 and 3)
14 | - 4 → ❌ Not Prime (1, 2, 4)
15 | - 5 → Prime
16 | - 6 → ❌ Not Prime (1, 2, 3, 6)
17 |
18 | ---
19 |
20 | ## 📘 What’s Covered?
21 |
22 | This file demonstrates **three distinct approaches** to determine if a number is prime:
23 |
24 | | Approach | Description |
25 | |----------------|---------------------------------------------------|
26 | | Brute Force | Try all numbers from 2 to n-1 |
27 | | Optimized | Try only up to √n (square root) |
28 | | Recursive | Use recursion to divide from 2 up to √n |
29 |
30 | ---
31 |
32 | ## 🗂 File Structure
33 |
34 | Prime/
35 | │
36 | ├── prime_number.cpp # All three approaches with comments
37 | ├── README.md # This file
38 |
39 | ├── Makefile # Build and run commands
40 |
41 | ---
42 |
43 | ## 🔍 Sample Usage
44 |
45 | ```cpp
46 | #include
47 | using namespace std;
48 |
49 | int main() {
50 | int n = 29;
51 |
52 | cout << "Brute Force: " << isPrimeBruteForce(n) << endl;
53 | cout << "Optimized: " << isPrimeOptimized(n) << endl;
54 | cout << "Recursive: " << isPrimeRecursive(n) << endl;
55 |
56 | return 0;
57 | }
58 |
59 |
--------------------------------------------------------------------------------
/Level 1/Week 02/Sliding windows/424. Longest Repeating Character Replacement/README.md:
--------------------------------------------------------------------------------
1 | Medium
You are given a string s and an integer k. You can choose any character of the string and change it to any other uppercase English character. You can perform this operation at most k times.
2 |
3 | Return the length of the longest substring containing the same letter you can get after performing the above operations.
4 |
5 |
6 | Example 1:
7 |
8 |
9 | Input: s = "ABAB", k = 2
10 | Output: 4
11 | Explanation: Replace the two 'A's with two 'B's or vice versa.
12 |
13 |
14 | Example 2:
15 |
16 |
17 | Input: s = "AABABBA", k = 1
18 | Output: 4
19 | Explanation: Replace the one 'A' in the middle with 'B' and form "AABBBBA".
20 | The substring "BBBB" has the longest repeating letters, which is 4.
21 | There may exists other ways to achieve this answer too.
22 |
23 |
24 | Constraints:
25 |
26 |
27 | 1 <= s.length <= 105s consists of only uppercase English letters.0 <= k <= s.length
31 |
--------------------------------------------------------------------------------
/Level 1/Week 10/Recursion/206. Reverse Linked List/code.cpp:
--------------------------------------------------------------------------------
1 | /*
2 | Problem: 206. Reverse Linked List
3 |
4 | This is a classic recursion problem for reversing a linked list.
5 | Key insights:
6 | 1. Base case: if head is null or only one node remains
7 | 2. Recursive case: reverse the rest of the list
8 | 3. Make the current node point to the reversed list
9 | 4. Return the new head (which is the last node of original list)
10 | 5. The recursive approach naturally handles the reversal by working backwards
11 |
12 | Time Complexity: O(n) - we visit each node once
13 | Space Complexity: O(n) - recursion stack depth
14 | */
15 |
16 | /**
17 | * Definition for singly-linked list.
18 | * struct ListNode {
19 | * int val;
20 | * ListNode *next;
21 | * ListNode() : val(0), next(nullptr) {}
22 | * ListNode(int x) : val(x), next(nullptr) {}
23 | * ListNode(int x, ListNode *next) : val(x), next(next) {}
24 | * };
25 | */
26 |
27 | class Solution {
28 | public:
29 | ListNode* reverseList(ListNode* head) {
30 | // Base case: if head is null or only one node remains
31 | if (head == nullptr || head->next == nullptr) {
32 | return head;
33 | }
34 |
35 | // Recursively reverse the rest of the list
36 | ListNode* reversedRest = reverseList(head->next);
37 |
38 | // Make the current node point to the reversed list
39 | head->next->next = head;
40 | head->next = nullptr;
41 |
42 | // Return the new head (which is the last node of original list)
43 | return reversedRest;
44 | }
45 | };
46 |
--------------------------------------------------------------------------------
 8 |
8 |  10 |
10 |  6 |
6 |  6 |
6 |  13 |
13 |  6 |
6 |  13 |
13 |  6 |
6 |  15 |
15 |  6 |
6 |  6 |
6 |  13 |
13 |  10 |
10 |  6 |
6 |  13 |
13 |  18 |
18 |  25 |
25 |  8 |
8 |