├── autobound
├── example_bounds.png
├── __init__.py
├── jax
│ ├── __init__.py
│ ├── jaxpr_editor_test.py
│ ├── jaxpr_editor.py
│ ├── jax_bound_test.py
│ └── jax_bound.py
├── types_test.py
├── graph_editor_test.py
├── test_utils.py
├── polynomials_test.py
├── graph_editor.py
├── polynomials.py
├── interval_arithmetic_test.py
├── enclosure_arithmetic_test.py
├── primitive_enclosures.py
├── elementwise_functions_test.py
├── elementwise_functions.py
├── interval_arithmetic.py
└── enclosure_arithmetic.py
├── .gitignore
├── CONTRIBUTING.md
├── .github
└── workflows
│ └── ci-build.yaml
├── pyproject.toml
├── README.md
├── LICENSE
└── .pylintrc
/autobound/example_bounds.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/dpsanders/autobound/main/autobound/example_bounds.png
--------------------------------------------------------------------------------
/.gitignore:
--------------------------------------------------------------------------------
1 | # Compiled python modules.
2 | *.pyc
3 |
4 | # Byte-compiled
5 | _pycache__/
6 | .cache/
7 |
8 | # Poetry, setuptools, PyPI distribution artifacts.
9 | /*.egg-info
10 | .eggs/
11 | build/
12 | dist/
13 | poetry.lock
14 |
15 | # Tests
16 | .pytest_cache/
17 |
18 | # Type checking
19 | .pytype/
20 |
21 | # Other
22 | *.DS_Store
23 |
24 | # PyCharm
25 | .idea
26 |
--------------------------------------------------------------------------------
/autobound/__init__.py:
--------------------------------------------------------------------------------
1 | # Copyright 2023 The autobound Authors.
2 | #
3 | # Licensed under the Apache License, Version 2.0 (the "License");
4 | # you may not use this file except in compliance with the License.
5 | # You may obtain a copy of the License at
6 | #
7 | # http://www.apache.org/licenses/LICENSE-2.0
8 | #
9 | # Unless required by applicable law or agreed to in writing, software
10 | # distributed under the License is distributed on an "AS IS" BASIS,
11 | # WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
12 | # See the License for the specific language governing permissions and
13 | # limitations under the License.
14 |
15 | __version__ = "0.1.2"
16 |
--------------------------------------------------------------------------------
/autobound/jax/__init__.py:
--------------------------------------------------------------------------------
1 | # Copyright 2023 The autobound Authors.
2 | #
3 | # Licensed under the Apache License, Version 2.0 (the "License");
4 | # you may not use this file except in compliance with the License.
5 | # You may obtain a copy of the License at
6 | #
7 | # http://www.apache.org/licenses/LICENSE-2.0
8 | #
9 | # Unless required by applicable law or agreed to in writing, software
10 | # distributed under the License is distributed on an "AS IS" BASIS,
11 | # WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
12 | # See the License for the specific language governing permissions and
13 | # limitations under the License.
14 |
15 | """Package for computing Taylor polynomial enclosures in JAX."""
16 |
17 | from autobound.jax.jax_bound import taylor_bounds
18 |
--------------------------------------------------------------------------------
/autobound/types_test.py:
--------------------------------------------------------------------------------
1 | # Copyright 2023 The autobound Authors.
2 | #
3 | # Licensed under the Apache License, Version 2.0 (the "License");
4 | # you may not use this file except in compliance with the License.
5 | # You may obtain a copy of the License at
6 | #
7 | # http://www.apache.org/licenses/LICENSE-2.0
8 | #
9 | # Unless required by applicable law or agreed to in writing, software
10 | # distributed under the License is distributed on an "AS IS" BASIS,
11 | # WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
12 | # See the License for the specific language governing permissions and
13 | # limitations under the License.
14 |
15 | from absl.testing import absltest
16 | from autobound import test_utils
17 | from autobound import types
18 |
19 |
20 | class TestCase(test_utils.TestCase):
21 |
22 | def test_ndarray(self):
23 | for np_like in self.backends:
24 | self.assertIsInstance(np_like.eye(3), types.NDArray)
25 |
26 | def test_numpy_like(self):
27 | for np_like in self.backends:
28 | self.assertIsInstance(np_like, types.NumpyLike)
29 |
30 |
31 | if __name__ == '__main__':
32 | absltest.main()
33 |
--------------------------------------------------------------------------------
/CONTRIBUTING.md:
--------------------------------------------------------------------------------
1 | # How to Contribute
2 |
3 | We'd love to accept your patches and contributions to this project. There are
4 | just a few small guidelines you need to follow.
5 |
6 | ## Contributor License Agreement
7 |
8 | Contributions to this project must be accompanied by a Contributor License
9 | Agreement (CLA). You (or your employer) retain the copyright to your
10 | contribution; this simply gives us permission to use and redistribute your
11 | contributions as part of the project. Head over to
12 | to see your current agreements on file or
13 | to sign a new one.
14 |
15 | You generally only need to submit a CLA once, so if you've already submitted one
16 | (even if it was for a different project), you probably don't need to do it
17 | again.
18 |
19 | ## Code Reviews
20 |
21 | All submissions, including submissions by project members, require review. We
22 | use GitHub pull requests for this purpose. Consult
23 | [GitHub Help](https://help.github.com/articles/about-pull-requests/) for more
24 | information on using pull requests.
25 |
26 | ## Community Guidelines
27 |
28 | This project follows
29 | [Google's Open Source Community Guidelines](https://opensource.google/conduct/).
30 |
--------------------------------------------------------------------------------
/.github/workflows/ci-build.yaml:
--------------------------------------------------------------------------------
1 | # This workflow will install Python dependencies, run tests and lint with a variety of Python versions
2 | # For more information see: https://docs.github.com/en/actions/automating-builds-and-tests/building-and-testing-python
3 |
4 | name: CI
5 |
6 | on:
7 | push:
8 | branches: [ "main" ]
9 | pull_request:
10 | branches: [ "main" ]
11 |
12 | jobs:
13 | build:
14 |
15 | runs-on: ubuntu-latest
16 | strategy:
17 | fail-fast: false
18 | matrix:
19 | python-version: ["3.9", "3.10"]
20 |
21 | steps:
22 | - uses: actions/checkout@v3
23 | - name: Set up Python ${{ matrix.python-version }}
24 | uses: actions/setup-python@v3
25 | with:
26 | python-version: ${{ matrix.python-version }}
27 | - name: Install dependencies
28 | run: |
29 | python -m pip install --upgrade pip
30 | python -m pip install flake8 .[dev]
31 | - name: Lint with flake8
32 | run: |
33 | # stop the build if there are Python syntax errors or undefined names
34 | flake8 . --count --select=E9,F63,F7,F82 --show-source --statistics
35 | # exit-zero treats all errors as warnings. The GitHub editor is 127 chars wide
36 | flake8 . --count --exit-zero --max-complexity=10 --max-line-length=127 --statistics
37 | - name: Test with pytest
38 | run: |
39 | pytest
40 |
--------------------------------------------------------------------------------
/pyproject.toml:
--------------------------------------------------------------------------------
1 | [project]
2 | name = "autobound"
3 | description = ""
4 | readme = "README.md"
5 | requires-python = ">=3.7"
6 | license = {file = "LICENSE"}
7 | authors = [{name = "AutoBound authors", email="autobound@google.com"}]
8 | classifiers = [
9 | "Programming Language :: Python :: 3",
10 | "Programming Language :: Python :: 3 :: Only",
11 | "License :: OSI Approved :: Apache Software License",
12 | "Intended Audience :: Science/Research",
13 | ]
14 | keywords = []
15 |
16 | # pip dependencies of the project
17 | dependencies = [
18 | "jax>=0.4.6"
19 | ]
20 |
21 | # This is set automatically by flit using `autobound.__version__`
22 | dynamic = ["version"]
23 |
24 | [project.urls]
25 | homepage = "https://github.com/google/autobound"
26 | repository = "https://github.com/google/autobound"
27 | # Other: `documentation`, `changelog`
28 |
29 | [project.optional-dependencies]
30 | # Development deps (unittest, linting, formating,...)
31 | # Installed through `pip install .[dev]`
32 | dev = [
33 | "absl-py>=1.3.0",
34 | "flax>=0.6.7",
35 | "pytest",
36 | "pytest-xdist",
37 | "pylint>=2.6.0",
38 | "pyink",
39 | "typing_extensions>=4.4.0",
40 | ]
41 |
42 | [tool.pyink]
43 | # Formatting configuration to follow Google style-guide
44 | pyink-indentation = 2
45 | pyink-use-majority-quotes = true
46 |
47 | [build-system]
48 | requires = ["flit_core >=3.5,<4"]
49 | build-backend = "flit_core.buildapi"
50 |
--------------------------------------------------------------------------------
/autobound/graph_editor_test.py:
--------------------------------------------------------------------------------
1 | # Copyright 2023 The autobound Authors.
2 | #
3 | # Licensed under the Apache License, Version 2.0 (the "License");
4 | # you may not use this file except in compliance with the License.
5 | # You may obtain a copy of the License at
6 | #
7 | # http://www.apache.org/licenses/LICENSE-2.0
8 | #
9 | # Unless required by applicable law or agreed to in writing, software
10 | # distributed under the License is distributed on an "AS IS" BASIS,
11 | # WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
12 | # See the License for the specific language governing permissions and
13 | # limitations under the License.
14 |
15 | from absl.testing import absltest
16 | from absl.testing import parameterized
17 | from autobound import graph_editor
18 | from autobound.graph_editor import ComputationGraph, Operation
19 |
20 |
21 | class TestCase(parameterized.TestCase):
22 |
23 | @parameterized.parameters(
24 | (
25 | Operation('foo', ['a', 'b'], ['x', 'y']),
26 | {'a': 'A', 'y': 'Y'},
27 | Operation('foo', ['A', 'b'], ['x', 'Y']),
28 | )
29 | )
30 | def test_edge_subs(self, edge, mapping, expected):
31 | actual = edge.subs(mapping)
32 | self.assertEqual(expected, actual)
33 |
34 | @parameterized.parameters(
35 | (
36 | ComputationGraph(['a', 'b'], ['z'],
37 | [Operation('foo', ['a'], ['y']),
38 | Operation('bar', ['y'], ['z'])]),
39 | {'a', 'b', 'y', 'z'}
40 | ),
41 | )
42 | def test_intermediate_variables(self, graph, expected):
43 | actual = graph.intermediate_variables()
44 | self.assertSetEqual(expected, actual)
45 |
46 | @parameterized.parameters(
47 | (
48 | [Operation('foo', ['x'], ['y'])],
49 | [Operation('foo', ['x'], ['y'])],
50 | lambda u, v: True,
51 | {'x': 'x', 'y': 'y'}
52 | ),
53 | (
54 | [Operation('foo', ['x'], ['y'])],
55 | [Operation('foo', ['x'], ['y'])],
56 | lambda u, v: False,
57 | None
58 | ),
59 | (
60 | [Operation('foo', ['x'], ['y'])],
61 | [Operation('foo', ['a'], ['b'])],
62 | lambda u, v: True,
63 | {'x': 'a', 'y': 'b'}
64 | ),
65 | (
66 | [Operation('foo', ['x'], ['y'])],
67 | [Operation('bar', ['x'], ['y'])],
68 | lambda u, v: True,
69 | None
70 | ),
71 | )
72 | def test_match(self, pattern, subject, can_bind, expected):
73 | actual = graph_editor.match(pattern, subject, can_bind)
74 | self.assertEqual(expected, actual)
75 | if actual is not None:
76 | self.assertTrue(all(can_bind(u, v) for u, v in actual.items()))
77 | self.assertEqual([e.subs(actual) for e in pattern], subject)
78 |
79 | @parameterized.parameters(
80 | (
81 | [Operation('foo', ['x'], ['y'])],
82 | [Operation('bar', ['x'], ['y'])],
83 | ComputationGraph(['a'], ['b'], [Operation('foo', ['a'], ['b'])]),
84 | lambda u, v: True,
85 | ComputationGraph(['a'], ['b'], [Operation('bar', ['a'], ['b'])]),
86 | ),
87 | )
88 | def test_replace(self, pattern, replacement, subject, can_bind, expected):
89 | actual = graph_editor.replace(pattern, replacement, subject, can_bind)
90 | self.assertEqual(expected, actual)
91 |
92 |
93 | if __name__ == '__main__':
94 | absltest.main()
95 |
--------------------------------------------------------------------------------
/README.md:
--------------------------------------------------------------------------------
1 | # AutoBound: Automatically Bounding Functions
2 |
3 | 
4 | 
5 |
6 | AutoBound is a generalization of automatic differentiation. In addition to
7 | computing a Taylor polynomial approximation of a function, it computes upper
8 | and lower bounds that are guaranteed to hold over a user-specified
9 | _trust region_.
10 |
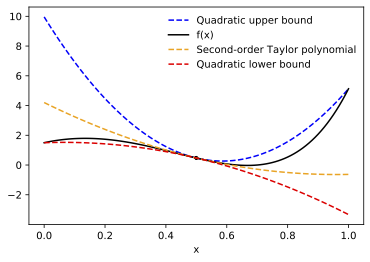
11 | As an example, here are the quadratic upper and lower bounds AutoBound computes
12 | for the function `f(x) = 1.5*exp(3*x) - 25*(x**2)`, centered at `0.5`, and
13 | valid over the trust region `[0, 1]`.
14 |
15 |
16 |
17 |
 17 |
17 |  17 |
17 |