| 407 | | rounds | 408 |mi_mean | 409 |mi_error | 410 |delta | 411 |num_feat | 412 |features | 413 |
|---|---|---|---|---|---|---|
| 0 | 418 |0 | 419 |0.000000 | 420 |0.000000 | 421 |0.000000 | 422 |0 | 423 |[] | 424 |
| 1 | 427 |1 | 428 |0.139542 | 429 |0.005217 | 430 |0.000000 | 431 |1 | 432 |[3] | 433 |
| 2 | 436 |2 | 437 |0.280835 | 438 |0.006377 | 439 |1.012542 | 440 |2 | 441 |[3, 0] | 442 |
| 3 | 445 |3 | 446 |0.503872 | 447 |0.006499 | 448 |0.794196 | 449 |3 | 450 |[3, 0, 1] | 451 |
| 4 | 454 |4 | 455 |0.617048 | 456 |0.006322 | 457 |0.224612 | 458 |4 | 459 |[3, 0, 1, 4] | 460 |
| 5 | 463 |5 | 464 |0.745933 | 465 |0.005135 | 466 |0.208874 | 467 |5 | 468 |[3, 0, 1, 4, 2] | 469 |
| 6 | 472 |6 | 473 |0.745549 | 474 |0.005202 | 475 |-0.000515 | 476 |6 | 477 |[3, 0, 1, 4, 2, 5] | 478 |
| 7 | 481 |7 | 482 |0.740968 | 483 |0.005457 | 484 |-0.006144 | 485 |7 | 486 |[3, 0, 1, 4, 2, 5, 6] | 487 |
\n", 207 | "\\begin{align}\n", 208 | "Y_i &= f(X_{0,i},...,X_{6,i}) + \\epsilon_i \\\\[.5em]\n", 209 | "&=10\\cdot \\sin(\\pi X_{0,i} X_{1,i}) + 20 (X_{2,i}-0.5)^2 + 10 X_{3,i} + 5 X_{4,i} + \\epsilon_i\n", 210 | "\\end{align}\n", 211 | "
\n", 212 | "\n", 213 | "Where $X_{0,i},...,X_{6,i} \\overset{iid}{\\sim} U[0,1]$ and $\\epsilon_i \\sim N(0,1)$ independent from all the other random variables for all $i\\in [n]$. In the following we set $n=20000$:" 214 | ] 215 | }, 216 | { 217 | "cell_type": "code", 218 | "execution_count": 3, 219 | "metadata": { 220 | "id": "8Y4_HMDDmTLZ" 221 | }, 222 | "outputs": [], 223 | "source": [ 224 | "def f(X,e): return 10*np.sin(np.pi*X[:,0]*X[:,1]) + 20*(X[:,2]-.5)**2 + 10*X[:,3] + 5*X[:,4] + e" 225 | ] 226 | }, 227 | { 228 | "cell_type": "code", 229 | "execution_count": 4, 230 | "metadata": { 231 | "colab": { 232 | "base_uri": "https://localhost:8080/" 233 | }, 234 | "id": "isQqEnhDmTLl", 235 | "outputId": "cd966641-eadb-40cc-ec64-67cb54ae8f31" 236 | }, 237 | "outputs": [ 238 | { 239 | "data": { 240 | "text/plain": [ 241 | "((20000, 7), (20000,))" 242 | ] 243 | }, 244 | "execution_count": 4, 245 | "metadata": {}, 246 | "output_type": "execute_result" 247 | } 248 | ], 249 | "source": [ 250 | "n=20000\n", 251 | "d=7\n", 252 | "\n", 253 | "X = np.random.uniform(0,1,d*n).reshape((n,d))\n", 254 | "e = np.random.normal(0,1,n)\n", 255 | "y = f(X,e)\n", 256 | "\n", 257 | "X.shape, y.shape" 258 | ] 259 | }, 260 | { 261 | "cell_type": "markdown", 262 | "metadata": { 263 | "id": "Sgl9V_enmTL2" 264 | }, 265 | "source": [ 266 | "### 1.2\\. Selecting Features for a Regression Task" 267 | ] 268 | }, 269 | { 270 | "cell_type": "markdown", 271 | "metadata": { 272 | "id": "J-KknWzDmTL4" 273 | }, 274 | "source": [ 275 | "Training (and validating) GMM:" 276 | ] 277 | }, 278 | { 279 | "cell_type": "code", 280 | "execution_count": 228, 281 | "metadata": { 282 | "colab": { 283 | "base_uri": "https://localhost:8080/" 284 | }, 285 | "id": "KKg_aU1hmTL8", 286 | "outputId": "e0071c65-ee69-4627-b4f1-519111c87d5c" 287 | }, 288 | "outputs": [ 289 | { 290 | "ename": "TypeError", 291 | "evalue": "get_gmm() got an unexpected keyword argument 'covariance_type'", 292 | "output_type": "error", 293 | "traceback": [ 294 | "\u001b[0;31m---------------------------------------------------------------------------\u001b[0m", 295 | "\u001b[0;31mTypeError\u001b[0m Traceback (most recent call last)", 296 | "\u001b[0;32m
\n",
405 | "\n",
418 | "\n",
419 | " \n",
420 | "
\n",
496 | "
"
497 | ],
498 | "text/plain": [
499 | " rounds mi_mean mi_error delta num_feat features\n",
500 | "0 0 1.483969 0.006147 0.000000 7 [0, 1, 2, 3, 4, 5, 6]\n",
501 | "1 1 1.483101 0.006139 -0.000585 6 [0, 1, 2, 3, 4, 5]\n",
502 | "2 2 1.481667 0.006135 -0.000967 5 [0, 1, 2, 3, 4]\n",
503 | "3 3 1.001292 0.005613 -0.324212 4 [0, 1, 3, 4]\n",
504 | "4 4 0.751952 0.005343 -0.249018 3 [0, 1, 3]\n",
505 | "5 5 0.390138 0.005015 -0.481166 2 [1, 3]\n",
506 | "6 6 0.212257 0.003765 -0.455946 1 [3]"
507 | ]
508 | },
509 | "execution_count": 8,
510 | "metadata": {
511 | "tags": []
512 | },
513 | "output_type": "execute_result"
514 | }
515 | ],
516 | "source": [
517 | "select.get_info()"
518 | ]
519 | },
520 | {
521 | "cell_type": "markdown",
522 | "metadata": {
523 | "id": "CtsYNrEsmTMc"
524 | },
525 | "source": [
526 | "It is possible to see that the estimated mutual information is untouched until Round 2, when it varies around -$30\\%$.\n",
527 | "\n",
528 | "Since there is a 'break' in Round 2, we should choose to stop the algorithm at theta round. This will be clear in the Mutual Information history plot that follows:"
529 | ]
530 | },
531 | {
532 | "cell_type": "code",
533 | "execution_count": null,
534 | "metadata": {
535 | "colab": {
536 | "base_uri": "https://localhost:8080/",
537 | "height": 279
538 | },
539 | "id": "5G8kBvEvmTMd",
540 | "outputId": "f9ed0da4-762e-48dd-d9ce-3f94e8db2c81"
541 | },
542 | "outputs": [
543 | {
544 | "data": {
545 | "image/png": "iVBORw0KGgoAAAANSUhEUgAAAYIAAAEGCAYAAABo25JHAAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADh0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uMy4yLjIsIGh0dHA6Ly9tYXRwbG90bGliLm9yZy+WH4yJAAAgAElEQVR4nO3dd5hU5fnG8e+zBZa6CCxFOggWqrAUNYJGMdggFlQQLFEpxhaNPzXRqDGJMRq7UgSDoqJYg7FgB5W6C4gUQZqwqFQp0hee3x8zqwNsGZedPTs79+e6zrUz5z1zzj0X5dlz3nPe19wdERFJXElBBxARkWCpEIiIJDgVAhGRBKdCICKS4FQIREQSXErQAX6p2rVre9OmTYOOISISV7Kzs9e7e0Z+bXFXCJo2bUpWVlbQMURE4oqZfVNQmy4NiYgkOBUCEZEEp0IgIpLgVAhERBKcCoGISIJTIRARSXAqBCIiCU6FQEQkwcXdA2XFdcYjk/l2804ym9TELLTOIOJ16IXZwevYb3uLXBXa/qfX+7dh+++3sGP+/PPg7X8+Tujde/O/B6BXm3o/HzPcnpcn9D3Cn8inLe/4P+UPb1vQfgo8xkHfIXI/4feFHCPJoEerOtRLT0NEgpEwhWCfw+7cfazetAOAyAl58l46HvGa/bbziJWRbZ7PPvLeHzjnT5HbH9BGAXm27swF4I053/68z/Dn896H9uc/7/eA9/llCUrFlCSm3XYKh1WpEGwQkQSVMIXg3Ru6Bx2hzHM/uFBEFhQ4uMBEbpdXbH7e7uD9/FywQu+Xrt3G78bM5LoXZzPm8i4kJ1k+yUQklhKmEEjR8i7jhN+VyjHrp1fint+25pZXv+T+iYu49fSjSuW4IvIzdRZL4C7s3JiLuzZm+KSlvDX3u6DjiCQcFQIpE+48uzWdmhzGza98waLvtwYdRyShqBBImVAhJYknL+5IlYopDBqbxebte4KOJJIwVAikzKhbPY1hF3fk2007uP6l2ezdF/DtTCIJQoVAypTMpjW58+zWfLJoHQ9/sDjoOCIJIWaFwMyeNrO1ZjaviO06m1mumZ0fqywSXy7u2pgLMxvx2EdLmBh+eE5EYieWZwRjgF6FbWBmycB9wHsxzCFxxsy4u09r2jdM56bxX7BkrTqPRWIpZoXA3ScDG4vY7FrgVWBtrHJIfEpLTWbYgE6kpSYxaGw2W3aq81gkVgLrIzCzBsA5wLAoth1kZllmlrVu3brYh5My4fAalXiif0dWbtjOjS99wT51HovERJCdxQ8Dt7j7vqI2dPeR7p7p7pkZGRmlEE3Kiq7Na3H7mUfzwcI1PP7xkqDjiJRLQQ4xkQm8GB7ZsjZwhpnluvsbAWaSMujS45syd/VmHvpgMa0Pr84pR9cNOpJIuRLYGYG7N3P3pu7eFHgFuFpFQPJjZvzjnLa0Prw6N7w4h2Xrfgw6kki5EsvbR8cBU4EjzSzHzK4wsyFmNiRWx5TyKy01meEDOpGSbAwem82Pu3KDjiRSbpgHPRj9L5SZmelZWVlBx5CATFmyngGjp/Ob1vV48uKOP02aIyKFM7Nsd8/Mr01PFktcOf6I2vzpjKN5Z973DJu0NOg4IuWCCoHEnSt+1Yyz2x/O/RMX8ckiPYIicqhUCCTumBn3ndeWI+tW47pxs/lmw7agI4nENRUCiUuVK6QwcmAmZqHO4+271XksUlwqBBK3GteqzGP9jmXxmq3c8uqXxNuNDyJlhQqBxLXurTK4+TdH8eYX3zLq0+VBxxGJSyoEEveG9GjOGW3rce87C/ns6/VBxxGJOyoEEvfMjPvPb88Rdapy7bhZrNq4PehIInFFhUDKhSoVUxgxMJPcfc6Q57LZuWdv0JFE4oYKgZQbzWpX4ZGLOrDguy3c9po6j0WipUIg5cqvj6rLH05txeuzVzNmyoqg44jEBRUCKXeuOfkIeh5Tl7+9tZBpyzYEHUekzFMhkHInKcl48IL2NKlVmd8/P4tvN+0IOpJImaZCIOVStbRURg7MZFfuPoaq81ikUCoEUm4dUacqD17Qni9yNnPHG/PUeSxSABUCKddOa12P6359BC9n5/Dc9JVBxxEpk1QIpNy74dRWnHxkBndPmM/MFRuDjiNS5qgQSLmXlGQ8fNGxNDysElc/P4s1W3YGHUmkTInlnMVPm9laM5tXQPvFZjbXzL40sylm1j5WWUTSK6Uy8pJMtu3KZehz2ezKVeexSJ5YnhGMAXoV0r4c6OHubYF7gJExzCJCq7rVeKBve2at3MTdby4IOo5ImRGzQuDuk4ECL8i6+xR3/yH8dhrQMFZZRPKc0bY+Q09qwQvTVzJuhjqPRaDs9BFcAbxTUKOZDTKzLDPLWrduXSnGkvLoj6cdyYkta3Pnf+cze+UPRX9ApJwLvBCY2cmECsEtBW3j7iPdPdPdMzMyMkovnJRLyUnGY/2OpW56RYY+N4u1W9V5LIkt0EJgZu2AUUAfd9egMFJqalSuwMiBmWzesYffPz+L3bn7go4kEpjACoGZNQZeAwa6++KgckjiOrp+de47vx0zV/zA399S57EkrpRY7djMxgEnAbXNLAe4E0gFcPfhwF+AWsCTZgaQ6+6Zscojkp/e7Q/ny5xNPPXpcto0SKdvZqOgI4mUupgVAnfvV0T7lcCVsTq+SLRu6XUU87/dwp/fmMeR9arRrmGNoCOJlKrAO4tFgpaSnMTj/TuSUbUiQ8Zms+HHXUFHEilVKgQiQM0qFRgxsBMbtu3m9y/MInevOo8lcagQiIS1aZDOvee2Zdqyjdz7zldBxxEpNTHrIxCJR+d2bMjcnM2M/mw57Rqm06dDg6AjicSczghEDvDnM4+mS7Oa3PLqXOZ/uznoOCIxp0IgcoDU5CSe6N+RwypXYPDYbH7YtjvoSCIxpUIgko+MahUZNqATa7fs4tpxs9V5LOWaCoFIATo0qsHfftuGz5as5/73FgUdRyRmouosNrMGQJPI7cPDTIuUaxd0bsTc1ZsYMWkZbRukc1a7w4OOJFLiiiwEZnYfcCGwAMib1skBFQJJCH85qzULv9vKzS/P5Yg6VTmqXvWgI4mUqGguDf0WONLdz3D3s8NL71gHEykrKqQkMezijlRLS2Hw2Gw2b98TdCSREhVNIVhGeLA4kURVp3oawwZ05NtNO7j+pdns3edBRxIpMdEUgu3AHDMbYWaP5i2xDiZS1nRqUpO7erfmk0XreOh9jZwu5Uc0ncUTwotIwuvfpTFf5mzm8Y+X0KZBOr3a1As6ksghK7IQuPszZlYBaBVetcjddZFUEpKZcXef1nz1/VZuGj+HI+qcwBF1qgUdS+SQFHlpyMxOAr4GngCeBBabWfcY5xIpsyqmJDNsQEcqVUhm0LPZbNmp34skvkXTR/Bv4DR37+Hu3YHfAA/FNpZI2VY/vRJP9O/Iyo3bufGlOexT57HEsWgKQaq7//RYZXh+4SLvIjKzp81srZnNK6Ddwh3PS8xsrpl1jD62SPC6Nq/FHWcdwwcL1/LYR0uCjiNSbNEUgiwzG2VmJ4WXp4CsKD43BuhVSPvpQMvwMggYFsU+RcqUS45rwnkdG/LQB4v5cOGaoOOIFEs0hWAooaeKrwsvC8LrChUegmJjIZv0AZ71kGlADTOrH0UekTLDzPj7OW1o06A6g57N5oxH9MC9xJ8iC4G773L3B9393PDykLuXxKSuDYBVEe9zwusOYmaDzCzLzLLWrVtXAocWKTlpqcmMGJhJSrKx4Lut3DVhPtt25QYdSyRqBRYCMxsf/vll+Br+fkvpRQR3H+nume6emZGRUZqHFolKgxqVmHVHTy47vinPTF3Bbx6ezGdfrw86lkhUCnuO4Prwz7NidOzVQKOI9w3D60TiUpWKKdzVuzVntqvPLa/MZcDo6VyQ2ZA/n3kM6ZU0SouUXQWeEbj7d+GXV7v7N5ELcHUJHHsCcEn47qFuwOaIY4rErc5Na/L29Scy9KQWvDprNT0fnMR7878POpZIgaLpLO6Zz7rTi/qQmY0DpgJHmlmOmV1hZkPMbEh4k7cJDWi3BHiKkikuImVCWmoyt/Q6ijeuPoGaVSowaGw217wwiw0/lkT3mkjJMvf8H4Qxs6GE/nNuDiyNaKoGfO7uA2If72CZmZmelRXN3asiZcPu3H2MmLSUxz5aQpWKydzVuzW92x+OmQUdTRKImWW7e2a+bYUUgnTgMOBe4NaIpq3uXthtoTGlQiDx6us1W7n5lbnMWbWJU46qw9/PaUu99LSgY0mCKKwQFNZHsNndV7h7v3C/wA5CM5NVNbPGMcoqUm61rFuNV4cez+1nHs3nS9fT88FJjJuxkoJ+GRMpLdEMOne2mX0NLAcmASuAd2KcS6RcSk4yrjyxORNv6E6bBunc9tqX9H9qOt9s2BZ0NElg0XQW/w3oBix292bAKcC0mKYSKeea1KrCC1d15R/ntOXL1Zv5zcOTGfXpMs18JoGIphDscfcNQJKZJbn7x0C+15lEJHpmRv+ujXn/xu4c36I2f3trIecPn8LXa7YGHU0STDSFYJOZVQUmA8+b2SOAzmNFSkj99EqMvjSThy/swIr12zjz0c947MOv2bN3X9DRJEFEUwj6EOoo/gPwLqFbSc+OZSiRRGNm/PbYBrx/Yw96tq7Lv99fTO/HP2fe6s1BR5MEEM2gc9vcfS9QGXgTeI7Q3UMiUsJqV63IE/07MmJgJzb8uIs+T3zOfe9+xc49e4OOJuVYNHcNDTaz74G5hOYhyCa6+QhEpJh+07oe7/+hB+d1bMCwT5ZyxqOfkrUisMd3pJyL5tLQH4E27t7U3Zu7ezN3bx7rYCKJLr1yKv86vz1jr+jCrj376Dtiqoa4lpiIphAsBbbHOoiI5O/Elhm894fuXHpcaIjr0x6azKdfa14OKTkFDjHx0wZmxwL/AaYDP42Y5e7XxTZa/jTEhCSymSs2csurc1m2bht9OzXk9jOPIb2yhriWohVriIkII4CPCD1Elh2xiEgp69y0Jm9fFxri+rXZq+n50CQmaohrOUTRnBHMdvdjSylPkXRGIBIyb/Vmbn5lLgu/28KZ7epzd+/W1K5aMehYUkYd6hnBO+E5g+ubWc28pYQzisgv1KZBOhOuOYGberbi/flr6PngJN6YvVqD2MkvFs0ZwfJ8VntQdw7pjEDkYJFDXP/6qDr8/Zw21E+vFHQsKUOKfUZgZknAreFbRiMX3T4qUoZEDnE9Zel6TntwMi9M1xDXEp1CC4G77wNuLqUsInII8oa4fu+GHrRtmM6fXtcQ1xKdaPoIPjCzP5pZo1/aR2BmvcxskZktMbNb82lvbGYfm9lsM5trZmf84m8gIvtpXKsyz1/ZlXvPbcs8DXEtUYhZH4GZJQOLgZ5ADjAT6OfuCyK2GQnMdvdhZnYM8La7Ny1sv+ojEIned5t3cPvr8/jwq7V0aFSDf53fjlZ1qwUdSwJwSHcN5dM/EG0fQRdgibsvc/fdwIuERjLdb/dA9fDrdODbKPYrIlGqn16JUZdm8shFHfhmwzbOevQzHtUQ13KAaAadSzWz68zslfByjZlF8yhjA2BVxPuc8LpIdwEDzCwHeBu4toAMg8wsy8yy1q3To/Uiv4SZ0adDaIjr01rX5cH3F3P2Y5/xZY6GuJaQaPoIhgGdgCfDS6fwupLQDxjj7g2BM4Cx4TuV9uPuI909090zMzIySujQIomldtWKPN6/IyMHdmLjtt389snP+ec7GuJaICWKbTq7e/uI9x+Z2RdRfG410CjifcPwukhXAL0A3H2qmaUBtYG1UexfRIrhtNb16Nq8Fn9/awHDJy3lvfnfc9/57ejcVM+JJqpozgj2mlmLvDdm1hyI5leImUBLM2tmZhWAi4AJB2yzEjglvN+jgTRA135EYiy90s9DXO/eu48LRkzlzv/O0xDXCSqaQnAz8LGZfWJmkwgNQHdTUR9y91zgGmAisBAY7+7zzeyvZtY7vNlNwFXhM4xxwGWuJ2BESs2JLTOYeENoiOtnp33DaQ9NZvJi/S6WaAq8fdTM+rr7y2bWjNDdPEeGmxa5+658P1QKdPuoSGxkrdjI/4WHuM6oWoFPb/k1aanJQceSElLc20dvC/981d13ufvc8BJYERCR2MkMD3FdPz2NdT/u5spnsti+W5eKEkFhhWCDmb0HNDOzCQcupRVQREpPWmoyU287hQf6tmfK0vUMHD2DzTv2BB1LYqywu4bOBDoCY4F/l04cESkLzu/UkMoVkrn+xdn0GzmNsVd0oZbmOii3CiwE4aeBp5nZ8e6u3iORBHNG2/pUqpDMkLHZXDBiKs9f2Y166WlBx5IYiOauocPMbKSZvWdmH+UtMU8mIoE7+cg6PPu7LqzZsou+I6awcsP2oCNJDERTCF4GZgO3E7qVNG8RkQTQtXktnr+yK1t35nL+8Cl8vWZr0JGkhEVTCHLdfZi7z3D37Lwl5slEpMxo36gGLw06jn0OF46cxrzVGqeoPImmELxpZldrzmKRxHZkvWq8POQ4KqUm02/kNLJWbAw6kpSQaArBpYQuBU0BssOLnugSSUDNalfh5SHHkVGtIgNHz+DTr3UfSXkQy/kIRKQcOrxGJV4afBxNalXmijFZTJz/fdCR5BAVePuomZ1b2Afd/bWSjyMi8SCjWkVeGnQcl/5nBlc/P4sH+rbjnGMbBh1LiqmwB8rOLqTNARUCkQSWXjmV567sylXPZHHj+C/YtmsvA7o1CTqWFENhD5RdXppBRCT+VK2Ywn8u78zVz8/i9jdCw1gP7tGi6A9KmRJNZ7GISIHSUpMZMbATZ7Wrz73vfMW/31uERpOPL9HMUCYiUqjU5CQeuehYqlRI4bGPlrB1Zy5/OesYkpIs6GgSBRUCESkRyUnGP89rS5WKKTz9+XK2787l3nPbkaxiUObpriERKTFmxh1nHU3VtBQe/fBrtu3ay0MXdqBCiq5Cl2UxvWvIzHoBjwDJwCh3/2c+21wA3BXe5xfu3r+o/YpI2WVm3NizFVUrJvOPt79i++5chg3opNnOyrCY3TVkZsnAE0BPIAeYaWYT3H1BxDYtCc2EdoK7/2BmdQ7lmCJSdgzq3oKqFVP58xtfctl/ZjDq0s5Urair0WVRVH8qZnYm0Br4aTByd/9rER/rAixx92XhfbwI9AEWRGxzFfCEu/8Q3ufa6KOLSFnXv2tjqlRM5sbxX3DxqOk8c3lnalSuEHQsOUCRF+7MbDhwIXAtYEBfIJqnRhoAqyLe54TXRWoFtDKzz81sWvhSUn4ZBplZlpllrVunsU1E4kmfDg0YdnFHFn67hYtGTmPdVk17XtZE04NzvLtfAvzg7ncDxxH6D7wkpAAtgZOAfsBTZlbjwI3cfaS7Z7p7ZkZGRgkdWkRKy2mt6/H0ZZ35ZsN2LhgxldWbdgQdSSJEUwjy/sS2m9nhwB6gfhSfWw00injfMLwuUg4wwd33uPtyYDGhwiAi5cyvWtbmuSu7sP7HXfQdNoXl67cFHUnCoikE/wv/ln4/MAtYAYyL4nMzgZZm1szMKgAXARMO2OYNQmcDmFltQmcay6JKLiJxp1OTmoy7qhs7c/fRd/hUvvp+S9CRhOiGob7H3Te5+6uE+gaOcvc7ovhcLnANMBFYCIx39/lm9lcz6x3ebCKwwcwWAB8DN7v7huJ+GREp+9o0SGf84G6kJBkXjpjGnFWbgo6U8KyoMUHM7JL81rv7szFJVITMzEzPytK8OCLxbtXG7fQfNY2NP+5m9GWd6da8VtCRyjUzy3b3zPzaork01DliOZHQw1+9C/uAiEhRGtWszMuDj6d+jUpc+vQMPv5Kd48HJZpLQ9dGLFcBHYGqsY8mIuVdvfQ0xg8+jpZ1qzJobBZvzf0u6EgJqTgDgGwDmpV0EBFJTDWrVOCFq7rRvmENrh03i/FZq4r+kJSoIp8sNrM3CY0DBKHCcQzwcixDiUhiqZ6WyrNXdGHw2Gz+75W5bN+Vy2Un6PfN0hLNEBMPRLzOBb5x95wY5RGRBFW5QgqjLs3kunGzuevNBWzbvZerT2qBmYaxjrVoLg2d4e6Twsvn7p5jZvfFPJmIJJyKKck80b8j5xzbgPsnLuKf736l2c5KQTSFoGc+604v6SAiIgApyUn8u297BnRrzIhJy7jjv/PYt0/FIJYKm5hmKHA10MLM5kY0VQM+j3UwEUlcSUnGPX3aUKViCiMmLWP7rr386/x2pCRrgptYKKyP4AXgHeBe4NaI9VvdfWNMU4lIwjMzbu11FNXTUrl/4iK27c7l0X7HUjFFE9yUtALLq7tvdvcVwC2E7hrKW6qaWePSiSciiczM+P3JR3Dn2ccwcf4arnwmi+27c4OOVe5Ec9fQW4QKgBGamKYZsIjQRDUiIjF3+QnNqFIxhVtfnculT89g9GWdqZ6WGnSsciOaJ4vbunu78M+WhGYemxr7aCIiP7sgsxGP9evI7JWb6P/UNDZu2x10pHLjF/e8uPssoGsMsoiIFOrMdvV56pJMvl7zIxeOmMqaLTuDjlQuRDNV5Y0Ryx/N7AXg21LIJiJykJOPqsMzv+vCt5t20Hf4VFZt3B50pLgXzRlBtYilIqE+gz6xDCUiUphuzWvx/FXd2LxjD32HT2XJ2h+DjhTXipyPoKzRfAQikuer77cwYNQM3J1nfteFNg3Sg45UZhU2H0GBhcDMDpxWcj/uHsicBCoEIhJp+fptXPzUNLbuymXM5Z3p1KRm0JHKpOIWgnXAKkLzE08ndPvoT9x9UgnnjIoKgYgcaPWmHQwYNZ3vN+/kqUsy+VXL2kFHKnOKO0NZPeBPQBvgEUJjDq3PG4AuygP3MrNFZrbEzG4tZLvzzMzNLN+QIiKFaVCjEi8N7kaTWpX53ZiZvL9gTdCR4kphTxbvdfd33f1SoBuwBPjEzK6JZsdmlgw8QWiAumOAfmZ2TD7bVQOuJ3TWISJSLHWqpfHioG4cfXh1hjyXzX/nrA46Utwo9K4hM6toZucCzwG/Bx4FXo9y312AJe6+zN13Ay+S/91G9wD3AbohWEQOSY3KFXj+yq50bnoYN7w0hxemrww6UlwosBCY2bOEniDuCNzt7p3d/R53j7bMNiDUx5AnJ7wu8hgdgUbu/lZhOzKzQWaWZWZZ69ati/LwIpKIqlZMYczlXTipVQZ/ev1Ljr/3Q7bu3BN0rDKtsDOCAUBLQpdtppjZlvCy1cy2HOqBzSwJeBC4qaht3X2ku2e6e2ZGRsahHlpEyrm01GRGDMykVpUKfLt5J8f/8yPue/cr1m7VhYf8FDjonLsf6sDfq4FGEe8bhtflqUaoI/qT8FR09YAJZtbb3XVbkIgckgopSWTf0ZO5OZsYMWkZIyYtZfRnyzmvY0MGdW9Os9pVgo5YZsTsgTIzSwEWA6cQKgAzgf7uPr+A7T8B/lhUEdDtoyJSHCvWb2Pkp8t4JTuHPXv3cXqbegzp0YJ2DWsEHa1UFPf20UPi7rnANcBEYCEw3t3nm9lfzSyQh9FEJHE1rV2Ff5zTls9uOZmhPVrw6dfr6f345/R/ahqTF69L6LmRNcSEiCSkrTv3MG7GSkZ/tpw1W3bR+vDqDOnRgtPb1CuXU2IW68niskqFQERK0q7cvbwxezUjJi9j2bptNK5ZmatObEbfzEakpZafaTFVCEREirBvn/PegjUMn7SUOas2UatKBS4/oSkDuzUlvXL8z4amQiAiEiV3Z/ryjQyftJRPFq2jSoVk+nVpzBUnNqN+eqWg4xWbCoGISDEs/G4LIyYt5c2535Fk0KdDA4b0aM4RdaoFHe0XUyEQETkEqzZuZ/Rny3lx5kp27tnHqUfXZehJzeNqyGsVAhGRErBx226embKCZ6auYNP2PXRuehhDerTg5CPrkJRkRX4+SCoEIiIlaPvuXF6csYrRny1n9aYdtKpblcHdW9C7w+GkltFbT1UIRERiYM/efbz5xbeMmLSMRWu20qBGJa74VTMu6tKIyhUKHMEnECoEIiIx5O58vGgtwz9ZxowVG6lROZVLjmvKZcc3pWaVCkHHA1QIRERKTfY3PzB80lLeX7CGtNQkLsxsxJUnNqdRzcqB5lIhEBEpZUvWbmXEpGW8MWc1+xzOalefwd1bcMzh1QPJo0IgIhKQ7zbv4OnPlvPC9JVs272XHq0yGNKjBd2a1yQ8BH+pUCEQEQnY5u17eG76N/zn8+Ws/3E37RvVYGiPFpx2TN1SufVUhUBEpIzYuWcvL2fn8NTkZazcuJ3mGVUY3L05vz22ARVTYjfInQqBiEgZs3ef88687xj2yVLmf7uFOtUqcsWvmtG/a2OqpZX8IHcqBCIiZZS789mS9QyftJTPl2ygWloKA7o14fITmlKnWlqJHUeFQEQkDuTNr/zOvO9ISU4q0fmVAysEZtYLeARIBka5+z8PaL8RuBLIBdYBv3P3bwrbpwqBiJR3sZhfOZBCYGbJhCav7wnkEJq8vp+7L4jY5mRgurtvN7OhwEnufmFh+1UhEJFEsXbrTsZ8voKx075h685c6qenMfW2U4q1r8IKQSwHw+gCLHH3ZeEQLwJ9gJ8Kgbt/HLH9NGBADPOIiMSVOtXS+L9eRzH0pBaMm7GSDo0Oi8lxYlkIGgCrIt7nAF0L2f4K4J38GsxsEDAIoHHjxiWVT0QkLlRLS2VQ9xYx23+ZGC/VzAYAmcD9+bW7+0h3z3T3zIyMjNINJyJSzsXyjGA10CjifcPwuv2Y2anAn4Ee7r4rhnlERCQfsTwjmAm0NLNmZlYBuAiYELmBmR0LjAB6u/vaGGYREZECxKwQuHsucA0wEVgIjHf3+Wb2VzPrHd7sfqAq8LKZzTGzCQXsTkREYiSmU+i4+9vA2wes+0vE61NjeXwRESlamegsFhGR4KgQiIgkOBUCEZEEp0IgIpLgVAhERBKcCoGISIJTIRARSXAqBCIiCU6FQEQkwakQiIgkOBUCEZEEp0IgIpLgVAhERBKcCoGISIJTIRARSXAqBCIiCU6FQEQkwakQiIgkuJgWAjPrZWaLzGyJmd2aT3tFM3sp3D7dzJrGMo+IiBwsZoXAzJKBJ4DTgWOAfmZ2zAGbXQH84O5HAA8B98Uqj4iI5C+Wk9d3AZa4+4T25BYAAAe1SURBVDIAM3sR6AMsiNimD3BX+PUrwONmZu7uBe100YZFnDTmpP3WXdD6Aq7ufDXb92znjOfPOOgzl3W4jMs6XMb67es5f/z5B7UPzRzKhW0uZNXmVQx8feBB7TcddxNnH3k2i9YvYvD/Bh/Ufnv32zm1+anM+X4ON7x7w0Ht/zjlHxzf6HimrJrCnz7800HtD/d6mA71OvDBsg/42+S/HdQ+4qwRHFn7SN5c9Cb/nvrvg9rHnjOWRumNeGneSwzLGnZQ+ysXvELtyrUZM2cMY+aMOaj97YvfpnJqZZ6c+STj548/qP2Tyz4B4IEpD/C/xf/br61SaiXeufgdAO6ZdA8fLv9wv/ZalWvx6gWvAnDbB7cxNWfqfu0NqzfkuXOfA+CGd29gzvdz9mtvVasVI88eCcCgNwexeMPi/do71OvAw70eBmDAawPI2ZKzX/txDY/j3lPvBeC88eexYfuG/dpPaXYKd/S4A4DTnz+dHXt27Nd+Vquz+OPxfwQ46O8d6O+e/u7F79+9SLG8NNQAWBXxPie8Lt9t3D0X2AzUOnBHZjbIzLLMLGvPnj0xiisikpiskF++D23HZucDvdz9yvD7gUBXd78mYpt54W1ywu+XhrdZX9B+MzMzPSsrKyaZRUTKKzPLdvfM/NpieUawGmgU8b5heF2+25hZCpAObEBEREpNLAvBTKClmTUzswrARcCEA7aZAFwafn0+8FFh/QMiIlLyYtZZ7O65ZnYNMBFIBp529/lm9lcgy90nAKOBsWa2BNhIqFiIiEgpiuVdQ7j728DbB6z7S8TrnUDfWGYQEZHC6cliEZEEp0IgIpLgVAhERBKcCoGISIKL2QNlsWJm64Bvivnx2kCBD6vFGX2Xsqm8fJfy8j1A3yVPE3fPyK8h7grBoTCzrIKerIs3+i5lU3n5LuXle4C+SzR0aUhEJMGpEIiIJLhEKwQjgw5QgvRdyqby8l3Ky/cAfZciJVQfgYiIHCzRzghEROQAKgQiIgkuYQqBmfUys0VmtsTMbg06T3GZ2dNmtjY8qU/cMrNGZvaxmS0ws/lmdn3QmYrLzNLMbIaZfRH+LncHnelQmVmymc02s/8VvXXZZWYrzOxLM5tjZnE7o5WZ1TCzV8zsKzNbaGbHlej+E6GPwMySgcVAT0JTZs4E+rn7gkI/WAaZWXfgR+BZd28TdJ7iMrP6QH13n2Vm1YBs4Ldx+mdiQBV3/9HMUoHPgOvdfVrA0YrNzG4EMoHq7n5W0HmKy8xWAJmFzXoYD8zsGeBTdx8Vnt+lsrtvKqn9J8oZQRdgibsvc/fdwItAn4AzFYu7TyY0d0Ncc/fv3H1W+PVWYCEHz2kdFzzkx/Db1PASt79hmVlD4ExgVNBZBMwsHehOaP4W3H13SRYBSJxC0ABYFfE+hzj9T6c8MrOmwLHA9GCTFF/4UsocYC3wvrvH7XcBHgb+D9gXdJAS4MB7ZpZtZoOCDlNMzYB1wH/Cl+tGmVmVkjxAohQCKaPMrCrwKnCDu28JOk9xufted+9AaG7uLmYWl5ftzOwsYK27ZwedpYT8yt07AqcDvw9fWo03KUBHYJi7HwtsA0q0nzNRCsFqoFHE+4bhdRKg8PX0V4Hn3f21oPOUhPAp+8dAr6CzFNMJQO/wtfUXgV+b2XPBRio+d18d/rkWeJ3QZeJ4kwPkRJxlvkKoMJSYRCkEM4GWZtYs3NFyETAh4EwJLdzBOhpY6O4PBp3nUJhZhpnVCL+uROimhK+CTVU87n6buzd096aE/p185O4DAo5VLGZWJXwjAuFLKacBcXe3nbt/D6wysyPDq04BSvSmipjOWVxWuHuumV0DTASSgafdfX7AsYrFzMYBJwG1zSwHuNPdRwebqlhOAAYCX4avrQP8KTzPdbypDzwTvjstCRjv7nF922U5URd4PfQ7BynAC+7+brCRiu1a4PnwL7LLgMtLcucJcfuoiIgULFEuDYmISAFUCEREEpwKgYhIglMhEBFJcCoEIiIJToVABDCzveERKueZ2Zt5zwXE8HiXmdnjsTyGSLRUCERCdrh7h/CIrhuB3wcdSKS0qBCIHGwq4UEJzayDmU0zs7lm9rqZHRZe/4mZZYZf1w4PyZD3m/5rZvaumX1tZv/K26mZXW5mi81sBqEH6vLW9w2fiXxhZpNL8XuKACoEIvsJPx18Cj8PQfIscIu7twO+BO6MYjcdgAuBtsCF4Ul46gN3EyoAvwKOidj+L8Bv3L090LtEvojIL6BCIBJSKTzUxfeEhiZ4PzwOfA13nxTe5hlC48IX5UN33+zuOwmNCdME6Ap84u7rwnNivBSx/efAGDO7itAQKCKlSoVAJGRHeBjpJoBRdB9BLj//+0k7oG1XxOu9FDGml7sPAW4nNEJutpnVija0SElQIRCJ4O7bgeuAmwiN+/6DmZ0Ybh4I5J0drAA6hV+fH8WupwM9zKxWePjtvnkNZtbC3ae7+18ITUDSqKCdiMRCQow+KvJLuPtsM5sL9AMuBYabWWX2H/XxAWB8eNart6LY53dmdhehjuhNwJyI5vvNrCWhM5EPgS9K6ruIREOjj4qIJDhdGhIRSXAqBCIiCU6FQEQkwakQiIgkOBUCEZEEp0IgIpLgVAhERBLc/wMse/8DbELtlwAAAABJRU5ErkJggg==\n",
546 | "text/plain": [
547 | "| \n", 422 | " | rounds | \n", 423 | "mi_mean | \n", 424 | "mi_error | \n", 425 | "delta | \n", 426 | "num_feat | \n", 427 | "features | \n", 428 | "
|---|---|---|---|---|---|---|
| 0 | \n", 433 | "0 | \n", 434 | "1.483969 | \n", 435 | "0.006147 | \n", 436 | "0.000000 | \n", 437 | "7 | \n", 438 | "[0, 1, 2, 3, 4, 5, 6] | \n", 439 | "
| 1 | \n", 442 | "1 | \n", 443 | "1.483101 | \n", 444 | "0.006139 | \n", 445 | "-0.000585 | \n", 446 | "6 | \n", 447 | "[0, 1, 2, 3, 4, 5] | \n", 448 | "
| 2 | \n", 451 | "2 | \n", 452 | "1.481667 | \n", 453 | "0.006135 | \n", 454 | "-0.000967 | \n", 455 | "5 | \n", 456 | "[0, 1, 2, 3, 4] | \n", 457 | "
| 3 | \n", 460 | "3 | \n", 461 | "1.001292 | \n", 462 | "0.005613 | \n", 463 | "-0.324212 | \n", 464 | "4 | \n", 465 | "[0, 1, 3, 4] | \n", 466 | "
| 4 | \n", 469 | "4 | \n", 470 | "0.751952 | \n", 471 | "0.005343 | \n", 472 | "-0.249018 | \n", 473 | "3 | \n", 474 | "[0, 1, 3] | \n", 475 | "
| 5 | \n", 478 | "5 | \n", 479 | "0.390138 | \n", 480 | "0.005015 | \n", 481 | "-0.481166 | \n", 482 | "2 | \n", 483 | "[1, 3] | \n", 484 | "
| 6 | \n", 487 | "6 | \n", 488 | "0.212257 | \n", 489 | "0.003765 | \n", 490 | "-0.455946 | \n", 491 | "1 | \n", 492 | "[3] | \n", 493 | "
"
548 | ]
549 | },
550 | "metadata": {
551 | "needs_background": "light",
552 | "tags": []
553 | },
554 | "output_type": "display_data"
555 | }
556 | ],
557 | "source": [
558 | "select.plot_mi()"
559 | ]
560 | },
561 | {
562 | "cell_type": "markdown",
563 | "metadata": {
564 | "id": "uYZoCp1vmTMh"
565 | },
566 | "source": [
567 | "Plotting the percentual variations of the mutual information between rounds:"
568 | ]
569 | },
570 | {
571 | "cell_type": "code",
572 | "execution_count": null,
573 | "metadata": {
574 | "colab": {
575 | "base_uri": "https://localhost:8080/",
576 | "height": 279
577 | },
578 | "id": "BBV2ciMkmTMh",
579 | "outputId": "d8ee110e-0245-42e1-ebb6-5a14f21b4b5d"
580 | },
581 | "outputs": [
582 | {
583 | "data": {
584 | "image/png": "iVBORw0KGgoAAAANSUhEUgAAAYoAAAEGCAYAAAB7DNKzAAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADh0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uMy4yLjIsIGh0dHA6Ly9tYXRwbG90bGliLm9yZy+WH4yJAAAgAElEQVR4nO3dd3xV9f3H8dcnG0iYgbAJAcIQBCWKCMQBuBVntVZx1GKnWlt/om1tq9Zqq9YOa0W04mjVigrOiijLRUGQJXvvJSNswuf3x71ggORyIbn35Cbv5+NxHvfcc773nPeNwU/O+n7N3RERESlLUtABRESkclOhEBGRiFQoREQkIhUKERGJSIVCREQiSgk6QEXLzs723NzcoGOIiCSUyZMnr3f3hqWtq3KFIjc3l0mTJgUdQ0QkoZjZkrLW6dSTiIhEpEIhIiIRqVCIiEhEKhQiIhKRCoWIiEQUaKEws3PMbI6ZzTezwaWsTzezl8PrPzez3PinFBGp3gIrFGaWDDwOnAt0Ar5tZp0OafZd4Gt3bwv8CXgovilFRCTI5yhOBua7+0IAM3sJGADMKtFmAPCb8PyrwN/MzDxS3+hz5sDppx+87Fvfgh/+ELZvh/POO/wz11/P9quv4dkRk7jw/lsAO7DKgGkXfpt5p59P1rpVnPXgHaHl3zRh6hU3sqRXX+ouXchpj/6qxKdDG5hy7Y9YWdCbBvNn0fOv9x+2+y9u/jlru3Sn0fTJdB/y8GHrJ912D5vyj6PxxAl0efav32w4vKNJgx+gKLcNTcd/QPsXnzroswZMvPfP7GzclOajRpL36vMHlgMkmVH7rTdIyWkEzz4bmg71zjtQsyb8/e/wyiuHrx8zJvT68MPw1lsHr6tRA959NzR/330wevTB6xs0gOHDQ/N33QWffnrw+ubN4YUXQvO33QZTpx68Pj8fhgwJzQ8aBHPnHry+Wzd47LHQ/DXXwPLlB6/v2RN+//vQ/GWXwYYNB6/v2xd+9avQ/Lnnwo4dB6+/4AL4+c9D84f+3kFUv3tcfz2sXw+XX374+h/8AK68EpYtg2uvPXz9z34GF14Y+r2/+ebD1//yl9CvX+jndttth69/4AE49VT45BO4++7D1z/2WOhn+MEHcP/hv7s8+SS0bw9vvgmPPHL4+uefhxYt4OWX4YknDl//6quQna3fvcr4u1dCkIWiGbCsxPvlQI+y2rj7XjPbDDQA1pdsZGaDgEEAx6enH1OYHbuLGTphISd+veOwde9MX8Vbe+fSZMs6On29/bD1r01Zweitc8jbsJy8jYev/9fEZXy89is6rVlE0w3bDlv/9ITFfLG4BicuX0yD9Yev//tHC5g1y+m1eDE/KWX9I+/PZWGD7fSdv5jvrSs6bP39b89iVe11XPDVEq5Ze/j6pVNW8K1zGh22XEQEwIIauMjMLgfOcfebwu+vBXq4+49LtJkRbrM8/H5BuM360rYJUFBQ4BX1ZPb+n407eIll38zD/nclf4yHLi/rs/vfRNPWv2lc5v4P+uwhecraz20vTWHTjj18+LPTSU466FhIRKoRM5vs7gWlrQvyiGIF0KLE++bhZaW1WW5mKUAd4JDjs9ix8PklO/RcUhXy/dPa8IMXv+D9mas5t0uToOOISCUU5F1P/wPamVlrM0sDrgJGHtJmJHBdeP5y4MOI1yfkqJ11XGNyG9TkH+MWoh+tiJQmsELh7nuBHwP/Bb4CXnH3mWZ2r5ldFG72NNDAzOYDtwOH3UIr5ZOcZHy3Tx5fLtvExEUbg44jIpVQYNcoYqUir1FUFzv3FHPqgx9yQou6PH39SUHHEZEARLpGoSezhYzUZAb2bMXo2WuZt2Zr0HFEpJJRoRAABvbMJSM1iafGLww6iohUMioUAkD9Wml8q6AFr09ZwZotO4OOIyKViAqFHHBT7zyK9zn//Hhx0FFEpBJRoZADWjaoybmdm/Di50so2rU36DgiUkmoUMhBBhXmsXXnXl6auDToKCJSSahQyEG6tqjLKXn1eXrCIvYU7ws6johUAioUcpibC9uwavNO3vxyZdBRRKQSUKGQw5zeviH5OZkMUbceIoIKhZTCzPhenzxmr97KuHlldtQrItWECoWUakC3ZuTUTmfIuAVBRxGRgKlQSKnSUpK4sVdrPp6/gRkrNgcdR0QCpEIhZfp2j5Zkpqfw5Dh16yFSnalQSJlqZ6RydY+WvDN9FctKGeJVRKoHFQqJ6IZeuRjw9IRFQUcRkYCoUEhETerU4KJuTXn5f8vYtH130HFEJAAqFHJEgwrz2LGnmBc+WxJ0FBEJgAqFHFGHxrU5vX1Dnv1kMTv3FAcdR0TiTIVCojKoMI/1Rbt57YsVQUcRkThToZCo9MxrQJdmdRg6fiH79qlbD5HqRIVComJmDCrMY+H6bYz6ak3QcUQkjlQoJGrndm5Mi/o1eHKsuvUQqU5UKCRqKclJ3NQ7jy+WbmLS4o1BxxGROFGhkKNyRUFz6tZMVbceItWICoUclZppKQw8pRUffLWGBeuKgo4jInGgQiFHbeCpuaQlJzF0vI4qRKoDFQo5atmZ6VzevTnDJ69g7dadQccRkRhToZBjclOfPPbs28ewTxYHHUVEYkyFQo5J6+xanN2pMS98tpRtu/YGHUdEYkiFQo7ZoNPy2LxjDy//b1nQUUQkhlQo5Jid2LIeJ+XW4+kJi9hTvC/oOCISIyoUUi43F7ZhxaYdvDN9VdBRRCRGAikUZlbfzEaZ2bzwa70y2r1nZpvM7K14Z5TonNmhEW0a1uLJsQtxV2eBIlVRUEcUg4HR7t4OGB1+X5o/AtfGLZUctaSkUGeBs1Zt4eP5G4KOIyIxEFShGAAMC88PAy4urZG7jwa2xiuUHJuLT2hGw6x0nhynzgJFqqKgCkWOu+8/qb0ayCnPxsxskJlNMrNJ69atK386OSrpKclcf2ou4+etZ9bKLUHHEZEKFrNCYWYfmNmMUqYBJdt56MR2uU5uu/sQdy9w94KGDRuWK7ccm2t6tKJWWjJDdFQhUuWkxGrD7t6vrHVmtsbMmrj7KjNrAqyNVQ6Jjzo1U7nq5JY8+8li7jinA83q1gg6kohUkCMeUZhZQzO728yGmNkz+6dy7nckcF14/jpgRDm3J5XAjb1bA/DMhEUBJxGRihTNqacRQB3gA+DtElN5PAj0N7N5QL/we8yswMyG7m9kZuOB/wB9zWy5mZ1dzv1KDDWrW4MLj2/CSxOXsnnHnqDjiEgFiebUU013v7Mid+ruG4C+pSyfBNxU4n2fityvxN6gwja8MXUlL36+hB+e3jboOCJSAaI5onjLzM6LeRKpEjo1rU2fdtn88+PF7NpbHHQcEakA0RSKWwkVi51mtjU86R5IKdPNhW1Yt3UXb0xZEXQUEakARywU7p7l7knunhGez3L32vEIJ4mpV9sGdGpSmyHjFrJvn7r1EEl0UT1HYWYXmdnD4emCWIeSxGZm3HxaHgvWbePD2brzWSTRRXN77IOETj/NCk+3mtnvYx1MEtt5XZrQrG4NhozTuNoiiS6aI4rzgP7u/oy7PwOcA5wf21iS6FKTk/hu79ZMXLyRL5Z+HXQcESmHaLvwqFtivk4sgkjVc+VJLahTI5UhY3VUIZLIoikUvwemmNmzZjYMmAz8LraxpCqolZ7CNae05L+zVrNo/bag44jIMYrmrqd/A6cArwHDgZ7u/nKsg0nVcN2puaQmJTF0vI4qRBJVmYXCzDqEX08EmgDLw1PT8DKRI2qUlcGlJzbj1cnLWV+0K+g4InIMInXhcTswCHiklHUOnBmTRFLlfK8wj5cnLeO5TxZz+1ntg44jIkepzELh7oPCs+e6+86S68wsI6appEpp0zCTfh1zeO6zJXz/9DbUTItZ7/YiEgPRXMz+JMplImW6uTCPTdv38J9Jy4OOIiJHqcw/7cysMdAMqGFmJwAWXlUbqBmHbFKFFOTW58SWdRk6YSHf6dGSlOSgRuEVkaMV6RzA2cD1QHPg0RLLtwJ3xzCTVFGDCtvw/Rcm8+6M1VzYtWnQcUQkSpGuUQwDhpnZZe4+PI6ZpIrq3ymHvOxaDBm3kAuOb4KZHflDIhK4I15VdPfhZnY+cByQUWL5vbEMJlVPcpJxU5887n59Op8u3MCpbbKDjiQiUYimU8B/AFcCPyF0neIKoFWMc0kVdemJzcjOTFNngSIJJJoriqe6+0Dga3f/LdATyI9tLKmqMlKTua5nLmPmrGP2ao1/JZIIoikUO8Kv282sKbCH0JPaIsfkmlNaUSM1WUcVIgki2jGz6wJ/BL4AFgP/jmUoqdrq1UrjypNaMHLqSlZt3nHkD4hIoKLpFPA+d98UvvOpFdDB3X8V+2hSlX23d2sc+OfHi4OOIiJHcMS7nswsmdBARbn725sZ7v5opM+JRNKifk3O69KEf32+lB+f2ZbaGalBRxKRMkRz6ulNQg/eNQCySkwi5XJzYR5Fu/by78+XBh1FRCKIpne25u5+fMyTSLXTuVkdTm3TgGc+XsQNvVqTlqJuPUQqo2j+Zb5rZmfFPIlUSzef1oY1W3YxYuqKoKOISBmiKRSfAa+b2Q4z22JmW81MN8BLhShsl02Hxlk8NX4h7h50HBEpRTSF4lFCD9nVdPfa7p7l7rVjnEuqCTNjUGEec9cUMWbOuqDjiEgpoikUy4AZrj/3JEYu7NqUJnUyeHLcgqCjiEgpormYvRAYY2bvAgcGPdbtsVJRUpOTuLFXa373zld8uWwTXVvUDTqSiJQQzRHFImA0kIZuj5UYuerkFmRlpKhbD5FKKOIRRfhhu3x3/06c8kg1lZWRynd6tGLIuAUs3bCdlg00iKJIZRHxiMLdi4FWZpZWkTs1s/pmNsrM5oVf65XSppuZfWpmM81smpldWZEZpPK5oVcuyUnG0Ak6qhCpTKI59bQQ+NjMfmVmt++fyrnfwcBod29H6LTW4FLabAcGuvtxwDnAY+HOCaWKyqmdwcXdmvHKpGVs3LY76DgiEhZNoVgAvBVuW1HXKAYAw8Lzw4CLD23g7nPdfV54fiWwFmhYzv1KJTeoMI+de/bx3KeLg44iImHRDIX6WwAzywy/L6qA/ea4+6rw/GogJ1JjMzuZ0MX0Uu+fNLNBwCCAli1bVkA8CUq7nCz6dmjEc58u4ebCNtRISw46kki1F81QqJ3NbAowE5hpZpPN7LgoPveBmc0oZRpQsl34+Ywyn9EwsybA88AN7r6vtDbuPsTdC9y9oGFDHXQkukGFeWzctptXv1gedBQRIbrnKIYAt7v7RwBmdjrwFHBqpA+5e7+y1pnZGjNr4u6rwoVgbRntagNvA79w98+iyCpVwMmt69O1RV2Gjl/I1Se3JDnJgo4kUq1Fc42i1v4iAeDuY4Ba5dzvSOC68Px1wIhDG4TvtHodeM7dXy3n/iSBmBk3F+axZMN23p+5Oug4ItVeVHc9he94yg1PvyR0J1R5PAj0N7N5QL/we8yswMyGhtt8CygErjezqeGpWzn3Kwni7OMa06pBTf4xTp0FigQtmkJxI6G7jV4DhgPZ4WXHzN03uHtfd2/n7v3cfWN4+SR3vyk8/4K7p7p7txLT1PLsVxJHcpJxU588vly2iYmLNgYdR6RaK7NQmNnz4dmB7n6Lu5/o7t3d/TZ3/zpO+aQau6J7c+rXSlO3HiIBi3RE0d3MmgI3mlm98NPUB6Z4BZTqKyM1mYE9WzF69lrmrdkadByRaitSofgHoaemOwCTD5kmxT6aCAzsmUtGahJPjddRhUhQyiwU7v4Xd+8IPOPuee7eusSUF8eMUo3Vr5XGFd1b8PqUFazZsjPoOCLV0hEvZrv7D8ws2cyamlnL/VM8wokA3NSnNcX7nH9+vDjoKCLVUjRPZv8YWAOMIvTw29uE+n4SiYtWDWpxbucmvPj5Eop27Q06jki1E83tsbcB7d39OHfvEp6Oj3UwkZIGFeaxdedeXpq4NOgoItVOtGNmb451EJFIuraoS4/W9Xl6wiL2FJfa5ZeIxEi041GMMbO7KnA8CpGjdvNpeazavJM3v1wZdBSRaiWaQrGU0PUJjZktgTo9vxH5OZkMUbceInEV9XgUIkFLSjK+1yePO16dxrh56zktX13Ki8RDmYXCzN4kwjgR7n5RTBKJRDCgWzMefn8OQ8YtUKEQiZNIRxQPxy2FSJTSUpK4oVdrHnx3NjNWbKZzszpBRxKp8iI9mT020hTPkCIlXd2jJZnpKTypzgKjsmn7bmas0I2LcuyiuZgtUqnUzkjl6h4teWf6KpZt3B50nEpr8449PPr+HHo/9BEX/m0Ck5eou3Y5NioUkpBu6JWLAU9PWBR0lEpn6849/GX0PHo/9CF/+XA+hfnZNK1Tg8HDp7Nrb3HQ8SQBqVBIQmpSpwYXdWvKy/9bxtfbdgcdp1Io2rWXxz+aT++HPuLRUXPpmdeAd27pw9+/0537L+nMvLVF/GOMTtfJ0dNdT5KwBhXm8doXK3jhsyX8pG+7oOMEZvvuvTz/6RKeHLeQjdt207dDI27rl0+X5t9c6D+jfSMu6tqUxz+az/nHN6ZtIz0KJdHTXU+SsDo0rs3p7Rsy7NPFfK8wj4zU5KAjxdXOPcW88NkS/jF2AeuLdnNafkN+2j+fbi3qltr+ngs7MW7eOgYPn84rN/ckKcninFgSVZmFQnc2SSIYVJjH1U99zmtfrODqHtWj9/ude4p5aeJSHh+zgHVbd9G7bTY/7d+O7q0iDzyZnZnOL87ryB2vTuNfE5dyzSmt4pRYEt0Rn8w2s3bA74FOQMb+5Rq8SCqDnnkN6NKsDkPHL+Sqk1pU6b+Sd+0t5pVJy3n8w/ms3rKTHq3r87dvn0CPvAZRb+Py7s15Y+oKHnp3Nv065tC4TsaRPyTVXjQXs/8JPAHsBc4AngNeiGUokWiZGYMK81i4fhujvloTdJyY2FO8j39PXMqZD4/lV2/MoHm9Gvzrph68NOiUoyoSEPp5PXBJF3YX7+PXI2fEKLFUNdEUihruPhowd1/i7r8Bzo9tLJHondu5Mc3r1eDJsQuCjlKh9hbv45VJyzjzkTHc9dp0Gmal89yNJ/Of7/fk1LbZmB3b0VOrBrX4af98/jtzDe/NWFXBqaUqOuKpJ2CXmSUB88Kj3a0AMmMbSyR6KclJfK9PHr8eOZNJizdSkBv5XH1lV7zPGfnlCv78wTwWb9hOl2Z1uPf6zpzevuExF4dD3dS7NSOnruSeETPp2SabOjVSK2S7UjVFc0RxK1ATuAXoDlwLXBfLUCJH64qC5tStmZrQ3XqECsRK+v9pLD99+UtqpKXw1MACRv64F2d0aFRhRQJCxfWhy45nfdEuHnpvdoVtV6qmaLoZ/194tgi4IbZxRI5NzbQUBp7Sir9+NJ8F64po0zBxDnr37XPem7maxz6Yy9w1RbTPyeIf15zIWZ0ax/TifJfmdbixV2uGTljExd2acXLrxD4Sk9g54hGFmX1kZh8eOsUjnMjRGHhqLmnJSQwdnxhHFe7Of2eu5ry/jOeHL37BPoe/XX0C797ah3M6N4nLHVy3n5VP83o1uOu1aezco+49pHTRXKP4eYn5DOAyQndAiVQq2ZnpXNa9Oa9OWs5P++fTKKty3vrp7nw4ey2PjprLzJVbaJ1diz9f1Y0Ljm9Kcpxv762ZlsIDl3Rh4DMT+ftH87n9rPZx3b8khmhOPU0+ZNHHZjYxRnlEyuV7ffL498SlDPtkMXec3SHoOAdxd8bOXcefRs3ly+WbaVm/Jg9f0ZWLuzUlJTm4btcK8xtyyQnNeGLsAi7o2pT8HHXvIQeL5tRT/RJTtpmdDWi0GKmUWmfX4uxOjXnhs6Vs21U5DnzdnQnz1nPZE59w/T//x/qi3Tx0WRdG/+w0Lu/ePNAisd8vz+9IZnoKg4dPY98+jUcuB4vm1NNkQp0DGqFTTouA78YylEh5DDotj/dmrubl/y3jxt6tA83y2cINPDpqLhMXbaRJnQx+d0lnrujegrSU4ItDSQ0y0/nVBZ24/ZUveeHzJQzsmRt0JKlEoikUHd19Z8kFZpYeozwi5XZiy3qclFuPpycs4tqerUgN4C/2/y3eyJ9GzeWTBRtolJXOvQOO48qTWpCeUnk7LrzkhGa8PmUFf3hvDv065tC0bo2gI0klEc2/oE9KWfZpeXYaPo01yszmhV/rldKmlZl9YWZTzWymmX2/PPuU6mVQYRtWbNrBO9Pj++TxF0u/5tqnP+eKf3zK3DVF3HNBJ8b93xkM7JlbqYsEfNO9R/E+554RM3DXKSgJiTQeRWOgGVDDzE4gdOoJoDahB/DKYzAw2t0fNLPB4fd3HtJmFdDT3XeZWSYww8xGuvvKcu5bqoG+HRrRpmEtnhy7kIu6Nq3Qh9VKM235Jv40ai4fzVlH/Vpp/OK8jlxzSitqpFXu4nCoFvVrcnv/fH73zle8M3015x/fJOhIUglEOvV0NnA90Bx4tMTyrcDd5dzvAOD08PwwYAyHFAp3LzlsWToajU+OQlJSqLPAO4dP5+P5G+jdLjsm+5mxYjOPfTCPD75aQ92aqdx5TgcG9mxFrfRozupWTjf0ymXklyv59ciZ9G6bTZ2a6t6jurMjHV6a2WXuPrxCd2q2yd3rhucN+Hr/+0PatQDeBtoCd7j742VsbxAwCKBly5bdlyxZUpFxJUHt2ltM74c+okPjLJ7/bo8K3fbs1Vt4bNQ83pu5mtoZKXyvTx7X98olK6Nq/E91xorNDHj8Y67o3pwHLzs+6DgSB2Y22d0LSlsXzZ89nc3suEMXuvu9R9jpB0DjUlb94pDtuJmVWq3cfRlwvJk1Bd4ws1fd/bC+pN19CDAEoKCgQCdWBYD0lGSuPzWXP/53DrNWbqFT09rl3ua8NVt5bPQ83p62iqz0FG7t244be7eucp3qdW5Wh5v6tObJsQsZ0K0ZPdscXXfmUrVEczqnCNgWnoqBc4HcI33I3fu5e+dSphHAGjNrAhB+XXuEba0EZgB9osgrcsA1PVpRMy2ZIePK1wX5gnVF3PrSFM56bBxjZq/lx2e0ZfydZ/DT/vlVrkjsd1vffFrWr8ndr09X9x7V3BELhbs/UmL6HaFrC+Ud3W4k3/RAex0w4tAGZtbczGqE5+sBvYE55dyvVDN1aqby7ZNb8ua0VazYtOOoP79kwzZuf2Uq/R8dy/sz13BzYRvG33kmPz+7PXVrpsUgceVRIy2ZBy7pwqL12/jrh/OCjiMBOpYLxDUJXeAujweB/mY2D+gXfo+ZFZjZ0HCbjsDnZvYlMBZ42N2nl3O/Ug3tf+jumQmLov7Mso3bufPVaZz5yFjenraK7/Zuzfg7z2DwuR2oX6tqF4iSerfL5rITm/Pk2IV8tWpL0HEkINFczJ5O6MlsgGSgIXCvu/8txtmOSUFBgU+aNCnoGFLJ3PbSFEbNWsMng/tGvItnxaYdPP7RfF753zKSkozv9GjJD05rQ6PalbODwXj4ettu+j06lub1a/LaD06Ne8eFEh/lvZh9QYn5vcAad68cneiIRGlQYRvemLqSFz5fwo/OaHvY+tWbd/L3MfN5aeIyHOfbJ7fkR2e0pXGd6lsg9qtXK417LuzErS9N5blPF3NDr2C7RZH4i/TA3f5RTLYesqq2meHuG2MXS6RidWpamz7tsnn2k8Xc1Kf1gaek127dyRNjFvDi50vZt8+5oqAFPz6zLc3UfcVBLuralNenrOCP/51D/045NK9X3mduJZFEOqJYDyznm7EnSh5vOuW/oC0SVzcXtuGapz/njSkr6NsxhyfHLuD5z5awp9i57MRm/OTMdrSor/8BlsbMuP/izpz1p3H86o0ZPHP9STF/2l0qj0iF4i/AGcDHwL+BCa7OXySB9WrbgE5NavOH9+bwm5Gz2LW3mItPaMYtZ7YjN7tW0PEqveb1avKzs9pz31uzeHPaKi7q2jToSBInZd715O63Ad2A/wDXAlPM7A9mphOUkpDMjFv6tuXr7bs567gcRt1+Go9+q5uKxFG4/tRcujavw71vzmTT9t1H/oBUCUe86wnAzOoCVwH3AXe7+1OxDnasdNeTHMnOPcVkpCZWZ32VyayVW7jobxO45IRm/PGKrkHHkQoS6a6nMo8ozKyWmV1tZiOAd4BMoHtlLhIi0VCRKJ9OTWszqDCP/0xezsfz1wcdR+Ig0gN3a4H/IzT2xCPAQqDAzC41s0vjEU5EKqdb+rYjt4G696guIhWK/wBTgPaEnqW4sMR0QYTPiUgVl5GazAOXdmHJhu089oG696jqyrzryd2vj2MOEUkwp7bJ5lsFzXlq/EIu7NqE45rWCTqSxIgGAxKRY3b3eR2pVzONwcOns7d4X9BxJEZUKETkmNWtmcZvLurE9BWbefaTxUHHkRhRoRCRcjm/SxP6dmjEI+/PZdnG7UHHkRiIulCYWVsze8HMhptZz1iGEpHEYWbcd3Fnkgx+8cYM1IFD1RPpOYpDu828D7gLuA14IpahRCSxNK1bgzvObs+4uesYMXVl0HGkgkU6onjTzAaWeL+H0BCorQgNiSoicsC1PXM5oWVd7n1rFhu3qXuPqiRSoTiHUJfi75lZIfBz4GzgEuA78QgnIokjOcl48NLj2bpzD/e/NSvoOFKBInUKWBwexe5K4CLgz8A/3f1n7j47XgFFJHG0b5zF909rw2tTVjBu7rqg40gFiXSNooeZvUroesSzwC+B35nZI+FOAkVEDvOjM9qS17AWv3hjOtt3azDMqiDSqacngVuA3wBPuvsCd78KGAm8HIdsIpKAMlKT+f0lXVi2cYe696giIhWKvXxz8frAlSl3H+vuZ8c4l4gksB55Dfj2yS0ZOn4h05dvDjqOlFOkQnE1cBlwJjAwQjsRkcMMPrcD2ZnpDH5tmrr3SHCRLmbPDV+4vsvdl+1fbma9zezx+MQTkURVp0Yqv73oOGau3MLTExYFHUfKIaons83sBDP7o5ktITQ2xTWxjSUiVcE5nRvTv1MOf/pgLks3qHuPRBXprqd8M/u1mc0BngLWA6e7ew9gY7wCikjiMjPuG9CZlKQk7n59urr3SFCRjihmA+cBl7t7gbs/5O77jx/1X1tEotK4TgZ3ntuBCfPXMzxogQ8AAA1HSURBVPyLFUHHkWMQqVBcCiwC3jez583sQjNLjVMuEalCvnNySwpa1eP+t2exvmhX0HHkKEW6mP1G+LmJtsC7wCBguZn9E6gdp3wiUgUkJRm/v7QL23bt5T5175Fwjngx2923ufu/3P1CoAPwKTAt5slEpEppl5PFD09vy4ipK/loztqg48hROKqBi9z9a3cf4u5nxiqQiFRdPzyjDW0bZfLL12ewbZe690gUGuFOROImPSWZBy/twopNO3jk/blBx5EoqVCISFwV5NbnmlNa8uwni/hy2aag40gUAikUZlbfzEaZ2bzwa70IbWub2XIz+1s8M4pI7PzfOR1omJXOncOnsUfde1R6QR1RDAZGu3s7YHT4fVnuA8bFJZWIxEXtjFTuHdCZ2au38tT4hUHHkSMIqlAMAIaF54cBF5fWyMy6AznA+3HKJSJxcvZxjTnnuMb8+YN5LFq/Leg4EkFQhSLH3VeF51cTKgYHMbMkQv1K/TyewUQkfn474DjSUpK4+zV171GZxaxQmNkHZjajlGlAyXYe+u0o7Tfkh8A77r48in0NMrNJZjZp3ToNvyiSKHJqZ3DXuR35dOEG/jPpiP/UJSApsdqwu/cra52ZrTGzJu6+ysyaAKU9fdMT6GNmPwQygTQzK3L3w65nuPsQYAhAQUGB/iwRSSBXndSCN6as4HfvfMUZHRrRMCs96EhyiKBOPY0ErgvPXweMOLSBu3/H3Vu6ey6h00/PlVYkRCSxJSUZD1zahR27i/ntmzODjiOlCKpQPAj0N7N5QL/we8yswMyGBpRJRALStlEmPz6zLW9NW8Xor9YEHUcOYVXtAlJBQYFPmjQp6BgicpR2793HBX8dz9adexl1+2lkpsfszLiUwswmu3tBaev0ZLaIVAppKUk8eNnxrN6yk4f/OyfoOFKCCoWIVBontqzHwFNaMezTxXyx9Oug40iYCoWIVCp3nNOBxrUzuGv4dHbvVfcelYEKhYhUKpnpKdw3oDNz1mxlyLgFQccRVChEpBLq1ymH849vwl9Gz2fBuqKg41R7KhQiUin9+sJOZKQmcddr09m3r2rdnZloVChEpFJqlJXBL87vyMRFG3l50rKg41RrKhQiUml9q6AFp+TV54F3vmLtlp1Bx6m2VChEpNIyM35/6fHs2ruP36h7j8CoUIhIpdY6uxa39m3HO9NX8/7M1UHHqZZUKESk0htUmEeHxlncM2ImW3fuCTpOtaNCISKVXmpyqHuPNVt38of31L1HvKlQiEhC6NaiLtefmssLny9h8pKNQcepVlQoRCRh/Pys9jStU4M7h09n197ioONUGyoUIpIwaqWncP8lnZm/tognxqh7j3hRoRCRhHJG+0Zc1LUpf/9oAfPXbg06TrWgQiEiCeeeCztRMz2ZwcPVvQfAvn3O0g3bmbVyS0y2ryGkRCThZGem84vzOnLHq9P418SlXHNKq6AjxYW7s3rLTuas3sq8NUXMWbOVeWu2MndNETv2FNO1RV1G/KhXhe9XhUJEEtLl3ZvzxtQVPPTubPp1zKFxnYygI1Wo9UW7mLt6K3PXbGXOmiLmrgnNb92590Cb7Mx02jfO5KqTW5Cfk0WnJrVjkkWFQkQSkpnxwCVdOOtP47hnxAyGDCx1uOdKb/P2PcxduzV8lLCVOeEjhI3bdh9oU6dGKu1zshjQrSntc7Jol5NFfk4W9WulxSWjCoWIJKxWDWrx0/75PPjubN6bsYpzOjcJOlKZtu3ay7y1RSWOEkKva7bsOtCmVloy+Y2z6N8xh/zGWeTnZNI+J4uGWemYWWDZVShEJKHd1Ls1I6eu5J4RM+nZJps6NVIDzbNzTzEL1oVOFc1ZXXTgKGH51zsOtElPSaJdTia92mST3zgrfJSQSbO6NQItCGVRoRCRhJaSnMRDlx3PgMcn8NB7s3ngki5x2e+e4n0sWr8tdO1g9dbwheUiFm/Yxv4bsVKTjbzsTE5oWY8rC1ocKAot6tckOanyFYSyqFCISMLr0rwON/ZqzdAJi7i4WzNObl2/wrZdvM9ZunH7YQVh4foi9hSHKkKSQW6DWuTnZHFB16YHThnlZtciNTnxn0JQoRCRKuH2s/J5b+ZqBr82jXdu6UNGavJRfd7dWbFpR/juoqIDRWH+2iJ27d13oF2L+jXIb5TFmR0bkZ+TSX5OFm0aZh71/hKJCoWIVAk101J44JIuDHxmIn//aD63n9W+1Hbuzrqtuw7cXVSyIBTt+ubW08a1M2iXk8m1p7QKX1jOol2jTGqlV7//bVa/bywiVVZhfkMuOaEZT4xdwAVdm5KdmX7g+YPQqaPQQ2qbd3wzpkX9Wmm0z8nishObHSgI+Y2yqFMz2IvilYkKhYhUKb88vyNj5qzlgr9MYHfxN6eMsjJSaJ+TxfnHNyG/UeaBopCdmR5g2sSgQiEiVUqDzHT+fNUJvD1tFW3DBaF9ThY5tYN9FiGRqVCISJVTmN+QwvyGQceoMhL/vi0REYkpFQoREYlIhUJERCIKpFCYWX0zG2Vm88Kv9cpoV2xmU8PTyHjnFBGR4I4oBgOj3b0dMDr8vjQ73L1beLoofvFERGS/oArFAGBYeH4YcHFAOURE5AiCKhQ57r4qPL8ayCmjXYaZTTKzz8yszGJiZoPC7SatW7euwsOKiFRnMXuOwsw+ABqXsuoXJd+4u5tZWaOjt3L3FWaWB3xoZtPdfcGhjdx9CDAEoKCgQCOti4hUIHOP//9XzWwOcLq7rzKzJsAYdy+9B69vPvMs8Ja7v3qEduuAJeWIlw2sL8fnE1F1+87V7fuCvnN1UZ7v3MrdS31KMagns0cC1wEPhl9HHNogfCfUdnffZWbZQC/gD0facFlfNFpmNsndE3Pw3WNU3b5zdfu+oO9cXcTqOwd1jeJBoL+ZzQP6hd9jZgVmNjTcpiMwycy+BD4CHnT3WYGkFRGpxgI5onD3DUDfUpZPAm4Kz38CxGdMQxERKZOezD7ckKADBKC6fefq9n1B37m6iMl3DuRitoiIJA4dUYiISEQqFCIiEpEKRZiZPWNma81sRtBZ4sHMWpjZR2Y2y8xmmtmtQWeKNTPLMLOJZvZl+Dv/NuhM8WJmyWY2xczeCjpLPJjZYjObHu5QdFLQeeLBzOqa2atmNtvMvjKznhW2bV2jCDGzQqAIeM7dOwedJ9bCDzo2cfcvzCwLmAxcXJVvQbbQOJi13L3IzFKBCcCt7v5ZwNFizsxuBwqA2u5+QdB5Ys3MFgMF7l5tHrgzs2HAeHcfamZpQE1331QR29YRRZi7jwM2Bp0jXtx9lbt/EZ7fCnwFNAs2VWx5SFH4bWp4qvJ/KZlZc+B8YOiR2kpiMrM6QCHwNIC7766oIgEqFAKYWS5wAvB5sEliL3wKZiqwFhjl7lX+OwOPAf8H7As6SBw58L6ZTTazQUGHiYPWwDrgn+FTjEPNrFZFbVyFopozs0xgOHCbu28JOk+suXuxu3cDmgMnm1mVPs1oZhcAa919ctBZ4qy3u58InAv8KHxquSpLAU4EnnD3E4BtlD3Oz1FToajGwufphwMvuvtrQeeJp/Bh+UfAOUFnibFewEXhc/YvAWea2QvBRoo9d18Rfl0LvA6cHGyimFsOLC9xhPwqocJRIVQoqqnwhd2nga/c/dGg88SDmTU0s7rh+RpAf2B2sKliy93vcvfm7p4LXAV86O7XBBwrpsysVvgGDcKnX84CqvTdjO6+GlhmZvt74e4LVNiNKUH1HlvpmNm/gdOBbDNbDvza3Z8ONlVM9QKuBaaHz9kD3O3u7wSYKdaaAMPMLJnQH0mvuHu1uF20mskBXg/9LUQK8C93fy/YSHHxE+DF8B1PC4EbKmrDuj1WREQi0qknERGJSIVCREQiUqEQEZGIVChERCQiFQoREYlIhUIkCmZWHO6JdIaZvbn/eYwY7u96M/tbLPchEi0VCpHo7HD3buGehTcCPwo6kEi8qFCIHL1PCfe0a2bdzOwzM5tmZq+bWb3w8jFmVhCezw53obH/SOE1M3vPzOaZ2R/2b9TMbjCzuWY2kdADkfuXXxE+kvnSzMbF8XuKACoUIkcl/FR3X2BkeNFzwJ3ufjwwHfh1FJvpBlwJdAGuDA8i1QT4LaEC0RvoVKL9PcDZ7t4VuKhCvojIUVChEIlOjXBXJ6sJdRExKjwGQF13HxtuM4zQmABHMtrdN7v7TkL98bQCegBj3H2du+8GXi7R/mPgWTP7HpBcQd9HJGoqFCLR2RHunrwVYBz5GsVevvn3lXHIul0l5os5Qp9r7v594JdAC2CymTWINrRIRVChEDkK7r4duAX4GaE+/782sz7h1dcC+48uFgPdw/OXR7Hpz4HTzKxBuPv3K/avMLM27v65u99DaHCaFuX+IiJHQb3Hihwld59iZtOAbwPXAf8ws5oc3GPnw8Ar4dHV3o5im6vM7DeELpRvAqaWWP1HM2tH6EhmNPBlRX0XkWio91gREYlIp55ERCQiFQoREYlIhUJERCJSoRARkYhUKEREJCIVChERiUiFQkREIvp/A2vhVt3huvYAAAAASUVORK5CYII=\n",
585 | "text/plain": [
586 | "
"
587 | ]
588 | },
589 | "metadata": {
590 | "needs_background": "light",
591 | "tags": []
592 | },
593 | "output_type": "display_data"
594 | }
595 | ],
596 | "source": [
597 | "select.plot_delta()"
598 | ]
599 | },
600 | {
601 | "cell_type": "markdown",
602 | "metadata": {
603 | "id": "5QAhk35EmTMo"
604 | },
605 | "source": [
606 | "Making the selection choosing to stop at Round 2:"
607 | ]
608 | },
609 | {
610 | "cell_type": "code",
611 | "execution_count": null,
612 | "metadata": {
613 | "colab": {
614 | "base_uri": "https://localhost:8080/"
615 | },
616 | "id": "u6qtvG8vmTMp",
617 | "outputId": "04946e63-1d8b-4a6b-c233-bb85e9cb54a2"
618 | },
619 | "outputs": [
620 | {
621 | "data": {
622 | "text/plain": [
623 | "(20000, 5)"
624 | ]
625 | },
626 | "execution_count": 11,
627 | "metadata": {
628 | "tags": []
629 | },
630 | "output_type": "execute_result"
631 | }
632 | ],
633 | "source": [
634 | "X_new = select.transform(X, rd=2)\n",
635 | "\n",
636 | "X_new.shape"
637 | ]
638 | },
639 | {
640 | "cell_type": "markdown",
641 | "metadata": {
642 | "id": "OzXhfro9mTMx"
643 | },
644 | "source": [
645 | "### 1.3\\. Selecting Features for a Classification Task"
646 | ]
647 | },
648 | {
649 | "cell_type": "markdown",
650 | "metadata": {
651 | "id": "Upuhc2UqmTMy"
652 | },
653 | "source": [
654 | "Categorizing $Y$:"
655 | ]
656 | },
657 | {
658 | "cell_type": "code",
659 | "execution_count": null,
660 | "metadata": {
661 | "id": "wDOrI5yRmTMz"
662 | },
663 | "outputs": [],
664 | "source": [
665 | "ind0 = (y\n",
848 | "\n",
861 | "\n",
862 | " \n",
863 | "
\n",
948 | ""
949 | ],
950 | "text/plain": [
951 | " rounds mi_mean mi_error delta num_feat features\n",
952 | "0 0 0.000000 0.000000 0.000000 0 []\n",
953 | "1 1 0.144904 0.003717 0.000000 1 [3]\n",
954 | "2 2 0.280840 0.004493 0.938110 2 [3, 1]\n",
955 | "3 3 0.524522 0.004559 0.867691 3 [3, 1, 0]\n",
956 | "4 4 0.636269 0.004315 0.213045 4 [3, 1, 0, 4]\n",
957 | "5 5 0.795123 0.003400 0.249667 5 [3, 1, 0, 4, 2]\n",
958 | "6 6 0.792673 0.003550 -0.003082 6 [3, 1, 0, 4, 2, 6]\n",
959 | "7 7 0.791315 0.003708 -0.001712 7 [3, 1, 0, 4, 2, 6, 5]"
960 | ]
961 | },
962 | "execution_count": 16,
963 | "metadata": {
964 | "tags": []
965 | },
966 | "output_type": "execute_result"
967 | }
968 | ],
969 | "source": [
970 | "select.get_info()"
971 | ]
972 | },
973 | {
974 | "cell_type": "markdown",
975 | "metadata": {
976 | "id": "wFTKMAtJmTN4"
977 | },
978 | "source": [
979 | "It is possible to see that the estimated mutual information is untouched from Round 6 onwards.\n",
980 | "\n",
981 | "Since there is a 'break' in Round 5, we should choose to stop the algorithm at theta round. This will be clear in the Mutual Information history plot that follows:"
982 | ]
983 | },
984 | {
985 | "cell_type": "code",
986 | "execution_count": null,
987 | "metadata": {
988 | "colab": {
989 | "base_uri": "https://localhost:8080/",
990 | "height": 279
991 | },
992 | "id": "SX0Le6YMmTN6",
993 | "outputId": "54053b01-dcd5-46ce-c1b6-4357536aa11b"
994 | },
995 | "outputs": [
996 | {
997 | "data": {
998 | "image/png": "iVBORw0KGgoAAAANSUhEUgAAAYIAAAEGCAYAAABo25JHAAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADh0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uMy4yLjIsIGh0dHA6Ly9tYXRwbG90bGliLm9yZy+WH4yJAAAgAElEQVR4nO3dd5hU5fnG8e+zC7h0lCJIEVBEaQKuIGrQKEasREUFK7Fgw66xxBhLooklxV8QJYqIKMWWgGKLNVFUli4IuCBlUWClF4Hdnef3xwxmWLYMsGfPzM79ua65Zs55z5y5FxaeOee8533N3RERkfSVEXYAEREJlwqBiEiaUyEQEUlzKgQiImlOhUBEJM1VCzvA7mrUqJG3bt067BgiIill6tSpP7h745LaUq4QtG7dmpycnLBjiIikFDNbUlqbTg2JiKQ5FQIRkTSnQiAikuZUCERE0pwKgYhImgu0EJhZXzObb2a5ZnZnCe2tzOxDM5tuZrPM7NQg84iIyK4CKwRmlgkMBU4BOgADzaxDsc3uAca7ezdgAPBkUHlERKRkQR4R9ABy3X2Ru28HxgL9im3jQL3Y6/rAdwHmERGREgR5Q1lzYFncch7Qs9g29wHvmtn1QG2gT0k7MrPBwGCAVq1aVXhQEdl7m7YV0ufxj9he5PRu14iMDKNahpEZe1TLyCDDjGqZFn3OsBK2sT3YJoOMDKiWkVHmfnZqi3vOMCPDIMMMiz3vWGdmYf+xVoqw7yweCIx098fNrBfwgpl1cvdI/EbuPhwYDpCdna2ZdESSTP7Gbfxq5Jes2LCNrOoZTF+2jsIiJ+JOYcSJRKLPRfEPjz4nu4y44vC/QhFXODJ2Lhzlbl+8LWNHW/x7d93X7OXr2L9eFu/efFyF/4xBFoLlQMu45RaxdfEuB/oCuPtkM8sCGgGrAswlIhVoyerNXDLiS1Zu2MqIQdmccOj+Cb/X3Yk4FEYiRCLR5+LFIr6gFBV7FEZibUXxxSVCUYSfnkvaZ1HEefY/3+I4Fx/VmkgsR8T9p0w71kWX49shEtnN7YvvP5LI9tF1RZFI7DnaFoQgC8EUoJ2ZtSFaAAYAFxTbZilwIjDSzA4DsoD8ADOJSAX6avl6Bj33JYUR56Urj6J7q3136/1mRqZBZkZmbE1mmdtXpEt6ta60z0p2gRUCdy80syHAO0T/dke4+xwzewDIcfcJwK3AP8zsZqIXjge5JlEWSQmf5f7A4BemUi+rGmMH9+DgJnXDjiR7KNBrBO4+CZhUbN29ca/nAscEmUFEKt4bs77j5nEzaNOoNs9f1oNm9WuGHUn2QtgXi0UkxYz89Fvuf2Mu2QfuyzOXHEn9WtXDjiR7SYVARBLi7jz27nyGfriQkzrsz/8N7EZW9co7py/BUSEQkXIVFkW4+/XZjM/JY2CPljzYrxPVMjVUWVWhQiAiZfpxexFDXprG+/NWccMJB3PzSYekzY1W6UKFQERKtW7Ldi4bOYXpy9bxYL+OXKwul1WSCoGIlOi7dT9yyYgvWbp6C0Mv6M6pnZuFHUkCokIgIrtYsHIjl474kk1bC3n+sh70Oqhh2JEkQCoEIrKTqUvWcNnIHGpUy2DcVb3ocEC98t8kKU2FQER+8u+5K7nupWkc0KAmoy7rQcv9aoUdSSqBCoGIADB+yjLuen02HQ+ox3ODjqRhnX3CjiSVRIVAJM25O09+tJBH35nPz9o14qmLjqD2PvqvIZ3ob1skjUUizgNvzGXkZ4v5ZdcDeKT/4dSophvF0o0KgUia2lZYxC3jZ/LmrO+54tg23H3qYWRk6EaxdKRCIJKGNm4t4KoXpvLZwtXcfeqhDO59UNiRJEQqBCJpZtXGrfzquSnMW7GRx889nHOOaBF2JAlZoCcDzayvmc03s1wzu7OE9r+Y2YzYY4GZrQsyj0i6W/zDZvoPm8yi/M08c2m2ioAAAR4RmFkmMBQ4CcgDppjZhNhkNAC4+81x218PdAsqj0i62zGtZFHEeenKnnTbzWklpeoK8oigB5Dr7ovcfTswFuhXxvYDgTEB5hFJW//95gfOf3oy+1TL5JVrjlYRkJ0EWQiaA8vilvNi63ZhZgcCbYAPAswjkpYmzPyOX438khb71uLVa47moMZ1wo4kSSZZOgwPAF5x96KSGs1ssJnlmFlOfn5+JUcTSV3PffotN4yZTreW+zL+6l40rZ8VdiRJQkEWguVAy7jlFrF1JRlAGaeF3H24u2e7e3bjxo0rMKJI1eTu/Ontedw/cS4nd9yfUZf3oH5NzS0sJQuy++gUoJ2ZtSFaAAYAFxTfyMwOBfYFJgeYRSRtFBZFuOu12bw8NY8LerbiwX6dyNSNYlKGwAqBuxea2RDgHSATGOHuc8zsASDH3SfENh0AjHV3DyqLSLqIn1bypj7tuPHEdppWUsoV6A1l7j4JmFRs3b3Flu8LMoNIuli7eTuXPz+FGcvW8ftfduKiow4MO5KkCN1ZLFIF/DSt5JotPHlhd/p20rSSkjgVApEUt2DlRi559ks2bytk1GU9OKqtppWU3aNCIJLCchav4bKRU8iqnsn4q3txWDNNKym7T4VAJEW9N3clQ16aRvMGNXle00rKXlAhEElB46Ys5a7XZtO5RQNGXJqtaSVlr6gQiKQQd2foh7k89u4Ceh/SmGEXdte0krLX9BskkiKKIs4DE+fw/OQlnNWtOY/070L1zGQZJUZSmQqBSArYVljELeNm8ubs7xncuy139j1U00pKhVEhEElyG7YWcNWoqUxetJrfnHoYV/ZuG3YkqWJUCESS2FlDP2X+yo1sL4zwl/MP56xumlFMKp4KgUgScnfGTVnGrOXrcXdGDDqS49s3CTuWVFEqBCJJZmH+Ju5+bTZffLuGnm324+GzO9NWk8lIgFQIRJLE9sIIT3+8kP/7MJesahn86ZzOnJfdUqOHSuBUCESSwLSla7nr1dnMX7mR07o043dndKBJXc0mJpVDhUAkRJu2FfLo2/MY9fkSmtbL4plLsunTYf+wY0maUSEQCcl7c1dy77++YsWGrVzaqzW3ndyeOrpLWEIQ6G+dmfUF/kZ0hrJn3P2PJWxzHnAf4MBMd99lOkuRqmTVhq3cN3EOk2avoP3+dRl6YXe6t9o37FiSxgIrBGaWCQwFTgLygClmNsHd58Zt0w64CzjG3deamfrHSZUViTjjcpbx0KSv2VYY4faT23Plz9pSo5qGiZBwBXlE0APIdfdFAGY2FugHzI3b5kpgqLuvBXD3VQHmEQnNwvxN3PXabL78dg1Htd2Ph85Sl1BJHkEWgubAsrjlPKBnsW0OATCzT4mePrrP3d8uviMzGwwMBmjVqlUgYUWCsL0wwlMfL+TvH+SSVV1dQiU5hX1lqhrQDjgeaAF8Ymad3X1d/EbuPhwYDpCdne2VHVJkT0xdspa7XpvFgpWb1CVUklqQhWA50DJuuUVsXbw84At3LwC+NbMFRAvDlABziQRq49YCHn1nPi/EuoQ+e2k2Jx6mLqGSvIIsBFOAdmbWhmgBGAAU7xH0T2Ag8JyZNSJ6qmhRgJlEAvXe3JX89p9fsXKjuoRK6kjoN9TMmgMHxm/v7p+U9R53LzSzIcA7RM//j3D3OWb2AJDj7hNibb8ws7lAEXC7u6/esx9FJDzxXUIPbVqXYRd1p5u6hEqKMPeyT7mb2Z+A84n29imKrXZ3PzPgbCXKzs72nJycMD5aZBeRiDN2yjIefivaJfTGE9sxuHdbzRwmScfMprp7dkltiRwR/BJo7+7bKjaWSGrLXbWJu19Xl1BJfYkUgkVAdUCFQAR1CZWqJ5FCsAWYYWbvE1cM3P2GwFKJJKn4LqGnd2nGveoSKlVAIoVgQuwhkrY2bi3gkbfnM/qLJTSrl8WIQdmccKi6hErVUG4hcPfnzawGsbuAgfmxfv8iaeHdOSu4919z1CVUqqxyf5vN7HjgeWAxYEBLM7u0vO6jIqlu1Yat/G7CHN76Sl1CpWpL5GvN48Av3H0+gJkdAowBjggymEhYincJvf3k9uoSKlVaIoWg+o4iAODuC8yseoCZREKTuyo6cfyXi9fQq21DHjq7M20a1Q47lkigEikEOWb2DDA6tnwhoDu6pErZXhhh2EcLGfphLjVrZPLIOV04N7uFuoRKWkikEFwDXAfs6C76H+DJwBKJVLKpS9Zw56uz+WZVtEvo787oSOO6+4QdS6TSJNJraBvw59hDpMpQl1CRqFILgZmNd/fzzGw20fmEd+LuXQJNJhIgdQkV+Z+yfvNvjD2fXhlBRCpDYVGEng+9z+rN29UlVCSm1P5w7v597OW17r4k/gFcWznxRCrWEx/ksnrzdpo3yGLi9ceqCIhQRiGIc1IJ606p6CAiQfvy2zX8/YNvOLt7cz6980TdFyASU9Y1gmuIfvNva2az4prqAp8GHUykIq3fUsBNY6fTcr9aPNCvU9hxRJJKWV+JXgLOIDrg3BlxjyPc/aJEdm5mfc1svpnlmtmdJbQPMrN8M5sRe1yxBz+DSJncnbten8Wqjdt4YkA3XRQWKabUfxHuvh5YT3ROYcysCZAF1DGzOu6+tKwdm1kmMJToqaU8YIqZTXD3ucU2HefuQ/biZxAp0/icZUyavYI7+h7K4S0bhB1HJOmUe5LUzM4ws2+Ab4GPiQ4+91YC++4B5Lr7InffDowF+u1FVpHdtjB/E/dNmMvRBzXkqt5tw44jkpQSuVr2e+AoYIG7twFOBD5P4H3NgWVxy3mxdcWdY2azzOwVM2tZ0o7MbLCZ5ZhZTn5+fgIfLQLbCou4Ycx0sqpn8OfzupKRoeEiREqSSCEocPfVQIaZZbj7h0CJEyDvgYlA69jNae8RHe56F+4+3N2z3T27cePGFfTRUtU99s585ny3gT+d04Wm9TWLmEhpErlqts7M6gCfAC+a2SpgcwLvWw7Ef8NvEVv3k1iB2eEZ4JEE9itSro8X5POP/3zLxUcdyC86Ng07jkhSS+SIoB/wI3Az8DawkGjvofJMAdqZWZvYDGcDKDblpZk1i1s8E/g6kdAiZflh0zZuHT+TQ/avw29OOyzsOCJJL5FB5zYDmFk9oqdyEuLuhWY2BHgHyARGuPscM3sAyHH3CcANZnYmUAisAQbt/o8g8j/uzu0vz2TD1gJGX9GDrOqZYUcSSXqJTFV5FXA/sBWIEJ2u0oFyu2C4+yRgUrF198a9vgu4a/cii5Ru5GeL+XB+Pvef2ZFDm9YLO45ISkjkGsFtQCd3/yHoMCJ7Y+53G3h40jxOPLQJl/Q6MOw4IikjkWsEC4EtQQcR2Rs/bi/ihrHTaVCrOo/076KZxUR2QyJHBHcBn5nZF8C2HSvd/YbS3yJSuR58cy65qzYx+vKeNKyj2cVEdkciheBp4ANgNtFrBCJJ5e2vVvDSF0u5qndbjm3XKOw4IiknkUJQ3d1vCTyJyB74fv2P3PnaLDo3r8+tv2gfdhyRlJTINYK3YkM8NDOz/XY8Ak8mUo6iiHPzuBlsL4zwxMBu1Kim+QVE9kQiRwQDY8/x3TwT6j4qEqSnPl7I54vW8Gj/LrRpVDvsOCIpq8xCYGYZwJ3uPq6S8ogkZNrStfz5vQWc3qUZ/Y9oEXYckZRW5rG0u0eA2yspi0hCNm4t4Max02laL4s/nNVZXUVF9lIiJ1X/bWa3mVlLXSOQZPDbf37F8rU/8rcBXalfs3rYcURSXiLXCM6PPV8Xt07XCCQUr0/P458zvuPmPoeQ3VrfR0QqQiKDzrWpjCAi5VmyejP3vP4VPVrvx5ATDg47jkiVkcigc9WBa4DesVUfAU+7e0GAuUR2UlAU4YaxM8jMMP4yoCuZmm1MpMIkcmpoGFAdeDK2fHFs3RVBhRIp7i/vLWDmsnU8eWF3mjeoGXYckSolkUJwpLsfHrf8gZnNDCqQSHGfLfyBYR8v5PzslpzauVn5bxCR3ZJIr6EiMztox4KZtQWKgosk8j9rN2/nlnEzadOwNr87s0PYcUSqpEQKwe3Ah2b2kZl9THQAulsT2bmZ9TWz+WaWa2Z3lrHdOWbmZpadWGxJB+7OHa/OYvXmbTwxsBu1aiRyACsiu6vUf1lmdq67vwwsAtoBO0b0mu/u20p7X9z7M4GhwElAHjDFzCa4+9xi29UFbgS+2LMfQaqqF79YyrtzV3LPaYfRqXn9sOOIVFllHRHsGFvoVXff5u6zYo9yi0BMDyDX3Re5+3ZgLNCvhO0eBP5EdCpMEQC+WbmRB9+Yy8/aNeKyY9SDWSRIZR1rrzazd4E2ZjaheKO7n1nOvpsDy+KW84Ce8RuYWXegpbu/aWalDmVhZoOBwQCtWrUq52Ml1W0tKOL6MdOps081Hj/vcDLUVVQkUGUVgtOA7sALwOMV/cGxAe3+DAwqb1t3Hw4MB8jOzvaKziLJ5Y9vzWPeio08N+hImtTNCjuOSJVXaiGInc753MyOdvf8Pdj3cqBl3HKL2Lod6gKdgI9ig4Y1BSaY2ZnunrMHnydVwAfzVjLys8X86pjW/PzQJmHHEUkLiXTD2NfM/gC0jt/e3U8o531TgHZm1oZoARgAXBD3/vXAT/MKmtlHwG0qAulr1Yat3PbyLA5rVo87+h4adhyRtJFIIXgZeAp4ht24f8DdC81sCPAOkAmMcPc5ZvYAkOPuu1x3kPQViTi3vjyTLdsLeWJAV7KqZ4YdSSRtJFIICt192J7s3N0nAZOKrbu3lG2P35PPkKrh2f9+y3+++YE/nNWJdvvXDTuOSFpJ5IayiWZ2reYslqDMzlvPI+/M4+SO+3NBD/UKE6lsiRwRXBp7ju/eqfkIpEJs3lbIDWOn07D2Pvzx7C6abUwkBJqPQEJ1/8Q5LF69mZeuOIp9a9cIO45IWipriImzy3qju79W8XEknbwx6zvG5+Rx3c8PotdBDcOOI5K2yjoiOKOMNgdUCGSP5a3dwl2vzaZrywbc1OeQsOOIpLWybij7VWUGkfRRWBThprEzcIcnBnSjemYifRZEJCga11cq3d8/zCVnyVr+en5XWjWsFXYckbSnr2JSqXIWr+GJ97/h7G7N+WW35mHHERFUCKQSrf+xgBvHzqDFvrW4v1/HsOOISIx6DUmlcHfufn02Kzds5ZVrjqZuVvWwI4lIjHoNSaV4eWoeb876nttPbk/Xlg3CjiMicdRrSAK3KH8T902YQ6+2Dbn6uIPCjiMixSTUa8jMTgM6Aj/NEuLuDwQVSqqO7YURbhw7gxrVMvjL+V3J1GxjIkmn3EJgZk8BtYCfEx2Kuj/wZcC5pIp4/N35zF6+nqcvPoKm9TXbmEgySqTX0NHufgmw1t3vB3oBuhVUyvWfb/J5+pNFXNizFSd3bBp2HBEpRSKF4MfY8xYzOwAoAJolsnMz62tm880s18zuLKH9ajObbWYzzOy/ZtYh8eiSzFZv2sYt42fSrkkd7jlNf60iySyRQvCGmTUAHgWmAYuBMeW9ycwygaHAKUAHYGAJ/9G/5O6d3b0r8AjRyewlxbk7t78yi/U/FvDEwG7UrKHZxkSSWSLDUD8Ye/mqmb0BZMXmGy5PDyDX3RcBmNlYoB8wN27fG+K2r020W6qkuFGTl/DBvFXcd0YHDmtWL+w4IlKORC4WX1LCOtx9VDlvbQ4si1vOA3qWsK/rgFuAGsAJ5eWR5Pb19xv4w6SvOeHQJlx6dOuw44hIAhI5NXRk3ONnwH3AmRUVwN2HuvtBwB3APSVtY2aDzSzHzHLy8/Mr6qOlgm0tKOKGMdOpX7M6j/bXbGMiqSKRU0PXxy/HrheMTWDfy4GWccstYutKMxYYVkqG4cBwgOzsbJ0+SlK/f3Mu36zaxKjLetCwzj5hxxGRBO3JoHObgUSmr5wCtDOzNmZWAxgATIjfwMzaxS2eBnyzB3kkCbw7ZwWjP1/K4N5t6X1I47DjiMhuSOQawUT+dxE3g2gPoJfLe5+7F5rZEOAdIBMY4e5zzOwBIMfdJwBDzKwP0S6pa4FL9+zHkDD9cuinfLV8PZ2a1+O2X7QPO46I7KZEhph4LO51IbDE3fMS2bm7TwImFVt3b9zrGxPZjySvqUvWMue79UTceWJAN2pU08jmIqkmkX+1p7r7x7HHp+6eZ2Z/CjyZJDV3Z+Sn33L+05PJMKNDs3q0bVwn7FgisgcSOSI4iWiPnninlLBO0sTmbYXc+dpsJs78jj6HNeHxc7tSv5bmFxBJVWVNTHMNcC1wkJnNimuqC3wadDBJTrmrNnH16Kksyt/E7Se355rjDiJDI4qKpLSyjgheAt4CHgbixwna6O5rAk0lSenNWd/z61dmklU9kxcu78kxBzcKO5KIVICyJqZZD6w3s+KngOqYWR13XxpsNEkWBUUR/vjWPJ7977d0a9WAJy/sTrP6NcOOJSIVJJFrBG8S7T5qRCemaQPMJzpRjVRxKzds5boXp5GzZC2Djm7N3acepp5BIlVMIncWd45fNrPuRK8dSBU3eeFqrh8zjc3bivjbgK7069o87EgiEoCEpqqM5+7TzGyXweOk6nB3nv5kEY+8PY/WjWrz0pVHccj+dcOOJSIBSeTO4lviFjOA7sB3gSWSUG3YWsBt42fy7tyVnNq5KY/0P5w6++z29wURSSGJ/AuP/ypYSPSawavBxJEwff39Bq4ZPZW8tT/y29M7cNkxrTWCqEgaSOQawf2VEUTC9dq0PO5+fTb1sqozZvBRHNl6v7AjiUglKeuGsgmltQG4e4XNSSDh2VZYxAMT5/LiF0s5qu1+PDGwG03qZoUdS0QqUVlHBL2IzjA2BviCaPdRqULy1m7h2henMStvPVcfdxC3/eIQqmWqa6hIuimrEDQlOs7QQOACotcGxrj7nMoIJsH6eEE+N46dTlGR8/TFR3Byx6ZhRxKRkJT69c/di9z9bXe/FDgKyAU+is0xICkqEnH++u8FDHruS5rWy2LC9ceqCIikuTIvFpvZPkRnDhsItAaeAF4PPpYEYe3m7dw0bgYfL8jn7G7N+cNZnalZIzPsWCISsrIuFo8COhGdWOZ+d/9qd3duZn2BvxGdoewZd/9jsfZbgCuIdkvNBy5z9yW7+zlSvll567hm9DTyN27jD2d14oIerdQ1VESAsiemuQhoB9wIfGZmG2KPjWa2obwdm1kmMJTo3AUdgIFm1qHYZtOBbHfvArwCPLInP4SUzt156Yul9B82GYCXr+7FhT0PVBEQkZ+UNfro3nYf6QHkuvsiADMbC/QD5sZ9xodx239OtPhIBflxexH3/PMrXp2Wx8/aNeJvA7qxX+0aYccSkSQT5NgBzYl2P90hDyhrjKLLic5/sAszGwwMBmjVqlVF5avSFv+wmatHT2X+yo3ceGI7bjixHZmaQEZESpAUg8iY2UVANnBcSe3uPhwYDpCdne2VGC0lvTtnBbeOn0lmpjFi0JH8vH2TsCOJSBILshAsB1rGLbeIrduJmfUBfgMc5+7bAsxT5RUWRXj8vQUM+2ghnZvX58kLu9Nyv1phxxKRJBdkIZgCtDOzNkQLwACiN6b9xMy6AU8Dfd19VYBZqrz8jdu4Ycx0Ji9azcAerfjdGR3Iqq6uoSJSvsAKgbsXxm4+e4do99ER7j7HzB4Actx9AvAoUAd4OdaLZanGMNp9OYvXcN1L01i3pYBH+3fh3OyW5b9JRCQm0GsE7j6J6H0I8evujXvdJ8jPr+rcnec+XcxDk76m+b41ef3aHnQ4oF7YsUQkxSTFxWLZfZu2FXLHq7N4c9b39Dlsfx4/73Dq16wediwRSUEqBCkod9VGrh49jUX5m7ij76Fc1bstGeoaKiJ7SIUgxUyc+R13vDqLWjUyGX1FT44+qFHYkUQkxakQpIjthREefutrnvt0MUccuC9DL+hO0/qaQEZE9p4KQQpYsX4r1700jalL1nLZMW2469RDqa4JZESkgqgQJLnPcn/ghrHT2bK9iL9f0I3TuxwQdiQRqWJUCJJUJOI89clCHntnPm0a1Wbs4KM4uEndsGOJSBWkQpCENm4toPcjH7J2SwGnd2nGH8/pQp199FclIsHQ/y5JZunqLVwxagprtxRw4H61+L+B3TR3gIgESoUgiUxeuJprX5xKxOHFK3pyzMHqGioiwVMhSBKjP1/CfRPmcGDDWjx76ZG0blQ77EgikiZUCEJWUBThgYlzeeHzJRzfvjFPDOxGvSwNFSEilUeFIETrtmzn2hen8dnC1Qzu3ZY7+h6qWcREpNKpEITkm5UbuWJUDt+v28pj5x5O/yNahB1JRNKUCkEIPpy3iuvHTCereiZjBh/FEQfuG3YkEUljKgSVyN35x38W8fBb8+jQrB7/uCSbAxrUDDuWiKS5QAesMbO+ZjbfzHLN7M4S2nub2TQzKzSz/kFmCdvWgiJufXkmD02ax6mdmvHy1b1UBEQkKQR2RGBmmcBQ4CQgD5hiZhPcfW7cZkuBQcBtQeVIBqs2buWqF6Yyfek6bu5zCDeceLBuEhORpBHkqaEeQK67LwIws7FAP+CnQuDui2NtkQBzhOqr5eu5clQO67YUMOzC7pzSuVnYkUREdhLkqaHmwLK45bzYut1mZoPNLMfMcvLz8yskXGV4c9b39H/qMwx45ZpeKgIikpRSYlB7dx/u7tnunt24ceOw45QrEnH+/N4CrntpGh0PqM+/hhxLxwPqhx1LRKREQZ4aWg60jFtuEVtXpW3ZXsgt42by9pwVnHtEC35/Vif2qZYZdiwRkVIFWQimAO3MrA3RAjAAuCDAzwtd3totXDlqKvNXbOCe0w7j8mPb6KKwiCS9wAqBuxea2RDgHSATGOHuc8zsASDH3SeY2ZHA68C+wBlmdr+7dwwqU5ByFq/hqhemsr0wwohBR3J8+yZhRxIRSUigN5S5+yRgUrF198a9nkL0lFFKGz9lGb/552xa7FuLf1ySzcFN6oQdSUQkYbqzeC8UFkV4+K15PPvfbzn24EYMvaA79Wtp5FARSS0qBHto/Y8FXD9mOp8syGfQ0a2557TDqJaZEp2wRER2okKwBxblb+KKUTksW7OFh8/uzMAercKOJCKyx1QIdtN/vsnnuhenUS0zg9GX96Rn24ZhRxIR2SsqBAlyd0Z+tpjfv/k17ZrU4R+XZNNyv1phx2PECUYAAAnwSURBVBIR2WsqBAnYXhjh3n99xdgpyzipw/785fyu1NlHf3QiUjXof7NyrN60jWtGT+PLxWsY8vODueWkQ8jQdJIiUoWoEJTh6+83cMXzOfywaRt/G9CVfl33aMw8EZGkpkJQinfnrOCmcTOom1WN8Vf14vCWDcKOJCISCBWCYtydoR/m8ti7Czi8ZQOGX3wE+9fLCjuWiEhgVAjibC0o4vZXZjFx5nf8susB/PGcLmRV18ihIlK1qRDErFi/lcEv5DB7+Xp+3bc91xx3kEYOFZG0oEIAzFi2jsGjcti8rZB/XJxNnw77hx1JRKTSpH0h+Of05fz61VnsX28fXrj8GNo3rRt2JBGRSpW2hSAScR59dz7DPlpIzzb7MeyiI9ivdo2wY4mIVLq0LAQbtxZw87gZ/PvrVVzQsxX3ndGRGtU0cqiIpKdA//czs75mNt/Mcs3szhLa9zGzcbH2L8ysdZB5AJau3sI5wz7jw/n5PNivIw+d1VlFQETSWmBHBGaWCQwFTgLygClmNsHd58Ztdjmw1t0PNrMBwJ+A84PKNHnhaq59cSoRh1GX9eCYgxsF9VEiIikjyFNDPYBcd18EYGZjgX5AfCHoB9wXe/0K8HczM3f30nY6f/V8jh95/E7rzut4HtceeS1bCrZw6oun7vKeQV0HUaeoD3e8OouMavk0afE6v/nvOvhvtP2a7Gs4v9P5LFu/jItfv3iX99/a61bOaH8G83+Yz1VvXLVL+z2976FP2z7MWDGDm96+aZf2h058iKNbHs1nyz7j7vfv3qX9r33/StemXfn3on/z+09+v0v706c/TftG7Zk4fyKPT358l/YXznqBlvVbMu6rcQzLGbZL+yvnvUKjWo0YOWMkI2eM3KV90oWTqFW9Fk9OeZLxc8bv0v7RoI8AeOyzx3hjwRs7tdWsXpO3LnwLgAc/fpD3v31/p/aGtRry6nmvAnDXv+9ict7kndpb1GvB6LNHA3DT2zcxY8WMndoPaXgIw88YDsDgiYNZsHrBTu1dm3blr33/CsBFr11E3oa8ndp7tejFw30eBuCc8eewesvqndpPbHMivz3utwCc8uIp/Fjw407tpx9yOrcdfRvALr93kNjv3qCug/hhyw/0H99/l3b97ul3D8L53YsX5DmR5sCyuOW82LoSt3H3QmA9sMsA/2Y22MxyzCynoKBgj8K0aVSL3oc0oNmBL1K9xro92oeISFVkZXz53rsdm/UH+rr7FbHli4Ge7j4kbpuvYtvkxZYXxrb5obT9Zmdne05OTiCZRUSqKjOb6u7ZJbUFeUSwHGgZt9witq7EbcysGlAfWI2IiFSaIAvBFKCdmbUxsxrAAGBCsW0mAJfGXvcHPijr+oCIiFS8wC4Wu3uhmQ0B3gEygRHuPsfMHgBy3H0C8CzwgpnlAmuIFgsREalEgd5Q5u6TgEnF1t0b93orcG6QGUREpGy6k0pEJM2pEIiIpDkVAhGRNKdCICKS5gK7oSwoZpYPLNnDtzcCSr1ZLQmlUt5UygqplTeVskJq5U2lrLB3eQ9098YlNaRcIdgbZpZT2p11ySiV8qZSVkitvKmUFVIrbyplheDy6tSQiEiaUyEQEUlz6VYIhocdYDelUt5UygqplTeVskJq5U2lrBBQ3rS6RiAiIrtKtyMCEREpRoVARCTNpU0hMLO+ZjbfzHLN7M6w85TFzEaY2arYxD1JzcxamtmHZjbXzOaY2Y1hZyqNmWWZ2ZdmNjOW9f6wMyXCzDLNbLqZvVH+1uExs8VmNtvMZphZ0s8eZWYNzOwVM5tnZl+bWa+wM5XEzNrH/kx3PDaY2a7zku7NZ6TDNQIzywQWACcRnTJzCjDQ3eeW+caQmFlvYBMwyt07hZ2nLGbWDGjm7tPMrC4wFfhlMv7ZmpkBtd19k5lVJzpr9Y3u/nnI0cpkZrcA2UA9dz897DylMbPFQHZZMwwmEzN7HviPuz8TmzOllrsn9Ty2sf/LlhOdyXFPb6zdRbocEfQAct19kbtvB8YC/ULOVCp3/4To/AxJz92/d/dpsdcbga/ZdW7qpOBRm2KL1WOPpP4mZGYtgNOAZ8LOUpWYWX2gN9E5UXD37cleBGJOBBZWZBGA9CkEzYFlcct5JOl/VqnMzFoD3YAvwk1SuthplhnAKuA9d0/arDF/BX4NRMIOkgAH3jWzqWY2OOww5WgD5APPxU67PWNmtcMOlYABwJiK3mm6FAIJmJnVAV4FbnL3DWHnKY27F7l7V6JzaPcws6Q99WZmpwOr3H1q2FkSdKy7dwdOAa6LneJMVtWA7sAwd+8GbAaS/dphDeBM4OWK3ne6FILlQMu45RaxdVIBYufbXwVedPfXws6TiNhpgA+BvmFnKcMxwJmxc+9jgRPMbHS4kUrn7stjz6uA14mekk1WeUBe3BHhK0QLQzI7BZjm7isresfpUgimAO3MrE2sqg4AJoScqUqIXYB9Fvja3f8cdp6ymFljM2sQe12TaOeBeeGmKp273+XuLdy9NdHf2Q/c/aKQY5XIzGrHOgsQO8XyCyBpe725+wpgmZm1j606EUi6Dg7FDCSA00IQ8JzFycLdC81sCPAOkAmMcPc5IccqlZmNAY4HGplZHvA7d3823FSlOga4GJgdO/cOcHdsvupk0wx4PtbzIgMY7+5J3SUzhewPvB79XkA14CV3fzvcSOW6Hngx9uVwEfCrkPOUKlZcTwKuCmT/6dB9VERESpcup4ZERKQUKgQiImlOhUBEJM2pEIiIpDkVAhGRNKdCIAKYWVFsZMevzGzijvsNAvy8QWb29yA/QyRRKgQiUT+6e9fYaK9rgOvCDiRSWVQIRHY1mdighGbW1cw+N7NZZva6me0bW/+RmWXHXjeKDQOx45v+a2b2tpl9Y2aP7Nipmf3KzBaY2ZdEb8Tbsf7c2JHITDP7pBJ/ThFAhUBkJ7G7jk/kf0OQjALucPcuwGzgdwnspitwPtAZOD82eU8z4H6iBeBYoEPc9vcCJ7v74UQHFROpVCoEIlE1Y0NkrCA6XMJ7sTHrG7j7x7Ftnic6hn153nf39e6+lej4NQcCPYGP3D0/NifGuLjtPwVGmtmVRIdAEalUKgQiUT/Ghqc+EDDKv0ZQyP/+/WQVa9sW97qIcsb0cvergXuIjpA71cwaJhpapCKoEIjEcfctwA3ArUTHqF9rZj+LNV8M7Dg6WAwcEXvdP4FdfwEcZ2YNY8N2n7ujwcwOcvcv3P1eopOltCxtJyJBSIvRR0V2h7tPN7NZRIf9vRR4ysxqsfMIlY8B42Mzcb2ZwD6/N7P7iF6IXgfMiGt+1MzaET0SeR+YWVE/i0giNPqoiEia06khEZE0p0IgIpLmVAhERNKcCoGISJpTIRARSXMqBCIiaU6FQEQkzf0/ZyDX/BxEzAYAAAAASUVORK5CYII=\n",
999 | "text/plain": [
1000 | ""
1001 | ]
1002 | },
1003 | "metadata": {
1004 | "needs_background": "light",
1005 | "tags": []
1006 | },
1007 | "output_type": "display_data"
1008 | }
1009 | ],
1010 | "source": [
1011 | "select.plot_mi()"
1012 | ]
1013 | },
1014 | {
1015 | "cell_type": "markdown",
1016 | "metadata": {
1017 | "id": "NbCXcBoCmTN_"
1018 | },
1019 | "source": [
1020 | "Plotting the percentual variations of the mutual information between rounds:"
1021 | ]
1022 | },
1023 | {
1024 | "cell_type": "code",
1025 | "execution_count": null,
1026 | "metadata": {
1027 | "colab": {
1028 | "base_uri": "https://localhost:8080/",
1029 | "height": 279
1030 | },
1031 | "id": "k145NZeOmTOA",
1032 | "outputId": "07354713-4f34-4c28-ac69-084d2fe2d1ff"
1033 | },
1034 | "outputs": [
1035 | {
1036 | "data": {
1037 | "image/png": "iVBORw0KGgoAAAANSUhEUgAAAYIAAAEGCAYAAABo25JHAAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADh0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uMy4yLjIsIGh0dHA6Ly9tYXRwbG90bGliLm9yZy+WH4yJAAAgAElEQVR4nO3deXyU5bn/8c812VdCNpaEJWEVBCEgm1bFahUXVLBV616t/dljjx49v7Zaa1trT9tTa8/vnNpatS5VW7WCFvdaRU/bRATCIrtMQEjYkgkJhOzJ9ftjJhoCJEPI5JmZ53q/Xs/LmWeemfkO4Fzz3Pf93LeoKsYYY9zL43QAY4wxzrJCYIwxLmeFwBhjXM4KgTHGuJwVAmOMcblYpwMcr+zsbB05cqTTMYwxJqKsXLmySlVzjvZYxBWCkSNHsmLFCqdjGGNMRBGRT4/1mDUNGWOMy1khMMYYl7NCYIwxLmeFwBhjXM4KgTHGuJwVAmOMcTkrBMYY43JWCCLQqh37ef6jHeyqaXA6ijEmCkTcBWUGvrvoYzbvPQjA+MFpzB2fy9njc5k6LIPYGKvtxpjjY4UgwlQebGLz3oNcN3sE+QOTeG/TPh773zJ++76XAUlxnDE2h7PH53Dm2FwyU+KdjmuMiQBWCCLMh2U+AC6bmsfU4QO55YxRHGhs4R+fVPHepn28v3kfr67ZhQhMGZbB2eNymTs+l4lD0xERh9MbY8KRFYIIU+z1kZoQy6S8AZ/tS0+M44JJQ7hg0hDa25V1u2p5b9M+lm7axy/f2cIv39lCbloCc8flMnd8DqePySE1wf7qjTF+9m0QYUq8VcwsyDxmX4DHI0zOz2ByfgZ3nDOWyoNNfLClkqWb9vHGut28sGIncTHCjILMQGHIpTA7xc4WjHExKwQRZFdNA9t99Vwza0TQz8lJS+DyaflcPi2flrZ2Vn66n6Wb/WcLD7y+kQde38iIrOTPisLMgkwS42JC+CmMMeHGCkEEKfH6+wfmjMru1fPjYjzMKsxiVmEWd887iZ3V9bwfOFt4fvkOnireTlJcDKeNzmLu+FzmjstlaEZSX34EY0wYskIQQYq9PgYmxzF+cFqfvN6wzGSunTWCa2eNoLGljZIyH0s37eO9Tfv428Z9gH946lnj/MNTi4bb8FRjopEVggihqpR4q5g9KguPp+/b8xPjYvzNQ+Ny+dF8Zeu+OpZu9heFx/9exiMfeElPjA0MT83lzLE5ZKUm9HkOY0z/s0IQIT711bOrtpFbe9ksdDxEhDGD0hgzKO0ow1MreW3tbkTglPwMzg5czDZhSHpICpQxJvSsEESI4s/6B7L6/b2POTx1cyW/+tsWHnpnCzlpCcwd5z9bOG10NmmJcf2e0xjTO1YIIkSxt4pB6QkUZqc4mqPr8NSquibe31zJ0s37eHPdHl5cUU5cjHDqyM+Hp47KseGpxoQzKwQRwN8/4OOMsTlh94WanXrs4ak/eWMjP3ljI8Mzk5k7Loe543OZVZhlw1ONCTNWCCLAlr11+A41M9uBZqHj0XV4avn+epZu9g9PfWHFTp4u+ZTEOA+njcr2D08dn0ueDU81xnFWCCJAsbcKgNmF4V0IusofeOzhqe9u8g9PHTcojZ9fPpkpwzIcTmuMe1khiADFXh/DMpMYlpnsdJRe6zo81VtZx9JNlTzygZeH3tnCH742w+mIxriWFYIw19auLCvzMe/kIU5H6TMiwujcNEbnpnGgsYWHl25l74FGBqUnOh3NGFeyy0TD3IZdBzjQ2Mqc0ZHVLBSsy6bm0a7wyqoKp6MY41pWCMJcpPYPBKswJ5Wi4RksKi1HVZ2OY4wrWSEIc8VeH6NzU8mN4maTBUX5bNlbx/pdB5yOYowrWSEIY82t7SzfXu3I1cT96aLJQ4iP8fDSynKnoxjjSlYIwtja8hrqm9uivhBkJMdzzoRclqzZRUtbu9NxjHEdKwRhrNjrQwRmFkR3IQBYMDWf6kPNvL+50ukoxriOFYIwVuytYsKQdAamxDsdJeTOHJdDVko8i0uteciY/maFIEw1trRR+mlN1DcLdYiL8TB/ylDe3biPmvpmp+MY4ypWCMLUyk/309zWHvbzC/WlhUX5NLe18+ra3U5HMcZVQloIROR8EdksIltF5LtHeXy4iCwVkVUislZELghlnkhS7K0ixuOfztktJg5NZ9ygNGseMqafhawQiEgM8DAwD5gAXCUiE7ocdi/woqpOBa4EfhOqPJGmxOtjcv4AVy3wIiIsnJbHqh01eCvrnI5jjGuE8oxgBrBVVctUtRl4HrikyzEKpAduDwB2hTBPxKhramVNea1r+gc6u3RKHh6Bl0ttyglj+ksoC0EesLPT/fLAvs5+CFwjIuXAG8C3jvZCInKLiKwQkRWVldE/vHD5tmra2pU5/bA+cbjJTU/kC2NyeHlVBe3tNuWEMf3B6c7iq4CnVDUfuAB4RkSOyKSqj6rqdFWdnpOT0+8h+1uxt4r4GA/TRgx0OoojFhTlUVHTwIfbfE5HMcYVQlkIKoBhne7nB/Z1dhPwIoCqlgCJgPt+BndR7PVRNCLDtUs6fmnCYFITYlm00pqHjOkPoSwEy4ExIlIgIvH4O4OXdDlmB/BFABE5CX8hiP62n27sP9TMht0HXNks1CEpPoYLJw3hzXW7qW9udTqOMVEvZIVAVVuB24C3gY34RwetF5H7RWR+4LC7gK+LyBrgT8AN6vK5iJdt86GKKzuKO1tQlEd9cxtvr9/jdBRjol5IVyhT1TfwdwJ33ndfp9sbgNNCmSHSFHt9JMfHMDnf3Wv4njoyk2GZSSxaWcFlU/OdjmNMVHO6s9h0Uez1cerITOJj3f1X4/EIl03N55/eKnbXNjgdx5io5u5vmzCz70AjW/fVub5ZqMPCojxU4WVbxtKYkLJCEEZKyvzDJd00v1B3RmSlMH3EQBaXVtgylsaEkBWCMFLi9ZGWGMvEoQOcjhI2Fk7LZ+u+OtaW1zodxZioZYUgjBR7fcwqzCLGI05HCRsXTBpCfKzHJqIzJoSsEISJndX17Kiut/6BLgYkxXHuhEEsWbOL5lZbxtKYULBCECY6+gfcfCHZsVxelM/++haWbt7ndBRjopIVgjBR4vWRlRLP2EGpTkcJO18Yk012agKLVlrzkDGhYIUgDKgqxd4qZo/KQsT6B7qKjfFw6ZShLN28j+pDtoylMX2tx0IgIjkico+IPCoiT3Rs/RHOLcqqDrH3QJM1C3VjQVE+LW3Ka2ttyQpj+lowZwR/wb9ozN+A1zttpo8Uezv6B6yj+FgmDE3npCHp1jxkTAgEM9dQsqp+J+RJXKzEW8XQAYmMyEp2OkpYW1iUxwOvb2TrvoOMzk1zOo4xUSOYM4LXbFH50GlvV0q8PmaPyrb+gR7MnzKUGI+wyJaxNKZPBVMIbsdfDBpF5GBgOxDqYG6xac9B9te32LQSQchNS+SMMdm8sqqCNlvG0pg+02MhUNU0VfWoamLgdpqqpvf0PBMcm1/o+Cwoymd3bSMlXlvG0pi+EtTwURGZLyIPBraLQh3KTUq8VYzMSiYvI8npKBHh3AmDSEuMtSknjOlDwQwf/Rn+5qENge12EflpqIO5QWtbO8vKqpltw0aDlhgXw0WTh/Dmuj3UNdkylsb0hWDOCC4AzlXVJ1T1CeB84MLQxnKHdbsOcLCp1YaNHqeFRfk0tLTx1jpbxtKYvhDslcWd1020OZL7SLG3CoBZhVYIjse0EQMZkZVszUPG9JFgCsFPgVUi8pSIPA2sBH4S2ljuUOL1MW5QGjlpCU5HiSgiwoKp+ZSU+aiosWUsjTlRwYwa+hMwC1gMLAJmq+oLoQ4W7Zpa21i+vdpGC/XSgsAylq/YMpbGnLBjFgIRGR/4bxEwBCgPbEMD+8wJWL2jhsaWdusf6KVhmcnMKMhk0cpyW8bSmBPU3RQTdwK3AL88ymMKnB2SRC5R7PXhEZhp/QO9trAoj+8s+pjVO2uYOnyg03GMiVjHPCNQ1VsCN+ep6tzOG/6RROYElHh9nJw3gAFJcU5HiVjzJg0hIdbDIus0NuaEBNNZXBzkPhOk+uZWVu3cz2w7Gzgh6YlxnDdxMK+u2U1Ta5vTcYyJWN31EQwWkWlAkohMFZGiwHYWYNNknoAV2/fT0qbWUdwHFhTlUdvQwnsbbRlLY3qruz6C84AbgHzgoU77DwL3hDBT1Csp8xHrEU4dmel0lIh3+uhsctMSWFRawbxJQ5yOY0xEOmYhUNWngadFZKGqLurHTFGv2OtjyrAMUhKCWQ7CdCc2xsOlU/N44h/b8NU1kZVq12QYc7yCuY5gkYhcKCLfFpH7Orb+CBeNDjS28HF5jQ0b7UMLi/JpbVeWrLFlLI3pjWAmnXsEuAL4FiDAl4ERIc4VtT4qq6ZdsYnm+tC4wWlMHJrOYluwxpheCWbU0BxVvQ7Yr6o/AmYDY0MbK3oVe30kxHqYOjyj54NN0BYW5fNxRS1b9h50OooxESeYQtAxmUu9iAwFWvBfaWx6odhbxfSRA0mMi3E6SlT5fBlLu6bAmOMV7JrFGcAvgFJgO/CnUIaKVr66JjbtOcgcaxbqc9mpCZw1NseWsTSmF4LpLP6xqtYERg6NAMar6veDeXEROV9ENovIVhH57jGO+YqIbBCR9SLyx+OLH1k+LKsGbFnKUFk4LZ+9B5r459Yqp6MYE1F6HL8oIjH4F6IZ2XG8iKCqDwXxvIeBc/FPVrdcRJao6oZOx4wB7gZOU9X9IpLb2w8SCYq9VaQmxDI5z5Z0CIWzx+eSnhjLotJyzhib43QcYyJGMAPZXwUagY+B9uN47RnAVlUtAxCR54FL8C932eHrwMOquh9AVaP68tASr48ZBZnExgS7HpA5HolxMVx8ylAWlZZzsLGFtESbx8mYYARTCPJVdXIvXjsP2Nnpfjkws8sxYwFE5J9ADPBDVX2r6wuJyC34Z0Jl+PDhvYjivD21jZRVHeKqGZGZP1IsKMrnuWU7ePPjPXzl1GFOxzEmIgTz0/RNEflSiN4/FhgDnAVcBTwW6Jg+jKo+qqrTVXV6Tk5knvKXlPnbra1/ILSKhmdQkJ1io4eMOQ7BFIIPgZdFpEFEDojIQRE5EMTzKoDOP8nyA/s6KweWqGqLqm4DtuAvDFGneKuPAUlxTBiS7nSUqOZfxjKPZduq2Vld73QcYyJCMIXgIfwXkSWrarqqpqlqMN9my4ExIlIgIvHAlcCSLse8gv9sABHJxt9UVBZs+EihqhR7fcwuzMLjEafjRL3LivIAeNmWsTQmKMEUgp3AOj3O9QBVtRW4DXgb2Ai8qKrrReR+EZkfOOxtwCciG4ClwP9VVd/xvE8k2FndQEVNA3NGW7NQf8gfmMyswkwWl9oylsYEI5jO4jLgfRF5E2jq2NnT8NHAMW8Ab3TZd1+n24p/Scw7gw0ciYq9/v4Bm2iu/ywoyufbL62ldMd+po2w6b6N6U4wZwTbgHeBeCCt02aCVOz1kZOWwKicVKejuMYFk4aQGOdhkU1EZ0yPuj0jCFwUNlZVr+6nPFGno3/gtNFZiFj/QH9JTYjl/ImDeW3NLu67aILN7WRMN7o9I1DVNmBEoLPX9MLWfXVU1TVZs5ADFk7L50BjK+/aMpbGdCvYPoJ/isgS4FDHzmD6CIy/WQiwieYcMGdUNoPTE1lUWs6Fk23CXGOOJZg+Ai/wWuBY6yM4TsXeKvIHJjEsM9npKK4T4xEunZrHB1sqqTzY1PMTjHGpHs8IAovRICKpgft1oQ4VLdrblQ/LqvnShEFOR3GthUV5PPKBl7+sruDmLxQ6HceYsBTMUpUni8gqYD2wXkRWisjE0EeLfBt2H6C2ocWuH3DQmEFpTM4fYMtYGtONYJqGHgXuVNURqjoCuAt4LLSxokNJoH9gdqH1DzhpwdQ8Nuw+wMbdwcyMYoz7BFMIUlR1accdVX0fSAlZoihS7K2iMCeFwQMSnY7iahefMpRYj7DYJqIz5qiCKQRlIvJ9ERkZ2O4lCucD6mstbe18tK3aho2GgazUBOaOz+WV1btobTueJTWMcYdgCsHXgBxgMbAIyA7sM91YW17LoeY2GzYaJhYW5VF5sIm/2zKWxhzhmKOGROQZVb0WuE5V/7UfM0WFksD8QrMK7YwgHMwdn0tGchyLSyuYOy6qV0Q15rh1d0YwTUSGAl8TkYEiktl566+AkarY6+OkIelkpthF2eEgITaGiycP5a/r93CgscXpOMaEle4KwSP4J5sbD6zssq0IfbTI1djSxopP91v/QJhZOC2fptZ23li72+koxoSVYxYCVf1vVT0JeEJVC1W1oNNmV+Z0o3THfppb260QhJlT8gdQmGPLWBrTVY+dxap6q4jEiMhQERnesfVHuEhV4vUR4xFmFFgLWjgRERYW5bN8+34+9R3q+QnGuEQwVxbfBuwF3gFeD2yvhThXRCv2+piUN4C0xDino5guLp2ahwh2pbExnQQzfPQOYJyqTlTVSYFtcqiDRapDTa2s2VnDbGsWCkt5GUnMLsxi8SpbxtKYDsGuWVwb6iDRYvn2alrb1foHwtjConx2Vjew4tP9TkcxJiwEdWUx/jWL7xaROzu2UAeLVCVeH3ExwnRbJzdsnX/yYJLjY1i00jqNjYHgCsEO/P0DtmZxEIq9PqYOH0hSvC2NGK5SEmI5/+TBvL52N40tbU7HMcZxQa9HYHpWW9/Cul213P7FMU5HMT1YWJTP4tIK/rphL/NPGep0HGMc1d0UE68Cx+xNU9X5IUkUwT7c5kPVlqWMBLMLsxg6IJHFpeVWCIzrdXdG8GC/pYgSJV4fiXEepgzLcDqK6YEnsIzlIx942Xegkdx0myrcuNcxC4GqftCfQaJBsbeKU0dmEh8bTNeLcdqConx+876Xv6zexdfPsIvljXvZN1YfqTzYxJa9ddYsFEFG56ZyyrAMFpXaNQXG3awQ9JGSMv+ylHb9QGRZWJTHpj0H2WDLWBoXs0LQR0q8VaQlxjJxaLrTUcxxuHjyUOJixKacMK5mo4b6SInXx8yCTGJjrLZGkoEp8Zw9Ppe/rK7gu/PGE2d/f8aFbNRQH6ioaWC7r55rZ490OorphYVF+by9fi9//6SSs8cPcjqOMf3ORg31gRKv9Q9EsrPG5TIwOY5FKyusEBhXCmYa6jEi8pKIbBCRso6tP8JFimJvFZkp8YwbZDNvRKL4WA+XTMnjnY17qa23ZSyN+wTTIPok8FugFZgL/AF4NpShIomqUuL1MbswC49HnI5jemlBUR7Nre289vEup6MY0++CKQRJqvouIKr6qar+ELgwmBcXkfNFZLOIbBWR73Zz3EIRURGZHlzs8LHdV8/u2kZbfyDCTcobwJjcVBs9ZFwpmELQJCIe4BMRuU1ELgNSe3qSiMQADwPzgAnAVSIy4SjHpQG3A8uOK3mYKPZWAdY/EOlEhAVF+az8dD/bqmwZS+MuwRSC24Fk4F+BacC1wPVBPG8GsFVVy1S1GXgeuOQox/0Y+DnQGFTiMFPs9TE4PZGC7BSno5gTdFlgGcuXbXF74zLBLF6/XFXrVLVcVW9U1QWq+mEQr52Hf3WzDuWBfZ8RkSJgmKq+3t0LicgtIrJCRFZUVlYG8db9o71d+dDrY86oLESsfyDSDR6QyOmjs1lUWkF7u005YdwjmFFDS0Xkva7bib5xoLnpIeCuno5V1UdVdbqqTs/JyTnRt+4zW/YdxHeo2foHosiCojwqahr4aHu101GM6Tc9LkwD/Hun24nAQvwjiHpSAQzrdD8/sK9DGnAy/mUwAQYDS0RkvqquCOL1HVe81X/9gBWC6HHexMGkxK9jcWk5swrt79W4QzBNQys7bf9U1TuBs4J47eXAGBEpEJF44EpgSafXrVXVbFUdqaojgQ+BiCkC4J9obnhmMvkDk52OYvpIcnws8yYN4Y2P99DQbMtYGncIpmkos9OWLSLnAQN6ep6qtgK3AW8DG4EXVXW9iNwvIhE/T1Fbu/Jhmc9GC0WhhUX51DW18tcNe5yOYky/CKZpaCX+yecEf5PQNuCmYF5cVd8A3uiy775jHHtWMK8ZLtbvquVgY6s1C0WhmQWZ5GUk8dLKci6ZktfzE4yJcMEUgpNU9bChnSKSEKI8EaPYa/0D0crjERYU5fHw0q3sqW1k8ABbxtJEt2CuIyg+yr6Svg4SaYq9PsbkppKbZl8S0eiyqXm0K7yy2q40NtHvmIVARAaLyDQgSUSmikhRYDsL/wVmrtXc2s7ybdXWPxDFCnNSKRqewaKVtoyliX7dNQ2dB9yAf9jnQ532HwTuCWGmsLemvIaGljZm2/rEUW1BUT73vrKOdRUHmJTf4/gIYyLWMc8IVPVpVZ0L3KCqcztt81V1cT9mDDvFW32IwKzCTKejmBC6aPIQ4mM8LLIpJ0yUC6az+GQRmdh1p6reH4I8EaHYW8XEoelkJMc7HcWEUEZyPOdMyGXJml1878KTbBlLE7WC+ZddBxwKbG34ZxMdGcJMYa2huY1VO2qYY81CrrBgaj7Vh5p5f3P4zHFlTF/r8YxAVX/Z+b6IPIj/IjFXWvnpfprb2m3YqEucOS6HrJR4FpeWc+4EW8bSRKfenOsm4+9AdqWSsipiPcKpI61/wA3iYjzMnzKUdzfuo6a+2ek4xoREMFNMfCwiawPbemAz8F+hjxaeir0+JucPIDUhmO4VEw0WFuXT3NbOq2t3Ox3FmJAI5tvsok63W4G9gXmEXOdgYwtry2u59cxRTkcx/Wji0HTGDUpj0cpyrp01wuk4xvS57i4oyxSRTPzXDXRsDUB6YL/rLN9eTVu72oVkLiMiLJyWx+qdNXgr65yOY0yf665pqApYDawIbCs7bREzVXRfKt7qIz7WQ9GIgU5HMf3skil5eAQW2zUFJgp1Vwj+G9gPvIV/jeJCVS0IbIX9ki7MFHt9TBs+kMS4GKejmH42KD2R08fk8LItY2miUHdXFt8BTAH+jH/B+lUi8p8iUtBf4cLJ/kPNbNh9wJqFXGxhUR67ahv5sMzndBRj+lS3o4bUbynwbeAR4EbgnP4IFm46/uefM9oKgVt9acJgUhNiWVRqM5Ka6NJdZ3GKiHxVRP6Cf3GZVGCaqj7Wb+nCSLHXR3J8DJPzM5yOYhySFB/DhZOG8Oa63dQ3u3LgnIlS3Z0R7MN/JlAC/BIoA6aLyAIRWdAf4cJJsbeKGQWZNt+Myy0oyqO+uY231tkyliZ6dHcdwZ/xL1E5LrB1poBrZiDde6ARb+Uhrjh1mNNRjMNOHZnJsMwkFpdWsKDItRfYmyhzzEKgqjf0Y46wVhJYltImmjMej3DZ1Hz+571P2FXTwNCMJKcjGXPCrJ0jCCVeH+mJsZw0JN3pKCYMLCzKQ20ZSxNFrBAEobisilmFWcR4xOkoJgyMyEph+oiBtoyliRpWCHqws7qendUNdv2AOcyCony8lYdYW17rdBRjTljQhUBERovIsyKySERmhzJUOPmsf2C09Q+Yz104eQjxsbaMpYkO3V1HkNhl14+Bu4E7gN+GMlQ4KfZWkZ0az5jcVKejmDAyICmOcycMYsmaXTS3tjsdx5gT0t3w0VdF5BlV/UPgfgv+JSoV/5KVUU9VKfb6mD0qGxHrHzCHu7won9fX7mbp5n2cN3Gw03F6pba+BW9VHWWVh9gW+G9Z5SEGpsTx668WkZ2a4HRE0w+6KwTnA7eKyFvAfwD/DvwrkARc3Q/ZHOetPMS+g03WP2CO6gtjsslOTWDRyvKwLgTNre3sqK6nrLKOsqpDlFXWsa3K/4XvO/T5qmsxHmFEZjIjs1Mo9lZx7e8/4vmvz2JAcpyD6U1/6O46gjbg1yLyDPB94FbgXlX19lc4p5V4qwCsEJijio3xcOmUoTxdsp3qQ81kpsQ7lkVVqaxr+uwXfceX/raqQ+yorqet04yp2anxFGancu6EQRRkp1CYk0phTgrDM5M/u3L+f7dUcvPTK7j+yY949uaZtiJflDvm366IzAT+L9CM/4ygAfiJiFQAP1bVmv6J6Jxir4+8jCSGZyY7HcWEqQVF+Tz+j228umYX188ZGfL3a2hu8/+a/6wZJ/CFX3mIg02fz3+UEOuhIDuFk4akceGkIRTmpHz2pT8gqedf+GeMzeHXX53Krc+V8rWnlvP0jTNIirfp16NVd2X+d8AF+Cebe1JVTwOuFJEzgReA8/ohn2Pa25WSMh/nnDTI+gfMMU0Yms5JQ9JZXFreZ4WgvV2pqGkINN90NOf4b++qbTzs2KEDEinMSeWyojwKA1/0Bdkp5GUk4TnB616+NHEwv7piCrc/v4pvPLuSx66bRkKsFYNo1F0haMXfOZyC/6wAAFX9APggtLGct3HPAWrqW6xZyPRoYVEeD7y+ka37DjI6Ny3o59U2tBzWXl/2WaftIZo6jURKTYilMCeFGQWZnzXjFGb7v/BD/St9/ilDaWxu49uL1vKtP67i4auLbOLFKNRdIfgq8A38ReC6/okTPjquH5hthcD0YP6Uofz0zU0sKq3gO+ePP+yxlraOjtrDR+WUVdVRVXd4R+3wzGQKs1M4fXT251/4OSnkpCY4elb6lVOH0dDSxg+WrOeuF9fwqyum2FX2Uaa7zuItwF1d94vI6cBVqvovoQzmtBKvj4LsFIYMsEnFTPdy0xI5Y0w2L5dWMDwz+fMmnUp/R21rp47arJR4CnNS+OL4QYe12w/PTCY+Nnx/aV8/ZyT1zW38/K1NJMXF8NMFk0646cmEj6CGAojIVPxnCF8B9gDjgR4LgYicD/w/IAZ4XFV/1uXxO4Gb8TdDVQJfU9VPj+cDhEJrWzvLtlUzf8pQp6OYCPHl6cP45nOl3L34Y+JjPRRkpTBucBrzJg32N+PkpDAqOzWih2LeetYo6ptb+Z/3tpIUH8MPLp5g/WdRortRQ2OBq/AXgIP41yc4S1W3ici2nl5YRGKAh4FzgXJguYgsUdUNnQ5bBUxX1XoRuRX4T+CKXn+aPvJxRS11Ta3WP2CCNu/kwbz8zTlkpyYwNCMpaptO7jx3LPXNbfz+H9tIjo/h212awkxk6u6MYBOwHLhcVT/u8lgwUy7OALaqahmAiDwPXAJ8VkwUETkAABBNSURBVAgC6yF3+BC4JpjQoVYc6B+YVWiFwARHRJg6fKDTMUJORLj3wpOob27jN+97SUmI5V/mjnY6ljlB3TVKLgC2AX8VkWdE5GIROZ7z2jxgZ6f75YF9x3IT8ObRHhCRW0RkhYisqKysPI4IvVPi9TF+cJpdXm/MUYgIP7n0ZC6bmscv3t7M7//RYwOBCXPHLASq+oqqXgmMxv8FfQtQLiJPAn26QouIXANMB35xjCyPqup0VZ2ek5PTl299hKbWNpZvr7bRQsZ0w+MRfnH5ZM6fOJgfv7aBP320w+lI5gT0OExBVQ+p6h9V9WL8ncQlwNogXrsC6LzIb35g32FE5Bzge8B8VW0KKnUIrdpRQ1Nruy1LaUwPYmM8/PdVUzlrXA73vPwxr6yyFdsi1XGNV1PV/YFf52cHcfhyYIyIFIhIPHAlsKTzAYHRSL/DXwT2HU+WUCn2+vAIzCjIdDqKMWEvPtbDI9dMY1ZBFnf9eQ1vrdvjdCTTCyEbuKyqrcBtwNvARuBFVV0vIveLyPzAYb/AP4XFn0VktYgsOcbL9ZsSbxWT8gYENR+LMQYS42J4/PrpnJI/gG/9qZT3N4fFbzpzHEJ6BYuqvqGqY1V1lKr+JLDvPlVdErh9jqoOUtUpgW1+968YWvXNrazeWcNsaxYy5rikJMTy5I0zGDsojW88s/KzK/NNZAjfSxkdsGL7flra1K4fMKYXBiTF8cxNMxmemcxNTy+ndMd+pyOZIFkh6KTY6yMuRpg+MvrHgxsTCpkp8Tx380xy0hK4/omPWFdR63QkEwQrBJ2UeKuYMiyD5HhbhMOY3spNT+S5m2eSlhDLdU98xCd7DzodyfTACkFAbUMLH1fUWv+AMX0gf2Ayz319FjEe4erHl7G96pDTkUw3rBAEfLStmna1ZSmN6SsF2Sk8d/NMWtraufrxZVTUNDgdyRyDFYKAYm8VCbEepg7PcDqKMVFj7KA0nrlpJgcaW7jm8WXsO9jY85NMv7NCEFDi9XHqyExbis+YPnZy3gCeuvFU9h5o5JrHl1F9qLnnJ5l+ZYUAqKprYtOegza/kDEhMm1EJo9fN53tvnque2IZBxpbnI5kOrFCAHxY5r/4xfoHjAmdOaOz+d0109i85yA3PrmcQ02tTkcyAVYI8F8/kJoQy6S8AU5HMSaqzR2fy39fOZVVO/bz9T+soLGlzelIBisEgL9/YGZBJrEx9sdhTKjNmzSEB798CiVlPr75XCnNre1OR3I913/z7a5tYFvVIesfMKYfLSjK54FLT+a9Tfu444VVtLZZMXCS6y+h7Zgcy9YfMKZ/XT1zBA3NbTzw+kYS49by4OWn4InStZ7DnesLQbHXx8DkOMYPTnM6ijGuc/MXCqlvbuOhd7aQFBfDA5eejIgVg/7m6kKgqpR4fcwqzLJfIsY45Ftnj6a+uY1HPvCSHB/DPRecZMWgn7m6EOyorqeipoH/c2ah01GMcS0R4Tvnj6OhuZXH/r6N5PhY/u3csU7HchVXF4LiQP+ATTRnjLNEhB9cPJH65jb+37ufkBwfwzfOHOV0LNdwfSHITUtgVE6K01GMcT2PR/jZwsk0tLTx0zc3kRQfw3WzRzodyxVcWwj8/QNVnD4629ojjQkTMR7hV1dMobGlnfv+sp6kuBi+PH2Y07GinmuvI/hkXx1Vdc02bNSYMBMX4+HXX53KF8Zk851Fa3l1zS6nI0U91xaC4q1VAHYhmTFhKDEuhkevnc70EZn82wur+duGvU5HimruLQReH8MykxiWmex0FGPMUSTFx/D7G6YzcWg633yulH98UuV0pKjlykLQ1q4s21bNnEJrFjImnKUlxvH012ZQmJPC1/+wguXbq52OFJVcWQg27j5AbUMLc0Zbs5Ax4S4jOZ5nbprJkIxEbnxyOWt21jgdKeq4shAUewP9A4VWCIyJBDlpCTx380wGpsRx3RMfsXH3AacjRRWXFgIfo3JSyE1PdDqKMSZIQwYk8cebZ5EUF8O1v1+Gt7LO6UhRw3WFoKWtnY+2VduwUWMi0LDMZJ69eSaqcPVjy9hZXe90pKjgukKwtryG+uY2W5bSmAg1OjeVZ2+eSUNLG199/EP21DY6HSniua4QFG/1zy80y/oHjIlYJw1J5w9fm8H+Qy1c/fiHVNU1OR0pormvEHh9TBiSzsCUeKejGGNOwCnDMnjihlOpqGngmseXUVPf7HSkiOWqQtDY0sbKHfutWciYKDGjIJPHrptOWeUhrn9yOQcbW5yOFJFcVQhKP91Pc2u7XT9gTBT5wpgcHr66iHUVtdz01AoamtucjhRxXFUIir0+YjzCqSMznY5ijOlD504YxK+umMLyT6u55ZkVNLVaMTgeIS0EInK+iGwWka0i8t2jPJ4gIi8EHl8mIiNDmaekzMfk/AGkJcaF8m2MMQ6Yf8pQfr5wMn//pIrb/riKlrZ2pyNFjJAVAhGJAR4G5gETgKtEZEKXw24C9qvqaOBXwM9DlaeuqZU1O2usf8CYKPaV6cP40fyJvLNhL3e+uIa2dnU6UkQI5cI0M4CtqloGICLPA5cAGzodcwnww8Dtl4Bfi4io6rH/9jZvhrPOOnzfV74C3/wm1NfDBRcc+ZwbbmD57AtIq6vhlvtugp92OSO49Va44grYuROuvfbI5991F1x8sf+9v/GNIx+/91445xxYvRruuOPIx//jP2DOHCguhnvuOfLx//ovmDIF/vY3eOCBIx//3e9g3Dh49VX45S+PfPyZZ2DYMHjhBfjtb498/KWXIDsbnnrKv3X1xhuQnAy/+Q28+OKRj7//vv+/Dz4Ir712+GNJSfDmm/7bP/4xvPvu4Y9nZcGiRf7bd98NJSWHP56fD88+6799xx3+P8POxo6FRx/1377lFtiy5fDHp0zx//kBXHMNlJcf/vjs2fDTn/pvL1wIPt/hj3/xi/D97/tvz5sHDQ2HP37RRfDv/+6/3fXfHQT1b48bboCqKrj88iMft397ff5v73rgnJoG1r4cy91xv+FnCybj+d49/fpvTwGdNYv2n/wHCni+fDni86GdDmidO5fG734PFJIvvQgaGgH97Jim8+Zx6Fv/RrsqWRedB0CsR4jxBBbSOtF/e52EshDkATs73S8HZh7rGFVtFZFaIAs4bL5ZEbkFuAVgckJCr8Js3H2A+BgPqYmuXZTNGNfIy0iiPjWeW1eUU1Lm49ZlO5gQmKyu44t2X20s9//sPdpVuX35Tsbs2v/Z8xXYUVfO/ff/FVX4/spyRviqD/si31i/nZ/c+yaqyoOrKxh04PAfGaVNXv7ze/5C9dv1exnYcPj8SP98byv/0/RXAJ7a6iOx9fBrId59dyuP1fmL2/M7/NkKslMYFIKpcaS7H98n9MIilwPnq+rNgfvXAjNV9bZOx6wLHFMeuO8NHHPMicenT5+uK1as6FWmmvpmMpLt+gFj3EBVeeKf2yn9dD8iICII4Om4LSBI4D54OvYFjvtsH58f33Hf4zl8v/91pcv7dDzn6O8nfH68p+M1PEd/v47jioYPZHRuaq/+PERkpapOP9pjofx5XAF0Xmw0P7DvaMeUi0gsMADocu7ed6wIGOMeIsJNpxdw0+kFTkcJe6EcNbQcGCMiBSISD1wJLOlyzBL8TXoAlwPvdds/YIwxps+F7Iwg0OZ/G/A2EAM8oarrReR+YIWqLgF+DzwjIluBavzFwhhjTD8Kac+pqr4BvNFl332dbjcCXw5lBmOMMd1z1ZXFxhhjjmSFwBhjXM4KgTHGuJwVAmOMcTkrBMYY43Ihu7I4VESkEvi0l0/Ppsv0FRHMPkv4iZbPAfZZwtWJfJYRqppztAcirhCcCBFZcaxLrCONfZbwEy2fA+yzhKtQfRZrGjLGGJezQmCMMS7ntkLwqNMB+pB9lvATLZ8D7LOEq5B8Flf1ERhjjDmS284IjDHGdGGFwBhjXM4VhUBEnhCRfYEV0SKaiAwTkaUiskFE1ovI7U5n6g0RSRSRj0RkTeBz/MjpTCdKRGJEZJWIvNbz0eFLRLaLyMcislpEerccYBgQkQwReUlENonIRhGZ7XSm3hCRcYG/i47tgIgcZYHqE3gPN/QRiMgZQB3wB1U92ek8J0JEhgBDVLVURNKAlcClqrrB4WjHRUQESFHVOhGJA/4B3K6qHzocrddE5E5gOpCuqhc5nae3RGQ7ML27JWMjgYg8DfxdVR8PLI6VrKo1Tuc6ESISg39lx5mq2tsLa4/gijMCVf1f/AvfRDxV3a2qpYHbB4GNQJ6zqY6f+tUF7sYFtoj9VSIi+cCFwONOZzEgIgOAM/AvfoWqNkd6EQj4IuDtyyIALikE0UpERgJTgWXOJumdQFPKamAf8I6qRuTnCPgv4NtAu9NB+oACfxWRlSJyi9NheqkAqASeDDTXPS4iKU6H6gNXAn/q6xe1QhChRCQVWATcoaoHnM7TG6rapqpTgHxghohEZLOdiFwE7FPVlU5n6SOnq2oRMA/4l0DTaqSJBYqA36rqVOAQ8F1nI52YQPPWfODPff3aVggiUKBNfRHwnKoudjrPiQqcsi8Fznc6Sy+dBswPtK0/D5wtIs86G6n3VLUi8N99wMvADGcT9Uo5UN7pLPMl/IUhks0DSlV1b1+/sBWCCBPoZP09sFFVH3I6T2+JSI6IZARuJwHnApucTdU7qnq3quar6kj8p+7vqeo1DsfqFRFJCQxCINCU8iUg4kbbqeoeYKeIjAvs+iIQUQMqjuIqQtAsBCFevD5ciMifgLOAbBEpB36gqr93NlWvnQZcC3wcaF8HuEdV33AwU28MAZ4OjILwAC+qakQPu4wSg4CX/b83iAX+qKpvORup174FPBdoUikDbnQ4T68FivK5wDdC8vpuGD5qjDHm2KxpyBhjXM4KgTHGuJwVAmOMcTkrBMYY43JWCIwxxuWsEBgDiEhbYGbHdSLyasc1DiF8vxtE5NehfA9jgmWFwBi/BlWdEpidthr4F6cDGdNfrBAYc6QSAjO6isgUEflQRNaKyMsiMjCw/30RmR64nR2YXqLjl/5iEXlLRD4Rkf/seFERuVFEtojIR/gvDOzY/+XAmcgaEfnffvycxgBWCIw5TOBK5y8CSwK7/gB8R1UnAx8DPwjiZaYAVwCTgCsCiwkNAX6EvwCcDkzodPx9wHmqegr+ScWM6VdWCIzxSwpM2bEH/zQL7wTmtM9Q1Q8CxzyNf477nryrqrWq2oh/fpsRwEzgfVWtVNVm4IVOx/8TeEpEvg7E9NHnMSZoVgiM8WsITIk9AhB67iNo5fP/fxK7PNbU6XYbPczppar/B7gXGAasFJGsYEMb0xesEBjTiarWA/8K3IV/Dvv9IvKFwMPXAh1nB9uBaYHblwfx0suAM0UkKzCN+Jc7HhCRUaq6TFXvw7+YyrAT/iDGHAdXzD5qzPFQ1VUishb/tL/XA4+ISDKHz2D5IPBiYAWv14N4zd0i8kP8HdE1wOpOD/9CRMbgPxN5F1jTV5/FmGDY7KPGGONy1jRkjDEuZ4XAGGNczgqBMca4nBUCY4xxOSsExhjjclYIjDHG5awQGGOMy/1/PRRbkhdFX+kAAAAASUVORK5CYII=\n",
1038 | "text/plain": [
1039 | ""
1040 | ]
1041 | },
1042 | "metadata": {
1043 | "needs_background": "light",
1044 | "tags": []
1045 | },
1046 | "output_type": "display_data"
1047 | }
1048 | ],
1049 | "source": [
1050 | "select.plot_delta()\n"
1051 | ]
1052 | },
1053 | {
1054 | "cell_type": "markdown",
1055 | "metadata": {
1056 | "id": "E0X_P7NgmTOE"
1057 | },
1058 | "source": [
1059 | "Making the selection choosing to stop at Round 5:"
1060 | ]
1061 | },
1062 | {
1063 | "cell_type": "code",
1064 | "execution_count": null,
1065 | "metadata": {
1066 | "colab": {
1067 | "base_uri": "https://localhost:8080/"
1068 | },
1069 | "id": "GgwHXp-PmTOF",
1070 | "outputId": "b1482802-a4a5-4b77-d09f-2b419bb35c45"
1071 | },
1072 | "outputs": [
1073 | {
1074 | "data": {
1075 | "text/plain": [
1076 | "(20000, 5)"
1077 | ]
1078 | },
1079 | "execution_count": 19,
1080 | "metadata": {
1081 | "tags": []
1082 | },
1083 | "output_type": "execute_result"
1084 | }
1085 | ],
1086 | "source": [
1087 | "X_new = select.transform(X, rd=5)\n",
1088 | "\n",
1089 | "X_new.shape"
1090 | ]
1091 | },
1092 | {
1093 | "cell_type": "markdown",
1094 | "metadata": {
1095 | "id": "JwdP1J8W2m8G"
1096 | },
1097 | "source": [
1098 | "\n",
1099 | "## 5\\. References\n",
1100 | "\n",
1101 | "[1] Eirola, E., Lendasse, A., & Karhunen, J. (2014, July). Variable selection for regression problems using Gaussian mixture models to estimate mutual information. In 2014 International Joint Conference on Neural Networks (IJCNN) (pp. 1606-1613). IEEE.\n",
1102 | "\n",
1103 | "[2] Lan, T., Erdogmus, D., Ozertem, U., & Huang, Y. (2006, July). Estimating mutual information using gaussian mixture model for feature ranking and selection. In The 2006 IEEE International Joint Conference on Neural Network Proceedings (pp. 5034-5039). IEEE.\n",
1104 | "\n",
1105 | "[3] Maia Polo, F., & Vicente, R. (2022). Effective sample size, dimensionality, and generalization in covariate shift adaptation. Neural Computing and Applications, 1-13.\n",
1106 | "\n",
1107 | "\n"
1108 | ]
1109 | },
1110 | {
1111 | "cell_type": "code",
1112 | "execution_count": null,
1113 | "metadata": {
1114 | "id": "GvWp_Cmd20WX"
1115 | },
1116 | "outputs": [],
1117 | "source": []
1118 | }
1119 | ],
1120 | "metadata": {
1121 | "colab": {
1122 | "collapsed_sections": [],
1123 | "include_colab_link": true,
1124 | "name": "InfoSelect.ipynb",
1125 | "provenance": []
1126 | },
1127 | "kernelspec": {
1128 | "display_name": "Python 3 (ipykernel)",
1129 | "language": "python",
1130 | "name": "python3"
1131 | },
1132 | "language_info": {
1133 | "codemirror_mode": {
1134 | "name": "ipython",
1135 | "version": 3
1136 | },
1137 | "file_extension": ".py",
1138 | "mimetype": "text/x-python",
1139 | "name": "python",
1140 | "nbconvert_exporter": "python",
1141 | "pygments_lexer": "ipython3",
1142 | "version": "3.7.13"
1143 | }
1144 | },
1145 | "nbformat": 4,
1146 | "nbformat_minor": 1
1147 | }
1148 |
--------------------------------------------------------------------------------
| \n", 865 | " | rounds | \n", 866 | "mi_mean | \n", 867 | "mi_error | \n", 868 | "delta | \n", 869 | "num_feat | \n", 870 | "features | \n", 871 | "
|---|---|---|---|---|---|---|
| 0 | \n", 876 | "0 | \n", 877 | "0.000000 | \n", 878 | "0.000000 | \n", 879 | "0.000000 | \n", 880 | "0 | \n", 881 | "[] | \n", 882 | "
| 1 | \n", 885 | "1 | \n", 886 | "0.144904 | \n", 887 | "0.003717 | \n", 888 | "0.000000 | \n", 889 | "1 | \n", 890 | "[3] | \n", 891 | "
| 2 | \n", 894 | "2 | \n", 895 | "0.280840 | \n", 896 | "0.004493 | \n", 897 | "0.938110 | \n", 898 | "2 | \n", 899 | "[3, 1] | \n", 900 | "
| 3 | \n", 903 | "3 | \n", 904 | "0.524522 | \n", 905 | "0.004559 | \n", 906 | "0.867691 | \n", 907 | "3 | \n", 908 | "[3, 1, 0] | \n", 909 | "
| 4 | \n", 912 | "4 | \n", 913 | "0.636269 | \n", 914 | "0.004315 | \n", 915 | "0.213045 | \n", 916 | "4 | \n", 917 | "[3, 1, 0, 4] | \n", 918 | "
| 5 | \n", 921 | "5 | \n", 922 | "0.795123 | \n", 923 | "0.003400 | \n", 924 | "0.249667 | \n", 925 | "5 | \n", 926 | "[3, 1, 0, 4, 2] | \n", 927 | "
| 6 | \n", 930 | "6 | \n", 931 | "0.792673 | \n", 932 | "0.003550 | \n", 933 | "-0.003082 | \n", 934 | "6 | \n", 935 | "[3, 1, 0, 4, 2, 6] | \n", 936 | "
| 7 | \n", 939 | "7 | \n", 940 | "0.791315 | \n", 941 | "0.003708 | \n", 942 | "-0.001712 | \n", 943 | "7 | \n", 944 | "[3, 1, 0, 4, 2, 6, 5] | \n", 945 | "
 302 |
303 |
304 | Plotting the percentual variations of the mutual information between rounds:
305 |
306 |
307 | ```python
308 | select.plot_delta()
309 | ```
310 |
311 |
312 | 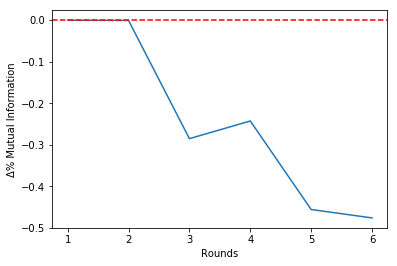
313 |
314 |
315 | Making the selection choosing to stop at Round 2:
316 |
317 |
318 | ```python
319 | X_new = select.transform(X, rd=2)
320 |
321 | X_new.shape
322 | ```
323 |
324 |
325 |
326 |
327 | (10000, 5)
328 |
329 |
330 |
331 | ### 4.3\. Selecting Features for a Classification Task
332 |
333 | Categorizing Y:
334 |
335 |
336 | ```python
337 | ind0 = (y
302 |
303 |
304 | Plotting the percentual variations of the mutual information between rounds:
305 |
306 |
307 | ```python
308 | select.plot_delta()
309 | ```
310 |
311 |
312 | 
313 |
314 |
315 | Making the selection choosing to stop at Round 2:
316 |
317 |
318 | ```python
319 | X_new = select.transform(X, rd=2)
320 |
321 | X_new.shape
322 | ```
323 |
324 |
325 |
326 |
327 | (10000, 5)
328 |
329 |
330 |
331 | ### 4.3\. Selecting Features for a Classification Task
332 |
333 | Categorizing Y:
334 |
335 |
336 | ```python
337 | ind0 = (y