├── .DS_Store ├── .babelrc ├── .gitignore ├── .idea ├── .gitignore ├── Algorithm-365-Days.iml ├── misc.xml ├── modules.xml └── vcs.xml ├── CS-Books ├── .DS_Store ├── 1000本编程电子书下载.md ├── 1000本编程电子书下载地址.png ├── README.md └── 算法学习资料 │ ├── 数据结构和算法知识框架.xmind │ └── 算法视频下载.md ├── Day01-17 ├── 01-1.数据结构和算法的重要性.md ├── 01-2.时间复杂度学习.md ├── 01-3.最基础的数据结构-数组.md ├── 02.链表.md ├── 03.双向链表.md ├── 04.队列.md ├── 05.栈.md ├── 06.哈希表.md ├── 07.堆.md ├── 08.优先队列.md ├── 09.字典树.md ├── 10.树.md ├── 11.二叉搜索树.md ├── 12.AVL树.md ├── 13.红黑树.md ├── 14.树状数组.md ├── 15.图.md ├── 16.并查集.md ├── 17.布隆过滤器.md ├── config │ └── img │ │ ├── 01-001.jpg │ │ ├── 01-1-001.png │ │ ├── 01-3-01.jpg │ │ ├── 01-3-02.jpg │ │ ├── 01-3-03.jpg │ │ ├── 01-3-04.jpg │ │ ├── 04-001.png │ │ ├── 04-002.png │ │ ├── 04-003.png │ │ ├── 13-001.png │ │ ├── 13-002.png │ │ ├── 13-003.png │ │ ├── 13-004.png │ │ ├── 15-001.png │ │ ├── 15-002.png │ │ ├── 15-003.png │ │ └── 15-004.png └── english │ ├── 01.The Importance of Algorithms.md │ ├── 02.Linked List.md │ ├── 03.Doubly Linked List.md │ ├── 04.Queue.md │ ├── 05.Stack.md │ ├── 06.Hash Table.md │ ├── 07.Heap.md │ ├── 08.Priority Queue.md │ ├── 09.Trie.md │ ├── 10.Tree.md │ ├── 11.Binary Search Tree.md │ ├── 12.AVL Tree.md │ ├── 13.Red-Black Tree.md │ ├── 14.Fenwick Tree.md │ ├── 15.Graph.md │ ├── 16.Disjoint Set.md │ └── 17.Bloom Filter.md ├── Day18-28 ├── 18.笛卡尔积.md ├── 19.洗牌算法.md ├── 20.子集.md ├── 21.排列.md ├── 22.组合.md ├── 23.最长公共子序列.md ├── 24.最长递增子序列.md ├── 25.最短公共父序列.md ├── 26.背包问题.md ├── 27.最大子数列问题.md └── 28.组合求和.md ├── Day29-36 ├── 29.汉明距离.md ├── 30.莱温斯坦距离.md ├── 31.KMP.md ├── 32.Sunday.md ├── 33.字符串快速查找.md ├── 34.Rabin Karp 算法.md ├── 35.最长公共子串.md └── 36.正则表达式匹配.md ├── Day37-40 ├── 37.线性搜索.md ├── 38.跳转搜索.md ├── 39.二分查找.md └── 40.插值搜索.md ├── Day41-49 ├── 41.冒泡排序.md ├── 42.选择排序.md ├── 43.插入排序.md ├── 44.堆排序.md ├── 45.归并排序.md ├── 46.快速排序.md ├── 47.希尔排序.md ├── 48.计数排序.md └── 49.基数排序.md ├── Day50-51 ├── 50.链表遍历.md └── 51.链表反转.md ├── Day52-53 ├── 52.树的深搜.md └── 53.树的广搜.md ├── Day54-55 ├── 54.图的深搜.md ├── 55.图的广搜.md ├── 56.寻找加权无向图的最小生成树.md ├── 57.找到图中所有顶点的最短路径.md ├── 58.找到所有顶点对之间的最短路径.md ├── 59.判圈算法.md ├── 60.寻找加权无向图的最小生成树.md ├── 61.拓扑排序.md ├── 62.Tarjan算法.md ├── 63.Fleury算法.md ├── 64.哈密顿图.md └── 65.旅行推销员问题.md ├── Day70-80 ├── 70.欧几里得算法.md ├── 71.最小公倍数.md ├── 72.素数筛.md ├── 73.判断2次方数.md ├── 74.杨辉三角形.md ├── 75.复数.md ├── 76.弧度和角.md ├── 77.位操作.md ├── 78.阶乘.md ├── 79.斐波那契数.md └── 80.素数检测.md ├── Day81-88 ├── 81.LRU算法.md ├── 82.八皇后问题.md ├── 83.骑士巡逻.md ├── 84.递归楼梯.md ├── 85.旋转矩阵.md ├── 86.跳跃游戏.md ├── 87.雨水收集.md └── 88.汉诺塔.md ├── Day89-98 ├── 89.递推DP.md ├── 90.背包九讲.md ├── 91.LIS.md ├── 92.LCS.md ├── 93.区间DP.md ├── 94.树形DP.md ├── 95.数位DP.md ├── 96.概率DP.md ├── 97.状压DP.md └── 98.结构DP.md ├── Day99 └── 99.毕业证书.md ├── README.md ├── jest.config.js ├── package-lock.json ├── package.json └── src ├── Day01-17 ├── bloom-filter │ ├── BloomFilter.js │ └── __test__ │ │ └── BloomFilter.test.js ├── disjoint-set │ ├── DisjointSet.js │ ├── DisjointSetItem.js │ └── __test__ │ │ ├── DisjointSet.test.js │ │ └── DisjointSetItem.test.js ├── doubly-linked-list │ ├── DoublyLinkedList.js │ ├── DoublyLinkedListNode.js │ └── __test__ │ │ ├── DoublyLinkedList.test.js │ │ └── DoublyLinkedListNode.test.js ├── graph │ ├── Graph.js │ ├── GraphEdge.js │ ├── GraphVertex.js │ └── __test__ │ │ ├── Graph.test.js │ │ ├── GraphEdge.test.js │ │ └── GraphVertex.test.js ├── hash-table │ ├── HashTable.js │ └── __test__ │ │ └── HashTable.test.js ├── heap │ ├── Heap.js │ ├── MaxHeap.js │ ├── MinHeap.js │ └── __test__ │ │ ├── Heap.test.js │ │ ├── MaxHeap.test.js │ │ └── MinHeap.test.js ├── linked-list │ ├── LinkedList.js │ ├── LinkedListNode.js │ └── __test__ │ │ ├── LinkedList.test.js │ │ └── LinkedListNode.test.js ├── priority-queue │ ├── PriorityQueue.js │ └── __test__ │ │ └── PriorityQueue.test.js ├── queue │ ├── Queue.js │ └── __test__ │ │ └── Queue.test.js ├── stack │ ├── Stack.js │ └── __test__ │ │ └── Stack.test.js ├── tree │ ├── BinaryTreeNode.js │ ├── __test__ │ │ └── BinaryTreeNode.test.js │ ├── avl-tree │ │ ├── AvlTree.js │ │ └── __test__ │ │ │ └── AvlTRee.test.js │ ├── binary-search-tree │ │ ├── BinarySearchTree.js │ │ ├── BinarySearchTreeNode.js │ │ └── __test__ │ │ │ ├── BinarySearchTree.test.js │ │ │ └── BinarySearchTreeNode.test.js │ ├── fenwick-tree │ │ ├── FenwickTree.js │ │ └── __test__ │ │ │ └── FenwickTree.test.js │ ├── red-black-tree │ │ ├── RedBlackTree.js │ │ └── __test__ │ │ │ └── RedBlackTree.test.js │ └── segment-tree │ │ ├── SegmentTree.js │ │ └── __test__ │ │ └── SegmentTree.test.js └── trie │ ├── Trie.js │ ├── TrieNode.js │ └── __test__ │ ├── Trie.test.js │ └── TrieNode.test.js └── utils └── comparator ├── Comparator.js └── __test__ └── Comparator.test.js /.DS_Store: -------------------------------------------------------------------------------- https://raw.githubusercontent.com/geekxh/hello-interview/807bb7f8e6a6421deccd0f51b24f1d4660f65b81/.DS_Store -------------------------------------------------------------------------------- /.babelrc: -------------------------------------------------------------------------------- 1 | { 2 | "presets": ["@babel/preset-env"] 3 | } 4 | -------------------------------------------------------------------------------- /.gitignore: -------------------------------------------------------------------------------- 1 | node_modules 2 | .idea 3 | coverage 4 | .vscode 5 | .DS_Store 6 | -------------------------------------------------------------------------------- /.idea/.gitignore: -------------------------------------------------------------------------------- 1 | # Default ignored files 2 | /workspace.xml 3 | -------------------------------------------------------------------------------- /.idea/Algorithm-365-Days.iml: -------------------------------------------------------------------------------- 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | -------------------------------------------------------------------------------- /.idea/misc.xml: -------------------------------------------------------------------------------- 1 | 2 | 3 | 4 | 6 | -------------------------------------------------------------------------------- /.idea/modules.xml: -------------------------------------------------------------------------------- 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | -------------------------------------------------------------------------------- /.idea/vcs.xml: -------------------------------------------------------------------------------- 1 | 2 | 3 | 4 | 5 | 6 | -------------------------------------------------------------------------------- /CS-Books/.DS_Store: -------------------------------------------------------------------------------- https://raw.githubusercontent.com/geekxh/hello-interview/807bb7f8e6a6421deccd0f51b24f1d4660f65b81/CS-Books/.DS_Store -------------------------------------------------------------------------------- /CS-Books/1000本编程电子书下载.md: -------------------------------------------------------------------------------- https://raw.githubusercontent.com/geekxh/hello-interview/807bb7f8e6a6421deccd0f51b24f1d4660f65b81/CS-Books/1000本编程电子书下载.md -------------------------------------------------------------------------------- /CS-Books/1000本编程电子书下载地址.png: -------------------------------------------------------------------------------- https://raw.githubusercontent.com/geekxh/hello-interview/807bb7f8e6a6421deccd0f51b24f1d4660f65b81/CS-Books/1000本编程电子书下载地址.png -------------------------------------------------------------------------------- /CS-Books/README.md: -------------------------------------------------------------------------------- 1 | ## 资源下载 2 | 3 | > 计算机的书籍很昂贵，但作为一个好的程序员却应该做到书不离身。 4 | > 任何书都买纸质书当然是不现实的，咱们也不知道哪些书好哪些书不好。 5 | > 所以，为了方便各位小伙伴能方便找到适合自己的学习书籍， 6 | > 我花了大功夫从全网各个网站找来近1000本超清电子书。 7 | 8 | ![](https://www.geekxh.com/allbook.png) 9 | 10 | 如果大家只是要下载算法相关的书籍，直接进入这个目录就可以了： 11 | 12 | [算法相关书籍下载]() 13 | 14 | 如果大家要下载全部书籍，可以通过下方链接进行下载： 15 | 16 | [获取全部]() 17 | -------------------------------------------------------------------------------- /CS-Books/算法学习资料/数据结构和算法知识框架.xmind: -------------------------------------------------------------------------------- https://raw.githubusercontent.com/geekxh/hello-interview/807bb7f8e6a6421deccd0f51b24f1d4660f65b81/CS-Books/算法学习资料/数据结构和算法知识框架.xmind -------------------------------------------------------------------------------- /CS-Books/算法学习资料/算法视频下载.md: -------------------------------------------------------------------------------- 1 | 小甲鱼数据结构和算法 2 | 3 | 链接:https://pan.baidu.com/s/1yGvXPY3Az5-9iVLyEXwsbw 密码:3bnz 4 | 5 | 其他更多学习视频，下方扫码回复【999】获取： 6 | 7 | > [![点击查看](https://www.geekxh.com/code.png)](https://www.geekxh.com/code.png) -------------------------------------------------------------------------------- /Day01-17/01-1.数据结构和算法的重要性.md: -------------------------------------------------------------------------------- 1 | ## Day01：数据结构和算法的重要性 2 | 3 | > 你也许会觉得数据结构和算法，是脱离实际工作的知识！认为除了面试，这辈子也用不着。但事实真的是这样吗? 4 | 5 | ### 1. 什么是“数据结构”？ 6 | 7 | *数据结构是一种抽象的封装。* 8 | 9 | 说简单点就是，把一堆基本的数据，按照某种顺序给揉成一坨。 10 | 11 | 比如做一道菜需要放各种调料，如盐、味精，还有肉等，把它们混在一起就做成了一道菜。 12 | 13 | 如果我们抽象来展示： 14 | 15 | ``` 16 | struct 水煮肉片 { 17 | 牛肉 = [] 18 | 葱 = [] 19 | 姜 = [] 20 | 盐 = [] 21 | 花椒 = [] 22 | 植物油 = [] 23 | } 24 | ``` 25 | 26 | 我们完全可以将上述这个结构体当成一个自定义的数据结构，将很多种不同的东西融合在一起；而计算机中的数据结构，则是把一些基本的数据类型，融合成一些复杂的数据结构，如map、队列。 27 | 28 | ### 2. 数据结构为什么重要？ 29 | 30 | 哪怕只写过几行代码的人都会发现，编程基本上就是在跟数据打交道。计算机程序总是在接收数据、操作数据或返回数据。不管是求两数之和的小程序，还是管理公司的企业级软件，都运行在数据之上。 31 | 32 | 数据结构不只是用于组织数据，它还极大地影响着代码的运行速度。因为数据结构不同，程序的运行速度可能相差多个数量级。如果你写的程序要处理大量的数据，或者要让数千人同时使用，那么你采用何种数据结构，将决定它是能够运行，还是会因为不堪重负而崩溃。 33 | 34 | 一旦对各种数据结构有了深刻的理解，并明白它们对程序性能方面的影响，你就能写出快速而优雅的代码，从而使软件运行得快速且流畅。当然，你的编程技能也会更上一层楼。 35 | 36 | ### 视频学习 37 | 38 | [Data Structures Easy to Advanced Course](https://www.youtube.com/watch?v=RBSGKlAvoiM) 39 | [中：什么是数据结构？](https://www.youtube.com/watch?v=hkwi2rQlPak&list=PLV5qT67glKSGFkKRDyuMfwcL-hwXOc4q_) 40 | 41 | ### 3. 最基础的数据结构 - 数组 42 | 43 | 数组是最简单、也是使用最广泛的数据结构。栈、队列等其他数据结构均可由数组演变而来。下图是一个包含元素（1，2，3 和 4）的简单数组，数组长度为4。 44 | 45 | ![](./config/img/01-001.jpg) 46 | 47 | 每个数据元素都关联一个正数值，我们称之为索引，它表明数组中每个元素所在的位置。大部分语言将初始索引定义为零。 48 | 49 | 以下是数组的两种类型： 50 | 51 | - 一维数组（如上所示） 52 | - 多维数组（数组的数组） 53 | 54 | 数组的基本操作 55 | - Insert——在指定索引位置插入一个元素 56 | - Get——返回指定索引位置的元素 57 | - Delete——删除指定索引位置的元素 58 | - Size——得到数组所有元素的数量 59 | 60 | 面试中关于数组的常见问题 61 | - 寻找数组中第二小的元素 62 | - 找到数组中第一个不重复出现的整数 63 | - 合并两个有序数组 64 | - 重新排列数组中的正值和负值 65 | 66 | 现在，我们给出一系列的关于数组的学习视频： 67 | 68 | [小甲鱼数组学习-1](https://www.youtube.com/watch?v=13bNE3pGcIg) 69 | 70 | [小甲鱼数组学习-2](https://www.youtube.com/watch?v=Msm84syHpHQ) 71 | 72 | [小甲鱼数组学习-3](https://www.youtube.com/watch?v=QYdHN67R1hk) 73 | 74 | --- 75 | 76 | 接下来，我们完成其他常见数据结构的学习： 77 | 78 | | 数据结构 | 难度 | 79 | | --- | --- | 80 | | [链表](./02.链表.md) | 81 | | [双向链表](./03.双向链表.md) | 82 | | [队列](./04.队列.md) | 83 | | [栈](./05.栈.md) | 84 | | [哈希表](./06.哈希表.md) | 85 | | [堆](./07.堆.md) | 86 | | [优先队列](./08.优先队列.md) | 87 | | [字典树](./09.字典树.md) | 88 | | [树](./10.树.md) | 89 | | [二叉查找树](./11.二叉搜索树.md) | 90 | | [AVL 树](./12.AVL树.md) | 91 | | [红黑树](./13.红黑树.md) | 92 | | [树状数组](./14.树状数组.md) | 93 | | [图](./15.图.md) | 94 | | [并查集](./16.并查集.md) | 95 | | [布隆过滤器](./17.布隆过滤器.md) | 96 | -------------------------------------------------------------------------------- /Day01-17/01-2.时间复杂度学习.md: -------------------------------------------------------------------------------- 1 | ## 时间复杂度学习 2 | 3 | 本文作者：raymondCaptain 4 | 5 | > 我们假设计算机运行一行基础代码需要执行一次运算。 6 | 7 | ``` 8 | int aFunc(void) { 9 | printf("Hello, World!\n"); // 需要执行 1 次 10 | return 0; // 需要执行 1 次 11 | } 12 | ``` 13 | 14 | 那么上面这个方法需要执行 2 次运算 15 | 16 | ``` 17 | int aFunc(int n) { 18 | for(int i = 0; i 定义：存在常数 c 和函数 f(N)，使得当 N >= c 时 T(N) <= f(N)，表示为 T(n) = O(f(n)) 。 31 | 32 | 如图： 33 | 34 | ![](config/img/01-1-001.png) 35 | 36 | 当 N >= 2 的时候，f(n) = n^2 总是大于 T(n) = n + 2 的，于是我们说 f(n) 的增长速度是大于或者等于 T(n) 的，也说 f(n) 是 T(n) 的上界，可以表示为 T(n) = O(f(n))。 37 | 38 | 因为f(n) 的增长速度是大于或者等于 T(n) 的，即T(n) = O(f(n))，所以我们可以用 f(n) 的增长速度来度量 T(n) 的增长速度，所以我们说这个算法的时间复杂度是 O(f(n))。 39 | 40 | > 算法的时间复杂度，用来度量算法的运行时间，记作: T(n) = O(f(n))。它表示随着 输入大小 n 的增大，算法执行需要的时间的增长速度可以用 f(n) 来描述。 41 | 42 | 显然如果 T(n) = n^2，那么 T(n) = O(n^2)，T(n) = O(n^3)，T(n) = O(n^4) 都是成立的，但是因为第一个 f(n) 的增长速度与 T(n) 是最接近的，所以第一个是最好的选择，所以我们说这个算法的复杂度是 O(n^2) 。 43 | 44 | 那么当我们拿到算法的执行次数函数 T(n) 之后怎么得到算法的时间复杂度呢？ 45 | 46 | * 我们知道常数项对函数的增长速度影响并不大，所以当 T(n) = c，c 为一个常数的时候，我们说这个算法的时间复杂度为 O(1)；如果 T(n) 不等于一个常数项时，直接将常数项省略。 47 | ``` 48 | 比如 49 | 第一个 Hello, World 的例子中 T(n) = 2，所以我们说那个函数(算法)的时间复杂度为 O(1)。 50 | T(n) = n + 29，此时时间复杂度为 O(n)。 51 | ``` 52 | 53 | * 我们知道高次项对于函数的增长速度的影响是最大的。n^3 的增长速度是远超 n^2 的，同时 n^2 的增长速度是远超 n 的。 同时因为要求的精度不高，所以我们直接忽略低此项。 54 | ``` 55 | 比如 56 | T(n) = n^3 + n^2 + 29，此时时间复杂度为 O(n^3)。 57 | ``` 58 | 59 | * 因为函数的阶数对函数的增长速度的影响是最显著的，所以我们忽略与最高阶相乘的常数。 60 | ``` 61 | 比如 62 | T(n) = 3n^3，此时时间复杂度为 O(n^3)。 63 | ``` 64 | 65 | > 综合起来：如果一个算法的执行次数是 T(n)，那么只保留最高次项，同时忽略最高项的系数后得到函数 f(n)，此时算法的时间复杂度就是 O(f(n))。为了方便描述，下文称此为 大O推导法。 66 | 67 | 由此可见，由执行次数 T(n) 得到时间复杂度并不困难，很多时候困难的是从算法通过分析和数学运算得到 T(n)。对此，提供下列四个便利的法则，这些法则都是可以简单推导出来的，总结出来以便提高效率。 68 | 69 | 对于一个循环，假设循环体的时间复杂度为 O(n)，循环次数为 m，则这个 70 | 循环的时间复杂度为 O(n×m)。 71 | ``` 72 | void aFunc(int n) { 73 | for(int i = 0; i < n; i++) { // 循环次数为 n 74 | printf("Hello, World!\n"); // 循环体时间复杂度为 O(1) 75 | } 76 | } 77 | ``` 78 | 此时时间复杂度为 O(n × 1)，即 O(n)。 79 | 80 | 对于多个循环，假设循环体的时间复杂度为 O(n)，各个循环的循环次数分别是a, b, c...，则这个循环的时间复杂度为 O(n×a×b×c...)。分析的时候应该由里向外分析这些循环。 81 | ``` 82 | void aFunc(int n) { 83 | for(int i = 0; i < n; i++) { // 循环次数为 n 84 | for(int j = 0; j < n; j++) { // 循环次数为 n 85 | printf("Hello, World!\n"); // 循环体时间复杂度为 O(1) 86 | } 87 | } 88 | } 89 | ``` 90 | 此时时间复杂度为 O(n × n × 1)，即 O(n^2)。 91 | 92 | 对于顺序执行的语句或者算法，总的时间复杂度等于其中最大的时间复杂度。 93 | ``` 94 | void aFunc(int n) { 95 | // 第一部分时间复杂度为 O(n^2) 96 | for(int i = 0; i < n; i++) { 97 | for(int j = 0; j < n; j++) { 98 | printf("Hello, World!\n"); 99 | } 100 | } 101 | // 第二部分时间复杂度为 O(n) 102 | for(int j = 0; j < n; j++) { 103 | printf("Hello, World!\n"); 104 | } 105 | } 106 | ``` 107 | 此时时间复杂度为 max(O(n^2), O(n))，即 O(n^2)。 108 | 109 | 对于条件判断语句，总的时间复杂度等于其中 时间复杂度最大的路径 的时间复杂度。 110 | ``` 111 | void aFunc(int n) { 112 | if (n >= 0) { 113 | // 第一条路径时间复杂度为 O(n^2) 114 | for(int i = 0; i < n; i++) { 115 | for(int j = 0; j < n; j++) { 116 | printf("输入数据大于等于零\n"); 117 | } 118 | } 119 | } else { 120 | // 第二条路径时间复杂度为 O(n) 121 | for(int j = 0; j < n; j++) { 122 | printf("输入数据小于零\n"); 123 | } 124 | } 125 | } 126 | ``` 127 | 此时时间复杂度为 max(O(n^2), O(n))，即 O(n^2)。 128 | 129 | 时间复杂度分析的基本策略是：从内向外分析，从最深层开始分析。如果遇到函数调用，要深入函数进行分析。 130 | 131 | 最后，我们来练习一下 132 | 133 | 一. 基础题 134 | 求该方法的时间复杂度 135 | ``` 136 | void aFunc(int n) { 137 | for (int i = 0; i < n; i++) { 138 | for (int j = i; j < n; j++) { 139 | printf("Hello World\n"); 140 | } 141 | } 142 | } 143 | ``` 144 | 参考答案： 145 | 当 i = 0 时，内循环执行 n 次运算，当 i = 1 时，内循环执行 n - 1 次运算……当 i = n - 1 时，内循环执行 1 次运算。 146 | 所以，执行次数 T(n) = n + (n - 1) + (n - 2)……+ 1 = n(n + 1) / 2 = n^2 / 2 + n / 2。 147 | 根据上文说的 大O推导法 可以知道，此时时间复杂度为 O(n^2)。 148 | 149 | 二. 进阶题 150 | 求该方法的时间复杂度 151 | 152 | ``` 153 | void aFunc(int n) { 154 | for (int i = 2; i < n; i++) { 155 | i *= 2; 156 | printf("%i\n", i); 157 | } 158 | } 159 | ``` 160 | 参考答案： 161 | 假设循环次数为 t，则循环条件满足 2^t < n。 162 | 可以得出，执行次数t = log(2)(n)，即 T(n) = log(2)(n)，可见时间复杂度为 O(log(2)(n))，即 O(log n)。 163 | 164 | 三. 再次进阶 165 | 求该方法的时间复杂度 166 | ``` 167 | long aFunc(int n) { 168 | if (n <= 1) { 169 | return 1; 170 | } else { 171 | return aFunc(n - 1) + aFunc(n - 2); 172 | } 173 | } 174 | ``` 175 | 参考答案： 176 | 显然运行次数，T(0) = T(1) = 1，同时 T(n) = T(n - 1) + T(n - 2) + 1，这里的 1 是其中的加法算一次执行。 177 | 显然 T(n) = T(n - 1) + T(n - 2) 是一个斐波那契数列，通过归纳证明法可以证明，当 n >= 1 时 T(n) < (5/3)^n，同时当 n > 4 时 T(n) >= (3/2)^n。 178 | 所以该方法的时间复杂度可以表示为 O((5/3)^n)，简化后为 O(2^n)。 179 | 可见这个方法所需的运行时间是以指数的速度增长的。如果大家感兴趣，可以试下分别用 1，10，100 的输入大小来测试下算法的运行时间，相信大家会感受到时间复杂度的无穷魅力。 180 | 181 | ### 学习视频 182 | 183 | [时间和空间复杂度 ](https://www.youtube.com/watch?v=7_UkcocEmDs&list=PLV5qT67glKSGFkKRDyuMfwcL-hwXOc4q_&index=2) 184 | 185 | -------------------------------------------------------------------------------- /Day01-17/01-3.最基础的数据结构-数组.md: -------------------------------------------------------------------------------- 1 | ## 最基础的数据结构-数组 2 | 3 | ### 数组 4 | 5 | 提到数组，相信大家的都不陌生，毕竟每个编程语言都会有它的影子。 6 | 7 | 数组是最基础的数据结构，尽管数组看起来非常的基础简单，但这个基础的数据结构要掌握其精髓，也不是那么简单事。 8 | 9 | ### 开门见山 10 | 数组（Array）是一种线性表数据结构，它用一组连续的内存空间，来存储一组具有相同类型的数据。 11 | 12 | 这个定义有几个关键词，也是数组的精髓所在。下面就从这几个关键词进一步理解数组。 13 | 14 | 第一个是线性表。顾名思义，线性表的特征就是数据排成像一条线一样的结构。每个线性表的数据最多只有前和后两个方向。除了数组，链表、队列、栈等数据结构也是线性表结构。 15 | 16 | 举个栗子，糖葫芦串就与线性表的特征非常相似。糖葫芦（数据）串成在一条直线的竹签，并且每个糖葫芦（数据）最多只有前和后两个方向。 17 | 18 | 第二个是连续的内存空间和相同的类型的数据。因为这两个条件的限制，数组有了非常重要的特性：随机访问元素，随机访问元素的时间复杂度为O(1)。但有利必有弊，这两个条件的限制导致数据在进行插入和删除一个数据的时候，为了保证数据的连续性，就需要做数据的搬移操作。 19 | 20 | ### 随机访问 21 | 数组是如何实现根据下表随机访问数组元素的呢？ 22 | 23 | 我们拿一个长度为5的int类型的数组int a[5]，来举例子。在我们定义这个数组时，计算机会给数组int a[5]，分配了一块连续的内存空间。 24 | 25 | ![](config/img/01-3-01.jpg) 26 | 27 | 假设，数组int a[5]内存块的首地址为base_address=100，那么 28 | 29 | a[0]的地址就是100（首地址） 30 | a[2]的地址就是104 31 | a[3]的地址就是108 32 | a[3]的地址就是112 33 | a[4]的地址就是116 34 | 计算机是通过访内存地址，来访问内存中存储的数据。那么，当计算机要随机访问数组中的某个元素时，会通过下面这条寻址公式，计算出对应元素的内存地址，从而通过内存地址访问数据。 35 | 36 | ``` 37 | a[i]_address = base_address + i * data_type_size 38 | ``` 39 | 40 | a[i]_address表示对应数组下标的内存地址，data_type_size表示数组存储的数据类型的大小，数组int a[5]。存储的是5个int类型的数据，它的data_type_size就为4个字节。 41 | 42 | 二维数组的寻址公式，假设二位数组的维度是m*n，则公式为： 43 | ``` 44 | a[i][j]_address = base_address + ( i * n + j ) * data_type_size 45 | ``` 46 | 47 | ![](config/img/01-3-02.jpg) 48 | 49 | ### 为什么数组下标从0开始? 50 | 要先解答这个问题时，我们试想假设数组下标从1开始，a[1]表示数组的首地址，那么计算机的寻址公式就会变成为： 51 | ``` 52 | a[i]_address = base_address + (i - 1) * data_type_size 53 | ``` 54 | 对比数组下标从0开始和设数组下标从1开始的寻址公式，我们不难看出，从1开始编号，每次随机访问数组元素都多了一次减法运算，对于CPU来说，就是多了一次减法指令。 55 | 56 | 更何况数组是非常基础的数据结构，使用频率非常的高，所以效率优化必须要做到极致。所以为了减少CPU的一次减法指令，数组选择了从0开始编号，而不是从1开始。 57 | 58 | 以上是从计算机寻址公式角度分析的，当然其实还有历史等原因。 59 | 60 | ### 数组的插入和删除过程 61 | 前面提到对于数组的定义，数组为了保持内存数据的连续性，就会导致插入和删除这两个操作比比较低效。接下来通过代码来阐述为什么导致低效呢？又有哪些方法改进？ 62 | 63 | 插入操作过程 64 | 插入操作对于数据的不同的场景和不同的插入位置，时间复杂度都略有不同。接下来以数组的数据是有序和没有规律的两种场景分析插入操作。 65 | 66 | 不管什么场景，如果在数组的末尾插入元素，那么就非常简单，不需要搬移数据，直接将元素放入到数组的末尾，这时空间复杂度就为O(1)。 67 | 68 | 如果在数组的开头或中间插入数据呢？这时可以根据场景的不同，采用不同的方式。 69 | 70 | 如果数组的数据是有序（从小到大或从大到小），在第k位置插入一个新的元素时，就必须把k之后的数据往后移动一位，此时最坏时间复杂度是O(n)。 71 | 72 | 如果数组的数据没有任何规律，那么在第k位置插入一个新的元素时，先将旧的第k位置的数据搬移到数据末尾，在把新的元素数据直接放入到第k位置。那么在这种特定场景下，在第k个位置插入一个元素的时间复杂度就为O(1)。 73 | 74 | 一图胜千言，我们以图的方式展现数组的数据是有序和没有规律场景的插入元素的过程。 75 | 76 | ![](config/img/01-3-03.jpg) 77 | 78 | 79 | ### 删除操作过程 80 | 跟插入数据类似，如果我们要删除第k位置的数据，为了内存的连续性，也是需要数据搬移，不然中间就会出现空洞，内存就不连续了。 81 | 82 | 如果删除数组末尾的数据，则时间复杂度为O(1)；如果删除开头的数据，因需把k位置之后的数据往前搬移一位，那么时间复杂度就为O(n)。 83 | 84 | 一图胜千言，我们以图的方式展现数组删除操作。 85 | 86 | ![](config/img/01-3-04.jpg) 87 | 88 | --- 89 | 90 | 总结：数组是最基础、最简单的数据结构。数组用一块连续的内存空间，来存储相同类型的一组数据，最大的特点就是随机访问元素，并且时间复杂度为O(1)。但是插入、删除操作也因此比较低效，时间复杂度为O(n)。 91 | 92 | -------------------------------------------------------------------------------- /Day01-17/02.链表.md: -------------------------------------------------------------------------------- 1 | # 链表 2 | 3 | 在计算机科学中, 一个 **链表** 是数据元素的线性集合, 元素的线性顺序不是由它们在内存中的物理位置给出的。 相反, 每个元素指向下一个元素。它是由一组节点组成的数据结构,这些节点一起,表示序列。 4 | 5 | 在最简单的形式下，每个节点由数据和到序列中下一个节点的引用(换句话说，链接)组成。这种结构允许在迭代期间有效地从序列中的任何位置插入或删除元素。 6 | 7 | 更复杂的变体添加额外的链接，允许有效地插入或删除任意元素引用。链表的一个缺点是访问时间是线性的(而且难以管道化)。 8 | 9 | 更快的访问，如随机访问，是不可行的。与链表相比，数组具有更好的缓存位置。 10 | 11 | ![Linked List](https://upload.wikimedia.org/wikipedia/commons/6/6d/Singly-linked-list.svg) 12 | 13 | ## 基本操作的伪代码 14 | 15 | ### 插入 16 | 17 | ```text 18 | Add(value) 19 | Pre: value is the value to add to the list 20 | Post: value has been placed at the tail of the list 21 | n ← node(value) 22 | if head = ø 23 | head ← n 24 | tail ← n 25 | else 26 | tail.next ← n 27 | tail ← n 28 | end if 29 | end Add 30 | ``` 31 | 32 | ``` 33 | Prepend(value) 34 | Pre: value is the value to add to the list 35 | Post: value has been placed at the head of the list 36 | n ← node(value) 37 | n.next ← head 38 | head ← n 39 | if tail = ø 40 | tail ← n 41 | end 42 | end Prepend 43 | ``` 44 | 45 | ### 搜索 46 | 47 | ```text 48 | Contains(head, value) 49 | Pre: head is the head node in the list 50 | value is the value to search for 51 | Post: the item is either in the linked list, true; otherwise false 52 | n ← head 53 | while n != ø and n.value != value 54 | n ← n.next 55 | end while 56 | if n = ø 57 | return false 58 | end if 59 | return true 60 | end Contains 61 | ``` 62 | 63 | ### 删除 64 | 65 | ```text 66 | Remove(head, value) 67 | Pre: head is the head node in the list 68 | value is the value to remove from the list 69 | Post: value is removed from the list, true, otherwise false 70 | if head = ø 71 | return false 72 | end if 73 | n ← head 74 | if n.value = value 75 | if head = tail 76 | head ← ø 77 | tail ← ø 78 | else 79 | head ← head.next 80 | end if 81 | return true 82 | end if 83 | while n.next != ø and n.next.value != value 84 | n ← n.next 85 | end while 86 | if n.next != ø 87 | if n.next = tail 88 | tail ← n 89 | end if 90 | n.next ← n.next.next 91 | return true 92 | end if 93 | return false 94 | end Remove 95 | ``` 96 | 97 | ### 遍历 98 | 99 | ```text 100 | Traverse(head) 101 | Pre: head is the head node in the list 102 | Post: the items in the list have been traversed 103 | n ← head 104 | while n != 0 105 | yield n.value 106 | n ← n.next 107 | end while 108 | end Traverse 109 | ``` 110 | 111 | ### 反向遍历 112 | 113 | ```text 114 | ReverseTraversal(head, tail) 115 | Pre: head and tail belong to the same list 116 | Post: the items in the list have been traversed in reverse order 117 | if tail != ø 118 | curr ← tail 119 | while curr != head 120 | prev ← head 121 | while prev.next != curr 122 | prev ← prev.next 123 | end while 124 | yield curr.value 125 | curr ← prev 126 | end while 127 | yield curr.value 128 | end if 129 | end ReverseTraversal 130 | ``` 131 | 132 | ## 复杂度 133 | 134 | ### 时间复杂度 135 | 136 | | Access | Search | Insertion | Deletion | 137 | | :-------: | :-------: | :-------: | :-------: | 138 | | O(n) | O(n) | O(1) | O(1) | 139 | 140 | ### 空间复杂度 141 | 142 | O(n) 143 | 144 | ### 学习视频 145 | 146 | [链表数据结构学习](https://www.youtube.com/watch?v=Vw7f6NqHCJk) 147 | 148 | [链表刷题找工作](https://www.youtube.com/watch?v=-UBiYuIVErM&list=PLLuMmzMTgVK6a-2aAwPieEIIuIJY6JTSq) 149 | 150 | ## 参考 151 | 152 | - [Wikipedia](https://en.wikipedia.org/wiki/Linked_list) 153 | - [YouTube](https://www.youtube.com/watch?v=njTh_OwMljA&index=2&t=1s&list=PLLXdhg_r2hKA7DPDsunoDZ-Z769jWn4R8) 154 | -------------------------------------------------------------------------------- /Day01-17/03.双向链表.md: -------------------------------------------------------------------------------- 1 | # 双向链表 2 | 3 | 在计算机科学中, 一个 **双向链表(doubly linked list)** 是由一组称为节点的顺序链接记录组成的链接数据结构。每个节点包含两个字段，称为链接，它们是对节点序列中上一个节点和下一个节点的引用。开始节点和结束节点的上一个链接和下一个链接分别指向某种终止节点，通常是前哨节点或null，以方便遍历列表。如果只有一个前哨节点，则列表通过前哨节点循环链接。它可以被概念化为两个由相同数据项组成的单链表，但顺序相反。 4 | 5 | ![Doubly Linked List](https://upload.wikimedia.org/wikipedia/commons/5/5e/Doubly-linked-list.svg) 6 | 7 | 两个节点链接允许在任一方向上遍历列表。 8 | 9 | 在双向链表中进行添加或者删除节点时,需做的链接更改要比单向链表复杂得多。这种操作在单向链表中更简单高效,因为不需要关注一个节点（除第一个和最后一个节点以外的节点）的两个链接,而只需要关注一个链接即可。 10 | 11 | ## 基础操作的伪代码 12 | 13 | ### 插入 14 | 15 | ```text 16 | Add(value) 17 | Pre: value is the value to add to the list 18 | Post: value has been placed at the tail of the list 19 | n ← node(value) 20 | if head = ø 21 | head ← n 22 | tail ← n 23 | else 24 | n.previous ← tail 25 | tail.next ← n 26 | tail ← n 27 | end if 28 | end Add 29 | ``` 30 | 31 | ### 删除 32 | 33 | ```text 34 | Remove(head, value) 35 | Pre: head is the head node in the list 36 | value is the value to remove from the list 37 | Post: value is removed from the list, true; otherwise false 38 | if head = ø 39 | return false 40 | end if 41 | if value = head.value 42 | if head = tail 43 | head ← ø 44 | tail ← ø 45 | else 46 | head ← head.next 47 | head.previous ← ø 48 | end if 49 | return true 50 | end if 51 | n ← head.next 52 | while n = ø and value = n.value 53 | n ← n.next 54 | end while 55 | if n = tail 56 | tail ← tail.previous 57 | tail.next ← ø 58 | return true 59 | else if n = ø 60 | n.previous.next ← n.next 61 | n.next.previous ← n.previous 62 | return true 63 | end if 64 | return false 65 | end Remove 66 | ``` 67 | 68 | ### 反向遍历 69 | 70 | ```text 71 | ReverseTraversal(tail) 72 | Pre: tail is the node of the list to traverse 73 | Post: the list has been traversed in reverse order 74 | n ← tail 75 | while n = ø 76 | yield n.value 77 | n ← n.previous 78 | end while 79 | end Reverse Traversal 80 | ``` 81 | 82 | ## 复杂度 83 | 84 | ## 时间复杂度 85 | 86 | | Access | Search | Insertion | Deletion | 87 | | :-------: | :-------: | :-------: | :-------: | 88 | | O(n) | O(n) | O(1) | O(1) | 89 | 90 | ### 空间复杂度 91 | 92 | O(n) 93 | 94 | ### 学习视频 95 | 96 | [双向链表学习-1](https://www.youtube.com/watch?v=J6j_5oFqvgs) 97 | 98 | [双向链表学习-2](https://www.youtube.com/watch?v=NXSq1jexwGE) 99 | 100 | [双向链表学习-3](https://www.youtube.com/watch?v=IyJaOlxD_Lc) 101 | 102 | [双向链表学习-4](https://www.youtube.com/watch?v=WYdaztL3l7k) 103 | 104 | ## 参考 105 | 106 | - [Wikipedia](https://en.wikipedia.org/wiki/Doubly_linked_list) 107 | - [YouTube](https://www.youtube.com/watch?v=JdQeNxWCguQ&t=7s&index=72&list=PLLXdhg_r2hKA7DPDsunoDZ-Z769jWn4R8) 108 | -------------------------------------------------------------------------------- /Day01-17/04.队列.md: -------------------------------------------------------------------------------- 1 | # 队列 2 | 3 | > 本文主要讲解了队列的定义和队列主要功能实现的算法。最后会列举一些队列在程序设计当中常见的应用实例！ 4 | 5 | ### 队列的定义 6 | 队列 (Queue)是一种先进先出(first in first out : FIFO)的线性表。它只允许在表的一端进行插入，在另一端进行删除元素。这和我们平时战队买票很一样。最早进入队列的元素最先离开，在队列中，允许插入的一端叫做队尾(rear),允许删除的一段则称为队头(front).示意图如下： 7 | 8 | ![](./config/img/04-001.png) 9 | 10 | ### 队列的分类 11 | 12 | 队列主要分为两类： 13 | - 链式队列：链式队列即用链表实现的队列 14 | - 顺序队列：顺序队列是用数组实现的队列，顺序队列通常必须是循环队列 15 | 16 | 顺序队列本身是一种数组表示。在队列的顺序存储结构中，除了用一组连续的存储单元依次存放从队列头到队列尾的元素之外，尚需附设两个指针 front 和 rear 分别指示队列头元素及队列尾元素的位置。为了在C语言中描述方便，通常有如下约定：初始化创建空队列时，令 front = rear = 0，每当插入新的队列尾元素时，“尾指针增 1”；每当删除队列头元素时，“头指针增 1”；因此，在非空队列下，头指针始终指向队列头元素，而尾指针始终指向队列尾元素的下一个位置，如图所示： 17 | 18 | ![](./config/img/04-002.png) 19 | 20 | 假设当前队列分配最大空间为6，则当队列处于上图(d)的状态时，不可再继续插入新的队尾元素，否则会因为数组越界而导致程序代码被破坏。然而此时又不宜进行存储再分配扩大数组空间，因为队列的实际可用空间并未占满。一个巧妙的办法是将顺序队列臆造为一个环状的空间，如图所示，称之为循环队列： 21 | 22 | ![](./config/img/04-003.png) 23 | 24 | 如图，指针和队列之间的关系不变，上图 (a) 所示循环队列中，队列头元素是 J3 ，队列尾元素是 J5,之后J6,J7和J8相继插入，则队列空间均被占满，如图 (b) 所示，此时 Q.front = Q.rear; 反之，若 J3,J4 和 J5 相继从图 (a) 队列中删除，使队列呈“空”的状态，如图 (c) 所示，此时存在关系为 Q.front = Q.rear, 由此可见只凭等式 Q.front = Q.rear无法判断队列是“空”还是“满”。有两种可处理方式：一种是另外设置一个标志以区别队列是 “空” 还是 “满”；另一种是少用一个元素空间，约定以“队列头指针在队列尾指针的下一位置(指环状的下一位置)”作为队列呈“满”状态的标志。 25 | 26 | 从此分析中可见，在C语言中不能用动态分配的一维数组来实现循环队列，如果用户的应用程序中设有循环队列，则必须为它设定一个最大队列长度，若用户无法预估所用队列的最大长度，则宜采用链式队列。 27 | 28 | > front && rear 不同场合下含义不同。 29 | 30 | - 队列初始化 -- front 和 rear 的值都是零 31 | - 队列非空 -- front 代表队列的第一个元素，rear 代表队列的最后一个有效元素的下一个元素 32 | - 队列为空 -- front 和 rear 相等，但不一定是零 33 | 34 | ### 入队伪算法 35 | 36 | > 尾部入队，分两步完成 37 | 38 | 将值存入r所代表的位置 39 | 错误写法 r = r + 1; 正确写法： r = (r + 1) % 数组的长度 【n-1对n取余，结果就是n-1】 40 | 41 | ### 出队伪算法 42 | 43 | > 头部出队，分两步完成 44 | 45 | 将f出队的值保存起来（可以根据具体需求确定是否要保存） 46 | f 的指针变动正确写法： f = (f + 1) % 数组的长度 【n-1对n取余，结果就是n-1】 47 | 48 | ### 如何判断循环队列是否为空 49 | 50 | > 如果front == rear ，则该队列一定为空 51 | 52 | ### 如何判断循环队列已满 53 | 54 | 预备知识： 55 | front 的值可能比 rear 大 56 | front 的值也可能比 rear 小 57 | 当然两者也完全可能相等 58 | 59 | 判断已满两种方式： 60 | 61 | ### 什么时候该使用顺序队列？什么时候该使用链式队列？ 62 | 如果用户的应用程序中设有循环队列，则必须为它设定一个最大队列长度，若用户无法预估所用队列的最大长度，则宜采用链式队列 63 | 64 | ### 队列的伪算法和实现 65 | 此小节实现的是一个最大队列长度为 6 的环形队列，下面是本队列的定义和相关实现。 66 | 67 | ### 队列类型的定义 68 | 69 | ``` 70 | #define kQueueMaxLength 6 // 假设最大长度为 6 71 | typedef struct Queue{ 72 | int * pBase; // 队列中操作的数组 73 | int front; // 队头 74 | int rear; // 对尾 75 | }QUEUE; 76 | ``` 77 | 78 | ### 队列的初始化 79 | 80 | ``` 81 | void init_queue(QUEUE *pQueue){ 82 | pQueue->pBase = (int *)malloc(sizeof(int) * kQueueMaxLength); // 初始化，pBase指向长度6的 int* 数组 83 | pQueue->front = pQueue->rear = 0; 84 | } 85 | ``` 86 | 87 | ### 元素入队 88 | 89 | ``` 90 | /** 91 | 入队 92 | 93 | @param pQueue 要入队的队列地址 94 | @param val 入队元素的值 95 | @return 入队成功/失败 96 | */ 97 | bool en_queue(QUEUE *pQueue , int val){ 98 | 99 | if (full_queue(pQueue)) { // 队列已满，直接返回入队失败 100 | return false; 101 | }else 102 | { // 队列未满，执行入队操作 103 | 104 | // 1.元素插入数组中 105 | pQueue->pBase[pQueue->rear] = val; 106 | // 2.队头队尾的表示 107 | pQueue->rear = (pQueue->rear + 1) % kQueueMaxLength; 108 | 109 | return true; 110 | } 111 | } 112 | ``` 113 | 114 | ### 元素出队 115 | 116 | ``` 117 | /** 118 | 出队 119 | 120 | @param pQueue 要出队队列地址 121 | @param val 被出队元素地址 122 | @return 出队成功/失败 123 | */ 124 | bool de_queue(QUEUE *pQueue , int *val){ 125 | 126 | if (empty_queue(pQueue)) { // 如果是空队列，直接出队失败 127 | return false; 128 | }else 129 | { 130 | // 出队->保存被出队元素的值 131 | *val = pQueue->pBase[pQueue->front]; 132 | // 修改队头位置 133 | pQueue->front = (pQueue->front + 1) % kQueueMaxLength; 134 | 135 | } 136 | return true; 137 | } 138 | ``` 139 | 140 | ### 遍历队列 141 | 142 | ``` 143 | /** 144 | 遍历队列 145 | 146 | @param pQueue 要遍历的队列的地址 147 | */ 148 | void tranverce_queue(QUEUE *pQueue){ 149 | 150 | int i = pQueue->front; 151 | int lenght = 0; 152 | while (i != pQueue->rear) { 153 | lenght ++; 154 | i = (i + 1) % kQueueMaxLength; 155 | } 156 | printf("队列中共有 %d 个元素\n",lenght); 157 | 158 | i = pQueue->front; 159 | while (i != pQueue->rear) { 160 | 161 | printf("第 %d 个元素为 %d\n",i + 1,pQueue->pBase[i]); 162 | i = (i + 1) % kQueueMaxLength; 163 | } 164 | } 165 | ``` 166 | 167 | 队列中元素先进先出 FIFO (first in, first out)的示意 168 | 169 | ![Queue](https://upload.wikimedia.org/wikipedia/commons/5/52/Data_Queue.svg) 170 | 171 | ## 学习视频 172 | 173 | [栈和队列](https://www.youtube.com/watch?v=KaMUAVCf1Rc) 174 | 175 | [为什么要学习消息队列](https://www.youtube.com/watch?v=KoccSL_56sM) 176 | 177 | ## 参考 178 | 179 | - [Wikipedia](https://en.wikipedia.org/wiki/Queue_(abstract_data_type)) 180 | - [YouTube](https://www.youtube.com/watch?v=wjI1WNcIntg&list=PLLXdhg_r2hKA7DPDsunoDZ-Z769jWn4R8&index=3&) 181 | -------------------------------------------------------------------------------- /Day01-17/05.栈.md: -------------------------------------------------------------------------------- 1 | # 栈 2 | 3 | 在计算机科学中, 一个 **栈(stack)** 是一种抽象数据类型,用作表示元素的集合,具有两种主要操作: 4 | 5 | * **push**, 添加元素到栈的顶端(末尾); 6 | * **pop**, 移除栈最顶端(末尾)的元素. 7 | 8 | 以上两种操作可以简单概括为“后进先出(LIFO = last in, first out)”。 9 | 10 | 此外,应有一个 `peek` 操作用于访问栈当前顶端(末尾)的元素。 11 | 12 | "栈"这个名称,可类比于一组物体的堆叠(一摞书,一摞盘子之类的)。 13 | 14 | 栈的 push 和 pop 操作的示意 15 | 16 | ![Stack](https://upload.wikimedia.org/wikipedia/commons/b/b4/Lifo_stack.png) 17 | 18 | ### 学习视频 19 | 20 | [栈和队列](https://www.youtube.com/watch?v=KaMUAVCf1Rc) 21 | 22 | ## 参考 23 | 24 | - [Wikipedia](https://en.wikipedia.org/wiki/Stack_(abstract_data_type)) 25 | - [YouTube](https://www.youtube.com/watch?v=wjI1WNcIntg&list=PLLXdhg_r2hKA7DPDsunoDZ-Z769jWn4R8&index=3&) 26 | -------------------------------------------------------------------------------- /Day01-17/06.哈希表.md: -------------------------------------------------------------------------------- 1 | # 哈希表 2 | 3 | 在计算中, 一个 **哈希表(hash table 或hash map)** 是一种实现 *关联数组(associative array)* 4 | 的抽象数据；类型, 该结构可以将 *键映射到值*。 5 | 6 | 哈希表使用 *哈希函数/散列函数* 来计算一个值在数组或桶(buckets)中或槽(slots)中对应的索引,可使用该索引找到所需的值。 7 | 8 | 理想情况下,散列函数将为每个键分配给一个唯一的桶(bucket),但是大多数哈希表设计采用不完美的散列函数,这可能会导致"哈希冲突(hash collisions)",也就是散列函数为多个键(key)生成了相同的索引,这种碰撞必须 9 | 以某种方式进行处理。 10 | 11 | ![Hash Table](https://upload.wikimedia.org/wikipedia/commons/7/7d/Hash_table_3_1_1_0_1_0_0_SP.svg) 12 | 13 | 通过单独的链接解决哈希冲突 14 | 15 | ![Hash Collision](https://upload.wikimedia.org/wikipedia/commons/d/d0/Hash_table_5_0_1_1_1_1_1_LL.svg) 16 | 17 | ### 学习视频 18 | 19 | [哈希表学习基础](https://www.youtube.com/watch?v=CaF_RipLLh4) 20 | 21 | ## 参考 22 | 23 | - [Wikipedia](https://en.wikipedia.org/wiki/Hash_table) 24 | - [YouTube](https://www.youtube.com/watch?v=shs0KM3wKv8&index=4&list=PLLXdhg_r2hKA7DPDsunoDZ-Z769jWn4R8) 25 | -------------------------------------------------------------------------------- /Day01-17/07.堆.md: -------------------------------------------------------------------------------- 1 | # 堆 (数据结构) 2 | 3 | 在计算机科学中, 一个 **堆(heap)** 是一种特殊的基于树的数据结构，它满足下面描述的堆属性。 4 | 5 | 在一个 *最小堆(min heap)* 中, 如果 `P` 是 `C` 的一个父级节点, 那么 `P` 的key(或value)应小于或等于 `C` 的对应值. 6 | 7 | ![最小堆](https://upload.wikimedia.org/wikipedia/commons/6/69/Min-heap.png) 8 | 9 | 在一个 *最大堆(max heap)* 中, `P` 的key(或value)大于 `C` 的对应值。 10 | 11 | ![堆](https://upload.wikimedia.org/wikipedia/commons/3/38/Max-Heap.svg) 12 | 13 | 在堆“顶部”的没有父级节点的节点,被称之为根节点。 14 | 15 | ### 学习视频 16 | 17 | [堆结构讲解](https://www.youtube.com/watch?v=j-DqQcNPGbE) 18 | 19 | ## 参考 20 | 21 | - [Wikipedia](https://en.wikipedia.org/wiki/Heap_(data_structure)) 22 | - [YouTube](https://www.youtube.com/watch?v=t0Cq6tVNRBA&index=5&t=0s&list=PLLXdhg_r2hKA7DPDsunoDZ-Z769jWn4R8) 23 | -------------------------------------------------------------------------------- /Day01-17/08.优先队列.md: -------------------------------------------------------------------------------- 1 | # 优先队列 2 | 3 | 在计算机科学中, **优先级队列(priority queue)** 是一种抽象数据类型, 它类似于常规的队列或栈, 但每个元素都有与之关联的“优先级”。 4 | 5 | 在优先队列中, 低优先级的元素之前前面应该是高优先级的元素。 如果两个元素具有相同的优先级, 则根据它们在队列中的顺序是它们的出现顺序即可。 6 | 7 | 优先队列虽通常用堆来实现,但它在概念上与堆不同。优先队列是一个抽象概念，就像“列表”或“图”这样的抽象概念一样; 8 | 9 | 正如列表可以用链表或数组实现一样，优先队列可以用堆或各种其他方法实现,例如无序数组。 10 | 11 | ### 学习视频 12 | 13 | [优先队列讲解](https://www.youtube.com/watch?v=wTAoOhytiQs) 14 | 15 | ## 参考 16 | 17 | - [Wikipedia](https://en.wikipedia.org/wiki/Priority_queue) 18 | - [YouTube](https://www.youtube.com/watch?v=wptevk0bshY&list=PLLXdhg_r2hKA7DPDsunoDZ-Z769jWn4R8&index=6) 19 | -------------------------------------------------------------------------------- /Day01-17/09.字典树.md: -------------------------------------------------------------------------------- 1 | # 字典树 2 | 3 | 在计算机科学中, **字典树(trie,中文又被称为”单词查找树“或 ”键树“)**, 也称为数字树,有时候也被称为基数树或前缀树（因为它们可以通过前缀搜索）,它是一种搜索树--一种已排序的数据结构,通常用于存储动态集或键为字符串的关联数组。 4 | 5 | 与二叉搜索树不同, 树上没有节点存储与该节点关联的键; 相反,节点在树上的位置定义了与之关联的键。一个节点的全部后代节点都有一个与该节点关联的通用的字符串前缀, 与根节点关联的是空字符串。 6 | 7 | 值对于字典树中关联的节点来说,不是必需的,相反,值往往和相关的叶子相关,以及与一些键相关的内部节点相关。 8 | 9 | 有关字典树的空间优化示意,请参阅紧凑前缀树 10 | 11 | ![Trie](https://upload.wikimedia.org/wikipedia/commons/b/be/Trie_example.svg) 12 | 13 | ### 学习视频 14 | 15 | [什么是字典树](https://www.youtube.com/watch?v=GCGolin7Ffk) 16 | 17 | ## 参考 18 | 19 | - [Wikipedia](https://en.wikipedia.org/wiki/Trie) 20 | - [YouTube](https://www.youtube.com/watch?v=zIjfhVPRZCg&list=PLLXdhg_r2hKA7DPDsunoDZ-Z769jWn4R8&index=7&t=0s) 21 | -------------------------------------------------------------------------------- /Day01-17/10.树.md: -------------------------------------------------------------------------------- 1 | # 树 2 | 3 | 在计算机科学中, **树(tree)** 是一种广泛使用的抽象数据类型(ADT)— 或实现此ADT的数据结构 — 模拟分层树结构, 具有根节点和有父节点的子树,表示为一组链接节点。 4 | 5 | 树可以被(本地地)递归定义为一个(始于一个根节点的)节点集, 每个节点都是一个包含了值的数据结构, 除了值,还有该节点的节点引用列表(子节点)一起。 6 | 树的节点之间没有引用重复的约束。 7 | 8 | 一棵简单的无序树; 在下图中: 9 | 10 | 标记为7的节点具有两个子节点, 标记为2和6; 11 | 一个父节点,标记为2,作为根节点, 在顶部,没有父节点。 12 | 13 | ![Tree](https://upload.wikimedia.org/wikipedia/commons/f/f7/Binary_tree.svg) 14 | 15 | ### 学习视频 16 | 17 | [Data structures: Introduction to Trees](https://www.youtube.com/watch?v=qH6yxkw0u78) 18 | 19 | ## 参考 20 | 21 | - [Wikipedia](https://en.wikipedia.org/wiki/Tree_(data_structure)) 22 | - [YouTube](https://www.youtube.com/watch?v=oSWTXtMglKE&list=PLLXdhg_r2hKA7DPDsunoDZ-Z769jWn4R8&index=8) 23 | -------------------------------------------------------------------------------- /Day01-17/11.二叉搜索树.md: -------------------------------------------------------------------------------- 1 | # 二叉搜索树 2 | 3 | ### 二叉查找树（英语：Binary Search Tree），也称为二叉搜索树、有序二叉树（ordered binary tree）或排序二叉树（sorted binary tree），是指一棵空树或者具有下列性质的二叉树： 4 | 5 | >若任意节点的左子树不空，则左子树上所有节点的值均小于它的根节点的值； 6 | > 7 | >若任意节点的右子树不空，则右子树上所有节点的值均大于或等于它的根节点的值； 8 | > 9 | >任意节点的左、右子树也分别为二叉查找树； 10 | 11 | 二叉查找树相比于其他数据结构的优势在于查找、插入的时间复杂度较低。为{\displaystyle O(\log n)}O(\log n)。二叉查找树是基础性数据结构，用于构建更为抽象的数据结构，如集合、多重集、关联数组等。 12 | 13 | ![BST](https://zh.wikipedia.org/wiki/%E4%BA%8C%E5%85%83%E6%90%9C%E5%B0%8B%E6%A8%B9#/media/File:Binary_search_tree.svg) 14 | 15 | ### 学习视频 16 | 17 | [二叉搜索树](https://www.youtube.com/watch?v=GtflM7nUrU0) -------------------------------------------------------------------------------- /Day01-17/12.AVL树.md: -------------------------------------------------------------------------------- 1 | # AVL树 2 | 3 | > 在计算机科学中，AVL树是最早被发明的自平衡二叉查找树。在AVL树中，任一节点对应的两棵子树的最大高度差为1，因此它也被称为高度平衡树。查找、插入和删除在平均和最坏情况下的时间复杂度都是{\displaystyle O(\log 4 | {n})}O(\log{n})。增加和删除元素的操作则可能需要借由一次或多次树旋转，以实现树的重新平衡。 5 | 6 | ### 学习视频 7 | 8 | [AVL Tree](https://www.youtube.com/watch?v=jDM6_TnYIqE) 9 | 10 | [AVL 平衡二叉树](https://www.youtube.com/watch?v=NAiBAph8cGk) 11 | 12 | -------------------------------------------------------------------------------- /Day01-17/14.树状数组.md: -------------------------------------------------------------------------------- 1 | # 树状数组 2 | 3 | > 其初衷是解决数据压缩里的累积频率（Cumulative Frequency）的计算问题，现多用于高效计算数列的前缀和， 区间和。它可以以{\displaystyle O(\log n)}O(\log n)的时间得到任意前缀和{\displaystyle \sum _{i=1}^{j}A[i],1<=j<=N}，并同时支持在{\displaystyle O(\log n)}O(\log n)时间内支持动态单点值的修改。空间复杂度{\displaystyle O(n)}O(n)。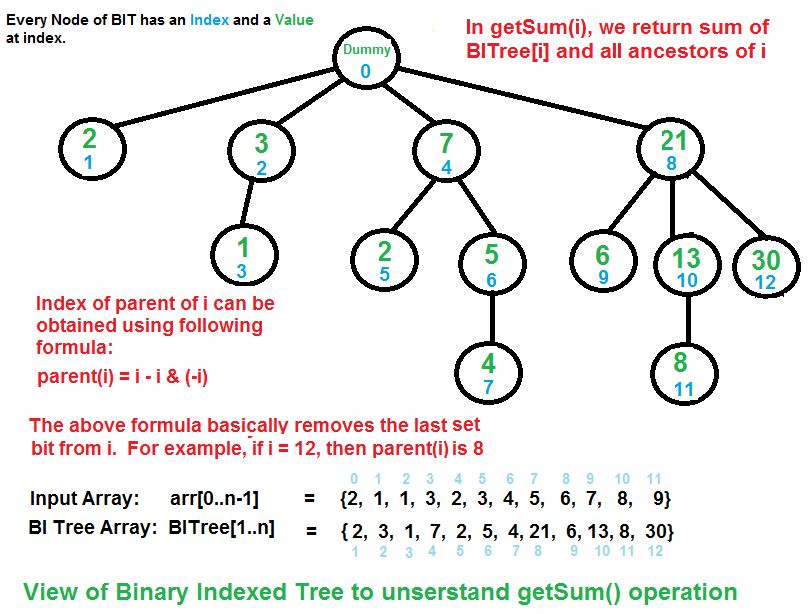 4 | 5 | ![Fenwick Tree](https://upload.wikimedia.org/wikipedia/commons/d/dc/BITDemo.gif) 6 | 7 | ![Binary Indexed Tree](https://www.geeksforgeeks.org/wp-content/uploads/BITSum.png) 8 | 9 | ### 学习视频 10 | 11 | [树状数组讲解](https://www.youtube.com/watch?v=v_wj_mOAlig) -------------------------------------------------------------------------------- /Day01-17/15.图.md: -------------------------------------------------------------------------------- 1 | # 图 2 | 3 | 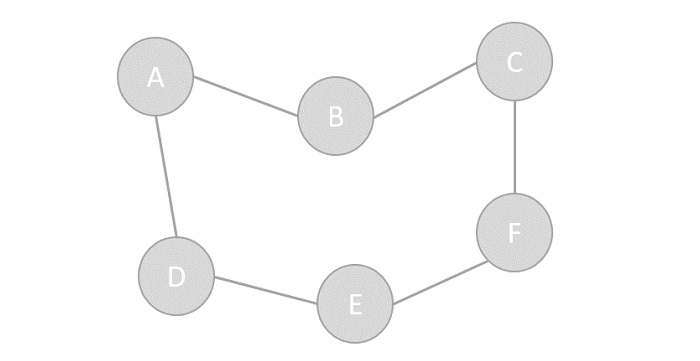![Graph](https://www.tutorialspoint.com/data_structures_algorithms/images/graph.jpg) 4 | 5 | > 我们知道，数据之间的关系有 3 种，分别是 "一对一"、"一对多" 和 "多对多"，前两种关系的数据可分别用线性表和树结构存储，本节学习存储具有"多对多"逻辑关系数据的结构——图存储结构。 6 | 7 | ![](./config/img/15-001.png) 8 | 9 | 图 1 所示为存储 V1、V2、V3、V4 的图结构，从图中可以清楚的看出数据之间具有的"多对多"关系。例如，V1 与 V4 和 V2 建立着联系，V4 与 V1 和 V3 建立着联系，以此类推。 10 | 11 | 与链表不同，图中存储的各个数据元素被称为顶点（而不是节点）。拿图 1 来说，该图中含有 4 个顶点，分别为顶点 V1、V2、V3 和 V4。 12 | 图存储结构中，习惯上用 Vi 表示图中的顶点，且所有顶点构成的集合通常用 V 表示，如图 1 中顶点的集合为 V={V1,V2,V3,V4}。 13 | 14 | 注意，图 1 中的图仅是图存储结构的其中一种，数据之间 "多对多" 的关系还可能用如图 2 所示的图结构表示： 15 | 16 | ![](./config/img/15-002.png) 17 | 18 | 可以看到，各个顶点之间的关系并不是"双向"的。比如，V4 只与 V1 存在联系（从 V4 可直接找到 V1），而与 V3 没有直接联系；同样，V3 只与 V4 存在联系（从 V3 可直接找到 V4），而与 V1 没有直接联系，以此类推。 19 | 20 | 因此，图存储结构可细分两种表现类型，分别为无向图（图 1）和有向图（图 2）。 21 | 22 | ### 图的基本常识 23 | 24 | #### 弧头和弧尾 25 | 26 | 有向图中，无箭头一端的顶点通常被称为"初始点"或"弧尾"，箭头直线的顶点被称为"终端点"或"弧头"。 27 | 28 | #### 入度和出度 29 | 30 | 对于有向图中的一个顶点 V 来说，箭头指向 V 的弧的数量为 V 的入度（InDegree，记为 ID(V)）；箭头远离 V 的弧的数量为 V 的出度（OutDegree，记为OD(V)）。拿图 2 中的顶点 V1来说，该顶点的入度为 1，出度为 2（该顶点的度为 3）。 31 | 32 | #### (V1,V2) 和 的区别 33 | 34 | 无向图中描述两顶点（V1 和 V2）之间的关系可以用 (V1,V2) 来表示，而有向图中描述从 V1 到 V2 的"单向"关系用 来表示。 35 | 36 | --- 37 | 38 | 由于图存储结构中顶点之间的关系是用线来表示的，因此 (V1,V2) 还可以用来表示无向图中连接 V1 和 V2 的线，又称为边；同样， 也可用来表示有向图中从 V1 到 V2 带方向的线，又称为弧。 39 | 40 | #### 集合 VR 的含义 41 | 42 | 并且，图中习惯用 VR 表示图中所有顶点之间关系的集合。例如，图 1 中无向图的集合 VR={(v1,v2),(v1,v4),(v1,v3),(v3,v4)}，图 2 中有向图的集合 VR={,,,}。 43 | 44 | #### 路径和回路 45 | 46 | 无论是无向图还是有向图，从一个顶点到另一顶点途径的所有顶点组成的序列（包含这两个顶点），称为一条路径。如果路径中第一个顶点和最后一个顶点相同，则此路径称为"回路"（或"环"）。 47 | 48 | 并且，若路径中各顶点都不重复，此路径又被称为"简单路径"；同样，若回路中的顶点互不重复，此回路被称为"简单回路"（或简单环）。 49 | 50 | 拿图 1 来说，从 V1 存在一条路径还可以回到 V1，此路径为 {V1,V3,V4,V1}，这是一个回路（环），而且还是一个简单回路（简单环）。 51 | >在有向图中，每条路径或回路都是有方向的。 52 | 53 | #### 权和网的含义 54 | 55 | 在某些实际场景中，图中的每条边（或弧）会赋予一个实数来表示一定的含义，这种与边（或弧）相匹配的实数被称为"权"，而带权的图通常称为网。如图 3 所示，就是一个网结构： 56 | 57 | ![](./config/img/15-003.png) 58 | 59 | 子图：指的是由图中一部分顶点和边构成的图，称为原图的子图。 60 | 61 | ### 图存储结构的分类 62 | 63 | 根据不同的特征，图又可分为完全图，连通图、稀疏图和稠密图： 64 | 65 | 完全图：若图中各个顶点都与除自身外的其他顶点有关系，这样的无向图称为完全图（如图 4a)）。同时，满足此条件的有向图则称为有向完全图（图 4b)）。 66 | 67 | ![](./config/img/15-004.png) 68 | 69 | >具有 n 个顶点的完全图，图中边的数量为 n(n-1)/2；而对于具有 n 个顶点的有向完全图，图中弧的数量为 n(n-1)。 70 | 71 | 稀疏图和稠密图：这两种图是相对存在的，即如果图中具有很少的边（或弧），此图就称为"稀疏图"；反之，则称此图为"稠密图"。 72 | 73 | >稀疏和稠密的判断条件是：e 在计算机科学中，并查集是一种树型的数据结构，用于处理一些不交集（Disjoint Sets）的合并及查询问题。 4 | 5 | ### 概念 6 | 7 | 并查集是一种树型的数据结构，其保持着用于处理一些不相交集合（Disjoint Sets）的合并及查询问题。 8 | 9 | ### 基本操作 10 | 11 | - 1.初始化（init） 12 | - 2.查询（Find）: 确定元素属于哪一个子集。它可以被用来确定两个元素是否属于同一子集 13 | - 3.合并（Union）: 将两个子集合并成同一个集合 14 | 15 | > 由于支持这两种操作，一个不相交集也常被称为联合-查找数据结构（union-find data structure）或合并-查找集合（merge-find set）。其他的重要方法，MakeSet，用于创建单元素集合。有了这些方法，许多经典的划分问题可以被解决。 16 | 17 | ### 初始化 18 | 19 | 我们用 par 数组表示i结点的父亲，rank数组表示树的高度，当par[x] = x 时，x就是所在树的根，因为刚开始没有边，每个结点就是自己的根。 20 | 21 | ``` 22 | void init(int n) 23 | { 24 | for(int i = 0; i < n; i++) 25 | { 26 | par[i] = i; 27 | rank[i] = 0; 28 | } 29 | } 30 | ``` 31 | 32 | ### 查询 33 | 34 | 写法1（递归） 35 | ``` 36 | int find( int x) 37 | { 38 | if(par[x] == x) 39 | return x; 40 | else 41 | return par[x] = find( par[x]);//路径压缩 42 | } 43 | ``` 44 | 45 | 写法2 46 | ``` 47 | int find(int x) 48 | { 49 | int root, temp; 50 | root = x; 51 | while(root != par[root])//查找位置 52 | root = par[root]; 53 | while(x != root)//路径压缩 54 | { 55 | temp = par[x]; 56 | par[temp] = root; 57 | x = temp; 58 | } 59 | return root; 60 | } 61 | ``` 62 | 63 | ### 合并 64 | 65 | ``` 66 | void union(int x,int y)//合并x,y所在集合 67 | { 68 | x = find(x); 69 | y = find(y); 70 | if(x == y)//判断x,y是否属于同一集合 71 | return ; 72 | //防止树退化（辉哥说用了很多年从来发现有明显优化的现象发生。。。） 73 | if(rank[x] < rank[y]) 74 | par[x] = y; 75 | else 76 | { 77 | par[y] = x; 78 | if(rank[x] == rank[y]) 79 | rank[x]++; 80 | } 81 | } 82 | ``` 83 | 84 | ### 学习视频 85 | 86 | [并查集讲解](https://www.youtube.com/watch?v=YKE4Vd1ysPI) -------------------------------------------------------------------------------- /Day01-17/17.布隆过滤器.md: -------------------------------------------------------------------------------- 1 | # 布隆过滤器 2 | 3 | > 布隆过滤器（Bloom Filter）是1970年由布隆提出的。它实际上是一个很长的二进制向量和一系列随机映射函数。布隆过滤器可以用于检索一个元素是否在一个集合中。它的优点是空间效率和查询时间都比一般的算法要好的多，缺点是有一定的误识别率和删除困难。 4 | 5 | ![Bloom Filter](https://upload.wikimedia.org/wikipedia/commons/a/ac/Bloom_filter.svg) 6 | 7 | ### 理论基础 8 | 9 | 如果想要判断一个元素是不是在一个集合里，一般想到的是将所有元素保存起来，然后通过比较确定。链表，树等等数据结构都是这种思路. 但是随着集合中元素的增加，我们需要的存储空间越来越大，检索速度也越来越慢(O(n),O(logn))。不过世界上还有一种叫作散列表（又叫哈希表，Hash table）的数据结构。它可以通过一个Hash函数将一个元素映射成一个位阵列（Bit array）中的一个点。这样一来，我们只要看看这个点是不是1就可以知道集合中有没有它了。这就是布隆过滤器的基本思想。 10 | 11 | ### 优点 12 | 13 | 相比于其它的数据结构，布隆过滤器在空间和时间方面都有巨大的优势。布隆过滤器存储空间和插入/查询时间都是常数。另外, Hash函数相互之间没有关系，方便由硬件并行实现。布隆过滤器不需要存储元素本身，在某些对保密要求非常严格的场合有优势。 14 | 布隆过滤器可以表示全集，其它任何数据结构都不能。 15 | 16 | ### 学习视频 17 | 18 | [布隆过滤器：理论讲解](https://www.youtube.com/watch?v=skmTPIKIks4) -------------------------------------------------------------------------------- /Day01-17/config/img/01-001.jpg: -------------------------------------------------------------------------------- https://raw.githubusercontent.com/geekxh/hello-interview/807bb7f8e6a6421deccd0f51b24f1d4660f65b81/Day01-17/config/img/01-001.jpg -------------------------------------------------------------------------------- /Day01-17/config/img/01-1-001.png: -------------------------------------------------------------------------------- https://raw.githubusercontent.com/geekxh/hello-interview/807bb7f8e6a6421deccd0f51b24f1d4660f65b81/Day01-17/config/img/01-1-001.png -------------------------------------------------------------------------------- /Day01-17/config/img/01-3-01.jpg: -------------------------------------------------------------------------------- https://raw.githubusercontent.com/geekxh/hello-interview/807bb7f8e6a6421deccd0f51b24f1d4660f65b81/Day01-17/config/img/01-3-01.jpg -------------------------------------------------------------------------------- /Day01-17/config/img/01-3-02.jpg: -------------------------------------------------------------------------------- https://raw.githubusercontent.com/geekxh/hello-interview/807bb7f8e6a6421deccd0f51b24f1d4660f65b81/Day01-17/config/img/01-3-02.jpg -------------------------------------------------------------------------------- /Day01-17/config/img/01-3-03.jpg: -------------------------------------------------------------------------------- https://raw.githubusercontent.com/geekxh/hello-interview/807bb7f8e6a6421deccd0f51b24f1d4660f65b81/Day01-17/config/img/01-3-03.jpg -------------------------------------------------------------------------------- /Day01-17/config/img/01-3-04.jpg: -------------------------------------------------------------------------------- https://raw.githubusercontent.com/geekxh/hello-interview/807bb7f8e6a6421deccd0f51b24f1d4660f65b81/Day01-17/config/img/01-3-04.jpg -------------------------------------------------------------------------------- /Day01-17/config/img/04-001.png: -------------------------------------------------------------------------------- https://raw.githubusercontent.com/geekxh/hello-interview/807bb7f8e6a6421deccd0f51b24f1d4660f65b81/Day01-17/config/img/04-001.png -------------------------------------------------------------------------------- /Day01-17/config/img/04-002.png: -------------------------------------------------------------------------------- https://raw.githubusercontent.com/geekxh/hello-interview/807bb7f8e6a6421deccd0f51b24f1d4660f65b81/Day01-17/config/img/04-002.png -------------------------------------------------------------------------------- /Day01-17/config/img/04-003.png: -------------------------------------------------------------------------------- https://raw.githubusercontent.com/geekxh/hello-interview/807bb7f8e6a6421deccd0f51b24f1d4660f65b81/Day01-17/config/img/04-003.png -------------------------------------------------------------------------------- /Day01-17/config/img/13-001.png: -------------------------------------------------------------------------------- https://raw.githubusercontent.com/geekxh/hello-interview/807bb7f8e6a6421deccd0f51b24f1d4660f65b81/Day01-17/config/img/13-001.png -------------------------------------------------------------------------------- /Day01-17/config/img/13-002.png: -------------------------------------------------------------------------------- https://raw.githubusercontent.com/geekxh/hello-interview/807bb7f8e6a6421deccd0f51b24f1d4660f65b81/Day01-17/config/img/13-002.png -------------------------------------------------------------------------------- /Day01-17/config/img/13-003.png: -------------------------------------------------------------------------------- https://raw.githubusercontent.com/geekxh/hello-interview/807bb7f8e6a6421deccd0f51b24f1d4660f65b81/Day01-17/config/img/13-003.png -------------------------------------------------------------------------------- /Day01-17/config/img/13-004.png: -------------------------------------------------------------------------------- https://raw.githubusercontent.com/geekxh/hello-interview/807bb7f8e6a6421deccd0f51b24f1d4660f65b81/Day01-17/config/img/13-004.png -------------------------------------------------------------------------------- /Day01-17/config/img/15-001.png: -------------------------------------------------------------------------------- https://raw.githubusercontent.com/geekxh/hello-interview/807bb7f8e6a6421deccd0f51b24f1d4660f65b81/Day01-17/config/img/15-001.png -------------------------------------------------------------------------------- /Day01-17/config/img/15-002.png: -------------------------------------------------------------------------------- https://raw.githubusercontent.com/geekxh/hello-interview/807bb7f8e6a6421deccd0f51b24f1d4660f65b81/Day01-17/config/img/15-002.png -------------------------------------------------------------------------------- /Day01-17/config/img/15-003.png: -------------------------------------------------------------------------------- https://raw.githubusercontent.com/geekxh/hello-interview/807bb7f8e6a6421deccd0f51b24f1d4660f65b81/Day01-17/config/img/15-003.png -------------------------------------------------------------------------------- /Day01-17/config/img/15-004.png: -------------------------------------------------------------------------------- https://raw.githubusercontent.com/geekxh/hello-interview/807bb7f8e6a6421deccd0f51b24f1d4660f65b81/Day01-17/config/img/15-004.png -------------------------------------------------------------------------------- /Day01-17/english/01.The Importance of Algorithms.md: -------------------------------------------------------------------------------- 1 | The Importance of Studying Algorithms 2 | 3 | After working in Silicon Valley, and with tech students and alumni for the past seven years, one common thing really stood out about individuals that were best prepared for interviews: the dedication to practicing algorithms. 4 | 5 | Interview Prep 6 | Many of the individuals I have coached over my career have asked how to gain the competitive advantage during the job search process. One of the most important tips I share is for individuals to practice algorithms daily. Software engineering and programming interviews often include whiteboard algorithms questions. Stories from people who have gone through the interview process at some of the top tech companies in the world explain in detail how algorithms are used during the process. And my recruiter contacts have shared that when they interview candidates for programming jobs, they are trying to quickly find out how adept candidates are at solving complex problems. Algorithm and data-set exercises mimic real life; complex problems present themselves in everyday work as a programmer. Whiteboarding exercises during program interviews offer insight into the candidate’s problem solving skills, ability to keep track of details, and communication skills. 7 | 8 | Keeping Your Programming Skills Sharp 9 | I teach job seekers that practice makes perfect. During the bootcamp, students learn three stacks of technology and practice their skills via projects, exams, and project pitch days. But it is important to keep learning after the 14 weeks of the bootcamp. Job seekers should strive to increase their baseline of knowledge, and there are various resources available to practice algorithms. It is highly encouraged that you code on a whiteboard, paper, and computer. Practicing algorithms will help you start to recognize common questions and patterns, as well as make you very familiar with algorithmic problem solving. 10 | 11 | Long Term Career Goals 12 | If an individual wants to grow and solve projects for a team then they should be proficient in algorithms. As a developer, your everyday work is to solve problems and algorithms solve problems very efficiently. Practicing algorithms will increase you skill and your visibility at work. -------------------------------------------------------------------------------- /Day01-17/english/02.Linked List.md: -------------------------------------------------------------------------------- 1 | # Linked List 2 | 3 | In computer science, a **linked list** is a linear collection 4 | of data elements, in which linear order is not given by 5 | their physical placement in memory. Instead, each 6 | element points to the next. It is a data structure 7 | consisting of a group of nodes which together represent 8 | a sequence. Under the simplest form, each node is 9 | composed of data and a reference (in other words, 10 | a link) to the next node in the sequence. This structure 11 | allows for efficient insertion or removal of elements 12 | from any position in the sequence during iteration. 13 | More complex variants add additional links, allowing 14 | efficient insertion or removal from arbitrary element 15 | references. A drawback of linked lists is that access 16 | time is linear (and difficult to pipeline). Faster 17 | access, such as random access, is not feasible. Arrays 18 | have better cache locality as compared to linked lists. 19 | 20 | ![Linked List](https://upload.wikimedia.org/wikipedia/commons/6/6d/Singly-linked-list.svg) 21 | 22 | ## Pseudocode for Basic Operations 23 | 24 | ### Insert 25 | 26 | ```text 27 | Add(value) 28 | Pre: value is the value to add to the list 29 | Post: value has been placed at the tail of the list 30 | n ← node(value) 31 | if head = ø 32 | head ← n 33 | tail ← n 34 | else 35 | tail.next ← n 36 | tail ← n 37 | end if 38 | end Add 39 | ``` 40 | 41 | ```text 42 | Prepend(value) 43 | Pre: value is the value to add to the list 44 | Post: value has been placed at the head of the list 45 | n ← node(value) 46 | n.next ← head 47 | head ← n 48 | if tail = ø 49 | tail ← n 50 | end 51 | end Prepend 52 | ``` 53 | 54 | ### Search 55 | 56 | ```text 57 | Contains(head, value) 58 | Pre: head is the head node in the list 59 | value is the value to search for 60 | Post: the item is either in the linked list, true; otherwise false 61 | n ← head 62 | while n != ø and n.value != value 63 | n ← n.next 64 | end while 65 | if n = ø 66 | return false 67 | end if 68 | return true 69 | end Contains 70 | ``` 71 | 72 | ### Delete 73 | 74 | ```text 75 | Remove(head, value) 76 | Pre: head is the head node in the list 77 | value is the value to remove from the list 78 | Post: value is removed from the list, true, otherwise false 79 | if head = ø 80 | return false 81 | end if 82 | n ← head 83 | if n.value = value 84 | if head = tail 85 | head ← ø 86 | tail ← ø 87 | else 88 | head ← head.next 89 | end if 90 | return true 91 | end if 92 | while n.next != ø and n.next.value != value 93 | n ← n.next 94 | end while 95 | if n.next != ø 96 | if n.next = tail 97 | tail ← n 98 | end if 99 | n.next ← n.next.next 100 | return true 101 | end if 102 | return false 103 | end Remove 104 | ``` 105 | 106 | ### Traverse 107 | 108 | ```text 109 | Traverse(head) 110 | Pre: head is the head node in the list 111 | Post: the items in the list have been traversed 112 | n ← head 113 | while n != ø 114 | yield n.value 115 | n ← n.next 116 | end while 117 | end Traverse 118 | ``` 119 | 120 | ### Traverse in Reverse 121 | 122 | ```text 123 | ReverseTraversal(head, tail) 124 | Pre: head and tail belong to the same list 125 | Post: the items in the list have been traversed in reverse order 126 | if tail != ø 127 | curr ← tail 128 | while curr != head 129 | prev ← head 130 | while prev.next != curr 131 | prev ← prev.next 132 | end while 133 | yield curr.value 134 | curr ← prev 135 | end while 136 | yield curr.value 137 | end if 138 | end ReverseTraversal 139 | ``` 140 | 141 | ## Complexities 142 | 143 | ### Time Complexity 144 | 145 | | Access | Search | Insertion | Deletion | 146 | | :-------: | :-------: | :-------: | :-------: | 147 | | O(n) | O(n) | O(1) | O(n) | 148 | 149 | ### Space Complexity 150 | 151 | O(n) 152 | 153 | ## References 154 | 155 | - [Wikipedia](https://en.wikipedia.org/wiki/Linked_list) 156 | - [YouTube](https://www.youtube.com/watch?v=njTh_OwMljA&index=2&t=1s&list=PLLXdhg_r2hKA7DPDsunoDZ-Z769jWn4R8) 157 | -------------------------------------------------------------------------------- /Day01-17/english/03.Doubly Linked List.md: -------------------------------------------------------------------------------- 1 | # Doubly Linked List 2 | 3 | In computer science, a **doubly linked list** is a linked data structure that 4 | consists of a set of sequentially linked records called nodes. Each node contains 5 | two fields, called links, that are references to the previous and to the next 6 | node in the sequence of nodes. The beginning and ending nodes' previous and next 7 | links, respectively, point to some kind of terminator, typically a sentinel 8 | node or null, to facilitate traversal of the list. If there is only one 9 | sentinel node, then the list is circularly linked via the sentinel node. It can 10 | be conceptualized as two singly linked lists formed from the same data items, 11 | but in opposite sequential orders. 12 | 13 | ![Doubly Linked List](https://upload.wikimedia.org/wikipedia/commons/5/5e/Doubly-linked-list.svg) 14 | 15 | The two node links allow traversal of the list in either direction. While adding 16 | or removing a node in a doubly linked list requires changing more links than the 17 | same operations on a singly linked list, the operations are simpler and 18 | potentially more efficient (for nodes other than first nodes) because there 19 | is no need to keep track of the previous node during traversal or no need 20 | to traverse the list to find the previous node, so that its link can be modified. 21 | 22 | ## Pseudocode for Basic Operations 23 | 24 | ### Insert 25 | 26 | ```text 27 | Add(value) 28 | Pre: value is the value to add to the list 29 | Post: value has been placed at the tail of the list 30 | n ← node(value) 31 | if head = ø 32 | head ← n 33 | tail ← n 34 | else 35 | n.previous ← tail 36 | tail.next ← n 37 | tail ← n 38 | end if 39 | end Add 40 | ``` 41 | 42 | ### Delete 43 | 44 | ```text 45 | Remove(head, value) 46 | Pre: head is the head node in the list 47 | value is the value to remove from the list 48 | Post: value is removed from the list, true; otherwise false 49 | if head = ø 50 | return false 51 | end if 52 | if value = head.value 53 | if head = tail 54 | head ← ø 55 | tail ← ø 56 | else 57 | head ← head.next 58 | head.previous ← ø 59 | end if 60 | return true 61 | end if 62 | n ← head.next 63 | while n != ø and value !== n.value 64 | n ← n.next 65 | end while 66 | if n = tail 67 | tail ← tail.previous 68 | tail.next ← ø 69 | return true 70 | else if n != ø 71 | n.previous.next ← n.next 72 | n.next.previous ← n.previous 73 | return true 74 | end if 75 | return false 76 | end Remove 77 | ``` 78 | 79 | ### Reverse Traversal 80 | 81 | ```text 82 | ReverseTraversal(tail) 83 | Pre: tail is the node of the list to traverse 84 | Post: the list has been traversed in reverse order 85 | n ← tail 86 | while n != ø 87 | yield n.value 88 | n ← n.previous 89 | end while 90 | end Reverse Traversal 91 | ``` 92 | 93 | ## Complexities 94 | 95 | ## Time Complexity 96 | 97 | | Access | Search | Insertion | Deletion | 98 | | :-------: | :-------: | :-------: | :-------: | 99 | | O(n) | O(n) | O(1) | O(n) | 100 | 101 | ### Space Complexity 102 | 103 | O(n) 104 | 105 | ## References 106 | 107 | - [Wikipedia](https://en.wikipedia.org/wiki/Doubly_linked_list) 108 | - [YouTube](https://www.youtube.com/watch?v=JdQeNxWCguQ&t=7s&index=72&list=PLLXdhg_r2hKA7DPDsunoDZ-Z769jWn4R8) 109 | -------------------------------------------------------------------------------- /Day01-17/english/04.Queue.md: -------------------------------------------------------------------------------- 1 | # Queue 2 | 3 | In computer science, a **queue** is a particular kind of abstract data 4 | type or collection in which the entities in the collection are 5 | kept in order and the principle (or only) operations on the 6 | collection are the addition of entities to the rear terminal 7 | position, known as enqueue, and removal of entities from the 8 | front terminal position, known as dequeue. This makes the queue 9 | a First-In-First-Out (FIFO) data structure. In a FIFO data 10 | structure, the first element added to the queue will be the 11 | first one to be removed. This is equivalent to the requirement 12 | that once a new element is added, all elements that were added 13 | before have to be removed before the new element can be removed. 14 | Often a peek or front operation is also entered, returning the 15 | value of the front element without dequeuing it. A queue is an 16 | example of a linear data structure, or more abstractly a 17 | sequential collection. 18 | 19 | Representation of a FIFO (first in, first out) queue 20 | 21 | ![Queue](https://upload.wikimedia.org/wikipedia/commons/5/52/Data_Queue.svg) 22 | 23 | ## References 24 | 25 | - [Wikipedia](https://en.wikipedia.org/wiki/Queue_(abstract_data_type)) 26 | - [YouTube](https://www.youtube.com/watch?v=wjI1WNcIntg&list=PLLXdhg_r2hKA7DPDsunoDZ-Z769jWn4R8&index=3&) 27 | -------------------------------------------------------------------------------- /Day01-17/english/05.Stack.md: -------------------------------------------------------------------------------- 1 | # Stack 2 | 3 | In computer science, a **stack** is an abstract data type that serves 4 | as a collection of elements, with two principal operations: 5 | 6 | * **push**, which adds an element to the collection, and 7 | * **pop**, which removes the most recently added element that was not yet removed. 8 | 9 | The order in which elements come off a stack gives rise to its 10 | alternative name, LIFO (last in, first out). Additionally, a 11 | peek operation may give access to the top without modifying 12 | the stack. The name "stack" for this type of structure comes 13 | from the analogy to a set of physical items stacked on top of 14 | each other, which makes it easy to take an item off the top 15 | of the stack, while getting to an item deeper in the stack 16 | may require taking off multiple other items first. 17 | 18 | Simple representation of a stack runtime with push and pop operations. 19 | 20 | ![Stack](https://upload.wikimedia.org/wikipedia/commons/b/b4/Lifo_stack.png) 21 | 22 | ## References 23 | 24 | - [Wikipedia](https://en.wikipedia.org/wiki/Stack_(abstract_data_type)) 25 | - [YouTube](https://www.youtube.com/watch?v=wjI1WNcIntg&list=PLLXdhg_r2hKA7DPDsunoDZ-Z769jWn4R8&index=3&) 26 | -------------------------------------------------------------------------------- /Day01-17/english/06.Hash Table.md: -------------------------------------------------------------------------------- 1 | # Hash Table 2 | 3 | In computing, a **hash table** (hash map) is a data 4 | structure which implements an *associative array* 5 | abstract data type, a structure that can *map keys 6 | to values*. A hash table uses a *hash function* to 7 | compute an index into an array of buckets or slots, 8 | from which the desired value can be found 9 | 10 | Ideally, the hash function will assign each key to a 11 | unique bucket, but most hash table designs employ an 12 | imperfect hash function, which might cause hash 13 | collisions where the hash function generates the same 14 | index for more than one key. Such collisions must be 15 | accommodated in some way. 16 | 17 | ![Hash Table](https://upload.wikimedia.org/wikipedia/commons/7/7d/Hash_table_3_1_1_0_1_0_0_SP.svg) 18 | 19 | Hash collision resolved by separate chaining. 20 | 21 | ![Hash Collision](https://upload.wikimedia.org/wikipedia/commons/d/d0/Hash_table_5_0_1_1_1_1_1_LL.svg) 22 | 23 | ## References 24 | 25 | - [Wikipedia](https://en.wikipedia.org/wiki/Hash_table) 26 | - [YouTube](https://www.youtube.com/watch?v=shs0KM3wKv8&index=4&list=PLLXdhg_r2hKA7DPDsunoDZ-Z769jWn4R8) 27 | -------------------------------------------------------------------------------- /Day01-17/english/07.Heap.md: -------------------------------------------------------------------------------- 1 | # Heap (data-structure) 2 | 3 | In computer science, a **heap** is a specialized tree-based 4 | data structure that satisfies the heap property described 5 | below. 6 | 7 | In a *min heap*, if `P` is a parent node of `C`, then the 8 | key (the value) of `P` is less than or equal to the 9 | key of `C`. 10 | 11 | ![MinHeap](https://upload.wikimedia.org/wikipedia/commons/6/69/Min-heap.png) 12 | 13 | In a *max heap*, the key of `P` is greater than or equal 14 | to the key of `C` 15 | 16 | ![Heap](https://upload.wikimedia.org/wikipedia/commons/3/38/Max-Heap.svg) 17 | 18 | The node at the "top" of the heap with no parents is 19 | called the root node. 20 | 21 | ## References 22 | 23 | - [Wikipedia](https://en.wikipedia.org/wiki/Heap_(data_structure)) 24 | - [YouTube](https://www.youtube.com/watch?v=t0Cq6tVNRBA&index=5&t=0s&list=PLLXdhg_r2hKA7DPDsunoDZ-Z769jWn4R8) 25 | -------------------------------------------------------------------------------- /Day01-17/english/08.Priority Queue.md: -------------------------------------------------------------------------------- 1 | # Priority Queue 2 | 3 | In computer science, a **priority queue** is an abstract data type 4 | which is like a regular queue or stack data structure, but where 5 | additionally each element has a "priority" associated with it. 6 | In a priority queue, an element with high priority is served before 7 | an element with low priority. If two elements have the same 8 | priority, they are served according to their order in the queue. 9 | 10 | While priority queues are often implemented with heaps, they are 11 | conceptually distinct from heaps. A priority queue is an abstract 12 | concept like "a list" or "a map"; just as a list can be implemented 13 | with a linked list or an array, a priority queue can be implemented 14 | with a heap or a variety of other methods such as an unordered 15 | array. 16 | 17 | ## References 18 | 19 | - [Wikipedia](https://en.wikipedia.org/wiki/Priority_queue) 20 | - [YouTube](https://www.youtube.com/watch?v=wptevk0bshY&list=PLLXdhg_r2hKA7DPDsunoDZ-Z769jWn4R8&index=6) 21 | -------------------------------------------------------------------------------- /Day01-17/english/09.Trie.md: -------------------------------------------------------------------------------- 1 | # Trie 2 | 3 | In computer science, a **trie**, also called digital tree and sometimes 4 | radix tree or prefix tree (as they can be searched by prefixes), 5 | is a kind of search tree—an ordered tree data structure that is 6 | used to store a dynamic set or associative array where the keys 7 | are usually strings. Unlike a binary search tree, no node in the 8 | tree stores the key associated with that node; instead, its 9 | position in the tree defines the key with which it is associated. 10 | All the descendants of a node have a common prefix of the string 11 | associated with that node, and the root is associated with the 12 | empty string. Values are not necessarily associated with every 13 | node. Rather, values tend only to be associated with leaves, 14 | and with some inner nodes that correspond to keys of interest. 15 | For the space-optimized presentation of prefix tree, see compact 16 | prefix tree. 17 | 18 | ![Trie](https://upload.wikimedia.org/wikipedia/commons/b/be/Trie_example.svg) 19 | 20 | ## References 21 | 22 | - [Wikipedia](https://en.wikipedia.org/wiki/Trie) 23 | - [YouTube](https://www.youtube.com/watch?v=zIjfhVPRZCg&list=PLLXdhg_r2hKA7DPDsunoDZ-Z769jWn4R8&index=7&t=0s) 24 | -------------------------------------------------------------------------------- /Day01-17/english/10.Tree.md: -------------------------------------------------------------------------------- 1 | # AVL Tree 2 | 3 | In computer science, an **AVL tree** (named after inventors 4 | Adelson-Velsky and Landis) is a self-balancing binary search 5 | tree. It was the first such data structure to be invented. 6 | In an AVL tree, the heights of the two child subtrees of any 7 | node differ by at most one; if at any time they differ by 8 | more than one, rebalancing is done to restore this property. 9 | Lookup, insertion, and deletion all take `O(log n)` time in 10 | both the average and worst cases, where n is the number of 11 | nodes in the tree prior to the operation. Insertions and 12 | deletions may require the tree to be rebalanced by one or 13 | more tree rotations. 14 | 15 | Animation showing the insertion of several elements into an AVL 16 | tree. It includes left, right, left-right and right-left rotations. 17 | 18 | ![AVL Tree](https://upload.wikimedia.org/wikipedia/commons/f/fd/AVL_Tree_Example.gif) 19 | 20 | AVL tree with balance factors (green) 21 | 22 | ![AVL Tree](https://upload.wikimedia.org/wikipedia/commons/a/ad/AVL-tree-wBalance_K.svg) 23 | 24 | ### AVL Tree Rotations 25 | 26 | **Left-Left Rotation** 27 | 28 | ![Left-Left Rotation](http://btechsmartclass.com/data_structures/ds_images/LL%20Rotation.png) 29 | 30 | **Right-Right Rotation** 31 | 32 | ![Right-Right Rotation](http://btechsmartclass.com/data_structures/ds_images/RR%20Rotation.png) 33 | 34 | **Left-Right Rotation** 35 | 36 | ![Left-Right Rotation](http://btechsmartclass.com/data_structures/ds_images/LR%20Rotation.png) 37 | 38 | **Right-Left Rotation** 39 | 40 | ![Right-Right Rotation](http://btechsmartclass.com/data_structures/ds_images/RL%20Rotation.png) 41 | 42 | ## References 43 | 44 | * [Wikipedia](https://en.wikipedia.org/wiki/AVL_tree) 45 | * [Tutorials Point](https://www.tutorialspoint.com/data_structures_algorithms/avl_tree_algorithm.htm) 46 | * [BTech](http://btechsmartclass.com/data_structures/avl-trees.html) 47 | * [AVL Tree Insertion on YouTube](https://www.youtube.com/watch?v=rbg7Qf8GkQ4&list=PLLXdhg_r2hKA7DPDsunoDZ-Z769jWn4R8&index=12&) 48 | * [AVL Tree Interactive Visualisations](https://www.cs.usfca.edu/~galles/visualization/AVLtree.html) 49 | -------------------------------------------------------------------------------- /Day01-17/english/12.AVL Tree.md: -------------------------------------------------------------------------------- 1 | # AVL Tree 2 | 3 | In computer science, an **AVL tree** (named after inventors 4 | Adelson-Velsky and Landis) is a self-balancing binary search 5 | tree. It was the first such data structure to be invented. 6 | In an AVL tree, the heights of the two child subtrees of any 7 | node differ by at most one; if at any time they differ by 8 | more than one, rebalancing is done to restore this property. 9 | Lookup, insertion, and deletion all take `O(log n)` time in 10 | both the average and worst cases, where n is the number of 11 | nodes in the tree prior to the operation. Insertions and 12 | deletions may require the tree to be rebalanced by one or 13 | more tree rotations. 14 | 15 | Animation showing the insertion of several elements into an AVL 16 | tree. It includes left, right, left-right and right-left rotations. 17 | 18 | ![AVL Tree](https://upload.wikimedia.org/wikipedia/commons/f/fd/AVL_Tree_Example.gif) 19 | 20 | AVL tree with balance factors (green) 21 | 22 | ![AVL Tree](https://upload.wikimedia.org/wikipedia/commons/a/ad/AVL-tree-wBalance_K.svg) 23 | 24 | ### AVL Tree Rotations 25 | 26 | **Left-Left Rotation** 27 | 28 | ![Left-Left Rotation](http://btechsmartclass.com/data_structures/ds_images/LL%20Rotation.png) 29 | 30 | **Right-Right Rotation** 31 | 32 | ![Right-Right Rotation](http://btechsmartclass.com/data_structures/ds_images/RR%20Rotation.png) 33 | 34 | **Left-Right Rotation** 35 | 36 | ![Left-Right Rotation](http://btechsmartclass.com/data_structures/ds_images/LR%20Rotation.png) 37 | 38 | **Right-Left Rotation** 39 | 40 | ![Right-Right Rotation](http://btechsmartclass.com/data_structures/ds_images/RL%20Rotation.png) 41 | 42 | ## References 43 | 44 | * [Wikipedia](https://en.wikipedia.org/wiki/AVL_tree) 45 | * [Tutorials Point](https://www.tutorialspoint.com/data_structures_algorithms/avl_tree_algorithm.htm) 46 | * [BTech](http://btechsmartclass.com/data_structures/avl-trees.html) 47 | * [AVL Tree Insertion on YouTube](https://www.youtube.com/watch?v=rbg7Qf8GkQ4&list=PLLXdhg_r2hKA7DPDsunoDZ-Z769jWn4R8&index=12&) 48 | * [AVL Tree Interactive Visualisations](https://www.cs.usfca.edu/~galles/visualization/AVLtree.html) 49 | -------------------------------------------------------------------------------- /Day01-17/english/13.Red-Black Tree.md: -------------------------------------------------------------------------------- 1 | # Red–Black Tree 2 | 3 | A **red–black tree** is a kind of self-balancing binary search 4 | tree in computer science. Each node of the binary tree has 5 | an extra bit, and that bit is often interpreted as the 6 | color (red or black) of the node. These color bits are used 7 | to ensure the tree remains approximately balanced during 8 | insertions and deletions. 9 | 10 | Balance is preserved by painting each node of the tree with 11 | one of two colors in a way that satisfies certain properties, 12 | which collectively constrain how unbalanced the tree can 13 | become in the worst case. When the tree is modified, the 14 | new tree is subsequently rearranged and repainted to 15 | restore the coloring properties. The properties are 16 | designed in such a way that this rearranging and recoloring 17 | can be performed efficiently. 18 | 19 | The balancing of the tree is not perfect, but it is good 20 | enough to allow it to guarantee searching in `O(log n)` time, 21 | where `n` is the total number of elements in the tree. 22 | The insertion and deletion operations, along with the tree 23 | rearrangement and recoloring, are also performed 24 | in `O(log n)` time. 25 | 26 | An example of a red–black tree: 27 | 28 | ![red-black tree](https://upload.wikimedia.org/wikipedia/commons/6/66/Red-black_tree_example.svg) 29 | 30 | ## Properties 31 | 32 | In addition to the requirements imposed on a binary search 33 | tree the following must be satisfied by a red–black tree: 34 | 35 | - Each node is either red or black. 36 | - The root is black. This rule is sometimes omitted. 37 | Since the root can always be changed from red to black, 38 | but not necessarily vice versa, this rule has little 39 | effect on analysis. 40 | - All leaves (NIL) are black. 41 | - If a node is red, then both its children are black. 42 | - Every path from a given node to any of its descendant 43 | NIL nodes contains the same number of black nodes. 44 | 45 | Some definitions: the number of black nodes from the root 46 | to a node is the node's **black depth**; the uniform 47 | number of black nodes in all paths from root to the leaves 48 | is called the **black-height** of the red–black tree. 49 | 50 | These constraints enforce a critical property of red–black 51 | trees: _the path from the root to the farthest leaf is no more than twice as long as the path from the root to the nearest leaf_. 52 | The result is that the tree is roughly height-balanced. 53 | Since operations such as inserting, deleting, and finding 54 | values require worst-case time proportional to the height 55 | of the tree, this theoretical upper bound on the height 56 | allows red–black trees to be efficient in the worst case, 57 | unlike ordinary binary search trees. 58 | 59 | ## Balancing during insertion 60 | 61 | ### If uncle is RED 62 | ![Red Black Tree Balancing](https://www.geeksforgeeks.org/wp-content/uploads/redBlackCase2.png) 63 | 64 | ### If uncle is BLACK 65 | 66 | - Left Left Case (`p` is left child of `g` and `x` is left child of `p`) 67 | - Left Right Case (`p` is left child of `g` and `x` is right child of `p`) 68 | - Right Right Case (`p` is right child of `g` and `x` is right child of `p`) 69 | - Right Left Case (`p` is right child of `g` and `x` is left child of `p`) 70 | 71 | #### Left Left Case (See g, p and x) 72 | 73 | ![Red Black Tree Balancing](https://www.geeksforgeeks.org/wp-content/uploads/redBlackCase3a1.png) 74 | 75 | #### Left Right Case (See g, p and x) 76 | 77 | 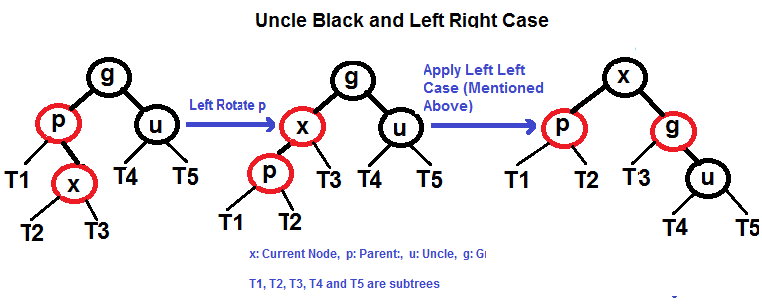![Red Black Tree Balancing](https://www.geeksforgeeks.org/wp-content/uploads/redBlackCase3b.png) 78 | 79 | #### Right Right Case (See g, p and x) 80 | 81 | 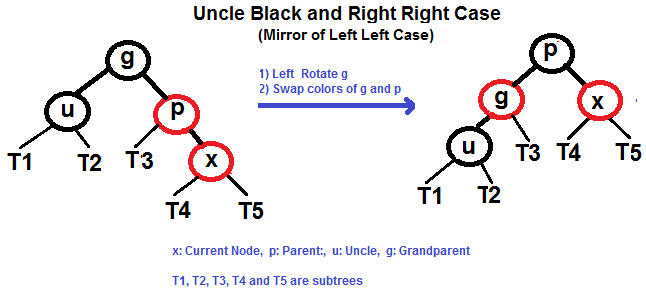![Red Black Tree Balancing](https://www.geeksforgeeks.org/wp-content/uploads/redBlackCase3c.png) 82 | 83 | #### Right Left Case (See g, p and x) 84 | 85 | 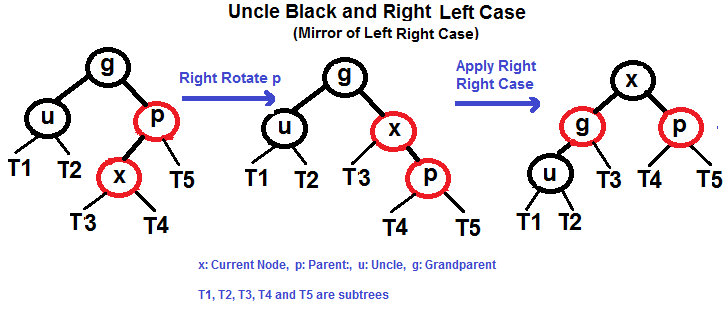![Red Black Tree Balancing](https://www.geeksforgeeks.org/wp-content/uploads/redBlackCase3d.png) 86 | 87 | ## References 88 | 89 | - [Wikipedia](https://en.wikipedia.org/wiki/Red%E2%80%93black_tree) 90 | - [Red Black Tree Insertion by Tushar Roy (YouTube)](https://www.youtube.com/watch?v=UaLIHuR1t8Q&list=PLLXdhg_r2hKA7DPDsunoDZ-Z769jWn4R8&index=63) 91 | - [Red Black Tree Deletion by Tushar Roy (YouTube)](https://www.youtube.com/watch?v=CTvfzU_uNKE&t=0s&list=PLLXdhg_r2hKA7DPDsunoDZ-Z769jWn4R8&index=64) 92 | - [Red Black Tree Insertion on GeeksForGeeks](https://www.geeksforgeeks.org/red-black-tree-set-2-insert/) 93 | - [Red Black Tree Interactive Visualisations](https://www.cs.usfca.edu/~galles/visualization/RedBlack.html) 94 | -------------------------------------------------------------------------------- /Day01-17/english/14.Fenwick Tree.md: -------------------------------------------------------------------------------- 1 | # Fenwick Tree / Binary Indexed Tree 2 | 3 | A **Fenwick tree** or **binary indexed tree** is a data 4 | structure that can efficiently update elements and 5 | calculate prefix sums in a table of numbers. 6 | 7 | When compared with a flat array of numbers, the Fenwick tree achieves a 8 | much better balance between two operations: element update and prefix sum 9 | calculation. In a flat array of `n` numbers, you can either store the elements, 10 | or the prefix sums. In the first case, computing prefix sums requires linear 11 | time; in the second case, updating the array elements requires linear time 12 | (in both cases, the other operation can be performed in constant time). 13 | Fenwick trees allow both operations to be performed in `O(log n)` time. 14 | This is achieved by representing the numbers as a tree, where the value of 15 | each node is the sum of the numbers in that subtree. The tree structure allows 16 | operations to be performed using only `O(log n)` node accesses. 17 | 18 | ## Implementation Notes 19 | 20 | Binary Indexed Tree is represented as an array. Each node of Binary Indexed Tree 21 | stores sum of some elements of given array. Size of Binary Indexed Tree is equal 22 | to `n` where `n` is size of input array. In current implementation we have used 23 | size as `n+1` for ease of implementation. All the indexes are 1-based. 24 | 25 | ![Binary Indexed Tree](https://www.geeksforgeeks.org/wp-content/uploads/BITSum.png) 26 | 27 | On the picture below you may see animated example of 28 | creation of binary indexed tree for the 29 | array `[1, 2, 3, 4, 5]` by inserting one by one. 30 | 31 | ![Fenwick Tree](https://upload.wikimedia.org/wikipedia/commons/d/dc/BITDemo.gif) 32 | 33 | ## References 34 | 35 | - [Wikipedia](https://en.wikipedia.org/wiki/Fenwick_tree) 36 | - [GeeksForGeeks](https://www.geeksforgeeks.org/binary-indexed-tree-or-fenwick-tree-2/) 37 | - [YouTube](https://www.youtube.com/watch?v=CWDQJGaN1gY&index=18&t=0s&list=PLLXdhg_r2hKA7DPDsunoDZ-Z769jWn4R8) 38 | -------------------------------------------------------------------------------- /Day01-17/english/15.Graph.md: -------------------------------------------------------------------------------- 1 | # Graph 2 | 3 | In computer science, a **graph** is an abstract data type 4 | that is meant to implement the undirected graph and 5 | directed graph concepts from mathematics, specifically 6 | the field of graph theory 7 | 8 | A graph data structure consists of a finite (and possibly 9 | mutable) set of vertices or nodes or points, together 10 | with a set of unordered pairs of these vertices for an 11 | undirected graph or a set of ordered pairs for a 12 | directed graph. These pairs are known as edges, arcs, 13 | or lines for an undirected graph and as arrows, 14 | directed edges, directed arcs, or directed lines 15 | for a directed graph. The vertices may be part of 16 | the graph structure, or may be external entities 17 | represented by integer indices or references. 18 | 19 | ![Graph](https://www.tutorialspoint.com/data_structures_algorithms/images/graph.jpg) 20 | 21 | ## References 22 | 23 | - [Wikipedia](https://en.wikipedia.org/wiki/Graph_(abstract_data_type)) 24 | - [Introduction to Graphs on YouTube](https://www.youtube.com/watch?v=gXgEDyodOJU&index=9&list=PLLXdhg_r2hKA7DPDsunoDZ-Z769jWn4R8) 25 | - [Graphs representation on YouTube](https://www.youtube.com/watch?v=k1wraWzqtvQ&index=10&list=PLLXdhg_r2hKA7DPDsunoDZ-Z769jWn4R8)~~ 26 | -------------------------------------------------------------------------------- /Day01-17/english/16.Disjoint Set.md: -------------------------------------------------------------------------------- 1 | # Disjoint Set 2 | 3 | **Disjoint-set** data structure (also called a union–find data structure or merge–find set) is a data 4 | structure that tracks a set of elements partitioned into a number of disjoint (non-overlapping) subsets. 5 | It provides near-constant-time operations (bounded by the inverse Ackermann function) to *add new sets*, 6 | to *merge existing sets*, and to *determine whether elements are in the same set*. 7 | In addition to many other uses (see the Applications section), disjoint-sets play a key role in Kruskal's algorithm for finding the minimum spanning tree of a graph. 8 | 9 | ![disjoint set](https://upload.wikimedia.org/wikipedia/commons/6/67/Dsu_disjoint_sets_init.svg) 10 | 11 | *MakeSet* creates 8 singletons. 12 | 13 | ![disjoint set](https://upload.wikimedia.org/wikipedia/commons/a/ac/Dsu_disjoint_sets_final.svg) 14 | 15 | After some operations of *Union*, some sets are grouped together. 16 | 17 | ## References 18 | 19 | - [Wikipedia](https://en.wikipedia.org/wiki/Disjoint-set_data_structure) 20 | - [By Abdul Bari on YouTube](https://www.youtube.com/watch?v=wU6udHRIkcc&index=14&t=0s&list=PLLXdhg_r2hKA7DPDsunoDZ-Z769jWn4R8) 21 | -------------------------------------------------------------------------------- /Day01-17/english/17.Bloom Filter.md: -------------------------------------------------------------------------------- 1 | # Bloom Filter 2 | 3 | A **bloom filter** is a space-efficient probabilistic 4 | data structure designed to test whether an element 5 | is present in a set. It is designed to be blazingly 6 | fast and use minimal memory at the cost of potential 7 | false positives. False positive matches are possible, 8 | but false negatives are not – in other words, a query 9 | returns either "possibly in set" or "definitely not in set". 10 | 11 | Bloom proposed the technique for applications where the 12 | amount of source data would require an impractically large 13 | amount of memory if "conventional" error-free hashing 14 | techniques were applied. 15 | 16 | ## Algorithm description 17 | 18 | An empty Bloom filter is a bit array of `m` bits, all 19 | set to `0`. There must also be `k` different hash functions 20 | defined, each of which maps or hashes some set element to 21 | one of the `m` array positions, generating a uniform random 22 | distribution. Typically, `k` is a constant, much smaller 23 | than `m`, which is proportional to the number of elements 24 | to be added; the precise choice of `k` and the constant of 25 | proportionality of `m` are determined by the intended 26 | false positive rate of the filter. 27 | 28 | Here is an example of a Bloom filter, representing the 29 | set `{x, y, z}`. The colored arrows show the positions 30 | in the bit array that each set element is mapped to. The 31 | element `w` is not in the set `{x, y, z}`, because it 32 | hashes to one bit-array position containing `0`. For 33 | this figure, `m = 18` and `k = 3`. 34 | 35 | ![Bloom Filter](https://upload.wikimedia.org/wikipedia/commons/a/ac/Bloom_filter.svg) 36 | 37 | ## Operations 38 | 39 | There are two main operations a bloom filter can 40 | perform: _insertion_ and _search_. Search may result in 41 | false positives. Deletion is not possible. 42 | 43 | In other words, the filter can take in items. When 44 | we go to check if an item has previously been 45 | inserted, it can tell us either "no" or "maybe". 46 | 47 | Both insertion and search are `O(1)` operations. 48 | 49 | ## Making the filter 50 | 51 | A bloom filter is created by allotting a certain size. 52 | In our example, we use `100` as a default length. All 53 | locations are initialized to `false`. 54 | 55 | ### Insertion 56 | 57 | During insertion, a number of hash functions, 58 | in our case `3` hash functions, are used to create 59 | hashes of the input. These hash functions output 60 | indexes. At every index received, we simply change 61 | the value in our bloom filter to `true`. 62 | 63 | ### Search 64 | 65 | During a search, the same hash functions are called 66 | and used to hash the input. We then check if the 67 | indexes received _all_ have a value of `true` inside 68 | our bloom filter. If they _all_ have a value of 69 | `true`, we know that the bloom filter may have had 70 | the value previously inserted. 71 | 72 | However, it's not certain, because it's possible 73 | that other values previously inserted flipped the 74 | values to `true`. The values aren't necessarily 75 | `true` due to the item currently being searched for. 76 | Absolute certainty is impossible unless only a single 77 | item has previously been inserted. 78 | 79 | While checking the bloom filter for the indexes 80 | returned by our hash functions, if even one of them 81 | has a value of `false`, we definitively know that the 82 | item was not previously inserted. 83 | 84 | ## False Positives 85 | 86 | The probability of false positives is determined by 87 | three factors: the size of the bloom filter, the 88 | number of hash functions we use, and the number 89 | of items that have been inserted into the filter. 90 | 91 | The formula to calculate probablity of a false positive is: 92 | 93 | ( 1 - e -kn/m ) k 94 | 95 | `k` = number of hash functions 96 | 97 | `m` = filter size 98 | 99 | `n` = number of items inserted 100 | 101 | These variables, `k`, `m`, and `n`, should be picked based 102 | on how acceptable false positives are. If the values 103 | are picked and the resulting probability is too high, 104 | the values should be tweaked and the probability 105 | re-calculated. 106 | 107 | ## Applications 108 | 109 | A bloom filter can be used on a blogging website. If 110 | the goal is to show readers only articles that they 111 | have never seen before, a bloom filter is perfect. 112 | It can store hashed values based on the articles. After 113 | a user reads a few articles, they can be inserted into 114 | the filter. The next time the user visits the site, 115 | those articles can be filtered out of the results. 116 | 117 | Some articles will inevitably be filtered out by mistake, 118 | but the cost is acceptable. It's ok if a user never sees 119 | a few articles as long as they have other, brand new ones 120 | to see every time they visit the site. 121 | 122 | ## References 123 | 124 | - [Wikipedia](https://en.wikipedia.org/wiki/Bloom_filter) 125 | - [Bloom Filters by Example](http://llimllib.github.io/bloomfilter-tutorial/) 126 | - [Calculating False Positive Probability](https://hur.st/bloomfilter/?n=4&p=&m=18&k=3) 127 | - [Bloom Filters on Medium](https://blog.medium.com/what-are-bloom-filters-1ec2a50c68ff) 128 | - [Bloom Filters on YouTube](https://www.youtube.com/watch?v=bEmBh1HtYrw) 129 | -------------------------------------------------------------------------------- /Day18-28/18.笛卡尔积.md: -------------------------------------------------------------------------------- 1 | # 笛卡尔积 2 | 3 | -------------------------------------------------------------------------------- /Day18-28/19.洗牌算法.md: -------------------------------------------------------------------------------- 1 | # 洗牌算法 2 | 3 | -------------------------------------------------------------------------------- /Day18-28/20.子集.md: -------------------------------------------------------------------------------- 1 | # 子集 2 | 3 | -------------------------------------------------------------------------------- /Day18-28/21.排列.md: -------------------------------------------------------------------------------- 1 | # 排列 2 | 3 | -------------------------------------------------------------------------------- /Day18-28/22.组合.md: -------------------------------------------------------------------------------- 1 | # 组合 2 | 3 | -------------------------------------------------------------------------------- /Day18-28/23.最长公共子序列.md: -------------------------------------------------------------------------------- 1 | # 最长公共子序列 2 | 3 | -------------------------------------------------------------------------------- /Day18-28/24.最长递增子序列.md: -------------------------------------------------------------------------------- 1 | # 24.最长递增子序列.md 2 | 3 | -------------------------------------------------------------------------------- /Day18-28/25.最短公共父序列.md: -------------------------------------------------------------------------------- 1 | # 25.最短公共父序列.md 2 | 3 | -------------------------------------------------------------------------------- /Day18-28/26.背包问题.md: -------------------------------------------------------------------------------- 1 | # 26.背包问题.md 2 | 3 | -------------------------------------------------------------------------------- /Day18-28/27.最大子数列问题.md: -------------------------------------------------------------------------------- 1 | # 27.最大子数列问题.md 2 | 3 | -------------------------------------------------------------------------------- /Day18-28/28.组合求和.md: -------------------------------------------------------------------------------- 1 | # 28.组合求和.md 2 | 3 | -------------------------------------------------------------------------------- /Day29-36/29.汉明距离.md: -------------------------------------------------------------------------------- 1 | # 29.汉明距离.md 2 | 3 | -------------------------------------------------------------------------------- /Day29-36/30.莱温斯坦距离.md: -------------------------------------------------------------------------------- 1 | # 30.莱温斯坦距离.md 2 | 3 | -------------------------------------------------------------------------------- /Day29-36/31.KMP.md: -------------------------------------------------------------------------------- 1 | # 31.KMP.md 2 | 3 | -------------------------------------------------------------------------------- /Day29-36/32.Sunday.md: -------------------------------------------------------------------------------- 1 | # 32.Sunday.md 2 | 3 | -------------------------------------------------------------------------------- /Day29-36/33.字符串快速查找.md: -------------------------------------------------------------------------------- 1 | # 33.字符串快速查找.md 2 | 3 | -------------------------------------------------------------------------------- /Day29-36/34.Rabin Karp 算法.md: -------------------------------------------------------------------------------- 1 | # 34.Rabin Karp 算法.md 2 | 3 | -------------------------------------------------------------------------------- /Day29-36/35.最长公共子串.md: -------------------------------------------------------------------------------- 1 | # 35.最长公共子串.md 2 | 3 | -------------------------------------------------------------------------------- /Day29-36/36.正则表达式匹配.md: -------------------------------------------------------------------------------- 1 | # 37.线性搜索.md 2 | 3 | -------------------------------------------------------------------------------- /Day37-40/37.线性搜索.md: -------------------------------------------------------------------------------- 1 | # 布隆过滤器 2 | 3 | -------------------------------------------------------------------------------- /Day37-40/38.跳转搜索.md: -------------------------------------------------------------------------------- 1 | # 38.跳转搜索.md 2 | 3 | -------------------------------------------------------------------------------- /Day37-40/39.二分查找.md: -------------------------------------------------------------------------------- 1 | # 39.二分查找.md 2 | 3 | -------------------------------------------------------------------------------- /Day37-40/40.插值搜索.md: -------------------------------------------------------------------------------- 1 | # 40.插值搜索.md 2 | 3 | -------------------------------------------------------------------------------- /Day41-49/41.冒泡排序.md: -------------------------------------------------------------------------------- 1 | # 41.冒泡排序.md 2 | 3 | -------------------------------------------------------------------------------- /Day41-49/42.选择排序.md: -------------------------------------------------------------------------------- 1 | # 42.选择排序.md 2 | 3 | -------------------------------------------------------------------------------- /Day41-49/43.插入排序.md: -------------------------------------------------------------------------------- 1 | # 43.插入排序.md 2 | 3 | -------------------------------------------------------------------------------- /Day41-49/44.堆排序.md: -------------------------------------------------------------------------------- 1 | # 44.堆排序.md 2 | 3 | -------------------------------------------------------------------------------- /Day41-49/45.归并排序.md: -------------------------------------------------------------------------------- 1 | # 45.归并排序.md 2 | 3 | -------------------------------------------------------------------------------- /Day41-49/46.快速排序.md: -------------------------------------------------------------------------------- 1 | # 46.快速排序.md 2 | 3 | -------------------------------------------------------------------------------- /Day41-49/47.希尔排序.md: -------------------------------------------------------------------------------- 1 | # 47.希尔排序.md 2 | 3 | -------------------------------------------------------------------------------- /Day41-49/48.计数排序.md: -------------------------------------------------------------------------------- 1 | # 48.计数排序.md 2 | 3 | -------------------------------------------------------------------------------- /Day41-49/49.基数排序.md: -------------------------------------------------------------------------------- 1 | # 49.基数排序.md 2 | 3 | -------------------------------------------------------------------------------- /Day50-51/50.链表遍历.md: -------------------------------------------------------------------------------- 1 | # 50.链表遍历.md 2 | 3 | -------------------------------------------------------------------------------- /Day50-51/51.链表反转.md: -------------------------------------------------------------------------------- 1 | # 51.链表反转.md 2 | 3 | -------------------------------------------------------------------------------- /Day52-53/52.树的深搜.md: -------------------------------------------------------------------------------- 1 | # 52.树的深搜.md 2 | 3 | -------------------------------------------------------------------------------- /Day52-53/53.树的广搜.md: -------------------------------------------------------------------------------- 1 | # 53.树的广搜.md 2 | 3 | -------------------------------------------------------------------------------- /Day54-55/54.图的深搜.md: -------------------------------------------------------------------------------- 1 | # 54.图的深搜.md 2 | 3 | -------------------------------------------------------------------------------- /Day54-55/55.图的广搜.md: -------------------------------------------------------------------------------- 1 | # 55.图的广搜.md 2 | 3 | -------------------------------------------------------------------------------- /Day54-55/56.寻找加权无向图的最小生成树.md: -------------------------------------------------------------------------------- 1 | # 56.寻找加权无向图的最小生成树.md 2 | 3 | -------------------------------------------------------------------------------- /Day54-55/57.找到图中所有顶点的最短路径.md: -------------------------------------------------------------------------------- 1 | # 57.找到图中所有顶点的最短路径.md 2 | 3 | -------------------------------------------------------------------------------- /Day54-55/58.找到所有顶点对之间的最短路径.md: -------------------------------------------------------------------------------- 1 | # 58.找到所有顶点对之间的最短路径.md 2 | 3 | -------------------------------------------------------------------------------- /Day54-55/59.判圈算法.md: -------------------------------------------------------------------------------- 1 | # 59.判圈算法.md 2 | 3 | -------------------------------------------------------------------------------- /Day54-55/60.寻找加权无向图的最小生成树.md: -------------------------------------------------------------------------------- 1 | # 60.寻找加权无向图的最小生成树.md 2 | 3 | -------------------------------------------------------------------------------- /Day54-55/61.拓扑排序.md: -------------------------------------------------------------------------------- 1 | # 61.拓扑排序.md 2 | 3 | -------------------------------------------------------------------------------- /Day54-55/62.Tarjan算法.md: -------------------------------------------------------------------------------- 1 | # 62.Tarjan算法.md 2 | 3 | -------------------------------------------------------------------------------- /Day54-55/63.Fleury算法.md: -------------------------------------------------------------------------------- 1 | # 63.Fleury算法.md 2 | 3 | -------------------------------------------------------------------------------- /Day54-55/64.哈密顿图.md: -------------------------------------------------------------------------------- 1 | # 64.哈密顿图.md 2 | 3 | -------------------------------------------------------------------------------- /Day54-55/65.旅行推销员问题.md: -------------------------------------------------------------------------------- 1 | # 65.旅行推销员问题.md 2 | 3 | -------------------------------------------------------------------------------- /Day70-80/70.欧几里得算法.md: -------------------------------------------------------------------------------- 1 | # 70.欧几里得算法.md 2 | 3 | -------------------------------------------------------------------------------- /Day70-80/71.最小公倍数.md: -------------------------------------------------------------------------------- 1 | # 71.最小公倍数.md 2 | 3 | -------------------------------------------------------------------------------- /Day70-80/72.素数筛.md: -------------------------------------------------------------------------------- 1 | # 72.素数筛.md 2 | 3 | -------------------------------------------------------------------------------- /Day70-80/73.判断2次方数.md: -------------------------------------------------------------------------------- 1 | # 73.判断2次方数.md 2 | 3 | -------------------------------------------------------------------------------- /Day70-80/74.杨辉三角形.md: -------------------------------------------------------------------------------- 1 | # 74.杨辉三角形.md 2 | 3 | -------------------------------------------------------------------------------- /Day70-80/75.复数.md: -------------------------------------------------------------------------------- 1 | # 75.复数.md 2 | 3 | -------------------------------------------------------------------------------- /Day70-80/76.弧度和角.md: -------------------------------------------------------------------------------- 1 | # 76.弧度和角.md 2 | 3 | -------------------------------------------------------------------------------- /Day70-80/77.位操作.md: -------------------------------------------------------------------------------- 1 | # 77.位操作.md 2 | 3 | -------------------------------------------------------------------------------- /Day70-80/78.阶乘.md: -------------------------------------------------------------------------------- 1 | # 78.阶乘.md 2 | 3 | -------------------------------------------------------------------------------- /Day70-80/79.斐波那契数.md: -------------------------------------------------------------------------------- 1 | # 79.斐波那契数.md 2 | 3 | -------------------------------------------------------------------------------- /Day70-80/80.素数检测.md: -------------------------------------------------------------------------------- 1 | # 80.素数检测.md 2 | 3 | -------------------------------------------------------------------------------- /Day81-88/81.LRU算法.md: -------------------------------------------------------------------------------- 1 | # 81.LRU算法.md 2 | 3 | -------------------------------------------------------------------------------- /Day81-88/82.八皇后问题.md: -------------------------------------------------------------------------------- 1 | # 82.八皇后问题.md 2 | 3 | -------------------------------------------------------------------------------- /Day81-88/83.骑士巡逻.md: -------------------------------------------------------------------------------- 1 | # 83.骑士巡逻.md 2 | 3 | -------------------------------------------------------------------------------- /Day81-88/84.递归楼梯.md: -------------------------------------------------------------------------------- 1 | # 84.递归楼梯.md 2 | 3 | -------------------------------------------------------------------------------- /Day81-88/85.旋转矩阵.md: -------------------------------------------------------------------------------- 1 | # 85.旋转矩阵.md 2 | 3 | -------------------------------------------------------------------------------- /Day81-88/86.跳跃游戏.md: -------------------------------------------------------------------------------- 1 | # 86.跳跃游戏.md 2 | 3 | -------------------------------------------------------------------------------- /Day81-88/87.雨水收集.md: -------------------------------------------------------------------------------- 1 | # 87.雨水收集.md 2 | 3 | -------------------------------------------------------------------------------- /Day81-88/88.汉诺塔.md: -------------------------------------------------------------------------------- 1 | # 88.汉诺塔.md 2 | 3 | -------------------------------------------------------------------------------- /Day89-98/89.递推DP.md: -------------------------------------------------------------------------------- 1 | # 89.递推DP.md 2 | 3 | -------------------------------------------------------------------------------- /Day89-98/90.背包九讲.md: -------------------------------------------------------------------------------- 1 | # 90.背包九讲.md 2 | 3 | -------------------------------------------------------------------------------- /Day89-98/91.LIS.md: -------------------------------------------------------------------------------- 1 | # 91.LIS.md 2 | 3 | -------------------------------------------------------------------------------- /Day89-98/92.LCS.md: -------------------------------------------------------------------------------- 1 | # 92.LCS.md 2 | 3 | -------------------------------------------------------------------------------- /Day89-98/93.区间DP.md: -------------------------------------------------------------------------------- 1 | # 93.区间DP.md 2 | 3 | -------------------------------------------------------------------------------- /Day89-98/94.树形DP.md: -------------------------------------------------------------------------------- 1 | # 94.树形DP.md 2 | 3 | -------------------------------------------------------------------------------- /Day89-98/95.数位DP.md: -------------------------------------------------------------------------------- 1 | # 95.数位DP.md 2 | 3 | -------------------------------------------------------------------------------- /Day89-98/96.概率DP.md: -------------------------------------------------------------------------------- 1 | # 96.概率DP.md 2 | 3 | -------------------------------------------------------------------------------- /Day89-98/97.状压DP.md: -------------------------------------------------------------------------------- 1 | # 97.状压DP.md 2 | 3 | -------------------------------------------------------------------------------- /Day89-98/98.结构DP.md: -------------------------------------------------------------------------------- 1 | # 98.结构DP.md 2 | 3 | -------------------------------------------------------------------------------- /Day99/99.毕业证书.md: -------------------------------------------------------------------------------- 1 | # 毕业证书 2 | 3 | -------------------------------------------------------------------------------- /README.md: -------------------------------------------------------------------------------- 1 | # Algorithm - 100天摆脱算法小白 2 | > **作者**：小浩 3 | > 4 | > **说明**：我曾发起一个项目 [hello-algorithm](https://github.com/geekxh/hello-algorithm)，从上线到获得 8k star 只用了不到半个月的时间，且登上过 github trending 日榜榜首的位置。但是该项目在我看来却有一定局限性，由于资源性质过重，并不能让大家真正参与进来。同时，也没有系统的给出一套完整的算法训练步骤。在这样的背景下，我重新创建了现在这个项目：Algorithm-100-Days，期望可以提供**一套完整的算法训练，并对每一节学习内容都提供了视频**。 5 | > 6 | > 同时该项目也会尽可能的提供算法相关学习资料，包括但不限于：国内外优质算法算法视频（Youtube、Bilibili）、算法相关书籍下载（百度云）、算法面试题目汇总（leetcode、flag、bat）、算法题目源码解析（我会尽可能组织更多的人来提供代码以及代码分析） 7 | > 8 | > *最后：所有对该项目有兴趣的人，都可以参与进来，你的任何行为都可以使你成为 contributor。哪怕只是提供一个学习链接！* 9 | 10 | ### 如何进行学习？ 11 | 12 | 1、通过阅读文档，进行基础知识的学习。 13 | 14 | 2、通过文档下方的视频链接，进行内容巩固。 15 | 16 | 3、通过代码，进行提升。 17 | 18 | ### 如何运行代码： 19 | 20 | ``` 21 | 第一步：安装依赖文件 22 | npm install 23 | 第二步：测试单一文件 24 | npm test -- 'LinkedList' 25 | 第三步：测试全部 26 | npm test 27 | ``` 28 | 29 | ### 提示 30 | 31 | > 数据结构和算法的学习主要在于思想的掌握，并不需要纠结语言层面的东西。 32 | 33 | 难度 A：基础 B：进阶 34 | 35 | | 学习目录 | 难度 | 描述 | 36 | | --- | --- | --- | 37 | | [01.数据结构和算法的重要性](./Day01-17/01-1.数据结构和算法的重要性.md) | A | | 38 | | [02.链表](./Day01-17/02.链表.md) | A | | 39 | | [03.双向链表](./Day01-17/03.双向链表.md) | A | | 40 | | [04.队列](./Day01-17/04.队列.md) | A | | 41 | | [05.栈](./Day01-17/05.栈.md) | A | | 42 | | [06.哈希表](./Day01-17/06.哈希表.md) | A | | 43 | | [07.堆](./Day01-17/07.堆.md) | A | | 44 | | [08.优先队列](./Day01-17/08.优先队列.md) | B | | 45 | | [09.字典树](./Day01-17/09.字典树.md) | B | | 46 | | [10.树](./Day01-17/10.树.md) | A | | 47 | | [11.二叉搜索树](./Day01-17/11.二叉搜索树.md) | A | | 48 | | [12.AVL树](./Day01-17/12.AVL树.md) | B | | 49 | | [13.红黑树](./Day01-17/13.红黑树.md) | B | | 50 | | [14.树状数组](./Day01-17/14.树状数组.md) | B | | 51 | | [15.图](./Day01-17/15.图.md) | A | | 52 | | [16.并查集](./Day01-17/16.并查集.md) | B | | 53 | | [17.布隆过滤器](./Day01-17/17.布隆过滤器.md) | B | | 54 | | [18.笛卡尔积]() | | | 55 | | [19.洗牌算法]() | | | 56 | | [20.子集]() | | | 57 | | [21.排列]() | | | 58 | | [22.组合]() | | | 59 | | [23.最长公共子序列]() | | | 60 | | [24.最长递增子序列]() | | | 61 | | [25.最短公共父序列]() | | | 62 | | [26.背包问题]() | | | 63 | | [27.最大子数列问题]() | | | 64 | | [28.组合求和]() | | | 65 | | [29.汉明距离]() | | | 66 | | [30.莱温斯坦距离]() | | | 67 | | [31.KMP]() | | | 68 | | [32.Sun./Day]() | | | 69 | | [33.字符串快速查找]() | | | 70 | | [34.Rabin Karp 算法]() | | | 71 | | [35.最长公共子串]() | | | 72 | | [36.正则表达式匹配]() | | | 73 | | [37.线性搜索]() | | | 74 | | [38.跳转搜索]() | | | 75 | | [39.二分查找]() | | | 76 | | [40.插值搜索]() | | | 77 | | [41.冒泡排序]() | | | 78 | | [42.选择排序]() | | | 79 | | [43.插入排序]() | | | 80 | | [44.堆排序]() | | | 81 | | [45.归并排序]() | | | 82 | | [46.快速排序]() | | | 83 | | [47.希尔排序]() | | | 84 | | [48.计数排序]() | | | 85 | | [49.基数排序]() | | | 86 | | [50.链表遍历]() | | | 87 | | [51.链表反转]() | | | 88 | | [52.树的深搜]() | | | 89 | | [53.树的广搜]() | | | 90 | | [54.图的深搜]() | | | 91 | | [55.图的广搜]() | | | 92 | | [56.寻找加权无向图的最小生成树]() | | | 93 | | [57.找到图中所有顶点的最短路径]() | | | 94 | | [58.找到所有顶点对之间的最短路径]() | | | 95 | | [59.判圈算法]() | | | 96 | | [60.寻找加权无向图的最小生成树]() | | | 97 | | [61.拓扑排序]() | | | 98 | | [62.Tarjan算法]() | | | 99 | | [63.Fleury算法]() | | | 100 | | [64.哈密顿图]() | | | 101 | | [65.旅行推销员问题]() | | | 102 | | [70.欧几里得算法]() | | | 103 | | [71.最小公倍数]() | | | 104 | | [72.素数筛]() | | | 105 | | [73.判断2次方数]() | | | 106 | | [74.杨辉三角形]() | | | 107 | | [75.复数]() | | | 108 | | [76.弧度和角]() | | | 109 | | [77.位操作]() | | | 110 | | [78.阶乘]() | | | 111 | | [79.斐波那契数]() | | | 112 | | [80.素数检测]() | | | 113 | | [81.LRU算法]() | | | 114 | | [82.八皇后问题]() | | | 115 | | [83.骑士巡逻]() | | | 116 | | [84.递归楼梯]() | | | 117 | | [85.旋转矩阵]() | | | 118 | | [86.跳跃游戏]() | | | 119 | | [87.雨水收集]() | | | 120 | | [88.汉诺塔]() | | | 121 | | [89.递推DP]() | | | 122 | | [90.背包九讲]() | | | 123 | | [91.LIS]() | | | 124 | | [92.LCS]() | | | 125 | | [93.区间DP]() | | | 126 | | [94.树形DP]() | | | 127 | | [95.数位DP]() | | | 128 | | [96.概率DP]() | | | 129 | | [97.状压DP]() | | | 130 | | [98.结构DP]() | | | 131 | | [99.DP总结]() | | | 132 | | [100.毕业证书]() | | | 133 | 134 | -------------------------------------------------------------------------------- /jest.config.js: -------------------------------------------------------------------------------- 1 | module.exports = { 2 | // The bail config option can be used here to have Jest stop running tests after 3 | // the first failure. 4 | bail: false, 5 | 6 | // Indicates whether each individual test should be reported during the run. 7 | verbose: false, 8 | 9 | // Indicates whether the coverage information should be collected while executing the test 10 | collectCoverage: false, 11 | 12 | // The directory where Jest should output its coverage files. 13 | coverageDirectory: './coverage/', 14 | 15 | // If the test path matches any of the patterns, it will be skipped. 16 | testPathIgnorePatterns: ['/node_modules/'], 17 | 18 | // If the file path matches any of the patterns, coverage information will be skipped. 19 | coveragePathIgnorePatterns: ['/node_modules/'], 20 | 21 | // The pattern Jest uses to detect test files. 22 | testRegex: '(/__tests__/.*|(\\.|/)(test|spec))\\.jsx?$', 23 | 24 | // This option sets the URL for the jsdom environment. 25 | // It is reflected in properties such as location.href. 26 | // @see: https://github.com/facebook/jest/issues/6769 27 | testURL: 'http://localhost/', 28 | }; 29 | -------------------------------------------------------------------------------- /package.json: -------------------------------------------------------------------------------- 1 | { 2 | "name": "javascript-algorithms-and-data-structures", 3 | "version": "0.0.4", 4 | "description": "Algorithms and data-structures implemented on JavaScript", 5 | "main": "index.js", 6 | "scripts": { 7 | "test": "jest", 8 | }, 9 | "repository": { 10 | "type": "git", 11 | "url": "git+https://github.com/trekhleb/javascript-algorithms.git" 12 | }, 13 | "keywords": [ 14 | "computer-science", 15 | "cs", 16 | "algorithms", 17 | "data-structures", 18 | "javascript", 19 | "algorithm", 20 | "javascript-algorithms", 21 | "sorting-algorithms", 22 | "graph", 23 | "tree", 24 | "interview", 25 | "interview-preparation" 26 | ], 27 | "author": "Oleksii Trekhleb (https://www.linkedin.com/in/trekhleb/)", 28 | "license": "MIT", 29 | "bugs": { 30 | "url": "https://github.com/trekhleb/javascript-algorithms/issues" 31 | }, 32 | "homepage": "https://github.com/trekhleb/javascript-algorithms#readme", 33 | "devDependencies": { 34 | "@babel/cli": "^7.10.5", 35 | "@babel/preset-env": "^7.10.4", 36 | "@types/jest": "^26.0.7", 37 | "eslint": "^7.5.0", 38 | "eslint-config-airbnb": "^18.2.0", 39 | "eslint-plugin-import": "^2.22.0", 40 | "eslint-plugin-jest": "^23.18.2", 41 | "eslint-plugin-jsx-a11y": "^6.3.1", 42 | "eslint-plugin-react": "^7.20.3", 43 | "husky": "^4.2.5", 44 | "jest": "^26.1.0" 45 | }, 46 | "dependencies": {} 47 | } 48 | -------------------------------------------------------------------------------- /src/Day01-17/bloom-filter/BloomFilter.js: -------------------------------------------------------------------------------- 1 | export default class BloomFilter { 2 | /** 3 | * @param {number} size - the size of the storage. 4 | */ 5 | constructor(size = 100) { 6 | // Bloom filter size directly affects the likelihood of false positives. 7 | // The bigger the size the lower the likelihood of false positives. 8 | this.size = size; 9 | this.storage = this.createStore(size); 10 | } 11 | 12 | /** 13 | * @param {string} item 14 | */ 15 | insert(item) { 16 | const hashValues = this.getHashValues(item); 17 | 18 | // Set each hashValue index to true. 19 | hashValues.forEach((val) => this.storage.setValue(val)); 20 | } 21 | 22 | /** 23 | * @param {string} item 24 | * @return {boolean} 25 | */ 26 | mayContain(item) { 27 | const hashValues = this.getHashValues(item); 28 | 29 | for (let hashIndex = 0; hashIndex < hashValues.length; hashIndex += 1) { 30 | if (!this.storage.getValue(hashValues[hashIndex])) { 31 | // We know that the item was definitely not inserted. 32 | return false; 33 | } 34 | } 35 | 36 | // The item may or may not have been inserted. 37 | return true; 38 | } 39 | 40 | /** 41 | * Creates the data store for our filter. 42 | * We use this method to generate the store in order to 43 | * encapsulate the data itself and only provide access 44 | * to the necessary methods. 45 | * 46 | * @param {number} size 47 | * @return {Object} 48 | */ 49 | createStore(size) { 50 | const storage = []; 51 | 52 | // Initialize all indexes to false 53 | for (let storageCellIndex = 0; storageCellIndex < size; storageCellIndex += 1) { 54 | storage.push(false); 55 | } 56 | 57 | const storageInterface = { 58 | getValue(index) { 59 | return storage[index]; 60 | }, 61 | setValue(index) { 62 | storage[index] = true; 63 | }, 64 | }; 65 | 66 | return storageInterface; 67 | } 68 | 69 | /** 70 | * @param {string} item 71 | * @return {number} 72 | */ 73 | hash1(item) { 74 | let hash = 0; 75 | 76 | for (let charIndex = 0; charIndex < item.length; charIndex += 1) { 77 | const char = item.charCodeAt(charIndex); 78 | hash = (hash << 5) + hash + char; 79 | hash &= hash; // Convert to 32bit integer 80 | hash = Math.abs(hash); 81 | } 82 | 83 | return hash % this.size; 84 | } 85 | 86 | /** 87 | * @param {string} item 88 | * @return {number} 89 | */ 90 | hash2(item) { 91 | let hash = 5381; 92 | 93 | for (let charIndex = 0; charIndex < item.length; charIndex += 1) { 94 | const char = item.charCodeAt(charIndex); 95 | hash = (hash << 5) + hash + char; /* hash * 33 + c */ 96 | } 97 | 98 | return Math.abs(hash % this.size); 99 | } 100 | 101 | /** 102 | * @param {string} item 103 | * @return {number} 104 | */ 105 | hash3(item) { 106 | let hash = 0; 107 | 108 | for (let charIndex = 0; charIndex < item.length; charIndex += 1) { 109 | const char = item.charCodeAt(charIndex); 110 | hash = (hash << 5) - hash; 111 | hash += char; 112 | hash &= hash; // Convert to 32bit integer 113 | } 114 | 115 | return Math.abs(hash % this.size); 116 | } 117 | 118 | /** 119 | * Runs all 3 hash functions on the input and returns an array of results. 120 | * 121 | * @param {string} item 122 | * @return {number[]} 123 | */ 124 | getHashValues(item) { 125 | return [ 126 | this.hash1(item), 127 | this.hash2(item), 128 | this.hash3(item), 129 | ]; 130 | } 131 | } 132 | -------------------------------------------------------------------------------- /src/Day01-17/bloom-filter/__test__/BloomFilter.test.js: -------------------------------------------------------------------------------- 1 | import BloomFilter from '../BloomFilter'; 2 | 3 | describe('BloomFilter', () => { 4 | let bloomFilter; 5 | const people = [ 6 | 'Bruce Wayne', 7 | 'Clark Kent', 8 | 'Barry Allen', 9 | ]; 10 | 11 | beforeEach(() => { 12 | bloomFilter = new BloomFilter(); 13 | }); 14 | 15 | it('should have methods named "insert" and "mayContain"', () => { 16 | expect(typeof bloomFilter.insert).toBe('function'); 17 | expect(typeof bloomFilter.mayContain).toBe('function'); 18 | }); 19 | 20 | it('should create a new filter store with the appropriate methods', () => { 21 | const store = bloomFilter.createStore(18); 22 | expect(typeof store.getValue).toBe('function'); 23 | expect(typeof store.setValue).toBe('function'); 24 | }); 25 | 26 | it('should hash deterministically with all 3 hash functions', () => { 27 | const str1 = 'apple'; 28 | 29 | expect(bloomFilter.hash1(str1)).toEqual(bloomFilter.hash1(str1)); 30 | expect(bloomFilter.hash2(str1)).toEqual(bloomFilter.hash2(str1)); 31 | expect(bloomFilter.hash3(str1)).toEqual(bloomFilter.hash3(str1)); 32 | 33 | expect(bloomFilter.hash1(str1)).toBe(14); 34 | expect(bloomFilter.hash2(str1)).toBe(43); 35 | expect(bloomFilter.hash3(str1)).toBe(10); 36 | 37 | const str2 = 'orange'; 38 | 39 | expect(bloomFilter.hash1(str2)).toEqual(bloomFilter.hash1(str2)); 40 | expect(bloomFilter.hash2(str2)).toEqual(bloomFilter.hash2(str2)); 41 | expect(bloomFilter.hash3(str2)).toEqual(bloomFilter.hash3(str2)); 42 | 43 | expect(bloomFilter.hash1(str2)).toBe(0); 44 | expect(bloomFilter.hash2(str2)).toBe(61); 45 | expect(bloomFilter.hash3(str2)).toBe(10); 46 | }); 47 | 48 | it('should create an array with 3 hash values', () => { 49 | expect(bloomFilter.getHashValues('abc').length).toBe(3); 50 | expect(bloomFilter.getHashValues('abc')).toEqual([66, 63, 54]); 51 | }); 52 | 53 | it('should insert strings correctly and return true when checking for inserted values', () => { 54 | people.forEach((person) => bloomFilter.insert(person)); 55 | 56 | expect(bloomFilter.mayContain('Bruce Wayne')).toBe(true); 57 | expect(bloomFilter.mayContain('Clark Kent')).toBe(true); 58 | expect(bloomFilter.mayContain('Barry Allen')).toBe(true); 59 | 60 | expect(bloomFilter.mayContain('Tony Stark')).toBe(false); 61 | }); 62 | }); 63 | -------------------------------------------------------------------------------- /src/Day01-17/disjoint-set/DisjointSet.js: -------------------------------------------------------------------------------- 1 | import DisjointSetItem from './DisjointSetItem'; 2 | 3 | export default class DisjointSet { 4 | /** 5 | * @param {function(value: *)} [keyCallback] 6 | */ 7 | constructor(keyCallback) { 8 | this.keyCallback = keyCallback; 9 | this.items = {}; 10 | } 11 | 12 | /** 13 | * @param {*} itemValue 14 | * @return {DisjointSet} 15 | */ 16 | makeSet(itemValue) { 17 | const disjointSetItem = new DisjointSetItem(itemValue, this.keyCallback); 18 | 19 | if (!this.items[disjointSetItem.getKey()]) { 20 | // Add new item only in case if it not presented yet. 21 | this.items[disjointSetItem.getKey()] = disjointSetItem; 22 | } 23 | 24 | return this; 25 | } 26 | 27 | /** 28 | * Find set representation node. 29 | * 30 | * @param {*} itemValue 31 | * @return {(string|null)} 32 | */ 33 | find(itemValue) { 34 | const templateDisjointItem = new DisjointSetItem(itemValue, this.keyCallback); 35 | 36 | // Try to find item itself; 37 | const requiredDisjointItem = this.items[templateDisjointItem.getKey()]; 38 | 39 | if (!requiredDisjointItem) { 40 | return null; 41 | } 42 | 43 | return requiredDisjointItem.getRoot().getKey(); 44 | } 45 | 46 | /** 47 | * Union by rank. 48 | * 49 | * @param {*} valueA 50 | * @param {*} valueB 51 | * @return {DisjointSet} 52 | */ 53 | union(valueA, valueB) { 54 | const rootKeyA = this.find(valueA); 55 | const rootKeyB = this.find(valueB); 56 | 57 | if (rootKeyA === null || rootKeyB === null) { 58 | throw new Error('One or two values are not in sets'); 59 | } 60 | 61 | if (rootKeyA === rootKeyB) { 62 | // In case if both elements are already in the same set then just return its key. 63 | return this; 64 | } 65 | 66 | const rootA = this.items[rootKeyA]; 67 | const rootB = this.items[rootKeyB]; 68 | 69 | if (rootA.getRank() < rootB.getRank()) { 70 | // If rootB's tree is bigger then make rootB to be a new root. 71 | rootB.addChild(rootA); 72 | 73 | return this; 74 | } 75 | 76 | // If rootA's tree is bigger then make rootA to be a new root. 77 | rootA.addChild(rootB); 78 | 79 | return this; 80 | } 81 | 82 | /** 83 | * @param {*} valueA 84 | * @param {*} valueB 85 | * @return {boolean} 86 | */ 87 | inSameSet(valueA, valueB) { 88 | const rootKeyA = this.find(valueA); 89 | const rootKeyB = this.find(valueB); 90 | 91 | if (rootKeyA === null || rootKeyB === null) { 92 | throw new Error('One or two values are not in sets'); 93 | } 94 | 95 | return rootKeyA === rootKeyB; 96 | } 97 | } 98 | -------------------------------------------------------------------------------- /src/Day01-17/disjoint-set/DisjointSetItem.js: -------------------------------------------------------------------------------- 1 | export default class DisjointSetItem { 2 | /** 3 | * @param {*} value 4 | * @param {function(value: *)} [keyCallback] 5 | */ 6 | constructor(value, keyCallback) { 7 | this.value = value; 8 | this.keyCallback = keyCallback; 9 | /** @var {DisjointSetItem} this.parent */ 10 | this.parent = null; 11 | this.children = {}; 12 | } 13 | 14 | /** 15 | * @return {*} 16 | */ 17 | getKey() { 18 | // Allow user to define custom key generator. 19 | if (this.keyCallback) { 20 | return this.keyCallback(this.value); 21 | } 22 | 23 | // Otherwise use value as a key by default. 24 | return this.value; 25 | } 26 | 27 | /** 28 | * @return {DisjointSetItem} 29 | */ 30 | getRoot() { 31 | return this.isRoot() ? this : this.parent.getRoot(); 32 | } 33 | 34 | /** 35 | * @return {boolean} 36 | */ 37 | isRoot() { 38 | return this.parent === null; 39 | } 40 | 41 | /** 42 | * Rank basically means the number of all ancestors. 43 | * 44 | * @return {number} 45 | */ 46 | getRank() { 47 | if (this.getChildren().length === 0) { 48 | return 0; 49 | } 50 | 51 | let rank = 0; 52 | 53 | /** @var {DisjointSetItem} child */ 54 | this.getChildren().forEach((child) => { 55 | // Count child itself. 56 | rank += 1; 57 | 58 | // Also add all children of current child. 59 | rank += child.getRank(); 60 | }); 61 | 62 | return rank; 63 | } 64 | 65 | /** 66 | * @return {DisjointSetItem[]} 67 | */ 68 | getChildren() { 69 | return Object.values(this.children); 70 | } 71 | 72 | /** 73 | * @param {DisjointSetItem} parentItem 74 | * @param {boolean} forceSettingParentChild 75 | * @return {DisjointSetItem} 76 | */ 77 | setParent(parentItem, forceSettingParentChild = true) { 78 | this.parent = parentItem; 79 | if (forceSettingParentChild) { 80 | parentItem.addChild(this); 81 | } 82 | 83 | return this; 84 | } 85 | 86 | /** 87 | * @param {DisjointSetItem} childItem 88 | * @return {DisjointSetItem} 89 | */ 90 | addChild(childItem) { 91 | this.children[childItem.getKey()] = childItem; 92 | childItem.setParent(this, false); 93 | 94 | return this; 95 | } 96 | } 97 | -------------------------------------------------------------------------------- /src/Day01-17/disjoint-set/__test__/DisjointSet.test.js: -------------------------------------------------------------------------------- 1 | import DisjointSet from '../DisjointSet'; 2 | 3 | describe('DisjointSet', () => { 4 | it('should throw error when trying to union and check not existing sets', () => { 5 | function mergeNotExistingSets() { 6 | const disjointSet = new DisjointSet(); 7 | 8 | disjointSet.union('A', 'B'); 9 | } 10 | 11 | function checkNotExistingSets() { 12 | const disjointSet = new DisjointSet(); 13 | 14 | disjointSet.inSameSet('A', 'B'); 15 | } 16 | 17 | expect(mergeNotExistingSets).toThrow(); 18 | expect(checkNotExistingSets).toThrow(); 19 | }); 20 | 21 | it('should do basic manipulations on disjoint set', () => { 22 | const disjointSet = new DisjointSet(); 23 | 24 | expect(disjointSet.find('A')).toBeNull(); 25 | expect(disjointSet.find('B')).toBeNull(); 26 | 27 | disjointSet.makeSet('A'); 28 | 29 | expect(disjointSet.find('A')).toBe('A'); 30 | expect(disjointSet.find('B')).toBeNull(); 31 | 32 | disjointSet.makeSet('B'); 33 | 34 | expect(disjointSet.find('A')).toBe('A'); 35 | expect(disjointSet.find('B')).toBe('B'); 36 | 37 | disjointSet.makeSet('C'); 38 | 39 | expect(disjointSet.inSameSet('A', 'B')).toBe(false); 40 | 41 | disjointSet.union('A', 'B'); 42 | 43 | expect(disjointSet.find('A')).toBe('A'); 44 | expect(disjointSet.find('B')).toBe('A'); 45 | expect(disjointSet.inSameSet('A', 'B')).toBe(true); 46 | expect(disjointSet.inSameSet('B', 'A')).toBe(true); 47 | expect(disjointSet.inSameSet('A', 'C')).toBe(false); 48 | 49 | disjointSet.union('A', 'A'); 50 | 51 | disjointSet.union('B', 'C'); 52 | 53 | expect(disjointSet.find('A')).toBe('A'); 54 | expect(disjointSet.find('B')).toBe('A'); 55 | expect(disjointSet.find('C')).toBe('A'); 56 | 57 | expect(disjointSet.inSameSet('A', 'B')).toBe(true); 58 | expect(disjointSet.inSameSet('B', 'C')).toBe(true); 59 | expect(disjointSet.inSameSet('A', 'C')).toBe(true); 60 | 61 | disjointSet 62 | .makeSet('E') 63 | .makeSet('F') 64 | .makeSet('G') 65 | .makeSet('H') 66 | .makeSet('I'); 67 | 68 | disjointSet 69 | .union('E', 'F') 70 | .union('F', 'G') 71 | .union('G', 'H') 72 | .union('H', 'I'); 73 | 74 | expect(disjointSet.inSameSet('A', 'I')).toBe(false); 75 | expect(disjointSet.inSameSet('E', 'I')).toBe(true); 76 | 77 | disjointSet.union('I', 'C'); 78 | 79 | expect(disjointSet.find('I')).toBe('E'); 80 | expect(disjointSet.inSameSet('A', 'I')).toBe(true); 81 | }); 82 | 83 | it('should union smaller set with bigger one making bigger one to be new root', () => { 84 | const disjointSet = new DisjointSet(); 85 | 86 | disjointSet 87 | .makeSet('A') 88 | .makeSet('B') 89 | .makeSet('C') 90 | .union('B', 'C') 91 | .union('A', 'C'); 92 | 93 | expect(disjointSet.find('A')).toBe('B'); 94 | }); 95 | 96 | it('should do basic manipulations on disjoint set with custom key extractor', () => { 97 | const keyExtractor = (value) => value.key; 98 | 99 | const disjointSet = new DisjointSet(keyExtractor); 100 | 101 | const itemA = { key: 'A', value: 1 }; 102 | const itemB = { key: 'B', value: 2 }; 103 | const itemC = { key: 'C', value: 3 }; 104 | 105 | expect(disjointSet.find(itemA)).toBeNull(); 106 | expect(disjointSet.find(itemB)).toBeNull(); 107 | 108 | disjointSet.makeSet(itemA); 109 | 110 | expect(disjointSet.find(itemA)).toBe('A'); 111 | expect(disjointSet.find(itemB)).toBeNull(); 112 | 113 | disjointSet.makeSet(itemB); 114 | 115 | expect(disjointSet.find(itemA)).toBe('A'); 116 | expect(disjointSet.find(itemB)).toBe('B'); 117 | 118 | disjointSet.makeSet(itemC); 119 | 120 | expect(disjointSet.inSameSet(itemA, itemB)).toBe(false); 121 | 122 | disjointSet.union(itemA, itemB); 123 | 124 | expect(disjointSet.find(itemA)).toBe('A'); 125 | expect(disjointSet.find(itemB)).toBe('A'); 126 | expect(disjointSet.inSameSet(itemA, itemB)).toBe(true); 127 | expect(disjointSet.inSameSet(itemB, itemA)).toBe(true); 128 | expect(disjointSet.inSameSet(itemA, itemC)).toBe(false); 129 | 130 | disjointSet.union(itemA, itemC); 131 | 132 | expect(disjointSet.find(itemA)).toBe('A'); 133 | expect(disjointSet.find(itemB)).toBe('A'); 134 | expect(disjointSet.find(itemC)).toBe('A'); 135 | 136 | expect(disjointSet.inSameSet(itemA, itemB)).toBe(true); 137 | expect(disjointSet.inSameSet(itemB, itemC)).toBe(true); 138 | expect(disjointSet.inSameSet(itemA, itemC)).toBe(true); 139 | }); 140 | }); 141 | -------------------------------------------------------------------------------- /src/Day01-17/disjoint-set/__test__/DisjointSetItem.test.js: -------------------------------------------------------------------------------- 1 | import DisjointSetItem from '../DisjointSetItem'; 2 | 3 | describe('DisjointSetItem', () => { 4 | it('should do basic manipulation with disjoint set item', () => { 5 | const itemA = new DisjointSetItem('A'); 6 | const itemB = new DisjointSetItem('B'); 7 | const itemC = new DisjointSetItem('C'); 8 | const itemD = new DisjointSetItem('D'); 9 | 10 | expect(itemA.getRank()).toBe(0); 11 | expect(itemA.getChildren()).toEqual([]); 12 | expect(itemA.getKey()).toBe('A'); 13 | expect(itemA.getRoot()).toEqual(itemA); 14 | expect(itemA.isRoot()).toBe(true); 15 | expect(itemB.isRoot()).toBe(true); 16 | 17 | itemA.addChild(itemB); 18 | itemD.setParent(itemC); 19 | 20 | expect(itemA.getRank()).toBe(1); 21 | expect(itemC.getRank()).toBe(1); 22 | 23 | expect(itemB.getRank()).toBe(0); 24 | expect(itemD.getRank()).toBe(0); 25 | 26 | expect(itemA.getChildren().length).toBe(1); 27 | expect(itemC.getChildren().length).toBe(1); 28 | 29 | expect(itemA.getChildren()[0]).toEqual(itemB); 30 | expect(itemC.getChildren()[0]).toEqual(itemD); 31 | 32 | expect(itemB.getChildren().length).toBe(0); 33 | expect(itemD.getChildren().length).toBe(0); 34 | 35 | expect(itemA.getRoot()).toEqual(itemA); 36 | expect(itemB.getRoot()).toEqual(itemA); 37 | 38 | expect(itemC.getRoot()).toEqual(itemC); 39 | expect(itemD.getRoot()).toEqual(itemC); 40 | 41 | expect(itemA.isRoot()).toBe(true); 42 | expect(itemB.isRoot()).toBe(false); 43 | expect(itemC.isRoot()).toBe(true); 44 | expect(itemD.isRoot()).toBe(false); 45 | 46 | itemA.addChild(itemC); 47 | 48 | expect(itemA.isRoot()).toBe(true); 49 | expect(itemB.isRoot()).toBe(false); 50 | expect(itemC.isRoot()).toBe(false); 51 | expect(itemD.isRoot()).toBe(false); 52 | 53 | expect(itemA.getRank()).toEqual(3); 54 | expect(itemB.getRank()).toEqual(0); 55 | expect(itemC.getRank()).toEqual(1); 56 | }); 57 | 58 | it('should do basic manipulation with disjoint set item with custom key extractor', () => { 59 | const keyExtractor = (value) => { 60 | return value.key; 61 | }; 62 | 63 | const itemA = new DisjointSetItem({ key: 'A', value: 1 }, keyExtractor); 64 | const itemB = new DisjointSetItem({ key: 'B', value: 2 }, keyExtractor); 65 | const itemC = new DisjointSetItem({ key: 'C', value: 3 }, keyExtractor); 66 | const itemD = new DisjointSetItem({ key: 'D', value: 4 }, keyExtractor); 67 | 68 | expect(itemA.getRank()).toBe(0); 69 | expect(itemA.getChildren()).toEqual([]); 70 | expect(itemA.getKey()).toBe('A'); 71 | expect(itemA.getRoot()).toEqual(itemA); 72 | expect(itemA.isRoot()).toBe(true); 73 | expect(itemB.isRoot()).toBe(true); 74 | 75 | itemA.addChild(itemB); 76 | itemD.setParent(itemC); 77 | 78 | expect(itemA.getRank()).toBe(1); 79 | expect(itemC.getRank()).toBe(1); 80 | 81 | expect(itemB.getRank()).toBe(0); 82 | expect(itemD.getRank()).toBe(0); 83 | 84 | expect(itemA.getChildren().length).toBe(1); 85 | expect(itemC.getChildren().length).toBe(1); 86 | 87 | expect(itemA.getChildren()[0]).toEqual(itemB); 88 | expect(itemC.getChildren()[0]).toEqual(itemD); 89 | 90 | expect(itemB.getChildren().length).toBe(0); 91 | expect(itemD.getChildren().length).toBe(0); 92 | 93 | expect(itemA.getRoot()).toEqual(itemA); 94 | expect(itemB.getRoot()).toEqual(itemA); 95 | 96 | expect(itemC.getRoot()).toEqual(itemC); 97 | expect(itemD.getRoot()).toEqual(itemC); 98 | 99 | expect(itemA.isRoot()).toBe(true); 100 | expect(itemB.isRoot()).toBe(false); 101 | expect(itemC.isRoot()).toBe(true); 102 | expect(itemD.isRoot()).toBe(false); 103 | 104 | itemA.addChild(itemC); 105 | 106 | expect(itemA.isRoot()).toBe(true); 107 | expect(itemB.isRoot()).toBe(false); 108 | expect(itemC.isRoot()).toBe(false); 109 | expect(itemD.isRoot()).toBe(false); 110 | 111 | expect(itemA.getRank()).toEqual(3); 112 | expect(itemB.getRank()).toEqual(0); 113 | expect(itemC.getRank()).toEqual(1); 114 | }); 115 | }); 116 | -------------------------------------------------------------------------------- /src/Day01-17/doubly-linked-list/DoublyLinkedListNode.js: -------------------------------------------------------------------------------- 1 | export default class DoublyLinkedListNode { 2 | constructor(value, next = null, previous = null) { 3 | this.value = value; 4 | this.next = next; 5 | this.previous = previous; 6 | } 7 | 8 | toString(callback) { 9 | return callback ? callback(this.value) : `${this.value}`; 10 | } 11 | } 12 | -------------------------------------------------------------------------------- /src/Day01-17/doubly-linked-list/__test__/DoublyLinkedListNode.test.js: -------------------------------------------------------------------------------- 1 | import DoublyLinkedListNode from '../DoublyLinkedListNode'; 2 | 3 | describe('DoublyLinkedListNode', () => { 4 | it('should create list node with value', () => { 5 | const node = new DoublyLinkedListNode(1); 6 | 7 | expect(node.value).toBe(1); 8 | expect(node.next).toBeNull(); 9 | expect(node.previous).toBeNull(); 10 | }); 11 | 12 | it('should create list node with object as a value', () => { 13 | const nodeValue = { value: 1, key: 'test' }; 14 | const node = new DoublyLinkedListNode(nodeValue); 15 | 16 | expect(node.value.value).toBe(1); 17 | expect(node.value.key).toBe('test'); 18 | expect(node.next).toBeNull(); 19 | expect(node.previous).toBeNull(); 20 | }); 21 | 22 | it('should link nodes together', () => { 23 | const node2 = new DoublyLinkedListNode(2); 24 | const node1 = new DoublyLinkedListNode(1, node2); 25 | const node3 = new DoublyLinkedListNode(10, node1, node2); 26 | 27 | expect(node1.next).toBeDefined(); 28 | expect(node1.previous).toBeNull(); 29 | expect(node2.next).toBeNull(); 30 | expect(node2.previous).toBeNull(); 31 | expect(node3.next).toBeDefined(); 32 | expect(node3.previous).toBeDefined(); 33 | expect(node1.value).toBe(1); 34 | expect(node1.next.value).toBe(2); 35 | expect(node3.next.value).toBe(1); 36 | expect(node3.previous.value).toBe(2); 37 | }); 38 | 39 | it('should convert node to string', () => { 40 | const node = new DoublyLinkedListNode(1); 41 | 42 | expect(node.toString()).toBe('1'); 43 | 44 | node.value = 'string value'; 45 | expect(node.toString()).toBe('string value'); 46 | }); 47 | 48 | it('should convert node to string with custom stringifier', () => { 49 | const nodeValue = { value: 1, key: 'test' }; 50 | const node = new DoublyLinkedListNode(nodeValue); 51 | const toStringCallback = (value) => `value: ${value.value}, key: ${value.key}`; 52 | 53 | expect(node.toString(toStringCallback)).toBe('value: 1, key: test'); 54 | }); 55 | }); 56 | -------------------------------------------------------------------------------- /src/Day01-17/graph/Graph.js: -------------------------------------------------------------------------------- 1 | export default class Graph { 2 | /** 3 | * @param {boolean} isDirected 4 | */ 5 | constructor(isDirected = false) { 6 | this.vertices = {}; 7 | this.edges = {}; 8 | this.isDirected = isDirected; 9 | } 10 | 11 | /** 12 | * @param {GraphVertex} newVertex 13 | * @returns {Graph} 14 | */ 15 | addVertex(newVertex) { 16 | this.vertices[newVertex.getKey()] = newVertex; 17 | 18 | return this; 19 | } 20 | 21 | /** 22 | * @param {string} vertexKey 23 | * @returns GraphVertex 24 | */ 25 | getVertexByKey(vertexKey) { 26 | return this.vertices[vertexKey]; 27 | } 28 | 29 | /** 30 | * @param {GraphVertex} vertex 31 | * @returns {GraphVertex[]} 32 | */ 33 | getNeighbors(vertex) { 34 | return vertex.getNeighbors(); 35 | } 36 | 37 | /** 38 | * @return {GraphVertex[]} 39 | */ 40 | getAllVertices() { 41 | return Object.values(this.vertices); 42 | } 43 | 44 | /** 45 | * @return {GraphEdge[]} 46 | */ 47 | getAllEdges() { 48 | return Object.values(this.edges); 49 | } 50 | 51 | /** 52 | * @param {GraphEdge} edge 53 | * @returns {Graph} 54 | */ 55 | addEdge(edge) { 56 | // Try to find and end start vertices. 57 | let startVertex = this.getVertexByKey(edge.startVertex.getKey()); 58 | let endVertex = this.getVertexByKey(edge.endVertex.getKey()); 59 | 60 | // Insert start vertex if it wasn't inserted. 61 | if (!startVertex) { 62 | this.addVertex(edge.startVertex); 63 | startVertex = this.getVertexByKey(edge.startVertex.getKey()); 64 | } 65 | 66 | // Insert end vertex if it wasn't inserted. 67 | if (!endVertex) { 68 | this.addVertex(edge.endVertex); 69 | endVertex = this.getVertexByKey(edge.endVertex.getKey()); 70 | } 71 | 72 | // Check if edge has been already added. 73 | if (this.edges[edge.getKey()]) { 74 | throw new Error('Edge has already been added before'); 75 | } else { 76 | this.edges[edge.getKey()] = edge; 77 | } 78 | 79 | // Add edge to the vertices. 80 | if (this.isDirected) { 81 | // If graph IS directed then add the edge only to start vertex. 82 | startVertex.addEdge(edge); 83 | } else { 84 | // If graph ISN'T directed then add the edge to both vertices. 85 | startVertex.addEdge(edge); 86 | endVertex.addEdge(edge); 87 | } 88 | 89 | return this; 90 | } 91 | 92 | /** 93 | * @param {GraphEdge} edge 94 | */ 95 | deleteEdge(edge) { 96 | // Delete edge from the list of edges. 97 | if (this.edges[edge.getKey()]) { 98 | delete this.edges[edge.getKey()]; 99 | } else { 100 | throw new Error('Edge not found in graph'); 101 | } 102 | 103 | // Try to find and end start vertices and delete edge from them. 104 | const startVertex = this.getVertexByKey(edge.startVertex.getKey()); 105 | const endVertex = this.getVertexByKey(edge.endVertex.getKey()); 106 | 107 | startVertex.deleteEdge(edge); 108 | endVertex.deleteEdge(edge); 109 | } 110 | 111 | /** 112 | * @param {GraphVertex} startVertex 113 | * @param {GraphVertex} endVertex 114 | * @return {(GraphEdge|null)} 115 | */ 116 | findEdge(startVertex, endVertex) { 117 | const vertex = this.getVertexByKey(startVertex.getKey()); 118 | 119 | if (!vertex) { 120 | return null; 121 | } 122 | 123 | return vertex.findEdge(endVertex); 124 | } 125 | 126 | /** 127 | * @return {number} 128 | */ 129 | getWeight() { 130 | return this.getAllEdges().reduce((weight, graphEdge) => { 131 | return weight + graphEdge.weight; 132 | }, 0); 133 | } 134 | 135 | /** 136 | * Reverse all the edges in directed graph. 137 | * @return {Graph} 138 | */ 139 | reverse() { 140 | /** @param {GraphEdge} edge */ 141 | this.getAllEdges().forEach((edge) => { 142 | // Delete straight edge from graph and from vertices. 143 | this.deleteEdge(edge); 144 | 145 | // Reverse the edge. 146 | edge.reverse(); 147 | 148 | // Add reversed edge back to the graph and its vertices. 149 | this.addEdge(edge); 150 | }); 151 | 152 | return this; 153 | } 154 | 155 | /** 156 | * @return {object} 157 | */ 158 | getVerticesIndices() { 159 | const verticesIndices = {}; 160 | this.getAllVertices().forEach((vertex, index) => { 161 | verticesIndices[vertex.getKey()] = index; 162 | }); 163 | 164 | return verticesIndices; 165 | } 166 | 167 | /** 168 | * @return {*[][]} 169 | */ 170 | getAdjacencyMatrix() { 171 | const vertices = this.getAllVertices(); 172 | const verticesIndices = this.getVerticesIndices(); 173 | 174 | // Init matrix with infinities meaning that there is no ways of 175 | // getting from one vertex to another yet. 176 | const adjacencyMatrix = Array(vertices.length).fill(null).map(() => { 177 | return Array(vertices.length).fill(Infinity); 178 | }); 179 | 180 | // Fill the columns. 181 | vertices.forEach((vertex, vertexIndex) => { 182 | vertex.getNeighbors().forEach((neighbor) => { 183 | const neighborIndex = verticesIndices[neighbor.getKey()]; 184 | adjacencyMatrix[vertexIndex][neighborIndex] = this.findEdge(vertex, neighbor).weight; 185 | }); 186 | }); 187 | 188 | return adjacencyMatrix; 189 | } 190 | 191 | /** 192 | * @return {string} 193 | */ 194 | toString() { 195 | return Object.keys(this.vertices).toString(); 196 | } 197 | } 198 | -------------------------------------------------------------------------------- /src/Day01-17/graph/GraphEdge.js: -------------------------------------------------------------------------------- 1 | export default class GraphEdge { 2 | /** 3 | * @param {GraphVertex} startVertex 4 | * @param {GraphVertex} endVertex 5 | * @param {number} [weight=1] 6 | */ 7 | constructor(startVertex, endVertex, weight = 0) { 8 | this.startVertex = startVertex; 9 | this.endVertex = endVertex; 10 | this.weight = weight; 11 | } 12 | 13 | /** 14 | * @return {string} 15 | */ 16 | getKey() { 17 | const startVertexKey = this.startVertex.getKey(); 18 | const endVertexKey = this.endVertex.getKey(); 19 | 20 | return `${startVertexKey}_${endVertexKey}`; 21 | } 22 | 23 | /** 24 | * @return {GraphEdge} 25 | */ 26 | reverse() { 27 | const tmp = this.startVertex; 28 | this.startVertex = this.endVertex; 29 | this.endVertex = tmp; 30 | 31 | return this; 32 | } 33 | 34 | /** 35 | * @return {string} 36 | */ 37 | toString() { 38 | return this.getKey(); 39 | } 40 | } 41 | -------------------------------------------------------------------------------- /src/Day01-17/graph/GraphVertex.js: -------------------------------------------------------------------------------- 1 | import LinkedList from '../linked-list/LinkedList'; 2 | 3 | export default class GraphVertex { 4 | /** 5 | * @param {*} value 6 | */ 7 | constructor(value) { 8 | if (value === undefined) { 9 | throw new Error('Graph vertex must have a value'); 10 | } 11 | 12 | /** 13 | * @param {GraphEdge} edgeA 14 | * @param {GraphEdge} edgeB 15 | */ 16 | const edgeComparator = (edgeA, edgeB) => { 17 | if (edgeA.getKey() === edgeB.getKey()) { 18 | return 0; 19 | } 20 | 21 | return edgeA.getKey() < edgeB.getKey() ? -1 : 1; 22 | }; 23 | 24 | // Normally you would store string value like vertex name. 25 | // But generally it may be any object as well 26 | this.value = value; 27 | this.edges = new LinkedList(edgeComparator); 28 | } 29 | 30 | /** 31 | * @param {GraphEdge} edge 32 | * @returns {GraphVertex} 33 | */ 34 | addEdge(edge) { 35 | this.edges.append(edge); 36 | 37 | return this; 38 | } 39 | 40 | /** 41 | * @param {GraphEdge} edge 42 | */ 43 | deleteEdge(edge) { 44 | this.edges.delete(edge); 45 | } 46 | 47 | /** 48 | * @returns {GraphVertex[]} 49 | */ 50 | getNeighbors() { 51 | const edges = this.edges.toArray(); 52 | 53 | /** @param {LinkedListNode} node */ 54 | const neighborsConverter = (node) => { 55 | return node.value.startVertex === this ? node.value.endVertex : node.value.startVertex; 56 | }; 57 | 58 | // Return either start or end vertex. 59 | // For undirected graphs it is possible that current vertex will be the end one. 60 | return edges.map(neighborsConverter); 61 | } 62 | 63 | /** 64 | * @return {GraphEdge[]} 65 | */ 66 | getEdges() { 67 | return this.edges.toArray().map((linkedListNode) => linkedListNode.value); 68 | } 69 | 70 | /** 71 | * @return {number} 72 | */ 73 | getDegree() { 74 | return this.edges.toArray().length; 75 | } 76 | 77 | /** 78 | * @param {GraphEdge} requiredEdge 79 | * @returns {boolean} 80 | */ 81 | hasEdge(requiredEdge) { 82 | const edgeNode = this.edges.find({ 83 | callback: (edge) => edge === requiredEdge, 84 | }); 85 | 86 | return !!edgeNode; 87 | } 88 | 89 | /** 90 | * @param {GraphVertex} vertex 91 | * @returns {boolean} 92 | */ 93 | hasNeighbor(vertex) { 94 | const vertexNode = this.edges.find({ 95 | callback: (edge) => edge.startVertex === vertex || edge.endVertex === vertex, 96 | }); 97 | 98 | return !!vertexNode; 99 | } 100 | 101 | /** 102 | * @param {GraphVertex} vertex 103 | * @returns {(GraphEdge|null)} 104 | */ 105 | findEdge(vertex) { 106 | const edgeFinder = (edge) => { 107 | return edge.startVertex === vertex || edge.endVertex === vertex; 108 | }; 109 | 110 | const edge = this.edges.find({ callback: edgeFinder }); 111 | 112 | return edge ? edge.value : null; 113 | } 114 | 115 | /** 116 | * @returns {string} 117 | */ 118 | getKey() { 119 | return this.value; 120 | } 121 | 122 | /** 123 | * @return {GraphVertex} 124 | */ 125 | deleteAllEdges() { 126 | this.getEdges().forEach((edge) => this.deleteEdge(edge)); 127 | 128 | return this; 129 | } 130 | 131 | /** 132 | * @param {function} [callback] 133 | * @returns {string} 134 | */ 135 | toString(callback) { 136 | return callback ? callback(this.value) : `${this.value}`; 137 | } 138 | } 139 | -------------------------------------------------------------------------------- /src/Day01-17/graph/__test__/GraphEdge.test.js: -------------------------------------------------------------------------------- 1 | import GraphEdge from '../GraphEdge'; 2 | import GraphVertex from '../GraphVertex'; 3 | 4 | describe('GraphEdge', () => { 5 | it('should create graph edge with default weight', () => { 6 | const startVertex = new GraphVertex('A'); 7 | const endVertex = new GraphVertex('B'); 8 | const edge = new GraphEdge(startVertex, endVertex); 9 | 10 | expect(edge.getKey()).toBe('A_B'); 11 | expect(edge.toString()).toBe('A_B'); 12 | expect(edge.startVertex).toEqual(startVertex); 13 | expect(edge.endVertex).toEqual(endVertex); 14 | expect(edge.weight).toEqual(0); 15 | }); 16 | 17 | it('should create graph edge with predefined weight', () => { 18 | const startVertex = new GraphVertex('A'); 19 | const endVertex = new GraphVertex('B'); 20 | const edge = new GraphEdge(startVertex, endVertex, 10); 21 | 22 | expect(edge.startVertex).toEqual(startVertex); 23 | expect(edge.endVertex).toEqual(endVertex); 24 | expect(edge.weight).toEqual(10); 25 | }); 26 | 27 | it('should be possible to do edge reverse', () => { 28 | const vertexA = new GraphVertex('A'); 29 | const vertexB = new GraphVertex('B'); 30 | const edge = new GraphEdge(vertexA, vertexB, 10); 31 | 32 | expect(edge.startVertex).toEqual(vertexA); 33 | expect(edge.endVertex).toEqual(vertexB); 34 | expect(edge.weight).toEqual(10); 35 | 36 | edge.reverse(); 37 | 38 | expect(edge.startVertex).toEqual(vertexB); 39 | expect(edge.endVertex).toEqual(vertexA); 40 | expect(edge.weight).toEqual(10); 41 | }); 42 | }); 43 | -------------------------------------------------------------------------------- /src/Day01-17/hash-table/HashTable.js: -------------------------------------------------------------------------------- 1 | import LinkedList from '../linked-list/LinkedList'; 2 | 3 | // Hash table size directly affects on the number of collisions. 4 | // The bigger the hash table size the less collisions you'll get. 5 | // For demonstrating purposes hash table size is small to show how collisions 6 | // are being handled. 7 | const defaultHashTableSize = 32; 8 | 9 | export default class HashTable { 10 | /** 11 | * @param {number} hashTableSize 12 | */ 13 | constructor(hashTableSize = defaultHashTableSize) { 14 | // Create hash table of certain size and fill each bucket with empty linked list. 15 | this.buckets = Array(hashTableSize).fill(null).map(() => new LinkedList()); 16 | 17 | // Just to keep track of all actual keys in a fast way. 18 | this.keys = {}; 19 | } 20 | 21 | /** 22 | * Converts key string to hash number. 23 | * 24 | * @param {string} key 25 | * @return {number} 26 | */ 27 | hash(key) { 28 | // For simplicity reasons we will just use character codes sum of all characters of the key 29 | // to calculate the hash. 30 | // 31 | // But you may also use more sophisticated approaches like polynomial string hash to reduce the 32 | // number of collisions: 33 | // 34 | // hash = charCodeAt(0) * PRIME^(n-1) + charCodeAt(1) * PRIME^(n-2) + ... + charCodeAt(n-1) 35 | // 36 | // where charCodeAt(i) is the i-th character code of the key, n is the length of the key and 37 | // PRIME is just any prime number like 31. 38 | const hash = Array.from(key).reduce( 39 | (hashAccumulator, keySymbol) => (hashAccumulator + keySymbol.charCodeAt(0)), 40 | 0, 41 | ); 42 | 43 | // Reduce hash number so it would fit hash table size. 44 | return hash % this.buckets.length; 45 | } 46 | 47 | /** 48 | * @param {string} key 49 | * @param {*} value 50 | */ 51 | set(key, value) { 52 | const keyHash = this.hash(key); 53 | this.keys[key] = keyHash; 54 | const bucketLinkedList = this.buckets[keyHash]; 55 | const node = bucketLinkedList.find({ callback: (nodeValue) => nodeValue.key === key }); 56 | 57 | if (!node) { 58 | // Insert new node. 59 | bucketLinkedList.append({ key, value }); 60 | } else { 61 | // Update value of existing node. 62 | node.value.value = value; 63 | } 64 | } 65 | 66 | /** 67 | * @param {string} key 68 | * @return {*} 69 | */ 70 | delete(key) { 71 | const keyHash = this.hash(key); 72 | delete this.keys[key]; 73 | const bucketLinkedList = this.buckets[keyHash]; 74 | const node = bucketLinkedList.find({ callback: (nodeValue) => nodeValue.key === key }); 75 | 76 | if (node) { 77 | return bucketLinkedList.delete(node.value); 78 | } 79 | 80 | return null; 81 | } 82 | 83 | /** 84 | * @param {string} key 85 | * @return {*} 86 | */ 87 | get(key) { 88 | const bucketLinkedList = this.buckets[this.hash(key)]; 89 | const node = bucketLinkedList.find({ callback: (nodeValue) => nodeValue.key === key }); 90 | 91 | return node ? node.value.value : undefined; 92 | } 93 | 94 | /** 95 | * @param {string} key 96 | * @return {boolean} 97 | */ 98 | has(key) { 99 | return Object.hasOwnProperty.call(this.keys, key); 100 | } 101 | 102 | /** 103 | * @return {string[]} 104 | */ 105 | getKeys() { 106 | return Object.keys(this.keys); 107 | } 108 | } 109 | -------------------------------------------------------------------------------- /src/Day01-17/hash-table/__test__/HashTable.test.js: -------------------------------------------------------------------------------- 1 | import HashTable from '../HashTable'; 2 | 3 | describe('HashTable', () => { 4 | it('should create hash table of certain size', () => { 5 | const defaultHashTable = new HashTable(); 6 | expect(defaultHashTable.buckets.length).toBe(32); 7 | 8 | const biggerHashTable = new HashTable(64); 9 | expect(biggerHashTable.buckets.length).toBe(64); 10 | }); 11 | 12 | it('should generate proper hash for specified keys', () => { 13 | const hashTable = new HashTable(); 14 | 15 | expect(hashTable.hash('a')).toBe(1); 16 | expect(hashTable.hash('b')).toBe(2); 17 | expect(hashTable.hash('abc')).toBe(6); 18 | }); 19 | 20 | it('should set, read and delete data with collisions', () => { 21 | const hashTable = new HashTable(3); 22 | 23 | expect(hashTable.hash('a')).toBe(1); 24 | expect(hashTable.hash('b')).toBe(2); 25 | expect(hashTable.hash('c')).toBe(0); 26 | expect(hashTable.hash('d')).toBe(1); 27 | 28 | hashTable.set('a', 'sky-old'); 29 | hashTable.set('a', 'sky'); 30 | hashTable.set('b', 'sea'); 31 | hashTable.set('c', 'earth'); 32 | hashTable.set('d', 'ocean'); 33 | 34 | expect(hashTable.has('x')).toBe(false); 35 | expect(hashTable.has('b')).toBe(true); 36 | expect(hashTable.has('c')).toBe(true); 37 | 38 | const stringifier = (value) => `${value.key}:${value.value}`; 39 | 40 | expect(hashTable.buckets[0].toString(stringifier)).toBe('c:earth'); 41 | expect(hashTable.buckets[1].toString(stringifier)).toBe('a:sky,d:ocean'); 42 | expect(hashTable.buckets[2].toString(stringifier)).toBe('b:sea'); 43 | 44 | expect(hashTable.get('a')).toBe('sky'); 45 | expect(hashTable.get('d')).toBe('ocean'); 46 | expect(hashTable.get('x')).not.toBeDefined(); 47 | 48 | hashTable.delete('a'); 49 | 50 | expect(hashTable.delete('not-existing')).toBeNull(); 51 | 52 | expect(hashTable.get('a')).not.toBeDefined(); 53 | expect(hashTable.get('d')).toBe('ocean'); 54 | 55 | hashTable.set('d', 'ocean-new'); 56 | expect(hashTable.get('d')).toBe('ocean-new'); 57 | }); 58 | 59 | it('should be possible to add objects to hash table', () => { 60 | const hashTable = new HashTable(); 61 | 62 | hashTable.set('objectKey', { prop1: 'a', prop2: 'b' }); 63 | 64 | const object = hashTable.get('objectKey'); 65 | expect(object).toBeDefined(); 66 | expect(object.prop1).toBe('a'); 67 | expect(object.prop2).toBe('b'); 68 | }); 69 | 70 | it('should track actual keys', () => { 71 | const hashTable = new HashTable(3); 72 | 73 | hashTable.set('a', 'sky-old'); 74 | hashTable.set('a', 'sky'); 75 | hashTable.set('b', 'sea'); 76 | hashTable.set('c', 'earth'); 77 | hashTable.set('d', 'ocean'); 78 | 79 | expect(hashTable.getKeys()).toEqual(['a', 'b', 'c', 'd']); 80 | expect(hashTable.has('a')).toBe(true); 81 | expect(hashTable.has('x')).toBe(false); 82 | 83 | hashTable.delete('a'); 84 | 85 | expect(hashTable.has('a')).toBe(false); 86 | expect(hashTable.has('b')).toBe(true); 87 | expect(hashTable.has('x')).toBe(false); 88 | }); 89 | }); 90 | -------------------------------------------------------------------------------- /src/Day01-17/heap/MaxHeap.js: -------------------------------------------------------------------------------- 1 | import Heap from './Heap'; 2 | 3 | export default class MaxHeap extends Heap { 4 | /** 5 | * Checks if pair of heap elements is in correct order. 6 | * For MinHeap the first element must be always smaller or equal. 7 | * For MaxHeap the first element must be always bigger or equal. 8 | * 9 | * @param {*} firstElement 10 | * @param {*} secondElement 11 | * @return {boolean} 12 | */ 13 | pairIsInCorrectOrder(firstElement, secondElement) { 14 | return this.compare.greaterThanOrEqual(firstElement, secondElement); 15 | } 16 | } 17 | -------------------------------------------------------------------------------- /src/Day01-17/heap/MinHeap.js: -------------------------------------------------------------------------------- 1 | import Heap from './Heap'; 2 | 3 | export default class MinHeap extends Heap { 4 | /** 5 | * Checks if pair of heap elements is in correct order. 6 | * For MinHeap the first element must be always smaller or equal. 7 | * For MaxHeap the first element must be always bigger or equal. 8 | * 9 | * @param {*} firstElement 10 | * @param {*} secondElement 11 | * @return {boolean} 12 | */ 13 | pairIsInCorrectOrder(firstElement, secondElement) { 14 | return this.compare.lessThanOrEqual(firstElement, secondElement); 15 | } 16 | } 17 | -------------------------------------------------------------------------------- /src/Day01-17/heap/__test__/Heap.test.js: -------------------------------------------------------------------------------- 1 | import Heap from '../Heap'; 2 | 3 | describe('Heap', () => { 4 | it('should not allow to create instance of the Heap directly', () => { 5 | const instantiateHeap = () => { 6 | const heap = new Heap(); 7 | heap.add(5); 8 | }; 9 | 10 | expect(instantiateHeap).toThrow(); 11 | }); 12 | }); 13 | -------------------------------------------------------------------------------- /src/Day01-17/heap/__test__/MaxHeap.test.js: -------------------------------------------------------------------------------- 1 | import MaxHeap from '../MaxHeap'; 2 | import Comparator from '../../../utils/comparator/Comparator'; 3 | 4 | describe('MaxHeap', () => { 5 | it('should create an empty max heap', () => { 6 | const maxHeap = new MaxHeap(); 7 | 8 | expect(maxHeap).toBeDefined(); 9 | expect(maxHeap.peek()).toBeNull(); 10 | expect(maxHeap.isEmpty()).toBe(true); 11 | }); 12 | 13 | it('should add items to the heap and heapify it up', () => { 14 | const maxHeap = new MaxHeap(); 15 | 16 | maxHeap.add(5); 17 | expect(maxHeap.isEmpty()).toBe(false); 18 | expect(maxHeap.peek()).toBe(5); 19 | expect(maxHeap.toString()).toBe('5'); 20 | 21 | maxHeap.add(3); 22 | expect(maxHeap.peek()).toBe(5); 23 | expect(maxHeap.toString()).toBe('5,3'); 24 | 25 | maxHeap.add(10); 26 | expect(maxHeap.peek()).toBe(10); 27 | expect(maxHeap.toString()).toBe('10,3,5'); 28 | 29 | maxHeap.add(1); 30 | expect(maxHeap.peek()).toBe(10); 31 | expect(maxHeap.toString()).toBe('10,3,5,1'); 32 | 33 | maxHeap.add(1); 34 | expect(maxHeap.peek()).toBe(10); 35 | expect(maxHeap.toString()).toBe('10,3,5,1,1'); 36 | 37 | expect(maxHeap.poll()).toBe(10); 38 | expect(maxHeap.toString()).toBe('5,3,1,1'); 39 | 40 | expect(maxHeap.poll()).toBe(5); 41 | expect(maxHeap.toString()).toBe('3,1,1'); 42 | 43 | expect(maxHeap.poll()).toBe(3); 44 | expect(maxHeap.toString()).toBe('1,1'); 45 | }); 46 | 47 | it('should poll items from the heap and heapify it down', () => { 48 | const maxHeap = new MaxHeap(); 49 | 50 | maxHeap.add(5); 51 | maxHeap.add(3); 52 | maxHeap.add(10); 53 | maxHeap.add(11); 54 | maxHeap.add(1); 55 | 56 | expect(maxHeap.toString()).toBe('11,10,5,3,1'); 57 | 58 | expect(maxHeap.poll()).toBe(11); 59 | expect(maxHeap.toString()).toBe('10,3,5,1'); 60 | 61 | expect(maxHeap.poll()).toBe(10); 62 | expect(maxHeap.toString()).toBe('5,3,1'); 63 | 64 | expect(maxHeap.poll()).toBe(5); 65 | expect(maxHeap.toString()).toBe('3,1'); 66 | 67 | expect(maxHeap.poll()).toBe(3); 68 | expect(maxHeap.toString()).toBe('1'); 69 | 70 | expect(maxHeap.poll()).toBe(1); 71 | expect(maxHeap.toString()).toBe(''); 72 | 73 | expect(maxHeap.poll()).toBeNull(); 74 | expect(maxHeap.toString()).toBe(''); 75 | }); 76 | 77 | it('should heapify down through the right branch as well', () => { 78 | const maxHeap = new MaxHeap(); 79 | 80 | maxHeap.add(3); 81 | maxHeap.add(12); 82 | maxHeap.add(10); 83 | 84 | expect(maxHeap.toString()).toBe('12,3,10'); 85 | 86 | maxHeap.add(11); 87 | expect(maxHeap.toString()).toBe('12,11,10,3'); 88 | 89 | expect(maxHeap.poll()).toBe(12); 90 | expect(maxHeap.toString()).toBe('11,3,10'); 91 | }); 92 | 93 | it('should be possible to find item indices in heap', () => { 94 | const maxHeap = new MaxHeap(); 95 | 96 | maxHeap.add(3); 97 | maxHeap.add(12); 98 | maxHeap.add(10); 99 | maxHeap.add(11); 100 | maxHeap.add(11); 101 | 102 | expect(maxHeap.toString()).toBe('12,11,10,3,11'); 103 | 104 | expect(maxHeap.find(5)).toEqual([]); 105 | expect(maxHeap.find(12)).toEqual([0]); 106 | expect(maxHeap.find(11)).toEqual([1, 4]); 107 | }); 108 | 109 | it('should be possible to remove items from heap with heapify down', () => { 110 | const maxHeap = new MaxHeap(); 111 | 112 | maxHeap.add(3); 113 | maxHeap.add(12); 114 | maxHeap.add(10); 115 | maxHeap.add(11); 116 | maxHeap.add(11); 117 | 118 | expect(maxHeap.toString()).toBe('12,11,10,3,11'); 119 | 120 | expect(maxHeap.remove(12).toString()).toEqual('11,11,10,3'); 121 | expect(maxHeap.remove(12).peek()).toEqual(11); 122 | expect(maxHeap.remove(11).toString()).toEqual('10,3'); 123 | expect(maxHeap.remove(10).peek()).toEqual(3); 124 | }); 125 | 126 | it('should be possible to remove items from heap with heapify up', () => { 127 | const maxHeap = new MaxHeap(); 128 | 129 | maxHeap.add(3); 130 | maxHeap.add(10); 131 | maxHeap.add(5); 132 | maxHeap.add(6); 133 | maxHeap.add(7); 134 | maxHeap.add(4); 135 | maxHeap.add(6); 136 | maxHeap.add(8); 137 | maxHeap.add(2); 138 | maxHeap.add(1); 139 | 140 | expect(maxHeap.toString()).toBe('10,8,6,7,6,4,5,3,2,1'); 141 | expect(maxHeap.remove(4).toString()).toEqual('10,8,6,7,6,1,5,3,2'); 142 | expect(maxHeap.remove(3).toString()).toEqual('10,8,6,7,6,1,5,2'); 143 | expect(maxHeap.remove(5).toString()).toEqual('10,8,6,7,6,1,2'); 144 | expect(maxHeap.remove(10).toString()).toEqual('8,7,6,2,6,1'); 145 | expect(maxHeap.remove(6).toString()).toEqual('8,7,1,2'); 146 | expect(maxHeap.remove(2).toString()).toEqual('8,7,1'); 147 | expect(maxHeap.remove(1).toString()).toEqual('8,7'); 148 | expect(maxHeap.remove(7).toString()).toEqual('8'); 149 | expect(maxHeap.remove(8).toString()).toEqual(''); 150 | }); 151 | 152 | it('should be possible to remove items from heap with custom finding comparator', () => { 153 | const maxHeap = new MaxHeap(); 154 | maxHeap.add('a'); 155 | maxHeap.add('bb'); 156 | maxHeap.add('ccc'); 157 | maxHeap.add('dddd'); 158 | 159 | expect(maxHeap.toString()).toBe('dddd,ccc,bb,a'); 160 | 161 | const comparator = new Comparator((a, b) => { 162 | if (a.length === b.length) { 163 | return 0; 164 | } 165 | 166 | return a.length < b.length ? -1 : 1; 167 | }); 168 | 169 | maxHeap.remove('hey', comparator); 170 | expect(maxHeap.toString()).toBe('dddd,a,bb'); 171 | }); 172 | }); 173 | -------------------------------------------------------------------------------- /src/Day01-17/heap/__test__/MinHeap.test.js: -------------------------------------------------------------------------------- 1 | import MinHeap from '../MinHeap'; 2 | import Comparator from '../../../utils/comparator/Comparator'; 3 | 4 | describe('MinHeap', () => { 5 | it('should create an empty min heap', () => { 6 | const minHeap = new MinHeap(); 7 | 8 | expect(minHeap).toBeDefined(); 9 | expect(minHeap.peek()).toBeNull(); 10 | expect(minHeap.isEmpty()).toBe(true); 11 | }); 12 | 13 | it('should add items to the heap and heapify it up', () => { 14 | const minHeap = new MinHeap(); 15 | 16 | minHeap.add(5); 17 | expect(minHeap.isEmpty()).toBe(false); 18 | expect(minHeap.peek()).toBe(5); 19 | expect(minHeap.toString()).toBe('5'); 20 | 21 | minHeap.add(3); 22 | expect(minHeap.peek()).toBe(3); 23 | expect(minHeap.toString()).toBe('3,5'); 24 | 25 | minHeap.add(10); 26 | expect(minHeap.peek()).toBe(3); 27 | expect(minHeap.toString()).toBe('3,5,10'); 28 | 29 | minHeap.add(1); 30 | expect(minHeap.peek()).toBe(1); 31 | expect(minHeap.toString()).toBe('1,3,10,5'); 32 | 33 | minHeap.add(1); 34 | expect(minHeap.peek()).toBe(1); 35 | expect(minHeap.toString()).toBe('1,1,10,5,3'); 36 | 37 | expect(minHeap.poll()).toBe(1); 38 | expect(minHeap.toString()).toBe('1,3,10,5'); 39 | 40 | expect(minHeap.poll()).toBe(1); 41 | expect(minHeap.toString()).toBe('3,5,10'); 42 | 43 | expect(minHeap.poll()).toBe(3); 44 | expect(minHeap.toString()).toBe('5,10'); 45 | }); 46 | 47 | it('should poll items from the heap and heapify it down', () => { 48 | const minHeap = new MinHeap(); 49 | 50 | minHeap.add(5); 51 | minHeap.add(3); 52 | minHeap.add(10); 53 | minHeap.add(11); 54 | minHeap.add(1); 55 | 56 | expect(minHeap.toString()).toBe('1,3,10,11,5'); 57 | 58 | expect(minHeap.poll()).toBe(1); 59 | expect(minHeap.toString()).toBe('3,5,10,11'); 60 | 61 | expect(minHeap.poll()).toBe(3); 62 | expect(minHeap.toString()).toBe('5,11,10'); 63 | 64 | expect(minHeap.poll()).toBe(5); 65 | expect(minHeap.toString()).toBe('10,11'); 66 | 67 | expect(minHeap.poll()).toBe(10); 68 | expect(minHeap.toString()).toBe('11'); 69 | 70 | expect(minHeap.poll()).toBe(11); 71 | expect(minHeap.toString()).toBe(''); 72 | 73 | expect(minHeap.poll()).toBeNull(); 74 | expect(minHeap.toString()).toBe(''); 75 | }); 76 | 77 | it('should heapify down through the right branch as well', () => { 78 | const minHeap = new MinHeap(); 79 | 80 | minHeap.add(3); 81 | minHeap.add(12); 82 | minHeap.add(10); 83 | 84 | expect(minHeap.toString()).toBe('3,12,10'); 85 | 86 | minHeap.add(11); 87 | expect(minHeap.toString()).toBe('3,11,10,12'); 88 | 89 | expect(minHeap.poll()).toBe(3); 90 | expect(minHeap.toString()).toBe('10,11,12'); 91 | }); 92 | 93 | it('should be possible to find item indices in heap', () => { 94 | const minHeap = new MinHeap(); 95 | 96 | minHeap.add(3); 97 | minHeap.add(12); 98 | minHeap.add(10); 99 | minHeap.add(11); 100 | minHeap.add(11); 101 | 102 | expect(minHeap.toString()).toBe('3,11,10,12,11'); 103 | 104 | expect(minHeap.find(5)).toEqual([]); 105 | expect(minHeap.find(3)).toEqual([0]); 106 | expect(minHeap.find(11)).toEqual([1, 4]); 107 | }); 108 | 109 | it('should be possible to remove items from heap with heapify down', () => { 110 | const minHeap = new MinHeap(); 111 | 112 | minHeap.add(3); 113 | minHeap.add(12); 114 | minHeap.add(10); 115 | minHeap.add(11); 116 | minHeap.add(11); 117 | 118 | expect(minHeap.toString()).toBe('3,11,10,12,11'); 119 | 120 | expect(minHeap.remove(3).toString()).toEqual('10,11,11,12'); 121 | expect(minHeap.remove(3).peek()).toEqual(10); 122 | expect(minHeap.remove(11).toString()).toEqual('10,12'); 123 | expect(minHeap.remove(3).peek()).toEqual(10); 124 | }); 125 | 126 | it('should be possible to remove items from heap with heapify up', () => { 127 | const minHeap = new MinHeap(); 128 | 129 | minHeap.add(3); 130 | minHeap.add(10); 131 | minHeap.add(5); 132 | minHeap.add(6); 133 | minHeap.add(7); 134 | minHeap.add(4); 135 | minHeap.add(6); 136 | minHeap.add(8); 137 | minHeap.add(2); 138 | minHeap.add(1); 139 | 140 | expect(minHeap.toString()).toBe('1,2,4,6,3,5,6,10,8,7'); 141 | expect(minHeap.remove(8).toString()).toEqual('1,2,4,6,3,5,6,10,7'); 142 | expect(minHeap.remove(7).toString()).toEqual('1,2,4,6,3,5,6,10'); 143 | expect(minHeap.remove(1).toString()).toEqual('2,3,4,6,10,5,6'); 144 | expect(minHeap.remove(2).toString()).toEqual('3,6,4,6,10,5'); 145 | expect(minHeap.remove(6).toString()).toEqual('3,5,4,10'); 146 | expect(minHeap.remove(10).toString()).toEqual('3,5,4'); 147 | expect(minHeap.remove(5).toString()).toEqual('3,4'); 148 | expect(minHeap.remove(3).toString()).toEqual('4'); 149 | expect(minHeap.remove(4).toString()).toEqual(''); 150 | }); 151 | 152 | it('should be possible to remove items from heap with custom finding comparator', () => { 153 | const minHeap = new MinHeap(); 154 | minHeap.add('dddd'); 155 | minHeap.add('ccc'); 156 | minHeap.add('bb'); 157 | minHeap.add('a'); 158 | 159 | expect(minHeap.toString()).toBe('a,bb,ccc,dddd'); 160 | 161 | const comparator = new Comparator((a, b) => { 162 | if (a.length === b.length) { 163 | return 0; 164 | } 165 | 166 | return a.length < b.length ? -1 : 1; 167 | }); 168 | 169 | minHeap.remove('hey', comparator); 170 | expect(minHeap.toString()).toBe('a,bb,dddd'); 171 | }); 172 | 173 | it('should remove values from heap and correctly re-order the tree', () => { 174 | const minHeap = new MinHeap(); 175 | 176 | minHeap.add(1); 177 | minHeap.add(2); 178 | minHeap.add(3); 179 | minHeap.add(4); 180 | minHeap.add(5); 181 | minHeap.add(6); 182 | minHeap.add(7); 183 | minHeap.add(8); 184 | minHeap.add(9); 185 | 186 | expect(minHeap.toString()).toBe('1,2,3,4,5,6,7,8,9'); 187 | 188 | minHeap.remove(2); 189 | expect(minHeap.toString()).toBe('1,4,3,8,5,6,7,9'); 190 | 191 | minHeap.remove(4); 192 | expect(minHeap.toString()).toBe('1,5,3,8,9,6,7'); 193 | }); 194 | }); 195 | -------------------------------------------------------------------------------- /src/Day01-17/linked-list/LinkedList.js: -------------------------------------------------------------------------------- 1 | import LinkedListNode from './LinkedListNode'; 2 | import Comparator from '../../utils/comparator/Comparator'; 3 | 4 | export default class LinkedList { 5 | /** 6 | * @param {Function} [comparatorFunction] 7 | */ 8 | constructor(comparatorFunction) { 9 | /** @var LinkedListNode */ 10 | this.head = null; 11 | 12 | /** @var LinkedListNode */ 13 | this.tail = null; 14 | 15 | this.compare = new Comparator(comparatorFunction); 16 | } 17 | 18 | /** 19 | * @param {*} value 20 | * @return {LinkedList} 21 | */ 22 | prepend(value) { 23 | // Make new node to be a head. 24 | const newNode = new LinkedListNode(value, this.head); 25 | this.head = newNode; 26 | 27 | // If there is no tail yet let's make new node a tail. 28 | if (!this.tail) { 29 | this.tail = newNode; 30 | } 31 | 32 | return this; 33 | } 34 | 35 | /** 36 | * @param {*} value 37 | * @return {LinkedList} 38 | */ 39 | append(value) { 40 | const newNode = new LinkedListNode(value); 41 | 42 | // If there is no head yet let's make new node a head. 43 | if (!this.head) { 44 | this.head = newNode; 45 | this.tail = newNode; 46 | 47 | return this; 48 | } 49 | 50 | // Attach new node to the end of linked list. 51 | this.tail.next = newNode; 52 | this.tail = newNode; 53 | 54 | return this; 55 | } 56 | 57 | /** 58 | * @param {*} value 59 | * @return {LinkedListNode} 60 | */ 61 | delete(value) { 62 | if (!this.head) { 63 | return null; 64 | } 65 | 66 | let deletedNode = null; 67 | 68 | // If the head must be deleted then make next node that is differ 69 | // from the head to be a new head. 70 | while (this.head && this.compare.equal(this.head.value, value)) { 71 | deletedNode = this.head; 72 | this.head = this.head.next; 73 | } 74 | 75 | let currentNode = this.head; 76 | 77 | if (currentNode !== null) { 78 | // If next node must be deleted then make next node to be a next next one. 79 | while (currentNode.next) { 80 | if (this.compare.equal(currentNode.next.value, value)) { 81 | deletedNode = currentNode.next; 82 | currentNode.next = currentNode.next.next; 83 | } else { 84 | currentNode = currentNode.next; 85 | } 86 | } 87 | } 88 | 89 | // Check if tail must be deleted. 90 | if (this.compare.equal(this.tail.value, value)) { 91 | this.tail = currentNode; 92 | } 93 | 94 | return deletedNode; 95 | } 96 | 97 | /** 98 | * @param {Object} findParams 99 | * @param {*} findParams.value 100 | * @param {function} [findParams.callback] 101 | * @return {LinkedListNode} 102 | */ 103 | find({ value = undefined, callback = undefined }) { 104 | if (!this.head) { 105 | return null; 106 | } 107 | 108 | let currentNode = this.head; 109 | 110 | while (currentNode) { 111 | // If callback is specified then try to find node by callback. 112 | if (callback && callback(currentNode.value)) { 113 | return currentNode; 114 | } 115 | 116 | // If value is specified then try to compare by value.. 117 | if (value !== undefined && this.compare.equal(currentNode.value, value)) { 118 | return currentNode; 119 | } 120 | 121 | currentNode = currentNode.next; 122 | } 123 | 124 | return null; 125 | } 126 | 127 | /** 128 | * @return {LinkedListNode} 129 | */ 130 | deleteTail() { 131 | const deletedTail = this.tail; 132 | 133 | if (this.head === this.tail) { 134 | // There is only one node in linked list. 135 | this.head = null; 136 | this.tail = null; 137 | 138 | return deletedTail; 139 | } 140 | 141 | // If there are many nodes in linked list... 142 | 143 | // Rewind to the last node and delete "next" link for the node before the last one. 144 | let currentNode = this.head; 145 | while (currentNode.next) { 146 | if (!currentNode.next.next) { 147 | currentNode.next = null; 148 | } else { 149 | currentNode = currentNode.next; 150 | } 151 | } 152 | 153 | this.tail = currentNode; 154 | 155 | return deletedTail; 156 | } 157 | 158 | /** 159 | * @return {LinkedListNode} 160 | */ 161 | deleteHead() { 162 | if (!this.head) { 163 | return null; 164 | } 165 | 166 | const deletedHead = this.head; 167 | 168 | if (this.head.next) { 169 | this.head = this.head.next; 170 | } else { 171 | this.head = null; 172 | this.tail = null; 173 | } 174 | 175 | return deletedHead; 176 | } 177 | 178 | /** 179 | * @param {*[]} values - Array of values that need to be converted to linked list. 180 | * @return {LinkedList} 181 | */ 182 | fromArray(values) { 183 | values.forEach((value) => this.append(value)); 184 | 185 | return this; 186 | } 187 | 188 | /** 189 | * @return {LinkedListNode[]} 190 | */ 191 | toArray() { 192 | const nodes = []; 193 | 194 | let currentNode = this.head; 195 | while (currentNode) { 196 | nodes.push(currentNode); 197 | currentNode = currentNode.next; 198 | } 199 | 200 | return nodes; 201 | } 202 | 203 | /** 204 | * @param {function} [callback] 205 | * @return {string} 206 | */ 207 | toString(callback) { 208 | return this.toArray().map((node) => node.toString(callback)).toString(); 209 | } 210 | 211 | /** 212 | * Reverse a linked list. 213 | * @returns {LinkedList} 214 | */ 215 | reverse() { 216 | let currNode = this.head; 217 | let prevNode = null; 218 | let nextNode = null; 219 | 220 | while (currNode) { 221 | // Store next node. 222 | nextNode = currNode.next; 223 | 224 | // Change next node of the current node so it would link to previous node. 225 | currNode.next = prevNode; 226 | 227 | // Move prevNode and currNode nodes one step forward. 228 | prevNode = currNode; 229 | currNode = nextNode; 230 | } 231 | 232 | // Reset head and tail. 233 | this.tail = this.head; 234 | this.head = prevNode; 235 | 236 | return this; 237 | } 238 | } 239 | -------------------------------------------------------------------------------- /src/Day01-17/linked-list/LinkedListNode.js: -------------------------------------------------------------------------------- 1 | export default class LinkedListNode { 2 | constructor(value, next = null) { 3 | this.value = value; 4 | this.next = next; 5 | } 6 | 7 | toString(callback) { 8 | return callback ? callback(this.value) : `${this.value}`; 9 | } 10 | } 11 | -------------------------------------------------------------------------------- /src/Day01-17/linked-list/__test__/LinkedListNode.test.js: -------------------------------------------------------------------------------- 1 | import LinkedListNode from '../LinkedListNode'; 2 | 3 | describe('LinkedListNode', () => { 4 | it('should create list node with value', () => { 5 | const node = new LinkedListNode(1); 6 | 7 | expect(node.value).toBe(1); 8 | expect(node.next).toBeNull(); 9 | }); 10 | 11 | it('should create list node with object as a value', () => { 12 | const nodeValue = { value: 1, key: 'test' }; 13 | const node = new LinkedListNode(nodeValue); 14 | 15 | expect(node.value.value).toBe(1); 16 | expect(node.value.key).toBe('test'); 17 | expect(node.next).toBeNull(); 18 | }); 19 | 20 | it('should link nodes together', () => { 21 | const node2 = new LinkedListNode(2); 22 | const node1 = new LinkedListNode(1, node2); 23 | 24 | expect(node1.next).toBeDefined(); 25 | expect(node2.next).toBeNull(); 26 | expect(node1.value).toBe(1); 27 | expect(node1.next.value).toBe(2); 28 | }); 29 | 30 | it('should convert node to string', () => { 31 | const node = new LinkedListNode(1); 32 | 33 | expect(node.toString()).toBe('1'); 34 | 35 | node.value = 'string value'; 36 | expect(node.toString()).toBe('string value'); 37 | }); 38 | 39 | it('should convert node to string with custom stringifier', () => { 40 | const nodeValue = { value: 1, key: 'test' }; 41 | const node = new LinkedListNode(nodeValue); 42 | const toStringCallback = (value) => `value: ${value.value}, key: ${value.key}`; 43 | 44 | expect(node.toString(toStringCallback)).toBe('value: 1, key: test'); 45 | }); 46 | }); 47 | -------------------------------------------------------------------------------- /src/Day01-17/priority-queue/PriorityQueue.js: -------------------------------------------------------------------------------- 1 | import MinHeap from '../heap/MinHeap'; 2 | import Comparator from '../../utils/comparator/Comparator'; 3 | 4 | // It is the same as min heap except that when comparing two elements 5 | // we take into account its priority instead of the element's value. 6 | export default class PriorityQueue extends MinHeap { 7 | constructor() { 8 | // Call MinHip constructor first. 9 | super(); 10 | 11 | // Setup priorities map. 12 | this.priorities = new Map(); 13 | 14 | // Use custom comparator for heap elements that will take element priority 15 | // instead of element value into account. 16 | this.compare = new Comparator(this.comparePriority.bind(this)); 17 | } 18 | 19 | /** 20 | * Add item to the priority queue. 21 | * @param {*} item - item we're going to add to the queue. 22 | * @param {number} [priority] - items priority. 23 | * @return {PriorityQueue} 24 | */ 25 | add(item, priority = 0) { 26 | this.priorities.set(item, priority); 27 | super.add(item); 28 | return this; 29 | } 30 | 31 | /** 32 | * Remove item from priority queue. 33 | * @param {*} item - item we're going to remove. 34 | * @param {Comparator} [customFindingComparator] - custom function for finding the item to remove 35 | * @return {PriorityQueue} 36 | */ 37 | remove(item, customFindingComparator) { 38 | super.remove(item, customFindingComparator); 39 | this.priorities.delete(item); 40 | return this; 41 | } 42 | 43 | /** 44 | * Change priority of the item in a queue. 45 | * @param {*} item - item we're going to re-prioritize. 46 | * @param {number} priority - new item's priority. 47 | * @return {PriorityQueue} 48 | */ 49 | changePriority(item, priority) { 50 | this.remove(item, new Comparator(this.compareValue)); 51 | this.add(item, priority); 52 | return this; 53 | } 54 | 55 | /** 56 | * Find item by ite value. 57 | * @param {*} item 58 | * @return {Number[]} 59 | */ 60 | findByValue(item) { 61 | return this.find(item, new Comparator(this.compareValue)); 62 | } 63 | 64 | /** 65 | * Check if item already exists in a queue. 66 | * @param {*} item 67 | * @return {boolean} 68 | */ 69 | hasValue(item) { 70 | return this.findByValue(item).length > 0; 71 | } 72 | 73 | /** 74 | * Compares priorities of two items. 75 | * @param {*} a 76 | * @param {*} b 77 | * @return {number} 78 | */ 79 | comparePriority(a, b) { 80 | if (this.priorities.get(a) === this.priorities.get(b)) { 81 | return 0; 82 | } 83 | return this.priorities.get(a) < this.priorities.get(b) ? -1 : 1; 84 | } 85 | 86 | /** 87 | * Compares values of two items. 88 | * @param {*} a 89 | * @param {*} b 90 | * @return {number} 91 | */ 92 | compareValue(a, b) { 93 | if (a === b) { 94 | return 0; 95 | } 96 | return a < b ? -1 : 1; 97 | } 98 | } 99 | -------------------------------------------------------------------------------- /src/Day01-17/priority-queue/__test__/PriorityQueue.test.js: -------------------------------------------------------------------------------- 1 | import PriorityQueue from '../PriorityQueue'; 2 | 3 | describe('PriorityQueue', () => { 4 | it('should create default priority queue', () => { 5 | const priorityQueue = new PriorityQueue(); 6 | 7 | expect(priorityQueue).toBeDefined(); 8 | }); 9 | 10 | it('should insert items to the queue and respect priorities', () => { 11 | const priorityQueue = new PriorityQueue(); 12 | 13 | priorityQueue.add(10, 1); 14 | expect(priorityQueue.peek()).toBe(10); 15 | 16 | priorityQueue.add(5, 2); 17 | expect(priorityQueue.peek()).toBe(10); 18 | 19 | priorityQueue.add(100, 0); 20 | expect(priorityQueue.peek()).toBe(100); 21 | }); 22 | 23 | it('should be possible to use objects in priority queue', () => { 24 | const priorityQueue = new PriorityQueue(); 25 | 26 | const user1 = { name: 'Mike' }; 27 | const user2 = { name: 'Bill' }; 28 | const user3 = { name: 'Jane' }; 29 | 30 | priorityQueue.add(user1, 1); 31 | expect(priorityQueue.peek()).toBe(user1); 32 | 33 | priorityQueue.add(user2, 2); 34 | expect(priorityQueue.peek()).toBe(user1); 35 | 36 | priorityQueue.add(user3, 0); 37 | expect(priorityQueue.peek()).toBe(user3); 38 | }); 39 | 40 | it('should poll from queue with respect to priorities', () => { 41 | const priorityQueue = new PriorityQueue(); 42 | 43 | priorityQueue.add(10, 1); 44 | priorityQueue.add(5, 2); 45 | priorityQueue.add(100, 0); 46 | priorityQueue.add(200, 0); 47 | 48 | expect(priorityQueue.poll()).toBe(100); 49 | expect(priorityQueue.poll()).toBe(200); 50 | expect(priorityQueue.poll()).toBe(10); 51 | expect(priorityQueue.poll()).toBe(5); 52 | }); 53 | 54 | it('should be possible to change priority of head node', () => { 55 | const priorityQueue = new PriorityQueue(); 56 | 57 | priorityQueue.add(10, 1); 58 | priorityQueue.add(5, 2); 59 | priorityQueue.add(100, 0); 60 | priorityQueue.add(200, 0); 61 | 62 | expect(priorityQueue.peek()).toBe(100); 63 | 64 | priorityQueue.changePriority(100, 10); 65 | priorityQueue.changePriority(10, 20); 66 | 67 | expect(priorityQueue.poll()).toBe(200); 68 | expect(priorityQueue.poll()).toBe(5); 69 | expect(priorityQueue.poll()).toBe(100); 70 | expect(priorityQueue.poll()).toBe(10); 71 | }); 72 | 73 | it('should be possible to change priority of internal nodes', () => { 74 | const priorityQueue = new PriorityQueue(); 75 | 76 | priorityQueue.add(10, 1); 77 | priorityQueue.add(5, 2); 78 | priorityQueue.add(100, 0); 79 | priorityQueue.add(200, 0); 80 | 81 | expect(priorityQueue.peek()).toBe(100); 82 | 83 | priorityQueue.changePriority(200, 10); 84 | priorityQueue.changePriority(10, 20); 85 | 86 | expect(priorityQueue.poll()).toBe(100); 87 | expect(priorityQueue.poll()).toBe(5); 88 | expect(priorityQueue.poll()).toBe(200); 89 | expect(priorityQueue.poll()).toBe(10); 90 | }); 91 | 92 | it('should be possible to change priority along with node addition', () => { 93 | const priorityQueue = new PriorityQueue(); 94 | 95 | priorityQueue.add(10, 1); 96 | priorityQueue.add(5, 2); 97 | priorityQueue.add(100, 0); 98 | priorityQueue.add(200, 0); 99 | 100 | priorityQueue.changePriority(200, 10); 101 | priorityQueue.changePriority(10, 20); 102 | 103 | priorityQueue.add(15, 15); 104 | 105 | expect(priorityQueue.poll()).toBe(100); 106 | expect(priorityQueue.poll()).toBe(5); 107 | expect(priorityQueue.poll()).toBe(200); 108 | expect(priorityQueue.poll()).toBe(15); 109 | expect(priorityQueue.poll()).toBe(10); 110 | }); 111 | 112 | it('should be possible to search in priority queue by value', () => { 113 | const priorityQueue = new PriorityQueue(); 114 | 115 | priorityQueue.add(10, 1); 116 | priorityQueue.add(5, 2); 117 | priorityQueue.add(100, 0); 118 | priorityQueue.add(200, 0); 119 | priorityQueue.add(15, 15); 120 | 121 | expect(priorityQueue.hasValue(70)).toBe(false); 122 | expect(priorityQueue.hasValue(15)).toBe(true); 123 | }); 124 | }); 125 | -------------------------------------------------------------------------------- /src/Day01-17/queue/Queue.js: -------------------------------------------------------------------------------- 1 | import LinkedList from '../linked-list/LinkedList'; 2 | 3 | export default class Queue { 4 | constructor() { 5 | // We're going to implement Queue based on LinkedList since the two 6 | // structures are quite similar. Namely, they both operate mostly on 7 | // the elements at the beginning and the end. Compare enqueue/dequeue 8 | // operations of Queue with append/deleteHead operations of LinkedList. 9 | this.linkedList = new LinkedList(); 10 | } 11 | 12 | /** 13 | * @return {boolean} 14 | */ 15 | isEmpty() { 16 | return !this.linkedList.head; 17 | } 18 | 19 | /** 20 | * Read the element at the front of the queue without removing it. 21 | * @return {*} 22 | */ 23 | peek() { 24 | if (!this.linkedList.head) { 25 | return null; 26 | } 27 | 28 | return this.linkedList.head.value; 29 | } 30 | 31 | /** 32 | * Add a new element to the end of the queue (the tail of the linked list). 33 | * This element will be processed after all elements ahead of it. 34 | * @param {*} value 35 | */ 36 | enqueue(value) { 37 | this.linkedList.append(value); 38 | } 39 | 40 | /** 41 | * Remove the element at the front of the queue (the head of the linked list). 42 | * If the queue is empty, return null. 43 | * @return {*} 44 | */ 45 | dequeue() { 46 | const removedHead = this.linkedList.deleteHead(); 47 | return removedHead ? removedHead.value : null; 48 | } 49 | 50 | /** 51 | * @param [callback] 52 | * @return {string} 53 | */ 54 | toString(callback) { 55 | // Return string representation of the queue's linked list. 56 | return this.linkedList.toString(callback); 57 | } 58 | } 59 | -------------------------------------------------------------------------------- /src/Day01-17/queue/__test__/Queue.test.js: -------------------------------------------------------------------------------- 1 | import Queue from '../Queue'; 2 | 3 | describe('Queue', () => { 4 | it('should create empty queue', () => { 5 | const queue = new Queue(); 6 | expect(queue).not.toBeNull(); 7 | expect(queue.linkedList).not.toBeNull(); 8 | }); 9 | 10 | it('should enqueue data to queue', () => { 11 | const queue = new Queue(); 12 | 13 | queue.enqueue(1); 14 | queue.enqueue(2); 15 | 16 | expect(queue.toString()).toBe('1,2'); 17 | }); 18 | 19 | it('should be possible to enqueue/dequeue objects', () => { 20 | const queue = new Queue(); 21 | 22 | queue.enqueue({ value: 'test1', key: 'key1' }); 23 | queue.enqueue({ value: 'test2', key: 'key2' }); 24 | 25 | const stringifier = (value) => `${value.key}:${value.value}`; 26 | 27 | expect(queue.toString(stringifier)).toBe('key1:test1,key2:test2'); 28 | expect(queue.dequeue().value).toBe('test1'); 29 | expect(queue.dequeue().value).toBe('test2'); 30 | }); 31 | 32 | it('should peek data from queue', () => { 33 | const queue = new Queue(); 34 | 35 | expect(queue.peek()).toBeNull(); 36 | 37 | queue.enqueue(1); 38 | queue.enqueue(2); 39 | 40 | expect(queue.peek()).toBe(1); 41 | expect(queue.peek()).toBe(1); 42 | }); 43 | 44 | it('should check if queue is empty', () => { 45 | const queue = new Queue(); 46 | 47 | expect(queue.isEmpty()).toBe(true); 48 | 49 | queue.enqueue(1); 50 | 51 | expect(queue.isEmpty()).toBe(false); 52 | }); 53 | 54 | it('should dequeue from queue in FIFO order', () => { 55 | const queue = new Queue(); 56 | 57 | queue.enqueue(1); 58 | queue.enqueue(2); 59 | 60 | expect(queue.dequeue()).toBe(1); 61 | expect(queue.dequeue()).toBe(2); 62 | expect(queue.dequeue()).toBeNull(); 63 | expect(queue.isEmpty()).toBe(true); 64 | }); 65 | }); 66 | -------------------------------------------------------------------------------- /src/Day01-17/stack/Stack.js: -------------------------------------------------------------------------------- 1 | import LinkedList from '../linked-list/LinkedList'; 2 | 3 | export default class Stack { 4 | constructor() { 5 | // We're going to implement Stack based on LinkedList since these 6 | // structures are quite similar. Compare push/pop operations of the Stack 7 | // with prepend/deleteHead operations of LinkedList. 8 | this.linkedList = new LinkedList(); 9 | } 10 | 11 | /** 12 | * @return {boolean} 13 | */ 14 | isEmpty() { 15 | // The stack is empty if its linked list doesn't have a head. 16 | return !this.linkedList.head; 17 | } 18 | 19 | /** 20 | * @return {*} 21 | */ 22 | peek() { 23 | if (this.isEmpty()) { 24 | // If the linked list is empty then there is nothing to peek from. 25 | return null; 26 | } 27 | 28 | // Just read the value from the start of linked list without deleting it. 29 | return this.linkedList.head.value; 30 | } 31 | 32 | /** 33 | * @param {*} value 34 | */ 35 | push(value) { 36 | // Pushing means to lay the value on top of the stack. Therefore let's just add 37 | // the new value at the start of the linked list. 38 | this.linkedList.prepend(value); 39 | } 40 | 41 | /** 42 | * @return {*} 43 | */ 44 | pop() { 45 | // Let's try to delete the first node (the head) from the linked list. 46 | // If there is no head (the linked list is empty) just return null. 47 | const removedHead = this.linkedList.deleteHead(); 48 | return removedHead ? removedHead.value : null; 49 | } 50 | 51 | /** 52 | * @return {*[]} 53 | */ 54 | toArray() { 55 | return this.linkedList 56 | .toArray() 57 | .map((linkedListNode) => linkedListNode.value); 58 | } 59 | 60 | /** 61 | * @param {function} [callback] 62 | * @return {string} 63 | */ 64 | toString(callback) { 65 | return this.linkedList.toString(callback); 66 | } 67 | } 68 | -------------------------------------------------------------------------------- /src/Day01-17/stack/__test__/Stack.test.js: -------------------------------------------------------------------------------- 1 | import Stack from '../Stack'; 2 | 3 | describe('Stack', () => { 4 | it('should create empty stack', () => { 5 | const stack = new Stack(); 6 | expect(stack).not.toBeNull(); 7 | expect(stack.linkedList).not.toBeNull(); 8 | }); 9 | 10 | it('should stack data to stack', () => { 11 | const stack = new Stack(); 12 | 13 | stack.push(1); 14 | stack.push(2); 15 | 16 | expect(stack.toString()).toBe('2,1'); 17 | }); 18 | 19 | it('should peek data from stack', () => { 20 | const stack = new Stack(); 21 | 22 | expect(stack.peek()).toBeNull(); 23 | 24 | stack.push(1); 25 | stack.push(2); 26 | 27 | expect(stack.peek()).toBe(2); 28 | expect(stack.peek()).toBe(2); 29 | }); 30 | 31 | it('should check if stack is empty', () => { 32 | const stack = new Stack(); 33 | 34 | expect(stack.isEmpty()).toBe(true); 35 | 36 | stack.push(1); 37 | 38 | expect(stack.isEmpty()).toBe(false); 39 | }); 40 | 41 | it('should pop data from stack', () => { 42 | const stack = new Stack(); 43 | 44 | stack.push(1); 45 | stack.push(2); 46 | 47 | expect(stack.pop()).toBe(2); 48 | expect(stack.pop()).toBe(1); 49 | expect(stack.pop()).toBeNull(); 50 | expect(stack.isEmpty()).toBe(true); 51 | }); 52 | 53 | it('should be possible to push/pop objects', () => { 54 | const stack = new Stack(); 55 | 56 | stack.push({ value: 'test1', key: 'key1' }); 57 | stack.push({ value: 'test2', key: 'key2' }); 58 | 59 | const stringifier = (value) => `${value.key}:${value.value}`; 60 | 61 | expect(stack.toString(stringifier)).toBe('key2:test2,key1:test1'); 62 | expect(stack.pop().value).toBe('test2'); 63 | expect(stack.pop().value).toBe('test1'); 64 | }); 65 | 66 | it('should be possible to convert stack to array', () => { 67 | const stack = new Stack(); 68 | 69 | expect(stack.peek()).toBeNull(); 70 | 71 | stack.push(1); 72 | stack.push(2); 73 | stack.push(3); 74 | 75 | expect(stack.toArray()).toEqual([3, 2, 1]); 76 | }); 77 | }); 78 | -------------------------------------------------------------------------------- /src/Day01-17/tree/BinaryTreeNode.js: -------------------------------------------------------------------------------- 1 | import Comparator from '../../utils/comparator/Comparator'; 2 | import HashTable from '../hash-table/HashTable'; 3 | 4 | export default class BinaryTreeNode { 5 | /** 6 | * @param {*} [value] - node value. 7 | */ 8 | constructor(value = null) { 9 | this.left = null; 10 | this.right = null; 11 | this.parent = null; 12 | this.value = value; 13 | 14 | // Any node related meta information may be stored here. 15 | this.meta = new HashTable(); 16 | 17 | // This comparator is used to compare binary tree nodes with each other. 18 | this.nodeComparator = new Comparator(); 19 | } 20 | 21 | /** 22 | * @return {number} 23 | */ 24 | get leftHeight() { 25 | if (!this.left) { 26 | return 0; 27 | } 28 | 29 | return this.left.height + 1; 30 | } 31 | 32 | /** 33 | * @return {number} 34 | */ 35 | get rightHeight() { 36 | if (!this.right) { 37 | return 0; 38 | } 39 | 40 | return this.right.height + 1; 41 | } 42 | 43 | /** 44 | * @return {number} 45 | */ 46 | get height() { 47 | return Math.max(this.leftHeight, this.rightHeight); 48 | } 49 | 50 | /** 51 | * @return {number} 52 | */ 53 | get balanceFactor() { 54 | return this.leftHeight - this.rightHeight; 55 | } 56 | 57 | /** 58 | * Get parent's sibling if it exists. 59 | * @return {BinaryTreeNode} 60 | */ 61 | get uncle() { 62 | // Check if current node has parent. 63 | if (!this.parent) { 64 | return undefined; 65 | } 66 | 67 | // Check if current node has grand-parent. 68 | if (!this.parent.parent) { 69 | return undefined; 70 | } 71 | 72 | // Check if grand-parent has two children. 73 | if (!this.parent.parent.left || !this.parent.parent.right) { 74 | return undefined; 75 | } 76 | 77 | // So for now we know that current node has grand-parent and this 78 | // grand-parent has two children. Let's find out who is the uncle. 79 | if (this.nodeComparator.equal(this.parent, this.parent.parent.left)) { 80 | // Right one is an uncle. 81 | return this.parent.parent.right; 82 | } 83 | 84 | // Left one is an uncle. 85 | return this.parent.parent.left; 86 | } 87 | 88 | /** 89 | * @param {*} value 90 | * @return {BinaryTreeNode} 91 | */ 92 | setValue(value) { 93 | this.value = value; 94 | 95 | return this; 96 | } 97 | 98 | /** 99 | * @param {BinaryTreeNode} node 100 | * @return {BinaryTreeNode} 101 | */ 102 | setLeft(node) { 103 | // Reset parent for left node since it is going to be detached. 104 | if (this.left) { 105 | this.left.parent = null; 106 | } 107 | 108 | // Attach new node to the left. 109 | this.left = node; 110 | 111 | // Make current node to be a parent for new left one. 112 | if (this.left) { 113 | this.left.parent = this; 114 | } 115 | 116 | return this; 117 | } 118 | 119 | /** 120 | * @param {BinaryTreeNode} node 121 | * @return {BinaryTreeNode} 122 | */ 123 | setRight(node) { 124 | // Reset parent for right node since it is going to be detached. 125 | if (this.right) { 126 | this.right.parent = null; 127 | } 128 | 129 | // Attach new node to the right. 130 | this.right = node; 131 | 132 | // Make current node to be a parent for new right one. 133 | if (node) { 134 | this.right.parent = this; 135 | } 136 | 137 | return this; 138 | } 139 | 140 | /** 141 | * @param {BinaryTreeNode} nodeToRemove 142 | * @return {boolean} 143 | */ 144 | removeChild(nodeToRemove) { 145 | if (this.left && this.nodeComparator.equal(this.left, nodeToRemove)) { 146 | this.left = null; 147 | return true; 148 | } 149 | 150 | if (this.right && this.nodeComparator.equal(this.right, nodeToRemove)) { 151 | this.right = null; 152 | return true; 153 | } 154 | 155 | return false; 156 | } 157 | 158 | /** 159 | * @param {BinaryTreeNode} nodeToReplace 160 | * @param {BinaryTreeNode} replacementNode 161 | * @return {boolean} 162 | */ 163 | replaceChild(nodeToReplace, replacementNode) { 164 | if (!nodeToReplace || !replacementNode) { 165 | return false; 166 | } 167 | 168 | if (this.left && this.nodeComparator.equal(this.left, nodeToReplace)) { 169 | this.left = replacementNode; 170 | return true; 171 | } 172 | 173 | if (this.right && this.nodeComparator.equal(this.right, nodeToReplace)) { 174 | this.right = replacementNode; 175 | return true; 176 | } 177 | 178 | return false; 179 | } 180 | 181 | /** 182 | * @param {BinaryTreeNode} sourceNode 183 | * @param {BinaryTreeNode} targetNode 184 | */ 185 | static copyNode(sourceNode, targetNode) { 186 | targetNode.setValue(sourceNode.value); 187 | targetNode.setLeft(sourceNode.left); 188 | targetNode.setRight(sourceNode.right); 189 | } 190 | 191 | /** 192 | * @return {*[]} 193 | */ 194 | traverseInOrder() { 195 | let traverse = []; 196 | 197 | // Add left node. 198 | if (this.left) { 199 | traverse = traverse.concat(this.left.traverseInOrder()); 200 | } 201 | 202 | // Add root. 203 | traverse.push(this.value); 204 | 205 | // Add right node. 206 | if (this.right) { 207 | traverse = traverse.concat(this.right.traverseInOrder()); 208 | } 209 | 210 | return traverse; 211 | } 212 | 213 | /** 214 | * @return {string} 215 | */ 216 | toString() { 217 | return this.traverseInOrder().toString(); 218 | } 219 | } 220 | -------------------------------------------------------------------------------- /src/Day01-17/tree/avl-tree/AvlTree.js: -------------------------------------------------------------------------------- 1 | import BinarySearchTree from '../binary-search-tree/BinarySearchTree'; 2 | 3 | export default class AvlTree extends BinarySearchTree { 4 | /** 5 | * @param {*} value 6 | */ 7 | insert(value) { 8 | // Do the normal BST insert. 9 | super.insert(value); 10 | 11 | // Let's move up to the root and check balance factors along the way. 12 | let currentNode = this.root.find(value); 13 | while (currentNode) { 14 | this.balance(currentNode); 15 | currentNode = currentNode.parent; 16 | } 17 | } 18 | 19 | /** 20 | * @param {*} value 21 | * @return {boolean} 22 | */ 23 | remove(value) { 24 | // Do standard BST removal. 25 | super.remove(value); 26 | 27 | // Balance the tree starting from the root node. 28 | this.balance(this.root); 29 | } 30 | 31 | /** 32 | * @param {BinarySearchTreeNode} node 33 | */ 34 | balance(node) { 35 | // If balance factor is not OK then try to balance the node. 36 | if (node.balanceFactor > 1) { 37 | // Left rotation. 38 | if (node.left.balanceFactor > 0) { 39 | // Left-Left rotation 40 | this.rotateLeftLeft(node); 41 | } else if (node.left.balanceFactor < 0) { 42 | // Left-Right rotation. 43 | this.rotateLeftRight(node); 44 | } 45 | } else if (node.balanceFactor < -1) { 46 | // Right rotation. 47 | if (node.right.balanceFactor < 0) { 48 | // Right-Right rotation 49 | this.rotateRightRight(node); 50 | } else if (node.right.balanceFactor > 0) { 51 | // Right-Left rotation. 52 | this.rotateRightLeft(node); 53 | } 54 | } 55 | } 56 | 57 | /** 58 | * @param {BinarySearchTreeNode} rootNode 59 | */ 60 | rotateLeftLeft(rootNode) { 61 | // Detach left node from root node. 62 | const leftNode = rootNode.left; 63 | rootNode.setLeft(null); 64 | 65 | // Make left node to be a child of rootNode's parent. 66 | if (rootNode.parent) { 67 | rootNode.parent.setLeft(leftNode); 68 | } else if (rootNode === this.root) { 69 | // If root node is root then make left node to be a new root. 70 | this.root = leftNode; 71 | } 72 | 73 | // If left node has a right child then detach it and 74 | // attach it as a left child for rootNode. 75 | if (leftNode.right) { 76 | rootNode.setLeft(leftNode.right); 77 | } 78 | 79 | // Attach rootNode to the right of leftNode. 80 | leftNode.setRight(rootNode); 81 | } 82 | 83 | /** 84 | * @param {BinarySearchTreeNode} rootNode 85 | */ 86 | rotateLeftRight(rootNode) { 87 | // Detach left node from rootNode since it is going to be replaced. 88 | const leftNode = rootNode.left; 89 | rootNode.setLeft(null); 90 | 91 | // Detach right node from leftNode. 92 | const leftRightNode = leftNode.right; 93 | leftNode.setRight(null); 94 | 95 | // Preserve leftRightNode's left subtree. 96 | if (leftRightNode.left) { 97 | leftNode.setRight(leftRightNode.left); 98 | leftRightNode.setLeft(null); 99 | } 100 | 101 | // Attach leftRightNode to the rootNode. 102 | rootNode.setLeft(leftRightNode); 103 | 104 | // Attach leftNode as left node for leftRight node. 105 | leftRightNode.setLeft(leftNode); 106 | 107 | // Do left-left rotation. 108 | this.rotateLeftLeft(rootNode); 109 | } 110 | 111 | /** 112 | * @param {BinarySearchTreeNode} rootNode 113 | */ 114 | rotateRightLeft(rootNode) { 115 | // Detach right node from rootNode since it is going to be replaced. 116 | const rightNode = rootNode.right; 117 | rootNode.setRight(null); 118 | 119 | // Detach left node from rightNode. 120 | const rightLeftNode = rightNode.left; 121 | rightNode.setLeft(null); 122 | 123 | if (rightLeftNode.right) { 124 | rightNode.setLeft(rightLeftNode.right); 125 | rightLeftNode.setRight(null); 126 | } 127 | 128 | // Attach rightLeftNode to the rootNode. 129 | rootNode.setRight(rightLeftNode); 130 | 131 | // Attach rightNode as right node for rightLeft node. 132 | rightLeftNode.setRight(rightNode); 133 | 134 | // Do right-right rotation. 135 | this.rotateRightRight(rootNode); 136 | } 137 | 138 | /** 139 | * @param {BinarySearchTreeNode} rootNode 140 | */ 141 | rotateRightRight(rootNode) { 142 | // Detach right node from root node. 143 | const rightNode = rootNode.right; 144 | rootNode.setRight(null); 145 | 146 | // Make right node to be a child of rootNode's parent. 147 | if (rootNode.parent) { 148 | rootNode.parent.setRight(rightNode); 149 | } else if (rootNode === this.root) { 150 | // If root node is root then make right node to be a new root. 151 | this.root = rightNode; 152 | } 153 | 154 | // If right node has a left child then detach it and 155 | // attach it as a right child for rootNode. 156 | if (rightNode.left) { 157 | rootNode.setRight(rightNode.left); 158 | } 159 | 160 | // Attach rootNode to the left of rightNode. 161 | rightNode.setLeft(rootNode); 162 | } 163 | } 164 | -------------------------------------------------------------------------------- /src/Day01-17/tree/binary-search-tree/BinarySearchTree.js: -------------------------------------------------------------------------------- 1 | import BinarySearchTreeNode from './BinarySearchTreeNode'; 2 | 3 | export default class BinarySearchTree { 4 | /** 5 | * @param {function} [nodeValueCompareFunction] 6 | */ 7 | constructor(nodeValueCompareFunction) { 8 | this.root = new BinarySearchTreeNode(null, nodeValueCompareFunction); 9 | 10 | // Steal node comparator from the root. 11 | this.nodeComparator = this.root.nodeComparator; 12 | } 13 | 14 | /** 15 | * @param {*} value 16 | * @return {BinarySearchTreeNode} 17 | */ 18 | insert(value) { 19 | return this.root.insert(value); 20 | } 21 | 22 | /** 23 | * @param {*} value 24 | * @return {boolean} 25 | */ 26 | contains(value) { 27 | return this.root.contains(value); 28 | } 29 | 30 | /** 31 | * @param {*} value 32 | * @return {boolean} 33 | */ 34 | remove(value) { 35 | return this.root.remove(value); 36 | } 37 | 38 | /** 39 | * @return {string} 40 | */ 41 | toString() { 42 | return this.root.toString(); 43 | } 44 | } 45 | -------------------------------------------------------------------------------- /src/Day01-17/tree/binary-search-tree/BinarySearchTreeNode.js: -------------------------------------------------------------------------------- 1 | import BinaryTreeNode from '../BinaryTreeNode'; 2 | import Comparator from '../../../utils/comparator/Comparator'; 3 | 4 | export default class BinarySearchTreeNode extends BinaryTreeNode { 5 | /** 6 | * @param {*} [value] - node value. 7 | * @param {function} [compareFunction] - comparator function for node values. 8 | */ 9 | constructor(value = null, compareFunction = undefined) { 10 | super(value); 11 | 12 | // This comparator is used to compare node values with each other. 13 | this.compareFunction = compareFunction; 14 | this.nodeValueComparator = new Comparator(compareFunction); 15 | } 16 | 17 | /** 18 | * @param {*} value 19 | * @return {BinarySearchTreeNode} 20 | */ 21 | insert(value) { 22 | if (this.nodeValueComparator.equal(this.value, null)) { 23 | this.value = value; 24 | 25 | return this; 26 | } 27 | 28 | if (this.nodeValueComparator.lessThan(value, this.value)) { 29 | // Insert to the left. 30 | if (this.left) { 31 | return this.left.insert(value); 32 | } 33 | 34 | const newNode = new BinarySearchTreeNode(value, this.compareFunction); 35 | this.setLeft(newNode); 36 | 37 | return newNode; 38 | } 39 | 40 | if (this.nodeValueComparator.greaterThan(value, this.value)) { 41 | // Insert to the right. 42 | if (this.right) { 43 | return this.right.insert(value); 44 | } 45 | 46 | const newNode = new BinarySearchTreeNode(value, this.compareFunction); 47 | this.setRight(newNode); 48 | 49 | return newNode; 50 | } 51 | 52 | return this; 53 | } 54 | 55 | /** 56 | * @param {*} value 57 | * @return {BinarySearchTreeNode} 58 | */ 59 | find(value) { 60 | // Check the root. 61 | if (this.nodeValueComparator.equal(this.value, value)) { 62 | return this; 63 | } 64 | 65 | if (this.nodeValueComparator.lessThan(value, this.value) && this.left) { 66 | // Check left nodes. 67 | return this.left.find(value); 68 | } 69 | 70 | if (this.nodeValueComparator.greaterThan(value, this.value) && this.right) { 71 | // Check right nodes. 72 | return this.right.find(value); 73 | } 74 | 75 | return null; 76 | } 77 | 78 | /** 79 | * @param {*} value 80 | * @return {boolean} 81 | */ 82 | contains(value) { 83 | return !!this.find(value); 84 | } 85 | 86 | /** 87 | * @param {*} value 88 | * @return {boolean} 89 | */ 90 | remove(value) { 91 | const nodeToRemove = this.find(value); 92 | 93 | if (!nodeToRemove) { 94 | throw new Error('Item not found in the tree'); 95 | } 96 | 97 | const { parent } = nodeToRemove; 98 | 99 | if (!nodeToRemove.left && !nodeToRemove.right) { 100 | // Node is a leaf and thus has no children. 101 | if (parent) { 102 | // Node has a parent. Just remove the pointer to this node from the parent. 103 | parent.removeChild(nodeToRemove); 104 | } else { 105 | // Node has no parent. Just erase current node value. 106 | nodeToRemove.setValue(undefined); 107 | } 108 | } else if (nodeToRemove.left && nodeToRemove.right) { 109 | // Node has two children. 110 | // Find the next biggest value (minimum value in the right branch) 111 | // and replace current value node with that next biggest value. 112 | const nextBiggerNode = nodeToRemove.right.findMin(); 113 | if (!this.nodeComparator.equal(nextBiggerNode, nodeToRemove.right)) { 114 | this.remove(nextBiggerNode.value); 115 | nodeToRemove.setValue(nextBiggerNode.value); 116 | } else { 117 | // In case if next right value is the next bigger one and it doesn't have left child 118 | // then just replace node that is going to be deleted with the right node. 119 | nodeToRemove.setValue(nodeToRemove.right.value); 120 | nodeToRemove.setRight(nodeToRemove.right.right); 121 | } 122 | } else { 123 | // Node has only one child. 124 | // Make this child to be a direct child of current node's parent. 125 | /** @var BinarySearchTreeNode */ 126 | const childNode = nodeToRemove.left || nodeToRemove.right; 127 | 128 | if (parent) { 129 | parent.replaceChild(nodeToRemove, childNode); 130 | } else { 131 | BinaryTreeNode.copyNode(childNode, nodeToRemove); 132 | } 133 | } 134 | 135 | // Clear the parent of removed node. 136 | nodeToRemove.parent = null; 137 | 138 | return true; 139 | } 140 | 141 | /** 142 | * @return {BinarySearchTreeNode} 143 | */ 144 | findMin() { 145 | if (!this.left) { 146 | return this; 147 | } 148 | 149 | return this.left.findMin(); 150 | } 151 | } 152 | -------------------------------------------------------------------------------- /src/Day01-17/tree/binary-search-tree/__test__/BinarySearchTree.test.js: -------------------------------------------------------------------------------- 1 | import BinarySearchTree from '../BinarySearchTree'; 2 | 3 | describe('BinarySearchTree', () => { 4 | it('should create binary search tree', () => { 5 | const bst = new BinarySearchTree(); 6 | 7 | expect(bst).toBeDefined(); 8 | expect(bst.root).toBeDefined(); 9 | expect(bst.root.value).toBeNull(); 10 | expect(bst.root.left).toBeNull(); 11 | expect(bst.root.right).toBeNull(); 12 | }); 13 | 14 | it('should insert values', () => { 15 | const bst = new BinarySearchTree(); 16 | 17 | const insertedNode1 = bst.insert(10); 18 | const insertedNode2 = bst.insert(20); 19 | bst.insert(5); 20 | 21 | expect(bst.toString()).toBe('5,10,20'); 22 | expect(insertedNode1.value).toBe(10); 23 | expect(insertedNode2.value).toBe(20); 24 | }); 25 | 26 | it('should check if value exists', () => { 27 | const bst = new BinarySearchTree(); 28 | 29 | bst.insert(10); 30 | bst.insert(20); 31 | bst.insert(5); 32 | 33 | expect(bst.contains(20)).toBe(true); 34 | expect(bst.contains(40)).toBe(false); 35 | }); 36 | 37 | it('should remove nodes', () => { 38 | const bst = new BinarySearchTree(); 39 | 40 | bst.insert(10); 41 | bst.insert(20); 42 | bst.insert(5); 43 | 44 | expect(bst.toString()).toBe('5,10,20'); 45 | 46 | const removed1 = bst.remove(5); 47 | expect(bst.toString()).toBe('10,20'); 48 | expect(removed1).toBe(true); 49 | 50 | const removed2 = bst.remove(20); 51 | expect(bst.toString()).toBe('10'); 52 | expect(removed2).toBe(true); 53 | }); 54 | 55 | it('should insert object values', () => { 56 | const nodeValueCompareFunction = (a, b) => { 57 | const normalizedA = a || { value: null }; 58 | const normalizedB = b || { value: null }; 59 | 60 | if (normalizedA.value === normalizedB.value) { 61 | return 0; 62 | } 63 | 64 | return normalizedA.value < normalizedB.value ? -1 : 1; 65 | }; 66 | 67 | const obj1 = { key: 'obj1', value: 1, toString: () => 'obj1' }; 68 | const obj2 = { key: 'obj2', value: 2, toString: () => 'obj2' }; 69 | const obj3 = { key: 'obj3', value: 3, toString: () => 'obj3' }; 70 | 71 | const bst = new BinarySearchTree(nodeValueCompareFunction); 72 | 73 | bst.insert(obj2); 74 | bst.insert(obj3); 75 | bst.insert(obj1); 76 | 77 | expect(bst.toString()).toBe('obj1,obj2,obj3'); 78 | }); 79 | 80 | it('should be traversed to sorted array', () => { 81 | const bst = new BinarySearchTree(); 82 | 83 | bst.insert(10); 84 | bst.insert(-10); 85 | bst.insert(20); 86 | bst.insert(-20); 87 | bst.insert(25); 88 | bst.insert(6); 89 | 90 | expect(bst.toString()).toBe('-20,-10,6,10,20,25'); 91 | expect(bst.root.height).toBe(2); 92 | 93 | bst.insert(4); 94 | 95 | expect(bst.toString()).toBe('-20,-10,4,6,10,20,25'); 96 | expect(bst.root.height).toBe(3); 97 | }); 98 | }); 99 | -------------------------------------------------------------------------------- /src/Day01-17/tree/fenwick-tree/FenwickTree.js: -------------------------------------------------------------------------------- 1 | export default class FenwickTree { 2 | /** 3 | * Constructor creates empty fenwick tree of size 'arraySize', 4 | * however, array size is size+1, because index is 1-based. 5 | * 6 | * @param {number} arraySize 7 | */ 8 | constructor(arraySize) { 9 | this.arraySize = arraySize; 10 | 11 | // Fill tree array with zeros. 12 | this.treeArray = Array(this.arraySize + 1).fill(0); 13 | } 14 | 15 | /** 16 | * Adds value to existing value at position. 17 | * 18 | * @param {number} position 19 | * @param {number} value 20 | * @return {FenwickTree} 21 | */ 22 | increase(position, value) { 23 | if (position < 1 || position > this.arraySize) { 24 | throw new Error('Position is out of allowed range'); 25 | } 26 | 27 | for (let i = position; i <= this.arraySize; i += (i & -i)) { 28 | this.treeArray[i] += value; 29 | } 30 | 31 | return this; 32 | } 33 | 34 | /** 35 | * Query sum from index 1 to position. 36 | * 37 | * @param {number} position 38 | * @return {number} 39 | */ 40 | query(position) { 41 | if (position < 1 || position > this.arraySize) { 42 | throw new Error('Position is out of allowed range'); 43 | } 44 | 45 | let sum = 0; 46 | 47 | for (let i = position; i > 0; i -= (i & -i)) { 48 | sum += this.treeArray[i]; 49 | } 50 | 51 | return sum; 52 | } 53 | 54 | /** 55 | * Query sum from index leftIndex to rightIndex. 56 | * 57 | * @param {number} leftIndex 58 | * @param {number} rightIndex 59 | * @return {number} 60 | */ 61 | queryRange(leftIndex, rightIndex) { 62 | if (leftIndex > rightIndex) { 63 | throw new Error('Left index can not be greater than right one'); 64 | } 65 | 66 | if (leftIndex === 1) { 67 | return this.query(rightIndex); 68 | } 69 | 70 | return this.query(rightIndex) - this.query(leftIndex - 1); 71 | } 72 | } 73 | -------------------------------------------------------------------------------- /src/Day01-17/tree/fenwick-tree/__test__/FenwickTree.test.js: -------------------------------------------------------------------------------- 1 | import FenwickTree from '../FenwickTree'; 2 | 3 | describe('FenwickTree', () => { 4 | it('should create empty fenwick tree of correct size', () => { 5 | const tree1 = new FenwickTree(5); 6 | expect(tree1.treeArray.length).toBe(5 + 1); 7 | 8 | for (let i = 0; i < 5; i += 1) { 9 | expect(tree1.treeArray[i]).toBe(0); 10 | } 11 | 12 | const tree2 = new FenwickTree(50); 13 | expect(tree2.treeArray.length).toBe(50 + 1); 14 | }); 15 | 16 | it('should create correct fenwick tree', () => { 17 | const inputArray = [3, 2, -1, 6, 5, 4, -3, 3, 7, 2, 3]; 18 | 19 | const tree = new FenwickTree(inputArray.length); 20 | expect(tree.treeArray.length).toBe(inputArray.length + 1); 21 | 22 | inputArray.forEach((value, index) => { 23 | tree.increase(index + 1, value); 24 | }); 25 | 26 | expect(tree.treeArray).toEqual([0, 3, 5, -1, 10, 5, 9, -3, 19, 7, 9, 3]); 27 | 28 | expect(tree.query(1)).toBe(3); 29 | expect(tree.query(2)).toBe(5); 30 | expect(tree.query(3)).toBe(4); 31 | expect(tree.query(4)).toBe(10); 32 | expect(tree.query(5)).toBe(15); 33 | expect(tree.query(6)).toBe(19); 34 | expect(tree.query(7)).toBe(16); 35 | expect(tree.query(8)).toBe(19); 36 | expect(tree.query(9)).toBe(26); 37 | expect(tree.query(10)).toBe(28); 38 | expect(tree.query(11)).toBe(31); 39 | 40 | expect(tree.queryRange(1, 1)).toBe(3); 41 | expect(tree.queryRange(1, 2)).toBe(5); 42 | expect(tree.queryRange(2, 4)).toBe(7); 43 | expect(tree.queryRange(6, 9)).toBe(11); 44 | 45 | tree.increase(3, 1); 46 | 47 | expect(tree.query(1)).toBe(3); 48 | expect(tree.query(2)).toBe(5); 49 | expect(tree.query(3)).toBe(5); 50 | expect(tree.query(4)).toBe(11); 51 | expect(tree.query(5)).toBe(16); 52 | expect(tree.query(6)).toBe(20); 53 | expect(tree.query(7)).toBe(17); 54 | expect(tree.query(8)).toBe(20); 55 | expect(tree.query(9)).toBe(27); 56 | expect(tree.query(10)).toBe(29); 57 | expect(tree.query(11)).toBe(32); 58 | 59 | expect(tree.queryRange(1, 1)).toBe(3); 60 | expect(tree.queryRange(1, 2)).toBe(5); 61 | expect(tree.queryRange(2, 4)).toBe(8); 62 | expect(tree.queryRange(6, 9)).toBe(11); 63 | }); 64 | 65 | it('should correctly execute queries', () => { 66 | const tree = new FenwickTree(5); 67 | 68 | tree.increase(1, 4); 69 | tree.increase(3, 7); 70 | 71 | expect(tree.query(1)).toBe(4); 72 | expect(tree.query(3)).toBe(11); 73 | expect(tree.query(5)).toBe(11); 74 | expect(tree.queryRange(2, 3)).toBe(7); 75 | 76 | tree.increase(2, 5); 77 | expect(tree.query(5)).toBe(16); 78 | 79 | tree.increase(1, 3); 80 | expect(tree.queryRange(1, 1)).toBe(7); 81 | expect(tree.query(5)).toBe(19); 82 | expect(tree.queryRange(1, 5)).toBe(19); 83 | }); 84 | 85 | it('should throw exceptions', () => { 86 | const tree = new FenwickTree(5); 87 | 88 | const increaseAtInvalidLowIndex = () => { 89 | tree.increase(0, 1); 90 | }; 91 | 92 | const increaseAtInvalidHighIndex = () => { 93 | tree.increase(10, 1); 94 | }; 95 | 96 | const queryInvalidLowIndex = () => { 97 | tree.query(0); 98 | }; 99 | 100 | const queryInvalidHighIndex = () => { 101 | tree.query(10); 102 | }; 103 | 104 | const rangeQueryInvalidIndex = () => { 105 | tree.queryRange(3, 2); 106 | }; 107 | 108 | expect(increaseAtInvalidLowIndex).toThrowError(); 109 | expect(increaseAtInvalidHighIndex).toThrowError(); 110 | expect(queryInvalidLowIndex).toThrowError(); 111 | expect(queryInvalidHighIndex).toThrowError(); 112 | expect(rangeQueryInvalidIndex).toThrowError(); 113 | }); 114 | }); 115 | -------------------------------------------------------------------------------- /src/Day01-17/tree/segment-tree/__test__/SegmentTree.test.js: -------------------------------------------------------------------------------- 1 | import SegmentTree from '../SegmentTree'; 2 | 3 | describe('SegmentTree', () => { 4 | it('should build tree for input array #0 with length of power of two', () => { 5 | const array = [-1, 2]; 6 | const segmentTree = new SegmentTree(array, Math.min, Infinity); 7 | 8 | expect(segmentTree.segmentTree).toEqual([-1, -1, 2]); 9 | expect(segmentTree.segmentTree.length).toBe((2 * array.length) - 1); 10 | }); 11 | 12 | it('should build tree for input array #1 with length of power of two', () => { 13 | const array = [-1, 2, 4, 0]; 14 | const segmentTree = new SegmentTree(array, Math.min, Infinity); 15 | 16 | expect(segmentTree.segmentTree).toEqual([-1, -1, 0, -1, 2, 4, 0]); 17 | expect(segmentTree.segmentTree.length).toBe((2 * array.length) - 1); 18 | }); 19 | 20 | it('should build tree for input array #0 with length not of power of two', () => { 21 | const array = [0, 1, 2]; 22 | const segmentTree = new SegmentTree(array, Math.min, Infinity); 23 | 24 | expect(segmentTree.segmentTree).toEqual([0, 0, 2, 0, 1, null, null]); 25 | expect(segmentTree.segmentTree.length).toBe((2 * 4) - 1); 26 | }); 27 | 28 | it('should build tree for input array #1 with length not of power of two', () => { 29 | const array = [-1, 3, 4, 0, 2, 1]; 30 | const segmentTree = new SegmentTree(array, Math.min, Infinity); 31 | 32 | expect(segmentTree.segmentTree).toEqual([ 33 | -1, -1, 0, -1, 4, 0, 1, -1, 3, null, null, 0, 2, null, null, 34 | ]); 35 | expect(segmentTree.segmentTree.length).toBe((2 * 8) - 1); 36 | }); 37 | 38 | it('should build max array', () => { 39 | const array = [-1, 2, 4, 0]; 40 | const segmentTree = new SegmentTree(array, Math.max, -Infinity); 41 | 42 | expect(segmentTree.segmentTree).toEqual([4, 2, 4, -1, 2, 4, 0]); 43 | expect(segmentTree.segmentTree.length).toBe((2 * array.length) - 1); 44 | }); 45 | 46 | it('should build sum array', () => { 47 | const array = [-1, 2, 4, 0]; 48 | const segmentTree = new SegmentTree(array, (a, b) => (a + b), 0); 49 | 50 | expect(segmentTree.segmentTree).toEqual([5, 1, 4, -1, 2, 4, 0]); 51 | expect(segmentTree.segmentTree.length).toBe((2 * array.length) - 1); 52 | }); 53 | 54 | it('should do min range query on power of two length array', () => { 55 | const array = [-1, 3, 4, 0, 2, 1]; 56 | const segmentTree = new SegmentTree(array, Math.min, Infinity); 57 | 58 | expect(segmentTree.rangeQuery(0, 5)).toBe(-1); 59 | expect(segmentTree.rangeQuery(0, 2)).toBe(-1); 60 | expect(segmentTree.rangeQuery(1, 3)).toBe(0); 61 | expect(segmentTree.rangeQuery(2, 4)).toBe(0); 62 | expect(segmentTree.rangeQuery(4, 5)).toBe(1); 63 | expect(segmentTree.rangeQuery(2, 2)).toBe(4); 64 | }); 65 | 66 | it('should do min range query on not power of two length array', () => { 67 | const array = [-1, 2, 4, 0]; 68 | const segmentTree = new SegmentTree(array, Math.min, Infinity); 69 | 70 | expect(segmentTree.rangeQuery(0, 4)).toBe(-1); 71 | expect(segmentTree.rangeQuery(0, 1)).toBe(-1); 72 | expect(segmentTree.rangeQuery(1, 3)).toBe(0); 73 | expect(segmentTree.rangeQuery(1, 2)).toBe(2); 74 | expect(segmentTree.rangeQuery(2, 3)).toBe(0); 75 | expect(segmentTree.rangeQuery(2, 2)).toBe(4); 76 | }); 77 | 78 | it('should do max range query', () => { 79 | const array = [-1, 3, 4, 0, 2, 1]; 80 | const segmentTree = new SegmentTree(array, Math.max, -Infinity); 81 | 82 | expect(segmentTree.rangeQuery(0, 5)).toBe(4); 83 | expect(segmentTree.rangeQuery(0, 1)).toBe(3); 84 | expect(segmentTree.rangeQuery(1, 3)).toBe(4); 85 | expect(segmentTree.rangeQuery(2, 4)).toBe(4); 86 | expect(segmentTree.rangeQuery(4, 5)).toBe(2); 87 | expect(segmentTree.rangeQuery(3, 3)).toBe(0); 88 | }); 89 | 90 | it('should do sum range query', () => { 91 | const array = [-1, 3, 4, 0, 2, 1]; 92 | const segmentTree = new SegmentTree(array, (a, b) => (a + b), 0); 93 | 94 | expect(segmentTree.rangeQuery(0, 5)).toBe(9); 95 | expect(segmentTree.rangeQuery(0, 1)).toBe(2); 96 | expect(segmentTree.rangeQuery(1, 3)).toBe(7); 97 | expect(segmentTree.rangeQuery(2, 4)).toBe(6); 98 | expect(segmentTree.rangeQuery(4, 5)).toBe(3); 99 | expect(segmentTree.rangeQuery(3, 3)).toBe(0); 100 | }); 101 | }); 102 | -------------------------------------------------------------------------------- /src/Day01-17/trie/Trie.js: -------------------------------------------------------------------------------- 1 | import TrieNode from './TrieNode'; 2 | 3 | // Character that we will use for trie tree root. 4 | const HEAD_CHARACTER = '*'; 5 | 6 | export default class Trie { 7 | constructor() { 8 | this.head = new TrieNode(HEAD_CHARACTER); 9 | } 10 | 11 | /** 12 | * @param {string} word 13 | * @return {Trie} 14 | */ 15 | addWord(word) { 16 | const characters = Array.from(word); 17 | let currentNode = this.head; 18 | 19 | for (let charIndex = 0; charIndex < characters.length; charIndex += 1) { 20 | const isComplete = charIndex === characters.length - 1; 21 | currentNode = currentNode.addChild(characters[charIndex], isComplete); 22 | } 23 | 24 | return this; 25 | } 26 | 27 | /** 28 | * @param {string} word 29 | * @return {Trie} 30 | */ 31 | deleteWord(word) { 32 | const depthFirstDelete = (currentNode, charIndex = 0) => { 33 | if (charIndex >= word.length) { 34 | // Return if we're trying to delete the character that is out of word's scope. 35 | return; 36 | } 37 | 38 | const character = word[charIndex]; 39 | const nextNode = currentNode.getChild(character); 40 | 41 | if (nextNode == null) { 42 | // Return if we're trying to delete a word that has not been added to the Trie. 43 | return; 44 | } 45 | 46 | // Go deeper. 47 | depthFirstDelete(nextNode, charIndex + 1); 48 | 49 | // Since we're going to delete a word let's un-mark its last character isCompleteWord flag. 50 | if (charIndex === (word.length - 1)) { 51 | nextNode.isCompleteWord = false; 52 | } 53 | 54 | // childNode is deleted only if: 55 | // - childNode has NO children 56 | // - childNode.isCompleteWord === false 57 | currentNode.removeChild(character); 58 | }; 59 | 60 | // Start depth-first deletion from the head node. 61 | depthFirstDelete(this.head); 62 | 63 | return this; 64 | } 65 | 66 | /** 67 | * @param {string} word 68 | * @return {string[]} 69 | */ 70 | suggestNextCharacters(word) { 71 | const lastCharacter = this.getLastCharacterNode(word); 72 | 73 | if (!lastCharacter) { 74 | return null; 75 | } 76 | 77 | return lastCharacter.suggestChildren(); 78 | } 79 | 80 | /** 81 | * Check if complete word exists in Trie. 82 | * 83 | * @param {string} word 84 | * @return {boolean} 85 | */ 86 | doesWordExist(word) { 87 | const lastCharacter = this.getLastCharacterNode(word); 88 | 89 | return !!lastCharacter && lastCharacter.isCompleteWord; 90 | } 91 | 92 | /** 93 | * @param {string} word 94 | * @return {TrieNode} 95 | */ 96 | getLastCharacterNode(word) { 97 | const characters = Array.from(word); 98 | let currentNode = this.head; 99 | 100 | for (let charIndex = 0; charIndex < characters.length; charIndex += 1) { 101 | if (!currentNode.hasChild(characters[charIndex])) { 102 | return null; 103 | } 104 | 105 | currentNode = currentNode.getChild(characters[charIndex]); 106 | } 107 | 108 | return currentNode; 109 | } 110 | } 111 | -------------------------------------------------------------------------------- /src/Day01-17/trie/TrieNode.js: -------------------------------------------------------------------------------- 1 | import HashTable from '../hash-table/HashTable'; 2 | 3 | export default class TrieNode { 4 | /** 5 | * @param {string} character 6 | * @param {boolean} isCompleteWord 7 | */ 8 | constructor(character, isCompleteWord = false) { 9 | this.character = character; 10 | this.isCompleteWord = isCompleteWord; 11 | this.children = new HashTable(); 12 | } 13 | 14 | /** 15 | * @param {string} character 16 | * @return {TrieNode} 17 | */ 18 | getChild(character) { 19 | return this.children.get(character); 20 | } 21 | 22 | /** 23 | * @param {string} character 24 | * @param {boolean} isCompleteWord 25 | * @return {TrieNode} 26 | */ 27 | addChild(character, isCompleteWord = false) { 28 | if (!this.children.has(character)) { 29 | this.children.set(character, new TrieNode(character, isCompleteWord)); 30 | } 31 | 32 | const childNode = this.children.get(character); 33 | 34 | // In cases similar to adding "car" after "carpet" we need to mark "r" character as complete. 35 | childNode.isCompleteWord = childNode.isCompleteWord || isCompleteWord; 36 | 37 | return childNode; 38 | } 39 | 40 | /** 41 | * @param {string} character 42 | * @return {TrieNode} 43 | */ 44 | removeChild(character) { 45 | const childNode = this.getChild(character); 46 | 47 | // Delete childNode only if: 48 | // - childNode has NO children, 49 | // - childNode.isCompleteWord === false. 50 | if ( 51 | childNode 52 | && !childNode.isCompleteWord 53 | && !childNode.hasChildren() 54 | ) { 55 | this.children.delete(character); 56 | } 57 | 58 | return this; 59 | } 60 | 61 | /** 62 | * @param {string} character 63 | * @return {boolean} 64 | */ 65 | hasChild(character) { 66 | return this.children.has(character); 67 | } 68 | 69 | /** 70 | * Check whether current TrieNode has children or not. 71 | * @return {boolean} 72 | */ 73 | hasChildren() { 74 | return this.children.getKeys().length !== 0; 75 | } 76 | 77 | /** 78 | * @return {string[]} 79 | */ 80 | suggestChildren() { 81 | return [...this.children.getKeys()]; 82 | } 83 | 84 | /** 85 | * @return {string} 86 | */ 87 | toString() { 88 | let childrenAsString = this.suggestChildren().toString(); 89 | childrenAsString = childrenAsString ? `:${childrenAsString}` : ''; 90 | const isCompleteString = this.isCompleteWord ? '*' : ''; 91 | 92 | return `${this.character}${isCompleteString}${childrenAsString}`; 93 | } 94 | } 95 | -------------------------------------------------------------------------------- /src/Day01-17/trie/__test__/Trie.test.js: -------------------------------------------------------------------------------- 1 | import Trie from '../Trie'; 2 | 3 | describe('Trie', () => { 4 | it('should create trie', () => { 5 | const trie = new Trie(); 6 | 7 | expect(trie).toBeDefined(); 8 | expect(trie.head.toString()).toBe('*'); 9 | }); 10 | 11 | it('should add words to trie', () => { 12 | const trie = new Trie(); 13 | 14 | trie.addWord('cat'); 15 | 16 | expect(trie.head.toString()).toBe('*:c'); 17 | expect(trie.head.getChild('c').toString()).toBe('c:a'); 18 | 19 | trie.addWord('car'); 20 | expect(trie.head.toString()).toBe('*:c'); 21 | expect(trie.head.getChild('c').toString()).toBe('c:a'); 22 | expect(trie.head.getChild('c').getChild('a').toString()).toBe('a:t,r'); 23 | expect(trie.head.getChild('c').getChild('a').getChild('t').toString()).toBe('t*'); 24 | }); 25 | 26 | it('should delete words from trie', () => { 27 | const trie = new Trie(); 28 | 29 | trie.addWord('carpet'); 30 | trie.addWord('car'); 31 | trie.addWord('cat'); 32 | trie.addWord('cart'); 33 | expect(trie.doesWordExist('carpet')).toBe(true); 34 | expect(trie.doesWordExist('car')).toBe(true); 35 | expect(trie.doesWordExist('cart')).toBe(true); 36 | expect(trie.doesWordExist('cat')).toBe(true); 37 | 38 | // Try to delete not-existing word first. 39 | trie.deleteWord('carpool'); 40 | expect(trie.doesWordExist('carpet')).toBe(true); 41 | expect(trie.doesWordExist('car')).toBe(true); 42 | expect(trie.doesWordExist('cart')).toBe(true); 43 | expect(trie.doesWordExist('cat')).toBe(true); 44 | 45 | trie.deleteWord('carpet'); 46 | expect(trie.doesWordExist('carpet')).toEqual(false); 47 | expect(trie.doesWordExist('car')).toEqual(true); 48 | expect(trie.doesWordExist('cart')).toBe(true); 49 | expect(trie.doesWordExist('cat')).toBe(true); 50 | 51 | trie.deleteWord('cat'); 52 | expect(trie.doesWordExist('car')).toEqual(true); 53 | expect(trie.doesWordExist('cart')).toBe(true); 54 | expect(trie.doesWordExist('cat')).toBe(false); 55 | 56 | trie.deleteWord('car'); 57 | expect(trie.doesWordExist('car')).toEqual(false); 58 | expect(trie.doesWordExist('cart')).toBe(true); 59 | 60 | trie.deleteWord('cart'); 61 | expect(trie.doesWordExist('car')).toEqual(false); 62 | expect(trie.doesWordExist('cart')).toBe(false); 63 | }); 64 | 65 | it('should suggests next characters', () => { 66 | const trie = new Trie(); 67 | 68 | trie.addWord('cat'); 69 | trie.addWord('cats'); 70 | trie.addWord('car'); 71 | trie.addWord('caption'); 72 | 73 | expect(trie.suggestNextCharacters('ca')).toEqual(['t', 'r', 'p']); 74 | expect(trie.suggestNextCharacters('cat')).toEqual(['s']); 75 | expect(trie.suggestNextCharacters('cab')).toBeNull(); 76 | }); 77 | 78 | it('should check if word exists', () => { 79 | const trie = new Trie(); 80 | 81 | trie.addWord('cat'); 82 | trie.addWord('cats'); 83 | trie.addWord('carpet'); 84 | trie.addWord('car'); 85 | trie.addWord('caption'); 86 | 87 | expect(trie.doesWordExist('cat')).toBe(true); 88 | expect(trie.doesWordExist('cats')).toBe(true); 89 | expect(trie.doesWordExist('carpet')).toBe(true); 90 | expect(trie.doesWordExist('car')).toBe(true); 91 | expect(trie.doesWordExist('cap')).toBe(false); 92 | expect(trie.doesWordExist('call')).toBe(false); 93 | }); 94 | }); 95 | -------------------------------------------------------------------------------- /src/Day01-17/trie/__test__/TrieNode.test.js: -------------------------------------------------------------------------------- 1 | import TrieNode from '../TrieNode'; 2 | 3 | describe('TrieNode', () => { 4 | it('should create trie node', () => { 5 | const trieNode = new TrieNode('c', true); 6 | 7 | expect(trieNode.character).toBe('c'); 8 | expect(trieNode.isCompleteWord).toBe(true); 9 | expect(trieNode.toString()).toBe('c*'); 10 | }); 11 | 12 | it('should add child nodes', () => { 13 | const trieNode = new TrieNode('c'); 14 | 15 | trieNode.addChild('a', true); 16 | trieNode.addChild('o'); 17 | 18 | expect(trieNode.toString()).toBe('c:a,o'); 19 | }); 20 | 21 | it('should get child nodes', () => { 22 | const trieNode = new TrieNode('c'); 23 | 24 | trieNode.addChild('a'); 25 | trieNode.addChild('o'); 26 | 27 | expect(trieNode.getChild('a').toString()).toBe('a'); 28 | expect(trieNode.getChild('a').character).toBe('a'); 29 | expect(trieNode.getChild('o').toString()).toBe('o'); 30 | expect(trieNode.getChild('b')).toBeUndefined(); 31 | }); 32 | 33 | it('should check if node has children', () => { 34 | const trieNode = new TrieNode('c'); 35 | 36 | expect(trieNode.hasChildren()).toBe(false); 37 | 38 | trieNode.addChild('a'); 39 | 40 | expect(trieNode.hasChildren()).toBe(true); 41 | }); 42 | 43 | it('should check if node has specific child', () => { 44 | const trieNode = new TrieNode('c'); 45 | 46 | trieNode.addChild('a'); 47 | trieNode.addChild('o'); 48 | 49 | expect(trieNode.hasChild('a')).toBe(true); 50 | expect(trieNode.hasChild('o')).toBe(true); 51 | expect(trieNode.hasChild('b')).toBe(false); 52 | }); 53 | 54 | it('should suggest next children', () => { 55 | const trieNode = new TrieNode('c'); 56 | 57 | trieNode.addChild('a'); 58 | trieNode.addChild('o'); 59 | 60 | expect(trieNode.suggestChildren()).toEqual(['a', 'o']); 61 | }); 62 | 63 | it('should delete child node if the child node has NO children', () => { 64 | const trieNode = new TrieNode('c'); 65 | trieNode.addChild('a'); 66 | expect(trieNode.hasChild('a')).toBe(true); 67 | 68 | trieNode.removeChild('a'); 69 | expect(trieNode.hasChild('a')).toBe(false); 70 | }); 71 | 72 | it('should NOT delete child node if the child node has children', () => { 73 | const trieNode = new TrieNode('c'); 74 | trieNode.addChild('a'); 75 | const childNode = trieNode.getChild('a'); 76 | childNode.addChild('r'); 77 | 78 | trieNode.removeChild('a'); 79 | expect(trieNode.hasChild('a')).toEqual(true); 80 | }); 81 | 82 | it('should NOT delete child node if the child node completes a word', () => { 83 | const trieNode = new TrieNode('c'); 84 | const IS_COMPLETE_WORD = true; 85 | trieNode.addChild('a', IS_COMPLETE_WORD); 86 | 87 | trieNode.removeChild('a'); 88 | expect(trieNode.hasChild('a')).toEqual(true); 89 | }); 90 | }); 91 | -------------------------------------------------------------------------------- /src/utils/comparator/Comparator.js: -------------------------------------------------------------------------------- 1 | export default class Comparator { 2 | /** 3 | * @param {function(a: *, b: *)} [compareFunction] - It may be custom compare function that, let's 4 | * say may compare custom objects together. 5 | */ 6 | constructor(compareFunction) { 7 | this.compare = compareFunction || Comparator.defaultCompareFunction; 8 | } 9 | 10 | /** 11 | * Default comparison function. It just assumes that "a" and "b" are strings or numbers. 12 | * @param {(string|number)} a 13 | * @param {(string|number)} b 14 | * @returns {number} 15 | */ 16 | static defaultCompareFunction(a, b) { 17 | if (a === b) { 18 | return 0; 19 | } 20 | 21 | return a < b ? -1 : 1; 22 | } 23 | 24 | /** 25 | * Checks if two variables are equal. 26 | * @param {*} a 27 | * @param {*} b 28 | * @return {boolean} 29 | */ 30 | equal(a, b) { 31 | return this.compare(a, b) === 0; 32 | } 33 | 34 | /** 35 | * Checks if variable "a" is less than "b". 36 | * @param {*} a 37 | * @param {*} b 38 | * @return {boolean} 39 | */ 40 | lessThan(a, b) { 41 | return this.compare(a, b) < 0; 42 | } 43 | 44 | /** 45 | * Checks if variable "a" is greater than "b". 46 | * @param {*} a 47 | * @param {*} b 48 | * @return {boolean} 49 | */ 50 | greaterThan(a, b) { 51 | return this.compare(a, b) > 0; 52 | } 53 | 54 | /** 55 | * Checks if variable "a" is less than or equal to "b". 56 | * @param {*} a 57 | * @param {*} b 58 | * @return {boolean} 59 | */ 60 | lessThanOrEqual(a, b) { 61 | return this.lessThan(a, b) || this.equal(a, b); 62 | } 63 | 64 | /** 65 | * Checks if variable "a" is greater than or equal to "b". 66 | * @param {*} a 67 | * @param {*} b 68 | * @return {boolean} 69 | */ 70 | greaterThanOrEqual(a, b) { 71 | return this.greaterThan(a, b) || this.equal(a, b); 72 | } 73 | 74 | /** 75 | * Reverses the comparison order. 76 | */ 77 | reverse() { 78 | const compareOriginal = this.compare; 79 | this.compare = (a, b) => compareOriginal(b, a); 80 | } 81 | } 82 | -------------------------------------------------------------------------------- /src/utils/comparator/__test__/Comparator.test.js: -------------------------------------------------------------------------------- 1 | import Comparator from '../Comparator'; 2 | 3 | describe('Comparator', () => { 4 | it('should compare with default comparator function', () => { 5 | const comparator = new Comparator(); 6 | 7 | expect(comparator.equal(0, 0)).toBe(true); 8 | expect(comparator.equal(0, 1)).toBe(false); 9 | expect(comparator.equal('a', 'a')).toBe(true); 10 | expect(comparator.lessThan(1, 2)).toBe(true); 11 | expect(comparator.lessThan(-1, 2)).toBe(true); 12 | expect(comparator.lessThan('a', 'b')).toBe(true); 13 | expect(comparator.lessThan('a', 'ab')).toBe(true); 14 | expect(comparator.lessThan(10, 2)).toBe(false); 15 | expect(comparator.lessThanOrEqual(10, 2)).toBe(false); 16 | expect(comparator.lessThanOrEqual(1, 1)).toBe(true); 17 | expect(comparator.lessThanOrEqual(0, 0)).toBe(true); 18 | expect(comparator.greaterThan(0, 0)).toBe(false); 19 | expect(comparator.greaterThan(10, 0)).toBe(true); 20 | expect(comparator.greaterThanOrEqual(10, 0)).toBe(true); 21 | expect(comparator.greaterThanOrEqual(10, 10)).toBe(true); 22 | expect(comparator.greaterThanOrEqual(0, 10)).toBe(false); 23 | }); 24 | 25 | it('should compare with custom comparator function', () => { 26 | const comparator = new Comparator((a, b) => { 27 | if (a.length === b.length) { 28 | return 0; 29 | } 30 | 31 | return a.length < b.length ? -1 : 1; 32 | }); 33 | 34 | expect(comparator.equal('a', 'b')).toBe(true); 35 | expect(comparator.equal('a', '')).toBe(false); 36 | expect(comparator.lessThan('b', 'aa')).toBe(true); 37 | expect(comparator.greaterThanOrEqual('a', 'aa')).toBe(false); 38 | expect(comparator.greaterThanOrEqual('aa', 'a')).toBe(true); 39 | expect(comparator.greaterThanOrEqual('a', 'a')).toBe(true); 40 | 41 | comparator.reverse(); 42 | 43 | expect(comparator.equal('a', 'b')).toBe(true); 44 | expect(comparator.equal('a', '')).toBe(false); 45 | expect(comparator.lessThan('b', 'aa')).toBe(false); 46 | expect(comparator.greaterThanOrEqual('a', 'aa')).toBe(true); 47 | expect(comparator.greaterThanOrEqual('aa', 'a')).toBe(false); 48 | expect(comparator.greaterThanOrEqual('a', 'a')).toBe(true); 49 | }); 50 | }); 51 | --------------------------------------------------------------------------------