├── .DS_Store
├── BST
├── .DS_Store
└── BST Problems Part #1.md
├── Heap
├── .DS_Store
└── Heap Tutorials.md
├── Math
└── .DS_Store
├── SQL
└── .DS_Store
├── Graph
├── .DS_Store
└── Graph Part #1.md
├── Recursion
├── .DS_Store
└── Recursion Problems Part #1.md
├── Binary Tree
├── .DS_Store
└── Binary Tree Tutorial.md
├── Hash Table
└── .DS_Store
├── Two Pointers
├── .DS_Store
└── Two Pointers Problems Part #1.md
├── Binary Search
├── .DS_Store
└── Binary Search Problems Part #1.md
├── Array and String
└── .DS_Store
├── LeeCode Summary.xlsx.xlsx
├── Dynamic Programming
└── .DS_Store
├── ~$LeeCode Summary.xlsx.xlsx
├── Common-method-cheet-sheet.md
├── README.md
├── Bit Manipulation
└── Bit Problems Part #1.md
├── Bit
└── Bit Manipulation Part #1.md
├── OA Summary
└── Online Assessment.md
├── System Design
├── System Design Tutorial.md
└── System Design Problem Part #1.md
├── Sort
└── Sorting Problems Part #1.md
├── Greedy
└── Greedy Algorithm Part #1.md
├── Trie
└── Trie Tutorial.md
├── Basic LeetCode Template.md
└── Queue & Stack
└── Queue Problems Part #1.md
/.DS_Store:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/hhhwenjun/leetcode-note-java/HEAD/.DS_Store
--------------------------------------------------------------------------------
/BST/.DS_Store:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/hhhwenjun/leetcode-note-java/HEAD/BST/.DS_Store
--------------------------------------------------------------------------------
/Heap/.DS_Store:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/hhhwenjun/leetcode-note-java/HEAD/Heap/.DS_Store
--------------------------------------------------------------------------------
/Math/.DS_Store:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/hhhwenjun/leetcode-note-java/HEAD/Math/.DS_Store
--------------------------------------------------------------------------------
/SQL/.DS_Store:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/hhhwenjun/leetcode-note-java/HEAD/SQL/.DS_Store
--------------------------------------------------------------------------------
/Graph/.DS_Store:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/hhhwenjun/leetcode-note-java/HEAD/Graph/.DS_Store
--------------------------------------------------------------------------------
/Recursion/.DS_Store:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/hhhwenjun/leetcode-note-java/HEAD/Recursion/.DS_Store
--------------------------------------------------------------------------------
/Binary Tree/.DS_Store:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/hhhwenjun/leetcode-note-java/HEAD/Binary Tree/.DS_Store
--------------------------------------------------------------------------------
/Hash Table/.DS_Store:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/hhhwenjun/leetcode-note-java/HEAD/Hash Table/.DS_Store
--------------------------------------------------------------------------------
/Two Pointers/.DS_Store:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/hhhwenjun/leetcode-note-java/HEAD/Two Pointers/.DS_Store
--------------------------------------------------------------------------------
/Binary Search/.DS_Store:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/hhhwenjun/leetcode-note-java/HEAD/Binary Search/.DS_Store
--------------------------------------------------------------------------------
/Array and String/.DS_Store:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/hhhwenjun/leetcode-note-java/HEAD/Array and String/.DS_Store
--------------------------------------------------------------------------------
/LeeCode Summary.xlsx.xlsx:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/hhhwenjun/leetcode-note-java/HEAD/LeeCode Summary.xlsx.xlsx
--------------------------------------------------------------------------------
/Dynamic Programming/.DS_Store:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/hhhwenjun/leetcode-note-java/HEAD/Dynamic Programming/.DS_Store
--------------------------------------------------------------------------------
/~$LeeCode Summary.xlsx.xlsx:
--------------------------------------------------------------------------------
1 | �Microsoft Office User ��M�i�c�r�o�s�o�f�t� �O�f�f�i�c�e� �U�s�e�r� � � � � � � � � � � � � � � � � � � � � � � � � � � � � � � � � �
--------------------------------------------------------------------------------
/Common-method-cheet-sheet.md:
--------------------------------------------------------------------------------
1 | # Commonly Used Method in LeetCode
2 | Authored by: hhhwenjun
3 |
4 | ## Integer, String, Character Transformation
5 | #### Char to Int
6 | 1. Subtract with '0' to find the value: `char - '0'`
7 | 2. Use built-in character method to get the numeric value: `Character.getNumericValue(char)`
8 | **Tips**: Do not use `Integer.valueOf` or `Integer.parseInt`, they would only show the char value, such as 'a' -> 67
9 |
--------------------------------------------------------------------------------
/README.md:
--------------------------------------------------------------------------------
1 | # LeetCode Solution and Learning Notes
2 |
3 | ## Introduction
4 | Leetcode summary of solutions and tutorial notes. Java only. For self use. Categorized by topics. Each of the note includes my solution, tips and summary, and solutions provided by Leetcode. Some of the notes are tutorial.
5 |
6 | ## Catalog
7 | https://docs.google.com/spreadsheets/d/15wv-zRllN9pYZhOTVzVBLuY03gyqo_AH/edit?usp=sharing&ouid=101695934894145863901&rtpof=true&sd=true
8 |
9 | Please use the spreadsheet to find the location of the problems. The spreadsheet contains problem number, category, summary and my check dates.
10 |
11 | ## Update
12 | Usually I solve 3 problems everyday. The repo is updated in a daily basis.
13 |
--------------------------------------------------------------------------------
/Bit Manipulation/Bit Problems Part #1.md:
--------------------------------------------------------------------------------
1 | # Bit Problems Part #1
2 |
3 | ## Sort Integers by The Number of 1 Bit (Easy #1356)
4 |
5 | **Question**: You are given an integer array `arr`. Sort the integers in the array in ascending order by the number of `1`'s in their binary representation and in case of two or more integers have the same number of `1`'s you have to sort them in ascending order.
6 |
7 | Return *the array after sorting it*.
8 |
9 | **Example 1:**
10 |
11 | ```
12 | Input: arr = [0,1,2,3,4,5,6,7,8]
13 | Output: [0,1,2,4,8,3,5,6,7]
14 | Explantion: [0] is the only integer with 0 bits.
15 | [1,2,4,8] all have 1 bit.
16 | [3,5,6] have 2 bits.
17 | [7] has 3 bits.
18 | The sorted array by bits is [0,1,2,4,8,3,5,6,7]
19 | ```
20 |
21 | **Example 2:**
22 |
23 | ```
24 | Input: arr = [1024,512,256,128,64,32,16,8,4,2,1]
25 | Output: [1,2,4,8,16,32,64,128,256,512,1024]
26 | Explantion: All integers have 1 bit in the binary representation, you should just sort them in ascending order.
27 | ```
28 |
29 | **Constraints:**
30 |
31 | - `1 <= arr.length <= 500`
32 | - `0 <= arr[i] <= 104`
33 |
34 | ### Standard Solution
35 |
36 | #### Solution #1 Bit Count
37 |
38 | * The **bitCount()** method of Integer class of java.lang package returns the count of the number of one-bits in the two’s complement binary representation of an int value. This function is sometimes referred to as the **population count**.
39 |
40 | ```java
41 | public int[] sortByBits(int[] arr) {
42 | Integer[] boxedArray = Arrays.stream(arr).boxed().toArray(Integer[]::new);
43 |
44 | Arrays.sort(boxedArray, (a,b) -> {
45 | int A = Integer.bitCount(a);
46 | int B = Integer.bitCount(b);
47 | if(A < B) return -1;
48 | if(A > B) return 1;
49 | return Integer.compare(a,b);
50 | });
51 |
52 | return Arrays.stream(boxedArray).mapToInt(Integer::intValue).toArray();
53 | }
54 | ```
55 |
56 |
--------------------------------------------------------------------------------
/Recursion/Recursion Problems Part #1.md:
--------------------------------------------------------------------------------
1 | # Recursion Problems Part #1
2 |
3 | ## Count Complete Tree Nodes(Medium #222)
4 |
5 | **Question**: Given the `root` of a **complete** binary tree, return the number of the nodes in the tree.
6 |
7 | According to **[Wikipedia](http://en.wikipedia.org/wiki/Binary_tree#Types_of_binary_trees)**, every level, except possibly the last, is completely filled in a complete binary tree, and all nodes in the last level are as far left as possible. It can have between `1` and `2h` nodes inclusive at the last level `h`.
8 |
9 | Design an algorithm that runs in less than `O(n)` time complexity.
10 |
11 |
12 |
13 | **Example 1:**
14 |
15 | 
16 |
17 | ```
18 | Input: root = [1,2,3,4,5,6]
19 | Output: 6
20 | ```
21 |
22 | **Example 2:**
23 |
24 | ```
25 | Input: root = []
26 | Output: 0
27 | ```
28 |
29 | **Example 3:**
30 |
31 | ```
32 | Input: root = [1]
33 | Output: 1
34 | ```
35 |
36 | **Constraints:**
37 |
38 | - The number of nodes in the tree is in the range `[0, 5 * 104]`.
39 | - `0 <= Node.val <= 5 * 104`
40 | - The tree is guaranteed to be **complete**.
41 |
42 | ### My Solution
43 |
44 | * Recursion method to do the counting
45 |
46 | ```java
47 | public int countNodes(TreeNode root) {
48 | return count(root);
49 | }
50 | public int count(TreeNode root){
51 | if (root == null){
52 | return 0;
53 | }
54 | return 1 + count(root.left) + count(root.right);
55 | }
56 | ```
57 |
58 | ### Standard Solution
59 |
60 | #### Solution #1 Linear Time
61 |
62 | * Same as my solution, but a more simplified version.
63 |
64 | ```java
65 | public int countNodes(TreeNode root){
66 | return root != null ? 1 + countNodes(root.right) + countNodes(root.left) : 0;
67 | }
68 | ```
69 |
70 | - Time complexity: $\mathcal{O}(N)$.
71 | - Space complexity: $\mathcal{O}(d) = \mathcal{O}(\log N)$ to keep the recursion stack, where d is a tree depth.
--------------------------------------------------------------------------------
/Bit/Bit Manipulation Part #1.md:
--------------------------------------------------------------------------------
1 | # Bit Manipulation Part #1
2 |
3 | ## Maximum XOR After Operations (Medium #2317)
4 |
5 | **Question**: You are given a **0-indexed** integer array `nums`. In one operation, select **any** non-negative integer `x` and an index `i`, then **update** `nums[i]` to be equal to `nums[i] AND (nums[i] XOR x)`.
6 |
7 | Note that `AND` is the bitwise AND operation and `XOR` is the bitwise XOR operation.
8 |
9 | Return *the **maximum** possible bitwise XOR of all elements of* `nums` *after applying the operation **any number** of times*.
10 |
11 | **Example 1:**
12 |
13 | ```
14 | Input: nums = [3,2,4,6]
15 | Output: 7
16 | Explanation: Apply the operation with x = 4 and i = 3, num[3] = 6 AND (6 XOR 4) = 6 AND 2 = 2.
17 | Now, nums = [3, 2, 4, 2] and the bitwise XOR of all the elements = 3 XOR 2 XOR 4 XOR 2 = 7.
18 | It can be shown that 7 is the maximum possible bitwise XOR.
19 | Note that other operations may be used to achieve a bitwise XOR of 7.
20 | ```
21 |
22 | **Example 2:**
23 |
24 | ```
25 | Input: nums = [1,2,3,9,2]
26 | Output: 11
27 | Explanation: Apply the operation zero times.
28 | The bitwise XOR of all the elements = 1 XOR 2 XOR 3 XOR 9 XOR 2 = 11.
29 | It can be shown that 11 is the maximum possible bitwise XOR.
30 | ```
31 |
32 | **Constraints:**
33 |
34 | - `1 <= nums.length <= 105`
35 | - `0 <= nums[i] <= 108`
36 |
37 | ### Standard Solution
38 |
39 | * Now we approve it's realizable. Assume result is `best = XOR(A[i])` and `best < res` above. There is at least one bit difference between `best` and `res`, assume it's `x = 1 << k`. We can find at least a `A[i]` that `A[i] && x = x`.
40 | * We apply `x` on `A[i]`, `A[i]` is updated to `A[i] && (A[i] ^ x) = A[i] ^ x`. We had `best = XOR(A[i])` as said above,
41 | now we have `best2 = XOR(A[i]) ^ x`, so we get a better `best2 > best`, where we prove by contradiction.
42 |
43 | ```java
44 | public int maximumXOR(int[] nums) {
45 | int res = 0;
46 | for (int a: nums)
47 | res |= a;
48 | return res;
49 | }
50 | ```
51 |
52 |
--------------------------------------------------------------------------------
/Graph/Graph Part #1.md:
--------------------------------------------------------------------------------
1 | # Graph Part #1
2 |
3 | ## Maximum Total Importance of Roads (Medium #2285)
4 |
5 | **Question**: You are given an int `n` denoting the number of cities in a country. The cities are numbered from `0` to `n - 1`.
6 |
7 | You are also given a 2D integer array `roads` where `roads[i] = [ai, bi]` denotes that there exists a **bidirectional** road connecting cities `ai` and `bi`.
8 |
9 | You need to assign each city with an integer value from `1` to `n`, where each value can only be used **once**. The **importance** of a road is then defined as the **sum** of the values of the two cities it connects.
10 |
11 | Return *the **maximum total importance** of all roads possible after assigning the values optimally.*
12 |
13 | **Example 1:**
14 |
15 | 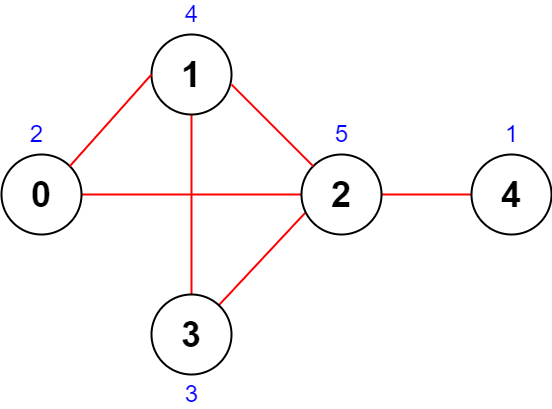 16 |
17 | ```
18 | Input: n = 5, roads = [[0,1],[1,2],[2,3],[0,2],[1,3],[2,4]]
19 | Output: 43
20 | Explanation: The figure above shows the country and the assigned values of [2,4,5,3,1].
21 | - The road (0,1) has an importance of 2 + 4 = 6.
22 | - The road (1,2) has an importance of 4 + 5 = 9.
23 | - The road (2,3) has an importance of 5 + 3 = 8.
24 | - The road (0,2) has an importance of 2 + 5 = 7.
25 | - The road (1,3) has an importance of 4 + 3 = 7.
26 | - The road (2,4) has an importance of 5 + 1 = 6.
27 | The total importance of all roads is 6 + 9 + 8 + 7 + 7 + 6 = 43.
28 | It can be shown that we cannot obtain a greater total importance than 43.
29 | ```
30 |
31 | **Example 2:**
32 |
33 |
16 |
17 | ```
18 | Input: n = 5, roads = [[0,1],[1,2],[2,3],[0,2],[1,3],[2,4]]
19 | Output: 43
20 | Explanation: The figure above shows the country and the assigned values of [2,4,5,3,1].
21 | - The road (0,1) has an importance of 2 + 4 = 6.
22 | - The road (1,2) has an importance of 4 + 5 = 9.
23 | - The road (2,3) has an importance of 5 + 3 = 8.
24 | - The road (0,2) has an importance of 2 + 5 = 7.
25 | - The road (1,3) has an importance of 4 + 3 = 7.
26 | - The road (2,4) has an importance of 5 + 1 = 6.
27 | The total importance of all roads is 6 + 9 + 8 + 7 + 7 + 6 = 43.
28 | It can be shown that we cannot obtain a greater total importance than 43.
29 | ```
30 |
31 | **Example 2:**
32 |
33 | 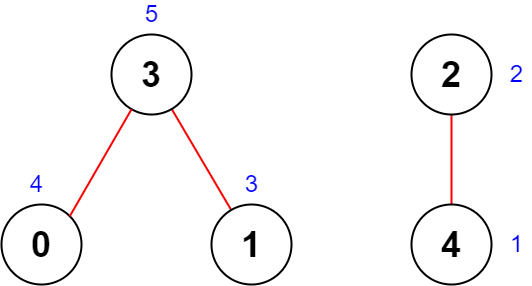 34 |
35 | ```
36 | Input: n = 5, roads = [[0,3],[2,4],[1,3]]
37 | Output: 20
38 | Explanation: The figure above shows the country and the assigned values of [4,3,2,5,1].
39 | - The road (0,3) has an importance of 4 + 5 = 9.
40 | - The road (2,4) has an importance of 2 + 1 = 3.
41 | - The road (1,3) has an importance of 3 + 5 = 8.
42 | The total importance of all roads is 9 + 3 + 8 = 20.
43 | It can be shown that we cannot obtain a greater total importance than 20.
44 | ```
45 |
46 | **Constraints:**
47 |
48 | - `2 <= n <= 5 * 104`
49 | - `1 <= roads.length <= 5 * 104`
50 | - `roads[i].length == 2`
51 | - `0 <= ai, bi <= n - 1`
52 | - `ai != bi`
53 | - There are no duplicate roads.
54 |
55 | ### Standard Solution
56 |
57 | #### Solution #1 Count Degree
58 |
59 | - The number assigned to any node will contribute to its neighbors, which is equal to its degree.
60 | - So, give the maximum number to the node with the maximum degree (edges connected to it).
61 |
62 | ```java
63 | public long maximumImportance(int n, int[][] roads) {
64 | long ans = 0, x = 1;
65 | long degree[] = new long[n];
66 | for(int road[] : roads){
67 | degree[road[0]]++; // count degree for node
68 | degree[road[1]]++;
69 | }
70 | Arrays.sort(degree);
71 | for(long i : degree) ans += i * (x++) ; // assign number to the degree
72 | return ans;
73 | }
74 | ```
75 |
76 | * The time complexity is $O(n \log n)$ due to sorting
77 | * The space complexity is $O(n)$ for the length of n
--------------------------------------------------------------------------------
/OA Summary/Online Assessment.md:
--------------------------------------------------------------------------------
1 | # Online Assessment
2 |
3 | ## Square Data Engineering Intern
4 |
5 | **Source**: [Credit to this link and author](https://leetcode.com/discuss/interview-question/1014660/samsara-oa-codesignal-summer-internship)
6 |
7 | #### Problem
8 |
9 | ```
10 | You have a passage of text that needs to be typed out, but some of the letter keys on your keyboard are broken! You are given an array letters representing the working letter keys, as well as a string text, and your task is to determine how many of the words from text can be typed using the broken keyboard. It is guaranteed that all of the non-letter keys are working (including all punctuation and special characters).
11 | A word is defined as a sequence of consecutive characters which does not contain any spaces.
12 | The given text is a string consisting of words, each separated by exactly one space.
13 | It is guaranteed that text does not contain any leading or trailing spaces.
14 | Note that the characters in letters are all lowercase, but since the shift key is working,
15 | it's possible to type the uppercase versions also.
16 | ```
17 |
18 | ```
19 | Example:
20 | 1. For text = "Hello, this is CodeSignal!" and letters = ['e', 'i', 'h', 'l', 'o', 's'],
21 | the output should be brokenKeyboard(text, letters) = 2.
22 | - "Hello," can be typed since the characters 'h', 'e', 'l' and 'o' are in letters.
23 | - Note that the symbol ',' also belongs to the current word and can by typed.
24 | - "this" cannot be typed because the character 't' is not in letters.
25 | - "is" can be typed (both 'i' and 's' appear in letters).
26 | - "CodeSignal!" cannot be typed because the character 'c' is not in letters (as well as 'd', 'g', 'n', and 'a').
27 | 2. For text = "Hi, this is Chris!" and letters = ['r', 's', 't', 'c', 'h'], the output should be
28 | brokenKeyboard(text, letters) = 0.
29 | - Each word contains the character 'i' which does not appear in letters and thus cannot be typed on the keyboard.
30 | 3. For text = "3 + 2 = 5" and letters = [], the output should be brokenKeyboard(text, letters) = 5.
31 | - There are no working letters on the keyboard, but since each of these words consists of numbers and
32 | special characters, they can all be typed, and there are 5 of them.
33 | ```
34 |
35 | **Solution**:
36 |
37 | ```java
38 | public static int checkBrokenLetter(String text, char[] letters) {
39 | // Build hashSet
40 | Set set = new HashSet<>();
41 | for (char c : letters) {
42 | set.add(c);
43 | }
44 | String[] words= text.split(" ");
45 | int count = 0;
46 | for (String word: words) {
47 | // important to learn how to clean the string, regular expression
48 | String cleanText = word.replaceAll("[^[a-zA-Z]]", "").toLowerCase();
49 | System.out.println(cleanText);
50 | boolean valid = true;
51 | for (int i = 0; i < cleanText.length(); i++) {
52 | if (! set.contains(cleanText.charAt(i))) {
53 | valid = false;
54 | break;
55 | }
56 | }
57 | if (valid) {
58 | count++;
59 | }
60 | }
61 | return count;
62 | }
63 | ```
64 |
65 |
--------------------------------------------------------------------------------
/System Design/System Design Tutorial.md:
--------------------------------------------------------------------------------
1 | # System Design Tutorial
2 |
3 | This course is divided into three main chapters -
4 |
5 | - **Basics**: This chapter is specially designed for novices to build a strong foundation of System Design fundamentals that are useful in understanding the dynamics of highly scalable systems.
6 | - **Case Studies**: This chapter aims to model the System Design of some of the most frequently asked interview questions, like designing an e-commerce app.
7 | - **Problem Solving**: This chapter lets you apply your understanding of the preceding chapters with the help of some practice problems and quizzes.
8 |
9 | ### **High-Level Design**
10 |
11 | #### Structure
12 |
13 | * Overall architecture
14 | * How can the system be built such that it takes care of scalability, latency, and other performance requirements
15 | * Systems and Services
16 | * In this part of high-level design, we need to decide how the system will be broken down, what the microservices will be, and their scope.
17 | * Interaction between Systems
18 | * How will the systems interact with each other?
19 | * What protocols will you use?
20 | * Will it be synchronous or asynchronous?
21 | * You need to make these decisions based on the requirements
22 | * Database(Design database schema)
23 | * What databases will you need?
24 | * What kind of data do you need to store?
25 | * SQL or NoSQL, what will be the database schema?
26 | * Examples
27 |
28 | #### Expectation
29 |
30 | * Requirements: fulfill requirements, highly scalable
31 | * Futuristic: open to future improvement, non-restrictive to specific items, modular
32 |
33 |
34 |
35 | ```
36 | Input: n = 5, roads = [[0,3],[2,4],[1,3]]
37 | Output: 20
38 | Explanation: The figure above shows the country and the assigned values of [4,3,2,5,1].
39 | - The road (0,3) has an importance of 4 + 5 = 9.
40 | - The road (2,4) has an importance of 2 + 1 = 3.
41 | - The road (1,3) has an importance of 3 + 5 = 8.
42 | The total importance of all roads is 9 + 3 + 8 = 20.
43 | It can be shown that we cannot obtain a greater total importance than 20.
44 | ```
45 |
46 | **Constraints:**
47 |
48 | - `2 <= n <= 5 * 104`
49 | - `1 <= roads.length <= 5 * 104`
50 | - `roads[i].length == 2`
51 | - `0 <= ai, bi <= n - 1`
52 | - `ai != bi`
53 | - There are no duplicate roads.
54 |
55 | ### Standard Solution
56 |
57 | #### Solution #1 Count Degree
58 |
59 | - The number assigned to any node will contribute to its neighbors, which is equal to its degree.
60 | - So, give the maximum number to the node with the maximum degree (edges connected to it).
61 |
62 | ```java
63 | public long maximumImportance(int n, int[][] roads) {
64 | long ans = 0, x = 1;
65 | long degree[] = new long[n];
66 | for(int road[] : roads){
67 | degree[road[0]]++; // count degree for node
68 | degree[road[1]]++;
69 | }
70 | Arrays.sort(degree);
71 | for(long i : degree) ans += i * (x++) ; // assign number to the degree
72 | return ans;
73 | }
74 | ```
75 |
76 | * The time complexity is $O(n \log n)$ due to sorting
77 | * The space complexity is $O(n)$ for the length of n
--------------------------------------------------------------------------------
/OA Summary/Online Assessment.md:
--------------------------------------------------------------------------------
1 | # Online Assessment
2 |
3 | ## Square Data Engineering Intern
4 |
5 | **Source**: [Credit to this link and author](https://leetcode.com/discuss/interview-question/1014660/samsara-oa-codesignal-summer-internship)
6 |
7 | #### Problem
8 |
9 | ```
10 | You have a passage of text that needs to be typed out, but some of the letter keys on your keyboard are broken! You are given an array letters representing the working letter keys, as well as a string text, and your task is to determine how many of the words from text can be typed using the broken keyboard. It is guaranteed that all of the non-letter keys are working (including all punctuation and special characters).
11 | A word is defined as a sequence of consecutive characters which does not contain any spaces.
12 | The given text is a string consisting of words, each separated by exactly one space.
13 | It is guaranteed that text does not contain any leading or trailing spaces.
14 | Note that the characters in letters are all lowercase, but since the shift key is working,
15 | it's possible to type the uppercase versions also.
16 | ```
17 |
18 | ```
19 | Example:
20 | 1. For text = "Hello, this is CodeSignal!" and letters = ['e', 'i', 'h', 'l', 'o', 's'],
21 | the output should be brokenKeyboard(text, letters) = 2.
22 | - "Hello," can be typed since the characters 'h', 'e', 'l' and 'o' are in letters.
23 | - Note that the symbol ',' also belongs to the current word and can by typed.
24 | - "this" cannot be typed because the character 't' is not in letters.
25 | - "is" can be typed (both 'i' and 's' appear in letters).
26 | - "CodeSignal!" cannot be typed because the character 'c' is not in letters (as well as 'd', 'g', 'n', and 'a').
27 | 2. For text = "Hi, this is Chris!" and letters = ['r', 's', 't', 'c', 'h'], the output should be
28 | brokenKeyboard(text, letters) = 0.
29 | - Each word contains the character 'i' which does not appear in letters and thus cannot be typed on the keyboard.
30 | 3. For text = "3 + 2 = 5" and letters = [], the output should be brokenKeyboard(text, letters) = 5.
31 | - There are no working letters on the keyboard, but since each of these words consists of numbers and
32 | special characters, they can all be typed, and there are 5 of them.
33 | ```
34 |
35 | **Solution**:
36 |
37 | ```java
38 | public static int checkBrokenLetter(String text, char[] letters) {
39 | // Build hashSet
40 | Set set = new HashSet<>();
41 | for (char c : letters) {
42 | set.add(c);
43 | }
44 | String[] words= text.split(" ");
45 | int count = 0;
46 | for (String word: words) {
47 | // important to learn how to clean the string, regular expression
48 | String cleanText = word.replaceAll("[^[a-zA-Z]]", "").toLowerCase();
49 | System.out.println(cleanText);
50 | boolean valid = true;
51 | for (int i = 0; i < cleanText.length(); i++) {
52 | if (! set.contains(cleanText.charAt(i))) {
53 | valid = false;
54 | break;
55 | }
56 | }
57 | if (valid) {
58 | count++;
59 | }
60 | }
61 | return count;
62 | }
63 | ```
64 |
65 |
--------------------------------------------------------------------------------
/System Design/System Design Tutorial.md:
--------------------------------------------------------------------------------
1 | # System Design Tutorial
2 |
3 | This course is divided into three main chapters -
4 |
5 | - **Basics**: This chapter is specially designed for novices to build a strong foundation of System Design fundamentals that are useful in understanding the dynamics of highly scalable systems.
6 | - **Case Studies**: This chapter aims to model the System Design of some of the most frequently asked interview questions, like designing an e-commerce app.
7 | - **Problem Solving**: This chapter lets you apply your understanding of the preceding chapters with the help of some practice problems and quizzes.
8 |
9 | ### **High-Level Design**
10 |
11 | #### Structure
12 |
13 | * Overall architecture
14 | * How can the system be built such that it takes care of scalability, latency, and other performance requirements
15 | * Systems and Services
16 | * In this part of high-level design, we need to decide how the system will be broken down, what the microservices will be, and their scope.
17 | * Interaction between Systems
18 | * How will the systems interact with each other?
19 | * What protocols will you use?
20 | * Will it be synchronous or asynchronous?
21 | * You need to make these decisions based on the requirements
22 | * Database(Design database schema)
23 | * What databases will you need?
24 | * What kind of data do you need to store?
25 | * SQL or NoSQL, what will be the database schema?
26 | * Examples
27 |
28 | #### Expectation
29 |
30 | * Requirements: fulfill requirements, highly scalable
31 | * Futuristic: open to future improvement, non-restrictive to specific items, modular
32 |
33 |  34 |
35 | #### Approach
36 |
37 | * Functional requirements
38 | * Features
39 | * User Journeys
40 | * Non-functional requirements
41 | * Scale
42 | * Latency
43 | * Consistency
44 |
45 | #### Approach Solution
46 |
47 |
34 |
35 | #### Approach
36 |
37 | * Functional requirements
38 | * Features
39 | * User Journeys
40 | * Non-functional requirements
41 | * Scale
42 | * Latency
43 | * Consistency
44 |
45 | #### Approach Solution
46 |
47 |  48 |
49 | * Propose a design
50 | * This means breaking down the system into multiple components and identifying which microservices are needed, setting up interactions between these microservices, finalizing databases, etc.
51 | * Talk about trade-offs
52 | * What database would be more suitable? Do you need SQL or NoSQL? You keep adjusting your design based on your **design decisions** and tradeoffs until the requirements have been satisfactorily met.
53 | * Discuss design choices
54 | * Limitations of the design
55 | * If your system does not have a monitoring component, it would be good to mention this at this stage.
56 |
57 | ### Low-Level Design
58 |
59 |
48 |
49 | * Propose a design
50 | * This means breaking down the system into multiple components and identifying which microservices are needed, setting up interactions between these microservices, finalizing databases, etc.
51 | * Talk about trade-offs
52 | * What database would be more suitable? Do you need SQL or NoSQL? You keep adjusting your design based on your **design decisions** and tradeoffs until the requirements have been satisfactorily met.
53 | * Discuss design choices
54 | * Limitations of the design
55 | * If your system does not have a monitoring component, it would be good to mention this at this stage.
56 |
57 | ### Low-Level Design
58 |
59 |  60 |
61 | #### Structure
62 |
63 | * Dive deeper into the implemention of the individual system
64 | * Covers a sub-system
65 | * Optimisations within the sub-system
66 | * Sample: Design a parking lot, Uber's pricing system
67 |
68 | #### Expection
69 |
70 | * Requirements:
71 | * fulfulls function and non-function requirement, good code structure, working + clean code
72 | * Modular, futuristic, non-restrictive
73 | * Code:
74 | * Interfaces
75 | * Class diagrams
76 | * Entities
77 | * Data model
78 | * Design patterns
79 | * Quality:
80 | * Working code, pass basic tests
81 | * Modular: able to add new features, code consistent when adding new features(old codes works well)
82 | * Testable: unit test cases
83 | * Expected Outcome (Example of Uber's pricing engine)
84 | * `getFareEstimate()` which fetches the `basePrice` and `surgePrice` and accordingly returns the total estimated fare.`getBasePrice()` will return the base price based on distance, time, and ride type. If there are too many requests from users for the current number of drivers, we will apply a surge price and increase the fare.
85 | * We could use the Factory Design Pattern here and add two factories, `BasePriceCalculatorFactory` for calculating `basePrice` and `SurgePriceCalculatorFactory` for calculating `surgePrice`.
86 |
87 | 
88 |
89 | #### How to Approach LLD Interview
90 |
91 | * Lock down the requirements, both functional and non-functional. The idea is to limit the scope early on so we don't get lost trying to build too many things.
92 | * The next step is the code. The first thing to do here will be to define the interfaces.
93 | * Next are class diagrams, where we define what classes we need, how they will interact, what hierarchy they will follow, etc.
94 | * We will further define our entities and data models, and while doing all this, we need to consider what design pattern will be most suitable.
95 | * Talking about design patterns, the next step would be to ensure code quality. This means we should have a working code with some basic test cases that are passing for the logic we have written.
--------------------------------------------------------------------------------
/Sort/Sorting Problems Part #1.md:
--------------------------------------------------------------------------------
1 | # Sorting Problems Part #1
2 |
3 | ## Sort List (Medium #148)
4 |
5 | **Question**: Given the `head` of a linked list, return *the list after sorting it in **ascending order***.
6 |
7 | **Example 1:**
8 |
9 |
60 |
61 | #### Structure
62 |
63 | * Dive deeper into the implemention of the individual system
64 | * Covers a sub-system
65 | * Optimisations within the sub-system
66 | * Sample: Design a parking lot, Uber's pricing system
67 |
68 | #### Expection
69 |
70 | * Requirements:
71 | * fulfulls function and non-function requirement, good code structure, working + clean code
72 | * Modular, futuristic, non-restrictive
73 | * Code:
74 | * Interfaces
75 | * Class diagrams
76 | * Entities
77 | * Data model
78 | * Design patterns
79 | * Quality:
80 | * Working code, pass basic tests
81 | * Modular: able to add new features, code consistent when adding new features(old codes works well)
82 | * Testable: unit test cases
83 | * Expected Outcome (Example of Uber's pricing engine)
84 | * `getFareEstimate()` which fetches the `basePrice` and `surgePrice` and accordingly returns the total estimated fare.`getBasePrice()` will return the base price based on distance, time, and ride type. If there are too many requests from users for the current number of drivers, we will apply a surge price and increase the fare.
85 | * We could use the Factory Design Pattern here and add two factories, `BasePriceCalculatorFactory` for calculating `basePrice` and `SurgePriceCalculatorFactory` for calculating `surgePrice`.
86 |
87 | 
88 |
89 | #### How to Approach LLD Interview
90 |
91 | * Lock down the requirements, both functional and non-functional. The idea is to limit the scope early on so we don't get lost trying to build too many things.
92 | * The next step is the code. The first thing to do here will be to define the interfaces.
93 | * Next are class diagrams, where we define what classes we need, how they will interact, what hierarchy they will follow, etc.
94 | * We will further define our entities and data models, and while doing all this, we need to consider what design pattern will be most suitable.
95 | * Talking about design patterns, the next step would be to ensure code quality. This means we should have a working code with some basic test cases that are passing for the logic we have written.
--------------------------------------------------------------------------------
/Sort/Sorting Problems Part #1.md:
--------------------------------------------------------------------------------
1 | # Sorting Problems Part #1
2 |
3 | ## Sort List (Medium #148)
4 |
5 | **Question**: Given the `head` of a linked list, return *the list after sorting it in **ascending order***.
6 |
7 | **Example 1:**
8 |
9 |  10 |
11 | ```
12 | Input: head = [4,2,1,3]
13 | Output: [1,2,3,4]
14 | ```
15 |
16 | **Example 2:**
17 |
18 |
10 |
11 | ```
12 | Input: head = [4,2,1,3]
13 | Output: [1,2,3,4]
14 | ```
15 |
16 | **Example 2:**
17 |
18 |  19 |
20 | ```
21 | Input: head = [-1,5,3,4,0]
22 | Output: [-1,0,3,4,5]
23 | ```
24 |
25 | **Example 3:**
26 |
27 | ```
28 | Input: head = []
29 | Output: []
30 | ```
31 |
32 | **Constraints:**
33 |
34 | - The number of nodes in the list is in the range `[0, 5 * 104]`.
35 | - `-105 <= Node.val <= 105`
36 |
37 | ### My Solution
38 |
39 | * Use an array list to record all the numbers, sort them using Collections
40 | * Then reassign them to the nodes
41 |
42 | ```java
43 | public ListNode sortList(ListNode head) {
44 | if (head == null){
45 | return null;
46 | }
47 | List nums = new ArrayList<>();
48 | ListNode current = head;
49 | while (current != null){
50 | nums.add(current.val);
51 | current = current.next;
52 | }
53 | Collections.sort(nums);
54 | current = head;
55 | while(nums.size() > 0){
56 | current.val = nums.remove(0);
57 | current = current.next;
58 | }
59 | return head;
60 | }
61 | ```
62 |
63 | ### Standard Solution
64 |
65 | #### Solution #1 Top-down Merge Sort
66 |
67 | * Recursively split the list into two halves, until only one node in the list (find mid)
68 | * Merge two lists also in recursion
69 |
70 | ```java
71 | public ListNode sortList(ListNode head){
72 | if (head == null || head.next == null){
73 | return head;
74 | }
75 | ListNode mid = getMid(head);
76 | ListNode left = sortList(head);
77 | ListNode right = sortList(mid);
78 | return merge(left, right);
79 | }
80 |
81 | public ListNode merge(ListNode list1, ListNode list2){
82 | ListNode dummyHead = new ListNode();
83 | ListNode tail = dummyHead;
84 | while (list1 != null && list2 != null){
85 | if {
86 | tail.next = list1;
87 | list1 = list1.next;
88 | tail = tail.next;
89 | } else {
90 | tail.next = list2;
91 | list2 = list2.next;
92 | tail = tail.next;
93 | }
94 | }
95 | tail.next = (list1 != null) ? list1 : list2;
96 | return dummyHead.next;
97 | }
98 | public ListNode getMid(ListNode head){
99 | ListNode midPrev = null;
100 | while(head != null && head.next != null){
101 | midPrev = (midPrev == null) ? head : midPrev.next;
102 | head = head.next.next;
103 | }
104 | ListNode mid = midPrev.next;
105 | midPrev.next = null;
106 | return mid;
107 | }
108 | ```
109 |
110 | - Time Complexity: $\mathcal{O}(n \log n)$, where n is the number of nodes in the linked list. The algorithm can be split into 2 phases, Split and Merge.
111 | - Space Complexity: $\mathcal{O}(\log n)$, where n is the number of nodes in the linked list. Since the problem is recursive, we need additional space to store the recursive call stack. The maximum depth of the recursion tree is $\log n$
112 |
113 | ## Largest Number (Medium #179)
114 |
115 | **Question**: Given a list of non-negative integers `nums`, arrange them such that they form the largest number and return it.
116 |
117 | Since the result may be very large, so you need to return a string instead of an integer.
118 |
119 | **Example 1:**
120 |
121 | ```
122 | Input: nums = [10,2]
123 | Output: "210"
124 | ```
125 |
126 | **Example 2:**
127 |
128 | ```
129 | Input: nums = [3,30,34,5,9]
130 | Output: "9534330"
131 | ```
132 |
133 | **Constraints:**
134 |
135 | - `1 <= nums.length <= 100`
136 | - `0 <= nums[i] <= 109`
137 |
138 | ### Standard Solution
139 |
140 | #### Solution #1 Sorting via Custom Comparator
141 |
142 | * Create a custom comparator, and compare the adding order (solve the problem: single digit vs. multiple digits)
143 | * Sort the string array
144 | * Add element to the string
145 |
146 | ```java
147 | private class LargeNumberComparator implements Comparator{
148 | @Override
149 | public int compare(String a, String b){
150 | String order1 = a + b;
151 | String order2 = b + a;
152 | return order2.compareTo(order1);
153 | }
154 | }
155 |
156 | public String largestNumber(int[] nums) {
157 | // get input integers as strings
158 | String[] strs = new String[nums.length];
159 | for (int i = 0; i < nums.length; i++){
160 | strs[i] = String.valueOf(nums[i]);
161 | }
162 |
163 | // sort strings according to custom comparator
164 | Arrays.sort(strs, new LargeNumberComparator());
165 |
166 | // if, after being sorted, the largest number is 0,
167 | // the entire number is 0.
168 | if (strs[0].equals("0")) return "0";
169 |
170 | // build largest number from sorted array
171 | String largestNumberStr = new String();
172 | for (String numStr : strs){
173 | largestNumberStr += numStr;
174 | }
175 | return largestNumberStr;
176 | }
177 | ```
178 |
179 | ```java
180 | // almost same but much faster solution
181 | public String largestNumber(int[] nums) {
182 | if (nums == null || nums.length == 0) return "";
183 | String[] strs = new String[nums.length];
184 | for (int i = 0; i < nums.length; i++) {
185 | strs[i] = nums[i]+"";
186 | }
187 | Arrays.sort(strs, new Comparator() {
188 | @Override
189 | public int compare(String i, String j) {
190 | String s1 = i+j;
191 | String s2 = j+i;
192 | return s1.compareTo(s2);
193 | }
194 | });
195 | if (strs[strs.length-1].charAt(0) == '0') return "0";
196 | String res = new String();
197 | for (int i = 0; i < strs.length; i++) {
198 | res = strs[i]+res;
199 | }
200 | return res;
201 | }
202 | ```
203 |
204 | - Time complexity: $\mathcal{O}(nlgn)$
205 |
206 | Although we are doing extra work in our comparator, it is only by a constant factor. Therefore, the overall runtime is dominated by the complexity of `sort`, which is $\mathcal{O}(nlgn)$ in Python and Java.
207 |
208 | - Space complexity: $\mathcal{O}(n)$
209 |
210 | Here, we allocate $\mathcal{O}(n)$ additional space to store the copy of `nums`. Although we could do that work in place (if we decide that it is okay to modify `nums`), we must allocate $\mathcal{O}(n)$ space for the final return string. Therefore, the overall memory footprint is linear in length of `nums`.
--------------------------------------------------------------------------------
/Greedy/Greedy Algorithm Part #1.md:
--------------------------------------------------------------------------------
1 | # Greedy Algorithm Part #1
2 |
3 | ## Remove Covered Intervals(Medium #1288)
4 |
5 | **Question**: Given an array `intervals` where `intervals[i] = [li, ri]` represent the interval `[li, ri)`, remove all intervals that are covered by another interval in the list.
6 |
7 | The interval `[a, b)` is covered by the interval `[c, d)` if and only if `c <= a` and `b <= d`.
8 |
9 | Return *the number of remaining intervals*.
10 |
11 | **Example 1:**
12 |
13 | ```
14 | Input: intervals = [[1,4],[3,6],[2,8]]
15 | Output: 2
16 | Explanation: Interval [3,6] is covered by [2,8], therefore it is removed.
17 | ```
18 |
19 | **Example 2:**
20 |
21 | ```
22 | Input: intervals = [[1,4],[2,3]]
23 | Output: 1
24 | ```
25 |
26 | **Constraints:**
27 |
28 | - `1 <= intervals.length <= 1000`
29 | - `intervals[i].length == 2`
30 | - `0 <= li <= ri <= 105`
31 | - All the given intervals are **unique**.
32 |
33 | ### Standard Solution
34 |
35 | #### Solution #1 Greedy Algorithm
36 |
37 | * The typical greedy solution has $\mathcal{O}(N \log N)$ time complexity and consists of two steps:
38 |
39 | - Figure out how to sort the input data. That would take $\mathcal{O}(N \log N)$ time, and could be done directly by sorting or indirectly by using the heap data structure. Usually sorting is better than heap usage because of gain in space.
40 | - Parse the sorted input in $\mathcal{O}(N)$ time to construct a solution.
41 |
42 |
19 |
20 | ```
21 | Input: head = [-1,5,3,4,0]
22 | Output: [-1,0,3,4,5]
23 | ```
24 |
25 | **Example 3:**
26 |
27 | ```
28 | Input: head = []
29 | Output: []
30 | ```
31 |
32 | **Constraints:**
33 |
34 | - The number of nodes in the list is in the range `[0, 5 * 104]`.
35 | - `-105 <= Node.val <= 105`
36 |
37 | ### My Solution
38 |
39 | * Use an array list to record all the numbers, sort them using Collections
40 | * Then reassign them to the nodes
41 |
42 | ```java
43 | public ListNode sortList(ListNode head) {
44 | if (head == null){
45 | return null;
46 | }
47 | List nums = new ArrayList<>();
48 | ListNode current = head;
49 | while (current != null){
50 | nums.add(current.val);
51 | current = current.next;
52 | }
53 | Collections.sort(nums);
54 | current = head;
55 | while(nums.size() > 0){
56 | current.val = nums.remove(0);
57 | current = current.next;
58 | }
59 | return head;
60 | }
61 | ```
62 |
63 | ### Standard Solution
64 |
65 | #### Solution #1 Top-down Merge Sort
66 |
67 | * Recursively split the list into two halves, until only one node in the list (find mid)
68 | * Merge two lists also in recursion
69 |
70 | ```java
71 | public ListNode sortList(ListNode head){
72 | if (head == null || head.next == null){
73 | return head;
74 | }
75 | ListNode mid = getMid(head);
76 | ListNode left = sortList(head);
77 | ListNode right = sortList(mid);
78 | return merge(left, right);
79 | }
80 |
81 | public ListNode merge(ListNode list1, ListNode list2){
82 | ListNode dummyHead = new ListNode();
83 | ListNode tail = dummyHead;
84 | while (list1 != null && list2 != null){
85 | if {
86 | tail.next = list1;
87 | list1 = list1.next;
88 | tail = tail.next;
89 | } else {
90 | tail.next = list2;
91 | list2 = list2.next;
92 | tail = tail.next;
93 | }
94 | }
95 | tail.next = (list1 != null) ? list1 : list2;
96 | return dummyHead.next;
97 | }
98 | public ListNode getMid(ListNode head){
99 | ListNode midPrev = null;
100 | while(head != null && head.next != null){
101 | midPrev = (midPrev == null) ? head : midPrev.next;
102 | head = head.next.next;
103 | }
104 | ListNode mid = midPrev.next;
105 | midPrev.next = null;
106 | return mid;
107 | }
108 | ```
109 |
110 | - Time Complexity: $\mathcal{O}(n \log n)$, where n is the number of nodes in the linked list. The algorithm can be split into 2 phases, Split and Merge.
111 | - Space Complexity: $\mathcal{O}(\log n)$, where n is the number of nodes in the linked list. Since the problem is recursive, we need additional space to store the recursive call stack. The maximum depth of the recursion tree is $\log n$
112 |
113 | ## Largest Number (Medium #179)
114 |
115 | **Question**: Given a list of non-negative integers `nums`, arrange them such that they form the largest number and return it.
116 |
117 | Since the result may be very large, so you need to return a string instead of an integer.
118 |
119 | **Example 1:**
120 |
121 | ```
122 | Input: nums = [10,2]
123 | Output: "210"
124 | ```
125 |
126 | **Example 2:**
127 |
128 | ```
129 | Input: nums = [3,30,34,5,9]
130 | Output: "9534330"
131 | ```
132 |
133 | **Constraints:**
134 |
135 | - `1 <= nums.length <= 100`
136 | - `0 <= nums[i] <= 109`
137 |
138 | ### Standard Solution
139 |
140 | #### Solution #1 Sorting via Custom Comparator
141 |
142 | * Create a custom comparator, and compare the adding order (solve the problem: single digit vs. multiple digits)
143 | * Sort the string array
144 | * Add element to the string
145 |
146 | ```java
147 | private class LargeNumberComparator implements Comparator{
148 | @Override
149 | public int compare(String a, String b){
150 | String order1 = a + b;
151 | String order2 = b + a;
152 | return order2.compareTo(order1);
153 | }
154 | }
155 |
156 | public String largestNumber(int[] nums) {
157 | // get input integers as strings
158 | String[] strs = new String[nums.length];
159 | for (int i = 0; i < nums.length; i++){
160 | strs[i] = String.valueOf(nums[i]);
161 | }
162 |
163 | // sort strings according to custom comparator
164 | Arrays.sort(strs, new LargeNumberComparator());
165 |
166 | // if, after being sorted, the largest number is 0,
167 | // the entire number is 0.
168 | if (strs[0].equals("0")) return "0";
169 |
170 | // build largest number from sorted array
171 | String largestNumberStr = new String();
172 | for (String numStr : strs){
173 | largestNumberStr += numStr;
174 | }
175 | return largestNumberStr;
176 | }
177 | ```
178 |
179 | ```java
180 | // almost same but much faster solution
181 | public String largestNumber(int[] nums) {
182 | if (nums == null || nums.length == 0) return "";
183 | String[] strs = new String[nums.length];
184 | for (int i = 0; i < nums.length; i++) {
185 | strs[i] = nums[i]+"";
186 | }
187 | Arrays.sort(strs, new Comparator() {
188 | @Override
189 | public int compare(String i, String j) {
190 | String s1 = i+j;
191 | String s2 = j+i;
192 | return s1.compareTo(s2);
193 | }
194 | });
195 | if (strs[strs.length-1].charAt(0) == '0') return "0";
196 | String res = new String();
197 | for (int i = 0; i < strs.length; i++) {
198 | res = strs[i]+res;
199 | }
200 | return res;
201 | }
202 | ```
203 |
204 | - Time complexity: $\mathcal{O}(nlgn)$
205 |
206 | Although we are doing extra work in our comparator, it is only by a constant factor. Therefore, the overall runtime is dominated by the complexity of `sort`, which is $\mathcal{O}(nlgn)$ in Python and Java.
207 |
208 | - Space complexity: $\mathcal{O}(n)$
209 |
210 | Here, we allocate $\mathcal{O}(n)$ additional space to store the copy of `nums`. Although we could do that work in place (if we decide that it is okay to modify `nums`), we must allocate $\mathcal{O}(n)$ space for the final return string. Therefore, the overall memory footprint is linear in length of `nums`.
--------------------------------------------------------------------------------
/Greedy/Greedy Algorithm Part #1.md:
--------------------------------------------------------------------------------
1 | # Greedy Algorithm Part #1
2 |
3 | ## Remove Covered Intervals(Medium #1288)
4 |
5 | **Question**: Given an array `intervals` where `intervals[i] = [li, ri]` represent the interval `[li, ri)`, remove all intervals that are covered by another interval in the list.
6 |
7 | The interval `[a, b)` is covered by the interval `[c, d)` if and only if `c <= a` and `b <= d`.
8 |
9 | Return *the number of remaining intervals*.
10 |
11 | **Example 1:**
12 |
13 | ```
14 | Input: intervals = [[1,4],[3,6],[2,8]]
15 | Output: 2
16 | Explanation: Interval [3,6] is covered by [2,8], therefore it is removed.
17 | ```
18 |
19 | **Example 2:**
20 |
21 | ```
22 | Input: intervals = [[1,4],[2,3]]
23 | Output: 1
24 | ```
25 |
26 | **Constraints:**
27 |
28 | - `1 <= intervals.length <= 1000`
29 | - `intervals[i].length == 2`
30 | - `0 <= li <= ri <= 105`
31 | - All the given intervals are **unique**.
32 |
33 | ### Standard Solution
34 |
35 | #### Solution #1 Greedy Algorithm
36 |
37 | * The typical greedy solution has $\mathcal{O}(N \log N)$ time complexity and consists of two steps:
38 |
39 | - Figure out how to sort the input data. That would take $\mathcal{O}(N \log N)$ time, and could be done directly by sorting or indirectly by using the heap data structure. Usually sorting is better than heap usage because of gain in space.
40 | - Parse the sorted input in $\mathcal{O}(N)$ time to construct a solution.
41 |
42 |  43 |
44 | * Let us consider two subsequent intervals after sorting. Since sorting ensures that `start1 < start2`, it's sufficient to compare the end boundaries:
45 | - If `end1 < end2`, the intervals won't completely cover one another, though they have some overlapping.
46 | - If `end1 >= end2`, interval 2 is covered by interval 1.
47 | * Edge case: **How to treat intervals that share start point**
48 | * If two intervals share the same start point, one has to put the longer interval in front.
49 |
50 |
43 |
44 | * Let us consider two subsequent intervals after sorting. Since sorting ensures that `start1 < start2`, it's sufficient to compare the end boundaries:
45 | - If `end1 < end2`, the intervals won't completely cover one another, though they have some overlapping.
46 | - If `end1 >= end2`, interval 2 is covered by interval 1.
47 | * Edge case: **How to treat intervals that share start point**
48 | * If two intervals share the same start point, one has to put the longer interval in front.
49 |
50 |  51 |
52 | ```java
53 | public int removeCoveredIntervals(int[][] intervals) {
54 | Arrays.sort(intervals, new Comparator(){
55 | @Override
56 | public int compare(int[] o1, int[] o2){
57 | // sort by start point
58 | // if two intervals share same start point,
59 | // put the longer one to be first
60 | return o1[0] == o2[0] ? o2[1] - o1[1] : o1[0] - o2[0];
61 | }
62 | });
63 | int count = 0;
64 | int end, prev_end = 0;
65 | for (int[] curr : intervals){
66 | end = curr[1];
67 | // if current interval is not covered
68 | // by the previous one
69 | if (prev_end < end){
70 | ++count;
71 | prev_end = end;
72 | }
73 | }
74 | return count;
75 | }
76 | ```
77 |
78 | * Time complexity: $\mathcal{O}(N \log N)$ since the sorting dominates the complexity of the algorithm.
79 | * Space complexity: $\mathcal{O}(N)$ or $\mathcal{O}(\log{N})$
80 | - The space complexity of the sorting algorithm depends on the implementation of each programming language.
81 | - For instance, the `sorted()` function in Python is implemented with the [Timsort](https://en.wikipedia.org/wiki/Timsort) algorithm whose space complexity is $\mathcal{O}(N)$
82 | - In Java, the [Arrays. sort()](https://docs.oracle.com/javase/8/docs/api/java/util/Arrays.html#sort-byte:A-) is implemented as a variant of quicksort algorithm whose space complexity is $\mathcal{O}(\log{N})$.
83 |
84 | ## Two City Scheduling(Medium #1029)
85 |
86 | **Question**: A company is planning to interview `2n` people. Given the array `costs` where `costs[i] = [aCosti, bCosti]`, the cost of flying the `ith` person to city `a` is `aCosti`, and the cost of flying the `ith` person to city `b` is `bCosti`.
87 |
88 | Return *the minimum cost to fly every person to a city* such that exactly `n` people arrive in each city.
89 |
90 | **Example 1:**
91 |
92 | ```
93 | Input: costs = [[10,20],[30,200],[400,50],[30,20]]
94 | Output: 110
95 | Explanation:
96 | The first person goes to city A for a cost of 10.
97 | The second person goes to city A for a cost of 30.
98 | The third person goes to city B for a cost of 50.
99 | The fourth person goes to city B for a cost of 20.
100 |
101 | The total minimum cost is 10 + 30 + 50 + 20 = 110 to have half the people interviewing in each city.
102 | ```
103 |
104 | **Example 2:**
105 |
106 | ```
107 | Input: costs = [[259,770],[448,54],[926,667],[184,139],[840,118],[577,469]]
108 | Output: 1859
109 | ```
110 |
111 | **Example 3:**
112 |
113 | ```
114 | Input: costs = [[515,563],[451,713],[537,709],[343,819],[855,779],[457,60],[650,359],[631,42]]
115 | Output: 3086
116 | ```
117 |
118 | **Constraints:**
119 |
120 | - `2 * n == costs.length`
121 | - `2 <= costs.length <= 100`
122 | - `costs.length` is even.
123 | - `1 <= aCosti, bCosti <= 1000`
124 |
125 | ### Standard Solution
126 |
127 | #### Solution #1 Greedy
128 |
129 | * Greedy problems usually look like "Find a minimum number of *something* to do *something*" or "Find a maximum number of *something* to fit in *some conditions*", and typically propose an unsorted input.
130 | * The idea of the greedy algorithm is to pick the *locally* optimal move at each step, that will lead to the *globally* optimal solution.
131 |
132 | * The standard solution has $\mathcal{O}(N \log N)$ time complexity and consists of two parts:
133 | - Figure out how to sort the input data ($\mathcal{O}(N \log N)$ time). That could be done directly by a sorting or indirectly by a heap usage. Typically sort is better than the heap usage because of gain in space.
134 | - Parse the sorted input to have a solution ($\mathcal{O}(N)$ time).
135 | * Sort the persons in the ascending order by `price_A - price_B` parameter, which indicates the company's additional costs(Based on the two group differences).
136 | * The first n persons choose group A, the last n persons choose group B.
137 |
138 | ```java
139 | public int twoCitySchedCost(int[][] costs) {
140 | // Sort by a gain which company has
141 | // by sending a person to city A and not to city B
142 | Arrays.sort(costs, new Comparator() {
143 | @Override
144 | public int compare(int[] o1, int[] o2) {
145 | return o1[0] - o1[1] - (o2[0] - o2[1]);
146 | }
147 | });
148 |
149 | int total = 0;
150 | int n = costs.length / 2;
151 | // To optimize the company expenses,
152 | // send the first n persons to the city A
153 | // and the others to the city B
154 | for (int i = 0; i < n; ++i) total += costs[i][0] + costs[i + n][1];
155 | return total;
156 | }
157 | ```
158 |
159 | - Time complexity: $\mathcal{O}(N \log N)$ because of sorting of input data.
160 | - Space complexity: $\mathcal{O}(1)$ since it's a constant space solution.
161 |
--------------------------------------------------------------------------------
/BST/BST Problems Part #1.md:
--------------------------------------------------------------------------------
1 | BST Problems Part #1
2 |
3 | ## Two Sum IV(Easy #653)
4 |
5 | **Question**: Given the `root` of a Binary Search Tree and a target number `k`, return *`true` if there exist two elements in the BST such that their sum is equal to the given target*.
6 |
7 | **Example 1:**
8 |
9 |
51 |
52 | ```java
53 | public int removeCoveredIntervals(int[][] intervals) {
54 | Arrays.sort(intervals, new Comparator(){
55 | @Override
56 | public int compare(int[] o1, int[] o2){
57 | // sort by start point
58 | // if two intervals share same start point,
59 | // put the longer one to be first
60 | return o1[0] == o2[0] ? o2[1] - o1[1] : o1[0] - o2[0];
61 | }
62 | });
63 | int count = 0;
64 | int end, prev_end = 0;
65 | for (int[] curr : intervals){
66 | end = curr[1];
67 | // if current interval is not covered
68 | // by the previous one
69 | if (prev_end < end){
70 | ++count;
71 | prev_end = end;
72 | }
73 | }
74 | return count;
75 | }
76 | ```
77 |
78 | * Time complexity: $\mathcal{O}(N \log N)$ since the sorting dominates the complexity of the algorithm.
79 | * Space complexity: $\mathcal{O}(N)$ or $\mathcal{O}(\log{N})$
80 | - The space complexity of the sorting algorithm depends on the implementation of each programming language.
81 | - For instance, the `sorted()` function in Python is implemented with the [Timsort](https://en.wikipedia.org/wiki/Timsort) algorithm whose space complexity is $\mathcal{O}(N)$
82 | - In Java, the [Arrays. sort()](https://docs.oracle.com/javase/8/docs/api/java/util/Arrays.html#sort-byte:A-) is implemented as a variant of quicksort algorithm whose space complexity is $\mathcal{O}(\log{N})$.
83 |
84 | ## Two City Scheduling(Medium #1029)
85 |
86 | **Question**: A company is planning to interview `2n` people. Given the array `costs` where `costs[i] = [aCosti, bCosti]`, the cost of flying the `ith` person to city `a` is `aCosti`, and the cost of flying the `ith` person to city `b` is `bCosti`.
87 |
88 | Return *the minimum cost to fly every person to a city* such that exactly `n` people arrive in each city.
89 |
90 | **Example 1:**
91 |
92 | ```
93 | Input: costs = [[10,20],[30,200],[400,50],[30,20]]
94 | Output: 110
95 | Explanation:
96 | The first person goes to city A for a cost of 10.
97 | The second person goes to city A for a cost of 30.
98 | The third person goes to city B for a cost of 50.
99 | The fourth person goes to city B for a cost of 20.
100 |
101 | The total minimum cost is 10 + 30 + 50 + 20 = 110 to have half the people interviewing in each city.
102 | ```
103 |
104 | **Example 2:**
105 |
106 | ```
107 | Input: costs = [[259,770],[448,54],[926,667],[184,139],[840,118],[577,469]]
108 | Output: 1859
109 | ```
110 |
111 | **Example 3:**
112 |
113 | ```
114 | Input: costs = [[515,563],[451,713],[537,709],[343,819],[855,779],[457,60],[650,359],[631,42]]
115 | Output: 3086
116 | ```
117 |
118 | **Constraints:**
119 |
120 | - `2 * n == costs.length`
121 | - `2 <= costs.length <= 100`
122 | - `costs.length` is even.
123 | - `1 <= aCosti, bCosti <= 1000`
124 |
125 | ### Standard Solution
126 |
127 | #### Solution #1 Greedy
128 |
129 | * Greedy problems usually look like "Find a minimum number of *something* to do *something*" or "Find a maximum number of *something* to fit in *some conditions*", and typically propose an unsorted input.
130 | * The idea of the greedy algorithm is to pick the *locally* optimal move at each step, that will lead to the *globally* optimal solution.
131 |
132 | * The standard solution has $\mathcal{O}(N \log N)$ time complexity and consists of two parts:
133 | - Figure out how to sort the input data ($\mathcal{O}(N \log N)$ time). That could be done directly by a sorting or indirectly by a heap usage. Typically sort is better than the heap usage because of gain in space.
134 | - Parse the sorted input to have a solution ($\mathcal{O}(N)$ time).
135 | * Sort the persons in the ascending order by `price_A - price_B` parameter, which indicates the company's additional costs(Based on the two group differences).
136 | * The first n persons choose group A, the last n persons choose group B.
137 |
138 | ```java
139 | public int twoCitySchedCost(int[][] costs) {
140 | // Sort by a gain which company has
141 | // by sending a person to city A and not to city B
142 | Arrays.sort(costs, new Comparator() {
143 | @Override
144 | public int compare(int[] o1, int[] o2) {
145 | return o1[0] - o1[1] - (o2[0] - o2[1]);
146 | }
147 | });
148 |
149 | int total = 0;
150 | int n = costs.length / 2;
151 | // To optimize the company expenses,
152 | // send the first n persons to the city A
153 | // and the others to the city B
154 | for (int i = 0; i < n; ++i) total += costs[i][0] + costs[i + n][1];
155 | return total;
156 | }
157 | ```
158 |
159 | - Time complexity: $\mathcal{O}(N \log N)$ because of sorting of input data.
160 | - Space complexity: $\mathcal{O}(1)$ since it's a constant space solution.
161 |
--------------------------------------------------------------------------------
/BST/BST Problems Part #1.md:
--------------------------------------------------------------------------------
1 | BST Problems Part #1
2 |
3 | ## Two Sum IV(Easy #653)
4 |
5 | **Question**: Given the `root` of a Binary Search Tree and a target number `k`, return *`true` if there exist two elements in the BST such that their sum is equal to the given target*.
6 |
7 | **Example 1:**
8 |
9 |  10 |
11 | ```
12 | Input: root = [5,3,6,2,4,null,7], k = 9
13 | Output: true
14 | ```
15 |
16 | **Example 2:**
17 |
18 |
10 |
11 | ```
12 | Input: root = [5,3,6,2,4,null,7], k = 9
13 | Output: true
14 | ```
15 |
16 | **Example 2:**
17 |
18 |  19 |
20 | ```
21 | Input: root = [5,3,6,2,4,null,7], k = 28
22 | Output: false
23 | ```
24 |
25 | **Constraints:**
26 |
27 | - The number of nodes in the tree is in the range `[1, 104]`.
28 | - `-104 <= Node.val <= 104`
29 | - `root` is guaranteed to be a **valid** binary search tree.
30 | - `-105 <= k <= 105`
31 |
32 | ### Standard Solution
33 |
34 | #### Solution #1 Using HashSet
35 |
36 | * Simplest solution is to traverse over the whole tree and consider every pair
37 | * For every node, check if the complement is in the set. Then put it to the set.
38 |
39 | ```java
40 | public boolean findTarget(TreeNode root, int k){
41 | Set set = new HashSet();
42 | return find(root, k, set);
43 | }
44 |
45 | public boolean find(TreeNode root, int k, Set set){
46 | if (root == null) return false;
47 | if (set.contains(k - root.val)) return true;
48 | set.add(root.val);
49 | return find(root.left, k, set) || find(root.right, k, set);//find left or right
50 | }
51 | ```
52 |
53 | * Time complexity : $O(n)$. The entire tree is traversed only once in the worst case. Here, n refers to the number of nodes in the given tree.
54 | * Space complexity : $O(n)$. The size of the set can grow up to n in the worst case.
55 |
56 | #### Solution #2 BFS and HashSet
57 |
58 | * BFS: **Breadth First Search** (traversal)
59 | * **Algorithm**:
60 | * Remove an element, $p$, from the front of the **queue**.
61 | * Check if the element $k-p$ already exists in the set. If so, return True.
62 | * Otherwise, add this element, $p$ to the set. Further, add the right and the left child nodes of the current node to the back of the **queue**.
63 | * Continue steps 1. to 3. till the **queue** becomes empty.
64 | * Return false if the **queue** becomes empty.
65 |
66 | ```java
67 | public boolean findTarget(TreeNode root, int k){
68 | Set set = new HashSet();
69 | Queue queue = new LinkedList();//only add, linkedlist is faster
70 | queue.add(root);
71 | while(!queue.isEmpty()){
72 | if (queue.peek() != null){
73 | TreeNode node = queue.remove();
74 | if (set.contains(k - node.val)) return true;
75 | set.add(node.val);
76 | queue.add(node.right);//put right to the last part of the queue
77 | queue.add(node.left);//put left to the front of the queue
78 | } else queue.remove();
79 | }
80 | return false;
81 | }
82 | ```
83 |
84 | * Time complexity : $O(n)$. We need to traverse over the whole tree once in the worst case. Here, n refers to the number of nodes in the given tree.
85 | * Space complexity : $O(n)$. The size of the set can grow at most up to n.
86 |
87 | #### Solution #3 Using BST + Two Pointers
88 |
89 | * Using BST, in order BST print as a sorted array
90 | * Get the sorted array, apply two pointers method to find the target
91 |
92 | ```java
93 | public boolean findTarget(TreeNode root, int k){
94 | List list = new ArrayList();//create arraylist to contain the sorted array
95 | inorder(root, list);
96 | int l = 0, r = list.size() - 1;
97 | while(l < r){
98 | int sum = list.get(l) + list.get(r);
99 | if (sum == k)return true;
100 | else if (sum < k) l++;
101 | else r--;
102 | }
103 | return false;
104 | }
105 |
106 | public void inorder(TreeNode root, List list){
107 | if (root == null) return;
108 | inorder(root.left, list);//go left
109 | list.add(root.val);//operation
110 | inorder(root.right, list);//then go right
111 | }
112 | ```
113 |
114 | * Time complexity : $O(n)$. We need to traverse over the whole tree once to do them in-order traversal. Here, n refers to the number of nodes in the given tree.
115 | * Space complexity : $O(n)$. The sorted list will contain n elements.
116 |
117 | ## Kth Smallest Element in a BST (Medium #230)
118 |
119 | **Question**: Given the `root` of a binary search tree, and an integer `k`, return *the* `kth` *smallest value (**1-indexed**) of all the values of the nodes in the tree*.
120 |
121 | **Example 1:**
122 |
123 | 
124 |
125 | ```
126 | Input: root = [3,1,4,null,2], k = 1
127 | Output: 1
128 | ```
129 |
130 | **Example 2:**
131 |
132 | 
133 |
134 | ```
135 | Input: root = [5,3,6,2,4,null,null,1], k = 3
136 | Output: 3
137 | ```
138 |
139 | **Constraints:**
140 |
141 | - The number of nodes in the tree is `n`.
142 | - `1 <= k <= n <= 104`
143 | - `0 <= Node.val <= 104`
144 |
145 | **Follow up:** If the BST is modified often (i.e., we can do insert and delete operations) and you need to find the kth smallest frequently, how would you optimize?
146 |
147 | ### My Solution
148 |
149 | ```java
150 | public int kthSmallest(TreeNode root, int k) {
151 | // 1. traverse the tree and put values in a list
152 | List treeList = new ArrayList<>();
153 |
154 | inorder(root, treeList);
155 | // 2. get the corresponding value in kth location
156 | return treeList.get(k - 1);
157 |
158 | }
159 |
160 | public void inorder(TreeNode root, List treeList){
161 | if (root == null) return;
162 | inorder(root.left, treeList);
163 | treeList.add(root.val);
164 | inorder(root.right, treeList);
165 | }
166 | ```
167 |
168 | ### Standard Solution
169 |
170 | #### Solution #1 Recursive Inorder Traversal
171 |
172 | * Same as my solution
173 |
174 | - Time complexity: $O(N)$ to build a traversal.
175 | - Space complexity: $O(N)$ to keep an inorder traversal.
176 |
177 | #### Solution #2 Iterative Inorder Traversal
178 |
179 | * With the help of a stack to do the iterative traversal, speed up the solution.
180 | * One could stop after the kth element.
181 |
182 | ```java
183 | public int kthSmallest(TreeNode root, int k){
184 | LinkedList stack = new LinkedList<>();
185 |
186 | while(true){
187 | while(root != null){
188 | stack.push(root);
189 | root = root.left;
190 | }
191 | root = stack.pop();
192 | if (--k == 0) return root.val;
193 | root = root.right;
194 | }
195 | }
196 | ```
197 |
198 | - Time complexity: $O(H + k)$, where H is a tree height. This complexity is defined by the stack, which contains at least. $H + k$ elements since before starting to pop out, one has to go down to a leaf. This results in $O(\log N + k)$ for the balanced tree and $O(N + k)$ for the completely unbalanced tree with all the nodes in the left subtree.
199 | - Space complexity: $O(H)$ to keep the stack, where H is a tree height. That makes $O(N)$ in the worst case of the skewed tree and $O(\log N)$ in the average case of the balanced tree.
200 |
--------------------------------------------------------------------------------
/System Design/System Design Problem Part #1.md:
--------------------------------------------------------------------------------
1 | # System Design Problem Part #1
2 |
3 | ## Design Search Autocomplete System (Hard #642)
4 |
5 | **Question**: Design a search autocomplete system for a search engine. Users may input a sentence (at least one word and end with a special character `'#'`).
6 |
7 | You are given a string array `sentences` and an integer array `times` both of length `n` where `sentences[i]` is a previously typed sentence and `times[i]` is the corresponding number of times the sentence was typed. For each input character except `'#'`, return the top `3` historical hot sentences that have the same prefix as the part of the sentence already typed.
8 |
9 | Here are the specific rules:
10 |
11 | - The hot degree for a sentence is defined as the number of times a user typed the exactly same sentence before.
12 | - The returned top `3` hot sentences should be sorted by hot degree (The first is the hottest one). If several sentences have the same hot degree, use ASCII-code order (smaller one appears first).
13 | - If less than `3` hot sentences exist, return as many as you can.
14 | - When the input is a special character, it means the sentence ends, and in this case, you need to return an empty list.
15 |
16 | Implement the `AutocompleteSystem` class:
17 |
18 | - `AutocompleteSystem(String[] sentences, int[] times)` Initializes the object with the `sentences` and `times` arrays.
19 | - `List input(char c)` This indicates that the user typed the character `c`
20 | - Returns an empty array `[]` if `c == '#'` and stores the inputted sentence in the system.
21 | - Returns the top `3` historical hot sentences that have the same prefix as the part of the sentence already typed. If there are fewer than `3` matches, return them all.
22 |
23 | **Example 1:**
24 |
25 | ```
26 | Input
27 | ["AutocompleteSystem", "input", "input", "input", "input"]
28 | [[["i love you", "island", "iroman", "i love leetcode"], [5, 3, 2, 2]], ["i"], [" "], ["a"], ["#"]]
29 | Output
30 | [null, ["i love you", "island", "i love leetcode"], ["i love you", "i love leetcode"], [], []]
31 |
32 | Explanation
33 | AutocompleteSystem obj = new AutocompleteSystem(["i love you", "island", "iroman", "i love leetcode"], [5, 3, 2, 2]);
34 | obj.input("i"); // return ["i love you", "island", "i love leetcode"]. There are four sentences that have prefix "i". Among them, "ironman" and "i love leetcode" have same hot degree. Since ' ' has ASCII code 32 and 'r' has ASCII code 114, "i love leetcode" should be in front of "ironman". Also we only need to output top 3 hot sentences, so "ironman" will be ignored.
35 | obj.input(" "); // return ["i love you", "i love leetcode"]. There are only two sentences that have prefix "i ".
36 | obj.input("a"); // return []. There are no sentences that have prefix "i a".
37 | obj.input("#"); // return []. The user finished the input, the sentence "i a" should be saved as a historical sentence in system. And the following input will be counted as a new search.
38 | ```
39 |
40 | **Constraints:**
41 |
42 | - `n == sentences.length`
43 | - `n == times.length`
44 | - `1 <= n <= 100`
45 | - `1 <= sentences[i].length <= 100`
46 | - `1 <= times[i] <= 50`
47 | - `c` is a lowercase English letter, a hash `'#'`, or space `' '`.
48 | - Each tested sentence will be a sequence of characters `c` that end with the character `'#'`.
49 | - Each tested sentence will have a length in the range `[1, 200]`.
50 | - The words in each input sentence are separated by single spaces.
51 | - At most `5000` calls will be made to `input`.
52 |
53 | ### Standard Solution
54 |
55 | ```java
56 | class AutocompleteSystem{
57 | class TrieNode implements Comparable {
58 | TrieNode[] children; // children array
59 | String s; // stored string
60 | int times; // times of call
61 | List hot; // top 3 hot strings
62 |
63 | public TrieNode(){
64 | children = new TrieNode[128];
65 | s = null;
66 | times = 0;
67 | hot = new ArrayList<>();
68 | }
69 |
70 | public int compareTo(TrieNode o){
71 | if (this.times == o.times){
72 | // compare the string alphebet
73 | return this.s.compareTo(o.s);
74 | }
75 | return o.times - this.times;
76 | }
77 |
78 | public void update(TrieNode node){
79 | if (!this.hot.contains(node)){
80 | this.hot.add(node);
81 | }
82 | Collections.sort(hot);
83 | if (hot.size() > 3){
84 | hot.remove(hot.size() - 1);
85 | }
86 | }
87 | }
88 |
89 | TrieNode root;
90 | TrieNode cur;
91 | StringBuilder sb;
92 |
93 | public AutocompleteSystem(String[] sentences, int[] times){
94 | root = new TrieNode();
95 | cur = root;
96 | sb = new StringBuilder();
97 |
98 | for (int i = 0; i < times.length; i++){
99 | add(sentences[i], times[i]);
100 | }
101 | }
102 |
103 | public void add(String sentence, int t){
104 | TrieNode tmp = root;
105 | List visited = new ArrayList<>();
106 | for (char c : sentence.toCharArray()){
107 | if (tmp.children[c] == null){
108 | tmp.children[c] = new TrieNode();
109 | }
110 | tmp = tmp.children[c];
111 | visited.add(tmp);
112 | }
113 |
114 | tmp.s = sentence;
115 | tmp.times += t;
116 |
117 | for (TrieNode node : visited){
118 | node.update(tmp);
119 | }
120 | }
121 |
122 | public List input(char c){
123 | List res = new ArrayList<>();
124 | if (c == '#'){
125 | add(sb.toString(), 1);
126 | sb = new StringBuilder();
127 | cur = root;
128 | return res;
129 | }
130 |
131 | sb.append(c);
132 | if (cur != null){
133 | cur = cur.children[c];
134 | }
135 |
136 | if (cur == null) return res;
137 | for (TrieNode node : cur.hot){
138 | res.add(node.s);
139 | }
140 | return res;
141 | }
142 | }
143 | ```
144 |
145 | ## Design Add and Search Words Data Structure (Medium #211)
146 |
147 | **Question**: Design a data structure that supports adding new words and finding if a string matches any previously added string.
148 |
149 | Implement the `WordDictionary` class:
150 |
151 | - `WordDictionary()` Initializes the object.
152 | - `void addWord(word)` Adds `word` to the data structure, it can be matched later.
153 | - `bool search(word)` Returns `true` if there is any string in the data structure that matches `word` or `false` otherwise. `word` may contain dots `'.'` where dots can be matched with any letter.
154 |
155 | **Example:**
156 |
157 | ```
158 | Input
159 | ["WordDictionary","addWord","addWord","addWord","search","search","search","search"]
160 | [[],["bad"],["dad"],["mad"],["pad"],["bad"],[".ad"],["b.."]]
161 | Output
162 | [null,null,null,null,false,true,true,true]
163 |
164 | Explanation
165 | WordDictionary wordDictionary = new WordDictionary();
166 | wordDictionary.addWord("bad");
167 | wordDictionary.addWord("dad");
168 | wordDictionary.addWord("mad");
169 | wordDictionary.search("pad"); // return False
170 | wordDictionary.search("bad"); // return True
171 | wordDictionary.search(".ad"); // return True
172 | wordDictionary.search("b.."); // return True
173 | ```
174 |
175 | **Constraints:**
176 |
177 | - `1 <= word.length <= 25`
178 | - `word` in `addWord` consists of lowercase English letters.
179 | - `word` in `search` consist of `'.'` or lowercase English letters.
180 | - There will be at most `3` dots in `word` for `search` queries.
181 | - At most `104` calls will be made to `addWord` and `search`.
182 |
183 | ### Standard Solution
184 |
185 | ```java
186 | class TrieNode {
187 | Map children = new HashMap();
188 | boolean word = false;
189 | public TrieNode(){}
190 | }
191 |
192 | class WordDictionary {
193 | TrieNode trie;
194 |
195 | /** Initialize your data structure here.**/
196 | public WordDictionary(){
197 | trie = new TrieNode();
198 | }
199 |
200 | /** Adds a word into the data structure **/
201 | public void addWord(String word){
202 | TrieNode node = trie;
203 |
204 | for (char ch : word.toCharArray()){
205 | if (!node.children.containsKey(ch)){
206 | node.children.put(ch, new TrieNode());
207 | }
208 | node = node.children.get(ch);
209 | }
210 | node.word = true;
211 | }
212 |
213 | /** returns if the word is in the node.**/
214 | public boolean searchInNode(String word, TrieNode node){
215 | for (int i = 0; i < word.length(); i++){
216 | char ch = word.charAt(i);
217 | if (!node.children.containsKey(ch)){
218 | // if the current char is '.'
219 | if (ch == '.'){
220 | for (char x : node.children.keySet()){
221 | TrieNode child = node.children.get(x);
222 | if (searchInNode(word.substring(i + 1), child)){
223 | return true;
224 | }
225 | }
226 | }
227 | // if no nodes lead to answer
228 | return false;
229 | } else {
230 | node = node.children.get(ch);
231 | }
232 | }
233 | return node.word;
234 | }
235 |
236 | public boolean search(String word){
237 | return searchInNode(word, trie);
238 | }
239 | }
240 | ```
241 |
242 | - Time complexity: $\mathcal{O}(M)$ for the "well-defined" words without dots, where M is the key length, and N is a number of keys, and $\mathcal{O}(N \cdot 26 ^ M)$ for the "undefined" words. That corresponds to the worst-case situation of searching an undefined word $\underbrace{.........}_\text{M times}$ which is one character longer than all inserted keys.
243 | - Space complexity: $\mathcal{O}(1)$ for the search of "well-defined" words without dots, and up to $\mathcal{O}(M)$ for the "undefined" words, to keep the recursion stack.
244 |
245 | ```java
246 | // another similar solution but easier to understand
247 | class WordDictionary {
248 | private WordDictionary[] children;
249 | boolean isEndOfWord;
250 | // Initialize your data structure here.
251 | public WordDictionary() {
252 | children = new WordDictionary[26];
253 | isEndOfWord = false;
254 | }
255 |
256 | // Adds a word into the data structure.
257 | public void addWord(String word) {
258 | WordDictionary curr = this;
259 | for(char c: word.toCharArray()){
260 | if(curr.children[c - 'a'] == null)
261 | curr.children[c - 'a'] = new WordDictionary();
262 | curr = curr.children[c - 'a'];
263 | }
264 | curr.isEndOfWord = true;
265 | }
266 |
267 | // Returns if the word is in the data structure. A word could contain the dot character '.' to represent any one letter.
268 | public boolean search(String word) {
269 | WordDictionary curr = this;
270 | for(int i = 0; i < word.length(); ++i){
271 | char c = word.charAt(i);
272 | if(c == '.'){
273 | for(WordDictionary ch: curr.children)
274 | if(ch != null && ch.search(word.substring(i+1))) return true;
275 | return false;
276 | }
277 | if(curr.children[c - 'a'] == null) return false;
278 | curr = curr.children[c - 'a'];
279 | }
280 | return curr != null && curr.isEndOfWord;
281 | }
282 | }
283 | ```
284 |
285 |
--------------------------------------------------------------------------------
/Trie/Trie Tutorial.md:
--------------------------------------------------------------------------------
1 | # Trie Tutorial
2 |
3 | ## Definition
4 |
5 | A `Trie` is a special form of a `Nary tree`. Typically, a trie is used to `store strings`. Each Trie node represents `a string` (`a prefix`). Each node might have several children nodes while the paths to different children nodes represent different characters. And the strings the child nodes represent will be the `origin string` represented by the node itself plus `the character on the path`.
6 |
7 |
19 |
20 | ```
21 | Input: root = [5,3,6,2,4,null,7], k = 28
22 | Output: false
23 | ```
24 |
25 | **Constraints:**
26 |
27 | - The number of nodes in the tree is in the range `[1, 104]`.
28 | - `-104 <= Node.val <= 104`
29 | - `root` is guaranteed to be a **valid** binary search tree.
30 | - `-105 <= k <= 105`
31 |
32 | ### Standard Solution
33 |
34 | #### Solution #1 Using HashSet
35 |
36 | * Simplest solution is to traverse over the whole tree and consider every pair
37 | * For every node, check if the complement is in the set. Then put it to the set.
38 |
39 | ```java
40 | public boolean findTarget(TreeNode root, int k){
41 | Set set = new HashSet();
42 | return find(root, k, set);
43 | }
44 |
45 | public boolean find(TreeNode root, int k, Set set){
46 | if (root == null) return false;
47 | if (set.contains(k - root.val)) return true;
48 | set.add(root.val);
49 | return find(root.left, k, set) || find(root.right, k, set);//find left or right
50 | }
51 | ```
52 |
53 | * Time complexity : $O(n)$. The entire tree is traversed only once in the worst case. Here, n refers to the number of nodes in the given tree.
54 | * Space complexity : $O(n)$. The size of the set can grow up to n in the worst case.
55 |
56 | #### Solution #2 BFS and HashSet
57 |
58 | * BFS: **Breadth First Search** (traversal)
59 | * **Algorithm**:
60 | * Remove an element, $p$, from the front of the **queue**.
61 | * Check if the element $k-p$ already exists in the set. If so, return True.
62 | * Otherwise, add this element, $p$ to the set. Further, add the right and the left child nodes of the current node to the back of the **queue**.
63 | * Continue steps 1. to 3. till the **queue** becomes empty.
64 | * Return false if the **queue** becomes empty.
65 |
66 | ```java
67 | public boolean findTarget(TreeNode root, int k){
68 | Set set = new HashSet();
69 | Queue queue = new LinkedList();//only add, linkedlist is faster
70 | queue.add(root);
71 | while(!queue.isEmpty()){
72 | if (queue.peek() != null){
73 | TreeNode node = queue.remove();
74 | if (set.contains(k - node.val)) return true;
75 | set.add(node.val);
76 | queue.add(node.right);//put right to the last part of the queue
77 | queue.add(node.left);//put left to the front of the queue
78 | } else queue.remove();
79 | }
80 | return false;
81 | }
82 | ```
83 |
84 | * Time complexity : $O(n)$. We need to traverse over the whole tree once in the worst case. Here, n refers to the number of nodes in the given tree.
85 | * Space complexity : $O(n)$. The size of the set can grow at most up to n.
86 |
87 | #### Solution #3 Using BST + Two Pointers
88 |
89 | * Using BST, in order BST print as a sorted array
90 | * Get the sorted array, apply two pointers method to find the target
91 |
92 | ```java
93 | public boolean findTarget(TreeNode root, int k){
94 | List list = new ArrayList();//create arraylist to contain the sorted array
95 | inorder(root, list);
96 | int l = 0, r = list.size() - 1;
97 | while(l < r){
98 | int sum = list.get(l) + list.get(r);
99 | if (sum == k)return true;
100 | else if (sum < k) l++;
101 | else r--;
102 | }
103 | return false;
104 | }
105 |
106 | public void inorder(TreeNode root, List list){
107 | if (root == null) return;
108 | inorder(root.left, list);//go left
109 | list.add(root.val);//operation
110 | inorder(root.right, list);//then go right
111 | }
112 | ```
113 |
114 | * Time complexity : $O(n)$. We need to traverse over the whole tree once to do them in-order traversal. Here, n refers to the number of nodes in the given tree.
115 | * Space complexity : $O(n)$. The sorted list will contain n elements.
116 |
117 | ## Kth Smallest Element in a BST (Medium #230)
118 |
119 | **Question**: Given the `root` of a binary search tree, and an integer `k`, return *the* `kth` *smallest value (**1-indexed**) of all the values of the nodes in the tree*.
120 |
121 | **Example 1:**
122 |
123 | 
124 |
125 | ```
126 | Input: root = [3,1,4,null,2], k = 1
127 | Output: 1
128 | ```
129 |
130 | **Example 2:**
131 |
132 | 
133 |
134 | ```
135 | Input: root = [5,3,6,2,4,null,null,1], k = 3
136 | Output: 3
137 | ```
138 |
139 | **Constraints:**
140 |
141 | - The number of nodes in the tree is `n`.
142 | - `1 <= k <= n <= 104`
143 | - `0 <= Node.val <= 104`
144 |
145 | **Follow up:** If the BST is modified often (i.e., we can do insert and delete operations) and you need to find the kth smallest frequently, how would you optimize?
146 |
147 | ### My Solution
148 |
149 | ```java
150 | public int kthSmallest(TreeNode root, int k) {
151 | // 1. traverse the tree and put values in a list
152 | List treeList = new ArrayList<>();
153 |
154 | inorder(root, treeList);
155 | // 2. get the corresponding value in kth location
156 | return treeList.get(k - 1);
157 |
158 | }
159 |
160 | public void inorder(TreeNode root, List treeList){
161 | if (root == null) return;
162 | inorder(root.left, treeList);
163 | treeList.add(root.val);
164 | inorder(root.right, treeList);
165 | }
166 | ```
167 |
168 | ### Standard Solution
169 |
170 | #### Solution #1 Recursive Inorder Traversal
171 |
172 | * Same as my solution
173 |
174 | - Time complexity: $O(N)$ to build a traversal.
175 | - Space complexity: $O(N)$ to keep an inorder traversal.
176 |
177 | #### Solution #2 Iterative Inorder Traversal
178 |
179 | * With the help of a stack to do the iterative traversal, speed up the solution.
180 | * One could stop after the kth element.
181 |
182 | ```java
183 | public int kthSmallest(TreeNode root, int k){
184 | LinkedList stack = new LinkedList<>();
185 |
186 | while(true){
187 | while(root != null){
188 | stack.push(root);
189 | root = root.left;
190 | }
191 | root = stack.pop();
192 | if (--k == 0) return root.val;
193 | root = root.right;
194 | }
195 | }
196 | ```
197 |
198 | - Time complexity: $O(H + k)$, where H is a tree height. This complexity is defined by the stack, which contains at least. $H + k$ elements since before starting to pop out, one has to go down to a leaf. This results in $O(\log N + k)$ for the balanced tree and $O(N + k)$ for the completely unbalanced tree with all the nodes in the left subtree.
199 | - Space complexity: $O(H)$ to keep the stack, where H is a tree height. That makes $O(N)$ in the worst case of the skewed tree and $O(\log N)$ in the average case of the balanced tree.
200 |
--------------------------------------------------------------------------------
/System Design/System Design Problem Part #1.md:
--------------------------------------------------------------------------------
1 | # System Design Problem Part #1
2 |
3 | ## Design Search Autocomplete System (Hard #642)
4 |
5 | **Question**: Design a search autocomplete system for a search engine. Users may input a sentence (at least one word and end with a special character `'#'`).
6 |
7 | You are given a string array `sentences` and an integer array `times` both of length `n` where `sentences[i]` is a previously typed sentence and `times[i]` is the corresponding number of times the sentence was typed. For each input character except `'#'`, return the top `3` historical hot sentences that have the same prefix as the part of the sentence already typed.
8 |
9 | Here are the specific rules:
10 |
11 | - The hot degree for a sentence is defined as the number of times a user typed the exactly same sentence before.
12 | - The returned top `3` hot sentences should be sorted by hot degree (The first is the hottest one). If several sentences have the same hot degree, use ASCII-code order (smaller one appears first).
13 | - If less than `3` hot sentences exist, return as many as you can.
14 | - When the input is a special character, it means the sentence ends, and in this case, you need to return an empty list.
15 |
16 | Implement the `AutocompleteSystem` class:
17 |
18 | - `AutocompleteSystem(String[] sentences, int[] times)` Initializes the object with the `sentences` and `times` arrays.
19 | - `List input(char c)` This indicates that the user typed the character `c`
20 | - Returns an empty array `[]` if `c == '#'` and stores the inputted sentence in the system.
21 | - Returns the top `3` historical hot sentences that have the same prefix as the part of the sentence already typed. If there are fewer than `3` matches, return them all.
22 |
23 | **Example 1:**
24 |
25 | ```
26 | Input
27 | ["AutocompleteSystem", "input", "input", "input", "input"]
28 | [[["i love you", "island", "iroman", "i love leetcode"], [5, 3, 2, 2]], ["i"], [" "], ["a"], ["#"]]
29 | Output
30 | [null, ["i love you", "island", "i love leetcode"], ["i love you", "i love leetcode"], [], []]
31 |
32 | Explanation
33 | AutocompleteSystem obj = new AutocompleteSystem(["i love you", "island", "iroman", "i love leetcode"], [5, 3, 2, 2]);
34 | obj.input("i"); // return ["i love you", "island", "i love leetcode"]. There are four sentences that have prefix "i". Among them, "ironman" and "i love leetcode" have same hot degree. Since ' ' has ASCII code 32 and 'r' has ASCII code 114, "i love leetcode" should be in front of "ironman". Also we only need to output top 3 hot sentences, so "ironman" will be ignored.
35 | obj.input(" "); // return ["i love you", "i love leetcode"]. There are only two sentences that have prefix "i ".
36 | obj.input("a"); // return []. There are no sentences that have prefix "i a".
37 | obj.input("#"); // return []. The user finished the input, the sentence "i a" should be saved as a historical sentence in system. And the following input will be counted as a new search.
38 | ```
39 |
40 | **Constraints:**
41 |
42 | - `n == sentences.length`
43 | - `n == times.length`
44 | - `1 <= n <= 100`
45 | - `1 <= sentences[i].length <= 100`
46 | - `1 <= times[i] <= 50`
47 | - `c` is a lowercase English letter, a hash `'#'`, or space `' '`.
48 | - Each tested sentence will be a sequence of characters `c` that end with the character `'#'`.
49 | - Each tested sentence will have a length in the range `[1, 200]`.
50 | - The words in each input sentence are separated by single spaces.
51 | - At most `5000` calls will be made to `input`.
52 |
53 | ### Standard Solution
54 |
55 | ```java
56 | class AutocompleteSystem{
57 | class TrieNode implements Comparable {
58 | TrieNode[] children; // children array
59 | String s; // stored string
60 | int times; // times of call
61 | List hot; // top 3 hot strings
62 |
63 | public TrieNode(){
64 | children = new TrieNode[128];
65 | s = null;
66 | times = 0;
67 | hot = new ArrayList<>();
68 | }
69 |
70 | public int compareTo(TrieNode o){
71 | if (this.times == o.times){
72 | // compare the string alphebet
73 | return this.s.compareTo(o.s);
74 | }
75 | return o.times - this.times;
76 | }
77 |
78 | public void update(TrieNode node){
79 | if (!this.hot.contains(node)){
80 | this.hot.add(node);
81 | }
82 | Collections.sort(hot);
83 | if (hot.size() > 3){
84 | hot.remove(hot.size() - 1);
85 | }
86 | }
87 | }
88 |
89 | TrieNode root;
90 | TrieNode cur;
91 | StringBuilder sb;
92 |
93 | public AutocompleteSystem(String[] sentences, int[] times){
94 | root = new TrieNode();
95 | cur = root;
96 | sb = new StringBuilder();
97 |
98 | for (int i = 0; i < times.length; i++){
99 | add(sentences[i], times[i]);
100 | }
101 | }
102 |
103 | public void add(String sentence, int t){
104 | TrieNode tmp = root;
105 | List visited = new ArrayList<>();
106 | for (char c : sentence.toCharArray()){
107 | if (tmp.children[c] == null){
108 | tmp.children[c] = new TrieNode();
109 | }
110 | tmp = tmp.children[c];
111 | visited.add(tmp);
112 | }
113 |
114 | tmp.s = sentence;
115 | tmp.times += t;
116 |
117 | for (TrieNode node : visited){
118 | node.update(tmp);
119 | }
120 | }
121 |
122 | public List input(char c){
123 | List res = new ArrayList<>();
124 | if (c == '#'){
125 | add(sb.toString(), 1);
126 | sb = new StringBuilder();
127 | cur = root;
128 | return res;
129 | }
130 |
131 | sb.append(c);
132 | if (cur != null){
133 | cur = cur.children[c];
134 | }
135 |
136 | if (cur == null) return res;
137 | for (TrieNode node : cur.hot){
138 | res.add(node.s);
139 | }
140 | return res;
141 | }
142 | }
143 | ```
144 |
145 | ## Design Add and Search Words Data Structure (Medium #211)
146 |
147 | **Question**: Design a data structure that supports adding new words and finding if a string matches any previously added string.
148 |
149 | Implement the `WordDictionary` class:
150 |
151 | - `WordDictionary()` Initializes the object.
152 | - `void addWord(word)` Adds `word` to the data structure, it can be matched later.
153 | - `bool search(word)` Returns `true` if there is any string in the data structure that matches `word` or `false` otherwise. `word` may contain dots `'.'` where dots can be matched with any letter.
154 |
155 | **Example:**
156 |
157 | ```
158 | Input
159 | ["WordDictionary","addWord","addWord","addWord","search","search","search","search"]
160 | [[],["bad"],["dad"],["mad"],["pad"],["bad"],[".ad"],["b.."]]
161 | Output
162 | [null,null,null,null,false,true,true,true]
163 |
164 | Explanation
165 | WordDictionary wordDictionary = new WordDictionary();
166 | wordDictionary.addWord("bad");
167 | wordDictionary.addWord("dad");
168 | wordDictionary.addWord("mad");
169 | wordDictionary.search("pad"); // return False
170 | wordDictionary.search("bad"); // return True
171 | wordDictionary.search(".ad"); // return True
172 | wordDictionary.search("b.."); // return True
173 | ```
174 |
175 | **Constraints:**
176 |
177 | - `1 <= word.length <= 25`
178 | - `word` in `addWord` consists of lowercase English letters.
179 | - `word` in `search` consist of `'.'` or lowercase English letters.
180 | - There will be at most `3` dots in `word` for `search` queries.
181 | - At most `104` calls will be made to `addWord` and `search`.
182 |
183 | ### Standard Solution
184 |
185 | ```java
186 | class TrieNode {
187 | Map children = new HashMap();
188 | boolean word = false;
189 | public TrieNode(){}
190 | }
191 |
192 | class WordDictionary {
193 | TrieNode trie;
194 |
195 | /** Initialize your data structure here.**/
196 | public WordDictionary(){
197 | trie = new TrieNode();
198 | }
199 |
200 | /** Adds a word into the data structure **/
201 | public void addWord(String word){
202 | TrieNode node = trie;
203 |
204 | for (char ch : word.toCharArray()){
205 | if (!node.children.containsKey(ch)){
206 | node.children.put(ch, new TrieNode());
207 | }
208 | node = node.children.get(ch);
209 | }
210 | node.word = true;
211 | }
212 |
213 | /** returns if the word is in the node.**/
214 | public boolean searchInNode(String word, TrieNode node){
215 | for (int i = 0; i < word.length(); i++){
216 | char ch = word.charAt(i);
217 | if (!node.children.containsKey(ch)){
218 | // if the current char is '.'
219 | if (ch == '.'){
220 | for (char x : node.children.keySet()){
221 | TrieNode child = node.children.get(x);
222 | if (searchInNode(word.substring(i + 1), child)){
223 | return true;
224 | }
225 | }
226 | }
227 | // if no nodes lead to answer
228 | return false;
229 | } else {
230 | node = node.children.get(ch);
231 | }
232 | }
233 | return node.word;
234 | }
235 |
236 | public boolean search(String word){
237 | return searchInNode(word, trie);
238 | }
239 | }
240 | ```
241 |
242 | - Time complexity: $\mathcal{O}(M)$ for the "well-defined" words without dots, where M is the key length, and N is a number of keys, and $\mathcal{O}(N \cdot 26 ^ M)$ for the "undefined" words. That corresponds to the worst-case situation of searching an undefined word $\underbrace{.........}_\text{M times}$ which is one character longer than all inserted keys.
243 | - Space complexity: $\mathcal{O}(1)$ for the search of "well-defined" words without dots, and up to $\mathcal{O}(M)$ for the "undefined" words, to keep the recursion stack.
244 |
245 | ```java
246 | // another similar solution but easier to understand
247 | class WordDictionary {
248 | private WordDictionary[] children;
249 | boolean isEndOfWord;
250 | // Initialize your data structure here.
251 | public WordDictionary() {
252 | children = new WordDictionary[26];
253 | isEndOfWord = false;
254 | }
255 |
256 | // Adds a word into the data structure.
257 | public void addWord(String word) {
258 | WordDictionary curr = this;
259 | for(char c: word.toCharArray()){
260 | if(curr.children[c - 'a'] == null)
261 | curr.children[c - 'a'] = new WordDictionary();
262 | curr = curr.children[c - 'a'];
263 | }
264 | curr.isEndOfWord = true;
265 | }
266 |
267 | // Returns if the word is in the data structure. A word could contain the dot character '.' to represent any one letter.
268 | public boolean search(String word) {
269 | WordDictionary curr = this;
270 | for(int i = 0; i < word.length(); ++i){
271 | char c = word.charAt(i);
272 | if(c == '.'){
273 | for(WordDictionary ch: curr.children)
274 | if(ch != null && ch.search(word.substring(i+1))) return true;
275 | return false;
276 | }
277 | if(curr.children[c - 'a'] == null) return false;
278 | curr = curr.children[c - 'a'];
279 | }
280 | return curr != null && curr.isEndOfWord;
281 | }
282 | }
283 | ```
284 |
285 |
--------------------------------------------------------------------------------
/Trie/Trie Tutorial.md:
--------------------------------------------------------------------------------
1 | # Trie Tutorial
2 |
3 | ## Definition
4 |
5 | A `Trie` is a special form of a `Nary tree`. Typically, a trie is used to `store strings`. Each Trie node represents `a string` (`a prefix`). Each node might have several children nodes while the paths to different children nodes represent different characters. And the strings the child nodes represent will be the `origin string` represented by the node itself plus `the character on the path`.
6 |
7 |  8 |
9 | ### Array Solution
10 |
11 | ```java
12 | class TrieNode {
13 | // change this value to adapt to different cases
14 | public static final N = 26;
15 | public TrieNode[] children = new TrieNode[N];
16 |
17 | // you might need some extra values according to different cases
18 | };
19 | ```
20 |
21 | ### Map Solution
22 |
23 | ```java
24 | class TrieNode {
25 | public Map children = new HashMap<>();
26 |
27 | // you might need some extra values according to different cases
28 | };
29 | ```
30 |
31 | ## Data Structure - Implement Trie(Prefix Tree)(Medium #208)
32 |
33 | ```java
34 | class Trie {
35 |
36 | private TrieNode root;
37 |
38 | public Trie() {
39 | root = new TrieNode();
40 | }
41 |
42 | // insert a word into trie
43 | // Time complexity : O(m), where m is the key length.
44 | // Space complexity : O(m).
45 | public void insert(String word) {
46 | TrieNode node = root;
47 | for (int i = 0; i < word.length(); i++){
48 | char currentChar = word.charAt(i);
49 | if (!node.containsKey(currentChar)){
50 | node.put(currentChar, new TrieNode());
51 | }
52 | node = node.get(currentChar);
53 | }
54 | node.setEnd();
55 | }
56 |
57 |
58 | // search prefix can be applied in search, but need to check isEnd
59 | // Time complexity : O(m) In each step of the algorithm we search for the next key character.
60 | // Space complexity : O(1)
61 | public boolean search(String word) {
62 | TrieNode node = searchPrefix(word);
63 | return node != null && node.isEnd();
64 | }
65 |
66 | private TrieNode searchPrefix(String word){
67 | TrieNode node = root;
68 | for (int i = 0; i < word.length(); i++){
69 | char currLetter = word.charAt(i);
70 | if (node.containsKey(currLetter)){
71 | node = node.get(currLetter);
72 | }
73 | else {
74 | return null;
75 | }
76 | }
77 | return node;
78 | }
79 |
80 | // apply the previous method
81 | // Time complexity : O(m)
82 | // Space complexity : O(1)
83 | public boolean startsWith(String prefix) {
84 | TrieNode node = searchPrefix(prefix);
85 | return node != null;
86 | }
87 | }
88 |
89 | class TrieNode {
90 | // R links to node children
91 | private TrieNode[] links;
92 | private final int R = 26;
93 | private boolean isEnd;
94 |
95 | public TrieNode(){
96 | links = new TrieNode[R];
97 | }
98 |
99 | public boolean containsKey(char ch){
100 | return links[ch - 'a'] != null;
101 | }
102 |
103 | public TrieNode get(char ch){
104 | return links[ch - 'a'];
105 | }
106 |
107 | public void put(char ch, TrieNode node){
108 | links[ch - 'a'] = node;
109 | }
110 |
111 | public void setEnd(){
112 | isEnd = true;
113 | }
114 |
115 | public boolean isEnd(){
116 | return isEnd;
117 | }
118 | }
119 |
120 | /**
121 | * Your Trie object will be instantiated and called as such:
122 | * Trie obj = new Trie();
123 | * obj.insert(word);
124 | * boolean param_2 = obj.search(word);
125 | * boolean param_3 = obj.startsWith(prefix);
126 | */
127 | ```
128 |
129 | ```java
130 | // map implementation
131 | class Trie {
132 | class TrieNode {
133 | public boolean isWord;
134 | public Map childrenMap = new HashMap<>();
135 | }
136 |
137 | private TrieNode root;
138 |
139 | /** Initialize your data structure here. */
140 | public Trie() {
141 | root = new TrieNode();
142 | }
143 |
144 | /** Inserts a word into the trie. */
145 | public void insert(String word) {
146 | TrieNode cur = root;
147 | for(int i = 0; i < word.length(); i++){
148 | char c = word.charAt(i);
149 | if(cur.childrenMap.get(c) == null){
150 | // insert a new node if the path does not exist
151 | cur.childrenMap.put(c, new TrieNode());
152 | }
153 | cur = cur.childrenMap.get(c);
154 | }
155 | cur.isWord = true;
156 | }
157 |
158 | /** Returns if the word is in the trie. */
159 | public boolean search(String word) {
160 | TrieNode cur = root;
161 | for(int i = 0; i < word.length(); i++) {
162 | char c = word.charAt(i);
163 | if(cur.childrenMap.get(c) == null) {
164 | return false;
165 | }
166 | cur = cur.childrenMap.get(c);
167 | }
168 | return cur.isWord;
169 | }
170 |
171 | /** Returns if there is any word in the trie that starts with the given prefix. */
172 | public boolean startsWith(String prefix) {
173 | TrieNode cur = root;
174 | for(int i = 0;i < prefix.length(); i++){
175 | char c = prefix.charAt(i);
176 | if(cur.childrenMap.get(c) == null) {
177 | return false;
178 | }
179 | cur = cur.childrenMap.get(c);
180 | }
181 | return true;
182 | }
183 | }
184 | ```
185 |
186 | * The time complexity to search in Trie is `O(M)`.
187 | * The space complexity of hash table is `O(M * N)`.
188 |
189 | ## Map Sum Pairs (Medium #677)
190 |
191 | **Question**: Design a map that allows you to do the following:
192 |
193 | - Maps a string key to a given value.
194 | - Returns the sum of the values that have a key with a prefix equal to a given string.
195 |
196 | Implement the `MapSum` class:
197 |
198 | - `MapSum()` Initializes the `MapSum` object.
199 | - `void insert(String key, int val)` Inserts the `key-val` pair into the map. If the `key` already existed, the original `key-value` pair will be overridden to the new one.
200 | - `int sum(string prefix)` Returns the sum of all the pairs' value whose `key` starts with the `prefix`.
201 |
202 | **Example 1:**
203 |
204 | ```
205 | Input
206 | ["MapSum", "insert", "sum", "insert", "sum"]
207 | [[], ["apple", 3], ["ap"], ["app", 2], ["ap"]]
208 | Output
209 | [null, null, 3, null, 5]
210 |
211 | Explanation
212 | MapSum mapSum = new MapSum();
213 | mapSum.insert("apple", 3);
214 | mapSum.sum("ap"); // return 3 (apple = 3)
215 | mapSum.insert("app", 2);
216 | mapSum.sum("ap"); // return 5 (apple + app = 3 + 2 = 5)
217 | ```
218 |
219 | **Constraints:**
220 |
221 | - `1 <= key.length, prefix.length <= 50`
222 | - `key` and `prefix` consist of only lowercase English letters.
223 | - `1 <= val <= 1000`
224 | - At most `50` calls will be made to `insert` and `sum`.
225 |
226 | ### Standard Solution
227 |
228 | #### Solution #1 Trie
229 |
230 | ```java
231 | class TrieNode {
232 | public Map children;
233 | public int score;
234 |
235 | public TrieNode() {
236 | children = new HashMap<>();
237 | score = 0;
238 | }
239 | }
240 |
241 | class MapSum {
242 | // trie data structure
243 | public TrieNode root;
244 | public Map map;
245 |
246 | public MapSum() {
247 | root = new TrieNode();
248 | map = new HashMap<>();
249 | }
250 |
251 | public void insert(String key, int val) {
252 | int delta = val - map.getOrDefault(key, 0);
253 | map.put(key, val);
254 | TrieNode curr = root;
255 | curr.score += delta;
256 | for (int i = 0; i < key.length(); i++){
257 | char currLetter = key.charAt(i);
258 | curr.children.putIfAbsent(currLetter, new TrieNode());
259 | curr = curr.children.get(currLetter);
260 | curr.score += delta;
261 | }
262 | }
263 |
264 | public int sum(String prefix) {
265 | TrieNode curr = root;
266 | for (char c : prefix.toCharArray()){
267 | curr = curr.children.get(c);
268 | if (curr == null) return 0;
269 | }
270 | return curr.score;
271 | }
272 | }
273 | ```
274 |
275 | - Time Complexity: Every inserts operation is $O(K)$, where K is the length of the key. Every sum operation is $O(K)$
276 | - Space Complexity: The space used is linear in the size of the total input.
277 |
278 | #### Solution #2 Prefix Hashmap
279 |
280 | ```java
281 | Map map;
282 | Map score;
283 | public MapSum() {
284 | map = new HashMap();
285 | score = new HashMap();
286 | }
287 | public void insert(String key, int val) {
288 | int delta = val - map.getOrDefault(key, 0);
289 | map.put(key, val);
290 | String prefix = "";
291 | for (char c: key.toCharArray()) {
292 | prefix += c;
293 | score.put(prefix, score.getOrDefault(prefix, 0) + delta);
294 | }
295 | }
296 | public int sum(String prefix) {
297 | return score.getOrDefault(prefix, 0);
298 | }
299 | ```
300 |
301 | - Time Complexity: Every insert operation is $O(K^2)$, where K is the length of the key, as K strings are made of an average length of K. Every sum operation is $O(1)$
302 | - Space Complexity: The space used by `map` and `score` is linear in the size of all input `key` and `val` values combined.
303 |
304 | ## Replace Words (Medium #648)
305 |
306 | **Question**: In English, we have a concept called **root**, which can be followed by some other word to form another longer word - let's call this word **successor**. For example, when the **root** `"an"` is followed by the **successor** word `"other"`, we can form a new word `"another"`.
307 |
308 | Given a `dictionary` consisting of many **roots** and a `sentence` consisting of words separated by spaces, replace all the **successors** in the sentence with the **root** forming it. If a **successor** can be replaced by more than one **root**, replace it with the **root** that has **the shortest length**.
309 |
310 | Return *the `sentence`* after the replacement.
311 |
312 | **Example 1:**
313 |
314 | ```
315 | Input: dictionary = ["cat","bat","rat"], sentence = "the cattle was rattled by the battery"
316 | Output: "the cat was rat by the bat"
317 | ```
318 |
319 | **Example 2:**
320 |
321 | ```
322 | Input: dictionary = ["a","b","c"], sentence = "aadsfasf absbs bbab cadsfafs"
323 | Output: "a a b c"
324 | ```
325 |
326 | **Constraints:**
327 |
328 | - `1 <= dictionary.length <= 1000`
329 | - `1 <= dictionary[i].length <= 100`
330 | - `dictionary[i]` consists of only lower-case letters.
331 | - `1 <= sentence.length <= 106`
332 | - `sentence` consists of only lower-case letters and spaces.
333 | - The number of words in `sentence` is in the range `[1, 1000]`
334 | - The length of each word in `sentence` is in the range `[1, 1000]`
335 | - Every two consecutive words in `sentence` will be separated by exactly one space.
336 | - `sentence` does not have leading or trailing spaces.
337 |
338 | ### Standard Solution
339 |
340 | #### Solution #1 Trie
341 |
342 | ```java
343 | class TrieNode {
344 | TrieNode[] children;
345 | String word;
346 | TrieNode(){
347 | children = new TrieNode[26];
348 | }
349 | }
350 | class Solution {
351 | public String replaceWords(List dictionary, String sentence) {
352 | // use a trie structure to store prefix to trie
353 | TrieNode trie = new TrieNode();
354 | for (String prefix : dictionary){
355 | TrieNode curr = trie;
356 | for (char letter : prefix.toCharArray()){
357 | // create a children trienode
358 | if (curr.children[letter - 'a'] == null){
359 | curr.children[letter - 'a'] = new TrieNode();
360 | }
361 | curr = curr.children[letter - 'a'];
362 | }
363 | curr.word = prefix;
364 | }
365 |
366 | // construct a new string to return
367 | StringBuilder res = new StringBuilder();
368 |
369 | for (String word : sentence.split("\\s+")){
370 | if (res.length() > 0) res.append(" ");
371 |
372 | TrieNode curr = trie;
373 | for (char letter : word.toCharArray()){
374 | if (curr.children[letter - 'a'] == null || curr.word != null){
375 | break;
376 | }
377 | curr = curr.children[letter - 'a'];
378 | }
379 | res.append(curr.word != null ? curr.word : word);
380 | }
381 | return res.toString();
382 | }
383 | }
384 | ```
385 |
386 | - Time Complexity: $O(N)$ where N is the length of the `sentence`. Every query of a word is in linear time.
387 | - Space Complexity: $O(N)$ the size of our trie.
--------------------------------------------------------------------------------
/Two Pointers/Two Pointers Problems Part #1.md:
--------------------------------------------------------------------------------
1 | # Two Pointers Problems Part #1
2 |
3 | ## Maximize Distance to Closest Person(Medium #849)
4 |
5 | **Question**: You are given an array representing a row of `seats` where `seats[i] = 1` represents a person sitting in the `ith` seat, and `seats[i] = 0` represents that the `ith` seat is empty **(0-indexed)**.
6 |
7 | There is at least one empty seat, and at least one person sitting.
8 |
9 | Alex wants to sit in the seat such that the distance between him and the closest person to him is maximized.
10 |
11 | Return *that maximum distance to the closest person*.
12 |
13 | **Example 1:**
14 |
15 |
8 |
9 | ### Array Solution
10 |
11 | ```java
12 | class TrieNode {
13 | // change this value to adapt to different cases
14 | public static final N = 26;
15 | public TrieNode[] children = new TrieNode[N];
16 |
17 | // you might need some extra values according to different cases
18 | };
19 | ```
20 |
21 | ### Map Solution
22 |
23 | ```java
24 | class TrieNode {
25 | public Map children = new HashMap<>();
26 |
27 | // you might need some extra values according to different cases
28 | };
29 | ```
30 |
31 | ## Data Structure - Implement Trie(Prefix Tree)(Medium #208)
32 |
33 | ```java
34 | class Trie {
35 |
36 | private TrieNode root;
37 |
38 | public Trie() {
39 | root = new TrieNode();
40 | }
41 |
42 | // insert a word into trie
43 | // Time complexity : O(m), where m is the key length.
44 | // Space complexity : O(m).
45 | public void insert(String word) {
46 | TrieNode node = root;
47 | for (int i = 0; i < word.length(); i++){
48 | char currentChar = word.charAt(i);
49 | if (!node.containsKey(currentChar)){
50 | node.put(currentChar, new TrieNode());
51 | }
52 | node = node.get(currentChar);
53 | }
54 | node.setEnd();
55 | }
56 |
57 |
58 | // search prefix can be applied in search, but need to check isEnd
59 | // Time complexity : O(m) In each step of the algorithm we search for the next key character.
60 | // Space complexity : O(1)
61 | public boolean search(String word) {
62 | TrieNode node = searchPrefix(word);
63 | return node != null && node.isEnd();
64 | }
65 |
66 | private TrieNode searchPrefix(String word){
67 | TrieNode node = root;
68 | for (int i = 0; i < word.length(); i++){
69 | char currLetter = word.charAt(i);
70 | if (node.containsKey(currLetter)){
71 | node = node.get(currLetter);
72 | }
73 | else {
74 | return null;
75 | }
76 | }
77 | return node;
78 | }
79 |
80 | // apply the previous method
81 | // Time complexity : O(m)
82 | // Space complexity : O(1)
83 | public boolean startsWith(String prefix) {
84 | TrieNode node = searchPrefix(prefix);
85 | return node != null;
86 | }
87 | }
88 |
89 | class TrieNode {
90 | // R links to node children
91 | private TrieNode[] links;
92 | private final int R = 26;
93 | private boolean isEnd;
94 |
95 | public TrieNode(){
96 | links = new TrieNode[R];
97 | }
98 |
99 | public boolean containsKey(char ch){
100 | return links[ch - 'a'] != null;
101 | }
102 |
103 | public TrieNode get(char ch){
104 | return links[ch - 'a'];
105 | }
106 |
107 | public void put(char ch, TrieNode node){
108 | links[ch - 'a'] = node;
109 | }
110 |
111 | public void setEnd(){
112 | isEnd = true;
113 | }
114 |
115 | public boolean isEnd(){
116 | return isEnd;
117 | }
118 | }
119 |
120 | /**
121 | * Your Trie object will be instantiated and called as such:
122 | * Trie obj = new Trie();
123 | * obj.insert(word);
124 | * boolean param_2 = obj.search(word);
125 | * boolean param_3 = obj.startsWith(prefix);
126 | */
127 | ```
128 |
129 | ```java
130 | // map implementation
131 | class Trie {
132 | class TrieNode {
133 | public boolean isWord;
134 | public Map childrenMap = new HashMap<>();
135 | }
136 |
137 | private TrieNode root;
138 |
139 | /** Initialize your data structure here. */
140 | public Trie() {
141 | root = new TrieNode();
142 | }
143 |
144 | /** Inserts a word into the trie. */
145 | public void insert(String word) {
146 | TrieNode cur = root;
147 | for(int i = 0; i < word.length(); i++){
148 | char c = word.charAt(i);
149 | if(cur.childrenMap.get(c) == null){
150 | // insert a new node if the path does not exist
151 | cur.childrenMap.put(c, new TrieNode());
152 | }
153 | cur = cur.childrenMap.get(c);
154 | }
155 | cur.isWord = true;
156 | }
157 |
158 | /** Returns if the word is in the trie. */
159 | public boolean search(String word) {
160 | TrieNode cur = root;
161 | for(int i = 0; i < word.length(); i++) {
162 | char c = word.charAt(i);
163 | if(cur.childrenMap.get(c) == null) {
164 | return false;
165 | }
166 | cur = cur.childrenMap.get(c);
167 | }
168 | return cur.isWord;
169 | }
170 |
171 | /** Returns if there is any word in the trie that starts with the given prefix. */
172 | public boolean startsWith(String prefix) {
173 | TrieNode cur = root;
174 | for(int i = 0;i < prefix.length(); i++){
175 | char c = prefix.charAt(i);
176 | if(cur.childrenMap.get(c) == null) {
177 | return false;
178 | }
179 | cur = cur.childrenMap.get(c);
180 | }
181 | return true;
182 | }
183 | }
184 | ```
185 |
186 | * The time complexity to search in Trie is `O(M)`.
187 | * The space complexity of hash table is `O(M * N)`.
188 |
189 | ## Map Sum Pairs (Medium #677)
190 |
191 | **Question**: Design a map that allows you to do the following:
192 |
193 | - Maps a string key to a given value.
194 | - Returns the sum of the values that have a key with a prefix equal to a given string.
195 |
196 | Implement the `MapSum` class:
197 |
198 | - `MapSum()` Initializes the `MapSum` object.
199 | - `void insert(String key, int val)` Inserts the `key-val` pair into the map. If the `key` already existed, the original `key-value` pair will be overridden to the new one.
200 | - `int sum(string prefix)` Returns the sum of all the pairs' value whose `key` starts with the `prefix`.
201 |
202 | **Example 1:**
203 |
204 | ```
205 | Input
206 | ["MapSum", "insert", "sum", "insert", "sum"]
207 | [[], ["apple", 3], ["ap"], ["app", 2], ["ap"]]
208 | Output
209 | [null, null, 3, null, 5]
210 |
211 | Explanation
212 | MapSum mapSum = new MapSum();
213 | mapSum.insert("apple", 3);
214 | mapSum.sum("ap"); // return 3 (apple = 3)
215 | mapSum.insert("app", 2);
216 | mapSum.sum("ap"); // return 5 (apple + app = 3 + 2 = 5)
217 | ```
218 |
219 | **Constraints:**
220 |
221 | - `1 <= key.length, prefix.length <= 50`
222 | - `key` and `prefix` consist of only lowercase English letters.
223 | - `1 <= val <= 1000`
224 | - At most `50` calls will be made to `insert` and `sum`.
225 |
226 | ### Standard Solution
227 |
228 | #### Solution #1 Trie
229 |
230 | ```java
231 | class TrieNode {
232 | public Map children;
233 | public int score;
234 |
235 | public TrieNode() {
236 | children = new HashMap<>();
237 | score = 0;
238 | }
239 | }
240 |
241 | class MapSum {
242 | // trie data structure
243 | public TrieNode root;
244 | public Map map;
245 |
246 | public MapSum() {
247 | root = new TrieNode();
248 | map = new HashMap<>();
249 | }
250 |
251 | public void insert(String key, int val) {
252 | int delta = val - map.getOrDefault(key, 0);
253 | map.put(key, val);
254 | TrieNode curr = root;
255 | curr.score += delta;
256 | for (int i = 0; i < key.length(); i++){
257 | char currLetter = key.charAt(i);
258 | curr.children.putIfAbsent(currLetter, new TrieNode());
259 | curr = curr.children.get(currLetter);
260 | curr.score += delta;
261 | }
262 | }
263 |
264 | public int sum(String prefix) {
265 | TrieNode curr = root;
266 | for (char c : prefix.toCharArray()){
267 | curr = curr.children.get(c);
268 | if (curr == null) return 0;
269 | }
270 | return curr.score;
271 | }
272 | }
273 | ```
274 |
275 | - Time Complexity: Every inserts operation is $O(K)$, where K is the length of the key. Every sum operation is $O(K)$
276 | - Space Complexity: The space used is linear in the size of the total input.
277 |
278 | #### Solution #2 Prefix Hashmap
279 |
280 | ```java
281 | Map map;
282 | Map score;
283 | public MapSum() {
284 | map = new HashMap();
285 | score = new HashMap();
286 | }
287 | public void insert(String key, int val) {
288 | int delta = val - map.getOrDefault(key, 0);
289 | map.put(key, val);
290 | String prefix = "";
291 | for (char c: key.toCharArray()) {
292 | prefix += c;
293 | score.put(prefix, score.getOrDefault(prefix, 0) + delta);
294 | }
295 | }
296 | public int sum(String prefix) {
297 | return score.getOrDefault(prefix, 0);
298 | }
299 | ```
300 |
301 | - Time Complexity: Every insert operation is $O(K^2)$, where K is the length of the key, as K strings are made of an average length of K. Every sum operation is $O(1)$
302 | - Space Complexity: The space used by `map` and `score` is linear in the size of all input `key` and `val` values combined.
303 |
304 | ## Replace Words (Medium #648)
305 |
306 | **Question**: In English, we have a concept called **root**, which can be followed by some other word to form another longer word - let's call this word **successor**. For example, when the **root** `"an"` is followed by the **successor** word `"other"`, we can form a new word `"another"`.
307 |
308 | Given a `dictionary` consisting of many **roots** and a `sentence` consisting of words separated by spaces, replace all the **successors** in the sentence with the **root** forming it. If a **successor** can be replaced by more than one **root**, replace it with the **root** that has **the shortest length**.
309 |
310 | Return *the `sentence`* after the replacement.
311 |
312 | **Example 1:**
313 |
314 | ```
315 | Input: dictionary = ["cat","bat","rat"], sentence = "the cattle was rattled by the battery"
316 | Output: "the cat was rat by the bat"
317 | ```
318 |
319 | **Example 2:**
320 |
321 | ```
322 | Input: dictionary = ["a","b","c"], sentence = "aadsfasf absbs bbab cadsfafs"
323 | Output: "a a b c"
324 | ```
325 |
326 | **Constraints:**
327 |
328 | - `1 <= dictionary.length <= 1000`
329 | - `1 <= dictionary[i].length <= 100`
330 | - `dictionary[i]` consists of only lower-case letters.
331 | - `1 <= sentence.length <= 106`
332 | - `sentence` consists of only lower-case letters and spaces.
333 | - The number of words in `sentence` is in the range `[1, 1000]`
334 | - The length of each word in `sentence` is in the range `[1, 1000]`
335 | - Every two consecutive words in `sentence` will be separated by exactly one space.
336 | - `sentence` does not have leading or trailing spaces.
337 |
338 | ### Standard Solution
339 |
340 | #### Solution #1 Trie
341 |
342 | ```java
343 | class TrieNode {
344 | TrieNode[] children;
345 | String word;
346 | TrieNode(){
347 | children = new TrieNode[26];
348 | }
349 | }
350 | class Solution {
351 | public String replaceWords(List dictionary, String sentence) {
352 | // use a trie structure to store prefix to trie
353 | TrieNode trie = new TrieNode();
354 | for (String prefix : dictionary){
355 | TrieNode curr = trie;
356 | for (char letter : prefix.toCharArray()){
357 | // create a children trienode
358 | if (curr.children[letter - 'a'] == null){
359 | curr.children[letter - 'a'] = new TrieNode();
360 | }
361 | curr = curr.children[letter - 'a'];
362 | }
363 | curr.word = prefix;
364 | }
365 |
366 | // construct a new string to return
367 | StringBuilder res = new StringBuilder();
368 |
369 | for (String word : sentence.split("\\s+")){
370 | if (res.length() > 0) res.append(" ");
371 |
372 | TrieNode curr = trie;
373 | for (char letter : word.toCharArray()){
374 | if (curr.children[letter - 'a'] == null || curr.word != null){
375 | break;
376 | }
377 | curr = curr.children[letter - 'a'];
378 | }
379 | res.append(curr.word != null ? curr.word : word);
380 | }
381 | return res.toString();
382 | }
383 | }
384 | ```
385 |
386 | - Time Complexity: $O(N)$ where N is the length of the `sentence`. Every query of a word is in linear time.
387 | - Space Complexity: $O(N)$ the size of our trie.
--------------------------------------------------------------------------------
/Two Pointers/Two Pointers Problems Part #1.md:
--------------------------------------------------------------------------------
1 | # Two Pointers Problems Part #1
2 |
3 | ## Maximize Distance to Closest Person(Medium #849)
4 |
5 | **Question**: You are given an array representing a row of `seats` where `seats[i] = 1` represents a person sitting in the `ith` seat, and `seats[i] = 0` represents that the `ith` seat is empty **(0-indexed)**.
6 |
7 | There is at least one empty seat, and at least one person sitting.
8 |
9 | Alex wants to sit in the seat such that the distance between him and the closest person to him is maximized.
10 |
11 | Return *that maximum distance to the closest person*.
12 |
13 | **Example 1:**
14 |
15 | 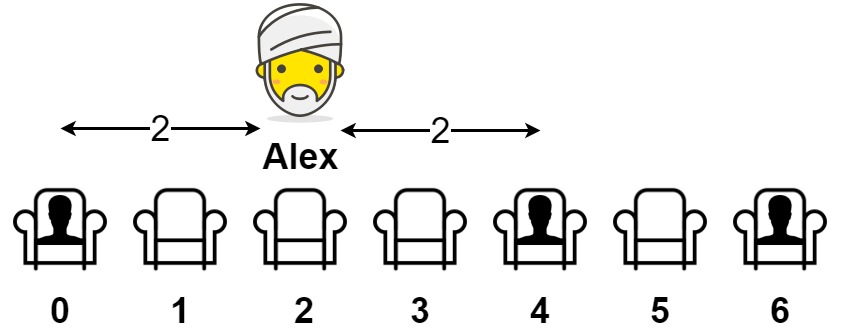 16 |
17 | ```
18 | Input: seats = [1,0,0,0,1,0,1]
19 | Output: 2
20 | Explanation:
21 | If Alex sits in the second open seat (i.e. seats[2]), then the closest person has distance 2.
22 | If Alex sits in any other open seat, the closest person has distance 1.
23 | Thus, the maximum distance to the closest person is 2.
24 | ```
25 |
26 | **Example 2:**
27 |
28 | ```
29 | Input: seats = [1,0,0,0]
30 | Output: 3
31 | Explanation:
32 | If Alex sits in the last seat (i.e. seats[3]), the closest person is 3 seats away.
33 | This is the maximum distance possible, so the answer is 3.
34 | ```
35 |
36 | **Example 3:**
37 |
38 | ```
39 | Input: seats = [0,1]
40 | Output: 1
41 | ```
42 |
43 | **Constraints:**
44 |
45 | - `2 <= seats.length <= 2 * 104`
46 | - `seats[i]` is `0` or `1`.
47 | - At least one seat is **empty**.
48 | - At least one seat is **occupied**.
49 |
50 | ### My Solution
51 |
52 | ```java
53 | public int maxDistToClosest(int[] seats) {
54 | int maxDist = 0, low, high;
55 |
56 | for (low = 0, high = 0; high < seats.length; ++high){
57 | if (seats[high] == 1){
58 | int totalDist = high - low;
59 | if (seats[low] == 1){
60 | maxDist = Math.max((int)Math.ceil(totalDist/2), maxDist);
61 | }
62 | else {
63 | maxDist = Math.max(totalDist, maxDist);
64 | }
65 | low = high;
66 | }
67 | }
68 | if (low == seats.length - 1) return Math.max(maxDist, high - low);
69 | return Math.max(maxDist, high - low - 1);
70 | }
71 | ```
72 |
73 | ### Standard Solution
74 |
75 | #### Solution #1 Next Array
76 |
77 | * Let `left[i]` be the distance from seat `i` to the closest person sitting to the left of `i`. Similarly, let `right[i]` be the distance to the closest person sitting to the right of `i`. This is motivated by the idea that the closest person in seat `i` sits a distance `min(left[i], right[i])` away.
78 |
79 | * **Algorithm**
80 |
81 | To construct `left[i]`, notice it is either `left[i-1] + 1` if the seat is empty, or `0` if it is full. `right[i]` is constructed in a similar way.
82 |
83 | ```java
84 | public int maxDistToClosest(int[] seats){
85 | int N = seats.length;
86 | int[] left = new int[N], right = new int[N];
87 | Arrays.fill(left, N);
88 | Arrays.fill(right, N);
89 |
90 | for (int i = 0; i < N; i++){
91 | if (seats[i] == 1) left[i] = 0; //distance to the cloest one would be 0
92 | else if (i > 0) left[i] = left[i - 1] + 1; //add 1 distance comparing to the previous one
93 | }
94 | for (int i = N - 1; i >= 0; i--){
95 | if (seats[i] == 1) right[i] = 0; //distance to the cloest one would be 0
96 | else if (i < N - 1) right[i] = right[i + 1] + 1; //add 1 distance comparing to the previous one
97 | }
98 |
99 | int ans = 0;
100 | for (int i = 0; i < N; i++){
101 | if (seats[i] == 0){
102 | ans = Math.max(ans, Math.min(left[i], right[i]));
103 | }
104 | }
105 | return ans;
106 | }
107 | ```
108 |
109 | * Time complexity: $O(N)$ where N is the length of seats
110 | * Space complexity: $O(N)$ where the space used by left and right
111 |
112 | #### Solution #2 Two Pointer
113 |
114 | * **Algorithm**:
115 | * Keep track of `prev`, the filled seat at or to the left of `i`, and `future`, the filled seat at or to the right of `i`.
116 | * Then at seat `i`, the closest person is `min(i - prev, future - i)`, with one exception. `i - prev` should be considered infinite if there is no person to the left of seat `i`, and similarly `future - i` is infinite if there is no one to the right of seat `i`.
117 |
118 | ```java
119 | public int maxDistToClosest(int[] seats){
120 | int N = seats.length;
121 | int prev = -1, future = 0;
122 | int ans = 0;
123 |
124 | for (int i = 0; i < N; i++){
125 | if (seats[i] == 1){
126 | prev = i;
127 | } else {
128 | while (future < N && seats[future] == 0 || future < i){
129 | future++;
130 | }
131 | int left = prev == -1 ? N : i - prev;
132 | int right = future == N ? N : future - i;
133 | ans = Math.max(ans, Math.min(left, right));
134 | }
135 | }
136 | return ans;
137 | }
138 | ```
139 |
140 | * Time Complexity: $O(N)$, where $N$ is the length of `seats`.
141 | * Space Complexity: $O(1)$
142 |
143 | #### Solution #3 Group by Zero
144 |
145 | * My solution is a combination of solution 2 and 3
146 | * In a group of `K` adjacent empty seats between two people, the answer is `(K+1) / 2`.
147 | * For groups of empty seats between the edge of the row and one other person, the answer is `K`, and we should take into account those answers too.
148 |
149 | ```java
150 | public int maxDistToClosest(int[] seats){
151 | int N = seats.length;
152 | int K = 0;//current longest group of empty seats
153 | int ans = 0;
154 |
155 | for (int i = 0; i < N; i++){
156 | if (seats[i] == 1){
157 | K = 0;
158 | } else {
159 | K++;
160 | ans = Math.max(ans, (K + 1) / 2);
161 | }
162 | }
163 |
164 | for (int i = 0; i < N; i++){// in case starts from 0
165 | if (seats[i] == 1){
166 | ans = Math.max(ans, i);
167 | break;
168 | }
169 | }
170 |
171 | for (int i = N - 1; i >= 0; i--){// in case ends with 0
172 | if (seats[i] == 1){
173 | ans = Math.max(ans, N - 1 - i);
174 | break;
175 | }
176 | }
177 | return ans;
178 | }
179 | ```
180 |
181 | * Time Complexity: $O(N)$, where N is the length of `seats`.
182 | * Space Complexity: $O(1)$.
183 |
184 | ## 3Sum (Medium #15)
185 |
186 | **Question**: Given an integer array nums, return all the triplets `[nums[i], nums[j], nums[k]]` such that `i != j`, `i != k`, and `j != k`, and `nums[i] + nums[j] + nums[k] == 0`.
187 |
188 | Notice that the solution set must not contain duplicate triplets.
189 |
190 | **Example 1:**
191 |
192 | ```
193 | Input: nums = [-1,0,1,2,-1,-4]
194 | Output: [[-1,-1,2],[-1,0,1]]
195 | Explanation:
196 | nums[0] + nums[1] + nums[2] = (-1) + 0 + 1 = 0.
197 | nums[1] + nums[2] + nums[4] = 0 + 1 + (-1) = 0.
198 | nums[0] + nums[3] + nums[4] = (-1) + 2 + (-1) = 0.
199 | The distinct triplets are [-1,0,1] and [-1,-1,2].
200 | Notice that the order of the output and the order of the triplets does not matter.
201 | ```
202 |
203 | **Example 2:**
204 |
205 | ```
206 | Input: nums = [0,1,1]
207 | Output: []
208 | Explanation: The only possible triplet does not sum up to 0.
209 | ```
210 |
211 | **Example 3:**
212 |
213 | ```
214 | Input: nums = [0,0,0]
215 | Output: [[0,0,0]]
216 | Explanation: The only possible triplet sums up to 0.
217 | ```
218 |
219 | **Constraints:**
220 |
221 | - `3 <= nums.length <= 3000`
222 | - `-105 <= nums[i] <= 105`
223 |
224 | ### My Solution
225 |
226 | ```java
227 | // two pointers
228 | // 1. sum to 0: location < 0
229 | // 2. low and high pointer
230 | List> res;
231 | int[] nums;
232 |
233 | public List> threeSum(int[] nums) {
234 | Arrays.sort(nums);
235 | res = new ArrayList<>();
236 | this.nums = nums;
237 | for (int i = 0; i < nums.length && nums[i] <= 0; i++){
238 | // in case duplicate situations
239 | if (i == 0 || nums[i - 1] != nums[i]){
240 | findSolution(i);
241 | }
242 | }
243 | return res;
244 | }
245 |
246 | public void findSolution(int loc){
247 |
248 | int low = loc + 1, high = nums.length - 1;
249 | while(low < high){
250 | int sum = nums[low] + nums[high] + nums[loc];
251 | if (sum == 0){
252 | res.add(Arrays.asList(nums[loc], nums[low++], nums[high--]));
253 | while(low < high && nums[low] == nums[low - 1]){
254 | low++;
255 | }
256 | }
257 | else if (sum < 0){
258 | low++;
259 | }
260 | else {
261 | high--;
262 | }
263 | }
264 | }
265 | ```
266 |
267 | ### Standard Solution
268 |
269 | #### Solution #1 Two pointer
270 |
271 | * Same as my solution
272 |
273 | ```java
274 | public List> threeSum(int[] nums) {
275 | Arrays.sort(nums);
276 | List> res = new ArrayList<>();
277 | for (int i = 0; i < nums.length && nums[i] <= 0; ++i)
278 | // skip the duplicate number
279 | if (i == 0 || nums[i - 1] != nums[i]) {
280 | twoSumII(nums, i, res);
281 | }
282 | return res;
283 | }
284 | void twoSumII(int[] nums, int i, List> res) {
285 | int lo = i + 1, hi = nums.length - 1;
286 | while (lo < hi) {
287 | int sum = nums[i] + nums[lo] + nums[hi];
288 | if (sum < 0) {
289 | ++lo;
290 | } else if (sum > 0) {
291 | --hi;
292 | } else {
293 | // continue to move low and high pointer to next possible solution
294 | res.add(Arrays.asList(nums[i], nums[lo++], nums[hi--]));
295 | // skip the duplicate number
296 | while (lo < hi && nums[lo] == nums[lo - 1])
297 | ++lo;
298 | }
299 | }
300 | }
301 | ```
302 |
303 | - Time Complexity: $\mathcal{O}(n^2)$. `twoSumII` is $\mathcal{O}(n)$, and we call it n times.
304 |
305 | Sorting the array takes $\mathcal{O}(n\log{n})$, so overall complexity is $\mathcal{O}(n\log{n} + n^2)$. This is asymptotically equivalent to $\mathcal{O}(n^2)$
306 |
307 | - Space Complexity: from $\mathcal{O}(\log{n})$ to $\mathcal{O}(n)$, depending on the implementation of the sorting algorithm. For the purpose of complexity analysis, we ignore the memory required for the output.
308 |
309 | #### Solution #2 HashSet
310 |
311 | ```java
312 | public List> threeSum(int[] nums) {
313 | Arrays.sort(nums);
314 | List> res = new ArrayList<>();
315 | for (int i = 0; i < nums.length && nums[i] <= 0; ++i)
316 | if (i == 0 || nums[i - 1] != nums[i]) {
317 | twoSum(nums, i, res);
318 | }
319 | return res;
320 | }
321 | void twoSum(int[] nums, int i, List> res) {
322 | var seen = new HashSet();
323 | for (int j = i + 1; j < nums.length; ++j) {
324 | int complement = -nums[i] - nums[j];
325 | if (seen.contains(complement)) {
326 | res.add(Arrays.asList(nums[i], nums[j], complement));
327 | while (j + 1 < nums.length && nums[j] == nums[j + 1])
328 | ++j;
329 | }
330 | seen.add(nums[j]);
331 | }
332 | }
333 | ```
334 |
335 | - Time Complexity: $\mathcal{O}(n^2)$. `twoSum` is $\mathcal{O}(n)$, and we call it n times.
336 |
337 | Sorting the array takes $\mathcal{O}(n\log{n})$, so overall complexity is $\mathcal{O}(n\log{n} + n^2)$. This is asymptotically equivalent to $\mathcal{O}(n^2)$
338 |
339 | - Space Complexity: $\mathcal{O}(n)$ for the hashset.
340 |
341 | ## Trapping Rain Water (Hard #42)
342 |
343 | **Question**: Given `n` non-negative integers representing an elevation map where the width of each bar is `1`, compute how much water it can trap after raining.
344 |
345 | **Example 1:**
346 |
347 | 
348 |
349 | ```
350 | Input: height = [0,1,0,2,1,0,1,3,2,1,2,1]
351 | Output: 6
352 | Explanation: The above elevation map (black section) is represented by array [0,1,0,2,1,0,1,3,2,1,2,1]. In this case, 6 units of rain water (blue section) are being trapped.
353 | ```
354 |
355 | **Example 2:**
356 |
357 | ```
358 | Input: height = [4,2,0,3,2,5]
359 | Output: 9
360 | ```
361 |
362 | **Constraints:**
363 |
364 | - `n == height.length`
365 | - `1 <= n <= 2 * 104`
366 | - `0 <= height[i] <= 105`
367 |
368 | ### Standard Solution
369 |
370 | #### Solution #1 Two Pointers
371 |
372 | * Use two pointers: left pointer and the right pointer.
373 | * Track the left maximum and right maximum.
374 | * Always keep the larger pointer, and move the lower pointer, in this way, we can calcuate the trapping rain water by `max - curr`
375 |
376 | ```java
377 | public int trap(int[] height) {
378 | // two pointers: low, high
379 | int left = 0, right = height.length - 1;
380 | int maxLeft = 0, maxRight = 0;
381 | int water = 0;
382 |
383 | while(left < right){
384 | // current right pointer is max right
385 | // 1. compare two pointer, always keep the high one
386 | if (height[left] < height[right]){
387 | if (height[left] >= maxLeft){
388 | maxLeft = height[left];
389 | }
390 | else water += maxLeft - height[left];
391 | // 2. move the lower pointer, record left and right max
392 | left++;
393 | }
394 | else {
395 | // 3. when move the lower one, record max - low value
396 | if (height[right] >= maxRight){
397 | maxRight = height[right];
398 | }
399 | else water += maxRight - height[right];
400 | right--;
401 | }
402 | }
403 | return water;
404 | }
405 | ```
406 |
407 | - Time complexity: $O(n)$. Single iteration of $O(n)$.
408 | - Space complexity: $O(1)$ extra space. Only constant space required for $\text{left}$, $\text{right}$, $\text{left\_max}$ and $\text{right\_max}$.
409 |
410 | ## Product of Array Except Self (Medium #238)
411 |
412 | **Question**: Given an integer array `nums`, return *an array* `answer` *such that* `answer[i]` *is equal to the product of all the elements of* `nums` *except* `nums[i]`.
413 |
414 | The product of any prefix or suffix of `nums` is **guaranteed** to fit in a **32-bit** integer.
415 |
416 | You must write an algorithm that runs in `O(n)` time and without using the division operation.
417 |
418 | **Example 1:**
419 |
420 | ```
421 | Input: nums = [1,2,3,4]
422 | Output: [24,12,8,6]
423 | ```
424 |
425 | **Example 2:**
426 |
427 | ```
428 | Input: nums = [-1,1,0,-3,3]
429 | Output: [0,0,9,0,0]
430 | ```
431 |
432 | **Constraints:**
433 |
434 | - `2 <= nums.length <= 105`
435 | - `-30 <= nums[i] <= 30`
436 | - The product of any prefix or suffix of `nums` is **guaranteed** to fit in a **32-bit** integer.
437 |
438 | **Follow up:** Can you solve the problem in `O(1) `extra space complexity? (The output array **does not** count as extra space for space complexity analysis.)
439 |
440 | ### My Solution
441 |
442 | ```java
443 | // correct but time limit exceeded
444 | public int[] productExceptSelf(int[] nums) {
445 | // product every digit in the array, then change i element back to origin
446 | int[] res = new int[nums.length];
447 | Arrays.fill(res, 1);
448 | for (int i = 0; i < nums.length; i++){
449 | int curr = nums[i];
450 | for (int j = 0; j < nums.length; j++){
451 | if (i == j) continue;
452 | res[j] = res[j] * curr;
453 | }
454 | }
455 | return res;
456 | }
457 | ```
458 |
459 | ### Standard Solution
460 |
461 | #### Solution #1 Left and Right Product Lists
462 |
463 | 
464 |
465 | * Use previous product times `nums[i - 1]` to avoid times themselves. Similarly, calculate the product starting from the right direction.
466 |
467 | ```java
468 | public int[] productExceptSelf(int[] nums){
469 | // the length of the input array
470 | int length = nums.length;
471 |
472 | // the left and right arrays as described in the algorithm
473 | int[] L = new int[length];
474 | int[] R = new int[length];
475 |
476 | // final answer array to be returned
477 | int[] answer = new int[length];
478 |
479 | // L[i] contains the product of all elements to the left
480 | // note: for the element at index '0', no elements to the left, L[0] would be 1
481 | L[0] = 1;
482 | for (int i = 1; i < length; i++){
483 | // L[i - 1] already contains the product of elements to the left of 'i - 1'
484 | L[i] = nums[i - 1] * L[i - 1];
485 | }
486 |
487 | R[length - 1] = 1;
488 | for (int i = length - 2; i >= 0; i--){
489 | // R[i + 1] already contains the product of elements to the right of 'i + 1'
490 | R[i] = nums[i + 1] * R[i + 1];
491 | }
492 |
493 | // constructing the answer array
494 | for (int i = 0; i < length; i++){
495 | // For the first element, R[i] would be product except for self
496 | // For the last element of the array, product except for self would be L[i]
497 | // Else, multiple product of all elements to the left and to the right
498 | answer[i] = L[i] * R[i];
499 | }
500 | return answer;
501 | }
502 | ```
503 |
504 | - Time complexity: $O(N)$ where N represents the number of elements in the input array. We use one iteration to construct the array L, one to construct the array R, and one last to construct the `answer` array using L and R.
505 | - Space complexity: $O(N)$ used up by the two intermediate arrays that we constructed to keep track of the product of elements to the left and right.
506 |
507 | #### Solution #2 O(1) Space Approach
508 |
509 | * Similar idea to the first solution, but more space efficient
510 |
511 | ```java
512 | public int[] productExceptSelf(int[] nums) {
513 | // The length of the input array
514 | int length = nums.length;
515 |
516 | // Final answer array to be returned
517 | int[] answer = new int[length];
518 |
519 | answer[0] = 1;
520 | for (int i = 1; i < length; i++) {
521 | answer[i] = nums[i - 1] * answer[i - 1];
522 | }
523 |
524 | int R = 1;
525 | for (int i = length - 1; i >= 0; i--) {
526 |
527 | // For the index 'i', R would contain the
528 | // product of all elements to the right. We update R accordingly
529 | answer[i] = answer[i] * R;
530 | R *= nums[i];
531 | }
532 | return answer;
533 | }
534 | ```
535 |
536 | * More simplified version
537 |
538 | ```java
539 | public int[] productExceptSelf(int[] nums) {
540 | int[] result = new int[nums.length];
541 | for (int i = 0, tmp = 1; i < nums.length; i++) {
542 | result[i] = tmp;
543 | tmp *= nums[i];
544 | }
545 | for (int i = nums.length - 1, tmp = 1; i >= 0; i--) {
546 | result[i] *= tmp;
547 | tmp *= nums[i];
548 | }
549 | return result;
550 | }
551 | ```
552 |
553 | - Time complexity: $O(N)$ where N represents the number of elements in the input array. We use one iteration to construct the array L, and one to update the array answer.
554 | - Space complexity: $O(1)$ since don't use any additional array for our computations. The problem statement mentions that using the answer array doesn't add to the space complexity.
--------------------------------------------------------------------------------
/Binary Tree/Binary Tree Tutorial.md:
--------------------------------------------------------------------------------
1 | # Binary Tree Tutorial
2 |
3 | Materials refer to: https://leetcode.com/explore/learn/card/recursion-i/
4 |
5 | # Introduction to Binary Tree
6 |
7 | * From graph view, a tree can also be defined as a directed acyclic graph which has `N nodes` and `N-1 edges`.
8 | * As the name suggests, a binary tree is a tree data structure in which each node has `at most two children`, which are referred to as the left child and the right child.
9 |
10 | ## Traverse a Tree
11 |
12 | * **Pre-order Traversal**
13 |
14 | * Pre-order traversal is to visit the root first. Then traverse the left subtree. Finally, traverse the right subtree.
15 |
16 | * **In-order Traversal**
17 |
18 | * In-order traversal is to traverse the left subtree first. Then visit the root. Finally, traverse the right subtree.
19 | * Typically, for `binary search tree`, we can retrieve all the data in sorted order using in-order traversal.
20 |
21 | * **Post-order Traversal**
22 |
23 | * Post-order traversal is to traverse the left subtree first. Then traverse the right subtree. Finally, visit the root.
24 | * It is worth noting that when you delete nodes in a tree, **deletion process will be in post-order**. That is to say, when you delete a node, you will delete its left child and its right child before you delete the node itself.
25 | * Post-order is widely use in mathematical expression. It is easier to write a program to parse a post-order expression.
26 |
27 |
16 |
17 | ```
18 | Input: seats = [1,0,0,0,1,0,1]
19 | Output: 2
20 | Explanation:
21 | If Alex sits in the second open seat (i.e. seats[2]), then the closest person has distance 2.
22 | If Alex sits in any other open seat, the closest person has distance 1.
23 | Thus, the maximum distance to the closest person is 2.
24 | ```
25 |
26 | **Example 2:**
27 |
28 | ```
29 | Input: seats = [1,0,0,0]
30 | Output: 3
31 | Explanation:
32 | If Alex sits in the last seat (i.e. seats[3]), the closest person is 3 seats away.
33 | This is the maximum distance possible, so the answer is 3.
34 | ```
35 |
36 | **Example 3:**
37 |
38 | ```
39 | Input: seats = [0,1]
40 | Output: 1
41 | ```
42 |
43 | **Constraints:**
44 |
45 | - `2 <= seats.length <= 2 * 104`
46 | - `seats[i]` is `0` or `1`.
47 | - At least one seat is **empty**.
48 | - At least one seat is **occupied**.
49 |
50 | ### My Solution
51 |
52 | ```java
53 | public int maxDistToClosest(int[] seats) {
54 | int maxDist = 0, low, high;
55 |
56 | for (low = 0, high = 0; high < seats.length; ++high){
57 | if (seats[high] == 1){
58 | int totalDist = high - low;
59 | if (seats[low] == 1){
60 | maxDist = Math.max((int)Math.ceil(totalDist/2), maxDist);
61 | }
62 | else {
63 | maxDist = Math.max(totalDist, maxDist);
64 | }
65 | low = high;
66 | }
67 | }
68 | if (low == seats.length - 1) return Math.max(maxDist, high - low);
69 | return Math.max(maxDist, high - low - 1);
70 | }
71 | ```
72 |
73 | ### Standard Solution
74 |
75 | #### Solution #1 Next Array
76 |
77 | * Let `left[i]` be the distance from seat `i` to the closest person sitting to the left of `i`. Similarly, let `right[i]` be the distance to the closest person sitting to the right of `i`. This is motivated by the idea that the closest person in seat `i` sits a distance `min(left[i], right[i])` away.
78 |
79 | * **Algorithm**
80 |
81 | To construct `left[i]`, notice it is either `left[i-1] + 1` if the seat is empty, or `0` if it is full. `right[i]` is constructed in a similar way.
82 |
83 | ```java
84 | public int maxDistToClosest(int[] seats){
85 | int N = seats.length;
86 | int[] left = new int[N], right = new int[N];
87 | Arrays.fill(left, N);
88 | Arrays.fill(right, N);
89 |
90 | for (int i = 0; i < N; i++){
91 | if (seats[i] == 1) left[i] = 0; //distance to the cloest one would be 0
92 | else if (i > 0) left[i] = left[i - 1] + 1; //add 1 distance comparing to the previous one
93 | }
94 | for (int i = N - 1; i >= 0; i--){
95 | if (seats[i] == 1) right[i] = 0; //distance to the cloest one would be 0
96 | else if (i < N - 1) right[i] = right[i + 1] + 1; //add 1 distance comparing to the previous one
97 | }
98 |
99 | int ans = 0;
100 | for (int i = 0; i < N; i++){
101 | if (seats[i] == 0){
102 | ans = Math.max(ans, Math.min(left[i], right[i]));
103 | }
104 | }
105 | return ans;
106 | }
107 | ```
108 |
109 | * Time complexity: $O(N)$ where N is the length of seats
110 | * Space complexity: $O(N)$ where the space used by left and right
111 |
112 | #### Solution #2 Two Pointer
113 |
114 | * **Algorithm**:
115 | * Keep track of `prev`, the filled seat at or to the left of `i`, and `future`, the filled seat at or to the right of `i`.
116 | * Then at seat `i`, the closest person is `min(i - prev, future - i)`, with one exception. `i - prev` should be considered infinite if there is no person to the left of seat `i`, and similarly `future - i` is infinite if there is no one to the right of seat `i`.
117 |
118 | ```java
119 | public int maxDistToClosest(int[] seats){
120 | int N = seats.length;
121 | int prev = -1, future = 0;
122 | int ans = 0;
123 |
124 | for (int i = 0; i < N; i++){
125 | if (seats[i] == 1){
126 | prev = i;
127 | } else {
128 | while (future < N && seats[future] == 0 || future < i){
129 | future++;
130 | }
131 | int left = prev == -1 ? N : i - prev;
132 | int right = future == N ? N : future - i;
133 | ans = Math.max(ans, Math.min(left, right));
134 | }
135 | }
136 | return ans;
137 | }
138 | ```
139 |
140 | * Time Complexity: $O(N)$, where $N$ is the length of `seats`.
141 | * Space Complexity: $O(1)$
142 |
143 | #### Solution #3 Group by Zero
144 |
145 | * My solution is a combination of solution 2 and 3
146 | * In a group of `K` adjacent empty seats between two people, the answer is `(K+1) / 2`.
147 | * For groups of empty seats between the edge of the row and one other person, the answer is `K`, and we should take into account those answers too.
148 |
149 | ```java
150 | public int maxDistToClosest(int[] seats){
151 | int N = seats.length;
152 | int K = 0;//current longest group of empty seats
153 | int ans = 0;
154 |
155 | for (int i = 0; i < N; i++){
156 | if (seats[i] == 1){
157 | K = 0;
158 | } else {
159 | K++;
160 | ans = Math.max(ans, (K + 1) / 2);
161 | }
162 | }
163 |
164 | for (int i = 0; i < N; i++){// in case starts from 0
165 | if (seats[i] == 1){
166 | ans = Math.max(ans, i);
167 | break;
168 | }
169 | }
170 |
171 | for (int i = N - 1; i >= 0; i--){// in case ends with 0
172 | if (seats[i] == 1){
173 | ans = Math.max(ans, N - 1 - i);
174 | break;
175 | }
176 | }
177 | return ans;
178 | }
179 | ```
180 |
181 | * Time Complexity: $O(N)$, where N is the length of `seats`.
182 | * Space Complexity: $O(1)$.
183 |
184 | ## 3Sum (Medium #15)
185 |
186 | **Question**: Given an integer array nums, return all the triplets `[nums[i], nums[j], nums[k]]` such that `i != j`, `i != k`, and `j != k`, and `nums[i] + nums[j] + nums[k] == 0`.
187 |
188 | Notice that the solution set must not contain duplicate triplets.
189 |
190 | **Example 1:**
191 |
192 | ```
193 | Input: nums = [-1,0,1,2,-1,-4]
194 | Output: [[-1,-1,2],[-1,0,1]]
195 | Explanation:
196 | nums[0] + nums[1] + nums[2] = (-1) + 0 + 1 = 0.
197 | nums[1] + nums[2] + nums[4] = 0 + 1 + (-1) = 0.
198 | nums[0] + nums[3] + nums[4] = (-1) + 2 + (-1) = 0.
199 | The distinct triplets are [-1,0,1] and [-1,-1,2].
200 | Notice that the order of the output and the order of the triplets does not matter.
201 | ```
202 |
203 | **Example 2:**
204 |
205 | ```
206 | Input: nums = [0,1,1]
207 | Output: []
208 | Explanation: The only possible triplet does not sum up to 0.
209 | ```
210 |
211 | **Example 3:**
212 |
213 | ```
214 | Input: nums = [0,0,0]
215 | Output: [[0,0,0]]
216 | Explanation: The only possible triplet sums up to 0.
217 | ```
218 |
219 | **Constraints:**
220 |
221 | - `3 <= nums.length <= 3000`
222 | - `-105 <= nums[i] <= 105`
223 |
224 | ### My Solution
225 |
226 | ```java
227 | // two pointers
228 | // 1. sum to 0: location < 0
229 | // 2. low and high pointer
230 | List> res;
231 | int[] nums;
232 |
233 | public List> threeSum(int[] nums) {
234 | Arrays.sort(nums);
235 | res = new ArrayList<>();
236 | this.nums = nums;
237 | for (int i = 0; i < nums.length && nums[i] <= 0; i++){
238 | // in case duplicate situations
239 | if (i == 0 || nums[i - 1] != nums[i]){
240 | findSolution(i);
241 | }
242 | }
243 | return res;
244 | }
245 |
246 | public void findSolution(int loc){
247 |
248 | int low = loc + 1, high = nums.length - 1;
249 | while(low < high){
250 | int sum = nums[low] + nums[high] + nums[loc];
251 | if (sum == 0){
252 | res.add(Arrays.asList(nums[loc], nums[low++], nums[high--]));
253 | while(low < high && nums[low] == nums[low - 1]){
254 | low++;
255 | }
256 | }
257 | else if (sum < 0){
258 | low++;
259 | }
260 | else {
261 | high--;
262 | }
263 | }
264 | }
265 | ```
266 |
267 | ### Standard Solution
268 |
269 | #### Solution #1 Two pointer
270 |
271 | * Same as my solution
272 |
273 | ```java
274 | public List> threeSum(int[] nums) {
275 | Arrays.sort(nums);
276 | List> res = new ArrayList<>();
277 | for (int i = 0; i < nums.length && nums[i] <= 0; ++i)
278 | // skip the duplicate number
279 | if (i == 0 || nums[i - 1] != nums[i]) {
280 | twoSumII(nums, i, res);
281 | }
282 | return res;
283 | }
284 | void twoSumII(int[] nums, int i, List> res) {
285 | int lo = i + 1, hi = nums.length - 1;
286 | while (lo < hi) {
287 | int sum = nums[i] + nums[lo] + nums[hi];
288 | if (sum < 0) {
289 | ++lo;
290 | } else if (sum > 0) {
291 | --hi;
292 | } else {
293 | // continue to move low and high pointer to next possible solution
294 | res.add(Arrays.asList(nums[i], nums[lo++], nums[hi--]));
295 | // skip the duplicate number
296 | while (lo < hi && nums[lo] == nums[lo - 1])
297 | ++lo;
298 | }
299 | }
300 | }
301 | ```
302 |
303 | - Time Complexity: $\mathcal{O}(n^2)$. `twoSumII` is $\mathcal{O}(n)$, and we call it n times.
304 |
305 | Sorting the array takes $\mathcal{O}(n\log{n})$, so overall complexity is $\mathcal{O}(n\log{n} + n^2)$. This is asymptotically equivalent to $\mathcal{O}(n^2)$
306 |
307 | - Space Complexity: from $\mathcal{O}(\log{n})$ to $\mathcal{O}(n)$, depending on the implementation of the sorting algorithm. For the purpose of complexity analysis, we ignore the memory required for the output.
308 |
309 | #### Solution #2 HashSet
310 |
311 | ```java
312 | public List> threeSum(int[] nums) {
313 | Arrays.sort(nums);
314 | List> res = new ArrayList<>();
315 | for (int i = 0; i < nums.length && nums[i] <= 0; ++i)
316 | if (i == 0 || nums[i - 1] != nums[i]) {
317 | twoSum(nums, i, res);
318 | }
319 | return res;
320 | }
321 | void twoSum(int[] nums, int i, List> res) {
322 | var seen = new HashSet();
323 | for (int j = i + 1; j < nums.length; ++j) {
324 | int complement = -nums[i] - nums[j];
325 | if (seen.contains(complement)) {
326 | res.add(Arrays.asList(nums[i], nums[j], complement));
327 | while (j + 1 < nums.length && nums[j] == nums[j + 1])
328 | ++j;
329 | }
330 | seen.add(nums[j]);
331 | }
332 | }
333 | ```
334 |
335 | - Time Complexity: $\mathcal{O}(n^2)$. `twoSum` is $\mathcal{O}(n)$, and we call it n times.
336 |
337 | Sorting the array takes $\mathcal{O}(n\log{n})$, so overall complexity is $\mathcal{O}(n\log{n} + n^2)$. This is asymptotically equivalent to $\mathcal{O}(n^2)$
338 |
339 | - Space Complexity: $\mathcal{O}(n)$ for the hashset.
340 |
341 | ## Trapping Rain Water (Hard #42)
342 |
343 | **Question**: Given `n` non-negative integers representing an elevation map where the width of each bar is `1`, compute how much water it can trap after raining.
344 |
345 | **Example 1:**
346 |
347 | 
348 |
349 | ```
350 | Input: height = [0,1,0,2,1,0,1,3,2,1,2,1]
351 | Output: 6
352 | Explanation: The above elevation map (black section) is represented by array [0,1,0,2,1,0,1,3,2,1,2,1]. In this case, 6 units of rain water (blue section) are being trapped.
353 | ```
354 |
355 | **Example 2:**
356 |
357 | ```
358 | Input: height = [4,2,0,3,2,5]
359 | Output: 9
360 | ```
361 |
362 | **Constraints:**
363 |
364 | - `n == height.length`
365 | - `1 <= n <= 2 * 104`
366 | - `0 <= height[i] <= 105`
367 |
368 | ### Standard Solution
369 |
370 | #### Solution #1 Two Pointers
371 |
372 | * Use two pointers: left pointer and the right pointer.
373 | * Track the left maximum and right maximum.
374 | * Always keep the larger pointer, and move the lower pointer, in this way, we can calcuate the trapping rain water by `max - curr`
375 |
376 | ```java
377 | public int trap(int[] height) {
378 | // two pointers: low, high
379 | int left = 0, right = height.length - 1;
380 | int maxLeft = 0, maxRight = 0;
381 | int water = 0;
382 |
383 | while(left < right){
384 | // current right pointer is max right
385 | // 1. compare two pointer, always keep the high one
386 | if (height[left] < height[right]){
387 | if (height[left] >= maxLeft){
388 | maxLeft = height[left];
389 | }
390 | else water += maxLeft - height[left];
391 | // 2. move the lower pointer, record left and right max
392 | left++;
393 | }
394 | else {
395 | // 3. when move the lower one, record max - low value
396 | if (height[right] >= maxRight){
397 | maxRight = height[right];
398 | }
399 | else water += maxRight - height[right];
400 | right--;
401 | }
402 | }
403 | return water;
404 | }
405 | ```
406 |
407 | - Time complexity: $O(n)$. Single iteration of $O(n)$.
408 | - Space complexity: $O(1)$ extra space. Only constant space required for $\text{left}$, $\text{right}$, $\text{left\_max}$ and $\text{right\_max}$.
409 |
410 | ## Product of Array Except Self (Medium #238)
411 |
412 | **Question**: Given an integer array `nums`, return *an array* `answer` *such that* `answer[i]` *is equal to the product of all the elements of* `nums` *except* `nums[i]`.
413 |
414 | The product of any prefix or suffix of `nums` is **guaranteed** to fit in a **32-bit** integer.
415 |
416 | You must write an algorithm that runs in `O(n)` time and without using the division operation.
417 |
418 | **Example 1:**
419 |
420 | ```
421 | Input: nums = [1,2,3,4]
422 | Output: [24,12,8,6]
423 | ```
424 |
425 | **Example 2:**
426 |
427 | ```
428 | Input: nums = [-1,1,0,-3,3]
429 | Output: [0,0,9,0,0]
430 | ```
431 |
432 | **Constraints:**
433 |
434 | - `2 <= nums.length <= 105`
435 | - `-30 <= nums[i] <= 30`
436 | - The product of any prefix or suffix of `nums` is **guaranteed** to fit in a **32-bit** integer.
437 |
438 | **Follow up:** Can you solve the problem in `O(1) `extra space complexity? (The output array **does not** count as extra space for space complexity analysis.)
439 |
440 | ### My Solution
441 |
442 | ```java
443 | // correct but time limit exceeded
444 | public int[] productExceptSelf(int[] nums) {
445 | // product every digit in the array, then change i element back to origin
446 | int[] res = new int[nums.length];
447 | Arrays.fill(res, 1);
448 | for (int i = 0; i < nums.length; i++){
449 | int curr = nums[i];
450 | for (int j = 0; j < nums.length; j++){
451 | if (i == j) continue;
452 | res[j] = res[j] * curr;
453 | }
454 | }
455 | return res;
456 | }
457 | ```
458 |
459 | ### Standard Solution
460 |
461 | #### Solution #1 Left and Right Product Lists
462 |
463 | 
464 |
465 | * Use previous product times `nums[i - 1]` to avoid times themselves. Similarly, calculate the product starting from the right direction.
466 |
467 | ```java
468 | public int[] productExceptSelf(int[] nums){
469 | // the length of the input array
470 | int length = nums.length;
471 |
472 | // the left and right arrays as described in the algorithm
473 | int[] L = new int[length];
474 | int[] R = new int[length];
475 |
476 | // final answer array to be returned
477 | int[] answer = new int[length];
478 |
479 | // L[i] contains the product of all elements to the left
480 | // note: for the element at index '0', no elements to the left, L[0] would be 1
481 | L[0] = 1;
482 | for (int i = 1; i < length; i++){
483 | // L[i - 1] already contains the product of elements to the left of 'i - 1'
484 | L[i] = nums[i - 1] * L[i - 1];
485 | }
486 |
487 | R[length - 1] = 1;
488 | for (int i = length - 2; i >= 0; i--){
489 | // R[i + 1] already contains the product of elements to the right of 'i + 1'
490 | R[i] = nums[i + 1] * R[i + 1];
491 | }
492 |
493 | // constructing the answer array
494 | for (int i = 0; i < length; i++){
495 | // For the first element, R[i] would be product except for self
496 | // For the last element of the array, product except for self would be L[i]
497 | // Else, multiple product of all elements to the left and to the right
498 | answer[i] = L[i] * R[i];
499 | }
500 | return answer;
501 | }
502 | ```
503 |
504 | - Time complexity: $O(N)$ where N represents the number of elements in the input array. We use one iteration to construct the array L, one to construct the array R, and one last to construct the `answer` array using L and R.
505 | - Space complexity: $O(N)$ used up by the two intermediate arrays that we constructed to keep track of the product of elements to the left and right.
506 |
507 | #### Solution #2 O(1) Space Approach
508 |
509 | * Similar idea to the first solution, but more space efficient
510 |
511 | ```java
512 | public int[] productExceptSelf(int[] nums) {
513 | // The length of the input array
514 | int length = nums.length;
515 |
516 | // Final answer array to be returned
517 | int[] answer = new int[length];
518 |
519 | answer[0] = 1;
520 | for (int i = 1; i < length; i++) {
521 | answer[i] = nums[i - 1] * answer[i - 1];
522 | }
523 |
524 | int R = 1;
525 | for (int i = length - 1; i >= 0; i--) {
526 |
527 | // For the index 'i', R would contain the
528 | // product of all elements to the right. We update R accordingly
529 | answer[i] = answer[i] * R;
530 | R *= nums[i];
531 | }
532 | return answer;
533 | }
534 | ```
535 |
536 | * More simplified version
537 |
538 | ```java
539 | public int[] productExceptSelf(int[] nums) {
540 | int[] result = new int[nums.length];
541 | for (int i = 0, tmp = 1; i < nums.length; i++) {
542 | result[i] = tmp;
543 | tmp *= nums[i];
544 | }
545 | for (int i = nums.length - 1, tmp = 1; i >= 0; i--) {
546 | result[i] *= tmp;
547 | tmp *= nums[i];
548 | }
549 | return result;
550 | }
551 | ```
552 |
553 | - Time complexity: $O(N)$ where N represents the number of elements in the input array. We use one iteration to construct the array L, and one to update the array answer.
554 | - Space complexity: $O(1)$ since don't use any additional array for our computations. The problem statement mentions that using the answer array doesn't add to the space complexity.
--------------------------------------------------------------------------------
/Binary Tree/Binary Tree Tutorial.md:
--------------------------------------------------------------------------------
1 | # Binary Tree Tutorial
2 |
3 | Materials refer to: https://leetcode.com/explore/learn/card/recursion-i/
4 |
5 | # Introduction to Binary Tree
6 |
7 | * From graph view, a tree can also be defined as a directed acyclic graph which has `N nodes` and `N-1 edges`.
8 | * As the name suggests, a binary tree is a tree data structure in which each node has `at most two children`, which are referred to as the left child and the right child.
9 |
10 | ## Traverse a Tree
11 |
12 | * **Pre-order Traversal**
13 |
14 | * Pre-order traversal is to visit the root first. Then traverse the left subtree. Finally, traverse the right subtree.
15 |
16 | * **In-order Traversal**
17 |
18 | * In-order traversal is to traverse the left subtree first. Then visit the root. Finally, traverse the right subtree.
19 | * Typically, for `binary search tree`, we can retrieve all the data in sorted order using in-order traversal.
20 |
21 | * **Post-order Traversal**
22 |
23 | * Post-order traversal is to traverse the left subtree first. Then traverse the right subtree. Finally, visit the root.
24 | * It is worth noting that when you delete nodes in a tree, **deletion process will be in post-order**. That is to say, when you delete a node, you will delete its left child and its right child before you delete the node itself.
25 | * Post-order is widely use in mathematical expression. It is easier to write a program to parse a post-order expression.
26 |
27 |  28 |
29 | * If you handle this tree in postorder, you can easily handle the expression using a stack.
30 | * Each time when you meet a operator, you can just **pop 2 elements from the stack**, **calculate the result and push the result back into the stack**.
31 |
32 | * Frequently come with **recursion and/or iteration** for code solution.
33 |
34 | * To be cautious, the complexity might be different due to a different implementation. It is comparatively easy to do traversal recursively but when the depth of the tree is too large, we might suffer from `stack overflow` problem. That's one of the main reasons why we want to solve this problem iteratively sometimes.
35 |
36 | ## Binary Tree Preorder Traversal(Easy #144)
37 |
38 | **Question**: Given the `root` of a binary tree, return *the preorder traversal of its nodes' values*.
39 |
40 | **Example 1:**
41 |
42 |
28 |
29 | * If you handle this tree in postorder, you can easily handle the expression using a stack.
30 | * Each time when you meet a operator, you can just **pop 2 elements from the stack**, **calculate the result and push the result back into the stack**.
31 |
32 | * Frequently come with **recursion and/or iteration** for code solution.
33 |
34 | * To be cautious, the complexity might be different due to a different implementation. It is comparatively easy to do traversal recursively but when the depth of the tree is too large, we might suffer from `stack overflow` problem. That's one of the main reasons why we want to solve this problem iteratively sometimes.
35 |
36 | ## Binary Tree Preorder Traversal(Easy #144)
37 |
38 | **Question**: Given the `root` of a binary tree, return *the preorder traversal of its nodes' values*.
39 |
40 | **Example 1:**
41 |
42 |  43 |
44 | ```
45 | Input: root = [1,null,2,3]
46 | Output: [1,2,3]
47 | ```
48 |
49 | **Example 2:**
50 |
51 | ```
52 | Input: root = []
53 | Output: []
54 | ```
55 |
56 | **Example 3:**
57 |
58 | ```
59 | Input: root = [1]
60 | Output: [1]
61 | ```
62 |
63 | **Constraints:**
64 |
65 | - The number of nodes in the tree is in the range `[0, 100]`.
66 | - `-100 <= Node.val <= 100`
67 |
68 | ### My Solution
69 |
70 | ```java
71 | /**
72 | * Definition for a binary tree node.
73 | * public class TreeNode {
74 | * int val;
75 | * TreeNode left;
76 | * TreeNode right;
77 | * TreeNode() {}
78 | * TreeNode(int val) { this.val = val; }
79 | * TreeNode(int val, TreeNode left, TreeNode right) {
80 | * this.val = val;
81 | * this.left = left;
82 | * this.right = right;
83 | * }
84 | * }
85 | */
86 | public List preorderTraversal(TreeNode root) {
87 | List nodes = new ArrayList<>();
88 | preorder(root, nodes);
89 | return nodes;
90 | }
91 |
92 | public void preorder(TreeNode root, List nodes){
93 | if (root == null){
94 | return;
95 | } else {
96 | nodes.add(root.val);
97 | preorder(root.left, nodes);
98 | preorder(root.right, nodes);
99 | }
100 | }
101 | ```
102 |
103 | * Recursion method:
104 | * Add the root first
105 | * Traverse the left tree
106 | * Traverse the right tree
107 | * The traversal method **return void**, separate it from the main method
108 | * While traverse, bring in the tree with the nodes record
109 | * Always use `if-else`, `if` for the base case and `return`
110 |
111 | ### Standard Solution
112 |
113 | * There are two general strategies to traverse a tree:
114 |
115 | - ***Breadth First Search* (`BFS`)**
116 |
117 | We scan through the tree level by level, following the order of height, from top to bottom. The nodes on higher level would be visited before the ones with lower levels.
118 |
119 | - ***Depth First Search* (`DFS`)**
120 |
121 | In this strategy, we adopt the `depth` as the priority, so that one would start from a root and reach all the way down to certain leaf, and then back to root to reach another branch.
122 |
123 | The DFS strategy can further be distinguished as `preorder`, `inorder`, and `postorder` depending on the relative order among the root node, left node and right node.
124 |
125 | 
126 |
127 | #### Solution #1 Recursion
128 |
129 | * Same as my solution
130 | * Time complexity: $O(N)$. N is the number of nodes, each node is traversed once.
131 | * Space complexity: $O(N)$. Average case should be $O(\log n)$, the worst case is a linked-list-like tree then it would be a $O(N)$
132 |
133 | #### Solution #2 Iteration
134 |
135 | * Use a stack to hold the values, each time we encouter a null, we pop one element from the stack
136 |
137 | ```java
138 | public List preorderTraversal(TreeNode root){
139 | Stack stack = new Stack<>();
140 | LinkedList output = new LinkedList<>();
141 | if (root == null){
142 | return output;
143 | }
144 |
145 | stack.add(root);
146 | while(!stack.isEmpty()){
147 | TreeNode node = stack.pop();
148 | output.add(node.val);
149 | if (node.right != null){// since it is a stack, we need to exchange the order here with left
150 | stack.add(node.right);
151 | }
152 | if (node.left != null){
153 | stack.add(node.left);
154 | }
155 | }
156 | }
157 | ```
158 |
159 | * Time complexity: $O(N)$. N is the number of nodes, each node is traversed once.
160 | * Space complexity: $O(N)$. Average case should be $O(\log n)$, the worst case is a linked-list-like tree then it would be a $O(N)$
161 |
162 | #### Solution #3 Morris Traversal(not important)
163 |
164 | * The algorithm does not use additional space for the computation, and the memory is only used to keep the output. If one prints the output directly along the computation, the space complexity would be $ \mathcal{O}(1)$.
165 | * Details refer to [morris traversal leetcode](https://leetcode.com/problems/binary-tree-preorder-traversal/solution/)
166 |
167 | ```java
168 | public List preorderTraversal(TreeNode root){
169 | LinkedList output = new LinkedList<>();
170 |
171 | TreeNode node = root;
172 | while(node != null){
173 | if(node.left == null){
174 | output.add(node.val);
175 | node = node.right;
176 | }
177 | else {
178 | TreeNode predecessor = node.left;
179 | while((predecessor.right != null) && (predecessor.right != node)){
180 | predecessor = predecessor.right;
181 | }
182 | if (predecessor.right == null){
183 | output.add(node.val);
184 | predecessor.right = node;
185 | node = node.left;
186 | }
187 | else {
188 | predecessor.right = null;
189 | node = node.right;
190 | }
191 | }
192 | }
193 | return output;
194 | }
195 | ```
196 |
197 | - Time complexity : we visit each predecessor exactly twice descending down from the node, thus the time complexity is $\mathcal{O}(N)$, where N is the number of nodes, *i.e.* the size of tree.
198 | - Space complexity : we use no additional memory for the computation itself, thus space complexity is $\mathcal{O}(1)$.
199 |
200 | ## Binary Tree Inorder Traversal(Easy #94)
201 |
202 | **Question**: Given the `root` of a binary tree, return *the inorder traversal of its nodes' values*.
203 |
204 | **Example 1:**
205 |
206 |
43 |
44 | ```
45 | Input: root = [1,null,2,3]
46 | Output: [1,2,3]
47 | ```
48 |
49 | **Example 2:**
50 |
51 | ```
52 | Input: root = []
53 | Output: []
54 | ```
55 |
56 | **Example 3:**
57 |
58 | ```
59 | Input: root = [1]
60 | Output: [1]
61 | ```
62 |
63 | **Constraints:**
64 |
65 | - The number of nodes in the tree is in the range `[0, 100]`.
66 | - `-100 <= Node.val <= 100`
67 |
68 | ### My Solution
69 |
70 | ```java
71 | /**
72 | * Definition for a binary tree node.
73 | * public class TreeNode {
74 | * int val;
75 | * TreeNode left;
76 | * TreeNode right;
77 | * TreeNode() {}
78 | * TreeNode(int val) { this.val = val; }
79 | * TreeNode(int val, TreeNode left, TreeNode right) {
80 | * this.val = val;
81 | * this.left = left;
82 | * this.right = right;
83 | * }
84 | * }
85 | */
86 | public List preorderTraversal(TreeNode root) {
87 | List nodes = new ArrayList<>();
88 | preorder(root, nodes);
89 | return nodes;
90 | }
91 |
92 | public void preorder(TreeNode root, List nodes){
93 | if (root == null){
94 | return;
95 | } else {
96 | nodes.add(root.val);
97 | preorder(root.left, nodes);
98 | preorder(root.right, nodes);
99 | }
100 | }
101 | ```
102 |
103 | * Recursion method:
104 | * Add the root first
105 | * Traverse the left tree
106 | * Traverse the right tree
107 | * The traversal method **return void**, separate it from the main method
108 | * While traverse, bring in the tree with the nodes record
109 | * Always use `if-else`, `if` for the base case and `return`
110 |
111 | ### Standard Solution
112 |
113 | * There are two general strategies to traverse a tree:
114 |
115 | - ***Breadth First Search* (`BFS`)**
116 |
117 | We scan through the tree level by level, following the order of height, from top to bottom. The nodes on higher level would be visited before the ones with lower levels.
118 |
119 | - ***Depth First Search* (`DFS`)**
120 |
121 | In this strategy, we adopt the `depth` as the priority, so that one would start from a root and reach all the way down to certain leaf, and then back to root to reach another branch.
122 |
123 | The DFS strategy can further be distinguished as `preorder`, `inorder`, and `postorder` depending on the relative order among the root node, left node and right node.
124 |
125 | 
126 |
127 | #### Solution #1 Recursion
128 |
129 | * Same as my solution
130 | * Time complexity: $O(N)$. N is the number of nodes, each node is traversed once.
131 | * Space complexity: $O(N)$. Average case should be $O(\log n)$, the worst case is a linked-list-like tree then it would be a $O(N)$
132 |
133 | #### Solution #2 Iteration
134 |
135 | * Use a stack to hold the values, each time we encouter a null, we pop one element from the stack
136 |
137 | ```java
138 | public List preorderTraversal(TreeNode root){
139 | Stack stack = new Stack<>();
140 | LinkedList output = new LinkedList<>();
141 | if (root == null){
142 | return output;
143 | }
144 |
145 | stack.add(root);
146 | while(!stack.isEmpty()){
147 | TreeNode node = stack.pop();
148 | output.add(node.val);
149 | if (node.right != null){// since it is a stack, we need to exchange the order here with left
150 | stack.add(node.right);
151 | }
152 | if (node.left != null){
153 | stack.add(node.left);
154 | }
155 | }
156 | }
157 | ```
158 |
159 | * Time complexity: $O(N)$. N is the number of nodes, each node is traversed once.
160 | * Space complexity: $O(N)$. Average case should be $O(\log n)$, the worst case is a linked-list-like tree then it would be a $O(N)$
161 |
162 | #### Solution #3 Morris Traversal(not important)
163 |
164 | * The algorithm does not use additional space for the computation, and the memory is only used to keep the output. If one prints the output directly along the computation, the space complexity would be $ \mathcal{O}(1)$.
165 | * Details refer to [morris traversal leetcode](https://leetcode.com/problems/binary-tree-preorder-traversal/solution/)
166 |
167 | ```java
168 | public List preorderTraversal(TreeNode root){
169 | LinkedList output = new LinkedList<>();
170 |
171 | TreeNode node = root;
172 | while(node != null){
173 | if(node.left == null){
174 | output.add(node.val);
175 | node = node.right;
176 | }
177 | else {
178 | TreeNode predecessor = node.left;
179 | while((predecessor.right != null) && (predecessor.right != node)){
180 | predecessor = predecessor.right;
181 | }
182 | if (predecessor.right == null){
183 | output.add(node.val);
184 | predecessor.right = node;
185 | node = node.left;
186 | }
187 | else {
188 | predecessor.right = null;
189 | node = node.right;
190 | }
191 | }
192 | }
193 | return output;
194 | }
195 | ```
196 |
197 | - Time complexity : we visit each predecessor exactly twice descending down from the node, thus the time complexity is $\mathcal{O}(N)$, where N is the number of nodes, *i.e.* the size of tree.
198 | - Space complexity : we use no additional memory for the computation itself, thus space complexity is $\mathcal{O}(1)$.
199 |
200 | ## Binary Tree Inorder Traversal(Easy #94)
201 |
202 | **Question**: Given the `root` of a binary tree, return *the inorder traversal of its nodes' values*.
203 |
204 | **Example 1:**
205 |
206 |  207 |
208 | ```
209 | Input: root = [1,null,2,3]
210 | Output: [1,3,2]
211 | ```
212 |
213 | **Example 2:**
214 |
215 | ```
216 | Input: root = []
217 | Output: []
218 | ```
219 |
220 | **Example 3:**
221 |
222 | ```
223 | Input: root = [1]
224 | Output: [1]
225 | ```
226 |
227 | **Constraints:**
228 |
229 | - The number of nodes in the tree is in the range `[0, 100]`.
230 | - `-100 <= Node.val <= 100`
231 |
232 | ### My Solution
233 |
234 | ```java
235 | public List inorderTraversal(TreeNode root){
236 | List nodes = new ArrayList<>();
237 | inorder(root, nodes);
238 | return nodes;
239 | }
240 |
241 | public void inorder(TreeNode root, List nodes){
242 | if (root == null) return;
243 | else {
244 | inorder(root.left, nodes);
245 | nodes.add(root.val);
246 | inorder(root.right, nodes);
247 | }
248 | }
249 | ```
250 |
251 | ### Standard Solution
252 |
253 | #### Solution #1 Recursion
254 |
255 | * Same as my solution
256 | * Time complexity: $O(N)$ because the recursive function is $T(n) = 2 \cdot T(n/2)+1$.
257 | * Space complexity: $O(N)$. The worst case space is $O(N)$, and in average case it is $O(\log n)$
258 |
259 | #### Solution #2 Interation using Stack
260 |
261 | ```java
262 | public List inorderTraversal(TreeNode root){
263 | List res = new ArrayList<>();
264 | Stack stack = new Stack<>();
265 | TreeNode curr = root;
266 | while (curr != null || !stack.isEmpty()){
267 | while (curr != null){
268 | stack.push(curr);
269 | curr = curr.left;
270 | }
271 | curr = stack.pop();
272 | res.add(curr.val);
273 | curr = curr.right;
274 | }
275 | }
276 | ```
277 |
278 | ```java
279 | class Solution {
280 | public List inorderTraversal(TreeNode root) {
281 | List result = new ArrayList<>();
282 | if (root == null){
283 | return result;
284 | }
285 | Stack stack = new Stack<>();
286 | TreeNode cur =root;
287 | while (cur!=null || !stack.isEmpty()) {
288 | if (cur!=null) {
289 | stack.push(cur);
290 | cur = cur.left;
291 | }else {
292 | cur = stack.pop();
293 | result.add(cur.val);
294 | cur = cur.right;
295 | }
296 | }
297 | return result;
298 | }
299 | }
300 |
301 | 作者:mulberry_qs
302 | 链接:https://leetcode-cn.com/problems/binary-tree-postorder-traversal/solution/duo-chong-bian-li-tou-da-by-mulberry_qs-02c9/
303 | 来源:力扣(LeetCode)
304 | 著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
305 | ```
306 |
307 | * Time complexity: $O(N)$ because the recursive function is $T(n) = 2 \cdot T(n/2)+1$.
308 | * Space complexity: $O(N)$. The worst case space is $O(N)$, and in average case it is $O(\log n)$
309 |
310 | #### Solution #3 Morris Traversal
311 |
312 | ```java
313 | class Solution {
314 | public List inorderTraversal(TreeNode root) {
315 | List res = new ArrayList<>();
316 | TreeNode curr = root;
317 | TreeNode pre;
318 | while (curr != null) {
319 | if (curr.left == null) {
320 | res.add(curr.val);
321 | curr = curr.right; // move to next right node
322 | } else { // has a left subtree
323 | pre = curr.left;
324 | while (pre.right != null) { // find rightmost
325 | pre = pre.right;
326 | }
327 | pre.right = curr; // put cur after the pre node
328 | TreeNode temp = curr; // store cur node
329 | curr = curr.left; // move cur to the top of the new tree
330 | temp.left = null; // original cur left be null, avoid infinite loops
331 | }
332 | }
333 | return res;
334 | }
335 | }
336 | ```
337 |
338 | * Time complexity: $O(N)$
339 | * Space complexity: $O(1)$
340 |
341 | ## Binary Tree Postorder Traversal(Easy #145)
342 |
343 | **Question**: Given the `root` of a binary tree, return *the postorder traversal of its nodes' values*.
344 |
345 | **Example 1:**
346 |
347 | 
348 |
349 | ```
350 | Input: root = [1,null,2,3]
351 | Output: [3,2,1]
352 | ```
353 |
354 | **Example 2:**
355 |
356 | ```
357 | Input: root = []
358 | Output: []
359 | ```
360 |
361 | **Example 3:**
362 |
363 | ```
364 | Input: root = [1]
365 | Output: [1]
366 | ```
367 |
368 | **Constraints:**
369 |
370 | - The number of the nodes in the tree is in the range `[0, 100]`.
371 | - `-100 <= Node.val <= 100`
372 |
373 | ### My Solution
374 |
375 | ```java
376 | public List postorderTraversal(TreeNode root){
377 | List nodes = new ArrayList<>();
378 | postorder(root, nodes);
379 | return nodes;
380 | }
381 |
382 | public void postorder(TreeNode root, List nodes){
383 | if (root == null){
384 | return;
385 | }
386 | else {
387 | postorder(root.left, nodes);
388 | postorder(root.right, nodes);
389 | nodes.add(root.val);
390 | }
391 | }
392 | ```
393 |
394 | ```java
395 | class Solution {
396 | public List postorderTraversal(TreeNode root) {
397 | List result = new ArrayList<>();
398 | if (root == null) {
399 | return result;
400 | }
401 | Stack stack = new Stack<>(); // 入栈为中左右 出栈为中右左
402 | stack.push(root);
403 | while (!stack.isEmpty()) {
404 | TreeNode treeNode = stack.pop();
405 | result.add(treeNode.val);
406 | if (treeNode.left != null) {
407 | stack.push(treeNode.left);
408 | }
409 | if (treeNode.right != null) {
410 | stack.push(treeNode.right);
411 | }
412 | }
413 | Collections.reverse(result); // 直接翻转中右左为左右中
414 | return result;
415 | }
416 | }
417 |
418 | 作者:mulberry_qs
419 | 链接:https://leetcode-cn.com/problems/binary-tree-postorder-traversal/solution/duo-chong-bian-li-tou-da-by-mulberry_qs-02c9/
420 | 来源:力扣(LeetCode)
421 | 著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
422 | ```
423 |
424 | * Time complexity and space complexity should be the same as previous problems
425 | * No given standard solution in leetcode but should be similar to previous problems
426 |
427 | # Level-order Traversal - Introduction
428 |
429 | * Level-order traversal is to traverse the tree level by level.
430 | * `Breadth-First Search` is an algorithm to traverse or search in data structures like a tree or a graph.
431 | * Typically, we use a **queue** to help us to do BFS.
432 |
433 | ## Binary Tree Level Order Traversal(Medium 102)
434 |
435 | **Question**: Given the `root` of a binary tree, return *the level order traversal of its nodes' values*. (i.e., from left to right, level by level).
436 |
437 | **Example 1:**
438 |
439 |
207 |
208 | ```
209 | Input: root = [1,null,2,3]
210 | Output: [1,3,2]
211 | ```
212 |
213 | **Example 2:**
214 |
215 | ```
216 | Input: root = []
217 | Output: []
218 | ```
219 |
220 | **Example 3:**
221 |
222 | ```
223 | Input: root = [1]
224 | Output: [1]
225 | ```
226 |
227 | **Constraints:**
228 |
229 | - The number of nodes in the tree is in the range `[0, 100]`.
230 | - `-100 <= Node.val <= 100`
231 |
232 | ### My Solution
233 |
234 | ```java
235 | public List inorderTraversal(TreeNode root){
236 | List nodes = new ArrayList<>();
237 | inorder(root, nodes);
238 | return nodes;
239 | }
240 |
241 | public void inorder(TreeNode root, List nodes){
242 | if (root == null) return;
243 | else {
244 | inorder(root.left, nodes);
245 | nodes.add(root.val);
246 | inorder(root.right, nodes);
247 | }
248 | }
249 | ```
250 |
251 | ### Standard Solution
252 |
253 | #### Solution #1 Recursion
254 |
255 | * Same as my solution
256 | * Time complexity: $O(N)$ because the recursive function is $T(n) = 2 \cdot T(n/2)+1$.
257 | * Space complexity: $O(N)$. The worst case space is $O(N)$, and in average case it is $O(\log n)$
258 |
259 | #### Solution #2 Interation using Stack
260 |
261 | ```java
262 | public List inorderTraversal(TreeNode root){
263 | List res = new ArrayList<>();
264 | Stack stack = new Stack<>();
265 | TreeNode curr = root;
266 | while (curr != null || !stack.isEmpty()){
267 | while (curr != null){
268 | stack.push(curr);
269 | curr = curr.left;
270 | }
271 | curr = stack.pop();
272 | res.add(curr.val);
273 | curr = curr.right;
274 | }
275 | }
276 | ```
277 |
278 | ```java
279 | class Solution {
280 | public List inorderTraversal(TreeNode root) {
281 | List result = new ArrayList<>();
282 | if (root == null){
283 | return result;
284 | }
285 | Stack stack = new Stack<>();
286 | TreeNode cur =root;
287 | while (cur!=null || !stack.isEmpty()) {
288 | if (cur!=null) {
289 | stack.push(cur);
290 | cur = cur.left;
291 | }else {
292 | cur = stack.pop();
293 | result.add(cur.val);
294 | cur = cur.right;
295 | }
296 | }
297 | return result;
298 | }
299 | }
300 |
301 | 作者:mulberry_qs
302 | 链接:https://leetcode-cn.com/problems/binary-tree-postorder-traversal/solution/duo-chong-bian-li-tou-da-by-mulberry_qs-02c9/
303 | 来源:力扣(LeetCode)
304 | 著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
305 | ```
306 |
307 | * Time complexity: $O(N)$ because the recursive function is $T(n) = 2 \cdot T(n/2)+1$.
308 | * Space complexity: $O(N)$. The worst case space is $O(N)$, and in average case it is $O(\log n)$
309 |
310 | #### Solution #3 Morris Traversal
311 |
312 | ```java
313 | class Solution {
314 | public List inorderTraversal(TreeNode root) {
315 | List res = new ArrayList<>();
316 | TreeNode curr = root;
317 | TreeNode pre;
318 | while (curr != null) {
319 | if (curr.left == null) {
320 | res.add(curr.val);
321 | curr = curr.right; // move to next right node
322 | } else { // has a left subtree
323 | pre = curr.left;
324 | while (pre.right != null) { // find rightmost
325 | pre = pre.right;
326 | }
327 | pre.right = curr; // put cur after the pre node
328 | TreeNode temp = curr; // store cur node
329 | curr = curr.left; // move cur to the top of the new tree
330 | temp.left = null; // original cur left be null, avoid infinite loops
331 | }
332 | }
333 | return res;
334 | }
335 | }
336 | ```
337 |
338 | * Time complexity: $O(N)$
339 | * Space complexity: $O(1)$
340 |
341 | ## Binary Tree Postorder Traversal(Easy #145)
342 |
343 | **Question**: Given the `root` of a binary tree, return *the postorder traversal of its nodes' values*.
344 |
345 | **Example 1:**
346 |
347 | 
348 |
349 | ```
350 | Input: root = [1,null,2,3]
351 | Output: [3,2,1]
352 | ```
353 |
354 | **Example 2:**
355 |
356 | ```
357 | Input: root = []
358 | Output: []
359 | ```
360 |
361 | **Example 3:**
362 |
363 | ```
364 | Input: root = [1]
365 | Output: [1]
366 | ```
367 |
368 | **Constraints:**
369 |
370 | - The number of the nodes in the tree is in the range `[0, 100]`.
371 | - `-100 <= Node.val <= 100`
372 |
373 | ### My Solution
374 |
375 | ```java
376 | public List postorderTraversal(TreeNode root){
377 | List nodes = new ArrayList<>();
378 | postorder(root, nodes);
379 | return nodes;
380 | }
381 |
382 | public void postorder(TreeNode root, List nodes){
383 | if (root == null){
384 | return;
385 | }
386 | else {
387 | postorder(root.left, nodes);
388 | postorder(root.right, nodes);
389 | nodes.add(root.val);
390 | }
391 | }
392 | ```
393 |
394 | ```java
395 | class Solution {
396 | public List postorderTraversal(TreeNode root) {
397 | List result = new ArrayList<>();
398 | if (root == null) {
399 | return result;
400 | }
401 | Stack stack = new Stack<>(); // 入栈为中左右 出栈为中右左
402 | stack.push(root);
403 | while (!stack.isEmpty()) {
404 | TreeNode treeNode = stack.pop();
405 | result.add(treeNode.val);
406 | if (treeNode.left != null) {
407 | stack.push(treeNode.left);
408 | }
409 | if (treeNode.right != null) {
410 | stack.push(treeNode.right);
411 | }
412 | }
413 | Collections.reverse(result); // 直接翻转中右左为左右中
414 | return result;
415 | }
416 | }
417 |
418 | 作者:mulberry_qs
419 | 链接:https://leetcode-cn.com/problems/binary-tree-postorder-traversal/solution/duo-chong-bian-li-tou-da-by-mulberry_qs-02c9/
420 | 来源:力扣(LeetCode)
421 | 著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
422 | ```
423 |
424 | * Time complexity and space complexity should be the same as previous problems
425 | * No given standard solution in leetcode but should be similar to previous problems
426 |
427 | # Level-order Traversal - Introduction
428 |
429 | * Level-order traversal is to traverse the tree level by level.
430 | * `Breadth-First Search` is an algorithm to traverse or search in data structures like a tree or a graph.
431 | * Typically, we use a **queue** to help us to do BFS.
432 |
433 | ## Binary Tree Level Order Traversal(Medium 102)
434 |
435 | **Question**: Given the `root` of a binary tree, return *the level order traversal of its nodes' values*. (i.e., from left to right, level by level).
436 |
437 | **Example 1:**
438 |
439 |  440 |
441 | ```
442 | Input: root = [3,9,20,null,null,15,7]
443 | Output: [[3],[9,20],[15,7]]
444 | ```
445 |
446 | **Example 2:**
447 |
448 | ```
449 | Input: root = [1]
450 | Output: [[1]]
451 | ```
452 |
453 | **Example 3:**
454 |
455 | ```
456 | Input: root = []
457 | Output: []
458 | ```
459 |
460 | **Constraints:**
461 |
462 | - The number of nodes in the tree is in the range `[0, 2000]`.
463 | - `-1000 <= Node.val <= 1000`
464 |
465 | ### My Solution
466 |
467 | * Use a queue to store the value from left to right
468 | * Use queue size to determine how many nodes in the same level and use array list to store the same level nodes
469 | * Add the level nodes to `levels` which is the return list
470 |
471 | ```java
472 | /**
473 | * Definition for a binary tree node.
474 | * public class TreeNode {
475 | * int val;
476 | * TreeNode left;
477 | * TreeNode right;
478 | * TreeNode() {}
479 | * TreeNode(int val) { this.val = val; }
480 | * TreeNode(int val, TreeNode left, TreeNode right) {
481 | * this.val = val;
482 | * this.left = left;
483 | * this.right = right;
484 | * }
485 | * }
486 | */
487 | public List> levelOrder(TreeNode root) {
488 | Queue treeQueue = new LinkedList<>();
489 | List> levels = new ArrayList<>();
490 | if (root == null) return levels;
491 | treeQueue.add(root);
492 | while(!treeQueue.isEmpty()){
493 | List list = new ArrayList<>();
494 | int level_length = treeQueue.size();
495 | for (int i = 0; i < level_length; i++){
496 | TreeNode node = treeQueue.remove();
497 | list.add(node.val);
498 | if (node.left != null){
499 | treeQueue.add(node.left);
500 | }
501 | if (node.right != null){
502 | treeQueue.add(node.right);
503 | }
504 | }
505 | levels.add(list);
506 | }
507 | return levels;
508 | }
509 | ```
510 |
511 | ```java
512 | // second attempt
513 | public List> levelOrder(TreeNode root) {
514 | List> res = new ArrayList<>();
515 | bfs(root, res, 0);
516 | return res;
517 | }
518 |
519 | public void bfs(TreeNode root, List> res, int level){
520 | if (root == null){
521 | return;
522 | }
523 | if (res.size() == level){
524 | res.add(new ArrayList());
525 | }
526 | res.get(level).add(root.val);
527 | bfs(root.left, res, level + 1);
528 | bfs(root.right, res, level + 1);
529 | }
530 | ```
531 |
532 | ```java
533 | // third attempt
534 | public List> levelOrder(TreeNode root) {
535 | // level order traversal: BFS
536 | // 1. create the res list, create a queue
537 | List> res = new ArrayList<>();
538 | Queue queue = new LinkedList<>();
539 | if (root == null) return res;
540 | queue.add(root);
541 | int level = 0;
542 | // 2. use queue to store the root node, left, right
543 | while(!queue.isEmpty()){
544 | res.add(new ArrayList());
545 | int levelLength = queue.size();
546 |
547 | for (int i = 0; i < levelLength; i++){
548 | // 3. poll from queue, put element to the list
549 | TreeNode curr = queue.poll();
550 | res.get(level).add(curr.val);
551 | if (curr.left != null) queue.add(curr.left);
552 | if (curr.right != null) queue.add(curr.right);
553 | }
554 | level++;
555 | }
556 | return res;
557 | }
558 | ```
559 |
560 |
561 |
562 | ### Standard Solution
563 |
564 | #### Solution #1 Iteration
565 |
566 | * Same as my solution
567 | * Time complexity : $\mathcal{O}(N)$ since each node is processed exactly once.
568 | * Space complexity : $\mathcal{O}(N)$ to keep the output structure which contains `N` node values.
569 |
570 | #### Solution #2 Recursion
571 |
572 | * Call recursive helper function
573 | * Same concept with the method 1 but using recursion
574 |
575 | ```java
576 | class Solution {
577 | List> levels = new ArrayList>();
578 | public void helper(TreeNode node, int level) {
579 | // start the current level
580 | if (levels.size() == level)
581 | levels.add(new ArrayList());
582 |
583 | // fulfil the current level
584 | levels.get(level).add(node.val);
585 |
586 | // process child nodes for the next level
587 | if (node.left != null)
588 | helper(node.left, level + 1);
589 | if (node.right != null)
590 | helper(node.right, level + 1);
591 | }
592 | public List> levelOrder(TreeNode root) {
593 | if (root == null) return levels;
594 | helper(root, 0);
595 | return levels;
596 | }
597 | }
598 | ```
599 |
600 | * Time complexity : $\mathcal{O}(N)$ since each node is processed exactly once.
601 | * Space complexity : $\mathcal{O}(N)$ to keep the output structure which contains `N` node values.
602 |
603 | # Solve Tree Problem Recursively
604 |
605 | As we know, a tree can be defined recursively as a node(the root node) that includes a value and a list of references to children nodes. Recursion is one of the natural features of a tree. Therefore, many tree problems can be solved recursively. For each recursive function call, we only focus on the problem for the current node and call the function recursively to solve its children.
606 |
607 | Typically, we can solve a tree problem recursively using a top-down approach or using a bottom-up approach.
608 |
609 | ## Top-down Solution
610 |
611 | * "Top-down" means that in each recursive call, we will visit the node first to come up with some values, and pass these values to its children when calling the function recursively.
612 |
613 | * So the "top-down" solution can be considered as a kind of **preorder** traversal.
614 |
615 | * To be specific, the recursive function `top_down(root, params)` works like this:
616 |
617 | ```
618 | 1. return specific value for null node
619 | 2. update the answer if needed // answer <-- params
620 | 3. left_ans = top_down(root.left, left_params) // left_params <-- root.val, params
621 | 4. right_ans = top_down(root.right, right_params) // right_params <-- root.val, params
622 | 5. return the answer if needed // answer <-- left_ans, right_ans
623 | ```
624 |
625 | * Find maximum depth of a binary tree:
626 |
627 | ```
628 | 1. return if root is null
629 | 2. if root is a leaf node:
630 | 3. answer = max(answer, depth) // update the answer if needed
631 | 4. maximum_depth(root.left, depth + 1) // call the function recursively for left child
632 | 5. maximum_depth(root.right, depth + 1) // call the function recursively for right child
633 | ```
634 |
635 | ```java
636 | private int answer; // don't forget to initialize answer before call maximum_depth
637 | private void maximum_depth(TreeNode root, int depth) {
638 | if (root == null) {
639 | return;
640 | }
641 | if (root.left == null && root.right == null) {
642 | answer = Math.max(answer, depth);
643 | }
644 | maximum_depth(root.left, depth + 1);
645 | maximum_depth(root.right, depth + 1);
646 | }
647 | ```
648 |
649 | ## Bottom-up Solution
650 |
651 | * In each recursive call, we will firstly call the function recursively for all the children nodes and then come up with the answer according to the returned values and the value of the current node itself.
652 |
653 | * This process can be regarded as a kind of **postorder** traversal.
654 |
655 | * Typically, a "bottom-up" recursive function `bottom_up(root)` will be something like this:
656 |
657 | ```
658 | 1. return specific value for null node
659 | 2. left_ans = bottom_up(root.left) // call function recursively for left child
660 | 3. right_ans = bottom_up(root.right) // call function recursively for right child
661 | 4. return answers // answer <-- left_ans, right_ans, root.val
662 | ```
663 |
664 | * Maximum depth:
665 |
666 | ```
667 | 1. return 0 if root is null // return 0 for null node
668 | 2. left_depth = maximum_depth(root.left)
669 | 3. right_depth = maximum_depth(root.right)
670 | 4. return max(left_depth, right_depth) + 1 // return depth of the subtree rooted at root
671 | ```
672 |
673 | ```java
674 | public int maximum_depth(TreeNode root) {
675 | if (root == null) {
676 | return 0; // return 0 for null node
677 | }
678 | int left_depth = maximum_depth(root.left);
679 | int right_depth = maximum_depth(root.right);
680 | return Math.max(left_depth, right_depth) + 1; // return depth of the subtree rooted at root
681 | }
682 | ```
683 |
684 |
--------------------------------------------------------------------------------
/Basic LeetCode Template.md:
--------------------------------------------------------------------------------
1 | # LeetCode Template 一页通
2 |
3 | ## Binary Search
4 |
5 | **Complexity**
6 |
7 | * Time complexity: $O(\log N)$ - 因为每次都从中间开始把数据split成一半一半,log的底数为2
8 | * Space complexity: $O(1)$ if not adding other structure
9 | * 通常使用constant space来存储mid以及需要return的结果
10 |
11 |
12 | #### **Template 1**
13 |
14 | ```java
15 | int binarySearch(int[] nums, int target){
16 | if(nums == null || nums.length == 0)
17 | return -1;
18 |
19 | int left = 0, right = nums.length - 1;
20 | while(left <= right){
21 | // Prevent (left + right) overflow
22 | int mid = left + (right - left) / 2;
23 | if(nums[mid] == target){ return mid; }
24 | else if(nums[mid] < target) { left = mid + 1; }
25 | else { right = mid - 1; }
26 | }
27 |
28 | // End Condition: left > right
29 | return -1;
30 | }
31 | ```
32 |
33 | #### **Template 2**
34 |
35 | ```java
36 | int binarySearch(int[] nums, int target){
37 | if(nums == null || nums.length == 0)
38 | return -1;
39 |
40 | int left = 0, right = nums.length;
41 | while(left < right){
42 | // Prevent (left + right) overflow
43 | int mid = left + (right - left) / 2;
44 | if(nums[mid] == target){ return mid; }
45 | else if(nums[mid] < target) { left = mid + 1; }
46 | else { right = mid; }
47 | }
48 |
49 | // Post-processing:
50 | // End Condition: left == right
51 | if(left != nums.length && nums[left] == target) return left;
52 | return -1;
53 | }
54 | ```
55 |
56 | #### **Template 3**
57 |
58 | ```java
59 | int binarySearch(int[] nums, int target) {
60 | if (nums == null || nums.length == 0)
61 | return -1;
62 |
63 | int left = 0, right = nums.length - 1;
64 | while (left + 1 < right){
65 | // Prevent (left + right) overflow
66 | int mid = left + (right - left) / 2;
67 | if (nums[mid] == target) {
68 | return mid;
69 | } else if (nums[mid] < target) {
70 | left = mid;
71 | } else {
72 | right = mid;
73 | }
74 | }
75 |
76 | // Post-processing:
77 | // End Condition: left + 1 == right
78 | if(nums[left] == target) return left;
79 | if(nums[right] == target) return right;
80 | return -1;
81 | }
82 | ```
83 |
84 | ## Dynamic Programming
85 |
86 | * **Top-down**: Recursion + Memoization(usually hashmap)
87 | * **Bottom-up**: Create an array to cumulatively store values or flags
88 |
89 | * 通常提问方式:
90 | * Maximum/minimum problems
91 | * How many ways
92 | * The result depends on optimal sub-problems solutions
93 | * **Process**:
94 | * 分析State variables的数量决定了array的dimension: what decisions are there to make, what information is needed
95 | * 如何进行递归: The recurrence relation to transition between states
96 | * Base cases
97 |
98 | ### Memoization(Top-down) + recursion
99 |
100 | * 使用array来记录每个sub-problem的cumulative的结果,储存的array最好是given条件的array
101 | * 在given array上进行修改,可以保持$O(1)$的space complexity
102 | * 该方法绑定recursion,且通常使用一个helper method来完成recursion
103 | * Base case
104 | * Recurrence relationship
105 | * Time complexity: $O(n)$
106 | * 因为我们使用了hashmap进行临时结果的存储,因此每次recursion的时候,对于已存储的结果是$O(1)$
107 | * 不过因为可能在决定action的时候,会从不同的可能性出发,因此这个$n$也可能是$2n$, $3n$,但总体converge to $n$
108 | * 值得注意的是,由于需要进行大量的recursion,尽管已经有hashmap来大大缩短时间,但与其他的dp模板相比较,总体运行时间并不会很快
109 | * Space complexity: $O(n)$
110 | * 存储hashmap所需要的空间
111 |
112 | #### **Template 1 - HashMap**
113 |
114 | ```java
115 | // step 1: 创建一个hashmap,用以记录对应的结果
116 | private HashMap memo = new HashMap<>();
117 | // 公开given variables,因为helper method也需要用
118 |
119 | public int mainFunct(int[][] costs){
120 | // 链接真正用来dp的helper method
121 | return Something;
122 | }
123 |
124 | // step2: 考虑具体有多少变量:
125 | // 1. state variables - 有多少个状态(日期, holding, color..),就有多少个dimension需要考虑
126 | // 2. actions - 可能产生的动作,以股票题为例(买入,售出等), 以及该动作应何时产生
127 |
128 | // step3: 创建一个dp的method,输入两个state用以进行recurrsion
129 | public int dp(state1, state2){
130 | // sub-step 1: 当变量触底,base cases
131 | if (day == array.length){
132 | return 0;
133 | }
134 | // sub-step 2: 检查是否已经存储了对应的数据
135 | if (memo.containsKey(state1)){
136 | return memo.get(state1));
137 | }
138 | // sub-step 3: recurrence relationship 链接下一个index,以及找到sub-problem的最优
139 | currentstate = dp(state1 + 1, state2);
140 | // sub-step 4: 记录进入memo hashmap,返回该数值
141 | memo.put(getKey(state1), totalCost);
142 | return totalCost;
143 | }
144 | ```
145 |
146 | **Example**
147 |
148 | ```java
149 | // 以 paint house 题目为例
150 |
151 | // step 1: 创建一个hashmap,用以记录对应的结果
152 | private HashMap memo = new HashMap<>();
153 | // 通常把given array先存起来,因为memoization通常需要另外再造方法
154 | private int[][] costs;
155 |
156 | public int mainFunct(int[][] costs){
157 | this.costs = costs;
158 | // 链接真正用来dp的helper method
159 | return Something // Math.min(Math.min(paintCost(0, 0), paintCost(0, 1)), paintCost(0, 2));
160 | }
161 |
162 | // step2: 考虑具体有多少变量:
163 | // 1. state variables - 有多少个状态(日期, holding, color..),就有多少个dimension需要考虑
164 | // 2. actions - 可能产生的动作,以股票题为例(买入,售出等), 以及该动作应何时产生
165 |
166 | // step3: 创建一个dp的method,输入两个state用以进行recurrsion
167 | public int paintCost(int day, int color){
168 | // Memoization template: ***************************************************************
169 | // sub-step 1: 当变量触底,base cases
170 | if (day == costs.length){
171 | return 0;
172 | }
173 | // sub-step 2: 检查是否已经存储了对应的数据
174 | if (memo.containsKey(getKey(day, color))){
175 | return memo.get(getKey(day, color));
176 | }
177 | // sub-step 3: recurrence relationship 链接下一个index,以及找到sub-problem的最优
178 | // the cost at current day and color
179 | int totalCost = costs[day][color];
180 | if (color == 0){
181 | // red color
182 | totalCost += Math.min(paintCost(day + 1, 1), paintCost(day + 1, 2));
183 | }
184 | else if (color == 1){
185 | // blue color
186 | totalCost += Math.min(paintCost(day + 1, 0), paintCost(day + 1, 2));
187 | }
188 | else {
189 | // green color
190 | totalCost += Math.min(paintCost(day + 1, 0), paintCost(day + 1, 1));
191 | }
192 | // sub-step 4: 记录进入memo hashmap,返回该数值
193 | memo.put(getKey(day, color), totalCost);
194 | return totalCost;
195 | }
196 | ```
197 |
198 | #### Template 2 - 多元或单元Array
199 |
200 | * 具体的思考过程与hashmap近似,但是使用了array来进行数据的存储
201 | * 适用于需要考虑多个状态变量的同时,某些变量(如日期等)并不需要在每个节点进行单一的动作
202 | * 以股票为例,动作分别有售出和hold两种动作/购买和hold,但是hashmap通常只有一个动作
203 | * 当涉及到某个状态的记录而非单纯数值的记录时,array会比hashmap更加通用,不过array的dimension会更高
204 | * 以股票为例,一个状态变量即为hold/unhold,既此时是否持有股票
205 | * Time and space complexity : $O(m*n)$, 分别都是多元array的长度
206 |
207 | ```java
208 | // step 1: 考虑具体有多少变量:
209 | // 1. state variables - 有多少个状态(日期, holding, color..),就有多少个dimension需要考虑
210 | // 2. actions - 可能产生的动作,以股票题为例(买入,售出等), 以及该动作应何时产生
211 |
212 | // step 2: 创建一个array,用以记录对应的结果
213 | private int[][] memo;
214 | // 公开given variables,因为helper method也需要用
215 |
216 | public int mainFunct(int[][] costs){
217 | memo = new int[prices.length + 1][2]; // 创建对应的memo array,通常对于given变量长度 + 1, 存储结果
218 | // 链接真正用来dp的helper method
219 | return Something;
220 | }
221 |
222 | // step3: 创建一个dp的method,输入两个state用以进行recurrsion
223 | public int dp(state1, state2){
224 | // sub-step 1: 当变量触底,base cases
225 | if (day == array.length){
226 | return 0;
227 | }
228 | // sub-step 2: 检查是否已经存储了对应的数据,但是检查的是array的内容
229 | if (memo[state1][state2] == 0){
230 | // sub-step 3: 分辨可能出现的动作,recurrence relationship 链接下一个index,以及找到sub-problem的最优
231 | int doNothing = dp(state1 + 1, state2); // 动作1 - 结果1
232 | int doSomething; // 动作2 - 结果2
233 |
234 | if (holding == 1){
235 | // doSomething, action 1
236 | }
237 | else {
238 | // doSomething, action 2
239 | }
240 | // sub-step 4: 对比两种动作的结果,记录进入memo array,返回该数值
241 | memo[state1][state2] = Math.max(doNothing, doSomething);
242 | }
243 | return memo[state1][state2];
244 | }
245 | ```
246 |
247 | **Example 以股票问题为例**
248 |
249 | ```java
250 | // step 1: 考虑具体有多少变量:
251 | // 1. state variables - 有多少个状态(日期, holding, color..),就有多少个dimension需要考虑
252 | // 2. actions - 可能产生的动作,以股票题为例(买入,售出等), 以及该动作应何时产生
253 |
254 | // step 2: 创建一个memo array,用以记录对应的结果, dimension = # state variables
255 | private int[] prices;
256 | private int[][] memo;
257 | private int fee;
258 |
259 | public int mainFunct(int[][] costs){
260 | this.prices = prices;
261 | this.fee = fee;
262 | // 该题的考量:
263 | // two state variables: day, holding stock or not
264 | // two actions: buy, sell
265 |
266 | memo = new int[prices.length + 1][2]; // 创建对应的memo array,通常对于given变量长度 + 1
267 | return dp(0, 0);
268 | }
269 |
270 | // step3: 创建一个dp的method,输入两个state用以进行recurrsion
271 | public int dp(int day, int holding){
272 | // sub-step 1: 当变量触底,base cases
273 | if (day == prices.length){
274 | return 0;
275 | }
276 | // sub-step 2: 检查是否已经存储了对应的数据,但是检查的是array的内容
277 | if (memo[day][holding] == 0){
278 | // sub-step3: 分辨可能出现的动作,recurrence relationship 链接下一个index,以及找到sub-problem的最优
279 | int doNothing = dp(day + 1, holding); // 动作1 - 结果1
280 | int doSomething; // 动作2 - 结果2
281 |
282 | // do something we have two actions
283 | // 1 - holding stock, 0 - does not hold
284 | if (holding == 1){
285 | // sell the stock?
286 | doSomething = prices[day] - fee + dp(day + 1, 0);
287 | }
288 | else {
289 | // buy a stock?
290 | doSomething = -prices[day] + dp(day + 1, 1);
291 | }
292 | // sub-step 4: 记录进入memo array,返回该数值
293 | memo[day][holding] = Math.max(doNothing, doSomething);
294 | }
295 | return memo[day][holding];
296 | }
297 | ```
298 |
299 | ### Bottom-up + No Recursion
300 |
301 | * 通常由top-down的方法转化,但是不需要进行recursion因此运行速度上快很多
302 | * 通常需要进行for loop
303 | * 视情况可以控制space complexity到$O(1)$的水平,是dp中较为好的方法,但是可能比较难想到
304 |
305 | #### Template 1 - Changing States
306 |
307 | * 使用一些state varibles来存储变量,在循环中不断更改value,通常需要两个或以上
308 | * 通常使用`Math.min()`或者`Math.max()`来进行关系上的传递
309 | * 通常时间complexity为$O(n)$, 空间的complexity为$O(1)$
310 | * **难点**: 如果寻找内部的recurrence relationship,这里可能会很难
311 |
312 | ```java
313 | public int maxProfit(int[] prices){
314 | // step 1: set up states and initial values, usually 0, min, max
315 | int sold = Integer.MIN_VALUE, held = Integer.MIN_VALUE, reset = 0;
316 |
317 | // step 2: for loop
318 | for (int price : prices){
319 | int preSold = sold;
320 | // step 3: states recurrence relationship
321 | sold = held + price;
322 | held = Math.max(held, reset - price);
323 | reset = Math.max(reset, preSold);
324 | }
325 | // step 4: return and compare max and min
326 | return Math.max(sold, reset);
327 | }
328 | ```
329 |
330 | ##### T 1.1 Kanede's Algorithm
331 |
332 | * Goal: find maximum subarray - find the contiguous subarray (containing at least one number) which has the largest sum
333 |
334 | ```java
335 | public int maxSubArray(int[] nums) {
336 | // kadene's algorithm
337 | int current = 0, max = Integer.MIN_VALUE;
338 | for (int num : nums){
339 | // should we abandon the previous values?
340 | current = Math.max(num, current + num);
341 | max = Math.max(max, current);
342 | }
343 | return max;
344 | }
345 | ```
346 |
347 | #### Template 2 - Sum-up Array
348 |
349 | * 与memoization的做法相似,但是不需要进行recursion,而是使用for-loop
350 | * 通常时间complexity为$O(n)$, 空间的complexity为$O(1)$
351 | * 通常使用`Math.min()`或者`Math.max()`来进行关系上的传递
352 | * 在array的最后一行或列中寻找最大或最小
353 | * **难点**: 如果寻找内部的recurrence relationship
354 |
355 | ```java
356 | public int minCost(int[][] costs) {
357 | // step 1: Use for loop 传递并递增信息,例如次数,cost,等
358 | for (int n = costs.length - 2; n >= 0; n--) {
359 | // step 2: 寻找array之中的递增联系以及关系,一直传递到最后一行
360 | // Total cost of painting the nth house red.
361 | costs[n][0] += Math.min(costs[n + 1][1], costs[n + 1][2]);
362 | // Total cost of painting the nth house green.
363 | costs[n][1] += Math.min(costs[n + 1][0], costs[n + 1][2]);
364 | // Total cost of painting the nth house blue.
365 | costs[n][2] += Math.min(costs[n + 1][0], costs[n + 1][1]);
366 | }
367 | if (costs.length == 0) return 0;
368 | // step 3: 在最后一行寻找答案
369 | return Math.min(Math.min(costs[0][0], costs[0][1]), costs[0][2]);
370 | }
371 | ```
372 |
373 | ## Backtracking
374 |
375 | * 通常提问方式:
376 |
377 | * **All** possible combinations/solutions/permutations,要详细的**所有**结果的情况
378 |
379 | * Return in list,结果为一个list,list中每个结果都是一个list
380 | * 通常需要另一个backtracking的helper method, helper method需要使用recursion
381 |
382 | #### Template 1 - 通用模版
383 |
384 | * 把所有给的variables public 作全局,包括需要return的结果(很可能是list,先做好return的空list)
385 | * 在主方法中调用backtracking,并在其中创建一个空list作为单个的结果
386 | * backtracking:
387 | * 通常下是void method,调用参数index
388 | * index在此处用于追踪我们在given array中的位置,记录是否达到了given array 的末端
389 | * 同时index也是下一个可能结果的先决条件
390 | * 写好base case for recursion:
391 | * 到达了target value
392 | * 到达了given array的末端
393 | * 注意需要重新建一个arraylist来结果当前结果list
394 | * for loop
395 | * 从loop中进行操作链接到下一个可能的结果
396 | * 把本次结果加入到结果集中
397 | * 进入下一个可能的结果
398 | * 把本次结果从结果集中**删除**:达到backtracking的目的
399 |
400 | ```java
401 | // step 1: 把所有给的variables public 作全局,创建res的list(通常list中list嵌套)
402 | List> res;
403 | int[] candidates;
404 |
405 | public List> main(int[] candidates) {
406 | res = new ArrayList<>();
407 | this.candidates = candidates;
408 | // step 2: 思考需要把什么带入backtracking的方法(target,index等),并套入一个空结果list
409 | backtracking(0, new ArrayList());
410 | // 直接return已经做好的result list
411 | return res;
412 | }
413 |
414 | // step 2: 思考需要把什么带入backtracking的方法(target,*index*等)
415 | // 并套入一个*空结果list(指代当前结果)*
416 | // 通常是void method
417 | public void backtracking(int start, List singleComb){
418 | // step 3: base case 刚好达成结果的条件,在此增加当前结果到结果集
419 | if (start == candidates.length){
420 | res.add(new ArrayList(singleComb));
421 | return;
422 | }
423 | // step 4: **最重要**,通常需要for-loop来进入下一个可能的结果 *****************
424 | // 从当前index出发,直到given array的末端,代表某个可能的路径
425 | for (int i = start; i < candidates.length; i++){
426 | // 加入到当前结果
427 | singleComb.add(candidates[i]);
428 | // 进入下一个可能的结果,注意此处 *********
429 | // * 可重复的结果则i
430 | // * 不可重复的记过则i + 1
431 | backtracking(i + 1, singleComb);
432 | // 移除出当前结果(实现backtracking)
433 | singleComb.remove(singleComb.size() - 1);
434 | }
435 | }
436 | ```
437 |
438 | 以combination sum为例
439 |
440 | ```java
441 | // step 1: 把所有给的variables public 作全局,创建res的list(通常list中list嵌套)
442 | List> res;
443 | int[] candidates;
444 | int target;
445 |
446 | public List> combinationSum(int[] candidates, int target) {
447 | res = new ArrayList<>();
448 | this.candidates = candidates;
449 | this.target = target;
450 | // step 2: 思考需要把什么带入backtracking的方法(target,index等),并套入一个空结果list
451 | backtracking(0, target, new ArrayList());
452 | // 直接return已经做好的result list
453 | return res;
454 | }
455 |
456 | // step 2: 思考需要把什么带入backtracking的方法(target,*index*等)
457 | // 并套入一个*空结果list(指代当前结果)*
458 | // 通常是void method
459 | public void backtracking(int start, int target, List singleComb){
460 | // step 3: base case 刚好达成结果的条件,在此增加当前结果到结果集
461 | if (target == 0){
462 | res.add(new ArrayList(singleComb)); // *重要*:建一个new list来接结果
463 | return;
464 | }
465 | // base case: not meet the requirement
466 | if (target < 0 || start == candidates.length){
467 | return;
468 | }
469 | // step 4: **最重要**,通常需要for-loop来进入下一个可能的结果 *****************
470 | // 从当前index出发,直到given array的末端,代表某个可能的路径
471 | for (int i = start; i < candidates.length; i++){
472 | // 加入到当前结果
473 | singleComb.add(candidates[i]);
474 | // 进入下一个可能的结果
475 | backtracking(i, target - candidates[i], singleComb);
476 | // 移除出当前结果(实现backtracking)
477 | singleComb.remove(singleComb.size() - 1);
478 | }
479 | }
480 | ```
481 |
482 | #### Template 2 - Permutation(通用模版变形)
483 |
484 | * 适用于可能的情况:
485 | * permutation
486 | * 每个return的结果,并不按照原来given array中element的排序,需要乱序处理
487 | * 本质上讲通用模版中的可能结果的元素增减,改变为元素的swap来换位
488 | * 需要将given array(如果有的话)转换成list,方便使用`Collections.swap()`,否则需要自己建立helper method来实现元素的交换
489 |
490 | 以permutation为例
491 |
492 | ```java
493 | // step 1: 把所有给的variables public 作全局,创建res的list(通常list中list嵌套)
494 | List> res;
495 | List nums;
496 |
497 | public List> permute(int[] nums) {
498 | res = new ArrayList<>();
499 | this.nums = new ArrayList<>();
500 | // step 2: array 不方便进行swap且不是list,现转换成list就不需要create new list for single result
501 | for (int num : nums){
502 | this.nums.add(num);
503 | }
504 | // step 3: 思考需要把什么带入backtracking的方法(target,index等)
505 | backtracking(0);
506 | return res;
507 | }
508 | public void backtracking(int index){
509 | // step 4: base case 刚好达成结果的条件,在此增加当前结果到结果集
510 | if (index == nums.size()){
511 | res.add(new ArrayList(nums));
512 | return;
513 | }
514 | // step 4: **最重要**,通常需要for-loop来进入下一个可能的结果 *****************
515 | // 从当前index出发,直到given array的末端,代表某个可能的路径,并进行swap
516 | for (int i = index; i < nums.size(); i++){
517 | Collections.swap(nums, i, index);
518 | //*****注意****************
519 | // 由于是swap并不按顺序排列结果,因此从index进行关联而不是i,保证swap到每个元素以及自己
520 | backtracking(index + 1);
521 | Collections.swap(nums, i, index);
522 | }
523 | }
524 | ```
525 |
526 | ## UNION FIND
527 |
528 | * Union-Find is all about remembering the patterns.
529 | * 每次使用这个class来进行cluster,对于每个cluster只需要找ancestor的数据(e.g rank,find)
530 | * Create a class called `UnionFind`
531 | * Initialize a `group` array and a `rank` array. Sometimes you may also need to create a `size` array
532 | * Create `find,` and `union` method
533 | * `find`: Find the ancestor(centroid) of the cluster, 用以进行union时确定存在于某个cluster
534 | * `union`: Union two groups. If true, we union them; if false, they are already in the same cluster
535 | * `rank`: Speeding up the `union` process, basically, calculates the path number of the cluster tree.
536 | * Always attach the cluster with a shorter path to the cluster with a longer path.
537 | * 使用方法为path compression
538 | * Time complexity: time complexity for find/union operation is $\alpha({N})$ (Here, $\alpha({N})$ is the inverse Ackermann function that grows so slowly. Suppose we have $N$ elements to go through, then the time compleXIty would be $O(N \alpha({N}))$
539 | * Space complexity: just using array so it would be $O(N)$
540 |
541 | ### Template 1 - 通用模版
542 |
543 | ```java
544 | class UnionFind {
545 | private int[] group;
546 | private int[] rank;
547 |
548 | public UnionFind(int n){
549 | group = new int[n];
550 | rank = new int[n];
551 | for (int i = 0; i < n; i++){
552 | group[i] = i; // initialization: each node is its own group
553 | rank[i] = 1; // each node has rank 1(path length: 1)
554 | }
555 | }
556 |
557 | public int find(int node){
558 | if (node != group[node]){
559 | group[node] = find(group[node]); // recursion find the ancestor
560 | }
561 | return group[node];
562 | }
563 |
564 | public boolean union(int i, int j){
565 | // find the ancestor
566 | int root1 = find(i);
567 | int root2 = find(j);
568 |
569 | if (root1 == root2){
570 | // already in same group
571 | return false;
572 | }
573 | // if they are not in the same group
574 | if (rank[root1] > rank[root2]){
575 | group[root2] = group[root1]; // attach shorter path cluster to the longer one
576 | }
577 | else if (rank[root2] > rank[root1]){
578 | group[root1] = group[root2];
579 | }
580 | else {
581 | group[root1] = group[root2];
582 | rank[root2]++; // same length, one of the cluster have to be ancestor, rank + 1
583 | }
584 | return true;
585 | }
586 | }
587 | ```
588 |
589 | * **模版的使用**
590 | * 通常在主method中进行class的实例化与使用,例子如下
591 |
592 | ```java
593 | // map to store the number and index, union-find to group the numbers
594 | Map numMap = new HashMap<>();
595 | UnionFind uf = new UnionFind(nums.length);
596 | for (int i = 0; i < nums.length; i++){
597 | int curr = nums[i];
598 | // in case duplicate
599 | if (numMap.containsKey(curr)) continue;
600 | // if map has consecutive elements for curr element
601 | if (numMap.containsKey(curr - 1)){
602 | uf.union(i, numMap.get(curr - 1));
603 | }
604 | if (numMap.containsKey(curr + 1)){
605 | uf.union(i, numMap.get(curr + 1));
606 | }
607 | numMap.put(curr, i);
608 | }
609 | ```
610 |
611 | * `rank`不是必须的,可以分情况使用,如果不需要优化time complexity也可以不用(最好用上)
612 | * 如果需要知道每个cluster的size,也可以使用size来替代rank(同样也是path compression)
613 |
614 | ### Template 2 - With Size
615 |
616 | * Path compression with size
617 |
618 | ```java
619 | class UnionFind {
620 | int representative[];
621 | int size[];
622 |
623 | public UnionFind(int size){
624 | representative = new int[size];
625 | this.size = new int[size];
626 |
627 | for (int i = 0; i < size; i++){
628 | representative[i] = i;
629 | this.size[i] = 1;
630 | }
631 | }
632 |
633 | public int find(int x){
634 | if (x != representative[x]){
635 | representative[x] = find(representative[x]);
636 | }
637 | return representative[x];
638 | }
639 |
640 | public void union(int a, int b){
641 | int root1 = find(a);
642 | int root2 = find(b);
643 |
644 | if (root1 == root2) return;
645 | if (size[root1] > size[root2]){
646 | size[root1] += size[root2];
647 | representative[root2] = representative[root1];
648 | }
649 | else {
650 | size[root2] += size[root1];
651 | representative[root1] = representative[root2];
652 | }
653 | }
654 | }
655 | ```
656 |
657 | ## DFS
658 |
659 | ### DFS - Line Graph
660 |
661 | * 需要创建`adjList`,可以是list或者map,用以存储相关联的nodes的信息(**important**)
662 |
663 | ## BFS
664 |
665 | * Traverse a tree/graph:通常要使用queue来进行
666 | * Traverse by layer
667 | * while循环,queue不为空
668 | * 事先存储一个node(通常为root),然后在循环中pop(poll)
669 | * 进行操作,接着把node的左子树和右子树存储在queue或者stack中,循环往复直到所有node都traverse完成
670 | * **DFS-stack, BFS-queue**
671 |
672 | * Time Complexity: $O(V + E)$. Here, V represents the number of vertices, and E represents the number of edges. We need to check every vertex and traverse through every edge in the graph. The time complexity is the same as it was for the DFS approach.
673 | * Space Complexity: $O(V)$. Generally, we will check if a vertex has been visited before adding it to the queue, so the queue will use most $O(V)$ space. Keeping track of which vertices have been visited will also require $O(V)$ space.
674 |
675 | ## Two Pointer
676 |
677 | ### Linked List
678 |
679 | * Usually **1 fast pointer, 1 slow pointer**, and different speeds of progress(hare and tortoise)
680 | * A fast pointer can move two steps each time, and a slow pointer move 1 step each time
681 | * **Always examine if the node is null before you call the next field.**
682 | * Getting the next node of a null node will cause the null-pointer error. For example, before we run `fast = fast.next.next`, we need to examine both `fast` and `fast.next` is not null.
683 | * **Carefully define the end conditions of your loop.**
684 |
685 | ```java
686 | // Initialize slow & fast pointers
687 | ListNode slow = head;
688 | ListNode fast = head;
689 | /**
690 | * Change this condition to fit the specific problem.
691 | * Attention: remember to avoid null-pointer error
692 | **/
693 | while (slow != null && fast != null && fast.next != null) {
694 | slow = slow.next; // move slow pointer one step each time
695 | fast = fast.next.next; // move fast pointer two steps each time
696 | if (slow == fast) { // change this condition to fit specific problem
697 | return true;
698 | }
699 | }
700 | return false; // change return value to fit specific problem
701 | ```
702 |
703 | * Or two pointers have the same speed but start from a different node (remove the nth node from the end)
704 | * **Complexity Analysis**
705 | * If you only use pointers without any other extra space, the space complexity will be `O(1)`.
706 | * However, it is more difficult to analyze the time complexity. In order to get the answer, we need to analyze `how many times we will run our loop` . In our previous finding cycle example, let's assume that we move the faster pointer 2 steps each time and move the slower pointer 1 step each time.
707 | * If there is no cycle, the fast pointer takes `N/2 times` to reach the end of the linked list, where N is the length of the linked list.
708 | * If there is a cycle, the fast pointer needs `M times` to catch up the slower pointer, where M is the length of the cycle in the list.
709 | * Obviously, M <= N. So we will run the loop `up to N times`. And for each loop, we only need constant time. So, the time complexity of this algorithm is `O(N)` in total.
710 |
711 | ## LinkedList一些技巧
712 |
713 | ### DummyHead/Sentinel Node的使用
714 |
715 | * dummy head/sentinel node/pseudo-head 即为在目前的head之前再加一个node,是一个fake node,数值没有意义
716 | * **作用**:
717 | * 在需要移除某个node,比如说head的时候,会非常方便移除(否则很麻烦)
718 | * 需要对list长度进行计数,但计数从1不从0开始时,计数容易错位,此时dummy head可以补足空位
719 | * 在某些题目中需要记录prev node的指针,此时dummy head可以帮助记录head的prev node
720 | * 一般在使用while loop的时候使用dummy head,recursion的情况下很少使用
721 |
--------------------------------------------------------------------------------
/Heap/Heap Tutorials.md:
--------------------------------------------------------------------------------
1 | # Heap Tutorials
2 |
3 | ## Priority Queue
4 |
5 | * A priority queue is an abstract data type similar to a regular queue or stack data structure in which each element additionally has a "priority" associated with it.
6 | * In a priority queue, an element with high priority is served before an element with low priority.
7 | * **Heap vs. PQ**
8 | * A priority queue is an abstract data type, while a Heap is a data structure.
9 | * Therefore, a Heap is not a Priority Queue, but a way to implement a Priority Queue.
10 |
11 | * **Implementation**:
12 | * There are multiple ways to implement a Priority Queue, such as array and linked list. However, these implementations only guarantee $O(1)$ the time complexity for either insertion or deletion, while the other operation will have a time complexity of $O(N)$.
13 | * On the other hand, implementing the priority queue with Heap will allow both insertion and deletion to have a time complexity of $O(\log N)$.
14 |
15 | ## Heap
16 |
17 | * A **Heap** is a special type of binary tree. A heap is a binary tree that meets the following criteria:
18 | * Is a **complete binary tree**;
19 | * The value of each node must be **no greater than (or no less than)** the value of its child nodes.
20 |
21 | * A Heap has the following properties:
22 |
23 | - Insertion of an element into the Heap has a time complexity of $O(\log N)$;
24 |
25 | - Deletion of an element from the Heap has a time complexity of $O(\log N)$;
26 |
27 | - The maximum/minimum value in the Heap can be obtained with $O(1)$ time complexity.
28 |
29 | ### Heap Classification
30 |
31 | There are two kinds of heaps: **Max Heap** and **Min Heap**.
32 |
33 | - Max Heap: Each node in the Heap has a value **no less than** its child nodes. Therefore, the top element (root node) has the **largest** value in the Heap.
34 | - Min Heap: Each node in the Heap has a value **no larger than** its child nodes. Therefore, the top element (root node) has the **smallest** value in the Heap.
35 |
36 |
440 |
441 | ```
442 | Input: root = [3,9,20,null,null,15,7]
443 | Output: [[3],[9,20],[15,7]]
444 | ```
445 |
446 | **Example 2:**
447 |
448 | ```
449 | Input: root = [1]
450 | Output: [[1]]
451 | ```
452 |
453 | **Example 3:**
454 |
455 | ```
456 | Input: root = []
457 | Output: []
458 | ```
459 |
460 | **Constraints:**
461 |
462 | - The number of nodes in the tree is in the range `[0, 2000]`.
463 | - `-1000 <= Node.val <= 1000`
464 |
465 | ### My Solution
466 |
467 | * Use a queue to store the value from left to right
468 | * Use queue size to determine how many nodes in the same level and use array list to store the same level nodes
469 | * Add the level nodes to `levels` which is the return list
470 |
471 | ```java
472 | /**
473 | * Definition for a binary tree node.
474 | * public class TreeNode {
475 | * int val;
476 | * TreeNode left;
477 | * TreeNode right;
478 | * TreeNode() {}
479 | * TreeNode(int val) { this.val = val; }
480 | * TreeNode(int val, TreeNode left, TreeNode right) {
481 | * this.val = val;
482 | * this.left = left;
483 | * this.right = right;
484 | * }
485 | * }
486 | */
487 | public List> levelOrder(TreeNode root) {
488 | Queue treeQueue = new LinkedList<>();
489 | List> levels = new ArrayList<>();
490 | if (root == null) return levels;
491 | treeQueue.add(root);
492 | while(!treeQueue.isEmpty()){
493 | List list = new ArrayList<>();
494 | int level_length = treeQueue.size();
495 | for (int i = 0; i < level_length; i++){
496 | TreeNode node = treeQueue.remove();
497 | list.add(node.val);
498 | if (node.left != null){
499 | treeQueue.add(node.left);
500 | }
501 | if (node.right != null){
502 | treeQueue.add(node.right);
503 | }
504 | }
505 | levels.add(list);
506 | }
507 | return levels;
508 | }
509 | ```
510 |
511 | ```java
512 | // second attempt
513 | public List> levelOrder(TreeNode root) {
514 | List> res = new ArrayList<>();
515 | bfs(root, res, 0);
516 | return res;
517 | }
518 |
519 | public void bfs(TreeNode root, List> res, int level){
520 | if (root == null){
521 | return;
522 | }
523 | if (res.size() == level){
524 | res.add(new ArrayList());
525 | }
526 | res.get(level).add(root.val);
527 | bfs(root.left, res, level + 1);
528 | bfs(root.right, res, level + 1);
529 | }
530 | ```
531 |
532 | ```java
533 | // third attempt
534 | public List> levelOrder(TreeNode root) {
535 | // level order traversal: BFS
536 | // 1. create the res list, create a queue
537 | List> res = new ArrayList<>();
538 | Queue queue = new LinkedList<>();
539 | if (root == null) return res;
540 | queue.add(root);
541 | int level = 0;
542 | // 2. use queue to store the root node, left, right
543 | while(!queue.isEmpty()){
544 | res.add(new ArrayList());
545 | int levelLength = queue.size();
546 |
547 | for (int i = 0; i < levelLength; i++){
548 | // 3. poll from queue, put element to the list
549 | TreeNode curr = queue.poll();
550 | res.get(level).add(curr.val);
551 | if (curr.left != null) queue.add(curr.left);
552 | if (curr.right != null) queue.add(curr.right);
553 | }
554 | level++;
555 | }
556 | return res;
557 | }
558 | ```
559 |
560 |
561 |
562 | ### Standard Solution
563 |
564 | #### Solution #1 Iteration
565 |
566 | * Same as my solution
567 | * Time complexity : $\mathcal{O}(N)$ since each node is processed exactly once.
568 | * Space complexity : $\mathcal{O}(N)$ to keep the output structure which contains `N` node values.
569 |
570 | #### Solution #2 Recursion
571 |
572 | * Call recursive helper function
573 | * Same concept with the method 1 but using recursion
574 |
575 | ```java
576 | class Solution {
577 | List> levels = new ArrayList>();
578 | public void helper(TreeNode node, int level) {
579 | // start the current level
580 | if (levels.size() == level)
581 | levels.add(new ArrayList());
582 |
583 | // fulfil the current level
584 | levels.get(level).add(node.val);
585 |
586 | // process child nodes for the next level
587 | if (node.left != null)
588 | helper(node.left, level + 1);
589 | if (node.right != null)
590 | helper(node.right, level + 1);
591 | }
592 | public List> levelOrder(TreeNode root) {
593 | if (root == null) return levels;
594 | helper(root, 0);
595 | return levels;
596 | }
597 | }
598 | ```
599 |
600 | * Time complexity : $\mathcal{O}(N)$ since each node is processed exactly once.
601 | * Space complexity : $\mathcal{O}(N)$ to keep the output structure which contains `N` node values.
602 |
603 | # Solve Tree Problem Recursively
604 |
605 | As we know, a tree can be defined recursively as a node(the root node) that includes a value and a list of references to children nodes. Recursion is one of the natural features of a tree. Therefore, many tree problems can be solved recursively. For each recursive function call, we only focus on the problem for the current node and call the function recursively to solve its children.
606 |
607 | Typically, we can solve a tree problem recursively using a top-down approach or using a bottom-up approach.
608 |
609 | ## Top-down Solution
610 |
611 | * "Top-down" means that in each recursive call, we will visit the node first to come up with some values, and pass these values to its children when calling the function recursively.
612 |
613 | * So the "top-down" solution can be considered as a kind of **preorder** traversal.
614 |
615 | * To be specific, the recursive function `top_down(root, params)` works like this:
616 |
617 | ```
618 | 1. return specific value for null node
619 | 2. update the answer if needed // answer <-- params
620 | 3. left_ans = top_down(root.left, left_params) // left_params <-- root.val, params
621 | 4. right_ans = top_down(root.right, right_params) // right_params <-- root.val, params
622 | 5. return the answer if needed // answer <-- left_ans, right_ans
623 | ```
624 |
625 | * Find maximum depth of a binary tree:
626 |
627 | ```
628 | 1. return if root is null
629 | 2. if root is a leaf node:
630 | 3. answer = max(answer, depth) // update the answer if needed
631 | 4. maximum_depth(root.left, depth + 1) // call the function recursively for left child
632 | 5. maximum_depth(root.right, depth + 1) // call the function recursively for right child
633 | ```
634 |
635 | ```java
636 | private int answer; // don't forget to initialize answer before call maximum_depth
637 | private void maximum_depth(TreeNode root, int depth) {
638 | if (root == null) {
639 | return;
640 | }
641 | if (root.left == null && root.right == null) {
642 | answer = Math.max(answer, depth);
643 | }
644 | maximum_depth(root.left, depth + 1);
645 | maximum_depth(root.right, depth + 1);
646 | }
647 | ```
648 |
649 | ## Bottom-up Solution
650 |
651 | * In each recursive call, we will firstly call the function recursively for all the children nodes and then come up with the answer according to the returned values and the value of the current node itself.
652 |
653 | * This process can be regarded as a kind of **postorder** traversal.
654 |
655 | * Typically, a "bottom-up" recursive function `bottom_up(root)` will be something like this:
656 |
657 | ```
658 | 1. return specific value for null node
659 | 2. left_ans = bottom_up(root.left) // call function recursively for left child
660 | 3. right_ans = bottom_up(root.right) // call function recursively for right child
661 | 4. return answers // answer <-- left_ans, right_ans, root.val
662 | ```
663 |
664 | * Maximum depth:
665 |
666 | ```
667 | 1. return 0 if root is null // return 0 for null node
668 | 2. left_depth = maximum_depth(root.left)
669 | 3. right_depth = maximum_depth(root.right)
670 | 4. return max(left_depth, right_depth) + 1 // return depth of the subtree rooted at root
671 | ```
672 |
673 | ```java
674 | public int maximum_depth(TreeNode root) {
675 | if (root == null) {
676 | return 0; // return 0 for null node
677 | }
678 | int left_depth = maximum_depth(root.left);
679 | int right_depth = maximum_depth(root.right);
680 | return Math.max(left_depth, right_depth) + 1; // return depth of the subtree rooted at root
681 | }
682 | ```
683 |
684 |
--------------------------------------------------------------------------------
/Basic LeetCode Template.md:
--------------------------------------------------------------------------------
1 | # LeetCode Template 一页通
2 |
3 | ## Binary Search
4 |
5 | **Complexity**
6 |
7 | * Time complexity: $O(\log N)$ - 因为每次都从中间开始把数据split成一半一半,log的底数为2
8 | * Space complexity: $O(1)$ if not adding other structure
9 | * 通常使用constant space来存储mid以及需要return的结果
10 |
11 |
12 | #### **Template 1**
13 |
14 | ```java
15 | int binarySearch(int[] nums, int target){
16 | if(nums == null || nums.length == 0)
17 | return -1;
18 |
19 | int left = 0, right = nums.length - 1;
20 | while(left <= right){
21 | // Prevent (left + right) overflow
22 | int mid = left + (right - left) / 2;
23 | if(nums[mid] == target){ return mid; }
24 | else if(nums[mid] < target) { left = mid + 1; }
25 | else { right = mid - 1; }
26 | }
27 |
28 | // End Condition: left > right
29 | return -1;
30 | }
31 | ```
32 |
33 | #### **Template 2**
34 |
35 | ```java
36 | int binarySearch(int[] nums, int target){
37 | if(nums == null || nums.length == 0)
38 | return -1;
39 |
40 | int left = 0, right = nums.length;
41 | while(left < right){
42 | // Prevent (left + right) overflow
43 | int mid = left + (right - left) / 2;
44 | if(nums[mid] == target){ return mid; }
45 | else if(nums[mid] < target) { left = mid + 1; }
46 | else { right = mid; }
47 | }
48 |
49 | // Post-processing:
50 | // End Condition: left == right
51 | if(left != nums.length && nums[left] == target) return left;
52 | return -1;
53 | }
54 | ```
55 |
56 | #### **Template 3**
57 |
58 | ```java
59 | int binarySearch(int[] nums, int target) {
60 | if (nums == null || nums.length == 0)
61 | return -1;
62 |
63 | int left = 0, right = nums.length - 1;
64 | while (left + 1 < right){
65 | // Prevent (left + right) overflow
66 | int mid = left + (right - left) / 2;
67 | if (nums[mid] == target) {
68 | return mid;
69 | } else if (nums[mid] < target) {
70 | left = mid;
71 | } else {
72 | right = mid;
73 | }
74 | }
75 |
76 | // Post-processing:
77 | // End Condition: left + 1 == right
78 | if(nums[left] == target) return left;
79 | if(nums[right] == target) return right;
80 | return -1;
81 | }
82 | ```
83 |
84 | ## Dynamic Programming
85 |
86 | * **Top-down**: Recursion + Memoization(usually hashmap)
87 | * **Bottom-up**: Create an array to cumulatively store values or flags
88 |
89 | * 通常提问方式:
90 | * Maximum/minimum problems
91 | * How many ways
92 | * The result depends on optimal sub-problems solutions
93 | * **Process**:
94 | * 分析State variables的数量决定了array的dimension: what decisions are there to make, what information is needed
95 | * 如何进行递归: The recurrence relation to transition between states
96 | * Base cases
97 |
98 | ### Memoization(Top-down) + recursion
99 |
100 | * 使用array来记录每个sub-problem的cumulative的结果,储存的array最好是given条件的array
101 | * 在given array上进行修改,可以保持$O(1)$的space complexity
102 | * 该方法绑定recursion,且通常使用一个helper method来完成recursion
103 | * Base case
104 | * Recurrence relationship
105 | * Time complexity: $O(n)$
106 | * 因为我们使用了hashmap进行临时结果的存储,因此每次recursion的时候,对于已存储的结果是$O(1)$
107 | * 不过因为可能在决定action的时候,会从不同的可能性出发,因此这个$n$也可能是$2n$, $3n$,但总体converge to $n$
108 | * 值得注意的是,由于需要进行大量的recursion,尽管已经有hashmap来大大缩短时间,但与其他的dp模板相比较,总体运行时间并不会很快
109 | * Space complexity: $O(n)$
110 | * 存储hashmap所需要的空间
111 |
112 | #### **Template 1 - HashMap**
113 |
114 | ```java
115 | // step 1: 创建一个hashmap,用以记录对应的结果
116 | private HashMap memo = new HashMap<>();
117 | // 公开given variables,因为helper method也需要用
118 |
119 | public int mainFunct(int[][] costs){
120 | // 链接真正用来dp的helper method
121 | return Something;
122 | }
123 |
124 | // step2: 考虑具体有多少变量:
125 | // 1. state variables - 有多少个状态(日期, holding, color..),就有多少个dimension需要考虑
126 | // 2. actions - 可能产生的动作,以股票题为例(买入,售出等), 以及该动作应何时产生
127 |
128 | // step3: 创建一个dp的method,输入两个state用以进行recurrsion
129 | public int dp(state1, state2){
130 | // sub-step 1: 当变量触底,base cases
131 | if (day == array.length){
132 | return 0;
133 | }
134 | // sub-step 2: 检查是否已经存储了对应的数据
135 | if (memo.containsKey(state1)){
136 | return memo.get(state1));
137 | }
138 | // sub-step 3: recurrence relationship 链接下一个index,以及找到sub-problem的最优
139 | currentstate = dp(state1 + 1, state2);
140 | // sub-step 4: 记录进入memo hashmap,返回该数值
141 | memo.put(getKey(state1), totalCost);
142 | return totalCost;
143 | }
144 | ```
145 |
146 | **Example**
147 |
148 | ```java
149 | // 以 paint house 题目为例
150 |
151 | // step 1: 创建一个hashmap,用以记录对应的结果
152 | private HashMap memo = new HashMap<>();
153 | // 通常把given array先存起来,因为memoization通常需要另外再造方法
154 | private int[][] costs;
155 |
156 | public int mainFunct(int[][] costs){
157 | this.costs = costs;
158 | // 链接真正用来dp的helper method
159 | return Something // Math.min(Math.min(paintCost(0, 0), paintCost(0, 1)), paintCost(0, 2));
160 | }
161 |
162 | // step2: 考虑具体有多少变量:
163 | // 1. state variables - 有多少个状态(日期, holding, color..),就有多少个dimension需要考虑
164 | // 2. actions - 可能产生的动作,以股票题为例(买入,售出等), 以及该动作应何时产生
165 |
166 | // step3: 创建一个dp的method,输入两个state用以进行recurrsion
167 | public int paintCost(int day, int color){
168 | // Memoization template: ***************************************************************
169 | // sub-step 1: 当变量触底,base cases
170 | if (day == costs.length){
171 | return 0;
172 | }
173 | // sub-step 2: 检查是否已经存储了对应的数据
174 | if (memo.containsKey(getKey(day, color))){
175 | return memo.get(getKey(day, color));
176 | }
177 | // sub-step 3: recurrence relationship 链接下一个index,以及找到sub-problem的最优
178 | // the cost at current day and color
179 | int totalCost = costs[day][color];
180 | if (color == 0){
181 | // red color
182 | totalCost += Math.min(paintCost(day + 1, 1), paintCost(day + 1, 2));
183 | }
184 | else if (color == 1){
185 | // blue color
186 | totalCost += Math.min(paintCost(day + 1, 0), paintCost(day + 1, 2));
187 | }
188 | else {
189 | // green color
190 | totalCost += Math.min(paintCost(day + 1, 0), paintCost(day + 1, 1));
191 | }
192 | // sub-step 4: 记录进入memo hashmap,返回该数值
193 | memo.put(getKey(day, color), totalCost);
194 | return totalCost;
195 | }
196 | ```
197 |
198 | #### Template 2 - 多元或单元Array
199 |
200 | * 具体的思考过程与hashmap近似,但是使用了array来进行数据的存储
201 | * 适用于需要考虑多个状态变量的同时,某些变量(如日期等)并不需要在每个节点进行单一的动作
202 | * 以股票为例,动作分别有售出和hold两种动作/购买和hold,但是hashmap通常只有一个动作
203 | * 当涉及到某个状态的记录而非单纯数值的记录时,array会比hashmap更加通用,不过array的dimension会更高
204 | * 以股票为例,一个状态变量即为hold/unhold,既此时是否持有股票
205 | * Time and space complexity : $O(m*n)$, 分别都是多元array的长度
206 |
207 | ```java
208 | // step 1: 考虑具体有多少变量:
209 | // 1. state variables - 有多少个状态(日期, holding, color..),就有多少个dimension需要考虑
210 | // 2. actions - 可能产生的动作,以股票题为例(买入,售出等), 以及该动作应何时产生
211 |
212 | // step 2: 创建一个array,用以记录对应的结果
213 | private int[][] memo;
214 | // 公开given variables,因为helper method也需要用
215 |
216 | public int mainFunct(int[][] costs){
217 | memo = new int[prices.length + 1][2]; // 创建对应的memo array,通常对于given变量长度 + 1, 存储结果
218 | // 链接真正用来dp的helper method
219 | return Something;
220 | }
221 |
222 | // step3: 创建一个dp的method,输入两个state用以进行recurrsion
223 | public int dp(state1, state2){
224 | // sub-step 1: 当变量触底,base cases
225 | if (day == array.length){
226 | return 0;
227 | }
228 | // sub-step 2: 检查是否已经存储了对应的数据,但是检查的是array的内容
229 | if (memo[state1][state2] == 0){
230 | // sub-step 3: 分辨可能出现的动作,recurrence relationship 链接下一个index,以及找到sub-problem的最优
231 | int doNothing = dp(state1 + 1, state2); // 动作1 - 结果1
232 | int doSomething; // 动作2 - 结果2
233 |
234 | if (holding == 1){
235 | // doSomething, action 1
236 | }
237 | else {
238 | // doSomething, action 2
239 | }
240 | // sub-step 4: 对比两种动作的结果,记录进入memo array,返回该数值
241 | memo[state1][state2] = Math.max(doNothing, doSomething);
242 | }
243 | return memo[state1][state2];
244 | }
245 | ```
246 |
247 | **Example 以股票问题为例**
248 |
249 | ```java
250 | // step 1: 考虑具体有多少变量:
251 | // 1. state variables - 有多少个状态(日期, holding, color..),就有多少个dimension需要考虑
252 | // 2. actions - 可能产生的动作,以股票题为例(买入,售出等), 以及该动作应何时产生
253 |
254 | // step 2: 创建一个memo array,用以记录对应的结果, dimension = # state variables
255 | private int[] prices;
256 | private int[][] memo;
257 | private int fee;
258 |
259 | public int mainFunct(int[][] costs){
260 | this.prices = prices;
261 | this.fee = fee;
262 | // 该题的考量:
263 | // two state variables: day, holding stock or not
264 | // two actions: buy, sell
265 |
266 | memo = new int[prices.length + 1][2]; // 创建对应的memo array,通常对于given变量长度 + 1
267 | return dp(0, 0);
268 | }
269 |
270 | // step3: 创建一个dp的method,输入两个state用以进行recurrsion
271 | public int dp(int day, int holding){
272 | // sub-step 1: 当变量触底,base cases
273 | if (day == prices.length){
274 | return 0;
275 | }
276 | // sub-step 2: 检查是否已经存储了对应的数据,但是检查的是array的内容
277 | if (memo[day][holding] == 0){
278 | // sub-step3: 分辨可能出现的动作,recurrence relationship 链接下一个index,以及找到sub-problem的最优
279 | int doNothing = dp(day + 1, holding); // 动作1 - 结果1
280 | int doSomething; // 动作2 - 结果2
281 |
282 | // do something we have two actions
283 | // 1 - holding stock, 0 - does not hold
284 | if (holding == 1){
285 | // sell the stock?
286 | doSomething = prices[day] - fee + dp(day + 1, 0);
287 | }
288 | else {
289 | // buy a stock?
290 | doSomething = -prices[day] + dp(day + 1, 1);
291 | }
292 | // sub-step 4: 记录进入memo array,返回该数值
293 | memo[day][holding] = Math.max(doNothing, doSomething);
294 | }
295 | return memo[day][holding];
296 | }
297 | ```
298 |
299 | ### Bottom-up + No Recursion
300 |
301 | * 通常由top-down的方法转化,但是不需要进行recursion因此运行速度上快很多
302 | * 通常需要进行for loop
303 | * 视情况可以控制space complexity到$O(1)$的水平,是dp中较为好的方法,但是可能比较难想到
304 |
305 | #### Template 1 - Changing States
306 |
307 | * 使用一些state varibles来存储变量,在循环中不断更改value,通常需要两个或以上
308 | * 通常使用`Math.min()`或者`Math.max()`来进行关系上的传递
309 | * 通常时间complexity为$O(n)$, 空间的complexity为$O(1)$
310 | * **难点**: 如果寻找内部的recurrence relationship,这里可能会很难
311 |
312 | ```java
313 | public int maxProfit(int[] prices){
314 | // step 1: set up states and initial values, usually 0, min, max
315 | int sold = Integer.MIN_VALUE, held = Integer.MIN_VALUE, reset = 0;
316 |
317 | // step 2: for loop
318 | for (int price : prices){
319 | int preSold = sold;
320 | // step 3: states recurrence relationship
321 | sold = held + price;
322 | held = Math.max(held, reset - price);
323 | reset = Math.max(reset, preSold);
324 | }
325 | // step 4: return and compare max and min
326 | return Math.max(sold, reset);
327 | }
328 | ```
329 |
330 | ##### T 1.1 Kanede's Algorithm
331 |
332 | * Goal: find maximum subarray - find the contiguous subarray (containing at least one number) which has the largest sum
333 |
334 | ```java
335 | public int maxSubArray(int[] nums) {
336 | // kadene's algorithm
337 | int current = 0, max = Integer.MIN_VALUE;
338 | for (int num : nums){
339 | // should we abandon the previous values?
340 | current = Math.max(num, current + num);
341 | max = Math.max(max, current);
342 | }
343 | return max;
344 | }
345 | ```
346 |
347 | #### Template 2 - Sum-up Array
348 |
349 | * 与memoization的做法相似,但是不需要进行recursion,而是使用for-loop
350 | * 通常时间complexity为$O(n)$, 空间的complexity为$O(1)$
351 | * 通常使用`Math.min()`或者`Math.max()`来进行关系上的传递
352 | * 在array的最后一行或列中寻找最大或最小
353 | * **难点**: 如果寻找内部的recurrence relationship
354 |
355 | ```java
356 | public int minCost(int[][] costs) {
357 | // step 1: Use for loop 传递并递增信息,例如次数,cost,等
358 | for (int n = costs.length - 2; n >= 0; n--) {
359 | // step 2: 寻找array之中的递增联系以及关系,一直传递到最后一行
360 | // Total cost of painting the nth house red.
361 | costs[n][0] += Math.min(costs[n + 1][1], costs[n + 1][2]);
362 | // Total cost of painting the nth house green.
363 | costs[n][1] += Math.min(costs[n + 1][0], costs[n + 1][2]);
364 | // Total cost of painting the nth house blue.
365 | costs[n][2] += Math.min(costs[n + 1][0], costs[n + 1][1]);
366 | }
367 | if (costs.length == 0) return 0;
368 | // step 3: 在最后一行寻找答案
369 | return Math.min(Math.min(costs[0][0], costs[0][1]), costs[0][2]);
370 | }
371 | ```
372 |
373 | ## Backtracking
374 |
375 | * 通常提问方式:
376 |
377 | * **All** possible combinations/solutions/permutations,要详细的**所有**结果的情况
378 |
379 | * Return in list,结果为一个list,list中每个结果都是一个list
380 | * 通常需要另一个backtracking的helper method, helper method需要使用recursion
381 |
382 | #### Template 1 - 通用模版
383 |
384 | * 把所有给的variables public 作全局,包括需要return的结果(很可能是list,先做好return的空list)
385 | * 在主方法中调用backtracking,并在其中创建一个空list作为单个的结果
386 | * backtracking:
387 | * 通常下是void method,调用参数index
388 | * index在此处用于追踪我们在given array中的位置,记录是否达到了given array 的末端
389 | * 同时index也是下一个可能结果的先决条件
390 | * 写好base case for recursion:
391 | * 到达了target value
392 | * 到达了given array的末端
393 | * 注意需要重新建一个arraylist来结果当前结果list
394 | * for loop
395 | * 从loop中进行操作链接到下一个可能的结果
396 | * 把本次结果加入到结果集中
397 | * 进入下一个可能的结果
398 | * 把本次结果从结果集中**删除**:达到backtracking的目的
399 |
400 | ```java
401 | // step 1: 把所有给的variables public 作全局,创建res的list(通常list中list嵌套)
402 | List> res;
403 | int[] candidates;
404 |
405 | public List> main(int[] candidates) {
406 | res = new ArrayList<>();
407 | this.candidates = candidates;
408 | // step 2: 思考需要把什么带入backtracking的方法(target,index等),并套入一个空结果list
409 | backtracking(0, new ArrayList());
410 | // 直接return已经做好的result list
411 | return res;
412 | }
413 |
414 | // step 2: 思考需要把什么带入backtracking的方法(target,*index*等)
415 | // 并套入一个*空结果list(指代当前结果)*
416 | // 通常是void method
417 | public void backtracking(int start, List singleComb){
418 | // step 3: base case 刚好达成结果的条件,在此增加当前结果到结果集
419 | if (start == candidates.length){
420 | res.add(new ArrayList(singleComb));
421 | return;
422 | }
423 | // step 4: **最重要**,通常需要for-loop来进入下一个可能的结果 *****************
424 | // 从当前index出发,直到given array的末端,代表某个可能的路径
425 | for (int i = start; i < candidates.length; i++){
426 | // 加入到当前结果
427 | singleComb.add(candidates[i]);
428 | // 进入下一个可能的结果,注意此处 *********
429 | // * 可重复的结果则i
430 | // * 不可重复的记过则i + 1
431 | backtracking(i + 1, singleComb);
432 | // 移除出当前结果(实现backtracking)
433 | singleComb.remove(singleComb.size() - 1);
434 | }
435 | }
436 | ```
437 |
438 | 以combination sum为例
439 |
440 | ```java
441 | // step 1: 把所有给的variables public 作全局,创建res的list(通常list中list嵌套)
442 | List> res;
443 | int[] candidates;
444 | int target;
445 |
446 | public List> combinationSum(int[] candidates, int target) {
447 | res = new ArrayList<>();
448 | this.candidates = candidates;
449 | this.target = target;
450 | // step 2: 思考需要把什么带入backtracking的方法(target,index等),并套入一个空结果list
451 | backtracking(0, target, new ArrayList());
452 | // 直接return已经做好的result list
453 | return res;
454 | }
455 |
456 | // step 2: 思考需要把什么带入backtracking的方法(target,*index*等)
457 | // 并套入一个*空结果list(指代当前结果)*
458 | // 通常是void method
459 | public void backtracking(int start, int target, List singleComb){
460 | // step 3: base case 刚好达成结果的条件,在此增加当前结果到结果集
461 | if (target == 0){
462 | res.add(new ArrayList(singleComb)); // *重要*:建一个new list来接结果
463 | return;
464 | }
465 | // base case: not meet the requirement
466 | if (target < 0 || start == candidates.length){
467 | return;
468 | }
469 | // step 4: **最重要**,通常需要for-loop来进入下一个可能的结果 *****************
470 | // 从当前index出发,直到given array的末端,代表某个可能的路径
471 | for (int i = start; i < candidates.length; i++){
472 | // 加入到当前结果
473 | singleComb.add(candidates[i]);
474 | // 进入下一个可能的结果
475 | backtracking(i, target - candidates[i], singleComb);
476 | // 移除出当前结果(实现backtracking)
477 | singleComb.remove(singleComb.size() - 1);
478 | }
479 | }
480 | ```
481 |
482 | #### Template 2 - Permutation(通用模版变形)
483 |
484 | * 适用于可能的情况:
485 | * permutation
486 | * 每个return的结果,并不按照原来given array中element的排序,需要乱序处理
487 | * 本质上讲通用模版中的可能结果的元素增减,改变为元素的swap来换位
488 | * 需要将given array(如果有的话)转换成list,方便使用`Collections.swap()`,否则需要自己建立helper method来实现元素的交换
489 |
490 | 以permutation为例
491 |
492 | ```java
493 | // step 1: 把所有给的variables public 作全局,创建res的list(通常list中list嵌套)
494 | List> res;
495 | List nums;
496 |
497 | public List> permute(int[] nums) {
498 | res = new ArrayList<>();
499 | this.nums = new ArrayList<>();
500 | // step 2: array 不方便进行swap且不是list,现转换成list就不需要create new list for single result
501 | for (int num : nums){
502 | this.nums.add(num);
503 | }
504 | // step 3: 思考需要把什么带入backtracking的方法(target,index等)
505 | backtracking(0);
506 | return res;
507 | }
508 | public void backtracking(int index){
509 | // step 4: base case 刚好达成结果的条件,在此增加当前结果到结果集
510 | if (index == nums.size()){
511 | res.add(new ArrayList(nums));
512 | return;
513 | }
514 | // step 4: **最重要**,通常需要for-loop来进入下一个可能的结果 *****************
515 | // 从当前index出发,直到given array的末端,代表某个可能的路径,并进行swap
516 | for (int i = index; i < nums.size(); i++){
517 | Collections.swap(nums, i, index);
518 | //*****注意****************
519 | // 由于是swap并不按顺序排列结果,因此从index进行关联而不是i,保证swap到每个元素以及自己
520 | backtracking(index + 1);
521 | Collections.swap(nums, i, index);
522 | }
523 | }
524 | ```
525 |
526 | ## UNION FIND
527 |
528 | * Union-Find is all about remembering the patterns.
529 | * 每次使用这个class来进行cluster,对于每个cluster只需要找ancestor的数据(e.g rank,find)
530 | * Create a class called `UnionFind`
531 | * Initialize a `group` array and a `rank` array. Sometimes you may also need to create a `size` array
532 | * Create `find,` and `union` method
533 | * `find`: Find the ancestor(centroid) of the cluster, 用以进行union时确定存在于某个cluster
534 | * `union`: Union two groups. If true, we union them; if false, they are already in the same cluster
535 | * `rank`: Speeding up the `union` process, basically, calculates the path number of the cluster tree.
536 | * Always attach the cluster with a shorter path to the cluster with a longer path.
537 | * 使用方法为path compression
538 | * Time complexity: time complexity for find/union operation is $\alpha({N})$ (Here, $\alpha({N})$ is the inverse Ackermann function that grows so slowly. Suppose we have $N$ elements to go through, then the time compleXIty would be $O(N \alpha({N}))$
539 | * Space complexity: just using array so it would be $O(N)$
540 |
541 | ### Template 1 - 通用模版
542 |
543 | ```java
544 | class UnionFind {
545 | private int[] group;
546 | private int[] rank;
547 |
548 | public UnionFind(int n){
549 | group = new int[n];
550 | rank = new int[n];
551 | for (int i = 0; i < n; i++){
552 | group[i] = i; // initialization: each node is its own group
553 | rank[i] = 1; // each node has rank 1(path length: 1)
554 | }
555 | }
556 |
557 | public int find(int node){
558 | if (node != group[node]){
559 | group[node] = find(group[node]); // recursion find the ancestor
560 | }
561 | return group[node];
562 | }
563 |
564 | public boolean union(int i, int j){
565 | // find the ancestor
566 | int root1 = find(i);
567 | int root2 = find(j);
568 |
569 | if (root1 == root2){
570 | // already in same group
571 | return false;
572 | }
573 | // if they are not in the same group
574 | if (rank[root1] > rank[root2]){
575 | group[root2] = group[root1]; // attach shorter path cluster to the longer one
576 | }
577 | else if (rank[root2] > rank[root1]){
578 | group[root1] = group[root2];
579 | }
580 | else {
581 | group[root1] = group[root2];
582 | rank[root2]++; // same length, one of the cluster have to be ancestor, rank + 1
583 | }
584 | return true;
585 | }
586 | }
587 | ```
588 |
589 | * **模版的使用**
590 | * 通常在主method中进行class的实例化与使用,例子如下
591 |
592 | ```java
593 | // map to store the number and index, union-find to group the numbers
594 | Map numMap = new HashMap<>();
595 | UnionFind uf = new UnionFind(nums.length);
596 | for (int i = 0; i < nums.length; i++){
597 | int curr = nums[i];
598 | // in case duplicate
599 | if (numMap.containsKey(curr)) continue;
600 | // if map has consecutive elements for curr element
601 | if (numMap.containsKey(curr - 1)){
602 | uf.union(i, numMap.get(curr - 1));
603 | }
604 | if (numMap.containsKey(curr + 1)){
605 | uf.union(i, numMap.get(curr + 1));
606 | }
607 | numMap.put(curr, i);
608 | }
609 | ```
610 |
611 | * `rank`不是必须的,可以分情况使用,如果不需要优化time complexity也可以不用(最好用上)
612 | * 如果需要知道每个cluster的size,也可以使用size来替代rank(同样也是path compression)
613 |
614 | ### Template 2 - With Size
615 |
616 | * Path compression with size
617 |
618 | ```java
619 | class UnionFind {
620 | int representative[];
621 | int size[];
622 |
623 | public UnionFind(int size){
624 | representative = new int[size];
625 | this.size = new int[size];
626 |
627 | for (int i = 0; i < size; i++){
628 | representative[i] = i;
629 | this.size[i] = 1;
630 | }
631 | }
632 |
633 | public int find(int x){
634 | if (x != representative[x]){
635 | representative[x] = find(representative[x]);
636 | }
637 | return representative[x];
638 | }
639 |
640 | public void union(int a, int b){
641 | int root1 = find(a);
642 | int root2 = find(b);
643 |
644 | if (root1 == root2) return;
645 | if (size[root1] > size[root2]){
646 | size[root1] += size[root2];
647 | representative[root2] = representative[root1];
648 | }
649 | else {
650 | size[root2] += size[root1];
651 | representative[root1] = representative[root2];
652 | }
653 | }
654 | }
655 | ```
656 |
657 | ## DFS
658 |
659 | ### DFS - Line Graph
660 |
661 | * 需要创建`adjList`,可以是list或者map,用以存储相关联的nodes的信息(**important**)
662 |
663 | ## BFS
664 |
665 | * Traverse a tree/graph:通常要使用queue来进行
666 | * Traverse by layer
667 | * while循环,queue不为空
668 | * 事先存储一个node(通常为root),然后在循环中pop(poll)
669 | * 进行操作,接着把node的左子树和右子树存储在queue或者stack中,循环往复直到所有node都traverse完成
670 | * **DFS-stack, BFS-queue**
671 |
672 | * Time Complexity: $O(V + E)$. Here, V represents the number of vertices, and E represents the number of edges. We need to check every vertex and traverse through every edge in the graph. The time complexity is the same as it was for the DFS approach.
673 | * Space Complexity: $O(V)$. Generally, we will check if a vertex has been visited before adding it to the queue, so the queue will use most $O(V)$ space. Keeping track of which vertices have been visited will also require $O(V)$ space.
674 |
675 | ## Two Pointer
676 |
677 | ### Linked List
678 |
679 | * Usually **1 fast pointer, 1 slow pointer**, and different speeds of progress(hare and tortoise)
680 | * A fast pointer can move two steps each time, and a slow pointer move 1 step each time
681 | * **Always examine if the node is null before you call the next field.**
682 | * Getting the next node of a null node will cause the null-pointer error. For example, before we run `fast = fast.next.next`, we need to examine both `fast` and `fast.next` is not null.
683 | * **Carefully define the end conditions of your loop.**
684 |
685 | ```java
686 | // Initialize slow & fast pointers
687 | ListNode slow = head;
688 | ListNode fast = head;
689 | /**
690 | * Change this condition to fit the specific problem.
691 | * Attention: remember to avoid null-pointer error
692 | **/
693 | while (slow != null && fast != null && fast.next != null) {
694 | slow = slow.next; // move slow pointer one step each time
695 | fast = fast.next.next; // move fast pointer two steps each time
696 | if (slow == fast) { // change this condition to fit specific problem
697 | return true;
698 | }
699 | }
700 | return false; // change return value to fit specific problem
701 | ```
702 |
703 | * Or two pointers have the same speed but start from a different node (remove the nth node from the end)
704 | * **Complexity Analysis**
705 | * If you only use pointers without any other extra space, the space complexity will be `O(1)`.
706 | * However, it is more difficult to analyze the time complexity. In order to get the answer, we need to analyze `how many times we will run our loop` . In our previous finding cycle example, let's assume that we move the faster pointer 2 steps each time and move the slower pointer 1 step each time.
707 | * If there is no cycle, the fast pointer takes `N/2 times` to reach the end of the linked list, where N is the length of the linked list.
708 | * If there is a cycle, the fast pointer needs `M times` to catch up the slower pointer, where M is the length of the cycle in the list.
709 | * Obviously, M <= N. So we will run the loop `up to N times`. And for each loop, we only need constant time. So, the time complexity of this algorithm is `O(N)` in total.
710 |
711 | ## LinkedList一些技巧
712 |
713 | ### DummyHead/Sentinel Node的使用
714 |
715 | * dummy head/sentinel node/pseudo-head 即为在目前的head之前再加一个node,是一个fake node,数值没有意义
716 | * **作用**:
717 | * 在需要移除某个node,比如说head的时候,会非常方便移除(否则很麻烦)
718 | * 需要对list长度进行计数,但计数从1不从0开始时,计数容易错位,此时dummy head可以补足空位
719 | * 在某些题目中需要记录prev node的指针,此时dummy head可以帮助记录head的prev node
720 | * 一般在使用while loop的时候使用dummy head,recursion的情况下很少使用
721 |
--------------------------------------------------------------------------------
/Heap/Heap Tutorials.md:
--------------------------------------------------------------------------------
1 | # Heap Tutorials
2 |
3 | ## Priority Queue
4 |
5 | * A priority queue is an abstract data type similar to a regular queue or stack data structure in which each element additionally has a "priority" associated with it.
6 | * In a priority queue, an element with high priority is served before an element with low priority.
7 | * **Heap vs. PQ**
8 | * A priority queue is an abstract data type, while a Heap is a data structure.
9 | * Therefore, a Heap is not a Priority Queue, but a way to implement a Priority Queue.
10 |
11 | * **Implementation**:
12 | * There are multiple ways to implement a Priority Queue, such as array and linked list. However, these implementations only guarantee $O(1)$ the time complexity for either insertion or deletion, while the other operation will have a time complexity of $O(N)$.
13 | * On the other hand, implementing the priority queue with Heap will allow both insertion and deletion to have a time complexity of $O(\log N)$.
14 |
15 | ## Heap
16 |
17 | * A **Heap** is a special type of binary tree. A heap is a binary tree that meets the following criteria:
18 | * Is a **complete binary tree**;
19 | * The value of each node must be **no greater than (or no less than)** the value of its child nodes.
20 |
21 | * A Heap has the following properties:
22 |
23 | - Insertion of an element into the Heap has a time complexity of $O(\log N)$;
24 |
25 | - Deletion of an element from the Heap has a time complexity of $O(\log N)$;
26 |
27 | - The maximum/minimum value in the Heap can be obtained with $O(1)$ time complexity.
28 |
29 | ### Heap Classification
30 |
31 | There are two kinds of heaps: **Max Heap** and **Min Heap**.
32 |
33 | - Max Heap: Each node in the Heap has a value **no less than** its child nodes. Therefore, the top element (root node) has the **largest** value in the Heap.
34 | - Min Heap: Each node in the Heap has a value **no larger than** its child nodes. Therefore, the top element (root node) has the **smallest** value in the Heap.
35 |
36 |  37 |
38 | * [Heap Insertion](https://leetcode.com/explore/learn/card/heap/643/heap/4019/)
39 | * [Heap Deletion](https://leetcode.com/explore/learn/card/heap/643/heap/4020/)
40 |
41 | ### Implementation of a Heap
42 |
43 | * Use an array to implement a heap
44 |
45 | * Min Heap
46 |
47 | ```java
48 | // Implementing "Min Heap"
49 | public class MinHeap {
50 | // Create a complete binary tree using an array
51 | // Then use the binary tree to construct a Heap
52 | int[] minHeap;
53 | // the number of elements is needed when instantiating an array
54 | // heapSize records the size of the array
55 | int heapSize;
56 | // realSize records the number of elements in the Heap
57 | int realSize = 0;
58 |
59 | public MinHeap(int heapSize) {
60 | this.heapSize = heapSize;
61 | minHeap = new int[heapSize + 1];
62 | // To better track the indices of the binary tree,
63 | // we will not use the 0-th element in the array
64 | // You can fill it with any value
65 | minHeap[0] = 0;
66 | }
67 |
68 | // Function to add an element
69 | public void add(int element) {
70 | realSize++;
71 | // If the number of elements in the Heap exceeds the preset heapSize
72 | // print "Added too many elements" and return
73 | if (realSize > heapSize) {
74 | System.out.println("Added too many elements!");
75 | realSize--;
76 | return;
77 | }
78 | // Add the element into the array
79 | minHeap[realSize] = element;
80 | // Index of the newly added element
81 | int index = realSize;
82 | // Parent node of the newly added element
83 | // Note if we use an array to represent the complete binary tree
84 | // and store the root node at index 1
85 | // index of the parent node of any node is [index of the node / 2]
86 | // index of the left child node is [index of the node * 2]
87 | // index of the right child node is [index of the node * 2 + 1]
88 | int parent = index / 2;
89 | // If the newly added element is smaller than its parent node,
90 | // its value will be exchanged with that of the parent node
91 | while ( minHeap[index] < minHeap[parent] && index > 1 ) {
92 | int temp = minHeap[index];
93 | minHeap[index] = minHeap[parent];
94 | minHeap[parent] = temp;
95 | index = parent;
96 | parent = index / 2;
97 | }
98 | }
99 |
100 | // Get the top element of the Heap
101 | public int peek() {
102 | return minHeap[1];
103 | }
104 |
105 | // Delete the top element of the Heap
106 | public int pop() {
107 | // If the number of elements in the current Heap is 0,
108 | // print "Don't have any elements" and return a default value
109 | if (realSize < 1) {
110 | System.out.println("Don't have any element!");
111 | return Integer.MAX_VALUE;
112 | } else {
113 | // When there are still elements in the Heap
114 | // realSize >= 1
115 | int removeElement = minHeap[1];
116 | // Put the last element in the Heap to the top of Heap
117 | minHeap[1] = minHeap[realSize];
118 | realSize--;
119 | int index = 1;
120 | // When the deleted element is not a leaf node
121 | while (index <= realSize / 2) {
122 | // the left child of the deleted element
123 | int left = index * 2;
124 | // the right child of the deleted element
125 | int right = (index * 2) + 1;
126 | // If the deleted element is larger than the left or right child
127 | // its value needs to be exchanged with the smaller value
128 | // of the left and right child
129 | if (minHeap[index] > minHeap[left] || minHeap[index] > minHeap[right]) {
130 | if (minHeap[left] < minHeap[right]) {
131 | int temp = minHeap[left];
132 | minHeap[left] = minHeap[index];
133 | minHeap[index] = temp;
134 | index = left;
135 | } else {
136 | // maxHeap[left] >= maxHeap[right]
137 | int temp = minHeap[right];
138 | minHeap[right] = minHeap[index];
139 | minHeap[index] = temp;
140 | index = right;
141 | }
142 | } else {
143 | break;
144 | }
145 | }
146 | return removeElement;
147 | }
148 | }
149 |
150 | // return the number of elements in the Heap
151 | public int size() {
152 | return realSize;
153 | }
154 |
155 | public String toString() {
156 | if (realSize == 0) {
157 | return "No element!";
158 | } else {
159 | StringBuilder sb = new StringBuilder();
160 | sb.append('[');
161 | for (int i = 1; i <= realSize; i++) {
162 | sb.append(minHeap[i]);
163 | sb.append(',');
164 | }
165 | sb.deleteCharAt(sb.length() - 1);
166 | sb.append(']');
167 | return sb.toString();
168 | }
169 | }
170 |
171 | public static void main(String[] args) {
172 | // Test case
173 | MinHeap minHeap = new MinHeap(3);
174 | minHeap.add(3);
175 | minHeap.add(1);
176 | minHeap.add(2);
177 | // [1,3,2]
178 | System.out.println(minHeap.toString());
179 | // 1
180 | System.out.println(minHeap.peek());
181 | // 1
182 | System.out.println(minHeap.pop());
183 | // [2, 3]
184 | System.out.println(minHeap.toString());
185 | minHeap.add(4);
186 | // Add too many elements
187 | minHeap.add(5);
188 | // [2,3,4]
189 | System.out.println(minHeap.toString());
190 | }
191 | }
192 |
193 | ```
194 |
195 | * Max Heap
196 |
197 | ```java
198 | // Implementing "Max Heap"
199 | public class MaxHeap {
200 | // Create a complete binary tree using an array
201 | // Then use the binary tree to construct a Heap
202 | int[] maxHeap;
203 | // the number of elements is needed when instantiating an array
204 | // heapSize records the size of the array
205 | int heapSize;
206 | // realSize records the number of elements in the Heap
207 | int realSize = 0;
208 |
209 | public MaxHeap(int heapSize) {
210 | this.heapSize = heapSize;
211 | maxHeap = new int[heapSize + 1];
212 | // To better track the indices of the binary tree,
213 | // we will not use the 0-th element in the array
214 | // You can fill it with any value
215 | maxHeap[0] = 0;
216 | }
217 |
218 | // Function to add an element
219 | public void add(int element) {
220 | realSize++;
221 | // If the number of elements in the Heap exceeds the preset heapSize
222 | // print "Added too many elements" and return
223 | if (realSize > heapSize) {
224 | System.out.println("Added too many elements!");
225 | realSize--;
226 | return;
227 | }
228 | // Add the element into the array
229 | maxHeap[realSize] = element;
230 | // Index of the newly added element
231 | int index = realSize;
232 | // Parent node of the newly added element
233 | // Note if we use an array to represent the complete binary tree
234 | // and store the root node at index 1
235 | // index of the parent node of any node is [index of the node / 2]
236 | // index of the left child node is [index of the node * 2]
237 | // index of the right child node is [index of the node * 2 + 1]
238 |
239 | int parent = index / 2;
240 | // If the newly added element is larger than its parent node,
241 | // its value will be exchanged with that of the parent node
242 | while ( maxHeap[index] > maxHeap[parent] && index > 1 ) {
243 | int temp = maxHeap[index];
244 | maxHeap[index] = maxHeap[parent];
245 | maxHeap[parent] = temp;
246 | index = parent;
247 | parent = index / 2;
248 | }
249 | }
250 |
251 | // Get the top element of the Heap
252 | public int peek() {
253 | return maxHeap[1];
254 | }
255 |
256 | // Delete the top element of the Heap
257 | public int pop() {
258 | // If the number of elements in the current Heap is 0,
259 | // print "Don't have any elements" and return a default value
260 | if (realSize < 1) {
261 | System.out.println("Don't have any element!");
262 | return Integer.MIN_VALUE;
263 | } else {
264 | // When there are still elements in the Heap
265 | // realSize >= 1
266 | int removeElement = maxHeap[1];
267 | // Put the last element in the Heap to the top of Heap
268 | maxHeap[1] = maxHeap[realSize];
269 | realSize--;
270 | int index = 1;
271 | // When the deleted element is not a leaf node
272 | while (index <= realSize / 2) {
273 | // the left child of the deleted element
274 | int left = index * 2;
275 | // the right child of the deleted element
276 | int right = (index * 2) + 1;
277 | // If the deleted element is smaller than the left or right child
278 | // its value needs to be exchanged with the larger value
279 | // of the left and right child
280 | if (maxHeap[index] < maxHeap[left] || maxHeap[index] < maxHeap[right]) {
281 | if (maxHeap[left] > maxHeap[right]) {
282 | int temp = maxHeap[left];
283 | maxHeap[left] = maxHeap[index];
284 | maxHeap[index] = temp;
285 | index = left;
286 | } else {
287 | // maxHeap[left] <= maxHeap[right]
288 | int temp = maxHeap[right];
289 | maxHeap[right] = maxHeap[index];
290 | maxHeap[index] = temp;
291 | index = right;
292 | }
293 | } else {
294 | break;
295 | }
296 | }
297 | return removeElement;
298 | }
299 | }
300 |
301 | // return the number of elements in the Heap
302 | public int size() {
303 | return realSize;
304 | }
305 |
306 | public String toString() {
307 | if (realSize == 0) {
308 | return "No element!";
309 | } else {
310 | StringBuilder sb = new StringBuilder();
311 | sb.append('[');
312 | for (int i = 1; i <= realSize; i++) {
313 | sb.append(maxHeap[i]);
314 | sb.append(',');
315 | }
316 | sb.deleteCharAt(sb.length() - 1);
317 | sb.append(']');
318 | return sb.toString();
319 | }
320 | }
321 |
322 | public static void main(String[] args) {
323 | // Test case
324 | MaxHeap maxheap = new MaxHeap(5);
325 | maxheap.add(1);
326 | maxheap.add(2);
327 | maxheap.add(3);
328 | // [3,1,2]
329 | System.out.println(maxheap.toString());
330 | // 3
331 | System.out.println(maxheap.peek());
332 | // 3
333 | System.out.println(maxheap.pop());
334 | System.out.println(maxheap.pop());
335 | System.out.println(maxheap.pop());
336 | // No element
337 | System.out.println(maxheap.toString());
338 | maxheap.add(4);
339 | // Add too many elements
340 | maxheap.add(5);
341 | // [4,1,2]
342 | System.out.println(maxheap.toString());
343 | }
344 | }
345 |
346 | ```
347 |
348 | ## Heap Construction
349 |
350 | * When creating a Heap, we can simultaneously perform the **heapify** operation. Heapify means converting a group of data into a Heap.
351 | * Time complexity: $O(N)$.
352 | * Space complexity: $O(N)$.
353 |
354 | ```java
355 | // In Java, a Heap is represented by a Priority Queue
356 | import java.util.Collections;
357 | import java.util.PriorityQueue;
358 | import java.util.Arrays;
359 |
360 | // Construct an empty Min Heap
361 | PriorityQueue minHeap = new PriorityQueue<>();
362 |
363 | // Construct an empty Max Heap
364 | PriorityQueue maxHeap = new PriorityQueue<>(Collections.reverseOrder());
365 |
366 | // Construct a Heap with initial elements.
367 | // This process is named "Heapify".
368 | // The Heap is a Min Heap
369 | PriorityQueue heapWithValues= new PriorityQueue<>(Arrays.asList(3, 1, 2));
370 | ```
371 |
372 | * Inserting an element
373 | * Time complexity: $O(\log N)$
374 | * Space complexity: $O(1)$
375 |
376 | ```java
377 | // Insert an element to the Min Heap
378 | minHeap.add(5);
379 |
380 | // Insert an element to the Max Heap
381 | maxHeap.add(5);
382 | ```
383 |
384 | * Getting the top element of the heap
385 | * Time complexity: $O(1)$
386 | * Space complexity: $O(1)$
387 |
388 | ```java
389 | // Get top element from the Min Heap
390 | // i.e. the smallest element
391 | minHeap.peek();
392 | // Get top element from the Max Heap
393 | // i.e. the largest element
394 | maxHeap.peek();
395 | ```
396 |
397 | * Deleting the top element
398 | * Time complexity: $O(\log N)$
399 | * Space complexity: $O(1)$
400 |
401 | ```java
402 | // Delete top element from the Min Heap
403 | minHeap.poll();
404 |
405 | // Delete top element from the Max Heap
406 | maxheap.poll();
407 | ```
408 |
409 | * Getting the length of a heap
410 | * Time complexity: $O(1)$
411 | * Space complexity: $O(1)$
412 |
413 | ```java
414 | // Length of the Min Heap
415 | minHeap.size();
416 |
417 | // Length of the Max Heap
418 | maxHeap.size();
419 |
420 | // Note, in Java, apart from checking if the length of the Heap is 0, we can also use isEmpty()
421 | // If there are no elements in the Heap, isEmpty() will return true;
422 | // If there are still elements in the Heap, isEmpty() will return false;
423 | ```
424 |
425 | * Time and Space Complexity:
426 |
427 | | Heap method | Time complexity | Space complexity |
428 | | ---------------------- | --------------- | ---------------- |
429 | | Construct a Heap | $O(N)$ | $O(N)$ |
430 | | Insert an element | $O(\log N)$ | $O(1)$ |
431 | | Get the top element | $O(1)$ | $O(1)$ |
432 | | Delete the top element | $O(\log N)$ | $O(1)$ |
433 | | Get the size of a Heap | $O(1)$ | $O(1)$ |
434 |
435 | ## Common Methods of Heap
436 |
437 | **Min Heap**
438 |
439 | ```java
440 | // Code for Min Heap
441 | import java.util.PriorityQueue;
442 |
443 | public class App {
444 | public static void main(String[] args) {
445 | // Construct an instance of Min Heap
446 | PriorityQueue minHeap = new PriorityQueue<>();
447 |
448 | // Add 3,1,2 respectively to the Min Heap
449 | minHeap.add(3);
450 | minHeap.add(1);
451 | minHeap.add(2);
452 |
453 | // Check all elements in the Min Heap, the result is [1, 3, 2]
454 | System.out.println("minHeap: " + minHeap.toString());
455 |
456 | // Get the top element of the Min Heap
457 | int peekNum = minHeap.peek();
458 |
459 | // The result is 1
460 | System.out.println("peek number: " + peekNum);
461 |
462 | // Delete the top element in the Min Heap
463 | int pollNum = minHeap.poll();
464 |
465 | // The reult is 1
466 | System.out.println("poll number: " + pollNum);
467 |
468 | // Check the top element after deleting 1, the result is 2
469 | System.out.println("peek number: " + minHeap.peek());
470 |
471 | // Check all elements in the Min Heap, the result is [2,3]
472 | System.out.println("minHeap: " + minHeap.toString());
473 |
474 | // Check the number of elements in the Min Heap
475 | // Which is also the length of the Min Heap
476 | int heapSize = minHeap.size();
477 |
478 | // The result is 2
479 | System.out.println("minHeap size: " + heapSize);
480 |
481 | // Check if the Min Heap is empty
482 | boolean isEmpty = minHeap.isEmpty();
483 |
484 | // The result is false
485 | System.out.println("isEmpty: " + isEmpty);
486 | }
487 | }
488 | ```
489 |
490 | **Max Heap**
491 |
492 | ```java
493 | // Code for Max Heap
494 | import java.util.Collections;
495 | import java.util.PriorityQueue;
496 |
497 | public class App {
498 | public static void main(String[] args) {
499 | // Construct an instance of Max Heap
500 | PriorityQueue maxHeap = new PriorityQueue<>(Collections.reverseOrder());
501 |
502 | // Add 1,3,2 respectively to the Max Heap
503 | maxHeap.add(1);
504 | maxHeap.add(3);
505 | maxHeap.add(2);
506 |
507 | // Check all elements in the Max Heap, the result is [3, 1, 2]
508 | System.out.println("maxHeap: " + maxHeap.toString());
509 |
510 | // Get the top element of the Max Heap
511 | int peekNum = maxHeap.peek();
512 |
513 | // The result is 3
514 | System.out.println("peek number: " + peekNum);
515 |
516 | // Delete the top element in the Max Heap
517 | int pollNum = maxHeap.poll();
518 |
519 | // The reult is 3
520 | System.out.println("poll number: " + pollNum);
521 |
522 | // Check the top element after deleting 3, the result is 2
523 | System.out.println("peek number: " + maxHeap.peek());
524 |
525 | // Check all elements in the Max Heap, the result is [2,1]
526 | System.out.println("maxHeap: " + maxHeap.toString());
527 |
528 | // Check the number of elements in the Max Heap
529 | // Which is also the length of the Max Heap
530 | int heapSize = maxHeap.size();
531 |
532 | // The result is 2
533 | System.out.println("maxHeap size: " + heapSize);
534 |
535 | // Check if the Max Heap is empty
536 | boolean isEmpty = maxHeap.isEmpty();
537 |
538 | // The result is false
539 | System.out.println("isEmpty: " + isEmpty);
540 | }
541 | }
542 | ```
543 |
544 | ## Heap Sort
545 |
546 | The sorting algorithm using a **Min Heap** is as follows:
547 |
548 | 1. Heapify all elements into a Min Heap.
549 | 2. Record and delete the top element.
550 | 3. Put the top element into an array T that stores all sorted elements. Now, the Heap will remain a Min Heap.
551 | 4. Repeat steps 2 and 3 until the Heap is empty. The array T will contain all elements sorted in ascending order.
552 |
553 | The sorting algorithm using a **Max Heap** is as follows:
554 |
555 | 1. Heapify all elements into a Max Heap.
556 | 2. Record and delete the top element.
557 | 3. Put the top element into an array T that stores all sorted elements. Now, the Heap will remain a Max Heap.
558 | 4. Repeat steps 2 and 3 until the Heap is empty. The array T will contain all elements sorted in descending order.
559 |
560 | * **Complexity Analysis:**
561 | * Let N be the total number of elements.
562 | * Time complexity: $O(N \log N)$
563 | * Space complexity: $O(N)$
564 |
565 | ## The Top K Problem
566 |
567 | Solution of the Top K largest elements:
568 |
569 | 1. Construct a Max Heap.
570 | 2. Add all elements into the Max Heap.
571 | 3. Traversing and deleting the top element (using pop() or poll() for instance), and storing the value into the result array T.
572 | 4. Repeat step 3 until we have removed the K largest elements.
573 |
574 | **Complexity Analysis**
575 |
576 | * Time complexity: $O(K \log N + N)$
577 | * Steps one and two require us to construct a Max Heap which requires $O(N)$ time using the previously discussed heapify method. Each element removed from the heap requires $O(\log N)$ time; this process is repeated K*K* times. Thus the total time complexity is $O(K \log N + N)$.
578 |
579 | * Space complexity: $O(N)$
580 | * After step 2, the heap will store all N elements.
581 |
582 | ## The K-th Element
583 |
584 | ### Approach 1
585 |
586 | * Solution of the K-th largest element:
587 |
588 | 1. Construct a Max Heap.
589 | 2. Add all elements into the Max Heap.
590 | 3. Traversing and deleting the top element (using pop() or poll() for instance).
591 | 4. Repeat Step 3 K times until we find the K-th largest element.
592 |
593 | * Let N be the total number of elements.
594 |
595 | Time complexity: $O(K \log N + N)$
596 |
597 | - Steps one and two require us to construct a Max Heap which requires O(N) time using the previously discussed heapify method. Each element removed from the heap requires $O(\log N)$ time; this process is repeated K times. Thus the total time complexity is $O(K \log N + N)$.
598 |
599 | Space complexity: $O(N)$
600 |
601 | - After step 2, the heap will store all N elements.
602 |
603 | ### Approach 2
604 |
605 | * Solution of the K-th largest element:
606 |
607 | 1. Construct a Min Heap with size K.
608 | 2. Add elements to the Min Heap one by one.
609 | 3. When there are K elements in the “Min Heap”, compare the current element with the top element of the Heap:
610 | - If the current element is not larger than the top element of the Heap, drop it and proceed to the next element.
611 | - If the current element is larger than the Heap’s top element, delete the Heap’s top element, and add the current element to the “Min Heap”.
612 | 4. Repeat Steps 2 and 3 until all elements have been iterated.
613 |
614 | Now the top element in the Min Heap is the K-th largest element.
615 |
616 | * Complexity:
617 |
618 | * Time complexity: $O(N \log K)$
619 |
620 | - Steps one and two will require $O(K \log K)$ time if the elements are added one by one to the heap, however using the heapify method, these two steps could be accomplished in $O(K)$ time. Steps 3 and 4 will require $O(\log K)$ time each time an element must be replaced in the heap. In the worst-case scenario, this will be done N - K times. Thus the total time complexity is $O((N - K) \log K + K \log K)$ which simplifies to $O(N \log K)$.
621 |
622 | Space complexity: $O(K)$
623 |
624 | - The heap will contain at most K elements at any given time.
625 |
626 |
--------------------------------------------------------------------------------
/Binary Search/Binary Search Problems Part #1.md:
--------------------------------------------------------------------------------
1 | # Binary Search Problems Part #1
2 |
3 | ## Closest Binary Search Tree Value(Easy #270)
4 |
5 | **Question**: Given the `root` of a binary search tree and a `target` value, return *the value in the BST that is closest to the* `target`
6 |
7 | **Example 1:**
8 |
9 | 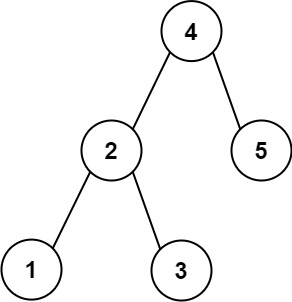
10 |
11 | ```
12 | Input: root = [4,2,5,1,3], target = 3.714286
13 | Output: 4
14 | ```
15 |
16 | **Example 2:**
17 |
18 | ```
19 | Input: root = [1], target = 4.428571
20 | Output: 1
21 | ```
22 |
23 | **Constraints:**
24 |
25 | - The number of nodes in the tree is in the range `[1, 104]`.
26 | - `0 <= Node.val <= 109`
27 | - `-109 <= target <= 109`
28 |
29 | ### My Solution
30 |
31 | * In order recursively find the distance between the value and the target
32 | * Compare the distance and record the root value
33 |
34 | ```java
35 | class Solution {
36 | int value = 0;
37 | public int closestValue(TreeNode root, double target) {
38 | double distance = Double.POSITIVE_INFINITY;
39 | findValue(root, target, distance);
40 | return value;
41 | }
42 | // recursively find the value near target
43 | public double findValue(TreeNode root, double target, double distance){
44 | if (root == null){
45 | return distance;
46 | }
47 | distance = findValue(root.left, target, distance);
48 | if ((double)Math.abs(target - root.val) < distance){
49 | distance = (double)Math.abs(target - root.val);
50 | value = root.val;
51 | }
52 | distance = findValue(root.right, target, distance);
53 | return distance;
54 | }
55 | }
56 | ```
57 |
58 | ### Standard Solution
59 |
60 | #### Solution #1 Recursive Inorder + Linear Search
61 |
62 | * Recursively use the list to record all the value
63 | * Create a customized comparator for comparison
64 |
65 | ```java
66 | public void inorder(TreeNode root, List nums){
67 | if (root == null) return;
68 | inorder(root.left, nums);
69 | nums.add(root.val);
70 | inorder(root.right, nums);
71 | }
72 | public int closestValue(TreeNode root, double target){
73 | List nums = new ArrayList();
74 | inorder(root, nums); // put all values to the list
75 | return Collections.min(nums, new Comparator(){
76 | @Override
77 | public int compare(Integer o1, Integer o2){
78 | return Math.abs(o1 - target) < Math.abs(o2 - target) ? -1 : 1;
79 | }
80 | });
81 | }
82 | ```
83 |
84 | - Time complexity: $\mathcal{O}(N)$ because to build in order traversal and then to perform linear search takes linear time.
85 | - Space complexity: $\mathcal{O}(N)$ to keep in order traversal.
86 |
87 | #### Solution #2 Binary Search, O(H) time
88 |
89 | * Use the properties of the binary search tree
90 |
91 |
37 |
38 | * [Heap Insertion](https://leetcode.com/explore/learn/card/heap/643/heap/4019/)
39 | * [Heap Deletion](https://leetcode.com/explore/learn/card/heap/643/heap/4020/)
40 |
41 | ### Implementation of a Heap
42 |
43 | * Use an array to implement a heap
44 |
45 | * Min Heap
46 |
47 | ```java
48 | // Implementing "Min Heap"
49 | public class MinHeap {
50 | // Create a complete binary tree using an array
51 | // Then use the binary tree to construct a Heap
52 | int[] minHeap;
53 | // the number of elements is needed when instantiating an array
54 | // heapSize records the size of the array
55 | int heapSize;
56 | // realSize records the number of elements in the Heap
57 | int realSize = 0;
58 |
59 | public MinHeap(int heapSize) {
60 | this.heapSize = heapSize;
61 | minHeap = new int[heapSize + 1];
62 | // To better track the indices of the binary tree,
63 | // we will not use the 0-th element in the array
64 | // You can fill it with any value
65 | minHeap[0] = 0;
66 | }
67 |
68 | // Function to add an element
69 | public void add(int element) {
70 | realSize++;
71 | // If the number of elements in the Heap exceeds the preset heapSize
72 | // print "Added too many elements" and return
73 | if (realSize > heapSize) {
74 | System.out.println("Added too many elements!");
75 | realSize--;
76 | return;
77 | }
78 | // Add the element into the array
79 | minHeap[realSize] = element;
80 | // Index of the newly added element
81 | int index = realSize;
82 | // Parent node of the newly added element
83 | // Note if we use an array to represent the complete binary tree
84 | // and store the root node at index 1
85 | // index of the parent node of any node is [index of the node / 2]
86 | // index of the left child node is [index of the node * 2]
87 | // index of the right child node is [index of the node * 2 + 1]
88 | int parent = index / 2;
89 | // If the newly added element is smaller than its parent node,
90 | // its value will be exchanged with that of the parent node
91 | while ( minHeap[index] < minHeap[parent] && index > 1 ) {
92 | int temp = minHeap[index];
93 | minHeap[index] = minHeap[parent];
94 | minHeap[parent] = temp;
95 | index = parent;
96 | parent = index / 2;
97 | }
98 | }
99 |
100 | // Get the top element of the Heap
101 | public int peek() {
102 | return minHeap[1];
103 | }
104 |
105 | // Delete the top element of the Heap
106 | public int pop() {
107 | // If the number of elements in the current Heap is 0,
108 | // print "Don't have any elements" and return a default value
109 | if (realSize < 1) {
110 | System.out.println("Don't have any element!");
111 | return Integer.MAX_VALUE;
112 | } else {
113 | // When there are still elements in the Heap
114 | // realSize >= 1
115 | int removeElement = minHeap[1];
116 | // Put the last element in the Heap to the top of Heap
117 | minHeap[1] = minHeap[realSize];
118 | realSize--;
119 | int index = 1;
120 | // When the deleted element is not a leaf node
121 | while (index <= realSize / 2) {
122 | // the left child of the deleted element
123 | int left = index * 2;
124 | // the right child of the deleted element
125 | int right = (index * 2) + 1;
126 | // If the deleted element is larger than the left or right child
127 | // its value needs to be exchanged with the smaller value
128 | // of the left and right child
129 | if (minHeap[index] > minHeap[left] || minHeap[index] > minHeap[right]) {
130 | if (minHeap[left] < minHeap[right]) {
131 | int temp = minHeap[left];
132 | minHeap[left] = minHeap[index];
133 | minHeap[index] = temp;
134 | index = left;
135 | } else {
136 | // maxHeap[left] >= maxHeap[right]
137 | int temp = minHeap[right];
138 | minHeap[right] = minHeap[index];
139 | minHeap[index] = temp;
140 | index = right;
141 | }
142 | } else {
143 | break;
144 | }
145 | }
146 | return removeElement;
147 | }
148 | }
149 |
150 | // return the number of elements in the Heap
151 | public int size() {
152 | return realSize;
153 | }
154 |
155 | public String toString() {
156 | if (realSize == 0) {
157 | return "No element!";
158 | } else {
159 | StringBuilder sb = new StringBuilder();
160 | sb.append('[');
161 | for (int i = 1; i <= realSize; i++) {
162 | sb.append(minHeap[i]);
163 | sb.append(',');
164 | }
165 | sb.deleteCharAt(sb.length() - 1);
166 | sb.append(']');
167 | return sb.toString();
168 | }
169 | }
170 |
171 | public static void main(String[] args) {
172 | // Test case
173 | MinHeap minHeap = new MinHeap(3);
174 | minHeap.add(3);
175 | minHeap.add(1);
176 | minHeap.add(2);
177 | // [1,3,2]
178 | System.out.println(minHeap.toString());
179 | // 1
180 | System.out.println(minHeap.peek());
181 | // 1
182 | System.out.println(minHeap.pop());
183 | // [2, 3]
184 | System.out.println(minHeap.toString());
185 | minHeap.add(4);
186 | // Add too many elements
187 | minHeap.add(5);
188 | // [2,3,4]
189 | System.out.println(minHeap.toString());
190 | }
191 | }
192 |
193 | ```
194 |
195 | * Max Heap
196 |
197 | ```java
198 | // Implementing "Max Heap"
199 | public class MaxHeap {
200 | // Create a complete binary tree using an array
201 | // Then use the binary tree to construct a Heap
202 | int[] maxHeap;
203 | // the number of elements is needed when instantiating an array
204 | // heapSize records the size of the array
205 | int heapSize;
206 | // realSize records the number of elements in the Heap
207 | int realSize = 0;
208 |
209 | public MaxHeap(int heapSize) {
210 | this.heapSize = heapSize;
211 | maxHeap = new int[heapSize + 1];
212 | // To better track the indices of the binary tree,
213 | // we will not use the 0-th element in the array
214 | // You can fill it with any value
215 | maxHeap[0] = 0;
216 | }
217 |
218 | // Function to add an element
219 | public void add(int element) {
220 | realSize++;
221 | // If the number of elements in the Heap exceeds the preset heapSize
222 | // print "Added too many elements" and return
223 | if (realSize > heapSize) {
224 | System.out.println("Added too many elements!");
225 | realSize--;
226 | return;
227 | }
228 | // Add the element into the array
229 | maxHeap[realSize] = element;
230 | // Index of the newly added element
231 | int index = realSize;
232 | // Parent node of the newly added element
233 | // Note if we use an array to represent the complete binary tree
234 | // and store the root node at index 1
235 | // index of the parent node of any node is [index of the node / 2]
236 | // index of the left child node is [index of the node * 2]
237 | // index of the right child node is [index of the node * 2 + 1]
238 |
239 | int parent = index / 2;
240 | // If the newly added element is larger than its parent node,
241 | // its value will be exchanged with that of the parent node
242 | while ( maxHeap[index] > maxHeap[parent] && index > 1 ) {
243 | int temp = maxHeap[index];
244 | maxHeap[index] = maxHeap[parent];
245 | maxHeap[parent] = temp;
246 | index = parent;
247 | parent = index / 2;
248 | }
249 | }
250 |
251 | // Get the top element of the Heap
252 | public int peek() {
253 | return maxHeap[1];
254 | }
255 |
256 | // Delete the top element of the Heap
257 | public int pop() {
258 | // If the number of elements in the current Heap is 0,
259 | // print "Don't have any elements" and return a default value
260 | if (realSize < 1) {
261 | System.out.println("Don't have any element!");
262 | return Integer.MIN_VALUE;
263 | } else {
264 | // When there are still elements in the Heap
265 | // realSize >= 1
266 | int removeElement = maxHeap[1];
267 | // Put the last element in the Heap to the top of Heap
268 | maxHeap[1] = maxHeap[realSize];
269 | realSize--;
270 | int index = 1;
271 | // When the deleted element is not a leaf node
272 | while (index <= realSize / 2) {
273 | // the left child of the deleted element
274 | int left = index * 2;
275 | // the right child of the deleted element
276 | int right = (index * 2) + 1;
277 | // If the deleted element is smaller than the left or right child
278 | // its value needs to be exchanged with the larger value
279 | // of the left and right child
280 | if (maxHeap[index] < maxHeap[left] || maxHeap[index] < maxHeap[right]) {
281 | if (maxHeap[left] > maxHeap[right]) {
282 | int temp = maxHeap[left];
283 | maxHeap[left] = maxHeap[index];
284 | maxHeap[index] = temp;
285 | index = left;
286 | } else {
287 | // maxHeap[left] <= maxHeap[right]
288 | int temp = maxHeap[right];
289 | maxHeap[right] = maxHeap[index];
290 | maxHeap[index] = temp;
291 | index = right;
292 | }
293 | } else {
294 | break;
295 | }
296 | }
297 | return removeElement;
298 | }
299 | }
300 |
301 | // return the number of elements in the Heap
302 | public int size() {
303 | return realSize;
304 | }
305 |
306 | public String toString() {
307 | if (realSize == 0) {
308 | return "No element!";
309 | } else {
310 | StringBuilder sb = new StringBuilder();
311 | sb.append('[');
312 | for (int i = 1; i <= realSize; i++) {
313 | sb.append(maxHeap[i]);
314 | sb.append(',');
315 | }
316 | sb.deleteCharAt(sb.length() - 1);
317 | sb.append(']');
318 | return sb.toString();
319 | }
320 | }
321 |
322 | public static void main(String[] args) {
323 | // Test case
324 | MaxHeap maxheap = new MaxHeap(5);
325 | maxheap.add(1);
326 | maxheap.add(2);
327 | maxheap.add(3);
328 | // [3,1,2]
329 | System.out.println(maxheap.toString());
330 | // 3
331 | System.out.println(maxheap.peek());
332 | // 3
333 | System.out.println(maxheap.pop());
334 | System.out.println(maxheap.pop());
335 | System.out.println(maxheap.pop());
336 | // No element
337 | System.out.println(maxheap.toString());
338 | maxheap.add(4);
339 | // Add too many elements
340 | maxheap.add(5);
341 | // [4,1,2]
342 | System.out.println(maxheap.toString());
343 | }
344 | }
345 |
346 | ```
347 |
348 | ## Heap Construction
349 |
350 | * When creating a Heap, we can simultaneously perform the **heapify** operation. Heapify means converting a group of data into a Heap.
351 | * Time complexity: $O(N)$.
352 | * Space complexity: $O(N)$.
353 |
354 | ```java
355 | // In Java, a Heap is represented by a Priority Queue
356 | import java.util.Collections;
357 | import java.util.PriorityQueue;
358 | import java.util.Arrays;
359 |
360 | // Construct an empty Min Heap
361 | PriorityQueue minHeap = new PriorityQueue<>();
362 |
363 | // Construct an empty Max Heap
364 | PriorityQueue maxHeap = new PriorityQueue<>(Collections.reverseOrder());
365 |
366 | // Construct a Heap with initial elements.
367 | // This process is named "Heapify".
368 | // The Heap is a Min Heap
369 | PriorityQueue heapWithValues= new PriorityQueue<>(Arrays.asList(3, 1, 2));
370 | ```
371 |
372 | * Inserting an element
373 | * Time complexity: $O(\log N)$
374 | * Space complexity: $O(1)$
375 |
376 | ```java
377 | // Insert an element to the Min Heap
378 | minHeap.add(5);
379 |
380 | // Insert an element to the Max Heap
381 | maxHeap.add(5);
382 | ```
383 |
384 | * Getting the top element of the heap
385 | * Time complexity: $O(1)$
386 | * Space complexity: $O(1)$
387 |
388 | ```java
389 | // Get top element from the Min Heap
390 | // i.e. the smallest element
391 | minHeap.peek();
392 | // Get top element from the Max Heap
393 | // i.e. the largest element
394 | maxHeap.peek();
395 | ```
396 |
397 | * Deleting the top element
398 | * Time complexity: $O(\log N)$
399 | * Space complexity: $O(1)$
400 |
401 | ```java
402 | // Delete top element from the Min Heap
403 | minHeap.poll();
404 |
405 | // Delete top element from the Max Heap
406 | maxheap.poll();
407 | ```
408 |
409 | * Getting the length of a heap
410 | * Time complexity: $O(1)$
411 | * Space complexity: $O(1)$
412 |
413 | ```java
414 | // Length of the Min Heap
415 | minHeap.size();
416 |
417 | // Length of the Max Heap
418 | maxHeap.size();
419 |
420 | // Note, in Java, apart from checking if the length of the Heap is 0, we can also use isEmpty()
421 | // If there are no elements in the Heap, isEmpty() will return true;
422 | // If there are still elements in the Heap, isEmpty() will return false;
423 | ```
424 |
425 | * Time and Space Complexity:
426 |
427 | | Heap method | Time complexity | Space complexity |
428 | | ---------------------- | --------------- | ---------------- |
429 | | Construct a Heap | $O(N)$ | $O(N)$ |
430 | | Insert an element | $O(\log N)$ | $O(1)$ |
431 | | Get the top element | $O(1)$ | $O(1)$ |
432 | | Delete the top element | $O(\log N)$ | $O(1)$ |
433 | | Get the size of a Heap | $O(1)$ | $O(1)$ |
434 |
435 | ## Common Methods of Heap
436 |
437 | **Min Heap**
438 |
439 | ```java
440 | // Code for Min Heap
441 | import java.util.PriorityQueue;
442 |
443 | public class App {
444 | public static void main(String[] args) {
445 | // Construct an instance of Min Heap
446 | PriorityQueue minHeap = new PriorityQueue<>();
447 |
448 | // Add 3,1,2 respectively to the Min Heap
449 | minHeap.add(3);
450 | minHeap.add(1);
451 | minHeap.add(2);
452 |
453 | // Check all elements in the Min Heap, the result is [1, 3, 2]
454 | System.out.println("minHeap: " + minHeap.toString());
455 |
456 | // Get the top element of the Min Heap
457 | int peekNum = minHeap.peek();
458 |
459 | // The result is 1
460 | System.out.println("peek number: " + peekNum);
461 |
462 | // Delete the top element in the Min Heap
463 | int pollNum = minHeap.poll();
464 |
465 | // The reult is 1
466 | System.out.println("poll number: " + pollNum);
467 |
468 | // Check the top element after deleting 1, the result is 2
469 | System.out.println("peek number: " + minHeap.peek());
470 |
471 | // Check all elements in the Min Heap, the result is [2,3]
472 | System.out.println("minHeap: " + minHeap.toString());
473 |
474 | // Check the number of elements in the Min Heap
475 | // Which is also the length of the Min Heap
476 | int heapSize = minHeap.size();
477 |
478 | // The result is 2
479 | System.out.println("minHeap size: " + heapSize);
480 |
481 | // Check if the Min Heap is empty
482 | boolean isEmpty = minHeap.isEmpty();
483 |
484 | // The result is false
485 | System.out.println("isEmpty: " + isEmpty);
486 | }
487 | }
488 | ```
489 |
490 | **Max Heap**
491 |
492 | ```java
493 | // Code for Max Heap
494 | import java.util.Collections;
495 | import java.util.PriorityQueue;
496 |
497 | public class App {
498 | public static void main(String[] args) {
499 | // Construct an instance of Max Heap
500 | PriorityQueue maxHeap = new PriorityQueue<>(Collections.reverseOrder());
501 |
502 | // Add 1,3,2 respectively to the Max Heap
503 | maxHeap.add(1);
504 | maxHeap.add(3);
505 | maxHeap.add(2);
506 |
507 | // Check all elements in the Max Heap, the result is [3, 1, 2]
508 | System.out.println("maxHeap: " + maxHeap.toString());
509 |
510 | // Get the top element of the Max Heap
511 | int peekNum = maxHeap.peek();
512 |
513 | // The result is 3
514 | System.out.println("peek number: " + peekNum);
515 |
516 | // Delete the top element in the Max Heap
517 | int pollNum = maxHeap.poll();
518 |
519 | // The reult is 3
520 | System.out.println("poll number: " + pollNum);
521 |
522 | // Check the top element after deleting 3, the result is 2
523 | System.out.println("peek number: " + maxHeap.peek());
524 |
525 | // Check all elements in the Max Heap, the result is [2,1]
526 | System.out.println("maxHeap: " + maxHeap.toString());
527 |
528 | // Check the number of elements in the Max Heap
529 | // Which is also the length of the Max Heap
530 | int heapSize = maxHeap.size();
531 |
532 | // The result is 2
533 | System.out.println("maxHeap size: " + heapSize);
534 |
535 | // Check if the Max Heap is empty
536 | boolean isEmpty = maxHeap.isEmpty();
537 |
538 | // The result is false
539 | System.out.println("isEmpty: " + isEmpty);
540 | }
541 | }
542 | ```
543 |
544 | ## Heap Sort
545 |
546 | The sorting algorithm using a **Min Heap** is as follows:
547 |
548 | 1. Heapify all elements into a Min Heap.
549 | 2. Record and delete the top element.
550 | 3. Put the top element into an array T that stores all sorted elements. Now, the Heap will remain a Min Heap.
551 | 4. Repeat steps 2 and 3 until the Heap is empty. The array T will contain all elements sorted in ascending order.
552 |
553 | The sorting algorithm using a **Max Heap** is as follows:
554 |
555 | 1. Heapify all elements into a Max Heap.
556 | 2. Record and delete the top element.
557 | 3. Put the top element into an array T that stores all sorted elements. Now, the Heap will remain a Max Heap.
558 | 4. Repeat steps 2 and 3 until the Heap is empty. The array T will contain all elements sorted in descending order.
559 |
560 | * **Complexity Analysis:**
561 | * Let N be the total number of elements.
562 | * Time complexity: $O(N \log N)$
563 | * Space complexity: $O(N)$
564 |
565 | ## The Top K Problem
566 |
567 | Solution of the Top K largest elements:
568 |
569 | 1. Construct a Max Heap.
570 | 2. Add all elements into the Max Heap.
571 | 3. Traversing and deleting the top element (using pop() or poll() for instance), and storing the value into the result array T.
572 | 4. Repeat step 3 until we have removed the K largest elements.
573 |
574 | **Complexity Analysis**
575 |
576 | * Time complexity: $O(K \log N + N)$
577 | * Steps one and two require us to construct a Max Heap which requires $O(N)$ time using the previously discussed heapify method. Each element removed from the heap requires $O(\log N)$ time; this process is repeated K*K* times. Thus the total time complexity is $O(K \log N + N)$.
578 |
579 | * Space complexity: $O(N)$
580 | * After step 2, the heap will store all N elements.
581 |
582 | ## The K-th Element
583 |
584 | ### Approach 1
585 |
586 | * Solution of the K-th largest element:
587 |
588 | 1. Construct a Max Heap.
589 | 2. Add all elements into the Max Heap.
590 | 3. Traversing and deleting the top element (using pop() or poll() for instance).
591 | 4. Repeat Step 3 K times until we find the K-th largest element.
592 |
593 | * Let N be the total number of elements.
594 |
595 | Time complexity: $O(K \log N + N)$
596 |
597 | - Steps one and two require us to construct a Max Heap which requires O(N) time using the previously discussed heapify method. Each element removed from the heap requires $O(\log N)$ time; this process is repeated K times. Thus the total time complexity is $O(K \log N + N)$.
598 |
599 | Space complexity: $O(N)$
600 |
601 | - After step 2, the heap will store all N elements.
602 |
603 | ### Approach 2
604 |
605 | * Solution of the K-th largest element:
606 |
607 | 1. Construct a Min Heap with size K.
608 | 2. Add elements to the Min Heap one by one.
609 | 3. When there are K elements in the “Min Heap”, compare the current element with the top element of the Heap:
610 | - If the current element is not larger than the top element of the Heap, drop it and proceed to the next element.
611 | - If the current element is larger than the Heap’s top element, delete the Heap’s top element, and add the current element to the “Min Heap”.
612 | 4. Repeat Steps 2 and 3 until all elements have been iterated.
613 |
614 | Now the top element in the Min Heap is the K-th largest element.
615 |
616 | * Complexity:
617 |
618 | * Time complexity: $O(N \log K)$
619 |
620 | - Steps one and two will require $O(K \log K)$ time if the elements are added one by one to the heap, however using the heapify method, these two steps could be accomplished in $O(K)$ time. Steps 3 and 4 will require $O(\log K)$ time each time an element must be replaced in the heap. In the worst-case scenario, this will be done N - K times. Thus the total time complexity is $O((N - K) \log K + K \log K)$ which simplifies to $O(N \log K)$.
621 |
622 | Space complexity: $O(K)$
623 |
624 | - The heap will contain at most K elements at any given time.
625 |
626 |
--------------------------------------------------------------------------------
/Binary Search/Binary Search Problems Part #1.md:
--------------------------------------------------------------------------------
1 | # Binary Search Problems Part #1
2 |
3 | ## Closest Binary Search Tree Value(Easy #270)
4 |
5 | **Question**: Given the `root` of a binary search tree and a `target` value, return *the value in the BST that is closest to the* `target`
6 |
7 | **Example 1:**
8 |
9 | 
10 |
11 | ```
12 | Input: root = [4,2,5,1,3], target = 3.714286
13 | Output: 4
14 | ```
15 |
16 | **Example 2:**
17 |
18 | ```
19 | Input: root = [1], target = 4.428571
20 | Output: 1
21 | ```
22 |
23 | **Constraints:**
24 |
25 | - The number of nodes in the tree is in the range `[1, 104]`.
26 | - `0 <= Node.val <= 109`
27 | - `-109 <= target <= 109`
28 |
29 | ### My Solution
30 |
31 | * In order recursively find the distance between the value and the target
32 | * Compare the distance and record the root value
33 |
34 | ```java
35 | class Solution {
36 | int value = 0;
37 | public int closestValue(TreeNode root, double target) {
38 | double distance = Double.POSITIVE_INFINITY;
39 | findValue(root, target, distance);
40 | return value;
41 | }
42 | // recursively find the value near target
43 | public double findValue(TreeNode root, double target, double distance){
44 | if (root == null){
45 | return distance;
46 | }
47 | distance = findValue(root.left, target, distance);
48 | if ((double)Math.abs(target - root.val) < distance){
49 | distance = (double)Math.abs(target - root.val);
50 | value = root.val;
51 | }
52 | distance = findValue(root.right, target, distance);
53 | return distance;
54 | }
55 | }
56 | ```
57 |
58 | ### Standard Solution
59 |
60 | #### Solution #1 Recursive Inorder + Linear Search
61 |
62 | * Recursively use the list to record all the value
63 | * Create a customized comparator for comparison
64 |
65 | ```java
66 | public void inorder(TreeNode root, List nums){
67 | if (root == null) return;
68 | inorder(root.left, nums);
69 | nums.add(root.val);
70 | inorder(root.right, nums);
71 | }
72 | public int closestValue(TreeNode root, double target){
73 | List nums = new ArrayList();
74 | inorder(root, nums); // put all values to the list
75 | return Collections.min(nums, new Comparator(){
76 | @Override
77 | public int compare(Integer o1, Integer o2){
78 | return Math.abs(o1 - target) < Math.abs(o2 - target) ? -1 : 1;
79 | }
80 | });
81 | }
82 | ```
83 |
84 | - Time complexity: $\mathcal{O}(N)$ because to build in order traversal and then to perform linear search takes linear time.
85 | - Space complexity: $\mathcal{O}(N)$ to keep in order traversal.
86 |
87 | #### Solution #2 Binary Search, O(H) time
88 |
89 | * Use the properties of the binary search tree
90 |
91 |  92 |
93 | ```java
94 | public int closestValue(TreeNode root, double target){
95 | int val, closest = root.val;
96 | while (root != null){
97 | val = root.val;
98 | closest = Math.abs(val - target) < Math.abs(closest - target) ? val : closest;
99 | root = target < root.val ? root.left : root.right;
100 | }
101 | return closest;
102 | }
103 | ```
104 |
105 | - Time complexity: $\mathcal{O}(H)$ since here one goes from root down to a leaf.
106 | - Space complexity: $\mathcal{O}(1)$.
107 |
108 | ## Search in a Sorted Array of Unknown Size(Medium #702)
109 |
110 | **Question**: This is an ***interactive problem***.
111 |
112 | You have a sorted array of **unique** elements and an **unknown size**. You do not have an access to the array but you can use the `ArrayReader` interface to access it. You can call `ArrayReader.get(i)` that:
113 |
114 | - returns the value at the `ith` index (**0-indexed**) of the secret array (i.e., `secret[i]`), or
115 | - returns `231 - 1` if the `i` is out of the boundary of the array.
116 |
117 | You are also given an integer `target`.
118 |
119 | Return the index `k` of the hidden array where `secret[k] == target` or return `-1` otherwise.
120 |
121 | You must write an algorithm with `O(log n)` runtime complexity.
122 |
123 | **Example 1:**
124 |
125 | ```
126 | Input: secret = [-1,0,3,5,9,12], target = 9
127 | Output: 4
128 | Explanation: 9 exists in secret and its index is 4.
129 | ```
130 |
131 | **Example 2:**
132 |
133 | ```
134 | Input: secret = [-1,0,3,5,9,12], target = 2
135 | Output: -1
136 | Explanation: 2 does not exist in secret so return -1.
137 | ```
138 |
139 | **Constraints:**
140 |
141 | - `1 <= secret.length <= 104`
142 | - `-104 <= secret[i], target <= 104`
143 | - `secret` is sorted in a strictly increasing order.
144 |
145 | ### My Solution
146 |
147 | * Binary search method
148 |
149 | ```java
150 | public int search(ArrayReader reader, int target) {
151 | int max = (int)Math.pow(10, 4);
152 | int low = 0;
153 | while (low < max){
154 | int mid = low + (max - low) / 2;
155 | int value = reader.get(mid);
156 | if (value > target){
157 | max = mid - 1;
158 | }
159 | else if (value < target){
160 | low = mid + 1;
161 | }
162 | else {
163 | return mid;
164 | }
165 | }
166 | return reader.get(low) == target ? low : -1;
167 | }
168 | ```
169 |
170 | ### Standard Solution
171 |
172 | #### Solution #1 Binary Search + Bit Operation
173 |
174 | ```java
175 | class Solution {
176 | public int search(ArrayReader reader, int target) {
177 | if (reader.get(0) == target) return 0;
178 | // search boundaries
179 | int left = 0, right = 1;
180 | while (reader.get(right) < target) {
181 | left = right;
182 | right <<= 1;
183 | }
184 | // binary search
185 | int pivot, num;
186 | while (left <= right) {
187 | pivot = left + ((right - left) >> 1);
188 | num = reader.get(pivot);
189 |
190 | if (num == target) return pivot;
191 | if (num > target) right = pivot - 1;
192 | else left = pivot + 1;
193 | }
194 | // there is no target element
195 | return -1;
196 | }
197 | }
198 | ```
199 |
200 | - Time complexity: $\mathcal{O}(\log T)$, where T is an index of the target value.
201 |
202 | There are two operations here: to define search boundaries and to perform a binary search.
203 |
204 | Let's first find the number of steps k to set up the boundaries. In the first step, the boundaries are $2^0 .. 2^{0 + 1}$, on the second step $2^1 .. 2^{1 + 1}$, etc. When everything is done, the boundaries are $2^k .. 2^{k + 1}$ and $2^k < T \le 2^{k + 1}$. That means one needs $k = \log T$ steps to set up the boundaries, that means $\mathcal{O}(\log T)$ time complexity.
205 |
206 | Now let's discuss the complexity of the binary search. There are $2^{k + 1} - 2^k = 2^k$ elements in the boundaries, i.e. $2^{\log T} = T2$ elements. Binary search has logarithmic complexity, which results in $\mathcal{O}(\log T)$ time complexity.
207 |
208 | - Space complexity: $\mathcal{O}(1)$ since it's a constant space solution.
209 |
210 | ## Valid Perfect Square(Easy #367)
211 |
212 | **Question**: Given a **positive** integer *num*, write a function that returns True if *num* is a perfect square else False.
213 |
214 | **Follow up:** **Do not** use any built-in library function such as `sqrt`.
215 |
216 | **Example 1:**
217 |
218 | ```
219 | Input: num = 16
220 | Output: true
221 | ```
222 |
223 | **Example 2:**
224 |
225 | ```
226 | Input: num = 14
227 | Output: false
228 | ```
229 |
230 | **Constraints:**
231 |
232 | - `1 <= num <= 2^31 - 1`
233 |
234 | ### My Solution
235 |
236 | * Use binary search to find mid, check if the square larger or smaller than the target
237 |
238 | ```java
239 | public boolean isPerfectSquare(int num) {
240 | if (num == 0 || num == 1){
241 | return true;
242 | }
243 | if (num < 0){
244 | return false;
245 | }
246 | int low = 1, high = num / 2;
247 | while (low < high){
248 | int mid = low + (high - low) / 2;
249 | if ((long)mid * mid < num){
250 | low = mid + 1;
251 | }
252 | else if ((long)mid * mid > num){
253 | high = mid - 1;
254 | }
255 | else {
256 | return true;
257 | }
258 | }
259 | return low * low == num ? true : false;
260 | }
261 | ```
262 |
263 | ### Standard Solution
264 |
265 | #### Solution #1 Binary Search
266 |
267 | * Almost the same as my solution
268 |
269 | ```java
270 | public boolean isPerfectSquare(int num) {
271 | if (num < 2) {
272 | return true;
273 | }
274 | long left = 2, right = num / 2, x, guessSquared;
275 | while (left <= right) {
276 | x = left + (right - left) / 2;
277 | guessSquared = x * x;
278 | if (guessSquared == num) {
279 | return true;
280 | }
281 | if (guessSquared > num) {
282 | right = x - 1;
283 | } else {
284 | left = x + 1;
285 | }
286 | }
287 | return false;
288 | }
289 | ```
290 |
291 | * Time complexity: $\mathcal{O}(\log N)$.
292 | * Space complexity: $\mathcal{O}(1)$.
293 |
294 | ## Find Smallest Letter Greater Than Target (Easy #744)
295 |
296 | **Question**: Given a characters array `letters` that is sorted in **non-decreasing** order and a character `target`, return *the smallest character in the array that is larger than* `target`.
297 |
298 | **Note** that the letters wrap around.
299 |
300 | - For example, if `target == 'z'` and `letters == ['a', 'b']`, the answer is `'a'`.
301 |
302 | **Example 1:**
303 |
304 | ```
305 | Input: letters = ["c","f","j"], target = "a"
306 | Output: "c"
307 | ```
308 |
309 | **Example 2:**
310 |
311 | ```
312 | Input: letters = ["c","f","j"], target = "c"
313 | Output: "f"
314 | ```
315 |
316 | **Example 3:**
317 |
318 | ```
319 | Input: letters = ["c","f","j"], target = "d"
320 | Output: "f"
321 | ```
322 |
323 | **Constraints:**
324 |
325 | - `2 <= letters.length <= 104`
326 | - `letters[i]` is a lowercase English letter.
327 | - `letters` are sorted in **non-decreasing** order.
328 | - `letters` contain at least two different characters.
329 | - `target` is a lowercase English letter.
330 |
331 | ### My Solution
332 |
333 | * Calculate the relative distance
334 |
335 | ```java
336 | public char nextGreatestLetter(char[] letters, char target) {
337 | int distance = 0;
338 | int minDistance = Integer.MAX_VALUE;
339 | char res = 'a';
340 | for (char letter : letters){
341 | if (letter >= target){
342 | distance = letter - target;
343 | }
344 | else {
345 | distance = 'z' - target + letter - 'a' + 1;
346 | }
347 | if (distance > 0 && distance < minDistance){
348 | minDistance = distance;
349 | res = letter;
350 | }
351 | }
352 | return res;
353 | }
354 | ```
355 |
356 | ### Standard Solution
357 |
358 | #### Solution #1 Linear Scan
359 |
360 | * The question asks for the letter, not distance, don't need to calculate the distance
361 | * Just loop through the letters and find the one that meets the requirement
362 |
363 | ```java
364 | class Solution {
365 | public char nextGreatestLetter(char[] letters, char target) {
366 | for (char c: letters)
367 | if (c > target) return c;
368 | return letters[0];
369 | }
370 | }
371 | ```
372 |
373 | - Time Complexity: $O(N)$, where N is the length of `letters`. We scan every element of the array.
374 | - Space Complexity: $O(1)$, as we maintain only pointers.
375 |
376 | #### Solution #2 Binary Search
377 |
378 | * Binary search method to check if the letter is larger than the target
379 |
380 | ```java
381 | public char nextGreatestLetter(char[] letters, char target) {
382 | int lo = 0, hi = letters.length;
383 | while (lo < hi) {
384 | int mi = lo + (hi - lo) / 2;
385 | if (letters[mi] <= target) lo = mi + 1;
386 | else hi = mi;
387 | }
388 | return letters[lo % letters.length];
389 | }
390 | ```
391 |
392 | - Time Complexity: $O(\log N)$, where N is the length of `letters`. We peek only at $\log N$ elements in the array.
393 | - Space Complexity: $O(1)$, as we maintain only pointers.
394 |
395 | ## Find Minimum in Rotated Sorted Array II (Hard #154)
396 |
397 | **Question**: Suppose an array of length `n` sorted in ascending order is **rotated** between `1` and `n` times. For example, the array `nums = [0,1,4,4,5,6,7]` might become:
398 |
399 | - `[4,5,6,7,0,1,4]` if it was rotated `4` times.
400 | - `[0,1,4,4,5,6,7]` if it was rotated `7` times.
401 |
402 | Notice that **rotating** an array `[a[0], a[1], a[2], ..., a[n-1]]` 1 time results in the array `[a[n-1], a[0], a[1], a[2], ..., a[n-2]]`.
403 |
404 | Given the sorted rotated array `nums` that may contain **duplicates**, return *the minimum element of this array*.
405 |
406 | You must decrease the overall operation steps as much as possible.
407 |
408 | **Example 1:**
409 |
410 | ```
411 | Input: nums = [1,3,5]
412 | Output: 1
413 | ```
414 |
415 | **Example 2:**
416 |
417 | ```
418 | Input: nums = [2,2,2,0,1]
419 | Output: 0
420 | ```
421 |
422 | **Constraints:**
423 |
424 | - `n == nums.length`
425 | - `1 <= n <= 5000`
426 | - `-5000 <= nums[i] <= 5000`
427 | - `nums` is sorted and rotated between `1` and `n` times.
428 |
429 | ### Standard Solution
430 |
431 | #### Solution #1 Variant of Binary Search
432 |
433 | * Compare the pivot element to the element pointed by the upper bound pointer
434 | * We use the upper bound of the search scope as the reference for the comparison with the pivot element, while in the classical binary search the reference would be the desired value.
435 | * When the result of the comparison is equal (*i.e.* Case #3), we further move the upper bound, while in the classical binary search normally we would return the value immediately.
436 |
437 | ```java
438 | public int findMin(int[] nums) {
439 | int low = 0, high = nums.length - 1;
440 | while (low < high){
441 | int mid = low + (high - low) / 2;
442 | if (nums[mid] > nums[high]){
443 | low = mid + 1;
444 | }
445 | else if (nums[mid] < nums[high]) {
446 | high = mid;
447 | }
448 | // change the edge value since it is valid
449 | else {
450 | high--;
451 | }
452 | }
453 | return nums[low];
454 | }
455 | ```
456 |
457 | - Time complexity: on average $\mathcal{O}(\log_{2}{N})$ where N is the length of the array, since in general, it is a binary search algorithm. However, in the worst case where the array contains identical elements (*i.e.* case #3 `nums[pivot]==nums[high]`), the algorithm would deteriorate to iterating each element, as a result, the time complexity becomes $\mathcal{O}(N)$.
458 | - Space complexity: $\mathcal{O}(1)$, it's a constant space solution.
459 |
460 | ## Median of Two Sorted Array(Hard #4)
461 |
462 | **Question**: Given two sorted arrays `nums1` and `nums2` of size `m` and `n` respectively, return **the median** of the two sorted arrays.
463 |
464 | The overall run time complexity should be `O(log (m+n))`.
465 |
466 | **Example 1:**
467 |
468 | ```
469 | Input: nums1 = [1,3], nums2 = [2]
470 | Output: 2.00000
471 | Explanation: merged array = [1,2,3] and median is 2.
472 | ```
473 |
474 | **Example 2:**
475 |
476 | ```
477 | Input: nums1 = [1,2], nums2 = [3,4]
478 | Output: 2.50000
479 | Explanation: merged array = [1,2,3,4] and median is (2 + 3) / 2 = 2.5.
480 | ```
481 |
482 | **Constraints:**
483 |
484 | - `nums1.length == m`
485 | - `nums2.length == n`
486 | - `0 <= m <= 1000`
487 | - `0 <= n <= 1000`
488 | - `1 <= m + n <= 2000`
489 | - `-106 <= nums1[i], nums2[i] <= 106`
490 |
491 | ### My Solution
492 |
493 | ```java
494 | public double findMedianSortedArrays(int[] nums1, int[] nums2) {
495 | int length = nums1.length + nums2.length;
496 | int[] nums = new int[length];
497 | for (int i = 0; i < nums1.length; i++){
498 | nums[i] = nums1[i];
499 | }
500 | for (int i = nums1.length; i < length; i++){
501 | nums[i] = nums2[i - nums1.length];
502 | }
503 | Arrays.sort(nums);
504 | double median = 0.0;
505 | // find the median of the aggregated array
506 | if (length % 2 == 1){
507 | median = nums[length/ 2];
508 | }
509 | else {
510 | median = ((double)nums[(length - 1)/ 2] + (double)nums[(length - 1) / 2 + 1]) / 2;
511 | }
512 | return median;
513 | }
514 | ```
515 |
516 | ### Other Solution
517 |
518 | * Binary search and compare two value
519 |
520 | ```java
521 | public double findMedianSortedArrays(int[] nums1, int[] nums2) {
522 | int index1 = 0;
523 | int index2 = 0;
524 | int med1 = 0;
525 | int med2 = 0;
526 | for (int i=0; i<=(nums1.length+nums2.length)/2; i++) {
527 | med1 = med2;
528 | if (index1 == nums1.length) {
529 | med2 = nums2[index2];
530 | index2++;
531 | } else if (index2 == nums2.length) {
532 | med2 = nums1[index1];
533 | index1++;
534 | } else if (nums1[index1] < nums2[index2] ) {
535 | med2 = nums1[index1];
536 | index1++;
537 | } else {
538 | med2 = nums2[index2];
539 | index2++;
540 | }
541 | }
542 |
543 | // the median is the average of two numbers
544 | if ((nums1.length+nums2.length)%2 == 0) {
545 | return (float)(med1+med2)/2;
546 | }
547 | return med2;
548 | }
549 | ```
550 |
551 | ## Find k-th Smallest Pair Distance (Hard #719)
552 |
553 | **Question**: The **distance of a pair** of integers `a` and `b` is defined as the absolute difference between `a` and `b`.
554 |
555 | Given an integer array `nums` and an integer `k`, return *the* `kth` *smallest **distance among all the pairs*** `nums[i]` *and* `nums[j]` *where* `0 <= i < j < nums.length`.
556 |
557 | **Example 1:**
558 |
559 | ```
560 | Input: nums = [1,3,1], k = 1
561 | Output: 0
562 | Explanation: Here are all the pairs:
563 | (1,3) -> 2
564 | (1,1) -> 0
565 | (3,1) -> 2
566 | Then the 1st smallest distance pair is (1,1), and its distance is 0.
567 | ```
568 |
569 | **Example 2:**
570 |
571 | ```
572 | Input: nums = [1,1,1], k = 2
573 | Output: 0
574 | ```
575 |
576 | **Example 3:**
577 |
578 | ```
579 | Input: nums = [1,6,1], k = 3
580 | Output: 5
581 | ```
582 |
583 | **Constraints:**
584 |
585 | - `n == nums.length`
586 | - `2 <= n <= 104`
587 | - `0 <= nums[i] <= 106`
588 | - `1 <= k <= n * (n - 1) / 2`
589 |
590 | ### Standard Solution
591 |
592 | #### Solution #1 Binary Search
593 |
594 | * Find low distance, and high distance, use binary search
595 |
596 | ```java
597 | public int smallestDistancePair(int[] nums, int k) {
598 | // sort the array and then do the binary search
599 | Arrays.sort(nums);
600 |
601 | int lo = 0;
602 | int hi = nums[nums.length - 1] - nums[0];
603 | while (lo < hi) {
604 | int mi = (lo + hi) / 2;
605 | int count = 0, left = 0;
606 | for (int right = 0; right < nums.length; right++){
607 | // find out how many count of pairs with distance <= mi
608 | while (nums[right] - nums[left] > mi) left++;
609 | count += right - left;
610 | }
611 | // count = number of pairs with distance <= mi
612 | if (count >= k) hi = mi;
613 | else lo = mi + 1;
614 | }
615 | return lo;
616 | }
617 | ```
618 |
619 | - Time Complexity: $O(N \log{W} + N \log{N})$, where N is the length of `nums`, and W*W* is equal to `nums[nums.length - 1] - nums[0]`. The $\log W$ factor comes from our binary search, and we do $O(N)$ work inside our call to `possible` (or to calculate `count` in Java). The final $O(N\log N)$ factor comes from sorting.
620 | - Space Complexity: $O(1)$. No additional space is used except for integer variables.
621 |
622 | ## Split Array Largest Sum (Hard #410)
623 |
624 | **Question**: Given an array `nums` which consists of non-negative integers and an integer `m`, you can split the array into `m` non-empty continuous subarrays.
625 |
626 | Write an algorithm to minimize the largest sum among these `m` subarrays.
627 |
628 | **Example 1:**
629 |
630 | ```
631 | Input: nums = [7,2,5,10,8], m = 2
632 | Output: 18
633 | Explanation:
634 | There are four ways to split nums into two subarrays.
635 | The best way is to split it into [7,2,5] and [10,8],
636 | where the largest sum among the two subarrays is only 18.
637 | ```
638 |
639 | **Example 2:**
640 |
641 | ```
642 | Input: nums = [1,2,3,4,5], m = 2
643 | Output: 9
644 | ```
645 |
646 | **Example 3:**
647 |
648 | ```
649 | Input: nums = [1,4,4], m = 3
650 | Output: 4
651 | ```
652 |
653 | **Constraints:**
654 |
655 | - `1 <= nums.length <= 1000`
656 | - `0 <= nums[i] <= 106`
657 | - `1 <= m <= min(50, nums.length)`
658 |
659 | ### Standard Solution
660 |
661 | #### Solution #1 Binary Search
662 |
663 | * Not only use binary search on array index but also use it for value search
664 | * Check if the target value converge
665 |
666 | ```java
667 | private int minimumSubarraysRequired(int[] nums, int maxSumAllowed) {
668 | int currentSum = 0;
669 | int splitsRequired = 0;
670 | for (int element : nums) {
671 | // Add element only if the sum doesn't exceed maxSumAllowed
672 | if (currentSum + element <= maxSumAllowed) {
673 | currentSum += element;
674 | } else {
675 | // If the element addition makes sum more than maxSumAllowed
676 | // Increment the splits required and reset sum
677 | currentSum = element;
678 | splitsRequired++;
679 | }
680 | }
681 | // Return the number of subarrays, which is the number of splits + 1
682 | return splitsRequired + 1;
683 | }
684 |
685 | public int splitArray(int[] nums, int m) {
686 | // Find the sum of all elements and the maximum element
687 | int sum = 0;
688 | int maxElement = Integer.MIN_VALUE;
689 | for (int element : nums) {
690 | sum += element;
691 | maxElement = Math.max(maxElement, element);
692 | }
693 | // Define the left and right boundary of binary search
694 | int left = maxElement;
695 | int right = sum;
696 | int minimumLargestSplitSum = 0;
697 | while (left <= right) {
698 | // Find the mid value
699 | int maxSumAllowed = left + (right - left) / 2;
700 | // Find the minimum splits. If splitsRequired is less than
701 | // or equal to m move towards left i.e., smaller values
702 | if (minimumSubarraysRequired(nums, maxSumAllowed) <= m) {
703 | right = maxSumAllowed - 1;
704 | minimumLargestSplitSum = maxSumAllowed;
705 | } else {
706 | // Move towards right if splitsRequired is more than m
707 | left = maxSumAllowed + 1;
708 | }
709 | }
710 | return minimumLargestSplitSum;
711 | }
712 | ```
713 |
714 | - Time complexity: $O(N \cdot \log(S))$, where N is the length of the array and S is the sum of integers in the array.
715 |
716 | The total number of iterations in the binary search is $\log(S)$, and for each such iteration, we call `minimumSubarraysRequired` which takes $O(N)$ time. Hence, the time complexity is equal to $O(N \cdot \log(S))$.
717 |
718 | - Space complexity: $O(1)$
719 |
720 | We do not use any data structures that require more than constant extra space.
721 |
722 | ## 3Sum Closest (Medium #16)
723 |
724 | **Question**: Given an integer array `nums` of length `n` and an integer `target`, find three integers in `nums` such that the sum is closest to `target`.
725 |
726 | Return *the sum of the three integers*.
727 |
728 | You may assume that each input would have exactly one solution.
729 |
730 | **Example 1:**
731 |
732 | ```
733 | Input: nums = [-1,2,1,-4], target = 1
734 | Output: 2
735 | Explanation: The sum that is closest to the target is 2. (-1 + 2 + 1 = 2).
736 | ```
737 |
738 | **Example 2:**
739 |
740 | ```
741 | Input: nums = [0,0,0], target = 1
742 | Output: 0
743 | ```
744 |
745 | **Constraints:**
746 |
747 | - `3 <= nums.length <= 1000`
748 | - `-1000 <= nums[i] <= 1000`
749 | - `-104 <= target <= 104`
750 |
751 | ### Standard Solution
752 |
753 | #### Solution #1 Two Pointers
754 |
755 | * Use for loop and three-pointers, calculate the sum
756 | * Compare the sum with the target, if smaller, move the low pointer, if higher, move the high pointer
757 |
758 | ```java
759 | public int threeSumClosest(int[] nums, int target) {
760 | int diff = Integer.MAX_VALUE;
761 | int sz = nums.length;
762 | Arrays.sort(nums);
763 | for (int i = 0; i < sz && diff != 0; i++){
764 | int lo = i + 1;
765 | int hi = sz - 1;
766 | while (lo < hi){
767 | int sum = nums[i] + nums[lo] + nums[hi];
768 | if (Math.abs(target - sum) < Math.abs(diff)){
769 | diff = target - sum;
770 | }
771 | if (sum < target){
772 | lo++;
773 | }
774 | else {
775 | hi--;
776 | }
777 | }
778 | }
779 | return target - diff;
780 | }
781 | ```
782 |
783 | - Time Complexity: $\mathcal{O}(n^2)$. We have outer and inner loops, each going through n elements.
784 |
785 | Sorting the array takes $\mathcal{O}(n\log{n})$, so overall complexity is $\mathcal{O}(n\log{n} + n^2)$. This is asymptotically equivalent to $\mathcal{O}(n^2)$.
786 |
787 | - Space Complexity: from $\mathcal{O}(\log{n})$ to $\mathcal{O}(n)$, depending on the implementation of the sorting algorithm.
788 |
789 | #### Solution #2 Binary Search
790 |
791 | ```java
792 | public int threeSumClosest(int[] nums, int target) {
793 | int diff = Integer.MAX_VALUE;
794 | int sz = nums.length;
795 | Arrays.sort(nums);
796 | for (int i = 0; i < sz && diff != 0; ++i) {
797 | for (int j = i + 1; j < sz - 1; ++j) {
798 | int complement = target - nums[i] - nums[j];
799 | var idx = Arrays.binarySearch(nums, j + 1, sz - 1, complement);
800 | int hi = idx >= 0 ? idx : ~idx, lo = hi - 1;
801 | if (hi < sz && Math.abs(complement - nums[hi]) < Math.abs(diff))
802 | diff = complement - nums[hi];
803 | if (lo > j && Math.abs(complement - nums[lo]) < Math.abs(diff))
804 | diff = complement - nums[lo];
805 | }
806 | }
807 | return target - diff;
808 | }
809 | ```
810 |
811 | - Time Complexity: $\mathcal{O}(n^2\log{n})$. Binary search takes $\mathcal{O}(\log{n})$, and we do it n times in the inner loop. Since we are going through n elements in the outer loop, the overall complexity is $\mathcal{O}(n^2\log{n})$.
812 | - Space Complexity: from $\mathcal{O}(\log{n})$ to $\mathcal{O}(n)$, depending on the implementation of the sorting algorithm.
--------------------------------------------------------------------------------
/Queue & Stack/Queue Problems Part #1.md:
--------------------------------------------------------------------------------
1 | # Queue Problems Part #1
2 |
3 | ## Design Hit Counter(Medium #362)
4 |
5 | **Question**: Design a hit counter which counts the number of hits received in the past `5` minutes (i.e., the past `300` seconds).
6 |
7 | Your system should accept a `timestamp` parameter (**in seconds** granularity), and you may assume that calls are being made to the system in chronological order (i.e., `timestamp` is monotonically increasing). Several hits may arrive roughly at the same time.
8 |
9 | Implement the `HitCounter` class:
10 |
11 | - `HitCounter()` Initializes the object of the hit counter system.
12 | - `void hit(int timestamp)` Records a hit that happened at `timestamp` (**in seconds**). Several hits may happen at the same `timestamp`.
13 | - `int getHits(int timestamp)` Returns the number of hits in the past 5 minutes from `timestamp` (i.e., the past `300` seconds).
14 |
15 | **Example 1:**
16 |
17 | ```
18 | Input
19 | ["HitCounter", "hit", "hit", "hit", "getHits", "hit", "getHits", "getHits"]
20 | [[], [1], [2], [3], [4], [300], [300], [301]]
21 | Output
22 | [null, null, null, null, 3, null, 4, 3]
23 |
24 | Explanation
25 | HitCounter hitCounter = new HitCounter();
26 | hitCounter.hit(1); // hit at timestamp 1.
27 | hitCounter.hit(2); // hit at timestamp 2.
28 | hitCounter.hit(3); // hit at timestamp 3.
29 | hitCounter.getHits(4); // get hits at timestamp 4, return 3.
30 | hitCounter.hit(300); // hit at timestamp 300.
31 | hitCounter.getHits(300); // get hits at timestamp 300, return 4.
32 | hitCounter.getHits(301); // get hits at timestamp 301, return 3.
33 | ```
34 |
35 | **Constraints:**
36 |
37 | - `1 <= timestamp <= 2 * 109`
38 | - All the calls are being made to the system in chronological order (i.e., `timestamp` is monotonically increasing).
39 | - At most `300` calls will be made to `hit` and `getHits`.
40 |
41 | ### My Solution
42 |
43 | ```java
44 | class HitCounter {
45 | private LinkedList hitQueue;
46 |
47 | public HitCounter() {
48 | hitQueue = new LinkedList();
49 | }
50 | public void hit(int timestamp) {
51 | this.hitQueue.addLast(timestamp);
52 | }
53 | /** return number of hits in the past 5 mins**/
54 | private int findHitsInPast5Min(int pastTime){
55 |
56 | while(this.hitQueue.peekFirst() != null){
57 | if (this.hitQueue.getFirst() <= pastTime){
58 | this.hitQueue.removeFirst();
59 | }
60 | else break;
61 | }
62 | return this.hitQueue.size();
63 | }
64 | public int getHits(int timestamp) {
65 | int pastTime = timestamp - 300;
66 | return findHitsInPast5Min(pastTime);
67 | }
68 | }
69 |
70 | /**
71 | * Your HitCounter object will be instantiated and called as such:
72 | * HitCounter obj = new HitCounter();
73 | * obj.hit(timestamp);
74 | * int param_2 = obj.getHits(timestamp);
75 | */
76 | ```
77 |
78 | ### Standard Solution
79 |
80 | #### Solution #1 Queue
81 |
82 | * Similar to my solution: all the timestamps that we will encounter are going to be in increasing order.
83 | * Should be clean of API doc comments
84 | * This is the case of considering the elements in the FIFO manner (First in first out) which is best solved by using the "queue" data structure.
85 |
86 | ```java
87 | class HitCounter{
88 | private Queue hits;
89 |
90 | /** Initialize your data structure here.**/
91 | public HitCounter(){
92 | this.hits = new LinkedList();
93 | }
94 |
95 | /**
96 | * Record a hit
97 | * @param timestamp
98 | */
99 | public void hit(int timestamp){
100 | this.hits.add(timestamp);
101 | }
102 |
103 | /**
104 | * Return the number of hits in the past 5 minutes
105 | * @param timestamp
106 | */
107 | public int getHits(int timestamp){
108 | while (!this.hits.isEmpty()){
109 | int diff = timestamp - this.hits.peek();
110 | if (diff >= 300) this.hits.remove();
111 | else break;
112 | }
113 | return this.hits.size();
114 | }
115 | }
116 | ```
117 |
118 | * Time complexity: `hit` is $O(1)$, while `getHits` is $O(N)$.
119 | * Space complexity: The queue can have up to N elements, hence overall space complexity of the approach is $O(N)$
120 |
121 | #### Solution #2 Using Deque with Pairs
122 |
123 | * Similar to the solution 1 but using deque
124 | * Similar to my solution
125 | * Avoid this repetitive removals of the same value
126 | * If we encounter the hit for the same timestamp, instead of appending a new entry in the deque, we simply increment the count of the latest timestamp.
127 |
128 | ```java
129 | class HitCounter{
130 | private int total;
131 | private Deque> hits;
132 |
133 | /** Initialize your data structure here.**/
134 | public HitCounter(){
135 | // Initialize total to 0
136 | this.total = 0;
137 | this.hits = new LinkedList>();
138 | }
139 |
140 | /**
141 | * Record a hit
142 | * @param timestamp
143 | */
144 | public void hit(int timestamp){
145 | if (this.hits.isEmpty() || this.hits.getLast().getKey() != timestamp){
146 | // Insert the new timestamp with count = 1
147 | this.hits.add(new Pair(timestamp, 1));
148 | }
149 | else {
150 | // Update the count of latest timestamp by incrementing the count by 1
151 | // Obtain the current count of the lastest timestamp
152 | int prevCount = this.hits.getLast().getValue();
153 | // Remove the last pair of (timestamp, count) from the deque
154 | this.hits.removeLast();
155 | // Insert a new pair of (timestamp, updated count) in the deque
156 | this.hits.add(new Pair(timestamp, prevCount + 1));
157 | }
158 | // Increment total
159 | this.total++;
160 | }
161 |
162 | /**
163 | * Return the number of hits in the past 5 minutes
164 | * @param timestamp
165 | */
166 | public int getHits(int timestamp){
167 | while (!this.hits.isEmpty()){
168 | int diff = timestamp - this.hits.getFirst().getKey();
169 | if (diff >= 300){
170 | // Decrement total by the count of the oldest timestamp
171 | this.total -= this.hits.getFirst().getValue();
172 | this.hits.removeFirst();
173 | }
174 | else break;
175 | }
176 | return this.total;
177 | }
178 | }
179 | ```
180 |
181 | - Time Complexity:
182 | - `hit` - $O(1)$.
183 | - `getHits` - If there are a total of n pairs present in the deque, worst case time complexity can be $O(n)$. However, by clubbing all the timestamps with same value together, for the $i^{th} $ timestamp with k repetitions, the time complexity is $O(1)$ as here, instead of removing all those k repetitions, we only remove a single entry from the deque.
184 | - Space complexity: If there are a total of $N$ elements that we encountered throughout, the space complexity is $O(N)$ (similar to Approach 1). However, in the case of repetitions, the space required for storing those k values $O(1)$.
185 |
186 | ## Design Circular Queue (Medium #622)
187 |
188 | **Question**: Design your implementation of the circular queue. The circular queue is a linear data structure in which the operations are performed based on FIFO (First In First Out) principle, and the last position is connected back to the first position to make a circle. It is also called "Ring Buffer".
189 |
190 | One of the benefits of the circular queue is that we can make use of the spaces in front of the queue. In a normal queue, once the queue becomes full, we cannot insert the next element even if there is a space in front of the queue. But using the circular queue, we can use the space to store new values.
191 |
192 | Implementation of the `MyCircularQueue` class:
193 |
194 | - `MyCircularQueue(k)` Initializes the object with the size of the queue to be `k`.
195 | - `int Front()` Gets the front item from the queue. If the queue is empty, return `-1`.
196 | - `int Rear()` Gets the last item from the queue. If the queue is empty, return `-1`.
197 | - `boolean enQueue(int value)` Inserts an element into the circular queue. Return `true` if the operation is successful.
198 | - `boolean deQueue()` Deletes an element from the circular queue. Return `true` if the operation is successful.
199 | - `boolean isEmpty()` Checks whether the circular queue is empty or not.
200 | - `boolean isFull()` Checks whether the circular queue is full or not.
201 |
202 | You must solve the problem without using the built-in queue data structure in your programming language.
203 |
204 | **Example 1:**
205 |
206 | ```
207 | Input
208 | ["MyCircularQueue", "enQueue", "enQueue", "enQueue", "enQueue", "Rear", "isFull", "deQueue", "enQueue", "Rear"]
209 | [[3], [1], [2], [3], [4], [], [], [], [4], []]
210 | Output
211 | [null, true, true, true, false, 3, true, true, true, 4]
212 |
213 | Explanation
214 | MyCircularQueue myCircularQueue = new MyCircularQueue(3);
215 | myCircularQueue.enQueue(1); // return True
216 | myCircularQueue.enQueue(2); // return True
217 | myCircularQueue.enQueue(3); // return True
218 | myCircularQueue.enQueue(4); // return False
219 | myCircularQueue.Rear(); // return 3
220 | myCircularQueue.isFull(); // return True
221 | myCircularQueue.deQueue(); // return True
222 | myCircularQueue.enQueue(4); // return True
223 | myCircularQueue.Rear(); // return 4
224 | ```
225 |
226 | **Constraints:**
227 |
228 | - `1 <= k <= 1000`
229 | - `0 <= value <= 1000`
230 | - At most `3000` calls will be made to `enQueue`, `deQueue`, `Front`, `Rear`, `isEmpty`, and `isFull`.
231 |
232 | ### My Solution
233 |
234 | ```java
235 | class MyCircularQueue {
236 | private int[] queue;
237 | private int size;
238 | // two pointers to track the queue
239 | private int front;
240 | private int rear;
241 | private int capacity;
242 |
243 | public MyCircularQueue(int k) {
244 | queue = new int[k];
245 | capacity = k;
246 | size = 0;
247 | front = 0;
248 | rear = 0;
249 | }
250 |
251 | public boolean enQueue(int value) {
252 | if (size >= capacity){
253 | return false;
254 | }
255 | // queue is empty
256 | if (size == 0){
257 | queue[rear] = value;
258 | }
259 | else {
260 | // in-case we pass the end or array(circular)
261 | rear = (rear + 1) % capacity;
262 | queue[rear] = value;
263 | }
264 | size++;
265 | return true;
266 | }
267 |
268 | public boolean deQueue() {
269 | if (size <= 0){
270 | return false;
271 | }
272 | // only 1 element left in the queue
273 | if (rear == front){
274 | queue[rear] = 0;
275 | }
276 | else {
277 | queue[front] = 0;
278 | front = (front + 1) % capacity;
279 | }
280 | size--;
281 | return true;
282 | }
283 |
284 | public int Front() {
285 | if (size <= 0){
286 | return -1;
287 | }
288 | return queue[front];
289 | }
290 | public int Rear() {
291 | if (size <= 0){
292 | return -1;
293 | }
294 | return queue[rear];
295 | }
296 | public boolean isEmpty() {
297 | return size == 0;
298 | }
299 | public boolean isFull() {
300 | return size == capacity;
301 | }
302 | }
303 | ```
304 |
305 | * The solution works well; the space complexity is $O(N)$ and the time complexity is $O(1)$
306 | * Two pointers solution is easy to find the front and rear
307 |
308 | ### Standard Solution
309 |
310 | #### Solution #1 Array
311 |
312 | * Similar idea but only using 1 pointer
313 |
314 | * A simplified code, don't need to clear the cell to 0, only left the new element cover the old element.
315 |
316 | ```java
317 | class MyCircularQueue {
318 |
319 | private int[] queue;
320 | private int headIndex;
321 | private int count;
322 | private int capacity;
323 |
324 | /** Initialize your data structure here. Set the size of the queue to be k. */
325 | public MyCircularQueue(int k) {
326 | this.capacity = k;
327 | this.queue = new int[k];
328 | this.headIndex = 0;
329 | this.count = 0;
330 | }
331 |
332 | /** Insert an element into the circular queue. Return true if the operation is successful. */
333 | public boolean enQueue(int value) {
334 | if (this.count == this.capacity)
335 | return false;
336 | this.queue[(this.headIndex + this.count) % this.capacity] = value;
337 | this.count += 1;
338 | return true;
339 | }
340 |
341 | /** Delete an element from the circular queue. Return true if the operation is successful. */
342 | public boolean deQueue() {
343 | if (this.count == 0)
344 | return false;
345 | this.headIndex = (this.headIndex + 1) % this.capacity;
346 | this.count -= 1;
347 | return true;
348 | }
349 |
350 | /** Get the front item from the queue. */
351 | public int Front() {
352 | if (this.count == 0)
353 | return -1;
354 | return this.queue[this.headIndex];
355 | }
356 |
357 | /** Get the last item from the queue. */
358 | public int Rear() {
359 | if (this.count == 0)
360 | return -1;
361 | int tailIndex = (this.headIndex + this.count - 1) % this.capacity;
362 | return this.queue[tailIndex];
363 | }
364 |
365 | /** Checks whether the circular queue is empty or not. */
366 | public boolean isEmpty() {
367 | return (this.count == 0);
368 | }
369 |
370 | /** Checks whether the circular queue is full or not. */
371 | public boolean isFull() {
372 | return (this.count == this.capacity);
373 | }
374 | }
375 | ```
376 |
377 | - Time complexity: $\mathcal{O}(1)$. All of the methods in our circular data structure are of constant time complexity.
378 | - Space Complexity: $\mathcal{O}(N)$. The overall space complexity of the data structure is linear, where N is the pre-assigned capacity of the queue. *However, it is worth mentioning that the memory consumption of the data structure remains at its pre-assigned capacity during its entire life cycle.*
379 |
380 | ## Moving Average from Data Stream (Easy #346)
381 |
382 | **Question**: Given a stream of integers and a window size, calculate the moving average of all integers in the sliding window.
383 |
384 | Implement the `MovingAverage` class:
385 |
386 | - `MovingAverage(int size)` Initializes the object with the size of the window `size`.
387 | - `double next(int val)` Returns the moving average of the last `size` values of the stream.
388 |
389 | **Example 1:**
390 |
391 | ```
392 | Input
393 | ["MovingAverage", "next", "next", "next", "next"]
394 | [[3], [1], [10], [3], [5]]
395 | Output
396 | [null, 1.0, 5.5, 4.66667, 6.0]
397 |
398 | Explanation
399 | MovingAverage movingAverage = new MovingAverage(3);
400 | movingAverage.next(1); // return 1.0 = 1 / 1
401 | movingAverage.next(10); // return 5.5 = (1 + 10) / 2
402 | movingAverage.next(3); // return 4.66667 = (1 + 10 + 3) / 3
403 | movingAverage.next(5); // return 6.0 = (10 + 3 + 5) / 3
404 | ```
405 |
406 | **Constraints:**
407 |
408 | - `1 <= size <= 1000`
409 | - `-105 <= val <= 105`
410 | - At most `104` calls will be made to `next`.
411 |
412 | ### My Solution
413 |
414 | * Each time only keep the same size of elements in the list
415 |
416 | ```java
417 | class MovingAverage {
418 |
419 | private int size;
420 | private List list;
421 |
422 | public MovingAverage(int size) {
423 | this.size = size;
424 | list = new ArrayList<>();
425 | }
426 |
427 | public double next(int val) {
428 | list.add(val);
429 | if (list.size() > size){
430 | list.remove(0);
431 | }
432 | int denominator = list.size();
433 | int sum = 0;
434 | for (int i = 0; i < denominator; i++){
435 | int curr = list.get(i);
436 | sum += curr;
437 | }
438 | return (double)sum / (double)denominator;
439 | }
440 | }
441 | ```
442 |
443 | ### Standard Solution
444 |
445 | #### Solution #1 Array or List
446 |
447 | ```java
448 | class MovingAverage {
449 | int size;
450 | List queue = new ArrayList();
451 | public MovingAverage(int size) {
452 | this.size = size;
453 | }
454 |
455 | public double next(int val) {
456 | queue.add(val);
457 | // calculate the sum of the moving window
458 | int windowSum = 0;
459 | for(int i = Math.max(0, queue.size() - size); i < queue.size(); ++i)
460 | windowSum += (int)queue.get(i);
461 |
462 | return windowSum * 1.0 / Math.min(queue.size(), size);
463 | }
464 | }
465 | ```
466 |
467 | - Time Complexity: $\mathcal{O}(N)$ where N is the size of the moving window since we need to retrieve N elements from the queue at each invocation of `next(val)` function.
468 | - Space Complexity: $\mathcal{O}(M)$, where M is the length of the queue which would grow at each invocation of the `next(val)` function.
469 |
470 | #### Solution #2 Deque
471 |
472 | * Each time add value to the sum, delete the value in the tail if exceed the specified size
473 |
474 | ```java
475 | class MovingAverage {
476 | int size, windowSum = 0, count = 0;
477 | Deque queue = new ArrayDeque();
478 |
479 | public MovingAverage(int size) {
480 | this.size = size;
481 | }
482 |
483 | public double next(int val) {
484 | ++count;
485 | // calculate the new sum by shifting the window
486 | queue.add(val);
487 | int tail = count > size ? (int)queue.poll() : 0;
488 |
489 | windowSum = windowSum - tail + val;
490 |
491 | return windowSum * 1.0 / Math.min(size, count);
492 | }
493 | }
494 | ```
495 |
496 | - Time Complexity: $\mathcal{O}(1)$, as we explained in intuition.
497 | - Space Complexity: $\mathcal{O}(N)$, where N is the size of the moving window.
498 |
499 | ## Flatten Nested List Iterator (Medium #341)
500 |
501 | **Question**: You are given a nested list of integers `nestedList`. Each element is either an integer or a list whose elements may also be integers or other lists. Implement an iterator to flatten it.
502 |
503 | Implement the `NestedIterator` class:
504 |
505 | - `NestedIterator(List nestedList)` Initializes the iterator with the nested list `nestedList`.
506 | - `int next()` Returns the next integer in the nested list.
507 | - `boolean hasNext()` Returns `true` if there are still some integers in the nested list and `false` otherwise.
508 |
509 | Your code will be tested with the following pseudocode:
510 |
511 | ```
512 | initialize iterator with nestedList
513 | res = []
514 | while iterator.hasNext()
515 | append iterator.next() to the end of res
516 | return res
517 | ```
518 |
519 | If `res` matches the expected flattened list, then your code will be judged as correct.
520 |
521 | **Example 1:**
522 |
523 | ```
524 | Input: nestedList = [[1,1],2,[1,1]]
525 | Output: [1,1,2,1,1]
526 | Explanation: By calling next repeatedly until hasNext returns false, the order of elements returned by next should be: [1,1,2,1,1].
527 | ```
528 |
529 | **Example 2:**
530 |
531 | ```
532 | Input: nestedList = [1,[4,[6]]]
533 | Output: [1,4,6]
534 | Explanation: By calling next repeatedly until hasNext returns false, the order of elements returned by next should be: [1,4,6].
535 | ```
536 |
537 | **Constraints:**
538 |
539 | - `1 <= nestedList.length <= 500`
540 | - The values of the integers in the nested list is in the range `[-106, 106]`.
541 |
542 | ### Standard Solution
543 |
544 | * Need to fully understand the `iterator`. `next()` would return the element
545 | * Flatten the elements into a list or other structure, then use `iterator` to iterate the structure.
546 |
547 | #### Solution #1 Recursion + List
548 |
549 | ```java
550 | import java.util.NoSuchElementException;
551 | public class NestedIterator implements Iterator {
552 |
553 | int curr;
554 | List list;
555 |
556 | public NestedIterator(List nestedList) {
557 | curr = 0;
558 | list = new ArrayList<>();
559 | flattenList(nestedList);
560 | }
561 |
562 | // recursively unpacks a nest list in dfs
563 | // flatten all the elements to a list before the iterator begins
564 | private void flattenList(List nestedList){
565 | for (NestedInteger nestedInteger : nestedList){
566 | if (nestedInteger.isInteger()){
567 | list.add(nestedInteger.getInteger());
568 | } else {
569 | flattenList(nestedInteger.getList());
570 | }
571 | }
572 | }
573 |
574 | @Override
575 | public Integer next() {
576 | if (!hasNext()) throw new NoSuchElementException();
577 | return list.get(curr++);
578 | }
579 |
580 | @Override
581 | public boolean hasNext() {
582 | return curr < list.size();
583 | }
584 | }
585 | ```
586 |
587 | - Let N be the total number of *integers* within the nested list, L be the total number of *lists* within the nested list, and D be the maximum nesting depth (maximum number of lists inside each other).
588 |
589 | - Time complexity:
590 |
591 | We'll analyze each of the methods separately.
592 |
593 | - **Constructor:** $O(N + L)$
594 |
595 | The constructor is where all the time-consuming work is done.
596 |
597 | For each list within the nested list, there will be one call to `flattenList(...)`. The loop within `flattenList(...)` will then iterate n times, where n is the number of integers within that list. Across all calls to `flattenList(...)`, there will be a total of N loop iterations. Therefore, the time complexity is the number of lists plus the number of integers, giving us $O(N + L)$
598 |
599 | Notice that the maximum depth of the nesting does not impact the time complexity.
600 |
601 | - **next():** $O(1)$
602 |
603 | Getting the next element requires incrementing `position` by 1 and accessing an element at a particular index of the `integers` list. Both of these are $O(1)$ operations.
604 |
605 | - **hasNext():** $O(1)$.
606 |
607 | Checking whether or not there is a next element requires comparing the length of the `integers` list to the `position` variable. This is an $O(1)$ operation.
608 |
609 | - Space complexity: $O(N + D)$.
610 |
611 | The most obvious auxiliary space is the `integers` list. The length of this is $O(N)$
612 |
613 | The less obvious auxiliary space is the space used by the `flattenList(...)` function. Recall that recursive functions need to keep track of where they're up to by putting stack frames on the runtime stack. Therefore, we need to determine what the maximum number of stack frames there could be at a time is. Each time we encounter a nested list, we call `flattenList(...)` and a stack frame is added. Each time we finish processing a nested list, `flattenList(...)` returns and a stack frame is removed. Therefore, the maximum number of stack frames on the runtime stack is the maximum nesting depth, D.
614 |
615 | Because these two operations happen one-after-the-other, and either could be the largest, we add their time complexities together giving a final result of $O(N + D)$
616 |
617 | #### Solution #2 Stack
618 |
619 | ```java
620 | import java.util.NoSuchElementException;
621 |
622 | public class NestedIterator implements Iterator {
623 |
624 | // In Java, the Stack class is considered deprecated. Best practice is to use
625 | // a Deque instead. We'll use addFirst() for push, and removeFirst() for pop.
626 | private Deque stack;
627 |
628 | public NestedIterator(List nestedList) {
629 | // The constructor puts them on in the order we require. No need to reverse.
630 | stack = new ArrayDeque(nestedList);
631 | }
632 |
633 |
634 | @Override
635 | public Integer next() {
636 | // As per java specs, throw an exception if there's no elements left.
637 | if (!hasNext()) throw new NoSuchElementException();
638 | // hasNext ensures the stack top is now an integer. Pop and return
639 | // this integer.
640 | return stack.removeFirst().getInteger();
641 | }
642 |
643 |
644 | @Override
645 | public boolean hasNext() {
646 | // Check if there are integers left by getting one onto the top of stack.
647 | makeStackTopAnInteger();
648 | // If there are any integers remaining, one will be on the top of the stack,
649 | // and therefore the stack can't possibly be empty.
650 | return !stack.isEmpty();
651 | }
652 |
653 |
654 | private void makeStackTopAnInteger() {
655 | // While there are items remaining on the stack and the front of
656 | // stack is a list (i.e. not integer), keep unpacking.
657 | while (!stack.isEmpty() && !stack.peekFirst().isInteger()) {
658 | // Put the NestedIntegers onto the stack in reverse order.
659 | List nestedList = stack.removeFirst().getList();
660 | for (int i = nestedList.size() - 1; i >= 0; i--) {
661 | stack.addFirst(nestedList.get(i));
662 | }
663 | }
664 | }
665 | }
666 | ```
667 |
668 | - Time complexity.
669 |
670 | - **Constructor:** $O(N + L)$
671 |
672 | The worst-case occurs when the initial input nestedList consists entirely of integers and empty lists (everything is in the top-level). In this case, every item is reversed and stored, giving a total time complexity of $O(N + L)$
673 |
674 | - **makeStackTopAnInteger():** $O(\dfrac{L}{N})$or $O(1)$
675 |
676 | If the top of the stack is an integer, then this function does nothing; taking $O(1)$ time.
677 |
678 | Otherwise, it needs to process the stack until an integer is on top. The best way of analyzing the time complexity is to look at the total cost across all calls to `makeStackTopAnInteger()` and then divide by the number of calls made. Once the iterator is exhausted `makeStackTopAnInteger()` must have seen every integer at least once, costing $O(N)$ time. Additionally, it has seen every list (except the first) on the stack at least once also, so this costs $O(L)$ time. Adding these together, we get $O(N + L)$ time.
679 |
680 | The amortized time of a single `makeStackTopAnInteger` is the total cost, $O(N + L)$, divided by the number of times it's called. In order to get all integers, we need to have called it N times. This gives us an amortized time complexity of $\dfrac{O(N + L)}{N} = O(\dfrac{N}{N} + \dfrac{L}{N}) = O(\dfrac{L}{N})$
681 |
682 | - **next():** $O(\dfrac{L}{N})$ or $O(1)$
683 |
684 | All of this method is $O(1)$, except for possibly the call to `makeStackTopAnInteger()`, giving us a time complexity the same as `makeStackTopAnInteger()`.
685 |
686 | - **hasNext():** $O(\dfrac{L}{N})$ or $O(1)$
687 |
688 | All of these methods is $O(1)$, except for possibly the call to `makeStackTopAnInteger()`, giving us a time complexity the same as `makeStackTopAnInteger()`.
689 |
690 | - Space complexity: $O(N + L)$
691 |
692 | In the worst case, where the top list contains N integers, or L empty lists, it will cost $O(N + L)$ space. Other expensive cases occur when the nesting is very deep. However, it's useful to remember that $D ≤ L$ (because each layer of nesting requires another list), and so we don't need to take this into account.
693 |
694 |
--------------------------------------------------------------------------------
92 |
93 | ```java
94 | public int closestValue(TreeNode root, double target){
95 | int val, closest = root.val;
96 | while (root != null){
97 | val = root.val;
98 | closest = Math.abs(val - target) < Math.abs(closest - target) ? val : closest;
99 | root = target < root.val ? root.left : root.right;
100 | }
101 | return closest;
102 | }
103 | ```
104 |
105 | - Time complexity: $\mathcal{O}(H)$ since here one goes from root down to a leaf.
106 | - Space complexity: $\mathcal{O}(1)$.
107 |
108 | ## Search in a Sorted Array of Unknown Size(Medium #702)
109 |
110 | **Question**: This is an ***interactive problem***.
111 |
112 | You have a sorted array of **unique** elements and an **unknown size**. You do not have an access to the array but you can use the `ArrayReader` interface to access it. You can call `ArrayReader.get(i)` that:
113 |
114 | - returns the value at the `ith` index (**0-indexed**) of the secret array (i.e., `secret[i]`), or
115 | - returns `231 - 1` if the `i` is out of the boundary of the array.
116 |
117 | You are also given an integer `target`.
118 |
119 | Return the index `k` of the hidden array where `secret[k] == target` or return `-1` otherwise.
120 |
121 | You must write an algorithm with `O(log n)` runtime complexity.
122 |
123 | **Example 1:**
124 |
125 | ```
126 | Input: secret = [-1,0,3,5,9,12], target = 9
127 | Output: 4
128 | Explanation: 9 exists in secret and its index is 4.
129 | ```
130 |
131 | **Example 2:**
132 |
133 | ```
134 | Input: secret = [-1,0,3,5,9,12], target = 2
135 | Output: -1
136 | Explanation: 2 does not exist in secret so return -1.
137 | ```
138 |
139 | **Constraints:**
140 |
141 | - `1 <= secret.length <= 104`
142 | - `-104 <= secret[i], target <= 104`
143 | - `secret` is sorted in a strictly increasing order.
144 |
145 | ### My Solution
146 |
147 | * Binary search method
148 |
149 | ```java
150 | public int search(ArrayReader reader, int target) {
151 | int max = (int)Math.pow(10, 4);
152 | int low = 0;
153 | while (low < max){
154 | int mid = low + (max - low) / 2;
155 | int value = reader.get(mid);
156 | if (value > target){
157 | max = mid - 1;
158 | }
159 | else if (value < target){
160 | low = mid + 1;
161 | }
162 | else {
163 | return mid;
164 | }
165 | }
166 | return reader.get(low) == target ? low : -1;
167 | }
168 | ```
169 |
170 | ### Standard Solution
171 |
172 | #### Solution #1 Binary Search + Bit Operation
173 |
174 | ```java
175 | class Solution {
176 | public int search(ArrayReader reader, int target) {
177 | if (reader.get(0) == target) return 0;
178 | // search boundaries
179 | int left = 0, right = 1;
180 | while (reader.get(right) < target) {
181 | left = right;
182 | right <<= 1;
183 | }
184 | // binary search
185 | int pivot, num;
186 | while (left <= right) {
187 | pivot = left + ((right - left) >> 1);
188 | num = reader.get(pivot);
189 |
190 | if (num == target) return pivot;
191 | if (num > target) right = pivot - 1;
192 | else left = pivot + 1;
193 | }
194 | // there is no target element
195 | return -1;
196 | }
197 | }
198 | ```
199 |
200 | - Time complexity: $\mathcal{O}(\log T)$, where T is an index of the target value.
201 |
202 | There are two operations here: to define search boundaries and to perform a binary search.
203 |
204 | Let's first find the number of steps k to set up the boundaries. In the first step, the boundaries are $2^0 .. 2^{0 + 1}$, on the second step $2^1 .. 2^{1 + 1}$, etc. When everything is done, the boundaries are $2^k .. 2^{k + 1}$ and $2^k < T \le 2^{k + 1}$. That means one needs $k = \log T$ steps to set up the boundaries, that means $\mathcal{O}(\log T)$ time complexity.
205 |
206 | Now let's discuss the complexity of the binary search. There are $2^{k + 1} - 2^k = 2^k$ elements in the boundaries, i.e. $2^{\log T} = T2$ elements. Binary search has logarithmic complexity, which results in $\mathcal{O}(\log T)$ time complexity.
207 |
208 | - Space complexity: $\mathcal{O}(1)$ since it's a constant space solution.
209 |
210 | ## Valid Perfect Square(Easy #367)
211 |
212 | **Question**: Given a **positive** integer *num*, write a function that returns True if *num* is a perfect square else False.
213 |
214 | **Follow up:** **Do not** use any built-in library function such as `sqrt`.
215 |
216 | **Example 1:**
217 |
218 | ```
219 | Input: num = 16
220 | Output: true
221 | ```
222 |
223 | **Example 2:**
224 |
225 | ```
226 | Input: num = 14
227 | Output: false
228 | ```
229 |
230 | **Constraints:**
231 |
232 | - `1 <= num <= 2^31 - 1`
233 |
234 | ### My Solution
235 |
236 | * Use binary search to find mid, check if the square larger or smaller than the target
237 |
238 | ```java
239 | public boolean isPerfectSquare(int num) {
240 | if (num == 0 || num == 1){
241 | return true;
242 | }
243 | if (num < 0){
244 | return false;
245 | }
246 | int low = 1, high = num / 2;
247 | while (low < high){
248 | int mid = low + (high - low) / 2;
249 | if ((long)mid * mid < num){
250 | low = mid + 1;
251 | }
252 | else if ((long)mid * mid > num){
253 | high = mid - 1;
254 | }
255 | else {
256 | return true;
257 | }
258 | }
259 | return low * low == num ? true : false;
260 | }
261 | ```
262 |
263 | ### Standard Solution
264 |
265 | #### Solution #1 Binary Search
266 |
267 | * Almost the same as my solution
268 |
269 | ```java
270 | public boolean isPerfectSquare(int num) {
271 | if (num < 2) {
272 | return true;
273 | }
274 | long left = 2, right = num / 2, x, guessSquared;
275 | while (left <= right) {
276 | x = left + (right - left) / 2;
277 | guessSquared = x * x;
278 | if (guessSquared == num) {
279 | return true;
280 | }
281 | if (guessSquared > num) {
282 | right = x - 1;
283 | } else {
284 | left = x + 1;
285 | }
286 | }
287 | return false;
288 | }
289 | ```
290 |
291 | * Time complexity: $\mathcal{O}(\log N)$.
292 | * Space complexity: $\mathcal{O}(1)$.
293 |
294 | ## Find Smallest Letter Greater Than Target (Easy #744)
295 |
296 | **Question**: Given a characters array `letters` that is sorted in **non-decreasing** order and a character `target`, return *the smallest character in the array that is larger than* `target`.
297 |
298 | **Note** that the letters wrap around.
299 |
300 | - For example, if `target == 'z'` and `letters == ['a', 'b']`, the answer is `'a'`.
301 |
302 | **Example 1:**
303 |
304 | ```
305 | Input: letters = ["c","f","j"], target = "a"
306 | Output: "c"
307 | ```
308 |
309 | **Example 2:**
310 |
311 | ```
312 | Input: letters = ["c","f","j"], target = "c"
313 | Output: "f"
314 | ```
315 |
316 | **Example 3:**
317 |
318 | ```
319 | Input: letters = ["c","f","j"], target = "d"
320 | Output: "f"
321 | ```
322 |
323 | **Constraints:**
324 |
325 | - `2 <= letters.length <= 104`
326 | - `letters[i]` is a lowercase English letter.
327 | - `letters` are sorted in **non-decreasing** order.
328 | - `letters` contain at least two different characters.
329 | - `target` is a lowercase English letter.
330 |
331 | ### My Solution
332 |
333 | * Calculate the relative distance
334 |
335 | ```java
336 | public char nextGreatestLetter(char[] letters, char target) {
337 | int distance = 0;
338 | int minDistance = Integer.MAX_VALUE;
339 | char res = 'a';
340 | for (char letter : letters){
341 | if (letter >= target){
342 | distance = letter - target;
343 | }
344 | else {
345 | distance = 'z' - target + letter - 'a' + 1;
346 | }
347 | if (distance > 0 && distance < minDistance){
348 | minDistance = distance;
349 | res = letter;
350 | }
351 | }
352 | return res;
353 | }
354 | ```
355 |
356 | ### Standard Solution
357 |
358 | #### Solution #1 Linear Scan
359 |
360 | * The question asks for the letter, not distance, don't need to calculate the distance
361 | * Just loop through the letters and find the one that meets the requirement
362 |
363 | ```java
364 | class Solution {
365 | public char nextGreatestLetter(char[] letters, char target) {
366 | for (char c: letters)
367 | if (c > target) return c;
368 | return letters[0];
369 | }
370 | }
371 | ```
372 |
373 | - Time Complexity: $O(N)$, where N is the length of `letters`. We scan every element of the array.
374 | - Space Complexity: $O(1)$, as we maintain only pointers.
375 |
376 | #### Solution #2 Binary Search
377 |
378 | * Binary search method to check if the letter is larger than the target
379 |
380 | ```java
381 | public char nextGreatestLetter(char[] letters, char target) {
382 | int lo = 0, hi = letters.length;
383 | while (lo < hi) {
384 | int mi = lo + (hi - lo) / 2;
385 | if (letters[mi] <= target) lo = mi + 1;
386 | else hi = mi;
387 | }
388 | return letters[lo % letters.length];
389 | }
390 | ```
391 |
392 | - Time Complexity: $O(\log N)$, where N is the length of `letters`. We peek only at $\log N$ elements in the array.
393 | - Space Complexity: $O(1)$, as we maintain only pointers.
394 |
395 | ## Find Minimum in Rotated Sorted Array II (Hard #154)
396 |
397 | **Question**: Suppose an array of length `n` sorted in ascending order is **rotated** between `1` and `n` times. For example, the array `nums = [0,1,4,4,5,6,7]` might become:
398 |
399 | - `[4,5,6,7,0,1,4]` if it was rotated `4` times.
400 | - `[0,1,4,4,5,6,7]` if it was rotated `7` times.
401 |
402 | Notice that **rotating** an array `[a[0], a[1], a[2], ..., a[n-1]]` 1 time results in the array `[a[n-1], a[0], a[1], a[2], ..., a[n-2]]`.
403 |
404 | Given the sorted rotated array `nums` that may contain **duplicates**, return *the minimum element of this array*.
405 |
406 | You must decrease the overall operation steps as much as possible.
407 |
408 | **Example 1:**
409 |
410 | ```
411 | Input: nums = [1,3,5]
412 | Output: 1
413 | ```
414 |
415 | **Example 2:**
416 |
417 | ```
418 | Input: nums = [2,2,2,0,1]
419 | Output: 0
420 | ```
421 |
422 | **Constraints:**
423 |
424 | - `n == nums.length`
425 | - `1 <= n <= 5000`
426 | - `-5000 <= nums[i] <= 5000`
427 | - `nums` is sorted and rotated between `1` and `n` times.
428 |
429 | ### Standard Solution
430 |
431 | #### Solution #1 Variant of Binary Search
432 |
433 | * Compare the pivot element to the element pointed by the upper bound pointer
434 | * We use the upper bound of the search scope as the reference for the comparison with the pivot element, while in the classical binary search the reference would be the desired value.
435 | * When the result of the comparison is equal (*i.e.* Case #3), we further move the upper bound, while in the classical binary search normally we would return the value immediately.
436 |
437 | ```java
438 | public int findMin(int[] nums) {
439 | int low = 0, high = nums.length - 1;
440 | while (low < high){
441 | int mid = low + (high - low) / 2;
442 | if (nums[mid] > nums[high]){
443 | low = mid + 1;
444 | }
445 | else if (nums[mid] < nums[high]) {
446 | high = mid;
447 | }
448 | // change the edge value since it is valid
449 | else {
450 | high--;
451 | }
452 | }
453 | return nums[low];
454 | }
455 | ```
456 |
457 | - Time complexity: on average $\mathcal{O}(\log_{2}{N})$ where N is the length of the array, since in general, it is a binary search algorithm. However, in the worst case where the array contains identical elements (*i.e.* case #3 `nums[pivot]==nums[high]`), the algorithm would deteriorate to iterating each element, as a result, the time complexity becomes $\mathcal{O}(N)$.
458 | - Space complexity: $\mathcal{O}(1)$, it's a constant space solution.
459 |
460 | ## Median of Two Sorted Array(Hard #4)
461 |
462 | **Question**: Given two sorted arrays `nums1` and `nums2` of size `m` and `n` respectively, return **the median** of the two sorted arrays.
463 |
464 | The overall run time complexity should be `O(log (m+n))`.
465 |
466 | **Example 1:**
467 |
468 | ```
469 | Input: nums1 = [1,3], nums2 = [2]
470 | Output: 2.00000
471 | Explanation: merged array = [1,2,3] and median is 2.
472 | ```
473 |
474 | **Example 2:**
475 |
476 | ```
477 | Input: nums1 = [1,2], nums2 = [3,4]
478 | Output: 2.50000
479 | Explanation: merged array = [1,2,3,4] and median is (2 + 3) / 2 = 2.5.
480 | ```
481 |
482 | **Constraints:**
483 |
484 | - `nums1.length == m`
485 | - `nums2.length == n`
486 | - `0 <= m <= 1000`
487 | - `0 <= n <= 1000`
488 | - `1 <= m + n <= 2000`
489 | - `-106 <= nums1[i], nums2[i] <= 106`
490 |
491 | ### My Solution
492 |
493 | ```java
494 | public double findMedianSortedArrays(int[] nums1, int[] nums2) {
495 | int length = nums1.length + nums2.length;
496 | int[] nums = new int[length];
497 | for (int i = 0; i < nums1.length; i++){
498 | nums[i] = nums1[i];
499 | }
500 | for (int i = nums1.length; i < length; i++){
501 | nums[i] = nums2[i - nums1.length];
502 | }
503 | Arrays.sort(nums);
504 | double median = 0.0;
505 | // find the median of the aggregated array
506 | if (length % 2 == 1){
507 | median = nums[length/ 2];
508 | }
509 | else {
510 | median = ((double)nums[(length - 1)/ 2] + (double)nums[(length - 1) / 2 + 1]) / 2;
511 | }
512 | return median;
513 | }
514 | ```
515 |
516 | ### Other Solution
517 |
518 | * Binary search and compare two value
519 |
520 | ```java
521 | public double findMedianSortedArrays(int[] nums1, int[] nums2) {
522 | int index1 = 0;
523 | int index2 = 0;
524 | int med1 = 0;
525 | int med2 = 0;
526 | for (int i=0; i<=(nums1.length+nums2.length)/2; i++) {
527 | med1 = med2;
528 | if (index1 == nums1.length) {
529 | med2 = nums2[index2];
530 | index2++;
531 | } else if (index2 == nums2.length) {
532 | med2 = nums1[index1];
533 | index1++;
534 | } else if (nums1[index1] < nums2[index2] ) {
535 | med2 = nums1[index1];
536 | index1++;
537 | } else {
538 | med2 = nums2[index2];
539 | index2++;
540 | }
541 | }
542 |
543 | // the median is the average of two numbers
544 | if ((nums1.length+nums2.length)%2 == 0) {
545 | return (float)(med1+med2)/2;
546 | }
547 | return med2;
548 | }
549 | ```
550 |
551 | ## Find k-th Smallest Pair Distance (Hard #719)
552 |
553 | **Question**: The **distance of a pair** of integers `a` and `b` is defined as the absolute difference between `a` and `b`.
554 |
555 | Given an integer array `nums` and an integer `k`, return *the* `kth` *smallest **distance among all the pairs*** `nums[i]` *and* `nums[j]` *where* `0 <= i < j < nums.length`.
556 |
557 | **Example 1:**
558 |
559 | ```
560 | Input: nums = [1,3,1], k = 1
561 | Output: 0
562 | Explanation: Here are all the pairs:
563 | (1,3) -> 2
564 | (1,1) -> 0
565 | (3,1) -> 2
566 | Then the 1st smallest distance pair is (1,1), and its distance is 0.
567 | ```
568 |
569 | **Example 2:**
570 |
571 | ```
572 | Input: nums = [1,1,1], k = 2
573 | Output: 0
574 | ```
575 |
576 | **Example 3:**
577 |
578 | ```
579 | Input: nums = [1,6,1], k = 3
580 | Output: 5
581 | ```
582 |
583 | **Constraints:**
584 |
585 | - `n == nums.length`
586 | - `2 <= n <= 104`
587 | - `0 <= nums[i] <= 106`
588 | - `1 <= k <= n * (n - 1) / 2`
589 |
590 | ### Standard Solution
591 |
592 | #### Solution #1 Binary Search
593 |
594 | * Find low distance, and high distance, use binary search
595 |
596 | ```java
597 | public int smallestDistancePair(int[] nums, int k) {
598 | // sort the array and then do the binary search
599 | Arrays.sort(nums);
600 |
601 | int lo = 0;
602 | int hi = nums[nums.length - 1] - nums[0];
603 | while (lo < hi) {
604 | int mi = (lo + hi) / 2;
605 | int count = 0, left = 0;
606 | for (int right = 0; right < nums.length; right++){
607 | // find out how many count of pairs with distance <= mi
608 | while (nums[right] - nums[left] > mi) left++;
609 | count += right - left;
610 | }
611 | // count = number of pairs with distance <= mi
612 | if (count >= k) hi = mi;
613 | else lo = mi + 1;
614 | }
615 | return lo;
616 | }
617 | ```
618 |
619 | - Time Complexity: $O(N \log{W} + N \log{N})$, where N is the length of `nums`, and W*W* is equal to `nums[nums.length - 1] - nums[0]`. The $\log W$ factor comes from our binary search, and we do $O(N)$ work inside our call to `possible` (or to calculate `count` in Java). The final $O(N\log N)$ factor comes from sorting.
620 | - Space Complexity: $O(1)$. No additional space is used except for integer variables.
621 |
622 | ## Split Array Largest Sum (Hard #410)
623 |
624 | **Question**: Given an array `nums` which consists of non-negative integers and an integer `m`, you can split the array into `m` non-empty continuous subarrays.
625 |
626 | Write an algorithm to minimize the largest sum among these `m` subarrays.
627 |
628 | **Example 1:**
629 |
630 | ```
631 | Input: nums = [7,2,5,10,8], m = 2
632 | Output: 18
633 | Explanation:
634 | There are four ways to split nums into two subarrays.
635 | The best way is to split it into [7,2,5] and [10,8],
636 | where the largest sum among the two subarrays is only 18.
637 | ```
638 |
639 | **Example 2:**
640 |
641 | ```
642 | Input: nums = [1,2,3,4,5], m = 2
643 | Output: 9
644 | ```
645 |
646 | **Example 3:**
647 |
648 | ```
649 | Input: nums = [1,4,4], m = 3
650 | Output: 4
651 | ```
652 |
653 | **Constraints:**
654 |
655 | - `1 <= nums.length <= 1000`
656 | - `0 <= nums[i] <= 106`
657 | - `1 <= m <= min(50, nums.length)`
658 |
659 | ### Standard Solution
660 |
661 | #### Solution #1 Binary Search
662 |
663 | * Not only use binary search on array index but also use it for value search
664 | * Check if the target value converge
665 |
666 | ```java
667 | private int minimumSubarraysRequired(int[] nums, int maxSumAllowed) {
668 | int currentSum = 0;
669 | int splitsRequired = 0;
670 | for (int element : nums) {
671 | // Add element only if the sum doesn't exceed maxSumAllowed
672 | if (currentSum + element <= maxSumAllowed) {
673 | currentSum += element;
674 | } else {
675 | // If the element addition makes sum more than maxSumAllowed
676 | // Increment the splits required and reset sum
677 | currentSum = element;
678 | splitsRequired++;
679 | }
680 | }
681 | // Return the number of subarrays, which is the number of splits + 1
682 | return splitsRequired + 1;
683 | }
684 |
685 | public int splitArray(int[] nums, int m) {
686 | // Find the sum of all elements and the maximum element
687 | int sum = 0;
688 | int maxElement = Integer.MIN_VALUE;
689 | for (int element : nums) {
690 | sum += element;
691 | maxElement = Math.max(maxElement, element);
692 | }
693 | // Define the left and right boundary of binary search
694 | int left = maxElement;
695 | int right = sum;
696 | int minimumLargestSplitSum = 0;
697 | while (left <= right) {
698 | // Find the mid value
699 | int maxSumAllowed = left + (right - left) / 2;
700 | // Find the minimum splits. If splitsRequired is less than
701 | // or equal to m move towards left i.e., smaller values
702 | if (minimumSubarraysRequired(nums, maxSumAllowed) <= m) {
703 | right = maxSumAllowed - 1;
704 | minimumLargestSplitSum = maxSumAllowed;
705 | } else {
706 | // Move towards right if splitsRequired is more than m
707 | left = maxSumAllowed + 1;
708 | }
709 | }
710 | return minimumLargestSplitSum;
711 | }
712 | ```
713 |
714 | - Time complexity: $O(N \cdot \log(S))$, where N is the length of the array and S is the sum of integers in the array.
715 |
716 | The total number of iterations in the binary search is $\log(S)$, and for each such iteration, we call `minimumSubarraysRequired` which takes $O(N)$ time. Hence, the time complexity is equal to $O(N \cdot \log(S))$.
717 |
718 | - Space complexity: $O(1)$
719 |
720 | We do not use any data structures that require more than constant extra space.
721 |
722 | ## 3Sum Closest (Medium #16)
723 |
724 | **Question**: Given an integer array `nums` of length `n` and an integer `target`, find three integers in `nums` such that the sum is closest to `target`.
725 |
726 | Return *the sum of the three integers*.
727 |
728 | You may assume that each input would have exactly one solution.
729 |
730 | **Example 1:**
731 |
732 | ```
733 | Input: nums = [-1,2,1,-4], target = 1
734 | Output: 2
735 | Explanation: The sum that is closest to the target is 2. (-1 + 2 + 1 = 2).
736 | ```
737 |
738 | **Example 2:**
739 |
740 | ```
741 | Input: nums = [0,0,0], target = 1
742 | Output: 0
743 | ```
744 |
745 | **Constraints:**
746 |
747 | - `3 <= nums.length <= 1000`
748 | - `-1000 <= nums[i] <= 1000`
749 | - `-104 <= target <= 104`
750 |
751 | ### Standard Solution
752 |
753 | #### Solution #1 Two Pointers
754 |
755 | * Use for loop and three-pointers, calculate the sum
756 | * Compare the sum with the target, if smaller, move the low pointer, if higher, move the high pointer
757 |
758 | ```java
759 | public int threeSumClosest(int[] nums, int target) {
760 | int diff = Integer.MAX_VALUE;
761 | int sz = nums.length;
762 | Arrays.sort(nums);
763 | for (int i = 0; i < sz && diff != 0; i++){
764 | int lo = i + 1;
765 | int hi = sz - 1;
766 | while (lo < hi){
767 | int sum = nums[i] + nums[lo] + nums[hi];
768 | if (Math.abs(target - sum) < Math.abs(diff)){
769 | diff = target - sum;
770 | }
771 | if (sum < target){
772 | lo++;
773 | }
774 | else {
775 | hi--;
776 | }
777 | }
778 | }
779 | return target - diff;
780 | }
781 | ```
782 |
783 | - Time Complexity: $\mathcal{O}(n^2)$. We have outer and inner loops, each going through n elements.
784 |
785 | Sorting the array takes $\mathcal{O}(n\log{n})$, so overall complexity is $\mathcal{O}(n\log{n} + n^2)$. This is asymptotically equivalent to $\mathcal{O}(n^2)$.
786 |
787 | - Space Complexity: from $\mathcal{O}(\log{n})$ to $\mathcal{O}(n)$, depending on the implementation of the sorting algorithm.
788 |
789 | #### Solution #2 Binary Search
790 |
791 | ```java
792 | public int threeSumClosest(int[] nums, int target) {
793 | int diff = Integer.MAX_VALUE;
794 | int sz = nums.length;
795 | Arrays.sort(nums);
796 | for (int i = 0; i < sz && diff != 0; ++i) {
797 | for (int j = i + 1; j < sz - 1; ++j) {
798 | int complement = target - nums[i] - nums[j];
799 | var idx = Arrays.binarySearch(nums, j + 1, sz - 1, complement);
800 | int hi = idx >= 0 ? idx : ~idx, lo = hi - 1;
801 | if (hi < sz && Math.abs(complement - nums[hi]) < Math.abs(diff))
802 | diff = complement - nums[hi];
803 | if (lo > j && Math.abs(complement - nums[lo]) < Math.abs(diff))
804 | diff = complement - nums[lo];
805 | }
806 | }
807 | return target - diff;
808 | }
809 | ```
810 |
811 | - Time Complexity: $\mathcal{O}(n^2\log{n})$. Binary search takes $\mathcal{O}(\log{n})$, and we do it n times in the inner loop. Since we are going through n elements in the outer loop, the overall complexity is $\mathcal{O}(n^2\log{n})$.
812 | - Space Complexity: from $\mathcal{O}(\log{n})$ to $\mathcal{O}(n)$, depending on the implementation of the sorting algorithm.
--------------------------------------------------------------------------------
/Queue & Stack/Queue Problems Part #1.md:
--------------------------------------------------------------------------------
1 | # Queue Problems Part #1
2 |
3 | ## Design Hit Counter(Medium #362)
4 |
5 | **Question**: Design a hit counter which counts the number of hits received in the past `5` minutes (i.e., the past `300` seconds).
6 |
7 | Your system should accept a `timestamp` parameter (**in seconds** granularity), and you may assume that calls are being made to the system in chronological order (i.e., `timestamp` is monotonically increasing). Several hits may arrive roughly at the same time.
8 |
9 | Implement the `HitCounter` class:
10 |
11 | - `HitCounter()` Initializes the object of the hit counter system.
12 | - `void hit(int timestamp)` Records a hit that happened at `timestamp` (**in seconds**). Several hits may happen at the same `timestamp`.
13 | - `int getHits(int timestamp)` Returns the number of hits in the past 5 minutes from `timestamp` (i.e., the past `300` seconds).
14 |
15 | **Example 1:**
16 |
17 | ```
18 | Input
19 | ["HitCounter", "hit", "hit", "hit", "getHits", "hit", "getHits", "getHits"]
20 | [[], [1], [2], [3], [4], [300], [300], [301]]
21 | Output
22 | [null, null, null, null, 3, null, 4, 3]
23 |
24 | Explanation
25 | HitCounter hitCounter = new HitCounter();
26 | hitCounter.hit(1); // hit at timestamp 1.
27 | hitCounter.hit(2); // hit at timestamp 2.
28 | hitCounter.hit(3); // hit at timestamp 3.
29 | hitCounter.getHits(4); // get hits at timestamp 4, return 3.
30 | hitCounter.hit(300); // hit at timestamp 300.
31 | hitCounter.getHits(300); // get hits at timestamp 300, return 4.
32 | hitCounter.getHits(301); // get hits at timestamp 301, return 3.
33 | ```
34 |
35 | **Constraints:**
36 |
37 | - `1 <= timestamp <= 2 * 109`
38 | - All the calls are being made to the system in chronological order (i.e., `timestamp` is monotonically increasing).
39 | - At most `300` calls will be made to `hit` and `getHits`.
40 |
41 | ### My Solution
42 |
43 | ```java
44 | class HitCounter {
45 | private LinkedList hitQueue;
46 |
47 | public HitCounter() {
48 | hitQueue = new LinkedList();
49 | }
50 | public void hit(int timestamp) {
51 | this.hitQueue.addLast(timestamp);
52 | }
53 | /** return number of hits in the past 5 mins**/
54 | private int findHitsInPast5Min(int pastTime){
55 |
56 | while(this.hitQueue.peekFirst() != null){
57 | if (this.hitQueue.getFirst() <= pastTime){
58 | this.hitQueue.removeFirst();
59 | }
60 | else break;
61 | }
62 | return this.hitQueue.size();
63 | }
64 | public int getHits(int timestamp) {
65 | int pastTime = timestamp - 300;
66 | return findHitsInPast5Min(pastTime);
67 | }
68 | }
69 |
70 | /**
71 | * Your HitCounter object will be instantiated and called as such:
72 | * HitCounter obj = new HitCounter();
73 | * obj.hit(timestamp);
74 | * int param_2 = obj.getHits(timestamp);
75 | */
76 | ```
77 |
78 | ### Standard Solution
79 |
80 | #### Solution #1 Queue
81 |
82 | * Similar to my solution: all the timestamps that we will encounter are going to be in increasing order.
83 | * Should be clean of API doc comments
84 | * This is the case of considering the elements in the FIFO manner (First in first out) which is best solved by using the "queue" data structure.
85 |
86 | ```java
87 | class HitCounter{
88 | private Queue hits;
89 |
90 | /** Initialize your data structure here.**/
91 | public HitCounter(){
92 | this.hits = new LinkedList();
93 | }
94 |
95 | /**
96 | * Record a hit
97 | * @param timestamp
98 | */
99 | public void hit(int timestamp){
100 | this.hits.add(timestamp);
101 | }
102 |
103 | /**
104 | * Return the number of hits in the past 5 minutes
105 | * @param timestamp
106 | */
107 | public int getHits(int timestamp){
108 | while (!this.hits.isEmpty()){
109 | int diff = timestamp - this.hits.peek();
110 | if (diff >= 300) this.hits.remove();
111 | else break;
112 | }
113 | return this.hits.size();
114 | }
115 | }
116 | ```
117 |
118 | * Time complexity: `hit` is $O(1)$, while `getHits` is $O(N)$.
119 | * Space complexity: The queue can have up to N elements, hence overall space complexity of the approach is $O(N)$
120 |
121 | #### Solution #2 Using Deque with Pairs
122 |
123 | * Similar to the solution 1 but using deque
124 | * Similar to my solution
125 | * Avoid this repetitive removals of the same value
126 | * If we encounter the hit for the same timestamp, instead of appending a new entry in the deque, we simply increment the count of the latest timestamp.
127 |
128 | ```java
129 | class HitCounter{
130 | private int total;
131 | private Deque> hits;
132 |
133 | /** Initialize your data structure here.**/
134 | public HitCounter(){
135 | // Initialize total to 0
136 | this.total = 0;
137 | this.hits = new LinkedList>();
138 | }
139 |
140 | /**
141 | * Record a hit
142 | * @param timestamp
143 | */
144 | public void hit(int timestamp){
145 | if (this.hits.isEmpty() || this.hits.getLast().getKey() != timestamp){
146 | // Insert the new timestamp with count = 1
147 | this.hits.add(new Pair(timestamp, 1));
148 | }
149 | else {
150 | // Update the count of latest timestamp by incrementing the count by 1
151 | // Obtain the current count of the lastest timestamp
152 | int prevCount = this.hits.getLast().getValue();
153 | // Remove the last pair of (timestamp, count) from the deque
154 | this.hits.removeLast();
155 | // Insert a new pair of (timestamp, updated count) in the deque
156 | this.hits.add(new Pair(timestamp, prevCount + 1));
157 | }
158 | // Increment total
159 | this.total++;
160 | }
161 |
162 | /**
163 | * Return the number of hits in the past 5 minutes
164 | * @param timestamp
165 | */
166 | public int getHits(int timestamp){
167 | while (!this.hits.isEmpty()){
168 | int diff = timestamp - this.hits.getFirst().getKey();
169 | if (diff >= 300){
170 | // Decrement total by the count of the oldest timestamp
171 | this.total -= this.hits.getFirst().getValue();
172 | this.hits.removeFirst();
173 | }
174 | else break;
175 | }
176 | return this.total;
177 | }
178 | }
179 | ```
180 |
181 | - Time Complexity:
182 | - `hit` - $O(1)$.
183 | - `getHits` - If there are a total of n pairs present in the deque, worst case time complexity can be $O(n)$. However, by clubbing all the timestamps with same value together, for the $i^{th} $ timestamp with k repetitions, the time complexity is $O(1)$ as here, instead of removing all those k repetitions, we only remove a single entry from the deque.
184 | - Space complexity: If there are a total of $N$ elements that we encountered throughout, the space complexity is $O(N)$ (similar to Approach 1). However, in the case of repetitions, the space required for storing those k values $O(1)$.
185 |
186 | ## Design Circular Queue (Medium #622)
187 |
188 | **Question**: Design your implementation of the circular queue. The circular queue is a linear data structure in which the operations are performed based on FIFO (First In First Out) principle, and the last position is connected back to the first position to make a circle. It is also called "Ring Buffer".
189 |
190 | One of the benefits of the circular queue is that we can make use of the spaces in front of the queue. In a normal queue, once the queue becomes full, we cannot insert the next element even if there is a space in front of the queue. But using the circular queue, we can use the space to store new values.
191 |
192 | Implementation of the `MyCircularQueue` class:
193 |
194 | - `MyCircularQueue(k)` Initializes the object with the size of the queue to be `k`.
195 | - `int Front()` Gets the front item from the queue. If the queue is empty, return `-1`.
196 | - `int Rear()` Gets the last item from the queue. If the queue is empty, return `-1`.
197 | - `boolean enQueue(int value)` Inserts an element into the circular queue. Return `true` if the operation is successful.
198 | - `boolean deQueue()` Deletes an element from the circular queue. Return `true` if the operation is successful.
199 | - `boolean isEmpty()` Checks whether the circular queue is empty or not.
200 | - `boolean isFull()` Checks whether the circular queue is full or not.
201 |
202 | You must solve the problem without using the built-in queue data structure in your programming language.
203 |
204 | **Example 1:**
205 |
206 | ```
207 | Input
208 | ["MyCircularQueue", "enQueue", "enQueue", "enQueue", "enQueue", "Rear", "isFull", "deQueue", "enQueue", "Rear"]
209 | [[3], [1], [2], [3], [4], [], [], [], [4], []]
210 | Output
211 | [null, true, true, true, false, 3, true, true, true, 4]
212 |
213 | Explanation
214 | MyCircularQueue myCircularQueue = new MyCircularQueue(3);
215 | myCircularQueue.enQueue(1); // return True
216 | myCircularQueue.enQueue(2); // return True
217 | myCircularQueue.enQueue(3); // return True
218 | myCircularQueue.enQueue(4); // return False
219 | myCircularQueue.Rear(); // return 3
220 | myCircularQueue.isFull(); // return True
221 | myCircularQueue.deQueue(); // return True
222 | myCircularQueue.enQueue(4); // return True
223 | myCircularQueue.Rear(); // return 4
224 | ```
225 |
226 | **Constraints:**
227 |
228 | - `1 <= k <= 1000`
229 | - `0 <= value <= 1000`
230 | - At most `3000` calls will be made to `enQueue`, `deQueue`, `Front`, `Rear`, `isEmpty`, and `isFull`.
231 |
232 | ### My Solution
233 |
234 | ```java
235 | class MyCircularQueue {
236 | private int[] queue;
237 | private int size;
238 | // two pointers to track the queue
239 | private int front;
240 | private int rear;
241 | private int capacity;
242 |
243 | public MyCircularQueue(int k) {
244 | queue = new int[k];
245 | capacity = k;
246 | size = 0;
247 | front = 0;
248 | rear = 0;
249 | }
250 |
251 | public boolean enQueue(int value) {
252 | if (size >= capacity){
253 | return false;
254 | }
255 | // queue is empty
256 | if (size == 0){
257 | queue[rear] = value;
258 | }
259 | else {
260 | // in-case we pass the end or array(circular)
261 | rear = (rear + 1) % capacity;
262 | queue[rear] = value;
263 | }
264 | size++;
265 | return true;
266 | }
267 |
268 | public boolean deQueue() {
269 | if (size <= 0){
270 | return false;
271 | }
272 | // only 1 element left in the queue
273 | if (rear == front){
274 | queue[rear] = 0;
275 | }
276 | else {
277 | queue[front] = 0;
278 | front = (front + 1) % capacity;
279 | }
280 | size--;
281 | return true;
282 | }
283 |
284 | public int Front() {
285 | if (size <= 0){
286 | return -1;
287 | }
288 | return queue[front];
289 | }
290 | public int Rear() {
291 | if (size <= 0){
292 | return -1;
293 | }
294 | return queue[rear];
295 | }
296 | public boolean isEmpty() {
297 | return size == 0;
298 | }
299 | public boolean isFull() {
300 | return size == capacity;
301 | }
302 | }
303 | ```
304 |
305 | * The solution works well; the space complexity is $O(N)$ and the time complexity is $O(1)$
306 | * Two pointers solution is easy to find the front and rear
307 |
308 | ### Standard Solution
309 |
310 | #### Solution #1 Array
311 |
312 | * Similar idea but only using 1 pointer
313 |
314 | * A simplified code, don't need to clear the cell to 0, only left the new element cover the old element.
315 |
316 | ```java
317 | class MyCircularQueue {
318 |
319 | private int[] queue;
320 | private int headIndex;
321 | private int count;
322 | private int capacity;
323 |
324 | /** Initialize your data structure here. Set the size of the queue to be k. */
325 | public MyCircularQueue(int k) {
326 | this.capacity = k;
327 | this.queue = new int[k];
328 | this.headIndex = 0;
329 | this.count = 0;
330 | }
331 |
332 | /** Insert an element into the circular queue. Return true if the operation is successful. */
333 | public boolean enQueue(int value) {
334 | if (this.count == this.capacity)
335 | return false;
336 | this.queue[(this.headIndex + this.count) % this.capacity] = value;
337 | this.count += 1;
338 | return true;
339 | }
340 |
341 | /** Delete an element from the circular queue. Return true if the operation is successful. */
342 | public boolean deQueue() {
343 | if (this.count == 0)
344 | return false;
345 | this.headIndex = (this.headIndex + 1) % this.capacity;
346 | this.count -= 1;
347 | return true;
348 | }
349 |
350 | /** Get the front item from the queue. */
351 | public int Front() {
352 | if (this.count == 0)
353 | return -1;
354 | return this.queue[this.headIndex];
355 | }
356 |
357 | /** Get the last item from the queue. */
358 | public int Rear() {
359 | if (this.count == 0)
360 | return -1;
361 | int tailIndex = (this.headIndex + this.count - 1) % this.capacity;
362 | return this.queue[tailIndex];
363 | }
364 |
365 | /** Checks whether the circular queue is empty or not. */
366 | public boolean isEmpty() {
367 | return (this.count == 0);
368 | }
369 |
370 | /** Checks whether the circular queue is full or not. */
371 | public boolean isFull() {
372 | return (this.count == this.capacity);
373 | }
374 | }
375 | ```
376 |
377 | - Time complexity: $\mathcal{O}(1)$. All of the methods in our circular data structure are of constant time complexity.
378 | - Space Complexity: $\mathcal{O}(N)$. The overall space complexity of the data structure is linear, where N is the pre-assigned capacity of the queue. *However, it is worth mentioning that the memory consumption of the data structure remains at its pre-assigned capacity during its entire life cycle.*
379 |
380 | ## Moving Average from Data Stream (Easy #346)
381 |
382 | **Question**: Given a stream of integers and a window size, calculate the moving average of all integers in the sliding window.
383 |
384 | Implement the `MovingAverage` class:
385 |
386 | - `MovingAverage(int size)` Initializes the object with the size of the window `size`.
387 | - `double next(int val)` Returns the moving average of the last `size` values of the stream.
388 |
389 | **Example 1:**
390 |
391 | ```
392 | Input
393 | ["MovingAverage", "next", "next", "next", "next"]
394 | [[3], [1], [10], [3], [5]]
395 | Output
396 | [null, 1.0, 5.5, 4.66667, 6.0]
397 |
398 | Explanation
399 | MovingAverage movingAverage = new MovingAverage(3);
400 | movingAverage.next(1); // return 1.0 = 1 / 1
401 | movingAverage.next(10); // return 5.5 = (1 + 10) / 2
402 | movingAverage.next(3); // return 4.66667 = (1 + 10 + 3) / 3
403 | movingAverage.next(5); // return 6.0 = (10 + 3 + 5) / 3
404 | ```
405 |
406 | **Constraints:**
407 |
408 | - `1 <= size <= 1000`
409 | - `-105 <= val <= 105`
410 | - At most `104` calls will be made to `next`.
411 |
412 | ### My Solution
413 |
414 | * Each time only keep the same size of elements in the list
415 |
416 | ```java
417 | class MovingAverage {
418 |
419 | private int size;
420 | private List list;
421 |
422 | public MovingAverage(int size) {
423 | this.size = size;
424 | list = new ArrayList<>();
425 | }
426 |
427 | public double next(int val) {
428 | list.add(val);
429 | if (list.size() > size){
430 | list.remove(0);
431 | }
432 | int denominator = list.size();
433 | int sum = 0;
434 | for (int i = 0; i < denominator; i++){
435 | int curr = list.get(i);
436 | sum += curr;
437 | }
438 | return (double)sum / (double)denominator;
439 | }
440 | }
441 | ```
442 |
443 | ### Standard Solution
444 |
445 | #### Solution #1 Array or List
446 |
447 | ```java
448 | class MovingAverage {
449 | int size;
450 | List queue = new ArrayList();
451 | public MovingAverage(int size) {
452 | this.size = size;
453 | }
454 |
455 | public double next(int val) {
456 | queue.add(val);
457 | // calculate the sum of the moving window
458 | int windowSum = 0;
459 | for(int i = Math.max(0, queue.size() - size); i < queue.size(); ++i)
460 | windowSum += (int)queue.get(i);
461 |
462 | return windowSum * 1.0 / Math.min(queue.size(), size);
463 | }
464 | }
465 | ```
466 |
467 | - Time Complexity: $\mathcal{O}(N)$ where N is the size of the moving window since we need to retrieve N elements from the queue at each invocation of `next(val)` function.
468 | - Space Complexity: $\mathcal{O}(M)$, where M is the length of the queue which would grow at each invocation of the `next(val)` function.
469 |
470 | #### Solution #2 Deque
471 |
472 | * Each time add value to the sum, delete the value in the tail if exceed the specified size
473 |
474 | ```java
475 | class MovingAverage {
476 | int size, windowSum = 0, count = 0;
477 | Deque queue = new ArrayDeque();
478 |
479 | public MovingAverage(int size) {
480 | this.size = size;
481 | }
482 |
483 | public double next(int val) {
484 | ++count;
485 | // calculate the new sum by shifting the window
486 | queue.add(val);
487 | int tail = count > size ? (int)queue.poll() : 0;
488 |
489 | windowSum = windowSum - tail + val;
490 |
491 | return windowSum * 1.0 / Math.min(size, count);
492 | }
493 | }
494 | ```
495 |
496 | - Time Complexity: $\mathcal{O}(1)$, as we explained in intuition.
497 | - Space Complexity: $\mathcal{O}(N)$, where N is the size of the moving window.
498 |
499 | ## Flatten Nested List Iterator (Medium #341)
500 |
501 | **Question**: You are given a nested list of integers `nestedList`. Each element is either an integer or a list whose elements may also be integers or other lists. Implement an iterator to flatten it.
502 |
503 | Implement the `NestedIterator` class:
504 |
505 | - `NestedIterator(List nestedList)` Initializes the iterator with the nested list `nestedList`.
506 | - `int next()` Returns the next integer in the nested list.
507 | - `boolean hasNext()` Returns `true` if there are still some integers in the nested list and `false` otherwise.
508 |
509 | Your code will be tested with the following pseudocode:
510 |
511 | ```
512 | initialize iterator with nestedList
513 | res = []
514 | while iterator.hasNext()
515 | append iterator.next() to the end of res
516 | return res
517 | ```
518 |
519 | If `res` matches the expected flattened list, then your code will be judged as correct.
520 |
521 | **Example 1:**
522 |
523 | ```
524 | Input: nestedList = [[1,1],2,[1,1]]
525 | Output: [1,1,2,1,1]
526 | Explanation: By calling next repeatedly until hasNext returns false, the order of elements returned by next should be: [1,1,2,1,1].
527 | ```
528 |
529 | **Example 2:**
530 |
531 | ```
532 | Input: nestedList = [1,[4,[6]]]
533 | Output: [1,4,6]
534 | Explanation: By calling next repeatedly until hasNext returns false, the order of elements returned by next should be: [1,4,6].
535 | ```
536 |
537 | **Constraints:**
538 |
539 | - `1 <= nestedList.length <= 500`
540 | - The values of the integers in the nested list is in the range `[-106, 106]`.
541 |
542 | ### Standard Solution
543 |
544 | * Need to fully understand the `iterator`. `next()` would return the element
545 | * Flatten the elements into a list or other structure, then use `iterator` to iterate the structure.
546 |
547 | #### Solution #1 Recursion + List
548 |
549 | ```java
550 | import java.util.NoSuchElementException;
551 | public class NestedIterator implements Iterator {
552 |
553 | int curr;
554 | List list;
555 |
556 | public NestedIterator(List nestedList) {
557 | curr = 0;
558 | list = new ArrayList<>();
559 | flattenList(nestedList);
560 | }
561 |
562 | // recursively unpacks a nest list in dfs
563 | // flatten all the elements to a list before the iterator begins
564 | private void flattenList(List nestedList){
565 | for (NestedInteger nestedInteger : nestedList){
566 | if (nestedInteger.isInteger()){
567 | list.add(nestedInteger.getInteger());
568 | } else {
569 | flattenList(nestedInteger.getList());
570 | }
571 | }
572 | }
573 |
574 | @Override
575 | public Integer next() {
576 | if (!hasNext()) throw new NoSuchElementException();
577 | return list.get(curr++);
578 | }
579 |
580 | @Override
581 | public boolean hasNext() {
582 | return curr < list.size();
583 | }
584 | }
585 | ```
586 |
587 | - Let N be the total number of *integers* within the nested list, L be the total number of *lists* within the nested list, and D be the maximum nesting depth (maximum number of lists inside each other).
588 |
589 | - Time complexity:
590 |
591 | We'll analyze each of the methods separately.
592 |
593 | - **Constructor:** $O(N + L)$
594 |
595 | The constructor is where all the time-consuming work is done.
596 |
597 | For each list within the nested list, there will be one call to `flattenList(...)`. The loop within `flattenList(...)` will then iterate n times, where n is the number of integers within that list. Across all calls to `flattenList(...)`, there will be a total of N loop iterations. Therefore, the time complexity is the number of lists plus the number of integers, giving us $O(N + L)$
598 |
599 | Notice that the maximum depth of the nesting does not impact the time complexity.
600 |
601 | - **next():** $O(1)$
602 |
603 | Getting the next element requires incrementing `position` by 1 and accessing an element at a particular index of the `integers` list. Both of these are $O(1)$ operations.
604 |
605 | - **hasNext():** $O(1)$.
606 |
607 | Checking whether or not there is a next element requires comparing the length of the `integers` list to the `position` variable. This is an $O(1)$ operation.
608 |
609 | - Space complexity: $O(N + D)$.
610 |
611 | The most obvious auxiliary space is the `integers` list. The length of this is $O(N)$
612 |
613 | The less obvious auxiliary space is the space used by the `flattenList(...)` function. Recall that recursive functions need to keep track of where they're up to by putting stack frames on the runtime stack. Therefore, we need to determine what the maximum number of stack frames there could be at a time is. Each time we encounter a nested list, we call `flattenList(...)` and a stack frame is added. Each time we finish processing a nested list, `flattenList(...)` returns and a stack frame is removed. Therefore, the maximum number of stack frames on the runtime stack is the maximum nesting depth, D.
614 |
615 | Because these two operations happen one-after-the-other, and either could be the largest, we add their time complexities together giving a final result of $O(N + D)$
616 |
617 | #### Solution #2 Stack
618 |
619 | ```java
620 | import java.util.NoSuchElementException;
621 |
622 | public class NestedIterator implements Iterator {
623 |
624 | // In Java, the Stack class is considered deprecated. Best practice is to use
625 | // a Deque instead. We'll use addFirst() for push, and removeFirst() for pop.
626 | private Deque stack;
627 |
628 | public NestedIterator(List nestedList) {
629 | // The constructor puts them on in the order we require. No need to reverse.
630 | stack = new ArrayDeque(nestedList);
631 | }
632 |
633 |
634 | @Override
635 | public Integer next() {
636 | // As per java specs, throw an exception if there's no elements left.
637 | if (!hasNext()) throw new NoSuchElementException();
638 | // hasNext ensures the stack top is now an integer. Pop and return
639 | // this integer.
640 | return stack.removeFirst().getInteger();
641 | }
642 |
643 |
644 | @Override
645 | public boolean hasNext() {
646 | // Check if there are integers left by getting one onto the top of stack.
647 | makeStackTopAnInteger();
648 | // If there are any integers remaining, one will be on the top of the stack,
649 | // and therefore the stack can't possibly be empty.
650 | return !stack.isEmpty();
651 | }
652 |
653 |
654 | private void makeStackTopAnInteger() {
655 | // While there are items remaining on the stack and the front of
656 | // stack is a list (i.e. not integer), keep unpacking.
657 | while (!stack.isEmpty() && !stack.peekFirst().isInteger()) {
658 | // Put the NestedIntegers onto the stack in reverse order.
659 | List nestedList = stack.removeFirst().getList();
660 | for (int i = nestedList.size() - 1; i >= 0; i--) {
661 | stack.addFirst(nestedList.get(i));
662 | }
663 | }
664 | }
665 | }
666 | ```
667 |
668 | - Time complexity.
669 |
670 | - **Constructor:** $O(N + L)$
671 |
672 | The worst-case occurs when the initial input nestedList consists entirely of integers and empty lists (everything is in the top-level). In this case, every item is reversed and stored, giving a total time complexity of $O(N + L)$
673 |
674 | - **makeStackTopAnInteger():** $O(\dfrac{L}{N})$or $O(1)$
675 |
676 | If the top of the stack is an integer, then this function does nothing; taking $O(1)$ time.
677 |
678 | Otherwise, it needs to process the stack until an integer is on top. The best way of analyzing the time complexity is to look at the total cost across all calls to `makeStackTopAnInteger()` and then divide by the number of calls made. Once the iterator is exhausted `makeStackTopAnInteger()` must have seen every integer at least once, costing $O(N)$ time. Additionally, it has seen every list (except the first) on the stack at least once also, so this costs $O(L)$ time. Adding these together, we get $O(N + L)$ time.
679 |
680 | The amortized time of a single `makeStackTopAnInteger` is the total cost, $O(N + L)$, divided by the number of times it's called. In order to get all integers, we need to have called it N times. This gives us an amortized time complexity of $\dfrac{O(N + L)}{N} = O(\dfrac{N}{N} + \dfrac{L}{N}) = O(\dfrac{L}{N})$
681 |
682 | - **next():** $O(\dfrac{L}{N})$ or $O(1)$
683 |
684 | All of this method is $O(1)$, except for possibly the call to `makeStackTopAnInteger()`, giving us a time complexity the same as `makeStackTopAnInteger()`.
685 |
686 | - **hasNext():** $O(\dfrac{L}{N})$ or $O(1)$
687 |
688 | All of these methods is $O(1)$, except for possibly the call to `makeStackTopAnInteger()`, giving us a time complexity the same as `makeStackTopAnInteger()`.
689 |
690 | - Space complexity: $O(N + L)$
691 |
692 | In the worst case, where the top list contains N integers, or L empty lists, it will cost $O(N + L)$ space. Other expensive cases occur when the nesting is very deep. However, it's useful to remember that $D ≤ L$ (because each layer of nesting requires another list), and so we don't need to take this into account.
693 |
694 |
--------------------------------------------------------------------------------
 34 |
35 | #### Approach
36 |
37 | * Functional requirements
38 | * Features
39 | * User Journeys
40 | * Non-functional requirements
41 | * Scale
42 | * Latency
43 | * Consistency
44 |
45 | #### Approach Solution
46 |
47 |
34 |
35 | #### Approach
36 |
37 | * Functional requirements
38 | * Features
39 | * User Journeys
40 | * Non-functional requirements
41 | * Scale
42 | * Latency
43 | * Consistency
44 |
45 | #### Approach Solution
46 |
47 |  48 |
49 | * Propose a design
50 | * This means breaking down the system into multiple components and identifying which microservices are needed, setting up interactions between these microservices, finalizing databases, etc.
51 | * Talk about trade-offs
52 | * What database would be more suitable? Do you need SQL or NoSQL? You keep adjusting your design based on your **design decisions** and tradeoffs until the requirements have been satisfactorily met.
53 | * Discuss design choices
54 | * Limitations of the design
55 | * If your system does not have a monitoring component, it would be good to mention this at this stage.
56 |
57 | ### Low-Level Design
58 |
59 |
48 |
49 | * Propose a design
50 | * This means breaking down the system into multiple components and identifying which microservices are needed, setting up interactions between these microservices, finalizing databases, etc.
51 | * Talk about trade-offs
52 | * What database would be more suitable? Do you need SQL or NoSQL? You keep adjusting your design based on your **design decisions** and tradeoffs until the requirements have been satisfactorily met.
53 | * Discuss design choices
54 | * Limitations of the design
55 | * If your system does not have a monitoring component, it would be good to mention this at this stage.
56 |
57 | ### Low-Level Design
58 |
59 |  60 |
61 | #### Structure
62 |
63 | * Dive deeper into the implemention of the individual system
64 | * Covers a sub-system
65 | * Optimisations within the sub-system
66 | * Sample: Design a parking lot, Uber's pricing system
67 |
68 | #### Expection
69 |
70 | * Requirements:
71 | * fulfulls function and non-function requirement, good code structure, working + clean code
72 | * Modular, futuristic, non-restrictive
73 | * Code:
74 | * Interfaces
75 | * Class diagrams
76 | * Entities
77 | * Data model
78 | * Design patterns
79 | * Quality:
80 | * Working code, pass basic tests
81 | * Modular: able to add new features, code consistent when adding new features(old codes works well)
82 | * Testable: unit test cases
83 | * Expected Outcome (Example of Uber's pricing engine)
84 | * `getFareEstimate()` which fetches the `basePrice` and `surgePrice` and accordingly returns the total estimated fare.`getBasePrice()` will return the base price based on distance, time, and ride type. If there are too many requests from users for the current number of drivers, we will apply a surge price and increase the fare.
85 | * We could use the Factory Design Pattern here and add two factories, `BasePriceCalculatorFactory` for calculating `basePrice` and `SurgePriceCalculatorFactory` for calculating `surgePrice`.
86 |
87 | 
88 |
89 | #### How to Approach LLD Interview
90 |
91 | * Lock down the requirements, both functional and non-functional. The idea is to limit the scope early on so we don't get lost trying to build too many things.
92 | * The next step is the code. The first thing to do here will be to define the interfaces.
93 | * Next are class diagrams, where we define what classes we need, how they will interact, what hierarchy they will follow, etc.
94 | * We will further define our entities and data models, and while doing all this, we need to consider what design pattern will be most suitable.
95 | * Talking about design patterns, the next step would be to ensure code quality. This means we should have a working code with some basic test cases that are passing for the logic we have written.
--------------------------------------------------------------------------------
/Sort/Sorting Problems Part #1.md:
--------------------------------------------------------------------------------
1 | # Sorting Problems Part #1
2 |
3 | ## Sort List (Medium #148)
4 |
5 | **Question**: Given the `head` of a linked list, return *the list after sorting it in **ascending order***.
6 |
7 | **Example 1:**
8 |
9 |
60 |
61 | #### Structure
62 |
63 | * Dive deeper into the implemention of the individual system
64 | * Covers a sub-system
65 | * Optimisations within the sub-system
66 | * Sample: Design a parking lot, Uber's pricing system
67 |
68 | #### Expection
69 |
70 | * Requirements:
71 | * fulfulls function and non-function requirement, good code structure, working + clean code
72 | * Modular, futuristic, non-restrictive
73 | * Code:
74 | * Interfaces
75 | * Class diagrams
76 | * Entities
77 | * Data model
78 | * Design patterns
79 | * Quality:
80 | * Working code, pass basic tests
81 | * Modular: able to add new features, code consistent when adding new features(old codes works well)
82 | * Testable: unit test cases
83 | * Expected Outcome (Example of Uber's pricing engine)
84 | * `getFareEstimate()` which fetches the `basePrice` and `surgePrice` and accordingly returns the total estimated fare.`getBasePrice()` will return the base price based on distance, time, and ride type. If there are too many requests from users for the current number of drivers, we will apply a surge price and increase the fare.
85 | * We could use the Factory Design Pattern here and add two factories, `BasePriceCalculatorFactory` for calculating `basePrice` and `SurgePriceCalculatorFactory` for calculating `surgePrice`.
86 |
87 | 
88 |
89 | #### How to Approach LLD Interview
90 |
91 | * Lock down the requirements, both functional and non-functional. The idea is to limit the scope early on so we don't get lost trying to build too many things.
92 | * The next step is the code. The first thing to do here will be to define the interfaces.
93 | * Next are class diagrams, where we define what classes we need, how they will interact, what hierarchy they will follow, etc.
94 | * We will further define our entities and data models, and while doing all this, we need to consider what design pattern will be most suitable.
95 | * Talking about design patterns, the next step would be to ensure code quality. This means we should have a working code with some basic test cases that are passing for the logic we have written.
--------------------------------------------------------------------------------
/Sort/Sorting Problems Part #1.md:
--------------------------------------------------------------------------------
1 | # Sorting Problems Part #1
2 |
3 | ## Sort List (Medium #148)
4 |
5 | **Question**: Given the `head` of a linked list, return *the list after sorting it in **ascending order***.
6 |
7 | **Example 1:**
8 |
9 |  10 |
11 | ```
12 | Input: head = [4,2,1,3]
13 | Output: [1,2,3,4]
14 | ```
15 |
16 | **Example 2:**
17 |
18 |
10 |
11 | ```
12 | Input: head = [4,2,1,3]
13 | Output: [1,2,3,4]
14 | ```
15 |
16 | **Example 2:**
17 |
18 |  19 |
20 | ```
21 | Input: head = [-1,5,3,4,0]
22 | Output: [-1,0,3,4,5]
23 | ```
24 |
25 | **Example 3:**
26 |
27 | ```
28 | Input: head = []
29 | Output: []
30 | ```
31 |
32 | **Constraints:**
33 |
34 | - The number of nodes in the list is in the range `[0, 5 * 104]`.
35 | - `-105 <= Node.val <= 105`
36 |
37 | ### My Solution
38 |
39 | * Use an array list to record all the numbers, sort them using Collections
40 | * Then reassign them to the nodes
41 |
42 | ```java
43 | public ListNode sortList(ListNode head) {
44 | if (head == null){
45 | return null;
46 | }
47 | List
19 |
20 | ```
21 | Input: head = [-1,5,3,4,0]
22 | Output: [-1,0,3,4,5]
23 | ```
24 |
25 | **Example 3:**
26 |
27 | ```
28 | Input: head = []
29 | Output: []
30 | ```
31 |
32 | **Constraints:**
33 |
34 | - The number of nodes in the list is in the range `[0, 5 * 104]`.
35 | - `-105 <= Node.val <= 105`
36 |
37 | ### My Solution
38 |
39 | * Use an array list to record all the numbers, sort them using Collections
40 | * Then reassign them to the nodes
41 |
42 | ```java
43 | public ListNode sortList(ListNode head) {
44 | if (head == null){
45 | return null;
46 | }
47 | List 43 |
44 | * Let us consider two subsequent intervals after sorting. Since sorting ensures that `start1 < start2`, it's sufficient to compare the end boundaries:
45 | - If `end1 < end2`, the intervals won't completely cover one another, though they have some overlapping.
46 | - If `end1 >= end2`, interval 2 is covered by interval 1.
47 | * Edge case: **How to treat intervals that share start point**
48 | * If two intervals share the same start point, one has to put the longer interval in front.
49 |
50 |
43 |
44 | * Let us consider two subsequent intervals after sorting. Since sorting ensures that `start1 < start2`, it's sufficient to compare the end boundaries:
45 | - If `end1 < end2`, the intervals won't completely cover one another, though they have some overlapping.
46 | - If `end1 >= end2`, interval 2 is covered by interval 1.
47 | * Edge case: **How to treat intervals that share start point**
48 | * If two intervals share the same start point, one has to put the longer interval in front.
49 |
50 |  51 |
52 | ```java
53 | public int removeCoveredIntervals(int[][] intervals) {
54 | Arrays.sort(intervals, new Comparator
51 |
52 | ```java
53 | public int removeCoveredIntervals(int[][] intervals) {
54 | Arrays.sort(intervals, new Comparator 10 |
11 | ```
12 | Input: root = [5,3,6,2,4,null,7], k = 9
13 | Output: true
14 | ```
15 |
16 | **Example 2:**
17 |
18 |
10 |
11 | ```
12 | Input: root = [5,3,6,2,4,null,7], k = 9
13 | Output: true
14 | ```
15 |
16 | **Example 2:**
17 |
18 |  19 |
20 | ```
21 | Input: root = [5,3,6,2,4,null,7], k = 28
22 | Output: false
23 | ```
24 |
25 | **Constraints:**
26 |
27 | - The number of nodes in the tree is in the range `[1, 104]`.
28 | - `-104 <= Node.val <= 104`
29 | - `root` is guaranteed to be a **valid** binary search tree.
30 | - `-105 <= k <= 105`
31 |
32 | ### Standard Solution
33 |
34 | #### Solution #1 Using HashSet
35 |
36 | * Simplest solution is to traverse over the whole tree and consider every pair
37 | * For every node, check if the complement is in the set. Then put it to the set.
38 |
39 | ```java
40 | public boolean findTarget(TreeNode root, int k){
41 | Set
19 |
20 | ```
21 | Input: root = [5,3,6,2,4,null,7], k = 28
22 | Output: false
23 | ```
24 |
25 | **Constraints:**
26 |
27 | - The number of nodes in the tree is in the range `[1, 104]`.
28 | - `-104 <= Node.val <= 104`
29 | - `root` is guaranteed to be a **valid** binary search tree.
30 | - `-105 <= k <= 105`
31 |
32 | ### Standard Solution
33 |
34 | #### Solution #1 Using HashSet
35 |
36 | * Simplest solution is to traverse over the whole tree and consider every pair
37 | * For every node, check if the complement is in the set. Then put it to the set.
38 |
39 | ```java
40 | public boolean findTarget(TreeNode root, int k){
41 | Set 8 |
9 | ### Array Solution
10 |
11 | ```java
12 | class TrieNode {
13 | // change this value to adapt to different cases
14 | public static final N = 26;
15 | public TrieNode[] children = new TrieNode[N];
16 |
17 | // you might need some extra values according to different cases
18 | };
19 | ```
20 |
21 | ### Map Solution
22 |
23 | ```java
24 | class TrieNode {
25 | public Map
8 |
9 | ### Array Solution
10 |
11 | ```java
12 | class TrieNode {
13 | // change this value to adapt to different cases
14 | public static final N = 26;
15 | public TrieNode[] children = new TrieNode[N];
16 |
17 | // you might need some extra values according to different cases
18 | };
19 | ```
20 |
21 | ### Map Solution
22 |
23 | ```java
24 | class TrieNode {
25 | public Map 16 |
17 | ```
18 | Input: seats = [1,0,0,0,1,0,1]
19 | Output: 2
20 | Explanation:
21 | If Alex sits in the second open seat (i.e. seats[2]), then the closest person has distance 2.
22 | If Alex sits in any other open seat, the closest person has distance 1.
23 | Thus, the maximum distance to the closest person is 2.
24 | ```
25 |
26 | **Example 2:**
27 |
28 | ```
29 | Input: seats = [1,0,0,0]
30 | Output: 3
31 | Explanation:
32 | If Alex sits in the last seat (i.e. seats[3]), the closest person is 3 seats away.
33 | This is the maximum distance possible, so the answer is 3.
34 | ```
35 |
36 | **Example 3:**
37 |
38 | ```
39 | Input: seats = [0,1]
40 | Output: 1
41 | ```
42 |
43 | **Constraints:**
44 |
45 | - `2 <= seats.length <= 2 * 104`
46 | - `seats[i]` is `0` or `1`.
47 | - At least one seat is **empty**.
48 | - At least one seat is **occupied**.
49 |
50 | ### My Solution
51 |
52 | ```java
53 | public int maxDistToClosest(int[] seats) {
54 | int maxDist = 0, low, high;
55 |
56 | for (low = 0, high = 0; high < seats.length; ++high){
57 | if (seats[high] == 1){
58 | int totalDist = high - low;
59 | if (seats[low] == 1){
60 | maxDist = Math.max((int)Math.ceil(totalDist/2), maxDist);
61 | }
62 | else {
63 | maxDist = Math.max(totalDist, maxDist);
64 | }
65 | low = high;
66 | }
67 | }
68 | if (low == seats.length - 1) return Math.max(maxDist, high - low);
69 | return Math.max(maxDist, high - low - 1);
70 | }
71 | ```
72 |
73 | ### Standard Solution
74 |
75 | #### Solution #1 Next Array
76 |
77 | * Let `left[i]` be the distance from seat `i` to the closest person sitting to the left of `i`. Similarly, let `right[i]` be the distance to the closest person sitting to the right of `i`. This is motivated by the idea that the closest person in seat `i` sits a distance `min(left[i], right[i])` away.
78 |
79 | * **Algorithm**
80 |
81 | To construct `left[i]`, notice it is either `left[i-1] + 1` if the seat is empty, or `0` if it is full. `right[i]` is constructed in a similar way.
82 |
83 | ```java
84 | public int maxDistToClosest(int[] seats){
85 | int N = seats.length;
86 | int[] left = new int[N], right = new int[N];
87 | Arrays.fill(left, N);
88 | Arrays.fill(right, N);
89 |
90 | for (int i = 0; i < N; i++){
91 | if (seats[i] == 1) left[i] = 0; //distance to the cloest one would be 0
92 | else if (i > 0) left[i] = left[i - 1] + 1; //add 1 distance comparing to the previous one
93 | }
94 | for (int i = N - 1; i >= 0; i--){
95 | if (seats[i] == 1) right[i] = 0; //distance to the cloest one would be 0
96 | else if (i < N - 1) right[i] = right[i + 1] + 1; //add 1 distance comparing to the previous one
97 | }
98 |
99 | int ans = 0;
100 | for (int i = 0; i < N; i++){
101 | if (seats[i] == 0){
102 | ans = Math.max(ans, Math.min(left[i], right[i]));
103 | }
104 | }
105 | return ans;
106 | }
107 | ```
108 |
109 | * Time complexity: $O(N)$ where N is the length of seats
110 | * Space complexity: $O(N)$ where the space used by left and right
111 |
112 | #### Solution #2 Two Pointer
113 |
114 | * **Algorithm**:
115 | * Keep track of `prev`, the filled seat at or to the left of `i`, and `future`, the filled seat at or to the right of `i`.
116 | * Then at seat `i`, the closest person is `min(i - prev, future - i)`, with one exception. `i - prev` should be considered infinite if there is no person to the left of seat `i`, and similarly `future - i` is infinite if there is no one to the right of seat `i`.
117 |
118 | ```java
119 | public int maxDistToClosest(int[] seats){
120 | int N = seats.length;
121 | int prev = -1, future = 0;
122 | int ans = 0;
123 |
124 | for (int i = 0; i < N; i++){
125 | if (seats[i] == 1){
126 | prev = i;
127 | } else {
128 | while (future < N && seats[future] == 0 || future < i){
129 | future++;
130 | }
131 | int left = prev == -1 ? N : i - prev;
132 | int right = future == N ? N : future - i;
133 | ans = Math.max(ans, Math.min(left, right));
134 | }
135 | }
136 | return ans;
137 | }
138 | ```
139 |
140 | * Time Complexity: $O(N)$, where $N$ is the length of `seats`.
141 | * Space Complexity: $O(1)$
142 |
143 | #### Solution #3 Group by Zero
144 |
145 | * My solution is a combination of solution 2 and 3
146 | * In a group of `K` adjacent empty seats between two people, the answer is `(K+1) / 2`.
147 | * For groups of empty seats between the edge of the row and one other person, the answer is `K`, and we should take into account those answers too.
148 |
149 | ```java
150 | public int maxDistToClosest(int[] seats){
151 | int N = seats.length;
152 | int K = 0;//current longest group of empty seats
153 | int ans = 0;
154 |
155 | for (int i = 0; i < N; i++){
156 | if (seats[i] == 1){
157 | K = 0;
158 | } else {
159 | K++;
160 | ans = Math.max(ans, (K + 1) / 2);
161 | }
162 | }
163 |
164 | for (int i = 0; i < N; i++){// in case starts from 0
165 | if (seats[i] == 1){
166 | ans = Math.max(ans, i);
167 | break;
168 | }
169 | }
170 |
171 | for (int i = N - 1; i >= 0; i--){// in case ends with 0
172 | if (seats[i] == 1){
173 | ans = Math.max(ans, N - 1 - i);
174 | break;
175 | }
176 | }
177 | return ans;
178 | }
179 | ```
180 |
181 | * Time Complexity: $O(N)$, where N is the length of `seats`.
182 | * Space Complexity: $O(1)$.
183 |
184 | ## 3Sum (Medium #15)
185 |
186 | **Question**: Given an integer array nums, return all the triplets `[nums[i], nums[j], nums[k]]` such that `i != j`, `i != k`, and `j != k`, and `nums[i] + nums[j] + nums[k] == 0`.
187 |
188 | Notice that the solution set must not contain duplicate triplets.
189 |
190 | **Example 1:**
191 |
192 | ```
193 | Input: nums = [-1,0,1,2,-1,-4]
194 | Output: [[-1,-1,2],[-1,0,1]]
195 | Explanation:
196 | nums[0] + nums[1] + nums[2] = (-1) + 0 + 1 = 0.
197 | nums[1] + nums[2] + nums[4] = 0 + 1 + (-1) = 0.
198 | nums[0] + nums[3] + nums[4] = (-1) + 2 + (-1) = 0.
199 | The distinct triplets are [-1,0,1] and [-1,-1,2].
200 | Notice that the order of the output and the order of the triplets does not matter.
201 | ```
202 |
203 | **Example 2:**
204 |
205 | ```
206 | Input: nums = [0,1,1]
207 | Output: []
208 | Explanation: The only possible triplet does not sum up to 0.
209 | ```
210 |
211 | **Example 3:**
212 |
213 | ```
214 | Input: nums = [0,0,0]
215 | Output: [[0,0,0]]
216 | Explanation: The only possible triplet sums up to 0.
217 | ```
218 |
219 | **Constraints:**
220 |
221 | - `3 <= nums.length <= 3000`
222 | - `-105 <= nums[i] <= 105`
223 |
224 | ### My Solution
225 |
226 | ```java
227 | // two pointers
228 | // 1. sum to 0: location < 0
229 | // 2. low and high pointer
230 | List
16 |
17 | ```
18 | Input: seats = [1,0,0,0,1,0,1]
19 | Output: 2
20 | Explanation:
21 | If Alex sits in the second open seat (i.e. seats[2]), then the closest person has distance 2.
22 | If Alex sits in any other open seat, the closest person has distance 1.
23 | Thus, the maximum distance to the closest person is 2.
24 | ```
25 |
26 | **Example 2:**
27 |
28 | ```
29 | Input: seats = [1,0,0,0]
30 | Output: 3
31 | Explanation:
32 | If Alex sits in the last seat (i.e. seats[3]), the closest person is 3 seats away.
33 | This is the maximum distance possible, so the answer is 3.
34 | ```
35 |
36 | **Example 3:**
37 |
38 | ```
39 | Input: seats = [0,1]
40 | Output: 1
41 | ```
42 |
43 | **Constraints:**
44 |
45 | - `2 <= seats.length <= 2 * 104`
46 | - `seats[i]` is `0` or `1`.
47 | - At least one seat is **empty**.
48 | - At least one seat is **occupied**.
49 |
50 | ### My Solution
51 |
52 | ```java
53 | public int maxDistToClosest(int[] seats) {
54 | int maxDist = 0, low, high;
55 |
56 | for (low = 0, high = 0; high < seats.length; ++high){
57 | if (seats[high] == 1){
58 | int totalDist = high - low;
59 | if (seats[low] == 1){
60 | maxDist = Math.max((int)Math.ceil(totalDist/2), maxDist);
61 | }
62 | else {
63 | maxDist = Math.max(totalDist, maxDist);
64 | }
65 | low = high;
66 | }
67 | }
68 | if (low == seats.length - 1) return Math.max(maxDist, high - low);
69 | return Math.max(maxDist, high - low - 1);
70 | }
71 | ```
72 |
73 | ### Standard Solution
74 |
75 | #### Solution #1 Next Array
76 |
77 | * Let `left[i]` be the distance from seat `i` to the closest person sitting to the left of `i`. Similarly, let `right[i]` be the distance to the closest person sitting to the right of `i`. This is motivated by the idea that the closest person in seat `i` sits a distance `min(left[i], right[i])` away.
78 |
79 | * **Algorithm**
80 |
81 | To construct `left[i]`, notice it is either `left[i-1] + 1` if the seat is empty, or `0` if it is full. `right[i]` is constructed in a similar way.
82 |
83 | ```java
84 | public int maxDistToClosest(int[] seats){
85 | int N = seats.length;
86 | int[] left = new int[N], right = new int[N];
87 | Arrays.fill(left, N);
88 | Arrays.fill(right, N);
89 |
90 | for (int i = 0; i < N; i++){
91 | if (seats[i] == 1) left[i] = 0; //distance to the cloest one would be 0
92 | else if (i > 0) left[i] = left[i - 1] + 1; //add 1 distance comparing to the previous one
93 | }
94 | for (int i = N - 1; i >= 0; i--){
95 | if (seats[i] == 1) right[i] = 0; //distance to the cloest one would be 0
96 | else if (i < N - 1) right[i] = right[i + 1] + 1; //add 1 distance comparing to the previous one
97 | }
98 |
99 | int ans = 0;
100 | for (int i = 0; i < N; i++){
101 | if (seats[i] == 0){
102 | ans = Math.max(ans, Math.min(left[i], right[i]));
103 | }
104 | }
105 | return ans;
106 | }
107 | ```
108 |
109 | * Time complexity: $O(N)$ where N is the length of seats
110 | * Space complexity: $O(N)$ where the space used by left and right
111 |
112 | #### Solution #2 Two Pointer
113 |
114 | * **Algorithm**:
115 | * Keep track of `prev`, the filled seat at or to the left of `i`, and `future`, the filled seat at or to the right of `i`.
116 | * Then at seat `i`, the closest person is `min(i - prev, future - i)`, with one exception. `i - prev` should be considered infinite if there is no person to the left of seat `i`, and similarly `future - i` is infinite if there is no one to the right of seat `i`.
117 |
118 | ```java
119 | public int maxDistToClosest(int[] seats){
120 | int N = seats.length;
121 | int prev = -1, future = 0;
122 | int ans = 0;
123 |
124 | for (int i = 0; i < N; i++){
125 | if (seats[i] == 1){
126 | prev = i;
127 | } else {
128 | while (future < N && seats[future] == 0 || future < i){
129 | future++;
130 | }
131 | int left = prev == -1 ? N : i - prev;
132 | int right = future == N ? N : future - i;
133 | ans = Math.max(ans, Math.min(left, right));
134 | }
135 | }
136 | return ans;
137 | }
138 | ```
139 |
140 | * Time Complexity: $O(N)$, where $N$ is the length of `seats`.
141 | * Space Complexity: $O(1)$
142 |
143 | #### Solution #3 Group by Zero
144 |
145 | * My solution is a combination of solution 2 and 3
146 | * In a group of `K` adjacent empty seats between two people, the answer is `(K+1) / 2`.
147 | * For groups of empty seats between the edge of the row and one other person, the answer is `K`, and we should take into account those answers too.
148 |
149 | ```java
150 | public int maxDistToClosest(int[] seats){
151 | int N = seats.length;
152 | int K = 0;//current longest group of empty seats
153 | int ans = 0;
154 |
155 | for (int i = 0; i < N; i++){
156 | if (seats[i] == 1){
157 | K = 0;
158 | } else {
159 | K++;
160 | ans = Math.max(ans, (K + 1) / 2);
161 | }
162 | }
163 |
164 | for (int i = 0; i < N; i++){// in case starts from 0
165 | if (seats[i] == 1){
166 | ans = Math.max(ans, i);
167 | break;
168 | }
169 | }
170 |
171 | for (int i = N - 1; i >= 0; i--){// in case ends with 0
172 | if (seats[i] == 1){
173 | ans = Math.max(ans, N - 1 - i);
174 | break;
175 | }
176 | }
177 | return ans;
178 | }
179 | ```
180 |
181 | * Time Complexity: $O(N)$, where N is the length of `seats`.
182 | * Space Complexity: $O(1)$.
183 |
184 | ## 3Sum (Medium #15)
185 |
186 | **Question**: Given an integer array nums, return all the triplets `[nums[i], nums[j], nums[k]]` such that `i != j`, `i != k`, and `j != k`, and `nums[i] + nums[j] + nums[k] == 0`.
187 |
188 | Notice that the solution set must not contain duplicate triplets.
189 |
190 | **Example 1:**
191 |
192 | ```
193 | Input: nums = [-1,0,1,2,-1,-4]
194 | Output: [[-1,-1,2],[-1,0,1]]
195 | Explanation:
196 | nums[0] + nums[1] + nums[2] = (-1) + 0 + 1 = 0.
197 | nums[1] + nums[2] + nums[4] = 0 + 1 + (-1) = 0.
198 | nums[0] + nums[3] + nums[4] = (-1) + 2 + (-1) = 0.
199 | The distinct triplets are [-1,0,1] and [-1,-1,2].
200 | Notice that the order of the output and the order of the triplets does not matter.
201 | ```
202 |
203 | **Example 2:**
204 |
205 | ```
206 | Input: nums = [0,1,1]
207 | Output: []
208 | Explanation: The only possible triplet does not sum up to 0.
209 | ```
210 |
211 | **Example 3:**
212 |
213 | ```
214 | Input: nums = [0,0,0]
215 | Output: [[0,0,0]]
216 | Explanation: The only possible triplet sums up to 0.
217 | ```
218 |
219 | **Constraints:**
220 |
221 | - `3 <= nums.length <= 3000`
222 | - `-105 <= nums[i] <= 105`
223 |
224 | ### My Solution
225 |
226 | ```java
227 | // two pointers
228 | // 1. sum to 0: location < 0
229 | // 2. low and high pointer
230 | List 28 |
29 | * If you handle this tree in postorder, you can easily handle the expression using a stack.
30 | * Each time when you meet a operator, you can just **pop 2 elements from the stack**, **calculate the result and push the result back into the stack**.
31 |
32 | * Frequently come with **recursion and/or iteration** for code solution.
33 |
34 | * To be cautious, the complexity might be different due to a different implementation. It is comparatively easy to do traversal recursively but when the depth of the tree is too large, we might suffer from `stack overflow` problem. That's one of the main reasons why we want to solve this problem iteratively sometimes.
35 |
36 | ## Binary Tree Preorder Traversal(Easy #144)
37 |
38 | **Question**: Given the `root` of a binary tree, return *the preorder traversal of its nodes' values*.
39 |
40 | **Example 1:**
41 |
42 |
28 |
29 | * If you handle this tree in postorder, you can easily handle the expression using a stack.
30 | * Each time when you meet a operator, you can just **pop 2 elements from the stack**, **calculate the result and push the result back into the stack**.
31 |
32 | * Frequently come with **recursion and/or iteration** for code solution.
33 |
34 | * To be cautious, the complexity might be different due to a different implementation. It is comparatively easy to do traversal recursively but when the depth of the tree is too large, we might suffer from `stack overflow` problem. That's one of the main reasons why we want to solve this problem iteratively sometimes.
35 |
36 | ## Binary Tree Preorder Traversal(Easy #144)
37 |
38 | **Question**: Given the `root` of a binary tree, return *the preorder traversal of its nodes' values*.
39 |
40 | **Example 1:**
41 |
42 |  43 |
44 | ```
45 | Input: root = [1,null,2,3]
46 | Output: [1,2,3]
47 | ```
48 |
49 | **Example 2:**
50 |
51 | ```
52 | Input: root = []
53 | Output: []
54 | ```
55 |
56 | **Example 3:**
57 |
58 | ```
59 | Input: root = [1]
60 | Output: [1]
61 | ```
62 |
63 | **Constraints:**
64 |
65 | - The number of nodes in the tree is in the range `[0, 100]`.
66 | - `-100 <= Node.val <= 100`
67 |
68 | ### My Solution
69 |
70 | ```java
71 | /**
72 | * Definition for a binary tree node.
73 | * public class TreeNode {
74 | * int val;
75 | * TreeNode left;
76 | * TreeNode right;
77 | * TreeNode() {}
78 | * TreeNode(int val) { this.val = val; }
79 | * TreeNode(int val, TreeNode left, TreeNode right) {
80 | * this.val = val;
81 | * this.left = left;
82 | * this.right = right;
83 | * }
84 | * }
85 | */
86 | public List
43 |
44 | ```
45 | Input: root = [1,null,2,3]
46 | Output: [1,2,3]
47 | ```
48 |
49 | **Example 2:**
50 |
51 | ```
52 | Input: root = []
53 | Output: []
54 | ```
55 |
56 | **Example 3:**
57 |
58 | ```
59 | Input: root = [1]
60 | Output: [1]
61 | ```
62 |
63 | **Constraints:**
64 |
65 | - The number of nodes in the tree is in the range `[0, 100]`.
66 | - `-100 <= Node.val <= 100`
67 |
68 | ### My Solution
69 |
70 | ```java
71 | /**
72 | * Definition for a binary tree node.
73 | * public class TreeNode {
74 | * int val;
75 | * TreeNode left;
76 | * TreeNode right;
77 | * TreeNode() {}
78 | * TreeNode(int val) { this.val = val; }
79 | * TreeNode(int val, TreeNode left, TreeNode right) {
80 | * this.val = val;
81 | * this.left = left;
82 | * this.right = right;
83 | * }
84 | * }
85 | */
86 | public List 207 |
208 | ```
209 | Input: root = [1,null,2,3]
210 | Output: [1,3,2]
211 | ```
212 |
213 | **Example 2:**
214 |
215 | ```
216 | Input: root = []
217 | Output: []
218 | ```
219 |
220 | **Example 3:**
221 |
222 | ```
223 | Input: root = [1]
224 | Output: [1]
225 | ```
226 |
227 | **Constraints:**
228 |
229 | - The number of nodes in the tree is in the range `[0, 100]`.
230 | - `-100 <= Node.val <= 100`
231 |
232 | ### My Solution
233 |
234 | ```java
235 | public List
207 |
208 | ```
209 | Input: root = [1,null,2,3]
210 | Output: [1,3,2]
211 | ```
212 |
213 | **Example 2:**
214 |
215 | ```
216 | Input: root = []
217 | Output: []
218 | ```
219 |
220 | **Example 3:**
221 |
222 | ```
223 | Input: root = [1]
224 | Output: [1]
225 | ```
226 |
227 | **Constraints:**
228 |
229 | - The number of nodes in the tree is in the range `[0, 100]`.
230 | - `-100 <= Node.val <= 100`
231 |
232 | ### My Solution
233 |
234 | ```java
235 | public List 440 |
441 | ```
442 | Input: root = [3,9,20,null,null,15,7]
443 | Output: [[3],[9,20],[15,7]]
444 | ```
445 |
446 | **Example 2:**
447 |
448 | ```
449 | Input: root = [1]
450 | Output: [[1]]
451 | ```
452 |
453 | **Example 3:**
454 |
455 | ```
456 | Input: root = []
457 | Output: []
458 | ```
459 |
460 | **Constraints:**
461 |
462 | - The number of nodes in the tree is in the range `[0, 2000]`.
463 | - `-1000 <= Node.val <= 1000`
464 |
465 | ### My Solution
466 |
467 | * Use a queue to store the value from left to right
468 | * Use queue size to determine how many nodes in the same level and use array list to store the same level nodes
469 | * Add the level nodes to `levels` which is the return list
470 |
471 | ```java
472 | /**
473 | * Definition for a binary tree node.
474 | * public class TreeNode {
475 | * int val;
476 | * TreeNode left;
477 | * TreeNode right;
478 | * TreeNode() {}
479 | * TreeNode(int val) { this.val = val; }
480 | * TreeNode(int val, TreeNode left, TreeNode right) {
481 | * this.val = val;
482 | * this.left = left;
483 | * this.right = right;
484 | * }
485 | * }
486 | */
487 | public List
440 |
441 | ```
442 | Input: root = [3,9,20,null,null,15,7]
443 | Output: [[3],[9,20],[15,7]]
444 | ```
445 |
446 | **Example 2:**
447 |
448 | ```
449 | Input: root = [1]
450 | Output: [[1]]
451 | ```
452 |
453 | **Example 3:**
454 |
455 | ```
456 | Input: root = []
457 | Output: []
458 | ```
459 |
460 | **Constraints:**
461 |
462 | - The number of nodes in the tree is in the range `[0, 2000]`.
463 | - `-1000 <= Node.val <= 1000`
464 |
465 | ### My Solution
466 |
467 | * Use a queue to store the value from left to right
468 | * Use queue size to determine how many nodes in the same level and use array list to store the same level nodes
469 | * Add the level nodes to `levels` which is the return list
470 |
471 | ```java
472 | /**
473 | * Definition for a binary tree node.
474 | * public class TreeNode {
475 | * int val;
476 | * TreeNode left;
477 | * TreeNode right;
478 | * TreeNode() {}
479 | * TreeNode(int val) { this.val = val; }
480 | * TreeNode(int val, TreeNode left, TreeNode right) {
481 | * this.val = val;
482 | * this.left = left;
483 | * this.right = right;
484 | * }
485 | * }
486 | */
487 | public List 37 |
38 | * [Heap Insertion](https://leetcode.com/explore/learn/card/heap/643/heap/4019/)
39 | * [Heap Deletion](https://leetcode.com/explore/learn/card/heap/643/heap/4020/)
40 |
41 | ### Implementation of a Heap
42 |
43 | * Use an array to implement a heap
44 |
45 | * Min Heap
46 |
47 | ```java
48 | // Implementing "Min Heap"
49 | public class MinHeap {
50 | // Create a complete binary tree using an array
51 | // Then use the binary tree to construct a Heap
52 | int[] minHeap;
53 | // the number of elements is needed when instantiating an array
54 | // heapSize records the size of the array
55 | int heapSize;
56 | // realSize records the number of elements in the Heap
57 | int realSize = 0;
58 |
59 | public MinHeap(int heapSize) {
60 | this.heapSize = heapSize;
61 | minHeap = new int[heapSize + 1];
62 | // To better track the indices of the binary tree,
63 | // we will not use the 0-th element in the array
64 | // You can fill it with any value
65 | minHeap[0] = 0;
66 | }
67 |
68 | // Function to add an element
69 | public void add(int element) {
70 | realSize++;
71 | // If the number of elements in the Heap exceeds the preset heapSize
72 | // print "Added too many elements" and return
73 | if (realSize > heapSize) {
74 | System.out.println("Added too many elements!");
75 | realSize--;
76 | return;
77 | }
78 | // Add the element into the array
79 | minHeap[realSize] = element;
80 | // Index of the newly added element
81 | int index = realSize;
82 | // Parent node of the newly added element
83 | // Note if we use an array to represent the complete binary tree
84 | // and store the root node at index 1
85 | // index of the parent node of any node is [index of the node / 2]
86 | // index of the left child node is [index of the node * 2]
87 | // index of the right child node is [index of the node * 2 + 1]
88 | int parent = index / 2;
89 | // If the newly added element is smaller than its parent node,
90 | // its value will be exchanged with that of the parent node
91 | while ( minHeap[index] < minHeap[parent] && index > 1 ) {
92 | int temp = minHeap[index];
93 | minHeap[index] = minHeap[parent];
94 | minHeap[parent] = temp;
95 | index = parent;
96 | parent = index / 2;
97 | }
98 | }
99 |
100 | // Get the top element of the Heap
101 | public int peek() {
102 | return minHeap[1];
103 | }
104 |
105 | // Delete the top element of the Heap
106 | public int pop() {
107 | // If the number of elements in the current Heap is 0,
108 | // print "Don't have any elements" and return a default value
109 | if (realSize < 1) {
110 | System.out.println("Don't have any element!");
111 | return Integer.MAX_VALUE;
112 | } else {
113 | // When there are still elements in the Heap
114 | // realSize >= 1
115 | int removeElement = minHeap[1];
116 | // Put the last element in the Heap to the top of Heap
117 | minHeap[1] = minHeap[realSize];
118 | realSize--;
119 | int index = 1;
120 | // When the deleted element is not a leaf node
121 | while (index <= realSize / 2) {
122 | // the left child of the deleted element
123 | int left = index * 2;
124 | // the right child of the deleted element
125 | int right = (index * 2) + 1;
126 | // If the deleted element is larger than the left or right child
127 | // its value needs to be exchanged with the smaller value
128 | // of the left and right child
129 | if (minHeap[index] > minHeap[left] || minHeap[index] > minHeap[right]) {
130 | if (minHeap[left] < minHeap[right]) {
131 | int temp = minHeap[left];
132 | minHeap[left] = minHeap[index];
133 | minHeap[index] = temp;
134 | index = left;
135 | } else {
136 | // maxHeap[left] >= maxHeap[right]
137 | int temp = minHeap[right];
138 | minHeap[right] = minHeap[index];
139 | minHeap[index] = temp;
140 | index = right;
141 | }
142 | } else {
143 | break;
144 | }
145 | }
146 | return removeElement;
147 | }
148 | }
149 |
150 | // return the number of elements in the Heap
151 | public int size() {
152 | return realSize;
153 | }
154 |
155 | public String toString() {
156 | if (realSize == 0) {
157 | return "No element!";
158 | } else {
159 | StringBuilder sb = new StringBuilder();
160 | sb.append('[');
161 | for (int i = 1; i <= realSize; i++) {
162 | sb.append(minHeap[i]);
163 | sb.append(',');
164 | }
165 | sb.deleteCharAt(sb.length() - 1);
166 | sb.append(']');
167 | return sb.toString();
168 | }
169 | }
170 |
171 | public static void main(String[] args) {
172 | // Test case
173 | MinHeap minHeap = new MinHeap(3);
174 | minHeap.add(3);
175 | minHeap.add(1);
176 | minHeap.add(2);
177 | // [1,3,2]
178 | System.out.println(minHeap.toString());
179 | // 1
180 | System.out.println(minHeap.peek());
181 | // 1
182 | System.out.println(minHeap.pop());
183 | // [2, 3]
184 | System.out.println(minHeap.toString());
185 | minHeap.add(4);
186 | // Add too many elements
187 | minHeap.add(5);
188 | // [2,3,4]
189 | System.out.println(minHeap.toString());
190 | }
191 | }
192 |
193 | ```
194 |
195 | * Max Heap
196 |
197 | ```java
198 | // Implementing "Max Heap"
199 | public class MaxHeap {
200 | // Create a complete binary tree using an array
201 | // Then use the binary tree to construct a Heap
202 | int[] maxHeap;
203 | // the number of elements is needed when instantiating an array
204 | // heapSize records the size of the array
205 | int heapSize;
206 | // realSize records the number of elements in the Heap
207 | int realSize = 0;
208 |
209 | public MaxHeap(int heapSize) {
210 | this.heapSize = heapSize;
211 | maxHeap = new int[heapSize + 1];
212 | // To better track the indices of the binary tree,
213 | // we will not use the 0-th element in the array
214 | // You can fill it with any value
215 | maxHeap[0] = 0;
216 | }
217 |
218 | // Function to add an element
219 | public void add(int element) {
220 | realSize++;
221 | // If the number of elements in the Heap exceeds the preset heapSize
222 | // print "Added too many elements" and return
223 | if (realSize > heapSize) {
224 | System.out.println("Added too many elements!");
225 | realSize--;
226 | return;
227 | }
228 | // Add the element into the array
229 | maxHeap[realSize] = element;
230 | // Index of the newly added element
231 | int index = realSize;
232 | // Parent node of the newly added element
233 | // Note if we use an array to represent the complete binary tree
234 | // and store the root node at index 1
235 | // index of the parent node of any node is [index of the node / 2]
236 | // index of the left child node is [index of the node * 2]
237 | // index of the right child node is [index of the node * 2 + 1]
238 |
239 | int parent = index / 2;
240 | // If the newly added element is larger than its parent node,
241 | // its value will be exchanged with that of the parent node
242 | while ( maxHeap[index] > maxHeap[parent] && index > 1 ) {
243 | int temp = maxHeap[index];
244 | maxHeap[index] = maxHeap[parent];
245 | maxHeap[parent] = temp;
246 | index = parent;
247 | parent = index / 2;
248 | }
249 | }
250 |
251 | // Get the top element of the Heap
252 | public int peek() {
253 | return maxHeap[1];
254 | }
255 |
256 | // Delete the top element of the Heap
257 | public int pop() {
258 | // If the number of elements in the current Heap is 0,
259 | // print "Don't have any elements" and return a default value
260 | if (realSize < 1) {
261 | System.out.println("Don't have any element!");
262 | return Integer.MIN_VALUE;
263 | } else {
264 | // When there are still elements in the Heap
265 | // realSize >= 1
266 | int removeElement = maxHeap[1];
267 | // Put the last element in the Heap to the top of Heap
268 | maxHeap[1] = maxHeap[realSize];
269 | realSize--;
270 | int index = 1;
271 | // When the deleted element is not a leaf node
272 | while (index <= realSize / 2) {
273 | // the left child of the deleted element
274 | int left = index * 2;
275 | // the right child of the deleted element
276 | int right = (index * 2) + 1;
277 | // If the deleted element is smaller than the left or right child
278 | // its value needs to be exchanged with the larger value
279 | // of the left and right child
280 | if (maxHeap[index] < maxHeap[left] || maxHeap[index] < maxHeap[right]) {
281 | if (maxHeap[left] > maxHeap[right]) {
282 | int temp = maxHeap[left];
283 | maxHeap[left] = maxHeap[index];
284 | maxHeap[index] = temp;
285 | index = left;
286 | } else {
287 | // maxHeap[left] <= maxHeap[right]
288 | int temp = maxHeap[right];
289 | maxHeap[right] = maxHeap[index];
290 | maxHeap[index] = temp;
291 | index = right;
292 | }
293 | } else {
294 | break;
295 | }
296 | }
297 | return removeElement;
298 | }
299 | }
300 |
301 | // return the number of elements in the Heap
302 | public int size() {
303 | return realSize;
304 | }
305 |
306 | public String toString() {
307 | if (realSize == 0) {
308 | return "No element!";
309 | } else {
310 | StringBuilder sb = new StringBuilder();
311 | sb.append('[');
312 | for (int i = 1; i <= realSize; i++) {
313 | sb.append(maxHeap[i]);
314 | sb.append(',');
315 | }
316 | sb.deleteCharAt(sb.length() - 1);
317 | sb.append(']');
318 | return sb.toString();
319 | }
320 | }
321 |
322 | public static void main(String[] args) {
323 | // Test case
324 | MaxHeap maxheap = new MaxHeap(5);
325 | maxheap.add(1);
326 | maxheap.add(2);
327 | maxheap.add(3);
328 | // [3,1,2]
329 | System.out.println(maxheap.toString());
330 | // 3
331 | System.out.println(maxheap.peek());
332 | // 3
333 | System.out.println(maxheap.pop());
334 | System.out.println(maxheap.pop());
335 | System.out.println(maxheap.pop());
336 | // No element
337 | System.out.println(maxheap.toString());
338 | maxheap.add(4);
339 | // Add too many elements
340 | maxheap.add(5);
341 | // [4,1,2]
342 | System.out.println(maxheap.toString());
343 | }
344 | }
345 |
346 | ```
347 |
348 | ## Heap Construction
349 |
350 | * When creating a Heap, we can simultaneously perform the **heapify** operation. Heapify means converting a group of data into a Heap.
351 | * Time complexity: $O(N)$.
352 | * Space complexity: $O(N)$.
353 |
354 | ```java
355 | // In Java, a Heap is represented by a Priority Queue
356 | import java.util.Collections;
357 | import java.util.PriorityQueue;
358 | import java.util.Arrays;
359 |
360 | // Construct an empty Min Heap
361 | PriorityQueue
37 |
38 | * [Heap Insertion](https://leetcode.com/explore/learn/card/heap/643/heap/4019/)
39 | * [Heap Deletion](https://leetcode.com/explore/learn/card/heap/643/heap/4020/)
40 |
41 | ### Implementation of a Heap
42 |
43 | * Use an array to implement a heap
44 |
45 | * Min Heap
46 |
47 | ```java
48 | // Implementing "Min Heap"
49 | public class MinHeap {
50 | // Create a complete binary tree using an array
51 | // Then use the binary tree to construct a Heap
52 | int[] minHeap;
53 | // the number of elements is needed when instantiating an array
54 | // heapSize records the size of the array
55 | int heapSize;
56 | // realSize records the number of elements in the Heap
57 | int realSize = 0;
58 |
59 | public MinHeap(int heapSize) {
60 | this.heapSize = heapSize;
61 | minHeap = new int[heapSize + 1];
62 | // To better track the indices of the binary tree,
63 | // we will not use the 0-th element in the array
64 | // You can fill it with any value
65 | minHeap[0] = 0;
66 | }
67 |
68 | // Function to add an element
69 | public void add(int element) {
70 | realSize++;
71 | // If the number of elements in the Heap exceeds the preset heapSize
72 | // print "Added too many elements" and return
73 | if (realSize > heapSize) {
74 | System.out.println("Added too many elements!");
75 | realSize--;
76 | return;
77 | }
78 | // Add the element into the array
79 | minHeap[realSize] = element;
80 | // Index of the newly added element
81 | int index = realSize;
82 | // Parent node of the newly added element
83 | // Note if we use an array to represent the complete binary tree
84 | // and store the root node at index 1
85 | // index of the parent node of any node is [index of the node / 2]
86 | // index of the left child node is [index of the node * 2]
87 | // index of the right child node is [index of the node * 2 + 1]
88 | int parent = index / 2;
89 | // If the newly added element is smaller than its parent node,
90 | // its value will be exchanged with that of the parent node
91 | while ( minHeap[index] < minHeap[parent] && index > 1 ) {
92 | int temp = minHeap[index];
93 | minHeap[index] = minHeap[parent];
94 | minHeap[parent] = temp;
95 | index = parent;
96 | parent = index / 2;
97 | }
98 | }
99 |
100 | // Get the top element of the Heap
101 | public int peek() {
102 | return minHeap[1];
103 | }
104 |
105 | // Delete the top element of the Heap
106 | public int pop() {
107 | // If the number of elements in the current Heap is 0,
108 | // print "Don't have any elements" and return a default value
109 | if (realSize < 1) {
110 | System.out.println("Don't have any element!");
111 | return Integer.MAX_VALUE;
112 | } else {
113 | // When there are still elements in the Heap
114 | // realSize >= 1
115 | int removeElement = minHeap[1];
116 | // Put the last element in the Heap to the top of Heap
117 | minHeap[1] = minHeap[realSize];
118 | realSize--;
119 | int index = 1;
120 | // When the deleted element is not a leaf node
121 | while (index <= realSize / 2) {
122 | // the left child of the deleted element
123 | int left = index * 2;
124 | // the right child of the deleted element
125 | int right = (index * 2) + 1;
126 | // If the deleted element is larger than the left or right child
127 | // its value needs to be exchanged with the smaller value
128 | // of the left and right child
129 | if (minHeap[index] > minHeap[left] || minHeap[index] > minHeap[right]) {
130 | if (minHeap[left] < minHeap[right]) {
131 | int temp = minHeap[left];
132 | minHeap[left] = minHeap[index];
133 | minHeap[index] = temp;
134 | index = left;
135 | } else {
136 | // maxHeap[left] >= maxHeap[right]
137 | int temp = minHeap[right];
138 | minHeap[right] = minHeap[index];
139 | minHeap[index] = temp;
140 | index = right;
141 | }
142 | } else {
143 | break;
144 | }
145 | }
146 | return removeElement;
147 | }
148 | }
149 |
150 | // return the number of elements in the Heap
151 | public int size() {
152 | return realSize;
153 | }
154 |
155 | public String toString() {
156 | if (realSize == 0) {
157 | return "No element!";
158 | } else {
159 | StringBuilder sb = new StringBuilder();
160 | sb.append('[');
161 | for (int i = 1; i <= realSize; i++) {
162 | sb.append(minHeap[i]);
163 | sb.append(',');
164 | }
165 | sb.deleteCharAt(sb.length() - 1);
166 | sb.append(']');
167 | return sb.toString();
168 | }
169 | }
170 |
171 | public static void main(String[] args) {
172 | // Test case
173 | MinHeap minHeap = new MinHeap(3);
174 | minHeap.add(3);
175 | minHeap.add(1);
176 | minHeap.add(2);
177 | // [1,3,2]
178 | System.out.println(minHeap.toString());
179 | // 1
180 | System.out.println(minHeap.peek());
181 | // 1
182 | System.out.println(minHeap.pop());
183 | // [2, 3]
184 | System.out.println(minHeap.toString());
185 | minHeap.add(4);
186 | // Add too many elements
187 | minHeap.add(5);
188 | // [2,3,4]
189 | System.out.println(minHeap.toString());
190 | }
191 | }
192 |
193 | ```
194 |
195 | * Max Heap
196 |
197 | ```java
198 | // Implementing "Max Heap"
199 | public class MaxHeap {
200 | // Create a complete binary tree using an array
201 | // Then use the binary tree to construct a Heap
202 | int[] maxHeap;
203 | // the number of elements is needed when instantiating an array
204 | // heapSize records the size of the array
205 | int heapSize;
206 | // realSize records the number of elements in the Heap
207 | int realSize = 0;
208 |
209 | public MaxHeap(int heapSize) {
210 | this.heapSize = heapSize;
211 | maxHeap = new int[heapSize + 1];
212 | // To better track the indices of the binary tree,
213 | // we will not use the 0-th element in the array
214 | // You can fill it with any value
215 | maxHeap[0] = 0;
216 | }
217 |
218 | // Function to add an element
219 | public void add(int element) {
220 | realSize++;
221 | // If the number of elements in the Heap exceeds the preset heapSize
222 | // print "Added too many elements" and return
223 | if (realSize > heapSize) {
224 | System.out.println("Added too many elements!");
225 | realSize--;
226 | return;
227 | }
228 | // Add the element into the array
229 | maxHeap[realSize] = element;
230 | // Index of the newly added element
231 | int index = realSize;
232 | // Parent node of the newly added element
233 | // Note if we use an array to represent the complete binary tree
234 | // and store the root node at index 1
235 | // index of the parent node of any node is [index of the node / 2]
236 | // index of the left child node is [index of the node * 2]
237 | // index of the right child node is [index of the node * 2 + 1]
238 |
239 | int parent = index / 2;
240 | // If the newly added element is larger than its parent node,
241 | // its value will be exchanged with that of the parent node
242 | while ( maxHeap[index] > maxHeap[parent] && index > 1 ) {
243 | int temp = maxHeap[index];
244 | maxHeap[index] = maxHeap[parent];
245 | maxHeap[parent] = temp;
246 | index = parent;
247 | parent = index / 2;
248 | }
249 | }
250 |
251 | // Get the top element of the Heap
252 | public int peek() {
253 | return maxHeap[1];
254 | }
255 |
256 | // Delete the top element of the Heap
257 | public int pop() {
258 | // If the number of elements in the current Heap is 0,
259 | // print "Don't have any elements" and return a default value
260 | if (realSize < 1) {
261 | System.out.println("Don't have any element!");
262 | return Integer.MIN_VALUE;
263 | } else {
264 | // When there are still elements in the Heap
265 | // realSize >= 1
266 | int removeElement = maxHeap[1];
267 | // Put the last element in the Heap to the top of Heap
268 | maxHeap[1] = maxHeap[realSize];
269 | realSize--;
270 | int index = 1;
271 | // When the deleted element is not a leaf node
272 | while (index <= realSize / 2) {
273 | // the left child of the deleted element
274 | int left = index * 2;
275 | // the right child of the deleted element
276 | int right = (index * 2) + 1;
277 | // If the deleted element is smaller than the left or right child
278 | // its value needs to be exchanged with the larger value
279 | // of the left and right child
280 | if (maxHeap[index] < maxHeap[left] || maxHeap[index] < maxHeap[right]) {
281 | if (maxHeap[left] > maxHeap[right]) {
282 | int temp = maxHeap[left];
283 | maxHeap[left] = maxHeap[index];
284 | maxHeap[index] = temp;
285 | index = left;
286 | } else {
287 | // maxHeap[left] <= maxHeap[right]
288 | int temp = maxHeap[right];
289 | maxHeap[right] = maxHeap[index];
290 | maxHeap[index] = temp;
291 | index = right;
292 | }
293 | } else {
294 | break;
295 | }
296 | }
297 | return removeElement;
298 | }
299 | }
300 |
301 | // return the number of elements in the Heap
302 | public int size() {
303 | return realSize;
304 | }
305 |
306 | public String toString() {
307 | if (realSize == 0) {
308 | return "No element!";
309 | } else {
310 | StringBuilder sb = new StringBuilder();
311 | sb.append('[');
312 | for (int i = 1; i <= realSize; i++) {
313 | sb.append(maxHeap[i]);
314 | sb.append(',');
315 | }
316 | sb.deleteCharAt(sb.length() - 1);
317 | sb.append(']');
318 | return sb.toString();
319 | }
320 | }
321 |
322 | public static void main(String[] args) {
323 | // Test case
324 | MaxHeap maxheap = new MaxHeap(5);
325 | maxheap.add(1);
326 | maxheap.add(2);
327 | maxheap.add(3);
328 | // [3,1,2]
329 | System.out.println(maxheap.toString());
330 | // 3
331 | System.out.println(maxheap.peek());
332 | // 3
333 | System.out.println(maxheap.pop());
334 | System.out.println(maxheap.pop());
335 | System.out.println(maxheap.pop());
336 | // No element
337 | System.out.println(maxheap.toString());
338 | maxheap.add(4);
339 | // Add too many elements
340 | maxheap.add(5);
341 | // [4,1,2]
342 | System.out.println(maxheap.toString());
343 | }
344 | }
345 |
346 | ```
347 |
348 | ## Heap Construction
349 |
350 | * When creating a Heap, we can simultaneously perform the **heapify** operation. Heapify means converting a group of data into a Heap.
351 | * Time complexity: $O(N)$.
352 | * Space complexity: $O(N)$.
353 |
354 | ```java
355 | // In Java, a Heap is represented by a Priority Queue
356 | import java.util.Collections;
357 | import java.util.PriorityQueue;
358 | import java.util.Arrays;
359 |
360 | // Construct an empty Min Heap
361 | PriorityQueue 92 |
93 | ```java
94 | public int closestValue(TreeNode root, double target){
95 | int val, closest = root.val;
96 | while (root != null){
97 | val = root.val;
98 | closest = Math.abs(val - target) < Math.abs(closest - target) ? val : closest;
99 | root = target < root.val ? root.left : root.right;
100 | }
101 | return closest;
102 | }
103 | ```
104 |
105 | - Time complexity: $\mathcal{O}(H)$ since here one goes from root down to a leaf.
106 | - Space complexity: $\mathcal{O}(1)$.
107 |
108 | ## Search in a Sorted Array of Unknown Size(Medium #702)
109 |
110 | **Question**: This is an ***interactive problem***.
111 |
112 | You have a sorted array of **unique** elements and an **unknown size**. You do not have an access to the array but you can use the `ArrayReader` interface to access it. You can call `ArrayReader.get(i)` that:
113 |
114 | - returns the value at the `ith` index (**0-indexed**) of the secret array (i.e., `secret[i]`), or
115 | - returns `231 - 1` if the `i` is out of the boundary of the array.
116 |
117 | You are also given an integer `target`.
118 |
119 | Return the index `k` of the hidden array where `secret[k] == target` or return `-1` otherwise.
120 |
121 | You must write an algorithm with `O(log n)` runtime complexity.
122 |
123 | **Example 1:**
124 |
125 | ```
126 | Input: secret = [-1,0,3,5,9,12], target = 9
127 | Output: 4
128 | Explanation: 9 exists in secret and its index is 4.
129 | ```
130 |
131 | **Example 2:**
132 |
133 | ```
134 | Input: secret = [-1,0,3,5,9,12], target = 2
135 | Output: -1
136 | Explanation: 2 does not exist in secret so return -1.
137 | ```
138 |
139 | **Constraints:**
140 |
141 | - `1 <= secret.length <= 104`
142 | - `-104 <= secret[i], target <= 104`
143 | - `secret` is sorted in a strictly increasing order.
144 |
145 | ### My Solution
146 |
147 | * Binary search method
148 |
149 | ```java
150 | public int search(ArrayReader reader, int target) {
151 | int max = (int)Math.pow(10, 4);
152 | int low = 0;
153 | while (low < max){
154 | int mid = low + (max - low) / 2;
155 | int value = reader.get(mid);
156 | if (value > target){
157 | max = mid - 1;
158 | }
159 | else if (value < target){
160 | low = mid + 1;
161 | }
162 | else {
163 | return mid;
164 | }
165 | }
166 | return reader.get(low) == target ? low : -1;
167 | }
168 | ```
169 |
170 | ### Standard Solution
171 |
172 | #### Solution #1 Binary Search + Bit Operation
173 |
174 | ```java
175 | class Solution {
176 | public int search(ArrayReader reader, int target) {
177 | if (reader.get(0) == target) return 0;
178 | // search boundaries
179 | int left = 0, right = 1;
180 | while (reader.get(right) < target) {
181 | left = right;
182 | right <<= 1;
183 | }
184 | // binary search
185 | int pivot, num;
186 | while (left <= right) {
187 | pivot = left + ((right - left) >> 1);
188 | num = reader.get(pivot);
189 |
190 | if (num == target) return pivot;
191 | if (num > target) right = pivot - 1;
192 | else left = pivot + 1;
193 | }
194 | // there is no target element
195 | return -1;
196 | }
197 | }
198 | ```
199 |
200 | - Time complexity: $\mathcal{O}(\log T)$, where T is an index of the target value.
201 |
202 | There are two operations here: to define search boundaries and to perform a binary search.
203 |
204 | Let's first find the number of steps k to set up the boundaries. In the first step, the boundaries are $2^0 .. 2^{0 + 1}$, on the second step $2^1 .. 2^{1 + 1}$, etc. When everything is done, the boundaries are $2^k .. 2^{k + 1}$ and $2^k < T \le 2^{k + 1}$. That means one needs $k = \log T$ steps to set up the boundaries, that means $\mathcal{O}(\log T)$ time complexity.
205 |
206 | Now let's discuss the complexity of the binary search. There are $2^{k + 1} - 2^k = 2^k$ elements in the boundaries, i.e. $2^{\log T} = T2$ elements. Binary search has logarithmic complexity, which results in $\mathcal{O}(\log T)$ time complexity.
207 |
208 | - Space complexity: $\mathcal{O}(1)$ since it's a constant space solution.
209 |
210 | ## Valid Perfect Square(Easy #367)
211 |
212 | **Question**: Given a **positive** integer *num*, write a function that returns True if *num* is a perfect square else False.
213 |
214 | **Follow up:** **Do not** use any built-in library function such as `sqrt`.
215 |
216 | **Example 1:**
217 |
218 | ```
219 | Input: num = 16
220 | Output: true
221 | ```
222 |
223 | **Example 2:**
224 |
225 | ```
226 | Input: num = 14
227 | Output: false
228 | ```
229 |
230 | **Constraints:**
231 |
232 | - `1 <= num <= 2^31 - 1`
233 |
234 | ### My Solution
235 |
236 | * Use binary search to find mid, check if the square larger or smaller than the target
237 |
238 | ```java
239 | public boolean isPerfectSquare(int num) {
240 | if (num == 0 || num == 1){
241 | return true;
242 | }
243 | if (num < 0){
244 | return false;
245 | }
246 | int low = 1, high = num / 2;
247 | while (low < high){
248 | int mid = low + (high - low) / 2;
249 | if ((long)mid * mid < num){
250 | low = mid + 1;
251 | }
252 | else if ((long)mid * mid > num){
253 | high = mid - 1;
254 | }
255 | else {
256 | return true;
257 | }
258 | }
259 | return low * low == num ? true : false;
260 | }
261 | ```
262 |
263 | ### Standard Solution
264 |
265 | #### Solution #1 Binary Search
266 |
267 | * Almost the same as my solution
268 |
269 | ```java
270 | public boolean isPerfectSquare(int num) {
271 | if (num < 2) {
272 | return true;
273 | }
274 | long left = 2, right = num / 2, x, guessSquared;
275 | while (left <= right) {
276 | x = left + (right - left) / 2;
277 | guessSquared = x * x;
278 | if (guessSquared == num) {
279 | return true;
280 | }
281 | if (guessSquared > num) {
282 | right = x - 1;
283 | } else {
284 | left = x + 1;
285 | }
286 | }
287 | return false;
288 | }
289 | ```
290 |
291 | * Time complexity: $\mathcal{O}(\log N)$.
292 | * Space complexity: $\mathcal{O}(1)$.
293 |
294 | ## Find Smallest Letter Greater Than Target (Easy #744)
295 |
296 | **Question**: Given a characters array `letters` that is sorted in **non-decreasing** order and a character `target`, return *the smallest character in the array that is larger than* `target`.
297 |
298 | **Note** that the letters wrap around.
299 |
300 | - For example, if `target == 'z'` and `letters == ['a', 'b']`, the answer is `'a'`.
301 |
302 | **Example 1:**
303 |
304 | ```
305 | Input: letters = ["c","f","j"], target = "a"
306 | Output: "c"
307 | ```
308 |
309 | **Example 2:**
310 |
311 | ```
312 | Input: letters = ["c","f","j"], target = "c"
313 | Output: "f"
314 | ```
315 |
316 | **Example 3:**
317 |
318 | ```
319 | Input: letters = ["c","f","j"], target = "d"
320 | Output: "f"
321 | ```
322 |
323 | **Constraints:**
324 |
325 | - `2 <= letters.length <= 104`
326 | - `letters[i]` is a lowercase English letter.
327 | - `letters` are sorted in **non-decreasing** order.
328 | - `letters` contain at least two different characters.
329 | - `target` is a lowercase English letter.
330 |
331 | ### My Solution
332 |
333 | * Calculate the relative distance
334 |
335 | ```java
336 | public char nextGreatestLetter(char[] letters, char target) {
337 | int distance = 0;
338 | int minDistance = Integer.MAX_VALUE;
339 | char res = 'a';
340 | for (char letter : letters){
341 | if (letter >= target){
342 | distance = letter - target;
343 | }
344 | else {
345 | distance = 'z' - target + letter - 'a' + 1;
346 | }
347 | if (distance > 0 && distance < minDistance){
348 | minDistance = distance;
349 | res = letter;
350 | }
351 | }
352 | return res;
353 | }
354 | ```
355 |
356 | ### Standard Solution
357 |
358 | #### Solution #1 Linear Scan
359 |
360 | * The question asks for the letter, not distance, don't need to calculate the distance
361 | * Just loop through the letters and find the one that meets the requirement
362 |
363 | ```java
364 | class Solution {
365 | public char nextGreatestLetter(char[] letters, char target) {
366 | for (char c: letters)
367 | if (c > target) return c;
368 | return letters[0];
369 | }
370 | }
371 | ```
372 |
373 | - Time Complexity: $O(N)$, where N is the length of `letters`. We scan every element of the array.
374 | - Space Complexity: $O(1)$, as we maintain only pointers.
375 |
376 | #### Solution #2 Binary Search
377 |
378 | * Binary search method to check if the letter is larger than the target
379 |
380 | ```java
381 | public char nextGreatestLetter(char[] letters, char target) {
382 | int lo = 0, hi = letters.length;
383 | while (lo < hi) {
384 | int mi = lo + (hi - lo) / 2;
385 | if (letters[mi] <= target) lo = mi + 1;
386 | else hi = mi;
387 | }
388 | return letters[lo % letters.length];
389 | }
390 | ```
391 |
392 | - Time Complexity: $O(\log N)$, where N is the length of `letters`. We peek only at $\log N$ elements in the array.
393 | - Space Complexity: $O(1)$, as we maintain only pointers.
394 |
395 | ## Find Minimum in Rotated Sorted Array II (Hard #154)
396 |
397 | **Question**: Suppose an array of length `n` sorted in ascending order is **rotated** between `1` and `n` times. For example, the array `nums = [0,1,4,4,5,6,7]` might become:
398 |
399 | - `[4,5,6,7,0,1,4]` if it was rotated `4` times.
400 | - `[0,1,4,4,5,6,7]` if it was rotated `7` times.
401 |
402 | Notice that **rotating** an array `[a[0], a[1], a[2], ..., a[n-1]]` 1 time results in the array `[a[n-1], a[0], a[1], a[2], ..., a[n-2]]`.
403 |
404 | Given the sorted rotated array `nums` that may contain **duplicates**, return *the minimum element of this array*.
405 |
406 | You must decrease the overall operation steps as much as possible.
407 |
408 | **Example 1:**
409 |
410 | ```
411 | Input: nums = [1,3,5]
412 | Output: 1
413 | ```
414 |
415 | **Example 2:**
416 |
417 | ```
418 | Input: nums = [2,2,2,0,1]
419 | Output: 0
420 | ```
421 |
422 | **Constraints:**
423 |
424 | - `n == nums.length`
425 | - `1 <= n <= 5000`
426 | - `-5000 <= nums[i] <= 5000`
427 | - `nums` is sorted and rotated between `1` and `n` times.
428 |
429 | ### Standard Solution
430 |
431 | #### Solution #1 Variant of Binary Search
432 |
433 | * Compare the pivot element to the element pointed by the upper bound pointer
434 | * We use the upper bound of the search scope as the reference for the comparison with the pivot element, while in the classical binary search the reference would be the desired value.
435 | * When the result of the comparison is equal (*i.e.* Case #3), we further move the upper bound, while in the classical binary search normally we would return the value immediately.
436 |
437 | ```java
438 | public int findMin(int[] nums) {
439 | int low = 0, high = nums.length - 1;
440 | while (low < high){
441 | int mid = low + (high - low) / 2;
442 | if (nums[mid] > nums[high]){
443 | low = mid + 1;
444 | }
445 | else if (nums[mid] < nums[high]) {
446 | high = mid;
447 | }
448 | // change the edge value since it is valid
449 | else {
450 | high--;
451 | }
452 | }
453 | return nums[low];
454 | }
455 | ```
456 |
457 | - Time complexity: on average $\mathcal{O}(\log_{2}{N})$ where N is the length of the array, since in general, it is a binary search algorithm. However, in the worst case where the array contains identical elements (*i.e.* case #3 `nums[pivot]==nums[high]`), the algorithm would deteriorate to iterating each element, as a result, the time complexity becomes $\mathcal{O}(N)$.
458 | - Space complexity: $\mathcal{O}(1)$, it's a constant space solution.
459 |
460 | ## Median of Two Sorted Array(Hard #4)
461 |
462 | **Question**: Given two sorted arrays `nums1` and `nums2` of size `m` and `n` respectively, return **the median** of the two sorted arrays.
463 |
464 | The overall run time complexity should be `O(log (m+n))`.
465 |
466 | **Example 1:**
467 |
468 | ```
469 | Input: nums1 = [1,3], nums2 = [2]
470 | Output: 2.00000
471 | Explanation: merged array = [1,2,3] and median is 2.
472 | ```
473 |
474 | **Example 2:**
475 |
476 | ```
477 | Input: nums1 = [1,2], nums2 = [3,4]
478 | Output: 2.50000
479 | Explanation: merged array = [1,2,3,4] and median is (2 + 3) / 2 = 2.5.
480 | ```
481 |
482 | **Constraints:**
483 |
484 | - `nums1.length == m`
485 | - `nums2.length == n`
486 | - `0 <= m <= 1000`
487 | - `0 <= n <= 1000`
488 | - `1 <= m + n <= 2000`
489 | - `-106 <= nums1[i], nums2[i] <= 106`
490 |
491 | ### My Solution
492 |
493 | ```java
494 | public double findMedianSortedArrays(int[] nums1, int[] nums2) {
495 | int length = nums1.length + nums2.length;
496 | int[] nums = new int[length];
497 | for (int i = 0; i < nums1.length; i++){
498 | nums[i] = nums1[i];
499 | }
500 | for (int i = nums1.length; i < length; i++){
501 | nums[i] = nums2[i - nums1.length];
502 | }
503 | Arrays.sort(nums);
504 | double median = 0.0;
505 | // find the median of the aggregated array
506 | if (length % 2 == 1){
507 | median = nums[length/ 2];
508 | }
509 | else {
510 | median = ((double)nums[(length - 1)/ 2] + (double)nums[(length - 1) / 2 + 1]) / 2;
511 | }
512 | return median;
513 | }
514 | ```
515 |
516 | ### Other Solution
517 |
518 | * Binary search and compare two value
519 |
520 | ```java
521 | public double findMedianSortedArrays(int[] nums1, int[] nums2) {
522 | int index1 = 0;
523 | int index2 = 0;
524 | int med1 = 0;
525 | int med2 = 0;
526 | for (int i=0; i<=(nums1.length+nums2.length)/2; i++) {
527 | med1 = med2;
528 | if (index1 == nums1.length) {
529 | med2 = nums2[index2];
530 | index2++;
531 | } else if (index2 == nums2.length) {
532 | med2 = nums1[index1];
533 | index1++;
534 | } else if (nums1[index1] < nums2[index2] ) {
535 | med2 = nums1[index1];
536 | index1++;
537 | } else {
538 | med2 = nums2[index2];
539 | index2++;
540 | }
541 | }
542 |
543 | // the median is the average of two numbers
544 | if ((nums1.length+nums2.length)%2 == 0) {
545 | return (float)(med1+med2)/2;
546 | }
547 | return med2;
548 | }
549 | ```
550 |
551 | ## Find k-th Smallest Pair Distance (Hard #719)
552 |
553 | **Question**: The **distance of a pair** of integers `a` and `b` is defined as the absolute difference between `a` and `b`.
554 |
555 | Given an integer array `nums` and an integer `k`, return *the* `kth` *smallest **distance among all the pairs*** `nums[i]` *and* `nums[j]` *where* `0 <= i < j < nums.length`.
556 |
557 | **Example 1:**
558 |
559 | ```
560 | Input: nums = [1,3,1], k = 1
561 | Output: 0
562 | Explanation: Here are all the pairs:
563 | (1,3) -> 2
564 | (1,1) -> 0
565 | (3,1) -> 2
566 | Then the 1st smallest distance pair is (1,1), and its distance is 0.
567 | ```
568 |
569 | **Example 2:**
570 |
571 | ```
572 | Input: nums = [1,1,1], k = 2
573 | Output: 0
574 | ```
575 |
576 | **Example 3:**
577 |
578 | ```
579 | Input: nums = [1,6,1], k = 3
580 | Output: 5
581 | ```
582 |
583 | **Constraints:**
584 |
585 | - `n == nums.length`
586 | - `2 <= n <= 104`
587 | - `0 <= nums[i] <= 106`
588 | - `1 <= k <= n * (n - 1) / 2`
589 |
590 | ### Standard Solution
591 |
592 | #### Solution #1 Binary Search
593 |
594 | * Find low distance, and high distance, use binary search
595 |
596 | ```java
597 | public int smallestDistancePair(int[] nums, int k) {
598 | // sort the array and then do the binary search
599 | Arrays.sort(nums);
600 |
601 | int lo = 0;
602 | int hi = nums[nums.length - 1] - nums[0];
603 | while (lo < hi) {
604 | int mi = (lo + hi) / 2;
605 | int count = 0, left = 0;
606 | for (int right = 0; right < nums.length; right++){
607 | // find out how many count of pairs with distance <= mi
608 | while (nums[right] - nums[left] > mi) left++;
609 | count += right - left;
610 | }
611 | // count = number of pairs with distance <= mi
612 | if (count >= k) hi = mi;
613 | else lo = mi + 1;
614 | }
615 | return lo;
616 | }
617 | ```
618 |
619 | - Time Complexity: $O(N \log{W} + N \log{N})$, where N is the length of `nums`, and W*W* is equal to `nums[nums.length - 1] - nums[0]`. The $\log W$ factor comes from our binary search, and we do $O(N)$ work inside our call to `possible` (or to calculate `count` in Java). The final $O(N\log N)$ factor comes from sorting.
620 | - Space Complexity: $O(1)$. No additional space is used except for integer variables.
621 |
622 | ## Split Array Largest Sum (Hard #410)
623 |
624 | **Question**: Given an array `nums` which consists of non-negative integers and an integer `m`, you can split the array into `m` non-empty continuous subarrays.
625 |
626 | Write an algorithm to minimize the largest sum among these `m` subarrays.
627 |
628 | **Example 1:**
629 |
630 | ```
631 | Input: nums = [7,2,5,10,8], m = 2
632 | Output: 18
633 | Explanation:
634 | There are four ways to split nums into two subarrays.
635 | The best way is to split it into [7,2,5] and [10,8],
636 | where the largest sum among the two subarrays is only 18.
637 | ```
638 |
639 | **Example 2:**
640 |
641 | ```
642 | Input: nums = [1,2,3,4,5], m = 2
643 | Output: 9
644 | ```
645 |
646 | **Example 3:**
647 |
648 | ```
649 | Input: nums = [1,4,4], m = 3
650 | Output: 4
651 | ```
652 |
653 | **Constraints:**
654 |
655 | - `1 <= nums.length <= 1000`
656 | - `0 <= nums[i] <= 106`
657 | - `1 <= m <= min(50, nums.length)`
658 |
659 | ### Standard Solution
660 |
661 | #### Solution #1 Binary Search
662 |
663 | * Not only use binary search on array index but also use it for value search
664 | * Check if the target value converge
665 |
666 | ```java
667 | private int minimumSubarraysRequired(int[] nums, int maxSumAllowed) {
668 | int currentSum = 0;
669 | int splitsRequired = 0;
670 | for (int element : nums) {
671 | // Add element only if the sum doesn't exceed maxSumAllowed
672 | if (currentSum + element <= maxSumAllowed) {
673 | currentSum += element;
674 | } else {
675 | // If the element addition makes sum more than maxSumAllowed
676 | // Increment the splits required and reset sum
677 | currentSum = element;
678 | splitsRequired++;
679 | }
680 | }
681 | // Return the number of subarrays, which is the number of splits + 1
682 | return splitsRequired + 1;
683 | }
684 |
685 | public int splitArray(int[] nums, int m) {
686 | // Find the sum of all elements and the maximum element
687 | int sum = 0;
688 | int maxElement = Integer.MIN_VALUE;
689 | for (int element : nums) {
690 | sum += element;
691 | maxElement = Math.max(maxElement, element);
692 | }
693 | // Define the left and right boundary of binary search
694 | int left = maxElement;
695 | int right = sum;
696 | int minimumLargestSplitSum = 0;
697 | while (left <= right) {
698 | // Find the mid value
699 | int maxSumAllowed = left + (right - left) / 2;
700 | // Find the minimum splits. If splitsRequired is less than
701 | // or equal to m move towards left i.e., smaller values
702 | if (minimumSubarraysRequired(nums, maxSumAllowed) <= m) {
703 | right = maxSumAllowed - 1;
704 | minimumLargestSplitSum = maxSumAllowed;
705 | } else {
706 | // Move towards right if splitsRequired is more than m
707 | left = maxSumAllowed + 1;
708 | }
709 | }
710 | return minimumLargestSplitSum;
711 | }
712 | ```
713 |
714 | - Time complexity: $O(N \cdot \log(S))$, where N is the length of the array and S is the sum of integers in the array.
715 |
716 | The total number of iterations in the binary search is $\log(S)$, and for each such iteration, we call `minimumSubarraysRequired` which takes $O(N)$ time. Hence, the time complexity is equal to $O(N \cdot \log(S))$.
717 |
718 | - Space complexity: $O(1)$
719 |
720 | We do not use any data structures that require more than constant extra space.
721 |
722 | ## 3Sum Closest (Medium #16)
723 |
724 | **Question**: Given an integer array `nums` of length `n` and an integer `target`, find three integers in `nums` such that the sum is closest to `target`.
725 |
726 | Return *the sum of the three integers*.
727 |
728 | You may assume that each input would have exactly one solution.
729 |
730 | **Example 1:**
731 |
732 | ```
733 | Input: nums = [-1,2,1,-4], target = 1
734 | Output: 2
735 | Explanation: The sum that is closest to the target is 2. (-1 + 2 + 1 = 2).
736 | ```
737 |
738 | **Example 2:**
739 |
740 | ```
741 | Input: nums = [0,0,0], target = 1
742 | Output: 0
743 | ```
744 |
745 | **Constraints:**
746 |
747 | - `3 <= nums.length <= 1000`
748 | - `-1000 <= nums[i] <= 1000`
749 | - `-104 <= target <= 104`
750 |
751 | ### Standard Solution
752 |
753 | #### Solution #1 Two Pointers
754 |
755 | * Use for loop and three-pointers, calculate the sum
756 | * Compare the sum with the target, if smaller, move the low pointer, if higher, move the high pointer
757 |
758 | ```java
759 | public int threeSumClosest(int[] nums, int target) {
760 | int diff = Integer.MAX_VALUE;
761 | int sz = nums.length;
762 | Arrays.sort(nums);
763 | for (int i = 0; i < sz && diff != 0; i++){
764 | int lo = i + 1;
765 | int hi = sz - 1;
766 | while (lo < hi){
767 | int sum = nums[i] + nums[lo] + nums[hi];
768 | if (Math.abs(target - sum) < Math.abs(diff)){
769 | diff = target - sum;
770 | }
771 | if (sum < target){
772 | lo++;
773 | }
774 | else {
775 | hi--;
776 | }
777 | }
778 | }
779 | return target - diff;
780 | }
781 | ```
782 |
783 | - Time Complexity: $\mathcal{O}(n^2)$. We have outer and inner loops, each going through n elements.
784 |
785 | Sorting the array takes $\mathcal{O}(n\log{n})$, so overall complexity is $\mathcal{O}(n\log{n} + n^2)$. This is asymptotically equivalent to $\mathcal{O}(n^2)$.
786 |
787 | - Space Complexity: from $\mathcal{O}(\log{n})$ to $\mathcal{O}(n)$, depending on the implementation of the sorting algorithm.
788 |
789 | #### Solution #2 Binary Search
790 |
791 | ```java
792 | public int threeSumClosest(int[] nums, int target) {
793 | int diff = Integer.MAX_VALUE;
794 | int sz = nums.length;
795 | Arrays.sort(nums);
796 | for (int i = 0; i < sz && diff != 0; ++i) {
797 | for (int j = i + 1; j < sz - 1; ++j) {
798 | int complement = target - nums[i] - nums[j];
799 | var idx = Arrays.binarySearch(nums, j + 1, sz - 1, complement);
800 | int hi = idx >= 0 ? idx : ~idx, lo = hi - 1;
801 | if (hi < sz && Math.abs(complement - nums[hi]) < Math.abs(diff))
802 | diff = complement - nums[hi];
803 | if (lo > j && Math.abs(complement - nums[lo]) < Math.abs(diff))
804 | diff = complement - nums[lo];
805 | }
806 | }
807 | return target - diff;
808 | }
809 | ```
810 |
811 | - Time Complexity: $\mathcal{O}(n^2\log{n})$. Binary search takes $\mathcal{O}(\log{n})$, and we do it n times in the inner loop. Since we are going through n elements in the outer loop, the overall complexity is $\mathcal{O}(n^2\log{n})$.
812 | - Space Complexity: from $\mathcal{O}(\log{n})$ to $\mathcal{O}(n)$, depending on the implementation of the sorting algorithm.
--------------------------------------------------------------------------------
/Queue & Stack/Queue Problems Part #1.md:
--------------------------------------------------------------------------------
1 | # Queue Problems Part #1
2 |
3 | ## Design Hit Counter(Medium #362)
4 |
5 | **Question**: Design a hit counter which counts the number of hits received in the past `5` minutes (i.e., the past `300` seconds).
6 |
7 | Your system should accept a `timestamp` parameter (**in seconds** granularity), and you may assume that calls are being made to the system in chronological order (i.e., `timestamp` is monotonically increasing). Several hits may arrive roughly at the same time.
8 |
9 | Implement the `HitCounter` class:
10 |
11 | - `HitCounter()` Initializes the object of the hit counter system.
12 | - `void hit(int timestamp)` Records a hit that happened at `timestamp` (**in seconds**). Several hits may happen at the same `timestamp`.
13 | - `int getHits(int timestamp)` Returns the number of hits in the past 5 minutes from `timestamp` (i.e., the past `300` seconds).
14 |
15 | **Example 1:**
16 |
17 | ```
18 | Input
19 | ["HitCounter", "hit", "hit", "hit", "getHits", "hit", "getHits", "getHits"]
20 | [[], [1], [2], [3], [4], [300], [300], [301]]
21 | Output
22 | [null, null, null, null, 3, null, 4, 3]
23 |
24 | Explanation
25 | HitCounter hitCounter = new HitCounter();
26 | hitCounter.hit(1); // hit at timestamp 1.
27 | hitCounter.hit(2); // hit at timestamp 2.
28 | hitCounter.hit(3); // hit at timestamp 3.
29 | hitCounter.getHits(4); // get hits at timestamp 4, return 3.
30 | hitCounter.hit(300); // hit at timestamp 300.
31 | hitCounter.getHits(300); // get hits at timestamp 300, return 4.
32 | hitCounter.getHits(301); // get hits at timestamp 301, return 3.
33 | ```
34 |
35 | **Constraints:**
36 |
37 | - `1 <= timestamp <= 2 * 109`
38 | - All the calls are being made to the system in chronological order (i.e., `timestamp` is monotonically increasing).
39 | - At most `300` calls will be made to `hit` and `getHits`.
40 |
41 | ### My Solution
42 |
43 | ```java
44 | class HitCounter {
45 | private LinkedList
92 |
93 | ```java
94 | public int closestValue(TreeNode root, double target){
95 | int val, closest = root.val;
96 | while (root != null){
97 | val = root.val;
98 | closest = Math.abs(val - target) < Math.abs(closest - target) ? val : closest;
99 | root = target < root.val ? root.left : root.right;
100 | }
101 | return closest;
102 | }
103 | ```
104 |
105 | - Time complexity: $\mathcal{O}(H)$ since here one goes from root down to a leaf.
106 | - Space complexity: $\mathcal{O}(1)$.
107 |
108 | ## Search in a Sorted Array of Unknown Size(Medium #702)
109 |
110 | **Question**: This is an ***interactive problem***.
111 |
112 | You have a sorted array of **unique** elements and an **unknown size**. You do not have an access to the array but you can use the `ArrayReader` interface to access it. You can call `ArrayReader.get(i)` that:
113 |
114 | - returns the value at the `ith` index (**0-indexed**) of the secret array (i.e., `secret[i]`), or
115 | - returns `231 - 1` if the `i` is out of the boundary of the array.
116 |
117 | You are also given an integer `target`.
118 |
119 | Return the index `k` of the hidden array where `secret[k] == target` or return `-1` otherwise.
120 |
121 | You must write an algorithm with `O(log n)` runtime complexity.
122 |
123 | **Example 1:**
124 |
125 | ```
126 | Input: secret = [-1,0,3,5,9,12], target = 9
127 | Output: 4
128 | Explanation: 9 exists in secret and its index is 4.
129 | ```
130 |
131 | **Example 2:**
132 |
133 | ```
134 | Input: secret = [-1,0,3,5,9,12], target = 2
135 | Output: -1
136 | Explanation: 2 does not exist in secret so return -1.
137 | ```
138 |
139 | **Constraints:**
140 |
141 | - `1 <= secret.length <= 104`
142 | - `-104 <= secret[i], target <= 104`
143 | - `secret` is sorted in a strictly increasing order.
144 |
145 | ### My Solution
146 |
147 | * Binary search method
148 |
149 | ```java
150 | public int search(ArrayReader reader, int target) {
151 | int max = (int)Math.pow(10, 4);
152 | int low = 0;
153 | while (low < max){
154 | int mid = low + (max - low) / 2;
155 | int value = reader.get(mid);
156 | if (value > target){
157 | max = mid - 1;
158 | }
159 | else if (value < target){
160 | low = mid + 1;
161 | }
162 | else {
163 | return mid;
164 | }
165 | }
166 | return reader.get(low) == target ? low : -1;
167 | }
168 | ```
169 |
170 | ### Standard Solution
171 |
172 | #### Solution #1 Binary Search + Bit Operation
173 |
174 | ```java
175 | class Solution {
176 | public int search(ArrayReader reader, int target) {
177 | if (reader.get(0) == target) return 0;
178 | // search boundaries
179 | int left = 0, right = 1;
180 | while (reader.get(right) < target) {
181 | left = right;
182 | right <<= 1;
183 | }
184 | // binary search
185 | int pivot, num;
186 | while (left <= right) {
187 | pivot = left + ((right - left) >> 1);
188 | num = reader.get(pivot);
189 |
190 | if (num == target) return pivot;
191 | if (num > target) right = pivot - 1;
192 | else left = pivot + 1;
193 | }
194 | // there is no target element
195 | return -1;
196 | }
197 | }
198 | ```
199 |
200 | - Time complexity: $\mathcal{O}(\log T)$, where T is an index of the target value.
201 |
202 | There are two operations here: to define search boundaries and to perform a binary search.
203 |
204 | Let's first find the number of steps k to set up the boundaries. In the first step, the boundaries are $2^0 .. 2^{0 + 1}$, on the second step $2^1 .. 2^{1 + 1}$, etc. When everything is done, the boundaries are $2^k .. 2^{k + 1}$ and $2^k < T \le 2^{k + 1}$. That means one needs $k = \log T$ steps to set up the boundaries, that means $\mathcal{O}(\log T)$ time complexity.
205 |
206 | Now let's discuss the complexity of the binary search. There are $2^{k + 1} - 2^k = 2^k$ elements in the boundaries, i.e. $2^{\log T} = T2$ elements. Binary search has logarithmic complexity, which results in $\mathcal{O}(\log T)$ time complexity.
207 |
208 | - Space complexity: $\mathcal{O}(1)$ since it's a constant space solution.
209 |
210 | ## Valid Perfect Square(Easy #367)
211 |
212 | **Question**: Given a **positive** integer *num*, write a function that returns True if *num* is a perfect square else False.
213 |
214 | **Follow up:** **Do not** use any built-in library function such as `sqrt`.
215 |
216 | **Example 1:**
217 |
218 | ```
219 | Input: num = 16
220 | Output: true
221 | ```
222 |
223 | **Example 2:**
224 |
225 | ```
226 | Input: num = 14
227 | Output: false
228 | ```
229 |
230 | **Constraints:**
231 |
232 | - `1 <= num <= 2^31 - 1`
233 |
234 | ### My Solution
235 |
236 | * Use binary search to find mid, check if the square larger or smaller than the target
237 |
238 | ```java
239 | public boolean isPerfectSquare(int num) {
240 | if (num == 0 || num == 1){
241 | return true;
242 | }
243 | if (num < 0){
244 | return false;
245 | }
246 | int low = 1, high = num / 2;
247 | while (low < high){
248 | int mid = low + (high - low) / 2;
249 | if ((long)mid * mid < num){
250 | low = mid + 1;
251 | }
252 | else if ((long)mid * mid > num){
253 | high = mid - 1;
254 | }
255 | else {
256 | return true;
257 | }
258 | }
259 | return low * low == num ? true : false;
260 | }
261 | ```
262 |
263 | ### Standard Solution
264 |
265 | #### Solution #1 Binary Search
266 |
267 | * Almost the same as my solution
268 |
269 | ```java
270 | public boolean isPerfectSquare(int num) {
271 | if (num < 2) {
272 | return true;
273 | }
274 | long left = 2, right = num / 2, x, guessSquared;
275 | while (left <= right) {
276 | x = left + (right - left) / 2;
277 | guessSquared = x * x;
278 | if (guessSquared == num) {
279 | return true;
280 | }
281 | if (guessSquared > num) {
282 | right = x - 1;
283 | } else {
284 | left = x + 1;
285 | }
286 | }
287 | return false;
288 | }
289 | ```
290 |
291 | * Time complexity: $\mathcal{O}(\log N)$.
292 | * Space complexity: $\mathcal{O}(1)$.
293 |
294 | ## Find Smallest Letter Greater Than Target (Easy #744)
295 |
296 | **Question**: Given a characters array `letters` that is sorted in **non-decreasing** order and a character `target`, return *the smallest character in the array that is larger than* `target`.
297 |
298 | **Note** that the letters wrap around.
299 |
300 | - For example, if `target == 'z'` and `letters == ['a', 'b']`, the answer is `'a'`.
301 |
302 | **Example 1:**
303 |
304 | ```
305 | Input: letters = ["c","f","j"], target = "a"
306 | Output: "c"
307 | ```
308 |
309 | **Example 2:**
310 |
311 | ```
312 | Input: letters = ["c","f","j"], target = "c"
313 | Output: "f"
314 | ```
315 |
316 | **Example 3:**
317 |
318 | ```
319 | Input: letters = ["c","f","j"], target = "d"
320 | Output: "f"
321 | ```
322 |
323 | **Constraints:**
324 |
325 | - `2 <= letters.length <= 104`
326 | - `letters[i]` is a lowercase English letter.
327 | - `letters` are sorted in **non-decreasing** order.
328 | - `letters` contain at least two different characters.
329 | - `target` is a lowercase English letter.
330 |
331 | ### My Solution
332 |
333 | * Calculate the relative distance
334 |
335 | ```java
336 | public char nextGreatestLetter(char[] letters, char target) {
337 | int distance = 0;
338 | int minDistance = Integer.MAX_VALUE;
339 | char res = 'a';
340 | for (char letter : letters){
341 | if (letter >= target){
342 | distance = letter - target;
343 | }
344 | else {
345 | distance = 'z' - target + letter - 'a' + 1;
346 | }
347 | if (distance > 0 && distance < minDistance){
348 | minDistance = distance;
349 | res = letter;
350 | }
351 | }
352 | return res;
353 | }
354 | ```
355 |
356 | ### Standard Solution
357 |
358 | #### Solution #1 Linear Scan
359 |
360 | * The question asks for the letter, not distance, don't need to calculate the distance
361 | * Just loop through the letters and find the one that meets the requirement
362 |
363 | ```java
364 | class Solution {
365 | public char nextGreatestLetter(char[] letters, char target) {
366 | for (char c: letters)
367 | if (c > target) return c;
368 | return letters[0];
369 | }
370 | }
371 | ```
372 |
373 | - Time Complexity: $O(N)$, where N is the length of `letters`. We scan every element of the array.
374 | - Space Complexity: $O(1)$, as we maintain only pointers.
375 |
376 | #### Solution #2 Binary Search
377 |
378 | * Binary search method to check if the letter is larger than the target
379 |
380 | ```java
381 | public char nextGreatestLetter(char[] letters, char target) {
382 | int lo = 0, hi = letters.length;
383 | while (lo < hi) {
384 | int mi = lo + (hi - lo) / 2;
385 | if (letters[mi] <= target) lo = mi + 1;
386 | else hi = mi;
387 | }
388 | return letters[lo % letters.length];
389 | }
390 | ```
391 |
392 | - Time Complexity: $O(\log N)$, where N is the length of `letters`. We peek only at $\log N$ elements in the array.
393 | - Space Complexity: $O(1)$, as we maintain only pointers.
394 |
395 | ## Find Minimum in Rotated Sorted Array II (Hard #154)
396 |
397 | **Question**: Suppose an array of length `n` sorted in ascending order is **rotated** between `1` and `n` times. For example, the array `nums = [0,1,4,4,5,6,7]` might become:
398 |
399 | - `[4,5,6,7,0,1,4]` if it was rotated `4` times.
400 | - `[0,1,4,4,5,6,7]` if it was rotated `7` times.
401 |
402 | Notice that **rotating** an array `[a[0], a[1], a[2], ..., a[n-1]]` 1 time results in the array `[a[n-1], a[0], a[1], a[2], ..., a[n-2]]`.
403 |
404 | Given the sorted rotated array `nums` that may contain **duplicates**, return *the minimum element of this array*.
405 |
406 | You must decrease the overall operation steps as much as possible.
407 |
408 | **Example 1:**
409 |
410 | ```
411 | Input: nums = [1,3,5]
412 | Output: 1
413 | ```
414 |
415 | **Example 2:**
416 |
417 | ```
418 | Input: nums = [2,2,2,0,1]
419 | Output: 0
420 | ```
421 |
422 | **Constraints:**
423 |
424 | - `n == nums.length`
425 | - `1 <= n <= 5000`
426 | - `-5000 <= nums[i] <= 5000`
427 | - `nums` is sorted and rotated between `1` and `n` times.
428 |
429 | ### Standard Solution
430 |
431 | #### Solution #1 Variant of Binary Search
432 |
433 | * Compare the pivot element to the element pointed by the upper bound pointer
434 | * We use the upper bound of the search scope as the reference for the comparison with the pivot element, while in the classical binary search the reference would be the desired value.
435 | * When the result of the comparison is equal (*i.e.* Case #3), we further move the upper bound, while in the classical binary search normally we would return the value immediately.
436 |
437 | ```java
438 | public int findMin(int[] nums) {
439 | int low = 0, high = nums.length - 1;
440 | while (low < high){
441 | int mid = low + (high - low) / 2;
442 | if (nums[mid] > nums[high]){
443 | low = mid + 1;
444 | }
445 | else if (nums[mid] < nums[high]) {
446 | high = mid;
447 | }
448 | // change the edge value since it is valid
449 | else {
450 | high--;
451 | }
452 | }
453 | return nums[low];
454 | }
455 | ```
456 |
457 | - Time complexity: on average $\mathcal{O}(\log_{2}{N})$ where N is the length of the array, since in general, it is a binary search algorithm. However, in the worst case where the array contains identical elements (*i.e.* case #3 `nums[pivot]==nums[high]`), the algorithm would deteriorate to iterating each element, as a result, the time complexity becomes $\mathcal{O}(N)$.
458 | - Space complexity: $\mathcal{O}(1)$, it's a constant space solution.
459 |
460 | ## Median of Two Sorted Array(Hard #4)
461 |
462 | **Question**: Given two sorted arrays `nums1` and `nums2` of size `m` and `n` respectively, return **the median** of the two sorted arrays.
463 |
464 | The overall run time complexity should be `O(log (m+n))`.
465 |
466 | **Example 1:**
467 |
468 | ```
469 | Input: nums1 = [1,3], nums2 = [2]
470 | Output: 2.00000
471 | Explanation: merged array = [1,2,3] and median is 2.
472 | ```
473 |
474 | **Example 2:**
475 |
476 | ```
477 | Input: nums1 = [1,2], nums2 = [3,4]
478 | Output: 2.50000
479 | Explanation: merged array = [1,2,3,4] and median is (2 + 3) / 2 = 2.5.
480 | ```
481 |
482 | **Constraints:**
483 |
484 | - `nums1.length == m`
485 | - `nums2.length == n`
486 | - `0 <= m <= 1000`
487 | - `0 <= n <= 1000`
488 | - `1 <= m + n <= 2000`
489 | - `-106 <= nums1[i], nums2[i] <= 106`
490 |
491 | ### My Solution
492 |
493 | ```java
494 | public double findMedianSortedArrays(int[] nums1, int[] nums2) {
495 | int length = nums1.length + nums2.length;
496 | int[] nums = new int[length];
497 | for (int i = 0; i < nums1.length; i++){
498 | nums[i] = nums1[i];
499 | }
500 | for (int i = nums1.length; i < length; i++){
501 | nums[i] = nums2[i - nums1.length];
502 | }
503 | Arrays.sort(nums);
504 | double median = 0.0;
505 | // find the median of the aggregated array
506 | if (length % 2 == 1){
507 | median = nums[length/ 2];
508 | }
509 | else {
510 | median = ((double)nums[(length - 1)/ 2] + (double)nums[(length - 1) / 2 + 1]) / 2;
511 | }
512 | return median;
513 | }
514 | ```
515 |
516 | ### Other Solution
517 |
518 | * Binary search and compare two value
519 |
520 | ```java
521 | public double findMedianSortedArrays(int[] nums1, int[] nums2) {
522 | int index1 = 0;
523 | int index2 = 0;
524 | int med1 = 0;
525 | int med2 = 0;
526 | for (int i=0; i<=(nums1.length+nums2.length)/2; i++) {
527 | med1 = med2;
528 | if (index1 == nums1.length) {
529 | med2 = nums2[index2];
530 | index2++;
531 | } else if (index2 == nums2.length) {
532 | med2 = nums1[index1];
533 | index1++;
534 | } else if (nums1[index1] < nums2[index2] ) {
535 | med2 = nums1[index1];
536 | index1++;
537 | } else {
538 | med2 = nums2[index2];
539 | index2++;
540 | }
541 | }
542 |
543 | // the median is the average of two numbers
544 | if ((nums1.length+nums2.length)%2 == 0) {
545 | return (float)(med1+med2)/2;
546 | }
547 | return med2;
548 | }
549 | ```
550 |
551 | ## Find k-th Smallest Pair Distance (Hard #719)
552 |
553 | **Question**: The **distance of a pair** of integers `a` and `b` is defined as the absolute difference between `a` and `b`.
554 |
555 | Given an integer array `nums` and an integer `k`, return *the* `kth` *smallest **distance among all the pairs*** `nums[i]` *and* `nums[j]` *where* `0 <= i < j < nums.length`.
556 |
557 | **Example 1:**
558 |
559 | ```
560 | Input: nums = [1,3,1], k = 1
561 | Output: 0
562 | Explanation: Here are all the pairs:
563 | (1,3) -> 2
564 | (1,1) -> 0
565 | (3,1) -> 2
566 | Then the 1st smallest distance pair is (1,1), and its distance is 0.
567 | ```
568 |
569 | **Example 2:**
570 |
571 | ```
572 | Input: nums = [1,1,1], k = 2
573 | Output: 0
574 | ```
575 |
576 | **Example 3:**
577 |
578 | ```
579 | Input: nums = [1,6,1], k = 3
580 | Output: 5
581 | ```
582 |
583 | **Constraints:**
584 |
585 | - `n == nums.length`
586 | - `2 <= n <= 104`
587 | - `0 <= nums[i] <= 106`
588 | - `1 <= k <= n * (n - 1) / 2`
589 |
590 | ### Standard Solution
591 |
592 | #### Solution #1 Binary Search
593 |
594 | * Find low distance, and high distance, use binary search
595 |
596 | ```java
597 | public int smallestDistancePair(int[] nums, int k) {
598 | // sort the array and then do the binary search
599 | Arrays.sort(nums);
600 |
601 | int lo = 0;
602 | int hi = nums[nums.length - 1] - nums[0];
603 | while (lo < hi) {
604 | int mi = (lo + hi) / 2;
605 | int count = 0, left = 0;
606 | for (int right = 0; right < nums.length; right++){
607 | // find out how many count of pairs with distance <= mi
608 | while (nums[right] - nums[left] > mi) left++;
609 | count += right - left;
610 | }
611 | // count = number of pairs with distance <= mi
612 | if (count >= k) hi = mi;
613 | else lo = mi + 1;
614 | }
615 | return lo;
616 | }
617 | ```
618 |
619 | - Time Complexity: $O(N \log{W} + N \log{N})$, where N is the length of `nums`, and W*W* is equal to `nums[nums.length - 1] - nums[0]`. The $\log W$ factor comes from our binary search, and we do $O(N)$ work inside our call to `possible` (or to calculate `count` in Java). The final $O(N\log N)$ factor comes from sorting.
620 | - Space Complexity: $O(1)$. No additional space is used except for integer variables.
621 |
622 | ## Split Array Largest Sum (Hard #410)
623 |
624 | **Question**: Given an array `nums` which consists of non-negative integers and an integer `m`, you can split the array into `m` non-empty continuous subarrays.
625 |
626 | Write an algorithm to minimize the largest sum among these `m` subarrays.
627 |
628 | **Example 1:**
629 |
630 | ```
631 | Input: nums = [7,2,5,10,8], m = 2
632 | Output: 18
633 | Explanation:
634 | There are four ways to split nums into two subarrays.
635 | The best way is to split it into [7,2,5] and [10,8],
636 | where the largest sum among the two subarrays is only 18.
637 | ```
638 |
639 | **Example 2:**
640 |
641 | ```
642 | Input: nums = [1,2,3,4,5], m = 2
643 | Output: 9
644 | ```
645 |
646 | **Example 3:**
647 |
648 | ```
649 | Input: nums = [1,4,4], m = 3
650 | Output: 4
651 | ```
652 |
653 | **Constraints:**
654 |
655 | - `1 <= nums.length <= 1000`
656 | - `0 <= nums[i] <= 106`
657 | - `1 <= m <= min(50, nums.length)`
658 |
659 | ### Standard Solution
660 |
661 | #### Solution #1 Binary Search
662 |
663 | * Not only use binary search on array index but also use it for value search
664 | * Check if the target value converge
665 |
666 | ```java
667 | private int minimumSubarraysRequired(int[] nums, int maxSumAllowed) {
668 | int currentSum = 0;
669 | int splitsRequired = 0;
670 | for (int element : nums) {
671 | // Add element only if the sum doesn't exceed maxSumAllowed
672 | if (currentSum + element <= maxSumAllowed) {
673 | currentSum += element;
674 | } else {
675 | // If the element addition makes sum more than maxSumAllowed
676 | // Increment the splits required and reset sum
677 | currentSum = element;
678 | splitsRequired++;
679 | }
680 | }
681 | // Return the number of subarrays, which is the number of splits + 1
682 | return splitsRequired + 1;
683 | }
684 |
685 | public int splitArray(int[] nums, int m) {
686 | // Find the sum of all elements and the maximum element
687 | int sum = 0;
688 | int maxElement = Integer.MIN_VALUE;
689 | for (int element : nums) {
690 | sum += element;
691 | maxElement = Math.max(maxElement, element);
692 | }
693 | // Define the left and right boundary of binary search
694 | int left = maxElement;
695 | int right = sum;
696 | int minimumLargestSplitSum = 0;
697 | while (left <= right) {
698 | // Find the mid value
699 | int maxSumAllowed = left + (right - left) / 2;
700 | // Find the minimum splits. If splitsRequired is less than
701 | // or equal to m move towards left i.e., smaller values
702 | if (minimumSubarraysRequired(nums, maxSumAllowed) <= m) {
703 | right = maxSumAllowed - 1;
704 | minimumLargestSplitSum = maxSumAllowed;
705 | } else {
706 | // Move towards right if splitsRequired is more than m
707 | left = maxSumAllowed + 1;
708 | }
709 | }
710 | return minimumLargestSplitSum;
711 | }
712 | ```
713 |
714 | - Time complexity: $O(N \cdot \log(S))$, where N is the length of the array and S is the sum of integers in the array.
715 |
716 | The total number of iterations in the binary search is $\log(S)$, and for each such iteration, we call `minimumSubarraysRequired` which takes $O(N)$ time. Hence, the time complexity is equal to $O(N \cdot \log(S))$.
717 |
718 | - Space complexity: $O(1)$
719 |
720 | We do not use any data structures that require more than constant extra space.
721 |
722 | ## 3Sum Closest (Medium #16)
723 |
724 | **Question**: Given an integer array `nums` of length `n` and an integer `target`, find three integers in `nums` such that the sum is closest to `target`.
725 |
726 | Return *the sum of the three integers*.
727 |
728 | You may assume that each input would have exactly one solution.
729 |
730 | **Example 1:**
731 |
732 | ```
733 | Input: nums = [-1,2,1,-4], target = 1
734 | Output: 2
735 | Explanation: The sum that is closest to the target is 2. (-1 + 2 + 1 = 2).
736 | ```
737 |
738 | **Example 2:**
739 |
740 | ```
741 | Input: nums = [0,0,0], target = 1
742 | Output: 0
743 | ```
744 |
745 | **Constraints:**
746 |
747 | - `3 <= nums.length <= 1000`
748 | - `-1000 <= nums[i] <= 1000`
749 | - `-104 <= target <= 104`
750 |
751 | ### Standard Solution
752 |
753 | #### Solution #1 Two Pointers
754 |
755 | * Use for loop and three-pointers, calculate the sum
756 | * Compare the sum with the target, if smaller, move the low pointer, if higher, move the high pointer
757 |
758 | ```java
759 | public int threeSumClosest(int[] nums, int target) {
760 | int diff = Integer.MAX_VALUE;
761 | int sz = nums.length;
762 | Arrays.sort(nums);
763 | for (int i = 0; i < sz && diff != 0; i++){
764 | int lo = i + 1;
765 | int hi = sz - 1;
766 | while (lo < hi){
767 | int sum = nums[i] + nums[lo] + nums[hi];
768 | if (Math.abs(target - sum) < Math.abs(diff)){
769 | diff = target - sum;
770 | }
771 | if (sum < target){
772 | lo++;
773 | }
774 | else {
775 | hi--;
776 | }
777 | }
778 | }
779 | return target - diff;
780 | }
781 | ```
782 |
783 | - Time Complexity: $\mathcal{O}(n^2)$. We have outer and inner loops, each going through n elements.
784 |
785 | Sorting the array takes $\mathcal{O}(n\log{n})$, so overall complexity is $\mathcal{O}(n\log{n} + n^2)$. This is asymptotically equivalent to $\mathcal{O}(n^2)$.
786 |
787 | - Space Complexity: from $\mathcal{O}(\log{n})$ to $\mathcal{O}(n)$, depending on the implementation of the sorting algorithm.
788 |
789 | #### Solution #2 Binary Search
790 |
791 | ```java
792 | public int threeSumClosest(int[] nums, int target) {
793 | int diff = Integer.MAX_VALUE;
794 | int sz = nums.length;
795 | Arrays.sort(nums);
796 | for (int i = 0; i < sz && diff != 0; ++i) {
797 | for (int j = i + 1; j < sz - 1; ++j) {
798 | int complement = target - nums[i] - nums[j];
799 | var idx = Arrays.binarySearch(nums, j + 1, sz - 1, complement);
800 | int hi = idx >= 0 ? idx : ~idx, lo = hi - 1;
801 | if (hi < sz && Math.abs(complement - nums[hi]) < Math.abs(diff))
802 | diff = complement - nums[hi];
803 | if (lo > j && Math.abs(complement - nums[lo]) < Math.abs(diff))
804 | diff = complement - nums[lo];
805 | }
806 | }
807 | return target - diff;
808 | }
809 | ```
810 |
811 | - Time Complexity: $\mathcal{O}(n^2\log{n})$. Binary search takes $\mathcal{O}(\log{n})$, and we do it n times in the inner loop. Since we are going through n elements in the outer loop, the overall complexity is $\mathcal{O}(n^2\log{n})$.
812 | - Space Complexity: from $\mathcal{O}(\log{n})$ to $\mathcal{O}(n)$, depending on the implementation of the sorting algorithm.
--------------------------------------------------------------------------------
/Queue & Stack/Queue Problems Part #1.md:
--------------------------------------------------------------------------------
1 | # Queue Problems Part #1
2 |
3 | ## Design Hit Counter(Medium #362)
4 |
5 | **Question**: Design a hit counter which counts the number of hits received in the past `5` minutes (i.e., the past `300` seconds).
6 |
7 | Your system should accept a `timestamp` parameter (**in seconds** granularity), and you may assume that calls are being made to the system in chronological order (i.e., `timestamp` is monotonically increasing). Several hits may arrive roughly at the same time.
8 |
9 | Implement the `HitCounter` class:
10 |
11 | - `HitCounter()` Initializes the object of the hit counter system.
12 | - `void hit(int timestamp)` Records a hit that happened at `timestamp` (**in seconds**). Several hits may happen at the same `timestamp`.
13 | - `int getHits(int timestamp)` Returns the number of hits in the past 5 minutes from `timestamp` (i.e., the past `300` seconds).
14 |
15 | **Example 1:**
16 |
17 | ```
18 | Input
19 | ["HitCounter", "hit", "hit", "hit", "getHits", "hit", "getHits", "getHits"]
20 | [[], [1], [2], [3], [4], [300], [300], [301]]
21 | Output
22 | [null, null, null, null, 3, null, 4, 3]
23 |
24 | Explanation
25 | HitCounter hitCounter = new HitCounter();
26 | hitCounter.hit(1); // hit at timestamp 1.
27 | hitCounter.hit(2); // hit at timestamp 2.
28 | hitCounter.hit(3); // hit at timestamp 3.
29 | hitCounter.getHits(4); // get hits at timestamp 4, return 3.
30 | hitCounter.hit(300); // hit at timestamp 300.
31 | hitCounter.getHits(300); // get hits at timestamp 300, return 4.
32 | hitCounter.getHits(301); // get hits at timestamp 301, return 3.
33 | ```
34 |
35 | **Constraints:**
36 |
37 | - `1 <= timestamp <= 2 * 109`
38 | - All the calls are being made to the system in chronological order (i.e., `timestamp` is monotonically increasing).
39 | - At most `300` calls will be made to `hit` and `getHits`.
40 |
41 | ### My Solution
42 |
43 | ```java
44 | class HitCounter {
45 | private LinkedList 16 |
17 | ```
18 | Input: n = 5, roads = [[0,1],[1,2],[2,3],[0,2],[1,3],[2,4]]
19 | Output: 43
20 | Explanation: The figure above shows the country and the assigned values of [2,4,5,3,1].
21 | - The road (0,1) has an importance of 2 + 4 = 6.
22 | - The road (1,2) has an importance of 4 + 5 = 9.
23 | - The road (2,3) has an importance of 5 + 3 = 8.
24 | - The road (0,2) has an importance of 2 + 5 = 7.
25 | - The road (1,3) has an importance of 4 + 3 = 7.
26 | - The road (2,4) has an importance of 5 + 1 = 6.
27 | The total importance of all roads is 6 + 9 + 8 + 7 + 7 + 6 = 43.
28 | It can be shown that we cannot obtain a greater total importance than 43.
29 | ```
30 |
31 | **Example 2:**
32 |
33 |
16 |
17 | ```
18 | Input: n = 5, roads = [[0,1],[1,2],[2,3],[0,2],[1,3],[2,4]]
19 | Output: 43
20 | Explanation: The figure above shows the country and the assigned values of [2,4,5,3,1].
21 | - The road (0,1) has an importance of 2 + 4 = 6.
22 | - The road (1,2) has an importance of 4 + 5 = 9.
23 | - The road (2,3) has an importance of 5 + 3 = 8.
24 | - The road (0,2) has an importance of 2 + 5 = 7.
25 | - The road (1,3) has an importance of 4 + 3 = 7.
26 | - The road (2,4) has an importance of 5 + 1 = 6.
27 | The total importance of all roads is 6 + 9 + 8 + 7 + 7 + 6 = 43.
28 | It can be shown that we cannot obtain a greater total importance than 43.
29 | ```
30 |
31 | **Example 2:**
32 |
33 |  34 |
35 | ```
36 | Input: n = 5, roads = [[0,3],[2,4],[1,3]]
37 | Output: 20
38 | Explanation: The figure above shows the country and the assigned values of [4,3,2,5,1].
39 | - The road (0,3) has an importance of 4 + 5 = 9.
40 | - The road (2,4) has an importance of 2 + 1 = 3.
41 | - The road (1,3) has an importance of 3 + 5 = 8.
42 | The total importance of all roads is 9 + 3 + 8 = 20.
43 | It can be shown that we cannot obtain a greater total importance than 20.
44 | ```
45 |
46 | **Constraints:**
47 |
48 | - `2 <= n <= 5 * 104`
49 | - `1 <= roads.length <= 5 * 104`
50 | - `roads[i].length == 2`
51 | - `0 <= ai, bi <= n - 1`
52 | - `ai != bi`
53 | - There are no duplicate roads.
54 |
55 | ### Standard Solution
56 |
57 | #### Solution #1 Count Degree
58 |
59 | - The number assigned to any node will contribute to its neighbors, which is equal to its degree.
60 | - So, give the maximum number to the node with the maximum degree (edges connected to it).
61 |
62 | ```java
63 | public long maximumImportance(int n, int[][] roads) {
64 | long ans = 0, x = 1;
65 | long degree[] = new long[n];
66 | for(int road[] : roads){
67 | degree[road[0]]++; // count degree for node
68 | degree[road[1]]++;
69 | }
70 | Arrays.sort(degree);
71 | for(long i : degree) ans += i * (x++) ; // assign number to the degree
72 | return ans;
73 | }
74 | ```
75 |
76 | * The time complexity is $O(n \log n)$ due to sorting
77 | * The space complexity is $O(n)$ for the length of n
--------------------------------------------------------------------------------
/OA Summary/Online Assessment.md:
--------------------------------------------------------------------------------
1 | # Online Assessment
2 |
3 | ## Square Data Engineering Intern
4 |
5 | **Source**: [Credit to this link and author](https://leetcode.com/discuss/interview-question/1014660/samsara-oa-codesignal-summer-internship)
6 |
7 | #### Problem
8 |
9 | ```
10 | You have a passage of text that needs to be typed out, but some of the letter keys on your keyboard are broken! You are given an array letters representing the working letter keys, as well as a string text, and your task is to determine how many of the words from text can be typed using the broken keyboard. It is guaranteed that all of the non-letter keys are working (including all punctuation and special characters).
11 | A word is defined as a sequence of consecutive characters which does not contain any spaces.
12 | The given text is a string consisting of words, each separated by exactly one space.
13 | It is guaranteed that text does not contain any leading or trailing spaces.
14 | Note that the characters in letters are all lowercase, but since the shift key is working,
15 | it's possible to type the uppercase versions also.
16 | ```
17 |
18 | ```
19 | Example:
20 | 1. For text = "Hello, this is CodeSignal!" and letters = ['e', 'i', 'h', 'l', 'o', 's'],
21 | the output should be brokenKeyboard(text, letters) = 2.
22 | - "Hello," can be typed since the characters 'h', 'e', 'l' and 'o' are in letters.
23 | - Note that the symbol ',' also belongs to the current word and can by typed.
24 | - "this" cannot be typed because the character 't' is not in letters.
25 | - "is" can be typed (both 'i' and 's' appear in letters).
26 | - "CodeSignal!" cannot be typed because the character 'c' is not in letters (as well as 'd', 'g', 'n', and 'a').
27 | 2. For text = "Hi, this is Chris!" and letters = ['r', 's', 't', 'c', 'h'], the output should be
28 | brokenKeyboard(text, letters) = 0.
29 | - Each word contains the character 'i' which does not appear in letters and thus cannot be typed on the keyboard.
30 | 3. For text = "3 + 2 = 5" and letters = [], the output should be brokenKeyboard(text, letters) = 5.
31 | - There are no working letters on the keyboard, but since each of these words consists of numbers and
32 | special characters, they can all be typed, and there are 5 of them.
33 | ```
34 |
35 | **Solution**:
36 |
37 | ```java
38 | public static int checkBrokenLetter(String text, char[] letters) {
39 | // Build hashSet
40 | Set
34 |
35 | ```
36 | Input: n = 5, roads = [[0,3],[2,4],[1,3]]
37 | Output: 20
38 | Explanation: The figure above shows the country and the assigned values of [4,3,2,5,1].
39 | - The road (0,3) has an importance of 4 + 5 = 9.
40 | - The road (2,4) has an importance of 2 + 1 = 3.
41 | - The road (1,3) has an importance of 3 + 5 = 8.
42 | The total importance of all roads is 9 + 3 + 8 = 20.
43 | It can be shown that we cannot obtain a greater total importance than 20.
44 | ```
45 |
46 | **Constraints:**
47 |
48 | - `2 <= n <= 5 * 104`
49 | - `1 <= roads.length <= 5 * 104`
50 | - `roads[i].length == 2`
51 | - `0 <= ai, bi <= n - 1`
52 | - `ai != bi`
53 | - There are no duplicate roads.
54 |
55 | ### Standard Solution
56 |
57 | #### Solution #1 Count Degree
58 |
59 | - The number assigned to any node will contribute to its neighbors, which is equal to its degree.
60 | - So, give the maximum number to the node with the maximum degree (edges connected to it).
61 |
62 | ```java
63 | public long maximumImportance(int n, int[][] roads) {
64 | long ans = 0, x = 1;
65 | long degree[] = new long[n];
66 | for(int road[] : roads){
67 | degree[road[0]]++; // count degree for node
68 | degree[road[1]]++;
69 | }
70 | Arrays.sort(degree);
71 | for(long i : degree) ans += i * (x++) ; // assign number to the degree
72 | return ans;
73 | }
74 | ```
75 |
76 | * The time complexity is $O(n \log n)$ due to sorting
77 | * The space complexity is $O(n)$ for the length of n
--------------------------------------------------------------------------------
/OA Summary/Online Assessment.md:
--------------------------------------------------------------------------------
1 | # Online Assessment
2 |
3 | ## Square Data Engineering Intern
4 |
5 | **Source**: [Credit to this link and author](https://leetcode.com/discuss/interview-question/1014660/samsara-oa-codesignal-summer-internship)
6 |
7 | #### Problem
8 |
9 | ```
10 | You have a passage of text that needs to be typed out, but some of the letter keys on your keyboard are broken! You are given an array letters representing the working letter keys, as well as a string text, and your task is to determine how many of the words from text can be typed using the broken keyboard. It is guaranteed that all of the non-letter keys are working (including all punctuation and special characters).
11 | A word is defined as a sequence of consecutive characters which does not contain any spaces.
12 | The given text is a string consisting of words, each separated by exactly one space.
13 | It is guaranteed that text does not contain any leading or trailing spaces.
14 | Note that the characters in letters are all lowercase, but since the shift key is working,
15 | it's possible to type the uppercase versions also.
16 | ```
17 |
18 | ```
19 | Example:
20 | 1. For text = "Hello, this is CodeSignal!" and letters = ['e', 'i', 'h', 'l', 'o', 's'],
21 | the output should be brokenKeyboard(text, letters) = 2.
22 | - "Hello," can be typed since the characters 'h', 'e', 'l' and 'o' are in letters.
23 | - Note that the symbol ',' also belongs to the current word and can by typed.
24 | - "this" cannot be typed because the character 't' is not in letters.
25 | - "is" can be typed (both 'i' and 's' appear in letters).
26 | - "CodeSignal!" cannot be typed because the character 'c' is not in letters (as well as 'd', 'g', 'n', and 'a').
27 | 2. For text = "Hi, this is Chris!" and letters = ['r', 's', 't', 'c', 'h'], the output should be
28 | brokenKeyboard(text, letters) = 0.
29 | - Each word contains the character 'i' which does not appear in letters and thus cannot be typed on the keyboard.
30 | 3. For text = "3 + 2 = 5" and letters = [], the output should be brokenKeyboard(text, letters) = 5.
31 | - There are no working letters on the keyboard, but since each of these words consists of numbers and
32 | special characters, they can all be typed, and there are 5 of them.
33 | ```
34 |
35 | **Solution**:
36 |
37 | ```java
38 | public static int checkBrokenLetter(String text, char[] letters) {
39 | // Build hashSet
40 | Set