├── README.md
├── example.py
├── hp_search.py
└── rocstar.py
/README.md:
--------------------------------------------------------------------------------
1 |
2 |
3 |
4 | # Roc-star : An objective function for ROC-AUC that actually works.
5 |
6 | For binary classification. everybody loves the Area Under the Curve (AUC) metric, but nobody directly targets it in their loss function. Instead folks use a proxy function like Binary Cross Entropy (BCE).
7 |
8 | This works fairly well, most of the time. But we're left with a nagging question : could we get a higher score with a loss function closer in nature to AUC?
9 |
10 | It seems likely since BCE really bears very little relation to AUC. There have been many attempts to find a loss function that more directly targets AUC. (One common tactic is some form of rank-loss function such as Hinge Rank-Loss.) In practice, however, no clear winner has ever emerged. There's been no serious challenge to BCE.
11 |
12 | There are also considerations beyond performance. Since BCE is essentially different than AUC, BCE tends to misbehave in the final stretch of training where we are trying to steer it toward the highest AUC score.
13 |
14 | A good deal of the AUC optimization actually ends up occurring in the tuning of hyper-parameters. Early Stopping becomes an uncomfortable necessity as the model may diverge sharply at any time from its high score.
15 |
16 | We'd like a loss function that gives us higher scores and less trouble.
17 |
18 | We present such a function here.
19 |
20 |
21 | ## The Problem : AUC is bumpy
22 |
23 | My favorite working definition of AUC is this: Let's call the binary class labels "Black" (0) and "White" (1). Pick one black element at random and let *x* be its predicted value. Now pick a random white element with value *y*. Then,
24 |
25 | AUC = the probability that the elements are in the right order. That is, *x*<*y* .
26 |
27 | That's it. For any given set of points like the Training Set, we can get this probability by doing a brute-force calculation. Scan the set of all possible black/white pairs , and count the portion that are right-ordered.
28 |
29 | We can see that the AUC score is not differentiable (a smooth curve with respect to any single *x* or *y*.) Take an element (any color) and move it slightly enough that it doesn't hit a neighboring element. The AUC stays the same. Once the point does cross a neighbor, we have a chance of flipping one of the x
78 |
79 |
80 |
81 | This is really just straining mathematical notation to say 'count the right-ordered pairs.' If we divide this sum by the total number of pairs , |**B**| * |**W**|, we get exactly the AUC metric. (Historically, this is called the normalized Wilcoxon-Mann-Whitney (WMW) statistic.)
82 |
83 | To make a loss function from this, we could just flip the x < y comparison to x > y in order to penalize wrong-ordered pairs. The problem, of course, is that discontinuous jump when *x* crosses y .
84 |
85 | *Yan et. al* surveys - and then rejects - past work-arounds using continuous approximations to the step (Heaviside) function, such as a Sigmoid curve. Then they pull this out of a hat :
86 |
87 | 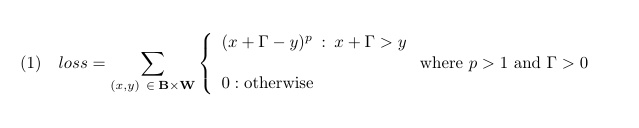 88 |
89 | Yann got this forumula by applying a series of changes to the WMW:
90 |
91 | 1. x1 is differentiable everywhere. OK, so p>1.
101 |
102 | Now back to Γ : Γ provides a 'padding' which is enforced between two points. We penalize not only wrong-ordered pairs, but also right-ordered pairs which are *too close*. If a right-ordered pair is too close, its elements are at risk of getting swapped in the future by the random jiggling of a stochastic neural net. The idea is to keep them moving apart until they reach a comfortable distance.
103 |
104 |
105 | And that's the basic idea as outlined in the paper. We now ake some refinements regarding Γ and p.
106 |
107 |
108 | ## About that Γ and p
109 |
110 |
111 | Here we break a bit with the paper. *Yan et. al* seem a little squeamish on the topic of choosing Γ and p, offering only that a *p* = 2 or *p* = 3 seems good and that Γ should be somewhere between 0.10 and 0.70. Yan essentially wishes us luck with these parameters and bows out.
112 |
113 | First, we permanently fix *p* = 2, because any self-respecting loss function should be a sum-of-squares. (One reason for this is that it ensures the loss function is not only differentiable, but also *convex*)
114 |
115 | Second and more importantly, let's take a look at Γ. The heuristic of 'somewhere from 0.10 to 0.70' looks strange on the face of it; even if the predictions were normalized to be 0x| = δ |**pairs** where y>x|
130 |
131 | In our experiments we found that δ can range from 0.5 to 2.0, and 1.0 is a good default choice.
132 |
133 | So we set δ to 1, p to 2, and forget about Γ altogether,
134 |
135 | ## Let's make code
136 |
137 | Our loss function (1) looks dismally expensive to compute. It requires that we scan the entire training set for each individual prediction.
138 |
139 | We bypass this problem with a performance tweak :
140 |
141 | Suppose we are calculating the loss function for a given white data point, *x*. To calculate (3), we need to compare *x* against the entire training set of black predictions, *y*.
142 | We take a short-cut and use a random sub-sample of the black data points. If we set the size of the sub-sample to be, say, 1000 - we get a very (very) close approximation to the true loss function. [1]
143 |
144 | Similar reasoning applies to the loss function of a black data-point; we use a random sub-sample of all white training elements.
145 |
146 | In this way, white and black subsamples fit easily into GPU memory. By reusing the same sub-sample throughout a given batch, we can parallelize the operation in batches. We end up with a loss function that's about as fast at BCE.
147 |
148 | Here's the batch-loss function in PyTorch:
149 |
150 |
151 | def roc_star_loss( _y_true, y_pred, gamma, _epoch_true, epoch_pred):
152 | """
153 | Nearly direct loss function for AUC.
154 | See article,
155 | C. Reiss, "Roc-star : An objective function for ROC-AUC that actually works."
156 | https://github.com/iridiumblue/articles/blob/master/roc_star.md
157 | _y_true: `Tensor`. Targets (labels). Float either 0.0 or 1.0 .
158 | y_pred: `Tensor` . Predictions.
159 | gamma : `Float` Gamma, as derived from last epoch.
160 | _epoch_true: `Tensor`. Targets (labels) from last epoch.
161 | epoch_pred : `Tensor`. Predicions from last epoch.
162 | """
163 | #convert labels to boolean
164 | y_true = (_y_true>=0.50)
165 | epoch_true = (_epoch_true>=0.50)
166 |
167 | # if batch is either all true or false return small random stub value.
168 | if torch.sum(y_true)==0 or torch.sum(y_true) == y_true.shape[0]: return torch.sum(y_pred)*1e-8
169 |
170 | pos = y_pred[y_true]
171 | neg = y_pred[~y_true]
172 |
173 | epoch_pos = epoch_pred[epoch_true]
174 | epoch_neg = epoch_pred[~epoch_true]
175 |
176 | # Take random subsamples of the training set, both positive and negative.
177 | max_pos = 1000 # Max number of positive training samples
178 | max_neg = 1000 # Max number of positive training samples
179 | cap_pos = epoch_pos.shape[0]
180 | cap_neg = epoch_neg.shape[0]
181 | epoch_pos = epoch_pos[torch.rand_like(epoch_pos) < max_pos/cap_pos]
182 | epoch_neg = epoch_neg[torch.rand_like(epoch_neg) < max_neg/cap_pos]
183 |
184 | ln_pos = pos.shape[0]
185 | ln_neg = neg.shape[0]
186 |
187 | # sum positive batch elements agaionst (subsampled) negative elements
188 | if ln_pos>0 :
189 | pos_expand = pos.view(-1,1).expand(-1,epoch_neg.shape[0]).reshape(-1)
190 | neg_expand = epoch_neg.repeat(ln_pos)
191 |
192 | diff2 = neg_expand - pos_expand + gamma
193 | l2 = diff2[diff2>0]
194 | m2 = l2 * l2
195 | len2 = l2.shape[0]
196 | else:
197 | m2 = torch.tensor([0], dtype=torch.float).cuda()
198 | len2 = 0
199 |
200 | # Similarly, compare negative batch elements against (subsampled) positive elements
201 | if ln_neg>0 :
202 | pos_expand = epoch_pos.view(-1,1).expand(-1, ln_neg).reshape(-1)
203 | neg_expand = neg.repeat(epoch_pos.shape[0])
204 |
205 | diff3 = neg_expand - pos_expand + gamma
206 | l3 = diff3[diff3>0]
207 | m3 = l3*l3
208 | len3 = l3.shape[0]
209 | else:
210 | m3 = torch.tensor([0], dtype=torch.float).cuda()
211 | len3=0
212 |
213 | if (torch.sum(m2)+torch.sum(m3))!=0 :
214 | res2 = torch.sum(m2)/max_pos+torch.sum(m3)/max_neg
215 | #code.interact(local=dict(globals(), **locals()))
216 | else:
217 | res2 = torch.sum(m2)+torch.sum(m3)
218 |
219 | res2 = torch.where(torch.isnan(res2), torch.zeros_like(res2), res2)
220 |
221 | return res2
222 |
223 |
224 | Note that there are some extra parameters. We are passing in the training set from the *last epoch*. Since the entire training set doesn't change much from one epoch to the next, the loss function can compare each prediction again a slightly out-of-date training set. This simplifies debugging, and appears to benefit performance as the 'background' epoch isn't changing from one batch to the next.
225 |
226 | Similarly, Γ is an expensive calculation. We again use the sub-sampling trick, but increase the size of the sub-samples to ~10,000 to ensure an accurate estimate. To keep performance clipping along, we recompute this value only once per epoch. Here's the function to do that :
227 |
228 | def epoch_update_gamma(y_true,y_pred, epoch=-1,delta=2):
229 | """
230 | Calculate gamma from last epoch's targets and predictions.
231 | Gamma is updated at the end of each epoch.
232 | y_true: `Tensor`. Targets (labels). Float either 0.0 or 1.0 .
233 | y_pred: `Tensor` . Predictions.
234 | """
235 | DELTA = delta
236 | SUB_SAMPLE_SIZE = 2000.0
237 | pos = y_pred[y_true==1]
238 | neg = y_pred[y_true==0] # yo pytorch, no boolean tensors or operators? Wassap?
239 | # subsample the training set for performance
240 | cap_pos = pos.shape[0]
241 | cap_neg = neg.shape[0]
242 | pos = pos[torch.rand_like(pos) < SUB_SAMPLE_SIZE/cap_pos]
243 | neg = neg[torch.rand_like(neg) < SUB_SAMPLE_SIZE/cap_neg]
244 | ln_pos = pos.shape[0]
245 | ln_neg = neg.shape[0]
246 | pos_expand = pos.view(-1,1).expand(-1,ln_neg).reshape(-1)
247 | neg_expand = neg.repeat(ln_pos)
248 | diff = neg_expand - pos_expand
249 | ln_All = diff.shape[0]
250 | Lp = diff[diff>0] # because we're taking positive diffs, we got pos and neg flipped.
251 | ln_Lp = Lp.shape[0]-1
252 | diff_neg = -1.0 * diff[diff<0]
253 | diff_neg = diff_neg.sort()[0]
254 | ln_neg = diff_neg.shape[0]-1
255 | ln_neg = max([ln_neg, 0])
256 | left_wing = int(ln_Lp*DELTA)
257 | left_wing = max([0,left_wing])
258 | left_wing = min([ln_neg,left_wing])
259 | default_gamma=torch.tensor(0.2, dtype=torch.float).cuda()
260 | if diff_neg.shape[0] > 0 :
261 | gamma = diff_neg[left_wing]
262 | else:
263 | gamma = default_gamma # default=torch.tensor(0.2, dtype=torch.float).cuda() #zoink
264 | L1 = diff[diff>-1.0*gamma]
265 | ln_L1 = L1.shape[0]
266 | if epoch > -1 :
267 | return gamma
268 | else :
269 | return default_gamma
270 |
271 |
272 | Here's the helicopter view showing how to use the two functions as we loop on epochs, then on batches :
273 |
274 |
275 |
276 | train_ds = CatDogDataset(train_files, transform)
277 | train_dl = DataLoader(train_ds, batch_size=BATCH_SIZE)
278 |
279 | #initialize last epoch with random values
280 | last_epoch_y_pred = torch.tensor( 1.0-numpy.random.rand(len(train_ds))/2.0, dtype=torch.float).cuda()
281 | last_epoch_y_t = torch.tensor([o for o in train_tt],dtype=torch.float).cuda()
282 | epoch_gamma = 0.20
283 | for epoch in range(epoches):
284 | epoch_y_pred=[]
285 | epoch_y_t=[]
286 | for X, y in train_dl:
287 | preds = model(X)
288 | # .
289 | # .
290 | loss = roc_star_loss(y,preds,epoch_gamma, last_epoch_y_t, last_epoch_y_pred)
291 | # .
292 | # .
293 | epoch_y_pred.extend(preds)
294 | epoch_y_t.extend(y)
295 | last_epoch_y_pred = torch.tensor(epoch_y_pred).cuda()
296 | last_epoch_y_t = torch.tensor(epoch_y_t).cuda()
297 | epoch_gamma = epoch_update_gamma(last_epoch_y_t, last_epoch_y_pred, epoch)
298 | #...
299 |
300 | A complete working example can be found here, [example.py](https://github.com/iridiumblue/roc-star/blob/master/example.py)
301 | For a faster jump-star you can fork this kernel on Kaggle : [kernel](https://www.kaggle.com/iridiumblue/roc-star-an-auc-loss-function-to-challenge-bxe)
302 |
303 | Below we chart the performance of roc-star against the same model using BCE. Experience shows that roc-star can often simply be swapped into any model using BCE with a good chance at a performance increase.
304 |
305 |
88 |
89 | Yann got this forumula by applying a series of changes to the WMW:
90 |
91 | 1. x1 is differentiable everywhere. OK, so p>1.
101 |
102 | Now back to Γ : Γ provides a 'padding' which is enforced between two points. We penalize not only wrong-ordered pairs, but also right-ordered pairs which are *too close*. If a right-ordered pair is too close, its elements are at risk of getting swapped in the future by the random jiggling of a stochastic neural net. The idea is to keep them moving apart until they reach a comfortable distance.
103 |
104 |
105 | And that's the basic idea as outlined in the paper. We now ake some refinements regarding Γ and p.
106 |
107 |
108 | ## About that Γ and p
109 |
110 |
111 | Here we break a bit with the paper. *Yan et. al* seem a little squeamish on the topic of choosing Γ and p, offering only that a *p* = 2 or *p* = 3 seems good and that Γ should be somewhere between 0.10 and 0.70. Yan essentially wishes us luck with these parameters and bows out.
112 |
113 | First, we permanently fix *p* = 2, because any self-respecting loss function should be a sum-of-squares. (One reason for this is that it ensures the loss function is not only differentiable, but also *convex*)
114 |
115 | Second and more importantly, let's take a look at Γ. The heuristic of 'somewhere from 0.10 to 0.70' looks strange on the face of it; even if the predictions were normalized to be 0x| = δ |**pairs** where y>x|
130 |
131 | In our experiments we found that δ can range from 0.5 to 2.0, and 1.0 is a good default choice.
132 |
133 | So we set δ to 1, p to 2, and forget about Γ altogether,
134 |
135 | ## Let's make code
136 |
137 | Our loss function (1) looks dismally expensive to compute. It requires that we scan the entire training set for each individual prediction.
138 |
139 | We bypass this problem with a performance tweak :
140 |
141 | Suppose we are calculating the loss function for a given white data point, *x*. To calculate (3), we need to compare *x* against the entire training set of black predictions, *y*.
142 | We take a short-cut and use a random sub-sample of the black data points. If we set the size of the sub-sample to be, say, 1000 - we get a very (very) close approximation to the true loss function. [1]
143 |
144 | Similar reasoning applies to the loss function of a black data-point; we use a random sub-sample of all white training elements.
145 |
146 | In this way, white and black subsamples fit easily into GPU memory. By reusing the same sub-sample throughout a given batch, we can parallelize the operation in batches. We end up with a loss function that's about as fast at BCE.
147 |
148 | Here's the batch-loss function in PyTorch:
149 |
150 |
151 | def roc_star_loss( _y_true, y_pred, gamma, _epoch_true, epoch_pred):
152 | """
153 | Nearly direct loss function for AUC.
154 | See article,
155 | C. Reiss, "Roc-star : An objective function for ROC-AUC that actually works."
156 | https://github.com/iridiumblue/articles/blob/master/roc_star.md
157 | _y_true: `Tensor`. Targets (labels). Float either 0.0 or 1.0 .
158 | y_pred: `Tensor` . Predictions.
159 | gamma : `Float` Gamma, as derived from last epoch.
160 | _epoch_true: `Tensor`. Targets (labels) from last epoch.
161 | epoch_pred : `Tensor`. Predicions from last epoch.
162 | """
163 | #convert labels to boolean
164 | y_true = (_y_true>=0.50)
165 | epoch_true = (_epoch_true>=0.50)
166 |
167 | # if batch is either all true or false return small random stub value.
168 | if torch.sum(y_true)==0 or torch.sum(y_true) == y_true.shape[0]: return torch.sum(y_pred)*1e-8
169 |
170 | pos = y_pred[y_true]
171 | neg = y_pred[~y_true]
172 |
173 | epoch_pos = epoch_pred[epoch_true]
174 | epoch_neg = epoch_pred[~epoch_true]
175 |
176 | # Take random subsamples of the training set, both positive and negative.
177 | max_pos = 1000 # Max number of positive training samples
178 | max_neg = 1000 # Max number of positive training samples
179 | cap_pos = epoch_pos.shape[0]
180 | cap_neg = epoch_neg.shape[0]
181 | epoch_pos = epoch_pos[torch.rand_like(epoch_pos) < max_pos/cap_pos]
182 | epoch_neg = epoch_neg[torch.rand_like(epoch_neg) < max_neg/cap_pos]
183 |
184 | ln_pos = pos.shape[0]
185 | ln_neg = neg.shape[0]
186 |
187 | # sum positive batch elements agaionst (subsampled) negative elements
188 | if ln_pos>0 :
189 | pos_expand = pos.view(-1,1).expand(-1,epoch_neg.shape[0]).reshape(-1)
190 | neg_expand = epoch_neg.repeat(ln_pos)
191 |
192 | diff2 = neg_expand - pos_expand + gamma
193 | l2 = diff2[diff2>0]
194 | m2 = l2 * l2
195 | len2 = l2.shape[0]
196 | else:
197 | m2 = torch.tensor([0], dtype=torch.float).cuda()
198 | len2 = 0
199 |
200 | # Similarly, compare negative batch elements against (subsampled) positive elements
201 | if ln_neg>0 :
202 | pos_expand = epoch_pos.view(-1,1).expand(-1, ln_neg).reshape(-1)
203 | neg_expand = neg.repeat(epoch_pos.shape[0])
204 |
205 | diff3 = neg_expand - pos_expand + gamma
206 | l3 = diff3[diff3>0]
207 | m3 = l3*l3
208 | len3 = l3.shape[0]
209 | else:
210 | m3 = torch.tensor([0], dtype=torch.float).cuda()
211 | len3=0
212 |
213 | if (torch.sum(m2)+torch.sum(m3))!=0 :
214 | res2 = torch.sum(m2)/max_pos+torch.sum(m3)/max_neg
215 | #code.interact(local=dict(globals(), **locals()))
216 | else:
217 | res2 = torch.sum(m2)+torch.sum(m3)
218 |
219 | res2 = torch.where(torch.isnan(res2), torch.zeros_like(res2), res2)
220 |
221 | return res2
222 |
223 |
224 | Note that there are some extra parameters. We are passing in the training set from the *last epoch*. Since the entire training set doesn't change much from one epoch to the next, the loss function can compare each prediction again a slightly out-of-date training set. This simplifies debugging, and appears to benefit performance as the 'background' epoch isn't changing from one batch to the next.
225 |
226 | Similarly, Γ is an expensive calculation. We again use the sub-sampling trick, but increase the size of the sub-samples to ~10,000 to ensure an accurate estimate. To keep performance clipping along, we recompute this value only once per epoch. Here's the function to do that :
227 |
228 | def epoch_update_gamma(y_true,y_pred, epoch=-1,delta=2):
229 | """
230 | Calculate gamma from last epoch's targets and predictions.
231 | Gamma is updated at the end of each epoch.
232 | y_true: `Tensor`. Targets (labels). Float either 0.0 or 1.0 .
233 | y_pred: `Tensor` . Predictions.
234 | """
235 | DELTA = delta
236 | SUB_SAMPLE_SIZE = 2000.0
237 | pos = y_pred[y_true==1]
238 | neg = y_pred[y_true==0] # yo pytorch, no boolean tensors or operators? Wassap?
239 | # subsample the training set for performance
240 | cap_pos = pos.shape[0]
241 | cap_neg = neg.shape[0]
242 | pos = pos[torch.rand_like(pos) < SUB_SAMPLE_SIZE/cap_pos]
243 | neg = neg[torch.rand_like(neg) < SUB_SAMPLE_SIZE/cap_neg]
244 | ln_pos = pos.shape[0]
245 | ln_neg = neg.shape[0]
246 | pos_expand = pos.view(-1,1).expand(-1,ln_neg).reshape(-1)
247 | neg_expand = neg.repeat(ln_pos)
248 | diff = neg_expand - pos_expand
249 | ln_All = diff.shape[0]
250 | Lp = diff[diff>0] # because we're taking positive diffs, we got pos and neg flipped.
251 | ln_Lp = Lp.shape[0]-1
252 | diff_neg = -1.0 * diff[diff<0]
253 | diff_neg = diff_neg.sort()[0]
254 | ln_neg = diff_neg.shape[0]-1
255 | ln_neg = max([ln_neg, 0])
256 | left_wing = int(ln_Lp*DELTA)
257 | left_wing = max([0,left_wing])
258 | left_wing = min([ln_neg,left_wing])
259 | default_gamma=torch.tensor(0.2, dtype=torch.float).cuda()
260 | if diff_neg.shape[0] > 0 :
261 | gamma = diff_neg[left_wing]
262 | else:
263 | gamma = default_gamma # default=torch.tensor(0.2, dtype=torch.float).cuda() #zoink
264 | L1 = diff[diff>-1.0*gamma]
265 | ln_L1 = L1.shape[0]
266 | if epoch > -1 :
267 | return gamma
268 | else :
269 | return default_gamma
270 |
271 |
272 | Here's the helicopter view showing how to use the two functions as we loop on epochs, then on batches :
273 |
274 |
275 |
276 | train_ds = CatDogDataset(train_files, transform)
277 | train_dl = DataLoader(train_ds, batch_size=BATCH_SIZE)
278 |
279 | #initialize last epoch with random values
280 | last_epoch_y_pred = torch.tensor( 1.0-numpy.random.rand(len(train_ds))/2.0, dtype=torch.float).cuda()
281 | last_epoch_y_t = torch.tensor([o for o in train_tt],dtype=torch.float).cuda()
282 | epoch_gamma = 0.20
283 | for epoch in range(epoches):
284 | epoch_y_pred=[]
285 | epoch_y_t=[]
286 | for X, y in train_dl:
287 | preds = model(X)
288 | # .
289 | # .
290 | loss = roc_star_loss(y,preds,epoch_gamma, last_epoch_y_t, last_epoch_y_pred)
291 | # .
292 | # .
293 | epoch_y_pred.extend(preds)
294 | epoch_y_t.extend(y)
295 | last_epoch_y_pred = torch.tensor(epoch_y_pred).cuda()
296 | last_epoch_y_t = torch.tensor(epoch_y_t).cuda()
297 | epoch_gamma = epoch_update_gamma(last_epoch_y_t, last_epoch_y_pred, epoch)
298 | #...
299 |
300 | A complete working example can be found here, [example.py](https://github.com/iridiumblue/roc-star/blob/master/example.py)
301 | For a faster jump-star you can fork this kernel on Kaggle : [kernel](https://www.kaggle.com/iridiumblue/roc-star-an-auc-loss-function-to-challenge-bxe)
302 |
303 | Below we chart the performance of roc-star against the same model using BCE. Experience shows that roc-star can often simply be swapped into any model using BCE with a good chance at a performance increase.
304 |
305 | 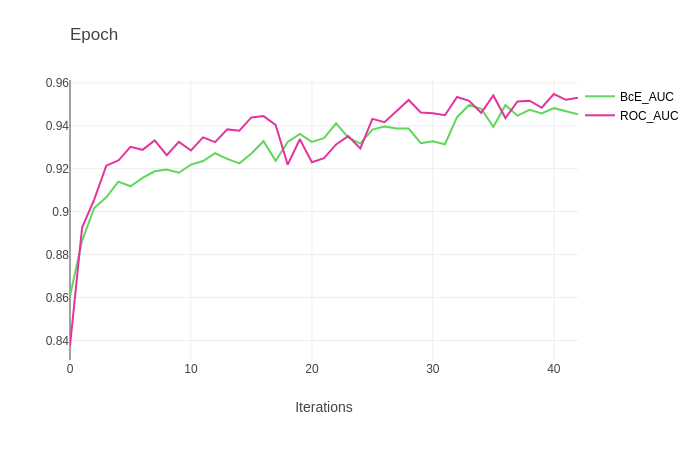 306 |
307 |
308 |
--------------------------------------------------------------------------------
/example.py:
--------------------------------------------------------------------------------
1 | '''
2 | A demonstration of a new and experimental loss function which directly targets AUC/ROC,
3 | and is seen to outperform BxE in early testing. See paper up here -
4 | https://github.com/iridiumblue/roc-star.
5 |
6 | The test is a simple sentiment analysis binary classifier turned loose on tweets from Twitter.
7 | Text embeddings have been precomputed and pickled for speed.
8 | TRUNC truncates the training set, set it to -1 for all 1.6 M sample tweets.
9 |
10 | Note that for the first epoch (only), the loss function is BxE. That is just to kickstart
11 | the new loss function roc_star_loss. That's a good practice to stick to if you want
12 | to give this a try for your model. Note also that roc_star_loss requires a call to
13 | epoch_update_gamma at the end of each epoch.
14 | '''
15 |
16 |
17 | from warnings import simplefilter
18 | import time
19 | from copy import copy
20 | import torch
21 | import torch.nn.functional as F
22 | import torch.nn as nn
23 | from torch.nn.utils.rnn import PackedSequence
24 | import numpy as np
25 | import _pickle
26 | import gc
27 | from pathlib2 import Path
28 | from sklearn.metrics import roc_auc_score
29 | from trains import Task
30 | from trains import StorageManager
31 | from pkbar import Kbar as Progbar
32 | import argparse
33 | import os
34 | from tempfile import gettempdir
35 |
36 |
37 | # ignore all future warnings
38 | simplefilter(action='ignore', category=FutureWarning)
39 | simplefilter(action='ignore', category=UserWarning)
40 |
41 | x_train_torch,x_valid_torch,y_train_torch,y_valid_torch = None,None,None,None
42 | embedding_matrix = None
43 | task=None
44 | logger=None
45 | best_result={}
46 | max_features = 200000
47 | embed_size = 300
48 |
49 |
50 | def init(h_params):
51 | global x_train_torch, x_valid_torch, y_train_torch, y_valid_torch
52 | global embedding_matrix
53 | global task, logger
54 |
55 | print("Recovering tokenized text from pickle ...")
56 | tokenized = StorageManager.get_local_copy(
57 | remote_url="https://allegro-datasets.s3.amazonaws.com/roc_star_data"
58 | "/tokenized.pkl.zip",
59 | name="tokenized",
60 | )
61 | embedding = StorageManager.get_local_copy(
62 | remote_url="https://allegro-datasets.s3.amazonaws.com/roc_star_data"
63 | "/embedding.pkl.zip",
64 | name="embedding",
65 | )
66 |
67 | x_train, x_valid, y_train, y_valid = _pickle.load(open(Path(tokenized, "tokenized.pkl"), "rb"))
68 | print("Reusing pickled embedding ...")
69 | embedding_matrix = _pickle.load(open(Path(embedding, "embedding.pkl"), "rb"))
70 |
71 | print("Moving data to GPU ...")
72 | if h_params.trunc>-1 :
73 | print(f"\r\r * * WARNING training set truncated to first {h_params.trunc} items.\r\r")
74 |
75 | x_train_torch = torch.tensor(x_train[:h_params.trunc], dtype=torch.long).cuda()
76 | x_valid_torch = torch.tensor(x_valid, dtype=torch.long).cuda()
77 | y_train_torch = torch.tensor(y_train[:h_params.trunc], dtype=torch.float32).cuda()
78 | y_valid_torch = torch.tensor(y_valid, dtype=torch.float32).cuda()
79 | del x_train, y_train, x_valid, y_valid; gc.collect(2)
80 |
81 | task_name = "ROC" if h_params.use_roc_star else "BxE"
82 | task = Task.init(project_name='Roc-star Loss', task_name='Roc star')
83 | logger = task.get_logger()
84 |
85 |
86 | def epoch_update_gamma(y_true, y_pred, epoch=-1, delta=2):
87 | """
88 | Calculate gamma from last epoch's targets and predictions.
89 | Gamma is updated at the end of each epoch.
90 | y_true: `Tensor`. Targets (labels). Float either 0.0 or 1.0 .
91 | y_pred: `Tensor` . Predictions.
92 | """
93 | sub_sample_size = 2000.0
94 | pos = y_pred[y_true==1]
95 | neg = y_pred[y_true==0] # yo pytorch, no boolean tensors or operators? Wassap?
96 | # subsample the training set for performance
97 | cap_pos = pos.shape[0]
98 | cap_neg = neg.shape[0]
99 | pos = pos[torch.rand_like(pos) < sub_sample_size/cap_pos]
100 | neg = neg[torch.rand_like(neg) < sub_sample_size/cap_neg]
101 | ln_pos = pos.shape[0]
102 | ln_neg = neg.shape[0]
103 | pos_expand = pos.view(-1,1).expand(-1,ln_neg).reshape(-1)
104 | neg_expand = neg.repeat(ln_pos)
105 | diff = neg_expand - pos_expand
106 | Lp = diff[diff>0] # because we're taking positive diffs, we got pos and neg flipped.
107 | ln_Lp = Lp.shape[0]-1
108 | diff_neg = -1.0 * diff[diff<0]
109 | diff_neg = diff_neg.sort()[0]
110 | ln_neg = diff_neg.shape[0]-1
111 | ln_neg = max([ln_neg, 0])
112 | left_wing = int(ln_Lp*delta)
113 | left_wing = max([0,left_wing])
114 | left_wing = min([ln_neg,left_wing])
115 | default_gamma = torch.tensor(0.2, dtype=torch.float).cuda()
116 | if diff_neg.shape[0] > 0 :
117 | gamma = diff_neg[left_wing]
118 | else:
119 | gamma = default_gamma # default=torch.tensor(0.2, dtype=torch.float).cuda() #zoink
120 | L1 = diff[diff>-1.0*gamma]
121 | if epoch > -1 :
122 | return gamma
123 | else :
124 | return default_gamma
125 |
126 |
127 | def roc_star_loss(_y_true, y_pred, gamma, _epoch_true, epoch_pred):
128 | """
129 | Nearly direct loss function for AUC.
130 | See article,
131 | C. Reiss, "Roc-star : An objective function for ROC-AUC that actually works."
132 | https://github.com/iridiumblue/articles/blob/master/roc_star.md
133 | _y_true: `Tensor`. Targets (labels). Float either 0.0 or 1.0 .
134 | y_pred: `Tensor` . Predictions.
135 | gamma : `Float` Gamma, as derived from last epoch.
136 | _epoch_true: `Tensor`. Targets (labels) from last epoch.
137 | epoch_pred : `Tensor`. Predicions from last epoch.
138 | """
139 | #convert labels to boolean
140 | y_true = (_y_true>=0.50)
141 | epoch_true = (_epoch_true>=0.50)
142 |
143 | # if batch is either all true or false return small random stub value.
144 | if torch.sum(y_true)==0 or torch.sum(y_true) == y_true.shape[0]: return torch.sum(y_pred)*1e-8
145 |
146 | pos = y_pred[y_true]
147 | neg = y_pred[~y_true]
148 |
149 | epoch_pos = epoch_pred[epoch_true]
150 | epoch_neg = epoch_pred[~epoch_true]
151 |
152 | # Take random subsamples of the training set, both positive and negative.
153 | max_pos = 1000 # Max number of positive training samples
154 | max_neg = 1000 # Max number of positive training samples
155 | cap_pos = epoch_pos.shape[0]
156 | epoch_pos = epoch_pos[torch.rand_like(epoch_pos) < max_pos/cap_pos]
157 | epoch_neg = epoch_neg[torch.rand_like(epoch_neg) < max_neg/cap_pos]
158 |
159 | ln_pos = pos.shape[0]
160 | ln_neg = neg.shape[0]
161 |
162 | # sum positive batch elements agaionst (subsampled) negative elements
163 | if ln_pos>0 :
164 | pos_expand = pos.view(-1,1).expand(-1,epoch_neg.shape[0]).reshape(-1)
165 | neg_expand = epoch_neg.repeat(ln_pos)
166 |
167 | diff2 = neg_expand - pos_expand + gamma
168 | l2 = diff2[diff2>0]
169 | m2 = l2 * l2
170 | else:
171 | m2 = torch.tensor([0], dtype=torch.float).cuda()
172 |
173 | # Similarly, compare negative batch elements against (subsampled) positive elements
174 | if ln_neg>0 :
175 | pos_expand = epoch_pos.view(-1,1).expand(-1, ln_neg).reshape(-1)
176 | neg_expand = neg.repeat(epoch_pos.shape[0])
177 |
178 | diff3 = neg_expand - pos_expand + gamma
179 | l3 = diff3[diff3>0]
180 | m3 = l3*l3
181 | else:
182 | m3 = torch.tensor([0], dtype=torch.float).cuda()
183 |
184 | if (torch.sum(m2)+torch.sum(m3))!=0 :
185 | res2 = torch.sum(m2)/max_pos+torch.sum(m3)/max_neg
186 | else:
187 | res2 = torch.sum(m2)+torch.sum(m3)
188 |
189 | res2 = torch.where(torch.isnan(res2), torch.zeros_like(res2), res2)
190 |
191 | return res2
192 |
193 |
194 | #https://github.com/keitakurita/Better_LSTM_PyTorch/blob/master/better_lstm/model.py
195 | class VariationalDropout(nn.Module):
196 | """
197 | Applies the same dropout mask across the temporal dimension
198 | See https://arxiv.org/abs/1512.05287 for more details.
199 | Note that this is not applied to the recurrent activations in the LSTM like the above paper.
200 | Instead, it is applied to the inputs and outputs of the recurrent layer.
201 | """
202 | def __init__(self, dropout, batch_first=False):
203 | super().__init__()
204 | self.dropout = dropout
205 | self.batch_first = batch_first
206 |
207 | def forward(self, x: torch.Tensor) -> torch.Tensor:
208 | if not self.training or self.dropout <= 0.:
209 | return x
210 |
211 | is_packed = isinstance(x, PackedSequence)
212 | if is_packed:
213 | x, batch_sizes = x
214 | max_batch_size = int(batch_sizes[0])
215 | else:
216 | batch_sizes = None
217 | max_batch_size = x.size(0)
218 |
219 | # Drop same mask across entire sequence
220 | if self.batch_first:
221 | m = x.new_empty(max_batch_size, 1, x.size(2), requires_grad=False).bernoulli_(1 - self.dropout)
222 | else:
223 | m = x.new_empty(1, max_batch_size, x.size(2), requires_grad=False).bernoulli_(1 - self.dropout)
224 | x = x.masked_fill(m == 0, 0) / (1 - self.dropout)
225 |
226 | if is_packed:
227 | return PackedSequence(x, batch_sizes)
228 | else:
229 | return x
230 |
231 |
232 | #https://github.com/keitakurita/Better_LSTM_PyTorch/blob/master/better_lstm/model.py
233 | class LSTM(nn.LSTM):
234 | def __init__(self, *args, dropouti: float=0.,
235 | dropoutw: float=0., dropouto: float=0.,
236 | batch_first=True, unit_forget_bias=True, **kwargs):
237 | super().__init__(*args, **kwargs, batch_first=batch_first)
238 | self.unit_forget_bias = unit_forget_bias
239 | self.dropoutw = dropoutw
240 | self.input_drop = VariationalDropout(dropouti,
241 | batch_first=batch_first)
242 | self.output_drop = VariationalDropout(dropouto,
243 | batch_first=batch_first)
244 | self._init_weights()
245 |
246 | def _init_weights(self):
247 | """
248 | Use orthogonal init for recurrent layers, xavier uniform for input layers
249 | Bias is 0 except for forget gate
250 | """
251 | for name, param in self.named_parameters():
252 | if "weight_hh" in name:
253 | nn.init.orthogonal_(param.data)
254 | elif "weight_ih" in name:
255 | nn.init.xavier_uniform_(param.data)
256 | elif "bias" in name and self.unit_forget_bias:
257 | nn.init.zeros_(param.data)
258 | param.data[self.hidden_size:2 * self.hidden_size] = 1
259 |
260 | def _drop_weights(self):
261 | for name, param in self.named_parameters():
262 | if "weight_hh" in name:
263 | getattr(self, name).data = \
264 | torch.nn.functional.dropout(param.data, p=self.dropoutw,
265 | training=self.training).contiguous()
266 |
267 | def forward(self, input, hx=None):
268 | self._drop_weights()
269 | input = self.input_drop(input)
270 | seq, state = super().forward(input, hx=hx)
271 | return self.output_drop(seq), state
272 |
273 |
274 |
275 | class NeuralNet(nn.Module):
276 | def __init__(self, embedding_matrix,h_params):
277 | super(NeuralNet, self).__init__()
278 | embed_size = embedding_matrix.shape[1]
279 |
280 | self.embedding = nn.Embedding(max_features, embed_size)
281 | self.embedding.weight = nn.Parameter(torch.tensor(embedding_matrix, dtype=torch.float32))
282 | self.embedding.weight.requires_grad = False
283 | self.h_params = copy(h_params)
284 |
285 | self.c1 = nn.Conv1d(300,kernel_size=2,out_channels=300,padding=1)
286 | LSTM_UNITS=h_params.lstm_units
287 | BIDIR = h_params.bidirectional
288 |
289 | LSTM_OUT = 2* LSTM_UNITS if BIDIR else LSTM_UNITS
290 |
291 | self.lstm1 = LSTM(embed_size, LSTM_UNITS, dropouti=h_params.dropout_i,dropoutw=h_params.dropout_w, dropouto=h_params.dropout_o,bidirectional=BIDIR, batch_first=True)
292 | self.lstm2 = LSTM(LSTM_OUT, LSTM_UNITS, dropouti=h_params.dropout_i,dropoutw=h_params.dropout_w, dropouto=h_params.dropout_o,bidirectional=BIDIR, batch_first=True)
293 |
294 |
295 | self.linear1 = nn.Linear(2*LSTM_OUT, 2*LSTM_OUT)
296 | self.linear2 = nn.Linear(2*LSTM_OUT, 2*LSTM_OUT)
297 |
298 | self.hey_norm = nn.LayerNorm(2*LSTM_OUT)
299 |
300 | self.linear_out = nn.Linear(2*LSTM_OUT, h_params.dense_hidden_units)
301 | self.linear_xtra = nn.Linear(h_params.dense_hidden_units,int(h_params.dense_hidden_units/2))
302 | self.linear_xtra2 = nn.Linear(int(h_params.dense_hidden_units/2),int(h_params.dense_hidden_units/4))
303 | self.linear_out2= nn.Linear(int(h_params.dense_hidden_units/4), 1)
304 |
305 |
306 |
307 | def forward(self, x):
308 | h_embedding = self.embedding(x)
309 | h1 = h_embedding.permute(0, 2, 1)
310 |
311 | q1 = self.c1(h1)
312 | f1 = q1.permute(0, 2, 1)
313 | h_lstm1, _ = self.lstm1(f1)
314 | h_lstm2, _ = self.lstm2(h_lstm1)
315 |
316 | # global average pooling
317 | avg_pool = torch.mean(h_lstm2, 1)
318 | # global max pooling
319 | max_pool, _ = torch.max(h_lstm2, 1)
320 |
321 | h_conc = torch.cat((max_pool, avg_pool), 1)
322 |
323 | h_conc_linear1 = self.linear1(h_conc)
324 | h_conc_linear2 = self.linear2(h_conc)
325 |
326 | hidden = h_conc + h_conc_linear1 + h_conc_linear2
327 | hidden = F.selu(self.linear_out(hidden))
328 | hidden = F.selu(self.linear_xtra(hidden))
329 | hidden = F.selu(self.linear_xtra2(hidden))
330 | hidden = F.sigmoid(self.linear_out2(hidden))
331 |
332 | result=hidden.flatten()
333 |
334 | return result
335 |
336 |
337 |
338 | def train_model(h_params, model, x_train, x_valid, y_train, y_valid, lr,
339 | batch_size=1000, n_epochs=20, title='', graph=''):
340 | global best_result
341 | param_lrs = [{'params': param, 'lr': lr} for param in model.parameters()]
342 | optimizer = torch.optim.AdamW(param_lrs, lr=h_params.initial_lr,
343 | betas=(0.9, 0.999),
344 | eps=1e-6,
345 | amsgrad=False
346 | )
347 |
348 | train_loader = torch.utils.data.DataLoader(torch.utils.data.TensorDataset(x_train, y_train), batch_size=batch_size, shuffle=True)
349 | valid_loader = torch.utils.data.DataLoader(torch.utils.data.TensorDataset(x_valid, y_valid), batch_size=batch_size, shuffle=False)
350 |
351 | num_batches = len(x_train)/batch_size
352 | print(len(x_train))
353 | results=[]
354 |
355 | for epoch in range(n_epochs):
356 | start_time = time.time()
357 | model.train()
358 | avg_loss = 0.
359 |
360 |
361 | progbar =Progbar(num_batches, stateful_metrics=['train-auc'])
362 |
363 | whole_y_pred=np.array([])
364 | whole_y_t=np.array([])
365 |
366 | for i,data in enumerate(train_loader):
367 | x_batch = data[:-1][0]
368 | y_batch = data[-1]
369 |
370 | y_pred = model(x_batch)
371 |
372 | if h_params.use_roc_star and epoch>0 :
373 |
374 | if i==0 : print('*Using Loss Roc-star')
375 | loss = roc_star_loss(y_batch,y_pred,epoch_gamma, last_whole_y_t, last_whole_y_pred)
376 |
377 | else:
378 | if i==0 : print('*Using Loss BxE')
379 | loss = F.binary_cross_entropy(y_pred, 1.0*y_batch)
380 |
381 | logger.report_scalar(title="Loss", series="trains loss",
382 | value=loss, iteration=epoch * len(x_train) + i)
383 |
384 | optimizer.zero_grad()
385 | loss.backward()
386 | # To prevent gradient explosions resulting in NaNs
387 | # https://discuss.pytorch.org/t/nan-loss-in-rnn-model/655/8
388 | # https://github.com/pytorch/examples/blob/master/word_language_model/main.py
389 | torch.nn.utils.clip_grad_norm_(model.parameters(), 0.5)
390 |
391 | optimizer.step()
392 |
393 | whole_y_pred = np.append(whole_y_pred, y_pred.clone().detach().cpu().numpy())
394 | whole_y_t = np.append(whole_y_t, y_batch.clone().detach().cpu().numpy())
395 |
396 | if i>0:
397 | if i%50==1 :
398 | try:
399 | train_roc_val = roc_auc_score(whole_y_t>=0.5, whole_y_pred)
400 | except:
401 |
402 | train_roc_val=-1
403 |
404 | progbar.update(
405 | i,
406 | values=[
407 | ("loss", np.mean(loss.detach().cpu().numpy())),
408 | ("train-auc", train_roc_val)
409 | ]
410 | )
411 |
412 | model.eval()
413 | last_whole_y_t = torch.tensor(whole_y_t).cuda()
414 | last_whole_y_pred = torch.tensor(whole_y_pred).cuda()
415 |
416 | all_valid_preds = np.array([])
417 | all_valid_t = np.array([])
418 | for i, valid_data in enumerate(valid_loader):
419 | x_batch = valid_data[:-1]
420 | y_batch = valid_data[-1]
421 |
422 | y_pred = model(*x_batch).detach().cpu().numpy()
423 | y_t = y_batch.detach().cpu().numpy()
424 |
425 | all_valid_preds=np.concatenate([all_valid_preds,y_pred],axis=0)
426 | all_valid_t = np.concatenate([all_valid_t,y_t],axis=0)
427 |
428 | epoch_gamma = epoch_update_gamma(last_whole_y_t, last_whole_y_pred, epoch,h_params.delta)
429 |
430 | try:
431 | valid_auc = roc_auc_score(all_valid_t>=0.5, all_valid_preds)
432 | except:
433 | valid_auc=-1
434 |
435 | try:
436 | train_roc_val = roc_auc_score(whole_y_t>=0.5, whole_y_pred)
437 | except:
438 | train_roc_val=-1
439 |
440 | elapsed_time = time.time() - start_time
441 | if epoch==0 :
442 | print("\n\n* * * * * * * * * * * Params :", title," :: ", graph)
443 | print('\nEpoch {}/{} \t loss={:.4f} \t time={:.2f}s'.format(
444 | epoch + 1, n_epochs, avg_loss, elapsed_time))
445 |
446 | print("Gamma = ", epoch_gamma)
447 | print("Validation AUC = ", valid_auc)
448 | if not ('auc' in best_result) or best_result['auc']0] # because we're taking positive diffs, we got pos and neg flipped.
24 | ln_Lp = Lp.shape[0]-1
25 | diff_neg = -1.0 * diff[diff<0]
26 | diff_neg = diff_neg.sort()[0]
27 | ln_neg = diff_neg.shape[0]-1
28 | ln_neg = max([ln_neg, 0])
29 | left_wing = int(ln_Lp*DELTA)
30 | left_wing = max([0,left_wing])
31 | left_wing = min([ln_neg,left_wing])
32 | default_gamma=torch.tensor(0.2, dtype=torch.float).cuda()
33 | if diff_neg.shape[0] > 0 :
34 | gamma = diff_neg[left_wing]
35 | else:
36 | gamma = default_gamma # default=torch.tensor(0.2, dtype=torch.float).cuda() #zoink
37 | L1 = diff[diff>-1.0*gamma]
38 | ln_L1 = L1.shape[0]
39 | if epoch > -1 :
40 | return gamma
41 | else :
42 | return default_gamma
43 |
44 |
45 |
46 | def roc_star_loss( _y_true, y_pred, gamma, _epoch_true, epoch_pred):
47 | """
48 | Nearly direct loss function for AUC.
49 | See article,
50 | C. Reiss, "Roc-star : An objective function for ROC-AUC that actually works."
51 | https://github.com/iridiumblue/articles/blob/master/roc_star.md
52 | _y_true: `Tensor`. Targets (labels). Float either 0.0 or 1.0 .
53 | y_pred: `Tensor` . Predictions.
54 | gamma : `Float` Gamma, as derived from last epoch.
55 | _epoch_true: `Tensor`. Targets (labels) from last epoch.
56 | epoch_pred : `Tensor`. Predicions from last epoch.
57 | """
58 | #convert labels to boolean
59 | y_true = (_y_true>=0.50)
60 | epoch_true = (_epoch_true>=0.50)
61 |
62 | # if batch is either all true or false return small random stub value.
63 | if torch.sum(y_true)==0 or torch.sum(y_true) == y_true.shape[0]: return torch.sum(y_pred)*1e-8
64 |
65 | pos = y_pred[y_true]
66 | neg = y_pred[~y_true]
67 |
68 | epoch_pos = epoch_pred[epoch_true]
69 | epoch_neg = epoch_pred[~epoch_true]
70 |
71 | # Take random subsamples of the training set, both positive and negative.
72 | max_pos = 1000 # Max number of positive training samples
73 | max_neg = 1000 # Max number of positive training samples
74 | cap_pos = epoch_pos.shape[0]
75 | cap_neg = epoch_neg.shape[0]
76 | epoch_pos = epoch_pos[torch.rand_like(epoch_pos) < max_pos/cap_pos]
77 | epoch_neg = epoch_neg[torch.rand_like(epoch_neg) < max_neg/cap_pos]
78 |
79 | ln_pos = pos.shape[0]
80 | ln_neg = neg.shape[0]
81 |
82 | # sum positive batch elements agaionst (subsampled) negative elements
83 | if ln_pos>0 :
84 | pos_expand = pos.view(-1,1).expand(-1,epoch_neg.shape[0]).reshape(-1)
85 | neg_expand = epoch_neg.repeat(ln_pos)
86 |
87 | diff2 = neg_expand - pos_expand + gamma
88 | l2 = diff2[diff2>0]
89 | m2 = l2 * l2
90 | len2 = l2.shape[0]
91 | else:
92 | m2 = torch.tensor([0], dtype=torch.float).cuda()
93 | len2 = 0
94 |
95 | # Similarly, compare negative batch elements against (subsampled) positive elements
96 | if ln_neg>0 :
97 | pos_expand = epoch_pos.view(-1,1).expand(-1, ln_neg).reshape(-1)
98 | neg_expand = neg.repeat(epoch_pos.shape[0])
99 |
100 | diff3 = neg_expand - pos_expand + gamma
101 | l3 = diff3[diff3>0]
102 | m3 = l3*l3
103 | len3 = l3.shape[0]
104 | else:
105 | m3 = torch.tensor([0], dtype=torch.float).cuda()
106 | len3=0
107 |
108 | if (torch.sum(m2)+torch.sum(m3))!=0 :
109 | res2 = torch.sum(m2)/max_pos+torch.sum(m3)/max_neg
110 | #code.interact(local=dict(globals(), **locals()))
111 | else:
112 | res2 = torch.sum(m2)+torch.sum(m3)
113 |
114 | res2 = torch.where(torch.isnan(res2), torch.zeros_like(res2), res2)
115 |
116 | return res2
--------------------------------------------------------------------------------
306 |
307 |
308 |
--------------------------------------------------------------------------------
/example.py:
--------------------------------------------------------------------------------
1 | '''
2 | A demonstration of a new and experimental loss function which directly targets AUC/ROC,
3 | and is seen to outperform BxE in early testing. See paper up here -
4 | https://github.com/iridiumblue/roc-star.
5 |
6 | The test is a simple sentiment analysis binary classifier turned loose on tweets from Twitter.
7 | Text embeddings have been precomputed and pickled for speed.
8 | TRUNC truncates the training set, set it to -1 for all 1.6 M sample tweets.
9 |
10 | Note that for the first epoch (only), the loss function is BxE. That is just to kickstart
11 | the new loss function roc_star_loss. That's a good practice to stick to if you want
12 | to give this a try for your model. Note also that roc_star_loss requires a call to
13 | epoch_update_gamma at the end of each epoch.
14 | '''
15 |
16 |
17 | from warnings import simplefilter
18 | import time
19 | from copy import copy
20 | import torch
21 | import torch.nn.functional as F
22 | import torch.nn as nn
23 | from torch.nn.utils.rnn import PackedSequence
24 | import numpy as np
25 | import _pickle
26 | import gc
27 | from pathlib2 import Path
28 | from sklearn.metrics import roc_auc_score
29 | from trains import Task
30 | from trains import StorageManager
31 | from pkbar import Kbar as Progbar
32 | import argparse
33 | import os
34 | from tempfile import gettempdir
35 |
36 |
37 | # ignore all future warnings
38 | simplefilter(action='ignore', category=FutureWarning)
39 | simplefilter(action='ignore', category=UserWarning)
40 |
41 | x_train_torch,x_valid_torch,y_train_torch,y_valid_torch = None,None,None,None
42 | embedding_matrix = None
43 | task=None
44 | logger=None
45 | best_result={}
46 | max_features = 200000
47 | embed_size = 300
48 |
49 |
50 | def init(h_params):
51 | global x_train_torch, x_valid_torch, y_train_torch, y_valid_torch
52 | global embedding_matrix
53 | global task, logger
54 |
55 | print("Recovering tokenized text from pickle ...")
56 | tokenized = StorageManager.get_local_copy(
57 | remote_url="https://allegro-datasets.s3.amazonaws.com/roc_star_data"
58 | "/tokenized.pkl.zip",
59 | name="tokenized",
60 | )
61 | embedding = StorageManager.get_local_copy(
62 | remote_url="https://allegro-datasets.s3.amazonaws.com/roc_star_data"
63 | "/embedding.pkl.zip",
64 | name="embedding",
65 | )
66 |
67 | x_train, x_valid, y_train, y_valid = _pickle.load(open(Path(tokenized, "tokenized.pkl"), "rb"))
68 | print("Reusing pickled embedding ...")
69 | embedding_matrix = _pickle.load(open(Path(embedding, "embedding.pkl"), "rb"))
70 |
71 | print("Moving data to GPU ...")
72 | if h_params.trunc>-1 :
73 | print(f"\r\r * * WARNING training set truncated to first {h_params.trunc} items.\r\r")
74 |
75 | x_train_torch = torch.tensor(x_train[:h_params.trunc], dtype=torch.long).cuda()
76 | x_valid_torch = torch.tensor(x_valid, dtype=torch.long).cuda()
77 | y_train_torch = torch.tensor(y_train[:h_params.trunc], dtype=torch.float32).cuda()
78 | y_valid_torch = torch.tensor(y_valid, dtype=torch.float32).cuda()
79 | del x_train, y_train, x_valid, y_valid; gc.collect(2)
80 |
81 | task_name = "ROC" if h_params.use_roc_star else "BxE"
82 | task = Task.init(project_name='Roc-star Loss', task_name='Roc star')
83 | logger = task.get_logger()
84 |
85 |
86 | def epoch_update_gamma(y_true, y_pred, epoch=-1, delta=2):
87 | """
88 | Calculate gamma from last epoch's targets and predictions.
89 | Gamma is updated at the end of each epoch.
90 | y_true: `Tensor`. Targets (labels). Float either 0.0 or 1.0 .
91 | y_pred: `Tensor` . Predictions.
92 | """
93 | sub_sample_size = 2000.0
94 | pos = y_pred[y_true==1]
95 | neg = y_pred[y_true==0] # yo pytorch, no boolean tensors or operators? Wassap?
96 | # subsample the training set for performance
97 | cap_pos = pos.shape[0]
98 | cap_neg = neg.shape[0]
99 | pos = pos[torch.rand_like(pos) < sub_sample_size/cap_pos]
100 | neg = neg[torch.rand_like(neg) < sub_sample_size/cap_neg]
101 | ln_pos = pos.shape[0]
102 | ln_neg = neg.shape[0]
103 | pos_expand = pos.view(-1,1).expand(-1,ln_neg).reshape(-1)
104 | neg_expand = neg.repeat(ln_pos)
105 | diff = neg_expand - pos_expand
106 | Lp = diff[diff>0] # because we're taking positive diffs, we got pos and neg flipped.
107 | ln_Lp = Lp.shape[0]-1
108 | diff_neg = -1.0 * diff[diff<0]
109 | diff_neg = diff_neg.sort()[0]
110 | ln_neg = diff_neg.shape[0]-1
111 | ln_neg = max([ln_neg, 0])
112 | left_wing = int(ln_Lp*delta)
113 | left_wing = max([0,left_wing])
114 | left_wing = min([ln_neg,left_wing])
115 | default_gamma = torch.tensor(0.2, dtype=torch.float).cuda()
116 | if diff_neg.shape[0] > 0 :
117 | gamma = diff_neg[left_wing]
118 | else:
119 | gamma = default_gamma # default=torch.tensor(0.2, dtype=torch.float).cuda() #zoink
120 | L1 = diff[diff>-1.0*gamma]
121 | if epoch > -1 :
122 | return gamma
123 | else :
124 | return default_gamma
125 |
126 |
127 | def roc_star_loss(_y_true, y_pred, gamma, _epoch_true, epoch_pred):
128 | """
129 | Nearly direct loss function for AUC.
130 | See article,
131 | C. Reiss, "Roc-star : An objective function for ROC-AUC that actually works."
132 | https://github.com/iridiumblue/articles/blob/master/roc_star.md
133 | _y_true: `Tensor`. Targets (labels). Float either 0.0 or 1.0 .
134 | y_pred: `Tensor` . Predictions.
135 | gamma : `Float` Gamma, as derived from last epoch.
136 | _epoch_true: `Tensor`. Targets (labels) from last epoch.
137 | epoch_pred : `Tensor`. Predicions from last epoch.
138 | """
139 | #convert labels to boolean
140 | y_true = (_y_true>=0.50)
141 | epoch_true = (_epoch_true>=0.50)
142 |
143 | # if batch is either all true or false return small random stub value.
144 | if torch.sum(y_true)==0 or torch.sum(y_true) == y_true.shape[0]: return torch.sum(y_pred)*1e-8
145 |
146 | pos = y_pred[y_true]
147 | neg = y_pred[~y_true]
148 |
149 | epoch_pos = epoch_pred[epoch_true]
150 | epoch_neg = epoch_pred[~epoch_true]
151 |
152 | # Take random subsamples of the training set, both positive and negative.
153 | max_pos = 1000 # Max number of positive training samples
154 | max_neg = 1000 # Max number of positive training samples
155 | cap_pos = epoch_pos.shape[0]
156 | epoch_pos = epoch_pos[torch.rand_like(epoch_pos) < max_pos/cap_pos]
157 | epoch_neg = epoch_neg[torch.rand_like(epoch_neg) < max_neg/cap_pos]
158 |
159 | ln_pos = pos.shape[0]
160 | ln_neg = neg.shape[0]
161 |
162 | # sum positive batch elements agaionst (subsampled) negative elements
163 | if ln_pos>0 :
164 | pos_expand = pos.view(-1,1).expand(-1,epoch_neg.shape[0]).reshape(-1)
165 | neg_expand = epoch_neg.repeat(ln_pos)
166 |
167 | diff2 = neg_expand - pos_expand + gamma
168 | l2 = diff2[diff2>0]
169 | m2 = l2 * l2
170 | else:
171 | m2 = torch.tensor([0], dtype=torch.float).cuda()
172 |
173 | # Similarly, compare negative batch elements against (subsampled) positive elements
174 | if ln_neg>0 :
175 | pos_expand = epoch_pos.view(-1,1).expand(-1, ln_neg).reshape(-1)
176 | neg_expand = neg.repeat(epoch_pos.shape[0])
177 |
178 | diff3 = neg_expand - pos_expand + gamma
179 | l3 = diff3[diff3>0]
180 | m3 = l3*l3
181 | else:
182 | m3 = torch.tensor([0], dtype=torch.float).cuda()
183 |
184 | if (torch.sum(m2)+torch.sum(m3))!=0 :
185 | res2 = torch.sum(m2)/max_pos+torch.sum(m3)/max_neg
186 | else:
187 | res2 = torch.sum(m2)+torch.sum(m3)
188 |
189 | res2 = torch.where(torch.isnan(res2), torch.zeros_like(res2), res2)
190 |
191 | return res2
192 |
193 |
194 | #https://github.com/keitakurita/Better_LSTM_PyTorch/blob/master/better_lstm/model.py
195 | class VariationalDropout(nn.Module):
196 | """
197 | Applies the same dropout mask across the temporal dimension
198 | See https://arxiv.org/abs/1512.05287 for more details.
199 | Note that this is not applied to the recurrent activations in the LSTM like the above paper.
200 | Instead, it is applied to the inputs and outputs of the recurrent layer.
201 | """
202 | def __init__(self, dropout, batch_first=False):
203 | super().__init__()
204 | self.dropout = dropout
205 | self.batch_first = batch_first
206 |
207 | def forward(self, x: torch.Tensor) -> torch.Tensor:
208 | if not self.training or self.dropout <= 0.:
209 | return x
210 |
211 | is_packed = isinstance(x, PackedSequence)
212 | if is_packed:
213 | x, batch_sizes = x
214 | max_batch_size = int(batch_sizes[0])
215 | else:
216 | batch_sizes = None
217 | max_batch_size = x.size(0)
218 |
219 | # Drop same mask across entire sequence
220 | if self.batch_first:
221 | m = x.new_empty(max_batch_size, 1, x.size(2), requires_grad=False).bernoulli_(1 - self.dropout)
222 | else:
223 | m = x.new_empty(1, max_batch_size, x.size(2), requires_grad=False).bernoulli_(1 - self.dropout)
224 | x = x.masked_fill(m == 0, 0) / (1 - self.dropout)
225 |
226 | if is_packed:
227 | return PackedSequence(x, batch_sizes)
228 | else:
229 | return x
230 |
231 |
232 | #https://github.com/keitakurita/Better_LSTM_PyTorch/blob/master/better_lstm/model.py
233 | class LSTM(nn.LSTM):
234 | def __init__(self, *args, dropouti: float=0.,
235 | dropoutw: float=0., dropouto: float=0.,
236 | batch_first=True, unit_forget_bias=True, **kwargs):
237 | super().__init__(*args, **kwargs, batch_first=batch_first)
238 | self.unit_forget_bias = unit_forget_bias
239 | self.dropoutw = dropoutw
240 | self.input_drop = VariationalDropout(dropouti,
241 | batch_first=batch_first)
242 | self.output_drop = VariationalDropout(dropouto,
243 | batch_first=batch_first)
244 | self._init_weights()
245 |
246 | def _init_weights(self):
247 | """
248 | Use orthogonal init for recurrent layers, xavier uniform for input layers
249 | Bias is 0 except for forget gate
250 | """
251 | for name, param in self.named_parameters():
252 | if "weight_hh" in name:
253 | nn.init.orthogonal_(param.data)
254 | elif "weight_ih" in name:
255 | nn.init.xavier_uniform_(param.data)
256 | elif "bias" in name and self.unit_forget_bias:
257 | nn.init.zeros_(param.data)
258 | param.data[self.hidden_size:2 * self.hidden_size] = 1
259 |
260 | def _drop_weights(self):
261 | for name, param in self.named_parameters():
262 | if "weight_hh" in name:
263 | getattr(self, name).data = \
264 | torch.nn.functional.dropout(param.data, p=self.dropoutw,
265 | training=self.training).contiguous()
266 |
267 | def forward(self, input, hx=None):
268 | self._drop_weights()
269 | input = self.input_drop(input)
270 | seq, state = super().forward(input, hx=hx)
271 | return self.output_drop(seq), state
272 |
273 |
274 |
275 | class NeuralNet(nn.Module):
276 | def __init__(self, embedding_matrix,h_params):
277 | super(NeuralNet, self).__init__()
278 | embed_size = embedding_matrix.shape[1]
279 |
280 | self.embedding = nn.Embedding(max_features, embed_size)
281 | self.embedding.weight = nn.Parameter(torch.tensor(embedding_matrix, dtype=torch.float32))
282 | self.embedding.weight.requires_grad = False
283 | self.h_params = copy(h_params)
284 |
285 | self.c1 = nn.Conv1d(300,kernel_size=2,out_channels=300,padding=1)
286 | LSTM_UNITS=h_params.lstm_units
287 | BIDIR = h_params.bidirectional
288 |
289 | LSTM_OUT = 2* LSTM_UNITS if BIDIR else LSTM_UNITS
290 |
291 | self.lstm1 = LSTM(embed_size, LSTM_UNITS, dropouti=h_params.dropout_i,dropoutw=h_params.dropout_w, dropouto=h_params.dropout_o,bidirectional=BIDIR, batch_first=True)
292 | self.lstm2 = LSTM(LSTM_OUT, LSTM_UNITS, dropouti=h_params.dropout_i,dropoutw=h_params.dropout_w, dropouto=h_params.dropout_o,bidirectional=BIDIR, batch_first=True)
293 |
294 |
295 | self.linear1 = nn.Linear(2*LSTM_OUT, 2*LSTM_OUT)
296 | self.linear2 = nn.Linear(2*LSTM_OUT, 2*LSTM_OUT)
297 |
298 | self.hey_norm = nn.LayerNorm(2*LSTM_OUT)
299 |
300 | self.linear_out = nn.Linear(2*LSTM_OUT, h_params.dense_hidden_units)
301 | self.linear_xtra = nn.Linear(h_params.dense_hidden_units,int(h_params.dense_hidden_units/2))
302 | self.linear_xtra2 = nn.Linear(int(h_params.dense_hidden_units/2),int(h_params.dense_hidden_units/4))
303 | self.linear_out2= nn.Linear(int(h_params.dense_hidden_units/4), 1)
304 |
305 |
306 |
307 | def forward(self, x):
308 | h_embedding = self.embedding(x)
309 | h1 = h_embedding.permute(0, 2, 1)
310 |
311 | q1 = self.c1(h1)
312 | f1 = q1.permute(0, 2, 1)
313 | h_lstm1, _ = self.lstm1(f1)
314 | h_lstm2, _ = self.lstm2(h_lstm1)
315 |
316 | # global average pooling
317 | avg_pool = torch.mean(h_lstm2, 1)
318 | # global max pooling
319 | max_pool, _ = torch.max(h_lstm2, 1)
320 |
321 | h_conc = torch.cat((max_pool, avg_pool), 1)
322 |
323 | h_conc_linear1 = self.linear1(h_conc)
324 | h_conc_linear2 = self.linear2(h_conc)
325 |
326 | hidden = h_conc + h_conc_linear1 + h_conc_linear2
327 | hidden = F.selu(self.linear_out(hidden))
328 | hidden = F.selu(self.linear_xtra(hidden))
329 | hidden = F.selu(self.linear_xtra2(hidden))
330 | hidden = F.sigmoid(self.linear_out2(hidden))
331 |
332 | result=hidden.flatten()
333 |
334 | return result
335 |
336 |
337 |
338 | def train_model(h_params, model, x_train, x_valid, y_train, y_valid, lr,
339 | batch_size=1000, n_epochs=20, title='', graph=''):
340 | global best_result
341 | param_lrs = [{'params': param, 'lr': lr} for param in model.parameters()]
342 | optimizer = torch.optim.AdamW(param_lrs, lr=h_params.initial_lr,
343 | betas=(0.9, 0.999),
344 | eps=1e-6,
345 | amsgrad=False
346 | )
347 |
348 | train_loader = torch.utils.data.DataLoader(torch.utils.data.TensorDataset(x_train, y_train), batch_size=batch_size, shuffle=True)
349 | valid_loader = torch.utils.data.DataLoader(torch.utils.data.TensorDataset(x_valid, y_valid), batch_size=batch_size, shuffle=False)
350 |
351 | num_batches = len(x_train)/batch_size
352 | print(len(x_train))
353 | results=[]
354 |
355 | for epoch in range(n_epochs):
356 | start_time = time.time()
357 | model.train()
358 | avg_loss = 0.
359 |
360 |
361 | progbar =Progbar(num_batches, stateful_metrics=['train-auc'])
362 |
363 | whole_y_pred=np.array([])
364 | whole_y_t=np.array([])
365 |
366 | for i,data in enumerate(train_loader):
367 | x_batch = data[:-1][0]
368 | y_batch = data[-1]
369 |
370 | y_pred = model(x_batch)
371 |
372 | if h_params.use_roc_star and epoch>0 :
373 |
374 | if i==0 : print('*Using Loss Roc-star')
375 | loss = roc_star_loss(y_batch,y_pred,epoch_gamma, last_whole_y_t, last_whole_y_pred)
376 |
377 | else:
378 | if i==0 : print('*Using Loss BxE')
379 | loss = F.binary_cross_entropy(y_pred, 1.0*y_batch)
380 |
381 | logger.report_scalar(title="Loss", series="trains loss",
382 | value=loss, iteration=epoch * len(x_train) + i)
383 |
384 | optimizer.zero_grad()
385 | loss.backward()
386 | # To prevent gradient explosions resulting in NaNs
387 | # https://discuss.pytorch.org/t/nan-loss-in-rnn-model/655/8
388 | # https://github.com/pytorch/examples/blob/master/word_language_model/main.py
389 | torch.nn.utils.clip_grad_norm_(model.parameters(), 0.5)
390 |
391 | optimizer.step()
392 |
393 | whole_y_pred = np.append(whole_y_pred, y_pred.clone().detach().cpu().numpy())
394 | whole_y_t = np.append(whole_y_t, y_batch.clone().detach().cpu().numpy())
395 |
396 | if i>0:
397 | if i%50==1 :
398 | try:
399 | train_roc_val = roc_auc_score(whole_y_t>=0.5, whole_y_pred)
400 | except:
401 |
402 | train_roc_val=-1
403 |
404 | progbar.update(
405 | i,
406 | values=[
407 | ("loss", np.mean(loss.detach().cpu().numpy())),
408 | ("train-auc", train_roc_val)
409 | ]
410 | )
411 |
412 | model.eval()
413 | last_whole_y_t = torch.tensor(whole_y_t).cuda()
414 | last_whole_y_pred = torch.tensor(whole_y_pred).cuda()
415 |
416 | all_valid_preds = np.array([])
417 | all_valid_t = np.array([])
418 | for i, valid_data in enumerate(valid_loader):
419 | x_batch = valid_data[:-1]
420 | y_batch = valid_data[-1]
421 |
422 | y_pred = model(*x_batch).detach().cpu().numpy()
423 | y_t = y_batch.detach().cpu().numpy()
424 |
425 | all_valid_preds=np.concatenate([all_valid_preds,y_pred],axis=0)
426 | all_valid_t = np.concatenate([all_valid_t,y_t],axis=0)
427 |
428 | epoch_gamma = epoch_update_gamma(last_whole_y_t, last_whole_y_pred, epoch,h_params.delta)
429 |
430 | try:
431 | valid_auc = roc_auc_score(all_valid_t>=0.5, all_valid_preds)
432 | except:
433 | valid_auc=-1
434 |
435 | try:
436 | train_roc_val = roc_auc_score(whole_y_t>=0.5, whole_y_pred)
437 | except:
438 | train_roc_val=-1
439 |
440 | elapsed_time = time.time() - start_time
441 | if epoch==0 :
442 | print("\n\n* * * * * * * * * * * Params :", title," :: ", graph)
443 | print('\nEpoch {}/{} \t loss={:.4f} \t time={:.2f}s'.format(
444 | epoch + 1, n_epochs, avg_loss, elapsed_time))
445 |
446 | print("Gamma = ", epoch_gamma)
447 | print("Validation AUC = ", valid_auc)
448 | if not ('auc' in best_result) or best_result['auc']0] # because we're taking positive diffs, we got pos and neg flipped.
24 | ln_Lp = Lp.shape[0]-1
25 | diff_neg = -1.0 * diff[diff<0]
26 | diff_neg = diff_neg.sort()[0]
27 | ln_neg = diff_neg.shape[0]-1
28 | ln_neg = max([ln_neg, 0])
29 | left_wing = int(ln_Lp*DELTA)
30 | left_wing = max([0,left_wing])
31 | left_wing = min([ln_neg,left_wing])
32 | default_gamma=torch.tensor(0.2, dtype=torch.float).cuda()
33 | if diff_neg.shape[0] > 0 :
34 | gamma = diff_neg[left_wing]
35 | else:
36 | gamma = default_gamma # default=torch.tensor(0.2, dtype=torch.float).cuda() #zoink
37 | L1 = diff[diff>-1.0*gamma]
38 | ln_L1 = L1.shape[0]
39 | if epoch > -1 :
40 | return gamma
41 | else :
42 | return default_gamma
43 |
44 |
45 |
46 | def roc_star_loss( _y_true, y_pred, gamma, _epoch_true, epoch_pred):
47 | """
48 | Nearly direct loss function for AUC.
49 | See article,
50 | C. Reiss, "Roc-star : An objective function for ROC-AUC that actually works."
51 | https://github.com/iridiumblue/articles/blob/master/roc_star.md
52 | _y_true: `Tensor`. Targets (labels). Float either 0.0 or 1.0 .
53 | y_pred: `Tensor` . Predictions.
54 | gamma : `Float` Gamma, as derived from last epoch.
55 | _epoch_true: `Tensor`. Targets (labels) from last epoch.
56 | epoch_pred : `Tensor`. Predicions from last epoch.
57 | """
58 | #convert labels to boolean
59 | y_true = (_y_true>=0.50)
60 | epoch_true = (_epoch_true>=0.50)
61 |
62 | # if batch is either all true or false return small random stub value.
63 | if torch.sum(y_true)==0 or torch.sum(y_true) == y_true.shape[0]: return torch.sum(y_pred)*1e-8
64 |
65 | pos = y_pred[y_true]
66 | neg = y_pred[~y_true]
67 |
68 | epoch_pos = epoch_pred[epoch_true]
69 | epoch_neg = epoch_pred[~epoch_true]
70 |
71 | # Take random subsamples of the training set, both positive and negative.
72 | max_pos = 1000 # Max number of positive training samples
73 | max_neg = 1000 # Max number of positive training samples
74 | cap_pos = epoch_pos.shape[0]
75 | cap_neg = epoch_neg.shape[0]
76 | epoch_pos = epoch_pos[torch.rand_like(epoch_pos) < max_pos/cap_pos]
77 | epoch_neg = epoch_neg[torch.rand_like(epoch_neg) < max_neg/cap_pos]
78 |
79 | ln_pos = pos.shape[0]
80 | ln_neg = neg.shape[0]
81 |
82 | # sum positive batch elements agaionst (subsampled) negative elements
83 | if ln_pos>0 :
84 | pos_expand = pos.view(-1,1).expand(-1,epoch_neg.shape[0]).reshape(-1)
85 | neg_expand = epoch_neg.repeat(ln_pos)
86 |
87 | diff2 = neg_expand - pos_expand + gamma
88 | l2 = diff2[diff2>0]
89 | m2 = l2 * l2
90 | len2 = l2.shape[0]
91 | else:
92 | m2 = torch.tensor([0], dtype=torch.float).cuda()
93 | len2 = 0
94 |
95 | # Similarly, compare negative batch elements against (subsampled) positive elements
96 | if ln_neg>0 :
97 | pos_expand = epoch_pos.view(-1,1).expand(-1, ln_neg).reshape(-1)
98 | neg_expand = neg.repeat(epoch_pos.shape[0])
99 |
100 | diff3 = neg_expand - pos_expand + gamma
101 | l3 = diff3[diff3>0]
102 | m3 = l3*l3
103 | len3 = l3.shape[0]
104 | else:
105 | m3 = torch.tensor([0], dtype=torch.float).cuda()
106 | len3=0
107 |
108 | if (torch.sum(m2)+torch.sum(m3))!=0 :
109 | res2 = torch.sum(m2)/max_pos+torch.sum(m3)/max_neg
110 | #code.interact(local=dict(globals(), **locals()))
111 | else:
112 | res2 = torch.sum(m2)+torch.sum(m3)
113 |
114 | res2 = torch.where(torch.isnan(res2), torch.zeros_like(res2), res2)
115 |
116 | return res2
--------------------------------------------------------------------------------
 306 |
307 |
308 |
--------------------------------------------------------------------------------
/example.py:
--------------------------------------------------------------------------------
1 | '''
2 | A demonstration of a new and experimental loss function which directly targets AUC/ROC,
3 | and is seen to outperform BxE in early testing. See paper up here -
4 | https://github.com/iridiumblue/roc-star.
5 |
6 | The test is a simple sentiment analysis binary classifier turned loose on tweets from Twitter.
7 | Text embeddings have been precomputed and pickled for speed.
8 | TRUNC truncates the training set, set it to -1 for all 1.6 M sample tweets.
9 |
10 | Note that for the first epoch (only), the loss function is BxE. That is just to kickstart
11 | the new loss function roc_star_loss. That's a good practice to stick to if you want
12 | to give this a try for your model. Note also that roc_star_loss requires a call to
13 | epoch_update_gamma at the end of each epoch.
14 | '''
15 |
16 |
17 | from warnings import simplefilter
18 | import time
19 | from copy import copy
20 | import torch
21 | import torch.nn.functional as F
22 | import torch.nn as nn
23 | from torch.nn.utils.rnn import PackedSequence
24 | import numpy as np
25 | import _pickle
26 | import gc
27 | from pathlib2 import Path
28 | from sklearn.metrics import roc_auc_score
29 | from trains import Task
30 | from trains import StorageManager
31 | from pkbar import Kbar as Progbar
32 | import argparse
33 | import os
34 | from tempfile import gettempdir
35 |
36 |
37 | # ignore all future warnings
38 | simplefilter(action='ignore', category=FutureWarning)
39 | simplefilter(action='ignore', category=UserWarning)
40 |
41 | x_train_torch,x_valid_torch,y_train_torch,y_valid_torch = None,None,None,None
42 | embedding_matrix = None
43 | task=None
44 | logger=None
45 | best_result={}
46 | max_features = 200000
47 | embed_size = 300
48 |
49 |
50 | def init(h_params):
51 | global x_train_torch, x_valid_torch, y_train_torch, y_valid_torch
52 | global embedding_matrix
53 | global task, logger
54 |
55 | print("Recovering tokenized text from pickle ...")
56 | tokenized = StorageManager.get_local_copy(
57 | remote_url="https://allegro-datasets.s3.amazonaws.com/roc_star_data"
58 | "/tokenized.pkl.zip",
59 | name="tokenized",
60 | )
61 | embedding = StorageManager.get_local_copy(
62 | remote_url="https://allegro-datasets.s3.amazonaws.com/roc_star_data"
63 | "/embedding.pkl.zip",
64 | name="embedding",
65 | )
66 |
67 | x_train, x_valid, y_train, y_valid = _pickle.load(open(Path(tokenized, "tokenized.pkl"), "rb"))
68 | print("Reusing pickled embedding ...")
69 | embedding_matrix = _pickle.load(open(Path(embedding, "embedding.pkl"), "rb"))
70 |
71 | print("Moving data to GPU ...")
72 | if h_params.trunc>-1 :
73 | print(f"\r\r * * WARNING training set truncated to first {h_params.trunc} items.\r\r")
74 |
75 | x_train_torch = torch.tensor(x_train[:h_params.trunc], dtype=torch.long).cuda()
76 | x_valid_torch = torch.tensor(x_valid, dtype=torch.long).cuda()
77 | y_train_torch = torch.tensor(y_train[:h_params.trunc], dtype=torch.float32).cuda()
78 | y_valid_torch = torch.tensor(y_valid, dtype=torch.float32).cuda()
79 | del x_train, y_train, x_valid, y_valid; gc.collect(2)
80 |
81 | task_name = "ROC" if h_params.use_roc_star else "BxE"
82 | task = Task.init(project_name='Roc-star Loss', task_name='Roc star')
83 | logger = task.get_logger()
84 |
85 |
86 | def epoch_update_gamma(y_true, y_pred, epoch=-1, delta=2):
87 | """
88 | Calculate gamma from last epoch's targets and predictions.
89 | Gamma is updated at the end of each epoch.
90 | y_true: `Tensor`. Targets (labels). Float either 0.0 or 1.0 .
91 | y_pred: `Tensor` . Predictions.
92 | """
93 | sub_sample_size = 2000.0
94 | pos = y_pred[y_true==1]
95 | neg = y_pred[y_true==0] # yo pytorch, no boolean tensors or operators? Wassap?
96 | # subsample the training set for performance
97 | cap_pos = pos.shape[0]
98 | cap_neg = neg.shape[0]
99 | pos = pos[torch.rand_like(pos) < sub_sample_size/cap_pos]
100 | neg = neg[torch.rand_like(neg) < sub_sample_size/cap_neg]
101 | ln_pos = pos.shape[0]
102 | ln_neg = neg.shape[0]
103 | pos_expand = pos.view(-1,1).expand(-1,ln_neg).reshape(-1)
104 | neg_expand = neg.repeat(ln_pos)
105 | diff = neg_expand - pos_expand
106 | Lp = diff[diff>0] # because we're taking positive diffs, we got pos and neg flipped.
107 | ln_Lp = Lp.shape[0]-1
108 | diff_neg = -1.0 * diff[diff<0]
109 | diff_neg = diff_neg.sort()[0]
110 | ln_neg = diff_neg.shape[0]-1
111 | ln_neg = max([ln_neg, 0])
112 | left_wing = int(ln_Lp*delta)
113 | left_wing = max([0,left_wing])
114 | left_wing = min([ln_neg,left_wing])
115 | default_gamma = torch.tensor(0.2, dtype=torch.float).cuda()
116 | if diff_neg.shape[0] > 0 :
117 | gamma = diff_neg[left_wing]
118 | else:
119 | gamma = default_gamma # default=torch.tensor(0.2, dtype=torch.float).cuda() #zoink
120 | L1 = diff[diff>-1.0*gamma]
121 | if epoch > -1 :
122 | return gamma
123 | else :
124 | return default_gamma
125 |
126 |
127 | def roc_star_loss(_y_true, y_pred, gamma, _epoch_true, epoch_pred):
128 | """
129 | Nearly direct loss function for AUC.
130 | See article,
131 | C. Reiss, "Roc-star : An objective function for ROC-AUC that actually works."
132 | https://github.com/iridiumblue/articles/blob/master/roc_star.md
133 | _y_true: `Tensor`. Targets (labels). Float either 0.0 or 1.0 .
134 | y_pred: `Tensor` . Predictions.
135 | gamma : `Float` Gamma, as derived from last epoch.
136 | _epoch_true: `Tensor`. Targets (labels) from last epoch.
137 | epoch_pred : `Tensor`. Predicions from last epoch.
138 | """
139 | #convert labels to boolean
140 | y_true = (_y_true>=0.50)
141 | epoch_true = (_epoch_true>=0.50)
142 |
143 | # if batch is either all true or false return small random stub value.
144 | if torch.sum(y_true)==0 or torch.sum(y_true) == y_true.shape[0]: return torch.sum(y_pred)*1e-8
145 |
146 | pos = y_pred[y_true]
147 | neg = y_pred[~y_true]
148 |
149 | epoch_pos = epoch_pred[epoch_true]
150 | epoch_neg = epoch_pred[~epoch_true]
151 |
152 | # Take random subsamples of the training set, both positive and negative.
153 | max_pos = 1000 # Max number of positive training samples
154 | max_neg = 1000 # Max number of positive training samples
155 | cap_pos = epoch_pos.shape[0]
156 | epoch_pos = epoch_pos[torch.rand_like(epoch_pos) < max_pos/cap_pos]
157 | epoch_neg = epoch_neg[torch.rand_like(epoch_neg) < max_neg/cap_pos]
158 |
159 | ln_pos = pos.shape[0]
160 | ln_neg = neg.shape[0]
161 |
162 | # sum positive batch elements agaionst (subsampled) negative elements
163 | if ln_pos>0 :
164 | pos_expand = pos.view(-1,1).expand(-1,epoch_neg.shape[0]).reshape(-1)
165 | neg_expand = epoch_neg.repeat(ln_pos)
166 |
167 | diff2 = neg_expand - pos_expand + gamma
168 | l2 = diff2[diff2>0]
169 | m2 = l2 * l2
170 | else:
171 | m2 = torch.tensor([0], dtype=torch.float).cuda()
172 |
173 | # Similarly, compare negative batch elements against (subsampled) positive elements
174 | if ln_neg>0 :
175 | pos_expand = epoch_pos.view(-1,1).expand(-1, ln_neg).reshape(-1)
176 | neg_expand = neg.repeat(epoch_pos.shape[0])
177 |
178 | diff3 = neg_expand - pos_expand + gamma
179 | l3 = diff3[diff3>0]
180 | m3 = l3*l3
181 | else:
182 | m3 = torch.tensor([0], dtype=torch.float).cuda()
183 |
184 | if (torch.sum(m2)+torch.sum(m3))!=0 :
185 | res2 = torch.sum(m2)/max_pos+torch.sum(m3)/max_neg
186 | else:
187 | res2 = torch.sum(m2)+torch.sum(m3)
188 |
189 | res2 = torch.where(torch.isnan(res2), torch.zeros_like(res2), res2)
190 |
191 | return res2
192 |
193 |
194 | #https://github.com/keitakurita/Better_LSTM_PyTorch/blob/master/better_lstm/model.py
195 | class VariationalDropout(nn.Module):
196 | """
197 | Applies the same dropout mask across the temporal dimension
198 | See https://arxiv.org/abs/1512.05287 for more details.
199 | Note that this is not applied to the recurrent activations in the LSTM like the above paper.
200 | Instead, it is applied to the inputs and outputs of the recurrent layer.
201 | """
202 | def __init__(self, dropout, batch_first=False):
203 | super().__init__()
204 | self.dropout = dropout
205 | self.batch_first = batch_first
206 |
207 | def forward(self, x: torch.Tensor) -> torch.Tensor:
208 | if not self.training or self.dropout <= 0.:
209 | return x
210 |
211 | is_packed = isinstance(x, PackedSequence)
212 | if is_packed:
213 | x, batch_sizes = x
214 | max_batch_size = int(batch_sizes[0])
215 | else:
216 | batch_sizes = None
217 | max_batch_size = x.size(0)
218 |
219 | # Drop same mask across entire sequence
220 | if self.batch_first:
221 | m = x.new_empty(max_batch_size, 1, x.size(2), requires_grad=False).bernoulli_(1 - self.dropout)
222 | else:
223 | m = x.new_empty(1, max_batch_size, x.size(2), requires_grad=False).bernoulli_(1 - self.dropout)
224 | x = x.masked_fill(m == 0, 0) / (1 - self.dropout)
225 |
226 | if is_packed:
227 | return PackedSequence(x, batch_sizes)
228 | else:
229 | return x
230 |
231 |
232 | #https://github.com/keitakurita/Better_LSTM_PyTorch/blob/master/better_lstm/model.py
233 | class LSTM(nn.LSTM):
234 | def __init__(self, *args, dropouti: float=0.,
235 | dropoutw: float=0., dropouto: float=0.,
236 | batch_first=True, unit_forget_bias=True, **kwargs):
237 | super().__init__(*args, **kwargs, batch_first=batch_first)
238 | self.unit_forget_bias = unit_forget_bias
239 | self.dropoutw = dropoutw
240 | self.input_drop = VariationalDropout(dropouti,
241 | batch_first=batch_first)
242 | self.output_drop = VariationalDropout(dropouto,
243 | batch_first=batch_first)
244 | self._init_weights()
245 |
246 | def _init_weights(self):
247 | """
248 | Use orthogonal init for recurrent layers, xavier uniform for input layers
249 | Bias is 0 except for forget gate
250 | """
251 | for name, param in self.named_parameters():
252 | if "weight_hh" in name:
253 | nn.init.orthogonal_(param.data)
254 | elif "weight_ih" in name:
255 | nn.init.xavier_uniform_(param.data)
256 | elif "bias" in name and self.unit_forget_bias:
257 | nn.init.zeros_(param.data)
258 | param.data[self.hidden_size:2 * self.hidden_size] = 1
259 |
260 | def _drop_weights(self):
261 | for name, param in self.named_parameters():
262 | if "weight_hh" in name:
263 | getattr(self, name).data = \
264 | torch.nn.functional.dropout(param.data, p=self.dropoutw,
265 | training=self.training).contiguous()
266 |
267 | def forward(self, input, hx=None):
268 | self._drop_weights()
269 | input = self.input_drop(input)
270 | seq, state = super().forward(input, hx=hx)
271 | return self.output_drop(seq), state
272 |
273 |
274 |
275 | class NeuralNet(nn.Module):
276 | def __init__(self, embedding_matrix,h_params):
277 | super(NeuralNet, self).__init__()
278 | embed_size = embedding_matrix.shape[1]
279 |
280 | self.embedding = nn.Embedding(max_features, embed_size)
281 | self.embedding.weight = nn.Parameter(torch.tensor(embedding_matrix, dtype=torch.float32))
282 | self.embedding.weight.requires_grad = False
283 | self.h_params = copy(h_params)
284 |
285 | self.c1 = nn.Conv1d(300,kernel_size=2,out_channels=300,padding=1)
286 | LSTM_UNITS=h_params.lstm_units
287 | BIDIR = h_params.bidirectional
288 |
289 | LSTM_OUT = 2* LSTM_UNITS if BIDIR else LSTM_UNITS
290 |
291 | self.lstm1 = LSTM(embed_size, LSTM_UNITS, dropouti=h_params.dropout_i,dropoutw=h_params.dropout_w, dropouto=h_params.dropout_o,bidirectional=BIDIR, batch_first=True)
292 | self.lstm2 = LSTM(LSTM_OUT, LSTM_UNITS, dropouti=h_params.dropout_i,dropoutw=h_params.dropout_w, dropouto=h_params.dropout_o,bidirectional=BIDIR, batch_first=True)
293 |
294 |
295 | self.linear1 = nn.Linear(2*LSTM_OUT, 2*LSTM_OUT)
296 | self.linear2 = nn.Linear(2*LSTM_OUT, 2*LSTM_OUT)
297 |
298 | self.hey_norm = nn.LayerNorm(2*LSTM_OUT)
299 |
300 | self.linear_out = nn.Linear(2*LSTM_OUT, h_params.dense_hidden_units)
301 | self.linear_xtra = nn.Linear(h_params.dense_hidden_units,int(h_params.dense_hidden_units/2))
302 | self.linear_xtra2 = nn.Linear(int(h_params.dense_hidden_units/2),int(h_params.dense_hidden_units/4))
303 | self.linear_out2= nn.Linear(int(h_params.dense_hidden_units/4), 1)
304 |
305 |
306 |
307 | def forward(self, x):
308 | h_embedding = self.embedding(x)
309 | h1 = h_embedding.permute(0, 2, 1)
310 |
311 | q1 = self.c1(h1)
312 | f1 = q1.permute(0, 2, 1)
313 | h_lstm1, _ = self.lstm1(f1)
314 | h_lstm2, _ = self.lstm2(h_lstm1)
315 |
316 | # global average pooling
317 | avg_pool = torch.mean(h_lstm2, 1)
318 | # global max pooling
319 | max_pool, _ = torch.max(h_lstm2, 1)
320 |
321 | h_conc = torch.cat((max_pool, avg_pool), 1)
322 |
323 | h_conc_linear1 = self.linear1(h_conc)
324 | h_conc_linear2 = self.linear2(h_conc)
325 |
326 | hidden = h_conc + h_conc_linear1 + h_conc_linear2
327 | hidden = F.selu(self.linear_out(hidden))
328 | hidden = F.selu(self.linear_xtra(hidden))
329 | hidden = F.selu(self.linear_xtra2(hidden))
330 | hidden = F.sigmoid(self.linear_out2(hidden))
331 |
332 | result=hidden.flatten()
333 |
334 | return result
335 |
336 |
337 |
338 | def train_model(h_params, model, x_train, x_valid, y_train, y_valid, lr,
339 | batch_size=1000, n_epochs=20, title='', graph=''):
340 | global best_result
341 | param_lrs = [{'params': param, 'lr': lr} for param in model.parameters()]
342 | optimizer = torch.optim.AdamW(param_lrs, lr=h_params.initial_lr,
343 | betas=(0.9, 0.999),
344 | eps=1e-6,
345 | amsgrad=False
346 | )
347 |
348 | train_loader = torch.utils.data.DataLoader(torch.utils.data.TensorDataset(x_train, y_train), batch_size=batch_size, shuffle=True)
349 | valid_loader = torch.utils.data.DataLoader(torch.utils.data.TensorDataset(x_valid, y_valid), batch_size=batch_size, shuffle=False)
350 |
351 | num_batches = len(x_train)/batch_size
352 | print(len(x_train))
353 | results=[]
354 |
355 | for epoch in range(n_epochs):
356 | start_time = time.time()
357 | model.train()
358 | avg_loss = 0.
359 |
360 |
361 | progbar =Progbar(num_batches, stateful_metrics=['train-auc'])
362 |
363 | whole_y_pred=np.array([])
364 | whole_y_t=np.array([])
365 |
366 | for i,data in enumerate(train_loader):
367 | x_batch = data[:-1][0]
368 | y_batch = data[-1]
369 |
370 | y_pred = model(x_batch)
371 |
372 | if h_params.use_roc_star and epoch>0 :
373 |
374 | if i==0 : print('*Using Loss Roc-star')
375 | loss = roc_star_loss(y_batch,y_pred,epoch_gamma, last_whole_y_t, last_whole_y_pred)
376 |
377 | else:
378 | if i==0 : print('*Using Loss BxE')
379 | loss = F.binary_cross_entropy(y_pred, 1.0*y_batch)
380 |
381 | logger.report_scalar(title="Loss", series="trains loss",
382 | value=loss, iteration=epoch * len(x_train) + i)
383 |
384 | optimizer.zero_grad()
385 | loss.backward()
386 | # To prevent gradient explosions resulting in NaNs
387 | # https://discuss.pytorch.org/t/nan-loss-in-rnn-model/655/8
388 | # https://github.com/pytorch/examples/blob/master/word_language_model/main.py
389 | torch.nn.utils.clip_grad_norm_(model.parameters(), 0.5)
390 |
391 | optimizer.step()
392 |
393 | whole_y_pred = np.append(whole_y_pred, y_pred.clone().detach().cpu().numpy())
394 | whole_y_t = np.append(whole_y_t, y_batch.clone().detach().cpu().numpy())
395 |
396 | if i>0:
397 | if i%50==1 :
398 | try:
399 | train_roc_val = roc_auc_score(whole_y_t>=0.5, whole_y_pred)
400 | except:
401 |
402 | train_roc_val=-1
403 |
404 | progbar.update(
405 | i,
406 | values=[
407 | ("loss", np.mean(loss.detach().cpu().numpy())),
408 | ("train-auc", train_roc_val)
409 | ]
410 | )
411 |
412 | model.eval()
413 | last_whole_y_t = torch.tensor(whole_y_t).cuda()
414 | last_whole_y_pred = torch.tensor(whole_y_pred).cuda()
415 |
416 | all_valid_preds = np.array([])
417 | all_valid_t = np.array([])
418 | for i, valid_data in enumerate(valid_loader):
419 | x_batch = valid_data[:-1]
420 | y_batch = valid_data[-1]
421 |
422 | y_pred = model(*x_batch).detach().cpu().numpy()
423 | y_t = y_batch.detach().cpu().numpy()
424 |
425 | all_valid_preds=np.concatenate([all_valid_preds,y_pred],axis=0)
426 | all_valid_t = np.concatenate([all_valid_t,y_t],axis=0)
427 |
428 | epoch_gamma = epoch_update_gamma(last_whole_y_t, last_whole_y_pred, epoch,h_params.delta)
429 |
430 | try:
431 | valid_auc = roc_auc_score(all_valid_t>=0.5, all_valid_preds)
432 | except:
433 | valid_auc=-1
434 |
435 | try:
436 | train_roc_val = roc_auc_score(whole_y_t>=0.5, whole_y_pred)
437 | except:
438 | train_roc_val=-1
439 |
440 | elapsed_time = time.time() - start_time
441 | if epoch==0 :
442 | print("\n\n* * * * * * * * * * * Params :", title," :: ", graph)
443 | print('\nEpoch {}/{} \t loss={:.4f} \t time={:.2f}s'.format(
444 | epoch + 1, n_epochs, avg_loss, elapsed_time))
445 |
446 | print("Gamma = ", epoch_gamma)
447 | print("Validation AUC = ", valid_auc)
448 | if not ('auc' in best_result) or best_result['auc']
306 |
307 |
308 |
--------------------------------------------------------------------------------
/example.py:
--------------------------------------------------------------------------------
1 | '''
2 | A demonstration of a new and experimental loss function which directly targets AUC/ROC,
3 | and is seen to outperform BxE in early testing. See paper up here -
4 | https://github.com/iridiumblue/roc-star.
5 |
6 | The test is a simple sentiment analysis binary classifier turned loose on tweets from Twitter.
7 | Text embeddings have been precomputed and pickled for speed.
8 | TRUNC truncates the training set, set it to -1 for all 1.6 M sample tweets.
9 |
10 | Note that for the first epoch (only), the loss function is BxE. That is just to kickstart
11 | the new loss function roc_star_loss. That's a good practice to stick to if you want
12 | to give this a try for your model. Note also that roc_star_loss requires a call to
13 | epoch_update_gamma at the end of each epoch.
14 | '''
15 |
16 |
17 | from warnings import simplefilter
18 | import time
19 | from copy import copy
20 | import torch
21 | import torch.nn.functional as F
22 | import torch.nn as nn
23 | from torch.nn.utils.rnn import PackedSequence
24 | import numpy as np
25 | import _pickle
26 | import gc
27 | from pathlib2 import Path
28 | from sklearn.metrics import roc_auc_score
29 | from trains import Task
30 | from trains import StorageManager
31 | from pkbar import Kbar as Progbar
32 | import argparse
33 | import os
34 | from tempfile import gettempdir
35 |
36 |
37 | # ignore all future warnings
38 | simplefilter(action='ignore', category=FutureWarning)
39 | simplefilter(action='ignore', category=UserWarning)
40 |
41 | x_train_torch,x_valid_torch,y_train_torch,y_valid_torch = None,None,None,None
42 | embedding_matrix = None
43 | task=None
44 | logger=None
45 | best_result={}
46 | max_features = 200000
47 | embed_size = 300
48 |
49 |
50 | def init(h_params):
51 | global x_train_torch, x_valid_torch, y_train_torch, y_valid_torch
52 | global embedding_matrix
53 | global task, logger
54 |
55 | print("Recovering tokenized text from pickle ...")
56 | tokenized = StorageManager.get_local_copy(
57 | remote_url="https://allegro-datasets.s3.amazonaws.com/roc_star_data"
58 | "/tokenized.pkl.zip",
59 | name="tokenized",
60 | )
61 | embedding = StorageManager.get_local_copy(
62 | remote_url="https://allegro-datasets.s3.amazonaws.com/roc_star_data"
63 | "/embedding.pkl.zip",
64 | name="embedding",
65 | )
66 |
67 | x_train, x_valid, y_train, y_valid = _pickle.load(open(Path(tokenized, "tokenized.pkl"), "rb"))
68 | print("Reusing pickled embedding ...")
69 | embedding_matrix = _pickle.load(open(Path(embedding, "embedding.pkl"), "rb"))
70 |
71 | print("Moving data to GPU ...")
72 | if h_params.trunc>-1 :
73 | print(f"\r\r * * WARNING training set truncated to first {h_params.trunc} items.\r\r")
74 |
75 | x_train_torch = torch.tensor(x_train[:h_params.trunc], dtype=torch.long).cuda()
76 | x_valid_torch = torch.tensor(x_valid, dtype=torch.long).cuda()
77 | y_train_torch = torch.tensor(y_train[:h_params.trunc], dtype=torch.float32).cuda()
78 | y_valid_torch = torch.tensor(y_valid, dtype=torch.float32).cuda()
79 | del x_train, y_train, x_valid, y_valid; gc.collect(2)
80 |
81 | task_name = "ROC" if h_params.use_roc_star else "BxE"
82 | task = Task.init(project_name='Roc-star Loss', task_name='Roc star')
83 | logger = task.get_logger()
84 |
85 |
86 | def epoch_update_gamma(y_true, y_pred, epoch=-1, delta=2):
87 | """
88 | Calculate gamma from last epoch's targets and predictions.
89 | Gamma is updated at the end of each epoch.
90 | y_true: `Tensor`. Targets (labels). Float either 0.0 or 1.0 .
91 | y_pred: `Tensor` . Predictions.
92 | """
93 | sub_sample_size = 2000.0
94 | pos = y_pred[y_true==1]
95 | neg = y_pred[y_true==0] # yo pytorch, no boolean tensors or operators? Wassap?
96 | # subsample the training set for performance
97 | cap_pos = pos.shape[0]
98 | cap_neg = neg.shape[0]
99 | pos = pos[torch.rand_like(pos) < sub_sample_size/cap_pos]
100 | neg = neg[torch.rand_like(neg) < sub_sample_size/cap_neg]
101 | ln_pos = pos.shape[0]
102 | ln_neg = neg.shape[0]
103 | pos_expand = pos.view(-1,1).expand(-1,ln_neg).reshape(-1)
104 | neg_expand = neg.repeat(ln_pos)
105 | diff = neg_expand - pos_expand
106 | Lp = diff[diff>0] # because we're taking positive diffs, we got pos and neg flipped.
107 | ln_Lp = Lp.shape[0]-1
108 | diff_neg = -1.0 * diff[diff<0]
109 | diff_neg = diff_neg.sort()[0]
110 | ln_neg = diff_neg.shape[0]-1
111 | ln_neg = max([ln_neg, 0])
112 | left_wing = int(ln_Lp*delta)
113 | left_wing = max([0,left_wing])
114 | left_wing = min([ln_neg,left_wing])
115 | default_gamma = torch.tensor(0.2, dtype=torch.float).cuda()
116 | if diff_neg.shape[0] > 0 :
117 | gamma = diff_neg[left_wing]
118 | else:
119 | gamma = default_gamma # default=torch.tensor(0.2, dtype=torch.float).cuda() #zoink
120 | L1 = diff[diff>-1.0*gamma]
121 | if epoch > -1 :
122 | return gamma
123 | else :
124 | return default_gamma
125 |
126 |
127 | def roc_star_loss(_y_true, y_pred, gamma, _epoch_true, epoch_pred):
128 | """
129 | Nearly direct loss function for AUC.
130 | See article,
131 | C. Reiss, "Roc-star : An objective function for ROC-AUC that actually works."
132 | https://github.com/iridiumblue/articles/blob/master/roc_star.md
133 | _y_true: `Tensor`. Targets (labels). Float either 0.0 or 1.0 .
134 | y_pred: `Tensor` . Predictions.
135 | gamma : `Float` Gamma, as derived from last epoch.
136 | _epoch_true: `Tensor`. Targets (labels) from last epoch.
137 | epoch_pred : `Tensor`. Predicions from last epoch.
138 | """
139 | #convert labels to boolean
140 | y_true = (_y_true>=0.50)
141 | epoch_true = (_epoch_true>=0.50)
142 |
143 | # if batch is either all true or false return small random stub value.
144 | if torch.sum(y_true)==0 or torch.sum(y_true) == y_true.shape[0]: return torch.sum(y_pred)*1e-8
145 |
146 | pos = y_pred[y_true]
147 | neg = y_pred[~y_true]
148 |
149 | epoch_pos = epoch_pred[epoch_true]
150 | epoch_neg = epoch_pred[~epoch_true]
151 |
152 | # Take random subsamples of the training set, both positive and negative.
153 | max_pos = 1000 # Max number of positive training samples
154 | max_neg = 1000 # Max number of positive training samples
155 | cap_pos = epoch_pos.shape[0]
156 | epoch_pos = epoch_pos[torch.rand_like(epoch_pos) < max_pos/cap_pos]
157 | epoch_neg = epoch_neg[torch.rand_like(epoch_neg) < max_neg/cap_pos]
158 |
159 | ln_pos = pos.shape[0]
160 | ln_neg = neg.shape[0]
161 |
162 | # sum positive batch elements agaionst (subsampled) negative elements
163 | if ln_pos>0 :
164 | pos_expand = pos.view(-1,1).expand(-1,epoch_neg.shape[0]).reshape(-1)
165 | neg_expand = epoch_neg.repeat(ln_pos)
166 |
167 | diff2 = neg_expand - pos_expand + gamma
168 | l2 = diff2[diff2>0]
169 | m2 = l2 * l2
170 | else:
171 | m2 = torch.tensor([0], dtype=torch.float).cuda()
172 |
173 | # Similarly, compare negative batch elements against (subsampled) positive elements
174 | if ln_neg>0 :
175 | pos_expand = epoch_pos.view(-1,1).expand(-1, ln_neg).reshape(-1)
176 | neg_expand = neg.repeat(epoch_pos.shape[0])
177 |
178 | diff3 = neg_expand - pos_expand + gamma
179 | l3 = diff3[diff3>0]
180 | m3 = l3*l3
181 | else:
182 | m3 = torch.tensor([0], dtype=torch.float).cuda()
183 |
184 | if (torch.sum(m2)+torch.sum(m3))!=0 :
185 | res2 = torch.sum(m2)/max_pos+torch.sum(m3)/max_neg
186 | else:
187 | res2 = torch.sum(m2)+torch.sum(m3)
188 |
189 | res2 = torch.where(torch.isnan(res2), torch.zeros_like(res2), res2)
190 |
191 | return res2
192 |
193 |
194 | #https://github.com/keitakurita/Better_LSTM_PyTorch/blob/master/better_lstm/model.py
195 | class VariationalDropout(nn.Module):
196 | """
197 | Applies the same dropout mask across the temporal dimension
198 | See https://arxiv.org/abs/1512.05287 for more details.
199 | Note that this is not applied to the recurrent activations in the LSTM like the above paper.
200 | Instead, it is applied to the inputs and outputs of the recurrent layer.
201 | """
202 | def __init__(self, dropout, batch_first=False):
203 | super().__init__()
204 | self.dropout = dropout
205 | self.batch_first = batch_first
206 |
207 | def forward(self, x: torch.Tensor) -> torch.Tensor:
208 | if not self.training or self.dropout <= 0.:
209 | return x
210 |
211 | is_packed = isinstance(x, PackedSequence)
212 | if is_packed:
213 | x, batch_sizes = x
214 | max_batch_size = int(batch_sizes[0])
215 | else:
216 | batch_sizes = None
217 | max_batch_size = x.size(0)
218 |
219 | # Drop same mask across entire sequence
220 | if self.batch_first:
221 | m = x.new_empty(max_batch_size, 1, x.size(2), requires_grad=False).bernoulli_(1 - self.dropout)
222 | else:
223 | m = x.new_empty(1, max_batch_size, x.size(2), requires_grad=False).bernoulli_(1 - self.dropout)
224 | x = x.masked_fill(m == 0, 0) / (1 - self.dropout)
225 |
226 | if is_packed:
227 | return PackedSequence(x, batch_sizes)
228 | else:
229 | return x
230 |
231 |
232 | #https://github.com/keitakurita/Better_LSTM_PyTorch/blob/master/better_lstm/model.py
233 | class LSTM(nn.LSTM):
234 | def __init__(self, *args, dropouti: float=0.,
235 | dropoutw: float=0., dropouto: float=0.,
236 | batch_first=True, unit_forget_bias=True, **kwargs):
237 | super().__init__(*args, **kwargs, batch_first=batch_first)
238 | self.unit_forget_bias = unit_forget_bias
239 | self.dropoutw = dropoutw
240 | self.input_drop = VariationalDropout(dropouti,
241 | batch_first=batch_first)
242 | self.output_drop = VariationalDropout(dropouto,
243 | batch_first=batch_first)
244 | self._init_weights()
245 |
246 | def _init_weights(self):
247 | """
248 | Use orthogonal init for recurrent layers, xavier uniform for input layers
249 | Bias is 0 except for forget gate
250 | """
251 | for name, param in self.named_parameters():
252 | if "weight_hh" in name:
253 | nn.init.orthogonal_(param.data)
254 | elif "weight_ih" in name:
255 | nn.init.xavier_uniform_(param.data)
256 | elif "bias" in name and self.unit_forget_bias:
257 | nn.init.zeros_(param.data)
258 | param.data[self.hidden_size:2 * self.hidden_size] = 1
259 |
260 | def _drop_weights(self):
261 | for name, param in self.named_parameters():
262 | if "weight_hh" in name:
263 | getattr(self, name).data = \
264 | torch.nn.functional.dropout(param.data, p=self.dropoutw,
265 | training=self.training).contiguous()
266 |
267 | def forward(self, input, hx=None):
268 | self._drop_weights()
269 | input = self.input_drop(input)
270 | seq, state = super().forward(input, hx=hx)
271 | return self.output_drop(seq), state
272 |
273 |
274 |
275 | class NeuralNet(nn.Module):
276 | def __init__(self, embedding_matrix,h_params):
277 | super(NeuralNet, self).__init__()
278 | embed_size = embedding_matrix.shape[1]
279 |
280 | self.embedding = nn.Embedding(max_features, embed_size)
281 | self.embedding.weight = nn.Parameter(torch.tensor(embedding_matrix, dtype=torch.float32))
282 | self.embedding.weight.requires_grad = False
283 | self.h_params = copy(h_params)
284 |
285 | self.c1 = nn.Conv1d(300,kernel_size=2,out_channels=300,padding=1)
286 | LSTM_UNITS=h_params.lstm_units
287 | BIDIR = h_params.bidirectional
288 |
289 | LSTM_OUT = 2* LSTM_UNITS if BIDIR else LSTM_UNITS
290 |
291 | self.lstm1 = LSTM(embed_size, LSTM_UNITS, dropouti=h_params.dropout_i,dropoutw=h_params.dropout_w, dropouto=h_params.dropout_o,bidirectional=BIDIR, batch_first=True)
292 | self.lstm2 = LSTM(LSTM_OUT, LSTM_UNITS, dropouti=h_params.dropout_i,dropoutw=h_params.dropout_w, dropouto=h_params.dropout_o,bidirectional=BIDIR, batch_first=True)
293 |
294 |
295 | self.linear1 = nn.Linear(2*LSTM_OUT, 2*LSTM_OUT)
296 | self.linear2 = nn.Linear(2*LSTM_OUT, 2*LSTM_OUT)
297 |
298 | self.hey_norm = nn.LayerNorm(2*LSTM_OUT)
299 |
300 | self.linear_out = nn.Linear(2*LSTM_OUT, h_params.dense_hidden_units)
301 | self.linear_xtra = nn.Linear(h_params.dense_hidden_units,int(h_params.dense_hidden_units/2))
302 | self.linear_xtra2 = nn.Linear(int(h_params.dense_hidden_units/2),int(h_params.dense_hidden_units/4))
303 | self.linear_out2= nn.Linear(int(h_params.dense_hidden_units/4), 1)
304 |
305 |
306 |
307 | def forward(self, x):
308 | h_embedding = self.embedding(x)
309 | h1 = h_embedding.permute(0, 2, 1)
310 |
311 | q1 = self.c1(h1)
312 | f1 = q1.permute(0, 2, 1)
313 | h_lstm1, _ = self.lstm1(f1)
314 | h_lstm2, _ = self.lstm2(h_lstm1)
315 |
316 | # global average pooling
317 | avg_pool = torch.mean(h_lstm2, 1)
318 | # global max pooling
319 | max_pool, _ = torch.max(h_lstm2, 1)
320 |
321 | h_conc = torch.cat((max_pool, avg_pool), 1)
322 |
323 | h_conc_linear1 = self.linear1(h_conc)
324 | h_conc_linear2 = self.linear2(h_conc)
325 |
326 | hidden = h_conc + h_conc_linear1 + h_conc_linear2
327 | hidden = F.selu(self.linear_out(hidden))
328 | hidden = F.selu(self.linear_xtra(hidden))
329 | hidden = F.selu(self.linear_xtra2(hidden))
330 | hidden = F.sigmoid(self.linear_out2(hidden))
331 |
332 | result=hidden.flatten()
333 |
334 | return result
335 |
336 |
337 |
338 | def train_model(h_params, model, x_train, x_valid, y_train, y_valid, lr,
339 | batch_size=1000, n_epochs=20, title='', graph=''):
340 | global best_result
341 | param_lrs = [{'params': param, 'lr': lr} for param in model.parameters()]
342 | optimizer = torch.optim.AdamW(param_lrs, lr=h_params.initial_lr,
343 | betas=(0.9, 0.999),
344 | eps=1e-6,
345 | amsgrad=False
346 | )
347 |
348 | train_loader = torch.utils.data.DataLoader(torch.utils.data.TensorDataset(x_train, y_train), batch_size=batch_size, shuffle=True)
349 | valid_loader = torch.utils.data.DataLoader(torch.utils.data.TensorDataset(x_valid, y_valid), batch_size=batch_size, shuffle=False)
350 |
351 | num_batches = len(x_train)/batch_size
352 | print(len(x_train))
353 | results=[]
354 |
355 | for epoch in range(n_epochs):
356 | start_time = time.time()
357 | model.train()
358 | avg_loss = 0.
359 |
360 |
361 | progbar =Progbar(num_batches, stateful_metrics=['train-auc'])
362 |
363 | whole_y_pred=np.array([])
364 | whole_y_t=np.array([])
365 |
366 | for i,data in enumerate(train_loader):
367 | x_batch = data[:-1][0]
368 | y_batch = data[-1]
369 |
370 | y_pred = model(x_batch)
371 |
372 | if h_params.use_roc_star and epoch>0 :
373 |
374 | if i==0 : print('*Using Loss Roc-star')
375 | loss = roc_star_loss(y_batch,y_pred,epoch_gamma, last_whole_y_t, last_whole_y_pred)
376 |
377 | else:
378 | if i==0 : print('*Using Loss BxE')
379 | loss = F.binary_cross_entropy(y_pred, 1.0*y_batch)
380 |
381 | logger.report_scalar(title="Loss", series="trains loss",
382 | value=loss, iteration=epoch * len(x_train) + i)
383 |
384 | optimizer.zero_grad()
385 | loss.backward()
386 | # To prevent gradient explosions resulting in NaNs
387 | # https://discuss.pytorch.org/t/nan-loss-in-rnn-model/655/8
388 | # https://github.com/pytorch/examples/blob/master/word_language_model/main.py
389 | torch.nn.utils.clip_grad_norm_(model.parameters(), 0.5)
390 |
391 | optimizer.step()
392 |
393 | whole_y_pred = np.append(whole_y_pred, y_pred.clone().detach().cpu().numpy())
394 | whole_y_t = np.append(whole_y_t, y_batch.clone().detach().cpu().numpy())
395 |
396 | if i>0:
397 | if i%50==1 :
398 | try:
399 | train_roc_val = roc_auc_score(whole_y_t>=0.5, whole_y_pred)
400 | except:
401 |
402 | train_roc_val=-1
403 |
404 | progbar.update(
405 | i,
406 | values=[
407 | ("loss", np.mean(loss.detach().cpu().numpy())),
408 | ("train-auc", train_roc_val)
409 | ]
410 | )
411 |
412 | model.eval()
413 | last_whole_y_t = torch.tensor(whole_y_t).cuda()
414 | last_whole_y_pred = torch.tensor(whole_y_pred).cuda()
415 |
416 | all_valid_preds = np.array([])
417 | all_valid_t = np.array([])
418 | for i, valid_data in enumerate(valid_loader):
419 | x_batch = valid_data[:-1]
420 | y_batch = valid_data[-1]
421 |
422 | y_pred = model(*x_batch).detach().cpu().numpy()
423 | y_t = y_batch.detach().cpu().numpy()
424 |
425 | all_valid_preds=np.concatenate([all_valid_preds,y_pred],axis=0)
426 | all_valid_t = np.concatenate([all_valid_t,y_t],axis=0)
427 |
428 | epoch_gamma = epoch_update_gamma(last_whole_y_t, last_whole_y_pred, epoch,h_params.delta)
429 |
430 | try:
431 | valid_auc = roc_auc_score(all_valid_t>=0.5, all_valid_preds)
432 | except:
433 | valid_auc=-1
434 |
435 | try:
436 | train_roc_val = roc_auc_score(whole_y_t>=0.5, whole_y_pred)
437 | except:
438 | train_roc_val=-1
439 |
440 | elapsed_time = time.time() - start_time
441 | if epoch==0 :
442 | print("\n\n* * * * * * * * * * * Params :", title," :: ", graph)
443 | print('\nEpoch {}/{} \t loss={:.4f} \t time={:.2f}s'.format(
444 | epoch + 1, n_epochs, avg_loss, elapsed_time))
445 |
446 | print("Gamma = ", epoch_gamma)
447 | print("Validation AUC = ", valid_auc)
448 | if not ('auc' in best_result) or best_result['auc']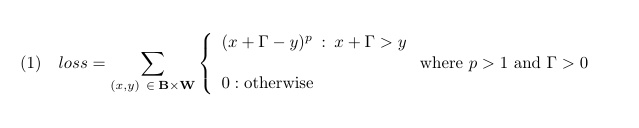 88 |
89 | Yann got this forumula by applying a series of changes to the WMW:
90 |
91 | 1. x
88 |
89 | Yann got this forumula by applying a series of changes to the WMW:
90 |
91 | 1. x