├── .gitignore
├── README.md
├── .github
└── workflows
│ └── build.yml
├── fiziko.mkiv
├── LICENSE.md
├── fiziko.tex
└── fiziko.mp
/.gitignore:
--------------------------------------------------------------------------------
1 | .DS_Store
2 | *.log
3 | *.tu?
4 |
--------------------------------------------------------------------------------
/README.md:
--------------------------------------------------------------------------------
1 | # fiziko
2 |
3 | 
4 |
5 | This MetaPost library was initially written to automate some elements of black and white illustrations for a physics textbook. First and foremost it provides functions to draw things like lines of variable width, shaded spheres and tubes of different kinds, which can be used to produce images of a variety of objects. The library also contains functions to draw some objects constructed from these primitives.
6 |
7 | 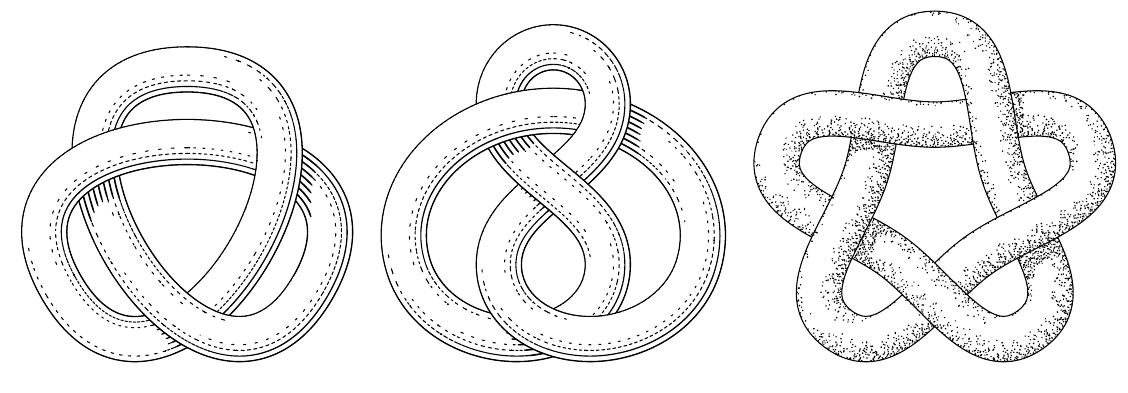
8 |
9 | Here's a [blog post](https://m.habr.com/en/post/454376/) describing the project in more detail.
10 |
--------------------------------------------------------------------------------
/.github/workflows/build.yml:
--------------------------------------------------------------------------------
1 | # This is a basic workflow to help you get started with Actions
2 |
3 | name: CI
4 |
5 | # Controls when the workflow will run
6 | on:
7 | # Triggers the workflow on push or pull request events but only for the "master" branch
8 | push:
9 | branches: [ "master" ]
10 | pull_request:
11 | branches: [ "master" ]
12 |
13 | # Allows you to run this workflow manually from the Actions tab
14 | workflow_dispatch:
15 |
16 | # A workflow run is made up of one or more jobs that can run sequentially or in parallel
17 | jobs:
18 | build:
19 | runs-on: ubuntu-latest
20 | container: texlive/texlive:latest
21 | steps:
22 | - uses: actions/checkout@v3
23 |
24 | # Runs a single command using the runners shell
25 | - name: Build the pdf
26 | run: lualatex -interaction=nonstopmode fiziko.tex
27 |
28 | - uses: actions/upload-artifact@v3
29 | with:
30 | name: pdf
31 | path: fiziko.pdf
32 |
--------------------------------------------------------------------------------
/fiziko.mkiv:
--------------------------------------------------------------------------------
1 | \startMPinclusions
2 | input fiziko.mp;
3 | \stopMPinclusions
4 |
5 | \setuptyping[
6 | option=mp,
7 | numbering=file,
8 | keeptogether=yes,
9 | ]
10 | \setuplinenumbering[
11 | style={\ss\bfxx},
12 | color=gray,
13 | ]
14 | \setupinteraction[
15 | state=start
16 | ]
17 |
18 | \usesymbols[cc]
19 |
20 | \startsetups document:start
21 | \startalignment[middle]
22 | \documentvariable{author}\par
23 | \blank[3*line]
24 |
25 | {\ss\bfa\documentvariable{title}}
26 |
27 | \vfill
28 |
29 | \documentvariable{abstract}
30 |
31 | \vfill
32 |
33 | \goto{\documentvariable{url}}[url(\documentvariable{url})]\par
34 | \blank[line]
35 |
36 | \documentvariable{license}
37 |
38 | \stopalignment
39 | \page
40 | \completecontent[criterium=all]
41 | \page
42 | \stopsetups
43 |
44 |
45 | \startdocument[
46 | author=Sergey Slyusarev,
47 | title={\type{fiziko}\par v.0.2.1 package for \MetaPost},
48 | abstract={This document describes a bunch of macros provided by the \quotation{fiziko} library for \MetaPost.},
49 | license={This document is distributed under the CC-BY-SA 4.0 license\par\symbol[cc][by]~\symbol[cc][sa]},
50 | url={https://github.com/jemmybutton/fiziko},
51 | ]
52 |
53 | \section{Introduction}
54 | This MetaPost library was initially written to automate some elements of black and white illustrations for a physics textbook. First and foremost it provides functions to draw things like lines of variable width, shaded spheres and tubes of different kinds, which can be used to produce images of a variety of objects. The library also contains functions to draw some objects constructed from these primitives.
55 |
56 | \section{Usage}
57 | Simply include this in the beginning of your \MetaPost\ document:
58 |
59 | \startMP[numbering=no]
60 | input fiziko.mp
61 | \stopMP
62 |
63 | \section{Global variables}
64 | A few global variables control different aspects of the behavior of the provided macros. Not all possible values are meaningful and some will definitely result in ugly pictures or errors.
65 |
66 | \subsection{minStrokeWidth}
67 | This variable controls minimal thickness of lines that are used for shading. Below this value lines are not getting thinner, but become dashed instead, maintaining roughly the same amount of ink per unit length as a thinner line would take. Default value is one fifth of a point. There are several things that depend on this value, so it’s convenient to change it using a macro:
68 |
69 | \startMP[numbering=no]
70 | defineMinStrokeWidth(1/2pt);
71 | \stopMP
72 |
73 | \subsection{lightDirection}
74 | This variable controls direction from which light falls on shaded objects. It’s of \type{pair} type and is set in radians. Default direction is top-left:
75 |
76 | \startMP[numbering=no]
77 | lightDirection := (-1/8pi, 1/8pi);
78 | \stopMP
79 |
80 | \subsection{lightDirection}
81 | This variable determines whether the light is inverted. This comes in handy when you need to have your shaded objects white on black. It's of \type{boolean} type. Default value is false:
82 |
83 | \def\BufferName{lightDirection}
84 | \startbuffer[\BufferName]
85 | draw sphere.c(1cm);
86 | invertedLight := true;
87 | fill ((unitsquare shifted (-1/2,-1/2)) scaled 3/2cm) shifted (3/2cm, 0) withcolor black;
88 | draw sphere.c(1cm) shifted (3/2cm, 0) withcolor white;
89 | invertedLight := false;
90 | \stopbuffer
91 | \typebuffer[\BufferName] \processMPbuffer[\BufferName]
92 |
93 |
94 | \section{\quotation{Lower level} macros}
95 | Currently, algorithms are quite stupid and will produce decent results only in certain simple circumstances.
96 |
97 | \subsection{offsetPath (\emph{path})(\emph{offset function})}
98 | This macro returns offset path (of type \type{path}) to a current path with a distance from the original path controlled by some arbitrary function; typically, it is a function of path length, set as either \type{offsetPathTime} or \type{offsetPathLength}. Former is simply \type{time} on current path and changes from 0 to \type{length(path)}, and latter changes from 0 to 1 over the path \type{arctime} (as a function of \type{arclength}).
99 |
100 | \def\BufferName{offsetPath}
101 | \startbuffer[\BufferName]
102 | path p, q;
103 | p := (0,0){dir(30)}..(5cm, 0)..{dir(30)}(10cm, 0);
104 | q := offsetPath(p)(1cm*sin(offsetPathLength*pi));
105 | draw p;
106 | draw q dashed evenly;
107 | \stopbuffer
108 | \typebuffer[\BufferName] \processMPbuffer[\BufferName]
109 |
110 | \subsection{brush (\emph{path})(\emph{offset function})}
111 | This macro returns a \type{picture} of a line of variable width along given path, which is controlled by some arbitrary function, analogous to \type{offsetPath}. If line is getting thinner than \type{minStrokeWith}, it is drawn dashed.
112 |
113 | \def\BufferName{brush}
114 | \startbuffer[\BufferName]
115 | path p;
116 | p := (0,0){dir(30)}..(5cm, 0)..{dir(30)}(10cm, 0);
117 | draw brush (p)(2minStrokeWidth*sin(offsetPathLength*pi));
118 | \stopbuffer
119 | \typebuffer[\BufferName] \processMPbuffer[\BufferName]
120 |
121 | \subsection{sphere.c (\emph{diameter})}
122 | This macro returns a \type{picture} of a sphere with specified diameter shaded with concentric strokes. Strokes are arranged to fit those of \type{tube.l}.
123 |
124 | \def\BufferName{sphere.c}
125 | \startbuffer[\BufferName]
126 | for i := 1 step 1 until 6:
127 | draw sphere.c(i*1/4cm) shifted (1/2cm*(i*(i+1))/2, 0);
128 | endfor;
129 | \stopbuffer
130 | \typebuffer[\BufferName] \processMPbuffer[\BufferName]
131 |
132 | \subsection{sphere.s (\emph{diameter})}
133 | This macro returns a \type{picture} of a sphere with specified diameter shaded with stipples.
134 |
135 | \def\BufferName{sphere.s}
136 | \startbuffer[\BufferName]
137 | for i := 1 step 1 until 6:
138 | draw sphere.s(i*1/4cm) shifted (1/2cm*(i*(i+1))/2, 0);
139 | endfor;
140 | \stopbuffer
141 | \typebuffer[\BufferName] \processMPbuffer[\BufferName]
142 |
143 | \subsection{sphereLat (\emph{diameter, angle})}
144 | This macro returns a \type{picture} of a shaded sphere with specified diameter. Unlike \type{sphere.c} macro, this one draws latitudinal strokes around axis rotated at specified \type{angle}.
145 |
146 | \def\BufferName{sphereLat}
147 | \startbuffer[\BufferName]
148 | for i := 1 step 1 until 6:
149 | draw sphereLat(i*1/4cm, -90 + i*30)
150 | shifted (1/2cm*(i*(i+1))/2, 0);
151 | endfor;
152 | \stopbuffer
153 | \typebuffer[\BufferName] \processMPbuffer[\BufferName]
154 |
155 | \subsection{tube.l (\emph{path})(\emph{offset function})}
156 | This macro returns a \type{picture} of a shaded \quotation{tube} of a variable width along a given path, which is controlled by some arbitrary function, analogous to \type{offsetPath}. \quotation{Tube} drawn by this macro is shaded be longitudal strokes. Once tube is generated, you can call \type{tubeOutline} path global variable, if you need one.
157 |
158 | \def\BufferName{tube.l}
159 | \startbuffer[\BufferName]
160 | path p;
161 | p := (0,0){dir(30)}..(5cm, 0)..{dir(30)}(10cm, 0);
162 | draw tube.l (p)(1/2cm*sin(offsetPathLength*pi));
163 | \stopbuffer
164 | \typebuffer[\BufferName] \processMPbuffer[\BufferName]
165 |
166 | \subsection{tube.t (\emph{path})(\emph{offset function})}
167 | This macro returns a \type{picture} of a shaded \quotation{tube} of variable width along given path, which is controlled by some arbitrary function, analogous to \type{offsetPath}. \quotation{Tube} drawn by this macro is shaded be transverse strokes. Once tube is generated, you can call \type{tubeOutline} path global variable, if you need one.
168 |
169 | \def\BufferName{tube.t}
170 | \startbuffer[\BufferName]
171 | path p;
172 | p := (0,0){dir(30)}..(5cm, 0)..{dir(30)}(10cm, 0);
173 | draw tube.t (p)(1/2cm*sin(offsetPathLength*pi));
174 | \stopbuffer
175 | \typebuffer[\BufferName] \processMPbuffer[\BufferName]
176 |
177 | \subsection{tube.s (\emph{path})(\emph{offset function})}
178 | This macro returns a \type{picture} of a shaded \quotation{tube} of variable width along given path, which is controlled by some arbitrary function, analogous to \type{offsetPath}. \quotation{Tube} drawn by this macro is shaded with stipples. Once tube is generated, you can call \type{tubeOutline} path global variable, if you need one.
179 |
180 | \def\BufferName{tube.s}
181 | \startbuffer[\BufferName]
182 | path p;
183 | p := (0,0){dir(30)}..(5cm, 0)..{dir(30)}(10cm, 0);
184 | draw tube.s (p)(1/2cm*sin(offsetPathLength*pi));
185 | \stopbuffer
186 | \typebuffer[\BufferName] \processMPbuffer[\BufferName]
187 |
188 | \subsection{tube.e (\emph{path})(\emph{offset function})}
189 | This macro returns the outline of a tube as a path.
190 |
191 | \section{\quotation{Higher level} macros}
192 | Using macros described in the previous section it is possible to construct more complex images. Macros for drawing some often used images are present in this package.
193 |
194 | \subsection{eye (\emph{angle})}
195 | This macro returns a \type{picture} of an eye pointed at the direction \type{angle} (in degrees). Eye size is controlled by a global variable \type{eyescale}, which has default value of \type{eyescale := 1/2cm;}.
196 |
197 | \def\BufferName{eye}
198 | \startbuffer[\BufferName]
199 | save eyescale;
200 | for i := 1 step 1 until 6:
201 | eyescale := 1/6cm*i;
202 | draw eye(i*60) shifted (1/2cm*(i*(i+1))/2, 0);
203 | endfor;
204 | \stopbuffer
205 | \typebuffer[\BufferName] \processMPbuffer[\BufferName]
206 |
207 | \subsection{pulley (\emph{diameter, angle})}
208 | This macro returns a \type{picture} of a pulley with specified \type{diameter} and its support pointed at the direction \type{angle} (in degrees). Note that pulley’s support protrudes from its center by \type{pulleySupportSize*diameter} and by default \type{pulleySupportSize} = 3/2. Once pulley is generated, you can call \type{pulleyOutline} path global variable, if you need one.
209 |
210 | \def\BufferName{pulley}
211 | \startbuffer[\BufferName]
212 | draw (-1/8cm, 0)--(12cm, 0);
213 | for i := 1 step 1 until 6:
214 | r := 1/7cm*i;
215 | draw image(
216 | draw pulley(2r, 0) shifted (0, -4/3r);
217 | draw (r, -4/3r) -- (r, -2cm);
218 | drawarrow (-r, -4/3r) -- (-r, -2cm);
219 | ) shifted (1/2cm*(i*(i+1))/2, 0);
220 | endfor;
221 | \stopbuffer
222 | \typebuffer[\BufferName] \processMPbuffer[\BufferName]
223 |
224 | \subsection{pulleyWheel (\emph{diameter})}
225 | This macro returns a \type{picture} of a pulley wheel with specified \type{diameter}.
226 |
227 | \def\BufferName{pulleyWheel}
228 | \startbuffer[\BufferName]
229 | for i := 1 step 1 until 6:
230 | r := 1/7cm*i;
231 | draw image(
232 | draw pulleyWheel(2r);
233 | draw (r, 0) -- (r, 1cm);
234 | drawarrow (-r, 0) -- (-r, 1cm);
235 | ) shifted (1/2cm*(i*(i+1))/2, 0);
236 | endfor;
237 | \stopbuffer
238 | \typebuffer[\BufferName] \processMPbuffer[\BufferName]
239 |
240 | \subsection{wheel (\emph{diameter, angle})}
241 | This macro returns a \type{picture} of a wheel with specified \type{diameter} and its support pointed at the direction \type{angle} (in degrees).
242 |
243 | \def\BufferName{wheel}
244 | \startbuffer[\BufferName]
245 | draw (-1/8cm, 0)--(12cm, 0);
246 | for i := 1 step 1 until 6:
247 | r := 1/7cm*i;
248 | draw wheel(2r, 0) shifted (0, -r) shifted (1/2cm*(i*(i+1))/2, 0);
249 | endfor;
250 | \stopbuffer
251 | \typebuffer[\BufferName] \processMPbuffer[\BufferName]
252 |
253 | \subsection{weight.s (\emph{height})}
254 | This macro returns a \type{picture} of a weight of a specific \type{height} that is standing on the point \type{(0, 0)}.
255 |
256 | \def\BufferName{weight.s}
257 | \startbuffer[\BufferName]
258 | for i := 1 step 1 until 6:
259 | draw weight.s(1/4cm + i*1/4cm) shifted (1/2cm*(i*(i+1))/2, 0);
260 | endfor;
261 | draw (-1/8cm, 0)--(12cm, 0);
262 | \stopbuffer
263 | \typebuffer[\BufferName] \processMPbuffer[\BufferName]
264 |
265 | \subsection{weight.h (\emph{height})}
266 | This macro returns a \type{picture} of a weight of a specific \type{height} that is is hanging from the point \type{(0, 0)}.
267 |
268 | \def\BufferName{weight.h}
269 | \startbuffer[\BufferName]
270 | for i := 1 step 1 until 6:
271 | draw weight.h(1/4cm + i*1/4cm) shifted (1/2cm*(i*(i+1))/2, 0);
272 | endfor;
273 | draw (12cm, 0)--(-1/8cm, 0);
274 | \stopbuffer
275 | \typebuffer[\BufferName] \processMPbuffer[\BufferName]
276 |
277 | \subsection{spring (\emph{point a, point b, number of steps})}
278 | This macro returns a \type{picture} of a spring stretched between points \type{a} and \type{b} (of type \type{pair}), with specified \type{number of steps}. Spring width is controlled by global variable \type{springwidth} with the default value \type{springwidth := 1/8cm;}.
279 |
280 | \def\BufferName{spring}
281 | \startbuffer[\BufferName]
282 | pair a, b;
283 | a := (0, 0);
284 | for i := 1 step 1 until 6:
285 | springwidth := 1/16cm + i*1/48cm;
286 | b := (i*1/3cm, - i*1/5cm);
287 | draw spring (a, b, 10) shifted (2/5cm*(i*(i+1))/2, 0);
288 | endfor;
289 | \stopbuffer
290 | \typebuffer[\BufferName] \processMPbuffer[\BufferName]
291 |
292 | \subsection{solidSurface (\emph{path})}
293 | This macro returns a \type{picture} of a solid surface on the right side of a given \type{path}.
294 |
295 | \def\BufferName{solidSurface}
296 | \startbuffer[\BufferName]
297 | path p;
298 | p := (0,0){dir(30)}..(5cm, 0)..{dir(30)}(10cm, 0);
299 | draw solidSurface(p);
300 | \stopbuffer
301 | \typebuffer[\BufferName] \processMPbuffer[\BufferName]
302 |
303 | \subsection{solid (\emph{path, angle, type})}
304 | Fills given \type{path} with strokes of specific type at a given \type{angle}. \type{type} can be 0 (\quotation{solid} strokes) and 1 (\quotation{glass} strokes).
305 |
306 | \def\BufferName{solid}
307 | \startbuffer[\BufferName]
308 | path p[];
309 | p1 := unitsquare scaled 2cm;
310 | p2 := p1 shifted (4cm, 0);
311 | draw solid(p1, 45, 0);
312 | draw solid(p2, -45, 1);
313 | \stopbuffer
314 | \typebuffer[\BufferName] \processMPbuffer[\BufferName]
315 |
316 | \subsection{woodBlock (\emph{width, height})}
317 | Returns a \type{picture} of a rectangular block of wood with its bottom-left corner in the origin.
318 |
319 | \def\BufferName{woodBlock}
320 | \startbuffer[\BufferName]
321 | draw woodBlock(10cm, 1/2cm);
322 | \stopbuffer
323 | \typebuffer[\BufferName] \processMPbuffer[\BufferName]
324 |
325 | \subsection{woodenThing (\emph{path, angle})}
326 | Returns a \type{picture} of a wood texture at a given \type{angle} fitted into a given \type{path}.
327 |
328 | \def\BufferName{woodenThing}
329 | \startbuffer[\BufferName]
330 | path p, q;
331 | p := dir(-60) scaled 1/2 -- dir(90) scaled 2/3 -- dir (-120) scaled 3/5 -- cycle;
332 | for i := 1 step 1 until 6:
333 | q := (p scaled 3/2cm) rotated (i*60);
334 | draw woodenThing (q, i*60) shifted (2cm*i, 0);
335 | endfor;
336 | \stopbuffer
337 | \typebuffer[\BufferName] \processMPbuffer[\BufferName]
338 |
339 | \subsection{woodenSurface (\emph{path, angle})}
340 | Returns a \type{picture} similar to that of a solid surface on the right side of a given \type{path}, but with wood texture .
341 |
342 | \def\BufferName{woodenSurface}
343 | \startbuffer[\BufferName]
344 | path p;
345 | p := (0,0){dir(30)}..(5cm, 0)..{dir(30)}(10cm, 0);
346 | draw woodenSurface(p);
347 | \stopbuffer
348 | \typebuffer[\BufferName] \processMPbuffer[\BufferName]
349 |
350 | \subsection{globe (\emph{radius, longitude, latitude})}
351 | This macro returns a \type{picture} of the globe of specified \type{radius} centered at specific \type{longitude} and \type{latitude};
352 |
353 | \def\BufferName{globe}
354 | \startbuffer[\BufferName]
355 | for i := 1 step 1 until 6:
356 | draw globe(i*1/4cm, i*60, -90 + i*30)
357 | shifted (1/2cm*(i*(i+1))/2, 0);
358 | endfor;
359 | \stopbuffer
360 | \typebuffer[\BufferName] \processMPbuffer[\BufferName]
361 |
362 | \subsection{Knots}
363 | There are two macros to handle knot drawing: \type{addStrandToKnot} and \type{knotFromStrands}. Currently the algorithm is not especially stable.
364 |
365 | \subsubsection{addStrandToKnot (\emph{knotName}) (\emph{path, ropeWidth, ropeType, intersectionOrder})}
366 | This macro adds a strand to knot named \type{knotName} and returns nothing. Strand follows the given \type{path} and has a given \type{ropeWidth}. \type{ropeType} can be \type{"l"}, \type{"t"} (as in \type{tube.l} and \type{tube.t}) or \type{"e"} (for an unshaded strand). \type{intersectionOrder} is a string of comma separated numbers which represent a \quotation{layer} to which intersections along the strand go.
367 |
368 | \subsubsection{knotFromStrands (\emph{knotName})}
369 | This macro returns a picture of a knot with a given \type{knotName}.
370 |
371 | \def\BufferName{knotFromStrands}
372 | \startbuffer[\BufferName]
373 | path p[];
374 | p1 := (dir(90)*4/3cm) {dir(0)} .. tension 3/2
375 | .. (dir(90 + 120)*4/3cm){dir(90 + 30)} .. tension 3/2
376 | .. (dir(90 - 120)*4/3cm){dir(-90 - 30)} .. tension 3/2
377 | .. cycle;
378 | p2 := (fullcircle scaled 3cm) shifted (0, -3/2cm);
379 | p3 := (fullcircle scaled 4cm);
380 | addStrandToKnot (theknot) (p1 shifted (4cm, -4cm), 1/5cm, "l",
381 | "-1,1,-1,1,-1,1,-1,1,-1");
382 | addStrandToKnot (theknot) (p2 shifted (4cm, -4cm), 1/6cm, "s",
383 | "");
384 | addStrandToKnot (theknot) (p3 shifted (4cm, -4cm), 1/7cm, "e",
385 | "-1,1");
386 | draw knotFromStrands (theknot);
387 | \stopbuffer
388 | \typebuffer[\BufferName] \processMPbuffer[\BufferName]
389 |
390 | \subsection{Other 3D contraptions}
391 | Some macros can be used to shade 3D polygons. Currently only flat surfaces are supported
392 |
393 | \subsubsection{flatSurface\emph{\#@}(\emph{surface outline path, normal vector, hatch angle})}
394 | This macro returns a \type{picture} of a flat surface with the specified \type{surface outline path} with the given \type{normal vector}, illuminated from the direction determined by \type{lightDirection} and with hatches aligned at the andle \type{hatch angle}. If \type{\#@} is \type{".hatches"} then the surface is shaded with hatches, if it’s \type{".stipples"}, then the surface is shaded with stipples.
395 |
396 | \def\BufferName{flatSurface}
397 | \startbuffer[\BufferName]
398 | path p[];
399 | p1 := unitsquare xscaled 1cm yscaled 2cm;
400 | p2 := p1 shifted (1cm, 0);
401 | draw flatSurface.hatches(p1, (-1,0,1), 45);
402 | draw flatSurface.hatches(p2, (1,0,1), 45);
403 | draw p1; draw p2;
404 | \stopbuffer
405 | \typebuffer[\BufferName] \processMPbuffer[\BufferName]
406 |
407 | \section{Other macros}
408 | Some macros that are not directly related to drawing are listed below
409 |
410 | \subsection{refractionPath (\emph{initial ray, shape, refraction coefficient})}
411 | This macro returns a \type{path} that represent refraction of some \type{ray} (any variable of type \type{path}, point next to last in a given path is considered a source of a \quotation{ray}, and last point determines its direction) through some \type{shape} with given \type{refraction coefficient}. When appropriate, the \quotation{ray} is fully internally reflected.
412 |
413 | Setting \type{refraction coefficient} to 0 results in reflection instead of refraction in all cases.
414 |
415 | \def\BufferName{refractionPath}
416 | \startbuffer[\BufferName]
417 | path r, p;
418 | p := fullcircle scaled 2.1cm;
419 | draw p;
420 | for i:= 1cm step -1/4cm until -1cm:
421 | r := (-4cm, i) -- (-1cm, i);
422 | draw refractionPath(r, p, 1.5);
423 | endfor;
424 | \stopbuffer
425 | \typebuffer[\BufferName] \processMPbuffer[\BufferName]
426 |
427 |
428 | \subsection{lens (\emph{(left radius, right radius), thickness, diameter, units})}
429 | This macro returns a \type{path} that represent a section of a lens with given radii of curvature (positive value for convex, negative --- for concave), thickness (i. e. distance benween sides' centers) and diameter (i. e. height) in given arbitrary units.
430 |
431 | \def\BufferName{lens}
432 | \startbuffer[\BufferName]
433 | draw lens((5, 10), 1/2, 2, cm);
434 | draw lens((-10, -5), 1/4, 2, cm) shifted (2cm, 0);
435 | draw lens((infinity, 7), 1/4, 2, cm) shifted (4cm, 0);
436 | \stopbuffer
437 | \typebuffer[\BufferName] \processMPbuffer[\BufferName]
438 |
439 | \section{Auxilary macros}
440 | Some macros that not related to physical problems at all are listed below.
441 |
442 | \subsection{\emph{picture} maskedWith \emph{path}}
443 | This macro masks a part of a \type{picture} with closed \type{path}. In fact this is inversion of metapost’s built-in \type{clip} but, in contrast to the latter, it does not modify original image. Note that it requires that counter-clockwise \type{path} to work properly.
444 |
445 | \subsection{\emph{path} firstIntersectionTimes \emph{path}}
446 | This macro is similar to metapost’s \type{intersectiontimes} but it returns intersection times with smallest time on first path.
447 |
448 | \subsection{pathSubdivide \emph{path, n}}
449 | This macro returns original \type{path} with \type{n}-times more points.
450 |
451 | \subsection{drawmidarrow (\emph{path})}
452 | Draws \type{path} with arrows in the middles of segments with length no less than \type{midArrowLimit} (another global variable, 1cm by default).
453 |
454 | \subsection{markAngle (\emph{point a, point o, point b})(\emph{text})}
455 | This macro marks an angle \type{aob} (counter-clockwise) with some \type{text}
456 |
457 | \def\BufferName{markAngle}
458 | \startbuffer[\BufferName]
459 | pair a, o, b;
460 | for i:= 30 step 60 until 390:
461 | o := (10cm*(i/360), 0);
462 | a := dir(i/2)*4/3cm shifted o;
463 | b := dir(i)*4/3cm shifted o;
464 | draw (a--o--b);
465 | markAngle(a, o, b)(btex $\alpha$ etex);
466 | endfor;
467 | \stopbuffer
468 | \typebuffer[\BufferName] \processMPbuffer[\BufferName]
469 |
470 |
471 | \section{Some examples}
472 |
473 | \subsection{Gregory-Maksutov type telescope}
474 | Lines 3--11 define parameters of lenses and mirrors\footnote{Taken from here http://www.google.ru/patents/US2701983}. Lines 12--16 generate lenses. On line 20 shape of prism is defined. Line 22 cuts part of the rear mirror. Line 26 describes mirror part of the front lens. On lines 31--33 all the glass parts are drawn. On lines 34--36 all the mirror ones. On lines 39--44 rays are traced through all system in order specified in loop on line 41. Lines 49--56 are about the telescope frame.
475 |
476 | \def\BufferName{GMtt}
477 | \startbuffer[\BufferName]
478 | path p[], q[], axis[], f[]; pair o;
479 | u := 6mm;
480 | r1 := -36.979; r2 := -r1; t1 := 0.7; n1 := 1.517; d1 := 5;
481 | l1 := 8.182;
482 | r3 := -11.657; r4 := r3; t2 := 0.2; n2 := n1; d2 := 3/2;
483 | l2 := 0.4;
484 | r5 := -30.433; r6 := 9.598; t3 := 0.39; n3 := 1.621; d3 := d2;
485 | l3 := 0.828;
486 | r7 := -35.512; r8 := infinity; t4 := 0.7; n4 := 0; d4 := d1;
487 | l4 := 5.272;
488 | ll0 := 0;
489 | for i := 1 upto 4:
490 | ll[i] := ll[i-1] + t[i] + l[i];
491 | p[i] := lens ((r[i*2 - 1], r[i*2]), t[i], d[i], u)
492 | shifted (ll[i-1]*u, 0);
493 | endfor;
494 | axis1 := (0, 0) -- (ll4*u, 0);
495 | axis2 := reverse(axis1);
496 | ll5 := ll4 - 1/2l4;
497 | p5 := ((-1,-1) -- (1,1) -- (-1,1) -- cycle)
498 | scaled (1/2d2*u) shifted (ll5*u, 0);
499 | p6 := (subpath
500 | (ypart((axis1 shifted (0, 1/2d2*u)) firstIntersectionTimes p4),
501 | ypart((axis2 shifted (0, 1/2d2*u)) firstIntersectionTimes p4))
502 | of p4) -- cycle;
503 | p7 := (subpath
504 | (ypart((axis2 shifted (0, 3/4d2*u)) firstIntersectionTimes p1),
505 | ypart((axis2 shifted (0, -3/4d2*u)) firstIntersectionTimes p1))
506 | of p1);
507 | p7 := p7 -- (reverse(p7) shifted ((-1/3t1)*u, 0)) -- cycle;
508 | for i := 1, 2, 3, 5:
509 | draw p[i] withpen thickpen; draw solid (p[i], 45, 1);
510 | endfor;
511 | draw solid (p7, -45, 0);
512 | draw p6 withpen thickpen; draw solid (p6, -45, 0);
513 | draw p6 yscaled -1 withpen thickpen;
514 | draw solid (p6 yscaled -1, -45, 0);
515 | n7 := 0; n5 := n1;
516 | for i := 0, 1:
517 | q[i] := (-3/2u, -2u + i*4u) -- (16u, -2u + i*4u);
518 | for j = 1, 4, 7, 2, 3, 5:
519 | q[i] := refractionPath(q[i], p[j], n[j]);
520 | endfor;
521 | endfor;
522 | o := whatever[point length(q0) of q0, point length(q0)-1 of q0]
523 | = whatever[point length(q1) of q1, point length(q1)-1 of q1];
524 | for i := 0, 1: drawmidarrow (q[i] -- o) withpen thinpen; endfor;
525 | draw eye(-91) shifted o shifted (0, u);
526 | f1 := (-1/4u, 1/2d1*u) -- ((ll3 + t4)*u, 1/2d1*u)
527 | -- ((ll3 + t4)*u, 1/2d2*u);
528 | f2 := (ll1*u - 1/8u, 1/2d2*u) -- (ll5*u - 1/2d2*u, 1/2d2*u)
529 | -- (ll5*u - 1/2d2*u, ypart(o));
530 | f3 := (ll1*u - 1/8u, -1/2d2*u) -- (ll5*u + 1/2d2*u, -1/2d2*u)
531 | -- (ll5*u + 1/2d2*u, ypart(o));
532 | draw f1 withpen fatpen; draw f1 yscaled -1 withpen fatpen;
533 | draw f2 withpen fatpen; draw f3 withpen fatpen;
534 | \stopbuffer
535 | \typebuffer[\BufferName][keeptogether=no] \processMPbuffer[\BufferName]
536 |
537 |
538 | \subsection{L’Hôpital’s Pulley Problem}
539 | Line 3 describe initial setup. Line 4 is problem’s solution. Lines 8–11 set all the points where they belong. Lines 12–16 are needed to decide where to put the pulley.
540 |
541 | \def\BufferName{PulleyProblem}
542 | \startbuffer[\BufferName]
543 | pair p[], o[];
544 | numeric a, d[], l[], x[], y[];
545 | l0 := 6; l1 := 4; l2 := 4;
546 | x1 := (l1**2 + abs(l1)*((sqrt(8)*l0)++l1))/4l0;
547 | y1 := l1+-+x1;
548 | y2 := l2 - ((l0-x1)++y1);
549 | d1 := 2/3cm; d2 := 4/3cm; d3 := 5/6d1;
550 | p1 := (0, 0);
551 | p2 := (l0*cm, 0);
552 | p3 := (x1*cm, -y1*cm);
553 | p4 := p3 shifted (0, -y2*cm);
554 | o1 := (unitvector(p4-p3) rotated 90 scaled 1/2d3);
555 | o2 := (unitvector(p3-p2) rotated 90 scaled 1/2d3);
556 | p5 := whatever [p3 shifted o1, p4 shifted o1]
557 | = whatever [p3 shifted o2, p2 shifted o2];
558 | a := angle(p1-p3);
559 | draw solidSurface(11/10[p1,p2] -- 11/10[p2, p1]);
560 | draw pulley (d1, a - 90) shifted p5;
561 | draw image(
562 | draw p1 -- p3 -- p2 withpen thickpen;
563 | draw p3 -- p4 withpen thickpen;
564 | ) maskedWith (pulleyOutline shifted p5);
565 | draw sphere.c(d2) shifted p4 shifted (0, -1/2d2);
566 | dotlabel.llft(btex $A$ etex, p1);
567 | dotlabel.lrt(btex $B$ etex, p2);
568 | dotlabel.ulft(btex $C$ etex, p4);
569 | label.llft(btex $l$ etex, 1/2[p1, p3]);
570 | markAngle(p3, p1, p2)(btex $\alpha$ etex);
571 | \stopbuffer
572 | \typebuffer[\BufferName][keeptogether=no] \processMPbuffer[\BufferName]
573 |
574 | \subsection{Hooke’s law}
575 |
576 | \def\BufferName{HookesLaw}
577 | \startbuffer[\BufferName]
578 | numeric l[],d, h;
579 | pair p[], q[];
580 | l0 := 3/2cm; l1 := 1cm;
581 | d := 1cm; h := 7/8cm;
582 | p1 := (0, 0); p2 := (0, -l0);
583 | p3 := (d, 0); p4 := (d, -l0-l1);
584 | p5 := (2d, 0); p6 := (2d, -l0-2l1); p7 := (2d, -l0-2l1-h);
585 | draw solidSurface((2d + 1/2cm, 0)--(-1/2cm, 0));
586 | draw spring(p1, p2, 20);
587 | draw spring(p3, p4, 20);
588 | draw weight.h(h) shifted p4;
589 | draw spring(p5, p6, 20);
590 | draw weight.h(h) shifted p6;
591 | draw weight.h(h) shifted p7;
592 | q1 := (0, ypart(p2));
593 | q2 := (0, ypart(p4));
594 | q3 := (0, ypart(p6));
595 | draw p2 -- q1 withpen thinpen;
596 | draw p4 -- q2 withpen thinpen;
597 | draw p6 -- q3 withpen thinpen;
598 | drawdblarrow q1--q2 withpen thinpen;
599 | drawdblarrow q2--q3 withpen thinpen;
600 | label.lft (btex $x$ etex, 1/2[q1, q2]);
601 | label.lft (btex $x$ etex, 1/2[q2, q3]);
602 | \stopbuffer
603 | \typebuffer[\BufferName][keeptogether=no] \processMPbuffer[\BufferName]
604 |
605 | \subsection{Weight on a cart}
606 |
607 | \def\BufferName{Weight}
608 | \startbuffer[\BufferName]
609 | numeric l, w, r, h;
610 | l := 4cm;
611 | w := 1/4cm;
612 | r := 2/3cm;
613 | h := 1cm;
614 | draw solidSurface((-1/5l, 0) -- (6/5l, 0));
615 | draw woodBlock (l, w) shifted (0, r);
616 | draw wheel (r, 0) shifted (r, 1/2r);
617 | draw wheel (r, 0) shifted (l-r, 1/2r);
618 | draw weight.s(h) shifted (1/2l, r + w);
619 | \stopbuffer
620 | \typebuffer[\BufferName] \processMPbuffer[\BufferName]
621 |
622 | \subsection{Some knots}
623 |
624 | \def\BufferName{Knots}
625 | \startbuffer[\BufferName]
626 | path p[];
627 | p1 := (dir(90)*4/3cm) {dir(0)} .. tension 3/2
628 | .. (dir(90 + 120)*4/3cm){dir(90 + 30)} .. tension 3/2
629 | .. (dir(90 - 120)*4/3cm){dir(-90 - 30)} .. tension 3/2
630 | .. cycle;
631 | p1 := p1 scaled 6/5;
632 | addStrandToKnot (primeOne) (p1, 1/4cm, "l", "1, -1, 1");
633 | draw knotFromStrands (primeOne);
634 | p2 := (0, 2cm) .. (1/2cm, 3/2cm) .. (-1/2cm, 0)
635 | .. (1/2cm, -2/3cm) .. (4/3cm, 0) .. (0, 17/12cm)
636 | .. (-4/3cm, 0) .. (-1/2cm, -2/3cm) .. (1/2cm, 0)
637 | .. (-1/2cm, 3/2cm) .. cycle;
638 | p2 := p2 scaled 6/5;
639 | addStrandToKnot (primeTwo) (p2, 1/4cm, "l", "1, -1, 1, -1, 1");
640 | draw knotFromStrands (primeTwo) shifted (4cm, 0);
641 | p3 := (dir(0)*3/2cm) .. (dir(1*72)*2/3cm)
642 | .. (dir(2*72)*3/2cm) .. (dir(3*72)*2/3cm)
643 | .. (dir(4*72)*3/2cm) .. (dir(0)*2/3cm)
644 | .. (dir(1*72)*3/2cm) .. (dir(2*72)*2/3cm)
645 | .. (dir(3*72)*3/2cm) .. (dir(4*72)*2/3cm)
646 | .. cycle;
647 | p3 := (p3 rotated (72/4)) scaled 6/5;
648 | addStrandToKnot (primeThree) (p3, 1/4cm, "l", "-1, 1, -1, 1, -1");
649 | draw knotFromStrands (primeThree) shifted (8cm, 0);
650 | \stopbuffer
651 | \typebuffer[\BufferName][keeptogether=no] \processMPbuffer[\BufferName]
652 |
653 | \stopdocument
654 |
--------------------------------------------------------------------------------
/LICENSE.md:
--------------------------------------------------------------------------------
1 | GNU GENERAL PUBLIC LICENSE
2 |
3 | Version 3, 29 June 2007
4 |
5 | Copyright © 2007 Free Software Foundation, Inc.
6 |
7 | Everyone is permitted to copy and distribute verbatim copies of this license document, but changing it is not allowed.
8 | Preamble
9 |
10 | The GNU General Public License is a free, copyleft license for software and other kinds of works.
11 |
12 | The licenses for most software and other practical works are designed to take away your freedom to share and change the works. By contrast, the GNU General Public License is intended to guarantee your freedom to share and change all versions of a program--to make sure it remains free software for all its users. We, the Free Software Foundation, use the GNU General Public License for most of our software; it applies also to any other work released this way by its authors. You can apply it to your programs, too.
13 |
14 | When we speak of free software, we are referring to freedom, not price. Our General Public Licenses are designed to make sure that you have the freedom to distribute copies of free software (and charge for them if you wish), that you receive source code or can get it if you want it, that you can change the software or use pieces of it in new free programs, and that you know you can do these things.
15 |
16 | To protect your rights, we need to prevent others from denying you these rights or asking you to surrender the rights. Therefore, you have certain responsibilities if you distribute copies of the software, or if you modify it: responsibilities to respect the freedom of others.
17 |
18 | For example, if you distribute copies of such a program, whether gratis or for a fee, you must pass on to the recipients the same freedoms that you received. You must make sure that they, too, receive or can get the source code. And you must show them these terms so they know their rights.
19 |
20 | Developers that use the GNU GPL protect your rights with two steps: (1) assert copyright on the software, and (2) offer you this License giving you legal permission to copy, distribute and/or modify it.
21 |
22 | For the developers' and authors' protection, the GPL clearly explains that there is no warranty for this free software. For both users' and authors' sake, the GPL requires that modified versions be marked as changed, so that their problems will not be attributed erroneously to authors of previous versions.
23 |
24 | Some devices are designed to deny users access to install or run modified versions of the software inside them, although the manufacturer can do so. This is fundamentally incompatible with the aim of protecting users' freedom to change the software. The systematic pattern of such abuse occurs in the area of products for individuals to use, which is precisely where it is most unacceptable. Therefore, we have designed this version of the GPL to prohibit the practice for those products. If such problems arise substantially in other domains, we stand ready to extend this provision to those domains in future versions of the GPL, as needed to protect the freedom of users.
25 |
26 | Finally, every program is threatened constantly by software patents. States should not allow patents to restrict development and use of software on general-purpose computers, but in those that do, we wish to avoid the special danger that patents applied to a free program could make it effectively proprietary. To prevent this, the GPL assures that patents cannot be used to render the program non-free.
27 |
28 | The precise terms and conditions for copying, distribution and modification follow.
29 | TERMS AND CONDITIONS
30 | 0. Definitions.
31 |
32 | “This License” refers to version 3 of the GNU General Public License.
33 |
34 | “Copyright” also means copyright-like laws that apply to other kinds of works, such as semiconductor masks.
35 |
36 | “The Program” refers to any copyrightable work licensed under this License. Each licensee is addressed as “you”. “Licensees” and “recipients” may be individuals or organizations.
37 |
38 | To “modify” a work means to copy from or adapt all or part of the work in a fashion requiring copyright permission, other than the making of an exact copy. The resulting work is called a “modified version” of the earlier work or a work “based on” the earlier work.
39 |
40 | A “covered work” means either the unmodified Program or a work based on the Program.
41 |
42 | To “propagate” a work means to do anything with it that, without permission, would make you directly or secondarily liable for infringement under applicable copyright law, except executing it on a computer or modifying a private copy. Propagation includes copying, distribution (with or without modification), making available to the public, and in some countries other activities as well.
43 |
44 | To “convey” a work means any kind of propagation that enables other parties to make or receive copies. Mere interaction with a user through a computer network, with no transfer of a copy, is not conveying.
45 |
46 | An interactive user interface displays “Appropriate Legal Notices” to the extent that it includes a convenient and prominently visible feature that (1) displays an appropriate copyright notice, and (2) tells the user that there is no warranty for the work (except to the extent that warranties are provided), that licensees may convey the work under this License, and how to view a copy of this License. If the interface presents a list of user commands or options, such as a menu, a prominent item in the list meets this criterion.
47 | 1. Source Code.
48 |
49 | The “source code” for a work means the preferred form of the work for making modifications to it. “Object code” means any non-source form of a work.
50 |
51 | A “Standard Interface” means an interface that either is an official standard defined by a recognized standards body, or, in the case of interfaces specified for a particular programming language, one that is widely used among developers working in that language.
52 |
53 | The “System Libraries” of an executable work include anything, other than the work as a whole, that (a) is included in the normal form of packaging a Major Component, but which is not part of that Major Component, and (b) serves only to enable use of the work with that Major Component, or to implement a Standard Interface for which an implementation is available to the public in source code form. A “Major Component”, in this context, means a major essential component (kernel, window system, and so on) of the specific operating system (if any) on which the executable work runs, or a compiler used to produce the work, or an object code interpreter used to run it.
54 |
55 | The “Corresponding Source” for a work in object code form means all the source code needed to generate, install, and (for an executable work) run the object code and to modify the work, including scripts to control those activities. However, it does not include the work's System Libraries, or general-purpose tools or generally available free programs which are used unmodified in performing those activities but which are not part of the work. For example, Corresponding Source includes interface definition files associated with source files for the work, and the source code for shared libraries and dynamically linked subprograms that the work is specifically designed to require, such as by intimate data communication or control flow between those subprograms and other parts of the work.
56 |
57 | The Corresponding Source need not include anything that users can regenerate automatically from other parts of the Corresponding Source.
58 |
59 | The Corresponding Source for a work in source code form is that same work.
60 | 2. Basic Permissions.
61 |
62 | All rights granted under this License are granted for the term of copyright on the Program, and are irrevocable provided the stated conditions are met. This License explicitly affirms your unlimited permission to run the unmodified Program. The output from running a covered work is covered by this License only if the output, given its content, constitutes a covered work. This License acknowledges your rights of fair use or other equivalent, as provided by copyright law.
63 |
64 | You may make, run and propagate covered works that you do not convey, without conditions so long as your license otherwise remains in force. You may convey covered works to others for the sole purpose of having them make modifications exclusively for you, or provide you with facilities for running those works, provided that you comply with the terms of this License in conveying all material for which you do not control copyright. Those thus making or running the covered works for you must do so exclusively on your behalf, under your direction and control, on terms that prohibit them from making any copies of your copyrighted material outside their relationship with you.
65 |
66 | Conveying under any other circumstances is permitted solely under the conditions stated below. Sublicensing is not allowed; section 10 makes it unnecessary.
67 | 3. Protecting Users' Legal Rights From Anti-Circumvention Law.
68 |
69 | No covered work shall be deemed part of an effective technological measure under any applicable law fulfilling obligations under article 11 of the WIPO copyright treaty adopted on 20 December 1996, or similar laws prohibiting or restricting circumvention of such measures.
70 |
71 | When you convey a covered work, you waive any legal power to forbid circumvention of technological measures to the extent such circumvention is effected by exercising rights under this License with respect to the covered work, and you disclaim any intention to limit operation or modification of the work as a means of enforcing, against the work's users, your or third parties' legal rights to forbid circumvention of technological measures.
72 | 4. Conveying Verbatim Copies.
73 |
74 | You may convey verbatim copies of the Program's source code as you receive it, in any medium, provided that you conspicuously and appropriately publish on each copy an appropriate copyright notice; keep intact all notices stating that this License and any non-permissive terms added in accord with section 7 apply to the code; keep intact all notices of the absence of any warranty; and give all recipients a copy of this License along with the Program.
75 |
76 | You may charge any price or no price for each copy that you convey, and you may offer support or warranty protection for a fee.
77 | 5. Conveying Modified Source Versions.
78 |
79 | You may convey a work based on the Program, or the modifications to produce it from the Program, in the form of source code under the terms of section 4, provided that you also meet all of these conditions:
80 |
81 | a) The work must carry prominent notices stating that you modified it, and giving a relevant date.
82 | b) The work must carry prominent notices stating that it is released under this License and any conditions added under section 7. This requirement modifies the requirement in section 4 to “keep intact all notices”.
83 | c) You must license the entire work, as a whole, under this License to anyone who comes into possession of a copy. This License will therefore apply, along with any applicable section 7 additional terms, to the whole of the work, and all its parts, regardless of how they are packaged. This License gives no permission to license the work in any other way, but it does not invalidate such permission if you have separately received it.
84 | d) If the work has interactive user interfaces, each must display Appropriate Legal Notices; however, if the Program has interactive interfaces that do not display Appropriate Legal Notices, your work need not make them do so.
85 |
86 | A compilation of a covered work with other separate and independent works, which are not by their nature extensions of the covered work, and which are not combined with it such as to form a larger program, in or on a volume of a storage or distribution medium, is called an “aggregate” if the compilation and its resulting copyright are not used to limit the access or legal rights of the compilation's users beyond what the individual works permit. Inclusion of a covered work in an aggregate does not cause this License to apply to the other parts of the aggregate.
87 | 6. Conveying Non-Source Forms.
88 |
89 | You may convey a covered work in object code form under the terms of sections 4 and 5, provided that you also convey the machine-readable Corresponding Source under the terms of this License, in one of these ways:
90 |
91 | a) Convey the object code in, or embodied in, a physical product (including a physical distribution medium), accompanied by the Corresponding Source fixed on a durable physical medium customarily used for software interchange.
92 | b) Convey the object code in, or embodied in, a physical product (including a physical distribution medium), accompanied by a written offer, valid for at least three years and valid for as long as you offer spare parts or customer support for that product model, to give anyone who possesses the object code either (1) a copy of the Corresponding Source for all the software in the product that is covered by this License, on a durable physical medium customarily used for software interchange, for a price no more than your reasonable cost of physically performing this conveying of source, or (2) access to copy the Corresponding Source from a network server at no charge.
93 | c) Convey individual copies of the object code with a copy of the written offer to provide the Corresponding Source. This alternative is allowed only occasionally and noncommercially, and only if you received the object code with such an offer, in accord with subsection 6b.
94 | d) Convey the object code by offering access from a designated place (gratis or for a charge), and offer equivalent access to the Corresponding Source in the same way through the same place at no further charge. You need not require recipients to copy the Corresponding Source along with the object code. If the place to copy the object code is a network server, the Corresponding Source may be on a different server (operated by you or a third party) that supports equivalent copying facilities, provided you maintain clear directions next to the object code saying where to find the Corresponding Source. Regardless of what server hosts the Corresponding Source, you remain obligated to ensure that it is available for as long as needed to satisfy these requirements.
95 | e) Convey the object code using peer-to-peer transmission, provided you inform other peers where the object code and Corresponding Source of the work are being offered to the general public at no charge under subsection 6d.
96 |
97 | A separable portion of the object code, whose source code is excluded from the Corresponding Source as a System Library, need not be included in conveying the object code work.
98 |
99 | A “User Product” is either (1) a “consumer product”, which means any tangible personal property which is normally used for personal, family, or household purposes, or (2) anything designed or sold for incorporation into a dwelling. In determining whether a product is a consumer product, doubtful cases shall be resolved in favor of coverage. For a particular product received by a particular user, “normally used” refers to a typical or common use of that class of product, regardless of the status of the particular user or of the way in which the particular user actually uses, or expects or is expected to use, the product. A product is a consumer product regardless of whether the product has substantial commercial, industrial or non-consumer uses, unless such uses represent the only significant mode of use of the product.
100 |
101 | “Installation Information” for a User Product means any methods, procedures, authorization keys, or other information required to install and execute modified versions of a covered work in that User Product from a modified version of its Corresponding Source. The information must suffice to ensure that the continued functioning of the modified object code is in no case prevented or interfered with solely because modification has been made.
102 |
103 | If you convey an object code work under this section in, or with, or specifically for use in, a User Product, and the conveying occurs as part of a transaction in which the right of possession and use of the User Product is transferred to the recipient in perpetuity or for a fixed term (regardless of how the transaction is characterized), the Corresponding Source conveyed under this section must be accompanied by the Installation Information. But this requirement does not apply if neither you nor any third party retains the ability to install modified object code on the User Product (for example, the work has been installed in ROM).
104 |
105 | The requirement to provide Installation Information does not include a requirement to continue to provide support service, warranty, or updates for a work that has been modified or installed by the recipient, or for the User Product in which it has been modified or installed. Access to a network may be denied when the modification itself materially and adversely affects the operation of the network or violates the rules and protocols for communication across the network.
106 |
107 | Corresponding Source conveyed, and Installation Information provided, in accord with this section must be in a format that is publicly documented (and with an implementation available to the public in source code form), and must require no special password or key for unpacking, reading or copying.
108 | 7. Additional Terms.
109 |
110 | “Additional permissions” are terms that supplement the terms of this License by making exceptions from one or more of its conditions. Additional permissions that are applicable to the entire Program shall be treated as though they were included in this License, to the extent that they are valid under applicable law. If additional permissions apply only to part of the Program, that part may be used separately under those permissions, but the entire Program remains governed by this License without regard to the additional permissions.
111 |
112 | When you convey a copy of a covered work, you may at your option remove any additional permissions from that copy, or from any part of it. (Additional permissions may be written to require their own removal in certain cases when you modify the work.) You may place additional permissions on material, added by you to a covered work, for which you have or can give appropriate copyright permission.
113 |
114 | Notwithstanding any other provision of this License, for material you add to a covered work, you may (if authorized by the copyright holders of that material) supplement the terms of this License with terms:
115 |
116 | a) Disclaiming warranty or limiting liability differently from the terms of sections 15 and 16 of this License; or
117 | b) Requiring preservation of specified reasonable legal notices or author attributions in that material or in the Appropriate Legal Notices displayed by works containing it; or
118 | c) Prohibiting misrepresentation of the origin of that material, or requiring that modified versions of such material be marked in reasonable ways as different from the original version; or
119 | d) Limiting the use for publicity purposes of names of licensors or authors of the material; or
120 | e) Declining to grant rights under trademark law for use of some trade names, trademarks, or service marks; or
121 | f) Requiring indemnification of licensors and authors of that material by anyone who conveys the material (or modified versions of it) with contractual assumptions of liability to the recipient, for any liability that these contractual assumptions directly impose on those licensors and authors.
122 |
123 | All other non-permissive additional terms are considered “further restrictions” within the meaning of section 10. If the Program as you received it, or any part of it, contains a notice stating that it is governed by this License along with a term that is a further restriction, you may remove that term. If a license document contains a further restriction but permits relicensing or conveying under this License, you may add to a covered work material governed by the terms of that license document, provided that the further restriction does not survive such relicensing or conveying.
124 |
125 | If you add terms to a covered work in accord with this section, you must place, in the relevant source files, a statement of the additional terms that apply to those files, or a notice indicating where to find the applicable terms.
126 |
127 | Additional terms, permissive or non-permissive, may be stated in the form of a separately written license, or stated as exceptions; the above requirements apply either way.
128 | 8. Termination.
129 |
130 | You may not propagate or modify a covered work except as expressly provided under this License. Any attempt otherwise to propagate or modify it is void, and will automatically terminate your rights under this License (including any patent licenses granted under the third paragraph of section 11).
131 |
132 | However, if you cease all violation of this License, then your license from a particular copyright holder is reinstated (a) provisionally, unless and until the copyright holder explicitly and finally terminates your license, and (b) permanently, if the copyright holder fails to notify you of the violation by some reasonable means prior to 60 days after the cessation.
133 |
134 | Moreover, your license from a particular copyright holder is reinstated permanently if the copyright holder notifies you of the violation by some reasonable means, this is the first time you have received notice of violation of this License (for any work) from that copyright holder, and you cure the violation prior to 30 days after your receipt of the notice.
135 |
136 | Termination of your rights under this section does not terminate the licenses of parties who have received copies or rights from you under this License. If your rights have been terminated and not permanently reinstated, you do not qualify to receive new licenses for the same material under section 10.
137 | 9. Acceptance Not Required for Having Copies.
138 |
139 | You are not required to accept this License in order to receive or run a copy of the Program. Ancillary propagation of a covered work occurring solely as a consequence of using peer-to-peer transmission to receive a copy likewise does not require acceptance. However, nothing other than this License grants you permission to propagate or modify any covered work. These actions infringe copyright if you do not accept this License. Therefore, by modifying or propagating a covered work, you indicate your acceptance of this License to do so.
140 | 10. Automatic Licensing of Downstream Recipients.
141 |
142 | Each time you convey a covered work, the recipient automatically receives a license from the original licensors, to run, modify and propagate that work, subject to this License. You are not responsible for enforcing compliance by third parties with this License.
143 |
144 | An “entity transaction” is a transaction transferring control of an organization, or substantially all assets of one, or subdividing an organization, or merging organizations. If propagation of a covered work results from an entity transaction, each party to that transaction who receives a copy of the work also receives whatever licenses to the work the party's predecessor in interest had or could give under the previous paragraph, plus a right to possession of the Corresponding Source of the work from the predecessor in interest, if the predecessor has it or can get it with reasonable efforts.
145 |
146 | You may not impose any further restrictions on the exercise of the rights granted or affirmed under this License. For example, you may not impose a license fee, royalty, or other charge for exercise of rights granted under this License, and you may not initiate litigation (including a cross-claim or counterclaim in a lawsuit) alleging that any patent claim is infringed by making, using, selling, offering for sale, or importing the Program or any portion of it.
147 | 11. Patents.
148 |
149 | A “contributor” is a copyright holder who authorizes use under this License of the Program or a work on which the Program is based. The work thus licensed is called the contributor's “contributor version”.
150 |
151 | A contributor's “essential patent claims” are all patent claims owned or controlled by the contributor, whether already acquired or hereafter acquired, that would be infringed by some manner, permitted by this License, of making, using, or selling its contributor version, but do not include claims that would be infringed only as a consequence of further modification of the contributor version. For purposes of this definition, “control” includes the right to grant patent sublicenses in a manner consistent with the requirements of this License.
152 |
153 | Each contributor grants you a non-exclusive, worldwide, royalty-free patent license under the contributor's essential patent claims, to make, use, sell, offer for sale, import and otherwise run, modify and propagate the contents of its contributor version.
154 |
155 | In the following three paragraphs, a “patent license” is any express agreement or commitment, however denominated, not to enforce a patent (such as an express permission to practice a patent or covenant not to sue for patent infringement). To “grant” such a patent license to a party means to make such an agreement or commitment not to enforce a patent against the party.
156 |
157 | If you convey a covered work, knowingly relying on a patent license, and the Corresponding Source of the work is not available for anyone to copy, free of charge and under the terms of this License, through a publicly available network server or other readily accessible means, then you must either (1) cause the Corresponding Source to be so available, or (2) arrange to deprive yourself of the benefit of the patent license for this particular work, or (3) arrange, in a manner consistent with the requirements of this License, to extend the patent license to downstream recipients. “Knowingly relying” means you have actual knowledge that, but for the patent license, your conveying the covered work in a country, or your recipient's use of the covered work in a country, would infringe one or more identifiable patents in that country that you have reason to believe are valid.
158 |
159 | If, pursuant to or in connection with a single transaction or arrangement, you convey, or propagate by procuring conveyance of, a covered work, and grant a patent license to some of the parties receiving the covered work authorizing them to use, propagate, modify or convey a specific copy of the covered work, then the patent license you grant is automatically extended to all recipients of the covered work and works based on it.
160 |
161 | A patent license is “discriminatory” if it does not include within the scope of its coverage, prohibits the exercise of, or is conditioned on the non-exercise of one or more of the rights that are specifically granted under this License. You may not convey a covered work if you are a party to an arrangement with a third party that is in the business of distributing software, under which you make payment to the third party based on the extent of your activity of conveying the work, and under which the third party grants, to any of the parties who would receive the covered work from you, a discriminatory patent license (a) in connection with copies of the covered work conveyed by you (or copies made from those copies), or (b) primarily for and in connection with specific products or compilations that contain the covered work, unless you entered into that arrangement, or that patent license was granted, prior to 28 March 2007.
162 |
163 | Nothing in this License shall be construed as excluding or limiting any implied license or other defenses to infringement that may otherwise be available to you under applicable patent law.
164 | 12. No Surrender of Others' Freedom.
165 |
166 | If conditions are imposed on you (whether by court order, agreement or otherwise) that contradict the conditions of this License, they do not excuse you from the conditions of this License. If you cannot convey a covered work so as to satisfy simultaneously your obligations under this License and any other pertinent obligations, then as a consequence you may not convey it at all. For example, if you agree to terms that obligate you to collect a royalty for further conveying from those to whom you convey the Program, the only way you could satisfy both those terms and this License would be to refrain entirely from conveying the Program.
167 | 13. Use with the GNU Affero General Public License.
168 |
169 | Notwithstanding any other provision of this License, you have permission to link or combine any covered work with a work licensed under version 3 of the GNU Affero General Public License into a single combined work, and to convey the resulting work. The terms of this License will continue to apply to the part which is the covered work, but the special requirements of the GNU Affero General Public License, section 13, concerning interaction through a network will apply to the combination as such.
170 | 14. Revised Versions of this License.
171 |
172 | The Free Software Foundation may publish revised and/or new versions of the GNU General Public License from time to time. Such new versions will be similar in spirit to the present version, but may differ in detail to address new problems or concerns.
173 |
174 | Each version is given a distinguishing version number. If the Program specifies that a certain numbered version of the GNU General Public License “or any later version” applies to it, you have the option of following the terms and conditions either of that numbered version or of any later version published by the Free Software Foundation. If the Program does not specify a version number of the GNU General Public License, you may choose any version ever published by the Free Software Foundation.
175 |
176 | If the Program specifies that a proxy can decide which future versions of the GNU General Public License can be used, that proxy's public statement of acceptance of a version permanently authorizes you to choose that version for the Program.
177 |
178 | Later license versions may give you additional or different permissions. However, no additional obligations are imposed on any author or copyright holder as a result of your choosing to follow a later version.
179 | 15. Disclaimer of Warranty.
180 |
181 | THERE IS NO WARRANTY FOR THE PROGRAM, TO THE EXTENT PERMITTED BY APPLICABLE LAW. EXCEPT WHEN OTHERWISE STATED IN WRITING THE COPYRIGHT HOLDERS AND/OR OTHER PARTIES PROVIDE THE PROGRAM “AS IS” WITHOUT WARRANTY OF ANY KIND, EITHER EXPRESSED OR IMPLIED, INCLUDING, BUT NOT LIMITED TO, THE IMPLIED WARRANTIES OF MERCHANTABILITY AND FITNESS FOR A PARTICULAR PURPOSE. THE ENTIRE RISK AS TO THE QUALITY AND PERFORMANCE OF THE PROGRAM IS WITH YOU. SHOULD THE PROGRAM PROVE DEFECTIVE, YOU ASSUME THE COST OF ALL NECESSARY SERVICING, REPAIR OR CORRECTION.
182 | 16. Limitation of Liability.
183 |
184 | IN NO EVENT UNLESS REQUIRED BY APPLICABLE LAW OR AGREED TO IN WRITING WILL ANY COPYRIGHT HOLDER, OR ANY OTHER PARTY WHO MODIFIES AND/OR CONVEYS THE PROGRAM AS PERMITTED ABOVE, BE LIABLE TO YOU FOR DAMAGES, INCLUDING ANY GENERAL, SPECIAL, INCIDENTAL OR CONSEQUENTIAL DAMAGES ARISING OUT OF THE USE OR INABILITY TO USE THE PROGRAM (INCLUDING BUT NOT LIMITED TO LOSS OF DATA OR DATA BEING RENDERED INACCURATE OR LOSSES SUSTAINED BY YOU OR THIRD PARTIES OR A FAILURE OF THE PROGRAM TO OPERATE WITH ANY OTHER PROGRAMS), EVEN IF SUCH HOLDER OR OTHER PARTY HAS BEEN ADVISED OF THE POSSIBILITY OF SUCH DAMAGES.
185 | 17. Interpretation of Sections 15 and 16.
186 |
187 | If the disclaimer of warranty and limitation of liability provided above cannot be given local legal effect according to their terms, reviewing courts shall apply local law that most closely approximates an absolute waiver of all civil liability in connection with the Program, unless a warranty or assumption of liability accompanies a copy of the Program in return for a fee.
188 |
189 | END OF TERMS AND CONDITIONS
190 | How to Apply These Terms to Your New Programs
191 |
192 | If you develop a new program, and you want it to be of the greatest possible use to the public, the best way to achieve this is to make it free software which everyone can redistribute and change under these terms.
193 |
194 | To do so, attach the following notices to the program. It is safest to attach them to the start of each source file to most effectively state the exclusion of warranty; and each file should have at least the “copyright” line and a pointer to where the full notice is found.
195 |
196 |
197 | Copyright (C)
198 |
199 | This program is free software: you can redistribute it and/or modify
200 | it under the terms of the GNU General Public License as published by
201 | the Free Software Foundation, either version 3 of the License, or
202 | (at your option) any later version.
203 |
204 | This program is distributed in the hope that it will be useful,
205 | but WITHOUT ANY WARRANTY; without even the implied warranty of
206 | MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE. See the
207 | GNU General Public License for more details.
208 |
209 | You should have received a copy of the GNU General Public License
210 | along with this program. If not, see .
211 |
212 | Also add information on how to contact you by electronic and paper mail.
213 |
214 | If the program does terminal interaction, make it output a short notice like this when it starts in an interactive mode:
215 |
216 | Copyright (C)
217 | This program comes with ABSOLUTELY NO WARRANTY; for details type `show w'.
218 | This is free software, and you are welcome to redistribute it
219 | under certain conditions; type `show c' for details.
220 |
221 | The hypothetical commands `show w' and `show c' should show the appropriate parts of the General Public License. Of course, your program's commands might be different; for a GUI interface, you would use an “about box”.
222 |
223 | You should also get your employer (if you work as a programmer) or school, if any, to sign a “copyright disclaimer” for the program, if necessary. For more information on this, and how to apply and follow the GNU GPL, see .
224 |
225 | The GNU General Public License does not permit incorporating your program into proprietary programs. If your program is a subroutine library, you may consider it more useful to permit linking proprietary applications with the library. If this is what you want to do, use the GNU Lesser General Public License instead of this License. But first, please read .
226 |
--------------------------------------------------------------------------------
/fiziko.tex:
--------------------------------------------------------------------------------
1 | \documentclass{ltxdoc}
2 |
3 | \usepackage{luamplib, listings, bxtexlogo, ccicons}
4 | \everymplib{verbatimtex \leavevmode etex; input fiziko.mp; beginfig(1);}
5 | \everyendmplib{endfig;}
6 |
7 | \lstset{
8 | language=MetaPost,
9 | numbers=left,
10 | numberstyle=\tiny,
11 | basicstyle=\scriptsize
12 | }
13 |
14 | \author{Sergey Slyusarev}
15 | \title{``fiziko'' v. 0.2.1 package for \METAPOST}
16 |
17 | \begin{document}
18 | \maketitle
19 |
20 | \begin{abstract}
21 | This document describes a bunch of macros provided by ``fiziko'' library for \METAPOST.
22 | \end{abstract}
23 |
24 | \begin{centering}
25 |
26 | This document is distributed under CC-BY-SA 4.0 license
27 |
28 | \ccbysa
29 |
30 | https://github.com/jemmybutton/fiziko
31 |
32 | \end{centering}
33 |
34 | \section{Introduction}
35 | This \METAPOST\ library was initially written to automate some elements of black and white illustrations for a physics textbook. First and foremost it provides functions to draw things like lines of variable width, shaded spheres and tubes of different kinds, which can be used to produce images of a variety of objects. The library also contains functions to draw some objects constructed from these primitives.
36 |
37 | \section{Usage}
38 | Simply include this in the beginning of your \METAPOST\ document:
39 |
40 | \begin{lstlisting}
41 | input fiziko.mp
42 | \end{lstlisting}
43 |
44 | \section{Global variables}
45 | A few global variables control different aspects of the behavior of the provided macros. Not all possible values are meaningful and some will definitely result in ugly pictures or errors.
46 |
47 | \subsection{minStrokeWidth}
48 | This variable controls minimal thickness of lines that are used for shading. Below this value lines are not getting thinner, but become dashed instead, maintaining roughly the same amount of ink per unit length as a thinner line would take. Default value is one fifth of a point. There are several things that depend on this value, so it's convenient to change it using a macro:
49 |
50 | \begin{lstlisting}
51 | defineMinStrokeWidth(1/2pt);
52 | \end{lstlisting}
53 |
54 | \subsection{lightDirection}
55 | This variable controls direction from which light falls on shaded objects. It's of \texttt{pair} type and is set in radians. Default direction is top-left:
56 | \begin{lstlisting}
57 | lightDirection := (-1/8pi, 1/8pi);
58 | \end{lstlisting}
59 |
60 |
61 | \subsection{invertedLight}
62 | This variable determines whether the light is inverted. This comes in handy when you need to have your shaded objects white on black. It's of \texttt{boolean} type. Default value is false:
63 |
64 | \begin{lstlisting}
65 | draw sphere.s(1cm);
66 | invertedLight := true;
67 | fill ((unitsquare shifted (-1/2,-1/2)) scaled 3/2cm) shifted (3/2cm, 0) withcolor black;
68 | draw sphere.s(1cm) shifted (3/2cm, 0) withcolor white;
69 | \end{lstlisting}
70 |
71 | \begin{mplibcode}
72 | draw sphere.c(1cm);
73 | invertedLight := true;
74 | fill ((unitsquare shifted (-1/2,-1/2)) scaled 3/2cm) shifted (3/2cm, 0) withcolor black;
75 | draw sphere.c(1cm) shifted (3/2cm, 0) withcolor white;
76 | invertedLight := false;
77 | \end{mplibcode}
78 |
79 | \section{``Lower level'' macros}
80 | Currently, algorithms are quite stupid and will produce decent results only in certain simple circumstances.
81 |
82 | \subsection{offsetPath (\emph{path})(\emph{offset function})}
83 | This macro returns offset path (of type \texttt{path}) to a current path with a distance from the original path controlled by some arbitrary function; typically, it is a function of path length, set as either \texttt{offsetPathTime} or \texttt{offsetPathLength}. Former is simply \texttt{time} on current path and changes from 0 to \texttt{length(path)}, and latter changes from 0 to 1 over the path \texttt{arctime} (as a function of \texttt{arclength}).
84 |
85 | \begin{lstlisting}
86 | path p, q;
87 | p := (0,0){dir(30)}..(5cm, 0)..{dir(30)}(10cm, 0);
88 | q := offsetPath(p)(1cm*sin(offsetPathLength*pi));
89 | draw p;
90 | draw q dashed evenly;
91 | \end{lstlisting}
92 |
93 | \begin{mplibcode}
94 | path p, q;
95 | p := (0,0){dir(30)}..(5cm, 0)..{dir(30)}(10cm, 0);
96 | q := offsetPath(p)(1cm*sin(offsetPathLength*pi));
97 | draw p;
98 | draw q dashed evenly;
99 | \end{mplibcode}
100 |
101 | \subsection{brush (\emph{path})(\emph{offset function})}
102 | This macro returns a \texttt{picture} of a line of variable width along given path, which is controlled by some arbitrary function, analogous to \texttt{offsetPath}. If line is getting thinner than \texttt{minStrokeWith}, it is drawn dashed.
103 |
104 | \begin{lstlisting}
105 | path p;
106 | p := (0,0){dir(30)}..(5cm, 0)..{dir(30)}(10cm, 0);
107 | draw brush (p)(2minStrokeWidth*sin(offsetPathLength*pi));
108 | \end{lstlisting}
109 |
110 | \begin{mplibcode}
111 | path p;
112 | p := (0,0){dir(30)}..(5cm, 0)..{dir(30)}(10cm, 0);
113 | draw brush (p)(2minStrokeWidth*sin(offsetPathLength*pi));
114 | \end{mplibcode}
115 |
116 | \subsection{sphere.c (\emph{diameter})}
117 | This macro returns a \texttt{picture} of a sphere with specified diameter shaded with concentric strokes. Strokes are arranged to fit those of \texttt{tube.l}.
118 |
119 | \begin{lstlisting}
120 | for i := 1 step 1 until 6:
121 | draw sphere.c(i*1/4cm) shifted (1/2cm*(i*(i+1))/2, 0);
122 | endfor;
123 | \end{lstlisting}
124 |
125 | \begin{mplibcode}
126 | for i := 1 step 1 until 6:
127 | draw sphere.c(i*1/4cm) shifted (1/2cm*(i*(i+1))/2, 0);
128 | endfor;
129 | \end{mplibcode}
130 |
131 | \subsection{sphere.s (\emph{diameter})}
132 | This macro returns a \texttt{picture} of a sphere with specified diameter shaded with stipples.
133 |
134 | \begin{lstlisting}
135 | for i := 1 step 1 until 6:
136 | draw sphere.s(i*1/4cm) shifted (1/2cm*(i*(i+1))/2, 0);
137 | endfor;
138 | \end{lstlisting}
139 |
140 | \begin{mplibcode}
141 | for i := 1 step 1 until 6:
142 | draw sphere.s(i*1/4cm) shifted (1/2cm*(i*(i+1))/2, 0);
143 | endfor;
144 | \end{mplibcode}
145 |
146 | \subsection{sphereLat (\emph{diameter, angle})}
147 | This macro returns a \texttt{picture} of a shaded sphere with specified diameter. Unlike \texttt{sphere.c} macro, this one draws latitudinal strokes around axis rotated at specified \texttt{angle}.
148 |
149 | \begin{lstlisting}
150 | for i := 1 step 1 until 6:
151 | draw sphereLat(i*1/4cm, -90 + i*30)
152 | shifted (1/2cm*(i*(i+1))/2, 0);
153 | endfor;
154 | \end{lstlisting}
155 |
156 | \begin{mplibcode}
157 | for i := 1 step 1 until 6:
158 | draw sphereLat(i*1/4cm, -90 + i*30)
159 | shifted (1/2cm*(i*(i+1))/2, 0);
160 | endfor;
161 | \end{mplibcode}
162 |
163 | \subsection{tube.l (\emph{path})(\emph{offset function})}
164 | This macro returns a \texttt{picture} of a shaded ``tube'' of a variable width along a given path, which is controlled by some arbitrary function, analogous to \texttt{offsetPath}. ``Tube'' drawn by this macro is shaded be longitudal strokes. Once tube is generated, you can call \texttt{tubeOutline} path global variable, if you need one.
165 |
166 | \begin{lstlisting}
167 | path p;
168 | p := (0,0){dir(30)}..(5cm, 0)..{dir(30)}(10cm, 0);
169 | draw tube.l (p)(1/2cm*sin(offsetPathLength*pi));
170 | \end{lstlisting}
171 |
172 | \begin{mplibcode}
173 | path p;
174 | p := (0,0){dir(30)}..(5cm, 0)..{dir(30)}(10cm, 0);
175 | draw tube.l (p)(1/2cm*sin(offsetPathLength*pi));
176 | \end{mplibcode}
177 |
178 | \subsection{tube.t (\emph{path})(\emph{offset function})}
179 | This macro returns a \texttt{picture} of a shaded ``tube'' of variable width along given path, which is controlled by some arbitrary function, analogous to \texttt{offsetPath}. ``Tube'' drawn by this macro is shaded be transverse strokes. Once tube is generated, you can call \texttt{tubeOutline} path global variable, if you need one.
180 |
181 | \begin{lstlisting}
182 | path p;
183 | p := (0,0){dir(30)}..(5cm, 0)..{dir(30)}(10cm, 0);
184 | draw tube.t (p)(1/2cm*sin(offsetPathLength*pi));
185 | \end{lstlisting}
186 |
187 | \begin{mplibcode}
188 | path p;
189 | p := (0,0){dir(30)}..(5cm, 0)..{dir(30)}(10cm, 0);
190 | draw tube.t (p)(1/2cm*sin(offsetPathLength*pi));
191 | \end{mplibcode}
192 |
193 | \subsection{tube.s (\emph{path})(\emph{offset function})}
194 | This macro returns a \texttt{picture} of a shaded ``tube'' of variable width along given path, which is controlled by some arbitrary function, analogous to \texttt{offsetPath}. ``Tube'' drawn by this macro is shaded with stipples. Once tube is generated, you can call \texttt{tubeOutline} path global variable, if you need one.
195 |
196 | \begin{lstlisting}
197 | path p;
198 | p := (0,0){dir(30)}..(5cm, 0)..{dir(30)}(10cm, 0);
199 | draw tube.s (p)(1/2cm*sin(offsetPathLength*pi));
200 | \end{lstlisting}
201 |
202 | \begin{mplibcode}
203 | path p;
204 | p := (0,0){dir(30)}..(5cm, 0)..{dir(30)}(10cm, 0);
205 | draw tube.s (p)(1/2cm*sin(offsetPathLength*pi));
206 | \end{mplibcode}
207 |
208 | \subsection{tube.e (\emph{path})(\emph{offset function})}
209 | This macro returns the outline of a tube as a path.
210 |
211 | \section{``Higher level'' macros}
212 | Using macros described in the previous section it is possible to construct more complex images. Macros for drawing some often used images are present in this package.
213 |
214 | \subsection{eye (\emph{angle})}
215 | This macro returns a \texttt{picture} of an eye pointed at the direction \texttt{angle} (in degrees). Eye size is controlled by a global variable \texttt{eyescale}, which has default value of \texttt{eyescale := 1/2cm;}.
216 |
217 | \begin{lstlisting}
218 | save eyescale;
219 | for i := 1 step 1 until 6:
220 | eyescale := 1/6cm*i;
221 | draw eye(i*60) shifted (1/2cm*(i*(i+1))/2, 0);
222 | endfor;
223 | \end{lstlisting}
224 |
225 | \begin{mplibcode}
226 | save eyescale;
227 | for i := 1 step 1 until 6:
228 | eyescale := 1/6cm*i;
229 | draw eye(i*60) shifted (1/2cm*(i*(i+1))/2, 0);
230 | endfor;
231 | \end{mplibcode}
232 |
233 | \subsection{pulley (\emph{diameter, angle})}
234 | This macro returns a \texttt{picture} of a pulley with specified \texttt{diameter} and its support pointed at the direction \texttt{angle} (in degrees). Note that pulley's support protrudes from its center by \texttt{pulleySupportSize*diameter} and by default \texttt{pulleySupportSize} = 3/2. Once pulley is generated, you can call \texttt{pulleyOutline} path global variable, if you need one.
235 |
236 | \begin{lstlisting}
237 | draw (-1/8cm, 0)--(12cm, 0);
238 | for i := 1 step 1 until 6:
239 | r := 1/7cm*i;
240 | draw image(
241 | draw pulley(2r, 0) shifted (0, -4/3r);
242 | draw (r, -4/3r) -- (r, -2cm);
243 | drawarrow (-r, -4/3r) -- (-r, -2cm);
244 | ) shifted (1/2cm*(i*(i+1))/2, 0);
245 | endfor;
246 | \end{lstlisting}
247 |
248 | \noindent\begin{mplibcode}
249 | draw (-1/8cm, 0)--(12cm, 0);
250 | for i := 1 step 1 until 6:
251 | r := 1/7cm*i;
252 | draw image(
253 | draw pulley(2r, 0) shifted (0, -4/3r);
254 | draw (r, -4/3r) -- (r, -2cm);
255 | drawarrow (-r, -4/3r) -- (-r, -2cm);
256 | ) shifted (1/2cm*(i*(i+1))/2, 0);
257 | endfor;
258 | \end{mplibcode}
259 |
260 | \subsection{pulleyWheel (\emph{diameter})}
261 | This macro returns a \texttt{picture} of a pulley wheel with specified \texttt{diameter}.
262 |
263 | \begin{lstlisting}
264 | for i := 1 step 1 until 6:
265 | r := 1/7cm*i;
266 | draw image(
267 | draw pulleyWheel(2r);
268 | draw (r, 0) -- (r, 1cm);
269 | drawarrow (-r, 0) -- (-r, 1cm);
270 | ) shifted (1/2cm*(i*(i+1))/2, 0);
271 | endfor;
272 | \end{lstlisting}
273 |
274 | \begin{mplibcode}
275 | for i := 1 step 1 until 6:
276 | r := 1/7cm*i;
277 | draw image(
278 | draw pulleyWheel(2r);
279 | draw (r, 0) -- (r, 1cm);
280 | drawarrow (-r, 0) -- (-r, 1cm);
281 | ) shifted (1/2cm*(i*(i+1))/2, 0);
282 | endfor;
283 | \end{mplibcode}
284 |
285 | \subsection{wheel (\emph{diameter, angle})}
286 | This macro returns a \texttt{picture} of a wheel with specified \texttt{diameter} and its support pointed at the direction \texttt{angle} (in degrees).
287 |
288 | \begin{lstlisting}
289 | draw (-1/8cm, 0)--(12cm, 0);
290 | for i := 1 step 1 until 6:
291 | r := 1/7cm*i;
292 | draw wheel(2r, 0) shifted (0, -r) shifted (1/2cm*(i*(i+1))/2, 0);
293 | endfor;
294 | \end{lstlisting}
295 |
296 |
297 | \noindent\begin{mplibcode}
298 | draw (-1/8cm, 0)--(12cm, 0);
299 | for i := 1 step 1 until 6:
300 | r := 1/7cm*i;
301 | draw wheel(2r, 0) shifted (0, -r) shifted (1/2cm*(i*(i+1))/2, 0);
302 | endfor;
303 | \end{mplibcode}
304 |
305 |
306 | \subsection{weight.s (\emph{height})}
307 | This macro returns a \texttt{picture} of a weight of a specific \texttt{height} that is standing on the point \texttt{(0, 0)}.
308 |
309 | \begin{lstlisting}
310 | for i := 1 step 1 until 6:
311 | draw weight.s(1/4cm + i*1/4cm) shifted (1/2cm*(i*(i+1))/2, 0);
312 | endfor;
313 | draw (-1/8cm, 0)--(12cm, 0);
314 | \end{lstlisting}
315 |
316 | \noindent\begin{mplibcode}
317 | for i := 1 step 1 until 6:
318 | draw weight.s(1/4cm + i*1/4cm) shifted (1/2cm*(i*(i+1))/2, 0);
319 | endfor;
320 | draw (-1/8cm, 0)--(12cm, 0);
321 | \end{mplibcode}
322 |
323 | \subsection{weight.h (\emph{height})}
324 | This macro returns a \texttt{picture} of a weight of a specific \texttt{height} that is is hanging from the point \texttt{(0, 0)}.
325 |
326 | \begin{lstlisting}
327 | for i := 1 step 1 until 6:
328 | draw weight.h(1/4cm + i*1/4cm) shifted (1/2cm*(i*(i+1))/2, 0);
329 | endfor;
330 | draw (12cm, 0)--(-1/8cm, 0);
331 | \end{lstlisting}
332 |
333 | \noindent\begin{mplibcode}
334 | for i := 1 step 1 until 6:
335 | draw weight.h(1/4cm + i*1/4cm) shifted (1/2cm*(i*(i+1))/2, 0);
336 | endfor;
337 | draw (12cm, 0)--(-1/8cm, 0);
338 | \end{mplibcode}
339 |
340 |
341 | \subsection{spring (\emph{point a, point b, number of steps})}
342 | This macro returns a \texttt{picture} of a spring stretched between points \texttt{a} and \texttt{b} (of type \texttt{pair}), with specified \texttt{number of steps}. Spring width is controlled by global variable \texttt{springwidth} with the default value \texttt{springwidth := 1/8cm;}.
343 |
344 | \begin{lstlisting}
345 | pair a, b;
346 | a := (0, 0);
347 | for i := 1 step 1 until 6:
348 | springwidth := 1/16cm + i*1/48cm;
349 | b := (i*1/3cm, - i*1/5cm);
350 | draw spring (a, b, 10) shifted (2/5cm*(i*(i+1))/2, 0);
351 | endfor;
352 | \end{lstlisting}
353 |
354 | \begin{mplibcode}
355 | pair a, b;
356 | a := (0, 0);
357 | for i := 1 step 1 until 6:
358 | springwidth := 1/16cm + i*1/48cm;
359 | b := (i*1/3cm, - i*1/5cm);
360 | draw spring (a, b, 10) shifted (2/5cm*(i*(i+1))/2, 0);
361 | endfor;
362 | \end{mplibcode}
363 |
364 | \subsection{solidSurface (\emph{path})}
365 | This macro returns a \texttt{picture} of a solid surface on the right side of a given \texttt{path}.
366 |
367 | \begin{lstlisting}
368 | path p;
369 | p := (0,0){dir(30)}..(5cm, 0)..{dir(30)}(10cm, 0);
370 | draw solidSurface(p);
371 | \end{lstlisting}
372 |
373 | \begin{mplibcode}
374 | path p;
375 | p := (0,0){dir(30)}..(5cm, 0)..{dir(30)}(10cm, 0);
376 | draw solidSurface(p);
377 | \end{mplibcode}
378 |
379 | \subsection{solid (\emph{path, angle, type})}
380 | Fills given \texttt{path} with strokes of specific type at a given \texttt{angle}. \texttt{type} can be 0 (``solid'' strokes) and 1 (``glass'' strokes).
381 |
382 | \begin{lstlisting}
383 | path p[];
384 | p1 := unitsquare scaled 2cm;
385 | p2 := p1 shifted (4cm, 0);
386 | draw solid(p1, 45, 0);
387 | draw solid(p2, -45, 1);
388 | \end{lstlisting}
389 |
390 | \begin{mplibcode}
391 | path p[];
392 | p1 := unitsquare scaled 2cm;
393 | p2 := p1 shifted (4cm, 0);
394 | draw solid(p1, 45, 0);
395 | draw solid(p2, -45, 1);
396 | \end{mplibcode}
397 |
398 | \subsection{woodBlock (\emph{width, height})}
399 | Returns a \texttt{picture} of a rectangular block of wood with its bottom-left corner in the origin.
400 |
401 | \begin{lstlisting}
402 | draw woodBlock(10cm, 1/2cm);
403 | \end{lstlisting}
404 |
405 | \begin{mplibcode}
406 | draw woodBlock(10cm, 1/2cm);
407 | \end{mplibcode}
408 |
409 | \subsection{woodenThing (\emph{path, angle})}
410 | Returns a \texttt{picture} of a wood texture at a given \texttt{angle} fitted into a given \texttt{path}.
411 |
412 | \begin{lstlisting}
413 | path p, q;
414 | p := dir(-60) scaled 1/2 -- dir(90) scaled 2/3 -- dir (-120) scaled 3/5 -- cycle;
415 | for i := 1 step 1 until 6:
416 | q := (p scaled 3/2cm) rotated (i*60);
417 | draw woodenThing (q, i*60) shifted (2cm*i, 0);
418 | endfor;
419 | \end{lstlisting}
420 |
421 | \begin{mplibcode}
422 | path p, q;
423 | p := dir(-60) scaled 1/2 -- dir(90) scaled 2/3 -- dir (-120) scaled 3/5 -- cycle;
424 | for i := 1 step 1 until 6:
425 | q := (p scaled 3/2cm) rotated (i*60);
426 | draw woodenThing (q, i*60) shifted (2cm*i, 0);
427 | endfor;
428 | \end{mplibcode}
429 |
430 | \subsection{woodenSurface (\emph{path})}
431 |
432 | Returns a \texttt{picture} similar to that of a solid surface on the right side of a given \texttt{path}, but with wood texture .
433 |
434 | \begin{lstlisting}
435 | path p;
436 | p := (0,0){dir(30)}..(5cm, 0)..{dir(30)}(10cm, 0);
437 | draw woodenSurface(p);
438 | \end{lstlisting}
439 |
440 | \begin{mplibcode}
441 | path p;
442 | p := (0,0){dir(30)}..(5cm, 0)..{dir(30)}(10cm, 0);
443 | draw woodenSurface(p);
444 | \end{mplibcode}
445 |
446 | \subsection{globe (\emph{radius, longitude, latitude})}
447 | This macro returns a \texttt{picture} of the globe of specified \texttt{radius} centered at specific \texttt{longitude} and \texttt{latitude};
448 |
449 | \begin{lstlisting}
450 | for i := 1 step 1 until 6:
451 | draw globe(i*1/4cm, i*60, -90 + i*30)
452 | shifted (1/2cm*(i*(i+1))/2, 0);
453 | endfor;
454 | \end{lstlisting}
455 |
456 | \begin{mplibcode}
457 | for i := 1 step 1 until 6:
458 | draw globe(i*1/4cm, i*60, -90 + i*30)
459 | shifted (1/2cm*(i*(i+1))/2, 0);
460 | endfor;
461 | \end{mplibcode}
462 |
463 | \subsection{Knots}
464 | There are two macros to handle knot drawing: \texttt{addStrandToKnot} and \texttt{knot\-From\-Strands}. Currently the algorithm is not especially stable.
465 |
466 | % \subsubsection{initKnot (\emph{knotName})}
467 | % This macro creates an empty knot with no strands named \texttt{knotName} and returns nothing. Useful if a knot is redefined with the same name repeatedly.
468 |
469 | \subsubsection{addStrandToKnot (\emph{knotName}) (\emph{path, ropeWidth, ropeType, intersectionOrder})}
470 | This macro adds a strand to knot named \texttt{knotName} and returns nothing. Strand follows the given \texttt{path} and has a given \texttt{ropeWidth}. \texttt{ropeType} can be \texttt{"l"}, \texttt{"t"} (as in \texttt{tube.l} and \texttt{tube.t}) or \texttt{"e"} (for an unshaded strand). \texttt{intersectionOrder} is a string of comma separated numbers which represent a ``layer'' to which intersections along the strand go.
471 |
472 | \subsubsection{knotFromStrands (\emph{knotName})}
473 | This macro returns a picture of a knot with a given \texttt{knotName}.
474 |
475 | \begin{lstlisting}
476 | path p[];
477 | p1 := (dir(90)*4/3cm) {dir(0)} .. tension 3/2
478 | .. (dir(90 + 120)*4/3cm){dir(90 + 30)} .. tension 3/2
479 | .. (dir(90 - 120)*4/3cm){dir(-90 - 30)} .. tension 3/2
480 | .. cycle;
481 | p2 := (fullcircle scaled 3cm) shifted (0, -3/2cm);
482 | p3 := (fullcircle scaled 4cm);
483 | addStrandToKnot (theknot) (p1 shifted (4cm, -4cm), 1/5cm, "l",
484 | "-1,1,-1,1,-1,1,-1,1,-1");
485 | addStrandToKnot (theknot) (p2 shifted (4cm, -4cm), 1/6cm, "s",
486 | "");
487 | addStrandToKnot (theknot) (p3 shifted (4cm, -4cm), 1/7cm, "e",
488 | "-1,1");
489 | draw knotFromStrands (theknot);
490 | \end{lstlisting}
491 |
492 | \begin{mplibcode}
493 | path p[];
494 | p1 := (dir(90)*4/3cm) {dir(0)} .. tension 3/2
495 | .. (dir(90 + 120)*4/3cm){dir(90 + 30)} .. tension 3/2
496 | .. (dir(90 - 120)*4/3cm){dir(-90 - 30)} .. tension 3/2
497 | .. cycle;
498 | p2 := (fullcircle scaled 3cm) shifted (0, -3/2cm);
499 | p3 := (fullcircle scaled 4cm);
500 | addStrandToKnot (theknot) (p1 shifted (4cm, -4cm), 1/5cm, "l",
501 | "-1,1,-1,1,-1,1,-1,1,-1");
502 | addStrandToKnot (theknot) (p2 shifted (4cm, -4cm), 1/6cm, "s",
503 | "");
504 | addStrandToKnot (theknot) (p3 shifted (4cm, -4cm), 1/7cm, "e",
505 | "-1,1");
506 | draw knotFromStrands (theknot);
507 | \end{mplibcode}
508 |
509 | \subsection{Other 3D contraptions}
510 | Some macros can be used to shade 3D polygons. Currently only flat surfaces re supported
511 |
512 | \subsubsection{flatSurface\emph{\#@}(\emph{surface outline path, normal vector, hatch angle})}
513 | This macro returns a \texttt{picture} of a flat surface with the specified \texttt{surface outline path} with the given \texttt{normal vector}, illuminated from the direction determined by \texttt{lightDirection} and with hatches aligned at the andle \texttt{hatch angle}. If \texttt{\#@} is \texttt{".hatches"} then the surface is shaded with hatches, if it's \texttt{".stipples"}, then the surface is shaded with stipples.
514 |
515 | \begin{mplibcode}
516 | path p[];
517 | p1 := unitsquare xscaled 1cm yscaled 2cm;
518 | p2 := p1 shifted (1cm, 0);
519 | draw flatSurface.hatches(p1, (-1,0,1), 45);
520 | draw flatSurface.hatches(p2, (1,0,1), 45);
521 | draw p1; draw p2;
522 | \end{mplibcode}
523 |
524 | \section{Other macros}
525 | Some macros that are not directly related to drawing are listed below
526 |
527 | \subsection{refractionPath (\emph{initial ray, shape, refraction coefficient})}
528 | This macro returns a \texttt{path} that represent refraction of some \texttt{ray} (any variable of type \texttt{path}, point next to last in a given path is considered a source of a ``ray'', and last point determines its direction) through some \texttt{shape} with given \texttt{refraction coefficient}. When appropriate, the ``ray'' is fully internally reflected.
529 |
530 | Setting \texttt{refraction coefficient} to 0 results in reflection instead of refraction in all cases.
531 |
532 | \begin{lstlisting}
533 | path r, p;
534 | p := fullcircle scaled 2.1cm;
535 | draw p;
536 | for i:= 1cm step -1/4cm until -1cm:
537 | r := (-4cm, i) -- (-1cm, i);
538 | draw refractionPath(r, p, 1.5);
539 | endfor;
540 | \end{lstlisting}
541 |
542 | \begin{mplibcode}
543 | path r, p;
544 | p := fullcircle scaled 2.1cm;
545 | draw p;
546 | for i:= 1cm step -1/4cm until -1cm:
547 | r := (-4cm, i) -- (-1cm, i);
548 | draw refractionPath(r, p, 1.5);
549 | endfor;
550 | \end{mplibcode}
551 |
552 |
553 | \subsection{lens (\emph{(left radius, right radius), thickness, diameter, units})}
554 | This macro returns a \texttt{path} that represent a section of a lens with given radii of curvature (positive value for convex, negative --- for concave), thickness (i. e. distance benween sides' centers) and diameter (i. e. height) in given arbitrary units.
555 |
556 | \begin{lstlisting}
557 | draw lens((5, 10), 1/2, 2, cm);
558 | draw lens((-10, -5), 1/4, 2, cm) shifted (2cm, 0);
559 | draw lens((infinity, 7), 1/4, 2, cm) shifted (4cm, 0);
560 | \end{lstlisting}
561 |
562 | \begin{mplibcode}
563 | draw lens((5, 10), 1/2, 2, cm);
564 | draw lens((-10, -5), 1/4, 2, cm) shifted (2cm, 0);
565 | draw lens((infinity, 7), 1/4, 2, cm) shifted (4cm, 0);
566 | \end{mplibcode}
567 |
568 | \section{Auxilary macros}
569 | Some macros that not related to physical problems at all are listed below.
570 |
571 | \subsection{\emph{picture} maskedWith \emph{path}}
572 | This macro masks a part of a \texttt{picture} with closed \texttt{path}. In fact this is inversion of \METAPOST's built-in \texttt{clip} but, in contrast to the latter, it does not modify original image. Note that it requires that counter-clockwise \texttt{path} to work properly.
573 |
574 | \subsection{\emph{path} firstIntersectionTimes \emph{path}}
575 | This macro is similar to \METAPOST's \texttt{intersectiontimes} but it returns intersection times with smallest time on first path.
576 |
577 | \subsection{pathSubdivide \emph{path, n}}
578 | This macro returns original \texttt{path} with \texttt{n}-times more points.
579 |
580 | \subsection{drawmidarrow (\emph{path})}
581 | Draws \texttt{path} with arrows in the middles of segments with length no less than \texttt{midArrowLimit} (another global variable, 1cm by default).
582 |
583 | \subsection{markAngle (\emph{point a, point o, point b})(\emph{text})}
584 | This macro marks an angle \texttt{aob} (counter-clockwise) with some \texttt{text}
585 |
586 | \begin{lstlisting}
587 | pair a, o, b;
588 | for i:= 30 step 60 until 390:
589 | o := (10cm*(i/360), 0);
590 | a := dir(i/2)*4/3cm shifted o;
591 | b := dir(i)*4/3cm shifted o;
592 | draw (a--o--b);
593 | markAngle(a, o, b)(btex $\alpha$ etex);
594 | endfor;
595 | \end{lstlisting}
596 |
597 | \begin{mplibcode}
598 | pair a, o, b;
599 | for i:= 30 step 60 until 390:
600 | o := (10cm*(i/360), 0);
601 | a := dir(i/2)*4/3cm shifted o;
602 | b := dir(i)*4/3cm shifted o;
603 | draw (a--o--b);
604 | markAngle(a, o, b)(btex $\alpha$ etex);
605 | endfor;
606 | \end{mplibcode}
607 |
608 |
609 | \section{Some examples}
610 |
611 | \subsection{Gregory-Maksutov type telescope}
612 | Lines 3--11 define parameters of lenses and mirrors\footnote{Taken from here http://www.google.ru/patents/US2701983}. Lines 12--16 generate lenses. On line 20 shape of prism is defined. Line 22 cuts part of the rear mirror. Line 26 describes mirror part of the front lens. On lines 31--33 all the glass parts are drawn. On lines 34--36 all the mirror ones. On lines 39--44 rays are traced through all system in order specified in loop on line 41. Lines 49--56 are about the telescope frame.
613 | \begin{lstlisting}
614 | path p[], q[], axis[], f[]; pair o;
615 | u := 6mm;
616 | r1 := -36.979; r2 := -r1; t1 := 0.7; n1 := 1.517; d1 := 5;
617 | l1 := 8.182;
618 | r3 := -11.657; r4 := r3; t2 := 0.2; n2 := n1; d2 := 3/2;
619 | l2 := 0.4;
620 | r5 := -30.433; r6 := 9.598; t3 := 0.39; n3 := 1.621; d3 := d2;
621 | l3 := 0.828;
622 | r7 := -35.512; r8 := infinity; t4 := 0.7; n4 := 0; d4 := d1;
623 | l4 := 5.272;
624 | ll0 := 0;
625 | for i := 1 upto 4:
626 | ll[i] := ll[i-1] + t[i] + l[i];
627 | p[i] := lens ((r[i*2 - 1], r[i*2]), t[i], d[i], u)
628 | shifted (ll[i-1]*u, 0);
629 | endfor;
630 | axis1 := (0, 0) -- (ll4*u, 0);
631 | axis2 := reverse(axis1);
632 | ll5 := ll4 - 1/2l4;
633 | p5 := ((-1,-1) -- (1,1) -- (-1,1) -- cycle)
634 | scaled (1/2d2*u) shifted (ll5*u, 0);
635 | p6 := (subpath
636 | (ypart((axis1 shifted (0, 1/2d2*u)) firstIntersectionTimes p4),
637 | ypart((axis2 shifted (0, 1/2d2*u)) firstIntersectionTimes p4))
638 | of p4) -- cycle;
639 | p7 := (subpath
640 | (ypart((axis2 shifted (0, 3/4d2*u)) firstIntersectionTimes p1),
641 | ypart((axis2 shifted (0, -3/4d2*u)) firstIntersectionTimes p1))
642 | of p1);
643 | p7 := p7 -- (reverse(p7) shifted ((-1/3t1)*u, 0)) -- cycle;
644 | for i := 1, 2, 3, 5:
645 | draw p[i] withpen thickpen; draw solid (p[i], 45, 1);
646 | endfor;
647 | draw solid (p7, -45, 0);
648 | draw p6 withpen thickpen; draw solid (p6, -45, 0);
649 | draw p6 yscaled -1 withpen thickpen;
650 | draw solid (p6 yscaled -1, -45, 0);
651 | n7 := 0; n5 := n1;
652 | for i := 0, 1:
653 | q[i] := (-3/2u, -2u + i*4u) -- (16u, -2u + i*4u);
654 | for j = 1, 4, 7, 2, 3, 5:
655 | q[i] := refractionPath(q[i], p[j], n[j]);
656 | endfor;
657 | endfor;
658 | o := whatever[point length(q0) of q0, point length(q0)-1 of q0]
659 | = whatever[point length(q1) of q1, point length(q1)-1 of q1];
660 | for i := 0, 1: drawmidarrow (q[i] -- o) withpen thinpen; endfor;
661 | draw eye(-91) shifted o shifted (0, u);
662 | f1 := (-1/4u, 1/2d1*u) -- ((ll3 + t4)*u, 1/2d1*u)
663 | -- ((ll3 + t4)*u, 1/2d2*u);
664 | f2 := (ll1*u - 1/8u, 1/2d2*u) -- (ll5*u - 1/2d2*u, 1/2d2*u)
665 | -- (ll5*u - 1/2d2*u, ypart(o));
666 | f3 := (ll1*u - 1/8u, -1/2d2*u) -- (ll5*u + 1/2d2*u, -1/2d2*u)
667 | -- (ll5*u + 1/2d2*u, ypart(o));
668 | draw f1 withpen fatpen; draw f1 yscaled -1 withpen fatpen;
669 | draw f2 withpen fatpen; draw f3 withpen fatpen;
670 | \end{lstlisting}
671 |
672 | \begin{mplibcode}
673 | path p[], q[], axis[], f[]; pair o;
674 | u := 6mm;
675 | r1 := -36.979; r2 := -r1; t1 := 0.7; n1 := 1.517; d1 := 5;
676 | l1 := 8.182;
677 | r3 := -11.657; r4 := r3; t2 := 0.2; n2 := n1; d2 := 3/2;
678 | l2 := 0.4;
679 | r5 := -30.433; r6 := 9.598; t3 := 0.39; n3 := 1.621; d3 := d2;
680 | l3 := 0.828;
681 | r7 := -35.512; r8 := infinity; t4 := 0.7; n4 := 0; d4 := d1;
682 | l4 := 5.272;
683 | ll0 := 0;
684 | for i := 1 upto 4:
685 | ll[i] := ll[i-1] + t[i] + l[i];
686 | p[i] := lens ((r[i*2 - 1], r[i*2]), t[i], d[i], u)
687 | shifted (ll[i-1]*u, 0);
688 | endfor;
689 | axis1 := (0, 0) -- (ll4*u, 0);
690 | axis2 := reverse(axis1);
691 | ll5 := ll4 - 1/2l4;
692 | p5 := ((-1,-1) -- (1,1) -- (-1,1) -- cycle)
693 | scaled (1/2d2*u) shifted (ll5*u, 0);
694 | p6 := (subpath
695 | (ypart((axis1 shifted (0, 1/2d2*u)) firstIntersectionTimes p4),
696 | ypart((axis2 shifted (0, 1/2d2*u)) firstIntersectionTimes p4))
697 | of p4) -- cycle;
698 | p7 := (subpath
699 | (ypart((axis2 shifted (0, 3/4d2*u)) firstIntersectionTimes p1),
700 | ypart((axis2 shifted (0, -3/4d2*u)) firstIntersectionTimes p1))
701 | of p1);
702 | p7 := p7 -- (reverse(p7) shifted ((-1/3t1)*u, 0)) -- cycle;
703 | for i := 1, 2, 3, 5:
704 | draw p[i] withpen thickpen; draw solid (p[i], 45, 1);
705 | endfor;
706 | draw solid (p7, -45, 0);
707 | draw p6 withpen thickpen; draw solid (p6, -45, 0);
708 | draw p6 yscaled -1 withpen thickpen;
709 | draw solid (p6 yscaled -1, -45, 0);
710 | n7 := 0; n5 := n1;
711 | for i := 0, 1:
712 | q[i] := (-3/2u, -2u + i*4u) -- (16u, -2u + i*4u);
713 | for j = 1, 4, 7, 2, 3, 5:
714 | q[i] := refractionPath(q[i], p[j], n[j]);
715 | endfor;
716 | endfor;
717 | o := whatever[point length(q0) of q0, point length(q0)-1 of q0]
718 | = whatever[point length(q1) of q1, point length(q1)-1 of q1];
719 | for i := 0, 1: drawmidarrow (q[i] -- o) withpen thinpen; endfor;
720 | draw eye(-91) shifted o shifted (0, u);
721 | f1 := (-1/4u, 1/2d1*u) -- ((ll3 + t4)*u, 1/2d1*u)
722 | -- ((ll3 + t4)*u, 1/2d2*u);
723 | f2 := (ll1*u - 1/8u, 1/2d2*u) -- (ll5*u - 1/2d2*u, 1/2d2*u)
724 | -- (ll5*u - 1/2d2*u, ypart(o));
725 | f3 := (ll1*u - 1/8u, -1/2d2*u) -- (ll5*u + 1/2d2*u, -1/2d2*u)
726 | -- (ll5*u + 1/2d2*u, ypart(o));
727 | draw f1 withpen fatpen; draw f1 yscaled -1 withpen fatpen;
728 | draw f2 withpen fatpen; draw f3 withpen fatpen;
729 | \end{mplibcode}
730 |
731 | \subsection{L'H\^{o}pital's Pulley Problem}
732 | Line 3 describe initial setup. Line 4 is problem's solution. Lines 8--11 set all the points where they belong. Lines 12--16 are needed to decide where to put the pulley.
733 |
734 | \begin{lstlisting}
735 | pair p[], o[];
736 | numeric a, d[], l[], x[], y[];
737 | l0 := 6; l1 := 4; l2 := 4;
738 | x1 := (l1**2 + abs(l1)*((sqrt(8)*l0)++l1))/4l0;
739 | y1 := l1+-+x1;
740 | y2 := l2 - ((l0-x1)++y1);
741 | d1 := 2/3cm; d2 := 4/3cm; d3 := 5/6d1;
742 | p1 := (0, 0);
743 | p2 := (l0*cm, 0);
744 | p3 := (x1*cm, -y1*cm);
745 | p4 := p3 shifted (0, -y2*cm);
746 | o1 := (unitvector(p4-p3) rotated 90 scaled 1/2d3);
747 | o2 := (unitvector(p3-p2) rotated 90 scaled 1/2d3);
748 | p5 := whatever [p3 shifted o1, p4 shifted o1]
749 | = whatever [p3 shifted o2, p2 shifted o2];
750 | a := angle(p1-p3);
751 | draw solidSurface(11/10[p1,p2] -- 11/10[p2, p1]);
752 | draw pulley (d1, a - 90) shifted p5;
753 | draw image(
754 | draw p1 -- p3 -- p2 withpen thickpen;
755 | draw p3 -- p4 withpen thickpen;
756 | ) maskedWith (pulleyOutline shifted p5);
757 | draw sphere.c(d2) shifted p4 shifted (0, -1/2d2);
758 | dotlabel.llft(btex $A$ etex, p1);
759 | dotlabel.lrt(btex $B$ etex, p2);
760 | dotlabel.ulft(btex $C$ etex, p4);
761 | label.llft(btex $l$ etex, 1/2[p1, p3]);
762 | markAngle(p3, p1, p2)(btex $\alpha$ etex);
763 | \end{lstlisting}
764 |
765 | \begin{mplibcode}
766 | pair p[], o[];
767 | numeric a, d[], l[], x[], y[];
768 | l0 := 6; l1 := 4; l2 := 4;
769 | x1 := (l1**2 + abs(l1)*((sqrt(8)*l0)++l1))/4l0;
770 | y1 := l1+-+x1;
771 | y2 := l2 - ((l0-x1)++y1);
772 | d1 := 2/3cm; d2 := 4/3cm; d3 := 5/6d1;
773 | p1 := (0, 0);
774 | p2 := (l0*cm, 0);
775 | p3 := (x1*cm, -y1*cm);
776 | p4 := p3 shifted (0, -y2*cm);
777 | o1 := (unitvector(p4-p3) rotated 90 scaled 1/2d3);
778 | o2 := (unitvector(p3-p2) rotated 90 scaled 1/2d3);
779 | p5 := whatever [p3 shifted o1, p4 shifted o1]
780 | = whatever [p3 shifted o2, p2 shifted o2];
781 | a := angle(p1-p3);
782 | draw solidSurface(11/10[p1,p2] -- 11/10[p2, p1]);
783 | draw pulley (d1, a - 90) shifted p5;
784 | draw image(
785 | draw p1 -- p3 -- p2 withpen thickpen;
786 | draw p3 -- p4 withpen thickpen;
787 | ) maskedWith (pulleyOutline shifted p5);
788 | draw sphere.c(d2) shifted p4 shifted (0, -1/2d2);
789 | dotlabel.llft(btex $A$ etex, p1);
790 | dotlabel.lrt(btex $B$ etex, p2);
791 | dotlabel.ulft(btex $C$ etex, p4);
792 | label.llft(btex $l$ etex, 1/2[p1, p3]);
793 | markAngle(p3, p1, p2)(btex $\alpha$ etex);
794 | \end{mplibcode}
795 |
796 | \subsection{Hooke's law}
797 |
798 | \begin{lstlisting}
799 | numeric l[],d, h;
800 | pair p[], q[];
801 | l0 := 3/2cm; l1 := 1cm;
802 | d := 1cm; h := 7/8cm;
803 | p1 := (0, 0); p2 := (0, -l0);
804 | p3 := (d, 0); p4 := (d, -l0-l1);
805 | p5 := (2d, 0); p6 := (2d, -l0-2l1); p7 := (2d, -l0-2l1-h);
806 | draw solidSurface((2d + 1/2cm, 0)--(-1/2cm, 0));
807 | draw spring(p1, p2, 20);
808 | draw spring(p3, p4, 20);
809 | draw weight.h(h) shifted p4;
810 | draw spring(p5, p6, 20);
811 | draw weight.h(h) shifted p6;
812 | draw weight.h(h) shifted p7;
813 | q1 := (0, ypart(p2));
814 | q2 := (0, ypart(p4));
815 | q3 := (0, ypart(p6));
816 | draw p2 -- q1 withpen thinpen;
817 | draw p4 -- q2 withpen thinpen;
818 | draw p6 -- q3 withpen thinpen;
819 | drawdblarrow q1--q2 withpen thinpen;
820 | drawdblarrow q2--q3 withpen thinpen;
821 | label.lft (btex $x$ etex, 1/2[q1, q2]);
822 | label.lft (btex $x$ etex, 1/2[q2, q3]);
823 | \end{lstlisting}
824 |
825 | \begin{mplibcode}
826 | numeric l[],d, h;
827 | pair p[], q[];
828 | l0 := 3/2cm; l1 := 1cm;
829 | d := 1cm; h := 7/8cm;
830 | p1 := (0, 0); p2 := (0, -l0);
831 | p3 := (d, 0); p4 := (d, -l0-l1);
832 | p5 := (2d, 0); p6 := (2d, -l0-2l1); p7 := (2d, -l0-2l1-h);
833 | draw solidSurface((2d + 1/2cm, 0)--(-1/2cm, 0));
834 | draw spring(p1, p2, 20);
835 | draw spring(p3, p4, 20);
836 | draw weight.h(h) shifted p4;
837 | draw spring(p5, p6, 20);
838 | draw weight.h(h) shifted p6;
839 | draw weight.h(h) shifted p7;
840 | q1 := (0, ypart(p2));
841 | q2 := (0, ypart(p4));
842 | q3 := (0, ypart(p6));
843 | draw p2 -- q1 withpen thinpen;
844 | draw p4 -- q2 withpen thinpen;
845 | draw p6 -- q3 withpen thinpen;
846 | drawdblarrow q1--q2 withpen thinpen;
847 | drawdblarrow q2--q3 withpen thinpen;
848 | label.lft (btex $x$ etex, 1/2[q1, q2]);
849 | label.lft (btex $x$ etex, 1/2[q2, q3]);
850 | \end{mplibcode}
851 |
852 | \subsection{Weight on a cart}
853 |
854 | \begin{lstlisting}
855 | numeric l, w, r, h;
856 | l := 4cm;
857 | w := 1/4cm;
858 | r := 2/3cm;
859 | h := 1cm;
860 | draw solidSurface((-1/5l, 0) -- (6/5l, 0));
861 | draw woodBlock (l, w) shifted (0, r);
862 | draw wheel (r, 0) shifted (r, 1/2r);
863 | draw wheel (r, 0) shifted (l-r, 1/2r);
864 | draw weight.s(h) shifted (1/2l, r + w);
865 | \end{lstlisting}
866 |
867 | \begin{mplibcode}
868 | numeric l, w, r, h;
869 | l := 4cm;
870 | w := 1/4cm;
871 | r := 2/3cm;
872 | h := 1cm;
873 | draw solidSurface((-1/5l, 0) -- (6/5l, 0));
874 | draw woodBlock (l, w) shifted (0, r);
875 | draw wheel (r, 0) shifted (r, 1/2r);
876 | draw wheel (r, 0) shifted (l-r, 1/2r);
877 | draw weight.s(h) shifted (1/2l, r + w);
878 | \end{mplibcode}
879 |
880 | \subsection{Some knots}
881 |
882 | \begin{lstlisting}
883 | path p[];
884 | p1 := (dir(90)*4/3cm) {dir(0)} .. tension 3/2
885 | .. (dir(90 + 120)*4/3cm){dir(90 + 30)} .. tension 3/2
886 | .. (dir(90 - 120)*4/3cm){dir(-90 - 30)} .. tension 3/2
887 | .. cycle;
888 | p1 := p1 scaled 6/5;
889 | addStrandToKnot (primeOne) (p1, 1/4cm, "l", "1, -1, 1");
890 | draw knotFromStrands (primeOne);
891 | p2 := (0, 2cm) .. (1/2cm, 3/2cm) .. (-1/2cm, 0)
892 | .. (1/2cm, -2/3cm) .. (4/3cm, 0) .. (0, 17/12cm)
893 | .. (-4/3cm, 0) .. (-1/2cm, -2/3cm) .. (1/2cm, 0)
894 | .. (-1/2cm, 3/2cm) .. cycle;
895 | p2 := p2 scaled 6/5;
896 | addStrandToKnot (primeTwo) (p2, 1/4cm, "l", "1, -1, 1, -1, 1");
897 | draw knotFromStrands (primeTwo) shifted (4cm, 0);
898 | p3 := (dir(0)*3/2cm) .. (dir(1*72)*2/3cm)
899 | .. (dir(2*72)*3/2cm) .. (dir(3*72)*2/3cm)
900 | .. (dir(4*72)*3/2cm) .. (dir(0)*2/3cm)
901 | .. (dir(1*72)*3/2cm) .. (dir(2*72)*2/3cm)
902 | .. (dir(3*72)*3/2cm) .. (dir(4*72)*2/3cm)
903 | .. cycle;
904 | p3 := (p3 rotated (72/4)) scaled 6/5;
905 | addStrandToKnot (primeThree) (p3, 1/4cm, "l", "-1, 1, -1, 1, -1");
906 | draw knotFromStrands (primeThree) shifted (8cm, 0);
907 | \end{lstlisting}
908 |
909 | \begin{mplibcode}
910 | path p[];
911 | p1 := (dir(90)*4/3cm) {dir(0)} .. tension 3/2
912 | .. (dir(90 + 120)*4/3cm){dir(90 + 30)} .. tension 3/2
913 | .. (dir(90 - 120)*4/3cm){dir(-90 - 30)} .. tension 3/2
914 | .. cycle;
915 | p1 := p1 scaled 6/5;
916 | addStrandToKnot (primeOne) (p1, 1/4cm, "l", "1, -1, 1");
917 | draw knotFromStrands (primeOne);
918 | p2 := (0, 2cm) .. (1/2cm, 3/2cm) .. (-1/2cm, 0)
919 | .. (1/2cm, -2/3cm) .. (4/3cm, 0) .. (0, 17/12cm)
920 | .. (-4/3cm, 0) .. (-1/2cm, -2/3cm) .. (1/2cm, 0)
921 | .. (-1/2cm, 3/2cm) .. cycle;
922 | p2 := p2 scaled 6/5;
923 | addStrandToKnot (primeTwo) (p2, 1/4cm, "s", "1, -1, 1, -1, 1");
924 | draw knotFromStrands (primeTwo) shifted (4cm, -2cm);
925 | p3 := (dir(0)*3/2cm) .. (dir(1*72)*2/3cm)
926 | .. (dir(2*72)*3/2cm) .. (dir(3*72)*2/3cm)
927 | .. (dir(4*72)*3/2cm) .. (dir(0)*2/3cm)
928 | .. (dir(1*72)*3/2cm) .. (dir(2*72)*2/3cm)
929 | .. (dir(3*72)*3/2cm) .. (dir(4*72)*2/3cm)
930 | .. cycle;
931 | p3 := (p3 rotated (72/4)) scaled 6/5;
932 | addStrandToKnot (primeThree) (p3, 1/4cm, "e", "-1, 1, -1, 1, -1");
933 | draw knotFromStrands (primeThree) shifted (8cm, 0);
934 | \end{mplibcode}
935 |
936 |
937 | \end{document}
--------------------------------------------------------------------------------
/fiziko.mp:
--------------------------------------------------------------------------------
1 | % fiziko 0.2.1
2 | % MetaPost library for physics textbook illustrations
3 | % Copyright 2023 Sergey Slyusarev
4 | %
5 | % This program is free software: you can redistribute it and/or modify
6 | % it under the terms of the GNU General Public License as published by
7 | % the Free Software Foundation, either version 3 of the License, or
8 | % (at your option) any later version.
9 | %
10 | % This program is distributed in the hope that it will be useful,
11 | % but WITHOUT ANY WARRANTY; without even the implied warranty of
12 | % MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE. See the
13 | % GNU General Public License for more details.
14 | %
15 | % You should have received a copy of the GNU General Public License
16 | % along with this program. If not, see .
17 |
18 | % https://github.com/jemmybutton/fiziko
19 |
20 | %
21 | % Here we define some things of general interest
22 | %
23 |
24 | pi := 3.1415926;
25 | radian := 180/pi;
26 |
27 | vardef sin primary x = (sind(x*radian)) enddef;
28 |
29 | vardef cos primary x = (cosd(x*radian)) enddef;
30 |
31 | vardef log (expr n, b) =
32 | save rv;
33 | numeric rv;
34 | if n > 0:
35 | rv := (mlog(n)/mlog(b));
36 | else:
37 | rv := 0;
38 | fi;
39 | rv
40 | enddef;
41 |
42 | vardef arcsind primary x = angle((1+-+x,x)) enddef;
43 |
44 | vardef arccosd primary x = angle((x,1+-+x)) enddef;
45 |
46 | vardef arcsin primary x = ((arcsind(x))/radian) enddef;
47 |
48 | vardef arccos primary x = ((arccosd(x))/radian) enddef;
49 |
50 | vardef angleRad primary x = angle(x)/radian enddef;
51 |
52 | vardef dirRad primary x = dir(x*radian) enddef;
53 |
54 | % used here and there.
55 |
56 | vardef sign (expr x)=
57 | if x > 0: 1 fi
58 | if x < 0: -1 fi
59 | if x = 0: 1 fi
60 | enddef;
61 |
62 | % This is inverted `clip`
63 |
64 | primarydef i maskedWith p =
65 | begingroup
66 | save q, invertedmask, resultimage, breakpoint;
67 | pair q[];
68 | path invertedmask;
69 | picture resultimage;
70 | resultimage := i;
71 | q1 := ulcorner(i) shifted (-1, 1);
72 | q3 := lrcorner(i) shifted (1, -1);
73 | q2 := (xpart(q3), ypart(q1));
74 | q4 := (xpart(q1), ypart(q3));
75 | breakpoint := ypart((ulcorner(p)--llcorner(p)) firstIntersectionTimes p);
76 | invertedmask := (subpath (breakpoint, length(p) + breakpoint) of p) -- q1 -- q2 -- q3 -- q4 -- q1 -- cycle;
77 | clip resultimage to invertedmask;
78 | resultimage
79 | endgroup
80 | enddef;
81 |
82 | %
83 | % Since metapost is somewhat unpredictable in determining where paths intersect, here's macro
84 | % that returns first intersection times with first path (ray) priority.
85 | % Actually, it is so in most cases, but sometimes second path can take precedence,
86 | % so the macro just checks whether reversing 'q' changes something
87 | %
88 |
89 | primarydef p firstIntersectionTimes q =
90 | begingroup
91 | save t;
92 | pair t[];
93 | t1 := p intersectiontimes q;
94 | t2 := p intersectiontimes reverse(q);
95 | if xpart(t1) < xpart(t2):
96 | t3 := t1;
97 | else:
98 | t3 := (xpart(t2), length(q) - ypart(t2));
99 | fi;
100 | if xpart(t1) < 0: t3 := t2; fi;
101 | t3
102 | endgroup
103 | enddef;
104 |
105 | % This checks if point a is inside of closed path p
106 |
107 | primarydef a isInside p =
108 | begingroup
109 | save ang, v, i, rv, pp;
110 | boolean rv;
111 | pair pp[];
112 | ang := 0;
113 | for i := 0 step 1/4 until (length(p)):
114 | pp1 := (point i of p) - a;
115 | pp2 := (point i + 1/4 of p) - a;
116 | if (pp1 <> (0, 0)) and (pp2 <> (0, 0)):
117 | v := angle(pp1) - angle(pp2);
118 | if v > 180: v := v - 360; fi; if v < -180: v := v + 360; fi;
119 | ang := ang + v;
120 | fi;
121 | endfor;
122 | if abs(ang) > 355:
123 | rv := true;
124 | else:
125 | rv := false;
126 | fi;
127 | rv
128 | endgroup
129 | enddef;
130 |
131 | % rotation in radians
132 |
133 | primarydef somethingToRotate radRotated radAngle =
134 | somethingToRotate rotated ((radAngle/pi)*180)
135 | enddef;
136 |
137 | %
138 | % some 3D stuff
139 | %
140 |
141 | % this one's from byrne.mp
142 |
143 | primarydef colorone dotprodXYZ colortwo =
144 | begingroup
145 | save xp, yp, zp;
146 | numeric xp[], yp[], zp[];
147 | xp1 := (redpart colorone);
148 | yp1 := (greenpart colorone);
149 | zp1 := (bluepart colorone);
150 | xp2 := (redpart colortwo);
151 | yp2 := (greenpart colortwo);
152 | zp2 := (bluepart colortwo);
153 | xp1*xp2 + yp1*yp2 + zp1*zp2
154 | endgroup
155 | enddef;
156 |
157 | %
158 | % sometimes it's useful to put some arrows along the path. this macro puts them
159 | % in the middles of the segments that have length no less than midArrowLimit;
160 | %
161 |
162 | midArrowLimit := 1cm;
163 |
164 | def drawmidarrow (expr p) text t =
165 | begingroup
166 | save i, j, q;
167 | path q;
168 | j := 0;
169 | for i := 1 upto length(p):
170 | if arclength(subpath(i-1, i) of p) >= midArrowLimit:
171 | q := subpath(j, i - 1/2) of p;
172 | j := i - 1/2;
173 | draw q t;
174 | filldraw arrowhead q t;
175 | fi;
176 | endfor;
177 | draw subpath(j, length(p)) of p t;
178 | endgroup
179 | enddef;
180 |
181 | % This macro marks angles, unsurprisingly
182 |
183 | def markAngle (expr a, o, b) (text t) =
184 | begingroup
185 | save p, an, d;
186 | numeric an[], d[];
187 | pair p;
188 | an1 := angle(a-o);
189 | an2 := angle(b-o) - an1;
190 | if (an2 < 0): an2 := an2 + 360; fi;
191 | an3 := an1 + 1/2an2;
192 | p := center(t);
193 | d1 := abs(ulcorner(t)-lrcorner(t));
194 | if (an2 < 90) and (an2 > 0):
195 | d2 := max(1/3cm, (d1/(abs(sind(an2))*1/3cm))*1/3cm);
196 | else:
197 | d2 := 1/3cm;
198 | fi;
199 | draw subpath (0, 8an2/360) of fullcircle scaled 2d2 rotated an1 shifted o withpen thinpen;
200 | draw (t) shifted -p shifted o shifted (dir(an3)*(d2 + d1));
201 | endgroup
202 | enddef;
203 |
204 | %
205 | % Here we define some auxilary global variables
206 | %
207 |
208 | % Offset path algorithm can subdivide original path in order to be more precise
209 | offsetPathSteps := 4;
210 |
211 | % The following macro sets all the values related to minimal stroke width at once.
212 | % It can be used to easily redefine all of them.
213 | def defineMinStrokeWidth (expr msw) =
214 | % We don't want to display strokes that are too thin to print. Default value
215 | % is subject to change when needed.
216 | minStrokeWidth := msw;
217 | maxShadingStrokeWidth := 3/2minStrokeWidth;
218 |
219 | % At some point it's useless to display even dashes
220 | minDashStrokeWidth := 1/3minStrokeWidth;
221 |
222 | % this value corresponds to particular dashing algorithm and is subject to change whenever this algorithm changes
223 | minDashStrokeLength := 6minStrokeWidth;
224 |
225 | dashStrokeWidthStep := (minStrokeWidth - minDashStrokeWidth)/16;
226 |
227 | % all the shading algorithms need to know how close lines should be packed
228 | shadingDensity := 3maxShadingStrokeWidth;
229 |
230 | stippleSize := 3/2minStrokeWidth;
231 | minStippleStep := 1/2stippleSize;
232 | stippleShadingDensity := 3minStippleStep;
233 | minStippleStrokeWidth := 1/20stippleSize;
234 |
235 | % here are some pens
236 | pen thinpen, thickpen, fatpen, stipplepen;
237 |
238 | thinpen := pencircle scaled minStrokeWidth;
239 | thickpen := pencircle scaled 3minStrokeWidth;
240 | fatpen := pencircle scaled 6minStrokeWidth;
241 | stipplepen := pencircle scaled stippleSize;
242 | enddef;
243 |
244 | defineMinStrokeWidth(1/5pt);
245 |
246 | % here we set global light direction
247 |
248 | def defineLightDirection (expr ldx, ldy) =
249 | pair lightDirection;
250 | color lightDirectionVectorXYZ;
251 | lightDirection := (ldx, ldy);
252 | lightDirectionVectorXYZ := (0, 0, 1);
253 | lightDirectionVectorXYZ := rotateXYZaround.x(lightDirectionVectorXYZ, ldy);
254 | lightDirectionVectorXYZ := rotateXYZaround.y(lightDirectionVectorXYZ, ldx);
255 | enddef;
256 |
257 | vardef rotateXYZaround@# (expr p, a) =
258 | save partProj, rv;
259 | pair partProj;
260 | color rv;
261 | if str @# = "x":
262 | partProj := (greenpart(p), bluepart(p)) radRotated -a;
263 | rv := (redpart(p), xpart(partProj), ypart(partProj));
264 | elseif str @# = "y":
265 | partProj := (redpart(p), bluepart(p)) radRotated -a;
266 | rv := (xpart(partProj), greenpart(p), ypart(partProj));
267 | elseif str @# = "z":
268 | partProj := (redpart(p), greenpart(p)) radRotated -a;
269 | rv := (xpart(partProj), ypart(partProj), bluepart(p));
270 | else:
271 | errmessage("What axis is " & str @# & "?");
272 | fi;
273 | rv
274 | enddef;
275 |
276 | defineLightDirection(-1/8pi, 1/8pi);
277 |
278 | boolean shadowsEnabled;
279 | shadowsEnabled := false;
280 |
281 | %
282 | % To simplify further calculations we need subdivided original path
283 | %
284 |
285 | vardef pathSubdivideBase (expr p, subdivideStep, i) =
286 | save returnPath, sp;
287 | path returnPath, sp;
288 | returnPath := point i of p;
289 | if i 0):
328 | offsetPathLength := arclength(subpath (0, i) of p)/arclength(p);
329 | else:
330 | offsetPathLength := 0;
331 | fi;
332 | returnPath := (arclength(subpath (0, i) of p), offsetFunction);
333 | if (i < length(p)):
334 | % this thing is glitchy, but should be more accurate
335 | %if (arclength(subpath (0, i) of p) < arclength(subpath (0, i + 1/4) of p)):
336 | % offsetPathTime := i + 1/4;
337 | % offsetPathLength := arclength(subpath (0, i + 1/4) of p)/arclength(p);
338 | % instantDirection := unitvector((arclength(subpath (0, i + 1/4) of p), offsetFunction) - point 0 of returnPath);
339 | % offsetPathTime := i + 1;
340 | % offsetPathLength := arclength(subpath (0, i + 1) of p)/arclength(p);
341 | % nextDirection := (arclength(subpath (0, i + 1) of p), offsetFunction);
342 | % offsetPathTime := i + 3/4;
343 | % offsetPathLength := arclength(subpath (0, i + 3/4) of p)/arclength(p);
344 | % nextDirection := unitvector(nextDirection - (arclength(subpath (0, i + 3/4) of p), offsetFunction));
345 | % returnPath := returnPath{instantDirection} .. {nextDirection}offsetPathTemplate(p, i + 1)(offsetFunction);
346 | % returnPath := returnPath -- offsetPathTemplate(p, i + 1)(offsetFunction);
347 | %else:
348 | returnPath := returnPath -- offsetPathTemplate(p, i + 1)(offsetFunction);
349 | %fi;
350 | fi;
351 | returnPath
352 | enddef;
353 |
354 | %
355 | % This macro creates offset path p based on previously built template q, instead of function itself
356 | % It is loosely based on something called Tiller-Hanson heuristic as described here:
357 | % http://math.stackexchange.com/questions/465782/control-points-of-offset-bezier-curve
358 | %
359 |
360 | vardef offsetPathGenerate (expr p, q, i) =
361 | save returnPath, c, d, a, pl, ps;
362 | path returnPath, pl[];
363 | pair c[], d[];
364 | numeric a[];
365 | c1 := precontrol i of p;
366 | c2 := point i of p;
367 | c3 := postcontrol i of p;
368 | if abs(c1-c2) = 0:
369 | c1 := c2 shifted (c2-c3);
370 | fi;
371 | if abs(c3-c2) = 0:
372 | c3 := c2 shifted (c2-c1);
373 | fi;
374 | if (abs(c1-c2) > 0) and (abs(c2-c3) > 0):
375 | d1 := unitvector(c1-c2) rotated -90;
376 | d2 := unitvector(c2-c3) rotated -90;
377 | pl1 := (unitvector(c2-c1)--unitvector(c1-c2))
378 | scaled arclength(subpath (i - 1/2, i + 1/2) of p)
379 | shifted (point i of p shifted (d1 scaled ypart(point i of q)));
380 | pl2 := (unitvector(c2-c3)--unitvector(c3-c2))
381 | scaled arclength(subpath (i - 1/2, i + 1/2) of p)
382 | shifted (point i of p shifted (d2 scaled ypart(point i of q)));
383 | if (abs(angle(d1) - angle(d2)) > 2) and (xpart(pl1 intersectiontimes pl2) > 0):
384 | c4 := pl1 intersectionpoint pl2;
385 | else:
386 | c4 := c2 shifted (d1 scaled ypart(point i of q));
387 | fi;
388 | returnPath := c4;
389 | else:
390 | returnPath := c2 shifted (unitvector( (point i-1 of p) - (point i+1 of p) rotated -90) scaled ypart (point i of q));
391 | fi;
392 | if i < length(p):
393 | path ps;
394 | ps := subpath (i, i + 1) of p;
395 | c1 := point 0 of ps;
396 | c2 := postcontrol 0 of ps;
397 | c3 := precontrol 1 of ps;
398 | c4 := point 1 of ps;
399 | c5 := point 0 of returnPath;
400 | if (abs(c3-c4)>0)
401 | and (abs(c1-c2)>0)
402 | and (abs(c1-c4)>0)
403 | and (abs(direction i of q) > 0):
404 | c6 := c4 shifted (unitvector(c4 - c3) rotated 90 scaled ypart(point i + 1 of q));
405 | %if abs(direction i of q) > 0:
406 | a1 := angle(direction i of q);
407 | %else:
408 | % a1 := angle((point (i + 1/10) of q) - (point (i - 1/10) of q));
409 | %fi;
410 | %if abs(direction i + 1 of q) > 0:
411 | a2 := angle(direction i + 1 of q);
412 | %else:
413 | % a2 := angle((point (i + 1 + 1/10) of q) - (point (i + 1 - 1/10) of q));
414 | %fi;
415 | c7 := (c2 - c1) scaled (abs(c5-c6)/abs(c1-c4)) rotated a1 shifted c5;
416 | c8 := (c3 - c4) scaled (abs(c5-c6)/abs(c1-c4)) rotated a2 shifted c6;
417 | returnPath := returnPath .. controls c7 and c8 .. offsetPathGenerate (p, q, i + 1);
418 | else:
419 | returnPath := returnPath -- offsetPathGenerate (p, q, i + 1);
420 | fi;
421 | fi;
422 | returnPath
423 | enddef;
424 |
425 | %
426 | % Frontend for offsetPathGenerate and offsetPathTemplate
427 | %
428 |
429 | vardef offsetPath (expr p)(text offsetFunction) =
430 | offsetPathGenerate (p, offsetPathTemplate(p, 0)(offsetFunction), 0)
431 | enddef;
432 |
433 | %
434 | % Brush macro. It draws line with brush of variable width.
435 | % For parts thicker than minStrokeWidth it uses offsetPath functions'
436 | % results, for thiner parts it draws dashed lines of fixed width
437 | %
438 |
439 | def brushGenerate (expr p, q, i) =
440 | begingroup
441 | save w, brushPath, bt, t;
442 | numeric w[], t[];
443 | path brushPath[], bt;
444 | bt := q;
445 | w0 := (ypart(urcorner(bt)));
446 | w1 := (ypart(lrcorner(bt)));
447 | t := cutPathTime(bt, minStrokeWidth);
448 | if ((w0 > minStrokeWidth)
449 | and (w1 < minStrokeWidth)
450 | and (t > 0)
451 | and (t < length(p))
452 | and (arclength(p) > minDashStrokeLength)
453 | and (i < 10)):
454 | brushGenerate (subpath (0, t) of p, subpath (0, t) of q, i + 1);
455 | brushGenerate (subpath (t, length(p)) of p, subpath (t, length(q)) of q, i + 1);
456 | elseif (arclength(p) > 0):
457 | if (w0 > 99/100minStrokeWidth)
458 | and (w1 > 99/100minStrokeWidth):
459 | brushPath1 := offsetPathGenerate (p, q yscaled 1/2, 0);
460 | brushPath2 := offsetPathGenerate (p, q yscaled -1/2, 0);
461 | fill brushPath1 -- reverse(brushPath2) -- cycle;
462 | elseif (w0 < 101/100minStrokeWidth) and (w1 < 101/100minStrokeWidth):
463 | thinBrushGenerate (p, q, 0)
464 | fi;
465 | fi;
466 | endgroup
467 | enddef;
468 |
469 | %
470 | % macro for thin lines which are actually dashed
471 | %
472 |
473 | vardef thinBrushGenerate@#(expr p, q, i) =
474 | begingroup
475 | save w, brushPath, bt, t, h, minLength, minWidth, dashPatternImage;
476 | numeric w[], t[];
477 | path brushPath[], bt;
478 | picture dashPatternImage;
479 | if (str @# = "") or (str @# = "hatches"):
480 | minLength := minDashStrokeLength;
481 | minWidth := minDashStrokeWidth;
482 | elseif str @# = "stipples":
483 | minLength := minStippleStep;
484 | minWidth := minStippleStrokeWidth;
485 | fi;
486 | bt := q;
487 | w0 := ypart(urcorner(bt));
488 | w1 := ypart(lrcorner(bt));
489 | if (w0 > minWidth + 1/100):
490 | if (w1 > minWidth - 1/100):
491 | w2 := floor((1/2(w0 + w1) - minWidth)/dashStrokeWidthStep)*dashStrokeWidthStep + minWidth;
492 | else:
493 | w2 := minWidth;
494 | fi;
495 | t := cutPathTime(bt, w2);
496 | brushPath1 := subpath (0, t) of p;
497 | brushPath2 := subpath (t, length(p)) of p;
498 | if (((w0 - w1) >= dashStrokeWidthStep) and (i < 15))
499 | and ((arclength(brushPath1) > minLength)
500 | or (arclength(brushPath2) > minLength))
501 | and (t > 1/100) and (t < length(p) - 1/100):
502 | thinBrushGenerate@#(brushPath1, subpath (0, t) of q, i + 1);
503 | thinBrushGenerate@#(brushPath2, subpath (t, length(q)) of q, i + 1);
504 | else:
505 | if (str @# = "") or (str @# = "hatches"):
506 | if (w2 > minStrokeWidth):
507 | w2 := minStrokeWidth;
508 | fi;
509 | if (w2 >= minWidth) and (arclength(p) > 0):
510 | if (w2 < minStrokeWidth) and (arclength(p) > minLength):
511 | draw p withpen thinpen dashed thinBrushPattern(w2, arclength(p));
512 | else:
513 | draw p withpen thinpen;
514 | fi;
515 | fi;
516 | elseif str @# = "stipples":
517 | begingroup
518 | interim linecap := rounded;
519 | save stippleSizeVar;
520 | stippleSizeVar := stippleSize;
521 | save stippleSize;
522 | w2 := 1/3w2;
523 | if (w2 >= minWidth) and (arclength(p) > 0):
524 | stippleSize := stippleSizeVar * (0.9 + uniformdeviate(0.3));
525 | dashPatternImage := stipplesBrushPattern(w2, arclength(p));
526 | if urcorner(dashPatternImage) <> (0,0):
527 | brushPath1 := offsetPathGenerate (p, (q yscaled 0) shifted (0, 1/3stippleShadingDensity), 0);
528 | draw brushPath1 withpen (pencircle scaled stippleSize) dashed dashPatternImage;
529 | fi;
530 | stippleSize := stippleSizeVar * (0.9 + uniformdeviate(0.3));
531 | dashPatternImage := stipplesBrushPattern(w2, arclength(p));
532 | if urcorner(dashPatternImage) <> (0,0):
533 | brushPath2 := offsetPathGenerate (p, (q yscaled 0) shifted (0, -1/3stippleShadingDensity), 0);
534 | draw brushPath2 withpen (pencircle scaled stippleSize) dashed dashPatternImage;
535 | fi;
536 | stippleSize := stippleSizeVar * (0.9 + uniformdeviate(0.3));
537 | dashPatternImage := stipplesBrushPattern(w2, arclength(p));
538 | if urcorner(dashPatternImage) <> (0,0):
539 | draw p withpen (pencircle scaled stippleSize) dashed dashPatternImage;
540 | fi;
541 | fi;
542 | endgroup
543 | fi;
544 | fi;
545 | fi;
546 | endgroup
547 | enddef;
548 |
549 | %
550 | % this macro returns path as a shaded edge
551 | %
552 |
553 | vardef shadedEdge (expr p) =
554 | image(
555 | brushGenerate (p,
556 | offsetPathTemplate (p, 0) (
557 | 1/2minStrokeWidth + 2*minStrokeWidth
558 | * normalVectorToLightness(
559 | sphereAnglesToNormalVector(
560 | (angleRad(point offsetPathTime of p), arcsin(1/2))
561 | ), 0, point offsetPathTime of p
562 | )
563 | ), 0);
564 | )
565 | enddef;
566 |
567 | %
568 | % Whenever we have brush thinner than minStrokeWidth we call this dash pattern macro
569 | %
570 |
571 | vardef thinBrushPattern (expr w, l) =
572 | save d;
573 | numeric d[];
574 | d0 := w;
575 | if d0 > minStrokeWidth: d0 := minStrokeWidth; fi;
576 | % d1 is a result of some arbitrary function of line width
577 | % we do not use simple linear function because minimal dash length
578 | % also shouldn't be less than minStrokeWidth.
579 | % After we get d1 other measurements are calculated,
580 | % so filled area per unit length remains adequate and dashes are aligned
581 | % with segments
582 | % d1*mSW = (d1*w + d2*w) -> d2=d1(mSW-w)/w
583 | d1 := (1/2minDashStrokeLength) + (((d0/minStrokeWidth)**(5/2))*1/2minDashStrokeLength);
584 | d1 := d1 + 1/2uniformdeviate(d1);
585 | d2 := (minStrokeWidth - d0)*(d1/d0);
586 | d3 := round(l/(d2 + d1));
587 | if (d3 < 1): d3 := 1; fi;
588 | d4 := (l/d3)/(d2 + d1);
589 | d1 := d1*d4;
590 | d2 := d2*d4;
591 | if (uniformdeviate(2) > 1):
592 | dashpattern (on d1/2 off d2 on d1/2)
593 | else:
594 | dashpattern (off d2/2 on d1 off d2/2)
595 | fi
596 | enddef;
597 |
598 |
599 | %
600 | % Stipples are also dashes
601 | %
602 |
603 | vardef stipplesBrushPattern (expr w, l) =
604 | save d, n, rn, rv, ss;
605 | ss := 1/1000;
606 | numeric d[];
607 | picture rv;
608 | %if w > stippleSize:
609 | % d0 := minStippleStep;
610 | %else:
611 | n := (w*l)/(stippleSize**2);
612 | rn := floor(n);
613 | if rn > 0:
614 | d0 := l/rn;
615 | fi;
616 | %fi;
617 | if rn > 0:
618 | d1 := uniformdeviate(d0);
619 | d2 := d0-d1;
620 | if rn >=3:
621 | d3 := uniformdeviate(d0);
622 | d4 := d0-d3;
623 | %if uniformdeviate(2) > 1:
624 | % d5 := uniformdeviate(d0);
625 | % d6 := d0-d5;
626 | % rv := dashpattern (off d1 on ss off (d2+d5)-ss on ss off (d4+d6)-ss on ss off d3-ss);
627 | %else:
628 | rv := dashpattern (off d1 on ss off (d2+d3)-ss on ss off d4-ss);
629 | %fi;
630 | else:
631 | rv := dashpattern (off d1 on ss off d2-ss);
632 | fi;
633 | else:
634 | if uniformdeviate(1) < n:
635 | rv := dashpattern (off uniformdeviate(l-ss) on ss off l);
636 | else:
637 | rv := image();
638 | fi;
639 | fi;
640 | rv
641 | enddef;
642 |
643 | %
644 | % macro that actually draws line of variable width
645 | %
646 |
647 | vardef brush (expr p) (text offsetFunction) =
648 | image(
649 | brushGenerate (p, offsetPathTemplate(p, 0)(offsetFunction), 0);
650 | )
651 | enddef;
652 |
653 | %
654 | % same, but only for thin brushes
655 | %
656 |
657 | vardef thinBrush@#(expr p) (text offsetFunction) =
658 | image(
659 | thinBrushGenerate@#(p, offsetPathTemplate(p, 0)(offsetFunction), 0);
660 | )
661 | enddef;
662 |
663 | %
664 | % This macro generates tube between paths p and q, of variable width d
665 | % Tube is subdivided into segments in such a way that within every segment
666 | % we need 2**n lines to generate even fill
667 | %
668 |
669 | vardef tubeGenerate@#(expr p, q, d, i) =
670 | save w, bw, k, t, tubeWidth, sp, currentPath, currentTubePath, currentDepth, lineDensity;
671 | numeric w[], bw[], t, currentDepth;
672 | path tubeWidth, sp, currentPath, currentTubePath;
673 | tubeWidth := d yscaled 2;
674 | if (str @# = "") or (str @# = "hatches"):
675 | lineDensity := shadingDensity;
676 | elseif (str @# = "stipples"):
677 | lineDensity := stippleShadingDensity;
678 | fi;
679 | w0 := (ypart(urcorner(tubeWidth))) - 1/1000;
680 | w1 := (ypart(lrcorner(tubeWidth))) + 1/1000;
681 | w2 := ceiling(log(w0/lineDensity, 2));
682 | w3 := ceiling(log(w1/lineDensity, 2));
683 | if ((w2 > w3) and (i<20)):
684 | t := cutPathTime(tubeWidth, lineDensity*(2**(w2-1)));
685 | tubeGenerate@#(subpath (0, t) of p, subpath (0, t) of q, subpath (0, t) of d, i + 1);
686 | tubeGenerate@#(subpath (t, length(p)) of p, subpath (t, length(q)) of q, subpath (t, length(d)) of d, i + 1);
687 | else:
688 | if (arclength(p) > 0) and (arclength(q) > 0):
689 | bw1 := 2**w2;
690 | currentTubePath := interpath (1/2, q, p);
691 | for k := 0 upto bw1:
692 | currentPath := interpath (k/bw1, q, p);
693 | angleOnTube := arcsin(((k/bw1)*2) - 1);
694 | currentDepth := -abs((1-sin(angleOnTube + 1/2pi))*w0);
695 | if shadowsEnabled:
696 | currentPath := shadowCut(currentPath, currentDepth);
697 | fi;
698 | if (str @# = "") or (str @# = "hatches"):
699 | brushGenerate (currentPath,
700 | offsetPathTemplate(currentPath, 0)(
701 | maxShadingStrokeWidth
702 | if odd (k): * (abs(ypart(point offsetPathTime of tubeWidth)/bw1) - 1/2lineDensity) fi
703 | * normalVectorToLightness(
704 | tubeAnglesToNormalVector((
705 | angleOnTube,
706 | angleRad(direction offsetPathTime of currentTubePath),
707 | angleRad(direction offsetPathTime of (tubeWidth yscaled 1/2))
708 | )), currentDepth, point offsetPathTime of currentPath)
709 | ), 0);
710 | elseif (str @# = "stipples"):
711 | begingroup
712 | save stippleShadingDensity;
713 | if w2 > 0:
714 | stippleShadingDensity := 2w0/(2**w2); % When the distance between the lines changes, wtipples should spread further apart
715 | else:
716 | stippleShadingDensity := w0;
717 | fi;
718 | thinBrushGenerate.@#(currentPath,
719 | offsetPathTemplate(currentPath, 0)(
720 | stippleSize
721 | if odd (k): * (abs(ypart(point offsetPathTime of tubeWidth)/bw1) - 1/2lineDensity) fi
722 | * normalVectorToLightness(
723 | tubeAnglesToNormalVector((
724 | angleOnTube,
725 | angleRad(direction offsetPathTime of currentTubePath),
726 | angleRad(direction offsetPathTime of (tubeWidth yscaled 1/2))
727 | )), currentDepth, point offsetPathTime of currentPath)
728 | ), 0);
729 | endgroup
730 | fi;
731 | endfor;
732 | fi;
733 | fi;
734 | enddef;
735 |
736 | %
737 | % This macro is analogous to tubeGenerate, but draws transverse strokes
738 | % result is somewhat suboptimal for now, but in simple cases it works ok
739 | %
740 |
741 | def tubeGenerateAlt (expr p, q, d) =
742 | begingroup
743 | save spth, lpth, currentPath, pos, t, pthdir, corr, o, l, i, j, k, tubeAngle, pathAngle, scorr, dt;
744 | numeric l[];
745 | path spth, lpth, currentPath;
746 | pos := 0;
747 | j := 0;
748 | forever:
749 | dt := (xpart(point pos of d) + 1/2shadingDensity);
750 | scorr := cosd(angle(direction xpart(d intersectiontimes ((dt, ypart(lrcorner(d))) -- (dt, ypart(urcorner(d))))) of d));
751 | t1 := arctime ((arclength(subpath(0, pos) of p)) + shadingDensity/scorr) of p;
752 | t2 := arctime ((arclength(subpath(0, pos) of q)) + shadingDensity/scorr) of q;
753 | if (arclength(subpath(pos, t1) of p) < arclength(subpath(pos, t1) of q)):
754 | pthdir := -1;
755 | t3 := t1;
756 | else:
757 | pthdir := 1;
758 | t3 := t2;
759 | fi;
760 | corr := round(arclength(subpath(pos, t3) of if pthdir = 1: p else: q fi)/(shadingDensity/scorr));
761 | if (corr < 1): corr := 1; fi;
762 | corr := (arclength(subpath(pos, t3) of if pthdir = 1: p else: q fi) - (corr*(shadingDensity/scorr)))/corr;
763 | t3 := arctime (arclength(subpath(0, t3) of if pthdir = 1: q else: p fi) - 1/3corr) of if pthdir = 1: q else: p fi;
764 | spth := subpath(pos, t3) of if pthdir = 1: q else: p fi;
765 | lpth := subpath(pos, t3) of if pthdir = 1: p else: q fi;
766 | tubeAngle := angleRad(direction 1/2[pos, t3] of d);
767 | pathAngle := angleRad(direction 1/2 of interpath (1/2, spth, lpth));
768 | pos := t3;
769 | l1 := round(arclength(lpth)/(shadingDensity/scorr));
770 | if (l1 < 1): l1 := 1; fi;
771 | l2 := arclength(lpth)/(l1*(shadingDensity/scorr));
772 | for i := 0 upto l1 - 1:
773 | j := j + 1;
774 | k := i*(arclength(lpth)/l1);
775 | currentPath := point (arctime k of lpth) of spth -- point (arctime k of lpth) of lpth;
776 | currentPath := offsetPathSubdivide(currentPath);
777 | brushGenerate (
778 | currentPath,
779 | offsetPathTemplate(currentPath, 0)(
780 | maxShadingStrokeWidth
781 | * orderFade(offsetPathLength[1/l1, l2], j)
782 | * normalVectorToLightness(
783 | tubeAnglesToNormalVector((
784 | arcsin(pthdir*((offsetPathLength*2)-1)),
785 | pathAngle,
786 | tubeAngle)
787 | ), -2(1/2arclength(currentPath))+sqrt(1 - (2offsetPathLength - 1)**2)*(1/2arclength(currentPath)), point offsetPathTime of currentPath)
788 | )
789 | , 0);
790 | endfor;
791 | exitif pos >= length(p);
792 | endfor;
793 | endgroup
794 | enddef;
795 |
796 | %
797 | % This macro converts some measurements of point on tube to absolute angle.
798 | % Since there are three such measurements, macro gets them as as a single
799 | % argument of "color" type, in case it would eventually appear as a result
800 | % of some other macro.
801 | %
802 | % redpart is the angle on the tube's circumference
803 | % greenpart is the angle of the tube path
804 | % bluepart is the angle of the tube's outline
805 | %
806 |
807 | vardef tubeAnglesToNormalVector (expr p) =
808 | save normalVector;
809 | color normalVector;
810 | normalVector := (0, 0, 1);
811 | normalVector := rotateXYZaround.y(normalVector, -bluepart(p));
812 | normalVector := rotateXYZaround.x(normalVector, redpart(p));
813 | normalVector := rotateXYZaround.z(normalVector, -greenpart(p));
814 | normalVector
815 | enddef;
816 |
817 | %
818 | % frontend to simplify tube drawing. tubeOutline variable changes on every call
819 | % of the function and can be used afterwards.
820 | %
821 |
822 | path tubeOutline;
823 | boolean drawTubeEnds;
824 | drawTubeEnds := true;
825 |
826 | vardef tube@#(expr p)(text offsetFunction)=
827 | save q, respic;
828 | path q[];
829 | picture respic;
830 | q0 := offsetPathSubdivide(p);
831 | q1 := offsetPathTemplate(q0, 0)(offsetFunction);
832 | q2 := offsetPathGenerate (q0, q1, 0);
833 | q3 := offsetPathGenerate (q0, q1 yscaled -1, 0);
834 | tubeOutline := q3--reverse(q2)--cycle;
835 | if str @# = "e":
836 | if not drawTubeEnds:
837 | image(
838 | draw q2 withpen thinpen;
839 | draw q3 withpen thinpen;
840 | )
841 | else:
842 | tubeOutline
843 | fi
844 | else:
845 | image(
846 | if str @# = "l":
847 | respic := image(tubeGenerate (q2, q3, q1, 0););
848 | elseif str @# = "s":
849 | respic := image(tubeGenerate.stipples(q2, q3, q1, 0);)
850 | elseif str @# = "t":
851 | respic := image(tubeGenerateAlt (q2, q3, q1););
852 | fi;
853 | if (cycle p) or (not drawTubeEnds):
854 | draw q2 withpen thinpen;
855 | draw q3 withpen thinpen;
856 | else:
857 | draw q2--reverse(q3)--cycle withpen thinpen;
858 | fi;
859 | clip respic to (q2--reverse(q3)--cycle);
860 | draw respic;
861 | )
862 | fi
863 | enddef;
864 |
865 | %
866 | % Sphere can be used as a cap for a tube, so it has same 2**n lines.
867 | %
868 |
869 | vardef sphere@#(expr d) =
870 | save currentCircle, origCircle, currentRadius, currentDepth, order, circleThickness, lineDensity, shadingPicture;
871 | path currentCircle, origCircle;
872 | numeric currentRadius, currentDepth, order;
873 | picture shadingPicture;
874 | if (str @# = "") or (str @# = "c"):
875 | lineDensity := shadingDensity;
876 | elseif (str @# = "s"):
877 | lineDensity := stippleShadingDensity;
878 | fi;
879 | origCircle := fullcircle;
880 | order := 2**ceiling(log((1/2d)/lineDensity, 2));
881 | image(
882 | draw fullcircle scaled d withpen thinpen;
883 | shadingPicture := image(
884 | for i := 1 upto order:
885 | currentRadius := i/order;
886 | currentCircle := origCircle scaled (currentRadius*d) rotated uniformdeviate (1/4pi);
887 | if odd(i):
888 | circleThickness := maxShadingStrokeWidth * ((abs(d - (lineDensity*order)))/order);
889 | else:
890 | circleThickness := maxShadingStrokeWidth;
891 | fi;
892 | currentDepth:= -(1-sqrt(1-currentRadius**2))*(1/2d);
893 | if shadowsEnabled:
894 | currentCircle := shadowCut(currentCircle, currentDepth);
895 | fi;
896 | if (str @# = "") or (str @# = "c"):
897 | brushGenerate (currentCircle,
898 | offsetPathTemplate (currentCircle, 0) (
899 | circleThickness
900 | * normalVectorToLightness(
901 | sphereAnglesToNormalVector(
902 | (angleRad(point offsetPathTime of currentCircle), arcsin(currentRadius))
903 | ), currentDepth, point offsetPathTime of currentCircle
904 | )
905 | ), 0);
906 | elseif (str @# = "s"):
907 | begingroup
908 | save stippleShadingDensity;
909 | if order > 0:
910 | stippleShadingDensity := d/order; % When the distance between the lines changes, wtipples should spread further ap
911 | else:
912 | stippleShadingDensity := 1/2d;
913 | fi;
914 | thinBrushGenerate.stipples(currentCircle,
915 | offsetPathTemplate (currentCircle, 0) (
916 | circleThickness
917 | * normalVectorToLightness(
918 | sphereAnglesToNormalVector(
919 | (angleRad(point offsetPathTime of currentCircle), arcsin(currentRadius))
920 | ), currentDepth, point offsetPathTime of currentCircle
921 | )
922 | ), 0);
923 | endgroup
924 | fi;
925 | endfor;
926 | );
927 | clip shadingPicture to (fullcircle scaled d);
928 | draw shadingPicture;
929 | )
930 | enddef;
931 |
932 | %
933 | % Alternative sphere macro. It's all about latitudinal strokes.
934 | % The idea is: when we have a sphere with evenly distributed parallel strokes
935 | % we know how their density rises towards edge in a projection,
936 | % so all we need to do is to fade lines correspondingly
937 | %
938 |
939 | vardef sphereLat (expr d, lat) =
940 | save p, a, x, y, sphlat, latrad, n, c, currentPath, nline, tlat;
941 | path p[], currentPath, currentArc;
942 | sphlat := 0;
943 | nline := 0;
944 | latrad := (2pi*lat/360);
945 | n := ceiling((pi*1/2d)/shadingDensity);
946 | if (cosd(lat) <> 0): tlat := (sind(lat)/cosd(lat)); fi;
947 | image(
948 | draw fullcircle scaled d withpen thinpen;
949 | p0 := fullcircle rotated 90;
950 | for nline := 1 upto n-1:
951 | sphlat := nline*(pi/n);
952 | if (sphlat + latrad < pi) and (sphlat + latrad > 0):
953 | if (cosd(lat) <> 0):
954 | if (sin(sphlat) <> 0):
955 | x := tlat*(cos(sphlat)/sin(sphlat));
956 | else:
957 | x := 0;
958 | fi;
959 | else:
960 | if ((sphlat > 1/2pi) and (lat > 0)) or ((sphlat < 1/2pi) and (lat < 0)):
961 | x := -2;
962 | else:
963 | x := 2;
964 | fi;
965 | fi;
966 | if (abs(x) <= 1):
967 | y := arcsin(x);
968 | p1 := subpath(6 + 8y/2pi, 2 - 8y/2pi) of p0;
969 | else:
970 | p1 := p0;
971 | fi;
972 | if (x > -1) and (arclength(p1) > 0):
973 | currentPath := (p1 scaled (d*sin(sphlat)) yscaled sind(lat)) shifted (0, 1/2d*cos(sphlat)*cosd(lat));
974 | currentPath := offsetPathSubdivide(currentPath);
975 | brushGenerate(currentPath,
976 | offsetPathTemplate(currentPath, 0)(
977 | maxShadingStrokeWidth * orderFade(
978 | sqrt(1 -
979 | abs(
980 | ypart(point offsetPathTime of currentPath)/(1/2d),
981 | 1 - abs(
982 | 1 - abs(
983 | xpart(point offsetPathTime of currentPath)
984 | /(1/2d)
985 | )
986 | )**abs(sind(lat))
987 | )**2)
988 | , nline)
989 | * normalVectorToLightness(
990 | sphereAnglesToNormalVector((
991 | (
992 | if (abs(point offsetPathTime of currentPath) > 0):
993 | angleRad(point offsetPathTime of currentPath)
994 | else:
995 | 0
996 | fi
997 | ), arcsin(2abs(point offsetPathTime of currentPath)/(d+1)))
998 | ), 0, point offsetPathTime of currentPath)
999 | ), 0);
1000 | fi;
1001 | fi;
1002 | endfor;
1003 | )
1004 | enddef;
1005 |
1006 | vardef orderFade (expr v, n)=
1007 | save o;
1008 | if (v > 1/256):
1009 | o := 2**ceiling(log(1/v, 2));
1010 | if ((n mod 1/2o) = 0):
1011 | if ((n mod o) = 0):
1012 | 1
1013 | else:
1014 | (v*o) - 1
1015 | fi
1016 | else:
1017 | 0
1018 | fi
1019 | else:
1020 | 0
1021 | fi
1022 | enddef;
1023 |
1024 | %
1025 | % This one converts point location on sphere to normal vector
1026 | %
1027 |
1028 | vardef sphereAnglesToNormalVector (expr p) =
1029 | save normalVector;
1030 | color normalVector;
1031 | normalVector := (0, 0, 1);
1032 | normalVector := rotateXYZaround.y(normalVector, ypart(p));
1033 | normalVector := rotateXYZaround.z(normalVector, -xpart(p));
1034 | normalVector
1035 | enddef;
1036 |
1037 | %
1038 | % Once we get two angles at some point of some surface, we can compute light intensity there.
1039 | %
1040 |
1041 | % In case you need to have your shaded objects white-on-black,
1042 | % you can just switch invertedLight invertedLight to 'true'
1043 |
1044 | boolean invertedLight;
1045 | invertedLight := false;
1046 |
1047 | vardef normalVectorToLightness (expr normalVector, d, q) =
1048 | save returnValue, shiftedShadowPath;
1049 | path shiftedShadowPath;
1050 | if shadowsEnabled:
1051 | for i := 0 step 1 until numberOfShadows:
1052 | shiftedShadowPath := shadowPath[i] shifted
1053 | ((redpart(lightDirectionVectorXYZ), greenpart(lightDirectionVectorXYZ))
1054 | scaled ((d-shadowDepth[i])*bluepart(lightDirectionVectorXYZ)));
1055 | if q isInside shiftedShadowPath:
1056 | returnValue := 1;
1057 | fi;
1058 | endfor;
1059 | fi;
1060 | if not known returnValue:
1061 | returnValue := 1 - (normalVector dotprodXYZ lightDirectionVectorXYZ);
1062 | returnValue := lightnessPP(returnValue);
1063 | fi;
1064 | if returnValue > 1:
1065 | returnValue := 1;
1066 | fi;
1067 | if returnValue < 0:
1068 | returnValue := 0;
1069 | fi;
1070 | if invertedLight:
1071 | returnValue := 1 - returnValue;
1072 | fi;
1073 | returnValue
1074 | enddef;
1075 |
1076 | vardef lightnessPP (expr v) =
1077 | v
1078 | enddef;
1079 |
1080 | % Shadows are global
1081 |
1082 | path shadowPath[];
1083 | numeric shadowDepth[];
1084 |
1085 | % Shadows either require high path resolution, or some points
1086 | % on a path in just the right place for shadows.
1087 | % This macro adds such points.
1088 |
1089 | vardef shadowCut (expr pathToCut, currentDepth)=
1090 | save shiftedShadowPath, pathShadowIntersection, pathShadowCut, currentPath;
1091 | path shiftedShadowPath, currentPath;
1092 | pair pathShadowIntersection;
1093 | numeric pathShadowCut;
1094 | currentPath := pathToCut;
1095 | for j := 0 step 1 until numberOfShadows:
1096 | shiftedShadowPath := shadowPath[j] shifted
1097 | ((redpart(lightDirectionVectorXYZ), greenpart(lightDirectionVectorXYZ))
1098 | scaled ((currentDepth - shadowDepth[j])*bluepart(lightDirectionVectorXYZ)));
1099 | forever:
1100 | pathShadowIntersection := shiftedShadowPath firstIntersectionTimes currentPath;
1101 | pathShadowCut := ypart(pathShadowIntersection);
1102 | if (pathShadowCut > 1/10) and (pathShadowCut < length(currentPath) - 1/10):
1103 | currentPath := (subpath (0, pathShadowCut - 1/20) of currentPath) .. (subpath (pathShadowCut + 1/20, length(currentPath)) of currentPath);
1104 | fi;
1105 | shiftedShadowPath := subpath (xpart(pathShadowIntersection) + 1/5, length(shiftedShadowPath)) of shiftedShadowPath;
1106 | exitif (pathShadowCut = -1);
1107 | endfor;
1108 | endfor;
1109 | currentPath
1110 | enddef;
1111 |
1112 | %
1113 | % Several macros rely on cutting offset path template at given height.
1114 | % Taking cutting points closer to the middle gives better results, and that's
1115 | % just what this macro tries to do.
1116 | %
1117 |
1118 | vardef cutPathTime (expr p, h) =
1119 | save cutTime, d;
1120 | numeric cutTime[], d[];
1121 | d1 := xpart(urcorner(p));
1122 | d2 := xpart(ulcorner(p));
1123 | if (d2 < d1):
1124 | d3 := 1/2(d1 + d2);
1125 | cutTime1 := ypart(((d3, h) -- (d1, h)) firstIntersectionTimes p);
1126 | cutTime2 := ypart(((d3, h) -- (d2, h)) firstIntersectionTimes p);
1127 | d4 := xpart (point cutTime1 of p);
1128 | d5 := xpart (point cutTime2 of p);
1129 | if abs(d4-d3) < abs(d5-d3):
1130 | cutTime3 := cutTime1
1131 | else:
1132 | cutTime3 := cutTime2
1133 | fi;
1134 | else:
1135 | cutTime3 := -1;
1136 | fi;
1137 | cutTime3
1138 | enddef;
1139 |
1140 | %
1141 | % This macro calculates ray angle after refraction. It takes raw angles (one of ray — p and one of surface — q)
1142 | % and refraction indices ratio. Whether ray comes from opticaly denser material is determined by direction of q
1143 | % relative to that of p
1144 | %
1145 |
1146 | vardef refractionAngle (expr p, q, n) =
1147 | save a;
1148 | numeric a[];
1149 | a0 := p - q;
1150 | if (sin(a0) < 0):
1151 | a1 := cos(a0 + pi) * n;
1152 | a2 := pi;
1153 | else:
1154 | a1 := cos(a0) / n;
1155 | a2 := 0;
1156 | fi;
1157 | if abs(a1) <= 1:
1158 | a3 := arccos(a1) + q + a2;
1159 | else:
1160 | a3 := -1000;
1161 | fi;
1162 | a3
1163 | enddef;
1164 |
1165 | %
1166 | % Same thing for reflection angle, just in case
1167 | %
1168 |
1169 | vardef reflectionAngle (expr p, q) =
1170 | (2pi - p + 2q)
1171 | enddef;
1172 |
1173 | %
1174 | % This macro returns path of ray 'sa' (which can actually be any path, but only ray from next to last to last point
1175 | % will count) refracted with coef. n through some shape p; if ray can't be refracted and, therefore, totally reflected,
1176 | % it will contunue as reflected from that point. i is total number of refractions to compute;
1177 | %
1178 |
1179 | vardef refractionPathR (expr sa, p, n, i, mn) =
1180 | save ray, resultRay, d, s, a, iT;
1181 | path ray, resultRay;
1182 | pair s, iT;
1183 | numeric d[], a;
1184 | s := point (length(sa) - 1) of sa;
1185 | a := angleRad((point (length(sa)) of sa)-(point (length(sa) - 1) of sa));
1186 | ray := (s shifted (-dirRad(a) scaled 2)) -- s -- (s shifted (dirRad(a) scaled (abs(llcorner(p)-(urcorner(p))) + abs(s-(center(p))))));
1187 | if (i > 0): ray := subpath (1 + 1/1000, 2) of ray; fi;
1188 | iT := ray firstIntersectionTimes p;
1189 | d1 := xpart(iT);
1190 | d2 := ypart(iT);
1191 | d3 := a;
1192 | d4 := angleRad(direction d2 of p);
1193 | if (n > 0):
1194 | d5 := refractionAngle(d3, d4, n);
1195 | if (d5 < -100) and (d2 >= 0):
1196 | d5 := reflectionAngle(d3, d4);
1197 | fi;
1198 | else:
1199 | d5 := reflectionAngle(d3, d4);
1200 | fi;
1201 | if (d1 >= 0) and (i < mn) and (d5 > -100):
1202 | resultRay := (subpath (0, length(sa) - 1) of sa) -- refractionPathR(point d2 of p -- (point d2 of p shifted dirRad(d5)), p, n, i + 1, mn);
1203 | else:
1204 | if (d5 > -100) or (d1 < 0):
1205 | resultRay := subpath (0, 1/2) of ray;
1206 | else:
1207 | resultRay := subpath (0, d1) of ray;
1208 | fi;
1209 | fi;
1210 | resultRay
1211 | enddef;
1212 |
1213 | vardef refractionPath (expr sa, p, n) =
1214 | refractionPathR(sa, p, n, 0, 10)
1215 | enddef;
1216 |
1217 | %
1218 | % These macros are for isolines. cLine draws continuous line and is called by isoLines.
1219 | % For now they are only used to draw wood texture, but can be used elsewhere
1220 | %
1221 |
1222 | %
1223 | % isoLines goes through i by j matrix of nodes (xy), looking for a square, that has some of its
1224 | % angles below zero and some - above, when found, it calls cLine, that tries to build segment of
1225 | % isoline, that happen to go through abovementioned square. Thickness of line is
1226 | % controlled by values in v array.
1227 | % All squares with lines already drawn through are ignored.
1228 | %
1229 |
1230 | vardef isoLines (suffix xy)(expr cs, l, s) =
1231 | save xxyy, i, j, c, v, sqB, iL, lvl, isNotMasked;
1232 | numeric c[], v[], sqB, sqbM;
1233 | boolean isNotMasked, xxyy[][];
1234 | isNotMasked := true;
1235 | lvl := l;
1236 | path iL;
1237 | image(
1238 | for i := 0 step 1 until xpart(cs) - 1:
1239 | for j := 0 step 1 until ypart(cs) - 1:
1240 | if (boolean isoLinesMask[i][j]):
1241 | isNotMasked := isoLinesMask[i][j];
1242 | fi;
1243 | if isNotMasked:
1244 | if (unknown xxyy[i][j]):
1245 | c1 := xy[i][j]+lvl;
1246 | c2 := xy[i][j+1]+lvl;
1247 | c3 := xy[i+1][j]+lvl;
1248 | c4 := xy[i+1][j+1]+lvl;
1249 | sqB := 0;
1250 | sqBm := 0;
1251 | if (abs(sign(c1)+sign(c2)+sign(c3)+sign(c4)) < 4):
1252 | iL := cLine (xy)((i, j), (0, 0), 0, cs) scaled s;
1253 | brushGenerate (reverse(iL),
1254 | offsetPathTemplate(iL, 0)(
1255 | 1/16minStrokeWidth
1256 | /(1/64 + 2(
1257 | if (offsetPathTime < length(iL) - 1):
1258 | (offsetPathTime - floor(offsetPathTime))
1259 | [v[floor(sqB + offsetPathTime)],
1260 | v[ceiling(sqB + offsetPathTime)]]
1261 | else:
1262 | 1
1263 | fi
1264 | ))
1265 | )
1266 | , 0);
1267 | fi;
1268 | fi;
1269 | fi;
1270 | endfor;
1271 | endfor;
1272 | draw (0,0);
1273 | )
1274 | enddef;
1275 |
1276 | % cLine tries to generate continouos segment of an isoline
1277 |
1278 | vardef cLine (suffix xy)(expr ij, dr, st, cs) =
1279 | save p, d, dd, n, i, j, k, outputPath, sqS, cp, dp, nd, isNotMasked;
1280 | pair p[], d[], dd[], cp[], dp[];
1281 | path outputPath;
1282 | boolean isNotMasked;
1283 | isNotMasked := true;
1284 | i := xpart(ij);
1285 | j := ypart(ij);
1286 | sqS := 0;
1287 | if (boolean isoLinesMask[i][j]):
1288 | isNotMasked := isoLinesMask[i][j];
1289 | fi;
1290 | if (i >= 0) and (i <= xpart(cs)-1) and (j >= 0) and (j <= ypart(cs)-1):
1291 | n := 0;
1292 | c1 := xy[i][j] + lvl; d1:= (i, j);
1293 | c2 := xy[i][j+1] + lvl; d2:= (i, j+1);
1294 | c3 := xy[i+1][j] + lvl; d3:= (i+1, j);
1295 | c4 := xy[i+1][j+1] + lvl; d4:= (i+1, j+1);
1296 | cp1 := (1, 2); dp1 := (-1, 0);
1297 | cp2 := (1, 3); dp2 := (0, -1);
1298 | cp3 := (2, 4); dp3 := (0, 1);
1299 | cp4 := (3, 4); dp4 := (1, 0);
1300 | for k := 1 upto 4:
1301 | c5 := c[xpart(cp[k])]; d5 := d[xpart(cp[k])];
1302 | c6 := c[ypart(cp[k])]; d6 := d[ypart(cp[k])];
1303 | if (sign(c5)) <> (sign(c6)):
1304 | n := n + 1;
1305 | p[n] := (abs(-c5/(c6-c5)))[d5, d6];
1306 | dd[n] := dp[k];
1307 | fi;
1308 | endfor;
1309 | sqS := max(c1, c2, c3, c4) - min(c1, c2, c3, c4);
1310 | if (unknown xxyy[i][j]) and isNotMasked:
1311 | xxyy[i][j] := true;
1312 | if (boolean isoLinesMask[i][j]):
1313 | isoLinesMask[i][j] := false;
1314 | fi;
1315 | if (dr = (0, 0)):
1316 | outputPath := cLine (xy)(ij shifted dd2, dd2, st + 1,cs) -- p1 -- p2 -- cLine (xy)(ij shifted dd1, dd1, st - 1,cs);
1317 | else:
1318 | nd := 0;
1319 | if (unknown(xxyy[i + xpart(dd1)][j + ypart(dd1)])):
1320 | nd := 1;
1321 | elseif (unknown(xxyy[i + xpart(dd2)][j + ypart(dd2)])):
1322 | nd := 2;
1323 | fi;
1324 | if nd > 0:
1325 | outputPath := cLine (xy)(ij shifted dd[nd], dd[nd], st + sign(st),cs);
1326 | p3 := p[nd];
1327 | if (st > 0):
1328 | outputPath := outputPath -- p3;
1329 | else:
1330 | outputPath := p3 -- outputPath;
1331 | fi;
1332 | else:
1333 | outputPath := 1/2[p1, p2];
1334 | fi;
1335 | fi;
1336 | else:
1337 | outputPath := 1/2[p1, p2];
1338 | fi;
1339 | else:
1340 | outputPath := (i, j);
1341 | xxyy[i][j] := true;
1342 | if (boolean isoLinesMask[i][j]):
1343 | isoLinesMask[i][j] := false;
1344 | fi;
1345 | fi;
1346 | if (st < sqB): sqB := st; fi;
1347 | if (st > sqBm): sqBm := st; fi;
1348 | v[st] := sqS;
1349 | outputPath
1350 | enddef;
1351 |
1352 | %
1353 | %
1354 | %
1355 | % In following section are gathered all the things for some commonly used
1356 | % real life objects
1357 | %
1358 | %
1359 | %
1360 |
1361 | %
1362 | % Though there's a decent library to deal with geography for mp already
1363 | % (http://melusine.eu.org/lab/bmp/a_mp-geo), here's some basic globe-drawing
1364 | % routine for simple cases, note that latitude starts from the pole,
1365 | % not from the equator (for convenience sake)
1366 | % Below some landmasses are defined
1367 | %
1368 |
1369 | path landmass[];
1370 | landmass1 := (206, 122.33)--(211.07, 116)--(213.3, 109.94)--(218.57, 106.03)--(218.38, 97.36)--(220.28, 91.28)--(229.75, 78.07)--(221.41, 78.29)--(220.78, 76.52)--(218.07, 74.48)--(213.8, 66.08)--(213.38, 62.04)--(222.31, 77.1)--(233.88, 72.27)--(237.79, 68.59)--(234.88, 64.69)--(229.83, 65.57)--(228.98, 64.73)--(227.37, 59.82)--(250.57, 68.12)--(254.63, 80.83)--(257.07, 80.93)--(257.38, 80.52)--(258.64, 75.5)--(266.4, 68.48)--(269.56, 67.49)--(271.88, 70.43)--(272.67, 74.49)--(275.36, 72.94)--(276.87, 78.6)--(276.68, 79.04)--(276.11, 79.28)--(276.3, 80.22)--(276.75, 79.96)--(276.56, 82.38)--(277.05, 82.04)--(280.5, 86.44)--(277.25, 85.56)--(276.55, 88.03)--(279.47, 92.77)--(283.29, 92.25)--(282.68, 90.91)--(283.74, 90.4)--(282.53, 89.58)--(283.03, 88.6)--(278.44, 80.08)--(279.15, 76.64)--(281.08, 78.25)--(282.29, 80.21)--(285.35, 79.72)--(288, 77.83)--(284.21, 71.22)--(287.94, 68.57)--(288, 68.6)--(288.74, 69.82)--(300.09, 61.89)--(300.86, 59.94)--(299.36, 59.63)--(297.64, 55.13)--(301.24, 52.55)--(296.1, 51.5)--(300.45, 49.51)--(299.83, 50.75)--(299.84, 50.82)--(299.44, 51.42)--(303.59, 50.57)--(302.72, 51.9)--(302.96, 52.12)--(304.97, 52.87)--(304.12, 55.13)--(307.89, 53.38)--(306.37, 50.11)--(308.65, 47.92)--(315.01, 45.12)--(319.69, 40.31)--(320.43, 44.25)--(321.66, 44.31)--(323.19, 41.66)--(320.37, 35.59)--(318.47, 37.21)--(315.99, 36.32)--(313.68, 35.16)--(320.43, 31.11)--(332.73, 30.38)--(338.5, 28.24)--(340.91, 28.61)--(334.92, 32.27)--(335, 39.2)--(340.58, 35.32)--(341.69, 32.15)--(340.43, 31.93)--(344.49, 29.68)--(352.49, 28.33)--(355.9, 25.35)--(358.67, 24.01)--(366.1, 25.61)--(368.78, 23.99)--(319.11, 17.34)--(309.82, 19)--(308.23, 18.4)--(307.69, 16.74)--(297.49, 16.63)--(290.61, 13.26)--(285.38, 13.37)--(284.06, 12.79)--(258.59, 16.61)--(260.79, 18.13)--(254.13, 18.01)--(253.53, 17.04)--(252.25, 17.02)--(252.44, 18.56)--(253.69, 19.64)--(251.71, 20.89)--(249.66, 16.97)--(245.54, 19.39)--(236.64, 19.73)--(239.08, 21)--(237.57, 21.46)--(232.4, 21.62)--(232.29, 21.34)--(225.16, 22.27)--(221.46, 21.23)--(218.52, 25.09)--(216.81, 24.69)--(214.76, 24.93)--(214.95, 25.52)--(213.66, 25.25)--(211.67, 23.33)--(215.44, 23.49)--(217.75, 21.65)--(200.52, 19.57)--(194.37, 21.1)--(186.19, 26.3)--(183.33, 30.4)--(187.61, 31.42)--(191.44, 33.88)--(194.61, 33.54)--(197.17, 30.74)--(196.08, 28.46)--(196.04, 27.66)--(203.54, 24.58)--(203.45, 24.88)--(200.38, 27.18)--(200.91, 27.54)--(200.05, 29.69)--(199.62, 29.91)--(201.03, 30.25)--(207.36, 29.93)--(205.2, 31.05)--(199.88, 30.97)--(199.94, 31.44)--(200.26, 32.2)--(202.19, 31.76)--(202.85, 32.2)--(199.62, 32.83)--(199.15, 34.61)--(189.46, 35.87)--(189.93, 35.46)--(191.12, 35.08)--(190.83, 34.56)--(188.1, 33.45)--(186.87, 34.75)--(187.11, 36.02)--(176.39, 40.19)--(176.65, 41.24)--(173.41, 42.02)--(176.82, 43.77)--(169.68, 46.56)--(169.15, 53.05)--(171.1, 53.62)--(173.12, 53.39)--(178.7, 51.26)--(183.17, 46.73)--(186.38, 46.75)--(192.72, 49.52)--(191.46, 52.64)--(193.74, 52.83)--(196.74, 50.32)--(190.71, 44.65)--(191.74, 44.4)--(198.11, 50.06)--(198.89, 52.03)--(200.95, 53.75)--(202.49, 51.99)--(201.15, 49.3)--(204.15, 49.28)--(206.54, 53.44)--(214.39, 53.25)--(211.18, 58.75)--(198.36, 57.7)--(197.88, 59.47)--(188.5, 55.87)--(189.63, 53.18)--(189.49, 52.79)--(173.31, 54.75)--(168.56, 58.21)--(161.34, 69.75)--(160.58, 75.18)--(161.25, 77.58)--(162.08, 79.09)--(163.71, 80.23)--(165.04, 82.46)--(168.88, 84.86)--(182.72, 83.77)--(184.88, 85.79)--(187.22, 85.99)--(186.79, 90.34)--(190.56, 95.97)--(190.23, 105.47)--(193.05, 115.74)--(196.18, 121.46)--(196.92, 124.65)--(206, 122.33)--(206, 122.33);
1371 | landmass2 := (111.44, 45.06)--(113.41, 44.75)--(111.77, 46)--(111.77, 46.07)--(118.69, 43.98)--(118.13, 42.88)--(116.49, 43.6)--(114.48, 42.7)--(114.1, 43.65)--(114.04, 41.9)--(113.28, 42.04)--(108.57, 42.18)--(114.57, 39.81)--(120.91, 38.84)--(119.04, 41.38)--(119.53, 41.59)--(122.9, 42.64)--(121.94, 42.77)--(121.82, 43.31)--(124.3, 42.48)--(125.29, 42.37)--(125.59, 41.84)--(125.41, 41.3)--(124.75, 41.38)--(122.58, 40.38)--(122.97, 39.95)--(121.71, 40.06)--(123.02, 38.38)--(121.65, 38.53)--(120.78, 35.69)--(116.8, 33.48)--(114.09, 29.59)--(110.59, 31.42)--(108.79, 28.81)--(104.18, 27.54)--(99.54, 29.42)--(100.85, 30.15)--(100.61, 31.83)--(100.51, 34.6)--(98.7, 35.56)--(99.11, 36.37)--(99.33, 38.41)--(96.3, 36.78)--(85.98, 32.83)--(83.79, 29.73)--(86.02, 28)--(87.63, 26.53)--(92.02, 23.6)--(94.53, 23.9)--(94.57, 23.59)--(95.6, 23.75)--(96.08, 21.63)--(96.05, 20.47)--(99.61, 19.73)--(103.5, 21.33)--(105.9, 22.76)--(103.75, 23.87)--(104.54, 24.37)--(101.78, 25.83)--(112.52, 27.74)--(113.4, 27.33)--(113.39, 27.23)--(110.6, 24.25)--(110.62, 24.18)--(111.27, 23.6)--(116.34, 23.81)--(117.17, 23.3)--(110.5, 21.34)--(111.78, 20.87)--(110.82, 20.4)--(111.3, 20.21)--(109.74, 19.84)--(110.11, 19.43)--(102.09, 17.29)--(97.38, 16.64)--(92.88, 17.67)--(92.21, 18.01)--(91.83, 17.28)--(89.16, 18.82)--(92.76, 20.05)--(93.22, 20.96)--(92.06, 21.98)--(91.69, 22.39)--(88.11, 21.59)--(87.79, 20.91)--(86.11, 20.22)--(86.94, 19.77)--(84.28, 18.1)--(84.81, 17.32)--(85.92, 16.37)--(82.62, 16.82)--(82.26, 18.46)--(82.22, 20.63)--(80.29, 21.42)--(73.81, 21.72)--(73.19, 21.56)--(73.02, 21.15)--(75.97, 21.21)--(75.92, 20.34)--(77.6, 20.64)--(73.05, 17.2)--(70.79, 18.11)--(67.81, 17.27)--(64.31, 17.23)--(54.27, 15.93)--(52.31, 18.03)--(60.06, 17.29)--(60.43, 18.73)--(59.79, 19.06)--(65.44, 20.05)--(71.86, 20.7)--(72.16, 20.95)--(69.43, 21.73)--(70.4, 21.96)--(70.06, 22.49)--(69.48, 22.4)--(63.3, 21.97)--(48.4, 19.77)--(41.64, 20.99)--(22.72, 18.59)--(11.06, 21.67)--(16.58, 23.75)--(14.57, 23.75)--(10.29, 24.54)--(17.36, 25.3)--(17.42, 26.18)--(12.61, 29.54)--(15.96, 29.89)--(15.52, 31.43)--(20.94, 31.31)--(13.31, 35.43)--(16.05, 35.66)--(19.1, 35.11)--(18.12, 34.75)--(27.83, 28.87)--(28.89, 30.18)--(33.87, 29.92)--(33.36, 30.35)--(38.31, 30.44)--(42.27, 33.16)--(42.87, 32.94)--(47.84, 35.37)--(50.85, 39.13)--(53.79, 42.3)--(54.39, 50.26)--(64.16, 61.59)--(63.13, 61.47)--(62.78, 61.95)--(64.93, 63.33)--(66.24, 65.62)--(67.78, 65.49)--(65.67, 61.75)--(65.09, 58.99)--(66.42, 61.44)--(68.81, 63.42)--(72.94, 69.36)--(81.5, 74.4)--(83.61, 73.92)--(85.99, 75.53)--(90.7, 76.75)--(93.55, 80.26)--(95.61, 82.43)--(96.7, 82.3)--(98.47, 82.54)--(101.05, 86.23)--(98.22, 93.14)--(100.55, 101.04)--(102.97, 105.27)--(107.45, 108.16)--(104.04, 132.27)--(104.08, 133.7)--(103.49, 134.62)--(102.5, 136.82)--(104.04, 136.98)--(103.44, 141.15)--(104.17, 143.63)--(108.08, 144.9)--(110.27, 145.35)--(111.35, 145.04)--(113.34, 144.63)--(109.31, 140.79)--(112.69, 137.21)--(111.47, 135.36)--(113.17, 133.67)--(113.34, 130.92)--(116.56, 129.1)--(119.97, 124.37)--(128.41, 119.87)--(133.19, 114.17)--(136.37, 113.08)--(138.56, 109.76)--(141.63, 100.78)--(139.94, 93.61)--(133.56, 91.17)--(129.89, 90.92)--(128.12, 89.29)--(123.75, 83.93)--(119.97, 83.01)--(117.24, 81.38)--(117.85, 80.79)--(116.9, 80.06)--(117.65, 79.02)--(114.24, 79.23)--(110.12, 78.93)--(108.35, 77.69)--(102.27, 80.15)--(102.6, 80.45)--(101.42, 81.66)--(96.3, 80.94)--(95.6, 75.16)--(91.88, 73.8)--(89.69, 73.89)--(91.19, 69.61)--(91.08, 68.3)--(87.73, 69.96)--(81.32, 69.32)--(81.63, 61.96)--(88.41, 60.66)--(88.78, 61.23)--(92.41, 60.31)--(95.93, 65.23)--(96.7, 65.47)--(97.12, 65.14)--(97.12, 59.81)--(100.34, 56.62)--(103.22, 54.85)--(104.21, 50.99)--(106.28, 48.84)--(108.51, 48.83)--(108.23, 48.05)--(111.68, 45.41);
1372 | landmass3 := (309.58, 101.89)--(307.85, 104.82)--(304.23, 104.36)--(301.98, 106.89)--(301.81, 107.2)--(301.39, 106.32)--(297.9, 109.91)--(292.61, 112.27)--(292.42, 116.24)--(291.76, 116.34)--(293.22, 123.3)--(295.54, 125.57)--(300.79, 123.84)--(313.31, 124.74)--(314.35, 125.13)--(314.72, 125.92)--(316.53, 125.74)--(318.45, 127.71)--(324.06, 128.78)--(326.88, 127.94)--(328.82, 125.64)--(331.64, 120.19)--(331.26, 115.24)--(328.34, 111.83)--(327.46, 109.78)--(327.32, 109.75)--(323.91, 106.24)--(320.57, 100.41)--(318.09, 106.52)--(315.29, 105.19)--(314.65, 104.27)--(314.4, 103.64)--(314.38, 101.88)--(314.02, 100.8)--(310.93, 100.72)--(310, 101.21)--(309.58, 101.89);
1373 | landmass4 := (360, 173.94)--(347.31, 173.02)--(337.83, 170.31)--(340.03, 168.66)--(345.63, 168.61)--(346.01, 167.92)--(341.09, 166.89)--(341.61, 165.5)--(343.88, 164.64)--(343.24, 163.51)--(349.37, 161.91)--(322.58, 157.73)--(323.11, 157.14)--(263.4, 156.39)--(263.26, 156.59)--(263.82, 157.03)--(245.18, 163.09)--(245.85, 157.68)--(234.93, 156.8)--(226.52, 156.65)--(194.69, 160.02)--(194.23, 160.12)--(182.27, 160.22)--(175.88, 161.21)--(175.09, 160.92)--(174.87, 161.24)--(171.99, 160.65)--(165.8, 161.33)--(163.91, 162.6)--(161.68, 163.73)--(141.54, 169.39)--(118.58, 172.13)--(116.78, 171.69)--(102.46, 169.67)--(94.78, 168.49)--(97.74, 167.88)--(101.28, 166.75)--(117.86, 164.33)--(118.52, 163.02)--(117.24, 161.46)--(117.41, 160.81)--(114.93, 158.64)--(113.38, 158.53)--(113.67, 158.17)--(112.94, 157.45)--(115.93, 156.83)--(115.81, 156.34)--(116.18, 155.88)--(116.84, 155.67)--(119.7, 154.63)--(119.77, 154.11)--(121.16, 153.99)--(121.76, 153.53)--(116.74, 154)--(113.84, 154.79)--(110.65, 157.28)--(111.18, 157.79)--(111.19, 159.12)--(104.73, 163.13)--(104.3, 163)--(90.27, 162.69)--(86.46, 162.59)--(74.77, 162.74)--(78.14, 164.63)--(64.48, 164.84)--(65.31, 164.46)--(50.04, 164.22)--(50.29, 164.61)--(32.44, 165.76)--(29.52, 166.6)--(27.21, 166.74)--(27.17, 166.97)--(22.41, 166.97)--(23.06, 168.33)--(21.43, 168.63)--(29.78, 169.97)--(27.58, 170.36)--(29.1, 170.81)--(23.15, 171.94)--(24.93, 172.46)--(17.69, 173.06)--(13.37, 172.69)--(3.71, 172.63)--(13.68, 173.98)--(0, 174.21);
1374 | landmass5 := (124.62, 19.08)--(123.98, 19.56)--(126.36, 20.09)--(127.24, 20.59)--(124.98, 23.19)--(130.77, 29.28)--(135.8, 28.99)--(137.84, 25.04)--(141.86, 24.34)--(146.13, 22.18)--(157, 19.51)--(155.91, 17.98)--(155.55, 16.8)--(159.25, 15.48)--(158.44, 14.93)--(159.9, 14.05)--(157.97, 12.46)--(159.52, 10.77)--(159.19, 10.3)--(167.06, 8.42)--(159.95, 8.2)--(156.76, 8.73)--(153.02, 7.87)--(131.44, 7.07)--(130.82, 7.37)--(127.12, 7.44)--(116.94, 8.32)--(111.03, 9.65)--(105.32, 11.75)--(107.03, 12.86)--(108.98, 13.43)--(112.23, 14.12)--(119.83, 14.46)--(121.54, 15.67)--(120.54, 15.91)--(122.91, 16.69)--(121.82, 17.23)--(124.62, 19.08);
1375 | landmass6 := (307.49, 56.47)--(307.06, 57.11)--(308.22, 57.5)--(310.39, 56.79)--(310.75, 57.43)--(312.59, 56.96)--(313.38, 56.17)--(316.84, 55.24)--(317.14, 55.51)--(319.46, 54.34)--(320.21, 51.88)--(320.32, 48.77)--(319.72, 48.29)--(319.35, 47.51)--(322.01, 46.93)--(323.56, 45.58)--(319.79, 44.82)--(319.05, 44.6)--(318.2, 46.06)--(317.67, 48.01)--(318.7, 48.63)--(315.73, 52.34)--(311.83, 54.71)--(307.49, 56.47);
1376 | landmass7 := (172.44, 33.8)--(171.76, 34.44)--(174.73, 35.22)--(173.52, 37.33)--(172.83, 38.17)--(172.56, 39.98)--(179.32, 38.52)--(178.63, 37.06)--(175.74, 33.85)--(176.19, 30.59)--(172.04, 32.2)--(171.52, 33.36)--(172.44, 33.8);
1377 | landmass8 := (222.04, 111.1)--(224.53, 115.35)--(228.6, 106.45)--(226.81, 103.35)--(222.04, 111.1);
1378 |
1379 | %
1380 | % This macro draws contures for a landmass on globe centered on lon,lat
1381 | %
1382 |
1383 | vardef drawLandMass (expr p, lon, lat) =
1384 | save i, j, k, l, horizon, currentPoint, horizonTimes, outHorizon, inHorizon, visibleContours, pathNumber, horizonArc, arcTimes, resultPath;
1385 | path resultPath, visibleContours[], horizon, horizonArc;
1386 | pair currentPoint, horizonTimes[];
1387 | numeric pathNumber, outHorizon, arcTimes[];
1388 | horizon := fullcircle scaled 2;
1389 | pathNumber := 0;
1390 | outHorizon := -1;
1391 | inHorizon := -1;
1392 |
1393 | % In the following loop visible segments of landmass and points of
1394 | % horizon-crossing are calculated
1395 | % visibleContours are just what they are called and horizonTimes are
1396 | % times on horizon circle where visible segment should cross it
1397 | for i := 0 upto length(p):
1398 | currentPoint := pointOnGlobe (point i of p, lon, lat);
1399 | if (horizonOnGlobe (point i of p, lon, lat) < 0):
1400 | if (unknown visibleContours[pathNumber]):
1401 | visibleContours[pathNumber] := currentPoint;
1402 | if (i > 0):
1403 | outHorizon := xpart(horizon intersectiontimes ((0,0) -- (findHorizonPoint (subpath(i-1, i) of p, lon, lat, 0) scaled 5)));
1404 | if (outHorizon < inHorizon): outHorizon := outHorizon + 8; fi;
1405 | horizonTimes[pathNumber - 1] := (inHorizon, outHorizon);
1406 | fi;
1407 | else:
1408 | visibleContours[pathNumber] := visibleContours[pathNumber] -- currentPoint;
1409 | fi;
1410 | else:
1411 | if (known visibleContours[pathNumber]):
1412 | pathNumber := pathNumber + 1;
1413 | inHorizon := xpart(horizon intersectiontimes ((0,0) -- (findHorizonPoint (subpath(i, i-1) of p, lon, lat, 0) scaled 5)));
1414 | fi;
1415 | fi;
1416 | endfor;
1417 | if (unknown visibleContours0):
1418 | resultPath := (1,0);
1419 | else:
1420 | if (unknown visibleContours[pathNumber]): pathNumber := pathNumber - 1; fi;
1421 | if (unknown horizonTimes[-1]):
1422 | if (pathNumber > 0):
1423 | visibleContours0 := visibleContours[pathNumber] -- visibleContours0;
1424 | fi;
1425 | pathNumber := pathNumber - 1;
1426 | else:
1427 | if (ypart(horizonTimes[-1]) < inHorizon):
1428 | horizonTimes[pathNumber] := (inHorizon, ypart(horizonTimes[-1]) + 8);
1429 | else:
1430 | horizonTimes[pathNumber] := (inHorizon, ypart(horizonTimes[-1]));
1431 | fi;
1432 | fi;
1433 | % In these loops horizon arcs directions should be handled
1434 | % The idea is that when we have path with no self-intersections arcs should
1435 | % not cross one another, these conflicts are resolved here
1436 | % It's important to note, that horizon-time detecting algorithm is
1437 | % not absolutely precise for now, so at times in will work incorrect.
1438 | for i := 0 upto pathNumber - 1:
1439 | for j := i + 1 upto pathNumber:
1440 | l := 0;
1441 | for k := -8, 0, 8:
1442 | if (xpart(horizonTimes[j]) > xpart(horizonTimes[i]) + k) and (xpart(horizonTimes[j]) < ypart(horizonTimes[i]) + k): l := l + 1; fi;
1443 | if (xpart(horizonTimes[i]) > xpart(horizonTimes[j]) + k) and (xpart(horizonTimes[i]) < ypart(horizonTimes[j]) + k): l := l + 1; fi;
1444 | endfor;
1445 | if (l > 1): horizonTimes[j] := (xpart(horizonTimes[j]) + 8, ypart(horizonTimes[j])); fi;
1446 | endfor;
1447 | endfor;
1448 |
1449 | % In the following loop previously calculated segments of a landmass and
1450 | % arcs of the horizon are sewed together in order
1451 | resultPath := visibleContours0
1452 | for i := 1 upto pathNumber + 1:
1453 | if (known horizonTimes[i-1]): -- (subpath horizonTimes[i-1] of horizon) fi
1454 | if (i <= pathNumber): -- visibleContours[i] fi
1455 | endfor
1456 | fi;
1457 | resultPath -- cycle
1458 | enddef;
1459 |
1460 | % This thing just converts coordinates on globe rotated by lon, lat to screen coordinates
1461 |
1462 | vardef pointOnGlobe (expr p, lon, lat) =
1463 | (cosd(lon + xpart(p)) * sind(ypart(p)),
1464 | cosd(ypart(p)) * cosd(lat)
1465 | + sind(lon + xpart(p)) * sind(ypart(p)) * sind(lat))
1466 | enddef;
1467 |
1468 | % This one is needed to check if point on globe is in view
1469 |
1470 | vardef horizonOnGlobe (expr p, lon, lat) =
1471 | (sind(lon + xpart(p)) * cosd(lat) * sind(ypart(p))) - (cosd(ypart(p)) * sind(lat))
1472 | enddef;
1473 |
1474 | % This macro calculates horizon crossing point with given precision (recursion depth).
1475 | % Likely, this could be done analytically, though.
1476 |
1477 | vardef findHorizonPoint (expr p, lon, lat, i) =
1478 | save selecthalf, returnpoint;
1479 | pair selecthalf, returnpoint;
1480 | if (horizonOnGlobe (point 1/2 of p, lon, lat) < 0):
1481 | selecthalf := (0, 1/2);
1482 | else:
1483 | selecthalf := (1/2, 1);
1484 | fi;
1485 | if (i < 5):
1486 | returnpoint := findHorizonPoint (subpath selecthalf of p, lon, lat, i + 1)
1487 | else:
1488 | returnpoint := pointOnGlobe (point 1/2 of p, lon, lat);
1489 | fi;
1490 | returnpoint
1491 | enddef;
1492 |
1493 | vardef globe (expr s, lon, lat) =
1494 | save i, p, lm;
1495 | picture p[];
1496 | path lm;
1497 | begingroup
1498 | save lightnessPP;
1499 | vardef lightnessPP (expr v) =
1500 | 1/2v
1501 | enddef;
1502 | p1 := image(draw sphereLat(2s, lat));
1503 | vardef lightnessPP (expr v) =
1504 | if (abs(cos(sphlat)) > 7/8 + uniformdeviate (1/20)):
1505 | 1/4v
1506 | else:
1507 | 1/3v + 2/3
1508 | fi
1509 | enddef;
1510 | p2 := image(draw sphereLat(2s, lat));
1511 | endgroup;
1512 | image(
1513 | draw fullcircle scaled 2s withpen thinpen;
1514 | for i := 1 upto 8:
1515 | lm := drawLandMass(landmass[i], lon + 90, lat) scaled s;
1516 | p3 := p2;
1517 | clip p3 to lm;
1518 | draw p3;
1519 | thinBrushGenerate (lm,
1520 | offsetPathTemplate (lm, 0) (
1521 | 2/3minStrokeWidth + 1/3minStrokeWidth
1522 | * normalVectorToLightness(
1523 | sphereAnglesToNormalVector(
1524 | (angleRad(point offsetPathTime of lm), arcsin(abs(point offsetPathTime of lm)/2s))
1525 | ), 0, point offsetPathTime of lm
1526 | )
1527 | ), 0);
1528 | p1 := p1 maskedWith lm;
1529 | endfor;
1530 | draw p1;
1531 | )
1532 | enddef;
1533 |
1534 | %
1535 | % This macro draws an eye pointed in the direction a (in degrees)
1536 | % Eye is opened at random angle and pupil is scaled randomly by design
1537 | % Scaling below some level, dependent on minStrokeWidth, simplifies image
1538 | %
1539 |
1540 | eyescale := 1/2cm;
1541 |
1542 | vardef eye (expr a) =
1543 | save s, eyelids, pupil, eyeball, eyelash, loopstep, p, o;
1544 | path eyelids[], pupil[], eyelash;
1545 | pair p[];
1546 | picture eyeball;
1547 | numeric s, loopstep;
1548 | o := 10 + (15/(1 + 2**(3/2normaldeviate)));
1549 | s := eyescale;
1550 | p1 := (-3/4s, 0);
1551 | pupil1 := ((subpath (-2, 2) of fullcircle xscaled 3/5) .. (subpath (3, 5) of fullcircle xscaled 2/5) .. cycle) scaled 3/5s;
1552 | pupil2 := fullcircle scaled (1/3s + uniformdeviate(1/5s)) xscaled 1/3;
1553 | p2 := ((p1 -- ((1/2s, 0) rotatedabout (p1, o - 5))) intersectionpoint (subpath (0, 4) of pupil1));
1554 | eyelids1 := (p1 shifted (0, -1/16s)){dir(1/3o)} .. {dir(0)}p2;
1555 | eyelids2 := p1 {dir(-1/3o)} .. {dir(0)}((1/6s, 0) rotatedabout (p1, -2/3o - 5));
1556 | eyelids2 := subpath(xpart(eyelids2 intersectiontimes eyelids1), length(eyelids2)) of eyelids2;
1557 | eyelids3 := (p1){dir(2/3o)} .. tension 3/2 .. {dir(o-1/3o)}p2 rotatedabout (p1, 1/3o + 7);
1558 | eyelids3 := subpath (1/8, length(eyelids3)) of eyelids3;
1559 | eyelids4 := (p1 shifted (0, -1/16s)) .. {dir(1/4o - 2/3o)}((1/6s, -1/6s) rotatedabout (p1, -2/3o - 5));
1560 | eyelids4 := subpath (1/2, length(eyelids4)) of eyelids4;
1561 | loopstep := length(eyelids1)/20;
1562 | if (arclength(subpath(0, loopstep) of eyelids1) < 5minStrokeWidth):
1563 | loopstep := arctime (5minStrokeWidth) of eyelids1;
1564 | fi;
1565 | eyeball := image(
1566 | if (5loopstep <= 1):
1567 | draw pupil1 withpen thinpen;
1568 | fill pupil2;
1569 | for i := 0 step 5loopstep until length pupil1:
1570 | draw brush ((point i of pupil1) -- (point i + 6 of pupil2 scaled 5/6 yscaled 1/2))(cos(offsetPathLength*1/2pi)*2minStrokeWidth);
1571 | endfor;
1572 | else:
1573 | fill pupil1;
1574 | fi;
1575 | );
1576 | clip eyeball to (eyelids1{(1, 0)} .. (s, 0) .. {-1, 0}reverse(eyelids2) -- cycle);
1577 | eyeball := eyeball maskedWith ((fullcircle scaled (1/4s) xscaled 1/2 rotated 2 shifted (1/12s, 0) rotatedabout (p1, 1/3o + 2)));
1578 | image(
1579 | draw brush (eyelids1 .. tension 2.5 .. reverse (eyelids3))((1-offsetPathLength)*2minStrokeWidth);
1580 | draw brush (eyelids2)((offsetPathLength)*2minStrokeWidth);
1581 | draw brush (eyelids4)(sin(offsetPathLength*pi)*minStrokeWidth);
1582 | draw eyeball;
1583 | for i := length(eyelids1) step -loopstep until 0:
1584 | eyelash := (point i of eyelids1) {dir(angle(direction i of eyelids1) - 60 + 50*(i/length(eyelids1)))}
1585 | .. (point i of eyelids1) shifted (1/16s + (i/length(eyelids1))*1/4s, (i/length(eyelids1))*1/5s);
1586 | if (arclength(eyelash) > 2/3minDashStrokeLength):
1587 | draw brush (eyelash shifted ((-1/32s, uniformdeviate(1/12s)) scaled ((length(eyelids1)-i)/length(eyelids1))) )(minStrokeWidth + (1-offsetPathLength)*minStrokeWidth);
1588 | fi;
1589 | endfor;
1590 | for i := length(eyelids2) step -3/2loopstep until 0:
1591 | eyelash := (point i of eyelids2) {dir(angle(direction i of eyelids2) + 20 - 40*(i/length(eyelids2)))}
1592 | .. (point i of eyelids2) shifted (1/16s + (i/length(eyelids2))**2*1/7s, 1/16s - (i/length(eyelids2))*1/5s);
1593 | if (arclength(eyelash) > minDashStrokeLength):
1594 | draw brush (eyelash shifted (-1/32s, -uniformdeviate(1/24s)))(minStrokeWidth + (1-offsetPathLength)*minStrokeWidth);
1595 | fi;
1596 | endfor;
1597 | ) if cosd(a) < 0: yscaled -1 rotated (a) else: rotated a fi
1598 | enddef;
1599 |
1600 | %
1601 | % This macro draws solid surface
1602 | %
1603 |
1604 | numeric solidSurfaceThickness;
1605 | solidSurfaceThickness := 1/4cm;
1606 |
1607 | vardef solidSurface (expr p) =
1608 | save q, s, d, stripes;
1609 | path q, s;
1610 | picture stripes;
1611 | q := offsetPath(p) (-solidSurfaceThickness);
1612 | s := p -- reverse(q) -- cycle;
1613 | image(
1614 | draw solid (s, 45, 0);
1615 | draw p withpen thinpen;
1616 | )
1617 | enddef;
1618 |
1619 | vardef solid (expr p, a, t) =
1620 | save stripes, stripeskind, d, i, j, c, strokeVariation;
1621 | picture stripes, stripeskind;
1622 | pair c;
1623 | stripes := image(
1624 | d1 := abs(ulcorner(p rotated (90 - a)) - urcorner(p rotated (90 - a)));
1625 | d2 := abs(ulcorner(p rotated (90 - a)) - llcorner(p rotated (90 - a)));
1626 | stripeskind := dashpattern (on 1mm);
1627 | c := 1/2[ulcorner(p rotated (90 - a)), lrcorner(p rotated (90 - a))] rotated (a - 90);
1628 | for i:= 0 step (3/2shadingDensity)/d1 until 1:
1629 | if (t = 1):
1630 | strokeVariation := uniformdeviate(1)-1/2;
1631 | j := round(i*d1/(3/2shadingDensity));
1632 | if (j mod 4) = 0:
1633 | stripeskind := dashpattern (on (8-strokeVariation)*shadingDensity off (4+strokeVariation)*shadingDensity);
1634 | fi;
1635 | if ((j mod 4) = 1) or ((j mod 4) = 3):
1636 | stripeskind := dashpattern (off 1shadingDensity on (6-strokeVariation)*shadingDensity off (5+strokeVariation)*shadingDensity);
1637 | fi;
1638 | if (j mod 4) = 2:
1639 | stripeskind := dashpattern (on 0 off 12shadingDensity);
1640 | fi;
1641 | fi;
1642 | draw ((dir(a) scaled 1/2(d2-uniformdeviate(3shadingDensity))) -- (dir(a + 180) scaled 1/2d2)) shifted c shifted i[dir(a + 90) scaled 1/2d1, dir(a -90) scaled 1/2d1] withpen thinpen
1643 | dashed stripeskind;
1644 | endfor;
1645 | );
1646 | clip stripes to p;
1647 | stripes
1648 | enddef;
1649 |
1650 | %
1651 | % Returns a picture of shaded gradient inside shape p at an angle a
1652 | %
1653 |
1654 | vardef gradientShade (expr p, a) =
1655 | save stripes, stripeshd, d, i, j, s;
1656 | picture stripes;
1657 | path s;
1658 | stripes := image(
1659 | d1 := abs(ulcorner(p rotated (90 - a)) - urcorner(p rotated (90 - a)));
1660 | d2 := abs(ulcorner(p rotated (90 - a)) - llcorner(p rotated (90 - a)));
1661 | for i:= 0 step (shadingDensity)/d1 until 1:
1662 | s := ((dir(a) scaled 1/2d2) -- (dir(a + 180) scaled 1/2d2)) shifted 1/2[ulcorner(p), lrcorner(p)] shifted i[dir(a + 90) scaled 1/2d1, dir(a -90) scaled 1/2d1];
1663 | stripeshd := 1/4 + 3/4i;
1664 | draw brush(s)(minStrokeWidth*stripeshd);
1665 | endfor;
1666 | );
1667 | clip stripes to p;
1668 | stripes
1669 | enddef;
1670 |
1671 | %
1672 | % This one draws a spring between points p and q with n steps
1673 | % if stretched more than possible, displayed as a straight line
1674 | % if compressed too much, displayed as having less steps
1675 | %
1676 |
1677 | springwidth := 1/8cm;
1678 |
1679 | vardef spring (expr p, q, n) =
1680 | save sp, ss, t, x, springstep, springcoef, springsegment;
1681 | transform t;
1682 | path ss[];
1683 | pair sp;
1684 | picture springsegment;
1685 | springstep := (arclength(p--q) - 2springwidth)/(n+1);
1686 | if (springstep < 6minStrokeWidth): springstep := arclength(p--q)/round(arclength(p--q)/6minStrokeWidth); fi;
1687 | if (springstep < (springwidth*pi)):
1688 | springcoef := (1-(springstep/(springwidth*pi)));
1689 | else:
1690 | springcoef := 0;
1691 | fi;
1692 | image(
1693 | for i := 0 step 30 until 360:
1694 | sp := ((cosd(i - 90), sind(i - 90)) scaled springwidth xscaled 1/4 yscaled springcoef) shifted (springstep*(i/360) - 1/2springstep, 0);
1695 | if (i = 0):
1696 | ss1 := sp;
1697 | else:
1698 | ss1 := ss1 -- sp;
1699 | fi;
1700 | endfor;
1701 | ss2 := subpath (0, 6) of ss1;
1702 | ss3 := subpath (6, 12) of ss1;
1703 | ss4 := subpath (0, ypart(ss2 shifted (-3minStrokeWidth, 0) intersectiontimes ss3)) of ss3;
1704 | x := ypart(ss2 shifted (3minStrokeWidth, 0) intersectiontimes ss3);
1705 | if (x > 0):
1706 | ss5 := subpath (x, length(ss3)) of ss3;
1707 | else:
1708 | ss5 := point length(ss3) of ss3;
1709 | fi;
1710 | if (xpart(llcorner(ss4)) - 3minStrokeWidth < xpart(urcorner(ss2 shifted (-springstep, 0)))):
1711 | x := ypart((subpath (3, 6) of ss2 shifted (-springstep + 3minStrokeWidth, 0)) intersectiontimes ss4);
1712 | if (x > 0):
1713 | ss6 := subpath (0, x) of ss4;
1714 | else:
1715 | ss6 := point 0 of ss4;
1716 | fi;
1717 | x := ypart((subpath (0, 3) of ss2 shifted (-springstep + 3minStrokeWidth, 0)) intersectiontimes ss4);
1718 | if (x > 0):
1719 | ss7 := subpath (x, length(ss4)) of ss4;
1720 | else:
1721 | ss7 := point length(ss4) of ss4;
1722 | fi;
1723 | fi;
1724 | springsegment := image(
1725 | draw brush (ss2)(minStrokeWidth + sin(offsetPathLength*pi)*minStrokeWidth);
1726 | if (unknown(ss6)):
1727 | if (arclength(ss4) > minStrokeWidth): draw ss4 withpen thinpen; fi;
1728 | else:
1729 | if (arclength(ss6) > minStrokeWidth): draw ss6 withpen thinpen; fi
1730 | if (arclength(ss7) > minStrokeWidth): draw ss7 withpen thinpen; fi
1731 | fi;
1732 | if (arclength(ss5) > minStrokeWidth): draw ss5 withpen thinpen; fi;
1733 | );
1734 | ss8 := (ss2 shifted (-2minStrokeWidth, 0)) rotated angle(q-p) shifted ((springwidth + 1/2springstep)/arclength(p--q))[p, q];
1735 | for i := springwidth + 1/2springstep step springstep until arclength(p--q) - springwidth - 1/2springstep + 1:
1736 | t := identity rotated angle(q-p) shifted (i/arclength(p--q))[p, q];
1737 | draw springsegment transformed t;
1738 | if (i <= springwidth + 1/2springstep + 2/3springwidth):
1739 | ss9 := ss3 transformed t;
1740 | ss10 := subpath (
1741 | xpart(ss9 intersectiontimes (subpath (0, 3) of ss8)),
1742 | xpart(ss9 intersectiontimes (subpath (3, 6) of ss8))
1743 | ) of ss9;
1744 | if (arclength(ss10) > minStrokeWidth): draw ss10 withpen thinpen; fi;
1745 | fi;
1746 | endfor;
1747 | draw brush (((springwidth)/arclength(p--q))[p, q] shifted (dir(angle(p-q) + 90)*springwidth * springcoef){(p-q)} .. {(p-q)}p)(minStrokeWidth);
1748 | draw brush (((springwidth)/arclength(p--q))[q, p] shifted (dir(angle(p-q) + 90)*springwidth * springcoef){(q-p)} .. {(q-p)}q)(minStrokeWidth);
1749 | )
1750 | enddef;
1751 |
1752 | %
1753 | % This macro draws some kind of weight. Not very nice one at the moment
1754 | %
1755 |
1756 | vardef weight.h (expr h) =
1757 | save auricle, q, r;
1758 | path q[];
1759 | auricle.d := 2mm;
1760 | auricle.t := 2shadingDensity;
1761 | r := 2/5(h-auricle.d);
1762 | image(
1763 | q0 := offsetPathSubdivide((0, -h) -- (0, -auricle.d - 1/6h));
1764 | q1 := offsetPathTemplate(q0, 0)(r-(offsetPathLength*(1/8r)));
1765 | q2 := offsetPathGenerate (q0, q1, 0);
1766 | q3 := offsetPathGenerate (q0, q1 yscaled -1, 0);
1767 | tubeGenerate (q2, q3, q1, 0);
1768 | draw reverse(q2) -- q3 withpen thinpen;
1769 | q0 := offsetPathSubdivide((0, -auricle.d - 1/6h) -- (0, -auricle.d));
1770 | q1 := offsetPathTemplate(q0, 0)(2/8r + 5/8r*(sqrt(1-offsetPathLength**2)));
1771 | q2 := offsetPathGenerate (q0, q1, 0);
1772 | q3 := offsetPathGenerate (q0, q1 yscaled -1, 0);
1773 | tubeGenerateAlt (q2, q3, q1);
1774 | draw q3 -- reverse(q2) withpen thinpen;
1775 | q5 := offsetPathSubdivide(point 0 of q3 -- point 0 of q2);
1776 | q6 := tube.e((0,0) -- (0, -3/2auricle.t))(1/2auricle.t);
1777 | draw image(
1778 | q4 := (((0, -1/2) {dir(90)} .. (1/2, 1/2) .. (0, 1) .. {dir(-90)}(-1/2, 1/4)) shifted (0, -1)) scaled 2/3auricle.d;
1779 | draw shadedEdge(tube.e(q4) (1/4auricle.t)) shifted (0, -1/2auricle.t);
1780 | ) maskedWith (q3 -- reverse(q2) -- (q2 yscaled 0 shifted (0, -h)) -- (reverse(q3) yscaled 0 shifted (0, -h)) -- cycle)
1781 | maskedWith q6;
1782 | draw shadedEdge(q6);
1783 | )
1784 | enddef;
1785 |
1786 | vardef weight.s (expr h) =
1787 | save q,r;
1788 | path q[];
1789 | r := 2/5h;
1790 | image(
1791 | q0 := offsetPathSubdivide((0, 0) -- (0, h-2/3r));
1792 | q1 := offsetPathTemplate(q0, 0)(r);
1793 | q2 := offsetPathGenerate (q0, q1, 0);
1794 | q3 := offsetPathGenerate (q0, q1 yscaled -1, 0);
1795 | tubeGenerate (q2, q3, q1, 0);
1796 | draw reverse(q2)--q3 withpen thinpen;
1797 | q0 := offsetPathSubdivide((0, h-2/3r) -- (0, h - 1/8r));
1798 | q1 := offsetPathTemplate(q0, 0)(r-sqrt(1- (1- offsetPathLength*2)**2)*1/3r - 1/6r*offsetPathLength);
1799 | q2 := offsetPathGenerate (q0, q1, 0);
1800 | q3 := offsetPathGenerate (q0, q1 yscaled -1, 0);
1801 | tubeGenerateAlt (q2, q3, q1);
1802 | draw q2 withpen thinpen;
1803 | draw q3 withpen thinpen;
1804 | q0 := offsetPathSubdivide((0, h-1/8r) -- (0, h));
1805 | q1 := offsetPathTemplate(q0, 0)((r-1/6r)+sqrt(1- (1- offsetPathLength*2)**2)*1/16r);
1806 | q2 := offsetPathGenerate (q0, q1, 0);
1807 | q3 := offsetPathGenerate (q0, q1 yscaled -1, 0);
1808 | tubeGenerateAlt (q2, q3, q1);
1809 | draw q2 --reverse(q3) withpen thinpen;
1810 | )
1811 | enddef;
1812 |
1813 | %
1814 | % This macro makes a lens-shaped clockwise path with radii
1815 | % r = (left radius, right radius), thickness t and diameter d
1816 | %
1817 |
1818 | vardef lens (expr r, t, d, s) =
1819 | save p, q, m, c;
1820 | pair c[];
1821 | path p[], q[];
1822 | if (xpart(r) = infinity):
1823 | p1 := (0, d) -- (0, -d);
1824 | else:
1825 | p1 := subpath (2, 6) of fullcircle scaled 2xpart(r);
1826 | fi;
1827 | if (ypart(r) = infinity):
1828 | p2 := (0, d) -- (0, -d);
1829 | else:
1830 | p2 := subpath (-2, 2) of fullcircle scaled 2ypart(r);
1831 | fi;
1832 | q1 := (min(xpart(ulcorner(p1)), xpart(ulcorner(p2))) - 1, -1/2d)--(max(xpart(urcorner(p1)), xpart(urcorner(p2))) + 1,-1/2d);
1833 | q2 := q1 shifted (0, d);
1834 | q3 := q1 shifted (0, 1/2d);
1835 | c1 := p1 intersectiontimes q1;
1836 | c2 := p1 intersectiontimes q2;
1837 | c3 := p2 intersectiontimes q2;
1838 | c4 := p2 intersectiontimes q1;
1839 | if (xpart(c1) > 0):
1840 | p1 := subpath (xpart(c1), xpart(c2)) of p1;
1841 | fi;
1842 | if (xpart(c3) > 0):
1843 | p2 := subpath (xpart(c3), xpart(c4)) of p2;
1844 | fi;
1845 | p1 := p1 shifted (-xpart(point xpart(p1 intersectiontimes q3) of p1), 0);
1846 | p2 := p2 shifted (-xpart(point xpart(p2 intersectiontimes q3) of p2) + t, 0);
1847 | reverse(p1--p2--cycle) scaled s
1848 | enddef;
1849 |
1850 | %
1851 | % This one returns a picture of a pulley with diameter d and it's support rotated
1852 | % at angle a. pulleyOutline path changes every time
1853 | %
1854 |
1855 | path pulleyOutline;
1856 | numeric pulleySupportSize;
1857 | pulleySupportSize := 2/3;
1858 |
1859 | vardef pulley (expr d, a) =
1860 | save pw, p, r;
1861 | picture pw;
1862 | path p[];
1863 | r1 := 3/5d;
1864 | r2 := 1/6d;
1865 | image(
1866 | p0 := fullcircle scaled d;
1867 | p1 := (subpath (3, 9) of fullcircle) scaled r1;
1868 | p0 := subpath (
1869 | xpart(p0 intersectiontimes ((point 0 of p1) -- (point 0 of p1 shifted (0, d)))),
1870 | 8 + xpart(p0 intersectiontimes ((point 0 of reverse(p1)) -- (point 0 of reverse(p1) shifted (0, d)))))
1871 | of p0;
1872 | p0 := ((xpart(point 0 of reverse(p0)), pulleySupportSize*d) -- (xpart(point 0 of p0), pulleySupportSize*d) -- p0 -- cycle) rotated a;
1873 | pulleyOutline := p0;
1874 | p1 := (p1 -- (xpart(point 0 of reverse(p1)), pulleySupportSize*d) -- (xpart(point 0 of p1), pulleySupportSize*d) -- cycle) rotated a;
1875 | pw := pulleyWheel(d) maskedWith p1;
1876 | draw pw;
1877 | draw p1 withpen thinpen;
1878 | draw shadedEdge(reverse(fullcircle) scaled r2);
1879 | )
1880 | enddef;
1881 |
1882 | vardef pulleyWheel (expr d) =
1883 | save pw, r, i;
1884 | picture pw;
1885 | r1 := 7/9d;
1886 | r2 := 8/9d;
1887 | r3 := 3/5d;
1888 | r4 := 1/8d;
1889 | if (r2-r1) > shadingDensity:
1890 | pw := image(
1891 | for i := r3 step 2shadingDensity until r2:
1892 | if (i <= r1) or (i >= r2):
1893 | thinBrushGenerate (fullcircle scaled i,
1894 | offsetPathTemplate (fullcircle scaled i, 0) (
1895 | 2/3minStrokeWidth + minStrokeWidth
1896 | * normalVectorToLightness(
1897 | sphereAnglesToNormalVector(
1898 | (angleRad(point offsetPathTime of fullcircle), arcsin(i/4d))
1899 | ), 0, point offsetPathTime of fullcircle scaled i
1900 | )
1901 | ), 0);
1902 | else:
1903 | thinBrushGenerate (fullcircle scaled i,
1904 | offsetPathTemplate (fullcircle scaled i, 0) (
1905 | 1/4minStrokeWidth + minStrokeWidth
1906 | * normalVectorToLightness(
1907 | sphereAnglesToNormalVector(
1908 | (angleRad(point offsetPathTime of fullcircle) + pi, arcsin(1/2))
1909 | ), 0, point offsetPathTime of fullcircle scaled i
1910 | )
1911 | ), 0);
1912 | fi;
1913 | endfor;
1914 | draw brush (fullcircle scaled r1)(minStrokeWidth);
1915 | draw brush (fullcircle scaled r2)(minStrokeWidth);
1916 | draw fullcircle scaled d withpen thinpen;
1917 | draw fullcircle scaled r3 withpen thinpen;
1918 | draw shadedEdge(reverse(fullcircle) scaled r4);
1919 | );
1920 | else:
1921 | pw := image(
1922 | draw shadedEdge (reverse(fullcircle) scaled r1);
1923 | draw fullcircle scaled d withpen thinpen;
1924 | draw fullcircle scaled r4 withpen thickpen;
1925 | )
1926 | fi;
1927 | pw
1928 | enddef;
1929 |
1930 | %
1931 | % This macro draws a wheel
1932 | %
1933 |
1934 | vardef wheel (expr d, a) =
1935 | save pc, p, r, i;
1936 | picture pc[];
1937 | path p[];
1938 | r1 := 2/8d;
1939 | r2 := d-6minStrokeWidth;
1940 | r3 := 7/8d-2shadingDensity;
1941 | if r1 > 3shadingDensity:
1942 | pc1 := image(
1943 | for i := r1 step 2shadingDensity until r3:
1944 | thinBrushGenerate (fullcircle scaled i,
1945 | offsetPathTemplate (fullcircle scaled i, 0) (
1946 | 2/3minStrokeWidth + minStrokeWidth
1947 | * normalVectorToLightness(
1948 | sphereAnglesToNormalVector(
1949 | (angleRad(point offsetPathTime of fullcircle) + pi, arcsin(i/4d))
1950 | ), 0, point offsetPathTime of fullcircle scaled i
1951 | )
1952 | ), 0);
1953 | endfor;
1954 | draw sphere.c(r1);
1955 | draw shadedEdge (reverse(fullcircle) scaled r3);
1956 | );
1957 | else:
1958 | pc1 := image(
1959 | draw shadedEdge (fullcircle scaled d);
1960 | draw shadedEdge (fullcircle scaled r1);
1961 | draw shadedEdge (reverse(fullcircle) scaled r2);
1962 | );
1963 | fi;
1964 | pc2 := image(fill fullcircle scaled d;) maskedWith (fullcircle scaled r2);
1965 | pc3 := image(
1966 | p1 := reverse((1/3d, 1/4d) -- (-1/3d, 1/4d) -- (-1/2d, 1/2d) -- (1/2d, 1/2d) -- cycle) rotated a;
1967 | draw p1 withpen thinpen;
1968 | draw gradientShade(p1, 180);
1969 | );
1970 | pc3 := pc3 maskedWith (fullcircle scaled d);
1971 | image(
1972 | draw pc1;
1973 | draw pc2;
1974 | draw pc3;
1975 | )
1976 | enddef;
1977 |
1978 |
1979 | %
1980 | % This one roughly finds the center of mass for a closed shape
1981 | %
1982 |
1983 | vardef shapeCenterOfMass (expr p) =
1984 | save i, a, aTotal, q;
1985 | numeric i, a, aTotal;
1986 | pair rv, q[];
1987 | q0 := point 0 of p;
1988 | aTotal := 0;
1989 | rv := (0, 0);
1990 | for i := 1 step 1 until (length(p)-2):
1991 | q1 := point i of p;
1992 | q2 := point (i+1) of p;
1993 | if (xpart(q1-q0) = 0):
1994 | a := (abs(ypart(q1-q0)/cm)*abs(xpart(q2-q0)/cm))/2;
1995 | elseif (ypart(q1-q0) = 0):
1996 | a := (abs(xpart(q1-q0)/cm)*abs(ypart(q2-q0)/cm))/2;
1997 | elseif (abs(xpart(q1-q0)) > abs(ypart(q1-q0))):
1998 | begingroup
1999 | save qA;
2000 | pair qA;
2001 | qA = whatever[q0, q0 + (0,1)];
2002 | qA = whatever[q2, q2 + (q1-q0)];
2003 | a := (abs(ypart(qA-q0)/cm)*abs(xpart(q1-q0)/cm))/2;
2004 | endgroup
2005 | else:
2006 | begingroup
2007 | save qA;
2008 | pair qA;
2009 | qA = whatever[q0, q0 + (1,0)];
2010 | qA = whatever[q2, q2 + (q1-q0)];
2011 | a := (abs(xpart(qA-q0)/cm)*abs(ypart(q1-q0)/cm))/2;
2012 | endgroup
2013 | fi;
2014 | %a := 2;
2015 | aTotal := aTotal + a;
2016 | rv := rv + ((q0 + q1 + q2) scaled (a/3));
2017 | endfor;
2018 | if (aTotal > 0):
2019 | rv := rv scaled (1/aTotal);
2020 | else:
2021 | rv := (0, 0);
2022 | fi;
2023 | rv
2024 | enddef;
2025 |
2026 | %
2027 | % This macro is for drawing shaded flat surfaces
2028 | %
2029 |
2030 | vardef flatSurface@#(expr surfPath, normalVector, hatchAngle) =
2031 | save p, aHatch, hatchImage, surfLight, totalHeight, totalWidth, lineDensity, distFromEdge, hatchLength;
2032 | path p, aHatch;
2033 | picture hatchImage;
2034 | numeric distFromEdge, hatchLength;
2035 | surfLight := normalVectorToLightness(normalVector, 0, (0, 0));
2036 | p := surfPath rotated -hatchAngle;
2037 | if (str @# = "") or (str @# = "hatches"):
2038 | lineDensity := shadingDensity;
2039 | elseif (str @# = "stipples"):
2040 | lineDensity := stippleShadingDensity;
2041 | fi;
2042 | hatchImage := image(
2043 | totalHeight := abs(ypart(llcorner(p)) - ypart(urcorner(p)));
2044 | totalWidth := abs(xpart(llcorner(p)) - xpart(urcorner(p)));
2045 | %fill surfPath withcolor (surfLight, surfLight, surfLight);
2046 | for i := ypart(llcorner(p)) step (totalHeight/round(totalHeight/lineDensity)) until ypart(urcorner(p)):
2047 | distFromEdge := abs((i - ypart(llcorner(p)))/(ypart(urcorner(p))-ypart(llcorner(p))));
2048 | aHatch := (xpart(llcorner(p)),i) -- (xpart(lrcorner(p)), i);
2049 | aHatch := (point xpart(aHatch firstIntersectionTimes p) of aHatch) --
2050 | (point xpart(reverse(aHatch) firstIntersectionTimes p) of reverse(aHatch));
2051 | hatchLength := arclength(aHatch);
2052 | if arclength(aHatch) > 0:
2053 | aHatch := aHatch rotated hatchAngle;
2054 | aHatch := pathSubdivide(aHatch,3+round(uniformdeviate(2)));
2055 | if (str @# = "") or (str @# = "hatches"):
2056 | draw brush(aHatch)(
2057 | (2minStrokeWidth*(1/15+surfLight))*
2058 | (1-6/7sqrt(
2059 | sin(offsetPathLength*pi)*(hatchLength/totalWidth)*
2060 | sin(distFromEdge*pi)
2061 | ))
2062 | );
2063 | elseif (str @# = "stipples"):
2064 | draw thinBrush.stipples(aHatch)(
2065 | (stippleSize*(1/15+surfLight))*
2066 | (1-5/6sqrt(
2067 | sin(offsetPathLength*pi)*(hatchLength/totalWidth)*
2068 | sin(distFromEdge*pi)
2069 | ))
2070 | );
2071 | fi;
2072 | fi;
2073 | endfor;
2074 | );
2075 | clip hatchImage to surfPath;
2076 | image(
2077 | draw hatchImage;
2078 | )
2079 | enddef;
2080 |
2081 | %
2082 | % These macros are for drawing wood texture. A bunch of wood-related global
2083 | % variables are also here.
2084 | %
2085 |
2086 | woodBlockRes := 1/3mm;
2087 | woodBlockDetail := 1/5;
2088 | woodBlockYRdensity := 1/24;
2089 | woodKnotAngle := 1/3pi;
2090 | woodKnotRadius := 1/8cm;
2091 | woodKnotDensity := 2cm;
2092 |
2093 | % wField returns a value on a scalar field, that is surface of year ring
2094 |
2095 | vardef wField (suffix wk)(expr i, j, cs, nwk)=
2096 | save x, y, csx, csy, ba, a, r, outputValue, k, bd;
2097 | csx := xpart(cs);
2098 | csy := ypart(cs);
2099 | x := i*woodBlockDetail;
2100 | y := j*woodBlockDetail;
2101 | bd := 1/2(woodKnotRadius/woodBlockRes)*woodBlockDetail;
2102 | outputValue := 0;
2103 | for k := 0 upto nwk:
2104 | r := (abs(((x, y) shifted -wk[k]) yscaled (sin(woodKnotAngle))));
2105 | a := angleRad((x, y) shifted -wk[k]);
2106 | if (r >= 2bd) and (1/2r-bd < 8):
2107 | outputValue := outputValue + ((sqrt(1/2r-bd)/(3**(1/2r-bd)))*(sin(woodKnotAngle)*(1/2sin(-a)) + 1)*(1/3 + 2/3abs(cos(a))))**2;
2108 | elseif (r < 2bd):
2109 | outputValue := outputValue - 10sqrt(1-(r/2bd)**4);
2110 | fi;
2111 | outputValue := outputValue + 1/64cos(2pi*1/30r);
2112 | endfor;
2113 | outputValue := outputValue - (i*woodBlockYRdensity)/5 + 1/32sin(pi*i/xpart(cs) + 4pi*j/ypart(cs));
2114 | outputValue
2115 | enddef;
2116 |
2117 | % woodBlock generates coordinates of knots, calls wField to
2118 | % generate matrix of heights (one for all years, that's simplification, of course)
2119 | % and then calls isoLines for each year ring (shifting values in matrix by woodBlockYRdensity)
2120 |
2121 | vardef woodBlock (expr w, l) =
2122 | save wood, isoLinesMask, maskCoordinates, minWithinMask, maxWithinMask, isNotMasked, wKnot, nwKnot, p, q, i, j, k, cl, tr, wS, lS;
2123 | numeric wood[][];
2124 | boolean isNotMasked, isoLinesMask[][];
2125 | isNotMasked := true;
2126 | pair wKnot[], maskCoordinates;
2127 | path q;
2128 | picture p;
2129 | if (l > w):
2130 | wS := round(w/woodBlockRes);
2131 | lS := round(l/woodBlockRes);
2132 | else:
2133 | wS := round(l/woodBlockRes);
2134 | lS := round(w/woodBlockRes);
2135 | fi;
2136 | for i := -1 step 1 until wS + 1:
2137 | for j := -1 step 1 until lS + 1:
2138 | isoLinesMask[i][j] := true;
2139 | if (path woodBlockMaskPath):
2140 | if (l > w):
2141 | maskCoordinates := (i, j);
2142 | else:
2143 | maskCoordinates := (j, i);
2144 | fi;
2145 | if not (maskCoordinates*woodBlockRes isInside woodBlockMaskPath):
2146 | isoLinesMask[i][j] := false;
2147 | fi;
2148 | fi;
2149 | endfor;
2150 | endfor;
2151 | image(
2152 | p := image(
2153 | i := -1;
2154 | j := 0;
2155 | forever:
2156 | wKnot[-1] := (uniformdeviate(wS*woodBlockDetail + woodKnotRadius*woodBlockDetail/woodBlockRes), uniformdeviate(lS*woodBlockDetail + woodKnotRadius*woodBlockDetail/woodBlockRes)) shifted (-1/2woodKnotRadius*woodBlockDetail/woodBlockRes, -1/2woodKnotRadius*woodBlockDetail/woodBlockRes);
2157 | cl := 0;
2158 | if (i > -1):
2159 | for k := 0 step 1 until i:
2160 | if (woodBlockRes*abs(wKnot[k]-wKnot[-1])/woodBlockDetail) < woodKnotDensity:
2161 | cl := 1;
2162 | fi;
2163 | endfor;
2164 | fi;
2165 | if cl > 0:
2166 | j := j + 1;
2167 | else:
2168 | i := i + 1;
2169 | wKnot[i] := wKnot[-1];
2170 | for tr := 2woodKnotRadius step -8minStrokeWidth until 2minStrokeWidth:
2171 | draw brush(
2172 | ((fullcircle scaled tr yscaled (1/sin(woodKnotAngle))) shifted (woodBlockRes*wKnot[i]/woodBlockDetail))
2173 | )(
2174 | minStrokeWidth*(1/2+abs(sin(woodKnotAngle))*abs(sin(angleRad(point offsetPathTime of fullcircle))))
2175 | );
2176 | endfor;
2177 | fi;
2178 | exitif (j >= 10) or (i >= 1/2((w/cm)*(l*cm))/(woodKnotDensity/cm));
2179 | endfor;
2180 | nwKnot := i;
2181 | minWithinMask := infinity;
2182 | maxWithinMask := -infinity;
2183 | for i := 0 step 1 until wS:
2184 | k := uniformdeviate(1/8woodBlockYRdensity);
2185 | for j := 0 step 1 until lS:
2186 | if (boolean isoLinesMask[i][j]):
2187 | isNotMasked := isoLinesMask[i][j];
2188 | fi;
2189 | wood[i][j] := wField (wKnot)(i, j, (wS, lS), nwKnot) + k;
2190 | if isNotMasked:
2191 | if wood[i][j] > maxWithinMask:
2192 | maxWithinMask := wood[i][j];
2193 | fi;
2194 | if wood[i][j] < minWithinMask:
2195 | minWithinMask := wood[i][j];
2196 | fi;
2197 | fi;
2198 | endfor;
2199 | endfor;
2200 | for i := -maxWithinMask/woodBlockYRdensity - 1 upto -minWithinMask/woodBlockYRdensity + 1:
2201 | if (((minWithinMask + woodBlockYRdensity*i) < 0) and ((maxWithinMask + woodBlockYRdensity*i) > 0)):
2202 | draw isoLines(wood)((wS, lS), woodBlockYRdensity*i + uniformdeviate(1/8woodBlockYRdensity), woodBlockRes);
2203 | fi;
2204 | endfor;
2205 | );
2206 | q := (0, 0) -- (w, 0) -- (w, l) -- (0, l) -- cycle;
2207 | if (w > l): q := q xscaled -1 rotated -90; fi;
2208 | clip p to q;
2209 | draw p;
2210 | draw q withpen thinpen;
2211 | ) if (l < w): xscaled -1 rotated -90 fi
2212 | enddef;
2213 |
2214 | % woodenThing fits a woodBlock into thingOutline at a given woodAngle
2215 |
2216 | vardef woodenThing (expr thingOutline, woodAngle) =
2217 | save shiftedThing, woodBlockMaskPath, thingOrigin, thingWoodBlock;
2218 | path shiftedThing, woodBlockMaskPath;
2219 | pair thingOrigin;
2220 | picture thingWoodBlock;
2221 | shiftedThing := thingOutline rotated -woodAngle;
2222 | thingOrigin := llcorner(shiftedThing);
2223 | shiftedThing := shiftedThing shifted -thingOrigin;
2224 | if turningnumber(shiftedThing) > 0:
2225 | woodBlockMaskPath := offsetPath(shiftedThing, -woodBlockRes);
2226 | else:
2227 | woodBlockMaskPath := offsetPath(shiftedThing, woodBlockRes);
2228 | fi;
2229 | thingWoodBlock := woodBlock(xpart(urcorner(shiftedThing)), ypart(urcorner(shiftedThing)));
2230 | clip thingWoodBlock to shiftedThing;
2231 | thingWoodBlock := (thingWoodBlock shifted thingOrigin) rotated woodAngle;
2232 | image(
2233 | draw thingOutline withpen thinpen;
2234 | draw thingWoodBlock;
2235 | )
2236 | enddef;
2237 |
2238 | % similar to solidSurfece, but with wood texture
2239 |
2240 | vardef woodenSurface (expr p) =
2241 | save surfaceOutline, surfaceAngle;
2242 | numeric surfaceAngle;
2243 | path surfaceOutline;
2244 | surfaceOutline := p -- reverse(offsetPath(p) (-solidSurfaceThickness)) -- cycle;
2245 | surfaceAngle := findNarrowest(surfaceOutline);
2246 | woodenThing (surfaceOutline,-surfaceAngle)
2247 | enddef;
2248 |
2249 | % finds the orientation for path p in which it is the narrowest
2250 |
2251 | vardef findNarrowest (expr p) =
2252 | save minWidth, currentWidth, minWidthAngle, rotatedPath, i;
2253 | numeric minWidth, currentWidth, minWidthAngle, i;
2254 | path rotatedPath;
2255 | minWidth := infinity;
2256 | for i := 0 step 10 until 170:
2257 | rotatedPath := p rotated i;
2258 | currentWidth := ypart(urcorner(rotatedPath)-llcorner(rotatedPath));
2259 | if currentWidth < minWidth:
2260 | minWidth := currentWidth;
2261 | minWidthAngle := i;
2262 | fi;
2263 | endfor;
2264 | for i := minWidthAngle -9 step 1 until minWidthAngle + 9:
2265 | rotatedPath := p rotated i;
2266 | currentWidth := ypart(urcorner(rotatedPath)-llcorner(rotatedPath));
2267 | if currentWidth < minWidth:
2268 | minWidth := currentWidth;
2269 | minWidthAngle := i;
2270 | fi;
2271 | endfor;
2272 | minWidthAngle
2273 | enddef;
2274 |
2275 | %
2276 | % This part is related to knots
2277 | %
2278 |
2279 | % lists are only used in knots so far.
2280 | % The following two macros are taken from byrne.mp
2281 |
2282 | vardef appendList@#(suffix listName)(expr valueToAdd, whereToAdd, omitDuplicates) =
2283 | save v, valueExists;
2284 | string v;
2285 | boolean valueExists;
2286 | if str @# = "":
2287 | if not string listName:
2288 | string listName;
2289 | fi;
2290 | else:
2291 | if not string listName0:
2292 | string listName[];
2293 | fi;
2294 | fi;
2295 | if unknown listName@#:
2296 | listName@# := "";
2297 | fi;
2298 | valueExists := false;
2299 | if omitDuplicates:
2300 | valueExists := isInList@#(valueToAdd, listName)
2301 | fi;
2302 | if not valueExists:
2303 | if string valueToAdd:
2304 | v := valueToAdd;
2305 | else:
2306 | v := decimal(valueToAdd);
2307 | fi;
2308 | if length(listName@#) = 0:
2309 | listName@# := v;
2310 | else:
2311 | if (whereToAdd = 1):
2312 | listName@# := listName@# & ", " & v;
2313 | else:
2314 | listName@# := v & ", " & listName@#;
2315 | fi;
2316 | fi;
2317 | fi;
2318 | enddef;
2319 |
2320 | vardef isInList@#(expr valueToLookFor)(suffix listName) =
2321 | save rv, i;
2322 | boolean rv;
2323 | rv := false;
2324 | if str @# = "":
2325 | if not string listName:
2326 | string listName;
2327 | fi;
2328 | else:
2329 | if not string listName0:
2330 | string listName[];
2331 | fi;
2332 | fi;
2333 | if unknown listName@#:
2334 | listName@# := "";
2335 | fi;
2336 | if string valueToLookFor:
2337 | forsuffixes i=scantokens(listName@#):
2338 | if (str i = valueToLookFor):
2339 | rv := true;
2340 | fi;
2341 | endfor;
2342 | else:
2343 | for i=scantokens(listName@#):
2344 | if (i = valueToLookFor):
2345 | rv := true;
2346 | fi;
2347 | endfor;
2348 | fi;
2349 | rv
2350 | enddef;
2351 |
2352 | vardef sortList (expr listToSort, ascending) =
2353 | save nPre, nPost, pivot, isSorted, lastValue, preList, postList, rv;
2354 | numeric nPre, nPost, pivot;
2355 | boolean isSorted;
2356 | string preList, postList, rv;
2357 | nPre := 0;
2358 | nPost := 0;
2359 | isSorted := true;
2360 | if ascending:
2361 | lastValue := -infinity;
2362 | else:
2363 | lastValue := infinity;
2364 | fi;
2365 | for i=scantokens(listToSort):
2366 | if (unknown pivot):
2367 | pivot := i;
2368 | fi;
2369 | if ((i < pivot) and ascending) or ((i > pivot) and not ascending):
2370 | appendList (preList, i, -1, false);
2371 | nPre := nPre + 1;
2372 | else:
2373 | appendList (postList, i, -1, false);
2374 | nPost := nPost + 1;
2375 | fi;
2376 | if ((lastValue > i) and ascending) or ((lastValue < i) and not ascending):
2377 | isSorted := false;
2378 | fi;
2379 | lastValue := i;
2380 | endfor;
2381 | if isSorted:
2382 | rv := listToSort;
2383 | else:
2384 | if nPre > 1:
2385 | preList := sortList(preList, ascending);
2386 | fi;
2387 | if nPre > 0:
2388 | preList := preList & ", ";
2389 | else:
2390 | preList := "";
2391 | fi;
2392 | if nPost > 1:
2393 | postList := sortList(postList, ascending);
2394 | fi;
2395 | rv := preList & postList;
2396 | fi;
2397 | rv
2398 | enddef;
2399 |
2400 |
2401 | % When looking for intersections, knot is browsed with knotStepSize step.
2402 | % Affects nothing interesting.
2403 | numeric knotStepSize;
2404 | knotStepSize := 1/8;
2405 |
2406 | vardef knotFromStrands (suffix knotName) =
2407 | save slidingSegment, timeToAdd, pathSegments, intTimes, tSegWidth, tSegStyle, numberOfSegments, segmentWidth, totalNumberOfSegments, intersections, intersectionsList, layerContents, layersList, b, e, n, layerContents, segmentPicture;
2408 | save shadowsEnabled, allShadowPaths, totalNumberOfShadows, numberOfShadows, shadowPath, tmpShadows;
2409 | boolean shadowsEnabled;
2410 | path shadowPath[], allShadowPaths[];
2411 | numeric timeToAdd, numberOfShadows, totalNumberOfShadows;
2412 | totalNumberOfShadows := -1;
2413 | tmpShadows := -1;
2414 | path inspectedPath, slidingSegment, pathSegments[];
2415 | pair intTimes[];
2416 | numeric intersections[], numberOfSegments[], segmentWidth[], totalNumberOfSegments, tSegWidth, b, e, n;
2417 | picture layerPicture[];
2418 | string layerContents[], segmentStyle[], tSegStyle;
2419 | totalNumberOfSegments := 0;
2420 | for sNa := 1 step 1 until knotName.nStrands:
2421 | inspectedPath := knotName.strandPath[sNa];
2422 | tSegWidth := knotName.strandWidth[sNa];
2423 | tSegStyle := knotName.strandStyle[sNa];
2424 | for sNb := 1 step 1 until knotName.nStrands:
2425 | for i := -knotStepSize step knotStepSize until length(knotName.strandPath[sNb]):
2426 | slidingSegment := subpath (i, i + 2knotStepSize) of knotName.strandPath[sNb];
2427 | intTimes0 := (inspectedPath firstIntersectionTimes slidingSegment);
2428 | intTimes1 := (reverse(inspectedPath) firstIntersectionTimes slidingSegment);
2429 | if (sNb = sNa):
2430 | if (xpart(intTimes0) >= i)
2431 | and (xpart(intTimes0) <= i + 2knotStepSize):
2432 | intTimes0 := (-1, -1);
2433 | fi;
2434 | if ((length(inspectedPath) - xpart(intTimes1)) >= i)
2435 | and ((length(inspectedPath) - xpart(intTimes1)) <= i + 2knotStepSize):
2436 | intTimes1 := (-1, -1);
2437 | fi;
2438 | if (i+knotStepSize >= length(inspectedPath)):
2439 | if (xpart(intTimes0) <= knotStepSize)
2440 | or (xpart(intTimes0) = length(inspectedPath)):
2441 | intTimes0 := (-1, -1);
2442 | fi;
2443 | if ((length(inspectedPath) - xpart(intTimes1)) <= knotStepSize)
2444 | or (xpart(intTimes1) = 0):
2445 | intTimes1 := (-1, -1);
2446 | fi;
2447 | fi;
2448 | if (i-knotStepSize <= length(inspectedPath)):
2449 | if (xpart(intTimes0) >= (length(inspectedPath) - knotStepSize))
2450 | or (xpart(intTimes0) = 0):
2451 | intTimes0 := (-1, -1);
2452 | fi;
2453 | if ((length(inspectedPath) - xpart(intTimes1)) >= (length(inspectedPath) - knotStepSize))
2454 | or (xpart(intTimes1) = length(inspectedPath)):
2455 | intTimes1 := (-1, -1);
2456 | fi;
2457 | fi;
2458 | fi;
2459 | timeToAdd := -1;
2460 | if ((ypart(intTimes0) > 0) and (ypart(intTimes0) < length(slidingSegment)))
2461 | and ((xpart(intTimes0) >= 0) and (xpart(intTimes0) <= length(inspectedPath)))
2462 | and ((sNb <> sNa) or ((xpart(intTimes0) < i) or (xpart(intTimes0) > i + 1))):
2463 | timeToAdd := xpart(intTimes0);
2464 | elseif (sNb = sNa):
2465 | if ((ypart(intTimes1) > 0) and (ypart(intTimes1) < length(slidingSegment)))
2466 | and ((xpart(intTimes1) >= 0) and (xpart(intTimes1) <= length(inspectedPath)))
2467 | and ((length(inspectedPath) - xpart(intTimes1) < i) or (length(inspectedPath) - xpart(intTimes1) > i + 1)):
2468 | timeToAdd := length(inspectedPath) - xpart(intTimes1);
2469 | fi;
2470 | fi;
2471 | if (timeToAdd >= 0):
2472 | if (timeToAdd = length(inspectedPath)):
2473 | timeToAdd := 0;
2474 | fi;
2475 | appendList[sNa](intersectionsList, round(timeToAdd*10)/10, 1, true);
2476 | fi;
2477 | endfor;
2478 | endfor;
2479 | if known intersectionsList[sNa]:
2480 | numberOfSegments[sNa] := 0;
2481 | for i := scantokens(sortList(intersectionsList[sNa], true)):
2482 | numberOfSegments[sNa] := numberOfSegments[sNa] + 1;
2483 | intersections[numberOfSegments[sNa]] := i;
2484 | endfor;
2485 | intersections[0] := 0;
2486 | if (not cycle knotName.strandPath[sNa]):
2487 | intersections[numberOfSegments[sNa] + 1] := length(knotName.strandPath[sNa]);
2488 | fi;
2489 | for i := 1 step 1 until numberOfSegments[sNa]:
2490 | totalNumberOfSegments := totalNumberOfSegments + 1;
2491 | if (i > 1):
2492 | b := 1/2[intersections[i-1], intersections[i]];
2493 | else:
2494 | if (not cycle knotName.strandPath[sNa]):
2495 | b := 0;
2496 | else:
2497 | b := 1/2[intersections[numberOfSegments[sNa]] - length(knotName.strandPath[sNa]), intersections[i]];
2498 | fi;
2499 | fi;
2500 | if (i < numberOfSegments[sNa]):
2501 | e := 1/2[intersections[i], intersections[i+1]];
2502 | else:
2503 | if (not cycle knotName.strandPath[sNa]):
2504 | e := length(inspectedPath);
2505 | else:
2506 | e := 1/2[intersections[i], intersections[1] + length(knotName.strandPath[sNa])];
2507 | fi;
2508 | fi;
2509 | pathSegments[totalNumberOfSegments] := subpath (b, e) of inspectedPath;
2510 | if (length(pathSegments[totalNumberOfSegments])<=2):
2511 | pathSegments[totalNumberOfSegments] := pathSubdivide(pathSegments[totalNumberOfSegments], 2);
2512 | fi;
2513 | segmentWidth[totalNumberOfSegments] := tSegWidth;
2514 | segmentStyle[totalNumberOfSegments] := tSegStyle;
2515 | endfor;
2516 | else:
2517 | totalNumberOfSegments := totalNumberOfSegments + 1;
2518 | numberOfSegments[sNa] := 1;
2519 | pathSegments[totalNumberOfSegments] := inspectedPath;
2520 | segmentWidth[totalNumberOfSegments] := tSegWidth;
2521 | segmentStyle[totalNumberOfSegments] := tSegStyle;
2522 | fi;
2523 | n := 0;
2524 | for i := scantokens(knotName.intLayers[sNa]):
2525 | n := n + 1;
2526 | if (n <= numberOfSegments[sNa]):
2527 | appendList[i](layerContents, totalNumberOfSegments - numberOfSegments[sNa] + n, 1, true);
2528 | appendList(layersList, i, 1, true);
2529 | fi;
2530 | endfor;
2531 | if n > 0:
2532 | if n < numberOfSegments[sNa]:
2533 | for i := n + 1 step 1 until numberOfSegments[sNa]:
2534 | appendList0(layerContents, totalNumberOfSegments - numberOfSegments[sNa] + i, 1, true);
2535 | endfor;
2536 | appendList(layersList, 0, 1, true);
2537 | fi;
2538 | else:
2539 | for i := 1 step 1 until numberOfSegments[sNa]:
2540 | appendList0(layerContents, totalNumberOfSegments - numberOfSegments[sNa] + i, 1, true);
2541 | endfor;
2542 | appendList(layersList, 0, 1, true);
2543 | fi;
2544 | endfor;
2545 | image(
2546 | for i := scantokens(sortList(layersList, false)):
2547 | layerPicture[i] := image(
2548 | for j := scantokens(layerContents[i]):
2549 | numberOfShadows := -1;
2550 | shadowsEnabled := false;
2551 | for k := 0 step 1 until totalNumberOfShadows:
2552 | if xpart((subpath (1/10, length(pathSegments[j]) - 1/10) of pathSegments[j])
2553 | intersectiontimes allShadowPaths[k]) > 0:
2554 | shadowsEnabled := true;
2555 | numberOfShadows := numberOfShadows + 1;
2556 | shadowPath[numberOfShadows] := allShadowPaths[k];
2557 | shadowDepth[numberOfShadows] := 3/2segmentWidth[j];
2558 | fi;
2559 | endfor;
2560 | save drawTubeEnds;
2561 | boolean drawTubeEnds;
2562 | drawTubeEnds := false;
2563 | draw tube.scantokens(segmentStyle[j])(pathSegments[j])(segmentWidth[j]) if segmentStyle[j] = "e": withpen thickpen fi;
2564 | tmpShadows := tmpShadows + 1;
2565 | allShadowPaths[tmpShadows] := tubeOutline;
2566 | endfor;
2567 | );
2568 | for j := 0 step 1 until totalNumberOfShadows:
2569 | layerPicture[i] := layerPicture[i] maskedWith allShadowPaths[j];
2570 | endfor;
2571 | totalNumberOfShadows := tmpShadows;
2572 | endfor;
2573 | for i := scantokens(sortList(layersList, true)):
2574 | draw layerPicture[i];
2575 | endfor;
2576 | )
2577 | enddef;
2578 |
2579 | vardef initKnot (suffix knotName) =
2580 | numeric knotName.nStrands;
2581 | knotName.nStrands := 0;
2582 | path knotName.strandPath[];
2583 | numeric knotName.strandWidth[];
2584 | string knotName.strandStyle[];
2585 | string knotName.intLayers[];
2586 | enddef;
2587 |
2588 | vardef addStrandToKnot (suffix knotName) (expr p, w, s, intersectionLayers) =
2589 | save n;
2590 | if not known knotName.nStrands:
2591 | numeric knotName.nStrands;
2592 | knotName.nStrands := 0;
2593 | fi;
2594 | if not path knotName.strandPath0:
2595 | path knotName.strandPath[];
2596 | fi;
2597 | if not numeric knotName.strandWidth0:
2598 | numeric knotName.strandWidth[];
2599 | fi;
2600 | if not string knotName.strandStyle0:
2601 | string knotName.strandStyle[];
2602 | fi;
2603 | if not string knotName.intLayers0:
2604 | string knotName.intLayers[];
2605 | fi;
2606 | knotName.nStrands := knotName.nStrands + 1;
2607 | n := knotName.nStrands;
2608 | knotName.strandPath[n] := p;
2609 | knotName.strandWidth[n] := w;
2610 | knotName.strandStyle[n] := s;
2611 | knotName.intLayers[n] := intersectionLayers;
2612 | enddef;
2613 |
--------------------------------------------------------------------------------