├── 8.01 Classical Mechanics
├── 01. Units, Dimensions, and Scaling Arguments.md
├── 02. Introduction to Kinematics.md
├── 03. Vectors.md
├── 04. The Motion of Projectiles.md
├── 05. Uniform Circular Motion.md
├── 06. Newton's First, Second, and Third Laws.md
├── 07. Weight, Perceived Gravity, and Weightlessness.md
├── 08. Frictional Forces.md
├── 09. Review of Lecture 1 through 5.md
├── 1. Introduction to Mechanics
│ └── MIT8_01SC_coursenotes01.pdf
├── 10. Hooke's Law, Simple Harmonic Oscillator.md
├── 11. Work, Energy, and Universal Gravitation.md
├── 12. Resistive Forces.md
├── 13. Equation of Motion for Simple Harmonic Oscillators.md
├── 14. Orbits and Escape Velocity.md
├── 15. Momentum and its Conservation.md
├── 16. Elastic and Inelastic Collisions.md
├── 17. Momentum of Individual Objects.md
├── 18. Review of Lectures 6 through 15.md
├── 19. Rotating Rigid Bodies, Inertia, and Axis Theorems.md
├── 20. Angular Momentum.md
├── 21. Torque.md
├── 22. Kepler's Laws, Elliptical Orbits, and Change of Orbits.md
├── 23. Doppler's Effect, Binary Stars, Neutron Stars and Black Holes.md
├── 24. Rolling Motion, Gyroscopes.md
├── 25. Static Equilibrium, Stability, Rope Walker.md
├── 26. Elasticity and Young's Modulus.md
├── 27. Gases and Incompressible Liquids.md
├── 28. Hydrostatics, Archimedes' Principle, and Fluid Dynamics.md
├── 29. Review of Lectures 16 through 24.md
├── 30. Simple Harmonic Oscillations of Suspended Solid Bodies.md
├── 31. Pendulums and Springs.md
├── 32. Thermal Expansion.md
├── 33. Ideal-Gas Law.md
├── 34. Heisenberg's Uncertainty Principle.md
├── 35. Professor Lewin's Early Days at MIT.md
└── images
│ ├── L01_01.png
│ ├── L01_02.png
│ ├── L02_01.png
│ ├── L02_02.png
│ ├── L02_03.png
│ ├── L02_04.png
│ ├── L02_05.png
│ ├── L02_06.png
│ ├── L02_07.png
│ ├── L03_01.png
│ ├── L03_02.png
│ ├── L03_03.png
│ ├── L03_04.png
│ ├── L03_05.png
│ ├── L03_06.png
│ ├── L03_07.png
│ ├── L03_08.png
│ ├── L03_09.png
│ ├── L03_10.png
│ ├── L03_11.png
│ ├── L03_12.png
│ ├── L03_13.png
│ ├── L03_14.png
│ ├── L04_01.png
│ ├── L04_02.png
│ ├── L05_01.png
│ ├── L05_02.png
│ ├── L05_03.png
│ ├── L05_04.png
│ ├── L05_05.png
│ ├── L05_06.png
│ ├── L05_07.png
│ ├── L06_01.png
│ ├── L06_02.png
│ ├── L06_03.png
│ ├── L06_04.png
│ ├── L06_05.png
│ ├── L06_06.png
│ ├── L06_07.png
│ ├── L06_08.png
│ ├── L06_09.png
│ ├── L06_10.png
│ ├── L07_01.png
│ ├── L07_02.png
│ ├── L07_03.png
│ ├── L07_04.png
│ ├── L07_05.png
│ ├── L07_06.png
│ ├── L07_07.png
│ ├── L07_08.png
│ ├── L07_09.png
│ ├── L08_01.png
│ ├── L08_02.png
│ ├── L08_03.png
│ ├── L08_04.png
│ ├── L08_05.png
│ ├── L10_01.png
│ ├── L10_02.png
│ ├── L10_03.png
│ ├── L10_04.png
│ ├── L10_05.png
│ ├── L11_01.png
│ ├── L11_02.png
│ ├── L11_03.png
│ ├── L11_04.png
│ ├── L11_05.png
│ ├── L11_06.png
│ ├── L12_01.png
│ ├── L12_02.png
│ ├── L12_03.png
│ ├── L12_04.png
│ ├── L12_05.png
│ ├── L13_01.png
│ ├── L13_02.png
│ ├── L13_03.png
│ ├── L13_04.png
│ ├── L13_05.png
│ ├── L13_06.png
│ ├── L13_07.png
│ ├── L13_08.png
│ ├── L13_09.png
│ ├── L14_01.png
│ ├── L14_02.png
│ ├── L14_03.png
│ ├── L14_04.png
│ ├── L15_01.png
│ ├── L15_02.png
│ ├── L15_03.png
│ ├── L15_04.png
│ ├── L15_05.png
│ ├── L15_06.png
│ ├── L16_01.png
│ ├── L16_02.png
│ ├── L16_03.png
│ ├── L16_04.png
│ ├── L22
│ ├── 01.png
│ ├── 02.png
│ ├── 03.png
│ ├── 04.png
│ ├── 05.png
│ ├── 06.png
│ ├── 07.png
│ └── 08.png
│ ├── L25
│ ├── 01.png
│ ├── 02.png
│ ├── 03.png
│ ├── 04.png
│ ├── 05.png
│ ├── 06.png
│ ├── 07.png
│ ├── 08.png
│ ├── 09.png
│ ├── 10.png
│ ├── 11.png
│ └── 12.png
│ ├── L26
│ ├── 01.png
│ ├── 02.png
│ ├── 03.png
│ ├── 04.png
│ ├── 05.png
│ ├── 06.png
│ ├── 07.png
│ ├── 08.png
│ ├── 09.png
│ └── 10.png
│ └── L27
│ └── 06.png
├── 8.02 Electricity and Magnetism
├── 01. What holds our world together.md
├── 02. Electric Field and Dipoles.md
├── 03. Electric Flux and Gauss's Law.md
├── 04. Electrostatic Potential and Electric Energy.md
├── 05. Electrostatic Shielding (Faraday Cage).md
├── 06. High-Voltage Breakdown and Lightning.md
├── 07. Capacitance and Field Energy.md
├── 08. Polarization and Dielectrics.md
├── 09. Currents, Resistivity and Ohm's Law.md
├── 10. Batteries and EMF.md
├── 11. Magnetic Field and Lorentz Force.md
├── 12. Review Exam 1 (Secret Top!).md
├── 13. Moving Charges in B-fields.md
├── 14. Biot-Savart Law.md
├── 15. Ampere's Law.md
├── 16. Electromagnetic Induction.md
├── 17. Motional EMF and Dynamos.md
├── 18. Displacement Current and Synchronous Motors.md
├── 19. How do magicians levitate women.md
├── 20. Inductance and RL Circuit.md
├── 21. Magnetic Materials.md
├── 22. Hysteresis and Electromagnets.md
├── 23. Review for Exam 2.md
├── 24. Transformers, Car Coils and RC Circuits.md
├── 25. Driven LRC Circuits and Resonance.md
├── 26. Traveling Waves and Standing Waves.md
├── 27. Resonance and Destructive Resonance.md
├── 28. Index of Refraction and Poynting Vector.md
├── 29. Snell's Law, Refraction and Total Reflection.md
├── 30. Polarizers and Malus's Law.md
├── 31. Rainbows.md
├── 32. Review for Exam 3.md
├── 33. Double-Slit Interference and Interferometers.md
├── 34. Gratings and Resolving Power.md
├── 35. Dopper Effect and the Big Bang.md
├── 36. Farewell Special.md
└── images
│ ├── L01_01.png
│ ├── L01_02.png
│ ├── L01_03.png
│ ├── L01_04.png
│ ├── L01_05.png
│ ├── L01_06.png
│ ├── L01_07.png
│ ├── L01_08.png
│ └── L01_09.png
├── 8.03 Waves and Vibrations
├── 01. Periodic Oscillations, Physical Pendulum.md
├── 02. Beats, Damped Free Oscillations, Quality Q.md
├── 03. Forced Oscillations with Damping, Destructive Resonance.md
├── 04. Forced Oscillations, Power at Resonance, Transient Phenomena.md
├── 05. Coupled Oscillators.md
├── 06. Driven Coupled Oscillators and Cramer's Rule.md
├── 07. Coupled Oscillators, Transverse Traveling Pulses and Waves.md
├── 08. Traveling Waves, Sound Waves and Energy in Waves.md
├── 09. Musical Instruments, Sound Cavities, Normal Modes.md
├── 10. Exam 1 Review.md
├── 11. Fourier Analysis, Time Evolution of Pulses on Strings.md
├── 12. Dispersion, Phase Velocity, Group Velocity.md
├── 13. Electromagnetic Waves, Polarization.md
├── 14. Acceleration Changes, Poynting Vector, and Power.md
├── 15. Doppler Effect, EM Radiation and Expanding Universe.md
├── 16. Interactions of Electromagnetic Waves with Perfect Conductors.md
├── 17. Wave Guides, Resonance Cavities of EM-radiation and Sound.md
├── 18. Boundary Conditions for Dielectrics.md
├── 19. Exam 2 Review.md
├── 20. Huygens' Principle, Interference, Thin films, Soap, Oil, Light.md
├── 21. Diffraction, Gratings, Pin Holes, Angular Resolution.md
├── 22. Rainbows, Haloes, Coronae, Glories.md
└── 23, Farewell Lecture.md
└── README.md
/8.01 Classical Mechanics/01. Units, Dimensions, and Scaling Arguments.md:
--------------------------------------------------------------------------------
1 | # Lecture 1: Units Dimensions, and Scaling Arguments
2 |
3 | Walter Lewin, 8.01 Physics I: Classical Mechanics, Fall 1999.
4 | (Massachusetts Institute of Technology: MIT OpenCourseWare).
5 | [http://ocw.mit.edu](http://ocw.mit.edu) (accessed 04 08, 2013).
6 | License: Creative Commons Attribution-Noncommercial-Share Alike.
7 |
8 | ## Fundamental Units
9 |
10 | __In physics, we explore the very small to the very large.__
11 |
12 | The very small is a small fraction of a proton and the very large is the universe itself.
13 |
14 | They span 45 orders of magnitude--a 1 with 45 zeroes.
15 |
16 | __To express measurements quantitatively, we have to introduce units.__
17 |
18 | * the unit of __length__: the __meter__, m
19 | * the unit of __time__: the __second__, s
20 | * the unit of __mass__: the __kilogram__, kg.
21 |
22 | > TODO: add reference to definition and evolution of these units
23 |
24 | Many __derived units__ are defined for conveience, and some are tailored toward specific fields.
25 |
26 | * centimeters, millimeters, kilometers
27 | * inches, feet, miles
28 | * astronomical unit (mean distance between the earth and the sun)
29 | * light-year (the distance that light travels in one year)
30 | * milliseconds, microseconds, days, weeks, hours, centuries, months
31 | * milligrams, pounds, metric tons
32 |
33 | ## Discussion of Powers of Ten
34 |
35 | __Movie__: [The Power of 10][1]
36 |
37 | * covers 40 orders of magnitude
38 | * originally conceived by a Dutchman named Kees Boeke in the early '50s
39 | * second-generation movie, voice over by Professor Morrison, a MIT professor
40 |
41 | ## Dimensions
42 |
43 | __Three fundamental quantities in physics__:
44 |
45 | * length: symbol L
46 | * time: symbol T
47 | * mass: symbol M
48 |
49 | __All other quantities in physics can be derived from these fundamental quantities.__
50 |
51 | __Notation for dimension__: bracket
52 |
53 | ### Examples:
54 |
55 | [speed]: means the dimension of speed
56 |
57 | * \\( [ \text{speed} ] = {[\text{L}] \over [\text{T}]} \\)
58 | * \\( [ \text{volume} ] = [ \text{L} ]^3 \\)
59 | * \\( [ \text{density} ] = {[\text{M}] \over [\text{L}]^3} \\)
60 | * \\( [ \text{acceleration} ] = {[\text{L}] \over [\text{T}]^2} \\)
61 |
62 | ## The Art of Making Measurements
63 |
64 | __Any measurement that you make without any knowledge of the uncertainty is meaningless.__
65 |
66 | ### Demo: Someone who is lying in bed is longer than someone who stands up?
67 |
68 | Have a setup to measure something horizontally and vertically
69 |
70 | 1. Aluminum bar (calibration):
71 |
72 | vertical: \\( 150.0 \pm 0.1\ cm \\)
73 | horizontal: \\( 149.9 \pm 0.1\ cm \\)
74 |
75 | 2. Student
76 |
77 | stand up: \\( 183.2 \pm 0.1\ cm \\)
78 | lie down: \\( 185.7 \pm 0.1\ cm \\)
79 |
80 | ## Was Galileo Galilei's Reasoning Correct?
81 |
82 | Galileo Galilei: __Why are mammals as large as they are and not much larger?__
83 |
84 | He argued that if the mammal becomes too massive that the bones will break and he thought that that was a limiting factor.
85 |
86 | Model of a Mammal:
87 |
88 | * has a size, \\( S \\) (大約是身長)
89 | * has a mass, \\( m \\)
90 | * has a thigh bone, called the __femur (大腿骨)__
91 | * the femur carries the body, to a large extent
92 | * has a length, \\( l \\)
93 | * has a thickness, \\( d \\)
94 | * has a cross-sectional area, \\( A \\)
95 |
96 | ![Sketch of animal and femur][2]
97 |
98 | A __scaling argument__:
99 |
100 | 1. If an animal is 4 times larger than another, you would need 4 times longer legs
101 |
102 | \\( l \propto S \\)
103 |
104 | 2. The mass of an animal is proportional to the third power of the size because that's related to its volume
105 |
106 | \\( m \propto S^3 \\)
107 |
108 | 3. From 1 and 2, the mass of an animal must also be proportional to the third power of the length of the femur
109 |
110 | \\( m \propto l^3 \\)
111 |
112 | 4. Pressure on the femur is proportional to the weight of the animal divided by the cross-section \\( A \\) of the femur
113 |
114 | \\( P \propto {m \over d^2} \\)
115 |
116 | 5. If the pressure is higher than a certain level, the bones will break. Therefore, for an animal not to break its bones when the mass goes up by a certain factor, say a factor of four, \\( d^2 \\) must also go up by a factor of 4
117 |
118 | \\( m \uparrow 4 \Rightarrow d^2 \uparrow 4 \\)
119 |
120 | 6. Therefore, the mass must be proportional to \\( d^2 \\).
121 |
122 | \\( m \propto d^2 \\)
123 |
124 | 7. Compare 3 and 6
125 |
126 | \\( m \propto l^3 \wedge m \propto d^2 \\)
127 |
128 | 8. \\( \therefore d \propto l^{3/2} \\)
129 |
130 | __What is this result telling you?__
131 |
132 | * If animal 1 is 10 times larger than animal 2, then the lengths of the legs are 10 times larger, but the thickness of the femur is 31.6 times larger (\\( 10^{1.5} \\))
133 |
134 | __Comparing the femurs of various animals:__
135 |
136 | * mouse (鼠)
137 | * oppossum (負鼠)
138 | * raccoon (浣熊)
139 | * antelope (羚羊)
140 | * horse (馬)
141 | * moose (麋鹿)
142 | * elephant (象)
143 |
144 | ![Femur of animals][3]
145 |
146 | There is no evidence whatsoever that \\( d \over l \\) is really larger for the elephant than for the mouse.
147 |
148 | These vertical bars indicate my uncertainty in measurements of thickness and the horizontal scale, is in logarithmic scale...
149 |
150 | The \\( d \over l \\) for the mouse is really not all that different from the elephant
151 |
152 | ## Dimensional Analysis
153 |
154 | __If I drop an apple from a certain height and I change that height, what will happen with the time for the apple to fall?__
155 |
156 | Drop the apple from a height, \\( h \\):
157 |
158 | 1. If the height is larger, it takes longer for the apple to fall
159 | 2. If something is more massive, it will probably take less time
160 | 3. If gravity is stronger, it will take less time to fall
161 |
162 | $$ t \propto h^\alpha m^\beta g^\gamma $$
163 |
164 | __The dimensions on the left and right hand side of the equation must be the same.__
165 |
166 | What is the dimension here?
167 |
168 | $$ [T]^1 = [L]^\alpha [M]^\beta {[L]^\gamma \over [T]^{2 \gamma}} $$
169 |
170 | LHS = RHS:
171 |
172 | * [M]: \\( \beta = 0 \\)
173 | * [L]: \\( \alpha + \gamma = 0 \\)
174 | * [T]: \\( 1 = -2 \gamma \\)
175 |
176 | Solve:
177 |
178 | * \\( \gamma = -1/2 \\)
179 | * \\( \alpha = +1/2 \\)
180 |
181 | Conclusion:
182 |
183 | * \\( t = C \sqrt{h \over g} \propto \sqrt{h} \\)
184 | * Cannot predict the time to fall, but can compare two different heights
185 | * e.g. drop from 8 m takes twice as long as drop from 2 m
186 |
187 | ### Demo: drop an apple from 2 different heights
188 |
189 | Setup:
190 |
191 | * \\( h_1 = 3.000 \pm 0.003\ m \\)
192 | * \\( h_2 = 1.500 \pm 0.003\ m \\)
193 |
194 | Prediction:
195 |
196 | * \\( {h_1 \over h_2} = 2.000 \pm 0.006 \\)
197 | * \\( {t_1 \over t_2} = \sqrt{h_1 \over h_2} = 1.414 \pm 0.002 \\)
198 |
199 | Observation:
200 |
201 | * \\( t_1 = 0.781 \pm 0.002\ s \\)
202 | * \\( t_2 = 0.551 \pm 0.002\ s \\)
203 | * \\( {t_1 \over t_2} = 1.417 \pm 0.008 \\)
204 |
205 | We have demonstrated that the time that it takes for an object to fall is independent of its mass.
206 |
207 | __Is this dimensional analysis perhaps not quite kosher?__
208 |
209 | Maybe.
210 |
211 | __Is this dimensional analysis perhaps one that could have been done differently?__
212 |
213 | 1. the higher it is, the more it will take
214 | 2. the heavier it is, probably the less it will take
215 | 3. increase the mass of the Earth, the apple will fall faster
216 |
217 | --> DEAD END
218 |
219 | __Is there something wrong with the analysis that we did?__
220 |
221 | __Is ours perhaps better than this one?__
222 |
223 | Well, it's a different one.
224 |
225 | We came to the conclusion that the time that it takes for the apple to fall is independent of the mass.
226 |
227 | __Do we believe that?__
228 |
229 | Yes, we do.
230 |
231 | On the other hand, there are very prestigious physicists who even nowadays do very fancy experiments and they try to demonstrate that the time for an apple to fall does depend on its mass even though it probably is only very small, if it's true but they try to prove that.
232 |
233 | So we do believe that it's independent of the mass.
234 |
235 | However, this was not a proof because if you do it this way, you get stuck.
236 |
237 | [1]: http://www.youtube.com/watch?v=0fKBhvDjuy0 "Power of 10"
238 | [2]: https://raw.github.com/leeyt/Physics/master/8.01%20Classical%20Mechanics/images/L01_01.png "Sketch of Animal and its Femur"
239 | [3]: https://raw.github.com/leeyt/Physics/master/8.01%20Classical%20Mechanics/images/L01_02.png "Femur of mammals"
--------------------------------------------------------------------------------
/8.01 Classical Mechanics/02. Introduction to Kinematics.md:
--------------------------------------------------------------------------------
1 | # Lecture 02: Introduction to Kinematics
2 |
3 | Walter Lewin, 8.01 Physics I: Classical Mechanics, Fall 1999.
4 | (Massachusetts Institute of Technology: MIT OpenCourseWare).
5 | [http://ocw.mit.edu](http://ocw.mit.edu) (accessed 04 08, 2013).
6 | License: Creative Commons Attribution-Noncommercial-Share Alike.
7 |
8 | ## Introduction to 1-Dimensional Motion
9 |
10 | I have a motion of an object along a straight line--
11 |
12 | We'll call that __one-dimensional motion__.
13 |
14 | Diagram below shows the position of the object, x, at various points in time ( $ t_1, t_2, t_3, t_4, t_5 $ )
15 |
16 | ![1D motion of an object at various points in time][1]
17 |
18 | Now we will introduce what we call the __average velocity__.
19 |
20 | * I put a bar over it.
21 | * That stands for average between time $ t_1 $ and time $ t_2 $.
22 |
23 | $$ \bar{v}_{t_1 t_2} = {{x_{t_2} - x_{t_1}} \over {t_2 - t_1}} $$
24 |
25 | * could be > 0 ($ t_1 $ -> $ t_2 $), = 0 ($ t_1 $ -> $ t_5 $), < 0 ($ t_2 $ -> $ t_4 $)
26 | * choice of 0 on $x$-axis is unimportant
27 | * choice of +ve direction of $x$-axis is important
28 | * __the direction determines the signs__.
29 | * __Signs in physics do matter.__
30 |
31 | Diagram below is an $x$-$t$ diagram that shows exactly where the object is at any moment in time.
32 |
33 | ![x-t diagram of an object in 1D motion][2]
34 |
35 | * choice of 0-point is unimportant but need it to make a graph
36 |
37 | $$ \bar{v} = {\Delta x \over \Delta t} $$
38 |
39 | * be careful about the sign convention
40 | * sign of average velocity depends on the angle of the secant line
41 |
42 | ## Average Speed vs. Average Velocity
43 |
44 | There is a very big difference in physics between speed and velocity.
45 |
46 | $$ \text{average speed} = {\text{distance traveled} \over \text{time taken}} $$
47 |
48 | __What is the distance that the object traveled between time $t_1$ and time $t_5$?__
49 |
50 | * have to add up all the distances, irrespective to what direction the object is travelling
51 |
52 | ![average speed needs the distance travelled][3]
53 |
54 | e.g. If the distance altogether were $300\ m$ and the time between $t_1$ and $t_5$ were $3\ s$, then the average speed would be $300\ m / 3\ s = 100\ m/s$. Yet yet the average velocity would be $0\ m/s$.
55 |
56 | ## Instantaneous Velocity
57 |
58 | __The instantaneous velocity__, $v$, at time $t$ is defined to be
59 |
60 | $$ v_t = \lim_{\Delta t \to 0} \frac{x_{t+\Delta t} - x_t}{\Delta t} = \frac{dx}{dt} $$
61 |
62 | * can be recognized as the first derivative of the position w.r.t. time
63 |
64 | > $ v = \frac{dx}{dt} $
65 |
66 | * can be either > 0, = 0, or < 0, depending on tangential angle
67 | * look for velocity is zero where the derivative is zero
68 |
69 | __What are the times that the velocity is positive?__
70 |
71 | * look for positive slope
72 |
73 | __What is the instantaneous speed?__
74 |
75 | * speed is not sign-sensitive
76 | * __the speed is the magnitude of the velocity__
77 |
78 | e.g. the velocity of $-100\ m/s$ is lower than the velocity of $+30\ m/s$, but the speed is higher
79 |
80 | ## Measuring the Average Speed of a Bullet
81 |
82 | __How can I measure the average speed of a bullet?__
83 |
84 | * two parallel wires, seperated by $D$ meters
85 | * bullet would break those wires
86 | * when wire I breaks, timer starts
87 | * when wire II breaks, timer stops
88 |
89 | ![Setup for measuring the average speed of a bullet][4]
90 |
91 | > the wire are not exactly parallel, the wire may be deformed upon bullet impact before breaking
92 | > Hence, the uncertainly in measuring $D$ would be higher
93 |
94 | So the distance between the 2 wires, $D$, is measured to be
95 |
96 | $148.5 \pm 0.5\ cm$
97 |
98 | > only about 5/1500 or 1/300 = 1/3% error (__relative error__)
99 |
100 | I want to measure the accuracy of the speed of the bullet to about 2%.
101 |
102 | __How accurate should I do the timing?__
103 |
104 | Suppose the speed of the bullet is lower than the speed of sound, which is 340 m/s, say 300 m/s
105 |
106 | Then it would take $5\ ms$ for this bullet to travel the distance between the wires.
107 |
108 | And if I want to make a measurement to 2% accuracy, the timing error must be less than about $1/10\ ms$ because $1/10\ ms$ is about 2% of $5\ ms$.
109 |
110 | The timing measurement is
111 |
112 | $5.8 \pm 0.1\ ms$
113 |
114 | And so this is the result.
115 |
116 | $$ \frac{D}{t} = \frac{148.5 \pm 0.5 cm}{5.8 \pm 0.1 ms} = 256 \pm 4\ m/s$$
117 |
118 | ## Introducing Average Acceleration
119 |
120 | The __average acceleration__ between time $t_1$ and time $t_2$ would be
121 |
122 | $$ \bar{a}_{t_1 t_2} = \frac{v_{t_2} - v_{t_1}}{t_2 - t_1}\ m/s^2 $$
123 |
124 | * this number can be > 0, = 0, < 0
125 | * the sign depends on the direction of positive $x$-axis, not the zero point
126 |
127 | You can also write down that average acceleration using the difference quotient but you must be careful about the sign convention.
128 |
129 | $$\bar{a} = \frac{\Delta v}{\Delta t}$$
130 |
131 | ### Example:
132 |
133 | I have here a tennis ball and I can bounce this tennis ball, I can throw it down.
134 |
135 | Assume that it hits the floor at about $5\ m/s$, and it also bounces back with a velocity of about $5\ m/s$.
136 |
137 | ![Tennis ball bouncing off the floor][5]
138 |
139 | __What is the average acceleration?__
140 |
141 | I would have to know the time that it takes for this change in direction.
142 |
143 | In other words, we call that the __impact time__.
144 |
145 | Assume the impact time to be about $1/100\ s$
146 |
147 | $$ \bar{a} = \frac{10}{10^2} = +10^3\ m/s^2 $$
148 |
149 | ### Example:
150 |
151 | I have also here a tomato and I have here some eggs.
152 |
153 | Now, imagine now that I throw the tomato or the egg down and that they hit the floor at $5\ m/s$. They would not come back up. Therefore, the change in velocity would only be $5\ m/s$.
154 |
155 | The impact time would probably be much longer, maybe a $1/4\ s$.
156 |
157 | So therefore the average acceleration during the impact would only be
158 |
159 | $5 / (1/4) = 20\ m/s^2$.
160 |
161 | > Sign convention matters for the calculation; but Physics does not change
162 |
163 | __Something breaks because the magnitude of acceleration becomes too high.__
164 |
165 | > Professor Lewin told a Sherlock Holmes story about a guy crushed his skull when fell on the floor
166 |
167 | And when the impact time is short even if you hit the floor with a modest speed the acceleration is high...that was too much and so that's why his skull was crushed.
168 |
169 | __What matters is this changing velocity and the impact time__.
170 |
171 | ## Instantaneous Acceleration
172 |
173 | The acceleration at any moment in time will be
174 |
175 | $$ a_t = \lim_{\Delta t \to 0} \frac{v_{t + \Delta t}}{\Delta t} = \frac{dv}{dt} = \frac{d^2 x}{dt^2} $$
176 |
177 | That is the __instantaneous acceleration__.
178 |
179 | And this, you will recognize is the __first derivative of velocity versus time__, which is also the __second derivative of position versus time__.
180 |
181 | > Remember this
182 |
183 | > $ a = \frac{dv}{dt} = \frac{d^2 x}{dt^2} $
184 |
185 | We can go to our plot and ask:
186 |
187 | __Where is the acceleration = 0, > 0, < 0?__
188 |
189 | Look at how the slope is changing.
190 |
191 | ## Quadratic Equation of Position in Time
192 |
193 | I'm going to give you the position $x$ as a function of time and then ask you lots of questions about it.
194 |
195 | ### Example:
196 |
197 | $$ x = 8 - 6t + t^2\ m $$
198 |
199 | __What is the velocity at any moment in time?__
200 |
201 | Well, that's the derivative $ \frac{dx}{dt}$ and I will be using the differentiation rule for $ x = t^n $
202 |
203 | Then, as most of you should know
204 |
205 | $$ \frac{dx}{dt} = n t^{n-1} $$
206 |
207 | Then, I would get $ v = -6 + 2t\ m/s$
208 |
209 | and the acceleration $a = +2\ m/s^2$
210 |
211 | So notice that the acceleration is constant in time but the velocity is changing.
212 |
213 | At time $t = 0$, $x$ is $+8$, the velocity is $-6\ m/s$ and the acceleration equals $+2$.
214 |
215 | __At what time does $x = 0$?__
216 |
217 | Solve the quadratic equation to get $t = +2$ or $t = +4$.
218 |
219 | __When is the velocity zero?__
220 |
221 | $t = 3$
222 |
223 | __What is, at that moment, the position?__
224 |
225 | Substitute $t = 3$ and that gives me $x = -1$.
226 |
227 | So now I'm ready to plot $x$ as a function of $t$.
228 |
229 | ![Plot x-v diagram][6]
230 |
231 | ## 1D Motion with Constant Acceleration
232 |
233 | I now would like to write down, in most general form the equation for the position and the velocity as a function of time for a one-dimensional motion whereby the acceleration is constant.
234 |
235 | So it's going to be one-dimensional again and the acceleration, $a$, is going to be a constant.
236 |
237 | So we're going to get
238 |
239 | $$ x = C_1 + C_2 t + C_3 t^2 $$
240 |
241 | I can now take the derivative and so I get
242 |
243 | $$ v = C_2 + 2 C_3 t $$
244 |
245 | and
246 |
247 | $$ a= 2 C_3 $$
248 |
249 | Clearly, $C_1$ is the position of $x$ at time $t = 0$
250 |
251 | $$ C_1 = x_0 $$
252 |
253 | $C_2$ is really the velocity at time $t = 0$
254 |
255 | $$ C_2 = v_0 $$
256 |
257 | And the acceleration is not changing with time. It's $2C_3$.
258 |
259 | Therefore,
260 |
261 | $$ C_3 = \frac{1}{2} a $$
262 |
263 | When an object is influenced by the gravitational acceleration and the gravitational acceleration is a constant.
264 |
265 | And we write, often for that gravitational acceleration, the letter "$g$".
266 |
267 | In Boston, $g$ is $9.80\ m/s^2$ and it varies a little bit for different places on Earth.
268 |
269 | $$ g = 9.80\ m/s^2$$
270 |
271 | This gravitational acceleration is independent
272 |
273 | * of the mass of the object that I drop,
274 | * of the speed of the object,
275 | * of the chemical composition of the object,
276 | * of the size of the object and
277 | * of the shape of the object
278 |
279 | assuming that we have no air drag, that these experiments are done in...in vacuum.
280 |
281 | __Is it obvious that the gravitational acceleration is independent of all these quantities?__
282 |
283 | By no means.
284 |
285 | __Is it true?__
286 |
287 | We think so, but it is not obvious and it cannot be proven from first principles.
288 |
289 | > last lecture, Professor Lewin dropped an apple from $3\ m$ and another one from $1.5\ m$.
290 | > Based on the drop times, gravitational acceleration could be calculated.
291 |
292 | Suppose I dropped an apple at time $t = 0$, call that position $x_0$, with zero speed.
293 |
294 | The general equations, now, which deal with gravity...is the following.
295 |
296 | $$ x = x_0 + v_0 t + \frac{1}{2} gt^2 $$
297 |
298 | and
299 |
300 | $$ g = 9.80\ m/s^2$$
301 |
302 | The velocity, at any moment in time equals $ v_0 + g t $ and the acceleration is constant. It's simply $g$.
303 |
304 | Now, in my case, I have chosen at $t = 0$, $x_0 = 0$, $v_0 = 0$
305 |
306 | $$ x = \frac{1}{2} gt^2 $$
307 |
308 | > $ g = \frac{2x}{t^2} $
309 | > $ h_1 = 3.000 \pm 0.003\ m $; $ t_1 = 0.781 \pm 0.002\ s $ => $ g = 9.84 \pm 0.06\ m/s$
310 | > $ h_2 = 1.500 \pm 0.003\ m $; $ t_2 = 0.551 \pm 0.002\ s $ => $ g = 9.88 \pm 0.09\ m/s$
311 |
312 | Remember that we derived, last time, that the time it takes for the apple to fall was
313 |
314 | $$ C \sqrt{h \over g} $$
315 |
316 | and we never knew what that $C$ was.
317 |
318 | Now you know, because now you have the equations here and you see that
319 |
320 | $$ C = \sqrt 2 $$
321 |
322 | But I could not derive that from my dimensional analysis.
323 |
324 | ## Strobing an Object in Free Fall
325 |
326 | Look at this situation, $v = gt$.
327 |
328 | That means when I drop an apple--that the velocity increases with time.
329 |
330 | So if I strobe this apple while it was falling I would see the separation to increase with time, because the velocity goes up with time.
331 |
332 | I have here an apple that I am going to drop at a height of about $3\ m$ from the floor--
333 |
334 | We know from last time, that it took about $780\ ms$ to hit the floor.
335 |
336 | 1. Strobe at $2\ Hz$
337 | 2. Strobe at $10\ Hz$
338 |
339 | ![Strobing an Object in Free Fall][7]
340 |
341 | [1]: https://raw.github.com/leeyt/Physics/master/8.01%20Classical%20Mechanics/images/L02_01.png "1D motion of an object at various points in time"
342 | [2]: https://raw.github.com/leeyt/Physics/master/8.01%20Classical%20Mechanics/images/L02_02.png "x-t diagram of an object in 1D motion"
343 | [3]: https://raw.github.com/leeyt/Physics/master/8.01%20Classical%20Mechanics/images/L02_03.png "average speed needs the distance travelled"
344 | [4]: https://raw.github.com/leeyt/Physics/master/8.01%20Classical%20Mechanics/images/L02_04.png "Setup for measuring the average speed of a bullet"
345 | [5]: https://raw.github.com/leeyt/Physics/master/8.01%20Classical%20Mechanics/images/L02_05.png "Tennis ball bouncing off the floor"
346 | [6]: https://raw.github.com/leeyt/Physics/master/8.01%20Classical%20Mechanics/images/L02_06.png "Plot x-v diagram"
347 | [7]: https://raw.github.com/leeyt/Physics/master/8.01%20Classical%20Mechanics/images/L02_07.png "Strobing an Object in Free Fall"
348 |
--------------------------------------------------------------------------------
/8.01 Classical Mechanics/06. Newton's First, Second, and Third Laws.md:
--------------------------------------------------------------------------------
1 | # Lecture 06: Newton's First, Second and Third Laws
2 |
3 | Walter Lewin, 8.01 Physics I: Classical Mechanics, Fall 1999.
4 | (Massachusetts Institute of Technology: MIT OpenCourseWare).
5 | [http://ocw.mit.edu](http://ocw.mit.edu) (accessed 04 08, 2013).
6 | License: Creative Commons Attribution-Noncommercial-Share Alike.
7 |
8 | ## Newton's First Law and Inertial Reference Frames
9 |
10 | * The first law goes back to the first part of the 17th century
11 |
12 | Galileo expressed what he called __the law of inertia__:
13 |
14 | > A body at rest remains at rest and a body in motion continues to move at constant velocity along a straight line unless acted upon by an external force.
15 |
16 | Newton's own words in his famous book, Principia:
17 |
18 | > Every body perseveres in its state of rest or of uniform motion in a right line unless it is compelled to change that state by forces impressed upon it.
19 |
20 | Newton's First Law is clearly against our daily experiences:
21 |
22 | * Things that move don't move along a straight line
23 | * Things don't continue to move
24 | * the reason is
25 | * there's gravity.
26 | * there is friction (e.g. air drag)
27 |
28 | __Newtons' first law does not hold in all reference frames.__
29 |
30 | * For instance, doesn't hold in a reference frame which itself is being accelerated
31 |
32 | ### Example:
33 |
34 | Imagine that Professor Lewin is accelerating towards the audience
35 |
36 | Stationary observer:
37 |
38 | * Professor's velocity is changing so there must be a force on him
39 | * Professor does feel the push
40 |
41 | Professor Lewin:
42 |
43 | * The audience is accelerating towards him
44 | * However, the audience does not feel the push or pull
45 |
46 | __When does the First Law work?__
47 |
48 | "__inertial__" frame of reference: a frame in which there are no accelerations of any kind.
49 |
50 | __Is 26.100, this lecture hall, an inertial reference frame?__
51 |
52 | 1. the earth rotates about its own axis
53 | 2. the earth goes around the sun.
54 | 3. the sun goes around the Milky Way
55 |
56 | So clearly 26.100 is not an inertial reference frame.
57 |
58 | Estimate the effect of these accelerations:
59 |
60 | Due to the earth's rotation:
61 |
62 | ![Acceleration due to earth's rotation][1]
63 |
64 | * rotating with angular velocity: 
65 | * the earth has a certain radius: 
66 |
67 | Period of rotation, 
68 |
69 | So,
70 |
71 | 
72 |
73 | Hence, the centripetal acceleration at the equator is,
74 |
75 | 
76 |
77 | This is 300 times smaller than the gravitational acceleration that you experience here on Earth.
78 |
79 | The motion of the earth around the sun is an additional factor of 5 times lower.
80 |
81 | In other words, these accelerations even though they're real and they can be measured easily with today's high-tech instrumentation--
82 |
83 | they are much, much lower than what we are used to which is the gravitational acceleration.
84 |
85 | And therefore, in spite of these accelerations, we will accept this hall as a reasonably good inertial frame of reference in which the First Law then should hold.
86 |
87 | __Can Newton's Law be proven?__
88 |
89 | * The answer is no, because it's impossible to be sure that your reference frame is without any accelerations.
90 |
91 | __Do we believe in this?__
92 |
93 | Yes, we do.
94 |
95 | We believe in it since it is consistent within the uncertainty of the measurements with all experiments that have been done.
96 |
97 | ## Newton's Second Law
98 |
99 | ![An spring that is extended][2]
100 |
101 | I have a spring...
102 |
103 | * somewhere in outer space, no gravity
104 | * I extend the spring over a certain distance
105 | * experimental fact: 
106 |
107 | __Definition of force__: ma
108 |
109 | __The Second Law__:
110 |
111 | > A force action on a body gives it an __acceleration which is in the direction of the force__ and has __a magnitude given by ma__.
112 |
113 | 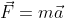
114 |
115 | The unit of this force is , or "newton", N.
116 |
117 | __The Second Law only holds in inertial reference frames.__
118 |
119 | __Can the Second Law be proven?__
120 |
121 | No.
122 |
123 | __Do we believe in it?__
124 |
125 | Yes.
126 |
127 | __Why do we believe in it?__
128 |
129 | Because all experiments and all measurements within the uncertainty of the measurements are in agreement with the Second Law.
130 |
131 | __How can you ever determine a mass if there is no force somewhere?__
132 |
133 | * If the mass were determined by a scale, you were making use of gravitational force.
134 | * Is this some kind of a circular argument that you're using? The answer is NO.
135 | * Mass is determined by the number of molecules (e.g. cheese in outer space, twice the cheese, twice the mass) so don't need gravity to have relative scales of masses
136 |
137 | ## Superposition of Forces and Net Force
138 |
139 | Since all objects in this lecture hall and the earth fall with the constant acceleration, which is g, we can write down that
140 |
141 | 
142 |
143 | Suppose I have here this softball in my hands.
144 |
145 | ![Softball in hand][3]
146 |
147 | In the reference frame of 26.100...an inertial reference frame
148 |
149 | * the force on the softball must be zero.
150 |
151 | 
152 |
153 | * Notice that there is no statement made on velocity or speed.
154 |
155 | If we take gravity and an object was falling down with 5 m/s, that the law would hold; as it would with falling speed of 5,000 m/s
156 |
157 | __Will it always hold?__
158 |
159 | No.
160 |
161 | Once your speed approaches the speed of light then Newtonian mechanics no longer works. Then you have to use _Einstein's theory of special relativity_.
162 |
163 | So this is only valid as long as we have speeds that are substantially smaller, say, than the speed of light.
164 |
165 | ## Newton's Third Law, Action = -Reaction
166 |
167 | Newton's Third Law:
168 |
169 | > If one object exerts a force on another, the other exerts the same force in opposite direction on the one.
170 |
171 | OR simply, "Action = - Reaction"
172 |
173 | e.g. Sit on your seats.
174 |
175 | * You are pulled down on your seats because of gravity
176 | * the seats will push back on you with the same force.
177 |
178 | e.g. I held the baseball in my hand.
179 |
180 | * The baseball pushes on my hand with a certain force.
181 | * I push on the baseball with the same force.
182 |
183 | e.g. I push against the wall
184 |
185 | * I push against the wall with a certain force.
186 | * the wall pushes back on me with exactly the same force.
187 |
188 | __The Third Law always holds.__
189 |
190 | * Whether the objects are moving or accelerated makes no difference.
191 |
192 | ### Simple example:
193 |
194 | ![2 masses being pushed][4].
195 |
196 | * m1 = 5 kg
197 | * m2 = 15 kg
198 | * F = 20 N
199 |
200 | __What is the acceleration of this system?__
201 |
202 | 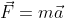
203 |
204 | 
205 |
206 |  m/s^2
207 |
208 | ![Force diagram of object number 2][5]
209 |
210 | Let the force, F_12, be the force that one exerts on two.
211 |
212 | 
213 |
214 | ![Force diagram of object number 1][6]
215 |
216 | 
217 |
218 | 
219 |
220 | In these two examples--
221 |
222 | 1. the baseball on my hand--consistent with the Third Law.
223 | 2. pushing on two masses--consistent with the Third Law.
224 |
225 | Is this a proof?
226 |
227 | No.
228 |
229 | __Can the Third Law be proven?__
230 |
231 | No.
232 |
233 | __Do we believe in it?__
234 |
235 | Yes.
236 |
237 | __Why do we believe in it?__
238 |
239 | Because all measurements, all experiments within the uncertainties are consistent with the Third Law.
240 |
241 | ### Examples:
242 |
243 | * garden hose snake backwards when faucet is turned on
244 | * balloon flies backward when air is rushed out--basic idea behind the rocket
245 | * If you fire a gun, the gun exerts a force on the bullet the bullet exerts an equal force on the gun which is called the _recoil_.
246 | * walking, the floor is pushing back on you
247 |
248 | ### Demo: hero's engine
249 |
250 | ![Hero's Engine][7]
251 |
252 | * a reservoir of water, which we will heat up.
253 | * the steam will squirt out these hollow tubes
254 |
255 | ### Demo: hero's engine made from a Soda Can
256 |
257 | * pop four holes in the soda can at the bottom
258 | * when you put a nail in there, you bend every time the nail to the same side so the holes are slanted.
259 | * put it in water and lift it out of water and you have a Hero's engine.
260 |
261 | ## Consequences of Newton's Third Law
262 |
263 | Some bizarre consequences of these laws:
264 |
265 | * Imagine that an object is falling towards the earth
266 | * the object is 0.5 kg
267 | * the earth exerts a force, mg = 5 N, on the object
268 | * the object would also exert an equal but opposite force on earth
269 |
270 | ### Example:
271 |
272 | Drop an apple from h = 100 m.
273 |
274 | __How long would it hit the earth?__
275 |
276 | * 
277 | * 
278 |
279 | So after 4 seconds, it hits the earth--
280 |
281 | But now, according to the Third Law, the earth must enxperience exactly the same force as the apple does but in opposite direction.
282 |
283 | __What is the earth going to do?__
284 |
285 | Well, the earth is going to fall towards the apple--
286 |
287 | 
288 |
289 | 
290 |
291 | __How long will the earth fall?__
292 |
293 | Well, the earth will fall roughly 4 seconds before they collide.
294 |
295 | __How far does the earth move in the 4 seconds?__
296 |
297 | 
298 |
299 | ## Decomposing Forces in x and y Directions
300 |
301 | ![An object hanged by two strings][8]
302 |
303 | This object is hanging there, it's not being accelerated, so the net acceleration must be zero.
304 |
305 | __How large is T1 and how large is T2?__
306 |
307 | *  because there's no acceleration in the x direction
308 | * 
309 |
310 | x: 
311 |
312 | y: 
313 |
314 | 
315 |
316 | 
317 |
318 | Suppose we take a mass of 4 kg--
319 |
320 | * m = 4 kg
321 | * mg = 40 N for simplicity
322 | * T_1 = 29.3 N
323 | * T_2 = 20.7 N
324 |
325 | ### Another way to solve the tensions without decomposition
326 |
327 | ![Another way to solve the tensions][9]
328 |
329 | * If the two tension forces must cancel out mg, why don't I flip mg over?
330 | * T1 and T2 now, together, must add up to the flipped over mg.
331 |
332 | __How do we measure tension?__
333 |
334 | * Use scales and tension meters
335 | * The scales are not very accurate
336 |
337 | ## Bizarre Demo with a 2kg Block and 2 Strings
338 |
339 | ![Which string would break first?][10]
340 |
341 | __Which of the strings will break first?__
342 |
343 | 1. pull down very fast --> the bottom one will break first
344 | 2. pull down slowly --> the top one will break first
345 |
346 | [1]: images/L06_01.png "Acceleration due to earth's rotation"
347 | [2]: images/L06_02.png "A spring that is extended"
348 | [3]: images/L06_03.png "A softball on the hand"
349 | [4]: images/L06_04.png "Push on two masses"
350 | [5]: images/L06_05.png "Force diagram of mass 2"
351 | [6]: images/L06_06.png "Force diagram of mass 1"
352 | [7]: images/L06_07.png "Hero's Engine"
353 | [8]: images/L06_08.png "An object hanged by 2 strings"
354 | [9]: images/L06_09.png "Another way to solve the tensions"
355 | [10]: images/L06_10.png "Which string would break first?"
--------------------------------------------------------------------------------
/8.01 Classical Mechanics/07. Weight, Perceived Gravity, and Weightlessness.md:
--------------------------------------------------------------------------------
1 | # Lecture 07: Weight, Perceived Gravity, and Weightlessness
2 |
3 | Walter Lewin, 8.01 Physics I: Classical Mechanics, Fall 1999.
4 | (Massachusetts Institute of Technology: MIT OpenCourseWare).
5 | [http://ocw.mit.edu](http://ocw.mit.edu) (accessed 04 08, 2013).
6 | License: Creative Commons Attribution-Noncommercial-Share Alike.
7 |
8 | ## What is Weight?
9 |
10 | __What is weight?__
11 |
12 | ![Define weight][1]
13 |
14 | * You stand on a bathroom scale
15 | * Gravity is acting upon you, the force is mg, your mass is m.
16 | * The bathroom scale is pushing on you with a force F_scale
17 | * F_scale = mg
18 | * F_scale is defined as weight
19 |
20 | ### Example: Weight in an elevator accelerating upwards
21 |
22 | ![Weight inside an elevator accelerating upwards][2]
23 |
24 | * You stand on a bathroom scale inside an elevator
25 | * The elevator is accelerating upwards
26 |
27 | 
28 |
29 | 
30 |
31 | And You have gained weight.
32 |
33 | ### Example: Weight in an elevator accelerating downwards
34 |
35 | ![Weight inside an elevator accelerating downwards][3]
36 |
37 | * You stand on a bathroom scale inside an elevator
38 | * The elevator is accelerating downwards
39 |
40 | 
41 |
42 | 
43 |
44 | And You've lost weight.
45 |
46 | ### Example: Weight in a free fall
47 |
48 | * Suppose now I cut the cable...
49 | * F_s = m(g - a) = 0
50 |
51 | You are now __weightless__, you are __free-fall__ing.
52 |
53 | * If you had a glass with water, you could turn it over and the water would not fall out.
54 | * the shuttle in orbit with the astronauts being weightless
55 |
56 | __What exactly is free fall?__
57 |
58 | * Free fall is when the forces acting upon you are exclusively gravitational.
59 |
60 | __How could I determine your weight if I hang you from a string?__
61 |
62 | ![Determine weight when hanging from a string][4]
63 |
64 | 
65 |
66 | I read the scale and I read my weight.
67 |
68 | * For accelerating upwards and downwards, the analysis stays the same
69 |
70 | ## Tension in Massless String
71 |
72 | ![Hanging two masses over a frictionless pin][5]
73 |
74 | * a frictionless pin
75 | * a massless string wrapped around the pin
76 | * two objects with mass m1 and m2, hanged on each side
77 | * m2 > m1
78 | * m2 will be accelerated down
79 | * m1 will be accelerated up
80 |
81 | Claim: 
82 |
83 | __Why is that?__
84 |
85 | * because the pin is frictionless, and the string is massless.
86 | * Take a little section of the string
87 | * If the tensions were different, the section of the string would get an infinite acceleration (since it is massless).
88 |
89 | If there is friction in the pin--then that's not the case.
90 |
91 | Given the fact that the tension left and the tension right are the same, I must now conclude that __these two objects have the same weight__.
92 |
93 | Let us calculate the acceleration of this system and let's calculate the tension and let's see what comes out.
94 |
95 | ![Force diagram of object number 1][5]
96 |
97 | 
98 |
99 | 
100 |
101 | Notice m1 gains weight.
102 |
103 | ![Force diagram of object number 2][6]
104 |
105 | 
106 |
107 | 
108 |
109 | Two equations with two unknowns.
110 |
111 | Solve these two equations, we get
112 |
113 | 
114 |
115 | 
116 |
117 | Let's scrutinize these equations a little.
118 |
119 | e.g. m1 = m2 = m, a = 0, T = mg
120 |
121 | e.g. m2 >> m1, a = g, T = 0
122 |
123 | Return to the case where m2 > m1
124 |
125 | * since m1 is being accelerated upwards, it gained weight
126 | * since m2 is being accelerated downwards, it lost weight
127 |
128 | Prediction:
129 |
130 | 
131 |
132 | e.g. m1 = 1.1 kg, m2 = 1.25 kg
133 |
134 | __What is the acceleration "a" of the system?__
135 |
136 | a ~ 0.064 g
137 |
138 | __What is the tension?__
139 |
140 | T ~ 1.17 g
141 |
142 | ## Weight, when Swinging around on a String
143 |
144 | Return to swinging around in a vertical plane
145 |
146 | ![Swinging around in a vertical plane][8]
147 |
148 | * radius, R
149 | * constant angular velocity, omega
150 |
151 | Look at the bottom point P first
152 |
153 | 
154 |
155 | * similar to being accelerated upwards in an elevator
156 |
157 | Let's now look at the situation at S.
158 |
159 | 
160 |
161 | * similar to being accelerated upwards in an elevator
162 | * This object is losing weight.
163 |
164 | e.g. a_c = 10, T = 0, weightless!
165 |
166 | e.g. a_c > 10, T > 0, T = your weight
167 |
168 | e.g. a_c < 10, meaningless, T can never be negative. What it means is that the bucket of water would never have made it to this point.
169 |
170 | ## Objects in Free Fall are Weightless
171 |
172 | Professor Lewin jumps off a table with a jug of water in his hand
173 |
174 | 1. Stand on a table: Normal weight
175 | 2. Jump off a table: Weightless
176 | 3. Impact time: Weight more
177 | 4. Stop: Normal weight
178 |
179 | How can I show you that we are weightless?
180 |
181 | Well, if I don't have to use my muscles to push on this bottle upwards I might as well lower my hands a little bit during this free fall.
182 |
183 | And you will see that __the bottle will just stay above my hands__ without my having to push up.
184 |
185 | What happens when I hit the floor?
186 |
187 | * I hit the floor with a downward velocity of about 5 m/s
188 | * assume impact time to about 2/10 s
189 | * then the average acceleration will be 25 m/s^2 or 2.5 g
190 | * that means I will weigh 3.5 times of my normal weight.
191 |
192 | ## Weight Measurements of a Free Falling Object
193 |
194 | * Jump off the table with bathroom scale tied under the feet
195 | * However, bathroom scales have very slow response time
196 |
197 | Professor Dave made a scale with response time of 10 ms
198 |
199 | * 4.5 pounds for the platform
200 | * tape down a 10 lb barbell on top
201 | * drop it from a height to a cushioned box
202 | * also showed on an electronic scale in fractions of a second
203 | * sees oscillation since it is being thrown back to the air
204 |
205 | ## Professor Young's "Zero Gravity" Experiments
206 |
207 | Professor Young and Professor Oman here at the Aeronautics Department have done what they call "zero gravity experiments" from airplanes--
208 |
209 | ![Professor Young's "Zero Gravity" Experiment][9]
210 |
211 | "zero gravity" is a complete misnomer.
212 |
213 | "Zero weight," yes--
214 | "zero gravity," no.
215 |
216 | * They fly an airplane, which is the KC-135
217 | * They do these experiments at an altitude of about 30,000 feet.
218 | * The plane comes in at an angle of about 45 degrees.
219 | * The speed is about 425 mi/hr
220 | * The horizontal component is about 300 mi/hr
221 | * The vertical component is about 300 mi/hr
222 |
223 | The engine is then cut; the plane goes to free-fall; the plane will follow the path of a parabola.
224 |
225 | __What is the time that the velocity in the y direction comes to zero?__
226 |
227 | ~15 sec
228 |
229 | __How much higher would it have travelled?__
230 |
231 | ~900 m
232 |
233 | It will take about 30 seconds to go from where the engine is cut off to being at the same level again.
234 |
235 | In those 30 seconds, the horizontal displacement is about 3.5 km.
236 |
237 | The plane is going to pull up, it goes into this phase and then the plane flies horizontally for a while.
238 |
239 | During this phase, there will be weight increase since there is an acceleration upwards.
240 |
241 | And then when flying horizontally, they have again normal weight.
242 |
243 | * the reason why these flights are done is to study motion sickness under weightless conditions.
244 |
245 | [1]: images/L07_01.png "Define weight"
246 | [2]: images/L07_02.png "Weight when accelerating upwards"
247 | [3]: images/L07_03.png "Weight when accelerating downwards"
248 | [4]: images/L07_04.png "Weight when hanging from a string"
249 | [5]: images/L07_05.png "Hanging two masses over a frictionless pin"
250 | [6]: images/L07_06.png "Force diagram of object number 1"
251 | [7]: images/L07_07.png "Force diagram of object number 2"
252 | [8]: images/L07_08.png "Swinging around in a vertical plane"
253 | [9]: images/L07_09.png "Prefessor Young's 'zero-gravity' experiment"
--------------------------------------------------------------------------------
/8.01 Classical Mechanics/08. Frictional Forces.md:
--------------------------------------------------------------------------------
1 | # Lecture 08: Frictional Forces
2 |
3 | Walter Lewin, 8.01 Physics I: Classical Mechanics, Fall 1999.
4 | (Massachusetts Institute of Technology: MIT OpenCourseWare).
5 | [http://ocw.mit.edu](http://ocw.mit.edu) (accessed 04 08, 2013).
6 | License: Creative Commons Attribution-Noncommercial-Share Alike.
7 |
8 | ## Normal and Frictional Forces
9 |
10 | ![Object on a horizontal surface][1]
11 |
12 | Forces on the object
13 |
14 | * gravitational force, mg
15 | * __normal force__, N = mg
16 | * force by Walter Lewin
17 |
18 | The object is not accelerating in x-diretion at first, so there must be a frictional force to counter the force given by Walter Lewin.
19 |
20 | As Professor Lewin pushes harder, the frictional force would also increase until it reaches a reaches a maximum value which it cannot exceed.
21 |
22 | Experimental fact:
23 |
24 | 
25 |
26 | where 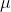 is called __the friction coefficient__, and has no dimension
27 |
28 | Distinction between __static__ friction coefficients and __kinetic__ friction
29 | coefficient.
30 |
31 | * static: to break it loose, to get it going
32 | * kinetic: to keep it going when it already has a certain velocity
33 |
34 | * 
35 |
36 | ## Measurements of the Coefficient of Static Friction
37 |
38 | It is fairly easy to measure a friction coefficient by putting an object on an incline and by changing the angle of the incline, increasing it.
39 |
40 | ![Object on an incline][2]
41 |
42 | Forces on the object:
43 |
44 | * gravity, mg
45 |
46 | * x-direction: 
47 | * y-direction: 
48 |
49 | * normal force: 
50 |
51 | * friction: 
52 |
53 | As the tilt is increased, the frictional force would eventually reach its maximum value, and the object will start to slide down.
54 |
55 | 
56 |
57 | 
58 |
59 | 
60 |
61 | 
62 |
63 | The friction coefficient is
64 |
65 | * independent of the mass.
66 | * independent of the contact surface area
67 | * only depends on the materials
68 |
69 | e.g. park a car with the brakes on, since the friction coefficient for rubber on concrete is about 1, so the car would slide on the hill of 45 degree.
70 |
71 | ### Demo: various objects on an incline
72 |
73 | * plastic bin vs rubber puck
74 | * mass independence
75 | * surface area independent
76 |
77 | The width of the tires of your car does not matter.
78 |
79 | But __why race cars have very wide tires?__
80 |
81 | ## Another Way to Measure Friction
82 |
83 | ![Object on an incline with a pulley][3]
84 |
85 | Problem:
86 |
87 | * do not know in which direction the system will accelerate or whether it will not accelerate at all--
88 |
89 | All these three cases have to be dealt with independently.
90 |
91 | 1. about to accelerate uphill
92 |
93 | 
94 |
95 | 
96 |
97 | 2. about to accelerate downhill
98 |
99 | 
100 |
101 | 
102 |
103 | 3. neight 1 or 2:
104 |
105 | * friction would adjust itself to balance out the force in x-direction
106 |
107 | ### Example:
108 |
109 | * m1 = 1 kg, m2 = 2 kg
110 | * 
111 | * 
112 |
113 | Is it going to be accelerated uphill or accelerated downhill or no acceleration at all?
114 |
115 | * 
116 | * 
117 | * 
118 |
119 | Let's first test whether condition one is met.
120 |
121 | 20 > 5 + 4.33?
122 |
123 | And the answer is yes, it is.
124 |
125 | So we know that it's going to be accelerated uphill.
126 |
127 | __What is the acceleration and what is the tension in the string?__
128 |
129 | * need to change  since it is now moving
130 |
131 | 
132 |
133 | 
134 |
135 | Solve to get.
136 |
137 | * a = 3.85 m/s^2
138 | * T = 12.3 N
139 |
140 | ### Example:
141 |
142 | * m1 = 1 kg, m2 = 0.4 kg
143 | * 
144 | * 
145 |
146 | * 
147 |
148 | Now, test the conditions
149 |
150 | 1. 4 > 5 + 4.33? NO
151 | 2. 4 < 5 - 4.33? NO
152 |
153 | Conclusion:
154 |
155 | a = 0
156 |
157 | The object will not be accelerated and the frictional force is going to adjust along the x direction so that the acceleration indeed is zero.
158 |
159 | __How does the frictional force do that?__
160 |
161 | * 
162 | * 
163 |
164 | Five newtons downhill, four newtons uphill.
165 |
166 | __What will the friction be?__
167 |
168 | Uphill, 1 N.
169 |
170 | ### Demo: measure coefficient of friction
171 |
172 | __Experiment 1: Slide down an incline__
173 |
174 | * m =  g
175 | * 
176 |
177 | > 
178 |
179 | __Experiment 2: Slide up an incline with a pulley__
180 |
181 | * 
182 | *  g
183 |
184 | __Would you find exactly the same number in these two experiments?__
185 |
186 | Not very likely.
187 |
188 | Wood has grain, and the grain could not be the same in every direction.
189 |
190 | __What happened during experiment #2?__
191 |
192 | * at first, it wants to slide downhill. So the friction is uphill
193 | * as m2 is increased, the friction becomes less and less
194 | * There comes a time that the friction becomes zero.
195 | * as m2 is further increased, the friction flips direction to downhill
196 | * as m2 is again increased, the friction is also increased until its maximum value
197 | * Then, the box starts to slide uphill
198 |
199 | ## Ways to Reduce Friction - Fleas are Good for Something!
200 |
201 | Friction is often a pain in the neck
202 | * friction causes wear and tear
203 | * friction costs fuel.
204 |
205 | With a car, there's a lot of friction with the road.
206 |
207 | People try to reduce friction
208 | * with bearings
209 | * with lubrication (e.g. oil, water)
210 |
211 | e.g. early part of the rain, the water is mixed with a little of dust
212 |
213 | e.g. cover of a pan becomes frictionless as water accumulated around the rim
214 |
215 | e.g. hovercrafts
216 |
217 | e.g. air track
218 |
219 | ![air track][4]
220 |
221 | e.g. a container of dry ice...
222 |
223 | * shows a film to demonstrate even a flea can pull the container if there is no friction
224 |
225 | [1]: images/L08_01.png "Object on a horizontal surface"
226 | [2]: images/L08_02.png "Object on an incline"
227 | [3]: images/L08_03.png "Object on an incline with a pulley"
228 | [4]: images/L08_04.png "Air track"
229 | [5]: images/L08_05.png "Container of dry ice"
230 |
--------------------------------------------------------------------------------
/8.01 Classical Mechanics/1. Introduction to Mechanics/MIT8_01SC_coursenotes01.pdf:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/leeyt/Physics/e33aa87cd6f9fee00272fbfce7321f4bd5a55f00/8.01 Classical Mechanics/1. Introduction to Mechanics/MIT8_01SC_coursenotes01.pdf
--------------------------------------------------------------------------------
/8.01 Classical Mechanics/10. Hooke's Law, Simple Harmonic Oscillator.md:
--------------------------------------------------------------------------------
1 | # Lecture 10: Hooke's Law, Simple Harmonic Oscillator
2 |
3 | Walter Lewin, 8.01 Physics I: Classical Mechanics, Fall 1999.
4 | (Massachusetts Institute of Technology: MIT OpenCourseWare).
5 | [http://ocw.mit.edu](http://ocw.mit.edu) (accessed 04 08, 2013).
6 | License: Creative Commons Attribution-Noncommercial-Share Alike.
7 |
8 | ## Restoring Force of a Spring
9 |
10 | If I have a spring...
11 |
12 | ![Spring in a horizontal position][1]
13 |
14 | And I extend the string...then there is a force that wants to drive this spring back to equilibrium.
15 |
16 | And it is an experimental fact that many springs--called __ideal springs__--
17 |
18 | 
19 |
20 | This is a one-dimensional problem, so to avoid the vector notation, we can simply say
21 |
22 | 
23 |
24 | where k is called the __spring constant__--
25 |
26 | * k is in N/m
27 | * it is a __restoring force__
28 | * __Hooke's Law__
29 |
30 | __How can we measure the spring constant?__
31 |
32 | ![Spring in a vertical position][2]
33 |
34 | * I hang on the spring a mass, m
35 | * plot displacement vs mass
36 |
37 | 
38 |
39 | ### Demo: Spring force is proportional to the displacement
40 |
41 | * a spring extends 13 cm per 1 kg
42 | * goes back to original length once the load is off
43 |
44 | ### Demo: Hooke's Law has its limit
45 |
46 | * permanent deformation of a spring
47 |
48 | ![Permanent deformation of a spring][3]
49 |
50 | So Hooke's Law holds only within certain limitations.
51 |
52 | ## Dynamic Equations of a Displaced Spring
53 |
54 | There are ways that you can also measure the spring constant in a dynamic way, which is actually very interesting.
55 |
56 | ![Spring oscillating horizontally][4]
57 |
58 | * attach an object to the spring
59 | * extend the spring and release it, it would start to oscillate
60 |
61 | The period of oscillation is
62 |
63 | 
64 |
65 | In other words, if you measured the period and you knew the mass, then you can calculate k.
66 |
67 | Alternatively, if you knew k and you measure the period, you can calculate the mass, even in the absence of gravity.
68 |
69 | * The period is not dependent on how far the spring was initially extended (or __amplitude__)
70 |
71 | Derivation of the period:
72 |
73 | 
74 |
75 | 
76 |
77 | 
78 |
79 | ### Demo: Shape of an oscillating spring
80 |
81 | * a spray paint suspended vertically by 2 springs
82 | * set the spray paint into oscillation
83 | * let it spray on a roll of paper pulled in a constant speed
84 |
85 | The curve looks like a sine or a cosine function.
86 |
87 | __What would a solution be to this differential equation?__
88 |
89 | So I'm going to substitute in this equation--
90 |
91 | 
92 |
93 | * A is called the __amplitude__
94 | * omega is called the __angular frequency__
95 |
96 | If I advance the time by , then the angle increases by 2 pi radians, which is 360 degrees.
97 |
98 | So that's the time it takes for the oscillation to repeat itself.
99 |
100 | The period is
101 |
102 | 
103 |
104 | You can define the __frequency__ of the oscillations to be 1/T, which we express always in terms of __Hz__.
105 |
106 | * phi is called the __phase angle__
107 |
108 | First, calculate the second derivate of x
109 |
110 | 
111 |
112 | 
113 |
114 | 
115 |
116 | Now, ready to substitute this result into that differential equation
117 |
118 | 
119 |
120 | This must hold for any x
121 |
122 | 
123 |
124 | And therefore, we now have the solution to this problem.
125 |
126 | 
127 |
128 | and
129 |
130 | 
131 |
132 | * independent of amplitude
133 | * independent of phase angle
134 |
135 | What is this business of this phase angle?
136 |
137 | When I start this oscillation, I could either:
138 |
139 | * release it with zero velocity
140 | * release it with a certain velocity
141 |
142 | Amplitude and phase angle do not determine the period, but they result from my __initial conditions__.
143 |
144 | ### Example:
145 |
146 | * Release the object at x = 0 and t = 0.
147 | * Give it a velocity, v = -3 m/s
148 | * k = 10 N/m
149 | * m = 0.1 kg
150 |
151 | What now is x as a function of time?
152 |
153 |  rad/s
154 |
155 |  sec
156 |
157 |  Hz
158 |
159 | I know that at t = 0, x = 0
160 |
161 | 
162 |
163 | Now, I go to my next initial condition, that the v = -3
164 |
165 | 
166 |
167 | If I pick pi / 2, then
168 |
169 | 
170 |
171 | And so the solution now, which includes now phi and A, is that
172 |
173 | 
174 |
175 | ## Measuring the Period of a Spring System
176 |
177 | * spring-mass system on an air track
178 | *  g
179 |
180 | ### Demo: Period is independent of the amplitude:
181 |
182 | * A = 20 cm,  sec
183 | * A = 40 cm,  sec
184 |
185 | ### Demo: Period is dependent on the mass
186 |
187 | *  g
188 |
189 | 
190 |
191 | Prediction:
192 |
193 |  sec
194 |
195 | > Professor Lewin made a comment about the uncertainty
196 |
197 | Observation:
198 |
199 |  sec
200 |
201 | ## Dynamic Equations of a Pendulum
202 |
203 | Here is the pendulum.
204 |
205 | ![Pendulum][5]
206 |
207 | And now I'm going to write down the differential equations of motion, first in the x direction.
208 |
209 | 
210 |
211 | Now the y direction.
212 |
213 | 
214 |
215 | It looks like a zoo, and it is a zoo.
216 |
217 | And now we're going to make an approximations which we will often see in physics when something oscillates--
218 |
219 | What we call the __small-angle approximations__.
220 |
221 | 
222 |
223 | Consequence of small angle approximations:
224 |
225 | 1. 
226 | 2. excursion in y-direction is way smaller than the excursion in x-direction so that 
227 |
228 | With these two conclusions, which follow from the small-angle approximation, I go back to my equation number two, and I find that
229 |
230 | 0 = T - mg
231 |
232 | So I find that T = mg.
233 |
234 | I substitute this back in my equation number one.
235 |
236 | 
237 |
238 | And now comes the wonderful result:
239 |
240 | 
241 |
242 | This is a __simple harmonic oscillation__.
243 |
244 | So you can write down immediately the solution to this differential equation.
245 |
246 | 
247 |
248 | where
249 |
250 | 
251 |
252 | So, the period of the pendulum will be
253 |
254 | 
255 |
256 | ## Comparing the Spring and Pendulum Periods
257 |
258 | I now want to compare with you the results that we have for the spring with the results that we have from the pendulum to give you some further insight.
259 |
260 | Spring:
261 |
262 | 
263 |
264 | * restoring force does not depend on mass
265 | * stiff springs gives larger restoring force, resulting in larger acceleration; hence, shorter period
266 | * will oscillate in outer space, could be used to measure the mass
267 |
268 | Pendulum:
269 |
270 | 
271 |
272 | * restoring force is proportional to the mass
273 | * will not swing in outer space
274 |
275 | ### Demo: Professor Lewin swings with a pendulum
276 |
277 | * m = 15 kg
278 | *  m
279 |
280 | Prediction:
281 |
282 |  sec
283 |
284 | Observation:
285 |
286 | 1. ,  sec
287 | 2. ,  sec
288 |
289 | One of the most remarkable things I just mentioned to you is that the period of the oscillations is independent of the mass of the object.
290 |
291 | That would mean if I joined the bob and I swing down with the bob that you should get that same period.
292 |
293 | __Would the period come out to be the same or not?__
294 |
295 | * it would be a little shorter, since Professor Lewin is not at exactly the same level as the mass and may shorten the length in the equation
296 |
297 | LEWIN: Ten T with Walter Lewin.
298 |
299 |  sec
300 |
301 | [1]: images/L10_01.png "Spring in a horizontal position"
302 | [2]: images/L10_02.png "Spring in a vertical position"
303 | [3]: images/L10_03.png "Permanent deformation of a spring"
304 | [4]: images/L10_04.png "Spring oscillating horizontally"
305 | [5]: images/L10_05.png "Pendulum"
306 |
--------------------------------------------------------------------------------
/8.01 Classical Mechanics/11. Work, Energy, and Universal Gravitation.md:
--------------------------------------------------------------------------------
1 | # Lecture 11: Work, Energy, and Universal Gravitation
2 |
3 | Walter Lewin, 8.01 Physics I: Classical Mechanics, Fall 1999.
4 | (Massachusetts Institute of Technology: MIT OpenCourseWare).
5 | [http://ocw.mit.edu](http://ocw.mit.edu) (accessed 04 08, 2013).
6 | License: Creative Commons Attribution-Noncommercial-Share Alike.
7 |
8 | ## 1D Work and Kinetic Energy
9 |
10 | The work that a force is doing, when that force is moving from point A to point B--
11 |
12 | 
13 |
14 | The unit of work is N m, for which we...call that "__joule__", J.
15 |
16 | If there's more than one force in this direction, you have to add these forces in this direction vectorially, and then this is the work that the forces do together.
17 |
18 | __Work is a scalar__, so it can be > 0, = 0, or < 0.
19 |
20 | F = ma, so therefore, F = m dv/dt.
21 |
22 | And I can write down for dx = v dt.
23 |
24 | I substitute that in there, so the work in going from A to B is
25 |
26 | 
27 |
28 | That's a very easy integral.
29 |
30 | 
31 |
32 | __kinetic energy__
33 |
34 | 
35 |
36 | __work-energy theorem__
37 |
38 | 
39 |
40 | * work is positive ==> KE increases when going from A to B
41 | * work is negative ==> KE decreases when going from A to B
42 | * work is zero ==> KE does not change when going from A to B
43 |
44 | ### Example
45 |
46 | ![Example 1][1]
47 |
48 | * I have an object that I want to move from A to B.
49 | * I give it a velocity at point A
50 | * when it reaches point B, it comes to a halt
51 |
52 | __What is the value of h?__
53 |
54 | 
55 |
56 | So you find that
57 |
58 | 
59 |
60 | m cancels, and so you'll find that
61 |
62 | 
63 |
64 | ### Example:
65 |
66 | ![Example 2][2]
67 |
68 | * Professor Lewin lifts an object from A to B
69 | * at point A and B, the velocities are all zero
70 |
71 | The work that Walter Lewin is doing is +mgh when the object goes from A to B.
72 |
73 | The work that gravity was doing was -mgh.
74 |
75 | So the net work that is done is zero, and you see there is indeed no change in kinetic energy.
76 |
77 | ### Example:
78 |
79 | * bring a briefcase up and down
80 | * bring up => positive work
81 | * bring down => negative work
82 | * gravity does opposite amount of work
83 | * net work is zero
84 |
85 | __Don't confuse getting tired with doing work.__
86 |
87 | __I would have done no work and I would be very tired.__
88 |
89 | ## Work Calculated in 3-Dimensions
90 |
91 | Now the work that the force is doing in going from A to B is
92 |
93 | 
94 |
95 | r is the position in three-dimensional space where the force is at that moment, and dr is a small displacement.
96 |
97 | ![F and dr][3]
98 |
99 | So let the force be...
100 |
101 | 
102 |
103 | And let dr--
104 |
105 | 
106 |
107 | So the work that this force is doing when it moves from A to B is
108 |
109 | 
110 |
111 | So we have that this is
112 |
113 | 
114 |
115 | If you add up these three terms, you get
116 |
117 | 
118 |
119 | and you get exactly the same result that you had before, namely that the __work done is the difference in kinetic energy__.
120 |
121 | ## Gravity is a Conservative Force
122 |
123 | ![Work done by gravity][4]
124 |
125 | 
126 |
127 | And so if I calculate now the work in going from A to B, this is
128 |
129 | 
130 |
131 | And what you see here, that it is completely __independent of the path__ that I have chosen.
132 |
133 | Whenever the work that is done by a force is independent of its path--it's only determined by the starting point and the end point--that force is called a "__conservative force__."
134 |
135 | __Gravity is a conservative force.__
136 |
137 | ## When Gravity is the only Force
138 |
139 | 
140 |
141 | I can rearrange this, and I then get
142 |
143 | 
144 |
145 | We call mgy..."__gravitational potential energy__." Often we write for that __PE__, or we write for that a __U__.
146 |
147 | And what you're seeing here is that
148 |
149 | 
150 |
151 | One can be converted into the other and it can be converted back.
152 |
153 | Sum of kinetic energy and potential energy--called "__mechanical energy__"--
154 | is conserved.
155 |
156 | And __mechanical energy is only conserved if the force is a conservative force__.
157 |
158 | * Spring forces are also conservative
159 | * Friction is not a conservative force
160 |
161 | ## What Matters is the Difference in Potential Energy
162 |
163 | If the object has no velocity, then there is no kinetic energy.
164 |
165 | __How about potential energy?__
166 |
167 | Well, you will say, sure, potential energy must be zero when y is zero.
168 |
169 | __But where is y a zero?__
170 |
171 | Well, you are completely free to choose where you put U = 0.
172 |
173 | It doesn't matter as long as point A and point B are close enough together that the gravitational acceleration, g, is very closely the same for both points.
174 |
175 | The only thing that matters then is how far they are separated vertically.
176 |
177 | The only thing that matters is that
178 |
179 | 
180 |
181 | ## A Roller Coaster, Upside-down
182 |
183 | Here is that roller coaster.
184 |
185 | ![Roller Coaster][5]
186 |
187 | 
188 |
189 | If there is no friction, if there are no other forces, only gravity.
190 |
191 | So no energy goes lost in terms of friction.
192 |
193 | And so now I can write this in general terms of y...
194 |
195 | 
196 |
197 | This should hold...for every point that I have here.
198 |
199 | and we summarize it as
200 |
201 | 
202 |
203 | Therefore, it should also hold for point D.
204 |
205 | However, at point D, it requires a centripetal acceleration.
206 |
207 | 
208 |
209 | So I have
210 |
211 | 
212 |
213 | But y for that point D is 2R,
214 |
215 | 
216 |
217 | Hence,
218 |
219 | 
220 |
221 | ## Newton's Law of Universal Gravitation
222 |
223 | Let's now look at the situation whereby A and B are so far apart that the gravitational acceleration is no longer constant, and so you can no longer simply say that the difference in potential energy between point B and point A is simply mgh.
224 |
225 | The formal definition of the gravitational potential energy at a point P is the work that I, Walter Lewin, have to do to bring that mass from infinity to that point P, or equivalently, the negative work the gravity does.
226 |
227 | __Newton's Universal Law of Gravity__
228 |
229 | 
230 |
231 | __Gravity is always attractive__.
232 |
233 | The gravitational constant G is an extremely low number--
234 |
235 |  N m^2/kg^2
236 |
237 | That's an extremely low number.
238 |
239 | e.g. 2 objects, each 1 kg, are 1 m apart, they would only experience 6.67 x 10^-11 newtons.
240 |
241 | 
242 |
243 | 
244 |
245 | You substitute in there
246 |
247 |  kg
248 |
249 | 
250 |
251 |  m
252 |
253 | out pops our well-known number of 9.8 m/s^2.
254 |
255 | Okay, my goal was to evaluate the gravitational potential energy that is defined in general, not in a special case when we are near the Earth.
256 |
257 | 
258 |
259 | And this is the gravitational potential energy at any distance capital R away from this object.
260 |
261 | At infinity, it's now always zero.
262 |
263 | Earlier, you had a choice where you chose your zero.
264 |
265 | Now you no longer have a choice.
266 |
267 | Now __the gravitational potential energy at infinity is fixed at zero__.
268 |
269 | So let's look at this function, and let us make a plot of this function as a function of distance.
270 |
271 | ![Plot gravitational potential energy vs r][6]
272 |
273 | If you move an object from A to B and this separation is h, and if A and B are very apart, the difference in potential energy is no longer mgh, but the difference in potential energy is the difference between U\_A and U\_B.
274 |
275 | So it increases when you go further away from the Earth if you look at the Earth, or from the sun if you look at the sun.
276 |
277 | Is there any disagreement between this `-mMG/r` result and the `mgh` result that we found there?
278 |
279 | The answer is __NO__.
280 |
281 | I invite you to go through the following exercise.
282 |
283 | 
284 |
285 | 
286 |
287 | And h << the radius of the Earth.
288 |
289 | So I can calculate now what the difference in potential energy is between point B and point A.
290 |
291 | And when I use the general equation and apply the first order of Taylor's expansion, you will immediately see that the result collapses into mgh because the g at the two points is so close that you will find then that it is approximately mgh.
292 |
293 | We will, many, many times in the future, use the 1/r relationship for gravitational potential energy.
294 |
295 | We will get very used to the idea that __gravitational potential energy is negative everywhere__, and we will get used to the idea that __at infinity, the gravitational potential energy is zero__.
296 |
297 | But whenever we deal with near-Earth situations like in 26.100, then, of course, it is way more convenient to use the simplification that the difference in gravitational potential energy is given by mgh.
298 |
299 | ## Conservation of Mechanical Energy and a Wrecking Ball
300 |
301 | I have here a pendulum.
302 |
303 | * 15 kg, lifted 1m higher
304 | * potential energy is increased by about 150 J
305 | * 150 J is enough to kill a person
306 |
307 | They use these devices--it's called a __wrecker ball__--
308 |
309 | __Demo: release the pendulum to break a glass pane__
310 |
311 | ### Demo: Conservation of Mechanical Energy
312 |
313 | * Professor Lewin standing with his back against a wall, holding a 15-kg pendulum under his chin, and let it go
314 | * The pendulum swings back and barely touches Professor Lewin's chin
315 |
316 | [1]: images/L11_01.png "Example 1"
317 | [2]: images/L11_02.png "Example 2"
318 | [3]: images/L11_03.png "F and dr"
319 | [4]: images/L11_04.png "Work done by gravity"
320 | [5]: images/L11_05.png "Roller Coaster"
321 | [6]: images/L11_06.png "Gravitational Potential Energy vs r"
--------------------------------------------------------------------------------
/8.01 Classical Mechanics/12. Resistive Forces.md:
--------------------------------------------------------------------------------
1 | # Lecture 12: Resistive Forces
2 |
3 | Walter Lewin, 8.01 Physics I: Classical Mechanics, Fall 1999.
4 | (Massachusetts Institute of Technology: MIT OpenCourseWare).
5 | [http://ocw.mit.edu](http://ocw.mit.edu) (accessed 04 08, 2013).
6 | License: Creative Commons Attribution-Noncommercial-Share Alike.
7 |
8 | ## Resistive and Drag Forces
9 |
10 | When you move an object through a medium, whether it's a gas or whether it's a liquid, it experiences a __drag force__.
11 |
12 | This drag force depends on
13 |
14 | * the shape of the object
15 | * the size of the object
16 | * the medium through which you move it
17 | * the speed of the object.
18 |
19 | The medium is immediately obvious.
20 |
21 | For example,
22 |
23 | * If you move through air, you feel the wind through your hair--
24 | * If you swim in water, you feel this drag force.
25 | * In oil, the drag force would be even larger.
26 |
27 | __This drag force, this resistive force is very, very different from the frictional force__.
28 |
29 | * the kinetic friction coefficient remains constant independent of the speed
30 | * the drag forces and the resistive forces are not independent of the speed
31 |
32 | In very general terms,
33 |
34 | 
35 |
36 | For spheres, we're going to get that
37 |
38 | 
39 |
40 | C1 is km / m / s and C2 has the dimension of density, kg / m^3
41 |
42 | We call the first term the __viscous__ term, and the second term the __pressure__ term.
43 |
44 | The viscous term has to do with the stickiness of the medium.
45 |
46 | Physicists also refer to that as __viscosity__.
47 |
48 | The C1 is a strong function of temperature.
49 |
50 | e.g. heated tar is less sticky than when it is cold
51 |
52 | C2 is not very dependent on the temperature.
53 |
54 | It's not so easy to see why this pressure term here has a v^2.
55 |
56 | > it has something to do with transfer of momentum
57 |
58 | But the r^2 is very easy to see, because the sphere has a cross-sectional area which is proportional to r^2.
59 |
60 | Two liquids with the very same density could have very different values for C1. They could differ by 4 or 5 orders of magnitude.
61 |
62 | But if they have the same density, then the C2 is very much the same.
63 |
64 | C2 is almost the density rho of the liquid--not quite but almost--
65 | there is a very strong correlation between the C2 and the density.
66 |
67 | If I drop an object and I just let it go--
68 |
69 | as it picks up speed, the resistive force will grow, and there comes a time that the resistive force and the gravitational force are equal.
70 |
71 | And when the two are equal, then there is no longer acceleration, so the object has a constant speed, and we call that the __terminal velocity__, and that will be the case when
72 |
73 | 
74 |
75 | If you know what m is, the radius, and the values for C1 or C2 of that medium in which you move it, then you can calculate what the terminal velocity is.
76 |
77 | ## Two Regimes and the Critical Velocity
78 |
79 | * Regime I: the viscous term is dominating
80 | * Regime II: the pressure term is dominating
81 |
82 | When the viscous force and the pressure force are the same,
83 |
84 | 
85 |
86 | We call that velocity __the critical velocity__, even though there is nothing critical about it.
87 |
88 | And that, of course,
89 |
90 | 
91 |
92 | Now we're going to make a clear distinction between the regimes I and II.
93 |
94 | Regime I:
95 |
96 | 
97 |
98 | So we then have that
99 |
100 | ,
101 |
102 | and therefore
103 |
104 | 
105 |
106 | If you take objects of the same material (same density), the density of the objects that you drop in the liquid or that you drop in the gas--
107 |
108 | so that
109 |
110 | 
111 |
112 | this rho is the density of the object; not the density of the medium--
113 |
114 | then you can immediately see, since you get an r^3 here, that the terminal velocity is proportional to r^2 if you drop objects in there with the same density.
115 |
116 | Regime II:
117 |
118 | 
119 |
120 | so then
121 |
122 | 
123 |
124 | So the terminal velocity is then
125 |
126 | 
127 |
128 | And if you take objects with the same density and you compare their radii, m is proportional to r^3 so the terminal velocity is now proportional to the square root of r.
129 |
130 | ## Measurements with Steel Balls in Syrup
131 |
132 | * drop ball bearings in Karo light corn syrup
133 | * C_1 = 1.6 x 10^2 (kg/m)/sec (strongly temperature dependent)
134 | * C_2 = 1.2 x 10^3 kg/m^3
135 | * rho_syrup = 1.7 x 10^3 kg/m^3
136 | * rho_ball = 7.8 x 10^3 kg/m^3
137 |
138 | And I'm going to drop in that Karo syrup four ball bearings, and they have diameters of an 1/8, 5/32, 3/16 and 1/4 of an inch.
139 |
140 | And what I calculated was the terminal velocity as a function of radius of these ball bearings.
141 |
142 | ![Drop Steel Ball Bearings in Corn Syrup][1]
143 |
144 | Our ball bearings are exclusively operating in regime I where the viscous term dominates.
145 |
146 | Now you could say, "Well, what is the meaning of this critical speed here if they never reach that speed anyhow?"
147 |
148 | Well, this critical speed for a small ball bearing would be some 100 m/s.
149 |
150 | That's about 200 mi/hr.
151 |
152 | There is nothing wrong with injecting a ball bearing with 400 mi/hr into this syrup, in which case, you would be above the critical speed and so for a short while would the motion be controlled by the pressure term.
153 |
154 | But of course when gravity takes over, then you ultimately end up in regime I.
155 |
156 | Now we are going to look at the various ball bearings, the various sizes, and I'll show you how we do the experiment.
157 |
158 | * there are seven marks which are 1 cm apart
159 | * when it reaches the second mark, I will start my timer.
160 | * when it reaches the sixth mark, I will stop my timer
161 | * this journey is about 4 cm
162 |
163 | And we will measure the time that it takes to go from here to here.
164 |
165 | 
166 |
167 | So we're going to get a list here of the diameters of the ball bearings, and the diameters is in inches.
168 |
169 |
178 |
179 |
180 | | diameter |
181 | d (1/32") |
182 | 100/d^2 |
183 | t (sec) |
184 |
185 |
186 | | 1/8" |
187 | 4 |
188 | 6.25 |
189 | 5.93 (5.66) ± 0.1 |
190 |
191 |
192 | | 5/32" |
193 | 5 |
194 | 4.00 |
195 | 3.80 ± 0.1 |
196 |
197 |
198 | | 3/16" |
199 | 6 |
200 | 2.78 |
201 | 2.69 ± 0.1 |
202 |
203 |
204 | | 1/4" |
205 | 8 |
206 | 1.56 |
207 | 1.66 (1.40) ± 0.2 sec |
208 |
209 |
210 |
211 | If the measurements were done correctly and if we really work in regime I, then if I plot 100 / d^2 versus t on linear paper, then it should be a straight line.
212 |
213 | Now... is this a straight line or is it not? A gorgeous straight line.
214 |
215 | And so you see you are really working here in the regime where the terminal velocity is proportional to the radius squared.
216 |
217 | ## Reaching Terminal Velocity in the Blink of an Eye
218 |
219 | How long does it take for the terminal speed to be reached?
220 |
221 | 
222 |
223 | Let a = dv/dt, then I have here a differential equation in v
224 |
225 | 
226 |
227 | What you're going to see is that the speed as a function of time is going to build up to a maximum value...
228 |
229 | ![Build up of terminal speed][2]
230 |
231 | __How long does it take to reach a speed of about 99% of the terminal speed
232 | for the 1/4" ball bearing?__
233 |
234 | That is only 9 ms.
235 |
236 | In other words, once it has broken through the surface--then in 9 ms will I already be at 99% of the terminal speed, and so there was no problem at all; when I waited for the object to cross the first mark, it was already clearly going at the terminal speed.
237 |
238 | ## Air Drag and the Pressure Term
239 |
240 | If we take air at 1 atm, and we take it at room temperature, then
241 |
242 | 
243 |
244 | and C_2 is about 0.85.
245 |
246 | And so the critical speed,
247 |
248 |  m/s
249 |
250 | And that is about 400 times lower than the critical speed in the Karo syrup for the same value of r.
251 |
252 | So if I drop the 1/4" ball bearing in the Karo syrup, then the terminal velocity is way below the critical velocity of the Karo syrup.
253 |
254 | The critical velocity of the Karo syrup would be 100 mi/hr for a 1/4" ball bearing.
255 |
256 | Here, in air, the critical velocity is something like 11 cm/s.
257 |
258 | We know when you drop a 1/4" ball bearing in air that the speed is way larger, and therefore in the case of air, a 1/4" ball bearing would have a speed way above the critical speed, and so you are now exclusively in regime II.
259 |
260 | Almost all spheres that you drop in air operate exclusively in regime two.
261 |
262 | Whether it is a raindrop or whether it is a baseball that you hit, or a golf ball, or even a beach ball, or you throw a pebble off a high building, or whether you jump out of an airplane, with or without a parachute, makes no difference, you're always dominated by the pressure term, by the v^2 term, and you always are in a range whereby the terminal speed is proportional to the square root of the radius for a given density of the object.
263 |
264 | If you take a pebble with a radius of about 1 cm and you throw it off a high building, it will reach a speed which will not exceed 75 mi/hr because of the air drag.
265 |
266 | If you jump out of a plane and you have no parachute and I make the assumption that your mass is about 70 kg--
267 |
268 | If I can approximate you by a sphere with a radius of about 40 cm--
269 | then the terminal velocity is 150 mi/hr.
270 |
271 | I just read an article yesterday about sky divers who jump out of planes, and they want to open the parachute at the very last possible, and they reach terminal velocities of 120 mi/hr, which doesn't surprise me.
272 |
273 | Of course, then they open the parachute and then the air drag increases enormously and then they slow down even further.
274 |
275 | I told you almost all raindrops operate in regime II when they fall.
276 |
277 | So the terminal velocity is dictated by the v^2 term.
278 |
279 | However, if you make the drops exceedingly small, there comes a time that you really enter regime I.
280 |
281 | I have here a ball--weighs approximately 34 g.
282 |
283 | and the radius is about 35 cm.
284 |
285 | It's about 70 centimeters across.
286 |
287 | I can calculate what the terminal velocity is--and so I find that to be about 1.8 m/s.
288 |
289 | So if I drop it from a height of 3 m, then you would think that the time that it takes to hit the floor would be about 1.7 s.
290 |
291 | However, it will, of course, take longer, and the reason is that the terminal velocity is not achieved instantaneously.
292 |
293 | Now, if you want to calculate the time that it takes to get close to terminal speed, that is not an easy task, because you are going to end up with a nasty differential equation.
294 |
295 | You see, we have
296 |
297 | 
298 |
299 | and this cannot be solved analytically.
300 |
301 | But I've asked my graduate student Dave Pooley to solve this for me numerically.
302 |
303 | ![Falling Balloon with and without Air Drag][3]
304 |
305 | So let's try this.
306 |
307 | And we're going to throw this object, and you may get something that is larger than 1.8 seconds, and the reasons are the following.
308 |
309 | 1. this is not a perfect sphere
310 | 2. this balloon is very springy, and creates turbulence.
311 |
312 | Turbulence is extremely hard to understand and predict.
313 |
314 | The prediction was 1.8; you get 2.0.
315 |
316 | ## Numerical Calculations of Air Drag Examples
317 |
318 | Throw a pebble off the Empire State Building.
319 |
320 | * radius of 1 cm
321 | * with air drag, the terminal speed would be about 75 mi/hr
322 | * without air drag, the speed would reach 225 mi/hr
323 |
324 | Empire State Building has a height of 475 m. If there had been no air drag, it would hit the ground a little less than 10 s, but now it will hit the ground more like 16, 17 seconds.
325 |
326 | And you see that the terminal speed builds up in about 5, 6 seconds.
327 |
328 | Now, you may remember that we dropped an apple from 3 m and that we calculated the gravitational acceleration given the time that it takes to fall.
329 |
330 | * the effect of air drag on the 3 m drop is only a delay of 2 ms
331 |
332 | ## Resistive Forces and Trajectories
333 |
334 | __How does air drag influence trajectories?__
335 |
336 | The motion of an object in liquid, giving an initial speed in the x direction
337 |
338 | ![Trajectory in a liquid][4]
339 |
340 | If there were no drag, then the trajectory would be a parabola, and the horizontal velocity would always be the same.
341 |
342 | Because of the drag force by the liquid, the object is going to get a component of the resistive force in the vertical direction.
343 |
344 | It has a horizontal speed, so there's also going to be a component of the resistive force in the x-direction.
345 |
346 | And then ultimately, there would be no horizontal speed, and the object would go vertically down with the terminal speed that you can find from dropping an object just into the liquid vertically.
347 |
348 | ### Example:
349 |
350 | Suppose I take a tennis ball and I throw up a tennis ball in 26.100.
351 |
352 | In the absence of any air drag, I would get a nice parabola which will be completely symmetric.
353 |
354 | But with air drag, there's going to be an air drag force in the y direction, there will also be a resistive force in the x direction. The trajectory would be asymmetric.
355 |
356 | ![Trajectory with and without air drag][5]
357 |
358 | Clearly you don't reach the highest point that you would have reached without air drag.
359 |
360 | __Demo: air drag effect on tennis ball and styrofoam ball__
361 |
362 | * tennis ball and styrofoam ball has about the same radius, so the resistive force is the same on both
363 | * styrofoam ball has way smaller mass than tennis ball, so air drag would have larger effect on styrofoam ball.
364 |
365 | When this object goes from O to P, that takes a certain amount of time.
366 |
367 | When it goes from P to S, back to the ground, that takes also a certain amount of time.
368 |
369 | Is OP time the same as PS time?
370 |
371 | -OR-
372 |
373 | Is OP time longer than OS time?
374 |
375 | -OR-
376 |
377 | Is OP time shorter than OS time?
378 |
379 | [1]: images/L12_01.png "Drop Steel Ball Bearings in Corn Syrup"
380 | [2]: images/L12_02.png "Build up of terminal speed"
381 | [3]: images/L12_03.png "Falling Balloon with and without Air Drag"
382 | [4]: images/L12_04.png "Trajectory in a liquid"
383 | [5]: images/L12_05.png "Trajectory with and without air drag"
384 |
--------------------------------------------------------------------------------
/8.01 Classical Mechanics/13. Equation of Motion for Simple Harmonic Oscillators.md:
--------------------------------------------------------------------------------
1 | # Lecture 13: Equation of Motion for Simple Harmonic Oscillators
2 |
3 | Walter Lewin, 8.01 Physics I: Classical Mechanics, Fall 1999.
4 | (Massachusetts Institute of Technology: MIT OpenCourseWare).
5 | [http://ocw.mit.edu](http://ocw.mit.edu) (accessed 04 08, 2013).
6 | License: Creative Commons Attribution-Noncommercial-Share Alike.
7 |
8 | ## Gravitational Potential Energy
9 |
10 | If I have an object, mass m, in gravitational field,
11 |
12 | ![Object in gravitational field][1]
13 |
14 | then the gravitational force, vectorially written,
15 |
16 | 
17 |
18 | Since this is a one-dimensional problem, we will often simply write
19 |
20 | F = -mg
21 |
22 | This minus sign is important because that's in the decreasing value of y.
23 |
24 | If the bottom level here is y = 0, then I could call this level U = 0.
25 |
26 | And the top level is y...its gravitational potential energy here, U = +mgy.
27 |
28 | So if I make a plot of the gravitational potential energy as a function of y, then I would get a straight line.
29 |
30 | ![Gravitational potential energy near Earth][2]
31 |
32 | If I move the object from point A to point B, I, Walter Lewin, have to do positive work. Notice that the gravitational potential energy increases. The gravity is doing negative work.
33 |
34 | If I move the object from point A to some other point, call it B'--then I do negative work. Notice the gravitational potential energy goes down. The gravity then is doing positive work.
35 |
36 | I could have chosen my zero point of potential energy anywhere I please.
37 |
38 | Nothing would change other than that I offset the zero point of my potential energy.
39 |
40 | But again, if I go from A to B, the gravitational potential energy increases by exactly the same amount--I have to do exactly the same work.
41 |
42 | So when you are near Earth, you are free to choose where the zero is.
43 |
44 | ### Gravitational Potential Energy not near the Earth
45 |
46 | Now we take the situation whereby we are not so close to the Earth.
47 |
48 | ![Gravitational Potential Energy not near the Earth][3]
49 |
50 | According to Newton's Universal Law of Gravity--the gravitational force on this object equals
51 |
52 | 
53 |
54 | Since it is really one-dimensional, we could simply write it this way.
55 |
56 | 
57 |
58 | The gravitational potential energy we derived last time equals
59 |
60 | --
61 |
62 | and if you plot that, then the plot goes sort of like this.
63 |
64 | ![U vs r][4]
65 |
66 | If I move away from the earth, with a mass m in my hand, notice that the gravitational potential energy increases. I have to do positive work, there is no difference.
67 |
68 | If I move closer to the Earth, notice that the gravitational potential energy decreases. I do negative work.
69 |
70 | Right here near Earth, where this 1/r curve hits the Earth, the tangent line would be exactly U = mgy so then you can simplify matters when you are near Earth.
71 |
72 | __The force is always in the direction opposite the increasing potential energy__.
73 |
74 | If I release an object at zero speed, it therefore will always move towards a lower potential energy because the force will drive it to lower potential energy.
75 |
76 | ## Calculating U(x) from F(x) and Vice Versa
77 |
78 | I have a spring which is relaxed length l--call this x = 0--
79 |
80 | and I extend it over a distance x and there's a mass m at the end
81 |
82 | and there will be a spring force.
83 |
84 | And that spring force...
85 |
86 | F = -kx.
87 |
88 | ![Extending a spring][5]
89 |
90 | I can calculate the work that I have to do to bring it from A to B.
91 |
92 | 
93 |
94 | And this is what we call __the potential energy of the spring__.
95 |
96 | At x = 0, we define potential energy to be zero.
97 |
98 | So if you now make a plot of the potential energy as a function of x, you get a parabola.
99 |
100 | ![Potential Energy of a Spring][6]
101 |
102 | The force is always in the direction opposing the increasing potential energy.
103 |
104 | You see, it's a restoring force.
105 |
106 | If we know the force--we were able to calculate the potential energy.
107 |
108 | __Suppose we knew the potential energy, can we find the force?__
109 |
110 | And the answer is yes, we can.
111 |
112 | Let's take the situation of the spring first.
113 |
114 | We have that the potential energy
115 |
116 | 
117 |
118 | and if I take the derivative of that versus x then I get +kx, but the force, the spring force itself, is -kx, so
119 |
120 | 
121 |
122 | The minus sign is telling you that the force is always pointing in the direction which is opposite to increasing values of the potential energy.
123 |
124 | If we have a three-dimensional situation that we know the potential energy as a function of x, y and z, then we can go back and find the forces as a function of x, y and z.
125 |
126 | It doesn't matter whether these are springs or whether it is gravity or whether it's electric forces or nuclear forces, you then find that
127 |
128 | 
129 |
130 | 
131 |
132 | 
133 |
134 | If we go back to the situation where we had gravity near Earth.
135 |
136 | We had U = mgy, so what is dU/dy?
137 |
138 | That is +mg, and notice that the gravitational force was -mg.
139 |
140 | And so you see that here, indeed,
141 |
142 | 
143 |
144 | Now we take the situation that we are not near Earth--
145 |
146 | Here we have
147 |
148 | 
149 |
150 | So the gravitational force equals
151 |
152 | 
153 |
154 | So whenever you know the potential as a function of space, you can always find the three components of the forces in the three orthogonal directions.
155 |
156 | ## Equilibrium Points
157 |
158 | Suppose I have a curved surface--
159 |
160 | ![Curved surface][7]
161 |
162 | So this is a function y = f(x) and the curve itself represents effectively the gravitational potential energy.
163 |
164 | So the gravitational potential energy U = mgy = mg f(x)
165 |
166 | There are points here where dU/dx = 0.
167 |
168 | It means that the component of the force in the x direction--is zero.
169 |
170 | So if we visit those points, then there is, of course, gravity, mg, in the -y direction and there is a normal force in the +y direction and these two exactly cancel each other.
171 |
172 | So the net result is that there is no force on the object at all, so the object is going to stay put.
173 |
174 | However, some points are __stable equilibrium__, and some points are __unstable equilibrium__.
175 |
176 | We have a curved track here, and I would like to show you how that will work.
177 |
178 | * put a little ball at various equilibrium points
179 | * At the stable point, the second derivative of the potential energy versus x is positive.
180 | * At the unstable point, the second derivative is negative.
181 |
182 | ## Parabolic Potential Energy Well ==> SHO
183 |
184 | I'm going to return now to my spring and I'm going to show you that if you use the potential energy of the spring alone that you can show that an object that oscillates on a spring follows a simple harmonic motion.
185 |
186 | ![Potential energy of a spring][8]
187 |
188 | Since spring forces are conservative forces, I can now apply the conservation of mechanical energy.
189 |
190 | We call this a __potential well__.
191 |
192 | The object is going to oscillate in a potential well.
193 |
194 | 
195 |
196 | 
197 |
198 | 
199 |
200 | 
201 |
202 | And now I'm going to take the time derivative of this equation.
203 |
204 | 
205 |
206 | 
207 |
208 | And this is a simple harmonic oscillation.
209 |
210 | We know the solution to this equation...
211 |
212 | 
213 |
214 | 
215 |
216 | We were able to apply the conservation of mechanical energy because spring forces are conservative forces.
217 |
218 | ## Circular Potential Energy Well ==> SHO
219 |
220 | Now I'm going to try something similar to another potential well and that potential well is a track and the track is a perfect circle.
221 |
222 | And I'm going to slide down that track an object mass m, and I'm going to evaluate the oscillation along a perfect circular track.
223 |
224 | ![Circular Track][9]
225 |
226 | 
227 |
228 | The velocity of that object is given by
229 |
230 | 
231 |
232 | So I can now apply the conservation of mechanical energy
233 |
234 | 
235 |
236 | And this is always the same, independent of the angle of theta, because gravity is a conservative force.
237 |
238 | This cosine theta is really a pain in the neck, and therefore we are going to make a small angle approximation...
239 |
240 | And we're going to write
241 |
242 | 
243 |
244 | We cannot use the earlier approximation that simply said cos(θ) = 0.
245 |
246 | If we did this, we would end up with nonsense, because it would say that the mechanical energy is changing all the time because this velocity is changing all the time.
247 |
248 | The approximation is really amazingly good.
249 |
250 |
259 |
260 |
261 | | θ (radian) |
262 | cos(θ) |
263 | 1-θ2/2 |
264 |
265 |
266 | | 1/60 |
267 | 0.999861114 |
268 | 0.999861111 |
269 |
270 |
271 | | 1/5 |
272 | 0.98007 |
273 | 0.98000 |
274 |
275 |
276 |
277 | So with this in mind, I feel comfortable to pursue my conservation of mechanical energy.
278 |
279 | And I'm going to replace this cos(θ) by 1 - θ2/2
280 |
281 | 
282 |
283 | And now I take the time derivative...
284 |
285 | 
286 |
287 | and what do I find?
288 |
289 | 
290 |
291 | And this tells me that the motion is that of a simple harmonic oscillation.
292 |
293 | And the solution is
294 |
295 | 
296 |
297 | where
298 |
299 |  is the angular frequency
300 |
301 | and
302 |
303 |  is the period.
304 |
305 | We have seen this before!
306 |
307 | We had a pendulum whereby we had length l of a massless string.
308 |
309 | Gravity is the only force that does work and so it is justified to use the conservation of mechanical energy because gravity is a conservative force.
310 |
311 | In the case of the spring, we had that the potential energy was proportional to x2 and out came a perfect simple harmonic oscillation, no approximation necessary.
312 |
313 | Now we forced this potential energy...into being dependent on θ2.
314 |
315 | And by the approximation of cos(θ) being 1 - θ2/2, we forced this term to become quadratic in θ and therefore now, with that approximation it becomes a perfect simple harmonic oscillation.
316 |
317 | Now comes a key question.
318 |
319 | __Is gravity is really the only force that does work?__
320 |
321 | YES.
322 |
323 | __Is the tension not doing any work? Is the normal force not doing any work?__
324 |
325 | YES. The force is always perpendicular to the direction of motion.
326 |
327 | ## Sliding on a Circular Track ==> SHO
328 |
329 | We do have a circular track.
330 |
331 | * a circular arc, radius = 115 ± 5 m
332 |
333 | Prediction:
334 |
335 |  sec
336 |
337 | Observation:
338 |
339 | 3T = 64.05 ± 0.1 sec
340 |
341 | T = 21.35 ± 0.03 sec
342 |
343 | ### Demo: Rolling ball on a circular track
344 |
345 | * the radius is 85 ± 1 cm
346 |
347 | Prediction:
348 |
349 | T = 1.85 ± 0.01 sec
350 |
351 | Observation:
352 |
353 | 10T = 22.7 ± 0.1 sec
354 |
355 | T = 2.27 ± 0.01 sec
356 |
357 | > the difference is that one is sliding, the other is rolling
358 |
359 | [1]: images/L13_01.png "Object in gravitational field"
360 | [2]: images/L13_02.png "Gravitational potential energy near the Earth"
361 | [3]: images/L13_03.png "Object not near the Earth"
362 | [4]: images/L13_04.png "Gravitational potential energy not near the Earth"
363 | [5]: images/L13_05.png "Extending a spring"
364 | [6]: images/L13_06.png "Potential energy of a spring"
365 | [7]: images/L13_07.png "Curved surface"
366 | [8]: images/L13_08.png "Potential energy of a spring"
367 | [9]: images/L13_09.png "Circular track"
368 |
--------------------------------------------------------------------------------
/8.01 Classical Mechanics/15. Momentum and its Conservation.md:
--------------------------------------------------------------------------------
1 | # Lecture 15: Momentum and its Conservation
2 |
3 | Walter Lewin, 8.01 Physics I: Classical Mechanics, Fall 1999.
4 | (Massachusetts Institute of Technology: MIT OpenCourseWare).
5 | [http://ocw.mit.edu](http://ocw.mit.edu) (accessed 04 08, 2013).
6 | License: Creative Commons Attribution-Noncommercial-Share Alike.
7 |
8 | ## Conservation of Momentum
9 |
10 | In physics, momentum is a vector
11 |
12 |  kg m/s
13 |
14 | 
15 |
16 | So you see--the force is dp/dt, and that means __if a particle changes its momentum, a force must have acted upon it__.
17 |
18 | It also means __if a force acts on a particle, it will change its momentum__.
19 |
20 | Let us now envision that we have a whole set of particles which are interacting with each other.
21 |
22 | ![System of particles with external forces][1]
23 |
24 | I pick one here, call it mi, and I pick another here, call it mj.
25 |
26 | And there is an external force on them, and so on mi, there is a force Fi,external, and on mj, there is Fj,external.
27 |
28 | But they're interacting with each other
29 |
30 | So there would be internal forces between each pair of particles, and they obey Newton's Third Law.
31 |
32 | The net force is ultimately the sum of the external force and all the internal forces.
33 |
34 | __What is the total momentum of these zillions of particles?__
35 |
36 | Well, that's the sum of the individual momenta.
37 |
38 | 
39 |
40 | I take the derivative of this--
41 |
42 | 
43 |
44 | And when we add up all these forces, obviously that is the total force on the entire system.
45 |
46 | If we view the system as a whole, the internal forces cancel each other out.
47 |
48 | Therefore,
49 |
50 | 
51 |
52 | This means that if the net external force on the whole system is zero, the momentum cannot change.
53 |
54 | Momentum is conserved, and that's called __the conservation of momentum__.
55 |
56 | ## Kinetic Energy and Momentum for a 1D Collision
57 |
58 | ![1D tail collision][2]
59 |
60 | And so now I can apply the conservation of momentum.
61 |
62 | The momentum before must be the same as the momentum afterwards because there are no external forces on the system.
63 |
64 | 
65 |
66 | And suppose m1 = 1 kg, and v1 = 5 m/s
67 |
68 | Let m2 = 2 kg, and v2 = 3 m/s.
69 |
70 | And you see, since they are both in the same direction,
71 |
72 | 5 + 6 = 3 v'
73 |
74 | so v' = 11/3 m/s.
75 |
76 | So the conservation of momentum tells you what the speed is after the collision.
77 |
78 | When we deal with collisions, __the velocities of the objects before the collision are unprimed__. __The velocities after the collisions, by convention, are primed__.
79 |
80 | Now if after the collision, object 1 and object 2 have different velocities, we will call them v1' and v2'.
81 |
82 | With an inelastic collision, m1 and m2 are stuck together.
83 |
84 | Now, there was a certain amount of kinetic energy before the collision, and of course, we can all calculate that-- kinetic energy before the collision.
85 |
86 | 
87 |
88 | __How much is it?__
89 |
90 | If you add that up, you will find 21.5 J.
91 |
92 | __What is the kinetic energy after the collision?__
93 |
94 | 
95 |
96 | That would give us 20.2 J.
97 |
98 | So the kinetic energy went down.
99 |
100 | Now, change the situation to a head-on collision.
101 |
102 | __What is the momentum of particle number one?__
103 |
104 | Well, that is m1v1 = 5.
105 |
106 | __What is the momentum of particle number two?__
107 |
108 | Well, that is m2v2 = -6.
109 |
110 | __What is the total momentum?__
111 |
112 | -1 kg m/s
113 |
114 | __What now is v'?__
115 |
116 | (m1 + m2)v' = -1
117 |
118 | and so v' = -1/3 m/s.
119 |
120 | The kinetic energy before has not changed--still is 21.5 J.
121 |
122 | __What now is the kinetic energy afterwards?__
123 |
124 | Now, there is only 0.17 J left.
125 |
126 | Almost all kinetic energy has been destroyed.
127 |
128 | So kinetic energy can be destroyed, but momentum cannot be destroyed in the absence of external forces.
129 |
130 | Suppose we have another head-on collision
131 |
132 | * particle one has a mass 5; the velocity is 1
133 | * particle two has a mass 1; the velocity is 5
134 | * total momentum before and after is 0
135 | * total kinetic energy before is 15
136 | * total kinetic energy after is 0
137 |
138 | ## Energy and Momentum for a 2D Car Collision
139 |
140 | If you have a car collision, and two cars hit each other, and I compare the situation just before the collision with just after the collision--
141 |
142 | The impact time is so short that the change in momentum due to friction with the road--that would be an external force--can be ignored.
143 |
144 | So momentum is approximately conserved if we can ignore the friction from the road during the impact time.
145 |
146 | ![2D Car Collision][3]
147 |
148 | __In what direction and what will be the speed after the collision?__
149 |
150 | Well, the net momentum is the vectorial sum of the momemtum of the two cars. That is never going to change before and after the collision.
151 |
152 | And therefore if you knew the angle of incidents, p1 and p2, then you can calculate in what direction the objects are going to slide, and also the velocity after the impact.
153 |
154 | And that's what the police is doing when they find wrecks on the road.
155 |
156 | They actually use the skidding tracks of the wreck to calculate v', and then they can try to reconstruct the situation as it was before the collision.
157 |
158 | We've only considered cases where they stick together, in which case we call them "__completely inelastic collisions__."
159 |
160 | __In completely inelastic collisions, you always lose kinetic energy__
161 |
162 | ## Scenarios that Increase the Kinetic Energy
163 |
164 | __Can we have, in a collision, an increase of kinetic energy?__
165 |
166 | Yes.
167 |
168 | e.g. exploding block
169 |
170 | ![Exploding block][4]
171 |
172 | Clearly, momentum must be conserved.
173 |
174 | __What happened with the kinetic energy?__
175 |
176 | Well, kinetic energy has clearly increased.
177 |
178 | __Where did the kinetric energy come from?__
179 |
180 | Well, it was from the chemical reaction of the explosion.
181 |
182 | __Never confuse momentum with energy.__
183 |
184 | ### Demo:
185 |
186 | * Set up on air track so there is a minimum of friction.
187 | * push two cars together and hold them together with a spring
188 | * they are held together with a string
189 | * take a burner and burn away this thread
190 |
191 | __How do we measure the speed?__
192 |
193 | Well, we actually measure the time for the cars to move 10 cm.
194 |
195 | Each car has a 10-cm long metal plate and it blanks out a light-emitting diode.
196 |
197 | And the moment that the LED is occluded, the timer starts, and the moment that the LED emerges again, the timer stops.
198 |
199 | __Experiment 1:__
200 |
201 | 1. m1 = 244 ± 1 g
202 | 2. m2 = 244 ± 1 g
203 |
204 | Prediction:
205 |
206 | I would predict that the times of these two cars will be the same to within roughly 5%.
207 |
208 | Observation:
209 |
210 | 1. t1 = 0.219 ± 0.001 s
211 | 2. t2 = 0.223 ± 0.001 s
212 |
213 | __Experiment 2:__
214 |
215 | 1. m1 = 488 ± 1 g
216 | 2. m2 = 244 ± 1 g
217 |
218 | Prediction:
219 |
220 | t2 should be 2 x t1 to within 5% of uncertainty.
221 |
222 | Observation:
223 |
224 | 1. t1 = 0.406 ± 0.001 s
225 | 2. t2 = 0.193 ± 0.001 s
226 |
227 | ## Center of Mass of a System
228 |
229 | The center of mass of a system is defined as follows:
230 |
231 | ![Center of mass][5]
232 |
233 | 
234 |
235 | Take the derivative of this equation, we have
236 |
237 | 
238 |
239 | So, we have
240 |
241 | 
242 |
243 | And so now you come to another very important statement in physics, and that is __the total momentum of an object is the total mass of that object times the velocity of the center of mass__.
244 |
245 | And if I take the derivative of this, then
246 |
247 | 
248 |
249 | This says F = ma.
250 |
251 | The center of mass behaves as if all the mass of the entire object was right at that center of mass.
252 |
253 | For the center of mass, the total momentum is the total mass times the velocity of the center of mass.
254 |
255 | And you take the derivative of that equation and you get F = ma.
256 |
257 | ### Example
258 |
259 | ![3 mass system][6]
260 |
261 | Where is the center of mass?
262 |
263 | We break it up into components.
264 |
265 | For the x component, we have
266 |
267 | 
268 |
269 | 
270 |
271 | Now, in the y direction, do the same thing would obtain
272 |
273 | 
274 |
275 | And so you have calculated the center of mass.
276 |
277 | ### Demo: Uniform motion of the center of the mass
278 |
279 | * connect two cars with springs
280 | * slide them across the air track
281 | * center of mass will travel in a constant speed
282 | * while the two cars would oscillate in a weird way
283 |
284 | ### Demo: Uniform motion of the center of the mass of a squash racquet
285 |
286 | * attach the center of the mass with a UV dot
287 | * throw the racquet at an angle
288 | * the center of the mass traverses a path of parabola
289 |
290 | [1]: images/L15_01.png "System of particles with external forces"
291 | [2]: images/L15_02.png "1D tail collision"
292 | [3]: images/L15_03.png "2D car collision"
293 | [4]: images/L15_04.png "Exploding block"
294 | [5]: images/L15_05.png "Center of mass"
295 | [6]: images/L15_06.png "3 mass system"
296 |
--------------------------------------------------------------------------------
/8.01 Classical Mechanics/16. Elastic and Inelastic Collisions.md:
--------------------------------------------------------------------------------
1 | # Lecture 16: Elastic and Inelastic Collisions
2 |
3 | Walter Lewin, 8.01 Physics I: Classical Mechanics, Fall 1999.
4 | (Massachusetts Institute of Technology: MIT OpenCourseWare).
5 | [http://ocw.mit.edu](http://ocw.mit.edu) (accessed 04 08, 2013).
6 | License: Creative Commons Attribution-Noncommercial-Share Alike.
7 |
8 | ## 1D Elastic Collisions
9 |
10 | Today I will talk about collisions in more general terms.
11 |
12 | Let's take a one-dimensional case.
13 |
14 | ![1D Elastic Collision][1]
15 |
16 | * 2 masses, m1 and m2
17 | * Before: v1, v2 = 0
18 | * After: v1', v2'
19 |
20 | To find v1' and v2', we need two equations.
21 |
22 | If no net external force is on the system during the collisions, then momentum is conserved.
23 |
24 | 
25 |
26 | Now, we need a second equation.
27 |
28 | Now, in physics we believe very strongly in the conservation of energy, not necessarily in the conservation of kinetic energy.
29 |
30 | We believe that if you destroy energy, it must come out in some other form, and you cannot create energy out of nothing.
31 |
32 | In the case of the completely inelastic collisions, we lost kinetic energy, which was converted to heat.
33 |
34 | There was internal friction.
35 |
36 | When the car wreck plowed into each other, there was internal friction--no external friction--and that took out kinetic energy.
37 |
38 | And so, in its most general form, you can write down that
39 |
40 | 
41 |
42 | If you know Q, then you have a second equation, and then you can solve for v1' and for v2'.
43 |
44 | * Q > 0, gained kinetic energy, called __superelastic collision__
45 | * Q = 0, conserved kinetic energy, called __(completely) elastic collision__
46 | * Q < 0, lost kinetic energy, called __completely inelastic collision__
47 |
48 | Now I want to continue a case whereby I have a completely elastic collision. So Q = 0.
49 |
50 | Momentum is conserved, because there was no net external force, but now kinetic energy is also conserved.
51 |
52 | And so I can write down now
53 |
54 | 
55 |
56 | Solving these two equations, we would get
57 |
58 | 
59 |
60 | and
61 |
62 | 
63 |
64 | This is the result which holds under three conditions:
65 |
66 | 1. kinetic energy is conserved, so Q = 0
67 | 2. momentum is conserved
68 | 3. v2 before the collision equals zero.
69 |
70 | Let's look at 3 interesting cases whereby we go to extremes.
71 |
72 | 1. m1 >> m2
73 |
74 | 
75 |
76 | 
77 |
78 | 2. m1 << m2
79 |
80 | 
81 |
82 | 
83 |
84 | 3. m1 = m2
85 |
86 | 
87 |
88 | 
89 |
90 | e.g. Newton's cradle
91 |
92 | ### Demo: Billiard ball vs. Ping-pong ball
93 |
94 | * Billard ball and ping-pong ball suspended as pendulumns
95 | * mass ratio is 500:1
96 |
97 | 1. Swing ping-pong ball onto billiard ball
98 | 2. Swing billiard ball onto ping-pong ball
99 |
100 | ### Demo: Elastic collision on air track
101 |
102 | * object m1 banged against object m2
103 | * object m2 stands still initially
104 | * using springs to make the collision ellastic
105 |
106 | #### Experiment 1:
107 |
108 | * m1 = 241 ± 1 g
109 | * m2 = 241 ± 1 g
110 |
111 | Prediction:
112 |
113 | * v1' = 0
114 | * v2' = v1
115 |
116 | Observation:
117 |
118 | * t1 = 0.194
119 | * t1' = 0.000
120 | * t2' = 0.196
121 |
122 | #### Experiment 2:
123 |
124 | * m1 = 241 ± 1 g
125 | * m2 = 482 ± 1 g
126 |
127 | Prediction:
128 |
129 | * v1' = -1/3 v1
130 | * v2' = +2/3 v1
131 |
132 | Observation:
133 |
134 | * t1 = 0.123
135 | * t1' = 0.375 * (1/3) = 0.125
136 | * t2' = 0.186 * (2/3) = 0.124
137 |
138 | ## Brain Teaser - Elastic Collision with a Wall
139 |
140 | ![Tennis ball bounced off a wall][2]
141 |
142 | * elastic collision => kinetic energy is conserved, entirely in the tennis ball
143 | * the momentum of this tennis ball has changed by an amount 2 mv
144 | * that momentum must be in the wall--because momentum must be conserved
145 |
146 | __How can the wall have no kinetic energy yet acquired momentum?__
147 |
148 | ## Center of Mass (CM) Frame of Reference
149 |
150 | In the absence of any net external forces on a system as a whole, the center of mass will always have the same velocity.
151 |
152 | If you jump into the frame of the center of mass, which means you move with the same velocity as the center of mass, the center of mass stands still in your frame of reference.
153 |
154 | And if the center of mass stands still, the momentum of the particles in this frame of reference, is zero.
155 |
156 | ![Collision in the center-of-mass frame][3]
157 |
158 | 
159 |
160 | Q is zero--and so kinetic energy must be conserved.
161 |
162 | 
163 |
164 | The result in the center of mass is that
165 |
166 | 
167 |
168 | and
169 |
170 | 
171 |
172 | In the center of mass, all that happens is that velocities reverse directions, but the speeds remain the same.
173 |
174 | __How do we calculate the velocity of the center of mass?__
175 |
176 | First, move back to laboratory frame.
177 |
178 | 
179 |
180 | If you take the derivative of this equation, then
181 |
182 | 
183 |
184 | Now, if you want to know what the velocity is in the center-of-mass frame,
185 |
186 | 
187 |
188 | 
189 |
190 | It sometimes pays off to move into the center-of-mass frame.
191 |
192 | The momentum in the center-of-mass frame is always zero before and after the collision, independent of whether it is an elastic, an inelastic, or a superelastic collision.
193 |
194 | ## 1D Inelastic Collision and Internal Energy
195 |
196 | The kinetic energy and the momentum depend on your reference frame.
197 |
198 | In general, the total momentum as seen from the lab frame is not zero.
199 |
200 | In the case of the center of mass, the total momentum is always zero.
201 |
202 | In general, the kinetic energy as seen from the lab frame is not the same as the kinetic energy from the center-of-mass frame.
203 |
204 | If I have a completely inelastic collision, then all energy in the center-of-mass frame is lost.
205 |
206 | This lost in kinetic energy--as observed in the center-of-mass frame--is called the internal energy.
207 |
208 | That would be the maximum energy in a collision that can ever be converted into heat.
209 |
210 | ### Example:
211 |
212 | ![Completely inelastic collision][4]
213 |
214 | Momentum is conserved if there's no net external force on the system, and so I can write down that
215 |
216 | 
217 |
218 | And so
219 |
220 | 
221 |
222 | This is also the velocity of the center of mass.
223 |
224 | Now we can calculate what the difference is between the kinetic energies after and before the collision.
225 |
226 | This equals
227 |
228 | 
229 |
230 | We lose kinetic energy when there is a completely inelastic collision.
231 |
232 | This is Q. You lose kinetic energy and that goes into heat.
233 |
234 | Now I'm going to do the same calculation in the center-of-mass frame.
235 |
236 | 
237 |
238 | 
239 |
240 | Now we are going to calculate the kinetic energy in the center-of-mass frame.
241 |
242 | 
243 |
244 | That's all we have before the collision occurs.
245 |
246 | This is the maximum you can ever lose, and this is what we call the internal kinetic energy of the system.
247 |
248 | And so going to the center-of-mass system, you can always immediately calculate what the maximum heat is that you can expect from a collision.
249 |
250 | ### Special case:
251 |
252 | If we take m2 going to ∞, like slam a piece of putty onto the wall.
253 |
254 | 
255 |
256 | ### Demo: Completely elastic collision on air track
257 |
258 | * object m1 banged against object m2
259 | * object m2 stands still initially
260 | * using Velcro to make the collision completely inellastic
261 |
262 | #### Experiment 1:
263 |
264 | * m1 = 237 ± 1 g
265 | * m2 = 237 ± 1 g
266 |
267 | Prediction:
268 |
269 | * v' = 1/2 v1
270 |
271 | Observation:
272 |
273 | * t1 = 0.138
274 | * t' = 0.288 * (1/2) = 0.144
275 |
276 | #### Experiment 2:
277 |
278 | * m1 = 237 ± 1 g
279 | * m2 = 474 ± 1 g
280 |
281 | Prediction:
282 |
283 | * v' = 1/3 v1
284 |
285 | Observation:
286 |
287 | * t1 = 0.187
288 | * t' = 0.603 * (1/3) = 0.201
289 |
290 | ## Newton's Cradle Demonstration
291 |
292 | * 8 billiard balls total
293 |
294 | * 2 banged onto 6 => out comes the 2
295 | * 3 banged onto 5 => out comes the 3
296 | * 5 banged onto 3 => out comes the 5
297 |
298 | [1]: images/L16_01.png "1D Elastic Collision"
299 | [2]: images/L16_02.png "Tennis ball bounced off a wall"
300 | [3]: images/L16_03.png "Collision in the center-of-mass frame"
301 | [4]: images/L16_04.png "Completely inelatic collision"
302 |
--------------------------------------------------------------------------------
/8.01 Classical Mechanics/images/L01_01.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/leeyt/Physics/e33aa87cd6f9fee00272fbfce7321f4bd5a55f00/8.01 Classical Mechanics/images/L01_01.png
--------------------------------------------------------------------------------
/8.01 Classical Mechanics/images/L01_02.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/leeyt/Physics/e33aa87cd6f9fee00272fbfce7321f4bd5a55f00/8.01 Classical Mechanics/images/L01_02.png
--------------------------------------------------------------------------------
/8.01 Classical Mechanics/images/L02_01.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/leeyt/Physics/e33aa87cd6f9fee00272fbfce7321f4bd5a55f00/8.01 Classical Mechanics/images/L02_01.png
--------------------------------------------------------------------------------
/8.01 Classical Mechanics/images/L02_02.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/leeyt/Physics/e33aa87cd6f9fee00272fbfce7321f4bd5a55f00/8.01 Classical Mechanics/images/L02_02.png
--------------------------------------------------------------------------------
/8.01 Classical Mechanics/images/L02_03.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/leeyt/Physics/e33aa87cd6f9fee00272fbfce7321f4bd5a55f00/8.01 Classical Mechanics/images/L02_03.png
--------------------------------------------------------------------------------
/8.01 Classical Mechanics/images/L02_04.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/leeyt/Physics/e33aa87cd6f9fee00272fbfce7321f4bd5a55f00/8.01 Classical Mechanics/images/L02_04.png
--------------------------------------------------------------------------------
/8.01 Classical Mechanics/images/L02_05.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/leeyt/Physics/e33aa87cd6f9fee00272fbfce7321f4bd5a55f00/8.01 Classical Mechanics/images/L02_05.png
--------------------------------------------------------------------------------
/8.01 Classical Mechanics/images/L02_06.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/leeyt/Physics/e33aa87cd6f9fee00272fbfce7321f4bd5a55f00/8.01 Classical Mechanics/images/L02_06.png
--------------------------------------------------------------------------------
/8.01 Classical Mechanics/images/L02_07.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/leeyt/Physics/e33aa87cd6f9fee00272fbfce7321f4bd5a55f00/8.01 Classical Mechanics/images/L02_07.png
--------------------------------------------------------------------------------
/8.01 Classical Mechanics/images/L03_01.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/leeyt/Physics/e33aa87cd6f9fee00272fbfce7321f4bd5a55f00/8.01 Classical Mechanics/images/L03_01.png
--------------------------------------------------------------------------------
/8.01 Classical Mechanics/images/L03_02.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/leeyt/Physics/e33aa87cd6f9fee00272fbfce7321f4bd5a55f00/8.01 Classical Mechanics/images/L03_02.png
--------------------------------------------------------------------------------
/8.01 Classical Mechanics/images/L03_03.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/leeyt/Physics/e33aa87cd6f9fee00272fbfce7321f4bd5a55f00/8.01 Classical Mechanics/images/L03_03.png
--------------------------------------------------------------------------------
/8.01 Classical Mechanics/images/L03_04.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/leeyt/Physics/e33aa87cd6f9fee00272fbfce7321f4bd5a55f00/8.01 Classical Mechanics/images/L03_04.png
--------------------------------------------------------------------------------
/8.01 Classical Mechanics/images/L03_05.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/leeyt/Physics/e33aa87cd6f9fee00272fbfce7321f4bd5a55f00/8.01 Classical Mechanics/images/L03_05.png
--------------------------------------------------------------------------------
/8.01 Classical Mechanics/images/L03_06.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/leeyt/Physics/e33aa87cd6f9fee00272fbfce7321f4bd5a55f00/8.01 Classical Mechanics/images/L03_06.png
--------------------------------------------------------------------------------
/8.01 Classical Mechanics/images/L03_07.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/leeyt/Physics/e33aa87cd6f9fee00272fbfce7321f4bd5a55f00/8.01 Classical Mechanics/images/L03_07.png
--------------------------------------------------------------------------------
/8.01 Classical Mechanics/images/L03_08.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/leeyt/Physics/e33aa87cd6f9fee00272fbfce7321f4bd5a55f00/8.01 Classical Mechanics/images/L03_08.png
--------------------------------------------------------------------------------
/8.01 Classical Mechanics/images/L03_09.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/leeyt/Physics/e33aa87cd6f9fee00272fbfce7321f4bd5a55f00/8.01 Classical Mechanics/images/L03_09.png
--------------------------------------------------------------------------------
/8.01 Classical Mechanics/images/L03_10.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/leeyt/Physics/e33aa87cd6f9fee00272fbfce7321f4bd5a55f00/8.01 Classical Mechanics/images/L03_10.png
--------------------------------------------------------------------------------
/8.01 Classical Mechanics/images/L03_11.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/leeyt/Physics/e33aa87cd6f9fee00272fbfce7321f4bd5a55f00/8.01 Classical Mechanics/images/L03_11.png
--------------------------------------------------------------------------------
/8.01 Classical Mechanics/images/L03_12.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/leeyt/Physics/e33aa87cd6f9fee00272fbfce7321f4bd5a55f00/8.01 Classical Mechanics/images/L03_12.png
--------------------------------------------------------------------------------
/8.01 Classical Mechanics/images/L03_13.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/leeyt/Physics/e33aa87cd6f9fee00272fbfce7321f4bd5a55f00/8.01 Classical Mechanics/images/L03_13.png
--------------------------------------------------------------------------------
/8.01 Classical Mechanics/images/L03_14.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/leeyt/Physics/e33aa87cd6f9fee00272fbfce7321f4bd5a55f00/8.01 Classical Mechanics/images/L03_14.png
--------------------------------------------------------------------------------
/8.01 Classical Mechanics/images/L04_01.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/leeyt/Physics/e33aa87cd6f9fee00272fbfce7321f4bd5a55f00/8.01 Classical Mechanics/images/L04_01.png
--------------------------------------------------------------------------------
/8.01 Classical Mechanics/images/L04_02.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/leeyt/Physics/e33aa87cd6f9fee00272fbfce7321f4bd5a55f00/8.01 Classical Mechanics/images/L04_02.png
--------------------------------------------------------------------------------
/8.01 Classical Mechanics/images/L05_01.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/leeyt/Physics/e33aa87cd6f9fee00272fbfce7321f4bd5a55f00/8.01 Classical Mechanics/images/L05_01.png
--------------------------------------------------------------------------------
/8.01 Classical Mechanics/images/L05_02.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/leeyt/Physics/e33aa87cd6f9fee00272fbfce7321f4bd5a55f00/8.01 Classical Mechanics/images/L05_02.png
--------------------------------------------------------------------------------
/8.01 Classical Mechanics/images/L05_03.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/leeyt/Physics/e33aa87cd6f9fee00272fbfce7321f4bd5a55f00/8.01 Classical Mechanics/images/L05_03.png
--------------------------------------------------------------------------------
/8.01 Classical Mechanics/images/L05_04.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/leeyt/Physics/e33aa87cd6f9fee00272fbfce7321f4bd5a55f00/8.01 Classical Mechanics/images/L05_04.png
--------------------------------------------------------------------------------
/8.01 Classical Mechanics/images/L05_05.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/leeyt/Physics/e33aa87cd6f9fee00272fbfce7321f4bd5a55f00/8.01 Classical Mechanics/images/L05_05.png
--------------------------------------------------------------------------------
/8.01 Classical Mechanics/images/L05_06.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/leeyt/Physics/e33aa87cd6f9fee00272fbfce7321f4bd5a55f00/8.01 Classical Mechanics/images/L05_06.png
--------------------------------------------------------------------------------
/8.01 Classical Mechanics/images/L05_07.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/leeyt/Physics/e33aa87cd6f9fee00272fbfce7321f4bd5a55f00/8.01 Classical Mechanics/images/L05_07.png
--------------------------------------------------------------------------------
/8.01 Classical Mechanics/images/L06_01.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/leeyt/Physics/e33aa87cd6f9fee00272fbfce7321f4bd5a55f00/8.01 Classical Mechanics/images/L06_01.png
--------------------------------------------------------------------------------
/8.01 Classical Mechanics/images/L06_02.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/leeyt/Physics/e33aa87cd6f9fee00272fbfce7321f4bd5a55f00/8.01 Classical Mechanics/images/L06_02.png
--------------------------------------------------------------------------------
/8.01 Classical Mechanics/images/L06_03.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/leeyt/Physics/e33aa87cd6f9fee00272fbfce7321f4bd5a55f00/8.01 Classical Mechanics/images/L06_03.png
--------------------------------------------------------------------------------
/8.01 Classical Mechanics/images/L06_04.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/leeyt/Physics/e33aa87cd6f9fee00272fbfce7321f4bd5a55f00/8.01 Classical Mechanics/images/L06_04.png
--------------------------------------------------------------------------------
/8.01 Classical Mechanics/images/L06_05.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/leeyt/Physics/e33aa87cd6f9fee00272fbfce7321f4bd5a55f00/8.01 Classical Mechanics/images/L06_05.png
--------------------------------------------------------------------------------
/8.01 Classical Mechanics/images/L06_06.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/leeyt/Physics/e33aa87cd6f9fee00272fbfce7321f4bd5a55f00/8.01 Classical Mechanics/images/L06_06.png
--------------------------------------------------------------------------------
/8.01 Classical Mechanics/images/L06_07.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/leeyt/Physics/e33aa87cd6f9fee00272fbfce7321f4bd5a55f00/8.01 Classical Mechanics/images/L06_07.png
--------------------------------------------------------------------------------
/8.01 Classical Mechanics/images/L06_08.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/leeyt/Physics/e33aa87cd6f9fee00272fbfce7321f4bd5a55f00/8.01 Classical Mechanics/images/L06_08.png
--------------------------------------------------------------------------------
/8.01 Classical Mechanics/images/L06_09.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/leeyt/Physics/e33aa87cd6f9fee00272fbfce7321f4bd5a55f00/8.01 Classical Mechanics/images/L06_09.png
--------------------------------------------------------------------------------
/8.01 Classical Mechanics/images/L06_10.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/leeyt/Physics/e33aa87cd6f9fee00272fbfce7321f4bd5a55f00/8.01 Classical Mechanics/images/L06_10.png
--------------------------------------------------------------------------------
/8.01 Classical Mechanics/images/L07_01.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/leeyt/Physics/e33aa87cd6f9fee00272fbfce7321f4bd5a55f00/8.01 Classical Mechanics/images/L07_01.png
--------------------------------------------------------------------------------
/8.01 Classical Mechanics/images/L07_02.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/leeyt/Physics/e33aa87cd6f9fee00272fbfce7321f4bd5a55f00/8.01 Classical Mechanics/images/L07_02.png
--------------------------------------------------------------------------------
/8.01 Classical Mechanics/images/L07_03.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/leeyt/Physics/e33aa87cd6f9fee00272fbfce7321f4bd5a55f00/8.01 Classical Mechanics/images/L07_03.png
--------------------------------------------------------------------------------
/8.01 Classical Mechanics/images/L07_04.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/leeyt/Physics/e33aa87cd6f9fee00272fbfce7321f4bd5a55f00/8.01 Classical Mechanics/images/L07_04.png
--------------------------------------------------------------------------------
/8.01 Classical Mechanics/images/L07_05.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/leeyt/Physics/e33aa87cd6f9fee00272fbfce7321f4bd5a55f00/8.01 Classical Mechanics/images/L07_05.png
--------------------------------------------------------------------------------
/8.01 Classical Mechanics/images/L07_06.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/leeyt/Physics/e33aa87cd6f9fee00272fbfce7321f4bd5a55f00/8.01 Classical Mechanics/images/L07_06.png
--------------------------------------------------------------------------------
/8.01 Classical Mechanics/images/L07_07.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/leeyt/Physics/e33aa87cd6f9fee00272fbfce7321f4bd5a55f00/8.01 Classical Mechanics/images/L07_07.png
--------------------------------------------------------------------------------
/8.01 Classical Mechanics/images/L07_08.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/leeyt/Physics/e33aa87cd6f9fee00272fbfce7321f4bd5a55f00/8.01 Classical Mechanics/images/L07_08.png
--------------------------------------------------------------------------------
/8.01 Classical Mechanics/images/L07_09.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/leeyt/Physics/e33aa87cd6f9fee00272fbfce7321f4bd5a55f00/8.01 Classical Mechanics/images/L07_09.png
--------------------------------------------------------------------------------
/8.01 Classical Mechanics/images/L08_01.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/leeyt/Physics/e33aa87cd6f9fee00272fbfce7321f4bd5a55f00/8.01 Classical Mechanics/images/L08_01.png
--------------------------------------------------------------------------------
/8.01 Classical Mechanics/images/L08_02.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/leeyt/Physics/e33aa87cd6f9fee00272fbfce7321f4bd5a55f00/8.01 Classical Mechanics/images/L08_02.png
--------------------------------------------------------------------------------
/8.01 Classical Mechanics/images/L08_03.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/leeyt/Physics/e33aa87cd6f9fee00272fbfce7321f4bd5a55f00/8.01 Classical Mechanics/images/L08_03.png
--------------------------------------------------------------------------------
/8.01 Classical Mechanics/images/L08_04.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/leeyt/Physics/e33aa87cd6f9fee00272fbfce7321f4bd5a55f00/8.01 Classical Mechanics/images/L08_04.png
--------------------------------------------------------------------------------
/8.01 Classical Mechanics/images/L08_05.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/leeyt/Physics/e33aa87cd6f9fee00272fbfce7321f4bd5a55f00/8.01 Classical Mechanics/images/L08_05.png
--------------------------------------------------------------------------------
/8.01 Classical Mechanics/images/L10_01.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/leeyt/Physics/e33aa87cd6f9fee00272fbfce7321f4bd5a55f00/8.01 Classical Mechanics/images/L10_01.png
--------------------------------------------------------------------------------
/8.01 Classical Mechanics/images/L10_02.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/leeyt/Physics/e33aa87cd6f9fee00272fbfce7321f4bd5a55f00/8.01 Classical Mechanics/images/L10_02.png
--------------------------------------------------------------------------------
/8.01 Classical Mechanics/images/L10_03.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/leeyt/Physics/e33aa87cd6f9fee00272fbfce7321f4bd5a55f00/8.01 Classical Mechanics/images/L10_03.png
--------------------------------------------------------------------------------
/8.01 Classical Mechanics/images/L10_04.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/leeyt/Physics/e33aa87cd6f9fee00272fbfce7321f4bd5a55f00/8.01 Classical Mechanics/images/L10_04.png
--------------------------------------------------------------------------------
/8.01 Classical Mechanics/images/L10_05.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/leeyt/Physics/e33aa87cd6f9fee00272fbfce7321f4bd5a55f00/8.01 Classical Mechanics/images/L10_05.png
--------------------------------------------------------------------------------
/8.01 Classical Mechanics/images/L11_01.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/leeyt/Physics/e33aa87cd6f9fee00272fbfce7321f4bd5a55f00/8.01 Classical Mechanics/images/L11_01.png
--------------------------------------------------------------------------------
/8.01 Classical Mechanics/images/L11_02.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/leeyt/Physics/e33aa87cd6f9fee00272fbfce7321f4bd5a55f00/8.01 Classical Mechanics/images/L11_02.png
--------------------------------------------------------------------------------
/8.01 Classical Mechanics/images/L11_03.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/leeyt/Physics/e33aa87cd6f9fee00272fbfce7321f4bd5a55f00/8.01 Classical Mechanics/images/L11_03.png
--------------------------------------------------------------------------------
/8.01 Classical Mechanics/images/L11_04.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/leeyt/Physics/e33aa87cd6f9fee00272fbfce7321f4bd5a55f00/8.01 Classical Mechanics/images/L11_04.png
--------------------------------------------------------------------------------
/8.01 Classical Mechanics/images/L11_05.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/leeyt/Physics/e33aa87cd6f9fee00272fbfce7321f4bd5a55f00/8.01 Classical Mechanics/images/L11_05.png
--------------------------------------------------------------------------------
/8.01 Classical Mechanics/images/L11_06.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/leeyt/Physics/e33aa87cd6f9fee00272fbfce7321f4bd5a55f00/8.01 Classical Mechanics/images/L11_06.png
--------------------------------------------------------------------------------
/8.01 Classical Mechanics/images/L12_01.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/leeyt/Physics/e33aa87cd6f9fee00272fbfce7321f4bd5a55f00/8.01 Classical Mechanics/images/L12_01.png
--------------------------------------------------------------------------------
/8.01 Classical Mechanics/images/L12_02.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/leeyt/Physics/e33aa87cd6f9fee00272fbfce7321f4bd5a55f00/8.01 Classical Mechanics/images/L12_02.png
--------------------------------------------------------------------------------
/8.01 Classical Mechanics/images/L12_03.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/leeyt/Physics/e33aa87cd6f9fee00272fbfce7321f4bd5a55f00/8.01 Classical Mechanics/images/L12_03.png
--------------------------------------------------------------------------------
/8.01 Classical Mechanics/images/L12_04.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/leeyt/Physics/e33aa87cd6f9fee00272fbfce7321f4bd5a55f00/8.01 Classical Mechanics/images/L12_04.png
--------------------------------------------------------------------------------
/8.01 Classical Mechanics/images/L12_05.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/leeyt/Physics/e33aa87cd6f9fee00272fbfce7321f4bd5a55f00/8.01 Classical Mechanics/images/L12_05.png
--------------------------------------------------------------------------------
/8.01 Classical Mechanics/images/L13_01.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/leeyt/Physics/e33aa87cd6f9fee00272fbfce7321f4bd5a55f00/8.01 Classical Mechanics/images/L13_01.png
--------------------------------------------------------------------------------
/8.01 Classical Mechanics/images/L13_02.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/leeyt/Physics/e33aa87cd6f9fee00272fbfce7321f4bd5a55f00/8.01 Classical Mechanics/images/L13_02.png
--------------------------------------------------------------------------------
/8.01 Classical Mechanics/images/L13_03.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/leeyt/Physics/e33aa87cd6f9fee00272fbfce7321f4bd5a55f00/8.01 Classical Mechanics/images/L13_03.png
--------------------------------------------------------------------------------
/8.01 Classical Mechanics/images/L13_04.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/leeyt/Physics/e33aa87cd6f9fee00272fbfce7321f4bd5a55f00/8.01 Classical Mechanics/images/L13_04.png
--------------------------------------------------------------------------------
/8.01 Classical Mechanics/images/L13_05.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/leeyt/Physics/e33aa87cd6f9fee00272fbfce7321f4bd5a55f00/8.01 Classical Mechanics/images/L13_05.png
--------------------------------------------------------------------------------
/8.01 Classical Mechanics/images/L13_06.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/leeyt/Physics/e33aa87cd6f9fee00272fbfce7321f4bd5a55f00/8.01 Classical Mechanics/images/L13_06.png
--------------------------------------------------------------------------------
/8.01 Classical Mechanics/images/L13_07.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/leeyt/Physics/e33aa87cd6f9fee00272fbfce7321f4bd5a55f00/8.01 Classical Mechanics/images/L13_07.png
--------------------------------------------------------------------------------
/8.01 Classical Mechanics/images/L13_08.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/leeyt/Physics/e33aa87cd6f9fee00272fbfce7321f4bd5a55f00/8.01 Classical Mechanics/images/L13_08.png
--------------------------------------------------------------------------------
/8.01 Classical Mechanics/images/L13_09.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/leeyt/Physics/e33aa87cd6f9fee00272fbfce7321f4bd5a55f00/8.01 Classical Mechanics/images/L13_09.png
--------------------------------------------------------------------------------
/8.01 Classical Mechanics/images/L14_01.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/leeyt/Physics/e33aa87cd6f9fee00272fbfce7321f4bd5a55f00/8.01 Classical Mechanics/images/L14_01.png
--------------------------------------------------------------------------------
/8.01 Classical Mechanics/images/L14_02.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/leeyt/Physics/e33aa87cd6f9fee00272fbfce7321f4bd5a55f00/8.01 Classical Mechanics/images/L14_02.png
--------------------------------------------------------------------------------
/8.01 Classical Mechanics/images/L14_03.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/leeyt/Physics/e33aa87cd6f9fee00272fbfce7321f4bd5a55f00/8.01 Classical Mechanics/images/L14_03.png
--------------------------------------------------------------------------------
/8.01 Classical Mechanics/images/L14_04.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/leeyt/Physics/e33aa87cd6f9fee00272fbfce7321f4bd5a55f00/8.01 Classical Mechanics/images/L14_04.png
--------------------------------------------------------------------------------
/8.01 Classical Mechanics/images/L15_01.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/leeyt/Physics/e33aa87cd6f9fee00272fbfce7321f4bd5a55f00/8.01 Classical Mechanics/images/L15_01.png
--------------------------------------------------------------------------------
/8.01 Classical Mechanics/images/L15_02.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/leeyt/Physics/e33aa87cd6f9fee00272fbfce7321f4bd5a55f00/8.01 Classical Mechanics/images/L15_02.png
--------------------------------------------------------------------------------
/8.01 Classical Mechanics/images/L15_03.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/leeyt/Physics/e33aa87cd6f9fee00272fbfce7321f4bd5a55f00/8.01 Classical Mechanics/images/L15_03.png
--------------------------------------------------------------------------------
/8.01 Classical Mechanics/images/L15_04.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/leeyt/Physics/e33aa87cd6f9fee00272fbfce7321f4bd5a55f00/8.01 Classical Mechanics/images/L15_04.png
--------------------------------------------------------------------------------
/8.01 Classical Mechanics/images/L15_05.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/leeyt/Physics/e33aa87cd6f9fee00272fbfce7321f4bd5a55f00/8.01 Classical Mechanics/images/L15_05.png
--------------------------------------------------------------------------------
/8.01 Classical Mechanics/images/L15_06.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/leeyt/Physics/e33aa87cd6f9fee00272fbfce7321f4bd5a55f00/8.01 Classical Mechanics/images/L15_06.png
--------------------------------------------------------------------------------
/8.01 Classical Mechanics/images/L16_01.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/leeyt/Physics/e33aa87cd6f9fee00272fbfce7321f4bd5a55f00/8.01 Classical Mechanics/images/L16_01.png
--------------------------------------------------------------------------------
/8.01 Classical Mechanics/images/L16_02.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/leeyt/Physics/e33aa87cd6f9fee00272fbfce7321f4bd5a55f00/8.01 Classical Mechanics/images/L16_02.png
--------------------------------------------------------------------------------
/8.01 Classical Mechanics/images/L16_03.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/leeyt/Physics/e33aa87cd6f9fee00272fbfce7321f4bd5a55f00/8.01 Classical Mechanics/images/L16_03.png
--------------------------------------------------------------------------------
/8.01 Classical Mechanics/images/L16_04.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/leeyt/Physics/e33aa87cd6f9fee00272fbfce7321f4bd5a55f00/8.01 Classical Mechanics/images/L16_04.png
--------------------------------------------------------------------------------
/8.01 Classical Mechanics/images/L22/01.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/leeyt/Physics/e33aa87cd6f9fee00272fbfce7321f4bd5a55f00/8.01 Classical Mechanics/images/L22/01.png
--------------------------------------------------------------------------------
/8.01 Classical Mechanics/images/L22/02.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/leeyt/Physics/e33aa87cd6f9fee00272fbfce7321f4bd5a55f00/8.01 Classical Mechanics/images/L22/02.png
--------------------------------------------------------------------------------
/8.01 Classical Mechanics/images/L22/03.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/leeyt/Physics/e33aa87cd6f9fee00272fbfce7321f4bd5a55f00/8.01 Classical Mechanics/images/L22/03.png
--------------------------------------------------------------------------------
/8.01 Classical Mechanics/images/L22/04.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/leeyt/Physics/e33aa87cd6f9fee00272fbfce7321f4bd5a55f00/8.01 Classical Mechanics/images/L22/04.png
--------------------------------------------------------------------------------
/8.01 Classical Mechanics/images/L22/05.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/leeyt/Physics/e33aa87cd6f9fee00272fbfce7321f4bd5a55f00/8.01 Classical Mechanics/images/L22/05.png
--------------------------------------------------------------------------------
/8.01 Classical Mechanics/images/L22/06.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/leeyt/Physics/e33aa87cd6f9fee00272fbfce7321f4bd5a55f00/8.01 Classical Mechanics/images/L22/06.png
--------------------------------------------------------------------------------
/8.01 Classical Mechanics/images/L22/07.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/leeyt/Physics/e33aa87cd6f9fee00272fbfce7321f4bd5a55f00/8.01 Classical Mechanics/images/L22/07.png
--------------------------------------------------------------------------------
/8.01 Classical Mechanics/images/L22/08.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/leeyt/Physics/e33aa87cd6f9fee00272fbfce7321f4bd5a55f00/8.01 Classical Mechanics/images/L22/08.png
--------------------------------------------------------------------------------
/8.01 Classical Mechanics/images/L25/01.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/leeyt/Physics/e33aa87cd6f9fee00272fbfce7321f4bd5a55f00/8.01 Classical Mechanics/images/L25/01.png
--------------------------------------------------------------------------------
/8.01 Classical Mechanics/images/L25/02.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/leeyt/Physics/e33aa87cd6f9fee00272fbfce7321f4bd5a55f00/8.01 Classical Mechanics/images/L25/02.png
--------------------------------------------------------------------------------
/8.01 Classical Mechanics/images/L25/03.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/leeyt/Physics/e33aa87cd6f9fee00272fbfce7321f4bd5a55f00/8.01 Classical Mechanics/images/L25/03.png
--------------------------------------------------------------------------------
/8.01 Classical Mechanics/images/L25/04.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/leeyt/Physics/e33aa87cd6f9fee00272fbfce7321f4bd5a55f00/8.01 Classical Mechanics/images/L25/04.png
--------------------------------------------------------------------------------
/8.01 Classical Mechanics/images/L25/05.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/leeyt/Physics/e33aa87cd6f9fee00272fbfce7321f4bd5a55f00/8.01 Classical Mechanics/images/L25/05.png
--------------------------------------------------------------------------------
/8.01 Classical Mechanics/images/L25/06.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/leeyt/Physics/e33aa87cd6f9fee00272fbfce7321f4bd5a55f00/8.01 Classical Mechanics/images/L25/06.png
--------------------------------------------------------------------------------
/8.01 Classical Mechanics/images/L25/07.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/leeyt/Physics/e33aa87cd6f9fee00272fbfce7321f4bd5a55f00/8.01 Classical Mechanics/images/L25/07.png
--------------------------------------------------------------------------------
/8.01 Classical Mechanics/images/L25/08.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/leeyt/Physics/e33aa87cd6f9fee00272fbfce7321f4bd5a55f00/8.01 Classical Mechanics/images/L25/08.png
--------------------------------------------------------------------------------
/8.01 Classical Mechanics/images/L25/09.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/leeyt/Physics/e33aa87cd6f9fee00272fbfce7321f4bd5a55f00/8.01 Classical Mechanics/images/L25/09.png
--------------------------------------------------------------------------------
/8.01 Classical Mechanics/images/L25/10.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/leeyt/Physics/e33aa87cd6f9fee00272fbfce7321f4bd5a55f00/8.01 Classical Mechanics/images/L25/10.png
--------------------------------------------------------------------------------
/8.01 Classical Mechanics/images/L25/11.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/leeyt/Physics/e33aa87cd6f9fee00272fbfce7321f4bd5a55f00/8.01 Classical Mechanics/images/L25/11.png
--------------------------------------------------------------------------------
/8.01 Classical Mechanics/images/L25/12.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/leeyt/Physics/e33aa87cd6f9fee00272fbfce7321f4bd5a55f00/8.01 Classical Mechanics/images/L25/12.png
--------------------------------------------------------------------------------
/8.01 Classical Mechanics/images/L26/01.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/leeyt/Physics/e33aa87cd6f9fee00272fbfce7321f4bd5a55f00/8.01 Classical Mechanics/images/L26/01.png
--------------------------------------------------------------------------------
/8.01 Classical Mechanics/images/L26/02.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/leeyt/Physics/e33aa87cd6f9fee00272fbfce7321f4bd5a55f00/8.01 Classical Mechanics/images/L26/02.png
--------------------------------------------------------------------------------
/8.01 Classical Mechanics/images/L26/03.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/leeyt/Physics/e33aa87cd6f9fee00272fbfce7321f4bd5a55f00/8.01 Classical Mechanics/images/L26/03.png
--------------------------------------------------------------------------------
/8.01 Classical Mechanics/images/L26/04.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/leeyt/Physics/e33aa87cd6f9fee00272fbfce7321f4bd5a55f00/8.01 Classical Mechanics/images/L26/04.png
--------------------------------------------------------------------------------
/8.01 Classical Mechanics/images/L26/05.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/leeyt/Physics/e33aa87cd6f9fee00272fbfce7321f4bd5a55f00/8.01 Classical Mechanics/images/L26/05.png
--------------------------------------------------------------------------------
/8.01 Classical Mechanics/images/L26/06.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/leeyt/Physics/e33aa87cd6f9fee00272fbfce7321f4bd5a55f00/8.01 Classical Mechanics/images/L26/06.png
--------------------------------------------------------------------------------
/8.01 Classical Mechanics/images/L26/07.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/leeyt/Physics/e33aa87cd6f9fee00272fbfce7321f4bd5a55f00/8.01 Classical Mechanics/images/L26/07.png
--------------------------------------------------------------------------------
/8.01 Classical Mechanics/images/L26/08.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/leeyt/Physics/e33aa87cd6f9fee00272fbfce7321f4bd5a55f00/8.01 Classical Mechanics/images/L26/08.png
--------------------------------------------------------------------------------
/8.01 Classical Mechanics/images/L26/09.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/leeyt/Physics/e33aa87cd6f9fee00272fbfce7321f4bd5a55f00/8.01 Classical Mechanics/images/L26/09.png
--------------------------------------------------------------------------------
/8.01 Classical Mechanics/images/L26/10.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/leeyt/Physics/e33aa87cd6f9fee00272fbfce7321f4bd5a55f00/8.01 Classical Mechanics/images/L26/10.png
--------------------------------------------------------------------------------
/8.01 Classical Mechanics/images/L27/06.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/leeyt/Physics/e33aa87cd6f9fee00272fbfce7321f4bd5a55f00/8.01 Classical Mechanics/images/L27/06.png
--------------------------------------------------------------------------------
/8.02 Electricity and Magnetism/03. Electric Flux and Gauss's Law.md:
--------------------------------------------------------------------------------
1 | # Lecture 03: Electric Flux and Gauss's Law
2 |
3 | Walter Lewin, 8.02 Physics II: Electricity and Magnetism, Spring 2002.
4 | (Massachusetts Institute of Technology: MIT OpenCourseWare).
5 | [http://ocw.mit.edu](http://ocw.mit.edu) (accessed 04 08, 2013).
6 | License: Creative Commons Attribution-Noncommercial-Share Alike.
7 |
--------------------------------------------------------------------------------
/8.02 Electricity and Magnetism/04. Electrostatic Potential and Electric Energy.md:
--------------------------------------------------------------------------------
1 | # Lecture 04: Electricstatic Potential and Electric Energy
2 |
3 | Walter Lewin, 8.02 Physics II: Electricity and Magnetism, Spring 2002.
4 | (Massachusetts Institute of Technology: MIT OpenCourseWare).
5 | [http://ocw.mit.edu](http://ocw.mit.edu) (accessed 04 08, 2013).
6 | License: Creative Commons Attribution-Noncommercial-Share Alike.
7 |
--------------------------------------------------------------------------------
/8.02 Electricity and Magnetism/05. Electrostatic Shielding (Faraday Cage).md:
--------------------------------------------------------------------------------
1 | # Lecture 05: Electrostatic Shielding (Faraday's Cage)
2 |
3 | Walter Lewin, 8.02 Physics II: Electricity and Magnetism, Spring 2002.
4 | (Massachusetts Institute of Technology: MIT OpenCourseWare).
5 | [http://ocw.mit.edu](http://ocw.mit.edu) (accessed 04 08, 2013).
6 | License: Creative Commons Attribution-Noncommercial-Share Alike.
--------------------------------------------------------------------------------
/8.02 Electricity and Magnetism/06. High-Voltage Breakdown and Lightning.md:
--------------------------------------------------------------------------------
1 | # Lecture 06: High-Voltage Breakdown and Lightning
2 |
3 | Walter Lewin, 8.02 Physics II: Electricity and Magnetism, Spring 2002.
4 | (Massachusetts Institute of Technology: MIT OpenCourseWare).
5 | [http://ocw.mit.edu](http://ocw.mit.edu) (accessed 04 08, 2013).
6 | License: Creative Commons Attribution-Noncommercial-Share Alike.
--------------------------------------------------------------------------------
/8.02 Electricity and Magnetism/07. Capacitance and Field Energy.md:
--------------------------------------------------------------------------------
1 | # Lecture 07: Capacitance and Field Energy
2 |
3 | Walter Lewin, 8.02 Physics II: Electricity and Magnetism, Spring 2002.
4 | (Massachusetts Institute of Technology: MIT OpenCourseWare).
5 | [http://ocw.mit.edu](http://ocw.mit.edu) (accessed 04 08, 2013).
6 | License: Creative Commons Attribution-Noncommercial-Share Alike.
--------------------------------------------------------------------------------
/8.02 Electricity and Magnetism/08. Polarization and Dielectrics.md:
--------------------------------------------------------------------------------
1 | # Lecture 08: Polarization and Dielectrics
2 |
3 | Walter Lewin, 8.02 Physics II: Electricity and Magnetism, Spring 2002.
4 | (Massachusetts Institute of Technology: MIT OpenCourseWare).
5 | [http://ocw.mit.edu](http://ocw.mit.edu) (accessed 04 08, 2013).
6 | License: Creative Commons Attribution-Noncommercial-Share Alike.
--------------------------------------------------------------------------------
/8.02 Electricity and Magnetism/09. Currents, Resistivity and Ohm's Law.md:
--------------------------------------------------------------------------------
1 | # Lecture 09: Currents, Resistivity, and Ohm's Law
2 |
3 | Walter Lewin, 8.02 Physics II: Electricity and Magnetism, Spring 2002.
4 | (Massachusetts Institute of Technology: MIT OpenCourseWare).
5 | [http://ocw.mit.edu](http://ocw.mit.edu) (accessed 04 08, 2013).
6 | License: Creative Commons Attribution-Noncommercial-Share Alike.
--------------------------------------------------------------------------------
/8.02 Electricity and Magnetism/10. Batteries and EMF.md:
--------------------------------------------------------------------------------
1 | # Lecture 10: Batteries and EMF
2 |
3 | Walter Lewin, 8.02 Physics II: Electricity and Magnetism, Spring 2002.
4 | (Massachusetts Institute of Technology: MIT OpenCourseWare).
5 | [http://ocw.mit.edu](http://ocw.mit.edu) (accessed 04 08, 2013).
6 | License: Creative Commons Attribution-Noncommercial-Share Alike.
--------------------------------------------------------------------------------
/8.02 Electricity and Magnetism/11. Magnetic Field and Lorentz Force.md:
--------------------------------------------------------------------------------
1 | # Lecture 11: Magnetic Field and Lorentz Force
2 |
3 | Walter Lewin, 8.02 Physics II: Electricity and Magnetism, Spring 2002.
4 | (Massachusetts Institute of Technology: MIT OpenCourseWare).
5 | [http://ocw.mit.edu](http://ocw.mit.edu) (accessed 04 08, 2013).
6 | License: Creative Commons Attribution-Noncommercial-Share Alike.
--------------------------------------------------------------------------------
/8.02 Electricity and Magnetism/12. Review Exam 1 (Secret Top!).md:
--------------------------------------------------------------------------------
1 | # Lecture 12: Review Exam 1 (Secret Top!)
2 |
3 | Walter Lewin, 8.02 Physics II: Electricity and Magnetism, Spring 2002.
4 | (Massachusetts Institute of Technology: MIT OpenCourseWare).
5 | [http://ocw.mit.edu](http://ocw.mit.edu) (accessed 04 08, 2013).
6 | License: Creative Commons Attribution-Noncommercial-Share Alike.
--------------------------------------------------------------------------------
/8.02 Electricity and Magnetism/13. Moving Charges in B-fields.md:
--------------------------------------------------------------------------------
1 | # Lecture 13: Moving Charges in B-fields
2 |
3 | Walter Lewin, 8.02 Physics II: Electricity and Magnetism, Spring 2002.
4 | (Massachusetts Institute of Technology: MIT OpenCourseWare).
5 | [http://ocw.mit.edu](http://ocw.mit.edu) (accessed 04 08, 2013).
6 | License: Creative Commons Attribution-Noncommercial-Share Alike.
--------------------------------------------------------------------------------
/8.02 Electricity and Magnetism/14. Biot-Savart Law.md:
--------------------------------------------------------------------------------
1 | # Lecture 14: Biot-Savart Law
2 |
3 | Walter Lewin, 8.02 Physics II: Electricity and Magnetism, Spring 2002.
4 | (Massachusetts Institute of Technology: MIT OpenCourseWare).
5 | [http://ocw.mit.edu](http://ocw.mit.edu) (accessed 04 08, 2013).
6 | License: Creative Commons Attribution-Noncommercial-Share Alike.
--------------------------------------------------------------------------------
/8.02 Electricity and Magnetism/15. Ampere's Law.md:
--------------------------------------------------------------------------------
1 | # Lecture 15: Ampere's Law
2 |
3 | Walter Lewin, 8.02 Physics II: Electricity and Magnetism, Spring 2002.
4 | (Massachusetts Institute of Technology: MIT OpenCourseWare).
5 | [http://ocw.mit.edu](http://ocw.mit.edu) (accessed 04 08, 2013).
6 | License: Creative Commons Attribution-Noncommercial-Share Alike.
--------------------------------------------------------------------------------
/8.02 Electricity and Magnetism/16. Electromagnetic Induction.md:
--------------------------------------------------------------------------------
1 | # Lecture 16: Electromagnetic Induction
2 |
3 | Walter Lewin, 8.02 Physics II: Electricity and Magnetism, Spring 2002.
4 | (Massachusetts Institute of Technology: MIT OpenCourseWare).
5 | [http://ocw.mit.edu](http://ocw.mit.edu) (accessed 04 08, 2013).
6 | License: Creative Commons Attribution-Noncommercial-Share Alike.
--------------------------------------------------------------------------------
/8.02 Electricity and Magnetism/17. Motional EMF and Dynamos.md:
--------------------------------------------------------------------------------
1 | # Lecture 17: Motional EMF and Dynamos
2 |
3 | Walter Lewin, 8.02 Physics II: Electricity and Magnetism, Spring 2002.
4 | (Massachusetts Institute of Technology: MIT OpenCourseWare).
5 | [http://ocw.mit.edu](http://ocw.mit.edu) (accessed 04 08, 2013).
6 | License: Creative Commons Attribution-Noncommercial-Share Alike.
--------------------------------------------------------------------------------
/8.02 Electricity and Magnetism/18. Displacement Current and Synchronous Motors.md:
--------------------------------------------------------------------------------
1 | # Lecture 18: Displacement Current and Synchronous Motors
2 |
3 | Walter Lewin, 8.02 Physics II: Electricity and Magnetism, Spring 2002.
4 | (Massachusetts Institute of Technology: MIT OpenCourseWare).
5 | [http://ocw.mit.edu](http://ocw.mit.edu) (accessed 04 08, 2013).
6 | License: Creative Commons Attribution-Noncommercial-Share Alike.
--------------------------------------------------------------------------------
/8.02 Electricity and Magnetism/19. How do magicians levitate women.md:
--------------------------------------------------------------------------------
1 | # Lecture 19: How do magicians levitate women?
2 |
3 | Walter Lewin, 8.02 Physics II: Electricity and Magnetism, Spring 2002.
4 | (Massachusetts Institute of Technology: MIT OpenCourseWare).
5 | [http://ocw.mit.edu](http://ocw.mit.edu) (accessed 04 08, 2013).
6 | License: Creative Commons Attribution-Noncommercial-Share Alike.
--------------------------------------------------------------------------------
/8.02 Electricity and Magnetism/20. Inductance and RL Circuit.md:
--------------------------------------------------------------------------------
1 | # Lecture 20: Inductance and RL Circuit
2 |
3 | Walter Lewin, 8.02 Physics II: Electricity and Magnetism, Spring 2002.
4 | (Massachusetts Institute of Technology: MIT OpenCourseWare).
5 | [http://ocw.mit.edu](http://ocw.mit.edu) (accessed 04 08, 2013).
6 | License: Creative Commons Attribution-Noncommercial-Share Alike.
--------------------------------------------------------------------------------
/8.02 Electricity and Magnetism/21. Magnetic Materials.md:
--------------------------------------------------------------------------------
1 | # Lecture 21: Magnetic Materials
2 |
3 | Walter Lewin, 8.02 Physics II: Electricity and Magnetism, Spring 2002.
4 | (Massachusetts Institute of Technology: MIT OpenCourseWare).
5 | [http://ocw.mit.edu](http://ocw.mit.edu) (accessed 04 08, 2013).
6 | License: Creative Commons Attribution-Noncommercial-Share Alike.
--------------------------------------------------------------------------------
/8.02 Electricity and Magnetism/22. Hysteresis and Electromagnets.md:
--------------------------------------------------------------------------------
1 | # Lecture 22: Hysteresis and Electromagnets
2 |
3 | Walter Lewin, 8.02 Physics II: Electricity and Magnetism, Spring 2002.
4 | (Massachusetts Institute of Technology: MIT OpenCourseWare).
5 | [http://ocw.mit.edu](http://ocw.mit.edu) (accessed 04 08, 2013).
6 | License: Creative Commons Attribution-Noncommercial-Share Alike.
--------------------------------------------------------------------------------
/8.02 Electricity and Magnetism/23. Review for Exam 2.md:
--------------------------------------------------------------------------------
1 | # Lecture 23: Review for Exam 2
2 |
3 | Walter Lewin, 8.02 Physics II: Electricity and Magnetism, Spring 2002.
4 | (Massachusetts Institute of Technology: MIT OpenCourseWare).
5 | [http://ocw.mit.edu](http://ocw.mit.edu) (accessed 04 08, 2013).
6 | License: Creative Commons Attribution-Noncommercial-Share Alike.
--------------------------------------------------------------------------------
/8.02 Electricity and Magnetism/24. Transformers, Car Coils and RC Circuits.md:
--------------------------------------------------------------------------------
1 | # Lecture 24: Transformers, Car Coils, and RC Circuits
2 |
3 | Walter Lewin, 8.02 Physics II: Electricity and Magnetism, Spring 2002.
4 | (Massachusetts Institute of Technology: MIT OpenCourseWare).
5 | [http://ocw.mit.edu](http://ocw.mit.edu) (accessed 04 08, 2013).
6 | License: Creative Commons Attribution-Noncommercial-Share Alike.
--------------------------------------------------------------------------------
/8.02 Electricity and Magnetism/25. Driven LRC Circuits and Resonance.md:
--------------------------------------------------------------------------------
1 | # Lecture 25: Driven LRC Circuits and Resonance
2 |
3 | Walter Lewin, 8.02 Physics II: Electricity and Magnetism, Spring 2002.
4 | (Massachusetts Institute of Technology: MIT OpenCourseWare).
5 | [http://ocw.mit.edu](http://ocw.mit.edu) (accessed 04 08, 2013).
6 | License: Creative Commons Attribution-Noncommercial-Share Alike.
--------------------------------------------------------------------------------
/8.02 Electricity and Magnetism/26. Traveling Waves and Standing Waves.md:
--------------------------------------------------------------------------------
1 | # Lecture 26: Traveling Waves and Standing Waves
2 |
3 | Walter Lewin, 8.02 Physics II: Electricity and Magnetism, Spring 2002.
4 | (Massachusetts Institute of Technology: MIT OpenCourseWare).
5 | [http://ocw.mit.edu](http://ocw.mit.edu) (accessed 04 08, 2013).
6 | License: Creative Commons Attribution-Noncommercial-Share Alike.
--------------------------------------------------------------------------------
/8.02 Electricity and Magnetism/27. Resonance and Destructive Resonance.md:
--------------------------------------------------------------------------------
1 | # Lecture 27: Resonance and Destructive Resonance
2 |
3 | Walter Lewin, 8.02 Physics II: Electricity and Magnetism, Spring 2002.
4 | (Massachusetts Institute of Technology: MIT OpenCourseWare).
5 | [http://ocw.mit.edu](http://ocw.mit.edu) (accessed 04 08, 2013).
6 | License: Creative Commons Attribution-Noncommercial-Share Alike.
--------------------------------------------------------------------------------
/8.02 Electricity and Magnetism/28. Index of Refraction and Poynting Vector.md:
--------------------------------------------------------------------------------
1 | # Lecture 28: Index of Refraction and Poynting Vector
2 |
3 | Walter Lewin, 8.02 Physics II: Electricity and Magnetism, Spring 2002.
4 | (Massachusetts Institute of Technology: MIT OpenCourseWare).
5 | [http://ocw.mit.edu](http://ocw.mit.edu) (accessed 04 08, 2013).
6 | License: Creative Commons Attribution-Noncommercial-Share Alike.
--------------------------------------------------------------------------------
/8.02 Electricity and Magnetism/29. Snell's Law, Refraction and Total Reflection.md:
--------------------------------------------------------------------------------
1 | # Lecture 29: Snell's Law, Refraction and Total Reflection
2 |
3 | Walter Lewin, 8.02 Physics II: Electricity and Magnetism, Spring 2002.
4 | (Massachusetts Institute of Technology: MIT OpenCourseWare).
5 | [http://ocw.mit.edu](http://ocw.mit.edu) (accessed 04 08, 2013).
6 | License: Creative Commons Attribution-Noncommercial-Share Alike.
--------------------------------------------------------------------------------
/8.02 Electricity and Magnetism/30. Polarizers and Malus's Law.md:
--------------------------------------------------------------------------------
1 | # Lecture 30: Polarizers and Malus's Law
2 |
3 | Walter Lewin, 8.02 Physics II: Electricity and Magnetism, Spring 2002.
4 | (Massachusetts Institute of Technology: MIT OpenCourseWare).
5 | [http://ocw.mit.edu](http://ocw.mit.edu) (accessed 04 08, 2013).
6 | License: Creative Commons Attribution-Noncommercial-Share Alike.
--------------------------------------------------------------------------------
/8.02 Electricity and Magnetism/31. Rainbows.md:
--------------------------------------------------------------------------------
1 | # Lecture 31: Rainbows
2 |
3 | Walter Lewin, 8.02 Physics II: Electricity and Magnetism, Spring 2002.
4 | (Massachusetts Institute of Technology: MIT OpenCourseWare).
5 | [http://ocw.mit.edu](http://ocw.mit.edu) (accessed 04 08, 2013).
6 | License: Creative Commons Attribution-Noncommercial-Share Alike.
--------------------------------------------------------------------------------
/8.02 Electricity and Magnetism/32. Review for Exam 3.md:
--------------------------------------------------------------------------------
1 | # Lecture 32: Review for Exam 3
2 |
3 | Walter Lewin, 8.02 Physics II: Electricity and Magnetism, Spring 2002.
4 | (Massachusetts Institute of Technology: MIT OpenCourseWare).
5 | [http://ocw.mit.edu](http://ocw.mit.edu) (accessed 04 08, 2013).
6 | License: Creative Commons Attribution-Noncommercial-Share Alike.
--------------------------------------------------------------------------------
/8.02 Electricity and Magnetism/33. Double-Slit Interference and Interferometers.md:
--------------------------------------------------------------------------------
1 | # Lecture 33: Double-Slit Interference and Interferometers
2 |
3 | Walter Lewin, 8.02 Physics II: Electricity and Magnetism, Spring 2002.
4 | (Massachusetts Institute of Technology: MIT OpenCourseWare).
5 | [http://ocw.mit.edu](http://ocw.mit.edu) (accessed 04 08, 2013).
6 | License: Creative Commons Attribution-Noncommercial-Share Alike.
--------------------------------------------------------------------------------
/8.02 Electricity and Magnetism/34. Gratings and Resolving Power.md:
--------------------------------------------------------------------------------
1 | # Lecture 34: Gratings and Resolving Power
2 |
3 | Walter Lewin, 8.02 Physics II: Electricity and Magnetism, Spring 2002.
4 | (Massachusetts Institute of Technology: MIT OpenCourseWare).
5 | [http://ocw.mit.edu](http://ocw.mit.edu) (accessed 04 08, 2013).
6 | License: Creative Commons Attribution-Noncommercial-Share Alike.
--------------------------------------------------------------------------------
/8.02 Electricity and Magnetism/35. Dopper Effect and the Big Bang.md:
--------------------------------------------------------------------------------
1 | # Lecture 34: Dopper Effect and the Big Bang
2 |
3 | Walter Lewin, 8.02 Physics II: Electricity and Magnetism, Spring 2002.
4 | (Massachusetts Institute of Technology: MIT OpenCourseWare).
5 | [http://ocw.mit.edu](http://ocw.mit.edu) (accessed 04 08, 2013).
6 | License: Creative Commons Attribution-Noncommercial-Share Alike.
--------------------------------------------------------------------------------
/8.02 Electricity and Magnetism/images/L01_01.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/leeyt/Physics/e33aa87cd6f9fee00272fbfce7321f4bd5a55f00/8.02 Electricity and Magnetism/images/L01_01.png
--------------------------------------------------------------------------------
/8.02 Electricity and Magnetism/images/L01_02.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/leeyt/Physics/e33aa87cd6f9fee00272fbfce7321f4bd5a55f00/8.02 Electricity and Magnetism/images/L01_02.png
--------------------------------------------------------------------------------
/8.02 Electricity and Magnetism/images/L01_03.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/leeyt/Physics/e33aa87cd6f9fee00272fbfce7321f4bd5a55f00/8.02 Electricity and Magnetism/images/L01_03.png
--------------------------------------------------------------------------------
/8.02 Electricity and Magnetism/images/L01_04.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/leeyt/Physics/e33aa87cd6f9fee00272fbfce7321f4bd5a55f00/8.02 Electricity and Magnetism/images/L01_04.png
--------------------------------------------------------------------------------
/8.02 Electricity and Magnetism/images/L01_05.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/leeyt/Physics/e33aa87cd6f9fee00272fbfce7321f4bd5a55f00/8.02 Electricity and Magnetism/images/L01_05.png
--------------------------------------------------------------------------------
/8.02 Electricity and Magnetism/images/L01_06.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/leeyt/Physics/e33aa87cd6f9fee00272fbfce7321f4bd5a55f00/8.02 Electricity and Magnetism/images/L01_06.png
--------------------------------------------------------------------------------
/8.02 Electricity and Magnetism/images/L01_07.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/leeyt/Physics/e33aa87cd6f9fee00272fbfce7321f4bd5a55f00/8.02 Electricity and Magnetism/images/L01_07.png
--------------------------------------------------------------------------------
/8.02 Electricity and Magnetism/images/L01_08.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/leeyt/Physics/e33aa87cd6f9fee00272fbfce7321f4bd5a55f00/8.02 Electricity and Magnetism/images/L01_08.png
--------------------------------------------------------------------------------
/8.02 Electricity and Magnetism/images/L01_09.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/leeyt/Physics/e33aa87cd6f9fee00272fbfce7321f4bd5a55f00/8.02 Electricity and Magnetism/images/L01_09.png
--------------------------------------------------------------------------------
/8.03 Waves and Vibrations/01. Periodic Oscillations, Physical Pendulum.md:
--------------------------------------------------------------------------------
1 | # Lecture 01: Periodic Oscillations, Physical Pendulum
2 |
3 | Walter Lewin, 8.03 Physics III: Waves and Oscillations, Fall 2004.
4 | (Massachusetts Institute of Technology: MIT OpenCourseWare).
5 | [http://ocw.mit.edu](http://ocw.mit.edu) (accessed 04 08, 2013).
6 | License: Creative Commons Attribution-Noncommercial-Share Alike.
--------------------------------------------------------------------------------
/8.03 Waves and Vibrations/02. Beats, Damped Free Oscillations, Quality Q.md:
--------------------------------------------------------------------------------
1 | # Lecture 02: Beats, Damped Free Oscillations, Quality Q
2 |
3 | Walter Lewin, 8.03 Physics III: Waves and Oscillations, Fall 2004.
4 | (Massachusetts Institute of Technology: MIT OpenCourseWare).
5 | [http://ocw.mit.edu](http://ocw.mit.edu) (accessed 04 08, 2013).
6 | License: Creative Commons Attribution-Noncommercial-Share Alike.
--------------------------------------------------------------------------------
/8.03 Waves and Vibrations/03. Forced Oscillations with Damping, Destructive Resonance.md:
--------------------------------------------------------------------------------
1 | # Lecture 03: Forced Oscillations with Damping, Destructive Resonance
2 |
3 | Walter Lewin, 8.03 Physics III: Waves and Oscillations, Fall 2004.
4 | (Massachusetts Institute of Technology: MIT OpenCourseWare).
5 | [http://ocw.mit.edu](http://ocw.mit.edu) (accessed 04 08, 2013).
6 | License: Creative Commons Attribution-Noncommercial-Share Alike.
--------------------------------------------------------------------------------
/8.03 Waves and Vibrations/04. Forced Oscillations, Power at Resonance, Transient Phenomena.md:
--------------------------------------------------------------------------------
1 | # Lecture 04: Forced Oscillations, Power at Resonance, Transient Phenomenon
2 |
3 | Walter Lewin, 8.03 Physics III: Waves and Oscillations, Fall 2004.
4 | (Massachusetts Institute of Technology: MIT OpenCourseWare).
5 | [http://ocw.mit.edu](http://ocw.mit.edu) (accessed 04 08, 2013).
6 | License: Creative Commons Attribution-Noncommercial-Share Alike.
--------------------------------------------------------------------------------
/8.03 Waves and Vibrations/05. Coupled Oscillators.md:
--------------------------------------------------------------------------------
1 | # Lecture 05: Coupled Oscillators
2 |
3 | Walter Lewin, 8.03 Physics III: Waves and Oscillations, Fall 2004.
4 | (Massachusetts Institute of Technology: MIT OpenCourseWare).
5 | [http://ocw.mit.edu](http://ocw.mit.edu) (accessed 04 08, 2013).
6 | License: Creative Commons Attribution-Noncommercial-Share Alike.
--------------------------------------------------------------------------------
/8.03 Waves and Vibrations/06. Driven Coupled Oscillators and Cramer's Rule.md:
--------------------------------------------------------------------------------
1 | # Lecture 06: Driven Coupled Oscillators and Cramer's Rule
2 |
3 | Walter Lewin, 8.03 Physics III: Waves and Oscillations, Fall 2004.
4 | (Massachusetts Institute of Technology: MIT OpenCourseWare).
5 | [http://ocw.mit.edu](http://ocw.mit.edu) (accessed 04 08, 2013).
6 | License: Creative Commons Attribution-Noncommercial-Share Alike.
--------------------------------------------------------------------------------
/8.03 Waves and Vibrations/07. Coupled Oscillators, Transverse Traveling Pulses and Waves.md:
--------------------------------------------------------------------------------
1 | # Lecture 07: Coupled Oscillators, Transverse Traveling Pulses and Waves
2 |
3 | Walter Lewin, 8.03 Physics III: Waves and Oscillations, Fall 2004.
4 | (Massachusetts Institute of Technology: MIT OpenCourseWare).
5 | [http://ocw.mit.edu](http://ocw.mit.edu) (accessed 04 08, 2013).
6 | License: Creative Commons Attribution-Noncommercial-Share Alike.
--------------------------------------------------------------------------------
/8.03 Waves and Vibrations/08. Traveling Waves, Sound Waves and Energy in Waves.md:
--------------------------------------------------------------------------------
1 | # Lecture 08: Traveling Waves, Sound Waves and Energy in Waves
2 |
3 | Walter Lewin, 8.03 Physics III: Waves and Oscillations, Fall 2004.
4 | (Massachusetts Institute of Technology: MIT OpenCourseWare).
5 | [http://ocw.mit.edu](http://ocw.mit.edu) (accessed 04 08, 2013).
6 | License: Creative Commons Attribution-Noncommercial-Share Alike.
--------------------------------------------------------------------------------
/8.03 Waves and Vibrations/09. Musical Instruments, Sound Cavities, Normal Modes.md:
--------------------------------------------------------------------------------
1 | # Lecture 09: Musical Instruments, Sound Cavities, Normal Modes
2 |
3 | Walter Lewin, 8.03 Physics III: Waves and Oscillations, Fall 2004.
4 | (Massachusetts Institute of Technology: MIT OpenCourseWare).
5 | [http://ocw.mit.edu](http://ocw.mit.edu) (accessed 04 08, 2013).
6 | License: Creative Commons Attribution-Noncommercial-Share Alike.
--------------------------------------------------------------------------------
/8.03 Waves and Vibrations/10. Exam 1 Review.md:
--------------------------------------------------------------------------------
1 | # Lecture 10: Exam 1 Review
2 |
3 | Walter Lewin, 8.03 Physics III: Waves and Oscillations, Fall 2004.
4 | (Massachusetts Institute of Technology: MIT OpenCourseWare).
5 | [http://ocw.mit.edu](http://ocw.mit.edu) (accessed 04 08, 2013).
6 | License: Creative Commons Attribution-Noncommercial-Share Alike.
--------------------------------------------------------------------------------
/8.03 Waves and Vibrations/11. Fourier Analysis, Time Evolution of Pulses on Strings.md:
--------------------------------------------------------------------------------
1 | # Lecture 11: Fourier Analysis, Time Evolution of Pulses on Strings
2 |
3 | Walter Lewin, 8.03 Physics III: Waves and Oscillations, Fall 2004.
4 | (Massachusetts Institute of Technology: MIT OpenCourseWare).
5 | [http://ocw.mit.edu](http://ocw.mit.edu) (accessed 04 08, 2013).
6 | License: Creative Commons Attribution-Noncommercial-Share Alike.
--------------------------------------------------------------------------------
/8.03 Waves and Vibrations/12. Dispersion, Phase Velocity, Group Velocity.md:
--------------------------------------------------------------------------------
1 | # Lecture 12: Dispersion, Phase Velocity, Group Velocity
2 |
3 | Walter Lewin, 8.03 Physics III: Waves and Oscillations, Fall 2004.
4 | (Massachusetts Institute of Technology: MIT OpenCourseWare).
5 | [http://ocw.mit.edu](http://ocw.mit.edu) (accessed 04 08, 2013).
6 | License: Creative Commons Attribution-Noncommercial-Share Alike.
--------------------------------------------------------------------------------
/8.03 Waves and Vibrations/13. Electromagnetic Waves, Polarization.md:
--------------------------------------------------------------------------------
1 | # Lecture 13: Electromagnetic Waves, Polarization
2 |
3 | Walter Lewin, 8.03 Physics III: Waves and Oscillations, Fall 2004.
4 | (Massachusetts Institute of Technology: MIT OpenCourseWare).
5 | [http://ocw.mit.edu](http://ocw.mit.edu) (accessed 04 08, 2013).
6 | License: Creative Commons Attribution-Noncommercial-Share Alike.
--------------------------------------------------------------------------------
/8.03 Waves and Vibrations/14. Acceleration Changes, Poynting Vector, and Power.md:
--------------------------------------------------------------------------------
1 | # Lecture 14: Acceleration Changes, Poynting Vector, and Power
2 |
3 | Walter Lewin, 8.03 Physics III: Waves and Oscillations, Fall 2004.
4 | (Massachusetts Institute of Technology: MIT OpenCourseWare).
5 | [http://ocw.mit.edu](http://ocw.mit.edu) (accessed 04 08, 2013).
6 | License: Creative Commons Attribution-Noncommercial-Share Alike.
--------------------------------------------------------------------------------
/8.03 Waves and Vibrations/15. Doppler Effect, EM Radiation and Expanding Universe.md:
--------------------------------------------------------------------------------
1 | # Lecture 15: Doppler Effect, EM Radiation and Expanding Universe
2 |
3 | Walter Lewin, 8.03 Physics III: Waves and Oscillations, Fall 2004.
4 | (Massachusetts Institute of Technology: MIT OpenCourseWare).
5 | [http://ocw.mit.edu](http://ocw.mit.edu) (accessed 04 08, 2013).
6 | License: Creative Commons Attribution-Noncommercial-Share Alike.
--------------------------------------------------------------------------------
/8.03 Waves and Vibrations/16. Interactions of Electromagnetic Waves with Perfect Conductors.md:
--------------------------------------------------------------------------------
1 | # Lecture 16: Interactions of Electromagnetic Waves with Perfect Conductors
2 |
3 | Walter Lewin, 8.03 Physics III: Waves and Oscillations, Fall 2004.
4 | (Massachusetts Institute of Technology: MIT OpenCourseWare).
5 | [http://ocw.mit.edu](http://ocw.mit.edu) (accessed 04 08, 2013).
6 | License: Creative Commons Attribution-Noncommercial-Share Alike.
--------------------------------------------------------------------------------
/8.03 Waves and Vibrations/17. Wave Guides, Resonance Cavities of EM-radiation and Sound.md:
--------------------------------------------------------------------------------
1 | # Lecture 17: Wave Guides, Resonance Cavities of EM-radiation and Sound
2 |
3 | Walter Lewin, 8.03 Physics III: Waves and Oscillations, Fall 2004.
4 | (Massachusetts Institute of Technology: MIT OpenCourseWare).
5 | [http://ocw.mit.edu](http://ocw.mit.edu) (accessed 04 08, 2013).
6 | License: Creative Commons Attribution-Noncommercial-Share Alike.
--------------------------------------------------------------------------------
/8.03 Waves and Vibrations/18. Boundary Conditions for Dielectrics.md:
--------------------------------------------------------------------------------
1 | # Lecture 18: Boundary Conditions for Dielectrics
2 |
3 | Walter Lewin, 8.03 Physics III: Waves and Oscillations, Fall 2004.
4 | (Massachusetts Institute of Technology: MIT OpenCourseWare).
5 | [http://ocw.mit.edu](http://ocw.mit.edu) (accessed 04 08, 2013).
6 | License: Creative Commons Attribution-Noncommercial-Share Alike.
--------------------------------------------------------------------------------
/8.03 Waves and Vibrations/19. Exam 2 Review.md:
--------------------------------------------------------------------------------
1 | # Lecture 19: Exam 2 Review
2 |
3 | Walter Lewin, 8.03 Physics III: Waves and Oscillations, Fall 2004.
4 | (Massachusetts Institute of Technology: MIT OpenCourseWare).
5 | [http://ocw.mit.edu](http://ocw.mit.edu) (accessed 04 08, 2013).
6 | License: Creative Commons Attribution-Noncommercial-Share Alike.
--------------------------------------------------------------------------------
/8.03 Waves and Vibrations/20. Huygens' Principle, Interference, Thin films, Soap, Oil, Light.md:
--------------------------------------------------------------------------------
1 | # Lecture 20: Huygen's Principle, Interference, Thin films, Soap, Oil, Light
2 |
3 | Walter Lewin, 8.03 Physics III: Waves and Oscillations, Fall 2004.
4 | (Massachusetts Institute of Technology: MIT OpenCourseWare).
5 | [http://ocw.mit.edu](http://ocw.mit.edu) (accessed 04 08, 2013).
6 | License: Creative Commons Attribution-Noncommercial-Share Alike.
--------------------------------------------------------------------------------
/8.03 Waves and Vibrations/21. Diffraction, Gratings, Pin Holes, Angular Resolution.md:
--------------------------------------------------------------------------------
1 | # Lecture 21: Diffraction, Gratings, Pin Holes, Angular Resolution
2 |
3 | Walter Lewin, 8.03 Physics III: Waves and Oscillations, Fall 2004.
4 | (Massachusetts Institute of Technology: MIT OpenCourseWare).
5 | [http://ocw.mit.edu](http://ocw.mit.edu) (accessed 04 08, 2013).
6 | License: Creative Commons Attribution-Noncommercial-Share Alike.
--------------------------------------------------------------------------------
/8.03 Waves and Vibrations/22. Rainbows, Haloes, Coronae, Glories.md:
--------------------------------------------------------------------------------
1 | # Lecture 22: Rainbows, Haloes, Coronae, Glories
2 |
3 | Walter Lewin, 8.03 Physics III: Waves and Oscillations, Fall 2004.
4 | (Massachusetts Institute of Technology: MIT OpenCourseWare).
5 | [http://ocw.mit.edu](http://ocw.mit.edu) (accessed 04 08, 2013).
6 | License: Creative Commons Attribution-Noncommercial-Share Alike.
--------------------------------------------------------------------------------
/8.03 Waves and Vibrations/23, Farewell Lecture.md:
--------------------------------------------------------------------------------
1 | # Lecture 23: Farewell Lecture
2 |
3 | Walter Lewin, 8.03 Physics III: Waves and Oscillations, Fall 2004.
4 | (Massachusetts Institute of Technology: MIT OpenCourseWare).
5 | [http://ocw.mit.edu](http://ocw.mit.edu) (accessed 04 08, 2013).
6 | License: Creative Commons Attribution-Noncommercial-Share Alike.
7 |
--------------------------------------------------------------------------------
/README.md:
--------------------------------------------------------------------------------
1 | Physics is a very fascinating subject.
2 |
3 | Prof. Walter Lewin, the renowned professor emeritus at MIT, will make you love physics, and see the world in a different way.
4 |
5 | As I watch his lecture videos on iTunes U, I would like to take down some notes so I won't forget easily and it won't be a waste of time.
6 |
7 | Please visit [MIT OpenCourseWare][1] to search for these three courses complete with homeworks, exams, etc.
8 |
9 | # Physics I: Classical Mechanics, Fall 1999
10 |
11 | Walter Lewin, 8.01 Physics I: Classical Mechanics, Fall 1999.
12 | (Massachusetts Institute of Technology: MIT OpenCourseWare).
13 | [http://ocw.mit.edu][1] (accessed 04 08, 2013).
14 | License: Creative Commons Attribution-Noncommercial-Share Alike.
15 |
16 | # Physics II: Electricity and Magnetism, Spring 2002
17 |
18 | Walter Lewin, 8.02 Physics II: Electricity and Magnetism, Spring 2002.
19 | (Massachusetts Institute of Technology: MIT OpenCourseWare).
20 | [http://ocw.mit.edu][1] (accessed 04 08, 2013).
21 | License: Creative Commons Attribution-Noncommercial-Share Alike.
22 |
23 | # Physics III: Vibrations and Waves, Fall 2004
24 |
25 | Walter Lewin, 8.03 Physics III: Vibrations and Waves, Fall 2004.
26 | (Massachusetts Institute of Technology: MIT OpenCourseWare).
27 | [http://ocw.mit.edu][1] (accessed 04 08, 2013).
28 | License: Creative Commons Attribution-Noncommercial-Share Alike.
29 |
30 | [1]: http://ocw.mit.edu "MIT OpenCourseWare"
31 | [2]: http://www.apple.com/education/itunes-u/ "iTunes U"
--------------------------------------------------------------------------------