2 |
3 |
30 | 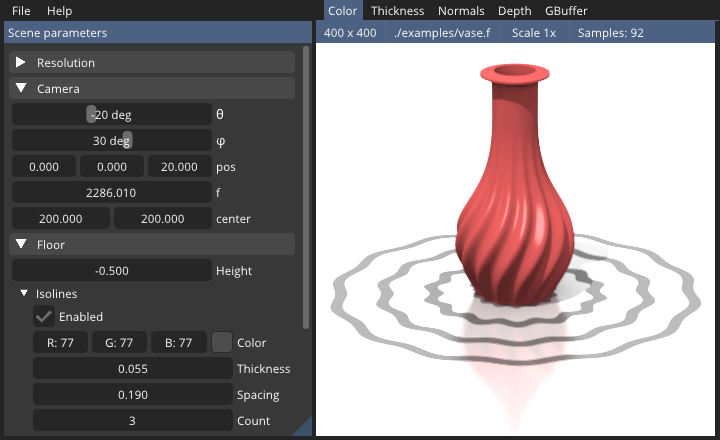 31 |
31 |
34 | 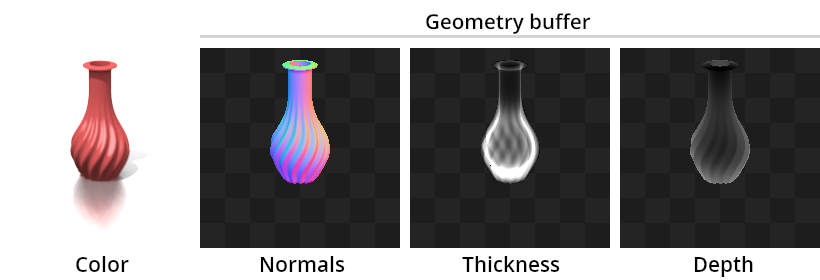 35 |
35 |
.
93 | // Unless otherwise noted, (if the object has an intrinsic "up"
94 | // side or direction) the y axis is "up" and the object is
95 | // centered at the origin.
96 | //
97 | ////////////////////////////////////////////////////////////////
98 |
99 | float fSphere(vec3 p, float r) {
100 | return length(p) - r;
101 | }
102 |
103 | // Plane with normal n (n is normalized) at some distance from the origin
104 | float fPlane(vec3 p, vec3 n, float distanceFromOrigin) {
105 | return dot(p, n) + distanceFromOrigin;
106 | }
107 |
108 | // Cheap Box: distance to corners is overestimated
109 | float fBoxCheap(vec3 p, vec3 b) { //cheap box
110 | return vmax(abs(p) - b);
111 | }
112 |
113 | // Box: correct distance to corners
114 | float fBox(vec3 p, vec3 b) {
115 | vec3 d = abs(p) - b;
116 | return length(max(d, vec3(0))) + vmax(min(d, vec3(0)));
117 | }
118 |
119 | // Same as above, but in two dimensions (an endless box)
120 | float fBox2Cheap(vec2 p, vec2 b) {
121 | return vmax(abs(p)-b);
122 | }
123 |
124 | float fBox2(vec2 p, vec2 b) {
125 | vec2 d = abs(p) - b;
126 | return length(max(d, vec2(0))) + vmax(min(d, vec2(0)));
127 | }
128 |
129 |
130 | // Endless "corner"
131 | float fCorner (vec2 p) {
132 | return length(max(p, vec2(0))) + vmax(min(p, vec2(0)));
133 | }
134 |
135 | // Blobby ball object. You've probably seen it somewhere. This is not a correct distance bound, beware.
136 | float fBlob(vec3 p) {
137 | p = abs(p);
138 | if (p.x < max(p.y, p.z)) p = p.yzx;
139 | if (p.x < max(p.y, p.z)) p = p.yzx;
140 | float b = max(max(max(
141 | dot(p, normalize(vec3(1, 1, 1))),
142 | dot(p.xz, normalize(vec2(PHI+1, 1)))),
143 | dot(p.yx, normalize(vec2(1, PHI)))),
144 | dot(p.xz, normalize(vec2(1, PHI))));
145 | float l = length(p);
146 | return l - 1.5 - 0.2 * (1.5 / 2)* cos(min(sqrt(1.01 - b / l)*(PI / 0.25), PI));
147 | }
148 |
149 | // Cylinder standing upright on the xz plane
150 | float fCylinder(vec3 p, float r, float height) {
151 | vec2 d = abs(vec2(length(p.xz),p.y)) - vec2(r, height);
152 | return min(max(d.x,d.y),0.0) + length(max(d,0.0));
153 | // return d;
154 | }
155 |
156 | // Capsule: A Cylinder with round caps on both sides
157 | float fCapsule(vec3 p, float r, float c) {
158 | return mix(length(p.xz) - r, length(vec3(p.x, abs(p.y) - c, p.z)) - r, step(c, abs(p.y)));
159 | }
160 |
161 | // Distance to line segment between and , used for fCapsule() version 2below
162 | float fLineSegment(vec3 p, vec3 a, vec3 b) {
163 | vec3 ab = b - a;
164 | float t = saturate(dot(p - a, ab) / dot(ab, ab));
165 | return length((ab*t + a) - p);
166 | }
167 |
168 | // Capsule version 2: between two end points and with radius r
169 | float fCapsule(vec3 p, vec3 a, vec3 b, float r) {
170 | return fLineSegment(p, a, b) - r;
171 | }
172 |
173 | // Torus in the XZ-plane
174 | float fTorus(vec3 p, float smallRadius, float largeRadius) {
175 | return length(vec2(length(p.xz) - largeRadius, p.y)) - smallRadius;
176 | }
177 |
178 | // A circle line. Can also be used to make a torus by subtracting the smaller radius of the torus.
179 | float fCircle(vec3 p, float r) {
180 | float l = length(p.xz) - r;
181 | return length(vec2(p.y, l));
182 | }
183 |
184 | // A circular disc with no thickness (i.e. a cylinder with no height).
185 | // Subtract some value to make a flat disc with rounded edge.
186 | float fDisc(vec3 p, float r) {
187 | float l = length(p.xz) - r;
188 | return l < 0 ? abs(p.y) : length(vec2(p.y, l));
189 | }
190 |
191 | // Hexagonal prism, circumcircle variant
192 | float fHexagonCircumcircle(vec3 p, vec2 h) {
193 | vec3 q = abs(p);
194 | return max(q.y - h.y, max(q.x*sqrt(3)*0.5 + q.z*0.5, q.z) - h.x);
195 | //this is mathematically equivalent to this line, but less efficient:
196 | //return max(q.y - h.y, max(dot(vec2(cos(PI/3), sin(PI/3)), q.zx), q.z) - h.x);
197 | }
198 |
199 | // Hexagonal prism, incircle variant
200 | float fHexagonIncircle(vec3 p, vec2 h) {
201 | return fHexagonCircumcircle(p, vec2(h.x*sqrt(3)*0.5, h.y));
202 | }
203 |
204 | float fTriPrism(vec3 p, float hx, float hy)
205 | {
206 | vec3 q = abs(p);
207 | return max(q.z-hy,max(q.x*0.866025+p.y*0.5,-p.y)-hx*0.5);
208 | }
209 |
210 | // Cone with correct distances to tip and base circle. Y is up, 0 is in the middle of the base.
211 | float fCone(vec3 p, float radius, float height) {
212 | vec2 q = vec2(length(p.xz), p.y);
213 | vec2 tip = q - vec2(0, height);
214 | vec2 mantleDir = normalize(vec2(height, radius));
215 | float mantle = dot(tip, mantleDir);
216 | float d = max(mantle, -q.y);
217 | float projected = dot(tip, vec2(mantleDir.y, -mantleDir.x));
218 |
219 | // distance to tip
220 | if ((q.y > height) && (projected < 0)) {
221 | d = max(d, length(tip));
222 | }
223 |
224 | // distance to base ring
225 | if ((q.x > radius) && (projected > length(vec2(height, radius)))) {
226 | d = max(d, length(q - vec2(radius, 0)));
227 | }
228 | return d;
229 | }
230 |
231 | //
232 | // "Generalized Distance Functions" by Akleman and Chen.
233 | // see the Paper at https://www.viz.tamu.edu/faculty/ergun/research/implicitmodeling/papers/sm99.pdf
234 | //
235 | // This set of constants is used to construct a large variety of geometric primitives.
236 | // Indices are shifted by 1 compared to the paper because we start counting at Zero.
237 | // Some of those are slow whenever a driver decides to not unroll the loop,
238 | // which seems to happen for fIcosahedron und fTruncatedIcosahedron on nvidia 350.12 at least.
239 | // Specialized implementations can well be faster in all cases.
240 | //
241 |
242 | const vec3 GDFVectors[19] = vec3[](
243 | normalize(vec3(1, 0, 0)),
244 | normalize(vec3(0, 1, 0)),
245 | normalize(vec3(0, 0, 1)),
246 |
247 | normalize(vec3(1, 1, 1 )),
248 | normalize(vec3(-1, 1, 1)),
249 | normalize(vec3(1, -1, 1)),
250 | normalize(vec3(1, 1, -1)),
251 |
252 | normalize(vec3(0, 1, PHI+1)),
253 | normalize(vec3(0, -1, PHI+1)),
254 | normalize(vec3(PHI+1, 0, 1)),
255 | normalize(vec3(-PHI-1, 0, 1)),
256 | normalize(vec3(1, PHI+1, 0)),
257 | normalize(vec3(-1, PHI+1, 0)),
258 |
259 | normalize(vec3(0, PHI, 1)),
260 | normalize(vec3(0, -PHI, 1)),
261 | normalize(vec3(1, 0, PHI)),
262 | normalize(vec3(-1, 0, PHI)),
263 | normalize(vec3(PHI, 1, 0)),
264 | normalize(vec3(-PHI, 1, 0))
265 | );
266 |
267 | // Version with variable exponent.
268 | // This is slow and does not produce correct distances, but allows for bulging of objects.
269 | float fGDF(vec3 p, float r, float e, int begin, int end) {
270 | float d = 0;
271 | for (int i = begin; i <= end; ++i)
272 | d += pow(abs(dot(p, GDFVectors[i])), e);
273 | return pow(d, 1/e) - r;
274 | }
275 |
276 | // Version with without exponent, creates objects with sharp edges and flat faces
277 | float fGDF(vec3 p, float r, int begin, int end) {
278 | float d = 0;
279 | for (int i = begin; i <= end; ++i)
280 | d = max(d, abs(dot(p, GDFVectors[i])));
281 | return d - r;
282 | }
283 |
284 | // Primitives follow:
285 |
286 | float fOctahedron(vec3 p, float r, float e) {
287 | return fGDF(p, r, e, 3, 6);
288 | }
289 |
290 | float fDodecahedron(vec3 p, float r, float e) {
291 | return fGDF(p, r, e, 13, 18);
292 | }
293 |
294 | float fIcosahedron(vec3 p, float r, float e) {
295 | return fGDF(p, r, e, 3, 12);
296 | }
297 |
298 | float fTruncatedOctahedron(vec3 p, float r, float e) {
299 | return fGDF(p, r, e, 0, 6);
300 | }
301 |
302 | float fTruncatedIcosahedron(vec3 p, float r, float e) {
303 | return fGDF(p, r, e, 3, 18);
304 | }
305 |
306 | float fOctahedron(vec3 p, float r) {
307 | return fGDF(p, r, 3, 6);
308 | }
309 |
310 | float fDodecahedron(vec3 p, float r) {
311 | return fGDF(p, r, 13, 18);
312 | }
313 |
314 | float fIcosahedron(vec3 p, float r) {
315 | return fGDF(p, r, 3, 12);
316 | }
317 |
318 | float fTruncatedOctahedron(vec3 p, float r) {
319 | return fGDF(p, r, 0, 6);
320 | }
321 |
322 | float fTruncatedIcosahedron(vec3 p, float r) {
323 | return fGDF(p, r, 3, 18);
324 | }
325 |
326 | // Rotate around a coordinate axis (i.e. in a plane perpendicular to that axis) by angle .
327 | // Read like this: R(p.xz, a) rotates "x towards z".
328 | // This is fast if is a compile-time constant and slower (but still practical) if not.
329 | void pR(inout vec2 p, float a) {
330 | p = cos(a)*p + sin(a)*vec2(p.y, -p.x);
331 | }
332 |
333 | vec2 pOpRotate(in vec2 p, float a) {
334 | return cos(a)*p + sin(a)*vec2(p.y, -p.x);
335 | }
336 |
337 | // Shortcut for 45-degrees rotation
338 | void pR45(inout vec2 p) {
339 | p = (p + vec2(p.y, -p.x))*sqrt(0.5);
340 | }
341 |
342 | // Repeat space along one axis. Use like this to repeat along the x axis:
343 | //