├── .DS_Store
├── images
├── IP协议.png
├── 递归导图.jpg
├── UDP协议.png
├── 以太网协议.png
├── 函数变量压栈.png
├── 应用层协议.png
├── 递归树重复.png
├── 递归系列目录.png
├── 八皇后问题正确.png
├── 小鹿的blog.png
├── 八皇后问题error.png
├── 数据结构与算法之链表系列目录.png
└── 数据结构与算法之链表系列【题型篇】思维导图.png
├── articel
├── 2021
│ ├── 【2021 第三期】被面试官最爱问的作用域与作用域链.md
│ ├── 【2021 第一期】日常开发 26 个常见的 JavaScript 代码优化方案.md
│ └── 【2021 第二期】简而不单,单而不简的执行上下文.md
├── .DS_Store
├── 网络原理
│ ├── images
│ │ ├── ACK.gif
│ │ ├── FIN.gif
│ │ ├── SYN.gif
│ │ ├── Sqn.gif
│ │ ├── 三次握手图.png
│ │ ├── 初始化状态.png
│ │ ├── 四次挥手
│ │ │ ├── 2.gif
│ │ │ ├── 3.gif
│ │ │ ├── 4.gif
│ │ │ ├── 5.png
│ │ │ ├── 发送延迟.gif
│ │ │ ├── 思维导图.png
│ │ │ ├── 第一次分手.gif
│ │ │ ├── 第三次分手.gif
│ │ │ ├── 第二次分手.gif
│ │ │ ├── 第四次分手.gif
│ │ │ └── 三次四次示意图.png
│ │ ├── 头部报文.png
│ │ ├── 思维导图.png
│ │ ├── 源目的端口号.png
│ │ ├── 第一次握手.gif
│ │ ├── 第三次握手.gif
│ │ └── 第二次握手.gif
│ ├── TCP之四次挥手.md
│ ├── 网络层次模型划分(下).md
│ ├── 网络分层模型划分(上).md
│ └── TCP 之三次握手.md
└── 数据结构与算法系列
│ ├── 数据结构与算法之递归系列.md
│ ├── 数据结构与算法之二叉树系列[题型篇].md
│ └── 数据结构与算法之链表系列[题型篇].md
└── README.md
/.DS_Store:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/luxiangqiang/Blog/HEAD/.DS_Store
--------------------------------------------------------------------------------
/images/IP协议.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/luxiangqiang/Blog/HEAD/images/IP协议.png
--------------------------------------------------------------------------------
/images/递归导图.jpg:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/luxiangqiang/Blog/HEAD/images/递归导图.jpg
--------------------------------------------------------------------------------
/articel/.DS_Store:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/luxiangqiang/Blog/HEAD/articel/.DS_Store
--------------------------------------------------------------------------------
/images/UDP协议.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/luxiangqiang/Blog/HEAD/images/UDP协议.png
--------------------------------------------------------------------------------
/images/以太网协议.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/luxiangqiang/Blog/HEAD/images/以太网协议.png
--------------------------------------------------------------------------------
/images/函数变量压栈.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/luxiangqiang/Blog/HEAD/images/函数变量压栈.png
--------------------------------------------------------------------------------
/images/应用层协议.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/luxiangqiang/Blog/HEAD/images/应用层协议.png
--------------------------------------------------------------------------------
/images/递归树重复.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/luxiangqiang/Blog/HEAD/images/递归树重复.png
--------------------------------------------------------------------------------
/images/递归系列目录.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/luxiangqiang/Blog/HEAD/images/递归系列目录.png
--------------------------------------------------------------------------------
/images/八皇后问题正确.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/luxiangqiang/Blog/HEAD/images/八皇后问题正确.png
--------------------------------------------------------------------------------
/images/小鹿的blog.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/luxiangqiang/Blog/HEAD/images/小鹿的blog.png
--------------------------------------------------------------------------------
/images/八皇后问题error.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/luxiangqiang/Blog/HEAD/images/八皇后问题error.png
--------------------------------------------------------------------------------
/images/数据结构与算法之链表系列目录.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/luxiangqiang/Blog/HEAD/images/数据结构与算法之链表系列目录.png
--------------------------------------------------------------------------------
/articel/网络原理/images/ACK.gif:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/luxiangqiang/Blog/HEAD/articel/网络原理/images/ACK.gif
--------------------------------------------------------------------------------
/articel/网络原理/images/FIN.gif:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/luxiangqiang/Blog/HEAD/articel/网络原理/images/FIN.gif
--------------------------------------------------------------------------------
/articel/网络原理/images/SYN.gif:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/luxiangqiang/Blog/HEAD/articel/网络原理/images/SYN.gif
--------------------------------------------------------------------------------
/articel/网络原理/images/Sqn.gif:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/luxiangqiang/Blog/HEAD/articel/网络原理/images/Sqn.gif
--------------------------------------------------------------------------------
/articel/网络原理/images/三次握手图.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/luxiangqiang/Blog/HEAD/articel/网络原理/images/三次握手图.png
--------------------------------------------------------------------------------
/articel/网络原理/images/初始化状态.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/luxiangqiang/Blog/HEAD/articel/网络原理/images/初始化状态.png
--------------------------------------------------------------------------------
/articel/网络原理/images/四次挥手/2.gif:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/luxiangqiang/Blog/HEAD/articel/网络原理/images/四次挥手/2.gif
--------------------------------------------------------------------------------
/articel/网络原理/images/四次挥手/3.gif:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/luxiangqiang/Blog/HEAD/articel/网络原理/images/四次挥手/3.gif
--------------------------------------------------------------------------------
/articel/网络原理/images/四次挥手/4.gif:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/luxiangqiang/Blog/HEAD/articel/网络原理/images/四次挥手/4.gif
--------------------------------------------------------------------------------
/articel/网络原理/images/四次挥手/5.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/luxiangqiang/Blog/HEAD/articel/网络原理/images/四次挥手/5.png
--------------------------------------------------------------------------------
/articel/网络原理/images/头部报文.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/luxiangqiang/Blog/HEAD/articel/网络原理/images/头部报文.png
--------------------------------------------------------------------------------
/articel/网络原理/images/思维导图.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/luxiangqiang/Blog/HEAD/articel/网络原理/images/思维导图.png
--------------------------------------------------------------------------------
/articel/网络原理/images/源目的端口号.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/luxiangqiang/Blog/HEAD/articel/网络原理/images/源目的端口号.png
--------------------------------------------------------------------------------
/articel/网络原理/images/第一次握手.gif:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/luxiangqiang/Blog/HEAD/articel/网络原理/images/第一次握手.gif
--------------------------------------------------------------------------------
/articel/网络原理/images/第三次握手.gif:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/luxiangqiang/Blog/HEAD/articel/网络原理/images/第三次握手.gif
--------------------------------------------------------------------------------
/articel/网络原理/images/第二次握手.gif:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/luxiangqiang/Blog/HEAD/articel/网络原理/images/第二次握手.gif
--------------------------------------------------------------------------------
/images/数据结构与算法之链表系列【题型篇】思维导图.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/luxiangqiang/Blog/HEAD/images/数据结构与算法之链表系列【题型篇】思维导图.png
--------------------------------------------------------------------------------
/articel/网络原理/images/四次挥手/发送延迟.gif:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/luxiangqiang/Blog/HEAD/articel/网络原理/images/四次挥手/发送延迟.gif
--------------------------------------------------------------------------------
/articel/网络原理/images/四次挥手/思维导图.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/luxiangqiang/Blog/HEAD/articel/网络原理/images/四次挥手/思维导图.png
--------------------------------------------------------------------------------
/articel/网络原理/images/四次挥手/第一次分手.gif:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/luxiangqiang/Blog/HEAD/articel/网络原理/images/四次挥手/第一次分手.gif
--------------------------------------------------------------------------------
/articel/网络原理/images/四次挥手/第三次分手.gif:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/luxiangqiang/Blog/HEAD/articel/网络原理/images/四次挥手/第三次分手.gif
--------------------------------------------------------------------------------
/articel/网络原理/images/四次挥手/第二次分手.gif:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/luxiangqiang/Blog/HEAD/articel/网络原理/images/四次挥手/第二次分手.gif
--------------------------------------------------------------------------------
/articel/网络原理/images/四次挥手/第四次分手.gif:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/luxiangqiang/Blog/HEAD/articel/网络原理/images/四次挥手/第四次分手.gif
--------------------------------------------------------------------------------
/articel/网络原理/images/四次挥手/三次四次示意图.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/luxiangqiang/Blog/HEAD/articel/网络原理/images/四次挥手/三次四次示意图.png
--------------------------------------------------------------------------------
/articel/2021/【2021 第三期】被面试官最爱问的作用域与作用域链.md:
--------------------------------------------------------------------------------
1 |
2 | # 2021 第三期。
3 |
4 | 本文继上篇文章详细讲解的 JavaScript 执行上下文继续深入作用域与作用域链。
5 |
6 | 在上一篇文章中《[【2021 第二期】简而不单,单而不简的执行上下文](https://github.com/luxiangqiang/Blog/blob/master/articel/2021/%E3%80%902021%20%E7%AC%AC%E4%BA%8C%E6%9C%9F%E3%80%91%E7%AE%80%E8%80%8C%E4%B8%8D%E5%8D%95%EF%BC%8C%E5%8D%95%E8%80%8C%E4%B8%8D%E7%AE%80%E7%9A%84%E6%89%A7%E8%A1%8C%E4%B8%8A%E4%B8%8B%E6%96%87.md)》,主要分享到了执行上下文的概念,而作用域和作用域链是基于执行上下文的概念去理解的,如果还没了解执行上下文,不建议看本篇内容。
7 |
8 | > 本文章已在 [Github blog]() 收录,欢迎大伙儿~ Star,文章中若存在不足或者 issues,欢迎在下方或 Github 留言!
9 |
10 |
11 | ## 一、作用域
12 |
13 | 如果说执行上下文是代码的执行环境,那么作用域就是执行环境中的一套执行规则,既然是规则,`JavaScript` 引擎执行代码时要遵守这套规则,同时开发人员在写代码时,同样也要遵守这套规则。
14 |
15 | ### 1、什么是作用域?
16 |
17 | 我们先来看这样一个例子:
18 |
19 | ```javascript
20 | function foo () {
21 | var bar = 'xiaolu'
22 | }
23 | foo()
24 | console.log(bar)
25 | ```
26 |
27 | 上述的运行结果很明显,控制台会报错 `bar is not defined`,我们可以通过这个小例子就可以发现在函数外部访问函数内部声明的变量是不可访问的,这背后的原因就是 `JavaScript` 作用域存在导致的结果。
28 |
29 | ### 2、什么是词法环境?
30 |
31 | 说到作用域,那什么是作用域?我们先来认识一下这位老朋友词法环境。
32 |
33 | > `ECMAScript` 规范中对词法环境的描述如下:词法环境是用来定义基于词法嵌套结构的 `ECMAScript` 代码内的标识符与变量值和函数值之间的关联关系的一种规范类型。
34 |
35 | 说的直白一点,词法环境就是一套规范和规则,它用来规定某些函数和变量的可访问范围等,我们也称词法环境为「词法作用域」。
36 |
37 | 既然词法作用域是一套约定好的规则,那么词法作用域的作用范围是开发人员在写代码的时候就已经是确定了的。
38 |
39 | 当代码执行的时候, `JavaScript` 引擎就会根据这套规范通过标识符名称来查找相对应的变量和函数。
40 |
41 | 好吧,最后给它做个总结性的定义。
42 |
43 | > 作用域:作用域是一套约定好的规范和规则,它用来规定某些函数和变量的可访问性等。
44 |
45 | ## 2、作用域链
46 |
47 | 作用域我们弄明白了,我们再来看作用域链。作用域链和作用域却大不相同,咱们分别从「执行栈层面」和「代码层面」来体验一下什么是作用域链。
48 |
49 | ```javascript
50 | var name = "xiaolu";
51 | function fn () {
52 | console.log(name);
53 | function getName(){
54 | console.log(name);
55 | }
56 | getName();
57 | }
58 | fn();
59 | ```
60 |
61 | 执行栈中的作用域链示意图:
62 |
63 | 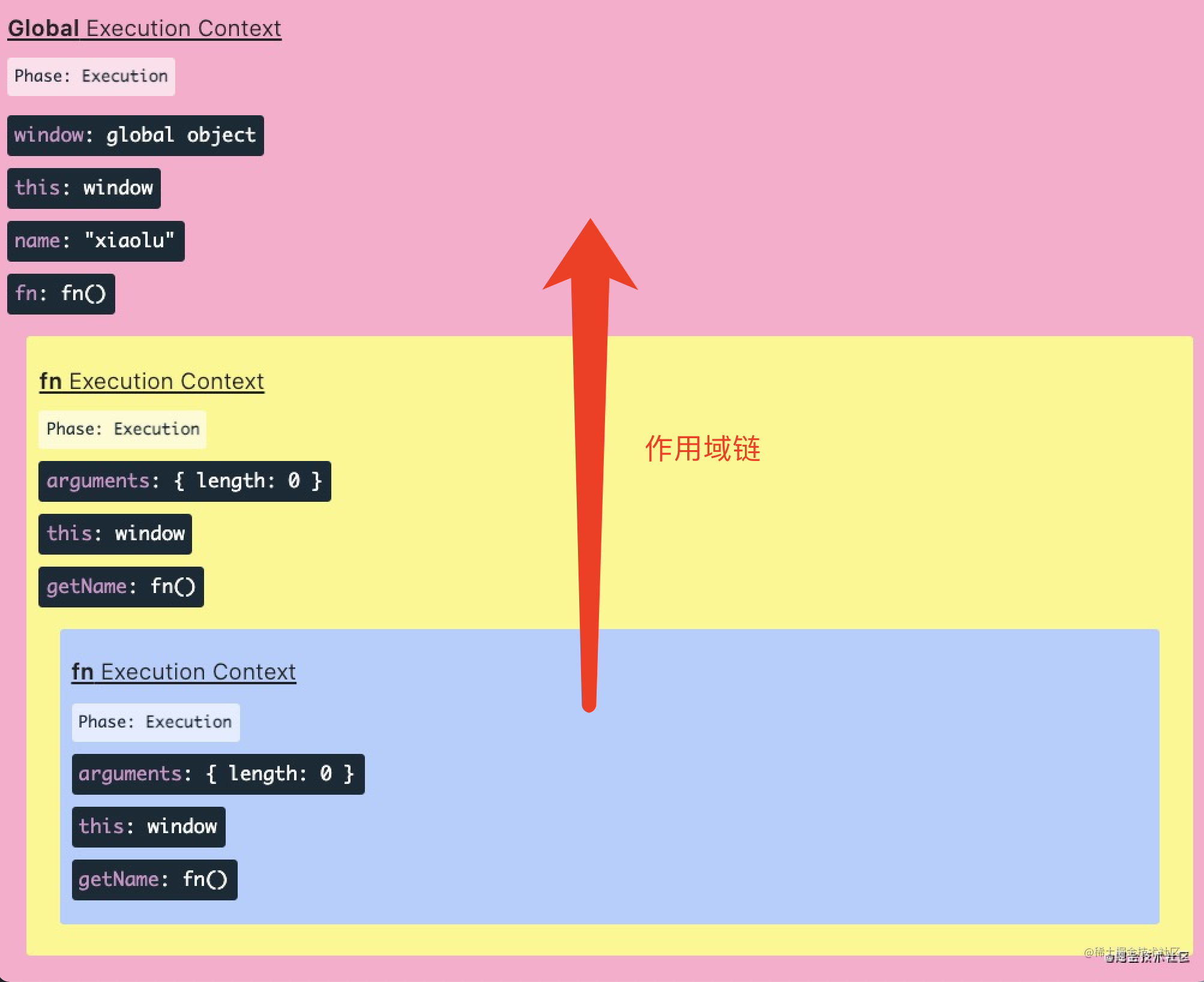
64 |
65 | 该示意图为上述代码的执行情况,在上述示意图中,不同的色块缩进形成的可访问链就是我们所说的作用域链。
66 |
67 | 虽然上述示意图是抽象出来的,如果我们在代码层面来理解作用域链,又是如何实现的呢?
68 |
69 | 在上一篇中分享到,每当创建一个新的执行上下文时,都会创建一个「变量对象」用于存放当前执行上下文中的变量和函数。(记住:这个变量对象很重要)
70 |
71 | 如果我们把这些执行上下文的「变量对象」关联起来,就形成了一条链,我们把这条链的实现称为「作用域链」。
72 |
73 | 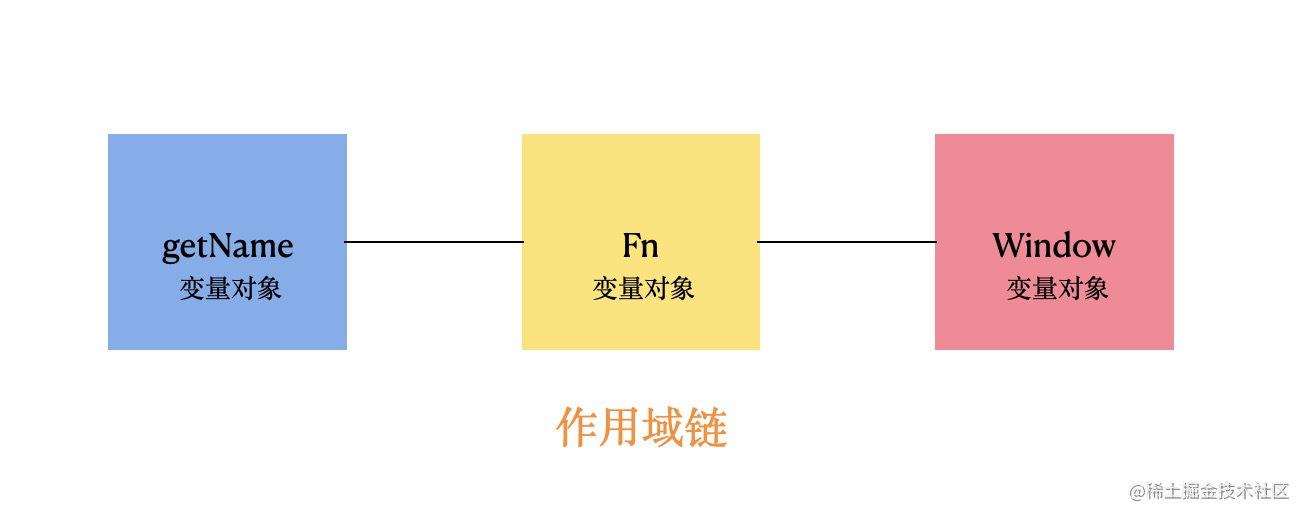
74 |
75 | 上述代码的执行结果是打印输出:
76 |
77 | ```javascript
78 | var name = "xiaolu";
79 | function fn () {
80 | console.log(name); // "xiaolu"
81 | function getName(){
82 | console.log(name); // "xiaolu"
83 | }
84 | getName();
85 | }
86 | fn();
87 | ```
88 | 当内部的 `getName` 执行时,`JavaScript` 引擎就在 `getName` 作用域内查找变量 `name`,发现并没有,就会沿着上图中的作用域链往上层寻找,在 `fn` 的作用域中也没有发现 `name` 变量,然后继续沿着作用域链往上层的寻找,直到全局作用域中,发现存在变量 `name`,然后输出 `name` 的值。
89 |
90 |
--------------------------------------------------------------------------------
/README.md:
--------------------------------------------------------------------------------
1 | 
2 |
3 | # 小鹿的博客
4 |
5 | ### 更新日志
6 |
7 | - #### 2019/4/1
8 |
9 | 开始发布 LeetCode 算法题解题思路,30天锻炼自己多种解题思路,用心记录每道算法题的收获,后续会转化为动画版本。
10 |
11 | - #### 2019 5/16
12 |
13 | 接下来一段时间将分享**数据结构与算法系列**的文章,通过半年数据结构与算法的学习,加上一个月 Leetcode 刷题,对数据结构与算法难点进行归纳、总结,编写成一系列的文章分享给每个人学习。
14 |
15 | - #### 2019/9/1
16 |
17 | 开始逐渐更新**网络原理**相关知识,最近去面试,公司很注重这部分的功底,那么就学起来,然后进行总结归纳和分享。
18 |
19 | - #### 2020/1/7
20 |
21 | 开始将所有的**剑指 offer** 题目以「**动画的形式**」展现,代码包括 **JavaScript 版、Java版本、Python版本**解题思路、总结、代码测试。
22 |
23 | - #### 2020/1/13
24 |
25 | 开始整理《大前端吊打面试官系列》面试知识点,从面试前简历的准备到知识点的总结,全面复盘大前端面试知识,实时更新,实时补充。
26 |
27 | - #### 2020/2/18
28 |
29 | 开始整理 2021 javascript 进阶,每周持续更新中~
30 |
31 | ## 目录
32 |
33 | #### 《LeetCode 系列》
34 |
35 | [LeetCode 题目全面解析](https://github.com/luxiangqiang/JS-LeetCode)
36 |
37 |
38 |
39 | #### 《数据结构与算法系列》
40 |
41 | **第一期:**[数据结构与算法之递归系列](https://github.com/luxiangqiang/Blog/blob/master/articel/%E6%95%B0%E6%8D%AE%E7%BB%93%E6%9E%84%E4%B8%8E%E7%AE%97%E6%B3%95%E7%B3%BB%E5%88%97/%E6%95%B0%E6%8D%AE%E7%BB%93%E6%9E%84%E4%B8%8E%E7%AE%97%E6%B3%95%E4%B9%8B%E9%80%92%E5%BD%92%E7%B3%BB%E5%88%97.md)
42 |
43 | **第二期:**[数据结构与算法之链表系列【题型篇】](https://github.com/luxiangqiang/Blog/blob/master/articel/%E6%95%B0%E6%8D%AE%E7%BB%93%E6%9E%84%E4%B8%8E%E7%AE%97%E6%B3%95%E7%B3%BB%E5%88%97/%E6%95%B0%E6%8D%AE%E7%BB%93%E6%9E%84%E4%B8%8E%E7%AE%97%E6%B3%95%E4%B9%8B%E9%93%BE%E8%A1%A8%E7%B3%BB%E5%88%97%5B%E9%A2%98%E5%9E%8B%E7%AF%87%5D.md)
44 |
45 | **第三期:** [数据结构与算法之二叉树系列【题型篇】](https://github.com/luxiangqiang/Blog/blob/master/articel/%E6%95%B0%E6%8D%AE%E7%BB%93%E6%9E%84%E4%B8%8E%E7%AE%97%E6%B3%95%E7%B3%BB%E5%88%97/%E6%95%B0%E6%8D%AE%E7%BB%93%E6%9E%84%E4%B8%8E%E7%AE%97%E6%B3%95%E4%B9%8B%E4%BA%8C%E5%8F%89%E6%A0%91%E7%B3%BB%E5%88%97%5B%E9%A2%98%E5%9E%8B%E7%AF%87%5D.md)
46 |
47 |
48 |
49 | #### 《网络原理系列》
50 |
51 | **第一期:**[网络层次模型划分(上)](https://github.com/luxiangqiang/Blog/blob/master/articel/%E7%BD%91%E7%BB%9C%E5%8E%9F%E7%90%86/%E7%BD%91%E7%BB%9C%E5%88%86%E5%B1%82%E5%88%92%E5%88%86%EF%BC%88%E4%B8%8A%EF%BC%89.md)
52 |
53 | **第二期:**[网络层次模型划分(下)](https://github.com/luxiangqiang/Blog/blob/master/articel/%E7%BD%91%E7%BB%9C%E5%8E%9F%E7%90%86/%E7%BD%91%E7%BB%9C%E5%B1%82%E6%AC%A1%E6%A8%A1%E5%9E%8B%E5%88%92%E5%88%86%EF%BC%88%E4%B8%8B%EF%BC%89.md)
54 |
55 | **第三期:** [动画:TCP 三次握手](https://github.com/luxiangqiang/Blog/blob/master/articel/%E7%BD%91%E7%BB%9C%E5%8E%9F%E7%90%86/TCP%20%E4%B9%8B%E4%B8%89%E6%AC%A1%E6%8F%A1%E6%89%8B.md)
56 |
57 | **第四期:**[动画:TCP 四次挥手](https://github.com/luxiangqiang/Blog/blob/master/articel/%E7%BD%91%E7%BB%9C%E5%8E%9F%E7%90%86/TCP%E4%B9%8B%E5%9B%9B%E6%AC%A1%E6%8C%A5%E6%89%8B.md)
58 |
59 |
60 |
61 | #### 《剑指 offer 系列》
62 |
63 | [剑指 offer 所有题型动画解析仓库](https://github.com/luxiangqiang/JianZhi-Offer_JavaScript)
64 |
65 |
66 |
67 | #### 《大前端吊打面试官系列》
68 |
69 | [大前端面试系列入口](https://github.com/luxiangqiang/Web-interview)
70 |
71 |
72 |
73 |
74 | #### JavaScript 进阶
75 |
76 | #### 2021
77 |
78 | **第一期:**[【2021 第一期】日常开发 26 个常见的 JavaScript 代码优化方案](https://github.com/luxiangqiang/Blog/blob/master/articel/2021/%E3%80%902021%20%E7%AC%AC%E4%B8%80%E6%9C%9F%E3%80%91%E6%97%A5%E5%B8%B8%E5%BC%80%E5%8F%91%2026%20%E4%B8%AA%E5%B8%B8%E8%A7%81%E7%9A%84%20JavaScript%20%E4%BB%A3%E7%A0%81%E4%BC%98%E5%8C%96%E6%96%B9%E6%A1%88.md)
79 |
80 | **第二期:**[【2021 第二期】简而不单,单而不简的执行上下文](https://github.com/luxiangqiang/Blog/blob/master/articel/2021/%E3%80%902021%20%E7%AC%AC%E4%BA%8C%E6%9C%9F%E3%80%91%E7%AE%80%E8%80%8C%E4%B8%8D%E5%8D%95%EF%BC%8C%E5%8D%95%E8%80%8C%E4%B8%8D%E7%AE%80%E7%9A%84%E6%89%A7%E8%A1%8C%E4%B8%8A%E4%B8%8B%E6%96%87.md)
81 |
82 |
83 | **第三期:**[【2021 第三期】被面试官最爱问的作用域与作用域链](https://github.com/luxiangqiang/Blog/blob/master/articel/2021/%E3%80%902021%20%E7%AC%AC%E4%B8%89%E6%9C%9F%E3%80%91%E8%A2%AB%E9%9D%A2%E8%AF%95%E5%AE%98%E6%9C%80%E7%88%B1%E9%97%AE%E7%9A%84%E4%BD%9C%E7%94%A8%E5%9F%9F%E4%B8%8E%E4%BD%9C%E7%94%A8%E5%9F%9F%E9%93%BE.md)
84 |
85 |
86 |
--------------------------------------------------------------------------------
/articel/网络原理/TCP之四次挥手.md:
--------------------------------------------------------------------------------
1 | ## 动画:TCP 四次挥手
2 |
3 | ### 写在前边
4 |
5 | 大家好,我们又见面了,做为一个业余的动画师,上次的用动画的形式讲解 TCP 三次握手过程再各大平台收到了广大读者的喜爱,说文章有趣、有货、有内容,也受到了很多读者的关注。很多读者留言说什么时候用动画讲一讲 TCP 四次挥手的过程,为了应大家的要求,今天我们就生动有趣的用动画给大家分享 TCP 四次挥手(分手)过程。
6 |
7 |
8 |
9 | #### [动画:TCP 三次握手](https://github.com/luxiangqiang/Blog/blob/master/articel/网络原理/TCP之四次挥手.md)
10 |
11 |
12 |
13 | 上次的三次握手动画是给面试官看的,那么今天咱们换种更加有乐趣的方式,用动画和你女(男)朋友讲解 TCP 四次分手过程,讲解完,考验一下你女(男)朋友和不和你分手呢。什么?首先你先有一个女(男)朋友,这一点小鹿早就考虑到了各大单身人士。
14 |
15 |
16 |
17 | **获取方式:**
18 |
19 | > 如果你没有女朋友,公众号后台回复“女朋友”,即可获取。小鹿不要脸的说,作为一个优秀的动画师,女性读者也是很多的,哈哈,公众号回复“男朋友”,小鹿会给你随机发放一个,嘿嘿,不信你试试。还等什么,把你女(男)朋友拉过来给她(他)讲吧。
20 |
21 |
22 |
23 | ### 一、思维导图
24 |
25 | 
26 |
27 |
28 |
29 | ### 二、为何要进行 TCP 三次握手/四次分手?
30 |
31 | TCP 的三次握手和四次分手和你恋爱是一模一样的,从相识到相恋到分手,然后认识另一个女孩再不管重复这个过程就是数据传输在网络中不断建立起三次握手和四次分手过程。
32 |
33 | 恋爱就恋爱吧,分手就分手吧,握手握来握去,挥手挥来挥去不嫌麻烦吗?
34 |
35 | 因为上篇文章 TCP 三次握手中的为什么要进行三次握手部分讲解的不怎么详细,小鹿课下就收集了一些资料,做了一个总结,在这里补充下。
36 |
37 |
38 |
39 | #### 2.1 为什么要进行三次握手?
40 |
41 | > 在谢希仁著《计算机网络》第四版中讲“三次握手”的目的是“为了防止已失效的连接请求报文段突然又传送到了服务端,因而产生错误”。
42 |
43 | 举个简单易懂的例子,你在微信对一个女孩表白,这条信息由于网络问题延迟发送了。
44 |
45 |
46 |
47 | 
48 |
49 |
50 |
51 | 然后此时你不耐烦了,去和微信另一个女孩表白,然后另一个女孩告诉你同意了,然后你心里很高兴,把高兴的心情分享给了女孩,女孩知道了你和她在一起很高兴,此时三次握完毕,你恋爱了。
52 |
53 |
54 |
55 | 
56 |
57 |
58 |
59 | 突然,到了第二天,发给第一个女孩的信息才收到,女孩认为你要和他表白,此时你已经和另一个女孩恋爱了,然后第一个女孩给你发微信同意了你的表白,但是你不理睬,那个女孩还在苦苦等待你给她分享此时的高兴心情。现在我们发现如果没有分享高兴的心情给女孩(也就是第三次握手过程),那么那个女孩一直等待,白白浪费了心思,所谓的千年都等不了一回。
60 |
61 | 
62 |
63 |
64 |
65 | 如果你是客户端,女孩是服务端,服务端收到延迟的报文,以为你要和它连接,所以会给你发送确认同意连接,但你一直不搭理它,所以服务端的资源也就这么白白浪费掉了。所以知道为什么要进行三次握手了吧。
66 |
67 |
68 |
69 | > 在《计算机网络》书中讲“三次握手”的目的是为了解决“网络中存在延迟的重复分组”的问题。
70 |
71 |
72 |
73 | #### 2.2 为什么要 TCP 四次分手?
74 |
75 | 我们知道,TCP协议是一种面向连接的、可靠的、基于字节流的运输层通信协议,而且TCP是全双工模式。
76 |
77 | 对于初学者来说,定义太枯燥、无味,其实意思就是你和你女朋友聊天是面向连接的,只有连接起来才可以通信的,可靠就是你发送的信息可以保证送达到对方,全双工意思就是你不仅可以给你女朋友发消息,而且她也可以给你发信息。
78 |
79 | 为什么非要进行 TCP 四次分手?我们接着上回说到,你现在和第二个女孩子恋爱了,突然有一天发现第一个女孩子是因为没有收到你的表白而错过了在一起的时机,那么你要和第二个女孩子分手,那过程对应在 TCP 四次分手是怎么样子的?
80 |
81 |
82 |
83 | 
84 |
85 |
86 |
87 | 你要给第二个女孩子微信发消息,我们分手吧,此时第二个女孩子收到消息知道了,非常伤心,就屏蔽了你。但是,此时你还没有屏蔽她,她完全可以给你继续发消息,她给你发消息说,好吧,此时你收到了确认消息,此时是第二次分手过程。那么女孩又给你发送消息,渣男,永远不要来找我。此时你又接收到消息,看到消息之后发了一个拜拜,然后你就直接屏蔽拉黑了对方,此时女孩微信显示你删除了对方,然后就把你也拉黑删除了。那么四次分手到此为止,恭喜你,成功获得下一个女孩子。
88 |
89 | 上述过程就阐述了为什么要进行 TCP 四次分手,为了能够让对方屏蔽你直至最后双方互相删除掉,然后你又可以和另一个女孩三次握手了。
90 |
91 |
92 | ### 三、TCP 四次分手过程
93 |
94 | 初始化状态:客户端和服务端都在连接状态,接下来开始进行四次分手断开连接操作。
95 |
96 | 
97 |
98 |
99 |
100 | - 第一次分手:第一次分手无论是客户端还是服务端都可以发起,因为 TCP 是全双工的。
101 |
102 | > 假如客户端发送的数据已经发送完毕,发送FIN = 1 告诉服务端,客户端所有数据已经全发完了,服务端你可以关闭接收了,但是如果你们服务端有数据要发给客户端,客户端照样可以接收的。此时客户端处于FIN = 1等待服务端确认释放连接状态。
103 |
104 | 
105 |
106 |
107 |
108 | - 第二次分手:服务端接收到客户端的释放请求连接之后,知道客户端没有数据要发给自己了,然后服务端发送ACK = 1告诉客户端受到你发给我的信息,此时服务端处于 CLOSE_WAIT 等待关闭状态。
109 |
110 | 
111 |
112 |
113 |
114 | - 第三次分手:此时服务端向客户端把所有的数据发送完了,然后发送一个FIN = 1,用于告诉客户端,服务端的所有数据发送完毕,客户端你也可以关闭接受数据连接了。此时服务端状态处于LAT_ACK状态,来等待确认客户端是否收到了自己的请求。
115 |
116 | 
117 |
118 |
119 |
120 | - 第四次分手:此时如果客户端收到了服务端发送完的信息之后,就发送ACK = 1,告诉服务端,客户端已经收到了你的信息。但是我们发现上图中有一个 2 MSL 的延迟等待。
121 |
122 | 
123 |
124 |
125 |
126 | ### 四、为什要有 2 MSL 等待延迟?
127 |
128 | 对应这样一种情况,最后客户端发送的ACK = 1给服务端的过程中丢失了,服务端没收到,服务端怎么认为的?我已经发送完数据了,怎么客户端没回应我?是不是中途丢失了?然后服务端再次发起断开连接的请求,一个来回就是2MSL,这里的两个来回由那一个来回组成的?
129 |
130 | 客户端给服务端发送的ACK = 1丢失,服务端等待 1MSL没收到,然后重新发送消息需要1MSL。如果再次接收到服务端的消息,则重启2MSL计时器,发送确认请求。客户端只需等待2MSL,如果没有再次收到服务端的消息,就说明服务端已经接收到自己确认消息;此时双方都关闭的连接,TCP 四次分手完毕。
131 |
132 |
133 |
134 | #### 五、如果双方建立连接,一方出问题怎么办?
135 |
136 | 如果双方建立连接,一方出问题怎么办?为了防止出现上述恋爱故事中千年等一回的情况,已经建立连接,但是服务端一直等待接收,发送端出现问题一直不能发送。
137 |
138 | 所以设计一个保活的计时器,如果一方出现问题,另一方过了这个计时器的时间,就发送试探报文,以后每隔 75 秒发送一次。若一连发送10个探测报文仍然没反应,服务器就认为客户端出了故障,接着就关闭连接。
139 |
140 |
141 |
142 | ### 六、小结
143 |
144 | 今天用动画的形式给你女(男)朋友讲了 TCP 四次分手的过程,文章的内容以及展现形式是最基础的内容。
145 |
146 | 最后小鹿为大家整理的三次握手和四次分手整张图,如下:
147 |
148 | 
149 |
150 | 最后希望你和你的女朋友永远三次握手,永不四次分手。
151 |
152 |
--------------------------------------------------------------------------------
/articel/网络原理/网络层次模型划分(下).md:
--------------------------------------------------------------------------------
1 | **上一篇:**[网络层次模型划分(上)](https://github.com/luxiangqiang/Blog/blob/master/articel/网络原理/网络分层模型划分(上).md)
2 |
3 |
4 |
5 | # 网络层次模型划分(下)
6 |
7 | ### 写在前边
8 |
9 | 上一篇主要分享了网络分层的基本概念,为什么要进行网络分层?又是如何进行分层?每一层的基本功能是什么?而且对于每一层的的功能细节方面,比如数据包的组成以及每层包含的一些协议的使用都没有细说,那么这一篇文章将会分享网络分层每层中协议等深入讲解。(PS:可能里边有的讲解不正确,还请大佬指出改正)
10 |
11 |
12 |
13 | ### 1、物理层
14 |
15 | 物理层里边涉及到最多的是硬件底层的一些内容,没有需要过多了解的内容,我们直接看数据链路层。
16 |
17 |
18 |
19 | ### 2、数据链路层
20 |
21 | 上回讲到数据链路层中规定的“以太网协议”来规定电信号的分组形式,什么是以太网,以太网的数据包是什么样子的?
22 |
23 |
24 |
25 | #### 2.1 **以太网协议**
26 |
27 | 以太网规定,每组的电信号就是一个数据包,每个数据包我们可以成为“帧”。每帧的组成是由标头(Head)和数据(Data)组成。
28 |
29 | 
30 |
31 | 那么你会问,标头里有什么信息?Data 数据又会存放写什么?为什么分为两部分?放在一块不好吗?
32 |
33 | **1、标头**
34 |
35 | 为什么传输数据会有标头,我们想呀,在传输数据的时候,接收端怎么判断是不是给自己发送的,那么就只取出标头来进行判断。
36 |
37 | 数据包的标头中通常会存放一些有关数据包的说明、发送者是谁、接受者又是谁等相关识别信息。
38 |
39 | 标头的长度固定为 18 字节,也就是说,一些标头识别信息的大小不能超过 18 字节。
40 |
41 |
42 |
43 | **2、数据**
44 |
45 | 数据,顾名思义,你要传输给接收端什么数据都会放到数据包中,也就是整个数据包的具体内容,比如文件、字符串之类的。
46 |
47 | 数据部分的长度最小至少为 46 个字节,最长 1500 字节。我们可能会想到,如果小于 46 字节没啥问题可以存放开,那么大于 1500 字节怎么处理呢?很简单,我们就分成两个包处理(分割),两个包存放不下就分割成三个包......
48 |
49 |
50 |
51 | #### 2.2 广播
52 |
53 | 上回说到,广播的作用就是用来查找接收端的 MAC 地址,从而进行下一步的数据传输。注意,广播只是一种发送数据的形式,而计算机想要知道另一台计算机的 MAC 地址是通过 ARP 协议解决的,ARP 协议会在讲完 IP 协议后再说,因为它会涉及到 IP 协议的一点内容,现在讲可能会有点乱。
54 |
55 |
56 |
57 | 如果你觉的上边稍微有点乱,那怎们稍微屡一下,我们想要发送数据,首先要知道对方的唯一标识(MAC 地址),要想知道对方的 MAC 地址,需要使用 ARP 协议,假设我们通过 ARP 协议拿到了接收方的 MAC 地址。
58 |
59 |
60 |
61 | 我们开始发送数据,将发送方的 MAC 地址和接收方的 MAC 地址封装在数据包中,然后发送端向同一子网络中(同一局域网)中的所有计算机发送该数据包,所有的计算机接收到该包之后,就对数据包的头部进行提取,提取出里边封装好的接收端 MAC 地址和自己的 MAC 地址作比对,如果相同,就说明该数据包是给自己发送的,否则,就会丢弃该数据包,这个过程就是广播的过程。
62 |
63 |
64 |
65 | 上一篇文章在这个地方留下的一个问题就以上是在同一局域网中,如果不在同一局域网中我们怎么处理?我们平常使用无线网都知道每个无线局域网都会有一个路由器,我们先通过以上的方法将数据发送到路由器,然后路由器转发数据到其他局域网中的计算机。
66 |
67 |
68 |
69 | ### 3、网络层
70 |
71 | 网络层中最重要的一个协议就是 IP 协议,我们一般发送端给服务端发送数据同时要知道两个地址才能准确送达到对方,分别为 IP 地址和 MAC 地址。停!stop! 上边讲到的明明知道对方的 MAC 地址就可以传输数据了,为什么现在需要两个地址呢?你给我说明白,说不明白取关!
72 |
73 |
74 |
75 | 上边确实是一个 MAC 地址就可以通信,但是前提是通过 ARP 协议获得的 MAC 地址,而 ARP 协议正是利用的接收端的 IP 地址才获取到接收端的 MAC 地址的,所以这两个地址很重要,那么如果实现的,下边会继续讲。
76 |
77 |
78 |
79 | #### 3.1 IP 协议
80 |
81 | IP 的数据包是直接放入到以太网数据包的“数据”部分的,这样做有一个好处就是“上层的变动完全涉及不到下层的结构”。然后数据包就变成这个样子了。
82 |
83 | 
84 |
85 | IP 数据包也分为标头(Head)和数据(Data)两部分。
86 |
87 |
88 |
89 | **1、标头**
90 |
91 | IP 数据包的标头是 20 ~ 60 字节,主要包括版本、IP 地址等信息。
92 |
93 |
94 |
95 | **2、数据**
96 |
97 | 数据的最大长度为 65515 字节。整个 IP 数据包的最大总长度为 65535 字节。主要存放 IP 数据包的具体内容。
98 |
99 | 问题来了,以太网的数据部分最长为 1500 字节,你把一个长度为 65535 字节的 IP 数据包放到以太网的数据包汇总,不会被撑破吗?你在逗我么?确实是呀,那我们就分割数据包吧,分割成几个以太网数据包分开发送。
100 |
101 |
102 |
103 | #### 3.2 **AND 运算**
104 |
105 | IP 协议上篇文章中最重要的作用就是判断两个设备是否属于同一子网中(同一局域网中)。
106 |
107 |
108 |
109 | 将两个IP地址与子网掩码分别进行AND运算(两个数位都为1,运算结果为1,否则为0),然后比较结果是否相同,如果是的话,就表明它们在同一个子网络中,否则就不是。
110 |
111 |
112 |
113 | > PS:看这篇文章之前,一定先要看之前写的入门网络分层的文章,不然会有很多疑问点。
114 |
115 |
116 |
117 | 我们可以通过 DNS 解析知道对方的 IP ,除了判断两个计算机是否在同一局域网中,还有一个作用就是然后通过 ARP 协议获取到对方的 MAC 地址。停!真想让我取关吗?ARP 就 TN 的说了多少遍了,该详细说一下了吧?
118 |
119 |
120 |
121 | #### 3.3 ARP 协议
122 |
123 | > 前提:对方的 IP 地址是已知的,通过 DNS 解析得到。
124 |
125 |
126 |
127 | ARP 协议发出一个数据包,包含在以太网的数据包中(其中包含对方的 IP 地址,对方的 MAC 地址栏是 FF:FF:FF:FF:FF:FF)。子网络中的每台主机都会收到这个包,然后从中取出 IP 地址与自身对比,如果两者相同,都做出回复,向对方报告自己的 MAC 地址,否则就丢弃这个包。
128 |
129 |
130 |
131 | ### 4、传输层
132 |
133 | 传输层主要涉及到两个重要协议,UDP 和 TCP 协议,上篇讲过主要用来确定端口到端口的通信,计算机中不同运行的程序端口号不相同。
134 |
135 |
136 |
137 | "端口"是 0 到 65535 之间的一个整数,正好 16 个二进制位。0 到 1023的端口被系统占用,我们只能选用大于1023 的端口。
138 |
139 |
140 |
141 | #### 4.1 UDP 协议
142 |
143 | UDP 协议也分为标头(Head)和数据(Data)两部分。
144 |
145 |
146 |
147 | **1、标头**
148 |
149 | 标头的长度为 8 字节。主要存放了发送和接收端口号。
150 |
151 |
152 |
153 | **2、数据**
154 |
155 | 数据部分和标头部分的总长度不超过 65535 字节,正好放进一个IP数据包。
156 |
157 |
158 |
159 | 前边也讲过,数据包之间是包含关系的,所以 UDP 的数据包是放到 IP 数据包的“数据”部分的,IP 数据包又放在以太网数据包的“数据”部分的。
160 |
161 |
162 |
163 | 
164 |
165 |
166 |
167 | #### 4.2 TCP 协议
168 |
169 | TCP 和 UDP 是相同的,上一篇讲了 UDP 和 TCP 的优缺点,TCP 保证了网络的可靠性,TCP 三次握手和四次挥手就是这部分内容。
170 |
171 |
172 |
173 | TCP 的数据包和 UDP 相同嵌入在 IP 协议的“数据”部分,TCP 并没有长度限制,但是为了保证传输效率,肯定要进行限制的,TCP 的数据包的长度一般不会超过 IP 数据包的长度了,保证单个的 TCP 数据包不再进行分割。
174 |
175 |
176 |
177 | ### 5、应用层
178 |
179 | 应用层是最高一层,直接面向用户,它的数据包会放在 TCP 的数据包的“数据”部分,那么整个五层的数据包就会变成一下这样。
180 |
181 |
182 | 
183 |
184 | 以上五层中的内容基本讲完了,我是从下到上逐层写的,这两篇文章可以让你入门网络五层协议的基本内容了。
185 |
186 |
187 |
188 | 里边还有一些 DNS 解析、如何分配 IP 地址以及TCP 三次握手四次挥手后续会单独拿出来写。老规矩,点赞、转发,小鹿谢谢你的支持,我们下期再见!
189 |
190 |
191 |
192 |
193 |
194 |
195 |
196 |
197 |
198 |
199 |
200 |
201 |
202 |
203 |
204 |
205 |
206 |
207 |
--------------------------------------------------------------------------------
/articel/网络原理/网络分层模型划分(上).md:
--------------------------------------------------------------------------------
1 | ## 写在前边
2 |
3 | 整个暑假去面试,面试了很多家公司(无论是小厂还是大厂)问到的深度不同,网络原理是面试最容易问到的问题,虽然我们在项目中很少去实践它,但是了解其原理,会让我们背后网络通信是如果工作的,既能在面试官面前体现出你的基础是否扎实,也能对以后深入网络这部分学习有更多的了解。
4 |
5 |
6 |
7 | 很多同学面试在准备这部分的时候,都会去背,这部分确实很难掌握,我个人总结的最好的学习网络原理的方法就是不用刻意的去记忆而是完全的结合实际去讲整个原理融会贯通。虽然一开始学习起来很吃力,但是稍微用点心,多看几遍,多问自己为什么,把自己当做是开发网络原理的开发者,面试前的准备只要理清逻辑就足够了,而不是去背这部分内容。
8 |
9 |
10 |
11 | 而且这部分相同的知识点面试官有多种提问方式,但是其中很多都是换汤不换药。我记得最多的问的是输入URL,到页面呈现出来,其中经历了什么?这道面试题的背后,涉及到了很多网络原理的知识,我们这篇文章不会全部分享到,而是先把由来和网络层次划分弄清楚,就完成了这篇文章的目的。
12 |
13 |
14 |
15 | ## 一、为什么要进行网络层次划分?
16 |
17 | 说到网络层次划分并不陌生,我刚刚接触到网络层次的时候一脸懵逼,这么多层,一层不就行了嘛?层与层之间好多协议,还有各种数据包,第一次我放弃了。
18 |
19 |
20 |
21 | 当我从新拾起网络层次的时候,我下定决心从根上理解它。首先弄明白它的原理,那必定要知道它的由来,也就是为什么要进行网络层次划分?这个问题问的好。
22 |
23 |
24 |
25 | 假如“小鹿”是网络的开发人员,起初认为计算机与计算机之间的通信只需要一根线就可以完成通信,对没错,但是世界那么大,那么多计算机,距离又远,不但浪费线,还没出现各种线被你偷偷剪断的情况,毋庸置疑,那计算机之间通信就不行了。(后边出来了无线网,虽然其中网关、路由之间也需要连线,但不是让每台计算机两两连接,而是一个区域为单位计算机相互连接通信)
26 |
27 |
28 |
29 | 不行,老板说,“小鹿”你给我想法子改,改不出来今晚不能睡觉,“小鹿”仔细想了想,这还是个技术活,需要进行全面的改进,也发现所谓的计算机之间的连线只能传送0、1信号,另一台计算并不知道那么多0、1代表什么,而且“小鹿”又发现不同厂商的生产的计算机既然有连线实现通信也是很麻烦的,干脆定义一套规则吧,无论“某硕”计算机还是“某想”计算机,都必须遵守这套规则,其实所说的这套规则就是我们经常说的“网络协议”。
30 |
31 |
32 |
33 | 不是说网络层次的由来吗,怎么讲到网络协议了。咱们继续,通过上面的问题,那个计算机之间通过连线传送0、1信号的问题虽然规定了通信规则,但是除了像0、1这种无意义的信号之外,网络中还存在着其他各种各样的问题,两个计算机之间怎么进行识别?以及怎么才能知道对方的地址?以及不同计算机应用程序怎么知道是给自己传递的数据,还有不同的通信数据格式怎么来规定等等一系列的问题都出来了。
34 |
35 |
36 |
37 |
38 | “小鹿”发现,如果各种问题都写成一套协议来规定双方通信的规则,但是呢?万一其中哪些规则通信中出现问题,影响到了其他规则,最常见的就是数据包,一个数据包中如果包含各种各样的协议,不就乱套了。
39 |
40 |
41 | “小鹿”为了能够把它设计的更好,决定采用分层划分的结构,既能规定不同层的完成的功能,又能实现层与层之间的改动而不相互影响,这就是我们经常听到网络划分层次的好处。
42 |
43 |
44 |
45 | ## 二、 网络分层是如何进行分层的?
46 |
47 | 既然我们决定要分层,那么分为几层才好呢?
48 |
49 |
50 | 起初网络分层是标准的七层,也就是我们所说的 OSI 七层模型。
51 |
52 | > 参考模型是国际标准化组织(ISO)制定的一个用于计算机或通信系统间互联的标准体系,一般称为OSI参考模型或七层模型。
53 |
54 | 
55 |
56 | 我们所知道的还有 TCP/IP 四层模型和 TCP/IP 五层模型。这又是怎么出来的,其实所谓的 TCP/IP 四层模型和 TCP/IP 五层模型是以 OSI 七层优化而来,把某些层进行合并了,其实本质上还是相同的,但是我个人最喜欢用五层来解释。
57 |
58 |
59 |
60 | 
61 |
62 |
63 |
64 | ## 三、每一层的作用是什么?
65 |
66 | 这一部分涉及到每一层的很多协议和知识点,但是我们这一节不具体分享,为什么?我们具体深入之前必须大脑里有个具体的网络分层结构图,先要知道每层是做什么的,层与层之间的关系,然后下一节再深入每层中的每个协议怎么通信的,这样的好处学起来条理清晰,而不至于当时我学习的时候表面还不懂,就深入最后懵逼状态。
67 |
68 |
69 |
70 | ### 3.1 物理层
71 |
72 | 物理层,顾名思义,用物理手段将电脑连接起来,就像我们上边讲到的计算机之间的物理连线。主要用来传输0、1信号,上边也分析过了,0、1信号毕竟没有任何的现实意义,所有我们用另一层用来规定不同0、1组合的意义是什么。
73 |
74 |
75 |
76 | ### 3.2 数据链路层
77 |
78 | 下层的物理层既然不能规定不同0、1组合的信号代表什么意义,那么我们在数据链路层规定一套协议,专门的给0、1信号进行分组,以及规定不同的组代表什么意思,从而双方计算机都能够进行识别,这个协议就是“以太网协议”(具体的以太网协议内容下节内容详细讲解)。
79 |
80 | 但是问题又来了,我们要发送给对方计算机,怎么标识对方以及怎么知道对方的地址呢?
81 |
82 |
83 |
84 | #### 3.2.1 MAC 地址
85 |
86 | 我们所说的MAC地址到底的作用是啥?说白了它就是作为网络中计算机设备的唯一标识,从计算机在厂商生产出来就被十六进制的数标识为MAC地址。
87 |
88 |
89 | 既然我们知道了用MAC地址作为标识,那么怎么才能知道我们要进行通信的计算机MAC地址呢?
90 |
91 |
92 |
93 | #### 3.2.2 广播
94 |
95 | 这里广播详细的在下一节讲,这一节你只需要知道广播可以帮助我们能够知道对方的 MAC 地址。那么既然知道了MAC地址就可以通信了?没有想得那么简单,广播中还存在两种情况,一种是,在同一子网络下(同一局域网下)的计算机是通过 ARP 协议获取到对方 MAC地址的。不同自网络中(不同局域网)中是交给两个局域网的网关(路由器)去处理的。这里边涉及到很多细节的知识,都会集中到下一节,但是这一节你了解怎么进行标识计算机和怎么获取到MAC地址就可以了。
96 |
97 |
98 |
99 | ### 3.3 网络层
100 |
101 | 物理层和数据链路层都有自己的事情要做,也就是我们上边所讲到的这些(里边很多细节不在这节多说)。上边两层在我看来可以完成正常通信了,那么网络层出来干啥子?
102 |
103 |
104 | 网络层的由来是因为在数据链路层中我们说说两台计算机之间的通信是分为同一子网络和不同子网络之间,那么问题就来了,怎么判断两台计算机是否在同一子网络(局域网)中?这就是网络层要解决的问题。
105 |
106 |
107 |
108 | #### 3.3.1 IP 协议
109 |
110 | 我们通常用到的 IP 地址,就是网络层中的东西,所规定的的协议就是 IP 协议。很多小伙伴问,IP 地址想必也是地址吧,上边都有唯一标识的 MAC 地址了,IP 地址出来是混饭吃的?为了能够让大家更方便的理解 IP 地址和 MAC 地址,我们可以将 IP 地址抽象成一种逻辑上的地址,也就是说 MAC 地址是物理上的地址,就是定死了。IP 地址呢,是动态分配的,不是固定死的。
111 |
112 |
113 | 我们就是通过 IP 地址来判断两个计算机设备是否在同一子网络中的,那么你会问它是怎么判断的,以及 IP 地址谁给他分配的?又是如何分配的等一些列问题,我们不着急,这里只说一下大体的流程,详细会后续写一大篇。
114 |
115 |
116 | 既然我们通过 IP 地址来判断两个计算机是否处于同一局域网中,那么首先要知道对方的 IP 地址吧?DNS 解析想必大家都知道,可以将域名解析为 IP 地址。好了,我们知道两台计算机的 IP 地址了,怎么进行判断是否同一局域网中?
117 |
118 |
119 |
120 | #### 3.3.2 子网掩码
121 |
122 | 嘿嘿,又是一个只听说过,但是不知道这个什么作用的一个名词,没事,等我聊完,你就明白是做什么的了。
123 |
124 |
125 | 子网掩码就是用来标识同一局域网中的 IP 地址的信息的?什么信息?IP 地址是由 32 个二进制位组成的,也就是四个十进制(如:255.255.255.000)。
126 |
127 |
128 | 子网掩码也是由 32 个二进制位组成的,但是只能用 0 或 1 来表示,如11111111.11111111.11111111.00000000。
129 |
130 |
131 | 到底什么意思呢?有 1 的部分表示网络部分,有 0 表示主机部分,这和判断两台计算机是否在同一局域网中有什么关系?没错,是有关系的!两台计算机的 IP 地址分别和子网掩码进行一种运算(AND 运算),如果结果相同,两台计算机就在同一局域网中,否则就不在同一局域网中。
132 |
133 |
134 | AND 是如何进行运算的,IP 的数据包的组成等问题,不在这里多陈述。
135 |
136 |
137 |
138 | ### 3.4 传输层
139 |
140 | 好了,如果你认为计算机可以进行通信了,那么“小鹿”恭喜你,你已经基本知道了以上几层划分的作用,但是如果你正在一边打 LOL,一边和朋友在 QQ 聊天,突然,游戏中队友聊天信息出现在了 QQ 窗口中,咦?出现了什么情况?
141 |
142 |
143 | 其实是以上层级还是不够,出现上边的原因就是,两台计算机虽然可以通信了,但是每天计算机运行着好多的程序,谁知道你们传输的信息是属于哪些程序的,怨不得 LOL 的聊天信息跑到了 QQ 窗口中。
144 |
145 |
146 | 想必大家猜到了传输层主要用来干啥滴,是的,传输层的主要功能就是为了能够实现“端口到端口”的通信。计算机上运行的不同程序都会分配不同的端口,所以才能使得数据能够正确的传送给不同的应用程序。
147 |
148 |
149 |
150 | #### 3.4.1 UDP 协议
151 |
152 | 加入端口号也需要一套规则,那就是 UDP 协议,但是 UDP协议有个缺点,一旦进行通信,就不知道对方是否接收到数据了,我们再定义一套规则,让其可以和对方进行确认,那么 TCP 出现了。
153 |
154 |
155 |
156 | #### 3.4.2 TCP 协议
157 |
158 | 我们通常说 TCP 三次握手和四次挥手,没错,这就是传输层中完成的,TCP 三次握手涉及到的内容贼多,都可以单独写一篇长文,这里不多陈述,知道它是在传输层中完成的以及它的作用是什么,能够认识到它就好了。
159 |
160 |
161 |
162 | ### 3.5 应用层协议
163 |
164 | “喂,你发给我的是什么破数据,乱七八糟的,我TM能解析吗?能不能按照我的规定给我传送?“
165 |
166 |
167 | “好的,下次不敢了”
168 |
169 |
170 | 想必大家已经猜到了应用层的协议,应用层的功能就是规定了应用程序的数据格式。我们经常用得到的电子邮件、HTTP协议、以及FTP数据的格式,就是在应用层定义的。
171 |
172 | **如果觉得本文对你有帮助,点个star,我希望能够让更多处在递归困惑的人看到,谢谢各位支持!**下一篇我打算出一篇完整关于链表的文章,终极目标:将数据结构与算法每个知识点写成一系列的文章。
173 |
174 |
175 |
176 | **下一篇:** [网络层次模型划分(下)](https://github.com/luxiangqiang/Blog/blob/master/articel/网络原理/网络层次模型划分(下).md)
177 |
178 |
179 | **作者: 小鹿**
180 |
181 | **原创公众号:小鹿动画学编程。**
182 |
183 | **简介:** 和小鹿同学一起用动画的方式从零基础学编程,将 Web前端领域、数据结构与算法、网络原理等通俗易懂的呈献给小伙伴。先定个小目标,原创 1000 篇的动画技术文章,和各位小伙伴共同努力一起学习!
184 |
185 |
186 |
187 |
188 |
189 |
190 |
191 |
192 |
--------------------------------------------------------------------------------
/articel/2021/【2021 第一期】日常开发 26 个常见的 JavaScript 代码优化方案.md:
--------------------------------------------------------------------------------
1 | # 【2021 第一期】:日常开发 26 个常见的 JavaScript 代码优化方案
2 |
3 | 本篇文章整理了在日常开发中 26 个常见的 JavaScript 代码优化方案。
4 |
5 | >本文章已在 [Github blog](https://github.com/luxiangqiang/Blog) 收录,也可在掘金社会同步阅读([戳我](https://juejin.cn/post/6930398744684789774/))。欢迎大伙儿~ Star,文章中若存在不足或者 issues,欢迎在下方或 Github 留言!
6 |
7 | ## 1、`NUll`、`Undefined`、`''`检查
8 | 我们在创建新变量赋予一个存在的变量值的时候,并不希望赋予 `null` 或 `undefined`,我们可以采用一下简洁的赋值方式。
9 | ```javascript
10 | if(test !== null || test !== undefined || test !== ''){
11 | let a1 = test;
12 | }
13 |
14 | // 优化后
15 | let a1 = test || ''
16 | ```
17 |
18 |
19 | ## 2、`null` 值检查并赋予默认值
20 |
21 | ```javascript
22 | let test = null;
23 | let a1 = test || '';
24 | ```
25 |
26 | ## 3、`undefined` 值检查并赋予默认值
27 |
28 | ```javascript
29 | let test = undefined;
30 | let a1 = test || '';
31 | ```
32 |
33 | ## 4、空值合并运算符(`??`)
34 | 空值合并操作符(`??`)是一个逻辑操作符,当左侧的操作数为 `null` 或者 `undefined` 时,返回其右侧操作数,否则返回左侧操作数。
35 | ```javascript
36 | const test= null ?? 'default string';
37 | console.log(test);
38 |
39 | console.log(foo); // expected output: "default string"
40 |
41 | const test = 0 ?? 42;
42 | console.log(test); // expected output: 0
43 | ```
44 | 具体介绍可戳这 [MDN](https://developer.mozilla.org/zh-CN/docs/Web/JavaScript/Reference/Operators/Nullish_coalescing_operator)
45 |
46 | ## 5、声明变量
47 | 当我们想要声明多个共同类型或者相同值的变量时,我们可以采用一下简写的方式。
48 | ```javascript
49 | let test1;
50 | let test2 = 0;
51 |
52 | // 优化后
53 | let test1, test2 = 0;
54 | ```
55 |
56 | ## 6、`if` 多条件判断
57 | 当我们进行多个条件判断时,我们可以采用数组 `includes` 的方式来实现简写。
58 | ```javascript
59 | if(test === '1' || test === '2' || test === '3' || test === '4'){
60 | // 逻辑
61 | }
62 |
63 | // 优化后
64 | if(['1','2','3','4'].includes(test)){
65 | // 逻辑处理
66 | }
67 | ```
68 | ## 7、`if...else` 的简写
69 | 当存在一层或两层 `if...else`嵌套时,我们可以使用三元运算符来简写。
70 | ```javascript
71 | let test = null;
72 | if(a > 10) {
73 | test = true;
74 | } else {
75 | test = false;
76 | }
77 |
78 | // 优化后
79 | let test = a > 10 ? true : false;
80 | // 或者
81 | let test = a > 10;
82 | ```
83 |
84 | ## 8、多变量赋值
85 | 当我们想给多个变量赋不同的值的时候,我们可以采用一下简洁的速记方案。
86 | ```javascript
87 | let a = 1;
88 | let b = 2;
89 | let c = 3;
90 |
91 | // 优化
92 | let [a, b, c] = [1, 2, 3];
93 | ```
94 |
95 | ## 9、算术运算简写优化
96 | 当我们在开发中经常用到算数运算符时,我们可以使用一下方式进行优化和简写。
97 | ```javascript
98 | let a = 1;
99 | a = a + 1;
100 | a = a - 1;
101 | a = a * 2;
102 |
103 | // 优化
104 | a++;
105 | a--;
106 | a *= 2;
107 | ```
108 |
109 | ## 10、有效值判断
110 | 我们经常会在开发中用到的,在这也简单整理一下。
111 | ```javascript
112 | if (test1 === true)
113 | if (test1 !== "")
114 | if (test1 !== null)
115 |
116 | // 优化
117 | if (test1)
118 | ```
119 |
120 | ## 11、多条件(`&&`)判断
121 | 我们通常在项目中遇到条件判断后跟函数执行,我们可以使用一下简写方式。
122 | ```javascript
123 | if (test) {
124 | foo();
125 | }
126 |
127 | //优化
128 | test && foo();
129 | ```
130 |
131 | ## 12、多个比较 `return`
132 |
133 | 在 return 的语句中使用比较,可以将其进行缩写的形式如下。
134 |
135 | ```javascript
136 | let test;
137 | function checkReturn() {
138 | if (!(test === undefined)) {
139 | return test;
140 | } else {
141 | return foo('test');
142 | }
143 | }
144 |
145 | // 优化
146 | function checkReturn() {
147 | return test || foo('test');
148 | }
149 | ```
150 |
151 | ## 13、`Switch` 的缩写
152 | 遇到如下形式的 switch 语句,我们可以将其条件和表达式以键值对的形式存储。
153 | ```javascript
154 | switch (type) {
155 | case 1:
156 | test1();
157 | break;
158 | case 2:
159 | test2();
160 | break;
161 | case 3:
162 | test();
163 | break;
164 | // ......
165 | }
166 |
167 | // 优化
168 | var obj = {
169 | 1: test1,
170 | 2: test2,
171 | 3: test
172 | };
173 |
174 | obj[type] && obj[type]();
175 | ```
176 |
177 | ## 14、for 循环缩写
178 |
179 | ```javascript
180 | for (let i = 0; i < arr.length; i++)
181 |
182 | // 优化
183 | for (let i in arr) or for (let i of arr)
184 | ```
185 |
186 | ## 15、箭头函数
187 |
188 | ```javascript
189 | function add() {
190 | return a + b;
191 | }
192 |
193 | // 优化
194 | const add = (a, b) => a + b;
195 | ```
196 |
197 | ## 16、短函数调用
198 |
199 | ```javascript
200 | function fn1(){
201 | console.log('fn1');
202 | }
203 |
204 | function fn2(){
205 | console.log('fn1');
206 | }
207 |
208 | if(type === 1){
209 | fn1();
210 | }else{
211 | fn2();
212 | }
213 |
214 | // 优化
215 | (type === 1 ? fn1 : fn2)();
216 |
217 | ```
218 |
219 | ## 17、数组合并与克隆
220 |
221 | ```javascript
222 | const data1 = [1, 2, 3];
223 | const data2 = [4 ,5 , 6].concat(data1);
224 |
225 | // 优化
226 | const data2 = [4 ,5 , 6, ...data1];
227 | ```
228 | 数组克隆:
229 |
230 | ```javascript
231 | const data1 = [1, 2, 3];
232 | const data2 = test1.slice()
233 |
234 | // 优化
235 | const data1 = [1, 2, 3];
236 | const data2 = [...data1];
237 | ```
238 |
239 | ## 18、字符串模版
240 |
241 | ```javascript
242 | const test = 'hello ' + text1 + '.'
243 |
244 | // 优化
245 | const test = `hello ${text}.`
246 | ```
247 |
248 | ## 19、数据解构
249 |
250 | ```javascript
251 | const a1 = this.data.a1;
252 | const a2 = this.data.a2;
253 | const a3 = this.data.a3;
254 |
255 | // 优化
256 | const { a1, a2, a3 } = this.data;
257 | ```
258 |
259 | ## 20、数组查找特定值
260 |
261 | 数组按照索引来查找特定值,我们可以通过逻辑位运算符 `~` 来代替判断。
262 | >“~”运算符(位非)用于对一个二进制操作数逐位进行取反操作
263 | ```javascript
264 | if(arr.indexOf(item) > -1)
265 |
266 | // 优化
267 | if(~arr.indexOf(item))
268 |
269 | // 或
270 | if(arr.includes(item))
271 | ```
272 |
273 | ## 21、`Object.entries()`
274 | 我们可以通过 Object.values() 将对象的内容转化为数组。如下:
275 | ```javascript
276 | const data = { a1: 'abc', a2: 'cde', a3: 'efg' };
277 | Object.entries(data);
278 |
279 | /** 输出:
280 | [ [ 'a1', 'abc' ],
281 | [ 'a2', 'cde' ],
282 | [ 'a3', 'efg' ]
283 | ]
284 | **/
285 | ```
286 |
287 | ## 22、`Object.values()`
288 |
289 | ```javascript
290 | const data = { a1: 'abc', a2: 'cde' };
291 | Object.values(data);
292 |
293 | /** 输出:
294 | [ 'abc', 'cde']
295 | **/
296 | ```
297 |
298 | ## 23、求平方
299 |
300 | ```javacript
301 | Math.pow(2,3);
302 |
303 | // 优化
304 | 2**3;
305 | ```
306 |
307 | ## 24、指数简写
308 |
309 | ```javascript
310 | for (var i = 0; i < 100000; i++)
311 |
312 | // 优化
313 | for (var i = 0; i < 1e4; i++) {
314 | ```
315 |
316 | ## 25、对象属性简写
317 |
318 | ```javascript
319 | let key1 = '1';
320 | let key2 = 'b';
321 | let obj = {key1: key1, key2: key2};
322 |
323 | // 简写
324 | let obj = {
325 | key1,
326 | key2
327 | };
328 | ```
329 |
330 | ## 26、字符串转数字
331 |
332 | ```javascript
333 | let a1 = parseInt('100');
334 | let a2 = parseFloat('10.1');
335 |
336 | // 简写
337 | let a1 = +'100';
338 | let a2 = +'10.1';
339 | ```
340 |
--------------------------------------------------------------------------------
/articel/2021/【2021 第二期】简而不单,单而不简的执行上下文.md:
--------------------------------------------------------------------------------
1 | # 2021 第二期。
2 |
3 | 想必大伙儿看到本期的标题很有疑惑,为什么是**简而不单,单而不简的执行上下文**呢?我来先解释一下,对于 javaScript 上一些抽象的概念,我们可以把它讲的非常复杂,也可以把它讲的极其简单,更可以把它讲的既复杂又简单。
4 |
5 | 嗯~ 最近重新回顾了这些抽象的概念,发现有些概念之前并不能很好的融会贯通,所以把这些相对抽象难以理解的概念作为几期文章来写。
6 |
7 | 不妨打开在谷歌搜「执行上下文」关键词,几篇相对排名靠前的优秀文章回呈现出来。
8 |
9 | - [[译] 理解 JavaScript 中的执行上下文和执行栈](https://juejin.cn/post/6844903682283143181)
10 |
11 | - [深入理解JavaScript执行上下文和执行栈](https://segmentfault.com/a/1190000018550118)
12 |
13 | - [JavaScript深入之执行上下文](https://github.com/mqyqingfeng/Blog/issues/8)
14 |
15 | 看到这几篇文章,作者尽心尽力的去解释这些比较抽象的概念,文字很多,图相对较少。我个人觉得要想更好的理解抽象概念,不得不借助可视化的图像减少作者和读者之间的理解力和理解差错。所以,不用担心,这篇文章小鹿会通过加入更多的图片深入浅出的解释这些抽象的概念。
16 |
17 | ```!
18 | 本文章已在 [Github blog 第二期]() 收录,欢迎大伙儿~ Star,文章中若存在不足或者 issues,欢迎在下方或 Github 留言!
19 | ```
20 |
21 | ## 本期目录
22 |
23 | - [1、执行上下文](1、执行上下文)
24 |
25 | - [1.1 JavaScript 引擎]()
26 |
27 | - [1.2 执行栈]()
28 |
29 | - [1.3 执行上下文]()
30 |
31 | - [2、执行上下文的分类]()
32 |
33 | - [2.1 全局执行上下文]()
34 |
35 | - [2.2 局部执行上下文]()
36 |
37 | - [3、执行上下文两个阶段]()
38 |
39 | - [3.1 创建阶段]()
40 |
41 | - [3.2 执行阶段]()
42 |
43 |
44 | ## 1、执行上下文
45 |
46 | ### 1.1 JavaScript 引擎
47 |
48 | 说到执行上下文,不得不先扯扯 JavaScript 引擎,[JavaScript 引擎](https://zh.wikipedia.org/wiki/JavaScript%E5%BC%95%E6%93%8E)是什么?考虑到这篇文章不专门写 JavaScript 引擎,可以自己谷歌一下。说白了,`JavaScript` 引擎就是用来「**解释**」、「**编译**」和「**执行**」`JavaScript` 代码的,毕竟开发人员写的 JS 代码只能够让开发者认得出来,交给计算机,由于计算机只识别二进制,所以中间需要进行一系列的解释和转化才能看懂执行这些 `JavaScript` 代码。
49 |
50 | 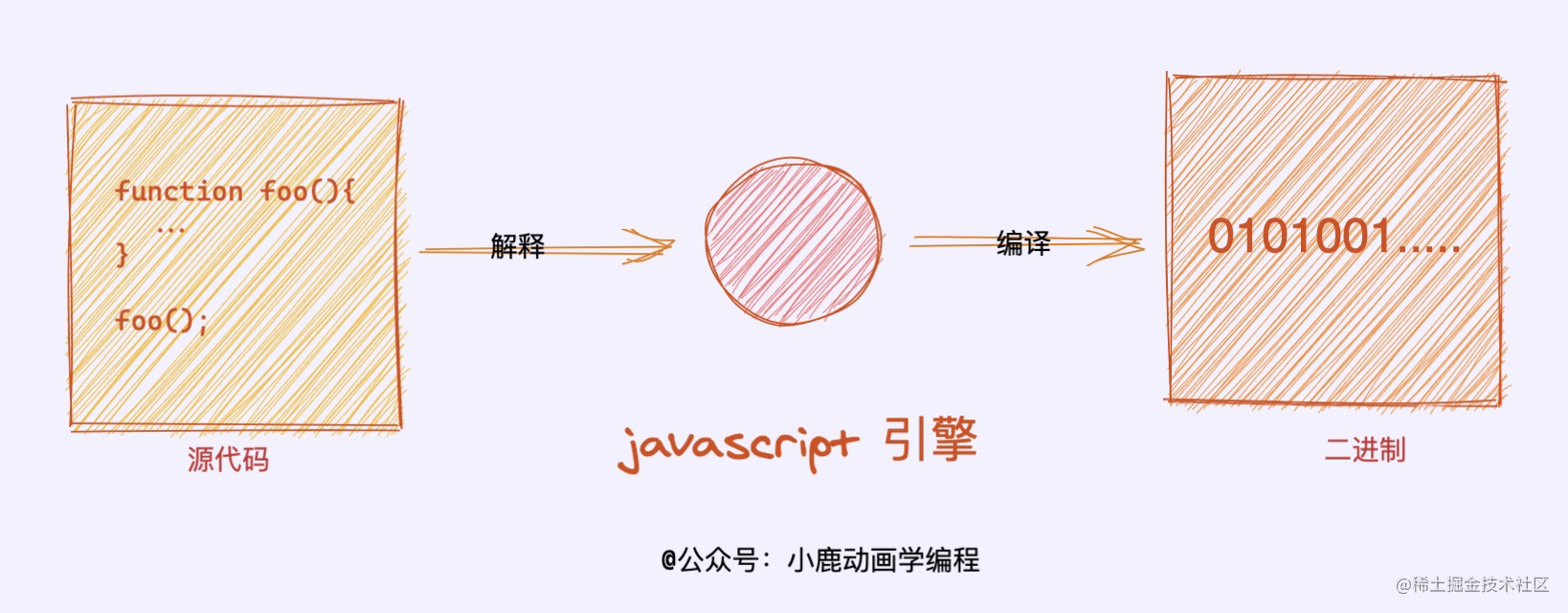
51 |
52 | ### 1.2 执行栈 (`Execution stack`)
53 |
54 | ```!
55 | 小鹿注:保证 JavaScript 代码的执行"顺序"。
56 | ```
57 |
58 | `JavaScript` 引擎既然可以执行 `JS` 的代码,那么是按照什么顺序执行的,又是怎么保证这些顺序而不被所打乱的。先看一段简单的代码:
59 |
60 | ```javaScript
61 | var foo2 = function () {
62 | console.log('foo2');
63 | }
64 |
65 | var foo1 = function () {
66 | console.log('foo1');
67 | foo2()
68 | console.log('foo3')
69 | }
70 |
71 | foo1(); // 输出:“foo1 foo2 foo3”
72 | ```
73 |
74 | 通过上述代码片段的执行,输出的顺序为`'foo1 foo2 foo3'`。
75 |
76 | 代码执行,`foo1()`函数先执行,首先输出`'foo1'`,遇到 `foo2()` 函数的执行命令,将执行权交给 `foo2`, `foo2` 函数体执行,输出`'foo2'`。`foo2` 执行完毕后,将执行权交回 `foo1` 函数,最后输出`'foo3'`。
77 |
78 | 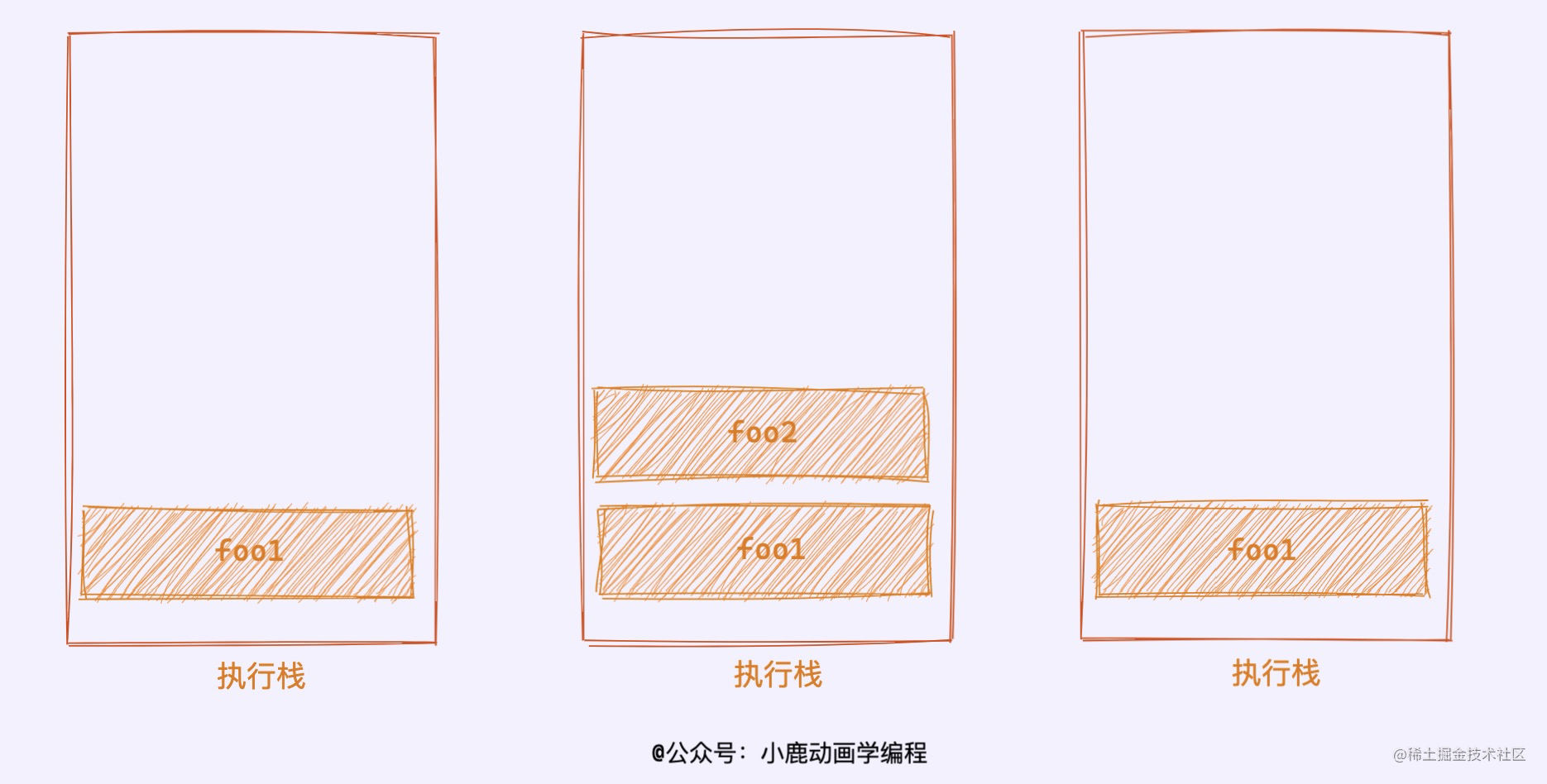
79 |
80 | 我们可以找出上述代码执行的规律,先执行的函数,会在最后退出,后执行的函数,先执行完毕。这个执行顺序不就是“栈”的`“先进后出”``“后进先出”`的结构嘛。`JavaScript` 引擎将其这种执行结构称为「**执行栈**」,用于保证 `JavaScript` 代码的顺序。
81 |
82 |
83 | ### 1.3 执行上下文(`Exception Context`)
84 |
85 | ```!
86 | 小鹿注:将执行的代码"模块化" —— 执行上下文的分类。
87 | ```
88 |
89 | 什么是执行上下文?虽然我们在“执行上下文”词义上很难直接理解,但是它具体代表的是什么,是很容易理解的,下面我把“执行上下文”的抽象概念进行具体化。
90 |
91 | 上述我们已经解释了 `JavaScript` 引擎是使用执行栈来保证代码的执行顺序的,但是执行过程中需要涉及到一些变量的作用范围界定(作用域)、闭包等复杂情况,我们需要 JavaScript 引擎引入一种机制来解决这些看起来复杂的问题,所以「`执行上下文`」的概念产生了。
92 |
93 | 
94 |
95 | 但是,执行上下文是什么?这不得不让我想起组件的模块化开发,之前的一个网页应用代码从上到下一个文件写下来几千行代码,难以阅读、难以维护,所以有了后来的模块化开发。每个模块都有自己的功能,都有属于自己的局部变量和样式。
96 |
97 | 我们可以理解为 `JavaScript` 引擎为了更好的解释和执行代码,所以引入类似于像组件模块的“`执行上下文`”的概念用于管理运行时代码的复杂度。
98 |
99 |
100 | ## 2、执行上下文的分类
101 |
102 | 上述我们把抽象的“执行上下文”类似于“模块”的具体概念便于理解。当然,执行上下文也就是所谓的“模块”也有不同的分类,在这里具体只展开两种,「`全局执行上下文`」和「`局部执行上下文`」。
103 |
104 |
105 | ### 2.1 全局执行上下文(`Global Exception Context`)
106 |
107 | 全局上下文这个“模块”由两部分组成,「`全局对象`」和「`this`」。
108 |
109 |
110 | 下图是全局执行上下文的最基本形式。包含一个 `window` 对象,以及一个 `this` 变量,而这个 `this` 变量是指向 `window` 对象的,如最右图的打印结果。
111 |
112 | 
113 |
114 | 从这里我们看出,执行上下文可以理解为是一个在内存中的「`对象和变量`」集合的模块(或者说是片段),这也是为什么我们可以把它看作类似“模块”的原因(除此之外还有其他作用)。
115 |
116 | > 小鹿注:为了便于理解,定义是我自己总结的,如有欠缺欢迎指出~
117 |
118 | ### 2.2 局部执行上下文
119 |
120 | 局部执行上下文和全局执行上下文类似,但不完全相同,在函数局部执行上下文中,需要注意的有一下两点:
121 |
122 | - 函数传入的参数会作为局部执行上下文的变量来存储
123 |
124 | - 局部上下文有一个 `arguments` 参数对象(参考)
125 |
126 | 局部执行上下文内容会在下面的两个阶段中详细讲到。
127 |
128 | ## 3、执行上下文两个阶段
129 |
130 | 无论是全局执行上下文还是局部的执行上下文,都会经历两个阶段,分别是「`创建`」和「`执行`」。
131 |
132 | 如下我们有一段代码:
133 |
134 | ```javascript
135 | var name = "小鹿";
136 | var age = 23;
137 |
138 | function getInfo(){
139 | return {
140 | name: name,
141 | age: age
142 | };
143 | }
144 | ```
145 |
146 | ### 3.1 创建阶段(`Creation`)
147 |
148 | 创建阶段要完成的事情,如下:
149 |
150 | - 在堆内存中创建全局对象(`global object`)—— 浏览器环境是 `windows`,`Node` 环境是 `Global`
151 | - 让 `this` 变量指向这个全局对象
152 | - 设置当前执行上下文中「变量和函数」的内存空间
153 | - 将声明的变量加入内存中(同时挂在到全局对象上),为变量赋值 `undifined`,函数存储的是字符串形式
154 |
155 |
156 | 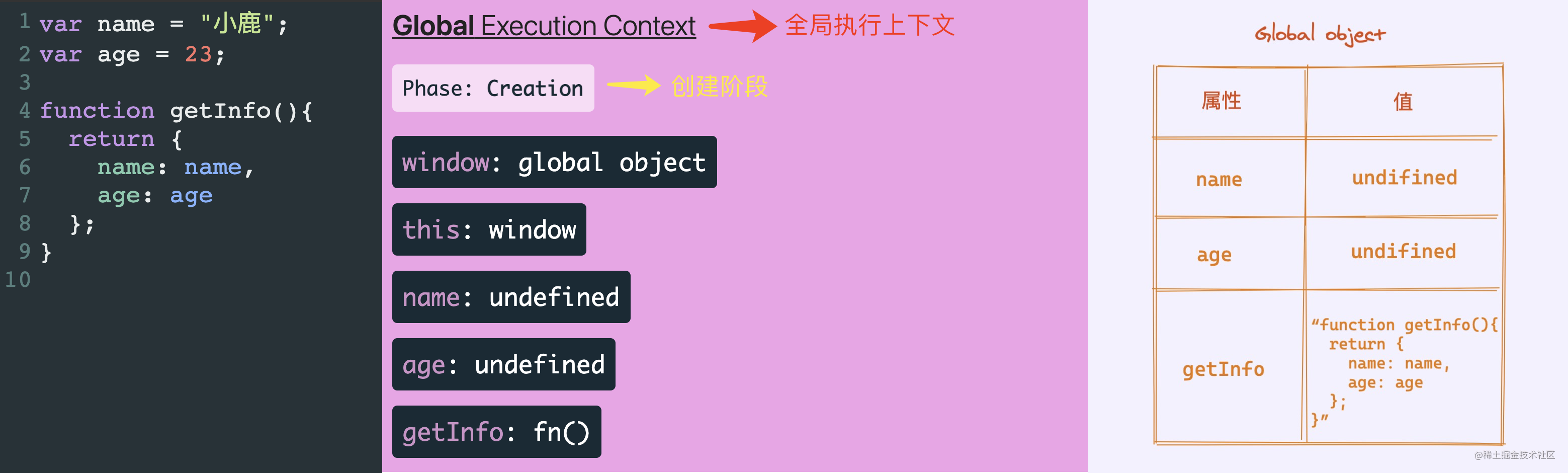
157 |
158 | >小鹿注:左 (1) 图执行的代码,左 (2) 图创建阶段完成后的执行上下文内存中状态,右 (1) 创建阶段全局对象的状态。
159 |
160 | `JavaScript` 引擎在执行代码之前,先在堆内存中创建全局执行上下文,生成全局对象(`global object`),然后让 `this` 变量指向这个变量。`JavaScript` 发现代码中声明的两个变量 `name` 和 `age`,然后在全局执行上下文中申请内存空间,将变量存储到该内存空间内,然后为该变量赋值 `undefined`,函数就以字符串的形式存储在内存中。
161 |
162 | ```!
163 | 小鹿注:在创建阶段为变量声明指定默认值(`undefined`)的过程称为「变量提升」。
164 | ```
165 |
166 | ### 3.2 执行阶段(`Execution`)
167 |
168 | 全局执行上下文创建完成之后,开始由创建状态(`Creation`)变为执行状态( `Execution`)。`JavaScript` 引擎开始逐行运行和执行代码,并为在创建阶段放入内存的变量赋予值。
169 |
170 | 
171 |
172 | >小鹿注:左 (1) 图执行的代码,左 (2) 图执行阶段完成后的执行上下文内存中状态,右 (1) 执行阶段全局对象的状态。
173 |
174 | 局部执行上下文和全局执行上下文的创建和执行过程是一模一样的。但是全局执行上下文创建一次,而函数局部执行上下文是随着函数的每次调用都要创建一个局部执行上下文。
175 |
176 | 还是上述例子,执行结果如下:
177 |
178 | ```javascript
179 | var name = "小鹿";
180 | var age = 23;
181 |
182 | function getInfo(name){
183 | console.log(name);
184 | return {
185 | name: name,
186 | age: age
187 | };
188 | }
189 |
190 | getInfo(name);
191 | ```
192 |
193 | 函数局部上下文执行状态如下:
194 |
195 | 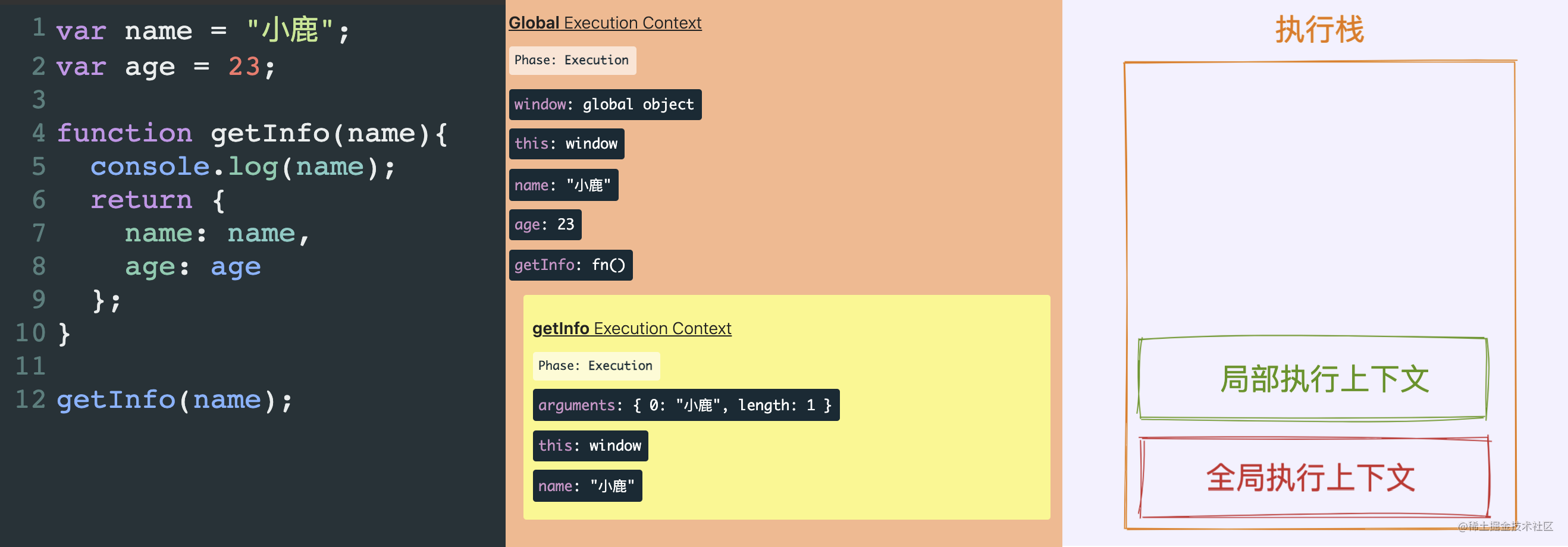
196 |
197 | >小鹿注:由于函数中没有定义新的变量,所以在这里没有变量提升。
198 |
199 | 我们了解了什么是函数局部上下文,当函数局部上下文执行完毕之后,就会执行出栈操作,将执行权交给父级执行上下文(可能是局部执行上下文,也可能是全局执行上下文),上述 `getInfo` 函数执行完毕的状态如下图所示。
200 |
201 | 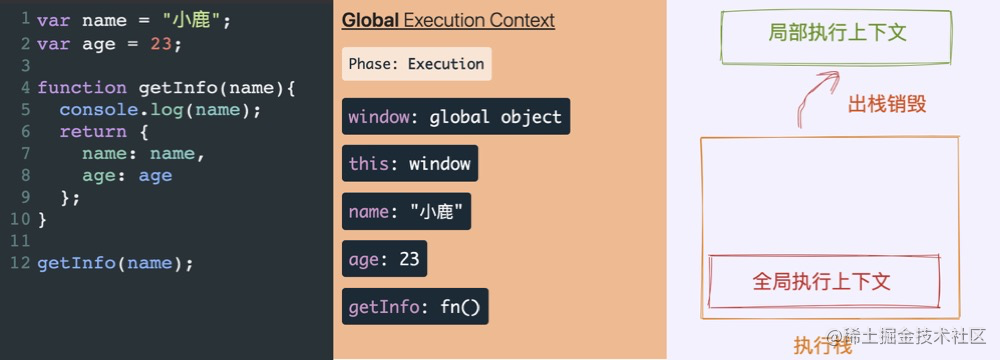
202 |
203 | 此时的函数执行完毕,局部执行上下文出栈销毁,执行权交给全局执行上下文继续执行其他代码。
204 |
205 | 由于 JavaScript 是单线程的,一次只能执行一个任务,为了方便大伙儿理解,左(3)图 是执行栈的调用情况。当然,我们也可以发现,左(2)图是以嵌套的方式来模拟执行栈的操作,每一个嵌套选项都是堆栈中一个新的执行上下文。
206 |
207 | ## ❤️ 原创不易,欢迎 star
208 |
209 | > 我是小鹿,文章同步更新 [Github](https://github.com/luxiangqiang/Blog/blob/master/articel/2021/%E3%80%902021%20%E7%AC%AC%E4%B8%80%E6%9C%9F%E3%80%91%E6%97%A5%E5%B8%B8%E5%BC%80%E5%8F%91%2026%20%E4%B8%AA%E5%B8%B8%E8%A7%81%E7%9A%84%20JavaScript%20%E4%BB%A3%E7%A0%81%E4%BC%98%E5%8C%96%E6%96%B9%E6%A1%88.md),也可以在微信搜一搜「**小鹿动画学编程**」第一时间接收文章更新通知,回复“**前端**”可获取小鹿整理的备战面试小册。
--------------------------------------------------------------------------------
/articel/网络原理/TCP 之三次握手.md:
--------------------------------------------------------------------------------
1 | ## 动画:TCP 三次握手
2 |
3 | ### 写在前边
4 |
5 | TCP 三次握手过程对于面试是必考的一个,所以不但要掌握 TCP 整个握手的过程,其中有些小细节也更受到面试官的青睐。
6 |
7 | 对于这部分掌握以及 TCP 的四次挥手,小鹿将会以动画的形式呈现给每个人,这样将复杂的知识简单化,理解起来也容易了很多,尤其对于一个初学者来说。
8 |
9 |
10 |
11 | ### 学习导图
12 |
13 | 
14 |
15 |
16 |
17 | ### 一、TCP 是什么?
18 |
19 | `TCP(Transmission Control Protocol 传输控制协议)`是一种面向连接的、可靠的、基于字节流的传输层通信协议。
20 |
21 | 我们知道了上述了解到了 `TCP `的定义,通俗一点的讲,`TCP `就是一个双方通信的一个规范标准(协议)。
22 |
23 | 我们在学习 `TCP` 握手过程之前,首先必须了解 `TCP` 报文头部的一些标志信息,因为在 `TCP `握手的过程中,会使用到这些报文信息,如果没有掌握这些信息,在学习握手过程中,整个人处于懵逼状态,也是为了能够深入 `TCP` 三次握手的原理。
24 |
25 |
26 |
27 | ### 二、TCP 头部报文
28 |
29 | 
30 |
31 |
32 |
33 | #### 2.1 `source port` 和 `destination port`
34 |
35 | > 两者分别为「源端口号」和「目的端口号」。源端口号就是指本地端口,目的端口就是远程端口。
36 |
37 | 一个数据包(`pocket`)被解封装成数据段(`segment`)后就会涉及到连接上层协议的端口问题。
38 |
39 | 可以这么理解,我们可以想象发送方很多的窗户,接收方也有很多的窗户,这些窗口都标有不同的端口号,源端口号和目的端口号就分别代表从哪个规定的串口发送到对方接收的窗口。不同的应用程度都有着不同的端口,之前网络分层的文章中有提到过。
40 |
41 | 
42 |
43 |
44 |
45 | > 扩展:应用程序的端口号和应用程序所在主机的 IP 地址统称为 socket(套接字),IP:端口号, 在互联网上 socket 唯一标识每一个应用程序,源端口+源IP+目的端口+目的IP称为”套接字对“,一对套接字就是一个连接,一个客户端与服务器之间的连接。
46 |
47 |
48 |
49 | #### 2.2 `Sequence Numbe`
50 | >称为「序列号」。用于 TCP 通信过程中某一传输方向上字节流的每个字节的编号,为了确保数据通信的有序性,避免网络中乱序的问题。接收端根据这个编号进行确认,保证分割的数据段在原始数据包的位置。
51 |
52 |
53 |
54 | 
55 |
56 |
57 |
58 | 再通俗一点的讲,每个字段在传送中用序列号来标记自己位置的,而这个字段就是用来完成双方传输中确保字段原始位置是按照传输顺序的。(发送方是数据是怎样一个顺序,到了接受方也要确保是这个顺序)
59 |
60 | >PS:初始序列号由自己定,而后绪的序列号由对端的 ACK 决定:SN_x = ACK_y (x 的序列号 = y 发给 x 的 ACK),这里后边会讲到。
61 |
62 |
63 |
64 | #### 2.3 `Acknowledgment Numbe`
65 | >称为「确认序列号」。确认序列号是接收确认端所期望收到的下一序列号。确认序号应当是上次已成功收到数据字节序号加1,只有当标志位中的 ACK 标志为 1 时该确认序列号的字段才有效。主要用来解决不丢包的问题。
66 |
67 | 若确认号=N,则表明:到序号N-1为止的所有数据都已正确收到。
68 |
69 | 在这里,现在我们只需知道它的作用是什么,就是在数据传输的时候是一段一段的,都是由序列号进行标识的,所以说,接收端每接收一段,之后就想要的下一段的序列号就称为「确认序列号」。
70 |
71 |
72 |
73 | #### 2.4 `TCP Flag`
74 |
75 | `TCP` 首部中有 6 个标志比特,它们中的多个可同时被设置为 `1`,主要是用于操控 `TCP` 的状态机的,依次为`URG,ACK,PSH,RST,SYN,FIN`。
76 |
77 | 不要求初学者全部掌握,在这里只讲三个重点的标志:
78 |
79 |
80 |
81 | ##### 2.4.1 `ACK`
82 | 这个标识可以理解为发送端发送数据到接收端,发送的时候 ACK 为 0,标识接收端还未应答,一旦接收端接收数据之后,就将 ACK 置为 1,发送端接收到之后,就知道了接收端已经接收了数据。
83 |
84 | 
85 |
86 |
87 |
88 | > 此标志表示「应答域有效」,就是说前面所说的TCP应答号将会包含在 TCP 数据包中;有两个取值:0 和 1,为 1 的时候表示应答域有效,反之为 0;
89 |
90 |
91 |
92 | ##### 2.4.2 `SYN`
93 | >表示「同步序列号」,是 TCP 握手的发送的第一个数据包。
94 |
95 | 用来建立 TCP 的连接。SYN 标志位和 ACK 标志位搭配使用,当连接请求的时候,SYN=1,ACK=0连接被响应的时候,SYN=1,ACK=1;这个标志的数据包经常被用来进行端口扫描。扫描者发送一个只有 SYN 的数据包,如果对方主机响应了一个数据包回来 ,就表明这台主机存在这个端口。看下面动画:
96 |
97 | 
98 |
99 |
100 |
101 | ##### 2.4.3 `FIN`
102 | >表示发送端已经达到数据末尾,也就是说双方的数据传送完成,没有数据可以传送了,发送FIN标志位的 TCP 数据包后,连接将被断开。这个标志的数据包也经常被用于进行端口扫描。
103 |
104 | 这个很好理解,就是说,发送端只剩最后的一段数据了,同时要告诉接收端后边没有数据可以接受了,所以用FIN标识一下,接收端看到这个FIN之后,哦!这是接受的最后的数据,接受完就关闭了。动画如下:
105 |
106 | 
107 |
108 | #### 2.5 `Window size`
109 | 称为滑动窗口大小。所说的滑动窗口,用来进行流量控制。
110 |
111 |
112 |
113 | ### 3、为什么进行 TCP 三次握手?
114 | 如果之前你不了解网络分层的话,建议看看写的文章。
115 |
116 | [网络分层协议]([https://github.com/luxiangqiang/Blog/blob/master/articel/%E7%BD%91%E7%BB%9C%E5%8E%9F%E7%90%86/%E7%BD%91%E7%BB%9C%E5%88%86%E5%B1%82%E5%88%92%E5%88%86%EF%BC%88%E4%B8%8A%EF%BC%89.md](https://github.com/luxiangqiang/Blog/blob/master/articel/网络原理/网络分层划分(上).md))
117 |
118 | 第一,为了确认双方的接收与发送能力是否正常。第二,指定自己的初始化序列号,为后面的可靠传送做准备。第三,如果是 https 协议的话,三次握手这个过程,还会进行数字证书的验证以及加密密钥的生成到。
119 |
120 | 如果你了解 UDP 的话,TCP 的出现正式弥补了 UDP 不可靠传输的缺点。但是 TCP 的诞生,也必然增加了连接的复杂性。
121 |
122 |
123 |
124 | ### 4、TCP 三次握手过程?
125 | TCP 三次握手的过程掌握最重要的两点就是客户端和服务端状态的变化,另一个是三次握手过程标志信息的变化,那么掌握 TCP 的三次握手就简单多了。下面我们就以动画形式进行拆解三次握手过程。
126 |
127 | 
128 |
129 | - **初始状态**:客户端处于 `closed(关闭) `状态,服务器处于 `listen(监听) ` 状态。
130 |
131 | [](https://github.com/luxiangqiang/Blog/blob/master/articel/%E7%BD%91%E7%BB%9C%E5%8E%9F%E7%90%86/images/%E5%88%9D%E5%A7%8B%E5%8C%96%E7%8A%B6%E6%80%81.png)
132 |
133 |
134 |
135 | - **第一次握手**:客户端发送请求报文将 `SYN = 1 `同步序列号和初始化序列号`seq = x`发送给服务端,发送完之后客户端处于` SYN_Send `状态。
136 |
137 | 
138 |
139 |
140 |
141 | - **第二次握手**:服务端受到 `SYN` 请求报文之后,如果同意连接,会以自己的同步序列号`SYN(服务端) = 1`、初始化序列号 `seq = y`和确认序列号(期望下次收到的数据包)`ack = x+ 1` 以及确认号`ACK = 1`报文作为应答,服务器为`SYN_Receive `状态。
142 |
143 | 
144 |
145 |
146 |
147 | - **第三次握手**: 客户端接收到服务端的 `SYN + ACK`之后,知道可以下次可以发送了下一序列的数据包了,然后发送同步序列号 `ack = y + 1`和数据包的序列号 `seq = x + 1`以及确认号`ACK = 1`确认包作为应答,客户端转为`established`状态。
148 |
149 | 
150 |
151 |
152 |
153 | ### 5、为什么不是一次、二次握手?
154 | >防止了服务器端的一直等待而浪费资源。
155 |
156 | 为了防止已失效的连接请求报文段突然又传送到了服务端,因而产生错误。如果此时客户端发送的延迟的握手信息服务器收到,然后服务器进行响应,认为客户端要和它建立连接,此时客户端并没有这个意思,但 `server` 却以为新的运输连接已经建立,并一直等待 `client` 发来数据。这样,`server` 的很多资源就白白浪费掉了。
157 |
158 |
--------------------------------------------------------------------------------
/articel/数据结构与算法系列/数据结构与算法之递归系列.md:
--------------------------------------------------------------------------------
1 | # 数据结构与算法之递归系列
2 |
3 | 
4 |
5 |
6 |
7 | ## 目录
8 |
9 | 
10 |
11 |
12 |
13 | ## 前言
14 |
15 | 几个月之前就想写这样一篇文章分享给大家,由于自己有心而力不足,没有把真正的学到的东西沉淀下来,所以一直在不断的自学。可能是因为在一所三流大学,资源也比较少,只能自己在网搜索相关资料,在互联网上遇到了一些朋友的帮助下去深入理解,然后自己抽出大量时间做题总结、归纳,才会把已有的知识概念所被自己吸收和理解,形成了自己的技术思想体系。
16 |
17 | 然后自己又用了一个星期的时间去整理、分类,才有了这篇 8000 字有关递归知识的分享,希望能够帮助正在学习递归的小伙伴们。而且有了这篇文章的支撑和动力,往后还会写出关于数据结构与算法一些难懂的概念简单化。如果文章中有错误的地方,希望大家指正,能够为他人分享出更有质量的内容!
18 |
19 |
20 |
21 | ## 为什么要写这篇递归文章
22 |
23 | 看了很多关于递归的文章,也总结了很多递归的文章,也看了多篇文章下方读者的评论。有的读者评论到文章清晰易懂,有的却喷作者写的存在很多错误,埋怨作者写出来很垃圾,还不如不写。我想从理性的角度说一下,创作者写文章的最初好意是能够帮助别人对此知识点有进一步的了解,并不代表一定能够满足每个人的要求。
24 |
25 | 另一方面,每篇文章的作者可能理解的不够透彻,很多地方可能存在许多错误,包括理解上的错误,笔误等,这也是写文章的第二个目的,能够让别人挑出自己文章中的不足,能够达到与别人共同进步的目的,一举两得,两全其美。
26 |
27 | 接下来分享的文章是关于递归的,这篇文章不单单分享递归的一切,我觉得更重要的是向每位读者传递一个思想。思想?对的,没错!这篇文章不能说包含递归的边边角角,但是通过自己的理论上的学习和实践,有了自己的一套递归思想。
28 |
29 | 什么问题该用递归,什么问题用递归简洁,什么问题就不能使用递归解决,以及对于特定的问题用递归解决的陷阱,能不能进一步对递归进行二次优化,这些都是今天小鹿分享的内容。
30 |
31 |
32 |
33 | ## 什么是递归?
34 |
35 | > 递归,顾名思义,有递有归才叫递归,有递无归,有归无递那叫 “耍流氓” 。
36 |
37 |
38 |
39 | ## 为什么要学习递归?
40 |
41 | 我们学习一门技术也好,编程语言也好,首先学习之前我们知道它将能给我们带来什么,能帮助我们解决什么样的问题,这也是激励我们去学习它的动力所在。
42 |
43 | 从数组到链表、散列表,再到基本算法等,直到遇到递归之后,感觉非常的难理解。我相信每个人都有这种感觉,一开始觉得非常难,经历了九九八十一难之后,还是没有弄懂递归里边的猫腻,然后就自然而然的跳过了。
44 |
45 | 后来我就开始刷了一个月的 LeetCode 题,发现递归在数据结构与算法中有着一席之地,统治着江山。大部分的题都可以用递归去解决,如:二叉树的遍历、回溯算法、0-1 背包问题、深度优先遍历、回溯算法等等,我整理了至少二三十到关于递归的题,才发现递归的重要性,所以不得不重新深入递归学习,所有有了今天这篇文章。
46 |
47 |
48 |
49 | ## 怎么理解递归的过程?
50 |
51 | > 上方我对递归“耍流氓”式的定义并不能让你准确的理解递归是什么,那么我们就来活生生的举个生活中的例子。
52 |
53 |
54 |
55 | #### 1、问题
56 |
57 | > 比如你和小鹿我一样,在大学里喜欢插队打饭(作为一个三好学生,我怎么能干这种事呢?哈哈),那么队伍后边的同学本数着自己前边还有 5 个同学就改轮到自己了,由于前边同学不断的插队,这时他发现,怎么觉得自己离着打饭的窗口越来越远呢?这时如果他想知道自己在队队列中的的第几个(前提是前边不再有人插队),用递归思想来解决,我们怎么做呢?
58 |
59 |
60 |
61 | #### 2、“递”
62 |
63 | > 于是他问前边的同学是第几位,前边的同学也不只到呀,于是前边的同学问他前边的同学是第几位,直到前边第二个同学问到第一个正在打饭的同学是队伍的第几个(有点小尴尬)。打饭的同学不耐烦的说,没看到我是第一个正在打饭吗?**这个过程其实是就是一个递归中“递”的过程**。
64 |
65 |
66 |
67 | #### 3、“归”
68 |
69 | > 然后前边打饭的第二个同学不耐烦的又告诉第三个同学,我是第二个,没看单我前边有个家伙正在打饭吗?然后第三个传给第四个,以后往后传,直到那位逐渐远离窗口的同学的前一个人告诉他是第几个之后,他知道了自己目前在队伍中的第几个位置。**这个过程我们可以理解为递归中“归”的过程**。
70 |
71 |
72 |
73 | #### 4、终止条件
74 |
75 | > “打饭的同学不耐烦的说,没看到我是第一个正在打饭吗?”,在递归中,我们称为**终止条件**。
76 |
77 |
78 |
79 | #### 5、怎么理解递归?
80 |
81 | > 1)问题虽然是层层递归的分析,但是用程序表示的时候,不要层层的在大脑中调用递归代码去想,这样可能会使你完全陷入到 “递” 的过程中去,“归” 的时候,归不出来了,这些都是我们交给计算机干的事情。
82 | >
83 | > 2)那我们在写程序的时候怎么理解递归呢?我们只找问题之间存在的关系,**屏蔽掉递归的细节**,具体看(五)分析。
84 |
85 |
86 |
87 | ## 满足递归的三个条件
88 |
89 | > 通过上方的例子,我们可以很容易的总结出满足递归的三个条件。
90 |
91 |
92 |
93 | #### 1、一个问题能不能分解成多个子问题来解决
94 |
95 | > 想知道自己在队伍中的位置,将其问题分解为“每个人所处队伍中的位置”这样的多个子问题。
96 |
97 |
98 |
99 | #### 2、该问题是否和子问题的解决思路相同
100 |
101 | > 想要知道自己当前的位置,就要问前边人所处的位置。那么前边人想要知道自己所处的位置,就要知道他前边人的位置。所以说,该问题和子问题的解决思路相同,满足第二个条件。
102 |
103 |
104 |
105 | #### 3、该问题是否有终止条件
106 |
107 | > 第一个正在打饭的同学说自己是队伍中的第一人,这就是所谓的终止条件,找到终止条件之后就开始进行“归”的过程。
108 |
109 |
110 |
111 | ## 怎么编写递归代码?
112 |
113 | > 如果你对递归有了一定的了解,上边的例子对你来说小菜一碟,下边还有更大的难度来进行挑战。那么问题分析清楚了,怎么根据问题编写出递归代码来呢?
114 |
115 |
116 |
117 | #### 1、写出递推公式
118 |
119 | > 写递归公式最重要的一点就是找到该问题和子问题的关系,怎么找到之间存在的关系呢?这里我要强调注意的一点就是不要让大脑试图去想层层的递归过程,毕竟大脑的思考方式是顺势思考的(一开始学习递归总是把自己绕绕进去,归的时候,就完全乱套的)。那怎么找到每个子问题之间存在的某种关系呢?
120 |
121 | 我们只想其中一层(第一层关系),以上述为例,如果我想知道当前队伍的位置,所以我要之前前一个人的位置,然后 `+1` 就是我的位置了。对于他在什么位置,我丝毫不用关系,而是让递归去解决他的位置。我们可以写出递推公式如下:
122 |
123 | ```javascript
124 | // f(n) 代表当前我在队伍中的位置
125 | // f(n-1) 代表我前边那个人的位置
126 | // 递推公式
127 | f(n) = f(n-1) + 1
128 | ```
129 |
130 | > **※ 注意:**这个式子的含义就是 `f(n)` 求当前 n 这个人的位置, `f(n-1) + 1` 代表的就是前一个人的位置 `+ 1` 就是 `n` 的位置。
131 |
132 |
133 |
134 | #### 2、找到终止条件
135 |
136 | > 递推公式我们很轻松的写出来了,但是没有终止条件的递推公式会永远的执行下去的,所以我们要有一个终止条件终止程序的运行。那么怎么找到终止条件呢?
137 |
138 | 所谓的终止条件就是已知的条件,比如上述的排队打饭的例子中,第一个人正在窗口打饭,他的前边是没有人的,所以他是第一个。第一个人的位置为 1,我们应该怎么表示呢?
139 |
140 | ```javascript
141 | // 终止条件
142 | f(1) = 1;
143 | ```
144 |
145 | > **※ 注意:**有的问题终止条件不止一个哦,比如:斐波那契数列。具体问题具体分析。
146 |
147 |
148 |
149 | #### 3、转换递归代码
150 |
151 | > 递推公式和终止条件我们分析出来了,那么将递推公式转化为递归代码非常容易了。
152 |
153 | ```javascript
154 | function f(n){
155 | // 终止条件
156 | if(n == 1) retun 1;
157 | // 递推公式
158 | return f(n-1) + 1;
159 | }
160 | ```
161 |
162 |
163 |
164 | ## 递归的分类
165 |
166 | > 通过做大量的题,根据递归解决不同的问题,引申出来的几种解决和思考的方式。之所以将其分类,是为了能够更好的理解递归在不同的问题下起着什么作用,如:每层递归之间存在的关系、计算,以及递归枚举所有情况和面临选择性问题的递归。虽然分为了几类,但是递归的本质是一成不变的。
167 |
168 |
169 |
170 | #### 分类一:递归计算型
171 |
172 | > 将哪一类用递归解决的问题作为计算型呢?我简单总结了为两点,**层层计算和并列计算**。
173 |
174 |
175 |
176 | ##### 1、层层计算
177 |
178 | > 层层计算,顾名思义,能够用递归解决的问题都可以分为多个子问题,我们把每个子问题可以抽象成一层,子问题之间的关系可以表示为层与层之间的关系。我们通过层与层之间的计算关系用递推公式表达出来做计算,经过层层的递归,最终得到结果值。
179 |
180 |
181 |
182 | **▉ 例子:**
183 |
184 | > 我们再那上方排队打饭的例子来说明,我们的子问题已经分析出来了,就是我想知道当前在队伍中的位置,就是去问我前边人的位置加一就是我当前队伍的位置,这为一层。而前边这个人想知道当前自己的位置,需要用同样的解决思路,作为另一层。
185 |
186 | 层与层之间的关系是什么(我当前队伍中的位置与前边人的位置存在什么样的关系)?这时你会说,当前是 `+1`。这个大部分人都很容易找出,既然关系确定了,然后通过递推公式很容易写出递归代码。
187 |
188 | ```javascript
189 | // f(n) 为我所在的当前层
190 | // f(n-1) 为我前边的人所在的当前层
191 | // + 1 是层与层之间的计算关系
192 | f(n) = f(n-1) + 1
193 | ```
194 |
195 |
196 |
197 | **▉ 总结:**
198 |
199 | > 我将以上一类递归问题命名为「递归计算型」的「层层计算类型」。
200 |
201 |
202 |
203 | **▉ 举一反三:**
204 |
205 | > 求年龄的问题也是层层计算类型的问题,自己尝试分析一下(一定要自己尝试的去想,动手编码,才能进一步领悟到递归技巧)。
206 | >
207 | > **问题一:**有 5 个人坐在一起,问第 5 个人多少岁,他说比第 4 个人大 2 岁。问第 4 个人多少岁,他说比第 3 个人大2岁。问第 3 人多少岁,他说比第 2个 人大 2 岁。问第2个人多少岁,他说比第 1 个人大 2 岁。最后问第 1 个人,他说他是 10 岁。编写程序,当输入第几个人时求出其对应的年龄。
208 | >
209 | > **问题二:**单链表从尾到头一次输出结点值,用递归实现。
210 |
211 |
212 |
213 | ##### 2、并列计算
214 |
215 | > 并列计算,顾名思义,问题的解决方式是通过递归的并列计算来得到结果的。层与层之间并没有一定的计算关系,而只是简单的改变输入的参数值。
216 |
217 |
218 |
219 | **▉ 例子:**
220 |
221 | > 最经典的题型就是**斐波那契数列**。观察这样一组数据 0、 1、1、2、3、5、8、13、21、34...,去除第一个和第二个数据外,其余的数据等于前两个数据之和(如:`2 = 1 + 1`,`8 = 3 + 5`,`34 = 21 + 13`)。你可以尝试着根据「满足递归的三个条件」以及「怎么写出递归代码」的步骤自己动手动脑亲自分析一下。
222 |
223 | 我也在这里稍微做一个分析。
224 |
225 | 1)第一步:首先判断能不能将问题分解为多个子问题,上边我也分析过了,除了第一个和第二个数据,其他数据是前两个数据之和。那么前两个数据怎么知道呢?同样的解决方式,是他们前两个数之和。
226 |
227 | 2)第二步:找到终止条件,如果不断的找到前两个数之和,直到最前边三个数据 `0、1、1` 。如果递归求第一个 1 时,前边的数据不够,所以这也是我们找到的终止条件。
228 |
229 | 3)第三步:既然我们终止条件和关系找到了,递推公式也就不难写出 `f(n) = f(n-1) + f(n-2)`(n 为要求的第几个数字的值)。
230 |
231 | 4)转化为递归代码如下:
232 |
233 | ```javascript
234 | function f(n) {
235 | // 终止条件
236 | if(n == 0) return 0;
237 | if(n == 1) return 1;
238 | // 递推公式
239 | return f(n-1) + f(n-2);
240 | }
241 | ```
242 |
243 |
244 |
245 | **▉ 总结:**
246 |
247 | > 我将上方的问题总结为并列计算型。也可以归属为层层计算的一种,只不过是 + 1 改成了加一个 f 函数自身的递归(说白了,递归的结果也是一个确切的数值)。之所谓并列计算 `f(n-1)` 和 `f(n-2)` 互不打扰,各自递归计算各的值。最后我们将其计算的结果值相加是我们最想要的结果。
248 |
249 |
250 |
251 | **▉ 举一反三:**
252 |
253 | > 青蛙跳台阶的问题也是一种并列计算的一种,自己尝试着根据上边的思路分析一下,实践出真知(一定要自己尝试的去想,动手编码,才能进一步领悟到递归技巧)。
254 | >
255 | > **问题:**
256 | >
257 | > 一只青蛙一次可以跳上 1 级台阶,也可以跳上2 级。求该青蛙跳上一个n 级的台阶总共有多少种跳法。
258 |
259 |
260 |
261 | #### 分类二:递归枚举型
262 |
263 | > 递归枚举型最多的应用就是回溯算法,枚举出所有可能的情况,怎么枚举所有情况呢?通过递归编程技巧进行枚举。那什么是回溯算法?比如走迷宫,从入口走到出口,如果遇到死胡同,需要回退,退回上一个路口,然后走另一岔路口,重复上述方式,直到找到出口。
264 |
265 | 回溯算法最经典的问题又深度优先遍历、八皇后问题等,应用非常广泛,下边以八皇后问题为例子,展开分析,其他利用递归枚举型的回溯算法就很简单了。
266 |
267 |
268 |
269 | ##### 八皇后问题
270 |
271 | > 在 8 X 8 的网格中,放入八个皇后(棋子),满足的条件是,任意两个皇后(棋子)都不能处于同一行、同一列或同一斜线上,问有多少种摆放方式?
272 |
273 |
274 |
275 | 
276 |
277 | 
278 |
279 |
280 |
281 | **▉ 问题分析:**
282 |
283 | > 要想满足任意两个皇后(棋子)都不能处于同一行、同一列或同一斜线上,需要一一枚举皇后(棋子)的所有摆放情况,然后设定条件,筛选出满足条件的情况。
284 |
285 |
286 |
287 | **▉ 算法思路:**
288 |
289 | > 我们把问题分析清楚了之后,怎么通过递归实现回溯算法枚举八个皇后(棋子)出现的所有情况呢?
290 | >
291 | > 1)我们在 8 X 8 的网格中,先将第一枚皇后(棋子)摆放到第一行的第一列的位置(也就是坐标: (0,0))。
292 | >
293 | > 2)然后我们在第二行安置第二个皇后(棋子),先放到第一列的位置,然后判断同一行、同一列、同一斜线是否存在另一个皇后?如果存在,则该位置不合适,然后放到下一列的位置,然后在判断是否满足我们设定的条件。
294 | >
295 | > 3)第二个皇后(棋子)找到合适的位置之后,然后在第三行放置第三枚棋子,依次将八个皇后放到合适的位置。
296 | >
297 | > 4)这只是一种可能,因为我设定的第一个皇后是固定位置的,在网格坐标的(0,0) 位置,那么怎么枚举所有的情况呢?然后我们不断的改变第一个皇后位置,第二个皇后位置...... ,就可以枚举出所有的情况。如果你和我一样,看了这个题之后,如果还有点懵懵懂懂,那么直接分析代码吧。
298 |
299 |
300 |
301 | **▉ 代码实现:**
302 |
303 | > 虽然是用 `javascript` 实现的代码,相信学过编程的小伙伴基本的代码逻辑都可以看懂。根据上方总结的递归分析满足的三个条件以及怎么写出递归代码的步骤,一步步来分析八皇后问题。
304 |
305 |
306 |
307 | **1、将问题分解为多个子问题**
308 |
309 | > 在上述的代码分析和算法思路分析中,我们可以大体知道怎么分解该问题了,枚举出八个皇后(棋子)所有的满足情况可以分解为,先寻找每一种满足的情况这种子问题。比如,每个子问题的算法思路就是上方列出的四个步骤。
310 |
311 |
312 |
313 | **2、找出终止条件**
314 |
315 | > 当遍历到第八行的时候,递归结束。
316 |
317 | ```javascript
318 | // 终止条件
319 | if(row === 8){
320 | // 打印第 n 种满足的情况
321 | console.log(result)
322 | n++;
323 | return;
324 | }
325 | ```
326 |
327 |
328 |
329 | **3、写出递推公式**
330 |
331 | > `isOkCulomn()` 函数判断找到的该位置是否满足条件(不能处于同一行、同一列或同一斜线上)。如果满足条件,我们返回 `true`,进入 `if` 判断,`row `行数加一传入进行递归下一行的皇后位置。直至递归遇到终止条件位置,`column ++`,将第一行的皇后放到下一位置,进行继续递归,枚举出所有可能的摆放情况。
332 |
333 | ```javascript
334 | // 每一列的判断
335 | for(let column = 0; column < 8; column++){
336 | // 判断当前的列位置是否合适
337 | if(isOkCulomn(row,column)){
338 | // 保存皇后的位置
339 | result[row] = column;
340 | // 对下一行寻找数据
341 | cal8queens(row + 1);
342 | }
343 | // 此循环结束后,继续遍历下一种情况,就会形成一种枚举所有可能性
344 | }
345 | ```
346 |
347 | ```javascript
348 | // 判断当前列是否合适
349 | const isOkCulomn = (row,column) =>{
350 | // 左上角列的位置
351 | let leftcolumn = column - 1;
352 | // 右上角列的位置
353 | let rightcolumn = column + 1;
354 |
355 | for(let i = row - 1;i >= 0; i--){
356 | // 判断当前格子正上方是否有重复
357 | if(result[i] === column) return false;
358 |
359 | // 判断当前格子左上角是否有重复
360 | if(leftcolumn >= 0){
361 | if(result[i] === leftcolumn) return false;
362 | }
363 |
364 | // 判断当前格式右上角是否有重复
365 | if(leftcolumn < 8){
366 | if(result[i] === rightcolumn) return false;
367 | }
368 |
369 | // 继续遍历
370 | leftcolumn --;
371 | rightcolumn ++;
372 | }
373 | return true;
374 | }
375 |
376 | ```
377 |
378 |
379 |
380 | **4、转换为递归代码**
381 |
382 | ```javascript
383 |
384 | // 变量
385 | // result 为数组,下标为行,数组中存储的是每一行中皇后的存储的列的位置。
386 | // row 行
387 | // column 列
388 | // n 计数满足条件的多少种
389 | var result = [];
390 | let n = 0
391 | const cal8queens = (row) =>{
392 | // 终止条件
393 | if(row === 8){
394 | console.log(result)
395 | n++;
396 | return;
397 | }
398 | // 每一列的判断
399 | for(let column = 0; column < 8; column++){
400 | // 判断当前的列位置是否合适
401 | if(isOkCulomn(row,column)){
402 | // 保存皇后的位置
403 | result[row] = column;
404 | // 对下一行寻找数据
405 | cal8queens(row + 1);
406 | }
407 | // 此循环结束后,继续遍历下一种情况,就会形成一种枚举所有可能性
408 | }
409 | }
410 |
411 | // 判断当前列是否合适
412 | const isOkCulomn = (row,column) =>{
413 | // 设置左上角
414 | let leftcolumn = column - 1;
415 | let rightcolumn = column + 1;
416 |
417 | for(let i = row - 1;i >= 0; i--){
418 | // 判断当前格子正上方是否有重复
419 | if(result[i] === column) return false;
420 |
421 | // 判断当前格子左上角是否有重复
422 | if(leftcolumn >= 0){
423 | if(result[i] === leftcolumn) return false;
424 | }
425 |
426 | // 判断当前格式右上角是否有重复
427 | if(leftcolumn < 8){
428 | if(result[i] === rightcolumn) return false;
429 | }
430 |
431 | // 继续遍历
432 | leftcolumn --;
433 | rightcolumn ++;
434 | }
435 | return true;
436 | }
437 |
438 | // 递归打印所有情况
439 | const print = (result)=>{
440 | for(let i = 0;i < 8; i++){
441 | for(let j = 0;j < 8; j++){
442 | if(result[i] === j){
443 | console.log('Q' + ' ')
444 | }else{
445 | console.log('*' + ' ')
446 | }
447 | }
448 | }
449 | }
450 |
451 | // 测试
452 | cal8queens(0);
453 | console.log(n)
454 | ```
455 |
456 |
457 |
458 | **▉ 总结**
459 |
460 | > 上述八皇后的问题就是用递归来枚举所有情况,然后再从中设置条件,只筛选满足条件的选项。上述代码建议多看几遍,亲自动手实践一下。一开始解决八皇后问题,我自己看了好长时间才明白的,以及递归如何发挥技巧作用的。
461 |
462 |
463 |
464 | **▉ 举一反三:**
465 |
466 | > 如果你想练练手,可以自己实现图的深度优先遍历,这个理解起来并不难,可以自己动手尝试着写一写,我把代码传到我的 `Github` 上了。
467 |
468 |
469 |
470 | #### 分类三:递归选择型
471 |
472 | > 所谓的递归选择型,每个子问题都要面临选择,求最优解的情况。有的小伙伴会说,求最优解动态规划最适合,对的,没错,但是递归通过选择型「枚举所有情况」,设置条件,求得问题的最优解也是可以实现的,所有我呢将其这一类问题归为递归选择型问题,它也是一个回溯算法。
473 |
474 |
475 |
476 | ##### 0 -1 背包问题
477 |
478 | > `0 - 1` 背包问题,了解过的小伙伴也是很熟悉的了。其实这个问题也属于回溯算法的一种,废话不多说,直接上问题。有一个背包,背包总的承载重量是 `Wkg`。现在我们有 `n` 个物品,每个物品的重量不等,并且不可分割。我们现在期望选择几件物品,装载到背包中。在不超过背包所能装载重量的前提下,如何让背包中物品的总重量最大?
479 |
480 |
481 |
482 | **▉ 问题分析:**
483 |
484 | > 如果你对该问题看懵了,没关系,我们一点点的分析。假如每个物品我们有两种状态,总的装法就有 `2^n `种,怎么才能不重复的穷举这些可能呢?
485 | >
486 |
487 |
488 |
489 | **▉ 算法思路:**
490 |
491 | > 我们可以把物品依次排列,整个问题就分解为了 n 个阶段,每个阶段对应一个物品怎么选择。先对第一个物品进行处理,选择装进去或者不装进去,然后再递归地处理剩下的物品。
492 |
493 |
494 |
495 | ▉ **代码实现:**
496 |
497 | > 这里有个技巧就是设置了条件,自动筛选掉不满足条件的情况,提高了程序的执行效率。
498 |
499 | ```javascript
500 | // 用来存储背包中承受的最大重量
501 | var max = Number.MIN_VALUE;
502 | // i: 对第 i 个物品做出选择
503 | // currentw: 当前背包的总重量
504 | // goods:数组,存储每个物品的质量
505 | // n: 物品的数量
506 | // weight: 背包应承受的重量
507 | const f = (i, currentw, goods, n, weight) => {
508 | // 终止条件
509 | if(currentw === weight || i === n){
510 | if(currentw > max){
511 | // 保存满足条件的最大值
512 | max = currentw;
513 | }
514 | return ;
515 | }
516 |
517 | // 选择跳过当前物品不装入背包
518 | f(i+1, currentw, goods, n, weight)
519 |
520 | // 将当前物品装入背包
521 | // 判断当前物品装入背包之前是否超过背包的重量,如果已经超过当前背包重量,就不要就继续装了
522 | if(currentw + goods[i] <= weight){
523 | f(i+1 ,currentw + goods[i], goods, n, weight)
524 | }
525 | }
526 |
527 | let a = [2,2,4,6,3]
528 | f(0,0,a,5,10)
529 | console.log(max)
530 | ```
531 |
532 |
533 |
534 | ## 递归的缺点
535 |
536 | > 虽然递归的使用非常的简洁,但是也有很多缺点,也是我们在使用中需要额外注意的地方和优化的地方。
537 |
538 |
539 |
540 | #### 1、递归警惕堆栈溢出
541 |
542 | > 你可能会问,递归和系统中的堆栈有什么关联?不要急,听我慢慢细说。
543 |
544 |
545 |
546 | ##### ▉ 理解堆栈溢出
547 |
548 | > 1)递归的本质就是重复调用本身的过程,本身是什么?当然是一个函数,那好,函数中有参数以及一些局部的声明的变量,相信很多小伙伴只会用函数,而不知道函数中的变量是怎么存储的吧。没关系,等你听我分析完,你就会了。
549 | >
550 | > 2)函数中变量是存储到系统中的栈中的,栈数据结构的特点就是先进后出,后进先出。一个函数中的变量的使用情况就是随函数的声明周期变化的。当我们执行一个函数时,该函数的变量就会一直不断的压入栈中,当函数执行完毕销毁的时候,栈内的元素依次出栈。还是不懂,没关系,看下方示意图。
551 | >
552 | > 3)我们理解了上述过程之后,回到递归上来,我们的递归调用是在函数里调用自身,且当前函数并没有销毁,因为当前函数在执行自身层层递归进去了,所以递归的过程,函数中的变量一直不断的压栈,由于我们系统栈或虚拟机栈空间是非常小的,当栈压满之后,再压时,就会导致堆栈溢出。
553 |
554 | ```javascript
555 | // 函数
556 | function f(n){
557 | var a = 1;
558 | var b = 2;
559 | return a + b;
560 | }
561 | ```
562 |
563 |
564 |
565 | 
566 |
567 |
568 |
569 | ##### ▉ 解决办法
570 |
571 | > 那么遇到这种情况,我们怎么解决呢?
572 |
573 | 通常我们设置递归深度,简单的理解就是,如果递归超过我们设置的深度,我们就退出,不再递归下去。还是那排队打饭的例子,如下:
574 |
575 | ```javascript
576 | // 表示递归深度变量
577 | let depth = 0;
578 |
579 | function f(n){
580 | depth++;
581 | // 如果超过递归深度,抛出错误
582 | if(depth > 1000) throw 'error';
583 | // 终止条件
584 | if(n == 1) retun 1;
585 | // 递推公式
586 | return f(n-1) + 1;
587 | }
588 | ```
589 |
590 |
591 |
592 | #### 2、递归警惕重复元素
593 |
594 | > 有些递归问题中,存在重复计算问题,比如求斐波那契数列,我们画一下递归树如下图,我们会发现有很多重复递归计算的值,重复计算会导致程序的时间复杂度很高,而且是指数级别的,导致我们的程序效率低下。
595 |
596 | 如下图递归树中,求斐波那契数列 `f(5) `的值,需要多次递归求 `f(3)` 和 `f(2)` 的值。
597 |
598 | 
599 |
600 |
601 |
602 | ##### ▉ 解决办法
603 |
604 | > 重复计算问题,我们应该怎么解决?有的小伙伴想到了,我们把已经计算过的值保存起来,每次递归计算之前先检查一下保存的数据有没有该数据,如果有,我们拿出来直接用。如果没有,我们计算出来保存起来。一般我们用散列表来保存。(所谓的散列表就是键值对的形式,如 map )
605 |
606 | ```javascript
607 | // 斐波那契数列改进后
608 | let map = new Map();
609 | function f(n) {
610 | // 终止条件
611 | if(n == 0) return 0;
612 | if(n == 1) return 1;
613 |
614 | // 如果散列表中存在当前计算的值,就直接返回,不再进行递归计算
615 | if(map.has(n)){
616 | return map.get(n);
617 | }
618 |
619 | // 递推公式
620 | let num = f(n-1) + f(n-2);
621 | // 将当前的值保存到散列表中
622 | map.set(n,num)
623 | return num;
624 | }
625 | ```
626 |
627 |
628 |
629 | #### 3、递归高空间复杂度
630 |
631 | > 因为递归时函数的变量的存储需要额外的栈空间,当递归深度很深时,需要额外的内存占空间就会很多,所以递归有非常高的空间复杂度。
632 |
633 | 比如:` f(n) = f(n-1)+1` ,空间复杂度并不是 `O(1)`,而是 `O(n)` 。
634 |
635 |
636 |
637 | ## 小结
638 |
639 | > 我们一起对递归做一个简单的总结吧,如果你还是没有完全明白,没关系,多看几遍,说实话,我这个人比较笨,前期看递归还不知道看了几十遍才想明白,吃饭想,睡觉之前想,相信最后总会想明白的。
640 |
641 |
642 |
643 | #### 1、满足递归的三个条件
644 |
645 | - 一个问题能不能分解成多个子问题来解决;
646 | - 该问题是否和子问题的解决思路相同;
647 | - 该问题是否有终止条件。
648 |
649 |
650 |
651 | #### 2、怎么写出递归代码
652 |
653 | - 寻找递归终止条件;
654 | - 写出递推公式;
655 | - 转化成递归代码。
656 |
657 |
658 |
659 | #### 3、怎么理解递归?
660 |
661 | > 不要用大脑去想每一层递归的实现,记住这是计算机应该做的事情,我们要做的就是弄懂递归之间的关系,从而屏蔽掉层层递归的细节。
662 |
663 |
664 |
665 | #### 4、递归的缺点
666 |
667 | - 递归警惕堆栈溢出
668 | - 递归警惕重复计算
669 | - 递归的高空间复杂度
670 |
671 |
672 |
673 | ## 最后想说的话
674 |
675 | 最后可能说的比较打鸡血,很多人一遇到递归就会崩溃掉,比如我,哈哈。无论以后遇到什么困难,不要对它们产生恐惧,而是当做一种挑战,当你经过长时间的战斗,突破层层困难,最后突破挑战的时候,你会感激曾经的自己当初困难面前没有放弃。这一点我深有感触,有时候对于难题感到很无助,虽然自己没有在一所好的大学,没有好的资源,更没有人去专心的指导你,但是我一直相信这都是老天给我发出的挑战书,我会继续努力,写出更多高质量的文章。
676 |
677 | **如果觉得本文对你有帮助,点个赞,我希望能够让更多处在递归困惑的人看到,谢谢各位支持!**下一篇我打算出一篇完整关于链表的文章,终极目标:将数据结构与算法每个知识点写成一系列的文章。
678 |
679 |
680 | **作者:**小鹿
681 |
682 | **座右铭:**追求平淡不平凡,一生追求做一个不甘平凡的码农!
683 |
684 | **本文首发于 Github ,转载请说明出处:**[https://github.com/luxiangqiang/Blog/blob/master/articel/数据结构与算法系列/数据结构与算法之递归系列.md](https://github.com/luxiangqiang/Blog/blob/master/articel/数据结构与算法系列/数据结构与算法之递归系列.md)
685 |
686 | **个人公众号:一个不甘平凡的码农。**
687 |
688 |
689 |
690 | ### 其他链接:
691 |
692 | #### [1、LeetCode 30 道经典题详细解析](https://github.com/luxiangqiang/JS-LeetCode)
693 |
694 | #### [2、Github:入门必会的基本数据结构与算法代码剖析](https://github.com/luxiangqiang/Data-Structure-Coding)
695 |
696 | #### [3、Github:公众号留言小程序开源项目](https://github.com/luxiangqiang/WeiXin_MessageApplet)
697 |
698 |
699 |
700 |
701 |
702 |
703 |
704 |
--------------------------------------------------------------------------------
/articel/数据结构与算法系列/数据结构与算法之二叉树系列[题型篇].md:
--------------------------------------------------------------------------------
1 | ## 写在前边
2 |
3 | 不知道你有没有这种困惑,虽然刷了很多算法题,当我去面试的时候,面试官让你手写一个算法,可能你对此算法很熟悉,知道实现思路,但是总是不知道该在什么地方写,而且很多边界条件想不全面,一紧张,代码写的乱七八糟。如果遇到没有做过的算法题,思路也不知道从何寻找,那么这篇文章就主要为你解决这几个问题。
4 |
5 |
6 |
7 | 《剑指 offer》是准备数据结构与算法面试的一本好书,里边很多面试手写算法很多的注意的问题,但是基本都是用 C++ 实现的,书中每章节的分类都是按照性能和消耗以及手写代码的注意的几大点进行了分类,针对每个不同的点,进行数据结构与算法的混合实现。
8 |
9 |
10 |
11 | 二遍刷题,发现了还可以根据自身情况进行整理和分类。全部代码是用 JS 书写,都经过 Leetcode 标准测试(小部分Leetcode 没有的题目),对所有的算法题的特点进行总结分类,手写算法中,如何考虑到全部的边界条件;如果快速多种思路解决,如何将思路快速的转化为代码,这是这一篇重点分享的地方。
12 |
13 |
14 |
15 | 二叉树题目共有 11 题,我把这 11 题书中对实现方法和思路有详细的讲解,但是对于个人来说,以后遇到陌生的二叉树的题目怎么进行解决,通过对 11 个题的分析、整理,得出以下几个步骤,首先先来看这 11 个二叉树经典算法题。
16 |
17 |
18 |
19 | **PS:**如果你已经做过这几道题,而且能够顺利的手写出来,不妨滑到最底部,希望最后的二叉树思路、测试用例以及代码编写的总结对你在面试中有所帮助(这篇文章精华所在)。
20 |
21 |
22 |
23 | ### 一、面试题7:重建二叉树
24 |
25 | > 已知前序遍历为{1,2,4,7,3,5,6,8},中序遍历为{4,7,2,1,5,3,8,6},它的二叉树是怎么样的?
26 |
27 |
28 |
29 | #### 1、思路
30 |
31 | 根据前、中序遍历的特点,(根左右、左根右),先根据前序遍历确定根节点,然后在中序遍历知道该根节点的左右树的数量,反推出前序遍历中左子树的结点有哪些。根据该思路进行递归即可完成二叉树的重建。
32 |
33 |
34 |
35 | #### 2、测试用例
36 |
37 | - 完全二叉树、非完全二叉树 —— 普通测试。
38 |
39 | - 只有左子节点二叉树,只有右子节点、只有一个结点的二叉树 —— 特殊二叉树测试。
40 |
41 | - 空树、前序和中序不匹配 —— 输入测试。
42 |
43 |
44 |
45 | #### 3、代码实现
46 |
47 | ```javascript
48 | 1// 定义结点
49 | 2// class TreeNode{
50 | 3// constructor(data){
51 | 4// this.data = data;
52 | 5// this.left = null;
53 | 6// this.right = null;
54 | 7// }
55 | 8// }
56 | 9
57 | 10// 参数:前序遍历数组 ~ 中序遍历数组
58 | 11const reConstructBinaryTree = (pre, vin)=>{
59 | 12 // 判断前序数组和中序数组是否为空
60 | 13 if(!pre || pre.length === 0 || !vin || vin.length === 0){
61 | 14 return;
62 | 15 }
63 | 16 // 新建二叉树的根节点
64 | 17 var treeNode = {
65 | 18 val: pre[0]
66 | 19 }
67 | 20 // 查找中序遍历中的根节点
68 | 21 for(var i = 0; i < pre.length; i++) {
69 | 22 if (vin[i] === pre[0]) {
70 | 23 // 将左子树的前中序遍历分割开
71 | 24 treeNode.left = reConstructBinaryTree(pre.slice(1, i+1), vin.slice(0, i));
72 | 25 // 将右子树的前中序遍历分割开
73 | 26 treeNode.right = reConstructBinaryTree(pre.slice(i+1),vin.slice(i+1));
74 | 27 }
75 | 28 }
76 | 29 // 返回该根节点
77 | 30 return treeNode;
78 | 31}
79 | 32
80 | 33let pre = [1,2,4,7,3,5,6,8];
81 | 34let vin = [4,7,2,1,5,3,8,6];
82 | 35console.log(reConstructBinaryTree(pre,vin));
83 | ```
84 |
85 |
86 |
87 | ### 二、**面试题8:二叉树的下一节点**
88 |
89 | > 给定一个二叉树的节点,如何找出中序遍历的下一节点。有两个指向左右子树的指针,还有一个指向父节点的指针。
90 |
91 |
92 |
93 | #### 一、思路
94 |
95 | 求中序遍历的下一节点,就要分各种情况(明确中序遍历下一结点在二叉树中的位置有哪些),然后对某种情况详细分析。
96 |
97 | 下一结点可能存在的情况:
98 |
99 | - 有右子节点
100 | - 右子节点有无左子节点
101 | - 无 —— 右子节点就是当前结点下一节
102 | - 有 —— 递归寻找右子节点的左子节点就是下一节点
103 | - 无右子节点
104 | - 无父节点 —— 无下一结点
105 | - 有父节点
106 | - 当前结点作为父节点的左子节点 —— 下一结点为父节点
107 | - 当前结点作为父节点的右子节点 —— 向父节点递归寻找作为左子节点的结点就是下一节点
108 |
109 |
110 |
111 | #### 二、测试用例
112 |
113 | - 普通测试 —— 完全二叉树、非完全二叉树
114 | - 特殊测试 —— 只要左子节点的二叉树、只有右子节点的二叉树、只有一个结点
115 | - 输入测试 —— 空节点
116 |
117 |
118 |
119 | #### 三、代码实现
120 |
121 | ```javascript
122 | const getNextNode = (pNode)=>{
123 | // 判断该结点是否为 null
124 | if(pNode == null){
125 | return;
126 | }
127 |
128 | // 当前结点有右子树且左子树
129 | if(pNode.right !== null){
130 | pNode = pNode.right;
131 | // 判断右子树是否有左子树
132 | while(pNode.left !== null){
133 | pNode = pNode.left;
134 | }
135 | return pNode;
136 | }else{
137 | // 判断当前结点是否存在父节点(如果为空,没有下一结点)
138 | while(pNode.next !== null){
139 | if(pNode == pNode.next.left){
140 | return pNode.next;
141 | }else{
142 | pNode = pNode.next;
143 | }
144 | }
145 | // 没有下一结点
146 | return null;
147 | }
148 | }
149 | ```
150 |
151 |
152 |
153 | ### 三、面试题26:树的子结构
154 |
155 | > 输入两棵二叉树 A 和 B,判断 B 是不是 A 的子结构。
156 |
157 |
158 |
159 | #### 一、思路
160 |
161 | 通过判断两棵树的根节点否相同,如果相同,则递归判断树剩余的结点是否相同。如果不相同,则递归树的左右子节点进行对比找到相同的根节点。
162 |
163 |
164 |
165 | #### 二、测试用例
166 |
167 | - 是子结构、不是子结构 —— 普通测试。
168 | - 只有左子节点、只有右子节点、只有一个结点 —— 特殊测试。
169 | - 空树 —— 输入测试。
170 |
171 |
172 |
173 | #### 三、代码实现
174 |
175 | ```javascript
176 | const TreeConstrutor = (nodeA, nodeB)=>{
177 | const result = false;
178 | // 判断输入是否为 null
179 | // nodeA 为 null 不会有子结构
180 | if(nodeA == null){
181 | return false;
182 | }
183 | // 如果 nodeB 为 null,代表所有子结构比较完成
184 | if(nodeB == null){
185 | return true;
186 | }
187 |
188 | // 如果根节点相同,则进行子结构全部的验证,返回验证的结果
189 | if(nodeA.data === nodeB.data){
190 | result = match(nodeA, nodeB)
191 | }
192 |
193 | // 如果根节点不相同,继续递归遍历查找相同的根节点
194 | return TreeConstrutor(nodeA.left, nodeB) || TreeConstrutor(nodeA.right, nodeB)
195 | }
196 |
197 | // 匹配根节点相同的子结构
198 | const match = (nodeA, nodeB)=>{
199 | if(nodeA == null){
200 | return false;
201 | }
202 | if(nodeB == null){
203 | return true;
204 | }
205 | // 判断匹配的当前结点是否相同
206 | if(nodeA.data == nodeB.data){
207 | // 递归匹配其他子节点
208 | return match(nodeA.left, nodeB.left) && match(nodeA.right, nodeB.right);
209 | }
210 |
211 | // 如果不相同
212 | return false;
213 | }
214 | ```
215 |
216 |
217 |
218 | ### 四、**面试题27:二叉树的镜像**
219 |
220 | > 请完成一个函数,如果一个二叉树,该函数输出它的镜像。
221 | >
222 |
223 |
224 |
225 | #### 一、思路
226 |
227 | 根节点的左右子节点相互交换,继续递归遍历,将子节点的左右结点进行交换,知道遇到叶子节点。
228 |
229 |
230 |
231 | #### 二、测试用例
232 |
233 | - 普通二叉树 —— 普通测试
234 | - 只有左子节点、只有右子节点、只有一个结点 —— 特殊测试
235 | - 空树 —— 输入测试
236 |
237 |
238 |
239 | #### 三、代码实现
240 |
241 | ```javascript
242 | const insert = (root)=>{
243 | // 判断根节点是否为 null
244 | if(root == null){
245 | return;
246 | }
247 |
248 | // 进行结点交换
249 | Let tempNode = root.left;
250 | root.left = root.right;
251 | root.right = tempNode;
252 |
253 | // 递归遍历剩余的子节点
254 | insert(root.left);
255 | insert(root.right);
256 |
257 | // 返回根节点
258 | return root;
259 | }
260 | ```
261 |
262 |
263 |
264 | ### 五、**面试题28:对称二叉树**
265 |
266 | #### 一、思路
267 |
268 | 1、首先,观察一个对称的二叉树有什么特点?
269 |
270 | - 结构上:在结构上实对称的,某一节点的左子节点和某一节点的右子节点对称。
271 | - 规律上:我们如果进行前序遍历(根、左、右),然后对前序遍历进行改进(根、右、左),如果是对称的二叉树,他们的遍历结果是相同的。
272 |
273 | 2、考虑其他情况
274 |
275 | - 结点数量不对称
276 | - 结点值不对称
277 |
278 |
279 |
280 | #### 二、测试用例
281 |
282 | - 对称二叉树、不对称二叉树(结点数量不对称、结点结构不对称) —— 普通测试
283 |
284 | - 所有结点值都相同的二叉树 —— 特殊测试
285 | - 空二叉树 —— 输入测试
286 |
287 |
288 |
289 | #### 三、代码编写
290 |
291 | ```javascript
292 | var isSymmetric = (root)=>{
293 | // 判断二叉树是否为 null —— 输入测试, if(root == null){
294 | return true;
295 | }
296 |
297 | // 判断输入的二叉树,从根节点开始判断是否是对称二叉树
298 | var Symmetric = (lNode, rNode)=>{
299 | // 判断左右结点是否都为 null
300 | if(lNode == null && rNode == null){
301 | return true;
302 | }
303 | // 判断其中一个为 null 另一个不是 null
304 | if(lNode == null && rNode !== null){
305 | return false;
306 | }
307 | if(lNode !== null && rNode == null){
308 | return false;
309 | }
310 | // 判断两个结点的值是否相同
311 | if(lNode.val !== rNode.val){
312 | return false;
313 | }
314 | // 如果相同,继续递归判断其他的结点
315 | return Symmetric(lNode.left,rNode.right) && Symmetric(lNode.right,rNode.left)
316 | }
317 |
318 | Symmetric(root.left,root.right)
319 | }
320 | ```
321 |
322 |
323 |
324 |
325 | ### 六、面试题32:从上到下打印二叉树
326 |
327 | > 从上到下打印出二叉树的每个节点,同一层的节点按照从左到右的顺序打印。(按层遍历二叉树)
328 |
329 |
330 |
331 | #### 一、思路
332 |
333 | 从根节点开始按层遍历打印结点(自左往右),下一层的遍历是上一层的字节点,但是我们发现想要获取到上层结点的子节点时,上层的父节点已经遍历过去可,想要在获取到,必须存储父节点。然后下层遍历的时候,自左往右取出父节点,依次打印子节点。
334 |
335 | 上方的解题思路中父节点的存储和遍历让我们想到一个熟悉的数据结构,对了,“先进先出”的思想,那就是队列。在遍历上一层结点的时候,先打印结点值,然后判断是够存在左右子树,如果存在,将给结点入队,直到该层的结点全部遍历完成。然后队列出队,分别打印结点,循环此步骤。
336 |
337 |
338 |
339 | #### 二、测试用例
340 |
341 | - 完全二叉树、非完全二叉树 —— 普通测试
342 | - 只有左、右子节点的二叉树、只有一个节点的二叉树 —— 特殊测试
343 | - 空树 —— 输入测试
344 |
345 |
346 |
347 | #### 三、代码编写
348 |
349 | - 参数:树的根节点。
350 | - 判断是否为空。
351 | - 打印结点值,判断该结点是否存在子节点,如果存在就入队。
352 | - 出队,打印结点
353 | - 循环上述步骤
354 |
355 | ```javascript
356 | var levelOrder = function(root) {
357 | let result = []; // 存放遍历的结果
358 | // 判断根节点是否为 null
359 | if(root == null){
360 | return [];
361 | }
362 | // 声明一个队列
363 | let queue = [];
364 | queue.push(root)
365 |
366 | // 出队,打印结结点、判断是否存在子节点
367 | while(queue.length !== 0){
368 | let temp = []; // 存储每层的结点
369 | let len = queue.length;
370 | for(let j = 0;j < len;j++){
371 | // 出队
372 | let tempNode = queue.shift();
373 | // 存储结点值
374 | temp.push(tempNode.val)
375 | // 判断出队的根节点是否有子节点
376 | if(tempVal.left !== null){
377 | queue.push(tempVal.left)
378 | }
379 | if(tempVal.right !== null){
380 | queue.push(tempVal.left)
381 | }
382 | }
383 | //存储每层的遍历的结点值
384 | result.push(temp);
385 | }
386 | // 返回结果集
387 | return result;
388 | }
389 | ```
390 |
391 |
392 |
393 | ### 七、**面试题33:二叉树的后序遍历序列**
394 |
395 | 输入一个整数数组,判断该数组是不是某二叉搜索树的后续遍历。如果是返回 true,如果不是返回 false。假设输入的任意两个数字互不相同。
396 |
397 |
398 |
399 | #### 一、思路
400 |
401 | **根据后续遍历的规律和二叉树具备的特点**,可以找到的规律就是(左、右、根)序列的最后一个数为根节点,又根据二叉树的特点,左子节点小于根节点,右子节点大于根节点,分离出左右子节点,根据上边的规律,**递归**剩下的序列。
402 |
403 |
404 |
405 | #### 二、测试用例
406 |
407 | - 完全二叉树、不完全二叉树 —— 普通测试
408 | - 只有左子节点的二叉树、只有右子节点的二叉树、只有一个节点的二叉树 —— 特殊测试
409 | - 空树 —— 输入测试
410 |
411 |
412 |
413 | #### 三、代码编写
414 |
415 | - 参数:数组
416 | - 判断数组是否为空
417 | - 取数组的最后一个元素作为对比的根节点
418 | - 根据根节点值的大小分割数组(分割数组的同时判断是否都满足小于根节点的要求)
419 | - 判断分割数组是否是空
420 | - 递归上方的步骤
421 |
422 | ```javascript
423 | const isPostorder = (arr)=>{
424 | // 判断数组是否为 null
425 | if(arr.length == 0){
426 | return true;
427 | }
428 |
429 | // 取数组最后一个数字为根节点
430 | let rootVal = arr[arr.length - 1];
431 |
432 | // 搜索小于根节点的值,并记录该结点的下标(除根节点外)
433 | let i = 0;
434 | for(;i < arr.length - 1;i++){
435 | if(arr[i] > rootVal){
436 | break
437 | }
438 | }
439 |
440 | // 搜索大于根节点的值(除根节点外)
441 | let j = 0;
442 | for(;j < arr.length - 1; j++){
443 | if(rootVal > arr[j]){
444 | return false;
445 | }
446 | }
447 |
448 | // 递归判断左子节点的值(先判断左子节点是够有值),默认返回 true
449 | let left = true
450 | if(i > 0){
451 | left = isPostorder(arr.slice(0, i))
452 | }
453 | // 如果右子树不为空,判断右子树为二叉搜索树
454 | let right = true
455 | if(i < arr.length - 1){
456 | right = isPostorder(arr.slice(i,arr.length - 1))
457 | }
458 | return (left && right)
459 | }
460 | ```
461 |
462 |
463 |
464 | ### 八、**面试34:二叉树和为某一值路径**
465 |
466 | >
467 | > 输入一棵二叉树和一个整数,打印出二叉树中节点值的和为输出整数的所有路径。从树的根节点开始往下一直到叶子节点所经过的节点形成一条路径。
468 | >
469 |
470 |
471 |
472 | #### 一、思路
473 |
474 | **1、找规律:**需要遍历树的所有结点:我们会想到前、中、后遍历
475 |
476 | : 需要存储遍历过的路径(节点值):我们想到用数组存储
477 |
478 |
479 |
480 |
481 | **2、算法思想:**前序遍历(根、左、右)的特点,从根到叶子节点,会从树自左向右依次遍历二叉树,所有可能的路径都会遍历到,所以使用前序遍历更佳。
482 |
483 | 每遍历一个结点就将其累加,然后判断累加的值是否等于目标值且子节点为叶子节点。如果是,则打印输出该路径;如果不是,则回退到上一父节点,此时数组中的数据结点进行删除,然后不断的遍历下一子节点,递归。
484 |
485 | **3、综上所述,**存储结点路径的时候,涉及到累加结点和删除节点,我们可以将其抽象成入栈和出栈。然后遍历二叉树的所有路径可以用到递归的过程,让出栈和入栈与递归的状态达成一致,这到题就不难了。
486 |
487 |
488 |
489 | #### 二、测试用例
490 |
491 | - 完全二叉树、非完全二叉树(有一条路径满足、有多条路径满足、都不满足)—— **普通测试**。
492 | - 只有左子节点的二叉树、只有右子节点的二叉树、只有一个结点的二叉树 —— **特殊测试**。
493 | - 空二叉树、输入负数 —— **输入测试**。
494 |
495 |
496 |
497 | #### 三、代码编写
498 |
499 | - 参数:二叉树、目标值
500 | - 判断二叉树是否为空和目标是是否是负数
501 | - 开始进行递归遍历二叉树进行查找满足条件的路径
502 | - 将当前递归的根节点进行累加
503 | - 同时该结点入栈
504 | -
505 |
506 | ```javascript
507 | const treeSum = (root, targetSum)=>{
508 | // 判断输入的二叉树和整数
509 | if(root == null || targetSum < 0){
510 | return false;
511 | }
512 |
513 | // 开始进行递归遍历二叉树进行查找满足条件的路径
514 | let result = []; // 存放最后满足条件的路径
515 | let pathStack = []; // 储存当前路径的栈
516 | let currentSum = 0; // 当前累加的结果值
517 |
518 | // 进行路径查找
519 | FindPath(root, targetSum, currentSum, pathStack, result);
520 |
521 | // 返回结果
522 | return result;
523 | }
524 |
525 | const FindPath = (root, targetSum, currentSum, pathStack, result)=>{
526 | // 将当前跟根节点进行累加
527 | currentSum = currentSum + root.val;
528 |
529 | // 存储栈中
530 | pathStack.push(root.val);
531 |
532 | // 判断目标值是否相等且是否为叶子节点
533 | if(currentSum == targetSum && root.left == null && root.right == null){
534 | // 打印路径
535 | result.push(pathStack.slice(0))
536 | }
537 |
538 | // 如果左子节点不为空
539 | if(root.left !== null){
540 | FindPath(root.left, targetSum, currentSum, pathStack, result);
541 | }
542 |
543 | // 如果当前结点还有右子树,继续遍历
544 | if(root.right !== null){
545 | FindPath(root.right, targetSum, currentSum, pathStack, result);
546 | }
547 |
548 | // 该路径遍历到叶子节点,还没有满足条件,则退回到父节点,进行下一结点的累加判断
549 | pathStack.pop();
550 | }
551 | ```
552 |
553 |
554 |
555 | #### 四、小结
556 |
557 | - 当问题能够用递归去解决的时候,首先找到递归的点,比如二叉树的中的每个节点就是递归的点。
558 |
559 | - 当使用递归解决满足条件的问题时,直接每层递归进行判断,如果满足条件就处理,否则,递归自动跳过 if 判断。
560 |
561 |
562 |
563 | ### 九、**面试题37:序列化二叉树**
564 |
565 | 请实现两个函数,分别用来序列化二叉树和反序列化二叉树。
566 |
567 |
568 |
569 | #### 一、思路
570 |
571 | 1、序列化:遍历二叉树,遇到叶子节点,将其转化为 $ 表示。
572 |
573 | 2、反序列化:根据前序遍历的特点(根、左、右),进行二叉树的还原。
574 |
575 |
576 |
577 | #### 二、测试用例
578 |
579 | - 完全二叉树、非完全二叉树 —— 普通测试
580 | - 只有左子节点、只有右子节点、只有一个节点 —— 特殊测试
581 | - 空数组、空树 —— 输入测试
582 |
583 |
584 |
585 | #### 三、代码编写
586 |
587 | - 序列化:
588 |
589 | ```javascript
590 | let result = [];
591 | var serialize = function(root) {
592 | // 判空
593 | if(root == null){
594 | result.push('$');
595 | return;
596 | }
597 | // 前序遍历
598 | result.push(root.val)
599 | serialize(root.left)
600 | serialize(root.right)
601 | // 打印
602 | console.log(result)
603 | };
604 |
605 | serialize(symmetricalTree);
606 | ```
607 |
608 | - 反序列化:
609 |
610 | ```javascript
611 | // 反序列化二叉树
612 | var deserialize = function(arr) {
613 | // 判空
614 | if(arr.length == 0){
615 | return null;
616 | }
617 |
618 | // 出栈队判断
619 | let node = null;
620 | const val = arr.shift();
621 | if(val !== '$'){
622 | node = {
623 | val: val
624 | };
625 | node.left = deserialize(arr);
626 | node.right = deserialize(arr);
627 | }
628 | return node;
629 | };
630 | let str = '8,6,5,$,$,7,$,$,6,7,$,$,5,$,$';
631 | console.log(deserialize(str.split(',')));
632 | ```
633 |
634 |
635 |
636 | ### 十、**面试题54:二叉树的第 K 大节点**
637 |
638 | > 给定一棵二叉搜索树,请找出其中的第 K 大节点。
639 |
640 |
641 |
642 | #### 一、思路
643 |
644 | 要想找到第 K 大结点必要要知道排序,二叉树的前、中、后遍历中的中序遍历就是从小到大排序。然后遍历的同时计数找到第 K 大节点。
645 |
646 |
647 |
648 | #### 二、测试用例
649 |
650 | - 完全二叉树、非完全二叉树 —— 普通测试
651 | - 只有左子节点的二叉树、只有右子节点的二叉树、只有一个节点的二叉树 —— 特殊测试
652 | - K 的范围、空树 —— 输入测试
653 |
654 |
655 |
656 | #### 三、代码编写
657 |
658 | ```javascript
659 | // 求二叉树中第 K 大节点
660 | var kthTallest = function(root, k) {
661 | let res = []
662 | // 遍历
663 | const inorder = (root) => {
664 | if (root) {
665 | inorder(root.left);
666 | res.push(root.val);
667 | inorder(root.right);
668 | }
669 | }
670 | // 调用
671 | inorder(root);
672 | return res[res.length - k]
673 | };
674 |
675 | ```
676 |
677 |
678 |
679 | ### 十一、**面试题55:二叉树的深度**
680 |
681 | 输入一棵二叉树的根节点,求该树的深度。从根节点到叶子节点依次经过的节点(包含根、叶子节点)形成树的一条路径,最长路径的长度树的深度。
682 |
683 |
684 |
685 | #### 一、思路
686 |
687 | 1、思路一:按层遍历,对按层遍历的算法进行改进,每遍历一次层进行加一。
688 |
689 | 2、思路二:寻找最长路径,借助遍历最长路径的设计思路记性改进。只需记录两个子树最深的结点为主。
690 |
691 |
692 |
693 | #### 二、测试用例
694 |
695 | - 完全二叉树、非完全二叉树 —— 普通测试
696 | - 只有左子节点、只有右子节点、只有一个结点二叉树 —— 特殊测试
697 | - 空树 —— 输入测试
698 |
699 |
700 |
701 | #### 三、代码编写
702 |
703 | ```javascript
704 | var maxDepth = function(root) {
705 | // 如果根节点为 null
706 | if(root === null) return 0;
707 |
708 | // 递归左子树
709 | let depthLeft = maxDepth(root.left);
710 |
711 | // 递归右子树
712 | let depthRight = maxDepth(root.right);
713 |
714 | // 将子问题合并求总问题
715 | return Math.max(depthLeft,depthRight) + 1;
716 | };
717 | ```
718 |
719 |
720 |
721 | ## 总结
722 |
723 | ### 一、解题思路总结
724 |
725 | #### 1、根据树前(根左右)、中(左根右)、后(左右根)序遍历的规律来解决问题。
726 |
727 | > 通过二叉树的遍历来找到规律,从而找到解题思路。
728 |
729 | - 重建二叉树
730 |
731 | 根据前、中序遍历,找到二叉树的根节点和左右子树的规律,然后递归构建二叉树。
732 |
733 | - 二叉树的下一节点
734 |
735 | 根据中序遍历,找出包含任何节点的一下节点的所有可能情况,然后根据情况分别进行判断。
736 |
737 | - 二叉树的后续遍历序列
738 |
739 | 通过中序遍历找到打印二叉树结点的规律,可以判断此后续遍历是否为二叉树。
740 |
741 | - 二叉树和为某一值的路径
742 |
743 | 选择二叉树的遍历,对每个节点进行存储判断,然后根据二叉树叶子节点的特点,进行对问题的解决。
744 |
745 | - 二叉树的第 K 大结点
746 |
747 | 中序遍历的结果是从小到大,然后倒数找到第 K 大数据。
748 |
749 | - 序列化二叉树
750 |
751 | 遍历二叉树,遇到 null 转化为特殊符号。
752 |
753 |
754 |
755 | #### 2、根据树的结构寻找规律来解决问题
756 |
757 | > 通过二叉树的特点:左子节点小于父节点、右子节点大于父节点、树的节点可以进行递归等,以上特点又是更好的帮我们解决思路。
758 |
759 | - 树的子结构
760 |
761 | 根据子结构和主体树的特点,对其树的结构进行分析,可以找到解题的思路。
762 |
763 | - 镜像二叉树
764 |
765 | 观察镜像二叉树的左右子节点交换特点,可以找到解题思路。
766 |
767 | - 对称二叉树
768 |
769 | 观察对称二叉树有什么特点,在结构上和遍历上寻找特点和规律,可以找到解题思路。
770 |
771 | - 按层遍历二叉树
772 |
773 | 根据二叉树每层节点的结构关系(父子关系),可以进行每层遍历,通过上层找到下层的遍历结点。
774 |
775 | - 反序列化二叉树
776 |
777 | 根据遍历的规律和二叉树的规律,将遍历结果生成一棵二叉树。
778 |
779 |
780 |
781 | ### 二、测试用例
782 |
783 | 通过以上题目中,我将测试用例分为三大种,测试代码的时候,在这三大种进行想就可以了。
784 |
785 | - **普通测试**
786 | - **特殊测试**
787 | - **输入测试**
788 |
789 |
790 |
791 | #### 1、普通测试
792 |
793 | 普通测试从两个方面去想,第一个方面就是问题的本身,比如对称二叉树的判断,普通测试就是分别输入一个对称二叉树和非对称二叉树进行测试。第二个方面就是问题本身没有什么可以找到的测试,比如按层遍历二叉树,它的普通测试就是分别输入完全二叉树(普通二叉树也可以),非完全二叉树进行测试。
794 |
795 |
796 |
797 | #### 2、特殊测试
798 |
799 | 特殊测试强调的是树的特殊性,特殊的二叉树就那么几个,比如:只有左子节点的二叉树、只有右子节点的二叉树、只有一个节点的二叉树、没有结点的二叉树。
800 |
801 |
802 |
803 | #### 3、输入测试
804 |
805 | 输入测试,顾名思义,要对用户输入的参数进行判断,比如,你输入一棵树,要判断是否为空。再比如,求最大 K 结点,对 K 的取值范围进行判断。
806 |
807 |
808 |
809 | ### 三、代码编写
810 |
811 | 将二叉树的解题思路转化为代码除了熟练最基本的二叉树的增、删、改、查之外,最重要的就是二叉树的递归,因为二叉树的结构决定了用递归解决二叉树问题更加简便。但是递归的书写并不仅简单,因为它有递和归的过程,大脑并不能更好的去处理这些,可以去看之前总结递归的文章《[数据结构与算法之递归系列](https://github.com/luxiangqiang/Blog/blob/master/articel/%E6%95%B0%E6%8D%AE%E7%BB%93%E6%9E%84%E4%B8%8E%E7%AE%97%E6%B3%95%E7%B3%BB%E5%88%97/%E6%95%B0%E6%8D%AE%E7%BB%93%E6%9E%84%E4%B8%8E%E7%AE%97%E6%B3%95%E4%B9%8B%E9%80%92%E5%BD%92%E7%B3%BB%E5%88%97.md)》。
812 |
813 | 书写二叉树递归问题有一点特别重要,不要尝试的去想那个递归的过程,而是先去寻找到递归的终止条件,然后对每次递归的结果进行判断,然后让他递归去吧,再次强调千万别去思考过程。
814 |
815 |
816 |
817 |
818 |
819 |
820 |
821 |
822 |
823 |
824 |
825 |
826 |
827 |
828 |
829 |
830 |
831 |
832 |
833 |
834 |
835 |
836 |
837 |
838 |
839 |
--------------------------------------------------------------------------------
/articel/数据结构与算法系列/数据结构与算法之链表系列[题型篇].md:
--------------------------------------------------------------------------------
1 | # 数据结构与算法之链表系列【题型篇】
2 |
3 | 
4 |
5 |
6 |
7 | ## 目录
8 |
9 | 
10 |
11 |
12 |
13 | ## 写在前边
14 |
15 | 如果你和小鹿一样,刚开始对链表的操作代码实现很懵的话,不妨按照小鹿经过一个月的时间对链表相关操作以及题型的整理总结,由浅入深进行适当的练习,我相信,当你真正的练习完这些题目,不但会让你失去链表对你心理上的困惑,而且对你学习其他数据结构有很大的信心和帮助!
16 |
17 |
18 |
19 | #### 1、学习建议
20 |
21 | 小鹿不建议你一口气去看完这篇所有的题目和练习,给自己制定一个小计划,我当初整理该题目的时候,每天都计划认真整理一到题目,把每道题分析透,这样才能达到最好的吸收。
22 |
23 |
24 |
25 | #### 2、学习路径
26 |
27 | > 本篇分为三个阶段,基础练习阶段、进阶练习阶段、加强练习阶段。
28 | >
29 |
30 | 1)基础练习阶段
31 |
32 | 首先进行第一个阶段之前,你已经对链表的基础知识能够熟练掌握,但是对于没有动手写过链表代码,那么你从第一阶段最基础的开始进行。确保每一个基础点要亲自动手用自己熟悉的语言写出来,虽然本篇中基本都是 javascript 代码实现的,但是算法思路是一成不变的,如果遇到困难可以自行百度或谷歌,也可以下方给我进行留言。
33 |
34 | 2)进阶练习阶段
35 |
36 | 如果你对上述的链表基本代码已经完全熟练掌握了,那么恭喜你可以进行下一个阶段,进阶阶段,这一阶段增加的难度就是链表的操作是对于实际问题来解决的,所以非常锻炼你对问题的分析能力和解决能力,也考验你对代码的全面性、鲁棒性。这一阶段非常的重要,下面的每道题我都做出了详细的分析。
37 |
38 | 3)加强练习阶段
39 |
40 | 如果上述的进阶练习阶段的题型你都了如指掌了,那么不妨我们实战一下,LeetCode 汇聚了很多面试的题型,所以我在上边整理了几个经典的题目,你可以尝试着解答它们,相关题目的代码以及解题思路我都整理好了。这一阶段的题目小鹿会在后期不断的更新,这些题目你能够完全掌握,链表对你来说小菜一碟了。
41 |
42 |
43 |
44 | ## 一、链表基础练习(阶段一)
45 |
46 | > 自己首相尝试着一个个攻破下方的链表中最基础的操作,相关代码我也整理好了(先自己尝试着去解决哦)。
47 |
48 | - 单链表的插入、删除、查找操作([点击查看代码实现](https://github.com/luxiangqiang/Data-Structure-Coding/blob/master/Link_List/javascript/SinglyLinkedList.md))。
49 | - 循环链表的插入、删除、查找操作 ([点击查看代码实现](https://github.com/luxiangqiang/Data-Structure-Coding/blob/master/Link_List/javascript/CircularLinkedList.md))。
50 |
51 | - 双向链表的插入、删除、查找操作 ([点击查看代码实现](https://github.com/luxiangqiang/Data-Structure-Coding/blob/master/Link_List/javascript/DoubleLinkedList.md))。
52 |
53 |
54 |
55 | ## 二、链表进阶练习(阶段二)
56 |
57 | ### 1、单链表从尾到头打印
58 |
59 | > 题目:输入一个链表的头结点,从尾到头反过来打印出每个节点的值。
60 |
61 |
62 |
63 | #### 1.1 问题分析与解决
64 |
65 | ###### ▉ 问题分析
66 |
67 | 1)看到题目第一想到的就是反转链表在打印输出,一种反转链表的方法,但是这种方法改变了原有的链表结构。
68 |
69 | > 缺点:使得链表的结构发生改变了。如果不改变链表结构应该怎么解决?
70 | >
71 |
72 | 2)从问题中可以得出,我们想要从尾到头打印链表,正常情况下是从头到尾打印的,我们就会想到最后的数据先打印,开始的数据最后打印,有种“先进后出”的特点,我们就能想到用“栈”这种结构,用栈来实现。
73 |
74 | > 缺点:代码不够简洁。
75 | >
76 | > 优点:鲁棒性好(在不确定的情况下,程序仍然可以正确的执行)。
77 | >
78 |
79 | 3)提到栈这种数据结构,我们就会想到“递归”的实现就是用栈这种数据结构实现的。既然栈能实现,那么递归也能实现。
80 |
81 | > 缺点:如果链表很长,递归深度很深,导致堆栈溢出。
82 | >
83 | > 优点:代码简洁、明了。
84 |
85 |
86 |
87 | ###### ▉ 算法思路
88 |
89 | > 得出以下几种实现方式:
90 | >
91 | > - 反转链表法
92 | > - 栈实现
93 | > - 递归实现
94 | >
95 |
96 | 1)反转链表实现:
97 |
98 | 从尾到头输出链表的内容,一般的思路就是将链表反转过来,然后从头到尾输出数据。
99 |
100 | 2)栈实现:
101 |
102 | 从头到尾遍历单链表,将数据存储按照顺序存储到栈中。然后遍历整个栈,打印输出数据。
103 |
104 | 3)递归实现:
105 |
106 | 可以通过递归的方式来实现单链表从尾到头依次输出,递归过程涉及到“递”和“归”,反转链表输出数据,正式利用了循环“递”的过程,所以数据先从头部输出,那么递归采用的是“归”的过程来输出内容,输出当前结点先要输出当前节点的下一节点。
107 |
108 |
109 |
110 | ###### ▉ 测试用例
111 |
112 | > 在写代码之前,要想好测试用例才能写出健全、鲁棒性的代码,也是为了考虑到边界情况,往往也是整个程序最致命的地方,如果考虑不全面,就会出现 bug,导致程序崩溃。
113 |
114 | 测试用例:
115 |
116 | 1)输入空链表;
117 |
118 | 2)输入的链表只有一个结点;
119 |
120 | 3)输入的链表有多个结点。
121 |
122 |
123 |
124 | ###### ▉ 代码实现:反转链表法
125 |
126 | ```javascript
127 | //定义结点
128 | class Node{
129 | constructor(data){
130 | this.data = data;
131 | this.next = null;
132 | }
133 | }
134 | //定义链表
135 | class LinkedList{
136 | constructor(){
137 | this.head = new Node('head');
138 | }
139 |
140 | // 功能:单链表反转
141 | // 步骤:
142 | // 1、定义三个指针(pre=null/next/current)
143 | // 2、判断链表是否可反转(头节点是否为空、是否有第二个结点)
144 | // 3、尾指针指向第一个结点的 next
145 | // 4、尾指针向前移动
146 | // 5、当前指针(current)向后移动
147 | // 6、将 head 指向单转好的结点
148 | reverseList = () =>{
149 | //声明三个指针
150 | let current = this.head; //当前指针指向头节点
151 | let pre = null;//尾指针
152 | let next;//指向当前指针的下一个指针
153 |
154 | //判断单链表是否符合反转的条件(一个结点以上)?
155 | if(this.head == null || this.head.next == null) return -1;
156 |
157 | //开始反转
158 | while(current !== null){
159 | next = current.next;
160 | current.next = pre;
161 | pre = current;
162 | current = next;
163 | }
164 | this.head = pre;
165 | }
166 |
167 | //输出结点
168 | print = () =>{
169 | let currentNode = this.head
170 | //如果结点不为空
171 | while(currentNode !== null){
172 | console.log(currentNode.data)
173 | currentNode = currentNode.next;
174 | }
175 | }
176 | }
177 | ```
178 |
179 |
180 |
181 | ###### ▉ 代码实现:循环栈
182 |
183 | ```javascript
184 | //方法三:栈实现
185 | const tailToHeadOutput = (currentNode)=>{
186 | let stack = [];
187 | //遍历链表,将数据入栈
188 | while(currentNode !== null){
189 | stack.push(currentNode.data);
190 | currentNode = currentNode.next;
191 | }
192 | //遍历栈,数据出栈
193 | while(stack.length !== 0){
194 | console.log(stack.pop());
195 | }
196 | }
197 | ```
198 |
199 |
200 |
201 | ###### ▉ 代码实现:递归
202 |
203 | ```javascript
204 | // 步骤:
205 | // 1、判断是否为空链表
206 | // 2、终止条件(下一结点为空)
207 | // 3、递归打印下一结点信息
208 | const tailToHeadOutput = (head)=>{
209 | // 判断是否空链表
210 | if(head !== null){
211 | // 判断下一结点是否为空
212 | if(head.next !== null){
213 | // 下一结点不为空,先输出下一结点
214 | tailToHeadOutput(head.next)
215 | }
216 | console.log(head.data);
217 | }else{
218 | console.log("空链表");
219 | }
220 | }
221 | ```
222 |
223 |
224 |
225 | ###### ▉ 性能分析
226 |
227 | 反转链表实现:
228 |
229 | - 时间复杂度:O(n)。需要遍历整个链表,时间复杂度为 O(n)。
230 | - 空间复杂度:O(1)。不需要额外的栈存储空间,空间复杂度为 O(1)。
231 |
232 | 循环栈实现:
233 |
234 | - 时间复杂度:O(n)。需要遍历整个链表,时间复杂度为 O(n)。
235 | - 空间复杂度:O(n)。需要额外的栈存储空间,空间复杂度为 O(n)。
236 |
237 | 递归实现:
238 |
239 | - 时间复杂度:O(n)。需要遍历整个链表,时间复杂度为 O(n)。
240 | - 空间复杂度:O(n)。需要额外的栈存储空间,空间复杂度为 O(n)。
241 |
242 |
243 |
244 | #### 2.2 小结
245 |
246 | ###### ▉ 考察内容
247 |
248 | 1)对单链表的基本操作。
249 |
250 | 2)代码的鲁棒性。
251 |
252 | 3)循环、递归、栈的灵活运用。
253 |
254 |
255 |
256 | ###### ▉ 扩展思考:循环和递归
257 |
258 | **适用条件:**如果需要进行多次计算相同的问题,将采用循环或递归的方式。
259 |
260 | **递归的优点:**代码简洁。
261 |
262 | **递归的缺点:**
263 |
264 | 1)堆栈溢出:函数调用自身,函数的临时变量是压栈的操作,当函数执行完,栈才清空,如果递归的规模过大,在函数内部一直执行函数的自身调用,临时变量一直压栈,系统栈或虚拟机栈内存小,导致堆栈溢出。
265 |
266 | 2)重复计算:递归会出现很多的重复计算问题,重复计算对程序的性能有很大影响,导致消耗时间成指数增长,但是可以通过散列表的方式解决。
267 |
268 | 3)高空间复杂度:递归的每次函数调用都要涉及到在内存开辟空间,压栈、出栈等操作,即耗时又耗费空间,导致递归的效率并不如循环的效率。
269 |
270 | **扩展:**
271 |
272 | 1)递归—栈:递归的本质是栈,通常用栈循环解决的问题适合于递归。
273 |
274 | 2)递归-动态规划:动态规划解决问题经常用递归的思路分析问题。关于递归重复计算问题,我们通常使用自下而上的解决思路(动态规划)来解决递归重复计算的问题。
275 |
276 | ※ 具体看这篇之前写的 8000 字的完整章节:[数据结构与算法之递归系列](https://github.com/luxiangqiang/Blog/blob/master/articel/%E6%95%B0%E6%8D%AE%E7%BB%93%E6%9E%84%E4%B8%8E%E7%AE%97%E6%B3%95%E7%B3%BB%E5%88%97/%E6%95%B0%E6%8D%AE%E7%BB%93%E6%9E%84%E4%B8%8E%E7%AE%97%E6%B3%95%E4%B9%8B%E9%80%92%E5%BD%92%E7%B3%BB%E5%88%97.md)
277 |
278 |
279 |
280 | ###### ▉ 注意事项:
281 |
282 | 1)涉及到循环解决的问题,可以想一想能不能使用递归来解决。
283 |
284 | 2)用递归解决一定要铭记递归的缺点带来的性能问题。
285 |
286 | 3)递归解决的问题,能不能用动态规划来解决,使得性能更高。
287 |
288 | 4)用到栈这种数据结构,想一想递归是否可以实现呢。
289 |
290 |
291 |
292 | ### 2、删除链表结点
293 |
294 | > 题目:在 O(1)的时间复杂度内删除链表节点。
295 | >
296 | > 给定单向链表的头指针和一个节点指针,定义一个函数在 O(1)时间内删除该节点。
297 |
298 |
299 |
300 | #### 2.1 问题分析与解决
301 |
302 | ###### ▉ 问题分析
303 |
304 | 1)想必看到单链表删除节点的题,第一想到的就是删除链表结点需要以 O(n)时间复杂度遍历链表找到该结点的前结点,然后以 O(1)时间复杂度进行删除,时间复杂度为O(n)。而题目中的确实整体要求时间复杂度为 O(1)。
305 |
306 | 2)怎么才能达到 O(1)的时间复杂度删除链表?如果不遍历不就可以了?如果直接删除的时间复杂度为 O(1),前提是我们需要知道前结点才能做到。我们就会想怎么做到不用遍历数据才能获取到前结点呢?而且必须保证时间复杂度为 O(1)。
307 |
308 | 3)但是必须让自己多想一步就是如果删除的结点是尾结点怎么操作,如果删除的链表结点只有一个结点,即是尾结点又是头结点怎么办?
309 |
310 |
311 |
312 | ###### ▉ 算法思路
313 |
314 | 得出以下几种实现方式:
315 |
316 | - 交换结点法
317 |
318 | 1)这一有种技巧很难想到,就是我把当前结点的数据与下一结点的数据进行交换,删除下一结点不就可以达到时间复杂度为O(1)了吗。而且我们知道当前结点就是下一结点的前节点,perfect。
319 |
320 | 2)针对以上两种特殊情况,如果是尾结点,没有下一结点,我们就从头遍历链表删除节点;如果即是尾结点又是头结点,那么删除头结点,并置于 null。
321 |
322 |
323 |
324 | ###### ▉ 测试用例
325 |
326 | 1) 输入空链表;
327 |
328 | 2)在多个结点链表中删除中间结点;
329 |
330 | 3)在多个链表中删除头结点;
331 |
332 | 4)在多个链表总删除尾结点;
333 |
334 | 5)在只有一个结点链表中删除唯一结点;
335 |
336 |
337 |
338 | ###### ▉ 代码实现
339 |
340 | ```javascript
341 | // 定义结点
342 | class Node{
343 | constructor(data){
344 | this.data = data;
345 | this.next = null;
346 | }
347 | }
348 | // 定义链表
349 | class LinkedList{
350 | constructor(){
351 | this.head = new Node('head');
352 | }
353 |
354 | //根据 value 查找结点
355 | findByValue = (value) =>{
356 | let currentNode = this.head;
357 | while(currentNode !== null && currentNode.data !== value){
358 | currentNode = currentNode.next;
359 | }
360 | //判断该结点是否找到
361 | console.log(currentNode)
362 | return currentNode === null ? -1 : currentNode;
363 | }
364 |
365 | //插入元素(指定元素向后插入)
366 | insert = (value,element) =>{
367 | //先查找该元素
368 | let currentNode = this.findByValue(element);
369 | //如果没有找到
370 | if(currentNode == -1){
371 | console.log("未找到插入位置!")
372 | return;
373 | }
374 | let newNode = new Node(value);
375 | newNode.next = currentNode.next;
376 | currentNode.next = newNode;
377 | }
378 |
379 | //遍历所有结点
380 | print = () =>{
381 | let currentNode = this.head
382 | //如果结点不为空
383 | while(currentNode !== null){
384 | console.log(currentNode.data)
385 | currentNode = currentNode.next;
386 | }
387 | }
388 |
389 | // 删除节点(核心代码)
390 | deleteNode = node =>{
391 | // 判断当前查找的结点是否为 null
392 | if(node == null) return -1;
393 | // 1、查找删除的结点
394 | let d_node = this.findByValue(parseInt(node.data))
395 | // 2、判断该结点是否为尾结点
396 | if(d_node.next == null){
397 | // 重新遍历链表
398 | let p = null;
399 | let current = this.head;
400 | while(current.next !== null){
401 | p = current;
402 | current = current.next;
403 | }
404 | // 尾结点置为 null
405 | p.next = null;
406 | }else{
407 | // 3、将删除结点的值与下一结点交换
408 | d_node.data = d_node.next.data;
409 | // 4、删除下一结点
410 | d_node.next = d_node.next.next;
411 | }
412 | }
413 | }
414 |
415 | // 测试
416 | sortedList1 = new LinkedList()
417 | sortedList1.insert(1, 'head')
418 | sortedList1.insert(2, 1)
419 | sortedList1.insert(3, 2)
420 | sortedList1.insert(4, 3)
421 | sortedList1.print();
422 | console.log('------------------------------删除指定结点----------------------------')
423 | let dnode = new Node('1')
424 | sortedList1.deleteNode(dnode)
425 | sortedList1.print();
426 | ```
427 |
428 |
429 |
430 | ###### ▉ 性能分析
431 |
432 | - 时间复杂度:O(1)。经过上述的方法,删除一个链表的结点,除了删除一个链表的尾结点之外,其他删除节点的时间复杂度为 O(1),获取删除的结点的前一结点,时间复杂度为 O(1),删除节点的时间复杂度为 O(1)。只有删除尾结点才需要遍历整个链表,但大部分删除节点是 O(1)的。使用分析时间复杂度的一个方法摊还分析,将删除节点的时间复杂度平均分到其他大部分情况下,所以平均时间复杂度为 O(1)。
433 |
434 | - 空间复杂度:O(1)。不需要额外的内存空间。
435 |
436 |
437 |
438 | #### 2.2 小结
439 |
440 | ###### ▉ 内容考察
441 |
442 | 1)对单链表的删除基本操作。
443 |
444 | 2)对问题的有创新思维的解决能力:能不能将复杂问题的根源用另一种思维去优化。
445 |
446 | 3)问题考虑的全面性:考虑到问题出现的各种特殊情况,以及边界问题。
447 |
448 |
449 |
450 | ### 3、链表中的倒数第 K 个结点
451 |
452 | > 题目:输入一个链表,输出该链表中倒数第 K 个节点。为符合大多数人的习惯,从 1 开始计数,即链表的尾结点是倒数第一个节点。
453 |
454 |
455 |
456 | #### 3.1 问题分析与解决
457 |
458 | ###### ▉ 问题分析
459 |
460 | 1)看到这个题的第一想法就是从链表头遍历到链表尾部,然后尾部倒数 k 个数,因为是单链表,所以倒数并不能实现,想法行不通。
461 |
462 | 2)那我们只能将思路转移到头结点开始,怎么才能从头结点开始遍历到倒数第 k 个结点呢?大体我们可以得出至少需要遍历两次链表。
463 |
464 | 3)上述能不能再优化呢?遍历一次链表就可以完成查找?
465 |
466 |
467 |
468 | ###### ▉ 算法思路
469 |
470 | 得出以下几种实现方式:
471 |
472 | - 两次遍历法
473 | - 一次遍历法
474 |
475 | 前提条件:
476 |
477 | 1)**不要忘记判断单链表是否为环型结构**
478 |
479 | 两次遍历法:
480 |
481 | 1)有一个规律就是链表的长度 n 减去 k 加 1 就是倒数第 k 个数据。所以需要遍历链表得到链表的长度,然后再遍历两次找到链表的倒数第 k 个数据。整个过程需要遍历两遍链表。
482 |
483 | 一次遍历法:
484 |
485 | 1)那我们就用到双指针,第一个指针指向第一个结点,第二个指针指向 k - 1 个结点,同时向前移动,直到第二个节点指向尾结点位置,第一个节点就指向了倒数第 k 结点。遍历一遍链表就完成查找。
486 |
487 |
488 |
489 | ###### ▉ 测试用例
490 |
491 | 1)k 的取值范围(0 < k < n);输入不在范围内的数据。
492 |
493 | 2)输入空链表。
494 |
495 | 3)查找倒数第 k 结点为头结点/尾结点。
496 |
497 |
498 |
499 | ###### ▉ 代码实现
500 |
501 | ```javascript
502 | // 定义结点
503 | class Node{
504 | constructor(data){
505 | this.data = data;
506 | this.next = null;
507 | }
508 | }
509 | // 定义链表
510 | class LinkedList{
511 | constructor(){
512 | this.head = new Node('head');
513 | }
514 |
515 | //根据 value 查找结点
516 | findByValue = (value) =>{
517 | let currentNode = this.head;
518 | while(currentNode !== null && currentNode.data !== value){
519 | currentNode = currentNode.next;
520 | }
521 | //判断该结点是否找到
522 | console.log(currentNode)
523 | return currentNode === null ? -1 : currentNode;
524 | }
525 |
526 | //插入元素(指定元素向后插入)
527 | insert = (value,element) =>{
528 | //先查找该元素
529 | let currentNode = this.findByValue(element);
530 | //如果没有找到
531 | if(currentNode == -1){
532 | console.log("未找到插入位置!")
533 | return;
534 | }
535 | let newNode = new Node(value);
536 | newNode.next = currentNode.next;
537 | currentNode.next = newNode;
538 | }
539 |
540 | //遍历所有结点
541 | print = () =>{
542 | let currentNode = this.head
543 | //如果结点不为空
544 | while(currentNode !== null){
545 | console.log(currentNode.data)
546 | currentNode = currentNode.next;
547 | }
548 | }
549 |
550 | // 检测单链表是否为环
551 | checkCircle = ()=>{
552 | // 判断是否为空链表
553 | if(this.head == null) return fast;
554 | // 定义快慢指针
555 | let fast = this.head.next;
556 | let low = this.head;
557 | //进行循环判断(当前 fast 结点/fast 移动两步后的结点是否为 null)
558 | while(fast !== null && fast.next !== null){
559 | // fast 指针向前移动两步
560 | fast = fast.next.next;
561 | // low 指针向前移动一步
562 | low = low.next;
563 | // 如果为环,总有一天会相遇
564 | if(fast === low) return true;
565 | }
566 | return false;
567 | }
568 |
569 | // 查找倒数第 k 结点
570 | findByIndexFromEnd = k =>{
571 | //判断 k 是否大于0
572 | if(k < 1) return 'k 的大小不在搜索范围内';
573 | // 检测是否为环
574 | if(this.checkCircle()) return false;
575 | // 定义两个指针进行遍历
576 | let current = this.head;
577 | let fast = current;
578 | let low = current;
579 |
580 | let pos = 0;
581 | for(let i = 1;i <= k - 1;i++){
582 | if(fast.next !== null){
583 | fast = fast.next;
584 | }else{
585 | // k 的大小超出链表大小的范围
586 | return 'k 的大小超出链表的范围';
587 | }
588 | }
589 |
590 | // low 和 fast 指针同时移动
591 | while(fast.next !== null){
592 | fast = fast.next;
593 | low = low.next;
594 | }
595 |
596 | // 返回倒数第 k 结点
597 | return low;
598 | }
599 | }
600 | // 测试
601 | const list = new LinkedList();
602 | list.insert('1','head');
603 | // list.insert('2','1');
604 | // list.insert('3','2');
605 | // list.insert('4','3');
606 | // list.insert('5','4');
607 | // list.insert('6','5');
608 | list.print();
609 | console.log('-------------------查找倒数第 k 结点----------------')
610 | console.log(list.findByIndexFromEnd(8));
611 | ```
612 |
613 |
614 |
615 | ###### ▉ 性能分析
616 |
617 | 两次遍历法:
618 |
619 | - 时间复杂度:O(k*n)。当 k 趋近于 n 时,最坏时间复杂度为 O(n^2)。
620 | - 空间复杂度:O(1)。不需要额外的内存空间。
621 |
622 | 一次遍历法:
623 |
624 | - 时间复杂度:O(n)。只需要遍历一次单链表,所以时间复杂度为O(n)。
625 | - 空间复杂度:O(1)。不需要额外的内存空间。
626 |
627 |
628 |
629 | #### 3.2 小结
630 |
631 | ###### ▉ 内容考察
632 |
633 | 1)对单链表的基本操作。
634 |
635 | 2)代码的全面性、鲁棒性。
636 |
637 |
638 |
639 | ###### ▉ 注意事项
640 |
641 | 1)当我们用一个指针不能解决时,想一想两个指针能否解决?
642 |
643 |
644 |
645 | ###### ▉ 相关题目
646 |
647 | 1)求中间结点
648 |
649 | 2)求倒数第 k 个结点
650 |
651 | 3)检测环的存在
652 |
653 |
654 |
655 | ### 4、反转链表
656 |
657 | > 题目:定义一个函数,输入一个链表的头结点,反转该链表并输出反转链表的头结点。
658 |
659 |
660 |
661 | #### 4.1 问题分析与解决
662 |
663 | ###### ▉ 问题分析
664 |
665 | 1)反转链表的我们第一能够想到的方法就是最常用的方法,声明三个指针,把头结点变为尾结点,然后下一结点拼接到尾结点的头部,一次类推。说白了就是就是直接将链表指针反转就可以实现反转链表。
666 |
667 |
668 |
669 | ###### ▉ 算法思路
670 |
671 | 1)定义三个指针,分别为 Pnext、pre、current,current 存储当前结点, pre 指向反转好的结点的头结点,Pnext 存储下一结点信息。
672 |
673 | 2)判断当前结点是否可以反转(是否为空链表或链表大于 1 个结点)?
674 |
675 | **步骤:**
676 |
677 | 1)Pnext 指针存储下一结点 。
678 |
679 | 2)当前结点的 next 结点是否为 null (为 null 的话当前结点就是最后的一个结点),如果为 null,将当前节点赋值为 head 头指针(断裂处)。
680 |
681 | 3)将 pre 指针指向的结点赋值当前节点 current 的下一结点 next。
682 |
683 | 4)然后让 pre 指针指向当前节点 current。
684 |
685 | 5)current 继续遍历, 当前节点指向 current 指向 Pnext。
686 |
687 | **递归法(重点分析):**
688 |
689 | 1)先确定终止条件:当下一结点为 null 时,返回当前节点;
690 |
691 | 2)判断当前的链表是否为 null;
692 |
693 | 3)递归找到尾结点,将其存储为头结点。
694 |
695 | 4)此时递归的层次是第二层递归,所以要设置为头结点的下一结点就是当前第二层结点,并且将第二节点的下一结点设置为 bull。
696 |
697 |
698 |
699 | ###### ▉ 测试用例
700 |
701 | 1)链表是空链表。
702 |
703 | 2)当前链表的长度小于等于 1。
704 |
705 | 3)输入长度大于 1 的链表。
706 |
707 |
708 |
709 | ###### ▉ 代码实现
710 |
711 | ```javascript
712 | var reverseList = function(head) {
713 | // 判断当前链表是否为空链表
714 | if(head == null) return null;
715 |
716 | // 定义三个指针
717 | let [current,prev,next] = [head,null,null];
718 |
719 | while(current !== null){
720 | //1、存储下一结点
721 | next = current.next;
722 | if(next == null){
723 | head = current;
724 | }
725 | current.next = prev;
726 | prev = current;
727 | current = next;
728 | }
729 | return head;
730 | };
731 | ```
732 |
733 |
734 |
735 | ###### ▉ 递归法
736 |
737 | ```javascript
738 | const reverseList = (head)=>{
739 | //如果链表为空或者链表中只有一个元素
740 | if(head == null || head.next == null){
741 | return head;
742 | }else{
743 | //先反转后面的链表,走到链表的末端结点
744 | let newhead = reverseList(head.next);
745 | //再将当前节点设置为后面节点的后续节点
746 | head.next.next = head;
747 | head.next = null;
748 | return newhead;
749 | }
750 | }
751 | ```
752 |
753 |
754 |
755 | ###### ▉ 性能分析
756 |
757 | - 时间复杂度:O(n)。只需遍历整个链表就可以完成反转,时间复杂度为 O(n)。
758 | - 空间复杂度:O(1)。只需要常量级的空间,空间复杂度为 O(1)。
759 |
760 |
761 |
762 | #### 4.2 小结
763 |
764 | ###### ▉ 内容考察
765 |
766 | 1)对单链表的基本操作。
767 |
768 | 2)对指针操作顺序的逻辑性考察。
769 |
770 | 3)考察思维的全面性以及代码的鲁棒性。
771 |
772 |
773 |
774 | ###### ▉ 注意事项
775 |
776 | 1)边界条件。
777 |
778 | 2)写代码之前想好测试用例,写完代码一一验证测试用例的正确性。
779 |
780 |
781 |
782 | ### 5、合并两个有序链表
783 |
784 | > 题目:输入两个递增排序的链表,合并这两个链表并使新链表中的节点仍然是递增排序的。
785 |
786 |
787 |
788 | #### 5.1 问题分析与解决
789 |
790 | ###### ▉ 问题分析
791 |
792 | 1)合并两个链表,经常犯的错误就是没有弄清除指针的指向,导致链表合并的时候断裂以及代码全面性考虑的不全,也就是代码的鲁棒性存在问题。
793 |
794 | 2)递归。每次都要比较两个结点大小,是否可以使用递归来解决呢?
795 |
796 |
797 |
798 | ###### ▉ 算法思路
799 |
800 | **一般解决法:**
801 |
802 | 1)合并两个链表,首先需要两个指针,分别指向两个链表。
803 |
804 | 2)比较两个指针指向结点元素的大小,小的结点添加到新链表,然后指针向后移动继续比较。
805 |
806 | 3)直到其中一个链表没有结点了,另一个链表存在结点,将剩余的结点加入到新链表的尾部,完成合并。
807 |
808 | **递归法:(满足递归的三个条件)**
809 |
810 | 比较当前结点大小先比较下一结点的大小。
811 |
812 | 1)结点之间的比较可以分的子问题为每个节点的比较。
813 |
814 | 2)终止条件:其中一个链表结点为 null。
815 |
816 | 3)子问题和总问题具有相同的解决思路。
817 |
818 |
819 |
820 | ###### ▉ 测试用例
821 |
822 | 1)输入两个空链表。
823 |
824 | 2)其中一个链表为空链表。
825 |
826 | 3)输入两个完整的链表。
827 |
828 |
829 |
830 | ###### ▉ 代码实现
831 |
832 | ```javascript
833 | // 功能:两个有序链表的合并
834 | // 步骤:
835 | // 1、判断两个链表是否为 null,并将链表赋予临时变量
836 | // 2、声明合并链表,通过 currentNode 指向当前结点
837 | // 3、两个链表比较大小,数值小的添加到合并链表中,合并链表进行指针移动
838 | // 4、将链表剩余数据添加到合并链表后边
839 | const mergeSortList = (listA,listB) =>{
840 | //判断链表是否为空
841 | if(listA === null) return false;
842 | if(listB === null) return false;
843 | let a = listA;
844 | let b = listB;
845 |
846 | //声明合并链表,通过 currentNode 指向当前结点
847 | let resultList = undefined
848 |
849 | //两个链表比较大小,数值小的添加到合并链表中,合并链表进行指针移动
850 | if (a.data < b.data) {
851 | resultList = a
852 | a = a.next
853 | } else {
854 | resultList = b
855 | b = b.next
856 | }
857 | let currentNode = resultList;
858 | while (a !== null && b !== null) {
859 | if (a.data < b.data) {
860 | currentNode.next = a
861 | a = a.next
862 | } else {
863 | currentNode.next = b
864 | b = b.next
865 | }
866 | currentNode = currentNode.next
867 | }
868 |
869 | // 将链表剩余数据添加到合并链表后边
870 | if(a !== null){
871 | currentNode.next = a;
872 | }else{
873 | currentNode.next = b;
874 | }
875 | //返回合并链表
876 | return resultList;
877 | }
878 | ```
879 |
880 |
881 |
882 | ###### ▉ 递归实现
883 |
884 | ```javascript
885 | var mergeTwoLists = function(l1, l2) {
886 | let result = null;
887 | //终止条件
888 | if(l1 == null) return l2;
889 | if(l2 == null) return l1;
890 |
891 | //判断数值大小递归
892 | if(l1.val < l2.val){
893 | result = l1;
894 | result.next = mergeTwoLists(l1.next,l2);
895 | }else{
896 | result = l2;
897 | result.next = mergeTwoLists(l2.next,l1);
898 | }
899 |
900 | //返回结果
901 | return result;
902 | };
903 | ```
904 |
905 |
906 |
907 | ###### ▉ 代码测试
908 |
909 | ```javascript
910 | //定义结点
911 | class Node{
912 | constructor(data){
913 | this.data = data;
914 | this.next = null;
915 | }
916 | }
917 |
918 | //定义链表
919 | class LinkedList{
920 | constructor(){
921 | this.head = new Node('head');
922 | }
923 |
924 | //根据 value 查找结点
925 | findByValue = (value) =>{
926 | let currentNode = this.head;
927 | while(currentNode !== null && currentNode.data !== value){
928 | currentNode = currentNode.next;
929 | }
930 | //判断该结点是否找到
931 | console.log(currentNode)
932 | return currentNode === null ? -1 : currentNode;
933 | }
934 |
935 | //插入元素(指定元素向后插入)
936 | insert = (value,element) =>{
937 | //先查找该元素
938 | let currentNode = this.findByValue(element);
939 | //如果没有找到
940 | if(currentNode == -1){
941 | console.log("未找到插入位置!")
942 | return;
943 | }
944 | let newNode = new Node(value);
945 | newNode.next = currentNode.next;
946 | currentNode.next = newNode;
947 | }
948 |
949 | //遍历所有结点
950 | print = () =>{
951 | let currentNode = this.head
952 | //如果结点不为空
953 | while(currentNode !== null){
954 | console.log(currentNode.data)
955 | currentNode = currentNode.next;
956 | }
957 | }
958 | }
959 | // 合并两个链表
960 | var mergeSortList = function(l1, l2) {
961 | let result = null;
962 | //终止条件
963 | if(l1 == null) return l2;
964 | if(l2 == null) return l1;
965 |
966 | //判断数值大小递归
967 | if(l1.val < l2.val){
968 | result = l1;
969 | result.next = mergeSortList(l1.next,l2);
970 | }else{
971 | result = l2;
972 | result.next = mergeSortList(l2.next,l1);
973 | }
974 |
975 | //返回结果
976 | return result;
977 | };
978 |
979 | // 测试
980 | sortedList1 = new LinkedList()
981 | sortedList1.insert(9, 'head')
982 | sortedList1.insert(8, 'head')
983 | sortedList1.insert(7, 'head')
984 | sortedList1.insert(6, 'head')
985 | sortedList1.print();
986 | sortedList2 = new LinkedList()
987 | sortedList2.insert(21, 'head')
988 | sortedList2.insert(20, 'head')
989 | sortedList2.insert(19, 'head')
990 | sortedList2.insert(18, 'head')
991 | sortedList2.print();
992 | console.log('----------------合并两个有序的链表----------------')
993 | let resultList = mergeSortList(sortedList1.head.next,sortedList2.head.next)
994 | while (resultList !== null) {
995 | console.log(resultList.date);
996 | resultList = resultList.next;
997 | }
998 | ```
999 |
1000 |
1001 |
1002 | ###### ▉ 性能分析
1003 |
1004 | - 时间复杂度:O(n)。n 为较短的链表的长度。
1005 | - 空间复杂度:O(n+m)。需要额外的 n+m(两个链表长度之和) 大小的空间来存储合并的结点。
1006 |
1007 |
1008 |
1009 | #### 5.2 小结
1010 |
1011 | ###### ▉ 内容考察
1012 |
1013 | 1)对链表的基本操作。
1014 |
1015 | 2)写代码考虑问题的全面性和鲁棒性。
1016 |
1017 |
1018 |
1019 | ###### ▉ 注意事项
1020 |
1021 | 1)递归实现,注意递归解决问题的三个缺点。
1022 |
1023 | - 堆栈溢出
1024 | - 重复数据
1025 | - 高空间复杂度
1026 |
1027 |
1028 |
1029 | ## 三、LeetCode 加强练习阶段(阶段三)
1030 |
1031 | > 如果你对基本的链表操作已经掌握,想进一步提高对链表熟练度的操作,可以练习一下 LeetCode 题目。每道题我都做了详细的解析,如:问题分析、算法思路、代码实现、考查内容等,有关链表的相关题目会不断更新......
1032 |
1033 | - [环形链表 I](https://leetcode-cn.com/problems/linked-list-cycle/) ([题目解析](https://github.com/luxiangqiang/JS-LeetCode/blob/master/LinkedListCycle.md) )
1034 | - [环形链表 II](https://leetcode-cn.com/problems/linked-list-cycle-ii/) ([题目解析](https://github.com/luxiangqiang/JS-LeetCode/blob/master/LinkedListCycle2.md) )
1035 | - [合并K个排序链表](https://leetcode-cn.com/problems/merge-k-sorted-lists/) ([题目解析](https://github.com/luxiangqiang/JS-LeetCode/blob/master/MergekSortedLists.md) )
1036 |
1037 |
1038 |
1039 | ## 四、链表总结
1040 |
1041 | > 做了大量有关链表的题型之后,对链表的操作做一个总结和复盘,对链表有一个整体的把握和重新的认识。
1042 |
1043 |
1044 |
1045 | #### 1、结构上
1046 |
1047 | ① 存储链表的内存空间是不连续的,所有需要使用指针将这些零碎内存空间连接起来,导致需要通过指针来进行操作,这也是为什么链表中大多数都是关于指针的操作的原因。
1048 |
1049 | ② 链表在结构上有两个特殊的地方就是链表头和链表尾,很多操作都要对链表头和链表尾进行特殊处理,所以我们可以借助哨兵思想(在链表头添加一个哨兵),这样带头的链表可以简化问题的解决。
1050 |
1051 |
1052 |
1053 | #### 2、操作上
1054 |
1055 | ① 递归:链表中的很多操作都是可以用递归来进行解决的,因为链表的每个结点都有着相同的结构,再加上解决的问题可以分解为子问题进行解决。所以在链表中递归编程技巧还是非常常用的。如:从尾到头打印链表、合并两个有序链表、反转链表等。
1056 |
1057 | ② 双指针:链表中大部分都是进行指针操作,链表属于线性表结构(形如一条线的结构),很多问题可以使用双指针来解决,也是非常常用到的。如:查找倒数第K 结点、求链表的中间结点等。
1058 |
1059 |
1060 |
1061 | #### 3、性能上
1062 |
1063 | ① 链表正是因为存储空间不连续,对 CPU 缓存不友好,随时访问只能从头遍历链表,时间复杂度为 O(n),但是链表的这种结构也有个好处就是。可以动态的申请内存空间,不需要提前申请。
1064 |
1065 | ② 指针的存储是需要额外的内存空间的,如果存储的数据远大于存储指针的内存空间,可以进行忽略。
1066 |
1067 |
1068 |
1069 | **作者:**小鹿
1070 |
1071 | **座右铭:**追求平淡不平凡,一生追求做一个不甘平凡的码农!
1072 |
1073 | **本文首发于 Github ,转载请说明出处:**[https://github.com/luxiangqiang/Blog/blob/master/articel/数据结构与算法系列/数据结构与算法之链表系列[题型篇].md](https://github.com/luxiangqiang/Blog/blob/master/articel/数据结构与算法系列/数据结构与算法之链表系列[题型篇].md)
1074 |
1075 | **个人公众号:「一个不甘平凡的码农」。**
1076 |
1077 |
--------------------------------------------------------------------------------