├── .ipynb_checkpoints
├── DP-checkpoint.ipynb
├── Dubins-checkpoint.ipynb
├── PRM-checkpoint.ipynb
├── WAStar-checkpoint.ipynb
├── 多项式曲线-checkpoint.ipynb
├── 时空A-checkpoint.ipynb
├── HybirdAstar-checkpoint.ipynb
├── ReedsShepp-checkpoint.ipynb
├── 时空RRT star-checkpoint.ipynb
├── Informed RRT star-checkpoint.ipynb
├── B STAR-checkpoint.ipynb
├── D star lite-checkpoint.ipynb
├── 二次规划-checkpoint.ipynb
└── LPAstar-checkpoint.ipynb
├── README.md
└── 基于图搜索
├── WAStar.ipynb
├── LPAstar.ipynb
├── B STAR.ipynb
└── Dijkstra.ipynb
/.ipynb_checkpoints/DP-checkpoint.ipynb:
--------------------------------------------------------------------------------
1 | {
2 | "cells": [],
3 | "metadata": {},
4 | "nbformat": 4,
5 | "nbformat_minor": 5
6 | }
7 |
--------------------------------------------------------------------------------
/.ipynb_checkpoints/Dubins-checkpoint.ipynb:
--------------------------------------------------------------------------------
1 | {
2 | "cells": [],
3 | "metadata": {},
4 | "nbformat": 4,
5 | "nbformat_minor": 5
6 | }
7 |
--------------------------------------------------------------------------------
/.ipynb_checkpoints/PRM-checkpoint.ipynb:
--------------------------------------------------------------------------------
1 | {
2 | "cells": [],
3 | "metadata": {},
4 | "nbformat": 4,
5 | "nbformat_minor": 5
6 | }
7 |
--------------------------------------------------------------------------------
/.ipynb_checkpoints/WAStar-checkpoint.ipynb:
--------------------------------------------------------------------------------
1 | {
2 | "cells": [],
3 | "metadata": {},
4 | "nbformat": 4,
5 | "nbformat_minor": 5
6 | }
7 |
--------------------------------------------------------------------------------
/.ipynb_checkpoints/多项式曲线-checkpoint.ipynb:
--------------------------------------------------------------------------------
1 | {
2 | "cells": [],
3 | "metadata": {},
4 | "nbformat": 4,
5 | "nbformat_minor": 5
6 | }
7 |
--------------------------------------------------------------------------------
/.ipynb_checkpoints/时空A-checkpoint.ipynb:
--------------------------------------------------------------------------------
1 | {
2 | "cells": [],
3 | "metadata": {},
4 | "nbformat": 4,
5 | "nbformat_minor": 5
6 | }
7 |
--------------------------------------------------------------------------------
/.ipynb_checkpoints/HybirdAstar-checkpoint.ipynb:
--------------------------------------------------------------------------------
1 | {
2 | "cells": [],
3 | "metadata": {},
4 | "nbformat": 4,
5 | "nbformat_minor": 5
6 | }
7 |
--------------------------------------------------------------------------------
/.ipynb_checkpoints/ReedsShepp-checkpoint.ipynb:
--------------------------------------------------------------------------------
1 | {
2 | "cells": [],
3 | "metadata": {},
4 | "nbformat": 4,
5 | "nbformat_minor": 5
6 | }
7 |
--------------------------------------------------------------------------------
/.ipynb_checkpoints/时空RRT star-checkpoint.ipynb:
--------------------------------------------------------------------------------
1 | {
2 | "cells": [],
3 | "metadata": {},
4 | "nbformat": 4,
5 | "nbformat_minor": 5
6 | }
7 |
--------------------------------------------------------------------------------
/.ipynb_checkpoints/Informed RRT star-checkpoint.ipynb:
--------------------------------------------------------------------------------
1 | {
2 | "cells": [],
3 | "metadata": {},
4 | "nbformat": 4,
5 | "nbformat_minor": 5
6 | }
7 |
--------------------------------------------------------------------------------
/README.md:
--------------------------------------------------------------------------------
1 | # PlanningAlgorithms
2 | ---
3 | CSDN专栏|[自动驾驶规划入门(已完结)](https://blog.csdn.net/u013468614/category_11897666.html)
4 | ---
5 | > “他们利用各种办法包围成群的野马,逼迫马群向山顶上跑,野马跑到悬崖边收不住脚,就成群地跌下悬崖,跌得血肉狼藉,这样,人们就获得了大量的野马。”上面这段文字描述了原始人打猎的场景。我们只需要稍加思索便能发现以上描述背后藏着原始人精妙的计划。智能体(人类或某些其他生物)从空间的变化中抽象出“时间”,有了时间观念后,便同时拥有了前瞻(计划未来)后瞩(回忆过去)的能力,其中,回忆过去也是为了更好的预测与计划未来。
6 | >
7 | 
8 | ## 一、什么是规划
9 | 当你被师长问及新的一年你有什么计划时,当你被面试官问及你的职业规划时,你的回答是名词性质的规划(plan)——一份制定好的计划、策划书或方案。
10 |
11 | 当你面对一个任务时,思索得到解决方案的过程则是动词的规划(planning)——制定、拟定一份计划或方案的整个过程。
12 |
13 | 相对于作为产出物的名词性质的规划,我们更加关注作为一种能力的规划过程,也即动词性质的规划。博客中所述的规划则默认为是动词性质的规划,而用“规划结果”表示名词性质的规划。
14 | 
15 | ## 二、自主移动机器人领域中的规划
16 | 在不同的研究领域,规划的具体内容与内涵都有区别。而我们本专栏只针对机器人领域的规划理论与方法进行介绍。
17 |
18 | 在自主移动机器人领域,一个最基本的任务是:将人类的高阶任务转换成指示机器人如何移动的低阶描述。例如,自动驾驶任务就是将乘客或货物安全、省时、节能地从起点运送到目的地。运动规划(motion planning)、路径规划(path planning)与轨迹规划(trajectory planning)便是用于解决这类任务。
19 | 
20 |
21 | 《Planning Algorithms》[^1]中有对运动规划与轨迹规划的描述,现引出如下:
22 |
23 | >**运动规划**:Robot motion planning usually ignores dynamics and other differential constraints and focuses primarily on the translations androtations required to move the piano. Recent work, however, does consider other aspects, such as uncertainties, differential constraints, modeling errors, and optimality.
24 | **轨迹规划**:Trajectory planning usually refers to the problem of taking the solution from a robot motion planning algorithm and determining how to move along the solution in a way that respects the mechanical limitations of the robot.
25 |
26 | 书中的意思是轨迹规划是运动规划的下层(如下图所示),运动规划的结果通常忽略动力学与运动学约束,得到机器人(或机械臂)完成任务过程所需要的位置与姿态序列。然而,轨迹规划则需要考虑更加细致动力学与运动学约束,使机器人(或机械臂)能够按照运动规划的位姿序列移动以完成任务。
27 | 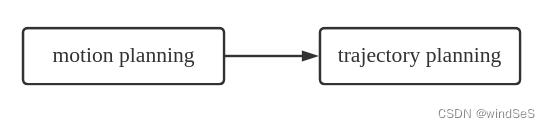
28 |
29 | 但是,书中在描述运动规划的最后加了一句:最近,不少运动规划方法开始考虑不确定性、微分约束(例如:一阶微分——速度、二阶微分——加速度等等)、建模误差以及最优性等其它方面。在这种情况下,运动规划与轨迹规划所做的事情就变得一样了。此时,轨迹规划则是被运动规划所包含:
30 |
31 | 
32 | 渐渐地,运动规划有了小弟——轨迹规划去描述更细的规划任务,那么运动规划中除了轨迹规划还剩一块空白仍需要用运动规划去描述,这时候我们就会觉得有点怪,因为运动规划的描述域时而大时而小容易让人困惑。此时,路径规划就出现用来替代最初运动规划的位置,而运动规划则完全抽身到更高的概念。
33 | 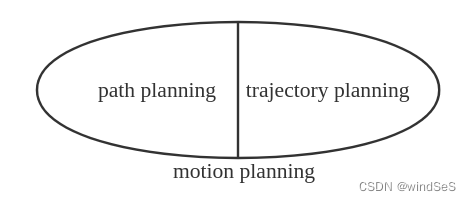
34 | 为了统一说法,本人延用如下定义:
35 |
36 | - **路径规划**(path planning):就是在给定位置A与位置B之间为机器人找到一条符合约束条件的路径,这个约束可以是碰撞、路径最短、能耗最小等;
37 | - **轨迹规划**(trajectory planning)以路径规划的结果作为参考路径,给出使机器人从位置A到达位置B,且满足机器人运动学与动力学约束时空轨迹;
38 | - **运动规划**(motion planning)由上层路径规划和下层轨迹规划组成。
39 |
40 | > **决策与规划的关系**:在心理学与传统人工智能领域,广义的决策是包含规划的,而自动驾驶领域里的行为决策(我们称之为狭义的决策)则是作为作为规划的前提,为规划提供依据与目标,规划则是对决策的具体落实与展开。还有一种说法可供参考:决策把规划问题约束成一个凸问题。
41 |
42 | ## 三、自主移动机器人领域中的规划算法
43 | 本专栏中会循序渐进地介绍自主移动机器人领域的经典规划算法,每篇博客会从背景、原理、示例代码演示、重要知识点、总结等五个方面对一个规划算法进行全方位的介绍。
44 |
45 | 要有序的对如此大量的规划算法进行介绍,对其进行分类是首要的事情。
46 |
47 | >第二小节根据任务对规划进行分层是一种对规划方法进行分类的方式,但是无益于我们去了解众多的规划算法之间的本质异同。因为,**同一类型的规划算法,按这样的目标、约束以及成本设计可以用于路径规划,按另外一种设计便可能可以用于轨迹规划了。**
48 |
49 | 本专栏的规划部分(本专栏还有一小部分是关于自主移动机器人控制)对规划算法按下图进行分类,并依据此图有序前进。根据下图所示,自主移动机器人规划算法主要包括图搜索、采样、优化等三大类方法。本专栏也会介绍一些占比较小部分的规划方法,如基于势场函数的方法、生物启发式类方法以及学习类方法。本专栏最后还对自主移动机器人规划算法中依赖的各种类型的运动基元开设专题对之进行介绍。
50 |
51 |
52 | 
53 |
54 |
55 |
56 |
57 | 学习完本专栏自主移动机器人规划部分,你应该:
58 |
59 | - 更加深刻地体会到规划是什么;
60 | - 熟悉各类自主移动机器人规划算法的核心思想、原理、优缺点;
61 | - 明白各类规划算法之间的本质异同;
62 | - 能够动手实现各规划算法;
63 | - 可以搭建一套自主移动机器人规划系统。
64 |
65 | ## 四、已经完成章节
66 | ### 4.1 基于图搜索的规划算法
67 | - [基于图搜索的规划算法之Dijkstra](https://windses.blog.csdn.net/article/details/125882452)
68 | - [基于图搜索的规划算法之 A* 家族(一):A* 算法](https://windses.blog.csdn.net/article/details/126024013)
69 | - [基于图搜索的规划算法之 A* 家族(二):双向 A* 算法](https://blog.csdn.net/u013468614/article/details/126085190?spm=1001.2014.3001.5501)
70 | - [基于图搜索的规划算法之 A* 家族(三):Anytime A* 算法](https://windses.blog.csdn.net/article/details/126196424)
71 | - [基于图搜索的规划算法之 A* 家族(四):Lifelong Planning A* 算法](https://windses.blog.csdn.net/article/details/126344705)
72 | - [基于图搜索的规划算法之 A* 家族(五):D* 算法](https://windses.blog.csdn.net/article/details/126356080)
73 | - [基于图搜索的规划算法之 A* 家族(六):D* Lite 算法](https://blog.csdn.net/u013468614/article/details/126578060?spm=1001.2014.3001.5501)
74 | - [基于图搜索的规划算法之 A* 家族(七):Field D* 算法](https://windses.blog.csdn.net/article/details/126652932)
75 | - [基于图搜索的规划算法之 A* 家族(八):Theta* 算法](https://blog.csdn.net/u013468614/article/details/126860201?spm=1001.2014.3001.5501)
76 | - [基于图搜索的规划算法之 A* 家族(九):Hybrid A* 算法](https://blog.csdn.net/u013468614/article/details/127040519?spm=1001.2014.3001.5501)
77 | - [基于图搜索的规划算法之 A* 家族(十):时空 A* 算法](https://blog.csdn.net/u013468614/article/details/127178132?spm=1001.2014.3001.5501)
78 | - [基于图搜索的规划算法之 A* 家族(十一):总结](https://blog.csdn.net/u013468614/article/details/127272352?spm=1001.2014.3001.5501)
79 | - [基于图搜索的规划算法之可视图法](https://blog.csdn.net/u013468614/article/details/127379218?spm=1001.2014.3001.5501)
80 | - [基于图搜索的规划算法之Voronoi图法](https://windses.blog.csdn.net/article/details/127454489?spm=1001.2014.3001.5502)
81 | ### 4.2 基于采样的规划算法
82 | - [基于采样的规划算法之概率路图(PRM)法](https://windses.blog.csdn.net/article/details/127643442)
83 | - [基于采样的规划算法之RRT家族(一):快速探索随机树(RRT)](https://windses.blog.csdn.net/article/details/127716172)
84 | - [基于采样的规划算法之RRT家族(二):RRT-Connect](https://windses.blog.csdn.net/article/details/127797445)
85 | - [基于采样的规划算法之RRT家族(三):RRT*](https://windses.blog.csdn.net/article/details/128058386)
86 | - [基于采样的规划算法之RRT家族(四):Informed RRT*](https://windses.blog.csdn.net/article/details/128227660)
87 | - [基于采样的规划算法之RRT家族(五):时空 RRT](https://windses.blog.csdn.net/article/details/128309038)
88 | - [基于采样的规划算法之RRT家族(六):总结](https://windses.blog.csdn.net/article/details/128413984)
89 | - [基于采样的规划算法之动态规划方法](https://windses.blog.csdn.net/article/details/128515996)
90 | - [基于采样的规划算法之动态窗口法(DWA)](https://windses.blog.csdn.net/article/details/128585386)
91 |
92 | ### 4.3 [基于连续优化的规划算法:以二次规划为例](https://windses.blog.csdn.net/article/details/128679625)
93 | ### 4.4 运动基元
94 | - [运动基元(一):Dubin‘s曲线【part1】](https://windses.blog.csdn.net/article/details/128749754)
95 | - [运动基元(一):Dubin‘s曲线【part2】](https://windses.blog.csdn.net/article/details/128758944)
96 | - [运动基元(一):Dubin‘s曲线【part3】](https://windses.blog.csdn.net/article/details/128766465)
97 | - [运动基元(二):贝塞尔曲线](https://windses.blog.csdn.net/article/details/128877012)
98 | - [运动基元(三):多项式曲线](https://windses.blog.csdn.net/article/details/129037343)
99 |
100 |
101 | ## 结语
102 | 人类在生活与工作中,规划无处不在。我们规划从家到公司的路线,我们有时也会规划从当前到未来的人生路线。自主移动机器人的终极目标就是替代人类的外出/出行任务:从起点如何高效、安全(有时还需要考虑舒适性)地到达目的地。在给出合适的目标、约束以及成本函数后,规划算法能够使移动机器人像人类一样给出一份出行计划(很多时候是一个由粗到精,由远及近、由静到动的多层规划结果)。
103 |
104 | 如果说使用和创造工具等是智能体智慧的主要表现形式,那么规划(计划)便是以智慧为音符在空间上写就的与时间相关的乐章(这个时间不一定是指规划的每一步包含显式的时间节点,规划步骤的先后同样也是一种时间的概念)。请将这作为阅读本专栏时的旁白,时时朗诵。
105 |
106 | ## 参考文献
107 | [^1]:Lavalle S M . Planning Algorithms[M]. Cambridge University Press, 2006.
108 |
--------------------------------------------------------------------------------
/.ipynb_checkpoints/B STAR-checkpoint.ipynb:
--------------------------------------------------------------------------------
1 | {
2 | "cells": [
3 | {
4 | "cell_type": "code",
5 | "execution_count": null,
6 | "id": "b16067a2",
7 | "metadata": {},
8 | "outputs": [],
9 | "source": [
10 | "import heapq\n",
11 | "import math\n",
12 | "import matplotlib.pyplot as plt\n",
13 | "import numpy as np\n",
14 | "import math\n",
15 | "import matplotlib\n",
16 | "%matplotlib inline\n",
17 | "#set up matplotlib\n",
18 | "is_ipython = 'inline' in matplotlib.get_backend()\n",
19 | "if is_ipython:\n",
20 | " from IPython import display\n",
21 | "plt.ion()\n",
22 | "plt.figure(figsize=(12, 12))\n",
23 | "\n",
24 | "\"\"\"\n",
25 | "\n",
26 | "\"\"\"\n",
27 | "\n",
28 | "class GridMap:\n",
29 | " def __init__(self, ox, oy, resolution):\n",
30 | " self.min_x = None\n",
31 | " self.min_y = None\n",
32 | " self.max_x = None\n",
33 | " self.max_y = None\n",
34 | " self.x_width = None\n",
35 | " self.y_width = None\n",
36 | " self.obstacle_map = None\n",
37 | " \n",
38 | " self.resolution = resolution\n",
39 | " self.calc_obstacle_map(ox, oy)\n",
40 | " \n",
41 | " def calc_obstacle_map(self, ox, oy):\n",
42 | "\n",
43 | " self.min_x = round(min(ox))\n",
44 | " self.min_y = round(min(oy))\n",
45 | " self.max_x = round(max(ox))\n",
46 | " self.max_y = round(max(oy))\n",
47 | " print(\"min_x:\", self.min_x)\n",
48 | " print(\"min_y:\", self.min_y)\n",
49 | " print(\"max_x:\", self.max_x)\n",
50 | " print(\"max_y:\", self.max_y)\n",
51 | "\n",
52 | " self.x_width = round((self.max_x - self.min_x) / self.resolution)+1\n",
53 | " self.y_width = round((self.max_y - self.min_y) / self.resolution)+1\n",
54 | " print(\"x_width:\", self.x_width)\n",
55 | " print(\"y_width:\", self.y_width)\n",
56 | "\n",
57 | " # obstacle map generation\n",
58 | " self.obstacle_map = np.zeros((self.x_width, self.y_width))\n",
59 | " for x, y in zip(ox, oy):\n",
60 | " ix, iy = self.calc_xy_index(x, self.min_x), self.calc_xy_index(y, self.min_y)\n",
61 | " if 0<=ix= self.x_width or node.ix < 0 or node.iy >= self.y_width or node.iy < 0:\n",
77 | " return False\n",
78 | " if abs(self.obstacle_map[node.ix, node.iy] - 10.0) < 0.01:\n",
79 | " return False \n",
80 | " return True\n",
81 | "\n",
82 | "sx = -5.0 # [m]\n",
83 | "sy = -5.0 # [m]\n",
84 | "gx = 50.0 # [m]\n",
85 | "gy = 50.0 # [m]\n",
86 | "grid_size = 5.0 # [m]\n",
87 | "robot_radius = 1.0 # [m]\n",
88 | "\n",
89 | "# set obstacle positions\n",
90 | "ox, oy = [], []\n",
91 | "for i in range(-10, 60):\n",
92 | " ox.append(i)\n",
93 | " oy.append(-10.0)\n",
94 | "for i in range(-10, 60):\n",
95 | " ox.append(60.0)\n",
96 | " oy.append(i)\n",
97 | "for i in range(-10, 61):\n",
98 | " ox.append(i)\n",
99 | " oy.append(60.0)\n",
100 | "for i in range(-10, 61):\n",
101 | " ox.append(-10.0)\n",
102 | " oy.append(i)\n",
103 | "# for i in range(-10, 40):\n",
104 | "# ox.append(20.0)\n",
105 | "# oy.append(i)\n",
106 | "for i in range(20, 40):\n",
107 | " ox.append(20.0)\n",
108 | " oy.append(60.0 - i) \n",
109 | "grid_map = GridMap(ox, oy, grid_size)\n",
110 | "\n",
111 | "\n",
112 | "\n",
113 | "class Node:\n",
114 | " def __init__(self, ix, iy, C=0.0, P=None):\n",
115 | " self.ix = ix\n",
116 | " self.iy = iy\n",
117 | " self.C = C\n",
118 | " self.P = P\n",
119 | " \n",
120 | "action_set = {'UP':[0, 1], 'DOWN':[0, -1], 'LEFT':[-1, 0], 'RIGHT':[1, 0]}\n",
121 | "\n",
122 | "def get_neighbors(current, grid_map):\n",
123 | " for a in action_set:\n",
124 | " node = Node(current.ix+action_set[a][0], \n",
125 | " current.iy+action_set[a][1], current.C+1.0, \n",
126 | " grid_map.calc_unique_index(current))\n",
127 | " if grid_map.verify_node(node):\n",
128 | " yield node\n",
129 | " \n",
130 | "def get_heuristic(node, end_node):\n",
131 | " dx = node.ix - end_node.ix\n",
132 | " dy = node.iy - end_node.iy\n",
133 | " return np.sqrt(dx*dx+dy*dy)\n",
134 | " \n",
135 | "\n",
136 | " \n",
137 | "def BAStar(grid_map, start_node, end_node):\n",
138 | " Closed_set_I, Open_set_I = {}, {}\n",
139 | " Closed_set_G, Open_set_G = {}, {}\n",
140 | " Open_set_I[grid_map.calc_unique_index(start_node)] = start_node\n",
141 | " Open_set_G[grid_map.calc_unique_index(end_node)] = end_node\n",
142 | " Q_I, Q_G = [],[]\n",
143 | " heapq.heappush(Q_I, (start_node.C+get_heuristic(start_node, end_node), \n",
144 | " grid_map.calc_unique_index(start_node)))\n",
145 | " heapq.heappush(Q_G, (end_node.C+get_heuristic(end_node, start_node), \n",
146 | " grid_map.calc_unique_index(end_node))) \n",
147 | " while True:\n",
148 | " if not Open_set_I and not Open_set_G:\n",
149 | " print(\"Bidirectional A* Algorithm Finished.\")\n",
150 | " return [], [], -1\n",
151 | " \n",
152 | " if Open_set_I:\n",
153 | " C, c_id = heapq.heappop(Q_I) \n",
154 | " if c_id in Open_set_I:\n",
155 | " current = Open_set_I.pop(c_id)\n",
156 | " Closed_set_I[c_id] = current\n",
157 | " if c_id in Closed_set_G:\n",
158 | " return ShortestPathFinder(grid_map, Closed_set_I, Closed_set_G, c_id)\n",
159 | " else:\n",
160 | " continue\n",
161 | "\n",
162 | " for node in get_neighbors(current, grid_map):\n",
163 | " neighbor_index = grid_map.calc_unique_index(node)\n",
164 | " if neighbor_index in Closed_set_I or neighbor_index in Closed_set_G: continue\n",
165 | " if neighbor_index not in Open_set_I or Open_set_I[neighbor_index].C > node.C:\n",
166 | " Open_set_I[neighbor_index] = node\n",
167 | " heapq.heappush(Q_I, (node.C+get_heuristic(node, end_node), neighbor_index))\n",
168 | " grid_map.obstacle_map[node.ix, node.iy] = 2\n",
169 | " plt.clf()\n",
170 | " plt.imshow(grid_map.obstacle_map)\n",
171 | " if is_ipython:\n",
172 | " display.clear_output(wait=True)\n",
173 | " display.display(plt.gcf()) \n",
174 | " \n",
175 | " if Open_set_G:\n",
176 | " C, c_id = heapq.heappop(Q_G) \n",
177 | " if c_id in Open_set_G:\n",
178 | " current = Open_set_G.pop(c_id)\n",
179 | " Closed_set_G[c_id] = current\n",
180 | " if c_id in Closed_set_I:\n",
181 | " return ShortestPathFinder(grid_map, Closed_set_I, Closed_set_G, start_node, end_node)\n",
182 | " else:\n",
183 | " continue\n",
184 | "\n",
185 | " for node in get_neighbors(current, grid_map):\n",
186 | " neighbor_index = grid_map.calc_unique_index(node)\n",
187 | " if neighbor_index in Closed_set_I or neighbor_index in Closed_set_G: continue\n",
188 | " if neighbor_index not in Open_set_G or Open_set_G[neighbor_index].C > node.C:\n",
189 | " Open_set_G[neighbor_index] = node\n",
190 | " heapq.heappush(Q_G, (node.C+get_heuristic(node, end_node), neighbor_index))\n",
191 | " grid_map.obstacle_map[node.ix, node.iy] = 2\n",
192 | " plt.clf()\n",
193 | " plt.imshow(grid_map.obstacle_map)\n",
194 | " if is_ipython:\n",
195 | " display.clear_output(wait=True)\n",
196 | " display.display(plt.gcf()) \n",
197 | "import collections\n",
198 | "\n",
199 | "def ShortestPathFinder(grid_map, Closed_set_I, Closed_set_G, start_node, end_node):\n",
200 | " if grid_map.verify_node(end_node) == False:\n",
201 | " print(\"the goal is unreachable!!!please change a reachable goal...\")\n",
202 | " return [], [], -1\n",
203 | " SPath_x = collections.deque()\n",
204 | " SPath_y = collections.deque()\n",
205 | " start_index = grid_map.calc_unique_index(start_node)\n",
206 | " end_index = grid_map.calc_unique_index(end_node)\n",
207 | " SPath_x = [Closed_set_I[end_index].ix]\n",
208 | " SPath_y = [Closed_set_I[end_index].iy] \n",
209 | " SPath_dist = Closed_set[end_index].C*grid_map.resolution\n",
210 | " v_index = Closed_set[end_index].P\n",
211 | " while v_index: \n",
212 | " SPath_x.append(Closed_set[v_index].ix)\n",
213 | " SPath_y.append(Closed_set[v_index].iy)\n",
214 | " v_index = Closed_set[v_index].P\n",
215 | " return list(reversed(SPath_x)), list(reversed(SPath_y)), SPath_dist\n",
216 | "\n",
217 | "start_node = Node(2, 7)\n",
218 | "end_node = Node(12, 7)\n",
219 | "grid_map.obstacle_map[start_node.ix, start_node.iy] = 8\n",
220 | "grid_map.obstacle_map[end_node.ix, end_node.iy] = 3\n",
221 | "plt.imshow(grid_map.obstacle_map)\n",
222 | "\n",
223 | "path_x, path_y, path_dist = AStar(grid_map, start_node, end_node)\n",
224 | "grid_map.obstacle_map[end_node.ix, end_node.iy] = 4\n",
225 | "for ix, iy in zip(path_x, path_y):\n",
226 | " grid_map.obstacle_map[ix, iy] = 4\n",
227 | " \n",
228 | "plt.clf()\n",
229 | "plt.imshow(grid_map.obstacle_map)\n",
230 | "if is_ipython:\n",
231 | " display.clear_output(wait=True)\n",
232 | " display.display(plt.gcf()) "
233 | ]
234 | }
235 | ],
236 | "metadata": {
237 | "kernelspec": {
238 | "display_name": "Python 3 (ipykernel)",
239 | "language": "python",
240 | "name": "python3"
241 | },
242 | "language_info": {
243 | "codemirror_mode": {
244 | "name": "ipython",
245 | "version": 3
246 | },
247 | "file_extension": ".py",
248 | "mimetype": "text/x-python",
249 | "name": "python",
250 | "nbconvert_exporter": "python",
251 | "pygments_lexer": "ipython3",
252 | "version": "3.9.5"
253 | }
254 | },
255 | "nbformat": 4,
256 | "nbformat_minor": 5
257 | }
258 |
--------------------------------------------------------------------------------
/.ipynb_checkpoints/D star lite-checkpoint.ipynb:
--------------------------------------------------------------------------------
1 | {
2 | "cells": [
3 | {
4 | "cell_type": "code",
5 | "execution_count": null,
6 | "id": "18358bb3",
7 | "metadata": {},
8 | "outputs": [
9 | {
10 | "name": "stdout",
11 | "output_type": "stream",
12 | "text": [
13 | "min_x: -10\n",
14 | "min_y: -10\n",
15 | "max_x: 60\n",
16 | "max_y: 60\n",
17 | "x_width: 15\n",
18 | "y_width: 15\n",
19 | "[70.71067811865476, 0.0] [9999.0, 9999.0]\n",
20 | "find a path.\n",
21 | "[[2, 2, 2, 2, 2, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12], [2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 11, 11, 11, 11, 11, 12]]\n"
22 | ]
23 | },
24 | {
25 | "data": {
26 | "image/png": "iVBORw0KGgoAAAANSUhEUgAAAPsAAAD4CAYAAAAq5pAIAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjUuMiwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy8qNh9FAAAACXBIWXMAAAsTAAALEwEAmpwYAAAMsUlEQVR4nO3db6xkdX3H8fenC9SCRBZRhGXbhYaQUNII2RCkxprSAlLC+sAHS7QFMSHG2EJjIktJatJHUhv7J7U1BGxpSsAUoRIDXbaoaRrLKmyXv4uwUgosyx+lAa0PYO23D+asud7euyxzzpk7u7/3K5ncM3N+c+e7Z+5nfzNnzplvqgpJB7+fW+kCJM2GYZcaYdilRhh2qRGGXWrEIbN8sGOOXlXr1h46y4eUmvLUM6/z/Zd/kqXWzTTs69Yeyrc3r53lQ0pNOfO8Z5Zd58t4qRGGXWpEr7AnOT/Jd5PsTLJpqKIkDW/qsCdZBXwB+ABwKnBxklOHKkzSsPrM7GcCO6vqyap6DbgF2DBMWZKG1ifsa4CFu/6e7W6TNIdG30GX5PIk9yW576Uf/GTsh5O0jD5h3wUs/ND8hO62n1FV11XV+qpa/463r+rxcJL66BP27wAnJzkxyWHARuCOYcqSNLSpj6Crqj1JPglsBlYBX6qqRwarTNKgeh0uW1V3AncOVIukEXkEndQIwy41YqZnvU3rvOPfvdIlSDO1+bntg/9OZ3apEYZdaoRhlxph2KVGGHapEYZdaoRhlxph2KVGGHapEYZdaoRhlxph2KVGGHapEQfEWW997Lrq7JUu4aC15tpvrXQJehOc2aVGGHapEYZdakSfXm9rk3wjyaNJHklyxZCFSRpWnx10e4BPVdW2JEcC9yfZUlWPDlSbpAFNPbNX1e6q2tYt/xDYgb3epLk1yHv2JOuA04GtQ/w+ScPrHfYkbwW+AlxZVa8usd7GjtIc6BX2JIcyCfpNVXXbUmNs7CjNhz574wPcAOyoqs8PV5KkMfSZ2X8N+B3gN5Js7y4XDFSXpIH16eL6b0AGrEXSiDyCTmqEYZcacdCf4uppmOPpc/qwz8vsObNLjTDsUiMMu9QIwy41wrBLjTDsUiMMu9QIwy41wrBLjTDsUiMMu9QIwy41wrBLjTjoz3rTePqcuTbtGXOeLTc9Z3apEYZdaoRhlxoxRJOIVUn+I8nXhihI0jiGmNmvYNLnTdIc69sR5gTgt4HrhylH0lj6zux/Dnwa+N/+pUgaU5/2TxcCL1bV/W8wzsaO0hzo2/7poiRPAbcwaQP1D4sH2dhRmg9Th72qrq6qE6pqHbAR+HpVfWSwyiQNys/ZpUYMcmx8VX0T+OYQv0vSOJzZpUYYdqkRnuKqFTHtqao2k5yeM7vUCMMuNcKwS40w7FIjDLvUCMMuNcKwS40w7FIjDLvUCMMuNcKwS40w7FIjDLvUCM960wHl4Sv+eur7nsYnprrfwXK2nDO71AjDLjXCsEuN6Nv+6agktyZ5LMmOJO8ZqjBJw+q7g+4vgH+uqg8lOQw4fICaJI1g6rAneRvwPuBSgKp6DXhtmLIkDa3Py/gTgZeAv+36s1+f5IiB6pI0sD5hPwQ4A/ibqjod+B9g0+JBNnaU5kOfsD8LPFtVW7vrtzIJ/8+wsaM0H/o0dnweeCbJKd1N5wCPDlKVpMH13Rv/e8BN3Z74J4GP9i9J0hh6hb2qtgPrhylF0pg8gk5qhGGXGmHYpUYYdqkRhl1qhGGXGmHYpUYYdqkRhl1qhGGXGmHYpUYYdqkRhl1qhGGXGmHYpUYYdqkRhl1qhGGXGmHYpUYYdqkRfRs7/kGSR5I8nOTmJG8ZqjBJw5o67EnWAL8PrK+q04BVwMahCpM0rL4v4w8BfiHJIUw6uD7XvyRJY+jTEWYX8KfA08Bu4JWqunuowiQNq8/L+NXABibdXI8HjkjykSXG2dhRmgN9Xsb/JvCfVfVSVb0O3AacvXiQjR2l+dAn7E8DZyU5PEmYNHbcMUxZkobW5z37ViZtmrcBD3W/67qB6pI0sL6NHT8DfGagWiSNyCPopEYYdqkRhl1qhGGXGmHYpUYYdqkRhl1qhGGXGmHYpUYYdqkRhl1qhGGXGmHYpUYYdqkRhl1qhGGXGtHryys0PzY/t32lS9Ccc2aXGmHYpUYYdqkRbxj2JF9K8mKShxfcdnSSLUme6H6uHrdMSX3tz8z+d8D5i27bBNxTVScD93TXJc2xNwx7Vf0r8PKimzcAN3bLNwIfHLYsSUOb9j37sVW1u1t+Hjh2oHokjaT3DrqqKqCWW29jR2k+TBv2F5IcB9D9fHG5gTZ2lObDtGG/A7ikW74E+Oow5Ugay/589HYz8O/AKUmeTfIx4LPAbyV5gknr5s+OW6akvt7w2PiquniZVecMXIukEXkEndQIwy41wlNcDxLnHf/ulS5h/l210gWsLGd2qRGGXWqEYZcaYdilRhh2qRGGXWqEYZcaYdilRhh2qRGGXWqEYZcaYdilRhh2qRGe9aZmrLn2W1Pdb9dVZ8/8McfgzC41wrBLjTDsUiOmbez4uSSPJXkwye1Jjhq1Skm9TdvYcQtwWlX9KvA4cPXAdUka2FSNHavq7qra0129FzhhhNokDWiI9+yXAXcN8HskjahX2JNcA+wBbtrHGBs7SnNg6rAnuRS4EPhw18l1STZ2lObDVEfQJTkf+DTw61X142FLkjSGaRs7/hVwJLAlyfYkXxy5Tkk9TdvY8YYRapE0Io+gkxph2KVGeIqr9Abm6TTVPpzZpUYYdqkRhl1qhGGXGmHYpUYYdqkRhl1qhGGXGmHYpUYYdqkRhl1qhGGXGmHYpUYcEGe9bX5u+0qXIB3wnNmlRhh2qRGGXWrEVI0dF6z7VJJKcsw45UkayrSNHUmyFjgXeHrgmiSNYKrGjp0/Y9IoYtluMJLmx1Tv2ZNsAHZV1QMD1yNpJG/6c/YkhwN/yOQl/P6Mvxy4HOAX1xwQH+tLB6VpZvZfBk4EHkjyFJPe7NuSvGupwTZ2lObDm55qq+oh4J17r3eBX19V3x+wLkkDm7axo6QDzLSNHReuXzdYNZJG4xF0UiMMu9SIVM3umJgkLwH/tczqY4B52sk3b/XA/NVkPfu2EvX8UlW9Y6kVMw37viS5r6rWr3Qde81bPTB/NVnPvs1bPb6Mlxph2KVGzFPYr1vpAhaZt3pg/mqynn2bq3rm5j27pHHN08wuaUSGXWrEzMOe5Pwk302yM8mmJdb/fJIvd+u3Jlk3Yi1rk3wjyaNJHklyxRJj3p/klSTbu8sfjVXPgsd8KslD3ePdt8T6JPnLbhs9mOSMEWs5ZcG/fXuSV5NcuWjMqNtoqa9GS3J0ki1Jnuh+rl7mvpd0Y55IcsmI9XwuyWPd83F7kqOWue8+n9tRVdXMLsAq4HvAScBhwAPAqYvGfAL4Yre8EfjyiPUcB5zRLR8JPL5EPe8Hvjbj7fQUcMw+1l8A3AUEOAvYOsPn73kmB27MbBsB7wPOAB5ecNufAJu65U3AtUvc72jgye7n6m559Uj1nAsc0i1fu1Q9+/PcjnmZ9cx+JrCzqp6sqteAW4ANi8ZsAG7slm8FzkmSMYqpqt1Vta1b/iGwA1gzxmMNbAPw9zVxL3BUkuNm8LjnAN+rquWOghxFLf3VaAv/Tm4EPrjEXc8DtlTVy1X138AWlvg+xSHqqaq7q2pPd/VeJt/zMFdmHfY1wDMLrj/L/w/XT8d0G+8V4O1jF9a9XTgd2LrE6vckeSDJXUl+ZexamHyv391J7u++6Wex/dmOY9gI3LzMullvo2Orane3/Dxw7BJjVmo7XcbklddS3ui5HY3fEwUkeSvwFeDKqnp10eptTF62/ijJBcA/ASePXNJ7q2pXkncCW5I81s0mKybJYcBFwNVLrF6JbfRTVVVJ5uIz5CTXAHuAm5YZsmLP7axn9l3A2gXXT+huW3JMkkOAtwE/GKugJIcyCfpNVXXb4vVV9WpV/ahbvhM4dOzvya+qXd3PF4Hbmbz9WWh/tuPQPgBsq6oXFq9YiW0EvLD3rUv388Ulxsx0OyW5FLgQ+HB1b9AX24/ndjSzDvt3gJOTnNjNFBuBOxaNuQPYu9f0Q8DXl9twfXX7Am4AdlTV55cZ8669+wySnMlkm435n88RSY7cu8xkx8/iBh13AL/b7ZU/C3hlwUvasVzMMi/hZ72NOgv/Ti4BvrrEmM3AuUlWd3vrz+1uG1yS85l8tfpFVfXjZcbsz3M7nlnvEWSyJ/lxJnvlr+lu+2MmGwngLcA/AjuBbwMnjVjLe5m8h3oQ2N5dLgA+Dny8G/NJ4BEmnxzcC5w98vY5qXusB7rH3buNFtYU4AvdNnyIyXcAjlnTEUzC+7YFt81sGzH5T2Y38DqT990fY7If5x7gCeBfgKO7seuB6xfc97Lub2kn8NER69nJZP/A3r+jvZ8oHQ/cua/ndlYXD5eVGuERdFIjDLvUCMMuNcKwS40w7FIjDLvUCMMuNeL/AEr61kWxO0/3AAAAAElFTkSuQmCC\n",
27 | "text/plain": [
28 | ""
29 | ]
30 | },
31 | "metadata": {
32 | "needs_background": "light"
33 | },
34 | "output_type": "display_data"
35 | },
36 | {
37 | "name": "stdout",
38 | "output_type": "stream",
39 | "text": [
40 | "if you want change environment, please input [ok] to start changingok\n",
41 | "please input ix number (Type: Int) in [0, 15):9\n",
42 | "please input iy number (Type: Int) in [0, 15):11\n",
43 | "change [ix: 9, iy: 11] from free to obs\n",
44 | "if you want change environment, please input [ok] to start changingok\n",
45 | "please input ix number (Type: Int) in [0, 15):9\n",
46 | "please input iy number (Type: Int) in [0, 15):12\n",
47 | "change [ix: 9, iy: 12] from free to obs\n",
48 | "if you want change environment, please input [ok] to start changingok\n",
49 | "please input ix number (Type: Int) in [0, 15):9\n",
50 | "please input iy number (Type: Int) in [0, 15):13\n",
51 | "change [ix: 9, iy: 13] from free to obs\n",
52 | "if you want change environment, please input [ok] to start changingstop\n",
53 | "changed map: 10.0\n",
54 | "changed map: 10.0\n",
55 | "changed map: 10.0\n",
56 | "[75.22179687553873, 17.071067811865476] [85.35533905932738, 80.35533905932738]\n",
57 | "find a path.\n",
58 | "[[2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 11, 11, 11, 11, 11, 12], [3, 3, 3, 3, 3, 3, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12]]\n"
59 | ]
60 | },
61 | {
62 | "data": {
63 | "image/png": "iVBORw0KGgoAAAANSUhEUgAAAPsAAAD4CAYAAAAq5pAIAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjUuMiwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy8qNh9FAAAACXBIWXMAAAsTAAALEwEAmpwYAAAMvElEQVR4nO3db6wldX3H8fenu1ALElhEEZZtFxpCQkkDZEOQGmtKC0gJ6wMfLNEWxIQYYwuNiUBJatJHUhv7J7U1BGxpSsCIUImBLlvUNI1lFbbLf4SVUmBZ/igNaH0Aa799cGbN9Xrv7npm5tzD/t6v5OTOOfM7d74753525syZOd9UFZIOfL+w0gVImg3DLjXCsEuNMOxSIwy71IjVs1zYUUeuqvXrDprlIqWmPP3sG3zvlR9nqXkzDfv6dQfxrc3rZrlIqSlnnPvssvPcjZcaYdilRvQKe5LzknwnyY4kVw1VlKThTR32JKuAzwHvA04GLkpy8lCFSRpWny37GcCOqnqqql4HbgE2DlOWpKH1CftaYOGhv+e6xyTNodEP0CW5LMl9Se57+fs/HntxkpbRJ+w7gYUfmh/XPfZTquq6qtpQVRve/rZVPRYnqY8+Yf82cGKS45McDGwC7himLElDm/oMuqraneTjwGZgFfCFqnpksMokDarX6bJVdSdw50C1SBqRZ9BJjTDsUiNmetXbtM499tSVLkGaqc3Pbx/8d7pllxph2KVGGHapEYZdaoRhlxph2KVGGHapEYZdaoRhlxph2KVGGHapEYZdaoRhlxrxprjqbaXsvPKsqZ639tpvDlyJ1J9bdqkRhl1qhGGXGtGn19u6JF9P8miSR5JcPmRhkobV5wDdbuATVbUtyWHA/Um2VNWjA9UmaUBTb9mraldVbeumfwA8hr3epLk1yHv2JOuB04CtQ/w+ScPrHfYkbwW+DFxRVa8tMd/GjtIc6BX2JAcxCfpNVXXbUmNs7CjNhz5H4wPcADxWVZ8driRJY+izZf8N4PeA30qyvbudP1BdkgbWp4vrvwMZsBZJI/IMOqkRhl1qhGGXGmHYpUYYdqkRhl1qhGGXGmHYpUYYdqkRhl1qhGGXGmHYpUYYdqkRhl1qhGGXGmHYpUYYdqkRhl1qhGGXGmHYpUYM0SRiVZL/TPLVIQqSNI4htuyXM+nzJmmO9e0Icxzwu8D1w5QjaSx9t+x/CXwS+L/+pUgaU5/2TxcAL1XV/fsYZ2NHaQ70bf90YZKngVuYtIH6p8WDbOwozYepw15VV1fVcVW1HtgEfK2qPjRYZZIG5efsUiOmbuy4UFV9A/jGEL9L0jjcskuNMOxSIwy71AjDLjXCsEuNMOxSIwy71AjDLjXCsEuNMOxSIwy71AjDLjXCsEuNMOxSIwy71AjDLjVikC+vkGZl8/Pbp37uuceeOlgdb0Zu2aVGGHapEYZdakTf9k9HJLk1yeNJHkvyrqEKkzSsvgfo/gr4l6r6QJKDgUMGqEnSCKYOe5LDgfcAlwBU1evA68OUJWlofXbjjwdeBv6+689+fZJDB6pL0sD6hH01cDrwd1V1GvC/wFWLB9nYUZoPfcL+HPBcVW3t7t/KJPw/xcaO0nzo09jxBeDZJCd1D50NPDpIVZIG1/do/B8AN3VH4p8CPty/JElj6BX2qtoObBimFElj8gw6qRGGXWqEYZcaYdilRhh2qRGGXWqEYZcaYdilRhh2qRGGXWqEYZcaYdilRhh2qRGGXWqEYZcaYdilRhh2qRGGXWqEYZcaYdilRvRt7PhHSR5J8nCSm5O8ZajCJA1r6rAnWQv8IbChqk4BVgGbhipM0rD67savBn4pyWomHVyf71+SpDH06QizE/hz4BlgF/BqVd09VGGShtVnN34NsJFJN9djgUOTfGiJcTZ2lOZAn9343wb+q6perqo3gNuAsxYPsrGjNB/6hP0Z4MwkhyQJk8aOjw1TlqSh9XnPvpVJm+ZtwEPd77puoLokDaxvY8dPAZ8aqBZJI/IMOqkRhl1qRK/d+APd2mu/OdXzdl75Mx9KjL5M7dvm57evdAkryi271AjDLjXCsEuNMOxSIwy71AjDLjXCsEuNMOxSIwy71AjDLjXCsEuNMOxSIwy71AivehtBnyvXpr1i7uHL/3bqZbbi3GNPXekS9tsYV+i5ZZcaYdilRhh2qRH7DHuSLyR5KcnDCx47MsmWJE92P9eMW6akvvZny/4PwHmLHrsKuKeqTgTu6e5LmmP7DHtV/RvwyqKHNwI3dtM3Au8ftixJQ5v2PfvRVbWrm34BOHqgeiSNpPcBuqoqoJabb2NHaT5MG/YXkxwD0P18abmBNnaU5sO0Yb8DuLibvhj4yjDlSBrL/nz0djPwH8BJSZ5L8hHg08DvJHmSSevmT49bpqS+9nlufFVdtMyssweuRdKIPINOaoRhlxrhJa5zZtrLY0/hYwNXcgC6crqnHSjNNt2yS40w7FIjDLvUCMMuNcKwS40w7FIjDLvUCMMuNcKwS40w7FIjDLvUCMMuNcKwS43wqrcDxIFyZdY8mrbZJszX6+KWXWqEYZcaYdilRkzb2PEzSR5P8mCS25McMWqVknqbtrHjFuCUqvp14Ang6oHrkjSwqRo7VtXdVbW7u3svcNwItUka0BDv2S8F7hrg90gaUa+wJ7kG2A3ctJcxNnaU5sDUYU9yCXAB8MGuk+uSbOwozYepzqBLch7wSeA3q+pHw5YkaQzTNnb8G+AwYEuS7Uk+P3KdknqatrHjDSPUImlEnkEnNcKwS43wEldpH+bpMtU+3LJLjTDsUiMMu9QIwy41wrBLjTDsUiMMu9QIwy41wrBLjTDsUiMMu9QIwy41wrBLjXhTXPW2+fntK12C9Kbnll1qhGGXGmHYpUZM1dhxwbxPJKkkR41TnqShTNvYkSTrgHOAZwauSdIIpmrs2PkLJo0ilu0GI2l+TPWePclGYGdVPTBwPZJG8nN/zp7kEOCPmezC78/4y4DLAH557ZviY33pgDTNlv1XgeOBB5I8zaQ3+7Yk71xqsI0dpfnwc29qq+oh4B177neB31BV3xuwLkkDm7axo6Q3mWkbOy6cv36waiSNxjPopEYYdqkRqZrdOTFJXgb+e5nZRwHzdJBv3uqB+avJevZuJer5lap6+1IzZhr2vUlyX1VtWOk69pi3emD+arKevZu3etyNlxph2KVGzFPYr1vpAhaZt3pg/mqynr2bq3rm5j27pHHN05Zd0ogMu9SImYc9yXlJvpNkR5Krlpj/i0m+2M3fmmT9iLWsS/L1JI8meSTJ5UuMeW+SV5Ns725/MlY9C5b5dJKHuuXdt8T8JPnrbh09mOT0EWs5acG/fXuS15JcsWjMqOtoqa9GS3Jkki1Jnux+rlnmuRd3Y55McvGI9XwmyePd63F7kiOWee5eX9tRVdXMbsAq4LvACcDBwAPAyYvGfAz4fDe9CfjiiPUcA5zeTR8GPLFEPe8Fvjrj9fQ0cNRe5p8P3AUEOBPYOsPX7wUmJ27MbB0B7wFOBx5e8NifAVd101cB1y7xvCOBp7qfa7rpNSPVcw6wupu+dql69ue1HfM26y37GcCOqnqqql4HbgE2LhqzEbixm74VODtJxiimqnZV1bZu+gfAY8DaMZY1sI3AP9bEvcARSY6ZwXLPBr5bVcudBTmKWvqr0Rb+ndwIvH+Jp54LbKmqV6rqf4AtLPF9ikPUU1V3V9Xu7u69TL7nYa7MOuxrgWcX3H+Onw3XT8Z0K+9V4G1jF9a9XTgN2LrE7HcleSDJXUl+bexamHyv391J7u++6Wex/VmPY9gE3LzMvFmvo6Oralc3/QJw9BJjVmo9Xcpkz2sp+3ptR+P3RAFJ3gp8Gbiiql5bNHsbk93WHyY5H/hn4MSRS3p3Ve1M8g5gS5LHu63JiklyMHAhcPUSs1diHf1EVVWSufgMOck1wG7gpmWGrNhrO+st+05g3YL7x3WPLTkmyWrgcOD7YxWU5CAmQb+pqm5bPL+qXquqH3bTdwIHjf09+VW1s/v5EnA7k7c/C+3Pehza+4BtVfXi4hkrsY6AF/e8del+vrTEmJmupySXABcAH6zuDfpi+/HajmbWYf82cGKS47stxSbgjkVj7gD2HDX9APC15VZcX92xgBuAx6rqs8uMeeeeYwZJzmCyzsb8z+fQJIftmWZy4Gdxg447gN/vjsqfCby6YJd2LBexzC78rNdRZ+HfycXAV5YYsxk4J8ma7mj9Od1jg0tyHpOvVr+wqn60zJj9eW3HM+sjgkyOJD/B5Kj8Nd1jf8pkJQG8BfgSsAP4FnDCiLW8m8l7qAeB7d3tfOCjwEe7MR8HHmHyycG9wFkjr58TumU90C13zzpaWFOAz3Xr8CEm3wE4Zk2HMgnv4Qsem9k6YvKfzC7gDSbvuz/C5DjOPcCTwL8CR3ZjNwDXL3jupd3f0g7gwyPWs4PJ8YE9f0d7PlE6Frhzb6/trG6eLis1wjPopEYYdqkRhl1qhGGXGmHYpUYYdqkRhl1qxP8DYiPXRo5VY5sAAAAASUVORK5CYII=\n",
64 | "text/plain": [
65 | ""
66 | ]
67 | },
68 | "metadata": {
69 | "needs_background": "light"
70 | },
71 | "output_type": "display_data"
72 | },
73 | {
74 | "name": "stdout",
75 | "output_type": "stream",
76 | "text": [
77 | "one iter planning timecost: 22.050686597824097\n"
78 | ]
79 | }
80 | ],
81 | "source": [
82 | "import heapq\n",
83 | "import math\n",
84 | "import matplotlib.pyplot as plt\n",
85 | "import numpy as np\n",
86 | "import math\n",
87 | "import matplotlib\n",
88 | "%matplotlib inline\n",
89 | "#set up matplotlib\n",
90 | "MAX_INT = 9999.0\n",
91 | "class GridMap:\n",
92 | " def __init__(self, ox, oy, resolution):\n",
93 | " self.min_x = None\n",
94 | " self.min_y = None\n",
95 | " self.max_x = None\n",
96 | " self.max_y = None\n",
97 | " self.x_width = None\n",
98 | " self.y_width = None\n",
99 | " self.obstacle_map = None\n",
100 | " \n",
101 | " self.resolution = resolution\n",
102 | " self.calc_obstacle_map(ox, oy)\n",
103 | " \n",
104 | " def calc_obstacle_map(self, ox, oy):\n",
105 | "\n",
106 | " self.min_x = round(min(ox))\n",
107 | " self.min_y = round(min(oy))\n",
108 | " self.max_x = round(max(ox))\n",
109 | " self.max_y = round(max(oy))\n",
110 | " print(\"min_x:\", self.min_x)\n",
111 | " print(\"min_y:\", self.min_y)\n",
112 | " print(\"max_x:\", self.max_x)\n",
113 | " print(\"max_y:\", self.max_y)\n",
114 | "\n",
115 | " self.x_width = round((self.max_x - self.min_x) / self.resolution)+1\n",
116 | " self.y_width = round((self.max_y - self.min_y) / self.resolution)+1\n",
117 | " print(\"x_width:\", self.x_width)\n",
118 | " print(\"y_width:\", self.y_width)\n",
119 | "\n",
120 | " # obstacle map generation\n",
121 | " self.obstacle_map = np.zeros((self.x_width, self.y_width))\n",
122 | " for x, y in zip(ox, oy):\n",
123 | " ix, iy = self.calc_xy_index(x, self.min_x), self.calc_xy_index(y, self.min_y)\n",
124 | " if 0<=ix= self.x_width or ix < 0 or iy >= self.y_width or iy < 0:\n",
140 | " return False \n",
141 | " return True\n",
142 | "\n",
143 | "sx = -5.0 # [m]\n",
144 | "sy = -5.0 # [m]\n",
145 | "gx = 50.0 # [m]\n",
146 | "gy = 50.0 # [m]\n",
147 | "grid_size = 5.0 # [m]\n",
148 | "robot_radius = 1.0 # [m]\n",
149 | "\n",
150 | "# set obstacle positions\n",
151 | "ox, oy = [], []\n",
152 | "for i in range(-10, 60):\n",
153 | " ox.append(i)\n",
154 | " oy.append(-10.0)\n",
155 | "for i in range(-10, 60):\n",
156 | " ox.append(60.0)\n",
157 | " oy.append(i)\n",
158 | "for i in range(-10, 61):\n",
159 | " ox.append(i)\n",
160 | " oy.append(60.0)\n",
161 | "for i in range(-10, 61):\n",
162 | " ox.append(-10.0)\n",
163 | " oy.append(i)\n",
164 | "# for i in range(-10, 40):\n",
165 | "# ox.append(20.0)\n",
166 | "# oy.append(i)\n",
167 | "for i in range(20, 40):\n",
168 | " ox.append(40.0)\n",
169 | " oy.append(60.0 - i) \n",
170 | " \n",
171 | "for i in range(20, 40):\n",
172 | " oy.append(40.0)\n",
173 | " ox.append(i) \n",
174 | "grid_map = GridMap(ox, oy, grid_size)\n",
175 | "\n",
176 | "\n",
177 | "class Node:\n",
178 | " def __init__(self, ix, iy, g=9999.0, rhs=9999.0, P=None):\n",
179 | " self.ix = ix\n",
180 | " self.iy = iy\n",
181 | " self.g = g\n",
182 | " self.rhs = rhs\n",
183 | " self.P = P\n",
184 | " \n",
185 | "action_set = {'UP':[0, 1], 'DOWN':[0, -1], 'LEFT':[-1, 0], 'RIGHT':[1, 0], 'UL':[-1, 1], 'UR':[1, 1], 'DL':[-1, -1], 'DR':[1, -1]}\n",
186 | "\n",
187 | "class DstarLite(object):\n",
188 | " def __init__(self, grid_map, start_node, end_node):\n",
189 | " self.grid_map = grid_map\n",
190 | " self.start_uid = self.grid_map.calc_unique_index(start_node.ix, start_node.iy)\n",
191 | " self.end_uid = self.grid_map.calc_unique_index(end_node.ix, end_node.iy)\n",
192 | " \n",
193 | " self.SPath = [] # 最优轨迹\n",
194 | " self.km = 0.0\n",
195 | " \n",
196 | " self.ANB = {} # all node buffer\n",
197 | " self.init_ANB()\n",
198 | " self.U = {}\n",
199 | " self.Qu = []\n",
200 | " self.ANB[self.end_uid] = end_node\n",
201 | " self.U[self.end_uid] = end_node\n",
202 | " heapq.heappush(self.Qu, (self.calculatekey(end_node), self.end_uid)) \n",
203 | " self.main()\n",
204 | " \n",
205 | " def init_ANB(self):\n",
206 | " for ix in range(self.grid_map.x_width):\n",
207 | " for iy in range(self.grid_map.y_width):\n",
208 | " self.ANB[self.grid_map.calc_unique_index(ix, iy)] = Node(ix, iy)\n",
209 | " \n",
210 | " def get_neighbors(self, current):\n",
211 | " for a in action_set:\n",
212 | " ix, iy = current.ix+action_set[a][0], current.iy+action_set[a][1]\n",
213 | " if self.grid_map.verify_node(ix, iy):\n",
214 | " cx1x2 = np.sqrt(action_set[a][0]*action_set[a][0]+action_set[a][1]*action_set[a][1])*self.grid_map.resolution\n",
215 | " if (abs(self.grid_map.obstacle_map[ix, iy]-10.0) < 0.01 or \n",
216 | " abs(self.grid_map.obstacle_map[current.ix, current.iy]-10.0) < 0.01):\n",
217 | " cx1x2 = MAX_INT \n",
218 | " yield (self.grid_map.calc_unique_index(ix, iy), cx1x2) \n",
219 | " \n",
220 | " def get_heuristic(self, node):\n",
221 | " dx = node.ix - self.ANB[self.start_uid].ix\n",
222 | " dy = node.iy - self.ANB[self.start_uid].iy\n",
223 | " return np.sqrt(dx*dx+dy*dy)*self.grid_map.resolution \n",
224 | " \n",
225 | " def calculatekey(self, node):\n",
226 | " return [min(node.g, node.rhs)+self.get_heuristic(node)+self.km, min(node.g, node.rhs)]\n",
227 | " \n",
228 | " def calculate_rhs(self, node):\n",
229 | " node.rhs = MAX_INT\n",
230 | " for pre_uid, cx1x2 in self.get_neighbors(node):\n",
231 | " pre_node = self.ANB[pre_uid]\n",
232 | " if pre_node.g+cx1x2 < node.rhs:\n",
233 | " node.rhs = pre_node.g+cx1x2\n",
234 | " node.P = pre_uid\n",
235 | " return node\n",
236 | " \n",
237 | " def updatenode(self, node_uid): \n",
238 | " if node_uid != self.end_uid: # line 06\n",
239 | " self.ANB[node_uid] = self.calculate_rhs(self.ANB[node_uid])\n",
240 | " \n",
241 | " if node_uid in self.U: # line 07\n",
242 | " del self.U[node_uid]\n",
243 | " if abs(self.ANB[node_uid].g - self.ANB[node_uid].rhs) > 0.00001: # line 08\n",
244 | " self.U[node_uid] = self.ANB[node_uid]\n",
245 | " heapq.heappush(self.Qu, (self.calculatekey(self.ANB[node_uid]), node_uid)) \n",
246 | "\n",
247 | " def waitenvchange(self):\n",
248 | " change_ixiy = []\n",
249 | " while input(\"if you want change environment, please input [ok] to start changing\") == \"ok\":\n",
250 | " ix = int(input(\"please input ix number (Type: Int) in [0, \"+str(self.grid_map.x_width)+\"):\"))\n",
251 | " iy = int(input(\"please input iy number (Type: Int) in [0, \"+str(self.grid_map.y_width)+\"):\")) \n",
252 | " if ix >= 0 and ix < self.grid_map.x_width and iy >= 0 and iy current.rhs:\n",
290 | " self.ANB[c_id].g = current.rhs\n",
291 | " else:\n",
292 | " self.ANB[c_id].g = MAX_INT\n",
293 | " self.updatenode(c_id)\n",
294 | " for succ_uid, cx1x2 in self.get_neighbors(self.ANB[c_id]):\n",
295 | " self.updatenode(succ_uid) \n",
296 | " \n",
297 | " is_into_while = True\n",
298 | " while self.Qu[0][1] not in self.U: # 保证堆项元系的确在U列表中 \n",
299 | " k, c_id = heapq.heappop(self.Qu) \n",
300 | " \n",
301 | " if is_into_while: \n",
302 | " print(\"find a path.\")\n",
303 | " self.shortestpathfinder()\n",
304 | " print(self.SPath)\n",
305 | " \n",
306 | " def plot_result(self): \n",
307 | " for ix, iy in zip(self.SPath[0], self.SPath[1]):\n",
308 | " self.grid_map.obstacle_map[ix, iy] = 4 \n",
309 | " plt.imshow(self.grid_map.obstacle_map)\n",
310 | " plt.show()\n",
311 | " for ix, iy in zip(self.SPath[0], self.SPath[1]):\n",
312 | " self.grid_map.obstacle_map[ix, iy] = 0\n",
313 | " \n",
314 | " def is_node_on_optpath(self, node):\n",
315 | " for ix, iy in zip(self.SPath[0], self.SPath[1]):\n",
316 | " if ix == node.ix and iy == node.iy:\n",
317 | " return True\n",
318 | " return False\n",
319 | " \n",
320 | " \n",
321 | " def main(self):\n",
322 | " last_uid = self.start_uid\n",
323 | " self.computeshortestpath()\n",
324 | " self.plot_result()\n",
325 | " while self.start_uid != self.end_uid:\n",
326 | " import time\n",
327 | " t0 = time.time() \n",
328 | " if self.ANB[self.start_uid].g > 1000.0:\n",
329 | " print(\"there is no known path.\")\n",
330 | " return;\n",
331 | " self.start_uid = self.get_new_start(self.start_uid)\n",
332 | " change_ixiy = self.waitenvchange()\n",
333 | " if len(change_ixiy) > 0:\n",
334 | " self.km += self.get_heuristic(self.ANB[last_uid])\n",
335 | " last_uid = self.start_uid \n",
336 | " for ix, iy in change_ixiy:\n",
337 | " print(\"changed map:\", self.grid_map.obstacle_map[ix, iy])\n",
338 | " change_index = self.grid_map.calc_unique_index(ix, iy)\n",
339 | "# if ((abs(self.grid_map.obstacle_map[ix, iy] - 10.0) < 0.01 and \n",
340 | "# self.is_node_on_optpath(self.ANB[change_index])) or \n",
341 | "# (abs(self.grid_map.obstacle_map[ix, iy] - 10.0) > 0.01 and\n",
342 | "# self.calculate_rhs(self.ANB[change_index]).rhs+self.get_heuristic(self.ANB[change_index]) < self.ANB[self.end_uid].g)):\n",
343 | "# self.updatenode(change_index)\n",
344 | " self.updatenode(change_index) # 如果使用定理一与定理二,则注释该行,并取消上面五行的注释 \n",
345 | " \n",
346 | " self.computeshortestpath()\n",
347 | " self.plot_result()\n",
348 | " print(\"one iter planning timecost:\", time.time()-t0)\n",
349 | " \n",
350 | " \n",
351 | "start_node = Node(2, 2)\n",
352 | "end_node = Node(12, 12, rhs=0.0)\n",
353 | "grid_map.obstacle_map[start_node.ix, start_node.iy] = 8\n",
354 | "grid_map.obstacle_map[end_node.ix, end_node.iy] = 3\n",
355 | "plt.imshow(grid_map.obstacle_map)\n",
356 | "planner = DstarLite(grid_map, start_node, end_node)"
357 | ]
358 | },
359 | {
360 | "cell_type": "code",
361 | "execution_count": null,
362 | "id": "7ea45902",
363 | "metadata": {},
364 | "outputs": [],
365 | "source": []
366 | }
367 | ],
368 | "metadata": {
369 | "kernelspec": {
370 | "display_name": "Python 3 (ipykernel)",
371 | "language": "python",
372 | "name": "python3"
373 | },
374 | "language_info": {
375 | "codemirror_mode": {
376 | "name": "ipython",
377 | "version": 3
378 | },
379 | "file_extension": ".py",
380 | "mimetype": "text/x-python",
381 | "name": "python",
382 | "nbconvert_exporter": "python",
383 | "pygments_lexer": "ipython3",
384 | "version": "3.9.5"
385 | }
386 | },
387 | "nbformat": 4,
388 | "nbformat_minor": 5
389 | }
390 |
--------------------------------------------------------------------------------
/基于图搜索/WAStar.ipynb:
--------------------------------------------------------------------------------
1 | {
2 | "cells": [
3 | {
4 | "cell_type": "code",
5 | "execution_count": 12,
6 | "id": "435e30d4",
7 | "metadata": {},
8 | "outputs": [
9 | {
10 | "data": {
11 | "image/png": "iVBORw0KGgoAAAANSUhEUgAAAq4AAAKrCAYAAAAwMg+1AAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjUuMiwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy8qNh9FAAAACXBIWXMAAAsTAAALEwEAmpwYAAAZZElEQVR4nO3db6imh1nn8d+1c9poarFtGkdNwiZIyRKCu21OSrXgwqS6UUvjC180bKTVQF64apVCSRX03VJQ1IKiDE1MoSFliRWLqGlIlLJQu5lJ0zZ/qi21m0yaJtOEVVFIOvHaF+dUZiYzZuac58yd65nPB8Kc588594+b5Mx37jzznOruAADAK91/WHoAAACcCeEKAMAIwhUAgBGEKwAAIwhXAABG2DiXB3vjG/b15Ze96lweEgCAQb72xLfyzederFM9dk7D9fLLXpX/c89l5/KQAAAM8tb/9sRpH/NSAQAARhCuAACMIFwBABhBuAIAMIJwBQBgBOEKAMAIwhUAgBGEKwAAIwhXAABGEK4AAIwgXAEAGEG4AgAwgnAFAGAE4QoAwAjCFQCAEYQrAAAjCFcAAEbYVbhW1fVV9bdV9ZWqunVVowAA4GQ7Dteq2pfk95P8eJKrktxYVVetahgAABxvN1dc35rkK9391e5+IcnHk9ywmlkAAHCi3YTrJUmeOO72ke37TlBVt1TVoao6dPTZF3dxOAAAzmd7/pezuvtgd2929+bFF+3b68MBALCmdhOuTya57Ljbl27fBwAAK7ebcH0gyZuq6oqqenWSdyf55GpmAQDAiTZ2+ondfayqfiHJPUn2Jbm9ux9Z2TIAADjOjsM1Sbr7z5P8+Yq2AADAafnJWQAAjCBcAQAYQbgCADCCcAUAYAThCgDACMIVAIARhCsAACMIVwAARhCuAACMIFwBABhBuAIAMIJwBQBgBOEKAMAIwhUAgBGEKwAAI2wsPeCV6rqbbl56AgCvQBv3H156Apy1e77+0NITVsIVVwAARhCuAACMIFwBABhBuAIAMIJwBQBgBOEKAMAIwhUAgBGEKwAAIwhXAABGEK4AAIwgXAEAGEG4AgAwgnAFAGAE4QoAwAjCFQCAEYQrAAAjCFcAAEYQrgAAjCBcAQAYQbgCADCCcAUAYAThCgDACMIVAIARhCsAACMIVwAARhCuAACMIFwBABhBuAIAMIJwBQBgBOEKAMAIwhUAgBGEKwAAIwhXAABGEK4AAIwgXAEAGEG4AgAwgnAFAGAE4QoAwAjCFQCAEYQrAAAjCFcAAEYQrgAAjCBcAQAYYWPpAazG09desPSEM7b/geeXngCwY8cOXLP0hLOycf/hpSfAyrjiCgDACMIVAIARhCsAACMIVwAARhCuAACMIFwBABhBuAIAMIJwBQBgBOEKAMAIwhUAgBGEKwAAIwhXAABGEK4AAIwgXAEAGEG4AgAwgnAFAGAE4QoAwAjCFQCAEXYcrlV1WVX9VVU9WlWPVNX7VjkMAACOt7GLzz2W5P3d/WBVvTbJ4aq6t7sfXdE2AAD4Nzu+4trdT3X3g9sf/1OSx5JcsqphAABwvJW8xrWqLk/y5iSfPcVjt1TVoao6dPTZF1dxOAAAzkO7Dteq+q4kf5zkl7v7H09+vLsPdvdmd29efNG+3R4OAIDz1K7Ctapela1ovbO7P7GaSQAA8FK7eVeBSnJbkse6+7dXNwkAAF5qN1dc357kZ5IcqKqHtv/5iRXtAgCAE+z47bC6+38nqRVuAQCA0/KTswAAGEG4AgAwgnAFAGAE4QoAwAjCFQCAEYQrAAAjCFcAAEYQrgAAjCBcAQAYQbgCADCCcAUAYAThCgDACMIVAIARhCsAACMIVwAARhCuAACMsLH0AFZj/wPPLz3hjD197QVLTzgrk84tAKwzV1wBABhBuAIAMIJwBQBgBOEKAMAIwhUAgBGEKwAAIwhXAABGEK4AAIwgXAEAGEG4AgAwgnAFAGAE4QoAwAjCFQCAEYQrAAAjCFcAAEYQrgAAjCBcAQAYQbgCADCCcAUAYAThCgDACMIVAIARhCsAACMIVwAARhCuAACMIFwBABhBuAIAMIJwBQBgBOEKAMAIwhUAgBGEKwAAIwhXAABGEK4AAIwgXAEAGEG4AgAwgnAFAGAE4QoAwAjCFQCAEYQrAAAjCFcAAEYQrgAAjCBcAQAYQbgCADDCxtIDAIC9c+zANUtPOGMb9x9eegKvcK64AgAwgnAFAGAE4QoAwAjCFQCAEYQrAAAjCFcAAEYQrgAAjCBcAQAYQbgCADCCcAUAYAThCgDACMIVAIARhCsAACMIVwAARhCuAACMIFwBABhBuAIAMIJwBQBghF2Ha1Xtq6rPVdWfrWIQAACcyiquuL4vyWMr+DoAAHBauwrXqro0yU8m+chq5gAAwKnt9orr7yb5QJJ/Pd0TquqWqjpUVYeOPvviLg8HAMD5asfhWlXvTPJMdx/+957X3Qe7e7O7Ny++aN9ODwcAwHluN1dc357kXVX1tSQfT3Kgqj62klUAAHCSHYdrd3+wuy/t7suTvDvJ/d1908qWAQDAcbyPKwAAI2ys4ot0918n+etVfC0AADgVV1wBABhBuAIAMIJwBQBgBOEKAMAIwhUAgBGEKwAAIwhXAABGEK4AAIwgXAEAGEG4AgAwgnAFAGAE4QoAwAjCFQCAEYQrAAAjCFcAAEYQrgAAjLCx9ADOP/sfeH7pCWfl6WsvWHrCWZl2fgG+7diBa5aecFY27j+89ITzjiuuAACMIFwBABhBuAIAMIJwBQBgBOEKAMAIwhUAgBGEKwAAIwhXAABGEK4AAIwgXAEAGEG4AgAwgnAFAGAE4QoAwAjCFQCAEYQrAAAjCFcAAEYQrgAAjCBcAQAYQbgCADCCcAUAYAThCgDACMIVAIARhCsAACMIVwAARhCuAACMIFwBABhBuAIAMIJwBQBgBOEKAMAIwhUAgBGEKwAAIwhXAABGEK4AAIwgXAEAGEG4AgAwgnAFAGAE4QoAwAjCFQCAEYQrAAAjCFcAAEYQrgAAjCBcAQAYYWPpAfBKt/+B55eecFaevvaCpSecsWnnFpLkvo/dtvSEs3LdTTcvPWFtHTtwzdITzsJDSw9YCVdcAQAYQbgCADCCcAUAYAThCgDACMIVAIARhCsAACMIVwAARhCuAACMIFwBABhBuAIAMIJwBQBgBOEKAMAIwhUAgBGEKwAAIwhXAABGEK4AAIwgXAEAGEG4AgAwwq7CtapeV1V3V9WXquqxqvqhVQ0DAIDjbezy8z+c5C+7+6er6tVJLlzBJgAAeIkdh2tVfXeSH0ny3iTp7heSvLCaWQAAcKLdvFTgiiRHk/xRVX2uqj5SVa85+UlVdUtVHaqqQ0effXEXhwMA4Hy2m3DdSPKWJH/Q3W9O8s9Jbj35Sd19sLs3u3vz4ov27eJwAACcz3YTrkeSHOnuz27fvjtbIQsAACu343Dt7m8keaKqrty+67okj65kFQAAnGS37yrwi0nu3H5Hga8m+dndTwIAgJfaVbh290NJNlczBQAATs9PzgIAYAThCgDACMIVAIARhCsAACMIVwAARhCuAACMIFwBABhBuAIAMIJwBQBgBOEKAMAIwhUAgBGEKwAAIwhXAABGEK4AAIwgXAEAGEG4AgAwgnAFAGAE4QoAwAjCFQCAEYQrAAAjCFcAAEYQrgAAjCBcAQAYQbgCADCCcAUAYAThCgDACMIVAIARhCsAACMIVwAARhCuAACMIFwBABhBuAIAMIJwBQBgBOEKAMAIwhUAgBGEKwAAIwhXAABGEK4AAIwgXAEAGEG4AgAwgnAFAGAE4QoAwAjCFQCAEYQrAAAjCFcAAEYQrgAAjCBcAQAYQbgCADCCcAUAYAThCgDACMIVAIARhCsAACMIVwAARhCuAACMIFwBABhBuAIAMIJwBQBgBOEKAMAIwhUAgBGEKwAAIwhXAABGEK4AAIwgXAEAGEG4AgAwgnAFAGAE4QoAwAjCFQCAEYQrAAAjCFcAAEYQrgAAjCBcAQAYQbgCADCCcAUAYAThCgDACMIVAIARhCsAACMIVwAARhCuAACMsKtwrapfqapHqurhqrqrqr5jVcMAAOB4Ow7XqrokyS8l2ezuq5PsS/LuVQ0DAIDj7falAhtJvrOqNpJcmOTru58EAAAvteNw7e4nk/xWkseTPJXkH7r7Uyc/r6puqapDVXXo6LMv7nwpAADntd28VOD1SW5IckWS70/ymqq66eTndffB7t7s7s2LL9q386UAAJzXdvNSgXck+fvuPtrd30ryiSQ/vJpZAABwot2E6+NJ3lZVF1ZVJbkuyWOrmQUAACfazWtcP5vk7iQPJvni9tc6uKJdAABwgo3dfHJ3/0aS31jRFgAAOC0/OQsAgBGEKwAAIwhXAABGEK4AAIwgXAEAGEG4AgAwgnAFAGAE4QoAwAjCFQCAEYQrAAAjCFcAAEYQrgAAjCBcAQAYQbgCADCCcAUAYAThCgDACMIVAIARhCsAACMIVwAARhCuAACMIFwBABhBuAIAMIJwBQBgBOEKAMAIwhUAgBGEKwAAIwhXAABGEK4AAIwgXAEAGEG4AgAwgnAFAGAE4QoAwAjCFQCAEYQrAAAjCFcAAEYQrgAAjCBcAQAYQbgCADCCcAUAYAThCgDACMIVAIARhCsAACMIVwAARhCuAACMIFwBABhBuAIAMIJwBQBgBOEKAMAIwhUAgBGEKwAAIwhXAABGEK4AAIwgXAEAGEG4AgAwgnAFAGAE4QoAwAjCFQCAEYQrAAAjCFcAAEbYWHrAK9XG/YeXnnBWjh24ZukJcNbu+9htS08AYBBXXAEAGEG4AgAwgnAFAGAE4QoAwAjCFQCAEYQrAAAjCFcAAEYQrgAAjCBcAQAYQbgCADCCcAUAYAThCgDACMIVAIARhCsAACMIVwAARhCuAACMIFwBABhBuAIAMMLLhmtV3V5Vz1TVw8fd94aqureqvrz96+v3diYAAOe7M7niekeS60+679Yk93X3m5Lct30bAAD2zMuGa3d/OslzJ919Q5KPbn/80SQ/tdpZAABwop2+xnV/dz+1/fE3kuw/3ROr6paqOlRVh44+++IODwcAwPlu1385q7s7Sf87jx/s7s3u3rz4on27PRwAAOepnYbr01X1fUmy/eszq5sEAAAvtdNw/WSS92x//J4kf7qaOQAAcGpn8nZYdyX5TJIrq+pIVd2c5ENJfrSqvpzkHdu3AQBgz2y83BO6+8bTPHTdircAAMBp+clZAACMIFwBABhBuAIAMIJwBQBgBOEKAMAIwhUAgBGEKwAAIwhXAABGEK4AAIwgXAEAGEG4AgAwgnAFAGAE4QoAwAjCFQCAEYQrAAAjCFcAAEbYWHoAq7Fx/+GlJ6ytYweuWXrCWdn/wPNLTzhjV3/455eeAOvv2qUHnLlJ379YhiuuAACMIFwBABhBuAIAMIJwBQBgBOEKAMAIwhUAgBGEKwAAIwhXAABGEK4AAIwgXAEAGEG4AgAwgnAFAGAE4QoAwAjCFQCAEYQrAAAjCFcAAEYQrgAAjCBcAQAYQbgCADCCcAUAYAThCgDACMIVAIARhCsAACMIVwAARhCuAACMIFwBABhBuAIAMIJwBQBgBOEKAMAIwhUAgBGEKwAAIwhXAABGEK4AAIwgXAEAGEG4AgAwgnAFAGAE4QoAwAjCFQCAEYQrAAAjCFcAAEYQrgAAjCBcAQAYYWPpAfBKt3H/4aUnnJVjB65ZesIZ2//A80tPAF5Bnr72gqUnnBXfw849V1wBABhBuAIAMIJwBQBgBOEKAMAIwhUAgBGEKwAAIwhXAABGEK4AAIwgXAEAGEG4AgAwgnAFAGAE4QoAwAjCFQCAEYQrAAAjCFcAAEYQrgAAjCBcAQAYQbgCADDCy4ZrVd1eVc9U1cPH3febVfWlqvpCVf1JVb1uT1cCAHDeO5Mrrnckuf6k++5NcnV3/2CSv0vywRXvAgCAE7xsuHb3p5M8d9J9n+ruY9s3/ybJpXuwDQAA/s0qXuP6c0n+4nQPVtUtVXWoqg4dffbFFRwOAIDz0a7Ctap+LcmxJHee7jndfbC7N7t78+KL9u3mcAAAnMc2dvqJVfXeJO9Mcl1398oWAQDAKewoXKvq+iQfSPJfu/tfVjsJAABe6kzeDuuuJJ9JcmVVHamqm5P8XpLXJrm3qh6qqj/c450AAJznXvaKa3ffeIq7b9uDLQAAcFp+chYAACMIVwAARhCuAACMIFwBABhBuAIAMIJwBQBgBOEKAMAIwhUAgBGEKwAAIwhXAABGEK4AAIwgXAEAGEG4AgAwgnAFAGAE4QoAwAjCFQCAETaWHgCs1sb9h5eecMaOHbhm6QnAK8j+B55fesJZmfT9dl244goAwAjCFQCAEYQrAAAjCFcAAEYQrgAAjCBcAQAYQbgCADCCcAUAYAThCgDACMIVAIARhCsAACMIVwAARhCuAACMIFwBABhBuAIAMIJwBQBgBOEKAMAIwhUAgBGEKwAAIwhXAABGEK4AAIwgXAEAGEG4AgAwgnAFAGAE4QoAwAjCFQCAEYQrAAAjCFcAAEYQrgAAjCBcAQAYQbgCADCCcAUAYAThCgDACMIVAIARhCsAACMIVwAARhCuAACMIFwBABhBuAIAMIJwBQBgBOEKAMAIwhUAgBE2lh7wSnXP1x9aegKcBx5aegAAg7jiCgDACMIVAIARhCsAACMIVwAARhCuAACMIFwBABhBuAIAMIJwBQBgBOEKAMAIwhUAgBGEKwAAIwhXAABGEK4AAIwgXAEAGEG4AgAwgnAFAGAE4QoAwAjCFQCAEV42XKvq9qp6pqoePsVj76+qrqo37s08AADYciZXXO9Icv3Jd1bVZUl+LMnjK94EAAAv8bLh2t2fTvLcKR76nSQfSNKrHgUAACfb0Wtcq+qGJE929+fP4Lm3VNWhqjp09NkXd3I4AAA4+3CtqguT/GqSXz+T53f3we7e7O7Niy/ad7aHAwCAJDu74voDSa5I8vmq+lqSS5M8WFXfu8phAABwvI2z/YTu/mKS7/n27e143ezub65wFwAAnOBM3g7rriSfSXJlVR2pqpv3fhYAAJzoZa+4dveNL/P45StbAwAAp+EnZwEAMIJwBQBgBOEKAMAIwhUAgBGEKwAAIwhXAABGEK4AAIwgXAEAGEG4AgAwgnAFAGAE4QoAwAjCFQCAEYQrAAAjCFcAAEYQrgAAjCBcAQAYobr73B2s6miS/7sHX/qNSb65B18X53YvObd7x7ndO87t3nFu945zu3f24tz+x+6++FQPnNNw3StVdai7N5fesY6c273j3O4d53bvOLd7x7ndO87t3jnX59ZLBQAAGEG4AgAwwrqE68GlB6wx53bvOLd7x7ndO87t3nFu945zu3fO6bldi9e4AgCw/tbliisAAGtOuAIAMMLocK2q66vqb6vqK1V169J71kVVXVZVf1VVj1bVI1X1vqU3rZuq2ldVn6uqP1t6yzqpqtdV1d1V9aWqeqyqfmjpTeuiqn5l+/vBw1V1V1V9x9Kbpqqq26vqmap6+Lj73lBV91bVl7d/ff2SG6c6zbn9ze3vCV+oqj+pqtctOHGsU53b4x57f1V1Vb1xr3eMDdeq2pfk95P8eJKrktxYVVctu2ptHEvy/u6+KsnbkvwP53bl3pfksaVHrKEPJ/nL7v5PSf5znOOVqKpLkvxSks3uvjrJviTvXnbVaHckuf6k+25Ncl93vynJfdu3OXt35KXn9t4kV3f3Dyb5uyQfPNej1sQdeem5TVVdluTHkjx+LkaMDdckb03yle7+ane/kOTjSW5YeNNa6O6nuvvB7Y//KVu/+V+y7Kr1UVWXJvnJJB9Zess6qarvTvIjSW5Lku5+obv/36Kj1stGku+sqo0kFyb5+sJ7xuruTyd57qS7b0jy0e2PP5rkp87lpnVxqnPb3Z/q7mPbN/8myaXnfNgaOM2/t0nyO0k+kOSc/G3/yeF6SZInjrt9JOJq5arq8iRvTvLZhaesk9/N1n/k/7rwjnVzRZKjSf5o+2UYH6mq1yw9ah1095NJfitbV1SeSvIP3f2pZVetnf3d/dT2x99Isn/JMWvs55L8xdIj1kVV3ZDkye7+/Lk65uRwZY9V1Xcl+eMkv9zd/7j0nnVQVe9M8kx3H156yxraSPKWJH/Q3W9O8s/xv1tXYvv1ljdk6w8H35/kNVV107Kr1ldvvU+l96pcsar6tWy9FO7Opbesg6q6MMmvJvn1c3ncyeH6ZJLLjrt96fZ9rEBVvSpb0Xpnd39i6T1r5O1J3lVVX8vWy1sOVNXHlp20No4kOdLd3/6/A3dnK2TZvXck+fvuPtrd30ryiSQ/vPCmdfN0VX1fkmz/+szCe9ZKVb03yTuT/Pf2Bvar8gPZ+sPs57d/T7s0yYNV9b17edDJ4fpAkjdV1RVV9eps/UWBTy68aS1UVWXrdYKPdfdvL71nnXT3B7v70u6+PFv/zt7f3a5crUB3fyPJE1V15fZd1yV5dMFJ6+TxJG+rqgu3vz9cF3/xbdU+meQ92x+/J8mfLrhlrVTV9dl6eda7uvtflt6zLrr7i939Pd19+fbvaUeSvGX7e/GeGRuu2y+0/oUk92TrG+j/6u5Hll21Nt6e5GeydTXwoe1/fmLpUXAGfjHJnVX1hST/Jcn/XHbOeti+in13kgeTfDFbv3f4EZo7VFV3JflMkiur6khV3ZzkQ0l+tKq+nK0r3B9acuNUpzm3v5fktUnu3f797A8XHTnUac7tud/hijkAABOMveIKAMD5RbgCADCCcAUAYAThCgDACMIVAIARhCsAACMIVwAARvj/PAeB/4zyUKMAAAAASUVORK5CYII=\n",
12 | "text/plain": [
13 | ""
14 | ]
15 | },
16 | "metadata": {},
17 | "output_type": "display_data"
18 | },
19 | {
20 | "data": {
21 | "image/png": "iVBORw0KGgoAAAANSUhEUgAAAq4AAAKrCAYAAAAwMg+1AAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjUuMiwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy8qNh9FAAAACXBIWXMAAAsTAAALEwEAmpwYAAAZZElEQVR4nO3db6imh1nn8d+1c9poarFtGkdNwiZIyRKCu21OSrXgwqS6UUvjC180bKTVQF64apVCSRX03VJQ1IKiDE1MoSFliRWLqGlIlLJQu5lJ0zZ/qi21m0yaJtOEVVFIOvHaF+dUZiYzZuac58yd65nPB8Kc588594+b5Mx37jzznOruAADAK91/WHoAAACcCeEKAMAIwhUAgBGEKwAAIwhXAABG2DiXB3vjG/b15Ze96lweEgCAQb72xLfyzederFM9dk7D9fLLXpX/c89l5/KQAAAM8tb/9sRpH/NSAQAARhCuAACMIFwBABhBuAIAMIJwBQBgBOEKAMAIwhUAgBGEKwAAIwhXAABGEK4AAIwgXAEAGEG4AgAwgnAFAGAE4QoAwAjCFQCAEYQrAAAjCFcAAEbYVbhW1fVV9bdV9ZWqunVVowAA4GQ7Dteq2pfk95P8eJKrktxYVVetahgAABxvN1dc35rkK9391e5+IcnHk9ywmlkAAHCi3YTrJUmeOO72ke37TlBVt1TVoao6dPTZF3dxOAAAzmd7/pezuvtgd2929+bFF+3b68MBALCmdhOuTya57Ljbl27fBwAAK7ebcH0gyZuq6oqqenWSdyf55GpmAQDAiTZ2+ondfayqfiHJPUn2Jbm9ux9Z2TIAADjOjsM1Sbr7z5P8+Yq2AADAafnJWQAAjCBcAQAYQbgCADCCcAUAYAThCgDACMIVAIARhCsAACMIVwAARhCuAACMIFwBABhBuAIAMIJwBQBgBOEKAMAIwhUAgBGEKwAAI2wsPeCV6rqbbl56AgCvQBv3H156Apy1e77+0NITVsIVVwAARhCuAACMIFwBABhBuAIAMIJwBQBgBOEKAMAIwhUAgBGEKwAAIwhXAABGEK4AAIwgXAEAGEG4AgAwgnAFAGAE4QoAwAjCFQCAEYQrAAAjCFcAAEYQrgAAjCBcAQAYQbgCADCCcAUAYAThCgDACMIVAIARhCsAACMIVwAARhCuAACMIFwBABhBuAIAMIJwBQBgBOEKAMAIwhUAgBGEKwAAIwhXAABGEK4AAIwgXAEAGEG4AgAwgnAFAGAE4QoAwAjCFQCAEYQrAAAjCFcAAEYQrgAAjCBcAQAYYWPpAazG09desPSEM7b/geeXngCwY8cOXLP0hLOycf/hpSfAyrjiCgDACMIVAIARhCsAACMIVwAARhCuAACMIFwBABhBuAIAMIJwBQBgBOEKAMAIwhUAgBGEKwAAIwhXAABGEK4AAIwgXAEAGEG4AgAwgnAFAGAE4QoAwAjCFQCAEXYcrlV1WVX9VVU9WlWPVNX7VjkMAACOt7GLzz2W5P3d/WBVvTbJ4aq6t7sfXdE2AAD4Nzu+4trdT3X3g9sf/1OSx5JcsqphAABwvJW8xrWqLk/y5iSfPcVjt1TVoao6dPTZF1dxOAAAzkO7Dteq+q4kf5zkl7v7H09+vLsPdvdmd29efNG+3R4OAIDz1K7Ctapela1ovbO7P7GaSQAA8FK7eVeBSnJbkse6+7dXNwkAAF5qN1dc357kZ5IcqKqHtv/5iRXtAgCAE+z47bC6+38nqRVuAQCA0/KTswAAGEG4AgAwgnAFAGAE4QoAwAjCFQCAEYQrAAAjCFcAAEYQrgAAjCBcAQAYQbgCADCCcAUAYAThCgDACMIVAIARhCsAACMIVwAARhCuAACMsLH0AFZj/wPPLz3hjD197QVLTzgrk84tAKwzV1wBABhBuAIAMIJwBQBgBOEKAMAIwhUAgBGEKwAAIwhXAABGEK4AAIwgXAEAGEG4AgAwgnAFAGAE4QoAwAjCFQCAEYQrAAAjCFcAAEYQrgAAjCBcAQAYQbgCADCCcAUAYAThCgDACMIVAIARhCsAACMIVwAARhCuAACMIFwBABhBuAIAMIJwBQBgBOEKAMAIwhUAgBGEKwAAIwhXAABGEK4AAIwgXAEAGEG4AgAwgnAFAGAE4QoAwAjCFQCAEYQrAAAjCFcAAEYQrgAAjCBcAQAYQbgCADDCxtIDAIC9c+zANUtPOGMb9x9eegKvcK64AgAwgnAFAGAE4QoAwAjCFQCAEYQrAAAjCFcAAEYQrgAAjCBcAQAYQbgCADCCcAUAYAThCgDACMIVAIARhCsAACMIVwAARhCuAACMIFwBABhBuAIAMIJwBQBghF2Ha1Xtq6rPVdWfrWIQAACcyiquuL4vyWMr+DoAAHBauwrXqro0yU8m+chq5gAAwKnt9orr7yb5QJJ/Pd0TquqWqjpUVYeOPvviLg8HAMD5asfhWlXvTPJMdx/+957X3Qe7e7O7Ny++aN9ODwcAwHluN1dc357kXVX1tSQfT3Kgqj62klUAAHCSHYdrd3+wuy/t7suTvDvJ/d1908qWAQDAcbyPKwAAI2ys4ot0918n+etVfC0AADgVV1wBABhBuAIAMIJwBQBgBOEKAMAIwhUAgBGEKwAAIwhXAABGEK4AAIwgXAEAGEG4AgAwgnAFAGAE4QoAwAjCFQCAEYQrAAAjCFcAAEYQrgAAjLCx9ADOP/sfeH7pCWfl6WsvWHrCWZl2fgG+7diBa5aecFY27j+89ITzjiuuAACMIFwBABhBuAIAMIJwBQBgBOEKAMAIwhUAgBGEKwAAIwhXAABGEK4AAIwgXAEAGEG4AgAwgnAFAGAE4QoAwAjCFQCAEYQrAAAjCFcAAEYQrgAAjCBcAQAYQbgCADCCcAUAYAThCgDACMIVAIARhCsAACMIVwAARhCuAACMIFwBABhBuAIAMIJwBQBgBOEKAMAIwhUAgBGEKwAAIwhXAABGEK4AAIwgXAEAGEG4AgAwgnAFAGAE4QoAwAjCFQCAEYQrAAAjCFcAAEYQrgAAjCBcAQAYYWPpAfBKt/+B55eecFaevvaCpSecsWnnFpLkvo/dtvSEs3LdTTcvPWFtHTtwzdITzsJDSw9YCVdcAQAYQbgCADCCcAUAYAThCgDACMIVAIARhCsAACMIVwAARhCuAACMIFwBABhBuAIAMIJwBQBgBOEKAMAIwhUAgBGEKwAAIwhXAABGEK4AAIwgXAEAGEG4AgAwwq7CtapeV1V3V9WXquqxqvqhVQ0DAIDjbezy8z+c5C+7+6er6tVJLlzBJgAAeIkdh2tVfXeSH0ny3iTp7heSvLCaWQAAcKLdvFTgiiRHk/xRVX2uqj5SVa85+UlVdUtVHaqqQ0effXEXhwMA4Hy2m3DdSPKWJH/Q3W9O8s9Jbj35Sd19sLs3u3vz4ov27eJwAACcz3YTrkeSHOnuz27fvjtbIQsAACu343Dt7m8keaKqrty+67okj65kFQAAnGS37yrwi0nu3H5Hga8m+dndTwIAgJfaVbh290NJNlczBQAATs9PzgIAYAThCgDACMIVAIARhCsAACMIVwAARhCuAACMIFwBABhBuAIAMIJwBQBgBOEKAMAIwhUAgBGEKwAAIwhXAABGEK4AAIwgXAEAGEG4AgAwgnAFAGAE4QoAwAjCFQCAEYQrAAAjCFcAAEYQrgAAjCBcAQAYQbgCADCCcAUAYAThCgDACMIVAIARhCsAACMIVwAARhCuAACMIFwBABhBuAIAMIJwBQBgBOEKAMAIwhUAgBGEKwAAIwhXAABGEK4AAIwgXAEAGEG4AgAwgnAFAGAE4QoAwAjCFQCAEYQrAAAjCFcAAEYQrgAAjCBcAQAYQbgCADCCcAUAYAThCgDACMIVAIARhCsAACMIVwAARhCuAACMIFwBABhBuAIAMIJwBQBgBOEKAMAIwhUAgBGEKwAAIwhXAABGEK4AAIwgXAEAGEG4AgAwgnAFAGAE4QoAwAjCFQCAEYQrAAAjCFcAAEYQrgAAjCBcAQAYQbgCADCCcAUAYAThCgDACMIVAIARhCsAACMIVwAARhCuAACMsKtwrapfqapHqurhqrqrqr5jVcMAAOB4Ow7XqrokyS8l2ezuq5PsS/LuVQ0DAIDj7falAhtJvrOqNpJcmOTru58EAAAvteNw7e4nk/xWkseTPJXkH7r7Uyc/r6puqapDVXXo6LMv7nwpAADntd28VOD1SW5IckWS70/ymqq66eTndffB7t7s7s2LL9q386UAAJzXdvNSgXck+fvuPtrd30ryiSQ/vJpZAABwot2E6+NJ3lZVF1ZVJbkuyWOrmQUAACfazWtcP5vk7iQPJvni9tc6uKJdAABwgo3dfHJ3/0aS31jRFgAAOC0/OQsAgBGEKwAAIwhXAABGEK4AAIwgXAEAGEG4AgAwgnAFAGAE4QoAwAjCFQCAEYQrAAAjCFcAAEYQrgAAjCBcAQAYQbgCADCCcAUAYAThCgDACMIVAIARhCsAACMIVwAARhCuAACMIFwBABhBuAIAMIJwBQBgBOEKAMAIwhUAgBGEKwAAIwhXAABGEK4AAIwgXAEAGEG4AgAwgnAFAGAE4QoAwAjCFQCAEYQrAAAjCFcAAEYQrgAAjCBcAQAYQbgCADCCcAUAYAThCgDACMIVAIARhCsAACMIVwAARhCuAACMIFwBABhBuAIAMIJwBQBgBOEKAMAIwhUAgBGEKwAAIwhXAABGEK4AAIwgXAEAGEG4AgAwgnAFAGAE4QoAwAjCFQCAEYQrAAAjCFcAAEbYWHrAK9XG/YeXnnBWjh24ZukJcNbu+9htS08AYBBXXAEAGEG4AgAwgnAFAGAE4QoAwAjCFQCAEYQrAAAjCFcAAEYQrgAAjCBcAQAYQbgCADCCcAUAYAThCgDACMIVAIARhCsAACMIVwAARhCuAACMIFwBABhBuAIAMMLLhmtV3V5Vz1TVw8fd94aqureqvrz96+v3diYAAOe7M7niekeS60+679Yk93X3m5Lct30bAAD2zMuGa3d/OslzJ919Q5KPbn/80SQ/tdpZAABwop2+xnV/dz+1/fE3kuw/3ROr6paqOlRVh44+++IODwcAwPlu1385q7s7Sf87jx/s7s3u3rz4on27PRwAAOepnYbr01X1fUmy/eszq5sEAAAvtdNw/WSS92x//J4kf7qaOQAAcGpn8nZYdyX5TJIrq+pIVd2c5ENJfrSqvpzkHdu3AQBgz2y83BO6+8bTPHTdircAAMBp+clZAACMIFwBABhBuAIAMIJwBQBgBOEKAMAIwhUAgBGEKwAAIwhXAABGEK4AAIwgXAEAGEG4AgAwgnAFAGAE4QoAwAjCFQCAEYQrAAAjCFcAAEbYWHoAq7Fx/+GlJ6ytYweuWXrCWdn/wPNLTzhjV3/455eeAOvv2qUHnLlJ379YhiuuAACMIFwBABhBuAIAMIJwBQBgBOEKAMAIwhUAgBGEKwAAIwhXAABGEK4AAIwgXAEAGEG4AgAwgnAFAGAE4QoAwAjCFQCAEYQrAAAjCFcAAEYQrgAAjCBcAQAYQbgCADCCcAUAYAThCgDACMIVAIARhCsAACMIVwAARhCuAACMIFwBABhBuAIAMIJwBQBgBOEKAMAIwhUAgBGEKwAAIwhXAABGEK4AAIwgXAEAGEG4AgAwgnAFAGAE4QoAwAjCFQCAEYQrAAAjCFcAAEYQrgAAjCBcAQAYYWPpAfBKt3H/4aUnnJVjB65ZesIZ2//A80tPAF5Bnr72gqUnnBXfw849V1wBABhBuAIAMIJwBQBgBOEKAMAIwhUAgBGEKwAAIwhXAABGEK4AAIwgXAEAGEG4AgAwgnAFAGAE4QoAwAjCFQCAEYQrAAAjCFcAAEYQrgAAjCBcAQAYQbgCADDCy4ZrVd1eVc9U1cPH3febVfWlqvpCVf1JVb1uT1cCAHDeO5Mrrnckuf6k++5NcnV3/2CSv0vywRXvAgCAE7xsuHb3p5M8d9J9n+ruY9s3/ybJpXuwDQAA/s0qXuP6c0n+4nQPVtUtVXWoqg4dffbFFRwOAIDz0a7Ctap+LcmxJHee7jndfbC7N7t78+KL9u3mcAAAnMc2dvqJVfXeJO9Mcl1398oWAQDAKewoXKvq+iQfSPJfu/tfVjsJAABe6kzeDuuuJJ9JcmVVHamqm5P8XpLXJrm3qh6qqj/c450AAJznXvaKa3ffeIq7b9uDLQAAcFp+chYAACMIVwAARhCuAACMIFwBABhBuAIAMIJwBQBgBOEKAMAIwhUAgBGEKwAAIwhXAABGEK4AAIwgXAEAGEG4AgAwgnAFAGAE4QoAwAjCFQCAETaWHgCs1sb9h5eecMaOHbhm6QnAK8j+B55fesJZmfT9dl244goAwAjCFQCAEYQrAAAjCFcAAEYQrgAAjCBcAQAYQbgCADCCcAUAYAThCgDACMIVAIARhCsAACMIVwAARhCuAACMIFwBABhBuAIAMIJwBQBgBOEKAMAIwhUAgBGEKwAAIwhXAABGEK4AAIwgXAEAGEG4AgAwgnAFAGAE4QoAwAjCFQCAEYQrAAAjCFcAAEYQrgAAjCBcAQAYQbgCADCCcAUAYAThCgDACMIVAIARhCsAACMIVwAARhCuAACMIFwBABhBuAIAMIJwBQBgBOEKAMAIwhUAgBE2lh7wSnXP1x9aegKcBx5aegAAg7jiCgDACMIVAIARhCsAACMIVwAARhCuAACMIFwBABhBuAIAMIJwBQBgBOEKAMAIwhUAgBGEKwAAIwhXAABGEK4AAIwgXAEAGEG4AgAwgnAFAGAE4QoAwAjCFQCAEV42XKvq9qp6pqoePsVj76+qrqo37s08AADYciZXXO9Icv3Jd1bVZUl+LMnjK94EAAAv8bLh2t2fTvLcKR76nSQfSNKrHgUAACfb0Wtcq+qGJE929+fP4Lm3VNWhqjp09NkXd3I4AAA4+3CtqguT/GqSXz+T53f3we7e7O7Niy/ad7aHAwCAJDu74voDSa5I8vmq+lqSS5M8WFXfu8phAABwvI2z/YTu/mKS7/n27e143ezub65wFwAAnOBM3g7rriSfSXJlVR2pqpv3fhYAAJzoZa+4dveNL/P45StbAwAAp+EnZwEAMIJwBQBgBOEKAMAIwhUAgBGEKwAAIwhXAABGEK4AAIwgXAEAGEG4AgAwgnAFAGAE4QoAwAjCFQCAEYQrAAAjCFcAAEYQrgAAjCBcAQAYobr73B2s6miS/7sHX/qNSb65B18X53YvObd7x7ndO87t3nFu945zu3f24tz+x+6++FQPnNNw3StVdai7N5fesY6c273j3O4d53bvOLd7x7ndO87t3jnX59ZLBQAAGEG4AgAwwrqE68GlB6wx53bvOLd7x7ndO87t3nFu945zu3fO6bldi9e4AgCw/tbliisAAGtOuAIAMMLocK2q66vqb6vqK1V169J71kVVXVZVf1VVj1bVI1X1vqU3rZuq2ldVn6uqP1t6yzqpqtdV1d1V9aWqeqyqfmjpTeuiqn5l+/vBw1V1V1V9x9Kbpqqq26vqmap6+Lj73lBV91bVl7d/ff2SG6c6zbn9ze3vCV+oqj+pqtctOHGsU53b4x57f1V1Vb1xr3eMDdeq2pfk95P8eJKrktxYVVctu2ptHEvy/u6+KsnbkvwP53bl3pfksaVHrKEPJ/nL7v5PSf5znOOVqKpLkvxSks3uvjrJviTvXnbVaHckuf6k+25Ncl93vynJfdu3OXt35KXn9t4kV3f3Dyb5uyQfPNej1sQdeem5TVVdluTHkjx+LkaMDdckb03yle7+ane/kOTjSW5YeNNa6O6nuvvB7Y//KVu/+V+y7Kr1UVWXJvnJJB9Zess6qarvTvIjSW5Lku5+obv/36Kj1stGku+sqo0kFyb5+sJ7xuruTyd57qS7b0jy0e2PP5rkp87lpnVxqnPb3Z/q7mPbN/8myaXnfNgaOM2/t0nyO0k+kOSc/G3/yeF6SZInjrt9JOJq5arq8iRvTvLZhaesk9/N1n/k/7rwjnVzRZKjSf5o+2UYH6mq1yw9ah1095NJfitbV1SeSvIP3f2pZVetnf3d/dT2x99Isn/JMWvs55L8xdIj1kVV3ZDkye7+/Lk65uRwZY9V1Xcl+eMkv9zd/7j0nnVQVe9M8kx3H156yxraSPKWJH/Q3W9O8s/xv1tXYvv1ljdk6w8H35/kNVV107Kr1ldvvU+l96pcsar6tWy9FO7Opbesg6q6MMmvJvn1c3ncyeH6ZJLLjrt96fZ9rEBVvSpb0Xpnd39i6T1r5O1J3lVVX8vWy1sOVNXHlp20No4kOdLd3/6/A3dnK2TZvXck+fvuPtrd30ryiSQ/vPCmdfN0VX1fkmz/+szCe9ZKVb03yTuT/Pf2Bvar8gPZ+sPs57d/T7s0yYNV9b17edDJ4fpAkjdV1RVV9eps/UWBTy68aS1UVWXrdYKPdfdvL71nnXT3B7v70u6+PFv/zt7f3a5crUB3fyPJE1V15fZd1yV5dMFJ6+TxJG+rqgu3vz9cF3/xbdU+meQ92x+/J8mfLrhlrVTV9dl6eda7uvtflt6zLrr7i939Pd19+fbvaUeSvGX7e/GeGRuu2y+0/oUk92TrG+j/6u5Hll21Nt6e5GeydTXwoe1/fmLpUXAGfjHJnVX1hST/Jcn/XHbOeti+in13kgeTfDFbv3f4EZo7VFV3JflMkiur6khV3ZzkQ0l+tKq+nK0r3B9acuNUpzm3v5fktUnu3f797A8XHTnUac7tud/hijkAABOMveIKAMD5RbgCADCCcAUAYAThCgDACMIVAIARhCsAACMIVwAARvj/PAeB/4zyUKMAAAAASUVORK5CYII=\n",
22 | "text/plain": [
23 | ""
24 | ]
25 | },
26 | "metadata": {
27 | "needs_background": "light"
28 | },
29 | "output_type": "display_data"
30 | }
31 | ],
32 | "source": [
33 | "import heapq\n",
34 | "import math\n",
35 | "import matplotlib.pyplot as plt\n",
36 | "import numpy as np\n",
37 | "import math\n",
38 | "import matplotlib\n",
39 | "%matplotlib inline\n",
40 | "#set up matplotlib\n",
41 | "is_ipython = 'inline' in matplotlib.get_backend()\n",
42 | "if is_ipython:\n",
43 | " from IPython import display\n",
44 | "plt.ion()\n",
45 | "plt.figure(figsize=(12, 12))\n",
46 | "\n",
47 | "\"\"\"\n",
48 | "\n",
49 | "\"\"\"\n",
50 | "\n",
51 | "class GridMap:\n",
52 | " def __init__(self, ox, oy, resolution):\n",
53 | " self.min_x = None\n",
54 | " self.min_y = None\n",
55 | " self.max_x = None\n",
56 | " self.max_y = None\n",
57 | " self.x_width = None\n",
58 | " self.y_width = None\n",
59 | " self.obstacle_map = None\n",
60 | " \n",
61 | " self.resolution = resolution\n",
62 | " self.calc_obstacle_map(ox, oy)\n",
63 | " \n",
64 | " def calc_obstacle_map(self, ox, oy):\n",
65 | "\n",
66 | " self.min_x = round(min(ox))\n",
67 | " self.min_y = round(min(oy))\n",
68 | " self.max_x = round(max(ox))\n",
69 | " self.max_y = round(max(oy))\n",
70 | " print(\"min_x:\", self.min_x)\n",
71 | " print(\"min_y:\", self.min_y)\n",
72 | " print(\"max_x:\", self.max_x)\n",
73 | " print(\"max_y:\", self.max_y)\n",
74 | "\n",
75 | " self.x_width = round((self.max_x - self.min_x) / self.resolution)+1\n",
76 | " self.y_width = round((self.max_y - self.min_y) / self.resolution)+1\n",
77 | " print(\"x_width:\", self.x_width)\n",
78 | " print(\"y_width:\", self.y_width)\n",
79 | "\n",
80 | " # obstacle map generation\n",
81 | " self.obstacle_map = np.zeros((self.x_width, self.y_width))\n",
82 | " for x, y in zip(ox, oy):\n",
83 | " ix, iy = self.calc_xy_index(x, self.min_x), self.calc_xy_index(y, self.min_y)\n",
84 | " if 0<=ix= self.x_width or node.ix < 0 or node.iy >= self.y_width or node.iy < 0:\n",
100 | " return False\n",
101 | " if abs(self.obstacle_map[node.ix, node.iy] - 10.0) < 0.01:\n",
102 | " return False \n",
103 | " return True\n",
104 | "\n",
105 | "sx = -5.0 # [m]\n",
106 | "sy = -5.0 # [m]\n",
107 | "gx = 50.0 # [m]\n",
108 | "gy = 50.0 # [m]\n",
109 | "grid_size = 5.0 # [m]\n",
110 | "robot_radius = 1.0 # [m]\n",
111 | "\n",
112 | "# set obstacle positions\n",
113 | "ox, oy = [], []\n",
114 | "for i in range(-10, 60):\n",
115 | " ox.append(i)\n",
116 | " oy.append(-10.0)\n",
117 | "for i in range(-10, 60):\n",
118 | " ox.append(60.0)\n",
119 | " oy.append(i)\n",
120 | "for i in range(-10, 61):\n",
121 | " ox.append(i)\n",
122 | " oy.append(60.0)\n",
123 | "for i in range(-10, 61):\n",
124 | " ox.append(-10.0)\n",
125 | " oy.append(i)\n",
126 | "# for i in range(-10, 40):\n",
127 | "# ox.append(20.0)\n",
128 | "# oy.append(i)\n",
129 | "for i in range(20, 40):\n",
130 | " ox.append(40.0)\n",
131 | " oy.append(60.0 - i) \n",
132 | " \n",
133 | "for i in range(20, 40):\n",
134 | " oy.append(40.0)\n",
135 | " ox.append(i) \n",
136 | "grid_map = GridMap(ox, oy, grid_size)\n",
137 | "\n",
138 | "\n",
139 | "\n",
140 | "class Node:\n",
141 | " def __init__(self, ix, iy, C=0.0, P=None):\n",
142 | " self.ix = ix\n",
143 | " self.iy = iy\n",
144 | " self.C = C\n",
145 | " self.P = P\n",
146 | " \n",
147 | "action_set = {'UP':[0, 1], 'DOWN':[0, -1], 'LEFT':[-1, 0], 'RIGHT':[1, 0], 'UL':[-1, 1], 'UR':[1, 1], 'DL':[-1, -1], 'DR':[1, -1]}\n",
148 | "\n",
149 | "def get_neighbors(current, grid_map):\n",
150 | " for a in action_set:\n",
151 | " node = Node(current.ix+action_set[a][0], \n",
152 | " current.iy+action_set[a][1], current.C+np.sqrt(action_set[a][0]*action_set[a][0]+action_set[a][1]*action_set[a][1]), \n",
153 | " grid_map.calc_unique_index(current))\n",
154 | " if grid_map.verify_node(node):\n",
155 | " yield node\n",
156 | "\n",
157 | " \n",
158 | "def get_weight(d):\n",
159 | " return np.exp(0.3*d)\n",
160 | "def get_heuristic(node, end_node):\n",
161 | " dx = node.ix - end_node.ix\n",
162 | " dy = node.iy - end_node.iy\n",
163 | " d = np.sqrt(dx*dx+dy*dy)\n",
164 | " print(d, get_weight(d))\n",
165 | " return d\n",
166 | " \n",
167 | "\n",
168 | " \n",
169 | "def AStar(grid_map, start_node, end_node):\n",
170 | " Closed_set, Open_set = {}, {}\n",
171 | " Open_set[grid_map.calc_unique_index(start_node)] = start_node\n",
172 | " Q = []\n",
173 | " heapq.heappush(Q, (start_node.C+get_heuristic(start_node, end_node), \n",
174 | " grid_map.calc_unique_index(start_node)))\n",
175 | " while True:\n",
176 | " if not Open_set:\n",
177 | " print(\"Dijkstra Algorithm Finished.\")\n",
178 | " return [], [], -1\n",
179 | " \n",
180 | " C, c_id = heapq.heappop(Q)\n",
181 | " \n",
182 | " if c_id in Open_set:\n",
183 | " current = Open_set.pop(c_id)\n",
184 | " Closed_set[c_id] = current\n",
185 | " if current.ix == end_node.ix and current.iy == end_node.iy:\n",
186 | " return ShortestPathFinder(grid_map, Closed_set, end_node)\n",
187 | " else:\n",
188 | " continue\n",
189 | " \n",
190 | " for node in get_neighbors(current, grid_map):\n",
191 | " neighbor_index = grid_map.calc_unique_index(node)\n",
192 | " if neighbor_index in Closed_set: continue\n",
193 | " if neighbor_index not in Open_set or Open_set[neighbor_index].C > node.C:\n",
194 | " Open_set[neighbor_index] = node\n",
195 | " heapq.heappush(Q, (node.C+get_heuristic(node, end_node), neighbor_index))\n",
196 | " grid_map.obstacle_map[node.ix, node.iy] = 2\n",
197 | " plt.clf()\n",
198 | " plt.imshow(grid_map.obstacle_map)\n",
199 | " if is_ipython:\n",
200 | " display.clear_output(wait=True)\n",
201 | " display.display(plt.gcf()) \n",
202 | " \n",
203 | " \n",
204 | "def ShortestPathFinder(grid_map, Closed_set, end_node):\n",
205 | " if grid_map.verify_node(end_node) == False:\n",
206 | " print(\"the goal is unreachable!!!please change a reachable goal...\")\n",
207 | " return [], [], -1\n",
208 | " \n",
209 | " end_index = grid_map.calc_unique_index(end_node)\n",
210 | " SPath_x = [Closed_set[end_index].ix]\n",
211 | " SPath_y = [Closed_set[end_index].iy] \n",
212 | " SPath_dist = Closed_set[end_index].C*grid_map.resolution\n",
213 | " v_index = Closed_set[end_index].P\n",
214 | " while v_index: \n",
215 | " SPath_x.append(Closed_set[v_index].ix)\n",
216 | " SPath_y.append(Closed_set[v_index].iy)\n",
217 | " v_index = Closed_set[v_index].P\n",
218 | " return list(reversed(SPath_x)), list(reversed(SPath_y)), SPath_dist\n",
219 | "\n",
220 | "start_node = Node(2, 2)\n",
221 | "end_node = Node(12, 12)\n",
222 | "grid_map.obstacle_map[start_node.ix, start_node.iy] = 8\n",
223 | "grid_map.obstacle_map[end_node.ix, end_node.iy] = 3\n",
224 | "plt.imshow(grid_map.obstacle_map)\n",
225 | "\n",
226 | "path_x, path_y, path_dist = AStar(grid_map, start_node, end_node)\n",
227 | "grid_map.obstacle_map[end_node.ix, end_node.iy] = 4\n",
228 | "for ix, iy in zip(path_x, path_y):\n",
229 | " grid_map.obstacle_map[ix, iy] = 4\n",
230 | " \n",
231 | "plt.clf()\n",
232 | "plt.imshow(grid_map.obstacle_map)\n",
233 | "if is_ipython:\n",
234 | " display.clear_output(wait=True)\n",
235 | " display.display(plt.gcf()) "
236 | ]
237 | },
238 | {
239 | "cell_type": "code",
240 | "execution_count": null,
241 | "id": "715a33c4",
242 | "metadata": {},
243 | "outputs": [],
244 | "source": []
245 | }
246 | ],
247 | "metadata": {
248 | "kernelspec": {
249 | "display_name": "Python 3 (ipykernel)",
250 | "language": "python",
251 | "name": "python3"
252 | },
253 | "language_info": {
254 | "codemirror_mode": {
255 | "name": "ipython",
256 | "version": 3
257 | },
258 | "file_extension": ".py",
259 | "mimetype": "text/x-python",
260 | "name": "python",
261 | "nbconvert_exporter": "python",
262 | "pygments_lexer": "ipython3",
263 | "version": "3.9.5"
264 | }
265 | },
266 | "nbformat": 4,
267 | "nbformat_minor": 5
268 | }
269 |
--------------------------------------------------------------------------------
/基于图搜索/LPAstar.ipynb:
--------------------------------------------------------------------------------
1 | {
2 | "cells": [
3 | {
4 | "cell_type": "code",
5 | "execution_count": null,
6 | "id": "716e00fd",
7 | "metadata": {},
8 | "outputs": [
9 | {
10 | "name": "stdout",
11 | "output_type": "stream",
12 | "text": [
13 | "min_x: -10\n",
14 | "min_y: -10\n",
15 | "max_x: 60\n",
16 | "max_y: 60\n",
17 | "x_width: 15\n",
18 | "y_width: 15\n",
19 | "[70.71067811865476, 0.0] [9999.0, 9999.0]\n",
20 | "find a path.\n",
21 | "one iter planning timecost: 0.02177882194519043\n"
22 | ]
23 | },
24 | {
25 | "data": {
26 | "image/png": "iVBORw0KGgoAAAANSUhEUgAAAPsAAAD4CAYAAAAq5pAIAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjUuMiwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy8qNh9FAAAACXBIWXMAAAsTAAALEwEAmpwYAAAMpElEQVR4nO3db6xkdX3H8fenC9SCRBZRhGXbhYaQUNII2RCkxprSAiJhfeCDJdqCmBBjbKEx0aUkNekjqY39k5oaArY0JWCKUImBLlvUNI0Fhe3yH2GlFFiWP0oDWh/A2m8fzFlzvZ27rHPOmTvL7/1KJvfMnN/c+e6Z+9nfzJlz5puqQtIb3y+sdgGS5sOwS40w7FIjDLvUCMMuNeKgeT7YUUeuqQ3rD57nQ0pNefLp1/j+Sz/JtHVzDfuG9Qfz7a3r5/mQUlNOP+fpFdf5Ml5qhGGXGtEr7EnOTfLdJDuTbBmqKEnDmznsSdYAXwDeB5wMXJjk5KEKkzSsPjP76cDOqnqiql4FbgQ2DVOWpKH1Cfs6YOmuv2e62yQtoNF30CW5NMk9Se558Qc/GfvhJK2gT9h3AUs/ND+uu+1nVNXVVbWxqja+7a1rejycpD76hP07wIlJjk9yCLAZuHWYsiQNbeYj6KpqT5JPAFuBNcCXquqhwSqTNKheh8tW1W3AbQPVImlEHkEnNcKwS42Y61lvszrn2HeudgnSXG19dsfgv9OZXWqEYZcaYdilRhh2qRGGXWqEYZcaYdilRhh2qRGGXWqEYZcaYdilRhh2qRGGXWrEAXHWWx+7Pn3mzPddd9W3BqxEWl3O7FIjDLvUCMMuNaJPr7f1Sb6R5OEkDyW5bMjCJA2rzw66PcAnq2p7ksOBe5Nsq6qHB6pN0oBmntmrandVbe+Wfwg8gr3epIU1yHv2JBuAU4G7h/h9kobXO+xJ3gx8Bbi8ql6Zst7GjtIC6BX2JAczCfr1VXXztDE2dpQWQ5+98QGuBR6pqs8PV5KkMfSZ2X8D+F3gt5Ls6C7nDVSXpIH16eL6b0AGrEXSiDyCTmqEYZca8YY/xbXPaaqznh7rqbFaRM7sUiMMu9QIwy41wrBLjTDsUiMMu9QIwy41wrBLjTDsUiMMu9QIwy41wrBLjTDsUiPe8Ge99THr2Ws2k9QicmaXGmHYpUYYdqkRQzSJWJPkP5J8bYiCJI1jiJn9MiZ93iQtsL4dYY4D3g9cM0w5ksbSd2b/C+BTwP/2L0XSmPq0fzofeKGq7n2dcTZ2lBZA3/ZPFyR5EriRSRuof1g+yMaO0mKYOexVdUVVHVdVG4DNwNer6sODVSZpUH7OLjVikGPjq+qbwDeH+F2SxuHMLjXCsEuN8BTXEdhMUovImV1qhGGXGmHYpUYYdqkRhl1qhGGXGmHYpUYYdqkRhl1qhGGXGmHYpUYYdqkRhl1qhGe96YCy9dkdM9/3nGPfOVgdByJndqkRhl1qhGGXGtG3/dMRSW5K8miSR5K8a6jCJA2r7w66vwT+uao+mOQQ4NABapI0gpnDnuQtwHuAiwGq6lXg1WHKkjS0Pi/jjwdeBP62689+TZLDBqpL0sD6hP0g4DTgb6rqVOB/gC3LB9nYUVoMfcL+DPBMVd3dXb+JSfh/ho0dpcXQp7Hjc8DTSU7qbjoLeHiQqiQNru/e+N8Hru/2xD8BfKR/SZLG0CvsVbUD2DhMKZLG5BF0UiMMu9QIwy41wrBLjTDsUiMMu9QIwy41wrBLjTDsUiMMu9QIwy41wrBLjTDsUiMMu9QIwy41wrBLjTDsUiMMu9QIwy41wrBLjejb2PEPkzyU5MEkNyR501CFSRrWzGFPsg74A2BjVZ0CrAE2D1WYpGH1fRl/EPBLSQ5i0sH12f4lSRpDn44wu4A/A54CdgMvV9UdQxUmaVh9XsavBTYx6eZ6LHBYkg9PGWdjR2kB9HkZ/9vAf1bVi1X1GnAzcObyQTZ2lBZDn7A/BZyR5NAkYdLY8ZFhypI0tD7v2e9m0qZ5O/BA97uuHqguSQPr29jxM8BnBqpF0og8gk5qhGGXGmHYpUYYdqkRhl1qhGGXGmHYpUYYdqkRhl1qhGGXGmHYpUYYdqkRhl1qhGGXGmHYpUYYdqkRvb68Qotj67M7VrsELThndqkRhl1qhGGXGvG6YU/ypSQvJHlwyW1HJtmW5PHu59pxy5TU1/7M7H8HnLvsti3AnVV1InBnd13SAnvdsFfVvwIvLbt5E3Bdt3wd8IFhy5I0tFnfsx9dVbu75eeAoweqR9JIeu+gq6oCaqX1NnaUFsOsYX8+yTEA3c8XVhpoY0dpMcwa9luBi7rli4CvDlOOpLHsz0dvNwD/DpyU5JkkHwU+C/xOkseZtG7+7LhlSurrdY+Nr6oLV1h11sC1SBqRR9BJjTDsUiM8xXXBrLvqWzPd7xQ+PvfH1IHFmV1qhGGXGmHYpUYYdqkRhl1qhGGXGmHYpUYYdqkRhl1qhGGXGmHYpUYYdqkRhl1qhGe9vUH0OXNt16fPHLASLbVIZxQ6s0uNMOxSIwy71IhZGzt+LsmjSe5PckuSI0atUlJvszZ23AacUlW/DjwGXDFwXZIGNlNjx6q6o6r2dFfvAo4boTZJAxriPfslwO0D/B5JI+oV9iRXAnuA6/cxxsaO0gKYOexJLgbOBz7UdXKdysaO0mKY6Qi6JOcCnwJ+s6p+PGxJksYwa2PHvwYOB7Yl2ZHkiyPXKamnWRs7XjtCLZJG5BF0UiMMu9QIT3HVQp2GqfE4s0uNMOxSIwy71AjDLjXCsEuNMOxSIwy71AjDLjXCsEuNMOxSIwy71AjDLjXCsEuNOCDOetv67I7VLkE64DmzS40w7FIjDLvUiJkaOy5Z98kkleSoccqTNJRZGzuSZD1wNvDUwDVJGsFMjR07f86kUcSK3WAkLY6Z3rMn2QTsqqr7Bq5H0kh+7s/ZkxwK/BGTl/D7M/5S4FKAX153QHysL70hzTKz/ypwPHBfkieZ9GbfnuQd0wbb2FFaDD/3VFtVDwBv33u9C/zGqvr+gHVJGtisjR0lHWBmbey4dP2GwaqRNBqPoJMaYdilRqRqfsfEJHkR+K8VVh8FLNJOvkWrBxavJuvZt9Wo51eq6m3TVsw17PuS5J6q2rjadey1aPXA4tVkPfu2aPX4Ml5qhGGXGrFIYb96tQtYZtHqgcWryXr2baHqWZj37JLGtUgzu6QRGXapEXMPe5Jzk3w3yc4kW6as/8UkX+7W351kw4i1rE/yjSQPJ3koyWVTxrw3yctJdnSXPx6rniWP+WSSB7rHu2fK+iT5q24b3Z/ktBFrOWnJv31HkleSXL5szKjbaNpXoyU5Msm2JI93P9eucN+LujGPJ7loxHo+l+TR7vm4JckRK9x3n8/tqKpqbhdgDfA94ATgEOA+4ORlYz4OfLFb3gx8ecR6jgFO65YPBx6bUs97ga/NeTs9CRy1j/XnAbcDAc4A7p7j8/cckwM35raNgPcApwEPLrntT4Et3fIW4Kop9zsSeKL7ubZbXjtSPWcDB3XLV02rZ3+e2zEv857ZTwd2VtUTVfUqcCOwadmYTcB13fJNwFlJMkYxVbW7qrZ3yz8EHgHWjfFYA9sE/H1N3AUckeSYOTzuWcD3qmqloyBHUdO/Gm3p38l1wAem3PUcYFtVvVRV/w1sY8r3KQ5RT1XdUVV7uqt3Mfmeh4Uy77CvA55ecv0Z/n+4fjqm23gvA28du7Du7cKpwN1TVr8ryX1Jbk/ya2PXwuR7/e5Icm/3TT/L7c92HMNm4IYV1s17Gx1dVbu75eeAo6eMWa3tdAmTV17TvN5zOxq/JwpI8mbgK8DlVfXKstXbmbxs/VGS84B/Ak4cuaR3V9WuJG8HtiV5tJtNVk2SQ4ALgCumrF6NbfRTVVVJFuIz5CRXAnuA61cYsmrP7bxn9l3A+iXXj+tumzomyUHAW4AfjFVQkoOZBP36qrp5+fqqeqWqftQt3wYcPPb35FfVru7nC8AtTN7+LLU/23Fo7wO2V9Xzy1esxjYCnt/71qX7+cKUMXPdTkkuBs4HPlTdG/Tl9uO5Hc28w/4d4MQkx3czxWbg1mVjbgX27jX9IPD1lTZcX92+gGuBR6rq8yuMecfefQZJTmeyzcb8z+ewJIfvXWay42d5g45bgd/r9sqfAby85CXtWC5khZfw895GnaV/JxcBX50yZitwdpK13d76s7vbBpfkXCZfrX5BVf14hTH789yOZ957BJnsSX6MyV75K7vb/oTJRgJ4E/CPwE7g28AJI9bybibvoe4HdnSX84CPAR/rxnwCeIjJJwd3AWeOvH1O6B7rvu5x926jpTUF+EK3DR9g8h2AY9Z0GJPwvmXJbXPbRkz+k9kNvMbkffdHmezHuRN4HPgX4Mhu7EbgmiX3vaT7W9oJfGTEenYy2T+w9+9o7ydKxwK37eu5ndfFw2WlRngEndQIwy41wrBLjTDsUiMMu9QIwy41wrBLjfg/xIfXzm2li8QAAAAASUVORK5CYII=\n",
27 | "text/plain": [
28 | ""
29 | ]
30 | },
31 | "metadata": {
32 | "needs_background": "light"
33 | },
34 | "output_type": "display_data"
35 | },
36 | {
37 | "name": "stdout",
38 | "output_type": "stream",
39 | "text": [
40 | "if you want change environment, please input [ok] to start changingok\n",
41 | "please input ix number (Type: Int) in [0, 15):12\n",
42 | "please input iy number (Type: Int) in [0, 15):7\n",
43 | "change [ix: 12, iy: 7] from free to obs\n",
44 | "if you want change environment, please input [ok] to start changingstop\n",
45 | "changed map: 10.0\n",
46 | "[85.35533905932738, 60.35533905932738] [85.35533905932738, 85.35533905932738]\n",
47 | "find a path.\n",
48 | "one iter planning timecost: 0.0008754730224609375\n"
49 | ]
50 | },
51 | {
52 | "data": {
53 | "image/png": "iVBORw0KGgoAAAANSUhEUgAAAPsAAAD4CAYAAAAq5pAIAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjUuMiwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy8qNh9FAAAACXBIWXMAAAsTAAALEwEAmpwYAAAMsElEQVR4nO3db6xkdX3H8fenu1ALElhEEZZtFxpCQkkDZEOQGmtKC4iE9YEPlmgLYkKMsYXGxC4lqUkfSW3sn9TUELClKQFThEoMdNmipmksq7Bd/i7CSimwLH+UBrQ+AOy3D+asvd7eu7vOOWfuLL/3K5ncM3N+c+e7Z+5nfzNnzplvqgpJb34/t9IFSJoNwy41wrBLjTDsUiMMu9SI1bN8sGOOXlXr1x0yy4eUmvLUM6/zvZd/nKXWzTTs69cdwre2rJvlQ0pNOev8Z5Zd58t4qRGGXWpEr7AnuSDJd5LsSrJ5qKIkDW/qsCdZBXweeB9wKnBJklOHKkzSsPrM7GcBu6rqyap6DbgF2DhMWZKG1ifsa4GFu/6e7W6TNIdG30GX5Iok9yW576Xv/3jsh5O0jD5h3w0s/ND8hO62n1JV11XVhqra8Pa3rerxcJL66BP2bwMnJzkxyaHAJuCOYcqSNLSpj6CrqjeSfALYAqwCvlhVjwxWmaRB9TpctqruBO4cqBZJI/IIOqkRhl1qxEzPepvW+cefvtIlSDO15bkdg/9OZ3apEYZdaoRhlxph2KVGGHapEYZdaoRhlxph2KVGGHapEYZdaoRhlxph2KVGGHapEQfFWW997P6Dc6a+79prvzlgJdLKcmaXGmHYpUYYdqkRfXq9rUvy9SSPJnkkyZVDFiZpWH120L0BfLKqtic5Arg/ydaqenSg2iQNaOqZvar2VNX2bvkHwE7s9SbNrUHesydZD5wBbBvi90kaXu+wJ3kr8GXgqqp6dYn1NnaU5kCvsCc5hEnQb6qq25YaY2NHaT702Rsf4AZgZ1V9briSJI2hz8z+a8BvA7+RZEd3uXCguiQNrE8X138FMmAtkkbkEXRSIwy71Ig3/SmufU5Tnfb0WE+N1TxyZpcaYdilRhh2qRGGXWqEYZcaYdilRhh2qRGGXWqEYZcaYdilRhh2qRGGXWqEYZca8aY/662Pac9es5mk5pEzu9QIwy41wrBLjRiiScSqJP+e5KtDFCRpHEPM7Fcy6fMmaY717QhzAvB+4PphypE0lr4z+58DnwL+p38pksbUp/3TRcCLVXX/fsbZ2FGaA33bP12c5CngFiZtoP5+8SAbO0rzYeqwV9XVVXVCVa0HNgFfq6oPD1aZpEH5ObvUiEGOja+qbwDfGOJ3SRqHM7vUCMMuNcJTXEdgM0nNI2d2qRGGXWqEYZcaYdilRhh2qRGGXWqEYZcaYdilRhh2qRGGXWqEYZcaYdilRhh2qRGe9aaDypbndkx93/OPP32wOg5GzuxSIwy71AjDLjWib/uno5LcmuSxJDuTvGuowiQNq+8Our8A/qmqPpjkUOCwAWqSNIKpw57kSOA9wGUAVfUa8NowZUkaWp+X8ScCLwF/0/Vnvz7J4QPVJWlgfcK+GjgT+OuqOgP4b2Dz4kE2dpTmQ5+wPws8W1Xbuuu3Mgn/T7GxozQf+jR2fB54Jskp3U3nAo8OUpWkwfXdG/+7wE3dnvgngY/0L0nSGHqFvap2ABuGKUXSmDyCTmqEYZcaYdilRhh2qRGGXWqEYZcaYdilRhh2qRGGXWqEYZcaYdilRhh2qRGGXWqEYZcaYdilRhh2qRGGXWqEYZcaYdilRhh2qRF9Gzv+fpJHkjyc5OYkbxmqMEnDmjrsSdYCvwdsqKrTgFXApqEKkzSsvi/jVwO/kGQ1kw6uz/UvSdIY+nSE2Q38KfA0sAd4paruHqowScPq8zJ+DbCRSTfX44HDk3x4iXE2dpTmQJ+X8b8J/EdVvVRVrwO3AecsHmRjR2k+9An708DZSQ5LEiaNHXcOU5akofV5z76NSZvm7cBD3e+6bqC6JA2sb2PHTwOfHqgWSSPyCDqpEYZdaoRhlxph2KVGGHapEYZdaoRhlxph2KVGGHapEYZdaoRhlxph2KVGGHapEYZdaoRhlxph2KVG9PryCs2PLc/tWOkSNOec2aVGGHapEYZdasR+w57ki0leTPLwgtuOTrI1yRPdzzXjlimprwOZ2f8WuGDRbZuBe6rqZOCe7rqkObbfsFfVvwAvL7p5I3Bjt3wj8IFhy5I0tGnfsx9bVXu65eeBYweqR9JIeu+gq6oCarn1NnaU5sO0YX8hyXEA3c8XlxtoY0dpPkwb9juAS7vlS4GvDFOOpLEcyEdvNwP/BpyS5NkkHwU+A/xWkieYtG7+zLhlSuprv8fGV9Uly6w6d+BaJI3II+ikRhh2qRGe4jpn1l77zanudxofH7iS/Zu2Vq0MZ3apEYZdaoRhlxph2KVGGHapEYZdaoRhlxph2KVGGHapEYZdaoRhlxph2KVGGHapEZ719ibR5wy0aZtCrsSZdgebeToz0JldaoRhlxph2KVGTNvY8bNJHkvyYJLbkxw1apWSepu2seNW4LSq+lXgceDqgeuSNLCpGjtW1d1V9UZ39V7ghBFqkzSgId6zXw7cNcDvkTSiXmFPcg3wBnDTPsbY2FGaA1OHPcllwEXAh7pOrkuysaM0H6Y6gi7JBcCngF+vqh8NW5KkMUzb2PGvgCOArUl2JPnCyHVK6mnaxo43jFCLpBF5BJ3UCMMuNcJTXMX5x58+1f3WMj+nb2r/nNmlRhh2qRGGXWqEYZcaYdilRhh2qRGGXWqEYZcaYdilRhh2qRGGXWqEYZcaYdilRhwUZ71N23hQ0v9xZpcaYdilRhh2qRFTNXZcsO6TSSrJMeOUJ2ko0zZ2JMk64Dzg6YFrkjSCqRo7dv6MSaOIZbvBSJofU71nT7IR2F1VDwxcj6SR/Myfsyc5DPhDJi/hD2T8FcAVAL+49qD4WF96U5pmZv9l4ETggSRPMenNvj3JO5cabGNHaT78zFNtVT0EvGPv9S7wG6rqewPWJWlg0zZ2lHSQmbax48L16werRtJoPIJOaoRhlxqRqtkdE5PkJeA/l1l9DDBPO/nmrR6Yv5qsZ99Wop5fqqq3L7VipmHflyT3VdWGla5jr3mrB+avJuvZt3mrx5fxUiMMu9SIeQr7dStdwCLzVg/MX03Ws29zVc/cvGeXNK55mtkljciwS42YediTXJDkO0l2Jdm8xPqfT/Klbv22JOtHrGVdkq8neTTJI0muXGLMe5O8kmRHd/mjsepZ8JhPJXmoe7z7llifJH/ZbaMHk5w5Yi2nLPi370jyapKrFo0ZdRst9dVoSY5OsjXJE93PNcvc99JuzBNJLh2xns8meax7Pm5PctQy993nczuqqprZBVgFfBc4CTgUeAA4ddGYjwNf6JY3AV8asZ7jgDO75SOAx5eo573AV2e8nZ4CjtnH+guBu4AAZwPbZvj8Pc/kwI2ZbSPgPcCZwMMLbvsTYHO3vBm4don7HQ082f1c0y2vGame84DV3fK1S9VzIM/tmJdZz+xnAbuq6smqeg24Bdi4aMxG4MZu+Vbg3CQZo5iq2lNV27vlHwA7gbVjPNbANgJ/VxP3AkclOW4Gj3su8N2qWu4oyFHU0l+NtvDv5EbgA0vc9Xxga1W9XFX/BWxlie9THKKeqrq7qt7ort7L5Hse5sqsw74WeGbB9Wf5/+H6yZhu470CvG3swrq3C2cA25ZY/a4kDyS5K8mvjF0Lk+/1uzvJ/d03/Sx2INtxDJuAm5dZN+ttdGxV7emWnweOXWLMSm2ny5m88lrK/p7b0fg9UUCStwJfBq6qqlcXrd7O5GXrD5NcCPwjcPLIJb27qnYneQewNclj3WyyYpIcClwMXL3E6pXYRj9RVZVkLj5DTnIN8AZw0zJDVuy5nfXMvhtYt+D6Cd1tS45Jsho4Evj+WAUlOYRJ0G+qqtsWr6+qV6vqh93yncAhY39PflXt7n6+CNzO5O3PQgeyHYf2PmB7Vb2weMVKbCPghb1vXbqfLy4xZqbbKcllwEXAh6p7g77YATy3o5l12L8NnJzkxG6m2ATcsWjMHcDevaYfBL623Ibrq9sXcAOws6o+t8yYd+7dZ5DkLCbbbMz/fA5PcsTeZSY7fhY36LgD+J1ur/zZwCsLXtKO5RKWeQk/623UWfh3cinwlSXGbAHOS7Km21t/Xnfb4JJcwOSr1S+uqh8tM+ZAntvxzHqPIJM9yY8z2St/TXfbHzPZSABvAf4B2AV8CzhpxFrezeQ91IPAju5yIfAx4GPdmE8AjzD55OBe4JyRt89J3WM90D3u3m20sKYAn++24UNMvgNwzJoOZxLeIxfcNrNtxOQ/mT3A60zed3+UyX6ce4AngH8Gju7GbgCuX3Dfy7u/pV3AR0asZxeT/QN7/472fqJ0PHDnvp7bWV08XFZqhEfQSY0w7FIjDLvUCMMuNcKwS40w7FIjDLvUiP8Fdo7ZRQMZNOAAAAAASUVORK5CYII=\n",
54 | "text/plain": [
55 | ""
56 | ]
57 | },
58 | "metadata": {
59 | "needs_background": "light"
60 | },
61 | "output_type": "display_data"
62 | },
63 | {
64 | "name": "stdout",
65 | "output_type": "stream",
66 | "text": [
67 | "if you want change environment, please input [ok] to start changingok\n",
68 | "please input ix number (Type: Int) in [0, 15):12\n",
69 | "please input iy number (Type: Int) in [0, 15):7\n",
70 | "change [ix: 12, iy: 7] from obs to free\n",
71 | "if you want change environment, please input [ok] to start changingstop\n",
72 | "changed map: 0.0\n",
73 | "[85.37319187990755, 44.14213562373095] [85.35533905932738, 85.35533905932738]\n",
74 | "one iter planning timecost: 0.00010752677917480469\n"
75 | ]
76 | },
77 | {
78 | "data": {
79 | "image/png": "iVBORw0KGgoAAAANSUhEUgAAAPsAAAD4CAYAAAAq5pAIAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjUuMiwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy8qNh9FAAAACXBIWXMAAAsTAAALEwEAmpwYAAAMrElEQVR4nO3db6xkdX3H8fenu1ALEllEEZZtFxpCQkkjZEOQGmtKC4iE9YEPlmgLYkKMsYXGRJeS1KSPpDb2T2pqCNjSlIApQiUGumxR0zSWVdgufxdhpRRYlj9KA1ofwNpvH8xZc729d3edc87cWX7vVzK5Z+b85s53z9zP/mbOnDPfVBWS3vh+YaULkDQbhl1qhGGXGmHYpUYYdqkRq2f5YMces6rWrztslg8pNeWpZ17n+y//JEutm2nY1687jG9vWTfLh5Sactb5zyy7zpfxUiMMu9SIXmFPckGS7ybZlWTzUEVJGt7UYU+yCvgC8D7gNOCSJKcNVZikYfWZ2c8CdlXVk1X1GnALsHGYsiQNrU/Y1wILd/09290maQ6NvoMuyRVJ7kty30s/+MnYDydpGX3CvhtY+KH5id1tP6OqrquqDVW14W1vXdXj4ST10Sfs3wFOSXJSksOBTcAdw5QlaWhTH0FXVXuTfALYAqwCvlRVjwxWmaRB9TpctqruBO4cqBZJI/IIOqkRhl1qxEzPepvW+Se8c6VLkGZqy3M7Bv+dzuxSIwy71AjDLjXCsEuNMOxSIwy71AjDLjXCsEuNMOxSIwy71AjDLjXCsEuNMOxSIw6Js9762P3pc6a+79prvzVgJdLKcmaXGmHYpUYYdqkRfXq9rUvyjSSPJnkkyZVDFiZpWH120O0FPllV25McBdyfZGtVPTpQbZIGNPXMXlV7qmp7t/xDYCf2epPm1iDv2ZOsB84Atg3x+yQNr3fYk7wZ+ApwVVW9usR6GztKc6BX2JMcxiToN1XVbUuNsbGjNB/67I0PcAOws6o+P1xJksbQZ2b/DeB3gd9KsqO7XDhQXZIG1qeL678BGbAWSSPyCDqpEYZdasQb/hTXPqepTnt6rKfGah45s0uNMOxSIwy71AjDLjXCsEuNMOxSIwy71AjDLjXCsEuNMOxSIwy71AjDLjXCsEuNeMOf9dbHtGev2UxS88iZXWqEYZcaYdilRgzRJGJVkv9I8rUhCpI0jiFm9iuZ9HmTNMf6doQ5EXg/cP0w5UgaS9+Z/S+ATwH/278USWPq0/7pIuDFqrr/AONs7CjNgb7tny5O8hRwC5M2UP+weJCNHaX5MHXYq+rqqjqxqtYDm4CvV9WHB6tM0qD8nF1qxCDHxlfVN4FvDvG7JI3DmV1qhGGXGuEpriOwmaTmkTO71AjDLjXCsEuNMOxSIwy71AjDLjXCsEuNMOxSIwy71AjDLjXCsEuNMOxSIwy71AjPetMhZctzO6a+7/knvHOwOg5FzuxSIwy71AjDLjWib/uno5PcmuSxJDuTvGuowiQNq+8Our8E/rmqPpjkcOCIAWqSNIKpw57kLcB7gMsAquo14LVhypI0tD4v408CXgL+tuvPfn2SIweqS9LA+oR9NXAm8DdVdQbwP8DmxYNs7CjNhz5hfxZ4tqq2dddvZRL+n2FjR2k+9Gns+DzwTJJTu5vOBR4dpCpJg+u7N/73gZu6PfFPAh/pX5KkMfQKe1XtADYMU4qkMXkEndQIwy41wrBLjTDsUiMMu9QIwy41wrBLjTDsUiMMu9QIwy41wrBLjTDsUiMMu9QIwy41wrBLjTDsUiMMu9QIwy41wrBLjTDsUiP6Nnb8wySPJHk4yc1J3jRUYZKGNXXYk6wF/gDYUFWnA6uATUMVJmlYfV/GrwZ+KclqJh1cn+tfkqQx9OkIsxv4M+BpYA/wSlXdPVRhkobV52X8GmAjk26uJwBHJvnwEuNs7CjNgT4v438b+M+qeqmqXgduA85ZPMjGjtJ86BP2p4GzkxyRJEwaO+4cpixJQ+vznn0bkzbN24GHut913UB1SRpY38aOnwE+M1AtkkbkEXRSIwy71AjDLjXCsEuNMOxSIwy71AjDLjXCsEuNMOxSIwy71AjDLjXCsEuNMOxSIwy71AjDLjXCsEuN6PXlFZofW57bsdIlaM45s0uNMOxSIwy71IgDhj3Jl5K8mOThBbcdk2Rrkie6n2vGLVNSXwczs/8dcMGi2zYD91TVKcA93XVJc+yAYa+qfwVeXnTzRuDGbvlG4APDliVpaNO+Zz+uqvZ0y88Dxw1Uj6SR9N5BV1UF1HLrbewozYdpw/5CkuMBup8vLjfQxo7SfJg27HcAl3bLlwJfHaYcSWM5mI/ebgb+HTg1ybNJPgp8FvidJE8wad382XHLlNTXAY+Nr6pLlll17sC1SBqRR9BJjTDsUiM8xXXOrL32W1Pd73Q+PnAlBzZtrVoZzuxSIwy71AjDLjXCsEuNMOxSIwy71AjDLjXCsEuNMOxSIwy71AjDLjXCsEuNMOxSIzzr7Q1iJc5A2/3pc2b+mIeaeToz0JldaoRhlxph2KVGTNvY8XNJHkvyYJLbkxw9apWSepu2seNW4PSq+nXgceDqgeuSNLCpGjtW1d1Vtbe7ei9w4gi1SRrQEO/ZLwfuGuD3SBpRr7AnuQbYC9y0nzE2dpTmwNRhT3IZcBHwoa6T65Js7CjNh6mOoEtyAfAp4Der6sfDliRpDNM2dvxr4Chga5IdSb44cp2Sepq2seMNI9QiaUQeQSc1wrBLjfAUV01tnk7f1IE5s0uNMOxSIwy71AjDLjXCsEuNMOxSIwy71AjDLjXCsEuNMOxSIwy71AjDLjXCsEuNOCTOetvy3I6VLkE65DmzS40w7FIjDLvUiKkaOy5Y98kkleTYccqTNJRpGzuSZB1wHvD0wDVJGsFUjR07f86kUcSy3WAkzY+p3rMn2QjsrqoHBq5H0kh+7s/ZkxwB/BGTl/AHM/4K4AqAX157SHysL70hTTOz/ypwEvBAkqeY9GbfnuQdSw22saM0H37uqbaqHgLevu96F/gNVfX9AeuSNLBpGztKOsRM29hx4fr1g1UjaTQeQSc1wrBLjUjV7I6JSfIS8F/LrD4WmKedfPNWD8xfTdazfytRz69U1duWWjHTsO9PkvuqasNK17HPvNUD81eT9ezfvNXjy3ipEYZdasQ8hf26lS5gkXmrB+avJuvZv7mqZ27es0sa1zzN7JJGZNilRsw87EkuSPLdJLuSbF5i/S8m+XK3fluS9SPWsi7JN5I8muSRJFcuMea9SV5JsqO7/PFY9Sx4zKeSPNQ93n1LrE+Sv+q20YNJzhyxllMX/Nt3JHk1yVWLxoy6jZb6arQkxyTZmuSJ7ueaZe57aTfmiSSXjljP55I81j0ftyc5epn77ve5HVVVzewCrAK+B5wMHA48AJy2aMzHgS92y5uAL49Yz/HAmd3yUcDjS9TzXuBrM95OTwHH7mf9hcBdQICzgW0zfP6eZ3Lgxsy2EfAe4Ezg4QW3/SmwuVveDFy7xP2OAZ7sfq7plteMVM95wOpu+dql6jmY53bMy6xn9rOAXVX1ZFW9BtwCbFw0ZiNwY7d8K3BukoxRTFXtqart3fIPgZ3A2jEea2Abgb+viXuBo5McP4PHPRf4XlUtdxTkKGrpr0Zb+HdyI/CBJe56PrC1ql6uqv8GtrLE9ykOUU9V3V1Ve7ur9zL5noe5MuuwrwWeWXD9Wf5/uH46ptt4rwBvHbuw7u3CGcC2JVa/K8kDSe5K8mtj18Lke/3uTnJ/900/ix3MdhzDJuDmZdbNehsdV1V7uuXngeOWGLNS2+lyJq+8lnKg53Y0fk8UkOTNwFeAq6rq1UWrtzN52fqjJBcC/wScMnJJ766q3UneDmxN8lg3m6yYJIcDFwNXL7F6JbbRT1VVJZmLz5CTXAPsBW5aZsiKPbezntl3A+sWXD+xu23JMUlWA28BfjBWQUkOYxL0m6rqtsXrq+rVqvpRt3wncNjY35NfVbu7ny8CtzN5+7PQwWzHob0P2F5VLyxesRLbCHhh31uX7ueLS4yZ6XZKchlwEfCh6t6gL3YQz+1oZh327wCnJDmpmyk2AXcsGnMHsG+v6QeBry+34frq9gXcAOysqs8vM+Yd+/YZJDmLyTYb8z+fI5MctW+ZyY6fxQ067gB+r9srfzbwyoKXtGO5hGVews96G3UW/p1cCnx1iTFbgPOSrOn21p/X3Ta4JBcw+Wr1i6vqx8uMOZjndjyz3iPIZE/y40z2yl/T3fYnTDYSwJuAfwR2Ad8GTh6xlnczeQ/1ILCju1wIfAz4WDfmE8AjTD45uBc4Z+Ttc3L3WA90j7tvGy2sKcAXum34EJPvAByzpiOZhPctC26b2TZi8p/MHuB1Ju+7P8pkP849wBPAvwDHdGM3ANcvuO/l3d/SLuAjI9azi8n+gX1/R/s+UToBuHN/z+2sLh4uKzXCI+ikRhh2qRGGXWqEYZcaYdilRhh2qRGGXWrE/wHNSNfOyPULSwAAAABJRU5ErkJggg==\n",
80 | "text/plain": [
81 | ""
82 | ]
83 | },
84 | "metadata": {
85 | "needs_background": "light"
86 | },
87 | "output_type": "display_data"
88 | }
89 | ],
90 | "source": [
91 | "import heapq\n",
92 | "import math\n",
93 | "import matplotlib.pyplot as plt\n",
94 | "import numpy as np\n",
95 | "import math\n",
96 | "import matplotlib\n",
97 | "%matplotlib inline\n",
98 | "#set up matplotlib\n",
99 | "MAX_INT = 9999.0\n",
100 | "class GridMap:\n",
101 | " def __init__(self, ox, oy, resolution):\n",
102 | " self.min_x = None\n",
103 | " self.min_y = None\n",
104 | " self.max_x = None\n",
105 | " self.max_y = None\n",
106 | " self.x_width = None\n",
107 | " self.y_width = None\n",
108 | " self.obstacle_map = None\n",
109 | " \n",
110 | " self.resolution = resolution\n",
111 | " self.calc_obstacle_map(ox, oy)\n",
112 | " \n",
113 | " def calc_obstacle_map(self, ox, oy):\n",
114 | "\n",
115 | " self.min_x = round(min(ox))\n",
116 | " self.min_y = round(min(oy))\n",
117 | " self.max_x = round(max(ox))\n",
118 | " self.max_y = round(max(oy))\n",
119 | " print(\"min_x:\", self.min_x)\n",
120 | " print(\"min_y:\", self.min_y)\n",
121 | " print(\"max_x:\", self.max_x)\n",
122 | " print(\"max_y:\", self.max_y)\n",
123 | "\n",
124 | " self.x_width = round((self.max_x - self.min_x) / self.resolution)+1\n",
125 | " self.y_width = round((self.max_y - self.min_y) / self.resolution)+1\n",
126 | " print(\"x_width:\", self.x_width)\n",
127 | " print(\"y_width:\", self.y_width)\n",
128 | "\n",
129 | " # obstacle map generation\n",
130 | " self.obstacle_map = np.zeros((self.x_width, self.y_width))\n",
131 | " for x, y in zip(ox, oy):\n",
132 | " ix, iy = self.calc_xy_index(x, self.min_x), self.calc_xy_index(y, self.min_y)\n",
133 | " if 0<=ix= self.x_width or ix < 0 or iy >= self.y_width or iy < 0:\n",
149 | " return False \n",
150 | " return True\n",
151 | "\n",
152 | "sx = -5.0 # [m]\n",
153 | "sy = -5.0 # [m]\n",
154 | "gx = 50.0 # [m]\n",
155 | "gy = 50.0 # [m]\n",
156 | "grid_size = 5.0 # [m]\n",
157 | "robot_radius = 1.0 # [m]\n",
158 | "\n",
159 | "# set obstacle positions\n",
160 | "ox, oy = [], []\n",
161 | "for i in range(-10, 60):\n",
162 | " ox.append(i)\n",
163 | " oy.append(-10.0)\n",
164 | "for i in range(-10, 60):\n",
165 | " ox.append(60.0)\n",
166 | " oy.append(i)\n",
167 | "for i in range(-10, 61):\n",
168 | " ox.append(i)\n",
169 | " oy.append(60.0)\n",
170 | "for i in range(-10, 61):\n",
171 | " ox.append(-10.0)\n",
172 | " oy.append(i)\n",
173 | "# for i in range(-10, 40):\n",
174 | "# ox.append(20.0)\n",
175 | "# oy.append(i)\n",
176 | "for i in range(20, 40):\n",
177 | " ox.append(40.0)\n",
178 | " oy.append(60.0 - i) \n",
179 | " \n",
180 | "for i in range(20, 40):\n",
181 | " oy.append(40.0)\n",
182 | " ox.append(i) \n",
183 | "grid_map = GridMap(ox, oy, grid_size)\n",
184 | "\n",
185 | "\n",
186 | "class Node:\n",
187 | " def __init__(self, ix, iy, g=9999.0, rhs=9999.0, P=None):\n",
188 | " self.ix = ix\n",
189 | " self.iy = iy\n",
190 | " self.g = g\n",
191 | " self.rhs = rhs\n",
192 | " self.P = P\n",
193 | " \n",
194 | "action_set = {'UP':[0, 1], 'DOWN':[0, -1], 'LEFT':[-1, 0], 'RIGHT':[1, 0], 'UL':[-1, 1], 'UR':[1, 1], 'DL':[-1, -1], 'DR':[1, -1]}\n",
195 | "\n",
196 | "class LPAstar(object):\n",
197 | " def __init__(self, grid_map, start_node, end_node):\n",
198 | " self.grid_map = grid_map\n",
199 | " self.start_uid = self.grid_map.calc_unique_index(start_node.ix, start_node.iy)\n",
200 | " self.end_uid = self.grid_map.calc_unique_index(end_node.ix, end_node.iy)\n",
201 | " \n",
202 | " self.SPath = [] # 最优轨迹\n",
203 | " \n",
204 | " self.ANB = {} # all node buffer\n",
205 | " self.init_ANB()\n",
206 | " self.U = {}\n",
207 | " self.Qu = []\n",
208 | " self.ANB[self.start_uid] = start_node\n",
209 | " self.U[self.start_uid] = start_node\n",
210 | " heapq.heappush(self.Qu, (self.calculatekey(start_node), self.start_uid)) \n",
211 | " self.main()\n",
212 | " \n",
213 | " def init_ANB(self):\n",
214 | " for ix in range(self.grid_map.x_width):\n",
215 | " for iy in range(self.grid_map.y_width):\n",
216 | " self.ANB[self.grid_map.calc_unique_index(ix, iy)] = Node(ix, iy)\n",
217 | " \n",
218 | " def get_neighbors(self, current):\n",
219 | " for a in action_set:\n",
220 | " ix, iy = current.ix+action_set[a][0], current.iy+action_set[a][1]\n",
221 | " if self.grid_map.verify_node(ix, iy):\n",
222 | " cx1x2 = np.sqrt(action_set[a][0]*action_set[a][0]+action_set[a][1]*action_set[a][1])*self.grid_map.resolution\n",
223 | " if (abs(self.grid_map.obstacle_map[ix, iy]-10.0) < 0.01 or \n",
224 | " abs(self.grid_map.obstacle_map[current.ix, current.iy]-10.0) < 0.01):\n",
225 | " cx1x2 = MAX_INT \n",
226 | " yield (self.grid_map.calc_unique_index(ix, iy), cx1x2) \n",
227 | " \n",
228 | " def get_heuristic(self, node):\n",
229 | " dx = node.ix - self.ANB[self.end_uid].ix\n",
230 | " dy = node.iy - self.ANB[self.end_uid].iy\n",
231 | " return np.sqrt(dx*dx+dy*dy)*self.grid_map.resolution \n",
232 | " \n",
233 | " def calculatekey(self, node):\n",
234 | " return [min(node.g, node.rhs)+self.get_heuristic(node), min(node.g, node.rhs)]\n",
235 | " \n",
236 | " def calculate_rhs(self, node):\n",
237 | " node.rhs = MAX_INT\n",
238 | " for pre_uid, cx1x2 in self.get_neighbors(node):\n",
239 | " pre_node = self.ANB[pre_uid]\n",
240 | " if pre_node.g+cx1x2 < node.rhs:\n",
241 | " node.rhs = pre_node.g+cx1x2\n",
242 | " node.P = pre_uid\n",
243 | " return node\n",
244 | " \n",
245 | " def updatenode(self, node_uid):\n",
246 | " \n",
247 | " if node_uid != self.start_uid: # line 06\n",
248 | " self.ANB[node_uid] = self.calculate_rhs(self.ANB[node_uid])\n",
249 | " \n",
250 | " if node_uid in self.U: # line 07\n",
251 | " del self.U[node_uid]\n",
252 | " if abs(self.ANB[node_uid].g - self.ANB[node_uid].rhs) > 0.00001: # line 08\n",
253 | " self.U[node_uid] = self.ANB[node_uid]\n",
254 | " heapq.heappush(self.Qu, (self.calculatekey(self.ANB[node_uid]), node_uid)) \n",
255 | " \n",
256 | "\n",
257 | " def waitenvchange(self):\n",
258 | " change_ixiy = []\n",
259 | " while input(\"if you want change environment, please input [ok] to start changing\") == \"ok\":\n",
260 | " ix = int(input(\"please input ix number (Type: Int) in [0, \"+str(self.grid_map.x_width)+\"):\"))\n",
261 | " iy = int(input(\"please input iy number (Type: Int) in [0, \"+str(self.grid_map.y_width)+\"):\")) \n",
262 | " if ix >= 0 and ix < self.grid_map.x_width and iy >= 0 and iy current.rhs:\n",
293 | " self.ANB[c_id].g = current.rhs\n",
294 | " else:\n",
295 | " self.ANB[c_id].g = MAX_INT\n",
296 | " self.updatenode(c_id)\n",
297 | " \n",
298 | " for succ_uid, cx1x2 in self.get_neighbors(self.ANB[c_id]):\n",
299 | " self.updatenode(succ_uid) \n",
300 | " \n",
301 | " is_into_while = True\n",
302 | " while self.Qu[0][1] not in self.U: # 保证堆项元系的确在U列表中 \n",
303 | " k, c_id = heapq.heappop(self.Qu) \n",
304 | " \n",
305 | " if is_into_while: \n",
306 | " print(\"find a path.\")\n",
307 | " self.shortestpathfinder()\n",
308 | " \n",
309 | " def plot_result(self): \n",
310 | " for ix, iy in zip(self.SPath[0], self.SPath[1]):\n",
311 | " self.grid_map.obstacle_map[ix, iy] = 4 \n",
312 | " plt.imshow(self.grid_map.obstacle_map)\n",
313 | " plt.show()\n",
314 | " for ix, iy in zip(self.SPath[0], self.SPath[1]):\n",
315 | " self.grid_map.obstacle_map[ix, iy] = 0\n",
316 | " \n",
317 | " def is_node_on_optpath(self, node):\n",
318 | " for ix, iy in zip(self.SPath[0], self.SPath[1]):\n",
319 | " if ix == node.ix and iy == node.iy:\n",
320 | " return True\n",
321 | " return False\n",
322 | " \n",
323 | " \n",
324 | " def main(self):\n",
325 | " while True:\n",
326 | " import time\n",
327 | " t0 = time.time()\n",
328 | " self.computeshortestpath()\n",
329 | " print(\"one iter planning timecost:\", time.time()-t0)\n",
330 | " self.plot_result()\n",
331 | " change_ixiy = self.waitenvchange()\n",
332 | " \n",
333 | " for ix, iy in change_ixiy:\n",
334 | " print(\"changed map:\", self.grid_map.obstacle_map[ix, iy])\n",
335 | " change_index = self.grid_map.calc_unique_index(ix, iy)\n",
336 | "# if ((abs(self.grid_map.obstacle_map[ix, iy] - 10.0) < 0.01 and \n",
337 | "# self.is_node_on_optpath(self.ANB[change_index])) or \n",
338 | "# (abs(self.grid_map.obstacle_map[ix, iy] - 10.0) > 0.01 and\n",
339 | "# self.calculate_rhs(self.ANB[change_index]).rhs+self.get_heuristic(self.ANB[change_index]) < self.ANB[self.end_uid].g)):\n",
340 | "# self.updatenode(change_index)\n",
341 | " self.updatenode(change_index) # 如果使用定理一与定理二,则注释该行,并取消上面五行的注释 \n",
342 | " \n",
343 | " \n",
344 | "start_node = Node(2, 2, rhs=0.0)\n",
345 | "end_node = Node(12, 12)\n",
346 | "grid_map.obstacle_map[start_node.ix, start_node.iy] = 8\n",
347 | "grid_map.obstacle_map[end_node.ix, end_node.iy] = 3\n",
348 | "plt.imshow(grid_map.obstacle_map)\n",
349 | "planner = LPAstar(grid_map, start_node, end_node)"
350 | ]
351 | },
352 | {
353 | "cell_type": "code",
354 | "execution_count": null,
355 | "id": "cb766005",
356 | "metadata": {},
357 | "outputs": [],
358 | "source": []
359 | }
360 | ],
361 | "metadata": {
362 | "kernelspec": {
363 | "display_name": "Python 3 (ipykernel)",
364 | "language": "python",
365 | "name": "python3"
366 | },
367 | "language_info": {
368 | "codemirror_mode": {
369 | "name": "ipython",
370 | "version": 3
371 | },
372 | "file_extension": ".py",
373 | "mimetype": "text/x-python",
374 | "name": "python",
375 | "nbconvert_exporter": "python",
376 | "pygments_lexer": "ipython3",
377 | "version": "3.9.5"
378 | }
379 | },
380 | "nbformat": 4,
381 | "nbformat_minor": 5
382 | }
383 |
--------------------------------------------------------------------------------
/基于图搜索/B STAR.ipynb:
--------------------------------------------------------------------------------
1 | {
2 | "cells": [
3 | {
4 | "cell_type": "code",
5 | "execution_count": 5,
6 | "id": "3bda9080",
7 | "metadata": {},
8 | "outputs": [
9 | {
10 | "data": {
11 | "image/png": "iVBORw0KGgoAAAANSUhEUgAAAq4AAAKrCAYAAAAwMg+1AAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjUuMiwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy8qNh9FAAAACXBIWXMAAAsTAAALEwEAmpwYAAAZGklEQVR4nO3dbaimh13n8d9/57TR1GLbNEabCZsgJUsobtuclGrBhaTaqKXxhS8attKugbxZtUqhpAr6bikoPoCuMrQxBUPKEisWUdPQKGWhdjOTpm0eqi21m0yaJtOEVVFIOvG/L85R5tGZnHOfufK/z+cDYc79cM714yI5850r99ynujsAAPBS9x+WHgAAAOdDuAIAMIJwBQBgBOEKAMAIwhUAgBE2LuTBXvuaA33lFS+7kIcEAGCQrz/+7Xzr2RfqTI9d0HC98oqX5f/cc8WFPCQAAIO85R2Pn/UxLxUAAGAE4QoAwAjCFQCAEYQrAAAjCFcAAEYQrgAAjCBcAQAYQbgCADCCcAUAYAThCgDACMIVAIARhCsAACMIVwAARhCuAACMIFwBABhBuAIAMIJwBQBghF2Fa1XdWFV/U1VfrarbVjUKAABOteNwraoDSX43yY8luSbJzVV1zaqGAQDAiXZzxfUtSb7a3V/r7ueTfDzJTauZBQAAJ9tNuF6e5PETbh/dvu8kVXVrVR2uqsPHnnlhF4cDAGA/2/O/nNXdh7p7s7s3L73kwF4fDgCANbWbcH0iyRUn3D64fR8AAKzcbsL1/iSvr6qrqurlSd6d5JOrmQUAACfb2OkndvfxqvrZJPckOZDk9u5+eGXLAADgBDsO1yTp7j9L8mcr2gIAAGflJ2cBADCCcAUAYAThCgDACMIVAIARhCsAACMIVwAARhCuAACMIFwBABhBuAIAMIJwBQBgBOEKAMAIwhUAgBGEKwAAIwhXAABGEK4AAIywsfSAl6p3vO6NS0+AHTl+/bVLT4C1tnHfkaUnwIt2zzceXHrCSrjiCgDACMIVAIARhCsAACMIVwAARhCuAACMIFwBABhBuAIAMIJwBQBgBOEKAMAIwhUAgBGEKwAAIwhXAABGEK4AAIwgXAEAGEG4AgAwgnAFAGAE4QoAwAjCFQCAEYQrAAAjCFcAAEYQrgAAjCBcAQAYQbgCADCCcAUAYAThCgDACMIVAIARhCsAACMIVwAARhCuAACMIFwBABhBuAIAMIJwBQBgBOEKAMAIwhUAgBGEKwAAIwhXAABGEK4AAIwgXAEAGEG4AgAwgnAFAGAE4QoAwAjCFQCAEYQrAAAjbCw9AF7qjl9/7dITeIl46rqLlp5w3i67/7mlJ6ytad8TNu47svQEWBlXXAEAGEG4AgAwgnAFAGAE4QoAwAjCFQCAEYQrAAAjCFcAAEYQrgAAjCBcAQAYQbgCADCCcAUAYAThCgDACMIVAIARhCsAACMIVwAARhCuAACMIFwBABhBuAIAMMKOw7Wqrqiqv6yqR6rq4ap6/yqHAQDAiTZ28bnHk3ygux+oqlcmOVJV93b3IyvaBgAA/2bHV1y7+8nufmD7439M8miSy1c1DAAATrSS17hW1ZVJ3pTkc2d47NaqOlxVh48988IqDgcAwD6063Ctqu9K8kdJfqG7/+HUx7v7UHdvdvfmpZcc2O3hAADYp3YVrlX1smxF653d/YnVTAIAgNPt5l0FKslHkzza3b+xukkAAHC63VxxfVuSn05yfVU9uP3Pj69oFwAAnGTHb4fV3f87Sa1wCwAAnJWfnAUAwAjCFQCAEYQrAAAjCFcAAEYQrgAAjCBcAQAYQbgCADCCcAUAYAThCgDACMIVAIARhCsAACMIVwAARhCuAACMIFwBABhBuAIAMIJwBQBgBOEKAMAIwhUAgBGEKwAAIwhXAABGEK4AAIwgXAEAGEG4AgAwgnAFAGAE4QoAwAjCFQCAEYQrAAAjCFcAAEYQrgAAjCBcAQAYQbgCADCCcAUAYAThCgDACMIVAIARhCsAACMIVwAARhCuAACMIFwBABhBuAIAMIJwBQBgBOEKAMAIwhUAgBGEKwAAIwhXAABGEK4AAIwgXAEAGEG4AgAwgnAFAGAE4QoAwAjCFQCAEYQrAAAjCFcAAEYQrgAAjCBcAQAYQbgCADCCcAUAYAThCgDACMIVAIARhCsAACMIVwAARhCuAACMIFwBABhBuAIAMIJwBQBgBOEKAMAIwhUAgBGEKwAAIwhXAABGEK4AAIwgXAEAGEG4AgAwgnAFAGAE4QoAwAjCFQCAEYQrAAAjCFcAAEYQrgAAjCBcAQAYYdfhWlUHqurzVfWnqxgEAABnsoorru9P8ugKvg4AAJzVrsK1qg4m+YkkH1nNHAAAOLPdXnH9rSQfTPIvZ3tCVd1aVYer6vCxZ17Y5eEAANivdhyuVfXOJE9395F/73ndfai7N7t789JLDuz0cAAA7HO7ueL6tiTvqqqvJ/l4kuur6g9XsgoAAE6x43Dt7g9198HuvjLJu5Pc193vWdkyAAA4gfdxBQBghI1VfJHu/qskf7WKrwUAAGfiiisAACMIVwAARhCuAACMIFwBABhBuAIAMIJwBQBgBOEKAMAIwhUAgBGEKwAAIwhXAABGEK4AAIwgXAEAGEG4AgAwgnAFAGAE4QoAwAjCFQCAETaWHgCs1lPXXbT0BADYE664AgAwgnAFAGAE4QoAwAjCFQCAEYQrAAAjCFcAAEYQrgAAjCBcAQAYQbgCADCCcAUAYAThCgDACMIVAIARhCsAACMIVwAARhCuAACMIFwBABhBuAIAMIJwBQBgBOEKAMAIwhUAgBGEKwAAIwhXAABGEK4AAIwgXAEAGEG4AgAwgnAFAGAE4QoAwAjCFQCAEYQrAAAjCFcAAEYQrgAAjCBcAQAYQbgCADCCcAUAYAThCgDACMIVAIARhCsAACMIVwAARhCuAACMIFwBABhBuAIAMIJwBQBghI2lBwD710Pv/59LT4C1947XvXHpCbAyrrgCADCCcAUAYAThCgDACMIVAIARhCsAACMIVwAARhCuAACMIFwBABhBuAIAMIJwBQBgBOEKAMAIwhUAgBGEKwAAIwhXAABGEK4AAIwgXAEAGEG4AgAwgnAFAGCEXYVrVb2qqu6uqi9X1aNV9YOrGgYAACfa2OXn/3aSv+jun6qqlye5eAWbAADgNDsO16r67iQ/nOR9SdLdzyd5fjWzAADgZLt5qcBVSY4l+YOq+nxVfaSqXnHqk6rq1qo6XFWHjz3zwi4OBwDAfrabcN1I8uYkv9fdb0ryT0luO/VJ3X2ouze7e/PSSw7s4nAAAOxnuwnXo0mOdvfntm/fna2QBQCAldtxuHb3N5M8XlVXb991Q5JHVrIKAABOsdt3Ffi5JHduv6PA15L8t91PAgCA0+0qXLv7wSSbq5kCAABn5ydnAQAwgnAFAGAE4QoAwAjCFQCAEYQrAAAjCFcAAEYQrgAAjCBcAQAYQbgCADCCcAUAYAThCgDACMIVAIARhCsAACMIVwAARhCuAACMIFwBABhhY+kBwP51w3tuWXrC2tq478jSEwBWzhVXAABGEK4AAIwgXAEAGEG4AgAwgnAFAGAE4QoAwAjCFQCAEYQrAAAjCFcAAEYQrgAAjCBcAQAYQbgCADCCcAUAYAThCgDACMIVAIARhCsAACMIVwAARhCuAACMIFwBABhBuAIAMIJwBQBgBOEKAMAIwhUAgBGEKwAAIwhXAABGEK4AAIwgXAEAGEG4AgAwgnAFAGAE4QoAwAjCFQCAEYQrAAAjCFcAAEYQrgAAjCBcAQAYQbgCADCCcAUAYAThCgDACMIVAIARhCsAACMIVwAARhCuAACMsLH0AABW7/j11y494UXZuO/I0hOAAVxxBQBgBOEKAMAIwhUAgBGEKwAAIwhXAABGEK4AAIwgXAEAGEG4AgAwgnAFAGAE4QoAwAjCFQCAEYQrAAAjCFcAAEYQrgAAjCBcAQAYQbgCADCCcAUAYAThCgDACLsK16r6xap6uKoeqqq7quo7VjUMAABOtONwrarLk/x8ks3ufkOSA0nevaphAABwot2+VGAjyXdW1UaSi5N8Y/eTAADgdDsO1+5+IsmvJ3ksyZNJ/r67P3Xq86rq1qo6XFWHjz3zws6XAgCwr+3mpQKvTnJTkquSvC7JK6rqPac+r7sPdfdmd29eesmBnS8FAGBf281LBd6e5O+6+1h3fzvJJ5L80GpmAQDAyXYTro8leWtVXVxVleSGJI+uZhYAAJxsN69x/VySu5M8kORL21/r0Ip2AQDASTZ288nd/atJfnVFWwAA4Kz85CwAAEYQrgAAjCBcAQAYQbgCADCCcAUAYAThCgDACMIVAIARhCsAACMIVwAARhCuAACMIFwBABhBuAIAMIJwBQBgBOEKAMAIwhUAgBGEKwAAI2wsPQDYv5667qKlJ7wol93/3NIT1tbx669desJ527jvyNITYN9yxRUAgBGEKwAAIwhXAABGEK4AAIwgXAEAGEG4AgAwgnAFAGAE4QoAwAjCFQCAEYQrAAAjCFcAAEYQrgAAjCBcAQAYQbgCADCCcAUAYAThCgDACMIVAIARhCsAACMIVwAARhCuAACMIFwBABhBuAIAMIJwBQBgBOEKAMAIwhUAgBGEKwAAIwhXAABGEK4AAIwgXAEAGEG4AgAwgnAFAGAE4QoAwAjCFQCAEYQrAAAjCFcAAEYQrgAAjCBcAQAYQbgCADCCcAUAYAThCgDACMIVAIARhCsAACNsLD0AWK3L7n9u6Qnn7anrLlp6Arxox6+/dukJL8rGfUeWngAr44orAAAjCFcAAEYQrgAAjCBcAQAYQbgCADCCcAUAYAThCgDACMIVAIARhCsAACMIVwAARhCuAACMIFwBABhBuAIAMIJwBQBgBOEKAMAIwhUAgBGEKwAAIwhXAABGOGe4VtXtVfV0VT10wn2vqap7q+or27++em9nAgCw353PFdc7ktx4yn23Jfl0d78+yae3bwMAwJ45Z7h292eSPHvK3Tcl+dj2xx9L8pOrnQUAACfb6WtcL+vuJ7c//maSy872xKq6taoOV9XhY8+8sMPDAQCw3+36L2d1dyfpf+fxQ9292d2bl15yYLeHAwBgn9ppuD5VVd+XJNu/Pr26SQAAcLqdhusnk7x3++P3JvmT1cwBAIAzO5+3w7oryWeTXF1VR6vqliQfTvIjVfWVJG/fvg0AAHtm41xP6O6bz/LQDSveAgAAZ+UnZwEAMIJwBQBgBOEKAMAIwhUAgBGEKwAAIwhXAABGEK4AAIwgXAEAGEG4AgAwgnAFAGAE4QoAwAjCFQCAEYQrAAAjCFcAAEYQrgAAjCBcAQAYYWPpAew/x6+/dukJAPvGpO+5G/cdWXoCL3GuuAIAMIJwBQBgBOEKAMAIwhUAgBGEKwAAIwhXAABGEK4AAIwgXAEAGEG4AgAwgnAFAGAE4QoAwAjCFQCAEYQrAAAjCFcAAEYQrgAAjCBcAQAYQbgCADCCcAUAYAThCgDACMIVAIARhCsAACMIVwAARhCuAACMIFwBABhBuAIAMIJwBQBgBOEKAMAIwhUAgBGEKwAAIwhXAABGEK4AAIwgXAEAGEG4AgAwgnAFAGAE4QoAwAjCFQCAEYQrAAAjCFcAAEYQrgAAjCBcAQAYQbgCADCCcAUAYISNpQcATPHUdRctPeG8XXb/c0tPAFg5V1wBABhBuAIAMIJwBQBgBOEKAMAIwhUAgBGEKwAAIwhXAABGEK4AAIwgXAEAGEG4AgAwgnAFAGAE4QoAwAjCFQCAEYQrAAAjCFcAAEYQrgAAjCBcAQAYQbgCADDCOcO1qm6vqqer6qET7vu1qvpyVX2xqv64ql61pysBANj3zueK6x1JbjzlvnuTvKG7fyDJ3yb50Ip3AQDASc4Zrt39mSTPnnLfp7r7+PbNv05ycA+2AQDAv1nFa1x/Jsmfn+3Bqrq1qg5X1eFjz7ywgsMBALAf7Spcq+qXkxxPcufZntPdh7p7s7s3L73kwG4OBwDAPrax00+sqvcleWeSG7q7V7YIAADOYEfhWlU3Jvlgkv/S3f+82kkAAHC683k7rLuSfDbJ1VV1tKpuSfI7SV6Z5N6qerCqfn+PdwIAsM+d84prd998hrs/ugdbAADgrPzkLAAARhCuAACMIFwBABhBuAIAMIJwBQBgBOEKAMAIwhUAgBGEKwAAIwhXAABGEK4AAIwgXAEAGEG4AgAwgnAFAGAE4QoAwAjCFQCAEYQrAAAjbCw9ANi/Lrv/uaUnADCIK64AAIwgXAEAGEG4AgAwgnAFAGAE4QoAwAjCFQCAEYQrAAAjCFcAAEYQrgAAjCBcAQAYQbgCADCCcAUAYAThCgDACMIVAIARhCsAACMIVwAARhCuAACMIFwBABhBuAIAMIJwBQBgBOEKAMAIwhUAgBGEKwAAIwhXAABGEK4AAIwgXAEAGEG4AgAwgnAFAGAE4QoAwAjCFQCAEYQrAAAjCFcAAEYQrgAAjCBcAQAYQbgCADCCcAUAYAThCgDACMIVAIARhCsAACMIVwAARhCuAACMIFwBABhhY+kBL1X3fOPBpSessQeXHgAADOSKKwAAIwhXAABGEK4AAIwgXAEAGEG4AgAwgnAFAGAE4QoAwAjCFQCAEYQrAAAjCFcAAEYQrgAAjCBcAQAYQbgCADCCcAUAYAThCgDACMIVAIARhCsAACMIVwAARjhnuFbV7VX1dFU9dIbHPlBVXVWv3Zt5AACw5XyuuN6R5MZT76yqK5L8aJLHVrwJAABOc85w7e7PJHn2DA/9ZpIPJulVjwIAgFPt6DWuVXVTkie6+wvn8dxbq+pwVR0+9swLOzkcAAC8+HCtqouT/FKSXzmf53f3oe7e7O7NSy858GIPBwAASXZ2xfX7k1yV5AtV9fUkB5M8UFXfu8phAABwoo0X+wnd/aUk3/Ovt7fjdbO7v7XCXQAAcJLzeTusu5J8NsnVVXW0qm7Z+1kAAHCyc15x7e6bz/H4lStbAwAAZ+EnZwEAMIJwBQBgBOEKAMAIwhUAgBGEKwAAIwhXAABGEK4AAIwgXAEAGEG4AgAwgnAFAGAE4QoAwAjCFQCAEYQrAAAjCFcAAEYQrgAAjCBcAQAYobr7wh2s6liS/7sHX/q1Sb61B18X53YvObd7x7ndO87t3nFu945zu3f24tz+x+6+9EwPXNBw3StVdbi7N5fesY6c273j3O4d53bvOLd7x7ndO87t3rnQ59ZLBQAAGEG4AgAwwrqE66GlB6wx53bvOLd7x7ndO87t3nFu945zu3cu6Lldi9e4AgCw/tbliisAAGtOuAIAMMLocK2qG6vqb6rqq1V129J71kVVXVFVf1lVj1TVw1X1/qU3rZuqOlBVn6+qP116yzqpqldV1d1V9eWqerSqfnDpTeuiqn5x+/vBQ1V1V1V9x9Kbpqqq26vq6ap66IT7XlNV91bVV7Z/ffWSG6c6y7n9te3vCV+sqj+uqlctOHGsM53bEx77QFV1Vb12r3eMDdeqOpDkd5P8WJJrktxcVdcsu2ptHE/yge6+Jslbk/x353bl3p/k0aVHrKHfTvIX3f2fkvznOMcrUVWXJ/n5JJvd/YYkB5K8e9lVo92R5MZT7rstyae7+/VJPr19mxfvjpx+bu9N8obu/oEkf5vkQxd61Jq4I6ef21TVFUl+NMljF2LE2HBN8pYkX+3ur3X380k+nuSmhTethe5+srsf2P74H7P1m//ly65aH1V1MMlPJPnI0lvWSVV9d5IfTvLRJOnu57v7/y06ar1sJPnOqtpIcnGSbyy8Z6zu/kySZ0+5+6YkH9v++GNJfvJCbloXZzq33f2p7j6+ffOvkxy84MPWwFn+vU2S30zywSQX5G/7Tw7Xy5M8fsLtoxFXK1dVVyZ5U5LPLTxlnfxWtv4j/5eFd6ybq5IcS/IH2y/D+EhVvWLpUeugu59I8uvZuqLyZJK/7+5PLbtq7VzW3U9uf/zNJJctOWaN/UySP196xLqoqpuSPNHdX7hQx5wcruyxqvquJH+U5Be6+x+W3rMOquqdSZ7u7iNLb1lDG0nenOT3uvtNSf4p/nfrSmy/3vKmbP3h4HVJXlFV71l21frqrfep9F6VK1ZVv5ytl8LdufSWdVBVFyf5pSS/ciGPOzlcn0hyxQm3D27fxwpU1cuyFa13dvcnlt6zRt6W5F1V9fVsvbzl+qr6w2UnrY2jSY5297/+34G7sxWy7N7bk/xddx/r7m8n+USSH1p407p5qqq+L0m2f3164T1rparel+SdSf5rewP7Vfn+bP1h9gvbv6cdTPJAVX3vXh50crjen+T1VXVVVb08W39R4JMLb1oLVVXZep3go939G0vvWSfd/aHuPtjdV2br39n7utuVqxXo7m8mebyqrt6+64Ykjyw4aZ08luStVXXx9veHG+Ivvq3aJ5O8d/vj9yb5kwW3rJWqujFbL896V3f/89J71kV3f6m7v6e7r9z+Pe1okjdvfy/eM2PDdfuF1j+b5J5sfQP9X9398LKr1sbbkvx0tq4GPrj9z48vPQrOw88lubOqvpjkjUn+x7Jz1sP2Vey7kzyQ5EvZ+r3Dj9Dcoaq6K8lnk1xdVUer6pYkH07yI1X1lWxd4f7wkhunOsu5/Z0kr0xy7/bvZ7+/6MihznJuL/wOV8wBAJhg7BVXAAD2F+EKAMAIwhUAgBGEKwAAIwhXAABGEK4AAIwgXAEAGOH/A0Klbbc+kh1DAAAAAElFTkSuQmCC\n",
12 | "text/plain": [
13 | ""
14 | ]
15 | },
16 | "metadata": {},
17 | "output_type": "display_data"
18 | },
19 | {
20 | "data": {
21 | "image/png": "iVBORw0KGgoAAAANSUhEUgAAAq4AAAKrCAYAAAAwMg+1AAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjUuMiwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy8qNh9FAAAACXBIWXMAAAsTAAALEwEAmpwYAAAZGklEQVR4nO3dbaimh13n8d9/57TR1GLbNEabCZsgJUsobtuclGrBhaTaqKXxhS8attKugbxZtUqhpAr6bikoPoCuMrQxBUPKEisWUdPQKGWhdjOTpm0eqi21m0yaJtOEVVFIOvG/L85R5tGZnHOfufK/z+cDYc79cM714yI5850r99ynujsAAPBS9x+WHgAAAOdDuAIAMIJwBQBgBOEKAMAIwhUAgBE2LuTBXvuaA33lFS+7kIcEAGCQrz/+7Xzr2RfqTI9d0HC98oqX5f/cc8WFPCQAAIO85R2Pn/UxLxUAAGAE4QoAwAjCFQCAEYQrAAAjCFcAAEYQrgAAjCBcAQAYQbgCADCCcAUAYAThCgDACMIVAIARhCsAACMIVwAARhCuAACMIFwBABhBuAIAMIJwBQBghF2Fa1XdWFV/U1VfrarbVjUKAABOteNwraoDSX43yY8luSbJzVV1zaqGAQDAiXZzxfUtSb7a3V/r7ueTfDzJTauZBQAAJ9tNuF6e5PETbh/dvu8kVXVrVR2uqsPHnnlhF4cDAGA/2/O/nNXdh7p7s7s3L73kwF4fDgCANbWbcH0iyRUn3D64fR8AAKzcbsL1/iSvr6qrqurlSd6d5JOrmQUAACfb2OkndvfxqvrZJPckOZDk9u5+eGXLAADgBDsO1yTp7j9L8mcr2gIAAGflJ2cBADCCcAUAYAThCgDACMIVAIARhCsAACMIVwAARhCuAACMIFwBABhBuAIAMIJwBQBgBOEKAMAIwhUAgBGEKwAAIwhXAABGEK4AAIywsfSAl6p3vO6NS0+AHTl+/bVLT4C1tnHfkaUnwIt2zzceXHrCSrjiCgDACMIVAIARhCsAACMIVwAARhCuAACMIFwBABhBuAIAMIJwBQBgBOEKAMAIwhUAgBGEKwAAIwhXAABGEK4AAIwgXAEAGEG4AgAwgnAFAGAE4QoAwAjCFQCAEYQrAAAjCFcAAEYQrgAAjCBcAQAYQbgCADCCcAUAYAThCgDACMIVAIARhCsAACMIVwAARhCuAACMIFwBABhBuAIAMIJwBQBgBOEKAMAIwhUAgBGEKwAAIwhXAABGEK4AAIwgXAEAGEG4AgAwgnAFAGAE4QoAwAjCFQCAEYQrAAAjbCw9AF7qjl9/7dITeIl46rqLlp5w3i67/7mlJ6ytad8TNu47svQEWBlXXAEAGEG4AgAwgnAFAGAE4QoAwAjCFQCAEYQrAAAjCFcAAEYQrgAAjCBcAQAYQbgCADCCcAUAYAThCgDACMIVAIARhCsAACMIVwAARhCuAACMIFwBABhBuAIAMMKOw7Wqrqiqv6yqR6rq4ap6/yqHAQDAiTZ28bnHk3ygux+oqlcmOVJV93b3IyvaBgAA/2bHV1y7+8nufmD7439M8miSy1c1DAAATrSS17hW1ZVJ3pTkc2d47NaqOlxVh48988IqDgcAwD6063Ctqu9K8kdJfqG7/+HUx7v7UHdvdvfmpZcc2O3hAADYp3YVrlX1smxF653d/YnVTAIAgNPt5l0FKslHkzza3b+xukkAAHC63VxxfVuSn05yfVU9uP3Pj69oFwAAnGTHb4fV3f87Sa1wCwAAnJWfnAUAwAjCFQCAEYQrAAAjCFcAAEYQrgAAjCBcAQAYQbgCADCCcAUAYAThCgDACMIVAIARhCsAACMIVwAARhCuAACMIFwBABhBuAIAMIJwBQBgBOEKAMAIwhUAgBGEKwAAIwhXAABGEK4AAIwgXAEAGEG4AgAwgnAFAGAE4QoAwAjCFQCAEYQrAAAjCFcAAEYQrgAAjCBcAQAYQbgCADCCcAUAYAThCgDACMIVAIARhCsAACMIVwAARhCuAACMIFwBABhBuAIAMIJwBQBgBOEKAMAIwhUAgBGEKwAAIwhXAABGEK4AAIwgXAEAGEG4AgAwgnAFAGAE4QoAwAjCFQCAEYQrAAAjCFcAAEYQrgAAjCBcAQAYQbgCADCCcAUAYAThCgDACMIVAIARhCsAACMIVwAARhCuAACMIFwBABhBuAIAMIJwBQBgBOEKAMAIwhUAgBGEKwAAIwhXAABGEK4AAIwgXAEAGEG4AgAwgnAFAGAE4QoAwAjCFQCAEYQrAAAjCFcAAEYQrgAAjCBcAQAYYdfhWlUHqurzVfWnqxgEAABnsoorru9P8ugKvg4AAJzVrsK1qg4m+YkkH1nNHAAAOLPdXnH9rSQfTPIvZ3tCVd1aVYer6vCxZ17Y5eEAANivdhyuVfXOJE9395F/73ndfai7N7t789JLDuz0cAAA7HO7ueL6tiTvqqqvJ/l4kuur6g9XsgoAAE6x43Dt7g9198HuvjLJu5Pc193vWdkyAAA4gfdxBQBghI1VfJHu/qskf7WKrwUAAGfiiisAACMIVwAARhCuAACMIFwBABhBuAIAMIJwBQBgBOEKAMAIwhUAgBGEKwAAIwhXAABGEK4AAIwgXAEAGEG4AgAwgnAFAGAE4QoAwAjCFQCAETaWHgCs1lPXXbT0BADYE664AgAwgnAFAGAE4QoAwAjCFQCAEYQrAAAjCFcAAEYQrgAAjCBcAQAYQbgCADCCcAUAYAThCgDACMIVAIARhCsAACMIVwAARhCuAACMIFwBABhBuAIAMIJwBQBgBOEKAMAIwhUAgBGEKwAAIwhXAABGEK4AAIwgXAEAGEG4AgAwgnAFAGAE4QoAwAjCFQCAEYQrAAAjCFcAAEYQrgAAjCBcAQAYQbgCADCCcAUAYAThCgDACMIVAIARhCsAACMIVwAARhCuAACMIFwBABhBuAIAMIJwBQBghI2lBwD710Pv/59LT4C1947XvXHpCbAyrrgCADCCcAUAYAThCgDACMIVAIARhCsAACMIVwAARhCuAACMIFwBABhBuAIAMIJwBQBgBOEKAMAIwhUAgBGEKwAAIwhXAABGEK4AAIwgXAEAGEG4AgAwgnAFAGCEXYVrVb2qqu6uqi9X1aNV9YOrGgYAACfa2OXn/3aSv+jun6qqlye5eAWbAADgNDsO16r67iQ/nOR9SdLdzyd5fjWzAADgZLt5qcBVSY4l+YOq+nxVfaSqXnHqk6rq1qo6XFWHjz3zwi4OBwDAfrabcN1I8uYkv9fdb0ryT0luO/VJ3X2ouze7e/PSSw7s4nAAAOxnuwnXo0mOdvfntm/fna2QBQCAldtxuHb3N5M8XlVXb991Q5JHVrIKAABOsdt3Ffi5JHduv6PA15L8t91PAgCA0+0qXLv7wSSbq5kCAABn5ydnAQAwgnAFAGAE4QoAwAjCFQCAEYQrAAAjCFcAAEYQrgAAjCBcAQAYQbgCADCCcAUAYAThCgDACMIVAIARhCsAACMIVwAARhCuAACMIFwBABhhY+kBwP51w3tuWXrC2tq478jSEwBWzhVXAABGEK4AAIwgXAEAGEG4AgAwgnAFAGAE4QoAwAjCFQCAEYQrAAAjCFcAAEYQrgAAjCBcAQAYQbgCADCCcAUAYAThCgDACMIVAIARhCsAACMIVwAARhCuAACMIFwBABhBuAIAMIJwBQBgBOEKAMAIwhUAgBGEKwAAIwhXAABGEK4AAIwgXAEAGEG4AgAwgnAFAGAE4QoAwAjCFQCAEYQrAAAjCFcAAEYQrgAAjCBcAQAYQbgCADCCcAUAYAThCgDACMIVAIARhCsAACMIVwAARhCuAACMsLH0AABW7/j11y494UXZuO/I0hOAAVxxBQBgBOEKAMAIwhUAgBGEKwAAIwhXAABGEK4AAIwgXAEAGEG4AgAwgnAFAGAE4QoAwAjCFQCAEYQrAAAjCFcAAEYQrgAAjCBcAQAYQbgCADCCcAUAYAThCgDACLsK16r6xap6uKoeqqq7quo7VjUMAABOtONwrarLk/x8ks3ufkOSA0nevaphAABwot2+VGAjyXdW1UaSi5N8Y/eTAADgdDsO1+5+IsmvJ3ksyZNJ/r67P3Xq86rq1qo6XFWHjz3zws6XAgCwr+3mpQKvTnJTkquSvC7JK6rqPac+r7sPdfdmd29eesmBnS8FAGBf281LBd6e5O+6+1h3fzvJJ5L80GpmAQDAyXYTro8leWtVXVxVleSGJI+uZhYAAJxsN69x/VySu5M8kORL21/r0Ip2AQDASTZ288nd/atJfnVFWwAA4Kz85CwAAEYQrgAAjCBcAQAYQbgCADCCcAUAYAThCgDACMIVAIARhCsAACMIVwAARhCuAACMIFwBABhBuAIAMIJwBQBgBOEKAMAIwhUAgBGEKwAAI2wsPQDYv5667qKlJ7wol93/3NIT1tbx669desJ527jvyNITYN9yxRUAgBGEKwAAIwhXAABGEK4AAIwgXAEAGEG4AgAwgnAFAGAE4QoAwAjCFQCAEYQrAAAjCFcAAEYQrgAAjCBcAQAYQbgCADCCcAUAYAThCgDACMIVAIARhCsAACMIVwAARhCuAACMIFwBABhBuAIAMIJwBQBgBOEKAMAIwhUAgBGEKwAAIwhXAABGEK4AAIwgXAEAGEG4AgAwgnAFAGAE4QoAwAjCFQCAEYQrAAAjCFcAAEYQrgAAjCBcAQAYQbgCADCCcAUAYAThCgDACMIVAIARhCsAACNsLD0AWK3L7n9u6Qnn7anrLlp6Arxox6+/dukJL8rGfUeWngAr44orAAAjCFcAAEYQrgAAjCBcAQAYQbgCADCCcAUAYAThCgDACMIVAIARhCsAACMIVwAARhCuAACMIFwBABhBuAIAMIJwBQBgBOEKAMAIwhUAgBGEKwAAIwhXAABGOGe4VtXtVfV0VT10wn2vqap7q+or27++em9nAgCw353PFdc7ktx4yn23Jfl0d78+yae3bwMAwJ45Z7h292eSPHvK3Tcl+dj2xx9L8pOrnQUAACfb6WtcL+vuJ7c//maSy872xKq6taoOV9XhY8+8sMPDAQCw3+36L2d1dyfpf+fxQ9292d2bl15yYLeHAwBgn9ppuD5VVd+XJNu/Pr26SQAAcLqdhusnk7x3++P3JvmT1cwBAIAzO5+3w7oryWeTXF1VR6vqliQfTvIjVfWVJG/fvg0AAHtm41xP6O6bz/LQDSveAgAAZ+UnZwEAMIJwBQBgBOEKAMAIwhUAgBGEKwAAIwhXAABGEK4AAIwgXAEAGEG4AgAwgnAFAGAE4QoAwAjCFQCAEYQrAAAjCFcAAEYQrgAAjCBcAQAYYWPpAew/x6+/dukJAPvGpO+5G/cdWXoCL3GuuAIAMIJwBQBgBOEKAMAIwhUAgBGEKwAAIwhXAABGEK4AAIwgXAEAGEG4AgAwgnAFAGAE4QoAwAjCFQCAEYQrAAAjCFcAAEYQrgAAjCBcAQAYQbgCADCCcAUAYAThCgDACMIVAIARhCsAACMIVwAARhCuAACMIFwBABhBuAIAMIJwBQBgBOEKAMAIwhUAgBGEKwAAIwhXAABGEK4AAIwgXAEAGEG4AgAwgnAFAGAE4QoAwAjCFQCAEYQrAAAjCFcAAEYQrgAAjCBcAQAYQbgCADCCcAUAYISNpQcATPHUdRctPeG8XXb/c0tPAFg5V1wBABhBuAIAMIJwBQBgBOEKAMAIwhUAgBGEKwAAIwhXAABGEK4AAIwgXAEAGEG4AgAwgnAFAGAE4QoAwAjCFQCAEYQrAAAjCFcAAEYQrgAAjCBcAQAYQbgCADDCOcO1qm6vqqer6qET7vu1qvpyVX2xqv64ql61pysBANj3zueK6x1JbjzlvnuTvKG7fyDJ3yb50Ip3AQDASc4Zrt39mSTPnnLfp7r7+PbNv05ycA+2AQDAv1nFa1x/Jsmfn+3Bqrq1qg5X1eFjz7ywgsMBALAf7Spcq+qXkxxPcufZntPdh7p7s7s3L73kwG4OBwDAPrax00+sqvcleWeSG7q7V7YIAADOYEfhWlU3Jvlgkv/S3f+82kkAAHC683k7rLuSfDbJ1VV1tKpuSfI7SV6Z5N6qerCqfn+PdwIAsM+d84prd998hrs/ugdbAADgrPzkLAAARhCuAACMIFwBABhBuAIAMIJwBQBgBOEKAMAIwhUAgBGEKwAAIwhXAABGEK4AAIwgXAEAGEG4AgAwgnAFAGAE4QoAwAjCFQCAEYQrAAAjbCw9ANi/Lrv/uaUnADCIK64AAIwgXAEAGEG4AgAwgnAFAGAE4QoAwAjCFQCAEYQrAAAjCFcAAEYQrgAAjCBcAQAYQbgCADCCcAUAYAThCgDACMIVAIARhCsAACMIVwAARhCuAACMIFwBABhBuAIAMIJwBQBgBOEKAMAIwhUAgBGEKwAAIwhXAABGEK4AAIwgXAEAGEG4AgAwgnAFAGAE4QoAwAjCFQCAEYQrAAAjCFcAAEYQrgAAjCBcAQAYQbgCADCCcAUAYAThCgDACMIVAIARhCsAACMIVwAARhCuAACMIFwBABhhY+kBL1X3fOPBpSessQeXHgAADOSKKwAAIwhXAABGEK4AAIwgXAEAGEG4AgAwgnAFAGAE4QoAwAjCFQCAEYQrAAAjCFcAAEYQrgAAjCBcAQAYQbgCADCCcAUAYAThCgDACMIVAIARhCsAACMIVwAARjhnuFbV7VX1dFU9dIbHPlBVXVWv3Zt5AACw5XyuuN6R5MZT76yqK5L8aJLHVrwJAABOc85w7e7PJHn2DA/9ZpIPJulVjwIAgFPt6DWuVXVTkie6+wvn8dxbq+pwVR0+9swLOzkcAAC8+HCtqouT/FKSXzmf53f3oe7e7O7NSy858GIPBwAASXZ2xfX7k1yV5AtV9fUkB5M8UFXfu8phAABwoo0X+wnd/aUk3/Ovt7fjdbO7v7XCXQAAcJLzeTusu5J8NsnVVXW0qm7Z+1kAAHCyc15x7e6bz/H4lStbAwAAZ+EnZwEAMIJwBQBgBOEKAMAIwhUAgBGEKwAAIwhXAABGEK4AAIwgXAEAGEG4AgAwgnAFAGAE4QoAwAjCFQCAEYQrAAAjCFcAAEYQrgAAjCBcAQAYobr7wh2s6liS/7sHX/q1Sb61B18X53YvObd7x7ndO87t3nFu945zu3f24tz+x+6+9EwPXNBw3StVdbi7N5fesY6c273j3O4d53bvOLd7x7ndO87t3rnQ59ZLBQAAGEG4AgAwwrqE66GlB6wx53bvOLd7x7ndO87t3nFu945zu3cu6Lldi9e4AgCw/tbliisAAGtOuAIAMMLocK2qG6vqb6rqq1V129J71kVVXVFVf1lVj1TVw1X1/qU3rZuqOlBVn6+qP116yzqpqldV1d1V9eWqerSqfnDpTeuiqn5x+/vBQ1V1V1V9x9Kbpqqq26vq6ap66IT7XlNV91bVV7Z/ffWSG6c6y7n9te3vCV+sqj+uqlctOHGsM53bEx77QFV1Vb12r3eMDdeqOpDkd5P8WJJrktxcVdcsu2ptHE/yge6+Jslbk/x353bl3p/k0aVHrKHfTvIX3f2fkvznOMcrUVWXJ/n5JJvd/YYkB5K8e9lVo92R5MZT7rstyae7+/VJPr19mxfvjpx+bu9N8obu/oEkf5vkQxd61Jq4I6ef21TVFUl+NMljF2LE2HBN8pYkX+3ur3X380k+nuSmhTethe5+srsf2P74H7P1m//ly65aH1V1MMlPJPnI0lvWSVV9d5IfTvLRJOnu57v7/y06ar1sJPnOqtpIcnGSbyy8Z6zu/kySZ0+5+6YkH9v++GNJfvJCbloXZzq33f2p7j6+ffOvkxy84MPWwFn+vU2S30zywSQX5G/7Tw7Xy5M8fsLtoxFXK1dVVyZ5U5LPLTxlnfxWtv4j/5eFd6ybq5IcS/IH2y/D+EhVvWLpUeugu59I8uvZuqLyZJK/7+5PLbtq7VzW3U9uf/zNJJctOWaN/UySP196xLqoqpuSPNHdX7hQx5wcruyxqvquJH+U5Be6+x+W3rMOquqdSZ7u7iNLb1lDG0nenOT3uvtNSf4p/nfrSmy/3vKmbP3h4HVJXlFV71l21frqrfep9F6VK1ZVv5ytl8LdufSWdVBVFyf5pSS/ciGPOzlcn0hyxQm3D27fxwpU1cuyFa13dvcnlt6zRt6W5F1V9fVsvbzl+qr6w2UnrY2jSY5297/+34G7sxWy7N7bk/xddx/r7m8n+USSH1p407p5qqq+L0m2f3164T1rparel+SdSf5rewP7Vfn+bP1h9gvbv6cdTPJAVX3vXh50crjen+T1VXVVVb08W39R4JMLb1oLVVXZep3go939G0vvWSfd/aHuPtjdV2br39n7utuVqxXo7m8mebyqrt6+64Ykjyw4aZ08luStVXXx9veHG+Ivvq3aJ5O8d/vj9yb5kwW3rJWqujFbL896V3f/89J71kV3f6m7v6e7r9z+Pe1okjdvfy/eM2PDdfuF1j+b5J5sfQP9X9398LKr1sbbkvx0tq4GPrj9z48vPQrOw88lubOqvpjkjUn+x7Jz1sP2Vey7kzyQ5EvZ+r3Dj9Dcoaq6K8lnk1xdVUer6pYkH07yI1X1lWxd4f7wkhunOsu5/Z0kr0xy7/bvZ7+/6MihznJuL/wOV8wBAJhg7BVXAAD2F+EKAMAIwhUAgBGEKwAAIwhXAABGEK4AAIwgXAEAGOH/A0Klbbc+kh1DAAAAAElFTkSuQmCC\n",
22 | "text/plain": [
23 | ""
24 | ]
25 | },
26 | "metadata": {
27 | "needs_background": "light"
28 | },
29 | "output_type": "display_data"
30 | }
31 | ],
32 | "source": [
33 | "import heapq\n",
34 | "import math\n",
35 | "import matplotlib.pyplot as plt\n",
36 | "import numpy as np\n",
37 | "import math\n",
38 | "import matplotlib\n",
39 | "%matplotlib inline\n",
40 | "#set up matplotlib\n",
41 | "is_ipython = 'inline' in matplotlib.get_backend()\n",
42 | "if is_ipython:\n",
43 | " from IPython import display\n",
44 | "plt.ion()\n",
45 | "plt.figure(figsize=(12, 12))\n",
46 | "\n",
47 | "\"\"\"\n",
48 | "\n",
49 | "\"\"\"\n",
50 | "\n",
51 | "class GridMap:\n",
52 | " def __init__(self, ox, oy, resolution):\n",
53 | " self.min_x = None\n",
54 | " self.min_y = None\n",
55 | " self.max_x = None\n",
56 | " self.max_y = None\n",
57 | " self.x_width = None\n",
58 | " self.y_width = None\n",
59 | " self.obstacle_map = None\n",
60 | " \n",
61 | " self.resolution = resolution\n",
62 | " self.calc_obstacle_map(ox, oy)\n",
63 | " \n",
64 | " def calc_obstacle_map(self, ox, oy):\n",
65 | "\n",
66 | " self.min_x = round(min(ox))\n",
67 | " self.min_y = round(min(oy))\n",
68 | " self.max_x = round(max(ox))\n",
69 | " self.max_y = round(max(oy))\n",
70 | " print(\"min_x:\", self.min_x)\n",
71 | " print(\"min_y:\", self.min_y)\n",
72 | " print(\"max_x:\", self.max_x)\n",
73 | " print(\"max_y:\", self.max_y)\n",
74 | "\n",
75 | " self.x_width = round((self.max_x - self.min_x) / self.resolution)+1\n",
76 | " self.y_width = round((self.max_y - self.min_y) / self.resolution)+1\n",
77 | " print(\"x_width:\", self.x_width)\n",
78 | " print(\"y_width:\", self.y_width)\n",
79 | "\n",
80 | " # obstacle map generation\n",
81 | " self.obstacle_map = np.zeros((self.x_width, self.y_width))\n",
82 | " for x, y in zip(ox, oy):\n",
83 | " ix, iy = self.calc_xy_index(x, self.min_x), self.calc_xy_index(y, self.min_y)\n",
84 | " if 0<=ix= self.x_width or node.ix < 0 or node.iy >= self.y_width or node.iy < 0:\n",
100 | " return False\n",
101 | " if abs(self.obstacle_map[node.ix, node.iy] - 10.0) < 0.01:\n",
102 | " return False \n",
103 | " return True\n",
104 | "\n",
105 | "sx = -5.0 # [m]\n",
106 | "sy = -5.0 # [m]\n",
107 | "gx = 50.0 # [m]\n",
108 | "gy = 50.0 # [m]\n",
109 | "grid_size = 5.0 # [m]\n",
110 | "robot_radius = 1.0 # [m]\n",
111 | "\n",
112 | "# set obstacle positions\n",
113 | "ox, oy = [], []\n",
114 | "for i in range(-10, 60):\n",
115 | " ox.append(i)\n",
116 | " oy.append(-10.0)\n",
117 | "for i in range(-10, 60):\n",
118 | " ox.append(60.0)\n",
119 | " oy.append(i)\n",
120 | "for i in range(-10, 61):\n",
121 | " ox.append(i)\n",
122 | " oy.append(60.0)\n",
123 | "for i in range(-10, 61):\n",
124 | " ox.append(-10.0)\n",
125 | " oy.append(i)\n",
126 | "# for i in range(-10, 40):\n",
127 | "# ox.append(20.0)\n",
128 | "# oy.append(i)\n",
129 | "for i in range(20, 40):\n",
130 | " ox.append(20.0)\n",
131 | " oy.append(60.0 - i) \n",
132 | "grid_map = GridMap(ox, oy, grid_size)\n",
133 | "\n",
134 | "\n",
135 | "\n",
136 | "class Node:\n",
137 | " def __init__(self, ix, iy, C=0.0, P=None):\n",
138 | " self.ix = ix\n",
139 | " self.iy = iy\n",
140 | " self.C = C\n",
141 | " self.P = P\n",
142 | " \n",
143 | "action_set = {'UP':[0, 1], 'DOWN':[0, -1], 'LEFT':[-1, 0], 'RIGHT':[1, 0]}\n",
144 | "\n",
145 | "def get_neighbors(current, grid_map):\n",
146 | " for a in action_set:\n",
147 | " node = Node(current.ix+action_set[a][0], \n",
148 | " current.iy+action_set[a][1], current.C+1.0, \n",
149 | " grid_map.calc_unique_index(current))\n",
150 | " if grid_map.verify_node(node):\n",
151 | " yield node\n",
152 | " \n",
153 | "def get_heuristic(node, end_node):\n",
154 | " dx = node.ix - end_node.ix\n",
155 | " dy = node.iy - end_node.iy\n",
156 | " return np.sqrt(dx*dx+dy*dy)\n",
157 | " \n",
158 | "\n",
159 | " \n",
160 | "def BAStar(grid_map, start_node, end_node):\n",
161 | " Closed_set_I, Open_set_I = {}, {}\n",
162 | " Closed_set_G, Open_set_G = {}, {}\n",
163 | " Open_set_I[grid_map.calc_unique_index(start_node)] = start_node\n",
164 | " Open_set_G[grid_map.calc_unique_index(end_node)] = end_node\n",
165 | " Q_I, Q_G = [],[]\n",
166 | " heapq.heappush(Q_I, (start_node.C+get_heuristic(start_node, end_node), \n",
167 | " grid_map.calc_unique_index(start_node)))\n",
168 | " heapq.heappush(Q_G, (end_node.C+get_heuristic(end_node, start_node), \n",
169 | " grid_map.calc_unique_index(end_node))) \n",
170 | " while True:\n",
171 | " if not Open_set_I and not Open_set_G:\n",
172 | " print(\"Bidirectional A* Algorithm Finished.\")\n",
173 | " return [], [], -1\n",
174 | " \n",
175 | " if Open_set_I:\n",
176 | " C, c_id = heapq.heappop(Q_I) \n",
177 | " if c_id in Open_set_I:\n",
178 | " current = Open_set_I.pop(c_id)\n",
179 | " Closed_set_I[c_id] = current\n",
180 | " if c_id in Closed_set_G:\n",
181 | " return ShortestPathFinder(grid_map, Closed_set_I, Closed_set_G, c_id)\n",
182 | " else:\n",
183 | " continue\n",
184 | "\n",
185 | " for node in get_neighbors(current, grid_map):\n",
186 | " neighbor_index = grid_map.calc_unique_index(node)\n",
187 | " if neighbor_index in Closed_set_I or neighbor_index in Closed_set_G: continue\n",
188 | " if neighbor_index not in Open_set_I or Open_set_I[neighbor_index].C > node.C:\n",
189 | " Open_set_I[neighbor_index] = node\n",
190 | " heapq.heappush(Q_I, (node.C+get_heuristic(node, end_node), neighbor_index))\n",
191 | " grid_map.obstacle_map[node.ix, node.iy] = 2\n",
192 | " plt.clf()\n",
193 | " plt.imshow(grid_map.obstacle_map)\n",
194 | " if is_ipython:\n",
195 | " display.clear_output(wait=True)\n",
196 | " display.display(plt.gcf()) \n",
197 | " \n",
198 | " if Open_set_G:\n",
199 | " C, c_id = heapq.heappop(Q_G) \n",
200 | " if c_id in Open_set_G:\n",
201 | " current = Open_set_G.pop(c_id)\n",
202 | " Closed_set_G[c_id] = current\n",
203 | " if c_id in Closed_set_I:\n",
204 | " return ShortestPathFinder(grid_map, Closed_set_I, Closed_set_G, c_id)\n",
205 | " else:\n",
206 | " continue\n",
207 | "\n",
208 | " for node in get_neighbors(current, grid_map):\n",
209 | " neighbor_index = grid_map.calc_unique_index(node)\n",
210 | " if neighbor_index in Closed_set_I or neighbor_index in Closed_set_G: continue\n",
211 | " if neighbor_index not in Open_set_G or Open_set_G[neighbor_index].C > node.C:\n",
212 | " Open_set_G[neighbor_index] = node\n",
213 | " heapq.heappush(Q_G, (node.C+get_heuristic(node, end_node), neighbor_index))\n",
214 | " grid_map.obstacle_map[node.ix, node.iy] = 2\n",
215 | " plt.clf()\n",
216 | " plt.imshow(grid_map.obstacle_map)\n",
217 | " if is_ipython:\n",
218 | " display.clear_output(wait=True)\n",
219 | " display.display(plt.gcf()) \n",
220 | "import collections\n",
221 | "\n",
222 | "def ShortestPathFinder(grid_map, Closed_set_I, Closed_set_G, c_id):\n",
223 | " print(Closed_set_I, Closed_set_G)\n",
224 | " print(c_id)\n",
225 | " if grid_map.verify_node(end_node) == False:\n",
226 | " print(\"the goal is unreachable!!!please change a reachable goal...\")\n",
227 | " return [], [], -1\n",
228 | " \n",
229 | " SPath_x = collections.deque()\n",
230 | " SPath_y = collections.deque()\n",
231 | "\n",
232 | " SPath_x.append(Closed_set_I[c_id].ix)\n",
233 | " SPath_y.append(Closed_set_I[c_id].iy)\n",
234 | " \n",
235 | " u_I_id = Closed_set_I[c_id].P\n",
236 | " u_G_id = Closed_set_G[c_id].P \n",
237 | " \n",
238 | " \n",
239 | " SPath_dist = (Closed_set_I[c_id].C+Closed_set_G[c_id].C)*grid_map.resolution \n",
240 | " while u_I_id or u_G_id: \n",
241 | " if u_I_id:\n",
242 | " SPath_x.append(Closed_set_I[u_I_id].ix)\n",
243 | " SPath_y.append(Closed_set_I[u_I_id].iy)\n",
244 | " u_I_id = Closed_set_I[u_I_id].P\n",
245 | " if u_G_id:\n",
246 | " SPath_x.appendleft(Closed_set_G[u_G_id].ix)\n",
247 | " SPath_y.appendleft(Closed_set_G[u_G_id].iy) \n",
248 | " u_G_id = Closed_set_G[u_G_id].P\n",
249 | " return SPath_x, SPath_y, SPath_dist\n",
250 | "\n",
251 | "start_node = Node(2, 7)\n",
252 | "end_node = Node(12, 7)\n",
253 | "grid_map.obstacle_map[start_node.ix, start_node.iy] = 8\n",
254 | "grid_map.obstacle_map[end_node.ix, end_node.iy] = 3\n",
255 | "plt.imshow(grid_map.obstacle_map)\n",
256 | "\n",
257 | "path_x, path_y, path_dist = BAStar(grid_map, start_node, end_node)\n",
258 | "grid_map.obstacle_map[end_node.ix, end_node.iy] = 4\n",
259 | "for ix, iy in zip(path_x, path_y):\n",
260 | " grid_map.obstacle_map[ix, iy] = 4\n",
261 | " \n",
262 | "plt.clf()\n",
263 | "plt.imshow(grid_map.obstacle_map)\n",
264 | "if is_ipython:\n",
265 | " display.clear_output(wait=True)\n",
266 | " display.display(plt.gcf()) "
267 | ]
268 | },
269 | {
270 | "cell_type": "code",
271 | "execution_count": null,
272 | "id": "703df07c",
273 | "metadata": {},
274 | "outputs": [],
275 | "source": [
276 | "\n",
277 | "\n",
278 | "\n",
279 | "\n",
280 | "\n",
281 | "\n",
282 | "\n",
283 | "\n",
284 | "\n",
285 | "\n",
286 | "\n",
287 | "\n",
288 | "\n",
289 | "\n",
290 | "\n",
291 | "\n",
292 | "\n",
293 | "\n",
294 | "\n",
295 | "\n",
296 | "\n",
297 | "\n",
298 | "\n",
299 | "\n",
300 | "\n",
301 | "\n",
302 | "\n",
303 | "\n",
304 | "\n",
305 | "\n",
306 | "\n",
307 | "\n",
308 | "\n",
309 | "\n",
310 | "\n",
311 | "\n",
312 | "\n",
313 | "\n"
314 | ]
315 | }
316 | ],
317 | "metadata": {
318 | "kernelspec": {
319 | "display_name": "Python 3 (ipykernel)",
320 | "language": "python",
321 | "name": "python3"
322 | },
323 | "language_info": {
324 | "codemirror_mode": {
325 | "name": "ipython",
326 | "version": 3
327 | },
328 | "file_extension": ".py",
329 | "mimetype": "text/x-python",
330 | "name": "python",
331 | "nbconvert_exporter": "python",
332 | "pygments_lexer": "ipython3",
333 | "version": "3.9.5"
334 | }
335 | },
336 | "nbformat": 4,
337 | "nbformat_minor": 5
338 | }
339 |
--------------------------------------------------------------------------------
/.ipynb_checkpoints/二次规划-checkpoint.ipynb:
--------------------------------------------------------------------------------
1 | {
2 | "cells": [
3 | {
4 | "cell_type": "code",
5 | "execution_count": 1,
6 | "id": "bb73a0cc",
7 | "metadata": {},
8 | "outputs": [],
9 | "source": [
10 | "import numpy as np\n",
11 | "import math\n",
12 | "import matplotlib.pyplot as plt\n",
13 | "\n",
14 | "class Box2D:\n",
15 | " def __init__(self, x, y, yaw, corner_points=None, v=0.0):\n",
16 | " self.x0 = x\n",
17 | " self.y0 = y\n",
18 | " self.x = x\n",
19 | " self.y = y\n",
20 | " self.yaw = yaw\n",
21 | " self.corner_points = corner_points\n",
22 | " self.inflat_cpoints = []\n",
23 | " self.v = v\n",
24 | " def reset_xy(self):\n",
25 | " self.x = self.x0\n",
26 | " self.y = self.y0\n",
27 | " \n",
28 | " def update_once(self, dt):\n",
29 | " self.x += self.v*dt*math.cos(self.yaw)\n",
30 | " self.y += self.v*dt*math.sin(self.yaw)\n",
31 | " def inflation_obs(self, r):\n",
32 | " A = []\n",
33 | " for i in range(len(self.corner_points[0])-1):\n",
34 | " v1 = [self.corner_points[0, i], self.corner_points[1, i]]\n",
35 | " v2 = [self.corner_points[0, i+1], self.corner_points[1, i+1]]\n",
36 | " a = v2[0] - v1[0]\n",
37 | " b = v1[1] - v2[1]\n",
38 | " c = v1[1]*a+v1[0]*b\n",
39 | " inflat_c = -r*math.sqrt(a*a+b*b)+c\n",
40 | " A.append([a, b, inflat_c])\n",
41 | " pre_ind = -1\n",
42 | " for i in range(len(A)):\n",
43 | " a1, b1, c1 = A[pre_ind][1], A[pre_ind][0], A[pre_ind][2]\n",
44 | " a2, b2, c2 = A[i][1], A[i][0], A[i][2]\n",
45 | " x = (b2*c1-b1*c2)/(a1*b2-a2*b1)\n",
46 | " y = (a1*c2-a2*c1)/(a1*b2-a2*b1) \n",
47 | " self.inflat_cpoints.append([x, y])\n",
48 | " pre_ind = i\n",
49 | " self.inflat_cpoints.append(self.inflat_cpoints[0]) \n",
50 | " self.inflat_cpoints = np.array(self.inflat_cpoints).T\n",
51 | " \n",
52 | " \n",
53 | "car_corner_points = np.array([[2.0, -2.0, -2.0, 2.0, 2.0],\n",
54 | " [1.0, 1.0, -1.0, -1.0, 1.0]])\n",
55 | "road_bound_points = np.array([[100.0, -15.0, -15.0, 100.0, 100.0],\n",
56 | " [0.1, 0.1, -0.1, -0.1, 0.1]])\n",
57 | "\n",
58 | "\n",
59 | "road_bound_left = Box2D(0.0, 3.5, 0.0, corner_points=road_bound_points)\n",
60 | "road_bound_right = Box2D(0.0, -3.5, 0.0, corner_points=road_bound_points)\n",
61 | "\n",
62 | "car1 = Box2D(1.0, 1.7, 0.0, corner_points=car_corner_points, v=0.0)\n",
63 | "car2 = Box2D(20.0, -1.7, 0.0, corner_points=car_corner_points, v=0.0)\n",
64 | "car3 = Box2D(45.0, 1.7, 0.0, corner_points=car_corner_points, v=0.0)\n",
65 | "ego = Box2D(0.0, -1.7, 0.0, corner_points=car_corner_points, v=0.0)\n",
66 | "obs_buf = [car1, car2, car3]\n",
67 | "road_bound_left.inflation_obs(1.4)\n",
68 | "road_bound_right.inflation_obs(1.4)\n",
69 | "for obs in obs_buf:\n",
70 | " obs.inflation_obs(1.4)\n",
71 | " \n",
72 | "def local2global(x0, y0, yaw0, corner_points):\n",
73 | " R = np.array([[math.cos(yaw0), -math.sin(yaw0)],\n",
74 | " [math.sin(yaw0), math.cos(yaw0)]])\n",
75 | " corner_arr = np.array(corner_points)\n",
76 | " return np.dot(R, corner_arr)+np.array([[x0],[y0]])\n",
77 | "\n",
78 | "\n",
79 | "MAP_lines = []\n",
80 | "MAP_cars = []\n",
81 | "for obs in obs_buf:\n",
82 | " gcp0 = local2global(obs.x, obs.y, obs.yaw, obs.inflat_cpoints)\n",
83 | " for j in range(len(gcp0[0])-1):\n",
84 | " MAP_lines.append([gcp0[0][j], gcp0[1][j], gcp0[0][j+1], gcp0[1][j+1]]) \n",
85 | " \n",
86 | " gcp_car = local2global(obs.x, obs.y, obs.yaw, obs.corner_points)\n",
87 | " for j in range(len(gcp_car[0])-1):\n",
88 | " MAP_cars.append([gcp_car[0][j], gcp_car[1][j], gcp_car[0][j+1], gcp_car[1][j+1]]) "
89 | ]
90 | },
91 | {
92 | "cell_type": "code",
93 | "execution_count": 2,
94 | "id": "4129c0e8",
95 | "metadata": {},
96 | "outputs": [
97 | {
98 | "data": {
99 | "image/png": "iVBORw0KGgoAAAANSUhEUgAAA3IAAAEvCAYAAAAAWPPhAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjUuMiwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy8qNh9FAAAACXBIWXMAAAsTAAALEwEAmpwYAAAT6klEQVR4nO3dbYylZ33f8d8/XjupvKgkeDDgB5bWViKnitftyAXFFcujjOvGrUQTkzQlaaQNUZBAShWRINEUKS/SJqFtjGK5YJVWPKVJDFZqiE2CBXkBYda7BAOmGSwjvLj2QILtbdKgpf++mLPNZDSz9vrcu2evPZ+PNJr7ae/rsuaWz/nOOeee6u4AAAAwju9Y9AQAAAA4NUIOAABgMEIOAABgMEIOAABgMEIOAABgMEIOAABgMHsWPYGTueiii3rfvn2LngYAAMBCHDp06OvdvbJ9+1kdcvv27cva2tqipwEAALAQVfWVnbZ7ayUAAMBghBwAAMBghBwAAMBghBwAAMBghBwAAMBghBwAAMBghBwAAMBghBwAAMBghBwAAMBghBwAAMBghBwAAMBghBwAAMBghBwAAMBghBwAAMBghBwAAMBghBwAAMBghBwAAMBghBwAAMBg5g65qvreqjqy5euJqnrztmMOVNXjW45527zjAgAALKs9856gu7+UZH+SVNV5SY4muWOHQz/Z3TfOOx4AAMCym/qtla9I8uXu/srE5wUAAGBm6pC7Ocn7d9n3kqr6bFV9pKq+f+JxAQAAlsZkIVdVFyT5oST/fYfd9yV5YXdfneQ3knzoJOc5WFVrVbW2sbEx1fQAAADOGVO+IveaJPd196Pbd3T3E919bLZ8V5Lzq+qinU7S3bd192p3r66srEw4PQAAgHPDlCH3uuzytsqqel5V1Wz52tm435hwbAAAgKUx910rk6SqLkzyqiQ/vWXbG5Kku29N8tokP1NVx5P8ZZKbu7unGBsAAGDZTBJy3f2/kzxn27ZbtyzfkuSWKcYCAABYdlPftRIAAIDTTMgBAAAMRsgBAAAMRsgBAAAMRsgBAAAMRsgBAAAMRsgBAAAMRsgBAAAMRsgBAAAMRsgBAAAMRsgBAAAMRsgBAAAMRsgBAAAMRsgBAAAMRsgBAAAMRsgBAAAMRsgBAAAMRsgBAAAMRsgBAAAMRsgBAAAMRsgBAAAMRsgBAAAMRsgBAAAMRsgBAAAMRsgBAAAMRsgBAAAMRsgBAAAMRsgBAAAMZrKQq6qHqupzVXWkqtZ22F9V9Z+qar2q/qSq/v5UYwMAACyTPROf72Xd/fVd9r0myZWzr3+Y5Ddn3wEAADgFZ/KtlTcl+a+96VNJnl1Vzz+D4wMAAJwTpgy5TnJ3VR2qqoM77L8kyVe3rD882wYAAMApmPKtldd199Gqem6Se6rqge7+xKmeZBaBB5Pk8ssvn3B6AAAA54bJXpHr7qOz748luSPJtdsOOZrksi3rl862bT/Pbd292t2rKysrU00PAADgnDFJyFXVhVX1rBPLSV6d5P5th92Z5F/O7l754iSPd/cjU4wPAACwTKZ6a+XFSe6oqhPnfF93f7Sq3pAk3X1rkruS3JBkPclfJPnJicYGAABYKpOEXHc/mOTqHbbfumW5k/zsFOMBAAAsszP55wcAAACYgJADAAAYjJADAAAYjJADAAAYjJADAAAYjJADAAAYjJADAAAYzFR/EHxpXHPNNdnY2MgVV1yx6Kkws76+npWVlRw+fHjRUwEAOCnPJc9OIz6fFHKnaGNjI8eOHVv0NNjCzwMAGIXnkmenEX8mQu4Unfjtyb333rvYifD/HThwYNFTAAB4WjyXPDuN+HzSZ+QAAAAGI+QAAAAGI+QAAAAGI+QAAAAGI+QAAAAGI+QAAAAGI+QAAAAGI+QAAAAGI+QAAAAGI+QAAAAGI+QAAAAGI+QAAAAGI+QAAAAGI+QAAAAGI+QAAAAGI+QAAAAGI+QAAAAGI+QAAAAGI+QAAAAGM3fIVdVlVfXxqvpCVX2+qt60wzEHqurxqjoy+3rbvOMCAAAsqz0TnON4kp/r7vuq6llJDlXVPd39hW3HfbK7b5xgPAAAgKU29yty3f1Id983W34yyReTXDLveQEAANjZpJ+Rq6p9Sa5J8ukddr+kqj5bVR+pqu8/yTkOVtVaVa1tbGxMOT0AAIBzwmQhV1V7k/xOkjd39xPbdt+X5IXdfXWS30jyod3O0923dfdqd6+urKxMNT0AAIBzxiQhV1XnZzPi3tvdv7t9f3c/0d3HZst3JTm/qi6aYmwAAIBlM8VdKyvJu5N8sbt/fZdjnjc7LlV17Wzcb8w7NgAAwDKa4q6VP5jkx5N8rqqOzLb9YpLLk6S7b03y2iQ/U1XHk/xlkpu7uycYGwAAYOnMHXLd/UdJ6imOuSXJLfOOBQAAwMR3rQQAAOD0E3IAAACDEXIAAACDEXIAAACDEXIAAACDEXIAAACDEXIAAACDEXIAAACDEXIAAACDEXIAAACDEXIAAACDEXIAAACDEXIAAACDEXIAAACDEXIAAACDEXIAAACDEXIAAACDEXIAAACDEXIAAACDEXIAAACD2bPoCQCws2uuuSYbGxu54oorFj0VtlhfX8/KykoOHz686KkAsMSEHMBZamNjI8eOHVv0NNjGzwSAs4GQAzhLnXgl7t57713sRPgbDhw4sOgpAIDPyAEAAIxGyAEAAAxGyAEAAAxGyAEAAAxGyAEAAAxmkpCrquur6ktVtV5Vb9lh/3dW1Qdn+z9dVfumGBcAAGAZzR1yVXVekncmeU2Sq5K8rqqu2nbYTyX58+6+Isk7kvzKvOMCAAAsqylekbs2yXp3P9jd30rygSQ3bTvmpiTvmS3/dpJXVFVNMDYAAMDSmSLkLkny1S3rD8+27XhMdx9P8niS50wwNgAAwNI56252UlUHq2qtqtY2NjYWPR0AAICzzhQhdzTJZVvWL51t2/GYqtqT5G8n+cZOJ+vu27p7tbtXV1ZWJpgeAADAuWWKkPtMkiur6kVVdUGSm5Pcue2YO5O8frb82iR/2N09wdgAAABLZ8+8J+ju41X1xiS/n+S8JLd39+er6u1J1rr7ziTvTvLfqmo9yZ9lM/YAAAB4BuYOuSTp7ruS3LVt29u2LP+fJP98irEAAACW3Vl3sxMAAABOTsgBAAAMRsgBAAAMRsgBAAAMZpKbnSyT9fX1HDt2LAcOHPibOx55JHn00YXMaSEef3zz+0tfuth5JDly5Ej27t276GkAADylXZ9LslAjPp8Ucqdo1z9S/uijybFjyWAXwLlg7969u/9cAADOIp6znJ1GfD4p5E7R4cOHd95x4rcq9957pqayWMv23wsAMIFdn0vCKfIZOQAAgMEIOQAAgMEIOQAAgMEIOQAAgMEIOQAAgMEIOQAAgMEIOQAAgMEIOQAAgMEIOQAAgMEIOQAAgMEIOQAAgMEIOQAAgMEIOQAAgMEIOQAAgMEIOQAAgMEIOQAAgMEIOQAAgMEIOQAAgMEIOQAAgMEIOQAAgMEIOQAAgMEIOQAAgMHsmecfV9W/T/JPknwryZeT/GR3f3OH4x5K8mSSbyc53t2r84wLAACwzOZ9Re6eJH+vu38gyf9M8gsnOfZl3b1fxAEAAMxnrpDr7ru7+/hs9VNJLp1/SgAAAJzMlJ+R+1dJPrLLvk5yd1UdqqqDJztJVR2sqrWqWtvY2JhwegAAAOeGp/yMXFV9LMnzdtj11u7+8OyYtyY5nuS9u5zmuu4+WlXPTXJPVT3Q3Z/Y6cDuvi3JbUmyurraT+O/AQAAYKk8Zch19ytPtr+qfiLJjUle0d07hld3H519f6yq7khybZIdQ25oR44kBw4sehZnxpEjyf79i54FAAAspXnvWnl9kp9P8tLu/otdjrkwyXd095Oz5Vcnefs8456VfvRHFz2DM2v//uX7bwYAgLPEXCGX5JYk35nNt0smyae6+w1V9YIk7+ruG5JcnOSO2f49Sd7X3R+dc9yzz8GDm18AAACn2Vwh191X7LL9a0lumC0/mOTqecYBAADgr01510oAAADOACEHAAAwGCEHAAAwGCEHAAAwGCEHAAAwGCEHAAAwGCEHAAAwGCEHAAAwGCEHAAAwGCEHAAAwGCEHAAAwGCEHAAAwGCEHAAAwGCEHAAAwGCEHAAAwGCEHAAAwGCEHAAAwmD2LngAAO1tfX8+xY8dy4MCBRU+FLY4cOZK9e/cuehoALDkhB3CWWllZWfQU2MHevXv9bABYOCEHcJY6fPjwoqcAAJylfEYOAABgMEIOAABgMEIOAABgMEIOAABgMEIOAABgMEIOAABgMEIOAABgMEIOAABgMHOFXFX9UlUdraojs68bdjnu+qr6UlWtV9Vb5hkTAABg2e2Z4Bzv6O5f3W1nVZ2X5J1JXpXk4SSfqao7u/sLE4wNAACwdM7EWyuvTbLe3Q9297eSfCDJTWdgXAAAgHPSFCH3xqr6k6q6vaq+e4f9lyT56pb1h2fbAAAAeAaeMuSq6mNVdf8OXzcl+c0kfzfJ/iSPJPm1eSdUVQeraq2q1jY2NuY9HQAAwDnnKT8j192vfDonqqr/nOT3dth1NMllW9YvnW3bbbzbktyWJKurq/10xgYAAFgm89618vlbVv9Zkvt3OOwzSa6sqhdV1QVJbk5y5zzjAgAALLN571r576pqf5JO8lCSn06SqnpBknd19w3dfbyq3pjk95Ocl+T27v78nOMCAAAsrblCrrt/fJftX0tyw5b1u5LcNc9YAAAAbDoTf34AAACACQk5AACAwQg5AACAwQg5AACAwQg5AACAwQg5AACAwQg5AACAwQg5AACAwQg5AACAwQg5AACAwQg5AACAwQg5AACAwQg5AACAwQg5AACAwQg5AACAwQg5AACAwQg5AACAwQg5AACAwQg5AACAwQg5AACAwQg5AACAwQg5AACAwQg5AACAwQg5AACAwQg5AACAwQg5AACAwQg5AACAwQg5AACAweyZ5x9X1QeTfO9s9dlJvtnd+3c47qEkTyb5dpLj3b06z7gAAADLbK6Q6+4fObFcVb+W5PGTHP6y7v76POMBAAAwZ8idUFWV5IeTvHyK8wEAALC7qT4j94+SPNrdf7rL/k5yd1UdqqqDE40JAACwlJ7yFbmq+liS5+2w663d/eHZ8uuSvP8kp7muu49W1XOT3FNVD3T3J3YZ72CSg0ly+eWXP9X0AAAAlk5193wnqNqT5GiSf9DdDz+N438pybHu/tWnOnZ1dbXX1tbmmh8AAMCoqurQTjeLnOKtla9M8sBuEVdVF1bVs04sJ3l1kvsnGBcAAGApTRFyN2fb2yqr6gVVddds9eIkf1RVn03yx0n+R3d/dIJxAQAAltLcd63s7p/YYdvXktwwW34wydXzjgMAAMCmqe5aCQAAwBki5AAAAAYj5AAAAAYj5AAAAAYj5AAAAAYj5AAAAAYj5AAAAAYj5AAAAAYj5AAAAAYj5AAAAAYj5AAAAAYj5AAAAAYj5AAAAAYj5AAAAAYj5AAAAAYj5AAAAAYj5AAAAAYj5AAAAAYj5AAAAAZT3b3oOeyqqjaSfGXR8xjARUm+vuhJcE5xTXE6uK44HVxXnA6uK6Y2zzX1wu5e2b7xrA45np6qWuvu1UXPg3OHa4rTwXXF6eC64nRwXTG103FNeWslAADAYIQcAADAYITcueG2RU+Ac45ritPBdcXp4LridHBdMbXJrymfkQMAABiMV+QAAAAGI+QGVlXXV9WXqmq9qt6y6Pkwpqq6vaoeq6r7t2z7nqq6p6r+dPb9uxc5R8ZTVZdV1cer6gtV9fmqetNsu2uLZ6Sqvquq/riqPju7pv7tbPuLqurTs8fCD1bVBYueK+OpqvOq6nBV/d5s3XXFXKrqoar6XFUdqaq12bZJHwOF3KCq6rwk70zymiRXJXldVV212FkxqP+S5Ppt296S5A+6+8okfzBbh1NxPMnPdfdVSV6c5Gdn/49ybfFM/VWSl3f31Un2J7m+ql6c5FeSvKO7r0jy50l+anFTZGBvSvLFLeuuK6bwsu7ev+XPDkz6GCjkxnVtkvXufrC7v5XkA0luWvCcGFB3fyLJn23bfFOS98yW35Pkn57JOTG+7n6ku++bLT+ZzSdIl8S1xTPUm47NVs+ffXWSlyf57dl21xSnrKouTfKPk7xrtl5xXXF6TPoYKOTGdUmSr25Zf3i2DaZwcXc/Mlv+X0kuXuRkGFtV7UtyTZJPx7XFHGZvfzuS5LEk9yT5cpJvdvfx2SEeC3km/kOSn0/yf2frz4nrivl1krur6lBVHZxtm/QxcM88/xg493V3V5Xb2/KMVNXeJL+T5M3d/cTmL7o3ubY4Vd397ST7q+rZSe5I8n2LnRGjq6obkzzW3Yeq6sCCp8O55bruPlpVz01yT1U9sHXnFI+BXpEb19Ekl21Zv3S2DabwaFU9P0lm3x9b8HwYUFWdn82Ie293/+5ss2uLuXX3N5N8PMlLkjy7qk78YtpjIafqB5P8UFU9lM2Pqbw8yX+M64o5dffR2ffHsvmLp2sz8WOgkBvXZ5JcObur0gVJbk5y54LnxLnjziSvny2/PsmHFzgXBjT7jMm7k3yxu399yy7XFs9IVa3MXolLVf2tJK/K5mcvP57ktbPDXFOcku7+he6+tLv3ZfO51B9294/FdcUcqurCqnrWieUkr05yfyZ+DPQHwQdWVTdk833d5yW5vbt/ebEzYkRV9f4kB5JclOTRJP8myYeS/FaSy5N8JckPd/f2G6LArqrquiSfTPK5/PXnTn4xm5+Tc21xyqrqB7J5c4DzsvmL6N/q7rdX1d/J5isp35PkcJJ/0d1/tbiZMqrZWyv/dXff6LpiHrPr547Z6p4k7+vuX66q52TCx0AhBwAAMBhvrQQAABiMkAMAABiMkAMAABiMkAMAABiMkAMAABiMkAMAABiMkAMAABiMkAMAABjM/wNOMKElSDgAGAAAAABJRU5ErkJggg==\n",
100 | "text/plain": [
101 | ""
102 | ]
103 | },
104 | "metadata": {
105 | "needs_background": "light"
106 | },
107 | "output_type": "display_data"
108 | }
109 | ],
110 | "source": [
111 | "plt.figure(figsize=(15,5)) \n",
112 | "ego_cps = local2global(ego.x, ego.y, ego.yaw, ego.corner_points)\n",
113 | "plt.plot(ego_cps[0], ego_cps[1], 'r')\n",
114 | "for line in MAP_lines:\n",
115 | " plt.plot([line[0], line[2]], [line[1], line[3]], 'k')\n",
116 | "plt.axis('equal') \n",
117 | "plt.show()"
118 | ]
119 | },
120 | {
121 | "cell_type": "code",
122 | "execution_count": 3,
123 | "id": "e8caba9f",
124 | "metadata": {},
125 | "outputs": [
126 | {
127 | "name": "stdout",
128 | "output_type": "stream",
129 | "text": [
130 | "-16.4 101.4 -5.0 -2.0\n",
131 | "-16.4 101.4 2.0 5.0\n",
132 | "-2.4 4.4 -0.7 4.1\n",
133 | "16.6 23.4 -4.1 0.7\n",
134 | "41.6 48.4 -0.7 4.1\n",
135 | "[-2. -2. -2. -2. -2. -2. -2. -2. -2. -2. -2. -2. -2. -2.\n",
136 | " -2. -2. -2. -2. -2. -2. -2. -2. -2. -2. -2. -2. -2. 0.7\n",
137 | " 0.7 0.7 0.7 0.7 0.7 0.7 0.7 0.7 0.7 0.7 0.7 -2. -2. -2.\n",
138 | " -2. -2. -2. -2. -2. -2. -2. -2. -2. -2. -2. -2. -2. -2.\n",
139 | " -2. -2. -2. -2. -2. -2. -2. -2. -2. -2. -2. -2. -2. -2.\n",
140 | " -2. -2. -2. -2. -2. -2. -2. -2. -2. -2. -2. -2. -2. -2.\n",
141 | " -2. -2. -2. -2. -2. -2. -2. -2. -2. -2. -2. -2. -2. -2.\n",
142 | " -2. -2. ] [-0.7 -0.7 -0.7 -0.7 -0.7 -0.7 -0.7 2. 2. 2. 2. 2. 2. 2.\n",
143 | " 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2.\n",
144 | " 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2.\n",
145 | " 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2.\n",
146 | " 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. -0.7\n",
147 | " -0.7 -0.7 -0.7 -0.7 -0.7 -0.7 -0.7 -0.7 -0.7 -0.7 2. 2. 2. 2.\n",
148 | " 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2. 2.\n",
149 | " 2. 2. ]\n"
150 | ]
151 | }
152 | ],
153 | "source": [
154 | "class AABB:\n",
155 | " def __init__(self, x_min, x_max, y_min, y_max):\n",
156 | " self.x_min = x_min\n",
157 | " self.x_max = x_max\n",
158 | " self.y_min = y_min\n",
159 | " self.y_max = y_max\n",
160 | " \n",
161 | " \n",
162 | "def BOX2AABB(obs):\n",
163 | " gcp0 = local2global(obs.x, obs.y, obs.yaw, obs.inflat_cpoints)\n",
164 | " x_min = np.min(gcp0[0, :])\n",
165 | " x_max = np.max(gcp0[0, :])\n",
166 | " y_min = np.min(gcp0[1, :])\n",
167 | " y_max = np.max(gcp0[1, :]) \n",
168 | " print(x_min, x_max, y_min, y_max)\n",
169 | " return AABB(x_min, x_max, y_min, y_max)\n",
170 | " \n",
171 | "\n",
172 | "N = 100\n",
173 | "x_end = 60.0\n",
174 | "dx = x_end/N\n",
175 | "X = np.linspace(0, x_end, N)\n",
176 | "\n",
177 | "# init by road boundary\n",
178 | "LB = np.ones(N)*BOX2AABB(road_bound_right).y_max\n",
179 | "UB = np.ones(N)*BOX2AABB(road_bound_left).y_min\n",
180 | "\n",
181 | "\n",
182 | "# update by obs\n",
183 | "for obs in obs_buf:\n",
184 | " obs_aabb = BOX2AABB(obs)\n",
185 | " start_x_idx = min(max(int(obs_aabb.x_min/dx), 0), N-1)\n",
186 | " end_x_idx = min(max(int(obs_aabb.x_max/dx), 0), N-1)\n",
187 | " if obs_aabb.y_min > LB[start_x_idx] and obs_aabb.y_min < UB[start_x_idx]:\n",
188 | " for i in range(start_x_idx, end_x_idx):\n",
189 | " UB[i] = obs_aabb.y_min\n",
190 | " if obs_aabb.y_max < UB[start_x_idx] and obs_aabb.y_max > LB[start_x_idx]:\n",
191 | " for i in range(start_x_idx, end_x_idx):\n",
192 | " LB[i] = obs_aabb.y_max \n",
193 | "print(LB, UB) "
194 | ]
195 | },
196 | {
197 | "cell_type": "code",
198 | "execution_count": 4,
199 | "id": "df207629",
200 | "metadata": {},
201 | "outputs": [
202 | {
203 | "data": {
204 | "image/png": "iVBORw0KGgoAAAANSUhEUgAAA3gAAAEvCAYAAAAXemMoAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjUuMiwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy8qNh9FAAAACXBIWXMAAAsTAAALEwEAmpwYAAAefklEQVR4nO3dfbRdZX0n8O/PBLQljihEkJcYLWiFLgh4RRIdG9+oUqe0U3Wwo6UdV1O77Gq7rKtqXbUdZ3XWdMbWmY4dXKhMmbXq26hUqlRFi8uXewUSCQqIY/ClgCjBFyD1BSPP/HFO2mu8gZB799k5+3w+a9119tvd+5c8yTn7e/bez1OttQAAADD9HtB3AQAAAKwMAQ8AAGAgBDwAAICBEPAAAAAGQsADAAAYCAEPAABgIFb3XcCBOPLII9v69ev7LgMAAKAX27Ztu721tnbv5VMZ8NavX5+tW7f2XQYAAEAvquorSy13iyYAAMBACHgAAAADIeABAAAMhIAHAAAwEAIeAADAQAh4AAAAAyHgAQAADMSKBLyqurCqbquqaxcte1hVXVZVXxi/PnQfv3veeJsvVNV5K1EPAADALFqpK3h/neRZey17ZZKPtNZOTPKR8fyPqKqHJfnjJE9MckaSP95XEAQAAODerUjAa619LMk391p8TpKLxtMXJfnFJX7155Jc1lr7ZmvtW0kuy48HRQAAAPZDl8/gHdVau3U8/bUkRy2xzbFJblo0f/N4GQAAAPfTRDpZaa21JG05+6iqLVW1taq27ty5c4UqAwAAGI4uA97Xq+oRSTJ+vW2JbW5Jcvyi+ePGy35Ma+2C1tpca21u7dq1K14sAADAtOsy4F2SZE+vmOclee8S23wwyVlV9dBx5ypnjZcBAABwP63UMAlvS7KQ5LFVdXNVvTjJf0nyzKr6QpJnjOdTVXNV9eYkaa19M8l/SnLV+Oe142UAAADcTzV6PG66zM3Nta1bt/ZdBgAAQC+qaltrbW7v5RPpZAUAAIDuCXgAAAADIeABAAAMhIAHAAAwEAIeAADAQAh4AAAAAyHgAQAADISABwAAMBACHgAAwEAIeAAAAAMh4AEAAAyEgAcAADAQAh4AAMBACHgAAAADIeABAAAMhIAHAAAwEAIeAADAQAh4AAAAAyHgAQAADISABwAAMBACHgAAwEAIeAAAAAPRacCrqsdW1fZFP3dW1e/ttc3mqrpj0Tav6bImAACAoVrd5c5ba59PsiFJqmpVkluSXLzEph9vrT2ny1oAAACGbpK3aD49yY2tta9M8JgAAAAzY5IB79wkb9vHuo1VdU1V/X1VnTzBmgAAAAZjIgGvqg5N8gtJ/u8Sqz+d5JGttVOT/M8kf7uPfWypqq1VtXXnzp2d1QoAADCtJnUF79lJPt1a+/reK1prd7bWdo2nL01ySFUducR2F7TW5lprc2vXru2+YgAAgCkzqYD3guzj9syqOrqqajx9xrimb0yoLgAAgMHotBfNJKmqw5I8M8lvLlr2kiRprb0xyXOT/FZV7U7y3STnttZa13UBAAAMTecBr7X2T0mO2GvZGxdNvyHJG7quAwAAYOgm2YsmAAAAHRLwAAAABkLAAwAAGAgBDwAAYCAEPAAAgIEQ8AAAAAZCwAMAABgIAQ8AAGAgBDwAAICBEPAAAAAGQsADAAAYCAEPAABgIAQ8AACAgRDwAAAABkLAAwAAGAgBDwAAYCAEPAAAgIEQ8AAAAAZCwAMAABgIAQ8AAGAgBDwAAICBEPAAAAAGovOAV1VfrqrPVtX2qtq6xPqqqr+sqh1V9ZmqOr3rmgAAAIZo9YSO89TW2u37WPfsJCeOf56Y5PzxKwAAAPfDwXCL5jlJ/k8b+VSSw6vqEX0XBQAAMG0mEfBakg9V1baq2rLE+mOT3LRo/ubxMgAAAO6HSdyi+eTW2i1V9fAkl1XVDa21j93fnYzD4ZYkWbdu3UrXCAAAMPU6v4LXWrtl/HpbkouTnLHXJrckOX7R/HHjZXvv54LW2lxrbW7t2rVdlQsAADC1Og14VXVYVT14z3SSs5Jcu9dmlyT51XFvmmcmuaO1dmuXdQEAAAxR17doHpXk4qrac6y3ttY+UFUvSZLW2huTXJrk7CQ7knwnya93XBMAAMAgdRrwWmtfTHLqEsvfuGi6JXlpl3UAAADMgoNhmAQAAABWgIAHAAAwEAIeAADAQAh4AAAAAyHgAQAADISABwAAMBACHgAAwEAIeAAAAAMh4AEAAAyEgAcAADAQAh4AAMBACHgAAAADIeABAAAMhIAHAAAwEAIeAADAQAh4AAAAAyHgAQAADISABwAAMBACHgAAwEAIeAAAAAMh4AEAAAxEZwGvqo6vqsur6vqquq6qfneJbTZX1R1VtX3885qu6gEAABi61R3ue3eS32+tfbqqHpxkW1Vd1lq7fq/tPt5ae06HdRyUTjvttOzcuTMnnHBC36UcsB07dmTt2rW5+uqr+y4FAFiC8w2YPZ0FvNbarUluHU/fVVWfS3Jskr0D3kzauXNndu3a1XcZyzLt9QPA0DnfgNnT5RW8f1ZV65OcluSKJVZvrKprknw1yctba9dNoqa+7fkm7aMf/Wi/hSzD5s2b+y4BALgXzjdg9nQe8KpqTZJ3J/m91tqde63+dJJHttZ2VdXZSf42yYn72M+WJFuSZN26dd0VDAAAMKU67UWzqg7JKNz9TWvtPXuvb63d2VrbNZ6+NMkhVXXkUvtqrV3QWptrrc2tXbu2y7IBAACmUpe9aFaStyT5XGvtL/axzdHj7VJVZ4zr+UZXNQEAAAxZl7doPinJi5J8tqq2j5f9YZJ1SdJae2OS5yb5raraneS7Sc5trbUOawIAABisLnvR/ESSuo9t3pDkDV3VAAAAMEsm0osm7G3XruRd70p+8IO+KwGAg8PjH5+cfnrfVQzXnXcm7353snt335UwbZ70pOSkk/quYv8JePTiTW9KXvayvqsAgIPH+vXJl77UdxXDdf75yStf2XcVTKPzzxfw4D598pOjD7JPfKLvSgCgfxdemLzmNclXv5occ0zf1QzTJz+ZnHhicvnlfVfCtDn88L4ruH8EPCautWRhIdm8OTn22L6rAYD+nXXWKOAtLCS//Mt9VzM8e849nvMc5x4MX6fj4MFS/vEfR99QbtrUdyUAcHA47bTkgQ9M5uf7rmSYduxIbr/duQezQcBj4hYWRq8bN/ZbBwAcLA49NJmb+5fPSFaWcw9miYDHxM3PJz/5k8kpp/RdCQAcPDZtSrZtS77//b4rGZ75+eRf/avp6igDDpSAx8QtLCRnnJGs9gQoAPyzjRuTu+9OPv3pvisZnoWF5Mwzkwc482UG+GfORH3nO8n27e6BB4C97bl90HN4K+vOO5PPfta5B7NDwGOitm4dDTDqHngA+FFHH5086lGew1tpV1456kXTuQezQsBjovZ8K3nmmf3WAQAHo40bR5+VrfVdyXDMzydVyROf2HclMBkCHhO1sJA85jHJkUf2XQkAHHw2bUpuvXU0pBArY2EhOfnk5CEP6bsSmAwBj4nZM8ioWyQAYGl7PiPdprky7rln9Hfp+TtmiYDHxNx4Y7JzpzdZANiXU04ZDSWko5WVccMNyR13+HKZ2SLgMTEGGQWAe7d69WgoIVfwVsaeoOzLZWaJgMfEGGQUAO7bpk2jIYW+852+K5l+CwvJEUckJ57YdyUwOYaa7smOHTuya9eubN68ue9SDtj27duzZs2a/d5+YWHUg9WqVR0Wxcz6wheS972v7yqG4ayzRh0SAP3YuHE0pNDWrclTnrK8fc3i+cZi8/Ojv8+qFS4KDmICXk/Wrl3bdwnLtmbNmv3+c9x112iQ0T/6o46LYma9/OXJJZf0XcUwbN6cXH5531XA7NozlND8/PID3qydbyz2zW+OnsF70Ys6KAoOYgJeT66++uq+S5ioK68c9WTl+Tu60NroROiFL0ze8Ia+q5lur3pVctFFo6sHq31CQC+OPHI0pNBKPIc3a+cbi33qU6NXz98xa3x8MxEGGaVLO3Ykt98++qbbOEfL85SnJOefn3zmM8npp/ddDcyuTZtGt5235vbCA7WwMHos5AlP6LsSmCydrDARCwujzlUOP7zvShgivaStnD1X2XXRDv3auHH0xdWNN/ZdyfSan09OPTU57LC+K4HJEvDo3D33jG6TcHsmXVlYGF25e9zj+q5k+q1blxxzjC7aoW8GPF+e3btHj4c492AWdR7wqupZVfX5qtpRVa9cYv0Dq+od4/VXVNX6rmtisj7/+eRb33J1he7Mz486JXiAr6yWrWp0QuSkEvp10kmjoYVcTT8w116b7Nrl3IPZ1OnpUFWtSvJXSZ6d5KQkL6iqvUdBe3GSb7XWTkjy+iR/1mVNTJ4BzunSnXeOPsj9+1o5mzYlX/pS8rWv9V0JzK5Vq0bPrfuy5cA492CWdf199xlJdrTWvthauzvJ25Ocs9c25yS5aDz9riRPr/I48ZDMzycPe9ioRzBYaVdcMeqEwIf4ynFrGBwcNm0aDTF01119VzJ95ueTo45K1q/vuxKYvK4D3rFJblo0f/N42ZLbtNZ2J7kjyREd18UELSy4fY7uLCzooXWlnX56cuihbg2Dvm3cOHqO/cor+65k+iwsjAKySwbMoqk55a6qLVW1taq27ty5s+9y2E/f+lZy/fXugac78/PJyScbHmElPfCByeMf7woe9O2JTxwFFF+23D+33TbqfdSdHcyqrgPeLUmOXzR/3HjZkttU1eokD0nyjb131Fq7oLU211qbW7t2bUflstKuuGL06k2WLuzpodUXCCtv06Zk69bk7rv7rgRm1+GHjzpb8WXL/bPn78tnA7Oq64B3VZITq+pRVXVoknOTXLLXNpckOW88/dwk/9Baax3XxYTMz49uzTzjjL4rYYhuuCG54w5fIHRh48bk+99Prr6670pgtm3aNAos99zTdyXTY2EhOeSQ0Z0IMIs6DXjjZ+p+O8kHk3wuyTtba9dV1Wur6hfGm70lyRFVtSPJy5L82FAKTK+FheSUU5I1a/quhCEywHl3DHgOB4eNG5Nvf3s05BD7Z35+9Czxgx7UdyXQj86fwWutXdpae0xr7adaa386Xvaa1tol4+nvtdae11o7obV2Rmvti13XxGT88IcGOKdbCwvJEUckJ57YdyXDc8wxySMf6dYw6JsvW+6fH/wgueoq5x7MtqnpZIXpc911BhmlW/Pzow9xvaR1w4Dn0L/HPGY01JD/i/tn+/bke99z7sFsE/DojEFG6dI3vzl6Bs+/r+5s2pTcfHNy0033vS3QjQc8YDTUkIC3f5x7QLK67wIG44ILkre+tbPdf+V7R+XG7x7T2f6TJJ+5ZvT6kX9Ykd393d8lD3948uhHr8ju4Ed86lOj166+pT3ttNOyc+fOnHDCCd0cYAJ27NiRtWvX5uoD7Cll8YDnxx9/79sC3dm0Kbn00tGP58ru3fvfP3q/Ou64viuB/gh4K+Wtbx3dF7BhQye7f8dtT80rvvSSTvb9Y56+crt63vPcPkc3FhaSVauSJzyhm/3v3Lkzu3bt6mbnE7Lc+k89NfmJnxjdCvv8569QUcD99rM/O3r9+Z/vt45p8cIX9l0B9EvAW0kbNiQf/Wgnu37BTcmZX+pk1//id35n9PqXf7liuzz11BXbFfyI+fnRv6/DDutm/3uu3H20o//Tk7B58+Zl/f4hh4wCtFvDoF9PelKybdvouXbuW0fftcPUEPCmxPHHT+AWqcM/M3p9SsfHgWXavTu58srkvPPue1uWZ9Om5HWvS7773dHVPGDyqkbd/gPsD52sAFPn2mv10DopGzeOAvW2bX1XAgDsDwEPmDp6SZscY3ABwHQR8ICpMz+fHH10sn5935UM39q1yQkneA4PAKaFgAdMnYUFA5xP0saNo1DdWt+VAAD3RcADpspttyU33uj5u0natGn09/6lrnvyBQCWTcADporn7yZv8YDnAMDBTcADpsr8/Gh8tsc/vu9KZsfP/EyyZo2OVgBgGgh4wFRZWBiNB/WgB/VdyexYtSp54hNdwQOAaSDgAVPj7ruTq67y/F0fNm1KrrlmNP4gAHDwEvCAqXHNNcn3vuf5uz5s3Jjcc88oYAMABy8BD5gae54BE/Am78wzR6+ewwOAg5uAB0yNhYXk+OOT447ru5LZ89CHJo97nOfwAOBgt7rvAtg/O3Yk11/f8UFuHz/YdEnHx4ED9PGPJ09+ct9VzK6NG5OLL04u8R4BwAw55ZRk/fq+q9h/At6UeM97kle8ouuj/OfRyzldHwcO3FOf2ncFs+tpT0suvDA5x3sEADPk/POTl7yk7yr2n4A3JX71V5NnPKPjg/zGb4xe3/Smjg8EB2b16uTkk/uuYna94AXJqaeOejMFgFlx/PF9V3D/CHhT4uijRz+devAXRq+nd3wcYCo94AGjQc8BgINXJwGvqv5bkn+T5O4kNyb59dbat5fY7stJ7krywyS7W2tzXdQDAAAwC7rqRfOyJD/TWjslyf9L8qp72faprbUNwh0AAMDydBLwWmsfaq3tHs9+KolOzQEAADo2iXHw/kOSv9/HupbkQ1W1raq2TKAWAACAwTrgZ/Cq6sNJlur249WttfeOt3l1kt1J/mYfu3lya+2Wqnp4ksuq6obW2sf2cbwtSbYkybp16w60bAAAgME64IDXWrvXTvur6teSPCfJ01trbR/7uGX8eltVXZzkjCRLBrzW2gVJLkiSubm5JffXu+3bk82b+67iwG3fnmzY0HcVcFDYsWNHdu3alc1T/H96+/btWbNmTd9lAAAT1FUvms9K8gdJfra19p19bHNYkge01u4aT5+V5LVd1DMRv/IrfVewfBs2DOPPAStg7dq1fZewbGvWrBnEnwMA2H+1j4try9tp1Y4kD0zyjfGiT7XWXlJVxyR5c2vt7Kp6dJKLx+tXJ3lra+1P92f/c3NzbevWrSteNwAAwDSoqm1LjUTQyRW81toJ+1j+1SRnj6e/mOTULo4PAAAwiybRiyYAAAATIOABAAAMhIAHAAAwEAIeAADAQAh4AAAAAyHgAQAADISABwAAMBACHgAAwEAIeAAAAAMh4AEAAAyEgAcAADAQAh4AAMBACHgAAAADIeABAAAMhIAHAAAwEAIeAADAQAh4AAAAAyHgAQAADISABwAAMBACHgAAwEAIeAAAAAPRWcCrqj+pqluqavv45+x9bPesqvp8Ve2oqld2VQ8AAMDQre54/69vrb1uXyuralWSv0ryzCQ3J7mqqi5prV3fcV0AAACD0/ctmmck2dFa+2Jr7e4kb09yTs81AQAATKWuA95vV9VnqurCqnroEuuPTXLTovmbx8sAAAC4n5YV8Krqw1V17RI/5yQ5P8lPJdmQ5NYkf77MY22pqq1VtXXnzp3L2RUAAMAgLesZvNbaM/Znu6p6U5L3LbHqliTHL5o/brxsqWNdkOSCJJmbm2v3r1IAAIDh67IXzUcsmv2lJNcusdlVSU6sqkdV1aFJzk1ySVc1AQAADFmXvWj+16rakKQl+XKS30ySqjomyZtba2e31nZX1W8n+WCSVUkubK1d12FNAAAAg9VZwGutvWgfy7+a5OxF85cmubSrOgAAAGZF38MkAAAAsEIEPAAAgIEQ8AAAAAZCwAMAABgIAQ8AAGAgBDwAAICBEPAAAAAGQsADAAAYCAEPAABgIAQ8AACAgRDwAAAABkLAAwAAGAgBDwAAYCAEPAAAgIEQ8AAAAAZCwAMAABgIAQ8AAGAgBDwAAICBEPAAAAAGQsADAAAYCAEPAABgIAQ8AACAgVjdxU6r6h1JHjuePTzJt1trG5bY7stJ7krywyS7W2tzXdQDAAAwCzoJeK21f7dnuqr+PMkd97L5U1trt3dRBwAAwCzpJODtUVWV5PlJntblcQAAAOj+Gbx/neTrrbUv7GN9S/KhqtpWVVs6rgUAAGDQDvgKXlV9OMnRS6x6dWvtvePpFyR5273s5smttVuq6uFJLquqG1prH9vH8bYk2ZIk69atO9CyAQAABqtaa93suGp1kluSPL61dvN+bP8nSXa11l53X9vOzc21rVu3Lr9IAACAKVRV25bqpLLLWzSfkeSGfYW7qjqsqh68ZzrJWUmu7bAeAACAQesy4J2bvW7PrKpjqurS8exRST5RVdckuTLJ+1trH+iwHgAAgEHrrBfN1tqvLbHsq0nOHk9/McmpXR0fAABg1nTdiyYAAAATIuABAAAMhIAHAAAwEAIeAADAQAh4AAAAAyHgAQAADISABwAAMBACHgAAwEAIeAAAAAMh4AEAAAyEgAcAADAQAh4AAMBACHgAAAADIeABAAAMhIAHAAAwEAIeAADAQAh4AAAAAyHgAQAADISABwAAMBACHgAAwEAIeAAAAAMh4AEAAAzEsgJeVT2vqq6rqnuqam6vda+qqh1V9fmq+rl9/P6jquqK8XbvqKpDl1MPAADALFvuFbxrk/zbJB9bvLCqTkpybpKTkzwryf+qqlVL/P6fJXl9a+2EJN9K8uJl1gMAADCzlhXwWmufa619folV5yR5e2vt+621LyXZkeSMxRtUVSV5WpJ3jRddlOQXl1MPAADALOvqGbxjk9y0aP7m8bLFjkjy7dba7nvZBgAAgP20+r42qKoPJzl6iVWvbq29d+VL2mcdW5JsSZJ169ZN6rAAAABT4z4DXmvtGQew31uSHL9o/rjxssW+keTwqlo9voq31DaL67ggyQVJMjc31w6gJgAAgEHr6hbNS5KcW1UPrKpHJTkxyZWLN2ittSSXJ3nueNF5SSZ2RRAAAGBoljtMwi9V1c1JNiZ5f1V9MElaa9cleWeS65N8IMlLW2s/HP/OpVV1zHgXr0jysqrakdEzeW9ZTj0AAACzrEYX0qbL3Nxc27p1a99lAAAA9KKqtrXW5vZe3tUtmgAAAEyYgAcAADAQAh4AAMBACHgAAAADIeABAAAMhIAHAAAwEAIeAADAQAh4AAAAAzGVA51X1c4kX+m7jh4cmeT2votgIrT17NDWs0E7zw5tPTu09ew4WNv6ka21tXsvnMqAN6uqautSo9UzPNp6dmjr2aCdZ4e2nh3aenZMW1u7RRMAAGAgBDwAAICBEPCmywV9F8DEaOvZoa1ng3aeHdp6dmjr2TFVbe0ZPAAAgIFwBQ8AAGAgBLwpUVXPqqrPV9WOqnpl3/Wwcqrqwqq6raquXbTsYVV1WVV9Yfz60D5rZPmq6viquryqrq+q66rqd8fLtfXAVNWDqurKqrpm3Nb/cbz8UVV1xfh9/B1VdWjftbJ8VbWqqq6uqveN57XzAFXVl6vqs1W1vaq2jpd5/x6gqjq8qt5VVTdU1eeqauO0tbWANwWqalWSv0ry7CQnJXlBVZ3Ub1WsoL9O8qy9lr0yyUdaaycm+ch4num2O8nvt9ZOSnJmkpeO/x9r6+H5fpKntdZOTbIhybOq6swkf5bk9a21E5J8K8mL+yuRFfS7ST63aF47D9dTW2sbFnWX7/17mP5Hkg+01n46yakZ/f+eqrYW8KbDGUl2tNa+2Fq7O8nbk5zTc02skNbax5J8c6/F5yS5aDx9UZJfnGRNrLzW2q2ttU+Pp+/K6APj2GjrwWkju8azh4x/WpKnJXnXeLm2HoCqOi7Jzyd583i+op1niffvgamqhyR5SpK3JElr7e7W2rczZW0t4E2HY5PctGj+5vEyhuuo1tqt4+mvJTmqz2JYWVW1PslpSa6Ith6k8W1725PcluSyJDcm+XZrbfd4E+/jw/Dfk/xBknvG80dEOw9VS/KhqtpWVVvGy7x/D8+jkuxM8r/Ht16/uaoOy5S1tYAHB7k26upWd7cDUVVrkrw7ye+11u5cvE5bD0dr7YettQ1JjsvoLoyf7rciVlpVPSfJba21bX3XwkQ8ubV2ekaPy7y0qp6yeKX378FYneT0JOe31k5L8k/Z63bMaWhrAW863JLk+EXzx42XMVxfr6pHJMn49bae62EFVNUhGYW7v2mtvWe8WFsP2PjWnsuTbExyeFWtHq/yPj79npTkF6rqyxk9OvG0jJ7d0c4D1Fq7Zfx6W5KLM/rixvv38Nyc5ObW2hXj+XdlFPimqq0FvOlwVZITxz1zHZrk3CSX9FwT3bokyXnj6fOSvLfHWlgB42dz3pLkc621v1i0SlsPTFWtrarDx9M/keSZGT1zeXmS544309ZTrrX2qtbaca219Rl9Lv9Da+3fRzsPTlUdVlUP3jOd5Kwk18b79+C01r6W5Kaqeux40dOTXJ8pa2sDnU+Jqjo7o3v9VyW5sLX2p/1WxEqpqrcl2ZzkyCRfT/LHSf42yTuTrEvylSTPb63t3RELU6Sqnpzk40k+m395XucPM3oOT1sPSFWdktFD+Ksy+iL1na2111bVozO60vOwJFcneWFr7fv9VcpKqarNSV7eWnuOdh6ecZtePJ5dneStrbU/raoj4v17cKpqQ0YdJx2a5ItJfj3j9/JMSVsLeAAAAAPhFk0AAICBEPAAAAAGQsADAAAYCAEPAABgIAQ8AACAgRDwAAAABkLAAwAAGAgBDwAAYCD+P06i2Ejf73/7AAAAAElFTkSuQmCC\n",
205 | "text/plain": [
206 | ""
207 | ]
208 | },
209 | "metadata": {
210 | "needs_background": "light"
211 | },
212 | "output_type": "display_data"
213 | }
214 | ],
215 | "source": [
216 | "plt.figure(figsize=(15,5)) \n",
217 | "ego_cps = local2global(ego.x, ego.y, ego.yaw, ego.corner_points)\n",
218 | "plt.plot(ego_cps[0], ego_cps[1], 'r')\n",
219 | "for line in MAP_cars:\n",
220 | " plt.plot([line[0], line[2]], [line[1], line[3]], 'k')\n",
221 | "plt.plot(X, LB, 'b')\n",
222 | "plt.plot(X, UB, 'b')\n",
223 | "plt.axis('equal') \n",
224 | "plt.show()"
225 | ]
226 | },
227 | {
228 | "cell_type": "code",
229 | "execution_count": 7,
230 | "id": "8d3e2ad9",
231 | "metadata": {},
232 | "outputs": [],
233 | "source": [
234 | "from pyomo.environ import *\n",
235 | "from pyomo.dae import *\n",
236 | "\n",
237 | "s = 3\n",
238 | "m = ConcreteModel()\n",
239 | "lb = {}\n",
240 | "ub = {}\n",
241 | "for i in range(N):\n",
242 | " lb[i] = LB[i]\n",
243 | " ub[i] = UB[i]\n",
244 | "# Parameters\n",
245 | "m.p0 = Param(initialize=ego.y, mutable=True)\n",
246 | "m.coeffs = Param(RangeSet(0, 5), initialize={0:10.0, 1:10.0, 2:10.0, 3:10.0})\n",
247 | "m.LB = Param(RangeSet(0, N-1), initialize=lb)\n",
248 | "m.UB = Param(RangeSet(0, N-1), initialize=ub)\n",
249 | "m.c = Var(RangeSet(0, 2*s-1))\n",
250 | "m.pt = Var(RangeSet(0, 3), RangeSet(0, N-1))\n",
251 | "\n",
252 | "# px = np.array([m.pk[i,0]() for i in range(len(tpath))])\n",
253 | "# py = np.array([m.pk[i,1]() for i in range(len(tpath))])\n",
254 | "# print(tpath, px, py)\n",
255 | "\n",
256 | "#Constrainsts\n",
257 | "pw = {(0, 0):1.0, (0, 1):1.0, (0, 2):1.0, (0, 3):1.0, (0, 4):1.0, (0, 5):1.0,\n",
258 | " (1, 0):0.0, (1, 1):5.0, (1, 2):4.0, (1, 3):3.0, (1, 4):2.0, (1, 5):1.0,\n",
259 | " (2, 0):0.0, (2, 1):0.0, (2, 2):20.0,(2, 3):12.0,(2, 4):6.0, (2, 5):2.0,\n",
260 | " (3, 0):0.0, (3, 1):0.0, (3, 2):0.0, (3, 3):60.0,(3, 4):24.0,(3, 5):6.0}\n",
261 | "\n",
262 | "m.pw = Param(RangeSet(0, 3), RangeSet(0, 5), initialize=pw)\n",
263 | "\n",
264 | "m.dx = Param(initialize=dx)\n",
265 | "\n",
266 | "def _polyfun(m, k, i):\n",
267 | " return (m.pt[k, i] == m.pw[k, 0]*m.c[max(0-k, 0)]*(m.dx*i)**5+\n",
268 | " m.pw[k, 1]*m.c[max(1-k, 0)]*(m.dx*i)**4+\n",
269 | " m.pw[k, 2]*m.c[max(2-k, 0)]*(m.dx*i)**3+\n",
270 | " m.pw[k, 3]*m.c[max(3-k, 0)]*(m.dx*i)**2+\n",
271 | " m.pw[k, 4]*m.c[max(4-k, 0)]*(m.dx*i)**1+\n",
272 | " m.pw[k, 5]*m.c[max(5-k, 0)])\n",
273 | "\n",
274 | "m.pt = Constraint(RangeSet(0, 3), RangeSet(0, N-1), rule=_polyfun)\n",
275 | "# m.pt_bound = Constraint(RangeSet(0, N-1), rule=lambda m, i : m.LB[i] <= m.pt[0, i] <= m.UB[i])\n",
276 | "# m.p0_con = Constraint(rule=lambda m : m.pt[0, 0] == m.p0)\n",
277 | "\n",
278 | "# m.dyobj = m.coeffs[0]*sum(m.pt[1, k]**2 for k in RangeSet(0, N-1))\n",
279 | "# m.ddyobj = m.coeffs[1]*sum(m.pt[2, k]**2 for k in RangeSet(0, N-1))\n",
280 | "# m.dddyobj = m.coeffs[2]*sum(m.pt[3, k]**2 for k in RangeSet(0, N-1))\n",
281 | "# m.refyobj = m.coeffs[3]*sum((m.pt[0, k]-ego.y)**2 for k in RangeSet(0, N-1))\n",
282 | "# m.obj = Objective(expr=m.dyobj+m.ddyobj+m.dddyobj+m.refyobj, sense=minimize)\n",
283 | "# %time SolverFactory('ipopt').solve(m)\n",
284 | "# m.display()"
285 | ]
286 | },
287 | {
288 | "cell_type": "code",
289 | "execution_count": null,
290 | "id": "40f7a3aa",
291 | "metadata": {},
292 | "outputs": [],
293 | "source": []
294 | }
295 | ],
296 | "metadata": {
297 | "kernelspec": {
298 | "display_name": "Python 3 (ipykernel)",
299 | "language": "python",
300 | "name": "python3"
301 | },
302 | "language_info": {
303 | "codemirror_mode": {
304 | "name": "ipython",
305 | "version": 3
306 | },
307 | "file_extension": ".py",
308 | "mimetype": "text/x-python",
309 | "name": "python",
310 | "nbconvert_exporter": "python",
311 | "pygments_lexer": "ipython3",
312 | "version": "3.9.5"
313 | }
314 | },
315 | "nbformat": 4,
316 | "nbformat_minor": 5
317 | }
318 |
--------------------------------------------------------------------------------
/.ipynb_checkpoints/LPAstar-checkpoint.ipynb:
--------------------------------------------------------------------------------
1 | {
2 | "cells": [
3 | {
4 | "cell_type": "code",
5 | "execution_count": null,
6 | "id": "716e00fd",
7 | "metadata": {},
8 | "outputs": [
9 | {
10 | "name": "stdout",
11 | "output_type": "stream",
12 | "text": [
13 | "min_x: -10\n",
14 | "min_y: -10\n",
15 | "max_x: 60\n",
16 | "max_y: 60\n",
17 | "x_width: 15\n",
18 | "y_width: 15\n",
19 | "[70.71067811865476, 0.0] [9999.0, 9999.0]\n",
20 | "find a path.\n",
21 | "one iter planning timecost: 0.023613452911376953\n"
22 | ]
23 | },
24 | {
25 | "data": {
26 | "image/png": "iVBORw0KGgoAAAANSUhEUgAAAPsAAAD4CAYAAAAq5pAIAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjUuMSwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy/YYfK9AAAACXBIWXMAAAsTAAALEwEAmpwYAAAMpElEQVR4nO3db6xkdX3H8fenC9SCRBZRhGXbhYaQUNII2RCkxprSAiJhfeCDJdqCmBBjbKEx0aUkNekjqY39k5oaArY0JWCKUImBLlvUNI0Fhe3yH2GlFFiWP0oDWh/A2m8fzFlzvZ27rHPOmTvL7/1KJvfMnN/c+e6Z+9nfzJlz5puqQtIb3y+sdgGS5sOwS40w7FIjDLvUCMMuNeKgeT7YUUeuqQ3rD57nQ0pNefLp1/j+Sz/JtHVzDfuG9Qfz7a3r5/mQUlNOP+fpFdf5Ml5qhGGXGtEr7EnOTfLdJDuTbBmqKEnDmznsSdYAXwDeB5wMXJjk5KEKkzSsPjP76cDOqnqiql4FbgQ2DVOWpKH1Cfs6YOmuv2e62yQtoNF30CW5NMk9Se558Qc/GfvhJK2gT9h3AUs/ND+uu+1nVNXVVbWxqja+7a1rejycpD76hP07wIlJjk9yCLAZuHWYsiQNbeYj6KpqT5JPAFuBNcCXquqhwSqTNKheh8tW1W3AbQPVImlEHkEnNcKwS42Y61lvszrn2HeudgnSXG19dsfgv9OZXWqEYZcaYdilRhh2qRGGXWqEYZcaYdilRhh2qRGGXWqEYZcaYdilRhh2qRGGXWrEAXHWWx+7Pn3mzPddd9W3BqxEWl3O7FIjDLvUCMMuNaJPr7f1Sb6R5OEkDyW5bMjCJA2rzw66PcAnq2p7ksOBe5Nsq6qHB6pN0oBmntmrandVbe+Wfwg8gr3epIU1yHv2JBuAU4G7h/h9kobXO+xJ3gx8Bbi8ql6Zst7GjtIC6BX2JAczCfr1VXXztDE2dpQWQ5+98QGuBR6pqs8PV5KkMfSZ2X8D+F3gt5Ls6C7nDVSXpIH16eL6b0AGrEXSiDyCTmqEYZca8YY/xbXPaaqznh7rqbFaRM7sUiMMu9QIwy41wrBLjTDsUiMMu9QIwy41wrBLjTDsUiMMu9QIwy41wrBLjTDsUiPe8Ge99THr2Ws2k9QicmaXGmHYpUYYdqkRQzSJWJPkP5J8bYiCJI1jiJn9MiZ93iQtsL4dYY4D3g9cM0w5ksbSd2b/C+BTwP/2L0XSmPq0fzofeKGq7n2dcTZ2lBZA3/ZPFyR5EriRSRuof1g+yMaO0mKYOexVdUVVHVdVG4DNwNer6sODVSZpUH7OLjVikGPjq+qbwDeH+F2SxuHMLjXCsEuN8BTXEdhMUovImV1qhGGXGmHYpUYYdqkRhl1qhGGXGmHYpUYYdqkRhl1qhGGXGmHYpUYYdqkRhl1qhGe96YCy9dkdM9/3nGPfOVgdByJndqkRhl1qhGGXGtG3/dMRSW5K8miSR5K8a6jCJA2r7w66vwT+uao+mOQQ4NABapI0gpnDnuQtwHuAiwGq6lXg1WHKkjS0Pi/jjwdeBP62689+TZLDBqpL0sD6hP0g4DTgb6rqVOB/gC3LB9nYUVoMfcL+DPBMVd3dXb+JSfh/ho0dpcXQp7Hjc8DTSU7qbjoLeHiQqiQNru/e+N8Hru/2xD8BfKR/SZLG0CvsVbUD2DhMKZLG5BF0UiMMu9QIwy41wrBLjTDsUiMMu9QIwy41wrBLjTDsUiMMu9QIwy41wrBLjTDsUiMMu9QIwy41wrBLjTDsUiMMu9QIwy41wrBLjejb2PEPkzyU5MEkNyR501CFSRrWzGFPsg74A2BjVZ0CrAE2D1WYpGH1fRl/EPBLSQ5i0sH12f4lSRpDn44wu4A/A54CdgMvV9UdQxUmaVh9XsavBTYx6eZ6LHBYkg9PGWdjR2kB9HkZ/9vAf1bVi1X1GnAzcObyQTZ2lBZDn7A/BZyR5NAkYdLY8ZFhypI0tD7v2e9m0qZ5O/BA97uuHqguSQPr29jxM8BnBqpF0og8gk5qhGGXGmHYpUYYdqkRhl1qhGGXGmHYpUYYdqkRhl1qhGGXGmHYpUYYdqkRhl1qhGGXGmHYpUYYdqkRvb68Qotj67M7VrsELThndqkRhl1qhGGXGvG6YU/ypSQvJHlwyW1HJtmW5PHu59pxy5TU1/7M7H8HnLvsti3AnVV1InBnd13SAnvdsFfVvwIvLbt5E3Bdt3wd8IFhy5I0tFnfsx9dVbu75eeAoweqR9JIeu+gq6oCaqX1NnaUFsOsYX8+yTEA3c8XVhpoY0dpMcwa9luBi7rli4CvDlOOpLHsz0dvNwD/DpyU5JkkHwU+C/xOkseZtG7+7LhlSurrdY+Nr6oLV1h11sC1SBqRR9BJjTDsUiM8xXXBrLvqWzPd7xQ+PvfH1IHFmV1qhGGXGmHYpUYYdqkRhl1qhGGXGmHYpUYYdqkRhl1qhGGXGmHYpUYYdqkRhl1qhGe9vUH0OXNt16fPHLASLbVIZxQ6s0uNMOxSIwy71IhZGzt+LsmjSe5PckuSI0atUlJvszZ23AacUlW/DjwGXDFwXZIGNlNjx6q6o6r2dFfvAo4boTZJAxriPfslwO0D/B5JI+oV9iRXAnuA6/cxxsaO0gKYOexJLgbOBz7UdXKdysaO0mKY6Qi6JOcCnwJ+s6p+PGxJksYwa2PHvwYOB7Yl2ZHkiyPXKamnWRs7XjtCLZJG5BF0UiMMu9QIT3HVQp2GqfE4s0uNMOxSIwy71AjDLjXCsEuNMOxSIwy71AjDLjXCsEuNMOxSIwy71AjDLjXCsEuNOCDOetv67I7VLkE64DmzS40w7FIjDLvUiJkaOy5Z98kkleSoccqTNJRZGzuSZD1wNvDUwDVJGsFMjR07f86kUcSK3WAkLY6Z3rMn2QTsqqr7Bq5H0kh+7s/ZkxwK/BGTl/D7M/5S4FKAX153QHysL70hzTKz/ypwPHBfkieZ9GbfnuQd0wbb2FFaDD/3VFtVDwBv33u9C/zGqvr+gHVJGtisjR0lHWBmbey4dP2GwaqRNBqPoJMaYdilRqRqfsfEJHkR+K8VVh8FLNJOvkWrBxavJuvZt9Wo51eq6m3TVsw17PuS5J6q2rjadey1aPXA4tVkPfu2aPX4Ml5qhGGXGrFIYb96tQtYZtHqgcWryXr2baHqWZj37JLGtUgzu6QRGXapEXMPe5Jzk3w3yc4kW6as/8UkX+7W351kw4i1rE/yjSQPJ3koyWVTxrw3yctJdnSXPx6rniWP+WSSB7rHu2fK+iT5q24b3Z/ktBFrOWnJv31HkleSXL5szKjbaNpXoyU5Msm2JI93P9eucN+LujGPJ7loxHo+l+TR7vm4JckRK9x3n8/tqKpqbhdgDfA94ATgEOA+4ORlYz4OfLFb3gx8ecR6jgFO65YPBx6bUs97ga/NeTs9CRy1j/XnAbcDAc4A7p7j8/cckwM35raNgPcApwEPLrntT4Et3fIW4Kop9zsSeKL7ubZbXjtSPWcDB3XLV02rZ3+e2zEv857ZTwd2VtUTVfUqcCOwadmYTcB13fJNwFlJMkYxVbW7qrZ3yz8EHgHWjfFYA9sE/H1N3AUckeSYOTzuWcD3qmqloyBHUdO/Gm3p38l1wAem3PUcYFtVvVRV/w1sY8r3KQ5RT1XdUVV7uqt3Mfmeh4Uy77CvA55ecv0Z/n+4fjqm23gvA28du7Du7cKpwN1TVr8ryX1Jbk/ya2PXwuR7/e5Icm/3TT/L7c92HMNm4IYV1s17Gx1dVbu75eeAo6eMWa3tdAmTV17TvN5zOxq/JwpI8mbgK8DlVfXKstXbmbxs/VGS84B/Ak4cuaR3V9WuJG8HtiV5tJtNVk2SQ4ALgCumrF6NbfRTVVVJFuIz5CRXAnuA61cYsmrP7bxn9l3A+iXXj+tumzomyUHAW4AfjFVQkoOZBP36qrp5+fqqeqWqftQt3wYcPPb35FfVru7nC8AtTN7+LLU/23Fo7wO2V9Xzy1esxjYCnt/71qX7+cKUMXPdTkkuBs4HPlTdG/Tl9uO5Hc28w/4d4MQkx3czxWbg1mVjbgX27jX9IPD1lTZcX92+gGuBR6rq8yuMecfefQZJTmeyzcb8z+ewJIfvXWay42d5g45bgd/r9sqfAby85CXtWC5khZfw895GnaV/JxcBX50yZitwdpK13d76s7vbBpfkXCZfrX5BVf14hTH789yOZ957BJnsSX6MyV75K7vb/oTJRgJ4E/CPwE7g28AJI9bybibvoe4HdnSX84CPAR/rxnwCeIjJJwd3AWeOvH1O6B7rvu5x926jpTUF+EK3DR9g8h2AY9Z0GJPwvmXJbXPbRkz+k9kNvMbkffdHmezHuRN4HPgX4Mhu7EbgmiX3vaT7W9oJfGTEenYy2T+w9+9o7ydKxwK37eu5ndfFw2WlRngEndQIwy41wrBLjTDsUiMMu9QIwy41wrBLjfg/xIfXzm2li8QAAAAASUVORK5CYII=\n",
27 | "text/plain": [
28 | ""
29 | ]
30 | },
31 | "metadata": {
32 | "needs_background": "light"
33 | },
34 | "output_type": "display_data"
35 | },
36 | {
37 | "name": "stdout",
38 | "output_type": "stream",
39 | "text": [
40 | "if you want change environment, please input [ok] to start changingok\n",
41 | "please input ix number (Type: Int) in [0, 15):12\n",
42 | "please input iy number (Type: Int) in [0, 15):7\n",
43 | "change [ix: 12, iy: 7] from free to obs\n",
44 | "if you want change environment, please input [ok] to start changingstop\n",
45 | "changed map: 10.0\n",
46 | "[85.35533905932738, 60.35533905932738] [85.35533905932738, 85.35533905932738]\n",
47 | "find a path.\n",
48 | "one iter planning timecost: 0.0003542900085449219\n"
49 | ]
50 | },
51 | {
52 | "data": {
53 | "image/png": "iVBORw0KGgoAAAANSUhEUgAAAPsAAAD4CAYAAAAq5pAIAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjUuMSwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy/YYfK9AAAACXBIWXMAAAsTAAALEwEAmpwYAAAMsElEQVR4nO3db6xkdX3H8fenu1ALElhEEZZtFxpCQkkDZEOQGmtKC4iE9YEPlmgLYkKMsYXGxC4lqUkfSW3sn9TUELClKQFThEoMdNmipmksq7Bd/i7CSimwLH+UBrQ+AOy3D+asvd7eu7vOOWfuLL/3K5ncM3N+c+e7Z+5nfzNnzplvqgpJb34/t9IFSJoNwy41wrBLjTDsUiMMu9SI1bN8sGOOXlXr1x0yy4eUmvLUM6/zvZd/nKXWzTTs69cdwre2rJvlQ0pNOev8Z5Zd58t4qRGGXWpEr7AnuSDJd5LsSrJ5qKIkDW/qsCdZBXweeB9wKnBJklOHKkzSsPrM7GcBu6rqyap6DbgF2DhMWZKG1ifsa4GFu/6e7W6TNIdG30GX5Iok9yW576Xv/3jsh5O0jD5h3w0s/ND8hO62n1JV11XVhqra8Pa3rerxcJL66BP2bwMnJzkxyaHAJuCOYcqSNLSpj6CrqjeSfALYAqwCvlhVjwxWmaRB9TpctqruBO4cqBZJI/IIOqkRhl1qxEzPepvW+cefvtIlSDO15bkdg/9OZ3apEYZdaoRhlxph2KVGGHapEYZdaoRhlxph2KVGGHapEYZdaoRhlxph2KVGGHapEQfFWW997P6Dc6a+79prvzlgJdLKcmaXGmHYpUYYdqkRfXq9rUvy9SSPJnkkyZVDFiZpWH120L0BfLKqtic5Arg/ydaqenSg2iQNaOqZvar2VNX2bvkHwE7s9SbNrUHesydZD5wBbBvi90kaXu+wJ3kr8GXgqqp6dYn1NnaU5kCvsCc5hEnQb6qq25YaY2NHaT702Rsf4AZgZ1V9briSJI2hz8z+a8BvA7+RZEd3uXCguiQNrE8X138FMmAtkkbkEXRSIwy71Ig3/SmufU5Tnfb0WE+N1TxyZpcaYdilRhh2qRGGXWqEYZcaYdilRhh2qRGGXWqEYZcaYdilRhh2qRGGXWqEYZca8aY/662Pac9es5mk5pEzu9QIwy41wrBLjRiiScSqJP+e5KtDFCRpHEPM7Fcy6fMmaY717QhzAvB+4PphypE0lr4z+58DnwL+p38pksbUp/3TRcCLVXX/fsbZ2FGaA33bP12c5CngFiZtoP5+8SAbO0rzYeqwV9XVVXVCVa0HNgFfq6oPD1aZpEH5ObvUiEGOja+qbwDfGOJ3SRqHM7vUCMMuNcJTXEdgM0nNI2d2qRGGXWqEYZcaYdilRhh2qRGGXWqEYZcaYdilRhh2qRGGXWqEYZcaYdilRhh2qRGe9aaDypbndkx93/OPP32wOg5GzuxSIwy71AjDLjWib/uno5LcmuSxJDuTvGuowiQNq+8Our8A/qmqPpjkUOCwAWqSNIKpw57kSOA9wGUAVfUa8NowZUkaWp+X8ScCLwF/0/Vnvz7J4QPVJWlgfcK+GjgT+OuqOgP4b2Dz4kE2dpTmQ5+wPws8W1Xbuuu3Mgn/T7GxozQf+jR2fB54Jskp3U3nAo8OUpWkwfXdG/+7wE3dnvgngY/0L0nSGHqFvap2ABuGKUXSmDyCTmqEYZcaYdilRhh2qRGGXWqEYZcaYdilRhh2qRGGXWqEYZcaYdilRhh2qRGGXWqEYZcaYdilRhh2qRGGXWqEYZcaYdilRhh2qRF9Gzv+fpJHkjyc5OYkbxmqMEnDmjrsSdYCvwdsqKrTgFXApqEKkzSsvi/jVwO/kGQ1kw6uz/UvSdIY+nSE2Q38KfA0sAd4paruHqowScPq8zJ+DbCRSTfX44HDk3x4iXE2dpTmQJ+X8b8J/EdVvVRVrwO3AecsHmRjR2k+9An708DZSQ5LEiaNHXcOU5akofV5z76NSZvm7cBD3e+6bqC6JA2sb2PHTwOfHqgWSSPyCDqpEYZdaoRhlxph2KVGGHapEYZdaoRhlxph2KVGGHapEYZdaoRhlxph2KVGGHapEYZdaoRhlxph2KVG9PryCs2PLc/tWOkSNOec2aVGGHapEYZdasR+w57ki0leTPLwgtuOTrI1yRPdzzXjlimprwOZ2f8WuGDRbZuBe6rqZOCe7rqkObbfsFfVvwAvL7p5I3Bjt3wj8IFhy5I0tGnfsx9bVXu65eeBYweqR9JIeu+gq6oCarn1NnaU5sO0YX8hyXEA3c8XlxtoY0dpPkwb9juAS7vlS4GvDFOOpLEcyEdvNwP/BpyS5NkkHwU+A/xWkieYtG7+zLhlSuprv8fGV9Uly6w6d+BaJI3II+ikRhh2qRGe4jpn1l77zanudxofH7iS/Zu2Vq0MZ3apEYZdaoRhlxph2KVGGHapEYZdaoRhlxph2KVGGHapEYZdaoRhlxph2KVGGHapEZ719ibR5wy0aZtCrsSZdgebeToz0JldaoRhlxph2KVGTNvY8bNJHkvyYJLbkxw1apWSepu2seNW4LSq+lXgceDqgeuSNLCpGjtW1d1V9UZ39V7ghBFqkzSgId6zXw7cNcDvkTSiXmFPcg3wBnDTPsbY2FGaA1OHPcllwEXAh7pOrkuysaM0H6Y6gi7JBcCngF+vqh8NW5KkMUzb2PGvgCOArUl2JPnCyHVK6mnaxo43jFCLpBF5BJ3UCMMuNcJTXMX5x58+1f3WMj+nb2r/nNmlRhh2qRGGXWqEYZcaYdilRhh2qRGGXWqEYZcaYdilRhh2qRGGXWqEYZcaYdilRhwUZ71N23hQ0v9xZpcaYdilRhh2qRFTNXZcsO6TSSrJMeOUJ2ko0zZ2JMk64Dzg6YFrkjSCqRo7dv6MSaOIZbvBSJofU71nT7IR2F1VDwxcj6SR/Myfsyc5DPhDJi/hD2T8FcAVAL+49qD4WF96U5pmZv9l4ETggSRPMenNvj3JO5cabGNHaT78zFNtVT0EvGPv9S7wG6rqewPWJWlg0zZ2lHSQmbax48L16werRtJoPIJOaoRhlxqRqtkdE5PkJeA/l1l9DDBPO/nmrR6Yv5qsZ99Wop5fqqq3L7VipmHflyT3VdWGla5jr3mrB+avJuvZt3mrx5fxUiMMu9SIeQr7dStdwCLzVg/MX03Ws29zVc/cvGeXNK55mtkljciwS42YediTXJDkO0l2Jdm8xPqfT/Klbv22JOtHrGVdkq8neTTJI0muXGLMe5O8kmRHd/mjsepZ8JhPJXmoe7z7llifJH/ZbaMHk5w5Yi2nLPi370jyapKrFo0ZdRst9dVoSY5OsjXJE93PNcvc99JuzBNJLh2xns8meax7Pm5PctQy993nczuqqprZBVgFfBc4CTgUeAA4ddGYjwNf6JY3AV8asZ7jgDO75SOAx5eo573AV2e8nZ4CjtnH+guBu4AAZwPbZvj8Pc/kwI2ZbSPgPcCZwMMLbvsTYHO3vBm4don7HQ082f1c0y2vGame84DV3fK1S9VzIM/tmJdZz+xnAbuq6smqeg24Bdi4aMxG4MZu+Vbg3CQZo5iq2lNV27vlHwA7gbVjPNbANgJ/VxP3AkclOW4Gj3su8N2qWu4oyFHU0l+NtvDv5EbgA0vc9Xxga1W9XFX/BWxlie9THKKeqrq7qt7ort7L5Hse5sqsw74WeGbB9Wf5/+H6yZhu470CvG3swrq3C2cA25ZY/a4kDyS5K8mvjF0Lk+/1uzvJ/d03/Sx2INtxDJuAm5dZN+ttdGxV7emWnweOXWLMSm2ny5m88lrK/p7b0fg9UUCStwJfBq6qqlcXrd7O5GXrD5NcCPwjcPLIJb27qnYneQewNclj3WyyYpIcClwMXL3E6pXYRj9RVZVkLj5DTnIN8AZw0zJDVuy5nfXMvhtYt+D6Cd1tS45Jsho4Evj+WAUlOYRJ0G+qqtsWr6+qV6vqh93yncAhY39PflXt7n6+CNzO5O3PQgeyHYf2PmB7Vb2weMVKbCPghb1vXbqfLy4xZqbbKcllwEXAh6p7g77YATy3o5l12L8NnJzkxG6m2ATcsWjMHcDevaYfBL623Ibrq9sXcAOws6o+t8yYd+7dZ5DkLCbbbMz/fA5PcsTeZSY7fhY36LgD+J1ur/zZwCsLXtKO5RKWeQk/623UWfh3cinwlSXGbAHOS7Km21t/Xnfb4JJcwOSr1S+uqh8tM+ZAntvxzHqPIJM9yY8z2St/TXfbHzPZSABvAf4B2AV8CzhpxFrezeQ91IPAju5yIfAx4GPdmE8AjzD55OBe4JyRt89J3WM90D3u3m20sKYAn++24UNMvgNwzJoOZxLeIxfcNrNtxOQ/mT3A60zed3+UyX6ce4AngH8Gju7GbgCuX3Dfy7u/pV3AR0asZxeT/QN7/472fqJ0PHDnvp7bWV08XFZqhEfQSY0w7FIjDLvUCMMuNcKwS40w7FIjDLvUiP8Fdo7ZRQMZNOAAAAAASUVORK5CYII=\n",
54 | "text/plain": [
55 | ""
56 | ]
57 | },
58 | "metadata": {
59 | "needs_background": "light"
60 | },
61 | "output_type": "display_data"
62 | },
63 | {
64 | "name": "stdout",
65 | "output_type": "stream",
66 | "text": [
67 | "if you want change environment, please input [ok] to start changingok\n",
68 | "please input ix number (Type: Int) in [0, 15):12\n",
69 | "please input iy number (Type: Int) in [0, 15):7\n",
70 | "change [ix: 12, iy: 7] from obs to free\n",
71 | "if you want change environment, please input [ok] to start changingstop\n",
72 | "changed map: 0.0\n",
73 | "[85.35533905932738, 60.35533905932738] [85.35533905932738, 85.35533905932738]\n",
74 | "find a path.\n",
75 | "one iter planning timecost: 0.00032711029052734375\n"
76 | ]
77 | },
78 | {
79 | "data": {
80 | "image/png": "iVBORw0KGgoAAAANSUhEUgAAAPsAAAD4CAYAAAAq5pAIAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjUuMSwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy/YYfK9AAAACXBIWXMAAAsTAAALEwEAmpwYAAAMpElEQVR4nO3db6xkdX3H8fenC9SCRBZRhGXbhYaQUNII2RCkxprSAiJhfeCDJdqCmBBjbKEx0aUkNekjqY39k5oaArY0JWCKUImBLlvUNI0Fhe3yH2GlFFiWP0oDWh/A2m8fzFlzvZ27rHPOmTvL7/1KJvfMnN/c+e6Z+9nfzJlz5puqQtIb3y+sdgGS5sOwS40w7FIjDLvUCMMuNeKgeT7YUUeuqQ3rD57nQ0pNefLp1/j+Sz/JtHVzDfuG9Qfz7a3r5/mQUlNOP+fpFdf5Ml5qhGGXGtEr7EnOTfLdJDuTbBmqKEnDmznsSdYAXwDeB5wMXJjk5KEKkzSsPjP76cDOqnqiql4FbgQ2DVOWpKH1Cfs6YOmuv2e62yQtoNF30CW5NMk9Se558Qc/GfvhJK2gT9h3AUs/ND+uu+1nVNXVVbWxqja+7a1rejycpD76hP07wIlJjk9yCLAZuHWYsiQNbeYj6KpqT5JPAFuBNcCXquqhwSqTNKheh8tW1W3AbQPVImlEHkEnNcKwS42Y61lvszrn2HeudgnSXG19dsfgv9OZXWqEYZcaYdilRhh2qRGGXWqEYZcaYdilRhh2qRGGXWqEYZcaYdilRhh2qRGGXWrEAXHWWx+7Pn3mzPddd9W3BqxEWl3O7FIjDLvUCMMuNaJPr7f1Sb6R5OEkDyW5bMjCJA2rzw66PcAnq2p7ksOBe5Nsq6qHB6pN0oBmntmrandVbe+Wfwg8gr3epIU1yHv2JBuAU4G7h/h9kobXO+xJ3gx8Bbi8ql6Zst7GjtIC6BX2JAczCfr1VXXztDE2dpQWQ5+98QGuBR6pqs8PV5KkMfSZ2X8D+F3gt5Ls6C7nDVSXpIH16eL6b0AGrEXSiDyCTmqEYZca8YY/xbXPaaqznh7rqbFaRM7sUiMMu9QIwy41wrBLjTDsUiMMu9QIwy41wrBLjTDsUiMMu9QIwy41wrBLjTDsUiPe8Ge99THr2Ws2k9QicmaXGmHYpUYYdqkRQzSJWJPkP5J8bYiCJI1jiJn9MiZ93iQtsL4dYY4D3g9cM0w5ksbSd2b/C+BTwP/2L0XSmPq0fzofeKGq7n2dcTZ2lBZA3/ZPFyR5EriRSRuof1g+yMaO0mKYOexVdUVVHVdVG4DNwNer6sODVSZpUH7OLjVikGPjq+qbwDeH+F2SxuHMLjXCsEuN8BTXEdhMUovImV1qhGGXGmHYpUYYdqkRhl1qhGGXGmHYpUYYdqkRhl1qhGGXGmHYpUYYdqkRhl1qhGe96YCy9dkdM9/3nGPfOVgdByJndqkRhl1qhGGXGtG3/dMRSW5K8miSR5K8a6jCJA2r7w66vwT+uao+mOQQ4NABapI0gpnDnuQtwHuAiwGq6lXg1WHKkjS0Pi/jjwdeBP62689+TZLDBqpL0sD6hP0g4DTgb6rqVOB/gC3LB9nYUVoMfcL+DPBMVd3dXb+JSfh/ho0dpcXQp7Hjc8DTSU7qbjoLeHiQqiQNru/e+N8Hru/2xD8BfKR/SZLG0CvsVbUD2DhMKZLG5BF0UiMMu9QIwy41wrBLjTDsUiMMu9QIwy41wrBLjTDsUiMMu9QIwy41wrBLjTDsUiMMu9QIwy41wrBLjTDsUiMMu9QIwy41wrBLjejb2PEPkzyU5MEkNyR501CFSRrWzGFPsg74A2BjVZ0CrAE2D1WYpGH1fRl/EPBLSQ5i0sH12f4lSRpDn44wu4A/A54CdgMvV9UdQxUmaVh9XsavBTYx6eZ6LHBYkg9PGWdjR2kB9HkZ/9vAf1bVi1X1GnAzcObyQTZ2lBZDn7A/BZyR5NAkYdLY8ZFhypI0tD7v2e9m0qZ5O/BA97uuHqguSQPr29jxM8BnBqpF0og8gk5qhGGXGmHYpUYYdqkRhl1qhGGXGmHYpUYYdqkRhl1qhGGXGmHYpUYYdqkRhl1qhGGXGmHYpUYYdqkRvb68Qotj67M7VrsELThndqkRhl1qhGGXGvG6YU/ypSQvJHlwyW1HJtmW5PHu59pxy5TU1/7M7H8HnLvsti3AnVV1InBnd13SAnvdsFfVvwIvLbt5E3Bdt3wd8IFhy5I0tFnfsx9dVbu75eeAoweqR9JIeu+gq6oCaqX1NnaUFsOsYX8+yTEA3c8XVhpoY0dpMcwa9luBi7rli4CvDlOOpLHsz0dvNwD/DpyU5JkkHwU+C/xOkseZtG7+7LhlSurrdY+Nr6oLV1h11sC1SBqRR9BJjTDsUiM8xXXBrLvqWzPd7xQ+PvfH1IHFmV1qhGGXGmHYpUYYdqkRhl1qhGGXGmHYpUYYdqkRhl1qhGGXGmHYpUYYdqkRhl1qhGe9vUH0OXNt16fPHLASLbVIZxQ6s0uNMOxSIwy71IhZGzt+LsmjSe5PckuSI0atUlJvszZ23AacUlW/DjwGXDFwXZIGNlNjx6q6o6r2dFfvAo4boTZJAxriPfslwO0D/B5JI+oV9iRXAnuA6/cxxsaO0gKYOexJLgbOBz7UdXKdysaO0mKY6Qi6JOcCnwJ+s6p+PGxJksYwa2PHvwYOB7Yl2ZHkiyPXKamnWRs7XjtCLZJG5BF0UiMMu9QIT3HVQp2GqfE4s0uNMOxSIwy71AjDLjXCsEuNMOxSIwy71AjDLjXCsEuNMOxSIwy71AjDLjXCsEuNOCDOetv67I7VLkE64DmzS40w7FIjDLvUiJkaOy5Z98kkleSoccqTNJRZGzuSZD1wNvDUwDVJGsFMjR07f86kUcSK3WAkLY6Z3rMn2QTsqqr7Bq5H0kh+7s/ZkxwK/BGTl/D7M/5S4FKAX153QHysL70hzTKz/ypwPHBfkieZ9GbfnuQd0wbb2FFaDD/3VFtVDwBv33u9C/zGqvr+gHVJGtisjR0lHWBmbey4dP2GwaqRNBqPoJMaYdilRqRqfsfEJHkR+K8VVh8FLNJOvkWrBxavJuvZt9Wo51eq6m3TVsw17PuS5J6q2rjadey1aPXA4tVkPfu2aPX4Ml5qhGGXGrFIYb96tQtYZtHqgcWryXr2baHqWZj37JLGtUgzu6QRGXapEXMPe5Jzk3w3yc4kW6as/8UkX+7W351kw4i1rE/yjSQPJ3koyWVTxrw3yctJdnSXPx6rniWP+WSSB7rHu2fK+iT5q24b3Z/ktBFrOWnJv31HkleSXL5szKjbaNpXoyU5Msm2JI93P9eucN+LujGPJ7loxHo+l+TR7vm4JckRK9x3n8/tqKpqbhdgDfA94ATgEOA+4ORlYz4OfLFb3gx8ecR6jgFO65YPBx6bUs97ga/NeTs9CRy1j/XnAbcDAc4A7p7j8/cckwM35raNgPcApwEPLrntT4Et3fIW4Kop9zsSeKL7ubZbXjtSPWcDB3XLV02rZ3+e2zEv857ZTwd2VtUTVfUqcCOwadmYTcB13fJNwFlJMkYxVbW7qrZ3yz8EHgHWjfFYA9sE/H1N3AUckeSYOTzuWcD3qmqloyBHUdO/Gm3p38l1wAem3PUcYFtVvVRV/w1sY8r3KQ5RT1XdUVV7uqt3Mfmeh4Uy77CvA55ecv0Z/n+4fjqm23gvA28du7Du7cKpwN1TVr8ryX1Jbk/ya2PXwuR7/e5Icm/3TT/L7c92HMNm4IYV1s17Gx1dVbu75eeAo6eMWa3tdAmTV17TvN5zOxq/JwpI8mbgK8DlVfXKstXbmbxs/VGS84B/Ak4cuaR3V9WuJG8HtiV5tJtNVk2SQ4ALgCumrF6NbfRTVVVJFuIz5CRXAnuA61cYsmrP7bxn9l3A+iXXj+tumzomyUHAW4AfjFVQkoOZBP36qrp5+fqqeqWqftQt3wYcPPb35FfVru7nC8AtTN7+LLU/23Fo7wO2V9Xzy1esxjYCnt/71qX7+cKUMXPdTkkuBs4HPlTdG/Tl9uO5Hc28w/4d4MQkx3czxWbg1mVjbgX27jX9IPD1lTZcX92+gGuBR6rq8yuMecfefQZJTmeyzcb8z+ewJIfvXWay42d5g45bgd/r9sqfAby85CXtWC5khZfw895GnaV/JxcBX50yZitwdpK13d76s7vbBpfkXCZfrX5BVf14hTH789yOZ957BJnsSX6MyV75K7vb/oTJRgJ4E/CPwE7g28AJI9bybibvoe4HdnSX84CPAR/rxnwCeIjJJwd3AWeOvH1O6B7rvu5x926jpTUF+EK3DR9g8h2AY9Z0GJPwvmXJbXPbRkz+k9kNvMbkffdHmezHuRN4HPgX4Mhu7EbgmiX3vaT7W9oJfGTEenYy2T+w9+9o7ydKxwK37eu5ndfFw2WlRngEndQIwy41wrBLjTDsUiMMu9QIwy41wrBLjfg/xIfXzm2li8QAAAAASUVORK5CYII=\n",
81 | "text/plain": [
82 | ""
83 | ]
84 | },
85 | "metadata": {
86 | "needs_background": "light"
87 | },
88 | "output_type": "display_data"
89 | }
90 | ],
91 | "source": [
92 | "import heapq\n",
93 | "import math\n",
94 | "import matplotlib.pyplot as plt\n",
95 | "import numpy as np\n",
96 | "import math\n",
97 | "import matplotlib\n",
98 | "%matplotlib inline\n",
99 | "#set up matplotlib\n",
100 | "MAX_INT = 9999.0\n",
101 | "class GridMap:\n",
102 | " def __init__(self, ox, oy, resolution):\n",
103 | " self.min_x = None\n",
104 | " self.min_y = None\n",
105 | " self.max_x = None\n",
106 | " self.max_y = None\n",
107 | " self.x_width = None\n",
108 | " self.y_width = None\n",
109 | " self.obstacle_map = None\n",
110 | " \n",
111 | " self.resolution = resolution\n",
112 | " self.calc_obstacle_map(ox, oy)\n",
113 | " \n",
114 | " def calc_obstacle_map(self, ox, oy):\n",
115 | "\n",
116 | " self.min_x = round(min(ox))\n",
117 | " self.min_y = round(min(oy))\n",
118 | " self.max_x = round(max(ox))\n",
119 | " self.max_y = round(max(oy))\n",
120 | " print(\"min_x:\", self.min_x)\n",
121 | " print(\"min_y:\", self.min_y)\n",
122 | " print(\"max_x:\", self.max_x)\n",
123 | " print(\"max_y:\", self.max_y)\n",
124 | "\n",
125 | " self.x_width = round((self.max_x - self.min_x) / self.resolution)+1\n",
126 | " self.y_width = round((self.max_y - self.min_y) / self.resolution)+1\n",
127 | " print(\"x_width:\", self.x_width)\n",
128 | " print(\"y_width:\", self.y_width)\n",
129 | "\n",
130 | " # obstacle map generation\n",
131 | " self.obstacle_map = np.zeros((self.x_width, self.y_width))\n",
132 | " for x, y in zip(ox, oy):\n",
133 | " ix, iy = self.calc_xy_index(x, self.min_x), self.calc_xy_index(y, self.min_y)\n",
134 | " if 0<=ix= self.x_width or ix < 0 or iy >= self.y_width or iy < 0:\n",
150 | " return False \n",
151 | " return True\n",
152 | "\n",
153 | "sx = -5.0 # [m]\n",
154 | "sy = -5.0 # [m]\n",
155 | "gx = 50.0 # [m]\n",
156 | "gy = 50.0 # [m]\n",
157 | "grid_size = 5.0 # [m]\n",
158 | "robot_radius = 1.0 # [m]\n",
159 | "\n",
160 | "# set obstacle positions\n",
161 | "ox, oy = [], []\n",
162 | "for i in range(-10, 60):\n",
163 | " ox.append(i)\n",
164 | " oy.append(-10.0)\n",
165 | "for i in range(-10, 60):\n",
166 | " ox.append(60.0)\n",
167 | " oy.append(i)\n",
168 | "for i in range(-10, 61):\n",
169 | " ox.append(i)\n",
170 | " oy.append(60.0)\n",
171 | "for i in range(-10, 61):\n",
172 | " ox.append(-10.0)\n",
173 | " oy.append(i)\n",
174 | "# for i in range(-10, 40):\n",
175 | "# ox.append(20.0)\n",
176 | "# oy.append(i)\n",
177 | "for i in range(20, 40):\n",
178 | " ox.append(40.0)\n",
179 | " oy.append(60.0 - i) \n",
180 | " \n",
181 | "for i in range(20, 40):\n",
182 | " oy.append(40.0)\n",
183 | " ox.append(i) \n",
184 | "grid_map = GridMap(ox, oy, grid_size)\n",
185 | "\n",
186 | "\n",
187 | "class Node:\n",
188 | " def __init__(self, ix, iy, g=9999.0, rhs=9999.0, P=None):\n",
189 | " self.ix = ix\n",
190 | " self.iy = iy\n",
191 | " self.g = g\n",
192 | " self.rhs = rhs\n",
193 | " self.P = P\n",
194 | " \n",
195 | "action_set = {'UP':[0, 1], 'DOWN':[0, -1], 'LEFT':[-1, 0], 'RIGHT':[1, 0], 'UL':[-1, 1], 'UR':[1, 1], 'DL':[-1, -1], 'DR':[1, -1]}\n",
196 | "\n",
197 | "class LPAstar(object):\n",
198 | " def __init__(self, grid_map, start_node, end_node):\n",
199 | " self.grid_map = grid_map\n",
200 | " self.start_uid = self.grid_map.calc_unique_index(start_node.ix, start_node.iy)\n",
201 | " self.end_uid = self.grid_map.calc_unique_index(end_node.ix, end_node.iy)\n",
202 | " \n",
203 | " self.SPath = [] # 最优轨迹\n",
204 | " \n",
205 | " self.ANB = {} # all node buffer\n",
206 | " self.init_ANB()\n",
207 | " self.U = {}\n",
208 | " self.Qu = []\n",
209 | " self.ANB[self.start_uid] = start_node\n",
210 | " self.U[self.start_uid] = start_node\n",
211 | " heapq.heappush(self.Qu, (min(start_node.g, start_node.rhs)+self.get_heuristic(start_node), \n",
212 | " min(start_node.g, start_node.rhs),\n",
213 | " self.start_uid)) \n",
214 | " self.main()\n",
215 | " \n",
216 | " def init_ANB(self):\n",
217 | " for ix in range(self.grid_map.x_width):\n",
218 | " for iy in range(self.grid_map.y_width):\n",
219 | " self.ANB[self.grid_map.calc_unique_index(ix, iy)] = Node(ix, iy)\n",
220 | " \n",
221 | " def get_neighbors(self, current):\n",
222 | " for a in action_set:\n",
223 | " ix, iy = current.ix+action_set[a][0], current.iy+action_set[a][1]\n",
224 | " if self.grid_map.verify_node(ix, iy):\n",
225 | " cx1x2 = np.sqrt(action_set[a][0]*action_set[a][0]+action_set[a][1]*action_set[a][1])*self.grid_map.resolution\n",
226 | " if (abs(self.grid_map.obstacle_map[ix, iy]-10.0) < 0.01 or \n",
227 | " abs(self.grid_map.obstacle_map[current.ix, current.iy]-10.0) < 0.01):\n",
228 | " cx1x2 = MAX_INT \n",
229 | " yield (self.grid_map.calc_unique_index(ix, iy), cx1x2) \n",
230 | " \n",
231 | " def get_heuristic(self, node):\n",
232 | " dx = node.ix - self.ANB[self.end_uid].ix\n",
233 | " dy = node.iy - self.ANB[self.end_uid].iy\n",
234 | " return np.sqrt(dx*dx+dy*dy)*self.grid_map.resolution \n",
235 | " \n",
236 | " def calculatekey(self, node):\n",
237 | " return [min(node.g, node.rhs)+self.get_heuristic(node), min(node.g, node.rhs)]\n",
238 | " \n",
239 | " def calculate_rhs(self, node):\n",
240 | " node.rhs = MAX_INT\n",
241 | " for pre_uid, cx1x2 in self.get_neighbors(node):\n",
242 | " pre_node = self.ANB[pre_uid]\n",
243 | " if pre_node.g+cx1x2 < node.rhs:\n",
244 | " node.rhs = pre_node.g+cx1x2\n",
245 | " node.P = pre_uid\n",
246 | " return node\n",
247 | " \n",
248 | " def updatenode(self, node_uid):\n",
249 | " \n",
250 | " if node_uid != self.start_uid: # line 06\n",
251 | " self.ANB[node_uid] = self.calculate_rhs(self.ANB[node_uid])\n",
252 | " \n",
253 | " if node_uid in self.U: # line 07\n",
254 | " del self.U[node_uid]\n",
255 | " if abs(self.ANB[node_uid].g - self.ANB[node_uid].rhs) > 0.00001: # line 08\n",
256 | " self.U[node_uid] = self.ANB[node_uid]\n",
257 | " heapq.heappush(self.Qu, (min(self.ANB[node_uid].g, self.ANB[node_uid].rhs)+\n",
258 | " self.get_heuristic(self.ANB[node_uid]), \n",
259 | " min(self.ANB[node_uid].g, self.ANB[node_uid].rhs),\n",
260 | " node_uid)) \n",
261 | " \n",
262 | "\n",
263 | " def waitenvchange(self):\n",
264 | " change_ixiy = []\n",
265 | " while input(\"if you want change environment, please input [ok] to start changing\") == \"ok\":\n",
266 | " ix = int(input(\"please input ix number (Type: Int) in [0, \"+str(self.grid_map.x_width)+\"):\"))\n",
267 | " iy = int(input(\"please input iy number (Type: Int) in [0, \"+str(self.grid_map.y_width)+\"):\")) \n",
268 | " if ix >= 0 and ix < self.grid_map.x_width and iy >= 0 and iy current.rhs:\n",
299 | " self.ANB[c_id].g = current.rhs\n",
300 | " else:\n",
301 | " self.ANB[c_id].g = MAX_INT\n",
302 | " self.updatenode(c_id)\n",
303 | " \n",
304 | " for succ_uid, cx1x2 in self.get_neighbors(self.ANB[c_id]):\n",
305 | " self.updatenode(succ_uid) \n",
306 | " \n",
307 | " is_into_while = True\n",
308 | " while self.Qu[0][2] not in self.U: # 保证堆项元系的确在U列表中 \n",
309 | " k1, k2, c_id = heapq.heappop(self.Qu) \n",
310 | " \n",
311 | " if is_into_while: \n",
312 | " print(\"find a path.\")\n",
313 | " self.shortestpathfinder()\n",
314 | " \n",
315 | " def plot_result(self): \n",
316 | " for ix, iy in zip(self.SPath[0], self.SPath[1]):\n",
317 | " self.grid_map.obstacle_map[ix, iy] = 4 \n",
318 | " plt.imshow(self.grid_map.obstacle_map)\n",
319 | " plt.show()\n",
320 | " for ix, iy in zip(self.SPath[0], self.SPath[1]):\n",
321 | " self.grid_map.obstacle_map[ix, iy] = 0\n",
322 | " \n",
323 | " def is_node_on_optpath(self, node):\n",
324 | " for ix, iy in zip(self.SPath[0], self.SPath[1]):\n",
325 | " if ix == node.ix and iy == node.iy:\n",
326 | " return True\n",
327 | " return False\n",
328 | " \n",
329 | " \n",
330 | " def main(self):\n",
331 | " while True:\n",
332 | " import time\n",
333 | " t0 = time.time()\n",
334 | " self.computeshortestpath()\n",
335 | " print(\"one iter planning timecost:\", time.time()-t0)\n",
336 | " self.plot_result()\n",
337 | " change_ixiy = self.waitenvchange()\n",
338 | " \n",
339 | " for ix, iy in change_ixiy:\n",
340 | " print(\"changed map:\", self.grid_map.obstacle_map[ix, iy])\n",
341 | " change_index = self.grid_map.calc_unique_index(ix, iy)\n",
342 | " if ((abs(self.grid_map.obstacle_map[ix, iy] - 10.0) < 0.01 and \n",
343 | " self.is_node_on_optpath(self.ANB[change_index])) or \n",
344 | " (abs(self.grid_map.obstacle_map[ix, iy] - 10.0) > 0.01 and\n",
345 | " self.calculate_rhs(self.ANB[change_index]).rhs+self.get_heuristic(self.ANB[change_index]) < self.ANB[self.end_uid].g)):\n",
346 | " self.updatenode(change_index)\n",
347 | "# self.updatenode(change_index) # 如果使用定理一与定理二,则注释该行,并取消上面五行的注释 \n",
348 | " \n",
349 | " \n",
350 | "start_node = Node(2, 2, rhs=0.0)\n",
351 | "end_node = Node(12, 12)\n",
352 | "grid_map.obstacle_map[start_node.ix, start_node.iy] = 8\n",
353 | "grid_map.obstacle_map[end_node.ix, end_node.iy] = 3\n",
354 | "plt.imshow(grid_map.obstacle_map)\n",
355 | "planner = LPAstar(grid_map, start_node, end_node)"
356 | ]
357 | },
358 | {
359 | "cell_type": "code",
360 | "execution_count": null,
361 | "id": "70bb71d2",
362 | "metadata": {},
363 | "outputs": [],
364 | "source": []
365 | }
366 | ],
367 | "metadata": {
368 | "kernelspec": {
369 | "display_name": "Python 3 (ipykernel)",
370 | "language": "python",
371 | "name": "python3"
372 | },
373 | "language_info": {
374 | "codemirror_mode": {
375 | "name": "ipython",
376 | "version": 3
377 | },
378 | "file_extension": ".py",
379 | "mimetype": "text/x-python",
380 | "name": "python",
381 | "nbconvert_exporter": "python",
382 | "pygments_lexer": "ipython3",
383 | "version": "3.9.5"
384 | }
385 | },
386 | "nbformat": 4,
387 | "nbformat_minor": 5
388 | }
389 |
--------------------------------------------------------------------------------
/基于图搜索/Dijkstra.ipynb:
--------------------------------------------------------------------------------
1 | {
2 | "cells": [
3 | {
4 | "cell_type": "code",
5 | "execution_count": 6,
6 | "id": "59c4fb02",
7 | "metadata": {},
8 | "outputs": [],
9 | "source": [
10 | "import heapq\n",
11 | "import math\n",
12 | "\n",
13 | "\n",
14 | "class Edge:\n",
15 | " def __init__(self, source, destine, weight):\n",
16 | " self.weight = weight\n",
17 | " self.source = source\n",
18 | " self.destine = destine\n",
19 | "\n",
20 | "class Graph:\n",
21 | " def __init__(self):\n",
22 | " self.vertices = set([])\n",
23 | " self.adjacents = {}\n",
24 | " self.inf = 99999.\n",
25 | " \n",
26 | " def add_startnode(self, vertice):\n",
27 | " self.vertices.add(vertice)\n",
28 | " self.adjacents[vertice] = {}\n",
29 | "\n",
30 | " def add_edge(self, edge):\n",
31 | " self.vertices.add(edge.source)\n",
32 | " self.vertices.add(edge.destine)\n",
33 | " if edge.source not in self.adjacents.keys():\n",
34 | " self.adjacents[edge.source] = {}\n",
35 | " self.adjacents[edge.source][edge.destine] = edge.weight\n",
36 | " if edge.destine not in self.adjacents.keys():\n",
37 | " self.adjacents[edge.destine] = {}\n",
38 | " self.adjacents[edge.destine][edge.source] = edge.weight\n",
39 | " else:\n",
40 | " self.adjacents[edge.destine][edge.source] = edge.weight\n",
41 | " else:\n",
42 | " self.adjacents[edge.source][edge.destine] = edge.weight\n",
43 | " if edge.destine not in self.adjacents.keys():\n",
44 | " self.adjacents[edge.destine] = {}\n",
45 | " self.adjacents[edge.destine][edge.source] = edge.weight\n",
46 | " else:\n",
47 | " self.adjacents[edge.destine][edge.source] = edge.weight\n",
48 | " # print(\"add edge from {} to {}, weight {}\".format(edge.source, edge.destine, edge.weight))\n",
49 | "\n",
50 | " def delete_edge(self, source, destine):\n",
51 | " if source not in self.vertices or destine not in self.vertices:\n",
52 | " return False\n",
53 | " if destine in self.adjacents[source].keys():\n",
54 | " self.adjacents[source].pop(destine) \n",
55 | " \n",
56 | " if source in self.adjacents[destine].keys():\n",
57 | " self.adjacents[destine].pop(source) \n",
58 | "\n",
59 | " def get_adjacents(self, vertex):\n",
60 | " # print(\"get the adjacent vertices of vertex {}\".format(vertex))\n",
61 | " if vertex not in self.adjacents.keys():\n",
62 | " return set([])\n",
63 | " return self.adjacents[vertex]\n",
64 | "\n",
65 | " def vertex_number(self):\n",
66 | " return len(self.vertices)\n",
67 | " \n",
68 | " def printgraph(self):\n",
69 | " for d in self.adjacents.keys():\n",
70 | " print(\"%d :\"% d)\n",
71 | " for b in self.adjacents[d].keys():\n",
72 | " print(d, b, self.adjacents[d][b]) \n",
73 | " \n",
74 | " def get_adjacents(self):\n",
75 | " return self.adjacents\n",
76 | " \n",
77 | "class Node:\n",
78 | " def __init__(self, C=0.0, P=None):\n",
79 | " self.C = C\n",
80 | " self.P = P\n",
81 | " \n",
82 | "def Dijkstra(G, start):\n",
83 | " Closed_set, Open_set = {}, {}\n",
84 | " Open_set[start] = Node()\n",
85 | " Q = []\n",
86 | " heapq.heappush(Q, (0.0, start))\n",
87 | " while True:\n",
88 | " if not Open_set:\n",
89 | " print(\"Dijkstra Algorithm Finished.\")\n",
90 | " return Closed_set\n",
91 | " \n",
92 | " C, u = heapq.heappop(Q)\n",
93 | " if u in Open_set:\n",
94 | " current = Open_set.pop(u)\n",
95 | " Closed_set[u] = current\n",
96 | " else:\n",
97 | " continue\n",
98 | " \n",
99 | " for v in G.adjacents[u].keys():\n",
100 | " if v not in Closed_set:\n",
101 | " v_temp_C = C + G.adjacents[u][v]\n",
102 | " if v not in Open_set:\n",
103 | " Open_set[v] = Node(v_temp_C, u)\n",
104 | " heapq.heappush(Q, (v_temp_C, v))\n",
105 | " elif Open_set[v].C > C + G.adjacents[u][v]:\n",
106 | " Open_set[v].C = v_temp_C\n",
107 | " Open_set[v].P = u\n",
108 | " heapq.heappush(Q, (v_temp_C, v))\n",
109 | "\n",
110 | "def ShortestPathFinder(Closed_set, start, end):\n",
111 | " SPath = [end]\n",
112 | " SPath_dist = Closed_set[end].C\n",
113 | " v = Closed_set[end].P\n",
114 | " while v != None:\n",
115 | " SPath.append(v)\n",
116 | " v = Closed_set[v].P\n",
117 | "\n",
118 | " return list(reversed(SPath)), SPath_dist"
119 | ]
120 | },
121 | {
122 | "cell_type": "code",
123 | "execution_count": 9,
124 | "id": "5e788083",
125 | "metadata": {},
126 | "outputs": [
127 | {
128 | "name": "stdout",
129 | "output_type": "stream",
130 | "text": [
131 | "Dijkstra Algorithm Finished.\n",
132 | "CPU times: user 670 µs, sys: 76 µs, total: 746 µs\n",
133 | "Wall time: 610 µs\n",
134 | "([0, 1, 4, 8, 11, 12], 17.0)\n"
135 | ]
136 | }
137 | ],
138 | "source": [
139 | "G = Graph()\n",
140 | "gmat = {}\n",
141 | "gmat[0] = {1:4, 2:5}\n",
142 | "gmat[1] = {0:4, 3:2, 4:3, 5:6}\n",
143 | "gmat[2] = {0:5, 4:8, 5:7, 6:7}\n",
144 | "gmat[3] = {1:2, 7:5, 8:8}\n",
145 | "gmat[4] = {1:3, 2:8, 7:4, 8:5}\n",
146 | "gmat[5] = {1:6, 2:7, 8:3, 9:4}\n",
147 | "gmat[6] = {2:7, 8:8, 9:4}\n",
148 | "gmat[7] = {3:5, 4:4, 10:3, 11:5}\n",
149 | "gmat[8] = {3:8, 4:5, 5:4, 6:8, 10:6, 11:2}\n",
150 | "gmat[9] = {5:4, 6:4, 10:1, 11:3}\n",
151 | "gmat[10] = {7:3, 8:6, 9:1, 12:4}\n",
152 | "gmat[11] = {7:5, 8:2, 9:3, 12:3}\n",
153 | "gmat[12] = {10:4, 11:3}\n",
154 | "for key_i in gmat.keys():\n",
155 | " for key_j in gmat[key_i].keys():\n",
156 | " e = Edge(key_i, key_j, gmat[key_i][key_j])\n",
157 | " G.add_edge(e)\n",
158 | "\n",
159 | "%time Closed_set = Dijkstra(G, 0)\n",
160 | "print(ShortestPathFinder(Closed_set, 0, 12))"
161 | ]
162 | },
163 | {
164 | "cell_type": "code",
165 | "execution_count": 1,
166 | "id": "143d9078",
167 | "metadata": {},
168 | "outputs": [
169 | {
170 | "data": {
171 | "image/png": "iVBORw0KGgoAAAANSUhEUgAAAq4AAAKrCAYAAAAwMg+1AAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjUuMiwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy8qNh9FAAAACXBIWXMAAAsTAAALEwEAmpwYAAAYwElEQVR4nO3df6jl913n8dd757bo1GLbNFaTCZsgJUsoblsubbWsC021UUtjwT8attKuhewf/qhSKKmC/rcUFH+AogxtTMGQssQGi6hpqEpZqFmn6bTNj2pL7SaTpGaasCrmjzTxvX/co8xPZ3LPOXPyPvfxgOGe8z3n3u+bD8m9z/nM955T3R0AAHih+w+bHgAAAC6GcAUAYAThCgDACMIVAIARhCsAACPsXMqTvfIVh/rqq150KU8JAMAgX3/kW/nmU8/VuR67pOF69VUvyv+5+6pLeUoAAAZ5w9seOe9jLhUAAGAE4QoAwAjCFQCAEYQrAAAjCFcAAEYQrgAAjCBcAQAYQbgCADCCcAUAYAThCgDACMIVAIARhCsAACMIVwAARhCuAACMIFwBABhBuAIAMIJwBQBghKXCtapuqKq/qaqvVtUtqxoKAADOtO9wrapDSX4nyY8kuS7JTVV13aoGAwCAUy2z4/qGJF/t7q919zNJPp7kxtWMBQAAp1smXK9M8sgp908sjp2mqm6uqmNVdezkk88tcToAAA6ytf9yVncf7e7d7t69/LJD6z4dAABbaplwfTTJVafcP7I4BgAAK7dMuP51kldX1TVV9eIk70ryydWMBQAAp9vZ7yd297NV9TNJ7k5yKMmt3f3AyiYDAIBT7Dtck6S7/yTJn6xoFgAAOC/vnAUAwAjCFQCAEYQrAAAjCFcAAEYQrgAAjCBcAQAYQbgCADCCcAUAYAThCgDACMIVAIARhCsAACMIVwAARhCuAACMIFwBABhBuAIAMMLOpgd4oXrbFa/d9AgAACtx92PHNz3CSthxBQBgBOEKAMAIwhUAgBGEKwAAIwhXAABGEK4AAIwgXAEAGEG4AgAwgnAFAGAE4QoAwAjCFQCAEYQrAAAjCFcAAEYQrgAAjCBcAQAYQbgCADCCcAUAYAThCgDACMIVAIARhCsAACMIVwAARhCuAACMIFwBABhBuAIAMIJwBQBgBOEKAMAIwhUAgBGEKwAAIwhXAABGEK4AAIwgXAEAGEG4AgAwgnAFAGAE4QoAwAjCFQCAEYQrAAAjCFcAAEYQrgAAjCBcAQAYQbgCADCCcAUAYAThCgDACMIVAIARdjY9AKvx9DvfuOkRLtrhu+7d9AgAwEB2XAEAGEG4AgAwgnAFAGAE4QoAwAjCFQCAEYQrAAAjCFcAAEYQrgAAjCBcAQAYQbgCADCCcAUAYAThCgDACMIVAIARhCsAACMIVwAARhCuAACMIFwBABhBuAIAMMK+w7Wqrqqqv6iqB6vqgap6/yoHAwCAU+0s8bnPJvlAd99XVS9N8rmquqe7H1zRbAAA8G/2vePa3Y93932L2/+U5KEkV65qMAAAONVKrnGtqquTvC7Jved47OaqOlZVx04++dwqTgcAwAG0dLhW1Xck+cMkP9/d/3jm4919tLt3u3v38ssOLXs6AAAOqKXCtapelL1ovb27P7GakQAA4GzLvKpAJflokoe6+9dXNxIAAJxtmR3XNyf5ySRvqarjiz8/uqK5AADgNPt+Oazu/t9JaoWzAADAeXnnLAAARhCuAACMIFwBABhBuAIAMIJwBQBgBOEKAMAIwhUAgBGEKwAAIwhXAABGEK4AAIwgXAEAGEG4AgAwgnAFAGAE4QoAwAjCFQCAEYQrAAAjCFcAAEYQrgAAjCBcAQAYQbgCADCCcAUAYAThCgDACMIVAIARhCsAACMIVwAARhCuAACMIFwBABhBuAIAMIJwBQBgBOEKAMAIwhUAgBGEKwAAIwhXAABGEK4AAIwgXAEAGEG4AgAwgnAFAGAE4QoAwAjCFQCAEYQrAAAjCFcAAEYQrgAAjCBcAQAYQbgCADCCcAUAYAThCgDACMIVAIARhCsAACMIVwAARhCuAACMIFwBABhBuAIAMIJwBQBgBOEKAMAIwhUAgBGEKwAAIwhXAABGEK4AAIwgXAEAGEG4AgAwgnAFAGAE4QoAwAjCFQCAEYQrAAAjCFcAAEYQrgAAjCBcAQAYQbgCADCCcAUAYAThCgDACMIVAIARhCsAACMIVwAARhCuAACMIFwBABhBuAIAMIJwBQBgBOEKAMAIS4drVR2qqs9X1R+vYiAAADiXVey4vj/JQyv4OgAAcF5LhWtVHUnyY0k+sppxAADg3Jbdcf3NJB9M8i/ne0JV3VxVx6rq2Mknn1vydAAAHFT7DteqenuSJ7r7c//e87r7aHfvdvfu5Zcd2u/pAAA44JbZcX1zkndU1deTfDzJW6rqD1YyFQAAnGHf4drdH+ruI919dZJ3Jfnz7n73yiYDAIBTeB1XAABG2FnFF+nuv0zyl6v4WgAAcC52XAEAGEG4AgAwgnAFAGAE4QoAwAjCFQCAEYQrAAAjCFcAAEYQrgAAjCBcAQAYQbgCADCCcAUAYAThCgDACMIVAIARhCsAACMIVwAARhCuAACMsLPpATh4nn7nGzc9AgAvQIfvunfTI/ACZ8cVAIARhCsAACMIVwAARhCuAACMIFwBABhBuAIAMIJwBQBgBOEKAMAIwhUAgBGEKwAAIwhXAABGEK4AAIwgXAEAGEG4AgAwgnAFAGAE4QoAwAjCFQCAEYQrAAAjCFcAAEYQrgAAjCBcAQAYQbgCADCCcAUAYAThCgDACMIVAIARhCsAACMIVwAARhCuAACMIFwBABhBuAIAMIJwBQBgBOEKAMAIwhUAgBGEKwAAIwhXAABGEK4AAIwgXAEAGEG4AgAwgnAFAGAE4QoAwAjCFQCAEYQrAAAj7Gx6gBequx87vukRnqfjmx4AgBeg//LT/2PTI8DK2HEFAGAE4QoAwAjCFQCAEYQrAAAjCFcAAEYQrgAAjCBcAQAYQbgCADCCcAUAYAThCgDACMIVAIARhCsAACMIVwAARhCuAACMIFwBABhBuAIAMIJwBQBgBOEKAMAIS4VrVb2squ6sqi9X1UNV9f2rGgwAAE61s+Tn/1aSP+vun6iqFyc5vIKZAADgLPsO16r6ziQ/mOS9SdLdzyR5ZjVjAQDA6Za5VOCaJCeT/H5Vfb6qPlJVLznzSVV1c1Udq6pjJ598bonTAQBwkC0TrjtJXp/kd7v7dUn+OcktZz6pu4929253715+2aElTgcAwEG2TLieSHKiu+9d3L8zeyELAAArt+9w7e5vJHmkqq5dHLo+yYMrmQoAAM6w7KsK/GyS2xevKPC1JP99+ZEAAOBsS4Vrdx9PsruaUQAA4Py8cxYAACMIVwAARhCuAACMIFwBABhBuAIAMIJwBQBgBOEKAMAIwhUAgBGEKwAAIwhXAABGEK4AAIwgXAEAGEG4AgAwgnAFAGAE4QoAwAjCFQCAEXY2PcAL1duueO2mR4B9efqdb9z0CACwFnZcAQAYQbgCADCCcAUAYAThCgDACMIVAIARhCsAACMIVwAARhCuAACMIFwBABhBuAIAMIJwBQBgBOEKAMAIwhUAgBGEKwAAIwhXAABGEK4AAIwgXAEAGEG4AgAwgnAFAGAE4QoAwAjCFQCAEYQrAAAjCFcAAEYQrgAAjCBcAQAYQbgCADCCcAUAYAThCgDACMIVAIARhCsAACMIVwAARhCuAACMIFwBABhBuAIAMIJwBQBgBOEKAMAIwhUAgBGEKwAAIwhXAABGEK4AAIwgXAEAGEG4AgAwws6mBwAOrsN33bvpEQAYxI4rAAAjCFcAAEYQrgAAjCBcAQAYQbgCADCCcAUAYAThCgDACMIVAIARhCsAACMIVwAARhCuAACMIFwBABhBuAIAMIJwBQBgBOEKAMAIwhUAgBGEKwAAIwhXAABGWCpcq+oXquqBqrq/qu6oqm9b1WAAAHCqfYdrVV2Z5OeS7Hb3a5IcSvKuVQ0GAACnWvZSgZ0k315VO0kOJ3ls+ZEAAOBs+w7X7n40ya8leTjJ40n+obs/debzqurmqjpWVcdOPvnc/icFAOBAW+ZSgZcnuTHJNUmuSPKSqnr3mc/r7qPdvdvdu5dfdmj/kwIAcKAtc6nAW5P8XXef7O5vJflEkh9YzVgAAHC6ZcL14SRvqqrDVVVJrk/y0GrGAgCA0y1zjeu9Se5Mcl+SLy2+1tEVzQUAAKfZWeaTu/tXkvzKimYBAIDz8s5ZAACMIFwBABhBuAIAMIJwBQBgBOEKAMAIwhUAgBGEKwAAIwhXAABGEK4AAIwgXAEAGEG4AgAwgnAFAGAE4QoAwAjCFQCAEYQrAAAjCFcAAEYQrgAAjCBcAQAYQbgCADCCcAUAYAThCgDACMIVAIARhCsAACMIVwAARhCuAACMIFwBABhBuAIAMIJwBQBgBOEKAMAIwhUAgBGEKwAAIwhXAABGEK4AAIwgXAEAGEG4AgAwgnAFAGAE4QoAwAjCFQCAEYQrAAAjCFcAAEYQrgAAjCBcAQAYQbgCADCCcAUAYAThCgDACMIVAIARhCsAACMIVwAARhCuAACMIFwBABhBuAIAMIJwBQBgBOEKAMAIwhUAgBGEKwAAIwhXAABGEK4AAIwgXAEAGEG4AgAwws6mBwAOrrsfO77pEQAYxI4rAAAjCFcAAEYQrgAAjCBcAQAYQbgCADCCcAUAYAThCgDACMIVAIARhCsAACMIVwAARhCuAACMIFwBABhBuAIAMIJwBQBgBOEKAMAIwhUAgBGEKwAAIwhXAABGuGC4VtWtVfVEVd1/yrFXVNU9VfWVxceXr3dMAAAOuovZcb0tyQ1nHLslyae7+9VJPr24DwAAa3PBcO3uzyR56ozDNyb52OL2x5L8+GrHAgCA0+33GtdXdffji9vfSPKq8z2xqm6uqmNVdezkk8/t83QAABx0S/9yVnd3kv53Hj/a3bvdvXv5ZYeWPR0AAAfUfsP176vqe5Jk8fGJ1Y0EAABn22+4fjLJexa335Pkj1YzDgAAnNvFvBzWHUk+m+TaqjpRVe9L8uEkP1RVX0ny1sV9AABYm50LPaG7bzrPQ9eveBYAADgv75wFAMAIwhUAgBGEKwAAIwhXAABGEK4AAIwgXAEAGEG4AgAwgnAFAGAE4QoAwAjCFQCAEYQrAAAjCFcAAEYQrgAAjCBcAQAYQbgCADCCcAUAYISdTQ8AHFxvu+K1mx4B4EC4+7Hjmx5hJey4AgAwgnAFAGAE4QoAwAjCFQCAEYQrAAAjCFcAAEYQrgAAjCBcAQAYQbgCADCCcAUAYAThCgDACMIVAIARhCsAACMIVwAARhCuAACMIFwBABhBuAIAMIJwBQBgBOEKAMAIwhUAgBGEKwAAIwhXAABGEK4AAIwgXAEAGEG4AgAwgnAFAGAE4QoAwAjCFQCAEYQrAAAjCFcAAEYQrgAAjCBcAQAYQbgCADCCcAUAYAThCgDACMIVAIARhCsAACMIVwAARhCuAACMIFwBABhBuAIAMIJwBQBghJ1NDwAcXE+/842bHgFg3w7fde+mRzhw7LgCADCCcAUAYAThCgDACMIVAIARhCsAACMIVwAARhCuAACMIFwBABhBuAIAMIJwBQBgBOEKAMAIwhUAgBGEKwAAIwhXAABGEK4AAIwgXAEAGEG4AgAwgnAFAGCEC4ZrVd1aVU9U1f2nHPvVqvpyVX2xqu6qqpetdUoAAA68i9lxvS3JDWccuyfJa7r7+5L8bZIPrXguAAA4zQXDtbs/k+SpM459qrufXdz9qyRH1jAbAAD8m1Vc4/pTSf70fA9W1c1Vdayqjp188rkVnA4AgINoqXCtql9K8myS28/3nO4+2t273b17+WWHljkdAAAH2M5+P7Gq3pvk7Umu7+5e2UQAAHAO+wrXqrohyQeT/Nfufnq1IwEAwNku5uWw7kjy2STXVtWJqnpfkt9O8tIk91TV8ar6vTXPCQDAAXfBHdfuvukchz+6hlkAAOC8vHMWAAAjCFcAAEYQrgAAjCBcAQAYQbgCADCCcAUAYAThCgDACMIVAIARhCsAACMIVwAARhCuAACMIFwBABhBuAIAMIJwBQBgBOEKAMAIwhUAgBF2Nj0AsFqH77p30yMAwFrYcQUAYAThCgDACMIVAIARhCsAACMIVwAARhCuAACMIFwBABhBuAIAMIJwBQBgBOEKAMAIwhUAgBGEKwAAIwhXAABGEK4AAIwgXAEAGEG4AgAwgnAFAGAE4QoAwAjCFQCAEYQrAAAjCFcAAEYQrgAAjCBcAQAYQbgCADCCcAUAYAThCgDACMIVAIARhCsAACMIVwAARhCuAACMIFwBABhBuAIAMIJwBQBgBOEKAMAIwhUAgBGEKwAAIwhXAABGEK4AAIwgXAEAGEG4AgAwgnAFAGAE4QoAwAg7mx7gherux45vegQAAE5hxxUAgBGEKwAAIwhXAABGEK4AAIwgXAEAGEG4AgAwgnAFAGAE4QoAwAjCFQCAEYQrAAAjCFcAAEYQrgAAjCBcAQAYQbgCADCCcAUAYAThCgDACMIVAIARhCsAACNcMFyr6taqeqKq7j/HYx+oqq6qV65nPAAA2HMxO663JbnhzINVdVWSH07y8IpnAgCAs1wwXLv7M0meOsdDv5Hkg0l61UMBAMCZ9nWNa1XdmOTR7v7CRTz35qo6VlXHTj753H5OBwAAzz9cq+pwkl9M8ssX8/zuPtrdu929e/llh57v6QAAIMn+dly/N8k1Sb5QVV9PciTJfVX13ascDAAATrXzfD+hu7+U5Lv+9f4iXne7+5srnAsAAE5zMS+HdUeSzya5tqpOVNX71j8WAACc7oI7rt190wUev3pl0wAAwHl45ywAAEYQrgAAjCBcAQAYQbgCADCCcAUAYAThCgDACMIVAIARhCsAACMIVwAARhCuAACMIFwBABhBuAIAMIJwBQBgBOEKAMAIwhUAgBGEKwAAI1R3X7qTVZ1M8n/X8KVfmeSba/i6WNt1srbrY23Xx9quj7VdH2u7PutY2//Y3Zef64FLGq7rUlXHunt303NsI2u7PtZ2fazt+ljb9bG262Nt1+dSr61LBQAAGEG4AgAwwraE69FND7DFrO36WNv1sbbrY23Xx9quj7Vdn0u6tltxjSsAANtvW3ZcAQDYcsIVAIARRodrVd1QVX9TVV+tqls2Pc+2qKqrquovqurBqnqgqt6/6Zm2TVUdqqrPV9Ufb3qWbVJVL6uqO6vqy1X1UFV9/6Zn2hZV9QuL7wf3V9UdVfVtm55pqqq6taqeqKr7Tzn2iqq6p6q+svj48k3OONV51vZXF98TvlhVd1XVyzY44ljnWttTHvtAVXVVvXLdc4wN16o6lOR3kvxIkuuS3FRV1212qq3xbJIPdPd1Sd6U5Ket7cq9P8lDmx5iC/1Wkj/r7v+U5D/HGq9EVV2Z5OeS7Hb3a5IcSvKuzU412m1Jbjjj2C1JPt3dr07y6cV9nr/bcvba3pPkNd39fUn+NsmHLvVQW+K2nL22qaqrkvxwkocvxRBjwzXJG5J8tbu/1t3PJPl4khs3PNNW6O7Hu/u+xe1/yt4P/ys3O9X2qKojSX4syUc2Pcs2qarvTPKDST6aJN39THf/v40OtV12knx7Ve0kOZzksQ3PM1Z3fybJU2ccvjHJxxa3P5bkxy/lTNviXGvb3Z/q7mcXd/8qyZFLPtgWOM9/t0nyG0k+mOSS/Lb/5HC9Mskjp9w/EXG1clV1dZLXJbl3w6Nsk9/M3v/k/7LhObbNNUlOJvn9xWUYH6mql2x6qG3Q3Y8m+bXs7ag8nuQfuvtTm51q67yqux9f3P5Gkldtcpgt9lNJ/nTTQ2yLqroxyaPd/YVLdc7J4cqaVdV3JPnDJD/f3f+46Xm2QVW9PckT3f25Tc+yhXaSvD7J73b365L8c/xz60osrre8MXt/ObgiyUuq6t2bnWp79d7rVHqtyhWrql/K3qVwt296lm1QVYeT/GKSX76U550cro8mueqU+0cWx1iBqnpR9qL19u7+xKbn2SJvTvKOqvp69i5veUtV/cFmR9oaJ5Kc6O5//deBO7MXsizvrUn+rrtPdve3knwiyQ9seKZt8/dV9T1Jsvj4xIbn2SpV9d4kb0/y39oL2K/K92bvL7NfWPxMO5Lkvqr67nWedHK4/nWSV1fVNVX14uz9osAnNzzTVqiqyt51gg91969vep5t0t0f6u4j3X119v6b/fPutnO1At39jSSPVNW1i0PXJ3lwgyNtk4eTvKmqDi++P1wfv/i2ap9M8p7F7fck+aMNzrJVquqG7F2e9Y7ufnrT82yL7v5Sd39Xd1+9+Jl2IsnrF9+L12ZsuC4utP6ZJHdn7xvo/+ruBzY71dZ4c5KfzN5u4PHFnx/d9FBwEX42ye1V9cUkr03yPzc7znZY7GLfmeS+JF/K3s8Ob6G5T1V1R5LPJrm2qk5U1fuSfDjJD1XVV7K3w/3hTc441XnW9reTvDTJPYufZ7+30SGHOs/aXvo57JgDADDB2B1XAAAOFuEKAMAIwhUAgBGEKwAAIwhXAABGEK4AAIwgXAEAGOH/A89DW9jQzVAiAAAAAElFTkSuQmCC\n",
172 | "text/plain": [
173 | ""
174 | ]
175 | },
176 | "metadata": {},
177 | "output_type": "display_data"
178 | },
179 | {
180 | "data": {
181 | "image/png": "iVBORw0KGgoAAAANSUhEUgAAAq4AAAKrCAYAAAAwMg+1AAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjUuMiwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy8qNh9FAAAACXBIWXMAAAsTAAALEwEAmpwYAAAYwElEQVR4nO3df6jl913n8dd757bo1GLbNFaTCZsgJUsoblsubbWsC021UUtjwT8attKuhewf/qhSKKmC/rcUFH+AogxtTMGQssQGi6hpqEpZqFmn6bTNj2pL7SaTpGaasCrmjzTxvX/co8xPZ3LPOXPyPvfxgOGe8z3n3u+bD8m9z/nM955T3R0AAHih+w+bHgAAAC6GcAUAYAThCgDACMIVAIARhCsAACPsXMqTvfIVh/rqq150KU8JAMAgX3/kW/nmU8/VuR67pOF69VUvyv+5+6pLeUoAAAZ5w9seOe9jLhUAAGAE4QoAwAjCFQCAEYQrAAAjCFcAAEYQrgAAjCBcAQAYQbgCADCCcAUAYAThCgDACMIVAIARhCsAACMIVwAARhCuAACMIFwBABhBuAIAMIJwBQBghKXCtapuqKq/qaqvVtUtqxoKAADOtO9wrapDSX4nyY8kuS7JTVV13aoGAwCAUy2z4/qGJF/t7q919zNJPp7kxtWMBQAAp1smXK9M8sgp908sjp2mqm6uqmNVdezkk88tcToAAA6ytf9yVncf7e7d7t69/LJD6z4dAABbaplwfTTJVafcP7I4BgAAK7dMuP51kldX1TVV9eIk70ryydWMBQAAp9vZ7yd297NV9TNJ7k5yKMmt3f3AyiYDAIBT7Dtck6S7/yTJn6xoFgAAOC/vnAUAwAjCFQCAEYQrAAAjCFcAAEYQrgAAjCBcAQAYQbgCADCCcAUAYAThCgDACMIVAIARhCsAACMIVwAARhCuAACMIFwBABhBuAIAMMLOpgd4oXrbFa/d9AgAACtx92PHNz3CSthxBQBgBOEKAMAIwhUAgBGEKwAAIwhXAABGEK4AAIwgXAEAGEG4AgAwgnAFAGAE4QoAwAjCFQCAEYQrAAAjCFcAAEYQrgAAjCBcAQAYQbgCADCCcAUAYAThCgDACMIVAIARhCsAACMIVwAARhCuAACMIFwBABhBuAIAMIJwBQBgBOEKAMAIwhUAgBGEKwAAIwhXAABGEK4AAIwgXAEAGEG4AgAwgnAFAGAE4QoAwAjCFQCAEYQrAAAjCFcAAEYQrgAAjCBcAQAYQbgCADCCcAUAYAThCgDACMIVAIARdjY9AKvx9DvfuOkRLtrhu+7d9AgAwEB2XAEAGEG4AgAwgnAFAGAE4QoAwAjCFQCAEYQrAAAjCFcAAEYQrgAAjCBcAQAYQbgCADCCcAUAYAThCgDACMIVAIARhCsAACMIVwAARhCuAACMIFwBABhBuAIAMMK+w7Wqrqqqv6iqB6vqgap6/yoHAwCAU+0s8bnPJvlAd99XVS9N8rmquqe7H1zRbAAA8G/2vePa3Y93932L2/+U5KEkV65qMAAAONVKrnGtqquTvC7Jved47OaqOlZVx04++dwqTgcAwAG0dLhW1Xck+cMkP9/d/3jm4919tLt3u3v38ssOLXs6AAAOqKXCtapelL1ovb27P7GakQAA4GzLvKpAJflokoe6+9dXNxIAAJxtmR3XNyf5ySRvqarjiz8/uqK5AADgNPt+Oazu/t9JaoWzAADAeXnnLAAARhCuAACMIFwBABhBuAIAMIJwBQBgBOEKAMAIwhUAgBGEKwAAIwhXAABGEK4AAIwgXAEAGEG4AgAwgnAFAGAE4QoAwAjCFQCAEYQrAAAjCFcAAEYQrgAAjCBcAQAYQbgCADCCcAUAYAThCgDACMIVAIARhCsAACMIVwAARhCuAACMIFwBABhBuAIAMIJwBQBgBOEKAMAIwhUAgBGEKwAAIwhXAABGEK4AAIwgXAEAGEG4AgAwgnAFAGAE4QoAwAjCFQCAEYQrAAAjCFcAAEYQrgAAjCBcAQAYQbgCADCCcAUAYAThCgDACMIVAIARhCsAACMIVwAARhCuAACMIFwBABhBuAIAMIJwBQBgBOEKAMAIwhUAgBGEKwAAIwhXAABGEK4AAIwgXAEAGEG4AgAwgnAFAGAE4QoAwAjCFQCAEYQrAAAjCFcAAEYQrgAAjCBcAQAYQbgCADCCcAUAYAThCgDACMIVAIARhCsAACMIVwAARhCuAACMIFwBABhBuAIAMIJwBQBgBOEKAMAIS4drVR2qqs9X1R+vYiAAADiXVey4vj/JQyv4OgAAcF5LhWtVHUnyY0k+sppxAADg3Jbdcf3NJB9M8i/ne0JV3VxVx6rq2Mknn1vydAAAHFT7DteqenuSJ7r7c//e87r7aHfvdvfu5Zcd2u/pAAA44JbZcX1zkndU1deTfDzJW6rqD1YyFQAAnGHf4drdH+ruI919dZJ3Jfnz7n73yiYDAIBTeB1XAABG2FnFF+nuv0zyl6v4WgAAcC52XAEAGEG4AgAwgnAFAGAE4QoAwAjCFQCAEYQrAAAjCFcAAEYQrgAAjCBcAQAYQbgCADCCcAUAYAThCgDACMIVAIARhCsAACMIVwAARhCuAACMsLPpATh4nn7nGzc9AgAvQIfvunfTI/ACZ8cVAIARhCsAACMIVwAARhCuAACMIFwBABhBuAIAMIJwBQBgBOEKAMAIwhUAgBGEKwAAIwhXAABGEK4AAIwgXAEAGEG4AgAwgnAFAGAE4QoAwAjCFQCAEYQrAAAjCFcAAEYQrgAAjCBcAQAYQbgCADCCcAUAYAThCgDACMIVAIARhCsAACMIVwAARhCuAACMIFwBABhBuAIAMIJwBQBgBOEKAMAIwhUAgBGEKwAAIwhXAABGEK4AAIwgXAEAGEG4AgAwgnAFAGAE4QoAwAjCFQCAEYQrAAAj7Gx6gBequx87vukRnqfjmx4AgBeg//LT/2PTI8DK2HEFAGAE4QoAwAjCFQCAEYQrAAAjCFcAAEYQrgAAjCBcAQAYQbgCADCCcAUAYAThCgDACMIVAIARhCsAACMIVwAARhCuAACMIFwBABhBuAIAMIJwBQBgBOEKAMAIS4VrVb2squ6sqi9X1UNV9f2rGgwAAE61s+Tn/1aSP+vun6iqFyc5vIKZAADgLPsO16r6ziQ/mOS9SdLdzyR5ZjVjAQDA6Za5VOCaJCeT/H5Vfb6qPlJVLznzSVV1c1Udq6pjJ598bonTAQBwkC0TrjtJXp/kd7v7dUn+OcktZz6pu4929253715+2aElTgcAwEG2TLieSHKiu+9d3L8zeyELAAArt+9w7e5vJHmkqq5dHLo+yYMrmQoAAM6w7KsK/GyS2xevKPC1JP99+ZEAAOBsS4Vrdx9PsruaUQAA4Py8cxYAACMIVwAARhCuAACMIFwBABhBuAIAMIJwBQBgBOEKAMAIwhUAgBGEKwAAIwhXAABGEK4AAIwgXAEAGEG4AgAwgnAFAGAE4QoAwAjCFQCAEXY2PcAL1duueO2mR4B9efqdb9z0CACwFnZcAQAYQbgCADCCcAUAYAThCgDACMIVAIARhCsAACMIVwAARhCuAACMIFwBABhBuAIAMIJwBQBgBOEKAMAIwhUAgBGEKwAAIwhXAABGEK4AAIwgXAEAGEG4AgAwgnAFAGAE4QoAwAjCFQCAEYQrAAAjCFcAAEYQrgAAjCBcAQAYQbgCADCCcAUAYAThCgDACMIVAIARhCsAACMIVwAARhCuAACMIFwBABhBuAIAMIJwBQBgBOEKAMAIwhUAgBGEKwAAIwhXAABGEK4AAIwgXAEAGEG4AgAwws6mBwAOrsN33bvpEQAYxI4rAAAjCFcAAEYQrgAAjCBcAQAYQbgCADCCcAUAYAThCgDACMIVAIARhCsAACMIVwAARhCuAACMIFwBABhBuAIAMIJwBQBgBOEKAMAIwhUAgBGEKwAAIwhXAABGWCpcq+oXquqBqrq/qu6oqm9b1WAAAHCqfYdrVV2Z5OeS7Hb3a5IcSvKuVQ0GAACnWvZSgZ0k315VO0kOJ3ls+ZEAAOBs+w7X7n40ya8leTjJ40n+obs/debzqurmqjpWVcdOPvnc/icFAOBAW+ZSgZcnuTHJNUmuSPKSqnr3mc/r7qPdvdvdu5dfdmj/kwIAcKAtc6nAW5P8XXef7O5vJflEkh9YzVgAAHC6ZcL14SRvqqrDVVVJrk/y0GrGAgCA0y1zjeu9Se5Mcl+SLy2+1tEVzQUAAKfZWeaTu/tXkvzKimYBAIDz8s5ZAACMIFwBABhBuAIAMIJwBQBgBOEKAMAIwhUAgBGEKwAAIwhXAABGEK4AAIwgXAEAGEG4AgAwgnAFAGAE4QoAwAjCFQCAEYQrAAAjCFcAAEYQrgAAjCBcAQAYQbgCADCCcAUAYAThCgDACMIVAIARhCsAACMIVwAARhCuAACMIFwBABhBuAIAMIJwBQBgBOEKAMAIwhUAgBGEKwAAIwhXAABGEK4AAIwgXAEAGEG4AgAwgnAFAGAE4QoAwAjCFQCAEYQrAAAjCFcAAEYQrgAAjCBcAQAYQbgCADCCcAUAYAThCgDACMIVAIARhCsAACMIVwAARhCuAACMIFwBABhBuAIAMIJwBQBgBOEKAMAIwhUAgBGEKwAAIwhXAABGEK4AAIwgXAEAGEG4AgAwws6mBwAOrrsfO77pEQAYxI4rAAAjCFcAAEYQrgAAjCBcAQAYQbgCADCCcAUAYAThCgDACMIVAIARhCsAACMIVwAARhCuAACMIFwBABhBuAIAMIJwBQBgBOEKAMAIwhUAgBGEKwAAIwhXAABGuGC4VtWtVfVEVd1/yrFXVNU9VfWVxceXr3dMAAAOuovZcb0tyQ1nHLslyae7+9VJPr24DwAAa3PBcO3uzyR56ozDNyb52OL2x5L8+GrHAgCA0+33GtdXdffji9vfSPKq8z2xqm6uqmNVdezkk8/t83QAABx0S/9yVnd3kv53Hj/a3bvdvXv5ZYeWPR0AAAfUfsP176vqe5Jk8fGJ1Y0EAABn22+4fjLJexa335Pkj1YzDgAAnNvFvBzWHUk+m+TaqjpRVe9L8uEkP1RVX0ny1sV9AABYm50LPaG7bzrPQ9eveBYAADgv75wFAMAIwhUAgBGEKwAAIwhXAABGEK4AAIwgXAEAGEG4AgAwgnAFAGAE4QoAwAjCFQCAEYQrAAAjCFcAAEYQrgAAjCBcAQAYQbgCADCCcAUAYISdTQ8AHFxvu+K1mx4B4EC4+7Hjmx5hJey4AgAwgnAFAGAE4QoAwAjCFQCAEYQrAAAjCFcAAEYQrgAAjCBcAQAYQbgCADCCcAUAYAThCgDACMIVAIARhCsAACMIVwAARhCuAACMIFwBABhBuAIAMIJwBQBgBOEKAMAIwhUAgBGEKwAAIwhXAABGEK4AAIwgXAEAGEG4AgAwgnAFAGAE4QoAwAjCFQCAEYQrAAAjCFcAAEYQrgAAjCBcAQAYQbgCADCCcAUAYAThCgDACMIVAIARhCsAACMIVwAARhCuAACMIFwBABhBuAIAMIJwBQBghJ1NDwAcXE+/842bHgFg3w7fde+mRzhw7LgCADCCcAUAYAThCgDACMIVAIARhCsAACMIVwAARhCuAACMIFwBABhBuAIAMIJwBQBgBOEKAMAIwhUAgBGEKwAAIwhXAABGEK4AAIwgXAEAGEG4AgAwgnAFAGCEC4ZrVd1aVU9U1f2nHPvVqvpyVX2xqu6qqpetdUoAAA68i9lxvS3JDWccuyfJa7r7+5L8bZIPrXguAAA4zQXDtbs/k+SpM459qrufXdz9qyRH1jAbAAD8m1Vc4/pTSf70fA9W1c1Vdayqjp188rkVnA4AgINoqXCtql9K8myS28/3nO4+2t273b17+WWHljkdAAAH2M5+P7Gq3pvk7Umu7+5e2UQAAHAO+wrXqrohyQeT/Nfufnq1IwEAwNku5uWw7kjy2STXVtWJqnpfkt9O8tIk91TV8ar6vTXPCQDAAXfBHdfuvukchz+6hlkAAOC8vHMWAAAjCFcAAEYQrgAAjCBcAQAYQbgCADCCcAUAYAThCgDACMIVAIARhCsAACMIVwAARhCuAACMIFwBABhBuAIAMIJwBQBgBOEKAMAIwhUAgBF2Nj0AsFqH77p30yMAwFrYcQUAYAThCgDACMIVAIARhCsAACMIVwAARhCuAACMIFwBABhBuAIAMIJwBQBgBOEKAMAIwhUAgBGEKwAAIwhXAABGEK4AAIwgXAEAGEG4AgAwgnAFAGAE4QoAwAjCFQCAEYQrAAAjCFcAAEYQrgAAjCBcAQAYQbgCADCCcAUAYAThCgDACMIVAIARhCsAACMIVwAARhCuAACMIFwBABhBuAIAMIJwBQBgBOEKAMAIwhUAgBGEKwAAIwhXAABGEK4AAIwgXAEAGEG4AgAwgnAFAGAE4QoAwAg7mx7gherux45vegQAAE5hxxUAgBGEKwAAIwhXAABGEK4AAIwgXAEAGEG4AgAwgnAFAGAE4QoAwAjCFQCAEYQrAAAjCFcAAEYQrgAAjCBcAQAYQbgCADCCcAUAYAThCgDACMIVAIARhCsAACNcMFyr6taqeqKq7j/HYx+oqq6qV65nPAAA2HMxO663JbnhzINVdVWSH07y8IpnAgCAs1wwXLv7M0meOsdDv5Hkg0l61UMBAMCZ9nWNa1XdmOTR7v7CRTz35qo6VlXHTj753H5OBwAAzz9cq+pwkl9M8ssX8/zuPtrdu929e/llh57v6QAAIMn+dly/N8k1Sb5QVV9PciTJfVX13ascDAAATrXzfD+hu7+U5Lv+9f4iXne7+5srnAsAAE5zMS+HdUeSzya5tqpOVNX71j8WAACc7oI7rt190wUev3pl0wAAwHl45ywAAEYQrgAAjCBcAQAYQbgCADCCcAUAYAThCgDACMIVAIARhCsAACMIVwAARhCuAACMIFwBABhBuAIAMIJwBQBgBOEKAMAIwhUAgBGEKwAAI1R3X7qTVZ1M8n/X8KVfmeSba/i6WNt1srbrY23Xx9quj7VdH2u7PutY2//Y3Zef64FLGq7rUlXHunt303NsI2u7PtZ2fazt+ljb9bG262Nt1+dSr61LBQAAGEG4AgAwwraE69FND7DFrO36WNv1sbbrY23Xx9quj7Vdn0u6tltxjSsAANtvW3ZcAQDYcsIVAIARRodrVd1QVX9TVV+tqls2Pc+2qKqrquovqurBqnqgqt6/6Zm2TVUdqqrPV9Ufb3qWbVJVL6uqO6vqy1X1UFV9/6Zn2hZV9QuL7wf3V9UdVfVtm55pqqq6taqeqKr7Tzn2iqq6p6q+svj48k3OONV51vZXF98TvlhVd1XVyzY44ljnWttTHvtAVXVVvXLdc4wN16o6lOR3kvxIkuuS3FRV1212qq3xbJIPdPd1Sd6U5Ket7cq9P8lDmx5iC/1Wkj/r7v+U5D/HGq9EVV2Z5OeS7Hb3a5IcSvKuzU412m1Jbjjj2C1JPt3dr07y6cV9nr/bcvba3pPkNd39fUn+NsmHLvVQW+K2nL22qaqrkvxwkocvxRBjwzXJG5J8tbu/1t3PJPl4khs3PNNW6O7Hu/u+xe1/yt4P/ys3O9X2qKojSX4syUc2Pcs2qarvTPKDST6aJN39THf/v40OtV12knx7Ve0kOZzksQ3PM1Z3fybJU2ccvjHJxxa3P5bkxy/lTNviXGvb3Z/q7mcXd/8qyZFLPtgWOM9/t0nyG0k+mOSS/Lb/5HC9Mskjp9w/EXG1clV1dZLXJbl3w6Nsk9/M3v/k/7LhObbNNUlOJvn9xWUYH6mql2x6qG3Q3Y8m+bXs7ag8nuQfuvtTm51q67yqux9f3P5Gkldtcpgt9lNJ/nTTQ2yLqroxyaPd/YVLdc7J4cqaVdV3JPnDJD/f3f+46Xm2QVW9PckT3f25Tc+yhXaSvD7J73b365L8c/xz60osrre8MXt/ObgiyUuq6t2bnWp79d7rVHqtyhWrql/K3qVwt296lm1QVYeT/GKSX76U550cro8mueqU+0cWx1iBqnpR9qL19u7+xKbn2SJvTvKOqvp69i5veUtV/cFmR9oaJ5Kc6O5//deBO7MXsizvrUn+rrtPdve3knwiyQ9seKZt8/dV9T1Jsvj4xIbn2SpV9d4kb0/y39oL2K/K92bvL7NfWPxMO5Lkvqr67nWedHK4/nWSV1fVNVX14uz9osAnNzzTVqiqyt51gg91969vep5t0t0f6u4j3X119v6b/fPutnO1At39jSSPVNW1i0PXJ3lwgyNtk4eTvKmqDi++P1wfv/i2ap9M8p7F7fck+aMNzrJVquqG7F2e9Y7ufnrT82yL7v5Sd39Xd1+9+Jl2IsnrF9+L12ZsuC4utP6ZJHdn7xvo/+ruBzY71dZ4c5KfzN5u4PHFnx/d9FBwEX42ye1V9cUkr03yPzc7znZY7GLfmeS+JF/K3s8Ob6G5T1V1R5LPJrm2qk5U1fuSfDjJD1XVV7K3w/3hTc441XnW9reTvDTJPYufZ7+30SGHOs/aXvo57JgDADDB2B1XAAAOFuEKAMAIwhUAgBGEKwAAIwhXAABGEK4AAIwgXAEAGOH/A89DW9jQzVAiAAAAAElFTkSuQmCC\n",
182 | "text/plain": [
183 | ""
184 | ]
185 | },
186 | "metadata": {
187 | "needs_background": "light"
188 | },
189 | "output_type": "display_data"
190 | }
191 | ],
192 | "source": [
193 | "import heapq\n",
194 | "import math\n",
195 | "import matplotlib.pyplot as plt\n",
196 | "import numpy as np\n",
197 | "import math\n",
198 | "import matplotlib\n",
199 | "%matplotlib inline\n",
200 | "#set up matplotlib\n",
201 | "is_ipython = 'inline' in matplotlib.get_backend()\n",
202 | "if is_ipython:\n",
203 | " from IPython import display\n",
204 | "plt.ion()\n",
205 | "plt.figure(figsize=(12, 12))\n",
206 | "\n",
207 | "class GridMap:\n",
208 | " def __init__(self, ox, oy, resolution):\n",
209 | " self.min_x = None\n",
210 | " self.min_y = None\n",
211 | " self.max_x = None\n",
212 | " self.max_y = None\n",
213 | " self.x_width = None\n",
214 | " self.y_width = None\n",
215 | " self.obstacle_map = None\n",
216 | " \n",
217 | " self.resolution = resolution\n",
218 | " self.calc_obstacle_map(ox, oy)\n",
219 | " \n",
220 | " def calc_obstacle_map(self, ox, oy):\n",
221 | "\n",
222 | " self.min_x = round(min(ox))\n",
223 | " self.min_y = round(min(oy))\n",
224 | " self.max_x = round(max(ox))\n",
225 | " self.max_y = round(max(oy))\n",
226 | " print(\"min_x:\", self.min_x)\n",
227 | " print(\"min_y:\", self.min_y)\n",
228 | " print(\"max_x:\", self.max_x)\n",
229 | " print(\"max_y:\", self.max_y)\n",
230 | "\n",
231 | " self.x_width = round((self.max_x - self.min_x) / self.resolution)+1\n",
232 | " self.y_width = round((self.max_y - self.min_y) / self.resolution)+1\n",
233 | " print(\"x_width:\", self.x_width)\n",
234 | " print(\"y_width:\", self.y_width)\n",
235 | "\n",
236 | " # obstacle map generation\n",
237 | " self.obstacle_map = np.zeros((self.x_width, self.y_width))\n",
238 | " for x, y in zip(ox, oy):\n",
239 | " ix, iy = self.calc_xy_index(x, self.min_x), self.calc_xy_index(y, self.min_y)\n",
240 | " if 0<=ix= self.x_width or node.ix < 0 or node.iy >= self.y_width or node.iy < 0:\n",
256 | " return False\n",
257 | " if abs(self.obstacle_map[node.ix, node.iy] - 10.0) < 0.01:\n",
258 | " return False \n",
259 | " return True\n",
260 | "\n",
261 | "sx = -5.0 # [m]\n",
262 | "sy = -5.0 # [m]\n",
263 | "gx = 50.0 # [m]\n",
264 | "gy = 50.0 # [m]\n",
265 | "grid_size = 5.0 # [m]\n",
266 | "robot_radius = 1.0 # [m]\n",
267 | "\n",
268 | "# set obstacle positions\n",
269 | "ox, oy = [], []\n",
270 | "for i in range(-10, 60):\n",
271 | " ox.append(i)\n",
272 | " oy.append(-10.0)\n",
273 | "for i in range(-10, 60):\n",
274 | " ox.append(60.0)\n",
275 | " oy.append(i)\n",
276 | "for i in range(-10, 61):\n",
277 | " ox.append(i)\n",
278 | " oy.append(60.0)\n",
279 | "for i in range(-10, 61):\n",
280 | " ox.append(-10.0)\n",
281 | " oy.append(i)\n",
282 | "for i in range(-10, 40):\n",
283 | " ox.append(20.0)\n",
284 | " oy.append(i)\n",
285 | "for i in range(0, 40):\n",
286 | " ox.append(40.0)\n",
287 | " oy.append(60.0 - i) \n",
288 | "grid_map = GridMap(ox, oy, grid_size)\n",
289 | "\n",
290 | "\n",
291 | "\n",
292 | "class Node:\n",
293 | " def __init__(self, ix, iy, C=0.0, P=None):\n",
294 | " self.ix = ix\n",
295 | " self.iy = iy\n",
296 | " self.C = C\n",
297 | " self.P = P\n",
298 | " \n",
299 | "action_set = {'UP':[0, 1], 'DOWN':[0, -1], 'LEFT':[-1, 0], 'RIGHT':[1, 0]}\n",
300 | "\n",
301 | "def get_neighbors(current, grid_map):\n",
302 | " for a in action_set:\n",
303 | " node = Node(current.ix+action_set[a][0], \n",
304 | " current.iy+action_set[a][1], current.C+1.0, \n",
305 | " grid_map.calc_unique_index(current))\n",
306 | " if grid_map.verify_node(node):\n",
307 | " yield node\n",
308 | " \n",
309 | "\n",
310 | " \n",
311 | "def Dijkstra(grid_map, start_node):\n",
312 | " Closed_set, Open_set = {}, {}\n",
313 | " Open_set[grid_map.calc_unique_index(start_node)] = start_node\n",
314 | " Q = []\n",
315 | " heapq.heappush(Q, (0.0, grid_map.calc_unique_index(start_node)))\n",
316 | " while True:\n",
317 | " if not Open_set:\n",
318 | " print(\"Dijkstra Algorithm Finished.\")\n",
319 | " return Closed_set\n",
320 | " \n",
321 | " C, c_id = heapq.heappop(Q)\n",
322 | " if c_id in Open_set:\n",
323 | " current = Open_set.pop(c_id)\n",
324 | " Closed_set[c_id] = current\n",
325 | " else:\n",
326 | " continue\n",
327 | " \n",
328 | " for node in get_neighbors(current, grid_map):\n",
329 | " neighbor_index = grid_map.calc_unique_index(node)\n",
330 | " if neighbor_index in Closed_set: continue\n",
331 | " if neighbor_index not in Open_set or Open_set[neighbor_index].C > node.C:\n",
332 | " Open_set[neighbor_index] = node\n",
333 | " heapq.heappush(Q, (node.C, neighbor_index))\n",
334 | " grid_map.obstacle_map[node.ix, node.iy] = 2\n",
335 | " plt.clf()\n",
336 | " plt.imshow(grid_map.obstacle_map)\n",
337 | " if is_ipython:\n",
338 | " display.clear_output(wait=True)\n",
339 | " display.display(plt.gcf()) \n",
340 | " \n",
341 | " \n",
342 | "def ShortestPathFinder(grid_map, Closed_set, end_node):\n",
343 | " if grid_map.verify_node(end_node) == False:\n",
344 | " print(\"the goal is unreachable!!!please change a reachable goal...\")\n",
345 | " return [], [], -1\n",
346 | " \n",
347 | " end_index = grid_map.calc_unique_index(end_node)\n",
348 | " SPath_x = [Closed_set[end_index].ix]\n",
349 | " SPath_y = [Closed_set[end_index].iy] \n",
350 | " SPath_dist = Closed_set[end_index].C*grid_map.resolution\n",
351 | " v_index = Closed_set[end_index].P\n",
352 | " while v_index: \n",
353 | " SPath_x.append(Closed_set[v_index].ix)\n",
354 | " SPath_y.append(Closed_set[v_index].iy)\n",
355 | " v_index = Closed_set[v_index].P\n",
356 | " return list(reversed(SPath_x)), list(reversed(SPath_y)), SPath_dist\n",
357 | "\n",
358 | "start_node = Node(2, 2)\n",
359 | "end_node = Node(12, 12)\n",
360 | "grid_map.obstacle_map[start_node.ix, start_node.iy] = 8\n",
361 | "\n",
362 | "plt.imshow(grid_map.obstacle_map)\n",
363 | "\n",
364 | "Closed_set = Dijkstra(grid_map, start_node)\n",
365 | "path_x, path_y, path_dist = ShortestPathFinder(grid_map, Closed_set, end_node)\n",
366 | "grid_map.obstacle_map[end_node.ix, end_node.iy] = 4\n",
367 | "for ix, iy in zip(path_x, path_y):\n",
368 | " grid_map.obstacle_map[ix, iy] = 4\n",
369 | " \n",
370 | "plt.clf()\n",
371 | "plt.imshow(grid_map.obstacle_map)\n",
372 | "if is_ipython:\n",
373 | " display.clear_output(wait=True)\n",
374 | " display.display(plt.gcf()) "
375 | ]
376 | },
377 | {
378 | "cell_type": "code",
379 | "execution_count": null,
380 | "id": "9697c895",
381 | "metadata": {},
382 | "outputs": [],
383 | "source": [
384 | "\n",
385 | "\n",
386 | "\n",
387 | "\n",
388 | "\n",
389 | "\n",
390 | "\n",
391 | "\n",
392 | "\n",
393 | "\n",
394 | "\n",
395 | "\n",
396 | "\n",
397 | "\n",
398 | "\n",
399 | "\n",
400 | "\n",
401 | "\n",
402 | "\n",
403 | "\n",
404 | "\n",
405 | "\n",
406 | "\n",
407 | "\n",
408 | "\n",
409 | "\n",
410 | "\n",
411 | "\n",
412 | "\n",
413 | "\n",
414 | "\n",
415 | "\n",
416 | "\n",
417 | "\n",
418 | "\n"
419 | ]
420 | }
421 | ],
422 | "metadata": {
423 | "kernelspec": {
424 | "display_name": "Python 3 (ipykernel)",
425 | "language": "python",
426 | "name": "python3"
427 | },
428 | "language_info": {
429 | "codemirror_mode": {
430 | "name": "ipython",
431 | "version": 3
432 | },
433 | "file_extension": ".py",
434 | "mimetype": "text/x-python",
435 | "name": "python",
436 | "nbconvert_exporter": "python",
437 | "pygments_lexer": "ipython3",
438 | "version": "3.9.5"
439 | }
440 | },
441 | "nbformat": 4,
442 | "nbformat_minor": 5
443 | }
444 |
--------------------------------------------------------------------------------