├── common
├── __init__.py
└── multiprocessing_env.py
├── README.md
├── 1.actor-critic.ipynb
├── 2.gae.ipynb
├── 5.ddpg.ipynb
├── 8.gail.ipynb
└── 3.ppo.ipynb
/common/__init__.py:
--------------------------------------------------------------------------------
1 | import multiprocessing_env
--------------------------------------------------------------------------------
/README.md:
--------------------------------------------------------------------------------
1 | # RL-Adventure-2: Policy Gradients
2 |
3 | Use CUDA "
38 | ]
39 | },
40 | {
41 | "cell_type": "code",
42 | "execution_count": 3,
43 | "metadata": {},
44 | "outputs": [],
45 | "source": [
46 | "use_cuda = torch.cuda.is_available()\n",
47 | "device = torch.device(\"cuda\" if use_cuda else \"cpu\")"
48 | ]
49 | },
50 | {
51 | "cell_type": "markdown",
52 | "metadata": {},
53 | "source": [
54 | "Create Environments "
55 | ]
56 | },
57 | {
58 | "cell_type": "code",
59 | "execution_count": 4,
60 | "metadata": {},
61 | "outputs": [],
62 | "source": [
63 | "from common.multiprocessing_env import SubprocVecEnv\n",
64 | "\n",
65 | "num_envs = 16\n",
66 | "env_name = \"CartPole-v0\"\n",
67 | "\n",
68 | "def make_env():\n",
69 | " def _thunk():\n",
70 | " env = gym.make(env_name)\n",
71 | " return env\n",
72 | "\n",
73 | " return _thunk\n",
74 | "\n",
75 | "envs = [make_env() for i in range(num_envs)]\n",
76 | "envs = SubprocVecEnv(envs)\n",
77 | "\n",
78 | "env = gym.make(env_name)"
79 | ]
80 | },
81 | {
82 | "cell_type": "markdown",
83 | "metadata": {},
84 | "source": [
85 | "Neural Network "
86 | ]
87 | },
88 | {
89 | "cell_type": "code",
90 | "execution_count": 19,
91 | "metadata": {},
92 | "outputs": [],
93 | "source": [
94 | "class ActorCritic(nn.Module):\n",
95 | " def __init__(self, num_inputs, num_outputs, hidden_size, std=0.0):\n",
96 | " super(ActorCritic, self).__init__()\n",
97 | " \n",
98 | " self.critic = nn.Sequential(\n",
99 | " nn.Linear(num_inputs, hidden_size),\n",
100 | " nn.ReLU(),\n",
101 | " nn.Linear(hidden_size, 1)\n",
102 | " )\n",
103 | " \n",
104 | " self.actor = nn.Sequential(\n",
105 | " nn.Linear(num_inputs, hidden_size),\n",
106 | " nn.ReLU(),\n",
107 | " nn.Linear(hidden_size, num_outputs),\n",
108 | " nn.Softmax(dim=1),\n",
109 | " )\n",
110 | " \n",
111 | " def forward(self, x):\n",
112 | " value = self.critic(x)\n",
113 | " probs = self.actor(x)\n",
114 | " dist = Categorical(probs)\n",
115 | " return dist, value"
116 | ]
117 | },
118 | {
119 | "cell_type": "code",
120 | "execution_count": 20,
121 | "metadata": {},
122 | "outputs": [],
123 | "source": [
124 | "def plot(frame_idx, rewards):\n",
125 | " clear_output(True)\n",
126 | " plt.figure(figsize=(20,5))\n",
127 | " plt.subplot(131)\n",
128 | " plt.title('frame %s. reward: %s' % (frame_idx, rewards[-1]))\n",
129 | " plt.plot(rewards)\n",
130 | " plt.show()\n",
131 | " \n",
132 | "def test_env(vis=False):\n",
133 | " state = env.reset()\n",
134 | " if vis: env.render()\n",
135 | " done = False\n",
136 | " total_reward = 0\n",
137 | " while not done:\n",
138 | " state = torch.FloatTensor(state).unsqueeze(0).to(device)\n",
139 | " dist, _ = model(state)\n",
140 | " next_state, reward, done, _ = env.step(dist.sample().cpu().numpy()[0])\n",
141 | " state = next_state\n",
142 | " if vis: env.render()\n",
143 | " total_reward += reward\n",
144 | " return total_reward"
145 | ]
146 | },
147 | {
148 | "cell_type": "markdown",
149 | "metadata": {},
150 | "source": [
151 | "A2C: Synchronous Advantage Actor Critic \n",
152 | "\n",
153 | "The Asynchronous Advantage Actor Critic method (A3C) has been very influential since the paper was published. The algorithm combines a few key ideas:
\n",
154 | "\n",
155 | "\n",
156 | " An updating scheme that operates on fixed-length segments of experience (say, 20 timesteps) and uses these segments to compute estimators of the returns and advantage function. \n",
157 | " Architectures that share layers between the policy and value function. \n",
158 | " Asynchronous updates. \n",
159 | " \n",
160 | "\n",
161 | "After reading the paper, AI researchers wondered whether the asynchrony led to improved performance (e.g. “perhaps the added noise would provide some regularization or exploration?“), or if it was just an implementation detail that allowed for faster training with a CPU-based implementation.
\n",
162 | "\n",
163 | "As an alternative to the asynchronous implementation, researchers found you can write a synchronous, deterministic implementation that waits for each actor to finish its segment of experience before performing an update, averaging over all of the actors. One advantage of this method is that it can more effectively use of GPUs, which perform best with large batch sizes. This algorithm is naturally called A2C, short for advantage actor critic. (This term has been used in several papers.)
"
164 | ]
165 | },
166 | {
167 | "cell_type": "code",
168 | "execution_count": 21,
169 | "metadata": {},
170 | "outputs": [],
171 | "source": [
172 | "def compute_returns(next_value, rewards, masks, gamma=0.99):\n",
173 | " R = next_value\n",
174 | " returns = []\n",
175 | " for step in reversed(range(len(rewards))):\n",
176 | " R = rewards[step] + gamma * R * masks[step]\n",
177 | " returns.insert(0, R)\n",
178 | " return returns"
179 | ]
180 | },
181 | {
182 | "cell_type": "code",
183 | "execution_count": 22,
184 | "metadata": {},
185 | "outputs": [],
186 | "source": [
187 | "num_inputs = envs.observation_space.shape[0]\n",
188 | "num_outputs = envs.action_space.n\n",
189 | "\n",
190 | "#Hyper params:\n",
191 | "hidden_size = 256\n",
192 | "lr = 3e-4\n",
193 | "num_steps = 5\n",
194 | "\n",
195 | "model = ActorCritic(num_inputs, num_outputs, hidden_size).to(device)\n",
196 | "optimizer = optim.Adam(model.parameters())"
197 | ]
198 | },
199 | {
200 | "cell_type": "code",
201 | "execution_count": 23,
202 | "metadata": {},
203 | "outputs": [],
204 | "source": [
205 | "max_frames = 20000\n",
206 | "frame_idx = 0\n",
207 | "test_rewards = []"
208 | ]
209 | },
210 | {
211 | "cell_type": "code",
212 | "execution_count": 17,
213 | "metadata": {},
214 | "outputs": [
215 | {
216 | "data": {
217 | "image/png": "iVBORw0KGgoAAAANSUhEUgAAAXQAAAE/CAYAAABW/Dj8AAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDIuMi4yLCBodHRwOi8vbWF0cGxvdGxpYi5vcmcvhp/UCwAAIABJREFUeJzt3Xl8XHW5+PHPk71Zm3TSLUmbpE0L3WnTsrXsAgIKaEVQAQFFLsK9iFcvV/yp93LdrnJV1CuCoKBS2QW9rIJCy9ampU3TPWnTNkubfd8z398fc6ZMQ9JMMss5M3ner9e8MnOWOU/OJE9Ovt/nfL9ijEEppVTki7E7AKWUUsGhCV0ppaKEJnSllIoSmtCVUipKaEJXSqkooQldKaWihCb0KCEi80Vkq4i0i8g/2x2PCi0RqRSRC+yOQzmLJvTo8XXg78aYNGPMfXYH40tE5onIcyJSLyJNIvKyiMwfss1XROSIiLSJyMMikuizLl9E/i4iXSKye2giC2TfiUBEviYiZdYf+wMi8rUh68d9foc51vnWe3RZ7zk7VN+X+jBN6NFjNrBjpJUiEhvGWIaaDDwPzAemARuB57wrReQi4C7gfDzfRyHwHz77rwPeB6YAdwNPiUh2oPuOhYjEjXWfYAjScQW4DsgELgZuE5GrfdYHcn59Y3UBzwD/D8gCSoDHgxC/8pcxRh8R/gBeBwaBHqADmAf8DvgV8ALQCVwAXIrnF7cNOAx8x+c98gED3GCtawZuAVYCpUAL8Ishx70R2GVt+zIw2894s6xjTbFePwZ8z2f9+cAR6/k8oBdI81m/Hrgl0H39iLMS+Dfr++8F4oCZwNNAPXAA+Gdr2ySgG3BZr+8GBoB06/U9wE+t5/58DjcBh4A3reXXAgeBRuu9K4ELxvnzch/w80DP7zDvezPwts/rFOucnGT378hEeegVehQwxpyH55fwNmNMqjFmr7XqM8B3gTRgA57Efh2eK+ZLgX8SkSuGvN2pQBHwaeCneJLHBcBC4CoRORtARC4HvgF8Asi2jr/Oz5DPwpMUGq3XC4FtPuu3AdNEZIq1br8xpn3I+oVB2Ncf1+A5V5MBN/AX6z1y8CS3O0TkImNMD7AJONva72w8CfhMn9dvWM/9+RzOBk4GLhKRBXj+OF+L5w/KFCDXu6GIrBaRFn++GRERYA0f/DcXyPkd6rhtjTGdQAVjO98qAJrQo9tzxpi3jDFuY0yPMeYfxpjt1utSPAn47CH73GNt+wqexLPOGFNnjKnGk7RPsba7Bfi+MWaXMWYA+B6wbLQ2UxHJBX4J3OmzOBVo9XntfZ42zDrv+rQg7OuP+4wxh40x3Xj+W8k2xvynMabPGLMfeBDwNl+8AZxtNZMswXMlfLaIJFn7vgng5+fwHWNMp3XctcBfjTFvGmN68TRpuL0bGmM2GGMm+/n9fAfP7/1vrdeBnN+hgnG+VQA0oUe3w74vRORUq6OqXkRa8SRl15B9jvo87x7mdar1fDbwMxFpsa4Om/C01eaMFIzVLvsK8L/GGN+r+Q4g3ee193n7MOu8671XlIHs6w/fczgbmOn9nq3v+xt4+gXAk9DPAZYD24FX8STq04By738kfn4Ovsed6fvauvJtZIxE5DY8/xlcav1hgMDO71DBON8qAJrQo9vQoTQfw9M5mWeMyQDux5OEx+Mw8CVjzGSfxyRjzNvDbSwimXiS+fPGmO8OWb0DWOrzeilw1EqAO4BCEUkbsn5HEPb1h+85PAwcGPI9pxljLrHWv42n4/dK4A1jzE5gFnAJHzS3gH+fg+9xa4E87wsRScbT7OI3EbkRq3PTGFPlsyqQ8zvUcduKSAowh7GdbxUATegTSxrQZIzpEZFVeNrYx+t+4N9FZCGAiGSIyKeG21BE0vF0mr5ljLlrmE0eBW4SkQUiMhn4Jp5OXaz+gK3At0UkSUSuxNOc8XQQ9h2rjUC7iPybiEwSkVgRWSQiK63jdQGbgS/zQQJ/G88VuG9CH+vn8BRwmdVWngD8J2P43RWRz+JpEvuI1Ux0TCDndxjPAotE5JNWM9O3gFJjzG5/Y1UBsrtXVh/BeQD/AL7g8/p3wH8N2WYtno66duCvwC+AP1jr8vFcFcb5bF8FnOPz+g/AN31eX4unacFbrfHwCLFdb713J55/y72PWT7b3ImneacNT/tuos+6fOv76wb2MKS6Y7z7Ap8FdpzgnFYOc6yZeNq8j+Cp7nl3yHt+3zpWovX6Nut7nzbez8HnHB5imCoXPJ2cHSf4Pg4A/UPO/f1BOr87gM/6vL4A2G291z+AfLt/NybSQ6wPQSmlVITTJhellIoSmtCVUipKaEJXSqkooQldKaWihCZ0pZSKEraMIDeUy+Uy+fn5doehlFKOtHnz5gZjzKijhDoioefn51NSUmJ3GEop5UgictCf7bTJRSmlooQmdKWUihKa0JVSKkpoQldKqSihCV0ppaKEJnSllIoSmtCVUipKjJrQRSTPmi5rp4jsEJF/sZZnicirIrLP+pppLRcRuU9EykWkVESWh/qbUEop5d8V+gDwVWPMAjxzI37ZmoX8LuA1Y0wR8Jr1GuCjeGaNLwJuxjNbuVJKqRAbNaEbY2qNMVus5+3ALjwTAV8OPGJt9ghwhfX8cuBR4/EuMFlEZgQ9cqVUWFW3dFNW3Wp3GBFnYNDNb986wP76jpAfa0xt6CKSD5wCvIdnSq1aa9URPpj5PIfjZyyvYpiZ4EXkZhEpEZGS+vr6MYatlAont9tw86MlXPfwRgbdOsvZWBxu7uY//rKTzQebQ36ssUw0m4pn4tg7jDFtvuuMZx67MX3KxpgHjDHFxpji7OxRx5xRStnoxbIj7Khpo6mzjx01epU+FhV1nivzuVNTQ34svxK6iMTjSeZ/NMY8Yy0+6m1Ksb7WWcurgTyf3XOtZUqpCDQw6ObeV/eQlzUJgPX7GmyOKLJUWE0thdkOSOgiIsBDwC5jzP/4rHoez0zkWF+f81l+nVXtchrQ6tM0o5SKMM++X83++k7uvuRkTpqexgZN6GNSXtdBdloiGZPiQ34sf67QzwSuBc4Tka3W4xLgB8BHRGQfcIH1GuAFYD9QDjwI3Br8sJVS4dA7MMhP/7aPxTkZXLRwOmuKXGw+2Ex336DdoUWMivoO5mSnhOVYo46HbozZAMgIq88fZnsDfDnAuJRSDvD4psNUt3TzvU8sRkRYXZTNg+sP8N6BRs6ZP9Xu8BzPGENFfSeXLQlPoZ/eKaqUGlZ33yA/f72cVQVZnFXkAmBVfhYJsTHa7OKnxs4+Wrv7w9IhCprQlVIjeOSdSurbe/naRfPxdKXBpIRYivMz2VCuCd0f5VaFy5wwdIiCJnSl1DDaevr51T8qOGd+Nivzs45bt7rIxe4j7dS199gUXeTwVrjM0St0pZRdfrP+AK3d/fzrhfM/tG7NXM99I2/pVfqoKuo6mRQfy4z0pLAcTxO6UhGio3eAe/66k22HW0J6nMaOXh5av59LFk9nUU7Gh9YvnJlOZnK81qP7oaK+gzlTU4iJGamuJLg0oSsVAZo7+/jsg+/y0IYD3PTIJmpaukN2rPvfqKC7f5A7PzJv2PUxMcKZc11s2NeAp6hNjaS8riNs7eegCV0pxzvS2sNVv36HXUfa+dZlC+jpd/Ol32+mpz/4teBHWnt45J2DXHlKLnOnpo243ZoiF3Xtvew9GvoBpyJVd98g1S3dmtCVUh4HGztZe//b1LR088gNq7hxdQE//fQyympauevp0qBfIf/89X0YY7jjgqITbre6yNOOvn6fDqw3kv0N4a1wAU3oSjnWrto21t7/Dp29A6y7+TROnzMFgAsWTOPOC+bx5601/Gb9gaAd71BjF49vOszVK2eRl5V8wm1zJk+i0JWi5YsnUFHfCcCcqeG5SxQ0oSvlSJsPNvPpX79DrAhP3nI6S3InH7f+tvPmcsni6Xz/xV28uTc4V8k//dte4mKF28+b69f2q4tcvLe/id4BHQZgOBV1HcQI5E/RhK7UhLV+Xz2f+817ZKUk8OQtpw/bli0i/GjtUuZNS+P2de9T2dAZ0DH3Hm3n2a3VXH96PlP9LLFbPddFd/8gWw6GtuomUpXXd5CXlUxSfGzYjqkJXSkHeXF7LTf+bhOzpyTzxC2nn7DpIyUxjgevK0YEvvhoCR29A+M+7r2v7CElIY5bzp7j9z6nzZlCbIywoVzb0YdTEeYKF9CErpRjPLHpMF9+bAtLcifz+JdOZ2ra6FfKeVnJ/PIzy9nf0Mmdj2/FPY7ZhLYdbuHlHUf54ppCMlMS/N4vPSmeZXmTdVyXYQy6DQcaOsM2yqKXJnSlHOA36/fz9adLWV2Uze9vWjWmsbPPnOvi7ktO5pWdR7nv9X1jPvaPX9lDZnI8N67OH/O+a4pclFa30tLVN+Z9o1lNSze9A269QldqIjHGcO8re/iv/9vFpYtn8JvriklOGHVU6w+54cx8Prk8l5/+bR8vlR3xe7939zeyfl8Dt54zl7SksU/AsKbIhTHwdkXjmPeNZuVhnHbOlyZ0pWzidhu+/fwOfv56OVevzOO+a04hIW58v5IiwnevXMTSvMl89Ymt7D3aPuo+xhh+/PIepqUncu3ps8d13KW5k0lLjNNhAIY4NiiXXqErFf36B93c+cRWHn3nIF86q5Dvf2IxsQGO95EUH8sD164gOTGOLz5aMmozyD/21lNysJnbzysadyVGXGwMp82Zwvp99ToMgI+K+g6yUhLG1CcRDJrQlQqznv5B/ukPm/nz1hq+dtF87vroScfGGw/UtPQk7v/cCmpberh93fsMDLqH3c7t9lyd52VN4qrivGG38deaIhdVzd0cbOwK6H2iSUVd+DtEQRO6UmHV3tPP9Q9v5LXdddxzxSK+fO7coCVzrxWzM7nnioWs39fAD1/aPew2L+04wo6aNr5ywbxxN/N4rZ7rmc1ovd41ekxFfUfY289BE7pSYbPnSDtrf/UOmw8289NPL+Pa08bXbu2PT6+cxfWnz+bB9Qd49v2q49YNuj0dsUVTU7l8WU7AxypwpZAzeRIbdFwXwDMyZmNnX9jbz0ETulIhZ4zhkbcr+dgvNtDY2ctvb1gZlEQ6mm9etoDTCrP4t6e3U1r1wd2cz75fTUV9J1+9cF7A7fbg6ZBdPdfF2xWNIzbxTCR2dYiCJnSlQqqho5cvPFLCt5/fwRlzpvDiv5zFGmukwlCLj43hl59ZTnZqIl/6/Wbq23vpG3Dz07/tZXFOBhctnB60Y60uctHeM0BpdWvQ3jNSaUJXKgq9sbeei3+6nvXlDXznYwv47edXkp2WGNYYpqQm8sB1K2ju6uOf/rCZ3797kKrmbv7VZ+LnYDhzrgsR9K5RPKMsJsTFkJM5KezH1oSuVJD1Dgxyz193cv3DG8lKief5287k82cWBL3z018LZ2bwo7VLKTnYzD1/3cmqgizOKnIF9RhZKQksmpmhCR3PTUWFrpSgNGeN1agJXUQeFpE6ESnzWfa4iGy1HpUistVani8i3T7r7g9l8Eo5TXldO1f88m0e2nCA60+fzfO3reak6el2h8XHls7k1nPmECPwtSBfnXutLnKx5VBzQIOERQPPPKLhb24B8Oce498BvwAe9S4wxnza+1xE7gV8G84qjDHLghWgUpHAGMNjGw9xz193kpwQx0PXF3P+ydPsDus4X7toPjeuLsCVGppmnzVzXfzqHxW8t7/Rcd97uPT0D3K4qSssnd7DGTWhG2PeFJH84daJ58/8VcB5wQ1LqcjR1NnHvz1dyqs7j7KmyMW9n1rq95ji4SQiIUvmACvyM0mKj2H9voYJm9APNnbhNthyUxH4d4V+ImuAo8YY3yHeCkTkfaAN+KYxZn2Ax1DKsd4qb+Arj2+luauPb156MjeeWUCMDW2nTpAYF8uqgikTep5Ruwbl8gq0U/QaYJ3P61pgljHmFOBO4DERGbYBUURuFpESESmpr5+4PwAqMvUNuPn+C7v43EPvkZYUx7O3nskX1hRO2GTutWaui4r6Tmpbu+0OxRbeksVCV4QldBGJAz4BPO5dZozpNcY0Ws83AxXAvOH2N8Y8YIwpNsYUZ2eHpy5XqWDYX9/BJ3/1Nr9+cz/XrJrFX29fw6KcDLvDcoTVVvXMRB19saK+g5zJk5iUEL5p53wFcoV+AbDbGHPsvmIRyRaRWOt5IVAE7A8sRKWcY/PBZi69bwOHm7v49bUr+N6Vi2375XWik6an4UpNnLDli3ZWuIB/ZYvrgHeA+SJSJSI3Wauu5vjmFoCzgFKrjPEp4BZjTFMwA1bKTn9+v5rYGOGlfzkrqHdaRgsRYU2Ri7fKG8Y1HV4kc7uNbaMsevlT5XLNCMs/P8yyp4GnAw9LKWcqrWphcU4G0zOcV8XiFKvnunj2/Wp2HWlj4cyJ0xRV29ZDd/+gbR2ioHeKKuW3vgE3u2rbWZI3cZLUeHjb0Sdas0tFnX1juHhpQldht2FfA/e+ssfuMMZs95E2+gbdLM2dbHcojjYtPYl501LZMMHGR7dzUC4vTegqrIwxfPeFXfz89XLeirBf+G1Vnhuil+TqFfpoVs/NZuOBJnr6B+0OJWwq6jtIT4rDlRreaed8aUJXYVVa1cqu2jZE4Ecv74moeShLD7eQlZJAzuTwj6IXadYUuegdcFNS2Wx3KGFTXuepcLFrEDbQhK7CbN3GQ0yKj+XuS05m6+EWXttVZ3dIfiutamVJboatv7CR4tTCLOJjZULdNVpR38lcG5tbQBO6CqOO3gGe31bDZUtmcP0Z+eRPSebHr+yJiPK2rr4B9tW1s0Tbz/2SnBDH8lmZE+YGo9bufurbe22tQQdN6CqMnt9aQ1ffINecOov42Bi+8pF57D7Szv9tr7U7tFGVVbfhNrBU28/9dta8bHbWttHQ0Wt3KCG33wEdoqAJXYXRnzYd4qTpaZyS57nK/diSmcyflsZPXt3r+LkovXNy6hW6/1bP9ZQvRlrn93hU1HcC9o2y6KUJXYVFWXUrpVWtXL0y71gbdEyMcOeF89jf0Mkz71fbHOGJlVa1MjMjKexTyEWyRTkZZEyKnxD16OV1HcTHCrOykm2NQxO6Cos/bTpEYlwMV56Se9zyCxdMY2luBj/72z56B5xb4lZa1aJX52MUGyOcOXcKG8obIqqaaTwq6jvIn5JCXKy9KVUTugq5rr4B/vx+DZcunkFGcvxx60SEr144n+qWbh7fdNimCE+staufysYuvUN0HFbPzaa2tedYk0S0qqjvsL39HDShqzD467ZaOnoHuObUWcOuX1PkYlVBFj9/vZzuPuddpZdWe9rP9Q7RsVtzbBiA6C1f7B90c6ixizlT7W0/B03oKgzWbTrE3KmpFM/OHHa9iPC1i+ZT397Lo+9UhjU2f5Rad4jqmOdjl5eVzOwpyVE9DMDBxk4G3Eav0FX0232kjfcPtRzXGTqclflZnD0vm1+9UUF7T38YIxzdtsMtFLpSyJgUP/rG6kNWz3XxTkUj/Q6vZBqv8jpPc5Kdoyx6aUJXIfWnjYdJiI3hE8tzR932Xy+cT0tXPw9vqAx9YGPgvUNUjc+aomw6+wZ5/1CL3aGExLFp5/QKXUWznv5BntlSxcWLppOVMvqARYtzM7h44XR+s34/LV19YYhwdHVtPRxp69EKlwCcPmcKMRK97egV9R1MT08iNXHU6SVCThO6CpkXttfS1jPA1avy/N7nzgvn0dE3wP1vOGPmQu8Ii0u1wmXcMibFszRvMuujtB29oq7DER2ioAldhdC6jYfIn5LM6YVT/N5n3rQ0Ll86k9+9fYC69p4QRuef0qoWYmOEBTM0oQdizVwX2w630NrtrP6RQBljHDEol5cmdBUS5XXtbKps5ppVs8Y8OuEdF8yjf9Dwv3+vCFF0/ttW1cq8aWk6EXSAVhdl4zbwTkWj3aEEVV17Lx29A7YPyuWlCV2FxLqNh4mPFT65YvTO0KHyXSlcVZzLY+8dorqlOwTR+ccY47lDVMsVA3bKrMkkJ8Ty7v7oSuhOmHbOlyZ0FXTeztALF0zHlTq+sU9uP68IgPv+ti+YoY3J4aZuWrr69Q7RIIiPjWFOduqxipBo4YRp53xpQldB9/KOIzR39Y+pM3SomZMn8dnTZvHUlioONNhz2/i2Kr1DNJgKs1Ns+yxDpbyug9TEOKalO2PQNk3oKuj+tPEweVmTOHOOK6D3ufWcuSTExvCTV/cGKbKxKa1qISEuhvnT02w5frQpcKVQ3dIdVfOMVtR3Mic7xTGzWGlCV0F1oKGTd/Y3cvXKWcTEBPZDnp2WyA1n5vOX0hp2H2kLUoT+21bVyoIZ6cTbPIJetChwpWAMHGrqsjuUoHHKoFxe+pOqgupPmw4RGyN8ahydocP50llzSE2M495XwnuVPug2lFW36gxFQVTo8iS+/VEy8mJH7wC1rT2OqXABPxK6iDwsInUiUuaz7DsiUi0iW63HJT7r/l1EykVkj4hcFKrAlfP0Dbh5qqSK80+aytT0pKC8Z0ZyPDevKeTVnUfZejh8t45X1HfQ1Teod4gGUb7LM/lDtLSjfzDtnDNuKgL/rtB/B1w8zPKfGGOWWY8XAERkAXA1sNDa539FRAt4J4hXdx6lsbNvxGFyx+uG1QVkpSRw7yt7gvq+J7LN+uOhd4gGT1pSPNlpiRxoiI5KF6dVuIAfCd0Y8ybQ5Of7XQ78yRjTa4w5AJQDqwKIT0WQP206RM7kSZxVlB3U901NjOPWc+awfl9D2OqYt1e3kpoYd6yZQAVHgSt6Kl0q6jqJjRFmT4msK/SR3CYipVaTjHeg6xzAd9qZKmuZinKHGrtYv6+Bq4rziA2wM3Q4nzttNtPSE/nxy3vCMp3ZtqpWFuWkB9yxq45XGE0Jvb6D2VnJJMQ5pytyvJH8CpgDLANqgXvH+gYicrOIlIhISX19dI7CNpE8XnKIGIGrVganM3SopPhYbj+viJKDzfxjb2h/XvoG3OyqadP68xAocKXQ0NEXFWO6lNd1OGLIXF/jSujGmKPGmEFjjBt4kA+aVaoB37tJcq1lw73HA8aYYmNMcXZ2cP9FV+HVP+jmiZIqzp0/lRkZk0J2nKuK88jLmsS9r4T2Kn3PkXb6Bt3aIRoCBS5P80SkX6UPDLqpbOx0zCiLXuNK6CIyw+fllYC3AuZ54GoRSRSRAqAI2BhYiMrpXt9dR317L9esCm5n6FAJcTHccf48yqrbeKnsSMiO471DVCe1CD7vFW2kd4webu6mf9A4ZpRFL3/KFtcB7wDzRaRKRG4C/ltEtotIKXAu8BUAY8wO4AlgJ/AS8GVjTPTcFqaGtW7jIaalJ3LO/ND/p3XFKTkUulL4zYYDITtGaVULWSkJ5GaG7r+NiWpWVjIxAgcivBb92KBcDqpBBxh1ig1jzDXDLH7oBNt/F/huIEGpyFHd0s0be+u5/dy5xIXhjsrYGOGqlXn84MXd7K8PTRumd8o5p9zOHU0S4mLIy0pmf4Q3uRwrWXRYFZRzumdVRHp8k6eo6aqV4x+Ia6w+cUoOsTHCU5urgv7eXX0D7D3aru3nIRQNpYvldR24UhPJSHbWxOGa0NW4DQy6ebLkMGcVZZObmRy2405NT+Lsedk8s6WaQXdwO0d31LThNugY6CHkTejhKD8NFc8YLs7qEAVN6CoAb+ytp7a1h2sCGCZ3vNauyOVIWw8bgjxPpfcOUR0DPXQKXSl09Q1S195rdyjjcmzaOYe1n4MmdBWAdRsP40pN5PyTp4X92OefPJXJyfFBb3YprWplRkYSU9OCMxaN+rCCCB+kq7HTU0fvpFv+vTShq3E50trD67uPclVxri3DyybGxXL50pm8vOMIrV3Bu0mltKpFyxVDrCA7smvRyx1a4QKa0NU4PVFyGLeBT4exM3SoTxXn0Tfg5vnSmqC8X2tXP5WNXdohGmIz0pNIio85NlphpKlw4CiLXprQ1ZgNug2PbzrM6rkuWwcmWjgznZOmpwWt2aW0WqecC4eYGCF/SuRWulTUdTIpPpaZIbwrerw0oasxe29/I9Ut3QHNGRoMIsLaFblsO9zCvqPtAb9faVUrAIu1ySXkInl+0Yr6DgqzUxw5cJsmdDVmb+5rIC5GOHf+VLtD4YpTcogLUk36tsMtFLhSyJjkrNriaFTgSuFQUxf9g267Qxkzp00750sTuhqztysaWD4rk5TEUW80DjlXaiLnnjSVZ96vZiDA5OC9Q1SFXoErlQG3oaq52+5QxqS7b5Dqlm5N6Co6tHT1sb26lTPnuuwO5ZhPrcilvr2XN/eNf1jdurYejrT1aIdomHww6mJkdYzub+jAGBw3yqKXJnQ1Ju/ub8QYOHPuFLtDOebck6YyJSWBJ0vG3+yyzWo/10mhw6PQSuiRVoteYcXrxJuKQBO6GqMN5Q2kJMSyNM85V7LxsTFccUoOf9t1lKbOvnG9R2lVC7ExwsKZmtDDITMlgcnJ8RHXMVpR14EI5Dto2jlfmtDVmLxd3siphVNsuZnoRNauyKV/0PD81mHnUxlVaVUrRVNTmZSgc5qHSyQO0lVe30FeZjJJ8c78OXHWb6VytJqWbvY3dDqq/dzr5BnpLMpJ58lxVLsYYyitatH68zCLxIReUefMQbm8NKErv71lDYTlpPZzX2uX57Kjpo2dNW1j2q+quZvmrn4dkCvM5mSnUtvaQ1ffgN2h+GXQbTjQ0OnYChfQhK7G4K3yBlypCcyflmZ3KMO6fFkO8bFjr0n3TjmnV+jhFWnzi9a0dNM74HZshyhoQld+MsbwVkUjZ8xxOXYmn8yUBC44eRp/3lpN34D/NemlVa0kxMYwz6F/qKJVpCV0Jw/K5aUJXfllX10H9e29rHZg+7mvTxXn0tTZx9/31Pm9z7bDLZw8M52EOP11CCdvpUikzC/6waBcmtBVhNuwz9N+foZD28+9zirKJjst0e+a9EG3oay6VevPbTApIZaZGUkRc4VeUd9BZnI8WSkJdocyIk3oyi9vVzSQPyU5rFPNjUdcbAyfOCWHv++po96PGXH213fQ2Teod4japCA7JWImjK6oc+YsRb40oatRDQy6eXd/E2c4vLnFa+2KXAbdhuf8qEnXO0TtVeDUvRNZAAAgAElEQVRKYX99R0TML+rkQbm8NKGrUW2raqWjd8Dx7edeRdPSWJo3mSdLqkZNFKVVLaQkxFLo8F/UaFXgSqWtZ4DmIM46FQrNnX00dvZpQleR763yBkTg9EJnt5/7+tSKXPYcbaes+sQ16duqWlmUk0GsA8e2nggKI2SQrmMdog4dlMtLE7oa1VvlDSycmU6mgzuDhvrYkpkkxMXw1ObDI27TN+BmV02bo8almWi8pYsVDq90iYQKF/AjoYvIwyJSJyJlPst+JCK7RaRURJ4VkcnW8nwR6RaRrdbj/lAGr0Kvq2+ALYeaOXNOZDS3eGUkx3PRwuk8t62G3oHBYbfZc6SdvkG3joFuo9zMScTHiuMrXSrqO0mIi3F8UYA/V+i/Ay4esuxVYJExZgmwF/h3n3UVxphl1uOW4ISp7LKpspn+QePI8VtGs3ZFLi1d/fxt5/A16XqHqP3iYmOYlZXs+Fr08roOCl0pjm+aGzWhG2PeBJqGLHvFGOMdgOFdIDcEsSkHeKu8gYTYGFbmZ9kdypitnutiRkbSiM0upVUtZCbHk5vpvMl+J5ICV6rjr9D3Hm139B2iXsFoQ78ReNHndYGIvC8ib4jImiC8v7LRW+UNLJ89OSKHlY2NET6xPIc39tZztK3nQ+s9U85NduxQBhNFYXYKBxo7cbudWbrY3NlHVXM3iyJgrPyAErqI3A0MAH+0FtUCs4wxpwB3Ao+JSPoI+94sIiUiUlJfP/6pw1ToNHX2saOmLWLKFYfzyeW5uA08+/7xNeldfQPsPdqu9ecOUOBKoW/ATU2rM+cX3WGN3rkoZ9hU5ijjTugi8nngMuCzxir2Ncb0GmMareebgQpg3nD7G2MeMMYUG2OKs7OzxxuGCqF3KhoBIuaGouEUZqdSPDuTJ0sOH1eTvqOmDbdB7xB1AKcP0lVW47n5LGqv0EXkYuDrwMeNMV0+y7NFJNZ6XggUAfuDEagKvw3lDaQlxrEkx/k/yCeydkUuFfWdbD3ccmzZNuu5VrjYr9DhCX17dSs5kydFRNmuP2WL64B3gPkiUiUiNwG/ANKAV4eUJ54FlIrIVuAp4BZjTNOwb6wc7+2KBk4tnEKcw6abG6tLl8wgKT7muNmMSqtamZ6exNT0JBsjUwDZaYmkJMQ6dsLoHdWtEdHcAhA32gbGmGuGWfzQCNs+DTwdaFDKfoebujjY2MUNZ+TbHUrA0pLi+eiiGfxlWw3fumwBSfGxbK9u1atzhxARCrKdOR1dW08/lY1drF0RGYV8kX3ppULm7QrvdHOR237u61MrcmnvGeDlHUdo7e7nQEOn3iHqIIWuVPY78PZ/73SGCyOk2VETuhrWhvJGpqYlOn64UH+dVjiFnMmTeGpzFdutERb1Ct05ClwpVDV3j3hXr13KqiOnQxQ0oathuN2Gt8sbOHOuc6ebG6uYGOGTK3LZUN7ASztqAViSo1foTlGYnYIxcKixa/SNw6is2tPXkp2WaHcoftGErj5kz9F2Gjv7oqa5xWvt8lyMgXUbD5M/JZmM5Hi7Q1IWb+mi0ya7KKtpi5gOUdCErobxVrm3/Txyhsv1x6wpyZxakMWg22j9ucPkO7B0sbN3gIr6DhZGSHMLaEJXw3irvIHC7BRmZETfGCefKs4DtP3cadKT4nGlJjpqkK5dtW0YA4sjpEMU/ChbVBNL34Cb9w408cnlkVGmNVaXLZnBniNtfHzZTLtDUUMUupxVunisQzSCErpeoavjbKtqoatvMOraz72S4mO5+9IFTE3TG4qcpsDlrAmjt1e34UpNYFp6ZHSIgiZ0NcSGfQ3ERNh0cyo6FGSn0NDRS1uPM+YX3VHjmZ4wkiq9NKFHqNd2HeVpn1vZg+XtigYW52RoBYgKO++YLpUOuErv6R9kX11HxNSfe2kbegTaeKCJL/1+M4PGkJs5iVODdDXd2TvA+4da+OJZhUF5P6XGojDbKl2s77S9CmlXbRuDbhNR7eegV+gRp6alm1v/uJm8rGTyMpP516e20dk7MPqOfth4oIkBt4no8c9V5MrLSiZGnFGLXhZBY6D70oQeQXr6B7n59yX09Lt58LoV/PhTS6lq7ua7L+wKyvtvKG8gIS6GFbMzg/J+So1FYlwsuZnJjqh02VHdyuTkeHImR1bprib0CGGM4a6nS9lR08ZPP72MuVPTWFWQxRfXFPLYe4d4Y2/gsz69Vd7AyvxMkuIjb7o5FR0KXCkccMAgXdurW1kcYR2ioAk9Yjy4fj9/3lrDVz8yjwsWTDu2/M6PzKNoaipff2obrV3jrw5o6Ohl95H2qC1XVJGhwJXCgfrO42aXCrfegUH2Hm2PqDtEvTShR4A39tbzgxd3c8ni6Xz53LnHrUuKj+V/rlpGQ0cf3/nLjnEf421rurkz52hCV/YpzE6hs2+Q+vZe22LYd7SD/kETce3noAnd8SobOrn9sS3Mm5bGj9YuHfZfwMW5Gdx27lyefb+al8pqx3Wct/Y1kJ4UF3G9+iq6OGGQru3WHaKRdMu/lyZ0B+voHeCLj5YQGyM8eF0xKYkjV5nedt5cFuWkc/ezZTR0jO3qxhjDhvIGTp8zhdiYyGozVNHFCRNGl1W3kpYUx6ysZNtiGC9N6A7ldhu+8vhW9jd08svPLCdvlB+u+NgY/ueqZbT3DPCNZ7aPqQ3yUFMX1S3dWq6obDczYxKJcTH2JvSaNhbOTI+4DlHQhO5YP3ttH6/uPMrdl5zMGX4m2nnT0vjqhfN4ZedR/ry12u9jbbCGy/X3OEqFSkyMeMZ0sWnUxf5BN7tq2yKyuQU0oTvSS2W1/Oy1faxdkcsNZ+aPad8vrCmkeHYm33puB7Wt3X7t83Z5IzMyko7deq2UnTyDdNlTulhe10HfgDti+5I0oTvMniPt3PnENpbmTea/rlg05n/7YmOEH39qKQODhq8/VTpq04vbbXi7ooEz5kTPdHMqshW4UjjU2MXAoDvsx/YOmRuJJYugCd1RWrr6+OKjJaQkxvHAtSvGfYNPviuFb1xyEuv3NfDH9w6dcNudtW00d/WzukhHV1TOUOBKYcBtqGr27z/MYCqrbiUlITZi/1vVhO4QA4NubnvsfY609nD/51YwLT2w8bo/d9ps1hS5+N4LuzjYOHJ7pHe6uTO0/lw5hHeQLjs6Rstq2lgwM52YCK320oTuED94cTcbyhv4rysWBWUsFRHhh59cQqwIX3uylEH38E0vb1U0UjQ1NeA/IEoFS4ErFQh/Lfqg27Czpi1im1vAz4QuIg+LSJ2IlPksyxKRV0Vkn/U101ouInKfiJSLSKmILA9V8NHimS1V/GbDAa4/fTZXrcwL2vvOnDyJb398IRsrm3h4w4EPre8dGGTjgUa93V85SmZyPBmT4sM+psv++g66+wcjtsIF/L9C/x1w8ZBldwGvGWOKgNes1wAfBYqsx83ArwIPM3qVVrVw1zPbOa0wi29etiDo7//J5Tl8ZME0fvTKHvYdbT9u3fuHWujpd2tCV44iItYgXeG9Qi+ribw5RIfyK6EbY94EmoYsvhx4xHr+CHCFz/JHjce7wGQRmRGMYKNNXXsPNz+6mezURH75meXExwa/BUxE+N6Vi0lJiOXOJ7bR71M58Fa5Z7q5Uwuzgn5cpQJRaA3SFU5l1W0kxccwJzsyO0QhsDb0acYY78AhRwDvEIA5wGGf7aqsZcpH34CbW/+whZbuPh64bgVTUkM3EW12WiLfvXIx26tb+d+/Vxxb/lZ5A0vzJpOepNPNKWcpzE6hprWH7r7BsB1ze3UrJ89IJy4EF1bhEpTIjafYeUzjXYrIzSJSIiIl9fWBj+UdaZ7aXEXJwWb+e+3SsHTCXLJ4Bpcvm8nPX99HWXUr7T39bKtq1dEVlSN5O0YrT1ChFUxuq0M00uYQHSqQhH7U25Rifa2zllcDvj17uday4xhjHjDGFBtjirOzswMIIzK9u7+RaemJfGxJ+Fqj/uPjC8lKSeDOJ7by5t4GBt1G28+VIx0bdTFMzS4Hm7ro6B2IyCFzfQWS0J8HrreeXw8857P8Oqva5TSg1adpRuEZ3XBTZRPF+VlhvTtzcnICP1y7hL1HO/jGs9tJio9h+Wx7J+NVajj5Ls9gdOGqdPEOmRvJHaLgf9niOuAdYL6IVInITcAPgI+IyD7gAus1wAvAfqAceBC4NehRR7iq5m5qW3tYlR/+zshz50/lmlV5tHb3szI/i8Q4nW5OOU9yQhwzMpLCVou+o7qVhNgYiqamheV4oTLyANs+jDHXjLDq/GG2NcCXAwkq2m2q9BQMrbQhoQPcfekCyus6WLsi15bjK+WPcJYultW0Mn96GglxkdshCn4mdBVcmyqbSUuKY/50e64GUhPjePKWM2w5tlL+KnCl8H/bQ99aa4yhrLqNSxZHfnV1ZP85ilCbKptYMTtTZwdS6gQKXCm0dPXT3NkX0uNUNXfT2t0f8R2ioAk97Jo6+yiv67CtuUWpSOEdpCvU7ejeIXMjvWQRNKGHnbf9fFWBJnSlTqTQqkUPdTv69upW4mLEtibQYNKEHmYllU0kxMWwJDfyrwaUCqXczEnExUjISxfLatoompY27vkHnEQTephtrGxmaW6GlgsqNYq42BhmTUkO6c1Fxhh2VLeyaGbkt5+DJvSw6uobYEd1q7afK+WnwhCXLta29tDY2cfiKPmPWRN6GG091MKA27BS28+V8ou3Ft09wgQtgYr0OUSH0oQeRhsrmxAhKDMSKTURFLhS6R1wU9vWE5L3L6tpI0ZgwQxtclFjtKmyiZOmp+twtUr5yTtIV6jGRi+rbmXu1FQmJURHn5Ym9DDpH3Sz5WALq/L16lwpf30wYXRoKl3Kqlujov7cSxN6mOysaaO7f1Dbz5Uag6lpiaQkxIbk5qK6th7q2nsjfoRFX5rQw8TuAbmUikQiQkF2aCpdomEO0aE0oYfJxgNNzMpKZlp6kt2hKBVRClypoUno1W2IwIIoqUEHTehhYYyh5GCzXp0rNQ4FrhQON3XRN+AefeMxKKtupcCVQmpi9Aw6qwk9DCrqO2nq7GNVgXaIKjVWha4U3AYONQX3Kj3aOkRBE3pYaPu5UuMXivlFGzt6qWntiYohc31pQg+DTQeacKUmHPvBVEr5L99bix7EdvQdNW1AdHWIgib0sNhY2UTx7PBOCK1UtMiYFI8rNSGoCX17lN3y76UJPcRqW7upau7W+nOlAlDgSglqLfqOmlZmZSWTMSm67trWhB5imyqbAVil7edKjVuwJ4wuq25jcZQ1t4Am9JDbdKCJlIRYTp4R+bOhKGWXAlcq9e29tPf0B/xerV39HGrqYmGUdYiCJvSQ21TZxPLZmcTF6qlWary8Y7rstDozA7GjJnrmEB1Ks0wItXb1s+dou5YrKhWg4tmZTElJ4I7Ht3K4qSug94rGW/69NKGH0OZDTRij9edKBWpKaiJ/+MKpdPcPcvUD71Ld0j3u99pe3UbO5ElkpSQEMUJnGHdCF5H5IrLV59EmIneIyHdEpNpn+SXBDDiSbDzQTHyssCxvst2hKBXxTp6Rzh9uOpW2nn6ueeBdjrSOb9KLHdWtLIyi8Vt8jTuhG2P2GGOWGWOWASuALuBZa/VPvOuMMS8EI9BItKmyiUU5GVEzeL5SdluUk8GjN66iqbOPzzz4LnXtY0vq7T397G/ojMoKFwhek8v5QIUx5mCQ3i/i9fQPUlrVouWKSgXZKbMy+e0NKznS1sNnH3yPxo5ev/fdGaV3iHoFK6FfDazzeX2biJSKyMMiMiFHpNp2uIX+QaPt50qFwMr8LH5zfTGHmrr43EMbaenq82u/MiuhR2PJIgQhoYtIAvBx4Elr0a+AOcAyoBa4d4T9bhaREhEpqa+vDzQMx/EOyFWsU84pFRJnzHHx4HXFVNR1cO1DG2ntHr1GfUd1K9PSE5maFp3zEgTjCv2jwBZjzFEAY8xRY8ygMcYNPAisGm4nY8wDxphiY0xxdnZ2EMJwlo2Vzcyblsrk5OjrSVfKKc6al8391y5n95E2Pv/bjXT0Dpxw++1ROGSur2Ak9GvwaW4RkRk+664EyoJwjIgy6DZs0QktlAqL806axs+vWU5pVSs3/HYjXX3DJ/WuvgEq6jtYGKXt5xBgQheRFOAjwDM+i/9bRLaLSClwLvCVQI4RiXbVttHRO8AqHZBLqbC4eNF0fnb1MjYfbOYLj5TQ0z/4oW121bbjNkRthQtAQHMvGWM6gSlDll0bUERRQCe0UCr8Llsyk4FBw1ee2MoXHy3hweuKSYr/oGS4rNp7h2h0doiC3ikaEpsqm8iZPImZkyfZHYpSE8oVp+Tww08sYf2+Bm7945bj5iEtq25lSkoC06N4onZN6EFmjGFTZTMrtbpFKVtctTKP/7piEa/vruP2dVvoH/Qk9bKaNhblZET1RDOa0IPsYGMX9e29OqGFUjb63Gmz+fbHFvDyjqN85fGtdPUNsO9oe1Q3t0CAbejqwzZa7ed6h6hS9rrhzAL6Btx8/8Xd1Lb2MOA2UV2yCJrQg66ksonJyfHMyU61OxSlJrwvnT2HvgE39766F4jeW/69NKEH2abKZopnZxETE73tdEpFktvPL0IE3tzXQG5mdBcqaBt6ENW193CgoZNVBdohqpST3HZeEU986fSo7hAFTehBVWJNCK3150opO2hCD6JNlU0kxcewMMo7XpRSzqQJPYg2VTZxSl4mCXF6WpVS4aeZJ0jae/rZWdOm9edKKdtoQg+SLYdacButP1dK2UcTepCUVDYRGyOcMksnhFZK2UMTepBsPNDEwpnppCRqab9Syh6a0IOgd2CQrYdbtFxRKWUrTehBUFbdSu+AWxO6UspWmtCDYJN1Q5FOCK2UspMm9CDYdKCJwuwUXKmJdoeilJrANKEHyO02lBxs1nJFpZTtNKEHaG9dO63d/dp+rpSynSb0AHnbz1fpHaJKKZtpQg/QpgNNTEtPjPpxlpVSzqcJPQCeCaGbWJmfFfXjLCulnE8TegCqmrupbe3R5hallCNoQg9AyUHPhNDaIaqUcoKABx4RkUqgHRgEBowxxSKSBTwO5AOVwFXGmOZAj+U0Gw80k5YUx7xpaXaHopRSQbtCP9cYs8wYU2y9vgt4zRhTBLxmvY46myqbKJ6dSaxOCK2UcoBQNblcDjxiPX8EuCJEx7FNRX0H5XUdOqGFUsoxgpHQDfCKiGwWkZutZdOMMbXW8yPAtCAcxzHcbsNdT5eSnhTH2hW5doejlFJAENrQgdXGmGoRmQq8KiK7fVcaY4yImKE7Wcn/ZoBZs2YFIYzw+cN7B9lU2cyP1i5halqS3eEopRQQhCt0Y0y19bUOeBZYBRwVkRkA1te6YfZ7wBhTbIwpzs7ODjSMsKlq7uKHL+5mTZFLr86VUo4SUEIXkRQRSfM+By4EyoDngeutza4HngvkOE5hjOEbz5ZhgO9duVhvJlJKOUqgTS7TgGetxBYHPGaMeUlENgFPiMhNwEHgqgCP4whPb6nmzb31/MfHF5KXlWx3OEopdZyAEroxZj+wdJjljcD5gby309S193DPX3dSPDuTa0+bbXc4Sin1IXqnqJ++/dwOuvsH+eHaJcRo3blSyoE0ofvhxe21vFh2hDsuKGJOdqrd4Sil1LA0oY+ipauP//fcDhbOTOeLawrtDkcppUYUjDr0qHbPX3fR3NXHIzeuJD5W//4ppZxLM9QJvLG3nqe3VHHL2YUsnJlhdzhKKXVCmtBH0NE7wDee2c6c7BRuP6/I7nCUUmpU2uQygh+9tJua1m6euuV0kuJj7Q5HKaVGpVfow9hU2cQj7xzk+tPzWTFbR1NUSkUGTehD9PQP8m9PlZKbOYmvXTTf7nCUUspv2uQyxM9e28f+hk5+f9MqUhL19CilIodeofsoq27lgTf3c1VxLmuKImcESKWUAk3ox/QPuvnaU6VkpSRw9yUL7A5HKaXGTNsULL9+o4JdtW38+toVZCTH2x2OUkqNmV6hA+V17dz3WjmXLp7BRQun2x2OUkqNy4RP6INuw9efKiU5MZbvfHyh3eEopdS4TfiE/sjblWw51MK3P7aA7LREu8NRSqlxm9AJ/XBTFz96eQ/nzM/mimU5doejlFIBmbAJ3dvUEiM6P6hSKjpM2IT+s7/t5Z39jXz74wuZOXmS3eEopVTAJmRCf2NvPT//ezlrV+RyVXGe3eEopVRQTLiEXtPSzR1/ep/509K45/JFdoejlFJBM6ESev+gm9se20LfgJtffnY5kxJ0WFylVPSYUHeK/uDF3Ww51MIvPnOKTvaslIo6E+YK/aWyWh7acIDrT5/NZUtm2h2OUkoF3YRI6JUNnXztyVKW5mbwjUtPtjscpZQKiXEndBHJE5G/i8hOEdkhIv9iLf+OiFSLyFbrcUnwwh27nv5Bbv3jFmJihF9+djmJcdpurpSKToG0oQ8AXzXGbBGRNGCziLxqrfuJMebHgYcXuP/4yw521rbx8OeLyc1MtjscpZQKmXEndGNMLVBrPW8XkV2Ao+6ff2ZLFes2HuafzpnDeSdNszscpZQKqaC0oYtIPnAK8J616DYRKRWRh0UkMxjHGKu9R9u5+9kyTi3I4qsfmWdHCEopFVYBJ3QRSQWeBu4wxrQBvwLmAMvwXMHfO8J+N4tIiYiU1NfXBxrGcTp7B/inP2wmJTGOn19zCnGxE6LvVyk1wQWU6UQkHk8y/6Mx5hkAY8xRY8ygMcYNPAisGm5fY8wDxphiY0xxdnbw5u80xvDvz2znQEMn912zjKnpSUF7b6WUcrJAqlwEeAjYZYz5H5/lM3w2uxIoG394Y/eH9w7x/LYa7vzIPM6Y4wrnoZVSylaBVLmcCVwLbBeRrdaybwDXiMgywACVwJcCinAMSqtauOcvOzlnfja3njM3XIdVSilHCKTKZQMw3CDiL4w/nPFr7ern1j9uwZWawE+uWkZMjI5vrpSaWKJiLBdjDF99chtH23p4/Eunk5mSYHdISikVdlFR/vHAm/v5266jfOOSk1k+y5YqSaWUsl3EJ/SNB5r475f3cOniGXz+jHy7w1FKKdtEdEJv6Ojl9nVbmJWVzA8+qfOCKqUmtohO6L94vZyWrn7+97PLSUuKtzscpZSyVUR3iv77JSdx2ZIZnDwj3e5QlFLKdhF9hZ4YF0txfpbdYSillCNEdEJXSin1AU3oSikVJTShK6VUlNCErpRSUUITulJKRQlN6EopFSU0oSulVJTQhK6UUlFCE7pSSkUJTehKKRUlxBhjdwyISD1wcJy7u4CGIIYTbE6OT2MbHyfHBs6OT2Mbn9nGmOzRNnJEQg+EiJQYY4rtjmMkTo5PYxsfJ8cGzo5PYwstbXJRSqkooQldKaWiRDQk9AfsDmAUTo5PYxsfJ8cGzo5PYwuhiG9DV0op5RENV+hKKaWIoIQuIheLyB4RKReRu4ZZnygij1vr3xOR/DDFlScifxeRnSKyQ0T+ZZhtzhGRVhHZaj2+FY7YfI5fKSLbrWOXDLNeROQ+69yVisjyMMU13+ecbBWRNhG5Y8g2YTt3IvKwiNSJSJnPsiwReVVE9llfM0fY93prm30icn2YYvuRiOy2PrNnRWTyCPue8PMPYXzfEZFqn8/ukhH2PeHvdohie9wnrkoR2TrCviE/d0FljHH8A4gFKoBCIAHYBiwYss2twP3W86uBx8MU2wxgufU8Ddg7TGznAH+18fxVAq4TrL8EeBEQ4DTgPZs+4yN46m1tOXfAWcByoMxn2X8Dd1nP7wJ+OMx+WcB+62um9TwzDLFdCMRZz384XGz+fP4hjO87wL/68bmf8Hc7FLENWX8v8C27zl0wH5Fyhb4KKDfG7DfG9AF/Ai4fss3lwCPW86eA80VEQh2YMabWGLPFet4O7AJyQn3cILsceNR4vAtMFpEZYY7hfKDCGDPeG8wCZox5E2gastj35+oR4Iphdr0IeNUY02SMaQZeBS4OdWzGmFeMMQPWy3eB3GAecyxGOHf+8Od3O2SxWTniKmBdMI9pl0hJ6DnAYZ/XVXw4aR7bxvohbwWmhCU6i9XMcwrw3jCrTxeRbSLyoogsDGdcgAFeEZHNInLzMOv9Ob+hdjUj/1LZee6mGWNqredHgGnDbOOE83cjnv+yhjPa5x9Kt1lNQg+P0Fxl97lbAxw1xuwbYb2d527MIiWhO56IpAJPA3cYY9qGrN6CpylhKfBz4M9hDm+1MWY58FHgyyJyVpiPf0IikgB8HHhymNV2n7tjjOd/cMeVhYnI3cAA8McRNrHr8/8VMAdYBtTiadpwmms48dW5o393hoqUhF4N5Pm8zrWWDbuNiMQBGUBjOIITkXg8yfyPxphnhq43xrQZYzqs5y8A8SLiCkds1jGrra91wLN4/s315c/5DaWPAluMMUeHrrD73AFHvc1P1te6Ybax7fyJyOeBy4DPWn9wPsSPzz8kjDFHjTGDxhg38OAIx7Xz3MUBnwAeH2kbu87deEVKQt8EFIlIgXU1dzXw/JBtnge81QVrgddH+gEPJqsN7iFglzHmf0bYZrq3PV9EVuE57+H6Y5MiImne53g60sqGbPY8cJ1V7XIa0OrTzBAOI14l2XnuLL4/V9cDzw2zzcvAhSKSaTUrXGgtCykRuRj4OvBxY0zXCNv48/mHKj7ffpgrRziuP7/boXIBsNsYUzXcSjvP3bjZ3Svr7wNPJcZePD3id1vL/hPPDzNAEp5/2cuBjUBhmOJajeff8FJgq/W4BLgFuMXa5jZgB54e/HeBM8J43gqt426zYvCeO9/4BPildW63A8VhjC8FT4LO8Flmy7nD80elFujH05Z7E55+mNeAfcDfgCxr22LgNz773mj97JUDN4QptnI87c/enztvlddM4IUTff5hiu/31s9TKZ4kPWNofNbrD/1uhzo2a/nvvD9nPtuG/dwF86F3iiqlVJSIlCYXpZRSo5TNNOsAAAAySURBVNCErpRSUUITulJKRQlN6EopFSU0oSulVJTQhK6UUlFCE7pSSkUJTehKKRUl/j/uGOcosdriMAAAAABJRU5ErkJggg==\n",
218 | "text/plain": [
219 | ""
220 | ]
221 | },
222 | "metadata": {},
223 | "output_type": "display_data"
224 | }
225 | ],
226 | "source": [
227 | "state = envs.reset()\n",
228 | "\n",
229 | "while frame_idx < max_frames:\n",
230 | "\n",
231 | " log_probs = []\n",
232 | " values = []\n",
233 | " rewards = []\n",
234 | " masks = []\n",
235 | " entropy = 0\n",
236 | "\n",
237 | " for _ in range(num_steps):\n",
238 | " state = torch.FloatTensor(state).to(device)\n",
239 | " dist, value = model(state)\n",
240 | "\n",
241 | " action = dist.sample()\n",
242 | " next_state, reward, done, _ = envs.step(action.cpu().numpy())\n",
243 | "\n",
244 | " log_prob = dist.log_prob(action)\n",
245 | " entropy += dist.entropy().mean()\n",
246 | " \n",
247 | " log_probs.append(log_prob)\n",
248 | " values.append(value)\n",
249 | " rewards.append(torch.FloatTensor(reward).unsqueeze(1).to(device))\n",
250 | " masks.append(torch.FloatTensor(1 - done).unsqueeze(1).to(device))\n",
251 | " \n",
252 | " state = next_state\n",
253 | " frame_idx += 1\n",
254 | " \n",
255 | " if frame_idx % 1000 == 0:\n",
256 | " test_rewards.append(np.mean([test_env() for _ in range(10)]))\n",
257 | " plot(frame_idx, test_rewards)\n",
258 | " \n",
259 | " next_state = torch.FloatTensor(next_state).to(device)\n",
260 | " _, next_value = model(next_state)\n",
261 | " returns = compute_returns(next_value, rewards, masks)\n",
262 | " \n",
263 | " log_probs = torch.cat(log_probs)\n",
264 | " returns = torch.cat(returns).detach()\n",
265 | " values = torch.cat(values)\n",
266 | "\n",
267 | " advantage = returns - values\n",
268 | "\n",
269 | " actor_loss = -(log_probs * advantage.detach()).mean()\n",
270 | " critic_loss = advantage.pow(2).mean()\n",
271 | "\n",
272 | " loss = actor_loss + 0.5 * critic_loss - 0.001 * entropy\n",
273 | "\n",
274 | " optimizer.zero_grad()\n",
275 | " loss.backward()\n",
276 | " optimizer.step()"
277 | ]
278 | },
279 | {
280 | "cell_type": "code",
281 | "execution_count": 26,
282 | "metadata": {},
283 | "outputs": [
284 | {
285 | "data": {
286 | "text/plain": [
287 | "200.0"
288 | ]
289 | },
290 | "execution_count": 26,
291 | "metadata": {},
292 | "output_type": "execute_result"
293 | }
294 | ],
295 | "source": [
296 | "test_env(True)"
297 | ]
298 | }
299 | ],
300 | "metadata": {
301 | "kernelspec": {
302 | "display_name": "Python [conda env:pytorch4]",
303 | "language": "python",
304 | "name": "conda-env-pytorch4-py"
305 | },
306 | "language_info": {
307 | "codemirror_mode": {
308 | "name": "ipython",
309 | "version": 3
310 | },
311 | "file_extension": ".py",
312 | "mimetype": "text/x-python",
313 | "name": "python",
314 | "nbconvert_exporter": "python",
315 | "pygments_lexer": "ipython3",
316 | "version": "3.5.5"
317 | }
318 | },
319 | "nbformat": 4,
320 | "nbformat_minor": 2
321 | }
322 |
--------------------------------------------------------------------------------
/2.gae.ipynb:
--------------------------------------------------------------------------------
1 | {
2 | "cells": [
3 | {
4 | "cell_type": "code",
5 | "execution_count": 5,
6 | "metadata": {},
7 | "outputs": [],
8 | "source": [
9 | "import math\n",
10 | "import random\n",
11 | "\n",
12 | "import gym\n",
13 | "import numpy as np\n",
14 | "\n",
15 | "import torch\n",
16 | "import torch.nn as nn\n",
17 | "import torch.optim as optim\n",
18 | "import torch.nn.functional as F\n",
19 | "from torch.distributions import Normal"
20 | ]
21 | },
22 | {
23 | "cell_type": "code",
24 | "execution_count": 6,
25 | "metadata": {},
26 | "outputs": [],
27 | "source": [
28 | "from IPython.display import clear_output\n",
29 | "import matplotlib.pyplot as plt\n",
30 | "%matplotlib inline"
31 | ]
32 | },
33 | {
34 | "cell_type": "markdown",
35 | "metadata": {},
36 | "source": [
37 | "Use CUDA "
38 | ]
39 | },
40 | {
41 | "cell_type": "code",
42 | "execution_count": 7,
43 | "metadata": {},
44 | "outputs": [],
45 | "source": [
46 | "use_cuda = torch.cuda.is_available()\n",
47 | "device = torch.device(\"cuda\" if use_cuda else \"cpu\")"
48 | ]
49 | },
50 | {
51 | "cell_type": "markdown",
52 | "metadata": {},
53 | "source": [
54 | "Create Environments "
55 | ]
56 | },
57 | {
58 | "cell_type": "code",
59 | "execution_count": 22,
60 | "metadata": {},
61 | "outputs": [],
62 | "source": [
63 | "from common.multiprocessing_env import SubprocVecEnv\n",
64 | "\n",
65 | "num_envs = 16\n",
66 | "env_name = \"Pendulum-v0\"\n",
67 | "\n",
68 | "def make_env():\n",
69 | " def _thunk():\n",
70 | " env = gym.make(env_name)\n",
71 | " return env\n",
72 | "\n",
73 | " return _thunk\n",
74 | "\n",
75 | "envs = [make_env() for i in range(num_envs)]\n",
76 | "envs = SubprocVecEnv(envs)\n",
77 | "\n",
78 | "env = gym.make(env_name)"
79 | ]
80 | },
81 | {
82 | "cell_type": "markdown",
83 | "metadata": {},
84 | "source": [
85 | "Neural Network "
86 | ]
87 | },
88 | {
89 | "cell_type": "code",
90 | "execution_count": 10,
91 | "metadata": {},
92 | "outputs": [],
93 | "source": [
94 | "def init_weights(m):\n",
95 | " if isinstance(m, nn.Linear):\n",
96 | " nn.init.normal_(m.weight, mean=0., std=0.1)\n",
97 | " nn.init.constant_(m.bias, 0.1)\n",
98 | "\n",
99 | "\n",
100 | "class ActorCritic(nn.Module):\n",
101 | " def __init__(self, num_inputs, num_outputs, hidden_size, std=0.0):\n",
102 | " super(ActorCritic, self).__init__()\n",
103 | " \n",
104 | " self.critic = nn.Sequential(\n",
105 | " nn.Linear(num_inputs, hidden_size),\n",
106 | " nn.ReLU(),\n",
107 | " nn.Linear(hidden_size, 1)\n",
108 | " )\n",
109 | " \n",
110 | " self.actor = nn.Sequential(\n",
111 | " nn.Linear(num_inputs, hidden_size),\n",
112 | " nn.ReLU(),\n",
113 | " nn.Linear(hidden_size, num_outputs),\n",
114 | " )\n",
115 | " self.log_std = nn.Parameter(torch.ones(1, num_outputs) * std)\n",
116 | " \n",
117 | " self.apply(init_weights)\n",
118 | " \n",
119 | " def forward(self, x):\n",
120 | " value = self.critic(x)\n",
121 | " mu = self.actor(x)\n",
122 | " std = self.log_std.exp().expand_as(mu)\n",
123 | " dist = Normal(mu, std)\n",
124 | " return dist, value"
125 | ]
126 | },
127 | {
128 | "cell_type": "code",
129 | "execution_count": 11,
130 | "metadata": {},
131 | "outputs": [],
132 | "source": [
133 | "def plot(frame_idx, rewards):\n",
134 | " clear_output(True)\n",
135 | " plt.figure(figsize=(20,5))\n",
136 | " plt.subplot(131)\n",
137 | " plt.title('frame %s. reward: %s' % (frame_idx, rewards[-1]))\n",
138 | " plt.plot(rewards)\n",
139 | " plt.show()\n",
140 | " \n",
141 | "def test_env(vis=False):\n",
142 | " state = env.reset()\n",
143 | " if vis: env.render()\n",
144 | " done = False\n",
145 | " total_reward = 0\n",
146 | " while not done:\n",
147 | " state = torch.FloatTensor(state).unsqueeze(0).to(device)\n",
148 | " dist, _ = model(state)\n",
149 | " next_state, reward, done, _ = env.step(dist.sample().cpu().numpy()[0])\n",
150 | " state = next_state\n",
151 | " if vis: env.render()\n",
152 | " total_reward += reward\n",
153 | " return total_reward"
154 | ]
155 | },
156 | {
157 | "cell_type": "markdown",
158 | "metadata": {},
159 | "source": [
160 | "High-Dimensional Continuous Control Using Generalized Advantage Estimation \n",
161 | ""
162 | ]
163 | },
164 | {
165 | "cell_type": "code",
166 | "execution_count": 17,
167 | "metadata": {},
168 | "outputs": [],
169 | "source": [
170 | "def compute_gae(next_value, rewards, masks, values, gamma=0.99, tau=0.95):\n",
171 | " values = values + [next_value]\n",
172 | " gae = 0\n",
173 | " returns = []\n",
174 | " for step in reversed(range(len(rewards))):\n",
175 | " delta = rewards[step] + gamma * values[step + 1] * masks[step] - values[step]\n",
176 | " gae = delta + gamma * tau * masks[step] * gae\n",
177 | " returns.insert(0, gae + values[step])\n",
178 | " return returns"
179 | ]
180 | },
181 | {
182 | "cell_type": "code",
183 | "execution_count": 29,
184 | "metadata": {},
185 | "outputs": [],
186 | "source": [
187 | "num_inputs = envs.observation_space.shape[0]\n",
188 | "num_outputs = envs.action_space.shape[0]\n",
189 | "\n",
190 | "#Hyper params:\n",
191 | "hidden_size = 256\n",
192 | "lr = 3e-2\n",
193 | "num_steps = 20\n",
194 | "\n",
195 | "model = ActorCritic(num_inputs, num_outputs, hidden_size).to(device)\n",
196 | "optimizer = optim.Adam(model.parameters())"
197 | ]
198 | },
199 | {
200 | "cell_type": "code",
201 | "execution_count": 30,
202 | "metadata": {},
203 | "outputs": [],
204 | "source": [
205 | "max_frames = 100000\n",
206 | "frame_idx = 0\n",
207 | "test_rewards = []"
208 | ]
209 | },
210 | {
211 | "cell_type": "code",
212 | "execution_count": 31,
213 | "metadata": {},
214 | "outputs": [
215 | {
216 | "data": {
217 | "image/png": "iVBORw0KGgoAAAANSUhEUgAAAYIAAAE/CAYAAABLrsQiAAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDIuMi4yLCBodHRwOi8vbWF0cGxvdGxpYi5vcmcvhp/UCwAAIABJREFUeJzsvXeYnFd5sH+f6WV7VVlJK8myZMtFtoWN6dgGm0AwoZMAdmgJJR8h/BICJCEkQPIF8kEKJZA4QCCAIYANMTY2GJtmbLlLtpplde1qd7ZOb+f3x1vmndmZnZndnd3Z3ee+rrl2521z5p2Z85ynK601giAIwurFtdQDEARBEJYWEQSCIAirHBEEgiAIqxwRBIIgCKscEQSCIAirHBEEgiAIqxwRBDWglNqulHpEKTWtlPo/Sz0eYelQSt2olPrFUo9DEBYSEQS18WfA3VrrVq31Py/1YEpRSn1RKXVAKZVXSt1YZv/7lFJDSqkppdRNSim/Y9+gUupupVRcKbVfKXXNYpy7WlFKfUopdchcVOxXSr25ZP9VSqmHzHt2RCn1Dse+tUqpW5VSp5VSWik1WMPrvVcp9bRSKqaUelIpda5j3x+Z+6aUUnuUUs9x7PuRUirqeKSVUo879v+tUupxpVRWKfXXJa+plFIfVkodN6/9TaVUm2P/l83rOa/vNvcNmu/Nue8v67h/bqXUx8x7NK2Uelgp1WHu8yulPm3uG1dKfU4p5XWc+zWl1BlzzAeVUm8rufbblFKHzTHdrpRa59jnV0p9QSk1rJQaU0r9QCm1vtZrLzlaa3lUeQB3AW+bZb97icf3buBqYA9wY8m+a4FhYCfQCfwM+HvH/l8D/w8IAq8CJoDeRp9b5/vzLNF9nfG5AjcCv5jHNT8K7MBYhF0BjAPPMvd5gUngDwAFPAOIAheb+/uBdwFXAhoYrPJabwMeA843r7cV6DL3XQHEgMvMfe8ERip9l83P768cz28AXgLcAvx1ybE3APuBDUCLecxXHPu/DHyswusMmu+t7Gc+2/0z938M+CmwyXxfFwABc99HgJ8DXUAvcB/wUce5OwG/+f8OYAi4zHz+AuCseYwP+Dxwj+PcPwMeNT+jAPBV4Lu1XLsZHks+gGZ/mF+qHJA0f5Tnml/kzwO3mT+ma4CXAg8DU8AJ54/D8eX+fXPfOPCH5g/9MYwJ9F9LXvctwJPmsXcAm2oY6y+YKQj+G/iE4/nVwJD5/7lACmh17P858IeNPLeG93Ej8Evg00AEc9KodE8wJod/Mf/3mp/JJ83nQfOzsybAb5s/wkngXmCn43XLfa7dwK3m53o/8LfMQxCUea+3Au83/+83vychx/4HgDeUnOOhiiDAmChPAFdX2P864H7H87B5zbVljh3E+A3MeD3ga8wUBN8B/tTx/FnmZxBy3Oc5CYIq968T4ze6tcKxe4DXOJ7/LnCiwrHbgTPAa83nnwI+69i/zhznVvP554F/cOx/KXCglms3w0NMQ1XQWl+FMcG9R2vdorU+aO76XeDjQCvGBBwD3gx0YHwJ3qmUekXJ5a4AtmH8CD8DfBhjstkJvFYp9XwApdT1wIeAV2KsXH4OfGOOb2EnxkrF4lGgXynVbe47orWeLtm/s8Hn1sIVwBGMyfHjVe7JPRgrNjCE6xDwPPP5lRg/yDHz+Y8wPoM+4CHg6yWvW/q5fhZjEluLIYje4jxYKfVDpdSf1/ieilBKBc3x7gPQWg+b7+n3TRPHlRgr27n4JAbMxwVKqROmCeijSinrN/8jwK2UusI0y7wFeATj3pXyZuDnWuuj9by9kv/9GPfd4l2mCeVBpdSrypx/TCl1Uin1n0qpnrIvUHL/gAuBLPBq0yR5UCn17irjGlBKtTuu+TmlVBxDozmDsSiodC4YGgfAfwDPVkqtU0qFgN/DuMfO8c527aVlqSXRcnhgqMVvczz/MvDVKud8Bvi0+f8gxuphvWN/BHid4/n/AH9s/v8j4K2OfS4gThWtgPIawVPAdY7nXnMsg8CbgPtKjv848OVGnlvD/b4ROF6yreI9obDq7wb+HENgnMQwS3wU+OcKr9Nhjqm93OcKuIEMsMOx7RMskEYAfAW4HVCObb+NYVLLmo+3lzmvFo3gWeYx/2u+z0HgoHU9jInsQ+b7ywKjwDMqXOtw6ffKsa+cRvA287UGgXaMVbsGrjT3X2p+Vh7gt4Bp4NnmvhZgt7mvH0O7uKOW+4chxDXGpBwELsIwd73I3P8xDE2zF1gD/IYyWpD5uT8H+AvAa267xrxHF5nX/jcgj6mtme/zm+b1shjWga4yY55x7WZ4iEYwd044n5grq7uVUiNKqUkM00/pSmbY8X+izPMW8/9NwD8ppSaUUhPAGMYPdz31EwXaHM+t/6fL7LP2W6v8Rp1bCydKnle8J1rrBIba/3wMTeAe4FfAs81t94DtSPx7pdRTSqkp4Kh5befn5HzdXowJybntWI3jx3QeWg7PD5Xs+yTGavK12pqZldqBMZm8GcMOvRP4M6XUS2t9TQcJ8+8/aK0ntLGa/zeMiRfgrRimSsvm/Ubgh04HqDmm52BMmt+p47VvwtBsfoaxWr/b3H4SQGv9kNY6orXOaq1vw9DKXmnui2qt95j7hoH3AC9WSrWWjGvG/XO857/RWie01o9h3E/rPX8cY4J+BOP78X0MQej8HaK1zmmtf4GhUb3T3HYXho/hfzC+N0cxvssnzdM+i6H1dGOY2b5LiUZQ6drNgAiCuaNLnv83xspng9a6HfgCxapkPZwA/kBr3eF4BLXWv5rDtfYBFzueXwwMa60j5r4tJT+yiymo2o06txZK72+1e3IPcBVwCYZd/R4Mh/XlGL4AMFaM12Os7toxVqxQ/Dk5X3cEY3W3wbFtY43jR2v9h9owJ7ZorT9hbVdKfRTD0fpirfWU45QLgINa6zu01nmt9QGMFf1Lan1NBweANMXvx/n/LuCHWuuD5mvdjmGueFbJdW7AcHpGa31h83of0VoPaq0HML4Lp8xH2VOo/FuxxmzPVbPcv8dKzin63xQO79Far9dab8HQyh/UWucrvLYHw8Funf9ZrfU2rXU/hkDwAHvN3bswtOExrXUK+Bfg8kpmrdJrLzlLrZIshwflTUMfKznmLHCD+f/l5vOvmc8HKXGAYawkXuB4/jXgL8z/fwfjC7ZTF9TO18wyPh9GpMIvgbeb/7vMfddh2H3PxzAR/JTiyJ/7MBxhAfN1nZE/DTu3yv2+kRLzS7V7ArwYw6H7E/P5TvP5Pscx78JYDbZhrNo+Z34u58zyuX4LY1UZMt/LydKx1fld+iBwCFhTZt9WDE3qKgpRPoeBdziOCVBw7G7HjIip8FpfBX6I4e8YwLBNv9XcdwOG+WaL+VovwjC1Oc1gQQyn+lVlru01x/LfGCaXAGbEEUZUzlbzuuebn5vzPbwaQ/t1mZ/bNOZvAcM3tN3c123e/7truX/m/nsxNB8/cB7G7/Bqc996DCevAp6Jsbh4sbmvD3i9OS43xiIiBrzccd8vMM/diDEnOIMh/hNDOLSb9+ZDwKlart0MjyUfwHJ4UJsgeDWG2WDa/PH9K3MUBObzNwGPU4hCuqnK+HTJw3ntP8FQf6fML6zfsW/QPD+BsYq8puTajTp3H/B7Fd7PjZSZbGe7J+aPLAN8xHyuMCaBz5ccc4v5GR3DMMFUEwS95udZNmoIQ/3/UB3fJY0RbRV1PD7k2P9ajInTMjv8X0yh7ji/6OHY9wXgC47nbRhCbNq8X39FwZ6ugL8Bjpv7nwTeVDLWN5j3SZV5H18uM5YbzX3nmt+HuHn+n5Sc+3MMATOFEUTw+pLXfBpjojyDIczW1HH/1mP4DaIYwQZ/4Nj3PAyTTtwc3+859vViaJET5rgex+GfwVjMPGaOawj4OxyhthhC6+sY37kJDH/d5bVcuxke1pdCEARBWKWIj0AQBGGVI4JAEARhlSOCQBAEYZUjgkAQBGGVI4JAEARhleNZ6gHMl56eHj04OLjUwxAEQWg6HnzwwVGtdW+145a9IBgcHGTPnj1LPQxBEISmQylVU0kUMQ0JgiCsckQQCIIgrHJEEAiCIKxyRBAIgiCsckQQCIIgrHJEEAiCIKxyRBAIgiCsckQQCIIgrHJEEAiCIKxyRBAIgiAsAacmEjx5Zqr6gYuACAJBEIQl4B/vOMDvfuk+Mrn8Ug9FBIEgCMJSEE1lGY9n+MWh0aUeiggCQRCEpSBtagI/ePT0Eo9EBIEgCMKSYJmE7tg3RDKTW9KxiCAQBEFYAtLZPEGvm1g6x0/3n13SsYggEARBqMLX7jvGf/366IJeM53T7B7spKfFv+TmIREEgiAIVfjWAyf4j188vaDXzGTz+D1uXnrhGn6y/yzTycyCXr8eGiYIlFKfVErtV0o9ppT6nlKqw7Hvg0qpw0qpA0qpax3brzO3HVZK/XmjxiYIglAPY7E0x8bixFLZBbtmOpfH73Hx8l3rSGfz3PnE8IJdu14aqRHcCVygtb4IOAh8EEApdT7wemAncB3wOaWUWynlBj4LvAQ4H3iDeawgCMKSEoml0BoODk8v2DUzuTxet+LSjZ2s7why6xKahxomCLTWP9ZaW+LzPmDA/P964Jta65TW+mngMHC5+TistT6itU4D3zSPFQRBWDLi6SzJjBHhs39o4QRBOpvH63ahlOK523p4/OTkgl27XhbLR/AW4Efm/+uBE459J81tlbbPQCn1DqXUHqXUnpGRkQYMVxCExeYff3yAXx5e+uSqUsZiafv//QtYEiKTy+PzGFPw2vYgkViaVHZpwkjnJQiUUncppfaWeVzvOObDQBb4+nwHa6G1/qLWerfWendvb+9CXVYQhFn40eNniERTDbm21pov3PMUtz1+piHXnw9FgmABNYKUqREArG0PAHB2qjH3txqe+Zystb5mtv1KqRuBlwFXa621ufkUsMFx2IC5jVm2C4KwhAxPJXnn1x/iA9ft4J0v2Lrg109kcmRymkR6aROryhExBcF5a9vYPzSN1hql1LyvmzGdxQBrTEFwZjLJhq7QvK9dL42MGroO+DPg5VrruGPXrcDrlVJ+pdRmYBtwP/AAsE0ptVkp5cNwKN/aqPEJglA7B8yV8Hg8XeXIuTGZMEInE0ucYVuOsajxnp+1tZvJRIahqeSCXDft0AgsQbBQ166XRvoI/hVoBe5USj2ilPoCgNZ6H3Az8ARwO/BurXXOdCy/B7gDeBK42TxWEIQlxoqWGY/NLgjmWknTEgTxJtQILNPQs8/pBmD/mYJ56Ev3HuFzPztc9zVzeU1eY/sIbEEwmZjvcOdEI6OGztFab9Ba7zIff+jY93Gt9Vat9Xat9Y8c22/TWp9r7vt4o8YmCEJ9WIJgIlE56enoaIwrPvETvnH/8bqvPxk3NYImFASRWBqvW3HZpi4AnhwyHMbRVJZP33WQWx6uP+zTEpiWRtDq9xDyuRmaXBofgWQWC8Iy44Bpp17U1xyOAoUJu5RkJse7vv4QY7E0RyOxuq9vCZh4ZuESthaK8ViazpCP9qCX9R1BWyO47bEzxNM5JhL1m8tSWUMQWBqBUoo17QGGplaYRiAIwsJz+Ow0137mXu4+sHhFyvJ5zeHh2X0EH/3BPp44M4XbpeaUfWv7COrQCG7fe4a9p2bG3t++d4iHj4/P2H7znhPcsW+o7rFFYmm6wj4AdqxpZb+pEdy8x4h2H49n6hbMlkbgcxeczmvbA5yZXHk+AkEQFpijo0bcxZNnFi6MsRqnJhLE0jl8bldZ09B3HzrJN+4/wTtfsJW17QHiqfrNO1NzEAR/8f19fOGep2Zs/+gP9vGvP51pt//MnQd5/82Pcna6vsl2LJaiu8UUBGtbeWokxpNnpthzbJy+Vj/pbL5uJ3c6W2waAuhvCzAsgkAQhGpYUSVPj9ZvfnGSyeX5y+/vrek6ln9g14YOJktWv5lcnr+6ZR+Xb+7i/S86l7DPQyw9d40gXuOEms9rxuPpGXH3+bzm7HSKk+PFJpZ0Ns/QVJJoKssnbz9Q19jGTNMQwI41beTymr//0X7cLsUbn7kJMLSCerA1Ak9hCl7bHmB4OkUuv7hmPxBBIAjLirOmIDg6T0Gw/8w0/3XfMb73cPVUnYOmf+AZmztJ5/JFkT1jsTTRVJaXX7wOj9tFyO8mNgeNoN6ooclEhlxeM1yyuo/E0uTympPj8SKBNTSZJK9hQ1eQbz94kkdPTNQ8tkgsTbdpGjpvbSsA9xwc4YXb+zi3vwWAiTrDastpBGvaAuTyumFJe7MhgkAQmhCtNb88PEq+ZHU4bK6A56sRHDBX+eVs7KUcHJ5mbXuADZ1GopPTPDRqTlo9pumkxT83jWDCXFGns/maVsRWktfwVLJowh82BWUsnStapZ8cN0xqf/nS8+lp8fPXP9hX1q4fS2WLfByZXJ7pZJausB+Awe6wvYp/7e4BOkxNYaJOjSBdRiNY0x4EWBI/gQgCQWggc60x/4vDo/zev/+Gew4V19KyTEORWLpiBE8tHDAdno+XEQQ/O3CWqGMyPDA0zbn9rY5Jr7D6jZjJVt0txkQZ8rnn5COYdAiXWuzt1qo5mckzlSyM1Wn/tyZ/gBPm/+etbePPrtvOw8cn+PKvjhYJ2lsfPc2Vf/cT/vQ7j9rbrLyJLlPQedwutvW10NPi44U7+ugIeY3j6tQIMjnjdX3uYtMQiCAQhBXFr54aZdff3MmhOZQu/vkho/jasZKV//BU0l5FPu0I0xyLpbnuM/dy78HaijBa4aAj0ynb3ASGyenG/3yAT96+HzASnw6PRNm+ptWe9JwCKBIzJmTLdBL2eYqESK04BUG8Bo3CWf/HOf5hh8/A6Sc4OZ7A7VKsbQ/w6ksHuHywi4/+4Amu/cy9fOuB4/zxNx/m/3zjYWLpHI85qoBamof1/gA++vKd/MsbLsXrdtm+g3p9BOnsTI2gvy1gvgcRBIKwYvjBo2fI5TUPHpsZyliNX5iCoNTpOTyV5NKNRo+np0ej9vb7jkTYPzTN+771SNHEmMzk+Ppvjs2YnA8OTbPRrGnj1Ap+9VQEgJv3nGQ8luZYJEY6m2dbX4tj9esQBKZG0NNqaARhv6emibyUKadGUIOfIOIQBM7J3zmJOjWCk+MJ1rQF8LhduFyKr7/9Cj79uotxuxQf+J/H+cFjZ/iTF53LO5+/lVMTCbsKqCVwrAkfYPdgF1duNbKMC8KxXo1gpo+gO+zD61aiEQjCSiGf19z1pNFx6ok6SxdHoin7HKcgSGUNu/flg124FDw9WpjoHjkxgdetiKdzvO/mR8jnNZOJDG++6X4+/L29fO2+Y/axk3GjXs4rdq1DqWJB8OsjEVr8HhKZHP913zE7Ymj7mlZ7MnQmUI1EU/jcLlr9Rv3KkN9oxl4vk4mMHatfi8N4rEgQFGsEPS1+2gIeTow5NYI4A51B+7nX7eJ3LhngR+99Ljf/wZXc/t7n8n+u3sY5fS1oDccjxr21NYKWgiBw4ve4CfncC6IRuFyKvtaAaASCsFJ47NQkI9Mp3C7FE6crC4LjkTg33HR/0erVWpX3tPg5OVHYboVKDnSGGOgMFTmMHzk+wc517fz1y8/nl4cj/P3t+3ndv/2ah4+P0x708psjEftYy1F8ycZOtva22A5jrTX3HYlw9Xl9XLWjj6/86iiPnpxEKTinr4X2oLH6nSjRCLpbfHY1zrDPQzqbr6vmkNaaiUSGNaZppFZBYFXudEYOnZ1K0t/mZ6AzNEMjGOicWdVTKcXlm7vY1m9EAw32hIGCM972EYTLCwKAjqC3bh9B2tYIiquYGkllBQF2YGiaJ89MNTyTXASBIDSAu54Yxu1S/PZFa3nyzNSM6B8wJsC/uGUv9xwc4Uv3HrG3//LwKK0BDy86v69II7BWin1tfjb3hG3TUDaX5/FTk+za0MFrd2/gZRet5Yv3HuH4WJybbnwGv3XhWvYcHbejcSxBcO6aVi5c387eU4agemokxsh0iiu3dPOO520hEkvzlV8dZUNniJDPQ8DrJuB1lTiLU0Wr5bCpGdTjMI6lc+TymnUdhiBI1uIsjqVZ2x6gNeApyiUYnk7S3xZgQ1fQvndWDoFTI6jE5u5iQRCJpVHKmOwr0RHy1R81ZGoEfk/xFLymPcCQwzT0r3cf5o3//hsanVoggkAQGsCdTwyze1Mnz9raQyyds6NWnNy+d4h7D47Q1+rn5j0n7WStnx8a5Vlbu9nYFWYinrHt+5YtfE17wBAEIzG01hwcjpLI5Ni1oQOlFJ945YW86Zmb+OY7nslzt/XyzC1dTKeytmZycGiaVr+Hde0Bdq5rY2gqych0il+bWsMzt3RzxeYuLh5oJ57Oca65WgboCBZPekaMvd9+Hva5AeoKIbUcxVYFzto0ghRdYZ+RjVtiGipoBAm01pyeSKA1NQmC9pCX7rDPrpc0FkvRHvTicVeeKjvD3rrzCMr5CMDIJRgyQ2JT2Rx37z/LNef143bNv//BbIggEIQF5ngkzoHhaV50fj/nrW0DmGEeiqayfPQHT3De2jZuuvEZJDI5vvHAcY6PxTk1keA55/TYE9cpc2VrhY72twbY0hsmls4xEk3xiJkctWuD4URuC3j521dcwEUDxvNnbjEcm7952pjoDwxPc+6aVpRSXLi+HTDyCe57KsLa9gCbukMopXjH84wGNNvXtNjj7gh5i/IIItE0PS0FQRAyNYJ66g1ZUUgF01D1cyPRNF1hP/1tflsQZHN5RqMp+loDDHQGSWRyRGJpWzOoteHLYE+YIyOWIEjPahaC+WkEMwRBe4BkJs9kIsOvnooQTWW59oL+uq49F0QQCMICc6fpJH7R+f1s628x/AQlDuN//skhhqaSfOwVF3DB+naefU43X/7lUX52wAj/fLZDEFi27rNm6GhHyMugZcIYifHIiXE6Q142dZef6PrbAgx2h7jvyJipQUzbq/ydpiB47OQk9x2JcOWWbtvef90Fa3j3C7fyyksH7Gt1hAqrX601I9GUnUwG0OK3NILaTUMFjcB4v7VEDY2Z2b79rQFbUxqNptHaeL9W8tvJ8YR9/2rRCAA294RtjSASTReFjpZjLj6CciUmoLhBzY/3DdHi9/CsrT11XXsuiCAQhBLyeT2vzN27nhhmW18Lm7rDBLxuzultKdIIjoxE+Y9fPM3rn7GByzZ1AvC252xhaCrJZ+46yFrT9DPgmMzAmBz62/wopdjscGo+cmKCi02zUCWu2NzNA0fHGJpKMhHPsGONIQha/B629IS55ZFTRGJpnmmGRQK4XYo/vXYHW3sdGoHDNBRNZUln80U+gpBvDhqBGYVkJVRVSyjT2qgz1NXio68twNlpw5RiaQb9bX4GugpC1MohsDSOamzuCTM8lSKWytakEXSGfEwmMmX9QJVImwllpRqBdQ9OTyS484lhXrC9l4DXXfN154oIAkEo4X8fP8PV//gzTk/UXxt+Mp7h/qNjvOj8gjp//rq2Io3gG/cfRwHvf/F2e9vzz+1la2+Y8XiGZ5/Tg1KKnhYffo/LXtEOTyXtyWxdRxCfx8XjpyY5dDZqm4UqccWWLiYTGW59xGii4rT7X7C+nSOm4LtyS3fZ8y06wwXTkJ1V7PARtMzFNGReb22NPoKpZJZMThsaQZufTE4zHs84BEHAFqInxgyNYG17YFY7vxNLyB6NxAyB43h/5egIeclrmE7W/p4rO4sNAfbDx84wGk1z7c41NV9zPoggEIQS9g9Nkddw6Gy0+sEl3H3gLLm85urzHIJgbRtnJpOMxdKks3m++9Aprjmvn97WwgTjcine8pzNADznHMMUoJRifWeQU6ZAGp5K0WcKArdLMdgd4rbHz6A1NQgCY4L/2m+MfAKrWBpg+wkGOoNV7ejtQR8T8TRa60JWcZFGYKxe62k5aQmC3lY/LlXdNGSVl7CcxWAIyeFpY3tfq58Wv4fOkNfWCGo1CwG22e2pkRjj8Qxd4coRQ4Aju7h281AlZ3Ffqx+l4IePnsHndvGC7b01X3M+eBblVQRhGXHcTEQ6FokB9f0Q73pymJ4WH5c4Jubz1xkO4yfPTDGdzBCJpXndMzbMOPe1uzcQ8Lj5rQvX2tuc0S/DU0mu2tFn7xvsDtuVQasJgvUdQQY6g5wYS9DT4rdrA4GhEUB1bQCM1W8mp4mnc4xaWcWOa1nho/WUmZhMZHC7FC1+DyGfp6oQGXPE9rcGjNcbnkpydiqJSxXqHln37uR4gudsq93OPthjCMPHTkyQy+uaNAIwBMEg4ZpeI53N43apGdFAXreLnhY/I9MpXri9l9bA7EJooRCNQBBKOG46Co+Ozgz5nI10Ns89B0e4akcfLscP3IocevLMFDfvOUl/m5/nlpmYvG4Xr7psoMiBONBpxMNHU1ni6Rz9bYVJaXOvMels7gnbBeFm44rNxkRv+QcsLhpoZ2tvmN++eF3Va3Sak95EIuOoPDpTENRTZmIykaE96EUpRcDrJlGlXaWV7dvT4qev1dAIzk6lGJ5K0tvqtyfXgc4gT41EGZ6uLYfAIuTzsKYtwB6zNEhVZ7GdcV175FAml5+RTGZhmf8WyywEIgiEFcS+05P85ff31pXVWo7jY4YAODZL793TEwn+v28/ypSjuugDR8eYTmaLzEJgrFzXtAX46f6z/OzAWV516UDN9uqBziBjsbTtvO53ODy3mLbsatqAxRVbjObrTv8AGJP3T97/Ap53bnXtpz1YqEBq+QicztSg6dispyfBRDxjZy2HfO6qpiGnRtBnCsbhqaSZQ1C4Pxu6LG0KO4qoVjb3hNl3etJ+ndmwhWMdpqFUNl9UedTJmvYALgXXnN/4sFELEQTCiuFnB0b4r/uO8c37j8/5GlPJjF03ZrYm7L84PMp3HjzJV3911N5215PD+Dyusqv989e18aunIuS1YQKqlfUdxkrWKlznnOg29xh2/osH2mu61rPP6cHrVuzaWJvgKEdHqFBmIhJN0RbwFGkwbpci6HXX7SxucwiCekxDfo+bzpCX4ekkw1NJW0OA4nDRejQCMHIJrFLRtUQNAYzH6tMISkNHLV5z2QDvvfrcIk2r0YggEFYMljnin35yaE6lkKFQbGxzT5j0C89rAAAgAElEQVQTY4mKTVIss8h//vIoiXQOrY0ic8/e2m2HUDo53zQPXb65y65nUwtW9IslCJwhkJds7OCPrjqH63etr+la6zuC/OIDV/HbF62tfnAFOh2NWEZj6bKTVdjvqSuPYCpR0AiCPnfV8NFINE3Y57bDKo3s4hRnp1NFprMiQVBjMpnFFsdnVE0QtAW9KFWfRpDO5mc4ii1evHMN771mW83XWghEEAgrhng6h0sZiUVfdNTuqQfLLPTcbT2kc/miAmBORqeNH30klubbD57g0NkoJ8YSFdX5nabDuB5tAGCDOZk9ZAqCPsdE53W7eP+Lt9NZZaJy0t8WmDXfoBq2RpBIE4mmKggC95x8BGCYlqprBCm7UQxAX1uAE2NxxmLpYtOQKUQ9LkV/a32r68E6BIHbpWgLeOv2EVTSCJaC5hmJIMyTRDpHT4ufl120li/de6SoLn+tHItYgqC36Hkpo9EUG7tCXLapk3+75wi37x0C4Ood5QXB1ef186nXXMwrdlV3yDrpafHj87g4PZmkNeApq20sJs4KpKNm5dFSQj5P3aahjjp8BJFYcWx/f6ufw2aor1MjWG8K0bUdtecQWFi5BE7NYzY6Q966SlFncrqiRrAUNM9IBGGexNM5Qj43f3rtdrL5PJ++61Dd1zg+FqMr7OOC9cYKvpKfYNQsrfCuFxiNTD7/s6e4YH2bXSKgFJ/Hxasvq91JbOFyKQZMP0GtmbGNJOB1E/S6TWdxqqwgaKmjgb3VN6FgGvJUNQ1Z5SUs+tsCZE0TXp/jHoV8HrrDPgY66jMLAWzsCuFSFGkes2HUG1oYZ/FS0DwjEYR5Ek/nCPo8bOoO84bLN3LznhN1rUzBMA1t7ArR3xrA73HNqhH0tPh54fY+tve3ksjkuOa8xkR5WCvb/iYQBGCYhyLRNOPxTFFWsYWRC1DbfY+ms+R1QdMIeaublUrLPji1gP7W4nv05isHedVlA9SLz+NioDNEVw1huWDck3oTyrxiGhKEhSeZydmZrTvXtZHL67rstmCYgjZ1h3C5FJu6QxytUHNoNJqmp9WPy6V4z1Xn4FJGkbZGMNBkgqA96OUp8770lLG9h/3ump31VuVRp7N4Nh+BkdFcrBE4tQCnUAB47zXbePUcBAHA656xoabcCjCc6JUqkD50fJy7D5wt2pbO5vE3kUYgmcXCiiGezto2dCsjczqZAWoLHUxn85yeSPA7lxhROJu6w2U1gmwuz3i8EDHz2xev41lbu4uydRcSK3KodJJbKjpDPrurWU8ZR2q4huxgC6u8RJszamiWc61Cd10lpiEwun111riCr4V3v/Ccmo81qrKWFwSfvvMgw1NJXri9kBWeyeXxe5tHEDTPSARhnhimIUMjsEoPTCVqNw2dnkiQ19hN3Qe7QxyNxGZUlRyLGeWOex3240YJAShoBJX8D4tNR8jLtLniL/e+w/7ancVW03orGinkdZPN64pJgWNlWkdaArKvNVCU0b2YdIZ8tpAq5dREYoZgTOfERyAIDSHhMA0VawS1ccwMHbUEwabuMKlsvqgnLhgN24FFS/jZZBZBs5LLlhpr0obyTd1DPqOBfS19di3TndM0BJWL1pVrJt/TYhRq61tCjcnKLp4sMUVqrTkzkZyh5cyWR7AUNM9IBGGeWFFDUNAI6ikNbNUYsiZeqwplac0hu9hanbHpc+XigXa+8pbLeYHDtLCUWGUmAHrKOIvDfg+5vCZVZnVcymSJILBMe5XMQ2N2WYvifIrusJ++Rfo8ytEeKpTecDIRz5DI5GZEQjWbs1h8BMKKIZnOEfRaPgJLENSuERwfi+P3uOwJxer4dSwS40pHw5bR6cXVCJRSPL+GOkCLhbX69boVbcGZU0jYsaqvFoM/UxBY55YX4JZpqLQQ3F++7Ly6y0gsJJ12BdLi75tVQjyRMTQkK5kvnWsuZ3HDR6KUer9SSiulesznSin1z0qpw0qpx5RSlzqOvUEpdch83NDosQkrB6018UyOoM/4SreZpqGpOjSCY5E4G7pCtp15XUcQr1txNFKqEViCYOEck8sJyzTUHfaXzVIO19GcZjKRwetWtgCwBEc9piGA63et57JNXTW+g4WnUk8Cq7mR1hRpSJlscyWUNVQjUEptAF4MOKuAvQTYZj6uAD4PXKGU6gI+AuwGNPCgUupWrfV4I8corAzSuTy5vLZNCwGvG5/bVZ9paCzOJkdNGrdLsaErNKMK6Wg0hd/jsrtxrTYs01A5/wA4BEENuQTOEtRQ0AiSFZLKxmIpAl7XkmdYl2IJx8kSjeDMZMG/lMwUNKT0Kisx8WngzzAmdovrga9qg/uADqXUWuBa4E6t9Zg5+d8JXNfg8QkrBMumHHSYIloDnqIy0bOhteb4WHxGh67B7nAZjSBtOiiXJkJlqbHMIJUipazJvJbsYmflUee5s2kE5ZLYlpqOKhoBFPdizqwWZ7FS6nrglNb60ZJd64ETjucnzW2Vtpe79juUUnuUUntGRkYWcNTCcsWaOKyJBAxBUKtGMBpNE0/nbL+AxaZuQyNwRsCMRlOL5ihuRqxJr1wOAdTXt3jS0YsAqkcN1dJMfikI+9x43aqijwCK31OqyTSCeelXSqm7gHLplB8GPoRhFlpwtNZfBL4IsHv37uoxasKKx/qRBYsEgbdmZ/HxMStiaKZGEE/nGJku9AsemU4tqWNyqbHMIJWEoWW2qaXMxGQiU2RisjS6Sl3KmlUQKKXK1hsq0gjM76jWRp6Er0KHsqVgXiJJa32N1vqC0gdwBNgMPKqUOgoMAA8ppdYApwBnLd4Bc1ul7YJQFcumXGoaqlUjOGH2KS7tZHVOn9H8xeoNDAXT0GqlM+SjO+xje0mnM4uwvz7TUEeRacgKHy0fehqJpqu2jlwqOstkF5+ZTNpRaNZ3NJvXaE1TaQQNGYnW+nGtdZ/WelBrPYhh5rlUaz0E3Aq82YweeiYwqbU+A9wBvFgp1amU6sTQJu5oxPiElUfBNFRQcg1BUJtGYEUC9ZUULbP6++4fmgIgl9eMxcrX4V8t+Dwu7vvQ1bzy0vINcepxFk/E0xVMQzPPNeoMla942gx0BH1FPoJMLs/wVJKtvcZiwvIRWFnTq8JHMAu3YWgMh4EvAe8C0FqPAX8LPGA+/sbcJghVsSYOp2moLeCtWSMYj6dxqUL+gUV3i5Go9OSZafu4vF69oaMWXrerorM87LN8BLNrBNFUlqlklv52Z+lo0zRUxkcQT+dIZvINLecxHwY6gzw9WvAnDU8lyeuCVmm9p0zW2N9MgmBRYrBMrcD6XwPvrnDcTcBNizEmYWWRKOssrkcQZOgI+crWqtmxts3WCOwcglXsLK5GwOvCpar7CKywXCuDG4zJ0etWxMuEj44ucmmPerl4QwffffgUZyaTrOsI2qGjW3uN92dpBKmc8XfFm4YEYbGpFDUUTWUr9h12MhFPF9XQcXLemlYODUfJ5PJ2i8pmnYyaAaUUYZ+nailqqz/0xpKQ3YC3fAVSq7RHs5qGdm3oAOCRExNAwVG8pbdEI8gZ30cpOicIC0yigrMYIFqDVjAey1QsYXze2jbSuTxPj8aaflXaLIT8buJVTENWkb/SSK1K7Soj1r1vwjwCML4nPo/LFgSnbEFQrBFYFUpFIxCEBSZRJny0UGaiusN4PJ62E6VK2bHWcBg/eWbKFgS9IghmJezzVHUWH4vE6Qr77EqxFiGfp4JpyCr215wagc/jYue6Nh45XtAIOkJee9EgzmJBWEBS2VxRog5UjhqC2iqQTpg+gnJs6WnB61bsH5pmJJrC53aVLbYmFKilJ8GxSGyGWQgMrS5RRohYGkEz5hFY7NrQweOnJsnm8pyZSLKuPYjf40IpoygiiEYgCAvC1+87zrWfvreoeUk8k8XnceF2OHvr6Ukwm0bg87jY2ttiaATTabpbfKu2vEStWD0JZuNYJM5g90xBEKrQrjISS9Ma8OD3zF7RdCnZtaGDRCbHgeFpTk0kWNcRQCllCDfLNGRrBM3zHRJBICw7hqaSRFPZoiYgCUcvAgtr1V5NI0ikc6Sy+YoaAcD5a9vYf2bablovzE6Lf/YG9ulsnjOTCTY6IoYsgj73jPr9YEQNNbtJ7pINnYDhMD49kWCd2Uwo6C0IN9EIBGEBsKJRpkoEQbCk9r2tEaRm1wgmEobtebZ+tzvWtjI0leTw2eiqzyGohZDfM2sewcnxOHlNUbVXi2DFqKHmTSaz2NAVpCvs45eHR5lKZm1BEHBoBJYmK1FDgjAPrCggp0Zg9CIoFQS19S0ejxnXqWQaAtixpg0wIkFEI6hO2Oee1UdQKWIIZjENRZuz8qgTpRS7NnRw936jGKatEfjcdokJWxCIRiAIc8eaYKqZhmrtUmYVCpvNNGRFDoEkk9VC2O+pWEEUHDkEZQRB0Ff+3Egs3bQRQ04sPwHAOjNr2qnlWKYhiRoShHkQLSMI4uksIW9xJI/f48bnqd6cxiod3BmurBH0tQZsk5BoBNUJ+9zE0tmKDeyPRmKEfO6yNn8jj6D4M8vm8ozHm18jgEJiGRRrBAVncfOVmGiekQhCjVT0EfhmRpO0BTxV21VahcJm8xFAwTwkPoLqhPwetKas0xcMjWBjV6hs9JUVYeMUImPxNHqZ1Hi62BQEbpeyK48a78nQBCyNwC+mIUGYO5ZpyDnBx8s4i6G2ngQF01BljQAKlUibPXKlGSj0LS4vCI6Nxcv6B8BYPedLevxGosuntEd70MuW3jBr2gJ4zFW/MzeiGRPKJCtGWHaUMw0lMjN9BGBoBLWYhkI+d9X4dGult34VN6WplbDdrjJLb4lPJZ832oJetaOv7LnOCqRWj9+IXWeo+QUBwBuv2FRUkrrINNSE4aMiCIRlhy0I4tVNQ60Bb9USE+PxdFFzlEq89MK1bOkNs6lM7LtQjJXhXa7MxPB0knQ2Xzar2DjX7EmQydFpbrNKezR7+KjFW56zuei5UUjPEAAZSSgThPmRzeVJmrbWYmdxeY2gli5ls5WXcOJyKXaua69zxKsTq29xueifo6OVQ0cBWwtwOoyXe7G/oLcQPpqW8FFBmB9Om7O10s/nNYlMjqBvpoJbS5ey8Xh61oghoX5CZrvKcqWorf7QgxU0q3LtKiOxNF63oi2wPI0YIV/BAW6Hj7qaZ/ptnpEIQg1EHatESyNIZmeWoLaopTlNrRqBUDtWl7JypaiPReJ4XIq17YEZ+8BhGnJqBNMpusP+ZVvjKehzk8trMjmjcb3Xrco2QVoqRBAIyworq9jvcdmCoFx3MovWgJGclM2Vb4YOsxecE+aG3cC+jI/g2Ficgc6gHVFTStDhI7CIxNLLxj9QjoK5K0c6m2+qiCEQQSAsMyxTw7qOoC0I4mV6EVhY9YYqdcvK5zWTicpNaYS5UehbXMY0FImXLTZnUa5vcWSZF/uztNVEJkcmp0UQCMJ8KAiCANNJow2lFZZXKXwUKlcgnUpm0Hr28hJC/Vg+glJnsdaaY5FY2WJzFkHvTEEwGl3eGkHQZ0y1iYxR6baZHMUggkBYZlgrzPVm6n40mS3br9jC0gicEUZO7PISYhpaUPweN2Gfm5HpVNH28XiGqWS2YsQQzDQNaa2Xfflvp3DL5PJNVXkURBAIywynaQiMCd5yKgbKOIuraQS1lpcQ6mdTd5ijkVjRNuv55p7ZTENW1JDxmcXMfhHLobxEJayItkTG8BGIRiAI88ByFjsFQaJMm0qLal3Kai0vIdTP5p4wR0dLBIH5fLakPGv1bGl6VovK5VBwrhKlGkEzJZOBCAJhmVFqGppMZGb1EVTrW1zoRbB8V5vNymBPiBPjiaKWokcjcVzKaOBSCbdL4fe4bAG/3LKKy1HsLBaNQBDmRTRl9Ca2JgXDNDRbHsHsPQnENNQ4Nve0kMtrTo4n7G3HIjHWdQSr1nVqDXg5OWGcN7qMCs5VotRZLFFDgjAPoqksrX4P7WZtoKlkpkoegWUaKq8RTMQzuFRBYAgLx+YewyHsNA8dHY3N6h+weNlFa/nxviHOTiWXVeXRSlj+q6Q4iwVh/sRSWcIOQVCkEZQRBD6Pi4DXxXSFPILxeJqOkK+psjxXClYJiaedgiBSufy0k99/9iDZvOarvz5mm4a6wstXawuJs1gQFo6oKQiCXjdetzKdxWbUUAVzQ2vAW9TExolRXkIcxY2gK+yjNeCxBcF4LM1kIlOxxpCTTd1hXnReP1//zTFOjSdoD3qbbvKsB0koE4QFxDINKaVoC3htZ3HQ6664qp+tAqlRXmL5rjSbGaWUETlkhoxaf2sRBABvfc5mxuMZbnn01LJ2FEOhG1ncLDEhpiFBmAeGRmCsrtqDxkq/Uglqi9l6EozHM5JM1kAGu8O2RmALghp8BACXb+7igvVtJDN5epZx6CgYJcwDXhdJM2rI22TaTXONRhCqEEvlaDEdwG1Br51HUM4/YDFbl7LJeJr24PJebTYzm3vCnJ5IkMrmODpaPXTUiVKKt5oNXnpal/9nZLSrNEtMiEYgCHNnOpmlpYxGUC501GK2ngSiETSWzT1h8hpOjMU5WmPoqJOXXriOwe4Q5/S1NnCUi4PRwN7KI2iu4ASJmROWFbFU1u5+1Rb0ciwSoz3km9U01FahJ0EykyORydG5jKNRmh3LDPT0aJyjkXjN/gELn8fFj9/3/KbLxJ0LVt/iVRc+qpT6I6XUfqXUPqXUPzi2f1ApdVgpdUApda1j+3XmtsNKqT9v5NiE5YdVaTRsCoL2oIfJRIZkFdNQa8BT1kcwYRack6ihxrHZDiGNcnQ0xmBP9dDRUnwe17JtSOMk6HOTbNJ+BA3TCJRSLwSuBy7WWqeUUn3m9vOB1wM7gXXAXUqpc83TPgu8CDgJPKCUulVr/USjxigsL6yCcy22IPAylcwSz2Tpay3f7QoMZ3EykzdrvBR+gJJV3HjaQ146Q14eOTFRc+joSiXodRNPG+GjzRYK28jRvBP4e611CkBrfdbcfj3wTa11Smv9NHAYuNx8HNZaH9Fap4FvmscKAlCoM+QUBLm8ZnQ6PatG0N9mRJzcsW+oaPu4FJxbFAZ7wvz80Cgwe7G5lU7A6yaeyZHONZ9G0MjRnAs8Vyn1G6XUPUqpZ5jb1wMnHMedNLdV2j4DpdQ7lFJ7lFJ7RkZGGjB0oRmxNIKwQxAAnJ1OzuosfsUl67l0Ywd/+u3H2Hd60t4+EZeCc4vB5p6w7aPZPAfT0Eoh6HXbQQsrSiNQSt2llNpb5nE9htmpC3gm8KfAzWqBDH1a6y9qrXdrrXf39vYuxCWFReD0RIJfPTU65/Nt05BZF6jNDCPN6/J1hiz8HjdfeNNldIS8vOOrDzIyneK2x8/wqTsO4HEp+lqXd4x6s2P5CZSCgc5VLAh8bjvDvdmcxfPyEWitr6m0Tyn1TuC7WmsN3K+UygM9wClgg+PQAXMbs2wXVgD/dNch7nhiiEf+6sVzOr+cachiNtMQQF9rgC+9eTev/sKveP4n7yaeznFOXwv/9qbL6F7GxcyWA1bk0Lr2YNnmQauFkM9td8prtiioRoql7wMvBDCdwT5gFLgVeL1Syq+U2gxsA+4HHgC2KaU2K6V8GA7lWxs4PmGROTA8zVQig7E2qB+rKY0zfNQi5K2+prlgfTuffu0utva28KnXXMwdf/w8rj6vf05jEWrHqjY6l4ihlUTA6yaTM777vjpyKRaDRuYR3ATcpJTaC6SBG0ztYJ9S6mbgCSALvFtrnQNQSr0HuANwAzdprfc1cHzCIqK15vDZKHkNyUy+6gq+HOWihixmMw05ecmFa3nJhWvrfm1h7lgawWqOGILifhnNphE0TBCYkT9vrLDv48DHy2y/DbitUWMSlo6hqaQ9kUdT2QURBE6NIDCH6wmLQ4vfwweu28Fzt/Us9VCWFKcgaDZnsWQWC4vCoeGo/b/RbL5+u3ysJGrIqEIKWkNoFduelwPvfMHWpR7CkuNc/DSbs7i5RiOsWA6dLQiCaIUmMdWIpnL4PC57NeVyKTtyqFbTkCAsFUWCoMk0guYajbBiOXx22v7f6ihWL9FUxjYLWVh+grmYmgRhMSn2ETTX1NtcoxFWLIeGowS8xtdtrhpBLJWzexFY2IJATENCk9PMPoLmGo2wItFac+hslAvXtwMFW3+9GCWoi8tBtAUNDcHqCSsIzYozoEE0AmHVMRJNMZnIsGtDBwDx1NxMQ0YJ6goagZiGhCanSCMQQSCsNg6bEUO7NnQC83EWZyv6CMRZLDQ7YhoSVjVWxNDFGwzTkBE+Wj+xVNYOHbVoE0EgLBNCvuZNKBNBIDScQ2enaQt4WN8RxOd2EZ2jaSiaytIaKBYEg91h2oNe8REITU+giTUC+fUIDefQcJRt/a0opQj53XPWCKKpLOGSCf+1uzfwWxeubbofliCUIgllwqrm8Nko5/a3ABD2eebkI8jlNfF0zi5BbeF2qaKaQ4LQrIiPQFi1RKIpIrE05/S1AhD2u+cUPhpLF9cZEoTlRkASyoTVymHTUbytz9QI/J45ZRaX1hkShOWG26VsTUA0AmFVYUUMbTNNQy3+uZmGSpvSCMJyxIoc8rgkakhYJWit+dmBs7QGPKxpCwDGD2EuCWXTSREEwvIn6HXjc7tYoK69C4YIAqFh3LznBHc9eZZ3vmCr/cUPz1kjMIRHqbNYEJYTQa+76cxCIIJAaBCHz0b561uf4Flbu/nD5xVq0Yd9njmFj0ZTGft8QViuBLzupksmA8kjEBaI/3nwJN+4/zjPO7eXF27v4wP/8xgBr4tPv24XLoc9NOz32Kv7erCS0EoTygRhORH0NadGIL8qYUG4+8BZHj4xwYPHx/l/dx4E4N/fvJt+0zdgEfa5SefypLP5un4QEjUkrARCPnfThY6CCAJhgZhMZLhwfTtffPNl/PTJs3jdLq45v3/GcdZEHk9n8Xl8NV8/agsCqSkkLF8CTeojEEEgLAiTiQxdYR99rQFef/nGisdZUT/RVJaOUO2C4OhojJ4WH36PCAJh+XL9rnWcmUgu9TBmIIJAWBAm4hk294SrHhcyV/T1JpXtPT3FznXtcxqbIDQLL7to3VIPoSzNp6MIy5LJRKammj9hh0ZQK6lsjkPD01ywvm3O4xMEoTIiCIR5k89rppIZOmoRBGb4Zz1JZQeHomTzWjQCQWgQIgiEeTOdzKJ1oUnMbFjOXqdGcO/BET5yy96K5+w9PQnABSIIBKEhiCAQ5s1EIg1Qk/PX1ggcSWU/2jvE135zHK112XP2npqkNeBhQ1dwAUYrCEIpIgiEeTOZMLJ+6/EROEtRj0ZT5PKaTK68INh3eoqd69qarj6LIKwURBAI88YSBB2h6oKgED5a8BGMTKcASGRm+g2yuTxPnpkSs5AgNBARBMK8mYjXrhEEvC5cqtg0ZAmCZBlB8NRIjFQ2zwXrRRAIQqMQQSDMG1sjqEEQKKWK2lVqrRmNmhpBmdyCfaajeOc6CR0VhEYhgmCVoLUmm8s35NqWIKglagiMpDIrfHQ6lSWVNcZVzjS099QUAa+LLb0tCzRaQRBKEUGwSviTmx/l97/8QEOuPZnIEPC6inqyzkbY7yFqmoZGTbMQlM823nt6kvPXtuFuso5OgrCSaJggUErtUkrdp5R6RCm1Ryl1ubldKaX+WSl1WCn1mFLqUsc5NyilDpmPGxo1ttXI/U+P8fNDozw9Glvwa0/E0zX5ByzCPg9x0zQ04hAEpT6CfF7zxOkp8Q8IQoNppEbwD8BHtda7gL8ynwO8BNhmPt4BfB5AKdUFfAS4Argc+IhSqrOB41s1xFJZTk0kAPjuQycX/Pq1lpewCPvddk+CkWhBEJT6CI6PxYmmsuIfEIQG00hBoAHrF9wOnDb/vx74qja4D+hQSq0FrgXu1FqPaa3HgTuB6xo4vlXDYbOBfNjn5rsPnSKfLx+vP1cmExk6grVXEnU2sHeahkp9BHttR7FoBILQSBopCP4Y+KRS6gTwKeCD5vb1wAnHcSfNbZW2C/PkkCkI3vbcLZyaSHDf05Gyx50Yi3NgaLru60/EMzU7igFCjnaVRRpBiSA4OBzFpeDc/ta6xyQIQu3MSxAope5SSu0t87geeCfwPq31BuB9wH8sxIDN132H6XfYMzIyslCXXbEcOjuN1614+/O20Or38J0Hy5uH/uqWvbzr6w/Wff2pRKamZDILo4G9MemPTqfxmR2bSn0E08kMYZ+nKRt5CMJKYl6/MK31NVrrC8o8bgFuAL5rHvptDLs/wClgg+MyA+a2StvLve4Xtda7tda7e3t75/MWVgWHh6Ns6Wmhxe/hZRev5fa9Q0UlHiz2nZ7i6dFY2cSu2Zio10fgcxdpBAOdRg2h0qiheCpn9y8QBKFxNHKpdRp4vvn/VcAh8/9bgTeb0UPPBCa11meAO4AXK6U6TSfxi81twjw5dDbKOf1GHP6rLh0gns7xo71DRceMx9KcnU6R19QVWZTO5omnczUlk1mE/R7i6Rz5vGZkOsV6UxCUOotj6axdpE4QhMbRSEHwduAflVKPAp/AiBACuA04AhwGvgS8C0BrPQb8LfCA+fgbc5swDxLpHCfG42zrMwTBZZs6GewOccsjxcrWfodvwPIp1IJdcK4u05DZpSyTYzSaor8tgN/jmqGJJNKiEQjCYtCw5ZbW+hfAZWW2a+DdFc65CbipUWNajTw1EkVr2NZnOFyVUrxgex/feuAE2Vwej2mfPzA0ZZ9zeLh2h3E9lUct7C5lySyj0RQ9LX5CPvcMZ3EsnSUkGoEgNBzxwq1wrNDRbf2FEg2XbOwgkclxwDHhHxiepjPkZXNPuE6NwOhFUI8gsCqQnppIkMlpelv9BL3uGaaheDpHyCcagSA0GhEEK5xDZ6fxuBSD3YXG8pduNPL0Hjo+YW/bPzTN9jWtbOtrmZNpqJamNBbWKv9YxPBF9Lb6CZuksVwAABzGSURBVJTTCFLiIxCExUAEwQrn0HCUwZ5wUQjmQGeQnhY/Dx8fB4xSDgeHptmxpo1t/S0cHY2RztZWoG5upiFjlX80Egegp8VH0Oue4SMQjUAQFgcRBCucw2ejtqPYQinFJRs7eMTUCE5NJIilc6ZG0Eo2rzkaqS1yqJ5eBBbhEo2gzzQNzQgfTedsf4IgCI1DBMEKJpnJcTQSmyEIwPATHBmNMR5L8+QZw1G8fU0r55jHHhquzTxkl6AO1D5hW5P7UTNMtbclQLCMaSiezopGIAiLgCy3VjBPj8bIazinTIkGy0/wyIkJu6zEuf2tuJVCKcO3AGurvsZEPEOr32NHH9WC0zTkc7toC3oIet1FlUjT2TyZnBZBIAiLgAiCFYzl9C2nEVw00I5LwcPHx3lqNMaGrqAdzbOhM1Szw3gqkakrhwAKGsFkIsO69gBKKYK+Yh+BlXks4aOC0HjkV7aCOTw8jUvB5p7wjH0hn4cda9p4+MQEZyaTbO8vlHre1tfC4RpNQ/WWlwCKIoF6Wv0ARvhokSAw/g9LQpkgNBzxEaxgDgxPs6k7XLFz2KWbOnj4+ARPj8bYsaZgPjqnv4Ujo9GaWltO1llwDsDtUgS8xlevt8UQBIGSPALRCARh8RBBsEKJprL8/NAolw92VTzmkg2dRFNZcnnNdocg2NbXSianOTYWr/o69TalsbDMUL2WRlDiLLYa14hGIAiNRwTBCuXWR04TT+d4/eUbKh5zycYO+/8dRYKg9sihiXiG9jqa0lhYK/2eloJpKJPTZEwtJGZqBEGvaASC0GhEEKxQvnH/cXasaWXXho6Kx2zuCdMR8uJzuxh0+BG2moLg8NnZaw5prQ1n8Rw0gnCJRmBFB1kO47hoBIKwaIggWIHsPTXJ46cmef0zNqCUqnicUoort3Rz4UA7Xkf4Z4vfw/qOYNXIoUQmRzqXn5sgMCf+HoePwLomGJVJQXwEgrAYyK9sBfKN+4/j97j4nUsGqh77yddcTC43s4fx1r4Wu2BdJQp1huavEQRNQZBMG6ahuNk4RzQCQWg8ohGsMOLpLLc8cpqXXri2pvj+Fr+n7HG9LX67fEQl5lJewvm6UOwshoJGEEuLRiAIi4UIgibkwWPjHKqjJ4CTHz52hmgqyxuu2DivMbQGPEwnZxcEtkYwB0EQsk1DhqPZ0gissFFLI5DMYkFoPCIImpAPf+9xPvXjA3WfNzyV5F9+eohz+lrYvalzXmNo8XuIprIYfYTKY2kEbXMQBF1hH61+j60ZlPoIYukcPreryHchCEJjEL27CYmmsozHZl+NlzIaTfG7X7qPsWiar73tilmdxLXQEvCQ18bEXMk8MzUPH8Hbn7eF37pwrT3O0qihRDorbSoFYZEQQdCEJDN5pqqYZZxMxNO88d9/w6mJBF/5/cu5ZOP8tAEo2PCjycrtIufSi8Cip8VvRwyBw0eQtvIIctKURhAWCdG7m5BUJmdPsrXw4e/v5chojC+9eTdXbOlekDG0mmWlp5LZisdMJNK4XcoWGvMhWBo+KiWoBWHRkCVXE5LI5MjPYpsv5cDQNFdt7+O523oXbAyWIIimKgsCq7zEfM1QUMZHkJLuZIKwWIhG0GRkc3myeU0snbPLLVRjLJamu6X+Mg+z0eI3zD3RWTSC4amUHfUzXwqmITNqKF3ZJCUIwsIigqDJSDp6BU/PMglb5PKa8Xia7vBCCwJLI6hsojoeibOxa2aJ67lgm4ashLJ0TpLJBGGREEHQZDhLMdfiJ5iIp9HaCMdcSCzTUCVhpLXm+FicTd2hBXk9t0vh87gcPoLK0UqCICwsIgiaDGeXrqkaBEEklgag2xGBsxBU8xGMTKdIZHILJgjA0AqSto8gKxqBICwSIgiajFS2Po0gEjUFwQJrBFYtoEoagdWrYGPXwgoCSyOKp3NSgloQFgkRBE1GMlPwEdSSSzBmagRdC+ws9rpdBLyuihrBsYghCDZ1L4yPAArNabTWxNOiEQjCYiGCoMlIFJmGqjuLx2IpYOF9BGBEDlXSCI5HYrgUrO8ILtjrBcy+xalsnryWgnOCsFiIIGgynD6CmkxDpkbQGVp4QdAa8FTWCMbirOsI4vMs3Fco6HWRSOeISQlqQVhURBA0GfWahiLRNB0hb0OKs7X4PUQrjOFYZOEihiws01BcSlALwqIigqDJSNSpEYzF0g0xC4FVirqCaWhs4XIILIJej6ERpKUEtSAsJiIImgzLNOTzuGoMH00teMSQhVWKupTpZIaxWLohGkGySCMQQSAIi4EIgiYjZQqCvlb/kmsELRU0AjtiaAFDR8H0EWRyjsb1YhoShMVgXoJAKfUapdQ+pVReKbW7ZN8HlVKHlVIHlFLXOrZfZ247rJT6c8f2zUqp35jbv6WUaszs1uRYpqH+tsCslT8tDEGwsMlkFq0VNILjVg7BQmsEZtSQmIYEYXGZr0awF3glcK9zo1LqfOD1wE7gOuBzSim3UsoNfBZ4CXA+8AbzWID/C3xaa30OMA68dZ5jW5ZYzuL+Nn9V01A+rxmLpRes8FspLYHyXcqORmLAwuYQAAR8buLpnN2uUvoRCMLiMC9BoLV+Umtdrqfi9cA3tdYprfXTwGHgcvNxWGt9RGudBr4JXK+MOsZXAd8xz/8K8Ir5jG25kszk8LgUnSFfVUEwkciQb0CdIYvWgJdcXhc5sMEoNtcd9i1IHwInQa+bdDZvVzwVjUAQFodG+QjWAyccz0+a2ypt7wYmtNbZku2rjkQmR9Drpj3oZTKRmbVncCOTyaC4S5mTY5H4gpuFoDDxW7kRIfERCMKiUFUQKKXuUkrtLfO4fjEGWGFM71BK7VFK7RkZGVmqYTSEZCaP3+umLeglW2Y17qRQZ6hBPgKrAmmJn+D4WHzBHcVQKEVtvS/ruSAIjaXqkktrfc0crnsK2OB4PmBuo8L2CNChlPKYWoHz+HJj+iLwRYDdu3fX3sprGZDK5Ah4XXYf4KlE5QYtdp2hRdQIUtkcpycTbOweWPDXs7qURWIpgl43btf8O58JglCdRpmGbgVer5TyK6U2A9uA+4EHgG1mhJAPw6F8qzbsH3cDrzbPvwG4pUFja2os01BbwBAEs4WQjpqCoGHOYv/MUtQnxxNovfCho1DoUjYaTUt5CUFYROYbPvo7SqmTwJXA/yql7gDQWu8DbgaeAG4H3q21zpmr/fcAdwBPAjebxwJ8APgTpdRhDJ/Bf8xnbMuVZCZHwPQRwOxlJsZME0pnA53FYCSQWRy3q4420jSUsoWCIAiNZ17eOK3194DvVdj3ceDjZbbfBtxWZvsRjKiiVU0ykyfgddEWND6ayfgsgiCWoi3gaUidISjfpeyYGTraCGexLQhiada0BRb8+oIglEcyi5uMZLZ2jSASSy94ZzIn5UxDx8bihHxuehvwupYWMBHPSOioICwiIgiajETaEAS1+Agi0caVl4BCiQens/jEWIINnSGM1I+FxWkOkvISgrB4iCBoMlLZPAGv2zbLzNacZiyWbljBOTAK3/k9xV3KTk0kWN+5cM1onDjDRUUjEITFQwTBEhJNZYsa0YDpLPa48LhdtPg9s2sEsTTdDYoYsmgNeItqHp0ajy9oVzInxYJANAJBWCxEECwhv/ul+/i7254s2pbI5GwTSVvAU9FHkM9rxuONNQ1BcZey6WSGqWS2YRpBwCcagSAsBbLsWiKSmRx7T03SU+J0tcJHAdrMMhPlmEpmyOV1wyqPWji7lJ2aSAAL26fYiVMjEB+BICweohEsEU+Pxsjr4hh9rbURPmr2AW4LeisWnhu1y0s0ViNwNqc5NW4KggZpBF63C6/bcEKLRiAIi4cIgiXi0NkoUByjn8oaJagtE0n7LBqBVV6i0T4CZ3MaSyMYaJBGAIUyE1KCWhAWDxEES8Th4WmgWBBYjuOAx/IReCv2DG505VELZ9/iU+MJfG7XDHPWQmKZhySzWBAWDxEES0RBIyis+K2mNNaquH0W05BVqrlRlUctnF3KTk4kWNcRwNXAYnCWAJBaQ4KweIggWCIOmhqBswOYVXI66LN8BB6mU1ly+ZkFVgt1hrwNHaezS9mp8cblEFhYGoGEjwrC4iGCYAlIZ/McjcQJeF3kNcTThgAoNQ1ZZSamy4SQRmJpWgMe/J7Grpxb/EaXsmQmbySTNdA/AOIjEISlQATBEnA0EiOX11w00AEU/AS2IPAWfAT8/+3de2yd9X3H8ffXPvbx5Rxfkji2YycQiJPghHs2blGpgCDoBcrWaVs7wdZuSNuqlg5poqrUdVInrdK0C9KEROk2YB1dS2kJrSgFhlTUABkUCLmQOoZAnPgSJ3Yc3+2c3/54nsfnHPsc5+bzHHaez0uy7PM85/j5PfzC8/Xv+7uRe5mJYwWeVRxI+DOcB0enOHpyiraGpV9sLtNci0CpIZHQKBAUQVe/1z9w5ZogEHgP+iA1FK/wqiVzc5r5jo9NFbyjGLxJbQBdA14qq9CpoWDYqIaPioRHgaAIugZOYgZXrvYDgd8ZO+V3FldnTCiD3C2C/pEpmpKF7SiG9Aqk+3r9QFDo1FClUkMiYVMgKIKugVFWN9bMPcjzpob8PQnmLzPhnKNnaJzVjYVN00A6EOzv8wJBe2idxWoRiIRFgaAIDvSPsr45QSKe3Rk8OZsdCOrztAiOjU0zOZMq+EMZ0n0E+/u8VkxzgTeMCQKBlpgQCY8CQchmT6V4b3CUdSuTc0tNB+v9T0zPSw1VBX0E2YGgx1/qoT2EFkHSD1bdR0dpTlZRGSvsP5maynLKDOIFvo6IpOnPrpB9cHycmVOOjpWJBVtBplND3kOwprKcWJktaBH0DHn7BrcvK3yLICjjbMoVvKMY4LNXt7NmeWE2vhGR3BQIQhaMGOpoTlBbGcMsf2rIzLyF5yZztwgK3XEL2SmaMK7X0ZykozlZ8OuISJra3yE74A/DvLgpQVmZkaiMzY0amvQnlmWmRbxlJrKHj/YMjdNQU0GyqrCziiG9SxkUfuioiBSHAkHIugZGaWuonvtLO3NRt8nZFFUVZVlpkaZEnCP+qp+BnqGJUDqKA0F6KIwWgYiEL5KBYHRqlk8++DL/+eoHoV+7q3+UdSsTc6+9ZZ791FDGpjSB9S0J9vefnFuPCPxAUOAZvpmCIaRqEYiUpkgGgtrKcvpHJnn70HDo1+4fmcx6oCarKuZW95yYPpW1SxfAxpY6Tk7OcuTEJJCeQxBui8BLQRVyHwIRKZ5IBgIz45LWOvYcGQn1us45hidmaKhO5/YXpobmBwKv4/TdXq+sg6PhzSEIqEUgUtoiGQgAOlfV0TVwkml/V7AwBEtKN9ak1whKxGNZw0fnj59fHwQCf2ZvMHR09bIQU0NVMRprKrQ0tEiJiuz/2ZtW1TNzynFgYJTOVXWhXHN4zOsLqK/JbBFUZAWC+S2CuqoK2hqq55Z4CHMyWeBTl7WyeVV9aNcTkXBFNhB0tnoP/z1HToQXCCb8zWQyWgR18zqL5/cRgJcemh8IwkzT3HlFW2jXEpHwRTY1tHZFLdUV5eztDa+fYGjce+A3ZLQIEvEYU7MppmdTTM6k5mYVZ9rQkqT76CjTsyl6hsZprKmYy9uLiJyvyAaC8jJjY2uSvSF2GA+PBy2C7M5i8Ia0TuRIDQFsbK1jNuXoPjrqzyEILy0kIqUvsoEAvPTQ3t6RrDH6Z8M5x33ff5On3zp8Ru8fnmsRpFNDwdDMk5Mzi6aGwFsBNOyhoyJS+qIdCFZ5Y/SDvPvZeu394/zkrSM88/aRM3p/EAjqM4aPJjIWnpucSRHPEQjWrqilotzY1zsS+qxiESl9kQ4Em/yRMOc6n+DxV7yZycHQztMZGp8mGY9RUZ7+z565AunUzKmcfQQV5WWsW5nkV92DTM2mlBoSkSV1XoHAzH7PzPaYWcrMtmQc32Zmb5jZO/73mzLOXe0fP2BmD5q/sI6ZLTOz582sy//eeD5lOxMbmpOUGew9cuKsP9t3YpLn9vSRrIrRMzQxNzt4McPj01lDRyG958DJyRkm8qSGwEsP7T7sBSy1CERkKZ1vi2A38DvAL+cdHwQ+7Zy7FLgHeDzj3EPAnwEd/tdt/vEHgBedcx3Ai/7rgqquLOfipsQ5jRz6r50fcso57rtlPZDeynExwxMzWUNHIT1rd3h8htmUy9lZDN7IoYBaBCKylM4rEDjn9jnn9uc4/qZzLkic7wGqzSxuZq1AnXPuVef10D4GfMZ/353Ao/7Pj2YcL6jOVXVnPXJoejbFEzs/5OPrm7i1sxk4s0AwND6TNXQU0qmho6NTADlTQ5DuMAYt9SAiSyuMPoLfBX7tnJsC2oCejHM9/jGAZudcr/9zH9AcQtnobK3jyIlJhsam+eDYGPf/4G1efe/Yop95bk8fR09Ocff1F3pLSleWs7/v9MHkxPh01oghSHcWHz3pBYL8qSFv0pvmEIjIUjvtE8XMXgBacpz6unPu6dN8dhPwbeDWsymUc86ZWd4xnWZ2L3AvwJo1a87mVy8QdBh/Y/sefrGnj6nZFLOpFNdetDzvZx5/5QMuWF7DjR1NlJUZ61uSZ9RhPDQ+kzWHACAeK6cyVjbXIsg1agiguS5OfXVFqGsMiUg0nDYQOOduOZdfbGbtwI+Bu51z3f7hw0B7xtva/WMA/WbW6pzr9VNIA4uU6WHgYYAtW7ac2yQA3yWtXsrlmbePcPvmFo6PTbOrJ3/n8bHRKXYePM7929ZTVuZtILOxJcmzu/twzuXda/dUyjEymb3yaKCuKjbXIsjXR2Bm3HVlG8tqK3OeFxE5VwVJDZlZA/Az4AHn3K+C437qZ8TMrvVHC90NBK2K7Xgdy/jfF21tLJXliTh/8+lOHrl7Cw/90dV8bH0T7w+OLdgwPvCKnzba2rFi7tiG5iTD4zMM+A/zXEYmZnCOBakh8CaVDZ4mNQTwzTs28eWbO87ovkREztT5Dh+9y8x6gOuAn5nZc/6pLwHrgG+Y2Vv+10r/3F8AjwAHgG7gWf/43wPbzKwLuMV/HYo/uWEtt/idvpe2eami3Ydztwp2dB8jGY/NvQ9gg5+/Xyw9NDyxcJ2hQCKe2SKI9NQOESmC8+p1dM79GC/9M//4t4Bv5fnM68DmHMePATefT3mWwmXt3gP+7Z5hbli3YsH5HQcGueaiZcQyJoWll4AY4cb1TTl/79D4wpVHA8mq9Ab2+VJDIiKFoj8/52moqeSC5TXsOrSwRXB4eIKDx8a57uLsANFYW8nKZHzxFoEfCHK1CIIhpABVMQUCEQmXAkEOl7bV806O1NCOA4MA3LBu4YiiDS1JftO/WCBYuOBcIBFPB4fqSlWJiIRLT50cLm9v4PDwBIOj2Z2/O7qPsby2kg3NyQWf2diSpKt/lFOp3IOYgr0I5g8fhewWQVwtAhEJmQJBDkE/wa6e4bljzjl2dA9y3cXLcw4R3dBSx9RsioPHxnL+zhPj05ill53OVJeZGlIfgYiETIEgh01t9ZiRNZ+g++gY/SNTOTuQIXvPgFyGxmeor66gvGxhEElkBILqSgUCEQmXAkEOiXiMdU2JrECwo9vrH7j+4twzjtetTFBm8G6eBeyGJ3JPJoPsVkJVTFUiIuHSUyePy9ob2NUzPLd72Y4Dx2hrqGZNniUeqirKuXx1A8/s6iWVo59gOMc6Q4GgjyBWZlnDUkVEwqCnTh6XtdczODrN4eEJntj5IS/tH2DruhV5l5AA+MINa3l/cIwX9vUvODc0Pp2zoxjSS1EvNqtYRKRQFAjyCDqMP/ed1/jaU+9w1ZpGvrpt/aKfuX1zC20N1Tzy8vsLzg2PzyzSIvACRL4F50RECkmBII9LWuuIx8o4PjbN3921me/96TW01Fct+plYeRlf2LqWnQeP89ah4axzwzn2IggEo4a0vISIFIOePHlUVZTzoz+/nhf+6kY+f80FcyuNns7v/9ZqklUxvvPye3PHZk6lGJ2apaE6d4sgGDWk1JCIFIMCwSI2t9WfthUwXyIe43PXrOHZd3o5dHwcSM8qbqxdfNSQ5hCISDEoEBTAH19/IWVmPPbKQQBOTHjrDNXnGT5aW1mOmVJDIlIcevIUQGt9NTeub5rbrCa9vETu1JCZkYjH1CIQkaJQICiQWzc10zM0wb7ekwyN5V+COlBXVaFAICJFoUBQIDdtbMYMnt/bv+imNIFtnc1szbN8hYhIIZ3XxjSSX1MyztVrGvnF3j7uvGIVsHgg+OYdm8IqmohIFrUICujWTc3sOTLCniMjxMpsbgaxiMhHiQJBAW3rbAHg57v7aKipWHR5ChGRYlEgKKC1K2rpWJlgajaVd+ioiEixKRAU2K2bmoHFRwyJiBSTAkGBBemhfAvOiYgUmwJBgV3WVs8Fy2vy7mMgIlJsGsZSYGVlxvYvbdXyESLykaVAEAJ1FIvIR5n+TBURiTgFAhGRiFMgEBGJOAUCEZGIUyAQEYk4BQIRkYhTIBARiTgFAhGRiFMgEBGJOAUCEZGIM+dcsctwXszsKPDBOX58BTC4hMX5qNP9lr6o3bPud3EXOOeaTvem//eB4HyY2evOuS3FLkdYdL+lL2r3rPtdGkoNiYhEnAKBiEjERT0QPFzsAoRM91v6onbPut8lEOk+AhERUYtARCTyIhkIzOw2M9tvZgfM7IFil2epmdlqM3vJzPaa2R4z+4p/fJmZPW9mXf73xmKXdSmZWbmZvWlmP/VfrzWz1/x6/m8zqyx2GZeSmTWY2ZNm9q6Z7TOz60q5js3sq/6/591m9oSZVZVaHZvZv5nZgJntzjiWs07N86B/77vM7KpzvW7kAoGZlQP/CtwOdAJ/aGadxS3VkpsF7nfOdQLXAn/p3+MDwIvOuQ7gRf91KfkKsC/j9beBf3LOrQOGgC8WpVSF8y/Az51zG4HL8e69JOvYzNqALwNbnHObgXLgDyi9Ov4P4LZ5x/LV6e1Ah/91L/DQuV40coEA+G3ggHPuPefcNPB94M4il2lJOed6nXO/9n8+ifeAaMO7z0f9tz0KfKY4JVx6ZtYOfBJ4xH9twE3Ak/5bSu1+64GPAd8FcM5NO+eGKeE6xttjvdrMYkAN0EuJ1bFz7pfA8XmH89XpncBjzvMq0GBmredy3SgGgjbgUMbrHv9YSTKzC4ErgdeAZudcr3+qD2guUrEK4Z+BvwZS/uvlwLBzbtZ/XWr1vBY4Cvy7nw57xMxqKdE6ds4dBv4B+BAvAJwA3qC06ziQr06X7FkWxUAQGWaWAH4E3OecG8k857zhYiUxZMzMPgUMOOfeKHZZQhQDrgIecs5dCYwxLw1UYnXciPcX8FpgFVDLwhRKyStUnUYxEBwGVme8bvePlRQzq8ALAt9zzj3lH+4Pmo7+94FilW+J3QDcYWYH8VJ9N+Hlzxv8NAKUXj33AD3Oudf810/iBYZSreNbgPedc0edczPAU3j1Xsp1HMhXp0v2LItiIPhfoMMfbVCJ1+G0vchlWlJ+fvy7wD7n3D9mnNoO3OP/fA/wdNhlKwTn3Necc+3OuQvx6vN/nHOfB14CPuu/rWTuF8A51wccMrMN/qGbgb2UaB3jpYSuNbMa/993cL8lW8cZ8tXpduBuf/TQtcCJjBTS2XHORe4L+ATwG6Ab+Hqxy1OA+9uK13zcBbzlf30CL2/+ItAFvAAsK3ZZC3DvHwd+6v98EbATOAD8EIgXu3xLfK9XAK/79fwToLGU6xj4W+BdYDfwOBAvtToGnsDrA5nBa/V9MV+dAoY3ArIbeAdvRNU5XVczi0VEIi6KqSEREcmgQCAiEnEKBCIiEadAICIScQoEIiIRp0AgIhJxCgQiIhGnQCAiEnH/B5GPjRl6sxsTAAAAAElFTkSuQmCC\n",
218 | "text/plain": [
219 | ""
220 | ]
221 | },
222 | "metadata": {},
223 | "output_type": "display_data"
224 | }
225 | ],
226 | "source": [
227 | "state = envs.reset()\n",
228 | "\n",
229 | "while frame_idx < max_frames:\n",
230 | "\n",
231 | " log_probs = []\n",
232 | " values = []\n",
233 | " rewards = []\n",
234 | " masks = []\n",
235 | " entropy = 0\n",
236 | "\n",
237 | " for _ in range(num_steps):\n",
238 | " state = torch.FloatTensor(state).to(device)\n",
239 | " dist, value = model(state)\n",
240 | "\n",
241 | " action = dist.sample()\n",
242 | " next_state, reward, done, _ = envs.step(action.cpu().numpy())\n",
243 | "\n",
244 | " log_prob = dist.log_prob(action)\n",
245 | " entropy += dist.entropy().mean()\n",
246 | " \n",
247 | " log_probs.append(log_prob)\n",
248 | " values.append(value)\n",
249 | " rewards.append(torch.FloatTensor(reward).unsqueeze(1).to(device))\n",
250 | " masks.append(torch.FloatTensor(1 - done).unsqueeze(1).to(device))\n",
251 | " \n",
252 | " state = next_state\n",
253 | " frame_idx += 1\n",
254 | " \n",
255 | " if frame_idx % 1000 == 0:\n",
256 | " test_rewards.append(np.mean([test_env() for _ in range(10)]))\n",
257 | " plot(frame_idx, test_rewards)\n",
258 | " \n",
259 | " next_state = torch.FloatTensor(next_state).to(device)\n",
260 | " _, next_value = model(next_state)\n",
261 | " returns = compute_gae(next_value, rewards, masks, values)\n",
262 | " \n",
263 | " log_probs = torch.cat(log_probs)\n",
264 | " returns = torch.cat(returns).detach()\n",
265 | " values = torch.cat(values)\n",
266 | "\n",
267 | " advantage = returns - values\n",
268 | "\n",
269 | " actor_loss = -(log_probs * advantage.detach()).mean()\n",
270 | " critic_loss = advantage.pow(2).mean()\n",
271 | "\n",
272 | " loss = actor_loss + 0.5 * critic_loss - 0.001 * entropy\n",
273 | "\n",
274 | " optimizer.zero_grad()\n",
275 | " loss.backward()\n",
276 | " optimizer.step()"
277 | ]
278 | },
279 | {
280 | "cell_type": "code",
281 | "execution_count": 32,
282 | "metadata": {},
283 | "outputs": [
284 | {
285 | "data": {
286 | "text/plain": [
287 | "-283.0576102217745"
288 | ]
289 | },
290 | "execution_count": 32,
291 | "metadata": {},
292 | "output_type": "execute_result"
293 | }
294 | ],
295 | "source": [
296 | "test_env(True)"
297 | ]
298 | },
299 | {
300 | "cell_type": "code",
301 | "execution_count": null,
302 | "metadata": {},
303 | "outputs": [],
304 | "source": []
305 | }
306 | ],
307 | "metadata": {
308 | "kernelspec": {
309 | "display_name": "Python [conda env:pytorch4]",
310 | "language": "python",
311 | "name": "conda-env-pytorch4-py"
312 | },
313 | "language_info": {
314 | "codemirror_mode": {
315 | "name": "ipython",
316 | "version": 3
317 | },
318 | "file_extension": ".py",
319 | "mimetype": "text/x-python",
320 | "name": "python",
321 | "nbconvert_exporter": "python",
322 | "pygments_lexer": "ipython3",
323 | "version": "3.5.5"
324 | }
325 | },
326 | "nbformat": 4,
327 | "nbformat_minor": 2
328 | }
329 |
--------------------------------------------------------------------------------
/5.ddpg.ipynb:
--------------------------------------------------------------------------------
1 | {
2 | "cells": [
3 | {
4 | "cell_type": "code",
5 | "execution_count": 1,
6 | "metadata": {},
7 | "outputs": [],
8 | "source": [
9 | "import math\n",
10 | "import random\n",
11 | "\n",
12 | "import gym\n",
13 | "import numpy as np\n",
14 | "\n",
15 | "import torch\n",
16 | "import torch.nn as nn\n",
17 | "import torch.optim as optim\n",
18 | "import torch.nn.functional as F\n",
19 | "from torch.distributions import Normal"
20 | ]
21 | },
22 | {
23 | "cell_type": "code",
24 | "execution_count": 2,
25 | "metadata": {},
26 | "outputs": [],
27 | "source": [
28 | "from IPython.display import clear_output\n",
29 | "import matplotlib.pyplot as plt\n",
30 | "%matplotlib inline"
31 | ]
32 | },
33 | {
34 | "cell_type": "markdown",
35 | "metadata": {},
36 | "source": [
37 | "Use CUDA "
38 | ]
39 | },
40 | {
41 | "cell_type": "code",
42 | "execution_count": 3,
43 | "metadata": {},
44 | "outputs": [],
45 | "source": [
46 | "use_cuda = torch.cuda.is_available()\n",
47 | "device = torch.device(\"cuda\" if use_cuda else \"cpu\")"
48 | ]
49 | },
50 | {
51 | "cell_type": "markdown",
52 | "metadata": {},
53 | "source": [
54 | "Replay Buffer "
55 | ]
56 | },
57 | {
58 | "cell_type": "code",
59 | "execution_count": 5,
60 | "metadata": {},
61 | "outputs": [],
62 | "source": [
63 | "class ReplayBuffer:\n",
64 | " def __init__(self, capacity):\n",
65 | " self.capacity = capacity\n",
66 | " self.buffer = []\n",
67 | " self.position = 0\n",
68 | " \n",
69 | " def push(self, state, action, reward, next_state, done):\n",
70 | " if len(self.buffer) < self.capacity:\n",
71 | " self.buffer.append(None)\n",
72 | " self.buffer[self.position] = (state, action, reward, next_state, done)\n",
73 | " self.position = (self.position + 1) % self.capacity\n",
74 | " \n",
75 | " def sample(self, batch_size):\n",
76 | " batch = random.sample(self.buffer, batch_size)\n",
77 | " state, action, reward, next_state, done = map(np.stack, zip(*batch))\n",
78 | " return state, action, reward, next_state, done\n",
79 | " \n",
80 | " def __len__(self):\n",
81 | " return len(self.buffer)"
82 | ]
83 | },
84 | {
85 | "cell_type": "markdown",
86 | "metadata": {},
87 | "source": [
88 | "Normalize action space "
89 | ]
90 | },
91 | {
92 | "cell_type": "code",
93 | "execution_count": 8,
94 | "metadata": {},
95 | "outputs": [],
96 | "source": [
97 | "class NormalizedActions(gym.ActionWrapper):\n",
98 | "\n",
99 | " def _action(self, action):\n",
100 | " low_bound = self.action_space.low\n",
101 | " upper_bound = self.action_space.high\n",
102 | " \n",
103 | " action = low_bound + (action + 1.0) * 0.5 * (upper_bound - low_bound)\n",
104 | " action = np.clip(action, low_bound, upper_bound)\n",
105 | " \n",
106 | " return action\n",
107 | "\n",
108 | " def _reverse_action(self, action):\n",
109 | " low_bound = self.action_space.low\n",
110 | " upper_bound = self.action_space.high\n",
111 | " \n",
112 | " action = 2 * (action - low_bound) / (upper_bound - low_bound) - 1\n",
113 | " action = np.clip(action, low_bound, upper_bound)\n",
114 | " \n",
115 | " return actions"
116 | ]
117 | },
118 | {
119 | "cell_type": "markdown",
120 | "metadata": {},
121 | "source": [
122 | "Ornstein-Uhlenbeck process \n",
123 | "Adding time-correlated noise to the actions taken by the deterministic policywiki "
125 | ]
126 | },
127 | {
128 | "cell_type": "code",
129 | "execution_count": 12,
130 | "metadata": {},
131 | "outputs": [],
132 | "source": [
133 | "class OUNoise(object):\n",
134 | " def __init__(self, action_space, mu=0.0, theta=0.15, max_sigma=0.3, min_sigma=0.3, decay_period=100000):\n",
135 | " self.mu = mu\n",
136 | " self.theta = theta\n",
137 | " self.sigma = max_sigma\n",
138 | " self.max_sigma = max_sigma\n",
139 | " self.min_sigma = min_sigma\n",
140 | " self.decay_period = decay_period\n",
141 | " self.action_dim = action_space.shape[0]\n",
142 | " self.low = action_space.low\n",
143 | " self.high = action_space.high\n",
144 | " self.reset()\n",
145 | " \n",
146 | " def reset(self):\n",
147 | " self.state = np.ones(self.action_dim) * self.mu\n",
148 | " \n",
149 | " def evolve_state(self):\n",
150 | " x = self.state\n",
151 | " dx = self.theta * (self.mu - x) + self.sigma * np.random.randn(self.action_dim)\n",
152 | " self.state = x + dx\n",
153 | " return self.state\n",
154 | " \n",
155 | " def get_action(self, action, t=0):\n",
156 | " ou_state = self.evolve_state()\n",
157 | " self.sigma = self.max_sigma - (self.max_sigma - self.min_sigma) * min(1.0, t / self.decay_period)\n",
158 | " return np.clip(action + ou_state, self.low, self.high)\n",
159 | " \n",
160 | "#https://github.com/vitchyr/rlkit/blob/master/rlkit/exploration_strategies/ou_strategy.py"
161 | ]
162 | },
163 | {
164 | "cell_type": "code",
165 | "execution_count": 16,
166 | "metadata": {},
167 | "outputs": [],
168 | "source": [
169 | "def plot(frame_idx, rewards):\n",
170 | " clear_output(True)\n",
171 | " plt.figure(figsize=(20,5))\n",
172 | " plt.subplot(131)\n",
173 | " plt.title('frame %s. reward: %s' % (frame_idx, rewards[-1]))\n",
174 | " plt.plot(rewards)\n",
175 | " plt.show()"
176 | ]
177 | },
178 | {
179 | "cell_type": "markdown",
180 | "metadata": {},
181 | "source": [
182 | " Continuous control with deep reinforcement learning \n",
183 | ""
184 | ]
185 | },
186 | {
187 | "cell_type": "code",
188 | "execution_count": 18,
189 | "metadata": {},
190 | "outputs": [],
191 | "source": [
192 | "class ValueNetwork(nn.Module):\n",
193 | " def __init__(self, num_inputs, num_actions, hidden_size, init_w=3e-3):\n",
194 | " super(ValueNetwork, self).__init__()\n",
195 | " \n",
196 | " self.linear1 = nn.Linear(num_inputs + num_actions, hidden_size)\n",
197 | " self.linear2 = nn.Linear(hidden_size, hidden_size)\n",
198 | " self.linear3 = nn.Linear(hidden_size, 1)\n",
199 | " \n",
200 | " self.linear3.weight.data.uniform_(-init_w, init_w)\n",
201 | " self.linear3.bias.data.uniform_(-init_w, init_w)\n",
202 | " \n",
203 | " def forward(self, state, action):\n",
204 | " x = torch.cat([state, action], 1)\n",
205 | " x = F.relu(self.linear1(x))\n",
206 | " x = F.relu(self.linear2(x))\n",
207 | " x = self.linear3(x)\n",
208 | " return x\n",
209 | " \n",
210 | "\n",
211 | "class PolicyNetwork(nn.Module):\n",
212 | " def __init__(self, num_inputs, num_actions, hidden_size, init_w=3e-3):\n",
213 | " super(PolicyNetwork, self).__init__()\n",
214 | " \n",
215 | " self.linear1 = nn.Linear(num_inputs, hidden_size)\n",
216 | " self.linear2 = nn.Linear(hidden_size, hidden_size)\n",
217 | " self.linear3 = nn.Linear(hidden_size, num_actions)\n",
218 | " \n",
219 | " self.linear3.weight.data.uniform_(-init_w, init_w)\n",
220 | " self.linear3.bias.data.uniform_(-init_w, init_w)\n",
221 | " \n",
222 | " def forward(self, state):\n",
223 | " x = F.relu(self.linear1(state))\n",
224 | " x = F.relu(self.linear2(x))\n",
225 | " x = F.tanh(self.linear3(x))\n",
226 | " return x\n",
227 | " \n",
228 | " def get_action(self, state):\n",
229 | " state = torch.FloatTensor(state).unsqueeze(0).to(device)\n",
230 | " action = self.forward(state)\n",
231 | " return action.detach().cpu().numpy()[0, 0]"
232 | ]
233 | },
234 | {
235 | "cell_type": "markdown",
236 | "metadata": {},
237 | "source": [
238 | "DDPG Update "
239 | ]
240 | },
241 | {
242 | "cell_type": "code",
243 | "execution_count": 19,
244 | "metadata": {},
245 | "outputs": [],
246 | "source": [
247 | "def ddpg_update(batch_size, \n",
248 | " gamma = 0.99,\n",
249 | " min_value=-np.inf,\n",
250 | " max_value=np.inf,\n",
251 | " soft_tau=1e-2):\n",
252 | " \n",
253 | " state, action, reward, next_state, done = replay_buffer.sample(batch_size)\n",
254 | " \n",
255 | " state = torch.FloatTensor(state).to(device)\n",
256 | " next_state = torch.FloatTensor(next_state).to(device)\n",
257 | " action = torch.FloatTensor(action).to(device)\n",
258 | " reward = torch.FloatTensor(reward).unsqueeze(1).to(device)\n",
259 | " done = torch.FloatTensor(np.float32(done)).unsqueeze(1).to(device)\n",
260 | "\n",
261 | " policy_loss = value_net(state, policy_net(state))\n",
262 | " policy_loss = -policy_loss.mean()\n",
263 | "\n",
264 | " next_action = target_policy_net(next_state)\n",
265 | " target_value = target_value_net(next_state, next_action.detach())\n",
266 | " expected_value = reward + (1.0 - done) * gamma * target_value\n",
267 | " expected_value = torch.clamp(expected_value, min_value, max_value)\n",
268 | "\n",
269 | " value = value_net(state, action)\n",
270 | " value_loss = value_criterion(value, expected_value.detach())\n",
271 | "\n",
272 | "\n",
273 | " policy_optimizer.zero_grad()\n",
274 | " policy_loss.backward()\n",
275 | " policy_optimizer.step()\n",
276 | "\n",
277 | " value_optimizer.zero_grad()\n",
278 | " value_loss.backward()\n",
279 | " value_optimizer.step()\n",
280 | "\n",
281 | " for target_param, param in zip(target_value_net.parameters(), value_net.parameters()):\n",
282 | " target_param.data.copy_(\n",
283 | " target_param.data * (1.0 - soft_tau) + param.data * soft_tau\n",
284 | " )\n",
285 | "\n",
286 | " for target_param, param in zip(target_policy_net.parameters(), policy_net.parameters()):\n",
287 | " target_param.data.copy_(\n",
288 | " target_param.data * (1.0 - soft_tau) + param.data * soft_tau\n",
289 | " )"
290 | ]
291 | },
292 | {
293 | "cell_type": "code",
294 | "execution_count": 25,
295 | "metadata": {},
296 | "outputs": [
297 | {
298 | "name": "stdout",
299 | "output_type": "stream",
300 | "text": [
301 | "\u001b[33mWARN: gym.spaces.Box autodetected dtype as . Please provide explicit dtype.\u001b[0m\n",
302 | "\u001b[33mWARN: gym.spaces.Box autodetected dtype as . Please provide explicit dtype.\u001b[0m\n"
303 | ]
304 | }
305 | ],
306 | "source": [
307 | "env = NormalizedActions(gym.make(\"Pendulum-v0\"))\n",
308 | "ou_noise = OUNoise(env.action_space)\n",
309 | "\n",
310 | "state_dim = env.observation_space.shape[0]\n",
311 | "action_dim = env.action_space.shape[0]\n",
312 | "hidden_dim = 256\n",
313 | "\n",
314 | "value_net = ValueNetwork(state_dim, action_dim, hidden_dim).to(device)\n",
315 | "policy_net = PolicyNetwork(state_dim, action_dim, hidden_dim).to(device)\n",
316 | "\n",
317 | "target_value_net = ValueNetwork(state_dim, action_dim, hidden_dim).to(device)\n",
318 | "target_policy_net = PolicyNetwork(state_dim, action_dim, hidden_dim).to(device)\n",
319 | "\n",
320 | "for target_param, param in zip(target_value_net.parameters(), value_net.parameters()):\n",
321 | " target_param.data.copy_(param.data)\n",
322 | "\n",
323 | "for target_param, param in zip(target_policy_net.parameters(), policy_net.parameters()):\n",
324 | " target_param.data.copy_(param.data)\n",
325 | " \n",
326 | " \n",
327 | "value_lr = 1e-3\n",
328 | "policy_lr = 1e-4\n",
329 | "\n",
330 | "value_optimizer = optim.Adam(value_net.parameters(), lr=value_lr)\n",
331 | "policy_optimizer = optim.Adam(policy_net.parameters(), lr=policy_lr)\n",
332 | "\n",
333 | "value_criterion = nn.MSELoss()\n",
334 | "\n",
335 | "replay_buffer_size = 1000000\n",
336 | "replay_buffer = ReplayBuffer(replay_buffer_size)"
337 | ]
338 | },
339 | {
340 | "cell_type": "code",
341 | "execution_count": 28,
342 | "metadata": {},
343 | "outputs": [],
344 | "source": [
345 | "max_frames = 12000\n",
346 | "max_steps = 500\n",
347 | "frame_idx = 0\n",
348 | "rewards = []\n",
349 | "batch_size = 128"
350 | ]
351 | },
352 | {
353 | "cell_type": "code",
354 | "execution_count": 29,
355 | "metadata": {},
356 | "outputs": [
357 | {
358 | "data": {
359 | "image/png": "iVBORw0KGgoAAAANSUhEUgAAAYIAAAE/CAYAAABLrsQiAAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDIuMi4yLCBodHRwOi8vbWF0cGxvdGxpYi5vcmcvhp/UCwAAIABJREFUeJzsvXl8Y2d56P99JFmyJK+yZ/UynkwmewhJJjNkhxBCuC0NBdoCBQJdWEp7of2Ve+ntTqELvbe9UAptKEspULbLEtpASggQsmcSSDKTbfYZj2fsseVVkrW+vz/OOfKxrM22ZFvj5/v56GPpPYveI0vvc55djDEoiqIo6xfPak9AURRFWV1UECiKoqxzVBAoiqKsc1QQKIqirHNUECiKoqxzVBAoiqKsc1QQ1AAROV9EfiYi0yLy31d7Pkp9EZEfichvrPY8FKVWqCCoDf8D+KExptUY87HVnkwhInKHiDwvIjkReVvBtttF5HERmRKRQRH5iIj4XNsjIvJNEYmJyDEReVPB8W+yx2Mi8i0RiVR77HpFRLwi8iERGbJvHn4qIh2u7b8rIqft/8lnRCRQ5Bw3iogRkQ9V8X4RETkjIvcXjIdE5BMiMioikyJyn2vby0Tkh/b40YLjNorIv9vznxSRB0RkT8GxT4vIhIiM2d+BHtf2z4lISkRmXA+vvW3Avi73tj9exDW9XESeE5G4Pf9tBdtvFpEn7O/koIj8smvbi+3fQtz++2LXtu8WzCklIk8XHPsT+/MYLDbntYwKgtqwDdhfaqPzJV9FngR+C3iiyLYQ8D6gG9gDvBz4fdf2fwRSwCbgV4FPisjFAPbffwbeYm+PA5+o5tjFIBYr/l11C8Qa8+fANcDVQBvW5zdrv+crgQ9g/R+2AefY+7vn1QR8FHikyvf7G+DZIuN3ABHgQvvv77q2xYDPAO8vclwL8BhwpX3cvwL/KSIt9vZngFcaYzqArcAB4JMF5/iIMabF9cgWbO9wbfuLaq5JRLqBbwB/bM9rL/AV1/aLgC8Bfwi0A5cBj9vb/MC3gS8AnfY1fdsexxjzKvd8gQeBr7ne/kvAffb73gj8loj8QpF5r02MMfpYxgO4F8hi/ZBngPOAz2F98e/C+kHdDPwc8FNgCjgB/JnrHAOAAd5ubxsH3gVcBTwFTAAfL3jfX8P6IYwDdwPbqpjr/cDbKuzze8B37OdhrIX8PNf2fwP+2n7+l8CXXNt22Pu3Vjq2irn+CPgw8ACQAM7F+vF+GjgFnAQ+BHjt/Y8BV9rPf9X+PC+2X/868C37+W7gIfszPQV8HPC73tcA78FavI7YY68AngMm7f1/DPzGEr8vnfb3ZEeJ7V8C/tL1+uXA6YJ9PgB8xP6efajC+11jX+/bgftd4xfY38W2CsffDByt4rqmnM+/YDwA/BXwjGus5LxdvwXfEq7pHcCDrtdh+7tzgeuz/YsS57zF/k6Ja+w4cGuJOWaBAddYHLjI9fprwB8s5TuyGg/VCJaJMeYm4CfAbxvrbuEFe9ObsBayVqwFOAa8FejAEgrvFpHXFJxuD7AT+BXg/2LdudwMXAz8sojcCCAitwH/C3gtsMF+/3+v0SXdwJx2cx6QcV0TWNqFc1d/sf0aAGPMIezFv4pjq+EtWD/uVqyF/nNABksoXI7143Vs9T8GXmo/vxE4bF+L8/rH9vMs1p1vN9Yd+cuxtCU3r8H6X1zkusv8I/uYQ8C1zo4i0m+bQPqrvKZL7Wt4vW3+eUFE3uPaPu8ztZ9vEpEu+/22Yd0EfLDSG9ma6MeB38ZaXN3sxvpM/9w2DT0tIq+r8hoK3+fFgB846BrrF5EJrIX497EEl5vfEpGobYIp9r7HbBPLZ+3/QTXXVPh9jGH9v5zv3EvsczwtIqdE5AsyZ8q8GHjK2Ku4zVMU/76+FfiJMeaoa+z/Am8VkSYROR/ru3VPkWPXJCoI6se3jTEPGGNyxphZY8yPjDFP26+fwlq4byw45i/sff8LS3D8uzFmxBhzEmuxv9ze713AXxljnjXGZLDuzF9caA9dLCLya8Au4H/bQy1Yd3puJrEWZmf7ZIntlY6ths8ZY/bb1xgB/hvwPmNMzBgzAvw98AZ73x8z93lej3UX6rzOCwJjzOPGmIeNMRn7h/zPLPw//JUxJmqMSdjvud8Y83VjTBrrB3/a2dEYc9wY02GMOV7lNfViaTbnAduB1wN/JiKvsLcXfqbOc+dz+xjwx8aYmSre678DjxhjHi8xj0vs82/FWlj/VUQurPI6ABCRNixN78+NMfl5O58LlvD8IyyNyuFjWDc8G7HMOJ8TEUe4jmJpwtuwTE+twBervKZy30fnmt8CvM5+/yDwD1Ue6+atWDclbv4D63+ZwLrWTxtjHity7JpEBUH9OOF+ISJ7bOfVGRGZxFrMuwuOGXY9TxR57dhgtwEfte9EJ4AoIEAPS8TWTv4KeJUxZtQensGyYbtpA6ar2F7p2Gpwf4bbgCbglOu6/xlrMQFrob9eRLYAXuCrwLUiMoC18P7Mvs7zROQ/7LvxKSwhWvh/cL/vVvdr+47xBFVS4GDsx/o/AnzQGJOwbwq+jCVwYOHn5jyfFpFXA63GmK9QARHZirVo/mGJXRJAGstEkzLG/Bj4IZaWVe21BYHvAA8bY/6q2D7GmChz9nafPfaEMWbMFsZ3YS30r7W3zRhj9trbhrEE1C0i0lrFNVX6ziWAzxpjXrAF6V9S+nMvPNa55uuAzcDXXWMR4HtYWloz0Ae8UkQKNc01iwqC+lGotn4JuBPoM8a0A/+EtXgvhRPAO+07UecRNMY8uJSTicitwKeAVxtjnnZtegHwichO19hlzJmO9tuvnfOcg2UTfqGKY6vB/RmeAJJAt+ua24wxFwMYYw5i2Wl/B7jPGDOFdef+Diw7cs4+zyex7th2GmPasExshf8H9/uewvphO9co7tcVL2C+Q/Q4lrmh8D3cz+d9pvbzYWPMGJYZa5ctxE5jmRDfJyLfLvLWu4EtwDP2vh8FdtvHel3zmDfdaq9LrEimbwGDwDsr7O7DEtiFC637fUv9Fpw5eah8TYXfxzCW38r5zj1F+c/9Rfb/1+FFLPy+3g58o0AjOwfIGmM+bwuwQeYL97XPajspzoYHlmPzN1yvP0eBMwwYAW63n++2X3/Bfj1AgYMM6wf2UtfrLwB/ZD//RWAfc87QduCXyszPj3Wn8gDwm/Zzj73tJmAMuKHEsV/GMmOFsWzjk673vRjL/HO9vf0LwJerOXaxn6k99m2sH38b1sKwA7jRtf1L9nzeYr/+W/v1+137PAr8CdbCcwHwPPMdjgY41/W6G+uu8LVYC9p7sWz8S3IW2+e8D0ubCWBF7IwAL7e33YolwC7C8ifdy5xzvhXrbtR5fAXLPBYp8h6Bgn3fixVltNne3oRl0/9j+7quta/Tcax67O/Jq7B8Cc3YTnX72O9gCYIFTl37szrfPscGLO3sCdf212Nptx4sDWQa+7uO5Ztxju2yr/GHVV7TBvs79jp7vn+Dpa047/trwBGshTtkz+vfXL+RY/Y5A1iayDHmBxIE7fPfVHC9bVjBB2+y570Zy5n9l8X+/2vxseoTOBseVCcIXm9/saax7IkfZ4mCwH79FuBp5qKQPlNhfqbg8VJ72w+xFrYZ1+O7rmMj9g8+hhVF8aaCc7/JHo9hLdSRao7FEh4z1X6m9lg71h39oP2D/CnwBtf2d9rXts1+/fP26z2ufW7A0ghmsPwuH6SMILDHbsXScBZEDQH99rn6F/F96cEyJcxgObXfWbD997DMglPAZ4FAifPM+55hRUvtL7Hv29zXaY9djLVgxbBCPn/Rte2lRb4zP7K33Wi/jhd8b663t/8O1oIbwxJqX8YV1WZ/7pP29T1Z8D98o+vYU8DnsRf6Kq/pZvv/m7C/QwMF2/8cOGM//g3odG27HCucNIEVan15wbFvxPoNS5G53IQVUjtpX/OngFC91pxaP8S+CEVRFGWdoj4CRVGUdY4KAkVRlHWOCgJFUZR1jgoCRVGUdY4KAkVRlHVOvaorrhjd3d1mYGBgtaehKIqy5nj88cdHjTEbKu3X8IJgYGCAvXv3rvY0FEVR1hwicqya/dQ0pCiKss5RQaAoirLOUUGgKIqyzlFBoCiKss5RQaAoirLOUUGgKIqyzlFBoCiKss5RQaAoirLOUUGgKIqyzlFBoCiKsgT2D00yMjW72tOoCSoIFEWpC/c8M8z7vvzT1Z5G3XjbZx/j7+85sNrTqAkqCBRFqQt37z/Nt342RDqbW+2pVE0mm+PGv/0h33hisOx+sWSGM9NJhlUjUBRFKc2J8TgAU4n0Ks+kek5NznJsLM7eY+Nl9zs5kQBgLJZaiWnVHRUEiqLUhRNRa7GcbCBB4AivwfFE2f1O2tvHZpJ1n9NKoIJAUZSak87mODXZeILAEQCDtkAovZ+1PaoagaIoSnFOTcySM9bzhhIE0TmNIOdcQLH9bNNQPJUlkcquyNzqiQoCRVFqzgnXHXUjCYITtkaQyuQYLWP2OekyHY3FGt88pIJAUZSacyLaoIIgGsfrEet5GT/B4HgCezfGZhrfPKSCQFGUmnNifG5BnYw3jiAYHE9wSU+7/by0n+DkRIJzN7YAqhGURUT+VkSeE5GnROSbItLh2vYHInJQRJ4XkVe6xm+1xw6KyAfqNTdFUerLiWiCrR3NBJu8DaMRJDNZhqdneck5EaB05NBsOsuZ6SQv6rWWNNUIyvN94BJjzIuAF4A/ABCRi4A3ABcDtwKfEBGviHiBfwReBVwEvNHeV1GUBmNwPE5fZ4j2YFPDCIKT4wmMgZ0bW+luCZTUCE5NWklkl/VamsPZkEtQN0FgjPkvY0zGfvkw0Gs/vw34sjEmaYw5AhwEdtuPg8aYw8aYFPBle19FURqME+OJhhMEjgbQ1xmktzOYz4NYuJ8lIHZuaiXg85wVIaQr5SP4NeC79vMe4IRr26A9VmpcUZQGwjGd9EWCtIeamGgQQeBEOvVFQvR2BktqBE7EUG9nkO6WQNnookZhWYJARO4RkX1FHre59vlDIAN8cbmTdZ3zHSKyV0T2njlzplanVRSlBgy6FtT2YFPDlJg4EU3Q5BU2tTXTFwlxcqJ4LsHJiQRej7C5rZlI2H9WaAS+5RxsjLm53HYReRvw88DLjTHOJ3oS6HPt1muPUWa88H3vAO4A2LVrV+msD0VRVhzHpNLbGaQ92MS+BhEEg+NxtnYE8XqE3s4g6axheHqWLe3Bgv0SbG5rxuf10NXiV2dxOUTkVuB/AL9gjHHrWHcCbxCRgIhsB3YCjwKPATtFZLuI+LEcynfWa36KotSHvImlwXwEjl8DoNf+Wyxy6OR4gp5OSzicLRpBPX0EHwdage+LyM9E5J8AjDH7ga8CzwDfA95jjMnajuXfBu4GngW+au+rKEoDcSIaJ+DzsKE1QHuwiXgqSyqz9ktRD0bj9EWsBb7PXuiL+QlOTiTo7bC2Oz6COYNHY7Is01A5jDHnltn2YeDDRcbvAu6q15wUpVFJZrL4vR5EZLWnUpET0QS9nUFEhI5QE2BlF29oDazyzEoTS2YYi6XymsBWe6EvjBxyium5NYJkJkcslaUlULfltO5oZrGirHFiyQx7/vIHvPrj93Pvc8Nr/u7zxHicvoi1oLYH5wRBtRhjODgyzY+eH6nL/Irh9BfotRf45iYvG1sX5hKcnrSK6fXYgqIr7Acg2uB+gsYVYYqyTtg/NMVEPE02Z/i1z+3l8v4Ofu8V53Hdud111xA+c/8RJuIpfu+W86s+ZnA8wRX9nQC0VSkIUpkcjx2Ncs+zw/zg2RGO27WK/uN3rsuXfFguI1OzbGgNFP3MnNpIjgBznhf6COYEhrVfd4ul5YzGkvR3hWhUVCNQKmKM4Wt7TxBLZirvrNScfScnAfje+27gr157KcOTs7zl04/yK3c8PK+4Wz2488kh/t8TRYP3ijI1m2Yykc7fWTsaQbkQ0kcOj3HlX3yfX/2XR/jiI8fZsSHMB151gbXtSHQZs5/jzHSSa/76Xr7z1Kmi253P0Zm38/xEgUbgCAa3aQhqoxH8+6PH+cj3nlv2eZaCCgKlIofOxHj/15/iv545vdpTOevYd3KybN17gH1Dk2xoDdDTEeSNu/v54ftfygdvu5inByf5h3vr2zx9aCLB6alZMlX2HS68s3YEwUSi9EL52NEo08kM//yWK/nZn7yCz759N++6cQfbukI8cnhsmVdgMTSRIJMzJc1Ng+MJmps8bGiZ82P0dgY5NTH/2p1ksi3tzQB0tViCoBaF5+56+hTf/Gn1QreWqCBQKuK045uZVY2gkCeOj/OiP7ubkenFNzE/dGaGn/+H+/nOU0Nl99t/copLXeaRgM/LW68e4GUXbOAnB0br5jNIZrKMTCfJ5ky+vk4lHOeqE4bZ4ZiGylQgPTOdpLXZxysv3kzIP2et3j0Q4bGj0YqCshrG45YgerSEhnFiPE5vZ2ie2aivM0QmZzjtalB/ciLOxtYAzU1eALrCluCoRb2hM9NJxmZSq+IDUkGgVGTc/hHHzoJOTLXmuVPTTM1meOH0zKKPPTRiHfNwmbveRCrLgZFpLtnatmDb9Ts3cGpylkNnFv/e1TA8OXeX69jGKzGXVWyZTuZ8BKVvIkZnUvPuxB12b48wHk9zsAbX5wiCwfFE0WtxIp3cFMslGHTlEAAE/V5Cfm9NksrGYilS2RzTq2CCVUGgVGTC/hHF1UewAMcJOlTlQunGaXyy9+h4yX2ePT1FzsDFRRym1+/sBuDHL4wu+r2rYWhy/gJYDSeicVoDvrxJqMnrIewvX4r6zHSS7iKhpXu2dwG18RNEY3Pv/+iRhYLXqZbqpjefSzB37ScnEvmIIYdaJJXlciZ/jtXIVFZBoFTEKRo2k1SNoBBngav2jtmNc/d8YGQmL2wL2W87ii8tIgh6O0OcsyHMTw7Up96WW7idrFYQjCfojcw3sVTKLh6dSRbVCPoiQTa3NZc05yyG8VgKj0Brs2/B+SYTaaZmM3ktxmFrRxCROb9HLmc4NTGb1xQcumpQeG48niJrm8DGVqGInQoCpSKOWh1PqUZQyLI0gmgi38XriePFtYKnT04SCfvzzslCbti5gYcPjzGbrr2Qdq6pPdjEyYnqopNOROP5rFyH9pCfyTLO4jMzyaLJZiLC7u0RHj0ytmy7+Xg8RWfIz+6BCI8cni8I8g7uggXe7/Owua05rxGcmUmSyubmmYYAumugEbh9DKOqEShrkYmY+ghK4SxwbjNKtQyOx7n6nC58HilpHtp3coqLt7aVzBe44bxuZtM5Hj9W2ry0VIYmZ+kK+zlnQ7gq05AxhsHxxII75vagr6RGMJvOMj2boduOvilk9/YIw1PJfF7BUhmPp+gM+9m9PcLh0dg85/7g+PzcADfuctTO394ipqHlmnNGp+e0gNVofamCQKnIuPoISpI3DVVpOnEwxnAiGufcjS1cvLWNvUUW8mQmywvD00XNQg57tnfR5BXue6H25qGhiQRbOprp6QhWZfoai6VIpLMLTCzlTEOOSaVU+Yk92622kYV38YslGksRCfnZc47ld3jsyNznXejgdtPXOZdUVphD4NDVEmAstrx6Q2dc5iD1EShrkol81JAKgkLypqHJ2UWFOU7E08RSWfoiIa7cFuHJExMLCrM9f3qaTM6UzawNB3zs2hbhvgO1dxgPTSTY2h6kpzPIUIna/G5KmVjKCYIz9p1wdxEfAcC5G1uIhP3LdhiPx9J0hJq4eGsbIb+XR1wO40IHt5veziCnJhOks7m8MCx0FneF/aSzZlnRPo45yOsR9REoa5M5H4GahgpxFrhUJreoWPK5Us1Bdg10kszk2D80OW+ffSenALhka/kSC9ef182zp6aWlMtQjqGJWbZ2BOntDJHOGkamyy9QThSUu0wDVNIIrM+slEYgIuweiPDo0eUllo3HU0TCfpq8Hq7c1jnPYXzCDgktZn7r7QyRM1aNocHxBJ2hJsIFxeXySWXLuJMfm0ni8wh9nUFGV6GstQoCpSL5PAI1DS1gMp7O3yEuxmGcT7yKhNi1zarLU2jn3zc0SVuzr6jJws0NOzcAcH8NtYKp2TQzyQxbO5rzNvFKDuNiZRoAOkJ+ZtO5og7tShoBWH6CE9HEkhzyYJnhHB8BWOam505PMx5zcgviC4SXQ2/EqUIan9eHwE2+zMQybPujM0m6WvxsaA2oRqCsPYwxeYeoagTzyeYMU7MZLtxiJXstShCMzy2aG9ua6YsEFziM952c5JKe9oqF5S7a0kZX2F9TP4FzLZZGsDCevhiD43G6wv4Fd8xtZeoNOT6CrhLOYrAEAVilKJbCTDJDOmuIhPz2+bry57N8NYkF5iyHPldSmdWHYOF++cJzy9AIRmdSdLcE6AoH1EegrD1iqSzprGUbVo1gPtOz1sJ20ZZWYHG5BCeicTpCTbQ2W4vkVdsi7D0WzTsc09kcz52arqrypscjXLezm/sPjtakHAPMFwQ9VQqCE1Erh6CQcqWoz0wnaQ82EfB5S573wi1ttAZ8S/YTjNtRb05vhMv62vH7PDx6JJp3cBdqMQ6b25vxiCW4B8fjRTUCR4gtJ4R0bCZJV0vAan2ppiFlreGozxtbA8RT2TVfC38lcRa2/q4wIb+XoYnqbfSD4/PvQq8c6GR0JsWxMTvJbHiGVDZXdQnmG3ZuYHQmxTOnphZxBaVxrqWnI0jI7yMS9lcWBOPxogtqOUEwOpMsGTrq4PUIuwY6l1yAzvFxOSacgM/L5X0dPHIkmr+mUqahJq+HLe1BnhqcZDadW+Aodp93OSYdSyPw09USYDyeqrrIX61QQaCUxYkY6ukMkskZkg3QcnClcBa2jmATWzuCVSddgdO8ZW5R2bXNMn84YaRO6eliNYaK4ZSb+EmN/ARDEwl8HsmbPSqFkGZzhqGJ4iYWp/DcRJHCc6MlkskK2b29i0NnYkvK4I3agsDxEQDsOaeL/UOTPGsLznJ+mN7OIHtts1QxQRfweWkN+JZ8J2+MsZLqWgJ0t/gxZs4vt1KoIFDK4txNOXdC6ieYw1nY2kNN9HQEq9YIcjmzQCPYubGFtmYfjx+zFpx9Q5O0BHwMdIWrOufGtmYu2Nxas3ITQxMJNrc35zOfezqCnCzSv9fh9NQs6awpuqBWMg2VcxQ75P0ESzAPOVqt4yMAy2GcM/Atu+xzsWQyh97OUD6ZsphpCCDSsvSksplkhlQmR1eL31XNdGUdxioIlLLkBYH9A1A/wRzOwtZuawTVOovPzCRJZXLz7i49HuGKbZ15h/G+k5NctLUNj6f6DmQ3nLeBvUfHa1IKxAkddejttDSCUqbBwRI5BFDJNJSqSiO4tKedYJN3SX4Cx3bf6RIEV/R34vMIjxyJ0hlqKttv2C3cijmLwcolWOri7TiZu20fAax8UpkKAqUsedPQKmkE6Wxuxe2l1eIWBD0dzYzFUlXV/MmXKiiwS+/a1smBkRnGZpI8c2qqYv5AITfs3EAqm1t2Fi5YJTPc9vCeziCz6dK5EqVyCKB0u8pEKstMMlOVRuD3ebhiW8eSCtBNxNN4PUJr89xiH/R7eVFve8k5u3G0hZaAj7ZgcYERWUa0j2Pu6rZNQ+6xlUIFgVIWRxBsbbc1ghXMLr7/wCg3fOSHvPrjD3C6ysYoK0mhRgDVhZAWNm9xuNL2E3z98UFm0zku6anOP+Cwa6ATv8/DQ8vs6pXNGU5Pzs4rdFesNr+bE9E4IrC1Y2FxPK9HaA0srDdUqbxEIbsHunj29FTF/seFROMpOkNNC7Qrp9xEqdBRB0dz6y2RdAbQvYxonzFXCK1jGlpuEbvFooJAKct4PGWl39uhd/EVKEWdSGX5szv38+ZPP0KwycvxsRiv/cQDHBiervt7L4apRJqAz0Nzk9clCCoLrFKJVy/u68DnET7/0DGgeOnpcjQ3edneFebIaKzy3GfTJU1IZ6aTZHJmnmnI0Q5K1VR6YXia3s5gyTDQ9tDC7GInU7lYCepivLi/A2PguUVGRo3HUvPMQg6O36FU6KiDozEUixhyiIT9jMdSSwrfPeNkV7cEaA822WUmVBAoa4iJeIqOcBMhv/UDr7dG8OSJCX7uH37C5x48ytuvHeCu917PV955Nemc4XWffLAmtelrxUQ8nbd/91SZfQtWxNAGV7tDh6Dfy8Vb2zg5YfXPPWdDy6Ln1BcJVdXQ/u2ffYz/+f+eLrrNqaRaaBqC4tdnjOHRI1GusjWaYhQrM7FYjcBZsBdb6TVaQhBcNRChpyPIroHS8wbY3NaM3+spa0LqagmQyRmmZhcf7eNUHo2E/Xg8Qmdo6f6GpVJ3QSAi/5+IGBHptl+LiHxMRA6KyFMicoVr39tF5ID9uL3ec1MqMx5P0xnyE7Z7ydazJ8HnHjjCaz/5IIlUli/8+h7+9NUX09zk5ZKedr7x7mvobg3w5k8/wl1Pn6rbHBbDZGJOEGxub0YETlahEVgRQ8XvLh3z0EVb2vIRO4uhPxLieDReNt/DGMP+oUkeOFi837Fj3triMvO0B5tobfYVNQ0dOhNjLJbK32EXo5ggqKa8hBvHPLnYSq8T8TSd4YUF5VoCPh74wE284qJNZY/3eoRPv20X77zxnJL7dOeb2C/+Tn4slqQz1ITP68mfa6V7EtRVEIhIH3ALcNw1/Cpgp/14B/BJe98I8KfAHmA38Kci0lnP+SmVmYin6AjNlQ2I1ck0lMnm+Nu7n2f3QITvvfcGrrPj4h36IiH+37uu4dKedt7zpSf4ymPHS5ypPLmcqVkTF7cgaPJ62NTaXJ2PoExtm10D1ld+sWYhh/5IkHgqW3ZBGplOMpvOEY2lOFzEjOTOKnZjhZAuvD5HS1usIKimvISboN9LV9hflbB1E7ULzi2H63duYEt7edMQLC3aZ3Q6NU8YdrX4V7zeUL01gr8H/gfgvu24Dfi8sXgY6BCRLcArge8bY6LGmHHg+8CtdZ6fUgFLI2giHLBNQ0sIHz01mai4+D5zaopYKsub9vTn/RGFdIb9fPE39nBFfycfvefAkrKcP3bvAW7+ux+TrkEkklsQgOUorSQIMtkcQxOzJR268wZmAAAgAElEQVSUu7dHCPu9XHNud9Htlejvss5brpHLUdfiv7dI/Z6hiVlaAz7amuf/H3pdtfndPHpkjO6WANu7S+c8dBTxEYzOWHfCTd7ql6GtVfZGcDDGlPQR1JI5J+/iF3Aru9olCMKBFS8zUTdBICK3ASeNMU8WbOoBTrheD9pjpcaVVcRp8dfs8yKy+C5lsWSGW/7uPv7vPQfK7lfNXSVYDtHXXN7D0OQsR8cW37XqwYNjDI4nalKpczKRnie0qsklODU5SzZnSjoou1sC/PRPbuGWCuaKUvTbmkY5P4FTxqJUZ7ShicQCbQCK5xIYY3jkSJQ950TKFsdrCzYxGU/PO7baZDI3PYvI1wCYTmbI5Ez9BUE+7HMppqHUPK2oaxnJaUtlWYJARO4RkX1FHrcB/wv4k9pMc8H7vkNE9orI3jNn6tO4W7HuXqdnM7QHrdC7UJN30V3KfvT8GaaTGe59brjsfo8ciTLQFWJTW/HevG6u3WGF/T1wcHGLeTZn2GfX/P/Wz04u6thiFGoEPR3Big1qKtW2AStmvlLF0VI4YZ7HywjJo2MxfHahumItLocmE/P8A3PnDjKTzDCVmPsODI4nODU5m+8kVor2YBOpbI7Z9JwmVm0ymZuttnmqWm3QabPauUzTUCUcQbOUsM/RAoHY3RJgJpmpSx/qUixLEBhjbjbGXFL4AA4D24EnReQo0As8ISKbgZNAn+s0vfZYqfFi73uHMWaXMWbXhg0blnMJShkcVb7TvusNBXyL1gi+t/80AC8Mz5TMBcjlDI8djVbUBhy2d4fZ0t7Mg4cWJwgOn5khnsrS3eLnv/YPL8vxncnmmElmCkxDwYoNauYa0pSPXV8qzU1eNrUFypqGjkWt4nB7tndxeDS2wB5dmFXs4EQRnXCVmqhWkyuWXbwkjaAzSCKdLVq3qBjRfMG54ubGWuH3eWhr9i3atj+bzjKdzMwTiF3hpTuel0pdTEPGmKeNMRuNMQPGmAEsM88VxpjTwJ3AW+3ooZcAk8aYU8DdwC0i0mk7iW+xx5RVwil85dxNhf3eRS2es+ks9z47zIv7OgC4v8Qd/IGRGSbi6Xyd+EqICNfs6ObBQ2OLitt+atDSBt5383kk0lm+/0x5LaUcU7PW51CoEUD5ctSD0Tgeoegdd61wIodKcWwsxraucN4x7dYKZtNZorFU0Zj5uRDSuet79EiU9mAT521sLTunYoKg2oJz8+Zgf27V+gnGi5SXqBfdLYFFdxfLO8zDbtOQXW9oBR3Gq5FHcBeWxnAQ+BTwWwDGmCjwF8Bj9uOD9piySkzYd1Md9o8o5PctKmrogYOjxFJZ3nvzTrpbAiULoj1q94+tZF5wc93OLibi6UWVXX765CQhv5c3XNXH1vbmfMGxpZCvPFrgI4Dy2cUnxhNsaQ8uykG6WMrlEhhjODYaZ6ArxKU97fi9nnmCYC5iqJhpaGF28SNHxrhqIFKxJlJH0PoOOZ9bLJmxtbPFCgJrDtUKgmJ1hupFV4uf6CJt+2OuOkPu87i3rQQrIghszWDUfm6MMe8xxuwwxlxqjNnr2u8zxphz7cdnV2JuSmnyGoG92IUDi9MIvrfvNK3NPq7d0c31O7u5/0DxximPHImypb25Yoanm2t2WFE1i/ETPDU4wSVb2/F5PfzCi3u478Doku+63OUlHKppWTlYomZ/LemPhDg1NUsys1BoR2MpppMZtnWF7RyNtnmdv5zM6GKhkp2hJoJN3nwI6fCU5bCvRoC350tRW4vbYpPJHPJaSZW5BONFSlDXi8gSCs/l6wy5PofucGDetpVAM4uVkuR/RG6NoEofQTqb4/vPDnPzhZvw+zxcv7ObsdjCxilOVuru7eWjTgrZ1NbMuRtbeOBQdXV1Mtkc+4emuNQuNPaay7eSzRn+c4nJac6C5hYEbUEfYb+37N3qiWiiYpGz5dIfCWFM8cXSibTaZoeZ7hqIsO/kVN4x6QixYqYhEaG3M5gvmuf4B/acU70gcAToXDLZ4hbozlATzU2eqiOHxuMpvB6hrbl0ddFa0dUSWLSzeK7g3PyoITgLfATK2cGcacilEVQZNfTokSgT8TSvvHgzANedW7xxyrGxOCPTyaodxW6u3dHFY0eiRe98CzkwMkMyk8tXnLxgcxvnb2pdsnmomEYgImVDSJOZLMPTpXMIaoUTQlrMT3A8auUQbLP7HFy5rZNUNsfTdiOcockEIpSM3urpnIvjf/RIlLDfy0VbKhfHKxQES9UIRKRikxw30ZiVGb/UKKzF0BX2E11kvaHRIqahkN9Lc5PnrPcRKA3CeDyNzyP5Wu1hv6/qMtTf3XeKYJOXG8+zorpKNU551DZLLMY/4HDNud0k0ll+enyi4r5P245id8bubZdv5YnjE2VDLUvhNGJvC86PRunpLN2gxgp7rFzkbLmUyyU4OmpVCXVq7O/aZjmMnXyCoYkEG1sD+H3Fl4beAkFw5UAkXxqhHK3NPkTmPjd3obXFspjeD1YyWX0jhhy6wn5yBiYWUR11dCZJS8A3r+6UiKx4E3sVBEpJJuJpOkJN+bupcMDHTBUaQS5nuHv/MC89fwNB/9wX/Pqd3ew9Ok7CJUwePRIlEvazYwkF1l5yThcegQer8BM8dXKC1oKOX79w2VYA7nxy8VpBMY0Ayi9S5Wr215INrQECPk9RjeDYWIyt7XNVQrtaApzTHc53RhuamC1bSqGnI8REPM2JaJznh6erFuAej9DW3JRfJM9MJxFhSaUf3MKoEuPx1Ir4BwAiS4j2cXoVF9Ld4l90BNJyUEGglMSpM+QQqjJ89Inj45yZTnLrJZvnjV/vNE45MmfXf/RIlN0Di/MPOLQHm7i0t6MqP8HTg5Nc0tM+L7qltzPE7oEI3/rZ0KLLVUwm0gSbvAvKLvd0BBmLpeYJOwfHtl6uP24tEJGSIaRHx+IMdBf2Qejk8WPjGGMWNKQpxHHWfttOyFuMSc9db2h0Jkkk5K9Kmyhka3uQ0ZnqmgCNx1PzWlTWk+4lxP+PzSTz4aJuuloCahpS1gbj8flqdTjgI501pCo0sP/evtP4vR5uumDjvPHd2yP4fZ68n+DUZILj0ThXLcEs5HDtji6ePDFRVlNJZXI8e2o67x9w8wsv3srBkRn2Dy2uxr27BLUbJ+yyWKnkE9EETV5hU2v9cggcLEGwcA7Ho3H6I/NrAu0a6GQ8nubQmRm7vETp+TlmrW88cZKAz1P0My2FWxAsJZnMwRFG1ZiHorH0imkEc/H/1QsCq87Qwvl1hVe2zIQKAqUklmlovkYA5UtRG2P43v7TXHtuF60FRcuam7zs2R7J+wnyUSfLEQTndpPJmXwuQjFeGJ4mlc3lI4bc/NylW/B5JH+HWy2F5SUcnFLJxRapE+NxejqCi+pDvFScXAK3pjOZSBONpRjoKt4Z7b+eGWY2nStrGuq1tYXDozEu7+8o2YimGIUawWIdxQ7VNgEyxjARXzkfQb4C6SJCSC3TUAmNIJZcUmHFpaCCQCnJAo3A7klQLoR0/9AUg+MJXnXJlqLbrzu3O19u4tEjUVoCPi6sIuqkFFdus9ozPnCwtCBwMopf1NOxYFtn2M9Lz9/Ad548tagfXUlBUCaXYDBauvx0remPhJhJZvK5IDBXf2hb13yNYMeGMJ2hJr7zpBVKW6y8hEN3y5wjudpMcAd3lzJLI1janXq1TYCcgnPLLUFdLZ2hJkSq1wgy2Rzj8VRR01B3i5901uQz2OuNCgKlKMaYfFMah5BdirpcCOn39p3GI3BzieqZ1++0ooh+cuAMjx6Jsmugc0kNWByam7xcNdBZNrHs6ZMTtAebStrmr97Rzemp2XmLZiUKK486bG5vxlOiQc3geCKfnVtvioWQHh2zQkcLfQQiwpXbOnnWzvEo5yPweCS/fbGaXLurAulyNIJyn7GblSwvAeDzeugINlWtEUTjKYyBDcVMQ/ns4pXxE6ggUIqSSGdJZXLzTEPVaATf3XeKPdu7St6FXbC5le6WAHc+OcSBkZkl5Q8Ucs2Obp47PV0yE/OpwUle1Nte0iHtdAurpsWjQymNoMnrYVPbwr4EsWSGsViq7o5ih2J9CY7ZgqC/iFbibtdYzkcAlqDweYTL+xdqWOVwTENWZc3ckn0EzmdcKbvYSe5aKY0AqGpeDqPTC3MIHJz+BiuVVKaCQCnKREF5CXD5CEpoBDPJDIfOxBZ0F3Pj8QjX7+zOO4yX4x9wuNZOVnuwSPTQbDrL86eny3b8qqaZSyGlBAHMlUp242gsK6UROElrJ+YJgjgbWwOE/AuzbJ18goDPU3Hh/IXLtnL7NQNFz1OO9mATmZzJ90NYqkYA1eUSjBckRK4EL+7r4InjE1UllTmaQ/GoIdUIlDVAsR9Rvl1lCY3AUcUr/cCdLOOAz8OlRez2i+XSnnZam31F8wmeOz1NJmfKRrfkF83x6gRBOpsjnsqWFQRO1FAmm+P//NfzvPMLj7O9O5y/9noT9HvZ0BqYlyx3bCw+L4/CzSV2AbqtHcGKoby/fFUff/zzFy16Ts7ndejMDFB9r+JiVJNdPG73IlhJjWDXQITJRJoXRqYr7lusvISD89msVO9iFQRKURyNYJ5pKFC+gb0jPCrFbV9vawxX9HeWzGBdDF6PcMPODXznySFeGJ7/A3RKJ1zaW1rghAM+usL+qk1DxSqPutna0cypiVmOj8X55X9+iH+49yCvv6KX//id61Z0USrMJTg6FsvXGCqkucnLS3Z0cf6m8uWkl0OHIwhGLEGwXI3g1GSi7J33Shacc9htm9geK9L5rZC8aajI5+D4NVYqhFQFgVKUwoJzYPUjAErG7M/1Lyivim9sa+bt1w5w+zXbajFVAP7o5y8kFPDxG/+6N6+ZADw9OEFX2M/W9vJ2byvcsjrbbqmsYoeejiCpbI5bP3ofB4Zn+Ic3Xs7f/tJleUG6UvR1BvOCIJ7KMDKdZKBMX+F/evMV/P2vvLhu83E+r4O10Ag6g6SzhjNlTCfRWAqfR2hdwc+9LxJkY2uAx45UrqA/Gkvi93qKzs/v89AebFpSD+SloIJAKUphCWqwOpQBxEv0JHAW4I4qojT+9NUXc2uJENOlsKU9yD+/5UpOT87yW198It+c/ik7o7iSuaOvQjMXN462VFhnyMFp4n7B5lbueu/1vNouZbHS9EdCnJpMkMrk8nb5UhoBWNVl3SVBak1bXiOI4VlieQmHahrUjNuZ8StRcM5BRLhqe4S9R6sQBNNWeYlS8+tawTITKgiUokwUWdSDdmGsWAXT0EqF6xVyRX8nf/naS3no8Bgf+o9nSKSyHBiZqSr7tT9iOR8z2fJZ0zBXOK2URnDdud189Z1X89V3Xr1ieQPF6IuEyBkrpyEvCCKlNYJ643xeR0ZjRMKBZYUN5xvUlInQGY+l696ishi7ByIMTc7mS4qUYnQmWdQs5GBlF6+MRrCyuqrSMIzH04T93nk2fK9HCDZ5S1YgHY+nESm9QK4Er7+yl+dPT/Gpnxwhkc6SzZmyEUMOfZ0hMjnDqcnZiot3JdOQiNQkLHa5uHMJ8qGjZTSCeuP4VFLZ3JKTyRzypTzKaATReGpVbkqcFqB7j46XjRIbnUmysawgCOQd6/VGNQKlKBOJVFETTzjgJVbKRxBL0R5sWtadXi34wKsu5MbzNvDVvYMAvKiMo9ghX7q5isihvLN4FQVeNbjDYo+OxYmE/asqpFsCvvx3YzmOYoDW5ibamn3lTUOx1Io65x0u2NxGa8CXL7FeirES5SUculr8mkegrC4T8XRRp2+oTE+C8VW6AyvE6xE+9sbLOWdDmC3tzWxqq7zo9JWp4V/IZIleBGuNTa3N+L0eTtgaQTn/wEogMtcpbCl9CAoplq/hZjxe/Gam3ng9whXbOss6jI0xjMUqmIZaAozHU1WZK5eLCgKlKOPxVL7huJuQv7RGMBFPr1iBr0q0B5v4+ruu4Yu/sacqZ+GW9ma8HqnKYTxhm83q2YC+Fng8Qm8kaJuGSucQrCSORrJcjQDK9yVwSqSsho8ArEq7B0Zm5kWwuZlMpElnDV1lNJbuFj/GsKjSJ0tlbX+TlVXDaUpTSDhQWiOIxtaGRuAQCfs5p8qGNz6vh60dzVWFkJbLKl5r9EdCHByZYWgyseoaAcwJguWEjjpsLZNUNjWbIZszq/Z9zHd+O1Y8n8BJFCsnEOfKTNTfYayCQClKKTNPOOArGTVU2Mim0SjVzKWQyUR6zZuFHPojIQ6MzGBM+dDRlaLd/n7UQiPo6QgyPZthanbhHfP4KtQZcnNZXwd+r6dkGOlcVnF5HwGsTFKZCgJlAdmcYTJR3MwT9ntL5xGsoipeC/o6QxVD/sAKH13J+jXLwV1grrD89GpQa40AikcORVc5lLm5ycuLettLOowdQdBVJnrKiawqVUyxlqggUBYwlUhjTPHEsJC/eN/i2XSWRDrb0BpBXyTE6EyqpA/EoZFMQ+5Q2LXhI7CdxbXQCMp0KptYhfIShewaiPD04GTRtqXOXX5ZjcAxDTW6RiAivyMiz4nIfhH5iGv8D0TkoIg8LyKvdI3fao8dFJEP1HNuSmmcBuPFoobCgeJ9i1c7mawWOIvmYIUywhOJVMMIAkcjaG32rQlH/pxGsPzvSb5BTZH/V9QpOLeK38fd2zvJ5Aw/OzGxYNvoTBKPlP+9OKHYK+EjqFtCmYi8DLgNuMwYkxSRjfb4RcAbgIuBrcA9InKefdg/Aq8ABoHHROROY8wz9ZqjUpy5yqPFNYJi1UfnKj2u/mKzVNwJWOdvLl18rRE1goGu8IqWWijFS8/fyNDEbE1uGDa0BGjyStEGNfmmNKv4fbyyP4IIPHY0ytU75ndzG51JVsyu9niEyAr1Lq5nZvG7gb82xiQBjDEj9vhtwJft8SMichDYbW87aIw5DCAiX7b3VUGwwkyUubsP+72kMjnS2dy88MlywqNRqKZBTTKTZTadaxhB0BLwsaE1kK9/tNpcNRDhqoHaZF17PMKW9uKRQ9G4VXCuZYUL/blpDzVx/qZWHivwEyQzWZ47PV2VVtQV9q9IKep6mobOA64XkUdE5McicpU93gOccO03aI+VGldWGOfuvljmbL7wXIFWcDaYhiJhP2G/t2zkUL68RANd5z+9+Qp+/5bzV3sadaGnRIOaiXiKzvDKFpwrxlUDEZ44Np5PCjs+Fud1n3yQnx6f4PVX9lY8vttuYl9vliUuReQeYHORTX9onzsCvAS4CviqiJyznPdzve87gHcA9Pf31+KUiotyi7pTijqeysy7K662BPVaRkToi5SPHKpUcG4tcuW21a97VC+2dgSL9quOxlKr6h9w2DXQyb89fIznTk8zOJ7g/V9/Eo8I//LWXSX7ervpavFz/Hj1nfOWyrIEgTHm5lLbROTdwDeMMQZ4VERyQDdwEuhz7dprj1FmvPB97wDuANi1a1flnnDKopiIp/GI5WAsxNEIYgUhpPkS1EWykRuJvkgoX6CtGE4J6kYSBGczPZ1BhqdnF5oqY8VLpKw0TvHB93/9KZ49NcVlve18/E1XVF2V9oadG9hcoZdGLainaehbwMsAbGewHxgF7gTeICIBEdkO7AQeBR4DdorIdhHxYzmU76zj/JQSODVaPEUcWW6NoPCYloCvJh3HVpO+TqtBjXX/spBKlUeVlaWnoxlj4PTkfIfxalUeLWRLe5CejiDPnpribdcM8LV3XbOo0uSvu7KXP3jVhXWcoUU9PSmfAT4jIvuAFHC7rR3sF5GvYjmBM8B7jDFZABH5beBuwAt8xhizv47zU0owUSZhKlxCIyhVpK7R6I8ESaSzjM6kisa6N0rl0fWCkyT3d99/gQ/edjGtzdb/xfERrAX+zy9fRjKT48bzNqz2VEpSN0FgjEkBby6x7cPAh4uM3wXcVa85KdUxUeZuKux3BMF8jWCt1RlaKn2uENJygkA1grXBnu0R3vOyHXzyR4d47GiU//1Ll7F7IGJlua+R7+NLzumqvNMq09h6vFIXxmOlq4iGAsW7lDV6nSGH/nxSWXEHXaU2lcrKIiK8/5UX8LV3XY3XI7zxUw/zR9/eZxWcWyMaQSOggkBZQLlF3dEIFoaPpomsgczV5eJ0lDo+VlwQTCbStLoarChrgyu3Rbjrv1/Pr+7p50uPHAdYE5nUjYK2qlQWMB5Pl7SB5zWCAtPQeOzs0AiCfi8bWgMlO5VNNVDl0fVGOODjQ6+5lFdctJlP3Xd4TbQLbRRUECjzcIrHlVKrQ01O1NCcRpDO5phOZs4KHwGUL0c92UCVR9crN563YU07ZtciahpS5uHYwEstdj6vh4DPM89H4CSgNXKdITd9ncGSDWoaqc6QolSLCgJlHk46e7m7+3DAN68nwZzwOHs0glOTCdJFesVOqCBQzkJUECjz2HvUaq13QZnqmyG/d75GEGv8OkNueiMhcqZ4nXvVCJSzERUEyjzufW6Ec7rDZXv9thRoBPnaRGeJachdjroQFQTK2YgKAiVPLJnhoUNjvOyCjWX3W6AROAXnzhKNwEkqK/QTzKazpDI52tVZrJxlqCBQ8jxwcJRUNsfLKwiCcMA3L3z0bChB7WZzWzNNXlmgEWhWsXK2ooJAyXPvcyO0BnzsqtA4JOT3zgsfHY+laG7yELQL0jU6Xo/Q0xFckEuglUeVsxUVBAoAuZzh3udGuOG8DRUriIb9vgWmobNFG3Doi4QWdCpTjUA5W1FBoACwf2iKkekkN1UwC4GVXTw/fPTsyCp2Y/UliHNwZJrRmSSZbE4FgXLWopnFCmCZhUTgpedXzsgs1AisyqNn1+J47oYWJhNpbv67+/JjjqakgkA521BBoABw73PDXN7XQVfLwtLLhYT8PmbTObI5g9cjTMTTXLg1uAKzXDne/JJtnLeplbFYkol4mol4mvF4ipDfS19n9Y1FFKURUEGgMDI9y5ODk/z+LedVtX84MNelrLW5ifH42acR+H0ertvZvdrTUJQVQX0ECj967gwAN11QuZk2WBoBWIXnsjnDROLscxYrynpCNQKFHzw3zJb2Zi7cUrqshJuwqxS13+vBmLMnh0BR1iOqEaxzkpksPzkwyk0XbESkumYr7uY0Z1t5CUVZj6hGsM559EiUeCrLyy+sHDbq4DSnmUlmSGasMNKzLXxUUdYTKgjWOT94doTmJg/X7KjeMTqnEWTI2ZWa10qjcEVRFo+ahtYoI1OzPHJ4rK7vYYzhB88Nc82Obpqbqi8PMecjyJ51dYYUZT2igmCN8okfHeL2zz6KMaZu73HozAwnoomqsondhFwagSMIOtRHoCgNiwqCNcrh0Riz6Vy+xHM9uO+FUYBF93d1TEOWRpDG5xFaA2plVJRGRQXBGuXYWAywkr3qxYOHRtnWFcrX368Wp8poPJXJ1xmqNuJIUZS1R90EgYi8WEQeFpGficheEdltj4uIfExEDorIUyJyheuY20XkgP24vV5zW+tksjlOjltNUYanknV7j0cORxflJHbw+zz4vR5iqexZWWdIUdYb9dTnPwL8uTHmuyLy3+zXLwVeBey0H3uATwJ7RCQC/CmwCzDA4yJypzFmvI5zXJMMTcySyVm+gZGp+mgET52cZDqZ4bpzl1ZGIRzwEk9mrBLUYXUUK0ojU0/TkAHa7OftwJD9/Dbg88biYaBDRLYArwS+b4yJ2ov/94Fb6zi/NcuxaCz/fGS6PhrBAwcs/8DVO7qWdHzI7yOWyjJxFtYZUpT1Rj01gvcBd4vI/8YSONfY4z3ACdd+g/ZYqfEFiMg7gHcA9Pf313bWa4BjY1ZDFI/UTyN44NAoF21pI7LEu/lwwEs8lSEaS3NFv2oEitLILEsjEJF7RGRfkcdtwLuB3zXG9AG/C3y6FhMGMMbcYYzZZYzZtWHD4iJeGoHj0Th+n4ft3eG6+AgSqSxPHJvg2nOXpg2ApRHMJG2NQE1DitLQLEsjMMbcXGqbiHweeK/98mvAv9jPTwJ9rl177bGTWD4E9/iPljO/RuXYWIz+SIhNbYG6RA3tPRYllc1x7RL9A2BpBCNTli9DTUOK0tjU00cwBNxoP78JOGA/vxN4qx099BJg0hhzCrgbuEVEOkWkE7jFHlt3HBuLsy0SYmNrc100gvsPjtLkFXZvL9+kvhwhv49BO7JJ6wwpSmNTTx/BbwIfFREfMItt0wfuAv4bcBCIA28HMMZEReQvgMfs/T5ojInWcX5rEmMMx6Nxrt7Rhd/n4cx0EmNMTeP0Hzw4xuV9nfkM4aUQ9nuZSVrtKrXOkKI0NnUTBMaY+4Eri4wb4D0ljvkM8Jl6zakRODOTJJ7Ksi0SImsglc0xUcMQzYl4in1Dk7z35TuXdZ6QK5NYS1ArSmOjmcVrjON2xNC27jAbW63+wbUMIX3o0BjGsOT8AYewf65InZqGFKWxUUGwxnBCR7dFQmxqawZguIYhpA8cGiXs93JZX8eyzuM2K6lpSFEaG60UtsY4Fo3jEejtDOGx/QK11AgePDjG7u0RmrzLuwdosU1DItAWVNOQojQyqhGsMY6NxdjSHsTv87CxzTIN1UojGJpIcHg0tqywUQenS1l7sAmvRwvOKUojo4JgjXFsLM62LqsaaMjvozXg40yNNIIHDlplJWohCJxS1GoWUpTGRwXBGuN4dE4QAGxsC9RMI3jw0BhdYT/nb2pd9rlCtrO4Q5PJFKXhUUGwhpieTRONpeiPhPNjG1uba+IjMMbwwMFRrt7RhacGppyw7SPQFpWK0vios3gN4UQMDbg0gk1tAfYeW3wl7mNjMU5PzhKNpYjGUwyOJxiZTtbELARujUAFgaI0OioI1hDHo5Yg6J9nGrI0gsVkF39t7wne//WnFoxvbA3wsvMX15+4FI5GENFkMkVpeFQQrCGO2u0pt3W5TUMBUpkck4l0VXffmWyOj/7gAJf2tPM/b72ASNhPJOynM9xEwPDaMLQAABc6SURBVOeteHy1qEagKGcPKgjWEMfH4nSF/fkYfbA0ArByCapZdL/z1BCD4wn+7NUXc93O2piBitHdEuCiLW1c0d9Zt/dQFGVlUEGwhjg2Fp9nFgLY1DqXS3BehWifXM7wiR8e4oLNrdx0QW1MQKVobvJy13uvr+t7KIqyMmjU0BrieNQqP+0mrxFUUY76+88Oc2Bkhne/dEdNIoMURVkfqCBYIyQzWYYmE/S7/ANA1YXnjDF84ocH2dYV4ucu3VK3eSqKcvahgmCNMDiewJj5oaNgRee0BHwVk8oeODjGk4OTvOvGHfiWWUdIUZT1ha4Ya4Rj+Yih0IJtG9sCFctM/OMPD7KpLcBrr+ipy/wURTl7UUGwRnCSydxZxQ4bW8uXmXj82DgPHR7jN68/p6YhooqirA9UEKwRjo3FCfm9dLcsDBHd1Fa+zMQnf3SQzlATb9rTX88pKopylqKCYI1wPBqnPxIqmj3saARWl8/5PHtqinueHeHXrt2+rB7EiqKsX1QQrBGOjcWK+gfA0giSmRxTs5kF2779syGavMJbrx6o8wwVRTlbUUGwBsjlDCfGEwx0LfQPAGxwQkiL+AkeOjzGZb0dtGs5aEVRlogKgjXA6alZUpncgqxih02uMhNupmfT7Ds5ydU7uuo+R0VRzl5UEKwB8sXmikQMwVxSWWHk0GNHo2RzRgWBoijLQgXBGuC4HTpaykewsYRG8NChMfw+jxZ+UxRlWSxLEIjIL4nIfhHJiciugm1/ICIHReR5EXmla/xWe+ygiHzANb5dRB6xx78iIuumvvGxaByfR9jS3lx0e0vAR9jvXaARPHR4jCv6O2hu0twBRVGWznI1gn3Aa4H73IMichHwBuBi4FbgEyLiFREv8I/Aq4CLgDfa+wL8DfD3xphzgXHg15c5t4bh8JkZ+iOhsqUhCnMJJuNp9g9NcfU59Ss1rSjK+mBZgsAY86wx5vkim24DvmyMSRpjjgAHgd3246Ax5rAxJgV8GbhNrOD5m4Cv28f/K/Ca5cytkTgwPMPOTS1l99nQGpgXNfTIkTGMQf0DiqIsm3r5CHqAE67Xg/ZYqfEuYMIYkykYP+uZTWc5Ohar2GugUCN48NAYzU0eLutrr/cUFUU5y6mYiioi9wCbi2z6Q2PMt2s/pcqIyDuAdwD09zd2WYXDZ2LkDOysIAjc2cUiwsOHx9i1LaK1hRRFWTYVBYEx5uYlnPck0Od63WuPUWJ8DOgQEZ+tFbj3LzanO4A7AHbt2rWw7kIDcWBkGoDzKpiGNrU1M5vOMZ3MkM7keO70NO9/5daVmKKiKGc59TIN3Qm8QUQCIrId2Ak8CjwG7LQjhPxYDuU7jVVE54fA6+3jbwdWRdtYaV4YnsbrEbZ3F88hcNjYNpdd/MiRKAAvOUf9A4qiLJ/lho/+oogMAlcD/ykidwMYY/YDXwWeAb4HvMcYk7Xv9n8buBt4FviqvS/A/wR+T0QOYvkMPr2cuTUKLwzPsL07XNHEs7F1rmXlQ4fGCPm9vKhX/QOKoiyfZZWrNMZ8E/hmiW0fBj5cZPwu4K4i44exoorWFQeGp7loa1vF/RyNYHh6locOj3HVQIQm7USmKEoN0JVkFZlNZzkWjbNzY3lHMcyVmXhmaIqDIzMaNqooSs1QQbCKHByZwRgqho6ClV0c8nv5zpOnALha/QOKotQIFQSrSLURQwAiwsbWAKenZmkN+Li4CnOSoihKNaggWEVeGJ6hySsMVIgYcnCKz+05J1K2HIWiKMpi0NVkFTkwPM327nDVTl/HT6Bho4qi1BIVBKvIC8MzFTOK3TgNatRRrChKLVm33c5n01mAVSvhnEhlOTEe53VX9FZ9zMvO38ipyQQXblb/gKIotWNdagSpTI4L/vh7fOq+w6s2h7mIocqOYofrdnbziV+9Eo9H6jgzRVHWG+tSEPh9HgI+D9PJTOWd68QLw1bE0GJMQ4qiKPVgXQoCgLZgE1OJ9Kq9/wsj0/i9HgZKtKdUFEVZKdatIGht9jE9u3oawYHhGc7ZENYwUEVRVp11uwq1NTcxNbuKGsHwtJqFFEVZE6xbQdDa7GNqlTSCWDLD4HiC8zZW7yhWFEWpF+tWELQFm5heJR/BwZEZQB3FiqKsDdavIFhFjcCJGFpM6KiiKEq9WMeCYPV8BAdGZvD7PGzrqq7GkKIoSj1Zt4KgtdlHKpPLZxivJC8MT7NjQwteTQxTFGUNsG4FQVuwCWBVQkgPDM+oWUhRlDXDuhUErc1WmaXpFTYPzSQznJxIVNWMRlEUZSVYt4KgrdnSCFbaYXzAKS2hoaOKoqwR1q0gaG12TEMrqxEcGLZCR1UjUBRlrbBuy1C3Ba1Ln0rUTyMwxjARTzMynWR4apaR6SR3PjlEwOehL6I1hhRFWRusW0GwEhrBH31rH1985PiC8Vsu2qQRQ4qirBnWrSBos53F9cwl+OnxCS7a0sa7X7qDTW3NbGoLsLG1maB/dZrhKIqiFGNZPgIR+SUR2S8iORHZ5Rp/hYg8LiJP239vcm270h4/KCIfExGxxyMi8n0ROWD/7VzO3CoR9vsQqW/46OmpWS7v7+DVl21l9/YI27rCKgQURVlzLNdZvA94LXBfwfgo8GpjzKXA7cC/ubZ9EvhNYKf9uNUe/wDwA2PMTuAH9uu64fEIrQFf3XoSzKazRGMptrQ31+X8iqIotWJZgsAY86wx5vki4z81xgzZL/cDQREJiMgWoM0Y87AxxgCfB15j73cb8K/28391jdeN1uamumkEw1OzAGxuD9bl/IqiKLViJcJHXwc8YYxJAj3AoGvboD0GsMkYc8p+fhrYVO+JtQXrV2/o1KQlCFQjUBRlrVPRWSwi9wCbi2z6Q2PMtyscezHwN8Ati5mUMcaIiClz3ncA7wDo7+9fzKnnUc+eBKcnHY1ABYGiKGubioLAGHPzUk4sIr3AN4G3GmMO2cMngV7Xbr32GMCwiGwxxpyyTUgjZeZ0B3AHwK5du0oKjEq0NTcxOB5f6uFlcTSCzW0qCBRFWdvUxTQkIh3AfwIfMMY84Izbpp8pEXmJHS30VsDRKu7Ecixj/y2rbdSCtjr2LT49maCt2Uc4sG4jdBVFaRCWGz76iyIyCFwN/KeI3G1v+m3gXOBPRORn9mOjve23gH8BDgKHgO/a438NvEJEDgA326/rSr19BFvUUawoSgOwrNtVY8w3scw/heMfAj5U4pi9wCVFxseAly9nPoultdnHTDJDLmfw1DjT9/TUrPoHFEVpCNZt0TmwfATGwEyq9uYhSyNQQaAoytpnXQuCuZ4EtRUEqUyO0ZmkagSKojQE61oQOF3Kap1dPDI9izGaQ6AoSmOwrgVBvTSCuRwCdRYrirL2WdeCoK1Opag1q1hRlEZiXQuC1jqVotasYkVRGol1LQgcH0GtTUOnJmcJ+720ajKZoigNwLoWBHmNoMbO4tNTCTa3N2O3WlAURVnTrGtBEPB5Cfg8ddEINKtYUZRGYV0LArB6EtTDR6D+AUVRGoV1LwjagrUtRZ3J5hiZTmrEkKIoDcO6FwStzU019RGMzqTI5oxqBIqiNAzrXhDUuhT1qckEoDkEiqI0DioIauwjyOcQtKmzWFGUxkAFQbDWGoFmFSuK0lise0FQax/B6alZAj4PHaGmmp1TURSlnqx7QdDW7COZyZHMZGtyPqcPgSaTKYrSKKx7QdDaXNsyE6cnExoxpChKQ7HuBUFbcPGlqD/xo4N844nBots0q1hRlEZj3VdFaw0svjnNZx84Ssjv5Rcv75lnAsrlDMPaq1hRlAZDNYJFViB12lAeG4tzeDQ2b9tYLEU6azRiSFGUhmLdC4LF9iQYnrLaUALc++zIvG1zOQQqCBRFaRzWvSCY0wiqEwRDE1bmsNcj3PPs8Lxtc1nF6iNQFKVxWPeCYK4nQXWmISdh7BUXbmLvsXEm43MC5PSUdiZTFKXxWJYgEJFfEpH9IpITkV1FtveLyIyI/L5r7FYReV5EDorIB1zj20XkEXv8KyLiX87cqqXF70NkERqBfdf/5pdsI5sz/PjAmfy2U5OzNHmFrvCKTF1RFKUmLFcj2Ae89v9v7/6D6yrrPI6/P8ltfpAmDW1DtrRI+VGB6ipitDCLLhZW8ccIOKyK7m7/6MrujLujozMI48yO/rMz7h/+2F3HWRCVHVZdRREG0QoVh3+WH0GKFrKFKiz9kZKA3CAloU3y3T/Oc8ttm9570yS9Ofd+XjN37j3PObd8v/Q03zzPc55zgPuPsf/LwM9KG5Jaga8D7wXWA9dIWp92fwn4SkScDbwIbJ5jbDVpaRFL22u/FfVwcYJlnUu46KwVLO9q45dlw0P7xibo7+mgpcWLycwsP+ZUCCJiKCJ2zLRP0pXA08DjZc1vB3ZGxO8j4gDwfeAKZddgbgRuS8fdAlw5l9hmYzY3nttbHGfVsg5aW8Ql5/TxqydHmZyaBrI5Al8xZGZ5syBzBJKWAp8DvnjErtXArrLt3altBVCMiMkj2k+I7o5CzXMEe8cmOLU3mwy+7Lx+iq8c5NFdRaD0ZDJPFJtZvlQtBJLulbR9htcVFb72BbJhnpfnLdLDY7pW0qCkwdHR0epfqKKnc0nNcwTDY+Oc2pv91v+OdSsptIitQyNExKH7DJmZ5UnVlcURcdlx/LkbgKsl/QvQC0xLmgAeAU4rO24NsAd4AeiVVEi9glL7sWK6EbgRYGBgII4jvsP0dBTYU5yoetz4gSmKrxw8dHlod8cSNpy5nK1Dz/F37zyTVyenvYbAzHJnQYaGIuIdEbE2ItYCXwX+OSL+HXgYWJeuEGoDPgrcGREB3Adcnf6ITcAdCxHbTHo6ausRlK4YKvUIADae289TIy/z4NN/APwcAjPLn7lePnqVpN3ARcBPJW2pdHz6bf8fgC3AEPCDiChNJn8O+IyknWRzBjfPJbbZyOYIqheC4WLpoTOvzQNcdt4pAHz3oWcBryEws/yZ003nIuJ24PYqx3zhiO27gbtnOO73ZFcVnXA9nUt4+dVJpqej4qWfh3oEZYXg9BVdnNXXxf1PZnMVXlVsZnnT9CuLIesRTAfsP1D5yqFSj6B/Wfth7Zee1w9kt53o624/6ntmZouZCwHZHAFUvwPp8Ng4K5e2015oPax947nZ8NAp3e20ejGZmeWMCwGvPaWs2qKybA3B0XMAA6efTE9HwfMDZpZLTf9gGqj9KWV7i+Oc1dd1VHuhtYXPv/88Otv8v9PM8sc/uSjrEVS4cigiGC6Oc/HZK2fc/5G3vW5BYjMzW2geGiJbUAaVewQvTUyy/8AUq3t9VZCZNRYXAmqbIzj00JkZ5gjMzPLMhYDXHk5TqUcw02IyM7NG4EIAdCxppa3QUnGOYKbbS5iZNQIXgiR7JkHlHkFrizil24XAzBqLC0HS01GoOEewd2ycfi8YM7MG5EKQdHcuqTpHsMpXDJlZA3IhSHqq3IF0rx9DaWYNyoUgqfRMgtLTx051j8DMGpALQdLdUTjm0NAL+w9wYHLaPQIza0guBElP55JjThaX1hC4R2BmjciFIOluLzBxcJoDk9NH7ZvpgTRmZo3ChSDp6Sw9k+DoXsFw0beXMLPG5UKQVLrNxPDYBG2FFlZ0tZ3osMzMFpwLQdJT4cZze8cmWLWsA8mLycys8bgQJBV7BEWvITCzxuVCkJTmCGZaVDY8NuGJYjNrWC4EybF6BFPTwb6XJjxRbGYNy4UgOdQjOGKOYOSPE0xNh59DYGYNa06FQNJfSnpc0rSkgSP2vUnS/6T9v5XUkdrfmrZ3SvpXpRlYScsl3SPpqfR+8lxim62lbQWko4eG9qbFZH5EpZk1qrn2CLYDHwLuL2+UVABuBf4+It4AXAKUfsJ+A/gEsC69Lk/t1wNbI2IdsDVtnzAtLeKMFV187+Fd/G705UPtfkSlmTW6ORWCiBiKiB0z7Ho38JuIeCwd90JETElaBfRExAMREcB/Alem71wB3JI+31LWfsL8x1+/lenp4GM3PcAzz+8H/IhKM2t8CzVH8HogJG2R9GtJ16X21cDusuN2pzaA/ogYTp/3Af0LFNsxrevv5rufuJCDU8E1Nz3Asy+8wt6xcbraWulJk8lmZo2maiGQdK+k7TO8rqjwtQJwMfDx9H6VpEtrDSr1FqJCTNdKGpQ0ODo6WusfW5Nz/qSbWzdvYPzgFNfc9ADbdhVZ1dvpxWRm1rCqFoKIuCwi3jjD644KX9sN3B8Rz0fEK8DdwAXAHmBN2XFrUhvAc2noiPQ+UiGmGyNiICIG+vr6qqUwa+tP7eHWzRv448RBHn226MVkZtbQFmpoaAvwp5JOShPHfw48kYZ+XpJ0Ybpa6G+AUkG5E9iUPm8qa6+LN65exq1/u4HujgJnn7K0nqGYmS0oZaMwx/ll6Srg34A+oAhsi4j3pH1/BdxANsRzd0Rcl9oHgO8AncDPgH+MiJC0AvgB8Drg/4APR8QfqsUwMDAQg4ODx51DNS/uP8BJ7a20F1oX7L9hZrYQJD0SEQNVj5tLIVgMFroQmJnlVa2FwCuLzcyanAuBmVmTcyEwM2tyLgRmZk3OhcDMrMm5EJiZNTkXAjOzJudCYGbW5FwIzMyanAuBmVmTy/0tJiSNkt2b6HisBJ6fx3DqpVHygMbJpVHyAOeyGNWax+kRUfUWzbkvBHMhabCW+3Asdo2SBzROLo2SBziXxWi+8/DQkJlZk3MhMDNrcs1eCG6sdwDzpFHygMbJpVHyAOeyGM1rHk09R2BmZu4RmJk1vaYsBJIul7RD0k5J19c7ntmQ9C1JI5K2l7Utl3SPpKfS+8n1jLEWkk6TdJ+kJyQ9LulTqT2PuXRIekjSYymXL6b2MyQ9mM6z/5bUVu9YayGpVdKjku5K23nN4xlJv5W0TdJgasvd+QUgqVfSbZL+V9KQpIvmM5emKwSSWoGvA+8F1gPXSFpf36hm5TvA5Ue0XQ9sjYh1wNa0vdhNAp+NiPXAhcAn099DHnN5FdgYEW8Gzgcul3Qh8CXgKxFxNvAisLmOMc7Gp4Chsu285gHwrog4v+xSyzyeXwBfA34eEecCbyb7+5m/XCKiqV7ARcCWsu0bgBvqHdcsc1gLbC/b3gGsSp9XATvqHeNx5HQH8Bd5zwU4Cfg1sIFswU8htR923i3WF7Am/VDZCNwFKI95pFifAVYe0Za78wtYBjxNmtNdiFyarkcArAZ2lW3vTm151h8Rw+nzPqC/nsHMlqS1wFuAB8lpLmk4ZRswAtwD/A4oRsRkOiQv59lXgeuA6bS9gnzmARDALyQ9Iuna1JbH8+sMYBT4dhqy+6akLuYxl2YsBA0tsl8PcnMpmKSlwI+AT0fES+X78pRLRExFxPlkv1G/HTi3ziHNmqQPACMR8Ui9Y5knF0fEBWTDwJ+U9M7ynTk6vwrABcA3IuItwH6OGAaaay7NWAj2AKeVba9JbXn2nKRVAOl9pM7x1ETSErIi8F8R8ePUnMtcSiKiCNxHNoTSK6mQduXhPPsz4IOSngG+TzY89DXylwcAEbEnvY8At5MV6DyeX7uB3RHxYNq+jawwzFsuzVgIHgbWpSsh2oCPAnfWOaa5uhPYlD5vIhtvX9QkCbgZGIqIL5ftymMufZJ60+dOsrmOIbKCcHU6bNHnEhE3RMSaiFhL9u/ilxHxcXKWB4CkLkndpc/Au4Ht5PD8ioh9wC5J56SmS4EnmM9c6j0RUqfJl/cBT5KN436+3vHMMvbvAcPAQbLfFDaTjeNuBZ4C7gWW1zvOGvK4mKwr+xtgW3q9L6e5vAl4NOWyHfin1H4m8BCwE/gh0F7vWGeR0yXAXXnNI8X8WHo9Xvp3nsfzK8V9PjCYzrGfACfPZy5eWWxm1uSacWjIzMzKuBCYmTU5FwIzsybnQmBm1uRcCMzMmpwLgZlZk3MhMDNrci4EZmZN7v8BhdBpPRweFBgAAAAASUVORK5CYII=\n",
360 | "text/plain": [
361 | ""
362 | ]
363 | },
364 | "metadata": {},
365 | "output_type": "display_data"
366 | }
367 | ],
368 | "source": [
369 | "while frame_idx < max_frames:\n",
370 | " state = env.reset()\n",
371 | " ou_noise.reset()\n",
372 | " episode_reward = 0\n",
373 | " \n",
374 | " for step in range(max_steps):\n",
375 | " action = policy_net.get_action(state)\n",
376 | " action = ou_noise.get_action(action, step)\n",
377 | " next_state, reward, done, _ = env.step(action)\n",
378 | " \n",
379 | " replay_buffer.push(state, action, reward, next_state, done)\n",
380 | " if len(replay_buffer) > batch_size:\n",
381 | " ddpg_update(batch_size)\n",
382 | " \n",
383 | " state = next_state\n",
384 | " episode_reward += reward\n",
385 | " frame_idx += 1\n",
386 | " \n",
387 | " if frame_idx % max(1000, max_steps + 1) == 0:\n",
388 | " plot(frame_idx, rewards)\n",
389 | " \n",
390 | " if done:\n",
391 | " break\n",
392 | " \n",
393 | " rewards.append(episode_reward)"
394 | ]
395 | },
396 | {
397 | "cell_type": "code",
398 | "execution_count": null,
399 | "metadata": {},
400 | "outputs": [],
401 | "source": []
402 | }
403 | ],
404 | "metadata": {
405 | "kernelspec": {
406 | "display_name": "Python [conda env:pytorch4]",
407 | "language": "python",
408 | "name": "conda-env-pytorch4-py"
409 | },
410 | "language_info": {
411 | "codemirror_mode": {
412 | "name": "ipython",
413 | "version": 3
414 | },
415 | "file_extension": ".py",
416 | "mimetype": "text/x-python",
417 | "name": "python",
418 | "nbconvert_exporter": "python",
419 | "pygments_lexer": "ipython3",
420 | "version": "3.5.5"
421 | }
422 | },
423 | "nbformat": 4,
424 | "nbformat_minor": 2
425 | }
426 |
--------------------------------------------------------------------------------
/8.gail.ipynb:
--------------------------------------------------------------------------------
1 | {
2 | "cells": [
3 | {
4 | "cell_type": "code",
5 | "execution_count": 1,
6 | "metadata": {},
7 | "outputs": [],
8 | "source": [
9 | "import math\n",
10 | "import random\n",
11 | "\n",
12 | "import gym\n",
13 | "import numpy as np\n",
14 | "\n",
15 | "import torch\n",
16 | "import torch.nn as nn\n",
17 | "import torch.optim as optim\n",
18 | "import torch.nn.functional as F\n",
19 | "from torch.distributions import Normal"
20 | ]
21 | },
22 | {
23 | "cell_type": "code",
24 | "execution_count": 2,
25 | "metadata": {},
26 | "outputs": [],
27 | "source": [
28 | "from IPython.display import clear_output\n",
29 | "import matplotlib.pyplot as plt\n",
30 | "%matplotlib inline"
31 | ]
32 | },
33 | {
34 | "cell_type": "markdown",
35 | "metadata": {},
36 | "source": [
37 | "Use CUDA "
38 | ]
39 | },
40 | {
41 | "cell_type": "code",
42 | "execution_count": 3,
43 | "metadata": {},
44 | "outputs": [],
45 | "source": [
46 | "use_cuda = torch.cuda.is_available()\n",
47 | "device = torch.device(\"cuda\" if use_cuda else \"cpu\")"
48 | ]
49 | },
50 | {
51 | "cell_type": "markdown",
52 | "metadata": {},
53 | "source": [
54 | "Create Environments "
55 | ]
56 | },
57 | {
58 | "cell_type": "code",
59 | "execution_count": 4,
60 | "metadata": {},
61 | "outputs": [],
62 | "source": [
63 | "from common.multiprocessing_env import SubprocVecEnv\n",
64 | "\n",
65 | "num_envs = 16\n",
66 | "env_name = \"Pendulum-v0\"\n",
67 | "\n",
68 | "def make_env():\n",
69 | " def _thunk():\n",
70 | " env = gym.make(env_name)\n",
71 | " return env\n",
72 | "\n",
73 | " return _thunk\n",
74 | "\n",
75 | "envs = [make_env() for i in range(num_envs)]\n",
76 | "envs = SubprocVecEnv(envs)\n",
77 | "\n",
78 | "env = gym.make(env_name)"
79 | ]
80 | },
81 | {
82 | "cell_type": "markdown",
83 | "metadata": {},
84 | "source": [
85 | "Neural Network "
86 | ]
87 | },
88 | {
89 | "cell_type": "code",
90 | "execution_count": 6,
91 | "metadata": {},
92 | "outputs": [],
93 | "source": [
94 | "def init_weights(m):\n",
95 | " if isinstance(m, nn.Linear):\n",
96 | " nn.init.normal_(m.weight, mean=0., std=0.1)\n",
97 | " nn.init.constant_(m.bias, 0.1)\n",
98 | " \n",
99 | "\n",
100 | "class ActorCritic(nn.Module):\n",
101 | " def __init__(self, num_inputs, num_outputs, hidden_size, std=0.0):\n",
102 | " super(ActorCritic, self).__init__()\n",
103 | " \n",
104 | " self.critic = nn.Sequential(\n",
105 | " nn.Linear(num_inputs, hidden_size),\n",
106 | " nn.ReLU(),\n",
107 | " nn.Linear(hidden_size, 1)\n",
108 | " )\n",
109 | " \n",
110 | " self.actor = nn.Sequential(\n",
111 | " nn.Linear(num_inputs, hidden_size),\n",
112 | " nn.ReLU(),\n",
113 | " nn.Linear(hidden_size, num_outputs),\n",
114 | " )\n",
115 | " self.log_std = nn.Parameter(torch.ones(1, num_outputs) * std)\n",
116 | " \n",
117 | " self.apply(init_weights)\n",
118 | " \n",
119 | " def forward(self, x):\n",
120 | " value = self.critic(x)\n",
121 | " mu = self.actor(x)\n",
122 | " std = self.log_std.exp().expand_as(mu)\n",
123 | " dist = Normal(mu, std)\n",
124 | " return dist, value"
125 | ]
126 | },
127 | {
128 | "cell_type": "code",
129 | "execution_count": 7,
130 | "metadata": {},
131 | "outputs": [],
132 | "source": [
133 | "def plot(frame_idx, rewards):\n",
134 | " clear_output(True)\n",
135 | " plt.figure(figsize=(20,5))\n",
136 | " plt.subplot(131)\n",
137 | " plt.title('frame %s. reward: %s' % (frame_idx, rewards[-1]))\n",
138 | " plt.plot(rewards)\n",
139 | " plt.show()\n",
140 | " \n",
141 | "def test_env(vis=False):\n",
142 | " state = env.reset()\n",
143 | " if vis: env.render()\n",
144 | " done = False\n",
145 | " total_reward = 0\n",
146 | " while not done:\n",
147 | " state = torch.FloatTensor(state).unsqueeze(0).to(device)\n",
148 | " dist, _ = model(state)\n",
149 | " next_state, reward, done, _ = env.step(dist.sample().cpu().numpy()[0])\n",
150 | " state = next_state\n",
151 | " if vis: env.render()\n",
152 | " total_reward += reward\n",
153 | " return total_reward"
154 | ]
155 | },
156 | {
157 | "cell_type": "markdown",
158 | "metadata": {},
159 | "source": [
160 | "GAE "
161 | ]
162 | },
163 | {
164 | "cell_type": "code",
165 | "execution_count": 9,
166 | "metadata": {},
167 | "outputs": [],
168 | "source": [
169 | "def compute_gae(next_value, rewards, masks, values, gamma=0.99, tau=0.95):\n",
170 | " values = values + [next_value]\n",
171 | " gae = 0\n",
172 | " returns = []\n",
173 | " for step in reversed(range(len(rewards))):\n",
174 | " delta = rewards[step] + gamma * values[step + 1] * masks[step] - values[step]\n",
175 | " gae = delta + gamma * tau * masks[step] * gae\n",
176 | " returns.insert(0, gae + values[step])\n",
177 | " return returns"
178 | ]
179 | },
180 | {
181 | "cell_type": "markdown",
182 | "metadata": {},
183 | "source": [
184 | "PPO "
185 | ]
186 | },
187 | {
188 | "cell_type": "code",
189 | "execution_count": 33,
190 | "metadata": {},
191 | "outputs": [],
192 | "source": [
193 | "def ppo_iter(mini_batch_size, states, actions, log_probs, returns, advantage):\n",
194 | " batch_size = states.size(0)\n",
195 | " for _ in range(batch_size // mini_batch_size):\n",
196 | " rand_ids = np.random.randint(0, batch_size, mini_batch_size)\n",
197 | " yield states[rand_ids, :], actions[rand_ids, :], log_probs[rand_ids, :], returns[rand_ids, :], advantage[rand_ids, :]\n",
198 | " \n",
199 | " \n",
200 | "\n",
201 | "def ppo_update(ppo_epochs, mini_batch_size, states, actions, log_probs, returns, advantages, clip_param=0.2):\n",
202 | " for _ in range(ppo_epochs):\n",
203 | " for state, action, old_log_probs, return_, advantage in ppo_iter(mini_batch_size, states, actions, log_probs, returns, advantages):\n",
204 | " dist, value = model(state)\n",
205 | " entropy = dist.entropy().mean()\n",
206 | " new_log_probs = dist.log_prob(action)\n",
207 | "\n",
208 | " ratio = (new_log_probs - old_log_probs).exp()\n",
209 | " surr1 = ratio * advantage\n",
210 | " surr2 = torch.clamp(ratio, 1.0 - clip_param, 1.0 + clip_param) * advantage\n",
211 | "\n",
212 | " actor_loss = - torch.min(surr1, surr2).mean()\n",
213 | " critic_loss = (return_ - value).pow(2).mean()\n",
214 | "\n",
215 | " loss = 0.5 * critic_loss + actor_loss - 0.001 * entropy\n",
216 | "\n",
217 | " optimizer.zero_grad()\n",
218 | " loss.backward()\n",
219 | " optimizer.step()"
220 | ]
221 | },
222 | {
223 | "cell_type": "markdown",
224 | "metadata": {},
225 | "source": [
226 | "Loading expert trajectories from №3 notebook "
227 | ]
228 | },
229 | {
230 | "cell_type": "code",
231 | "execution_count": 23,
232 | "metadata": {},
233 | "outputs": [],
234 | "source": [
235 | "try:\n",
236 | " expert_traj = np.load(\"expert_traj.npy\")\n",
237 | "except:\n",
238 | " print(\"Train, generate and save expert trajectories in notebook №3\")\n",
239 | " assert False"
240 | ]
241 | },
242 | {
243 | "cell_type": "markdown",
244 | "metadata": {},
245 | "source": [
246 | "Generative Adversarial Imitation Learning \n",
247 | ""
248 | ]
249 | },
250 | {
251 | "cell_type": "code",
252 | "execution_count": 24,
253 | "metadata": {},
254 | "outputs": [],
255 | "source": [
256 | "class Discriminator(nn.Module):\n",
257 | " def __init__(self, num_inputs, hidden_size):\n",
258 | " super(Discriminator, self).__init__()\n",
259 | " \n",
260 | " self.linear1 = nn.Linear(num_inputs, hidden_size)\n",
261 | " self.linear2 = nn.Linear(hidden_size, hidden_size)\n",
262 | " self.linear3 = nn.Linear(hidden_size, 1)\n",
263 | " self.linear3.weight.data.mul_(0.1)\n",
264 | " self.linear3.bias.data.mul_(0.0)\n",
265 | " \n",
266 | " def forward(self, x):\n",
267 | " x = F.tanh(self.linear1(x))\n",
268 | " x = F.tanh(self.linear2(x))\n",
269 | " prob = F.sigmoid(self.linear3(x))\n",
270 | " return prob"
271 | ]
272 | },
273 | {
274 | "cell_type": "code",
275 | "execution_count": 25,
276 | "metadata": {},
277 | "outputs": [],
278 | "source": [
279 | "def expert_reward(state, action):\n",
280 | " state = state.cpu().numpy()\n",
281 | " state_action = torch.FloatTensor(np.concatenate([state, action], 1)).to(device)\n",
282 | " return -np.log(discriminator(state_action).cpu().data.numpy())"
283 | ]
284 | },
285 | {
286 | "cell_type": "code",
287 | "execution_count": 35,
288 | "metadata": {},
289 | "outputs": [],
290 | "source": [
291 | "num_inputs = envs.observation_space.shape[0]\n",
292 | "num_outputs = envs.action_space.shape[0]\n",
293 | "\n",
294 | "\n",
295 | "#Hyper params:\n",
296 | "a2c_hidden_size = 256\n",
297 | "discrim_hidden_size = 128\n",
298 | "lr = 3e-3\n",
299 | "num_steps = 20\n",
300 | "mini_batch_size = 5\n",
301 | "ppo_epochs = 4\n",
302 | "threshold_reward = -200\n",
303 | "\n",
304 | "\n",
305 | "model = ActorCritic(num_inputs, num_outputs, a2c_hidden_size).to(device)\n",
306 | "discriminator = Discriminator(num_inputs + num_outputs, discrim_hidden_size).to(device)\n",
307 | "\n",
308 | "discrim_criterion = nn.BCELoss()\n",
309 | "\n",
310 | "optimizer = optim.Adam(model.parameters(), lr=lr)\n",
311 | "optimizer_discrim = optim.Adam(discriminator.parameters(), lr=lr)"
312 | ]
313 | },
314 | {
315 | "cell_type": "code",
316 | "execution_count": 36,
317 | "metadata": {},
318 | "outputs": [],
319 | "source": [
320 | "test_rewards = []\n",
321 | "max_frames = 100000\n",
322 | "frame_idx = 0"
323 | ]
324 | },
325 | {
326 | "cell_type": "code",
327 | "execution_count": 37,
328 | "metadata": {},
329 | "outputs": [
330 | {
331 | "data": {
332 | "image/png": "iVBORw0KGgoAAAANSUhEUgAAAYIAAAE/CAYAAABLrsQiAAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDIuMi4yLCBodHRwOi8vbWF0cGxvdGxpYi5vcmcvhp/UCwAAIABJREFUeJzsnXl4XFd58H/v7NpGiyV5kSzvjmM7iZ04TkIWkhBCQqBJ2RqgJEDbUAptaft9FAoUCuXrvlGWNpQUKKUhFEgChGyQBJzdsR3HcuxYXmUt1r7OPnO+P+69o9HskmYkzej8nmcea869d+6Z6zv3Pe8uSik0Go1Gs3SxLfQENBqNRrOwaEGg0Wg0SxwtCDQajWaJowWBRqPRLHG0INBoNJoljhYEGo1Gs8TRgmCGiMh5InJARMZF5A8Wej6a4iIiT4rIby/0PDSaYqIFwcz5OPCEUqpGKfWlhZ5MMiJiF5G/FJFuU1jtF5E6c9u/ichEwisoIuMJxzaIyI9EZFJETovIe5I++z3m+KSI3C8iDfkeu1QRkbtF5KiIxETk/Unb3i8i0aT/k2sTtq8VkSdExCciR0Tkhizn+XsROWb+nx8RkTuStl8vIvtEZExETojIXQnbrhORV0RkREQGzf/Hlnw+W0QaReRp87gREXlWRK5M2J7rnvuoiOw1x7+Z5fv9uYio5GsgIjeY32tSRM6KyLvM8c0i8oCI9IvIkIg8IiLnJRznFpF/Mn8nwyLyVRFxJmyfSHpFReRfzW0uEflfETllzunapDm5ze99zjz3jxOv56JEKaVfM3gBjwO/nWW7fYHn95fAL4A1gADbAU+Gfb8J3JPw/n+A7wHVwFXAKLDN3LYNGAeuMbd/F7g3n2NnOH8BbAtw3RwZxp/M9v+dx+d+BHgDsBd4f9K29wN7shz7LPCPQAXwdmAEaMqw718AWzAWd5cBw8DrzG1O8//jQ+b1vRSYAC4yty8HVpl/u4G/BR7M87M9wHnmNgFuA4ayXM/ke+5t5jFfA76Z4ZgNwCtAN3BDwvhWoA+4GXAAy4AN5rbdwG8BDeb3/wJwJOHYzwK/Mrc3Ac8Bf5Hh/NXm9brGfO8CPmbe5z3AtUn7fxx42byuHuDbwA/n+56e0X260BMopRfGAzYKBMwbY7N5Y38NeAiYBG4AbgH2A2NAJ/C5hM9YCyjgA+a2YeB3zR/nQfPH/uWk834QeNXc9xFgTYb51Zvz2pDHd6nCeLC/PuF9CNicsM9/AX9t/v3/gO8mbNtg7l+T69g85vIk8EXgacAPbARqgW+YP7QuDAFnN/c/DVxi/v1e83paAuu3gPvNv3djPExHzM/5MuBKOK/CeFAfA06aY28EjmA8OL8MPMUcBEHCufYwA0Fg3ltBoCZh7FfA7+Z5vgeBPzH/Xm5+18qE7S8C705znBv4K+BwPp+dNG4D3mqeqznXPZe07S/JLAgeBt4MnGK6IPgu8IU8r0eDOa9l5vu9wDsTtr8H6Mxw7J3ACUDSbDtLqiD4GvC3Ce9vAY7O9R4q5kubhmaAUup6jB/jR5VS1Uqp18xN78F4kNVg/OAngTuAOoyb4MMiclvSx10GbAJ+A/hn4FMYQmQb8C4ReT2AiNwK/BnGyqnJPP//ZJjiBUAEeIeI9IrIayLykQz7vh3oB35pvt8MRBK+Exirmm3m39vM99a1OI758M/j2Hx4H3AXxjU8jSFgIxhCYSdwI2DZ6p8CrjX/fj3Gj/SahPdPmX9HgT8CGoErMFbmv5d03tsw/i+2ikgj8EPg0+Yxx4FEM0ebaf5om8H3ysVOERkw/68+IyIOc3wbcEIpNZ6wb17XVEQqMBYW7QBKqXMY98wHxDAdXoGhMe5JOKZNREYwBPH/wdAKcn52wvhBjAXSg8B/KKX60hyefM/lRETeCQSVUg+l2Xy5uc8rItIjIt9JNFcmcQ3Qq5QaTPz4pL9bRaQ2zbF3At9W5lM9D74BXCkiq0SkEmOx8rM8j10QtCAoDA8opZ5WSsWUUgGl1JNKqVfM9wcxfoSvTzrmC+a+j2IIjv9RSvUppbowHvY7zf1+F/grpdSrSqkIxsp8h4isSTOPVoyV9GZgHfAO4HMi8sY0+ybf3NUYGkwioxgPZmv7aIbtuY7Nh28qpdrN79iAsQL8mFJq0nyo/BNwu7nvU0xdz6sxVrDW+7ggUEq9pJR6TikVUUqdAv6d1P+Hv1JKDSml/OY525VS/6uUCmMI6F5rR6XUGaVUnVLqzAy+VzZ+iWG6a8Z4SL4b+L/mtmzXOxf/hiE0HkkY+x/gzzG0jF8Bn1JKdVobre+GIQA/jaEV5fvZKKUuBLwYi6I9aY6DGT5QRaQG437/wwy7tGIsIN6OsaiqAP41zee0Al8B/jhh+GHgD0WkSURWAFbgR2XSsWsw7plv5TNnk2MY2n4Xxu/ifODzMzh+3tGCoDB0Jr4RkctMJ1+/iIxiPMwbk445l/C3P837avPvNcC/mCvREQz7qwDpnE9+89/PK6X8phC6F+MBlzi/NowV9bcThicwfsiJeDFU+Vzbcx2bD4nXcA2GXbcn4Xv/O8YDE4wH/dUishKwA/dhrMDWYgjCAxB3GP7E1I7GMB4qyf8PieddlfjefGB1kidJzsWcWoNS6oRS6qS5YHgF42HxDnPzrK6piPwdhnB5l/XAFZEtGPfBHRj27W3Ax0XkljRzGsJ46D2QoJ1k/OykYwNKqf8BPiEiFyUdm+6ey8XngP8yhXg6/MB/KqVeU0pNYPz/Jt/rTcCjwFfNuVl8EcN8ewB4BrgfCDP9dwiGoNmjlDo5g3l/BcPEtgzDHPZDtEawJEj+UXwXQ0VerZSqxVhFScpR+dEJfMhciVqvCqXUM2n2PZhmPulWX+8DnlZKnUgYew1wiMimhLGLmDIBtJvvARCR9Rg3+2t5HJsPifPsxFi5NiZ8Z69SahuAUqoD8AG/D/xSKTWGsXK/C+NHGzM/52sYK9tNSikvhokt+f8h8bw9wOqE7yiJ73N+AcNcaL1mozWohPm1A+vNVbFF1msqIn+B4Ti90bwmFtuB15RSj5hC5yjwU3PfdDgwhG5cEGX57HQ4gfVJY+nuuVy8AfgDU5D3Yvxf3Ccif2puP0iWe11E6jGEwINKqS8mbjMXSh9VSrUopdYDg8BLCfeOxR3MTBsA2IGh4Q4ppYIYWspu0/S4KNGCoDjUAENKqYCI7MZQl2fLvwGfFJFtACJSa9pNUzDt9r8CPmWGsJ2PYU75SdKud2DY4BOPncRYuXxeRKrECAG8FcPpC/DfwFtF5GoRqcJYvf5QKTWex7EzQinVg/ED/gcR8YqITUQ2WH4Tk6eAjzLlD3gy6T0Y/w9jwIS5Kv5wjlP/FNgmIm8zV8N/AKyYzXewMEMNPRgPeKeIeETEZm67WUSWm39vAT4DPABg+lsOAJ81j/l14ELgBxnO80mM++yGJDs4GCvfTWKEkIqIbADegrlwML/veeZ1bsKIVNpvagdZP1tELheRq8zvWWE+pJcDzyfNIeWeM493mNfHDtjN72ppIm/AEGI7zFc3RuTTV8zt/4nh91hv2uI/gXmvi4gXw3z1tFLqE2nO22La8EVELse49p9N2ud1GJr399Mc7zbnDeAy520J8ReBO8zfqhPDL9WtlBpI/pxFw0y9y0v9RVI4IcbN/ZdJ+7wDw+E5jnFjfhn4jrltLcbKxZGw/7TIA+A7wKcT3r8PI3zOikK6J8v8WjDsnxMYTtQPJW2/AsMnUZPm2AYMFXkSOAO8J2n7e8zxSYwHVkM+x2LY8SfyvabmWC3Giv4shm18P3B7wvYPmddxjfn+Leb7yxL2uQZDI5jAEJCfJyFKx9x/Y9J5b8LQcFKihoA287PaZni/qKTXtea2v8cwRUya/1efB5wJx641j/cDR5keMfNeDH9G4ncJmvOzXn+WsP1dwCHznjwL/A1mmC6GZnXSnEcvhhlpTT6fjWE/f9n83CHzel0zg3vuc2muz+cyXMtTidfAHPsLDAd0P8bCo94cv9P8rMmkebcl3BunMDTLo8B705zv3zFMU5nmkjzvtea2ZRgLpz6MiLU9wO5iP5vm8hJz4hqNRqNZomjTkEaj0SxxtCDQaDSaJY4WBBqNRrPE0YJAo9FoljhaEGg0Gs0Sx5F7l8VNY2OjWrt27UJPQ6PRaBYdL7300oBSqinXfiUvCNauXcvevXsXehoajUaz6BCR0/nsp01DGo1Gs8TRgkCj0WiWOFoQaDQazRJHCwKNRqNZ4mhBoNFoNEscLQg0Go1miaMFgUaj0SxxtCDQaDSaJY4WBBqNRrPE0YJAo9FoFinPnxjk4UO9RGPFbSBW8iUmNBqNplz52lPHea13nBu3Li/qebRGoNFoNIuQ/vEgvzo2wK07W7DZpKjn0oJAo9FoFiE/OdhNNKb49Z0tRT+XFgQajUazCLn/QDdbV3rZvLym6OfSgkCj0WgWGSf6J3i5c2RetAEooiAQkb8TkSMiclBEfiQidQnbPikiHSJyVETelDB+kznWISKfKNbcNBqNZjFz/4FuRODXdqyal/MVUyN4DNiulLoQeA34JICIbAVuB7YBNwFfFRG7iNiBrwA3A1uBd5v7ajQazZJBKcX9+7t43YZlLPd65uWcRRMESqlHlVIR8+1zQKv5963AvUqpoFLqJNAB7DZfHUqpE0qpEHCvua9Go9EsGfadGeHMkI/bdsyPWQjmz0fwQeBn5t8tQGfCtrPmWKZxjUajWTI8cKALt8PGTdtXzNs555RQJiKPA+lm+yml1APmPp8CIsB/z+VcSee9C7gLoK2trVAfq9FoypiJYASHTfA47Qs9lYyEozF+/HI3b9y6nBqPc97OOydBoJS6Idt2EXk/8BbgDUopK0e6C1idsFurOUaW8eTz3g3cDbBr167i5l5rNJqy4L1ff471TdX802/sWOipZOSXr/Uz7AvPW7SQRTGjhm4CPg78mlLKl7DpQeB2EXGLyDpgE/AC8CKwSUTWiYgLw6H8YLHmp9Foyodnjw/S0TeRcfvgRJCXz47yq2MDTK1JFx8/2t9FfaWTazY3zet5i+kj+DJQAzwmIgdE5N8AlFLtwH3AYeBh4CNKqajpWP4o8AjwKnCfua9Go9FkJBZT/O53XuIvfpz5cfHiqSEABiaCnB32z9fUZsRYIMxjh8/x1otW4bTPb4pX0YrOKaU2Ztn2ReCLacYfAh4q1pw0moXEH4ryf77/MmuWVfLxm7Ys9HTKhpODk4z6w7xwcohAOJrWB/D8yaH43y+dHmZ1Q+V8TjEv7n3hDMFIjHftWp175wKjM4s1eTMeCC9qtXoxMxmM8IFvvsBPX+nh56/2LfR05oRSin989CivnRtf6KkAsP/MCADBSIyXTg+n3eeFk0Nctq6BKpc94z4LSSgS4549p7hi/TK2t9TO+/m1INDkxenBSS75wuPs6RhY6KmUHGOBMHfc8wIvnhpmy4oazg77Slqgdg75+dIvOvjOc6cXeioA7D8zTJXLjsMmae/PUX+Ywz1jXLFhGTva6th3ZvEJgp8c7KZ3LMBdr1+/IOfXgkCTF48dPkcoGqNzaHHaVxcrI74Qv/kfz/Ny5whffvdO3nFJK5OhKCO+8EJPbda0d48CLJoH6oHOEXa21XNxWz17jqUKgpdOD6EUXLZuGZe01fNqzxiTwUiaT1oYlFLc/csTbGqu5tp5dhJbaEGgyYsnj/YD4Astnh/QYmciGOHdX3+eIz3j/NtvXsLNF6yktd6wTS9Wh2U+HDIFwas94/hD0QWdiy8U4UjvODvb6rhqUyOHukcZngxN2+f5E0M47cLOtjp2rqknpuDlsyNpP++j393Hnz9waD6mHmdPxwBHesf5nWvWI1LcvgOZ0IJAk5PJYITnTw4CxsNNkx9Pdwzwas8Y//gbF3GD2WGqtb4CgLPDvmyHLmrau8cQgWhMcTDDA3W+eOXsKNGYYmdbHVdubEQpeOb44LR9nj85xEWtdXicdi5eXQ/AvjR+gt7RAD99pYefHeqdV9Pd3b88QXONm1vnqcBcOrQg0OTk6Y4BwlHjh+Fb4BVgKWGtTHe21cfHVpeDRtA1Fjdh7O9cWEFgnf+i1jouaq2lxuNgT0d/fPtkMMIrXaNctr4BgNpKJ5uaq9l3JnXePznYjVJGZ7Du0cC8zP9w9xi/OjbA+69ci9uxcBnPumexJidPHO2n2u3AbhOtEcyAYdMPUF85VSrAW+Ggxu2gayR/QRAIR/nKEx28a9fqBQ977BsLMDAR5OpNTZwcmGR/Bj+BUoo/+t4BescC1FW4qK9yUlvh4vyVNdxawGJqB86MsGZZJcuq3QBcsX5ZPGlMRNh3ZphoTLF73bL4MRe31fPI4V5iMTWtBeSDL3fj9TgYC0Q4cGaElrqKgs0zE1//1QkqXXbeu3tN0c+VDa0RaLKilOLJo31ctbGR2gonPi0I8mbYF8LtsFGRENcuIrTUV8zINPT4q+f411908JvfeJ6+8flZqWaivXsMgO0ttexsq2ffmZG0ZpRDXWPcf6CbwYkQx/snePzVPr6x5wR/eO+BgjlqlVLsOzPMztXxVidcvamRs8N+Tg8a1/eFk0PYbcIla6a0skvW1DPiC3NiYDI+dnJgkoNnR/nQ6zfgctg40FlYR/hkMMIf33eAL/zkMD/cd5ajveN0Dvn48cvd3H5pG7WV81dXKB1aI9Bk5ei5cXpGA3zshiZOD/mYCGrTUL4MT4aor3SlOABb6ytnJAie7hig0mWnfzzInfe8yL13XU5txcI8OA51GY7i81fWcHFbHT/a30XXiD/uBLd47HAvNoHvfegKGqpcANz3Yicf/8FBhn0hqtzpHz2RaIzesUDK56WjZzRA33hwmuntyo2NgOGAXdtYxfMnhti+ykt1wvkuXmMIjn1nhtnYXA3Ag2YjmLdd3MLPXz3HgQKbvH52qJcf7uvCZbcRisYAEAGbCB+4cm1BzzUbtEagycoTRwx767XnNVPlsuuooRkw7AtRl2al11pfwdlhf94OyT0dA1y5sZF/f98ldPSN89vfenHBonXau8dYu6ySGo8z/gBOZ29/9PA5dq1piAsBIH4tsoXO/nB/F9f/w1MMTgRzzsV6WO9I0AjWNVbRUlfBnmMDBMJRDnSOsHtdw7Tj1jdWU1vhjDuMlVI88HIXu9c2sLK2gh2r63mla5Sw+cAuBD852E1rfQXtn38Tj3zsGv7xXRfxwSvX8blf27bg5j7QgkCTgyeO9rF1pZflXg9Vbseiir9e7Az7wtMehBat9RVMBCOM+nPnEpwZ9NE55OeqjY1cvamJf/6Nnew9PcxHvruvoA+qfGnvGWWbmfm6ZUUNHqctxU/QOeTjSO84bzQjpSzqzWsx7Jse3pnI2SEfoUiMQ6YJKhv7zwzjctg4f6U3PiYiXLWxkWeOD7Dv9DChaIzLEvwDADabEUpq5UG0d49xon8y3hZyR1sdgXCMo72FyZwe8YXYc2yAWy5cidNu47wVNbzt4lY+85atvO/yhfUNWGhBoMnIqD/MS6eHuW6LESFS5bYzqaOG8mbYZ5iGkplJLsHTx40EqSs3Gg+zWy5cyRdvu4BfHOnjM/fPb7z7qC9M55CfbauMB6/DbuPC1roUjeDRw+cAUgRBnWnOGs6iEQyZQsIyQWVj/5kRLmipxeWY/hi7alMjY4EI/7HnJCJw6dqGlGMvaavntXMTjPrDPPhyNw6b8ObtKwHiPodMEVE/OdjN/3voVZ45PpCXMH6kvZdITPGWCxYuPDQXWhBoMrLn2ADRmOK685oBqHJpjWAmDE9mNg1BfrkEezoGWO51s6GpOj72nsva+O2r1vG9vZ109M1fvZ/2HuPhvG3VVC2ci9vqOdw9SiA8tUB47HAvm5dXs7axatrxdaZQHM2iEQxPGkLicA6NIByN8UrX6DRHscXrNhhC8xdH+tiywpvWEWs5j/edGebHL3dzzeamuMbSWl/BsioXB9KYvMLRGJ99oJ27f3mC93z9eS7+/GN85L/38cCBLmKx9Ka+nxzsoa2hku0t3rTbFwNaEGgy8sTRPmornHEbrDYN5U8sphj1ZzYNQW6NIBZTPHt8kCs3NqY4nH/vuo14HHa++sTxwk06B+1dxsPZ0ggAdrbVEY6qeNmJEV+IF08Np2gDMOUjyKYRWGYj6/MycaRnnGAkxo62VEGwrNodn+Nl61K1AYCLVtdhE/j3p47TMxqYlswlYpiO0kUO7Tk2wOBkiH+5fQf//r5LePMFK3nh1BB/eO8B/vOZUyn7D02GeOb4IG+5cOWCZQ3ngxYEmrTEYoonj/ZzzeYmHGZtdMs0VMoF0+aLsUCYmJpaBSdSW+Gk2u3IKQhe7R1jaDLElRsaU7Y1VLl472VtPPByN2cG5ydLub17lBVeD41mzD4YggCmKoD+4kgf0ZjijVtTO9g67TZq3I6sPoIhMwnv1KCP8UBmgbHffEgnRgwlctUm45olO4otqtwOtqzw8tyJISqcdm44f7rg2rG6juP9kyl+nPsPdFFX6eTm7St507YV/M07LuT5T76Bqzc18qWfH2Mk6bs9fKiXaExxy4UrM36XxYAWBJq0tHePMTAR5LrzpopgVbkdRGOKYGT+nZSlhvVAa6hKNUuIiBk5lP0B/nSH5R9IFQQAv3PNeuwifO2p2WsFZ4d9eRePa+8eSzFvNNd4aK2viH/Go+3naK5xc2GGUsp1Vc6sUUMjvjBNNYagyWYe2n9mhOYaN6tqPWm3v/3iVq5YvyzjtYOpMNIbti5PCWfdYZaiSCyhMRGM8Eh7L7dcsHKaX8JmEz59y1bGA2H++fFj0z7np690s76xiq0rF69ZCLQg0GTgiaN9iDCtZV6Vy/ixaPNQbizzRzqNAKZCSLPxdMcgG5urWZHhYbfc6+Gdu1r5wUtn6Z1FSYRnOga45Ut7uOvbe3Pu6w9FOd4/wdZVqQ/4i9vq2X9mhEA4yi+P9XPD1uXTMnYTqa90ZdQIlFIM+UJcZT6827MIggOdI+xYXZfR3LJ5eQ3/kyPfwnIi33pRqhP3wtW1iExpOgCPtvcSCMfS9hM+b0UNt+9u4zvPneZ4v9Eys388yLPHB7llkZuFQAsCTQb2nxnmvOU108wA1qpJ1xvKjVVnKF3UEFhJZZlzCYKRKC+cHOLKDcvSbrf43ddvIGqWMZ4J333+DHfc8wLjgTADEyFCObS8V3vHiKnp/gGLnW119IwG+MG+s/hCUW5M4x+wqKt0ZfQR+MNRQpEYm837LpMgGJ4McXJgMqNZKF/efMFK7n7fJbzh/OaUbV6Pkw1N1dMSy+4/YOQCJGYpJ/JHN2zG47TzVw+9CsDD7b3EFIveLARaEGgy0D0SSEl0qXIZpRLKqd5QNKZ4x9ee4eszfJD2jQX40/89OC1aJhFr1duQRSPIlkuw/8wI/nA0q2kDYHVDJbftaOG7L5zOKwkrGlN8/seH+bMfvcJVmxr5xM1Gy8yBHMe2m+Gc6bpnXWw+kL/082NUux1ckUV41VU4U+zoFonmtO0t3owOY+vhvDONo3gmOO02bty2IuNqfcfqOg50GiU0+sYD7DnWz207WjLu31Tj5iPXbeTxV/t4umOAn7zczcbmas5bXjOnec4HWhBoUlBK0TXiTym6NaURlI8gePhQL3tPD8ebm+fLsycG+d7ezoyrVssOXpfGRwC5I4ee6RjAJnB5Do0A4Peu20AwEuOep09m3S8SjXHXt/dyz9Mn+cCVa/mPO3axvtEIS+0bzyEIuseoq3Smtcmfv9KL22Hj3FiQ129uylpFs77SmdIvwGIkXqTPxbZVXo71TaQVtE8c7cPjtHFR69wEQS52rK5jaDJE55CfH7/cQ0zBbTuz5wJ84Mq1tNZX8On7D/HCqSFuuWDxm4VACwJNGsYCESaCkfjDyqLKbWkE5WEaUkrx1Sc7AOjPYzWdiFXioW8svW1+yBfCYRNqMtTUmUoqS+8w3tMxwIWtdXg9uWsKbWiq5s3bV/LtZ05nzVZ+9sQgPz/Sxydu3sJn37oNh91Gs9ed9XtYtHePsW2VN+1DzeWwcYGpKaQLG02krtLFWCBCNE3MvaUR1Fe52LaqlmhMpfRFjsUUDx/q5drNzVS4ilu2eUc8sWyYBw50sb3Fy8bm7Kt7j9POJ27ewsmBSZSCt5SAWQi0INCkoctcpa7KpBGUiWnol8cGaO8eo8bjoG9sZoLAWqmey/AAHfGFqEtTcM4im0YwFgjz8tnRuNM0H37vug2MByP84KWzGfd56JVeqlx23v+6tfExK0InmyAMR41yC9vTOIotLl3XgMthiycfZsIqyZ1OYFnmtPpKV/xcyRrX/s5h+saD3LQ9NTy10FglNH64r4uDZ0e5Lc/y2bdcsJLdaxvY3uJlUwmYhUBXH9WkoduslZ9iGjKjhsrFR/CVJzpYWevhpu0r+O/nz8Rr2OeDP2w4VzOZVIYmQ9P6ECSTLZfg+RNDRGMqp38gkW2ratne4uX+A1188Kp1Kdsj0RiPtvfyhvOX40koi20FA2QThMfOTRCKxtiaxlFs8dHrNvL2i1tyllNOrDeUnGw35WB30lDlosbjSCk18fChXpx24fo0Dt5C47DbuLCljqde68cm8NY00UXpEBG+9cHdRGKlE2atNQJNClbTlEwaQTmEj750eogXTg7x21evp6WuglAkxpg//+/lj2sE6R+gw75w/KGXjqlcglRB8HTHAB6nLR7nni+37Wjh4NlROvomUra9cHKIwckQb75g+kraabfRUOXKqhFYTtttWTSCKrcjp9kEpsJp0zmMh3xhRAwhKSJsXemdphEopfjZoV6u2tiYl8msEFiZy6/b0Mhyb/ow3nRUuOzUzNMcC4EWBJoUukb8uBw2GqunP8gqTZtsORSe++oTx6mvdPLu3asTzCP5x+JbpqFMjWJGfNk1AiBtUlk0pnikvZfXbWiccevCX7toFTaBBw50pWx76FAPFU47r9+cupJurnFn1QiO9I7jcdpYl1Q7aDZY18SqKZTIiC+E1+OMZ7JvW1XLkd6xuD+hvXuMs8N+bt4+f3Z3q5bRQvYTng+0INCkYEUMJZtJ3A4bDpuUvEbwas8YPz/SxweuXEely0HeZN7nAAAgAElEQVRzjbHSm4mfwHIWZ/IRDE2GM+YQWLTWV9KVlEvwdMcAPaMB3n5xa95zsWj2erhqUxM/2j+9AFo0pnj40Dmu35LewdpU46Y/S+ezrmGj8Yw9Q5LYTKiryFyKemhyurloe4uXQDjGCTNB62eHerDbJKdDupDcsHU5f//Oi7gtTRJZOVF0QSAifyIiSkQazfciIl8SkQ4ROSgiFyfse6eIHDNfdxZ7bpr0dA2nho6CYc6odNlLPqHsa08ep8pl584r1gL5OUyTCWQxDSmlDI0gi2kIDI1gPBiZZpK6b28ndZVObtg6Oxv4r+9cxdlhPy8llI3Ye2qIgYkgN1+Q3sFqCILM37171J9iJpwtVjhtujITI77wtGqtlinqUPdo3Cx0+fqGnNe1kDjtNt5xSStOe3mvmYv67URkNXAjcCZh+GZgk/m6C/iauW8D8FngMmA38FkRmVvqoGZWdI/4WVWX3h5a7XaUtLP49OAkPznYzXsvXxN3bE6FUM5AIzAFwag/nBLrPhGMEImpvExDAJ2meWjUF+bRw+e4bUfLjM1CFjduXUGF086P9k+Zh352qBd3loie5hoP/RPBjFnO3SN+WjLcDzOlxu3AYRNG/Bk0ggQtakNTFW6HjfauMTr6JjjRP8lN24ofLbQUKbaY+yfg40DiHXYr8G1l8BxQJyIrgTcBjymlhpRSw8BjwE1Fnp8miWAkSt94kJa69O3zKt2Okk4ou39/Nwr4rYTImhq3A7fDNiuNAEhZTVv271ymIesaWw7jB1/uIhSJ8Y5LZm4WsqhyO3jTtuX89GAPwUiUWEzxs0M9XHteU8Y+wc01bsJRlbb0QyAcZWAixKrawmgEIkJdpTPtuZK1KIfdxpYVNbR3j/GzQ72IwJu0ICgKRRMEInIr0KWUejlpUwvQmfD+rDmWaVwzj1jFyzJpBFVuR0knlD17YiDeetNCRGj2unMmVSXiTxAEyX6CxHj4bCQ3qLlv71m2rvSmLeMwE27b2cKoP8yTR/vZ3znMubEgb74gs4M1bhpLYx7qMe+HlQUyDYEROZQ+aijVwb6tpZZD3aM89EoPl7TV0zyDyB1N/sxJEIjI4yJyKM3rVuDPgD8vzDRTznuXiOwVkb39/f3FOMWSxUoma6lP/8OvctlLNqEsEI6y78wIV6xPLdvQVO2ekUbgD0XjMfjJfgKr3WJ9hvISFnWVTqpcds4O+3m1Z4xXukZ5567ZawMWV21spLHazY/2dfHTg7247Dau35LZ59BsCoJ0EVA98VDiwj2AjTIT0zUCfyhKIBxLsf9vW+VlPBDhSO/4vCSRLVXmlFCmlLoh3biIXACsA142I09agX0ishvoAlYn7N5qjnUB1yaNP5nhvHcDdwPs2rVLd0kpIF0ZksksqtwOhibnpxFKodl3ZphQJJa2KFpzjSdePjgfAuEYa5ZVMjARTHmAjuSpERi5BEYV0u/vPYvLbss7ezUbDruNX7toFd957jS1lU6u2dyYNabdWmWn0why3Q+zobbClRI2m0mLSsxd0IKgeBTFNKSUekUp1ayUWquUWoth5rlYKdULPAjcYUYPXQ6MKqV6gEeAG0Wk3nQS32iOaeaRrhE/ImSsgV9VwlFDzx0fxCZGOYRkmmrcOQuvJRIIR1lZ68FplxSNIF8fARjmoZMDE9x/oIsbtjYXLCLm13e2EIrG6B/PbhaCKdNQuu/fPWIIuUz3w2yor0xtTjOUoWz3lhU12G3Cha218fpMmsKzECUmHgLeDHQAPuADAEqpIRH5AvCiud/nlVIzKwmpmTNdw36aqt0Zo1ZKuW/xsycGuaClNm1WanONm1F/mGAkmlfEjj8cpcJpp7nGk+JbGPaFEAFvlqYoFq31Ffz8SB8A77xkdY6982d7i5cNTVWcGfLxhvOzx91Xux1Uuuxpo6a6R/w01WS+H2ZDfVVqc5qpyqPTr5nHaecj123kota5+U002ZkXQWBqBdbfCvhIhv3uAe6Zjzlp0tM96s/oHwBTEJRg1JA/FOVA50jaOjww3WGaz8rTH45S4bKz3Ovm3HiqIKircOaVgGWda7nXzdWb8q8tlAsR4c/fuo0zQ76sXbosmmvS+0i6R/0Z20HOlrpKJ8FIDH8oGk9ws/wqyfWHAP74jZsLen5NKrronGYaXcP+rFErVS4HgXCMSDQWLwVQCuw9PUQ4qtI6imEqlyBvQRCa0giSfQvDvtxZxRZW5NDbLm4t+PV8fUKb0Vw01aSPmuoe8bO5wBU0rWsz4g9R4TK+f9yvMo/JYpopSueXrCk6sZiiezSQ1TFo9STwZejMtVh59vggdpvE+9QmEy8zkYefIBZTBCMxPE5TI0g2DU3mziq22LW2gWs2N/Gbl6/Ja/9iYSWVJaKUonskULCsYot09YYsH0FdHtqLpvBoQaCJMzAZJBSJ5TQNQelVIH32xCAXttZmTKrKFkufTNDs71vhstPs9TAWiMRrD4GlEeT3QGuqcfPtD+4uaFTObGiqcdOf5CMY8YXxh6MFFwTpKpCO+MJ4PY6S0jLLCX3VNXGsCJFsWaTxCqQllFQ2EYxw8OxoRrMQwLIqFyL5aQRWMlmF0x5PTEsMIR2eDMUfdqVCU42b8eB0gTYVOlp4HwEwLbt4aAZalKbwaEGgiZMrmQyMCBMoLY3gxVNGo5dsTdUddhvLqlx5aQSWIPA4bQnJWFPHpWu6sthpTqMRxbOKC1RewsLyESRGDg37Qnn7VTSFRwsCTZzuDA1pEqk0u5SVUuTQcycGcdqFXWvS+wcsmmo8WcsxW1irZk+CRmD5CfyhKMFIbFoVzVKgKU12cT73w2ywrs1IiiAorWtWTmhBoInTNeKnxu3IGm44pRGUjmnoueOD7Fhdl7PZea5yzBaBaaah6WUm4mGQJba6Tecs7zYbFC0rsHbjdtipdNmnmYaGJ7N3dNMUFy0INHG6RnLXna+0ooZKRCMYC4R5pSu7f8CiOc/s4rggcNmprXDictjioZdW391S8xEkhs9adI0YOQS2AjSkSaa+0jUtu1ibhhYWLQg0cbqGsyeTwZRGUCo9CV48OURMweVZ/AMWTTVuBiaC07p7pSPRWSwi0wTIVM2c0jJzNFS6sNskxTRUaLOQRV2lM24aCoSj+ELRkvOrlBNaEGjidGVpSGNhRQ35SsQ09OzxQVwOGxe35e5xZNXlH/Gn1spPJNFHALDc64n7CCxzR6k91Gw2obHaleIsLrSj2KK+cqrMxFR5idK6ZuWEFgQawFjhj/rDGRvSWFjO4lLQCGIxxZ6OAS5uq4s/tLORby7BVNSQJQimksqsVW6pmYbA8BNYmk04GuPcWKDgoaMWtQmF56YKzpWWFlVOaEGgARIjRLL/8O02ocJpX/Q+AqUUX/jpYY70jnNrnqWdpxym2SOHEn0E1nFWwbZ4hmwJPtSMMhPG9zg3FiCmCh8xZFFf6UzQCHR5iYVGCwINMJU81JrDRwCl0aXsK0908J9Pn+KDV67j9kvzq+qZt0YQmvIRgGEaGg9G8IUijPjC1HgcJdnsPLHwXDy5sGiCwMWoP0wspqYa+ZSgFlUulN7dqikKVjJZPj/8Krd9USeUfee50/z9o6/xtp0tfPqW8zGbI+UkXXJYOgJWiQmnpRGYx40FSzr6panGzeBEkGhM5a0hzpa6ShcxZUR1WZFWuTq6aYqHFgQawDANOWwSN49ko8q1eBvY//RgD5954BDXb2nmb95x4YxCH6vMuvz5agRuh/HzSUwqK+VSCc01bmIKBieDdI8agqB4zuKpMhOWg72uojSvWzmgBYEGMExDK+s8edXQr3LbF6Wz+EDnCB/73n52rannK++5eFbmmXxyCQLhKG6HLS5k4kll40FGZlBwbrHRZPlIxoJ0j/iNnsoZivTNlfqEwnNDkyFq3A5cDv04Wij0ldcAZsx4nqu/KrdjUbarfOpoP+Go4ut37MqZRZyJ5jzKTFhNaeLHWIXnLI2ghE1DYPhIukcCed8Ps2GqzESYEV+IOm0WWlC0INAA+SWTWVS5HItSIxj1h6ly2ecUuplP72KrKY2F1+PA7bDRNx5kpIR9BM3TBEHxkslgKrx22BdiyBcuuZIc5YYWBBrC0Ri9Y9kb0iRS5bYvyoSyUX84r7aM2cin3lAgEpsmCESE5V4PnUM+JkPREjYNTRWe684juXAuJPoIRnyl61cpF7Qg0MRjxvMXBIuzgf2oP5xXw/hsNNW4GQ9E4rkC6fCHoikJasu9bo72jgOlGw/vcdrxehycGJhkLBApqkbg9TixyZSPoFS1qHJBCwJNPCt2eZ5NyqtcRgN7pbLX5JlvxgqgEaSry59MIMlHAIaf4NTgJFDa8fDNXg8vd44AxcshAKOkRW2FkVQ2MoMez5rioAWBJv7Qa6p257V/ldtBTEEgHCvmtGZMoUxDkD272B+O4nFO/+lYoZdQ2qUSmmvcHO83BFqxyktY1Fe66BsLMhGMlPQ1Kwe0INDQP2Ek9Fir4VxYDewXW3OaQpiGrDyKbBpBsrMYpnIJoHRNQzAlCKG4GgEYkUNxLaqEr1k5oAWBhv7xICL5V8ysci3OdpVjgUJqBNlNQ+l8BBalbOawFgP2PJML50JdpYtTAz6gtK9ZOaAFgYaBiSANlS4ceSZgxTWCRRQ5FI7G8IWicxYEDVVGXf6cPoJkQZDw0CzFgnMW1sN/hTe/5MK5UFfpJBQ1zIu6vMTCUlRBICK/LyJHRKRdRP42YfyTItIhIkdF5E0J4zeZYx0i8olizk0zxcB4kMY8/QNAPNt0MZmGRs0eAnMVBHabsKzKFa/CmY7khDKY6vBV6bLnVfJ6sWJpRMUMHbVI1AJKrX9DuVGc/HFARK4DbgUuUkoFRaTZHN8K3A5sA1YBj4vIZvOwrwBvBM4CL4rIg0qpw8Wao8agfyJIY03+P8TKRWgaKpQgAOOhblXhTIc/jUZgZReXuomjOS4IiusfgOlO9VK/bqVOMTWCDwN/rZQKAiil+szxW4F7lVJBpdRJoAPYbb46lFInlFIh4F5zX02RGZgI5h0xBIuzgX0hBUFTtTtj1FAspgiEY7iTBEGN20GF017yJg5LIyhWsblEEjPAS9mcVg4UUxBsBq4WkedF5CkRudQcbwE6E/Y7a45lGtcUEaUUA+OhGZmGrHaVi9E0NNeoIbDqDaXXCIJJJagtjOxid8mvbFvqK6itcHJRa23Rz2VdqyqXHbejdM1p5cCcTEMi8jiwIs2mT5mf3QBcDlwK3Cci6+dyvoTz3gXcBdDW1laIj1yyTIai+MPRaWGDuZjSCBaPIBgrpEZQ42ZgIkQ0plIcpvHuZM7UNdTHbthMbYmvbCtdDvZ95o0U2U8MTJmGdOjowjMnQaCUuiHTNhH5MPBDZaSfviAiMaAR6AISW0a1mmNkGU8+793A3QC7du1aXOmtJcaAufKdkUZgRg0tpgqkhfYRRGOKoclQioD0J7WpTOS2neWhwBY7WsjCEpqlrkWVA8U0Dd0PXAdgOoNdwADwIHC7iLhFZB2wCXgBeBHYJCLrRMSF4VB+sIjz00DcKdo4A43A7bDjtMuiqkA66iucILAiWKxeuokkN67XzB5LAGiNYOEpWtQQcA9wj4gcAkLAnaZ20C4i9wGHgQjwEaVUFEBEPgo8AtiBe5RS7UWcn4YpjWAmzmIwTAi+xSQI/GEqnPaCNDfxegxhMhYIp2yzupNpQTB34oKgxM1p5UDRBIEZ+fObGbZ9EfhimvGHgIeKNSdNKgNxjWBmq7LqRdbAvhB1hiwsh/OYP1XQTfkItCCYKxUuOzVuR96lTTTFo5gagaYE6B8PYhNYVjVTjcC+qPoWF1QQeBzxz0wmm49AM3O+/Vu7Wd1QudDTWPJoQbDE6Z8IxcsqzIQq9+LqUlZIQWB9TjrTkFVxVWsEhWFnW/1CT0GDrjW05BmYmFl5CYsqt31RhY8WovKoRY3lI8iiEWgfgaac0IJgidM/HpxRDoFFlWtxNbAvRFMaC5fDRoXTntY0FAhp05Cm/NCCYIkze42gfE1DYJiH0jmL4xpBAaKTNJrFgr6blzBKqdlrBG57XhpBLKYIRoqrOYSjMSYLUII6EW+FI334qHYWa8oQLQiWMBPBCMFIjMbqmSf0VLny0wi+/EQHb/3XPbOZXt5MlZcoXOyD1+NMbxqKawRaEGjKBy0IljADZovK2ZqGQpEY4Wj2vsWnBid57dxEUUNN4+UlCpiYVFvhzKgRuB02bPNUhkGjmQ+0IFjCxJvWz8I0ZFUg9eVIKrMii84O+2d8jnwpZJ0hC28GH0EglNqURqMpdbQgWMLEs4pnoRFU59mlzPIjnBn0zfgc+TIWMOZglYYoBF6PI2NCmc4h0JQbWhAsYeakEeRZitryI5wZKp4gKIZGUFvhZDwQJhabXtzWH47pHAJN2aEFwRJmYMIoLzGbMsDVVgP7HJFDlqDoHC4tQeCtcBJTqRpPIBzVgkBTdmhBsIQZmAjSUOWeVf35fPsWW+0sO4uoEYwVsDuZhWVmSjYPBcLRtE1pNJpSRt/RS5jZ5hBA/l3KrBV159DMnMXnxgJEckQkWYz6w7gdtoKu1L1mKGqyw9ivncWaMkQLgiVM/0RoVjkEkH/fYiuq6MyQD6MdRW6CkShv+Ien+PqvTua1/6ivsFnFkFCKOimEVDuLNeWIFgRLmIHx4Iwb0lhMaQSZfQShSIxQNEZjtRt/OBrPW8jFudEgE8EITxzty2v/QpeXgMymIX84ilsLAk2ZoQXBEkUpRf/E7E1D+UQNWUlk56+sAfJ3GPeOBQDYf2Y43hEsG8UQBPFS1Mk+gpDWCDTlhxYES5TxYIRQJDarHAKASmfuqCErdHTLClMQ5Okw7hk1/AnhqGLv6aGc+xdFI4ibhpKihiIxLQg0ZYcWBEuUueQQANhsQqUre08CK5nsvBVeIP+kst5RQyOwCTxzfDDn/sUQBDVuByJpTEPaWawpQ3SHsiWK1bR+thoBGPWGstUQsjSCZdUummrcMzINVbnsbFnp5dk8BMFYAZvSWNhsQrXbMc00pJTCr/MINGWI1giWKPGCczNsWp9IlcuetYG9pS1Uux20NVTmnV3cOxpgRa2HKzcs4+DZkbTF3yyiMcV4MFJwjQBSC88FI7pNpaY80YJgidI/bphfZhs1BKZGkMU0ZEUUVbrstDVU5p1L0DtmCILLNywjpuDFk5n9BGNFyCq28Hqc0zQCy3Ht0QllmjJD39FLlIGJEHabzKq8hEWungSJGsHq+gp6Rv2EIrmTxHpHA6zwVnBxWz0uhy2rn6AY5SUsvBWOaQllAbPBjtYINOWGFgRLlIGJIMuqXHOqq5+rS5nlP6h0OVjdUElMQfdIdq0gGlP0jQdZUevG47Sza039ggmCZNOQX/cr1pQpWhAsUfrHZ9erOJFKtyNr1JDlP7B8BJA7l2BgIkg0plhRWwHA6zYs49WeMYYn0yejFaMpjUVyl7J4v2KtEWjKDC0IligDE0EaZxk6alHjdqTE2SfiC0WwiWFTX20KglwO4x4zdHSF1wPAFRuWAfDcifRaQXFNQ9N9BFabSm0a0pQbRRMEIrJDRJ4TkQMisldEdpvjIiJfEpEOETkoIhcnHHOniBwzX3cWa24as+DcHDUCr1mzPxMTwQhVLgciwnKvB5fdllMQWDkEK2sNQXBhax2VLntG81BRBYHHyWQoGi9+5w+ZUUPaNKQpM4qpEfwt8BdKqR3An5vvAW4GNpmvu4CvAYhIA/BZ4DJgN/BZEakv4vyWLEopBiZCcwodBaOLVzASIxhJ7yfwBaNUmn0L7Dahpb6Cszkih3rNrOIVpiBw2m3sXtfAM8cH0u5fXB+BkWYzbmo9ft24XlOmFFMQKMBr/l0LdJt/3wp8Wxk8B9SJyErgTcBjSqkhpdQw8BhwUxHnt2QZC0QIRWNz1ghqzMJs4xnMQxOhCFXuqZzF1XnkEvSMBXDahYaEaKbXbVjG8f5Jzpk1iBIZ84dxFbgEtYWVpGYJm7hpyKUtqpryoph39MeAvxORTuDvgU+a4y1AZ8J+Z82xTOOaAjPX8hIWUzX705uHfMFIvEopQFtDRU5n8bnRAMu9nmnRTFesbwTS+wnGAoUvL2FhVSC1Ioe0s1hTrsxJEIjI4yJyKM3rVuDDwB8ppVYDfwR8oxATNs97l+l32Nvf31+oj10yzKVpfSLeHBrBZDAa71sAsLq+khFfOG1TeIue0UDcUWyxdZUXr8fBMx2pgmDUH8brKU6lFCsSycol0M5iTbkyJ0GglLpBKbU9zesB4E7gh+au38ew+wN0AasTPqbVHMs0nu68dyuldimldjU1Nc3lKyxJLEEwd40gffMWi4kUjcAMIc1iHjpnZhUnYrcJl69fxtNp/ATFKDhnkdyTQOcRaMqVYpqGuoHXm39fDxwz/34QuMOMHrocGFVK9QCPADeKSL3pJL7RHNMUmP4CFJwDqPGkb+do4QtF4r2NgXgI6dkM5iGlFD2jgXjEUCJXbFjG2WF/yrFFFQSW6SvZNKSdxZoyo5jVR38H+BcRcQABjAghgIeANwMdgA/4AIBSakhEvgC8aO73eaVU7mL0mhkzMBHEYRPq5vgAnTINZdIIoinOYsicSzDqDxOMxFjuTRUEl6838gmePzFE6yWV047Z2FQ9uy+Qg+TmNIFwDJfDNqdsbI1mMVI0QaCU2gNckmZcAR/JcMw9wD3FmpPGoH88yLLquZWXgNymIV8oQlWCGaW2wklthTOjIOiJ5xBUpGw7b3kNdZVOnjsxyNsvaY2PF6NfsUWF047DJtOihrR/QFOO6Di4JUghykuAUYbaJulNQ7GYwhearhEArG6oyFiF1EomW1GbOjebTdi9toHnTk45jGNFLEENICJGdnFgykegBYGmHNGCYAlyZsjH6vrK3DvmQESo8aTPLvaZ9vQq9/QHp1GOOr1GYPUqXpFGIwDDPNQ55KfLLFw3HoigFAVvSpNIbYUzLuj8Yd2dTFOeaEGwxIjFFJ3DftYsm7sgALNUc5rwUasYXapGUMnZYT+xmEo5pmc0gAg0Z4hmumx9AwDPm/kExcwqtvB6HFNRQ7o7maZM0YJgidE7FiAUidFWIEFQ43amTShL7EWQyOr6SkLRGOfGU7OEz40GaKx247Snvy3PX+GltsIZTyybF0GQYBoKhKO6KY2mLNF39RLjtNlAfk1DVUE+z9AI0gkCqzvZdEFg5RKka2TfM5Y+dNTCZhN2r2vgebNj2bwJAu0s1pQ5WhAsMU4PTgIUzjTkcabNLJ6Im4ZSfQSQPoS0d9SfNnQ0kcvWNXB60Ef3iL+ovQgsjJ4ECT4CLQg0ZYgWBEuM00M+nHZhVV16h+xMSa7Zb2F1J6tK0gha6iuodjvYd2Y45ZjeDMlkicTzCU4OzpNG4JgWNeTRzmJNGaIFwRLjzKCP1vpK7AVKiqrxpHcWT2RwFjvtNq7e1MgTR/oxUkoMfKEIY4FITo3g/JVG3aHnTwzNk7PYSSgSIxCOEgjHtEagKUu0IFhinB6ajJtnCoHX42QiGCGaFAVk9TJONg0BXLelmd6xAId7xuJjyQ1pMmG3CbvXLeO5E4ZG4LRLUR/OidnF2jSkKVe0IFhCKKU4PegrmH8ApmL4J5K0gkzhowDXnmcUCnziSF98bCqZLLsgALh8fQOnBn28dm6c2gonIsUr+ZCYPa2jhjTlir6rlxAjvjDjgUhBNYJ44bmkyKF41FCaFXRzjYcLW2v5RYIgSO5VnA3LT7CnY6CoyWRAvMT1qNYINGWMFgRLiFNmxNDaZYUJHYXU5i0Wk6EIHqcNR4acgOvOa2Z/5whDkyEgMas4tyA4f6WXGo+DUCRWVP8ATJmG+seDKIV2FmvKEi0IlhBWyGZhTUPpS1FPmo3rM3H9lmaUgqdeM7SC3tEAXo8jJe8gHXaz7hAU11EMU6ahc2NG6W6tEWjKES0IyoyTA5OcGphMu81KJltdYGcxpDMNRdL6BywuaKmlsdrNL44YHeZ6xwJpq45mwjIPFV0QeCxBYGgsWhBoyhEtCMoIpRQf/OaL/MG9+9NuPz3oY4XXU9B6OZnaVSb3IkjGZhOuPa+Jp472EYnG6B0NsDwPs5DFvAkCU+OxNAJda0hTjmhBUEa8eGqYkwOTHOoajcfxJ3JmaLJgNYYsMjWwT+5FkI7rtzQzFoiw78yIoRHk4Si22LrKy/rGKs5f6Z35pGeA22HH47TRZ9ZG0oJAU45oQVBGfH9vJwAxBftOp2bunhr0saaAZiGYKio3U9MQwFWbGnHYhEfbexmYCOblKLaw24Rf/J9reffutplPeoZ4Pc4p05B2FmvKEC0IyoTJYISfvtLDLResxCaw99T0Lp++UIT+8SBrGwsXMQTgsNuoctlTTEOToWjaZLJEvB4nl65t4If7u1Aqv4ihhaC2whnPc9A+Ak05ogVBmfDQKz34QlHef+Vatq7y8uKp6RqBFTFUyBwCi3T1hnJFDVlcv6U5HkK6WAWBUYraEHRaEGjKES0IyoTvv3SWdY1V7FpTz6VrG9jfOUwoEotvj5efLrCPAIyV/WxMQ2CUm7DIJ5lsIbCSygAqXPonoyk/9F1dBpwamOSFk0O845JWRIRL1zYQCMdo7x6N73OmwH0IEqnxOKblESil8jINAWxoqoprKbnqDC0UidnLbofWCDTlhxYEZcD/vnQWm8DbLm4BYNfaegD2JpiHTg9NUlvhLErtfm+Fk/HglEYQjMSIxlReyWEiws3bV7CsylX0UNDZkjgv7SzWlCNaEBSYw91jfPg7LxGMROflfNGY4gf7znL1pqZ4QlZzjYe1yyp5IcFhXOhic4l4kzSCTG0qM/HHN27mZ394dVGLx80FK1cCtI9AU55oQVBgHm7v5WeHejnUNZZ75wLwdMcAPaMB3rmrddr4rrUN7D01FK/5bwiCwpuFAGqSfARTJajzE4GRXH0AABjUSURBVARuh53mReofgKlcCdB5BJryRAuCAnO8fwKAwwn2+WLy/ZfOUlvh5Ibzl08bv3RtPcO+MMf7JwlHY3SN+AueQ2DhrXAwHojEhU68KU2ZmFEs05DLYStYQx+NZjGR35JNkzfH+wxBMB8awagvzCPtvdx+6eqUleqlZlG2F08N4bQL0ZgqeFaxhdfjJBpT+EJGWYlsvQhKEcs0pM1CmnJlThqBiLxTRNpFJCYiu5K2fVJEOkTkqIi8KWH8JnOsQ0Q+kTC+TkSeN8e/JyKuucxtIYjGFCfMgm/tPcXXCL76VAehSIzfuHR1yrZ1jVUsq3Lx4qmhqdDRomkE0wvPTWbpTlaKWN9PN6XRlCtzvbMPAW8Dfpk4KCJbgduBbcBNwFdFxC4iduArwM3AVuDd5r4AfwP8k1JqIzAM/NYc5zbvdA75CEViNFa7Odo7Pi2Ov9B09I3zjV+d5J2XtLJtVW3KdhFh19p69p4a5nS8/HSxfATGyt/KLi43jcAyDWmNQFOuzEkQKKVeVUodTbPpVuBepVRQKXUS6AB2m68OpdQJpVQIuBe4VYxwkeuB/zWP/xZw21zmthBY/oG3XrSScFRxrG+8KOdRSvGZ+9updNn505u3ZNzv0rUNnBny8cLJIdwOG8017qLMJ16K2swujguCPMJHSwHr+2lHsaZcKZau2wJ0Jrw/a45lGl8GjCilIknjaRGRu0Rkr4js7e/vL+jE50KH6R/4tYtWAdCewU+glIoXMZsND77czbMnBvm/N22hsTrzw93yEzza3ktbQyW2Ijk6U0xDZaYRWFFDOodAU67kFAQi8riIHErzunU+JpgOpdTdSqldSqldTU1NCzWNFDr6JmisdnNRax1VLvu0zN5Efnywh9f99S/ipY1nwnggzBd/+ioXtNTynhyVN7et8lLpshOMxIpmFoI0piHTR1BZJg/OGu0s1pQ5OZdsSqkbZvG5XUCiB7PVHCPD+CBQJyIOUytI3L9kON4/wcbmKmw2YduqWg51p9cIHj7UQzSm6B8P0lwzs/j5f378GP0TQe6+Y1fOUEaH3cbOtjqe7hgsWjIZpDcNOWyC21EezlW7TahxO7RpSFO2FOuX+iBwu4i4RWQdsAl4AXgR2GRGCLkwHMoPKiMA/QngHebxdwIPFGluRUEpRUffBBubqwGjccrh7jGiMTVtv3A0xq+ODQAwGZxZ9vGR3jG++cwpbr+0jR2r6/I6ZtcawzxUTEFgaQRWhU4rjHSxZgrPBm+FU2sEmrJlruGjvy4iZ4ErgJ+KyCMASql24D7gMPAw8BGlVNRc7X8UeAR4FbjP3BfgT4E/FpEODJ/BN+Yyt/mmfyLIWCDChiZDEGxvqcUfjnIyqX/wvtPDCSaU1C5imYjFFJ/+0SG8Hgcff9N5eR935cZGADYvr8n7mJnicdpxOWxxH8FEMHd3slLj4zedx52vW7vQ09BoisKcvHlKqR8BP8qw7YvAF9OMPwQ8lGb8BEZUUUliOYotjWDbKqOFYnv3aHwM4MnXppzbk2naSWbiW8+eYu/pYf7+nRdRX5V/isXudQ08/LGrOa+IggDMUtT+qfDRcnEUW9y6I2PsgkZT8pSHEXcRcLzfWPlbD/2NzdW4HDbak/wETxzpi5dd9uVpGjo9OMnfPnyUa89r4u0Xz/yBtGWFt+hmGm+FY1pCWWWZCQKNppzRgqBAHO+boMpljzdXcdptnL+ihkNdU5FDvaMBjvSO8+YLVgKkbTCfTCym+NMfHMRhE/7qbRcsWru7oRFMOYuryySrWKNZCmhBUCA6+ibY0Fw97UG9dVUt7d1j8WJsTx7tA+AWUxDkYxr67+dP89yJIT51y/nxMtOLkRqPY1pmcT69CDQazeJAC4ICcbx/go1N1dPGtrd4GfWHOTvsB+DJo/2srPWwvcWLy26Lx9tnonPIx1/97AhXb2pMW09oMWH09bVMQ5G8exFoNJqFRwuCAjARjNAzGmBD83RBYNUAau8eIxSJsadjgGvPa0JEqHTbs2oESik++cNXEOCv337hojUJWSQ6i33BaNkkk2k0SwG9bCsAVunpDUkawZYVNdhtQnv3KLUVTiaCEa49z2jWXuVyZA0ffeb4IHs6BvjCrdtoqVu8JiELr8fBeEL4qNYINJrSQf9aC0By6KiFx2lnY1O1oRFEYzjtEo/rr8qhEfSOGuUnXr+5uUizLizeCifBSAxfKEIwEiu78FGNppzRv9YCcLx/AodN0mbvbmvxsufYAF3DfnataYivlKvcjnhLx3RYEUXVntL4L/Ka87QEmDYNaTSlg/YRFICOvgnWLKvEaU+9nNtX1dI3HuTouXGu2zJVIK/a7cgaPhpv91giYZhWYbYeUxBo05BGUzpoQVAAOvonUsxCFlaGMRD3D4CxYs6WUDYeiOBy2HA7SkMQWKWaLUGgE8o0mtJBC4I5Eo7GODPoyygItpqCoKWugk0J+1Tl1AjC1JTQw9SqQNo7aoTK6oQyjaZ0KJ0nzSLl9OAkkZhKiRiyqPE42b2ugUvX1k8LAa1yOfBliRqaCERKxj8AU81p4hqBTijTaEoG/WudI5kihhK570NXpIxVuR1Zy1CXWgimVYpa+wg0mtJDm4bmSEeGHIJcVLnshKKxjA3uxwOlJQi8nmSNQJuGNJpSQQuCOXK8f5KVtZ4Zx81b+2cyD00EI/FVdilQ6bJjt0mCj6B05q7RLHW0IJgjiV3JZoIVFprJYVxqpiERocbjYNhnZBfrhDKNpnTQgmAOdI/4OdI7xtaV3tw7JzGlEaT3E5SasximzEOgG71rNKWEFgRz4KtPdgDwvivWzPjYKjOqJpNGMB6MUO12pt22WLFyCapcdmy2xV0kT6PRTKEFwSzpGvHzvRc7eeeu1bTWz7wxfFwjSBM5FIxECUViJeUjgCmNQCeTaTSlhRYEWfidb+/lW8+cSrvtK08Y2sBHrts4q8+2omrSaQQTZoOXUvIRwFQIaanNW6NZ6uhfbAYi0RiPHT7H46+eo6Wughu2Lo9vOzvs4/t7O/mNS1fPukR0dZaooXjBuRJ7oMY1Ah06qtGUFFojyMCYuSq3ifCH9+7ntXPj8W1feaIDQWatDcCUaShdKWqr5WPJOYvN7GIdMaTRlBZaEGTAasT+JzduptLt4Le/tZfhyRCdQz6+v/cst+9ePacewlb4aLp2lZZGUGo+Amu+VVoj0GhKCi0IMjBqCoLzltdw9/suoXcswIf/+yX++fFj2GzC7107e20AjPBKkfQageUjqCm1qCGP1gg0mlJEC4IMWIKgtsLJzrZ6/ubtF/DciSF+sO8s79ndxopaz5w+X0SMdpVpooZKrSmNRdw0pAvOaTQlxZwEgYi8U0TaRSQmIrsSxt8oIi+JyCvmv9cnbLvEHO8QkS+JWZJTRBpE5DEROWb+Wz+Xuc2VREEA8Os7W/n96zfSWO3iw9duKMg5MrWrHC9RZ3HcNFRi89Zoljpz1QgOAW8Dfpk0PgC8VSl1AXAn8F8J274G/A6wyXzdZI5/Avi5UmoT8HPz/YJhCYL/3979xshVnXcc//52h12za1wnAYyDcU0FBUEgJt0QrNI25V9JFBVDSJu0ErxAdaskEm3TJiCkiFRUgr4gSRUUySJtSRMVUlpKxJ+6QC2hNoXEBpMaXAeTULHUYEPBa6931zs7T1/cM/bdYdbL7njunen8PtLIc8+9O/vIvr7PnHPuPU/9Wy7AF644i6duvpQVy1rrDdTNVcD+8NBQt/UI0tCQaxGYdZeWEkFE7IiInU3an42I/0mbzwPHSxqUtBJYFhFPRUQA3wbWp+OuAu5J7+/JtZeisUdQV2lSjnKxsqWom90+Ok2lTwxWumvkrv5ksR8oM+suRVxpPgk8ExFTwKnAaG7faGoDWBERu9P714AVlGhsYpqBSh9L2rhmztBAf/O7htI6Q/lCNt2gnjS7bUjLrNfN+z9W0uPAKU123RIRD87zs+cCdwBXLCSoiAhJcZTP3QBsAFi9evVCPvpd2zcx/Y7ewLG2dLDCa2OT72jf32Urj9aduvx4/uyqc/n4eSvLDsXMFmDeq01EXLaYD5a0CngAuC4iXkrNrwKrcoetSm0Ar0taGRG70xDSnqPEtBHYCDAyMjJnwmjF2GT7E8HQXENDXVaUpk4S161bU3YYZrZAbRkakrQceBi4KSL+vd6ehn7GJF2U7ha6Dqj3Kr5PNrFM+vOovY12K6ZHMMfQUJcVpTGz7tbq7aNXSxoF1gEPS9qUdn0eOAP4sqRt6XVy2vdZ4G5gF/AS8Ghqvx24XNKLwGVpuzRFJIKhgeY9gm4rU2lm3a2lq01EPEA2/NPYfhtw2xw/swX4QJP2N4FLW4nnWNo3Mc2ZJ5/Q1t8xPFjh4KEZarWYtX7/gakqa04cbuvvNjOr6677Ewu07+A0y9o8PFO/3/7g9OzhIfcIzKxITgRN1GrB/qlqIUNDAAcbhocOTE17jsDMCuNE0MT+ySoRs58qbof6t/58cZrpmRqT0zX3CMysME4ETcz1VPGxVi/gki9gP96l6wyZWfdyImiiqETQrEfQrUVpzKx7ORE0MTZZUI+gSbnKelJo90S1mVmdE0ETh3sEQ+1/oAzgQK4mwZF6xd1VlMbMupcTQRPFzRG8866hAx4aMrOCORE0cbgWwZL2JoLhZnMEniw2s4I5ETSxbyKrBzDU5iLs9SLv+XKV3VqUxsy6lxNBE/V1htpdD6DS38dgpa9hsjjrjbhHYGZFcSJooogF5+qGByuzhoYOTFaRaHtvxMyszomgibGJ6bY/VVw3PNg/64GysbTOULdVJzOz7uVE0EShPYKBhh7BVJUTPCxkZgVyImhirOChoVlzBKlesZlZUZwImih+jmD2A2WeKDazIjkRNIgIxiarLDu+mIvx8ED/rAfK9k9VWdrm5xfMzPKcCBocmKoyU4tCewTjs+4amvYcgZkVyomgQVHLS9QND8wuYO+hITMrmhNBg8ITQeoRRATgyWIzK54TQYPD6wwVmAiqteDQTI2ZWjB+aMY9AjMrlK84DcZKGBqCbL2hSn8N8DpDZlYsX3EaFD00VC9OMz5Vpb8ve5rYicDMiuQrToOxiewOnqISQX0YaPxQlb60rISL0phZkZwIGuybmKZP2dIPRRg6PDRUBVIicI/AzArkK06DfWnBub6+YhZ9O9wjmJqhlu4c8mSxmRWppbuGJH1K0vOSapJGmuxfLemApD/JtV0paaekXZJuyrWfLunp1H6fpIFWYlusIpeXgCPlKsenqocXn/McgZkVqdXbR7cD1wBPzrH/TuDR+oakfuAu4GPAOcBnJJ2Tdt8BfDUizgDeAm5oMbZFKToRHJkjmDlSr9g9AjMrUEuJICJ2RMTOZvskrQd+Bjyfa74Q2BURP42IQ8C9wFXKFt+/BLg/HXcPsL6V2Bar6EQwPHhkjqDeI/AcgZkVqS0PlElaCnwJ+ErDrlOBV3Lbo6ntfcDbEVFtaC9ckUVp4EgB+/FDVfanHkFRE9VmZvAuJoslPQ6c0mTXLRHx4Bw/divZMM+BdlTakrQB2ACwevXqY/rZRfcIBit99PeJ8akqk9M1hgf6Dz9PYGZWhHkTQURctojP/QhwraS/AJYDNUmTwFbgtNxxq4BXgTeB5ZIqqVdQb58rpo3ARoCRkZFYRHxzfW7hiUASQwP9jE/NMHFoxsNCZla4tlx1IuJX6u8l3QociIhvSKoAZ0o6nexC/2ngdyIiJG0GriWbN7gemKu30TYT0zNUa8GygusBLE0Lzx30OkNmVoJWbx+9WtIosA54WNKmox2fvu1/HtgE7AC+FxH1yeQvAX8saRfZnMG3WoltMYpeXqJuaCArYO+iNGZWhpa+fkbEA8AD8xxza8P2I8AjTY77KdldRaUpKxEsHcwK2LsojZmVwctQ5+w7WFaPoHL49lEPDZlZ0ZwIcsrqEQwPVg4/UObJYjMrmhNBTnmJoJ/xqSr7p6peXsLMCudEkFNqjyANDXmOwMyK5kSQMzYxjVT8om/DA/3878FDRHh5CTMrnhNBzr6JaZYOVgpbgrpueLBCWoHaRWnMrHBOBDljk9XCh4Vg9mqj7hGYWdGcCHKKXl6ibii3yJznCMysaE4EOWUlgvpS1OAegZkVz4kgp7REkOsR+IEyMyuaE0FOeT0CJwIzK48TQU4nDA35gTIzK5oTQTI5PcOhaq3Q6mR1+R7BsHsEZlYwJ4Kk/lRxKYkgzREsOa6P4/r9T2JmxfJVJylreQk4MjTkh8nMrAxOBMlYiYmg/hyB5wfMrAxOBEmZPYL+PnH8cf2+Y8jMSuFEkJSZCCAbHnIiMLMyOBEk5SeCip8qNrNS+MoDzNSCx154naGBfpaVdDH+0984i5OWDpbyu82stzkRAHdt3sUPXnqTOz55HpWSbt/8xPnvL+X3mpn1/NDQD156g689/hOuvuBUfmvktLLDMTMrXE8ngr37p7jx3m2sOXGY29Z/AKnYgjRmZp2gZ4eGZmrBH923jbGJaf72hgu9tIOZ9ayevfrdtXkX/7brDW6/5jzOPmVZ2eGYmZWmJ4eG9oxN8o3Nu1i/9v389oc9L2Bmva2lRCDpU5Kel1STNNKw73xJ/5H2/6ekJan9l9L2Lkl/qTQwL+m9kh6T9GL68z2txHY0Jy9bwvd+fx1/fvV5nhcws57Xao9gO3AN8GS+UVIF+A7wBxFxLvBRYDrt/ibwe8CZ6XVlar8JeCIizgSeSNtts/a05Z4XMDOjxUQQETsiYmeTXVcAP46I59Jxb0bEjKSVwLKIeCoiAvg2sD79zFXAPen9Pbl2MzNro3bNEfwiEJI2SXpG0hdT+6nAaO640dQGsCIidqf3rwEr5vpwSRskbZG0Ze/evcc6djOznjLv2Iikx4FTmuy6JSIePMrnXgx8GDgIPCFpK7Dv3QQVESEpjrJ/I7ARYGRkZM7jzMxsfvMmgoi4bBGfOwo8GRFvAEh6BPgQ2bzBqtxxq4BX0/vXJa2MiN1pCGnPIn6vmZktULuGhjYB50kaShPHvwa8kIZ+xiRdlO4Wug6o9yq+D1yf3l+fazczszZq9fbRqyWNAuuAhyVtAoiIt4A7gR8B24BnIuLh9GOfBe4GdgEvAY+m9tuByyW9CFyWts3MrM2U3bzTvUZGRmLLli1lh2Fm1nEkbY2IkfmO68kni83M7AgnAjOzHudEYGbW47p+jkDSXuC/F/njJwJvHMNwiuCYi9GNMUN3xu2Y2+fnI+Kk+Q7q+kTQCklb3s1ESidxzMXoxpihO+N2zOXz0JCZWY9zIjAz63G9ngg2lh3AIjjmYnRjzNCdcTvmkvX0HIGZmblHYGbW83oyEUi6UtLOVC6zrZXQWiHpryTtkbQ911ZYSc/FkHSapM2SXkhlSm9M7R0bt6Qlkn4o6bkU81dS++mSnk7nyX2SBsqOtZGkfknPSnoobXd0zJJeTqVqt0nakto69twAkLRc0v2S/kvSDknrOj3mheq5RCCpH7gL+BhwDvAZSeeUG9Wc/oYjpTzrCi3puQhV4AsRcQ5wEfC59PfbyXFPAZdExAeBtcCVki4C7gC+GhFnAG8BN5QY41xuBHbktrsh5l+PiLW52y87+dwA+DrwzxFxNvBBsr/vTo95YSKip15kK6Vuym3fDNxcdlxHiXcNsD23vRNYmd6vBHaWHeM88T8IXN4tcQNDwDPAR8geGKo0O2864UVWz+MJ4BLgIUBdEPPLwIkNbR17bgA/B/yMNJ/aDTEv5tVzPQKy0piv5Lbz5TK7wbsu6Vk2SWuAC4Cn6fC40xDLNrKCSI+RLZH+dkRU0yGdeJ58DfgiUEvb76PzYw7gXyRtlbQhtXXyuXE6sBf46zQEd7ekYTo75gXrxUTw/0ZkX0c68rYvSUuBfwD+MCLG8vs6Me6ImImItWTfsi8Ezi45pKOS9AlgT0RsLTuWBbo4Ij5ENjT7OUm/mt/ZgedGhay64jcj4gJgnIZhoA6MecF6MRG8CpyW286Xy+wGr6dSnnRqSU9Jx5Elge9GxD+m5o6PGyAi3gY2kw2rLE8V9qDzzpNfBn5T0svAvWTDQ1+ns2MmIl5Nf+4BHiBLup18bowCoxHxdNq+nywxdHLMC9aLieBHwJnp7ooB4NNkZTK7RUeX9EwlSL8F7IiIO3O7OjZuSSdJWp7eH082p7GDLCFcmw7rqJgj4uaIWBURa8jO4X+NiN+lg2OWNCzphPp74ApgOx18bkTEa8Arks5KTZcCL9DBMS9K2ZMUZbyAjwM/IRsHvqXseI4S598Bu4Fpsm8mN5CNAz8BvAg8Dry37DgbYr6YrJv8Y7IypdvS33fHxg2cDzybYt4OfDm1/wLwQ7Kyqn8PDJYd6xzxfxR4qNNjTrE9l17P1//vdfK5keJbC2xJ58c/Ae/p9JgX+vKTxWZmPa4Xh4bMzCzHicDMrMc5EZiZ9TgnAjOzHudEYGbW45wIzMx6nBOBmVmPcyIwM+tx/wdpNokIb2lwBQAAAABJRU5ErkJggg==\n",
333 | "text/plain": [
334 | ""
335 | ]
336 | },
337 | "metadata": {},
338 | "output_type": "display_data"
339 | }
340 | ],
341 | "source": [
342 | "i_update = 0\n",
343 | "state = envs.reset()\n",
344 | "early_stop = False\n",
345 | "\n",
346 | "while frame_idx < max_frames and not early_stop:\n",
347 | " i_update += 1\n",
348 | " \n",
349 | " log_probs = []\n",
350 | " values = []\n",
351 | " states = []\n",
352 | " actions = []\n",
353 | " rewards = []\n",
354 | " masks = []\n",
355 | " entropy = 0\n",
356 | "\n",
357 | " for _ in range(num_steps):\n",
358 | " state = torch.FloatTensor(state).to(device)\n",
359 | " dist, value = model(state)\n",
360 | "\n",
361 | " action = dist.sample()\n",
362 | " next_state, reward, done, _ = envs.step(action.cpu().numpy())\n",
363 | " reward = expert_reward(state, action.cpu().numpy())\n",
364 | " \n",
365 | " log_prob = dist.log_prob(action)\n",
366 | " entropy += dist.entropy().mean()\n",
367 | " \n",
368 | " log_probs.append(log_prob)\n",
369 | " values.append(value)\n",
370 | " rewards.append(torch.FloatTensor(reward).to(device))\n",
371 | " masks.append(torch.FloatTensor(1 - done).unsqueeze(1).to(device))\n",
372 | " \n",
373 | " states.append(state)\n",
374 | " actions.append(action)\n",
375 | " \n",
376 | " state = next_state\n",
377 | " frame_idx += 1\n",
378 | " \n",
379 | " if frame_idx % 1000 == 0:\n",
380 | " test_reward = np.mean([test_env() for _ in range(10)])\n",
381 | " test_rewards.append(test_reward)\n",
382 | " plot(frame_idx, test_rewards)\n",
383 | " if test_reward > threshold_reward: early_stop = True\n",
384 | " \n",
385 | "\n",
386 | " next_state = torch.FloatTensor(next_state).to(device)\n",
387 | " _, next_value = model(next_state)\n",
388 | " returns = compute_gae(next_value, rewards, masks, values)\n",
389 | "\n",
390 | " returns = torch.cat(returns).detach()\n",
391 | " log_probs = torch.cat(log_probs).detach()\n",
392 | " values = torch.cat(values).detach()\n",
393 | " states = torch.cat(states)\n",
394 | " actions = torch.cat(actions)\n",
395 | " advantage = returns - values\n",
396 | " \n",
397 | " if i_update % 3 == 0:\n",
398 | " ppo_update(4, mini_batch_size, states, actions, log_probs, returns, advantage)\n",
399 | " \n",
400 | " \n",
401 | " expert_state_action = expert_traj[np.random.randint(0, expert_traj.shape[0], 2 * num_steps * num_envs), :]\n",
402 | " expert_state_action = torch.FloatTensor(expert_state_action).to(device)\n",
403 | " state_action = torch.cat([states, actions], 1)\n",
404 | " fake = discriminator(state_action)\n",
405 | " real = discriminator(expert_state_action)\n",
406 | " optimizer_discrim.zero_grad()\n",
407 | " discrim_loss = discrim_criterion(fake, torch.ones((states.shape[0], 1)).to(device)) + \\\n",
408 | " discrim_criterion(real, torch.zeros((expert_state_action.size(0), 1)).to(device))\n",
409 | " discrim_loss.backward()\n",
410 | " optimizer_discrim.step()"
411 | ]
412 | },
413 | {
414 | "cell_type": "code",
415 | "execution_count": null,
416 | "metadata": {},
417 | "outputs": [],
418 | "source": []
419 | },
420 | {
421 | "cell_type": "code",
422 | "execution_count": null,
423 | "metadata": {},
424 | "outputs": [],
425 | "source": [
426 | "test_env(True)"
427 | ]
428 | }
429 | ],
430 | "metadata": {
431 | "kernelspec": {
432 | "display_name": "Python [conda env:pytorch4]",
433 | "language": "python",
434 | "name": "conda-env-pytorch4-py"
435 | },
436 | "language_info": {
437 | "codemirror_mode": {
438 | "name": "ipython",
439 | "version": 3
440 | },
441 | "file_extension": ".py",
442 | "mimetype": "text/x-python",
443 | "name": "python",
444 | "nbconvert_exporter": "python",
445 | "pygments_lexer": "ipython3",
446 | "version": "3.5.5"
447 | }
448 | },
449 | "nbformat": 4,
450 | "nbformat_minor": 2
451 | }
452 |
--------------------------------------------------------------------------------
/3.ppo.ipynb:
--------------------------------------------------------------------------------
1 | {
2 | "cells": [
3 | {
4 | "cell_type": "code",
5 | "execution_count": 1,
6 | "metadata": {},
7 | "outputs": [],
8 | "source": [
9 | "import math\n",
10 | "import random\n",
11 | "\n",
12 | "import gym\n",
13 | "import numpy as np\n",
14 | "\n",
15 | "import torch\n",
16 | "import torch.nn as nn\n",
17 | "import torch.optim as optim\n",
18 | "import torch.nn.functional as F\n",
19 | "from torch.distributions import Normal"
20 | ]
21 | },
22 | {
23 | "cell_type": "code",
24 | "execution_count": 2,
25 | "metadata": {},
26 | "outputs": [],
27 | "source": [
28 | "from IPython.display import clear_output\n",
29 | "import matplotlib.pyplot as plt\n",
30 | "%matplotlib inline"
31 | ]
32 | },
33 | {
34 | "cell_type": "markdown",
35 | "metadata": {},
36 | "source": [
37 | "Use CUDA "
38 | ]
39 | },
40 | {
41 | "cell_type": "code",
42 | "execution_count": 3,
43 | "metadata": {},
44 | "outputs": [],
45 | "source": [
46 | "use_cuda = torch.cuda.is_available()\n",
47 | "device = torch.device(\"cuda\" if use_cuda else \"cpu\")"
48 | ]
49 | },
50 | {
51 | "cell_type": "markdown",
52 | "metadata": {},
53 | "source": [
54 | "Create Environments "
55 | ]
56 | },
57 | {
58 | "cell_type": "code",
59 | "execution_count": 4,
60 | "metadata": {},
61 | "outputs": [],
62 | "source": [
63 | "from common.multiprocessing_env import SubprocVecEnv\n",
64 | "\n",
65 | "num_envs = 16\n",
66 | "env_name = \"Pendulum-v0\"\n",
67 | "\n",
68 | "def make_env():\n",
69 | " def _thunk():\n",
70 | " env = gym.make(env_name)\n",
71 | " return env\n",
72 | "\n",
73 | " return _thunk\n",
74 | "\n",
75 | "envs = [make_env() for i in range(num_envs)]\n",
76 | "envs = SubprocVecEnv(envs)\n",
77 | "\n",
78 | "env = gym.make(env_name)"
79 | ]
80 | },
81 | {
82 | "cell_type": "markdown",
83 | "metadata": {},
84 | "source": [
85 | "Neural Network "
86 | ]
87 | },
88 | {
89 | "cell_type": "code",
90 | "execution_count": 71,
91 | "metadata": {},
92 | "outputs": [],
93 | "source": [
94 | "def init_weights(m):\n",
95 | " if isinstance(m, nn.Linear):\n",
96 | " nn.init.normal_(m.weight, mean=0., std=0.1)\n",
97 | " nn.init.constant_(m.bias, 0.1)\n",
98 | " \n",
99 | "\n",
100 | "class ActorCritic(nn.Module):\n",
101 | " def __init__(self, num_inputs, num_outputs, hidden_size, std=0.0):\n",
102 | " super(ActorCritic, self).__init__()\n",
103 | " \n",
104 | " self.critic = nn.Sequential(\n",
105 | " nn.Linear(num_inputs, hidden_size),\n",
106 | " nn.ReLU(),\n",
107 | " nn.Linear(hidden_size, 1)\n",
108 | " )\n",
109 | " \n",
110 | " self.actor = nn.Sequential(\n",
111 | " nn.Linear(num_inputs, hidden_size),\n",
112 | " nn.ReLU(),\n",
113 | " nn.Linear(hidden_size, num_outputs),\n",
114 | " )\n",
115 | " self.log_std = nn.Parameter(torch.ones(1, num_outputs) * std)\n",
116 | " \n",
117 | " self.apply(init_weights)\n",
118 | " \n",
119 | " def forward(self, x):\n",
120 | " value = self.critic(x)\n",
121 | " mu = self.actor(x)\n",
122 | " std = self.log_std.exp().expand_as(mu)\n",
123 | " dist = Normal(mu, std)\n",
124 | " return dist, value"
125 | ]
126 | },
127 | {
128 | "cell_type": "code",
129 | "execution_count": 72,
130 | "metadata": {},
131 | "outputs": [],
132 | "source": [
133 | "def plot(frame_idx, rewards):\n",
134 | " clear_output(True)\n",
135 | " plt.figure(figsize=(20,5))\n",
136 | " plt.subplot(131)\n",
137 | " plt.title('frame %s. reward: %s' % (frame_idx, rewards[-1]))\n",
138 | " plt.plot(rewards)\n",
139 | " plt.show()\n",
140 | " \n",
141 | "def test_env(vis=False):\n",
142 | " state = env.reset()\n",
143 | " if vis: env.render()\n",
144 | " done = False\n",
145 | " total_reward = 0\n",
146 | " while not done:\n",
147 | " state = torch.FloatTensor(state).unsqueeze(0).to(device)\n",
148 | " dist, _ = model(state)\n",
149 | " next_state, reward, done, _ = env.step(dist.sample().cpu().numpy()[0])\n",
150 | " state = next_state\n",
151 | " if vis: env.render()\n",
152 | " total_reward += reward\n",
153 | " return total_reward"
154 | ]
155 | },
156 | {
157 | "cell_type": "markdown",
158 | "metadata": {},
159 | "source": [
160 | "GAE "
161 | ]
162 | },
163 | {
164 | "cell_type": "code",
165 | "execution_count": 73,
166 | "metadata": {},
167 | "outputs": [],
168 | "source": [
169 | "def compute_gae(next_value, rewards, masks, values, gamma=0.99, tau=0.95):\n",
170 | " values = values + [next_value]\n",
171 | " gae = 0\n",
172 | " returns = []\n",
173 | " for step in reversed(range(len(rewards))):\n",
174 | " delta = rewards[step] + gamma * values[step + 1] * masks[step] - values[step]\n",
175 | " gae = delta + gamma * tau * masks[step] * gae\n",
176 | " returns.insert(0, gae + values[step])\n",
177 | " return returns"
178 | ]
179 | },
180 | {
181 | "cell_type": "markdown",
182 | "metadata": {},
183 | "source": [
184 | " Proximal Policy Optimization Algorithm \n",
185 | ""
186 | ]
187 | },
188 | {
189 | "cell_type": "code",
190 | "execution_count": 74,
191 | "metadata": {},
192 | "outputs": [],
193 | "source": [
194 | "def ppo_iter(mini_batch_size, states, actions, log_probs, returns, advantage):\n",
195 | " batch_size = states.size(0)\n",
196 | " for _ in range(batch_size // mini_batch_size):\n",
197 | " rand_ids = np.random.randint(0, batch_size, mini_batch_size)\n",
198 | " yield states[rand_ids, :], actions[rand_ids, :], log_probs[rand_ids, :], returns[rand_ids, :], advantage[rand_ids, :]\n",
199 | " \n",
200 | " \n",
201 | "\n",
202 | "def ppo_update(ppo_epochs, mini_batch_size, states, actions, log_probs, returns, advantages, clip_param=0.2):\n",
203 | " for _ in range(ppo_epochs):\n",
204 | " for state, action, old_log_probs, return_, advantage in ppo_iter(mini_batch_size, states, actions, log_probs, returns, advantages):\n",
205 | " dist, value = model(state)\n",
206 | " entropy = dist.entropy().mean()\n",
207 | " new_log_probs = dist.log_prob(action)\n",
208 | "\n",
209 | " ratio = (new_log_probs - old_log_probs).exp()\n",
210 | " surr1 = ratio * advantage\n",
211 | " surr2 = torch.clamp(ratio, 1.0 - clip_param, 1.0 + clip_param) * advantage\n",
212 | "\n",
213 | " actor_loss = - torch.min(surr1, surr2).mean()\n",
214 | " critic_loss = (return_ - value).pow(2).mean()\n",
215 | "\n",
216 | " loss = 0.5 * critic_loss + actor_loss - 0.001 * entropy\n",
217 | "\n",
218 | " optimizer.zero_grad()\n",
219 | " loss.backward()\n",
220 | " optimizer.step()"
221 | ]
222 | },
223 | {
224 | "cell_type": "code",
225 | "execution_count": 82,
226 | "metadata": {},
227 | "outputs": [],
228 | "source": [
229 | "num_inputs = envs.observation_space.shape[0]\n",
230 | "num_outputs = envs.action_space.shape[0]\n",
231 | "\n",
232 | "#Hyper params:\n",
233 | "hidden_size = 256\n",
234 | "lr = 3e-4\n",
235 | "num_steps = 20\n",
236 | "mini_batch_size = 5\n",
237 | "ppo_epochs = 4\n",
238 | "threshold_reward = -200\n",
239 | "\n",
240 | "model = ActorCritic(num_inputs, num_outputs, hidden_size).to(device)\n",
241 | "optimizer = optim.Adam(model.parameters(), lr=lr)"
242 | ]
243 | },
244 | {
245 | "cell_type": "code",
246 | "execution_count": 83,
247 | "metadata": {},
248 | "outputs": [],
249 | "source": [
250 | "max_frames = 15000\n",
251 | "frame_idx = 0\n",
252 | "test_rewards = []"
253 | ]
254 | },
255 | {
256 | "cell_type": "code",
257 | "execution_count": 86,
258 | "metadata": {},
259 | "outputs": [
260 | {
261 | "data": {
262 | "image/png": "iVBORw0KGgoAAAANSUhEUgAAAYIAAAE/CAYAAABLrsQiAAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDIuMi4yLCBodHRwOi8vbWF0cGxvdGxpYi5vcmcvhp/UCwAAIABJREFUeJzt3Xl8FPX9x/HXJydXCPd933IIQrjqLYpCtdrWA2+rglatte1Pq/X3a2vv22ptVVS8BTxbFJBi1VqrnIKEGwTkCoQzhCshyef3xwy6Ro5Aspkk+34+Hnlkd75zfHZ2d94735ndMXdHREQSV1LUBYiISLQUBCIiCU5BICKS4BQEIiIJTkEgIpLgFAQiIglOQVDBzKy7mc03s3wzuz3qeqT8zGyNmZ0ddR0i8aIgqHh3Ae+4e4a7Pxh1MaWZ2QVmttDMdpvZB2bWM6bNzOwXZrbBzPLM7F0z6xXT3sjMJprZNjPbambPm1n9mPYOZvaOme01s6XaeIKZpZnZy2GYuJmdUao93cweMbPNZrbdzF43s9Yx7R3MbIqZ7TCzTWb2kJmlHGZZLc1skpltDJfVoVR7azP7R7ic9WZ2c6l2N7M94Wtjt5k9HtP2UzM7ENO228w6xbSfZWYfmdkuM1tlZmNKzbupmb0Qvq52mNnzpdrPDqffE9Z2aUzbWDNbZmYlZnZdqemuNbO54XLXm9nvYtdP+Jp9LZzvp2Z2RUzbj0o9nn3hMpqE7X8wsxXhh7qlZnZNzLRNzOy/4Xthp5l9aGYnH+p5qRbcXX8V+Ae8Bdx4hPbkCGvrCuwCTgFSgHuAlUBK2H4psBHoBCQDvwY+ipn+b8A/gfpAZvhY/xTT/iHwJ6A28E1gJ9D0OOpMiWj9HHK5wBrg7OOcZxpwR7jOc4AzSrXfBXwMNAdqAc8Ar8a0TwGeCttaANnA7YdZVnPgFmAo4ECHUu3vAH8GUoG+wHbgzJh2B7ocZt4/BZ47TFsqkAfcBBgwENgN9I0Z5z/hayMzHP+kmLaeQC4wInxdNgY6x7TfCgwD5gDXlVr2t4FTw/XcGpgL3B3TPh6YCNQLn4M8oNcRHuPbMffvA3oQfGAeDOwAvhK21QK6h20GXBSuz0heu+V+7UddQE36A94GioH94RuhW/gmfjh8Q+8Bzga+Cswj2CivA34aM48O4RvyW2HbDuDm8M21gGDj+lCp5V4PLAnHnQa0P0x9twGTY+4nAfuAYeH9HwIvxrT3AvbH3J8K3BJz/1ZgWni7G1AAZMS0/we4uYzrbk24/AXhfFKAVsArwBZgNeEGMHwT7gOahPfvBYqA+uH9nwN/Dm+XZV3fAKwF3guHXw18CmwL572G4wyCUo9xPV8OgoeB38Xc/yqwLOb+EmBkzP3fA48eZTkplAoCgg2hExPMwFjg2Zj7xxsEzcNp68QMmw1cHt4eHq7DQ34IAl4Afl6G9fc+pYLgEON8H3g9vF0XKAS6xbQ/C/zmENMZsAq49gjzngT84BDDk4ALwnXQrLyvkyj+1DVUgdz9LIKN323uXs/dl4dNVwC/BDIIXsx7gGuABgRv/G+b2UWlZjeY4BP8ZQSf4u4lCJFewKVmdjqAmV0I/Aj4BtA0XP74I5RppW4b0Du8PwHobGbdzCwVuBZ4M2b8vwLnm1lDM2tI8Kl/atjWC1jl7vkx438cDi+rywnWRwOgBHg9nEdrgk+Ed5jZue6+n2BDc3o43ekEG+6TY+7/O7xdlnV9OnACcG7YVfYwQRi0Ivh02ubgiGZ2ipntPIbHdDRPACebWSszqwNcyefrFILnfpSZ1Qm7jEbwxeekrKzU/4O3e5ca772wC+rV0l1LwAVht9IiM/v2wYHuvpngNfctM0s2s6FAe4LXOsAQYBnwdNiVMvvg6zemHTPLNrMcM3vOzBodx2MEOA1YFN7uBhTFvA/h8K/JU4FmBB88vsTMahN8GFtUavgCgg9+k4DH3T33OOuOVtRJVNP+gHeJ6Roi2CN45ijT/Bm4P7zdgeCTReuY9m3AZTH3XwHuCG9PBW6IaUsC9nKIvQKC3dw9wBkEu9L/R7DBvSdsTwMeCJdfRPApvGPM9K0IuoNKwr/pQFrYdjUwo9Tyfgk8Vcb1tga4Pub+YGBtqXHuAZ4Mb/8ceJDg0+8m4LvAb/h8b6HxMazrTjHtPwYmxNw/+KkyXnsEmQQBfHCdzwMaxbSfQNDdURSO8xRgR1nOl/YIwuHvA38J11F/gq6M2L2P08LXQAPgIWAhn3cb9gyf/2TgKwTdXJfHTHsBsDmsswgYHdM2ls/3vFKBUQR7tgf36ArD578bwZ7LK8Dzh3hcR9wjINgzXh8z31OBTaXGGQ28e4hpnzjSaxV4miCAv7Tuw/V5OUfYm6jqf9ojqBzrYu+Y2eDwoOoWM8sj6PppUmqazTG39x3ifr3wdnvggfCA1U6CN7cRfIr+AndfSvAp/yGCN3ITYDHBmweCjeBAoC3Bi/s+4O3wkyrAi8Bygj2b+sAnwHNh2+5wWKz6QD5lF7ue2gOtDj6u8LH9iKAbAoJP/GcQbNCyCULpdIJPlyvdfRuUeV3HLrdV7H1330MQxEdlZu1iDz6W6REHe1npBHsedYFXCfcIzCyJYOPzatjWBGgI/LaM8y7tSqAjweN7mOC5O/jc4+7vuXuhu+8kCNaOBEGEuy92943uXuzuHxB8YLg4rLMHQZhdQxAkvYC7zOyr4az3AWvc/Ql3P+DuE8IaTo5pf9Ldl7v7buBXwMhjeWDhXt6vgRHuvjUcXKbXZPj6voRgY3+oef+eYM/pUg+3/LHcfb+7jwfuNrO+x1J3VaEgqBylXzwvEOxKtnX3TOARvrjLfizWATe5e4OYv9rhm/XLhbi/7O693b0x8BOCT8Wzw+Z+wER3X+/uRe7+FMGGp2dM+6Puvid8wz7C52/YRUAnM8uIWVxfSu1KH0XseloHrC71uDLc/eDyPiA4WPd14N/uvhhoF9bz75j5lGVdxy43hyAIgc82Eo3LVLz7Wg+6BOu5e72jTwEE6/Qpd9/u7gUEn9gHhWeuNAof00PuXhCG25Mc40Yypr5P3f18d2/q7oMJgmXWkSbh8K/L2LbewHJ3n+buJe6+DJhM0I0FwXGf0u+B2Pul27+0sT0SMzsPeAy4wN2zY5qWAylm1jVm2KFek18n+AD17iHmfR/B4xju7ruOUkoqwYkW1Y6CIBoZwHZ3329mgwiOIRyvR4B7LDzN08wyzeySw41sZgPCftymBLvsk8I9BQgC4RIza25mSWZ2NcGLe2VM+41mVjvsMx1D8CbGg37Y+cBPzKyWmX0dOJHD9LmWwSwg38x+GC4v2cx6m9nAcHl7CbpMbuXzDf8HBJ/4Y4PgWNf1ywTHQU4xszTgZ5TzfWLBKaK1wrtp4fo5uBGdDVwTPm+pBGf9bHT3reEn29UExzVSzKwBwR7dgiMsqxbBHgZA7HIxsxPMLMOCU1qvIjiI+6ewrZeZ9QvXcz3gj8AGgoPVmNmF4bEhC9fj7cA/wlnPA7pacAqpmVln4PyYOl8DGlpwqmeymV1McNzlv2H7kwTHFzqFwXs38EZM3Wnh4zAgNVx/SWHbWcDzwDfd/QuhFu7NvQr8zMzqWnB654UEB4xjXUvQffuFADKzewheL2cf3MOMaRty8DUSvj5/SLC3OvMQT0vVF3XfVE3749DHCH5RapyLCQ5u5hO84B8iPCODz/utU2LG/0LfMsEu/f/G3L+aoHvk4Jkx445Q3/vhcrcDjwJ1Y9pqEXRV5ITz+gg4L6a9I8EB3G3h9G8CXWPaO4SPfx/BwcGzY9quBBYdoa41lOqHJ+imGU9wDGAHMKPUPH8dLis9vH9buO6aH++6DodfS3AW0ZfOGiLod959jK+JNeFyYv86hG2NCTZkuQT95u8Dg2Km7Reu0x3AVoLuudjHtxs4NeZ+6eV4TNsdBGdg7QmXkxXTdlb4nO0Ja/l7qed2fLg+dgNLKXUKK8GpxwvD9byeoPsqKab9VILX6G6C00BPLTX9fWFtWwg21A1LvadKP64zwrZ3CI5J7I75mxozbaPwsewJn9MrSi23dTj9l86WCpdTUGrePwrbTic48HzwvfRv4LSotz/H+2fhgxIRkQSlriERkQSnIBARSXAKAhGRBKcgEBFJcAoCEZEEd8ifs61OmjRp4h06dIi6DBGRKmfu3Llb3b3p0car9kHQoUMH5syZE3UZIiJVjpl9Wpbx1DUkIpLgFAQiIglOQSAikuAUBCIiCU5BICKS4BQEIiIJTkEgIpLgFAQiIglOQSAikuCq/TeLRUTKy9354JNt7CssplvzDNo0rE1S0vFeRrz6URCISEJbvHEXP3tjETNWbf9sWO3UZLo0q0fX5vXo2iyDbs3r0a15Bq0b1MyAUBCISELatruAP05fzoRZa8msncrPL+xFz1aZrNicz/LNu1mRm89/V27l1Y82fDZNnbQwIJpl0LV5PbqFQVHdA0JBICIJpbCohGc+XMMD/1rBvsJirv1KB+4Y1o3MOqkADGjf8Avj5+07wMrcIByWb85nxebd/GfFFl75aP1n49RJS6Zrs3p0bZ7xWTh0bV6P1g1qY1b1A0JBICIJ452lufz8jcWs2rqH07s15f/O70mXZvWOOE1m7VQGtG/EgPaNvjA8b+8BlucGwbB8cz4rcvP59/ItvDz384Com5ZMl+YZdGsWdC11CbuYWmXWqlIBoSAQkRpvZW4+P39jCf9evoVOTevy5HUDObNHs3LNM7NOKgM7NGJghy8GxM69hZ/tPazMDf6/s2wLL8UERL30FLo0q/fZsYeuzTPo2qweLSMKCHP3Sl9oRcrKynJdj0BEDiVv7wHuf2s5z874lDppyXx3WFeuGdqBtJTKP3N+x55Clm/OZ3nublaEXUwrcvPZurvws3Ey0lOCvYbPjkEE/1vUP76AMLO57p511PHiFQRm9nvgAqAQ+AT4lrvvDNvuAW4AioHb3X1aOPw84AEgGXjc3X9ztOUoCESktKLiEsbPWsufpi8nb98BLh/Uju+f043G9dKjLu1LtocBEXuQesXm3WzbEwREo7ppfPR/5xzXvMsaBPHsGpoO3OPuRWb2W+Ae4Idm1hMYBfQCWgFvmVm3cJq/AucA64HZZjbJ3RfHsUYRqWHeX7GVn7+xmGWb8xnaqTE/vqAnJ7SsH3VZh9WobhpDOjVmSKfGXxi+bXcByzfvJm9f4WGmrDhxCwJ3/2fM3RnAxeHtC4EJ7l4ArDazlcCgsG2lu68CMLMJ4bgKAhE5qjVb9/DLKUuYvngz7RrV4ZGrBnBur+ZV6qDssWhcL52hlbQHU1kHi68HJoa3WxMEw0Hrw2EA60oNH3yomZnZGGAMQLt27Sq0UBGpXvL3H+Cht1cy7r+rSUtO4q7zunP9yR2plZocdWnVRrmCwMzeAlocouled/9HOM69QBHwfHmWFcvdxwJjIThGUFHzFZHqo7jEeXnuOn4/bRnb9hRycf823Hlud5rVrxV1adVOuYLA3c8+UruZXQecDwzzz49KbwDaxozWJhzGEYaLiHxm1urt3Pf6IhZt3EVW+4aMu24gJ7ZpEHVZ1VbcuobCM4DuAk53970xTZOAF8zsTwQHi7sCswADuppZR4IAGAVcEa/6RKT6Wb9jL7+eupTJC3JolVmLBy8/iQtObFltjwNUFfE8RvAQkA5MD5+kGe5+s7svMrMXCQ4CFwG3unsxgJndBkwjOH10nLsvimN9IlJN7C0s4uF3P2Hse6swg++d3Y0xp3WidpqOA1QEfaFMRKqskhLnHx9v4DdTl7J5VwEX9mvFD8/rQasGtaMurVqoCt8jEBE5bvPW7uC+1xczf91OTmyTyd+u7P+l3/uRiqEgEJEqZVPefn775lJem7eBphnp/OGSvnzjpNbV+meeqzoFgYhUCfsPFPPYe6v427ufUOzOLWd05pYzu1AvXZupeNMaFpFIuTtTsjfxqylL2LBzHyN6t+BHI0+gbaM6UZeWMBQEIhKZhRvy+Nnri5m1Zjs9WmQwfvQQhnZufPQJpUIpCESk0m3JL+AP05bx4tx1NKyTxq++3ofLBrYlWccBIqEgEJFKtX7HXkY+8B/2FhZzw8kd+c6wrmTWTo26rISmIBCRSvX3eRvYtb+IKbefSs9WVffnoRNJ5V+mR0QS2pTsTfRv10AhUIUoCESk0qzZuofFObsY2adl1KVIDAWBiFSaKQtzABihIKhSFAQiUmmmZOfQr20DWuu3gqoUBYGIVIq12/aycMMuRvY51LWsJEoKAhGpFJ91C/VWt1BVoyAQkUoxJTuHE9tk6qcjqiAFgYjE3brte1mwPk9nC1VRCgIRibupYbfQSHULVUkKAhGJuynZm+jduj7tGqtbqCpSEIhIXG3YuY/563aqW6gKUxCISFxNzVa3UFWnIBCRuJqSnUPPlvXp0KRu1KXIYSgIRCRuNu7cx0drd+pLZFWcgkBE4ubNhZsAdHygilMQiEjcTMnOoUeLDDo1rRd1KXIECgIRiYtNefuZ8+kO7Q1UAwoCEYmLNw9+iUxBUOUpCEQkLqYs3ES35vXo0kzdQlWdgkBEKlzurv3MXrNdewPVhIJARCrcm4s24a5uoepCQSAiFW5Kdg5dmtWjW/OMqEuRMlAQiEiF2pJfwKzV2xnZW18iqy4UBCJSoaYt2kSJw8gT1S1UXSgIRKRCTcnOoVPTunRXt1C1oSAQkQqzbXcBM1ZtY2TvlphZ1OVIGSkIRKTCTFu0OegW0tlC1YqCQEQqzJTsHDo0rsMJLdUtVJ0oCESkQmzfU8iHq7Yxso+6haobBYGIVIh/LtpEcYmrW6gaUhCISIWYsnAT7RrVoVer+lGXIsco7kFgZj8wMzezJuF9M7MHzWylmS0ws/4x415rZivCv2vjXZuIVIydewv5YOVWdQtVUynxnLmZtQWGA2tjBo8AuoZ/g4GHgcFm1gj4CZAFODDXzCa5+4541igi5ffPxZspKnFdkrKaivcewf3AXQQb9oMuBJ7xwAyggZm1BM4Fprv79nDjPx04L871iUgFmJKdQ5uGtenTOjPqUuQ4xC0IzOxCYIO7f1yqqTWwLub++nDY4YYfat5jzGyOmc3ZsmVLBVYtIscqb+8B/qtuoWqtXF1DZvYWcKh9wXuBHxF0C1U4dx8LjAXIysryo4wuInE0fclmDhTrbKHqrFxB4O5nH2q4mfUBOgIfh58Q2gAfmdkgYAPQNmb0NuGwDcAZpYa/W576RCT+pmTn0LpBbfq2UbdQdRWXriF3z3b3Zu7ewd07EHTz9Hf3TcAk4Jrw7KEhQJ675wDTgOFm1tDMGhLsTUyLR30iUjF27T/Af1ZsYUTvFuoWqsbietbQYUwBRgIrgb3AtwDcfbuZ/RyYHY73M3ffHkF9IlJGby0Ou4X0k9PVWqUEQbhXcPC2A7ceZrxxwLjKqElEym9K9iZaZtaiX5sGUZci5aBvFovIccnff4D3VmxhRO+WJCWpW6g6UxCIyHF5e2kuhUUl+hJZDaAgEJHjMnlBDs3rp9O/XcOoS5FyUhCIyDHbXVDEu8vVLVRTKAhE5Jh93i2ks4VqAgWBiByzKQtyaJqRzoD26haqCRQEInJM9hQU8c6yXEb0bkGyuoVqBAWBiByTd5blUqBuoRpFQSAix2Rq9iaa1EtnYIdGUZciFURBICJltq+wmLeX5nJe7+bqFqpBFAQiUmbvLMtl34FiRvZWt1BNoiAQkTKbkp1D47ppDOqobqGaREEgImWy/0DQLTS8VwtSkrXpqEn0bIpImby7bAt7C4v5qs4WqnEUBCJSJlOyc2hYJ5UhndQtVNMoCETkqPYfKOZfSzZzrrqFaiQ9oyJyVO8t38KewmJ9iayGUhCIyFFNXbiJBnVSGdq5cdSlSBwoCETkiAqKinlr8WaG92xOqrqFaiQ9qyJyRP9ZvpX8giJGqFuoxlIQiMgRTVmYQ/1aKZzcuUnUpUicKAhE5LAKioqZvngzw3u1IC1Fm4uaSs+siBzWByu3kb+/SBeor+EUBCJyWJOzc8iolcLJXdQtVJMpCETkkAqLSvjnok2cc0Jz0lOSoy5H4khBICKH9MEnW9m1v0hfIksACgIROaQp2TnUS0/hlK7qFqrpFAQi8iUHikv45+LNnH1CM2qlqluoplMQiMiXfPjJNnbuPaBuoQShIBCRL5m6MIe6acmc1q1p1KVIJVAQiMgXFBWXMG3RZoad0FzdQglCQSAiXzBz9Xa27ynUl8gSiIJARL5gcnYOddKSOaN7s6hLkUqiIBCRzxQVlzBt4SbO7KGzhRKJgkBEPjNrzXa27SnUBeoTjIJARD4zJTuHWqlJnNFdZwslEgWBiABQXOK8uXAzZ/VoRp20lKjLkUqkIBARAGav2c7W3QX6ElkCUhCICABTs3NIT0niTJ0tlHDiGgRm9h0zW2pmi8zsdzHD7zGzlWa2zMzOjRl+XjhspZndHc/aRORzJSXO1IWbOLN7M+qmq1so0cTtGTezM4ELgb7uXmBmzcLhPYFRQC+gFfCWmXULJ/srcA6wHphtZpPcfXG8ahSRwNy1O8jNL2CEvkSWkOIZ/d8GfuPuBQDunhsOvxCYEA5fbWYrgUFh20p3XwVgZhPCcRUEInE2eUEOaSlJDDuhedSlSATi2TXUDTjVzGaa2b/NbGA4vDWwLma89eGwww3/EjMbY2ZzzGzOli1b4lC6SOIIuoVyOL1bU+qpWyghletZN7O3gEPtS94bzrsRMAQYCLxoZp3Ks7yD3H0sMBYgKyvLK2KeIolq3rodbN5VoC+RJbByBYG7n324NjP7NvCquzswy8xKgCbABqBtzKhtwmEcYbiIxMnkBZtIS05i2Ak6WyhRxbNr6O/AmQDhweA0YCswCRhlZulm1hHoCswCZgNdzayjmaURHFCeFMf6RBLewW6h07o1IaNWatTlSETi2SE4DhhnZguBQuDacO9gkZm9SHAQuAi41d2LAczsNmAakAyMc/dFcaxPJOHNX7+TnLz93Hlu96hLkQjFLQjcvRC46jBtvwR+eYjhU4Ap8apJRL5oanYOqcmms4USnL5ZLJKg3J0p2Zs4tWtTMmurWyiRKQhEEtTH6/PYsHMfI3rrS2SJTkEgkqAOdgsN76kgSHQKApEE5O5Mzs7h5C5NyKyjbqFEpyAQSUALN+xi/Y59jOytL5GJgkAkIU3OziElyRjeS2cLiYJAJOG4B18iG9q5MQ3qpEVdjlQBCgKRBLNo4y4+3bZXvy0kn1EQiCSYKdk5JCcZw3vpbCEJKAhEEkjwJbIchnZqTKO66haSgIJAJIEsyclnzba9ukC9fIGCQCSBTF2YQ5Khs4XkCxQEIgni4JfIhnRqTJN66VGXI1WIgkAkQSzfvJtVW/YwQt1CUoqCQCRBTM7OwQzO09lCUoqCQCRBTM3OYVCHRjTNULeQfJGCQCQBrNicz4rc3Xz1RHULyZcpCEQSgLqF5EgUBCIJYGr2Jga2b0Sz+rWiLkWqIAWBSA23Mnc3yzbnM7KP9gbk0BQEIjXc1OwcAM7TtQfkMBQEIjXc5Owcsto3pEWmuoXk0BQEIjXYqi27WbopX18ikyNSEIjUUCUlzkNvrwRgRG8dH5DDUxCI1EDFJc5dryzg1Xkb+M5ZXWjVoHbUJUkVlhJ1ASJSsYqKS/iflz7m7/M38t1hXbnj7K5RlyRVnIJApAY5UFzC9ybO540FOfzP8G7cdpZCQI5OQSBSQxQWlXD7+Hm8uWgT94zowU2nd466JKkmFAQiNUBBUTG3Pv8Rby3J5cfn9+T6UzpGXZJUIwoCkWpu/4Fibnp2Lv9evoWfX9Sbq4e0j7okqWYUBCLV2L7CYkY/M4f/frKV336zD5cNbBd1SVINKQhEqqk9BUXc8PRsZq3ezh8u7ss3B7SJuiSpphQEItVQ/v4DfOvJ2cxbt5P7L+vHhf1aR12SVGMKApFqJm/fAa4dN4uFG/J4cNRJutiMlJuCQKQa2bm3kKufmMXSTbv465X9OVcXmpEKoCAQqSa27ynkysdn8knubh69egBn9WgedUlSQygIRKqBLfkFXPX4TNZs28Pj12ZxWremUZckNYiCQKSKy921n8sfm8HGnft58rqBfKVLk6hLkhpGQSBSheXk7eOKx2aSu2s/T18/iEEdG0VdktRAcfsZajPrZ2YzzGy+mc0xs0HhcDOzB81spZktMLP+MdNca2Yrwr9r41WbSHWwfsdeLnt0BlvzC3jmBoWAxE889wh+B9zn7lPNbGR4/wxgBNA1/BsMPAwMNrNGwE+ALMCBuWY2yd13xLFGkSpp7ba9XP7YDPL3H+DZGwfTr22DqEuSGiyeF6ZxoH54OxPYGN6+EHjGAzOABmbWEjgXmO7u28ON/3TgvDjWJ1Ilrd66h0sf/ZA9hUW8MHqIQkDiLp57BHcA08zsDwSB85VweGtgXcx468Nhhxv+JWY2BhgD0K6dfltFao6Vuflc8dhMikqc8aOHcELL+kefSKScyhUEZvYWcKhvtNwLDAO+5+6vmNmlwBPA2eVZ3kHuPhYYC5CVleUVMU+RqC3blM+Vj88AjAljhtCteUbUJUmCKFcQuPthN+xm9gzw3fDuS8Dj4e0NQNuYUduEwzYQHEOIHf5ueeoTqS4WbczjqsdnkpaSxAujh9C5ab2oS5IEEs9jBBuB08PbZwErwtuTgGvCs4eGAHnungNMA4abWUMzawgMD4eJ1GjZ6/O44rGZ1E5NZuKYoQoBqXTxPEYwGnjAzFKA/YR9+sAUYCSwEtgLfAvA3beb2c+B2eF4P3P37XGsTyRy89bu4Jpxs8isncr40UNo26hO1CVJAopbELj7+8CAQwx34NbDTDMOGBevmkSqkjlrtnPdk7NpXC+NF0YPoXWD2lGXJAkqnl1DInIYH36yjWvGzaJZRjoTxwxVCEikFAQilez9FVv51lOzaN2gNhNuGkKLzFpRlyQJTr81JFKJ3l2Wy5hn59KpSV2eu3EwTeqlR12SiIJApLK8tXgztzz/EV2b1+O5GwbTsG5a1CWJAOoaEqkUby7M4ebn5nJCywxeuHGIQkCqFO0RiMTZ6x9v5I6J8+nbJpOnrh9E/VqpUZdfop2xAAAVnklEQVQk8gUKApE4em3een7w4sdktW/EuG8NpF663nJS9ehVKRInL81Zx12vLGBIx8Y8cV0WddL0dpOqSccIROLghZlrufPlBZzSpQnjrhuoEJAqTa9OkQr2zIdr+PE/FnFm96Y8fNUAaqUmR12SyBEpCEQq0OP/WcUvJi/hnJ7NeeiKk0hPUQhI1acgEKkgB0NgZJ8WPDDqJFKT1fMq1YOCQKQCzFy1jV9NCULgwVEnkaIQkGpEr1aRctq5t5A7Js6nfeO6/P7ivgoBqXa0RyBSDu7O3a9ks3V3Aa9++2Tq6nsCUg3po4tIOUyYvY43F23iznO706dNZtTliBwXBYHIcVqZm899ry/i1K5NuPGUTlGXI3LcFAQix6GgqJjvjJ9PnbQU/nhJX5KSLOqSRI6bOjRFjsNvpy5jSc4uxl2XRbP6urCMVG/aIxA5Ru8sy2Xcf1dz3Vc6cFaP5lGXI1JuCgKRY7Alv4A7X/qYHi0yuHtEj6jLEakQ6hoSKaOSEucHL31M/v4ixo8eot8QkhpDewQiZTTuv6t5b/kW/u/8nnRtnhF1OSIVRkEgUgYLN+Tx2zeXMrxnc64c3C7qckQqlIJA5Cj2FhZx+4R5NK6bzm+/eSJmOlVUahYdIxA5ip+9vpjVW/fw/I2DddF5qZG0RyBH5e5RlxCZKdk5TJi9jlvO6MxXOjeJuhyRuNAegRzSvsJiJmfnMHH2WpZtymfsNVkM6dQ46rIq1Yad+7j7lQX0a9uAO87uFnU5InGjIJAvWLghj/Gz1jJp/kbyC4ro2KQujeqmcd2Ts3jsmixO7do06hIrRXGJc8eEeZQ4PKiLzEgNpyAQ8vYdYNL8DUyYvY5FG3eRnpLEV/u05LKBbRnUsRHb9hRy1eMzueHpOTxyVf+E+DbtQ2+vZPaaHfz5sn60a1wn6nJE4kpBkKDcnVmrtzNx9jomZ+dQUFTCCS3r87MLe3Fh39Zk1kn9bNwm9dIZP3oI14ybxU3PzuUvl/fnvN4tIqw+vuas2c4D/1rO109qzUUntY66HJG4s+p+IDArK8vnzJkTdRnVxpb8Al75aD0vzl7Hqq17yEhP4Wv9WjFqYDt6t65/xFMj8/Yd4LonZ7FgfR73X9aPr/VtVYmVV468fQcY+cB/SE4yJt9+Chm1Uo8+kUgVZWZz3T3raONpjyABFJc47y3fwoTZa/nXklyKSpyBHRpyy5ldGNmnBXXSyvYyyKydyrM3DOb6J2dzx4R5FBaVcPGANnGuvvK4O/e+ls3mXft56eahCgFJGAqCGmzd9r28NGcdL81dT07efhrXTeP6UzpyaVZbujSrd1zzrJeewlPXD2T0M3O48+WPKSwq4Yoa8k3bl+au540FOdx5bndOatcw6nJEKo2CoIYpKCrmrcW5TJi9lvdXbgXgtK5N+fH5PRl2QnPSUsp/9kudtBSeuHYg335uLj96LZvComKuO7ljuecbpVVbdvPTSYsY2qkxN5/eOepyRCqVgqCGWLE5n4mz1/HqvA1s31NIq8xafHdYVy7JakvrBrUrfHm1UpN55OoBfOeFefz09cUUFpcw5rTquQEtLCrhuxPmk5aSxP2X9SNZVxuTBKMgqMb2FhbxxoIcJs5ex9xPd5CSZAzv1ZzLBrbjlC5N4r5BS09J5q9X9ueOifP51ZSlFBwo4TvDusZ1mfHwh38uI3tDHmOvHkCLTF1tTBKPgqCacXcWrM9jwux1vP7xRnYXFNGpaV1+NLIH3+jfhib10iu1ntTkJB64rB/pyUn8cfpyCopK+MHwbtXmh9n+s2ILY99bxVVD2jG8V809JVbkSBQE1UTe3gP8PfzS15KcXdRKTeKrfVoxalBbsto3jHTDm5KcxO8v6UtaShIPvbOSwuIS7hnRo8qHwbbdBXz/xY/p2qwe947sGXU5IpEpVxCY2SXAT4ETgEHuPiem7R7gBqAYuN3dp4XDzwMeAJKBx939N+HwjsAEoDEwF7ja3QvLU1915+7MWLWdibPXMmXhJgqLSujTOpNfXNSbr/VrRf0qdHpjcpLxq6/3IS0libHvraLgQDE/uaAXSVW0v93dufPlBeTtO8CzNwyidpquNiaJq7x7BAuBbwCPxg40s57AKKAX0Ap4y8wO/mrXX4FzgPXAbDOb5O6Lgd8C97v7BDN7hCBEHi5nfdVS7q79vBx+6WvNtr1k1Eph1MC2XJrVlt6tM6Mu77CSkoz7vtaLtOQkHn9/NYXFJfzyoj5VMgye/mANby/N5b6v9aJHi/pRlyMSqXIFgbsvAQ7VBXAhMMHdC4DVZrYSGBS2rXT3VeF0E4ALzWwJcBZwRTjO0wR7GgkVBAvW7+Qvb6/k7aW5FJc4gzo24vZhXRnRu2W1+cRqZtz71RNIT03ir+98QkFRCb/75omkVKEfbVuSs4tfTV3KsB7NuGZo+6jLEYlcvI4RtAZmxNxfHw4DWFdq+GCC7qCd7l50iPG/xMzGAGMA2rWrGV9mWrVlN1c+PpO05CRuPLUjl2W1pVPT4/vSV9TMjDvP7UGtlGT+OH05hUUl3H9ZvyrxC577Cou5ffw8Mmun8ruLdbUxEShDEJjZW8ChTqe4193/UfElHZ27jwXGQvBbQ1HUUJHy9x9g9DNzSE1O4h+3nUybhjXj1y6/M6wraSlJ/HrqUgqLSvjLFSeRnhLtns0vJi9mRe5unr1hEI0r+QwrkarqqEHg7mcfx3w3AG1j7rcJh3GY4duABmaWEu4VxI5fo5WUON+bOJ812/by3A2Da0wIHHTT6Z1JT0nip68v5uZn5/LwVQOolRpNGLy5cBPPz1zLTad1SpjrKoiURbz21ScBo8wsPTwbqCswC5gNdDWzjmaWRnBAeZIHP4H6DnBxOP21QCR7G5Xt/reW89aSXH58fk+Gdq6ZVwC77uSO/OrrfXh3+RZufHoO+wqLK72GnLx93P3qAvq0zuQHw7tX+vJFqrJyBYGZfd3M1gNDgclmNg3A3RcBLwKLgTeBW929OPy0fxswDVgCvBiOC/BD4PvhgeXGwBPlqa06mJqdw1/eXsmlWW1q/EHLKwa34/cX9+WDT7Zy7ZOz2F1QdPSJKkhxuNdVWFTCg5efVCG/tyRSk+h6BBFZumkX3/jbB3RvkcGEMUMi7zuvLP+Yv4Hvv/gxfdtk8tT1gyrluxB/fWclv5+2jN9ffCKXZLU9+gQiNURZr0egj0YR2Lm3kNHPzKFeegqPXDUgYUIA4MJ+rfnrFSeRvSGPqx6fyc698f3O4Ly1O/jT9OVc0LdVjbp2gkhFUhBUsqLiEm57YR6b8wp45OoBNK+feD9ydl7vljxy1QCW5uRz+WMz2ba7IC7Lyd9/gNsnzKNF/Vr84qLeOlVU5DAUBJXsN1OX8v7Krfziot70T+CLnww7oTmPX5vF6q27GTV2Brn5+yt8Gf/394Vs3LmfBy/vR2btqvNzHCJVjYKgEr360Xoef3811w5tz6UD1Vd9WremPHndIDbs3MeoR2eQk7evwub92rz1/H3+Rr47rCsD2jeqsPmK1EQKgkqyYP1O7n41myGdGvG/5+uXLg8a2rkxz94wiC35BVz66Ies27633PP8dNse/ve1hQzq0Ihbz+xSAVWK1GwKgkqwJb+Am56dS9N66fz1iv5V4qcWqpIB7Rvx3I2Dydt7gMse/ZA1W/cc97wOFJdw+4T5JCcZ94/S1cZEykJbpDgrLCrh28/NZcfeQsZeM0A/a3AYfds2YPyYIew7UMylj37IytzdxzWf+6cv5+N1O/nNN0+MyyU6RWoiBUGc/fT1Rcz5dAe/v7gvvVpV3Z+Qrgp6tcpkwpihlDiMGvshSzftOqbpP1i5lYf//QmjBrZlZJ+WcapSpOZREMTR8zM/5YWZa7n59M5c0LdV1OVUC91bZDDxpiEkJxmjxs5g4Ya8Mk23Y08h33txPh2b1OXHF+gYjMixUBDEyew12/nJPxZxRvem3HmuftvmWHRuWo8XbxpK3bQUrnhsBvPW7jji+O7OXa8sYMeeAzw46iTqpOkKrCLHQkEQBxt37uPbz82lbaM6PDDqJB2wPA7tG9dl4k1DaFg3jaufmMXsNdsPO+5zM9cyffFm7jqve5W+gptIVaUgqGD7DxRz07Nz2X+ghMeuGaAvMpVDm4Z1mDhmKM3qp3PNE7P4YOXWL42zfHM+v3hjMad3a8r1J3eMoEqR6k9BUIHcnR+9mk32hjzuv6wfXZplRF1StdcisxYTxwylXaM6fOup2fx7+ZbP2vYfCK42llErhT9c0rdKXhtZpDpQEFSgJ95fzavzNvD9c7pxTs/mUZdTYzTNSGf8mCF0blqP0U/PYfrizQD8esoSlm7K5w+X9KVphk7LFTleCoIK8v6KrfxqyhLO69WC2/Rt1grXqG4a40cP4YSWGXz7ubnc9/oinv7wU244pSNndG8WdXki1ZqCoAKs3baX28Z/RNdmGfzxUnVRxEtmnVSeu3Ew/do24Mn/rqFny/rcdZ7OyBIpL51nV057CooY/cwc3GHsNQOom65VGk8ZtVJ5+vpBPPreKi7u3yahruUgEi/aapWDu/M/L33Mitx8nr5+EO0b1426pIRQNz2F75/TLeoyRGoMdQ2Vw0Nvr2Tqwk3cM+IETu3aNOpyRESOi4LgOL21eDN/nL6cr5/UmhtP1fnrIlJ9KQiOw8rcfO6YOJ8+rTP59Tf66BKIIlKtKQiOUd6+A4x+Zi61UpN49OoB1ErVwUoRqd50sPgYFJc4350wj3Xb9/LC6CG00u/di0gNoCA4Bn/85zLeXbaFX1zUm0EddR1cEakZ1DVURm8s2Mjf3v2Eywe146oh7aMuR0SkwigIymDxxl3c+dICsto35L6v9Yq6HBGRCqUgOIrtewoZ/cwcMmun8rer+pOWolUmIjWLjhEcwYHiEm59/iO27C7g5ZuH0iyjVtQliYhUOH28PYJfTl7Ch6u28Ztv9OHENg2iLkdEJC4UBIfx4px1PPXBGm44pSPf6N8m6nJEROJGQXAI89bu4H9fW8gpXZpwz4geUZcjIhJXCoJScnft5+bn5tI8M52/XH4SKclaRSJSs+lgcYyComJuem4u+fuLePWWr9CwblrUJYmIxJ2CIOTu/Pjvi5i3dicPX9mfHi3qR12SiEilUL9H6LkZnzJxzjpuO7MLI/q0jLocEZFKoyAAZq7axn2vL2ZYj2a68pWIJJyED4INO/dxy/Mf0a5xHe4f1U8XnheRhJPQQbCvsJgxz8yhsKiEx67Jon6t1KhLEhGpdAl7sNjd+eErC1ics4tx1w6kc9N6UZckIhKJcu0RmNklZrbIzErMLCtm+DlmNtfMssP/Z8W0DQiHrzSzBy28zqOZNTKz6Wa2IvzfsDy1Hc3Y91Yx6eON/M/w7pzZo1k8FyUiUqWVt2toIfAN4L1Sw7cCF7h7H+Ba4NmYtoeB0UDX8O+8cPjdwL/cvSvwr/B+XGzetZ8/Tl/OV09syS1ndI7XYkREqoVydQ25+xLgSxdvd/d5MXcXAbXNLB1oBNR39xnhdM8AFwFTgQuBM8JpngbeBX5YnvoOp3n9WkwcM4TuLTJ04XkRSXiVcbD4m8BH7l4AtAbWx7StD4cBNHf3nPD2JqD54WZoZmPMbI6ZzdmyZctxFXVSu4bUSUvYQyQiIp856pbQzN4CWhyi6V53/8dRpu0F/BYYfixFububmR+hfSwwFiArK+uw44mIyNEdNQjc/ezjmbGZtQFeA65x90/CwRuA2N90bhMOA9hsZi3dPcfMWgK5x7NcERE5NnHpGjKzBsBk4G53/+/B4WHXzy4zGxKeLXQNcHCvYhLBgWXC/0fc2xARkYpR3tNHv25m64GhwGQzmxY23QZ0AX5sZvPDv4PnaN4CPA6sBD4hOFAM8BvgHDNbAZwd3hcRkTgz9+rdxZ6VleVz5syJugwRkSrHzOa6e9bRxkvon5gQEREFgYhIwlMQiIgkOAWBiEiCUxCIiCS4an/WkJltAT49zsmbEPxAXlWimsquKtalmsquKtZV02pq7+5NjzZStQ+C8jCzOWU5taoyqaayq4p1qaayq4p1JWpN6hoSEUlwCgIRkQSX6EEwNuoCDkE1lV1VrEs1lV1VrCsha0roYwQiIqI9AhGRhJeQQWBm55nZMjNbaWZxuzbysTCzcWaWa2YLo67lIDNra2bvmNliM1tkZt+tAjXVMrNZZvZxWNN9Udd0kJklm9k8M3sj6loOMrM1ZpYd/gJwlfh1RjNrYGYvm9lSM1tiZkMjrqd7zK8kzzezXWZ2R5Q1HWRm3wtf5wvNbLyZ1YrLchKta8jMkoHlwDkEl8qcDVzu7osjrus0YDfwjLv3jrKWg8ILBLV094/MLAOYC1wU5boKr2NR1913m1kq8D7w3YPXwY6SmX0fyCK4Lvf5UdcDQRAAWe5eZc6NN7Ongf+4++NmlgbUcfedUdcFn20fNgCD3f14v59UUbW0Jnh993T3fWb2IjDF3Z+q6GUl4h7BIGClu69y90JgAnBhxDXh7u8B26OuI5a757j7R+HtfGAJn19jOqqa3N13h3dTw7/IP82EV+T7KsG1NuQwzCwTOA14AsDdC6tKCISGAZ9EHQIxUoDaZpYC1AE2xmMhiRgErYF1MffXE/HGrTowsw7AScDMaCv5rAtmPsHlTKe7e+Q1AX8G7gJKoi6kFAf+aWZzzWxM1MUAHYEtwJNhN9rjZlY36qJijALGR10EgLtvAP4ArAVygDx3/2c8lpWIQSDHyMzqAa8Ad7j7rqjrcfdid+9HcM3rQWYWaVeamZ0P5Lr73CjrOIxT3L0/MAK4NeyCjFIK0B942N1PAvYAVeU4XRrwNeClqGsBMLOGBL0VHYFWQF0zuyoey0rEINgAtI253yYcJocQ9sO/Ajzv7q9GXU+ssEvhHeC8iEs5Gfha2B8/ATjLzJ6LtqRA+KkSd88FXiPoGo3SemB9zF7cywTBUBWMAD5y981RFxI6G1jt7lvc/QDwKvCVeCwoEYNgNtDVzDqGnwBGAZMirqlKCg/MPgEscfc/RV0PgJk1NbMG4e3aBAf9l0ZZk7vf4+5t3L0DwevpbXePyye3Y2FmdcOD/ITdL8OBSM9Kc/dNwDoz6x4OGgZEeqJGjMupIt1CobXAEDOrE74XhxEcp6twKfGYaVXm7kVmdhswDUgGxrn7oojLwszGA2cATcxsPfATd38i2qo4GbgayA775AF+5O5TIqypJfB0eHZHEvCiu1eZ0zWrmObAa8E2hBTgBXd/M9qSAPgO8Hz4QWwV8K2I6zkYlOcAN0Vdy0HuPtPMXgY+AoqAecTpW8YJd/qoiIh8USJ2DYmISAwFgYhIglMQiIgkOAWBiEiCUxCIiCQ4BYGISIJTEIiIJDgFgYhIgvt//nuSY9dkQ+4AAAAASUVORK5CYII=\n",
263 | "text/plain": [
264 | ""
265 | ]
266 | },
267 | "metadata": {},
268 | "output_type": "display_data"
269 | }
270 | ],
271 | "source": [
272 | "state = envs.reset()\n",
273 | "early_stop = False\n",
274 | "\n",
275 | "while frame_idx < max_frames and not early_stop:\n",
276 | "\n",
277 | " log_probs = []\n",
278 | " values = []\n",
279 | " states = []\n",
280 | " actions = []\n",
281 | " rewards = []\n",
282 | " masks = []\n",
283 | " entropy = 0\n",
284 | "\n",
285 | " for _ in range(num_steps):\n",
286 | " state = torch.FloatTensor(state).to(device)\n",
287 | " dist, value = model(state)\n",
288 | "\n",
289 | " action = dist.sample()\n",
290 | " next_state, reward, done, _ = envs.step(action.cpu().numpy())\n",
291 | "\n",
292 | " log_prob = dist.log_prob(action)\n",
293 | " entropy += dist.entropy().mean()\n",
294 | " \n",
295 | " log_probs.append(log_prob)\n",
296 | " values.append(value)\n",
297 | " rewards.append(torch.FloatTensor(reward).unsqueeze(1).to(device))\n",
298 | " masks.append(torch.FloatTensor(1 - done).unsqueeze(1).to(device))\n",
299 | " \n",
300 | " states.append(state)\n",
301 | " actions.append(action)\n",
302 | " \n",
303 | " state = next_state\n",
304 | " frame_idx += 1\n",
305 | " \n",
306 | " if frame_idx % 1000 == 0:\n",
307 | " test_reward = np.mean([test_env() for _ in range(10)])\n",
308 | " test_rewards.append(test_reward)\n",
309 | " plot(frame_idx, test_rewards)\n",
310 | " if test_reward > threshold_reward: early_stop = True\n",
311 | " \n",
312 | "\n",
313 | " next_state = torch.FloatTensor(next_state).to(device)\n",
314 | " _, next_value = model(next_state)\n",
315 | " returns = compute_gae(next_value, rewards, masks, values)\n",
316 | "\n",
317 | " returns = torch.cat(returns).detach()\n",
318 | " log_probs = torch.cat(log_probs).detach()\n",
319 | " values = torch.cat(values).detach()\n",
320 | " states = torch.cat(states)\n",
321 | " actions = torch.cat(actions)\n",
322 | " advantage = returns - values\n",
323 | " \n",
324 | " ppo_update(ppo_epochs, mini_batch_size, states, actions, log_probs, returns, advantage)"
325 | ]
326 | },
327 | {
328 | "cell_type": "markdown",
329 | "metadata": {},
330 | "source": [
331 | "Saving trajectories for GAIL "
332 | ]
333 | },
334 | {
335 | "cell_type": "code",
336 | "execution_count": 87,
337 | "metadata": {},
338 | "outputs": [
339 | {
340 | "name": "stdout",
341 | "output_type": "stream",
342 | "text": [
343 | "episode: 0 reward: -133.5056485070341\n",
344 | "episode: 1 reward: -3.3737309166625002\n",
345 | "episode: 2 reward: -135.0328820133956\n",
346 | "episode: 3 reward: -131.27964142064513\n",
347 | "episode: 4 reward: -125.12845453838382\n",
348 | "episode: 5 reward: -4.247933460422459\n",
349 | "episode: 6 reward: -395.59297834503883\n",
350 | "episode: 7 reward: -253.25736991568547\n",
351 | "episode: 8 reward: -135.50603026103278\n",
352 | "episode: 9 reward: -132.72095459732952\n",
353 | "episode: 10 reward: -133.89608385869212\n",
354 | "episode: 11 reward: -4.5990508813314035\n",
355 | "episode: 12 reward: -134.44470210766775\n",
356 | "episode: 13 reward: -801.7661346371387\n",
357 | "episode: 14 reward: -131.97725229377644\n",
358 | "episode: 15 reward: -266.76940521674015\n",
359 | "episode: 16 reward: -247.5062278004002\n",
360 | "episode: 17 reward: -4.914595620774103\n",
361 | "episode: 18 reward: -138.7990887577753\n",
362 | "episode: 19 reward: -268.3754189751262\n",
363 | "episode: 20 reward: -363.28764882256417\n",
364 | "episode: 21 reward: -128.15870842354997\n",
365 | "episode: 22 reward: -134.94598918501788\n",
366 | "episode: 23 reward: -309.9577786212293\n",
367 | "episode: 24 reward: -131.91670030817002\n",
368 | "episode: 25 reward: -134.65823444568952\n",
369 | "episode: 26 reward: -134.5615349098279\n",
370 | "episode: 27 reward: -273.5740578550409\n",
371 | "episode: 28 reward: -265.05553942459926\n",
372 | "episode: 29 reward: -258.0591054576666\n",
373 | "episode: 30 reward: -128.91060595426686\n",
374 | "episode: 31 reward: -656.2461074160591\n",
375 | "episode: 32 reward: -136.84071690580248\n",
376 | "episode: 33 reward: -259.2365200533221\n",
377 | "episode: 34 reward: -132.68644155022494\n",
378 | "episode: 35 reward: -260.66364797902054\n",
379 | "episode: 36 reward: -128.8211009270027\n",
380 | "episode: 37 reward: -384.53615237759317\n",
381 | "episode: 38 reward: -4.612904346743044\n",
382 | "episode: 39 reward: -401.1162060114804\n",
383 | "episode: 40 reward: -126.25334578262932\n",
384 | "episode: 41 reward: -3.845934927726255\n",
385 | "episode: 42 reward: -132.44253012402612\n",
386 | "episode: 43 reward: -134.1267203432647\n",
387 | "episode: 44 reward: -128.56866661753938\n",
388 | "episode: 45 reward: -4.97856955649956\n",
389 | "episode: 46 reward: -392.498679426522\n",
390 | "episode: 47 reward: -4.756869243844947\n",
391 | "episode: 48 reward: -4.59189846851519\n",
392 | "episode: 49 reward: -4.7496626929539225\n",
393 | "episode: 50 reward: -131.08999767991665\n",
394 | "episode: 51 reward: -138.17235302513578\n",
395 | "episode: 52 reward: -3.751761058079555\n",
396 | "episode: 53 reward: -260.6317126814632\n",
397 | "episode: 54 reward: -4.535299319594524\n",
398 | "episode: 55 reward: -133.70892423024802\n",
399 | "episode: 56 reward: -134.8732103854694\n",
400 | "episode: 57 reward: -5.315182694344295\n",
401 | "episode: 58 reward: -265.04898120165\n",
402 | "episode: 59 reward: -124.99288470795233\n",
403 | "episode: 60 reward: -4.247632479535832\n",
404 | "episode: 61 reward: -3.68334723705883\n",
405 | "episode: 62 reward: -133.617727327027\n",
406 | "episode: 63 reward: -136.28353948776376\n",
407 | "episode: 64 reward: -5.056124136459314\n",
408 | "episode: 65 reward: -262.7844771770983\n",
409 | "episode: 66 reward: -251.52420165781922\n",
410 | "episode: 67 reward: -133.4014820950796\n",
411 | "episode: 68 reward: -7.0558924646711\n",
412 | "episode: 69 reward: -135.41150554590206\n",
413 | "episode: 70 reward: -131.8871841825757\n",
414 | "episode: 71 reward: -130.8724972571845\n",
415 | "episode: 72 reward: -367.7339135957503\n",
416 | "episode: 73 reward: -134.25198778254116\n",
417 | "episode: 74 reward: -133.86858295338342\n",
418 | "episode: 75 reward: -378.9443227440811\n",
419 | "episode: 76 reward: -3.5473336732949625\n",
420 | "episode: 77 reward: -261.5470895641183\n",
421 | "episode: 78 reward: -408.34135925288217\n",
422 | "episode: 79 reward: -257.6727990499033\n",
423 | "episode: 80 reward: -399.78682205537433\n",
424 | "episode: 81 reward: -266.08087229456055\n",
425 | "episode: 82 reward: -817.186490578741\n",
426 | "episode: 83 reward: -4.500140134501902\n",
427 | "episode: 84 reward: -508.65456581456573\n",
428 | "episode: 85 reward: -378.46002005145874\n",
429 | "episode: 86 reward: -137.76181809972095\n",
430 | "episode: 87 reward: -674.8280917415572\n",
431 | "episode: 88 reward: -128.65034230393303\n",
432 | "episode: 89 reward: -3.922315525193146\n",
433 | "episode: 90 reward: -131.00005239353024\n",
434 | "episode: 91 reward: -130.68974732718007\n",
435 | "episode: 92 reward: -135.21946982972375\n",
436 | "episode: 93 reward: -137.3667851983452\n",
437 | "episode: 94 reward: -136.9119001250973\n",
438 | "episode: 95 reward: -254.5371556381929\n",
439 | "episode: 96 reward: -374.827391591992\n",
440 | "episode: 97 reward: -523.9964989484117\n",
441 | "episode: 98 reward: -133.94200200894622\n",
442 | "episode: 99 reward: -133.74880434577523\n",
443 | "episode: 100 reward: -247.32247835568552\n",
444 | "episode: 101 reward: -138.75528548988993\n",
445 | "episode: 102 reward: -4.847096453940289\n",
446 | "episode: 103 reward: -136.62732481247133\n",
447 | "episode: 104 reward: -262.20300946977864\n",
448 | "episode: 105 reward: -6.5435854338994\n",
449 | "episode: 106 reward: -125.17361036750681\n",
450 | "episode: 107 reward: -690.5202921080676\n",
451 | "episode: 108 reward: -280.53617631459497\n",
452 | "episode: 109 reward: -135.40352441695322\n",
453 | "episode: 110 reward: -131.07617970631023\n",
454 | "episode: 111 reward: -247.0260554601557\n",
455 | "episode: 112 reward: -135.40673404514774\n",
456 | "episode: 113 reward: -395.03306256658476\n",
457 | "episode: 114 reward: -384.1784417792837\n",
458 | "episode: 115 reward: -128.4500742980931\n",
459 | "episode: 116 reward: -463.6977661877445\n",
460 | "episode: 117 reward: -130.94801971085445\n",
461 | "episode: 118 reward: -144.0228791279258\n",
462 | "episode: 119 reward: -667.2634492717342\n",
463 | "episode: 120 reward: -131.79948959004724\n",
464 | "episode: 121 reward: -138.03140142705894\n",
465 | "episode: 122 reward: -129.26779443720966\n",
466 | "episode: 123 reward: -3.2877798185337896\n",
467 | "episode: 124 reward: -134.72016283865193\n",
468 | "episode: 125 reward: -382.2159098741087\n",
469 | "episode: 126 reward: -264.6491917411121\n",
470 | "episode: 127 reward: -134.2254720027939\n",
471 | "episode: 128 reward: -424.8235005744391\n",
472 | "episode: 129 reward: -134.52619102883028\n",
473 | "episode: 130 reward: -537.7406839640856\n",
474 | "episode: 131 reward: -133.90654715605245\n",
475 | "episode: 132 reward: -132.20198118805123\n",
476 | "episode: 133 reward: -400.3589991495165\n",
477 | "episode: 134 reward: -130.12695949420717\n",
478 | "episode: 135 reward: -290.86810229081595\n",
479 | "episode: 136 reward: -394.9043391522139\n",
480 | "episode: 137 reward: -133.42125091255778\n",
481 | "episode: 138 reward: -134.96306459417266\n",
482 | "episode: 139 reward: -3.8499366797706336\n",
483 | "episode: 140 reward: -3.828788719469504\n",
484 | "episode: 141 reward: -5.554963437941836\n",
485 | "episode: 142 reward: -4.510403163975261\n",
486 | "episode: 143 reward: -325.97799775791754\n",
487 | "episode: 144 reward: -3.1174779530363375\n",
488 | "episode: 145 reward: -134.55262416681552\n",
489 | "episode: 146 reward: -350.45777263184095\n",
490 | "episode: 147 reward: -137.33235583532627\n",
491 | "episode: 148 reward: -452.0061280718382\n",
492 | "episode: 149 reward: -265.98673902850385\n",
493 | "episode: 150 reward: -284.8590382363739\n",
494 | "episode: 151 reward: -250.06981206461143\n",
495 | "episode: 152 reward: -129.50428228187013\n",
496 | "episode: 153 reward: -393.09302439930724\n",
497 | "episode: 154 reward: -5.075964808667517\n",
498 | "episode: 155 reward: -129.83816358490287\n",
499 | "episode: 156 reward: -266.1020126434327\n",
500 | "episode: 157 reward: -132.23463644630868\n",
501 | "episode: 158 reward: -779.5855091317233\n",
502 | "episode: 159 reward: -3.763971510946643\n",
503 | "episode: 160 reward: -132.67794144748086\n",
504 | "episode: 161 reward: -662.5587064643477\n",
505 | "episode: 162 reward: -135.2401324340408\n",
506 | "episode: 163 reward: -259.9633585943629\n",
507 | "episode: 164 reward: -6.232862086437321\n",
508 | "episode: 165 reward: -139.498411973157\n",
509 | "episode: 166 reward: -135.35070491390638\n",
510 | "episode: 167 reward: -135.1400077480551\n",
511 | "episode: 168 reward: -347.3664683729514\n",
512 | "episode: 169 reward: -427.1984854733556\n",
513 | "episode: 170 reward: -5.15672209428849\n",
514 | "episode: 171 reward: -525.916662268042\n",
515 | "episode: 172 reward: -133.7053511504196\n",
516 | "episode: 173 reward: -271.26784680564384\n",
517 | "episode: 174 reward: -124.85474506625023\n",
518 | "episode: 175 reward: -134.19873581079943\n",
519 | "episode: 176 reward: -255.83160338962983\n",
520 | "episode: 177 reward: -135.13400569542506\n",
521 | "episode: 178 reward: -4.960226836538054\n",
522 | "episode: 179 reward: -139.19809065222032\n",
523 | "episode: 180 reward: -140.05080094044732\n",
524 | "episode: 181 reward: -137.76647105767526\n",
525 | "episode: 182 reward: -403.1731636539886\n",
526 | "episode: 183 reward: -257.970427512537\n",
527 | "episode: 184 reward: -3.7473226459331066\n",
528 | "episode: 185 reward: -278.3098063643893\n",
529 | "episode: 186 reward: -255.99692458401518\n",
530 | "episode: 187 reward: -4.6365121508813445\n",
531 | "episode: 188 reward: -244.67627722290948\n",
532 | "episode: 189 reward: -131.21920785362062\n",
533 | "episode: 190 reward: -777.3698354491825\n",
534 | "episode: 191 reward: -132.07220706141683\n",
535 | "episode: 192 reward: -392.09434598281683\n",
536 | "episode: 193 reward: -136.06354238422503\n",
537 | "episode: 194 reward: -377.4409927865957\n",
538 | "episode: 195 reward: -132.18253486880235\n",
539 | "episode: 196 reward: -129.15162595976702\n",
540 | "episode: 197 reward: -396.5254064840202\n",
541 | "episode: 198 reward: -3.610361833207753\n",
542 | "episode: 199 reward: -245.53736015092704\n",
543 | "episode: 200 reward: -270.99181854480565\n",
544 | "episode: 201 reward: -247.4231450110685\n",
545 | "episode: 202 reward: -131.59894474370887\n",
546 | "episode: 203 reward: -144.7898370619998\n",
547 | "episode: 204 reward: -926.5588068852352\n",
548 | "episode: 205 reward: -133.39727923189105\n",
549 | "episode: 206 reward: -131.93566436017008\n",
550 | "episode: 207 reward: -6.40529176710689\n",
551 | "episode: 208 reward: -257.08448208556194\n",
552 | "episode: 209 reward: -130.92098423630432\n",
553 | "episode: 210 reward: -262.2927047192545\n",
554 | "episode: 211 reward: -6.859901180492491\n",
555 | "episode: 212 reward: -262.70877767928914\n",
556 | "episode: 213 reward: -134.56588203218894\n",
557 | "episode: 214 reward: -135.22465193371625\n",
558 | "episode: 215 reward: -137.9657247788344\n",
559 | "episode: 216 reward: -135.13425433384725\n",
560 | "episode: 217 reward: -132.3215993693809\n",
561 | "episode: 218 reward: -400.611961792729\n",
562 | "episode: 219 reward: -401.91908212383294\n",
563 | "episode: 220 reward: -282.5082305011229\n",
564 | "episode: 221 reward: -135.42191465289923\n",
565 | "episode: 222 reward: -399.7881535647735\n",
566 | "episode: 223 reward: -131.06522770318847\n",
567 | "episode: 224 reward: -130.7681491912167\n",
568 | "episode: 225 reward: -135.31477016876133\n",
569 | "episode: 226 reward: -3.914901001828447\n",
570 | "episode: 227 reward: -134.5129393394648\n",
571 | "episode: 228 reward: -376.1469783238271\n",
572 | "episode: 229 reward: -133.09045533066046\n",
573 | "episode: 230 reward: -383.2750315233141\n",
574 | "episode: 231 reward: -263.71240275232276\n",
575 | "episode: 232 reward: -500.0083919266878\n",
576 | "episode: 233 reward: -135.22531187168758\n",
577 | "episode: 234 reward: -135.17818433537522\n",
578 | "episode: 235 reward: -395.9834332194123\n",
579 | "episode: 236 reward: -126.08778928679216\n",
580 | "episode: 237 reward: -413.7495701300203\n",
581 | "episode: 238 reward: -131.37116502717876\n",
582 | "episode: 239 reward: -121.6506938627967\n",
583 | "episode: 240 reward: -653.7053929625495\n",
584 | "episode: 241 reward: -254.87183145095838\n",
585 | "episode: 242 reward: -129.71331746419523\n",
586 | "episode: 243 reward: -265.9795936355916\n",
587 | "episode: 244 reward: -400.65989274385277\n",
588 | "episode: 245 reward: -251.82522565834446\n",
589 | "episode: 246 reward: -3.95924871368981\n",
590 | "episode: 247 reward: -312.7505665224348\n",
591 | "episode: 248 reward: -135.5875093701436\n",
592 | "episode: 249 reward: -441.6053043293015\n"
593 | ]
594 | }
595 | ],
596 | "source": [
597 | "from itertools import count\n",
598 | "\n",
599 | "max_expert_num = 50000\n",
600 | "num_steps = 0\n",
601 | "expert_traj = []\n",
602 | "\n",
603 | "for i_episode in count():\n",
604 | " state = env.reset()\n",
605 | " done = False\n",
606 | " total_reward = 0\n",
607 | " \n",
608 | " while not done:\n",
609 | " state = torch.FloatTensor(state).unsqueeze(0).to(device)\n",
610 | " dist, _ = model(state)\n",
611 | " action = dist.sample().cpu().numpy()[0]\n",
612 | " next_state, reward, done, _ = env.step(action)\n",
613 | " state = next_state\n",
614 | " total_reward += reward\n",
615 | " expert_traj.append(np.hstack([state, action]))\n",
616 | " num_steps += 1\n",
617 | " \n",
618 | " print(\"episode:\", i_episode, \"reward:\", total_reward)\n",
619 | " \n",
620 | " if num_steps >= max_expert_num:\n",
621 | " break\n",
622 | " \n",
623 | "expert_traj = np.stack(expert_traj)\n",
624 | "print()\n",
625 | "print(expert_traj.shape)\n",
626 | "print()\n",
627 | "np.save(\"expert_traj.npy\", expert_traj)"
628 | ]
629 | }
630 | ],
631 | "metadata": {
632 | "kernelspec": {
633 | "display_name": "Python [conda env:pytorch4]",
634 | "language": "python",
635 | "name": "conda-env-pytorch4-py"
636 | },
637 | "language_info": {
638 | "codemirror_mode": {
639 | "name": "ipython",
640 | "version": 3
641 | },
642 | "file_extension": ".py",
643 | "mimetype": "text/x-python",
644 | "name": "python",
645 | "nbconvert_exporter": "python",
646 | "pygments_lexer": "ipython3",
647 | "version": "3.5.5"
648 | }
649 | },
650 | "nbformat": 4,
651 | "nbformat_minor": 2
652 | }
653 |
--------------------------------------------------------------------------------
 4 |
5 |
6 | PyTorch tutorial of: actor critic / proximal policy optimization / acer / ddpg / twin dueling ddpg / soft actor critic / generative adversarial imitation learning / hindsight experience replay
7 |
8 | The deep reinforcement learning community has made several improvements to the [policy gradient](http://rll.berkeley.edu/deeprlcourse/f17docs/lecture_4_policy_gradient.pdf) algorithms. This tutorial presents latest extensions in the following order:
9 |
10 | 1. Advantage Actor Critic (A2C)
11 | - [actor-critic.ipynb](https://github.com/higgsfield/RL-Adventure-2/blob/master/1.actor-critic.ipynb)
12 | - [A3C Paper](https://arxiv.org/pdf/1602.01783.pdf)
13 | - [OpenAI blog](https://blog.openai.com/baselines-acktr-a2c/#a2canda3c)
14 | 2. High-Dimensional Continuous Control Using Generalized Advantage Estimation
15 | - [gae.ipynb](https://github.com/higgsfield/RL-Adventure-2/blob/master/2.gae.ipynb)
16 | - [GAE Paper](https://arxiv.org/abs/1506.02438)
17 | 3. Proximal Policy Optimization Algorithms
18 | - [ppo.ipynb](https://github.com/higgsfield/RL-Adventure-2/blob/master/3.ppo.ipynb)
19 | - [PPO Paper](https://arxiv.org/abs/1707.06347)
20 | - [OpenAI blog](https://blog.openai.com/openai-baselines-ppo/)
21 | 4. Sample Efficient Actor-Critic with Experience Replay
22 | - [acer.ipynb](https://github.com/higgsfield/RL-Adventure-2/blob/master/4.acer.ipynb)
23 | - [ACER Paper](https://arxiv.org/abs/1611.01224)
24 | 5. Continuous control with deep reinforcement learning
25 | - [ddpg.ipynb](https://github.com/higgsfield/RL-Adventure-2/blob/master/5.ddpg.ipynb)
26 | - [DDPG Paper](https://arxiv.org/abs/1509.02971)
27 | 6. Addressing Function Approximation Error in Actor-Critic Methods
28 | - [td3.ipynb](https://github.com/higgsfield/RL-Adventure-2/blob/master/6.td3.ipynb)
29 | - [Twin Dueling DDPG Paper](https://arxiv.org/abs/1802.09477)
30 | 7. Soft Actor-Critic: Off-Policy Maximum Entropy Deep Reinforcement Learning with a Stochastic Actor
31 | - [soft actor-critic.ipynb](https://github.com/higgsfield/RL-Adventure-2/blob/master/7.soft%20actor-critic.ipynb)
32 | - [Soft Actor-Critic Paper](https://arxiv.org/abs/1801.01290)
33 | 8. Generative Adversarial Imitation Learning
34 | - [gail.ipynb](https://github.com/higgsfield/RL-Adventure-2/blob/master/8.gail.ipynb)
35 | - [GAIL Paper](https://arxiv.org/abs/1606.03476)
36 | 9. Hindsight Experience Replay
37 | - [her.ipynb](https://github.com/higgsfield/RL-Adventure-2/blob/master/9.her.ipynb)
38 | - [HER Paper](https://arxiv.org/abs/1707.01495)
39 | - [OpenAI Blog](https://blog.openai.com/ingredients-for-robotics-research/#understandingher)
40 |
41 | # If you get stuck…
42 | - Remember you are not stuck unless you have spent more than a week on a single algorithm. It is perfectly normal if you do not have all the required knowledge of mathematics and CS.
43 | - Carefully go through the paper. Try to see what is the problem the authors are solving. Understand a high-level idea of the approach, then read the code (skipping the proofs), and after go over the mathematical details and proofs.
44 |
45 | # RL Algorithms
46 | Deep Q Learning tutorial: [DQN Adventure: from Zero to State of the Art](https://github.com/higgsfield/RL-Adventure)
47 | [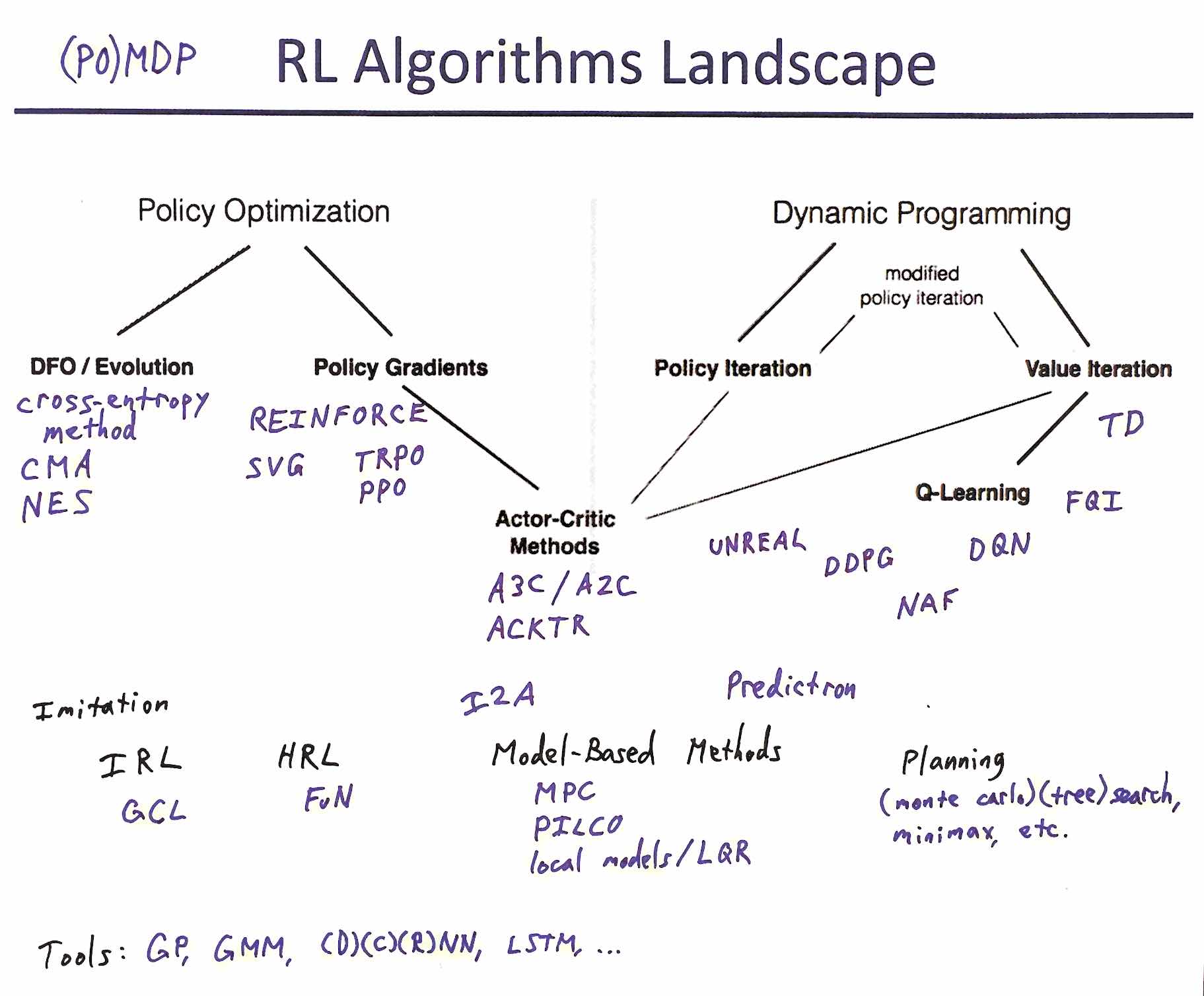]()
48 | Awesome RL libs: rlkit [@vitchyr](https://github.com/vitchyr), pytorch-a2c-ppo-acktr [@ikostrikov](https://github.com/ikostrikov),
49 | ACER [@Kaixhin](https://github.com/Kaixhin)
50 |
51 | # Best RL courses
52 | - Berkeley deep RL [link](http://rll.berkeley.edu/deeprlcourse/)
53 | - Deep RL Bootcamp [link](https://sites.google.com/view/deep-rl-bootcamp/lectures)
54 | - David Silver's course [link](http://www0.cs.ucl.ac.uk/staff/d.silver/web/Teaching.html)
55 | - Practical RL [link](https://github.com/yandexdataschool/Practical_RL)
56 |
--------------------------------------------------------------------------------
/common/multiprocessing_env.py:
--------------------------------------------------------------------------------
1 | #This code is from openai baseline
2 | #https://github.com/openai/baselines/tree/master/baselines/common/vec_env
3 |
4 | import numpy as np
5 | from multiprocessing import Process, Pipe
6 |
7 | def worker(remote, parent_remote, env_fn_wrapper):
8 | parent_remote.close()
9 | env = env_fn_wrapper.x()
10 | while True:
11 | cmd, data = remote.recv()
12 | if cmd == 'step':
13 | ob, reward, done, info = env.step(data)
14 | if done:
15 | ob = env.reset()
16 | remote.send((ob, reward, done, info))
17 | elif cmd == 'reset':
18 | ob = env.reset()
19 | remote.send(ob)
20 | elif cmd == 'reset_task':
21 | ob = env.reset_task()
22 | remote.send(ob)
23 | elif cmd == 'close':
24 | remote.close()
25 | break
26 | elif cmd == 'get_spaces':
27 | remote.send((env.observation_space, env.action_space))
28 | else:
29 | raise NotImplementedError
30 |
31 | class VecEnv(object):
32 | """
33 | An abstract asynchronous, vectorized environment.
34 | """
35 | def __init__(self, num_envs, observation_space, action_space):
36 | self.num_envs = num_envs
37 | self.observation_space = observation_space
38 | self.action_space = action_space
39 |
40 | def reset(self):
41 | """
42 | Reset all the environments and return an array of
43 | observations, or a tuple of observation arrays.
44 | If step_async is still doing work, that work will
45 | be cancelled and step_wait() should not be called
46 | until step_async() is invoked again.
47 | """
48 | pass
49 |
50 | def step_async(self, actions):
51 | """
52 | Tell all the environments to start taking a step
53 | with the given actions.
54 | Call step_wait() to get the results of the step.
55 | You should not call this if a step_async run is
56 | already pending.
57 | """
58 | pass
59 |
60 | def step_wait(self):
61 | """
62 | Wait for the step taken with step_async().
63 | Returns (obs, rews, dones, infos):
64 | - obs: an array of observations, or a tuple of
65 | arrays of observations.
66 | - rews: an array of rewards
67 | - dones: an array of "episode done" booleans
68 | - infos: a sequence of info objects
69 | """
70 | pass
71 |
72 | def close(self):
73 | """
74 | Clean up the environments' resources.
75 | """
76 | pass
77 |
78 | def step(self, actions):
79 | self.step_async(actions)
80 | return self.step_wait()
81 |
82 |
83 | class CloudpickleWrapper(object):
84 | """
85 | Uses cloudpickle to serialize contents (otherwise multiprocessing tries to use pickle)
86 | """
87 | def __init__(self, x):
88 | self.x = x
89 | def __getstate__(self):
90 | import cloudpickle
91 | return cloudpickle.dumps(self.x)
92 | def __setstate__(self, ob):
93 | import pickle
94 | self.x = pickle.loads(ob)
95 |
96 |
97 | class SubprocVecEnv(VecEnv):
98 | def __init__(self, env_fns, spaces=None):
99 | """
100 | envs: list of gym environments to run in subprocesses
101 | """
102 | self.waiting = False
103 | self.closed = False
104 | nenvs = len(env_fns)
105 | self.nenvs = nenvs
106 | self.remotes, self.work_remotes = zip(*[Pipe() for _ in range(nenvs)])
107 | self.ps = [Process(target=worker, args=(work_remote, remote, CloudpickleWrapper(env_fn)))
108 | for (work_remote, remote, env_fn) in zip(self.work_remotes, self.remotes, env_fns)]
109 | for p in self.ps:
110 | p.daemon = True # if the main process crashes, we should not cause things to hang
111 | p.start()
112 | for remote in self.work_remotes:
113 | remote.close()
114 |
115 | self.remotes[0].send(('get_spaces', None))
116 | observation_space, action_space = self.remotes[0].recv()
117 | VecEnv.__init__(self, len(env_fns), observation_space, action_space)
118 |
119 | def step_async(self, actions):
120 | for remote, action in zip(self.remotes, actions):
121 | remote.send(('step', action))
122 | self.waiting = True
123 |
124 | def step_wait(self):
125 | results = [remote.recv() for remote in self.remotes]
126 | self.waiting = False
127 | obs, rews, dones, infos = zip(*results)
128 | return np.stack(obs), np.stack(rews), np.stack(dones), infos
129 |
130 | def reset(self):
131 | for remote in self.remotes:
132 | remote.send(('reset', None))
133 | return np.stack([remote.recv() for remote in self.remotes])
134 |
135 | def reset_task(self):
136 | for remote in self.remotes:
137 | remote.send(('reset_task', None))
138 | return np.stack([remote.recv() for remote in self.remotes])
139 |
140 | def close(self):
141 | if self.closed:
142 | return
143 | if self.waiting:
144 | for remote in self.remotes:
145 | remote.recv()
146 | for remote in self.remotes:
147 | remote.send(('close', None))
148 | for p in self.ps:
149 | p.join()
150 | self.closed = True
151 |
152 | def __len__(self):
153 | return self.nenvs
--------------------------------------------------------------------------------
/1.actor-critic.ipynb:
--------------------------------------------------------------------------------
1 | {
2 | "cells": [
3 | {
4 | "cell_type": "code",
5 | "execution_count": 1,
6 | "metadata": {},
7 | "outputs": [],
8 | "source": [
9 | "import math\n",
10 | "import random\n",
11 | "\n",
12 | "import gym\n",
13 | "import numpy as np\n",
14 | "\n",
15 | "import torch\n",
16 | "import torch.nn as nn\n",
17 | "import torch.optim as optim\n",
18 | "import torch.nn.functional as F\n",
19 | "from torch.distributions import Categorical"
20 | ]
21 | },
22 | {
23 | "cell_type": "code",
24 | "execution_count": 2,
25 | "metadata": {},
26 | "outputs": [],
27 | "source": [
28 | "from IPython.display import clear_output\n",
29 | "import matplotlib.pyplot as plt\n",
30 | "%matplotlib inline"
31 | ]
32 | },
33 | {
34 | "cell_type": "markdown",
35 | "metadata": {},
36 | "source": [
37 | "
4 |
5 |
6 | PyTorch tutorial of: actor critic / proximal policy optimization / acer / ddpg / twin dueling ddpg / soft actor critic / generative adversarial imitation learning / hindsight experience replay
7 |
8 | The deep reinforcement learning community has made several improvements to the [policy gradient](http://rll.berkeley.edu/deeprlcourse/f17docs/lecture_4_policy_gradient.pdf) algorithms. This tutorial presents latest extensions in the following order:
9 |
10 | 1. Advantage Actor Critic (A2C)
11 | - [actor-critic.ipynb](https://github.com/higgsfield/RL-Adventure-2/blob/master/1.actor-critic.ipynb)
12 | - [A3C Paper](https://arxiv.org/pdf/1602.01783.pdf)
13 | - [OpenAI blog](https://blog.openai.com/baselines-acktr-a2c/#a2canda3c)
14 | 2. High-Dimensional Continuous Control Using Generalized Advantage Estimation
15 | - [gae.ipynb](https://github.com/higgsfield/RL-Adventure-2/blob/master/2.gae.ipynb)
16 | - [GAE Paper](https://arxiv.org/abs/1506.02438)
17 | 3. Proximal Policy Optimization Algorithms
18 | - [ppo.ipynb](https://github.com/higgsfield/RL-Adventure-2/blob/master/3.ppo.ipynb)
19 | - [PPO Paper](https://arxiv.org/abs/1707.06347)
20 | - [OpenAI blog](https://blog.openai.com/openai-baselines-ppo/)
21 | 4. Sample Efficient Actor-Critic with Experience Replay
22 | - [acer.ipynb](https://github.com/higgsfield/RL-Adventure-2/blob/master/4.acer.ipynb)
23 | - [ACER Paper](https://arxiv.org/abs/1611.01224)
24 | 5. Continuous control with deep reinforcement learning
25 | - [ddpg.ipynb](https://github.com/higgsfield/RL-Adventure-2/blob/master/5.ddpg.ipynb)
26 | - [DDPG Paper](https://arxiv.org/abs/1509.02971)
27 | 6. Addressing Function Approximation Error in Actor-Critic Methods
28 | - [td3.ipynb](https://github.com/higgsfield/RL-Adventure-2/blob/master/6.td3.ipynb)
29 | - [Twin Dueling DDPG Paper](https://arxiv.org/abs/1802.09477)
30 | 7. Soft Actor-Critic: Off-Policy Maximum Entropy Deep Reinforcement Learning with a Stochastic Actor
31 | - [soft actor-critic.ipynb](https://github.com/higgsfield/RL-Adventure-2/blob/master/7.soft%20actor-critic.ipynb)
32 | - [Soft Actor-Critic Paper](https://arxiv.org/abs/1801.01290)
33 | 8. Generative Adversarial Imitation Learning
34 | - [gail.ipynb](https://github.com/higgsfield/RL-Adventure-2/blob/master/8.gail.ipynb)
35 | - [GAIL Paper](https://arxiv.org/abs/1606.03476)
36 | 9. Hindsight Experience Replay
37 | - [her.ipynb](https://github.com/higgsfield/RL-Adventure-2/blob/master/9.her.ipynb)
38 | - [HER Paper](https://arxiv.org/abs/1707.01495)
39 | - [OpenAI Blog](https://blog.openai.com/ingredients-for-robotics-research/#understandingher)
40 |
41 | # If you get stuck…
42 | - Remember you are not stuck unless you have spent more than a week on a single algorithm. It is perfectly normal if you do not have all the required knowledge of mathematics and CS.
43 | - Carefully go through the paper. Try to see what is the problem the authors are solving. Understand a high-level idea of the approach, then read the code (skipping the proofs), and after go over the mathematical details and proofs.
44 |
45 | # RL Algorithms
46 | Deep Q Learning tutorial: [DQN Adventure: from Zero to State of the Art](https://github.com/higgsfield/RL-Adventure)
47 | []()
48 | Awesome RL libs: rlkit [@vitchyr](https://github.com/vitchyr), pytorch-a2c-ppo-acktr [@ikostrikov](https://github.com/ikostrikov),
49 | ACER [@Kaixhin](https://github.com/Kaixhin)
50 |
51 | # Best RL courses
52 | - Berkeley deep RL [link](http://rll.berkeley.edu/deeprlcourse/)
53 | - Deep RL Bootcamp [link](https://sites.google.com/view/deep-rl-bootcamp/lectures)
54 | - David Silver's course [link](http://www0.cs.ucl.ac.uk/staff/d.silver/web/Teaching.html)
55 | - Practical RL [link](https://github.com/yandexdataschool/Practical_RL)
56 |
--------------------------------------------------------------------------------
/common/multiprocessing_env.py:
--------------------------------------------------------------------------------
1 | #This code is from openai baseline
2 | #https://github.com/openai/baselines/tree/master/baselines/common/vec_env
3 |
4 | import numpy as np
5 | from multiprocessing import Process, Pipe
6 |
7 | def worker(remote, parent_remote, env_fn_wrapper):
8 | parent_remote.close()
9 | env = env_fn_wrapper.x()
10 | while True:
11 | cmd, data = remote.recv()
12 | if cmd == 'step':
13 | ob, reward, done, info = env.step(data)
14 | if done:
15 | ob = env.reset()
16 | remote.send((ob, reward, done, info))
17 | elif cmd == 'reset':
18 | ob = env.reset()
19 | remote.send(ob)
20 | elif cmd == 'reset_task':
21 | ob = env.reset_task()
22 | remote.send(ob)
23 | elif cmd == 'close':
24 | remote.close()
25 | break
26 | elif cmd == 'get_spaces':
27 | remote.send((env.observation_space, env.action_space))
28 | else:
29 | raise NotImplementedError
30 |
31 | class VecEnv(object):
32 | """
33 | An abstract asynchronous, vectorized environment.
34 | """
35 | def __init__(self, num_envs, observation_space, action_space):
36 | self.num_envs = num_envs
37 | self.observation_space = observation_space
38 | self.action_space = action_space
39 |
40 | def reset(self):
41 | """
42 | Reset all the environments and return an array of
43 | observations, or a tuple of observation arrays.
44 | If step_async is still doing work, that work will
45 | be cancelled and step_wait() should not be called
46 | until step_async() is invoked again.
47 | """
48 | pass
49 |
50 | def step_async(self, actions):
51 | """
52 | Tell all the environments to start taking a step
53 | with the given actions.
54 | Call step_wait() to get the results of the step.
55 | You should not call this if a step_async run is
56 | already pending.
57 | """
58 | pass
59 |
60 | def step_wait(self):
61 | """
62 | Wait for the step taken with step_async().
63 | Returns (obs, rews, dones, infos):
64 | - obs: an array of observations, or a tuple of
65 | arrays of observations.
66 | - rews: an array of rewards
67 | - dones: an array of "episode done" booleans
68 | - infos: a sequence of info objects
69 | """
70 | pass
71 |
72 | def close(self):
73 | """
74 | Clean up the environments' resources.
75 | """
76 | pass
77 |
78 | def step(self, actions):
79 | self.step_async(actions)
80 | return self.step_wait()
81 |
82 |
83 | class CloudpickleWrapper(object):
84 | """
85 | Uses cloudpickle to serialize contents (otherwise multiprocessing tries to use pickle)
86 | """
87 | def __init__(self, x):
88 | self.x = x
89 | def __getstate__(self):
90 | import cloudpickle
91 | return cloudpickle.dumps(self.x)
92 | def __setstate__(self, ob):
93 | import pickle
94 | self.x = pickle.loads(ob)
95 |
96 |
97 | class SubprocVecEnv(VecEnv):
98 | def __init__(self, env_fns, spaces=None):
99 | """
100 | envs: list of gym environments to run in subprocesses
101 | """
102 | self.waiting = False
103 | self.closed = False
104 | nenvs = len(env_fns)
105 | self.nenvs = nenvs
106 | self.remotes, self.work_remotes = zip(*[Pipe() for _ in range(nenvs)])
107 | self.ps = [Process(target=worker, args=(work_remote, remote, CloudpickleWrapper(env_fn)))
108 | for (work_remote, remote, env_fn) in zip(self.work_remotes, self.remotes, env_fns)]
109 | for p in self.ps:
110 | p.daemon = True # if the main process crashes, we should not cause things to hang
111 | p.start()
112 | for remote in self.work_remotes:
113 | remote.close()
114 |
115 | self.remotes[0].send(('get_spaces', None))
116 | observation_space, action_space = self.remotes[0].recv()
117 | VecEnv.__init__(self, len(env_fns), observation_space, action_space)
118 |
119 | def step_async(self, actions):
120 | for remote, action in zip(self.remotes, actions):
121 | remote.send(('step', action))
122 | self.waiting = True
123 |
124 | def step_wait(self):
125 | results = [remote.recv() for remote in self.remotes]
126 | self.waiting = False
127 | obs, rews, dones, infos = zip(*results)
128 | return np.stack(obs), np.stack(rews), np.stack(dones), infos
129 |
130 | def reset(self):
131 | for remote in self.remotes:
132 | remote.send(('reset', None))
133 | return np.stack([remote.recv() for remote in self.remotes])
134 |
135 | def reset_task(self):
136 | for remote in self.remotes:
137 | remote.send(('reset_task', None))
138 | return np.stack([remote.recv() for remote in self.remotes])
139 |
140 | def close(self):
141 | if self.closed:
142 | return
143 | if self.waiting:
144 | for remote in self.remotes:
145 | remote.recv()
146 | for remote in self.remotes:
147 | remote.send(('close', None))
148 | for p in self.ps:
149 | p.join()
150 | self.closed = True
151 |
152 | def __len__(self):
153 | return self.nenvs
--------------------------------------------------------------------------------
/1.actor-critic.ipynb:
--------------------------------------------------------------------------------
1 | {
2 | "cells": [
3 | {
4 | "cell_type": "code",
5 | "execution_count": 1,
6 | "metadata": {},
7 | "outputs": [],
8 | "source": [
9 | "import math\n",
10 | "import random\n",
11 | "\n",
12 | "import gym\n",
13 | "import numpy as np\n",
14 | "\n",
15 | "import torch\n",
16 | "import torch.nn as nn\n",
17 | "import torch.optim as optim\n",
18 | "import torch.nn.functional as F\n",
19 | "from torch.distributions import Categorical"
20 | ]
21 | },
22 | {
23 | "cell_type": "code",
24 | "execution_count": 2,
25 | "metadata": {},
26 | "outputs": [],
27 | "source": [
28 | "from IPython.display import clear_output\n",
29 | "import matplotlib.pyplot as plt\n",
30 | "%matplotlib inline"
31 | ]
32 | },
33 | {
34 | "cell_type": "markdown",
35 | "metadata": {},
36 | "source": [
37 | "