├── Markdown
├── Artificial Neural Networks.md
├── Associate Rule Mining.md
├── Cluster Analysis.md
├── Data Mining.md
├── Data Preprocessing.md
├── Data Warehouse.md
├── Decision Tree.md
├── Naive Bayes Analysis.md
├── Regression.md
└── Unclassified.md
├── PDF
├── Artificial Neural Networks.pdf
├── Associate Rule Mining.pdf
├── Cluster Analysis.pdf
├── Data Mining.pdf
├── Data Preprocessing.pdf
├── Data Warehouse.pdf
├── Decision Tree.pdf
├── Naive Bayes Analysis.pdf
├── Regression.pdf
└── Unclassified.pdf
├── README.md
└── python_tool
├── .gitignore
├── debug.py
├── example.py
├── main.py
└── tool.py
/Markdown/Artificial Neural Networks.md:
--------------------------------------------------------------------------------
1 | # Artificial Neural Networks (人工神經網路)
2 |
3 | > Reference:
4 | >
5 | > 1. Artificial Neural Networks - Dr. Tun-Wen Pai
6 | > 2. [Neural Networks Pt. 1: Inside the Black Box](https://www.youtube.com/watch?v=CqOfi41LfDw)
7 | > 3. [Neural Networks Pt. 2: Backpropagation Main Ideas](https://www.youtube.com/watch?v=IN2XmBhILt4)
8 | > 4. [Backpropagation Details Pt. 1: Optimizing 3 parameters simultaneously.](https://www.youtube.com/watch?v=iyn2zdALii8)
9 | > 5. [Backpropagation Details Pt. 2: Going bonkers with The Chain Rule](https://www.youtube.com/watch?v=GKZoOHXGcLo)
10 |
11 |
12 |
13 | ## 概述
14 |
15 | 人工神經網路(ANN)使用了**一種曲線**,能夠近乎完美的符合資料集。
16 |
17 | 使用的曲線為激勵函數,利用參數、權重等等來製作,藉由神經元來構造曲線,進而符合資料集。
18 |
19 | 本篇所講述的人工神經網路均屬於前饋神經網路(前饋神經網路)。
20 |
21 |
22 |
23 | 我們可以把他想成將一個參數放入 input 神經元後。
24 |
25 | 這個 input 神經元會隨著箭頭進入到 Hidden layer 的神經元,通常是一個激勵函數。
26 |
27 | 箭頭會逐漸塑造激勵函數,直到 output 神經元將曲線輸出。
28 |
29 |
30 |
31 | 下圖是一個簡單的 ANN,我們將藍色圈圈稱為 input,綠色圈圈稱為 hidden,粉紅色圈圈稱為 output
32 |
33 | $w_1, w_2, w_3, w_4$ 為 weight,$b_1, b_2, b_3$ 為 bias,而 $af_1, af_2$ 為[激勵函數](#激勵函數)。
34 |
35 |  36 |
37 | 而實際上可能會這麼複雜:
38 |
39 | > Artificial neural network.svg - 維基百科,自由嘅百科全書
40 |
41 |
36 |
37 | 而實際上可能會這麼複雜:
38 |
39 | > Artificial neural network.svg - 維基百科,自由嘅百科全書
40 |
41 | 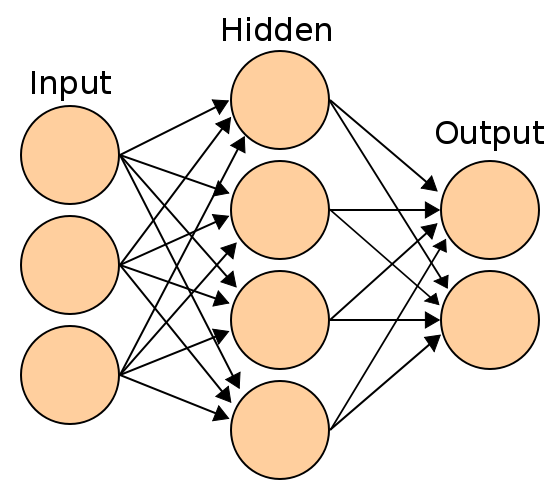 42 |
43 |
44 |
45 | ## 激勵函數
46 |
47 | 激勵函數在塑造曲線的時候扮演了重要的角色,主要分成四種:
48 |
49 | 1. Tanh:$f(x) = \tan x = \dfrac{e^x-e^{-x}}{e^x+e^{-x}}$
50 | 2. Sigmoid / Logistic:$f(x) = \dfrac{1}{1+e^{-x}}$
51 | 3. ReLu:$f(x) = x^{+} = \max(0, x)$
52 | 4. Softplus:$f(x) = \ln(1+e^x)$
53 |
54 |
55 |
56 | 所謂的激勵函數本質上就是函數,可以想像成把參數放入激勵函數後,可以使激勵函數最後塑造出我們想要的曲線。
57 |
58 |
59 |
60 | ## 建構簡單 ANN
61 |
62 |
63 |
64 | ### 建立概述
65 |
66 | 我們以簡單的例子來說明,以下圖為例。
67 |
68 |
42 |
43 |
44 |
45 | ## 激勵函數
46 |
47 | 激勵函數在塑造曲線的時候扮演了重要的角色,主要分成四種:
48 |
49 | 1. Tanh:$f(x) = \tan x = \dfrac{e^x-e^{-x}}{e^x+e^{-x}}$
50 | 2. Sigmoid / Logistic:$f(x) = \dfrac{1}{1+e^{-x}}$
51 | 3. ReLu:$f(x) = x^{+} = \max(0, x)$
52 | 4. Softplus:$f(x) = \ln(1+e^x)$
53 |
54 |
55 |
56 | 所謂的激勵函數本質上就是函數,可以想像成把參數放入激勵函數後,可以使激勵函數最後塑造出我們想要的曲線。
57 |
58 |
59 |
60 | ## 建構簡單 ANN
61 |
62 |
63 |
64 | ### 建立概述
65 |
66 | 我們以簡單的例子來說明,以下圖為例。
67 |
68 |  69 |
70 | 我們有一個*簡單的資料集*,分成三類,值域界於 $0$ 到 $1$:
71 |
72 | 1. 服用少數量 ntut-xuan 筆記的人 → 考不好 (0)
73 | 2. 服用中等數量 ntut-xuan 筆記的人 → 考得好 (1)
74 | 3. 服用多數量 ntut-xuan 筆記的人 → 考不好 (0)
75 |
76 | 可以得到左圖。
77 |
78 | 此時我們可能會想要用一條直線來分割這些資料,但這條直線可能不存在,因為不管怎麼畫都沒有辦法概括完全的資料。
79 |
80 | 如果這時候有一條*神奇的函數*來讓這些資料 match 就好,就像右圖。
81 |
82 | | | |
83 | | ------------------------------------------------------------ | ------------------------------------------------------------ |
84 | |
69 |
70 | 我們有一個*簡單的資料集*,分成三類,值域界於 $0$ 到 $1$:
71 |
72 | 1. 服用少數量 ntut-xuan 筆記的人 → 考不好 (0)
73 | 2. 服用中等數量 ntut-xuan 筆記的人 → 考得好 (1)
74 | 3. 服用多數量 ntut-xuan 筆記的人 → 考不好 (0)
75 |
76 | 可以得到左圖。
77 |
78 | 此時我們可能會想要用一條直線來分割這些資料,但這條直線可能不存在,因為不管怎麼畫都沒有辦法概括完全的資料。
79 |
80 | 如果這時候有一條*神奇的函數*來讓這些資料 match 就好,就像右圖。
81 |
82 | | | |
83 | | ------------------------------------------------------------ | ------------------------------------------------------------ |
84 | |  |
|  |
85 |
86 | 我們假設已經優化了類神經網路的 $w_1, w_2, b_1, b_2, w_3, w_4, b_3$ 參數,我們可以這樣建構我們的類神經網路。
87 |
88 | 假設我們使用的激勵函數 $af_1, af_2$ 為 Softplus:$f(x) = \ln(1+e^x)$
89 |
90 |
|
85 |
86 | 我們假設已經優化了類神經網路的 $w_1, w_2, b_1, b_2, w_3, w_4, b_3$ 參數,我們可以這樣建構我們的類神經網路。
87 |
88 | 假設我們使用的激勵函數 $af_1, af_2$ 為 Softplus:$f(x) = \ln(1+e^x)$
89 |
90 |  91 |
92 | 我們可以由我們建構的類神經網路,往上走建構出一條曲線,往下走建構出另一條曲線,如下圖:
93 |
94 | | 往上走 | 往下走 |
95 | | :----------------------------------------------------------: | :----------------------------------------------------------: |
96 | | $f\left(x\right)=-0.18\ln\left(1+e^{\left(-32.4x+18.34\right)}\right)$ | $g\left(x\right)=2.28\ln\left(1+e^{\left(-1.72x+2.55\right)}\right)$ |
97 | |
91 |
92 | 我們可以由我們建構的類神經網路,往上走建構出一條曲線,往下走建構出另一條曲線,如下圖:
93 |
94 | | 往上走 | 往下走 |
95 | | :----------------------------------------------------------: | :----------------------------------------------------------: |
96 | | $f\left(x\right)=-0.18\ln\left(1+e^{\left(-32.4x+18.34\right)}\right)$ | $g\left(x\right)=2.28\ln\left(1+e^{\left(-1.72x+2.55\right)}\right)$ |
97 | |  |
|  |
98 |
99 |
100 |
101 | 最後將兩個曲線加起來,並減去 $2.88$,得到以下的曲線,就能夠得到我們幾乎亂畫出來的曲線了!
102 |
103 | | $h(x)=-0.18\ln\left(1+e^{\left(-32.4x+18.34\right)}\right)+2.28\ln\left(1+e^{\left(-1.72x+2.55\right)}\right)-2.88$ | 我亂畫的 |
104 | | :----------------------------------------------------------: | :----------------------------------------------------------: |
105 | |  |
|
98 |
99 |
100 |
101 | 最後將兩個曲線加起來,並減去 $2.88$,得到以下的曲線,就能夠得到我們幾乎亂畫出來的曲線了!
102 |
103 | | $h(x)=-0.18\ln\left(1+e^{\left(-32.4x+18.34\right)}\right)+2.28\ln\left(1+e^{\left(-1.72x+2.55\right)}\right)-2.88$ | 我亂畫的 |
104 | | :----------------------------------------------------------: | :----------------------------------------------------------: |
105 | |  |  |
106 |
107 | 這時候我們就可以用這條曲線來判別我們特定資料集所出現的結果,所以人工神經網路*理論上*能夠成功分類所有的資料。
108 |
109 | **問題在於如何找出參數,來建構我們想要的曲線**。
110 |
111 |
112 |
113 | ### 簡單 ANN 的參數優化 (Backward Propagation)
114 |
115 | 對於找出參數,我們可以先給定一個初始值,然後進行參數優化。
116 |
117 | 對於 weight 的部分,我們的初始值可以先給定為**標準常態分布**的隨機一個值,而 bias 可以先預設為 $0$
118 |
119 |
|
106 |
107 | 這時候我們就可以用這條曲線來判別我們特定資料集所出現的結果,所以人工神經網路*理論上*能夠成功分類所有的資料。
108 |
109 | **問題在於如何找出參數,來建構我們想要的曲線**。
110 |
111 |
112 |
113 | ### 簡單 ANN 的參數優化 (Backward Propagation)
114 |
115 | 對於找出參數,我們可以先給定一個初始值,然後進行參數優化。
116 |
117 | 對於 weight 的部分,我們的初始值可以先給定為**標準常態分布**的隨機一個值,而 bias 可以先預設為 $0$
118 |
119 |  120 |
121 |
122 |
123 | 若要使曲線越來越擬合我們的資料集,我們得要先考慮是否能夠限縮 $\text{SSR}$,使他越小,讓曲線 $f(x_i)$ 越能擬合資料集。
124 |
125 | $\text{SSR}$ 即為殘差平方和,即為對於在 $x=i$ 上的資料集,其所有資料 $(y_i - f(x_i))^2$ 的和,可以定義為 $\text{SSR} = \displaystyle \sum^{n}_{i=1} (y_i - f(x_i))^2$
126 |
127 | 若我們想要優化參數,可以找出參數對 $\text{SSR}$ 的導函數,接著使用梯度下降法來同步優化所有參數
128 |
129 |
130 |
131 | 同樣以下圖為例:
132 |
133 |
120 |
121 |
122 |
123 | 若要使曲線越來越擬合我們的資料集,我們得要先考慮是否能夠限縮 $\text{SSR}$,使他越小,讓曲線 $f(x_i)$ 越能擬合資料集。
124 |
125 | $\text{SSR}$ 即為殘差平方和,即為對於在 $x=i$ 上的資料集,其所有資料 $(y_i - f(x_i))^2$ 的和,可以定義為 $\text{SSR} = \displaystyle \sum^{n}_{i=1} (y_i - f(x_i))^2$
126 |
127 | 若我們想要優化參數,可以找出參數對 $\text{SSR}$ 的導函數,接著使用梯度下降法來同步優化所有參數
128 |
129 |
130 |
131 | 同樣以下圖為例:
132 |
133 |  134 |
135 | 我們令 $af_1(x_i)$ 運算出的結果叫做 $y_{1,i}$,$af_2(x_i)$ 運算出的結果叫做 $y_{2,i}$
136 |
137 | 可以得到 $f(x_i) = w_3 \times y_{1, i} + w_4 \times y_{2, i} + b_3$
138 |
139 | 又 $y_{1, i} = \ln(1+e^{x_{1,i}}), y_{2, i} = \ln(1+e^{x_{2, i}}), x_{1,i}=x_i \times w_1+b_1, x_{2,i} = x_i \times w_2+b_2$,以 Softplus 為例。
140 |
141 |
142 |
143 | 找出導函數,可以使用鎖鏈法則來尋找。
144 |
145 | $\dfrac{d\text{SSR}}{db_3} = \dfrac{dSSR}{df(x_i)} \times \dfrac{df(x_i)}{db_3} = \displaystyle \sum^{n}_{i=1} -2(y_i-f(x_i)) \times 1$
146 |
147 | $\dfrac{d\text{SSR}}{dw_3} = \dfrac{dSSR}{df(x_i)} \times \dfrac{df(x_i)}{dw_3} = \displaystyle \sum^{n}_{i=1} -2(y_i-f(x_i)) \times y_{1, i}$
148 |
149 | $\dfrac{d\text{SSR}}{dw_4} = \dfrac{dSSR}{df(x_i)} \times \dfrac{df(x_i)}{dw_4} = \displaystyle \sum^{n}_{i=1} -2(y_i-f(x_i)) \times y_{2, i}$
150 |
151 | $\dfrac{d\text{SSR}}{db_1} = \dfrac{dSSR}{df(x_i)} \times \dfrac{df(x_i)}{dy_1} \times \dfrac{dy_1}{dx_1} \times \dfrac{dx_1}{db_1} = \displaystyle \sum^{n}_{i=1} -2(y_i-f(x_i)) \times w_3 \times \dfrac{e^{x_{1, i}}}{1+e^{x_{1, i}}}\times 1$
152 |
153 | $\dfrac{d\text{SSR}}{dw_1} = \dfrac{dSSR}{df(x_i)} \times \dfrac{df(x_i)}{dy_1} \times \dfrac{dy_1}{dx_1} \times \dfrac{dx_1}{dw_1} = \displaystyle \sum^{n}_{i=1} -2(y_i-f(x_i)) \times w_3 \times \dfrac{e^{x_{1, i}}}{1+e^{x_{1, i}}}\times x_{1i}$
154 |
155 | $\dfrac{d\text{SSR}}{db_2} = \dfrac{dSSR}{df(x_i)} \times \dfrac{df(x_i)}{dy_2} \times \dfrac{dy_2}{dx_2} \times \dfrac{dx_2}{db_2} = \displaystyle \sum^{n}_{i=1} -2(y_i-f(x_i)) \times w_4 \times \dfrac{e^{x_{2, i}}}{1+e^{x_{2, i}}}\times 1$
156 |
157 | $\dfrac{d\text{SSR}}{dw_2} = \dfrac{dSSR}{df(x_i)} \times \dfrac{df(x_i)}{dy_2} \times \dfrac{dy_2}{dx_2} \times \dfrac{dx_2}{dw_2} = \displaystyle \sum^{n}_{i=1} -2(y_i-f(x_i)) \times w_4 \times \dfrac{e^{x_{2, i}}}{1+e^{x_{2, i}}}\times x_{2i}$
158 |
159 | 接著使用梯度下降
160 |
161 | $\text{Step size} = \text{Derivative} \times \text{Learning Rate}$
162 |
163 | $\text{New value} = \text{Old value} - \text{Step size}$
164 |
165 | 不斷更新直到值變小到無法再小,或者步驟完成。
166 |
167 |
168 |
169 | ## 建構 2-input ANN
170 |
171 | ### 建立概述
172 |
173 | 我們以複雜的例子來說明,以下圖為例。
174 |
175 |
134 |
135 | 我們令 $af_1(x_i)$ 運算出的結果叫做 $y_{1,i}$,$af_2(x_i)$ 運算出的結果叫做 $y_{2,i}$
136 |
137 | 可以得到 $f(x_i) = w_3 \times y_{1, i} + w_4 \times y_{2, i} + b_3$
138 |
139 | 又 $y_{1, i} = \ln(1+e^{x_{1,i}}), y_{2, i} = \ln(1+e^{x_{2, i}}), x_{1,i}=x_i \times w_1+b_1, x_{2,i} = x_i \times w_2+b_2$,以 Softplus 為例。
140 |
141 |
142 |
143 | 找出導函數,可以使用鎖鏈法則來尋找。
144 |
145 | $\dfrac{d\text{SSR}}{db_3} = \dfrac{dSSR}{df(x_i)} \times \dfrac{df(x_i)}{db_3} = \displaystyle \sum^{n}_{i=1} -2(y_i-f(x_i)) \times 1$
146 |
147 | $\dfrac{d\text{SSR}}{dw_3} = \dfrac{dSSR}{df(x_i)} \times \dfrac{df(x_i)}{dw_3} = \displaystyle \sum^{n}_{i=1} -2(y_i-f(x_i)) \times y_{1, i}$
148 |
149 | $\dfrac{d\text{SSR}}{dw_4} = \dfrac{dSSR}{df(x_i)} \times \dfrac{df(x_i)}{dw_4} = \displaystyle \sum^{n}_{i=1} -2(y_i-f(x_i)) \times y_{2, i}$
150 |
151 | $\dfrac{d\text{SSR}}{db_1} = \dfrac{dSSR}{df(x_i)} \times \dfrac{df(x_i)}{dy_1} \times \dfrac{dy_1}{dx_1} \times \dfrac{dx_1}{db_1} = \displaystyle \sum^{n}_{i=1} -2(y_i-f(x_i)) \times w_3 \times \dfrac{e^{x_{1, i}}}{1+e^{x_{1, i}}}\times 1$
152 |
153 | $\dfrac{d\text{SSR}}{dw_1} = \dfrac{dSSR}{df(x_i)} \times \dfrac{df(x_i)}{dy_1} \times \dfrac{dy_1}{dx_1} \times \dfrac{dx_1}{dw_1} = \displaystyle \sum^{n}_{i=1} -2(y_i-f(x_i)) \times w_3 \times \dfrac{e^{x_{1, i}}}{1+e^{x_{1, i}}}\times x_{1i}$
154 |
155 | $\dfrac{d\text{SSR}}{db_2} = \dfrac{dSSR}{df(x_i)} \times \dfrac{df(x_i)}{dy_2} \times \dfrac{dy_2}{dx_2} \times \dfrac{dx_2}{db_2} = \displaystyle \sum^{n}_{i=1} -2(y_i-f(x_i)) \times w_4 \times \dfrac{e^{x_{2, i}}}{1+e^{x_{2, i}}}\times 1$
156 |
157 | $\dfrac{d\text{SSR}}{dw_2} = \dfrac{dSSR}{df(x_i)} \times \dfrac{df(x_i)}{dy_2} \times \dfrac{dy_2}{dx_2} \times \dfrac{dx_2}{dw_2} = \displaystyle \sum^{n}_{i=1} -2(y_i-f(x_i)) \times w_4 \times \dfrac{e^{x_{2, i}}}{1+e^{x_{2, i}}}\times x_{2i}$
158 |
159 | 接著使用梯度下降
160 |
161 | $\text{Step size} = \text{Derivative} \times \text{Learning Rate}$
162 |
163 | $\text{New value} = \text{Old value} - \text{Step size}$
164 |
165 | 不斷更新直到值變小到無法再小,或者步驟完成。
166 |
167 |
168 |
169 | ## 建構 2-input ANN
170 |
171 | ### 建立概述
172 |
173 | 我們以複雜的例子來說明,以下圖為例。
174 |
175 |  176 |
177 |
178 |
179 | 對於 weight 的部分,我們的初始值可以先給定為**標準常態分布**的隨機一個值,而 bias 可以先預設為 $0$
180 |
181 |
176 |
177 |
178 |
179 | 對於 weight 的部分,我們的初始值可以先給定為**標準常態分布**的隨機一個值,而 bias 可以先預設為 $0$
180 |
181 |  182 |
183 |
184 |
185 | ### 2-input ANN 的參數優化 (Backward Propagation)
186 |
187 | 若要使曲線越來越擬合我們的資料集,我們得要先考慮是否能夠限縮 $\text{SSR}$,使他越小,讓曲線 $f(x_i)$ 越能擬合資料集。
188 |
189 | $\text{SSR}$ 即為殘差平方和,即為對於在 $(x_1, x_2) = (i, j)$ 上的資料集,其所有資料 $(y(x_1, x_2) - f(x_1, x_2))^2$ 的和
190 |
191 | 可以定義為 $\text{SSR} = \displaystyle \sum^{}_{(x_1, x_2) \in S} (y(x_1, x_2) - f(x_1, x_2))^2$
192 |
193 | 若我們想要優化參數,可以找出參數對 $\text{SSR}$ 的導函數,接著使用梯度下降法來同步優化所有參數。
194 |
195 |
196 |
197 | 我們令 $af_1(x_{1i}, x_{2i})$ 運算出的結果叫做 $y_1(x_{1i}, x_{2i})$,$af_2(x_{1i}, x_{2i})$ 運算出的結果叫做 $y_2(x_{1i}, x_{2i})$
198 |
199 | 可以得到 $f(x_{1i}, x_{2i}) = w_5 \times y_1 + w_6 \times y_2 + b_3$
200 |
201 | 又 $y_1 = \ln(1+e^{x_{1}}), y_2 = \ln(1+e^{x_{2}})$,以 Softplus 為例。
202 |
203 | $x_{1}(x_{1i}, x_{2i})= x_{1i} \times w_1 + x_{2i} \times w_3$,$x_2(x_{1i}, x_{2i}) = x_{1i} \times w_2 + x_{2i} \times w_4$
204 |
205 |
206 |
207 | 找出導函數,可以使用鎖鏈法則來尋找。
208 |
209 |
210 |
211 | $\dfrac{d\text{SSR}}{db_3} = \dfrac{d\text{SSR}}{df(x_1, x_2)} \dfrac{df(x_1, x_2)}{db_3} = \displaystyle \sum_{(x_1, x_2) \in S} -2(y(x_1, x_2) - f(x_1, x_2)) \times 1$
212 |
213 | $\dfrac{d\text{SSR}}{dw_5} = \dfrac{d\text{SSR}}{df(x_1, x_2)} \times \dfrac{df(x_1, x_2)}{dw_5} = \displaystyle\sum_{(x_1, x_2) \in S} -2(y(x_1, x_2) - f(x_1, x_2)) \times y_{1}$
214 |
215 | $\dfrac{d\text{SSR}}{dw_6} = \dfrac{d\text{SSR}}{df(x_1, x_2)} \times \dfrac{df(x_1, x_2)}{dw_6} = \displaystyle \sum_{(x_1, x_2) \in S} -2(y(x_1, x_2) - f(x_1, x_2)) \times y_{2}$
216 |
217 | $\dfrac{d\text{SSR}}{db_1} = \dfrac{d\text{SSR}}{df(x_1, x_2)} \times \dfrac{df(x_1, x_2)}{dy_{1}} \times \dfrac{dy_1}{dx_1} \times \dfrac{dx_1}{db_1} = \displaystyle \sum_{(x_1, x_2) \in S} -2(y(x_1, x_2) - f(x_1, x_2)) \times w_5 \times \dfrac{e^{x_1}}{1+e^{x_1}} \times 1$
218 |
219 | $\dfrac{d\text{SSR}}{db_2} = \dfrac{d\text{SSR}}{df(x_1, x_2)} \times \dfrac{df(x_1, x_2)}{dy_{2}} \times \dfrac{dy_2}{dx_2} \times \dfrac{dx_2}{db_2} = \displaystyle \sum_{(x_1, x_2) \in S} -2(y(x_1, x_2) - f(x_1, x_2)) \times w_6 \times \dfrac{e^{x_2}}{1+e^{x_2}} \times 1$
220 |
221 | $\dfrac{d\text{SSR}}{dw_1} = \dfrac{d\text{SSR}}{df(x_1, x_2)} \times \dfrac{df(x_1, x_2)}{dy_{1}} \times \dfrac{dy_1}{dx_1} \times \dfrac{dx_1}{dw_1} = \displaystyle \sum_{(x_1, x_2) \in S} -2(y(x_1, x_2) - f(x_1, x_2)) \times w_5 \times \dfrac{e^{x_1}}{1+e^{x_1}} \times x_{1i}$
222 |
223 | $\dfrac{d\text{SSR}}{dw_2} = \dfrac{d\text{SSR}}{df(x_1, x_2)} \times \dfrac{df(x_1, x_2)}{dy_{2}} \times \dfrac{dy_2}{dx_2} \times \dfrac{dx_2}{dw_2} = \displaystyle \sum_{(x_1, x_2) \in S} -2(y(x_1, x_2) - f(x_1, x_2)) \times w_6 \times \dfrac{e^{x_2}}{1+e^{x_2}} \times x_{1i}$
224 |
225 | $\dfrac{d\text{SSR}}{dw_3} = \dfrac{d\text{SSR}}{df(x_1, x_2)} \times \dfrac{df(x_1, x_2)}{dy_{1}} \times \dfrac{dy_1}{dx_1} \times \dfrac{dx_1}{dw_3} = \displaystyle \sum_{(x_1, x_2) \in S} -2(y(x_1, x_2) - f(x_1, x_2)) \times w_5 \times \dfrac{e^{x_1}}{1+e^{x_1}} \times x_{2i}$
226 |
227 | $\dfrac{d\text{SSR}}{dw_4} = \dfrac{d\text{SSR}}{df(x_1, x_2)} \times \dfrac{df(x_1, x_2)}{dy_{2}} \times \dfrac{dy_2}{dx_2} \times \dfrac{dx_2}{dw_4} = \displaystyle \sum_{(x_1, x_2) \in S} -2(y(x_1, x_2) - f(x_1, x_2)) \times w_6 \times \dfrac{e^{x_2}}{1+e^{x_2}} \times x_{2i}$
228 |
229 | 接著使用梯度下降
230 |
231 | $\text{Step size} = \text{Derivative} \times \text{Learning Rate}$
232 |
233 | $\text{New value} = \text{Old value} - \text{Step size}$
234 |
235 | 不斷更新直到值變小到無法再小,或者步驟完成。
236 |
237 |
238 |
239 | ## ANN 的優缺點
240 |
241 | - 優點:
242 | 1. 準確度高
243 | 2. 可以處理很多種類的問題
244 | 3. 可以包含很多種類的資料(數值、名目...)
245 | 4. 可以得到非常好的 R-Score,只要訓練充足就可以
246 | - 缺點
247 | 1. 可能永遠訓練不完
248 | 2. 黑箱,所以很難向別人描述這個原理
249 | 3. 需要很大量的資料來訓練,才有準確度
250 | 4. 對於多變量來說可能會讓訓練過程變得非常長
--------------------------------------------------------------------------------
/Markdown/Associate Rule Mining.md:
--------------------------------------------------------------------------------
1 | # RS -- Associate Rule Mining(推薦系統 ─ 關聯規則探勘)
2 |
3 | > Reference:
4 | >
5 | > 1. Recommendation System -- Associate Rule Mining by Dr. Tun-Wen Pai
6 | > 2. [矩陣分解(Matrix Factorization): 交替最小平方法(Alternating least squares, ALS)和加權交替最小平方法(Alternating-least-squares with weighted-λ -regularization, ALS-WR)](https://chih-sheng-huang821.medium.com/%E7%9F%A9%E9%99%A3%E5%88%86%E8%A7%A3-matrix-factorization-%E4%BA%A4%E6%9B%BF%E6%9C%80%E5%B0%8F%E5%B9%B3%E6%96%B9%E6%B3%95-alternating-least-squares-2a71fd1393f7)
7 | > 3. [Day 07:初探推薦系統(Recommendation System)](https://ithelp.ithome.com.tw/articles/10219033)
8 |
9 |
10 |
11 | ## 推薦系統
12 |
13 | 啤酒對應到尿布是一個著名的關聯規則探勘例子,透過大量的銷售資料集探勘出了啤酒跟尿布同時購買的頻率很高。
14 |
15 | 在這份筆記,我們最主要會去探討要怎麼從大量的資料找到頻繁樣式,也就是找出哪種商品的購買組合頻率最高。
16 |
17 | 從大數據來說,找到東西的關聯是非常重要的。
18 |
19 | 推薦系統支持了我們找出頻繁樣式,進而從大量的資料分析出特定的組合,就能夠找出推薦的組合,稱為推薦系統。
20 |
21 |
22 |
23 | 主要有以下幾種不同的工具可以幫我們建立推薦系統。
24 |
25 | - Association Rule Mining(ARM),關聯規則探勘。
26 | - 我們可以用 Frequent pattern(頻繁樣式)來找出資料集的發生頻率。
27 | - Alternating Least Square(ALS),交替最小平方法。
28 | - 對一個隱含資料(Implicit Data)使用協同過濾演算法,例如 Matrix Factorization 來建立關聯。
29 | - Content Based Filtering
30 | - 以內容為基礎的過濾,比較商品的屬性,找出最相似的商品。
31 |
32 |
33 |
34 | ## 關聯規則探勘
35 |
36 | 關聯規則探勘 (Association Rule Mining),一種非監督式學習技巧,
37 |
38 | 利用大量的資料所產生的資料集來找出頻繁樣式、關聯、相關性、因果結構等等。
39 |
40 | 其中,Association Rule Mining 使用的是類別資料(Categorical Variable)。
41 |
42 |
43 |
44 | 若我們有 $N$ 個物品 $I_i$ 組成的物品集 $I$,對於一個輸入 Association Rule Mining 的資料集,
45 |
46 | 每筆資料 $T$ 都是資料集的子集合,稱為物品集,也就是 $T \subseteq I$。
47 |
48 |
49 |
50 | 例如我們有 6 個物品所組成的 $\{A, B, C, D, E, F\}$,我們有一個資料集:
51 |
52 | | ID | Item Set |
53 | | :--: | :------: |
54 | | 1 | A, B, C |
55 | | 2 | B, D, E |
56 | | 3 | D, E, F |
57 | | 4 | A, C, E |
58 | | 5 | B, E, F |
59 |
60 | 我們就能夠從這個資料集找出頻繁樣式。
61 |
62 |
63 |
64 | ### Support, Confidence and Lift
65 |
66 | 從大量的資料集,我們希望能夠量化出現頻率,來找到頻繁樣式,所以在 ARM 中將每個組合量化出了三種數值。
67 |
68 | 對於先發生事件 $A$ 再發生事件 $C$,我們可以量化出三種數值:
69 |
70 | - Support:$P(A \cap C)$,量化這個組合發生的機率。
71 | - Confidence:$P(C|A)$,量化這個組合發生 A 再發生 C 的機率。
72 | - Lift:$P(C|A)/P(C)$,用於量化這個組合的效力,通常大於 1 就代表這個組合是有效的。
73 |
74 |
75 |
76 | 那麼使用者可以設定一個門檻,用來採納這個頻繁組合該不該適用。
77 |
78 | 若使用者設定 Support > 40%,且 Confidence > 60%,使用者就可以接受這個組合為頻繁組合。
79 |
80 |
81 |
82 | ## 先驗演算法
83 |
84 | 對於一個很大的資料庫來說,我們可能同時會有很多個不同的頻繁組合。
85 |
86 | 我們希望可以制定頻繁組合必須要至少 Support 大於 k,來淘汰掉一些不太適用的組合。
87 |
88 |
89 |
90 | 先驗演算法的一些原則:
91 |
92 | 1. 一個組合的任意子集都在資料庫內,例如組合為 {a, b, c},則 {a}, {b}, {c}, {ab}, {ac}, {bc}, {abc} 都應發生在資料庫內。
93 |
94 | 2. Apriori pruning principle:當我們用任意兩種組合產生出另一個新組合,則這個新組合
95 |
96 | 也應該要符合第一點的原則,否則不該產生。
97 |
98 | 例如:透過 {a, c, e} 與 {a, e, f} 產生出了 {a, c, e, f} 這個組合,
99 |
100 | 但若 {c, e, f} 這個組合並沒有發生在資料庫內,則 {a, c, e, f} 這個組合無效。
101 |
102 |
103 |
104 | 下圖為演算法的產生過程。
105 |
106 | 1. 從原先的資料庫產生出了 1-item-set 的組合,並且刪去只有 support = 1 的組合(因為我們要求 min_support = 2)
107 |
108 | 2. 從 1-item-set 的任意兩種組合聯集,產生出了 **2**-item-set 的組合,並且刪去只有 support = 1 的組合
109 | 3. 從 i-item-set 產生出了 **(i+1)**-item-set 的組合...,直到能夠被分到只有一個。
110 |
111 |
182 |
183 |
184 |
185 | ### 2-input ANN 的參數優化 (Backward Propagation)
186 |
187 | 若要使曲線越來越擬合我們的資料集,我們得要先考慮是否能夠限縮 $\text{SSR}$,使他越小,讓曲線 $f(x_i)$ 越能擬合資料集。
188 |
189 | $\text{SSR}$ 即為殘差平方和,即為對於在 $(x_1, x_2) = (i, j)$ 上的資料集,其所有資料 $(y(x_1, x_2) - f(x_1, x_2))^2$ 的和
190 |
191 | 可以定義為 $\text{SSR} = \displaystyle \sum^{}_{(x_1, x_2) \in S} (y(x_1, x_2) - f(x_1, x_2))^2$
192 |
193 | 若我們想要優化參數,可以找出參數對 $\text{SSR}$ 的導函數,接著使用梯度下降法來同步優化所有參數。
194 |
195 |
196 |
197 | 我們令 $af_1(x_{1i}, x_{2i})$ 運算出的結果叫做 $y_1(x_{1i}, x_{2i})$,$af_2(x_{1i}, x_{2i})$ 運算出的結果叫做 $y_2(x_{1i}, x_{2i})$
198 |
199 | 可以得到 $f(x_{1i}, x_{2i}) = w_5 \times y_1 + w_6 \times y_2 + b_3$
200 |
201 | 又 $y_1 = \ln(1+e^{x_{1}}), y_2 = \ln(1+e^{x_{2}})$,以 Softplus 為例。
202 |
203 | $x_{1}(x_{1i}, x_{2i})= x_{1i} \times w_1 + x_{2i} \times w_3$,$x_2(x_{1i}, x_{2i}) = x_{1i} \times w_2 + x_{2i} \times w_4$
204 |
205 |
206 |
207 | 找出導函數,可以使用鎖鏈法則來尋找。
208 |
209 |
210 |
211 | $\dfrac{d\text{SSR}}{db_3} = \dfrac{d\text{SSR}}{df(x_1, x_2)} \dfrac{df(x_1, x_2)}{db_3} = \displaystyle \sum_{(x_1, x_2) \in S} -2(y(x_1, x_2) - f(x_1, x_2)) \times 1$
212 |
213 | $\dfrac{d\text{SSR}}{dw_5} = \dfrac{d\text{SSR}}{df(x_1, x_2)} \times \dfrac{df(x_1, x_2)}{dw_5} = \displaystyle\sum_{(x_1, x_2) \in S} -2(y(x_1, x_2) - f(x_1, x_2)) \times y_{1}$
214 |
215 | $\dfrac{d\text{SSR}}{dw_6} = \dfrac{d\text{SSR}}{df(x_1, x_2)} \times \dfrac{df(x_1, x_2)}{dw_6} = \displaystyle \sum_{(x_1, x_2) \in S} -2(y(x_1, x_2) - f(x_1, x_2)) \times y_{2}$
216 |
217 | $\dfrac{d\text{SSR}}{db_1} = \dfrac{d\text{SSR}}{df(x_1, x_2)} \times \dfrac{df(x_1, x_2)}{dy_{1}} \times \dfrac{dy_1}{dx_1} \times \dfrac{dx_1}{db_1} = \displaystyle \sum_{(x_1, x_2) \in S} -2(y(x_1, x_2) - f(x_1, x_2)) \times w_5 \times \dfrac{e^{x_1}}{1+e^{x_1}} \times 1$
218 |
219 | $\dfrac{d\text{SSR}}{db_2} = \dfrac{d\text{SSR}}{df(x_1, x_2)} \times \dfrac{df(x_1, x_2)}{dy_{2}} \times \dfrac{dy_2}{dx_2} \times \dfrac{dx_2}{db_2} = \displaystyle \sum_{(x_1, x_2) \in S} -2(y(x_1, x_2) - f(x_1, x_2)) \times w_6 \times \dfrac{e^{x_2}}{1+e^{x_2}} \times 1$
220 |
221 | $\dfrac{d\text{SSR}}{dw_1} = \dfrac{d\text{SSR}}{df(x_1, x_2)} \times \dfrac{df(x_1, x_2)}{dy_{1}} \times \dfrac{dy_1}{dx_1} \times \dfrac{dx_1}{dw_1} = \displaystyle \sum_{(x_1, x_2) \in S} -2(y(x_1, x_2) - f(x_1, x_2)) \times w_5 \times \dfrac{e^{x_1}}{1+e^{x_1}} \times x_{1i}$
222 |
223 | $\dfrac{d\text{SSR}}{dw_2} = \dfrac{d\text{SSR}}{df(x_1, x_2)} \times \dfrac{df(x_1, x_2)}{dy_{2}} \times \dfrac{dy_2}{dx_2} \times \dfrac{dx_2}{dw_2} = \displaystyle \sum_{(x_1, x_2) \in S} -2(y(x_1, x_2) - f(x_1, x_2)) \times w_6 \times \dfrac{e^{x_2}}{1+e^{x_2}} \times x_{1i}$
224 |
225 | $\dfrac{d\text{SSR}}{dw_3} = \dfrac{d\text{SSR}}{df(x_1, x_2)} \times \dfrac{df(x_1, x_2)}{dy_{1}} \times \dfrac{dy_1}{dx_1} \times \dfrac{dx_1}{dw_3} = \displaystyle \sum_{(x_1, x_2) \in S} -2(y(x_1, x_2) - f(x_1, x_2)) \times w_5 \times \dfrac{e^{x_1}}{1+e^{x_1}} \times x_{2i}$
226 |
227 | $\dfrac{d\text{SSR}}{dw_4} = \dfrac{d\text{SSR}}{df(x_1, x_2)} \times \dfrac{df(x_1, x_2)}{dy_{2}} \times \dfrac{dy_2}{dx_2} \times \dfrac{dx_2}{dw_4} = \displaystyle \sum_{(x_1, x_2) \in S} -2(y(x_1, x_2) - f(x_1, x_2)) \times w_6 \times \dfrac{e^{x_2}}{1+e^{x_2}} \times x_{2i}$
228 |
229 | 接著使用梯度下降
230 |
231 | $\text{Step size} = \text{Derivative} \times \text{Learning Rate}$
232 |
233 | $\text{New value} = \text{Old value} - \text{Step size}$
234 |
235 | 不斷更新直到值變小到無法再小,或者步驟完成。
236 |
237 |
238 |
239 | ## ANN 的優缺點
240 |
241 | - 優點:
242 | 1. 準確度高
243 | 2. 可以處理很多種類的問題
244 | 3. 可以包含很多種類的資料(數值、名目...)
245 | 4. 可以得到非常好的 R-Score,只要訓練充足就可以
246 | - 缺點
247 | 1. 可能永遠訓練不完
248 | 2. 黑箱,所以很難向別人描述這個原理
249 | 3. 需要很大量的資料來訓練,才有準確度
250 | 4. 對於多變量來說可能會讓訓練過程變得非常長
--------------------------------------------------------------------------------
/Markdown/Associate Rule Mining.md:
--------------------------------------------------------------------------------
1 | # RS -- Associate Rule Mining(推薦系統 ─ 關聯規則探勘)
2 |
3 | > Reference:
4 | >
5 | > 1. Recommendation System -- Associate Rule Mining by Dr. Tun-Wen Pai
6 | > 2. [矩陣分解(Matrix Factorization): 交替最小平方法(Alternating least squares, ALS)和加權交替最小平方法(Alternating-least-squares with weighted-λ -regularization, ALS-WR)](https://chih-sheng-huang821.medium.com/%E7%9F%A9%E9%99%A3%E5%88%86%E8%A7%A3-matrix-factorization-%E4%BA%A4%E6%9B%BF%E6%9C%80%E5%B0%8F%E5%B9%B3%E6%96%B9%E6%B3%95-alternating-least-squares-2a71fd1393f7)
7 | > 3. [Day 07:初探推薦系統(Recommendation System)](https://ithelp.ithome.com.tw/articles/10219033)
8 |
9 |
10 |
11 | ## 推薦系統
12 |
13 | 啤酒對應到尿布是一個著名的關聯規則探勘例子,透過大量的銷售資料集探勘出了啤酒跟尿布同時購買的頻率很高。
14 |
15 | 在這份筆記,我們最主要會去探討要怎麼從大量的資料找到頻繁樣式,也就是找出哪種商品的購買組合頻率最高。
16 |
17 | 從大數據來說,找到東西的關聯是非常重要的。
18 |
19 | 推薦系統支持了我們找出頻繁樣式,進而從大量的資料分析出特定的組合,就能夠找出推薦的組合,稱為推薦系統。
20 |
21 |
22 |
23 | 主要有以下幾種不同的工具可以幫我們建立推薦系統。
24 |
25 | - Association Rule Mining(ARM),關聯規則探勘。
26 | - 我們可以用 Frequent pattern(頻繁樣式)來找出資料集的發生頻率。
27 | - Alternating Least Square(ALS),交替最小平方法。
28 | - 對一個隱含資料(Implicit Data)使用協同過濾演算法,例如 Matrix Factorization 來建立關聯。
29 | - Content Based Filtering
30 | - 以內容為基礎的過濾,比較商品的屬性,找出最相似的商品。
31 |
32 |
33 |
34 | ## 關聯規則探勘
35 |
36 | 關聯規則探勘 (Association Rule Mining),一種非監督式學習技巧,
37 |
38 | 利用大量的資料所產生的資料集來找出頻繁樣式、關聯、相關性、因果結構等等。
39 |
40 | 其中,Association Rule Mining 使用的是類別資料(Categorical Variable)。
41 |
42 |
43 |
44 | 若我們有 $N$ 個物品 $I_i$ 組成的物品集 $I$,對於一個輸入 Association Rule Mining 的資料集,
45 |
46 | 每筆資料 $T$ 都是資料集的子集合,稱為物品集,也就是 $T \subseteq I$。
47 |
48 |
49 |
50 | 例如我們有 6 個物品所組成的 $\{A, B, C, D, E, F\}$,我們有一個資料集:
51 |
52 | | ID | Item Set |
53 | | :--: | :------: |
54 | | 1 | A, B, C |
55 | | 2 | B, D, E |
56 | | 3 | D, E, F |
57 | | 4 | A, C, E |
58 | | 5 | B, E, F |
59 |
60 | 我們就能夠從這個資料集找出頻繁樣式。
61 |
62 |
63 |
64 | ### Support, Confidence and Lift
65 |
66 | 從大量的資料集,我們希望能夠量化出現頻率,來找到頻繁樣式,所以在 ARM 中將每個組合量化出了三種數值。
67 |
68 | 對於先發生事件 $A$ 再發生事件 $C$,我們可以量化出三種數值:
69 |
70 | - Support:$P(A \cap C)$,量化這個組合發生的機率。
71 | - Confidence:$P(C|A)$,量化這個組合發生 A 再發生 C 的機率。
72 | - Lift:$P(C|A)/P(C)$,用於量化這個組合的效力,通常大於 1 就代表這個組合是有效的。
73 |
74 |
75 |
76 | 那麼使用者可以設定一個門檻,用來採納這個頻繁組合該不該適用。
77 |
78 | 若使用者設定 Support > 40%,且 Confidence > 60%,使用者就可以接受這個組合為頻繁組合。
79 |
80 |
81 |
82 | ## 先驗演算法
83 |
84 | 對於一個很大的資料庫來說,我們可能同時會有很多個不同的頻繁組合。
85 |
86 | 我們希望可以制定頻繁組合必須要至少 Support 大於 k,來淘汰掉一些不太適用的組合。
87 |
88 |
89 |
90 | 先驗演算法的一些原則:
91 |
92 | 1. 一個組合的任意子集都在資料庫內,例如組合為 {a, b, c},則 {a}, {b}, {c}, {ab}, {ac}, {bc}, {abc} 都應發生在資料庫內。
93 |
94 | 2. Apriori pruning principle:當我們用任意兩種組合產生出另一個新組合,則這個新組合
95 |
96 | 也應該要符合第一點的原則,否則不該產生。
97 |
98 | 例如:透過 {a, c, e} 與 {a, e, f} 產生出了 {a, c, e, f} 這個組合,
99 |
100 | 但若 {c, e, f} 這個組合並沒有發生在資料庫內,則 {a, c, e, f} 這個組合無效。
101 |
102 |
103 |
104 | 下圖為演算法的產生過程。
105 |
106 | 1. 從原先的資料庫產生出了 1-item-set 的組合,並且刪去只有 support = 1 的組合(因為我們要求 min_support = 2)
107 |
108 | 2. 從 1-item-set 的任意兩種組合聯集,產生出了 **2**-item-set 的組合,並且刪去只有 support = 1 的組合
109 | 3. 從 i-item-set 產生出了 **(i+1)**-item-set 的組合...,直到能夠被分到只有一個。
110 |
111 |  112 |
113 |
114 |
115 |
116 |
117 | ### 先驗演算法的缺點
118 |
119 | 對於大資料集來說,**為了產生候選組合,時間與效能耗費過大**。
120 |
121 |
122 |
123 |
124 |
125 | ## FP-Tree
126 |
127 | 樹狀結構很讚,能夠高效的處理大量資料。
128 |
129 |
112 |
113 |
114 |
115 |
116 |
117 | ### 先驗演算法的缺點
118 |
119 | 對於大資料集來說,**為了產生候選組合,時間與效能耗費過大**。
120 |
121 |
122 |
123 |
124 |
125 | ## FP-Tree
126 |
127 | 樹狀結構很讚,能夠高效的處理大量資料。
128 |
129 |  130 |
131 |
132 |
133 | FP-Tree 可以幫助我們建立出頻繁樣式,雖然高壓縮但頻繁樣式完整。
134 |
135 |
136 |
137 | ### frequent item table
138 |
139 | 若我們有左邊的資料表,由上至下的 ID 為 1、2、3、4、5。
140 |
141 | 首先我們應先設定一個 support 為門檻,淘汰掉不需要的資料。
142 |
143 |
144 |
145 | 以左邊為例,我們設定 min_support = 3。
146 |
147 | 經過淘汰掉不在門檻上的資料,得到右邊的 frequent item table。
148 |
149 | | Database | Frequent item table (unordered) |
150 | | :---------------------------------------------------------: | :---------------------------------------------------------: |
151 | |  |  |
152 |
153 | 我們需要對這個 table 做排序,根據物品出現的頻率由多至少排序,左圖呈現物品次數所建構的次數表,右圖呈現排序過後的表格。
154 |
155 | | Header Table | Frequent item table (ordered) |
156 | | :---------------------------------------------------------: | :---------------------------------------------------------: |
157 | |  |  |
158 |
159 | 接著只需要使用 Frequent item table,對於每一項逐一建樹即可。
160 |
161 | | Data1 | Data2 | Data3 |
162 | | :---------------------------------------------------------: | :----------------------------------------------------------: | :----------------------------------------------------------: |
163 | |  |  |
130 |
131 |
132 |
133 | FP-Tree 可以幫助我們建立出頻繁樣式,雖然高壓縮但頻繁樣式完整。
134 |
135 |
136 |
137 | ### frequent item table
138 |
139 | 若我們有左邊的資料表,由上至下的 ID 為 1、2、3、4、5。
140 |
141 | 首先我們應先設定一個 support 為門檻,淘汰掉不需要的資料。
142 |
143 |
144 |
145 | 以左邊為例,我們設定 min_support = 3。
146 |
147 | 經過淘汰掉不在門檻上的資料,得到右邊的 frequent item table。
148 |
149 | | Database | Frequent item table (unordered) |
150 | | :---------------------------------------------------------: | :---------------------------------------------------------: |
151 | |  |  |
152 |
153 | 我們需要對這個 table 做排序,根據物品出現的頻率由多至少排序,左圖呈現物品次數所建構的次數表,右圖呈現排序過後的表格。
154 |
155 | | Header Table | Frequent item table (ordered) |
156 | | :---------------------------------------------------------: | :---------------------------------------------------------: |
157 | |  |  |
158 |
159 | 接著只需要使用 Frequent item table,對於每一項逐一建樹即可。
160 |
161 | | Data1 | Data2 | Data3 |
162 | | :---------------------------------------------------------: | :----------------------------------------------------------: | :----------------------------------------------------------: |
163 | |  |  |  |
164 | | **Data 4** | **Data 5** | |
165 | |  |
|
164 | | **Data 4** | **Data 5** | |
165 | |  |  | |
166 |
167 | 藉此我們就能建構完整的 FP-Tree。
168 |
169 |
170 |
171 | ### conditional pattern base
172 |
173 | 對於一棵 FP-Tree,我們可以非常快速的查詢到樣式發生的次數。
174 |
175 | 以下圖為例,我們可以根據 Header Table 來逐一查詢。
176 |
177 | | Header Table | Frequent item table |
178 | | :---------------------------------------------------------: | :----------------------------------------------------------: |
179 | |  |
| |
166 |
167 | 藉此我們就能建構完整的 FP-Tree。
168 |
169 |
170 |
171 | ### conditional pattern base
172 |
173 | 對於一棵 FP-Tree,我們可以非常快速的查詢到樣式發生的次數。
174 |
175 | 以下圖為例,我們可以根據 Header Table 來逐一查詢。
176 |
177 | | Header Table | Frequent item table |
178 | | :---------------------------------------------------------: | :----------------------------------------------------------: |
179 | |  |  |
180 |
181 | 由於具有 BFS 的特性,所以我們可以很快速的查詢到相對的樣式。
182 |
183 | 我們會從 Header Table 第二項到第六項開始做向上尋訪(紅色節點)即可得到 Conditional Pattern Base
184 |
185 | 發生次數即為紫色節點的數字。
186 |
187 | | Item | Image | Conditional Pattern base |
188 | | :--: | :----------------------------------------------------------: | :----------------------: |
189 | | c |
|
180 |
181 | 由於具有 BFS 的特性,所以我們可以很快速的查詢到相對的樣式。
182 |
183 | 我們會從 Header Table 第二項到第六項開始做向上尋訪(紅色節點)即可得到 Conditional Pattern Base
184 |
185 | 發生次數即為紫色節點的數字。
186 |
187 | | Item | Image | Conditional Pattern base |
188 | | :--: | :----------------------------------------------------------: | :----------------------: |
189 | | c |  | f:3 |
190 | | a |
| f:3 |
190 | | a |  | fc:3 |
191 | | b |
| fc:3 |
191 | | b |  | fca: 1
| fca: 1
f:1
c:1 |
192 | | m |  | fca:2
| fca:2
fcab:1 |
193 | | p |  | fcam:2
| fcam:2
cb:1 |
194 |
195 |
196 |
197 | ### conditional FP-Tree
198 |
199 | 從前面的 conditional pattern base 之後,我們可以根據某一物品 $i$ 的所有 conditional pattern base 所建立出的分支取交集。
200 |
201 | 以 m 為例,我們已知 `fca:2, fcam:1`,即為兩個不同分支,我們可以將這些分支取交集合併,得到一個新的 conditional FP-Tree。
202 |
203 | | FP-Tree when item=m | conditional FP-Tree |
204 | | :----------------------------------------------------------: | :---------------------------------------------------------: |
205 | |  |  |
206 |
207 | 我們就能根據這個 conditional FP-Tree 窮舉出所有含有 m 的樣式,也就是`m, fm, cm, am, fcm, fam, cam, fcam`
208 |
209 | 我們還能根據 conditional FP-Tree 以遞迴的形式找出 am, cm, cam... 的 conditional FP-Tree,與上述同理。
210 |
211 |
212 |
213 | ## Collaborative Filtering
214 |
215 | 我們可以使用 Collaborative Filtering 來找出兩個相似的人或事物,分成以 User-Based 為主與以 Item-Based 為主。
216 |
217 | 我們會根據使用者或物品的 rating 來評估推薦
218 |
219 | 但也因此會有 cold start 的問題,也就是新東西或新的人進來之後會不知道要推薦什麼,因為沒有任何的評分紀錄。
220 |
221 |
222 |
223 | 要找出相似的人事物,我們需要算出相似度:
224 |
225 | - Jaccard similarity measure $\text{sim}(x, y) = \dfrac{|r_x \cap r_y|}{|r_x|+|r_y|-|r_x\cap r_y|}$,其中 $v_x, v_y$ 為 User rating set。
226 | - Cosine similarity:$\text{sim}(x, y) = \dfrac{r_x\cdot r_y}{||r_x||\cdot||r_y||}$
227 | - Pearson correlation coefficient:$\text{sim}(x,y)=\dfrac{\displaystyle \sum_{s\in s_{xy}} (r_{xs}-\overline{r_x})(r_{ys}-\overline{r_y})}{\sqrt{\sum_{s\in s_{xy}} (r_{xs}-\overline{r_x})^2} \sqrt{\sum_{s\in s_{xy}} (r_{ys}-\overline{r_y})^2}}$,$s_{xy}$ 為 x 與 y 對某物的評價。
228 |
229 |
230 |
231 | ### User-based collaborative filtering
232 |
233 | 我們可以使用 user-item rating matrix,找出 user 與 user 之間的關聯性。
234 |
235 | 只要找出兩個 user 有高相似度,就能把類似的行為推薦給 user。
236 |
237 |
238 |
239 | ### Item-based collaborative filtering
240 |
241 | 我們可以使用 user-item rating matrix,找出 item 與 item 之間的關聯性。
242 |
243 | 只要找出兩個 item 有高相似度,就能把類似的行為推薦給 user。
244 |
245 |
246 |
247 |
248 |
249 | ### Jaccard similarity measure
250 |
251 | 第一個提到的相似度計算即為 Jaccard similarity measure。
252 |
253 | Jaccard similarity measure 不管評分,只管該 index 有沒有評分,以下面的例子為例。
254 |
255 | | | 1 | 2 | 3 | 4 | 5 |
256 | | :--: | :--: | :--: | :--: | :--: | :--: |
257 | | x | 1 | | | 1 | 3 |
258 | | y | 1 | | 2 | 2 | |
259 |
260 | 我們可以得到 User rating set $r_x = \{1, 4, 5\}$,$r_y = \{1, 3, 4\}$,因為 $x$ 只有在 1、4、5 做評分,$y$ 只有在 1、3、4 做評分。
261 |
262 | 由於 $r_x$ 與 $r_y$ 有交集的數量只有 $2$,聯集則是 $4$,故 $\text{sim}(x, y) = \dfrac{2}{4} = 0.5$
263 |
264 |
265 |
266 | 缺點則是評分上是有意義的,故這樣做會忽略掉評分的意義。
267 |
268 |
269 |
270 | ### Cosine similarity
271 |
272 | 第二個提到的相似度計算即為 Cosine similarity。
273 |
274 | 以下面的例子為例。
275 |
276 | | | 1 | 2 | 3 | 4 | 5 |
277 | | :--: | :--: | :--: | :--: | :--: | :--: |
278 | | x | 1 | | | 1 | 3 |
279 | | y | 1 | | 2 | 2 | |
280 |
281 | 我們可以將 $r_x, r_y$ 視為點,則可以得到
282 | $$
283 | r_x = <1, 0, 0, 1, 3> \\
284 | r_y = <1, 0, 2, 2, 0>
285 | $$
286 | 故其 Cosine similarity 為 $\dfrac{1+0+0+2+0}{\sqrt{1^2+1^2+3^2}\sqrt{1^2+2^2+2^2}} \approx 30.2\%$
287 |
288 |
289 |
290 | ### Pearson correlation coefficient
291 |
292 | 定義上為 $\text{sim}(x,y)=\dfrac{\displaystyle \sum_{s\in s_{xy}} (r_{xs}-\overline{r_x})(r_{ys}-\overline{r_y})}{\sqrt{\sum_{s\in s_{xy}} (r_{xs}-\overline{r_x})^2} \sqrt{\sum_{s\in s_{xy}} (r_{ys}-\overline{r_y})^2}}$,$s_{xy}$ 為 x 與 y 對某物的評價。
293 |
294 | 雖然定義上是這樣,但,其實你只要算出列/行的平均,行/列存在的元素全部減去平均後砸 Cosine Similarity 也能做出來
295 |
296 | ~~安了我的算式恐懼症,這麼可怕的式子是啥鬼嗚嗚~~
297 |
298 |
299 |
300 | 以下面的例子為例。
301 |
302 | | | 1 | 2 | 3 | 4 | 5 |
303 | | :--: | :--: | :--: | :--: | :--: | :--: |
304 | | x | 2 | | | 1 | 3 |
305 | | y | 2 | | 2 | 2 | |
306 |
307 | 我們可以將 $r_x, r_y$ 視為點,則可以得到
308 | $$
309 | r_x = <1, 0, 0, 1, 3> \\
310 | r_y = <1, 0, 2, 2, 0>
311 | $$
312 | 平均 $\mu_x = 2$,$\mu_y = 2$,則
313 | $$
314 | r_x' = <-1, 0, 0, -1, 1> \\
315 | r_y' = <-1, 0, 0, 0, 0>
316 | $$
317 | 我們可以算出 Pearson correlation coefficient
318 | $$
319 | \text{sim}(x, y) = \dfrac{1}{((-1)^2+(-1)^2+1^2)((-1)^2)} = \dfrac{1}{3} \approx 0.333
320 | $$
321 |
322 |
323 | ### Prediction Function
324 |
325 | 若我們有一個物件與其他 $N$ 個物件相似,則我們可以用以下的式子來表達其預測值
326 | $$
327 | r_{xi} = \dfrac{\displaystyle \sum_{j\in N(i; x)} s_{ij} \cdot r_{xj}}{\displaystyle \sum_{j\in N(i; x)} s_{ij}}
328 | $$
329 | 見以下範例。
330 |
331 |
332 |
333 | ### Item-Item Collaborative Filtering
334 |
335 | 假設我們有一筆這樣的資料,欄為 User 且列為 Movie,表格上每個數字為 User 對 Movie 的評價
336 |
337 | | | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
338 | | :--: | :--: | :--: | :--: | :--: | :----: | :--: | :--: | :--: | :--: | :--: | :--: | :--: |
339 | | 1 | 1 | | 3 | | **?** | 5 | | | 5 | | 4 | |
340 | | 2 | | | 5 | 4 | | | 4 | | | 2 | 1 | 3 |
341 | | 3 | 2 | 4 | | 1 | 2 | | 3 | | 4 | 3 | 5 | |
342 | | 4 | | 2 | 4 | | 5 | | | 4 | | | 2 | |
343 | | 5 | | | 4 | 3 | 4 | 2 | | | | | 2 | |
344 | | 6 | 1 | | 3 | | 3 | | | 2 | | | 4 | |
345 |
346 | 可以看到 $D(1, 5)$ 的資料是問號,即為我們想要推演的資料。
347 |
348 | 我們使用 Pearson correlation coefficient 來**計算電影的相似度**,先算出每個電影的平均值,以及該列減去平均值的向量。
349 |
350 | $\mu_1 = (1+3+5+5+4)/5 = 3.6$,$v'_1 = <-2.6, 0, -0.6, 0, 0, 1.4, 0, 0, 1.4, 0, 0.4, 0>$
351 |
352 | $\mu_2 = (5+4+4+2+1+3)/6=3.167$,$v'_2 = <0, 0, 1.83, 0.83, 0, 0, 0.83, 0, 0, -1.17, -2.17, -0.17>$
353 |
354 | $\mu_3 = (2+4+1+2+3+4+3+5)/8=3$,$v'_3 = <-1, 1, 0, -2, -1, 0, 0, 0, 1, 0, 2, 0>$
355 |
356 | $\mu_4 = (2+4+5+4+2)/5=3.4$,$v'_4 = <0, -1.4, 0.6, 0, 1.6, 0, 0, 0.6, 0, 0, -1.4, 0>$
357 |
358 | $\mu_5 = (4+3+4+2+2)/5=3$,$v'_5 = <0, 0, 1, 0, 1, -1, 0, 0, 0, 0, -1, 0>$
359 |
360 | $\mu_6 = (1+3+3+2+4)/5=2.6$,$v'_6 = <-1.6, 0, 0.4, 0, 0.4, 0, 0, -0.6, 0, 0, 1.4. 0>$
361 |
362 | 我們可以算出 Pearson correlation coefficient,得到
363 |
364 | $\text{sim}(1, 2) = -0.17$,$\text{sim}(1, 3) = 0.41$,$\text{sim}(1, 4) = -0.1$,$\text{sim}(1, 5) = -0.36$,$\text{sim}(1, 6) = 0.59$
365 |
366 | 故我們選擇電影 3、6 與電影 1 有較高的關聯性。
367 |
368 |
369 |
370 | 因此我們可以套用預測函數,得到:
371 | $$
372 | \dfrac{0.41\times 2 + 0.59\times 3}{0.41+0.59} = 2.6
373 | $$
374 | 故 $D(1, 5)$ 可以被預測成 2.6 分。
375 |
376 |
377 |
378 | ### User-User Collaborative Filtering
379 |
380 | 與 [Item-Item Collaborative Filtering](#Item-Item Collaborative Filtering) 同理,跳過。
381 |
382 |
383 |
384 | ## Content-based Filtering
385 |
386 | 使用內容來進行評估,因為使用內容,所以不會有 cold start 的問題。
387 |
388 |
389 |
390 | ### TF-IDF
391 |
392 | TF-IDF (Term Frequency - Inverse Document Frequency),用來量化詞彙的重要性,但會隨著詞彙出現的頻率高而出現反比影響。
393 |
394 | 其定義為:
395 | $$
396 | TF_{ij} = \dfrac{n_{ij}}{\sum_{k} n_{kj}} \\
397 | IDF_{i} = \log(\dfrac{N}{n_i}) \\
398 | \text{TF-IDF}_{ij} = TF_{ij} \times IDF_{i}
399 | $$
400 | 其中 TF 的 $n_{ij}$ 為該詞彙在文件中的次數,分母則是在所有文件中該詞彙出現的次數,$N$ 為文件的總詞彙量。
401 |
402 |
--------------------------------------------------------------------------------
/Markdown/Cluster Analysis.md:
--------------------------------------------------------------------------------
1 | # 群聚分析(Cluster Analysis)
2 |
3 | > Reference:
4 | >
5 | > 1. Cluster Analysis - Dr. Tun-Wen Pai
6 |
7 | ## 群聚分析
8 |
9 | 主要分成兩種不同的群聚分析:
10 |
11 | 1. 分層式群聚:分成由上至下(top-down)或由下至上(bottom-up)演算法,層層迭代運算。
12 | 2. 分割式群聚:一次把所有的分群結果納入考慮。
13 |
14 |
15 |
16 | ## 分割式群聚
17 |
18 | 這邊舉一個最經典的例子:K-Mean。
19 |
20 |
21 |
22 | ### 簡單的步驟舉例
23 |
24 | 舉個例子,我們有個資料集。
25 |
26 |
|  |
206 |
207 | 我們就能根據這個 conditional FP-Tree 窮舉出所有含有 m 的樣式,也就是`m, fm, cm, am, fcm, fam, cam, fcam`
208 |
209 | 我們還能根據 conditional FP-Tree 以遞迴的形式找出 am, cm, cam... 的 conditional FP-Tree,與上述同理。
210 |
211 |
212 |
213 | ## Collaborative Filtering
214 |
215 | 我們可以使用 Collaborative Filtering 來找出兩個相似的人或事物,分成以 User-Based 為主與以 Item-Based 為主。
216 |
217 | 我們會根據使用者或物品的 rating 來評估推薦
218 |
219 | 但也因此會有 cold start 的問題,也就是新東西或新的人進來之後會不知道要推薦什麼,因為沒有任何的評分紀錄。
220 |
221 |
222 |
223 | 要找出相似的人事物,我們需要算出相似度:
224 |
225 | - Jaccard similarity measure $\text{sim}(x, y) = \dfrac{|r_x \cap r_y|}{|r_x|+|r_y|-|r_x\cap r_y|}$,其中 $v_x, v_y$ 為 User rating set。
226 | - Cosine similarity:$\text{sim}(x, y) = \dfrac{r_x\cdot r_y}{||r_x||\cdot||r_y||}$
227 | - Pearson correlation coefficient:$\text{sim}(x,y)=\dfrac{\displaystyle \sum_{s\in s_{xy}} (r_{xs}-\overline{r_x})(r_{ys}-\overline{r_y})}{\sqrt{\sum_{s\in s_{xy}} (r_{xs}-\overline{r_x})^2} \sqrt{\sum_{s\in s_{xy}} (r_{ys}-\overline{r_y})^2}}$,$s_{xy}$ 為 x 與 y 對某物的評價。
228 |
229 |
230 |
231 | ### User-based collaborative filtering
232 |
233 | 我們可以使用 user-item rating matrix,找出 user 與 user 之間的關聯性。
234 |
235 | 只要找出兩個 user 有高相似度,就能把類似的行為推薦給 user。
236 |
237 |
238 |
239 | ### Item-based collaborative filtering
240 |
241 | 我們可以使用 user-item rating matrix,找出 item 與 item 之間的關聯性。
242 |
243 | 只要找出兩個 item 有高相似度,就能把類似的行為推薦給 user。
244 |
245 |
246 |
247 |
248 |
249 | ### Jaccard similarity measure
250 |
251 | 第一個提到的相似度計算即為 Jaccard similarity measure。
252 |
253 | Jaccard similarity measure 不管評分,只管該 index 有沒有評分,以下面的例子為例。
254 |
255 | | | 1 | 2 | 3 | 4 | 5 |
256 | | :--: | :--: | :--: | :--: | :--: | :--: |
257 | | x | 1 | | | 1 | 3 |
258 | | y | 1 | | 2 | 2 | |
259 |
260 | 我們可以得到 User rating set $r_x = \{1, 4, 5\}$,$r_y = \{1, 3, 4\}$,因為 $x$ 只有在 1、4、5 做評分,$y$ 只有在 1、3、4 做評分。
261 |
262 | 由於 $r_x$ 與 $r_y$ 有交集的數量只有 $2$,聯集則是 $4$,故 $\text{sim}(x, y) = \dfrac{2}{4} = 0.5$
263 |
264 |
265 |
266 | 缺點則是評分上是有意義的,故這樣做會忽略掉評分的意義。
267 |
268 |
269 |
270 | ### Cosine similarity
271 |
272 | 第二個提到的相似度計算即為 Cosine similarity。
273 |
274 | 以下面的例子為例。
275 |
276 | | | 1 | 2 | 3 | 4 | 5 |
277 | | :--: | :--: | :--: | :--: | :--: | :--: |
278 | | x | 1 | | | 1 | 3 |
279 | | y | 1 | | 2 | 2 | |
280 |
281 | 我們可以將 $r_x, r_y$ 視為點,則可以得到
282 | $$
283 | r_x = <1, 0, 0, 1, 3> \\
284 | r_y = <1, 0, 2, 2, 0>
285 | $$
286 | 故其 Cosine similarity 為 $\dfrac{1+0+0+2+0}{\sqrt{1^2+1^2+3^2}\sqrt{1^2+2^2+2^2}} \approx 30.2\%$
287 |
288 |
289 |
290 | ### Pearson correlation coefficient
291 |
292 | 定義上為 $\text{sim}(x,y)=\dfrac{\displaystyle \sum_{s\in s_{xy}} (r_{xs}-\overline{r_x})(r_{ys}-\overline{r_y})}{\sqrt{\sum_{s\in s_{xy}} (r_{xs}-\overline{r_x})^2} \sqrt{\sum_{s\in s_{xy}} (r_{ys}-\overline{r_y})^2}}$,$s_{xy}$ 為 x 與 y 對某物的評價。
293 |
294 | 雖然定義上是這樣,但,其實你只要算出列/行的平均,行/列存在的元素全部減去平均後砸 Cosine Similarity 也能做出來
295 |
296 | ~~安了我的算式恐懼症,這麼可怕的式子是啥鬼嗚嗚~~
297 |
298 |
299 |
300 | 以下面的例子為例。
301 |
302 | | | 1 | 2 | 3 | 4 | 5 |
303 | | :--: | :--: | :--: | :--: | :--: | :--: |
304 | | x | 2 | | | 1 | 3 |
305 | | y | 2 | | 2 | 2 | |
306 |
307 | 我們可以將 $r_x, r_y$ 視為點,則可以得到
308 | $$
309 | r_x = <1, 0, 0, 1, 3> \\
310 | r_y = <1, 0, 2, 2, 0>
311 | $$
312 | 平均 $\mu_x = 2$,$\mu_y = 2$,則
313 | $$
314 | r_x' = <-1, 0, 0, -1, 1> \\
315 | r_y' = <-1, 0, 0, 0, 0>
316 | $$
317 | 我們可以算出 Pearson correlation coefficient
318 | $$
319 | \text{sim}(x, y) = \dfrac{1}{((-1)^2+(-1)^2+1^2)((-1)^2)} = \dfrac{1}{3} \approx 0.333
320 | $$
321 |
322 |
323 | ### Prediction Function
324 |
325 | 若我們有一個物件與其他 $N$ 個物件相似,則我們可以用以下的式子來表達其預測值
326 | $$
327 | r_{xi} = \dfrac{\displaystyle \sum_{j\in N(i; x)} s_{ij} \cdot r_{xj}}{\displaystyle \sum_{j\in N(i; x)} s_{ij}}
328 | $$
329 | 見以下範例。
330 |
331 |
332 |
333 | ### Item-Item Collaborative Filtering
334 |
335 | 假設我們有一筆這樣的資料,欄為 User 且列為 Movie,表格上每個數字為 User 對 Movie 的評價
336 |
337 | | | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
338 | | :--: | :--: | :--: | :--: | :--: | :----: | :--: | :--: | :--: | :--: | :--: | :--: | :--: |
339 | | 1 | 1 | | 3 | | **?** | 5 | | | 5 | | 4 | |
340 | | 2 | | | 5 | 4 | | | 4 | | | 2 | 1 | 3 |
341 | | 3 | 2 | 4 | | 1 | 2 | | 3 | | 4 | 3 | 5 | |
342 | | 4 | | 2 | 4 | | 5 | | | 4 | | | 2 | |
343 | | 5 | | | 4 | 3 | 4 | 2 | | | | | 2 | |
344 | | 6 | 1 | | 3 | | 3 | | | 2 | | | 4 | |
345 |
346 | 可以看到 $D(1, 5)$ 的資料是問號,即為我們想要推演的資料。
347 |
348 | 我們使用 Pearson correlation coefficient 來**計算電影的相似度**,先算出每個電影的平均值,以及該列減去平均值的向量。
349 |
350 | $\mu_1 = (1+3+5+5+4)/5 = 3.6$,$v'_1 = <-2.6, 0, -0.6, 0, 0, 1.4, 0, 0, 1.4, 0, 0.4, 0>$
351 |
352 | $\mu_2 = (5+4+4+2+1+3)/6=3.167$,$v'_2 = <0, 0, 1.83, 0.83, 0, 0, 0.83, 0, 0, -1.17, -2.17, -0.17>$
353 |
354 | $\mu_3 = (2+4+1+2+3+4+3+5)/8=3$,$v'_3 = <-1, 1, 0, -2, -1, 0, 0, 0, 1, 0, 2, 0>$
355 |
356 | $\mu_4 = (2+4+5+4+2)/5=3.4$,$v'_4 = <0, -1.4, 0.6, 0, 1.6, 0, 0, 0.6, 0, 0, -1.4, 0>$
357 |
358 | $\mu_5 = (4+3+4+2+2)/5=3$,$v'_5 = <0, 0, 1, 0, 1, -1, 0, 0, 0, 0, -1, 0>$
359 |
360 | $\mu_6 = (1+3+3+2+4)/5=2.6$,$v'_6 = <-1.6, 0, 0.4, 0, 0.4, 0, 0, -0.6, 0, 0, 1.4. 0>$
361 |
362 | 我們可以算出 Pearson correlation coefficient,得到
363 |
364 | $\text{sim}(1, 2) = -0.17$,$\text{sim}(1, 3) = 0.41$,$\text{sim}(1, 4) = -0.1$,$\text{sim}(1, 5) = -0.36$,$\text{sim}(1, 6) = 0.59$
365 |
366 | 故我們選擇電影 3、6 與電影 1 有較高的關聯性。
367 |
368 |
369 |
370 | 因此我們可以套用預測函數,得到:
371 | $$
372 | \dfrac{0.41\times 2 + 0.59\times 3}{0.41+0.59} = 2.6
373 | $$
374 | 故 $D(1, 5)$ 可以被預測成 2.6 分。
375 |
376 |
377 |
378 | ### User-User Collaborative Filtering
379 |
380 | 與 [Item-Item Collaborative Filtering](#Item-Item Collaborative Filtering) 同理,跳過。
381 |
382 |
383 |
384 | ## Content-based Filtering
385 |
386 | 使用內容來進行評估,因為使用內容,所以不會有 cold start 的問題。
387 |
388 |
389 |
390 | ### TF-IDF
391 |
392 | TF-IDF (Term Frequency - Inverse Document Frequency),用來量化詞彙的重要性,但會隨著詞彙出現的頻率高而出現反比影響。
393 |
394 | 其定義為:
395 | $$
396 | TF_{ij} = \dfrac{n_{ij}}{\sum_{k} n_{kj}} \\
397 | IDF_{i} = \log(\dfrac{N}{n_i}) \\
398 | \text{TF-IDF}_{ij} = TF_{ij} \times IDF_{i}
399 | $$
400 | 其中 TF 的 $n_{ij}$ 為該詞彙在文件中的次數,分母則是在所有文件中該詞彙出現的次數,$N$ 為文件的總詞彙量。
401 |
402 |
--------------------------------------------------------------------------------
/Markdown/Cluster Analysis.md:
--------------------------------------------------------------------------------
1 | # 群聚分析(Cluster Analysis)
2 |
3 | > Reference:
4 | >
5 | > 1. Cluster Analysis - Dr. Tun-Wen Pai
6 |
7 | ## 群聚分析
8 |
9 | 主要分成兩種不同的群聚分析:
10 |
11 | 1. 分層式群聚:分成由上至下(top-down)或由下至上(bottom-up)演算法,層層迭代運算。
12 | 2. 分割式群聚:一次把所有的分群結果納入考慮。
13 |
14 |
15 |
16 | ## 分割式群聚
17 |
18 | 這邊舉一個最經典的例子:K-Mean。
19 |
20 |
21 |
22 | ### 簡單的步驟舉例
23 |
24 | 舉個例子,我們有個資料集。
25 |
26 |  27 |
28 | 既然要分群,我們先***雖然說是隨機,但是為了做黑魔法所以不隨機的***挑選兩個群心。
29 |
30 |
27 |
28 | 既然要分群,我們先***雖然說是隨機,但是為了做黑魔法所以不隨機的***挑選兩個群心。
29 |
30 |  31 |
32 | 接下來我們開始迭代每個點,來知道距離哪個群心比較近,就屬於那個群心。
33 |
34 | 根據上圖來說,我們用眼睛可以看出這個分類結果,為了方便辨識群心在哪,我將群心用空心圓代替。
35 |
36 |
31 |
32 | 接下來我們開始迭代每個點,來知道距離哪個群心比較近,就屬於那個群心。
33 |
34 | 根據上圖來說,我們用眼睛可以看出這個分類結果,為了方便辨識群心在哪,我將群心用空心圓代替。
35 |
36 |  37 |
38 |
39 |
40 | 此時我們可以更新群心,利用每個向度 $x$, $y$ 的平均。
41 |
42 |
37 |
38 |
39 |
40 | 此時我們可以更新群心,利用每個向度 $x$, $y$ 的平均。
41 |
42 |  43 |
44 | 經過多次迭代之後就可以找到一個穩定的分群。
45 |
46 |
47 |
48 | ### 問題探討
49 |
50 | 顯然,我們用***雖然說是隨機,但是為了做黑魔法所以不隨機的***方式挑選群心是一個很大的問題。
51 |
52 | 因為隨機挑選群心可能會挑出一個完全不同的結果,舉個例子:
53 |
54 |
43 |
44 | 經過多次迭代之後就可以找到一個穩定的分群。
45 |
46 |
47 |
48 | ### 問題探討
49 |
50 | 顯然,我們用***雖然說是隨機,但是為了做黑魔法所以不隨機的***方式挑選群心是一個很大的問題。
51 |
52 | 因為隨機挑選群心可能會挑出一個完全不同的結果,舉個例子:
53 |
54 |  55 |
56 | 群心這樣挑選會得到這樣的結果。
57 |
58 |
55 |
56 | 群心這樣挑選會得到這樣的結果。
57 |
58 |  59 |
60 | 跟前面的結果幾乎完全不一樣,所以挑選適當的群心是非常重要的。
61 |
62 |
63 |
64 | ## 分層式群聚
65 |
66 | ### 簡介
67 |
68 | 分層式群聚可以將群聚的步驟畫成一樹枝狀圖。
69 |
70 | > Image source:[Hierarchical Clustering for Large Data Sets](https://www.researchgate.net/publication/278706094_Hierarchical_Clustering_for_Large_Data_Sets)
71 |
72 |
59 |
60 | 跟前面的結果幾乎完全不一樣,所以挑選適當的群心是非常重要的。
61 |
62 |
63 |
64 | ## 分層式群聚
65 |
66 | ### 簡介
67 |
68 | 分層式群聚可以將群聚的步驟畫成一樹枝狀圖。
69 |
70 | > Image source:[Hierarchical Clustering for Large Data Sets](https://www.researchgate.net/publication/278706094_Hierarchical_Clustering_for_Large_Data_Sets)
71 |
72 |  73 |
74 | 在這份筆記會介紹四種不同的分層式群聚。
75 |
76 | 令 $A$ 為某個群集的點,$B$ 為某個群集的點,以下是群集表格。
77 |
78 | | 分群演算法 | 群聚概念 | 演算表達式 |
79 | | :--------------: | :----------------------: | :----------------------------------------------------------: |
80 | | Single Linkage | 以兩個群聚的最近點 | $\text{min}\{d(a,b): a \in A, b \in B\}$ |
81 | | Complete Linkage | 以兩個群聚的最遠點 | $\text{max}\{d(a,b): a \in A, b \in B\}$ |
82 | | UPGMA | 以兩群的平均距離 | $\displaystyle \dfrac{1}{|A|+|B|}\sum_{a\in A}\sum_{b\in B}d(a,b)$ |
83 | | WPGMA | 以某點至兩群和的平均距離 | $d(i\cup j, k)=\dfrac{d(i, k)+d(j, k)}{2}$ |
84 |
85 |
86 |
87 | ### 群集步驟
88 |
89 | 以上的演算法其實都大同小異,只有差別在演算法更新「群集距離表」的方式不同。
90 |
91 | 群集距離表即為每個群集到其他群集的距離,與自己的群集距離為 0。
92 |
93 | 例如下方表格即為群集距離表。
94 |
95 | 以圖上來說,群集 A 至群集 B 的距離為 25,群集 B 至群集 C 的距離為 25,群集 A 至群集 C 的距離為 15。
96 |
97 | | | A | B | C |
98 | | :--: | :--: | :--: | :--: |
99 | | A | 0 | 25 | 15 |
100 | | B | 25 | 0 | 25 |
101 | | C | 15 | 25 | 0 |
102 |
103 |
104 |
105 | 這張流程圖是我自製的,用來解釋群集分析的流程。
106 |
107 |
73 |
74 | 在這份筆記會介紹四種不同的分層式群聚。
75 |
76 | 令 $A$ 為某個群集的點,$B$ 為某個群集的點,以下是群集表格。
77 |
78 | | 分群演算法 | 群聚概念 | 演算表達式 |
79 | | :--------------: | :----------------------: | :----------------------------------------------------------: |
80 | | Single Linkage | 以兩個群聚的最近點 | $\text{min}\{d(a,b): a \in A, b \in B\}$ |
81 | | Complete Linkage | 以兩個群聚的最遠點 | $\text{max}\{d(a,b): a \in A, b \in B\}$ |
82 | | UPGMA | 以兩群的平均距離 | $\displaystyle \dfrac{1}{|A|+|B|}\sum_{a\in A}\sum_{b\in B}d(a,b)$ |
83 | | WPGMA | 以某點至兩群和的平均距離 | $d(i\cup j, k)=\dfrac{d(i, k)+d(j, k)}{2}$ |
84 |
85 |
86 |
87 | ### 群集步驟
88 |
89 | 以上的演算法其實都大同小異,只有差別在演算法更新「群集距離表」的方式不同。
90 |
91 | 群集距離表即為每個群集到其他群集的距離,與自己的群集距離為 0。
92 |
93 | 例如下方表格即為群集距離表。
94 |
95 | 以圖上來說,群集 A 至群集 B 的距離為 25,群集 B 至群集 C 的距離為 25,群集 A 至群集 C 的距離為 15。
96 |
97 | | | A | B | C |
98 | | :--: | :--: | :--: | :--: |
99 | | A | 0 | 25 | 15 |
100 | | B | 25 | 0 | 25 |
101 | | C | 15 | 25 | 0 |
102 |
103 |
104 |
105 | 這張流程圖是我自製的,用來解釋群集分析的流程。
106 |
107 |  108 |
109 |
110 |
111 |
112 |
113 | ### 利用演算法更新群集距離表
114 |
115 | 基本上群聚的方法只差在利用演算法來合併群集與更新群聚分析表,也就是更新除了合併群集以外群集距離。
116 |
117 | | | A | B | C | D |
118 | | :--: | :--: | :--: | :--: | :--: |
119 | | A | 0 | 25 | 15 | 18 |
120 | | B | 25 | 0 | 25 | 35 |
121 | | C | 15 | 25 | 0 | 45 |
122 | | D | 18 | 35 | 45 | 0 |
123 |
124 | 以上方這個表格為例,要尋找最小距離進行合併,該合併的兩個群集即為 **A 與 C**。
125 |
126 |
127 |
128 | **請注意,$A$ 與 $C$ 非常重要。**
129 |
130 | 例如當你欲合併的結果為 $(B, C)$ 與 $D$ 得到 $(B, C, D)$ 時,你應該要在更新時使用 $(B, C)$ 欄的值與 $D$ 欄的值。
131 |
132 | 否則你可能會用 $B$ 與 $(C, D)$ 的值,但表格上 $(C, D)$ 的值並不存在,所以記住什麼與什麼合併是非常重要。
133 |
134 | | | (A, C) | B | D |
135 | | :----: | :----: | :--: | :--: |
136 | | (A, C) | 0 | ? | ? |
137 | | B | ? | 0 | 35 |
138 | | D | ? | 35 | 0 |
139 |
140 | 合併完成之後,此時我們想要知道群集 $(A, C)$ 與 $B$ 的距離,此時我們根據演算法的定義:$\dfrac{d(i, k) + d(j, k)}{2}$
141 |
142 | $d(i, k) = d(A, B) = 25$,$d(j, k) = d(C, B) = 25$,可以得到距離為 $d((A, C), B) = \dfrac{25+25}{2} = 25$。
143 |
144 | 故$d((A, C), B) = 25$
145 |
146 | 同理我們可以算出 $d((A, C), D) = \dfrac{d(A, D)+d(C, D)}{2} = \dfrac{18+45}{2} = \dfrac{63}{2} = 31.5$
147 |
148 | | | (A, C) | B | D |
149 | | :----: | :----: | :--: | :--: |
150 | | (A, C) | 0 | 25 | 31.5 |
151 | | B | 25 | 0 | 35 |
152 | | D | 31.5 | 35 | 0 |
153 |
154 | 且我們可以得到 branch length = $\dfrac{15}{2} = 7.5$,也就是我們合併時使用的最短距離除以 2。
155 |
156 | 通常來說會越來越大,就能在樹枝狀圖上畫出 branch length(或者你可以說他是 thoushold)。
157 |
158 |
159 |
160 | ### 舉例其他演算法更新群集距離表
161 |
162 | 此時就能完成表格更新的步驟,其餘的合併方法只差在演算法的不同,照著做就行。
163 |
164 | 以其他三種不同的演算法來說:
165 |
166 | 1. Single Linkage:更新其他群集距離的方式為,取合併群集與該群集的**最短距離**。
167 |
168 | 2. Complete Linkage:更新其他群集距離的方式為,取合併群集與該群集的**最長距離**。
169 |
170 | 3. UPGMA:更新其他群集距離的方式為,若合併群集為 $A$ 與 $B$ 的合併,且欲合併的群集為 $C$。
171 |
172 | 則距離更新方式為 $d((A, C), B) = \dfrac{|A| \times d(A, C) + |B| \times d(B, C)}{|A| + |B|}$,其中 $|A|$ 與 $|B|$ 為該群集的點數量。
173 |
174 | 4. WPGMA:更新其他群集距離的方式為,若合併群集為 $A$ 與 $B$ 的合併,且欲合併的群集為 $C$。
175 |
176 | 則距離更新方式為 $d((A, C), B) = \dfrac{d(A, C)+d(B, C)}{2}$
177 |
178 |
179 |
180 | ## 優化分群結果
181 |
182 | - 什麼樣的分群結果是好的?
183 | - 我們可以將不同的 $K$ 值進行計算 total variation,並且找出拐點。
--------------------------------------------------------------------------------
/Markdown/Data Mining.md:
--------------------------------------------------------------------------------
1 | # 資料探勘(Data Mining)
2 |
3 | > 參考資料:
4 | >
5 | > 資料探勘(Data Mining)Dr. Tun-Wen Pai
6 | >
7 | > Business Intelligence and Data Mining Anil K. Maheshwari, Ph.D.
8 |
9 |
10 |
11 | ## 資料探勘的介紹
12 |
13 | 資料探勘是一種技術,為了探索大量經過組織的資料中,得到有利的資訊、見解與模式。
14 |
15 | 資料探勘利用了統計學、人工智慧領域、機器學習的知識,挖掘資料中未知的資訊,例如發現資料的類別與結構、分類資料等等。
16 |
17 |
18 |
19 | ## 資料蒐集與資料選擇
20 |
21 | 從大量支離破碎的資料中很難探勘出有用的資訊,所以我們需要先做資料蒐集與資料選擇。
22 |
23 |
24 |
25 | 資料從大量的資料來源中被蒐集,此時資料是支離破碎的,所以我們需要經過一系列的處理(例如資料倉儲的 ETL)
26 |
27 | 在建立資料倉儲之前,我們可以使用企業模式的資料模型(Enterprise Data Model, EDM),為這些資料打造一個統一的框架。
28 |
29 | 經過資料倉儲一系列的處理之後得到組織過的資料,再從這些資料進行探勘。
30 |
31 |
32 |
33 | 這也是為什麼資料倉儲被用來幫助資料探勘,因為資料探勘需要整理過的資料,此時即完成了資料蒐集與資料選擇。
34 |
35 |
36 |
37 | ## 資料淨化
38 |
39 | 資料的品質會嚴重影響到資料探勘,所以我們會希望資料都是高品質的,也因此我們需要把資料淨化。
40 |
41 |
42 |
43 | 我們可以利用一些手段進行資料淨化,例如:填充遺失的欄位、處理異常值、劃分連續型變數等等。
44 |
45 | 經過資料淨化,就可以確保資料都是高品質,確保不會造成 Garbage in Garbage out 的問題。
46 |
47 |
48 |
49 | 以下列舉一些資料淨化的手段:
50 |
51 | 1. 重複的資料需要被移除,從各方資料來源蒐集資料可能會導致出現重複的資料,所以需要被移除。
52 |
53 | 2. 欄位若遺失值則需要被填上去,如果不該被填上去,則這個欄位應該被移除。
54 |
55 | 3. 資料元素從單一單位轉換成另一個單位。
56 |
57 | 例如透過總病人數量與總花費較難得到有利的資訊,但如果資料是病人與花費的對應關係,那麼我們可以從這邊得到更有利的資訊。
58 |
59 | 4. 連續型變數可以被劃分以利於資料探勘更佳。
60 |
61 | 例如工作經驗可以被劃分成低、中、高。
62 |
63 | 5. 資料元素可能需要經過調整,讓他能夠隨著時間的推移產生可比性。
64 |
65 | 例如大量不同的貨幣可以被調整成通用貨幣,用來評估通膨的情況。
66 |
67 | 6. 極值需要被移除。
68 |
69 | 7. 偏差數值需要經過矯正,來確保分析結果是正常的。
70 |
71 | 8. 資料應該保持同樣的顆粒度(Granularity),來讓資料能夠比較。
72 |
73 | 例如:櫃台銷售所產生的資料通常都是以日為單位,而銷售員的資料通常都是以月為單位。
74 |
75 | 為此我們應該將櫃台銷售調整成月為單位,兩個資料才做比較。
76 |
77 | 9. 資料需要足夠密集。
78 |
79 |
80 |
81 | ## Confusion Matrix
82 |
83 | Confusion Matrix 可用來監督學習、可以確定在機器學習中是否將兩個不同類型的資料混淆了。
84 |
85 |
86 |
87 | 以採檢病人是否為陽性反應為例,我們可以獲得以下的表格。
88 |
89 |
108 |
109 |
110 |
111 |
112 |
113 | ### 利用演算法更新群集距離表
114 |
115 | 基本上群聚的方法只差在利用演算法來合併群集與更新群聚分析表,也就是更新除了合併群集以外群集距離。
116 |
117 | | | A | B | C | D |
118 | | :--: | :--: | :--: | :--: | :--: |
119 | | A | 0 | 25 | 15 | 18 |
120 | | B | 25 | 0 | 25 | 35 |
121 | | C | 15 | 25 | 0 | 45 |
122 | | D | 18 | 35 | 45 | 0 |
123 |
124 | 以上方這個表格為例,要尋找最小距離進行合併,該合併的兩個群集即為 **A 與 C**。
125 |
126 |
127 |
128 | **請注意,$A$ 與 $C$ 非常重要。**
129 |
130 | 例如當你欲合併的結果為 $(B, C)$ 與 $D$ 得到 $(B, C, D)$ 時,你應該要在更新時使用 $(B, C)$ 欄的值與 $D$ 欄的值。
131 |
132 | 否則你可能會用 $B$ 與 $(C, D)$ 的值,但表格上 $(C, D)$ 的值並不存在,所以記住什麼與什麼合併是非常重要。
133 |
134 | | | (A, C) | B | D |
135 | | :----: | :----: | :--: | :--: |
136 | | (A, C) | 0 | ? | ? |
137 | | B | ? | 0 | 35 |
138 | | D | ? | 35 | 0 |
139 |
140 | 合併完成之後,此時我們想要知道群集 $(A, C)$ 與 $B$ 的距離,此時我們根據演算法的定義:$\dfrac{d(i, k) + d(j, k)}{2}$
141 |
142 | $d(i, k) = d(A, B) = 25$,$d(j, k) = d(C, B) = 25$,可以得到距離為 $d((A, C), B) = \dfrac{25+25}{2} = 25$。
143 |
144 | 故$d((A, C), B) = 25$
145 |
146 | 同理我們可以算出 $d((A, C), D) = \dfrac{d(A, D)+d(C, D)}{2} = \dfrac{18+45}{2} = \dfrac{63}{2} = 31.5$
147 |
148 | | | (A, C) | B | D |
149 | | :----: | :----: | :--: | :--: |
150 | | (A, C) | 0 | 25 | 31.5 |
151 | | B | 25 | 0 | 35 |
152 | | D | 31.5 | 35 | 0 |
153 |
154 | 且我們可以得到 branch length = $\dfrac{15}{2} = 7.5$,也就是我們合併時使用的最短距離除以 2。
155 |
156 | 通常來說會越來越大,就能在樹枝狀圖上畫出 branch length(或者你可以說他是 thoushold)。
157 |
158 |
159 |
160 | ### 舉例其他演算法更新群集距離表
161 |
162 | 此時就能完成表格更新的步驟,其餘的合併方法只差在演算法的不同,照著做就行。
163 |
164 | 以其他三種不同的演算法來說:
165 |
166 | 1. Single Linkage:更新其他群集距離的方式為,取合併群集與該群集的**最短距離**。
167 |
168 | 2. Complete Linkage:更新其他群集距離的方式為,取合併群集與該群集的**最長距離**。
169 |
170 | 3. UPGMA:更新其他群集距離的方式為,若合併群集為 $A$ 與 $B$ 的合併,且欲合併的群集為 $C$。
171 |
172 | 則距離更新方式為 $d((A, C), B) = \dfrac{|A| \times d(A, C) + |B| \times d(B, C)}{|A| + |B|}$,其中 $|A|$ 與 $|B|$ 為該群集的點數量。
173 |
174 | 4. WPGMA:更新其他群集距離的方式為,若合併群集為 $A$ 與 $B$ 的合併,且欲合併的群集為 $C$。
175 |
176 | 則距離更新方式為 $d((A, C), B) = \dfrac{d(A, C)+d(B, C)}{2}$
177 |
178 |
179 |
180 | ## 優化分群結果
181 |
182 | - 什麼樣的分群結果是好的?
183 | - 我們可以將不同的 $K$ 值進行計算 total variation,並且找出拐點。
--------------------------------------------------------------------------------
/Markdown/Data Mining.md:
--------------------------------------------------------------------------------
1 | # 資料探勘(Data Mining)
2 |
3 | > 參考資料:
4 | >
5 | > 資料探勘(Data Mining)Dr. Tun-Wen Pai
6 | >
7 | > Business Intelligence and Data Mining Anil K. Maheshwari, Ph.D.
8 |
9 |
10 |
11 | ## 資料探勘的介紹
12 |
13 | 資料探勘是一種技術,為了探索大量經過組織的資料中,得到有利的資訊、見解與模式。
14 |
15 | 資料探勘利用了統計學、人工智慧領域、機器學習的知識,挖掘資料中未知的資訊,例如發現資料的類別與結構、分類資料等等。
16 |
17 |
18 |
19 | ## 資料蒐集與資料選擇
20 |
21 | 從大量支離破碎的資料中很難探勘出有用的資訊,所以我們需要先做資料蒐集與資料選擇。
22 |
23 |
24 |
25 | 資料從大量的資料來源中被蒐集,此時資料是支離破碎的,所以我們需要經過一系列的處理(例如資料倉儲的 ETL)
26 |
27 | 在建立資料倉儲之前,我們可以使用企業模式的資料模型(Enterprise Data Model, EDM),為這些資料打造一個統一的框架。
28 |
29 | 經過資料倉儲一系列的處理之後得到組織過的資料,再從這些資料進行探勘。
30 |
31 |
32 |
33 | 這也是為什麼資料倉儲被用來幫助資料探勘,因為資料探勘需要整理過的資料,此時即完成了資料蒐集與資料選擇。
34 |
35 |
36 |
37 | ## 資料淨化
38 |
39 | 資料的品質會嚴重影響到資料探勘,所以我們會希望資料都是高品質的,也因此我們需要把資料淨化。
40 |
41 |
42 |
43 | 我們可以利用一些手段進行資料淨化,例如:填充遺失的欄位、處理異常值、劃分連續型變數等等。
44 |
45 | 經過資料淨化,就可以確保資料都是高品質,確保不會造成 Garbage in Garbage out 的問題。
46 |
47 |
48 |
49 | 以下列舉一些資料淨化的手段:
50 |
51 | 1. 重複的資料需要被移除,從各方資料來源蒐集資料可能會導致出現重複的資料,所以需要被移除。
52 |
53 | 2. 欄位若遺失值則需要被填上去,如果不該被填上去,則這個欄位應該被移除。
54 |
55 | 3. 資料元素從單一單位轉換成另一個單位。
56 |
57 | 例如透過總病人數量與總花費較難得到有利的資訊,但如果資料是病人與花費的對應關係,那麼我們可以從這邊得到更有利的資訊。
58 |
59 | 4. 連續型變數可以被劃分以利於資料探勘更佳。
60 |
61 | 例如工作經驗可以被劃分成低、中、高。
62 |
63 | 5. 資料元素可能需要經過調整,讓他能夠隨著時間的推移產生可比性。
64 |
65 | 例如大量不同的貨幣可以被調整成通用貨幣,用來評估通膨的情況。
66 |
67 | 6. 極值需要被移除。
68 |
69 | 7. 偏差數值需要經過矯正,來確保分析結果是正常的。
70 |
71 | 8. 資料應該保持同樣的顆粒度(Granularity),來讓資料能夠比較。
72 |
73 | 例如:櫃台銷售所產生的資料通常都是以日為單位,而銷售員的資料通常都是以月為單位。
74 |
75 | 為此我們應該將櫃台銷售調整成月為單位,兩個資料才做比較。
76 |
77 | 9. 資料需要足夠密集。
78 |
79 |
80 |
81 | ## Confusion Matrix
82 |
83 | Confusion Matrix 可用來監督學習、可以確定在機器學習中是否將兩個不同類型的資料混淆了。
84 |
85 |
86 |
87 | 以採檢病人是否為陽性反應為例,我們可以獲得以下的表格。
88 |
89 |  90 |
91 | 以理想的情況來說,採檢試劑要能夠分辨出陽性(True Positive)與陰性(True Negative)。
92 |
93 | 但必定會出現偽陰(False Negative)與偽陽(False Positive)的情況出現。
94 |
95 | 將這些數值填入表格,即可得到一個 Confusion Matrix。
96 |
97 |
98 |
99 | 我們可以擴展表格,得到更多的資訊。
100 |
101 | 
102 |
103 |
104 |
105 | 將同樣的概念,可以套用到機器分類數字、機器分類花...等情況,所以可以適用於績效評估機器學習。
106 |
107 |
108 |
109 | ## AUC - ROC Curve
110 |
111 | 我們可以使用 AUC - ROC Curve 來進行機器學習的績效評估。
112 |
113 | 對於上面表格,我們可以設定特定的閥值,用來得到在這個閥值中的真陽、真陰、偽陽、偽陰數量,進而劃出由兩個曲線組成的圖片。
114 |
115 |
116 |
117 | 例如我們預期在 TPR 閥值低於 0.5 時則為陰性,在閥值高於 0.5 時則為陽性。
118 |
119 | 此時我們可以預期沒有任何偽陰、偽陽的情況,所以可以得到以下這張圖。
120 |
121 |
90 |
91 | 以理想的情況來說,採檢試劑要能夠分辨出陽性(True Positive)與陰性(True Negative)。
92 |
93 | 但必定會出現偽陰(False Negative)與偽陽(False Positive)的情況出現。
94 |
95 | 將這些數值填入表格,即可得到一個 Confusion Matrix。
96 |
97 |
98 |
99 | 我們可以擴展表格,得到更多的資訊。
100 |
101 | 
102 |
103 |
104 |
105 | 將同樣的概念,可以套用到機器分類數字、機器分類花...等情況,所以可以適用於績效評估機器學習。
106 |
107 |
108 |
109 | ## AUC - ROC Curve
110 |
111 | 我們可以使用 AUC - ROC Curve 來進行機器學習的績效評估。
112 |
113 | 對於上面表格,我們可以設定特定的閥值,用來得到在這個閥值中的真陽、真陰、偽陽、偽陰數量,進而劃出由兩個曲線組成的圖片。
114 |
115 |
116 |
117 | 例如我們預期在 TPR 閥值低於 0.5 時則為陰性,在閥值高於 0.5 時則為陽性。
118 |
119 | 此時我們可以預期沒有任何偽陰、偽陽的情況,所以可以得到以下這張圖。
120 |
121 |  122 |
123 | 這時無論到哪點都不會出現偽陽性,故 ROC 曲線呈現直角,幾乎是完美分類。
124 |
125 |
126 |
127 | 另一個例子,若我們期望 TPR 閥值低於 0.5 時為陰性,高於 0.5 時則陽性。
128 |
129 | 然而結果不如預期,得到了以下這張圖。
130 |
131 |
122 |
123 | 這時無論到哪點都不會出現偽陽性,故 ROC 曲線呈現直角,幾乎是完美分類。
124 |
125 |
126 |
127 | 另一個例子,若我們期望 TPR 閥值低於 0.5 時為陰性,高於 0.5 時則陽性。
128 |
129 | 然而結果不如預期,得到了以下這張圖。
130 |
131 |  132 |
133 | 這時我們只需要反預測即可校正回上例。
134 |
135 |
136 |
137 | 換另一個不理想的例子,若可能出現偽陰偽陽的情況,
138 |
139 | 例如閥值是 0.46 時,陰性與陽性都出現,這時就會出真陽、偽陽的情況,得到以下這張圖。
140 |
141 | 可以發現,在出現 FPR 時,TPR 的數值稍微下跌,而在之後幾乎回到 1 的位置。
142 |
143 |
132 |
133 | 這時我們只需要反預測即可校正回上例。
134 |
135 |
136 |
137 | 換另一個不理想的例子,若可能出現偽陰偽陽的情況,
138 |
139 | 例如閥值是 0.46 時,陰性與陽性都出現,這時就會出真陽、偽陽的情況,得到以下這張圖。
140 |
141 | 可以發現,在出現 FPR 時,TPR 的數值稍微下跌,而在之後幾乎回到 1 的位置。
142 |
143 |  144 |
145 |
146 |
147 | 另一個例子,若無論在任何閥值出現的情況,真陰、真陽的人數都一樣,
148 |
149 | 則這個模型視同無效,因為檢驗一個人是否偽陰偽陽的機率相等於隨機。
150 |
151 |
144 |
145 |
146 |
147 | 另一個例子,若無論在任何閥值出現的情況,真陰、真陽的人數都一樣,
148 |
149 | 則這個模型視同無效,因為檢驗一個人是否偽陰偽陽的機率相等於隨機。
150 |
151 |  152 |
153 |
154 |
155 | 我們可以透過描點的方式畫出 ROC 曲線,就可以從 ROC 曲線中得出 AUC 值,若 AUC 值越大則模型越好。
156 |
157 |
158 |
159 | ## 機器學習的種類
160 |
161 | 1. 學習問題
162 | 1. 監督式學習:所有資料都被標註,給機器去學習與分類,通常來說對機器最簡單,對人類來說最累。
163 | 2. 非監督式學習:所有資料都沒有被標註,透過機器去尋找特徵的學習分式,對機器最困難,誤差較大。
164 | 3. 強化式學習:不標註任何資料,但告訴機器哪步正確,哪步錯誤,讓機器逐步自我修正。
165 | 2. 混合學習問題
166 | 1. 半監督式學習:對少部分資料進行標註,機器透過有標註的資料找出特徵並進行分類,能使非監督式學習的準確率提升。
167 | 2. 自我監督式學習:從一堆沒有 label 標註的資料,訓練出一個監督式模型,然後造出更多 label。
168 | 3. 多實例學習:輸入許多「包」,這些包都含有許多實例,若所有實例都是負例時則包即為負包,若有至少一個實例為正例時,包即為正包。
169 | 3. 推論統計學
170 | 1. 歸納學習:用來辨識汽車的知識可以用來提升辨識卡車的能力,以現有問題的解決模型利用在其他不同但相關的問題上。
171 | 2. 演繹學習:利用廣泛的前提去推論較具體的結論,通常依賴前提是否正確。
172 | 3. 轉導學習:通過觀察特定的訓練樣本,來預測特定測試樣本的方法。
173 | 4. 學習技術
174 | 1. 多任務學習:利用單一一個模型,解決多個問題
175 | 2. 主動學習:從每輪學習迭代中,尋找出一個最不確定的一個或一組樣本,來讓外部反饋者給予回饋。
176 | 3. 線上學習:利用當前的資料來直接更新模型,進而在預測前根據先前的資料給予預測。
177 | 4. 遷移學習:一個模型先訓練一個例子,接著所有模型用這個模型的訓練例子當成起始點,訓練其他的例子。
178 | 5. 集成學習:集成兩個以上合適的模型,接著從這個集成的模型上訓練。。
179 | 6. 聯盟式學習:從各式各樣的自訓練模型中,在不用給自己數據的情況下,也可以進行訓練得到模型。
180 |
181 |
182 |
183 | > Reference Website:
184 | >
185 | > 1. Marketing. (n.d.). *你知道機器學習(Machine Learning),有幾種學習方式嗎?* 伊雲谷eCloudvalley. Retrieved April 5, 2022, from https://www.ecloudvalley.com/zh-hant/machine-learning/
186 | > 2. *自監督學習 self-supervised learning 介紹*. (2021, June 11). 藏字閣. https://jigfopsda.com/zh/posts/2021/self_supervised_learning/
187 | > 3. *多實例學習*. (2021, August 31). 維基百科,自由的百科全書. https://zh.wikipedia.org/wiki/%E5%A4%9A%E7%A4%BA%E4%BE%8B%E5%AD%A6%E4%B9%A0
188 | > 4. *遷移學習*. (2020, September 19). 維基百科,自由的百科全書. https://zh.wikipedia.org/wiki/%E8%BF%81%E7%A7%BB%E5%AD%A6%E4%B9%A0
189 | > 5. *簡要介紹Active Learning(主動學習)思想框架,以及從IF(isolation forest)衍生出來的演算法:FBIF(Feedback-Guided Anomaly Discovery)*. (n.d.). IT人. Retrieved April 5, 2022, from https://iter01.com/420911.html
190 | > 6. Su, S. (2021, December 13). *聯盟式學習 (Federated Learning) - Sherry.AI*. Medium. https://medium.com/sherry-ai/%E8%81%AF%E7%9B%9F%E5%BC%8F%E5%AD%B8%E7%BF%92-federated-learning-b4cc5af7a9c0
--------------------------------------------------------------------------------
/Markdown/Data Preprocessing.md:
--------------------------------------------------------------------------------
1 | # 資料預處理(Data Preprocessing)
2 |
3 | > Reference:
4 | >
5 | > 1. Data Preprocessing by Dr. Tun-Wen Pai
6 |
7 | ## 資料預處理
8 |
9 | 對於一個資料集來說,若數值偏大或偏小的情況下,我們很難去做資料視覺化,甚至資料過大時會讓自然指數過大導致 overflow。
10 |
11 | 故我們希望可以把資料集的值域縮小,有以下幾種方法:
12 |
13 | 1. Z-score normalization
14 | 2. MinMaxScaler
15 | 3. MaxAbsScaler
16 | 4. Robust Scaling
17 | 5. QuantileTrasformation
18 |
19 |
20 |
21 | ### Z-score normalization
22 |
23 | 對於每個資料,我們利用常態分佈將他標準化(Standardization),定義為
24 | $$
25 | x'=\dfrac{x-\overline{x}}{\sigma}
26 | $$
27 | 用這樣的方式就能夠將其值域限縮至 $[-1, 1]$ 之間。
28 |
29 |
30 |
31 | ### MinMaxScaler
32 |
33 | 對於每個資料,我們使用最大與最小值的區間來限縮值域,定義如下:
34 | $$
35 | x' = \dfrac{x-\min(x)}{\max(x)-\min(x)}
36 | $$
37 | 用這樣的方式就能夠將其值域限縮至 $[0, 1]$ 之間。
38 |
39 |
40 |
41 | ### MaxAbsScaler
42 |
43 | 對於每個資料,我們單純使用最大與最小值的區間來限縮值域,定義如下:
44 | $$
45 | x' = \dfrac{x}{\max\{|x|\}}
46 | $$
47 |
48 |
49 | 用這樣的方式就能夠將其值域限縮至 $[-1, 1]$ 之間。
50 |
51 |
52 |
53 | ### Robust Scaling
54 |
55 | Robust Scaling 是一種非線性的限縮方式,使用第三分位與第一分位來進行限縮。
56 |
57 | 前面的方法,以最大值來說,若最大值過大則限縮資料會變小。
58 |
59 | Robust Scaling 優化了這個部分,他沒有特定的值域限縮範圍,但可以對極值有良好的抗噪性,定義如下:
60 | $$
61 | x' = \dfrac{x-Q_2}{(Q_3-Q_1)}
62 | $$
63 |
64 |
65 |
--------------------------------------------------------------------------------
/Markdown/Data Warehouse.md:
--------------------------------------------------------------------------------
1 | # Data Warehouse(資料倉儲)
2 |
3 | >主要的資料來源:
4 | >
5 | >Essentials of Database Management Jeffrey A. Hoffer, Heikki Topi, V. Ramesh
6 | >
7 | >資料倉儲(Data Warehouse, DW) Dr. Tun-Wen Pai
8 |
9 |
10 |
11 | ## 關於資料倉儲
12 |
13 | 資料倉儲具有主題式、經過整合、分析具有時變性、資料不會流失的優勢,用來支援商業智慧,例如分析。
14 |
15 |
16 |
17 | ## 關於資料超市
18 |
19 | 由資料倉儲的資料,分離出一個更具主題式的資料集,稱為資料超市。
20 |
21 |
22 |
23 | ## 資料倉儲的需求
24 |
25 | 從各方蒐集出來的資料通常來說都是支離破碎的(例如:包含編碼、形式不同、格式不一等等)。
26 |
27 | 所以通常一個企業需要的是從這堆支離破碎的資料中經過整合,提供出一個企業想要的簡潔有力的資訊。
28 |
29 | 因此資料倉儲主要就是蒐集這些破碎的資料,然後提供給企業一個高質量的資料。
30 |
31 |
32 |
33 | ## 資料倉儲的開發考慮
34 |
35 | 1. 主題式:僅對特定主題感興趣
36 | 2. 整合性:各式各樣的資料進入資料倉儲都會經過整合成統一格式的資料
37 | 3. 時變性:分析具有時變性,根據不同時間具有不同的分析結果
38 | 4. 穩定性:進入資料倉儲的資料並不會變動。
39 | 5. 摘要整理:進入的資料會盡可能地最佳化資料欄位與維度。
40 | 6. 非標準化:Data Warehouse 使用星狀綱要,因此不是標準化成一個表格做查詢。
41 | 7. 後設資料:可以衍伸出其他的資料變數。
42 | 8. 即時/合適的時間
43 |
44 |
45 |
46 | ## Operational System 與 Informational System
47 |
48 | Operational System 主要負責即時的商業活動運行,例如:訂單整合、預訂系統...
49 |
50 | Operational System 會將這個活動的資料完整的保存下來,但這些資料都是支離破碎的,會需要經過整合。
51 |
52 |
53 |
54 | Informational System 主要被設計來從資料倉儲的資料提供出對於特定時間的快照資料,以利於支援資料探勘、分析等等。
55 |
56 |
57 |
58 | 總歸來說,Operational System 與 Informational System 可以利用以下的表格來比較。
59 |
60 | | | Operational System | Informational System |
61 | | :----------: | :--------------------------------------------: | :------------------------------------: |
62 | | 主要用途 | 即時的商業活動運行 | 支援決策、分析等等 |
63 | | 資料型態 | 進行商業活動得到的數據(客戶、銷售商品...) | 特定時間的快照資料與預測 |
64 | | 給哪些人使用 | 銷售者 | 管理層級的人員、商業分析、客戶... |
65 | | 使用範圍 | 狹窄、易於更新與查詢 | 非常廣、特設、在詢問與分析上非常複雜 |
66 | | 設計目標 | 能夠被存取、能夠完整 | 易於使用與存取 |
67 | | 資料大小 | 在更新與存取時,得到的只有帶有幾列的表格資料 | 定期更新、詢問,通常需要非常大量的資料 |
68 |
69 |
70 |
71 | ## 資料倉儲的資料處理
72 |
73 | 一般遵循 `ETL` 的方式處理,也就是 Extract(萃取)、Transform(轉換)、Load(讀入)。
74 |
75 | 通常來說,會從各式資料源萃取資料,將資料進行整合(轉換)、接著讀入 Data Mart 或 Data Warehouse。
76 |
77 |
78 |
79 | ## 資料倉儲的開發方法
80 |
81 | 主要分成兩種:Top-Down、Buttom-Up。
82 |
83 |
84 |
85 | ### Bill Inmon – Top-down
86 |
87 | 先從各方提取資料,接著經過 `ETL` 後,放入 Data Warehouse。
88 |
89 | 接著從 Data Warehouse 再經過 `ETL` 後,轉成各式各樣的 Data Mart。
90 |
91 |
92 |
93 |
152 |
153 |
154 |
155 | 我們可以透過描點的方式畫出 ROC 曲線,就可以從 ROC 曲線中得出 AUC 值,若 AUC 值越大則模型越好。
156 |
157 |
158 |
159 | ## 機器學習的種類
160 |
161 | 1. 學習問題
162 | 1. 監督式學習:所有資料都被標註,給機器去學習與分類,通常來說對機器最簡單,對人類來說最累。
163 | 2. 非監督式學習:所有資料都沒有被標註,透過機器去尋找特徵的學習分式,對機器最困難,誤差較大。
164 | 3. 強化式學習:不標註任何資料,但告訴機器哪步正確,哪步錯誤,讓機器逐步自我修正。
165 | 2. 混合學習問題
166 | 1. 半監督式學習:對少部分資料進行標註,機器透過有標註的資料找出特徵並進行分類,能使非監督式學習的準確率提升。
167 | 2. 自我監督式學習:從一堆沒有 label 標註的資料,訓練出一個監督式模型,然後造出更多 label。
168 | 3. 多實例學習:輸入許多「包」,這些包都含有許多實例,若所有實例都是負例時則包即為負包,若有至少一個實例為正例時,包即為正包。
169 | 3. 推論統計學
170 | 1. 歸納學習:用來辨識汽車的知識可以用來提升辨識卡車的能力,以現有問題的解決模型利用在其他不同但相關的問題上。
171 | 2. 演繹學習:利用廣泛的前提去推論較具體的結論,通常依賴前提是否正確。
172 | 3. 轉導學習:通過觀察特定的訓練樣本,來預測特定測試樣本的方法。
173 | 4. 學習技術
174 | 1. 多任務學習:利用單一一個模型,解決多個問題
175 | 2. 主動學習:從每輪學習迭代中,尋找出一個最不確定的一個或一組樣本,來讓外部反饋者給予回饋。
176 | 3. 線上學習:利用當前的資料來直接更新模型,進而在預測前根據先前的資料給予預測。
177 | 4. 遷移學習:一個模型先訓練一個例子,接著所有模型用這個模型的訓練例子當成起始點,訓練其他的例子。
178 | 5. 集成學習:集成兩個以上合適的模型,接著從這個集成的模型上訓練。。
179 | 6. 聯盟式學習:從各式各樣的自訓練模型中,在不用給自己數據的情況下,也可以進行訓練得到模型。
180 |
181 |
182 |
183 | > Reference Website:
184 | >
185 | > 1. Marketing. (n.d.). *你知道機器學習(Machine Learning),有幾種學習方式嗎?* 伊雲谷eCloudvalley. Retrieved April 5, 2022, from https://www.ecloudvalley.com/zh-hant/machine-learning/
186 | > 2. *自監督學習 self-supervised learning 介紹*. (2021, June 11). 藏字閣. https://jigfopsda.com/zh/posts/2021/self_supervised_learning/
187 | > 3. *多實例學習*. (2021, August 31). 維基百科,自由的百科全書. https://zh.wikipedia.org/wiki/%E5%A4%9A%E7%A4%BA%E4%BE%8B%E5%AD%A6%E4%B9%A0
188 | > 4. *遷移學習*. (2020, September 19). 維基百科,自由的百科全書. https://zh.wikipedia.org/wiki/%E8%BF%81%E7%A7%BB%E5%AD%A6%E4%B9%A0
189 | > 5. *簡要介紹Active Learning(主動學習)思想框架,以及從IF(isolation forest)衍生出來的演算法:FBIF(Feedback-Guided Anomaly Discovery)*. (n.d.). IT人. Retrieved April 5, 2022, from https://iter01.com/420911.html
190 | > 6. Su, S. (2021, December 13). *聯盟式學習 (Federated Learning) - Sherry.AI*. Medium. https://medium.com/sherry-ai/%E8%81%AF%E7%9B%9F%E5%BC%8F%E5%AD%B8%E7%BF%92-federated-learning-b4cc5af7a9c0
--------------------------------------------------------------------------------
/Markdown/Data Preprocessing.md:
--------------------------------------------------------------------------------
1 | # 資料預處理(Data Preprocessing)
2 |
3 | > Reference:
4 | >
5 | > 1. Data Preprocessing by Dr. Tun-Wen Pai
6 |
7 | ## 資料預處理
8 |
9 | 對於一個資料集來說,若數值偏大或偏小的情況下,我們很難去做資料視覺化,甚至資料過大時會讓自然指數過大導致 overflow。
10 |
11 | 故我們希望可以把資料集的值域縮小,有以下幾種方法:
12 |
13 | 1. Z-score normalization
14 | 2. MinMaxScaler
15 | 3. MaxAbsScaler
16 | 4. Robust Scaling
17 | 5. QuantileTrasformation
18 |
19 |
20 |
21 | ### Z-score normalization
22 |
23 | 對於每個資料,我們利用常態分佈將他標準化(Standardization),定義為
24 | $$
25 | x'=\dfrac{x-\overline{x}}{\sigma}
26 | $$
27 | 用這樣的方式就能夠將其值域限縮至 $[-1, 1]$ 之間。
28 |
29 |
30 |
31 | ### MinMaxScaler
32 |
33 | 對於每個資料,我們使用最大與最小值的區間來限縮值域,定義如下:
34 | $$
35 | x' = \dfrac{x-\min(x)}{\max(x)-\min(x)}
36 | $$
37 | 用這樣的方式就能夠將其值域限縮至 $[0, 1]$ 之間。
38 |
39 |
40 |
41 | ### MaxAbsScaler
42 |
43 | 對於每個資料,我們單純使用最大與最小值的區間來限縮值域,定義如下:
44 | $$
45 | x' = \dfrac{x}{\max\{|x|\}}
46 | $$
47 |
48 |
49 | 用這樣的方式就能夠將其值域限縮至 $[-1, 1]$ 之間。
50 |
51 |
52 |
53 | ### Robust Scaling
54 |
55 | Robust Scaling 是一種非線性的限縮方式,使用第三分位與第一分位來進行限縮。
56 |
57 | 前面的方法,以最大值來說,若最大值過大則限縮資料會變小。
58 |
59 | Robust Scaling 優化了這個部分,他沒有特定的值域限縮範圍,但可以對極值有良好的抗噪性,定義如下:
60 | $$
61 | x' = \dfrac{x-Q_2}{(Q_3-Q_1)}
62 | $$
63 |
64 |
65 |
--------------------------------------------------------------------------------
/Markdown/Data Warehouse.md:
--------------------------------------------------------------------------------
1 | # Data Warehouse(資料倉儲)
2 |
3 | >主要的資料來源:
4 | >
5 | >Essentials of Database Management Jeffrey A. Hoffer, Heikki Topi, V. Ramesh
6 | >
7 | >資料倉儲(Data Warehouse, DW) Dr. Tun-Wen Pai
8 |
9 |
10 |
11 | ## 關於資料倉儲
12 |
13 | 資料倉儲具有主題式、經過整合、分析具有時變性、資料不會流失的優勢,用來支援商業智慧,例如分析。
14 |
15 |
16 |
17 | ## 關於資料超市
18 |
19 | 由資料倉儲的資料,分離出一個更具主題式的資料集,稱為資料超市。
20 |
21 |
22 |
23 | ## 資料倉儲的需求
24 |
25 | 從各方蒐集出來的資料通常來說都是支離破碎的(例如:包含編碼、形式不同、格式不一等等)。
26 |
27 | 所以通常一個企業需要的是從這堆支離破碎的資料中經過整合,提供出一個企業想要的簡潔有力的資訊。
28 |
29 | 因此資料倉儲主要就是蒐集這些破碎的資料,然後提供給企業一個高質量的資料。
30 |
31 |
32 |
33 | ## 資料倉儲的開發考慮
34 |
35 | 1. 主題式:僅對特定主題感興趣
36 | 2. 整合性:各式各樣的資料進入資料倉儲都會經過整合成統一格式的資料
37 | 3. 時變性:分析具有時變性,根據不同時間具有不同的分析結果
38 | 4. 穩定性:進入資料倉儲的資料並不會變動。
39 | 5. 摘要整理:進入的資料會盡可能地最佳化資料欄位與維度。
40 | 6. 非標準化:Data Warehouse 使用星狀綱要,因此不是標準化成一個表格做查詢。
41 | 7. 後設資料:可以衍伸出其他的資料變數。
42 | 8. 即時/合適的時間
43 |
44 |
45 |
46 | ## Operational System 與 Informational System
47 |
48 | Operational System 主要負責即時的商業活動運行,例如:訂單整合、預訂系統...
49 |
50 | Operational System 會將這個活動的資料完整的保存下來,但這些資料都是支離破碎的,會需要經過整合。
51 |
52 |
53 |
54 | Informational System 主要被設計來從資料倉儲的資料提供出對於特定時間的快照資料,以利於支援資料探勘、分析等等。
55 |
56 |
57 |
58 | 總歸來說,Operational System 與 Informational System 可以利用以下的表格來比較。
59 |
60 | | | Operational System | Informational System |
61 | | :----------: | :--------------------------------------------: | :------------------------------------: |
62 | | 主要用途 | 即時的商業活動運行 | 支援決策、分析等等 |
63 | | 資料型態 | 進行商業活動得到的數據(客戶、銷售商品...) | 特定時間的快照資料與預測 |
64 | | 給哪些人使用 | 銷售者 | 管理層級的人員、商業分析、客戶... |
65 | | 使用範圍 | 狹窄、易於更新與查詢 | 非常廣、特設、在詢問與分析上非常複雜 |
66 | | 設計目標 | 能夠被存取、能夠完整 | 易於使用與存取 |
67 | | 資料大小 | 在更新與存取時,得到的只有帶有幾列的表格資料 | 定期更新、詢問,通常需要非常大量的資料 |
68 |
69 |
70 |
71 | ## 資料倉儲的資料處理
72 |
73 | 一般遵循 `ETL` 的方式處理,也就是 Extract(萃取)、Transform(轉換)、Load(讀入)。
74 |
75 | 通常來說,會從各式資料源萃取資料,將資料進行整合(轉換)、接著讀入 Data Mart 或 Data Warehouse。
76 |
77 |
78 |
79 | ## 資料倉儲的開發方法
80 |
81 | 主要分成兩種:Top-Down、Buttom-Up。
82 |
83 |
84 |
85 | ### Bill Inmon – Top-down
86 |
87 | 先從各方提取資料,接著經過 `ETL` 後,放入 Data Warehouse。
88 |
89 | 接著從 Data Warehouse 再經過 `ETL` 後,轉成各式各樣的 Data Mart。
90 |
91 |
92 |
93 |  94 |
95 |
96 |
97 | ### Ralph Kimball – Bottom-up
98 |
99 | 先從各方提取資料,接著經過 `ETL` 後,轉置成 Data Mart 的形式。
100 |
101 | 再經由 `ETL` 的處理後,將這些 Data Mart 合併成一個大的 Data Warehouse。
102 |
103 |
104 |
105 |
94 |
95 |
96 |
97 | ### Ralph Kimball – Bottom-up
98 |
99 | 先從各方提取資料,接著經過 `ETL` 後,轉置成 Data Mart 的形式。
100 |
101 | 再經由 `ETL` 的處理後,將這些 Data Mart 合併成一個大的 Data Warehouse。
102 |
103 |
104 |
105 |  106 |
107 |
108 |
109 | ### 兩個開發方式的優缺點分析
110 |
111 | | 分類 | Top-Down | Buttom-up |
112 | | :------: | :------------------------------------------------: | :----------------------------------------------------------: |
113 | | 問題分解 | 將大問題分解成小問題 | 將小問題解決,並且推廣至大問題 |
114 | | 處理資料 | 處理資料的時候,架構是固定的
106 |
107 |
108 |
109 | ### 兩個開發方式的優缺點分析
110 |
111 | | 分類 | Top-Down | Buttom-up |
112 | | :------: | :------------------------------------------------: | :----------------------------------------------------------: |
113 | | 問題分解 | 將大問題分解成小問題 | 將小問題解決,並且推廣至大問題 |
114 | | 處理資料 | 處理資料的時候,架構是固定的
因此資料缺乏彈性 | 由於先建立 Data Mart
所以只需要增加 Data Mart 即可增加資料的彈性 |
115 | | 管理 | 集中管理 | 去中心化管理 |
116 | | 冗餘問題 | 可能包含冗餘的訊息 | 冗餘的訊息可以被移除 |
117 | | 運行速度 | 由於單一窗口,所以運行較快 | 由許多 Data Mart 當作窗口,所以運行較慢 |
118 |
119 |
120 |
121 | > Reference Website:
122 | >
123 | > 1. S, V. (2018, February 28). *Various data warehouse design approaches:top-down and bottom-up*. DWgeek.com. Retrieved April 4, 2022, from https://dwgeek.com/various-data-warehouse-design-approaches.html/
124 | >
125 | > 2. *Data Warehouse Design - javatpoint*. www.javatpoint.com. (n.d.). Retrieved April 4, 2022, from https://www.javatpoint.com/data-warehouse-design
126 |
127 |
128 |
129 | ## 資料倉儲的設計架構
130 |
131 |
132 |
133 | 以 top-down 為例,主要分成四大子架構:資料來源、資料轉換、資料超市或資料倉儲、應用。
134 |
135 | 基本按照 `ETL` 架構來進行資料處理(見 [資料倉儲的資料處理](#資料倉儲的資料處理)),轉換成 Data Warehouse 或 Data Mart。
136 |
137 |  138 |
139 |
140 |
141 | ## 資料倉儲的資料模型
142 |
143 | 在資料倉儲中,資料模型都是多維度的,包含一個以上的事實表格與多個維度表格。
144 |
145 | 以下介紹三種不同的資料模型:星狀綱要、雪花狀綱要、事實星座綱要。
146 |
147 |
148 |
149 | ### 星狀綱要
150 |
151 | 一個事實表格包含大量不重複的資料,與多個維度表格組成的綱要。
152 |
153 | 是目前最常用的綱要。
154 |
155 |
138 |
139 |
140 |
141 | ## 資料倉儲的資料模型
142 |
143 | 在資料倉儲中,資料模型都是多維度的,包含一個以上的事實表格與多個維度表格。
144 |
145 | 以下介紹三種不同的資料模型:星狀綱要、雪花狀綱要、事實星座綱要。
146 |
147 |
148 |
149 | ### 星狀綱要
150 |
151 | 一個事實表格包含大量不重複的資料,與多個維度表格組成的綱要。
152 |
153 | 是目前最常用的綱要。
154 |
155 |  156 |
157 |
158 |
159 | ### 雪花狀綱要
160 |
161 | 一個事實表格包含大量不重複的資料,與多個維度表格組成的綱要,多個維度可再經過細分分成更多個維度的表格。
162 |
163 |
156 |
157 |
158 |
159 | ### 雪花狀綱要
160 |
161 | 一個事實表格包含大量不重複的資料,與多個維度表格組成的綱要,多個維度可再經過細分分成更多個維度的表格。
162 |
163 |  164 |
165 |
166 |
167 | ### 事實星座綱要
168 |
169 | 由多個事實表格共用維度表格。
170 |
171 |
164 |
165 |
166 |
167 | ### 事實星座綱要
168 |
169 | 由多個事實表格共用維度表格。
170 |
171 |  172 |
173 |
174 |
175 | ## 資料倉儲的儲存架構
176 |
177 | 實際上的儲存可能是關聯式資料庫或資料立方體。
178 |
179 |
180 |
181 | ### 資料立方體 - 切塊與切片
182 |
183 | 由維度與事實組成,具有上捲、下鑽、切塊、切片、轉軸等操作,見以下例子。
184 |
185 |
186 |
187 | ### 操作方式 - 切片
188 |
189 | 例如下圖的資料方塊是由(產品類別、月份、數量)三種維度所組成。
190 |
191 | 若我們想要知道鞋子的資料,就相當於將產品類別固定為鞋子,得到一個降成二維的(月份、數量)資料。
192 |
193 | 
194 |
195 |
196 |
197 | ### 操作方式 - 切塊
198 |
199 | 延續上面的例子,若我們想要知道鞋子與衣服的資料,相當於將鞋子、衣服的立方塊切下來,此時資料依然是三維的。
200 |
201 |
202 |
203 | ### 操作方式 - 下鑽
204 |
205 | 延續上面的例子,若我們將這個鞋子的資料,想要知道某個月份的上旬、中旬或下旬的銷售資料。
206 |
207 | 則我們可以針對於資料立方體的月份下鑽,得到上旬、中旬、下旬的資料,藉此得到更詳細的資料。
208 |
209 |
210 |
211 | ### 操作方式 - 上捲
212 |
213 | 延續上面的例子,若我們想要知道整年的銷售資料,則我們可以針對於資料立方體的月份上捲,得到更為概觀的資料。
214 |
215 |
216 |
217 | ### 操作方式 - 轉軸
218 |
219 | 我們可以將立方體做旋轉,得到不同視角的資料。
220 |
221 |
222 |
223 |
224 |
225 | ## 資料倉儲的查詢處理
226 |
227 | - 若是為了快速查詢,在記憶空間充裕的情況下,可能會根據這些資料先建立出可能查詢的方式,
228 |
229 | 可藉由目前有的維度欄位慢慢上推整合合併成一個包含所有維度的資料。
230 |
231 | - 多維度的資料與一般的關聯式資料庫相比,一般的關聯式資料庫只能慢慢地計算累積,而多維度資料庫具有更好的效能。
232 |
--------------------------------------------------------------------------------
/Markdown/Decision Tree.md:
--------------------------------------------------------------------------------
1 | # Decision Tree(決策樹)
2 |
3 | > 主要參考資料:
4 | >
5 | > 決策樹 (Decision Tree) Dr. Tun-Wen Pai
6 | >
7 | > Business intelligence and data mining Anil K. Maheshwari, Ph.D.
8 |
9 |
10 |
11 | ## 決策樹
12 |
13 | 決策樹用來對於一個樹狀事件給出一條路線引導出一個決策,例如是否借款,或者更複雜的決策系統。
14 |
15 |
16 |
17 | 舉一個生活化的例子,若要決定是否要出遊,則我們可以畫出以下的樹狀事件。
18 |
19 |
172 |
173 |
174 |
175 | ## 資料倉儲的儲存架構
176 |
177 | 實際上的儲存可能是關聯式資料庫或資料立方體。
178 |
179 |
180 |
181 | ### 資料立方體 - 切塊與切片
182 |
183 | 由維度與事實組成,具有上捲、下鑽、切塊、切片、轉軸等操作,見以下例子。
184 |
185 |
186 |
187 | ### 操作方式 - 切片
188 |
189 | 例如下圖的資料方塊是由(產品類別、月份、數量)三種維度所組成。
190 |
191 | 若我們想要知道鞋子的資料,就相當於將產品類別固定為鞋子,得到一個降成二維的(月份、數量)資料。
192 |
193 | 
194 |
195 |
196 |
197 | ### 操作方式 - 切塊
198 |
199 | 延續上面的例子,若我們想要知道鞋子與衣服的資料,相當於將鞋子、衣服的立方塊切下來,此時資料依然是三維的。
200 |
201 |
202 |
203 | ### 操作方式 - 下鑽
204 |
205 | 延續上面的例子,若我們將這個鞋子的資料,想要知道某個月份的上旬、中旬或下旬的銷售資料。
206 |
207 | 則我們可以針對於資料立方體的月份下鑽,得到上旬、中旬、下旬的資料,藉此得到更詳細的資料。
208 |
209 |
210 |
211 | ### 操作方式 - 上捲
212 |
213 | 延續上面的例子,若我們想要知道整年的銷售資料,則我們可以針對於資料立方體的月份上捲,得到更為概觀的資料。
214 |
215 |
216 |
217 | ### 操作方式 - 轉軸
218 |
219 | 我們可以將立方體做旋轉,得到不同視角的資料。
220 |
221 |
222 |
223 |
224 |
225 | ## 資料倉儲的查詢處理
226 |
227 | - 若是為了快速查詢,在記憶空間充裕的情況下,可能會根據這些資料先建立出可能查詢的方式,
228 |
229 | 可藉由目前有的維度欄位慢慢上推整合合併成一個包含所有維度的資料。
230 |
231 | - 多維度的資料與一般的關聯式資料庫相比,一般的關聯式資料庫只能慢慢地計算累積,而多維度資料庫具有更好的效能。
232 |
--------------------------------------------------------------------------------
/Markdown/Decision Tree.md:
--------------------------------------------------------------------------------
1 | # Decision Tree(決策樹)
2 |
3 | > 主要參考資料:
4 | >
5 | > 決策樹 (Decision Tree) Dr. Tun-Wen Pai
6 | >
7 | > Business intelligence and data mining Anil K. Maheshwari, Ph.D.
8 |
9 |
10 |
11 | ## 決策樹
12 |
13 | 決策樹用來對於一個樹狀事件給出一條路線引導出一個決策,例如是否借款,或者更複雜的決策系統。
14 |
15 |
16 |
17 | 舉一個生活化的例子,若要決定是否要出遊,則我們可以畫出以下的樹狀事件。
18 |
19 |  20 |
21 |
22 |
23 | 可以發現從「是否出遊」到任意一種出遊決策都是唯一路徑,換言之,在這棵樹上共有 4 條路徑。
24 |
25 | 對於一個決策系統來說也可能會很複雜,例如判斷手寫數字時,龐大而精確的決策系統能夠有效的幫助我們判斷出手寫的數字。
26 |
27 |
28 |
29 |
30 |
31 | ## 使用決策樹的優點與缺點
32 |
33 | > Reference website:
34 | >
35 | > 1. https://scikit-learn.org/stable/modules/tree.html
36 | > 2. https://zh.wikipedia.org/wiki/%E5%86%B3%E7%AD%96%E6%A0%91%E5%AD%A6%E4%B9%A0
37 |
38 |
39 |
40 | - 優點
41 |
42 | 1. 樹可以被視覺化,方便理解
43 | 2. 資料需要被整理,資料的空值不被接受
44 | 3. 任何作出決策的操作都取決於樹的節點數量,且為對數時間複雜度
45 | 4. 支援輸出一種以上的結果(multi-output)
46 | 5. 使用白箱模型,因為決策樹可以簡單解釋決策的來源與邏輯
47 | 6. 可用統計測試來驗證模型
48 | 7. 對於噪聲有很強的控制性
49 |
50 |
51 |
52 | - 缺點
53 |
54 | 1. 可能會 overfitting
55 | 2. 因為可能會 overfitting,所以不好實行外推
56 | 3. 優化決策樹是 NP-Complete 問題,優化決策樹無法在多項式時間內解決
57 | 4. 有些概念沒有辦法清楚解釋(例如 XOR)
58 | 5. 資料集的平衡很重要,否則樹可能會被一些資料所支配,產生出帶有偏見的決策樹
59 |
60 |
61 |
62 | ## 建立決策樹的方式
63 |
64 | 我們以一個出遊的資料集為例,如下圖。
65 |
66 |
20 |
21 |
22 |
23 | 可以發現從「是否出遊」到任意一種出遊決策都是唯一路徑,換言之,在這棵樹上共有 4 條路徑。
24 |
25 | 對於一個決策系統來說也可能會很複雜,例如判斷手寫數字時,龐大而精確的決策系統能夠有效的幫助我們判斷出手寫的數字。
26 |
27 |
28 |
29 |
30 |
31 | ## 使用決策樹的優點與缺點
32 |
33 | > Reference website:
34 | >
35 | > 1. https://scikit-learn.org/stable/modules/tree.html
36 | > 2. https://zh.wikipedia.org/wiki/%E5%86%B3%E7%AD%96%E6%A0%91%E5%AD%A6%E4%B9%A0
37 |
38 |
39 |
40 | - 優點
41 |
42 | 1. 樹可以被視覺化,方便理解
43 | 2. 資料需要被整理,資料的空值不被接受
44 | 3. 任何作出決策的操作都取決於樹的節點數量,且為對數時間複雜度
45 | 4. 支援輸出一種以上的結果(multi-output)
46 | 5. 使用白箱模型,因為決策樹可以簡單解釋決策的來源與邏輯
47 | 6. 可用統計測試來驗證模型
48 | 7. 對於噪聲有很強的控制性
49 |
50 |
51 |
52 | - 缺點
53 |
54 | 1. 可能會 overfitting
55 | 2. 因為可能會 overfitting,所以不好實行外推
56 | 3. 優化決策樹是 NP-Complete 問題,優化決策樹無法在多項式時間內解決
57 | 4. 有些概念沒有辦法清楚解釋(例如 XOR)
58 | 5. 資料集的平衡很重要,否則樹可能會被一些資料所支配,產生出帶有偏見的決策樹
59 |
60 |
61 |
62 | ## 建立決策樹的方式
63 |
64 | 我們以一個出遊的資料集為例,如下圖。
65 |
66 |  67 |
68 |
69 |
70 | 決策樹是一種層級式的分支結構,我們可以分割表格,來計算錯誤合計。
71 |
72 | 我們將現有資訊加上規則,可以得到以下的表格,可以看出錯誤統計均是 4/18,因此我們可以任意選擇一個來建樹。
73 |
74 |
67 |
68 |
69 |
70 | 決策樹是一種層級式的分支結構,我們可以分割表格,來計算錯誤合計。
71 |
72 | 我們將現有資訊加上規則,可以得到以下的表格,可以看出錯誤統計均是 4/18,因此我們可以任意選擇一個來建樹。
73 |
74 |  75 |
76 | 例如我們選擇天氣,可以得到以下的事件樹狀圖。
77 |
78 | 
79 |
80 | 按照同樣方式進行推廣,可以得到以下的樹狀結構。
81 |
82 | 
83 |
84 |
85 |
86 | 這樣有點智障,因為晴天跟陰天應該可以合併,且冷跟溫和也該可以合併。
87 |
88 | 一個決策樹主要基於分支準則、停止條件與修剪而有所不同,也因此衍伸出了決策樹演算法。
89 |
90 |
91 |
92 | ## 決策樹的 Overfitting 問題
93 |
94 | 決策樹其中一個問題就是很容易 overfitting。
95 |
96 |
97 |
98 | ### Overfitting 簡介
99 |
100 | Overfitting 就是過度擬合,也就是對於一個訓練資料集,只對資料集的資料有作用,不利於推廣更多資料。
101 |
102 | 如果看不懂上面的文字,可以看下面找到的[一張圖](https://pbs.twimg.com/media/Ef5yDj2X0AIkHEe.jpg)。
103 |
104 |
75 |
76 | 例如我們選擇天氣,可以得到以下的事件樹狀圖。
77 |
78 | 
79 |
80 | 按照同樣方式進行推廣,可以得到以下的樹狀結構。
81 |
82 | 
83 |
84 |
85 |
86 | 這樣有點智障,因為晴天跟陰天應該可以合併,且冷跟溫和也該可以合併。
87 |
88 | 一個決策樹主要基於分支準則、停止條件與修剪而有所不同,也因此衍伸出了決策樹演算法。
89 |
90 |
91 |
92 | ## 決策樹的 Overfitting 問題
93 |
94 | 決策樹其中一個問題就是很容易 overfitting。
95 |
96 |
97 |
98 | ### Overfitting 簡介
99 |
100 | Overfitting 就是過度擬合,也就是對於一個訓練資料集,只對資料集的資料有作用,不利於推廣更多資料。
101 |
102 | 如果看不懂上面的文字,可以看下面找到的[一張圖](https://pbs.twimg.com/media/Ef5yDj2X0AIkHEe.jpg)。
103 |
104 |  105 |
106 | 由於只對資料集的資料有作用,因此若在預判不是資料集的資料時,很容易出現預判失敗的問題。
107 |
108 |
109 |
110 | ### 迴避 Overfitting 的方法
111 |
112 | 迴避 Overfitting 可以使用剪枝來迴避,分成先剪枝(prepruning)與後剪枝(postpruning)。
113 |
114 | 1. 先剪枝:可以設定一個條件,使得後面的子樹停止構建,當前的節點變成葉節點。
115 |
116 | 2. 後剪枝:先建照一個完整的決策樹,再將這個樹進行修剪。
117 |
118 | 當然,資料集也很重要,所以如同 data mining 一樣,需要對資料集的品質有所把持。
119 |
120 |
121 |
122 | ## 決策樹演算法
123 |
124 | 主要分成:ID3、CART、CHAID,這份筆記主要會講解 ID3、CART 演算法。
125 |
126 |
127 |
128 | ## ID3 演算法
129 |
130 | ### Entropy
131 |
132 | Entropy(資訊熵),一種量化資料同源的數值,介於 0 ~ 1 之間。
133 |
134 | 若一個資料是絕對同源,則 Entropy = 0,若一個資料絕對異源,則 Entropy = 1。
135 |
136 | 定義一個樣本的 Entropy 為:
137 | $$
138 | Entropy(S) = -\sum_{i} P(x_i)\log_2(P(x_i)) - \sum_{i} Q(x_i) \log_2(Q(x_i))
139 | $$
140 | 其中 $\displaystyle \lim_{p \rightarrow 0} p\log p = 0$。
141 |
142 |
143 |
144 | ### Information Gain
145 |
146 | Information Gain(訊息增益)為資訊熵經過分割 Attribute 後所減少的數值,介於 0 ~ 1 之間。
147 |
148 | 當我們在分割樹的時候,我們會選擇 Infomation Gain 大的來當作我們的父節點或根節點,若 Entropy = 0 時則為子節點。
149 |
150 | 我們可以定義一個樣本在分割成一個 Attribute 之後的 Infomation Gain 為
151 | $$
152 | IG(S, A) = Entropy(S) - \sum_{v\in D_A} \dfrac{|S_v|}{|S|} Entropy(S_v)
153 | $$
154 |
155 |
156 | ### 優缺點
157 |
158 | - 優點:
159 | 1. 好理解決策的邏輯,因為可以畫成一棵樹
160 | 2. 建立迅速
161 | 3. 建立較小的樹
162 | 4. 只需要足夠數量的測試資料
163 | 5. 只需要測試足夠多的屬性來讓所有資料都被分類
164 | 6. 在分類測試資料時可以被修剪,利於減少測試數量
165 | 7. 使用整個資料集,搜索空間完整
166 | - 缺點
167 | 1. 會因為測試資料過小導致 over-fitted 跟 over-classified,不利於推廣預測。
168 | 2. 每次預測只測試一個 Attribute。
169 | 3. 測試連續資料可能會導致大量運算,產生大量的樹。
170 |
171 |
172 |
173 | ### 範例
174 |
175 | 以這個資料為範例,利用 ID3 來建立決策樹。
176 |
177 |
105 |
106 | 由於只對資料集的資料有作用,因此若在預判不是資料集的資料時,很容易出現預判失敗的問題。
107 |
108 |
109 |
110 | ### 迴避 Overfitting 的方法
111 |
112 | 迴避 Overfitting 可以使用剪枝來迴避,分成先剪枝(prepruning)與後剪枝(postpruning)。
113 |
114 | 1. 先剪枝:可以設定一個條件,使得後面的子樹停止構建,當前的節點變成葉節點。
115 |
116 | 2. 後剪枝:先建照一個完整的決策樹,再將這個樹進行修剪。
117 |
118 | 當然,資料集也很重要,所以如同 data mining 一樣,需要對資料集的品質有所把持。
119 |
120 |
121 |
122 | ## 決策樹演算法
123 |
124 | 主要分成:ID3、CART、CHAID,這份筆記主要會講解 ID3、CART 演算法。
125 |
126 |
127 |
128 | ## ID3 演算法
129 |
130 | ### Entropy
131 |
132 | Entropy(資訊熵),一種量化資料同源的數值,介於 0 ~ 1 之間。
133 |
134 | 若一個資料是絕對同源,則 Entropy = 0,若一個資料絕對異源,則 Entropy = 1。
135 |
136 | 定義一個樣本的 Entropy 為:
137 | $$
138 | Entropy(S) = -\sum_{i} P(x_i)\log_2(P(x_i)) - \sum_{i} Q(x_i) \log_2(Q(x_i))
139 | $$
140 | 其中 $\displaystyle \lim_{p \rightarrow 0} p\log p = 0$。
141 |
142 |
143 |
144 | ### Information Gain
145 |
146 | Information Gain(訊息增益)為資訊熵經過分割 Attribute 後所減少的數值,介於 0 ~ 1 之間。
147 |
148 | 當我們在分割樹的時候,我們會選擇 Infomation Gain 大的來當作我們的父節點或根節點,若 Entropy = 0 時則為子節點。
149 |
150 | 我們可以定義一個樣本在分割成一個 Attribute 之後的 Infomation Gain 為
151 | $$
152 | IG(S, A) = Entropy(S) - \sum_{v\in D_A} \dfrac{|S_v|}{|S|} Entropy(S_v)
153 | $$
154 |
155 |
156 | ### 優缺點
157 |
158 | - 優點:
159 | 1. 好理解決策的邏輯,因為可以畫成一棵樹
160 | 2. 建立迅速
161 | 3. 建立較小的樹
162 | 4. 只需要足夠數量的測試資料
163 | 5. 只需要測試足夠多的屬性來讓所有資料都被分類
164 | 6. 在分類測試資料時可以被修剪,利於減少測試數量
165 | 7. 使用整個資料集,搜索空間完整
166 | - 缺點
167 | 1. 會因為測試資料過小導致 over-fitted 跟 over-classified,不利於推廣預測。
168 | 2. 每次預測只測試一個 Attribute。
169 | 3. 測試連續資料可能會導致大量運算,產生大量的樹。
170 |
171 |
172 |
173 | ### 範例
174 |
175 | 以這個資料為範例,利用 ID3 來建立決策樹。
176 |
177 |  178 |
179 | 首先先計算 $Entropy(Play)$,也就是
180 |
181 | $Entropy(Play) = -\dfrac{9}{14}\log_2 \dfrac{9}{14} - (\dfrac{5}{14}\log_2 \dfrac{5}{14}) \approx 0.94$
182 |
183 |
184 |
185 | 接著可以考慮
186 |
187 | 1. 三種不同類型的 Outlook 所產生出來的 $Entropy(Play, Outlook)$
188 |
189 | $Entropy(Sunny) = -\dfrac{2}{5}\log_2(\dfrac{2}{5}) - \dfrac{3}{5}\log_2(\dfrac{3}{5}) \approx 0.97$
190 |
191 | $Entropy(Overcast) = -\dfrac{4}{4}\log_2(\dfrac{4}{4}) - \dfrac{0}{4}\log_2(\dfrac{0}{4}) = 0$
192 |
193 | $Entropy(Rainy) = -\dfrac{3}{5}\log_2(\dfrac{3}{5}) - \dfrac{2}{5}\log_2(\dfrac{2}{5}) \approx 0.97$
194 |
195 | $Entropy(Play,Outlook) = \dfrac{5}{14}Entropy(Sunny) + \dfrac{4}{14}Entropy(Overcast) + \dfrac{5}{14}Entropy(Rainy) = 0.6936$
196 |
197 | 2. 三種不同類型的 Temperature 所產生出來的 $Entropy(Play, Temperature)$
198 |
199 | $Entropy(Hot) = -\dfrac{2}{4}\log_2(\dfrac{2}{4}) - \dfrac{2}{4}\log_2(\dfrac{2}{4})= 1$
200 |
201 | $Entropy(Mild) = -\dfrac{2}{6}\log_2(\dfrac{2}{6}) - \dfrac{4}{6}\log_2(\dfrac{4}{6}) \approx 0.92$
202 |
203 | $Entropy(Cold) = -\dfrac{3}{4}\log_2(\dfrac{3}{4})-\dfrac{1}{4}\log_2(\dfrac{1}{4}) \approx 0.81$
204 |
205 | $Entropy(Play, Temperature) \approx 0.911$
206 |
207 | 3. 兩種不同類型的 Humidity 所產生出來的 $Entropy(Play, Humidity)$
208 |
209 | $Entropy(High) = -\dfrac{3}{7}\log_2(\dfrac{3}{7})-\dfrac{4}{7}\log_2(\dfrac{4}{7}) \approx 0.985$
210 |
211 | $Entropy(Normal) = -\dfrac{6}{7}\log_2(\dfrac{6}{7})-\dfrac{6}{7}\log_2(\dfrac{6}{7}) \approx 0.592$
212 |
213 | $Entropy(Play, Humidity) \approx 0.7885$
214 |
215 | 4. 兩種不同類型的 Wind 所產生出來的 $Entropy(Play, Wind)$
216 |
217 | $Entropy(True) = -\dfrac{3}{6}\log_2(\dfrac{3}{6})-\dfrac{3}{6}\log_2(\dfrac{3}{6}) = 1$
218 |
219 | $Entropy(False) = -\dfrac{6}{8}\log_2(\dfrac{6}{8})-\dfrac{2}{8}\log_2(\dfrac{2}{8}) \approx 0.811$
220 |
221 | $Entropy(Play, Wind) \approx \dfrac{6}{14}\times 1 + \dfrac{8}{14}\times 0.811 \approx 0.892$
222 |
223 |
224 |
225 | 我們可以分別算出,分支這四種類型所產生的 $Information Gain$,得到
226 |
227 | $IG(Outlook) = Entropy(Play) - Entropy(Play, Outlook) = 0.2464$
228 |
229 | $IG(Temperature) = Entropy(Play) - Entropy(Play, Temperature) \approx 0.029$
230 |
231 | $IG(Humidity) = Entropy(Play) - Entropy(Play, Humidity) \approx 0.1515$
232 |
233 | $IG(Wind) = Entropy(Play) - Entropy(Play, Wind) \approx 0.048$
234 |
235 | 我們挑 $IG$ 最高的當作分支條件,所以 $Outlook$ 先分支,如圖。
236 |
237 |
178 |
179 | 首先先計算 $Entropy(Play)$,也就是
180 |
181 | $Entropy(Play) = -\dfrac{9}{14}\log_2 \dfrac{9}{14} - (\dfrac{5}{14}\log_2 \dfrac{5}{14}) \approx 0.94$
182 |
183 |
184 |
185 | 接著可以考慮
186 |
187 | 1. 三種不同類型的 Outlook 所產生出來的 $Entropy(Play, Outlook)$
188 |
189 | $Entropy(Sunny) = -\dfrac{2}{5}\log_2(\dfrac{2}{5}) - \dfrac{3}{5}\log_2(\dfrac{3}{5}) \approx 0.97$
190 |
191 | $Entropy(Overcast) = -\dfrac{4}{4}\log_2(\dfrac{4}{4}) - \dfrac{0}{4}\log_2(\dfrac{0}{4}) = 0$
192 |
193 | $Entropy(Rainy) = -\dfrac{3}{5}\log_2(\dfrac{3}{5}) - \dfrac{2}{5}\log_2(\dfrac{2}{5}) \approx 0.97$
194 |
195 | $Entropy(Play,Outlook) = \dfrac{5}{14}Entropy(Sunny) + \dfrac{4}{14}Entropy(Overcast) + \dfrac{5}{14}Entropy(Rainy) = 0.6936$
196 |
197 | 2. 三種不同類型的 Temperature 所產生出來的 $Entropy(Play, Temperature)$
198 |
199 | $Entropy(Hot) = -\dfrac{2}{4}\log_2(\dfrac{2}{4}) - \dfrac{2}{4}\log_2(\dfrac{2}{4})= 1$
200 |
201 | $Entropy(Mild) = -\dfrac{2}{6}\log_2(\dfrac{2}{6}) - \dfrac{4}{6}\log_2(\dfrac{4}{6}) \approx 0.92$
202 |
203 | $Entropy(Cold) = -\dfrac{3}{4}\log_2(\dfrac{3}{4})-\dfrac{1}{4}\log_2(\dfrac{1}{4}) \approx 0.81$
204 |
205 | $Entropy(Play, Temperature) \approx 0.911$
206 |
207 | 3. 兩種不同類型的 Humidity 所產生出來的 $Entropy(Play, Humidity)$
208 |
209 | $Entropy(High) = -\dfrac{3}{7}\log_2(\dfrac{3}{7})-\dfrac{4}{7}\log_2(\dfrac{4}{7}) \approx 0.985$
210 |
211 | $Entropy(Normal) = -\dfrac{6}{7}\log_2(\dfrac{6}{7})-\dfrac{6}{7}\log_2(\dfrac{6}{7}) \approx 0.592$
212 |
213 | $Entropy(Play, Humidity) \approx 0.7885$
214 |
215 | 4. 兩種不同類型的 Wind 所產生出來的 $Entropy(Play, Wind)$
216 |
217 | $Entropy(True) = -\dfrac{3}{6}\log_2(\dfrac{3}{6})-\dfrac{3}{6}\log_2(\dfrac{3}{6}) = 1$
218 |
219 | $Entropy(False) = -\dfrac{6}{8}\log_2(\dfrac{6}{8})-\dfrac{2}{8}\log_2(\dfrac{2}{8}) \approx 0.811$
220 |
221 | $Entropy(Play, Wind) \approx \dfrac{6}{14}\times 1 + \dfrac{8}{14}\times 0.811 \approx 0.892$
222 |
223 |
224 |
225 | 我們可以分別算出,分支這四種類型所產生的 $Information Gain$,得到
226 |
227 | $IG(Outlook) = Entropy(Play) - Entropy(Play, Outlook) = 0.2464$
228 |
229 | $IG(Temperature) = Entropy(Play) - Entropy(Play, Temperature) \approx 0.029$
230 |
231 | $IG(Humidity) = Entropy(Play) - Entropy(Play, Humidity) \approx 0.1515$
232 |
233 | $IG(Wind) = Entropy(Play) - Entropy(Play, Wind) \approx 0.048$
234 |
235 | 我們挑 $IG$ 最高的當作分支條件,所以 $Outlook$ 先分支,如圖。
236 |
237 |  238 |
239 | 接著我們考慮 Sunny,得到
240 |
241 | 1. 三種不同類型的 temperature。
242 |
243 | $Entropy(Hot) = - \dfrac{0}{2}\log_2\dfrac{0}{2} - \dfrac{2}{2}\log_2\dfrac{2}{2} = 0$。
244 |
245 | $Entropy(Mild) = -\dfrac{1}{2}\log_2\dfrac{1}{2} - \dfrac{1}{2}\log_2\dfrac{1}{2} = 1$
246 |
247 | $Entropy(Cold) = -\dfrac{1}{1}\log_2\dfrac{1}{1} - \dfrac{0}{1}\log_2\dfrac{0}{1} = 0$
248 |
249 | 可以得到 $\displaystyle Entropy(Sunny, Temperature) = \sum_{i}P(x_i)Entropy(x_i) = \dfrac{2}{5}$
250 |
251 | 2. 兩種不同類型的 humidity。
252 |
253 | $Entropy(High) = -\dfrac{0}{3}\log_2\dfrac{0}{3}-\dfrac{3}{3}\log_2\dfrac{3}{3} = 0$
254 |
255 | $Entropy(Normal) = -\dfrac{0}{2}\log_2\dfrac{0}{2} - \dfrac{2}{2}\log_2\dfrac{2}{2} = 0$
256 |
257 | 可以得到 $\displaystyle Entropy(Sunny, Humidity) = \sum_{i}P(x_i)Entropy(x_i) = 0$
258 |
259 | 3. 兩種不同類型的 wind。
260 |
261 | $Entropy(True) = -\dfrac{1}{2}\log_2\dfrac{1}{2} - \dfrac{1}{2}\log_2\dfrac{1}{2} = 1$
262 |
263 | $Entropy(False) = -\dfrac{1}{3}\log_2\dfrac{1}{3}-\dfrac{2}{3}\log_2\dfrac{2}{3} = 0.918$
264 |
265 | 可以得到 $\displaystyle Entropy(Sunny, Wind) = \sum_{i}P(x_i)Entropy(x_i) = 0.9508$
266 |
267 | 可以分別算出這三種分支的 Infomation Gain,也就是
268 |
269 | $IG(Temperature) = Entropy(Sunny) - Entropy(Sunny, Temperature) = 0.57$
270 |
271 | $IG(Humidity) = Entropy(Sunny) - Entropy(Sunny, Humidity) = 0.97$
272 |
273 | $IG(Wind) = Entropy(Sunny) - Entropy(Sunny, Wind) = 0.0192$
274 |
275 | 選擇 Infomation Gain 最高的來分支,得到下圖。
276 |
277 |
238 |
239 | 接著我們考慮 Sunny,得到
240 |
241 | 1. 三種不同類型的 temperature。
242 |
243 | $Entropy(Hot) = - \dfrac{0}{2}\log_2\dfrac{0}{2} - \dfrac{2}{2}\log_2\dfrac{2}{2} = 0$。
244 |
245 | $Entropy(Mild) = -\dfrac{1}{2}\log_2\dfrac{1}{2} - \dfrac{1}{2}\log_2\dfrac{1}{2} = 1$
246 |
247 | $Entropy(Cold) = -\dfrac{1}{1}\log_2\dfrac{1}{1} - \dfrac{0}{1}\log_2\dfrac{0}{1} = 0$
248 |
249 | 可以得到 $\displaystyle Entropy(Sunny, Temperature) = \sum_{i}P(x_i)Entropy(x_i) = \dfrac{2}{5}$
250 |
251 | 2. 兩種不同類型的 humidity。
252 |
253 | $Entropy(High) = -\dfrac{0}{3}\log_2\dfrac{0}{3}-\dfrac{3}{3}\log_2\dfrac{3}{3} = 0$
254 |
255 | $Entropy(Normal) = -\dfrac{0}{2}\log_2\dfrac{0}{2} - \dfrac{2}{2}\log_2\dfrac{2}{2} = 0$
256 |
257 | 可以得到 $\displaystyle Entropy(Sunny, Humidity) = \sum_{i}P(x_i)Entropy(x_i) = 0$
258 |
259 | 3. 兩種不同類型的 wind。
260 |
261 | $Entropy(True) = -\dfrac{1}{2}\log_2\dfrac{1}{2} - \dfrac{1}{2}\log_2\dfrac{1}{2} = 1$
262 |
263 | $Entropy(False) = -\dfrac{1}{3}\log_2\dfrac{1}{3}-\dfrac{2}{3}\log_2\dfrac{2}{3} = 0.918$
264 |
265 | 可以得到 $\displaystyle Entropy(Sunny, Wind) = \sum_{i}P(x_i)Entropy(x_i) = 0.9508$
266 |
267 | 可以分別算出這三種分支的 Infomation Gain,也就是
268 |
269 | $IG(Temperature) = Entropy(Sunny) - Entropy(Sunny, Temperature) = 0.57$
270 |
271 | $IG(Humidity) = Entropy(Sunny) - Entropy(Sunny, Humidity) = 0.97$
272 |
273 | $IG(Wind) = Entropy(Sunny) - Entropy(Sunny, Wind) = 0.0192$
274 |
275 | 選擇 Infomation Gain 最高的來分支,得到下圖。
276 |
277 |  278 |
279 |
280 |
281 | 接著我們考慮 Rainy,得到
282 |
283 | 1. 兩種不同類型的 temperature。
284 |
285 | $Entropy(Mild) = -\dfrac{2}{3}\log_2\dfrac{2}{3}-\dfrac{1}{3}\log_2\dfrac{1}{3} = 0.918$
286 |
287 | $Entropy(Cold) = -\dfrac{1}{2}\log_2\dfrac{1}{2} - \dfrac{1}{2}\log_2\dfrac{1}{2} = 1$
288 |
289 | $Entropy(Rainy, Temperature) = \dfrac{3}{5}Entropy(Mild) + \dfrac{2}{5}Entropy(Cold) = 0.951$
290 |
291 | 2. 兩種不同類型的 humidity。
292 |
293 | $Entropy(High) = -\dfrac{1}{2}\log_2\dfrac{1}{2} - \dfrac{1}{2}\log_2\dfrac{1}{2} = 1$
294 |
295 | $Entropy(Normal) = -\dfrac{2}{3}\log_2\dfrac{2}{3} - \dfrac{1}{3}\log_2\dfrac{1}{3} = 0.918$
296 |
297 | $Entropy(Rainy, Humidity) = \dfrac{2}{5}Entropy(High) + \dfrac{3}{5}Entropy(Normal) = 0.951$
298 |
299 | 3. 兩種不同類型的 wind。
300 |
301 | $Entropy(True) = -\dfrac{0}{2}\log_2\dfrac{0}{2} - \dfrac{2}{2}\log_2\dfrac{2}{2} = 0$
302 |
303 | $Entropy(False) = -\dfrac{3}{3}\log_2\dfrac{3}{3}-\dfrac{0}{3}\log_2\dfrac{0}{3} = 0$
304 |
305 | $Entropy(Rainy, Wind) = \dfrac{2}{5}Entropy(True) + \dfrac{3}{5}Entropy(False) = 0$
306 |
307 | 可以分別算出這三種分支的 Information Gain,如下:
308 |
309 | $IG(Temperature) = Entropy(Rainy) - Entropy(Rainy, Temperature) = 0.97 - 0.951 = 0.019$
310 |
311 | $IG(Humidity) = Entropy(Rainy) - Entropy(Rainy, Humidity) = 0.97 - 0.951 = 0.019$
312 |
313 | $IG(Wind) = Entropy(Rainy), Entropy(Rainy, Wind) = 0.97 - 0 = 0.97$
314 |
315 | 選擇 Information Gain 大的當作分支,得到下圖。
316 |
317 |
278 |
279 |
280 |
281 | 接著我們考慮 Rainy,得到
282 |
283 | 1. 兩種不同類型的 temperature。
284 |
285 | $Entropy(Mild) = -\dfrac{2}{3}\log_2\dfrac{2}{3}-\dfrac{1}{3}\log_2\dfrac{1}{3} = 0.918$
286 |
287 | $Entropy(Cold) = -\dfrac{1}{2}\log_2\dfrac{1}{2} - \dfrac{1}{2}\log_2\dfrac{1}{2} = 1$
288 |
289 | $Entropy(Rainy, Temperature) = \dfrac{3}{5}Entropy(Mild) + \dfrac{2}{5}Entropy(Cold) = 0.951$
290 |
291 | 2. 兩種不同類型的 humidity。
292 |
293 | $Entropy(High) = -\dfrac{1}{2}\log_2\dfrac{1}{2} - \dfrac{1}{2}\log_2\dfrac{1}{2} = 1$
294 |
295 | $Entropy(Normal) = -\dfrac{2}{3}\log_2\dfrac{2}{3} - \dfrac{1}{3}\log_2\dfrac{1}{3} = 0.918$
296 |
297 | $Entropy(Rainy, Humidity) = \dfrac{2}{5}Entropy(High) + \dfrac{3}{5}Entropy(Normal) = 0.951$
298 |
299 | 3. 兩種不同類型的 wind。
300 |
301 | $Entropy(True) = -\dfrac{0}{2}\log_2\dfrac{0}{2} - \dfrac{2}{2}\log_2\dfrac{2}{2} = 0$
302 |
303 | $Entropy(False) = -\dfrac{3}{3}\log_2\dfrac{3}{3}-\dfrac{0}{3}\log_2\dfrac{0}{3} = 0$
304 |
305 | $Entropy(Rainy, Wind) = \dfrac{2}{5}Entropy(True) + \dfrac{3}{5}Entropy(False) = 0$
306 |
307 | 可以分別算出這三種分支的 Information Gain,如下:
308 |
309 | $IG(Temperature) = Entropy(Rainy) - Entropy(Rainy, Temperature) = 0.97 - 0.951 = 0.019$
310 |
311 | $IG(Humidity) = Entropy(Rainy) - Entropy(Rainy, Humidity) = 0.97 - 0.951 = 0.019$
312 |
313 | $IG(Wind) = Entropy(Rainy), Entropy(Rainy, Wind) = 0.97 - 0 = 0.97$
314 |
315 | 選擇 Information Gain 大的當作分支,得到下圖。
316 |
317 |  318 |
319 | 此時決策樹已建立完成。
320 |
321 |
322 |
323 | ## CART 演算法
324 |
325 | > Reference:
326 | >
327 | > 1. **https://journals.plos.org/plosone/article/file?id=10.1371/journal.pone.0098450.s002&type=supplementary**
328 | > 2. https://www.youtube.com/watch?v=qrDzZMRm_Kw
329 |
330 |
331 |
332 | ### 演算法
333 |
334 | 一個基於吉尼不純度係數 (Gini Impurity) 作為分割標準的分類演算法,先前提到的 ID3 是基於 Information Gain。
335 |
336 | 演算法主要運行如下:
337 |
338 | 1. 尋找最佳特徵分割方式,例如有 K 種特徵,必有 K-1 種分割方式,對於每一種分割方式算出吉尼不純度係數。
339 |
340 | 2. 延續第一點,對於每一種特徵,算出每個特徵的吉尼不純度係數權重。
341 |
342 | 3. 選擇最低的吉尼不純度係數進行分割。
343 |
344 | 4. 重複1, 2, 3,直到達到結束條件。
345 |
346 |
347 |
348 | ### Gini Impurity
349 |
350 | 對於一個 CART 演算法的分割標準,主要以吉尼不純度係數(Gini Impurity)來做參考標準,定義如下。
351 | $$
352 | GI(A) = 1 - \sum^{m}_{k=1}p_k^2
353 | $$
354 | 其中 $0 \le GI(A) \le 1-\dfrac{1}{m}$,當 $GI(A) = 0$ 時,所有資料都被歸類在同一類,$GI(A) = 1 - \dfrac{1}{m}$ 時所有類別均不分類。
355 |
356 |
357 |
358 | ### 範例
359 |
360 | 以這個資料為範例,利用 CART 來建立決策樹。
361 |
362 |
318 |
319 | 此時決策樹已建立完成。
320 |
321 |
322 |
323 | ## CART 演算法
324 |
325 | > Reference:
326 | >
327 | > 1. **https://journals.plos.org/plosone/article/file?id=10.1371/journal.pone.0098450.s002&type=supplementary**
328 | > 2. https://www.youtube.com/watch?v=qrDzZMRm_Kw
329 |
330 |
331 |
332 | ### 演算法
333 |
334 | 一個基於吉尼不純度係數 (Gini Impurity) 作為分割標準的分類演算法,先前提到的 ID3 是基於 Information Gain。
335 |
336 | 演算法主要運行如下:
337 |
338 | 1. 尋找最佳特徵分割方式,例如有 K 種特徵,必有 K-1 種分割方式,對於每一種分割方式算出吉尼不純度係數。
339 |
340 | 2. 延續第一點,對於每一種特徵,算出每個特徵的吉尼不純度係數權重。
341 |
342 | 3. 選擇最低的吉尼不純度係數進行分割。
343 |
344 | 4. 重複1, 2, 3,直到達到結束條件。
345 |
346 |
347 |
348 | ### Gini Impurity
349 |
350 | 對於一個 CART 演算法的分割標準,主要以吉尼不純度係數(Gini Impurity)來做參考標準,定義如下。
351 | $$
352 | GI(A) = 1 - \sum^{m}_{k=1}p_k^2
353 | $$
354 | 其中 $0 \le GI(A) \le 1-\dfrac{1}{m}$,當 $GI(A) = 0$ 時,所有資料都被歸類在同一類,$GI(A) = 1 - \dfrac{1}{m}$ 時所有類別均不分類。
355 |
356 |
357 |
358 | ### 範例
359 |
360 | 以這個資料為範例,利用 CART 來建立決策樹。
361 |
362 |  363 |
364 |
365 |
366 | 先考慮四種不同的分割方式
367 |
368 | 1. 考慮第一種 Outlook
369 |
370 | $GI(Outlook, Sunny) = 1 - (\dfrac{2}{5})^2 - (\dfrac{3}{5})^2=0.48$
371 |
372 | $GI(Outlook, Overcast) = 1 - (\dfrac{4}{4})^2-(\dfrac{0}{4})^2=0$
373 |
374 | $GI(Outlook, Rainy) = 1-(\dfrac{3}{5})^2-(\dfrac{2}{5})^2=0.48$
375 |
376 | $GI(Outlook) = P(Sunny)GI(Sunny) + P(Overcast)GI(Overcast) + P(Rainy)GI(Rainy)$
377 |
378 | $= \dfrac{5}{14}\times 0.48 + \dfrac{4}{14}\times 0 + \dfrac{5}{14}\times 0.48 \approx 0.343$
379 |
380 | 2. 考慮第二種 Temperature
381 |
382 | $GI(Temperature, Hot) = 1 - (\dfrac{2}{4})^2 - (\dfrac{2}{4})^2 = 0.5$
383 |
384 | $GI(Temperature, Mild) = 1 - (\dfrac{4}{6})^2 - (\dfrac{2}{6})^2 \approx 0.44$
385 |
386 | $GI(Temperature, Cold) = 1 - (\dfrac{3}{4})^2 - (\dfrac{1}{4})^2 = 0.375$
387 |
388 | $GI(Temperature) = \dfrac{4}{14}\times 0.5 + \dfrac{6}{14}\times 0.44 + \dfrac{4}{14}\times 0.375 \approx 0.439$
389 |
390 | 3. 考慮第三種 Humidity
391 |
392 | $GI(Humidity, High) = 1 - (\dfrac{3}{7})^2 - (\dfrac{4}{7})^2 \approx 0.49$
393 |
394 | $GI(Humidity, Medium) = 1 - (\dfrac{6}{7})^2 - (\dfrac{1}{7})^2 \approx 0.245$
395 |
396 | $GI(Humidity) = \dfrac{7}{14}\times 0.49 + \dfrac{7}{14}\times 0.245 = 0.3675$
397 |
398 | 4. 考慮第四種 Wind
399 |
400 | $GI(Wind, True) = 1 - (\dfrac{3}{6})^2 - (\dfrac{3}{6})^2 = 0.5$
401 |
402 | $GI(Wind, False) = 1 - (\dfrac{6}{8})^2 - (\dfrac{2}{8})^2 = 0.375$
403 |
404 | $GI(Wind) = \dfrac{6}{14} \times 0.5 + \dfrac{8}{14} \times 0.375 \approx 0.429$
405 |
406 | 選擇最低的 GI 來當作分割標準,故選擇 Outlook 來當作分割節點。
407 |
408 |
363 |
364 |
365 |
366 | 先考慮四種不同的分割方式
367 |
368 | 1. 考慮第一種 Outlook
369 |
370 | $GI(Outlook, Sunny) = 1 - (\dfrac{2}{5})^2 - (\dfrac{3}{5})^2=0.48$
371 |
372 | $GI(Outlook, Overcast) = 1 - (\dfrac{4}{4})^2-(\dfrac{0}{4})^2=0$
373 |
374 | $GI(Outlook, Rainy) = 1-(\dfrac{3}{5})^2-(\dfrac{2}{5})^2=0.48$
375 |
376 | $GI(Outlook) = P(Sunny)GI(Sunny) + P(Overcast)GI(Overcast) + P(Rainy)GI(Rainy)$
377 |
378 | $= \dfrac{5}{14}\times 0.48 + \dfrac{4}{14}\times 0 + \dfrac{5}{14}\times 0.48 \approx 0.343$
379 |
380 | 2. 考慮第二種 Temperature
381 |
382 | $GI(Temperature, Hot) = 1 - (\dfrac{2}{4})^2 - (\dfrac{2}{4})^2 = 0.5$
383 |
384 | $GI(Temperature, Mild) = 1 - (\dfrac{4}{6})^2 - (\dfrac{2}{6})^2 \approx 0.44$
385 |
386 | $GI(Temperature, Cold) = 1 - (\dfrac{3}{4})^2 - (\dfrac{1}{4})^2 = 0.375$
387 |
388 | $GI(Temperature) = \dfrac{4}{14}\times 0.5 + \dfrac{6}{14}\times 0.44 + \dfrac{4}{14}\times 0.375 \approx 0.439$
389 |
390 | 3. 考慮第三種 Humidity
391 |
392 | $GI(Humidity, High) = 1 - (\dfrac{3}{7})^2 - (\dfrac{4}{7})^2 \approx 0.49$
393 |
394 | $GI(Humidity, Medium) = 1 - (\dfrac{6}{7})^2 - (\dfrac{1}{7})^2 \approx 0.245$
395 |
396 | $GI(Humidity) = \dfrac{7}{14}\times 0.49 + \dfrac{7}{14}\times 0.245 = 0.3675$
397 |
398 | 4. 考慮第四種 Wind
399 |
400 | $GI(Wind, True) = 1 - (\dfrac{3}{6})^2 - (\dfrac{3}{6})^2 = 0.5$
401 |
402 | $GI(Wind, False) = 1 - (\dfrac{6}{8})^2 - (\dfrac{2}{8})^2 = 0.375$
403 |
404 | $GI(Wind) = \dfrac{6}{14} \times 0.5 + \dfrac{8}{14} \times 0.375 \approx 0.429$
405 |
406 | 選擇最低的 GI 來當作分割標準,故選擇 Outlook 來當作分割節點。
407 |
408 |  409 |
410 |
411 |
412 | 考慮固定 Sunny,計算剩餘的 Temperature, Humidity, Wind。
413 |
414 | 1. 考慮 Temperature
415 |
416 | $GI(Temperature, Hot) = 1 - (\dfrac{0}{2})^2 - (\dfrac{2}{2})^2 = 0$
417 |
418 | $GI(Temperature, Mild) = 1 - (\dfrac{1}{2})^2 - (\dfrac{1}{2})^2 = 0.5$
419 |
420 | $GI(Temperature, Cold) = 1 - (\dfrac{1}{1})^2 - (\dfrac{0}{1})^2 = 0$
421 |
422 | $GI(Temperature) = \dfrac{2}{5} \times 0 + \dfrac{2}{5}\times 0.5 + \dfrac{1}{5}\times 0 = 0.2$
423 |
424 | 2. 考慮 Humidity
425 |
426 | $GI(Humidity, High) = 1 - (\dfrac{0}{3})^2 - (\dfrac{3}{3})^2 = 0$
427 |
428 | $GI(Humidity, Normal) = 1 - (\dfrac{2}{2})^2-(\dfrac{0}{2})^2 = 0$
429 |
430 | $GI(Humidity) = \dfrac{3}{5} \times 0 + \dfrac{2}{5} \times 0 = 0$
431 |
432 | 3. 考慮 Wind
433 |
434 | $GI(Wind, True) = 1 - (\dfrac{1}{2})^2 - (\dfrac{1}{2})^2 = 0.5$
435 |
436 | $GI(Wind, False) = 1 - (\dfrac{1}{3})^2 - (\dfrac{2}{3})^2 \approx 0.444$
437 |
438 | $GI(Wind) = \dfrac{2}{5}\times 0.5 + \dfrac{3}{5} \times 0.444 \approx 0.466$
439 |
440 | 選擇最低的 GI 來當作分割標準,故選擇 Humidity 當作分割節點。
441 |
442 |
409 |
410 |
411 |
412 | 考慮固定 Sunny,計算剩餘的 Temperature, Humidity, Wind。
413 |
414 | 1. 考慮 Temperature
415 |
416 | $GI(Temperature, Hot) = 1 - (\dfrac{0}{2})^2 - (\dfrac{2}{2})^2 = 0$
417 |
418 | $GI(Temperature, Mild) = 1 - (\dfrac{1}{2})^2 - (\dfrac{1}{2})^2 = 0.5$
419 |
420 | $GI(Temperature, Cold) = 1 - (\dfrac{1}{1})^2 - (\dfrac{0}{1})^2 = 0$
421 |
422 | $GI(Temperature) = \dfrac{2}{5} \times 0 + \dfrac{2}{5}\times 0.5 + \dfrac{1}{5}\times 0 = 0.2$
423 |
424 | 2. 考慮 Humidity
425 |
426 | $GI(Humidity, High) = 1 - (\dfrac{0}{3})^2 - (\dfrac{3}{3})^2 = 0$
427 |
428 | $GI(Humidity, Normal) = 1 - (\dfrac{2}{2})^2-(\dfrac{0}{2})^2 = 0$
429 |
430 | $GI(Humidity) = \dfrac{3}{5} \times 0 + \dfrac{2}{5} \times 0 = 0$
431 |
432 | 3. 考慮 Wind
433 |
434 | $GI(Wind, True) = 1 - (\dfrac{1}{2})^2 - (\dfrac{1}{2})^2 = 0.5$
435 |
436 | $GI(Wind, False) = 1 - (\dfrac{1}{3})^2 - (\dfrac{2}{3})^2 \approx 0.444$
437 |
438 | $GI(Wind) = \dfrac{2}{5}\times 0.5 + \dfrac{3}{5} \times 0.444 \approx 0.466$
439 |
440 | 選擇最低的 GI 來當作分割標準,故選擇 Humidity 當作分割節點。
441 |
442 |  443 |
444 |
445 |
446 | 考慮固定 Rainy,計算剩餘的 Temperature, Humidity, Wind。
447 |
448 | 1. 考慮 Temperature
449 |
450 | $GI(Temperature, Mild) = 1 - (\dfrac{2}{3})^2 - (\dfrac{1}{3})^2 \approx 0.444$
451 |
452 | $GI(Temperature, Cold) = 1 - (\dfrac{1}{2})^2 - (\dfrac{1}{2})^2 = 0.5$
453 |
454 | $GI(Temperature) = \dfrac{3}{5}\times 0.444 + \dfrac{2}{5}\times 0.5 = 0.4664$
455 |
456 | 2. 考慮 Humidity
457 |
458 | $GI(Humidity, High) = 1 - (\dfrac{1}{2})^2 - (\dfrac{1}{2})^2 = 0.5$
459 |
460 | $GI(Humidity, Normal) = 1 - (\dfrac{2}{3})^2 - (\dfrac{1}{3})^2 \approx 0.444$
461 |
462 | $GI(Humidity) = \dfrac{3}{5}\times 0.444 + \dfrac{2}{5}\times 0.5 = 0.4664$
463 |
464 | 3. 考慮 Wind
465 |
466 | $GI(Wind, True) = 1 - (\dfrac{0}{2})^2 - (\dfrac{2}{2})^2 = 0$
467 |
468 | $GI(Wind, False) = 1 - (\dfrac{3}{3})^2 - (\dfrac{0}{3})^2 = 0$
469 |
470 | $GI(Wind) = \dfrac{2}{5}\times 0 + \dfrac{3}{5}\times 0 = 0$
471 |
472 | 選擇最低的 GI 來當作分割標準,故選擇 Wind 當作分割節點。
473 |
474 |
443 |
444 |
445 |
446 | 考慮固定 Rainy,計算剩餘的 Temperature, Humidity, Wind。
447 |
448 | 1. 考慮 Temperature
449 |
450 | $GI(Temperature, Mild) = 1 - (\dfrac{2}{3})^2 - (\dfrac{1}{3})^2 \approx 0.444$
451 |
452 | $GI(Temperature, Cold) = 1 - (\dfrac{1}{2})^2 - (\dfrac{1}{2})^2 = 0.5$
453 |
454 | $GI(Temperature) = \dfrac{3}{5}\times 0.444 + \dfrac{2}{5}\times 0.5 = 0.4664$
455 |
456 | 2. 考慮 Humidity
457 |
458 | $GI(Humidity, High) = 1 - (\dfrac{1}{2})^2 - (\dfrac{1}{2})^2 = 0.5$
459 |
460 | $GI(Humidity, Normal) = 1 - (\dfrac{2}{3})^2 - (\dfrac{1}{3})^2 \approx 0.444$
461 |
462 | $GI(Humidity) = \dfrac{3}{5}\times 0.444 + \dfrac{2}{5}\times 0.5 = 0.4664$
463 |
464 | 3. 考慮 Wind
465 |
466 | $GI(Wind, True) = 1 - (\dfrac{0}{2})^2 - (\dfrac{2}{2})^2 = 0$
467 |
468 | $GI(Wind, False) = 1 - (\dfrac{3}{3})^2 - (\dfrac{0}{3})^2 = 0$
469 |
470 | $GI(Wind) = \dfrac{2}{5}\times 0 + \dfrac{3}{5}\times 0 = 0$
471 |
472 | 選擇最低的 GI 來當作分割標準,故選擇 Wind 當作分割節點。
473 |
474 |  475 |
476 | 此時分割已完成。
477 |
478 |
479 |
480 | ## 迴歸樹
481 |
482 | 迴歸樹是決策樹的一種種類,用來預判在某一種情況下時,能夠對應到的效果。
483 |
484 | 輸出值為連續變數,運作方式與分類樹較相同,與分類樹不同的地方是:
485 |
486 | 1. 對於一個二維的座標軸來說,迴歸樹通常是預判在這個二維座標軸特定條件所形成的一個長方形區塊內資料的平均值,
487 | 2. 判斷一個長方形區塊內資料的純度,使用了殘差平方和,定義為 $\displaystyle RSS = \sum^{n}_{i=1}(y_i - f(x_i))^2$。
488 | 3. 使用均方根誤差來測量效能。
489 |
490 |
491 |
492 | ### Cost Complexity Pruning
493 |
494 | > Reference: https://www.youtube.com/watch?v=D0efHEJsfHo
495 |
496 |
497 |
498 | 迴歸樹運作原理與分類樹較相同,但也同時會出現 over fitting 的問題。
499 |
500 | 為了避免 over fitting 的問題發生,需要對這棵樹進行適當的剪枝,以利於資料的預判。
501 |
502 |
503 |
504 | 對於剪枝的評斷,我們需要先窮舉每一種剪枝的方式,得到剪枝序列
505 |
506 | 根據每個序列每個區塊,做一次 $RSS$ 的測量總和,再計算一種基於 $RSS$ 出現的 Tree Score,定義為:
507 | $$
508 | Tree Score = RSS + aT
509 | $$
510 | 其中 $a$ 為一微調參數,且 $T$ 為葉節點樹量。
511 |
512 | 找到這個參數 $a$ 的方式是透過微調 $a$ 來使當前的樹算出的 Tree Score 變小。
513 |
514 | 再只使用測試資料來做幾次交叉測試,找出能夠使 $RSS$ 平均最小的子樹,即為最佳剪枝樹。
515 |
516 |
517 |
518 | ## Random Forest
519 |
520 | > Reference:
521 | >
522 | > 1. https://www.youtube.com/watch?v=J4Wdy0Wc_xQ
523 | > 2. https://www.youtube.com/watch?v=sQ870aTKqiM
524 |
525 |
526 |
527 | Random Forest 是一種包含多種決策樹的分類器,輸出的類別取決於所有決策樹的結果統計出的眾數。
528 |
529 | 大致上來說,Random Forest 使用以下的演算法:
530 |
531 | 1. 建立 bootstrapped table,隨機抽取一定數量的樣本來建立。
532 | 2. 建立決策樹的父節點,使用隨機不重複的變數來建立。
533 | 3. 重複第一步與第二步,利用這樣的方式建立多棵決策樹。
534 |
535 | 接下來即可將樣本丟入隨機森林,蒐集每一棵決策樹所產生出的結果,以及找出結果眾數。
536 |
537 |
538 |
539 | ### Bagging
540 |
541 | 我們將樣本隨機抽取來建立 bootstrapped table,然後利用總計來得出結果,這樣的方式稱為 Bagging。
542 |
543 |
544 |
545 | ### Out-of-bag dataset
546 |
547 | 由於我們前面說到,建立 bootstrapped table 的方式是使用隨機抽樣,那麼隨機抽樣這一步有可能會出現沒有抽到的資料。
548 |
549 | 我們將這些資料蒐集起來,稱為 Out-of-bag dataset。
550 |
551 |
552 |
553 | 處理這些 Out-of-bag dataset 的方式是,我們可以把這些資料集丟回去隨機森林,來確定所有的樹是否都回傳同一個結果。
554 |
555 | 就可以用這些結果來測量隨機森林的準確度,至於 Out-of-bag dataset 分類錯誤的部分即稱為 Out-of-bag error。
556 |
557 |
558 |
559 | 我們可以測量準確度,再來校正隨機抽取樣本的數量,來校正隨機森林。
560 |
561 |
562 |
563 | ### Missing Data
564 |
565 | 對於 Random Forest 的缺值問題,主要分成兩種。
566 |
567 | 1. 知道結果、但不知道資料變數的某些值。
568 | 2. 不知道結果、但也不知道資料變數的某些值。
569 |
570 | 對於這兩種問題,可以分成兩種不同的方式來解決。
571 |
572 |
573 |
574 | #### 缺值問題 1
575 |
576 | 我們可以先根據先前的資料集進行投票,並且去尋找相似的先前資料來設定值,再逐步調整。
577 |
578 | 逐步調整的方式可以利用 updated proximity matrix 來調整,經過多次迭代之後找到一個再迭代後也變化不大的結果。
579 |
580 |
581 |
582 | #### 缺值問題 2
583 |
584 | 我們可以根據剩餘的資料來進行建立隨機森林。
585 |
586 | 建立模型後,先是使用第一個缺值問題的方式來設定變數值,以及窮舉所有可能出現的結果,產生出多個候選資料。
587 |
588 | 將這些候選資料丟入模型進行預判,來得到隨機森林對於哪一種結果有更高的投票數,即可選定投票結果。
589 |
--------------------------------------------------------------------------------
/Markdown/Naive Bayes Analysis.md:
--------------------------------------------------------------------------------
1 | # Naive Bayes Analysis(單純貝氏分析)
2 |
3 | > Reference:
4 | >
5 | > 1. Naïve Bayes Analysis(單純貝氏) - Dr. Tun-Wen Pai
6 | > 2. [Naive Bayes, Clearly Explained!!! - StatQuest with Josh Starmer](https://www.youtube.com/watch?v=O2L2Uv9pdDA)
7 | > 3. [Bayes' Theorem, Clearly Explained!!!! - StatQuest with Josh Starmer](https://www.youtube.com/watch?v=9wCnvr7Xw4E)
8 | > 4. [Gaussian Naive Bayes, Clearly Explained!!! - StatQuest with Josh Starmer](https://www.youtube.com/watch?v=H3EjCKtlVog)
9 |
10 |
11 |
12 | ## 貝氏定理
13 |
14 | 貝氏定理是關於隨機事件 $A$ 和 $B$ 的條件機率的一則定理,定義如下:
15 | $$
16 | P(A|B) = \dfrac{P(A)P(B|A)}{P(B)}, P(B) \neq 0
17 | $$
18 | 其中 $P(A)$ 是事件 $A$ 的事前機率,$P(B)$ 是事件 $B$ 的事前機率。
19 |
20 | $P(B|A)$ 是事件 $A$ 發生後事件 $B$ 的條件機率(事後機率),同時,$P(B|A) = \dfrac{P(A \cap B)}{P(A)}$。
21 |
22 | $P(A|B)$ 是事件 $B$ 發生後事件 $A$ 的條件機率(事後機率),同時,$P(A|B) = \dfrac{P(A \cap B)}{P(B)}$。
23 |
24 |
25 |
26 | 以一張文氏圖來說,我們可以令藍色區塊為 $A$,黃色區塊為 $B$,則若我們想要知道事件 $B$ 發生後,發生 $A$ 的機率
27 |
28 | 就相比我們以藍色區塊點的數量去除以綠色區塊點的數量 $P(G|B) = \dfrac{N(G)}{N(B)}$,就能得到先發生 $B$ 後再發生 $A$ 的機率。
29 |
30 | > 文氏圖圖例,By StatQuest
31 |
32 | 
33 |
34 |
35 |
36 | ## 多項單純貝氏分類
37 |
38 | ### 概述
39 |
40 | 當我們要對一筆資料 $D$ 進行分類,我們可以根據資料的每個特徵 $C_i$,從訓練樣本中找出特徵 $C_i$ 是事件 $A$ 或事件 $B$ 的條件機率 $P(C_i|A)$ 或 $P(C_i|B)$ 的分數,用分數來進行分類,定義如下。
41 | $$
42 | P(D|E) = P(E) \times P(C_1|E)\times P(C_2|E) \times ... \times P(C_n|E)
43 | $$
44 | 其中 $D$ 為一筆資料,$E$ 為一個事件,$P(D|E)$ 為資料 $D$ 歸類在事件 $E$ 的分數,$C_i$ 為某特徵。
45 |
46 |
47 |
48 | 分類會出現有零值與沒有零值的情況。
49 |
50 |
51 |
52 | ### Example - 無零值
53 |
54 | | # | message | Happy |
55 | | :--: | :-----------------------: | :---: |
56 | | 1 | love happy joy joy love | Yes |
57 | | 2 | happy love kick joy happy | Yes |
58 | | 3 | love move joy good | Yes |
59 | | 4 | love happy joy pain love | Yes |
60 | | 5 | joy love pain kick pain | No |
61 | | 6 | pain pain love kick | No |
62 | | 7 | love pain joy love kick | ? |
63 |
64 | 我們想要找到第七筆應該被分類在哪一個類別(Happy = Yes/No),我們可以先算出事前機率:
65 | $$
66 | P(yes) = \dfrac{4}{6} = \dfrac{2}{3} \\
67 | P(no) = \dfrac{2}{6} = \dfrac{1}{3}
68 | $$
69 | 我們可以根據每個特徵來算出 $D_7$ 特徵值的事後機率。
70 |
71 | 
72 | $$
73 | P(love|yes) = \dfrac{6}{19}, P(love|no) = \dfrac{2}{9} \\
74 | P(pain|yes) = \dfrac{1}{19}, P(pain|no) = \dfrac{4}{9} \\
75 | P(joy|yes) = \dfrac{5}{19}, P(joy|no) = \dfrac{1}{9} \\
76 | P(kick|yes) = \dfrac{1}{19}, P(kick|no) = \dfrac{2}{9} \\
77 | $$
78 | 那我們就能夠根據定義來算出 $D_7$ 特徵值的分數。
79 | $$
80 | P(D_7|yes) = P(love|yes) \times P(pain|yes) \times P(joy|yes) \times P(love|yes) \times P(kick|yes) \approx 0.000004 \\
81 |
82 | P(D_7|no) = P(love|no) \times P(pain|no) \times P(joy|no) \times P(love|no) \times P(kick|no) \approx 0.00018
83 | $$
84 | 故 $D_7$ 在 $P(D_7|no)$ 有較高的分數,故選 $no$。
85 |
86 |
87 |
88 | ### Example - 有零值
89 |
90 | | # | message | Happy |
91 | | :--: | :----------------------------: | :---: |
92 | | 1 | love happy joy joy love | Yes |
93 | | 2 | happy love kick joy happy | Yes |
94 | | 3 | love move joy good | Yes |
95 | | 4 | love happy joy pain love | Yes |
96 | | 5 | joy love pain kick pain | No |
97 | | 6 | pain pain love kick | No |
98 | | 7 | love pain joy happy kick happy | ? |
99 |
100 | 我們想要找到第七筆應該被分類在哪一個類別(Happy = Yes/No),我們可以先算出事前機率:
101 | $$
102 | P(yes) = \dfrac{4}{6} = \dfrac{2}{3} \\
103 | P(no) = \dfrac{2}{6} = \dfrac{1}{3}
104 | $$
105 | 我們可以根據每個特徵來算出 $D_7$ 特徵值的事後機率。
106 |
107 | 但此時會發現 happy 這個特徵值並沒有出現在 No 裡面,通常來說,我們會把每一個特徵值重複加上去,如下:
108 |
109 | 
110 |
111 | 那我們就能夠根據定義來算出 $D_7$ 特徵值的分數。
112 | $$
113 | P(D_7|yes) = P(love|no) \times P(pain|yes) \times P(joy|yes) \times P(love|yes) \times P(kick|yes) \approx 9\times 10^{-6} \\
114 |
115 | P(D_7|no) = P(love|yes) \times P(pain|no) \times P(joy|no) \times P(love|no) \times P(kick|no) \approx 3\times 10^{-6}
116 | $$
117 | 故 $D_7$ 在 $P(D_7|yes)$ 有較高的分數,故選 $yes$。
118 |
119 |
120 |
121 | ## 常態單純貝氏分類
122 |
123 | > 另一種單純貝氏分類,屬於補充資料,有時間補。
124 |
--------------------------------------------------------------------------------
/Markdown/Regression.md:
--------------------------------------------------------------------------------
1 | # 迴歸 (Regression)
2 |
3 | > 筆記參考資料:
4 | >
5 | > 1. Regression (迴歸) Dr. Tun Wen Pai
6 |
7 | ## 線性回歸
8 |
9 | ### 線性迴歸簡介
10 |
11 | 一種統計學上分析資料的方法,目的在於了解多個獨立變數與一個應變數的關係。
12 |
13 | 通常來說,迴歸存在的意義,是造出一條曲線盡可能地滿足這些資料,以達到預測、了解關係的目的。
14 |
15 | 我們可以使用相關係數來比較這個造出來的曲線的好與壞。
16 |
17 |
18 |
19 | ### 相關係數
20 |
21 | 相關係數 $r$,用來評估兩個變數之間的關係是否相關,其定義如下:
22 | $$
23 | r= \dfrac{\displaystyle\sum^{n}_{i=1}(X_i-\overline{X})(Y_i-\overline{Y})}{\sqrt{\displaystyle\sum^n_{i=1}(X_i-\overline{X})^2}\sqrt{\displaystyle\sum^n_{i=1}(Y_i-\overline{Y})^2}}
24 | $$
25 | 定義 $\overline{X}、\overline{Y}$ 為變數 $X$ 、變數 $Y$ 的平均值。
26 |
27 | 其中 $-1 \le r \le 1$,其中若 $r = 0$ 時則代表完全無相關,$|r| = 1$ 時則代表完全相關,$0 < |r| < 1$ 時則代表存在一定的線性相關。
28 |
29 |
30 |
31 | ### 決定係數
32 |
33 | > Reference:https://www.youtube.com/watch?v=2AQKmw14mHM
34 |
35 |
36 |
37 | 決定係數 $r^2$,用來判斷回歸模型的解釋力,可以將相關係數平方,得到決定係數。
38 |
39 | 決定係數可以更好的幫助我們判斷兩個變數之間的關係,可以知道選擇的兩個變數能夠解釋多少比例的資料變異。
40 |
41 |
42 |
43 | ### 雙變數的圖形呈現
44 |
45 | 對於一個雙變數的資料集,我們可以畫出一張二維的散佈圖,可透過散佈圖來觀察出變數之間的關係。
46 |
47 |
475 |
476 | 此時分割已完成。
477 |
478 |
479 |
480 | ## 迴歸樹
481 |
482 | 迴歸樹是決策樹的一種種類,用來預判在某一種情況下時,能夠對應到的效果。
483 |
484 | 輸出值為連續變數,運作方式與分類樹較相同,與分類樹不同的地方是:
485 |
486 | 1. 對於一個二維的座標軸來說,迴歸樹通常是預判在這個二維座標軸特定條件所形成的一個長方形區塊內資料的平均值,
487 | 2. 判斷一個長方形區塊內資料的純度,使用了殘差平方和,定義為 $\displaystyle RSS = \sum^{n}_{i=1}(y_i - f(x_i))^2$。
488 | 3. 使用均方根誤差來測量效能。
489 |
490 |
491 |
492 | ### Cost Complexity Pruning
493 |
494 | > Reference: https://www.youtube.com/watch?v=D0efHEJsfHo
495 |
496 |
497 |
498 | 迴歸樹運作原理與分類樹較相同,但也同時會出現 over fitting 的問題。
499 |
500 | 為了避免 over fitting 的問題發生,需要對這棵樹進行適當的剪枝,以利於資料的預判。
501 |
502 |
503 |
504 | 對於剪枝的評斷,我們需要先窮舉每一種剪枝的方式,得到剪枝序列
505 |
506 | 根據每個序列每個區塊,做一次 $RSS$ 的測量總和,再計算一種基於 $RSS$ 出現的 Tree Score,定義為:
507 | $$
508 | Tree Score = RSS + aT
509 | $$
510 | 其中 $a$ 為一微調參數,且 $T$ 為葉節點樹量。
511 |
512 | 找到這個參數 $a$ 的方式是透過微調 $a$ 來使當前的樹算出的 Tree Score 變小。
513 |
514 | 再只使用測試資料來做幾次交叉測試,找出能夠使 $RSS$ 平均最小的子樹,即為最佳剪枝樹。
515 |
516 |
517 |
518 | ## Random Forest
519 |
520 | > Reference:
521 | >
522 | > 1. https://www.youtube.com/watch?v=J4Wdy0Wc_xQ
523 | > 2. https://www.youtube.com/watch?v=sQ870aTKqiM
524 |
525 |
526 |
527 | Random Forest 是一種包含多種決策樹的分類器,輸出的類別取決於所有決策樹的結果統計出的眾數。
528 |
529 | 大致上來說,Random Forest 使用以下的演算法:
530 |
531 | 1. 建立 bootstrapped table,隨機抽取一定數量的樣本來建立。
532 | 2. 建立決策樹的父節點,使用隨機不重複的變數來建立。
533 | 3. 重複第一步與第二步,利用這樣的方式建立多棵決策樹。
534 |
535 | 接下來即可將樣本丟入隨機森林,蒐集每一棵決策樹所產生出的結果,以及找出結果眾數。
536 |
537 |
538 |
539 | ### Bagging
540 |
541 | 我們將樣本隨機抽取來建立 bootstrapped table,然後利用總計來得出結果,這樣的方式稱為 Bagging。
542 |
543 |
544 |
545 | ### Out-of-bag dataset
546 |
547 | 由於我們前面說到,建立 bootstrapped table 的方式是使用隨機抽樣,那麼隨機抽樣這一步有可能會出現沒有抽到的資料。
548 |
549 | 我們將這些資料蒐集起來,稱為 Out-of-bag dataset。
550 |
551 |
552 |
553 | 處理這些 Out-of-bag dataset 的方式是,我們可以把這些資料集丟回去隨機森林,來確定所有的樹是否都回傳同一個結果。
554 |
555 | 就可以用這些結果來測量隨機森林的準確度,至於 Out-of-bag dataset 分類錯誤的部分即稱為 Out-of-bag error。
556 |
557 |
558 |
559 | 我們可以測量準確度,再來校正隨機抽取樣本的數量,來校正隨機森林。
560 |
561 |
562 |
563 | ### Missing Data
564 |
565 | 對於 Random Forest 的缺值問題,主要分成兩種。
566 |
567 | 1. 知道結果、但不知道資料變數的某些值。
568 | 2. 不知道結果、但也不知道資料變數的某些值。
569 |
570 | 對於這兩種問題,可以分成兩種不同的方式來解決。
571 |
572 |
573 |
574 | #### 缺值問題 1
575 |
576 | 我們可以先根據先前的資料集進行投票,並且去尋找相似的先前資料來設定值,再逐步調整。
577 |
578 | 逐步調整的方式可以利用 updated proximity matrix 來調整,經過多次迭代之後找到一個再迭代後也變化不大的結果。
579 |
580 |
581 |
582 | #### 缺值問題 2
583 |
584 | 我們可以根據剩餘的資料來進行建立隨機森林。
585 |
586 | 建立模型後,先是使用第一個缺值問題的方式來設定變數值,以及窮舉所有可能出現的結果,產生出多個候選資料。
587 |
588 | 將這些候選資料丟入模型進行預判,來得到隨機森林對於哪一種結果有更高的投票數,即可選定投票結果。
589 |
--------------------------------------------------------------------------------
/Markdown/Naive Bayes Analysis.md:
--------------------------------------------------------------------------------
1 | # Naive Bayes Analysis(單純貝氏分析)
2 |
3 | > Reference:
4 | >
5 | > 1. Naïve Bayes Analysis(單純貝氏) - Dr. Tun-Wen Pai
6 | > 2. [Naive Bayes, Clearly Explained!!! - StatQuest with Josh Starmer](https://www.youtube.com/watch?v=O2L2Uv9pdDA)
7 | > 3. [Bayes' Theorem, Clearly Explained!!!! - StatQuest with Josh Starmer](https://www.youtube.com/watch?v=9wCnvr7Xw4E)
8 | > 4. [Gaussian Naive Bayes, Clearly Explained!!! - StatQuest with Josh Starmer](https://www.youtube.com/watch?v=H3EjCKtlVog)
9 |
10 |
11 |
12 | ## 貝氏定理
13 |
14 | 貝氏定理是關於隨機事件 $A$ 和 $B$ 的條件機率的一則定理,定義如下:
15 | $$
16 | P(A|B) = \dfrac{P(A)P(B|A)}{P(B)}, P(B) \neq 0
17 | $$
18 | 其中 $P(A)$ 是事件 $A$ 的事前機率,$P(B)$ 是事件 $B$ 的事前機率。
19 |
20 | $P(B|A)$ 是事件 $A$ 發生後事件 $B$ 的條件機率(事後機率),同時,$P(B|A) = \dfrac{P(A \cap B)}{P(A)}$。
21 |
22 | $P(A|B)$ 是事件 $B$ 發生後事件 $A$ 的條件機率(事後機率),同時,$P(A|B) = \dfrac{P(A \cap B)}{P(B)}$。
23 |
24 |
25 |
26 | 以一張文氏圖來說,我們可以令藍色區塊為 $A$,黃色區塊為 $B$,則若我們想要知道事件 $B$ 發生後,發生 $A$ 的機率
27 |
28 | 就相比我們以藍色區塊點的數量去除以綠色區塊點的數量 $P(G|B) = \dfrac{N(G)}{N(B)}$,就能得到先發生 $B$ 後再發生 $A$ 的機率。
29 |
30 | > 文氏圖圖例,By StatQuest
31 |
32 | 
33 |
34 |
35 |
36 | ## 多項單純貝氏分類
37 |
38 | ### 概述
39 |
40 | 當我們要對一筆資料 $D$ 進行分類,我們可以根據資料的每個特徵 $C_i$,從訓練樣本中找出特徵 $C_i$ 是事件 $A$ 或事件 $B$ 的條件機率 $P(C_i|A)$ 或 $P(C_i|B)$ 的分數,用分數來進行分類,定義如下。
41 | $$
42 | P(D|E) = P(E) \times P(C_1|E)\times P(C_2|E) \times ... \times P(C_n|E)
43 | $$
44 | 其中 $D$ 為一筆資料,$E$ 為一個事件,$P(D|E)$ 為資料 $D$ 歸類在事件 $E$ 的分數,$C_i$ 為某特徵。
45 |
46 |
47 |
48 | 分類會出現有零值與沒有零值的情況。
49 |
50 |
51 |
52 | ### Example - 無零值
53 |
54 | | # | message | Happy |
55 | | :--: | :-----------------------: | :---: |
56 | | 1 | love happy joy joy love | Yes |
57 | | 2 | happy love kick joy happy | Yes |
58 | | 3 | love move joy good | Yes |
59 | | 4 | love happy joy pain love | Yes |
60 | | 5 | joy love pain kick pain | No |
61 | | 6 | pain pain love kick | No |
62 | | 7 | love pain joy love kick | ? |
63 |
64 | 我們想要找到第七筆應該被分類在哪一個類別(Happy = Yes/No),我們可以先算出事前機率:
65 | $$
66 | P(yes) = \dfrac{4}{6} = \dfrac{2}{3} \\
67 | P(no) = \dfrac{2}{6} = \dfrac{1}{3}
68 | $$
69 | 我們可以根據每個特徵來算出 $D_7$ 特徵值的事後機率。
70 |
71 | 
72 | $$
73 | P(love|yes) = \dfrac{6}{19}, P(love|no) = \dfrac{2}{9} \\
74 | P(pain|yes) = \dfrac{1}{19}, P(pain|no) = \dfrac{4}{9} \\
75 | P(joy|yes) = \dfrac{5}{19}, P(joy|no) = \dfrac{1}{9} \\
76 | P(kick|yes) = \dfrac{1}{19}, P(kick|no) = \dfrac{2}{9} \\
77 | $$
78 | 那我們就能夠根據定義來算出 $D_7$ 特徵值的分數。
79 | $$
80 | P(D_7|yes) = P(love|yes) \times P(pain|yes) \times P(joy|yes) \times P(love|yes) \times P(kick|yes) \approx 0.000004 \\
81 |
82 | P(D_7|no) = P(love|no) \times P(pain|no) \times P(joy|no) \times P(love|no) \times P(kick|no) \approx 0.00018
83 | $$
84 | 故 $D_7$ 在 $P(D_7|no)$ 有較高的分數,故選 $no$。
85 |
86 |
87 |
88 | ### Example - 有零值
89 |
90 | | # | message | Happy |
91 | | :--: | :----------------------------: | :---: |
92 | | 1 | love happy joy joy love | Yes |
93 | | 2 | happy love kick joy happy | Yes |
94 | | 3 | love move joy good | Yes |
95 | | 4 | love happy joy pain love | Yes |
96 | | 5 | joy love pain kick pain | No |
97 | | 6 | pain pain love kick | No |
98 | | 7 | love pain joy happy kick happy | ? |
99 |
100 | 我們想要找到第七筆應該被分類在哪一個類別(Happy = Yes/No),我們可以先算出事前機率:
101 | $$
102 | P(yes) = \dfrac{4}{6} = \dfrac{2}{3} \\
103 | P(no) = \dfrac{2}{6} = \dfrac{1}{3}
104 | $$
105 | 我們可以根據每個特徵來算出 $D_7$ 特徵值的事後機率。
106 |
107 | 但此時會發現 happy 這個特徵值並沒有出現在 No 裡面,通常來說,我們會把每一個特徵值重複加上去,如下:
108 |
109 | 
110 |
111 | 那我們就能夠根據定義來算出 $D_7$ 特徵值的分數。
112 | $$
113 | P(D_7|yes) = P(love|no) \times P(pain|yes) \times P(joy|yes) \times P(love|yes) \times P(kick|yes) \approx 9\times 10^{-6} \\
114 |
115 | P(D_7|no) = P(love|yes) \times P(pain|no) \times P(joy|no) \times P(love|no) \times P(kick|no) \approx 3\times 10^{-6}
116 | $$
117 | 故 $D_7$ 在 $P(D_7|yes)$ 有較高的分數,故選 $yes$。
118 |
119 |
120 |
121 | ## 常態單純貝氏分類
122 |
123 | > 另一種單純貝氏分類,屬於補充資料,有時間補。
124 |
--------------------------------------------------------------------------------
/Markdown/Regression.md:
--------------------------------------------------------------------------------
1 | # 迴歸 (Regression)
2 |
3 | > 筆記參考資料:
4 | >
5 | > 1. Regression (迴歸) Dr. Tun Wen Pai
6 |
7 | ## 線性回歸
8 |
9 | ### 線性迴歸簡介
10 |
11 | 一種統計學上分析資料的方法,目的在於了解多個獨立變數與一個應變數的關係。
12 |
13 | 通常來說,迴歸存在的意義,是造出一條曲線盡可能地滿足這些資料,以達到預測、了解關係的目的。
14 |
15 | 我們可以使用相關係數來比較這個造出來的曲線的好與壞。
16 |
17 |
18 |
19 | ### 相關係數
20 |
21 | 相關係數 $r$,用來評估兩個變數之間的關係是否相關,其定義如下:
22 | $$
23 | r= \dfrac{\displaystyle\sum^{n}_{i=1}(X_i-\overline{X})(Y_i-\overline{Y})}{\sqrt{\displaystyle\sum^n_{i=1}(X_i-\overline{X})^2}\sqrt{\displaystyle\sum^n_{i=1}(Y_i-\overline{Y})^2}}
24 | $$
25 | 定義 $\overline{X}、\overline{Y}$ 為變數 $X$ 、變數 $Y$ 的平均值。
26 |
27 | 其中 $-1 \le r \le 1$,其中若 $r = 0$ 時則代表完全無相關,$|r| = 1$ 時則代表完全相關,$0 < |r| < 1$ 時則代表存在一定的線性相關。
28 |
29 |
30 |
31 | ### 決定係數
32 |
33 | > Reference:https://www.youtube.com/watch?v=2AQKmw14mHM
34 |
35 |
36 |
37 | 決定係數 $r^2$,用來判斷回歸模型的解釋力,可以將相關係數平方,得到決定係數。
38 |
39 | 決定係數可以更好的幫助我們判斷兩個變數之間的關係,可以知道選擇的兩個變數能夠解釋多少比例的資料變異。
40 |
41 |
42 |
43 | ### 雙變數的圖形呈現
44 |
45 | 對於一個雙變數的資料集,我們可以畫出一張二維的散佈圖,可透過散佈圖來觀察出變數之間的關係。
46 |
47 |  48 |
49 | 可以發現,(a) 與 (b) 的圖形可以畫上一條直線,資料大部分都在這條線附近,所以是線性相關。
50 |
51 | (c) 與 (d) 可以畫上一條曲線,資料大部分都在這條曲線附近,所以是曲線相關。
52 |
53 | (e) 與 (f) 找不到直線、曲線能夠含括大部分的資料,故為無相關。
54 |
55 |
56 |
57 | 結合前一個小節所講的相關係數,我們可以從散佈圖上來找出與相關係數的關係,可以發現資料越散,取絕對值後的相關係數越小。
58 |
59 | 資料越集中於一條線,取絕對值後相關係數的係數越大。
60 |
61 |
48 |
49 | 可以發現,(a) 與 (b) 的圖形可以畫上一條直線,資料大部分都在這條線附近,所以是線性相關。
50 |
51 | (c) 與 (d) 可以畫上一條曲線,資料大部分都在這條曲線附近,所以是曲線相關。
52 |
53 | (e) 與 (f) 找不到直線、曲線能夠含括大部分的資料,故為無相關。
54 |
55 |
56 |
57 | 結合前一個小節所講的相關係數,我們可以從散佈圖上來找出與相關係數的關係,可以發現資料越散,取絕對值後的相關係數越小。
58 |
59 | 資料越集中於一條線,取絕對值後相關係數的係數越大。
60 |
61 |  62 |
63 |
64 |
65 |
66 |
67 | ## 羅吉斯迴歸
68 |
69 | ### 羅吉斯迴歸
70 |
71 |
62 |
63 |
64 |
65 |
66 |
67 | ## 羅吉斯迴歸
68 |
69 | ### 羅吉斯迴歸
70 |
71 |  72 |
73 | > Image from [equiskill](https://www.equiskill.com/understanding-logistic-regression/)
74 |
75 | 羅吉斯迴歸(Logistic Regression),是一種**對數分類器**而不是一種迴歸模型。
76 |
77 | 而羅吉斯迴歸又分成二元、多項式羅吉斯迴歸等等。
78 |
79 | 這邊主要介紹二元羅吉斯迴歸,也就是對於一個變量,評估結果是否發生。
80 |
81 |
82 |
83 | ### 羅吉斯迴歸的圖形
84 |
85 | 二元羅吉斯迴歸可以用一張二維平面圖來作圖。
86 |
87 | 其中,$x$ 軸是一種變量,而 $y$ 軸則是對於導致這個結果產生的機率,機率介於 $0$ 到 $1$ 之間。
88 |
89 | 圖上的點密集分布在 $y = 0$ 與 $y = 1$ 上,代表著對應的變量是否發生結果。
90 |
91 | 而圖上的的線即為線性迴歸模型,我們可以根據這個曲線對應到的變量,來預測對於一件事情的發生機率為何。
92 |
93 |
94 |
95 | 舉個例子,我們有一組資料為學生期中成績與通過課程與否的資料。
96 |
97 | | 期中考成績 | 44 | 53 | 23 | 67 | 79 | 91 | 100 | 58 | 82 | 52 |
98 | | ---------- | ---- | ---- | ---- | ---- | ---- | ---- | ---- | ---- | ---- | ---- |
99 | | 通過 | 0 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 0 |
100 |
101 | 我們可以根據這個資料,做一張 Logistic Regression 的圖。
102 |
103 |
72 |
73 | > Image from [equiskill](https://www.equiskill.com/understanding-logistic-regression/)
74 |
75 | 羅吉斯迴歸(Logistic Regression),是一種**對數分類器**而不是一種迴歸模型。
76 |
77 | 而羅吉斯迴歸又分成二元、多項式羅吉斯迴歸等等。
78 |
79 | 這邊主要介紹二元羅吉斯迴歸,也就是對於一個變量,評估結果是否發生。
80 |
81 |
82 |
83 | ### 羅吉斯迴歸的圖形
84 |
85 | 二元羅吉斯迴歸可以用一張二維平面圖來作圖。
86 |
87 | 其中,$x$ 軸是一種變量,而 $y$ 軸則是對於導致這個結果產生的機率,機率介於 $0$ 到 $1$ 之間。
88 |
89 | 圖上的點密集分布在 $y = 0$ 與 $y = 1$ 上,代表著對應的變量是否發生結果。
90 |
91 | 而圖上的的線即為線性迴歸模型,我們可以根據這個曲線對應到的變量,來預測對於一件事情的發生機率為何。
92 |
93 |
94 |
95 | 舉個例子,我們有一組資料為學生期中成績與通過課程與否的資料。
96 |
97 | | 期中考成績 | 44 | 53 | 23 | 67 | 79 | 91 | 100 | 58 | 82 | 52 |
98 | | ---------- | ---- | ---- | ---- | ---- | ---- | ---- | ---- | ---- | ---- | ---- |
99 | | 通過 | 0 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 0 |
100 |
101 | 我們可以根據這個資料,做一張 Logistic Regression 的圖。
102 |
103 |  104 |
105 | > Image from me with matplotlib and scikit-learn
106 |
107 | 圖中的橘線即為擬合後的線性迴歸模型,而點則是期中考成績對應到的通過與否。
108 |
109 |
110 |
111 | ### 勝算
112 |
113 | 我們定義勝算 (odds) 為,一件事情發生的機率,除以一件事情不發生的機率,也就是 $\dfrac{p}{1-p}$
114 |
115 | $\log(odds)$ 可以有效的讓勝算的起點設定在數線的 $0$ 上,並且隨著數值的大與小,顯示在數線上距離 $0$ 有多遠。
116 |
117 |
118 |
119 | ### 羅吉斯迴歸的圖形轉換
120 |
121 | 上面的圖似乎可以非常棒的看出對應的成績所造成的通過與否了,不過我們可以將這個圖形做一點轉換。
122 |
123 | 我們考慮將這條線性迴歸模型拉直,也就是轉成 $y=ax+b$ 的形式。
124 |
125 | 為此,我們可以考慮將 $y$ 軸每一點的機率值,映射到一個定義域為 $(-\infty, \infty)$ 的 $y$ 軸上
126 |
127 | 我們可以使用 Logit Function,定義為 $\ln(odds) = \ln(\dfrac{p}{1-p})$ ,來對 $y$ 軸進行映射,
128 |
129 | 再套用訓練出來的參數,將這個羅吉斯迴歸的圖形造成一條直線。
130 |
131 |
132 |
133 | 例如以上圖來說,可以將上圖轉成以下的平面。
134 |
135 | **請注意:圖形上的點應在 $y=-\infty$ 或 $y=\infty$,因坐標軸無法顯示,故以最大值表示。**
136 |
137 |
104 |
105 | > Image from me with matplotlib and scikit-learn
106 |
107 | 圖中的橘線即為擬合後的線性迴歸模型,而點則是期中考成績對應到的通過與否。
108 |
109 |
110 |
111 | ### 勝算
112 |
113 | 我們定義勝算 (odds) 為,一件事情發生的機率,除以一件事情不發生的機率,也就是 $\dfrac{p}{1-p}$
114 |
115 | $\log(odds)$ 可以有效的讓勝算的起點設定在數線的 $0$ 上,並且隨著數值的大與小,顯示在數線上距離 $0$ 有多遠。
116 |
117 |
118 |
119 | ### 羅吉斯迴歸的圖形轉換
120 |
121 | 上面的圖似乎可以非常棒的看出對應的成績所造成的通過與否了,不過我們可以將這個圖形做一點轉換。
122 |
123 | 我們考慮將這條線性迴歸模型拉直,也就是轉成 $y=ax+b$ 的形式。
124 |
125 | 為此,我們可以考慮將 $y$ 軸每一點的機率值,映射到一個定義域為 $(-\infty, \infty)$ 的 $y$ 軸上
126 |
127 | 我們可以使用 Logit Function,定義為 $\ln(odds) = \ln(\dfrac{p}{1-p})$ ,來對 $y$ 軸進行映射,
128 |
129 | 再套用訓練出來的參數,將這個羅吉斯迴歸的圖形造成一條直線。
130 |
131 |
132 |
133 | 例如以上圖來說,可以將上圖轉成以下的平面。
134 |
135 | **請注意:圖形上的點應在 $y=-\infty$ 或 $y=\infty$,因坐標軸無法顯示,故以最大值表示。**
136 |
137 |  138 |
139 | > Image from me with matplotlib and scikit-learn
140 |
141 |
--------------------------------------------------------------------------------
/Markdown/Unclassified.md:
--------------------------------------------------------------------------------
1 | # 資料科學概論筆記
2 |
3 | Author: [Uriah Xuan](https://ntut-xuan.github.io/) (109 NTUT CSIE)
4 |
5 |
6 |
7 | ## 大數據的 5V 特徵
8 |
9 | | 英文名稱 | 中文名稱 | 概念 |
10 | | :------: | :------: | :--------------------------------------------------: |
11 | | Volume | 大量化 | 大數據通常有著極大量的資料,因此需要注重保存與安全性 |
12 | | Variety | 多樣化 | 大數據的資料形式其實是不限的,文字、圖片等等 |
13 | | Velocity | 快速化 | 大數據的資料處理需要在一定時限內處理完成 |
14 | | Veracity | 真實性 | 大數據的資料需要有一定的真實性。 |
15 | | Value | 價值化 | 資料帶有價值意義,需要合理的運用,以低價值創造高價值 |
16 |
17 |
18 |
19 | ## 經營管理及數據導向決策問題
20 |
21 | 1. 決策時缺乏適合與即時有效的資訊參考。
22 | 2. 報表不夠齊全,格式與決策層需要的不同。
23 | 3. 花費大量人物力,製作使用率低與無效的報表。
24 | 4. 報表與管理規範結合困難,經常發生異常狀況。
25 | 5. 無法從報表分析產生新管理觀念,找出成功關鍵因素與核心競爭力。
26 |
27 |
28 |
29 | ## 商業智慧與資料探勘的循環
30 |
31 |
138 |
139 | > Image from me with matplotlib and scikit-learn
140 |
141 |
--------------------------------------------------------------------------------
/Markdown/Unclassified.md:
--------------------------------------------------------------------------------
1 | # 資料科學概論筆記
2 |
3 | Author: [Uriah Xuan](https://ntut-xuan.github.io/) (109 NTUT CSIE)
4 |
5 |
6 |
7 | ## 大數據的 5V 特徵
8 |
9 | | 英文名稱 | 中文名稱 | 概念 |
10 | | :------: | :------: | :--------------------------------------------------: |
11 | | Volume | 大量化 | 大數據通常有著極大量的資料,因此需要注重保存與安全性 |
12 | | Variety | 多樣化 | 大數據的資料形式其實是不限的,文字、圖片等等 |
13 | | Velocity | 快速化 | 大數據的資料處理需要在一定時限內處理完成 |
14 | | Veracity | 真實性 | 大數據的資料需要有一定的真實性。 |
15 | | Value | 價值化 | 資料帶有價值意義,需要合理的運用,以低價值創造高價值 |
16 |
17 |
18 |
19 | ## 經營管理及數據導向決策問題
20 |
21 | 1. 決策時缺乏適合與即時有效的資訊參考。
22 | 2. 報表不夠齊全,格式與決策層需要的不同。
23 | 3. 花費大量人物力,製作使用率低與無效的報表。
24 | 4. 報表與管理規範結合困難,經常發生異常狀況。
25 | 5. 無法從報表分析產生新管理觀念,找出成功關鍵因素與核心競爭力。
26 |
27 |
28 |
29 | ## 商業智慧與資料探勘的循環
30 |
31 |  32 |
33 |
34 |
35 | ## Business Intelligence Development Model
36 |
37 | (待補)
38 |
39 |
40 |
41 | ## 辨識模式
42 |
43 | 模式有助於解析複雜事務與展露趨勢、種類為時間、空間、功能。
44 |
45 |
46 |
47 | ### 帕金森定理(Parkinson's Law)
48 |
49 | 在工作能被完成的時限內,工作量會一直被增加,直到所有可用時間都被填充為止。
50 |
51 |
52 |
53 | ### 八二法則(Pareto Principle)
54 |
55 | 約僅有 20% 的變因操控著 80% 的局面,
56 |
57 | 也就是說:「所有變量中,最重要的僅有 20%,雖然 80% 佔多數,但控制的範圍卻遠低於關鍵的少數」。
58 |
59 |
60 |
61 | ## 資料處理鍊
62 |
63 | > 注意:這個條目還在建立與理解中,在服用時可能會承受一定的薛丁格錯誤風險。
64 |
65 |
66 |
67 | 
68 |
69 |
70 |
71 | ## 資料與變數
72 |
73 | 
74 |
75 | | 名詞 | 意義 |
76 | | ------ | ------------------------------------------------------------ |
77 | | 資料 | 經由蒐集、分析及彙總所得到,作為說明與解釋之用的事實與數值。 |
78 | | 資料集 | 為特定研究目的蒐集的所有資料,由許多元素所組成。 |
79 | | 元素 | 資料蒐集的實體,包含很多變數,例如上方表格的每個國家即為一個元素 |
80 | | 變數 | 元素的某一特性,例如上列表格的每個元素有以下四個變數:WTO狀態、GDP、Fitch Rating、Fitch Outlook |
81 | | 觀察值 | 對特定元素蒐集的一組衡量值就是觀察值,例如上表的第1個觀察值(Armenia)包含了一組衡量值:Member、3615、BB-及Stable |
82 |
83 |
84 |
85 | ## 衡量尺度
86 |
87 | 資料蒐集需要以下衡量尺度之一:名目尺度、順序尺度、區間尺度及比例尺度。
88 |
89 | 衡量尺度決定資料包含的資訊量,也指出資料彙整的或統計分析時的最適方法。
90 |
91 |
92 |
93 | ### 名目尺度(nominal scale)
94 |
95 | 用來表示元素屬性的標記或名稱,比較等於或不等於。
96 |
97 | 例如上表的國家WTO狀態可以分成「是WTO會員國」與「是WTO觀察員」,因此我們可以以數字1表示這個國家是WTO會員國,2表示這個國家是WTO觀察員,就能夠方便把資料輸入電腦,兩個國家的WTO狀態只能用相同與否來區分。
98 |
99 | 也因為名目尺度的意義是比較等於或不等於,因此詢問「WTO會員國與WTO觀察員哪個比較大」或者「兩個國家的WTO狀態相加等於多少」是完全毫無意義的行為。
100 |
101 |
102 |
103 | ### 順序尺度(ordinal scale)
104 |
105 | 與名目尺度不同,順序尺度的類別有一定的大小或順序,比起名目尺度只能比較相等,順序尺度能夠比較大小。
106 |
107 | 例如上表的Fitch Rating,其中AAA代表最好,F代表最差,因此可以根據評等排出高低,所以是順序尺度。
108 |
109 |
110 |
111 | ### 區間尺度(interval scale)
112 |
113 | 若變數具有順序資料的特性,且觀察值可以相加或相減,其結果仍有意義,這個變數的衡量尺度就是區間尺度,且一定以數值表示。
114 |
115 | 例如統測成績就是一個區間尺度,假設有三位學生的統測成績為699、560、350,則我們可以由高到低依序排序來衡量出成績表現的優劣,而他們的差距也存在意義,例如699的學生比560的學生高出139分。
116 |
117 |
118 |
119 | ### 比例尺度(ratio scale)
120 |
121 | 若變數具有順序資料的特性,且觀察值可以加減乘除,其結果仍有意義,這個變數的衡量尺度就是比例尺度,且一定以數值表示。
122 |
123 | 與區間尺度的差別在於,**比例尺度要求絕對零點,也就是值必須要大於等於0且在0上必須要是自然的不存在**。
124 |
125 | 例如年齡不存在0歲,而高度不存在0公分,而可以描述20歲比5歲大4倍。
126 |
127 |
128 |
129 | ## 百分位數
130 |
131 | 百分位數可以瞭解資料在最小值與最大值間的分布狀況,以pth百分位數可以把資料分成兩個部份。
132 |
133 | 大約pth百分比的觀察值會小於pth百分位數,而大約有(100-p)百分比的觀察值會大於pth百分位數。
134 |
135 | 計算時需要先「非嚴格遞增排序」,計算公式如下: $$ L_p = \dfrac{p}{100}(n+1) $$
136 |
137 |
138 |
139 | ## 四分位數
140 |
141 | 四分位數將整筆資料分成四個部份,每個部份大概含有25%的資料個數,定義如下:
142 |
143 | 1. $Q_1$為第一四分位數或 $25\text{th percentile}$
144 | 2. $Q_2$為第二四分位數或 $50\text{th percentile}$,也就是中位數
145 | 3. $Q_3$為第三四分位數或 $75\text{th percentile}$
146 |
147 |
148 |
149 | ## 四分位距(IQR)
150 |
151 | 四分位距較能克服極端值的影響,定義如下 $ \text{IQR} = Q_3-Q_1 $ 也就是中間資料$50%$的全距。
152 |
153 |
154 |
155 | ## 離群偵測
156 |
157 | 有時在一個資料集中會有極大與極小的數值,這些數值稱為離群。
158 |
159 | 我們可以利用$z$分數去偵測離群值,一般來說,約有$99.7%$的資料會落在標準差$\pm3$內,我們會希望資料的標準差與中心的距離不超過$3$。
160 |
161 | 另一種方式是使用第一分位、第三分位與四分位距來做偵測,能夠給定一個區間來要求值必須要在這個區間內,定義如下:
162 |
163 | $\text{Lower Limit} = Q_1 - 1.5(\text{IQR}) \ \text{Upper Limit} = Q_3 + 1.5(\text{IQR}) $
164 |
165 |
166 |
167 | ## 資料模型
168 |
169 | 資料模型是為了能有組織有效率地,將我們需求的資料儲存於資料庫系統中,以及有一個適當的表達方式。
170 |
171 |
172 |
173 | 主要分成三種模式的**演變**:
174 |
175 | 1. 階層式資料模型
176 | 2. 網路式資料模型
177 | 3. 關聯式資料模型
178 |
179 |
180 |
181 | ### 階層式資料模型
182 |
183 | 主要使用樹狀結構,將一筆一筆的紀錄組織起來,適合一對多的資料組成關係,但無法直接表達多對多的關係。
184 |
185 |
186 |
187 | ### 網路式資料模型
188 |
189 | 改善了階層式資料模型,可以供給多對多的關係。
190 |
191 | 在資料呈現上非常複雜、且無法確實表達資料與資料之間的網路連結關係。
192 |
193 |
194 |
195 | ### 關聯式資料模型
196 |
197 | 以表格來表達關係,每一列即為一個紀錄,通常會實體關聯圖作為輔助設計的依據。
198 |
199 |
200 |
201 | ## SQL 查詢
202 |
203 | SQL 全名為 結構化查詢語言(Structured Query Language),對於資料庫來說,我們可以用 SQL 語法來進行查詢。
204 |
205 | 
206 |
207 | 例如要從一張名為 Teacher 的資料表中,顯示出所有結果屬性,寫法可以寫成這樣。
208 |
209 | ```sql
210 | SELECT * FROM Teacher
211 | ```
212 |
213 | 若要從這堆老師中選出其中一個名為王小軒的老師,可以寫成這樣。
214 |
215 | ```sql
216 | SELECT * FROM Teacher WHERE name = '王小軒'
217 | ```
218 |
219 | 若只要得到王小軒老師的 ID,可以寫成這樣。
220 |
221 | ```sql
222 | SELECT ID FROM Teacher WHERE name = '王小軒'
223 | ```
224 |
225 |
226 |
227 | ## 非結構化資料
228 |
229 | ### 非結構化資料的介紹
230 |
231 | 非結構化資料形式涵蓋了聲音、圖像、影像、文字等等。
232 |
233 | > [結構化資料 vs. 非結構化資料 | Pure Storage](https://www.purestorage.com/tw/knowledge/big-data/structured-vs-unstructured-data.html)
234 |
235 |
236 |
237 | ### 非結構化資料的特性
238 |
239 | #### 數位化生成
240 |
241 | 大部分由機器生成的資料,並不一定能夠整齊的被資料庫的欄位所對應,因此會使得資料庫變成多維度,且非常難以預測。
242 |
243 |
244 |
245 | #### 多模式
246 |
247 | 資料經過蒐集之後,具有大量不同類別的資料,例如 e-mail、文檔、圖檔等等。
248 |
249 |
250 |
251 | #### 持續變動
252 |
253 | 大量資料被生成、處理、分析與即時運算。
254 |
255 |
256 |
257 | #### 地理分散
258 |
259 | 不同資料被儲存在不同的地方,來達成資安特性。
260 |
261 |
262 |
263 | > [結構化資料 vs. 非結構化資料 | Pure Storage](https://www.purestorage.com/tw/knowledge/big-data/structured-vs-unstructured-data.html)
264 | >
265 | > [Unified Fast File and Object: A New Category of Storage | Pure Storage](https://blog.purestorage.com/products/unified-fast-file-object-storage/)
266 | >
267 | > [Types and Examples of NoSQL Databases - Big Data Analytics News](https://bigdataanalyticsnews.com/types-examples-nosql-databases/)
268 | >
269 | > [淺談資料格式 — 結構化與非結構化資料. 進入大數據時代,資料成為挖掘商機的礦脈,對資料的管理不夠,想要利用大數據來開創新… | by 行銷資料科學 | Marketingdatascience | Medium](https://medium.com/marketingdatascience/%E6%B7%BA%E8%AB%87%E8%B3%87%E6%96%99%E6%A0%BC%E5%BC%8F-%E7%B5%90%E6%A7%8B%E5%8C%96%E8%88%87%E9%9D%9E%E7%B5%90%E6%A7%8B%E5%8C%96%E8%B3%87%E6%96%99-50c89a4b15e0)
270 |
271 |
272 |
273 | ### 結構化與非結構資料化的比較
274 |
275 | | | 結構化資料 | 非結構化資料 |
276 | | :----------: | :------------: | :----------: |
277 | | 呈現方面 | 表格 | 無法呈現 |
278 | | 處理方面 | 需正規化 | 不須正規化 |
279 | | 形式 | 有限的資料形式 | 不限 |
280 | | 儲存空間需求 | 較少 | 較大 |
281 | | 存取 | 較簡單 | 較困難 |
282 |
283 |
284 |
285 | ## 資料探勘
286 |
287 | 從一大群的資料中,利用技術(人工智慧、機器學習、統計學等等)探勘出有意義的資料。
288 |
289 |
290 |
291 | ### 資料的探勘任務
292 |
293 | 主要分成六種常見的任務。
294 |
295 | 1. 異常檢測:辨識不尋常的資料,或針對錯誤資料進一步調查。
296 | 2. 關聯規則學習:搜尋變數之間的關係。
297 | 3. 聚類:在未知資料的結構下,發現資料的類別與結構,利用演算法將資料分成更多子集,讓子集的資料都有相似的一些屬性。
298 | 4. 分類:對新的資料推廣成已知結構的任務,例如將一封新郵件分類成「正常郵件」與「垃圾郵件」,可利用決策樹來分析數據或輔助預測。
299 | 5. 迴歸:試圖找到最小誤差的建模函式。
300 | 6. 匯總:提供一個更緊湊的資料集表示,來生成視覺化或報表。
301 |
302 |
--------------------------------------------------------------------------------
/PDF/Artificial Neural Networks.pdf:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/ntut-xuan/DataScienceNote/c49735d5ffa0623e5f17974f95afcf68c413e15b/PDF/Artificial Neural Networks.pdf
--------------------------------------------------------------------------------
/PDF/Associate Rule Mining.pdf:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/ntut-xuan/DataScienceNote/c49735d5ffa0623e5f17974f95afcf68c413e15b/PDF/Associate Rule Mining.pdf
--------------------------------------------------------------------------------
/PDF/Cluster Analysis.pdf:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/ntut-xuan/DataScienceNote/c49735d5ffa0623e5f17974f95afcf68c413e15b/PDF/Cluster Analysis.pdf
--------------------------------------------------------------------------------
/PDF/Data Mining.pdf:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/ntut-xuan/DataScienceNote/c49735d5ffa0623e5f17974f95afcf68c413e15b/PDF/Data Mining.pdf
--------------------------------------------------------------------------------
/PDF/Data Preprocessing.pdf:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/ntut-xuan/DataScienceNote/c49735d5ffa0623e5f17974f95afcf68c413e15b/PDF/Data Preprocessing.pdf
--------------------------------------------------------------------------------
/PDF/Data Warehouse.pdf:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/ntut-xuan/DataScienceNote/c49735d5ffa0623e5f17974f95afcf68c413e15b/PDF/Data Warehouse.pdf
--------------------------------------------------------------------------------
/PDF/Decision Tree.pdf:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/ntut-xuan/DataScienceNote/c49735d5ffa0623e5f17974f95afcf68c413e15b/PDF/Decision Tree.pdf
--------------------------------------------------------------------------------
/PDF/Naive Bayes Analysis.pdf:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/ntut-xuan/DataScienceNote/c49735d5ffa0623e5f17974f95afcf68c413e15b/PDF/Naive Bayes Analysis.pdf
--------------------------------------------------------------------------------
/PDF/Regression.pdf:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/ntut-xuan/DataScienceNote/c49735d5ffa0623e5f17974f95afcf68c413e15b/PDF/Regression.pdf
--------------------------------------------------------------------------------
/PDF/Unclassified.pdf:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/ntut-xuan/DataScienceNote/c49735d5ffa0623e5f17974f95afcf68c413e15b/PDF/Unclassified.pdf
--------------------------------------------------------------------------------
/README.md:
--------------------------------------------------------------------------------
1 | # 資料科學導論筆記
2 |
3 |
4 |
5 | ## 作者
6 |
7 | 國立臺北科技大學 資訊工程系 [黃漢軒](https://ntut-xuan.github.io)
8 |
9 | 筆記上有任何問題,請丟 [issue](https://github.com/ntut-xuan/DataScienceNote/issues),支持這份筆記,請幫我點個 star,謝謝
10 |
11 |
12 |
13 | **超級注意:工具箱的部分只經過我本人測試過,並不保證他不會有任何問題,有任何問題不負任何責任,有遇到問題請丟 [issue](https://github.com/ntut-xuan/DataScienceNote/issues) 。**
14 |
15 |
16 |
17 | ## 主題式分析
18 |
19 | 這份筆記使用主題式的方式架構,主要分成以下幾個子主題。
20 |
21 |
22 |
23 | | 主題 | 完工進度 | ToolBox | 完工時間 |
24 | | :----------------------------------------: | :------: | :-----: | :------------: |
25 | | 還沒經過整理的主題 | SKIP | SKIP | SKIP |
26 | | 資料倉儲(Data Warehouse) | 100% | SKIP | 2022 / 04 / 04 |
27 | | 資料探勘(Data Mining) | 100% | SKIP | 2022 / 04 / 05 |
28 | | 決策樹(Decision Tree) | 100% | SKIP | 2022 / 04 / 12 |
29 | | 迴歸(Regression) | 100% | SKIP | 2022 / 04 / 14 |
30 | | 單純貝氏(Naïve Bayes Analysis) | 100% | OK | 2022 / 06 / 15 |
31 | | 人工神經網路(Artificial Neural Networks) | 100% | SKIP | 2022 / 06 / 15 |
32 | | 聚類分析(Cluster Analysis) | 100% | OK | 2022 / 06 / 22 |
33 | | 資料預處理(Data Preprocessing) | 100% | SKIP | 2022 / 06 / 22 |
34 | | 推薦系統(Recommandation System) | 100% | SKIP | 2022 / 06 / 22 |
35 |
36 |
37 |
--------------------------------------------------------------------------------
/python_tool/.gitignore:
--------------------------------------------------------------------------------
1 | .idea
2 | __pycache__
--------------------------------------------------------------------------------
/python_tool/debug.py:
--------------------------------------------------------------------------------
1 | import numpy as np
2 | import random
3 | import time
4 | import matplotlib.pyplot as plt
5 |
6 | def standard_random():
7 | std = np.array([0.1, 0.1, 0.1, 0.1, 0.1, 0.1, 0.1])
8 | return std
9 |
10 |
11 | def active_function(x):
12 | return np.log(1+np.exp(x))
13 |
14 |
15 | def calc(x_1s, x_2s, x_1, x_2, y_1, y_2, w, b):
16 | x_1s = np.transpose(data)[0]
17 | x_2s = np.transpose(data)[1]
18 | output = w[5] * y_1 + w[6] * y_2 + b[3]
19 | return (x_1s * w[1] + x_2s * w[3], x_1s * w[2] + x_2s * w[4], active_function(x_1), active_function(x_2), output)
20 |
21 | data = [[35, 67], [12, 75], [16, 89], [45, 56], [10, 90]]
22 | label = [1, 0, 1, 1, 0]
23 |
24 | data_array = np.array(data)
25 | label_array = np.array(label)
26 |
27 | w = standard_random()
28 | b = [0 for i in range(4)]
29 |
30 | print(w)
31 |
32 | x_1s = np.transpose(data)[0]
33 | x_2s = np.transpose(data)[1]
34 | x_1 = x_1s * w[1] + x_2s * w[3]
35 | x_2 = x_1s * w[2] + x_2s * w[4]
36 | y_1 = np.log(1+np.exp(x_1))
37 | y_2 = np.log(1+np.exp(x_2))
38 | output = w[5] * active_function(x_1*w[1]+x_2*w[3] + b[1]) + w[6] * active_function(x_1*w[2]+x_2*w[4] + b[2]) + b[3]
39 | learn_rate = 0.01
40 |
41 | for i in range(1000):
42 | x_1s = np.transpose(data)[0]
43 | x_2s = np.transpose(data)[1]
44 | x_1, x_2, y_1, y_2, output = calc(x_1s, x_2s, x_1, x_2, y_1, y_2, w, b)
45 | db3 = np.sum(-2 * (label_array - output))
46 | dw5 = np.sum((label_array - output) * y_1 * -2)
47 | dw6 = np.sum((label_array - output) * y_2 * -2)
48 | db1 = np.sum((label_array - output) * w[5] * (np.exp(x_1) / (1 + np.exp(x_1))) * -2)
49 | db2 = np.sum((label_array - output) * w[6] * (np.exp(x_2) / (1 + np.exp(x_2))) * -2)
50 | dw1 = np.sum((label_array - output) * w[5] * (np.exp(x_1) / (1 + np.exp(x_1))) * x_1s * -2)
51 | dw2 = np.sum((label_array - output) * w[6] * (np.exp(x_2) / (1 + np.exp(x_2))) * x_1s * -2)
52 | dw3 = np.sum((label_array - output) * w[5] * (np.exp(x_1) / (1 + np.exp(x_1))) * x_2s * -2)
53 | dw4 = np.sum((label_array - output) * w[6] * (np.exp(x_2) / (1 + np.exp(x_2))) * x_2s * -2)
54 | print("SSR =", np.sum(label_array - output) * np.sum(label_array - output))
55 | b[3] = b[3] - db3 * learn_rate
56 | b[2] = b[2] - db2 * learn_rate
57 | b[1] = b[1] - db1 * learn_rate
58 | w[6] = w[6] - dw6 * learn_rate
59 | w[5] = w[5] - dw5 * learn_rate
60 | w[4] = w[4] - dw4 * learn_rate
61 | w[3] = w[3] - dw3 * learn_rate
62 | w[2] = w[2] - dw2 * learn_rate
63 | w[1] = w[1] - dw1 * learn_rate
64 | print("b=", b)
65 | print("w=", w)
66 |
67 | fig = plt.figure(figsize=(10, 10))
68 | ax = fig.gca(projection='3d')
69 |
70 | plot_x = np.linspace(0, 100, num=100)
71 |
72 | table = np.array([[0 for _ in range(100)] for _ in range(100)])
73 |
74 | for i in range(100):
75 | for j in range(100):
76 | x1 = i
77 | x2 = j
78 | #print(x1, x2)
79 | table[i][j] = w[5] * (active_function(x1 * w[1] + x2 * w[3]) + b[1]) \
80 | + w[6] * (active_function(x1 * w[2] + x2 * w[4]) + b[2]) \
81 | + b[3]
82 |
83 | ax.scatter(np.transpose(data_array)[0], np.transpose(data_array)[1], label_array)
84 | ax.plot_surface(plot_x, plot_x, table, cmap='seismic')
85 | plt.show()
86 |
87 | print(table)
88 |
89 | print(table[45][56])
90 | print(table[25][70])
--------------------------------------------------------------------------------
/python_tool/example.py:
--------------------------------------------------------------------------------
1 | from tool import *
2 |
3 | naiveBayesClassifier = MultinomialNaiveBayesClassifier()
4 | data = [["love", "happy", "joy", "joy", "love"],
5 | ["happy", "love", "kick", "joy", "happy"],
6 | ["love", "move", "joy", "good"],
7 | ["love", "happy", "joy", "pain", "love"],
8 | ["joy", "love", "pain", "kick", "pain"],
9 | ["pain", "pain", "love", "kick"]]
10 | label = ["Yes", "Yes", "Yes", "Yes", "No", "No"]
11 | value = ["love", "pain", "joy", "happy", "kick", "happy"]
12 |
13 | naiveBayesClassifier.fit(np.array(data, dtype=object), np.array(label, dtype=object))
14 | print(naiveBayesClassifier.predict(value))
--------------------------------------------------------------------------------
/python_tool/main.py:
--------------------------------------------------------------------------------
1 | import numpy as np
2 | import tool
3 | import time
4 | import warnings
5 | import matplotlib.pyplot as plt
6 | from sklearn import cluster, datasets
7 | from sklearn.preprocessing import StandardScaler
8 | from itertools import cycle, islice
9 |
10 | n_samples = 300
11 | random_state = 170
12 | noisy_circles = datasets.make_circles(n_samples=n_samples, factor=0.5, noise=0.01)
13 |
14 | points = noisy_circles[0]
15 |
16 | array = np.zeros((n_samples, n_samples))
17 |
18 | for i in range(n_samples):
19 | for j in range(n_samples):
20 | array[i][j] = np.sqrt((points[i][0]-points[j][0])**2 + (points[i][1]-points[j][1])**2)
21 |
22 | algo = tool.WPGMAClustering(n_clusters=2)
23 | algo.fit(array)
24 | algo.clustering()
25 |
26 | print(algo.labels_)
27 |
28 | colors = np.array(
29 | list(
30 | islice(
31 | cycle(
32 | [
33 | "#377eb8",
34 | "#ff7f00",
35 | "#4daf4a",
36 | "#f781bf",
37 | "#a65628",
38 | "#984ea3",
39 | "#999999",
40 | "#e41a1c",
41 | "#dede00",
42 | ]
43 | ),
44 | int(max(algo.labels_) + 1),
45 | )
46 | ))
47 |
48 |
49 | plt.scatter(points[:, 0], points[:, 1], color=colors[algo.labels_])
50 | plt.show()
--------------------------------------------------------------------------------
/python_tool/tool.py:
--------------------------------------------------------------------------------
1 | import numpy as np
2 | import copy
3 |
4 |
5 | class MultinomialNaiveBayesClassifier:
6 | def __init__(self):
7 | self.value_map = {}
8 | self.result = np.array([])
9 | self.data = np.array([])
10 |
11 | def fit(self, x, y):
12 | self.result = y
13 | unique, counts = np.unique(self.result, return_counts=True)
14 | for v in unique:
15 | self.value_map[v] = []
16 | for i in range(len(y)):
17 | for s in x[i]:
18 | self.value_map[y[i]].append(s)
19 |
20 | def add_duplicated_value(self, temp_result, temp_value_map, missing_value):
21 | unique, counts = np.unique(temp_result, return_counts=True)
22 | for k in unique:
23 | value_unique = np.unique(temp_value_map[k])
24 | for v in value_unique:
25 | if missing_value == v:
26 | continue
27 | temp_value_map[k].append(v)
28 | for k in unique:
29 | temp_value_map[k].append(missing_value)
30 |
31 | def print_unique(self, y):
32 | for v in np.unique(self.result):
33 | unique, counts = np.unique(y[v], return_counts=True)
34 | result_dict = dict(zip(unique, counts))
35 | print(result_dict)
36 |
37 | def predict(self, y):
38 | temp_result = self.result
39 | temp_value_map = self.value_map
40 | unique, counts = np.unique(self.result, return_counts=True)
41 | result_dict = dict(zip(unique, counts))
42 | predict = {}
43 | for v in unique:
44 | print("calculate P(%s) = %d/%d" % (v, result_dict[v], int(np.sum(counts))))
45 | predict[v] = float(result_dict[v] / np.sum(counts))
46 | for s in y:
47 | for v in unique:
48 | if s not in self.value_map[v]:
49 | self.add_duplicated_value(temp_result, temp_value_map, s)
50 | self.print_unique(temp_value_map)
51 | for s in y:
52 | for v in unique:
53 | unique_s, counts_s = np.unique(self.value_map[v], return_counts=True)
54 | result_dict_s = dict(zip(unique_s, counts_s))
55 | total = np.sum(counts_s)
56 | print("calculate P(%s|%s) = %d/%d" % (s, v, result_dict_s[s], int(total)))
57 | predict[v] *= float(result_dict_s[s] / int(total))
58 | print(predict)
59 | return max(predict, key=predict.get)
60 |
61 |
62 | class UPGMAClustering:
63 |
64 | def __init__(self, n_clusters=2):
65 | self.labels_ = None
66 | self.n = None
67 | self.n_clusters = n_clusters
68 | self.cluster_list = None
69 | self.distance_table = None
70 | self.threshold = None
71 |
72 | def fit(self, distance_table):
73 | self.n = len(distance_table)
74 | self.distance_table = distance_table
75 | self.cluster_list = []
76 | self.threshold = []
77 | self.labels_ = [0 for _ in range(self.n)]
78 | for i in range(self.n):
79 | self.cluster_list.append([i])
80 |
81 | def clustering(self):
82 | for r in range(self.n - (self.n_clusters-1)):
83 |
84 | print("\n=============== Iter%5d ===============\n" % (r + 1))
85 |
86 | original_cluster_list = copy.deepcopy(self.cluster_list)
87 | self.distance_table[self.distance_table == 0] = np.iinfo(np.int32).max
88 |
89 | # choose minimum pair
90 | minimum_distance = np.min(self.distance_table)
91 | minimum_pair = np.unravel_index(np.argmin(self.distance_table, axis=None), self.distance_table.shape)
92 | print("Minimum pair: %s = %d" % (str(minimum_pair), minimum_distance))
93 |
94 | if r != self.n - self.n_clusters:
95 |
96 | # combine two cluster
97 | target_list1 = copy.deepcopy(self.cluster_list[minimum_pair[0]])
98 | target_list2 = copy.deepcopy(self.cluster_list[minimum_pair[1]])
99 | self.cluster_list[minimum_pair[0]] += (self.cluster_list[minimum_pair[1]])
100 | self.cluster_list.remove(self.cluster_list[minimum_pair[1]])
101 |
102 | print("target list l1=", target_list1, "- l2=", target_list2)
103 | print("combine list", original_cluster_list, "->", self.cluster_list)
104 |
105 | # recalculate distance between new cluster and another cluster
106 | self.distance_table[self.distance_table == np.iinfo(np.int32).max] = 0
107 | new_distance_table = np.zeros((len(self.cluster_list), len(self.cluster_list)))
108 | for i in range(len(self.cluster_list)):
109 | for j in range(len(self.cluster_list)):
110 | index1 = original_cluster_list.index(target_list1)
111 | index2 = original_cluster_list.index(target_list2)
112 | index4 = self.cluster_list.index(self.cluster_list[j])
113 | if i == index1 or j == index1:
114 | if index1 == index4:
115 | continue
116 | index3 = original_cluster_list.index(self.cluster_list[j])
117 | distance1 = self.distance_table[index1][index3]
118 | distance2 = self.distance_table[index2][index3]
119 | new_distance_table[index1][index4] = (len(target_list1) * distance1 + len(
120 | target_list2) * distance2) / float(len(target_list1) + len(target_list2))
121 | new_distance_table[index4][index1] = (len(target_list1) * distance1 + len(
122 | target_list2) * distance2) / float(len(target_list1) + len(target_list2))
123 | else:
124 | index3 = original_cluster_list.index(self.cluster_list[j])
125 | index5 = original_cluster_list.index(self.cluster_list[i])
126 | new_distance_table[i][j] = self.distance_table[index5][index3]
127 |
128 | self.distance_table = new_distance_table
129 |
130 | # print
131 | print("Update Table\n", str(new_distance_table))
132 | print(self.cluster_list)
133 |
134 | # calculate branch length estimation
135 | branch_length_estimation = minimum_distance / 2.0
136 | self.threshold += [branch_length_estimation]
137 | print("distance_threshold =", branch_length_estimation)
138 |
139 | for i in range(len(self.cluster_list)):
140 | for v in self.cluster_list[i]:
141 | self.labels_[v] = i+1
142 |
143 |
144 | class WPGMAClustering:
145 |
146 | def __init__(self, n_clusters=2):
147 | self.labels_ = None
148 | self.n = None
149 | self.n_clusters = n_clusters
150 | self.cluster_list = None
151 | self.distance_table = None
152 | self.threshold = None
153 |
154 | def fit(self, distance_table):
155 | self.n = len(distance_table)
156 | self.distance_table = distance_table
157 | self.cluster_list = []
158 | self.threshold = []
159 | self.labels_ = [0 for _ in range(self.n)]
160 | for i in range(self.n):
161 | self.cluster_list.append([i])
162 |
163 | def clustering(self):
164 | for r in range(self.n - (self.n_clusters-1)):
165 |
166 | print("\n=============== Iter%5d ===============\n" % (r + 1))
167 |
168 | original_cluster_list = copy.deepcopy(self.cluster_list)
169 | self.distance_table[self.distance_table == 0] = np.iinfo(np.int32).max
170 |
171 | # choose minimum pair
172 | minimum_distance = np.min(self.distance_table)
173 | minimum_pair = np.unravel_index(np.argmin(self.distance_table, axis=None), self.distance_table.shape)
174 | print("Minimum pair: %s = %d" % (str(minimum_pair), minimum_distance))
175 |
176 | if r != self.n - self.n_clusters:
177 |
178 | # combine two cluster
179 | target_list1 = copy.deepcopy(self.cluster_list[minimum_pair[0]])
180 | target_list2 = copy.deepcopy(self.cluster_list[minimum_pair[1]])
181 | self.cluster_list[minimum_pair[0]] += (self.cluster_list[minimum_pair[1]])
182 | self.cluster_list.remove(self.cluster_list[minimum_pair[1]])
183 |
184 | print("target list l1=", target_list1, "- l2=", target_list2)
185 | print("combine list", original_cluster_list, "->", self.cluster_list)
186 |
187 | # recalculate distance between new cluster and another cluster
188 | self.distance_table[self.distance_table == np.iinfo(np.int32).max] = 0
189 | new_distance_table = np.zeros((len(self.cluster_list), len(self.cluster_list)))
190 | for i in range(len(self.cluster_list)):
191 | for j in range(len(self.cluster_list)):
192 | index1 = original_cluster_list.index(target_list1)
193 | index2 = original_cluster_list.index(target_list2)
194 | index4 = self.cluster_list.index(self.cluster_list[j])
195 | if i == index1 or j == index1:
196 | if index1 == index4:
197 | continue
198 | index3 = original_cluster_list.index(self.cluster_list[j])
199 | distance1 = self.distance_table[index1][index3]
200 | distance2 = self.distance_table[index2][index3]
201 | new_distance_table[index1][index4] = (distance1 + distance2) / 2.0
202 | new_distance_table[index4][index1] = (distance1 + distance2) / 2.0
203 | else:
204 | index3 = original_cluster_list.index(self.cluster_list[j])
205 | index5 = original_cluster_list.index(self.cluster_list[i])
206 | new_distance_table[i][j] = self.distance_table[index5][index3]
207 |
208 | self.distance_table = new_distance_table
209 |
210 | # print
211 | print("Update Table\n", str(new_distance_table))
212 | print(self.cluster_list)
213 |
214 | # calculate branch length estimation
215 | branch_length_estimation = minimum_distance / 2.0
216 | self.threshold += [branch_length_estimation]
217 | print("distance_threshold =", branch_length_estimation)
218 |
219 | for i in range(len(self.cluster_list)):
220 | for v in self.cluster_list[i]:
221 | self.labels_[v] = i+1
222 |
--------------------------------------------------------------------------------
32 |
33 |
34 |
35 | ## Business Intelligence Development Model
36 |
37 | (待補)
38 |
39 |
40 |
41 | ## 辨識模式
42 |
43 | 模式有助於解析複雜事務與展露趨勢、種類為時間、空間、功能。
44 |
45 |
46 |
47 | ### 帕金森定理(Parkinson's Law)
48 |
49 | 在工作能被完成的時限內,工作量會一直被增加,直到所有可用時間都被填充為止。
50 |
51 |
52 |
53 | ### 八二法則(Pareto Principle)
54 |
55 | 約僅有 20% 的變因操控著 80% 的局面,
56 |
57 | 也就是說:「所有變量中,最重要的僅有 20%,雖然 80% 佔多數,但控制的範圍卻遠低於關鍵的少數」。
58 |
59 |
60 |
61 | ## 資料處理鍊
62 |
63 | > 注意:這個條目還在建立與理解中,在服用時可能會承受一定的薛丁格錯誤風險。
64 |
65 |
66 |
67 | 
68 |
69 |
70 |
71 | ## 資料與變數
72 |
73 | 
74 |
75 | | 名詞 | 意義 |
76 | | ------ | ------------------------------------------------------------ |
77 | | 資料 | 經由蒐集、分析及彙總所得到,作為說明與解釋之用的事實與數值。 |
78 | | 資料集 | 為特定研究目的蒐集的所有資料,由許多元素所組成。 |
79 | | 元素 | 資料蒐集的實體,包含很多變數,例如上方表格的每個國家即為一個元素 |
80 | | 變數 | 元素的某一特性,例如上列表格的每個元素有以下四個變數:WTO狀態、GDP、Fitch Rating、Fitch Outlook |
81 | | 觀察值 | 對特定元素蒐集的一組衡量值就是觀察值,例如上表的第1個觀察值(Armenia)包含了一組衡量值:Member、3615、BB-及Stable |
82 |
83 |
84 |
85 | ## 衡量尺度
86 |
87 | 資料蒐集需要以下衡量尺度之一:名目尺度、順序尺度、區間尺度及比例尺度。
88 |
89 | 衡量尺度決定資料包含的資訊量,也指出資料彙整的或統計分析時的最適方法。
90 |
91 |
92 |
93 | ### 名目尺度(nominal scale)
94 |
95 | 用來表示元素屬性的標記或名稱,比較等於或不等於。
96 |
97 | 例如上表的國家WTO狀態可以分成「是WTO會員國」與「是WTO觀察員」,因此我們可以以數字1表示這個國家是WTO會員國,2表示這個國家是WTO觀察員,就能夠方便把資料輸入電腦,兩個國家的WTO狀態只能用相同與否來區分。
98 |
99 | 也因為名目尺度的意義是比較等於或不等於,因此詢問「WTO會員國與WTO觀察員哪個比較大」或者「兩個國家的WTO狀態相加等於多少」是完全毫無意義的行為。
100 |
101 |
102 |
103 | ### 順序尺度(ordinal scale)
104 |
105 | 與名目尺度不同,順序尺度的類別有一定的大小或順序,比起名目尺度只能比較相等,順序尺度能夠比較大小。
106 |
107 | 例如上表的Fitch Rating,其中AAA代表最好,F代表最差,因此可以根據評等排出高低,所以是順序尺度。
108 |
109 |
110 |
111 | ### 區間尺度(interval scale)
112 |
113 | 若變數具有順序資料的特性,且觀察值可以相加或相減,其結果仍有意義,這個變數的衡量尺度就是區間尺度,且一定以數值表示。
114 |
115 | 例如統測成績就是一個區間尺度,假設有三位學生的統測成績為699、560、350,則我們可以由高到低依序排序來衡量出成績表現的優劣,而他們的差距也存在意義,例如699的學生比560的學生高出139分。
116 |
117 |
118 |
119 | ### 比例尺度(ratio scale)
120 |
121 | 若變數具有順序資料的特性,且觀察值可以加減乘除,其結果仍有意義,這個變數的衡量尺度就是比例尺度,且一定以數值表示。
122 |
123 | 與區間尺度的差別在於,**比例尺度要求絕對零點,也就是值必須要大於等於0且在0上必須要是自然的不存在**。
124 |
125 | 例如年齡不存在0歲,而高度不存在0公分,而可以描述20歲比5歲大4倍。
126 |
127 |
128 |
129 | ## 百分位數
130 |
131 | 百分位數可以瞭解資料在最小值與最大值間的分布狀況,以pth百分位數可以把資料分成兩個部份。
132 |
133 | 大約pth百分比的觀察值會小於pth百分位數,而大約有(100-p)百分比的觀察值會大於pth百分位數。
134 |
135 | 計算時需要先「非嚴格遞增排序」,計算公式如下: $$ L_p = \dfrac{p}{100}(n+1) $$
136 |
137 |
138 |
139 | ## 四分位數
140 |
141 | 四分位數將整筆資料分成四個部份,每個部份大概含有25%的資料個數,定義如下:
142 |
143 | 1. $Q_1$為第一四分位數或 $25\text{th percentile}$
144 | 2. $Q_2$為第二四分位數或 $50\text{th percentile}$,也就是中位數
145 | 3. $Q_3$為第三四分位數或 $75\text{th percentile}$
146 |
147 |
148 |
149 | ## 四分位距(IQR)
150 |
151 | 四分位距較能克服極端值的影響,定義如下 $ \text{IQR} = Q_3-Q_1 $ 也就是中間資料$50%$的全距。
152 |
153 |
154 |
155 | ## 離群偵測
156 |
157 | 有時在一個資料集中會有極大與極小的數值,這些數值稱為離群。
158 |
159 | 我們可以利用$z$分數去偵測離群值,一般來說,約有$99.7%$的資料會落在標準差$\pm3$內,我們會希望資料的標準差與中心的距離不超過$3$。
160 |
161 | 另一種方式是使用第一分位、第三分位與四分位距來做偵測,能夠給定一個區間來要求值必須要在這個區間內,定義如下:
162 |
163 | $\text{Lower Limit} = Q_1 - 1.5(\text{IQR}) \ \text{Upper Limit} = Q_3 + 1.5(\text{IQR}) $
164 |
165 |
166 |
167 | ## 資料模型
168 |
169 | 資料模型是為了能有組織有效率地,將我們需求的資料儲存於資料庫系統中,以及有一個適當的表達方式。
170 |
171 |
172 |
173 | 主要分成三種模式的**演變**:
174 |
175 | 1. 階層式資料模型
176 | 2. 網路式資料模型
177 | 3. 關聯式資料模型
178 |
179 |
180 |
181 | ### 階層式資料模型
182 |
183 | 主要使用樹狀結構,將一筆一筆的紀錄組織起來,適合一對多的資料組成關係,但無法直接表達多對多的關係。
184 |
185 |
186 |
187 | ### 網路式資料模型
188 |
189 | 改善了階層式資料模型,可以供給多對多的關係。
190 |
191 | 在資料呈現上非常複雜、且無法確實表達資料與資料之間的網路連結關係。
192 |
193 |
194 |
195 | ### 關聯式資料模型
196 |
197 | 以表格來表達關係,每一列即為一個紀錄,通常會實體關聯圖作為輔助設計的依據。
198 |
199 |
200 |
201 | ## SQL 查詢
202 |
203 | SQL 全名為 結構化查詢語言(Structured Query Language),對於資料庫來說,我們可以用 SQL 語法來進行查詢。
204 |
205 | 
206 |
207 | 例如要從一張名為 Teacher 的資料表中,顯示出所有結果屬性,寫法可以寫成這樣。
208 |
209 | ```sql
210 | SELECT * FROM Teacher
211 | ```
212 |
213 | 若要從這堆老師中選出其中一個名為王小軒的老師,可以寫成這樣。
214 |
215 | ```sql
216 | SELECT * FROM Teacher WHERE name = '王小軒'
217 | ```
218 |
219 | 若只要得到王小軒老師的 ID,可以寫成這樣。
220 |
221 | ```sql
222 | SELECT ID FROM Teacher WHERE name = '王小軒'
223 | ```
224 |
225 |
226 |
227 | ## 非結構化資料
228 |
229 | ### 非結構化資料的介紹
230 |
231 | 非結構化資料形式涵蓋了聲音、圖像、影像、文字等等。
232 |
233 | > [結構化資料 vs. 非結構化資料 | Pure Storage](https://www.purestorage.com/tw/knowledge/big-data/structured-vs-unstructured-data.html)
234 |
235 |
236 |
237 | ### 非結構化資料的特性
238 |
239 | #### 數位化生成
240 |
241 | 大部分由機器生成的資料,並不一定能夠整齊的被資料庫的欄位所對應,因此會使得資料庫變成多維度,且非常難以預測。
242 |
243 |
244 |
245 | #### 多模式
246 |
247 | 資料經過蒐集之後,具有大量不同類別的資料,例如 e-mail、文檔、圖檔等等。
248 |
249 |
250 |
251 | #### 持續變動
252 |
253 | 大量資料被生成、處理、分析與即時運算。
254 |
255 |
256 |
257 | #### 地理分散
258 |
259 | 不同資料被儲存在不同的地方,來達成資安特性。
260 |
261 |
262 |
263 | > [結構化資料 vs. 非結構化資料 | Pure Storage](https://www.purestorage.com/tw/knowledge/big-data/structured-vs-unstructured-data.html)
264 | >
265 | > [Unified Fast File and Object: A New Category of Storage | Pure Storage](https://blog.purestorage.com/products/unified-fast-file-object-storage/)
266 | >
267 | > [Types and Examples of NoSQL Databases - Big Data Analytics News](https://bigdataanalyticsnews.com/types-examples-nosql-databases/)
268 | >
269 | > [淺談資料格式 — 結構化與非結構化資料. 進入大數據時代,資料成為挖掘商機的礦脈,對資料的管理不夠,想要利用大數據來開創新… | by 行銷資料科學 | Marketingdatascience | Medium](https://medium.com/marketingdatascience/%E6%B7%BA%E8%AB%87%E8%B3%87%E6%96%99%E6%A0%BC%E5%BC%8F-%E7%B5%90%E6%A7%8B%E5%8C%96%E8%88%87%E9%9D%9E%E7%B5%90%E6%A7%8B%E5%8C%96%E8%B3%87%E6%96%99-50c89a4b15e0)
270 |
271 |
272 |
273 | ### 結構化與非結構資料化的比較
274 |
275 | | | 結構化資料 | 非結構化資料 |
276 | | :----------: | :------------: | :----------: |
277 | | 呈現方面 | 表格 | 無法呈現 |
278 | | 處理方面 | 需正規化 | 不須正規化 |
279 | | 形式 | 有限的資料形式 | 不限 |
280 | | 儲存空間需求 | 較少 | 較大 |
281 | | 存取 | 較簡單 | 較困難 |
282 |
283 |
284 |
285 | ## 資料探勘
286 |
287 | 從一大群的資料中,利用技術(人工智慧、機器學習、統計學等等)探勘出有意義的資料。
288 |
289 |
290 |
291 | ### 資料的探勘任務
292 |
293 | 主要分成六種常見的任務。
294 |
295 | 1. 異常檢測:辨識不尋常的資料,或針對錯誤資料進一步調查。
296 | 2. 關聯規則學習:搜尋變數之間的關係。
297 | 3. 聚類:在未知資料的結構下,發現資料的類別與結構,利用演算法將資料分成更多子集,讓子集的資料都有相似的一些屬性。
298 | 4. 分類:對新的資料推廣成已知結構的任務,例如將一封新郵件分類成「正常郵件」與「垃圾郵件」,可利用決策樹來分析數據或輔助預測。
299 | 5. 迴歸:試圖找到最小誤差的建模函式。
300 | 6. 匯總:提供一個更緊湊的資料集表示,來生成視覺化或報表。
301 |
302 |
--------------------------------------------------------------------------------
/PDF/Artificial Neural Networks.pdf:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/ntut-xuan/DataScienceNote/c49735d5ffa0623e5f17974f95afcf68c413e15b/PDF/Artificial Neural Networks.pdf
--------------------------------------------------------------------------------
/PDF/Associate Rule Mining.pdf:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/ntut-xuan/DataScienceNote/c49735d5ffa0623e5f17974f95afcf68c413e15b/PDF/Associate Rule Mining.pdf
--------------------------------------------------------------------------------
/PDF/Cluster Analysis.pdf:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/ntut-xuan/DataScienceNote/c49735d5ffa0623e5f17974f95afcf68c413e15b/PDF/Cluster Analysis.pdf
--------------------------------------------------------------------------------
/PDF/Data Mining.pdf:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/ntut-xuan/DataScienceNote/c49735d5ffa0623e5f17974f95afcf68c413e15b/PDF/Data Mining.pdf
--------------------------------------------------------------------------------
/PDF/Data Preprocessing.pdf:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/ntut-xuan/DataScienceNote/c49735d5ffa0623e5f17974f95afcf68c413e15b/PDF/Data Preprocessing.pdf
--------------------------------------------------------------------------------
/PDF/Data Warehouse.pdf:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/ntut-xuan/DataScienceNote/c49735d5ffa0623e5f17974f95afcf68c413e15b/PDF/Data Warehouse.pdf
--------------------------------------------------------------------------------
/PDF/Decision Tree.pdf:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/ntut-xuan/DataScienceNote/c49735d5ffa0623e5f17974f95afcf68c413e15b/PDF/Decision Tree.pdf
--------------------------------------------------------------------------------
/PDF/Naive Bayes Analysis.pdf:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/ntut-xuan/DataScienceNote/c49735d5ffa0623e5f17974f95afcf68c413e15b/PDF/Naive Bayes Analysis.pdf
--------------------------------------------------------------------------------
/PDF/Regression.pdf:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/ntut-xuan/DataScienceNote/c49735d5ffa0623e5f17974f95afcf68c413e15b/PDF/Regression.pdf
--------------------------------------------------------------------------------
/PDF/Unclassified.pdf:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/ntut-xuan/DataScienceNote/c49735d5ffa0623e5f17974f95afcf68c413e15b/PDF/Unclassified.pdf
--------------------------------------------------------------------------------
/README.md:
--------------------------------------------------------------------------------
1 | # 資料科學導論筆記
2 |
3 |
4 |
5 | ## 作者
6 |
7 | 國立臺北科技大學 資訊工程系 [黃漢軒](https://ntut-xuan.github.io)
8 |
9 | 筆記上有任何問題,請丟 [issue](https://github.com/ntut-xuan/DataScienceNote/issues),支持這份筆記,請幫我點個 star,謝謝
10 |
11 |
12 |
13 | **超級注意:工具箱的部分只經過我本人測試過,並不保證他不會有任何問題,有任何問題不負任何責任,有遇到問題請丟 [issue](https://github.com/ntut-xuan/DataScienceNote/issues) 。**
14 |
15 |
16 |
17 | ## 主題式分析
18 |
19 | 這份筆記使用主題式的方式架構,主要分成以下幾個子主題。
20 |
21 |
22 |
23 | | 主題 | 完工進度 | ToolBox | 完工時間 |
24 | | :----------------------------------------: | :------: | :-----: | :------------: |
25 | | 還沒經過整理的主題 | SKIP | SKIP | SKIP |
26 | | 資料倉儲(Data Warehouse) | 100% | SKIP | 2022 / 04 / 04 |
27 | | 資料探勘(Data Mining) | 100% | SKIP | 2022 / 04 / 05 |
28 | | 決策樹(Decision Tree) | 100% | SKIP | 2022 / 04 / 12 |
29 | | 迴歸(Regression) | 100% | SKIP | 2022 / 04 / 14 |
30 | | 單純貝氏(Naïve Bayes Analysis) | 100% | OK | 2022 / 06 / 15 |
31 | | 人工神經網路(Artificial Neural Networks) | 100% | SKIP | 2022 / 06 / 15 |
32 | | 聚類分析(Cluster Analysis) | 100% | OK | 2022 / 06 / 22 |
33 | | 資料預處理(Data Preprocessing) | 100% | SKIP | 2022 / 06 / 22 |
34 | | 推薦系統(Recommandation System) | 100% | SKIP | 2022 / 06 / 22 |
35 |
36 |
37 |
--------------------------------------------------------------------------------
/python_tool/.gitignore:
--------------------------------------------------------------------------------
1 | .idea
2 | __pycache__
--------------------------------------------------------------------------------
/python_tool/debug.py:
--------------------------------------------------------------------------------
1 | import numpy as np
2 | import random
3 | import time
4 | import matplotlib.pyplot as plt
5 |
6 | def standard_random():
7 | std = np.array([0.1, 0.1, 0.1, 0.1, 0.1, 0.1, 0.1])
8 | return std
9 |
10 |
11 | def active_function(x):
12 | return np.log(1+np.exp(x))
13 |
14 |
15 | def calc(x_1s, x_2s, x_1, x_2, y_1, y_2, w, b):
16 | x_1s = np.transpose(data)[0]
17 | x_2s = np.transpose(data)[1]
18 | output = w[5] * y_1 + w[6] * y_2 + b[3]
19 | return (x_1s * w[1] + x_2s * w[3], x_1s * w[2] + x_2s * w[4], active_function(x_1), active_function(x_2), output)
20 |
21 | data = [[35, 67], [12, 75], [16, 89], [45, 56], [10, 90]]
22 | label = [1, 0, 1, 1, 0]
23 |
24 | data_array = np.array(data)
25 | label_array = np.array(label)
26 |
27 | w = standard_random()
28 | b = [0 for i in range(4)]
29 |
30 | print(w)
31 |
32 | x_1s = np.transpose(data)[0]
33 | x_2s = np.transpose(data)[1]
34 | x_1 = x_1s * w[1] + x_2s * w[3]
35 | x_2 = x_1s * w[2] + x_2s * w[4]
36 | y_1 = np.log(1+np.exp(x_1))
37 | y_2 = np.log(1+np.exp(x_2))
38 | output = w[5] * active_function(x_1*w[1]+x_2*w[3] + b[1]) + w[6] * active_function(x_1*w[2]+x_2*w[4] + b[2]) + b[3]
39 | learn_rate = 0.01
40 |
41 | for i in range(1000):
42 | x_1s = np.transpose(data)[0]
43 | x_2s = np.transpose(data)[1]
44 | x_1, x_2, y_1, y_2, output = calc(x_1s, x_2s, x_1, x_2, y_1, y_2, w, b)
45 | db3 = np.sum(-2 * (label_array - output))
46 | dw5 = np.sum((label_array - output) * y_1 * -2)
47 | dw6 = np.sum((label_array - output) * y_2 * -2)
48 | db1 = np.sum((label_array - output) * w[5] * (np.exp(x_1) / (1 + np.exp(x_1))) * -2)
49 | db2 = np.sum((label_array - output) * w[6] * (np.exp(x_2) / (1 + np.exp(x_2))) * -2)
50 | dw1 = np.sum((label_array - output) * w[5] * (np.exp(x_1) / (1 + np.exp(x_1))) * x_1s * -2)
51 | dw2 = np.sum((label_array - output) * w[6] * (np.exp(x_2) / (1 + np.exp(x_2))) * x_1s * -2)
52 | dw3 = np.sum((label_array - output) * w[5] * (np.exp(x_1) / (1 + np.exp(x_1))) * x_2s * -2)
53 | dw4 = np.sum((label_array - output) * w[6] * (np.exp(x_2) / (1 + np.exp(x_2))) * x_2s * -2)
54 | print("SSR =", np.sum(label_array - output) * np.sum(label_array - output))
55 | b[3] = b[3] - db3 * learn_rate
56 | b[2] = b[2] - db2 * learn_rate
57 | b[1] = b[1] - db1 * learn_rate
58 | w[6] = w[6] - dw6 * learn_rate
59 | w[5] = w[5] - dw5 * learn_rate
60 | w[4] = w[4] - dw4 * learn_rate
61 | w[3] = w[3] - dw3 * learn_rate
62 | w[2] = w[2] - dw2 * learn_rate
63 | w[1] = w[1] - dw1 * learn_rate
64 | print("b=", b)
65 | print("w=", w)
66 |
67 | fig = plt.figure(figsize=(10, 10))
68 | ax = fig.gca(projection='3d')
69 |
70 | plot_x = np.linspace(0, 100, num=100)
71 |
72 | table = np.array([[0 for _ in range(100)] for _ in range(100)])
73 |
74 | for i in range(100):
75 | for j in range(100):
76 | x1 = i
77 | x2 = j
78 | #print(x1, x2)
79 | table[i][j] = w[5] * (active_function(x1 * w[1] + x2 * w[3]) + b[1]) \
80 | + w[6] * (active_function(x1 * w[2] + x2 * w[4]) + b[2]) \
81 | + b[3]
82 |
83 | ax.scatter(np.transpose(data_array)[0], np.transpose(data_array)[1], label_array)
84 | ax.plot_surface(plot_x, plot_x, table, cmap='seismic')
85 | plt.show()
86 |
87 | print(table)
88 |
89 | print(table[45][56])
90 | print(table[25][70])
--------------------------------------------------------------------------------
/python_tool/example.py:
--------------------------------------------------------------------------------
1 | from tool import *
2 |
3 | naiveBayesClassifier = MultinomialNaiveBayesClassifier()
4 | data = [["love", "happy", "joy", "joy", "love"],
5 | ["happy", "love", "kick", "joy", "happy"],
6 | ["love", "move", "joy", "good"],
7 | ["love", "happy", "joy", "pain", "love"],
8 | ["joy", "love", "pain", "kick", "pain"],
9 | ["pain", "pain", "love", "kick"]]
10 | label = ["Yes", "Yes", "Yes", "Yes", "No", "No"]
11 | value = ["love", "pain", "joy", "happy", "kick", "happy"]
12 |
13 | naiveBayesClassifier.fit(np.array(data, dtype=object), np.array(label, dtype=object))
14 | print(naiveBayesClassifier.predict(value))
--------------------------------------------------------------------------------
/python_tool/main.py:
--------------------------------------------------------------------------------
1 | import numpy as np
2 | import tool
3 | import time
4 | import warnings
5 | import matplotlib.pyplot as plt
6 | from sklearn import cluster, datasets
7 | from sklearn.preprocessing import StandardScaler
8 | from itertools import cycle, islice
9 |
10 | n_samples = 300
11 | random_state = 170
12 | noisy_circles = datasets.make_circles(n_samples=n_samples, factor=0.5, noise=0.01)
13 |
14 | points = noisy_circles[0]
15 |
16 | array = np.zeros((n_samples, n_samples))
17 |
18 | for i in range(n_samples):
19 | for j in range(n_samples):
20 | array[i][j] = np.sqrt((points[i][0]-points[j][0])**2 + (points[i][1]-points[j][1])**2)
21 |
22 | algo = tool.WPGMAClustering(n_clusters=2)
23 | algo.fit(array)
24 | algo.clustering()
25 |
26 | print(algo.labels_)
27 |
28 | colors = np.array(
29 | list(
30 | islice(
31 | cycle(
32 | [
33 | "#377eb8",
34 | "#ff7f00",
35 | "#4daf4a",
36 | "#f781bf",
37 | "#a65628",
38 | "#984ea3",
39 | "#999999",
40 | "#e41a1c",
41 | "#dede00",
42 | ]
43 | ),
44 | int(max(algo.labels_) + 1),
45 | )
46 | ))
47 |
48 |
49 | plt.scatter(points[:, 0], points[:, 1], color=colors[algo.labels_])
50 | plt.show()
--------------------------------------------------------------------------------
/python_tool/tool.py:
--------------------------------------------------------------------------------
1 | import numpy as np
2 | import copy
3 |
4 |
5 | class MultinomialNaiveBayesClassifier:
6 | def __init__(self):
7 | self.value_map = {}
8 | self.result = np.array([])
9 | self.data = np.array([])
10 |
11 | def fit(self, x, y):
12 | self.result = y
13 | unique, counts = np.unique(self.result, return_counts=True)
14 | for v in unique:
15 | self.value_map[v] = []
16 | for i in range(len(y)):
17 | for s in x[i]:
18 | self.value_map[y[i]].append(s)
19 |
20 | def add_duplicated_value(self, temp_result, temp_value_map, missing_value):
21 | unique, counts = np.unique(temp_result, return_counts=True)
22 | for k in unique:
23 | value_unique = np.unique(temp_value_map[k])
24 | for v in value_unique:
25 | if missing_value == v:
26 | continue
27 | temp_value_map[k].append(v)
28 | for k in unique:
29 | temp_value_map[k].append(missing_value)
30 |
31 | def print_unique(self, y):
32 | for v in np.unique(self.result):
33 | unique, counts = np.unique(y[v], return_counts=True)
34 | result_dict = dict(zip(unique, counts))
35 | print(result_dict)
36 |
37 | def predict(self, y):
38 | temp_result = self.result
39 | temp_value_map = self.value_map
40 | unique, counts = np.unique(self.result, return_counts=True)
41 | result_dict = dict(zip(unique, counts))
42 | predict = {}
43 | for v in unique:
44 | print("calculate P(%s) = %d/%d" % (v, result_dict[v], int(np.sum(counts))))
45 | predict[v] = float(result_dict[v] / np.sum(counts))
46 | for s in y:
47 | for v in unique:
48 | if s not in self.value_map[v]:
49 | self.add_duplicated_value(temp_result, temp_value_map, s)
50 | self.print_unique(temp_value_map)
51 | for s in y:
52 | for v in unique:
53 | unique_s, counts_s = np.unique(self.value_map[v], return_counts=True)
54 | result_dict_s = dict(zip(unique_s, counts_s))
55 | total = np.sum(counts_s)
56 | print("calculate P(%s|%s) = %d/%d" % (s, v, result_dict_s[s], int(total)))
57 | predict[v] *= float(result_dict_s[s] / int(total))
58 | print(predict)
59 | return max(predict, key=predict.get)
60 |
61 |
62 | class UPGMAClustering:
63 |
64 | def __init__(self, n_clusters=2):
65 | self.labels_ = None
66 | self.n = None
67 | self.n_clusters = n_clusters
68 | self.cluster_list = None
69 | self.distance_table = None
70 | self.threshold = None
71 |
72 | def fit(self, distance_table):
73 | self.n = len(distance_table)
74 | self.distance_table = distance_table
75 | self.cluster_list = []
76 | self.threshold = []
77 | self.labels_ = [0 for _ in range(self.n)]
78 | for i in range(self.n):
79 | self.cluster_list.append([i])
80 |
81 | def clustering(self):
82 | for r in range(self.n - (self.n_clusters-1)):
83 |
84 | print("\n=============== Iter%5d ===============\n" % (r + 1))
85 |
86 | original_cluster_list = copy.deepcopy(self.cluster_list)
87 | self.distance_table[self.distance_table == 0] = np.iinfo(np.int32).max
88 |
89 | # choose minimum pair
90 | minimum_distance = np.min(self.distance_table)
91 | minimum_pair = np.unravel_index(np.argmin(self.distance_table, axis=None), self.distance_table.shape)
92 | print("Minimum pair: %s = %d" % (str(minimum_pair), minimum_distance))
93 |
94 | if r != self.n - self.n_clusters:
95 |
96 | # combine two cluster
97 | target_list1 = copy.deepcopy(self.cluster_list[minimum_pair[0]])
98 | target_list2 = copy.deepcopy(self.cluster_list[minimum_pair[1]])
99 | self.cluster_list[minimum_pair[0]] += (self.cluster_list[minimum_pair[1]])
100 | self.cluster_list.remove(self.cluster_list[minimum_pair[1]])
101 |
102 | print("target list l1=", target_list1, "- l2=", target_list2)
103 | print("combine list", original_cluster_list, "->", self.cluster_list)
104 |
105 | # recalculate distance between new cluster and another cluster
106 | self.distance_table[self.distance_table == np.iinfo(np.int32).max] = 0
107 | new_distance_table = np.zeros((len(self.cluster_list), len(self.cluster_list)))
108 | for i in range(len(self.cluster_list)):
109 | for j in range(len(self.cluster_list)):
110 | index1 = original_cluster_list.index(target_list1)
111 | index2 = original_cluster_list.index(target_list2)
112 | index4 = self.cluster_list.index(self.cluster_list[j])
113 | if i == index1 or j == index1:
114 | if index1 == index4:
115 | continue
116 | index3 = original_cluster_list.index(self.cluster_list[j])
117 | distance1 = self.distance_table[index1][index3]
118 | distance2 = self.distance_table[index2][index3]
119 | new_distance_table[index1][index4] = (len(target_list1) * distance1 + len(
120 | target_list2) * distance2) / float(len(target_list1) + len(target_list2))
121 | new_distance_table[index4][index1] = (len(target_list1) * distance1 + len(
122 | target_list2) * distance2) / float(len(target_list1) + len(target_list2))
123 | else:
124 | index3 = original_cluster_list.index(self.cluster_list[j])
125 | index5 = original_cluster_list.index(self.cluster_list[i])
126 | new_distance_table[i][j] = self.distance_table[index5][index3]
127 |
128 | self.distance_table = new_distance_table
129 |
130 | # print
131 | print("Update Table\n", str(new_distance_table))
132 | print(self.cluster_list)
133 |
134 | # calculate branch length estimation
135 | branch_length_estimation = minimum_distance / 2.0
136 | self.threshold += [branch_length_estimation]
137 | print("distance_threshold =", branch_length_estimation)
138 |
139 | for i in range(len(self.cluster_list)):
140 | for v in self.cluster_list[i]:
141 | self.labels_[v] = i+1
142 |
143 |
144 | class WPGMAClustering:
145 |
146 | def __init__(self, n_clusters=2):
147 | self.labels_ = None
148 | self.n = None
149 | self.n_clusters = n_clusters
150 | self.cluster_list = None
151 | self.distance_table = None
152 | self.threshold = None
153 |
154 | def fit(self, distance_table):
155 | self.n = len(distance_table)
156 | self.distance_table = distance_table
157 | self.cluster_list = []
158 | self.threshold = []
159 | self.labels_ = [0 for _ in range(self.n)]
160 | for i in range(self.n):
161 | self.cluster_list.append([i])
162 |
163 | def clustering(self):
164 | for r in range(self.n - (self.n_clusters-1)):
165 |
166 | print("\n=============== Iter%5d ===============\n" % (r + 1))
167 |
168 | original_cluster_list = copy.deepcopy(self.cluster_list)
169 | self.distance_table[self.distance_table == 0] = np.iinfo(np.int32).max
170 |
171 | # choose minimum pair
172 | minimum_distance = np.min(self.distance_table)
173 | minimum_pair = np.unravel_index(np.argmin(self.distance_table, axis=None), self.distance_table.shape)
174 | print("Minimum pair: %s = %d" % (str(minimum_pair), minimum_distance))
175 |
176 | if r != self.n - self.n_clusters:
177 |
178 | # combine two cluster
179 | target_list1 = copy.deepcopy(self.cluster_list[minimum_pair[0]])
180 | target_list2 = copy.deepcopy(self.cluster_list[minimum_pair[1]])
181 | self.cluster_list[minimum_pair[0]] += (self.cluster_list[minimum_pair[1]])
182 | self.cluster_list.remove(self.cluster_list[minimum_pair[1]])
183 |
184 | print("target list l1=", target_list1, "- l2=", target_list2)
185 | print("combine list", original_cluster_list, "->", self.cluster_list)
186 |
187 | # recalculate distance between new cluster and another cluster
188 | self.distance_table[self.distance_table == np.iinfo(np.int32).max] = 0
189 | new_distance_table = np.zeros((len(self.cluster_list), len(self.cluster_list)))
190 | for i in range(len(self.cluster_list)):
191 | for j in range(len(self.cluster_list)):
192 | index1 = original_cluster_list.index(target_list1)
193 | index2 = original_cluster_list.index(target_list2)
194 | index4 = self.cluster_list.index(self.cluster_list[j])
195 | if i == index1 or j == index1:
196 | if index1 == index4:
197 | continue
198 | index3 = original_cluster_list.index(self.cluster_list[j])
199 | distance1 = self.distance_table[index1][index3]
200 | distance2 = self.distance_table[index2][index3]
201 | new_distance_table[index1][index4] = (distance1 + distance2) / 2.0
202 | new_distance_table[index4][index1] = (distance1 + distance2) / 2.0
203 | else:
204 | index3 = original_cluster_list.index(self.cluster_list[j])
205 | index5 = original_cluster_list.index(self.cluster_list[i])
206 | new_distance_table[i][j] = self.distance_table[index5][index3]
207 |
208 | self.distance_table = new_distance_table
209 |
210 | # print
211 | print("Update Table\n", str(new_distance_table))
212 | print(self.cluster_list)
213 |
214 | # calculate branch length estimation
215 | branch_length_estimation = minimum_distance / 2.0
216 | self.threshold += [branch_length_estimation]
217 | print("distance_threshold =", branch_length_estimation)
218 |
219 | for i in range(len(self.cluster_list)):
220 | for v in self.cluster_list[i]:
221 | self.labels_[v] = i+1
222 |
--------------------------------------------------------------------------------
 36 |
37 | 而實際上可能會這麼複雜:
38 |
39 | > Artificial neural network.svg - 維基百科,自由嘅百科全書
40 |
41 |
36 |
37 | 而實際上可能會這麼複雜:
38 |
39 | > Artificial neural network.svg - 維基百科,自由嘅百科全書
40 |
41 |  42 |
43 |
44 |
45 | ## 激勵函數
46 |
47 | 激勵函數在塑造曲線的時候扮演了重要的角色,主要分成四種:
48 |
49 | 1. Tanh:$f(x) = \tan x = \dfrac{e^x-e^{-x}}{e^x+e^{-x}}$
50 | 2. Sigmoid / Logistic:$f(x) = \dfrac{1}{1+e^{-x}}$
51 | 3. ReLu:$f(x) = x^{+} = \max(0, x)$
52 | 4. Softplus:$f(x) = \ln(1+e^x)$
53 |
54 |
55 |
56 | 所謂的激勵函數本質上就是函數,可以想像成把參數放入激勵函數後,可以使激勵函數最後塑造出我們想要的曲線。
57 |
58 |
59 |
60 | ## 建構簡單 ANN
61 |
62 |
63 |
64 | ### 建立概述
65 |
66 | 我們以簡單的例子來說明,以下圖為例。
67 |
68 |
42 |
43 |
44 |
45 | ## 激勵函數
46 |
47 | 激勵函數在塑造曲線的時候扮演了重要的角色,主要分成四種:
48 |
49 | 1. Tanh:$f(x) = \tan x = \dfrac{e^x-e^{-x}}{e^x+e^{-x}}$
50 | 2. Sigmoid / Logistic:$f(x) = \dfrac{1}{1+e^{-x}}$
51 | 3. ReLu:$f(x) = x^{+} = \max(0, x)$
52 | 4. Softplus:$f(x) = \ln(1+e^x)$
53 |
54 |
55 |
56 | 所謂的激勵函數本質上就是函數,可以想像成把參數放入激勵函數後,可以使激勵函數最後塑造出我們想要的曲線。
57 |
58 |
59 |
60 | ## 建構簡單 ANN
61 |
62 |
63 |
64 | ### 建立概述
65 |
66 | 我們以簡單的例子來說明,以下圖為例。
67 |
68 |  69 |
70 | 我們有一個*簡單的資料集*,分成三類,值域界於 $0$ 到 $1$:
71 |
72 | 1. 服用少數量 ntut-xuan 筆記的人 → 考不好 (0)
73 | 2. 服用中等數量 ntut-xuan 筆記的人 → 考得好 (1)
74 | 3. 服用多數量 ntut-xuan 筆記的人 → 考不好 (0)
75 |
76 | 可以得到左圖。
77 |
78 | 此時我們可能會想要用一條直線來分割這些資料,但這條直線可能不存在,因為不管怎麼畫都沒有辦法概括完全的資料。
79 |
80 | 如果這時候有一條*神奇的函數*來讓這些資料 match 就好,就像右圖。
81 |
82 | | | |
83 | | ------------------------------------------------------------ | ------------------------------------------------------------ |
84 | |
69 |
70 | 我們有一個*簡單的資料集*,分成三類,值域界於 $0$ 到 $1$:
71 |
72 | 1. 服用少數量 ntut-xuan 筆記的人 → 考不好 (0)
73 | 2. 服用中等數量 ntut-xuan 筆記的人 → 考得好 (1)
74 | 3. 服用多數量 ntut-xuan 筆記的人 → 考不好 (0)
75 |
76 | 可以得到左圖。
77 |
78 | 此時我們可能會想要用一條直線來分割這些資料,但這條直線可能不存在,因為不管怎麼畫都沒有辦法概括完全的資料。
79 |
80 | 如果這時候有一條*神奇的函數*來讓這些資料 match 就好,就像右圖。
81 |
82 | | | |
83 | | ------------------------------------------------------------ | ------------------------------------------------------------ |
84 | |  |
|  |
85 |
86 | 我們假設已經優化了類神經網路的 $w_1, w_2, b_1, b_2, w_3, w_4, b_3$ 參數,我們可以這樣建構我們的類神經網路。
87 |
88 | 假設我們使用的激勵函數 $af_1, af_2$ 為 Softplus:$f(x) = \ln(1+e^x)$
89 |
90 |
|
85 |
86 | 我們假設已經優化了類神經網路的 $w_1, w_2, b_1, b_2, w_3, w_4, b_3$ 參數,我們可以這樣建構我們的類神經網路。
87 |
88 | 假設我們使用的激勵函數 $af_1, af_2$ 為 Softplus:$f(x) = \ln(1+e^x)$
89 |
90 |  91 |
92 | 我們可以由我們建構的類神經網路,往上走建構出一條曲線,往下走建構出另一條曲線,如下圖:
93 |
94 | | 往上走 | 往下走 |
95 | | :----------------------------------------------------------: | :----------------------------------------------------------: |
96 | | $f\left(x\right)=-0.18\ln\left(1+e^{\left(-32.4x+18.34\right)}\right)$ | $g\left(x\right)=2.28\ln\left(1+e^{\left(-1.72x+2.55\right)}\right)$ |
97 | |
91 |
92 | 我們可以由我們建構的類神經網路,往上走建構出一條曲線,往下走建構出另一條曲線,如下圖:
93 |
94 | | 往上走 | 往下走 |
95 | | :----------------------------------------------------------: | :----------------------------------------------------------: |
96 | | $f\left(x\right)=-0.18\ln\left(1+e^{\left(-32.4x+18.34\right)}\right)$ | $g\left(x\right)=2.28\ln\left(1+e^{\left(-1.72x+2.55\right)}\right)$ |
97 | |  |
|  |
98 |
99 |
100 |
101 | 最後將兩個曲線加起來,並減去 $2.88$,得到以下的曲線,就能夠得到我們幾乎亂畫出來的曲線了!
102 |
103 | | $h(x)=-0.18\ln\left(1+e^{\left(-32.4x+18.34\right)}\right)+2.28\ln\left(1+e^{\left(-1.72x+2.55\right)}\right)-2.88$ | 我亂畫的 |
104 | | :----------------------------------------------------------: | :----------------------------------------------------------: |
105 | |  |
|
98 |
99 |
100 |
101 | 最後將兩個曲線加起來,並減去 $2.88$,得到以下的曲線,就能夠得到我們幾乎亂畫出來的曲線了!
102 |
103 | | $h(x)=-0.18\ln\left(1+e^{\left(-32.4x+18.34\right)}\right)+2.28\ln\left(1+e^{\left(-1.72x+2.55\right)}\right)-2.88$ | 我亂畫的 |
104 | | :----------------------------------------------------------: | :----------------------------------------------------------: |
105 | |  |  |
106 |
107 | 這時候我們就可以用這條曲線來判別我們特定資料集所出現的結果,所以人工神經網路*理論上*能夠成功分類所有的資料。
108 |
109 | **問題在於如何找出參數,來建構我們想要的曲線**。
110 |
111 |
112 |
113 | ### 簡單 ANN 的參數優化 (Backward Propagation)
114 |
115 | 對於找出參數,我們可以先給定一個初始值,然後進行參數優化。
116 |
117 | 對於 weight 的部分,我們的初始值可以先給定為**標準常態分布**的隨機一個值,而 bias 可以先預設為 $0$
118 |
119 |
|
106 |
107 | 這時候我們就可以用這條曲線來判別我們特定資料集所出現的結果,所以人工神經網路*理論上*能夠成功分類所有的資料。
108 |
109 | **問題在於如何找出參數,來建構我們想要的曲線**。
110 |
111 |
112 |
113 | ### 簡單 ANN 的參數優化 (Backward Propagation)
114 |
115 | 對於找出參數,我們可以先給定一個初始值,然後進行參數優化。
116 |
117 | 對於 weight 的部分,我們的初始值可以先給定為**標準常態分布**的隨機一個值,而 bias 可以先預設為 $0$
118 |
119 |  120 |
121 |
122 |
123 | 若要使曲線越來越擬合我們的資料集,我們得要先考慮是否能夠限縮 $\text{SSR}$,使他越小,讓曲線 $f(x_i)$ 越能擬合資料集。
124 |
125 | $\text{SSR}$ 即為殘差平方和,即為對於在 $x=i$ 上的資料集,其所有資料 $(y_i - f(x_i))^2$ 的和,可以定義為 $\text{SSR} = \displaystyle \sum^{n}_{i=1} (y_i - f(x_i))^2$
126 |
127 | 若我們想要優化參數,可以找出參數對 $\text{SSR}$ 的導函數,接著使用梯度下降法來同步優化所有參數
128 |
129 |
130 |
131 | 同樣以下圖為例:
132 |
133 |
120 |
121 |
122 |
123 | 若要使曲線越來越擬合我們的資料集,我們得要先考慮是否能夠限縮 $\text{SSR}$,使他越小,讓曲線 $f(x_i)$ 越能擬合資料集。
124 |
125 | $\text{SSR}$ 即為殘差平方和,即為對於在 $x=i$ 上的資料集,其所有資料 $(y_i - f(x_i))^2$ 的和,可以定義為 $\text{SSR} = \displaystyle \sum^{n}_{i=1} (y_i - f(x_i))^2$
126 |
127 | 若我們想要優化參數,可以找出參數對 $\text{SSR}$ 的導函數,接著使用梯度下降法來同步優化所有參數
128 |
129 |
130 |
131 | 同樣以下圖為例:
132 |
133 |  134 |
135 | 我們令 $af_1(x_i)$ 運算出的結果叫做 $y_{1,i}$,$af_2(x_i)$ 運算出的結果叫做 $y_{2,i}$
136 |
137 | 可以得到 $f(x_i) = w_3 \times y_{1, i} + w_4 \times y_{2, i} + b_3$
138 |
139 | 又 $y_{1, i} = \ln(1+e^{x_{1,i}}), y_{2, i} = \ln(1+e^{x_{2, i}}), x_{1,i}=x_i \times w_1+b_1, x_{2,i} = x_i \times w_2+b_2$,以 Softplus 為例。
140 |
141 |
142 |
143 | 找出導函數,可以使用鎖鏈法則來尋找。
144 |
145 | $\dfrac{d\text{SSR}}{db_3} = \dfrac{dSSR}{df(x_i)} \times \dfrac{df(x_i)}{db_3} = \displaystyle \sum^{n}_{i=1} -2(y_i-f(x_i)) \times 1$
146 |
147 | $\dfrac{d\text{SSR}}{dw_3} = \dfrac{dSSR}{df(x_i)} \times \dfrac{df(x_i)}{dw_3} = \displaystyle \sum^{n}_{i=1} -2(y_i-f(x_i)) \times y_{1, i}$
148 |
149 | $\dfrac{d\text{SSR}}{dw_4} = \dfrac{dSSR}{df(x_i)} \times \dfrac{df(x_i)}{dw_4} = \displaystyle \sum^{n}_{i=1} -2(y_i-f(x_i)) \times y_{2, i}$
150 |
151 | $\dfrac{d\text{SSR}}{db_1} = \dfrac{dSSR}{df(x_i)} \times \dfrac{df(x_i)}{dy_1} \times \dfrac{dy_1}{dx_1} \times \dfrac{dx_1}{db_1} = \displaystyle \sum^{n}_{i=1} -2(y_i-f(x_i)) \times w_3 \times \dfrac{e^{x_{1, i}}}{1+e^{x_{1, i}}}\times 1$
152 |
153 | $\dfrac{d\text{SSR}}{dw_1} = \dfrac{dSSR}{df(x_i)} \times \dfrac{df(x_i)}{dy_1} \times \dfrac{dy_1}{dx_1} \times \dfrac{dx_1}{dw_1} = \displaystyle \sum^{n}_{i=1} -2(y_i-f(x_i)) \times w_3 \times \dfrac{e^{x_{1, i}}}{1+e^{x_{1, i}}}\times x_{1i}$
154 |
155 | $\dfrac{d\text{SSR}}{db_2} = \dfrac{dSSR}{df(x_i)} \times \dfrac{df(x_i)}{dy_2} \times \dfrac{dy_2}{dx_2} \times \dfrac{dx_2}{db_2} = \displaystyle \sum^{n}_{i=1} -2(y_i-f(x_i)) \times w_4 \times \dfrac{e^{x_{2, i}}}{1+e^{x_{2, i}}}\times 1$
156 |
157 | $\dfrac{d\text{SSR}}{dw_2} = \dfrac{dSSR}{df(x_i)} \times \dfrac{df(x_i)}{dy_2} \times \dfrac{dy_2}{dx_2} \times \dfrac{dx_2}{dw_2} = \displaystyle \sum^{n}_{i=1} -2(y_i-f(x_i)) \times w_4 \times \dfrac{e^{x_{2, i}}}{1+e^{x_{2, i}}}\times x_{2i}$
158 |
159 | 接著使用梯度下降
160 |
161 | $\text{Step size} = \text{Derivative} \times \text{Learning Rate}$
162 |
163 | $\text{New value} = \text{Old value} - \text{Step size}$
164 |
165 | 不斷更新直到值變小到無法再小,或者步驟完成。
166 |
167 |
168 |
169 | ## 建構 2-input ANN
170 |
171 | ### 建立概述
172 |
173 | 我們以複雜的例子來說明,以下圖為例。
174 |
175 |
134 |
135 | 我們令 $af_1(x_i)$ 運算出的結果叫做 $y_{1,i}$,$af_2(x_i)$ 運算出的結果叫做 $y_{2,i}$
136 |
137 | 可以得到 $f(x_i) = w_3 \times y_{1, i} + w_4 \times y_{2, i} + b_3$
138 |
139 | 又 $y_{1, i} = \ln(1+e^{x_{1,i}}), y_{2, i} = \ln(1+e^{x_{2, i}}), x_{1,i}=x_i \times w_1+b_1, x_{2,i} = x_i \times w_2+b_2$,以 Softplus 為例。
140 |
141 |
142 |
143 | 找出導函數,可以使用鎖鏈法則來尋找。
144 |
145 | $\dfrac{d\text{SSR}}{db_3} = \dfrac{dSSR}{df(x_i)} \times \dfrac{df(x_i)}{db_3} = \displaystyle \sum^{n}_{i=1} -2(y_i-f(x_i)) \times 1$
146 |
147 | $\dfrac{d\text{SSR}}{dw_3} = \dfrac{dSSR}{df(x_i)} \times \dfrac{df(x_i)}{dw_3} = \displaystyle \sum^{n}_{i=1} -2(y_i-f(x_i)) \times y_{1, i}$
148 |
149 | $\dfrac{d\text{SSR}}{dw_4} = \dfrac{dSSR}{df(x_i)} \times \dfrac{df(x_i)}{dw_4} = \displaystyle \sum^{n}_{i=1} -2(y_i-f(x_i)) \times y_{2, i}$
150 |
151 | $\dfrac{d\text{SSR}}{db_1} = \dfrac{dSSR}{df(x_i)} \times \dfrac{df(x_i)}{dy_1} \times \dfrac{dy_1}{dx_1} \times \dfrac{dx_1}{db_1} = \displaystyle \sum^{n}_{i=1} -2(y_i-f(x_i)) \times w_3 \times \dfrac{e^{x_{1, i}}}{1+e^{x_{1, i}}}\times 1$
152 |
153 | $\dfrac{d\text{SSR}}{dw_1} = \dfrac{dSSR}{df(x_i)} \times \dfrac{df(x_i)}{dy_1} \times \dfrac{dy_1}{dx_1} \times \dfrac{dx_1}{dw_1} = \displaystyle \sum^{n}_{i=1} -2(y_i-f(x_i)) \times w_3 \times \dfrac{e^{x_{1, i}}}{1+e^{x_{1, i}}}\times x_{1i}$
154 |
155 | $\dfrac{d\text{SSR}}{db_2} = \dfrac{dSSR}{df(x_i)} \times \dfrac{df(x_i)}{dy_2} \times \dfrac{dy_2}{dx_2} \times \dfrac{dx_2}{db_2} = \displaystyle \sum^{n}_{i=1} -2(y_i-f(x_i)) \times w_4 \times \dfrac{e^{x_{2, i}}}{1+e^{x_{2, i}}}\times 1$
156 |
157 | $\dfrac{d\text{SSR}}{dw_2} = \dfrac{dSSR}{df(x_i)} \times \dfrac{df(x_i)}{dy_2} \times \dfrac{dy_2}{dx_2} \times \dfrac{dx_2}{dw_2} = \displaystyle \sum^{n}_{i=1} -2(y_i-f(x_i)) \times w_4 \times \dfrac{e^{x_{2, i}}}{1+e^{x_{2, i}}}\times x_{2i}$
158 |
159 | 接著使用梯度下降
160 |
161 | $\text{Step size} = \text{Derivative} \times \text{Learning Rate}$
162 |
163 | $\text{New value} = \text{Old value} - \text{Step size}$
164 |
165 | 不斷更新直到值變小到無法再小,或者步驟完成。
166 |
167 |
168 |
169 | ## 建構 2-input ANN
170 |
171 | ### 建立概述
172 |
173 | 我們以複雜的例子來說明,以下圖為例。
174 |
175 |  176 |
177 |
178 |
179 | 對於 weight 的部分,我們的初始值可以先給定為**標準常態分布**的隨機一個值,而 bias 可以先預設為 $0$
180 |
181 |
176 |
177 |
178 |
179 | 對於 weight 的部分,我們的初始值可以先給定為**標準常態分布**的隨機一個值,而 bias 可以先預設為 $0$
180 |
181 |  182 |
183 |
184 |
185 | ### 2-input ANN 的參數優化 (Backward Propagation)
186 |
187 | 若要使曲線越來越擬合我們的資料集,我們得要先考慮是否能夠限縮 $\text{SSR}$,使他越小,讓曲線 $f(x_i)$ 越能擬合資料集。
188 |
189 | $\text{SSR}$ 即為殘差平方和,即為對於在 $(x_1, x_2) = (i, j)$ 上的資料集,其所有資料 $(y(x_1, x_2) - f(x_1, x_2))^2$ 的和
190 |
191 | 可以定義為 $\text{SSR} = \displaystyle \sum^{}_{(x_1, x_2) \in S} (y(x_1, x_2) - f(x_1, x_2))^2$
192 |
193 | 若我們想要優化參數,可以找出參數對 $\text{SSR}$ 的導函數,接著使用梯度下降法來同步優化所有參數。
194 |
195 |
196 |
197 | 我們令 $af_1(x_{1i}, x_{2i})$ 運算出的結果叫做 $y_1(x_{1i}, x_{2i})$,$af_2(x_{1i}, x_{2i})$ 運算出的結果叫做 $y_2(x_{1i}, x_{2i})$
198 |
199 | 可以得到 $f(x_{1i}, x_{2i}) = w_5 \times y_1 + w_6 \times y_2 + b_3$
200 |
201 | 又 $y_1 = \ln(1+e^{x_{1}}), y_2 = \ln(1+e^{x_{2}})$,以 Softplus 為例。
202 |
203 | $x_{1}(x_{1i}, x_{2i})= x_{1i} \times w_1 + x_{2i} \times w_3$,$x_2(x_{1i}, x_{2i}) = x_{1i} \times w_2 + x_{2i} \times w_4$
204 |
205 |
206 |
207 | 找出導函數,可以使用鎖鏈法則來尋找。
208 |
209 |
210 |
211 | $\dfrac{d\text{SSR}}{db_3} = \dfrac{d\text{SSR}}{df(x_1, x_2)} \dfrac{df(x_1, x_2)}{db_3} = \displaystyle \sum_{(x_1, x_2) \in S} -2(y(x_1, x_2) - f(x_1, x_2)) \times 1$
212 |
213 | $\dfrac{d\text{SSR}}{dw_5} = \dfrac{d\text{SSR}}{df(x_1, x_2)} \times \dfrac{df(x_1, x_2)}{dw_5} = \displaystyle\sum_{(x_1, x_2) \in S} -2(y(x_1, x_2) - f(x_1, x_2)) \times y_{1}$
214 |
215 | $\dfrac{d\text{SSR}}{dw_6} = \dfrac{d\text{SSR}}{df(x_1, x_2)} \times \dfrac{df(x_1, x_2)}{dw_6} = \displaystyle \sum_{(x_1, x_2) \in S} -2(y(x_1, x_2) - f(x_1, x_2)) \times y_{2}$
216 |
217 | $\dfrac{d\text{SSR}}{db_1} = \dfrac{d\text{SSR}}{df(x_1, x_2)} \times \dfrac{df(x_1, x_2)}{dy_{1}} \times \dfrac{dy_1}{dx_1} \times \dfrac{dx_1}{db_1} = \displaystyle \sum_{(x_1, x_2) \in S} -2(y(x_1, x_2) - f(x_1, x_2)) \times w_5 \times \dfrac{e^{x_1}}{1+e^{x_1}} \times 1$
218 |
219 | $\dfrac{d\text{SSR}}{db_2} = \dfrac{d\text{SSR}}{df(x_1, x_2)} \times \dfrac{df(x_1, x_2)}{dy_{2}} \times \dfrac{dy_2}{dx_2} \times \dfrac{dx_2}{db_2} = \displaystyle \sum_{(x_1, x_2) \in S} -2(y(x_1, x_2) - f(x_1, x_2)) \times w_6 \times \dfrac{e^{x_2}}{1+e^{x_2}} \times 1$
220 |
221 | $\dfrac{d\text{SSR}}{dw_1} = \dfrac{d\text{SSR}}{df(x_1, x_2)} \times \dfrac{df(x_1, x_2)}{dy_{1}} \times \dfrac{dy_1}{dx_1} \times \dfrac{dx_1}{dw_1} = \displaystyle \sum_{(x_1, x_2) \in S} -2(y(x_1, x_2) - f(x_1, x_2)) \times w_5 \times \dfrac{e^{x_1}}{1+e^{x_1}} \times x_{1i}$
222 |
223 | $\dfrac{d\text{SSR}}{dw_2} = \dfrac{d\text{SSR}}{df(x_1, x_2)} \times \dfrac{df(x_1, x_2)}{dy_{2}} \times \dfrac{dy_2}{dx_2} \times \dfrac{dx_2}{dw_2} = \displaystyle \sum_{(x_1, x_2) \in S} -2(y(x_1, x_2) - f(x_1, x_2)) \times w_6 \times \dfrac{e^{x_2}}{1+e^{x_2}} \times x_{1i}$
224 |
225 | $\dfrac{d\text{SSR}}{dw_3} = \dfrac{d\text{SSR}}{df(x_1, x_2)} \times \dfrac{df(x_1, x_2)}{dy_{1}} \times \dfrac{dy_1}{dx_1} \times \dfrac{dx_1}{dw_3} = \displaystyle \sum_{(x_1, x_2) \in S} -2(y(x_1, x_2) - f(x_1, x_2)) \times w_5 \times \dfrac{e^{x_1}}{1+e^{x_1}} \times x_{2i}$
226 |
227 | $\dfrac{d\text{SSR}}{dw_4} = \dfrac{d\text{SSR}}{df(x_1, x_2)} \times \dfrac{df(x_1, x_2)}{dy_{2}} \times \dfrac{dy_2}{dx_2} \times \dfrac{dx_2}{dw_4} = \displaystyle \sum_{(x_1, x_2) \in S} -2(y(x_1, x_2) - f(x_1, x_2)) \times w_6 \times \dfrac{e^{x_2}}{1+e^{x_2}} \times x_{2i}$
228 |
229 | 接著使用梯度下降
230 |
231 | $\text{Step size} = \text{Derivative} \times \text{Learning Rate}$
232 |
233 | $\text{New value} = \text{Old value} - \text{Step size}$
234 |
235 | 不斷更新直到值變小到無法再小,或者步驟完成。
236 |
237 |
238 |
239 | ## ANN 的優缺點
240 |
241 | - 優點:
242 | 1. 準確度高
243 | 2. 可以處理很多種類的問題
244 | 3. 可以包含很多種類的資料(數值、名目...)
245 | 4. 可以得到非常好的 R-Score,只要訓練充足就可以
246 | - 缺點
247 | 1. 可能永遠訓練不完
248 | 2. 黑箱,所以很難向別人描述這個原理
249 | 3. 需要很大量的資料來訓練,才有準確度
250 | 4. 對於多變量來說可能會讓訓練過程變得非常長
--------------------------------------------------------------------------------
/Markdown/Associate Rule Mining.md:
--------------------------------------------------------------------------------
1 | # RS -- Associate Rule Mining(推薦系統 ─ 關聯規則探勘)
2 |
3 | > Reference:
4 | >
5 | > 1. Recommendation System -- Associate Rule Mining by Dr. Tun-Wen Pai
6 | > 2. [矩陣分解(Matrix Factorization): 交替最小平方法(Alternating least squares, ALS)和加權交替最小平方法(Alternating-least-squares with weighted-λ -regularization, ALS-WR)](https://chih-sheng-huang821.medium.com/%E7%9F%A9%E9%99%A3%E5%88%86%E8%A7%A3-matrix-factorization-%E4%BA%A4%E6%9B%BF%E6%9C%80%E5%B0%8F%E5%B9%B3%E6%96%B9%E6%B3%95-alternating-least-squares-2a71fd1393f7)
7 | > 3. [Day 07:初探推薦系統(Recommendation System)](https://ithelp.ithome.com.tw/articles/10219033)
8 |
9 |
10 |
11 | ## 推薦系統
12 |
13 | 啤酒對應到尿布是一個著名的關聯規則探勘例子,透過大量的銷售資料集探勘出了啤酒跟尿布同時購買的頻率很高。
14 |
15 | 在這份筆記,我們最主要會去探討要怎麼從大量的資料找到頻繁樣式,也就是找出哪種商品的購買組合頻率最高。
16 |
17 | 從大數據來說,找到東西的關聯是非常重要的。
18 |
19 | 推薦系統支持了我們找出頻繁樣式,進而從大量的資料分析出特定的組合,就能夠找出推薦的組合,稱為推薦系統。
20 |
21 |
22 |
23 | 主要有以下幾種不同的工具可以幫我們建立推薦系統。
24 |
25 | - Association Rule Mining(ARM),關聯規則探勘。
26 | - 我們可以用 Frequent pattern(頻繁樣式)來找出資料集的發生頻率。
27 | - Alternating Least Square(ALS),交替最小平方法。
28 | - 對一個隱含資料(Implicit Data)使用協同過濾演算法,例如 Matrix Factorization 來建立關聯。
29 | - Content Based Filtering
30 | - 以內容為基礎的過濾,比較商品的屬性,找出最相似的商品。
31 |
32 |
33 |
34 | ## 關聯規則探勘
35 |
36 | 關聯規則探勘 (Association Rule Mining),一種非監督式學習技巧,
37 |
38 | 利用大量的資料所產生的資料集來找出頻繁樣式、關聯、相關性、因果結構等等。
39 |
40 | 其中,Association Rule Mining 使用的是類別資料(Categorical Variable)。
41 |
42 |
43 |
44 | 若我們有 $N$ 個物品 $I_i$ 組成的物品集 $I$,對於一個輸入 Association Rule Mining 的資料集,
45 |
46 | 每筆資料 $T$ 都是資料集的子集合,稱為物品集,也就是 $T \subseteq I$。
47 |
48 |
49 |
50 | 例如我們有 6 個物品所組成的 $\{A, B, C, D, E, F\}$,我們有一個資料集:
51 |
52 | | ID | Item Set |
53 | | :--: | :------: |
54 | | 1 | A, B, C |
55 | | 2 | B, D, E |
56 | | 3 | D, E, F |
57 | | 4 | A, C, E |
58 | | 5 | B, E, F |
59 |
60 | 我們就能夠從這個資料集找出頻繁樣式。
61 |
62 |
63 |
64 | ### Support, Confidence and Lift
65 |
66 | 從大量的資料集,我們希望能夠量化出現頻率,來找到頻繁樣式,所以在 ARM 中將每個組合量化出了三種數值。
67 |
68 | 對於先發生事件 $A$ 再發生事件 $C$,我們可以量化出三種數值:
69 |
70 | - Support:$P(A \cap C)$,量化這個組合發生的機率。
71 | - Confidence:$P(C|A)$,量化這個組合發生 A 再發生 C 的機率。
72 | - Lift:$P(C|A)/P(C)$,用於量化這個組合的效力,通常大於 1 就代表這個組合是有效的。
73 |
74 |
75 |
76 | 那麼使用者可以設定一個門檻,用來採納這個頻繁組合該不該適用。
77 |
78 | 若使用者設定 Support > 40%,且 Confidence > 60%,使用者就可以接受這個組合為頻繁組合。
79 |
80 |
81 |
82 | ## 先驗演算法
83 |
84 | 對於一個很大的資料庫來說,我們可能同時會有很多個不同的頻繁組合。
85 |
86 | 我們希望可以制定頻繁組合必須要至少 Support 大於 k,來淘汰掉一些不太適用的組合。
87 |
88 |
89 |
90 | 先驗演算法的一些原則:
91 |
92 | 1. 一個組合的任意子集都在資料庫內,例如組合為 {a, b, c},則 {a}, {b}, {c}, {ab}, {ac}, {bc}, {abc} 都應發生在資料庫內。
93 |
94 | 2. Apriori pruning principle:當我們用任意兩種組合產生出另一個新組合,則這個新組合
95 |
96 | 也應該要符合第一點的原則,否則不該產生。
97 |
98 | 例如:透過 {a, c, e} 與 {a, e, f} 產生出了 {a, c, e, f} 這個組合,
99 |
100 | 但若 {c, e, f} 這個組合並沒有發生在資料庫內,則 {a, c, e, f} 這個組合無效。
101 |
102 |
103 |
104 | 下圖為演算法的產生過程。
105 |
106 | 1. 從原先的資料庫產生出了 1-item-set 的組合,並且刪去只有 support = 1 的組合(因為我們要求 min_support = 2)
107 |
108 | 2. 從 1-item-set 的任意兩種組合聯集,產生出了 **2**-item-set 的組合,並且刪去只有 support = 1 的組合
109 | 3. 從 i-item-set 產生出了 **(i+1)**-item-set 的組合...,直到能夠被分到只有一個。
110 |
111 |
182 |
183 |
184 |
185 | ### 2-input ANN 的參數優化 (Backward Propagation)
186 |
187 | 若要使曲線越來越擬合我們的資料集,我們得要先考慮是否能夠限縮 $\text{SSR}$,使他越小,讓曲線 $f(x_i)$ 越能擬合資料集。
188 |
189 | $\text{SSR}$ 即為殘差平方和,即為對於在 $(x_1, x_2) = (i, j)$ 上的資料集,其所有資料 $(y(x_1, x_2) - f(x_1, x_2))^2$ 的和
190 |
191 | 可以定義為 $\text{SSR} = \displaystyle \sum^{}_{(x_1, x_2) \in S} (y(x_1, x_2) - f(x_1, x_2))^2$
192 |
193 | 若我們想要優化參數,可以找出參數對 $\text{SSR}$ 的導函數,接著使用梯度下降法來同步優化所有參數。
194 |
195 |
196 |
197 | 我們令 $af_1(x_{1i}, x_{2i})$ 運算出的結果叫做 $y_1(x_{1i}, x_{2i})$,$af_2(x_{1i}, x_{2i})$ 運算出的結果叫做 $y_2(x_{1i}, x_{2i})$
198 |
199 | 可以得到 $f(x_{1i}, x_{2i}) = w_5 \times y_1 + w_6 \times y_2 + b_3$
200 |
201 | 又 $y_1 = \ln(1+e^{x_{1}}), y_2 = \ln(1+e^{x_{2}})$,以 Softplus 為例。
202 |
203 | $x_{1}(x_{1i}, x_{2i})= x_{1i} \times w_1 + x_{2i} \times w_3$,$x_2(x_{1i}, x_{2i}) = x_{1i} \times w_2 + x_{2i} \times w_4$
204 |
205 |
206 |
207 | 找出導函數,可以使用鎖鏈法則來尋找。
208 |
209 |
210 |
211 | $\dfrac{d\text{SSR}}{db_3} = \dfrac{d\text{SSR}}{df(x_1, x_2)} \dfrac{df(x_1, x_2)}{db_3} = \displaystyle \sum_{(x_1, x_2) \in S} -2(y(x_1, x_2) - f(x_1, x_2)) \times 1$
212 |
213 | $\dfrac{d\text{SSR}}{dw_5} = \dfrac{d\text{SSR}}{df(x_1, x_2)} \times \dfrac{df(x_1, x_2)}{dw_5} = \displaystyle\sum_{(x_1, x_2) \in S} -2(y(x_1, x_2) - f(x_1, x_2)) \times y_{1}$
214 |
215 | $\dfrac{d\text{SSR}}{dw_6} = \dfrac{d\text{SSR}}{df(x_1, x_2)} \times \dfrac{df(x_1, x_2)}{dw_6} = \displaystyle \sum_{(x_1, x_2) \in S} -2(y(x_1, x_2) - f(x_1, x_2)) \times y_{2}$
216 |
217 | $\dfrac{d\text{SSR}}{db_1} = \dfrac{d\text{SSR}}{df(x_1, x_2)} \times \dfrac{df(x_1, x_2)}{dy_{1}} \times \dfrac{dy_1}{dx_1} \times \dfrac{dx_1}{db_1} = \displaystyle \sum_{(x_1, x_2) \in S} -2(y(x_1, x_2) - f(x_1, x_2)) \times w_5 \times \dfrac{e^{x_1}}{1+e^{x_1}} \times 1$
218 |
219 | $\dfrac{d\text{SSR}}{db_2} = \dfrac{d\text{SSR}}{df(x_1, x_2)} \times \dfrac{df(x_1, x_2)}{dy_{2}} \times \dfrac{dy_2}{dx_2} \times \dfrac{dx_2}{db_2} = \displaystyle \sum_{(x_1, x_2) \in S} -2(y(x_1, x_2) - f(x_1, x_2)) \times w_6 \times \dfrac{e^{x_2}}{1+e^{x_2}} \times 1$
220 |
221 | $\dfrac{d\text{SSR}}{dw_1} = \dfrac{d\text{SSR}}{df(x_1, x_2)} \times \dfrac{df(x_1, x_2)}{dy_{1}} \times \dfrac{dy_1}{dx_1} \times \dfrac{dx_1}{dw_1} = \displaystyle \sum_{(x_1, x_2) \in S} -2(y(x_1, x_2) - f(x_1, x_2)) \times w_5 \times \dfrac{e^{x_1}}{1+e^{x_1}} \times x_{1i}$
222 |
223 | $\dfrac{d\text{SSR}}{dw_2} = \dfrac{d\text{SSR}}{df(x_1, x_2)} \times \dfrac{df(x_1, x_2)}{dy_{2}} \times \dfrac{dy_2}{dx_2} \times \dfrac{dx_2}{dw_2} = \displaystyle \sum_{(x_1, x_2) \in S} -2(y(x_1, x_2) - f(x_1, x_2)) \times w_6 \times \dfrac{e^{x_2}}{1+e^{x_2}} \times x_{1i}$
224 |
225 | $\dfrac{d\text{SSR}}{dw_3} = \dfrac{d\text{SSR}}{df(x_1, x_2)} \times \dfrac{df(x_1, x_2)}{dy_{1}} \times \dfrac{dy_1}{dx_1} \times \dfrac{dx_1}{dw_3} = \displaystyle \sum_{(x_1, x_2) \in S} -2(y(x_1, x_2) - f(x_1, x_2)) \times w_5 \times \dfrac{e^{x_1}}{1+e^{x_1}} \times x_{2i}$
226 |
227 | $\dfrac{d\text{SSR}}{dw_4} = \dfrac{d\text{SSR}}{df(x_1, x_2)} \times \dfrac{df(x_1, x_2)}{dy_{2}} \times \dfrac{dy_2}{dx_2} \times \dfrac{dx_2}{dw_4} = \displaystyle \sum_{(x_1, x_2) \in S} -2(y(x_1, x_2) - f(x_1, x_2)) \times w_6 \times \dfrac{e^{x_2}}{1+e^{x_2}} \times x_{2i}$
228 |
229 | 接著使用梯度下降
230 |
231 | $\text{Step size} = \text{Derivative} \times \text{Learning Rate}$
232 |
233 | $\text{New value} = \text{Old value} - \text{Step size}$
234 |
235 | 不斷更新直到值變小到無法再小,或者步驟完成。
236 |
237 |
238 |
239 | ## ANN 的優缺點
240 |
241 | - 優點:
242 | 1. 準確度高
243 | 2. 可以處理很多種類的問題
244 | 3. 可以包含很多種類的資料(數值、名目...)
245 | 4. 可以得到非常好的 R-Score,只要訓練充足就可以
246 | - 缺點
247 | 1. 可能永遠訓練不完
248 | 2. 黑箱,所以很難向別人描述這個原理
249 | 3. 需要很大量的資料來訓練,才有準確度
250 | 4. 對於多變量來說可能會讓訓練過程變得非常長
--------------------------------------------------------------------------------
/Markdown/Associate Rule Mining.md:
--------------------------------------------------------------------------------
1 | # RS -- Associate Rule Mining(推薦系統 ─ 關聯規則探勘)
2 |
3 | > Reference:
4 | >
5 | > 1. Recommendation System -- Associate Rule Mining by Dr. Tun-Wen Pai
6 | > 2. [矩陣分解(Matrix Factorization): 交替最小平方法(Alternating least squares, ALS)和加權交替最小平方法(Alternating-least-squares with weighted-λ -regularization, ALS-WR)](https://chih-sheng-huang821.medium.com/%E7%9F%A9%E9%99%A3%E5%88%86%E8%A7%A3-matrix-factorization-%E4%BA%A4%E6%9B%BF%E6%9C%80%E5%B0%8F%E5%B9%B3%E6%96%B9%E6%B3%95-alternating-least-squares-2a71fd1393f7)
7 | > 3. [Day 07:初探推薦系統(Recommendation System)](https://ithelp.ithome.com.tw/articles/10219033)
8 |
9 |
10 |
11 | ## 推薦系統
12 |
13 | 啤酒對應到尿布是一個著名的關聯規則探勘例子,透過大量的銷售資料集探勘出了啤酒跟尿布同時購買的頻率很高。
14 |
15 | 在這份筆記,我們最主要會去探討要怎麼從大量的資料找到頻繁樣式,也就是找出哪種商品的購買組合頻率最高。
16 |
17 | 從大數據來說,找到東西的關聯是非常重要的。
18 |
19 | 推薦系統支持了我們找出頻繁樣式,進而從大量的資料分析出特定的組合,就能夠找出推薦的組合,稱為推薦系統。
20 |
21 |
22 |
23 | 主要有以下幾種不同的工具可以幫我們建立推薦系統。
24 |
25 | - Association Rule Mining(ARM),關聯規則探勘。
26 | - 我們可以用 Frequent pattern(頻繁樣式)來找出資料集的發生頻率。
27 | - Alternating Least Square(ALS),交替最小平方法。
28 | - 對一個隱含資料(Implicit Data)使用協同過濾演算法,例如 Matrix Factorization 來建立關聯。
29 | - Content Based Filtering
30 | - 以內容為基礎的過濾,比較商品的屬性,找出最相似的商品。
31 |
32 |
33 |
34 | ## 關聯規則探勘
35 |
36 | 關聯規則探勘 (Association Rule Mining),一種非監督式學習技巧,
37 |
38 | 利用大量的資料所產生的資料集來找出頻繁樣式、關聯、相關性、因果結構等等。
39 |
40 | 其中,Association Rule Mining 使用的是類別資料(Categorical Variable)。
41 |
42 |
43 |
44 | 若我們有 $N$ 個物品 $I_i$ 組成的物品集 $I$,對於一個輸入 Association Rule Mining 的資料集,
45 |
46 | 每筆資料 $T$ 都是資料集的子集合,稱為物品集,也就是 $T \subseteq I$。
47 |
48 |
49 |
50 | 例如我們有 6 個物品所組成的 $\{A, B, C, D, E, F\}$,我們有一個資料集:
51 |
52 | | ID | Item Set |
53 | | :--: | :------: |
54 | | 1 | A, B, C |
55 | | 2 | B, D, E |
56 | | 3 | D, E, F |
57 | | 4 | A, C, E |
58 | | 5 | B, E, F |
59 |
60 | 我們就能夠從這個資料集找出頻繁樣式。
61 |
62 |
63 |
64 | ### Support, Confidence and Lift
65 |
66 | 從大量的資料集,我們希望能夠量化出現頻率,來找到頻繁樣式,所以在 ARM 中將每個組合量化出了三種數值。
67 |
68 | 對於先發生事件 $A$ 再發生事件 $C$,我們可以量化出三種數值:
69 |
70 | - Support:$P(A \cap C)$,量化這個組合發生的機率。
71 | - Confidence:$P(C|A)$,量化這個組合發生 A 再發生 C 的機率。
72 | - Lift:$P(C|A)/P(C)$,用於量化這個組合的效力,通常大於 1 就代表這個組合是有效的。
73 |
74 |
75 |
76 | 那麼使用者可以設定一個門檻,用來採納這個頻繁組合該不該適用。
77 |
78 | 若使用者設定 Support > 40%,且 Confidence > 60%,使用者就可以接受這個組合為頻繁組合。
79 |
80 |
81 |
82 | ## 先驗演算法
83 |
84 | 對於一個很大的資料庫來說,我們可能同時會有很多個不同的頻繁組合。
85 |
86 | 我們希望可以制定頻繁組合必須要至少 Support 大於 k,來淘汰掉一些不太適用的組合。
87 |
88 |
89 |
90 | 先驗演算法的一些原則:
91 |
92 | 1. 一個組合的任意子集都在資料庫內,例如組合為 {a, b, c},則 {a}, {b}, {c}, {ab}, {ac}, {bc}, {abc} 都應發生在資料庫內。
93 |
94 | 2. Apriori pruning principle:當我們用任意兩種組合產生出另一個新組合,則這個新組合
95 |
96 | 也應該要符合第一點的原則,否則不該產生。
97 |
98 | 例如:透過 {a, c, e} 與 {a, e, f} 產生出了 {a, c, e, f} 這個組合,
99 |
100 | 但若 {c, e, f} 這個組合並沒有發生在資料庫內,則 {a, c, e, f} 這個組合無效。
101 |
102 |
103 |
104 | 下圖為演算法的產生過程。
105 |
106 | 1. 從原先的資料庫產生出了 1-item-set 的組合,並且刪去只有 support = 1 的組合(因為我們要求 min_support = 2)
107 |
108 | 2. 從 1-item-set 的任意兩種組合聯集,產生出了 **2**-item-set 的組合,並且刪去只有 support = 1 的組合
109 | 3. 從 i-item-set 產生出了 **(i+1)**-item-set 的組合...,直到能夠被分到只有一個。
110 |
111 |  112 |
113 |
114 |
115 |
116 |
117 | ### 先驗演算法的缺點
118 |
119 | 對於大資料集來說,**為了產生候選組合,時間與效能耗費過大**。
120 |
121 |
122 |
123 |
124 |
125 | ## FP-Tree
126 |
127 | 樹狀結構很讚,能夠高效的處理大量資料。
128 |
129 |
112 |
113 |
114 |
115 |
116 |
117 | ### 先驗演算法的缺點
118 |
119 | 對於大資料集來說,**為了產生候選組合,時間與效能耗費過大**。
120 |
121 |
122 |
123 |
124 |
125 | ## FP-Tree
126 |
127 | 樹狀結構很讚,能夠高效的處理大量資料。
128 |
129 |  130 |
131 |
132 |
133 | FP-Tree 可以幫助我們建立出頻繁樣式,雖然高壓縮但頻繁樣式完整。
134 |
135 |
136 |
137 | ### frequent item table
138 |
139 | 若我們有左邊的資料表,由上至下的 ID 為 1、2、3、4、5。
140 |
141 | 首先我們應先設定一個 support 為門檻,淘汰掉不需要的資料。
142 |
143 |
144 |
145 | 以左邊為例,我們設定 min_support = 3。
146 |
147 | 經過淘汰掉不在門檻上的資料,得到右邊的 frequent item table。
148 |
149 | | Database | Frequent item table (unordered) |
150 | | :---------------------------------------------------------: | :---------------------------------------------------------: |
151 | |  |  |
152 |
153 | 我們需要對這個 table 做排序,根據物品出現的頻率由多至少排序,左圖呈現物品次數所建構的次數表,右圖呈現排序過後的表格。
154 |
155 | | Header Table | Frequent item table (ordered) |
156 | | :---------------------------------------------------------: | :---------------------------------------------------------: |
157 | |  |  |
158 |
159 | 接著只需要使用 Frequent item table,對於每一項逐一建樹即可。
160 |
161 | | Data1 | Data2 | Data3 |
162 | | :---------------------------------------------------------: | :----------------------------------------------------------: | :----------------------------------------------------------: |
163 | |  |  |
130 |
131 |
132 |
133 | FP-Tree 可以幫助我們建立出頻繁樣式,雖然高壓縮但頻繁樣式完整。
134 |
135 |
136 |
137 | ### frequent item table
138 |
139 | 若我們有左邊的資料表,由上至下的 ID 為 1、2、3、4、5。
140 |
141 | 首先我們應先設定一個 support 為門檻,淘汰掉不需要的資料。
142 |
143 |
144 |
145 | 以左邊為例,我們設定 min_support = 3。
146 |
147 | 經過淘汰掉不在門檻上的資料,得到右邊的 frequent item table。
148 |
149 | | Database | Frequent item table (unordered) |
150 | | :---------------------------------------------------------: | :---------------------------------------------------------: |
151 | |  |  |
152 |
153 | 我們需要對這個 table 做排序,根據物品出現的頻率由多至少排序,左圖呈現物品次數所建構的次數表,右圖呈現排序過後的表格。
154 |
155 | | Header Table | Frequent item table (ordered) |
156 | | :---------------------------------------------------------: | :---------------------------------------------------------: |
157 | |  |  |
158 |
159 | 接著只需要使用 Frequent item table,對於每一項逐一建樹即可。
160 |
161 | | Data1 | Data2 | Data3 |
162 | | :---------------------------------------------------------: | :----------------------------------------------------------: | :----------------------------------------------------------: |
163 | |  |  |  |
164 | | **Data 4** | **Data 5** | |
165 | |  |
|
164 | | **Data 4** | **Data 5** | |
165 | |  |  | |
166 |
167 | 藉此我們就能建構完整的 FP-Tree。
168 |
169 |
170 |
171 | ### conditional pattern base
172 |
173 | 對於一棵 FP-Tree,我們可以非常快速的查詢到樣式發生的次數。
174 |
175 | 以下圖為例,我們可以根據 Header Table 來逐一查詢。
176 |
177 | | Header Table | Frequent item table |
178 | | :---------------------------------------------------------: | :----------------------------------------------------------: |
179 | |  |
| |
166 |
167 | 藉此我們就能建構完整的 FP-Tree。
168 |
169 |
170 |
171 | ### conditional pattern base
172 |
173 | 對於一棵 FP-Tree,我們可以非常快速的查詢到樣式發生的次數。
174 |
175 | 以下圖為例,我們可以根據 Header Table 來逐一查詢。
176 |
177 | | Header Table | Frequent item table |
178 | | :---------------------------------------------------------: | :----------------------------------------------------------: |
179 | |  |  |
180 |
181 | 由於具有 BFS 的特性,所以我們可以很快速的查詢到相對的樣式。
182 |
183 | 我們會從 Header Table 第二項到第六項開始做向上尋訪(紅色節點)即可得到 Conditional Pattern Base
184 |
185 | 發生次數即為紫色節點的數字。
186 |
187 | | Item | Image | Conditional Pattern base |
188 | | :--: | :----------------------------------------------------------: | :----------------------: |
189 | | c |
|
180 |
181 | 由於具有 BFS 的特性,所以我們可以很快速的查詢到相對的樣式。
182 |
183 | 我們會從 Header Table 第二項到第六項開始做向上尋訪(紅色節點)即可得到 Conditional Pattern Base
184 |
185 | 發生次數即為紫色節點的數字。
186 |
187 | | Item | Image | Conditional Pattern base |
188 | | :--: | :----------------------------------------------------------: | :----------------------: |
189 | | c |  | f:3 |
190 | | a |
| f:3 |
190 | | a |  | fc:3 |
191 | | b |
| fc:3 |
191 | | b |  | fca: 1
| fca: 1 | fca:2
| fca:2 | fcam:2
| fcam:2 |  |
206 |
207 | 我們就能根據這個 conditional FP-Tree 窮舉出所有含有 m 的樣式,也就是`m, fm, cm, am, fcm, fam, cam, fcam`
208 |
209 | 我們還能根據 conditional FP-Tree 以遞迴的形式找出 am, cm, cam... 的 conditional FP-Tree,與上述同理。
210 |
211 |
212 |
213 | ## Collaborative Filtering
214 |
215 | 我們可以使用 Collaborative Filtering 來找出兩個相似的人或事物,分成以 User-Based 為主與以 Item-Based 為主。
216 |
217 | 我們會根據使用者或物品的 rating 來評估推薦
218 |
219 | 但也因此會有 cold start 的問題,也就是新東西或新的人進來之後會不知道要推薦什麼,因為沒有任何的評分紀錄。
220 |
221 |
222 |
223 | 要找出相似的人事物,我們需要算出相似度:
224 |
225 | - Jaccard similarity measure $\text{sim}(x, y) = \dfrac{|r_x \cap r_y|}{|r_x|+|r_y|-|r_x\cap r_y|}$,其中 $v_x, v_y$ 為 User rating set。
226 | - Cosine similarity:$\text{sim}(x, y) = \dfrac{r_x\cdot r_y}{||r_x||\cdot||r_y||}$
227 | - Pearson correlation coefficient:$\text{sim}(x,y)=\dfrac{\displaystyle \sum_{s\in s_{xy}} (r_{xs}-\overline{r_x})(r_{ys}-\overline{r_y})}{\sqrt{\sum_{s\in s_{xy}} (r_{xs}-\overline{r_x})^2} \sqrt{\sum_{s\in s_{xy}} (r_{ys}-\overline{r_y})^2}}$,$s_{xy}$ 為 x 與 y 對某物的評價。
228 |
229 |
230 |
231 | ### User-based collaborative filtering
232 |
233 | 我們可以使用 user-item rating matrix,找出 user 與 user 之間的關聯性。
234 |
235 | 只要找出兩個 user 有高相似度,就能把類似的行為推薦給 user。
236 |
237 |
238 |
239 | ### Item-based collaborative filtering
240 |
241 | 我們可以使用 user-item rating matrix,找出 item 與 item 之間的關聯性。
242 |
243 | 只要找出兩個 item 有高相似度,就能把類似的行為推薦給 user。
244 |
245 |
246 |
247 |
248 |
249 | ### Jaccard similarity measure
250 |
251 | 第一個提到的相似度計算即為 Jaccard similarity measure。
252 |
253 | Jaccard similarity measure 不管評分,只管該 index 有沒有評分,以下面的例子為例。
254 |
255 | | | 1 | 2 | 3 | 4 | 5 |
256 | | :--: | :--: | :--: | :--: | :--: | :--: |
257 | | x | 1 | | | 1 | 3 |
258 | | y | 1 | | 2 | 2 | |
259 |
260 | 我們可以得到 User rating set $r_x = \{1, 4, 5\}$,$r_y = \{1, 3, 4\}$,因為 $x$ 只有在 1、4、5 做評分,$y$ 只有在 1、3、4 做評分。
261 |
262 | 由於 $r_x$ 與 $r_y$ 有交集的數量只有 $2$,聯集則是 $4$,故 $\text{sim}(x, y) = \dfrac{2}{4} = 0.5$
263 |
264 |
265 |
266 | 缺點則是評分上是有意義的,故這樣做會忽略掉評分的意義。
267 |
268 |
269 |
270 | ### Cosine similarity
271 |
272 | 第二個提到的相似度計算即為 Cosine similarity。
273 |
274 | 以下面的例子為例。
275 |
276 | | | 1 | 2 | 3 | 4 | 5 |
277 | | :--: | :--: | :--: | :--: | :--: | :--: |
278 | | x | 1 | | | 1 | 3 |
279 | | y | 1 | | 2 | 2 | |
280 |
281 | 我們可以將 $r_x, r_y$ 視為點,則可以得到
282 | $$
283 | r_x = <1, 0, 0, 1, 3> \\
284 | r_y = <1, 0, 2, 2, 0>
285 | $$
286 | 故其 Cosine similarity 為 $\dfrac{1+0+0+2+0}{\sqrt{1^2+1^2+3^2}\sqrt{1^2+2^2+2^2}} \approx 30.2\%$
287 |
288 |
289 |
290 | ### Pearson correlation coefficient
291 |
292 | 定義上為 $\text{sim}(x,y)=\dfrac{\displaystyle \sum_{s\in s_{xy}} (r_{xs}-\overline{r_x})(r_{ys}-\overline{r_y})}{\sqrt{\sum_{s\in s_{xy}} (r_{xs}-\overline{r_x})^2} \sqrt{\sum_{s\in s_{xy}} (r_{ys}-\overline{r_y})^2}}$,$s_{xy}$ 為 x 與 y 對某物的評價。
293 |
294 | 雖然定義上是這樣,但,其實你只要算出列/行的平均,行/列存在的元素全部減去平均後砸 Cosine Similarity 也能做出來
295 |
296 | ~~安了我的算式恐懼症,這麼可怕的式子是啥鬼嗚嗚~~
297 |
298 |
299 |
300 | 以下面的例子為例。
301 |
302 | | | 1 | 2 | 3 | 4 | 5 |
303 | | :--: | :--: | :--: | :--: | :--: | :--: |
304 | | x | 2 | | | 1 | 3 |
305 | | y | 2 | | 2 | 2 | |
306 |
307 | 我們可以將 $r_x, r_y$ 視為點,則可以得到
308 | $$
309 | r_x = <1, 0, 0, 1, 3> \\
310 | r_y = <1, 0, 2, 2, 0>
311 | $$
312 | 平均 $\mu_x = 2$,$\mu_y = 2$,則
313 | $$
314 | r_x' = <-1, 0, 0, -1, 1> \\
315 | r_y' = <-1, 0, 0, 0, 0>
316 | $$
317 | 我們可以算出 Pearson correlation coefficient
318 | $$
319 | \text{sim}(x, y) = \dfrac{1}{((-1)^2+(-1)^2+1^2)((-1)^2)} = \dfrac{1}{3} \approx 0.333
320 | $$
321 |
322 |
323 | ### Prediction Function
324 |
325 | 若我們有一個物件與其他 $N$ 個物件相似,則我們可以用以下的式子來表達其預測值
326 | $$
327 | r_{xi} = \dfrac{\displaystyle \sum_{j\in N(i; x)} s_{ij} \cdot r_{xj}}{\displaystyle \sum_{j\in N(i; x)} s_{ij}}
328 | $$
329 | 見以下範例。
330 |
331 |
332 |
333 | ### Item-Item Collaborative Filtering
334 |
335 | 假設我們有一筆這樣的資料,欄為 User 且列為 Movie,表格上每個數字為 User 對 Movie 的評價
336 |
337 | | | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
338 | | :--: | :--: | :--: | :--: | :--: | :----: | :--: | :--: | :--: | :--: | :--: | :--: | :--: |
339 | | 1 | 1 | | 3 | | **?** | 5 | | | 5 | | 4 | |
340 | | 2 | | | 5 | 4 | | | 4 | | | 2 | 1 | 3 |
341 | | 3 | 2 | 4 | | 1 | 2 | | 3 | | 4 | 3 | 5 | |
342 | | 4 | | 2 | 4 | | 5 | | | 4 | | | 2 | |
343 | | 5 | | | 4 | 3 | 4 | 2 | | | | | 2 | |
344 | | 6 | 1 | | 3 | | 3 | | | 2 | | | 4 | |
345 |
346 | 可以看到 $D(1, 5)$ 的資料是問號,即為我們想要推演的資料。
347 |
348 | 我們使用 Pearson correlation coefficient 來**計算電影的相似度**,先算出每個電影的平均值,以及該列減去平均值的向量。
349 |
350 | $\mu_1 = (1+3+5+5+4)/5 = 3.6$,$v'_1 = <-2.6, 0, -0.6, 0, 0, 1.4, 0, 0, 1.4, 0, 0.4, 0>$
351 |
352 | $\mu_2 = (5+4+4+2+1+3)/6=3.167$,$v'_2 = <0, 0, 1.83, 0.83, 0, 0, 0.83, 0, 0, -1.17, -2.17, -0.17>$
353 |
354 | $\mu_3 = (2+4+1+2+3+4+3+5)/8=3$,$v'_3 = <-1, 1, 0, -2, -1, 0, 0, 0, 1, 0, 2, 0>$
355 |
356 | $\mu_4 = (2+4+5+4+2)/5=3.4$,$v'_4 = <0, -1.4, 0.6, 0, 1.6, 0, 0, 0.6, 0, 0, -1.4, 0>$
357 |
358 | $\mu_5 = (4+3+4+2+2)/5=3$,$v'_5 = <0, 0, 1, 0, 1, -1, 0, 0, 0, 0, -1, 0>$
359 |
360 | $\mu_6 = (1+3+3+2+4)/5=2.6$,$v'_6 = <-1.6, 0, 0.4, 0, 0.4, 0, 0, -0.6, 0, 0, 1.4. 0>$
361 |
362 | 我們可以算出 Pearson correlation coefficient,得到
363 |
364 | $\text{sim}(1, 2) = -0.17$,$\text{sim}(1, 3) = 0.41$,$\text{sim}(1, 4) = -0.1$,$\text{sim}(1, 5) = -0.36$,$\text{sim}(1, 6) = 0.59$
365 |
366 | 故我們選擇電影 3、6 與電影 1 有較高的關聯性。
367 |
368 |
369 |
370 | 因此我們可以套用預測函數,得到:
371 | $$
372 | \dfrac{0.41\times 2 + 0.59\times 3}{0.41+0.59} = 2.6
373 | $$
374 | 故 $D(1, 5)$ 可以被預測成 2.6 分。
375 |
376 |
377 |
378 | ### User-User Collaborative Filtering
379 |
380 | 與 [Item-Item Collaborative Filtering](#Item-Item Collaborative Filtering) 同理,跳過。
381 |
382 |
383 |
384 | ## Content-based Filtering
385 |
386 | 使用內容來進行評估,因為使用內容,所以不會有 cold start 的問題。
387 |
388 |
389 |
390 | ### TF-IDF
391 |
392 | TF-IDF (Term Frequency - Inverse Document Frequency),用來量化詞彙的重要性,但會隨著詞彙出現的頻率高而出現反比影響。
393 |
394 | 其定義為:
395 | $$
396 | TF_{ij} = \dfrac{n_{ij}}{\sum_{k} n_{kj}} \\
397 | IDF_{i} = \log(\dfrac{N}{n_i}) \\
398 | \text{TF-IDF}_{ij} = TF_{ij} \times IDF_{i}
399 | $$
400 | 其中 TF 的 $n_{ij}$ 為該詞彙在文件中的次數,分母則是在所有文件中該詞彙出現的次數,$N$ 為文件的總詞彙量。
401 |
402 |
--------------------------------------------------------------------------------
/Markdown/Cluster Analysis.md:
--------------------------------------------------------------------------------
1 | # 群聚分析(Cluster Analysis)
2 |
3 | > Reference:
4 | >
5 | > 1. Cluster Analysis - Dr. Tun-Wen Pai
6 |
7 | ## 群聚分析
8 |
9 | 主要分成兩種不同的群聚分析:
10 |
11 | 1. 分層式群聚:分成由上至下(top-down)或由下至上(bottom-up)演算法,層層迭代運算。
12 | 2. 分割式群聚:一次把所有的分群結果納入考慮。
13 |
14 |
15 |
16 | ## 分割式群聚
17 |
18 | 這邊舉一個最經典的例子:K-Mean。
19 |
20 |
21 |
22 | ### 簡單的步驟舉例
23 |
24 | 舉個例子,我們有個資料集。
25 |
26 |
|  |
206 |
207 | 我們就能根據這個 conditional FP-Tree 窮舉出所有含有 m 的樣式,也就是`m, fm, cm, am, fcm, fam, cam, fcam`
208 |
209 | 我們還能根據 conditional FP-Tree 以遞迴的形式找出 am, cm, cam... 的 conditional FP-Tree,與上述同理。
210 |
211 |
212 |
213 | ## Collaborative Filtering
214 |
215 | 我們可以使用 Collaborative Filtering 來找出兩個相似的人或事物,分成以 User-Based 為主與以 Item-Based 為主。
216 |
217 | 我們會根據使用者或物品的 rating 來評估推薦
218 |
219 | 但也因此會有 cold start 的問題,也就是新東西或新的人進來之後會不知道要推薦什麼,因為沒有任何的評分紀錄。
220 |
221 |
222 |
223 | 要找出相似的人事物,我們需要算出相似度:
224 |
225 | - Jaccard similarity measure $\text{sim}(x, y) = \dfrac{|r_x \cap r_y|}{|r_x|+|r_y|-|r_x\cap r_y|}$,其中 $v_x, v_y$ 為 User rating set。
226 | - Cosine similarity:$\text{sim}(x, y) = \dfrac{r_x\cdot r_y}{||r_x||\cdot||r_y||}$
227 | - Pearson correlation coefficient:$\text{sim}(x,y)=\dfrac{\displaystyle \sum_{s\in s_{xy}} (r_{xs}-\overline{r_x})(r_{ys}-\overline{r_y})}{\sqrt{\sum_{s\in s_{xy}} (r_{xs}-\overline{r_x})^2} \sqrt{\sum_{s\in s_{xy}} (r_{ys}-\overline{r_y})^2}}$,$s_{xy}$ 為 x 與 y 對某物的評價。
228 |
229 |
230 |
231 | ### User-based collaborative filtering
232 |
233 | 我們可以使用 user-item rating matrix,找出 user 與 user 之間的關聯性。
234 |
235 | 只要找出兩個 user 有高相似度,就能把類似的行為推薦給 user。
236 |
237 |
238 |
239 | ### Item-based collaborative filtering
240 |
241 | 我們可以使用 user-item rating matrix,找出 item 與 item 之間的關聯性。
242 |
243 | 只要找出兩個 item 有高相似度,就能把類似的行為推薦給 user。
244 |
245 |
246 |
247 |
248 |
249 | ### Jaccard similarity measure
250 |
251 | 第一個提到的相似度計算即為 Jaccard similarity measure。
252 |
253 | Jaccard similarity measure 不管評分,只管該 index 有沒有評分,以下面的例子為例。
254 |
255 | | | 1 | 2 | 3 | 4 | 5 |
256 | | :--: | :--: | :--: | :--: | :--: | :--: |
257 | | x | 1 | | | 1 | 3 |
258 | | y | 1 | | 2 | 2 | |
259 |
260 | 我們可以得到 User rating set $r_x = \{1, 4, 5\}$,$r_y = \{1, 3, 4\}$,因為 $x$ 只有在 1、4、5 做評分,$y$ 只有在 1、3、4 做評分。
261 |
262 | 由於 $r_x$ 與 $r_y$ 有交集的數量只有 $2$,聯集則是 $4$,故 $\text{sim}(x, y) = \dfrac{2}{4} = 0.5$
263 |
264 |
265 |
266 | 缺點則是評分上是有意義的,故這樣做會忽略掉評分的意義。
267 |
268 |
269 |
270 | ### Cosine similarity
271 |
272 | 第二個提到的相似度計算即為 Cosine similarity。
273 |
274 | 以下面的例子為例。
275 |
276 | | | 1 | 2 | 3 | 4 | 5 |
277 | | :--: | :--: | :--: | :--: | :--: | :--: |
278 | | x | 1 | | | 1 | 3 |
279 | | y | 1 | | 2 | 2 | |
280 |
281 | 我們可以將 $r_x, r_y$ 視為點,則可以得到
282 | $$
283 | r_x = <1, 0, 0, 1, 3> \\
284 | r_y = <1, 0, 2, 2, 0>
285 | $$
286 | 故其 Cosine similarity 為 $\dfrac{1+0+0+2+0}{\sqrt{1^2+1^2+3^2}\sqrt{1^2+2^2+2^2}} \approx 30.2\%$
287 |
288 |
289 |
290 | ### Pearson correlation coefficient
291 |
292 | 定義上為 $\text{sim}(x,y)=\dfrac{\displaystyle \sum_{s\in s_{xy}} (r_{xs}-\overline{r_x})(r_{ys}-\overline{r_y})}{\sqrt{\sum_{s\in s_{xy}} (r_{xs}-\overline{r_x})^2} \sqrt{\sum_{s\in s_{xy}} (r_{ys}-\overline{r_y})^2}}$,$s_{xy}$ 為 x 與 y 對某物的評價。
293 |
294 | 雖然定義上是這樣,但,其實你只要算出列/行的平均,行/列存在的元素全部減去平均後砸 Cosine Similarity 也能做出來
295 |
296 | ~~安了我的算式恐懼症,這麼可怕的式子是啥鬼嗚嗚~~
297 |
298 |
299 |
300 | 以下面的例子為例。
301 |
302 | | | 1 | 2 | 3 | 4 | 5 |
303 | | :--: | :--: | :--: | :--: | :--: | :--: |
304 | | x | 2 | | | 1 | 3 |
305 | | y | 2 | | 2 | 2 | |
306 |
307 | 我們可以將 $r_x, r_y$ 視為點,則可以得到
308 | $$
309 | r_x = <1, 0, 0, 1, 3> \\
310 | r_y = <1, 0, 2, 2, 0>
311 | $$
312 | 平均 $\mu_x = 2$,$\mu_y = 2$,則
313 | $$
314 | r_x' = <-1, 0, 0, -1, 1> \\
315 | r_y' = <-1, 0, 0, 0, 0>
316 | $$
317 | 我們可以算出 Pearson correlation coefficient
318 | $$
319 | \text{sim}(x, y) = \dfrac{1}{((-1)^2+(-1)^2+1^2)((-1)^2)} = \dfrac{1}{3} \approx 0.333
320 | $$
321 |
322 |
323 | ### Prediction Function
324 |
325 | 若我們有一個物件與其他 $N$ 個物件相似,則我們可以用以下的式子來表達其預測值
326 | $$
327 | r_{xi} = \dfrac{\displaystyle \sum_{j\in N(i; x)} s_{ij} \cdot r_{xj}}{\displaystyle \sum_{j\in N(i; x)} s_{ij}}
328 | $$
329 | 見以下範例。
330 |
331 |
332 |
333 | ### Item-Item Collaborative Filtering
334 |
335 | 假設我們有一筆這樣的資料,欄為 User 且列為 Movie,表格上每個數字為 User 對 Movie 的評價
336 |
337 | | | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
338 | | :--: | :--: | :--: | :--: | :--: | :----: | :--: | :--: | :--: | :--: | :--: | :--: | :--: |
339 | | 1 | 1 | | 3 | | **?** | 5 | | | 5 | | 4 | |
340 | | 2 | | | 5 | 4 | | | 4 | | | 2 | 1 | 3 |
341 | | 3 | 2 | 4 | | 1 | 2 | | 3 | | 4 | 3 | 5 | |
342 | | 4 | | 2 | 4 | | 5 | | | 4 | | | 2 | |
343 | | 5 | | | 4 | 3 | 4 | 2 | | | | | 2 | |
344 | | 6 | 1 | | 3 | | 3 | | | 2 | | | 4 | |
345 |
346 | 可以看到 $D(1, 5)$ 的資料是問號,即為我們想要推演的資料。
347 |
348 | 我們使用 Pearson correlation coefficient 來**計算電影的相似度**,先算出每個電影的平均值,以及該列減去平均值的向量。
349 |
350 | $\mu_1 = (1+3+5+5+4)/5 = 3.6$,$v'_1 = <-2.6, 0, -0.6, 0, 0, 1.4, 0, 0, 1.4, 0, 0.4, 0>$
351 |
352 | $\mu_2 = (5+4+4+2+1+3)/6=3.167$,$v'_2 = <0, 0, 1.83, 0.83, 0, 0, 0.83, 0, 0, -1.17, -2.17, -0.17>$
353 |
354 | $\mu_3 = (2+4+1+2+3+4+3+5)/8=3$,$v'_3 = <-1, 1, 0, -2, -1, 0, 0, 0, 1, 0, 2, 0>$
355 |
356 | $\mu_4 = (2+4+5+4+2)/5=3.4$,$v'_4 = <0, -1.4, 0.6, 0, 1.6, 0, 0, 0.6, 0, 0, -1.4, 0>$
357 |
358 | $\mu_5 = (4+3+4+2+2)/5=3$,$v'_5 = <0, 0, 1, 0, 1, -1, 0, 0, 0, 0, -1, 0>$
359 |
360 | $\mu_6 = (1+3+3+2+4)/5=2.6$,$v'_6 = <-1.6, 0, 0.4, 0, 0.4, 0, 0, -0.6, 0, 0, 1.4. 0>$
361 |
362 | 我們可以算出 Pearson correlation coefficient,得到
363 |
364 | $\text{sim}(1, 2) = -0.17$,$\text{sim}(1, 3) = 0.41$,$\text{sim}(1, 4) = -0.1$,$\text{sim}(1, 5) = -0.36$,$\text{sim}(1, 6) = 0.59$
365 |
366 | 故我們選擇電影 3、6 與電影 1 有較高的關聯性。
367 |
368 |
369 |
370 | 因此我們可以套用預測函數,得到:
371 | $$
372 | \dfrac{0.41\times 2 + 0.59\times 3}{0.41+0.59} = 2.6
373 | $$
374 | 故 $D(1, 5)$ 可以被預測成 2.6 分。
375 |
376 |
377 |
378 | ### User-User Collaborative Filtering
379 |
380 | 與 [Item-Item Collaborative Filtering](#Item-Item Collaborative Filtering) 同理,跳過。
381 |
382 |
383 |
384 | ## Content-based Filtering
385 |
386 | 使用內容來進行評估,因為使用內容,所以不會有 cold start 的問題。
387 |
388 |
389 |
390 | ### TF-IDF
391 |
392 | TF-IDF (Term Frequency - Inverse Document Frequency),用來量化詞彙的重要性,但會隨著詞彙出現的頻率高而出現反比影響。
393 |
394 | 其定義為:
395 | $$
396 | TF_{ij} = \dfrac{n_{ij}}{\sum_{k} n_{kj}} \\
397 | IDF_{i} = \log(\dfrac{N}{n_i}) \\
398 | \text{TF-IDF}_{ij} = TF_{ij} \times IDF_{i}
399 | $$
400 | 其中 TF 的 $n_{ij}$ 為該詞彙在文件中的次數,分母則是在所有文件中該詞彙出現的次數,$N$ 為文件的總詞彙量。
401 |
402 |
--------------------------------------------------------------------------------
/Markdown/Cluster Analysis.md:
--------------------------------------------------------------------------------
1 | # 群聚分析(Cluster Analysis)
2 |
3 | > Reference:
4 | >
5 | > 1. Cluster Analysis - Dr. Tun-Wen Pai
6 |
7 | ## 群聚分析
8 |
9 | 主要分成兩種不同的群聚分析:
10 |
11 | 1. 分層式群聚:分成由上至下(top-down)或由下至上(bottom-up)演算法,層層迭代運算。
12 | 2. 分割式群聚:一次把所有的分群結果納入考慮。
13 |
14 |
15 |
16 | ## 分割式群聚
17 |
18 | 這邊舉一個最經典的例子:K-Mean。
19 |
20 |
21 |
22 | ### 簡單的步驟舉例
23 |
24 | 舉個例子,我們有個資料集。
25 |
26 |  27 |
28 | 既然要分群,我們先***雖然說是隨機,但是為了做黑魔法所以不隨機的***挑選兩個群心。
29 |
30 |
27 |
28 | 既然要分群,我們先***雖然說是隨機,但是為了做黑魔法所以不隨機的***挑選兩個群心。
29 |
30 |  31 |
32 | 接下來我們開始迭代每個點,來知道距離哪個群心比較近,就屬於那個群心。
33 |
34 | 根據上圖來說,我們用眼睛可以看出這個分類結果,為了方便辨識群心在哪,我將群心用空心圓代替。
35 |
36 |
31 |
32 | 接下來我們開始迭代每個點,來知道距離哪個群心比較近,就屬於那個群心。
33 |
34 | 根據上圖來說,我們用眼睛可以看出這個分類結果,為了方便辨識群心在哪,我將群心用空心圓代替。
35 |
36 |  37 |
38 |
39 |
40 | 此時我們可以更新群心,利用每個向度 $x$, $y$ 的平均。
41 |
42 |
37 |
38 |
39 |
40 | 此時我們可以更新群心,利用每個向度 $x$, $y$ 的平均。
41 |
42 |  43 |
44 | 經過多次迭代之後就可以找到一個穩定的分群。
45 |
46 |
47 |
48 | ### 問題探討
49 |
50 | 顯然,我們用***雖然說是隨機,但是為了做黑魔法所以不隨機的***方式挑選群心是一個很大的問題。
51 |
52 | 因為隨機挑選群心可能會挑出一個完全不同的結果,舉個例子:
53 |
54 |
43 |
44 | 經過多次迭代之後就可以找到一個穩定的分群。
45 |
46 |
47 |
48 | ### 問題探討
49 |
50 | 顯然,我們用***雖然說是隨機,但是為了做黑魔法所以不隨機的***方式挑選群心是一個很大的問題。
51 |
52 | 因為隨機挑選群心可能會挑出一個完全不同的結果,舉個例子:
53 |
54 |  55 |
56 | 群心這樣挑選會得到這樣的結果。
57 |
58 |
55 |
56 | 群心這樣挑選會得到這樣的結果。
57 |
58 |  59 |
60 | 跟前面的結果幾乎完全不一樣,所以挑選適當的群心是非常重要的。
61 |
62 |
63 |
64 | ## 分層式群聚
65 |
66 | ### 簡介
67 |
68 | 分層式群聚可以將群聚的步驟畫成一樹枝狀圖。
69 |
70 | > Image source:[Hierarchical Clustering for Large Data Sets](https://www.researchgate.net/publication/278706094_Hierarchical_Clustering_for_Large_Data_Sets)
71 |
72 |
59 |
60 | 跟前面的結果幾乎完全不一樣,所以挑選適當的群心是非常重要的。
61 |
62 |
63 |
64 | ## 分層式群聚
65 |
66 | ### 簡介
67 |
68 | 分層式群聚可以將群聚的步驟畫成一樹枝狀圖。
69 |
70 | > Image source:[Hierarchical Clustering for Large Data Sets](https://www.researchgate.net/publication/278706094_Hierarchical_Clustering_for_Large_Data_Sets)
71 |
72 |  73 |
74 | 在這份筆記會介紹四種不同的分層式群聚。
75 |
76 | 令 $A$ 為某個群集的點,$B$ 為某個群集的點,以下是群集表格。
77 |
78 | | 分群演算法 | 群聚概念 | 演算表達式 |
79 | | :--------------: | :----------------------: | :----------------------------------------------------------: |
80 | | Single Linkage | 以兩個群聚的最近點 | $\text{min}\{d(a,b): a \in A, b \in B\}$ |
81 | | Complete Linkage | 以兩個群聚的最遠點 | $\text{max}\{d(a,b): a \in A, b \in B\}$ |
82 | | UPGMA | 以兩群的平均距離 | $\displaystyle \dfrac{1}{|A|+|B|}\sum_{a\in A}\sum_{b\in B}d(a,b)$ |
83 | | WPGMA | 以某點至兩群和的平均距離 | $d(i\cup j, k)=\dfrac{d(i, k)+d(j, k)}{2}$ |
84 |
85 |
86 |
87 | ### 群集步驟
88 |
89 | 以上的演算法其實都大同小異,只有差別在演算法更新「群集距離表」的方式不同。
90 |
91 | 群集距離表即為每個群集到其他群集的距離,與自己的群集距離為 0。
92 |
93 | 例如下方表格即為群集距離表。
94 |
95 | 以圖上來說,群集 A 至群集 B 的距離為 25,群集 B 至群集 C 的距離為 25,群集 A 至群集 C 的距離為 15。
96 |
97 | | | A | B | C |
98 | | :--: | :--: | :--: | :--: |
99 | | A | 0 | 25 | 15 |
100 | | B | 25 | 0 | 25 |
101 | | C | 15 | 25 | 0 |
102 |
103 |
104 |
105 | 這張流程圖是我自製的,用來解釋群集分析的流程。
106 |
107 |
73 |
74 | 在這份筆記會介紹四種不同的分層式群聚。
75 |
76 | 令 $A$ 為某個群集的點,$B$ 為某個群集的點,以下是群集表格。
77 |
78 | | 分群演算法 | 群聚概念 | 演算表達式 |
79 | | :--------------: | :----------------------: | :----------------------------------------------------------: |
80 | | Single Linkage | 以兩個群聚的最近點 | $\text{min}\{d(a,b): a \in A, b \in B\}$ |
81 | | Complete Linkage | 以兩個群聚的最遠點 | $\text{max}\{d(a,b): a \in A, b \in B\}$ |
82 | | UPGMA | 以兩群的平均距離 | $\displaystyle \dfrac{1}{|A|+|B|}\sum_{a\in A}\sum_{b\in B}d(a,b)$ |
83 | | WPGMA | 以某點至兩群和的平均距離 | $d(i\cup j, k)=\dfrac{d(i, k)+d(j, k)}{2}$ |
84 |
85 |
86 |
87 | ### 群集步驟
88 |
89 | 以上的演算法其實都大同小異,只有差別在演算法更新「群集距離表」的方式不同。
90 |
91 | 群集距離表即為每個群集到其他群集的距離,與自己的群集距離為 0。
92 |
93 | 例如下方表格即為群集距離表。
94 |
95 | 以圖上來說,群集 A 至群集 B 的距離為 25,群集 B 至群集 C 的距離為 25,群集 A 至群集 C 的距離為 15。
96 |
97 | | | A | B | C |
98 | | :--: | :--: | :--: | :--: |
99 | | A | 0 | 25 | 15 |
100 | | B | 25 | 0 | 25 |
101 | | C | 15 | 25 | 0 |
102 |
103 |
104 |
105 | 這張流程圖是我自製的,用來解釋群集分析的流程。
106 |
107 |  108 |
109 |
110 |
111 |
112 |
113 | ### 利用演算法更新群集距離表
114 |
115 | 基本上群聚的方法只差在利用演算法來合併群集與更新群聚分析表,也就是更新除了合併群集以外群集距離。
116 |
117 | | | A | B | C | D |
118 | | :--: | :--: | :--: | :--: | :--: |
119 | | A | 0 | 25 | 15 | 18 |
120 | | B | 25 | 0 | 25 | 35 |
121 | | C | 15 | 25 | 0 | 45 |
122 | | D | 18 | 35 | 45 | 0 |
123 |
124 | 以上方這個表格為例,要尋找最小距離進行合併,該合併的兩個群集即為 **A 與 C**。
125 |
126 |
127 |
128 | **請注意,$A$ 與 $C$ 非常重要。**
129 |
130 | 例如當你欲合併的結果為 $(B, C)$ 與 $D$ 得到 $(B, C, D)$ 時,你應該要在更新時使用 $(B, C)$ 欄的值與 $D$ 欄的值。
131 |
132 | 否則你可能會用 $B$ 與 $(C, D)$ 的值,但表格上 $(C, D)$ 的值並不存在,所以記住什麼與什麼合併是非常重要。
133 |
134 | | | (A, C) | B | D |
135 | | :----: | :----: | :--: | :--: |
136 | | (A, C) | 0 | ? | ? |
137 | | B | ? | 0 | 35 |
138 | | D | ? | 35 | 0 |
139 |
140 | 合併完成之後,此時我們想要知道群集 $(A, C)$ 與 $B$ 的距離,此時我們根據演算法的定義:$\dfrac{d(i, k) + d(j, k)}{2}$
141 |
142 | $d(i, k) = d(A, B) = 25$,$d(j, k) = d(C, B) = 25$,可以得到距離為 $d((A, C), B) = \dfrac{25+25}{2} = 25$。
143 |
144 | 故$d((A, C), B) = 25$
145 |
146 | 同理我們可以算出 $d((A, C), D) = \dfrac{d(A, D)+d(C, D)}{2} = \dfrac{18+45}{2} = \dfrac{63}{2} = 31.5$
147 |
148 | | | (A, C) | B | D |
149 | | :----: | :----: | :--: | :--: |
150 | | (A, C) | 0 | 25 | 31.5 |
151 | | B | 25 | 0 | 35 |
152 | | D | 31.5 | 35 | 0 |
153 |
154 | 且我們可以得到 branch length = $\dfrac{15}{2} = 7.5$,也就是我們合併時使用的最短距離除以 2。
155 |
156 | 通常來說會越來越大,就能在樹枝狀圖上畫出 branch length(或者你可以說他是 thoushold)。
157 |
158 |
159 |
160 | ### 舉例其他演算法更新群集距離表
161 |
162 | 此時就能完成表格更新的步驟,其餘的合併方法只差在演算法的不同,照著做就行。
163 |
164 | 以其他三種不同的演算法來說:
165 |
166 | 1. Single Linkage:更新其他群集距離的方式為,取合併群集與該群集的**最短距離**。
167 |
168 | 2. Complete Linkage:更新其他群集距離的方式為,取合併群集與該群集的**最長距離**。
169 |
170 | 3. UPGMA:更新其他群集距離的方式為,若合併群集為 $A$ 與 $B$ 的合併,且欲合併的群集為 $C$。
171 |
172 | 則距離更新方式為 $d((A, C), B) = \dfrac{|A| \times d(A, C) + |B| \times d(B, C)}{|A| + |B|}$,其中 $|A|$ 與 $|B|$ 為該群集的點數量。
173 |
174 | 4. WPGMA:更新其他群集距離的方式為,若合併群集為 $A$ 與 $B$ 的合併,且欲合併的群集為 $C$。
175 |
176 | 則距離更新方式為 $d((A, C), B) = \dfrac{d(A, C)+d(B, C)}{2}$
177 |
178 |
179 |
180 | ## 優化分群結果
181 |
182 | - 什麼樣的分群結果是好的?
183 | - 我們可以將不同的 $K$ 值進行計算 total variation,並且找出拐點。
--------------------------------------------------------------------------------
/Markdown/Data Mining.md:
--------------------------------------------------------------------------------
1 | # 資料探勘(Data Mining)
2 |
3 | > 參考資料:
4 | >
5 | > 資料探勘(Data Mining)Dr. Tun-Wen Pai
6 | >
7 | > Business Intelligence and Data Mining Anil K. Maheshwari, Ph.D.
8 |
9 |
10 |
11 | ## 資料探勘的介紹
12 |
13 | 資料探勘是一種技術,為了探索大量經過組織的資料中,得到有利的資訊、見解與模式。
14 |
15 | 資料探勘利用了統計學、人工智慧領域、機器學習的知識,挖掘資料中未知的資訊,例如發現資料的類別與結構、分類資料等等。
16 |
17 |
18 |
19 | ## 資料蒐集與資料選擇
20 |
21 | 從大量支離破碎的資料中很難探勘出有用的資訊,所以我們需要先做資料蒐集與資料選擇。
22 |
23 |
24 |
25 | 資料從大量的資料來源中被蒐集,此時資料是支離破碎的,所以我們需要經過一系列的處理(例如資料倉儲的 ETL)
26 |
27 | 在建立資料倉儲之前,我們可以使用企業模式的資料模型(Enterprise Data Model, EDM),為這些資料打造一個統一的框架。
28 |
29 | 經過資料倉儲一系列的處理之後得到組織過的資料,再從這些資料進行探勘。
30 |
31 |
32 |
33 | 這也是為什麼資料倉儲被用來幫助資料探勘,因為資料探勘需要整理過的資料,此時即完成了資料蒐集與資料選擇。
34 |
35 |
36 |
37 | ## 資料淨化
38 |
39 | 資料的品質會嚴重影響到資料探勘,所以我們會希望資料都是高品質的,也因此我們需要把資料淨化。
40 |
41 |
42 |
43 | 我們可以利用一些手段進行資料淨化,例如:填充遺失的欄位、處理異常值、劃分連續型變數等等。
44 |
45 | 經過資料淨化,就可以確保資料都是高品質,確保不會造成 Garbage in Garbage out 的問題。
46 |
47 |
48 |
49 | 以下列舉一些資料淨化的手段:
50 |
51 | 1. 重複的資料需要被移除,從各方資料來源蒐集資料可能會導致出現重複的資料,所以需要被移除。
52 |
53 | 2. 欄位若遺失值則需要被填上去,如果不該被填上去,則這個欄位應該被移除。
54 |
55 | 3. 資料元素從單一單位轉換成另一個單位。
56 |
57 | 例如透過總病人數量與總花費較難得到有利的資訊,但如果資料是病人與花費的對應關係,那麼我們可以從這邊得到更有利的資訊。
58 |
59 | 4. 連續型變數可以被劃分以利於資料探勘更佳。
60 |
61 | 例如工作經驗可以被劃分成低、中、高。
62 |
63 | 5. 資料元素可能需要經過調整,讓他能夠隨著時間的推移產生可比性。
64 |
65 | 例如大量不同的貨幣可以被調整成通用貨幣,用來評估通膨的情況。
66 |
67 | 6. 極值需要被移除。
68 |
69 | 7. 偏差數值需要經過矯正,來確保分析結果是正常的。
70 |
71 | 8. 資料應該保持同樣的顆粒度(Granularity),來讓資料能夠比較。
72 |
73 | 例如:櫃台銷售所產生的資料通常都是以日為單位,而銷售員的資料通常都是以月為單位。
74 |
75 | 為此我們應該將櫃台銷售調整成月為單位,兩個資料才做比較。
76 |
77 | 9. 資料需要足夠密集。
78 |
79 |
80 |
81 | ## Confusion Matrix
82 |
83 | Confusion Matrix 可用來監督學習、可以確定在機器學習中是否將兩個不同類型的資料混淆了。
84 |
85 |
86 |
87 | 以採檢病人是否為陽性反應為例,我們可以獲得以下的表格。
88 |
89 |
108 |
109 |
110 |
111 |
112 |
113 | ### 利用演算法更新群集距離表
114 |
115 | 基本上群聚的方法只差在利用演算法來合併群集與更新群聚分析表,也就是更新除了合併群集以外群集距離。
116 |
117 | | | A | B | C | D |
118 | | :--: | :--: | :--: | :--: | :--: |
119 | | A | 0 | 25 | 15 | 18 |
120 | | B | 25 | 0 | 25 | 35 |
121 | | C | 15 | 25 | 0 | 45 |
122 | | D | 18 | 35 | 45 | 0 |
123 |
124 | 以上方這個表格為例,要尋找最小距離進行合併,該合併的兩個群集即為 **A 與 C**。
125 |
126 |
127 |
128 | **請注意,$A$ 與 $C$ 非常重要。**
129 |
130 | 例如當你欲合併的結果為 $(B, C)$ 與 $D$ 得到 $(B, C, D)$ 時,你應該要在更新時使用 $(B, C)$ 欄的值與 $D$ 欄的值。
131 |
132 | 否則你可能會用 $B$ 與 $(C, D)$ 的值,但表格上 $(C, D)$ 的值並不存在,所以記住什麼與什麼合併是非常重要。
133 |
134 | | | (A, C) | B | D |
135 | | :----: | :----: | :--: | :--: |
136 | | (A, C) | 0 | ? | ? |
137 | | B | ? | 0 | 35 |
138 | | D | ? | 35 | 0 |
139 |
140 | 合併完成之後,此時我們想要知道群集 $(A, C)$ 與 $B$ 的距離,此時我們根據演算法的定義:$\dfrac{d(i, k) + d(j, k)}{2}$
141 |
142 | $d(i, k) = d(A, B) = 25$,$d(j, k) = d(C, B) = 25$,可以得到距離為 $d((A, C), B) = \dfrac{25+25}{2} = 25$。
143 |
144 | 故$d((A, C), B) = 25$
145 |
146 | 同理我們可以算出 $d((A, C), D) = \dfrac{d(A, D)+d(C, D)}{2} = \dfrac{18+45}{2} = \dfrac{63}{2} = 31.5$
147 |
148 | | | (A, C) | B | D |
149 | | :----: | :----: | :--: | :--: |
150 | | (A, C) | 0 | 25 | 31.5 |
151 | | B | 25 | 0 | 35 |
152 | | D | 31.5 | 35 | 0 |
153 |
154 | 且我們可以得到 branch length = $\dfrac{15}{2} = 7.5$,也就是我們合併時使用的最短距離除以 2。
155 |
156 | 通常來說會越來越大,就能在樹枝狀圖上畫出 branch length(或者你可以說他是 thoushold)。
157 |
158 |
159 |
160 | ### 舉例其他演算法更新群集距離表
161 |
162 | 此時就能完成表格更新的步驟,其餘的合併方法只差在演算法的不同,照著做就行。
163 |
164 | 以其他三種不同的演算法來說:
165 |
166 | 1. Single Linkage:更新其他群集距離的方式為,取合併群集與該群集的**最短距離**。
167 |
168 | 2. Complete Linkage:更新其他群集距離的方式為,取合併群集與該群集的**最長距離**。
169 |
170 | 3. UPGMA:更新其他群集距離的方式為,若合併群集為 $A$ 與 $B$ 的合併,且欲合併的群集為 $C$。
171 |
172 | 則距離更新方式為 $d((A, C), B) = \dfrac{|A| \times d(A, C) + |B| \times d(B, C)}{|A| + |B|}$,其中 $|A|$ 與 $|B|$ 為該群集的點數量。
173 |
174 | 4. WPGMA:更新其他群集距離的方式為,若合併群集為 $A$ 與 $B$ 的合併,且欲合併的群集為 $C$。
175 |
176 | 則距離更新方式為 $d((A, C), B) = \dfrac{d(A, C)+d(B, C)}{2}$
177 |
178 |
179 |
180 | ## 優化分群結果
181 |
182 | - 什麼樣的分群結果是好的?
183 | - 我們可以將不同的 $K$ 值進行計算 total variation,並且找出拐點。
--------------------------------------------------------------------------------
/Markdown/Data Mining.md:
--------------------------------------------------------------------------------
1 | # 資料探勘(Data Mining)
2 |
3 | > 參考資料:
4 | >
5 | > 資料探勘(Data Mining)Dr. Tun-Wen Pai
6 | >
7 | > Business Intelligence and Data Mining Anil K. Maheshwari, Ph.D.
8 |
9 |
10 |
11 | ## 資料探勘的介紹
12 |
13 | 資料探勘是一種技術,為了探索大量經過組織的資料中,得到有利的資訊、見解與模式。
14 |
15 | 資料探勘利用了統計學、人工智慧領域、機器學習的知識,挖掘資料中未知的資訊,例如發現資料的類別與結構、分類資料等等。
16 |
17 |
18 |
19 | ## 資料蒐集與資料選擇
20 |
21 | 從大量支離破碎的資料中很難探勘出有用的資訊,所以我們需要先做資料蒐集與資料選擇。
22 |
23 |
24 |
25 | 資料從大量的資料來源中被蒐集,此時資料是支離破碎的,所以我們需要經過一系列的處理(例如資料倉儲的 ETL)
26 |
27 | 在建立資料倉儲之前,我們可以使用企業模式的資料模型(Enterprise Data Model, EDM),為這些資料打造一個統一的框架。
28 |
29 | 經過資料倉儲一系列的處理之後得到組織過的資料,再從這些資料進行探勘。
30 |
31 |
32 |
33 | 這也是為什麼資料倉儲被用來幫助資料探勘,因為資料探勘需要整理過的資料,此時即完成了資料蒐集與資料選擇。
34 |
35 |
36 |
37 | ## 資料淨化
38 |
39 | 資料的品質會嚴重影響到資料探勘,所以我們會希望資料都是高品質的,也因此我們需要把資料淨化。
40 |
41 |
42 |
43 | 我們可以利用一些手段進行資料淨化,例如:填充遺失的欄位、處理異常值、劃分連續型變數等等。
44 |
45 | 經過資料淨化,就可以確保資料都是高品質,確保不會造成 Garbage in Garbage out 的問題。
46 |
47 |
48 |
49 | 以下列舉一些資料淨化的手段:
50 |
51 | 1. 重複的資料需要被移除,從各方資料來源蒐集資料可能會導致出現重複的資料,所以需要被移除。
52 |
53 | 2. 欄位若遺失值則需要被填上去,如果不該被填上去,則這個欄位應該被移除。
54 |
55 | 3. 資料元素從單一單位轉換成另一個單位。
56 |
57 | 例如透過總病人數量與總花費較難得到有利的資訊,但如果資料是病人與花費的對應關係,那麼我們可以從這邊得到更有利的資訊。
58 |
59 | 4. 連續型變數可以被劃分以利於資料探勘更佳。
60 |
61 | 例如工作經驗可以被劃分成低、中、高。
62 |
63 | 5. 資料元素可能需要經過調整,讓他能夠隨著時間的推移產生可比性。
64 |
65 | 例如大量不同的貨幣可以被調整成通用貨幣,用來評估通膨的情況。
66 |
67 | 6. 極值需要被移除。
68 |
69 | 7. 偏差數值需要經過矯正,來確保分析結果是正常的。
70 |
71 | 8. 資料應該保持同樣的顆粒度(Granularity),來讓資料能夠比較。
72 |
73 | 例如:櫃台銷售所產生的資料通常都是以日為單位,而銷售員的資料通常都是以月為單位。
74 |
75 | 為此我們應該將櫃台銷售調整成月為單位,兩個資料才做比較。
76 |
77 | 9. 資料需要足夠密集。
78 |
79 |
80 |
81 | ## Confusion Matrix
82 |
83 | Confusion Matrix 可用來監督學習、可以確定在機器學習中是否將兩個不同類型的資料混淆了。
84 |
85 |
86 |
87 | 以採檢病人是否為陽性反應為例,我們可以獲得以下的表格。
88 |
89 |  90 |
91 | 以理想的情況來說,採檢試劑要能夠分辨出陽性(True Positive)與陰性(True Negative)。
92 |
93 | 但必定會出現偽陰(False Negative)與偽陽(False Positive)的情況出現。
94 |
95 | 將這些數值填入表格,即可得到一個 Confusion Matrix。
96 |
97 |
98 |
99 | 我們可以擴展表格,得到更多的資訊。
100 |
101 | 
102 |
103 |
104 |
105 | 將同樣的概念,可以套用到機器分類數字、機器分類花...等情況,所以可以適用於績效評估機器學習。
106 |
107 |
108 |
109 | ## AUC - ROC Curve
110 |
111 | 我們可以使用 AUC - ROC Curve 來進行機器學習的績效評估。
112 |
113 | 對於上面表格,我們可以設定特定的閥值,用來得到在這個閥值中的真陽、真陰、偽陽、偽陰數量,進而劃出由兩個曲線組成的圖片。
114 |
115 |
116 |
117 | 例如我們預期在 TPR 閥值低於 0.5 時則為陰性,在閥值高於 0.5 時則為陽性。
118 |
119 | 此時我們可以預期沒有任何偽陰、偽陽的情況,所以可以得到以下這張圖。
120 |
121 |
90 |
91 | 以理想的情況來說,採檢試劑要能夠分辨出陽性(True Positive)與陰性(True Negative)。
92 |
93 | 但必定會出現偽陰(False Negative)與偽陽(False Positive)的情況出現。
94 |
95 | 將這些數值填入表格,即可得到一個 Confusion Matrix。
96 |
97 |
98 |
99 | 我們可以擴展表格,得到更多的資訊。
100 |
101 | 
102 |
103 |
104 |
105 | 將同樣的概念,可以套用到機器分類數字、機器分類花...等情況,所以可以適用於績效評估機器學習。
106 |
107 |
108 |
109 | ## AUC - ROC Curve
110 |
111 | 我們可以使用 AUC - ROC Curve 來進行機器學習的績效評估。
112 |
113 | 對於上面表格,我們可以設定特定的閥值,用來得到在這個閥值中的真陽、真陰、偽陽、偽陰數量,進而劃出由兩個曲線組成的圖片。
114 |
115 |
116 |
117 | 例如我們預期在 TPR 閥值低於 0.5 時則為陰性,在閥值高於 0.5 時則為陽性。
118 |
119 | 此時我們可以預期沒有任何偽陰、偽陽的情況,所以可以得到以下這張圖。
120 |
121 |  122 |
123 | 這時無論到哪點都不會出現偽陽性,故 ROC 曲線呈現直角,幾乎是完美分類。
124 |
125 |
126 |
127 | 另一個例子,若我們期望 TPR 閥值低於 0.5 時為陰性,高於 0.5 時則陽性。
128 |
129 | 然而結果不如預期,得到了以下這張圖。
130 |
131 |
122 |
123 | 這時無論到哪點都不會出現偽陽性,故 ROC 曲線呈現直角,幾乎是完美分類。
124 |
125 |
126 |
127 | 另一個例子,若我們期望 TPR 閥值低於 0.5 時為陰性,高於 0.5 時則陽性。
128 |
129 | 然而結果不如預期,得到了以下這張圖。
130 |
131 |  132 |
133 | 這時我們只需要反預測即可校正回上例。
134 |
135 |
136 |
137 | 換另一個不理想的例子,若可能出現偽陰偽陽的情況,
138 |
139 | 例如閥值是 0.46 時,陰性與陽性都出現,這時就會出真陽、偽陽的情況,得到以下這張圖。
140 |
141 | 可以發現,在出現 FPR 時,TPR 的數值稍微下跌,而在之後幾乎回到 1 的位置。
142 |
143 |
132 |
133 | 這時我們只需要反預測即可校正回上例。
134 |
135 |
136 |
137 | 換另一個不理想的例子,若可能出現偽陰偽陽的情況,
138 |
139 | 例如閥值是 0.46 時,陰性與陽性都出現,這時就會出真陽、偽陽的情況,得到以下這張圖。
140 |
141 | 可以發現,在出現 FPR 時,TPR 的數值稍微下跌,而在之後幾乎回到 1 的位置。
142 |
143 |  144 |
145 |
146 |
147 | 另一個例子,若無論在任何閥值出現的情況,真陰、真陽的人數都一樣,
148 |
149 | 則這個模型視同無效,因為檢驗一個人是否偽陰偽陽的機率相等於隨機。
150 |
151 |
144 |
145 |
146 |
147 | 另一個例子,若無論在任何閥值出現的情況,真陰、真陽的人數都一樣,
148 |
149 | 則這個模型視同無效,因為檢驗一個人是否偽陰偽陽的機率相等於隨機。
150 |
151 |  152 |
153 |
154 |
155 | 我們可以透過描點的方式畫出 ROC 曲線,就可以從 ROC 曲線中得出 AUC 值,若 AUC 值越大則模型越好。
156 |
157 |
158 |
159 | ## 機器學習的種類
160 |
161 | 1. 學習問題
162 | 1. 監督式學習:所有資料都被標註,給機器去學習與分類,通常來說對機器最簡單,對人類來說最累。
163 | 2. 非監督式學習:所有資料都沒有被標註,透過機器去尋找特徵的學習分式,對機器最困難,誤差較大。
164 | 3. 強化式學習:不標註任何資料,但告訴機器哪步正確,哪步錯誤,讓機器逐步自我修正。
165 | 2. 混合學習問題
166 | 1. 半監督式學習:對少部分資料進行標註,機器透過有標註的資料找出特徵並進行分類,能使非監督式學習的準確率提升。
167 | 2. 自我監督式學習:從一堆沒有 label 標註的資料,訓練出一個監督式模型,然後造出更多 label。
168 | 3. 多實例學習:輸入許多「包」,這些包都含有許多實例,若所有實例都是負例時則包即為負包,若有至少一個實例為正例時,包即為正包。
169 | 3. 推論統計學
170 | 1. 歸納學習:用來辨識汽車的知識可以用來提升辨識卡車的能力,以現有問題的解決模型利用在其他不同但相關的問題上。
171 | 2. 演繹學習:利用廣泛的前提去推論較具體的結論,通常依賴前提是否正確。
172 | 3. 轉導學習:通過觀察特定的訓練樣本,來預測特定測試樣本的方法。
173 | 4. 學習技術
174 | 1. 多任務學習:利用單一一個模型,解決多個問題
175 | 2. 主動學習:從每輪學習迭代中,尋找出一個最不確定的一個或一組樣本,來讓外部反饋者給予回饋。
176 | 3. 線上學習:利用當前的資料來直接更新模型,進而在預測前根據先前的資料給予預測。
177 | 4. 遷移學習:一個模型先訓練一個例子,接著所有模型用這個模型的訓練例子當成起始點,訓練其他的例子。
178 | 5. 集成學習:集成兩個以上合適的模型,接著從這個集成的模型上訓練。。
179 | 6. 聯盟式學習:從各式各樣的自訓練模型中,在不用給自己數據的情況下,也可以進行訓練得到模型。
180 |
181 |
182 |
183 | > Reference Website:
184 | >
185 | > 1. Marketing. (n.d.). *你知道機器學習(Machine Learning),有幾種學習方式嗎?* 伊雲谷eCloudvalley. Retrieved April 5, 2022, from https://www.ecloudvalley.com/zh-hant/machine-learning/
186 | > 2. *自監督學習 self-supervised learning 介紹*. (2021, June 11). 藏字閣. https://jigfopsda.com/zh/posts/2021/self_supervised_learning/
187 | > 3. *多實例學習*. (2021, August 31). 維基百科,自由的百科全書. https://zh.wikipedia.org/wiki/%E5%A4%9A%E7%A4%BA%E4%BE%8B%E5%AD%A6%E4%B9%A0
188 | > 4. *遷移學習*. (2020, September 19). 維基百科,自由的百科全書. https://zh.wikipedia.org/wiki/%E8%BF%81%E7%A7%BB%E5%AD%A6%E4%B9%A0
189 | > 5. *簡要介紹Active Learning(主動學習)思想框架,以及從IF(isolation forest)衍生出來的演算法:FBIF(Feedback-Guided Anomaly Discovery)*. (n.d.). IT人. Retrieved April 5, 2022, from https://iter01.com/420911.html
190 | > 6. Su, S. (2021, December 13). *聯盟式學習 (Federated Learning) - Sherry.AI*. Medium. https://medium.com/sherry-ai/%E8%81%AF%E7%9B%9F%E5%BC%8F%E5%AD%B8%E7%BF%92-federated-learning-b4cc5af7a9c0
--------------------------------------------------------------------------------
/Markdown/Data Preprocessing.md:
--------------------------------------------------------------------------------
1 | # 資料預處理(Data Preprocessing)
2 |
3 | > Reference:
4 | >
5 | > 1. Data Preprocessing by Dr. Tun-Wen Pai
6 |
7 | ## 資料預處理
8 |
9 | 對於一個資料集來說,若數值偏大或偏小的情況下,我們很難去做資料視覺化,甚至資料過大時會讓自然指數過大導致 overflow。
10 |
11 | 故我們希望可以把資料集的值域縮小,有以下幾種方法:
12 |
13 | 1. Z-score normalization
14 | 2. MinMaxScaler
15 | 3. MaxAbsScaler
16 | 4. Robust Scaling
17 | 5. QuantileTrasformation
18 |
19 |
20 |
21 | ### Z-score normalization
22 |
23 | 對於每個資料,我們利用常態分佈將他標準化(Standardization),定義為
24 | $$
25 | x'=\dfrac{x-\overline{x}}{\sigma}
26 | $$
27 | 用這樣的方式就能夠將其值域限縮至 $[-1, 1]$ 之間。
28 |
29 |
30 |
31 | ### MinMaxScaler
32 |
33 | 對於每個資料,我們使用最大與最小值的區間來限縮值域,定義如下:
34 | $$
35 | x' = \dfrac{x-\min(x)}{\max(x)-\min(x)}
36 | $$
37 | 用這樣的方式就能夠將其值域限縮至 $[0, 1]$ 之間。
38 |
39 |
40 |
41 | ### MaxAbsScaler
42 |
43 | 對於每個資料,我們單純使用最大與最小值的區間來限縮值域,定義如下:
44 | $$
45 | x' = \dfrac{x}{\max\{|x|\}}
46 | $$
47 |
48 |
49 | 用這樣的方式就能夠將其值域限縮至 $[-1, 1]$ 之間。
50 |
51 |
52 |
53 | ### Robust Scaling
54 |
55 | Robust Scaling 是一種非線性的限縮方式,使用第三分位與第一分位來進行限縮。
56 |
57 | 前面的方法,以最大值來說,若最大值過大則限縮資料會變小。
58 |
59 | Robust Scaling 優化了這個部分,他沒有特定的值域限縮範圍,但可以對極值有良好的抗噪性,定義如下:
60 | $$
61 | x' = \dfrac{x-Q_2}{(Q_3-Q_1)}
62 | $$
63 |
64 |
65 |
--------------------------------------------------------------------------------
/Markdown/Data Warehouse.md:
--------------------------------------------------------------------------------
1 | # Data Warehouse(資料倉儲)
2 |
3 | >主要的資料來源:
4 | >
5 | >Essentials of Database Management Jeffrey A. Hoffer, Heikki Topi, V. Ramesh
6 | >
7 | >資料倉儲(Data Warehouse, DW) Dr. Tun-Wen Pai
8 |
9 |
10 |
11 | ## 關於資料倉儲
12 |
13 | 資料倉儲具有主題式、經過整合、分析具有時變性、資料不會流失的優勢,用來支援商業智慧,例如分析。
14 |
15 |
16 |
17 | ## 關於資料超市
18 |
19 | 由資料倉儲的資料,分離出一個更具主題式的資料集,稱為資料超市。
20 |
21 |
22 |
23 | ## 資料倉儲的需求
24 |
25 | 從各方蒐集出來的資料通常來說都是支離破碎的(例如:包含編碼、形式不同、格式不一等等)。
26 |
27 | 所以通常一個企業需要的是從這堆支離破碎的資料中經過整合,提供出一個企業想要的簡潔有力的資訊。
28 |
29 | 因此資料倉儲主要就是蒐集這些破碎的資料,然後提供給企業一個高質量的資料。
30 |
31 |
32 |
33 | ## 資料倉儲的開發考慮
34 |
35 | 1. 主題式:僅對特定主題感興趣
36 | 2. 整合性:各式各樣的資料進入資料倉儲都會經過整合成統一格式的資料
37 | 3. 時變性:分析具有時變性,根據不同時間具有不同的分析結果
38 | 4. 穩定性:進入資料倉儲的資料並不會變動。
39 | 5. 摘要整理:進入的資料會盡可能地最佳化資料欄位與維度。
40 | 6. 非標準化:Data Warehouse 使用星狀綱要,因此不是標準化成一個表格做查詢。
41 | 7. 後設資料:可以衍伸出其他的資料變數。
42 | 8. 即時/合適的時間
43 |
44 |
45 |
46 | ## Operational System 與 Informational System
47 |
48 | Operational System 主要負責即時的商業活動運行,例如:訂單整合、預訂系統...
49 |
50 | Operational System 會將這個活動的資料完整的保存下來,但這些資料都是支離破碎的,會需要經過整合。
51 |
52 |
53 |
54 | Informational System 主要被設計來從資料倉儲的資料提供出對於特定時間的快照資料,以利於支援資料探勘、分析等等。
55 |
56 |
57 |
58 | 總歸來說,Operational System 與 Informational System 可以利用以下的表格來比較。
59 |
60 | | | Operational System | Informational System |
61 | | :----------: | :--------------------------------------------: | :------------------------------------: |
62 | | 主要用途 | 即時的商業活動運行 | 支援決策、分析等等 |
63 | | 資料型態 | 進行商業活動得到的數據(客戶、銷售商品...) | 特定時間的快照資料與預測 |
64 | | 給哪些人使用 | 銷售者 | 管理層級的人員、商業分析、客戶... |
65 | | 使用範圍 | 狹窄、易於更新與查詢 | 非常廣、特設、在詢問與分析上非常複雜 |
66 | | 設計目標 | 能夠被存取、能夠完整 | 易於使用與存取 |
67 | | 資料大小 | 在更新與存取時,得到的只有帶有幾列的表格資料 | 定期更新、詢問,通常需要非常大量的資料 |
68 |
69 |
70 |
71 | ## 資料倉儲的資料處理
72 |
73 | 一般遵循 `ETL` 的方式處理,也就是 Extract(萃取)、Transform(轉換)、Load(讀入)。
74 |
75 | 通常來說,會從各式資料源萃取資料,將資料進行整合(轉換)、接著讀入 Data Mart 或 Data Warehouse。
76 |
77 |
78 |
79 | ## 資料倉儲的開發方法
80 |
81 | 主要分成兩種:Top-Down、Buttom-Up。
82 |
83 |
84 |
85 | ### Bill Inmon – Top-down
86 |
87 | 先從各方提取資料,接著經過 `ETL` 後,放入 Data Warehouse。
88 |
89 | 接著從 Data Warehouse 再經過 `ETL` 後,轉成各式各樣的 Data Mart。
90 |
91 |
92 |
93 |
152 |
153 |
154 |
155 | 我們可以透過描點的方式畫出 ROC 曲線,就可以從 ROC 曲線中得出 AUC 值,若 AUC 值越大則模型越好。
156 |
157 |
158 |
159 | ## 機器學習的種類
160 |
161 | 1. 學習問題
162 | 1. 監督式學習:所有資料都被標註,給機器去學習與分類,通常來說對機器最簡單,對人類來說最累。
163 | 2. 非監督式學習:所有資料都沒有被標註,透過機器去尋找特徵的學習分式,對機器最困難,誤差較大。
164 | 3. 強化式學習:不標註任何資料,但告訴機器哪步正確,哪步錯誤,讓機器逐步自我修正。
165 | 2. 混合學習問題
166 | 1. 半監督式學習:對少部分資料進行標註,機器透過有標註的資料找出特徵並進行分類,能使非監督式學習的準確率提升。
167 | 2. 自我監督式學習:從一堆沒有 label 標註的資料,訓練出一個監督式模型,然後造出更多 label。
168 | 3. 多實例學習:輸入許多「包」,這些包都含有許多實例,若所有實例都是負例時則包即為負包,若有至少一個實例為正例時,包即為正包。
169 | 3. 推論統計學
170 | 1. 歸納學習:用來辨識汽車的知識可以用來提升辨識卡車的能力,以現有問題的解決模型利用在其他不同但相關的問題上。
171 | 2. 演繹學習:利用廣泛的前提去推論較具體的結論,通常依賴前提是否正確。
172 | 3. 轉導學習:通過觀察特定的訓練樣本,來預測特定測試樣本的方法。
173 | 4. 學習技術
174 | 1. 多任務學習:利用單一一個模型,解決多個問題
175 | 2. 主動學習:從每輪學習迭代中,尋找出一個最不確定的一個或一組樣本,來讓外部反饋者給予回饋。
176 | 3. 線上學習:利用當前的資料來直接更新模型,進而在預測前根據先前的資料給予預測。
177 | 4. 遷移學習:一個模型先訓練一個例子,接著所有模型用這個模型的訓練例子當成起始點,訓練其他的例子。
178 | 5. 集成學習:集成兩個以上合適的模型,接著從這個集成的模型上訓練。。
179 | 6. 聯盟式學習:從各式各樣的自訓練模型中,在不用給自己數據的情況下,也可以進行訓練得到模型。
180 |
181 |
182 |
183 | > Reference Website:
184 | >
185 | > 1. Marketing. (n.d.). *你知道機器學習(Machine Learning),有幾種學習方式嗎?* 伊雲谷eCloudvalley. Retrieved April 5, 2022, from https://www.ecloudvalley.com/zh-hant/machine-learning/
186 | > 2. *自監督學習 self-supervised learning 介紹*. (2021, June 11). 藏字閣. https://jigfopsda.com/zh/posts/2021/self_supervised_learning/
187 | > 3. *多實例學習*. (2021, August 31). 維基百科,自由的百科全書. https://zh.wikipedia.org/wiki/%E5%A4%9A%E7%A4%BA%E4%BE%8B%E5%AD%A6%E4%B9%A0
188 | > 4. *遷移學習*. (2020, September 19). 維基百科,自由的百科全書. https://zh.wikipedia.org/wiki/%E8%BF%81%E7%A7%BB%E5%AD%A6%E4%B9%A0
189 | > 5. *簡要介紹Active Learning(主動學習)思想框架,以及從IF(isolation forest)衍生出來的演算法:FBIF(Feedback-Guided Anomaly Discovery)*. (n.d.). IT人. Retrieved April 5, 2022, from https://iter01.com/420911.html
190 | > 6. Su, S. (2021, December 13). *聯盟式學習 (Federated Learning) - Sherry.AI*. Medium. https://medium.com/sherry-ai/%E8%81%AF%E7%9B%9F%E5%BC%8F%E5%AD%B8%E7%BF%92-federated-learning-b4cc5af7a9c0
--------------------------------------------------------------------------------
/Markdown/Data Preprocessing.md:
--------------------------------------------------------------------------------
1 | # 資料預處理(Data Preprocessing)
2 |
3 | > Reference:
4 | >
5 | > 1. Data Preprocessing by Dr. Tun-Wen Pai
6 |
7 | ## 資料預處理
8 |
9 | 對於一個資料集來說,若數值偏大或偏小的情況下,我們很難去做資料視覺化,甚至資料過大時會讓自然指數過大導致 overflow。
10 |
11 | 故我們希望可以把資料集的值域縮小,有以下幾種方法:
12 |
13 | 1. Z-score normalization
14 | 2. MinMaxScaler
15 | 3. MaxAbsScaler
16 | 4. Robust Scaling
17 | 5. QuantileTrasformation
18 |
19 |
20 |
21 | ### Z-score normalization
22 |
23 | 對於每個資料,我們利用常態分佈將他標準化(Standardization),定義為
24 | $$
25 | x'=\dfrac{x-\overline{x}}{\sigma}
26 | $$
27 | 用這樣的方式就能夠將其值域限縮至 $[-1, 1]$ 之間。
28 |
29 |
30 |
31 | ### MinMaxScaler
32 |
33 | 對於每個資料,我們使用最大與最小值的區間來限縮值域,定義如下:
34 | $$
35 | x' = \dfrac{x-\min(x)}{\max(x)-\min(x)}
36 | $$
37 | 用這樣的方式就能夠將其值域限縮至 $[0, 1]$ 之間。
38 |
39 |
40 |
41 | ### MaxAbsScaler
42 |
43 | 對於每個資料,我們單純使用最大與最小值的區間來限縮值域,定義如下:
44 | $$
45 | x' = \dfrac{x}{\max\{|x|\}}
46 | $$
47 |
48 |
49 | 用這樣的方式就能夠將其值域限縮至 $[-1, 1]$ 之間。
50 |
51 |
52 |
53 | ### Robust Scaling
54 |
55 | Robust Scaling 是一種非線性的限縮方式,使用第三分位與第一分位來進行限縮。
56 |
57 | 前面的方法,以最大值來說,若最大值過大則限縮資料會變小。
58 |
59 | Robust Scaling 優化了這個部分,他沒有特定的值域限縮範圍,但可以對極值有良好的抗噪性,定義如下:
60 | $$
61 | x' = \dfrac{x-Q_2}{(Q_3-Q_1)}
62 | $$
63 |
64 |
65 |
--------------------------------------------------------------------------------
/Markdown/Data Warehouse.md:
--------------------------------------------------------------------------------
1 | # Data Warehouse(資料倉儲)
2 |
3 | >主要的資料來源:
4 | >
5 | >Essentials of Database Management Jeffrey A. Hoffer, Heikki Topi, V. Ramesh
6 | >
7 | >資料倉儲(Data Warehouse, DW) Dr. Tun-Wen Pai
8 |
9 |
10 |
11 | ## 關於資料倉儲
12 |
13 | 資料倉儲具有主題式、經過整合、分析具有時變性、資料不會流失的優勢,用來支援商業智慧,例如分析。
14 |
15 |
16 |
17 | ## 關於資料超市
18 |
19 | 由資料倉儲的資料,分離出一個更具主題式的資料集,稱為資料超市。
20 |
21 |
22 |
23 | ## 資料倉儲的需求
24 |
25 | 從各方蒐集出來的資料通常來說都是支離破碎的(例如:包含編碼、形式不同、格式不一等等)。
26 |
27 | 所以通常一個企業需要的是從這堆支離破碎的資料中經過整合,提供出一個企業想要的簡潔有力的資訊。
28 |
29 | 因此資料倉儲主要就是蒐集這些破碎的資料,然後提供給企業一個高質量的資料。
30 |
31 |
32 |
33 | ## 資料倉儲的開發考慮
34 |
35 | 1. 主題式:僅對特定主題感興趣
36 | 2. 整合性:各式各樣的資料進入資料倉儲都會經過整合成統一格式的資料
37 | 3. 時變性:分析具有時變性,根據不同時間具有不同的分析結果
38 | 4. 穩定性:進入資料倉儲的資料並不會變動。
39 | 5. 摘要整理:進入的資料會盡可能地最佳化資料欄位與維度。
40 | 6. 非標準化:Data Warehouse 使用星狀綱要,因此不是標準化成一個表格做查詢。
41 | 7. 後設資料:可以衍伸出其他的資料變數。
42 | 8. 即時/合適的時間
43 |
44 |
45 |
46 | ## Operational System 與 Informational System
47 |
48 | Operational System 主要負責即時的商業活動運行,例如:訂單整合、預訂系統...
49 |
50 | Operational System 會將這個活動的資料完整的保存下來,但這些資料都是支離破碎的,會需要經過整合。
51 |
52 |
53 |
54 | Informational System 主要被設計來從資料倉儲的資料提供出對於特定時間的快照資料,以利於支援資料探勘、分析等等。
55 |
56 |
57 |
58 | 總歸來說,Operational System 與 Informational System 可以利用以下的表格來比較。
59 |
60 | | | Operational System | Informational System |
61 | | :----------: | :--------------------------------------------: | :------------------------------------: |
62 | | 主要用途 | 即時的商業活動運行 | 支援決策、分析等等 |
63 | | 資料型態 | 進行商業活動得到的數據(客戶、銷售商品...) | 特定時間的快照資料與預測 |
64 | | 給哪些人使用 | 銷售者 | 管理層級的人員、商業分析、客戶... |
65 | | 使用範圍 | 狹窄、易於更新與查詢 | 非常廣、特設、在詢問與分析上非常複雜 |
66 | | 設計目標 | 能夠被存取、能夠完整 | 易於使用與存取 |
67 | | 資料大小 | 在更新與存取時,得到的只有帶有幾列的表格資料 | 定期更新、詢問,通常需要非常大量的資料 |
68 |
69 |
70 |
71 | ## 資料倉儲的資料處理
72 |
73 | 一般遵循 `ETL` 的方式處理,也就是 Extract(萃取)、Transform(轉換)、Load(讀入)。
74 |
75 | 通常來說,會從各式資料源萃取資料,將資料進行整合(轉換)、接著讀入 Data Mart 或 Data Warehouse。
76 |
77 |
78 |
79 | ## 資料倉儲的開發方法
80 |
81 | 主要分成兩種:Top-Down、Buttom-Up。
82 |
83 |
84 |
85 | ### Bill Inmon – Top-down
86 |
87 | 先從各方提取資料,接著經過 `ETL` 後,放入 Data Warehouse。
88 |
89 | 接著從 Data Warehouse 再經過 `ETL` 後,轉成各式各樣的 Data Mart。
90 |
91 |
92 |
93 |  94 |
95 |
96 |
97 | ### Ralph Kimball – Bottom-up
98 |
99 | 先從各方提取資料,接著經過 `ETL` 後,轉置成 Data Mart 的形式。
100 |
101 | 再經由 `ETL` 的處理後,將這些 Data Mart 合併成一個大的 Data Warehouse。
102 |
103 |
104 |
105 |
94 |
95 |
96 |
97 | ### Ralph Kimball – Bottom-up
98 |
99 | 先從各方提取資料,接著經過 `ETL` 後,轉置成 Data Mart 的形式。
100 |
101 | 再經由 `ETL` 的處理後,將這些 Data Mart 合併成一個大的 Data Warehouse。
102 |
103 |
104 |
105 |  106 |
107 |
108 |
109 | ### 兩個開發方式的優缺點分析
110 |
111 | | 分類 | Top-Down | Buttom-up |
112 | | :------: | :------------------------------------------------: | :----------------------------------------------------------: |
113 | | 問題分解 | 將大問題分解成小問題 | 將小問題解決,並且推廣至大問題 |
114 | | 處理資料 | 處理資料的時候,架構是固定的
106 |
107 |
108 |
109 | ### 兩個開發方式的優缺點分析
110 |
111 | | 分類 | Top-Down | Buttom-up |
112 | | :------: | :------------------------------------------------: | :----------------------------------------------------------: |
113 | | 問題分解 | 將大問題分解成小問題 | 將小問題解決,並且推廣至大問題 |
114 | | 處理資料 | 處理資料的時候,架構是固定的 138 |
139 |
140 |
141 | ## 資料倉儲的資料模型
142 |
143 | 在資料倉儲中,資料模型都是多維度的,包含一個以上的事實表格與多個維度表格。
144 |
145 | 以下介紹三種不同的資料模型:星狀綱要、雪花狀綱要、事實星座綱要。
146 |
147 |
148 |
149 | ### 星狀綱要
150 |
151 | 一個事實表格包含大量不重複的資料,與多個維度表格組成的綱要。
152 |
153 | 是目前最常用的綱要。
154 |
155 |
138 |
139 |
140 |
141 | ## 資料倉儲的資料模型
142 |
143 | 在資料倉儲中,資料模型都是多維度的,包含一個以上的事實表格與多個維度表格。
144 |
145 | 以下介紹三種不同的資料模型:星狀綱要、雪花狀綱要、事實星座綱要。
146 |
147 |
148 |
149 | ### 星狀綱要
150 |
151 | 一個事實表格包含大量不重複的資料,與多個維度表格組成的綱要。
152 |
153 | 是目前最常用的綱要。
154 |
155 |  156 |
157 |
158 |
159 | ### 雪花狀綱要
160 |
161 | 一個事實表格包含大量不重複的資料,與多個維度表格組成的綱要,多個維度可再經過細分分成更多個維度的表格。
162 |
163 |
156 |
157 |
158 |
159 | ### 雪花狀綱要
160 |
161 | 一個事實表格包含大量不重複的資料,與多個維度表格組成的綱要,多個維度可再經過細分分成更多個維度的表格。
162 |
163 |  164 |
165 |
166 |
167 | ### 事實星座綱要
168 |
169 | 由多個事實表格共用維度表格。
170 |
171 |
164 |
165 |
166 |
167 | ### 事實星座綱要
168 |
169 | 由多個事實表格共用維度表格。
170 |
171 |  172 |
173 |
174 |
175 | ## 資料倉儲的儲存架構
176 |
177 | 實際上的儲存可能是關聯式資料庫或資料立方體。
178 |
179 |
180 |
181 | ### 資料立方體 - 切塊與切片
182 |
183 | 由維度與事實組成,具有上捲、下鑽、切塊、切片、轉軸等操作,見以下例子。
184 |
185 |
186 |
187 | ### 操作方式 - 切片
188 |
189 | 例如下圖的資料方塊是由(產品類別、月份、數量)三種維度所組成。
190 |
191 | 若我們想要知道鞋子的資料,就相當於將產品類別固定為鞋子,得到一個降成二維的(月份、數量)資料。
192 |
193 | 
194 |
195 |
196 |
197 | ### 操作方式 - 切塊
198 |
199 | 延續上面的例子,若我們想要知道鞋子與衣服的資料,相當於將鞋子、衣服的立方塊切下來,此時資料依然是三維的。
200 |
201 |
202 |
203 | ### 操作方式 - 下鑽
204 |
205 | 延續上面的例子,若我們將這個鞋子的資料,想要知道某個月份的上旬、中旬或下旬的銷售資料。
206 |
207 | 則我們可以針對於資料立方體的月份下鑽,得到上旬、中旬、下旬的資料,藉此得到更詳細的資料。
208 |
209 |
210 |
211 | ### 操作方式 - 上捲
212 |
213 | 延續上面的例子,若我們想要知道整年的銷售資料,則我們可以針對於資料立方體的月份上捲,得到更為概觀的資料。
214 |
215 |
216 |
217 | ### 操作方式 - 轉軸
218 |
219 | 我們可以將立方體做旋轉,得到不同視角的資料。
220 |
221 |
222 |
223 |
224 |
225 | ## 資料倉儲的查詢處理
226 |
227 | - 若是為了快速查詢,在記憶空間充裕的情況下,可能會根據這些資料先建立出可能查詢的方式,
228 |
229 | 可藉由目前有的維度欄位慢慢上推整合合併成一個包含所有維度的資料。
230 |
231 | - 多維度的資料與一般的關聯式資料庫相比,一般的關聯式資料庫只能慢慢地計算累積,而多維度資料庫具有更好的效能。
232 |
--------------------------------------------------------------------------------
/Markdown/Decision Tree.md:
--------------------------------------------------------------------------------
1 | # Decision Tree(決策樹)
2 |
3 | > 主要參考資料:
4 | >
5 | > 決策樹 (Decision Tree) Dr. Tun-Wen Pai
6 | >
7 | > Business intelligence and data mining Anil K. Maheshwari, Ph.D.
8 |
9 |
10 |
11 | ## 決策樹
12 |
13 | 決策樹用來對於一個樹狀事件給出一條路線引導出一個決策,例如是否借款,或者更複雜的決策系統。
14 |
15 |
16 |
17 | 舉一個生活化的例子,若要決定是否要出遊,則我們可以畫出以下的樹狀事件。
18 |
19 |
172 |
173 |
174 |
175 | ## 資料倉儲的儲存架構
176 |
177 | 實際上的儲存可能是關聯式資料庫或資料立方體。
178 |
179 |
180 |
181 | ### 資料立方體 - 切塊與切片
182 |
183 | 由維度與事實組成,具有上捲、下鑽、切塊、切片、轉軸等操作,見以下例子。
184 |
185 |
186 |
187 | ### 操作方式 - 切片
188 |
189 | 例如下圖的資料方塊是由(產品類別、月份、數量)三種維度所組成。
190 |
191 | 若我們想要知道鞋子的資料,就相當於將產品類別固定為鞋子,得到一個降成二維的(月份、數量)資料。
192 |
193 | 
194 |
195 |
196 |
197 | ### 操作方式 - 切塊
198 |
199 | 延續上面的例子,若我們想要知道鞋子與衣服的資料,相當於將鞋子、衣服的立方塊切下來,此時資料依然是三維的。
200 |
201 |
202 |
203 | ### 操作方式 - 下鑽
204 |
205 | 延續上面的例子,若我們將這個鞋子的資料,想要知道某個月份的上旬、中旬或下旬的銷售資料。
206 |
207 | 則我們可以針對於資料立方體的月份下鑽,得到上旬、中旬、下旬的資料,藉此得到更詳細的資料。
208 |
209 |
210 |
211 | ### 操作方式 - 上捲
212 |
213 | 延續上面的例子,若我們想要知道整年的銷售資料,則我們可以針對於資料立方體的月份上捲,得到更為概觀的資料。
214 |
215 |
216 |
217 | ### 操作方式 - 轉軸
218 |
219 | 我們可以將立方體做旋轉,得到不同視角的資料。
220 |
221 |
222 |
223 |
224 |
225 | ## 資料倉儲的查詢處理
226 |
227 | - 若是為了快速查詢,在記憶空間充裕的情況下,可能會根據這些資料先建立出可能查詢的方式,
228 |
229 | 可藉由目前有的維度欄位慢慢上推整合合併成一個包含所有維度的資料。
230 |
231 | - 多維度的資料與一般的關聯式資料庫相比,一般的關聯式資料庫只能慢慢地計算累積,而多維度資料庫具有更好的效能。
232 |
--------------------------------------------------------------------------------
/Markdown/Decision Tree.md:
--------------------------------------------------------------------------------
1 | # Decision Tree(決策樹)
2 |
3 | > 主要參考資料:
4 | >
5 | > 決策樹 (Decision Tree) Dr. Tun-Wen Pai
6 | >
7 | > Business intelligence and data mining Anil K. Maheshwari, Ph.D.
8 |
9 |
10 |
11 | ## 決策樹
12 |
13 | 決策樹用來對於一個樹狀事件給出一條路線引導出一個決策,例如是否借款,或者更複雜的決策系統。
14 |
15 |
16 |
17 | 舉一個生活化的例子,若要決定是否要出遊,則我們可以畫出以下的樹狀事件。
18 |
19 |  20 |
21 |
22 |
23 | 可以發現從「是否出遊」到任意一種出遊決策都是唯一路徑,換言之,在這棵樹上共有 4 條路徑。
24 |
25 | 對於一個決策系統來說也可能會很複雜,例如判斷手寫數字時,龐大而精確的決策系統能夠有效的幫助我們判斷出手寫的數字。
26 |
27 |
28 |
29 |
30 |
31 | ## 使用決策樹的優點與缺點
32 |
33 | > Reference website:
34 | >
35 | > 1. https://scikit-learn.org/stable/modules/tree.html
36 | > 2. https://zh.wikipedia.org/wiki/%E5%86%B3%E7%AD%96%E6%A0%91%E5%AD%A6%E4%B9%A0
37 |
38 |
39 |
40 | - 優點
41 |
42 | 1. 樹可以被視覺化,方便理解
43 | 2. 資料需要被整理,資料的空值不被接受
44 | 3. 任何作出決策的操作都取決於樹的節點數量,且為對數時間複雜度
45 | 4. 支援輸出一種以上的結果(multi-output)
46 | 5. 使用白箱模型,因為決策樹可以簡單解釋決策的來源與邏輯
47 | 6. 可用統計測試來驗證模型
48 | 7. 對於噪聲有很強的控制性
49 |
50 |
51 |
52 | - 缺點
53 |
54 | 1. 可能會 overfitting
55 | 2. 因為可能會 overfitting,所以不好實行外推
56 | 3. 優化決策樹是 NP-Complete 問題,優化決策樹無法在多項式時間內解決
57 | 4. 有些概念沒有辦法清楚解釋(例如 XOR)
58 | 5. 資料集的平衡很重要,否則樹可能會被一些資料所支配,產生出帶有偏見的決策樹
59 |
60 |
61 |
62 | ## 建立決策樹的方式
63 |
64 | 我們以一個出遊的資料集為例,如下圖。
65 |
66 |
20 |
21 |
22 |
23 | 可以發現從「是否出遊」到任意一種出遊決策都是唯一路徑,換言之,在這棵樹上共有 4 條路徑。
24 |
25 | 對於一個決策系統來說也可能會很複雜,例如判斷手寫數字時,龐大而精確的決策系統能夠有效的幫助我們判斷出手寫的數字。
26 |
27 |
28 |
29 |
30 |
31 | ## 使用決策樹的優點與缺點
32 |
33 | > Reference website:
34 | >
35 | > 1. https://scikit-learn.org/stable/modules/tree.html
36 | > 2. https://zh.wikipedia.org/wiki/%E5%86%B3%E7%AD%96%E6%A0%91%E5%AD%A6%E4%B9%A0
37 |
38 |
39 |
40 | - 優點
41 |
42 | 1. 樹可以被視覺化,方便理解
43 | 2. 資料需要被整理,資料的空值不被接受
44 | 3. 任何作出決策的操作都取決於樹的節點數量,且為對數時間複雜度
45 | 4. 支援輸出一種以上的結果(multi-output)
46 | 5. 使用白箱模型,因為決策樹可以簡單解釋決策的來源與邏輯
47 | 6. 可用統計測試來驗證模型
48 | 7. 對於噪聲有很強的控制性
49 |
50 |
51 |
52 | - 缺點
53 |
54 | 1. 可能會 overfitting
55 | 2. 因為可能會 overfitting,所以不好實行外推
56 | 3. 優化決策樹是 NP-Complete 問題,優化決策樹無法在多項式時間內解決
57 | 4. 有些概念沒有辦法清楚解釋(例如 XOR)
58 | 5. 資料集的平衡很重要,否則樹可能會被一些資料所支配,產生出帶有偏見的決策樹
59 |
60 |
61 |
62 | ## 建立決策樹的方式
63 |
64 | 我們以一個出遊的資料集為例,如下圖。
65 |
66 |  67 |
68 |
69 |
70 | 決策樹是一種層級式的分支結構,我們可以分割表格,來計算錯誤合計。
71 |
72 | 我們將現有資訊加上規則,可以得到以下的表格,可以看出錯誤統計均是 4/18,因此我們可以任意選擇一個來建樹。
73 |
74 |
67 |
68 |
69 |
70 | 決策樹是一種層級式的分支結構,我們可以分割表格,來計算錯誤合計。
71 |
72 | 我們將現有資訊加上規則,可以得到以下的表格,可以看出錯誤統計均是 4/18,因此我們可以任意選擇一個來建樹。
73 |
74 |  75 |
76 | 例如我們選擇天氣,可以得到以下的事件樹狀圖。
77 |
78 | 
79 |
80 | 按照同樣方式進行推廣,可以得到以下的樹狀結構。
81 |
82 | 
83 |
84 |
85 |
86 | 這樣有點智障,因為晴天跟陰天應該可以合併,且冷跟溫和也該可以合併。
87 |
88 | 一個決策樹主要基於分支準則、停止條件與修剪而有所不同,也因此衍伸出了決策樹演算法。
89 |
90 |
91 |
92 | ## 決策樹的 Overfitting 問題
93 |
94 | 決策樹其中一個問題就是很容易 overfitting。
95 |
96 |
97 |
98 | ### Overfitting 簡介
99 |
100 | Overfitting 就是過度擬合,也就是對於一個訓練資料集,只對資料集的資料有作用,不利於推廣更多資料。
101 |
102 | 如果看不懂上面的文字,可以看下面找到的[一張圖](https://pbs.twimg.com/media/Ef5yDj2X0AIkHEe.jpg)。
103 |
104 |
75 |
76 | 例如我們選擇天氣,可以得到以下的事件樹狀圖。
77 |
78 | 
79 |
80 | 按照同樣方式進行推廣,可以得到以下的樹狀結構。
81 |
82 | 
83 |
84 |
85 |
86 | 這樣有點智障,因為晴天跟陰天應該可以合併,且冷跟溫和也該可以合併。
87 |
88 | 一個決策樹主要基於分支準則、停止條件與修剪而有所不同,也因此衍伸出了決策樹演算法。
89 |
90 |
91 |
92 | ## 決策樹的 Overfitting 問題
93 |
94 | 決策樹其中一個問題就是很容易 overfitting。
95 |
96 |
97 |
98 | ### Overfitting 簡介
99 |
100 | Overfitting 就是過度擬合,也就是對於一個訓練資料集,只對資料集的資料有作用,不利於推廣更多資料。
101 |
102 | 如果看不懂上面的文字,可以看下面找到的[一張圖](https://pbs.twimg.com/media/Ef5yDj2X0AIkHEe.jpg)。
103 |
104 |  105 |
106 | 由於只對資料集的資料有作用,因此若在預判不是資料集的資料時,很容易出現預判失敗的問題。
107 |
108 |
109 |
110 | ### 迴避 Overfitting 的方法
111 |
112 | 迴避 Overfitting 可以使用剪枝來迴避,分成先剪枝(prepruning)與後剪枝(postpruning)。
113 |
114 | 1. 先剪枝:可以設定一個條件,使得後面的子樹停止構建,當前的節點變成葉節點。
115 |
116 | 2. 後剪枝:先建照一個完整的決策樹,再將這個樹進行修剪。
117 |
118 | 當然,資料集也很重要,所以如同 data mining 一樣,需要對資料集的品質有所把持。
119 |
120 |
121 |
122 | ## 決策樹演算法
123 |
124 | 主要分成:ID3、CART、CHAID,這份筆記主要會講解 ID3、CART 演算法。
125 |
126 |
127 |
128 | ## ID3 演算法
129 |
130 | ### Entropy
131 |
132 | Entropy(資訊熵),一種量化資料同源的數值,介於 0 ~ 1 之間。
133 |
134 | 若一個資料是絕對同源,則 Entropy = 0,若一個資料絕對異源,則 Entropy = 1。
135 |
136 | 定義一個樣本的 Entropy 為:
137 | $$
138 | Entropy(S) = -\sum_{i} P(x_i)\log_2(P(x_i)) - \sum_{i} Q(x_i) \log_2(Q(x_i))
139 | $$
140 | 其中 $\displaystyle \lim_{p \rightarrow 0} p\log p = 0$。
141 |
142 |
143 |
144 | ### Information Gain
145 |
146 | Information Gain(訊息增益)為資訊熵經過分割 Attribute 後所減少的數值,介於 0 ~ 1 之間。
147 |
148 | 當我們在分割樹的時候,我們會選擇 Infomation Gain 大的來當作我們的父節點或根節點,若 Entropy = 0 時則為子節點。
149 |
150 | 我們可以定義一個樣本在分割成一個 Attribute 之後的 Infomation Gain 為
151 | $$
152 | IG(S, A) = Entropy(S) - \sum_{v\in D_A} \dfrac{|S_v|}{|S|} Entropy(S_v)
153 | $$
154 |
155 |
156 | ### 優缺點
157 |
158 | - 優點:
159 | 1. 好理解決策的邏輯,因為可以畫成一棵樹
160 | 2. 建立迅速
161 | 3. 建立較小的樹
162 | 4. 只需要足夠數量的測試資料
163 | 5. 只需要測試足夠多的屬性來讓所有資料都被分類
164 | 6. 在分類測試資料時可以被修剪,利於減少測試數量
165 | 7. 使用整個資料集,搜索空間完整
166 | - 缺點
167 | 1. 會因為測試資料過小導致 over-fitted 跟 over-classified,不利於推廣預測。
168 | 2. 每次預測只測試一個 Attribute。
169 | 3. 測試連續資料可能會導致大量運算,產生大量的樹。
170 |
171 |
172 |
173 | ### 範例
174 |
175 | 以這個資料為範例,利用 ID3 來建立決策樹。
176 |
177 |
105 |
106 | 由於只對資料集的資料有作用,因此若在預判不是資料集的資料時,很容易出現預判失敗的問題。
107 |
108 |
109 |
110 | ### 迴避 Overfitting 的方法
111 |
112 | 迴避 Overfitting 可以使用剪枝來迴避,分成先剪枝(prepruning)與後剪枝(postpruning)。
113 |
114 | 1. 先剪枝:可以設定一個條件,使得後面的子樹停止構建,當前的節點變成葉節點。
115 |
116 | 2. 後剪枝:先建照一個完整的決策樹,再將這個樹進行修剪。
117 |
118 | 當然,資料集也很重要,所以如同 data mining 一樣,需要對資料集的品質有所把持。
119 |
120 |
121 |
122 | ## 決策樹演算法
123 |
124 | 主要分成:ID3、CART、CHAID,這份筆記主要會講解 ID3、CART 演算法。
125 |
126 |
127 |
128 | ## ID3 演算法
129 |
130 | ### Entropy
131 |
132 | Entropy(資訊熵),一種量化資料同源的數值,介於 0 ~ 1 之間。
133 |
134 | 若一個資料是絕對同源,則 Entropy = 0,若一個資料絕對異源,則 Entropy = 1。
135 |
136 | 定義一個樣本的 Entropy 為:
137 | $$
138 | Entropy(S) = -\sum_{i} P(x_i)\log_2(P(x_i)) - \sum_{i} Q(x_i) \log_2(Q(x_i))
139 | $$
140 | 其中 $\displaystyle \lim_{p \rightarrow 0} p\log p = 0$。
141 |
142 |
143 |
144 | ### Information Gain
145 |
146 | Information Gain(訊息增益)為資訊熵經過分割 Attribute 後所減少的數值,介於 0 ~ 1 之間。
147 |
148 | 當我們在分割樹的時候,我們會選擇 Infomation Gain 大的來當作我們的父節點或根節點,若 Entropy = 0 時則為子節點。
149 |
150 | 我們可以定義一個樣本在分割成一個 Attribute 之後的 Infomation Gain 為
151 | $$
152 | IG(S, A) = Entropy(S) - \sum_{v\in D_A} \dfrac{|S_v|}{|S|} Entropy(S_v)
153 | $$
154 |
155 |
156 | ### 優缺點
157 |
158 | - 優點:
159 | 1. 好理解決策的邏輯,因為可以畫成一棵樹
160 | 2. 建立迅速
161 | 3. 建立較小的樹
162 | 4. 只需要足夠數量的測試資料
163 | 5. 只需要測試足夠多的屬性來讓所有資料都被分類
164 | 6. 在分類測試資料時可以被修剪,利於減少測試數量
165 | 7. 使用整個資料集,搜索空間完整
166 | - 缺點
167 | 1. 會因為測試資料過小導致 over-fitted 跟 over-classified,不利於推廣預測。
168 | 2. 每次預測只測試一個 Attribute。
169 | 3. 測試連續資料可能會導致大量運算,產生大量的樹。
170 |
171 |
172 |
173 | ### 範例
174 |
175 | 以這個資料為範例,利用 ID3 來建立決策樹。
176 |
177 |  178 |
179 | 首先先計算 $Entropy(Play)$,也就是
180 |
181 | $Entropy(Play) = -\dfrac{9}{14}\log_2 \dfrac{9}{14} - (\dfrac{5}{14}\log_2 \dfrac{5}{14}) \approx 0.94$
182 |
183 |
184 |
185 | 接著可以考慮
186 |
187 | 1. 三種不同類型的 Outlook 所產生出來的 $Entropy(Play, Outlook)$
188 |
189 | $Entropy(Sunny) = -\dfrac{2}{5}\log_2(\dfrac{2}{5}) - \dfrac{3}{5}\log_2(\dfrac{3}{5}) \approx 0.97$
190 |
191 | $Entropy(Overcast) = -\dfrac{4}{4}\log_2(\dfrac{4}{4}) - \dfrac{0}{4}\log_2(\dfrac{0}{4}) = 0$
192 |
193 | $Entropy(Rainy) = -\dfrac{3}{5}\log_2(\dfrac{3}{5}) - \dfrac{2}{5}\log_2(\dfrac{2}{5}) \approx 0.97$
194 |
195 | $Entropy(Play,Outlook) = \dfrac{5}{14}Entropy(Sunny) + \dfrac{4}{14}Entropy(Overcast) + \dfrac{5}{14}Entropy(Rainy) = 0.6936$
196 |
197 | 2. 三種不同類型的 Temperature 所產生出來的 $Entropy(Play, Temperature)$
198 |
199 | $Entropy(Hot) = -\dfrac{2}{4}\log_2(\dfrac{2}{4}) - \dfrac{2}{4}\log_2(\dfrac{2}{4})= 1$
200 |
201 | $Entropy(Mild) = -\dfrac{2}{6}\log_2(\dfrac{2}{6}) - \dfrac{4}{6}\log_2(\dfrac{4}{6}) \approx 0.92$
202 |
203 | $Entropy(Cold) = -\dfrac{3}{4}\log_2(\dfrac{3}{4})-\dfrac{1}{4}\log_2(\dfrac{1}{4}) \approx 0.81$
204 |
205 | $Entropy(Play, Temperature) \approx 0.911$
206 |
207 | 3. 兩種不同類型的 Humidity 所產生出來的 $Entropy(Play, Humidity)$
208 |
209 | $Entropy(High) = -\dfrac{3}{7}\log_2(\dfrac{3}{7})-\dfrac{4}{7}\log_2(\dfrac{4}{7}) \approx 0.985$
210 |
211 | $Entropy(Normal) = -\dfrac{6}{7}\log_2(\dfrac{6}{7})-\dfrac{6}{7}\log_2(\dfrac{6}{7}) \approx 0.592$
212 |
213 | $Entropy(Play, Humidity) \approx 0.7885$
214 |
215 | 4. 兩種不同類型的 Wind 所產生出來的 $Entropy(Play, Wind)$
216 |
217 | $Entropy(True) = -\dfrac{3}{6}\log_2(\dfrac{3}{6})-\dfrac{3}{6}\log_2(\dfrac{3}{6}) = 1$
218 |
219 | $Entropy(False) = -\dfrac{6}{8}\log_2(\dfrac{6}{8})-\dfrac{2}{8}\log_2(\dfrac{2}{8}) \approx 0.811$
220 |
221 | $Entropy(Play, Wind) \approx \dfrac{6}{14}\times 1 + \dfrac{8}{14}\times 0.811 \approx 0.892$
222 |
223 |
224 |
225 | 我們可以分別算出,分支這四種類型所產生的 $Information Gain$,得到
226 |
227 | $IG(Outlook) = Entropy(Play) - Entropy(Play, Outlook) = 0.2464$
228 |
229 | $IG(Temperature) = Entropy(Play) - Entropy(Play, Temperature) \approx 0.029$
230 |
231 | $IG(Humidity) = Entropy(Play) - Entropy(Play, Humidity) \approx 0.1515$
232 |
233 | $IG(Wind) = Entropy(Play) - Entropy(Play, Wind) \approx 0.048$
234 |
235 | 我們挑 $IG$ 最高的當作分支條件,所以 $Outlook$ 先分支,如圖。
236 |
237 |
178 |
179 | 首先先計算 $Entropy(Play)$,也就是
180 |
181 | $Entropy(Play) = -\dfrac{9}{14}\log_2 \dfrac{9}{14} - (\dfrac{5}{14}\log_2 \dfrac{5}{14}) \approx 0.94$
182 |
183 |
184 |
185 | 接著可以考慮
186 |
187 | 1. 三種不同類型的 Outlook 所產生出來的 $Entropy(Play, Outlook)$
188 |
189 | $Entropy(Sunny) = -\dfrac{2}{5}\log_2(\dfrac{2}{5}) - \dfrac{3}{5}\log_2(\dfrac{3}{5}) \approx 0.97$
190 |
191 | $Entropy(Overcast) = -\dfrac{4}{4}\log_2(\dfrac{4}{4}) - \dfrac{0}{4}\log_2(\dfrac{0}{4}) = 0$
192 |
193 | $Entropy(Rainy) = -\dfrac{3}{5}\log_2(\dfrac{3}{5}) - \dfrac{2}{5}\log_2(\dfrac{2}{5}) \approx 0.97$
194 |
195 | $Entropy(Play,Outlook) = \dfrac{5}{14}Entropy(Sunny) + \dfrac{4}{14}Entropy(Overcast) + \dfrac{5}{14}Entropy(Rainy) = 0.6936$
196 |
197 | 2. 三種不同類型的 Temperature 所產生出來的 $Entropy(Play, Temperature)$
198 |
199 | $Entropy(Hot) = -\dfrac{2}{4}\log_2(\dfrac{2}{4}) - \dfrac{2}{4}\log_2(\dfrac{2}{4})= 1$
200 |
201 | $Entropy(Mild) = -\dfrac{2}{6}\log_2(\dfrac{2}{6}) - \dfrac{4}{6}\log_2(\dfrac{4}{6}) \approx 0.92$
202 |
203 | $Entropy(Cold) = -\dfrac{3}{4}\log_2(\dfrac{3}{4})-\dfrac{1}{4}\log_2(\dfrac{1}{4}) \approx 0.81$
204 |
205 | $Entropy(Play, Temperature) \approx 0.911$
206 |
207 | 3. 兩種不同類型的 Humidity 所產生出來的 $Entropy(Play, Humidity)$
208 |
209 | $Entropy(High) = -\dfrac{3}{7}\log_2(\dfrac{3}{7})-\dfrac{4}{7}\log_2(\dfrac{4}{7}) \approx 0.985$
210 |
211 | $Entropy(Normal) = -\dfrac{6}{7}\log_2(\dfrac{6}{7})-\dfrac{6}{7}\log_2(\dfrac{6}{7}) \approx 0.592$
212 |
213 | $Entropy(Play, Humidity) \approx 0.7885$
214 |
215 | 4. 兩種不同類型的 Wind 所產生出來的 $Entropy(Play, Wind)$
216 |
217 | $Entropy(True) = -\dfrac{3}{6}\log_2(\dfrac{3}{6})-\dfrac{3}{6}\log_2(\dfrac{3}{6}) = 1$
218 |
219 | $Entropy(False) = -\dfrac{6}{8}\log_2(\dfrac{6}{8})-\dfrac{2}{8}\log_2(\dfrac{2}{8}) \approx 0.811$
220 |
221 | $Entropy(Play, Wind) \approx \dfrac{6}{14}\times 1 + \dfrac{8}{14}\times 0.811 \approx 0.892$
222 |
223 |
224 |
225 | 我們可以分別算出,分支這四種類型所產生的 $Information Gain$,得到
226 |
227 | $IG(Outlook) = Entropy(Play) - Entropy(Play, Outlook) = 0.2464$
228 |
229 | $IG(Temperature) = Entropy(Play) - Entropy(Play, Temperature) \approx 0.029$
230 |
231 | $IG(Humidity) = Entropy(Play) - Entropy(Play, Humidity) \approx 0.1515$
232 |
233 | $IG(Wind) = Entropy(Play) - Entropy(Play, Wind) \approx 0.048$
234 |
235 | 我們挑 $IG$ 最高的當作分支條件,所以 $Outlook$ 先分支,如圖。
236 |
237 |  238 |
239 | 接著我們考慮 Sunny,得到
240 |
241 | 1. 三種不同類型的 temperature。
242 |
243 | $Entropy(Hot) = - \dfrac{0}{2}\log_2\dfrac{0}{2} - \dfrac{2}{2}\log_2\dfrac{2}{2} = 0$。
244 |
245 | $Entropy(Mild) = -\dfrac{1}{2}\log_2\dfrac{1}{2} - \dfrac{1}{2}\log_2\dfrac{1}{2} = 1$
246 |
247 | $Entropy(Cold) = -\dfrac{1}{1}\log_2\dfrac{1}{1} - \dfrac{0}{1}\log_2\dfrac{0}{1} = 0$
248 |
249 | 可以得到 $\displaystyle Entropy(Sunny, Temperature) = \sum_{i}P(x_i)Entropy(x_i) = \dfrac{2}{5}$
250 |
251 | 2. 兩種不同類型的 humidity。
252 |
253 | $Entropy(High) = -\dfrac{0}{3}\log_2\dfrac{0}{3}-\dfrac{3}{3}\log_2\dfrac{3}{3} = 0$
254 |
255 | $Entropy(Normal) = -\dfrac{0}{2}\log_2\dfrac{0}{2} - \dfrac{2}{2}\log_2\dfrac{2}{2} = 0$
256 |
257 | 可以得到 $\displaystyle Entropy(Sunny, Humidity) = \sum_{i}P(x_i)Entropy(x_i) = 0$
258 |
259 | 3. 兩種不同類型的 wind。
260 |
261 | $Entropy(True) = -\dfrac{1}{2}\log_2\dfrac{1}{2} - \dfrac{1}{2}\log_2\dfrac{1}{2} = 1$
262 |
263 | $Entropy(False) = -\dfrac{1}{3}\log_2\dfrac{1}{3}-\dfrac{2}{3}\log_2\dfrac{2}{3} = 0.918$
264 |
265 | 可以得到 $\displaystyle Entropy(Sunny, Wind) = \sum_{i}P(x_i)Entropy(x_i) = 0.9508$
266 |
267 | 可以分別算出這三種分支的 Infomation Gain,也就是
268 |
269 | $IG(Temperature) = Entropy(Sunny) - Entropy(Sunny, Temperature) = 0.57$
270 |
271 | $IG(Humidity) = Entropy(Sunny) - Entropy(Sunny, Humidity) = 0.97$
272 |
273 | $IG(Wind) = Entropy(Sunny) - Entropy(Sunny, Wind) = 0.0192$
274 |
275 | 選擇 Infomation Gain 最高的來分支,得到下圖。
276 |
277 |
238 |
239 | 接著我們考慮 Sunny,得到
240 |
241 | 1. 三種不同類型的 temperature。
242 |
243 | $Entropy(Hot) = - \dfrac{0}{2}\log_2\dfrac{0}{2} - \dfrac{2}{2}\log_2\dfrac{2}{2} = 0$。
244 |
245 | $Entropy(Mild) = -\dfrac{1}{2}\log_2\dfrac{1}{2} - \dfrac{1}{2}\log_2\dfrac{1}{2} = 1$
246 |
247 | $Entropy(Cold) = -\dfrac{1}{1}\log_2\dfrac{1}{1} - \dfrac{0}{1}\log_2\dfrac{0}{1} = 0$
248 |
249 | 可以得到 $\displaystyle Entropy(Sunny, Temperature) = \sum_{i}P(x_i)Entropy(x_i) = \dfrac{2}{5}$
250 |
251 | 2. 兩種不同類型的 humidity。
252 |
253 | $Entropy(High) = -\dfrac{0}{3}\log_2\dfrac{0}{3}-\dfrac{3}{3}\log_2\dfrac{3}{3} = 0$
254 |
255 | $Entropy(Normal) = -\dfrac{0}{2}\log_2\dfrac{0}{2} - \dfrac{2}{2}\log_2\dfrac{2}{2} = 0$
256 |
257 | 可以得到 $\displaystyle Entropy(Sunny, Humidity) = \sum_{i}P(x_i)Entropy(x_i) = 0$
258 |
259 | 3. 兩種不同類型的 wind。
260 |
261 | $Entropy(True) = -\dfrac{1}{2}\log_2\dfrac{1}{2} - \dfrac{1}{2}\log_2\dfrac{1}{2} = 1$
262 |
263 | $Entropy(False) = -\dfrac{1}{3}\log_2\dfrac{1}{3}-\dfrac{2}{3}\log_2\dfrac{2}{3} = 0.918$
264 |
265 | 可以得到 $\displaystyle Entropy(Sunny, Wind) = \sum_{i}P(x_i)Entropy(x_i) = 0.9508$
266 |
267 | 可以分別算出這三種分支的 Infomation Gain,也就是
268 |
269 | $IG(Temperature) = Entropy(Sunny) - Entropy(Sunny, Temperature) = 0.57$
270 |
271 | $IG(Humidity) = Entropy(Sunny) - Entropy(Sunny, Humidity) = 0.97$
272 |
273 | $IG(Wind) = Entropy(Sunny) - Entropy(Sunny, Wind) = 0.0192$
274 |
275 | 選擇 Infomation Gain 最高的來分支,得到下圖。
276 |
277 |  278 |
279 |
280 |
281 | 接著我們考慮 Rainy,得到
282 |
283 | 1. 兩種不同類型的 temperature。
284 |
285 | $Entropy(Mild) = -\dfrac{2}{3}\log_2\dfrac{2}{3}-\dfrac{1}{3}\log_2\dfrac{1}{3} = 0.918$
286 |
287 | $Entropy(Cold) = -\dfrac{1}{2}\log_2\dfrac{1}{2} - \dfrac{1}{2}\log_2\dfrac{1}{2} = 1$
288 |
289 | $Entropy(Rainy, Temperature) = \dfrac{3}{5}Entropy(Mild) + \dfrac{2}{5}Entropy(Cold) = 0.951$
290 |
291 | 2. 兩種不同類型的 humidity。
292 |
293 | $Entropy(High) = -\dfrac{1}{2}\log_2\dfrac{1}{2} - \dfrac{1}{2}\log_2\dfrac{1}{2} = 1$
294 |
295 | $Entropy(Normal) = -\dfrac{2}{3}\log_2\dfrac{2}{3} - \dfrac{1}{3}\log_2\dfrac{1}{3} = 0.918$
296 |
297 | $Entropy(Rainy, Humidity) = \dfrac{2}{5}Entropy(High) + \dfrac{3}{5}Entropy(Normal) = 0.951$
298 |
299 | 3. 兩種不同類型的 wind。
300 |
301 | $Entropy(True) = -\dfrac{0}{2}\log_2\dfrac{0}{2} - \dfrac{2}{2}\log_2\dfrac{2}{2} = 0$
302 |
303 | $Entropy(False) = -\dfrac{3}{3}\log_2\dfrac{3}{3}-\dfrac{0}{3}\log_2\dfrac{0}{3} = 0$
304 |
305 | $Entropy(Rainy, Wind) = \dfrac{2}{5}Entropy(True) + \dfrac{3}{5}Entropy(False) = 0$
306 |
307 | 可以分別算出這三種分支的 Information Gain,如下:
308 |
309 | $IG(Temperature) = Entropy(Rainy) - Entropy(Rainy, Temperature) = 0.97 - 0.951 = 0.019$
310 |
311 | $IG(Humidity) = Entropy(Rainy) - Entropy(Rainy, Humidity) = 0.97 - 0.951 = 0.019$
312 |
313 | $IG(Wind) = Entropy(Rainy), Entropy(Rainy, Wind) = 0.97 - 0 = 0.97$
314 |
315 | 選擇 Information Gain 大的當作分支,得到下圖。
316 |
317 |
278 |
279 |
280 |
281 | 接著我們考慮 Rainy,得到
282 |
283 | 1. 兩種不同類型的 temperature。
284 |
285 | $Entropy(Mild) = -\dfrac{2}{3}\log_2\dfrac{2}{3}-\dfrac{1}{3}\log_2\dfrac{1}{3} = 0.918$
286 |
287 | $Entropy(Cold) = -\dfrac{1}{2}\log_2\dfrac{1}{2} - \dfrac{1}{2}\log_2\dfrac{1}{2} = 1$
288 |
289 | $Entropy(Rainy, Temperature) = \dfrac{3}{5}Entropy(Mild) + \dfrac{2}{5}Entropy(Cold) = 0.951$
290 |
291 | 2. 兩種不同類型的 humidity。
292 |
293 | $Entropy(High) = -\dfrac{1}{2}\log_2\dfrac{1}{2} - \dfrac{1}{2}\log_2\dfrac{1}{2} = 1$
294 |
295 | $Entropy(Normal) = -\dfrac{2}{3}\log_2\dfrac{2}{3} - \dfrac{1}{3}\log_2\dfrac{1}{3} = 0.918$
296 |
297 | $Entropy(Rainy, Humidity) = \dfrac{2}{5}Entropy(High) + \dfrac{3}{5}Entropy(Normal) = 0.951$
298 |
299 | 3. 兩種不同類型的 wind。
300 |
301 | $Entropy(True) = -\dfrac{0}{2}\log_2\dfrac{0}{2} - \dfrac{2}{2}\log_2\dfrac{2}{2} = 0$
302 |
303 | $Entropy(False) = -\dfrac{3}{3}\log_2\dfrac{3}{3}-\dfrac{0}{3}\log_2\dfrac{0}{3} = 0$
304 |
305 | $Entropy(Rainy, Wind) = \dfrac{2}{5}Entropy(True) + \dfrac{3}{5}Entropy(False) = 0$
306 |
307 | 可以分別算出這三種分支的 Information Gain,如下:
308 |
309 | $IG(Temperature) = Entropy(Rainy) - Entropy(Rainy, Temperature) = 0.97 - 0.951 = 0.019$
310 |
311 | $IG(Humidity) = Entropy(Rainy) - Entropy(Rainy, Humidity) = 0.97 - 0.951 = 0.019$
312 |
313 | $IG(Wind) = Entropy(Rainy), Entropy(Rainy, Wind) = 0.97 - 0 = 0.97$
314 |
315 | 選擇 Information Gain 大的當作分支,得到下圖。
316 |
317 |  318 |
319 | 此時決策樹已建立完成。
320 |
321 |
322 |
323 | ## CART 演算法
324 |
325 | > Reference:
326 | >
327 | > 1. **https://journals.plos.org/plosone/article/file?id=10.1371/journal.pone.0098450.s002&type=supplementary**
328 | > 2. https://www.youtube.com/watch?v=qrDzZMRm_Kw
329 |
330 |
331 |
332 | ### 演算法
333 |
334 | 一個基於吉尼不純度係數 (Gini Impurity) 作為分割標準的分類演算法,先前提到的 ID3 是基於 Information Gain。
335 |
336 | 演算法主要運行如下:
337 |
338 | 1. 尋找最佳特徵分割方式,例如有 K 種特徵,必有 K-1 種分割方式,對於每一種分割方式算出吉尼不純度係數。
339 |
340 | 2. 延續第一點,對於每一種特徵,算出每個特徵的吉尼不純度係數權重。
341 |
342 | 3. 選擇最低的吉尼不純度係數進行分割。
343 |
344 | 4. 重複1, 2, 3,直到達到結束條件。
345 |
346 |
347 |
348 | ### Gini Impurity
349 |
350 | 對於一個 CART 演算法的分割標準,主要以吉尼不純度係數(Gini Impurity)來做參考標準,定義如下。
351 | $$
352 | GI(A) = 1 - \sum^{m}_{k=1}p_k^2
353 | $$
354 | 其中 $0 \le GI(A) \le 1-\dfrac{1}{m}$,當 $GI(A) = 0$ 時,所有資料都被歸類在同一類,$GI(A) = 1 - \dfrac{1}{m}$ 時所有類別均不分類。
355 |
356 |
357 |
358 | ### 範例
359 |
360 | 以這個資料為範例,利用 CART 來建立決策樹。
361 |
362 |
318 |
319 | 此時決策樹已建立完成。
320 |
321 |
322 |
323 | ## CART 演算法
324 |
325 | > Reference:
326 | >
327 | > 1. **https://journals.plos.org/plosone/article/file?id=10.1371/journal.pone.0098450.s002&type=supplementary**
328 | > 2. https://www.youtube.com/watch?v=qrDzZMRm_Kw
329 |
330 |
331 |
332 | ### 演算法
333 |
334 | 一個基於吉尼不純度係數 (Gini Impurity) 作為分割標準的分類演算法,先前提到的 ID3 是基於 Information Gain。
335 |
336 | 演算法主要運行如下:
337 |
338 | 1. 尋找最佳特徵分割方式,例如有 K 種特徵,必有 K-1 種分割方式,對於每一種分割方式算出吉尼不純度係數。
339 |
340 | 2. 延續第一點,對於每一種特徵,算出每個特徵的吉尼不純度係數權重。
341 |
342 | 3. 選擇最低的吉尼不純度係數進行分割。
343 |
344 | 4. 重複1, 2, 3,直到達到結束條件。
345 |
346 |
347 |
348 | ### Gini Impurity
349 |
350 | 對於一個 CART 演算法的分割標準,主要以吉尼不純度係數(Gini Impurity)來做參考標準,定義如下。
351 | $$
352 | GI(A) = 1 - \sum^{m}_{k=1}p_k^2
353 | $$
354 | 其中 $0 \le GI(A) \le 1-\dfrac{1}{m}$,當 $GI(A) = 0$ 時,所有資料都被歸類在同一類,$GI(A) = 1 - \dfrac{1}{m}$ 時所有類別均不分類。
355 |
356 |
357 |
358 | ### 範例
359 |
360 | 以這個資料為範例,利用 CART 來建立決策樹。
361 |
362 |  363 |
364 |
365 |
366 | 先考慮四種不同的分割方式
367 |
368 | 1. 考慮第一種 Outlook
369 |
370 | $GI(Outlook, Sunny) = 1 - (\dfrac{2}{5})^2 - (\dfrac{3}{5})^2=0.48$
371 |
372 | $GI(Outlook, Overcast) = 1 - (\dfrac{4}{4})^2-(\dfrac{0}{4})^2=0$
373 |
374 | $GI(Outlook, Rainy) = 1-(\dfrac{3}{5})^2-(\dfrac{2}{5})^2=0.48$
375 |
376 | $GI(Outlook) = P(Sunny)GI(Sunny) + P(Overcast)GI(Overcast) + P(Rainy)GI(Rainy)$
377 |
378 | $= \dfrac{5}{14}\times 0.48 + \dfrac{4}{14}\times 0 + \dfrac{5}{14}\times 0.48 \approx 0.343$
379 |
380 | 2. 考慮第二種 Temperature
381 |
382 | $GI(Temperature, Hot) = 1 - (\dfrac{2}{4})^2 - (\dfrac{2}{4})^2 = 0.5$
383 |
384 | $GI(Temperature, Mild) = 1 - (\dfrac{4}{6})^2 - (\dfrac{2}{6})^2 \approx 0.44$
385 |
386 | $GI(Temperature, Cold) = 1 - (\dfrac{3}{4})^2 - (\dfrac{1}{4})^2 = 0.375$
387 |
388 | $GI(Temperature) = \dfrac{4}{14}\times 0.5 + \dfrac{6}{14}\times 0.44 + \dfrac{4}{14}\times 0.375 \approx 0.439$
389 |
390 | 3. 考慮第三種 Humidity
391 |
392 | $GI(Humidity, High) = 1 - (\dfrac{3}{7})^2 - (\dfrac{4}{7})^2 \approx 0.49$
393 |
394 | $GI(Humidity, Medium) = 1 - (\dfrac{6}{7})^2 - (\dfrac{1}{7})^2 \approx 0.245$
395 |
396 | $GI(Humidity) = \dfrac{7}{14}\times 0.49 + \dfrac{7}{14}\times 0.245 = 0.3675$
397 |
398 | 4. 考慮第四種 Wind
399 |
400 | $GI(Wind, True) = 1 - (\dfrac{3}{6})^2 - (\dfrac{3}{6})^2 = 0.5$
401 |
402 | $GI(Wind, False) = 1 - (\dfrac{6}{8})^2 - (\dfrac{2}{8})^2 = 0.375$
403 |
404 | $GI(Wind) = \dfrac{6}{14} \times 0.5 + \dfrac{8}{14} \times 0.375 \approx 0.429$
405 |
406 | 選擇最低的 GI 來當作分割標準,故選擇 Outlook 來當作分割節點。
407 |
408 |
363 |
364 |
365 |
366 | 先考慮四種不同的分割方式
367 |
368 | 1. 考慮第一種 Outlook
369 |
370 | $GI(Outlook, Sunny) = 1 - (\dfrac{2}{5})^2 - (\dfrac{3}{5})^2=0.48$
371 |
372 | $GI(Outlook, Overcast) = 1 - (\dfrac{4}{4})^2-(\dfrac{0}{4})^2=0$
373 |
374 | $GI(Outlook, Rainy) = 1-(\dfrac{3}{5})^2-(\dfrac{2}{5})^2=0.48$
375 |
376 | $GI(Outlook) = P(Sunny)GI(Sunny) + P(Overcast)GI(Overcast) + P(Rainy)GI(Rainy)$
377 |
378 | $= \dfrac{5}{14}\times 0.48 + \dfrac{4}{14}\times 0 + \dfrac{5}{14}\times 0.48 \approx 0.343$
379 |
380 | 2. 考慮第二種 Temperature
381 |
382 | $GI(Temperature, Hot) = 1 - (\dfrac{2}{4})^2 - (\dfrac{2}{4})^2 = 0.5$
383 |
384 | $GI(Temperature, Mild) = 1 - (\dfrac{4}{6})^2 - (\dfrac{2}{6})^2 \approx 0.44$
385 |
386 | $GI(Temperature, Cold) = 1 - (\dfrac{3}{4})^2 - (\dfrac{1}{4})^2 = 0.375$
387 |
388 | $GI(Temperature) = \dfrac{4}{14}\times 0.5 + \dfrac{6}{14}\times 0.44 + \dfrac{4}{14}\times 0.375 \approx 0.439$
389 |
390 | 3. 考慮第三種 Humidity
391 |
392 | $GI(Humidity, High) = 1 - (\dfrac{3}{7})^2 - (\dfrac{4}{7})^2 \approx 0.49$
393 |
394 | $GI(Humidity, Medium) = 1 - (\dfrac{6}{7})^2 - (\dfrac{1}{7})^2 \approx 0.245$
395 |
396 | $GI(Humidity) = \dfrac{7}{14}\times 0.49 + \dfrac{7}{14}\times 0.245 = 0.3675$
397 |
398 | 4. 考慮第四種 Wind
399 |
400 | $GI(Wind, True) = 1 - (\dfrac{3}{6})^2 - (\dfrac{3}{6})^2 = 0.5$
401 |
402 | $GI(Wind, False) = 1 - (\dfrac{6}{8})^2 - (\dfrac{2}{8})^2 = 0.375$
403 |
404 | $GI(Wind) = \dfrac{6}{14} \times 0.5 + \dfrac{8}{14} \times 0.375 \approx 0.429$
405 |
406 | 選擇最低的 GI 來當作分割標準,故選擇 Outlook 來當作分割節點。
407 |
408 |  409 |
410 |
411 |
412 | 考慮固定 Sunny,計算剩餘的 Temperature, Humidity, Wind。
413 |
414 | 1. 考慮 Temperature
415 |
416 | $GI(Temperature, Hot) = 1 - (\dfrac{0}{2})^2 - (\dfrac{2}{2})^2 = 0$
417 |
418 | $GI(Temperature, Mild) = 1 - (\dfrac{1}{2})^2 - (\dfrac{1}{2})^2 = 0.5$
419 |
420 | $GI(Temperature, Cold) = 1 - (\dfrac{1}{1})^2 - (\dfrac{0}{1})^2 = 0$
421 |
422 | $GI(Temperature) = \dfrac{2}{5} \times 0 + \dfrac{2}{5}\times 0.5 + \dfrac{1}{5}\times 0 = 0.2$
423 |
424 | 2. 考慮 Humidity
425 |
426 | $GI(Humidity, High) = 1 - (\dfrac{0}{3})^2 - (\dfrac{3}{3})^2 = 0$
427 |
428 | $GI(Humidity, Normal) = 1 - (\dfrac{2}{2})^2-(\dfrac{0}{2})^2 = 0$
429 |
430 | $GI(Humidity) = \dfrac{3}{5} \times 0 + \dfrac{2}{5} \times 0 = 0$
431 |
432 | 3. 考慮 Wind
433 |
434 | $GI(Wind, True) = 1 - (\dfrac{1}{2})^2 - (\dfrac{1}{2})^2 = 0.5$
435 |
436 | $GI(Wind, False) = 1 - (\dfrac{1}{3})^2 - (\dfrac{2}{3})^2 \approx 0.444$
437 |
438 | $GI(Wind) = \dfrac{2}{5}\times 0.5 + \dfrac{3}{5} \times 0.444 \approx 0.466$
439 |
440 | 選擇最低的 GI 來當作分割標準,故選擇 Humidity 當作分割節點。
441 |
442 |
409 |
410 |
411 |
412 | 考慮固定 Sunny,計算剩餘的 Temperature, Humidity, Wind。
413 |
414 | 1. 考慮 Temperature
415 |
416 | $GI(Temperature, Hot) = 1 - (\dfrac{0}{2})^2 - (\dfrac{2}{2})^2 = 0$
417 |
418 | $GI(Temperature, Mild) = 1 - (\dfrac{1}{2})^2 - (\dfrac{1}{2})^2 = 0.5$
419 |
420 | $GI(Temperature, Cold) = 1 - (\dfrac{1}{1})^2 - (\dfrac{0}{1})^2 = 0$
421 |
422 | $GI(Temperature) = \dfrac{2}{5} \times 0 + \dfrac{2}{5}\times 0.5 + \dfrac{1}{5}\times 0 = 0.2$
423 |
424 | 2. 考慮 Humidity
425 |
426 | $GI(Humidity, High) = 1 - (\dfrac{0}{3})^2 - (\dfrac{3}{3})^2 = 0$
427 |
428 | $GI(Humidity, Normal) = 1 - (\dfrac{2}{2})^2-(\dfrac{0}{2})^2 = 0$
429 |
430 | $GI(Humidity) = \dfrac{3}{5} \times 0 + \dfrac{2}{5} \times 0 = 0$
431 |
432 | 3. 考慮 Wind
433 |
434 | $GI(Wind, True) = 1 - (\dfrac{1}{2})^2 - (\dfrac{1}{2})^2 = 0.5$
435 |
436 | $GI(Wind, False) = 1 - (\dfrac{1}{3})^2 - (\dfrac{2}{3})^2 \approx 0.444$
437 |
438 | $GI(Wind) = \dfrac{2}{5}\times 0.5 + \dfrac{3}{5} \times 0.444 \approx 0.466$
439 |
440 | 選擇最低的 GI 來當作分割標準,故選擇 Humidity 當作分割節點。
441 |
442 |  443 |
444 |
445 |
446 | 考慮固定 Rainy,計算剩餘的 Temperature, Humidity, Wind。
447 |
448 | 1. 考慮 Temperature
449 |
450 | $GI(Temperature, Mild) = 1 - (\dfrac{2}{3})^2 - (\dfrac{1}{3})^2 \approx 0.444$
451 |
452 | $GI(Temperature, Cold) = 1 - (\dfrac{1}{2})^2 - (\dfrac{1}{2})^2 = 0.5$
453 |
454 | $GI(Temperature) = \dfrac{3}{5}\times 0.444 + \dfrac{2}{5}\times 0.5 = 0.4664$
455 |
456 | 2. 考慮 Humidity
457 |
458 | $GI(Humidity, High) = 1 - (\dfrac{1}{2})^2 - (\dfrac{1}{2})^2 = 0.5$
459 |
460 | $GI(Humidity, Normal) = 1 - (\dfrac{2}{3})^2 - (\dfrac{1}{3})^2 \approx 0.444$
461 |
462 | $GI(Humidity) = \dfrac{3}{5}\times 0.444 + \dfrac{2}{5}\times 0.5 = 0.4664$
463 |
464 | 3. 考慮 Wind
465 |
466 | $GI(Wind, True) = 1 - (\dfrac{0}{2})^2 - (\dfrac{2}{2})^2 = 0$
467 |
468 | $GI(Wind, False) = 1 - (\dfrac{3}{3})^2 - (\dfrac{0}{3})^2 = 0$
469 |
470 | $GI(Wind) = \dfrac{2}{5}\times 0 + \dfrac{3}{5}\times 0 = 0$
471 |
472 | 選擇最低的 GI 來當作分割標準,故選擇 Wind 當作分割節點。
473 |
474 |
443 |
444 |
445 |
446 | 考慮固定 Rainy,計算剩餘的 Temperature, Humidity, Wind。
447 |
448 | 1. 考慮 Temperature
449 |
450 | $GI(Temperature, Mild) = 1 - (\dfrac{2}{3})^2 - (\dfrac{1}{3})^2 \approx 0.444$
451 |
452 | $GI(Temperature, Cold) = 1 - (\dfrac{1}{2})^2 - (\dfrac{1}{2})^2 = 0.5$
453 |
454 | $GI(Temperature) = \dfrac{3}{5}\times 0.444 + \dfrac{2}{5}\times 0.5 = 0.4664$
455 |
456 | 2. 考慮 Humidity
457 |
458 | $GI(Humidity, High) = 1 - (\dfrac{1}{2})^2 - (\dfrac{1}{2})^2 = 0.5$
459 |
460 | $GI(Humidity, Normal) = 1 - (\dfrac{2}{3})^2 - (\dfrac{1}{3})^2 \approx 0.444$
461 |
462 | $GI(Humidity) = \dfrac{3}{5}\times 0.444 + \dfrac{2}{5}\times 0.5 = 0.4664$
463 |
464 | 3. 考慮 Wind
465 |
466 | $GI(Wind, True) = 1 - (\dfrac{0}{2})^2 - (\dfrac{2}{2})^2 = 0$
467 |
468 | $GI(Wind, False) = 1 - (\dfrac{3}{3})^2 - (\dfrac{0}{3})^2 = 0$
469 |
470 | $GI(Wind) = \dfrac{2}{5}\times 0 + \dfrac{3}{5}\times 0 = 0$
471 |
472 | 選擇最低的 GI 來當作分割標準,故選擇 Wind 當作分割節點。
473 |
474 |  475 |
476 | 此時分割已完成。
477 |
478 |
479 |
480 | ## 迴歸樹
481 |
482 | 迴歸樹是決策樹的一種種類,用來預判在某一種情況下時,能夠對應到的效果。
483 |
484 | 輸出值為連續變數,運作方式與分類樹較相同,與分類樹不同的地方是:
485 |
486 | 1. 對於一個二維的座標軸來說,迴歸樹通常是預判在這個二維座標軸特定條件所形成的一個長方形區塊內資料的平均值,
487 | 2. 判斷一個長方形區塊內資料的純度,使用了殘差平方和,定義為 $\displaystyle RSS = \sum^{n}_{i=1}(y_i - f(x_i))^2$。
488 | 3. 使用均方根誤差來測量效能。
489 |
490 |
491 |
492 | ### Cost Complexity Pruning
493 |
494 | > Reference: https://www.youtube.com/watch?v=D0efHEJsfHo
495 |
496 |
497 |
498 | 迴歸樹運作原理與分類樹較相同,但也同時會出現 over fitting 的問題。
499 |
500 | 為了避免 over fitting 的問題發生,需要對這棵樹進行適當的剪枝,以利於資料的預判。
501 |
502 |
503 |
504 | 對於剪枝的評斷,我們需要先窮舉每一種剪枝的方式,得到剪枝序列
505 |
506 | 根據每個序列每個區塊,做一次 $RSS$ 的測量總和,再計算一種基於 $RSS$ 出現的 Tree Score,定義為:
507 | $$
508 | Tree Score = RSS + aT
509 | $$
510 | 其中 $a$ 為一微調參數,且 $T$ 為葉節點樹量。
511 |
512 | 找到這個參數 $a$ 的方式是透過微調 $a$ 來使當前的樹算出的 Tree Score 變小。
513 |
514 | 再只使用測試資料來做幾次交叉測試,找出能夠使 $RSS$ 平均最小的子樹,即為最佳剪枝樹。
515 |
516 |
517 |
518 | ## Random Forest
519 |
520 | > Reference:
521 | >
522 | > 1. https://www.youtube.com/watch?v=J4Wdy0Wc_xQ
523 | > 2. https://www.youtube.com/watch?v=sQ870aTKqiM
524 |
525 |
526 |
527 | Random Forest 是一種包含多種決策樹的分類器,輸出的類別取決於所有決策樹的結果統計出的眾數。
528 |
529 | 大致上來說,Random Forest 使用以下的演算法:
530 |
531 | 1. 建立 bootstrapped table,隨機抽取一定數量的樣本來建立。
532 | 2. 建立決策樹的父節點,使用隨機不重複的變數來建立。
533 | 3. 重複第一步與第二步,利用這樣的方式建立多棵決策樹。
534 |
535 | 接下來即可將樣本丟入隨機森林,蒐集每一棵決策樹所產生出的結果,以及找出結果眾數。
536 |
537 |
538 |
539 | ### Bagging
540 |
541 | 我們將樣本隨機抽取來建立 bootstrapped table,然後利用總計來得出結果,這樣的方式稱為 Bagging。
542 |
543 |
544 |
545 | ### Out-of-bag dataset
546 |
547 | 由於我們前面說到,建立 bootstrapped table 的方式是使用隨機抽樣,那麼隨機抽樣這一步有可能會出現沒有抽到的資料。
548 |
549 | 我們將這些資料蒐集起來,稱為 Out-of-bag dataset。
550 |
551 |
552 |
553 | 處理這些 Out-of-bag dataset 的方式是,我們可以把這些資料集丟回去隨機森林,來確定所有的樹是否都回傳同一個結果。
554 |
555 | 就可以用這些結果來測量隨機森林的準確度,至於 Out-of-bag dataset 分類錯誤的部分即稱為 Out-of-bag error。
556 |
557 |
558 |
559 | 我們可以測量準確度,再來校正隨機抽取樣本的數量,來校正隨機森林。
560 |
561 |
562 |
563 | ### Missing Data
564 |
565 | 對於 Random Forest 的缺值問題,主要分成兩種。
566 |
567 | 1. 知道結果、但不知道資料變數的某些值。
568 | 2. 不知道結果、但也不知道資料變數的某些值。
569 |
570 | 對於這兩種問題,可以分成兩種不同的方式來解決。
571 |
572 |
573 |
574 | #### 缺值問題 1
575 |
576 | 我們可以先根據先前的資料集進行投票,並且去尋找相似的先前資料來設定值,再逐步調整。
577 |
578 | 逐步調整的方式可以利用 updated proximity matrix 來調整,經過多次迭代之後找到一個再迭代後也變化不大的結果。
579 |
580 |
581 |
582 | #### 缺值問題 2
583 |
584 | 我們可以根據剩餘的資料來進行建立隨機森林。
585 |
586 | 建立模型後,先是使用第一個缺值問題的方式來設定變數值,以及窮舉所有可能出現的結果,產生出多個候選資料。
587 |
588 | 將這些候選資料丟入模型進行預判,來得到隨機森林對於哪一種結果有更高的投票數,即可選定投票結果。
589 |
--------------------------------------------------------------------------------
/Markdown/Naive Bayes Analysis.md:
--------------------------------------------------------------------------------
1 | # Naive Bayes Analysis(單純貝氏分析)
2 |
3 | > Reference:
4 | >
5 | > 1. Naïve Bayes Analysis(單純貝氏) - Dr. Tun-Wen Pai
6 | > 2. [Naive Bayes, Clearly Explained!!! - StatQuest with Josh Starmer](https://www.youtube.com/watch?v=O2L2Uv9pdDA)
7 | > 3. [Bayes' Theorem, Clearly Explained!!!! - StatQuest with Josh Starmer](https://www.youtube.com/watch?v=9wCnvr7Xw4E)
8 | > 4. [Gaussian Naive Bayes, Clearly Explained!!! - StatQuest with Josh Starmer](https://www.youtube.com/watch?v=H3EjCKtlVog)
9 |
10 |
11 |
12 | ## 貝氏定理
13 |
14 | 貝氏定理是關於隨機事件 $A$ 和 $B$ 的條件機率的一則定理,定義如下:
15 | $$
16 | P(A|B) = \dfrac{P(A)P(B|A)}{P(B)}, P(B) \neq 0
17 | $$
18 | 其中 $P(A)$ 是事件 $A$ 的事前機率,$P(B)$ 是事件 $B$ 的事前機率。
19 |
20 | $P(B|A)$ 是事件 $A$ 發生後事件 $B$ 的條件機率(事後機率),同時,$P(B|A) = \dfrac{P(A \cap B)}{P(A)}$。
21 |
22 | $P(A|B)$ 是事件 $B$ 發生後事件 $A$ 的條件機率(事後機率),同時,$P(A|B) = \dfrac{P(A \cap B)}{P(B)}$。
23 |
24 |
25 |
26 | 以一張文氏圖來說,我們可以令藍色區塊為 $A$,黃色區塊為 $B$,則若我們想要知道事件 $B$ 發生後,發生 $A$ 的機率
27 |
28 | 就相比我們以藍色區塊點的數量去除以綠色區塊點的數量 $P(G|B) = \dfrac{N(G)}{N(B)}$,就能得到先發生 $B$ 後再發生 $A$ 的機率。
29 |
30 | > 文氏圖圖例,By StatQuest
31 |
32 | 
33 |
34 |
35 |
36 | ## 多項單純貝氏分類
37 |
38 | ### 概述
39 |
40 | 當我們要對一筆資料 $D$ 進行分類,我們可以根據資料的每個特徵 $C_i$,從訓練樣本中找出特徵 $C_i$ 是事件 $A$ 或事件 $B$ 的條件機率 $P(C_i|A)$ 或 $P(C_i|B)$ 的分數,用分數來進行分類,定義如下。
41 | $$
42 | P(D|E) = P(E) \times P(C_1|E)\times P(C_2|E) \times ... \times P(C_n|E)
43 | $$
44 | 其中 $D$ 為一筆資料,$E$ 為一個事件,$P(D|E)$ 為資料 $D$ 歸類在事件 $E$ 的分數,$C_i$ 為某特徵。
45 |
46 |
47 |
48 | 分類會出現有零值與沒有零值的情況。
49 |
50 |
51 |
52 | ### Example - 無零值
53 |
54 | | # | message | Happy |
55 | | :--: | :-----------------------: | :---: |
56 | | 1 | love happy joy joy love | Yes |
57 | | 2 | happy love kick joy happy | Yes |
58 | | 3 | love move joy good | Yes |
59 | | 4 | love happy joy pain love | Yes |
60 | | 5 | joy love pain kick pain | No |
61 | | 6 | pain pain love kick | No |
62 | | 7 | love pain joy love kick | ? |
63 |
64 | 我們想要找到第七筆應該被分類在哪一個類別(Happy = Yes/No),我們可以先算出事前機率:
65 | $$
66 | P(yes) = \dfrac{4}{6} = \dfrac{2}{3} \\
67 | P(no) = \dfrac{2}{6} = \dfrac{1}{3}
68 | $$
69 | 我們可以根據每個特徵來算出 $D_7$ 特徵值的事後機率。
70 |
71 | 
72 | $$
73 | P(love|yes) = \dfrac{6}{19}, P(love|no) = \dfrac{2}{9} \\
74 | P(pain|yes) = \dfrac{1}{19}, P(pain|no) = \dfrac{4}{9} \\
75 | P(joy|yes) = \dfrac{5}{19}, P(joy|no) = \dfrac{1}{9} \\
76 | P(kick|yes) = \dfrac{1}{19}, P(kick|no) = \dfrac{2}{9} \\
77 | $$
78 | 那我們就能夠根據定義來算出 $D_7$ 特徵值的分數。
79 | $$
80 | P(D_7|yes) = P(love|yes) \times P(pain|yes) \times P(joy|yes) \times P(love|yes) \times P(kick|yes) \approx 0.000004 \\
81 |
82 | P(D_7|no) = P(love|no) \times P(pain|no) \times P(joy|no) \times P(love|no) \times P(kick|no) \approx 0.00018
83 | $$
84 | 故 $D_7$ 在 $P(D_7|no)$ 有較高的分數,故選 $no$。
85 |
86 |
87 |
88 | ### Example - 有零值
89 |
90 | | # | message | Happy |
91 | | :--: | :----------------------------: | :---: |
92 | | 1 | love happy joy joy love | Yes |
93 | | 2 | happy love kick joy happy | Yes |
94 | | 3 | love move joy good | Yes |
95 | | 4 | love happy joy pain love | Yes |
96 | | 5 | joy love pain kick pain | No |
97 | | 6 | pain pain love kick | No |
98 | | 7 | love pain joy happy kick happy | ? |
99 |
100 | 我們想要找到第七筆應該被分類在哪一個類別(Happy = Yes/No),我們可以先算出事前機率:
101 | $$
102 | P(yes) = \dfrac{4}{6} = \dfrac{2}{3} \\
103 | P(no) = \dfrac{2}{6} = \dfrac{1}{3}
104 | $$
105 | 我們可以根據每個特徵來算出 $D_7$ 特徵值的事後機率。
106 |
107 | 但此時會發現 happy 這個特徵值並沒有出現在 No 裡面,通常來說,我們會把每一個特徵值重複加上去,如下:
108 |
109 | 
110 |
111 | 那我們就能夠根據定義來算出 $D_7$ 特徵值的分數。
112 | $$
113 | P(D_7|yes) = P(love|no) \times P(pain|yes) \times P(joy|yes) \times P(love|yes) \times P(kick|yes) \approx 9\times 10^{-6} \\
114 |
115 | P(D_7|no) = P(love|yes) \times P(pain|no) \times P(joy|no) \times P(love|no) \times P(kick|no) \approx 3\times 10^{-6}
116 | $$
117 | 故 $D_7$ 在 $P(D_7|yes)$ 有較高的分數,故選 $yes$。
118 |
119 |
120 |
121 | ## 常態單純貝氏分類
122 |
123 | > 另一種單純貝氏分類,屬於補充資料,有時間補。
124 |
--------------------------------------------------------------------------------
/Markdown/Regression.md:
--------------------------------------------------------------------------------
1 | # 迴歸 (Regression)
2 |
3 | > 筆記參考資料:
4 | >
5 | > 1. Regression (迴歸) Dr. Tun Wen Pai
6 |
7 | ## 線性回歸
8 |
9 | ### 線性迴歸簡介
10 |
11 | 一種統計學上分析資料的方法,目的在於了解多個獨立變數與一個應變數的關係。
12 |
13 | 通常來說,迴歸存在的意義,是造出一條曲線盡可能地滿足這些資料,以達到預測、了解關係的目的。
14 |
15 | 我們可以使用相關係數來比較這個造出來的曲線的好與壞。
16 |
17 |
18 |
19 | ### 相關係數
20 |
21 | 相關係數 $r$,用來評估兩個變數之間的關係是否相關,其定義如下:
22 | $$
23 | r= \dfrac{\displaystyle\sum^{n}_{i=1}(X_i-\overline{X})(Y_i-\overline{Y})}{\sqrt{\displaystyle\sum^n_{i=1}(X_i-\overline{X})^2}\sqrt{\displaystyle\sum^n_{i=1}(Y_i-\overline{Y})^2}}
24 | $$
25 | 定義 $\overline{X}、\overline{Y}$ 為變數 $X$ 、變數 $Y$ 的平均值。
26 |
27 | 其中 $-1 \le r \le 1$,其中若 $r = 0$ 時則代表完全無相關,$|r| = 1$ 時則代表完全相關,$0 < |r| < 1$ 時則代表存在一定的線性相關。
28 |
29 |
30 |
31 | ### 決定係數
32 |
33 | > Reference:https://www.youtube.com/watch?v=2AQKmw14mHM
34 |
35 |
36 |
37 | 決定係數 $r^2$,用來判斷回歸模型的解釋力,可以將相關係數平方,得到決定係數。
38 |
39 | 決定係數可以更好的幫助我們判斷兩個變數之間的關係,可以知道選擇的兩個變數能夠解釋多少比例的資料變異。
40 |
41 |
42 |
43 | ### 雙變數的圖形呈現
44 |
45 | 對於一個雙變數的資料集,我們可以畫出一張二維的散佈圖,可透過散佈圖來觀察出變數之間的關係。
46 |
47 |
475 |
476 | 此時分割已完成。
477 |
478 |
479 |
480 | ## 迴歸樹
481 |
482 | 迴歸樹是決策樹的一種種類,用來預判在某一種情況下時,能夠對應到的效果。
483 |
484 | 輸出值為連續變數,運作方式與分類樹較相同,與分類樹不同的地方是:
485 |
486 | 1. 對於一個二維的座標軸來說,迴歸樹通常是預判在這個二維座標軸特定條件所形成的一個長方形區塊內資料的平均值,
487 | 2. 判斷一個長方形區塊內資料的純度,使用了殘差平方和,定義為 $\displaystyle RSS = \sum^{n}_{i=1}(y_i - f(x_i))^2$。
488 | 3. 使用均方根誤差來測量效能。
489 |
490 |
491 |
492 | ### Cost Complexity Pruning
493 |
494 | > Reference: https://www.youtube.com/watch?v=D0efHEJsfHo
495 |
496 |
497 |
498 | 迴歸樹運作原理與分類樹較相同,但也同時會出現 over fitting 的問題。
499 |
500 | 為了避免 over fitting 的問題發生,需要對這棵樹進行適當的剪枝,以利於資料的預判。
501 |
502 |
503 |
504 | 對於剪枝的評斷,我們需要先窮舉每一種剪枝的方式,得到剪枝序列
505 |
506 | 根據每個序列每個區塊,做一次 $RSS$ 的測量總和,再計算一種基於 $RSS$ 出現的 Tree Score,定義為:
507 | $$
508 | Tree Score = RSS + aT
509 | $$
510 | 其中 $a$ 為一微調參數,且 $T$ 為葉節點樹量。
511 |
512 | 找到這個參數 $a$ 的方式是透過微調 $a$ 來使當前的樹算出的 Tree Score 變小。
513 |
514 | 再只使用測試資料來做幾次交叉測試,找出能夠使 $RSS$ 平均最小的子樹,即為最佳剪枝樹。
515 |
516 |
517 |
518 | ## Random Forest
519 |
520 | > Reference:
521 | >
522 | > 1. https://www.youtube.com/watch?v=J4Wdy0Wc_xQ
523 | > 2. https://www.youtube.com/watch?v=sQ870aTKqiM
524 |
525 |
526 |
527 | Random Forest 是一種包含多種決策樹的分類器,輸出的類別取決於所有決策樹的結果統計出的眾數。
528 |
529 | 大致上來說,Random Forest 使用以下的演算法:
530 |
531 | 1. 建立 bootstrapped table,隨機抽取一定數量的樣本來建立。
532 | 2. 建立決策樹的父節點,使用隨機不重複的變數來建立。
533 | 3. 重複第一步與第二步,利用這樣的方式建立多棵決策樹。
534 |
535 | 接下來即可將樣本丟入隨機森林,蒐集每一棵決策樹所產生出的結果,以及找出結果眾數。
536 |
537 |
538 |
539 | ### Bagging
540 |
541 | 我們將樣本隨機抽取來建立 bootstrapped table,然後利用總計來得出結果,這樣的方式稱為 Bagging。
542 |
543 |
544 |
545 | ### Out-of-bag dataset
546 |
547 | 由於我們前面說到,建立 bootstrapped table 的方式是使用隨機抽樣,那麼隨機抽樣這一步有可能會出現沒有抽到的資料。
548 |
549 | 我們將這些資料蒐集起來,稱為 Out-of-bag dataset。
550 |
551 |
552 |
553 | 處理這些 Out-of-bag dataset 的方式是,我們可以把這些資料集丟回去隨機森林,來確定所有的樹是否都回傳同一個結果。
554 |
555 | 就可以用這些結果來測量隨機森林的準確度,至於 Out-of-bag dataset 分類錯誤的部分即稱為 Out-of-bag error。
556 |
557 |
558 |
559 | 我們可以測量準確度,再來校正隨機抽取樣本的數量,來校正隨機森林。
560 |
561 |
562 |
563 | ### Missing Data
564 |
565 | 對於 Random Forest 的缺值問題,主要分成兩種。
566 |
567 | 1. 知道結果、但不知道資料變數的某些值。
568 | 2. 不知道結果、但也不知道資料變數的某些值。
569 |
570 | 對於這兩種問題,可以分成兩種不同的方式來解決。
571 |
572 |
573 |
574 | #### 缺值問題 1
575 |
576 | 我們可以先根據先前的資料集進行投票,並且去尋找相似的先前資料來設定值,再逐步調整。
577 |
578 | 逐步調整的方式可以利用 updated proximity matrix 來調整,經過多次迭代之後找到一個再迭代後也變化不大的結果。
579 |
580 |
581 |
582 | #### 缺值問題 2
583 |
584 | 我們可以根據剩餘的資料來進行建立隨機森林。
585 |
586 | 建立模型後,先是使用第一個缺值問題的方式來設定變數值,以及窮舉所有可能出現的結果,產生出多個候選資料。
587 |
588 | 將這些候選資料丟入模型進行預判,來得到隨機森林對於哪一種結果有更高的投票數,即可選定投票結果。
589 |
--------------------------------------------------------------------------------
/Markdown/Naive Bayes Analysis.md:
--------------------------------------------------------------------------------
1 | # Naive Bayes Analysis(單純貝氏分析)
2 |
3 | > Reference:
4 | >
5 | > 1. Naïve Bayes Analysis(單純貝氏) - Dr. Tun-Wen Pai
6 | > 2. [Naive Bayes, Clearly Explained!!! - StatQuest with Josh Starmer](https://www.youtube.com/watch?v=O2L2Uv9pdDA)
7 | > 3. [Bayes' Theorem, Clearly Explained!!!! - StatQuest with Josh Starmer](https://www.youtube.com/watch?v=9wCnvr7Xw4E)
8 | > 4. [Gaussian Naive Bayes, Clearly Explained!!! - StatQuest with Josh Starmer](https://www.youtube.com/watch?v=H3EjCKtlVog)
9 |
10 |
11 |
12 | ## 貝氏定理
13 |
14 | 貝氏定理是關於隨機事件 $A$ 和 $B$ 的條件機率的一則定理,定義如下:
15 | $$
16 | P(A|B) = \dfrac{P(A)P(B|A)}{P(B)}, P(B) \neq 0
17 | $$
18 | 其中 $P(A)$ 是事件 $A$ 的事前機率,$P(B)$ 是事件 $B$ 的事前機率。
19 |
20 | $P(B|A)$ 是事件 $A$ 發生後事件 $B$ 的條件機率(事後機率),同時,$P(B|A) = \dfrac{P(A \cap B)}{P(A)}$。
21 |
22 | $P(A|B)$ 是事件 $B$ 發生後事件 $A$ 的條件機率(事後機率),同時,$P(A|B) = \dfrac{P(A \cap B)}{P(B)}$。
23 |
24 |
25 |
26 | 以一張文氏圖來說,我們可以令藍色區塊為 $A$,黃色區塊為 $B$,則若我們想要知道事件 $B$ 發生後,發生 $A$ 的機率
27 |
28 | 就相比我們以藍色區塊點的數量去除以綠色區塊點的數量 $P(G|B) = \dfrac{N(G)}{N(B)}$,就能得到先發生 $B$ 後再發生 $A$ 的機率。
29 |
30 | > 文氏圖圖例,By StatQuest
31 |
32 | 
33 |
34 |
35 |
36 | ## 多項單純貝氏分類
37 |
38 | ### 概述
39 |
40 | 當我們要對一筆資料 $D$ 進行分類,我們可以根據資料的每個特徵 $C_i$,從訓練樣本中找出特徵 $C_i$ 是事件 $A$ 或事件 $B$ 的條件機率 $P(C_i|A)$ 或 $P(C_i|B)$ 的分數,用分數來進行分類,定義如下。
41 | $$
42 | P(D|E) = P(E) \times P(C_1|E)\times P(C_2|E) \times ... \times P(C_n|E)
43 | $$
44 | 其中 $D$ 為一筆資料,$E$ 為一個事件,$P(D|E)$ 為資料 $D$ 歸類在事件 $E$ 的分數,$C_i$ 為某特徵。
45 |
46 |
47 |
48 | 分類會出現有零值與沒有零值的情況。
49 |
50 |
51 |
52 | ### Example - 無零值
53 |
54 | | # | message | Happy |
55 | | :--: | :-----------------------: | :---: |
56 | | 1 | love happy joy joy love | Yes |
57 | | 2 | happy love kick joy happy | Yes |
58 | | 3 | love move joy good | Yes |
59 | | 4 | love happy joy pain love | Yes |
60 | | 5 | joy love pain kick pain | No |
61 | | 6 | pain pain love kick | No |
62 | | 7 | love pain joy love kick | ? |
63 |
64 | 我們想要找到第七筆應該被分類在哪一個類別(Happy = Yes/No),我們可以先算出事前機率:
65 | $$
66 | P(yes) = \dfrac{4}{6} = \dfrac{2}{3} \\
67 | P(no) = \dfrac{2}{6} = \dfrac{1}{3}
68 | $$
69 | 我們可以根據每個特徵來算出 $D_7$ 特徵值的事後機率。
70 |
71 | 
72 | $$
73 | P(love|yes) = \dfrac{6}{19}, P(love|no) = \dfrac{2}{9} \\
74 | P(pain|yes) = \dfrac{1}{19}, P(pain|no) = \dfrac{4}{9} \\
75 | P(joy|yes) = \dfrac{5}{19}, P(joy|no) = \dfrac{1}{9} \\
76 | P(kick|yes) = \dfrac{1}{19}, P(kick|no) = \dfrac{2}{9} \\
77 | $$
78 | 那我們就能夠根據定義來算出 $D_7$ 特徵值的分數。
79 | $$
80 | P(D_7|yes) = P(love|yes) \times P(pain|yes) \times P(joy|yes) \times P(love|yes) \times P(kick|yes) \approx 0.000004 \\
81 |
82 | P(D_7|no) = P(love|no) \times P(pain|no) \times P(joy|no) \times P(love|no) \times P(kick|no) \approx 0.00018
83 | $$
84 | 故 $D_7$ 在 $P(D_7|no)$ 有較高的分數,故選 $no$。
85 |
86 |
87 |
88 | ### Example - 有零值
89 |
90 | | # | message | Happy |
91 | | :--: | :----------------------------: | :---: |
92 | | 1 | love happy joy joy love | Yes |
93 | | 2 | happy love kick joy happy | Yes |
94 | | 3 | love move joy good | Yes |
95 | | 4 | love happy joy pain love | Yes |
96 | | 5 | joy love pain kick pain | No |
97 | | 6 | pain pain love kick | No |
98 | | 7 | love pain joy happy kick happy | ? |
99 |
100 | 我們想要找到第七筆應該被分類在哪一個類別(Happy = Yes/No),我們可以先算出事前機率:
101 | $$
102 | P(yes) = \dfrac{4}{6} = \dfrac{2}{3} \\
103 | P(no) = \dfrac{2}{6} = \dfrac{1}{3}
104 | $$
105 | 我們可以根據每個特徵來算出 $D_7$ 特徵值的事後機率。
106 |
107 | 但此時會發現 happy 這個特徵值並沒有出現在 No 裡面,通常來說,我們會把每一個特徵值重複加上去,如下:
108 |
109 | 
110 |
111 | 那我們就能夠根據定義來算出 $D_7$ 特徵值的分數。
112 | $$
113 | P(D_7|yes) = P(love|no) \times P(pain|yes) \times P(joy|yes) \times P(love|yes) \times P(kick|yes) \approx 9\times 10^{-6} \\
114 |
115 | P(D_7|no) = P(love|yes) \times P(pain|no) \times P(joy|no) \times P(love|no) \times P(kick|no) \approx 3\times 10^{-6}
116 | $$
117 | 故 $D_7$ 在 $P(D_7|yes)$ 有較高的分數,故選 $yes$。
118 |
119 |
120 |
121 | ## 常態單純貝氏分類
122 |
123 | > 另一種單純貝氏分類,屬於補充資料,有時間補。
124 |
--------------------------------------------------------------------------------
/Markdown/Regression.md:
--------------------------------------------------------------------------------
1 | # 迴歸 (Regression)
2 |
3 | > 筆記參考資料:
4 | >
5 | > 1. Regression (迴歸) Dr. Tun Wen Pai
6 |
7 | ## 線性回歸
8 |
9 | ### 線性迴歸簡介
10 |
11 | 一種統計學上分析資料的方法,目的在於了解多個獨立變數與一個應變數的關係。
12 |
13 | 通常來說,迴歸存在的意義,是造出一條曲線盡可能地滿足這些資料,以達到預測、了解關係的目的。
14 |
15 | 我們可以使用相關係數來比較這個造出來的曲線的好與壞。
16 |
17 |
18 |
19 | ### 相關係數
20 |
21 | 相關係數 $r$,用來評估兩個變數之間的關係是否相關,其定義如下:
22 | $$
23 | r= \dfrac{\displaystyle\sum^{n}_{i=1}(X_i-\overline{X})(Y_i-\overline{Y})}{\sqrt{\displaystyle\sum^n_{i=1}(X_i-\overline{X})^2}\sqrt{\displaystyle\sum^n_{i=1}(Y_i-\overline{Y})^2}}
24 | $$
25 | 定義 $\overline{X}、\overline{Y}$ 為變數 $X$ 、變數 $Y$ 的平均值。
26 |
27 | 其中 $-1 \le r \le 1$,其中若 $r = 0$ 時則代表完全無相關,$|r| = 1$ 時則代表完全相關,$0 < |r| < 1$ 時則代表存在一定的線性相關。
28 |
29 |
30 |
31 | ### 決定係數
32 |
33 | > Reference:https://www.youtube.com/watch?v=2AQKmw14mHM
34 |
35 |
36 |
37 | 決定係數 $r^2$,用來判斷回歸模型的解釋力,可以將相關係數平方,得到決定係數。
38 |
39 | 決定係數可以更好的幫助我們判斷兩個變數之間的關係,可以知道選擇的兩個變數能夠解釋多少比例的資料變異。
40 |
41 |
42 |
43 | ### 雙變數的圖形呈現
44 |
45 | 對於一個雙變數的資料集,我們可以畫出一張二維的散佈圖,可透過散佈圖來觀察出變數之間的關係。
46 |
47 |  48 |
49 | 可以發現,(a) 與 (b) 的圖形可以畫上一條直線,資料大部分都在這條線附近,所以是線性相關。
50 |
51 | (c) 與 (d) 可以畫上一條曲線,資料大部分都在這條曲線附近,所以是曲線相關。
52 |
53 | (e) 與 (f) 找不到直線、曲線能夠含括大部分的資料,故為無相關。
54 |
55 |
56 |
57 | 結合前一個小節所講的相關係數,我們可以從散佈圖上來找出與相關係數的關係,可以發現資料越散,取絕對值後的相關係數越小。
58 |
59 | 資料越集中於一條線,取絕對值後相關係數的係數越大。
60 |
61 |
48 |
49 | 可以發現,(a) 與 (b) 的圖形可以畫上一條直線,資料大部分都在這條線附近,所以是線性相關。
50 |
51 | (c) 與 (d) 可以畫上一條曲線,資料大部分都在這條曲線附近,所以是曲線相關。
52 |
53 | (e) 與 (f) 找不到直線、曲線能夠含括大部分的資料,故為無相關。
54 |
55 |
56 |
57 | 結合前一個小節所講的相關係數,我們可以從散佈圖上來找出與相關係數的關係,可以發現資料越散,取絕對值後的相關係數越小。
58 |
59 | 資料越集中於一條線,取絕對值後相關係數的係數越大。
60 |
61 |  62 |
63 |
64 |
65 |
66 |
67 | ## 羅吉斯迴歸
68 |
69 | ### 羅吉斯迴歸
70 |
71 |
62 |
63 |
64 |
65 |
66 |
67 | ## 羅吉斯迴歸
68 |
69 | ### 羅吉斯迴歸
70 |
71 |  72 |
73 | > Image from [equiskill](https://www.equiskill.com/understanding-logistic-regression/)
74 |
75 | 羅吉斯迴歸(Logistic Regression),是一種**對數分類器**而不是一種迴歸模型。
76 |
77 | 而羅吉斯迴歸又分成二元、多項式羅吉斯迴歸等等。
78 |
79 | 這邊主要介紹二元羅吉斯迴歸,也就是對於一個變量,評估結果是否發生。
80 |
81 |
82 |
83 | ### 羅吉斯迴歸的圖形
84 |
85 | 二元羅吉斯迴歸可以用一張二維平面圖來作圖。
86 |
87 | 其中,$x$ 軸是一種變量,而 $y$ 軸則是對於導致這個結果產生的機率,機率介於 $0$ 到 $1$ 之間。
88 |
89 | 圖上的點密集分布在 $y = 0$ 與 $y = 1$ 上,代表著對應的變量是否發生結果。
90 |
91 | 而圖上的的線即為線性迴歸模型,我們可以根據這個曲線對應到的變量,來預測對於一件事情的發生機率為何。
92 |
93 |
94 |
95 | 舉個例子,我們有一組資料為學生期中成績與通過課程與否的資料。
96 |
97 | | 期中考成績 | 44 | 53 | 23 | 67 | 79 | 91 | 100 | 58 | 82 | 52 |
98 | | ---------- | ---- | ---- | ---- | ---- | ---- | ---- | ---- | ---- | ---- | ---- |
99 | | 通過 | 0 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 0 |
100 |
101 | 我們可以根據這個資料,做一張 Logistic Regression 的圖。
102 |
103 |
72 |
73 | > Image from [equiskill](https://www.equiskill.com/understanding-logistic-regression/)
74 |
75 | 羅吉斯迴歸(Logistic Regression),是一種**對數分類器**而不是一種迴歸模型。
76 |
77 | 而羅吉斯迴歸又分成二元、多項式羅吉斯迴歸等等。
78 |
79 | 這邊主要介紹二元羅吉斯迴歸,也就是對於一個變量,評估結果是否發生。
80 |
81 |
82 |
83 | ### 羅吉斯迴歸的圖形
84 |
85 | 二元羅吉斯迴歸可以用一張二維平面圖來作圖。
86 |
87 | 其中,$x$ 軸是一種變量,而 $y$ 軸則是對於導致這個結果產生的機率,機率介於 $0$ 到 $1$ 之間。
88 |
89 | 圖上的點密集分布在 $y = 0$ 與 $y = 1$ 上,代表著對應的變量是否發生結果。
90 |
91 | 而圖上的的線即為線性迴歸模型,我們可以根據這個曲線對應到的變量,來預測對於一件事情的發生機率為何。
92 |
93 |
94 |
95 | 舉個例子,我們有一組資料為學生期中成績與通過課程與否的資料。
96 |
97 | | 期中考成績 | 44 | 53 | 23 | 67 | 79 | 91 | 100 | 58 | 82 | 52 |
98 | | ---------- | ---- | ---- | ---- | ---- | ---- | ---- | ---- | ---- | ---- | ---- |
99 | | 通過 | 0 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 0 |
100 |
101 | 我們可以根據這個資料,做一張 Logistic Regression 的圖。
102 |
103 |  104 |
105 | > Image from me with matplotlib and scikit-learn
106 |
107 | 圖中的橘線即為擬合後的線性迴歸模型,而點則是期中考成績對應到的通過與否。
108 |
109 |
110 |
111 | ### 勝算
112 |
113 | 我們定義勝算 (odds) 為,一件事情發生的機率,除以一件事情不發生的機率,也就是 $\dfrac{p}{1-p}$
114 |
115 | $\log(odds)$ 可以有效的讓勝算的起點設定在數線的 $0$ 上,並且隨著數值的大與小,顯示在數線上距離 $0$ 有多遠。
116 |
117 |
118 |
119 | ### 羅吉斯迴歸的圖形轉換
120 |
121 | 上面的圖似乎可以非常棒的看出對應的成績所造成的通過與否了,不過我們可以將這個圖形做一點轉換。
122 |
123 | 我們考慮將這條線性迴歸模型拉直,也就是轉成 $y=ax+b$ 的形式。
124 |
125 | 為此,我們可以考慮將 $y$ 軸每一點的機率值,映射到一個定義域為 $(-\infty, \infty)$ 的 $y$ 軸上
126 |
127 | 我們可以使用 Logit Function,定義為 $\ln(odds) = \ln(\dfrac{p}{1-p})$ ,來對 $y$ 軸進行映射,
128 |
129 | 再套用訓練出來的參數,將這個羅吉斯迴歸的圖形造成一條直線。
130 |
131 |
132 |
133 | 例如以上圖來說,可以將上圖轉成以下的平面。
134 |
135 | **請注意:圖形上的點應在 $y=-\infty$ 或 $y=\infty$,因坐標軸無法顯示,故以最大值表示。**
136 |
137 |
104 |
105 | > Image from me with matplotlib and scikit-learn
106 |
107 | 圖中的橘線即為擬合後的線性迴歸模型,而點則是期中考成績對應到的通過與否。
108 |
109 |
110 |
111 | ### 勝算
112 |
113 | 我們定義勝算 (odds) 為,一件事情發生的機率,除以一件事情不發生的機率,也就是 $\dfrac{p}{1-p}$
114 |
115 | $\log(odds)$ 可以有效的讓勝算的起點設定在數線的 $0$ 上,並且隨著數值的大與小,顯示在數線上距離 $0$ 有多遠。
116 |
117 |
118 |
119 | ### 羅吉斯迴歸的圖形轉換
120 |
121 | 上面的圖似乎可以非常棒的看出對應的成績所造成的通過與否了,不過我們可以將這個圖形做一點轉換。
122 |
123 | 我們考慮將這條線性迴歸模型拉直,也就是轉成 $y=ax+b$ 的形式。
124 |
125 | 為此,我們可以考慮將 $y$ 軸每一點的機率值,映射到一個定義域為 $(-\infty, \infty)$ 的 $y$ 軸上
126 |
127 | 我們可以使用 Logit Function,定義為 $\ln(odds) = \ln(\dfrac{p}{1-p})$ ,來對 $y$ 軸進行映射,
128 |
129 | 再套用訓練出來的參數,將這個羅吉斯迴歸的圖形造成一條直線。
130 |
131 |
132 |
133 | 例如以上圖來說,可以將上圖轉成以下的平面。
134 |
135 | **請注意:圖形上的點應在 $y=-\infty$ 或 $y=\infty$,因坐標軸無法顯示,故以最大值表示。**
136 |
137 |  138 |
139 | > Image from me with matplotlib and scikit-learn
140 |
141 |
--------------------------------------------------------------------------------
/Markdown/Unclassified.md:
--------------------------------------------------------------------------------
1 | # 資料科學概論筆記
2 |
3 | Author: [Uriah Xuan](https://ntut-xuan.github.io/) (109 NTUT CSIE)
4 |
5 |
6 |
7 | ## 大數據的 5V 特徵
8 |
9 | | 英文名稱 | 中文名稱 | 概念 |
10 | | :------: | :------: | :--------------------------------------------------: |
11 | | Volume | 大量化 | 大數據通常有著極大量的資料,因此需要注重保存與安全性 |
12 | | Variety | 多樣化 | 大數據的資料形式其實是不限的,文字、圖片等等 |
13 | | Velocity | 快速化 | 大數據的資料處理需要在一定時限內處理完成 |
14 | | Veracity | 真實性 | 大數據的資料需要有一定的真實性。 |
15 | | Value | 價值化 | 資料帶有價值意義,需要合理的運用,以低價值創造高價值 |
16 |
17 |
18 |
19 | ## 經營管理及數據導向決策問題
20 |
21 | 1. 決策時缺乏適合與即時有效的資訊參考。
22 | 2. 報表不夠齊全,格式與決策層需要的不同。
23 | 3. 花費大量人物力,製作使用率低與無效的報表。
24 | 4. 報表與管理規範結合困難,經常發生異常狀況。
25 | 5. 無法從報表分析產生新管理觀念,找出成功關鍵因素與核心競爭力。
26 |
27 |
28 |
29 | ## 商業智慧與資料探勘的循環
30 |
31 |
138 |
139 | > Image from me with matplotlib and scikit-learn
140 |
141 |
--------------------------------------------------------------------------------
/Markdown/Unclassified.md:
--------------------------------------------------------------------------------
1 | # 資料科學概論筆記
2 |
3 | Author: [Uriah Xuan](https://ntut-xuan.github.io/) (109 NTUT CSIE)
4 |
5 |
6 |
7 | ## 大數據的 5V 特徵
8 |
9 | | 英文名稱 | 中文名稱 | 概念 |
10 | | :------: | :------: | :--------------------------------------------------: |
11 | | Volume | 大量化 | 大數據通常有著極大量的資料,因此需要注重保存與安全性 |
12 | | Variety | 多樣化 | 大數據的資料形式其實是不限的,文字、圖片等等 |
13 | | Velocity | 快速化 | 大數據的資料處理需要在一定時限內處理完成 |
14 | | Veracity | 真實性 | 大數據的資料需要有一定的真實性。 |
15 | | Value | 價值化 | 資料帶有價值意義,需要合理的運用,以低價值創造高價值 |
16 |
17 |
18 |
19 | ## 經營管理及數據導向決策問題
20 |
21 | 1. 決策時缺乏適合與即時有效的資訊參考。
22 | 2. 報表不夠齊全,格式與決策層需要的不同。
23 | 3. 花費大量人物力,製作使用率低與無效的報表。
24 | 4. 報表與管理規範結合困難,經常發生異常狀況。
25 | 5. 無法從報表分析產生新管理觀念,找出成功關鍵因素與核心競爭力。
26 |
27 |
28 |
29 | ## 商業智慧與資料探勘的循環
30 |
31 |  32 |
33 |
34 |
35 | ## Business Intelligence Development Model
36 |
37 | (待補)
38 |
39 |
40 |
41 | ## 辨識模式
42 |
43 | 模式有助於解析複雜事務與展露趨勢、種類為時間、空間、功能。
44 |
45 |
46 |
47 | ### 帕金森定理(Parkinson's Law)
48 |
49 | 在工作能被完成的時限內,工作量會一直被增加,直到所有可用時間都被填充為止。
50 |
51 |
52 |
53 | ### 八二法則(Pareto Principle)
54 |
55 | 約僅有 20% 的變因操控著 80% 的局面,
56 |
57 | 也就是說:「所有變量中,最重要的僅有 20%,雖然 80% 佔多數,但控制的範圍卻遠低於關鍵的少數」。
58 |
59 |
60 |
61 | ## 資料處理鍊
62 |
63 | > 注意:這個條目還在建立與理解中,在服用時可能會承受一定的薛丁格錯誤風險。
64 |
65 |
66 |
67 | 
68 |
69 |
70 |
71 | ## 資料與變數
72 |
73 | 
74 |
75 | | 名詞 | 意義 |
76 | | ------ | ------------------------------------------------------------ |
77 | | 資料 | 經由蒐集、分析及彙總所得到,作為說明與解釋之用的事實與數值。 |
78 | | 資料集 | 為特定研究目的蒐集的所有資料,由許多元素所組成。 |
79 | | 元素 | 資料蒐集的實體,包含很多變數,例如上方表格的每個國家即為一個元素 |
80 | | 變數 | 元素的某一特性,例如上列表格的每個元素有以下四個變數:WTO狀態、GDP、Fitch Rating、Fitch Outlook |
81 | | 觀察值 | 對特定元素蒐集的一組衡量值就是觀察值,例如上表的第1個觀察值(Armenia)包含了一組衡量值:Member、3615、BB-及Stable |
82 |
83 |
84 |
85 | ## 衡量尺度
86 |
87 | 資料蒐集需要以下衡量尺度之一:名目尺度、順序尺度、區間尺度及比例尺度。
88 |
89 | 衡量尺度決定資料包含的資訊量,也指出資料彙整的或統計分析時的最適方法。
90 |
91 |
92 |
93 | ### 名目尺度(nominal scale)
94 |
95 | 用來表示元素屬性的標記或名稱,比較等於或不等於。
96 |
97 | 例如上表的國家WTO狀態可以分成「是WTO會員國」與「是WTO觀察員」,因此我們可以以數字1表示這個國家是WTO會員國,2表示這個國家是WTO觀察員,就能夠方便把資料輸入電腦,兩個國家的WTO狀態只能用相同與否來區分。
98 |
99 | 也因為名目尺度的意義是比較等於或不等於,因此詢問「WTO會員國與WTO觀察員哪個比較大」或者「兩個國家的WTO狀態相加等於多少」是完全毫無意義的行為。
100 |
101 |
102 |
103 | ### 順序尺度(ordinal scale)
104 |
105 | 與名目尺度不同,順序尺度的類別有一定的大小或順序,比起名目尺度只能比較相等,順序尺度能夠比較大小。
106 |
107 | 例如上表的Fitch Rating,其中AAA代表最好,F代表最差,因此可以根據評等排出高低,所以是順序尺度。
108 |
109 |
110 |
111 | ### 區間尺度(interval scale)
112 |
113 | 若變數具有順序資料的特性,且觀察值可以相加或相減,其結果仍有意義,這個變數的衡量尺度就是區間尺度,且一定以數值表示。
114 |
115 | 例如統測成績就是一個區間尺度,假設有三位學生的統測成績為699、560、350,則我們可以由高到低依序排序來衡量出成績表現的優劣,而他們的差距也存在意義,例如699的學生比560的學生高出139分。
116 |
117 |
118 |
119 | ### 比例尺度(ratio scale)
120 |
121 | 若變數具有順序資料的特性,且觀察值可以加減乘除,其結果仍有意義,這個變數的衡量尺度就是比例尺度,且一定以數值表示。
122 |
123 | 與區間尺度的差別在於,**比例尺度要求絕對零點,也就是值必須要大於等於0且在0上必須要是自然的不存在**。
124 |
125 | 例如年齡不存在0歲,而高度不存在0公分,而可以描述20歲比5歲大4倍。
126 |
127 |
128 |
129 | ## 百分位數
130 |
131 | 百分位數可以瞭解資料在最小值與最大值間的分布狀況,以pth百分位數可以把資料分成兩個部份。
132 |
133 | 大約pth百分比的觀察值會小於pth百分位數,而大約有(100-p)百分比的觀察值會大於pth百分位數。
134 |
135 | 計算時需要先「非嚴格遞增排序」,計算公式如下: $$ L_p = \dfrac{p}{100}(n+1) $$
136 |
137 |
138 |
139 | ## 四分位數
140 |
141 | 四分位數將整筆資料分成四個部份,每個部份大概含有25%的資料個數,定義如下:
142 |
143 | 1. $Q_1$為第一四分位數或 $25\text{th percentile}$
144 | 2. $Q_2$為第二四分位數或 $50\text{th percentile}$,也就是中位數
145 | 3. $Q_3$為第三四分位數或 $75\text{th percentile}$
146 |
147 |
148 |
149 | ## 四分位距(IQR)
150 |
151 | 四分位距較能克服極端值的影響,定義如下 $ \text{IQR} = Q_3-Q_1 $ 也就是中間資料$50%$的全距。
152 |
153 |
154 |
155 | ## 離群偵測
156 |
157 | 有時在一個資料集中會有極大與極小的數值,這些數值稱為離群。
158 |
159 | 我們可以利用$z$分數去偵測離群值,一般來說,約有$99.7%$的資料會落在標準差$\pm3$內,我們會希望資料的標準差與中心的距離不超過$3$。
160 |
161 | 另一種方式是使用第一分位、第三分位與四分位距來做偵測,能夠給定一個區間來要求值必須要在這個區間內,定義如下:
162 |
163 | $\text{Lower Limit} = Q_1 - 1.5(\text{IQR}) \ \text{Upper Limit} = Q_3 + 1.5(\text{IQR}) $
164 |
165 |
166 |
167 | ## 資料模型
168 |
169 | 資料模型是為了能有組織有效率地,將我們需求的資料儲存於資料庫系統中,以及有一個適當的表達方式。
170 |
171 |
172 |
173 | 主要分成三種模式的**演變**:
174 |
175 | 1. 階層式資料模型
176 | 2. 網路式資料模型
177 | 3. 關聯式資料模型
178 |
179 |
180 |
181 | ### 階層式資料模型
182 |
183 | 主要使用樹狀結構,將一筆一筆的紀錄組織起來,適合一對多的資料組成關係,但無法直接表達多對多的關係。
184 |
185 |
186 |
187 | ### 網路式資料模型
188 |
189 | 改善了階層式資料模型,可以供給多對多的關係。
190 |
191 | 在資料呈現上非常複雜、且無法確實表達資料與資料之間的網路連結關係。
192 |
193 |
194 |
195 | ### 關聯式資料模型
196 |
197 | 以表格來表達關係,每一列即為一個紀錄,通常會實體關聯圖作為輔助設計的依據。
198 |
199 |
200 |
201 | ## SQL 查詢
202 |
203 | SQL 全名為 結構化查詢語言(Structured Query Language),對於資料庫來說,我們可以用 SQL 語法來進行查詢。
204 |
205 | 
206 |
207 | 例如要從一張名為 Teacher 的資料表中,顯示出所有結果屬性,寫法可以寫成這樣。
208 |
209 | ```sql
210 | SELECT * FROM Teacher
211 | ```
212 |
213 | 若要從這堆老師中選出其中一個名為王小軒的老師,可以寫成這樣。
214 |
215 | ```sql
216 | SELECT * FROM Teacher WHERE name = '王小軒'
217 | ```
218 |
219 | 若只要得到王小軒老師的 ID,可以寫成這樣。
220 |
221 | ```sql
222 | SELECT ID FROM Teacher WHERE name = '王小軒'
223 | ```
224 |
225 |
226 |
227 | ## 非結構化資料
228 |
229 | ### 非結構化資料的介紹
230 |
231 | 非結構化資料形式涵蓋了聲音、圖像、影像、文字等等。
232 |
233 | > [結構化資料 vs. 非結構化資料 | Pure Storage](https://www.purestorage.com/tw/knowledge/big-data/structured-vs-unstructured-data.html)
234 |
235 |
236 |
237 | ### 非結構化資料的特性
238 |
239 | #### 數位化生成
240 |
241 | 大部分由機器生成的資料,並不一定能夠整齊的被資料庫的欄位所對應,因此會使得資料庫變成多維度,且非常難以預測。
242 |
243 |
244 |
245 | #### 多模式
246 |
247 | 資料經過蒐集之後,具有大量不同類別的資料,例如 e-mail、文檔、圖檔等等。
248 |
249 |
250 |
251 | #### 持續變動
252 |
253 | 大量資料被生成、處理、分析與即時運算。
254 |
255 |
256 |
257 | #### 地理分散
258 |
259 | 不同資料被儲存在不同的地方,來達成資安特性。
260 |
261 |
262 |
263 | > [結構化資料 vs. 非結構化資料 | Pure Storage](https://www.purestorage.com/tw/knowledge/big-data/structured-vs-unstructured-data.html)
264 | >
265 | > [Unified Fast File and Object: A New Category of Storage | Pure Storage](https://blog.purestorage.com/products/unified-fast-file-object-storage/)
266 | >
267 | > [Types and Examples of NoSQL Databases - Big Data Analytics News](https://bigdataanalyticsnews.com/types-examples-nosql-databases/)
268 | >
269 | > [淺談資料格式 — 結構化與非結構化資料. 進入大數據時代,資料成為挖掘商機的礦脈,對資料的管理不夠,想要利用大數據來開創新… | by 行銷資料科學 | Marketingdatascience | Medium](https://medium.com/marketingdatascience/%E6%B7%BA%E8%AB%87%E8%B3%87%E6%96%99%E6%A0%BC%E5%BC%8F-%E7%B5%90%E6%A7%8B%E5%8C%96%E8%88%87%E9%9D%9E%E7%B5%90%E6%A7%8B%E5%8C%96%E8%B3%87%E6%96%99-50c89a4b15e0)
270 |
271 |
272 |
273 | ### 結構化與非結構資料化的比較
274 |
275 | | | 結構化資料 | 非結構化資料 |
276 | | :----------: | :------------: | :----------: |
277 | | 呈現方面 | 表格 | 無法呈現 |
278 | | 處理方面 | 需正規化 | 不須正規化 |
279 | | 形式 | 有限的資料形式 | 不限 |
280 | | 儲存空間需求 | 較少 | 較大 |
281 | | 存取 | 較簡單 | 較困難 |
282 |
283 |
284 |
285 | ## 資料探勘
286 |
287 | 從一大群的資料中,利用技術(人工智慧、機器學習、統計學等等)探勘出有意義的資料。
288 |
289 |
290 |
291 | ### 資料的探勘任務
292 |
293 | 主要分成六種常見的任務。
294 |
295 | 1. 異常檢測:辨識不尋常的資料,或針對錯誤資料進一步調查。
296 | 2. 關聯規則學習:搜尋變數之間的關係。
297 | 3. 聚類:在未知資料的結構下,發現資料的類別與結構,利用演算法將資料分成更多子集,讓子集的資料都有相似的一些屬性。
298 | 4. 分類:對新的資料推廣成已知結構的任務,例如將一封新郵件分類成「正常郵件」與「垃圾郵件」,可利用決策樹來分析數據或輔助預測。
299 | 5. 迴歸:試圖找到最小誤差的建模函式。
300 | 6. 匯總:提供一個更緊湊的資料集表示,來生成視覺化或報表。
301 |
302 |
--------------------------------------------------------------------------------
/PDF/Artificial Neural Networks.pdf:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/ntut-xuan/DataScienceNote/c49735d5ffa0623e5f17974f95afcf68c413e15b/PDF/Artificial Neural Networks.pdf
--------------------------------------------------------------------------------
/PDF/Associate Rule Mining.pdf:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/ntut-xuan/DataScienceNote/c49735d5ffa0623e5f17974f95afcf68c413e15b/PDF/Associate Rule Mining.pdf
--------------------------------------------------------------------------------
/PDF/Cluster Analysis.pdf:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/ntut-xuan/DataScienceNote/c49735d5ffa0623e5f17974f95afcf68c413e15b/PDF/Cluster Analysis.pdf
--------------------------------------------------------------------------------
/PDF/Data Mining.pdf:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/ntut-xuan/DataScienceNote/c49735d5ffa0623e5f17974f95afcf68c413e15b/PDF/Data Mining.pdf
--------------------------------------------------------------------------------
/PDF/Data Preprocessing.pdf:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/ntut-xuan/DataScienceNote/c49735d5ffa0623e5f17974f95afcf68c413e15b/PDF/Data Preprocessing.pdf
--------------------------------------------------------------------------------
/PDF/Data Warehouse.pdf:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/ntut-xuan/DataScienceNote/c49735d5ffa0623e5f17974f95afcf68c413e15b/PDF/Data Warehouse.pdf
--------------------------------------------------------------------------------
/PDF/Decision Tree.pdf:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/ntut-xuan/DataScienceNote/c49735d5ffa0623e5f17974f95afcf68c413e15b/PDF/Decision Tree.pdf
--------------------------------------------------------------------------------
/PDF/Naive Bayes Analysis.pdf:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/ntut-xuan/DataScienceNote/c49735d5ffa0623e5f17974f95afcf68c413e15b/PDF/Naive Bayes Analysis.pdf
--------------------------------------------------------------------------------
/PDF/Regression.pdf:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/ntut-xuan/DataScienceNote/c49735d5ffa0623e5f17974f95afcf68c413e15b/PDF/Regression.pdf
--------------------------------------------------------------------------------
/PDF/Unclassified.pdf:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/ntut-xuan/DataScienceNote/c49735d5ffa0623e5f17974f95afcf68c413e15b/PDF/Unclassified.pdf
--------------------------------------------------------------------------------
/README.md:
--------------------------------------------------------------------------------
1 | # 資料科學導論筆記
2 |
3 |
4 |
5 | ## 作者
6 |
7 | 國立臺北科技大學 資訊工程系 [黃漢軒](https://ntut-xuan.github.io)
8 |
9 | 筆記上有任何問題,請丟 [issue](https://github.com/ntut-xuan/DataScienceNote/issues),支持這份筆記,請幫我點個 star,謝謝
10 |
11 |
12 |
13 | **超級注意:工具箱的部分只經過我本人測試過,並不保證他不會有任何問題,有任何問題不負任何責任,有遇到問題請丟 [issue](https://github.com/ntut-xuan/DataScienceNote/issues) 。**
14 |
15 |
16 |
17 | ## 主題式分析
18 |
19 | 這份筆記使用主題式的方式架構,主要分成以下幾個子主題。
20 |
21 |
22 |
23 | | 主題 | 完工進度 | ToolBox | 完工時間 |
24 | | :----------------------------------------: | :------: | :-----: | :------------: |
25 | | 還沒經過整理的主題 | SKIP | SKIP | SKIP |
26 | | 資料倉儲(Data Warehouse) | 100% | SKIP | 2022 / 04 / 04 |
27 | | 資料探勘(Data Mining) | 100% | SKIP | 2022 / 04 / 05 |
28 | | 決策樹(Decision Tree) | 100% | SKIP | 2022 / 04 / 12 |
29 | | 迴歸(Regression) | 100% | SKIP | 2022 / 04 / 14 |
30 | | 單純貝氏(Naïve Bayes Analysis) | 100% | OK | 2022 / 06 / 15 |
31 | | 人工神經網路(Artificial Neural Networks) | 100% | SKIP | 2022 / 06 / 15 |
32 | | 聚類分析(Cluster Analysis) | 100% | OK | 2022 / 06 / 22 |
33 | | 資料預處理(Data Preprocessing) | 100% | SKIP | 2022 / 06 / 22 |
34 | | 推薦系統(Recommandation System) | 100% | SKIP | 2022 / 06 / 22 |
35 |
36 |
37 |
--------------------------------------------------------------------------------
/python_tool/.gitignore:
--------------------------------------------------------------------------------
1 | .idea
2 | __pycache__
--------------------------------------------------------------------------------
/python_tool/debug.py:
--------------------------------------------------------------------------------
1 | import numpy as np
2 | import random
3 | import time
4 | import matplotlib.pyplot as plt
5 |
6 | def standard_random():
7 | std = np.array([0.1, 0.1, 0.1, 0.1, 0.1, 0.1, 0.1])
8 | return std
9 |
10 |
11 | def active_function(x):
12 | return np.log(1+np.exp(x))
13 |
14 |
15 | def calc(x_1s, x_2s, x_1, x_2, y_1, y_2, w, b):
16 | x_1s = np.transpose(data)[0]
17 | x_2s = np.transpose(data)[1]
18 | output = w[5] * y_1 + w[6] * y_2 + b[3]
19 | return (x_1s * w[1] + x_2s * w[3], x_1s * w[2] + x_2s * w[4], active_function(x_1), active_function(x_2), output)
20 |
21 | data = [[35, 67], [12, 75], [16, 89], [45, 56], [10, 90]]
22 | label = [1, 0, 1, 1, 0]
23 |
24 | data_array = np.array(data)
25 | label_array = np.array(label)
26 |
27 | w = standard_random()
28 | b = [0 for i in range(4)]
29 |
30 | print(w)
31 |
32 | x_1s = np.transpose(data)[0]
33 | x_2s = np.transpose(data)[1]
34 | x_1 = x_1s * w[1] + x_2s * w[3]
35 | x_2 = x_1s * w[2] + x_2s * w[4]
36 | y_1 = np.log(1+np.exp(x_1))
37 | y_2 = np.log(1+np.exp(x_2))
38 | output = w[5] * active_function(x_1*w[1]+x_2*w[3] + b[1]) + w[6] * active_function(x_1*w[2]+x_2*w[4] + b[2]) + b[3]
39 | learn_rate = 0.01
40 |
41 | for i in range(1000):
42 | x_1s = np.transpose(data)[0]
43 | x_2s = np.transpose(data)[1]
44 | x_1, x_2, y_1, y_2, output = calc(x_1s, x_2s, x_1, x_2, y_1, y_2, w, b)
45 | db3 = np.sum(-2 * (label_array - output))
46 | dw5 = np.sum((label_array - output) * y_1 * -2)
47 | dw6 = np.sum((label_array - output) * y_2 * -2)
48 | db1 = np.sum((label_array - output) * w[5] * (np.exp(x_1) / (1 + np.exp(x_1))) * -2)
49 | db2 = np.sum((label_array - output) * w[6] * (np.exp(x_2) / (1 + np.exp(x_2))) * -2)
50 | dw1 = np.sum((label_array - output) * w[5] * (np.exp(x_1) / (1 + np.exp(x_1))) * x_1s * -2)
51 | dw2 = np.sum((label_array - output) * w[6] * (np.exp(x_2) / (1 + np.exp(x_2))) * x_1s * -2)
52 | dw3 = np.sum((label_array - output) * w[5] * (np.exp(x_1) / (1 + np.exp(x_1))) * x_2s * -2)
53 | dw4 = np.sum((label_array - output) * w[6] * (np.exp(x_2) / (1 + np.exp(x_2))) * x_2s * -2)
54 | print("SSR =", np.sum(label_array - output) * np.sum(label_array - output))
55 | b[3] = b[3] - db3 * learn_rate
56 | b[2] = b[2] - db2 * learn_rate
57 | b[1] = b[1] - db1 * learn_rate
58 | w[6] = w[6] - dw6 * learn_rate
59 | w[5] = w[5] - dw5 * learn_rate
60 | w[4] = w[4] - dw4 * learn_rate
61 | w[3] = w[3] - dw3 * learn_rate
62 | w[2] = w[2] - dw2 * learn_rate
63 | w[1] = w[1] - dw1 * learn_rate
64 | print("b=", b)
65 | print("w=", w)
66 |
67 | fig = plt.figure(figsize=(10, 10))
68 | ax = fig.gca(projection='3d')
69 |
70 | plot_x = np.linspace(0, 100, num=100)
71 |
72 | table = np.array([[0 for _ in range(100)] for _ in range(100)])
73 |
74 | for i in range(100):
75 | for j in range(100):
76 | x1 = i
77 | x2 = j
78 | #print(x1, x2)
79 | table[i][j] = w[5] * (active_function(x1 * w[1] + x2 * w[3]) + b[1]) \
80 | + w[6] * (active_function(x1 * w[2] + x2 * w[4]) + b[2]) \
81 | + b[3]
82 |
83 | ax.scatter(np.transpose(data_array)[0], np.transpose(data_array)[1], label_array)
84 | ax.plot_surface(plot_x, plot_x, table, cmap='seismic')
85 | plt.show()
86 |
87 | print(table)
88 |
89 | print(table[45][56])
90 | print(table[25][70])
--------------------------------------------------------------------------------
/python_tool/example.py:
--------------------------------------------------------------------------------
1 | from tool import *
2 |
3 | naiveBayesClassifier = MultinomialNaiveBayesClassifier()
4 | data = [["love", "happy", "joy", "joy", "love"],
5 | ["happy", "love", "kick", "joy", "happy"],
6 | ["love", "move", "joy", "good"],
7 | ["love", "happy", "joy", "pain", "love"],
8 | ["joy", "love", "pain", "kick", "pain"],
9 | ["pain", "pain", "love", "kick"]]
10 | label = ["Yes", "Yes", "Yes", "Yes", "No", "No"]
11 | value = ["love", "pain", "joy", "happy", "kick", "happy"]
12 |
13 | naiveBayesClassifier.fit(np.array(data, dtype=object), np.array(label, dtype=object))
14 | print(naiveBayesClassifier.predict(value))
--------------------------------------------------------------------------------
/python_tool/main.py:
--------------------------------------------------------------------------------
1 | import numpy as np
2 | import tool
3 | import time
4 | import warnings
5 | import matplotlib.pyplot as plt
6 | from sklearn import cluster, datasets
7 | from sklearn.preprocessing import StandardScaler
8 | from itertools import cycle, islice
9 |
10 | n_samples = 300
11 | random_state = 170
12 | noisy_circles = datasets.make_circles(n_samples=n_samples, factor=0.5, noise=0.01)
13 |
14 | points = noisy_circles[0]
15 |
16 | array = np.zeros((n_samples, n_samples))
17 |
18 | for i in range(n_samples):
19 | for j in range(n_samples):
20 | array[i][j] = np.sqrt((points[i][0]-points[j][0])**2 + (points[i][1]-points[j][1])**2)
21 |
22 | algo = tool.WPGMAClustering(n_clusters=2)
23 | algo.fit(array)
24 | algo.clustering()
25 |
26 | print(algo.labels_)
27 |
28 | colors = np.array(
29 | list(
30 | islice(
31 | cycle(
32 | [
33 | "#377eb8",
34 | "#ff7f00",
35 | "#4daf4a",
36 | "#f781bf",
37 | "#a65628",
38 | "#984ea3",
39 | "#999999",
40 | "#e41a1c",
41 | "#dede00",
42 | ]
43 | ),
44 | int(max(algo.labels_) + 1),
45 | )
46 | ))
47 |
48 |
49 | plt.scatter(points[:, 0], points[:, 1], color=colors[algo.labels_])
50 | plt.show()
--------------------------------------------------------------------------------
/python_tool/tool.py:
--------------------------------------------------------------------------------
1 | import numpy as np
2 | import copy
3 |
4 |
5 | class MultinomialNaiveBayesClassifier:
6 | def __init__(self):
7 | self.value_map = {}
8 | self.result = np.array([])
9 | self.data = np.array([])
10 |
11 | def fit(self, x, y):
12 | self.result = y
13 | unique, counts = np.unique(self.result, return_counts=True)
14 | for v in unique:
15 | self.value_map[v] = []
16 | for i in range(len(y)):
17 | for s in x[i]:
18 | self.value_map[y[i]].append(s)
19 |
20 | def add_duplicated_value(self, temp_result, temp_value_map, missing_value):
21 | unique, counts = np.unique(temp_result, return_counts=True)
22 | for k in unique:
23 | value_unique = np.unique(temp_value_map[k])
24 | for v in value_unique:
25 | if missing_value == v:
26 | continue
27 | temp_value_map[k].append(v)
28 | for k in unique:
29 | temp_value_map[k].append(missing_value)
30 |
31 | def print_unique(self, y):
32 | for v in np.unique(self.result):
33 | unique, counts = np.unique(y[v], return_counts=True)
34 | result_dict = dict(zip(unique, counts))
35 | print(result_dict)
36 |
37 | def predict(self, y):
38 | temp_result = self.result
39 | temp_value_map = self.value_map
40 | unique, counts = np.unique(self.result, return_counts=True)
41 | result_dict = dict(zip(unique, counts))
42 | predict = {}
43 | for v in unique:
44 | print("calculate P(%s) = %d/%d" % (v, result_dict[v], int(np.sum(counts))))
45 | predict[v] = float(result_dict[v] / np.sum(counts))
46 | for s in y:
47 | for v in unique:
48 | if s not in self.value_map[v]:
49 | self.add_duplicated_value(temp_result, temp_value_map, s)
50 | self.print_unique(temp_value_map)
51 | for s in y:
52 | for v in unique:
53 | unique_s, counts_s = np.unique(self.value_map[v], return_counts=True)
54 | result_dict_s = dict(zip(unique_s, counts_s))
55 | total = np.sum(counts_s)
56 | print("calculate P(%s|%s) = %d/%d" % (s, v, result_dict_s[s], int(total)))
57 | predict[v] *= float(result_dict_s[s] / int(total))
58 | print(predict)
59 | return max(predict, key=predict.get)
60 |
61 |
62 | class UPGMAClustering:
63 |
64 | def __init__(self, n_clusters=2):
65 | self.labels_ = None
66 | self.n = None
67 | self.n_clusters = n_clusters
68 | self.cluster_list = None
69 | self.distance_table = None
70 | self.threshold = None
71 |
72 | def fit(self, distance_table):
73 | self.n = len(distance_table)
74 | self.distance_table = distance_table
75 | self.cluster_list = []
76 | self.threshold = []
77 | self.labels_ = [0 for _ in range(self.n)]
78 | for i in range(self.n):
79 | self.cluster_list.append([i])
80 |
81 | def clustering(self):
82 | for r in range(self.n - (self.n_clusters-1)):
83 |
84 | print("\n=============== Iter%5d ===============\n" % (r + 1))
85 |
86 | original_cluster_list = copy.deepcopy(self.cluster_list)
87 | self.distance_table[self.distance_table == 0] = np.iinfo(np.int32).max
88 |
89 | # choose minimum pair
90 | minimum_distance = np.min(self.distance_table)
91 | minimum_pair = np.unravel_index(np.argmin(self.distance_table, axis=None), self.distance_table.shape)
92 | print("Minimum pair: %s = %d" % (str(minimum_pair), minimum_distance))
93 |
94 | if r != self.n - self.n_clusters:
95 |
96 | # combine two cluster
97 | target_list1 = copy.deepcopy(self.cluster_list[minimum_pair[0]])
98 | target_list2 = copy.deepcopy(self.cluster_list[minimum_pair[1]])
99 | self.cluster_list[minimum_pair[0]] += (self.cluster_list[minimum_pair[1]])
100 | self.cluster_list.remove(self.cluster_list[minimum_pair[1]])
101 |
102 | print("target list l1=", target_list1, "- l2=", target_list2)
103 | print("combine list", original_cluster_list, "->", self.cluster_list)
104 |
105 | # recalculate distance between new cluster and another cluster
106 | self.distance_table[self.distance_table == np.iinfo(np.int32).max] = 0
107 | new_distance_table = np.zeros((len(self.cluster_list), len(self.cluster_list)))
108 | for i in range(len(self.cluster_list)):
109 | for j in range(len(self.cluster_list)):
110 | index1 = original_cluster_list.index(target_list1)
111 | index2 = original_cluster_list.index(target_list2)
112 | index4 = self.cluster_list.index(self.cluster_list[j])
113 | if i == index1 or j == index1:
114 | if index1 == index4:
115 | continue
116 | index3 = original_cluster_list.index(self.cluster_list[j])
117 | distance1 = self.distance_table[index1][index3]
118 | distance2 = self.distance_table[index2][index3]
119 | new_distance_table[index1][index4] = (len(target_list1) * distance1 + len(
120 | target_list2) * distance2) / float(len(target_list1) + len(target_list2))
121 | new_distance_table[index4][index1] = (len(target_list1) * distance1 + len(
122 | target_list2) * distance2) / float(len(target_list1) + len(target_list2))
123 | else:
124 | index3 = original_cluster_list.index(self.cluster_list[j])
125 | index5 = original_cluster_list.index(self.cluster_list[i])
126 | new_distance_table[i][j] = self.distance_table[index5][index3]
127 |
128 | self.distance_table = new_distance_table
129 |
130 | # print
131 | print("Update Table\n", str(new_distance_table))
132 | print(self.cluster_list)
133 |
134 | # calculate branch length estimation
135 | branch_length_estimation = minimum_distance / 2.0
136 | self.threshold += [branch_length_estimation]
137 | print("distance_threshold =", branch_length_estimation)
138 |
139 | for i in range(len(self.cluster_list)):
140 | for v in self.cluster_list[i]:
141 | self.labels_[v] = i+1
142 |
143 |
144 | class WPGMAClustering:
145 |
146 | def __init__(self, n_clusters=2):
147 | self.labels_ = None
148 | self.n = None
149 | self.n_clusters = n_clusters
150 | self.cluster_list = None
151 | self.distance_table = None
152 | self.threshold = None
153 |
154 | def fit(self, distance_table):
155 | self.n = len(distance_table)
156 | self.distance_table = distance_table
157 | self.cluster_list = []
158 | self.threshold = []
159 | self.labels_ = [0 for _ in range(self.n)]
160 | for i in range(self.n):
161 | self.cluster_list.append([i])
162 |
163 | def clustering(self):
164 | for r in range(self.n - (self.n_clusters-1)):
165 |
166 | print("\n=============== Iter%5d ===============\n" % (r + 1))
167 |
168 | original_cluster_list = copy.deepcopy(self.cluster_list)
169 | self.distance_table[self.distance_table == 0] = np.iinfo(np.int32).max
170 |
171 | # choose minimum pair
172 | minimum_distance = np.min(self.distance_table)
173 | minimum_pair = np.unravel_index(np.argmin(self.distance_table, axis=None), self.distance_table.shape)
174 | print("Minimum pair: %s = %d" % (str(minimum_pair), minimum_distance))
175 |
176 | if r != self.n - self.n_clusters:
177 |
178 | # combine two cluster
179 | target_list1 = copy.deepcopy(self.cluster_list[minimum_pair[0]])
180 | target_list2 = copy.deepcopy(self.cluster_list[minimum_pair[1]])
181 | self.cluster_list[minimum_pair[0]] += (self.cluster_list[minimum_pair[1]])
182 | self.cluster_list.remove(self.cluster_list[minimum_pair[1]])
183 |
184 | print("target list l1=", target_list1, "- l2=", target_list2)
185 | print("combine list", original_cluster_list, "->", self.cluster_list)
186 |
187 | # recalculate distance between new cluster and another cluster
188 | self.distance_table[self.distance_table == np.iinfo(np.int32).max] = 0
189 | new_distance_table = np.zeros((len(self.cluster_list), len(self.cluster_list)))
190 | for i in range(len(self.cluster_list)):
191 | for j in range(len(self.cluster_list)):
192 | index1 = original_cluster_list.index(target_list1)
193 | index2 = original_cluster_list.index(target_list2)
194 | index4 = self.cluster_list.index(self.cluster_list[j])
195 | if i == index1 or j == index1:
196 | if index1 == index4:
197 | continue
198 | index3 = original_cluster_list.index(self.cluster_list[j])
199 | distance1 = self.distance_table[index1][index3]
200 | distance2 = self.distance_table[index2][index3]
201 | new_distance_table[index1][index4] = (distance1 + distance2) / 2.0
202 | new_distance_table[index4][index1] = (distance1 + distance2) / 2.0
203 | else:
204 | index3 = original_cluster_list.index(self.cluster_list[j])
205 | index5 = original_cluster_list.index(self.cluster_list[i])
206 | new_distance_table[i][j] = self.distance_table[index5][index3]
207 |
208 | self.distance_table = new_distance_table
209 |
210 | # print
211 | print("Update Table\n", str(new_distance_table))
212 | print(self.cluster_list)
213 |
214 | # calculate branch length estimation
215 | branch_length_estimation = minimum_distance / 2.0
216 | self.threshold += [branch_length_estimation]
217 | print("distance_threshold =", branch_length_estimation)
218 |
219 | for i in range(len(self.cluster_list)):
220 | for v in self.cluster_list[i]:
221 | self.labels_[v] = i+1
222 |
--------------------------------------------------------------------------------
32 |
33 |
34 |
35 | ## Business Intelligence Development Model
36 |
37 | (待補)
38 |
39 |
40 |
41 | ## 辨識模式
42 |
43 | 模式有助於解析複雜事務與展露趨勢、種類為時間、空間、功能。
44 |
45 |
46 |
47 | ### 帕金森定理(Parkinson's Law)
48 |
49 | 在工作能被完成的時限內,工作量會一直被增加,直到所有可用時間都被填充為止。
50 |
51 |
52 |
53 | ### 八二法則(Pareto Principle)
54 |
55 | 約僅有 20% 的變因操控著 80% 的局面,
56 |
57 | 也就是說:「所有變量中,最重要的僅有 20%,雖然 80% 佔多數,但控制的範圍卻遠低於關鍵的少數」。
58 |
59 |
60 |
61 | ## 資料處理鍊
62 |
63 | > 注意:這個條目還在建立與理解中,在服用時可能會承受一定的薛丁格錯誤風險。
64 |
65 |
66 |
67 | 
68 |
69 |
70 |
71 | ## 資料與變數
72 |
73 | 
74 |
75 | | 名詞 | 意義 |
76 | | ------ | ------------------------------------------------------------ |
77 | | 資料 | 經由蒐集、分析及彙總所得到,作為說明與解釋之用的事實與數值。 |
78 | | 資料集 | 為特定研究目的蒐集的所有資料,由許多元素所組成。 |
79 | | 元素 | 資料蒐集的實體,包含很多變數,例如上方表格的每個國家即為一個元素 |
80 | | 變數 | 元素的某一特性,例如上列表格的每個元素有以下四個變數:WTO狀態、GDP、Fitch Rating、Fitch Outlook |
81 | | 觀察值 | 對特定元素蒐集的一組衡量值就是觀察值,例如上表的第1個觀察值(Armenia)包含了一組衡量值:Member、3615、BB-及Stable |
82 |
83 |
84 |
85 | ## 衡量尺度
86 |
87 | 資料蒐集需要以下衡量尺度之一:名目尺度、順序尺度、區間尺度及比例尺度。
88 |
89 | 衡量尺度決定資料包含的資訊量,也指出資料彙整的或統計分析時的最適方法。
90 |
91 |
92 |
93 | ### 名目尺度(nominal scale)
94 |
95 | 用來表示元素屬性的標記或名稱,比較等於或不等於。
96 |
97 | 例如上表的國家WTO狀態可以分成「是WTO會員國」與「是WTO觀察員」,因此我們可以以數字1表示這個國家是WTO會員國,2表示這個國家是WTO觀察員,就能夠方便把資料輸入電腦,兩個國家的WTO狀態只能用相同與否來區分。
98 |
99 | 也因為名目尺度的意義是比較等於或不等於,因此詢問「WTO會員國與WTO觀察員哪個比較大」或者「兩個國家的WTO狀態相加等於多少」是完全毫無意義的行為。
100 |
101 |
102 |
103 | ### 順序尺度(ordinal scale)
104 |
105 | 與名目尺度不同,順序尺度的類別有一定的大小或順序,比起名目尺度只能比較相等,順序尺度能夠比較大小。
106 |
107 | 例如上表的Fitch Rating,其中AAA代表最好,F代表最差,因此可以根據評等排出高低,所以是順序尺度。
108 |
109 |
110 |
111 | ### 區間尺度(interval scale)
112 |
113 | 若變數具有順序資料的特性,且觀察值可以相加或相減,其結果仍有意義,這個變數的衡量尺度就是區間尺度,且一定以數值表示。
114 |
115 | 例如統測成績就是一個區間尺度,假設有三位學生的統測成績為699、560、350,則我們可以由高到低依序排序來衡量出成績表現的優劣,而他們的差距也存在意義,例如699的學生比560的學生高出139分。
116 |
117 |
118 |
119 | ### 比例尺度(ratio scale)
120 |
121 | 若變數具有順序資料的特性,且觀察值可以加減乘除,其結果仍有意義,這個變數的衡量尺度就是比例尺度,且一定以數值表示。
122 |
123 | 與區間尺度的差別在於,**比例尺度要求絕對零點,也就是值必須要大於等於0且在0上必須要是自然的不存在**。
124 |
125 | 例如年齡不存在0歲,而高度不存在0公分,而可以描述20歲比5歲大4倍。
126 |
127 |
128 |
129 | ## 百分位數
130 |
131 | 百分位數可以瞭解資料在最小值與最大值間的分布狀況,以pth百分位數可以把資料分成兩個部份。
132 |
133 | 大約pth百分比的觀察值會小於pth百分位數,而大約有(100-p)百分比的觀察值會大於pth百分位數。
134 |
135 | 計算時需要先「非嚴格遞增排序」,計算公式如下: $$ L_p = \dfrac{p}{100}(n+1) $$
136 |
137 |
138 |
139 | ## 四分位數
140 |
141 | 四分位數將整筆資料分成四個部份,每個部份大概含有25%的資料個數,定義如下:
142 |
143 | 1. $Q_1$為第一四分位數或 $25\text{th percentile}$
144 | 2. $Q_2$為第二四分位數或 $50\text{th percentile}$,也就是中位數
145 | 3. $Q_3$為第三四分位數或 $75\text{th percentile}$
146 |
147 |
148 |
149 | ## 四分位距(IQR)
150 |
151 | 四分位距較能克服極端值的影響,定義如下 $ \text{IQR} = Q_3-Q_1 $ 也就是中間資料$50%$的全距。
152 |
153 |
154 |
155 | ## 離群偵測
156 |
157 | 有時在一個資料集中會有極大與極小的數值,這些數值稱為離群。
158 |
159 | 我們可以利用$z$分數去偵測離群值,一般來說,約有$99.7%$的資料會落在標準差$\pm3$內,我們會希望資料的標準差與中心的距離不超過$3$。
160 |
161 | 另一種方式是使用第一分位、第三分位與四分位距來做偵測,能夠給定一個區間來要求值必須要在這個區間內,定義如下:
162 |
163 | $\text{Lower Limit} = Q_1 - 1.5(\text{IQR}) \ \text{Upper Limit} = Q_3 + 1.5(\text{IQR}) $
164 |
165 |
166 |
167 | ## 資料模型
168 |
169 | 資料模型是為了能有組織有效率地,將我們需求的資料儲存於資料庫系統中,以及有一個適當的表達方式。
170 |
171 |
172 |
173 | 主要分成三種模式的**演變**:
174 |
175 | 1. 階層式資料模型
176 | 2. 網路式資料模型
177 | 3. 關聯式資料模型
178 |
179 |
180 |
181 | ### 階層式資料模型
182 |
183 | 主要使用樹狀結構,將一筆一筆的紀錄組織起來,適合一對多的資料組成關係,但無法直接表達多對多的關係。
184 |
185 |
186 |
187 | ### 網路式資料模型
188 |
189 | 改善了階層式資料模型,可以供給多對多的關係。
190 |
191 | 在資料呈現上非常複雜、且無法確實表達資料與資料之間的網路連結關係。
192 |
193 |
194 |
195 | ### 關聯式資料模型
196 |
197 | 以表格來表達關係,每一列即為一個紀錄,通常會實體關聯圖作為輔助設計的依據。
198 |
199 |
200 |
201 | ## SQL 查詢
202 |
203 | SQL 全名為 結構化查詢語言(Structured Query Language),對於資料庫來說,我們可以用 SQL 語法來進行查詢。
204 |
205 | 
206 |
207 | 例如要從一張名為 Teacher 的資料表中,顯示出所有結果屬性,寫法可以寫成這樣。
208 |
209 | ```sql
210 | SELECT * FROM Teacher
211 | ```
212 |
213 | 若要從這堆老師中選出其中一個名為王小軒的老師,可以寫成這樣。
214 |
215 | ```sql
216 | SELECT * FROM Teacher WHERE name = '王小軒'
217 | ```
218 |
219 | 若只要得到王小軒老師的 ID,可以寫成這樣。
220 |
221 | ```sql
222 | SELECT ID FROM Teacher WHERE name = '王小軒'
223 | ```
224 |
225 |
226 |
227 | ## 非結構化資料
228 |
229 | ### 非結構化資料的介紹
230 |
231 | 非結構化資料形式涵蓋了聲音、圖像、影像、文字等等。
232 |
233 | > [結構化資料 vs. 非結構化資料 | Pure Storage](https://www.purestorage.com/tw/knowledge/big-data/structured-vs-unstructured-data.html)
234 |
235 |
236 |
237 | ### 非結構化資料的特性
238 |
239 | #### 數位化生成
240 |
241 | 大部分由機器生成的資料,並不一定能夠整齊的被資料庫的欄位所對應,因此會使得資料庫變成多維度,且非常難以預測。
242 |
243 |
244 |
245 | #### 多模式
246 |
247 | 資料經過蒐集之後,具有大量不同類別的資料,例如 e-mail、文檔、圖檔等等。
248 |
249 |
250 |
251 | #### 持續變動
252 |
253 | 大量資料被生成、處理、分析與即時運算。
254 |
255 |
256 |
257 | #### 地理分散
258 |
259 | 不同資料被儲存在不同的地方,來達成資安特性。
260 |
261 |
262 |
263 | > [結構化資料 vs. 非結構化資料 | Pure Storage](https://www.purestorage.com/tw/knowledge/big-data/structured-vs-unstructured-data.html)
264 | >
265 | > [Unified Fast File and Object: A New Category of Storage | Pure Storage](https://blog.purestorage.com/products/unified-fast-file-object-storage/)
266 | >
267 | > [Types and Examples of NoSQL Databases - Big Data Analytics News](https://bigdataanalyticsnews.com/types-examples-nosql-databases/)
268 | >
269 | > [淺談資料格式 — 結構化與非結構化資料. 進入大數據時代,資料成為挖掘商機的礦脈,對資料的管理不夠,想要利用大數據來開創新… | by 行銷資料科學 | Marketingdatascience | Medium](https://medium.com/marketingdatascience/%E6%B7%BA%E8%AB%87%E8%B3%87%E6%96%99%E6%A0%BC%E5%BC%8F-%E7%B5%90%E6%A7%8B%E5%8C%96%E8%88%87%E9%9D%9E%E7%B5%90%E6%A7%8B%E5%8C%96%E8%B3%87%E6%96%99-50c89a4b15e0)
270 |
271 |
272 |
273 | ### 結構化與非結構資料化的比較
274 |
275 | | | 結構化資料 | 非結構化資料 |
276 | | :----------: | :------------: | :----------: |
277 | | 呈現方面 | 表格 | 無法呈現 |
278 | | 處理方面 | 需正規化 | 不須正規化 |
279 | | 形式 | 有限的資料形式 | 不限 |
280 | | 儲存空間需求 | 較少 | 較大 |
281 | | 存取 | 較簡單 | 較困難 |
282 |
283 |
284 |
285 | ## 資料探勘
286 |
287 | 從一大群的資料中,利用技術(人工智慧、機器學習、統計學等等)探勘出有意義的資料。
288 |
289 |
290 |
291 | ### 資料的探勘任務
292 |
293 | 主要分成六種常見的任務。
294 |
295 | 1. 異常檢測:辨識不尋常的資料,或針對錯誤資料進一步調查。
296 | 2. 關聯規則學習:搜尋變數之間的關係。
297 | 3. 聚類:在未知資料的結構下,發現資料的類別與結構,利用演算法將資料分成更多子集,讓子集的資料都有相似的一些屬性。
298 | 4. 分類:對新的資料推廣成已知結構的任務,例如將一封新郵件分類成「正常郵件」與「垃圾郵件」,可利用決策樹來分析數據或輔助預測。
299 | 5. 迴歸:試圖找到最小誤差的建模函式。
300 | 6. 匯總:提供一個更緊湊的資料集表示,來生成視覺化或報表。
301 |
302 |
--------------------------------------------------------------------------------
/PDF/Artificial Neural Networks.pdf:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/ntut-xuan/DataScienceNote/c49735d5ffa0623e5f17974f95afcf68c413e15b/PDF/Artificial Neural Networks.pdf
--------------------------------------------------------------------------------
/PDF/Associate Rule Mining.pdf:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/ntut-xuan/DataScienceNote/c49735d5ffa0623e5f17974f95afcf68c413e15b/PDF/Associate Rule Mining.pdf
--------------------------------------------------------------------------------
/PDF/Cluster Analysis.pdf:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/ntut-xuan/DataScienceNote/c49735d5ffa0623e5f17974f95afcf68c413e15b/PDF/Cluster Analysis.pdf
--------------------------------------------------------------------------------
/PDF/Data Mining.pdf:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/ntut-xuan/DataScienceNote/c49735d5ffa0623e5f17974f95afcf68c413e15b/PDF/Data Mining.pdf
--------------------------------------------------------------------------------
/PDF/Data Preprocessing.pdf:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/ntut-xuan/DataScienceNote/c49735d5ffa0623e5f17974f95afcf68c413e15b/PDF/Data Preprocessing.pdf
--------------------------------------------------------------------------------
/PDF/Data Warehouse.pdf:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/ntut-xuan/DataScienceNote/c49735d5ffa0623e5f17974f95afcf68c413e15b/PDF/Data Warehouse.pdf
--------------------------------------------------------------------------------
/PDF/Decision Tree.pdf:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/ntut-xuan/DataScienceNote/c49735d5ffa0623e5f17974f95afcf68c413e15b/PDF/Decision Tree.pdf
--------------------------------------------------------------------------------
/PDF/Naive Bayes Analysis.pdf:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/ntut-xuan/DataScienceNote/c49735d5ffa0623e5f17974f95afcf68c413e15b/PDF/Naive Bayes Analysis.pdf
--------------------------------------------------------------------------------
/PDF/Regression.pdf:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/ntut-xuan/DataScienceNote/c49735d5ffa0623e5f17974f95afcf68c413e15b/PDF/Regression.pdf
--------------------------------------------------------------------------------
/PDF/Unclassified.pdf:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/ntut-xuan/DataScienceNote/c49735d5ffa0623e5f17974f95afcf68c413e15b/PDF/Unclassified.pdf
--------------------------------------------------------------------------------
/README.md:
--------------------------------------------------------------------------------
1 | # 資料科學導論筆記
2 |
3 |
4 |
5 | ## 作者
6 |
7 | 國立臺北科技大學 資訊工程系 [黃漢軒](https://ntut-xuan.github.io)
8 |
9 | 筆記上有任何問題,請丟 [issue](https://github.com/ntut-xuan/DataScienceNote/issues),支持這份筆記,請幫我點個 star,謝謝
10 |
11 |
12 |
13 | **超級注意:工具箱的部分只經過我本人測試過,並不保證他不會有任何問題,有任何問題不負任何責任,有遇到問題請丟 [issue](https://github.com/ntut-xuan/DataScienceNote/issues) 。**
14 |
15 |
16 |
17 | ## 主題式分析
18 |
19 | 這份筆記使用主題式的方式架構,主要分成以下幾個子主題。
20 |
21 |
22 |
23 | | 主題 | 完工進度 | ToolBox | 完工時間 |
24 | | :----------------------------------------: | :------: | :-----: | :------------: |
25 | | 還沒經過整理的主題 | SKIP | SKIP | SKIP |
26 | | 資料倉儲(Data Warehouse) | 100% | SKIP | 2022 / 04 / 04 |
27 | | 資料探勘(Data Mining) | 100% | SKIP | 2022 / 04 / 05 |
28 | | 決策樹(Decision Tree) | 100% | SKIP | 2022 / 04 / 12 |
29 | | 迴歸(Regression) | 100% | SKIP | 2022 / 04 / 14 |
30 | | 單純貝氏(Naïve Bayes Analysis) | 100% | OK | 2022 / 06 / 15 |
31 | | 人工神經網路(Artificial Neural Networks) | 100% | SKIP | 2022 / 06 / 15 |
32 | | 聚類分析(Cluster Analysis) | 100% | OK | 2022 / 06 / 22 |
33 | | 資料預處理(Data Preprocessing) | 100% | SKIP | 2022 / 06 / 22 |
34 | | 推薦系統(Recommandation System) | 100% | SKIP | 2022 / 06 / 22 |
35 |
36 |
37 |
--------------------------------------------------------------------------------
/python_tool/.gitignore:
--------------------------------------------------------------------------------
1 | .idea
2 | __pycache__
--------------------------------------------------------------------------------
/python_tool/debug.py:
--------------------------------------------------------------------------------
1 | import numpy as np
2 | import random
3 | import time
4 | import matplotlib.pyplot as plt
5 |
6 | def standard_random():
7 | std = np.array([0.1, 0.1, 0.1, 0.1, 0.1, 0.1, 0.1])
8 | return std
9 |
10 |
11 | def active_function(x):
12 | return np.log(1+np.exp(x))
13 |
14 |
15 | def calc(x_1s, x_2s, x_1, x_2, y_1, y_2, w, b):
16 | x_1s = np.transpose(data)[0]
17 | x_2s = np.transpose(data)[1]
18 | output = w[5] * y_1 + w[6] * y_2 + b[3]
19 | return (x_1s * w[1] + x_2s * w[3], x_1s * w[2] + x_2s * w[4], active_function(x_1), active_function(x_2), output)
20 |
21 | data = [[35, 67], [12, 75], [16, 89], [45, 56], [10, 90]]
22 | label = [1, 0, 1, 1, 0]
23 |
24 | data_array = np.array(data)
25 | label_array = np.array(label)
26 |
27 | w = standard_random()
28 | b = [0 for i in range(4)]
29 |
30 | print(w)
31 |
32 | x_1s = np.transpose(data)[0]
33 | x_2s = np.transpose(data)[1]
34 | x_1 = x_1s * w[1] + x_2s * w[3]
35 | x_2 = x_1s * w[2] + x_2s * w[4]
36 | y_1 = np.log(1+np.exp(x_1))
37 | y_2 = np.log(1+np.exp(x_2))
38 | output = w[5] * active_function(x_1*w[1]+x_2*w[3] + b[1]) + w[6] * active_function(x_1*w[2]+x_2*w[4] + b[2]) + b[3]
39 | learn_rate = 0.01
40 |
41 | for i in range(1000):
42 | x_1s = np.transpose(data)[0]
43 | x_2s = np.transpose(data)[1]
44 | x_1, x_2, y_1, y_2, output = calc(x_1s, x_2s, x_1, x_2, y_1, y_2, w, b)
45 | db3 = np.sum(-2 * (label_array - output))
46 | dw5 = np.sum((label_array - output) * y_1 * -2)
47 | dw6 = np.sum((label_array - output) * y_2 * -2)
48 | db1 = np.sum((label_array - output) * w[5] * (np.exp(x_1) / (1 + np.exp(x_1))) * -2)
49 | db2 = np.sum((label_array - output) * w[6] * (np.exp(x_2) / (1 + np.exp(x_2))) * -2)
50 | dw1 = np.sum((label_array - output) * w[5] * (np.exp(x_1) / (1 + np.exp(x_1))) * x_1s * -2)
51 | dw2 = np.sum((label_array - output) * w[6] * (np.exp(x_2) / (1 + np.exp(x_2))) * x_1s * -2)
52 | dw3 = np.sum((label_array - output) * w[5] * (np.exp(x_1) / (1 + np.exp(x_1))) * x_2s * -2)
53 | dw4 = np.sum((label_array - output) * w[6] * (np.exp(x_2) / (1 + np.exp(x_2))) * x_2s * -2)
54 | print("SSR =", np.sum(label_array - output) * np.sum(label_array - output))
55 | b[3] = b[3] - db3 * learn_rate
56 | b[2] = b[2] - db2 * learn_rate
57 | b[1] = b[1] - db1 * learn_rate
58 | w[6] = w[6] - dw6 * learn_rate
59 | w[5] = w[5] - dw5 * learn_rate
60 | w[4] = w[4] - dw4 * learn_rate
61 | w[3] = w[3] - dw3 * learn_rate
62 | w[2] = w[2] - dw2 * learn_rate
63 | w[1] = w[1] - dw1 * learn_rate
64 | print("b=", b)
65 | print("w=", w)
66 |
67 | fig = plt.figure(figsize=(10, 10))
68 | ax = fig.gca(projection='3d')
69 |
70 | plot_x = np.linspace(0, 100, num=100)
71 |
72 | table = np.array([[0 for _ in range(100)] for _ in range(100)])
73 |
74 | for i in range(100):
75 | for j in range(100):
76 | x1 = i
77 | x2 = j
78 | #print(x1, x2)
79 | table[i][j] = w[5] * (active_function(x1 * w[1] + x2 * w[3]) + b[1]) \
80 | + w[6] * (active_function(x1 * w[2] + x2 * w[4]) + b[2]) \
81 | + b[3]
82 |
83 | ax.scatter(np.transpose(data_array)[0], np.transpose(data_array)[1], label_array)
84 | ax.plot_surface(plot_x, plot_x, table, cmap='seismic')
85 | plt.show()
86 |
87 | print(table)
88 |
89 | print(table[45][56])
90 | print(table[25][70])
--------------------------------------------------------------------------------
/python_tool/example.py:
--------------------------------------------------------------------------------
1 | from tool import *
2 |
3 | naiveBayesClassifier = MultinomialNaiveBayesClassifier()
4 | data = [["love", "happy", "joy", "joy", "love"],
5 | ["happy", "love", "kick", "joy", "happy"],
6 | ["love", "move", "joy", "good"],
7 | ["love", "happy", "joy", "pain", "love"],
8 | ["joy", "love", "pain", "kick", "pain"],
9 | ["pain", "pain", "love", "kick"]]
10 | label = ["Yes", "Yes", "Yes", "Yes", "No", "No"]
11 | value = ["love", "pain", "joy", "happy", "kick", "happy"]
12 |
13 | naiveBayesClassifier.fit(np.array(data, dtype=object), np.array(label, dtype=object))
14 | print(naiveBayesClassifier.predict(value))
--------------------------------------------------------------------------------
/python_tool/main.py:
--------------------------------------------------------------------------------
1 | import numpy as np
2 | import tool
3 | import time
4 | import warnings
5 | import matplotlib.pyplot as plt
6 | from sklearn import cluster, datasets
7 | from sklearn.preprocessing import StandardScaler
8 | from itertools import cycle, islice
9 |
10 | n_samples = 300
11 | random_state = 170
12 | noisy_circles = datasets.make_circles(n_samples=n_samples, factor=0.5, noise=0.01)
13 |
14 | points = noisy_circles[0]
15 |
16 | array = np.zeros((n_samples, n_samples))
17 |
18 | for i in range(n_samples):
19 | for j in range(n_samples):
20 | array[i][j] = np.sqrt((points[i][0]-points[j][0])**2 + (points[i][1]-points[j][1])**2)
21 |
22 | algo = tool.WPGMAClustering(n_clusters=2)
23 | algo.fit(array)
24 | algo.clustering()
25 |
26 | print(algo.labels_)
27 |
28 | colors = np.array(
29 | list(
30 | islice(
31 | cycle(
32 | [
33 | "#377eb8",
34 | "#ff7f00",
35 | "#4daf4a",
36 | "#f781bf",
37 | "#a65628",
38 | "#984ea3",
39 | "#999999",
40 | "#e41a1c",
41 | "#dede00",
42 | ]
43 | ),
44 | int(max(algo.labels_) + 1),
45 | )
46 | ))
47 |
48 |
49 | plt.scatter(points[:, 0], points[:, 1], color=colors[algo.labels_])
50 | plt.show()
--------------------------------------------------------------------------------
/python_tool/tool.py:
--------------------------------------------------------------------------------
1 | import numpy as np
2 | import copy
3 |
4 |
5 | class MultinomialNaiveBayesClassifier:
6 | def __init__(self):
7 | self.value_map = {}
8 | self.result = np.array([])
9 | self.data = np.array([])
10 |
11 | def fit(self, x, y):
12 | self.result = y
13 | unique, counts = np.unique(self.result, return_counts=True)
14 | for v in unique:
15 | self.value_map[v] = []
16 | for i in range(len(y)):
17 | for s in x[i]:
18 | self.value_map[y[i]].append(s)
19 |
20 | def add_duplicated_value(self, temp_result, temp_value_map, missing_value):
21 | unique, counts = np.unique(temp_result, return_counts=True)
22 | for k in unique:
23 | value_unique = np.unique(temp_value_map[k])
24 | for v in value_unique:
25 | if missing_value == v:
26 | continue
27 | temp_value_map[k].append(v)
28 | for k in unique:
29 | temp_value_map[k].append(missing_value)
30 |
31 | def print_unique(self, y):
32 | for v in np.unique(self.result):
33 | unique, counts = np.unique(y[v], return_counts=True)
34 | result_dict = dict(zip(unique, counts))
35 | print(result_dict)
36 |
37 | def predict(self, y):
38 | temp_result = self.result
39 | temp_value_map = self.value_map
40 | unique, counts = np.unique(self.result, return_counts=True)
41 | result_dict = dict(zip(unique, counts))
42 | predict = {}
43 | for v in unique:
44 | print("calculate P(%s) = %d/%d" % (v, result_dict[v], int(np.sum(counts))))
45 | predict[v] = float(result_dict[v] / np.sum(counts))
46 | for s in y:
47 | for v in unique:
48 | if s not in self.value_map[v]:
49 | self.add_duplicated_value(temp_result, temp_value_map, s)
50 | self.print_unique(temp_value_map)
51 | for s in y:
52 | for v in unique:
53 | unique_s, counts_s = np.unique(self.value_map[v], return_counts=True)
54 | result_dict_s = dict(zip(unique_s, counts_s))
55 | total = np.sum(counts_s)
56 | print("calculate P(%s|%s) = %d/%d" % (s, v, result_dict_s[s], int(total)))
57 | predict[v] *= float(result_dict_s[s] / int(total))
58 | print(predict)
59 | return max(predict, key=predict.get)
60 |
61 |
62 | class UPGMAClustering:
63 |
64 | def __init__(self, n_clusters=2):
65 | self.labels_ = None
66 | self.n = None
67 | self.n_clusters = n_clusters
68 | self.cluster_list = None
69 | self.distance_table = None
70 | self.threshold = None
71 |
72 | def fit(self, distance_table):
73 | self.n = len(distance_table)
74 | self.distance_table = distance_table
75 | self.cluster_list = []
76 | self.threshold = []
77 | self.labels_ = [0 for _ in range(self.n)]
78 | for i in range(self.n):
79 | self.cluster_list.append([i])
80 |
81 | def clustering(self):
82 | for r in range(self.n - (self.n_clusters-1)):
83 |
84 | print("\n=============== Iter%5d ===============\n" % (r + 1))
85 |
86 | original_cluster_list = copy.deepcopy(self.cluster_list)
87 | self.distance_table[self.distance_table == 0] = np.iinfo(np.int32).max
88 |
89 | # choose minimum pair
90 | minimum_distance = np.min(self.distance_table)
91 | minimum_pair = np.unravel_index(np.argmin(self.distance_table, axis=None), self.distance_table.shape)
92 | print("Minimum pair: %s = %d" % (str(minimum_pair), minimum_distance))
93 |
94 | if r != self.n - self.n_clusters:
95 |
96 | # combine two cluster
97 | target_list1 = copy.deepcopy(self.cluster_list[minimum_pair[0]])
98 | target_list2 = copy.deepcopy(self.cluster_list[minimum_pair[1]])
99 | self.cluster_list[minimum_pair[0]] += (self.cluster_list[minimum_pair[1]])
100 | self.cluster_list.remove(self.cluster_list[minimum_pair[1]])
101 |
102 | print("target list l1=", target_list1, "- l2=", target_list2)
103 | print("combine list", original_cluster_list, "->", self.cluster_list)
104 |
105 | # recalculate distance between new cluster and another cluster
106 | self.distance_table[self.distance_table == np.iinfo(np.int32).max] = 0
107 | new_distance_table = np.zeros((len(self.cluster_list), len(self.cluster_list)))
108 | for i in range(len(self.cluster_list)):
109 | for j in range(len(self.cluster_list)):
110 | index1 = original_cluster_list.index(target_list1)
111 | index2 = original_cluster_list.index(target_list2)
112 | index4 = self.cluster_list.index(self.cluster_list[j])
113 | if i == index1 or j == index1:
114 | if index1 == index4:
115 | continue
116 | index3 = original_cluster_list.index(self.cluster_list[j])
117 | distance1 = self.distance_table[index1][index3]
118 | distance2 = self.distance_table[index2][index3]
119 | new_distance_table[index1][index4] = (len(target_list1) * distance1 + len(
120 | target_list2) * distance2) / float(len(target_list1) + len(target_list2))
121 | new_distance_table[index4][index1] = (len(target_list1) * distance1 + len(
122 | target_list2) * distance2) / float(len(target_list1) + len(target_list2))
123 | else:
124 | index3 = original_cluster_list.index(self.cluster_list[j])
125 | index5 = original_cluster_list.index(self.cluster_list[i])
126 | new_distance_table[i][j] = self.distance_table[index5][index3]
127 |
128 | self.distance_table = new_distance_table
129 |
130 | # print
131 | print("Update Table\n", str(new_distance_table))
132 | print(self.cluster_list)
133 |
134 | # calculate branch length estimation
135 | branch_length_estimation = minimum_distance / 2.0
136 | self.threshold += [branch_length_estimation]
137 | print("distance_threshold =", branch_length_estimation)
138 |
139 | for i in range(len(self.cluster_list)):
140 | for v in self.cluster_list[i]:
141 | self.labels_[v] = i+1
142 |
143 |
144 | class WPGMAClustering:
145 |
146 | def __init__(self, n_clusters=2):
147 | self.labels_ = None
148 | self.n = None
149 | self.n_clusters = n_clusters
150 | self.cluster_list = None
151 | self.distance_table = None
152 | self.threshold = None
153 |
154 | def fit(self, distance_table):
155 | self.n = len(distance_table)
156 | self.distance_table = distance_table
157 | self.cluster_list = []
158 | self.threshold = []
159 | self.labels_ = [0 for _ in range(self.n)]
160 | for i in range(self.n):
161 | self.cluster_list.append([i])
162 |
163 | def clustering(self):
164 | for r in range(self.n - (self.n_clusters-1)):
165 |
166 | print("\n=============== Iter%5d ===============\n" % (r + 1))
167 |
168 | original_cluster_list = copy.deepcopy(self.cluster_list)
169 | self.distance_table[self.distance_table == 0] = np.iinfo(np.int32).max
170 |
171 | # choose minimum pair
172 | minimum_distance = np.min(self.distance_table)
173 | minimum_pair = np.unravel_index(np.argmin(self.distance_table, axis=None), self.distance_table.shape)
174 | print("Minimum pair: %s = %d" % (str(minimum_pair), minimum_distance))
175 |
176 | if r != self.n - self.n_clusters:
177 |
178 | # combine two cluster
179 | target_list1 = copy.deepcopy(self.cluster_list[minimum_pair[0]])
180 | target_list2 = copy.deepcopy(self.cluster_list[minimum_pair[1]])
181 | self.cluster_list[minimum_pair[0]] += (self.cluster_list[minimum_pair[1]])
182 | self.cluster_list.remove(self.cluster_list[minimum_pair[1]])
183 |
184 | print("target list l1=", target_list1, "- l2=", target_list2)
185 | print("combine list", original_cluster_list, "->", self.cluster_list)
186 |
187 | # recalculate distance between new cluster and another cluster
188 | self.distance_table[self.distance_table == np.iinfo(np.int32).max] = 0
189 | new_distance_table = np.zeros((len(self.cluster_list), len(self.cluster_list)))
190 | for i in range(len(self.cluster_list)):
191 | for j in range(len(self.cluster_list)):
192 | index1 = original_cluster_list.index(target_list1)
193 | index2 = original_cluster_list.index(target_list2)
194 | index4 = self.cluster_list.index(self.cluster_list[j])
195 | if i == index1 or j == index1:
196 | if index1 == index4:
197 | continue
198 | index3 = original_cluster_list.index(self.cluster_list[j])
199 | distance1 = self.distance_table[index1][index3]
200 | distance2 = self.distance_table[index2][index3]
201 | new_distance_table[index1][index4] = (distance1 + distance2) / 2.0
202 | new_distance_table[index4][index1] = (distance1 + distance2) / 2.0
203 | else:
204 | index3 = original_cluster_list.index(self.cluster_list[j])
205 | index5 = original_cluster_list.index(self.cluster_list[i])
206 | new_distance_table[i][j] = self.distance_table[index5][index3]
207 |
208 | self.distance_table = new_distance_table
209 |
210 | # print
211 | print("Update Table\n", str(new_distance_table))
212 | print(self.cluster_list)
213 |
214 | # calculate branch length estimation
215 | branch_length_estimation = minimum_distance / 2.0
216 | self.threshold += [branch_length_estimation]
217 | print("distance_threshold =", branch_length_estimation)
218 |
219 | for i in range(len(self.cluster_list)):
220 | for v in self.cluster_list[i]:
221 | self.labels_[v] = i+1
222 |
--------------------------------------------------------------------------------