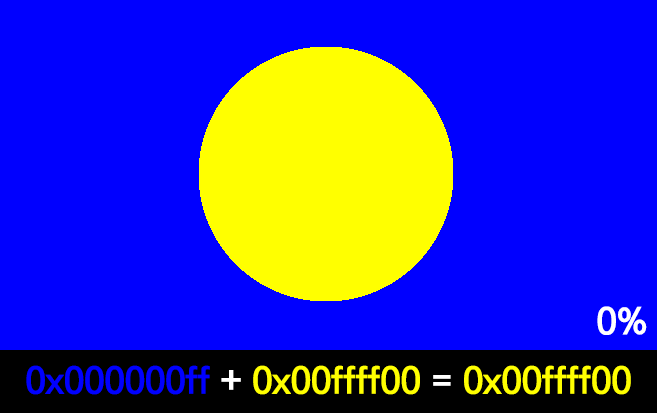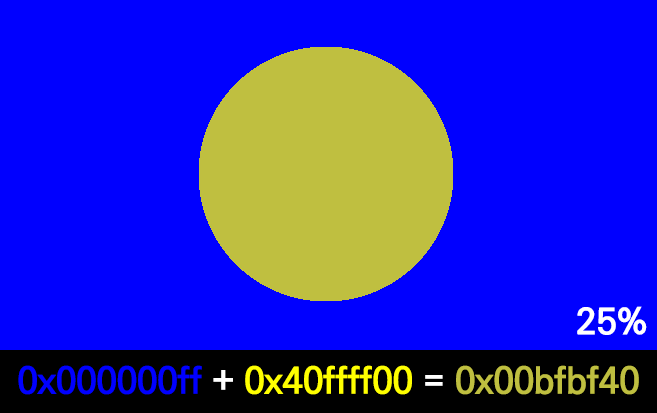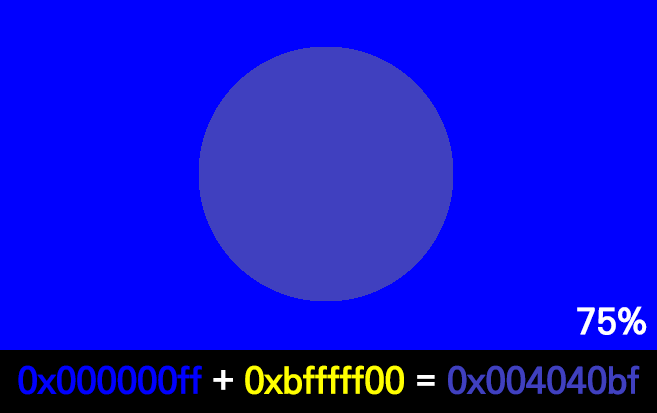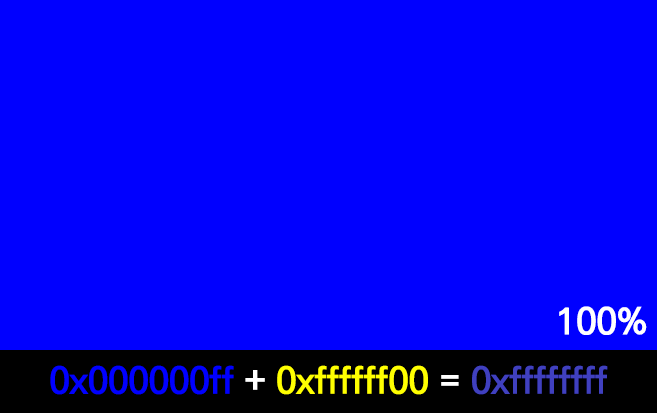├── 1.mlx_get_data_addr.md
├── 2.wall.md
├── 3.ceil.md
├── 4.transparency.md
└── README.md
/1.mlx_get_data_addr.md:
--------------------------------------------------------------------------------
1 | **mlx_get_data_addr 함수를 살펴보는 페이지.**
2 |
3 | 함수를 이해하는 데 필요했던 rgb, endian, bpp, 포인터 형변환 개념을 먼저 정리했습니다.
4 |
5 | mlx_get_data_addr에서 정리된 내용은 벽과 천장, rgb는 투명도 페이지에서 사용됩니다.
6 |
7 | [1. rgb](#rgb)
8 | [2. endian](#endian)
9 | [3. bpp](#bpp)
10 | [4. 포인터 형변환](#포인터-형변환)
11 | [5. mlx_get_data_addr](#mlx-get-data-addr)
12 |
13 | ---
14 |
15 | ## **rgb**
16 |
17 | Red, Green, Blue (빨강, 초록, 파랑) 세 종류의 기본 색을 이용하여 색을 표현한다.
18 |
19 | 각각의 요소는 0 ~ 255 의 값을 가질 수 있다. 이 값은 해당 색이 얼마나 섞였는지를 나타낸다.
20 |
21 | 완전 빨강: R = 255, G = 0, B = 0
22 | 완전 초록: R = 0, G = 255, B = 0
23 | 완전 파랑: R = 0, G = 0, B = 255
24 | 완전 검정: R = 0, G = 0, B = 0
25 | 완전 하양: R = 255, G = 255, B = 255
26 |
27 | 이런 방식으로 256 * 256 *256, 총 16,777,216 개의 색을 표현할 수 있다.
28 |
29 |
30 |
31 | #### **16진법**
32 |
33 | 색상을 표현할 때는 RGB를 16진법으로 변환해서 사용한다.
34 |
35 | (0 ~ 255)를 (00 ~ FF)로 변환해 0xRRGGBB 형식으로 나타낸다.
36 |
37 | 완전 빨강: 0xFF0000
38 | 완전 초록: 0x00FF00
39 | 완전 파랑: 0x0000FF
40 | 완전 검정: 0x000000
41 | 완전 하양: 0xFFFFFF
42 |
43 |
44 |
45 | #### **10진법**
46 |
47 | 특정 색상에서 R, G, B 값을 구해보자.
48 |
49 | 완전 빨강(0xFF0000): 255 * (256²) + 0 * (256) + 0 * (1)
50 |
51 | 여기서 R, G, B 값을 각각 구해보면
52 |
53 | B : 255 \* (256²) + 0 \* (256) + 0 \* (1) 를 256으로 나눈 나머지 = 0
54 |
55 | G : *255 \* (256²) + 0 \* (256) + 0 \* (1) 를 256으로 나눈 몫*을 다시 256으로 나눈 나머지
56 | = *255 \* (256) + 0 \* (1)* 을 256으로 나눈 나머지 = 0
57 |
58 | R : *255 \* (256²) + 0 \* (256) + 0 \* (1)를 256²으로 나눈 몫*을 다시 256으로 나눈 나머지
59 | = *255 \* (1)* 을 256으로 나눈 나머지 = 256
60 |
61 |
62 |
63 | #### **2진법, 비트연산**
64 |
65 | 이번엔 16진법 0xFF00000에서 R, G, B 값을 구해보자.
66 |
67 | 우리는 두 자리씩 딱 끊어서 R = FF, G = 00, B = 00 로 바로 파악할 수 있지만 컴퓨터는 못하니까..
68 |
69 | 이 계산을 위해 비트 연산이 필요하고 비트 연산을 이해하기 위해 색을 2진법으로 표현해본다.
70 |
71 | 16진법 각 자리의 수를 2진법으로 변환한다.
72 |
73 | 0xFF0000 : 1111 1111 / 0000 0000 / 0000 0000
74 |
75 | B 값을 구할 땐 앞의 16자리는 필요 없고 마지막 8자리만 필요하기 때문에 0xFF(255)와 & 연산을 해준다
76 |
77 | (10진법에서 256으로 나눠 나머지를 구하는 과정과 유사하다)
78 |
79 | 0xFF0000 : 1111 1111 / 0000 0000 / 0000 0000
80 | &
81 | 0x0000FF : 0000 0000 / 0000 0000 / 1111 1111
82 |
83 | 결과: 0000 0000 / 0000 0000 / **0000 0000**
84 |
85 |
86 |
87 |
88 | G: (10진법) 256으로 나눈 몫에서 256으로 나눈 나머지
89 | (2진법) 비트를 오른쪽으로 8칸 보내고 & 0xFF
90 |
91 | 0xFF0000 >> 8 = 0x00FF00
92 |
93 | 0x00FF00 : 0000 0000 / 1111 1111 / 0000 0000
94 | &
95 | 0x0000FF : 0000 0000 / 0000 0000 / 1111 1111
96 |
97 | 결과: 0000 0000 / 0000 0000 / **0000 0000**
98 |
99 |
100 |
101 | R : (10진법) 256²으로 나눈 몫에서 256으로 나눈 나머지
102 | (2진법) 비트를 오른쪽으로 16칸 보내고 & 0xFF
103 |
104 | 0xFF0000 >> 16 = 0x0000FF
105 |
106 | 0x00FF00 : 0000 0000 / 0000 0000 / 1111 1111
107 | &
108 | 0x0000FF : 0000 0000 / 0000 0000 / 1111 1111
109 |
110 | 결과: 0000 0000 / 0000 0000 / **1111 1111**
111 |
112 |
113 |
114 | #### **비트연산 정리**
115 |
116 | RGB color에서
117 |
118 | ```
119 | R = (color >> 16) & 0xFF
120 | G = (color >> 8 ) & 0xFF
121 | B = color & 0xFF
122 | ```
123 |
124 | 같은 원리로 R, G, B 값이 주어졌을 때 color를 구하는 방법
125 |
126 | ```
127 | color = R * 256² + G * 256 + B
128 | color = (R << 16) | ( G << 8) | B
129 | ```
130 |
131 |
132 |
133 | #### **ARGB**
134 |
135 | RGB에 투명도(Alpha)값을 추가해 ARGB 형식(0xAARRGGBB)으로 나타내기도 한다.
136 |
137 | A 또한 0(완전 불투명) ~ FF(완전 투명)의 값을 갖는다.
138 |
139 | 0xFF0000은 0x00FF0000와 동일하기 때문에 완전 불투명한 빨강
140 | 0xCCFF0000: 50% 투명한 빨강
141 | 0xFFFF0000: 완전 투명한 빨강
142 |
143 | ARGB가 가질 수 있는 값은 0x00000000 ~ 0xFFFFFFFF 로 (unsigned int) 범위와 동일하다.
144 |
145 |
146 | ---
147 |
148 | ## **endian**
149 |
150 | unsigned int color = 0x12345678; 를 선언하면 메모리에 아래처럼 저장된다.
151 |
152 |
153 |  154 |
154 |
155 |
156 | 우리가 눈으로 보는 것과 반대로 저장되는 이유는 리틀엔디언이라는 방식으로 값을 저장하기 때문이다.
157 |
158 | 엔디언은 숫자를 1바이트씩 쪼개서 저장할 때 저장순서를 나타낸다.
159 |
160 | 빅엔디언: 큰 자릿수가 앞에 저장됨
161 |
162 | 리틀엔디언: 작은 자릿수가 앞에 저장됨
163 |
164 |
165 | 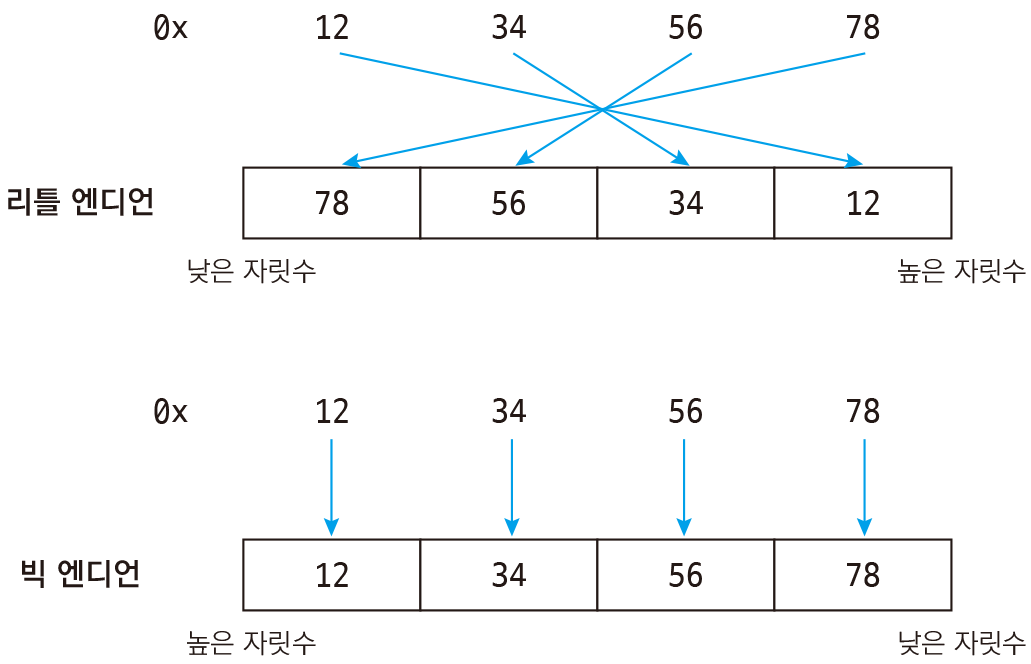
166 | 출처 코딩도장
167 |
168 |
169 |
170 | 리틀엔디언은 숫자를 읽는 방식이랑 반대라서 생소하게 보이지만, 우리가 보통 사용하는 x86(x86-64) 계열 CPU는 다 리틀 엔디언 방식이라고 한다.
171 |
172 | 리틀엔디언에서 color = 0x12345678 는 78 / 56 / 34 / 12 로 저장이 되고
173 |
174 | 순서대로 color = 0x78 + 0x5600 + 0x340000 + 0x12000000 = 0x12345678 로 계산이 된다.
175 |
176 | 우리는 0xF00FFF를 1111 0000 / 0000 1111 / 1111 1111 로 표현하지만
177 |
178 | 리틀엔디언에서는 실제로 1111 1111 / 0000 1111 / 1111 0000 으로 저장한다.
179 |
180 | 그래도 비트연산, 쉬프트연산 같은 계산은 엔디언의 영향을 받지 않기 때문에 그냥 사용하면 된다.
181 |
182 | 본 페이지에서는
183 |
184 | 0xRRGGBB 는 B / G / R
185 | 0xAARRGGBB는 B / G / R / A 순서로 저장되는 것을 알면 충분하다.
186 | cf) 엔디언이 계산에 영향을 미치는 예시 [확인하기](https://developer.ibm.com/articles/au-endianc/#list4)
187 |
188 |
189 |
190 | ---
191 |
192 | ## **bpp**
193 |
194 | **[mlx man]**
195 |
196 | > bits_per_pixel will be filled with the number of bits needed to represent a pixel color (also called the depth of the image).
197 | >
198 | > bpp = 픽셀 하나(색상 하나)를 표현하는 데 필요한 비트 수 (= depth of the image)
199 |
200 |
201 | RGB: 색상을 표현할때 BB / GG / RR 3바이트가 필요하기 때문에 bpp = 24비트
202 | ARGB : BB / RR / GG / AA 4바이트가 필요하기 때문에 bpp = 32비트
203 |
204 |
205 |
206 | 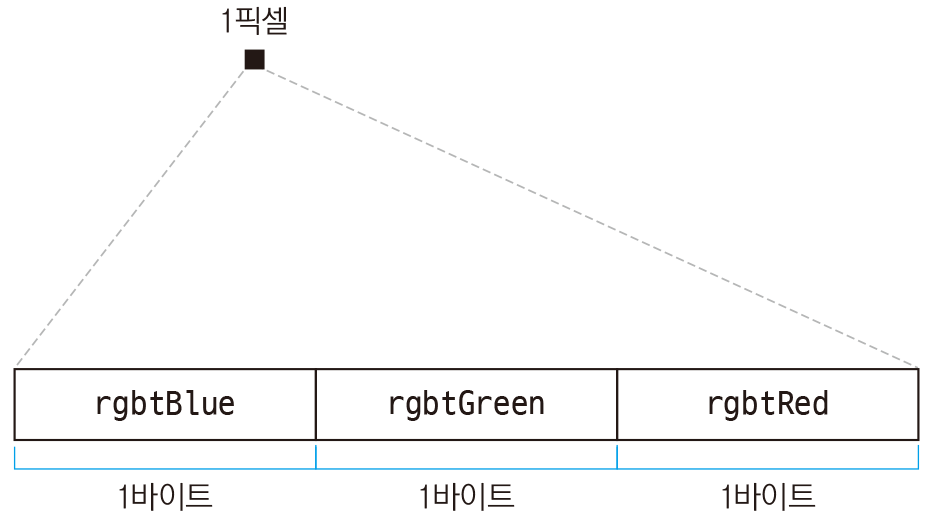
207 | 24비트 비트맵의 픽셀 저장. 출처 코딩도장
208 |
209 |
210 |
211 | ---
212 |
213 | ### **포인터 형변환**
214 |
215 | 색상을 char \*에 저장해놓고 주소값으로 접근해보자.
216 |
217 | char \*data = 할당;
218 |
219 |
220 |  221 |
221 |
222 |
223 | ```C
224 | unsigned int color_red = 0x00ff0000;
225 | *(unsigned int *)data = color_red;
226 | ```
227 |
228 | color_red를 0번에 넣을 때 형변환 없이 \*data = 0x00ff0000; 로 대입하면 1바이트 자리에 4바이트 값을 넣고 있기 때문에 오류가 난다.
229 |
230 | 따라서 data가 가리키는 곳의 타입을 unsigned int로 바꾸고 값을 넣어주어야 한다.
231 |
232 |
233 | 저장 결과
234 |
235 |
236 |  237 |
237 |
238 |
239 |
240 |
241 | 두 번째 색을 저장하려면 1번이 아니라 4번 주소에 저장한다. 첫 번째 색이 4바이트를 사용했기 때문에.
242 |
243 | ```C
244 | unsigned int color_2 = 0x12345678;
245 | *(unsigned int *)(data + 4) = color_2;
246 | ```
247 |
248 |
249 |  250 |
250 |
251 |
252 | 값을 가져올 때도 형 변환에 따라 결과가 달라진다. (data + 4)를 살펴보자.
253 |
254 |
255 |  256 |
256 |
257 |
258 | ```C
259 | *(data + 4) : 0x78
260 | *(short *)(data + 4) : 0x5678
261 | *(int *)(data + 4) : 0x12345678
262 | *(unsigned int *)(data + 4) : 0x12345678
263 | ```
264 |
265 |
266 | 색상과 색상 사이에 있는 중간 주소에 접근할 수도 있다.
267 |
268 | 다만 (data + 2)를 unsigned int로 접근하면 ff / 00 / 78 / 56 → 0x567800ff 가 뽑혀 저장했던 색상이 아닐 뿐.
269 |
270 |
271 | **정리:**
272 |
273 | char \* 포인터에 연속으로 색상을 저장할 때는 4칸 간격으로 저장하고, 저장한 값을 뽑아올 때도 4칸 간격으로 가져온다.
274 |
275 | (각각 unsigned int 캐스팅)
276 |
277 | ---
278 |
279 | ### **MiniLibX**
280 |
281 | **This library is a simple framework to help 42 students create simple graphical apps.**
282 |
283 | mlx에서는 색상을 ARGB, 0xAARRGGBB 형식으로 사용한다.
284 |
285 | 반투명한 색상을 넣고 띄워보면 투명도가 지원되는 것을 확인할 수 있다.
286 |
287 |
288 |
289 | 
290 | mlx함수로 뒷 배경이 투명한 X 그림 위에 투명도를 다르게 해서 0xAA00FF00(초록색)을 짝수 줄마다 입혀봄
291 |
292 |
293 | [투명도 참고](https://davidwalsh.name/hex-opacity)
294 |
295 |
296 | 투명도 50%일 때 코드는 다음과 같다.
297 |
298 | ```C
299 | int main(void)
300 | {
301 | void *mlx, *win, *img;
302 | unsigned int *data;
303 | int img_width, img_height;
304 | int bpp, size_l, endian;
305 |
306 | mlx = mlx_init();
307 | win = mlx_new_window(mlx, 640, 480, "mlx_title");
308 | img = mlx_xpm_file_to_image(mlx, "./textures/mark.xpm", &img_width, &img_height);
309 | data = (unsigned int *)mlx_get_data_addr(img, &bpp, &size_l, &endian);
310 |
311 | for(int i = 0; i < img_height; i++)
312 | for (int j = 0; j < img_width; j++)
313 | if (i % 2 == 0)
314 | data[size_l / 4 * i + j] = 0xCC00FF00;
315 |
316 | mlx_put_image_to_window(mlx, win, img, 0, 0);
317 | mlx_loop(mlx);
318 |
319 | }
320 | ```
321 |
322 | 여기서 **[size_l / 4 * i + j]** 이 무엇인지 알아보자. 해당 식은 cub3d에서 텍스쳐에 접근할 때 계속 사용된다.
323 |
324 | ---
325 |
326 | ## **mlx get data addr**
327 |
328 |
329 |  330 |
330 |
331 |
332 | 이 4pixel * 2pixel xpm 파일은 mlx에서 아래처럼 저장된다.
333 |
334 |
335 | 
336 |
337 |
338 |
339 | 가로로 4칸씩 저장되는 것은 앞의 포인터 형변환 파트에서 본 것과 동일하다.
340 |
341 | 이 과정은 라이브러리에서 확인할 수 있다.
342 |
343 | **[라이브러리 - mlx_xpm.c]**
344 |
345 | ```C
346 | void *mlx_int_parse_xpm(void *xvar, void *info, int info_size, char *(*f)(), int *width, int *height)
347 | {
348 | opp = 4;
349 | mlx_int_xpm_set_pixel(data, opp, col, x);
350 |
351 | }
352 |
353 | void *mlx_int_xpm_set_pixel(char *data, int opp, int col, int x)
354 | {
355 | *((unsigned int _)(data + 4 _ x)) = col; ← 4 대신 opp를 써야 했는데 하드코딩된 듯
356 | }
357 | ```
358 |
359 |
360 |
361 | 세로를 살펴보자.
362 |
363 |
364 | 원본 이미지를 생각하면 15번 주소에 이어서 16번 주소에 흰색이 들어갈 것 같지만
365 |
366 | 16부터 255는 건너 뛰고 256부터 두 번째 라인이 저장된다. 이때 **첫 번째 줄과 두 번째 줄의 간격이 바로 size_line이다.**
367 |
368 |
369 | **[mlx man]**
370 |
371 | > size_line is the number of bytes used to store one line of the image in memory.
372 | > This information is needed to move from one line to another in the image.
373 | >
374 | > size_line : 이미지 한 줄을 저장하는 데 쓰는 바이트. 줄을 넘어갈 때 이 값이 필요하다.
375 |
376 |
377 |
378 | '줄을 넘어간다'는 부분도 라이브러리에서 찾을 수 있다.
379 |
380 | **[라이브러리 - mlx_xpm.c]**
381 |
382 | ```C
383 | void *mlx_int_parse_xpm(void *xvar,void _info,int info_size,char _(*f)(), int *width, int \*height)
384 | {
385 | opp = 4;
386 |
387 | i = *height;
388 | while (i--)
389 | {
390 | x = 0;
391 | while (x < *width)
392 | {
393 | mlx_int_xpm_set_pixel(data, opp, col, x);
394 | x++;
395 | }
396 | data += size_line; //img->width*4;
397 | }
398 |
399 | }
400 | ```
401 |
402 | 안쪽 while문에서 width로 한 줄을 끝낸 후에 size_line 간격만큼 주소값을 건너 뛰고 있다.
403 |
404 |
405 |
406 | 그리고 이때 size_line의 값은 아래 함수에서 정해져서 오는 값이다.
407 |
408 | **[라이브러리 - mlx_img.swift]**
409 |
410 | ```Swift
411 | public class MlxImg
412 | {
413 | texture*sizeline = width * 4
414 | texture*sizeline = 256 * (texture_sizeline / 256 + (texture_sizeline % 256 >= 1 ? 1 : 0))
415 | }
416 | ```
417 |
418 |
419 |
420 | 0 ~ 64 : size_line = 256 * 1 = 256
421 | 65 ~ 128 : size_line = 256 * 2 = 512
422 | 129 ~ 192 : size_line = 256 * 3 = 768
423 | 193 ~ 256 : size_line = 256 * 4 = 1024
424 |
425 |
426 | 정리하자면 size_line은 이미지 한 줄이 저장된 후에 추가되는 간격, 이 값은 width 64마다 달라진다.
427 |
428 |
429 | ---
430 |
431 | 이를 바탕으로 데이터에서 [색상이 저장된 주소]를 계산하는 방법은 다음과 같다.
432 |
433 | 이미지는 첫 줄에서 다음 줄로 넘어갈 때 width를 더하겠지만, 데이터 접근은 size_line을 더해야 한다.
434 |
435 | 따라서 흰색의 주소는
436 |
437 | [width * 1 + 0] (x)
438 | [size_line * 1 + 0] (o)
439 |
440 |
441 | 그리고 가로로 접근할 때도 1이 아니라 4씩 더해야 한다.
442 |
443 | 노란색의 주소는
444 |
445 | [size_line * 0 + 2] (x)
446 | [size_line * 0 + 4 * 2] (o)
447 |
448 |
449 | 이 부분도 man에 나와있다.
450 |
451 | > From this adress, the first bits_per_pixel bits represent the color of the first pixel in the first line of the image.
452 | > The second group of bits_per_pixel bits represent the second pixel of the first line, and so on.
453 | > Add size_line to the adress to get the begining of the second line. You can reach any pixels of the image that way.
454 | >
455 | > 처음 32비트(4바이트)는 이미지 첫 줄의 첫 번째 픽셀을 나타낸다.
456 | > 그 다음 32비트는 이미지 첫 줄의 두 번째 픽셀을 나타낸다.
457 | > 처음 주소 값에 size_line을 더하면 이미지 둘째 줄로 갈 수 있다.
458 |
459 |
460 |
461 | 각 색상 데이터에 접근하는 방법은 아래처럼 정리된다.
462 |
463 | ```C
464 | int main(void)
465 | {
466 | char *data;
467 |
468 | data = mlx_get_data_addr(img, &bpp, &size_l, &endian);
469 |
470 | for(int i = 0; i < img_height; i++)
471 | for (int j = 0; j < img_width; j++)
472 | *(unsigned int *)(data + (size_l * i + 4 * j))
473 |
474 | }
475 | ```
476 |
477 |
478 |
479 | ---
480 |
481 | 여기까지 데이터에 접근하는 계산식은 찾았지만
482 |
483 | 바로 4라는 값을 어떻게 알지? 항상 라이브러리를 뜯어봐야 하나? 라는 의문이 생겼다.
484 |
485 |
486 | 사실 man에서는 4바이트라는 정확한 수치 대신 bits_per_pixel bits 단어를 사용한다.
487 |
488 | > From this adress, the first bits_per_pixel bits represent the color of the first pixel in the first line of the image.
489 | > The second group of bits_per_pixel bits represent the second pixel of the first line, and so on.
490 | > Add size_line to the adress to get the begining of the second line. You can reach any pixels of the image that way.
491 | >
492 | > ㅡㅡㅡㅡ아래는 bits_per_pixel bits를 곧바로 32비트로 해석한 것.ㅡㅡㅡㅡ
493 | >
494 | > 처음 32비트(4바이트)는 이미지 첫 줄의 첫 번째 픽셀을 나타낸다.
495 | > 그 다음 32비트는 이미지 첫 줄의 두 번째 픽셀을 나타낸다.
496 | > 처음 주소 값에 size_line을 더하면 이미지 둘째 줄로 갈 수 있다.
497 |
498 |
499 | bpp는 앞에서 정리했었다.
500 |
501 | 색을 RGB로 표현하면 3바이트, bpp = 24
502 | 색을 ARGB로 표현하면 4바이트, bpp = 32
503 |
504 | mlx에서는 색을 ARGB로 사용하기 때문에 bpp도 32고, 아래 문장은 전부 동일한 의미다.
505 |
506 | ARGB 형식을 사용한다
507 | = 색상을 4바이트로 표현한다
508 | = opp를 4로 둔다(4칸씩 띄워서 색상을 저장한다)
509 | = bits_per_pixel이 32다
510 |
511 |
512 | 그리고 get_data_addr함수에서 bpp에 32를 넣어서 우리한테 위 정보를 노출하고 있다.
513 | (cf) 엔디언을 0으로 주고 있는 것도 확인 가능)
514 |
515 | **[라이브러리 - interface.swift]**
516 |
517 | ```Swift
518 | @_cdecl("mlx_get_data_addr")
519 | public func mlx_get_data_addr_swift(_ imgptr:UnsafeRawPointer, _ bpp:UnsafeMutablePointer, _ sizeline:UnsafeMutablePointer, \_ endian:UnsafeMutablePointer) -> UnsafeMutablePointer
520 | {
521 | let img:MlxImg = \_mlx_bridge(ptr:imgptr)
522 | bpp.pointee = 32
523 | sizeline.pointee = Int32(img.texture_sizeline)
524 | endian.pointee = Int32(0)
525 | return img.texture_data
526 | }
527 | ```
528 |
529 |
530 |
531 | 그래서 "뜯어보지 않고 어떻게 4라는 값을 바로 알지?" 라는 의문에 대해서는
532 |
533 | get_data_addr 함수에서 bpp값(32)을 주고 있고, **[size_line * y + (bpp / 8) * x]** 가 정확한 접근이다. 라고 답할 수 있다.
534 |
535 | ```C
536 | int main(void)
537 | {
538 | char *data;
539 |
540 | data = mlx_get_data_addr(img, &bpp, &size_l, &endian);
541 |
542 | for(int i = 0; i < img_height; i++)
543 | for (int j = 0; j < img_width; j++)
544 | *(unsigned int *)(data + (size_l * i + (bpp / 8) * j))
545 |
546 | }
547 | ```
548 |
549 |
550 |
551 | ---
552 |
553 | #### **(unsigned int \*) 캐스팅**
554 |
555 | 매 4번째마다 색상이 들어있기 때문에 mlx_get_data_addr 전체를 (unsigned int \*)로 형변환해도 문제없이 사용 가능하다.
556 |
557 | 전체적으로 1/4 사이즈로 줄어든다고 보면 된다. (4 = bpp / 8)
558 |
559 | (아래 그림은 이해를 돕기 위한 그림으로 실제 메모리와 다름)
560 |
561 |
562 | 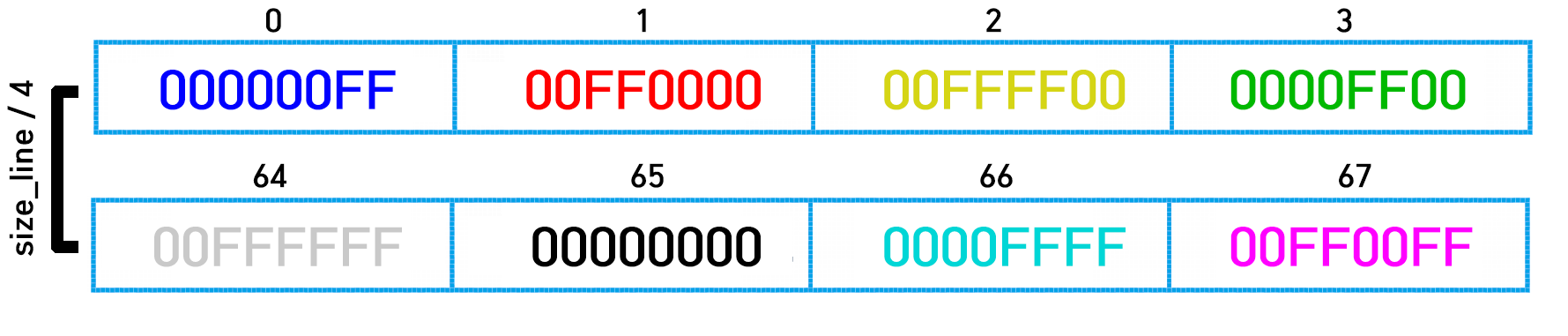
563 |
564 |
565 |
566 | (unsigned int \*)로 캐스팅했을 때 데이터 접근방법
567 |
568 | ```C
569 | int main(void)
570 | {
571 | unsigned int *data;
572 |
573 | data = (unsigned int *)mlx_get_data_addr(img, &bpp, &size_l, &endian);
574 |
575 | for(int i = 0; i < img_height; i++)
576 | for (int j = 0; j < img_width; j++)
577 | data[size_l / (bpp / 8) * i + j]
578 | }
579 |
580 | ```
581 |
582 |
583 | ----
584 | **cub3d에서 이미지 띄우는 흐름**
585 |
586 |
587 | 1. 윈도우 사이즈의 *새 이미지* 를 만든다.
588 |
589 | 2. 각 xpm 파일을 불러와 ^각 이미지 데이터^를 저장해놓는다. (img_width, img_height, bpp, size_l도 각각 저장)
590 |
591 | 3. floor, wall, sprite 순서로 스캔하면서, **저장한 ^이미지 데이터^들에서 색상을 뽑아와** 윈도우 사이즈의 버퍼에 저장한다.
592 |
593 | 4. 스캔이 모두 끝난 버퍼를 처음에 만들었던 *이미지 데이터* 에 넣는다.
594 |
595 | 5. *이미지* 를 윈도우에 띄운다.
596 |
597 |
598 | 3번 단계에서 **데이터 접근, \[size_l / (bpp / 8) * y + x\]** 가 사용된다.
599 |
--------------------------------------------------------------------------------
/2.wall.md:
--------------------------------------------------------------------------------
1 | **로데브 中 텍스쳐를 이해하는 페이지.**
2 |
3 | 이해했던 흐름 그대로의 정리라서 로데브 원본과 살짝 차이가 있습니다.
4 |
5 | **1 [벽 텍스쳐 (affine texture mapping)](https://github.com/p-eye/cub3d_texturing/blob/master/2.wall.md)**
6 | 2 [천장, 바닥 텍스쳐](https://github.com/p-eye/cub3d_texturing/blob/master/3.ceil.md)
7 | 3 [텍스쳐에 투명도 넣기](https://github.com/p-eye/cub3d_texturing/blob/master/4.transparency.md)
8 |
9 | ---
10 |
11 | ## **1. 벽 텍스쳐 (affine texture mapping)**
12 |
13 | 광선으로 벽의 높이를 구한 다음부터의 내용
14 |
15 | ```C
16 | int texNum = worldMap[mapX][mapY] - 1;
17 |
18 | double obj_x = (side == 0) ? posY + perpWallDist * rayDirY : posX + perpWallDist * rayDistX;
19 |
20 | int img_x = (int)(img_width * (obj_x - floor(obj_x)));
21 | if (wall->type == SOUTH || wall->type == WEST)
22 | img_x = img_width - img_x - 1;
23 |
24 | double obj_y = 0;
25 | if (draw_start == 0)
26 | obj_y = wall_height / 2 - sceenHeight / 2;
27 |
28 | y = draw_start;
29 | while (y < draw_end)
30 | {
31 | int img_y = (int)(img_height * obj_y / wall_height);
32 | int tex_point = size_l / (bpp / 8) * img_y + img_x;
33 | buf[y][x] = data[texNum][tex_point];
34 | obj_y++;
35 | y++;
36 | }
37 |
38 | ```
39 |
40 |
41 | 전체적인 흐름은 x좌표를 잡은 상태에서 수직으로 내려오면서 텍스쳐(이미지)를 가져오는 것이다.
42 |
43 |
44 | ```
45 | obj_x: 벽에 부딪혔을 때 가로 좌표
46 | obj_y: 그 위치에서 수직으로 올린 벽 시작점
47 |
48 | (img_x, img_y): 그 때 텍스쳐에 해당하는 위치
49 | img_height, img_width: 텍스쳐 각각의 가로세로 (각 텍스쳐 크기가 다른 경우 위 코드에서 보완 필요)
50 | ```
51 |
52 | 예시를 보면서 이해해보자.
53 |
54 | 왼쪽 벽에 오른쪽 4 \* 2 사이즈의 텍스쳐를 넣을 것이다.
55 |
56 | #### **가로 과정**
57 |
58 |
59 |
60 | 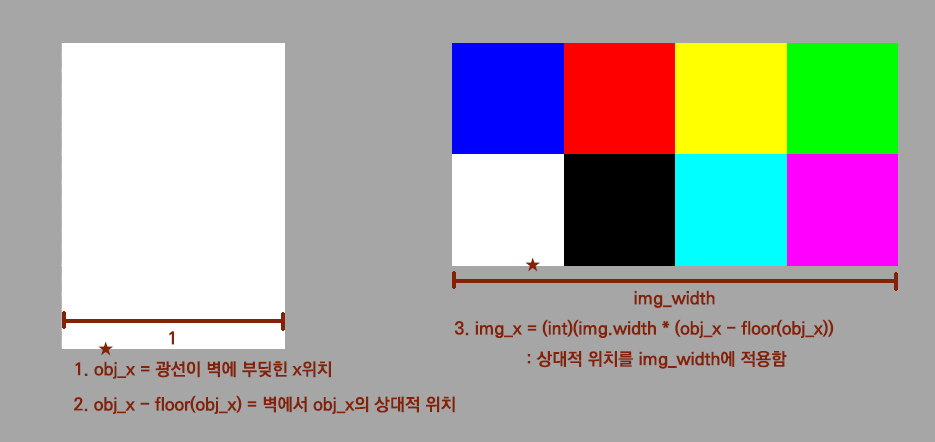 61 |
61 |
62 |
63 |
64 | ```
65 | 1. 광선이 벽에 부딪혔을 때 x 좌표를 구한다. (왼쪽 갈색별) (값은 레이캐스팅 과정에서 구해진다.)
66 | ex) obj_x = 44.23
67 |
68 | 2. 벽 가로에 대한 obj_x의 상대적 위치를 구한다. 가로가 1이기 때문에 정수부분을 빼서 소수부분으로 상대적 위치를 구할 수 있다.
69 | ex) obj_x - floor(obj_x) = 44.23 - 44 = 0.23
70 |
71 | 3. 상대적 위치를 원본 텍스쳐 width에 적용한다.
72 | ex) img_x = (int)(4 * 0.23) = (int) (0.92) = 0
73 |
74 | 4. [img_x = 0]이 실제 텍스쳐에서 가져올 가로 위치. (오른쪽 갈색별 위치를 int로 변환)
75 | ```
76 |
77 |
78 | #### **세로 과정**
79 |
80 |
81 | 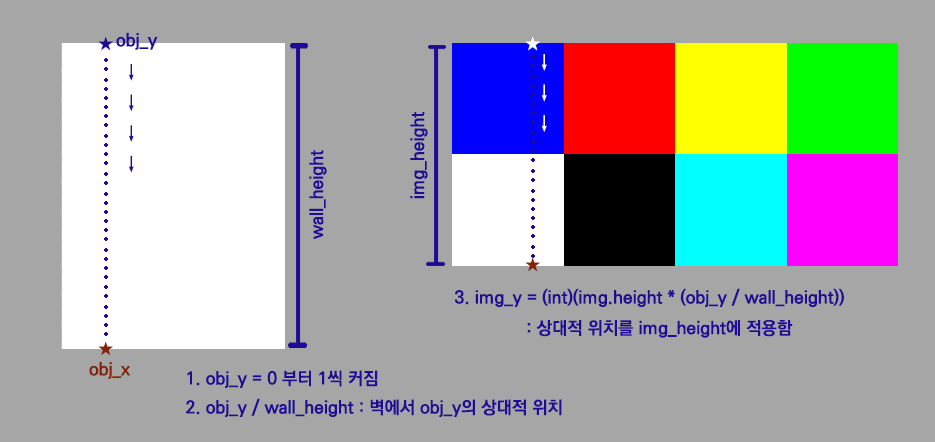 82 |
82 |
83 |
84 |
85 | ```
86 | 1. wall_height = 64라고 가정하자 (실제 구현에서는 texture 단계 이전에 wall_height를 구하는 과정이 있다.)
87 |
88 | 2. obj_x에서 수직으로 올라와 벽 시작점 obj_y를 잡는다. (왼쪽 파란별)
89 | (일단 스크린에 벽 전체가 보일 경우로 가정했다. 이때 obj_y는 0이다)
90 | ex) obj_y = 0
91 |
92 | 3. 벽 세로에 대한 obj_y의 상대적 위치를 구한다. 내 위치를 벽 높이로 나눠주면 상대적 위치를 구할 수 있다.
93 | ex) obj_y / 64 = 0
94 |
95 | 4. 상대적 위치를 원본 텍스쳐 height에 적용한다.
96 | ex) img_y = (int)(2 * 0) = 0
97 |
98 | 5. [img_y = 0]이 실제 텍스쳐에서 가져올 세로 위치. (오른쪽 흰색별 위치를 int로 변환)
99 | ```
100 |
101 | 종합하면 \[img\_x = 0, img\_y = 0\]으로 파란색 픽셀을 가져오게 된다.
102 |
103 |
104 |
105 | while문을 계속 돌아서 obj\_y = 40이 되었다면
106 |
107 | ```
108 | 1. obj_y = 40
109 |
110 | 2. obj_y의 상대적 위치는 40 / 64 = 5 / 8
111 |
112 | 3. img_y = (int) (2 * 5 / 8) = 1
113 | ```
114 |
115 | \[img\_x = 0, img\_y = 1\]으로 흰색 픽셀을 가져온다.
116 |
117 |
118 |
119 | ---
120 |
121 | 스킵했던 부분 설명
122 |
123 | ```C
124 | 1.
125 | img_x = (int)(img_width * (obj_x - floor(obj_x));
126 | if (wall->type == SOUTH || wall->type == WEST)
127 | img_x = img_width - img_x - 1;
128 |
129 |
130 | 2.
131 | obj_y = 0;
132 | if (draw_start == 0)
133 | obj_y = wall_height / 2 - sceenHeight / 2;
134 | ```
135 |
136 | 1.
137 |
138 | 스크린을 띄워보면 벽면이 가로로 뒤집혀서 그려지는 방향이 있다. (대칭이 아닌 텍스쳐를 넣어보면 바로 눈에 보인다.)
139 |
140 | **\[img\_x = img\_width - img\_x - 1\]** 이 찍은 위치를 다시 뒤집어서 정상적으로 돌려주는 부분이다.
141 |
142 | (side == 0 && rayDirX > 0) || (side == 1 && rayDirY < 0) 조건문을 그대로 써도 되고, cub3d 과제 내용 중 방향을 정하는 부분이 있기 때문에 위 코드처럼 단순화할 수도 있다.
143 |
144 |
145 |
146 | 2.
147 |
148 | **\[obj\_y= 0]** 은 벽 높이가 스크린 높이보다 작아서 화면에 벽 전체가 그려지는 경우를 가정한 것이었다. (멀리서 벽을 바라볼 때)
149 |
150 | 하지만 아래 그림처럼 벽 높이가 노란색 스크린보다 커지는 경우가 있다. (벽 바로 앞에 섰을 때)
151 |
152 |
153 | 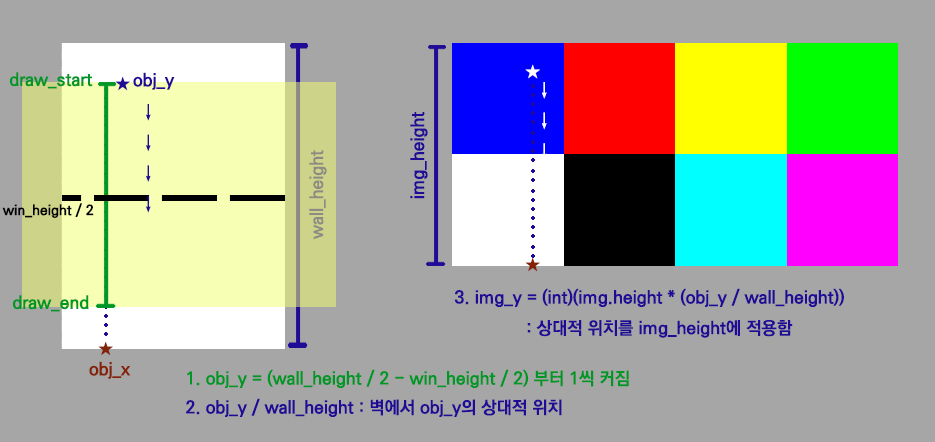 154 |
154 |
155 |
156 | texture 이전 단계에서 이런 경우를 draw_start = 0, draw_end =sceenHeight로 보정해주었다.
157 |
158 | 마찬가지로 보정이 필요한데, 이때는 벽 제일 윗부분을 시작점(obj\_y = 0)으로 잡으면 안되고, 화면에 그려주는 부분부터 시작해야 한다.
159 |
160 | 그 시작점이 벽 절반 높이에서 화면 절반 높이를 뺀 위치다.
161 |
162 | 그래서 draw\_start == 0일 땐 **\[obj\_y = wall\_height / 2 - sceenHeight / 2]**
163 |
164 |
165 |
166 | ---
167 |
168 | 마지막으로, 구한 텍스쳐 위치(img\_x, img\_y)로 데이터에서 색상을 가져와서 버퍼에 넣어준다.
169 |
170 | 텍스쳐 위치로 색상을 가져오는 계산은 [mlx_get_data_addr 페이지](https://github.com/p-eye/cub3d_texturing/blob/master/1.mlx_get_data_addr.md)에 설명되어 있다.
171 |
172 | ```C
173 | tex_point = size_l / (bpp / 8) * img_y + img_x;
174 | buf[y][x] = data[tex_point];
175 | ```
176 |
177 | x 하나에 대해서 수직으로 전부 내려오면 아래처럼 저장되고
178 |
179 | 이 작업을 모든 x에 대해(스크린 widht만큼) 실행하면 버퍼에 화면 전체 벽이 저장된다.
180 |
181 | 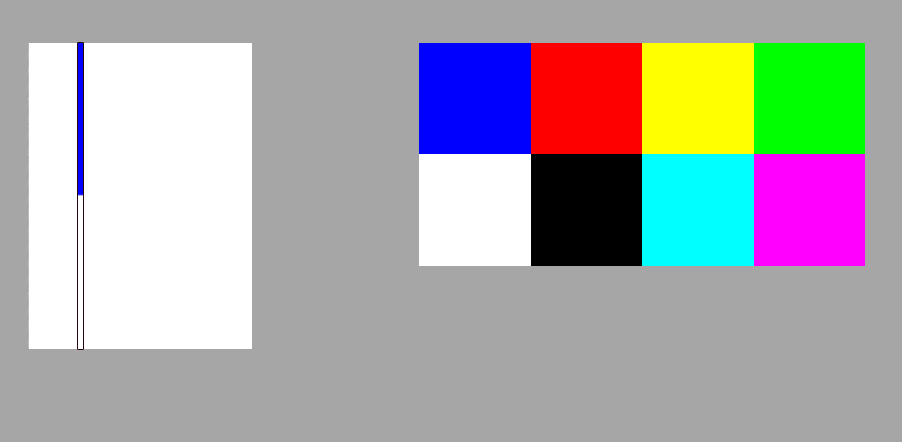 182 |
182 |
183 |
184 |
--------------------------------------------------------------------------------
/3.ceil.md:
--------------------------------------------------------------------------------
1 | **로데브 中 텍스쳐를 이해하는 페이지.**
2 |
3 | 이해했던 흐름 그대로의 정리라서 로데브 원본과 살짝 차이가 있습니다.
4 |
5 | 1 [벽 텍스쳐](https://github.com/p-eye/cub3d_texturing/blob/master/2.wall.md)
6 | **2 [천장, 바닥 텍스쳐 (scanline by scanline)](https://github.com/p-eye/cub3d_texturing/blob/master/3.ceil.md)**
7 | 3 [텍스쳐에 투명도 넣기](https://github.com/p-eye/cub3d_texturing/blob/master/4.transparency.md)
8 |
9 | ---
10 |
11 | ## **2. 천장, 바닥 텍스쳐 (scanline by scanline)**
12 |
13 |
14 | 벽은 x좌표를 잡고 위→아래, 수직으로 텍스쳐를 저장하는 방식이었다면
15 |
16 | 천장과 바닥은 y좌표를 잡고 왼→오, 수평으로 텍스쳐를 저장하는 방식이다.
17 |
18 |
19 |
20 | **1. 천장까지 수평거리 구하기**
21 |
22 | **2. 스크린 왼쪽 끝에 보이는 천장 좌표 구하기**
23 |
24 | **3. 왼쪽 끝에서 오른쪽 끝으로 갈 때 step 구하기**
25 |
26 | **4. 좌표에 해당하는 텍스쳐 저장하기**
27 |
28 | **5. 반복문 돌기**
29 |
30 |
31 |
32 | 순으로 진행된다.
33 |
34 |
35 |
36 |
37 | ----
38 |
39 | ### 1. 천장까지 수평거리 구하기
40 |
41 |
42 | 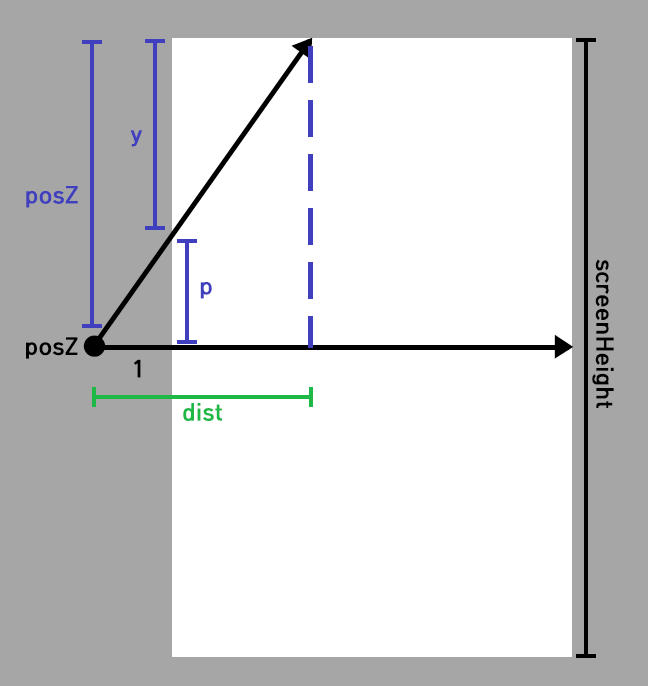
43 |
44 |
45 | ```C
46 | double posZ = 0.5 * screenHeight;
47 | int p = abs(y - screenHeight / 2);
48 | ```
49 |
50 | 광선시작점 posZ가 주어지고 y는 0부터 screenHeight / 2까지 움직인다.
51 |
52 | posZ가 y를 지나는 광선을 쏘았을 때 y와 스크린 중앙의 차이가 p, 광선이 천장에 닿았을 때 수평거리가 dist다.
53 |
54 |
55 | ```
56 | 1 : p = dist : posZ
57 | 따라서
58 | dist = posZ / p
59 | ```
60 |
61 |
62 | 다만 cub3d에서는 abs가 allowed function이 아니기 때문에.. 아래처럼 선언해준다.
63 | ```C
64 | double posZ = 0.5 * screenHeight;
65 | int p = y - screenHeight / 2;
66 | double dist = fabs(posZ / p);
67 | ```
68 |
69 |
70 | 직접 대입해보면 다음과 같다
71 | |screenHeihgt|480|480|480|480|480|
72 | |------|---|---|---|---|---|
73 | |y|0|60|120|180|239|
74 | |posZ|240|240|240|240|240|
75 | |p|-240|-180|-120|-6|-1|
76 | |dist|1|1.5|2|4|240|
77 |
78 |
79 | y = 0일 때 dist가 가장 짧고, y가 중앙(h /2)으로 갈수록 dist가 급격하게 커지는 관계를 확인하자.
80 |
81 | (y가 중앙으로 갈수록 삼각형이 눕고, dist는 더 커진다.)
82 |
83 |
84 |
85 |
86 |
87 | 
88 |
89 |
90 | 정면에서 볼 땐
91 |
92 | dist = 1 : 내 1칸 앞에 벽이 있음 → 천장이 1칸 보임
93 |
94 | dist = 2 : 내 2칸 앞에 벽이 있음 → 천장이 2칸 보임
95 |
96 | dist = 8 : 내 8칸 앞에 벽이 있음 → 천장이 8칸 보임
97 |
98 | dist = 240 : 내 240칸 앞에 벽이 있음 → 천장이 240칸 보임
99 |
100 |
101 | 로 생각하자
102 |
103 |
104 | ----
105 |
106 | ### 2. 스크린 왼쪽 끝에 보이는 천장 좌표 구하기
107 |
108 |
109 | ```C
110 | double rayDirX0 = dirX - planeX;
111 | double rayDirY0 = dirY - planeY;
112 | double rayDirX1 = dirX + planeX;
113 | double rayDirY1 = dirY + planeY;
114 |
115 | rayDir0 : 내 위치에서 스크린 왼쪽으로 끝으로 뻗어지는 광선
116 | rayDir1 : 내 위치에서 스크린 오른쪽 끝으로 뻗어지는 광선
117 | ```
118 |
119 |
120 | ```C
121 | double obj_x = posX + rayDirX0 * dist;
122 | double obj_y = posY + rayDirY0 * dist;
123 |
124 | (obj_x, obj_y) : (스크린 왼쪽 끝으로 광선을 뻗어서 * 천장에 닿을 때) 좌표
125 | ```
126 |
127 |
128 | 내 위치에서 스크린 왼쪽 끝으로 광선을 뻗었을 때 천장에 닿는 좌표를 (obj_x, obj_y)라고 하자.
129 |
130 |
131 | 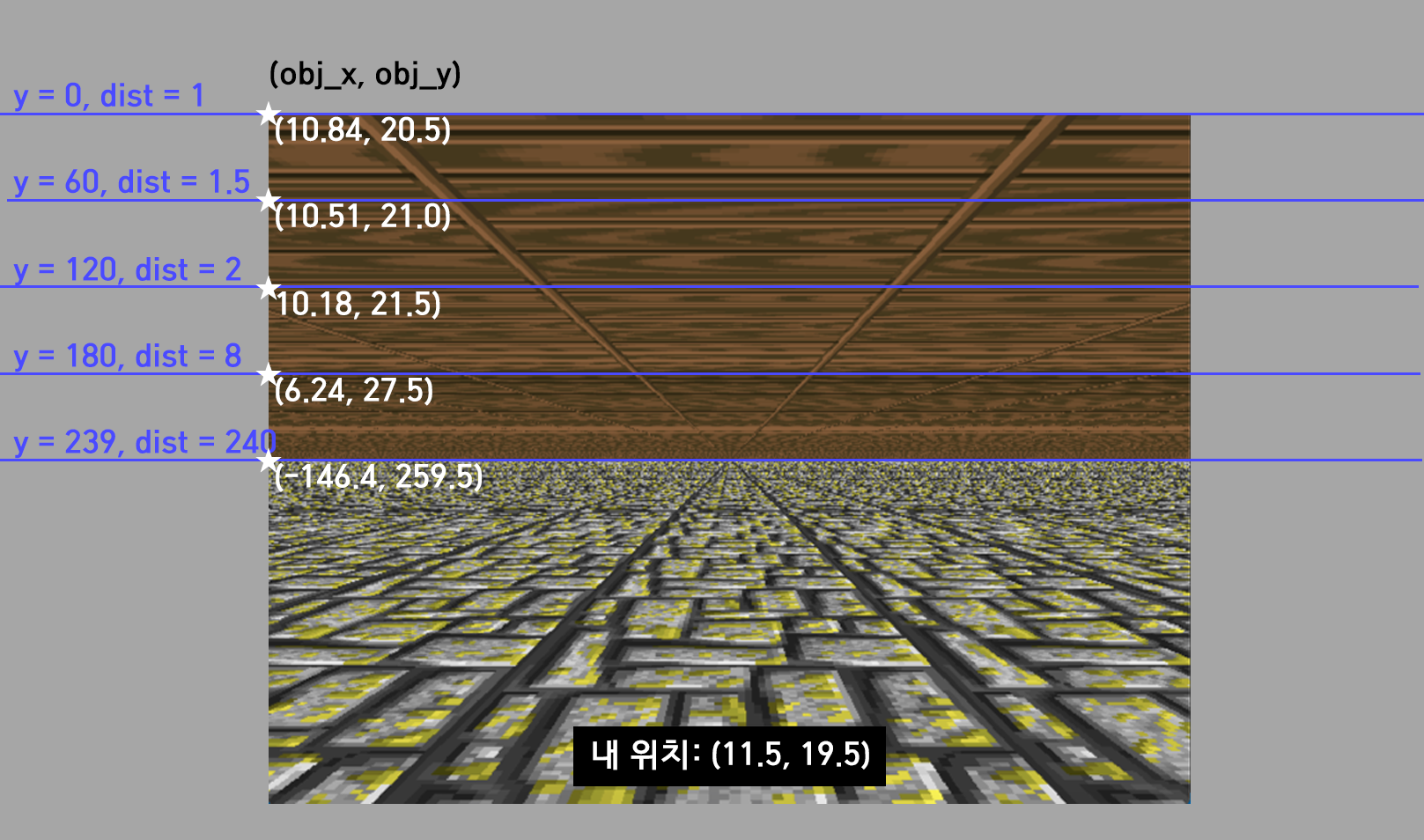
132 |
133 |
134 |
135 | 내 앞에 있던 벽이 멀어질수록 좌우로 시야가 넓어진다
136 |
137 | = dist가 커질수록 좌우로 시야가 넓어진다
138 |
139 | = y가 중앙으로 갈수록 좌우로 시야가 넓어진다
140 |
141 | = y가 중앙으로 갈수록 내 위치에서 obj_x, obj_y 좌표가 멀어진다
142 |
143 |
144 |
145 |
146 | 이해를 위해 스크린 오른쪽 끝 좌표도 한 번 더 확인해보자.
147 |
148 | ```
149 | double obj_x_end = posX + rayDirX1 * dist;
150 | double obj_y_end = posY + rayDirY1 * dist;
151 |
152 | (obj_x_end, obj_y_end) : (스크린 오른쪽 끝으로 광선을 뻗어서 * 천장에 닿을 때) 좌표
153 | ```
154 |
155 |
156 | 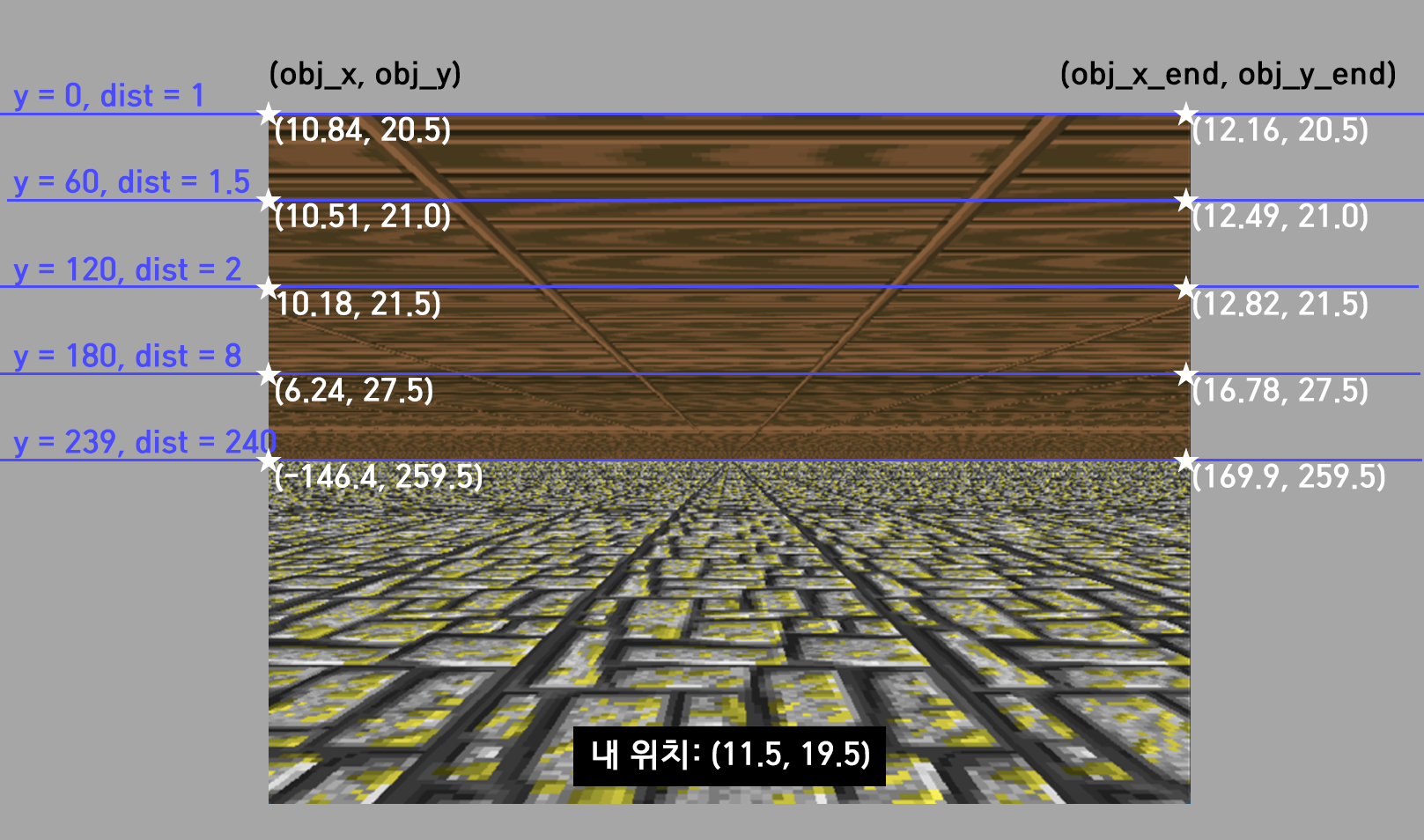
157 |
158 |
159 |
160 | 내 앞에 있던 벽이 멀어질수록 좌우로 시야가 넓어진다.
161 |
162 | dist = 1 : 눈에 보이는 좌표가 10 ~12
163 |
164 | dist = 8 : 눈에 보이는 좌표가 6 ~ 16
165 |
166 | dist = 240 : 눈에 보이는 좌표가 -146 ~ 16
167 |
168 |
169 |
170 | ----
171 | ### 3. 왼쪽 끝에서 오른쪽 끝으로 갈 때 step 구하기
172 |
173 |
174 | 이제 y위치를 잡아놓고 (obj_x, obj_y)에서 오른쪽으로 가면서 텍스쳐를 저장한다.
175 |
176 | 한 번에 얼만큼씩 움직여야 할까? 벽에서는 obj_y가 항상 동일하게 1씩 증가했지만, 천장은 조금 다르다.
177 |
178 |
179 | dist = 1 : 처음부터 끝까지 갔을 때 x 좌표 차이가 1.32
180 |
181 | dist = 8: 처음부터 끝까지 갔을 때 x 좌표 차이가 10.54
182 |
183 | dist = 240 : 처음부터 끝까지 갔을 때 x 좌표 차이가 326.3
184 |
185 |
186 |
187 | 이렇게 dist가 커질수록 좌표 차이가 크다는 것은 (거리가 멀어질수록 좌우로 시야가 넓어진다는 것은)
188 |
189 | dist = 1일 땐 obj에 더해주는 값이 작고 (가까운 곳을 볼 땐 시선을 움직일 때 시야의 변화가 작고)
190 |
191 | dist가 커질수록 더해주는 값이 커진다는 것을 의미한다. (멀리 볼수록 시선을 움직일 때 시야의 변화가 크다)
192 |
193 |
194 |
195 | 이때 더해주는 값이 step이다. step은 dist에 따라 달라지기 때문에 1로 둘 수 없고 값을 구해야 한다.
196 |
197 |
198 | 스크린 왼쪽 끝에서 오른쪽 끝으로 가는 과정은 왼쪽 끝 좌표인 (obj_x, obj_y)에서
199 |
200 | ```C
201 | double obj_x = posX + rayDirX0 * dist;
202 | double obj_y = posY + rayDirY0 * dist;
203 | ```
204 |
205 |
206 | (스크린 width)번 움직여서 오른쪽 끝 좌표인 (obj_x_end, obj_y_end)에 도착하는 과정이다.
207 |
208 | ```C
209 | double obj_x_end = posX + rayDirX1 * dist;
210 | double obj_y_end = posY + rayDirY1 * dist;
211 | ```
212 |
213 | 따라서
214 | ```C
215 | obj_x + (step_x * screenWidth) = obj_x_end
216 | obj_y + (step_y * screenWidth) = obj_y_end
217 | ```
218 | 를 만족하는 step_x, step_y를 구하면 된다.
219 |
220 |
221 |
222 | **step 유도과정**
223 | ```C
224 | obj_x + (step_x * screenWidth) = obj_x_end
225 | step_x * screenWidth = obj_x_end - obj_x
226 | step_x * screenWidth = (posX + rayDirX1 * dist) - (posX + rayDirX0 * dist)
227 | step_x * screenWidth = (rayDir1X - rayDir0x) * dist
228 |
229 | step_x = (rayDir1X - rayDir0X) * dist / screenWidth
230 |
231 | 동일한 방법으로
232 |
233 | step_y = (rayDir1Y - rayDir0Y) * dist / screenWidth
234 |
235 | dist에 따라 step이 바뀌는 관계도 식으로 확인할 수 있다.
236 | ```
237 |
238 |
239 | ----
240 |
241 | ### 4. 좌표에 해당하는 텍스쳐 가져오기
242 |
243 | 텍스쳐를 가져오는 방법은 벽과 동일하다.
244 |
245 | 1. 실제 천장 좌표(obj_x, obj_y)에서 소수부분만 구해서 = (1*1) 안에서 상대적 위치를 구해서
246 |
247 | 실제 텍스쳐에 상대적 위치를 적용해준다.
248 | ```C
249 | img_x = (int)(img_width * (obj_x - floor(obj_x)));
250 | img_y = (int)(img_height * (obj_y - floor(obj_y)));
251 | ```
252 |
253 |
254 | 2. 텍스쳐 위치(img_x, img_y)에 해당하는 색상을 가져온다.
255 | ```C
256 | tex_point = size_l / (bpp / 8) * img_y + img_x;
257 | buf[y][x] = data[tex_point];
258 | ```
259 |
260 |
261 | 상대적 위치를 구할 때 정수부분을 (int)obj_x 로 하지 않고 floor 함수로 구하는 것은 음수를 보정하기 위해서다.
262 |
263 | 천장좌표가 음수일 경우 상대적 위치가 정상범위(0 ~ 1)를 넘는 오류가 생긴다. (벽을 다 지우고 천장, 바닥만 그리면 오류를 확인할 수 있다.)
264 | ```C
265 | ex) obj_x = -1.4
266 |
267 | obj_x - (int)obj_x = -1.4 - (-1) = -0.4
268 | ```
269 |
270 | 따라서 좌표가 음수일 경우에도 상대적 위치는 양수가 되도록 floor함수를 사용했다.
271 |
272 | ```C
273 | ex) obj_x = -1.4
274 |
275 | obj_x - floor(obj_x) = -1.4 - (-2) = 0.6
276 | ```
277 |
278 |
279 | -0.4과 0.6의 상대적 위치가 동일하기 때문에 floor로 보정이 가능하다.
280 |
281 |
282 | 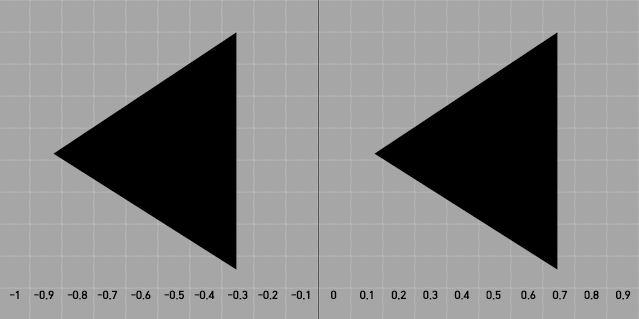
283 |
284 |
285 |
286 |
287 |
288 | ----
289 |
290 | ### 5. 반복문 돌기
291 |
292 |
293 |
294 | 반복문은 두가지 케이스가 있다.
295 |
296 | ```C
297 | 로데브 ver.
298 |
299 | for (int y = screenHeight / 2 + 1; y < screenHeight; y++)
300 | {
301 | for (int x = 0; x < screenWidth; ++x)
302 | {
303 | buf[y][x] = floor_color;
304 | buf[screenHeight - y - 1][x] = ceil_color;
305 | }
306 | }
307 | ```
308 |
309 | ```C
310 | for (int y = 0; y < sceenHeight / 2; y++)
311 | {
312 | for (int x = 0; x < screenWidth; ++x)
313 | {
314 | buf[y][x] = ceil_color;
315 | buf[screenHeight - y - 1][x] = floor_color;
316 | }
317 | }
318 | ```
319 |
320 |
321 |
322 | 1. 세로 반복문을 screenHeight만큼 전부 돌리지 않고 범위를 반으로 줄일 수 있다. 왜냐하면 screenHeignt / 2 기준으로 천장과 바닥이 완전 대칭이기 때문이다.
323 |
324 | screenHeight = 480일 때 y = 0과 y = 439 계산이 동일하고, y = 120과 y = 359 계산이 동일하다.
325 |
326 | 따라서 while문 안에서 buf[y][x]와 buf[screenHeignt - 1 - y][x]로 위아래를 한번에 처리해줄 수 있기 때문에 반복문을 절반만 돌린다.
327 |
328 |
329 | 2. 절반을 돌릴 때 기준을 floor과 ceil 중 선택할 수 있다.
330 |
331 | 로데브는 반복문 범위를 (h / 2 + 1) ~ (h - 1)으로 y를 floor에서 돌리고 있고
332 |
333 | 범위를 (0) ~ (h / 2 - 1)로 바꿔 y를 ceil에서 돌릴 수도 있다.
334 |
335 | 전자의 경우 h / 2 근처에서 1픽셀씩 범위가 비기 때문에 나는 (0) ~ (h / 2 - 1) 범위를 선택했다. (사실 눈에 보이지 않는 차이다.)
336 |
337 | 처음에 dist를 양수로 보정해주었기 때문에 이렇게 범위를 바꿔도 정상적으로 구현된다.
338 |
339 | ```C
340 | double dist = fabs(posZ / p);
341 | ```
342 |
343 |
344 |
345 | **전체적인 흐름**
346 |
347 | ```C
348 | y = 0;
349 | while (y < screenHeight / 2)
350 | {
351 | ...
352 | double dist = fabs(posZ / p);
353 |
354 | double obj_x = posX + rayDirX0 * dist;
355 | double obj_y = posY + rayDirY0 * dist;
356 |
357 | int step_x = (rayDir1X - rayDir0X) * dist / win_w;
358 | int step_y = (rayDir1Y - rayDir0Y) * dist / win_w;
359 |
360 | x = 0;
361 | while (x < screenWidth)
362 | {
363 | int img_x = (int)(img_width * (obj_x - floor(obj_x)));
364 | int img_y = (int)(img_height * (obj_y - floor(obj_y)));
365 | int tex_point = size_l / (bpp / 8) * img_y + img_x;
366 | buf[y][x] = data[tex_point]; // ceil
367 | buf[screenHeight - 1 - y][x] = data[tex_point]; // floor
368 | obj_x += step_x;
369 | obj_y += step_y;
370 | x++;
371 | }
372 | y++;
373 | }
374 | ```
375 |
376 | ceil 텍스쳐, floor 텍스쳐가 각자의 img_width, img_height, size_l, data를 사용할 수 있도록 코드 보완이 필요하다.
377 |
--------------------------------------------------------------------------------
/4.transparency.md:
--------------------------------------------------------------------------------
1 | **로데브 中 텍스쳐를 이해하는 페이지.**
2 |
3 | 이해했던 흐름 그대로의 정리라서 로데브 원본과 살짝 차이가 있습니다.
4 |
5 | 1 [벽 텍스쳐](https://github.com/p-eye/cub3d_texturing/blob/master/2.wall.md)
6 | 2 [천장, 바닥 텍스쳐](https://github.com/p-eye/cub3d_texturing/blob/master/3.ceil.md)
7 | **3 [텍스쳐에 투명도 넣기](https://github.com/p-eye/cub3d_texturing/blob/master/4.transparency.md)**
8 |
9 | ---
10 |
11 | ## **3. 텍스쳐에 투명도 넣기**
12 |
13 |
14 |
15 | 
16 |
17 |
18 | 앞에서 mlx에서는 0xAARRGGBB 색상 형식을 사용하고, 실제로 투명도를 지원하는 것도 확인해보았다. (위 움짤)
19 |
20 | alpha값이 있는 색상을 바로 mlx 함수로 띄웠던 경우다.
21 |
22 |
23 |
24 | 하지만 cub3d에서 buf[y][x]에 색을 저장하는 방식에서는 투명도를 다르게 구현해야 한다.
25 |
26 | '완전 투명'한 경우를 제외하고는, 아무리 반투명한 색을 넣어도 스크린에 띄워보면 '완전 불투명'한 이미지로 출력된다.
27 |
28 |
29 |
30 | 왜냐하면 buf[y][x] = color 과정에서 기존 색상을 남겨두지 않고 그냥 새로운 색상을 덮어 씌워버리기 때문이다.
31 |
32 | 지금은 파란색 위에 반투명한 노란색을 놓는다고 색이 섞이는 것이 아니라 그냥 노란색만 남겨진다.
33 |
34 | 따라서 투명도를 적용하기 위해서는 두 색을 섞어 새로운 색상을 만들어서 버퍼에 넣어야 한다.
35 |
36 |
37 |
38 | 이렇게
39 |
40 | 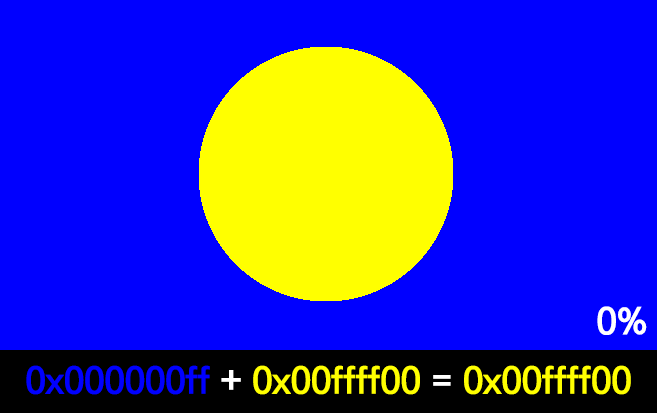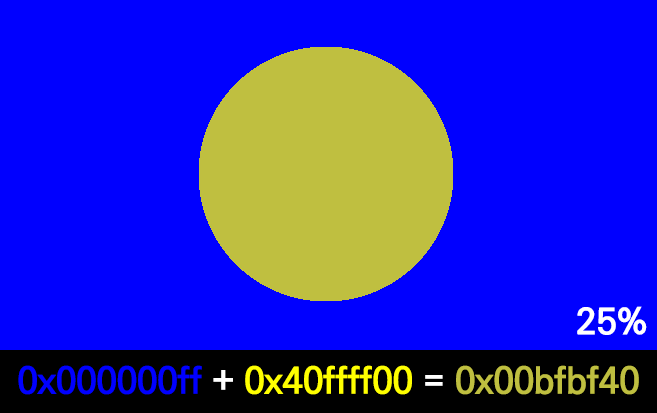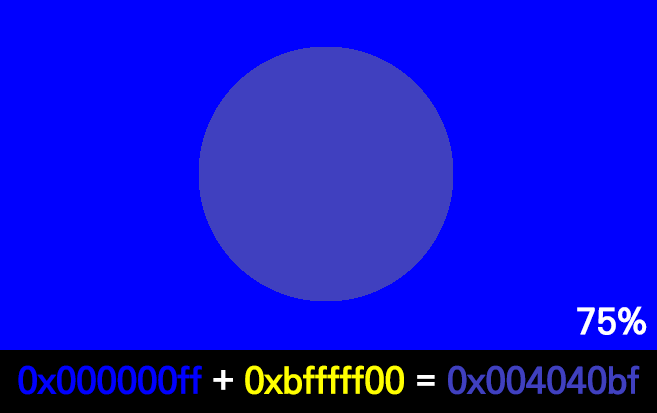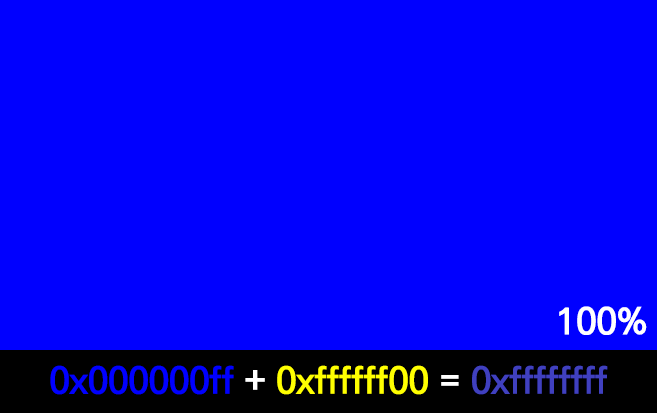
41 |
42 |
43 | [투명도 참고](https://davidwalsh.name/hex-opacity)
44 |
45 |
46 |
47 |
48 | 두 색을 섞을 땐 각 색상에 투명도 가중치를 주고 더해준다.
49 | ```C
50 | result = weight * new + (1 - weight) * old
51 |
52 |
53 | 여기서 가중치 weight는
54 | weight = (double) (255 - new_alpha) / 255;
55 | ```
56 |
57 |
58 | ```C
59 | ex) 완전 불투명한 색을 추가하면
60 |
61 | new_alpha = 0
62 | weihgt = 1
63 | result = new
64 |
65 | 이기 때문에 새로운 색만 보이게 된다.
66 | ```
67 |
68 |
69 |
70 | **새로 가져오는 색에 투명도가 적용된 경우**
71 |
72 | 1. new와 old를 각각 r, g, b로 분리한다.
73 |
74 | 2. new에서 alpha값을 뽑는다.
75 |
76 | 3. 가중치를 반영해서 r, g, b 각각 새로운 색을 만든다.
77 |
78 | 4. result color로 합쳐준다.
79 |
80 |
81 |
82 | **새로 가져오는 색은 불투명하지만, 투명도를 추가하고 싶은 경우**
83 |
84 | 1. new와 old를 각각 r, g, b로 분리한다.
85 |
86 | 2. new에 적용할 alpha값을 정한다.
87 |
88 | 3. 가중치를 반영해서 r, g, b 각각 새로운 색을 만든다.
89 |
90 | 4. result color로 합쳐준다.
91 |
92 |
93 |
94 | 과제에서는
95 | old: 기존 buf[y][x]에 저장된 색
96 | new: 새로 가져오는 data[tex_point] 색
97 | 이 될 것이다.
98 |
99 |
100 | 각각의 색상 요소를 분리하고 합치는 법은 [mlx_get_data_addr 페이지](https://github.com/p-eye/cub3d_texturing/blob/master/1.mlx_get_data_addr.md)에 설명되어 있다.
101 |
102 |
103 |
104 | 1) 벽 색이 0xCC00FF00 인 경우
105 |
106 | 
107 |
108 |
109 |
110 |
111 |
112 | 2) 완전 불투명한 벽에 0x80만큼의 투명도를 준 경우
113 |
114 | 
115 |
116 |
117 |
118 |
119 |
--------------------------------------------------------------------------------
/README.md:
--------------------------------------------------------------------------------
1 | # cub3d_texturing
2 | Description of cub3D texturing
3 |
4 | ----
5 |
6 | cub3d 과제를 진행하면서
7 | * [taelee님의 mlx 예제](https://github.com/taelee42/mlx_example)
8 | * [로데브 레이캐스팅 튜토리얼](https://lodev.org/cgtutor/raycasting.html)
9 | * [mihykim님의 로데브 번역본](https://github.com/365kim/raycasting_tutorial)
10 | * [yohlee님의 로데브 C 버전](https://github.com/l-yohai/cub3d)
11 |
12 | 자료들로부터 많은 도움을 받았습니다.
13 |
14 | 이 글도 위 자료들을 바탕으로 작성했기 때문에 참고하시면 좋을 것 같습니다.
15 |
16 |
17 | 이 글엔 제가 cub3d 진행 중 '텍스쳐 처리'를 학습한 과정이 정리되어 있습니다.
18 |
19 | 따라서 로데브 튜토리얼 중 아래 부분만 담겨 있습니다.
20 |
21 | * 벽에 텍스쳐 넣기 - 로데브 said, "affine texture mapping" (subejct mandatory)
22 | * 천장, 바닥에 텍스쳐 넣기 - 로데브 said, "scanline by scanline" (subject bonus)
23 | * 텍스쳐에 투명도 넣기 (extra)
24 |
25 | 그리고 이해를 돕기 위해 첫 페이지에 mlx_get_data_addr 함수를 정리했습니다.
26 |
27 | cub3d 텍스쳐 부분을 공부하는 분들에게 도움이 되었으면 좋겠습니다.
28 |
--------------------------------------------------------------------------------
 154 |
154 |  154 |
154 | 

 221 |
221 |  237 |
237 |  250 |
250 |  256 |
256 | 
 330 |
330 | 

 61 |
61 |  82 |
82 |  154 |
154 | 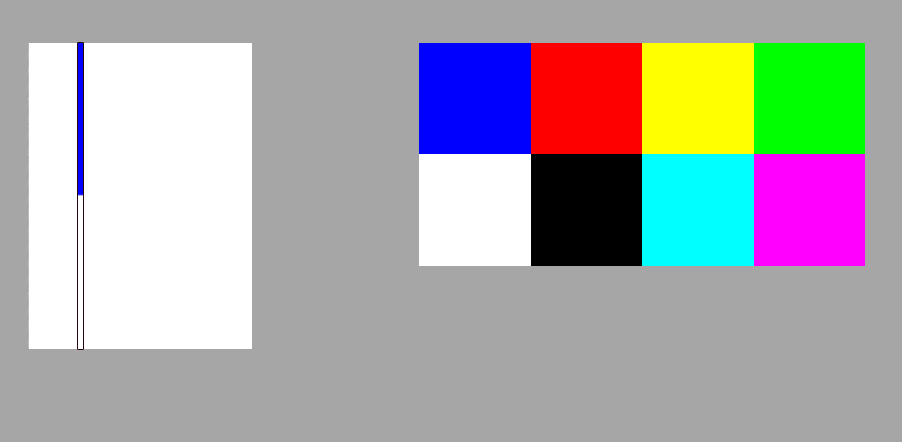 182 |
182 |