├── .gitignore
├── exams
├── exam1.pdf
├── exam2.pdf
└── exam1-solutions.ipynb
├── assignments
├── a7_q2.png
├── a7_q3.png
├── a7_q4.png
├── assignment1.pdf
├── assignment2.pdf
├── assignment3.pdf
├── assignment4.pdf
├── assignment5.pdf
├── assignment6.pdf
└── assignment7.pdf
├── math210-outline.pdf
├── projects
├── project1.pdf
├── project2.pdf
└── elections.csv
├── notes-week-13
├── StreetTrees_Downtown.csv
├── StreetTrees_WestEnd.csv
├── StreetTrees_Kitsilano.csv
├── StreetTrees_ArbutusRidge.csv
└── StreetTrees_WestPointGrey.csv
├── README.md
├── notes-week-04
├── number_theory.py
└── notes-01-25-16.ipynb
├── notes-week-11
├── canada_population_data.csv
└── gdp_data.csv
├── notes-week-01
├── notes-01-06-16.ipynb
└── notes-01-08-16.ipynb
├── notes-week-07
├── notes-02-22-16.ipynb
└── notes-02-24-16.ipynb
├── notes-week-03
├── notes-01-18-16.ipynb
└── notes-01-20-16.ipynb
├── notes-week-02
├── notes-01-13-16.ipynb
├── notes-01-11-16.ipynb
└── notes-01-15-16.ipynb
└── notes-week-10
└── notes-03-18-16.ipynb
/.gitignore:
--------------------------------------------------------------------------------
1 | .ipynb_checkpoints/
2 | .DS_Store
3 | solutions/
4 |
--------------------------------------------------------------------------------
/exams/exam1.pdf:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/patrickwalls/math210/HEAD/exams/exam1.pdf
--------------------------------------------------------------------------------
/exams/exam2.pdf:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/patrickwalls/math210/HEAD/exams/exam2.pdf
--------------------------------------------------------------------------------
/assignments/a7_q2.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/patrickwalls/math210/HEAD/assignments/a7_q2.png
--------------------------------------------------------------------------------
/assignments/a7_q3.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/patrickwalls/math210/HEAD/assignments/a7_q3.png
--------------------------------------------------------------------------------
/assignments/a7_q4.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/patrickwalls/math210/HEAD/assignments/a7_q4.png
--------------------------------------------------------------------------------
/math210-outline.pdf:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/patrickwalls/math210/HEAD/math210-outline.pdf
--------------------------------------------------------------------------------
/projects/project1.pdf:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/patrickwalls/math210/HEAD/projects/project1.pdf
--------------------------------------------------------------------------------
/projects/project2.pdf:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/patrickwalls/math210/HEAD/projects/project2.pdf
--------------------------------------------------------------------------------
/projects/elections.csv:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/patrickwalls/math210/HEAD/projects/elections.csv
--------------------------------------------------------------------------------
/assignments/assignment1.pdf:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/patrickwalls/math210/HEAD/assignments/assignment1.pdf
--------------------------------------------------------------------------------
/assignments/assignment2.pdf:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/patrickwalls/math210/HEAD/assignments/assignment2.pdf
--------------------------------------------------------------------------------
/assignments/assignment3.pdf:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/patrickwalls/math210/HEAD/assignments/assignment3.pdf
--------------------------------------------------------------------------------
/assignments/assignment4.pdf:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/patrickwalls/math210/HEAD/assignments/assignment4.pdf
--------------------------------------------------------------------------------
/assignments/assignment5.pdf:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/patrickwalls/math210/HEAD/assignments/assignment5.pdf
--------------------------------------------------------------------------------
/assignments/assignment6.pdf:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/patrickwalls/math210/HEAD/assignments/assignment6.pdf
--------------------------------------------------------------------------------
/assignments/assignment7.pdf:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/patrickwalls/math210/HEAD/assignments/assignment7.pdf
--------------------------------------------------------------------------------
/notes-week-13/StreetTrees_Downtown.csv:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/patrickwalls/math210/HEAD/notes-week-13/StreetTrees_Downtown.csv
--------------------------------------------------------------------------------
/notes-week-13/StreetTrees_WestEnd.csv:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/patrickwalls/math210/HEAD/notes-week-13/StreetTrees_WestEnd.csv
--------------------------------------------------------------------------------
/notes-week-13/StreetTrees_Kitsilano.csv:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/patrickwalls/math210/HEAD/notes-week-13/StreetTrees_Kitsilano.csv
--------------------------------------------------------------------------------
/notes-week-13/StreetTrees_ArbutusRidge.csv:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/patrickwalls/math210/HEAD/notes-week-13/StreetTrees_ArbutusRidge.csv
--------------------------------------------------------------------------------
/notes-week-13/StreetTrees_WestPointGrey.csv:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/patrickwalls/math210/HEAD/notes-week-13/StreetTrees_WestPointGrey.csv
--------------------------------------------------------------------------------
/README.md:
--------------------------------------------------------------------------------
1 | # MATH 210 Introduction to Mathematical Computing
2 |
3 | MATH 210 at the [University of British Columbia](http://www.math.ubc.ca) is an introduction to scientific computing in Python. We will start with basic Python programming including datatypes, logical statements, loops and functions and then focus on the scientific computing packages NumPy, SciPy, matplotlib and pandas. We will use these packages to solve problems in calculus, linear algebra, differential equations , statistics and data visualization.
--------------------------------------------------------------------------------
/notes-week-04/number_theory.py:
--------------------------------------------------------------------------------
1 | def is_prime(n):
2 | "Determine if a positive integer n is prime."
3 | if n <= 1:
4 | return False
5 | for d in range(2, round(n**0.5) + 1):
6 | if n % d == 0:
7 | return False
8 | return True
9 |
10 | def primes_up_to(N):
11 | "Create the list of primes p less than or equal to N."
12 | return [ p for p in range(2,N+1) if is_prime(p) ]
13 |
14 | def primes_interval(a,b):
15 | "Create the list of primes p contained in the closed interval [a,b]."
16 | return [ p for p in range(a,b+1) if is_prime(p) ]
17 |
18 | def divisors(n):
19 | "Create the list of positive divisors of an integer n."
20 | return [ d for d in range(1,n+1) if n % d == 0 ]
21 |
22 | def prime_divisors(n):
23 | "Create the list of prime divisors of an integer n."
24 | return [ p for p in range(2,n+1) if (n % p == 0 and is_prime(p)) ]
25 |
26 | def twin_primes(N):
27 | "Create the list of twin primes [p,p+2] with p less than or equal to N."
28 | prime_list = primes_up_to(N)
29 | return [ [p,p+2] for p in prime_list if p + 2 in prime_list ]
30 |
31 | def twin_primes_interval(a,b):
32 | "Create the list of twin primes [p,p+2] with p in the closed interval [a,b]."
33 | prime_list = primes_interval(a,b+2)
34 | return [ [p,p+2] for p in prime_list if p + 2 in prime_list ]
35 |
36 |
37 | #def sum_of_squares(n):
38 | # "Return the list of pairs [a,b] of integers such that n = a**2 + b**2 with 1 <= a <= b."
39 | # return [ [a,b] for b in range(1,round(n**0.5)+1) for a in range(1,b+1) if n == a**2 + b**2 ]
40 |
41 |
--------------------------------------------------------------------------------
/notes-week-11/canada_population_data.csv:
--------------------------------------------------------------------------------
1 | Year,Canada,Newfoundland and Labrador,Prince Edward Island,Nova Scotia,New Brunswick,Quebec,Ontario,Manitoba,Saskatchewan,Alberta,British Columbia,Yukon,Northwest Territories including Nunavut,Northwest Territories,Nunavut
2 | 1952,14436750,372750,100250,652250,525250,4167750,4779250,796000,842250,971500,1204500,9000,16000,,
3 | 1953,14833000,383000,101000,663250,532500,4267000,4935250,808500,859000,1010250,1248250,9000,16000,,
4 | 1954,15269500,394500,101000,672000,539750,4385000,5108250,822500,871750,1054250,1294000,9750,16750,,
5 | 1955,15681250,405500,100000,682750,547000,4510750,5258250,838750,878250,1089500,1341500,11250,17750,,
6 | 1956,16070250,415000,99250,693250,554500,4624750,5403000,848750,879750,1122250,1399000,12000,18750,,
7 | 1957,16579500,423500,99000,699000,561500,4762500,5624750,858250,878750,1161250,1479500,12250,19250,,
8 | 1958,17062250,431500,100000,708750,570500,4897500,5814250,874500,891000,1205250,1536000,13000,20000,,
9 | 1959,17467500,440000,101500,719000,581000,5019750,5962500,889750,905750,1247250,1567000,13000,21000,,
10 | 1960,17855250,448250,103250,726500,588000,5137500,6105500,905500,914250,1289750,1601000,14000,21750,,
11 | 1961,18224500,457750,104750,736250,597000,5254500,6231000,921250,924000,1330500,1629750,14500,23250,,
12 | 1962,18570750,467500,107000,745000,604500,5367000,6347500,935000,929250,1368500,1660000,15000,24500,,
13 | 1963,18919000,475750,108000,749750,608250,5476250,6478500,948500,931500,1402500,1699500,15000,25500,,
14 | 1964,19277250,482750,109000,754000,610750,5580250,6626750,958250,941000,1427750,1745000,15000,26750,,
15 | 1965,19633500,487000,109000,755000,614500,5681500,6783250,963500,949500,1448000,1800000,14750,27500,,
16 | 1966,19997500,493000,108500,755500,616500,5774250,6954000,961750,954750,1462500,1873750,14500,28500,,
17 | 1967,20363750,499000,109000,759500,620000,5857500,7121750,962250,956750,1488250,1945750,15000,29000,,
18 | 1968,20692000,506000,110250,767000,625250,5924500,7257750,970000,959750,1522750,2003250,15500,30000,,
19 | 1969,20994250,513750,111000,775000,627500,5981000,7385250,977500,957750,1558000,2060250,16000,31250,,
20 | 1970,21287500,517250,110250,781500,626750,6010750,7548750,981250,940750,1593000,2127750,17000,32500,,
21 | 1971,21747319,526331,111866,792274,637547,6081106,7767567,991958,928275,1645089,2211280,18613,35411,,
22 | 1972,22187095,538425,113424,802157,648586,6168675,7947178,1000587,920467,1691588,2297348,20074,38586,,
23 | 1973,22453742,544822,114569,811262,655909,6207238,8057794,1005965,911644,1722375,2360797,20951,40417,,
24 | 1974,22772043,548901,115780,818261,664456,6261372,8189190,1016226,908116,1752854,2434720,21068,41098,,
25 | 1975,23103010,555594,117520,826194,676037,6322332,8304342,1023105,915819,1802853,2494629,21848,42736,,
26 | 1976,23414354,561778,118534,834812,688276,6385255,8401757,1030789,930528,1864399,2531737,22368,44120,,
27 | 1977,23693935,564767,119695,839945,694403,6425092,8493530,1036468,942943,1942192,2567936,22445,44519,,
28 | 1978,23935460,567177,121354,844466,698544,6437989,8578040,1039574,951505,2017090,2611636,22945,45142,,
29 | 1979,24170164,569598,122567,848879,701924,6459979,8648592,1036582,958596,2092557,2662293,22924,45674,,
30 | 1980,24470715,572198,123391,852126,704867,6498485,8727944,1033998,966544,2184262,2737538,23027,46334,,
31 | 1981,24784554,574549,123412,854902,705612,6540880,8804010,1035375,975036,2282738,2816980,23707,47354,,
32 | 1982,25082944,574082,123517,859088,707284,6575840,8908938,1044148,985876,2359433,2871303,24465,48970,,
33 | 1983,25335951,578276,124849,867586,713683,6598969,9026909,1057957,999334,2389818,2904171,23741,50659,,
34 | 1984,25576735,579697,126382,877198,719514,6626718,9152063,1070580,1012931,2394104,2941539,23809,52198,,
35 | 1985,25813200,578856,127575,885198,722895,6660817,9279890,1081713,1023575,2402201,2972265,24308,53907,,
36 | 1986,26067486,576514,128344,888939,724758,6703313,9421117,1090618,1028305,2425855,3000682,24484,54558,,
37 | 1987,26397870,575181,128618,892881,726950,6772196,9612540,1097076,1031442,2437612,3043088,25506,54780,,
38 | 1988,26751474,574770,129252,896729,729875,6831143,9816491,1101103,1027949,2453974,3108064,26368,55754,,
39 | 1989,27214902,576057,130057,903024,734454,6914476,10068044,1102632,1019320,2493023,3189665,27079,57071,,
40 | 1990,27632360,576982,130394,909510,739547,6986226,10267345,1104302,1008330,2540902,3282328,27852,58642,,
41 | 1991,27987111,578742,130415,914386,744716,7054592,10409479,1108239,1002296,2587477,3367589,28682,,,
42 | 1992,28324154,579730,130861,918982,747418,7104606,10549810,1111732,1002730,2627162,3459366,29717,,39281,22761
43 | 1993,28651462,579840,132010,923593,748620,7153278,10676423,1116489,1005599,2663774,3558491,30107,,39776,23463
44 | 1994,28960064,574833,133255,926652,749965,7189008,10800283,1121910,1009113,2696102,3664473,29660,,40527,24282
45 | 1995,29263007,568009,134405,928296,750907,7215800,10931434,1127720,1013529,2730105,3766198,30336,,41356,24913
46 | 1996,29569874,560576,135543,930826,752062,7243693,11065044,1132782,1018106,2770298,3862540,31272,,41591,25543
47 | 1997,29867572,551774,136032,932330,752385,7272062,11208193,1135655,1017834,2822523,3939702,31661,,41558,25863
48 | 1998,30123874,541500,135821,932290,751072,7294436,11347200,1136941,1017422,2887726,3981074,31214,,40907,26272
49 | 1999,30367051,534147,136181,933496,750362,7320816,11484167,1141378,1014926,2945712,4007763,30686,,40639,26778
50 | 2000,30647400,529012,136400,934291,750524,7353293,11657472,1146449,1008478,2996032,4037128,30400,,40533,27388
51 | 2001,30971516,523045,136605,933058,749661,7391474,11864712,1150440,1001139,3051428,4071000,30126,,40817,28010
52 | 2002,31308560,520150,136928,934794,749076,7435910,12062619,1155384,997408,3118466,4097492,30226,,41504,28604
53 | 2003,31601594,518813,137208,936927,749354,7480516,12221288,1162043,996276,3176116,4120648,30789,,42418,29197
54 | 2004,31898942,517731,137628,939290,749290,7529704,12367823,1171467,997011,3232795,4151788,31465,,43258,29692
55 | 2005,32202766,515040,137918,938442,748348,7576590,12507353,1177691,994418,3310274,4191121,31913,,43457,30202
56 | 2006,32528626,511103,137878,937659,745966,7626106,12641896,1182247,992276,3410912,4236434,32224,,43198,30727
57 | 2007,32847675,509680,137814,935387,745319,7685354,12749822,1187953,1000495,3502678,4286244,32454,,43202,31273
58 | 2008,33198550,511789,138615,935986,746849,7753366,12865668,1196350,1015886,3582788,4343104,33028,,43335,31788
59 | 2009,33581080,516147,139730,938367,749640,7832800,12983106,1206574,1032532,3667912,4405052,33687,,43068,32466
60 | 2010,33958588,521561,141519,941983,752660,7918420,13117298,1219107,1049312,3724528,4461376,34408,,43171,33246
61 | 2011,34302909,524754,143732,944512,755285,7996821,13249885,1232071,1064673,3781472,4497034,35209,,43407,34054
62 | 2012,34698875,526722,145066,944934,756580,8073312,13393063,1248325,1084298,3873407,4538794,36020,,43675,34679
63 | 2013,35102353,528271,145340,943524,755810,8143836,13533970,1263560,1103406,3989191,4579968,36331,,43852,35296
64 | 2014,35496547,528839,145963,942932,755058,8206005,13664922,1278114,1120272,4104536,4633220,36733,,43968,35984
65 | 2015,35825433,528188,146406,943498,754306,8258662,13782341,1292286,1133028,4187166,4681500,37176,,44165,36711
--------------------------------------------------------------------------------
/notes-week-01/notes-01-06-16.ipynb:
--------------------------------------------------------------------------------
1 | {
2 | "cells": [
3 | {
4 | "cell_type": "markdown",
5 | "metadata": {},
6 | "source": [
7 | "# MATH 210 Introduction to Mathematical Computing\n",
8 | "## January 6, 2016"
9 | ]
10 | },
11 | {
12 | "cell_type": "markdown",
13 | "metadata": {
14 | "collapsed": true
15 | },
16 | "source": [
17 | "Today's Agenda:\n",
18 | "1. Jupyter Notebooks\n",
19 | "2. Markdown Language\n",
20 | "3. Latex\n",
21 | "4. Exercises"
22 | ]
23 | },
24 | {
25 | "cell_type": "markdown",
26 | "metadata": {},
27 | "source": [
28 | "## 1. Jupyter Notebooks\n",
29 | "\n",
30 | "Check out the official webpage [jupyter.org](http://jupyter.org)\n",
31 | "\n",
32 | "> The Jupyter Notebook is a web application that allows you to create and share documents that contain live code, equations, visualizations and explanatory text.\n",
33 | "\n",
34 | "See Help in the menu above for more **Notebook Help** and **User Interface Tour**.\n",
35 | "\n",
36 | "### Cells\n",
37 | "\n",
38 | "We will use two kinds of cells: markdown cells and code cells. Notice that the kind of cell is indicated in the toolbar above when the cell is selected.\n",
39 | "\n",
40 | "Hit `shift+enter` to execute the contents of a cell.\n",
41 | "\n",
42 | "**Markdown cells** contain:\n",
43 | "\n",
44 | "* Markdown code\n",
45 | "* HTML\n",
46 | "* LaTeX\n",
47 | "* Plain text\n",
48 | "\n",
49 | "This cell is a markdown cell and it contains plain text and markdown language. \n",
50 | "\n",
51 | "**Code cells** contain Python code (or whichever language the kernel is running). For example, the next cell is a code cell which contains Python code which displays the first 10 square numbers."
52 | ]
53 | },
54 | {
55 | "cell_type": "code",
56 | "execution_count": 1,
57 | "metadata": {
58 | "collapsed": false
59 | },
60 | "outputs": [
61 | {
62 | "name": "stdout",
63 | "output_type": "stream",
64 | "text": [
65 | "1\n",
66 | "4\n",
67 | "9\n",
68 | "16\n",
69 | "25\n",
70 | "36\n",
71 | "49\n",
72 | "64\n",
73 | "81\n",
74 | "100\n"
75 | ]
76 | }
77 | ],
78 | "source": [
79 | "# Python code to display the first 10 square numbers\n",
80 | "for n in range(1,11):\n",
81 | " print(n**2)"
82 | ]
83 | },
84 | {
85 | "cell_type": "markdown",
86 | "metadata": {},
87 | "source": [
88 | "### Modes\n",
89 | "\n",
90 | "There are 2 modes: **edit mode** and **command mode**. Press `escape` to enter command mode and `enter` for edit mode.\n",
91 | "\n",
92 | "Edit mode allows you to write code, text, markdown, etc. in the cell. The green border indicates when the cell is in edit mode.\n",
93 | "\n",
94 | "Command mode allows you to enter keyboard shortcuts to edit the notebook. For example,\n",
95 | "\n",
96 | "* hitting the `s` key in command mode saves the document\n",
97 | "* hitting the `x` key in command mode cuts the active cell\n",
98 | "* hitting the `a` key in command mode inserts a cell above the active cell\n",
99 | "\n",
100 | "See Help in the menu above to see the list of **keyboard shortcuts**."
101 | ]
102 | },
103 | {
104 | "cell_type": "markdown",
105 | "metadata": {
106 | "collapsed": true
107 | },
108 | "source": [
109 | "## 2. Markdown Language\n",
110 | "\n",
111 | "Markdown language is an easy-to-ready text format which converts to HTML. Check out [Markdown Basics](https://help.github.com/articles/markdown-basics/) on GitHub.\n",
112 | "\n",
113 | "We will only mention a few features of markdown:\n",
114 | "\n",
115 | "* create *italics* with asterisks `*italics*`\n",
116 | "* create **bold text** with double asterisks `**bold text**`\n",
117 | "* enclose text in single backticks \\` ... \\` to display text in `monospace` font without any formatting\n",
118 | "* create a link [UBC Math](https://www.math.ubc.ca) with brackets `[UBC Math](https://www.math.ubc.ca)`\n",
119 | "* display an image  similar to a link as above but with a leading exclamation point:
``\n",
120 | "\n",
121 | "* create headings with the number sign #\n",
122 | "\n",
123 | "# Heading 1\n",
124 | "`# Heading 1`\n",
125 | "\n",
126 | "## Heading 2\n",
127 | "`## Heading 2`\n",
128 | "\n",
129 | "### Heading 3\n",
130 | "`### Heading 3`\n",
131 | "\n",
132 | "#### Heading 4\n",
133 | "`#### Heading 4`\n",
134 | "\n",
135 | "##### Heading 5\n",
136 | "`##### Heading 5`\n",
137 | "\n",
138 | "\n",
139 | "* create ordered and unordered lists with numbers and asterisks. For example, my favourite sports teams are:\n",
140 | "\n",
141 | "```\n",
142 | "* NBA\n",
143 | " 1. Toronto Raptors\n",
144 | " 2. Oklahoma City Thunder\n",
145 | "* NHL\n",
146 | " 1. Calgary Flames\n",
147 | " 2. Montreal Canadiens\n",
148 | " 3. Los Angeles Kings\n",
149 | "* MLB\n",
150 | " 1. Toronto Blue Jays\n",
151 | " 2. Washington Nationals\n",
152 | "```\n",
153 | "\n",
154 | "* NBA\n",
155 | " 1. Toronto Raptors\n",
156 | " 2. Oklahoma City Thunder\n",
157 | "* NHL\n",
158 | " 1. Calgary Flames\n",
159 | " 2. Montreal Canadiens\n",
160 | " 3. Los Angeles Kings\n",
161 | "* MLB\n",
162 | " 1. Toronto Blue Jays\n",
163 | " 2. Washington Nationals"
164 | ]
165 | },
166 | {
167 | "cell_type": "markdown",
168 | "metadata": {},
169 | "source": [
170 | "## 3. LaTeX\n",
171 | "\n",
172 | "LaTeX is a markup language for typesetting documents. We will be using a *very* small part of the language to write mathematical expressions in Jupyter notebooks. See the [LaTeX WikiBook](https://en.wikibooks.org/wiki/LaTeX) for more information (especially the section on [mathematics](https://en.wikibooks.org/wiki/LaTeX/Mathematics)).\n",
173 | "\n",
174 | "Enclose LateX code in dollar signs `$ ... $` to display math inline. For example, the code `$\\int_a^b f(x) = F(b) - F(a)$` will render as $\\int_a^b f(x) = F(b) - F(a)$.\n",
175 | "\n",
176 | "Enclose LateX code in double dollar signs `$$ ... $$` to display expressions in a centered paragraph. For example, the code `$$f'(a) = \\lim_{x \\to a} \\frac{f(x) - f(a)}{x-a}$$` will render as $$f'(a) = \\lim_{x \\to a} \\frac{f(x) - f(a)}{x-a}$$\n",
177 | "\n",
178 | "The most commonly used mathematical symbols are:\n",
179 | "* the underscore `_` defines subscripts\n",
180 | " * `$x_n$` renders as $x_n$\n",
181 | "* the hat `^` defines superscripts\n",
182 | " * `$x^2$` renders as $x^2$\n",
183 | "* `\\int` is the integral sign $\\int$\n",
184 | " * `$\\int_a^b$` renders as $\\int_a^b$\n",
185 | "* `\\lim` is the limit $\\lim$\n",
186 | " * `$\\lim_{x \\to a}$` renders as $\\lim_{x \\to a}$\n",
187 | "* `\\frac` defines fractions\n",
188 | " * `$\\frac{a}{b}$` renders as $\\frac{a}{b}$\n",
189 | "* Greek symbols are `\\alpha`, `\\beta`, `\\gamma`, etc.\n",
190 | " * `$\\alpha$` renders as $\\alpha$\n",
191 | "* `$\\partial$` is the partial derivative symbol\n",
192 | " * `$\\frac{\\partial f}{\\partial x}$` renders as $\\frac{\\partial f}{\\partial x}$\n",
193 | " \n",
194 | "Check out the cool application [Detexify](http://detexify.kirelabs.org) to find any symbol you can imagine."
195 | ]
196 | },
197 | {
198 | "cell_type": "markdown",
199 | "metadata": {},
200 | "source": [
201 | "## 4. Exercises\n",
202 | "\n",
203 | "1. Make a list (in markdown language) of the top 5 websites you visit most often and include a link for each site.\n",
204 | "2. Make a list of courses you're taking this semester, provide links to the course pages and include pictures of the instructors.\n",
205 | "3. Go to the [Python Wikipedia page](https://en.wikipedia.org/wiki/Python_programming_language), copy the first paragraph of the introduction, paste it in this notebook and format it so that the word \"Python\" is bold and the words \"code\" and \"language\" are in italics.\n",
206 | "4. Write LaTeX code to display the [Navier-Stokes Equation for Incompressible Flow](https://en.wikipedia.org/wiki/Navier%E2%80%93Stokes_equations)\n",
207 | "\n",
208 | "5. Write LaTeX code to display [Green's Theorem](https://en.wikipedia.org/wiki/Green%27s_theorem)\n",
209 | "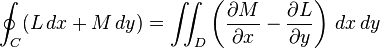\n",
210 | "6. Write LaTeX code to display the [Prime Number Theorem](https://en.wikipedia.org/wiki/Prime_number_theorem)\n",
211 | ""
212 | ]
213 | }
214 | ],
215 | "metadata": {
216 | "kernelspec": {
217 | "display_name": "Python 3",
218 | "language": "python",
219 | "name": "python3"
220 | },
221 | "language_info": {
222 | "codemirror_mode": {
223 | "name": "ipython",
224 | "version": 3
225 | },
226 | "file_extension": ".py",
227 | "mimetype": "text/x-python",
228 | "name": "python",
229 | "nbconvert_exporter": "python",
230 | "pygments_lexer": "ipython3",
231 | "version": "3.4.3"
232 | }
233 | },
234 | "nbformat": 4,
235 | "nbformat_minor": 0
236 | }
237 |
--------------------------------------------------------------------------------
/notes-week-07/notes-02-22-16.ipynb:
--------------------------------------------------------------------------------
1 | {
2 | "cells": [
3 | {
4 | "cell_type": "markdown",
5 | "metadata": {},
6 | "source": [
7 | "# MATH 210 Introduction to Mathematical Computing\n",
8 | "\n",
9 | "## February 22, 2016\n",
10 | "\n",
11 | "Today's Agenda:\n",
12 | "\n",
13 | "1. More about functions:\n",
14 | " * Defining functions with parameters that have default values\n",
15 | " * Calling functions with positional arguments or keyword arguments\n",
16 | "2. Approximating definite integrals with `scipy.integrate`\n",
17 | "3. Exercises"
18 | ]
19 | },
20 | {
21 | "cell_type": "code",
22 | "execution_count": 1,
23 | "metadata": {
24 | "collapsed": true
25 | },
26 | "outputs": [],
27 | "source": [
28 | "import numpy as np\n",
29 | "import matplotlib.pyplot as plt\n",
30 | "%matplotlib inline"
31 | ]
32 | },
33 | {
34 | "cell_type": "markdown",
35 | "metadata": {},
36 | "source": [
37 | "## 1. More about functions\n",
38 | "\n",
39 | "Be sure to read the section on [defining functions](https://docs.python.org/3/tutorial/controlflow.html#defining-functions) in the Python tutorial.\n",
40 | "\n",
41 | "### Defining functions with default values\n",
42 | "\n",
43 | "Look closely at the documentation string for the `numpy` function `linspace`:"
44 | ]
45 | },
46 | {
47 | "cell_type": "code",
48 | "execution_count": 2,
49 | "metadata": {
50 | "collapsed": true
51 | },
52 | "outputs": [],
53 | "source": [
54 | "np.linspace?"
55 | ]
56 | },
57 | {
58 | "cell_type": "markdown",
59 | "metadata": {},
60 | "source": [
61 | "The **variable names** in the **function definition** are called function **parameters**. But notice that there are 4 parameters with **default values**:\n",
62 | "\n",
63 | "* `num` is the number of points in the array (default value is `50`)\n",
64 | "* `endpoint` determines if the value `stop` is included as the last entry (default is `True`)\n",
65 | "* `retstep` determines if the function returns a tuple of length 2 including the array and the step value instead of just the array on its own (default is `False`)\n",
66 | "* `dtype` allows the user to specify the datatype of the entries (default is `False` which means that the function chooses what it thinks you want)\n",
67 | "\n",
68 | "This means that when we call the function, we **must** input 2 values for the parameters `start` and `stop` but the others are optional and we can change their default values if we choose."
69 | ]
70 | },
71 | {
72 | "cell_type": "markdown",
73 | "metadata": {},
74 | "source": [
75 | "For example, if we don't specify `num`, then we get an array with 50 points"
76 | ]
77 | },
78 | {
79 | "cell_type": "code",
80 | "execution_count": 3,
81 | "metadata": {
82 | "collapsed": false
83 | },
84 | "outputs": [
85 | {
86 | "name": "stdout",
87 | "output_type": "stream",
88 | "text": [
89 | "[ 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. 14. 15.\n",
90 | " 16. 17. 18. 19. 20. 21. 22. 23. 24. 25. 26. 27. 28. 29. 30.\n",
91 | " 31. 32. 33. 34. 35. 36. 37. 38. 39. 40. 41. 42. 43. 44. 45.\n",
92 | " 46. 47. 48. 49. 50.]\n"
93 | ]
94 | }
95 | ],
96 | "source": [
97 | "arr = np.linspace(1,50)\n",
98 | "print(arr)"
99 | ]
100 | },
101 | {
102 | "cell_type": "markdown",
103 | "metadata": {},
104 | "source": [
105 | "Or we can pass in arguments for all the parameters:"
106 | ]
107 | },
108 | {
109 | "cell_type": "code",
110 | "execution_count": 4,
111 | "metadata": {
112 | "collapsed": false
113 | },
114 | "outputs": [
115 | {
116 | "name": "stdout",
117 | "output_type": "stream",
118 | "text": [
119 | "(array([ 0, 5, 10, 15, 20, 25, 30, 35, 40, 45]), 5.0)\n"
120 | ]
121 | }
122 | ],
123 | "source": [
124 | "arr2 = np.linspace(0,50,10,False,True,int)\n",
125 | "print(arr2)"
126 | ]
127 | },
128 | {
129 | "cell_type": "markdown",
130 | "metadata": {},
131 | "source": [
132 | "### Calling functions with positional arguements or keyword arguments\n",
133 | "\n",
134 | "Notice that we called the function `np.linspace` in the previous cell above by specifying values for all the input parameters and we had to **keep track of the order in which they were entered**. This means we called the function with **positional arguments**: the first argument is the starting point, the second argument is the end point, the third argument is `num`, the fourth is `endpoint`, the fifth is `retstep`, and the sixth is `dtype`.\n",
135 | "\n",
136 | "What if we don't want to have to remember the order? More importantly, what if we want to call the function but **only** enter values to change some default values but not all? Do we have to enter values for all the arguments?\n",
137 | "\n",
138 | "No! We can call the function with **keyword arguments**. This just means that we call the function with the parameters names in the function call:"
139 | ]
140 | },
141 | {
142 | "cell_type": "code",
143 | "execution_count": 5,
144 | "metadata": {
145 | "collapsed": false
146 | },
147 | "outputs": [
148 | {
149 | "name": "stdout",
150 | "output_type": "stream",
151 | "text": [
152 | "[ 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25\n",
153 | " 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50]\n"
154 | ]
155 | }
156 | ],
157 | "source": [
158 | "arr3 = np.linspace(1,50,dtype=int)\n",
159 | "print(arr3)"
160 | ]
161 | },
162 | {
163 | "cell_type": "markdown",
164 | "metadata": {},
165 | "source": [
166 | "In fact, we can use keywords for all the arguments and the order doesn't matter!"
167 | ]
168 | },
169 | {
170 | "cell_type": "code",
171 | "execution_count": 6,
172 | "metadata": {
173 | "collapsed": false
174 | },
175 | "outputs": [
176 | {
177 | "name": "stdout",
178 | "output_type": "stream",
179 | "text": [
180 | "[ 0 4 8 12 16 20]\n"
181 | ]
182 | }
183 | ],
184 | "source": [
185 | "arr4 = np.linspace(stop=20,dtype=int,retstep=False,start=0,num=6,endpoint=True)\n",
186 | "print(arr4)"
187 | ]
188 | },
189 | {
190 | "cell_type": "markdown",
191 | "metadata": {},
192 | "source": [
193 | "But usually, we call the function with a **mix of positional arguments and keyword arguments**:"
194 | ]
195 | },
196 | {
197 | "cell_type": "code",
198 | "execution_count": 7,
199 | "metadata": {
200 | "collapsed": false
201 | },
202 | "outputs": [
203 | {
204 | "name": "stdout",
205 | "output_type": "stream",
206 | "text": [
207 | "[0 1 2 3 4 5 6 7 8 9]\n"
208 | ]
209 | }
210 | ],
211 | "source": [
212 | "arr5 = np.linspace(0,10,10,endpoint=False,dtype=int)\n",
213 | "print(arr5)"
214 | ]
215 | },
216 | {
217 | "cell_type": "markdown",
218 | "metadata": {
219 | "collapsed": true
220 | },
221 | "source": [
222 | "## 2. Approximating definite integrals with `scipy.integrate`\n",
223 | "\n",
224 | "See the notebook in `projects` folder to see an introduction to [`scipy.integrate`](http://docs.scipy.org/doc/scipy/reference/integrate.html)."
225 | ]
226 | },
227 | {
228 | "cell_type": "markdown",
229 | "metadata": {},
230 | "source": [
231 | "## 3. Exercises"
232 | ]
233 | },
234 | {
235 | "cell_type": "markdown",
236 | "metadata": {},
237 | "source": [
238 | "**Exercise.** Define a function called `my_int` with three parameters `y`, `x` and `method` (in that order) such that:\n",
239 | "* `y` and `x` are arrays of the same size which represent the values of a function $y = f(x)$ over the interval $[a,b]$\n",
240 | "* the first entry of `x` is the value $a$ and the last entry of `x` is the value $b$ (and the first and last entries of `y` are $f(a)$ and $f(b)$ respectively)\n",
241 | "* `method` is one of the strings `trapz` or `simps` (with **default value** `trapz`)\n",
242 | "* `my_int` returns the approximation of $\\int_a^b f(x) \\, dx$ using the method determined by `method`"
243 | ]
244 | },
245 | {
246 | "cell_type": "markdown",
247 | "metadata": {},
248 | "source": [
249 | "**Exercise.** Approximate the following definite integrals using all three methods `trapz`, `simps` and `quad`:\n",
250 | "\n",
251 | "$$\\int_0^{\\pi} e^{\\sin x} dx$$\n",
252 | "\n",
253 | "$$\\int_{-\\pi}^{\\pi} \\frac{\\sin x}{x} dx$$"
254 | ]
255 | },
256 | {
257 | "cell_type": "markdown",
258 | "metadata": {},
259 | "source": [
260 | "**Exercise.** (a) Write $\\LaTeX \\ $ code to display the definition of the Gamma function:\n",
261 | "\n",
262 | "\n",
263 | "\n",
264 | "(b) Define a function called `gamma_fun` with 2 parameters `t` and `b` which returns the value of the (partial) Gamma function\n",
265 | "\n",
266 | "$$\n",
267 | "\\int_0^b x^{t-1} e^{-x} dx\n",
268 | "$$\n",
269 | "\n",
270 | "and such that `b` has the **default value** $10$."
271 | ]
272 | }
273 | ],
274 | "metadata": {
275 | "kernelspec": {
276 | "display_name": "Python 3",
277 | "language": "python",
278 | "name": "python3"
279 | },
280 | "language_info": {
281 | "codemirror_mode": {
282 | "name": "ipython",
283 | "version": 3
284 | },
285 | "file_extension": ".py",
286 | "mimetype": "text/x-python",
287 | "name": "python",
288 | "nbconvert_exporter": "python",
289 | "pygments_lexer": "ipython3",
290 | "version": "3.4.3"
291 | }
292 | },
293 | "nbformat": 4,
294 | "nbformat_minor": 0
295 | }
296 |
--------------------------------------------------------------------------------
/notes-week-11/gdp_data.csv:
--------------------------------------------------------------------------------
1 | Year,Canada,China,Mexico,United Kingdom,United States,India,Japan,Spain,Kenya,Ghana,Nigeria,Saudi Arabia,Singapore
2 | 1960,2294.56881421577,88.722497622435,342.016187342239,1380.30624126257,3007.12344537862,83.7946836721907,478.995340162869,396.39225333761397,97.62153057863951,182.979246224725,92.8118675253452,,427.874822124962
3 | 1961,2231.2938237478,75.0489152135494,359.29099450970597,1452.54470901356,3066.56286916615,87.0311661449854,563.586759838827,450.053289246968,94.8352535524693,189.713214561876,96.811563813563,,448.953323596009
4 | 1962,2255.23004413036,70.1220819567229,374.445430155351,1513.6514485492596,3243.8430775498805,91.6579105818302,633.640315173776,520.206131380005,100.60425499174299,195.120016077062,104.194016425702,,471.87435357005205
5 | 1963,2354.83912197975,73.42039214025841,403.824180413223,1592.6144766156199,3374.51517105082,103.135871391376,717.866915230894,609.487384056513,104.012701298759,210.96897849835705,107.32921937644801,,510.98051928155195
6 | 1964,2529.5181790541,84.5733973268426,463.896331375075,1729.3999780356799,3573.94118474743,117.84282556275299,835.657252484116,675.241639141208,108.558932752822,230.43129191713902,112.933730562327,,485.296925203754
7 | 1965,2739.5858492818898,97.4700995061623,489.202771811987,1850.95476855498,3827.52710972039,121.704754280676,919.776688184802,774.761609330096,104.992173344736,266.318714877505,116.93053023763001,,516.289567126266
8 | 1966,3010.70590757947,103.181173206667,528.9442771060479,1959.6278296212602,4146.31664631665,91.7968816968293,1058.5035609090198,889.6598720115289,118.556282047262,269.45923557261904,124.02107987068999,,566.533791090293
9 | 1967,3173.07619352225,95.4966914845591,559.911919920292,2023.62756371118,4336.42658722171,98.26248565936741,1228.9092104006,968.3067817659828,121.38075149977502,216.841479579139,99.1666755249422,,625.715602873294
10 | 1968,3411.0601543445696,90.3713288302452,600.561804197751,1896.3867486073493,4695.92339043178,101.864956092725,1450.61965234374,950.545740593734,128.85766931067,202.761861045246,96.95829503901888,776.9751041422902,708.260498167471
11 | 1969,3703.990405255289,98.8898847120702,644.8579500822619,2032.3470096450305,5032.14474262003,109.76019029467,1669.09819990781,1077.67869994591,134.193723980301,233.651269791372,120.931169162556,800.795916424689,812.261674834967
12 | 1970,4115.65651596174,111.822722675711,683.102206184862,2347.54431773747,5246.88371730098,114.663703821518,2003.64704735892,1208.99666177967,142.49741854293,257.65203145901796,223.50680449796602,921.345154787928,925.281365186828
13 | 1971,4579.27254371988,117.181593075991,729.732129272449,2649.8015138722303,5623.44397840712,120.95237897719299,2234.26166584905,1359.76939667218,152.553677274524,273.822796409195,159.81154351959802,1178.5971302468902,1070.8170616846
14 | 1972,5133.78779554481,130.111264852008,814.311779701174,3030.43251411977,6109.92586804894,125.41655160581499,2917.65897572505,1709.19371762225,174.397946016905,232.539862332294,208.64453688130504,1514.25831293022,1263.659355126
15 | 1973,5861.661641198511,155.07843885033898,964.87535318316,3426.2762205037798,6741.3323643639515,146.625104408953,3931.3016274221995,2252.51385719224,199.69516250779702,263.685963969709,251.51791240796902,2231.7913525423,1684.3410852713198
16 | 1974,7032.74954107932,157.99938032732402,1218.0731085002099,3665.8627976419,7242.44110467889,166.71671770044398,4281.35992840974,2759.53994967487,228.76102299396703,301.36667320933,401.678582529331,6445.68967530052,2339.59880814999
17 | 1975,7478.535910759259,175.86574809627498,1445.71241045779,4299.74561799284,7820.065471146859,161.169257757703,4581.574389481621,3221.58639571399,241.679274139737,285.829466570477,437.01208670604103,6296.301631886379,2489.81517055462
18 | 1976,8770.346980354441,162.920523447144,1421.65110800311,4138.16778761535,8611.40183915427,164.289441861537,5111.29514922063,3288.45739531819,248.252989898807,275.87792294767297,554.9527957509598,8158.47274688513,2758.66456962643
19 | 1977,8879.22103986376,182.678574311367,1271.8171180305,4681.43993173038,9471.306171931401,189.916119229584,6230.33568811117,3631.82155193161,309.377091058443,312.999343901447,534.4482794263299,8943.31716666301,2845.83740321899
20 | 1978,9082.208530225029,155.184629765984,1552.6921351832502,5976.93816899991,10587.285756003299,209.792829493634,8675.01399673352,4343.71027217181,351.669291444554,353.709180539066,525.488257710168,9136.327872197591,3193.3309371308
21 | 1979,9997.19843230754,182.513532340627,1987.6383240985,7804.76208051155,11695.554420030701,228.47638196451697,8953.59152027864,5753.02733045419,398.0733141527781,381.03644863369794,659.8775375350821,11997.8757864119,3899.53993519642
22 | 1980,11118.482511433898,193.276832220606,2803.3188414344,10032.062080015,12597.6675101771,271.924889480832,9307.8392945921,6200.33627034647,446.60421148380897,411.518030874168,871.1458179680161,16598.720582053702,4927.14034313508
23 | 1981,12279.0603568666,195.564928628762,3524.7415848007795,9599.30622221965,13993.166743656999,275.916652537322,10212.378135896999,5359.143245637751,405.5628688855951,379.797675288649,806.5078395860139,17456.9401241101,5595.290915297839
24 | 1982,12437.625088418301,201.80802396478904,2394.56442167386,9146.077357018521,14438.9762759859,279.656851400964,9428.87465037061,5151.55399296785,366.267691841134,351.319205747966,661.232376300454,13624.776310516001,6075.54610216876
25 | 1983,13368.906739895801,223.734939337166,2008.09565081832,8691.51881306514,15561.4263961128,297.160496589153,10213.9582793056,4472.08823858807,327.783014508247,341.08707325448,444.649092091558,10798.2781628209,6629.784467065171
26 | 1984,13768.8791019052,248.915822103302,2319.45795959172,8179.19444064991,17134.2860171738,282.317665231223,10786.7861809452,4483.85195534637,326.852564974567,358.396586107534,348.52632599585297,9438.53720069303,7223.282937207508
27 | 1985,13991.2145509173,292.54793904355597,2385.7577824395003,8652.21654247593,18269.4221684235,302.510676668679,11465.7257816258,4693.07558925929,312.04536368057,354.219711284642,344.141083749821,7776.0376244895,6995.04602033271
28 | 1986,14335.7438678744,280.09804457441896,1639.74040986935,10611.112210096,19115.05290818,316.846113683895,16882.2739520677,6504.072932497571,354.968357762035,437.088948105851,240.617396617304,6204.223098591011,6793.60649254134
29 | 1987,16158.9874251888,250.314587134053,1740.8690134888095,13118.586534629,20100.8588916542,347.42508099660006,20355.6052224352,8228.71963465408,377.0430855224929,376.46042288959,272.507731472812,5852.60155347422,7531.162694172691
30 | 1988,18814.564547179198,282.056782845448,2227.405172532,15987.168077568798,21483.2330602579,361.45035799819397,24592.7720053564,9689.53885849796,381.541593358746,375.225019011649,256.375841257804,5791.395088953829,8902.507813621
31 | 1989,20586.5575115274,309.263385215471,2657.6004279976,16239.2821960944,22922.4370895271,353.255488535682,24505.7672958689,10662.9242467351,365.40619735778085,368.9981979909021,260.047569976104,6030.26897716685,10380.15486557
32 | 1990,21302.396912001,316.224430421825,3068.7024242419798,19095.4669984608,23954.4793548671,375.15201931464486,25123.6317862131,13773.365697854098,365.617821222712,402.588881651019,321.66837089409,7137.39224183787,11864.6582882248
33 | 1991,21591.1391612209,331.474915998499,3600.04518532238,19900.7266505069,24405.164814748907,309.327936127406,28540.771482599303,14782.0389005817,336.364188352272,438.5203726005809,279.275782314458,7775.70154164484,14504.941735979399
34 | 1992,20692.7220252261,364.759664140764,4080.4521751764396,20487.1707852878,25492.951651761694,323.524792197951,31013.6471483654,16105.418728516299,327.974824352508,414.56163970309194,291.283484505327,7834.23620797021,16143.998198073
35 | 1993,19936.3770646304,375.814293801228,5544.932462214821,18389.0195675099,26464.852511744,307.411043241706,35451.2975115738,13362.018345836399,222.724054761049,375.06533363794404,153.07566548763901,7386.668212502759,18302.270212181298
36 | 1994,19785.6790398347,471.760881219945,5690.674713130589,19709.238098365306,27776.635528226,353.2924952207009,38814.8943789814,13465.377826111599,268.645575252903,333.217824990775,171.024798212773,7310.9503451911,21578.7634766978
37 | 1995,20509.0030863168,607.568583122257,3640.833418872821,21330.276252903,28782.175020091803,381.527462218128,42522.0665906054,15561.9727455217,330.48312180175,385.725260199644,263.28803787451403,7555.96533208318,24936.8732805334
38 | 1996,21129.4354271046,707.029771302305,4131.80570593217,22462.509432358398,30068.2309182833,408.241774685944,37422.864142907405,16236.771679291101,428.433876388009,403.9197548286209,314.739902120504,8159.980674127802,26263.0448866015
39 | 1997,21709.2963371821,778.943905725537,4907.33315168627,24803.1474321952,31572.6902298492,424.086473791529,34304.1489712264,14872.565890678401,454.74177677799895,392.251816424239,314.29984936351,8328.97098487239,26386.7215887413
40 | 1998,20875.2483089147,825.547957082076,5038.62977470959,26281.0477516525,32949.1977640346,421.82159006749197,30969.7380327708,15534.359888909099,476.718513684413,416.326248548834,273.86979724431,7180.15043990568,21824.107820653302
41 | 1999,22109.603986218597,869.654882082718,5722.1221385730505,26675.9155954667,34620.928899082595,451.089144230562,35004.0612719044,15859.086025783601,425.593592101591,419.88555088473686,299.356765948378,7728.67638802958,21795.8235894758
42 | 2000,24031.951201788706,954.552291730423,6649.71653421574,26400.656438269598,36449.855115534905,452.41358466967597,37299.6441291293,14787.756063671,408.98186827212487,264.702576168061,377.50026934676805,8808.87536666471,23792.530279951603
43 | 2001,23573.750065110602,1047.4778628689,6952.28903930479,25980.22037934729,37273.6181034176,460.826199948675,32716.4186748897,15359.1084396669,407.5540065516809,275.47237205944,350.260182193982,8315.739301992131,21577.1407995835
44 | 2002,23995.016326533798,1141.75764437513,7023.78727594692,28301.2083322425,38166.0378407812,480.621442166669,31235.588184391407,17019.535413660502,402.17031549401605,311.61682502776796,457.39704755357803,8317.90857478937,22016.5691801331
45 | 2003,28026.006013044702,1280.60285480797,6673.16697380407,32575.091962619903,39677.1983481058,557.897365886494,33690.9377297154,21495.7074076474,444.233631050959,375.880704460924,510.296295281735,9186.310388435391,23573.7769924641
46 | 2004,31830.011871330298,1498.1737956253198,7115.12176872717,38305.8726859929,41921.8097617892,640.6005221609449,36441.5044939422,24918.645841999398,467.378752493262,426.159234240606,645.763871178843,10756.0162185009,27405.0345758398
47 | 2005,36028.2324902754,1740.0967263801099,7893.968233756529,40047.905967007006,44307.9205848603,729.000727040133,35781.1700525965,26510.717453342597,530.082157850254,501.72407455065996,804.005995170227,13273.653498638401,29869.5878981096
48 | 2006,40243.5522837141,2082.18336250102,8666.33535331064,42534.3062613449,46437.067117306506,816.733776198888,34075.978949411096,28482.6094833461,711.7211636716362,929.726628584054,1014.7347416177099,14826.916698381101,33579.5924481463
49 | 2007,44328.4753768925,2673.2941909354,9219.817782852859,48428.1574527987,48061.5376613353,1050.0248011225099,34033.701254936095,32709.4010383771,857.925688654194,1099.0223125795699,1131.1476946252699,15947.405786423898,39223.5733268202
50 | 2008,46400.441845675596,3441.221354570209,9578.570699611959,45195.156927388096,48401.4273403899,1022.5775919532699,37865.6180313874,35578.736189717005,938.571762345224,1234.0799001109401,1376.85744878293,19436.8571597589,39721.015350612004
51 | 2009,40764.14134688991,3800.4745416127703,7647.6847472833915,37166.2759654944,47001.555349681796,1124.51944550849,39322.6047284114,32333.4661042498,942.7431464663499,1095.50323245528,1091.96852722446,15655.083367533798,38577.349378883104
52 | 2010,47463.631192364905,4514.94052013381,8851.35051405824,38292.871131358304,48374.05645659661,1387.88008401297,42909.2341523544,30737.832270838506,991.850545143199,1323.09914056856,2314.96353665347,18753.981233207902,46569.9730490708
53 | 2011,52086.53352462701,5574.18709336902,9715.11259636147,41020.3769643089,49781.357490134,1471.65843924074,46203.7095189836,31832.2380807085,1012.8797726672999,1587.1908727476098,2514.14862151929,23256.0956126438,53121.2310437994
54 | 2012,52733.473689010185,6264.64387793993,9703.371017178159,41294.5148008666,51456.658728035305,1449.66487452505,46679.26543223031,28647.835242689198,1184.92325604363,1641.82592182439,2739.8521890390602,24883.1897146534,54577.1373654638
55 | 2013,52305.2583938465,6991.85386564447,10172.7225491296,42309.0399221273,52980.04362631191,1455.10219142081,38633.7080591795,29370.6638674201,1257.20283787002,1827.1013677999301,2979.8346788579493,24646.020873026402,55979.75704911281
56 | 2014,50235.3855086004,7590.01644054361,10325.646065875899,46331.9774103502,54629.495167891204,1581.5107030877402,36194.4156134427,29767.3515599958,1358.26221855626,1441.6364531116599,3203.29682449432,24160.958544678106,56284.5784053366
57 |
--------------------------------------------------------------------------------
/notes-week-04/notes-01-25-16.ipynb:
--------------------------------------------------------------------------------
1 | {
2 | "cells": [
3 | {
4 | "cell_type": "markdown",
5 | "metadata": {},
6 | "source": [
7 | "**IMPORTANT:** Make sure the kernel is set to Python 3\n",
8 | "\n",
9 | "---\n",
10 | "\n",
11 | "# MATH 210 Introduction to Mathematical Computing\n",
12 | "\n",
13 | "## January 25, 2016\n",
14 | "\n",
15 | "Today's Agenda:\n",
16 | "\n",
17 | "1. More List Comprehensions\n",
18 | "2. Modules and Packages\n",
19 | " * Example: Create our own Number Theory module\n",
20 | "\n",
21 | "See the Python 3 tutorial for more information about [modules](https://docs.python.org/3/tutorial/modules.html) and [packages](https://docs.python.org/3/tutorial/modules.html#packages).\n",
22 | "\n",
23 | "*Note: The original plan for the week was to do examples in combinatorics, sorting algorithms and do an example involving the general definition of the determinant of a matrix. However, we need to move on to the scientific somputing packages NumPy, SciPy, matplotlib and pandas.*"
24 | ]
25 | },
26 | {
27 | "cell_type": "markdown",
28 | "metadata": {},
29 | "source": [
30 | "## 1. More List Comprehensions\n",
31 | "\n",
32 | "A list comprehension is Python's simple syntax for creating lists. For example, we can easily construct a list of squares:"
33 | ]
34 | },
35 | {
36 | "cell_type": "code",
37 | "execution_count": 1,
38 | "metadata": {
39 | "collapsed": false
40 | },
41 | "outputs": [
42 | {
43 | "data": {
44 | "text/plain": [
45 | "[1, 4, 9, 16, 25, 36, 49, 64, 81, 100]"
46 | ]
47 | },
48 | "execution_count": 1,
49 | "metadata": {},
50 | "output_type": "execute_result"
51 | }
52 | ],
53 | "source": [
54 | "[ n**2 for n in range(1,11) ]"
55 | ]
56 | },
57 | {
58 | "cell_type": "markdown",
59 | "metadata": {},
60 | "source": [
61 | "We can use an `if` statement in a list comprehension. For example, we can create the list of divisors of an integer $N$:"
62 | ]
63 | },
64 | {
65 | "cell_type": "code",
66 | "execution_count": 2,
67 | "metadata": {
68 | "collapsed": false
69 | },
70 | "outputs": [
71 | {
72 | "data": {
73 | "text/plain": [
74 | "[1, 2, 3, 4, 6, 7, 9, 12, 14, 18, 21, 28, 36, 42, 63, 84, 126, 252]"
75 | ]
76 | },
77 | "execution_count": 2,
78 | "metadata": {},
79 | "output_type": "execute_result"
80 | }
81 | ],
82 | "source": [
83 | "N = 252\n",
84 | "[ divisor for divisor in range(1,N+1) if N % divisor == 0 ]"
85 | ]
86 | },
87 | {
88 | "cell_type": "markdown",
89 | "metadata": {},
90 | "source": [
91 | "We can use more than one `for` loop in a list comprehension. For example, let's create the list of all permutations of $\\{ 1,2,3 \\}$:"
92 | ]
93 | },
94 | {
95 | "cell_type": "code",
96 | "execution_count": 3,
97 | "metadata": {
98 | "collapsed": false
99 | },
100 | "outputs": [
101 | {
102 | "data": {
103 | "text/plain": [
104 | "[[1, 2, 3], [1, 3, 2], [2, 1, 3], [2, 3, 1], [3, 1, 2], [3, 2, 1]]"
105 | ]
106 | },
107 | "execution_count": 3,
108 | "metadata": {},
109 | "output_type": "execute_result"
110 | }
111 | ],
112 | "source": [
113 | "[ [a,b,c] for a in range(1,4) for b in range(1,4) for c in range(1,4) if (a != b and b != c and a != c) ]"
114 | ]
115 | },
116 | {
117 | "cell_type": "markdown",
118 | "metadata": {},
119 | "source": [
120 | "The `for` loops are executed from left to right therefore, in the example above, b is set to 1 first and then b and then c."
121 | ]
122 | },
123 | {
124 | "cell_type": "markdown",
125 | "metadata": {},
126 | "source": [
127 | "Let's construct the list triples $[a,b,a^2+b^2]$ to find all sums of squares $a^2 + b^2$ for $1 \\leq a \\leq b \\leq 5$. Note that if we loop variable `a` from `1` to `b`, we have to set `b` first and so the loop for `b` is written first."
128 | ]
129 | },
130 | {
131 | "cell_type": "code",
132 | "execution_count": 4,
133 | "metadata": {
134 | "collapsed": false
135 | },
136 | "outputs": [
137 | {
138 | "data": {
139 | "text/plain": [
140 | "[[1, 1, 2],\n",
141 | " [1, 2, 5],\n",
142 | " [2, 2, 8],\n",
143 | " [1, 3, 10],\n",
144 | " [2, 3, 13],\n",
145 | " [3, 3, 18],\n",
146 | " [1, 4, 17],\n",
147 | " [2, 4, 20],\n",
148 | " [3, 4, 25],\n",
149 | " [4, 4, 32],\n",
150 | " [1, 5, 26],\n",
151 | " [2, 5, 29],\n",
152 | " [3, 5, 34],\n",
153 | " [4, 5, 41],\n",
154 | " [5, 5, 50]]"
155 | ]
156 | },
157 | "execution_count": 4,
158 | "metadata": {},
159 | "output_type": "execute_result"
160 | }
161 | ],
162 | "source": [
163 | "[ [a,b,a**2+b**2] for b in range(1,6) for a in range(1,b+1) ]"
164 | ]
165 | },
166 | {
167 | "cell_type": "markdown",
168 | "metadata": {},
169 | "source": [
170 | "We can write nested list comprehensions. For example, let's create the list of lists of divisors for integers $n \\leq 20$:"
171 | ]
172 | },
173 | {
174 | "cell_type": "code",
175 | "execution_count": 5,
176 | "metadata": {
177 | "collapsed": false
178 | },
179 | "outputs": [
180 | {
181 | "data": {
182 | "text/plain": [
183 | "[[1],\n",
184 | " [1, 2],\n",
185 | " [1, 3],\n",
186 | " [1, 2, 4],\n",
187 | " [1, 5],\n",
188 | " [1, 2, 3, 6],\n",
189 | " [1, 7],\n",
190 | " [1, 2, 4, 8],\n",
191 | " [1, 3, 9],\n",
192 | " [1, 2, 5, 10],\n",
193 | " [1, 11],\n",
194 | " [1, 2, 3, 4, 6, 12],\n",
195 | " [1, 13],\n",
196 | " [1, 2, 7, 14],\n",
197 | " [1, 3, 5, 15],\n",
198 | " [1, 2, 4, 8, 16],\n",
199 | " [1, 17],\n",
200 | " [1, 2, 3, 6, 9, 18],\n",
201 | " [1, 19],\n",
202 | " [1, 2, 4, 5, 10, 20]]"
203 | ]
204 | },
205 | "execution_count": 5,
206 | "metadata": {},
207 | "output_type": "execute_result"
208 | }
209 | ],
210 | "source": [
211 | "[ [ divisor for divisor in range(1,n+1) if n % divisor == 0 ] for n in range(1,21) ]"
212 | ]
213 | },
214 | {
215 | "cell_type": "markdown",
216 | "metadata": {},
217 | "source": [
218 | "## 2. Modules and Packages\n",
219 | "\n",
220 | "We have been using some of the same functions over and over again. For example, we have `is_prime` to test if a postive integer is prime and `divisors` to return the list of divisors of a positive integer. Instead of re-writing these functions (or copying and pasting them) in every new notebook, we can write a Python module (and collect modules into packages) to store our functions for us to import into future notebooks. See the Python 3 tutorial for more about [modules](https://docs.python.org/3/tutorial/modules.html) and [packages](https://docs.python.org/3/tutorial/modules.html#packages).\n",
221 | "\n",
222 | "A Python **module** is a text file (with file extension `.py`) containing Python code including functions definitions, variables, et cetera.\n",
223 | "\n",
224 | "The built-in function `dir` lists the names that a module defines.\n",
225 | "\n",
226 | "Finally, a **package** is a collection of modules organzed under a single name. For example, we will be using the following packages:\n",
227 | "\n",
228 | "* NumPy\n",
229 | "* Matplotlib\n",
230 | "* SciPy\n",
231 | "* pandas\n",
232 | "\n",
233 | "And each of these packages contain subpackages and modules filled with lots of tools for scientific computing."
234 | ]
235 | },
236 | {
237 | "cell_type": "markdown",
238 | "metadata": {},
239 | "source": [
240 | "### Example: Create our own number theory package\n",
241 | "\n",
242 | "Create a new text file called `number_theory.py` (note the extension `.py`) and save it to the **same directory as this notebook**. In the new file `number_theory.py`, define the functions:\n",
243 | "\n",
244 | "* is_prime\n",
245 | "* primes_up_to\n",
246 | "* primes_interval\n",
247 | "* divisors\n",
248 | "* prime_divisors\n",
249 | "* twin_primes\n",
250 | "* twin_primes_interval\n",
251 | "\n",
252 | "To access our module `number_theory`, we use the `import` command. And if we want to import the module with a shorter name, such as `nt`, we write `import number_theory as nt`."
253 | ]
254 | },
255 | {
256 | "cell_type": "code",
257 | "execution_count": 6,
258 | "metadata": {
259 | "collapsed": false
260 | },
261 | "outputs": [],
262 | "source": [
263 | "import number_theory as nt"
264 | ]
265 | },
266 | {
267 | "cell_type": "code",
268 | "execution_count": 7,
269 | "metadata": {
270 | "collapsed": false
271 | },
272 | "outputs": [
273 | {
274 | "data": {
275 | "text/plain": [
276 | "True"
277 | ]
278 | },
279 | "execution_count": 7,
280 | "metadata": {},
281 | "output_type": "execute_result"
282 | }
283 | ],
284 | "source": [
285 | "nt.is_prime(16193)"
286 | ]
287 | },
288 | {
289 | "cell_type": "code",
290 | "execution_count": 8,
291 | "metadata": {
292 | "collapsed": false
293 | },
294 | "outputs": [
295 | {
296 | "data": {
297 | "text/plain": [
298 | "[2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67]"
299 | ]
300 | },
301 | "execution_count": 8,
302 | "metadata": {},
303 | "output_type": "execute_result"
304 | }
305 | ],
306 | "source": [
307 | "nt.primes_up_to(70)"
308 | ]
309 | },
310 | {
311 | "cell_type": "code",
312 | "execution_count": 9,
313 | "metadata": {
314 | "collapsed": false
315 | },
316 | "outputs": [
317 | {
318 | "data": {
319 | "text/plain": [
320 | "[2003,\n",
321 | " 2011,\n",
322 | " 2017,\n",
323 | " 2027,\n",
324 | " 2029,\n",
325 | " 2039,\n",
326 | " 2053,\n",
327 | " 2063,\n",
328 | " 2069,\n",
329 | " 2081,\n",
330 | " 2083,\n",
331 | " 2087,\n",
332 | " 2089,\n",
333 | " 2099]"
334 | ]
335 | },
336 | "execution_count": 9,
337 | "metadata": {},
338 | "output_type": "execute_result"
339 | }
340 | ],
341 | "source": [
342 | "nt.primes_interval(2000,2100)"
343 | ]
344 | },
345 | {
346 | "cell_type": "code",
347 | "execution_count": 10,
348 | "metadata": {
349 | "collapsed": false
350 | },
351 | "outputs": [
352 | {
353 | "data": {
354 | "text/plain": [
355 | "[[11, 13], [17, 19], [29, 31], [41, 43]]"
356 | ]
357 | },
358 | "execution_count": 10,
359 | "metadata": {},
360 | "output_type": "execute_result"
361 | }
362 | ],
363 | "source": [
364 | "nt.twin_primes_interval(10,43)"
365 | ]
366 | },
367 | {
368 | "cell_type": "code",
369 | "execution_count": 11,
370 | "metadata": {
371 | "collapsed": false
372 | },
373 | "outputs": [
374 | {
375 | "data": {
376 | "text/plain": [
377 | "[[3119, 3121], [3167, 3169]]"
378 | ]
379 | },
380 | "execution_count": 11,
381 | "metadata": {},
382 | "output_type": "execute_result"
383 | }
384 | ],
385 | "source": [
386 | "nt.twin_primes_interval(3000,3200)"
387 | ]
388 | },
389 | {
390 | "cell_type": "code",
391 | "execution_count": 13,
392 | "metadata": {
393 | "collapsed": false
394 | },
395 | "outputs": [
396 | {
397 | "data": {
398 | "text/plain": [
399 | "[2, 5]"
400 | ]
401 | },
402 | "execution_count": 13,
403 | "metadata": {},
404 | "output_type": "execute_result"
405 | }
406 | ],
407 | "source": [
408 | "nt.prime_divisors(100)"
409 | ]
410 | },
411 | {
412 | "cell_type": "code",
413 | "execution_count": 14,
414 | "metadata": {
415 | "collapsed": false
416 | },
417 | "outputs": [
418 | {
419 | "data": {
420 | "text/plain": [
421 | "['__builtins__',\n",
422 | " '__cached__',\n",
423 | " '__doc__',\n",
424 | " '__file__',\n",
425 | " '__loader__',\n",
426 | " '__name__',\n",
427 | " '__package__',\n",
428 | " '__spec__',\n",
429 | " 'divisors',\n",
430 | " 'is_prime',\n",
431 | " 'prime_divisors',\n",
432 | " 'primes_interval',\n",
433 | " 'primes_up_to',\n",
434 | " 'twin_primes',\n",
435 | " 'twin_primes_interval']"
436 | ]
437 | },
438 | "execution_count": 14,
439 | "metadata": {},
440 | "output_type": "execute_result"
441 | }
442 | ],
443 | "source": [
444 | "dir(nt)"
445 | ]
446 | },
447 | {
448 | "cell_type": "code",
449 | "execution_count": 15,
450 | "metadata": {
451 | "collapsed": true
452 | },
453 | "outputs": [],
454 | "source": [
455 | "nt.is_prime?"
456 | ]
457 | }
458 | ],
459 | "metadata": {
460 | "kernelspec": {
461 | "display_name": "Python 3",
462 | "language": "python",
463 | "name": "python3"
464 | },
465 | "language_info": {
466 | "codemirror_mode": {
467 | "name": "ipython",
468 | "version": 3
469 | },
470 | "file_extension": ".py",
471 | "mimetype": "text/x-python",
472 | "name": "python",
473 | "nbconvert_exporter": "python",
474 | "pygments_lexer": "ipython3",
475 | "version": "3.4.3"
476 | }
477 | },
478 | "nbformat": 4,
479 | "nbformat_minor": 0
480 | }
481 |
--------------------------------------------------------------------------------
/notes-week-03/notes-01-18-16.ipynb:
--------------------------------------------------------------------------------
1 | {
2 | "cells": [
3 | {
4 | "cell_type": "markdown",
5 | "metadata": {},
6 | "source": [
7 | "**IMPORTANT:** Make sure the kernel is set to Python 3\n",
8 | "\n",
9 | "---\n",
10 | "\n",
11 | "# MATH 210 Introduction to Mathematical Computing\n",
12 | "\n",
13 | "## January 18, 2016\n",
14 | "\n",
15 | "Today's Agenda:\n",
16 | "\n",
17 | "1. Writing comments in Python code\n",
18 | "2. Function documentation strings\n",
19 | "3. `while` loops\n",
20 | "4. Exercises\n",
21 | "\n",
22 | "For more exercises, check out [Project Euler](https://projecteuler.net/)."
23 | ]
24 | },
25 | {
26 | "cell_type": "markdown",
27 | "metadata": {},
28 | "source": [
29 | "## 1. Writing Comments in Python Code\n",
30 | "\n",
31 | "It is good practice to write comments within your Python code to explain what your code is doing. It is not enough for your code to make sense to you; your code must be clear to anyone who is reading it!\n",
32 | "\n",
33 | "Use the symbol `#` to turn a line of Python code into a comment. For example, let's construct the list of positive integers less than (or equal to) 200 which are multiples of either 7 or 11."
34 | ]
35 | },
36 | {
37 | "cell_type": "code",
38 | "execution_count": 1,
39 | "metadata": {
40 | "collapsed": false
41 | },
42 | "outputs": [
43 | {
44 | "name": "stdout",
45 | "output_type": "stream",
46 | "text": [
47 | "[7, 11, 14, 21, 22, 28, 33, 35, 42, 44, 49, 55, 56, 63, 66, 70, 77, 84, 88, 91, 98, 99, 105, 110, 112, 119, 121, 126, 132, 133, 140, 143, 147, 154, 161, 165, 168, 175, 176, 182, 187, 189, 196, 198]\n"
48 | ]
49 | }
50 | ],
51 | "source": [
52 | "# Initialize the list of multiples of 7 and 11\n",
53 | "multiples_of_7_and_11 = []\n",
54 | "\n",
55 | "# Write a for loop over all the integers up to 200\n",
56 | "for integer in range(1,201):\n",
57 | " # Test if the integer is a multiple of 7 or 11\n",
58 | " if ((integer % 7 == 0) or (integer % 11 == 0)):\n",
59 | " # Append the integer to the list of multiples\n",
60 | " multiples_of_7_and_11.append(integer)\n",
61 | " \n",
62 | "# Print the list when the loop is complete\n",
63 | "print(multiples_of_7_and_11)"
64 | ]
65 | },
66 | {
67 | "cell_type": "markdown",
68 | "metadata": {},
69 | "source": [
70 | "## 2. Function Documentation Strings\n",
71 | "\n",
72 | "In the definition of a function, the documentation string is a string written directly following the first line containing the `def` keyword. The following is taken from the Python 3 tutorial about [documentation strings](https://docs.python.org/3/tutorial/controlflow.html#documentation-strings):\n",
73 | "\n",
74 | "> The first line should always be a short, concise summary of the object’s purpose. For brevity, it should not explicitly state the object’s name or type, since these are available by other means (except if the name happens to be a verb describing a function’s operation). This line should begin with a capital letter and end with a period.\n",
75 | "\n",
76 | "> If there are more lines in the documentation string, the second line should be blank, visually separating the summary from the rest of the description. The following lines should be one or more paragraphs describing the object’s calling conventions, its side effects, etc.\n",
77 | "\n",
78 | "Note that we can write a long string over several lines using triple quotes `'''`."
79 | ]
80 | },
81 | {
82 | "cell_type": "code",
83 | "execution_count": 2,
84 | "metadata": {
85 | "collapsed": true
86 | },
87 | "outputs": [],
88 | "source": [
89 | "def mean(x,y):\n",
90 | " \"Compute the mean of x and y.\"\n",
91 | " return (x+y)/2"
92 | ]
93 | },
94 | {
95 | "cell_type": "markdown",
96 | "metadata": {},
97 | "source": [
98 | "And we can access the documentation string using the question mark `?`."
99 | ]
100 | },
101 | {
102 | "cell_type": "code",
103 | "execution_count": 3,
104 | "metadata": {
105 | "collapsed": true
106 | },
107 | "outputs": [],
108 | "source": [
109 | "mean?"
110 | ]
111 | },
112 | {
113 | "cell_type": "markdown",
114 | "metadata": {},
115 | "source": [
116 | "Try this on Python's built-in functions:"
117 | ]
118 | },
119 | {
120 | "cell_type": "code",
121 | "execution_count": 4,
122 | "metadata": {
123 | "collapsed": true
124 | },
125 | "outputs": [],
126 | "source": [
127 | "len?"
128 | ]
129 | },
130 | {
131 | "cell_type": "code",
132 | "execution_count": 5,
133 | "metadata": {
134 | "collapsed": true
135 | },
136 | "outputs": [],
137 | "source": [
138 | "int?"
139 | ]
140 | },
141 | {
142 | "cell_type": "markdown",
143 | "metadata": {},
144 | "source": [
145 | "Or we can use the help function `help()`"
146 | ]
147 | },
148 | {
149 | "cell_type": "code",
150 | "execution_count": 6,
151 | "metadata": {
152 | "collapsed": false
153 | },
154 | "outputs": [],
155 | "source": [
156 | "type?"
157 | ]
158 | },
159 | {
160 | "cell_type": "code",
161 | "execution_count": 7,
162 | "metadata": {
163 | "collapsed": false
164 | },
165 | "outputs": [],
166 | "source": [
167 | "abs?"
168 | ]
169 | },
170 | {
171 | "cell_type": "markdown",
172 | "metadata": {},
173 | "source": [
174 | "Let's define a long documentation string using triple quotes `'''`."
175 | ]
176 | },
177 | {
178 | "cell_type": "code",
179 | "execution_count": 8,
180 | "metadata": {
181 | "collapsed": true
182 | },
183 | "outputs": [],
184 | "source": [
185 | "def determinant(matrix):\n",
186 | " '''Compute the determinant of a 2 by 2 matrix.\n",
187 | " \n",
188 | " Input: list\n",
189 | " A Python list [a,b,c,d] to represent the matrix [a,b;c,d]\n",
190 | " Output: number\n",
191 | " The determinant a*d-b*c\n",
192 | " '''\n",
193 | " return matrix[0] * matrix[3] - matrix[1] * matrix[2]"
194 | ]
195 | },
196 | {
197 | "cell_type": "code",
198 | "execution_count": 9,
199 | "metadata": {
200 | "collapsed": true
201 | },
202 | "outputs": [],
203 | "source": [
204 | "determinant?"
205 | ]
206 | },
207 | {
208 | "cell_type": "markdown",
209 | "metadata": {},
210 | "source": [
211 | "Let's use the function `determinant` to computer the determinant of $\\begin{bmatrix} 2 & 3 \\\\ -1 & 1 \\end{bmatrix}$ and also $\\begin{bmatrix} 1 & -1 \\\\ -2 & 4 \\end{bmatrix}$:"
212 | ]
213 | },
214 | {
215 | "cell_type": "code",
216 | "execution_count": 10,
217 | "metadata": {
218 | "collapsed": false
219 | },
220 | "outputs": [
221 | {
222 | "data": {
223 | "text/plain": [
224 | "5"
225 | ]
226 | },
227 | "execution_count": 10,
228 | "metadata": {},
229 | "output_type": "execute_result"
230 | }
231 | ],
232 | "source": [
233 | "determinant([2,3,-1,1])"
234 | ]
235 | },
236 | {
237 | "cell_type": "code",
238 | "execution_count": 11,
239 | "metadata": {
240 | "collapsed": false
241 | },
242 | "outputs": [
243 | {
244 | "data": {
245 | "text/plain": [
246 | "2"
247 | ]
248 | },
249 | "execution_count": 11,
250 | "metadata": {},
251 | "output_type": "execute_result"
252 | }
253 | ],
254 | "source": [
255 | "determinant([1,-1,-2,4])"
256 | ]
257 | },
258 | {
259 | "cell_type": "markdown",
260 | "metadata": {},
261 | "source": [
262 | "## 3. `while` loops"
263 | ]
264 | },
265 | {
266 | "cell_type": "markdown",
267 | "metadata": {},
268 | "source": [
269 | "The syntax for writing a `while` loop is the following:\n",
270 | "\n",
271 | "```python\n",
272 | "while expression:\n",
273 | " Python code\n",
274 | " Python code\n",
275 | "```"
276 | ]
277 | },
278 | {
279 | "cell_type": "markdown",
280 | "metadata": {},
281 | "source": [
282 | "The loop will continue to execute its block of code until the expression evaluates to `False`. **BE CAREFUL TO AVOID INFINITE LOOPS!!!** If you create an infinite loop, interupt and restart the kernel (click the Stop button and then the Restart button in the toolbar)."
283 | ]
284 | },
285 | {
286 | "cell_type": "code",
287 | "execution_count": 12,
288 | "metadata": {
289 | "collapsed": false
290 | },
291 | "outputs": [
292 | {
293 | "name": "stdout",
294 | "output_type": "stream",
295 | "text": [
296 | "10!\n",
297 | "9!\n",
298 | "8!\n",
299 | "7!\n",
300 | "6!\n",
301 | "5!\n",
302 | "4!\n",
303 | "3!\n",
304 | "2!\n",
305 | "1!\n",
306 | "Blast off!\n"
307 | ]
308 | }
309 | ],
310 | "source": [
311 | "n = 10\n",
312 | "while n > 0:\n",
313 | " print(str(n) + '!')\n",
314 | " n = n - 1\n",
315 | "print('Blast off!')"
316 | ]
317 | },
318 | {
319 | "cell_type": "markdown",
320 | "metadata": {},
321 | "source": [
322 | "**Exercise 1.** Consider the sequence defined by the recursive formula\n",
323 | "$$\n",
324 | "\\begin{align*}\n",
325 | "x_0 &= 1 \\\\\n",
326 | "x_n &= \\sqrt{ 1 + x_{n-1} }\n",
327 | "\\end{align*}\n",
328 | "$$\n",
329 | "\n",
330 | "* Compute the limit $L = \\lim_{n \\to \\infty} x_n$\n",
331 | "* Find the smallest $n$ such that $x_n > 1.6$\n",
332 | "* Find the largest $n$ such that $x_n < 1.61803$"
333 | ]
334 | },
335 | {
336 | "cell_type": "markdown",
337 | "metadata": {},
338 | "source": [
339 | "First of all, let's compute the limit of the sequence. Let $L = \\lim_{n \\to \\infty} x_n$ and compute\n",
340 | "$$\n",
341 | "\\begin{align*}\n",
342 | "x_n &= \\sqrt{ 1 + x_{n-1} } \\\\\n",
343 | "\\lim_{n \\to \\infty} x_n &= \\lim_{n \\to \\infty} \\sqrt{ 1 + x_{n-1} } \\\\\n",
344 | "\\lim_{n \\to \\infty} x_n &= \\sqrt{ 1 + \\lim_{n \\to \\infty} x_{n-1} } \\\\\n",
345 | "L &= \\sqrt{ 1 + L } \\\\\n",
346 | "L^2 &= 1 + L \\\\\n",
347 | "L^2 - L - 1 &= 0 \\\\\n",
348 | "L &= \\frac{ 1 \\pm \\sqrt{5}}{2}\n",
349 | "\\end{align*}\n",
350 | "$$\n",
351 | "threfore $L = \\frac{ 1 + \\sqrt{5}}{2}$ since $L > 0$."
352 | ]
353 | },
354 | {
355 | "cell_type": "code",
356 | "execution_count": 13,
357 | "metadata": {
358 | "collapsed": false
359 | },
360 | "outputs": [
361 | {
362 | "data": {
363 | "text/plain": [
364 | "1.618033988749895"
365 | ]
366 | },
367 | "execution_count": 13,
368 | "metadata": {},
369 | "output_type": "execute_result"
370 | }
371 | ],
372 | "source": [
373 | "(1 + 5 ** 0.5)/2"
374 | ]
375 | },
376 | {
377 | "cell_type": "markdown",
378 | "metadata": {},
379 | "source": [
380 | "Use a `while` loop to find the smallest $n$ such that $x_n > 1.6$:"
381 | ]
382 | },
383 | {
384 | "cell_type": "code",
385 | "execution_count": 14,
386 | "metadata": {
387 | "collapsed": false
388 | },
389 | "outputs": [
390 | {
391 | "name": "stdout",
392 | "output_type": "stream",
393 | "text": [
394 | "n = 0 , x_n = 1\n",
395 | "n = 1 , x_n = 1.4142135623730951\n",
396 | "n = 2 , x_n = 1.5537739740300374\n",
397 | "n = 3 , x_n = 1.5980531824786175\n",
398 | "n = 4 , x_n = 1.6118477541252516\n"
399 | ]
400 | }
401 | ],
402 | "source": [
403 | "# Define the first number in the sequence\n",
404 | "x_n = 1\n",
405 | "n = 0\n",
406 | "while x_n <= 1.6:\n",
407 | " print('n =',n,', x_n =',x_n)\n",
408 | " # Compute the next number in the sequnce and increment n by 1\n",
409 | " x_n = (1 + x_n) ** 0.5\n",
410 | " n = n + 1\n",
411 | "# Print the value x_n and index n for the first number greater than 1.6\n",
412 | "print('n =',n,', x_n =',x_n)"
413 | ]
414 | },
415 | {
416 | "cell_type": "markdown",
417 | "metadata": {},
418 | "source": [
419 | "## 4. Exercises"
420 | ]
421 | },
422 | {
423 | "cell_type": "markdown",
424 | "metadata": {
425 | "collapsed": true
426 | },
427 | "source": [
428 | "**Exercise 2.** A Collatz sequence (see the [Collatz Conjecture](https://en.wikipedia.org/wiki/Collatz_conjecture)) is defined as follows. Given a starting integer $a$, the sequence is defined by:\n",
429 | "\n",
430 | "$$\n",
431 | "\\begin{align*}\n",
432 | "x_0 &= a \\\\\n",
433 | "x_n &= \\left\\{ \\begin{matrix} x_n / 2 & x_n \\text{ odd} \\\\ 3 x_n + 1 & x_n \\text{ even} \\end{matrix} \\right.\n",
434 | "\\end{align*}\n",
435 | "$$\n",
436 | "\n",
437 | "The Collatz conjecture states that every such sequence arrives at 1.\n",
438 | "\n",
439 | "* Write a function called `collatz` which takes an integer `a` and returns the Collatz sequence starting with $x_0 = a$ (terminated when it reaches 1).\n",
440 | "* Use the function `collatz` to find the length (and initial value $a$) of the longest Collatz sequence for $a \\leq 1000$.\n",
441 | "\n",
442 | "For example, `collatz(13)` return the list `[13,40,20,10,5,16,8,4,2,1]`."
443 | ]
444 | },
445 | {
446 | "cell_type": "markdown",
447 | "metadata": {},
448 | "source": [
449 | "**More Exercises.** Check out [Project Euler](http://projecteuler.net)."
450 | ]
451 | }
452 | ],
453 | "metadata": {
454 | "kernelspec": {
455 | "display_name": "Python 3",
456 | "language": "python",
457 | "name": "python3"
458 | },
459 | "language_info": {
460 | "codemirror_mode": {
461 | "name": "ipython",
462 | "version": 3
463 | },
464 | "file_extension": ".py",
465 | "mimetype": "text/x-python",
466 | "name": "python",
467 | "nbconvert_exporter": "python",
468 | "pygments_lexer": "ipython3",
469 | "version": "3.4.3"
470 | }
471 | },
472 | "nbformat": 4,
473 | "nbformat_minor": 0
474 | }
475 |
--------------------------------------------------------------------------------
/notes-week-07/notes-02-24-16.ipynb:
--------------------------------------------------------------------------------
1 | {
2 | "cells": [
3 | {
4 | "cell_type": "markdown",
5 | "metadata": {},
6 | "source": [
7 | "# MATH 210 Introduction to Mathematical Computing\n",
8 | "\n",
9 | "## February 24, 2016\n",
10 | "\n",
11 | "Today's Agenda:\n",
12 | "\n",
13 | "1. Unpacking lists and tuples\n",
14 | "2. Integration with `scipy.integrate`\n",
15 | "3. Exercises"
16 | ]
17 | },
18 | {
19 | "cell_type": "markdown",
20 | "metadata": {},
21 | "source": [
22 | "## 1. Unpacking lists and tuples\n",
23 | "\n",
24 | "### Tuples\n",
25 | "\n",
26 | "A Python **tuple** is like a list but it had a few technical differences. The major difference is that tuples are **immutable**. This means that we **cannot** change the entries of a tuple, or append to a tuple once it's been defined.\n",
27 | "\n",
28 | "We use parentheses to define tuples and so let's define a tuple and then try to modify it. Error!"
29 | ]
30 | },
31 | {
32 | "cell_type": "code",
33 | "execution_count": 1,
34 | "metadata": {
35 | "collapsed": false
36 | },
37 | "outputs": [
38 | {
39 | "name": "stdout",
40 | "output_type": "stream",
41 | "text": [
42 | "(1, 2, 3)\n"
43 | ]
44 | }
45 | ],
46 | "source": [
47 | "my_tuple = (1,2,3)\n",
48 | "print(my_tuple)"
49 | ]
50 | },
51 | {
52 | "cell_type": "code",
53 | "execution_count": 2,
54 | "metadata": {
55 | "collapsed": false
56 | },
57 | "outputs": [
58 | {
59 | "data": {
60 | "text/plain": [
61 | "tuple"
62 | ]
63 | },
64 | "execution_count": 2,
65 | "metadata": {},
66 | "output_type": "execute_result"
67 | }
68 | ],
69 | "source": [
70 | "type(my_tuple)"
71 | ]
72 | },
73 | {
74 | "cell_type": "code",
75 | "execution_count": 3,
76 | "metadata": {
77 | "collapsed": false
78 | },
79 | "outputs": [
80 | {
81 | "data": {
82 | "text/plain": [
83 | "1"
84 | ]
85 | },
86 | "execution_count": 3,
87 | "metadata": {},
88 | "output_type": "execute_result"
89 | }
90 | ],
91 | "source": [
92 | "my_tuple[0]"
93 | ]
94 | },
95 | {
96 | "cell_type": "code",
97 | "execution_count": 5,
98 | "metadata": {
99 | "collapsed": false
100 | },
101 | "outputs": [
102 | {
103 | "ename": "TypeError",
104 | "evalue": "'tuple' object does not support item assignment",
105 | "output_type": "error",
106 | "traceback": [
107 | "\u001b[0;31m---------------------------------------------------------------------------\u001b[0m",
108 | "\u001b[0;31mTypeError\u001b[0m Traceback (most recent call last)",
109 | "\u001b[0;32m\u001b[0m in \u001b[0;36m\u001b[0;34m()\u001b[0m\n\u001b[0;32m----> 1\u001b[0;31m \u001b[0mmy_tuple\u001b[0m\u001b[0;34m[\u001b[0m\u001b[0;36m0\u001b[0m\u001b[0;34m]\u001b[0m \u001b[0;34m=\u001b[0m \u001b[0;36m5\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[0m",
110 | "\u001b[0;31mTypeError\u001b[0m: 'tuple' object does not support item assignment"
111 | ]
112 | }
113 | ],
114 | "source": [
115 | "my_tuple[0] = 5"
116 | ]
117 | },
118 | {
119 | "cell_type": "code",
120 | "execution_count": 6,
121 | "metadata": {
122 | "collapsed": false
123 | },
124 | "outputs": [
125 | {
126 | "ename": "AttributeError",
127 | "evalue": "'tuple' object has no attribute 'append'",
128 | "output_type": "error",
129 | "traceback": [
130 | "\u001b[0;31m---------------------------------------------------------------------------\u001b[0m",
131 | "\u001b[0;31mAttributeError\u001b[0m Traceback (most recent call last)",
132 | "\u001b[0;32m\u001b[0m in \u001b[0;36m\u001b[0;34m()\u001b[0m\n\u001b[0;32m----> 1\u001b[0;31m \u001b[0mmy_tuple\u001b[0m\u001b[0;34m.\u001b[0m\u001b[0mappend\u001b[0m\u001b[0;34m(\u001b[0m\u001b[0;36m5\u001b[0m\u001b[0;34m)\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[0m",
133 | "\u001b[0;31mAttributeError\u001b[0m: 'tuple' object has no attribute 'append'"
134 | ]
135 | }
136 | ],
137 | "source": [
138 | "my_tuple.append(5)"
139 | ]
140 | },
141 | {
142 | "cell_type": "markdown",
143 | "metadata": {},
144 | "source": [
145 | "### Unpacking\n",
146 | "\n",
147 | "To access the entries in a list or tuple, we usually use indices. But we can also **unpack** the entries of a list or tuple into variables. This is a special feature of Python (like list comprehensions) and you'll see this a lot in other people's code (especially in documentation). We're going to ues unpacking in the next section when we use `scipy.integrate.quad`."
148 | ]
149 | },
150 | {
151 | "cell_type": "code",
152 | "execution_count": 7,
153 | "metadata": {
154 | "collapsed": true
155 | },
156 | "outputs": [],
157 | "source": [
158 | "my_tuple2 = ('Math','Chemistry',3.14159)"
159 | ]
160 | },
161 | {
162 | "cell_type": "code",
163 | "execution_count": 8,
164 | "metadata": {
165 | "collapsed": false
166 | },
167 | "outputs": [
168 | {
169 | "name": "stdout",
170 | "output_type": "stream",
171 | "text": [
172 | "Math\n",
173 | "Chemistry\n",
174 | "3.14159\n"
175 | ]
176 | }
177 | ],
178 | "source": [
179 | "most_favourite, least_favourite, pi = my_tuple2\n",
180 | "print(most_favourite)\n",
181 | "print(least_favourite)\n",
182 | "print(pi)"
183 | ]
184 | },
185 | {
186 | "cell_type": "markdown",
187 | "metadata": {},
188 | "source": [
189 | "## 2. Integration with `scipy.integrate`"
190 | ]
191 | },
192 | {
193 | "cell_type": "code",
194 | "execution_count": 9,
195 | "metadata": {
196 | "collapsed": true
197 | },
198 | "outputs": [],
199 | "source": [
200 | "import numpy as np\n",
201 | "import scipy.integrate as spi\n",
202 | "import matplotlib.pyplot as plt\n",
203 | "%matplotlib inline"
204 | ]
205 | },
206 | {
207 | "cell_type": "markdown",
208 | "metadata": {},
209 | "source": [
210 | "**Example.** Let's approximate $\\int_0^{\\pi} \\sin x \\, dx$ using `scipy.integrate.trapz`. Recall, all we need to do is create arrays `y` and `x` which correspond to the $x$ and $y$ values of $\\sin x$ over the interval $[0,\\pi]$. (We can solve this easily and it's equal to 2.)"
211 | ]
212 | },
213 | {
214 | "cell_type": "code",
215 | "execution_count": 10,
216 | "metadata": {
217 | "collapsed": false
218 | },
219 | "outputs": [
220 | {
221 | "data": {
222 | "text/plain": [
223 | "1.9999983517708519"
224 | ]
225 | },
226 | "execution_count": 10,
227 | "metadata": {},
228 | "output_type": "execute_result"
229 | }
230 | ],
231 | "source": [
232 | "x = np.linspace(0,np.pi,1000)\n",
233 | "y = np.sin(x)\n",
234 | "spi.trapz(y,x)"
235 | ]
236 | },
237 | {
238 | "cell_type": "markdown",
239 | "metadata": {},
240 | "source": [
241 | "**Example.** Let's approximate the [Fresnel integral](https://en.wikipedia.org/wiki/Fresnel_integral) evaluated at $x = 2$\n",
242 | "\n",
243 | "$$\n",
244 | "\\int_0^2 \\sin t^2 \\, dt\n",
245 | "$$\n",
246 | "\n",
247 | "using `scipy.integrate.simps`."
248 | ]
249 | },
250 | {
251 | "cell_type": "code",
252 | "execution_count": 11,
253 | "metadata": {
254 | "collapsed": false
255 | },
256 | "outputs": [
257 | {
258 | "data": {
259 | "text/plain": [
260 | "0.80477649360903636"
261 | ]
262 | },
263 | "execution_count": 11,
264 | "metadata": {},
265 | "output_type": "execute_result"
266 | }
267 | ],
268 | "source": [
269 | "x = np.linspace(0,2,1000)\n",
270 | "y = np.sin(x**2)\n",
271 | "spi.simps(y,x)"
272 | ]
273 | },
274 | {
275 | "cell_type": "markdown",
276 | "metadata": {},
277 | "source": [
278 | "**Example.** Let's approximate both sides of the integral equation\n",
279 | "\n",
280 | "$$\n",
281 | "\\int_0^{\\infty} \\frac{ x^2 e^x }{ \\sqrt{ (e^x - 1)^3 } } \\, dx = 8 \\pi \\ln 2\n",
282 | "$$\n",
283 | "\n",
284 | "using `scipy.integrate.quad`. Recall, this function works slightly differently than `trapz` and `simps`. First of all, its (first three) parameters are a function `f` and two values `a` an `b` (the limits of integration), instead of arrays `y` and `x`. Second, the output is a tuple `(y,abserr)` where `y` is the approximation for the integral $\\int_a^b f(x) \\, dx$ and `abserr` is an estimate for the error of the approximation.\n",
285 | "\n",
286 | "This means that if we want to use `quad` we first need to define the function `f` and then we need to unpack the returned tuple."
287 | ]
288 | },
289 | {
290 | "cell_type": "code",
291 | "execution_count": 12,
292 | "metadata": {
293 | "collapsed": true
294 | },
295 | "outputs": [],
296 | "source": [
297 | "def f(x):\n",
298 | " return x**2 * np.exp(x) / np.sqrt( (np.exp(x) - 1)**3 )"
299 | ]
300 | },
301 | {
302 | "cell_type": "code",
303 | "execution_count": 13,
304 | "metadata": {
305 | "collapsed": false
306 | },
307 | "outputs": [
308 | {
309 | "data": {
310 | "text/plain": [
311 | "(17.420688722431624, 1.7997925993995523e-07)"
312 | ]
313 | },
314 | "execution_count": 13,
315 | "metadata": {},
316 | "output_type": "execute_result"
317 | }
318 | ],
319 | "source": [
320 | "# Approximate the integral above over the interval [0,100]\n",
321 | "spi.quad(f,0,100)"
322 | ]
323 | },
324 | {
325 | "cell_type": "markdown",
326 | "metadata": {},
327 | "source": [
328 | "The first entry of the tuple that `quad` produces is the approximation for the integral and the second entry is an estimate for the error. Let's unpack the output into variables:"
329 | ]
330 | },
331 | {
332 | "cell_type": "code",
333 | "execution_count": 14,
334 | "metadata": {
335 | "collapsed": false
336 | },
337 | "outputs": [
338 | {
339 | "name": "stdout",
340 | "output_type": "stream",
341 | "text": [
342 | "17.420688722431624\n",
343 | "1.7997925993995523e-07\n"
344 | ]
345 | }
346 | ],
347 | "source": [
348 | "approximation, error = spi.quad(f,0,100)\n",
349 | "print(approximation)\n",
350 | "print(error)"
351 | ]
352 | },
353 | {
354 | "cell_type": "markdown",
355 | "metadata": {},
356 | "source": [
357 | "Now let's compute the true value of the infinite integral (the right hand side of the equation above):"
358 | ]
359 | },
360 | {
361 | "cell_type": "code",
362 | "execution_count": 15,
363 | "metadata": {
364 | "collapsed": false
365 | },
366 | "outputs": [
367 | {
368 | "name": "stdout",
369 | "output_type": "stream",
370 | "text": [
371 | "17.4206887224\n"
372 | ]
373 | }
374 | ],
375 | "source": [
376 | "true_value = 8 * np.pi * np.log(2)\n",
377 | "print(true_value)"
378 | ]
379 | },
380 | {
381 | "cell_type": "markdown",
382 | "metadata": {
383 | "collapsed": true
384 | },
385 | "source": [
386 | "Let's check if the approximation is indeed within the error estimate provided by `quad`:"
387 | ]
388 | },
389 | {
390 | "cell_type": "code",
391 | "execution_count": 16,
392 | "metadata": {
393 | "collapsed": false
394 | },
395 | "outputs": [
396 | {
397 | "data": {
398 | "text/plain": [
399 | "True"
400 | ]
401 | },
402 | "execution_count": 16,
403 | "metadata": {},
404 | "output_type": "execute_result"
405 | }
406 | ],
407 | "source": [
408 | "abs(approximation - true_value) < error"
409 | ]
410 | },
411 | {
412 | "cell_type": "markdown",
413 | "metadata": {},
414 | "source": [
415 | "## 3. Exercises"
416 | ]
417 | },
418 | {
419 | "cell_type": "markdown",
420 | "metadata": {},
421 | "source": [
422 | "**Exercise.** Use all three functions `trapz`, `simps` and `quad` to approximate the left side of the integral equation\n",
423 | "\n",
424 | "$$\n",
425 | "\\int_0^1 \\ln(x) \\ln(1-x) \\, dx = 2 - \\frac{\\pi^2}{6}\n",
426 | "$$\n",
427 | "\n",
428 | "and compare each with the right side. (Note that this is an improper integral since the integrand is not defined at 0 nor 1. To use `trapz` and `simps` consider using an array of $x$ values over an interval such as $[0.0001,0.9999]$.)"
429 | ]
430 | },
431 | {
432 | "cell_type": "markdown",
433 | "metadata": {},
434 | "source": [
435 | "**Exercise.** Use all three function `trapz`, `simps` and `quad` to approximate the left side of the integral equation\n",
436 | "\n",
437 | "$$\n",
438 | "\\int_0^{\\infty} \\frac{x^2}{\\sqrt{e^x - 1}} \\, dx = 4 \\pi \\left\\{ (\\ln 2)^2 + \\frac{\\pi^2}{12} \\right\\}\n",
439 | "$$\n",
440 | "\n",
441 | "and compare each with the right side. (Note this is an infinite integral therefore use a large interval such as $[0,100]$ for the approximation.)"
442 | ]
443 | },
444 | {
445 | "cell_type": "markdown",
446 | "metadata": {},
447 | "source": [
448 | "**Exercise.** Use all three function `trapz`, `simps` and `quad` to approximate the left side of the integral equation\n",
449 | "\n",
450 | "$$\n",
451 | "\\int_0^{\\pi/2} \\frac{x^3 \\cos x}{\\sin^3 x} \\, dx = \\frac{3}{2} \\pi \\ln 2 - \\frac{\\pi^3}{16}\n",
452 | "$$\n",
453 | "\n",
454 | "and compare each to the right side. (Note this is an improper integral since the integrand is not defined at $x=0$. Try using an interval such as $[0.0001,\\pi/2]$.)"
455 | ]
456 | },
457 | {
458 | "cell_type": "markdown",
459 | "metadata": {},
460 | "source": [
461 | "**Exercise.** Plot each of the functions appearing as the integrands in the integrals above."
462 | ]
463 | }
464 | ],
465 | "metadata": {
466 | "kernelspec": {
467 | "display_name": "Python 3",
468 | "language": "python",
469 | "name": "python3"
470 | },
471 | "language_info": {
472 | "codemirror_mode": {
473 | "name": "ipython",
474 | "version": 3
475 | },
476 | "file_extension": ".py",
477 | "mimetype": "text/x-python",
478 | "name": "python",
479 | "nbconvert_exporter": "python",
480 | "pygments_lexer": "ipython3",
481 | "version": "3.4.3"
482 | }
483 | },
484 | "nbformat": 4,
485 | "nbformat_minor": 0
486 | }
487 |
--------------------------------------------------------------------------------
/notes-week-03/notes-01-20-16.ipynb:
--------------------------------------------------------------------------------
1 | {
2 | "cells": [
3 | {
4 | "cell_type": "markdown",
5 | "metadata": {},
6 | "source": [
7 | "**IMPORTANT:** Make sure the kernel is set to Python 3\n",
8 | "\n",
9 | "---\n",
10 | "\n",
11 | "# MATH 210 Introduction to Mathematical Computing\n",
12 | "\n",
13 | "## January 20, 2016\n",
14 | "\n",
15 | "Today's Agenda:\n",
16 | "\n",
17 | "1. [Python Tutor](http://www.pythontutor.com/)\n",
18 | "2. Example: Pythagorean Triples"
19 | ]
20 | },
21 | {
22 | "cell_type": "markdown",
23 | "metadata": {},
24 | "source": [
25 | "## 1. Python Tutor"
26 | ]
27 | },
28 | {
29 | "cell_type": "markdown",
30 | "metadata": {},
31 | "source": [
32 | "[Python Tutor](http://www.pythontutor.com/) is a tool to visualize Python code. It's a great way to see how your code is working! Copy and paste the examples below (one at a time) into the visualizer and see how it works."
33 | ]
34 | },
35 | {
36 | "cell_type": "markdown",
37 | "metadata": {},
38 | "source": [
39 | "**Example.** Construct the list of Fibonacci numbers (up to $x_{10}$ where $x_0 = 1$ and $x_1 = 1$ and $x_n = x_{n-1} + x_{n-2}$)."
40 | ]
41 | },
42 | {
43 | "cell_type": "code",
44 | "execution_count": 1,
45 | "metadata": {
46 | "collapsed": false
47 | },
48 | "outputs": [
49 | {
50 | "name": "stdout",
51 | "output_type": "stream",
52 | "text": [
53 | "[1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89]\n"
54 | ]
55 | }
56 | ],
57 | "source": [
58 | "N = 10\n",
59 | "fib_list = [1,1]\n",
60 | "for n in range(2,N+1):\n",
61 | " next_fib = fib_list[n-1] + fib_list[n-2]\n",
62 | " fib_list.append( next_fib )\n",
63 | "print(fib_list)"
64 | ]
65 | },
66 | {
67 | "cell_type": "markdown",
68 | "metadata": {},
69 | "source": [
70 | "**Example.** Write a function which takes an integer $n$ and returns the factorial $n!$"
71 | ]
72 | },
73 | {
74 | "cell_type": "code",
75 | "execution_count": 2,
76 | "metadata": {
77 | "collapsed": false
78 | },
79 | "outputs": [
80 | {
81 | "name": "stdout",
82 | "output_type": "stream",
83 | "text": [
84 | "120\n"
85 | ]
86 | }
87 | ],
88 | "source": [
89 | "def factorial(n):\n",
90 | " \"Compute the factorial n! of a positive integer.\"\n",
91 | " product = 1\n",
92 | " if n == 0 or n == 1:\n",
93 | " return product\n",
94 | " else:\n",
95 | " for d in range(2,n+1):\n",
96 | " product = product * d\n",
97 | " return product\n",
98 | "\n",
99 | "print(factorial(5))"
100 | ]
101 | },
102 | {
103 | "cell_type": "markdown",
104 | "metadata": {},
105 | "source": [
106 | "**Example.** Use the function `factorial` above to write a new function called `e_approx` which takes an integer $N$ and returns the $N$th partial sum of the Taylor series of $e^x$ centered at $0$ and evaluated at $x=1$:\n",
107 | "$$\n",
108 | "\\sum_{n=0}^N \\frac{1}{n!}\n",
109 | "$$"
110 | ]
111 | },
112 | {
113 | "cell_type": "code",
114 | "execution_count": 3,
115 | "metadata": {
116 | "collapsed": false
117 | },
118 | "outputs": [
119 | {
120 | "name": "stdout",
121 | "output_type": "stream",
122 | "text": [
123 | "2.6666666666666665\n",
124 | "2.7182818011463845\n"
125 | ]
126 | }
127 | ],
128 | "source": [
129 | "def factorial(n):\n",
130 | " \"Compute the factorial n! of a positive integer.\"\n",
131 | " product = 1\n",
132 | " if n == 0 or n == 1:\n",
133 | " return product\n",
134 | " else:\n",
135 | " for d in range(2,n+1):\n",
136 | " product = product * d\n",
137 | " return product\n",
138 | "\n",
139 | "def e_approx(N):\n",
140 | " \"Compute the Nth partial sum of the Taylor series of e^x centered at 0 evaluated at x=1.\"\n",
141 | " terms_in_series = []\n",
142 | " for n in range(0,N+1):\n",
143 | " # We can use our factorial function defined above to compute the terms of the series\n",
144 | " terms_in_series.append(1 / factorial(n))\n",
145 | " return sum(terms_in_series)\n",
146 | "\n",
147 | "print(e_approx(3))\n",
148 | "print(e_approx(10))"
149 | ]
150 | },
151 | {
152 | "cell_type": "markdown",
153 | "metadata": {},
154 | "source": [
155 | "Here's another (perhaps more efficient way) to compute the sum of the series:"
156 | ]
157 | },
158 | {
159 | "cell_type": "code",
160 | "execution_count": 4,
161 | "metadata": {
162 | "collapsed": false
163 | },
164 | "outputs": [
165 | {
166 | "name": "stdout",
167 | "output_type": "stream",
168 | "text": [
169 | "2.6666666666666665\n",
170 | "2.7182818011463845\n"
171 | ]
172 | }
173 | ],
174 | "source": [
175 | "def factorial(n):\n",
176 | " \"Compute the factorial n! of a positive integer.\"\n",
177 | " product = 1\n",
178 | " if n == 0 or n == 1:\n",
179 | " return product\n",
180 | " else:\n",
181 | " for d in range(2,n+1):\n",
182 | " product = product * d\n",
183 | " return product\n",
184 | "\n",
185 | "def e_approx_2(N):\n",
186 | " \"Compute the Nth partial sum of the Taylor series of e^x centered at 0 evaluated at x=0.\"\n",
187 | " series_sum = 0\n",
188 | " for n in range(0,N+1):\n",
189 | " series_sum = series_sum + 1 / factorial(n)\n",
190 | " return series_sum\n",
191 | "\n",
192 | "print(e_approx_2(3))\n",
193 | "print(e_approx_2(10))"
194 | ]
195 | },
196 | {
197 | "cell_type": "markdown",
198 | "metadata": {},
199 | "source": [
200 | "## 2. Example: Pythagorean Triples"
201 | ]
202 | },
203 | {
204 | "cell_type": "markdown",
205 | "metadata": {},
206 | "source": [
207 | "A [Pythagorean triple](https://en.wikipedia.org/wiki/Pythagorean_triple) is a triple $[a,b,c]$ of integers (with $1 \\leq a < b$) such that $a^2 + b^2 = c^2$. Write a function called `pythagorean` which takes an integer $N$ and returns the list of all Pythagorean triples $[a,b,c]$ with $c \\leq N$. Use the function to compute:\n",
208 | "\n",
209 | "* The number of Pythagorean triples with $c \\leq 500$\n",
210 | "* The four different Pythagorean triples with $c=85$\n",
211 | "* The list of numbers $c \\leq 50$ which **do not** appear in a Pythagorean triple as the largest value $c$"
212 | ]
213 | },
214 | {
215 | "cell_type": "markdown",
216 | "metadata": {},
217 | "source": [
218 | "**Solution.** Let's make a plan. In other words, let's write some [pseudocode](https://en.wikipedia.org/wiki/Pseudocode)!\n",
219 | "\n",
220 | "* Input: N\n",
221 | " * Create an empty list called `py_triples` so that we can append Pythagorean triples to the list when we find them\n",
222 | " * Loop over all possible values of $a$ and $b$\n",
223 | " * Restrict to $1 \\leq a < b$\n",
224 | " * How big can $b$ be? We must have $b < N$ if $a^2 + b^2 = c^2 \\leq N^2$\n",
225 | " * Loop over $b$ from $1$ to $N$ and then $a$ from $1$ to $b$\n",
226 | " * Test if $a^2 + b^2$ is a square\n",
227 | " * Compute $\\sqrt{a^2 + b^2}$ and round to the nearest integer, and call it $n$\n",
228 | " * If $n^2 = a^2 + b^2$ then $[a,b,n]$ is a triple\n",
229 | " * If $a^2 + b^2$ is a square $c^2$ with $c \\leq N$, then add the triple $\\left[ a,b,\\sqrt{a^2 + b^2} \\right]$ to the list `py_triples`\n",
230 | "* Output: `py_triples`, a list of Pythagorean triples $[a,b,c]$ with $c \\leq N$"
231 | ]
232 | },
233 | {
234 | "cell_type": "code",
235 | "execution_count": 5,
236 | "metadata": {
237 | "collapsed": true
238 | },
239 | "outputs": [],
240 | "source": [
241 | "def pythagorean(N):\n",
242 | " \"Find all Pythagorean triples [a,b,c] with c less than or equal to N.\"\n",
243 | " \n",
244 | " # Create an empty list so that we can append Pythagorean triples to the list when we find them\n",
245 | " py_triples = []\n",
246 | " \n",
247 | " # Loop over all possible values of a and b\n",
248 | " # We can restrict to 1 <= a <= b < N\n",
249 | " # Loop over values of b up to N\n",
250 | " for b in range(1,N):\n",
251 | " \n",
252 | " # Loop over values of a up to b\n",
253 | " for a in range(1,b+1):\n",
254 | " \n",
255 | " # Test if a^2 + b^2 is equal to a square c^2 with c <= N, and append if True\n",
256 | " c = round( (a ** 2 + b ** 2) ** 0.5 )\n",
257 | " if (a ** 2 + b ** 2 == c ** 2) and (c <= N):\n",
258 | " py_triples.append([a,b,c])\n",
259 | " \n",
260 | " return py_triples"
261 | ]
262 | },
263 | {
264 | "cell_type": "markdown",
265 | "metadata": {},
266 | "source": [
267 | "Let's test our function with some inputs and we can check our answers against the [list of triples](http://www.tsm-resources.com/alists/trip.html)."
268 | ]
269 | },
270 | {
271 | "cell_type": "code",
272 | "execution_count": 6,
273 | "metadata": {
274 | "collapsed": false
275 | },
276 | "outputs": [
277 | {
278 | "name": "stdout",
279 | "output_type": "stream",
280 | "text": [
281 | "[[3, 4, 5], [6, 8, 10]]\n"
282 | ]
283 | }
284 | ],
285 | "source": [
286 | "print(pythagorean(10))"
287 | ]
288 | },
289 | {
290 | "cell_type": "code",
291 | "execution_count": 7,
292 | "metadata": {
293 | "collapsed": false
294 | },
295 | "outputs": [
296 | {
297 | "name": "stdout",
298 | "output_type": "stream",
299 | "text": [
300 | "[[3, 4, 5], [6, 8, 10], [5, 12, 13], [9, 12, 15], [8, 15, 17], [12, 16, 20], [15, 20, 25], [20, 21, 29], [7, 24, 25], [10, 24, 26], [18, 24, 30]]\n"
301 | ]
302 | }
303 | ],
304 | "source": [
305 | "print(pythagorean(30))"
306 | ]
307 | },
308 | {
309 | "cell_type": "markdown",
310 | "metadata": {},
311 | "source": [
312 | "We can use the function `len` to find the number of Pythagorean triples $[a,b,c]$ with $c \\leq 500$."
313 | ]
314 | },
315 | {
316 | "cell_type": "code",
317 | "execution_count": 8,
318 | "metadata": {
319 | "collapsed": false
320 | },
321 | "outputs": [
322 | {
323 | "data": {
324 | "text/plain": [
325 | "386"
326 | ]
327 | },
328 | "execution_count": 8,
329 | "metadata": {},
330 | "output_type": "execute_result"
331 | }
332 | ],
333 | "source": [
334 | "len(pythagorean(500))"
335 | ]
336 | },
337 | {
338 | "cell_type": "markdown",
339 | "metadata": {},
340 | "source": [
341 | "We can loop over the list of triples $[a,b,c]$ with $c \\leq 85$ to find the triples where $c = 85$"
342 | ]
343 | },
344 | {
345 | "cell_type": "code",
346 | "execution_count": 9,
347 | "metadata": {
348 | "collapsed": false
349 | },
350 | "outputs": [
351 | {
352 | "name": "stdout",
353 | "output_type": "stream",
354 | "text": [
355 | "[51, 68, 85]\n",
356 | "[40, 75, 85]\n",
357 | "[36, 77, 85]\n",
358 | "[13, 84, 85]\n"
359 | ]
360 | }
361 | ],
362 | "source": [
363 | "for triple in pythagorean(85):\n",
364 | " if triple[2] == 85:\n",
365 | " print(triple)"
366 | ]
367 | },
368 | {
369 | "cell_type": "markdown",
370 | "metadata": {},
371 | "source": [
372 | "Or we could just look at the last 10 triples in the list `pythagorean(85)` and pick out the ones with $c = 85$"
373 | ]
374 | },
375 | {
376 | "cell_type": "code",
377 | "execution_count": 10,
378 | "metadata": {
379 | "collapsed": false
380 | },
381 | "outputs": [
382 | {
383 | "data": {
384 | "text/plain": [
385 | "[[16, 63, 65],\n",
386 | " [48, 64, 80],\n",
387 | " [51, 68, 85],\n",
388 | " [24, 70, 74],\n",
389 | " [21, 72, 75],\n",
390 | " [30, 72, 78],\n",
391 | " [40, 75, 85],\n",
392 | " [36, 77, 85],\n",
393 | " [18, 80, 82],\n",
394 | " [13, 84, 85]]"
395 | ]
396 | },
397 | "execution_count": 10,
398 | "metadata": {},
399 | "output_type": "execute_result"
400 | }
401 | ],
402 | "source": [
403 | "pythagorean(85)[-10:]"
404 | ]
405 | },
406 | {
407 | "cell_type": "markdown",
408 | "metadata": {},
409 | "source": [
410 | "We can find those numbers which do not appear as $c$ in a triple $[a,b,c]$:\n",
411 | "\n",
412 | "* Make a list of values less than 50 which appear as $c$ in a triple\n",
413 | "* Loop over integers up to 50 and check if they're in the list of values $c$"
414 | ]
415 | },
416 | {
417 | "cell_type": "code",
418 | "execution_count": 11,
419 | "metadata": {
420 | "collapsed": false
421 | },
422 | "outputs": [
423 | {
424 | "name": "stdout",
425 | "output_type": "stream",
426 | "text": [
427 | "1 is not in the list.\n",
428 | "2 is not in the list.\n",
429 | "3 is not in the list.\n",
430 | "4 is not in the list.\n",
431 | "6 is not in the list.\n",
432 | "7 is not in the list.\n",
433 | "8 is not in the list.\n",
434 | "9 is not in the list.\n",
435 | "11 is not in the list.\n",
436 | "12 is not in the list.\n",
437 | "14 is not in the list.\n",
438 | "16 is not in the list.\n",
439 | "18 is not in the list.\n",
440 | "19 is not in the list.\n",
441 | "21 is not in the list.\n",
442 | "22 is not in the list.\n",
443 | "23 is not in the list.\n",
444 | "24 is not in the list.\n",
445 | "27 is not in the list.\n",
446 | "28 is not in the list.\n",
447 | "31 is not in the list.\n",
448 | "32 is not in the list.\n",
449 | "33 is not in the list.\n",
450 | "36 is not in the list.\n",
451 | "38 is not in the list.\n",
452 | "42 is not in the list.\n",
453 | "43 is not in the list.\n",
454 | "44 is not in the list.\n",
455 | "46 is not in the list.\n",
456 | "47 is not in the list.\n",
457 | "48 is not in the list.\n",
458 | "49 is not in the list.\n"
459 | ]
460 | }
461 | ],
462 | "source": [
463 | "list_of_c = []\n",
464 | "for triple in pythagorean(50):\n",
465 | " if triple[2] not in list_of_c:\n",
466 | " list_of_c.append(triple[2])\n",
467 | "for n in range(1,51):\n",
468 | " if n not in list_of_c:\n",
469 | " print(n,'is not in the list.')"
470 | ]
471 | }
472 | ],
473 | "metadata": {
474 | "kernelspec": {
475 | "display_name": "Python 3",
476 | "language": "python",
477 | "name": "python3"
478 | },
479 | "language_info": {
480 | "codemirror_mode": {
481 | "name": "ipython",
482 | "version": 3
483 | },
484 | "file_extension": ".py",
485 | "mimetype": "text/x-python",
486 | "name": "python",
487 | "nbconvert_exporter": "python",
488 | "pygments_lexer": "ipython3",
489 | "version": "3.4.3"
490 | }
491 | },
492 | "nbformat": 4,
493 | "nbformat_minor": 0
494 | }
495 |
--------------------------------------------------------------------------------
/notes-week-02/notes-01-13-16.ipynb:
--------------------------------------------------------------------------------
1 | {
2 | "cells": [
3 | {
4 | "cell_type": "markdown",
5 | "metadata": {},
6 | "source": [
7 | "**IMPORTANT:** Make sure the kernel is set to Python 3.\n",
8 | "\n",
9 | "------------\n",
10 | "\n",
11 | "# MATH 210 Introduction to Mathematical Computing\n",
12 | "\n",
13 | "## January 13, 2016\n",
14 | "\n",
15 | "Today's Agenda:\n",
16 | "\n",
17 | "1. `if/elif/else` statements\n",
18 | "2. Datatypes `list` and `str`\n",
19 | "3. Exercises\n",
20 | "\n",
21 | "See the [Python 3 tutorial](https://docs.python.org/3/tutorial/) for more information."
22 | ]
23 | },
24 | {
25 | "cell_type": "markdown",
26 | "metadata": {},
27 | "source": [
28 | "## 1. `if/elif/else` statements"
29 | ]
30 | },
31 | {
32 | "cell_type": "markdown",
33 | "metadata": {},
34 | "source": [
35 | "The syntax for an `if/elif/else` statement is:\n",
36 | "\n",
37 | "```python\n",
38 | "if expression1:\n",
39 | " ... Python code block 1 ...\n",
40 | " ... Python code block 1 ...\n",
41 | "elif expression2:\n",
42 | " ... Python code block 2 ...\n",
43 | " ... Python code block 2 ...\n",
44 | "elif expression3:\n",
45 | " ... Python code block 3 ...\n",
46 | " ... Python code block 3 ...\n",
47 | "else:\n",
48 | " ... Python code block 4 ...\n",
49 | " ... Python code block 4...\n",
50 | "```"
51 | ]
52 | },
53 | {
54 | "cell_type": "markdown",
55 | "metadata": {},
56 | "source": [
57 | "Notice the following **important** details:\n",
58 | "\n",
59 | "1. There are no brackets to disguish each block of Python code after each logical expression\n",
60 | "2. The indentation determines each block. In other words, the two lines after *expression1* are indented the standard 4 spaces and so they are executed if *expression1* is `True`.\n",
61 | "3. Each expression is evaluated in order **until** an expression is `True`, then the following indented code block is executed and then we exit the `if` statement without evaluating any of the subsequent expressions.\n",
62 | "4. The last block is executed only if none of the expressions above it are `True`\n",
63 | "5. An `if` statement does not require `elif` or `else` statements. Use them if you want to use them."
64 | ]
65 | },
66 | {
67 | "cell_type": "markdown",
68 | "metadata": {},
69 | "source": [
70 | "**Exercise 1.** Write an `if/elif/else` statement which tests a polynomial $ax^2 + bx + c$ has real distinct roots, real repeated roots or complex roots. In any case, print the corresponding statement as output."
71 | ]
72 | },
73 | {
74 | "cell_type": "markdown",
75 | "metadata": {},
76 | "source": [
77 | "Use the disciminant $b^2 -4ac$ in the quadratic formula: $$\\frac{-b \\pm \\sqrt{b^2 - 4ac}}{2a}$$"
78 | ]
79 | },
80 | {
81 | "cell_type": "code",
82 | "execution_count": 39,
83 | "metadata": {
84 | "collapsed": false
85 | },
86 | "outputs": [
87 | {
88 | "name": "stdout",
89 | "output_type": "stream",
90 | "text": [
91 | "f(x) = 1 x^2 + 2 x + 2\n",
92 | "The polynomial has complex roots.\n"
93 | ]
94 | }
95 | ],
96 | "source": [
97 | "a = 1\n",
98 | "b = 2\n",
99 | "c = 2\n",
100 | "discriminant = b**2 - 4*a*c\n",
101 | "print('f(x) = ',a,'x^2 +',b,'x +',c)\n",
102 | "if (discriminant > 0):\n",
103 | " print('The polynomial has real distinct roots.')\n",
104 | "elif (discriminant < 0):\n",
105 | " print('The polynomial has complex roots.')\n",
106 | "else:\n",
107 | " print('The polynomial has repeated roots.')"
108 | ]
109 | },
110 | {
111 | "cell_type": "markdown",
112 | "metadata": {},
113 | "source": [
114 | "**Exercise 2.** Write an `if/elif/else` statement which tests if a $2 \\times 2$ matrix $\\begin{bmatrix} a & b \\\\ c & d \\end{bmatrix}$ is invertible."
115 | ]
116 | },
117 | {
118 | "cell_type": "code",
119 | "execution_count": 40,
120 | "metadata": {
121 | "collapsed": false
122 | },
123 | "outputs": [
124 | {
125 | "name": "stdout",
126 | "output_type": "stream",
127 | "text": [
128 | "The matrix is invertible.\n"
129 | ]
130 | }
131 | ],
132 | "source": [
133 | "a = 1\n",
134 | "b = 2\n",
135 | "c = 3\n",
136 | "d = 4\n",
137 | "determinant = a*d - b*c\n",
138 | "if determinant != 0:\n",
139 | " print('The matrix is invertible.')\n",
140 | "else:\n",
141 | " print('The matrix is not invertible.')"
142 | ]
143 | },
144 | {
145 | "cell_type": "markdown",
146 | "metadata": {},
147 | "source": [
148 | "**Exercise 3.** Write an `if/elif/else` statement which tests if an integer $n$ is divisible by 3, 7 or 17."
149 | ]
150 | },
151 | {
152 | "cell_type": "markdown",
153 | "metadata": {},
154 | "source": [
155 | "## 2. Datatypes `list` and `str`"
156 | ]
157 | },
158 | {
159 | "cell_type": "markdown",
160 | "metadata": {},
161 | "source": [
162 | "So far we have seen two dataypes: `int` and `float`."
163 | ]
164 | },
165 | {
166 | "cell_type": "code",
167 | "execution_count": 41,
168 | "metadata": {
169 | "collapsed": false
170 | },
171 | "outputs": [
172 | {
173 | "data": {
174 | "text/plain": [
175 | "int"
176 | ]
177 | },
178 | "execution_count": 41,
179 | "metadata": {},
180 | "output_type": "execute_result"
181 | }
182 | ],
183 | "source": [
184 | "type(2)"
185 | ]
186 | },
187 | {
188 | "cell_type": "code",
189 | "execution_count": 42,
190 | "metadata": {
191 | "collapsed": false
192 | },
193 | "outputs": [
194 | {
195 | "data": {
196 | "text/plain": [
197 | "float"
198 | ]
199 | },
200 | "execution_count": 42,
201 | "metadata": {},
202 | "output_type": "execute_result"
203 | }
204 | ],
205 | "source": [
206 | "type(2.0)"
207 | ]
208 | },
209 | {
210 | "cell_type": "markdown",
211 | "metadata": {},
212 | "source": [
213 | "### `list`\n",
214 | "\n",
215 | "A `list` is simply a list of any Python datatypes and we use square brackets `[ ... ]` to define lists. See the [Python 3 tutorial](https://docs.python.org/3/tutorial/introduction.html#lists) and documentation for more infomation"
216 | ]
217 | },
218 | {
219 | "cell_type": "code",
220 | "execution_count": 43,
221 | "metadata": {
222 | "collapsed": false
223 | },
224 | "outputs": [
225 | {
226 | "name": "stdout",
227 | "output_type": "stream",
228 | "text": [
229 | "[1, 1.0, 3.14159]\n"
230 | ]
231 | }
232 | ],
233 | "source": [
234 | "my_list = [1,1.0,3.14159]\n",
235 | "print(my_list)"
236 | ]
237 | },
238 | {
239 | "cell_type": "code",
240 | "execution_count": 44,
241 | "metadata": {
242 | "collapsed": false
243 | },
244 | "outputs": [
245 | {
246 | "data": {
247 | "text/plain": [
248 | "list"
249 | ]
250 | },
251 | "execution_count": 44,
252 | "metadata": {},
253 | "output_type": "execute_result"
254 | }
255 | ],
256 | "source": [
257 | "type(my_list)"
258 | ]
259 | },
260 | {
261 | "cell_type": "markdown",
262 | "metadata": {},
263 | "source": [
264 | "We can access the elements in a list by its index. **But notice that the first element has index 0.**"
265 | ]
266 | },
267 | {
268 | "cell_type": "code",
269 | "execution_count": 45,
270 | "metadata": {
271 | "collapsed": false
272 | },
273 | "outputs": [
274 | {
275 | "name": "stdout",
276 | "output_type": "stream",
277 | "text": [
278 | "1\n",
279 | "1.0\n",
280 | "3.14159\n"
281 | ]
282 | }
283 | ],
284 | "source": [
285 | "print(my_list[0])\n",
286 | "print(my_list[1])\n",
287 | "print(my_list[2])"
288 | ]
289 | },
290 | {
291 | "cell_type": "markdown",
292 | "metadata": {},
293 | "source": [
294 | "A quick way to generate a list is to use the built-in Python function `range`. See the [documentation](https://docs.python.org/3/tutorial/controlflow.html#the-range-function) in the Python 3 tutorial about `range`."
295 | ]
296 | },
297 | {
298 | "cell_type": "code",
299 | "execution_count": 46,
300 | "metadata": {
301 | "collapsed": false
302 | },
303 | "outputs": [
304 | {
305 | "data": {
306 | "text/plain": [
307 | "range(0, 5)"
308 | ]
309 | },
310 | "execution_count": 46,
311 | "metadata": {},
312 | "output_type": "execute_result"
313 | }
314 | ],
315 | "source": [
316 | "range(5)"
317 | ]
318 | },
319 | {
320 | "cell_type": "markdown",
321 | "metadata": {},
322 | "source": [
323 | "The `range` function produces a Python `iterable`. The idea is that it is a very efficient list which **only computes the values in the list when you need them** which makes loops using `range` faster. Use the function `list` to produce the complete list."
324 | ]
325 | },
326 | {
327 | "cell_type": "code",
328 | "execution_count": 47,
329 | "metadata": {
330 | "collapsed": false
331 | },
332 | "outputs": [
333 | {
334 | "name": "stdout",
335 | "output_type": "stream",
336 | "text": [
337 | "[0, 1, 2, 3, 4]\n"
338 | ]
339 | }
340 | ],
341 | "source": [
342 | "new_list = list(range(0,5))\n",
343 | "print(new_list)"
344 | ]
345 | },
346 | {
347 | "cell_type": "code",
348 | "execution_count": 48,
349 | "metadata": {
350 | "collapsed": false
351 | },
352 | "outputs": [
353 | {
354 | "name": "stdout",
355 | "output_type": "stream",
356 | "text": [
357 | "[0, 2, 4, 6, 8]\n"
358 | ]
359 | }
360 | ],
361 | "source": [
362 | "another_list = list(range(0,10,2))\n",
363 | "print(another_list)"
364 | ]
365 | },
366 | {
367 | "cell_type": "markdown",
368 | "metadata": {},
369 | "source": [
370 | "**Exercise 4.** Make a list of all the multiples of 3 from 0 to 99."
371 | ]
372 | },
373 | {
374 | "cell_type": "code",
375 | "execution_count": 49,
376 | "metadata": {
377 | "collapsed": false
378 | },
379 | "outputs": [
380 | {
381 | "name": "stdout",
382 | "output_type": "stream",
383 | "text": [
384 | "[0, 3, 6, 9, 12, 15, 18, 21, 24, 27, 30, 33, 36, 39, 42, 45, 48, 51, 54, 57, 60, 63, 66, 69, 72, 75, 78, 81, 84, 87, 90, 93, 96, 99]\n"
385 | ]
386 | }
387 | ],
388 | "source": [
389 | "multiples_of_3 = list(range(0,100,3))\n",
390 | "print(multiples_of_3)"
391 | ]
392 | },
393 | {
394 | "cell_type": "markdown",
395 | "metadata": {},
396 | "source": [
397 | "### `str`\n",
398 | "\n",
399 | "A string `str` is any sequence of characters and we use either single quotes `' ... '` or double quotes `\" ... \"` to construct strings."
400 | ]
401 | },
402 | {
403 | "cell_type": "code",
404 | "execution_count": 50,
405 | "metadata": {
406 | "collapsed": false
407 | },
408 | "outputs": [
409 | {
410 | "name": "stdout",
411 | "output_type": "stream",
412 | "text": [
413 | "Patrick Walls\n"
414 | ]
415 | }
416 | ],
417 | "source": [
418 | "my_name = 'Patrick Walls'\n",
419 | "print(my_name)"
420 | ]
421 | },
422 | {
423 | "cell_type": "code",
424 | "execution_count": 51,
425 | "metadata": {
426 | "collapsed": false
427 | },
428 | "outputs": [
429 | {
430 | "data": {
431 | "text/plain": [
432 | "str"
433 | ]
434 | },
435 | "execution_count": 51,
436 | "metadata": {},
437 | "output_type": "execute_result"
438 | }
439 | ],
440 | "source": [
441 | "type(my_name)"
442 | ]
443 | },
444 | {
445 | "cell_type": "code",
446 | "execution_count": 52,
447 | "metadata": {
448 | "collapsed": false
449 | },
450 | "outputs": [
451 | {
452 | "name": "stdout",
453 | "output_type": "stream",
454 | "text": [
455 | "123456789 abcdefg +=!@\n"
456 | ]
457 | }
458 | ],
459 | "source": [
460 | "new_string = '123456789 abcdefg +=!@'\n",
461 | "print(new_string)"
462 | ]
463 | },
464 | {
465 | "cell_type": "markdown",
466 | "metadata": {},
467 | "source": [
468 | "We can turn other dataypes into strings using the function `str`."
469 | ]
470 | },
471 | {
472 | "cell_type": "code",
473 | "execution_count": 53,
474 | "metadata": {
475 | "collapsed": false
476 | },
477 | "outputs": [
478 | {
479 | "data": {
480 | "text/plain": [
481 | "'[1, 1.0, 3.14159]'"
482 | ]
483 | },
484 | "execution_count": 53,
485 | "metadata": {},
486 | "output_type": "execute_result"
487 | }
488 | ],
489 | "source": [
490 | "str(my_list)"
491 | ]
492 | },
493 | {
494 | "cell_type": "code",
495 | "execution_count": 54,
496 | "metadata": {
497 | "collapsed": false
498 | },
499 | "outputs": [
500 | {
501 | "data": {
502 | "text/plain": [
503 | "'3.14159'"
504 | ]
505 | },
506 | "execution_count": 54,
507 | "metadata": {},
508 | "output_type": "execute_result"
509 | }
510 | ],
511 | "source": [
512 | "str(3.14159)"
513 | ]
514 | },
515 | {
516 | "cell_type": "markdown",
517 | "metadata": {},
518 | "source": [
519 | "We can access the characters in a string just like a list."
520 | ]
521 | },
522 | {
523 | "cell_type": "code",
524 | "execution_count": 55,
525 | "metadata": {
526 | "collapsed": false
527 | },
528 | "outputs": [
529 | {
530 | "name": "stdout",
531 | "output_type": "stream",
532 | "text": [
533 | "P\n",
534 | "W\n"
535 | ]
536 | }
537 | ],
538 | "source": [
539 | "print(my_name[0])\n",
540 | "print(my_name[8])"
541 | ]
542 | },
543 | {
544 | "cell_type": "markdown",
545 | "metadata": {},
546 | "source": [
547 | "And we can also turn a string into a list."
548 | ]
549 | },
550 | {
551 | "cell_type": "code",
552 | "execution_count": 56,
553 | "metadata": {
554 | "collapsed": false
555 | },
556 | "outputs": [
557 | {
558 | "data": {
559 | "text/plain": [
560 | "['P', 'a', 't', 'r', 'i', 'c', 'k', ' ', 'W', 'a', 'l', 'l', 's']"
561 | ]
562 | },
563 | "execution_count": 56,
564 | "metadata": {},
565 | "output_type": "execute_result"
566 | }
567 | ],
568 | "source": [
569 | "list(my_name)"
570 | ]
571 | },
572 | {
573 | "cell_type": "markdown",
574 | "metadata": {},
575 | "source": [
576 | "Finally, we can test to see if a string is contained in another string using the operator `in`."
577 | ]
578 | },
579 | {
580 | "cell_type": "code",
581 | "execution_count": 57,
582 | "metadata": {
583 | "collapsed": false
584 | },
585 | "outputs": [
586 | {
587 | "name": "stdout",
588 | "output_type": "stream",
589 | "text": [
590 | "True\n"
591 | ]
592 | }
593 | ],
594 | "source": [
595 | "my_first_name = 'Patrick'\n",
596 | "my_full_name = 'Patrick Walls'\n",
597 | "print(my_first_name in my_full_name)"
598 | ]
599 | },
600 | {
601 | "cell_type": "markdown",
602 | "metadata": {},
603 | "source": [
604 | "## 3. Exercises"
605 | ]
606 | },
607 | {
608 | "cell_type": "markdown",
609 | "metadata": {},
610 | "source": [
611 | "**Exercise 5.** Make a list of all the multiples of 7 from 0 up to 1000."
612 | ]
613 | },
614 | {
615 | "cell_type": "markdown",
616 | "metadata": {},
617 | "source": [
618 | "**Exercise 6.** What happens when you add strings with the operator `+`?"
619 | ]
620 | },
621 | {
622 | "cell_type": "markdown",
623 | "metadata": {},
624 | "source": [
625 | "**Exercise 7.** What happens when you add lists with the operator `+`?"
626 | ]
627 | },
628 | {
629 | "cell_type": "markdown",
630 | "metadata": {},
631 | "source": [
632 | "**Exercise 8.** What happens when you multiply a `list` or `str` by an `int`?"
633 | ]
634 | },
635 | {
636 | "cell_type": "markdown",
637 | "metadata": {},
638 | "source": [
639 | "**Exercise 9.** Make a list with 20 entries which alternate between 0 and 1. In other words, `[0,1,0,1,0,1,...]`."
640 | ]
641 | },
642 | {
643 | "cell_type": "markdown",
644 | "metadata": {},
645 | "source": [
646 | "**Exercise 10.** Make a string which repeats `\"Math 210 Math 210 Math 210 ... \"` 10 times."
647 | ]
648 | },
649 | {
650 | "cell_type": "markdown",
651 | "metadata": {},
652 | "source": [
653 | "**Exercise 11.** Write an `if/elif/else` statement which tests if a string contains either the letter `x` or the letter `r`."
654 | ]
655 | },
656 | {
657 | "cell_type": "markdown",
658 | "metadata": {},
659 | "source": [
660 | "**Exercise 12.** Write an `if/elif/else` statement which tests if two vectors $\\mathbf{a} = [a_1 , a_2]$ and $\\mathbf{b} = [b_1 , b_2]$ are orthogonal. (Use lists to represent vectors.)"
661 | ]
662 | }
663 | ],
664 | "metadata": {
665 | "kernelspec": {
666 | "display_name": "Python 3",
667 | "language": "python",
668 | "name": "python3"
669 | },
670 | "language_info": {
671 | "codemirror_mode": {
672 | "name": "ipython",
673 | "version": 3
674 | },
675 | "file_extension": ".py",
676 | "mimetype": "text/x-python",
677 | "name": "python",
678 | "nbconvert_exporter": "python",
679 | "pygments_lexer": "ipython3",
680 | "version": "3.4.3"
681 | }
682 | },
683 | "nbformat": 4,
684 | "nbformat_minor": 0
685 | }
686 |
--------------------------------------------------------------------------------
/notes-week-01/notes-01-08-16.ipynb:
--------------------------------------------------------------------------------
1 | {
2 | "cells": [
3 | {
4 | "cell_type": "markdown",
5 | "metadata": {},
6 | "source": [
7 | "**IMPORTANT: Make sure the kernel (see `Kernel` in the toolbar above) is set to Python 3**\n",
8 | "\n",
9 | "--------\n",
10 | "\n",
11 | "# MATH 210 Introduction to Mathematical Computing\n",
12 | "\n",
13 | "## January 8, 2016\n",
14 | "\n",
15 | "Today's agenda:\n",
16 | "\n",
17 | "1. More Markdown and LaTeX\n",
18 | " * List and links\n",
19 | " * Matrices, braces and other symbols\n",
20 | "2. LaTeX Exercises\n",
21 | "3. Basic Python\n",
22 | " * Dataypes `int` and `float`\n",
23 | " * Arithmetic operators: `+`, `-`, `*`, `/`, `**`, `%` and `//`\n",
24 | "4. Python Exercises"
25 | ]
26 | },
27 | {
28 | "cell_type": "markdown",
29 | "metadata": {},
30 | "source": [
31 | "## 1. More Markdown and LaTeX"
32 | ]
33 | },
34 | {
35 | "cell_type": "markdown",
36 | "metadata": {},
37 | "source": [
38 | "### Lists and Links\n",
39 | "\n",
40 | "Let's practice making lists and links in markdown language by looking at the poll we conducted last class to see what courses everyone is taking this semester. The results were varied!\n",
41 | "\n",
42 | "* Second-year MATH courses:\n",
43 | " * MATH 210 [Introduction to Mathematical Computing](https://courses.students.ubc.ca/cs/main?pname=subjarea&tname=subjareas&req=3&dept=MATH&course=210)\n",
44 | " * MATH 215 [Elementary Differential Equations I](http://www.math.ubc.ca/~coombs/215/math215255common.html)\n",
45 | " * MATH 220 [Mathematical Proof](http://www.math.ubc.ca/~gor/Math220_2016/math220_201.html)\n",
46 | " * MATH 221 [Matrix Algebra](http://www.math.ubc.ca/~karu/m221/index.html)\n",
47 | " * MATH 227 [Advanced Calculus II](http://www.math.ubc.ca/~feldman/m227/)\n",
48 | "* Third-year MATH courses:\n",
49 | " * MATH 301 [Applied Analysis](http://www.math.ubc.ca/~jcwei/MATH301-2016.html)\n",
50 | " * MATH 302 [Introduction to Probability](https://courses.students.ubc.ca/cs/main?pname=subjarea&tname=subjareas&req=3&dept=MATH&course=302)\n",
51 | " * MATH 303 [Introduction to Stochastic Processes](https://www.sites.google.com/site/balkarichard/home/teaching-2)\n",
52 | " * MATH 307 [Applied Linear Algebra](https://courses.students.ubc.ca/cs/main?pname=subjarea&tname=subjareas&req=3&dept=MATH&course=307)\n",
53 | " * MATH 313 [Topics in Number Theory](https://courses.students.ubc.ca/cs/main?pname=subjarea&tname=subjareas&req=3&dept=MATH&course=313)\n",
54 | " * MATH 317 [Calculus IV](http://www.math.ubc.ca/~ollivier/Math317.html)\n",
55 | " * MATH 321 [Real Variables II](http://www.math.ubc.ca/~karu/m321/index.html)\n",
56 | " * MATH 323 [Introduction to Rings and Modules](http://www.math.ubc.ca/~miljan/math323/)\n",
57 | " * MATH 340 [Introduction to Linear Programming](http://www.math.ubc.ca/~anstee/math340/math340.html)\n",
58 | " * MATH 342 [Algebra, Coding Theory, and Cryptography](http://www.math.ubc.ca/~marcus/Math342/)\n",
59 | "* Other courses:\n",
60 | " * MATH 444 [Mathematical Research and Writing](http://www.math.ubc.ca/~steph/444/444.html)\n",
61 | " * ECON 234 [Wealth and Poverty of Nations](https://courses.students.ubc.ca/cs/main?pname=subjarea&tname=subjareas&req=3&dept=ECON&course=234)\n",
62 | " * ECON 325 [Introduction to Empirical Economics](https://courses.students.ubc.ca/cs/main?pname=subjarea&tname=subjareas&req=3&dept=ECON&course=325)\n",
63 | " * ARCL 419 [The Archaeology of Death](https://courses.students.ubc.ca/cs/main?pname=subjarea&tname=subjareas&req=5&dept=ARCL&course=419§ion=002)\n",
64 | " * BIOC 302 [General Biochemistry](https://courses.students.ubc.ca/cs/main?pname=subjarea&tname=subjareas&req=3&dept=BIOC&course=302)\n",
65 | " * VISA 210 [Digital Arts](https://courses.students.ubc.ca/cs/main?pname=subjarea&tname=subjareas&req=3&dept=VISA&course=210)\n",
66 | " * VISA 220 [Drawing](https://courses.students.ubc.ca/cs/main?pname=subjarea&tname=subjareas&req=3&dept=VISA&course=220)\n",
67 | " * JAPN 103 [Beginning Japanese II B](https://courses.students.ubc.ca/cs/main?pname=subjarea&tname=subjareas&req=3&dept=JAPN&course=103)\n",
68 | " * SWED 110 [Elementary Swedish II](https://courses.students.ubc.ca/cs/main?pname=subjarea&tname=subjareas&req=3&dept=SWED&course=110)\n",
69 | " * GERM 310 [Intermediate German IV](https://courses.students.ubc.ca/cs/main?pname=subjarea&tname=subjareas&req=3&dept=GERM&course=310)\n",
70 | " * CHIN 483 [Modern Chinese Literature II](https://courses.students.ubc.ca/cs/main?pname=subjarea&tname=subjareas&req=3&dept=CHIN&course=483)"
71 | ]
72 | },
73 | {
74 | "cell_type": "markdown",
75 | "metadata": {},
76 | "source": [
77 | "### Symbols and Matrices in LaTeX\n",
78 | "\n",
79 | "Let's explore some more common math symbols. Check out the [LaTeX WikiBook](https://en.wikibooks.org/wiki/LaTeX/Mathematics) and the [Detexify App](http://detexify.kirelabs.org/classify.html).\n",
80 | "\n",
81 | "* Matrices:\n",
82 | " * `$$\\begin{matrix} a & b \\\\ c & d \\end{matrix}$$` displays a matrix without braces $$\\begin{matrix} a & b \\\\ c & d \\end{matrix}$$\n",
83 | " * `$$\\begin{pmatrix} a & b \\\\ c & d \\end{pmatrix}$$` displays a matrix with parentheses $$\\begin{pmatrix} a & b \\\\ c & d \\end{pmatrix}$$\n",
84 | " * `$$\\begin{bmatrix} a & b \\\\ c & d \\end{bmatrix}$$` displays a matrix with square brackets $$\\begin{bmatrix} a & b \\\\ c & d \\end{bmatrix}$$\n",
85 | "* Braces:\n",
86 | " * use `\\left( ... \\right)` to enclose tall text in tall braces. For example, `$$\\left( \\frac{1}{2} - 1 \\right$$` renders as $$\\left( \\frac{1}{2} - 1 \\right)$$\n",
87 | "* Operators\n",
88 | " * `$\\bigcap$` $\\bigcap$\n",
89 | " * `$\\bigcup$` $\\bigcup$\n",
90 | " * `$\\prod$` $\\prod$\n",
91 | " * `$\\sum$` $\\sum$\n",
92 | "* Fonts\n",
93 | " * `$\\mathrm{Hom}$` $\\mathrm{Hom}$\n",
94 | " * `$\\mathbb{Z}$` $\\mathbb{Z}$\n",
95 | " * `$\\mathscr{L}$` $\\mathscr{L}$\n",
96 | " * `$\\mathfrak{g}$` $\\mathfrak{g}$\n",
97 | "* Other symbols\n",
98 | " * `$\\rightarrow$` $\\rightarrow$\n",
99 | " * `$\\leftarrow$` $\\leftarrow$\n",
100 | " * `$\\Rightarrow$` $\\Rightarrow$\n",
101 | " * `$\\Leftrightarrow$` $\\Leftrightarrow$\n",
102 | " * `$\\in$` $\\in$\n",
103 | " * `$\\notin$` $\\notin$\n",
104 | " * `$\\forall$` $\\forall$\n",
105 | " * `$\\infty$` $\\infty$"
106 | ]
107 | },
108 | {
109 | "cell_type": "markdown",
110 | "metadata": {},
111 | "source": [
112 | "## 2. LaTeX Exercises"
113 | ]
114 | },
115 | {
116 | "cell_type": "markdown",
117 | "metadata": {},
118 | "source": [
119 | "** Exercise 1.** Write LaTeX code to display the general formula for Taylor series 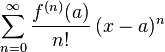"
120 | ]
121 | },
122 | {
123 | "cell_type": "markdown",
124 | "metadata": {},
125 | "source": [
126 | "** Exercise 2.** Write LaTeX code to display Stokes' Theorem "
127 | ]
128 | },
129 | {
130 | "cell_type": "markdown",
131 | "metadata": {},
132 | "source": [
133 | "**Exercise 3.** Write LaTeX code to display the adjoint property of the tensor product "
134 | ]
135 | },
136 | {
137 | "cell_type": "markdown",
138 | "metadata": {},
139 | "source": [
140 | "**Exercise 4.** Write LaTeX code to display the definition of the Laplace transform "
141 | ]
142 | },
143 | {
144 | "cell_type": "markdown",
145 | "metadata": {},
146 | "source": [
147 | "**Exercise 5.** Write LaTeX code to display the definition of the Jacobian matrix "
148 | ]
149 | },
150 | {
151 | "cell_type": "markdown",
152 | "metadata": {},
153 | "source": [
154 | "**Exercise 6.** Pick your favourite course from this semester and write the notes from your last class in LaTeX in this cell. "
155 | ]
156 | },
157 | {
158 | "cell_type": "markdown",
159 | "metadata": {},
160 | "source": [
161 | "## 3. Basic Python\n",
162 | "\n",
163 | "Let's dive into Python! Check out the [Python 3 documentation page](https://docs.python.org/3/) for all the info.\n",
164 | "\n",
165 | "**IMPORTANT: Make sure the kernel (see the toolbar above) is set to Python 3**\n",
166 | "\n",
167 | "### Dataypes\n",
168 | "\n",
169 | "There are several built-in dataypes in Python. Let's focus on the most basic and most commonly used datatypes: `int`, `float`, `list`, `string`."
170 | ]
171 | },
172 | {
173 | "cell_type": "markdown",
174 | "metadata": {},
175 | "source": [
176 | "### int\n",
177 | "\n",
178 | "An `int` is an integer and we can use the arithmetic operators `+`, `-`, `*`, `/`, `**` (exponent), `%` (modulo) and `//` (quotient) to do operations on them:"
179 | ]
180 | },
181 | {
182 | "cell_type": "code",
183 | "execution_count": 1,
184 | "metadata": {
185 | "collapsed": false
186 | },
187 | "outputs": [
188 | {
189 | "data": {
190 | "text/plain": [
191 | "7"
192 | ]
193 | },
194 | "execution_count": 1,
195 | "metadata": {},
196 | "output_type": "execute_result"
197 | }
198 | ],
199 | "source": [
200 | "2 + 5"
201 | ]
202 | },
203 | {
204 | "cell_type": "code",
205 | "execution_count": 2,
206 | "metadata": {
207 | "collapsed": false
208 | },
209 | "outputs": [
210 | {
211 | "data": {
212 | "text/plain": [
213 | "2"
214 | ]
215 | },
216 | "execution_count": 2,
217 | "metadata": {},
218 | "output_type": "execute_result"
219 | }
220 | ],
221 | "source": [
222 | "8 - 6"
223 | ]
224 | },
225 | {
226 | "cell_type": "code",
227 | "execution_count": 3,
228 | "metadata": {
229 | "collapsed": false
230 | },
231 | "outputs": [
232 | {
233 | "data": {
234 | "text/plain": [
235 | "-42"
236 | ]
237 | },
238 | "execution_count": 3,
239 | "metadata": {},
240 | "output_type": "execute_result"
241 | }
242 | ],
243 | "source": [
244 | "6 * -7"
245 | ]
246 | },
247 | {
248 | "cell_type": "code",
249 | "execution_count": 4,
250 | "metadata": {
251 | "collapsed": false
252 | },
253 | "outputs": [
254 | {
255 | "data": {
256 | "text/plain": [
257 | "11.0"
258 | ]
259 | },
260 | "execution_count": 4,
261 | "metadata": {},
262 | "output_type": "execute_result"
263 | }
264 | ],
265 | "source": [
266 | "121 / 11"
267 | ]
268 | },
269 | {
270 | "cell_type": "markdown",
271 | "metadata": {},
272 | "source": [
273 | "The operator `**` computes exponents:"
274 | ]
275 | },
276 | {
277 | "cell_type": "code",
278 | "execution_count": 5,
279 | "metadata": {
280 | "collapsed": false
281 | },
282 | "outputs": [
283 | {
284 | "data": {
285 | "text/plain": [
286 | "64"
287 | ]
288 | },
289 | "execution_count": 5,
290 | "metadata": {},
291 | "output_type": "execute_result"
292 | }
293 | ],
294 | "source": [
295 | "8 ** 2"
296 | ]
297 | },
298 | {
299 | "cell_type": "markdown",
300 | "metadata": {},
301 | "source": [
302 | "The operator `%` computes the remainder of integer disivion (ie. the modulo operator):"
303 | ]
304 | },
305 | {
306 | "cell_type": "code",
307 | "execution_count": 6,
308 | "metadata": {
309 | "collapsed": false
310 | },
311 | "outputs": [
312 | {
313 | "data": {
314 | "text/plain": [
315 | "1"
316 | ]
317 | },
318 | "execution_count": 6,
319 | "metadata": {},
320 | "output_type": "execute_result"
321 | }
322 | ],
323 | "source": [
324 | "9 % 4"
325 | ]
326 | },
327 | {
328 | "cell_type": "markdown",
329 | "metadata": {},
330 | "source": [
331 | "The operator `//` computes the quotient:"
332 | ]
333 | },
334 | {
335 | "cell_type": "code",
336 | "execution_count": 7,
337 | "metadata": {
338 | "collapsed": false
339 | },
340 | "outputs": [
341 | {
342 | "data": {
343 | "text/plain": [
344 | "2"
345 | ]
346 | },
347 | "execution_count": 7,
348 | "metadata": {},
349 | "output_type": "execute_result"
350 | }
351 | ],
352 | "source": [
353 | "9 // 4"
354 | ]
355 | },
356 | {
357 | "cell_type": "markdown",
358 | "metadata": {},
359 | "source": [
360 | "### float\n",
361 | "\n",
362 | "WAIT! Did you notice something different in the calculation `121/11` above? There's a decimal place in `11.0`. This type is called a `float`. It's just a real number with decimal places and the division operator always returns a `float` even if we're dividing by an `int`. **IMPORTANT: This is a feature of Python 3. Make sure the kernel (see `Kernel` in the toolbar above) is set to Python 3**."
363 | ]
364 | },
365 | {
366 | "cell_type": "code",
367 | "execution_count": 8,
368 | "metadata": {
369 | "collapsed": false
370 | },
371 | "outputs": [
372 | {
373 | "data": {
374 | "text/plain": [
375 | "int"
376 | ]
377 | },
378 | "execution_count": 8,
379 | "metadata": {},
380 | "output_type": "execute_result"
381 | }
382 | ],
383 | "source": [
384 | "type(11)"
385 | ]
386 | },
387 | {
388 | "cell_type": "code",
389 | "execution_count": 9,
390 | "metadata": {
391 | "collapsed": false
392 | },
393 | "outputs": [
394 | {
395 | "data": {
396 | "text/plain": [
397 | "float"
398 | ]
399 | },
400 | "execution_count": 9,
401 | "metadata": {},
402 | "output_type": "execute_result"
403 | }
404 | ],
405 | "source": [
406 | "type(11.0)"
407 | ]
408 | },
409 | {
410 | "cell_type": "code",
411 | "execution_count": 10,
412 | "metadata": {
413 | "collapsed": false
414 | },
415 | "outputs": [
416 | {
417 | "data": {
418 | "text/plain": [
419 | "12.443"
420 | ]
421 | },
422 | "execution_count": 10,
423 | "metadata": {},
424 | "output_type": "execute_result"
425 | }
426 | ],
427 | "source": [
428 | "2.3*5.41"
429 | ]
430 | },
431 | {
432 | "cell_type": "code",
433 | "execution_count": 11,
434 | "metadata": {
435 | "collapsed": false
436 | },
437 | "outputs": [
438 | {
439 | "data": {
440 | "text/plain": [
441 | "1.4142135623730951"
442 | ]
443 | },
444 | "execution_count": 11,
445 | "metadata": {},
446 | "output_type": "execute_result"
447 | }
448 | ],
449 | "source": [
450 | "2.0**0.5"
451 | ]
452 | },
453 | {
454 | "cell_type": "markdown",
455 | "metadata": {},
456 | "source": [
457 | "## 4. Python Exercises"
458 | ]
459 | },
460 | {
461 | "cell_type": "markdown",
462 | "metadata": {},
463 | "source": [
464 | "**Exercise 1.** An interger $p$ is prime if $1$ and $p$ are its only divisors. Find all the primes between $100$ and $150$. (Use the following fact: $p$ is prime if $p$ `%` $n \\not=0$ for all $n \\leq \\sqrt{p}$ where `%` is the modulo operator.)"
465 | ]
466 | },
467 | {
468 | "cell_type": "markdown",
469 | "metadata": {},
470 | "source": [
471 | "**Exercise 2.** [Fermat's theorem on the sum of two squares](https://en.wikipedia.org/wiki/Fermat%27s_theorem_on_sums_of_two_squares) states that every prime number $p$ of the form $4k+1$ can be expressed as the sum of two squares. For example, $5 = 2^2 + 1^2$ and $13 = 3^2 + 2^2$. For each prime $p < 50$ of the form $4k+1$, find integers $a$ and $b$ such that $p = a^2 + b^2$."
472 | ]
473 | },
474 | {
475 | "cell_type": "markdown",
476 | "metadata": {},
477 | "source": [
478 | "**Exercise 3.** We will continue with basic Python programming next week. In the meantime, check out this video from the SciPy 2015 Conference playlist on YouTube. It gives an introduction to Python and Juyter notebooks."
479 | ]
480 | },
481 | {
482 | "cell_type": "code",
483 | "execution_count": 12,
484 | "metadata": {
485 | "collapsed": false
486 | },
487 | "outputs": [
488 | {
489 | "data": {
490 | "text/html": [
491 | "\n",
492 | " \n",
499 | " "
500 | ],
501 | "text/plain": [
502 | ""
503 | ]
504 | },
505 | "execution_count": 12,
506 | "metadata": {},
507 | "output_type": "execute_result"
508 | }
509 | ],
510 | "source": [
511 | "from IPython.display import YouTubeVideo\n",
512 | "YouTubeVideo(\"pB3BFP001co\")"
513 | ]
514 | }
515 | ],
516 | "metadata": {
517 | "kernelspec": {
518 | "display_name": "Python 3",
519 | "language": "python",
520 | "name": "python3"
521 | },
522 | "language_info": {
523 | "codemirror_mode": {
524 | "name": "ipython",
525 | "version": 3
526 | },
527 | "file_extension": ".py",
528 | "mimetype": "text/x-python",
529 | "name": "python",
530 | "nbconvert_exporter": "python",
531 | "pygments_lexer": "ipython3",
532 | "version": "3.4.3"
533 | }
534 | },
535 | "nbformat": 4,
536 | "nbformat_minor": 0
537 | }
538 |
--------------------------------------------------------------------------------
/notes-week-02/notes-01-11-16.ipynb:
--------------------------------------------------------------------------------
1 | {
2 | "cells": [
3 | {
4 | "cell_type": "markdown",
5 | "metadata": {},
6 | "source": [
7 | "**IMPORTANT:** Make sure the kernel is set to Python 3\n",
8 | "\n",
9 | "------\n",
10 | "\n",
11 | "# MATH 210 Introduction to Mathematical Computing\n",
12 | "\n",
13 | "## January 11, 2016\n",
14 | "\n",
15 | "Today's Agenda:\n",
16 | "\n",
17 | "1. Python datatypes `int` and `float` and the assignment operator `=`\n",
18 | "2. Displaying output with `print`\n",
19 | "3. Logic\n",
20 | " * Comparison operators `<`, `>`, `<=`, `>=`, `==` and `!=`\n",
21 | " * Boolean operators `and`, `or` and `not`\n",
22 | " * `if` statements\n",
23 | "4. Exercises\n",
24 | "\n",
25 | "Check the [Python 3 tutorial](https://docs.python.org/3/tutorial/index.html) for more info."
26 | ]
27 | },
28 | {
29 | "cell_type": "markdown",
30 | "metadata": {},
31 | "source": [
32 | "## 1. Datatypes\n",
33 | "\n",
34 | "### `int`\n",
35 | "\n",
36 | "An `int` is simply an integer and we have the arithmetic operations: `+`, `-`, `*`, `/`, `**`, `%` and `//`. We can also use the assignment operator `=` to assign values to variables"
37 | ]
38 | },
39 | {
40 | "cell_type": "code",
41 | "execution_count": 47,
42 | "metadata": {
43 | "collapsed": true
44 | },
45 | "outputs": [],
46 | "source": [
47 | "a = 45\n",
48 | "b = 29"
49 | ]
50 | },
51 | {
52 | "cell_type": "code",
53 | "execution_count": 48,
54 | "metadata": {
55 | "collapsed": false
56 | },
57 | "outputs": [
58 | {
59 | "data": {
60 | "text/plain": [
61 | "74"
62 | ]
63 | },
64 | "execution_count": 48,
65 | "metadata": {},
66 | "output_type": "execute_result"
67 | }
68 | ],
69 | "source": [
70 | "a + b"
71 | ]
72 | },
73 | {
74 | "cell_type": "code",
75 | "execution_count": 49,
76 | "metadata": {
77 | "collapsed": false
78 | },
79 | "outputs": [
80 | {
81 | "data": {
82 | "text/plain": [
83 | "16"
84 | ]
85 | },
86 | "execution_count": 49,
87 | "metadata": {},
88 | "output_type": "execute_result"
89 | }
90 | ],
91 | "source": [
92 | "a - b"
93 | ]
94 | },
95 | {
96 | "cell_type": "code",
97 | "execution_count": 50,
98 | "metadata": {
99 | "collapsed": false
100 | },
101 | "outputs": [
102 | {
103 | "data": {
104 | "text/plain": [
105 | "1305"
106 | ]
107 | },
108 | "execution_count": 50,
109 | "metadata": {},
110 | "output_type": "execute_result"
111 | }
112 | ],
113 | "source": [
114 | "a * b"
115 | ]
116 | },
117 | {
118 | "cell_type": "code",
119 | "execution_count": 51,
120 | "metadata": {
121 | "collapsed": false
122 | },
123 | "outputs": [
124 | {
125 | "data": {
126 | "text/plain": [
127 | "1.5517241379310345"
128 | ]
129 | },
130 | "execution_count": 51,
131 | "metadata": {},
132 | "output_type": "execute_result"
133 | }
134 | ],
135 | "source": [
136 | "a / b"
137 | ]
138 | },
139 | {
140 | "cell_type": "code",
141 | "execution_count": 52,
142 | "metadata": {
143 | "collapsed": false
144 | },
145 | "outputs": [
146 | {
147 | "data": {
148 | "text/plain": [
149 | "877329837017924494095445366390049457550048828125"
150 | ]
151 | },
152 | "execution_count": 52,
153 | "metadata": {},
154 | "output_type": "execute_result"
155 | }
156 | ],
157 | "source": [
158 | "a ** b"
159 | ]
160 | },
161 | {
162 | "cell_type": "code",
163 | "execution_count": 53,
164 | "metadata": {
165 | "collapsed": false
166 | },
167 | "outputs": [
168 | {
169 | "data": {
170 | "text/plain": [
171 | "16"
172 | ]
173 | },
174 | "execution_count": 53,
175 | "metadata": {},
176 | "output_type": "execute_result"
177 | }
178 | ],
179 | "source": [
180 | "a % b"
181 | ]
182 | },
183 | {
184 | "cell_type": "code",
185 | "execution_count": 54,
186 | "metadata": {
187 | "collapsed": false
188 | },
189 | "outputs": [
190 | {
191 | "data": {
192 | "text/plain": [
193 | "1"
194 | ]
195 | },
196 | "execution_count": 54,
197 | "metadata": {},
198 | "output_type": "execute_result"
199 | }
200 | ],
201 | "source": [
202 | "a // b"
203 | ]
204 | },
205 | {
206 | "cell_type": "code",
207 | "execution_count": 55,
208 | "metadata": {
209 | "collapsed": false
210 | },
211 | "outputs": [
212 | {
213 | "data": {
214 | "text/plain": [
215 | "1.5517241379310345"
216 | ]
217 | },
218 | "execution_count": 55,
219 | "metadata": {},
220 | "output_type": "execute_result"
221 | }
222 | ],
223 | "source": [
224 | "a // b + (a % b) / b"
225 | ]
226 | },
227 | {
228 | "cell_type": "markdown",
229 | "metadata": {},
230 | "source": [
231 | "**Exercise 1.** Show that $149$ is a prime number."
232 | ]
233 | },
234 | {
235 | "cell_type": "code",
236 | "execution_count": 56,
237 | "metadata": {
238 | "collapsed": false
239 | },
240 | "outputs": [
241 | {
242 | "data": {
243 | "text/plain": [
244 | "2"
245 | ]
246 | },
247 | "execution_count": 56,
248 | "metadata": {},
249 | "output_type": "execute_result"
250 | }
251 | ],
252 | "source": [
253 | "149 % 3"
254 | ]
255 | },
256 | {
257 | "cell_type": "code",
258 | "execution_count": 57,
259 | "metadata": {
260 | "collapsed": false
261 | },
262 | "outputs": [
263 | {
264 | "data": {
265 | "text/plain": [
266 | "2"
267 | ]
268 | },
269 | "execution_count": 57,
270 | "metadata": {},
271 | "output_type": "execute_result"
272 | }
273 | ],
274 | "source": [
275 | "149 % 7"
276 | ]
277 | },
278 | {
279 | "cell_type": "code",
280 | "execution_count": 58,
281 | "metadata": {
282 | "collapsed": false
283 | },
284 | "outputs": [
285 | {
286 | "data": {
287 | "text/plain": [
288 | "6"
289 | ]
290 | },
291 | "execution_count": 58,
292 | "metadata": {},
293 | "output_type": "execute_result"
294 | }
295 | ],
296 | "source": [
297 | "149 % 11"
298 | ]
299 | },
300 | {
301 | "cell_type": "markdown",
302 | "metadata": {},
303 | "source": [
304 | "$\\Rightarrow$ $149$ is a prime number"
305 | ]
306 | },
307 | {
308 | "cell_type": "markdown",
309 | "metadata": {},
310 | "source": [
311 | "**Exercise 2.** Show that $149$ is of the form $4k+1$ and find numbers $a$ and $b$ such that $a^2 + b^2 =149$ (as in [Fermat's theorem on the sum of two squares](https://en.wikipedia.org/wiki/Fermat%27s_theorem_on_sums_of_two_squares))."
312 | ]
313 | },
314 | {
315 | "cell_type": "code",
316 | "execution_count": 59,
317 | "metadata": {
318 | "collapsed": false
319 | },
320 | "outputs": [
321 | {
322 | "data": {
323 | "text/plain": [
324 | "1"
325 | ]
326 | },
327 | "execution_count": 59,
328 | "metadata": {},
329 | "output_type": "execute_result"
330 | }
331 | ],
332 | "source": [
333 | "149 % 4"
334 | ]
335 | },
336 | {
337 | "cell_type": "code",
338 | "execution_count": 60,
339 | "metadata": {
340 | "collapsed": false
341 | },
342 | "outputs": [
343 | {
344 | "data": {
345 | "text/plain": [
346 | "149"
347 | ]
348 | },
349 | "execution_count": 60,
350 | "metadata": {},
351 | "output_type": "execute_result"
352 | }
353 | ],
354 | "source": [
355 | "7 ** 2 + 10 ** 2"
356 | ]
357 | },
358 | {
359 | "cell_type": "markdown",
360 | "metadata": {},
361 | "source": [
362 | "$\\Rightarrow 149 = 7^2 + 10^2$ "
363 | ]
364 | },
365 | {
366 | "cell_type": "markdown",
367 | "metadata": {},
368 | "source": [
369 | "**Exercise 3.** Find the largest prime number less than $1000$."
370 | ]
371 | },
372 | {
373 | "cell_type": "markdown",
374 | "metadata": {},
375 | "source": [
376 | "### `float`"
377 | ]
378 | },
379 | {
380 | "cell_type": "markdown",
381 | "metadata": {},
382 | "source": [
383 | "A `float` is a real number written with decimals and we have the operations: `+`, `-`, `*`, `/` and `**`."
384 | ]
385 | },
386 | {
387 | "cell_type": "code",
388 | "execution_count": 61,
389 | "metadata": {
390 | "collapsed": true
391 | },
392 | "outputs": [],
393 | "source": [
394 | "pi = 3.14159\n",
395 | "e = 2.71828"
396 | ]
397 | },
398 | {
399 | "cell_type": "code",
400 | "execution_count": 62,
401 | "metadata": {
402 | "collapsed": false
403 | },
404 | "outputs": [
405 | {
406 | "data": {
407 | "text/plain": [
408 | "5.85987"
409 | ]
410 | },
411 | "execution_count": 62,
412 | "metadata": {},
413 | "output_type": "execute_result"
414 | }
415 | ],
416 | "source": [
417 | "pi + e"
418 | ]
419 | },
420 | {
421 | "cell_type": "code",
422 | "execution_count": 63,
423 | "metadata": {
424 | "collapsed": false
425 | },
426 | "outputs": [
427 | {
428 | "data": {
429 | "text/plain": [
430 | "0.42330999999999985"
431 | ]
432 | },
433 | "execution_count": 63,
434 | "metadata": {},
435 | "output_type": "execute_result"
436 | }
437 | ],
438 | "source": [
439 | "pi - e"
440 | ]
441 | },
442 | {
443 | "cell_type": "code",
444 | "execution_count": 64,
445 | "metadata": {
446 | "collapsed": false
447 | },
448 | "outputs": [
449 | {
450 | "data": {
451 | "text/plain": [
452 | "8.539721265199999"
453 | ]
454 | },
455 | "execution_count": 64,
456 | "metadata": {},
457 | "output_type": "execute_result"
458 | }
459 | ],
460 | "source": [
461 | "pi * e"
462 | ]
463 | },
464 | {
465 | "cell_type": "code",
466 | "execution_count": 65,
467 | "metadata": {
468 | "collapsed": false
469 | },
470 | "outputs": [
471 | {
472 | "data": {
473 | "text/plain": [
474 | "1.1557271509925393"
475 | ]
476 | },
477 | "execution_count": 65,
478 | "metadata": {},
479 | "output_type": "execute_result"
480 | }
481 | ],
482 | "source": [
483 | "pi / e"
484 | ]
485 | },
486 | {
487 | "cell_type": "code",
488 | "execution_count": 66,
489 | "metadata": {
490 | "collapsed": false
491 | },
492 | "outputs": [
493 | {
494 | "data": {
495 | "text/plain": [
496 | "22.45905914251384"
497 | ]
498 | },
499 | "execution_count": 66,
500 | "metadata": {},
501 | "output_type": "execute_result"
502 | }
503 | ],
504 | "source": [
505 | "pi ** e"
506 | ]
507 | },
508 | {
509 | "cell_type": "markdown",
510 | "metadata": {},
511 | "source": [
512 | "## 2. Displaying output with `print`"
513 | ]
514 | },
515 | {
516 | "cell_type": "markdown",
517 | "metadata": {},
518 | "source": [
519 | "Notice that is we write several expressions within the same cell, the Jupyter notebook will only output the last expression."
520 | ]
521 | },
522 | {
523 | "cell_type": "code",
524 | "execution_count": 67,
525 | "metadata": {
526 | "collapsed": false
527 | },
528 | "outputs": [
529 | {
530 | "data": {
531 | "text/plain": [
532 | "2"
533 | ]
534 | },
535 | "execution_count": 67,
536 | "metadata": {},
537 | "output_type": "execute_result"
538 | }
539 | ],
540 | "source": [
541 | "2 ** 4\n",
542 | "8 * 13\n",
543 | "1 + 1"
544 | ]
545 | },
546 | {
547 | "cell_type": "markdown",
548 | "metadata": {},
549 | "source": [
550 | "Use the `print` function to display output."
551 | ]
552 | },
553 | {
554 | "cell_type": "code",
555 | "execution_count": 68,
556 | "metadata": {
557 | "collapsed": false
558 | },
559 | "outputs": [
560 | {
561 | "name": "stdout",
562 | "output_type": "stream",
563 | "text": [
564 | "16\n",
565 | "104\n",
566 | "2\n"
567 | ]
568 | }
569 | ],
570 | "source": [
571 | "print(2 ** 4)\n",
572 | "print(8 * 13)\n",
573 | "print(1 + 1)"
574 | ]
575 | },
576 | {
577 | "cell_type": "code",
578 | "execution_count": 69,
579 | "metadata": {
580 | "collapsed": false
581 | },
582 | "outputs": [
583 | {
584 | "name": "stdout",
585 | "output_type": "stream",
586 | "text": [
587 | "3\n",
588 | "-1.75\n",
589 | "0.00041649312786339027\n"
590 | ]
591 | }
592 | ],
593 | "source": [
594 | "x = 7\n",
595 | "y = -4\n",
596 | "print(x + y)\n",
597 | "print(x / y)\n",
598 | "print(x ** y)"
599 | ]
600 | },
601 | {
602 | "cell_type": "markdown",
603 | "metadata": {},
604 | "source": [
605 | "## 3. Logic"
606 | ]
607 | },
608 | {
609 | "cell_type": "markdown",
610 | "metadata": {},
611 | "source": [
612 | "### Comaprison and Boolean Operators"
613 | ]
614 | },
615 | {
616 | "cell_type": "markdown",
617 | "metadata": {},
618 | "source": [
619 | "We can use the comparison operators `<`, `>`, `<=`, `>=`, `==` and `!=` with the Boolean operators `and`, `or` and `not` to construct logical statements. These expressions return the Boolean values `True` or `False`."
620 | ]
621 | },
622 | {
623 | "cell_type": "code",
624 | "execution_count": 5,
625 | "metadata": {
626 | "collapsed": false
627 | },
628 | "outputs": [
629 | {
630 | "data": {
631 | "text/plain": [
632 | "True"
633 | ]
634 | },
635 | "execution_count": 5,
636 | "metadata": {},
637 | "output_type": "execute_result"
638 | }
639 | ],
640 | "source": [
641 | "5 < 7"
642 | ]
643 | },
644 | {
645 | "cell_type": "code",
646 | "execution_count": 7,
647 | "metadata": {
648 | "collapsed": false
649 | },
650 | "outputs": [
651 | {
652 | "data": {
653 | "text/plain": [
654 | "True"
655 | ]
656 | },
657 | "execution_count": 7,
658 | "metadata": {},
659 | "output_type": "execute_result"
660 | }
661 | ],
662 | "source": [
663 | "3.145 >= 3"
664 | ]
665 | },
666 | {
667 | "cell_type": "code",
668 | "execution_count": 8,
669 | "metadata": {
670 | "collapsed": false
671 | },
672 | "outputs": [
673 | {
674 | "data": {
675 | "text/plain": [
676 | "True"
677 | ]
678 | },
679 | "execution_count": 8,
680 | "metadata": {},
681 | "output_type": "execute_result"
682 | }
683 | ],
684 | "source": [
685 | "(3 < 4) and (4 < 5)"
686 | ]
687 | },
688 | {
689 | "cell_type": "code",
690 | "execution_count": 9,
691 | "metadata": {
692 | "collapsed": false
693 | },
694 | "outputs": [
695 | {
696 | "data": {
697 | "text/plain": [
698 | "True"
699 | ]
700 | },
701 | "execution_count": 9,
702 | "metadata": {},
703 | "output_type": "execute_result"
704 | }
705 | ],
706 | "source": [
707 | "(3 < 4) or (3 > 4)"
708 | ]
709 | },
710 | {
711 | "cell_type": "markdown",
712 | "metadata": {},
713 | "source": [
714 | "### `if` statement"
715 | ]
716 | },
717 | {
718 | "cell_type": "markdown",
719 | "metadata": {},
720 | "source": [
721 | "The syntax for an `if` statement is:"
722 | ]
723 | },
724 | {
725 | "cell_type": "markdown",
726 | "metadata": {},
727 | "source": [
728 | "```python\n",
729 | "if expression:\n",
730 | " ... Python code ...\n",
731 | " ... Python code ...\n",
732 | "```"
733 | ]
734 | },
735 | {
736 | "cell_type": "code",
737 | "execution_count": 10,
738 | "metadata": {
739 | "collapsed": false
740 | },
741 | "outputs": [
742 | {
743 | "name": "stdout",
744 | "output_type": "stream",
745 | "text": [
746 | "4 is less than 5\n"
747 | ]
748 | }
749 | ],
750 | "source": [
751 | "a = 4\n",
752 | "b = 5\n",
753 | "if a < b:\n",
754 | " print(a,'is less than',b)"
755 | ]
756 | },
757 | {
758 | "cell_type": "markdown",
759 | "metadata": {},
760 | "source": [
761 | "**The indentation in the definition of an `if` statement is very important!** In Python, we define blocks of code by indentation instead of brackets. This makes the code more readable. Check out the [Python 3 tutorial](https://docs.python.org/3/tutorial/introduction.html#first-steps-towards-programming) for more info."
762 | ]
763 | },
764 | {
765 | "cell_type": "markdown",
766 | "metadata": {},
767 | "source": [
768 | "## 4. Exercises"
769 | ]
770 | },
771 | {
772 | "cell_type": "markdown",
773 | "metadata": {},
774 | "source": [
775 | "**Exercise 4.** Calculate the length of the hypotenuse of a right angle triangle with shorter sides equal to $7$ and $11$."
776 | ]
777 | },
778 | {
779 | "cell_type": "markdown",
780 | "metadata": {},
781 | "source": [
782 | "**Exercise 5.** Write a logical expression which returns `True` if $1771$ is divisible by $23$ and $11$."
783 | ]
784 | },
785 | {
786 | "cell_type": "markdown",
787 | "metadata": {},
788 | "source": [
789 | "**Exercise 6.** Write a logical expression which tests if $20213$ is divisible by either $41$ or $43$. "
790 | ]
791 | },
792 | {
793 | "cell_type": "markdown",
794 | "metadata": {},
795 | "source": [
796 | "**Exercise 7.** Write a logical expression which tests if $20213$ is divisible by $41$ and $43$."
797 | ]
798 | },
799 | {
800 | "cell_type": "markdown",
801 | "metadata": {},
802 | "source": [
803 | "**Exercise 8.** Write an `if` statement which prints the statement `\"1771 is divisible by 7\"` if indeed $1771$ is divisible by $7$."
804 | ]
805 | }
806 | ],
807 | "metadata": {
808 | "kernelspec": {
809 | "display_name": "Python 3",
810 | "language": "python",
811 | "name": "python3"
812 | },
813 | "language_info": {
814 | "codemirror_mode": {
815 | "name": "ipython",
816 | "version": 3
817 | },
818 | "file_extension": ".py",
819 | "mimetype": "text/x-python",
820 | "name": "python",
821 | "nbconvert_exporter": "python",
822 | "pygments_lexer": "ipython3",
823 | "version": "3.4.3"
824 | }
825 | },
826 | "nbformat": 4,
827 | "nbformat_minor": 0
828 | }
829 |
--------------------------------------------------------------------------------
/notes-week-10/notes-03-18-16.ipynb:
--------------------------------------------------------------------------------
1 | {
2 | "cells": [
3 | {
4 | "cell_type": "markdown",
5 | "metadata": {},
6 | "source": [
7 | "# MATH 210 Introduction to Mathematical Computing\n",
8 | "\n",
9 | "## March 18, 2016\n",
10 | "\n",
11 | "Today's Agenda:\n",
12 | "\n",
13 | "1. Vector Geometry\n",
14 | " * Example: Volume of a Parallelpiped\n",
15 | " * Example: Projections\n",
16 | " * Example: Gram-Schmidt Algorithm\n",
17 | "2. Exercises"
18 | ]
19 | },
20 | {
21 | "cell_type": "code",
22 | "execution_count": 1,
23 | "metadata": {
24 | "collapsed": true
25 | },
26 | "outputs": [],
27 | "source": [
28 | "import numpy as np\n",
29 | "import scipy.linalg as la"
30 | ]
31 | },
32 | {
33 | "cell_type": "markdown",
34 | "metadata": {},
35 | "source": [
36 | "## 1. Vector Geometry\n",
37 | "\n",
38 | "We can represent vectors as 1-dimensional NumPy arrays and there are NumPy functions for the dot product and (in 3D) cross product of vectors: `np.dot` and `np.cross`. Note however that we need the linear algebra subpackage `scipy.linalg` to compute the norm of a vector.\n",
39 | "\n",
40 | "Let's create two vectors $\\mathbf{v}$ and $\\mathbf{w}$ in $\\mathbb{R}^3$ (with random integer entries contained in $[-5,5]$) and compute their dot product, cross product and norms."
41 | ]
42 | },
43 | {
44 | "cell_type": "code",
45 | "execution_count": 2,
46 | "metadata": {
47 | "collapsed": false
48 | },
49 | "outputs": [
50 | {
51 | "data": {
52 | "text/plain": [
53 | "array([-3, 1, -4])"
54 | ]
55 | },
56 | "execution_count": 2,
57 | "metadata": {},
58 | "output_type": "execute_result"
59 | }
60 | ],
61 | "source": [
62 | "v = np.random.randint(-5,5,3)\n",
63 | "v"
64 | ]
65 | },
66 | {
67 | "cell_type": "code",
68 | "execution_count": 3,
69 | "metadata": {
70 | "collapsed": false
71 | },
72 | "outputs": [
73 | {
74 | "data": {
75 | "text/plain": [
76 | "array([ 0, -3, -1])"
77 | ]
78 | },
79 | "execution_count": 3,
80 | "metadata": {},
81 | "output_type": "execute_result"
82 | }
83 | ],
84 | "source": [
85 | "w = np.random.randint(-5,5,3)\n",
86 | "w"
87 | ]
88 | },
89 | {
90 | "cell_type": "code",
91 | "execution_count": 4,
92 | "metadata": {
93 | "collapsed": false
94 | },
95 | "outputs": [
96 | {
97 | "data": {
98 | "text/plain": [
99 | "1"
100 | ]
101 | },
102 | "execution_count": 4,
103 | "metadata": {},
104 | "output_type": "execute_result"
105 | }
106 | ],
107 | "source": [
108 | "np.dot(v,w)"
109 | ]
110 | },
111 | {
112 | "cell_type": "code",
113 | "execution_count": 5,
114 | "metadata": {
115 | "collapsed": false
116 | },
117 | "outputs": [
118 | {
119 | "data": {
120 | "text/plain": [
121 | "array([-13, -3, 9])"
122 | ]
123 | },
124 | "execution_count": 5,
125 | "metadata": {},
126 | "output_type": "execute_result"
127 | }
128 | ],
129 | "source": [
130 | "np.cross(v,w)"
131 | ]
132 | },
133 | {
134 | "cell_type": "code",
135 | "execution_count": 6,
136 | "metadata": {
137 | "collapsed": false
138 | },
139 | "outputs": [
140 | {
141 | "data": {
142 | "text/plain": [
143 | "5.0990195135927845"
144 | ]
145 | },
146 | "execution_count": 6,
147 | "metadata": {},
148 | "output_type": "execute_result"
149 | }
150 | ],
151 | "source": [
152 | "la.norm(v)"
153 | ]
154 | },
155 | {
156 | "cell_type": "code",
157 | "execution_count": 7,
158 | "metadata": {
159 | "collapsed": false
160 | },
161 | "outputs": [
162 | {
163 | "data": {
164 | "text/plain": [
165 | "5.0990195135927845"
166 | ]
167 | },
168 | "execution_count": 7,
169 | "metadata": {},
170 | "output_type": "execute_result"
171 | }
172 | ],
173 | "source": [
174 | "sum([ entry**2 for entry in v ])**0.5"
175 | ]
176 | },
177 | {
178 | "cell_type": "markdown",
179 | "metadata": {},
180 | "source": [
181 | "### Volume of a Parallelpiped\n",
182 | "\n",
183 | "In 3D, the volume of the parallelpiped spanned by vectors $\\mathbf{u}$, $\\mathbf{v}$ and $\\mathbf{w}$ is\n",
184 | "\n",
185 | "$$\n",
186 | "V = \\left| \\, u \\cdot ( v \\times w ) \\, \\right|\n",
187 | "$$\n",
188 | "\n",
189 | "Define a function which takes three 1-dimensional NumPy arrays of length 3 and returns the volume of the parallelpiped spanned by those vectors."
190 | ]
191 | },
192 | {
193 | "cell_type": "code",
194 | "execution_count": 8,
195 | "metadata": {
196 | "collapsed": true
197 | },
198 | "outputs": [],
199 | "source": [
200 | "def vol_para(u,v,w):\n",
201 | " \"Compute the volume of the parallelpiped spanned by u,v and w.\"\n",
202 | " return abs( np.dot( u , np.cross(v,w) ) )"
203 | ]
204 | },
205 | {
206 | "cell_type": "code",
207 | "execution_count": 9,
208 | "metadata": {
209 | "collapsed": false
210 | },
211 | "outputs": [
212 | {
213 | "data": {
214 | "text/plain": [
215 | "1"
216 | ]
217 | },
218 | "execution_count": 9,
219 | "metadata": {},
220 | "output_type": "execute_result"
221 | }
222 | ],
223 | "source": [
224 | "u = np.array([1,0,0])\n",
225 | "v = np.array([0,1,0])\n",
226 | "w = np.array([0,0,1])\n",
227 | "vol_para(u,v,w)"
228 | ]
229 | },
230 | {
231 | "cell_type": "code",
232 | "execution_count": 10,
233 | "metadata": {
234 | "collapsed": false
235 | },
236 | "outputs": [
237 | {
238 | "data": {
239 | "text/plain": [
240 | "2"
241 | ]
242 | },
243 | "execution_count": 10,
244 | "metadata": {},
245 | "output_type": "execute_result"
246 | }
247 | ],
248 | "source": [
249 | "u = np.array([1,1,0])\n",
250 | "v = np.array([0,1,1])\n",
251 | "w = np.array([1,0,1])\n",
252 | "vol_para(u,v,w)"
253 | ]
254 | },
255 | {
256 | "cell_type": "markdown",
257 | "metadata": {},
258 | "source": [
259 | "Note that the function is written in a way that it will accept Python lists of length 3 and compute the corresponding volume."
260 | ]
261 | },
262 | {
263 | "cell_type": "code",
264 | "execution_count": 11,
265 | "metadata": {
266 | "collapsed": false
267 | },
268 | "outputs": [
269 | {
270 | "data": {
271 | "text/plain": [
272 | "2"
273 | ]
274 | },
275 | "execution_count": 11,
276 | "metadata": {},
277 | "output_type": "execute_result"
278 | }
279 | ],
280 | "source": [
281 | "vol_para([1,1,0],[0,1,1],[1,0,1])"
282 | ]
283 | },
284 | {
285 | "cell_type": "markdown",
286 | "metadata": {},
287 | "source": [
288 | "### Projections\n",
289 | "\n",
290 | "Define a function which takes two 1-dimensional NumPy arrays (or Python lists) $\\mathbf{v}$ and $\\mathbf{a}$ (in that order) and returns the projection of $v$ onto $a$:\n",
291 | "\n",
292 | "$$\n",
293 | "\\mathrm{proj}_{ \\mathbf{a} } (\\mathbf{v}) = \\frac{ \\mathbf{v} \\cdot \\mathbf{a} }{ \\mathbf{a} \\cdot \\mathbf{a} } \\ \\mathbf{a}\n",
294 | "$$"
295 | ]
296 | },
297 | {
298 | "cell_type": "code",
299 | "execution_count": 12,
300 | "metadata": {
301 | "collapsed": true
302 | },
303 | "outputs": [],
304 | "source": [
305 | "def proj(v,a):\n",
306 | " \"Compute the projection of v onto a.\"\n",
307 | " return np.dot(v,a) / np.dot(a,a) * np.array(a)"
308 | ]
309 | },
310 | {
311 | "cell_type": "code",
312 | "execution_count": 13,
313 | "metadata": {
314 | "collapsed": false
315 | },
316 | "outputs": [
317 | {
318 | "data": {
319 | "text/plain": [
320 | "array([ 1., 0.])"
321 | ]
322 | },
323 | "execution_count": 13,
324 | "metadata": {},
325 | "output_type": "execute_result"
326 | }
327 | ],
328 | "source": [
329 | "proj([1,1],[1,0])"
330 | ]
331 | },
332 | {
333 | "cell_type": "code",
334 | "execution_count": 14,
335 | "metadata": {
336 | "collapsed": false
337 | },
338 | "outputs": [
339 | {
340 | "data": {
341 | "text/plain": [
342 | "array([ 1., 1., 0.])"
343 | ]
344 | },
345 | "execution_count": 14,
346 | "metadata": {},
347 | "output_type": "execute_result"
348 | }
349 | ],
350 | "source": [
351 | "proj([1,1,1],[1,1,0])"
352 | ]
353 | },
354 | {
355 | "cell_type": "markdown",
356 | "metadata": {
357 | "collapsed": true
358 | },
359 | "source": [
360 | "### Gram-Schmidt Algorithm\n",
361 | "\n",
362 | "The Gram-Schmidt algorithm takes a basis $\\{ \\mathbf{v}_1, \\dots , \\mathbf{v}_n \\}$ of a vector space $V$ and produces an orthonormal basis $\\{ \\mathbf{e}_1, \\dots , \\mathbf{e}_n \\}$ of $V$:\n",
363 | "\n",
364 | "\\begin{align}\n",
365 | "\\mathbf{x}_1 &= \\mathbf{v}_1 \\\\\n",
366 | "\\mathbf{x}_2 &= \\mathbf{v}_2 - \\mathrm{proj}_{\\mathbf{x}_1}(\\mathbf{v}_2) \\\\\n",
367 | " & \\vdots \\\\\n",
368 | "\\mathbf{x}_n &= \\mathbf{v}_n - \\mathrm{proj}_{\\mathbf{x}_1}(\\mathbf{v}_n) - \\mathrm{proj}_{\\mathbf{x}_2}(\\mathbf{v}_n) - \\cdots - \\mathrm{proj}_{\\mathbf{x}_{n-1}}(\\mathbf{v}_n)\n",
369 | "\\end{align}\n",
370 | "\n",
371 | "and then normalize $\\mathbf{e}_i = \\mathbf{x}_i / ||\\mathbf{x}_i||$.\n",
372 | "\n",
373 | "Use the Gram-Schmidt algorithm to turn the following basis into a orthonormal basis of $\\mathbb{R}^4$:\n",
374 | "\n",
375 | "$$\n",
376 | "\\mathbf{v}_1 = \\begin{bmatrix} 1 & 2 & 3 & 4 \\end{bmatrix} \\ , \\ \\\n",
377 | "\\mathbf{v}_2 = \\begin{bmatrix} 1 & 2 & 3 & 2 \\end{bmatrix} \\ , \\ \\\n",
378 | "\\mathbf{v}_3 = \\begin{bmatrix} 1 & -2 & 3 & 4 \\end{bmatrix} \\ , \\ \\\n",
379 | "\\mathbf{v}_4 = \\begin{bmatrix} 3 & 2 & 3 & 4 \\end{bmatrix}\n",
380 | "$$\n",
381 | "\n",
382 | "First, let's check that this is a basis of $\\mathbb{R^4}$:"
383 | ]
384 | },
385 | {
386 | "cell_type": "code",
387 | "execution_count": 15,
388 | "metadata": {
389 | "collapsed": false
390 | },
391 | "outputs": [
392 | {
393 | "name": "stdout",
394 | "output_type": "stream",
395 | "text": [
396 | "[[ 1 2 3 4]\n",
397 | " [ 1 2 3 2]\n",
398 | " [ 1 -2 3 4]\n",
399 | " [ 3 2 3 4]]\n"
400 | ]
401 | }
402 | ],
403 | "source": [
404 | "V = np.array([[1,2,3,4],[1,2,3,2],[1,-2,3,4],[3,2,3,4]])\n",
405 | "print(V)"
406 | ]
407 | },
408 | {
409 | "cell_type": "code",
410 | "execution_count": 16,
411 | "metadata": {
412 | "collapsed": false
413 | },
414 | "outputs": [
415 | {
416 | "data": {
417 | "text/plain": [
418 | "-48.0"
419 | ]
420 | },
421 | "execution_count": 16,
422 | "metadata": {},
423 | "output_type": "execute_result"
424 | }
425 | ],
426 | "source": [
427 | "la.det(V)"
428 | ]
429 | },
430 | {
431 | "cell_type": "markdown",
432 | "metadata": {},
433 | "source": [
434 | "Therefore, these vectors are linearly independent. As we proceed with the Gram-Schmidt algorithm, let's assemble the vectors $\\mathbf{x}_i$ into the rows of a NumPy array $X$ which we intialize as a zero matrix."
435 | ]
436 | },
437 | {
438 | "cell_type": "code",
439 | "execution_count": 17,
440 | "metadata": {
441 | "collapsed": false
442 | },
443 | "outputs": [
444 | {
445 | "name": "stdout",
446 | "output_type": "stream",
447 | "text": [
448 | "[[ 0. 0. 0. 0.]\n",
449 | " [ 0. 0. 0. 0.]\n",
450 | " [ 0. 0. 0. 0.]\n",
451 | " [ 0. 0. 0. 0.]]\n"
452 | ]
453 | }
454 | ],
455 | "source": [
456 | "X = np.zeros((4,4))\n",
457 | "print(X)"
458 | ]
459 | },
460 | {
461 | "cell_type": "markdown",
462 | "metadata": {},
463 | "source": [
464 | "The first two steps of the Gram-Schmidt process are:"
465 | ]
466 | },
467 | {
468 | "cell_type": "code",
469 | "execution_count": 18,
470 | "metadata": {
471 | "collapsed": false
472 | },
473 | "outputs": [
474 | {
475 | "name": "stdout",
476 | "output_type": "stream",
477 | "text": [
478 | "[[ 1. 2. 3. 4. ]\n",
479 | " [ 0.26666667 0.53333333 0.8 -0.93333333]\n",
480 | " [ 0. 0. 0. 0. ]\n",
481 | " [ 0. 0. 0. 0. ]]\n"
482 | ]
483 | }
484 | ],
485 | "source": [
486 | "X[0,:] = V[0,:]\n",
487 | "X[1,:] = V[1,:] - proj(V[1,:],X[0,:])\n",
488 | "print(X)"
489 | ]
490 | },
491 | {
492 | "cell_type": "markdown",
493 | "metadata": {},
494 | "source": [
495 | "Let's check if $\\mathbf{x}_1$ and $\\mathbf{x}_2$ are perpendicular:"
496 | ]
497 | },
498 | {
499 | "cell_type": "code",
500 | "execution_count": 19,
501 | "metadata": {
502 | "collapsed": false
503 | },
504 | "outputs": [
505 | {
506 | "data": {
507 | "text/plain": [
508 | "1.7763568394002505e-15"
509 | ]
510 | },
511 | "execution_count": 19,
512 | "metadata": {},
513 | "output_type": "execute_result"
514 | }
515 | ],
516 | "source": [
517 | "np.dot( X[0,:] , X[1,:] )"
518 | ]
519 | },
520 | {
521 | "cell_type": "markdown",
522 | "metadata": {},
523 | "source": [
524 | "Success! Let's proceed with the next two steps:"
525 | ]
526 | },
527 | {
528 | "cell_type": "code",
529 | "execution_count": 20,
530 | "metadata": {
531 | "collapsed": false
532 | },
533 | "outputs": [
534 | {
535 | "name": "stdout",
536 | "output_type": "stream",
537 | "text": [
538 | "[[ 1.00000000e+00 2.00000000e+00 3.00000000e+00 4.00000000e+00]\n",
539 | " [ 2.66666667e-01 5.33333333e-01 8.00000000e-01 -9.33333333e-01]\n",
540 | " [ 5.71428571e-01 -2.85714286e+00 1.71428571e+00 1.33226763e-15]\n",
541 | " [ 1.80000000e+00 3.33066907e-16 -6.00000000e-01 6.99440506e-16]]\n"
542 | ]
543 | }
544 | ],
545 | "source": [
546 | "X[2,:] = V[2,:] - proj(V[2,:],X[0,:]) - proj(V[2,:],X[1,:])\n",
547 | "X[3,:] = V[3,:] - proj(V[3,:],X[0,:]) - proj(V[3,:],X[1,:]) - proj(V[3,:],X[2,:])\n",
548 | "print(X)"
549 | ]
550 | },
551 | {
552 | "cell_type": "markdown",
553 | "metadata": {},
554 | "source": [
555 | "Finally, let's normalize the vectors $\\mathbf{x}_i$ to obtain an orthonormal basis:"
556 | ]
557 | },
558 | {
559 | "cell_type": "code",
560 | "execution_count": 21,
561 | "metadata": {
562 | "collapsed": false
563 | },
564 | "outputs": [
565 | {
566 | "name": "stdout",
567 | "output_type": "stream",
568 | "text": [
569 | "[[ 1.82574186e-01 3.65148372e-01 5.47722558e-01 7.30296743e-01]\n",
570 | " [ 1.95180015e-01 3.90360029e-01 5.85540044e-01 -6.83130051e-01]\n",
571 | " [ 1.69030851e-01 -8.45154255e-01 5.07092553e-01 3.94090079e-16]\n",
572 | " [ 9.48683298e-01 1.75541673e-16 -3.16227766e-01 3.68637514e-16]]\n"
573 | ]
574 | }
575 | ],
576 | "source": [
577 | "for i in [0,1,2,3]:\n",
578 | " X[i,:] = X[i,:] / la.norm(X[i,:])\n",
579 | "\n",
580 | "print(X)"
581 | ]
582 | },
583 | {
584 | "cell_type": "markdown",
585 | "metadata": {},
586 | "source": [
587 | "To check our work, we turn the NumPy array $X$ into a NumPy matrix $Q$ and compute $Q Q^T$. If the rest is the identity, then we have succeeded!"
588 | ]
589 | },
590 | {
591 | "cell_type": "code",
592 | "execution_count": 22,
593 | "metadata": {
594 | "collapsed": false
595 | },
596 | "outputs": [
597 | {
598 | "name": "stdout",
599 | "output_type": "stream",
600 | "text": [
601 | "[[ 1.00000000e+00 1.94289029e-16 1.11022302e-16 -5.55111512e-17]\n",
602 | " [ 1.94289029e-16 1.00000000e+00 -3.88578059e-16 -6.38378239e-16]\n",
603 | " [ 1.11022302e-16 -3.88578059e-16 1.00000000e+00 -4.99600361e-16]\n",
604 | " [ -5.55111512e-17 -6.38378239e-16 -4.99600361e-16 1.00000000e+00]]\n"
605 | ]
606 | }
607 | ],
608 | "source": [
609 | "Q = np.matrix(X)\n",
610 | "I = Q * Q.T\n",
611 | "print(I)"
612 | ]
613 | },
614 | {
615 | "cell_type": "markdown",
616 | "metadata": {},
617 | "source": [
618 | "Let's round $I$ to 2 decimal places to see it more clearly."
619 | ]
620 | },
621 | {
622 | "cell_type": "code",
623 | "execution_count": 23,
624 | "metadata": {
625 | "collapsed": false
626 | },
627 | "outputs": [
628 | {
629 | "data": {
630 | "text/plain": [
631 | "array([[ 1., 0., 0., -0.],\n",
632 | " [ 0., 1., -0., -0.],\n",
633 | " [ 0., -0., 1., -0.],\n",
634 | " [-0., -0., -0., 1.]])"
635 | ]
636 | },
637 | "execution_count": 23,
638 | "metadata": {},
639 | "output_type": "execute_result"
640 | }
641 | ],
642 | "source": [
643 | "np.round(I,2)"
644 | ]
645 | },
646 | {
647 | "cell_type": "markdown",
648 | "metadata": {},
649 | "source": [
650 | "Finally, let's round $Q$ to two decimal places to see our final result more clearly:"
651 | ]
652 | },
653 | {
654 | "cell_type": "code",
655 | "execution_count": 24,
656 | "metadata": {
657 | "collapsed": false
658 | },
659 | "outputs": [
660 | {
661 | "data": {
662 | "text/plain": [
663 | "array([[ 0.18, 0.37, 0.55, 0.73],\n",
664 | " [ 0.2 , 0.39, 0.59, -0.68],\n",
665 | " [ 0.17, -0.85, 0.51, 0. ],\n",
666 | " [ 0.95, 0. , -0.32, 0. ]])"
667 | ]
668 | },
669 | "execution_count": 24,
670 | "metadata": {},
671 | "output_type": "execute_result"
672 | }
673 | ],
674 | "source": [
675 | "np.round(Q,2)"
676 | ]
677 | },
678 | {
679 | "cell_type": "markdown",
680 | "metadata": {},
681 | "source": [
682 | "## 2. Exercises"
683 | ]
684 | },
685 | {
686 | "cell_type": "markdown",
687 | "metadata": {},
688 | "source": [
689 | "**Exercise.** Compute the dot product, cross product and norms of the vectors $\\mathbf{v}$ and $\\mathbf{w}$:\n",
690 | "\n",
691 | "(a) $\\mathbf{v} = \\begin{bmatrix} 1 & -1 & 2 \\end{bmatrix}$ and $\\mathbf{w} = \\begin{bmatrix} 3 & 2 & -1 \\end{bmatrix}$\n",
692 | "\n",
693 | "(b) $\\mathbf{v} = \\begin{bmatrix} 3 & 4 & -1 \\end{bmatrix}$ and $\\mathbf{w} = \\begin{bmatrix} 0 & 1 & 3 \\end{bmatrix}$"
694 | ]
695 | },
696 | {
697 | "cell_type": "markdown",
698 | "metadata": {},
699 | "source": [
700 | "**Exercise.** Compute the projection of $\\mathbf{v} = \\begin{bmatrix} 2 & 5 & -1 \\end{bmatrix}$ onto the plane spanned by $\\mathbf{a} = \\begin{bmatrix} 1 & 1 & -1 \\end{bmatrix}$ and $\\mathbf{b} = \\begin{bmatrix} 4 & 0 & 1 \\end{bmatrix}$"
701 | ]
702 | },
703 | {
704 | "cell_type": "markdown",
705 | "metadata": {},
706 | "source": [
707 | "**Exercise.** Use the Gram-Schmidt algorithm to convert the following basis into an orthonormal basis of $\\mathbb{R}^3$:\n",
708 | "\n",
709 | "$$\n",
710 | "\\mathbf{v}_1 = \\begin{bmatrix} 1 & 1 & -1 \\end{bmatrix} \\ , \\ \\ \n",
711 | "\\mathbf{v}_2 = \\begin{bmatrix} 4 & -2 & 1 \\end{bmatrix} \\ , \\ \\\n",
712 | "\\mathbf{v}_3 = \\begin{bmatrix} 1 & 1 & 0 \\end{bmatrix}\n",
713 | "$$"
714 | ]
715 | }
716 | ],
717 | "metadata": {
718 | "kernelspec": {
719 | "display_name": "Python 3",
720 | "language": "python",
721 | "name": "python3"
722 | },
723 | "language_info": {
724 | "codemirror_mode": {
725 | "name": "ipython",
726 | "version": 3
727 | },
728 | "file_extension": ".py",
729 | "mimetype": "text/x-python",
730 | "name": "python",
731 | "nbconvert_exporter": "python",
732 | "pygments_lexer": "ipython3",
733 | "version": "3.4.3"
734 | }
735 | },
736 | "nbformat": 4,
737 | "nbformat_minor": 0
738 | }
739 |
--------------------------------------------------------------------------------
/notes-week-02/notes-01-15-16.ipynb:
--------------------------------------------------------------------------------
1 | {
2 | "cells": [
3 | {
4 | "cell_type": "markdown",
5 | "metadata": {},
6 | "source": [
7 | "**IMPORTANT:** Make sure the kernel is set to Python 3\n",
8 | "\n",
9 | "---\n",
10 | "\n",
11 | "# MATH 210 Introduction to Mathematical Computing\n",
12 | "\n",
13 | "## January 15, 2015\n",
14 | "\n",
15 | "Today's Agenda:\n",
16 | "\n",
17 | "1. More about lists and strings\n",
18 | " * Indexing and slicing lists and strings\n",
19 | " * Compute the length of a list or string with `len`\n",
20 | " * Changing and appending items in a list (but NOT a string)\n",
21 | "2. `for` loops\n",
22 | "3. Functions\n",
23 | "4. Exercises\n",
24 | "\n",
25 | "Check out the [Python 3 tutorial](https://docs.python.org/3/tutorial/index.html) for more information. In particular, check out the [documentation](https://docs.python.org/3/library/functions.html) for the list of built-in Python functions including some we have already used: `print()`, `range()`, `len()`, `type()`, `int()`, `float()`, `list()` and `str()`."
26 | ]
27 | },
28 | {
29 | "cell_type": "markdown",
30 | "metadata": {},
31 | "source": [
32 | "## 1. More about lists and strings"
33 | ]
34 | },
35 | {
36 | "cell_type": "markdown",
37 | "metadata": {},
38 | "source": [
39 | "### Indexing and slicing lists and strings\n",
40 | "\n",
41 | "We can access an item in a list by its index. Notice a couple of features:\n",
42 | "\n",
43 | "* a list (or string) starts at index 0\n",
44 | "* use negative indices to count backwards from the last item"
45 | ]
46 | },
47 | {
48 | "cell_type": "code",
49 | "execution_count": 1,
50 | "metadata": {
51 | "collapsed": false
52 | },
53 | "outputs": [
54 | {
55 | "name": "stdout",
56 | "output_type": "stream",
57 | "text": [
58 | "1\n",
59 | "16\n",
60 | "49\n",
61 | "25\n"
62 | ]
63 | }
64 | ],
65 | "source": [
66 | "squares = [1,4,9,16,25,36,49]\n",
67 | "print(squares[0])\n",
68 | "print(squares[3])\n",
69 | "print(squares[-1])\n",
70 | "print(squares[-3])"
71 | ]
72 | },
73 | {
74 | "cell_type": "markdown",
75 | "metadata": {},
76 | "source": [
77 | "We can access a sublist by slicing (see the [section](https://docs.python.org/3/tutorial/introduction.html#lists) about lists in the Python 3 tutorial):"
78 | ]
79 | },
80 | {
81 | "cell_type": "code",
82 | "execution_count": 2,
83 | "metadata": {
84 | "collapsed": false
85 | },
86 | "outputs": [
87 | {
88 | "name": "stdout",
89 | "output_type": "stream",
90 | "text": [
91 | "[4, 9, 16]\n",
92 | "[1, 9, 25]\n",
93 | "[1, 4]\n",
94 | "[9, 16, 25, 36, 49]\n"
95 | ]
96 | }
97 | ],
98 | "source": [
99 | "print(squares[1:4])\n",
100 | "print(squares[0:6:2])\n",
101 | "print(squares[:2])\n",
102 | "print(squares[2:])"
103 | ]
104 | },
105 | {
106 | "cell_type": "markdown",
107 | "metadata": {},
108 | "source": [
109 | "And the same indexing and slicing works for strings:"
110 | ]
111 | },
112 | {
113 | "cell_type": "code",
114 | "execution_count": 3,
115 | "metadata": {
116 | "collapsed": false
117 | },
118 | "outputs": [
119 | {
120 | "name": "stdout",
121 | "output_type": "stream",
122 | "text": [
123 | "i\n",
124 | "s\n",
125 | "trick\n",
126 | "tikW\n"
127 | ]
128 | }
129 | ],
130 | "source": [
131 | "name = 'Patrick Walls'\n",
132 | "print(name[4])\n",
133 | "print(name[-1])\n",
134 | "print(name[2:7])\n",
135 | "print(name[2:10:2])"
136 | ]
137 | },
138 | {
139 | "cell_type": "markdown",
140 | "metadata": {},
141 | "source": [
142 | "### The `len` function\n",
143 | "\n",
144 | "The `len` function simply returns the length of a list or string!"
145 | ]
146 | },
147 | {
148 | "cell_type": "code",
149 | "execution_count": 4,
150 | "metadata": {
151 | "collapsed": false
152 | },
153 | "outputs": [
154 | {
155 | "data": {
156 | "text/plain": [
157 | "10"
158 | ]
159 | },
160 | "execution_count": 4,
161 | "metadata": {},
162 | "output_type": "execute_result"
163 | }
164 | ],
165 | "source": [
166 | "len([0,1,2,3,4,5,6,7,8,9])"
167 | ]
168 | },
169 | {
170 | "cell_type": "code",
171 | "execution_count": 5,
172 | "metadata": {
173 | "collapsed": false
174 | },
175 | "outputs": [
176 | {
177 | "data": {
178 | "text/plain": [
179 | "26"
180 | ]
181 | },
182 | "execution_count": 5,
183 | "metadata": {},
184 | "output_type": "execute_result"
185 | }
186 | ],
187 | "source": [
188 | "len('abcdefghijklmnopqrstuvwxyz')"
189 | ]
190 | },
191 | {
192 | "cell_type": "markdown",
193 | "metadata": {},
194 | "source": [
195 | "Check out the list of built-in Python fucntions in the [documentation](https://docs.python.org/3/library/functions.html)."
196 | ]
197 | },
198 | {
199 | "cell_type": "markdown",
200 | "metadata": {},
201 | "source": [
202 | "### Manipulating lists (but NOT strings)"
203 | ]
204 | },
205 | {
206 | "cell_type": "markdown",
207 | "metadata": {},
208 | "source": [
209 | "We can reassign an item in a list:"
210 | ]
211 | },
212 | {
213 | "cell_type": "code",
214 | "execution_count": 6,
215 | "metadata": {
216 | "collapsed": false
217 | },
218 | "outputs": [
219 | {
220 | "name": "stdout",
221 | "output_type": "stream",
222 | "text": [
223 | "[1, 4, 9, 16, 25, 36, 49]\n",
224 | "[1, 'four', 9, 16, 25, 36, 49]\n"
225 | ]
226 | }
227 | ],
228 | "source": [
229 | "squares = [1,4,9,16,25,36,49]\n",
230 | "print(squares)\n",
231 | "squares[1] = 'four'\n",
232 | "print(squares)"
233 | ]
234 | },
235 | {
236 | "cell_type": "markdown",
237 | "metadata": {},
238 | "source": [
239 | "We can also append an item to a list using the **append method**:"
240 | ]
241 | },
242 | {
243 | "cell_type": "code",
244 | "execution_count": 7,
245 | "metadata": {
246 | "collapsed": false
247 | },
248 | "outputs": [
249 | {
250 | "name": "stdout",
251 | "output_type": "stream",
252 | "text": [
253 | "[1, 'four', 9, 16, 25, 36, 49, 64]\n"
254 | ]
255 | }
256 | ],
257 | "source": [
258 | "squares.append(64)\n",
259 | "print(squares)"
260 | ]
261 | },
262 | {
263 | "cell_type": "markdown",
264 | "metadata": {},
265 | "source": [
266 | "We will talk more about **methods** later in the course! For now, you can read about methods in object-oriented programming on [Wikipedia](https://en.wikipedia.org/wiki/Method_%28computer_programming%29)."
267 | ]
268 | },
269 | {
270 | "cell_type": "markdown",
271 | "metadata": {},
272 | "source": [
273 | "Notice what happens when we try to change a character in a string:"
274 | ]
275 | },
276 | {
277 | "cell_type": "code",
278 | "execution_count": 8,
279 | "metadata": {
280 | "collapsed": false
281 | },
282 | "outputs": [
283 | {
284 | "name": "stdout",
285 | "output_type": "stream",
286 | "text": [
287 | "mathematics\n"
288 | ]
289 | }
290 | ],
291 | "source": [
292 | "word = 'mathematics'\n",
293 | "print(word)"
294 | ]
295 | },
296 | {
297 | "cell_type": "code",
298 | "execution_count": 9,
299 | "metadata": {
300 | "collapsed": false
301 | },
302 | "outputs": [
303 | {
304 | "ename": "TypeError",
305 | "evalue": "'str' object does not support item assignment",
306 | "output_type": "error",
307 | "traceback": [
308 | "\u001b[0;31m---------------------------------------------------------------------------\u001b[0m",
309 | "\u001b[0;31mTypeError\u001b[0m Traceback (most recent call last)",
310 | "\u001b[0;32m\u001b[0m in \u001b[0;36m\u001b[0;34m()\u001b[0m\n\u001b[0;32m----> 1\u001b[0;31m \u001b[0mword\u001b[0m\u001b[0;34m[\u001b[0m\u001b[0;36m0\u001b[0m\u001b[0;34m]\u001b[0m \u001b[0;34m=\u001b[0m \u001b[0;34m'M'\u001b[0m\u001b[0;34m\u001b[0m\u001b[0m\n\u001b[0m",
311 | "\u001b[0;31mTypeError\u001b[0m: 'str' object does not support item assignment"
312 | ]
313 | }
314 | ],
315 | "source": [
316 | "word[0] = 'M'"
317 | ]
318 | },
319 | {
320 | "cell_type": "markdown",
321 | "metadata": {},
322 | "source": [
323 | "Strings are [immutable](https://docs.python.org/3/glossary.html#term-immutable)!"
324 | ]
325 | },
326 | {
327 | "cell_type": "markdown",
328 | "metadata": {},
329 | "source": [
330 | "## 2. `for` Loops"
331 | ]
332 | },
333 | {
334 | "cell_type": "markdown",
335 | "metadata": {},
336 | "source": [
337 | "To write a `for` loop, we use the syntax:\n",
338 | "\n",
339 | "```python\n",
340 | "for item in iterable:\n",
341 | " Write Python code here\n",
342 | " Write Python code here\n",
343 | " Write Python code here\n",
344 | "```"
345 | ]
346 | },
347 | {
348 | "cell_type": "markdown",
349 | "metadata": {},
350 | "source": [
351 | "Important notes:\n",
352 | "\n",
353 | "1. An **iterable** is any kind of Python object which looks like a sequence such as a **list** or a **string** (or a generator like `range(0,10)`).\n",
354 | "2. **Indentation is very important**. All the lines after the `for` statement are indented the same standard 4 spaces and therefore form the block of code which is executed for each iteration through the loop."
355 | ]
356 | },
357 | {
358 | "cell_type": "code",
359 | "execution_count": null,
360 | "metadata": {
361 | "collapsed": false
362 | },
363 | "outputs": [],
364 | "source": [
365 | "for number in [1,2,3,4,5,6,7,8,9]:\n",
366 | " square = number ** 2\n",
367 | " print('The square of', number, 'is', square)"
368 | ]
369 | },
370 | {
371 | "cell_type": "markdown",
372 | "metadata": {},
373 | "source": [
374 | "We can also use the `range` function:"
375 | ]
376 | },
377 | {
378 | "cell_type": "code",
379 | "execution_count": null,
380 | "metadata": {
381 | "collapsed": false
382 | },
383 | "outputs": [],
384 | "source": [
385 | "for number in range(0,10):\n",
386 | " square = number ** 2\n",
387 | " print('The square of', number, 'is', square)"
388 | ]
389 | },
390 | {
391 | "cell_type": "code",
392 | "execution_count": null,
393 | "metadata": {
394 | "collapsed": false
395 | },
396 | "outputs": [],
397 | "source": [
398 | "my_name = 'Patrick'\n",
399 | "for letter in my_name:\n",
400 | " print('Give me a', letter + '!')\n",
401 | "print('What does that spell?', my_name + '!')"
402 | ]
403 | },
404 | {
405 | "cell_type": "code",
406 | "execution_count": null,
407 | "metadata": {
408 | "collapsed": false
409 | },
410 | "outputs": [],
411 | "source": [
412 | "my_list = ['Hey!',3.14159,['a',1]]\n",
413 | "for item in my_list:\n",
414 | " print(item)"
415 | ]
416 | },
417 | {
418 | "cell_type": "markdown",
419 | "metadata": {},
420 | "source": [
421 | "**Exercise 1.** Write a `for` loop which tests if an integer $n$ is divisible by any integer $m \\leq \\sqrt{n}$."
422 | ]
423 | },
424 | {
425 | "cell_type": "code",
426 | "execution_count": null,
427 | "metadata": {
428 | "collapsed": false
429 | },
430 | "outputs": [],
431 | "source": [
432 | "n = 121\n",
433 | "N = int(n**0.5)\n",
434 | "for m in range(1,N+1):\n",
435 | " if (n % m == 0):\n",
436 | " print(n,'is divisible by',m)\n",
437 | " else:\n",
438 | " print(n,'is not divisible by',m)"
439 | ]
440 | },
441 | {
442 | "cell_type": "markdown",
443 | "metadata": {},
444 | "source": [
445 | "**Exercise 2.** The sequence of Fibonacci numbers 1, 1, 2, 3, 5, etc. is defined by the recursive formula\n",
446 | "$$\n",
447 | "\\begin{align*}\n",
448 | "x_0 &= 1 \\\\\n",
449 | "x_1 &= 1 \\\\\n",
450 | "x_n &= x_{n-1} + x_{n-2}\n",
451 | "\\end{align*}\n",
452 | "$$\n",
453 | "Let's say that the first Fibonacci number is 1 and the second is 2 (so that we don't count 1 twice as the first and second Fibonacci number). Then the first 5 Fibonacci numbers are: 1, 2, 3, 5, and 8. Given an integer $N$, write a `for` loop which constructs a Python list of the first $N$ Fibonacci numbers. What is the 100th Fibonacci number?"
454 | ]
455 | },
456 | {
457 | "cell_type": "code",
458 | "execution_count": null,
459 | "metadata": {
460 | "collapsed": false
461 | },
462 | "outputs": [],
463 | "source": [
464 | "N=101\n",
465 | "fib_list = [1,1]\n",
466 | "for n in range(2,N+1):\n",
467 | " fib_list.append( fib_list[n-1] + fib_list[n-2] )\n",
468 | "print(fib_list[100])"
469 | ]
470 | },
471 | {
472 | "cell_type": "markdown",
473 | "metadata": {},
474 | "source": [
475 | "Notice that we don't actually need to construct the complete list of Fibonacci numbers to find the 100th Fibonacci number. We could have just done the following:"
476 | ]
477 | },
478 | {
479 | "cell_type": "code",
480 | "execution_count": null,
481 | "metadata": {
482 | "collapsed": false
483 | },
484 | "outputs": [],
485 | "source": [
486 | "N = 100\n",
487 | "fib_n_minus_1 = 1\n",
488 | "fib_n_minus_2 = 1\n",
489 | "for n in range(2,N+1):\n",
490 | " # Calculate the nth Fibonacci number\n",
491 | " fib_n = fib_n_minus_1 + fib_n_minus_2\n",
492 | " # Redefine the two previous Fibonacci numbers for the next iteration of the loop\n",
493 | " fib_n_minus_2 = fib_n_minus_1\n",
494 | " fib_n_minus_1 = fib_n\n",
495 | "print(fib_n)"
496 | ]
497 | },
498 | {
499 | "cell_type": "markdown",
500 | "metadata": {},
501 | "source": [
502 | "**Exercise 3.** Given a string `s`, write a `for` loop which counts the number of vowels in `s`. Use the operator `in`. For example:"
503 | ]
504 | },
505 | {
506 | "cell_type": "code",
507 | "execution_count": null,
508 | "metadata": {
509 | "collapsed": false
510 | },
511 | "outputs": [],
512 | "source": [
513 | "'a' in ['a','b','c']"
514 | ]
515 | },
516 | {
517 | "cell_type": "markdown",
518 | "metadata": {},
519 | "source": [
520 | "**Exercise 4.** Create a list (in increasing order) of all the numbers less than 2000 which are multiples of either 7 or 8."
521 | ]
522 | },
523 | {
524 | "cell_type": "markdown",
525 | "metadata": {},
526 | "source": [
527 | "**Exercise 5.** A [Pythagorean triple](https://en.wikipedia.org/wiki/Pythagorean_triple) consists of three integers $a$, $b$ and $c$ which satisfy $a^2 + b^2 = c^2$. Given a number $N$, write a loop which constructs the list of all the Pythagorean triples with $c \\leq N$."
528 | ]
529 | },
530 | {
531 | "cell_type": "markdown",
532 | "metadata": {},
533 | "source": [
534 | "## 3. Functions"
535 | ]
536 | },
537 | {
538 | "cell_type": "markdown",
539 | "metadata": {},
540 | "source": [
541 | "To define a function, we use the syntax:\n",
542 | "\n",
543 | "```python\n",
544 | "def function_name(x,y,z):\n",
545 | " Python code to do calculations\n",
546 | " return Some result\n",
547 | "```"
548 | ]
549 | },
550 | {
551 | "cell_type": "markdown",
552 | "metadata": {},
553 | "source": [
554 | "For example, let's define a function which takes one numerical input $x$ and return the value $x^2$."
555 | ]
556 | },
557 | {
558 | "cell_type": "code",
559 | "execution_count": null,
560 | "metadata": {
561 | "collapsed": true
562 | },
563 | "outputs": [],
564 | "source": [
565 | "def squared(x):\n",
566 | " return x ** 2"
567 | ]
568 | },
569 | {
570 | "cell_type": "markdown",
571 | "metadata": {},
572 | "source": [
573 | "And now let's call our function `squared`:"
574 | ]
575 | },
576 | {
577 | "cell_type": "code",
578 | "execution_count": null,
579 | "metadata": {
580 | "collapsed": false
581 | },
582 | "outputs": [],
583 | "source": [
584 | "print(squared(2))\n",
585 | "print(squared(13))\n",
586 | "print(squared(245))"
587 | ]
588 | },
589 | {
590 | "cell_type": "markdown",
591 | "metadata": {},
592 | "source": [
593 | "Now let's define a function which takes two numeical inputs $x$ and $y$ and returns the mean $(x+y)/2$."
594 | ]
595 | },
596 | {
597 | "cell_type": "code",
598 | "execution_count": null,
599 | "metadata": {
600 | "collapsed": true
601 | },
602 | "outputs": [],
603 | "source": [
604 | "def mean(x,y):\n",
605 | " return (x+y)/2"
606 | ]
607 | },
608 | {
609 | "cell_type": "code",
610 | "execution_count": null,
611 | "metadata": {
612 | "collapsed": false
613 | },
614 | "outputs": [],
615 | "source": [
616 | "print(mean(2,3))\n",
617 | "print(mean(2023,1032))"
618 | ]
619 | },
620 | {
621 | "cell_type": "markdown",
622 | "metadata": {},
623 | "source": [
624 | "Let's define a function which takes a string (or a list) and returns the last letter in the string (or the last item in the list)."
625 | ]
626 | },
627 | {
628 | "cell_type": "code",
629 | "execution_count": null,
630 | "metadata": {
631 | "collapsed": true
632 | },
633 | "outputs": [],
634 | "source": [
635 | "def last(word):\n",
636 | " return word[-1]"
637 | ]
638 | },
639 | {
640 | "cell_type": "code",
641 | "execution_count": null,
642 | "metadata": {
643 | "collapsed": false
644 | },
645 | "outputs": [],
646 | "source": [
647 | "last('Mathematics')"
648 | ]
649 | },
650 | {
651 | "cell_type": "code",
652 | "execution_count": null,
653 | "metadata": {
654 | "collapsed": false
655 | },
656 | "outputs": [],
657 | "source": [
658 | "last(['Math','210'])"
659 | ]
660 | },
661 | {
662 | "cell_type": "markdown",
663 | "metadata": {},
664 | "source": [
665 | "**Exercise 6.** Write a function called `letter_count` which takes two string inputs, `word` and `letter`, and returns the number of times the letter appears in the word."
666 | ]
667 | },
668 | {
669 | "cell_type": "markdown",
670 | "metadata": {},
671 | "source": [
672 | "**Exercise 7.** Write a function called `det` which takes a list of 4 numbers `[a,b,c,d]` which represents the matrix $\\begin{bmatrix} a & b \\\\ c & d \\end{bmatrix}$ and returns the determinant."
673 | ]
674 | },
675 | {
676 | "cell_type": "markdown",
677 | "metadata": {},
678 | "source": [
679 | "**Exercise 8.** Write a function called `factorial` which takes an input $n$ and returns the factorial $n!$. (Do not import the `math` package or any other Python package.)"
680 | ]
681 | },
682 | {
683 | "cell_type": "markdown",
684 | "metadata": {},
685 | "source": [
686 | "## 4. Exercises"
687 | ]
688 | },
689 | {
690 | "cell_type": "markdown",
691 | "metadata": {},
692 | "source": [
693 | "**Exercise 9.** Write a function called `is_prime` which takes an integer $n$ and returns the Boolean value `True` if $n$ is prime and `False` if $n$ is not prime."
694 | ]
695 | },
696 | {
697 | "cell_type": "markdown",
698 | "metadata": {},
699 | "source": [
700 | "**Exercise 10.** Use the function `is_prime` above to find the following:\n",
701 | "\n",
702 | "1. The sum of all the primes less than 1000\n",
703 | "2. All the primes between 100 and 150\n",
704 | "3. The largest prime less than 4000"
705 | ]
706 | },
707 | {
708 | "cell_type": "markdown",
709 | "metadata": {},
710 | "source": [
711 | "**Exercise 11.** Use the function `is_prime` above to find the percentage of primes $p < 1000$ which are congruent to 1 modulo 4. (A number $n$ is congruent to 1 modulo 4 if the remainder of $n$ divided by 4 is 1.)"
712 | ]
713 | },
714 | {
715 | "cell_type": "markdown",
716 | "metadata": {},
717 | "source": [
718 | "**Exercise 12.** How many times does the letter o (uppercase or lowercase) appear in the English version of [Canadian National Anthem](http://pch.gc.ca/eng/1359402373291/1359402467746#a1.1)? (In other words, copy and paste the lyrics into your notebook as a string and write a `for` loop which iterates over the letters in the lyrics string to count the o's.)"
719 | ]
720 | },
721 | {
722 | "cell_type": "markdown",
723 | "metadata": {},
724 | "source": [
725 | "**Exercise 13.** A [Pythagorean triple](https://en.wikipedia.org/wiki/Pythagorean_triple) consists of three integers $a$, $b$ and $c$ which satisfy $a^2 + b^2 = c^2$. Let $N$ be a positive integer and suppose you choose positive integers $a$ and $b$ such that $0 < a,b \\leq N$. What is the probability of choosing $a$ and $b$ such that they form a Pythagorean triple?"
726 | ]
727 | },
728 | {
729 | "cell_type": "markdown",
730 | "metadata": {},
731 | "source": [
732 | "**Exercise 14.** A Pythagorean triple is called **primitive** if $a$, $b$ and $c$ have no common factors. Write a function which takes an input integer $N$ and returns a Python list of all the primitive Pythagorean triples with $c \\leq N$."
733 | ]
734 | },
735 | {
736 | "cell_type": "markdown",
737 | "metadata": {},
738 | "source": [
739 | "**Exercise 15.** The Taylor series of the function $f(x) = e^x$ is given by $$\\sum_{n=0}^{\\infty} \\frac{x^n}{n!}$$ Approximate the value of $e$ by computing the sum of the Taylor series up to $n=15$ with $x=1$ $$\\sum_{n=0}^{15} \\frac{1}{n!}$$\n",
740 | "(Hint: Use your factorial function from Exercise 8 above.)"
741 | ]
742 | }
743 | ],
744 | "metadata": {
745 | "kernelspec": {
746 | "display_name": "Python 3",
747 | "language": "python",
748 | "name": "python3"
749 | },
750 | "language_info": {
751 | "codemirror_mode": {
752 | "name": "ipython",
753 | "version": 3
754 | },
755 | "file_extension": ".py",
756 | "mimetype": "text/x-python",
757 | "name": "python",
758 | "nbconvert_exporter": "python",
759 | "pygments_lexer": "ipython3",
760 | "version": "3.4.3"
761 | }
762 | },
763 | "nbformat": 4,
764 | "nbformat_minor": 0
765 | }
766 |
--------------------------------------------------------------------------------
/exams/exam1-solutions.ipynb:
--------------------------------------------------------------------------------
1 | {
2 | "cells": [
3 | {
4 | "cell_type": "markdown",
5 | "metadata": {},
6 | "source": [
7 | "**QUESTION 1**"
8 | ]
9 | },
10 | {
11 | "cell_type": "markdown",
12 | "metadata": {},
13 | "source": [
14 | "$$\n",
15 | "\\frac{4 \\pi r^3}{3} = \\int_0^{2\\pi} \\int_0^{\\pi} \\int_0^r \\rho^2 \\sin(\\phi) \\, d\\rho \\, d\\phi \\, d\\theta\n",
16 | "$$"
17 | ]
18 | },
19 | {
20 | "cell_type": "markdown",
21 | "metadata": {
22 | "collapsed": true
23 | },
24 | "source": [
25 | "**QUESTION 2**"
26 | ]
27 | },
28 | {
29 | "cell_type": "code",
30 | "execution_count": 1,
31 | "metadata": {
32 | "collapsed": true
33 | },
34 | "outputs": [],
35 | "source": [
36 | "def fun(m,n,d):\n",
37 | " \"Compute the remainder of m*n divided by d.\"\n",
38 | " return m*n % d"
39 | ]
40 | },
41 | {
42 | "cell_type": "code",
43 | "execution_count": 2,
44 | "metadata": {
45 | "collapsed": false
46 | },
47 | "outputs": [
48 | {
49 | "data": {
50 | "text/plain": [
51 | "2"
52 | ]
53 | },
54 | "execution_count": 2,
55 | "metadata": {},
56 | "output_type": "execute_result"
57 | }
58 | ],
59 | "source": [
60 | "fun(4,5,3)"
61 | ]
62 | },
63 | {
64 | "cell_type": "markdown",
65 | "metadata": {},
66 | "source": [
67 | "**QUESTION 3**"
68 | ]
69 | },
70 | {
71 | "cell_type": "code",
72 | "execution_count": 3,
73 | "metadata": {
74 | "collapsed": false
75 | },
76 | "outputs": [],
77 | "source": [
78 | "def divide_either(m,n):\n",
79 | " \"Compute the list of positive integers which divide either m or n.\"\n",
80 | " N = max([m,n])\n",
81 | " return [ d for d in range(1,N+1) if ( m % d == 0 or n % d == 0 )]"
82 | ]
83 | },
84 | {
85 | "cell_type": "code",
86 | "execution_count": 4,
87 | "metadata": {
88 | "collapsed": false
89 | },
90 | "outputs": [
91 | {
92 | "data": {
93 | "text/plain": [
94 | "[1, 2, 3, 5, 6, 9, 15, 18]"
95 | ]
96 | },
97 | "execution_count": 4,
98 | "metadata": {},
99 | "output_type": "execute_result"
100 | }
101 | ],
102 | "source": [
103 | "divide_either(18,15)"
104 | ]
105 | },
106 | {
107 | "cell_type": "markdown",
108 | "metadata": {},
109 | "source": [
110 | "**QUESTION 4**"
111 | ]
112 | },
113 | {
114 | "cell_type": "code",
115 | "execution_count": 5,
116 | "metadata": {
117 | "collapsed": true
118 | },
119 | "outputs": [],
120 | "source": [
121 | "def a_sequence(a,N):\n",
122 | " \"Compute the Nth term in the recursive sequence given by x_1 = a and x_{n+1} = x_n + 2/x_n.\"\n",
123 | " x = a\n",
124 | " for n in range(2,N+1):\n",
125 | " x = x + 2/x\n",
126 | " return x"
127 | ]
128 | },
129 | {
130 | "cell_type": "code",
131 | "execution_count": 6,
132 | "metadata": {
133 | "collapsed": false
134 | },
135 | "outputs": [
136 | {
137 | "data": {
138 | "text/plain": [
139 | "3.0"
140 | ]
141 | },
142 | "execution_count": 6,
143 | "metadata": {},
144 | "output_type": "execute_result"
145 | }
146 | ],
147 | "source": [
148 | "a_sequence(1,2)"
149 | ]
150 | },
151 | {
152 | "cell_type": "code",
153 | "execution_count": 7,
154 | "metadata": {
155 | "collapsed": false
156 | },
157 | "outputs": [
158 | {
159 | "data": {
160 | "text/plain": [
161 | "8.727928256697213"
162 | ]
163 | },
164 | "execution_count": 7,
165 | "metadata": {},
166 | "output_type": "execute_result"
167 | }
168 | ],
169 | "source": [
170 | "a_sequence(8,4)"
171 | ]
172 | },
173 | {
174 | "cell_type": "markdown",
175 | "metadata": {},
176 | "source": [
177 | "**QUESTION 5(a)**"
178 | ]
179 | },
180 | {
181 | "cell_type": "markdown",
182 | "metadata": {},
183 | "source": [
184 | "$$\n",
185 | "\\arctan x = \\sum_{n = 0}^{\\infty} \\frac{(-1)^n}{2n+1} x^{2n+1}\n",
186 | "$$"
187 | ]
188 | },
189 | {
190 | "cell_type": "markdown",
191 | "metadata": {},
192 | "source": [
193 | "**QUESTION 5(b)**"
194 | ]
195 | },
196 | {
197 | "cell_type": "code",
198 | "execution_count": 8,
199 | "metadata": {
200 | "collapsed": true
201 | },
202 | "outputs": [],
203 | "source": [
204 | "def arctan_taylor(x,N):\n",
205 | " \"Compute the Nth partial sum of the Taylor series of arctan centered at 0 evaluated at x.\"\n",
206 | " if (abs(x) > 1):\n",
207 | " print('Error: x is not in the interval [-1,1]')\n",
208 | " return None\n",
209 | " else:\n",
210 | " return sum([ (-1)**n * x**(2*n+1) / (2*n+1) for n in range(0,N+1)])"
211 | ]
212 | },
213 | {
214 | "cell_type": "code",
215 | "execution_count": 9,
216 | "metadata": {
217 | "collapsed": false
218 | },
219 | "outputs": [
220 | {
221 | "data": {
222 | "text/plain": [
223 | "0.0"
224 | ]
225 | },
226 | "execution_count": 9,
227 | "metadata": {},
228 | "output_type": "execute_result"
229 | }
230 | ],
231 | "source": [
232 | "arctan_taylor(0,1)"
233 | ]
234 | },
235 | {
236 | "cell_type": "code",
237 | "execution_count": 10,
238 | "metadata": {
239 | "collapsed": false
240 | },
241 | "outputs": [
242 | {
243 | "name": "stdout",
244 | "output_type": "stream",
245 | "text": [
246 | "Error: x is not in the interval [-1,1]\n"
247 | ]
248 | }
249 | ],
250 | "source": [
251 | "arctan_taylor(10,1)"
252 | ]
253 | },
254 | {
255 | "cell_type": "code",
256 | "execution_count": 11,
257 | "metadata": {
258 | "collapsed": false
259 | },
260 | "outputs": [
261 | {
262 | "data": {
263 | "text/plain": [
264 | "0.46364760900080587"
265 | ]
266 | },
267 | "execution_count": 11,
268 | "metadata": {},
269 | "output_type": "execute_result"
270 | }
271 | ],
272 | "source": [
273 | "arctan_taylor(0.5,100000)"
274 | ]
275 | },
276 | {
277 | "cell_type": "markdown",
278 | "metadata": {},
279 | "source": [
280 | "**QUESTION 6(a)**"
281 | ]
282 | },
283 | {
284 | "cell_type": "markdown",
285 | "metadata": {},
286 | "source": [
287 | "The **Fourier series** of the **sawtooth wave** is the infinite series:\n",
288 | "\n",
289 | "$$\n",
290 | "y(t) = \\frac{1}{2} - \\frac{1}{\\pi} \\sum_{k=1}^{\\infty} \\frac{\\sin(2 \\pi k t)}{k}\n",
291 | "$$\n"
292 | ]
293 | },
294 | {
295 | "cell_type": "markdown",
296 | "metadata": {},
297 | "source": [
298 | "**QUESTION 6(b)**"
299 | ]
300 | },
301 | {
302 | "cell_type": "code",
303 | "execution_count": 12,
304 | "metadata": {
305 | "collapsed": true
306 | },
307 | "outputs": [],
308 | "source": [
309 | "import numpy as np\n",
310 | "import matplotlib.pyplot as plt\n",
311 | "%matplotlib inline"
312 | ]
313 | },
314 | {
315 | "cell_type": "code",
316 | "execution_count": 13,
317 | "metadata": {
318 | "collapsed": false
319 | },
320 | "outputs": [
321 | {
322 | "data": {
323 | "image/png": "iVBORw0KGgoAAAANSUhEUgAAAXkAAAEACAYAAABWLgY0AAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJztnXmcVdWV77+LoRBF0RJKJoEGBBQVooIT0XIENYnG0Il2\na9qkNaixO3aSFzvDi6Q/MWo6ne5npxXtNkZfTDTR14mmw6RWKSTIIChjQYGIzCiooEJRw35/rLpa\nFDWce898zvp+Pnyse+65+6zjOvt31t577b3FOYdhGIaRTbrEbYBhGIYRHibyhmEYGcZE3jAMI8OY\nyBuGYWQYE3nDMIwMYyJvGIaRYToVeRF5WER2iMiyDs65T0RqReRVERkXrImGYRhGqXiJ5B8BJrX3\npYhcBgx3zp0ATAWmB2SbYRiG4ZNORd45Nw94p4NTrgQeaz53AdBbRI4LxjzDMAzDD0H0yQ8ENrX4\nvKX5mGEYhhEzNvBqGIaRYboFUMYW4PgWnwc1HzsEEbGFcgzDMErAOSel/M5rJC/N/9riGeCLACJy\nFvCuc25HewU55zL7784774zdBrs/u7+83Vse7s8PnUbyIvIroBI4VkTeBO4EylSv3UPOuT+KyOUi\nsg74APiSL4sMwzCMwOhU5J1zf+XhnNuCMccwDMMIEht4DZDKysq4TQgVu7/0kuV7g+zfnx/Eb39P\nURcTcVFezzAMIwuICC7kgVfDMAwjhZjIG4ZhZBgT+ZyxfDncc0/cVhilct99sHBh3FYYpbB7N/zD\nP0BjY7TXtT75HPHOO3DGGbBtG9TUwODBcVtkFMNvfwvXXw8XXwx/+EPc1hjF0NgIV1wBVVXw1FPw\n6U8X93vrkzc6pakJrrtOH64bb4T//M+4LTKKYdUquPVWeO45mD8f3ngjbouMYpg2Derq4P774YEH\nor22RfI5Ydo0eOEFeP55qK2Fiy6CjRuhrCxuy4zOeO89mDABvv1tuOEGuP126NkT7r47bssML/z+\n9/B3fweLF8ORR2oLesECGDbMexl+InkT+RwwYwbcdJM+ZP366bHKSo0MP//5WE0zOsE5+Nzn1G/3\n36/Hamrg/PPhzTehR4947TM6Zt06OOccePZZOPNMPfaNb0C3bnDvvd7LMZE3OuTii+Hmm2HKlI+P\nPfkkTJ+ufYRGcnn9dRWJjRsPFvQLL9QX97XXxmeb0Tl33AEiByc71NbCuefCpk3eX9LWJ2+0S12d\nNg0vueTg45/9LKxerf+M5FJVpYLeWgxuuSX6vl2jeKqqYPLkg4+dcAKMHasDsFFgIp9xFiyA0aOh\nd++Dj5eVwd/+rUbzRnKpqoILLjj0+FVXaUS4YkX0NhneeO89HTA/66xDv4vyJW0in3HaEwmAr3wF\nfvlL+PDDaG0yvOFc+/7r3l2zpOwlnVzmztV++MMOO/S7z3wGNmzQeSthYyKfcToS+SFDYMQIWLo0\nWpsMb9TWQpcuMHx4299PmWJjKkmmo7rXrZu2xqLwn4l8htm3TzNqJk5s/5zRozVbw0geBZGQdobb\nRo6E9euhoSFauwxvdCTyEF3dM5HPMPPnwymnaG5ue5jIJ5fORKJnT+jfX5v9RrLYvVvTJ8ePb/8c\nE3nDN52JBJjIJxXnoLra/JdWXnoJzj6748mGJvKGb0zk08vq1RqpDx3a8Xnmv2Tipe4NHAh79mgW\nTpiYyGeUDz6AV1/VSRcdMXy4Tsqoq4vGLsMbXkQCTOSTihf/dekCo0bBmjXh2mIin1HmzYNPfAIO\nP7zj88rKNMtm/fpo7DK88cIL3kU+bJEwiuOtt3SG8umnd35uFC9pE/mM4jUSBIsGk0ZTE7z4okXy\naeXFFzWjrVu3zs81kTdKxkQ+vSxfDsccA4MGdX5uRYWuVf722+HbZXgjaXXPRD6DfPihCsXZZ3s7\n30Q+Wcydq6tMekHE/Jc0ivFfFN1tJvIZZNkyOPHEtqdTt4WJRLJYsqTj/OrWmP+Sw759mh9/6qne\nzj/hBF1pNMwJbSbyGWTJEjjtNO/njxqlImGrQCeDUv1nxM/y5frS9bqE8GGHhT+hzUQ+gyxdqpk1\nXikv14dt27bwbDK8UVcHa9fqTGWvWCSfHJYsKa7uQfj+M5HPIMVGgmBCkRRWrNBF47x2tYH5Lkkk\nse6ZyGeMAwd0tqTXPsEClm+dDEoRieHDYfNmm9CWBJYuNZE3QmblSt0guLNJUK2xaDAZlCLy3bvr\n8gfr1oVikuGR+nrdJKSUAMtE3vBMKSIBJvJJwfyXXlat0pftEUcU97vRo7X1HVbig4l8xih20LWA\niUT8NDRon/zYscX/1vwXP6UMugL07av/DWtCm4l8xig1EhwyBHbu1IXNjHioqdFZrh2t/98eJvLx\nU2rdC3tCm4l8hmhs1IlQ48YV/9uuXXVixtq1wdtleKNUkQAT+SSQVP+ZyGeINWt0YkXv3qX93oQi\nXvyIhE1oixc/ARaYyBse8SMSYDMn48aP/445RjOqtm4N1ibDG7W1cNxxcPTRpf0+zLpnIp8hSh10\nLTBkiOZbG9HT1KSbvJj/0kmpg64FwvSdJ5EXkckiUiMia0Xkjja+P0pEnhGRV0VkuYjcELilRqf4\njeQHDLBIMC7Wr9flJcrLSy/D/BcfSa57nYq8iHQBfgZMAsYA14rI6FanfRVY6ZwbB1wA/IuIeFgy\n3wiKpib/kfyAAbBlS3A2Gd7xKxJg/osTv/7r00f3eg1j1rKXSH4CUOuc2+icqweeAK5sdY4DColf\nRwK7nHMhLp5ptGbDBjjqqI9zbkvBIsH4CErkzX/R45z/7pouXaBfv3AWCfQi8gOBTS0+b24+1pKf\nASeJyFbgNeBrwZhneMXvQwYaTezda2ugxEEQ/hs40EQ+DjZsgF69dJcuP4Tlv6C6VCYBS51zF4rI\ncGCOiJzqnHu/9YnTpk376O/KykoqKysDMiHfLF4MZ5zhr4yW0cTQoYGYZXjAOXjlFW8bP3eERfLx\nEETdg4P9V11dTXV1tf9C8SbyW4DBLT4Paj7Wki8BdwM459aLyAZgNLC4dWEtRd4IjsWL4Zvf9F9O\noV/XRD46Xn9d1zvp189fOdYnHw9BinzBf60D4B/84Acll+ulu2YRMEJEhohIGXAN8EyrczYCFwOI\nyHHASOD1kq0yiqKpSSPBoKMJIxoWLSpuu7/2MN/Fw+LFyfZfp5G8c65RRG4DZqMvhYedc6tFZKp+\n7R4Cfgj8QkSWNf/sW8653cGba7TFunU6CcPPoGsB69eNnqAiwfJy3WP0ww+LX2raKI1CgOW3qw1U\n5Fet8l9Oazz1yTvnZgKjWh17sMXf29B+eSMGgookwKLBOFi8GL77Xf/liKj/tm3TjUSM8Kmt1Zdr\nnz7+yworwLIZrxlg0aJgIkEwkY+axkbNrAkiEgTzX9SkIcAykc8AQT9oNngXHWvXauqdn5muLTH/\nRUvQAVYYvjORTzkNDaXtK9ke1icfLUGKBFgkHzVBBli9e2t93rs3mPIKmMinnJoardilrn7XGhOJ\naAlq0LWAvaSjo6FBF5ULKsASUf8FPevVRD7lBJV+V+Coo7SfOOhowmiboP1nL+noWL1aRbnU/Rva\nIgz/mcinnKAjwUKGhglF+NTX60YTQUWCYH3yURJkV02BMPxnIp9ywnjQrMkfDatW6Tripezp2h72\ngo6OoMdTwCJ5oxUHDsCKFf4XtmqNCUU0hCkStg1g+ATdigYTeaMVK1bAsGG67kmQmMhHQxitsCOP\n1E3Z9+wJtlzjYMIKsMJoRZvIp5gwIkEwkY8K8196Wb5cZxWnIcAykU8xYTQXQaMJG7wLl/37NTtj\n7Njgy7bB1/AJq+7ZwKtxEH/6E5x5ZvDlWiQYPosXw+jR4SwkZv4Ln7DrXpBjKibyKWXTJnjrrWDT\n7wqYSITPrFkwKaQl/Sw7KlyammD2bLj00uDLPvxw6NkT3nknuDJN5FPKrFlwySW6m1PQWIZG+IQp\n8vaSDpdly3TS4LBh4ZQftP9M5FPKzJnhiUTPnhpR7LYdAULh7bdhzRo455xwyrc++XAJs+5B8P4z\nkU8hDQ3w/PPhNBcLWDQYHnPmQGUllJWFU775LlxmzYLJk8Mr3yJ5gwULdKZk//7hXcOEIjyiiATN\nd+Gwd68OmrfYfjVwTOSN0CMJMKEIC+d00C7sSHD7dh0gNIKlqkqzaoLOj29J0APnJvIpJMxBuwKW\noREOy5ZBr17hDdoB9OihM1937QrvGnklirpnkXzOefttnURz7rnhXscG78Ih7K6aAua/cIjCfzbw\nmnOeey7cQbsC1l0TDlF0tYH5LwzWrYN9++CUU8K9jkXyOSeK5iKYSITB++/rejVhDtoVMP8FT6Hu\niYR7nX79YOdO3bwnCEzkU4Rz0Ym8rV8TPFVVuupkr17hX8v8FzxRdbWVlcExx6jQB4GJfIp48UWd\naTdiRPjXqqjQZRNs1mtw/PrX8KlPRXOt444LTiQM2LED5s3TWeZREKT/TORTgnPwne/A974XzfXK\nyjRN7N13o7le1lm2DF54AW66KZrrVVSYyAfJXXfBDTfAscdGc70g/dctmGKMsPnDH3QixrXXRnfN\nwoN2zDHRXTOrfPe78O1vB7vVX0eYyAfHhg3w+ONQUxPdNYP0n0XyKaCxUaP4u+7SXX+iwoQiGP70\nJ91k4uabo7um+S44pk2D226Dvn2ju6ZF8jnj17/WCPDTn472uiYU/nFOI/hp03SSUlSY74JhxQod\ncK2tjfa6JvI54sAB+P734ec/Dz91qzUmFP6ZOVMnsF1/fbTXLS/XfV7r66F792ivnSW+9z341rc0\n4SFKKipg/fpgyrLumgSzaxfcfjuMHBlNbnVrTOT9sWABfP3r0Xezge4zcOyx+oIximf/frjvPnjl\nFbj11uivb5F8BtiyRUVg40Z48019qE48EU4+WVeXfPhheOQR+NznNIqPg759dQkF41BefhnWrlX/\nbdqkkfPJJ8OYMfpyvvtujcT+8R/hqqvisbEgFGGuVppG3nsP5s79uO7t3g0nnKC+O+EEeOYZ+OlP\n4fTT4dlndX+FqOnb10Q+1WzYoGvPjB8PQ4fC8cdryuLq1fDUU/r9lCnw2mswaFB8dlZUaG6+cTD/\n9m8qAuefr74bN06F/Q9/gHvv1Sj6G9/QTKg4u0qsJXYoH3wAF12kE9JOPFH9N3So9rk//7zWwXPO\ngRkzwtlk3SsWyaeY3bvhsss0pe6rX43bmo4xkTiUp5+Gf/5n+POfdU3/JGP+O5iGBrjmGhXv//qv\n6Me4iqEwGTEIrE8+Qurq4LOf1VmPSRd4MJFozfz5mgb57LPJF3gw/7XEOfja17QOTp+ebIEHbWk0\nNmrLwy8WyUeEc/DlL2vF+/GP47bGG0FGE2nn9dfh6qvh0UfhtNPitsYbffua/wr89KfaDz9vXjqy\njUQ+rn9+NyjxFMmLyGQRqRGRtSJyRzvnVIrIUhFZISJV/szKHn/+MyxcCI89pn22aaC8XAepGhri\ntiR+pk3TLIvLL4/bEu9YJK/s3g0//KGOmUSdCumHoPzXaSQvIl2AnwEXAVuBRSLye+dcTYtzegP/\nAVzqnNsiIn38m5Ytpk9XkYhjpL5UWqbh9esXtzXxsWuXZlysWxe3JcVhIq889hhccQUMHhy3JcUR\nlP+8xJQTgFrn3EbnXD3wBHBlq3P+CnjaObcFwDln2bkt2LVL+3H/5m/itqR4TCi0i+ZTn4I+KQtd\nzHfaTTp9OkydGrclxROlyA8ENrX4vLn5WEtGAuUiUiUii0Qk4vl9yebRR+Ezn9Huj7SRd6FwDh58\nMNp1Z4Ii774DeOklnYg2cWLclhRPZN01RZRzGnAhcAQwX0TmO+dS1sANnkIk8YtfxG1JaeRdKKqr\ndaAu7D11wyDvvgOtezffnPxsmraoqAhm4xcvIr8FaNmbNaj5WEs2A2875/YD+0XkJWAscIjIT5s2\n7aO/KysrqYxjvn6EVFXpwlRnnx23JaWRd6F48EFt6qdRJFqm4fnN0EgjO3fqpKYHHojbkuKprq5m\n3rxq1q/XQX8/iOtk6x8R6QqsQQdetwELgWudc6tbnDMa+HdgMtADWAB8wTm3qlVZrrPrZY3Pf15n\nRqYhL74tfvQj3Zv0Rz+K25Lo2blT1w164w04+ui4rSmNIUN01vLQoXFbEj333gtr1sS3LIhfZs2C\nf/kXmD0bRATnXEmhRqd98s65RuA2YDawEnjCObdaRKaKyFeaz6kBZgHLgJeBh1oLfB7ZsQPmzIHr\nrovbktLJcyRfWDsorQIP+fVfUxM89FA6x1IKRNon75ybCYxqdezBVp9/AvzEv0nZ4fHHdYZr795x\nW1I6eRUJUJFP61hKgbz6b+5c7a4aPz5uS0onyuwao0T++Mf4ViAMiiBXw0sT69frRLAzz4zbEn/k\nVeRnzNC6l8axlAJ9+uiM16Ymf+WYyIfE++/rUsIXXBC3Jf7Iq0jMmgWTJqVbJCC//ps5EyZPjtsK\nf/TooQPm777rrxwT+ZCortamYlQbN4eFiUS6yaP/tm7VNf7T3FVTIAj/mciHRFZEIsjV8NJCXZ1m\npFxySdyW+CePIj9rFlx8MXTLwPKLJvIJJisi33I1vLzwpz/phhLHHhu3Jf7Jo8hnpe5BMHXPRD4E\namvhww/hlFPitiQY8iYUM2ZkSyTy5LuGBk1bnjQpbkuCwSL5hFKIJNI+aFcgb0Ixc6bu3pUF8ua7\nRYt0S78BA+K2JBhM5BNKlpqLkC+h2LwZtm2DM86I25JgKGwc4jcNLy1Y3TsUE/mA2b9fV767+OK4\nLQmOPIn8rFk64Nq1a9yWBENZmQ6e+03DSwtZ6moDE/lEMneu9sWncVnh9siTyGctEoT8+O+tt3St\nmjSuGNoeJvIJJKsikYfsmoYGeO45uPTSuC0Jlrz4b84cqKzU1ktWMJFPIIWZklkiL5HgwoW6amP/\n/nFbEix5WZrC6l7bmMgHyM6dOnB3+ulxWxIseRH5qiq46KK4rQiePPjPuWz6r7wc9uzxV4aJfIBU\nV+s2Y1mYadeSvESCVVXa3M8aeRD5DRugvl7X/88SXbr4n5RnIh8g1dXpX5CsLQppeFne76WuTheU\nO++8uC0JnjyIfFWV1r2szE1pSd++/n5vIh8ghQcta/ToAYcfnu00vIULYfTodK/93x55EPmsBlig\n/vODiXxAbN+u/8aOjduScMi6UFRXZ7OrBrLvu0J/fJb95wcT+YCortamflYm0bQm60KR1VYYZN93\n69frf0eMiNeOsDCRTwhZjiRAH7QdO+K2Ihz279fumokT47YkHLLsO/i47mWxPx5gwgR/vzeRD4gs\n9wlCtifULFgAY8bAUUfFbUk4lJfD3r2afZJFstwKA/jrv/b3exP5ANi6VQXw1FPjtiQ8stzkz3or\nrJCG9/bbcVsSPM5lezwlCCIX+SyuhlddDeefr5Upq2RZ5LPeCoPs+m/tWp2XMmxY3JYkl8hlKYtp\neFlvLkJ2RWLfPli8OLv98QWy6r/CCzqr/fFBELnIZ/FBy3pzH7IrEvPn66qhvXrFbUm4ZNV/eah7\nfjGR98mmTdo6OfnkuC0Jl6yKRB66aiCb/iv0x+fBf36IXOSzlqExZw5ceGG2++MhmyIBMHt29ha1\naoss+m/5cjjiCBg6NG5Lko1F8j7J0n6gHVFYDS9LaXi7dsHq1dnvj4dsinxe6p5fTOR9UNhkImtr\nWLdFFtPw5szRrKgePeK2JHyyKvJZ26AnDEzkfbBwIQwenJ2d4Tsja0KRp0gwa77buxcWLbL+eC+Y\nyPsgb5FEloSiqSmbOwm1R5Z8B/DCC3DWWdonb3SMibwP8ijyWRk4X7ZMlzHIyySaLPkO8lf3/GAi\nXyKFneHPOSduS6IjSztE5U0kjjgCGhvhgw/itsQ/zuXPf34wkS+ROXO0PzBLO8N3Rpaa/HkTCZHs\nRPNr12rSw0knxW1JOohc5LOShjdjRr5EArIj8nv2wCuvaGZNnsiK/wovaFvKwBuRi3wW0vDyNmhX\nICsi8fzz2s12+OFxWxItWfFf3lphfolc5LPwoC1dqpOD/uIv4rYkWrLgO8ivSGTBf/v2wbx5+Zil\nHBSeRF5EJotIjYisFZE7OjhvvIjUi8jV7Z2ThQctj101kA3f5XnQLgv+q66GcePg6KPjtiQ9dCry\nItIF+BkwCRgDXCsio9s57x5gVkflpf1Bcw4eewz+8i/jtiR60u47UJE48kgYfcgTnH2y4L9HH81n\n3fODl0h+AlDrnNvonKsHngCubOO8vwOeAjp8jNL+oFVVwWGH5St1skCvXulPw3vwQbj55nwO2qW9\n7u3cqWNhX/xi3JakCy8iPxDY1OLz5uZjHyEiA4CrnHMPAB1Wn7SncU2fDlOn5lMk0p6Gt2OHdtVc\nd13clsRD2kX+kUfgs5+1rppiCWrg9d+Aln317Upgmh+07ds1Pz6vIgHp9t8jj8DnPpdfkUiz75qa\n4KGHtBVmFEc3D+dsAQa3+Dyo+VhLzgCeEBEB+gCXiUi9c+6Z1oU9//w0liyBadOgsrKSyhRt6/LI\nIzBlCvTuHbcl8ZFWoSiIxJNPxm1JfKTVd6CrvfbuDePHx21JNFRXV1NdXR1IWeKc6/gEka7AGuAi\nYBuwELjWObe6nfMfAZ51zv2/Nr5z8+c7br8dXn7Zt+2R0tgII0bAU0/B6afHbU18fOlL8MlPwpe/\nHLclxTFrFnznO7qfax672gAOHNDlDerq0rfJzdVXa0bUV74StyXxICI450p6cjt1tXOuEbgNmA2s\nBJ5wzq0Wkaki0tb/8g7fGmmNJmbP1olceRZ4SK//8jyWUqCsTAfP3303bkuKY+tWzYq69tq4LUkn\nXrprcM7NBEa1OvZgO+d2GOOlVSQKWRl5p6ICtrTurEs4W7bAiy9q6mveKdS/8vK4LfHOww/DF76g\nqa9G8UTeaDviCO0fTVMa3m9+A0uWwDXXxG1J/KTtJd3QADfeCDfdZCIB6fPfq6/Cv/873HZb3Jak\nl8hFPm1pePPm6QP27LPa1M07aRIJ5+DWW/Xvu+6K15akkCb/bdoEn/40/Md/wJgxcVuTXmIZfknL\ng7ZmjWbT/PKXMHZs3NYkg7T4DuCee3SLuN/8Brp56pjMPmnx33vvwRVXwN//vc1w9Ussj35SNp9Y\nsQJ+9zsYOlQjhdGjdRnkN9+EjRv1AfvRj+DSS+O2NDkkRSQaGuC3v9Vob8wYOPlkGDRIJzy9+Sa8\n9JIOts6fb900LUmK/7Zt0zGS8nL13Ukn6cDwpk3qv3vugYkT4ZvfjNvS9BOLyMf9oC1cqOL98sva\nz75iBdx7L9TWasQ3eLD++/rX05cqGDZ9+2pXW1NTPGl4+/fr+iX33quifvrpunTwihU6Wa1vX/Xd\nkCHwxz/mZ5N1r1RUwMqV8V3/9dfhxz/W1tWUKbB6tc5fWL1aX9yDBqn/zjhD62ies6GCIncif/fd\n8MAD8K1vwa9+dfCa4o2NKlz2YLVPWZkOnr/7bvQZGvv36wqEw4ap0H/ykwd/39gIXbtGa1PaiLMV\nPWOGzha/5RbtCu3b9+Pvmpr0v2nL308DsYl8HGl4O3bAT36iuwINHXro9yYQ3igMnEct8tOnw8iR\n8Mwh86gV81/nxJX00NgI/+t/aRfNFVcc+r2Je3jkauD1rrs0kmhL4A3vxOG/vXu1FWZZMv6Iq+49\n/riuGXT55dFfO+/kprvmjTf0QVvd5mIMRjHE4b+f/lQHwE85JdrrZo04fFdXB3feqVG8dYVGT2wi\nH3WTcdo0zZmuqIj2ulkkaqF46y247z5NhzT8UV6uG5nX10P37tFc86GH4MQTDx1DMaIhF5H8ypWa\naVFbG901s0zU/rv7bs2CGjYsumtmlS5ddA2mt9+G/v3Dv97772uWzIwZ4V/LaJvY8uTfektnJEbR\nfPv+9zWbJs9LBAdJRUV03V6bN8MvfhFv2l/WKLykoxD5++6DykrNijLiIZaB10Ia3jvvhH+tPXt0\nBUlbXCw4Kio0UykKnn5adwOKQpDyQpT+e/xxuP32aK5ltE1siUv9++ust7CpqoKzzrJ1Z4IkKt+B\nrgN/2WXRXCsvROW/TZv0ZXLGGeFfy2if2ER+4EBdJzpsZs6ESZPCv06eiMp3+/fD3Llw0UXhXytP\nROW/WbPgkkts/kLcxCbyAwaEPyHKOX3QJk8O9zp5oxAJdrKpmG/mzoVTT4Vjjgn3OnljwIDoRN7q\nXvzEKvJhP2jr1umWZ7ZMabD07KnLQezaFe51Zs2yVlgYRBFgNTTomkK2uF/8ZFrkZ87Uh8wmYARP\nVP4zkQ+eKHy3cCEcf7wNmCeBTIu8NRfDI2z/bd6sq0raoF3wWN3LF7EOvIbZZKyr0zXFL744vGvk\nmbAH72bNUt/ZoF3w9O+vL9DCyo9hYK2w5JDZSH7ePO2LT9OGxWki7H5diwTDo0cPnRgY1tIiu3ZB\nTQ2ce2445RvFEZvI9+unObRhRRM2aBcuYb6kGxrgueds0C5MwvTfc8/Beefpy8SIn9hEvqxMlx4N\nK5qw5mK4hCkSixbpDkG2q1N4hOk/q3vJItal+sPql9+6VQfuxo8PvmxDCbNP3rpqwics/zmny4iY\n/5JDrCIfVjQxd642F7vFsvxaPggzEnzpJbjggnDKNpSw/Ld+va50OWJE8GUbpZFJkV+82KL4sDnu\nOF3JsKEh2HKbmnR7RvNfuIQ1cG51L3lkUuQXLbIHLWy6d9d1yYNeV762VjOi+vQJtlzjYKzu5YfY\nRT7oaKKpCZYsgdNPD7Zc41DCEIrFi20CVBSE2Yo2/yWL2Adeg37Q1q7VTUmOPTbYco1DCcN/JhLR\nEIbvGhth6VLzX9KIPZIP+kFbtMgesqgIoyVmzf1oqKiA3bt1r9egWLNGy7VVQ5NF5kTeBn6iI2j/\nNTTAq6/CaacFV6bRNl27aot3+/bgyrS6l0xiFfm+fXULwAMHgivTIvnoCFrkV6/WboSjjw6uTKN9\ngvaf1b1kEqvId+2qqXhBRRMNDfDaaxYJRkXQ/brWHx8t5r98EKvIQ7DRxKpVMHgwHHVUMOUZHRN0\nJGgiES3Hz0duAAALpUlEQVRB+q++HpYtswAriWRK5K25GC1BD7zaoGu0BOm/lSthyBA48shgyjOC\nIxEiH9SDZgM/0dKnD+zZo2v3++XAAVixAsaN81+W4Y0gAyyre8nFk8iLyGQRqRGRtSJyRxvf/5WI\nvNb8b56InOLVAIvk00uXLrpk9LZt/stavhyGDYNevfyXZXjD6l4+6FTkRaQL8DNgEjAGuFZERrc6\n7XXgPOfcWOCHwH96NSCowZ+6Ou2Tt0gwWoLyn0WC0RPkwKuNpyQXL5H8BKDWObfROVcPPAFc2fIE\n59zLzrn3mj++DAz0akBQ0cTy5XDCCXD44f7LMrwTVHebiUT0BOW7/fs1/dUCrGTiReQHAptafN5M\nxyJ+IzDDqwFBPWjWXIyHoF7S5r/oKS+Hffvgww/9lbNsGYwcCT17BmOXESyBrrguIhcAXwImtnfO\ntGnTPvq7srKSU0+tDKy5byIRPUGI/L59OiV+7NhgbDK8IaKbem/bBsOHl16O1b3gqa6uprq6OpCy\nvIj8FmBwi8+Dmo8dhIicCjwETHbOvdNeYS1FHnQnmbo6+OADOOIILya3zZIlMHVq6b83SmPgQB0L\n8cPy5TBqFBx2WDA2Gd4p9Mv7EXlb9TV4Kisrqays/OjzD37wg5LL8tJdswgYISJDRKQMuAZ4puUJ\nIjIYeBq43jm3vhgDRDQa9JOhUVenkeApnnN6jKAIIpJfssQm0cSF+S/7dCryzrlG4DZgNrASeMI5\nt1pEporIV5pP+99AOXC/iCwVkYXFGOG3X37FCt1uzPoEoyeIMRUTifjw678DB6CmBk49NTibjGDx\n1CfvnJsJjGp17MEWf98E3FSqEX6jiaVLTSTiIohIcOlSuOGGQMwxisSv/1au1K4eC7CSS+wzXkH7\nBTdvLv33S5bAJz4RnD2Gd3r31s0i9uwp7ff19SoUNugaD1b3sk8iRH7ECN3bs1SsuR8fIv78t2oV\nDB3qb9DdKB2re9knESI/erQOnJZCQ4NmZ9hEjPjw4z+LBONl1CjdMtO50n5vIp98EiPyNTWl/bam\nBgYNstXv4sSP/0wk4uXoo3W9oFIGXxsadCKUBVjJJhEi37+/TojZvbv435pIxI+JfLop1X9r1mif\nvu3fkGwSIfIipTf5ly615n7clCoSjY0aCZr/4qVU/1ndSweJEHko/UGzSDB+Ro7UwbvGxuJ+V1sL\nFRW2p2vcWN3LNqkW+aYmiyaSwBFHqFhv3Fjc70wkkoGJfLZJjMiPGlX8g7Z+va6kd+yx4dhkeKcU\noTCRSAal1D0LsNJDYkTeRCLdlOo/E4n4GTxYkx727vX+m9df1262Pn3Cs8sIhsSI/IgR2tw/cMD7\nbyySSA7Firxz5r+k0KWLjqsUk/hgvksPiRH5Hj3g+OM1QvCKRfLJodjsqDfe0L78444LzSSjCIr1\nn9W99JAYkYfiokHn7EFLEsVG8ua7ZGH+yy6pFfk1a3Q/1/79w7XJ8Ea/fsVNaJs3D848M1ybDO8U\nU/caGuDll2HChHBtMoIhtSJfVQUXXBCuPYZ3ip3QZv5LFsXUvSVLtGu1oiJcm4xgSLXIX3hhuPYY\nxeHVf7t26djL+PHh22R4Y+RIWLfO24Q2q3vpIlEiX8jX7WxFPOegutoiwaThVeRffBHOOQe6dw/f\nJsMbhx+ukfkbb3R+rrXC0kWiRL5PH+jWDXbs6Pi8lSt11cnBgzs+z4gWryJvIpFMvPivvh7+/Gc4\n//xobDL8kyiRB28PmolEMjGRTzde/LdokW73V14ejU2Gf0zkjcAYPrzzCW07d+p2c5Z+lzys7mWT\n1Il8U5P26dqDljx69NAutPXr2z+nuhomTtRuOSNZmMhnk0SKfEdpeMuWad/9gAHR2WR4pzP/mUgk\nl858V1cHCxbAeedFZ5Phn8SJ/NixsHixPlBtYSKRbMaN04lO7WH+Sy79+ul8h7Vr2/5+wQJ9EfTu\nHa1dhj8SJ/LHH69C//TTbX9vIpFsvvhFeOwx2L//0O+2btU++bFjo7fL6BwRuOEGePDBtr+3updO\nEifyALfcAg88cOjxxkaYOxcqKyM3yfDIiBG6OuFTTx36XXW1NvW7do3cLMMjU6fCo4/qEhWtMZFP\nJ4kU+c98RmdELl9+8PGlS7Uv3lYuTDa33AL333/ocROJ5DNsmM5EfvLJg4/v26fdqBMnxmOXUTqJ\nFPnu3eGmm2D69I+POQf33ANXXRWfXYY3PvUp2LQJXnvt42Pr1sHvfw+XXx6fXYY3br310Jb0v/4r\nnHuuTkI00oW4ztYQCPJiIs7r9bZsgVNOgTffhF694Mc/1n76l17SVD0j2fzTP2kf/PTp8MEHcNZZ\nKh633BK3ZUZnNDZqRP/f/63zGWbP1r76RYtg4MC4rcsnIoJzTkr6bVJFHuDqq2HSJJ1kc/31+pAN\nGhSigUZgbN0KY8bo5KipU+Gww+DnP9fBPSP53HWXrmPz3e/qC/o3v7HUyTjJrMjPmQO33QbvvQe/\n/rX156aNKVNg+3btz503D3r2jNsiwyvbt8OJJ8KQIRrF33573Bblm8yKfFMTnHwy3HgjfP3rIRpm\nhEJ1NXz+87BwIQwdGrc1RrFcd52Ohf3yl9YCi5vMijzoOihlZSEZZISO+S+91Nfr8hMm8PGTaZE3\nDMPIO35EPpEplIZhGEYwmMgbhmFkGE8iLyKTRaRGRNaKyB3tnHOfiNSKyKsiMi5YMw3DMIxS6FTk\nRaQL8DNgEjAGuFZERrc65zJguHPuBGAqMP2QgnJAdXV13CaEit1fesnyvUH2788PXiL5CUCtc26j\nc64eeAK4stU5VwKPATjnFgC9RSR3K8xk/UGz+0svWb43yP79+cGLyA8ENrX4vLn5WEfnbGnjHMMw\nDCNibODVMAwjw3SaJy8iZwHTnHOTmz//I+Ccc/e2OGc6UOWce7L5cw1wvnNuR6uyLEneMAyjBErN\nk/eynfIiYISIDAG2AdcA17Y65xngq8CTzS+Fd1sLvB8jDcMwjNLoVOSdc40ichswG+3eedg5t1pE\npurX7iHn3B9F5HIRWQd8AHwpXLMNwzAML0S6rIFhGIYRLaEMvGZ98lRn9yci54vIuyKypPnf9+Kw\nsxRE5GER2SEiyzo4J82+6/D+Uu67QSLygoisFJHlIvL37ZyXSv95ub+U+6+HiCwQkaXN93dnO+cV\n5z/nXKD/0BfHOmAI0B14FRjd6pzLgP9p/vtM4OWg7Qjrn8f7Ox94Jm5bS7y/icA4YFk736fWdx7v\nL82+6weMa/67F7AmY3XPy/2l1n/N9h/e/N+uwMvABL/+CyOSz/rkKS/3B5DKQWbn3DzgnQ5OSbPv\nvNwfpNd3251zrzb//T6wmkPnq6TWfx7vD1LqPwDn3IfNf/ZAx0xb96cX7b8wRD7rk6e83B/A2c3N\nqf8RkZOiMS0S0uw7r6TedyIyFG2xLGj1VSb818H9QYr9JyJdRGQpsB2Y45xb1OqUov3nJYXSKJ5X\ngMHOuQ+b1/X5HTAyZpsMb6TedyLSC3gK+FpzxJspOrm/VPvPOdcEfEJEjgJ+JyInOedW+SkzjEh+\nCzC4xedBzcdan3N8J+cklU7vzzn3fqHZ5ZybAXQXkfLoTAyVNPuuU9LuOxHphgrg/3XO/b6NU1Lt\nv87uL+3+K+Cc2wNUAZNbfVW0/8IQ+Y8mT4lIGTp56plW5zwDfBE+mlHb5uSphNLp/bXsIxORCWiq\n6u5ozfSF0H6/Zpp9V6Dd+8uA734OrHLO/Z92vk+7/zq8vzT7T0T6iEjv5r97ApcANa1OK9p/gXfX\nuIxPnvJyf8AUEbkFqAf2AV+Iz+LiEJFfAZXAsSLyJnAnUEYGfAed3x/p9t25wF8Dy5v7dR3wHTQT\nLPX+83J/pNh/QH/gUdHl3bsATzb7y5d22mQowzCMDGOrUBqGYWQYE3nDMIwMYyJvGIaRYUzkDcMw\nMoyJvGEYRoYxkTcMw8gwJvKGYRgZxkTeMAwjw/x/fy9R1pOHaswAAAAASUVORK5CYII=\n",
324 | "text/plain": [
325 | ""
326 | ]
327 | },
328 | "metadata": {},
329 | "output_type": "display_data"
330 | }
331 | ],
332 | "source": [
333 | "t = np.linspace(0,3,100)\n",
334 | "y = 1/2 - 1/np.pi * ( np.sin(2*np.pi*t) + np.sin(4*np.pi*t)/2 + np.sin(6*np.pi*t)/3 )\n",
335 | "plt.plot(t,y);"
336 | ]
337 | },
338 | {
339 | "cell_type": "markdown",
340 | "metadata": {},
341 | "source": [
342 | "**QUESTION 7**"
343 | ]
344 | },
345 | {
346 | "cell_type": "code",
347 | "execution_count": 14,
348 | "metadata": {
349 | "collapsed": true
350 | },
351 | "outputs": [],
352 | "source": [
353 | "def is_square(n):\n",
354 | " \"Determine if the integer n is a square.\"\n",
355 | " if n < 0:\n",
356 | " return False\n",
357 | " else:\n",
358 | " if round(n**0.5)**2 == n:\n",
359 | " return True\n",
360 | "\n",
361 | "def elliptic(A,B,C,x_range):\n",
362 | " \"Compute the integer solutions of y**2 = A*x**3 + B*x + C for x in the interval x_range.\"\n",
363 | " a = x_range[0]\n",
364 | " b = x_range[1]\n",
365 | " solutions = []\n",
366 | " for x in range(a,b+1):\n",
367 | " # Compute the right hand side of the equation\n",
368 | " f = A*x**3+B*x+C\n",
369 | " if is_square(f):\n",
370 | " # If RHS is a square, we have a solution\n",
371 | " y = round(f**0.5)\n",
372 | " solutions.append([x,y])\n",
373 | " if f != 0:\n",
374 | " # If RHS is a nonzero square, then (x,y) and (x,-y) are both solutions\n",
375 | " solutions.append([x,-y])\n",
376 | " return solutions"
377 | ]
378 | },
379 | {
380 | "cell_type": "code",
381 | "execution_count": 15,
382 | "metadata": {
383 | "collapsed": false
384 | },
385 | "outputs": [
386 | {
387 | "data": {
388 | "text/plain": [
389 | "[[-1, 0], [0, 1], [0, -1], [2, 3], [2, -3]]"
390 | ]
391 | },
392 | "execution_count": 15,
393 | "metadata": {},
394 | "output_type": "execute_result"
395 | }
396 | ],
397 | "source": [
398 | "elliptic(1,0,1,[-1,2])"
399 | ]
400 | },
401 | {
402 | "cell_type": "code",
403 | "execution_count": 16,
404 | "metadata": {
405 | "collapsed": false
406 | },
407 | "outputs": [
408 | {
409 | "data": {
410 | "text/plain": [
411 | "[[0, 1], [0, -1], [3, 8], [3, -8]]"
412 | ]
413 | },
414 | "execution_count": 16,
415 | "metadata": {},
416 | "output_type": "execute_result"
417 | }
418 | ],
419 | "source": [
420 | "elliptic(2,3,1,[-10,10])"
421 | ]
422 | }
423 | ],
424 | "metadata": {
425 | "kernelspec": {
426 | "display_name": "Python 3",
427 | "language": "python",
428 | "name": "python3"
429 | },
430 | "language_info": {
431 | "codemirror_mode": {
432 | "name": "ipython",
433 | "version": 3
434 | },
435 | "file_extension": ".py",
436 | "mimetype": "text/x-python",
437 | "name": "python",
438 | "nbconvert_exporter": "python",
439 | "pygments_lexer": "ipython3",
440 | "version": "3.4.3"
441 | }
442 | },
443 | "nbformat": 4,
444 | "nbformat_minor": 0
445 | }
446 |
--------------------------------------------------------------------------------