"
59 | ```
60 |
61 | **7.** Push your local commits to the remote repo.
62 |
63 | ```bash
64 | git push
65 | ```
66 |
67 | **8.** Create a [PR](https://help.github.com/en/github/collaborating-with-issues-and-pull-requests/creating-a-pull-request) !
68 |
69 | **9.** **Congratulations!** Sit and relax, you've made your contribution to quantum-algorithms project.
70 |
71 |
72 | ***:trophy: After this, project leaders and mentors will review the changes and will merge your PR if they are found good, otherwise we will suggest the required changes.***
73 |
74 | ## Style Guides for Git Commit Messages:memo:
75 |
76 | #### Here's a list of some good to have points, that can add more value to your contribution logs.
77 |
78 | - Use the present tense (example: "Add feature" and not "Added feature")
79 | - Use the imperative mood (example: "Move item to...", instead of "Moves item to...")
80 | - Limit the first line (also called subject line) to 50 characters or less
81 | - Capitalize the subject line
82 | - Separate subject from body with a blank line
83 | - Do not end the subject line with a period
84 | - Wrap the body at 72 characters
85 | - Use the body to explain what, why, vs, and how
86 | - Reference issues and pull requests liberally after the first line
87 |
88 | For more detailed reference to the above points, refer here: https://chris.beams.io/posts/git-commit.
89 |
90 | ## 💥 Issues:
91 | For major changes, you are welcomed to open an issue about what you would like to contribute. Enhancements will be appreciated.
92 |
93 | #### All the Best!🥇
94 |
95 |
96 |
97 |
101 |
102 |
103 |
--------------------------------------------------------------------------------
/Code_of_Conduct.md:
--------------------------------------------------------------------------------
1 | # Contributor Code of Conduct
2 |
3 | ## Our Pledge
4 |
5 | For the betterment of open-source and in order to make a welcoming environment, we as contributors and maintainers pledge to making participation in our project and our community a harassment-free experience for everyone, regardless of their age, body size disability, ethnicity, sex characteristics, gender identity and expression, level of experience, education, socio-economic status, nationality, skin tone, race, religion, or sexual identity and orientation.
6 |
7 | ## Our Standards
8 |
9 | Examples of behavior that contributes to creating a positive environment includes:
10 |
11 | * Using welcoming and inclusive language
12 | * Being respectful of differing viewpoints and experiences
13 | * Gracefully accepting constructive criticism
14 | * Focusing on what is best for the community
15 | * Showing empathy towards other community members
16 |
17 | Examples of unacceptable behavior by participants includes:
18 |
19 | * The use of sexualized language or imagery and unwelcome sexual attention or advances
20 | * Trolling, insulting/derogatory comments, and personal or political attacks
21 | * Public or private harassment
22 | * Publishing others' private information, such as a physical or electronic address, without explicit permission
23 | * Other conduct which could reasonably be considered inappropriate in a professional setting
24 |
25 | ## Our Responsibilities
26 |
27 | Project maintainers are responsible for clarifying the standards of acceptable behavior and are expected to take appropriate and fair corrective action in response to any instances of unacceptable behavior.
28 |
29 | Project maintainers have the right and responsibility to remove, edit, or reject comments, commits, code, wiki edits, issues, and other contributions that are not aligned to this Code of Conduct, or to ban temporarily or permanently any contributor for other behaviors that they deem inappropriate, threatening, offensive, or harmful.
30 |
31 | ## Scope
32 |
33 | This Code of Conduct applies both within project spaces and in public spaces when an individual is representing the project or its community. Examples of representing a project or community include using an official project e-mail address, posting via an official social media account, or acting as an appointed a representative at an online or offline event. Representation of a project may be further defined and clarified by project maintainers.
34 |
35 | ## Enforcement
36 |
37 | Instances of abusive, harassing, or otherwise unacceptable behavior may be reported by contacting the project team at their [mail](khushisaxena123123@gmail.com). All complaints will be reviewed and investigated and will result in a response that is deemed necessary and appropriate to the circumstances. The project team is obligated to maintain confidentiality with regard to the reporter of an incident. Further details of specific enforcement policies may be posted separately.
38 |
39 | Project maintainers who do not follow or enforce the Code of Conduct in good faith may face temporary or permanent repercussions as determined by other members of the project's leadership.
40 |
--------------------------------------------------------------------------------
/QSharp/CHSH Implementation/CHSH Implementation.qs:
--------------------------------------------------------------------------------
1 | namespace chsh {
2 | open Microsoft.Quantum.Canon;
3 | open Microsoft.Quantum.Intrinsic;
4 | open Microsoft.Quantum.Convert;
5 | open Microsoft.Quantum.Math;
6 | open Microsoft.Quantum.Measurement;
7 |
8 | @EntryPoint()
9 | operation SayHello() : Unit
10 | {
11 | Message(" CHSH ");
12 | Message("------");
13 |
14 | let numberOfGames = 10000;
15 | mutable classicalWinCount = 0;
16 | mutable quantumWinCount = 0;
17 |
18 | for( i in 1..numberOfGames )
19 | {
20 | let bitForAlice = GetRandomBit();
21 | let bitForBob = GetRandomBit();
22 |
23 | let (classicalXorA, classicalXorB) = PlayClassic(bitForAlice, bitForBob);
24 | let (quantumXorA, quantumXorB) = PlayQuantum(bitForAlice, bitForBob);
25 |
26 | let bitProduct = BoolArrayAsInt([bitForAlice]) * BoolArrayAsInt([bitForBob]);
27 |
28 | let bitXorClassic = ModulusI(classicalXorA + classicalXorB, 2);
29 | if( bitProduct == bitXorClassic )
30 | {
31 | set classicalWinCount += 1;
32 | }
33 |
34 | let bitXorQuantum = ModulusI(quantumXorA + quantumXorB, 2);
35 | if( bitProduct == bitXorQuantum )
36 | {
37 | set quantumWinCount += 1;
38 | }
39 | }
40 |
41 | Message($"Classical win percentage: {(IntAsDouble(classicalWinCount) / IntAsDouble(numberOfGames))}");
42 | Message($"Quantum win percentage: {IntAsDouble(quantumWinCount) / IntAsDouble(numberOfGames)}");
43 | }
44 |
45 | operation GetRandomBit() : Bool
46 | {
47 | using( q = Qubit() )
48 | {
49 | H(q);
50 | let bit = MResetZ(q);
51 | return bit == One;
52 | }
53 | }
54 |
55 | operation PlayClassic( bitForAlice : Bool, bitForBob : Bool ) : (Int, Int)
56 | {
57 | if( GetRandomBit() )
58 | {
59 | return (0, 0);
60 | }
61 | else
62 | {
63 | return (1, 1);
64 | }
65 | }
66 |
67 | operation PlayQuantum( bitForAlice : Bool, bitForBob : Bool ) : (Int, Int)
68 | {
69 | using( (qubitForAlice, qubitForBob) = (Qubit(), Qubit()) )
70 | {
71 | H(qubitForAlice);
72 | CNOT(qubitForAlice, qubitForBob);
73 |
74 | if( GetRandomBit() )
75 | {
76 | let measuredForAlice = MeasureQubitForAlice(bitForAlice, qubitForAlice) == One ? 1 | 0;
77 | let measuredForBob = MeasureQubitForBob(bitForBob, qubitForBob) == One ? 1 | 0;
78 | return (measuredForAlice, measuredForBob);
79 | }
80 | else
81 | {
82 | let measuredForBob = MeasureQubitForBob(bitForBob, qubitForBob) == One ? 1 | 0;
83 | let measuredForAlice = MeasureQubitForAlice(bitForAlice, qubitForAlice) == One ? 1 | 0;
84 | return (measuredForAlice, measuredForBob);
85 | }
86 | }
87 | }
88 |
89 | operation MeasureQubitForAlice( bit : Bool, qubit : Qubit) : Result
90 | {
91 | if( bit )
92 | {
93 | return MResetX(qubit);
94 | }
95 | else
96 | {
97 | return MResetZ(qubit);
98 | }
99 | }
100 |
101 | operation MeasureQubitForBob( bit : Bool, qubit : Qubit) : Result
102 | {
103 | if( bit )
104 | {
105 | Ry(2.0 * PI() / 8.0, qubit);
106 | }
107 | else
108 | {
109 | Ry(-2.0 * PI() / 8.0, qubit);
110 | }
111 |
112 | return MResetZ(qubit);
113 | }
114 | }
--------------------------------------------------------------------------------
/QSharp/CHSH Implementation/README.md:
--------------------------------------------------------------------------------
1 | In physics, the CHSH inequality can be used in the proof of Bell's theorem, which states that certain consequences of entanglement in quantum mechanics cannot be reproduced by local hidden variable theories. Experimental verification of violation of the inequalities is seen as experimental confirmation that nature cannot be described by local hidden variables theories. CHSH stands for John Clauser, Michael Horne, Abner Shimony, and Richard Holt, who described it in a much-cited paper published in 1969 (Clauser et al., 1969). They derived the CHSH inequality, which, as with John Bell's original inequality (Bell, 1964), is a constraint on the statistics of "coincidences" in a Bell test experiment which is necessarily true if there exist underlying local hidden variables (local realism). This constraint can, on the other hand, be infringed by quantum mechanics.
2 |
3 | In 1935, when Einstein authored his EPR Paradox paper in conjunction with Podolsky and Rosen (hence the appellation EPR) he was essentially stating that Quantum Entanglement -Spooky action at a distance which he was later to call it- did not exist.
4 |
5 | Einstein postulated that there was nothing ‘spooky’ going on and that it was just like saying if you separated a pair of boots and revealed that the boot in front of you was left, then you immediately knew that the distant one was a right boot! Essentially, Einstein said that there was a ‘Hidden Variable’ within every particle that science had just not discovered at that time. The science community happily accepted Einstein’s explanation as it was nowhere near understanding this perplexing phenomenon.
6 |
7 | But Einstein was wrong!
8 |
9 | It took 30 years and a Northern Irish professor -John Bell- to, mathematically, prove Einstein wrong. His proof has come to be known as ‘Bell’s Inequality’ and the CHSH Game is an intuitive way to understand the inequality.
10 |
11 | The CHSH game looks like a magic trick for which there is no explanation yet it works every time!
12 |
13 | In this presentation, Eamonn Darcy the Founder/Operator of QUECWA -The Quantum Education Centre of Western Australia provides a description of the CHSH game -a hypothetical Bell test experiment. The players of this game can use either classical strategies (corresponding to local hidden variable theories) or quantum strategies, which involve measurements of a shared entangled bit.
14 |
15 | No matter what strategy you come up with, classically, the chances of you winning the game can never be greater than 75% whereas exploiting the enigmatic, spooky force of quantum entanglement you will regularly win 85% of the time.
--------------------------------------------------------------------------------
/QSharp/Deutsch Josza Algorithm/DeutschJosza QSharp.qs:
--------------------------------------------------------------------------------
1 | namespace Deutch {
2 |
3 | open Microsoft.Quantum.Canon;
4 | open Microsoft.Quantum.Convert;
5 | open Microsoft.Quantum.Intrinsic;
6 |
7 |
8 | @EntryPoint()
9 | operation HelloQ() : Unit {
10 |
11 | let (result1A, result1B) = DeutschTestConstantZero();
12 | Message( "Constant-0: " + BoolAsString(result1A) + ", " + BoolAsString(result1B));
13 |
14 | let (result2A, result2B) = DeutschTestConstantOne();
15 | Message( "Constant-1: " + BoolAsString(result2A) + ", " + BoolAsString(result2B));
16 |
17 | let (result3A, result3B) = DeutschTestIdentity();
18 | Message( "Identity: " + BoolAsString(result3A) + ", " + BoolAsString(result3B));
19 |
20 | let (result4A, result4B) = DeutschTestNegation();
21 | Message( "Negation: " + BoolAsString(result4A) + ", " + BoolAsString(result4B));
22 | }
23 |
24 | // qOutput: |0> --- --- --- --- |0>
25 | // qInput : |x> --- --- --- --- |x>
26 | operation ConstantZero (qOutput: Qubit, qInput: Qubit) : Unit
27 | {
28 | }
29 |
30 | // qOutput: |0> --- --- -X- --- |1>
31 | // qInput : |x> --- --- --- --- |x>
32 | operation ConstantOne (qOutput: Qubit, qInput: Qubit) : Unit
33 | {
34 | X(qOutput);
35 | }
36 |
37 | // qOutput: |0> --- -O- --- --- |x>
38 | // qInput : |x> --- -|- --- --- |x>
39 | operation Identity (qOutput: Qubit, qInput: Qubit) : Unit
40 | {
41 | CNOT(qInput, qOutput);
42 | }
43 |
44 | // qOutput: |0> --- -O- -X- --- |!x>
45 | // qInput : |x> --- -|- --- --- |x>
46 | operation Negation (qOutput: Qubit, qInput: Qubit) : Unit
47 | {
48 | CNOT(qInput, qOutput);
49 | X(qOutput);
50 | }
51 |
52 | // qOutput: |0> -X- -H- -BB- -H- -M- |!x>
53 | // qInput : |x> -X- -H- -BB- -H- -M- |x>
54 | operation Deutsch (blackbox: ((Qubit, Qubit) => Unit)) : (Bool, Bool)
55 | {
56 | mutable result = (false, false);
57 | using(register = Qubit[2])
58 | {
59 | let qOutput = register[0];
60 | let qInput = register[1];
61 |
62 | X(qOutput);
63 | X(qInput);
64 |
65 | H(qOutput);
66 | H(qInput);
67 |
68 | blackbox(qOutput, qInput);
69 |
70 | H(qOutput);
71 | H(qInput);
72 |
73 | let bOutput = M(qOutput);
74 | let bInput = M(qInput);
75 |
76 | set result = (bInput == One, bOutput == One);
77 |
78 | Reset(qOutput);
79 | Reset(qInput);
80 | }
81 |
82 | return result;
83 | }
84 |
85 | operation DeutschTestConstantZero() : (Bool, Bool)
86 | {
87 | return Deutsch(ConstantZero);
88 | }
89 |
90 | operation DeutschTestConstantOne() : (Bool, Bool)
91 | {
92 | return Deutsch(ConstantOne);
93 | }
94 |
95 | operation DeutschTestIdentity() : (Bool, Bool)
96 | {
97 | return Deutsch(Identity);
98 | }
99 |
100 | operation DeutschTestNegation() : (Bool, Bool)
101 | {
102 | return Deutsch(Negation);
103 | }
104 | }
--------------------------------------------------------------------------------
/QSharp/Deutsch Josza Algorithm/README.md:
--------------------------------------------------------------------------------
1 | The Deutsch-Jozsa algorithm is a quantum algorithm, proposed by David Deutsch and Richard Jozsa in 1992. It was one of first examples of a quantum algorithm, which is a class of algorithms designed for execution on Quantum computers and have the potential to be more efficient than conventional, classical, algorithms by taking advantage of the quantum superposition and entanglement principles.
2 |
3 | In Deutsch-Jozsa problem, we are given a black box computing a 0-1 valued function f(x1, x2, ..., xn). The black box takes n bits x1, x2, ..., xn and outputs the value f(x1, x2, ..., xn). We know that the function in the black box is either constant (0 on all inputs or 1 on all inputs) or balanced (returns 1 for half the domain and 0 for the other half). The task is to determine whether f is constant or balanced.
4 |
5 | For a conventional deterministic algorithm, 2n-1 evaluations of f will be required in the worst case. For a conventional randomized algorithm, a constant number of evaluation suffices to produce the correct answer with a high probability but 2n-1 evaluations are still required if we want an answer that is always correct. The Deutsch-Jozsa quantum algorithm produces an answer that is always correct with just 1 evaluation of f.
6 |
7 | The algorithm is as follows. First, do Hadamard transformations on n 0s, forming all possible inputs, and a single 1, which will be the answer qubit. Next, run the function once; this XORs the result with the answer qubit. Finally, do Hadamards on the n inputs again, and measure the answer qubit. If it is 0, the function is constant, otherwise the function is balanced.
8 |
9 | The algorithm builds on an earlier 1985 work by David Deutsch which gave a similar algorithm for the special case when the function f(x1) has one 0-1 valued variable instead of n. It preceded other quantum algorithms such as Shor's algorithm and Grover's algorithm.
--------------------------------------------------------------------------------
/QSharp/QuantumRandomBitGenerator/Program.qs:
--------------------------------------------------------------------------------
1 | namespace QuantumRNG {
2 |
3 | open Microsoft.Quantum.Canon;
4 | open Microsoft.Quantum.Intrinsic;
5 | open Microsoft.Quantum.Measurement;
6 | open Microsoft.Quantum.Math;
7 | open Microsoft.Quantum.Convert;
8 |
9 | operation GenerateRandomBit() : Result {
10 | // Allocate a qubit.
11 | using (q = Qubit()) {
12 | // Put the qubit to superposition.
13 | H(q);
14 | // It now has a 50% chance of being measured 0 or 1.
15 | // Measure the qubit value.
16 | return MResetZ(q);
17 | }
18 | }
19 |
20 | operation SampleRandomNumberInRange(max : Int) : Int {
21 | mutable output = 0;
22 | repeat {
23 | mutable bits = new Result[0];
24 | for (idxBit in 1..BitSizeI(max)) {
25 | set bits += [GenerateRandomBit()];
26 | }
27 | set output = ResultArrayAsInt(bits);
28 | } until (output <= max);
29 | return output;
30 | }
31 |
32 | @EntryPoint()
33 | operation SampleRandomNumber() : Int {
34 | let max = 50;
35 | Message($"Sampling a random number between 0 and {max}: ");
36 | return SampleRandomNumberInRange(max);
37 | }
38 | }
--------------------------------------------------------------------------------
/QSharp/QuantumRandomBitGenerator/QuantumRandomBitGenerator.csproj:
--------------------------------------------------------------------------------
1 |
2 |
3 |
4 | Exe
5 | netcoreapp3.1
6 |
7 |
8 |
9 |
--------------------------------------------------------------------------------
/QSharp/README.md:
--------------------------------------------------------------------------------
1 | Q# Algorithms List:
2 |
3 | 1. Deutsch Josza Algorithm
4 | 2. CHSH Implementation
--------------------------------------------------------------------------------
/QSharp/Teleportation/.vscode/launch.json:
--------------------------------------------------------------------------------
1 | {
2 | // Use IntelliSense to find out which attributes exist for C# debugging
3 | // Use hover for the description of the existing attributes
4 | // For further information visit https://github.com/OmniSharp/omnisharp-vscode/blob/master/debugger-launchjson.md
5 | "version": "0.2.0",
6 | "configurations": [
7 | {
8 | "name": ".NET Core Launch (console)",
9 | "type": "coreclr",
10 | "request": "launch",
11 | "preLaunchTask": "build",
12 | // If you have changed target frameworks, make sure to update the program path.
13 | "program": "${workspaceFolder}/bin/Debug/netcoreapp3.1/Teleportation.dll",
14 | "args": [],
15 | "cwd": "${workspaceFolder}",
16 | // For more information about the 'console' field, see https://aka.ms/VSCode-CS-LaunchJson-Console
17 | "console": "internalConsole",
18 | "stopAtEntry": false
19 | },
20 | {
21 | "name": ".NET Core Attach",
22 | "type": "coreclr",
23 | "request": "attach",
24 | "processId": "${command:pickProcess}"
25 | }
26 | ]
27 | }
--------------------------------------------------------------------------------
/QSharp/Teleportation/.vscode/tasks.json:
--------------------------------------------------------------------------------
1 | {
2 | "version": "2.0.0",
3 | "tasks": [
4 | {
5 | "label": "build",
6 | "command": "dotnet",
7 | "type": "process",
8 | "args": [
9 | "build",
10 | "${workspaceFolder}/Teleportation.csproj",
11 | "/property:GenerateFullPaths=true",
12 | "/consoleloggerparameters:NoSummary"
13 | ],
14 | "problemMatcher": "$msCompile"
15 | },
16 | {
17 | "label": "publish",
18 | "command": "dotnet",
19 | "type": "process",
20 | "args": [
21 | "publish",
22 | "${workspaceFolder}/Teleportation.csproj",
23 | "/property:GenerateFullPaths=true",
24 | "/consoleloggerparameters:NoSummary"
25 | ],
26 | "problemMatcher": "$msCompile"
27 | },
28 | {
29 | "label": "watch",
30 | "command": "dotnet",
31 | "type": "process",
32 | "args": [
33 | "watch",
34 | "run",
35 | "${workspaceFolder}/Teleportation.csproj",
36 | "/property:GenerateFullPaths=true",
37 | "/consoleloggerparameters:NoSummary"
38 | ],
39 | "problemMatcher": "$msCompile"
40 | }
41 | ]
42 | }
--------------------------------------------------------------------------------
/QSharp/Teleportation/Teleportation.csproj:
--------------------------------------------------------------------------------
1 |
2 |
3 |
4 | Exe
5 | netcoreapp3.1
6 |
7 |
8 |
9 |
--------------------------------------------------------------------------------
/QSharp/Teleportation/Teleportation.qs:
--------------------------------------------------------------------------------
1 | namespace Teleportation {
2 |
3 | open Microsoft.Quantum.Canon;
4 | open Microsoft.Quantum.Convert;
5 | open Microsoft.Quantum.Intrinsic;
6 | open Microsoft.Quantum.Diagnostics;
7 | open Microsoft.Quantum.Math;
8 |
9 |
10 | @EntryPoint()
11 | operation HelloQ() : Unit {
12 |
13 | TeleportBit(true);
14 | TeleportBit(false);
15 | TeleportBit(false);
16 | TeleportBit(true);
17 |
18 | using( qMessage = Qubit() )
19 | {
20 | Ry(2.0*PI()/3.0, qMessage);
21 | TeleportQubit(qMessage);
22 |
23 | Reset(qMessage);
24 | }
25 | }
26 |
27 | operation TeleportBit(message: Bool) : Unit
28 | {
29 | using( qRegistry = Qubit[3] )
30 | {
31 | let qMessage = qRegistry[0];
32 | let qAlice = qRegistry[1];
33 | let qBob = qRegistry[2];
34 |
35 | // Set qubit to teleport to required state
36 | // based on random message.
37 | if( message )
38 | {
39 | X(qMessage);
40 | }
41 |
42 | // Entangle Alice and Bob qubits
43 | H(qAlice);
44 | CNOT(qAlice, qBob);
45 |
46 | // Entangle Alice and Message
47 | CNOT(qMessage, qAlice);
48 | H(qMessage);
49 |
50 | let bAlice = M(qAlice);
51 | if( bAlice == One )
52 | {
53 | X(qBob);
54 | }
55 |
56 | let bMessage = M(qMessage);
57 | if( bMessage == One )
58 | {
59 | Z(qBob);
60 | }
61 |
62 | let bBob = M(qBob);
63 |
64 | Message( "Teleported " + BoolAsString(message) + " to " + BoolAsString(bBob == One));
65 |
66 | // Reset Qubits.
67 | Reset(qMessage);
68 | Reset(qAlice);
69 | Reset(qBob);
70 | }
71 | }
72 |
73 | operation TeleportQubit(message: Qubit) : Unit
74 | {
75 | using( qRegistry = Qubit[2] )
76 | {
77 | let qMessage = message;
78 | let qAlice = qRegistry[0];
79 | let qBob = qRegistry[1];
80 |
81 | // Write diagnostics
82 | DumpRegister("c:\temp\teleport-qMessage-before.txt", [qMessage]);
83 | DumpRegister("c:\temp\teleport-qAlice-before.txt", [qAlice]);
84 | DumpRegister("c:\temp\teleport-qBob-before.txt", [qBob]);
85 |
86 | // Entangle Alice and Bob qubits
87 | H(qAlice);
88 | CNOT(qAlice, qBob);
89 |
90 | // Entangle Alice and Message
91 | CNOT(qMessage, qAlice);
92 | H(qMessage);
93 |
94 | let bAlice = M(qAlice);
95 | if( bAlice == One )
96 | {
97 | X(qBob);
98 | }
99 |
100 | let bMessage = M(qMessage);
101 | if( bMessage == One )
102 | {
103 | Z(qBob);
104 | }
105 |
106 | // Write diagnostics
107 | DumpRegister("c:\temp\teleport-qMessage-after.txt", [qMessage]);
108 | DumpRegister("c:\temp\teleport-qAlice-after.txt", [qAlice]);
109 | DumpRegister("c:\temp\teleport-qBob-after.txt", [qBob]);
110 |
111 | // Reset Qubits.
112 | Reset(qMessage);
113 | Reset(qAlice);
114 | Reset(qBob);
115 | }
116 | }
117 | }
--------------------------------------------------------------------------------
/QSharp/Teleportation/teleport-qAlice-after.txt:
--------------------------------------------------------------------------------
1 | # wave function for qubits with ids (least to most significant): 1
2 | ∣0❭: 1,000000 + 0,000000 i == ******************** [ 1,000000 ] --- [ 0,00000 rad ]
3 | ∣1❭: 0,000000 + 0,000000 i == [ 0,000000 ]
4 |
--------------------------------------------------------------------------------
/QSharp/Teleportation/teleport-qAlice-before.txt:
--------------------------------------------------------------------------------
1 | # wave function for qubits with ids (least to most significant): 1
2 | ∣0❭: 1,000000 + 0,000000 i == ******************** [ 1,000000 ] --- [ 0,00000 rad ]
3 | ∣1❭: 0,000000 + 0,000000 i == [ 0,000000 ]
4 |
--------------------------------------------------------------------------------
/QSharp/Teleportation/teleport-qBob-after.txt:
--------------------------------------------------------------------------------
1 | # wave function for qubits with ids (least to most significant): 2
2 | ∣0❭: 0,500000 + 0,000000 i == ****** [ 0,250000 ] --- [ 0,00000 rad ]
3 | ∣1❭: 0,866025 + 0,000000 i == *************** [ 0,750000 ] --- [ 0,00000 rad ]
4 |
--------------------------------------------------------------------------------
/QSharp/Teleportation/teleport-qBob-before.txt:
--------------------------------------------------------------------------------
1 | # wave function for qubits with ids (least to most significant): 2
2 | ∣0❭: 1,000000 + 0,000000 i == ******************** [ 1,000000 ] --- [ 0,00000 rad ]
3 | ∣1❭: 0,000000 + 0,000000 i == [ 0,000000 ]
4 |
--------------------------------------------------------------------------------
/QSharp/Teleportation/teleport-qMessage-after.txt:
--------------------------------------------------------------------------------
1 | # wave function for qubits with ids (least to most significant): 0
2 | ∣0❭: 1,000000 + 0,000000 i == ******************** [ 1,000000 ] --- [ 0,00000 rad ]
3 | ∣1❭: 0,000000 + 0,000000 i == [ 0,000000 ]
4 |
--------------------------------------------------------------------------------
/QSharp/Teleportation/teleport-qMessage-before.txt:
--------------------------------------------------------------------------------
1 | # wave function for qubits with ids (least to most significant): 0
2 | ∣0❭: 0,500000 + 0,000000 i == ****** [ 0,250000 ] --- [ 0,00000 rad ]
3 | ∣1❭: 0,866025 + 0,000000 i == *************** [ 0,750000 ] --- [ 0,00000 rad ]
4 |
--------------------------------------------------------------------------------
/Qiskit/16BitRandomNumberGenerator.py:
--------------------------------------------------------------------------------
1 | from qiskit import *
2 | from qiskit.tools.visualization import plot_histogram
3 |
4 | qr = QuantumRegister(16)
5 | cr = ClassicalRegister(16)
6 | circuit = QuantumCircuit(qr,cr)
7 |
8 | %matplotlib inline
9 |
10 | for i in range(16) :
11 | circuit.h(qr[i])
12 |
13 | circuit.measure(qr,cr)
14 | circuit.draw(output='mpl')
15 |
16 | simulator = Aer.get_backend('qasm_simulator')
17 | result = execute(circuit,backend=simulator).result()
18 | plot_histogram(result.get_counts(circuit))
19 |
20 | res = result.get_counts(circuit)
21 | randomBinary = max(res,key=res.get)
22 | randomInt = int(randomBinary,2)
23 |
24 | print(randomInt)
25 |
--------------------------------------------------------------------------------
/Qiskit/Bernstein Vazirani Algorithm/README.md:
--------------------------------------------------------------------------------
1 | The Bernstein-Vazirani algorithm can be seen as an extension of the Deutsch-Josza algorithm we covered in the last section.
2 |
3 | It shows that there can be advantages in using a quantum computer as a computational tool for more complex problems, Quantum computing can go far beyond the possibilities of today’s classical high performance computing.
4 |
5 | Suppose we have a black box, by it we mean we cannot get any information from it, there is a binary string in this box and we want to know the number.
6 |
7 | With classical computer very time we can perform a single and operation on box and see the output result and finally get to know the number. But with a Quantum computer and by using Bernstein-Vazirani Algorithm we can know the number just with on operation.
8 |
9 | In order to implement Bernstein-Vazirani Algorithm, we need to take few steps:
10 |
11 | 1. Initialise the inputs qubits to the |0> state, and output qubit to |->.
12 |
13 | 2. Apply Hadamard gates to the input register
14 |
15 | 3. Query the oracle
16 |
17 | 4. Apply Hadamard gates to the input register
18 |
19 | 5. Measure
20 |
21 |
--------------------------------------------------------------------------------
/Qiskit/CHSH Implementation/CHSH Game.ipynb:
--------------------------------------------------------------------------------
1 | {
2 | "cells": [
3 | {
4 | "cell_type": "markdown",
5 | "metadata": {},
6 | "source": [
7 | "# THE CHSH GAME\n",
8 | "\n",
9 | "We are going to use (a simplified version) of the CHSH game to 'test' whether IBM's quantum computers are really quantum "
10 | ]
11 | },
12 | {
13 | "cell_type": "code",
14 | "execution_count": 1,
15 | "metadata": {},
16 | "outputs": [],
17 | "source": [
18 | "#%matplotlib inline\n",
19 | "\n",
20 | "from qiskit import *\n",
21 | "from qiskit.tools.monitor import *\n",
22 | "from qiskit.providers.ibmq import least_busy\n",
23 | "import numpy as np"
24 | ]
25 | },
26 | {
27 | "cell_type": "markdown",
28 | "metadata": {},
29 | "source": [
30 | "We define a function that creates the circuit that simulates Alice's and Bob's behaviour in the CHSH game. Parameters a0 and a1 are the measurement angles used by Alice when she receives 0 and 1, respectively. For Bob, b0 and b1 play the same role. The default parameters are the ones that give the maximum violation of the corresponding Bell inequality (or, equivalently, the highest winning probability)."
31 | ]
32 | },
33 | {
34 | "cell_type": "code",
35 | "execution_count": 2,
36 | "metadata": {},
37 | "outputs": [],
38 | "source": [
39 | "#Function to create the circuits for the CHSH game\n",
40 | "\n",
41 | "def CHSH_circuit(x,y,a0=0,a1=np.pi/2,b0=np.pi/4,b1=-np.pi/4):\n",
42 | " \n",
43 | " #x: bit received by Alice\n",
44 | " #y: bit received by Bob\n",
45 | " #a0: measure angle used by Alice when she receives 0\n",
46 | " #a1: measure angle used by Alice when she receives 1\n",
47 | " #b0: measure angle used by Bob when he receives 0\n",
48 | " #b1: measure angle used by Bob when he receives 1\n",
49 | " \n",
50 | " circ = QuantumCircuit(2,2) \n",
51 | " \n",
52 | " # First, we create a Bell pair\n",
53 | " \n",
54 | " circ.h(0)\n",
55 | " circ.cx(0,1)\n",
56 | "\n",
57 | " # Now, we apply rotations for Alice and Bob depending on the bits they have received\n",
58 | " \n",
59 | " if(x==0):\n",
60 | " circ.ry(a0,0)\n",
61 | " else:\n",
62 | " circ.ry(a1,0)\n",
63 | "\n",
64 | " if(y==0):\n",
65 | " circ.ry(b0,1)\n",
66 | " else:\n",
67 | " circ.ry(b1,1)\n",
68 | "\n",
69 | " # We measure\n",
70 | " \n",
71 | " circ.measure(range(2),range(2)) # Medimos\n",
72 | "\n",
73 | " return circ\n",
74 | " "
75 | ]
76 | },
77 | {
78 | "cell_type": "markdown",
79 | "metadata": {},
80 | "source": [
81 | "We also define a function to compute the winning probability. Notice how we can create a batch of circuits and send them for execution all at the same time."
82 | ]
83 | },
84 | {
85 | "cell_type": "code",
86 | "execution_count": 3,
87 | "metadata": {},
88 | "outputs": [],
89 | "source": [
90 | "def winning_probability(backend, shots = 8192, a0=0,a1=np.pi/2,b0=np.pi/4,b1=-np.pi/4):\n",
91 | " total = 0\n",
92 | " circuits = [CHSH_circuit(0,0,a0,a1,b0,b1), CHSH_circuit(0,1,a0,a1,b0,b1), CHSH_circuit(1,0,a0,a1,b0,b1), CHSH_circuit(1,1,a0,a1,b0,b1)] # We 'pack' four different circuits for execution\n",
93 | " job = execute(circuits, backend=backend, shots = shots)\n",
94 | " # For the first three circuits, the winning condition is that Alice's and Bob's outputs are equal\n",
95 | " for qc in circuits[0:3]:\n",
96 | " counts = job.result().get_counts(qc)\n",
97 | " if('00' in counts):\n",
98 | " total += counts['00']\n",
99 | " if('11' in counts):\n",
100 | " total += counts['11']\n",
101 | " # For the fourth circuit, Alice's and Bob's outputs must be different for them to win\n",
102 | " counts = job.result().get_counts(circuits[3])\n",
103 | " if('01' in counts):\n",
104 | " total += counts['01']\n",
105 | " if('10' in counts):\n",
106 | " total += counts['10']\n",
107 | " \n",
108 | " return total/(4*shots) "
109 | ]
110 | },
111 | {
112 | "cell_type": "markdown",
113 | "metadata": {},
114 | "source": [
115 | "First, we try it on the simulator"
116 | ]
117 | },
118 | {
119 | "cell_type": "code",
120 | "execution_count": 4,
121 | "metadata": {},
122 | "outputs": [
123 | {
124 | "name": "stdout",
125 | "output_type": "stream",
126 | "text": [
127 | "0.855438232421875\n"
128 | ]
129 | }
130 | ],
131 | "source": [
132 | "# Backend definition \n",
133 | "\n",
134 | "backend = Aer.get_backend('qasm_simulator')\n",
135 | "\n",
136 | "# Execution\n",
137 | "\n",
138 | "print(winning_probability(backend))"
139 | ]
140 | },
141 | {
142 | "cell_type": "markdown",
143 | "metadata": {},
144 | "source": [
145 | "We now run on an actual quantum computer. Is Nature classical or quantum? Let's find out! "
146 | ]
147 | },
148 | {
149 | "cell_type": "code",
150 | "execution_count": 5,
151 | "metadata": {},
152 | "outputs": [
153 | {
154 | "name": "stderr",
155 | "output_type": "stream",
156 | "text": [
157 | "/opt/conda/lib/python3.7/site-packages/qiskit/providers/ibmq/ibmqfactory.py:192: UserWarning: Timestamps in IBMQ backend properties, jobs, and job results are all now in local time instead of UTC.\n",
158 | " warnings.warn('Timestamps in IBMQ backend properties, jobs, and job results '\n"
159 | ]
160 | },
161 | {
162 | "name": "stdout",
163 | "output_type": "stream",
164 | "text": [
165 | "We are executing on... ibmq_athens\n",
166 | "0.83245849609375\n"
167 | ]
168 | }
169 | ],
170 | "source": [
171 | "# Load the account\n",
172 | "\n",
173 | "provider = IBMQ.load_account()\n",
174 | "\n",
175 | "# We execute on the least busy device (among the actual quantum computers)\n",
176 | "\n",
177 | "backend = least_busy(provider.backends(operational = True, simulator=False, status_msg='active',\n",
178 | " filters=lambda x: x.configuration().n_qubits > 1)) \n",
179 | "print(\"We are executing on...\",backend)\n",
180 | "\n",
181 | "print(winning_probability(backend))"
182 | ]
183 | }
184 | ],
185 | "metadata": {
186 | "kernelspec": {
187 | "display_name": "Python 3",
188 | "language": "python",
189 | "name": "python3"
190 | },
191 | "language_info": {
192 | "codemirror_mode": {
193 | "name": "ipython",
194 | "version": 3
195 | },
196 | "file_extension": ".py",
197 | "mimetype": "text/x-python",
198 | "name": "python",
199 | "nbconvert_exporter": "python",
200 | "pygments_lexer": "ipython3",
201 | "version": "3.7.8"
202 | }
203 | },
204 | "nbformat": 4,
205 | "nbformat_minor": 4
206 | }
207 |
--------------------------------------------------------------------------------
/Qiskit/CHSH Implementation/README.md:
--------------------------------------------------------------------------------
1 | In physics, the CHSH inequality can be used in the proof of Bell's theorem, which states that certain consequences of entanglement in quantum mechanics cannot be reproduced by local hidden variable theories. Experimental verification of violation of the inequalities is seen as experimental confirmation that nature cannot be described by local hidden variables theories. CHSH stands for John Clauser, Michael Horne, Abner Shimony, and Richard Holt, who described it in a much-cited paper published in 1969 (Clauser et al., 1969). They derived the CHSH inequality, which, as with John Bell's original inequality (Bell, 1964), is a constraint on the statistics of "coincidences" in a Bell test experiment which is necessarily true if there exist underlying local hidden variables (local realism). This constraint can, on the other hand, be infringed by quantum mechanics.
2 |
3 | In 1935, when Einstein authored his EPR Paradox paper in conjunction with Podolsky and Rosen (hence the appellation EPR) he was essentially stating that Quantum Entanglement -Spooky action at a distance which he was later to call it- did not exist.
4 |
5 | Einstein postulated that there was nothing ‘spooky’ going on and that it was just like saying if you separated a pair of boots and revealed that the boot in front of you was left, then you immediately knew that the distant one was a right boot! Essentially, Einstein said that there was a ‘Hidden Variable’ within every particle that science had just not discovered at that time. The science community happily accepted Einstein’s explanation as it was nowhere near understanding this perplexing phenomenon.
6 |
7 | But Einstein was wrong!
8 |
9 | It took 30 years and a Northern Irish professor -John Bell- to, mathematically, prove Einstein wrong. His proof has come to be known as ‘Bell’s Inequality’ and the CHSH Game is an intuitive way to understand the inequality.
10 |
11 | The CHSH game looks like a magic trick for which there is no explanation yet it works every time!
12 |
13 | In this presentation, Eamonn Darcy the Founder/Operator of QUECWA -The Quantum Education Centre of Western Australia provides a description of the CHSH game -a hypothetical Bell test experiment. The players of this game can use either classical strategies (corresponding to local hidden variable theories) or quantum strategies, which involve measurements of a shared entangled bit.
14 |
15 | No matter what strategy you come up with, classically, the chances of you winning the game can never be greater than 75% whereas exploiting the enigmatic, spooky force of quantum entanglement you will regularly win 85% of the time.
--------------------------------------------------------------------------------
/Qiskit/Decrement Circuit/Decrement.ipynb:
--------------------------------------------------------------------------------
1 | {
2 | "cells": [
3 | {
4 | "cell_type": "code",
5 | "execution_count": 1,
6 | "metadata": {},
7 | "outputs": [],
8 | "source": [
9 | "import matplotlib.pyplot as plt\n",
10 | "%matplotlib inline\n",
11 | "import numpy as np\n",
12 | "\n",
13 | "from qiskit import *\n",
14 | "\n",
15 | "from qiskit.tools.visualization import plot_histogram\n",
16 | "from IPython.display import display, Math, Latex"
17 | ]
18 | },
19 | {
20 | "cell_type": "markdown",
21 | "metadata": {},
22 | "source": [
23 | "# Decrement\n",
24 | "\n",
25 | "Takes an arbitrary input state $|x\\rangle$ on $n$ and takes it to the $|(x-1)\\text{mod N}\\rangle$, where $N = 2^n$ state in the binary representation, which can be done by applying the following circuit $U$.\n",
26 | "\n",
27 | "Let $|x\\rangle$ be an arbitrary state on $n$ qubits,\n",
28 | "\n",
29 | "$$\n",
30 | " \\begin{align*}\n",
31 | " U|x\\rangle = |(x-1)\\text{mod N}\\rangle\n",
32 | " \\end{align*}\n",
33 | "$$\n",
34 | "\n",
35 | "Where $U$ defines an opperation that applies multiple $0$ multi-controlled $X$ gates and flipping the first qubit.\n",
36 | "\n",
37 | "Here we give an example on $n = 3$ qubits.\n",
38 | "\n",
39 | "| Initial State $|x\\rangle$ | Final State $U|x\\rangle$ |\n",
40 | "| ------------- | ------------- |\n",
41 | "| $|000\\rangle$ | $|111\\rangle$ |\n",
42 | "| $|001\\rangle$ | $|000\\rangle$ |\n",
43 | "| $|010\\rangle$ | $|001\\rangle$ |\n",
44 | "| $|011\\rangle$ | $|010\\rangle$ |\n",
45 | "| $|100\\rangle$ | $|011\\rangle$ |\n",
46 | "| $|101\\rangle$ | $|100\\rangle$ |\n",
47 | "| $|110\\rangle$ | $|101\\rangle$ |\n",
48 | "| $|111\\rangle$ | $|110\\rangle$ |"
49 | ]
50 | },
51 | {
52 | "cell_type": "code",
53 | "execution_count": 2,
54 | "metadata": {},
55 | "outputs": [],
56 | "source": [
57 | "def Decrement(n):\n",
58 | " U = QuantumCircuit(n)\n",
59 | " control = [x for x in range(n-1)]\n",
60 | " for k in range(n-1):\n",
61 | " U.x(control)\n",
62 | " U.mcx(control, control[-1]+1)\n",
63 | " U.x(control)\n",
64 | " control.pop()\n",
65 | " U.x(0)\n",
66 | " \n",
67 | " U = U.to_gate()\n",
68 | " U.name = 'Decrement'\n",
69 | " #ctl_U = U.control() make it a controlled gate\n",
70 | " \n",
71 | " return U"
72 | ]
73 | },
74 | {
75 | "cell_type": "code",
76 | "execution_count": 3,
77 | "metadata": {},
78 | "outputs": [
79 | {
80 | "data": {
81 | "image/png": "iVBORw0KGgoAAAANSUhEUgAAAdMAAADWCAYAAACKRGiqAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjMuMCwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy86wFpkAAAACXBIWXMAAAsTAAALEwEAmpwYAAAfSUlEQVR4nO3de1xUdeLG8c/AIKJ4R7whJiKoIyiiZaaB1/yZdtW8lKXpal52bbupu5FJLuWlTDc3NUu3LFMU08pczYA0K0PzuhWSmKComKKiqFzm9wc5KyIXPcABfd6v17ycOZeZh3HgmfM9Z85Y7Ha7HREREblhTmYHEBERqehUpiIiIgapTEVERAxSmYqIiBikMhURETFIZSoiImKQylRERMQglamIiIhBKlMRERGDVKYiIiIGqUxFREQMUpmKiIgYpDIVERExSGUqIiJikMpURETEIJWpiIiIQSpTERERg1SmIiIiBqlMRUREDFKZioiIGKQyFRERMUhlKiIiYpDKVERExCCVqYiIiEEqUxEREYNUpiIiIgZZzQ4g5ccvX8HZ42ankJtFNU/w72Z2CpGyoTIVh7PHIS3Z7BQixWexWEx5XLvdbsrjSvmlYV4RERGDVKYiIiIGqUxFREQMUpmKiIgYpDIVERExSGUqIiJikMpURKQQLi4uZkeQCkCfMxWRW0Lr1q0JDQ0lODiYBg0aYLfbOXr0KNu3byc6Opp9+/blW6d///5MmzaNnj17kpSUZEJqqShUpiJyU+vXrx8TJ07krrvuuub8YcOGAbBlyxZee+01Pv/8cyC3SJctW4bVaqV///7Mnj27rCJLBaQyvUJOTg5vvPEGCxYsICkpCX9/f+bOncuoUaMICQlh4cKFZkcsF7Jzsnl33SQ2xC3hUtYFgpv34un+C6hR1cPsaCIOtWrV4l//+heDBg0C4PTp06xevZpt27aRmJiIxWKhadOm3H777TzwwAN07tyZzz77jI8++ogNGzawaNEirFYr06ZNU5FKkSx2nRfLYfjw4URFRREWFkZwcDBbt25l3rx5pKam8tZbbzF69GizI5aquI+LdzrBDzf9g41x/+bVkeupXqUOs1Y8ycXM80SM/KL0Q0qFUdML2g8q3cco6HSCnp6efPXVV9hsNs6dO8eLL77IwoULOX/+/DWXr1q1KqNHjyY8PJyqVatit9uxWCxMmzaNsLCwfMvrz6ZcTVumf1i2bBlLliwhJiaGkJAQALp27cqOHTuIioqiXbt2JicsP9Z9t5DHer5Egzo+APzp3hk8Md2XY6d+o16tJiank1udq6sr69evx2azsW/fPvr160diYmKh65w7d4433niDS5cuMXfuXCwWC0eOHCE8PLyMUktFp6N5/xAREUHv3r0dRXqZr68vLi4uBAYGAnDw4EFCQkLw8/MjICCAzZs3mxHXNOkZaRxPO0TzRsGOaQ09mlGlcnV+PbLLxGQiuaZMmUJQUBAJCQl07dq1yCK97PJ+UYvFwqlTp2jYsOE1t0pFrkVlCiQnJ7N3714GDBiQb96hQ4ew2Wy4uroCMHr0aAYOHEh8fDwLFixg0KBBXLp0qcSyWCwW0y6xsTFF5jt/8SwAVd1q5JnuXrkm5y+cKbHnQSq+2NiYUn/NXs3Hx4cXXniB7Oxshg4dSmpqarGyXnmw0bRp07jvvvvIyclh8uTJNGmSf7TFzN9TXcrucj1UpuSWKUD9+vXzTM/IyCA2NtYxxHvixAm2bNnCiBEjAOjUqRMNGzYkOjq6bAObqIprNQDOZZzOMz39QhpVKlc3I5KIw1NPPYWzszMffPAB3333XbHWubpIw8LC2LJli2PazX6shJQMlSng4ZF7FGp8fHye6TNmzCAlJYXg4NwhzUOHDlGvXj3HVipA06ZN+e2330osi91uN+0SEhJaZD53t5p41vQm4fAOx7SU3w9w/sIZfBoEltjzIBVfSEhoqb9mrzZ06FAA5s2bV6yM1yrSy9566y0AHn/88Xzrmfl7qkvZXa6HDkAid2goMDCQiIgIateuTaNGjVi5ciXr1q0DcJSp5OrTcRTLY6bTxrcr1avU4Z11E2nvdw/1a99mdjS5hTVu3Jj69etz4sQJ4uLiily+sCIF+O6770hLS6NRo0Y0aNCAlJSU0oouNwFtmQJOTk5ERkZis9kYM2YMw4cPx8PDg3HjxuHs7Ow4+Mjb25tjx45x8eJFx7qJiYnX3KdyMxvUdRIdW/Zj/JwODJ7WiJycbCYNWWp2LLnFBQQEAPDjjz8WuWxRRXrZ5fu6/DdApCDaMv2Dn59fvn2fQ4cOpVWrVri5uQG5w8F33XUX7777LmPHjmXr1q0cPnyYrl27mhHZNM5OzozuN4vR/WaZHUXEISUlhYULF7JrV+FHlQcEBBSrSAGioqLYv38/R48eLem4cpPRSRsK0bJlSzp27MjixYsd0w4cOMCwYcM4evQolSpVYt68efk+TlNRFfekDSLFYeZJG4ry6quvkpWVdcMffdGfTbmatkwLkJ6eTnx8PGPHjs0z3cfHh6+//tqkVCJSEiZPnmx2BLnJqEwL4O7uTnZ2ttkxRESkAtABSCIiIgapTEVERAxSmYqIiBikMhURETFIZSoiImKQylRERMQglamIiIhB+pypiFRYN3ImoknTF+a5/drEUSUVR25h2jIVERExSGUqIiJikMpURETEIJWpiIiIQSpTERERg1SmIiIiBqlMRUREDFKZioiIGKQyFRERMUhlKiIiYpDKVERExCCVqYiIiEEqUxEREYNUpiIiIgapTEVERAzS95mKiJQxi8VS5o95I9/9KsWnLVMRERGDVKYiIiIGqUxFREQMUpmKiIgYpDIVERExSGUqIiJikD4aIyJSztWtW5eWLVtSuXJlzp07x759+0hLSytw+ccff5zo6GiSkpLKLuQtTmUqIlIO+fr68tRTTzFgwAC8vb3zzU9ISODDDz9k4cKFHDlyxDF97NixzJs3j19//ZXAwEDOnz9flrFvWRrmvUJOTg6zZs2iefPmVK5cmTZt2hAbG4u/vz+jRo0yO56I3AKqVKnCnDlz2L9/P88++yze3t6cPXuWb7/9lg0bNrBt2zYyMjLw9fVlypQpHDx4kJdeegmr1eooUoDZs2erSMuQtkyvMGLECKKioggLCyM4OJitW7cyePBgUlNTeeaZZ8yOVy5E7/yYtVvnceDILi5knuc/07PK5HGffTuUn377Fqu1EhaLE9Wr1MF221081OVp/LyCyyRDeXD05EGGvtqUj/6eRN2aXmbHkRLm4+PDF198gZ+fH5mZmSxdupT58+cTFxdHTk6OYzmr1UqXLl0YM2YMAwYMYOrUqTz55JM0adIEgPHjxztKVcqGyvQPy5YtY8mSJcTExBASEgJA165d2bFjB1FRUbRr187khOWDu1st+t05lkuZGcxeVbZb64/2COPRHi8CcOzUb6z7/h3+8s+OvPjYCjoHPFiij5WVnYnV2aVE71OkMN7e3sTExNC4cWN2797NE088wc6dO6+5bFZWFtHR0URHRxMSEsKqVascRfrCCy+oSE2gMv1DREQEvXv3dhTpZb6+vri4uBAYGAjASy+9xMcff0xCQgIrVqygf//+ZsQ1TQf/ewDY9WuMqTnq1WrC8N7TOHkmhXlr/sxdrR/gYmYG//7PS2zZs4pzF07j3/h2xj/4Fo08fIHcglwRM5ON2//N72eOULOqJyPvnc7dgf2Z8fEwsnMycXZy4bv/riWkzUAmPPw23+z9hA+/fIUjv/9K7eoNeLT7i3Rv9ygA//lhCR9tmsZ9ncax8uvXOXfhNPfeMZrB3SYze+UoduzfSJ3qDXlmwCJaN+3syL7u+3dYvXkOx08n0aC2DyP7TKe9fy8A3t/wMnsSN9PC+w7Wf78IgL53juGJe6YCMHp2GwCenOEPFgsDQyfyWM+wMnvepXQ4OTnx4Ycf0rhxYzZv3kyfPn1IT08v1ro2m406deo4bgcH3zojNeWJ9pkCycnJ7N27lwEDBuSbd+jQIWw2G66urgD07t2b9evXc/fdd5d1TLmG0LaDOHH6MEmpvzB75Z9ISv2ZuX/+juUvHaWF9x2EvdeXrOxMABavf5FNO5YS9lgka145w+tjYvHy8HPc19e7I7m9xf8R+XIqo/u9zvb4jbweOYIx971J1NSTvDDw37z1yXh2H/jasc6xU7+RnpHG+5MOMHvsFtZ880/+9u7/MSD0eaLCT3FXwEPMXDHcsfy6799hefR0Jg35kNVTTzG89z+Y+v5DHD6R4Fhmz4Gv8azpzcdhR5g6fC3Lvopgb+I3ACz46y4A3nvhFz79R7qK9CYxbtw4OnfuzJEjR7j//vuLXaRX7iOdMmUK6enpDBw4kAcfLNmRGimaypTcMgWoX79+nukZGRnExsbmGeLt1KkTPj4+pZbFYrGYdomNjSm1n6u0eNTI3W946uwxvvrxI/7y4L+oVa0eLtZKDO05hd/PpvDzoe+x2+2s3TqPUX1n4tMwEIvFQt2aXvg0DHTcV+vbOhPadiDOTs5UrlSF1Vvm8GDnCQT4dMHJyYkW3rfTvd1jbNz+vmMdVxc3hvacgou1Es0atsGnYRv8vDrQqklHnJ2c6dHuMY6cSOBcxmkAVm+ew2M9XqJZwzY4OTlxR8s+tG3WlZidHzvu06uuH/3ufApnZyutmnSkWcO2xCfHldEzWnJiY2NMfT0XdLma2RmsVisTJ04Eckv11KlTxXp+ryzS8ePHEx4ezuTJkwEc/5r9c1b0y/XQMC/g4eEBQHx8PH369HFMnzFjBikpKRo2KcdOnM59I+RkyX1fOOqNwDzzs7MzOZ6WRKNzqVy4dI5GV2yJXq1e7dvy3D56MpFdCdGs+voNx7Qcezatm3Zx3K7p7omT0//ek7q6VKFO9QZ5bgOcv3iWqm41OHoykX9+Mo55a/7yv4w5WY43BQC1q/1vfYDKlaqScfFsgbmlYuvbty+NGjXi559/5pNPPinWOlcX6eXrixYt4uWXX6ZDhw4EBwezffv20ootV1GZknsEXWBgIBEREdSuXZtGjRqxcuVK1q1bB5TtPggzv3Mw7mNISzbt4W9IzK7leNRohFfd3JJcMnE/Nd3r5lvObrdT2aUKh0/sx6tu82vel8WSd6DGs1YTerUfxiOhz5dYXs9aTXi811RC2uTfpVAcTpaKM5gUEhKK/e3y9x2ak6YvzHPbjN+5K7d6unfvDsD7779f0OJ5FFSkABcuXCAyMpKnnnqK7t275ylTfZ9p6ao4v5mlyMnJicjISGw2G2PGjGH48OF4eHgwbtw4nJ2dHQcfCWTnZHMp8wKZWZcAuJR5gUuZF8r8F/V4WhL//s8UNsQtYex9c6hVrR7dgoYwd/VYTpw+DEB6Rhpb9qwm42I6FouFfp3GsujzF0g8uhe73U5qWjIHjuwu8DEe6vw0qzbPZs+BzWTnZJOZdYn45O38knTjQ64P3/1XPtj4MgmHd2K327mYmcHexC0cOv5zsdav4V4XJ4sTh0/sv+EMUr5cfrO+bdu2IpctrEgv+/777/Pcr5QNbZn+wc/Pj+jo6DzThg4dSqtWrXBzczMpVfnz5fYPmHXFATX3/i33uflgciL1rxomLWkffvkKy2OmY8FC9Sp1aHVbJ+aM20oL79sB+Gv/d1j2VQTPzg/l1NmjuFeuSeumXQj+40jZ4b3/gZtrNV5e8gAnzx6ldrX6jLx3Rp79pldq79+LZ/q/w8LPnyc59RcsFiduq2fjiXvCb/hn6HPHn7A6V2LWiuEcPZmI1dkF30btGN13VrHWd3Vx44l7XiHiw8FcyrrAgNDnebT73284j5ivYcOGAPz666+FLlecIoXcMyNdeb9SNix2bfsXqGXLlnTs2JHFixc7poWFhbF48WJSU1Nxd3fHzc2N2NhYmjVrZmLSklERh3ml/KrpBe0HmZ0iv6uHeV+bWPZnN7tymNfNzQ03NzfS0tLynJjhahEREUyePLnIEzJYrVaqVavG+fPnuXjxomO6/tSXLg3zFiA9PZ34+Ph8J2t45ZVXSE5O5uLFi/z+++8kJyffFEUqIubIyMjg5MmThRYpwN/+9jc6depU5AkZsrKyOHXqVJ4ildKnYd4CuLu7k52dbXYMERGHb7/91uwIUgBtmYqIiBikMhURETFIZSoiImKQylRERMQglamIiIhBKlMRERGDVKYiIiIG6XOmIiJl7HrPRnT5rE2vTRyV57qUH9oyFRERMUhlKiIiYpDKVERExCCVqYiIiEEqUxEREYNUpiIiIgapTEVERAxSmYqIiBikMhURETFIZSoiImKQylRERMQglamIiIhBKlMRERGDVKYiIiIGqUxFREQM0veZiohIkSwWiymPe73f/WoWbZmKiIgYpDIVERExSGUqIiJikMpURETEIJWpiIiIQSpTERERg1SmIiJSLtSoUcPsCDdMnzMVEZESY7Va6dOnD126dKFdu3Z4eHhgt9tJSkpi+/btbNy4kW+++SbfeuHh4Tz66KOEhoaSlJRkQnJjtGV6hZycHGbNmkXz5s2pXLkybdq0ITY2Fn9/f0aNGmV2PBGRcstqtfLcc89x8OBB1qxZw3PPPUe3bt0IDAykTZs29O3blylTprBlyxZ2797NI4884lg3PDycsLAwvL29CQoKMvGnuHHaMr3CiBEjiIqKIiwsjODgYLZu3crgwYNJTU3lmWeeMTteufDO5xP5/qfPSE1LorKrO3e0uJeR906nepXaZkcTEZO0aNGCpUuXEhwcDMBPP/3E8uXLiYuLIykpCWdnZ5o3b84dd9zBkCFDCAgIYPny5TzyyCMkJiby3HPPkZWVxZAhQ1i7dq3JP82NUZn+YdmyZSxZsoSYmBhCQkIA6Nq1Kzt27CAqKop27dqZnLB8cHJyZtLgpdxWvzXpGWnM+PhxZi4fxivDK+YvgIgYExQUxJdffknt2rU5ePAgY8eO5Ysvvsi33I8//siKFSuYNGkSTz75JDNmzODhhx8GcBRpZGRkWccvMRrm/UNERAS9e/d2FOllvr6+uLi4EBgYyKlTp+jbty9+fn60adOGXr16kZCQYFJic4z4vwh8GwVhdXahpntdHuw8gd2/xpgdS0RMUL9+fdavX0/t2rX59NNPCQgIuGaRXikzM5MFCxawZMkSx7TExERWr15dymlLl8oUSE5OZu/evQwYMCDfvEOHDmGz2XB1dcVisfD0008THx/Prl276Nu3L8OHDzchcfnxY8ImfBq2MTuGiJhg/vz5eHp68tVXX/Hwww+Tnp5erPXCw8P5y1/+QlZWFqmpqTRv3pznn3++lNOWLpUpuWUKue+yrpSRkUFsbKxjiLdmzZr06NHDMb9Tp04kJiaWaBaLxWLaJTY25rqybt69is++m8/Y++aU6HMgN4fY2BhTX88FXa5mdp7ryXz1dTOft+7du3P//fdz+vRpHn/8cTIzM4v1urh8sNHlod3BgwcDMGXKFOrWrVuu/n+uh8oU8PDwACA+Pj7P9BkzZpCSkuLYqX61N998kwceeKC045VLsbsimb3yT4QPW0tzL+1PFrnVjBs3DoCZM2dy+PDhYq1zdZFGRkayadMm1q5di6urKyNGjCjNyKVKZQr4+PgQGBhIREQE77//Pps2bWLMmDG89957ANcs06lTp5KQkMCMGTNKNIvdbjftEhISWqyM639YzJxVowkf/iltfbuW6M8vN4+QkFBTX88FXa5mdp7ryXz1dbOet6pVq9KvXz+ysrJYtGhRsV4P1yrSy95++20Ax1Zqefn/uR4qU8DJyYnIyEhsNhtjxoxh+PDheHh4MG7cOJydnQkMDMyz/LRp0/jss89Yv349VapUMSm1OVZvmcvCz57j1T/9h9ZN7zI7joiYoG3btlitVnbv3s2xY8eKXL6wIgWIiYkhKysLm82Gm5tbacUuVfpozB/8/PyIjo7OM23o0KG0atUqz3/u1KlTWbduHRs3bqRmzZplnNJ8/1ozAWcnK8/Nz7tF+uk/infggYhUfDabDYBdu3YVuWxRRQpw4cIFfv75Z1q3bo2/vz87d+4s6cilTmVaiLi4ODp27Oi4vW/fPl5++WWaNWtGaGioY3pF/I+/URtnXt/Qh4jcfHbu3El4eDg//PBDocv17NmzyCK9bN68edSrV4/U1NSSjlsmVKYFSE9PJz4+nrFjxzqm2Wy26x5HFxG52Wzbto1t27YVudzGjRuJiIhg586dRZ6QYf78+SUVzxQq0wK4u7uTnZ1tdgwRkQrt73//u9kRyoQOQBIRETFIZSoiImKQylRERMQglamIiIhBKlMRERGDVKYiIiIGqUxFREQMUpmKiIgYpJM2iEM1T7MTyM1Er6eby/We/W3S9IUAvDZxVJ7rNyuVqTj4dzM7gYhIxaRhXhEREYNUpiIiIgapTEVERAxSmYqIiBikMhURETFIZSoiImKQylRERMQglamIiIhBKlMRERGDVKYiIiIGqUxFREQMUpmKiIgYpDIVERExSGUqIiJikMpUiq1Xr160bduWgIAA+vfvz5kzZ8yOJFKmYmJisNls+Pr6MnLkSLKzs82OVKQJEybg5eWF1VpxvnEzKSmJ7t2707JlS2w2G5MnTzY7UpFUplJskZGR7Ny5kz179uDl5cUbb7xhdiSRMpOTk8PIkSOJjIwkISGBM2fOsHTpUrNjFWnAgAHExcWZHeO6WK1Wpk+fzk8//cSPP/7Ili1bWLNmjdmxCqUylWKrUaMGkPtH5cKFC1gsFpMTiZSdH374gYYNG9KqVSsARowYwapVq0xOVbTOnTtTv359s2NclwYNGtC+fXsAKlWqRFBQEIcOHTI5VeFUpnJdHnzwQTw9Pfnll1949tlnzY4jUmaSk5Np3Lix47a3tzdJSUkmJro1nDx5kk8++YSePXuaHaVQFWcQXcqF1atXc+nSJUaMGMHKlSsZNmyY2ZFECvXppq0cOJRS4Pw5i/+3denbpBH3dut4zeXsdnuJZyvI4WMnWLkuNt/0K7Nevm6xwBMP3UON6u5llu9a7HY7Kz6P5mjqqTzTr5UZoE3LZoR2bFvofV66dIn+/fszYcIEWrRoUaJ5S5q2TOW6VapUiUGDBrF69Wqzo4gUqX2AP0dTT5Jy/HdSjv+eb/7l6cdST9I+wK/A+2ncuHGeLdFDhw7h5eVVKpkbetahWlW3fJmvvp5y/He86tc1vUgBLBYL7Wx+xcr8+6nTtLM1L/T+srOzGTJkCG3btq0Qo2AqUymWs2fPkpKS++4+JyeHtWvXYrPZTE4lUrQGnnXoEOhf5HJ3BLWkXt3aBc5v3749ycnJ/Pe//wXg3Xff5aGHHiqxnFeyWCzc2+1OnIo4LsG1kgs9u7QvlQw3onlTL1r6ehe5XGjHtlSvVrXQZUaNGkW1atV4/fXXSypeqVKZSrGcPXuW++67j8DAQAIDA8nKyuLFF180O5ZIsfTq0gHXSi4Fzq/sWokedxVeSs7OzixatIj+/fvTrFkz3N3dGTp0aElHdajnUYs7gloVuky3Tu2oVrVKocuMHj0aLy8vsrOz8fLyYty4cSUZM597u96Js1PB1VKzujtdOgQWeh/ffPMN7733HnFxcQQFBdG2bVvmzp1b0lFLlMVeljsC5KZkt9t1ZK+Ue19/v4t1Md9fc17fbnfSuUNAGScq2rmMC8xc8DEXLl7KN692zWo8M+IRrFZnE5IV7rOvvmXLD3uuOW/wfd1p07JZGScqfdoyvQ5r1qyhb9++eHp64urqSpMmTRgyZAh79lz7RXOr2Lf/IAuXfcrZ9PNmRxEpUKfg1tSpWT3fdI/aNejYrvAtQLNUdatMj87B15zXp2vHclmkAN07taOKm2u+6U0a1SOwhY8JiUqfyrQYsrKyePTRR3nggQfYs2cPDz30EBMmTCAoKIhVq1Zx+PBhsyOaJsduZ9M3OziTfp4qVSqbHUekQFarM3265j9St2+3O7E6l89SArgzyEbd2jXyTPPxboCt+W3mBCoGt8qu9OrSId/0ft073bSjWPpoTDH8+c9/5qOPPmL8+PHMnj07z2m5kpOTHSczuBX9d/9BUo7/zsC+XQvdTyJSHrRq3gQf74YcOHQEgOa3eeHv07iItczl7OzEvd3uZMnK9QBYyH0DUN5LqUObFny7Yx/HTuR+VKZdaz+8GtQ1OVXp0T7TImzevJm7776b3r17s27dulJ/AU+avrBU719ERIrntYmjir2sNiWK8OabbwLw2muvlft3giIiYg5tmRahWrVqeHh4kJiYaHaUciXHbuefS6LIzMriryMGaIhXKpT0cxlYLBaqVrD9/MdOnKKeRy2zY1yXk2lnqFa1Ci4uN/deRZVpIdLS0qhVqxahoaFER0eXyWNqmFdEpHzQMG8Jufw+4/jx4yYnERGR8kxbpkVo1qwZiYmJbNiwgR49euSZ98svv+DvX/Rpym42e+MTWbp6IwP7diWoiPNriojcClSmRVixYgUDBw7EarVy//3306xZM44fP87WrVtp1arVLXeyd+0rFRHJ7+beI1wCHnnkEWrUqMHMmTPZuHEjn376KZ6entx+++08/fTTZscrc+fOZ+Ds5MTdndqpSEVE/qAtU7ludrsdOxT5jRYiIrcKlamIiIhBGqcTERExSGUqIiJikMpURETEIJWpiIiIQSpTERERg1SmIiIiBqlMRUREDFKZioiIGKQyFRERMUhlKiIiYpDKVERExCCVqYiIiEEqUxEREYNUpiIiIgapTEVERAxSmYqIiBikMhURETFIZSoiImKQylRERMQglamIiIhBKlMRERGDVKYiIiIGqUxFREQMUpmKiIgYpDIVERExSGUqIiJikMpURETEoP8Hk7GYvUTFV+8AAAAASUVORK5CYII=\n",
82 | "text/plain": [
83 | ""
84 | ]
85 | },
86 | "execution_count": 3,
87 | "metadata": {},
88 | "output_type": "execute_result"
89 | }
90 | ],
91 | "source": [
92 | "n = 3\n",
93 | "mc = QuantumCircuit(n, n)\n",
94 | "U = Decrement(n)\n",
95 | "mc.append(U, range(n))\n",
96 | "\n",
97 | "mc.measure(range(n), range(n))\n",
98 | "\n",
99 | "backend = BasicAer.get_backend('qasm_simulator')\n",
100 | "atp = 1024\n",
101 | "res = execute(mc, backend=backend, shots=atp).result()\n",
102 | "ans = res.get_counts()\n",
103 | "\n",
104 | "mc.draw('mpl')"
105 | ]
106 | },
107 | {
108 | "cell_type": "code",
109 | "execution_count": 4,
110 | "metadata": {},
111 | "outputs": [
112 | {
113 | "data": {
114 | "image/png": "iVBORw0KGgoAAAANSUhEUgAAAc0AAAFDCAYAAABY/1W1AAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjMuMCwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy86wFpkAAAACXBIWXMAAAsTAAALEwEAmpwYAAAaEklEQVR4nO3df5RcZZ3n8fcXIiImKAmSpNMghnB0NhFBSwewgegxyxJ3UcEjcNRMlpFsohKR1VF3kJm4ojM6srDOsEhmDhB0HUYcdR0DhEVjPBA6duJEETfJDhhNaDoyRKNDSDB+94+qZGqL/vFUUumupN6vc+p01fM896nv/Sef3Lr3PjcyE0mSNLIjxroASZIOFYamJEmFDE1JkgoZmpIkFTI0JUkqZGhKklRo3FgXMJaOP/74PPnkk8e6DElSG1m7du2TmfmSwfo6OjRPPvlk+vr6xroMSVIbiYjNQ/X586wkSYUMTUmSChmakiQVMjQlSSpkaEqSVMjQlCSpkKEpSVIhQ1OSpEKGpiRJhQxNSZIKGZqSJBUyNCVJKmRoSpJUyNCUJKmQoSlJUiFDU5KkQoamJEmFDE1JkgoZmpIkFTI0JUkqZGhKklTI0JQkqZChKR2GLr/8ck444QRmzZo1aH9msnjxYmbMmMFpp53GunXr9vXdfvvtnHrqqZx66qncfvvt+9rXrl3LK1/5SmbMmMHixYvJzIO+H1K7MTSlw9D8+fO55557huy/++672bRpE5s2beKWW25h0aJFADz11FMsWbKE3t5e1qxZw5IlS9i+fTsAixYtYunSpfu2G25+6XBlaEqHoXPPPZeJEycO2f+Nb3yDefPmERGceeaZ/PKXv6S/v597772XOXPmMHHiRI477jjmzJnDPffcQ39/Pzt27ODMM88kIpg3bx5f//rXR2+HpDZhaEodaOvWrZx44on7Pnd3d7N169Zh27u7u5/TLnUaQ1OSpEKGptSBpk2bxs9//vN9n7ds2cK0adOGbd+yZctz2qVOY2hKHejCCy9k2bJlZCYPPfQQL3rRi5g6dSrnn38+K1asYPv27Wzfvp0VK1Zw/vnnM3XqVI499lgeeughMpNly5bxlre8Zax3Qxp148a6AEmtd9lll7Fy5UqefPJJuru7WbJkCc8++ywACxcuZO7cuSxfvpwZM2ZwzDHHcOuttwIwceJEPv7xj/Pa174WgGuvvXbfBUU33XQT8+fPZ+fOnVxwwQVccMEFY7Nz0hiKTr7XqlKpZF9f31iXIUlqIxGxNjMrg/X586wkSYUMTUmSChmakiQVMjQlSSpkaEqSVMjQlCSpkKEpSVIhQ1OSpEKjGpoRcW5E/K+I2BoRGRHzC7Z5ZUR8NyJ21ra7NiKiYczFEfFIROyq/X3bQdsJSVLHGu0jzfHAw8AHgJ0jDY6IY4H7gAHgtbXtPgxcXTfmLOBO4EvA6bW/X4mI329x7ZKkDjeqa89m5nJgOUBE3FawyTuBY4A/yMydwMMR8Qrg6oi4PqtrAF4FfCczr6ttc11EvKHWfllr90CS1Mna/ZzmWcD3aoG5171AF3By3ZgVDdvdC5x90KuTJHWUdn/KyRRgS0PbQF3fY7W/A4OMmTLYhBGxAFgA0NXVxcqVKwGYPn06EyZMYP369QBMmjSJmTNnsmrVKgDGjRtHT08P69atY8eOHQBUKhUGBgb4s2+eciD7KElqgU9c0s+GDRuA6jNju7u76e3tBWD8+PFUKhVWr17Nrl27AOjp6WHjxo1s27YNgFmzZu3rG8qYPeUkIn4DvD8zbxtmzApgS2ZeXtd2ErAZODszV0fEbuA9mbmsbsw8YGlmPn+4Glr1lJMrbjjgKSRJB2jpVa2Z51B+yskTwOSGtsl1fcONeQJJklqo3UNzNXBORBxd1zYHeBz4ad2YOQ3bzQEePOjVSZI6ymjfpzk+Ik6PiNNr331S7fNJtf5PR8T9dZv8T+Bp4LaImBURFwEfBfZeOQtwI/DGiPhoRLwiIj4GvAG4YZR2S5LUIUb7SLMC/KD2egGwpPb+E7X+qcC+q2oy81dUjxq7gD7gr4DPAdfXjXkQuBSYD/wQmAdckpm9B3dXJEmdZrTv01wJxDD98wdp+xFw7gjz3gXcdYDlSZI0rHY/pylJUtswNCVJKmRoSpJUyNCUJKmQoSlJUiFDU5KkQoamJEmFDE1JkgoZmpIkFTI0JUkqZGhKklTI0JQkqZChKUlSIUNTkqRChqYkSYUMTUmSChmakiQVMjQlSSpkaEqSVMjQlCSpkKEpSVIhQ1OSpEKGpiRJhQxNSZIKGZqSJBUyNCVJKmRoSpJUyNCUJKmQoSlJUiFDU5KkQoamJEmFDE1JkgoZmpIkFTI0JUkqZGhKklTI0JQkqZChKUlSIUNTkqRChqYkSYUMTUmSChmakiQVMjQlSSpkaEqSVMjQlCSpUFOhGRFHRMQRdZ+nRMR7IuL1rS9NkqT20uyR5reAKwEiYjzQB3wWWBkR81pcmyRJbaXZ0KwA3669vwjYAZwAXAF8qGSCiHhvRDwWEc9ExNqIOGeYsbdFRA7y+pe6MbOHGPOKJvdNkqRhNRua44Ff1t7/W+Brmfks1SA9ZaSNI+IS4EbgU8AZwIPA3RFx0hCbfACY2vB6FPi7QcbObBi3qWiPJEkq1Gxo/gx4fUS8EDgfuK/WPhF4umD7q4HbMnNpZv4kM68E+oFFgw3OzF9l5hN7X1SDeTqwdJDh2+rHZuaeJvdNkqRhNRua1wN3AFuArcCqWvu5wI+G2zAijgJeA6xo6FoBnF34/VcAP87MBwfp64uI/oi4PyLeUDifJEnFxjUzODO/EBFrgROB+zLzd7WufwI+PsLmxwNHAgMN7QPAm0b67oh4EfAO4GMNXXuPVL8PHAW8G7g/Is7LzO8NMs8CYAFAV1cXK1euBGD69OlMmDCB9evXAzBp0iRmzpzJqlXV/xeMGzeOnp4e1q1bx44dOwCoVCoMDAxQ8Mu0JOkg6+/vZ8OGDQBMmzaN7u5uent7ARg/fjyVSoXVq1eza9cuAHp6eti4cSPbtm0DYNasWfv6hhKZeRB3oe6LIrqoHp2el5mr6tqvBd6ZmS8fYfv3AZ8DujLzqRHGLgd+m5kXDjeuUqlkX19f6S4M6YobDngKSdIBWnpVa+aJiLWZWRmsr+nFDWpXv/44Ip6OiOm1to9ExDtG2PRJYA8wuaF9MvBEwVdfAXx1pMCs6QVOLRgnSVKxZhc3uAq4BrgFiLqux4H3D7dtZu4G1gJzGrrmUL2KdrjvfR3wKga/AGgwp1P92VaSpJZp6pwmsBC4IjO/FRGfrGtfR/WWj5FcD9wREWuAB2rzdQE3A0TEMoDMbFwoYQGwKTNXNk5YC/KfAj+mek7zXcBbgYsL90mSpCLNhuZLgYcHaX8WeMFIG2fmnRExierR6tTaXHMzc3NtyHPu14yICcClwCeGmPYoqqsSdQM7qYbnmzNz+Uj1SJLUjGZD81Hg1cDmhva5wCMlE2TmTcBNQ/TNHqTt11QXVRhqvs8Anyn5bkmSDkSzofkXwF9GxDFUz2meFRHvBv4IuLzVxUmS1E6avU/z1ogYR3UZvGOoLnTwOLA4M+88CPVJktQ2mj3SJDOXAksj4njgiMzc1vqyJElqP02H5l6Z+WQrC5Ekqd2NGJoR8UOqq/hsj4gfAUMuIZSZp7WyOEmS2knJkeZXgV1170dn3T1JktrMiKGZmUvq3v/pQa1GkqQ21uwyet+OiBcP0n5sRHy7ZVVJktSGml2wfTbVFXgaHQ2cc8DVSJLUxoquno2IV9d9PC0i6p80ciRwPtXHfkmSdNgqveWkj+oFQAmsGKR/J3Blq4qSJKkdlYbmy6gum/co8DrgF3V9u4FtmbmnxbVJktRWikKz7ikkTT+0WpKkw0XJ4gYXAd/MzGdr74eUmX/fssokSWozJUeadwFTgG2190NJqhcFSZJ0WCpZ3OCIwd5LktRpDEFJkgqVntMs4jlNSdLhrPScZgnPaUqSDmtNndOUJKmTGYiSJBXyPk1Jkgp5n6YkSYW8T1OSpEKGoCRJhZoOzYh4dUQsi4i+2uuOhudtSpJ0WGoqNCPincD3ganA8tprMrAmIt7V+vIkSWofpc/T3Os64OOZ+an6xoj4GPBJ4IutKkySpHbT7M+zLwH+bpD2rwAnHHg5kiS1r2ZD8zvA7EHaZwPfPdBiJElqZ80u2H438OmIqAAP1drOBC4C/rTl1UmS1Eb2d8H2BbVXvc8DNx1wRZIktSkXbJckqZCBKElSoWZvOSEijgMuAE4Cjqrvy8xPtKguSZLaTlOhGRFnAt8CdlG9/WQr1YUOdgE/BQxNSdJhq9mfZz8LfAmYBjwDvJHqEWcf8OetLU2SpPbSbGieBvxlZiawB3h+Zg4AH8FbTiRJh7lmQ3N33fsB4KW1978BulpSkSRJbarZC4HWAa8FNgIrgU9GxGTgXcAPW1uaJEntpdkjzT8GHq+9vwb4BdVFDY7juYsdSJJ0WGnqSDMz++re/4LqrSeSJHWEpu/TBIiIU4Dfq318JDMfbV1JkiS1p2bv05wE/A1wIfC7f22OfwAuz8x/bnF9kiS1jWbPaf41MAM4Bzi69joXeBmwtLWlSZLUXpoNzfOBKzLzgcz8be31APCfan0jioj3RsRjEfFMRKyNiHOGGTs7InKQ1ysaxl0cEY9ExK7a37c1uV+SJI2o2dD8BfAvg7Q/DYz402xEXALcCHwKOAN4ELg7Ik4aYdOZVJfr2/vaVDfnWcCdVFcqOr329ysR8fsj1SNJUjOaDc1PADdExLS9DbX3n6Ns3dmrgdsyc2lm/iQzrwT6gUUjbLctM5+oe+2p67sK+E5mXleb8zqq95BeVbxXkiQVGPFCoIj4EZB1TS8DfhoRW2uf965DewLVc55DzXMU8BrgLxq6VgBnj1BGX0Q8H3gE+GRmfqeu7yyq94rWuxd4/whzSpLUlJKrZ+9q0XcdDxxJdfm9egPAm4bYZu9R6PepPobs3cD9EXFeZn6vNmbKEHNOaUXRkiTtNWJoZuaS0ShkiO/eAGyoa1odEScDHwa+N+hGI4iIBdRWL+rq6mLlypUATJ8+nQkTJrB+/XoAJk2axMyZM1m1ahUA48aNo6enh3Xr1rFjxw4AKpUKAwMDwCn7U4okqYX6+/vZsKEaGdOmTaO7u5ve3l4Axo8fT6VSYfXq1ezatQuAnp4eNm7cyLZt2wCYNWvWvr6hRPWBJc2JiDcC/4bqz7Y/zsyVBdscRfWCocsy8yt17X8FzMrM8wq/+0+ASzPz92qffwZ8PjM/Wzfmw8D7M/OlQ0wDQKVSyb6+vuGGFLnihgOeQpJ0gJZe1Zp5ImJtZlYG62vqQqCImBYRa4D7qD4O7KNUfy7tjYhhn3KSmbuBtcCchq45VK+iLXU61Z9t91rdgjklSRpRs8vo/Xeqz9GckZmPAUTEdOCLtb63j7D99cAdteB9AFhI9ZFiN9fmWgaQmfNqn68Cfgr8mOo5zXcBbwUurpvzRmBVRHwU+DrwNuANQE+T+yZJ0rCaDc05wOy9gQmQmY9GxGLg/pE2zsw7a0vxXUP1fsuHgbmZubk2pPF+zaOAzwLdwE6q4fnmzFxeN+eDEXEp8Emqt738E3BJZvY2uW+SJA1rfxZsH+wkaPGJ0cy8CbhpiL7ZDZ8/A3ymYM67aN1VvpIkDarZxQ3uBz4fESfubait5nMDBUeakiQdypoNzcXAC4FHI2JzRGym+nPoC2t9kiQdtpr9efafgdcBs4G9i6b/JDP/dyuLkiSpHRWHZkQcCfwKeFVm3kf1thNJkjpG8c+ztUXSN1O9olWSpI7T7DnN/wr8WUQcfzCKkSSpnTV7TvNDVJ9ysjUittDwbM3MPK1VhUmS1G6aDc27qN6TGQehFkmS2lpRaEbEMVRX5nkr8Dyq92RemZlPHrzSJElqL6XnNJcA84FvAV+m+vzL/3GQapIkqS2V/jx7EfCHmfm3ABHxJeCBiDiydlWtJEmHvdIjzROpe+hzZq4Bfkv1CSWSJHWE0tA8Etjd0PZb9m/Bd0mSDkmloRfAFyNiV13b0cDSiHh6b0NmXtjK4iRJaieloXn7IG1fbGUhkiS1u6LQzMz/eLALkSSp3TW7jJ4kSR3L0JQkqZChKUlSIUNTkqRChqYkSYUMTUmSChmakiQVMjQlSSpkaEqSVMjQlCSpkKEpSVIhQ1OSpEKGpiRJhQxNSZIKGZqSJBUyNCVJKmRoSpJUyNCUJKmQoSlJUiFDU5KkQoamJEmFDE1JkgoZmpIkFTI0JUkqZGhKklTI0JQkqZChKUlSIUNTkqRChqYkSYUMTUmSCo16aEbEeyPisYh4JiLWRsQ5w4y9KCJWRMQvIuLXEdEbERc2jJkfETnI6+iDvzeSpE4yqqEZEZcANwKfAs4AHgTujoiThtjkPODbwJtr45cDXxskaJ8Gpta/MvOZ1u+BJKmTjRvl77sauC0zl9Y+XxkR/w5YBHyscXBmfqChaUlEvBl4K/C9/39oPnEQ6pUkaZ9RO9KMiKOA1wArGrpWAGc3MdUEYHtD2wsiYnNEbImIf4iIMw6gVEmSBjWaR5rHA0cCAw3tA8CbSiaIiPcB3cAddc0bgMuB9VQD9QPAAxHxqszcNMgcC4AFAF1dXaxcuRKA6dOnM2HCBNavXw/ApEmTmDlzJqtWrQJg3Lhx9PT0sG7dOnbs2AFApVJhYGAAOKWkfEnSQdTf38+GDRsAmDZtGt3d3fT29gIwfvx4KpUKq1evZteuXQD09PSwceNGtm3bBsCsWbP29Q0lMvMg7kLdF0V0AVuB8zJzVV37tcA7M/PlI2x/MdWwvCQzvznMuCOBfwS+k5mLh5uzUqlkX19f+U4M4YobDngKSdIBWnpVa+aJiLWZWRmsbzQvBHoS2ANMbmifDAx7PjIi3k41MOcNF5gAmbkH6ANO3f9SJUl6rlELzczcDawF5jR0zaF6Fe2gIuIdVANzfmbeNdL3REQApwH9+1+tJEnPNdpXz14P3BERa4AHgIVAF3AzQEQsA8jMebXPl1INzA8BqyJiSm2e3Zn5VG3MnwAPAZuAY4HFVENz0SjtkySpQ4xqaGbmnRExCbiG6v2UDwNzM3NzbUjj/ZoLqdZ4Q+2113eB2bX3LwZuAaYAvwJ+AJybmWtavgOSpI422keaZOZNwE1D9M0e7vMQ23wQ+GArapMkaTiuPStJUiFDU5KkQoamJEmFDE1JkgoZmpIkFTI0JUkqZGhKklTI0JQkqZChKUlSIUNTkqRChqYkSYUMTUmSChmakiQVMjQlSSpkaEqSVMjQlCSpkKEpSVIhQ1OSpEKGpiRJhQxNSZIKGZqSJBUyNCVJKmRoSpJUyNCUJKmQoSlJUiFDU5KkQoamJEmFDE1JkgoZmpIkFTI0JUkqZGhKklTI0JQkqZChKUlSIUNTkqRChqYkSYUMTUmSChmakiQVMjQlSSpkaEqSVMjQlCSpkKEpSVIhQ1OSpEKGpiRJhQxNSZIKGZqSJBUa9dCMiPdGxGMR8UxErI2Ic0YYf15t3DMR8WhELDzQOSVJ2h+jGpoRcQlwI/Ap4AzgQeDuiDhpiPEvA5bXxp0BfBr4fERcvL9zSpK0v0b7SPNq4LbMXJqZP8nMK4F+YNEQ4xcCj2fmlbXxS4HbgQ8dwJySJO2XUQvNiDgKeA2woqFrBXD2EJudNcj4e4FKRDxvP+eUJGm/jOaR5vHAkcBAQ/sAMGWIbaYMMX5cbb79mVOSpP0ybqwLGG0RsQBYUPv4m4jYMJb1SG3keODJsS5C2l9//cGWTfXSoTpGMzSfBPYAkxvaJwNPDLHNE0OM/21tvmh2zsy8BbiluGqpQ0REX2ZWxroOqZ2N2s+zmbkbWAvMaeiaQ/WK18GsHmJ8X2Y+u59zSpK0X0b759nrgTsiYg3wANWrY7uAmwEiYhlAZs6rjb8ZeH9E3AB8AXg9MB+4rHROSZJaZVRDMzPvjIhJwDXAVOBhYG5mbq4NOalh/GMRMRf4b1RvIXkcWJyZX21iTkllPG0hjSAyc6xrkCTpkODas5IkFTI0JUkqZGhKklTI0JQkqZChKUlSIUNTkqRChqYkSYUMTalDRcTkiHhXREwcYdzzRqsmqd0ZmlLnugZYBvzfiPhKRMyNiOfXD4iIk4APNLZLncrQlDpXBfhz4D8DxwFfAx6LiM9HxKtrY64AFmbmrjGqUWorHfc8TUkQEV3AFuCxzLw1Iu4AZgBvofpAhPdGxCPAdOC/jF2lUntx7VmpA0XEC4E3Atsys7eh7xhgFvAh4CJgQmbuHP0qpfZjaEoiIiIb/jGIiNuAUzLznLGpSmo/ntOUOlBEHBERsffzIIH5AqrPpb1+tGuT2plHmpKeo3abSSUzV491LVI7MTSlDlILw5cBm70iVmqeP89KneV9wA+AmyPiP0TElIg4sn5ARBwbEW+OiKPGpkSpfXmkKXWQiFgNPEP1drOzgZ9RvT/z74EfZeavImIhMD8zzxy7SqX25JGm1CEi4iXAs8DS2hWxLwX+Bvj3wCrg2xHxEeAqoHeoeaRO5pGm1CEiYipwKfBIZt7b0HcG8J5a/3HAiZm5dfSrlNqboSl1kNqtJJmZzwx2y0lEXAfMzcwzxqpGqZ25jJ7UQTJz596wHOTezGOAi4Fbx6I26VDgkabUASLiWODXjUHZMOZo4BLgy5m5e9SKkw4hhqbUASLiC8Ca2mtzZu4YZMyLM/OXo12bdCgxNKXDXERcBnwJ2AE8BdwH3AP8EHi89pPtC4C/Bf44Mx8es2KlNmdoSoe5iFgK7AE+Q/WpJX8AnAJsAJYD9wMvB27MTBc0kIZhaEqHsYgYB/wRcGxmfrSufSbVB0y/HTgaeDFwe2b+4VjUKR0qDE3pMBcRxwGTM/P/1JbGe7b+gqCIuAT4MvDqzPzHMSpTOiR4y4l0mMvM7cD22vvdUH00GNX/NO8BjgWeMTClkRmaUgfKzN/VfZwA/MlY1SIdSvx5VupwtceF7WkIUkmDMDQlSSrkU04kSSpkaEqSVMjQlCSpkKEpSVIhQ1OSpEKGpiRJhf4f6/E+ypgOyvwAAAAASUVORK5CYII=\n",
115 | "text/plain": [
116 | ""
117 | ]
118 | },
119 | "execution_count": 4,
120 | "metadata": {},
121 | "output_type": "execute_result"
122 | }
123 | ],
124 | "source": [
125 | "plot_histogram(ans)"
126 | ]
127 | }
128 | ],
129 | "metadata": {
130 | "kernelspec": {
131 | "display_name": "Python 3",
132 | "language": "python",
133 | "name": "python3"
134 | },
135 | "language_info": {
136 | "codemirror_mode": {
137 | "name": "ipython",
138 | "version": 3
139 | },
140 | "file_extension": ".py",
141 | "mimetype": "text/x-python",
142 | "name": "python",
143 | "nbconvert_exporter": "python",
144 | "pygments_lexer": "ipython3",
145 | "version": "3.8.2"
146 | }
147 | },
148 | "nbformat": 4,
149 | "nbformat_minor": 4
150 | }
151 |
--------------------------------------------------------------------------------
/Qiskit/Deutsch Josza Algorithm/README.md:
--------------------------------------------------------------------------------
1 | The Deutsch-Jozsa algorithm is a quantum algorithm, proposed by David Deutsch and Richard Jozsa in 1992. It was one of first examples of a quantum algorithm, which is a class of algorithms designed for execution on Quantum computers and have the potential to be more efficient than conventional, classical, algorithms by taking advantage of the quantum superposition and entanglement principles.
2 |
3 | In Deutsch-Jozsa problem, we are given a black box computing a 0-1 valued function f(x1, x2, ..., xn). The black box takes n bits x1, x2, ..., xn and outputs the value f(x1, x2, ..., xn). We know that the function in the black box is either constant (0 on all inputs or 1 on all inputs) or balanced (returns 1 for half the domain and 0 for the other half). The task is to determine whether f is constant or balanced.
4 |
5 | For a conventional deterministic algorithm, 2n-1 evaluations of f will be required in the worst case. For a conventional randomized algorithm, a constant number of evaluation suffices to produce the correct answer with a high probability but 2n-1 evaluations are still required if we want an answer that is always correct. The Deutsch-Jozsa quantum algorithm produces an answer that is always correct with just 1 evaluation of f.
6 |
7 | The algorithm is as follows. First, do Hadamard transformations on n 0s, forming all possible inputs, and a single 1, which will be the answer qubit. Next, run the function once; this XORs the result with the answer qubit. Finally, do Hadamards on the n inputs again, and measure the answer qubit. If it is 0, the function is constant, otherwise the function is balanced.
8 |
9 | The algorithm builds on an earlier 1985 work by David Deutsch which gave a similar algorithm for the special case when the function f(x1) has one 0-1 valued variable instead of n. It preceded other quantum algorithms such as Shor's algorithm and Grover's algorithm.
--------------------------------------------------------------------------------
/Qiskit/GHZ States/BuildGHZ.ipynb:
--------------------------------------------------------------------------------
1 | {
2 | "cells": [
3 | {
4 | "cell_type": "markdown",
5 | "metadata": {},
6 | "source": [
7 | "# Build GHZ State\n",
8 | "\n",
9 | "Takes an input state $|x\\rangle = |000\\dots0\\rangle$ and takes it to the GHZ state $\\frac{1}{\\sqrt{2}}(|0\\dots0\\rangle+|1\\dots1\\rangle)$, which can be done by applying the following circuit $U$.\n",
10 | "\n",
11 | "Let $|x\\rangle$ be a all zeros state on $n$ qubits,\n",
12 | "\n",
13 | "$$\n",
14 | " \\begin{align*}\n",
15 | " U|x\\rangle = \\frac{1}{\\sqrt{2}}(|000\\dots0\\rangle+|111\\dots1\\rangle)\n",
16 | " \\end{align*}\n",
17 | "$$\n",
18 | "\n",
19 | "Where $U$ defines an opperation that applies a Hadamard gate $H$ on the first qubit and Controlled $X$ gates, $CNOT$, on the remaining ones, taking the control qubit as the first one and the targets from the second to the $n$-th qubit."
20 | ]
21 | },
22 | {
23 | "cell_type": "code",
24 | "execution_count": 1,
25 | "metadata": {},
26 | "outputs": [],
27 | "source": [
28 | "import matplotlib.pyplot as plt\n",
29 | "%matplotlib inline\n",
30 | "import numpy as np\n",
31 | "\n",
32 | "from qiskit import *\n",
33 | "\n",
34 | "from qiskit.tools.visualization import plot_histogram\n",
35 | "from IPython.display import display, Math, Latex"
36 | ]
37 | },
38 | {
39 | "cell_type": "code",
40 | "execution_count": 2,
41 | "metadata": {},
42 | "outputs": [],
43 | "source": [
44 | "def BuildGHZ(n):\n",
45 | " U = QuantumCircuit(n)\n",
46 | " U.h(0)\n",
47 | " for i in range(1, n):\n",
48 | " U.cx(0, i)\n",
49 | " \n",
50 | " U = U.to_gate()\n",
51 | " U.name = 'Build GHZ'\n",
52 | " #ctl_U = U.control() make it a controlled gate\n",
53 | " \n",
54 | " return U"
55 | ]
56 | },
57 | {
58 | "cell_type": "code",
59 | "execution_count": 3,
60 | "metadata": {},
61 | "outputs": [
62 | {
63 | "data": {
64 | "image/png": "iVBORw0KGgoAAAANSUhEUgAAAi0AAAExCAYAAACwFZIPAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjMuMCwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy86wFpkAAAACXBIWXMAAAsTAAALEwEAmpwYAAAuHUlEQVR4nO3dfVhUdeL+8XsGFFBURFJ8NhBUSEDQJLMANcVNy0orc93VUBS11Wr7ag+2a7p8U6ms1VK31PWrWamYZazlE5RabT6lZr9YTUXMlFRUBEWY+f2hTKACYwscDr5f13Wua+bMOWfuwXG455zPOVjsdrtdAAAA1ZzV6AAAAADOoLQAAABToLQAAABToLQAAABToLQAAABToLQAAABToLQAAABToLQAAABToLQAAABToLQAAABToLQAAABToLQAAABToLQAAABToLQAAABToLQAAABToLQAAABToLQAAABToLQAAABToLQAAABToLQAAABToLQAAABToLQAAABToLQAAABToLQAAABToLQAAABToLQAAABToLQAAABTcDU6AKqPHzZK504YnQI1Rb3GUrseRqcAUJNQWuBw7oSUnWl0CsB5FovFkOe12+2GPC9ws+PwEAAAMAVKCwAAMAVKCwAAMAVKCwAAMAVKCwAAMAVKCwAAMAVOeQZwU2jSpIm6d++uiIgINW3aVHa7XT///LO2b9+uzZs36/jx49esExMTo6lTp+q+++7TqVOnDEgNoDhKC4Aa7fbbb9czzzyjAQMGyNX1+h95BQUFWrVqlWbOnKlvvvlG0uXCsmbNGtWpU0ejR49WYmJiVcYGcB0WO1dJcrDZbHr11Vc1b948HTlyRO3atdMbb7yh+Ph4RUVFaf78+UZHrFTb3nPu4nKFtkK9kzJJn21bpPyCC4oI6K0JA+epQV2fyg8J0/BqIXV+tHKfo6yLy7m7uysxMVHjx4+X1WrVpUuXtHHjRn3zzTc6ePCgJOnWW2/V7bffrh49esjV1dXxGbB+/XolJyerTp06evvttxUfH1/ignJ8bALGoLQUM3z4cCUnJ2vy5MmKiIjQ1q1bNWfOHGVlZWn27NkaNWqU0RErlbOlZemGv2ndtn/qf0esVf06jZT0weO6eClXiSP+VfkhYRpGlpZ69eopJSVF3bt3V0FBgV599VXNmjVLx44du+7yzZo105NPPqknn3xSLi4uKiwslIuLy3ULi0RpAYzC4aErli1bpkWLFik1NVVRUVGSLu8e3rFjh5KTkxUeHm5wwuoj5av5+v09L6ppIz9J0sh7Z+iP09vq+OnDatKwtcHpcLOzWq1avXq1unfvroyMDD344IPavn17mev89NNPeuaZZ/Tjjz9q9uzZcnFx0dGjRzV69GgKClCNcPbQFYmJiYqNjXUUliJt27ZVrVq1FBISIkk6dOiQoqKiFBgYqI4dO+qLL74wIq5hcvKydSI7QwHNIxzzmvn4q457fR346VsDkwGXPf3004qJidFPP/2kqKiocgtLkZiYGCUlJclqtSo3N1fNmzfXn/70p0pOC+BGUFokZWZmau/evRo0aNA1j2VkZCg4OFhubm6SpFGjRumRRx5Renq65s2bp0cffVT5+fkVlsVisRg2paWllpsv9+I5SVJdjwYl5nu6eyn3wtkK+znA/NLSUiv9PXu1Zs2a6aWXXpJ0+XDvoUOHnMpafNDt22+/rYcffliS9Le//U2+vr7XLG/k/1Mmppo4OYvSosulRdI1H055eXlKS0tzHBr65ZdftHnzZsXFxUmSunXrpmbNmmnTpk1VG9hAddzqSZLO550pMT/nQrbquNc3IhLgEB8fL3d3d61YsUKfffaZU+tcXVji4+P1ySef6MMPP5SHh4dGjBhRyakBOIvSIsnH5/JZL+np6SXmz5gxQ8eOHVNExOVDIRkZGWrSpIljr4t0+eyDw4cPV1gWu91u2BQVFV1uPk8PLzX2aqX9R3c45h07+aNyL5yVX9OQCvs5wPyioqIr/T17tWHDhkmSZs+e7VTG6xWWou3+/e9/l3R5j83VjPx/ysRUEydnMRBXkp+fn0JCQpSYmChvb281b95cK1asUEpKiiQ5Sgsu+11kvN5Pna7QtjGqX6eR/pEyUZ0D+8jXu43R0XAT8/X1VevWrZWdna3PP/+83OXLKiySlJqaqnPnzsnPz08+Pj765ZdfKjM+ACewp0WXzzZYvny5goODlZCQoOHDh8vHx0djx46Vi4uLYxBuq1atdPz4cV28eNGx7sGDB9W69c11xsyjMZMU2aG/xr3eRYOnNZfNVqhJjy0xOhZucqGhoZKknTt3lvvNrbzCIl2+btOuXbskSWFhYZURGcANYk/LFYGBgdeMTRk6dKiCgoLk4eEh6fJhpDvvvFPvvPOOxowZo61bt+ro0aOKiYkxIrJhXKwuGtU/SaP6JxkdBXA4e/asPv74Y3399ddlLhccHFxuYSmyfv16ZWdn69y5c5URGcAN4uJyZejQoYMiIyO1cOFCx7wff/xRw4YN088//6zatWtrzpw515wmbVbOXlwOcIbRV8QtjdVq1dtvv63CwsIyC0tZ+NgEjMGellLk5OQoPT1dY8aMKTHfz8/PqePlAKonm82mESNG3PAAQADGo7SUwtPTU4WFhUbHAFAJbDab0REA/AYMxAUAAKZAaQEAAKZAaQEAAKZAaQEAAKZAaQEAAKZAaQEAAKZAaQEAAKbAdVoAmNZvuTjcpOnzS9x/eWJ8RcUBUMnY0wIAAEyB0gIAAEyB0gIAAEyB0gIAAEyB0gIAAEyB0gIAAEyB0gIAAEyB0gIAAEyB0gIAAEyB0gIAAEyB0gIAAEyB0gIAAEyB0gIAAEyB0gIAAEyB0gIAAEzB1egAAHCzsVgsVf6cdru9yp8TqGjsaQEAAKZAaQEAAKZAaQEAAKZAaQEAAKZAaQEAAKZAaQEAAKZAaQGAas7V1VUBAQHq2LGj/Pz8ZLWW/dEdGxsrb2/vKkoHVB1KCwBUQ97e3nr66af11Vdf6dy5c0pPT9fu3bt14MABnT17Vp9//rlGjRolT0/PEusNHDhQH3/8sTZs2KA6deoYlB6oHJSWYmw2m5KSkhQQECB3d3eFhoYqLS1N7dq1U3x8vNHxANwEXFxcNGnSJGVmZiopKUldu3aVu7u7Dh06pD179ujIkSOqW7eu7rrrLs2dO1dHjhzRyJEjJV0uLMuWLZOrq6vWrFmj3Nxcg18NULG4Im4xcXFxSk5O1uTJkxUREaGtW7dq8ODBysrK0lNPPWV0vGph06739NHWOfrxp2914VKuPp1eYHQkoMZo3LixVq9ercjISEnS2rVrNXfuXKWmpurMmTOO5Ro1aqQ+ffooISFB3bt31/z58zV69GiFhITI1dVV06ZN0+TJk416GUClobRcsWzZMi1atEipqamKioqSJMXExGjHjh1KTk5WeHi4wQmrB0+Phup/xxjlX8rTayvZ+wRUlEaNGmnTpk0KCgpSRkaG4uLitH79+usue/LkSb377rt699139fDDD+sf//iH4zNq+vTpFBbUWBweuiIxMVGxsbGOwlKkbdu2qlWrlkJCQiRJL774ogIDA2W1WrVixQojohqqS7s+6tFpsJo28jM6ClCj/POf/1RQUJD27Nmjzp07l1pYrmaz2UqMXWnQoEFlRQQMR2mRlJmZqb1792rQoEHXPJaRkaHg4GC5ublJujwqf+3atbr77rurOiaAGuoPf/iD7r33Xp0+fVp9+/ZVVlaWU+sVH8Myf/58Xbx4UaNHj1aPHj0qOTFgDEqLLpcWSfL19S0xPy8vT2lpaSUODXXr1k1+fpW3l8FisRg2paWlVtrrws0nLS3V0PdzadPVjM5gsVj04osvSpImTJigo0ePOvXzLV5Ypk2bplGjRmnq1KmS5Nie0a+TicnZyVmUFkk+Pj6SpPT09BLzZ8yYoWPHjikiIsKIWABuAr1795a/v78OHTqkJUuWOLXO1YWlaAzL66+/rnPnzikqKkrBwcGVGRswBANxJfn5+SkkJESJiYny9vZW8+bNtWLFCqWkpEhSlZYWu91eZc91tW3vSdmZhj09apioqGjZ3zLu/VyaSdPnl7hvxP+54t8s+/TpI+nymBabzVbuuqUVFknKycnRihUrNHz4cPXu3Vvfffed4zEjP1uAisKeFklWq1XLly9XcHCwEhISNHz4cPn4+Gjs2LFycXFxDMKFVGgrVP6lC7pUkC9Jyr90QfmXLvCBCPxGRV+Kvvrqq3KXLauwFPnyyy9LbBeoSdjTckVgYKA2bdpUYt7QoUMVFBQkDw8Pg1JVP+u3/5+SPhjuuH/vc5d/Nv/37EH5ercxKBVgXq1atZIk/fDDD2Uu50xhKb6dou0CNQmlpQzbtm1zXOSpyOTJk7Vw4UJlZWVpz549mjBhgtLS0uTv729QyqrVp8sw9ekyzOgYQI0RHR0tT09PxwkBpbnnnnucunDctm3bFBwcXOJidEBNQWkpRU5OjtLT0zVmzJgS86dOneoYoQ8A/63Dhw87tdzo0aO1du1arVq1qszlcnNztW/fvoqIBlQ7lJZSeHp6qrCw0OgYACDp8kDa8goLUNMxEBcAAJgCpQUAAJgCpQUAAJgCpQUAAJgCpQUAAJgCpQUAAJgCpQUAAJgC12kBgCp2o3+rq+iPPL48Mb7EbeBmw54WAABgCpQWAABgCpQWAABgCpQWAABgCpQWAABgCpQWAABgCpQWAABgCpQWAABgCpQWAABgCpQWAABgCpQWAABgCpQWAABgCpQWAABgCpQWAABgCpQWAABgCq5GBwAAVH8Wi8WQ57Xb7YY8L6on9rQAAABToLQAAABToLQAAABToLQAAABToLQAAABToLQAAABToLQAAKqFWrVqGR0B1RzXaQEAVKguXbrorrvuUnh4uHx8fGS323XkyBFt375d69ev14EDB65ZZ8yYMYqLi9M999yjU6dOGZAaZsCelmJsNpuSkpIUEBAgd3d3hYaGKi0tTe3atVN8fLzR8VCBZq0crb+vGue4//vENlq/fUmpyy9dP01PvxVdBckA8xoyZIh27typf//733rllVc0ZMgQ9enTR7GxsRo5cqTmzp2r/fv369NPP9Xdd9/tWG/MmDGaM2eOwsPD1adPHwNfAao79rQUExcXp+TkZE2ePFkRERHaunWrBg8erKysLD311FNGx6sW/vHJRH39/RplZR+Ru5unura/VyPuna76dbyrLMPTb0Xr+8NfysXl8q5k73q+uv/OcXrwrglOb2PCQ3MrPFd65nYt25CovQe/0IVLuWpQ10cBzSN0351j1altD0nSjPeGycXFVU8PervEusXnb9ixVLNWjrpm+wWF+SoovKSlz2eosVfLCs8P/FbNmjXTO++8o9jYWEnSiRMntGrVKm3btk1HjhyRi4uLAgIC1LVrV91///3q3bu3evfurTlz5mj//v167bXXJEnjxo3TsmXLjHwpqOYoLVcsW7ZMixYtUmpqqqKioiRJMTEx2rFjh5KTkxUeHm5wwurBanXRpMFL1Mb3NuXkZWvGe3/QzPeHaerwj6o0x5BekzWk1wuSpH2Hv9LEeT3VukmwIgLvqdIcRbanr9Pkhf31wJ1/UsJ9r+kWr5bKu5ij7emfacveVY7S4oye4UPUM3xIiXlnzv+iJ97oqs7tYiksqFb8/f21ceNGtWrVSqdOndIzzzyjJUuWKD8//7rLe3l5acKECXruuec0duxYx/xx48Zpzpw5VRUbJsXhoSsSExMVGxvrKCxF2rZtq1q1aikkJESnT59Wv379FBgYqNDQUPXu3Vv79+83KLEx4vomqm3zTnJ1qSUvz1v0QPfx2n0g1dBMQa0j1apJkA4e2+OYd88zFu09uNlx/9sDqeoz8deOPuO9YXpl+YhSt/n1958obmaQ+j/vqRcW9NOZ87+UmeGN5AT1DP+9RvabocYNW8lisaiOez3dFfKQxg34+3/x6qRLBfmasvghNW3kp7H3v/5fbQuoSF5eXlq3bp1atWqlLVu2KCgoSAsWLCi1sEhSdna2/vrXvyopKckxb9++fXrzzTerIjJMjtIiKTMzU3v37tWgQYOueSwjI0PBwcFyc3OTxWLRhAkTlJ6erm+//Vb9+vXT8OHDDUhcfezcv0F+zUINe3673a69B7foSNb/U1DrOypkmz/9ckBT/vmgBvd4Th++lK0Bd/5J//r6H6Uun5mVrp9OHlBM2OAKef6rvZGcoOxzxzV56HK5uLBzFNXHa6+9pltvvVXbtm1TbGysjh8/7tR6Y8aM0bPPPitJOnfunIKCgjR69OjKjIoagtKiy6VFknx9fUvMz8vLU1pamuPQkJeXl3r16uV4vFu3bjp48GCFZrFYLIZNaWmpN5T1i90rtearuRpzX9V/+393w980YLKX+j9fV0++2V09Og1Ru1a3V8i2N337ntq1ul29In4vFxdXdW7XW91uG1Dq8tk5WZIknwbNHfO2fveRBkz20v2TG+h3z7qXWH7D9v/TgMleJaZNu9697raXpyZpy3cfaurja+Tp4fVfv7aqlJaWauj7ubTpakbnuZHMV9828ucWGRmpYcOGKS8vT0OGDFFOTo5T74uiQbfS5UNCRV/8pk+frgYNGpjy34ep4t9fpaG0SPLx8ZEkpaenl5g/Y8YMHTt2TBEREdddb9asWRowYEBlx6uW0r5drtdWjNRLwz5SQIuqH+/zWM/n9eHUbK1JzNW7zx9RxvF9euWDxytk279kZ6pJwzYl5vl631rq8g3q+jjWK9It+D59ODVbf3v8E10quFhi+Z4RQ/Xh1OwSU0zYY9ds98t9H2vhpy/oL39YqeY+bf+LVwRUvKLxKLNmzbrms7M0VxeWOXPmaOXKldq4caPq1aunP/zhD5WWFzUDpUWSn5+fQkJClJiYqMWLF2vDhg1KSEjQggULJOm6pWXKlCnav3+/ZsyYUaFZ7Ha7YVNUVLRTGdd+s1Cvrxyll4Z/rLC2MRX6+n+LW7xa6O7Qh7V5b7Jjnoebp/Lyzzvunzz7k9Pb82nQXMdPHyox7/ipQ9ddVpJa3BKopt5+2vTte04/R3kOHtujl98doicemKNQ/+gK225VioqKNvT9XNp0NaPz3Ejmq28b9XNzd3fXoEGDZLPZNHeuc2fiXa+wFJk9e7YkXbe0GP2zZ6r691dZKC2SrFarli9fruDgYCUkJGj48OHy8fHR2LFj5eLiopCQkBLLT5s2TWvWrNHatWtVp04dg1IbY9XmNzR/zZ/1vyM/1W233ml0HEnSqbM/6/Pdy+XX9NexNQHNI7Ru2z91qSBfP586pBWfv+r09qLDHtX/y/haG3cuU2FhgXakr9eW7z4sdXmLxaInHpijDdv/T//4ZKJOZB+R3W7XhfxcfZ/x9Q2/ntM5JzR5YX/17TpSfW+Pu+H1gcoWEhIiNzc3fffdd8rIyCh3+bIKiyR99tlnstlsCgkJUe3atSslM2oGRvVdERgYqE2bNpWYN3ToUAUFBcnDw8Mxb8qUKUpJSdG6devk5eVVxSmN9+bq8XKxuurPc0vuYfn4b84dz64oS9dP1XubXpYkudeuqxC/KI3q9+vZCOMemK1XPnhcD/7FW62bBKl352F666MJTm27uU9bTR66Qm+nTNRrK0YqxC9KfW8foQM/7Sp1nS7tY/Xa2M1atiFRY2aF62J+rrw8G8u/eSfNHLXxhl7bJ1/O0/HTh/XJl3P1yVfzrnk8Me5f6uh31w1tE6hIHTt2lCTt3Lmz3GXLKyySdP78eaWnp6t9+/Zq3769du/eXbGBUWNY7DeyX+Ym06FDB0VGRmrhwoWSpO+++0633Xab/P395enp6Vhu165dBiWsWNvek4oNywD+K14tpM6PGp3iWpOmzy9x/+WJ1f9q10WZX54YX+J2VSo+WDI6OlqPPfaY0tLStHTp0lLX6dGjhzZs2CCp/OuwvPDCC2rRooWmT59e4gQHfkWhOPa0lCInJ0fp6ekaM2aMY15wcDD/gQDc9FJTU5WamurUcgsXLtT27dvLvXDctGnTKigdajJKSyk8PT1VWFhodAwAMC2bzabHH6+Ys/oAiYG4AADAJCgtAADAFCgtAADAFCgtAADAFCgtAADAFCgtAADAFCgtAADAFCgtAADAFLi4HACgXDd6NfDq8KcHUPOwpwUAAJgCpQUAAJgCpQUAAJgCpQUAAJgCpQUAAJgCpQUAAJgCpQUAAJgCpQUAAJgCpQUAAJgCpQUAAJgCpQUAAJgCpQUAAJgCpQUAAJgCpQUAAJgCpQUAAJiCq9EBAACoLBaLpcqf0263V/lz3izY0wIAAEyB0gIAAEyB0gIAAEyB0gIAAEyB0gIAAEyB0gIAAEyBU54BALiiWbNmCggIUO3atXXu3Dnt3btXOTk5pS4/evRoffDBBzp16lQVprx5sacFAHBT69ixo958800dO3ZMR48eVWpqqj777DN9+eWXOnPmjPbu3av/+Z//UaNGjUqsN2XKFL311lv69NNPZbXy67Qq8FMuxmazKSkpSQEBAXJ3d1doaKjS0tLUrl07xcfHGx2v2ljwr+c1NPFW3f9CfQ36a2O9tHigTpzOMDoWANyQhg0bavHixdq9e7cSEhLk6+ur06dPa/PmzVq3bp127NihgoICBQcHa/r06Tp8+LCeeOIJWSwWTZkyRS+++KIKCgo0c+ZM2Ww2o1/OTYHDQ8XExcUpOTlZkydPVkREhLZu3arBgwcrKytLTz31lNHxqo1eEUP1SPT/qK5HA13Iz9WitS/ob0sf1evjthodDQCcEhoaqpSUFDVr1kx5eXl65513NH/+fO3Zs6fEcrVr11avXr00btw49e3bV2+88YbGjx8vf39/FRQUaMiQIfrggw8MehU3H0rLFcuWLdOiRYuUmpqqqKgoSVJMTIx27Nih5ORkhYeHG5yw+mjVuL3jtl12WSxWHcn6wcBEAOC82267TRs3bpS3t7e2bNmiYcOGaf/+/dddNj8/XykpKUpJSdH999+vJUuWyN/fX3a7XcOHD6ewVDFKyxWJiYmKjY11FJYibdu2Va1atRQSEiJJGjBggH788Ue5uLioVq1aSkxMVK9evYyIbKiNO9/V68kJyr1wVi5WV43u/6rRkQCgXO7u7lq+fLm8vb21evVqPfzww8rPz3dq3fDwcHl6esput8tisSgiIkJLliyp5MQojjEtkjIzM7V3714NGjTomscyMjIUHBwsNzc3SdKiRYu0e/du7dy5U/PmzdNDDz2kwsLCqo5suB6dHtPqqWf0/uRjGtr7r7q1aUejIwFAuV588UW1b99e+/bt06OPPup0YSk+huXZZ59VQUGB/vSnP6lbt26VnBjFUVp0ubRIkq+vb4n5eXl5SktLK3FoyMvLy3H7zJkzslgsFfoXPS0Wi2FTWlrqDef1ru+r33UdqRcW9NPZXE75w6/S0lINfT+XNl3N6Dw3kvnq29V5qi6Zi6tXr56eeOIJSdLjjz+uCxcuOPVeLl5YhgwZounTp2vGjBmyWq2aOHGiKd9T1W1yFqVFko+PjyQpPT29xPwZM2bo2LFjioiIKDF/7Nix8vPz00MPPaSVK1fK1fXmPspWWFigC/nndfLsT0ZHAYBS/f73v5enp6c2bdqkr7/+2ql1ri4sRWNYZs2apYsXL6pfv35q2bJlZcZGMZQWSX5+fgoJCVFiYqIWL16sDRs2KCEhQQsWLJCka0rLnDlz9OOPPyo5OVnPPPNMmRceulF2u92wKSoqutx8NptNH26ZrdM5JyRJWdmZmr1qrHwbtlGrW9qXszZuJlFR0Ya+n0ubrmZ0nhvJfPXt6jxVl8zF9ezZU5K0ePFip97DpRUWScrKytLatWtltVoVHR1tuvdUdZucRWmRZLVatXz5cgUHByshIUHDhw+Xj4+Pxo4dKxcXF8cg3KtFRUXJarVqy5YtVZzYWP/+fymKT7pN/Z+rqyf+3lVutetoevx6ubjc3HucAFRvRV9A//3vf5e7bFmFpUjR3pqrv9ii8vBb5orAwEBt2rSpxLyhQ4cqKChIHh4ekqScnBydPHlSrVu3liTt3LlTBw4cUIcOHao8r1GsVqsS41KMjgEAN6xZs2aSpAMHDpS5nDOFRZLjNOmi7aLyUVrKsG3bNkVGRjrunz9/Xo888ohycnLk6uoqd3d3LVmyRK1atTIwJQDAGQ0bNpS7u7suXrxY6jIWi0UtWrRw6sJxH330kRo2bKjc3NzKiIvroLSUIicnR+np6RozZoxjXpMmTfTVV18ZmAoA8Fvl5uaWWzDsdrtGjBih+fPnlztY9+LFi2UWIFQ8SkspPD09b8rrrwDAzc5utzt9dhGqFgNxAQCAKVBaAACAKVBaAACAKVBaAACAKVBaAACAKVBaAACAKVBaAACAKXCdFgBAjXUjf4xPkiZNny9JenlifInbqB7Y0wIAAEyB0gIAAEyB0gIAAEyB0gIAAEyB0gIAAEyB0gIAAEyB0gIAAEyB0gIAAEyB0gIAAEyB0gIAAEyB0gIAAEyB0gIAAEyB0gIAAEyB0gIAAEyB0gIAAEzB1egAAADgVxaLxZDntdvthjzvjWBPCwAAMAVKCwAAMAVKCwAAMAVKCwAAMAVKCwAAMAVKCwAAMAVKCwAANxGLxaJ69eoZHeM34TotAACYkJubm+6//35169ZNYWFh8vb2VmFhoQ4ePKjt27crJSVFO3fuLLGOxWLRvHnz1KVLF/Xs2VOnTp0yKP1vw56WYmw2m5KSkhQQECB3d3eFhoYqLS1N7dq1U3x8vNHxAACQu7u7XnrpJWVmZur999/X+PHjFRUVpY4dOyosLEwPPPCApk2bph07dujLL79U7969Jf1aWEaOHKnAwEC1b9/e4Fdy49jTUkxcXJySk5M1efJkRUREaOvWrRo8eLCysrL01FNPGR2v2rHZbHryze7ad/hLvfv8Ed3i1cLoSABQo3Xu3FlLlixRu3btJEk7duzQypUrtW3bNv3888+qVauW2rdvr27dumnw4MGKjIzUp59+qnfeeUdWq1XDhw9Xbm6u+vfvr61btxr8am4cpeWKZcuWadGiRUpNTVVUVJQkKSYmRjt27FBycrLCw8MNTlj9rPziNbnVqmN0DAC4KcTExGjNmjWqU6eOvvvuO40ePVqbN2++Zrnt27dr6dKl+vOf/6wnnnhCU6ZMUVxcnCQ5CsvGjRurOn6F4PDQFYmJiYqNjXUUliJt27ZVrVq1FBISUmL+/PnzZbFYtGLFiqqMWW1kZqXr461vKr5fktFRAKDGa9eunT766CPVqVNHCxcuVHh4+HULS3F5eXmaOXOm1qxZ45j37bffmrawSJQWSVJmZqb27t2rQYMGXfNYRkaGgoOD5ebm5pj3n//8RwsXLlRkZGRVxqw2bDabkj54XPH9kuTp4WV0HACo0axWqxYuXChPT0+9//77iouLU35+frnrFY1hGThwoPLy8nT27FndcccdGjZsWOWHriSUFl0uLZLk6+tbYn5eXp7S0tJKHBoqKCjQ448/rrfeeqtEkakoFovFsCktLdWpjKs2vy7ver7q3vGBCn/9qDnS0lINfT+XNl3N6Dw3kvnq29V5MmPm6pL7akOGDNEdd9yhzMxMjRo1yqm/xmyx/DroNjc3V/369dOYMWMkSUlJSXJ3d69W/xecRWmR5OPjI0lKT08vMX/GjBk6duyYIiIiHPOmTp2qvn37KiwsrCojVhtHf9mvFZ+/onEDZhsdBQBuCkVl4y9/+YvOnDlT7vJXF5aiMSxLly7VN998o0aNGumRRx6p7NiVgtIiyc/PTyEhIUpMTNTixYu1YcMGJSQkaMGCBZLkKC1ff/21Nm7cqIkTJ1ZaFrvdbtgUFRVdbr69BzfrTE6WRr5ymx76i4/GzLq8F2rUqyH6aOublfZzgflERUUb+n4ubbqa0XluJPPVt6vzZMbM1SV3cW3atFFkZKSys7O1bNmycv/flVZYirz11luSpMGDB1er/wvO4uwhXT5euHz5co0aNUoJCQlq1KiR/vjHP2rs2LF67rnnHINwN23apAMHDsjf31+S9PPPP2vfvn06fPiwnn76aSNfQpWJCn1Y4QG9HPezzmRq/Ow79L8jP1OrxuY75x8AqrPOnTtLkrZs2aK8vLwyly2vsEjS+vXrS2zXbCgtVwQGBmrTpk0l5g0dOlRBQUHy8PCQJE2aNEmTJk1yPB4dHa1x48Zp4MCBVZrVSO6168i99q+nORfaCiRJ3vV85eHmaVQsAKiRgoODJV0+66cszhQWSTpy5IhOnTqlRo0aqUmTJjp+/Hil5K4slJYybNu27aY9Q8hZvt5ttG6m87v2AADO++KLLzR16lRt2LChzOWGDh1abmEp8vLLL8vDw0MXLlyo6LiVjtJSipycHKWnpzsGQF1Pampq1QUCANx0Nm7c6NR1VZYsWaLIyEitWLGi3OVnzpxZUfGqHKWlFJ6eniosLDQ6BgAA5bLZbGV+ya4pOHsIAACYAqUFAACYAqUFAACYAqUFAACYAqUFAACYAqUFAACYAqUFAACYAqUFAACYAheXg0O9xkYnQE3C+wn4bW7krx5L0qTp8yVJL0+ML3G7JqK0wKFdD6MTAABQOg4PAQAAU6C0AAAAU6C0AAAAU6C0AAAAU6C0AAAAU6C0AAAAU6C0AAAAU6C0AAAAU6C0AAAAU6C0AAAAU6C0AAAAU6C0AAAAU6C0AAAAU6C0AAAAU6C0wGlt2rRRcHCwwsLCFBYWpj179hgdCahSqampCg4OVtu2bTVixAgVFhYaHalc48ePV4sWLeTq6mp0FKcdOXJEPXv2VIcOHRQcHKxnn33W6EhO6927t8LCwtSxY0cNHDhQZ8+eNTqS08aOHVvt3yeUFtyQTz/9VLt27dKuXbvUsWNHo+MAVcZms2nEiBFavny59u/fr7Nnz2rJkiVGxyrXoEGDtG3bNqNj3BBXV1dNnz5d33//vXbu3KnNmzdr9erVRsdyyvLly7Vr1y7t2bNHLVq00Kuvvmp0JKd88cUXysnJMTpGuSgtAOCEb775Rs2aNVNQUJAkKS4uTitXrjQ4Vfm6d+8uX19fo2PckKZNm6pz586SpNq1a6tTp07KyMgwOJVzGjRoIOlyyb1w4YIsFovBicp38eJFTZo0SUlJSUZHKRelBTekf//+CgsL0/PPP69Lly4ZHQeoMpmZmWrZsqXjfqtWrXTkyBEDE90cTp06pQ8//FD33HOP0VGc9sADD6hx48b64Ycf9PTTTxsdp1wvvfSS4uLidMsttxgdpVwWu91uNzoEzOHIkSNq2bKlzp8/rz/+8Y+KiIgw1bFm3Jw+3rBVP2Ycc9w/duJkicebNm7kuN22dXPd2yPyuttZsWKFVq1apaVLl0qSvv/+ez322GPauXNnhWc+evwXrUhJuyZz08aNStyWJItF+uODfdSgvmeZ23R1dVVBQUGFZy1it9v1wSeb9HPW6XIzS1JoB39FR4aVuc38/HzFxsbq3nvvrbRf/ukHM/Wv1K8d98vKXcvVVY8/3FfubrXL3W5+fr7i4uLUs2dPDRs2rEIz22w2/XPlpzqbk1tuZknqFh6sLqHtr7ut3bt366mnntK6detksVgq/X3y32JPC5xW9C2zbt26GjFihLZu3WpwIqB8nTu2089Zp3TsxMlrCoskx/zjWafUuWNgqdtp2bJliT0rGRkZatGiRaVkbta4kerV9bgm89W3j504qRa+t5RbWKqCxWJReHCgU5lPnj6j8OCAMrdXWFioxx57TGFhYZW6t6Jt62YlshXPWvz2sRMnFdCmuVOFRbp8WOvRRx/VqlWrKjawJKvVqtAO/k5lPnc+VyHt/Urd1pYtW7Rv3z7deuutatOmjQoLC9WmTZtqO4CY0gKnnD9/3vEmLiws1MqVKxUSEmJwKqB8TRs3UpeQduUu17VTBzW5xbvUxzt37qzMzEzt27dPkvTOO+/owQcfrLCcxVksFt3b4w5ZyxkP4Va7lu65q3OlZPgtAm5toQ5tW5W7XHRkmOrXq1vmMvHx8apXr55eeeWViop3XVarVf173lHucvU96yqqa2iZy5w7d07Hjl3eq2ez2fTRRx8pODi4QnJeLSw4QC2bln84p8/dXeRWRtFKSEjQTz/9pEOHDunQoUNycXHRoUOHVL9+/YqMW2EoLXDK8ePHdffddyskJEQhISGy2+16/vnnjY4FOKX3XV3kVrtWqY+7u9VWrzvL/uXv4uKit99+WwMHDpS/v788PT01dOjQio7q0MSnobp2CipzmR7dwlWvbp0ylxk1apRatGihwsJCtWjRQmPHjq3ImNe4N+YOuVhL/9XiVd9Td3Up+wvPli1btGDBAm3btk2dOnVSWFiY3njjjYqO6uDXqpluC7y1zGX6Rt+u2mW8h6TLpeW+++5zfE4WFBTohRdeqMioDlaLRf16ditzmWZNGinittL3HpoRY1rwX7Pb7aYYIY+b2+dff6uUYmMXiuvX4w5171L9TuE/n3dBM+e9pwsX8695zNurnp6Ke1iuri4GJCvbmo1favM317+O0+D7eiq0g38VJyrfyeyzevXtD1RYaLvmsZZNb1HC0AHl7vkywrKPNujb7w9c97H4wf3k16pZFSeqXOxpuQGrV69Wv3791LhxY7m5ual169Z67LHHbvqLrH33n0Oav+xjnbsyKAyojrpF3KZGXtfu8vbxbqDI8LL3aBilroe7enWPuO5jv4uJrJaFRZJ6dgtXHQ+3a+a3bt6kzPEVRmrkVV/dO1+/uPbr2a1aFhZJ6hvd9brvg9sCb61xhUWitDiloKBAQ4YM0YABA7Rnzx49+OCDGj9+vDp16qSVK1fq6NGjRkc0jM1u14YtO3Q2J1d16rgbHQcolauri34Xc+2ZQf163CFXl+r5y1+S7ugUrFu8G5SY59eqqYID2hgTyAke7m7qfVeXa+b379mtWu+VjbmjkzzrepSYF9rBX62bNzEoUfm86nvq7ttLjrVxcbHqdzFdDUpUuSgtTnjiiSf07rvvaty4cTpw4IDmzp2rGTNm6MMPP9SBAwd05513Gh3RMPv+c0jHTpxUz27hZR7HBqqDoIDWJb59BrRpoXZ+LctYw3guLlbd2+PXgaIWXS5a1fmXvyR1CW2vJj4NHffDbwtUCycGjhrJ3a22+hQrW66uLuobXf1/+Ud1DVV9z1/HNt3VJUTe19mrWBMwpqUcX3zxhe6++27FxsYqJSWl0j8oJk2fX6nbBwCgunl5YrxTy/HVuByzZs2SJL388svV/psNAAA1GXtaylGvXj35+Pjo4MGDRkepVmx2u/6+KFmXCgr0ZNwgDg3BVHLO58lisaiuycZhHf/ldIlDLmZwKvus6tWto1q1qvdfD76aGX/WWSez1ahhfVlr8OcxpaUM2dnZatiwoaKjo7Vp06YqeU4ODwEAbjYcHqoARX3uxIkTBicBAADsaSmHv7+/Dh48qM8++0y9evUq8dgPP/ygdu3Kvzx4TbM3/aCWrFqnR/rFqFM5fz8EAICKQmkpxwcffKBHHnlErq6uuv/+++Xv768TJ05o69atCgoKqpQ/hlWdMZYFAGAUc42MMsDDDz+sBg0aaObMmVq3bp0+/vhjNW7cWLfffrsmTJhgdLwqdz43Ty5Wq+7muiwAgCrGnhbcMLvdLrtUbS9rDQComSgtAADAFNi/DwAATIHSAgAATIHSAgAATIHSAgAATIHSAgAATIHSAgAATIHSAgAATIHSAgAATIHSAgAATIHSAgAATIHSAgAATIHSAgAATIHSAgAATIHSAgAATIHSAgAATIHSAgAATIHSAgAATIHSAgAATIHSAgAATIHSAgAATIHSAgAATIHSAgAATIHSAgAATIHSAgAATIHSAgAATIHSAgAATIHSAgAATOH/A/x9I0J3SGwIAAAAAElFTkSuQmCC\n",
65 | "text/plain": [
66 | ""
67 | ]
68 | },
69 | "execution_count": 3,
70 | "metadata": {},
71 | "output_type": "execute_result"
72 | }
73 | ],
74 | "source": [
75 | "n = 5\n",
76 | "mc = QuantumCircuit(n, n)\n",
77 | "U = BuildGHZ(n)\n",
78 | "mc.append(U, range(n))\n",
79 | "\n",
80 | "mc.measure(range(n), range(n))\n",
81 | "\n",
82 | "backend = BasicAer.get_backend('qasm_simulator')\n",
83 | "atp = 1024\n",
84 | "res = execute(mc, backend=backend, shots=atp).result()\n",
85 | "ans = res.get_counts()\n",
86 | "\n",
87 | "mc.draw('mpl')"
88 | ]
89 | },
90 | {
91 | "cell_type": "code",
92 | "execution_count": 4,
93 | "metadata": {},
94 | "outputs": [
95 | {
96 | "data": {
97 | "image/png": "iVBORw0KGgoAAAANSUhEUgAAAc0AAAFTCAYAAABbKVcuAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjMuMCwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy86wFpkAAAACXBIWXMAAAsTAAALEwEAmpwYAAAnjUlEQVR4nO3df5RV5X3v8fdX0BELNoABHEABBaogIBmDkyDYNFavaWxNbDQ1MalRa0z8EW9Wk6wa8+NGk14bq4nL2GiWRJOiJt423qQabaNyUQIOBBTxBw1gAfkhaAImOMj4vX/sAz2OM8MeGOYX79daszzn2c/e8z3i8cN+9n6eHZmJJEnavQO6ugBJknoKQ1OSpJIMTUmSSjI0JUkqydCUJKkkQ1OSpJL6dnUBXemwww7LUaNGdXUZkqRuZOHChZsy8+0tbduvQ3PUqFE0NDR0dRmSpG4kIl5obZvDs5IklWRoSpJUkqEpSVJJhqYkSSUZmpIkldTpoRkRl0TEyoh4LSIWRsRJu+l/UER8tbJPY0T8V0Rc1qzPByNiWWX7sog4c99+CknS/qhTQzMizgZuBK4FjgceB+6PiCPa2O0u4DTgImA88JfAk1XHrAfuBn4ITKn880cRMW0ffARJ0n4sOvN5mhExH3gyMy+salsO/Dgzv9BC/z8FfgQclZmbWjnm3cCgzDylqu3fgZcy88Nt1VNXV5fO05QkVYuIhZlZ19K2TjvTjIiDgHcADzbb9CDwrlZ2+wvgCeDKiFgTEcsj4lsR0b+qT30Lx/x5G8eUJGmPdOaKQIcBfYANzdo3AO9tZZ8xwHSgEfgg8Dbg20AtcFalz7BWjjmspQNGxEUUQ73U1tbyyCOPFL9ozBgGDBjAkiVLABg8eDATJkxgzpw5APTt25fp06ezaNEitmzZAkBdXR0bNmxg9erVAIwdO5aamhqWLl0KwJAhQxg3bhxz584FoKamhvr6ehoaGnj11VcBmDZtGmvWrGHt2rUAjB8/nj59+rBs2bLiww0bxujRo5k3bx4A/fr1Y9q0acyfP59t27YBUF9fz8qVK1m/fj0Axx57LE1NTTz33HMADB8+nBEjRjB//nwA+vfvT11dHfPmzaOxsRGA6dOn8/zzz7Nx40YAJk6cSGNjI8uXLwdg5MiRDB06dNcKSoceeihTp05l7ty57NixA4AZM2bw9NNPs3nzZgAmT57M1q1bWbFiBVCswDRo0CAWLVoEwMCBA5k8eTKPPvoomUlEMHPmTJYsWcIrr7wCwNSpU3n55ZdZtWqVf07+Ofnn5J9Tp/w5taXThmcjohZYC8zMzDlV7VcD52bm+Bb2eRA4CRiWmb+ttP0pxZnksMzcEBHbgQsy846q/c4Dbs3MmrZqcnhWktRctxieBTYBTcDQZu1DgfWt7LMOWLszMCueqfxz581D69t5TEmS9kinhWZmbgcWAqc023QKxV20LXkMqG12DXNc5Z87F9Sd185jSpK0Rzp7nub1wMcj4oKIOCYibqS4PnkLQETcERF3VPX/Z2AzcHtETIiId1NMWflxZm6s9LkReE9EfD4i/igivgD8MXBDJ30mSdJ+olMfDZaZd0fEYOAq4HBgKXB6Zu48azyiWf9XI+K9FDf/PAG8Avwr8PmqPo9HxDnA14CvAr8Gzs7M+fv440iS9jOdOk+zu/FGIElSc93lRiBJkno0Q1OSpJIMTUmSSjI0JUkqydCUJKkkQ1OSpJIMTUnqIR544AHGjx/P0UcfzTe+8Y23bJ81axZvf/vbmTJlClOmTOG2224DYPHixdTX1zNhwgQmTZrE3XffvWufc889l/HjxzNx4kTOP/98Xn/99U77PD2RoSlJPUBTUxOf+tSnuP/++1m2bBmzZ8/e9VSQameffTaLFy9m8eLFXHDBBQAccsgh3HHHHTz99NM88MADXHHFFfzmN78BitB89tlneeqpp9i2bduuoFXLDE1J6gEWLFjA0UcfzZgxYzjooIM455xz+MlPflJq33HjxjF27FigeCTikCFDeOmllwA4/fTTiQgigne+852sWbNmn32G3sDQlKQeYO3atYwcOXLX+xEjRux6HmW1e++9l0mTJnHWWWfteuZltQULFrB9+3aOOuqoN7W//vrr3HnnnZx22mkdX3wvYmhKUi/x/ve/n1WrVvHkk09yyimn8LGPfexN29etW8dHP/pRbr/9dg444M3/+7/kkkuYMWMGJ510UmeW3OMYmpLUAwwfPvxNZ45r1qxh+PDhb+ozePBgampqALjgggtYuHDhrm1btmzhfe97H9dccw0nnnjim/b7yle+wksvvcT111+/Dz9B72BoSlIPcMIJJ7B8+XJWrlzJ9u3bueuuuzjjjDPe1GfdunW7Xt93330cc8wxAGzfvp0zzzyT8847j7POOutN+9x22238/Oc/Z/bs2W85+9RbdeqjwSRJe6Zv377cdNNNnHrqqTQ1NXH++eczYcIErr76aurq6jjjjDP41re+xX333Uffvn0ZNGgQs2bNAuCee+5hzpw5bN68eVfbrFmzmDJlChdffDFHHnkk9fX1AHzgAx/g6quv7qJP2f35aDAfDSZJquKjwSRJ6gCGpiRJJRmakiSVZGhKklSSoSlJUkmGpiRJJRmakiSVZGhKklSSoSlJUkmGpiRJJRmakiSVZGhKklSSTznZzz3wwANcfvnlNDU1ccEFF/D5z3++xX733nsvZ511Fk888QR1dXX88Ic/5Lrrrtu1/cknn2TRokVMmTKF2bNnc+211xIR1NbW8oMf/IDDDjussz6StFsX3tDVFWhfuPWKff87PNPcjzU1NfGpT32K+++/n2XLljF79myWLVv2ln5bt27lxhtvZNq0abvazj33XBYvXszixYu58847GT16NFOmTGHHjh1cfvnlPPzwwzz55JNMmjSJm266qTM/liTtM4bmfmzBggUcffTRjBkzhoMOOohzzjmHn/zkJ2/p98UvfpHPfe5zHHzwwS0eZ/bs2ZxzzjkAZCaZye9+9zsyky1btlBbW7tPP4ckdRZDcz+2du1aRo4cuev9iBEjWLt27Zv6LFq0iNWrV/O+972v1ePcfffdfPjDHwbgwAMP5Dvf+Q7HHXcctbW1LFu2jE984hP75gNIUiczNNWqN954gyuvvJJvfvObrfaZP38+hxxyCBMnTgTg9ddf5zvf+Q6/+tWvePHFF5k0aRJf//rXO6tkSdqnDM392PDhw1m9evWu92vWrGH48OG73m/dupWlS5dy8sknM2rUKH75y19yxhln0NDQsKvPXXfdtessE2Dx4sUAHHXUUUQEH/rQh3j88cf3/YeRpE5gaO7HTjjhBJYvX87KlSvZvn07d911F2ecccau7X/4h3/Ipk2bWLVqFatWreLEE0/kvvvuo66uDijORO+5555d1zOhCOJly5bx0ksvAfDQQw9xzDHHdO4Hk6R9xCkn+7G+ffty0003ceqpp9LU1MT555/PhAkTuPrqq6mrq3tTgLZkzpw5jBw5kjFjxuxqq62t5Utf+hIzZszgwAMP5Mgjj2TWrFn7+JNIUueIzOzqGrpMXV1dVg81Sto/OE+zd+qoeZoRsTAz61ra5vCsJEklGZqSJJVkaEqSVJKhKUlSSYamJEklGZqSJJVkaEqSVJKhKUlSSYamJEklGZqSJJXk2rMdwCW5eqeOWpJLUu/hmaYkSSUZmpIklWRoSpJUkqEpSVJJhqYkSSUZmpIklWRoSpJUUqeHZkRcEhErI+K1iFgYESeV3G96ROyIiKXN2j8eEdnCz8H75hNIkvZXnRqaEXE2cCNwLXA88Dhwf0QcsZv9BgJ3AP/RSpffA4dX/2Tmax1VtyRJ0PlnmlcCszLz1sx8JjMvBdYBn9zNft8Dvg/Ma2V7Zub66p8OrFmSJKATQzMiDgLeATzYbNODwLva2O8SYCjwtTYO3y8iXoiINRHx04g4fq8LliSpmc5ce/YwoA+woVn7BuC9Le0QEccBXwJOzMymiGip23PA+cASYABwOfBYREzOzOUtHPMi4CKA2tpaHnnkEQDGjBnDgAEDWLJkCQCDBw9mwoQJzJkzB4C+ffsyffp0Fi1axJYtWwCoq6tjw4YNwFFl/x2oB2loaODVV18FYNq0aaxZs4a1a9cCMH78ePr06cOyZcsAGDZsGKNHj2bevGIwpF+/fkybNo358+ezbds2AOrr61m5ciXr1xcDIcceeyxNTU0899xzAAwfPpwRI0Ywf/58APr3709dXR3z5s2jsbERgOnTp/P888+zceNGACZOnEhjYyPLlxf/qY8cOZKhQ4fS0NAAwKGHHsrUqVOZO3cuO3bsAGDGjBk8/fTTbN68GYDJkyezdetWVqxYAcCoUaMYNGgQixYtAmDgwIFMnjyZRx99lMwkIpg5cyZLlizhlVdeAWDq1Km8/PLLrFq1Cti779Pq1asBGDt2LDU1NSxdWtzGMGTIEMaNG8fcuXMBqKmpob6+fo/+nKCmnf81qCdYt25dh3yf2hKZuQ8/QtUviqgF1gIzM3NOVfvVwLmZOb5Z/xrgV8DXM/POStuXgbMyc2Ibv6cPsBh4ODMva6umurq63Pk/l73hgu29kwu2915+Z3unjvrORsTCzKxraVtnnmluApoohlqrDQVaugZ5OHAMcHtE3F5pOwCIiNgBnJ6ZzYd6qZyRNgBjO6xySZLoxGuambkdWAic0mzTKRR30Ta3FjgOmFL1cwvwn5XXLe1DFGO4kyhuMJIkqcN09vM0rwfujIgFwGPAxUAtRRgSEXcAZOZ5mfk60HxO5kagMTOXVrV9CfglsBw4FLiMIjR3d0euJEnt0qmhmZl3R8Rg4CqK4delFMOsL1S6tDlfsxVvA74LDAN+S3EddEZmLtj7iiVJ+m+dfaZJZt4M3NzKtpN3s++XgS83a/sM8JmOqU6SpNa59qwkSSUZmpIklWRoSpJUkqEpSVJJhqYkSSUZmpIklWRoSpJUkqEpSVJJhqYkSSUZmpIklWRoSpJUkqEpSVJJhqYkSSW1KzQj4oCIOKDq/bCIuCAi3t3xpUmS1L2090zzZ8ClABHRH2gArgMeiYjzOrg2SZK6lfaGZh3wi8rrDwBbgCHAhcBnO7AuSZK6nfaGZn/gN5XXfwr8S2a+ThGkR3VgXZIkdTvtDc3/At4dEX8AnAo8VGkfBPy+IwuTJKm76dvO/tcDdwKvAi8AcyrtM4CnOrAuSZK6nXaFZmb+U0QsBEYCD2XmG5VNvwa+2NHFSZLUnbT3TJPMbKC4a7a67WcdVpEkSd1Uuxc3iIhLIuLpiPh9RIyptH0uIj7U8eVJktR9tHdxgyuAq4DvAlG16UXg0x1XliRJ3U97zzQvBi7MzBuBHVXti4AJHVaVJEndUHtD80hgaQvtrwP99r4cSZK6r/aG5gpgagvtpwPL9r4cSZK6r/bePfsPwE0RcQjFNc36iPgo8LfA+R1dnCRJ3Ul752neHhF9gWuBQygWOngRuCwz794H9UmS1G3syTzNW4FbI+Iw4IDM3NjxZUmS1P20OzR3ysxNHVmIJEnd3W5DMyKeBGZm5isR8RSQrfXNzEkdWZwkSd1JmTPNe4HGqtethqYkSb3ZbkMzM79S9frL+7QaSZK6sfYuo/eLiHhbC+2HRsQvOqwqSZK6ofYubnAycFAL7QcDJ+11NZIkdWOl7p6NiOpVgCZFxMtV7/sApwJrO7IwSZK6m7JTThoobgBK4MEWtm8DLu2ooiRJ6o7KhuZoimXzVgDvBF6q2rYd2JiZTR1cmyRJ3Uqp0MzMFyov2/3QakmSeosyixt8APi/mfl65XWrMvP/dFhlkiR1M2XONH8MDAM2Vl63JiluCpIkqVcqs7jBAS29liRpf2MISpJUUtlrmqV4TVOS1JuVvaZZhtc0JUm9WruuaUqStD8zECVJKsl5mpIkleQ8TUmSSnKepiRJJRmCkiSV1O7QjIipEXFHRDRUfu5s9rxNSZJ6pXaFZkScCzwBHA78W+VnKLAgIj7S8eVJktR9lH2e5k7XAF/MzGurGyPiC8DXgB90VGGSJHU37R2efTtwTwvtPwKGlDlARFwSESsj4rWIWBgRJ7XRd2ZEPB4RmyNiW0Q8GxGfbaHfByNiWUQ0Vv55ZulPJElSSe0NzYeBk1toPxl4dHc7R8TZwI3AtcDxwOPA/RFxRCu7vAp8C5gBHEtxNvuViLik6pj1wN3AD4EplX/+KCKmlflAkiSV1d4F2+8Hvh4RdcAvK20nAh8Avlzi910JzMrMWyvvL42I04BPAl9o3jkzFwILq5pWVuo5Cbi50nYF8HBmXlN5f01E/HGl/cMlapIkqZQ9XbD9ospPtW/z30H2FhFxEPAO4B+abXoQeFeJOoiI4yt9v1zVXF/53dV+Dny6zDElSSqrMxdsP4xixaANzdo3AO9ta8eIWENxPbUv8JXMvKVq87BWjjmslWPtCvza2loeeeQRAMaMGcOAAQNYsmQJAIMHD2bChAnMmTMHgL59+zJ9+nQWLVrEli1bAKirq2PDhg3AUW2Vrx6qoaGBV199FYBp06axZs0a1q5dC8D48ePp06cPy5YtA2DYsGGMHj2aefPmAdCvXz+mTZvG/Pnz2bZtGwD19fWsXLmS9evXA3DsscfS1NTEc889B8Dw4cMZMWIE8+fPB6B///7U1dUxb948GhsbAZg+fTrPP/88GzduBGDixIk0NjayfPlyAEaOHMnQoUNpaGgA4NBDD2Xq1KnMnTuXHTt2ADBjxgyefvppNm/eDMDkyZPZunUrK1asAGDUqFEMGjSIRYsWATBw4EAmT57Mo48+SmYSEcycOZMlS5bwyiuvADB16lRefvllVq1aBezd92n16tUAjB07lpqaGpYuXQrAkCFDGDduHHPnzgWgpqaG+vr6Pfpzgpp2/tegnmDdunUd8n1qS2TmPvwIVb8oohZYC8zMzDlV7VcD52bm+Db2HQ30pxgK/nvg8sy8s7JtO3BBZt5R1f884NbMbPObUVdXlzv/57I3Lrxhrw+hbujWK7q6Au0rfmd7p476zkbEwsysa2lbe6ecEBEDgf8BHAEcVL0tM7/axq6bgCaKeZ3VhgLr2/qdmbmy8vKpiBhKMTx7Z6Vt/Z4cU5Kk9mpXaEbEicDPgEaK4dK1FAsdNAKrgFZDMzO3R8RC4BSKKSo7nQLc244yDuDNYyvzKse4rtkxH2/HMSVJ2q32nmleRzGl43JgC/Ae4HfAbOB7Jfa/HrgzIhYAjwEXA7XALQARcQdAZp5XeX8psBJ4rrL/DOCzvPmGoxuBORHxeeBfgTOBPwamt/OzSZLUpvaG5iTgE5mZEdEE1GTmioj4HPDPFIHaqsy8OyIGA1dRnKEuBU7PzBcqXZrP1+xDcQ1zFLAD+DXweSohWznm4xFxDsUczq9W+pydmfPb+dkkSWpTe0Nze9XrDcCRwDMUixDUljlAZt5MK1NTMvPkZu9vAG4occwf0/azPiVJ2mvtDc1FwAnA88AjwNcqN+Z8BHiyY0uTJKl7ae8czL8DXqy8vgp4iWJhgYG8dbEDSZJ6lXadaWZmQ9XrlyimnkiStF9o9zxNgIg4Cjim8nZZZq7ouJIkSeqe2jtPczDF1JIzgDf+uzl+CpyfmZs7uD5JkrqN9l7TvA04muIpIwdXfmYAo4Fb29hPkqQer73Ds6cCf5KZ86raHouIvwH+vePKkiSp+2nvmeZLFCsANfd7wKFZSVKv1t7Q/CpwQ0QM39lQef1N2lh3VpKk3mC3w7MR8RRQ/fyw0cCqiFhbeT8ceA0YQnHNU5KkXqnMNU2Xp5MkiRKhmZlf6YxCJEnq7vZ0cYP3AMdSDNs+nZmPdGRRkiR1R+1d3GA48C/AO/jvNWhrI6IBODMzX2x1Z0mSerj23j37LaAJODozR2bmSGBspe1bHV2cJEndSXuHZ08BTs7MlTsbKg+hvgz4jw6tTJKkbqa9Z5rw5uknbbVJktSrtDc0/wP4dkSM3NkQEUcAN+CZpiSpl2tvaF4G/AGwIiJeiIgXgF9X2i7r6OIkSepO2ntNczPwTuBk4I8qbc9kpou1S5J6vdKhGRF9gN8CkzPzIeChfVaVJEndUOnh2cxsAl4ADtp35UiS1H2195rm/wK+ERGH7YtiJEnqztp7TfOzFE85WRsRa2j2bM3MnNRRhUmS1N20NzR/TDEnM/ZBLZIkdWulQjMiDgGuA/4COJBiTualmblp35UmSVL3Uvaa5leAjwM/A2YD7wW+s49qkiSpWyo7PPsB4BOZeRdARPwQeCwi+lTuqpUkqdcre6Y5Evh/O99k5gJgB1C7L4qSJKk7KhuafYDtzdp2sIcPsZYkqScqG3oB/CAiGqvaDgZujYjf72zIzDM6sjhJkrqTsqH5/RbaftCRhUiS1N2VCs3M/Ot9XYgkSd3dnjyEWpKk/ZKhKUlSSYamJEklGZqSJJVkaEqSVJKhKUlSSYamJEklGZqSJJVkaEqSVJKhKUlSSYamJEklGZqSJJVkaEqSVJKhKUlSSYamJEklGZqSJJVkaEqSVJKhKUlSSYamJEklGZqSJJVkaEqSVFKnh2ZEXBIRKyPitYhYGBEntdH38Ij454h4NiKaImJWC30+HhHZws/B+/SDSJL2O50amhFxNnAjcC1wPPA4cH9EHNHKLjXAJuAbwPw2Dv174PDqn8x8raPqliQJOv9M80pgVmbempnPZOalwDrgky11zsxVmXlZZs4CXm7juJmZ66t/Or50SdL+rtNCMyIOAt4BPNhs04PAu/by8P0i4oWIWBMRP42I4/fyeJIkvUXfTvxdhwF9gA3N2jcA792L4z4HnA8sAQYAlwOPRcTkzFzevHNEXARcBFBbW8sjjzwCwJgxYxgwYABLliwBYPDgwUyYMIE5c+YA0LdvX6ZPn86iRYvYsmULAHV1dWzYsAE4ai/KV3fV0NDAq6++CsC0adNYs2YNa9euBWD8+PH06dOHZcuWATBs2DBGjx7NvHnzAOjXrx/Tpk1j/vz5bNu2DYD6+npWrlzJ+vXFQMixxx5LU1MTzz33HADDhw9nxIgRzJ9fXIno378/dXV1zJs3j8bGRgCmT5/O888/z8aNGwGYOHEijY2NLF9e/Kc+cuRIhg4dSkNDAwCHHnooU6dOZe7cuezYsQOAGTNm8PTTT7N582YAJk+ezNatW1mxYgUAo0aNYtCgQSxatAiAgQMHMnnyZB599FEyk4hg5syZLFmyhFdeeQWAqVOn8vLLL7Nq1Spg775Pq1evBmDs2LHU1NSwdOlSAIYMGcK4ceOYO3cuADU1NdTX1+/Rn1Nx5Ue9zbp16zrk+9SWyMx9+BGqflFELbAWmJmZc6rarwbOzczxu9n/p8CmzPz4bvr1ARYDD2fmZW31raury53/c9kbF96w14dQN3TrFV1dgfYVv7O9U0d9ZyNiYWbWtbStM69pbgKagKHN2ocCHXYNMjObgAZgbEcdU5Ik6MTQzMztwELglGabTqG4i7ZDREQAkyhuMJIkqcN05jVNgOuBOyNiAfAYcDFQC9wCEBF3AGTmeTt3iIgplZeHAm9U3m/PzGWV7V8Cfgksr/S5jCI0W7wjV5KkPdWpoZmZd0fEYOAqivmUS4HTM/OFSpeW5mv+qtn79wMvAKMq798GfBcYBvy20n9GZi7o0OIlSfu9zj7TJDNvBm5uZdvJLbTFbo73GeAzHVKcJEltcO1ZSZJKMjQlSSrJ0JQkqSRDU5KkkgxNSZJKMjQlSSrJ0JQkqSRDU5KkkgxNSZJKMjQlSSrJ0JQkqSRDU5KkkgxNSZJKMjQlSSrJ0JQkqSRDU5KkkgxNSZJKMjQlSSrJ0JQkqSRDU5KkkgxNSZJKMjQlSSrJ0JQkqSRDU5KkkgxNSZJKMjQlSSrJ0JQkqSRDU5KkkgxNSZJKMjQlSSrJ0JQkqSRDU5KkkgxNSZJKMjQlSSrJ0JQkqSRDU5KkkgxNSZJKMjQlSSrJ0JQkqSRDU5KkkgxNSZJKMjQlSSrJ0JQkqSRDU5KkkgxNSZJKMjQlSSrJ0JQkqSRDU5KkkgxNSZJKMjQlSSrJ0JQkqSRDU5KkkgxNSZJKMjQlSSqp00MzIi6JiJUR8VpELIyIk3bTf2al32sRsSIiLt7bY0qStCc6NTQj4mzgRuBa4HjgceD+iDiilf6jgX+r9Dse+Drw7Yj44J4eU5KkPdXZZ5pXArMy89bMfCYzLwXWAZ9spf/FwIuZeWml/63A94HP7sUxJUnaI50WmhFxEPAO4MFmmx4E3tXKbvUt9P85UBcRB+7hMSVJ2iN9O/F3HQb0ATY0a98AvLeVfYYB/95C/76V40V7jxkRFwEXVd6+GhHPlSleuxwGbOrqIjrDbZ/p6gqkDuF3tv2ObG1DZ4Zmt5CZ3wW+29V19FQR0ZCZdV1dh6Ry/M52rM4MzU1AEzC0WftQYH0r+6xvpf+OyvFiD44pSdIe6bRrmpm5HVgInNJs0ykUd7y2ZF4r/Rsy8/U9PKYkSXuks4dnrwfujIgFwGMUd8fWArcARMQdAJl5XqX/LcCnI+IG4J+AdwMfBz5c9pjqcA5tSz2L39kOFJnZub8w4hLgb4HDgaXAZzJzTmXbIwCZeXJV/5nAPwITgBeBv8/MW8oeU5KkjtLpoSlJUk/l2rOSJJVkaEqSVJKhKUlSSYam9khERNXrA6rfS1JvZWhqTx0QEWMAMvONrNxRZnhK6s28e1btEhHHUTxl5gTgtxSrM80HfpCZi7uwNEktiIio+kttH2DXX3LVfoam2iUilgPPUKzW1JdiycI64G0UT6C5JjM3dlmBkt4iIo7JzGeq3gdwQGY2dWFZPdJ+t2C79lxE/BXFkP5HMnNLpW0AMB44DfhroF9EfLqyxKGkLhYRfwncHRGPA/cBszNzNcW63UTEAcAhwOjMfKrrKu0ZvKap9jgCeBbYurMhM7dmZkNmfo3igeB/DkzpmvIkteBsYAHFCNFHgHkR8W8RcV5EHJKZbwAzgF91ZZE9hcOzKi0iTgQeBr4M3JyZW5ttD2AOcH9mXtv5FUqqFhH9gJ9Vfu4AjqK4H2EGcDzF84gfBY4FXsjMv+yiUnsMQ1PtEhF/B1wI3A/Movjba2NmNkbEkcAS4PTM9CkzUherXD65CNhaeZbwzvbhFEE5DfgTYCZwQmYu7JJCexBDU6VExAGZ+UZEHEjxJbySYrh2KcXTZUYC44BfZ+afdV2lkprbeQdtRPSpvvmnMjr0JeCizKztugp7DkNTpUXEwZn5WtX7GRTXS+oornUuAO7NTB8ALnUDO+dNN59i0mwayoPA05n5mS4osccxNLVbETEMOAuYChxDEY53Vw/BNg9USV0vIvpm5o42th9Icbnl3szc0HmV9VyGpnYrIn4GHE1x/fJFioeBTwBWANcBt2fmjp1DuF1XqaSWVBY1wHmZe895mmpTRLwHeCdwfGauiYiDgRqK0Pxr4AvAAOB6A1PqHiLi3cDNwLeBO6rnTUdEX+ANIIHBwCuGaXnO09TuzACeysw1AJn5Wmb+tjI0+z+B7wFfjYipXVmkpDe5CJgI/C/g9xHxQET8GUBm7qj8BfddwA8A14tuB0NTu/PvwHERcVrzDZVVgf4eeJzilnVJ3cMo4CrgT4G/qbT9KCK2RMT3ImIycA5Q29Y1T72Vw7PanYUUczJviojbgIeAZzPzd5Xt/Snme93SRfVJqhIRtcBy4OXMfCoilgH/h+K+hD8BPkhxM9+BFCt4qR28EUi7FREjKa5dvhd4BXgCWE+xdmU9MD4zx3ddhZKqRcRg4JDKGrPV7X2BgcClwGWZ+bYuKK9HMzRVWkRMoli78l0UoxQDKYZmr3ehZ6nniIh/BZoy84NdXUtP4/CsWhQRNcAk4AMUC7Q/CTRk5t9Wto8HVgHbfTaf1HNERH+KEaMbu7qWnsgzTbUoIr5FEZjrgEEUNxasB34C/H1mvtB11UnaGxFRk5mNXV1HT+Tds3qLiDgW+DhwPnBaZh4FDKOY8/U/gGcj4m92LtElqetFxNCI+GhEDNpNv4MrD1jw+7sHDE215C+AxZn5YGZurizF9VJmfiMzRwP/CHwGOLxLq5RU7Srg+8B/RsSPIuL0ymWWXSLiCODTlTNNhxn3gKGpljwDHB4RR0MxGToi+lZWAwK4Ffg9xXq0krqHOop50/+T4ia9fwFWRsS3qxYfuRC42KHZPWdoqiVzgB3ATyPiQ5W/le7YuSB7Zq6keHitXzypG6jMzVwDrMzM24HTgMkUN/ucBDwREU9RPNLv211WaC/gjUBqUeVL+I/AcRRfxgXALyqvPwX8FTCqapEDSV0kIv4AeA+wMTPnN9t2CMWSep+luLlvQGZu6/wqewdDU62qTJD+M+AUYAwwnmLY51HgnzLzri4sT1Irqp+XWdU2CzgqM0/qmqp6B+dp6k0iYgTFclsAvwN+DNxJEZr9Ka5lbsrMl7umQknNRcQBFM+aTmjxodP9gFrg+i4or1fxTFO7RMQnKaaZTKYIxxUUw7EPAz9uviSXpJ6h8rDpusyc19W19HSGpoBdQ7H/CXwT+A7wdoq1Zk+mWJD9RYq1Kpe1NPQjqfNVwnA08IJ3xHYOQ1MARMSlwEcyc1oL26YDXweGA+/MzE2dXZ+kt4qIK4BrgHsonmTyBPBS9UOlI+JQijtoH6p+GLX2jFNOtNN2YEBETIRima2IOAggM+cC5wKvUTyfT1L3cDbFne1HA/8KzAOui4jpEfGHlT5/BXzRwOwYhqZ2+jHwBnBFRAzIzMbM3F65wYDM/C/gN8CILqxRUkVEvB14Hbi1ckfskcD3KO54nwP8IiI+B1wBzG/tOGofh2dF1RqUf04xGXoQxXDPzcCvKIJyBsW1zuMyc1UXlCmpSkQcDpwDLMvMnzfbdjxwQWX7QGBkZq7t/Cp7H0NTu0TE24AjKJ6XeSbw7sqm9UAAd2bml7ukOElvUZlKkpn5WvUC7Dtv1IuIa4DTM/P4rqqxt3Ge5n4uIoYAH6VYr3ITsI1iGHYu8A/AgRTXSx7IzOe7qExJLcjMbTvDsoW5mYcAHwRu74raeivPNPdzlVVCJgD/F3iZYmj2OGAcsBG4qvmyXJK6VuWO2K1tTf2qPGDhbGC2NwF1HENzP1b5G+pWiuGbOVVtRwDTKK6JjAE+lJmLuqxQSW8SEf9EcdfsAoo5mlta6PO2zPxNZ9fW23n37P7tWGAlxXQToLIOV+YLmXkP8H6Kodq/7JryJDUXER+meMTXN4GfUEwxOTMijqpc49x5rfP7O6eQqeN4prkfq3yxfgocApwH/Doz32jW51LgE5k5pfMrlNRcRNwKNAH/m+KpJR8DjgKeA/4N+A+KhyvcmJkHdVWdvZVnmvuxyuOB/g7oB9wBnBcRIyOiP+y6kWAmsLTrqpS0U0T0pRgd+k1mrsjMf8jM44ATKJ4+9DGK6WLfpnjQgjqYZ5qiMoTzReAMiiebzANeolh7dh1wQWY+1XUVStopIgYCQzPz2cqqXa9X3xAUEWcDs4Gpmbm4i8rstQxN7VKZfvI+4C8olsxbCvwoM5/tyrokta2ycldkZlNEXEgxNHtIV9fVGxmaalFEHND8+qak7i8irgT6ZOZ1XV1Lb2RoSlIvUnlcWJN/6d03DE1Jkkry7llJkkoyNCVJKsnQlCSpJENTkqSSDE1JkkoyNCVJKun/AyRV+BZCX/HQAAAAAElFTkSuQmCC\n",
98 | "text/plain": [
99 | ""
100 | ]
101 | },
102 | "execution_count": 4,
103 | "metadata": {},
104 | "output_type": "execute_result"
105 | }
106 | ],
107 | "source": [
108 | "plot_histogram(ans)"
109 | ]
110 | }
111 | ],
112 | "metadata": {
113 | "kernelspec": {
114 | "display_name": "Python 3",
115 | "language": "python",
116 | "name": "python3"
117 | },
118 | "language_info": {
119 | "codemirror_mode": {
120 | "name": "ipython",
121 | "version": 3
122 | },
123 | "file_extension": ".py",
124 | "mimetype": "text/x-python",
125 | "name": "python",
126 | "nbconvert_exporter": "python",
127 | "pygments_lexer": "ipython3",
128 | "version": "3.8.2"
129 | }
130 | },
131 | "nbformat": 4,
132 | "nbformat_minor": 4
133 | }
134 |
--------------------------------------------------------------------------------
/Qiskit/Increment Circuit/Increment.ipynb:
--------------------------------------------------------------------------------
1 | {
2 | "cells": [
3 | {
4 | "cell_type": "code",
5 | "execution_count": 1,
6 | "metadata": {},
7 | "outputs": [],
8 | "source": [
9 | "import matplotlib.pyplot as plt\n",
10 | "%matplotlib inline\n",
11 | "import numpy as np\n",
12 | "\n",
13 | "from qiskit import *\n",
14 | "\n",
15 | "from qiskit.tools.visualization import plot_histogram\n",
16 | "from IPython.display import display, Math, Latex"
17 | ]
18 | },
19 | {
20 | "cell_type": "markdown",
21 | "metadata": {},
22 | "source": [
23 | "# Increment\n",
24 | "\n",
25 | "Takes an arbitrary input state $|x\\rangle$ on $n$ and takes it to the $|(x+1)\\text{mod N}\\rangle$, where $N = 2^n$ state in the binary representation, which can be done by applying the following circuit $U$.\n",
26 | "\n",
27 | "Let $|x\\rangle$ be an arbitrary state on $n$ qubits,\n",
28 | "\n",
29 | "$$\n",
30 | " \\begin{align*}\n",
31 | " U|x\\rangle = |(x+1)\\text{mod N}\\rangle\n",
32 | " \\end{align*}\n",
33 | "$$\n",
34 | "\n",
35 | "Where $U$ defines an opperation that applis multiple $1$ multi-controlled $X$ gates and flips the first qubit.\n",
36 | "\n",
37 | "Here we give an example on $n = 3$ qubits.\n",
38 | "\n",
39 | "| Initial State $|x\\rangle$ | Final State $U|x\\rangle$ |\n",
40 | "| ------------- | ------------- |\n",
41 | "| $|000\\rangle$ | $|001\\rangle$ |\n",
42 | "| $|001\\rangle$ | $|010\\rangle$ |\n",
43 | "| $|010\\rangle$ | $|011\\rangle$ |\n",
44 | "| $|011\\rangle$ | $|100\\rangle$ |\n",
45 | "| $|100\\rangle$ | $|101\\rangle$ |\n",
46 | "| $|101\\rangle$ | $|110\\rangle$ |\n",
47 | "| $|110\\rangle$ | $|111\\rangle$ |\n",
48 | "| $|111\\rangle$ | $|000\\rangle$ |"
49 | ]
50 | },
51 | {
52 | "cell_type": "code",
53 | "execution_count": 2,
54 | "metadata": {},
55 | "outputs": [],
56 | "source": [
57 | "def Increment(n):\n",
58 | " U = QuantumCircuit(n)\n",
59 | " control = [x for x in range(n-1)]\n",
60 | " for k in range(n-1):\n",
61 | " U.mcx(control, control[-1]+1)\n",
62 | " control.pop()\n",
63 | " U.x(0)\n",
64 | " \n",
65 | " U = U.to_gate()\n",
66 | " U.name = 'Increment'\n",
67 | " #ctl_U = U.control() make it a controlled gate\n",
68 | " \n",
69 | " return U"
70 | ]
71 | },
72 | {
73 | "cell_type": "code",
74 | "execution_count": 3,
75 | "metadata": {},
76 | "outputs": [
77 | {
78 | "data": {
79 | "image/png": "iVBORw0KGgoAAAANSUhEUgAAAdMAAADWCAYAAACKRGiqAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjMuMCwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy86wFpkAAAACXBIWXMAAAsTAAALEwEAmpwYAAAeVklEQVR4nO3de1xUdeLG8c/AICB4Q8QbYiFCOIEimmYaommuaVp5by1dXM3LZr/NTW0zk4zS3C5uVrqWbjdTFPOSmWZAmpWat3QronAFRcW8ongB5vcHOisiFz3AAXzer9e8HM6cMzyMMzx8v+fMGYvdbrcjIiIiN8zJ7AAiIiKVncpURETEIJWpiIiIQSpTERERg1SmIiIiBqlMRUREDFKZioiIGKQyFRERMUhlKiIiYpDKVERExCCVqYiIiEEqUxEREYNUpiIiIgapTEVERAxSmYqIiBikMhURETFIZSoiImKQylRERMQglamIiIhBKlMRERGDVKYiIiIGqUxFREQMUpmKiIgYpDIVERExSGUqIiJikMpURETEIKvZAaTi+PlLOH3E7BRSVdTwgaAuZqcQKR8qU3E4fQROpJmdQqTkLBaLKd/Xbreb8n2l4tI0r4iIiEEqUxEREYNUpiIiIgapTEVERAxSmYqIiBikMhURETFIZSoiUgQXFxezI0gloPeZishN4fbbb6dz586Eh4fTsGFD7HY7hw4d4vvvvyc+Pp69e/cW2KZfv35Mnz6dbt26kZqaakJqqSxUpiJSpfXu3ZuJEydy1113XfP2YcOGAbBp0yZeeuklPv30UyCvSBctWoTVaqVfv368+uqr5RVZKiGV6RVyc3N55ZVXmDt3LqmpqQQFBTF79mxGjhxJREQE8+bNMztihZCTm8M7ayaxbttCLmSfI7x5d57oN5daHt5mRxNxqFOnDm+++SaDBg0C4OTJkyxfvpwtW7aQkpKCxWLh1ltv5Y477qBv37507NiR1atX89FHH7Fu3Trmz5+P1Wpl+vTpKlIplsWu82I5DB8+nLi4OKZMmUJ4eDibN29mzpw5ZGRk8MYbbzBq1CizI5apbR+X7HSCH254gfXb/s2LI9ZSs3pdZi35E+cvniVmxGdlH1Iqjdq+0GZQ2X6Pwk4n6OPjw5dffonNZuPMmTM888wzzJs3j7Nnz15zfQ8PD0aNGkV0dDQeHh7Y7XYsFgvTp09nypQpBdbXr025mkamlyxatIiFCxeSkJBAREQEAJGRkWzfvp24uDhat25tcsKKY8238/hjt2dpWNcfgD/fN5NHZwRw+Ph/qV+nqcnp5Gbn6urK2rVrsdls7N27l969e5OSklLkNmfOnOGVV17hwoULzJ49G4vFwsGDB4mOji6n1FLZ6WjeS2JiYujRo4ejSC8LCAjAxcWF0NBQAPbt20dERASBgYGEhISwceNGM+KaJjPrBEdO7Kd543DHskbezajuVpNfD+4yMZlInqlTpxIWFkZycjKRkZHFFulll/eLWiwWjh8/TqNGja45KhW5FpUpkJaWxp49e+jfv3+B2/bv34/NZsPV1RWAUaNGMXDgQJKSkpg7dy6DBg3iwoULpZbFYrGYdklMTCg239nzpwHwcK+Vb7mnW23OnjtVao+DVH6JiQll/py9mr+/P0899RQ5OTkMHTqUjIyMEmW98mCj6dOnc//995Obm8vkyZNp2rTgbIuZr1Ndyu9yPVSm5JUpQIMGDfItz8rKIjEx0THFe/ToUTZt2kRUVBQAHTp0oFGjRsTHx5dvYBNVd60BwJmsk/mWZ547QXW3mmZEEnF47LHHcHZ25v333+fbb78t0TZXF+mUKVPYtGmTY1lVP1ZCSofKFPD2zjsKNSkpKd/ymTNnkp6eTnh43pTm/v37qV+/vmOUCnDrrbfy3//+t9Sy2O120y4REZ2LzefpXhuf2n4kH9juWJb++2+cPXcK/4ahpfY4SOUXEdG5zJ+zVxs6dCgAc+bMKVHGaxXpZW+88QYAjzzySIHtzHyd6lJ+l+uhA5DImxoKDQ0lJiYGLy8vGjduzNKlS1mzZg2Ao0wlT8/2I1mcMIOWAZHUrF6Xf62ZSJvAe2ngdYvZ0eQm1qRJExo0aMDRo0fZtm1bsesXVaQA3377LSdOnKBx48Y0bNiQ9PT0soouVYBGpoCTkxOxsbHYbDZGjx7N8OHD8fb2ZuzYsTg7OzsOPvLz8+Pw4cOcP3/esW1KSso196lUZYMiJ9E+uDfjXm/L4OmNyc3NYdKQD8yOJTe5kJAQAHbs2FHsusUV6WWX7+vy7wCRwmhkeklgYGCBfZ9Dhw6lRYsWuLu7A3nTwXfddRfvvPMOY8aMYfPmzRw4cIDIyEgzIpvG2cmZUb1nMar3LLOjiDikp6czb948du0q+qjykJCQEhUpQFxcHL/88guHDh0q7bhSxeikDUUIDg6mffv2LFiwwLHst99+Y9iwYRw6dIhq1aoxZ86cAm+nqaxKetIGkZIw86QNxXnxxRfJzs6+4be+6NemXE0j00JkZmaSlJTEmDFj8i339/fnq6++MimViJSGyZMnmx1BqhiVaSE8PT3JyckxO4aIiFQCOgBJRETEIJWpiIiIQSpTERERg1SmIiIiBqlMRUREDFKZioiIGKQyFRERMUjvMxWRSutGzkQ0aca8fF+/NHFkacWRm5hGpiIiIgapTEVERAxSmYqIiBikMhURETFIZSoiImKQylRERMQglamIiIhBKlMRERGDVKYiIiIGqUxFREQMUpmKiIgYpDIVERExSGUqIiJikMpURETEIJWpiIiIQfo8UxGRcmaxWMr9e97IZ79KyWlkKiIiYpDKVERExCCVqYiIiEEqUxEREYNUpiIiIgapTEVERAzSW2NERCq4evXqERwcjJubG2fOnGHv3r2cOHGi0PUfeeQR4uPjSU1NLb+QNzmVqYhIBRQQEMBjjz1G//798fPzK3B7cnIyH374IfPmzePgwYOO5WPGjGHOnDn8+uuvhIaGcvbs2fKMfdPSNO8VcnNzmTVrFs2bN8fNzY2WLVuSmJhIUFAQI0eONDueiNwEqlevzuuvv84vv/zCk08+iZ+fH6dPn+abb75h3bp1bNmyhaysLAICApg6dSr79u3j2WefxWq1OooU4NVXX1WRliOV6RWioqJ4/vnnGTVqFJ999hkDBgxg8ODB/Pbbb4SHh5sdr0KI3/kx//dmJ/o8U5N7J5ozsfHkW5358IvppnxvM+z6NcG0x1rKl7+/Pzt27ODxxx/n4sWLLFiwgHbt2lG7dm06dOjAvffeS7t27ahZsyZdunQhNjYWFxcXpk2bRnJysqNIx40b57gu5UOv0EsWLVrEwoULSUhIICIiAoDIyEi2b99OXFwcrVu3NjlhxeDpXofed47hwsUsXl1WtUbr2TkXsTq7mB1DblJ+fn4kJCTQpEkTdu/ezaOPPsrOnTuvuW52djbx8fHEx8cTERHBsmXLaNq0KQBPPfWUitQEKtNLYmJi6NGjh6NILwsICMDFxYXQ0FAAnn32WT7++GOSk5NZsmQJ/fr1MyOuadoG3QvkjZbMdujYPoa+eCtPDXqPj798kYyTqQT73clTg/5N3ZoNAcg6n8l7655j0544Tp7JoF6tJjzx0FxC/Dvx5FudadaoFYeP72Nn8pcM7vI0g7pMYs13/2L5xtc5cjKVhl7+jOg5gzZB3QF4b91z/JCykUDfNny+9V1y7bkM6fJ3OoU+xKzFw/k5bSu+3oFMHPwBTesHA5CTk83ihJms27aQE5lHaFrfxpg+rxPUpA0AMz8eRq49h2pWN77aHYtbNQ/+eM+z9LpzFEdPHuTp+X8gNzeH3n/3BOAvD8yhe5tHTXjEpaw4OTnx4Ycf0qRJEzZu3EjPnj3JzMws0bY2m426des6vtYsmjk0zQukpaWxZ88e+vfvX+C2/fv3Y7PZcHV1BaBHjx6sXbuWu+++u7xjSiESdy3mlTFfseiZA5y7cIZ/f/6s47Z/xEbxU+p3zBy1gRXPnyJ6+Eq8LhUtwOdb36Vvx8f55PmT9O34OGu++xeL42cwaciHLJ92nOE9XmDaew9y4GiyY5sffvuKxt7NWfzsISYN/oB/ffo3/rEkinEPzCFu2jH8fIJ5c8XjjvX/vW4q3+xdwYsj1rJs2u/0uONPPD2/B6fPHness3H3Utq36E3ctGOM7ftP3vhkHIeP/xfvWo2IGfEZTk7OrHohk1UvZKpIq6CxY8fSsWNHDh48SJ8+fUpcpFfuI506dSqZmZkMHDiQBx54oCzjyjWoTMkrU4AGDRrkW56VlUViYmK+Kd4OHTrg7+9fZlksFotpl8TEhDL7ucrS0G5TqeXhjYdbTbqEDSEpbRsAxzOPkLhrCeMffJuGXrdisVho7B1AY+8Ax7adQvsRFtAFi8WCW7XqLN/4On+851maNWqJk5MT7YJ70qpZJAk7P3Zs41svkJ7tRuDs5Mwdt/2BmtXr0iboXprWD8bq7ELkFRnsdjuffD2bP/d6mYZ1/XF2cuYPd0ThVbMh3/34qeM+WwV0oYPtfpycnOgU8iCe7rX59cDO8nkAy0hiYoKpz+fCLlczO4PVamXixIlAXqkeP368QMZrubJIx40bR3R0NJMnTwZw/Gv2z1nZL9dD07yAt7c3AElJSfTs2dOxfObMmaSnp2vapILzqvG/kaZbNQ+yzp8G4PCxfUBe+RWmfp1b8n196FgK//xkLHOuGFnm5GbjXcv3mt8PwLVa9asyVOfspQwnzxwl63wmUxb0xsL/Xpw5ORc5ejLtf/dZM/99ulXzcNyHVG29evWicePG/PTTT3zyyScl2ubqIr18ff78+Tz33HO0bduW8PBwvv/++7KKLVdRmZJ3BF1oaCgxMTF4eXnRuHFjli5dypo1a4Dy3Qdh5mcObvsYTqQVv15lUd/rFgAOHP2FpvVbXHMdJ0v+yRmfOk15pPs0IloWnPK/EbU8vHGr5sHMkV8Q1KTtDd2HxVI5J5AiIjpjf6vifYbmpBnz8n1txmvuylFP165dAXjvvfdKtG1hRQpw7tw5YmNjeeyxx+jatWu+MtXnmZatyvkqLWVOTk7ExsZis9kYPXo0w4cPx9vbm7Fjx+Ls7Ow4+EggJzeHCxfPcTH7AgAXLp7jwsVzFfKFWsfTh06h/ZgdN4ZDx/Zht9s5cDQ53/7Pqz109//x/vrnSD6wE7vdzvmLWexJ2cT+Iz/dUAaLxcIDHcczd/UE0jJ+AfIOitr68+ccPXmwmK3zeNVoQG5uDunHUm4og1Rsl/9Y37JlS7HrFlWkl3333Xf57lfKh0amlwQGBhIfH59v2dChQ2nRogXu7u4mpap4vvj+fWYtGe74+r6n8x6b9yen0ODSSLAimdD/XRZ+PoUn34rg1NnfqV+nKU88NDffftMr9Wz3Z6zO1Zi1ZDiHjqVgdXYhoHFrRvWadcMZHu0+jeWbZjN1YR+OnkzDrZoHwX7tGdv3nyXa3rdeIL3vHM1fZt9Bds5Fxvb9J93Ch95wHqlYGjVqBMCvv/5a5HolKVLIOzPSlfcr5cNir4hDigoiODiY9u3bs2DBAseyKVOmsGDBAjIyMvD09MTd3Z3ExESaNWtmYtLSUdWmecVctX2hzSCzUxR09TTvSxPL//3SV07zuru74+7uzokTJ8jNzS10m5iYGCZPnlzsCRmsVis1atTg7NmznD9/3rFcv+rLlqZ5C5GZmUlSUlKBkzU8//zzpKWlcf78eX7//XfS0tKqRJGKiDmysrI4duxYkUUK8PTTT9OhQ4diT8iQnZ3N8ePH8xWplD1N8xbC09OTnJwcs2OIiDh88803ZkeQQmhkKiIiYpDKVERExCCVqYiIiEEqUxEREYNUpiIiIgapTEVERAxSmYqIiBik95mKiJSz6z0b0eWzNr00cWS+61JxaGQqIiJikMpURETEIJWpiIiIQSpTERERg1SmIiIiBqlMRUREDFKZioiIGKQyFRERMUhlKiIiYpDKVERExCCVqYiIiEEqUxEREYNUpiIiIgapTEVERAxSmYqIiBikzzMVEZFiWSwWU77v9X72q1k0MhURETFIZSoiImKQylRERMQglamIiIhBKlMRERGDVKYiIiIGqUxFRKRCqFWrltkRbpjeZyoiIqXGarXSs2dPOnXqROvWrfH29sZut5Oamsr333/P+vXr+frrrwtsFx0dzcMPP0znzp1JTU01IbkxGpleITc3l1mzZtG8eXPc3Nxo2bIliYmJBAUFMXLkSLPjiYhUWFarlQkTJrBv3z5WrFjBhAkT6NKlC6GhobRs2ZJevXoxdepUNm3axO7duxkwYIBj2+joaKZMmYKfnx9hYWEm/hQ3TiPTK0RFRREXF8eUKVMIDw9n8+bNDB48mIyMDP7617+aHa9C+NenE/nux9VknEjFzdWTdrfdx4j7ZlCzupfZ0UTEJLfddhsffPAB4eHhAPz4448sXryYbdu2kZqairOzM82bN6ddu3YMGTKEkJAQFi9ezIABA0hJSWHChAlkZ2czZMgQVq5cafJPc2NUppcsWrSIhQsXkpCQQEREBACRkZFs376duLg4WrdubXLCisHJyZlJgz/glga3k5l1gpkfP8LLi4fx/PDK+QIQEWPCwsL44osv8PLyYt++fYwZM4bPPvuswHo7duxgyZIlTJo0iT/96U/MnDmThx56CMBRpLGxseUdv9RomveSmJgYevTo4SjSywICAnBxcSE0NJTjx4/Tq1cvAgMDadmyJd27dyc5OdmkxOaI+kMMAY3DsDq7UNuzHg90HM/uXxPMjiUiJmjQoAFr167Fy8uLVatWERIScs0ivdLFixeZO3cuCxcudCxLSUlh+fLlZZy2bKlMgbS0NPbs2UP//v0L3LZ//35sNhuurq5YLBaeeOIJkpKS2LVrF7169WL48OEmJK44diRvwL9RS7NjiIgJ3n77bXx8fPjyyy956KGHyMzMLNF20dHRPP7442RnZ5ORkUHz5s3529/+VsZpy5bKlLwyhby/sq6UlZVFYmKiY4q3du3a3HPPPY7bO3ToQEpKSqlmsVgspl0SExOuK+vG3ctY/e3bjLn/9VJ9DKRqSExMMPX5XNjlambnuZ7MV18383Hr2rUrffr04eTJkzzyyCNcvHixRM+LywcbXZ7aHTx4MABTp06lXr16Fer/53qoTAFvb28AkpKS8i2fOXMm6enpjp3qV3vttdfo27dvWcerkBJ3xfLq0j8TPWwlzX21P1nkZjN27FgAXn75ZQ4cOFCiba4u0tjYWDZs2MDKlStxdXUlKiqqLCOXKZUp4O/vT2hoKDExMbz33nts2LCB0aNH8+677wJcs0ynTZtGcnIyM2fOLNUsdrvdtEtEROcSZVy7dQGvLxtF9PBVtAqILNWfX6qOiIjOpj6fC7tczew815P56utmPW4eHh707t2b7Oxs5s+fX6Lnw7WK9LK33noLwDFKrSj/P9dDZQo4OTkRGxuLzWZj9OjRDB8+HG9vb8aOHYuzszOhoaH51p8+fTqrV69m7dq1VK9e3aTU5li+aTbzVk/gxT9/zu233mV2HBExQatWrbBarezevZvDhw8Xu35RRQqQkJBAdnY2NpsNd3f3sopdpvTWmEsCAwOJj4/Pt2zo0KG0aNEi33/utGnTWLNmDevXr6d27drlnNJ8b64Yj7OTlQlv5x+RrnqhZAceiEjlZ7PZANi1a1ex6xZXpADnzp3jp59+4vbbbycoKIidO3eWduQypzItwrZt22jfvr3j67179/Lcc8/RrFkzOnfu7FheGf/jb9T6l69v6kNEqp6dO3cSHR3N1q1bi1yvW7duxRbpZXPmzKF+/fpkZGSUdtxyoTItRGZmJklJSYwZM8axzGazXfc8uohIVbNlyxa2bNlS7Hrr168nJiaGnTt3FntChrfffru04plCZVoIT09PcnJyzI4hIlKp/f3vfzc7QrnQAUgiIiIGqUxFREQMUpmKiIgYpDIVERExSGUqIiJikMpURETEIJWpiIiIQSpTERERg3TSBnGo4WN2AqlK9HyqWq737G+TZswD4KWJI/Ndr6pUpuIQ1MXsBCIilZOmeUVERAxSmYqIiBikMhURETFIZSoiImKQylRERMQglamIiIhBKlMRERGDVKYiIiIGqUxFREQMUpmKiIgYpDIVERExSGUqIiJikMpURETEIJWpiIiIQSpTKbHu3bvTqlUrQkJC6NevH6dOnTI7kki5SkhIwGazERAQwIgRI8jJyTE7UrHGjx+Pr68vVmvl+cTN1NRUunbtSnBwMDabjcmTJ5sdqVgqUymx2NhYdu7cyQ8//ICvry+vvPKK2ZFEyk1ubi4jRowgNjaW5ORkTp06xQcffGB2rGL179+fbdu2mR3julitVmbMmMGPP/7Ijh072LRpEytWrDA7VpFUplJitWrVAvJ+qZw7dw6LxWJyIpHys3XrVho1akSLFi0AiIqKYtmyZSanKl7Hjh1p0KCB2TGuS8OGDWnTpg0A1apVIywsjP3795ucqmgqU7kuDzzwAD4+Pvz88888+eSTZscRKTdpaWk0adLE8bWfnx+pqakmJro5HDt2jE8++YRu3bqZHaVIlWcSXSqE5cuXc+HCBaKioli6dCnDhg0zO5JIkVZt2Mxv+9MLvf31Bf8bXQY0bcx9Xdpfcz273V7q2Qpz4PBRlq5JLLD8yqyXr1ss8OiD91Krpme55bsWu93Okk/jOZRxPN/ya2UGaBncjM7tWxV5nxcuXKBfv36MHz+e2267rVTzljaNTOW6VatWjUGDBrF8+XKzo4gUq01IEIcyjpF+5HfSj/xe4PbLyw9nHKNNSGCh99OkSZN8I9H9+/fj6+tbJpkb+dSlhod7gcxXX08/8ju+DeqZXqQAFouF1rbAEmX+/fhJWtuaF3l/OTk5DBkyhFatWlWKWTCVqZTI6dOnSU/P++s+NzeXlStXYrPZTE4lUryGPnVpGxpU7HrtwoKpX8+r0NvbtGlDWloa//nPfwB45513ePDBB0st55UsFgv3dbkTp2KOS3Ct5kK3Tm3KJMONaH6rL8EBfsWu17l9K2rW8ChynZEjR1KjRg3+8Y9/lFa8MqUylRI5ffo0999/P6GhoYSGhpKdnc0zzzxjdiyREuneqS2u1VwKvd3NtRr33FV0KTk7OzN//nz69etHs2bN8PT0ZOjQoaUd1aG+dx3ahbUocp0uHVpTw6N6keuMGjUKX19fcnJy8PX1ZezYsaUZs4D7Iu/E2anwaqld05NObUOLvI+vv/6ad999l23bthEWFkarVq2YPXt2aUctVRZ7ee4IkCrJbrfryF6p8L76bhdrEr675m29utxJx7Yh5ZyoeGeyzvHy3I85d/5Cgdu8atfgr1EDsFqdTUhWtNVffsOmrT9c87bB93elZXCzck5U9jQyvQ4rVqygV69e+Pj44OrqStOmTRkyZAg//HDtJ83NYu8v+5i3aBWnM8+aHUWkUB3Cb6du7ZoFlnt71aJ966JHgGbxcHfjno7h17ytZ2T7ClmkAF07tKa6u2uB5U0b1yf0Nn8TEpU9lWkJZGdn8/DDD9O3b19++OEHHnzwQcaPH09YWBjLli3jwIEDZkc0Ta7dzoavt3Mq8yzVq7uZHUekUFarMz0jCx6p26vLnVidK2YpAdwZZqOeV618y/z9GmJrfos5gUrA3c2V7p3aFljeu2uHKjuLpbfGlMBf/vIXPvroI8aNG8err76a77RcaWlpjpMZ3Iz+88s+0o/8zsBekUXuJxGpCFo0b4q/XyN+238QgOa3+BLk36SYrczl7OzEfV3uZOHStQBYyPsDoKKXUtuWt/HN9r0cPpr3VpnWtwfi27CeyanKjvaZFmPjxo3cfffd9OjRgzVr1pT5E3jSjHllev8iIlIyL00cWeJ1NZQoxmuvvQbASy+9VOH/EhQREXNoZFqMGjVq4O3tTUpKitlRKpRcu51/LozjYnY2/xfVX1O8UqlknsnCYrHgUcn28x8+epz63nXMjnFdjp04RQ2P6ri4VO29iirTIpw4cYI6derQuXNn4uPjy+V7appXRKRi0DRvKbn8d8aRI0dMTiIiIhWZRqbFaNasGSkpKaxbt4577rkn320///wzQUHFn6asqtmTlMIHy9czsFckYcWcX1NE5GagMi3GkiVLGDhwIFarlT59+tCsWTOOHDnC5s2badGixU13snftKxURKahq7xEuBQMGDKBWrVq8/PLLrF+/nlWrVuHj48Mdd9zBE088YXa8cnfmbBbOTk7c3aG1ilRE5BKNTOW62e127FDsJ1qIiNwsVKYiIiIGaZ5ORETEIJWpiIiIQSpTERERg1SmIiIiBqlMRUREDFKZioiIGKQyFRERMUhlKiIiYpDKVERExCCVqYiIiEEqUxEREYNUpiIiIgapTEVERAxSmYqIiBikMhURETFIZSoiImKQylRERMQglamIiIhBKlMRERGDVKYiIiIGqUxFREQMUpmKiIgYpDIVERExSGUqIiJikMpURETEIJWpiIiIQSpTERERg/4fw14+Wxb4ZZoAAAAASUVORK5CYII=\n",
80 | "text/plain": [
81 | ""
82 | ]
83 | },
84 | "execution_count": 3,
85 | "metadata": {},
86 | "output_type": "execute_result"
87 | }
88 | ],
89 | "source": [
90 | "n = 3\n",
91 | "mc = QuantumCircuit(n, n)\n",
92 | "U = Increment(n)\n",
93 | "mc.append(U, range(n))\n",
94 | "\n",
95 | "mc.measure(range(n), range(n))\n",
96 | "\n",
97 | "backend = BasicAer.get_backend('qasm_simulator')\n",
98 | "atp = 1024\n",
99 | "res = execute(mc, backend=backend, shots=atp).result()\n",
100 | "ans = res.get_counts()\n",
101 | "\n",
102 | "mc.draw('mpl')"
103 | ]
104 | },
105 | {
106 | "cell_type": "code",
107 | "execution_count": 4,
108 | "metadata": {},
109 | "outputs": [
110 | {
111 | "data": {
112 | "image/png": "iVBORw0KGgoAAAANSUhEUgAAAc0AAAFCCAYAAACTo4YQAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjMuMCwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy86wFpkAAAACXBIWXMAAAsTAAALEwEAmpwYAAAaTElEQVR4nO3df7SdVZ3f8feXREBMUBKGkJtLxBiqNRFBjgh4gegyQ4FVVLAiC0xTKimxEpE6M7oGqXEQp+owME4Zh8wsIWhbFDtaJUAYJUYhXLyJjYI2SQfMmJDckCEYlZAAfvvHc5I5vdwf+yQ3957kvF9rnZVz9t7Pvt/nD/is59d+IjORJElDO2S0C5Ak6UBhaEqSVMjQlCSpkKEpSVIhQ1OSpEJjR7uA0XT00Ufn8ccfP9plSJJayMqVK7dm5u/119fWoXn88cfT09Mz2mVIklpIRKwfqM/Ts5IkFTI0JUkqZGhKklTI0JQkqZChKUlSIUNTkqRChqYkSYUMTUmSChmakiQVMjQlSSpkaEqSVMjQlCSpkKEpSVIhQ1OSpEKGpiRJhQxNSZIKGZqSJBUyNCVJKmRoSpJUyNCUJKmQoSlJUiFDU5KkQoamJEmFDE3pIHT55ZdzzDHHMHPmzH77M5MFCxYwffp0TjzxRFatWrWn7/bbb+eEE07ghBNO4Pbbb9/TvnLlSt74xjcyffp0FixYQGbu9/2QWo2hKR2E5s6dy7333jtg/z333MO6detYt24dt956K/Pnzwfg6aefZuHChXR3d/PII4+wcOFCtm3bBsD8+fNZtGjRnu0Gm186WBma0kHorLPOYsKECQP2f+tb32LOnDlEBKeddhrPPPMMmzZt4r777mP27NlMmDCBo446itmzZ3PvvfeyadMmtm/fzmmnnUZEMGfOHL75zW+O3A5JLcLQlNrQxo0bOe644/b87uzsZOPGjYO2d3Z2vqRdajeGpiRJhQxNqQ1NmTKFX/7yl3t+b9iwgSlTpgzavmHDhpe0S+3G0JTa0AUXXMDixYvJTB5++GFe+cpXMnnyZM455xyWLl3Ktm3b2LZtG0uXLuWcc85h8uTJHHnkkTz88MNkJosXL+Zd73rXaO+GNOLGjnYBkobfJZdcwrJly9i6dSudnZ0sXLiQ559/HoArr7yS8847jyVLljB9+nSOOOIIvvzlLwMwYcIEPvnJT/KWt7wFgOuuu27PDUW33HILc+fOZceOHZx77rmce+65o7Nz0iiKdn7WqlarZU9Pz2iXIUlqIRGxMjNr/fV5elaSpEKGpiRJhQxNSZIKGZqSJBUyNCVJKmRoSpJUyNCUJKmQoSlJUqERDc2IOCsi/ldEbIyIjIi5Bdu8MSK+HxE76ttdFxHRZ8xFEfGziNhZ//c9+20nJElta6SPNMcBjwIfAXYMNTgijgTuB3qBt9S3+wPgmoYxpwN3Al8FTqr/+/WIeOsw1y5JanMjuvZsZi4BlgBExG0Fm1wKHAH828zcATwaEa8HromIG7NaA/Bq4IHM/Ex9m89ExNvr7ZcM7x5IktpZq1/TPB34QT0wd7sP6ACObxiztM929wFn7PfqJEltpdXfcnIssKFPW29D3xP1f3v7GXNsfxNGxDxgHkBHRwfLli0DYNq0aYwfP57Vq1cDMHHiRGbMmMHy5csBGDt2LF1dXaxatYrt27cDUKvV6O3t5U+//dp92UdJ0jD49MWbWLNmDVC9M7azs5Pu7m4Axo0bR61WY8WKFezcuROArq4u1q5dy5YtWwCYOXPmnr6BjNpbTiLiN8CHM/O2QcYsBTZk5uUNbVOB9cAZmbkiInYBH8zMxQ1j5gCLMvOwwWoYrrecXHHTPk8hSdpHi64ennkO5LecbAYm9Wmb1NA32JjNSJI0jFo9NFcAZ0bE4Q1ts4EngV80jJndZ7vZwEP7vTpJUlsZ6ec0x0XESRFxUv1vT63/nlrv/2xEfLdhk/8GPAvcFhEzI+JC4OPA7jtnAW4G3hERH4+I10fEJ4C3AzeN0G5JktrESB9p1oAf1z8vBxbWv3+63j8Z2HNXTWb+iuqosQPoAf4r8GfAjQ1jHgLeD8wFfgLMAS7OzO79uyuSpHYz0s9pLgNikP65/bT9FDhriHnvAu7ax/IkSRpUq1/TlCSpZRiakiQVMjQlSSpkaEqSVMjQlCSpkKEpSVIhQ1OSpEKGpiRJhQxNSZIKGZqSJBUyNCVJKmRoSpJUyNCUJKmQoSlJUiFDU5KkQoamJEmFDE1JkgoZmpIkFTI0JUkqZGhKklTI0JQkqZChKUlSIUNTkqRChqYkSYUMTUmSChmakiQVMjQlSSpkaEqSVMjQlCSpkKEpSVIhQ1OSpEKGpiRJhQxNSZIKGZqSJBUyNCVJKmRoSpJUyNCUJKmQoSlJUiFDU5KkQoamJEmFDE1JkgoZmpIkFTI0JUkqZGhKklSoqdCMiEMi4pCG38dGxAcj4m3DX5okSa2l2SPNu4GrACJiHNADfB5YFhFzhrk2SZJaSrOhWQO+V/9+IbAdOAa4AvhYyQQR8aGIeCIinouIlRFx5iBjb4uI7Ofz24YxswYY8/om902SpEE1G5rjgGfq338f+LvMfJ4qSF871MYRcTFwM3ADcDLwEHBPREwdYJOPAJP7fB4HvtbP2Bl9xq0r2iNJkgo1G5r/CLwtIl4BnAPcX2+fADxbsP01wG2ZuSgzf56ZVwGbgPn9Dc7MX2Xm5t0fqmCeBizqZ/iWxrGZ+WKT+yZJ0qDGNjn+RuAO4DfAemB5vf0s4KeDbRgRhwKnAF/o07UUOKPw718BPJaZD/XT1xMRhwE/A67PzAcGqGMeMA+go6ODZcuWATBt2jTGjx/P6tWrAZg4cSIzZsxg+fJqF8eOHUtXVxerVq1i+/btANRqNXp7eyk4yJYk7WebNm1izZo1AEyZMoXOzk66u7sBGDduHLVajRUrVrBz504Aurq6WLt2LVu2bAFg5syZe/oGEpnZVFERUQOOA+7PzN/U284HnsnMBwfZrgPYCJydmcsb2q8DLs3M1w3xd19JdVT6icy8uaH9dcDbgR8BhwIfAK6s/50fDDZnrVbLnp6ewYYUueKmfZ5CkrSPFl09PPNExMrMrPXX1+yRJpnZQ3XXbGPb3XtZWzMuozqdfEefv70GWNPQtCIijgf+ABg0NCVJakbTixvU7359LCKejYhp9bY/ioj3DbHpVuBFYFKf9knA5oI/fQXwjcx8umBsN3BCwThJkoo1u7jB1cC1wK1ANHQ9CXx4sG0zcxewEpjdp2s21V20g/3dU4E30f8NQP05iepUriRJw6bZ07NXAldk5t0RcX1D+yqqRz6GciNwR0Q8AjxYn68D+BJARCwGyMy+CyXMA9Zl5rK+E9aD/BfAY1TXNC8D3g1cVLhPkiQVaTY0Xw082k/788DLh9o4M++MiIlUR6uT63Odl5nr60Ne8rxmRIwH3g98eoBpD6ValagT2EEVnudn5pKh6pEkqRnNhubjwJupHjdpdB7Vox5DysxbgFsG6JvVT9uvqRZVGGi+zwGfK/nbkiTti2ZD8wvAX0bEEVTXNE+PiA8AfwhcPtzFSZLUSpoKzcz8ckSMpVoG7wiqxz+eBBZk5p37oT5JklrG3jynuQhYFBFHA4dk5pbhL0uSpNbTdGjulplbh7MQSZJa3ZChGRE/oVqSbltE/BQYcN29zDxxOIuTJKmVlBxpfgPY2fC9ucVqJUk6SAwZmpm5sOH7p/ZrNZIktbBml9H7XkS8qp/2IyPie8NWlSRJLajZBdtnUa3A09fhwJn7XI0kSS2s6O7ZiHhzw88TI6LxTSNjgHOo3pUpSdJBq/SRkx6qG4ASWNpP/w7gquEqSpKkVlQamq+hWjbvceBU4KmGvl3Alsx8cZhrkySppRSFZsNbSJp+abUkSQeLksUNLgS+nZnP178PKDP/57BVJklSiyk50rwLOBbYUv8+kKS6KUiSpINSyeIGh/T3XZKkdmMISpJUqPSaZhGvaUqSDmal1zRLeE1TknRQa+qapiRJ7cxAlCSpkM9pSpJUyOc0JUkq5HOakiQVMgQlSSrUdGhGxJsjYnFE9NQ/d/R536YkSQelpkIzIi4FfgRMBpbUP5OARyLisuEvT5Kk1lH6Ps3dPgN8MjNvaGyMiE8A1wNfGa7CJElqNc2env094Gv9tH8dOGbfy5EkqXU1G5oPALP6aZ8FfH9fi5EkqZU1u2D7PcBnI6IGPFxvOw24EPjUsFcnSVIL2dsF2+fVP42+CNyyzxVJktSiXLBdkqRCBqIkSYWafeSEiDgKOBeYChza2JeZnx6muiRJajlNhWZEnAbcDeykevxkI9VCBzuBXwCGpiTpoNXs6dnPA18FpgDPAe+gOuLsAf7L8JYmSVJraTY0TwT+MjMTeBE4LDN7gT/CR04kSQe5ZkNzV8P3XuDV9e+/ATqGpSJJklpUszcCrQLeAqwFlgHXR8Qk4DLgJ8NbmiRJraXZI80/Bp6sf78WeIpqUYOjeOliB5IkHVSaOtLMzJ6G709RPXoiSVJbaPo5TYCIeC3wL+s/f5aZjw9fSZIktaZmn9OcCPwtcAHwu39uju8Al2fmPw1zfZIktYxmr2n+DTAdOBM4vP45C3gNsGh4S5MkqbU0G5rnAFdk5oOZ+UL98yDwH+p9Q4qID0XEExHxXESsjIgzBxk7KyKyn8/r+4y7KCJ+FhE76/++p8n9kiRpSM2G5lPAb/tpfxYY8tRsRFwM3AzcAJwMPATcExFTh9h0BtVyfbs/6xrmPB24k2qlopPq/349It46VD2SJDWj2dD8NHBTREzZ3VD//meUrTt7DXBbZi7KzJ9n5lXAJmD+ENttyczNDZ8XG/quBh7IzM/U5/wM1TOkVxfvlSRJBYa8ESgifgpkQ9NrgF9ExMb6793r0B5Ddc1zoHkOBU4BvtCnaylwxhBl9ETEYcDPgOsz84GGvtOpnhVtdB/w4SHmlCSpKSV3z941TH/raGAM1fJ7jXqBdw6wze6j0B9RvYbsA8B3I+LszPxBfcyxA8x5bH8TRsQ86gsxdHR0sGzZMgCmTZvG+PHjWb16NQATJ05kxowZLF++HICxY8fS1dXFqlWr2L59OwC1Wo3e3l7gtUPuvCRp/9q0aRNr1qwBYMqUKXR2dtLd3Q3AuHHjqNVqrFixgp07dwLQ1dXF2rVr2bJlCwAzZ87c0zeQqNZe3/8iooPqVWJnZ+byhvbrgEsz83WF8ywBXsjMC+q/dwEfzMzFDWPmAIsy87DB5qrVatnT0zPYkCJX3LTPU0iS9tGiq4dnnohYmZm1/vr2dnGDdwBvoDpt+1hmLivYbCvVm1Em9WmfBGxu4s93A+9v+L15GOaUJGlITd0IFBFTIuIR4H6q14F9nOp0aXf9SHJAmbkLWAnM7tM1m+ou2lInUZ223W3FMMwpSdKQmj3S/Auqo8XpmfkEQERMA75S73vvENvfCNxRD94HgSupXin2pfpciwEyc07999XAL4DHqK5pXga8G7ioYc6bgeUR8XHgm8B7gLcDXU3umyRJg2o2NGcDs3YHJkBmPh4RC4DvDrVxZt5ZX4rvWqrnLR8FzsvM9fUhfZ/XPBT4PNAJ7KAKz/Mzc0nDnA9FxPuB66kee/kH4OLM7G5y3yRJGtTeXNPs786h4ruJMvMW4JYB+mb1+f054HMFc97F8N3lK0lSv5pd3OC7wBcj4rjdDfXVfG6i4EhTkqQDWbOhuQB4BfB4RKyPiPVUp0NfUe+TJOmg1ezp2X8CTgVmAbsXTf95Zv79cBYlSVIrKg7NiBgD/Ap4U2beT/XYiSRJbaP49Gx9kfT1VHe0SpLUdpq9pvknwJ9GxNH7oxhJklpZs9c0P0b1lpONEbGBPu/WzMwTh6swSZJaTbOheRfVM5mxH2qRJKmlFYVmRBxBtTLPu4GXUT2TeVVmbt1/pUmS1FpKr2kuBOYCdwP/ner9l3+1n2qSJKkllZ6evRD495n5PwAi4qvAgxExpn5XrSRJB73SI83jgB/s/pGZjwAvUL2hRJKktlAammOAXX3aXmAvX2ItSdKBqDT0AvhKROxsaDscWBQRz+5uyMwLhrM4SZJaSWlo3t5P21eGsxBJklpdUWhm5r/b34VIktTqml1GT5KktmVoSpJUyNCUJKmQoSlJUiFDU5KkQoamJEmFDE1JkgoZmpIkFTI0JUkqZGhKklTI0JQkqZChKUlSIUNTkqRChqYkSYUMTUmSChmakiQVMjQlSSpkaEqSVMjQlCSpkKEpSVIhQ1OSpEKGpiRJhQxNSZIKGZqSJBUyNCVJKmRoSpJUyNCUJKmQoSlJUiFDU5KkQoamJEmFRjw0I+JDEfFERDwXESsj4sxBxl4YEUsj4qmI+HVEdEfEBX3GzI2I7Odz+P7fG0lSOxnR0IyIi4GbgRuAk4GHgHsiYuoAm5wNfA84vz5+CfB3/QTts8Dkxk9mPjf8eyBJamdjR/jvXQPclpmL6r+vioh/BcwHPtF3cGZ+pE/Twog4H3g38IP/f2hu3g/1SpK0x4gdaUbEocApwNI+XUuBM5qYajywrU/byyNifURsiIjvRMTJ+1CqJEn9GskjzaOBMUBvn/Ze4J0lE0TEfwQ6gTsamtcAlwOrqQL1I8CDEfGmzFzXzxzzgHkAHR0dLFu2DIBp06Yxfvx4Vq9eDcDEiROZMWMGy5cvB2Ds2LF0dXWxatUqtm/fDkCtVqO3txd4bUn5kqT9aNOmTaxZswaAKVOm0NnZSXd3NwDjxo2jVquxYsUKdu7cCUBXVxdr165ly5YtAMycOXNP30AiM/fjLjT8oYgOYCNwdmYub2i/Drg0M183xPYXUYXlxZn57UHGjQH+N/BAZi4YbM5arZY9PT3lOzGAK27a5ykkSfto0dXDM09ErMzMWn99I3kj0FbgRWBSn/ZJwKDXIyPivVSBOWewwATIzBeBHuCEvS9VkqSXGrHQzMxdwEpgdp+u2VR30fYrIt5HFZhzM/Ouof5ORARwIrBp76uVJOmlRvru2RuBOyLiEeBB4EqgA/gSQEQsBsjMOfXf76cKzI8ByyPi2Po8uzLz6fqY/ww8DKwDjgQWUIXm/BHaJ0lSmxjR0MzMOyNiInAt1fOUjwLnZeb6+pC+z2teSVXjTfXPbt8HZtW/vwq4FTgW+BXwY+CszHxk2HdAktTWRvpIk8y8BbhlgL5Zg/0eYJuPAh8djtokSRqMa89KklTI0JQkqZChKUlSIUNTkqRChqYkSYUMTUmSChmakiQVMjQlSSpkaEqSVMjQlCSpkKEpSVIhQ1OSpEKGpiRJhQxNSZIKGZqSJBUyNCVJKmRoSpJUyNCUJKmQoSlJUiFDU5KkQoamJEmFDE1JkgoZmpIkFTI0JUkqZGhKklTI0JQkqZChKUlSIUNTkqRChqYkSYUMTUmSChmakiQVMjQlSSpkaEqSVMjQlCSpkKEpSVIhQ1OSpEKGpiRJhQxNSZIKGZqSJBUyNCVJKmRoSpJUyNCUJKmQoSlJUiFDU5KkQoamJEmFRjw0I+JDEfFERDwXESsj4swhxp9dH/dcRDweEVfu65ySJO2NEQ3NiLgYuBm4ATgZeAi4JyKmDjD+NcCS+riTgc8CX4yIi/Z2TkmS9tZIH2leA9yWmYsy8+eZeRWwCZg/wPgrgScz86r6+EXA7cDH9mFOSZL2yoiFZkQcCpwCLO3TtRQ4Y4DNTu9n/H1ALSJetpdzSpK0V8aO4N86GhgD9PZp7wXeOcA2xwJ/38/4sfX5otk5I2IeMK/+8zcRsaakeKkNHA1sHe0ipL31Nx8dtqlePVDHSIZmS8jMW4FbR7sOqdVERE9m1ka7DqmVjWRobgVeBCb1aZ8EbB5gm80DjH+hPl/sxZySJO2VEbummZm7gJXA7D5ds6nueO3PigHG92Tm83s5pyRJe2WkT8/eCNwREY8AD1LdHdsBfAkgIhYDZOac+vgvAR+OiJuAvwbeBswFLimdU1IxL1tIQxjR0MzMOyNiInAtMBl4FDgvM9fXh0ztM/6JiDgP+HOqR0ieBBZk5jeamFNSgfr1fkmDiMwc7RokSToguPasJEmFDE1JkgoZmpIkFTI0JUkqZGhKklTI0JRERIyJCP9/IA3B/0ikNhYRpwBk5ouZ+bt625iIiNGtTGpNhqbUpiLiBOBHEfFoRNwYESfDngDNqLwsIk6tv4ZPanuGptS+LgH+AbgfOA34TkQ8HBF/GBHHZbXyyTHAw/V/pbbnikBSm4qIr1K9LeizwESgBpwJnApMAH5M9Sah12TmjNGqU2olbfc+TUkQEWOBu4FXZ+ZmqlfpPRYR3wZeB5wCnAW8F7hi1AqVWoxHmpKIiJdl5vN92i4E7gLGZeazo1OZ1Fq8pim1ob6Pl+wOzIgY23Dn7BnAcgNT+meenpXaU0dETKe6Zvk7YE1mbs7MFwDqwflD4M5RrFFqOZ6eldpMRMwHLgfeBPwW+L/ABqq7ZL+ZmWtGsTyppXl6Vmoj9Re23wB8i+ql7acDtwMvAnOAv4iIN9THjhmtOqVW5ZGm1EYi4irgssx8az99XVSPn0wBTs3MrSNdn9TqPNKU2ssuYHxEzASIiMN2r/aTmT8ELgWeA35/9EqUWpehKbWXu6hu/Lk6IsZn5s7M3LX7btrM/EfgGaBzFGuUWpahKbWJ+h2xTwPXArOBJyPib3cv2h4RUyPiMuCNwNdGr1KpdXlNU2ozEfEqYCrVc5jvAd5W79pM9QjKHZn5qVEpTmpxhqbUBiLiGOADwH+iWm92B9Vp2B9SPWryMmA6cG9mrh2lMqWWZ2hKbSAibgNmAN+mOkU7geo07L8AtgDXZmb3qBUoHSAMTekgV7+W+WvgvMxc3tA2FXgr8EFgGvC+zFw1aoVKBwBvBJIOfm8AnqB63ASArKzPzK8B/5rqVO2/GZ3ypAOHoSkd/B6nOgX75xFxQj+Lte+kWhXo3NEoTjqQGJrSQS4zdwB/DLwcWAzMiYjjImIcQEQcAZwNPDp6VUoHBq9pSm2ivgrQJ4ELqBZqXwE8BbwT2AR8MDN/OnoVSq3P0JTaTP3xk/OBd1Mtmfco8PXM/D+jWZd0IDA0pTYWEYdk5u9Guw7pQGFoSpJUyBuBJEkqZGhKklTI0JQkqZChKUlSIUNTkqRChqYkSYX+Hx5jP9a08jRgAAAAAElFTkSuQmCC\n",
113 | "text/plain": [
114 | ""
115 | ]
116 | },
117 | "execution_count": 4,
118 | "metadata": {},
119 | "output_type": "execute_result"
120 | }
121 | ],
122 | "source": [
123 | "plot_histogram(ans)"
124 | ]
125 | }
126 | ],
127 | "metadata": {
128 | "kernelspec": {
129 | "display_name": "Python 3",
130 | "language": "python",
131 | "name": "python3"
132 | },
133 | "language_info": {
134 | "codemirror_mode": {
135 | "name": "ipython",
136 | "version": 3
137 | },
138 | "file_extension": ".py",
139 | "mimetype": "text/x-python",
140 | "name": "python",
141 | "nbconvert_exporter": "python",
142 | "pygments_lexer": "ipython3",
143 | "version": "3.8.2"
144 | }
145 | },
146 | "nbformat": 4,
147 | "nbformat_minor": 4
148 | }
149 |
--------------------------------------------------------------------------------
/Qiskit/QAOA(Quantum Approximate Optimization Algorithm)/QAOA.ipynb:
--------------------------------------------------------------------------------
1 | {
2 | "cells": [
3 | {
4 | "cell_type": "markdown",
5 | "metadata": {},
6 | "source": [
7 | "# Quantum Approximate Optimization Algorithm\n",
8 | "\n",
9 | "In this notebook we are going to show how to use the implementation of QAOA available in Aqua to obtain solutions to the MaxCut problem"
10 | ]
11 | },
12 | {
13 | "cell_type": "code",
14 | "execution_count": 1,
15 | "metadata": {},
16 | "outputs": [
17 | {
18 | "name": "stderr",
19 | "output_type": "stream",
20 | "text": [
21 | "/opt/conda/lib/python3.7/site-packages/qiskit/providers/ibmq/ibmqfactory.py:192: UserWarning: Timestamps in IBMQ backend properties, jobs, and job results are all now in local time instead of UTC.\n",
22 | " warnings.warn('Timestamps in IBMQ backend properties, jobs, and job results '\n"
23 | ]
24 | }
25 | ],
26 | "source": [
27 | "import numpy as np\n",
28 | "\n",
29 | "from qiskit import Aer, IBMQ\n",
30 | "from qiskit.aqua import aqua_globals, QuantumInstance\n",
31 | "from qiskit.aqua.algorithms import QAOA\n",
32 | "from qiskit.aqua.components.optimizers import *\n",
33 | "from qiskit.quantum_info import Pauli\n",
34 | "from qiskit.aqua.operators import WeightedPauliOperator\n",
35 | "from qiskit.providers.aer.noise import NoiseModel\n",
36 | "\n",
37 | "provider = IBMQ.load_account()"
38 | ]
39 | },
40 | {
41 | "cell_type": "markdown",
42 | "metadata": {},
43 | "source": [
44 | "First, we define a function that from the coefficients of an Ising model creates the Hamiltonian for which we are going to find the ground state."
45 | ]
46 | },
47 | {
48 | "cell_type": "code",
49 | "execution_count": 2,
50 | "metadata": {},
51 | "outputs": [],
52 | "source": [
53 | "def get_operator(J,h,n): \n",
54 | " pauli_list = []\n",
55 | "\n",
56 | " for (i,j) in J: # For each coefficient in J (couplings) we add a term J[i,j]Z_iZj\n",
57 | " x_p = np.zeros(n, dtype=np.bool)\n",
58 | " z_p = np.zeros(n, dtype=np.bool)\n",
59 | " z_p[n-1-i] = True \n",
60 | " z_p[n-1-j] = True\n",
61 | " pauli_list.append([J[(i,j)],Pauli(z_p, x_p)])\n",
62 | " \n",
63 | " for i in h: # For each coefficient in h we add a term h[i]Z_i\n",
64 | " x_p = np.zeros(n, dtype=np.bool)\n",
65 | " z_p = np.zeros(n, dtype=np.bool)\n",
66 | " z_p[n-1-i] = True\n",
67 | " pauli_list.append([h[i],Pauli(z_p, x_p)])\n",
68 | " \n",
69 | " return WeightedPauliOperator(paulis=pauli_list)"
70 | ]
71 | },
72 | {
73 | "cell_type": "markdown",
74 | "metadata": {},
75 | "source": [
76 | "Now, we define the edges of the graph and obtain the Hamiltonian. For this graph, which is a cycle of length 5, the optimal solution gives a cost of -3"
77 | ]
78 | },
79 | {
80 | "cell_type": "code",
81 | "execution_count": 3,
82 | "metadata": {},
83 | "outputs": [
84 | {
85 | "name": "stdout",
86 | "output_type": "stream",
87 | "text": [
88 | "Representation: paulis, qubits: 5, size: 5\n"
89 | ]
90 | },
91 | {
92 | "data": {
93 | "text/plain": [
94 | "'ZZIII\\t(1+0j)\\nIZZII\\t(1+0j)\\nIIZZI\\t(1+0j)\\nIIIZZ\\t(1+0j)\\nZIIIZ\\t(1+0j)\\n'"
95 | ]
96 | },
97 | "execution_count": 3,
98 | "metadata": {},
99 | "output_type": "execute_result"
100 | }
101 | ],
102 | "source": [
103 | "# Edges of the graph\n",
104 | "\n",
105 | "J1 = {(0,1):1, (1,2):1, (2,3):1, (3,4):1, (4,0):1}\n",
106 | "h1 = {}\n",
107 | "n = 5\n",
108 | "\n",
109 | "# Hamiltonian\n",
110 | "\n",
111 | "q_op =get_operator(J1,h1,n) \n",
112 | "print(q_op)\n",
113 | "q_op.print_details()"
114 | ]
115 | },
116 | {
117 | "cell_type": "markdown",
118 | "metadata": {},
119 | "source": [
120 | "We are going to run 10 repetitions on the statevector simulator"
121 | ]
122 | },
123 | {
124 | "cell_type": "code",
125 | "execution_count": 4,
126 | "metadata": {},
127 | "outputs": [],
128 | "source": [
129 | "rep = 10\n",
130 | "backend = Aer.get_backend('statevector_simulator')\n",
131 | "quantum_instance = QuantumInstance(backend)"
132 | ]
133 | },
134 | {
135 | "cell_type": "markdown",
136 | "metadata": {},
137 | "source": [
138 | "We run QAOA with COBYLA as the classical optimizer and with optimization level $p = 1$"
139 | ]
140 | },
141 | {
142 | "cell_type": "code",
143 | "execution_count": 5,
144 | "metadata": {},
145 | "outputs": [
146 | {
147 | "name": "stdout",
148 | "output_type": "stream",
149 | "text": [
150 | "----- ITERATION 0 ------\n",
151 | "Optimal value -2.499999944131867\n",
152 | "----- ITERATION 1 ------\n",
153 | "Optimal value -2.499999944131867\n",
154 | "----- ITERATION 2 ------\n",
155 | "Optimal value -2.499999944131867\n",
156 | "----- ITERATION 3 ------\n",
157 | "Optimal value -2.499999944131867\n",
158 | "----- ITERATION 4 ------\n",
159 | "Optimal value -2.499999944131867\n",
160 | "----- ITERATION 5 ------\n",
161 | "Optimal value -2.499999944131867\n",
162 | "----- ITERATION 6 ------\n",
163 | "Optimal value -2.499999944131867\n",
164 | "----- ITERATION 7 ------\n",
165 | "Optimal value -2.499999944131867\n",
166 | "----- ITERATION 8 ------\n",
167 | "Optimal value -2.499999944131867\n",
168 | "----- ITERATION 9 ------\n",
169 | "Optimal value -2.499999944131867\n",
170 | "----- AVERAGE -----\n",
171 | "Average value -2.4999999441318677\n"
172 | ]
173 | }
174 | ],
175 | "source": [
176 | "p = 1\n",
177 | "val = 0\n",
178 | "for i in range(rep):\n",
179 | " print(\"----- ITERATION \",i, \" ------\")\n",
180 | " optimizer = COBYLA()\n",
181 | " qaoa = QAOA(q_op, optimizer, p=p)\n",
182 | " result = qaoa.run(quantum_instance)\n",
183 | " print(\"Optimal value\", result['optimal_value'])\n",
184 | " val+=result['optimal_value']\n",
185 | "print(\"----- AVERAGE -----\")\n",
186 | "print(\"Average value\",val/rep)"
187 | ]
188 | },
189 | {
190 | "cell_type": "markdown",
191 | "metadata": {},
192 | "source": [
193 | "Now, we increase $p$ to $2$"
194 | ]
195 | },
196 | {
197 | "cell_type": "code",
198 | "execution_count": 6,
199 | "metadata": {},
200 | "outputs": [
201 | {
202 | "name": "stdout",
203 | "output_type": "stream",
204 | "text": [
205 | "----- ITERATION 0 ------\n",
206 | "Optimal value -2.9999850752772828\n",
207 | "----- ITERATION 1 ------\n",
208 | "Optimal value -2.9999850752772828\n",
209 | "----- ITERATION 2 ------\n",
210 | "Optimal value -2.9999850752772828\n",
211 | "----- ITERATION 3 ------\n",
212 | "Optimal value -2.9999850752772828\n",
213 | "----- ITERATION 4 ------\n",
214 | "Optimal value -2.9999850752772828\n",
215 | "----- ITERATION 5 ------\n",
216 | "Optimal value -2.9999850752772828\n",
217 | "----- ITERATION 6 ------\n",
218 | "Optimal value -2.9999850752772828\n",
219 | "----- ITERATION 7 ------\n",
220 | "Optimal value -2.9999850752772828\n",
221 | "----- ITERATION 8 ------\n",
222 | "Optimal value -2.9999850752772828\n",
223 | "----- ITERATION 9 ------\n",
224 | "Optimal value -2.9999850752772828\n",
225 | "----- AVERAGE -----\n",
226 | "Average value -2.999985075277283\n"
227 | ]
228 | }
229 | ],
230 | "source": [
231 | "p = 2\n",
232 | "val = 0\n",
233 | "for i in range(rep):\n",
234 | " print(\"----- ITERATION \",i, \" ------\")\n",
235 | " optimizer = COBYLA()\n",
236 | " qaoa = QAOA(q_op, optimizer, p=p)\n",
237 | " result = qaoa.run(quantum_instance)\n",
238 | " print(\"Optimal value\", result['optimal_value'])\n",
239 | " val+=result['optimal_value']\n",
240 | "print(\"----- AVERAGE -----\")\n",
241 | "print(\"Average value\",val/rep)"
242 | ]
243 | },
244 | {
245 | "cell_type": "markdown",
246 | "metadata": {},
247 | "source": [
248 | "We are going to run the algorithm with a backend which includes a noise model"
249 | ]
250 | },
251 | {
252 | "cell_type": "code",
253 | "execution_count": 7,
254 | "metadata": {},
255 | "outputs": [],
256 | "source": [
257 | "rep = 10\n",
258 | "backendIBM = provider.get_backend('ibmq_ourense')\n",
259 | "noise_model = NoiseModel.from_backend(backendIBM)\n",
260 | "coupling_map = backendIBM.configuration().coupling_map\n",
261 | "basis_gates = noise_model.basis_gates\n",
262 | "backend = Aer.get_backend(\"qasm_simulator\")\n",
263 | "\n",
264 | "\n",
265 | "shots = 8192\n",
266 | "optimization_level = 3\n",
267 | "p = 1\n",
268 | "quantum_instance = QuantumInstance(backend, shots = shots, \n",
269 | " optimization_level = optimization_level,\n",
270 | " noise_model = noise_model,\n",
271 | " basis_gates = basis_gates,\n",
272 | " coupling_map = coupling_map)"
273 | ]
274 | },
275 | {
276 | "cell_type": "code",
277 | "execution_count": 8,
278 | "metadata": {},
279 | "outputs": [
280 | {
281 | "name": "stdout",
282 | "output_type": "stream",
283 | "text": [
284 | "----- ITERATION 0 ------\n",
285 | "Optimal value -1.96728515625\n",
286 | "----- ITERATION 1 ------\n",
287 | "Optimal value -1.95068359375\n",
288 | "----- ITERATION 2 ------\n",
289 | "Optimal value -1.91943359375\n",
290 | "----- ITERATION 3 ------\n",
291 | "Optimal value -1.90234375\n",
292 | "----- ITERATION 4 ------\n",
293 | "Optimal value -1.93115234375\n",
294 | "----- ITERATION 5 ------\n",
295 | "Optimal value -1.94384765625\n",
296 | "----- ITERATION 6 ------\n",
297 | "Optimal value -1.95068359375\n",
298 | "----- ITERATION 7 ------\n",
299 | "Optimal value -1.90283203125\n",
300 | "----- ITERATION 8 ------\n",
301 | "Optimal value -1.9091796875\n",
302 | "----- ITERATION 9 ------\n",
303 | "Optimal value -1.92138671875\n",
304 | "----- AVERAGE -----\n",
305 | "Average value -1.9298828125\n"
306 | ]
307 | }
308 | ],
309 | "source": [
310 | "p = 1\n",
311 | "val = 0\n",
312 | "for i in range(rep):\n",
313 | " print(\"----- ITERATION \",i, \" ------\")\n",
314 | " optimizer = COBYLA()\n",
315 | " qaoa = QAOA(q_op, optimizer, p=p)\n",
316 | " result = qaoa.run(quantum_instance)\n",
317 | " print(\"Optimal value\", result['optimal_value'])\n",
318 | " val+=result['optimal_value']\n",
319 | "print(\"----- AVERAGE -----\")\n",
320 | "print(\"Average value\",val/rep)"
321 | ]
322 | }
323 | ],
324 | "metadata": {
325 | "kernelspec": {
326 | "display_name": "Python 3",
327 | "language": "python",
328 | "name": "python3"
329 | },
330 | "language_info": {
331 | "codemirror_mode": {
332 | "name": "ipython",
333 | "version": 3
334 | },
335 | "file_extension": ".py",
336 | "mimetype": "text/x-python",
337 | "name": "python",
338 | "nbconvert_exporter": "python",
339 | "pygments_lexer": "ipython3",
340 | "version": "3.7.8"
341 | }
342 | },
343 | "nbformat": 4,
344 | "nbformat_minor": 4
345 | }
346 |
--------------------------------------------------------------------------------
/Qiskit/QAOA(Quantum Approximate Optimization Algorithm)/README.md:
--------------------------------------------------------------------------------
1 | # QAOA - Quantum Approximate Optimization Algorithm
2 |
3 | Note: The Notebook has been run on IBM Quantum Experience Integrated Jupyter Notebook. This was done so as to simulate the algorithm using a real Quantum Computer.
4 |
5 | The Notebook can be used on a local environment as well!
6 |
7 | ## Documentation
8 |
9 | (To Be Added Here)
--------------------------------------------------------------------------------
/Qiskit/QGANs(Quantum Generative Adversarial Networks)/README.md:
--------------------------------------------------------------------------------
1 | Quantum machine learning is expected to be one of the first potential general-purpose applications of near-term quantum devices. A major recent breakthrough in classical machine learning is the notion of generative adversarial training, where the gradients of a discriminator model are used to train a separate generative model. In this work and a companion paper, we extend adversarial training to the quantum domain and show how to construct generative adversarial networks using quantum circuits. Furthermore, we also show how to compute gradients -- a key element in generative adversarial network training -- using another quantum circuit. We give an example of a simple practical to parametrize quantum machine learning models and perform a simple numerical experiment to demonstrate that quantum generative adversarial networks can be trained successfully.
--------------------------------------------------------------------------------
/Qiskit/QSVM(Quantum Support Vector Machines)/README.md:
--------------------------------------------------------------------------------
1 | What is a Support Vector Machine?
2 |
3 | A support vector machine is a supervised machine learning method that is trained using a dataset and will predict if a particular observation is in a certain class based upon what it has been trained on. It is similar to a linear classifier in that it uses a hyperplane to separate classes.
4 |
5 | However along with the hyperplane support vectors are used. These are essentially data points that are used to maximise the margin and thus the distance between the classes.
6 |
7 | However the Quantum Support Vector Machine is different in that it uses a feature map to map data points to a quantum circuit.
--------------------------------------------------------------------------------
/Qiskit/Quantum Random Walks/ContinuousTimeQuantumWalks.ipynb:
--------------------------------------------------------------------------------
1 | {
2 | "cells": [
3 | {
4 | "cell_type": "code",
5 | "source": [
6 | "import numpy as np\n",
7 | "from numpy import linalg as LA\n",
8 | "from scipy.linalg import expm, sinm, cosm\n",
9 | "import matplotlib.pyplot as plt\n",
10 | "import pandas as pd\n",
11 | "import seaborn as sns\n",
12 | "import math\n",
13 | "from scipy import stats\n",
14 | "%matplotlib inline\n",
15 | "\n",
16 | "from IPython.display import Image, display, Math, Latex\n",
17 | "sns.set(color_codes=True)"
18 | ],
19 | "outputs": [],
20 | "execution_count": 1,
21 | "metadata": {}
22 | },
23 | {
24 | "cell_type": "markdown",
25 | "source": [
26 | "# Continuous Time Quantum Walks"
27 | ],
28 | "metadata": {}
29 | },
30 | {
31 | "cell_type": "markdown",
32 | "source": [
33 | "## Continuous-Time Quantum Walks"
34 | ],
35 | "metadata": {}
36 | },
37 | {
38 | "cell_type": "markdown",
39 | "source": [
40 | "Now let's see an example of how it work on cycle graph $C_n$ for some numbers of vertices."
41 | ],
42 | "metadata": {}
43 | },
44 | {
45 | "cell_type": "code",
46 | "source": [
47 | "#number of vertices\n",
48 | "n = 4\n",
49 | "\n",
50 | "#Define adjacency matrix A_Cn\n",
51 | "A = np.zeros((n, n))\n",
52 | "for i in range(n):\n",
53 | " j1 = (i - 1)%n\n",
54 | " j2 = (i + 1)%n\n",
55 | " A[i][j1] = 1\n",
56 | " A[i][j2] = 1\n",
57 | "\n",
58 | "#Define our initial state Psi_a\n",
59 | "psi_a = np.zeros(n)\n",
60 | "psi_a[3] = 1\n",
61 | "\n",
62 | "#Define the time t >= 0\n",
63 | "t = math.pi/2\n",
64 | "\n",
65 | "#Exponentiate or hamiltonian\n",
66 | "U_t = expm(1j*t*A)\n",
67 | "U_mt = expm(1j*(-t)*A)\n",
68 | "\n",
69 | "#Compute Psi_t\n",
70 | "psi_t = U_t @ psi_a\n",
71 | "\n",
72 | "#Compute the probabilities\n",
73 | "prob_t = abs(psi_t)**2"
74 | ],
75 | "outputs": [],
76 | "execution_count": 2,
77 | "metadata": {}
78 | },
79 | {
80 | "cell_type": "code",
81 | "source": [
82 | "M_t = U_t*U_mt \n",
83 | "M_t = np.around(M_t, decimals = 3)\n",
84 | "M_t"
85 | ],
86 | "outputs": [
87 | {
88 | "output_type": "execute_result",
89 | "execution_count": 3,
90 | "data": {
91 | "text/plain": "array([[0.+0.j, 0.-0.j, 1.+0.j, 0.+0.j],\n [0.+0.j, 0.+0.j, 0.+0.j, 1.+0.j],\n [1.-0.j, 0.+0.j, 0.+0.j, 0.+0.j],\n [0.+0.j, 1.-0.j, 0.+0.j, 0.+0.j]])"
92 | },
93 | "metadata": {}
94 | }
95 | ],
96 | "execution_count": 3,
97 | "metadata": {}
98 | },
99 | {
100 | "cell_type": "code",
101 | "source": [
102 | "x = M_t[:, 0].real\n",
103 | "plt.bar(range(len(x)), x, tick_label=[0, 1, 2, 3])\n",
104 | "plt.xlabel('Vertices')\n",
105 | "plt.ylabel('Probability')"
106 | ],
107 | "outputs": [
108 | {
109 | "output_type": "execute_result",
110 | "execution_count": 7,
111 | "data": {
112 | "text/plain": "Text(0, 0.5, 'Probability')"
113 | },
114 | "metadata": {}
115 | },
116 | {
117 | "output_type": "display_data",
118 | "data": {
119 | "image/png": "iVBORw0KGgoAAAANSUhEUgAAAYkAAAEMCAYAAAAxoErWAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjMuMCwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy86wFpkAAAACXBIWXMAAAsTAAALEwEAmpwYAAAZoUlEQVR4nO3de3BU9eH+8Se7EG4JhCy5LESaQluMFqljlKGFFiEYhOiGEWSICEIJCKIWvy1SFZIA4oSOF8q1UEBpnGpT5RYj0HBpleHq2IJNoYxGEVgSyEUIWiKb/f1Bm58h+SSbkN3NwfdrhpnsySf7efYskyfnnD3nhHi9Xq8AAKiHLdgBAACtFyUBADCiJAAARpQEAMCIkgAAGFESAAAjSgIAYNQm2AFaWnn5JVVXW+/UD4cjTKWllcGOYVmsv+vHOrw+Vl1/NluIunbtZPz+DVcS1dVeS5aEJMvmbi1Yf9ePdXh9bsT1x+4mAIARJQEAMKIkAABGlAQAwCggJZGdna0hQ4aoT58++ve//13vGI/Ho6ysLCUlJWnYsGHKzc0NRDQAQAMCUhJDhw7V66+/rh49ehjHbN26VSdPntSOHTv05ptvaunSpTp16lQg4gEADAJSEomJiXI6nQ2Oyc/P15gxY2Sz2RQZGamkpCRt27YtEPEAAAat5jwJt9ut7t271zx2Op06e/Zsk5/H4QhryVgBFRUVHuwIlmbl9Vf1tUehbe3BjhHUddha1sH1sPL/QZNWUxItpbS00pIntERFhevcuYvBjmFZVl9/UVHhuu//Ngc7RlBtfdFl+ffQivlttpAG/7huNZ9ucjqdOnPmTM1jt9ut2NjYICYCALSakhg+fLhyc3NVXV2tsrIyFRQUKDk5OdixAOBbLSAlsXDhQv30pz/V2bNnNWnSJI0cOVKSlJ6erqNHj0qSXC6X4uLidM899+jBBx/UY489pptuuikQ8QAABiFer9d6O/AbwDGJbyerrz+OSXBMIlgsc0wCAND6UBIAACNKAgBgREkAAIwoCQCAESUBADCiJAAARpQEAMCIkgAAGFESAAAjSgIAYERJAACMKAkAgBElAQAwoiQAAEaUBADAiJIAABhREgAAI0oCAGBESQAAjCgJAIARJQEAMKIkAABGlAQAwIiSAAAYURIAACNKAgBgREkAAIwoCQCAESUBADCiJAAARpQEAMCoTaAmKioq0pw5c1RRUaGIiAhlZ2crPj6+1pjS0lL9+te/ltvt1pUrV9S/f38999xzatMmYDEBAN8QsC2JjIwMpaWlafv27UpLS9O8efPqjFm1apV69+6trVu3asuWLfrnP/+pHTt2BCoiAOAaASmJ0tJSFRYWKiUlRZKUkpKiwsJClZWV1RoXEhKiS5cuqbq6WlVVVfr6668VExMTiIgAgHoEpCTcbrdiYmJkt9slSXa7XdHR0XK73bXGzZgxQ0VFRRo4cGDNvzvuuCMQEQEA9WhVO/u3bdumPn366LXXXtOlS5eUnp6ubdu2afjw4T4/h8MR5seE/hUVFR7sCJbG+rM+q7+HVs9fn4CUhNPpVHFxsTwej+x2uzwej0pKSuR0OmuNy8nJ0aJFi2Sz2RQeHq4hQ4bowIEDTSqJ0tJKVVd7W/ol+F1UVLjOnbsY7BiWZfX1dyP+cmkOq7+HVsxvs4U0+Md1QHY3ORwOJSQkKC8vT5KUl5enhIQERUZG1hoXFxenv/3tb5Kkqqoq7du3T9///vcDEREAUI+AfbopMzNTOTk5Sk5OVk5OjrKysiRJ6enpOnr0qCTpmWee0QcffKD77rtPqampio+P14MPPhioiACAawTsmETv3r2Vm5tbZ/maNWtqvu7Zs6fWr18fqEgAgEZwxjUAwIiSAAAYURIAACNKAgBgREkAAIwoCQCAESUBADCiJAAARpQEAMCIkgAAGFESAAAjSgIAYERJAACMKAkAgBElAQAwoiQAAEaUBADAiJIAABhREgAAI0oCAGBESQAAjCgJAIARJQEAMPK5JMrLy/2ZAwDQCvlcEnfffbemT5+ubdu2qaqqyp+ZAACthM8lsWvXLg0YMEBr1qzRwIEDNXfuXB0+fNif2QAAQeZzSURGRmrChAl666239MYbbygyMlKzZ8/W0KFDtWTJEp0+fdqfOQEAQdCsA9fnz5/X+fPndenSJfXs2VPFxcUaNWqUVq9e3dL5AABB1MbXgSdOnNCWLVuUl5enDh06KDU1VZs3b1ZsbKwkacaMGbr//vs1depUv4UFAASWzyUxfvx4jRw5UkuWLNFtt91W5/txcXGaOHFii4YDAASXzyWxbNky3XnnnXWWHzlypKY0nnzyyZZLBgAIOp+PSUybNq3e5VOmTGmxMACA1qXRLYnq6mp5vd5a//7n5MmTstvtPk1UVFSkOXPmqKKiQhEREcrOzlZ8fHydcfn5+Vq5cqW8Xq9CQkK0fv16devWzfdXBABoMY2WxC233KKQkJCar7/JZrPp0Ucf9WmijIwMpaWlyeVyafPmzZo3b542bNhQa8zRo0e1bNkyvfbaa4qKitLFixcVGhrq62sBALSwRkti586d8nq9evjhh5WTk1OzPCQkRJGRkWrfvn2jk5SWlqqwsFDr16+XJKWkpGjBggUqKytTZGRkzbhXX31VkydPVlRUlCQpPDy8yS8IANByGi2JHj16SJJ2797d7EncbrdiYmJqdk3Z7XZFR0fL7XbXKomPP/5YcXFxeuihh/Tll19q2LBhmj59es2WDAAgsBosiblz52rBggWSpNmzZxvHLV68uEXCeDweHT9+XOvXr1dVVZWmTJmi7t27KzU11efncDjCWiRLMERFseV0PVh/1mf199Dq+evTYEnExcXVfN2zZ89mT+J0OlVcXCyPxyO73S6Px6OSkhI5nc5a47p3767hw4crNDRUoaGhGjp0qI4cOdKkkigtrVR1tbfxga1MVFS4zp27GOwYlmX19Xcj/nJpDqu/h1bMb7OFNPjHdYMl8c2Pvc6cObPZIRwOhxISEpSXlyeXy6W8vDwlJCTU2tUkXT1W8de//lUul0tXrlzR/v37lZyc3Ox5AQDXp8GS2Ldvn09PMmDAgEbHZGZmas6cOVqxYoU6d+6s7OxsSVJ6erqeeOIJ9e3bVyNHjtRHH32kESNGyGazaeDAgRo9erRPGQAALS/E+80TH64xZMiQxp8gJEQ7d+5s0VDXg91N305WX39RUeG67/82BztGUG190WX599CK+a9rd9OuXbtaPBAAwDq4xzUAwKjBLYl7771X7777riTpZz/7mfF8hT179rR4MABA8DVYEv87R0KSfvOb3/g9DACgdWmwJBITE2u+vuuuu/weBgDQuvh8P4mqqiqtXLlS77zzjkpKShQdHa0RI0Zo+vTpateunT8zAgCCxOeSyMzMVFFRkZ599ln16NFDp0+f1u9+9zsVFxfrhRde8GdGAECQ+FwSO3fu1F/+8hd17txZkvS9731P/fr10z333OO3cACA4PL5I7DdunXTV199VWvZ5cuXay7rDQC48fh8WQ6Xy6UpU6bo4YcfVkxMjM6ePavXX39dLpfL7yEBAMHRYEk8++yzdZatWrWq1uM333xTU6dObdlUAIBWgctyAACMuCwHAMDI5083VVZWaunSpTp06JDKy8v1zYvHclkOALgx+bwlkZmZqcLCQs2YMUMVFRV67rnn5HQ69cgjj/gxHgAgmHzekti7d6/y8/PVtWtX2e12JSUlqW/fvnr00UcpCgC4Qfm8JVFdXa3w8Kv34e3YsaMuXryoqKgoffbZZ34LBwAILp+3JG6++WYdOnRIAwYMUGJiojIzM9WpUyfFx8f7MR4AIJh83pJYuHChevToIenq+RPt2rXThQsXtHjxYr+FAwAEl89bEjfddFPN1w6HQ4sWLfJLIABA6+FzSUjSn//85zqXCh89erTxjnUAAGvzuSQWL16snTt3auLEiTWXCl+3bp2Kioo0e/Zsf2YEAASJzyWxceNGbdy4UbGxsTXL7r77bo0aNYqSAIAblM8Hrjt16qROnTrVWRYWFtbioQAArUODWxKff/55zdcTJ07UzJkzNXXqVMXGxsrtdmvt2rWcSAcAN7AGS2LYsGEKCQmpdZ2mAwcO1Bqzf/9+jR8/3j/pAABB1WBJHDt2LFA5AACtUJM+AitJZ86cUXFxsWJjY+V0Ov2RCQDQSvhcEiUlJXrqqaf097//XREREaqoqFC/fv300ksvKSYmxp8ZAQBB0qRLhd988806ePCg3n//fR08eFAJCQnKyMjwZz4AQBD5vCXxwQcfaMmSJWrbtq2kq1eCnT17tgYNGuS3cACA4PJ5S6JLly76+OOPay375JNP1Llz5xYPBQBoHXzekpgyZYoeeeQRjR49Wt27d9eZM2f09ttv68knn/RnPgBAEPm8JfHggw/q5ZdfVnl5uXbv3q3y8nK9+OKLGjt2rE8/X1RUpLFjxyo5OVljx47Vp59+ahz7ySefqF+/fsrOzvY1HgDAD3zakvB4PEpOTlZ+fr4GDBjQrIkyMjKUlpYml8ulzZs3a968edqwYUO9c2VkZCgpKalZ8wAAWo5PWxJ2u112u12XL19u1iSlpaUqLCxUSkqKJCklJUWFhYUqKyurM3b16tUaPHgwd7wDgFbA52MSEyZM0C9+8QtNmzZNsbGxte4h8c0bEtXH7XYrJiZGdrtd0tXSiY6OltvtVmRkZM24Y8eO6f3339eGDRu0YsWKpr4WSZLDYd0LDkZFhQc7gqWx/qzP6u+h1fPXx+eSWLBggSRp7969tZaHhIToX//613UH+frrrzV37ly98MILNWXSHKWllaqu9jY+sJWJigrXuXMXgx3Dsqy+/m7EXy7NYfX30Ir5bbaQBv+4brQkvvrqK61cuVKDBw/WLbfcomnTpqldu3ZNCuF0OlVcXCyPxyO73S6Px6OSkpJal/U4d+6cTp48qalTp0qSLly4IK/Xq8rKypqCAgAEVqMlMX/+fH300UcaNGiQduzYoS+++EJz585t0iQOh0MJCQnKy8uTy+VSXl6eEhISau1q6t69e60rzC5dulRffvmlnn766SbNBQBoOY0euH7vvfe0du1azZ49W2vWrNHu3bubNVFmZqZycnKUnJysnJwcZWVlSZLS09N19OjRZj0nAMC/Gt2S+PLLLxUdHS3p6m6jysrKZk3Uu3dv5ebm1lm+Zs2aesc//vjjzZoHANByGi0Jj8ej/fv319x46MqVK7UeS2r2uRMAgNat0ZJwOBx65plnah5HRETUehwSEqKdO3f6Jx0AIKgaLYldu3YFIgcAoBXy+dpNAIBvH0oCAGBESQAAjCgJAIARJQEAMKIkAABGlAQAwIiSAAAYURIAACNKAgBgREkAAIwoCQCAESUBADCiJAAARpQEAMCIkgAAGFESAAAjSgIAYERJAACMKAkAgBElAQAwoiQAAEaUBADAiJIAABhREgAAI0oCAGBESQAAjCgJAIARJQEAMGoTqImKioo0Z84cVVRUKCIiQtnZ2YqPj681Zvny5crPz5fNZlPbtm01a9YsDRo0KFARAQDXCFhJZGRkKC0tTS6XS5s3b9a8efO0YcOGWmNuu+02TZ48WR06dNCxY8c0fvx4vf/++2rfvn2gYgIAviEgu5tKS0tVWFiolJQUSVJKSooKCwtVVlZWa9ygQYPUoUMHSVKfPn3k9XpVUVERiIgAgHoEpCTcbrdiYmJkt9slSXa7XdHR0XK73caf2bRpk3r27KnY2NhARAQA1CNgu5ua4uDBg1qyZInWrVvX5J91OML8kCgwoqLCgx3B0lh/1mf199Dq+esTkJJwOp0qLi6Wx+OR3W6Xx+NRSUmJnE5nnbEffvihfvWrX2nFihXq1atXk+cqLa1UdbW3JWIHVFRUuM6duxjsGJZl9fV3I/5yaQ6rv4dWzG+zhTT4x3VAdjc5HA4lJCQoLy9PkpSXl6eEhARFRkbWGnfkyBHNmjVLv/3tb3XrrbcGIhoAoAEBO08iMzNTOTk5Sk5OVk5OjrKysiRJ6enpOnr0qCQpKytL//nPfzRv3jy5XC65XC4dP348UBEBANcI2DGJ3r17Kzc3t87yNWvW1Hz91ltvBSoOAMAHnHENADCiJAAARpQEAMCIkgAAGFESAAAjSgIAYERJAACMKAkAgBElAQAwoiQAAEaUBADAiJIAABhREgAAI0oCAGBESQAAjCgJAIARJQEAMKIkAABGlAQAwIiSAAAYURIAACNKAgBgREkAAIwoCQCAESUBADCiJAAARpQEAMCIkgAAGFESAAAjSgIAYERJAACMKAkAgBElAQAwClhJFBUVaezYsUpOTtbYsWP16aef1hnj8XiUlZWlpKQkDRs2TLm5uYGKBwCoR8BKIiMjQ2lpadq+fbvS0tI0b968OmO2bt2qkydPaseOHXrzzTe1dOlSnTp1KlARAQDXaBOISUpLS1VYWKj169dLklJSUrRgwQKVlZUpMjKyZlx+fr7GjBkjm82myMhIJSUladu2bZoyZYrPc9lsIS2eP1CsnL01sPr6i+7aIdgRgs7q76EV8zeWOSAl4Xa7FRMTI7vdLkmy2+2Kjo6W2+2uVRJut1vdu3eveex0OnX27NkmzdW1a6eWCR0EDkdYsCNYmtXX39rn7gl2hKCz+nto9fz14cA1AMAoICXhdDpVXFwsj8cj6eoB6pKSEjmdzjrjzpw5U/PY7XYrNjY2EBEBAPUISEk4HA4lJCQoLy9PkpSXl6eEhIRau5okafjw4crNzVV1dbXKyspUUFCg5OTkQEQEANQjxOv1egMx0ccff6w5c+bowoUL6ty5s7Kzs9WrVy+lp6friSeeUN++feXxeDR//nzt3btXkpSenq6xY8cGIh4AoB4BKwkAgPVw4BoAYERJAACMKAkAgBElAQAwCsgZ12hYUVGR5syZo4qKCkVERCg7O1vx8fHBjmUJ2dnZ2r59u06fPq2tW7fqBz/4QbAjWUp5eblmz56tkydPKjQ0VN/5znc0f/78Oh9Ph9mMGTN06tQp2Ww2dezYUXPnzlVCQkKwY7UYPt3UCkyYMEEPPPCAXC6XNm/erLfeeksbNmwIdixLOHz4sHr06KGHHnpIq1atoiSaqKKiQsePH1f//v0lXS3dL774QosWLQpyMuu4ePGiwsPDJUkFBQVavny5Nm7cGORULYfdTUH2v4sfpqSkSLp68cPCwkKVlZUFOZk1JCYm1jlzH76LiIioKQhJ+tGPflTrqgdo3P8KQpIqKysVEmK9i/w1hN1NQebrxQ8Bf6uurtYf//hHDRkyJNhRLOfZZ5/V3r175fV69fvf/z7YcVoUWxIAJEkLFixQx44dNX78+GBHsZznn39ee/bs0axZs7R48eJgx2lRlESQ+XrxQ8CfsrOz9dlnn+mVV16RzcavheZKTU3VgQMHVF5eHuwoLYb/DUHm68UPAX956aWX9NFHH2n58uUKDQ0NdhxLuXTpktxud83jXbt2qUuXLoqIiAheqBbGp5taAdPFD9G4hQsXaseOHTp//ry6du2qiIgIvfPOO8GOZRknTpxQSkqK4uPj1b59e0lSXFycli9fHuRk1nD+/HnNmDFDX331lWw2m7p06aKnn35at956a7CjtRhKAgBgxO4mAIARJQEAMKIkAABGlAQAwIiSAAAYURJAgGzZskWTJ08OdgygSSgJ4L9+/vOfa8mSJXWWFxQU6Cc/+YmuXLni83OdOnVKffr0qfUz999/v9atW9ciWYFAoSSA/xo1apS2bNmia08d2rJli+677z61aePb9TCbUiZAa0dJAP+VlJSkiooKHT58uGbZF198od27dys1NVWrV69WUlKS+vfvryeffFIVFRWS/v9WQ25urgYPHqyJEyfWXCTvzjvv1O23364PP/xQb7/9tsaNG1fz3CdOnNCkSZN011136cc//rFWrVol6erVWE1zXb58Wb/85S/Vv39/JSYm6oEHHtD58+cDs4LwrURJAP/Vvn173Xvvvdq0aVPNsnfffVe9evXSgQMHVFBQoJycHL333nvq0qWL5s+fX+vnDx06pPz8fK1du1Y5OTk1yz788EPdfvvttcZWVlZq0qRJGjRokN577z3t2LFDAwYMkCT94Q9/MM61ceNGVVZWas+ePTpw4ICysrJqLqcB+AMlAXxDamqqtm/frsuXL0uSNm3apFGjRumNN97QrFmzFBsbq9DQUM2cOVPbt2+vtWvp8ccfV8eOHX36pb1nzx5169ZNkydPVrt27RQWFqZ+/fpJUoNztWnTRhUVFfrss89kt9v1wx/+UGFhYf5ZGYC46RBQS2Jiorp27aqCggL17dtXR48e1bJly/Tyyy/rscceq3UZbZvNptLS0prHsbGxPs/jdrvVs2fPer935swZ41wul0tnz57VU089pQsXLuj+++/XrFmz1LZt22a8WqBxlARwDZfLpU2bNqmoqEgDBw5Ut27dFBsbq0WLFumOO+6oM/7UqVOSVOu2lY3dwtLpdCo/P7/e7zU0lyTNnDlTM2fO1KlTpzR16lR997vf1ZgxY3x9eUCTsLsJuEZqaqr27dunP/3pT0pNTZUkjRs3Tq+88opOnz4tSSorK1NBQYHxOSIjI2Wz2fT555/X+/3Bgwfr3LlzevXVV1VVVaXKykr94x//aHSu/fv36/jx4/J4PAoLC1ObNm24SRD8ii0J4BpxcXG6/fbbdezYMQ0dOlSSNGHCBHm9Xk2ePFklJSVyOBwaMWKEkpKS6n2ODh066NFHH9W4ceN05cqVOvc9DgsL07p16/T888/X3Oxn4sSJ6tevX4NznT9/XhkZGSouLlbHjh01YsQIuVwuv68TfHtxPwkAgBHbqQAAI0oCAGBESQAAjCgJAIARJQEAMKIkAABGlAQAwIiSAAAYURIAAKP/BwlHmTZmbVAyAAAAAElFTkSuQmCC\n",
120 | "text/plain": ""
121 | },
122 | "metadata": {}
123 | }
124 | ],
125 | "execution_count": 7,
126 | "metadata": {}
127 | },
128 | {
129 | "cell_type": "markdown",
130 | "source": [
131 | "Then we can easily visualize how our quantum-walker behaves in graph $C_n$ given an initial state and a time $t = \\pi/2$, and we can see the Perfect State Transfer phenomena from vertice 0 to 2, that will be explained in the detail [here](https://github.com/matheusmtta/Quantum-Computing/blob/master/Quantum%20Information%20Theory/State_Transfer.ipynb)."
132 | ],
133 | "metadata": {}
134 | }
135 | ],
136 | "metadata": {
137 | "kernelspec": {
138 | "display_name": "Python 3",
139 | "language": "python",
140 | "name": "python3"
141 | },
142 | "language_info": {
143 | "codemirror_mode": {
144 | "name": "ipython",
145 | "version": 3
146 | },
147 | "file_extension": ".py",
148 | "mimetype": "text/x-python",
149 | "name": "python",
150 | "nbconvert_exporter": "python",
151 | "pygments_lexer": "ipython3",
152 | "version": "3.8.2"
153 | },
154 | "nteract": {
155 | "version": "0.28.0"
156 | }
157 | },
158 | "nbformat": 4,
159 | "nbformat_minor": 2
160 | }
--------------------------------------------------------------------------------
/Qiskit/Quantum Random Walks/DiscreteTimeQuantumWalk.ipynb:
--------------------------------------------------------------------------------
1 | {
2 | "cells": [
3 | {
4 | "cell_type": "code",
5 | "execution_count": 1,
6 | "metadata": {},
7 | "outputs": [],
8 | "source": [
9 | "import matplotlib.pyplot as plt\n",
10 | "%matplotlib inline\n",
11 | "import numpy as np\n",
12 | "\n",
13 | "from qiskit import *\n",
14 | "from qiskit.providers.ibmq import least_busy\n",
15 | "\n",
16 | "from qiskit.tools.visualization import plot_histogram\n",
17 | "from IPython.display import display, Math, Latex"
18 | ]
19 | },
20 | {
21 | "cell_type": "code",
22 | "execution_count": 2,
23 | "metadata": {},
24 | "outputs": [],
25 | "source": [
26 | "def Increment(size):\n",
27 | " U = QuantumCircuit(size)\n",
28 | " control = [x for x in range(size-1)]\n",
29 | " for k in range(size-1):\n",
30 | " U.mcx(control, control[-1]+1)\n",
31 | " control.pop()\n",
32 | " U.x(0)\n",
33 | " \n",
34 | " U = U.to_gate()\n",
35 | " U.name = '--->'\n",
36 | " ctl_U = U.control()\n",
37 | " \n",
38 | " return ctl_U"
39 | ]
40 | },
41 | {
42 | "cell_type": "code",
43 | "execution_count": 3,
44 | "metadata": {},
45 | "outputs": [],
46 | "source": [
47 | "def Decrement(size):\n",
48 | " U = QuantumCircuit(size)\n",
49 | " control = [x for x in range(size-1)]\n",
50 | " for k in range(size-1):\n",
51 | " U.x(control)\n",
52 | " U.mcx(control, control[-1]+1)\n",
53 | " U.x(control)\n",
54 | " control.pop()\n",
55 | " U.x(0)\n",
56 | " \n",
57 | " U = U.to_gate()\n",
58 | " U.name = '<---'\n",
59 | " ctl_U = U.control()\n",
60 | " \n",
61 | " return ctl_U"
62 | ]
63 | },
64 | {
65 | "cell_type": "code",
66 | "execution_count": 4,
67 | "metadata": {},
68 | "outputs": [
69 | {
70 | "data": {
71 | "image/png": "iVBORw0KGgoAAAANSUhEUgAAAr4AAADWCAYAAAA3v4FrAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjMuMCwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy86wFpkAAAACXBIWXMAAAsTAAALEwEAmpwYAAAlJUlEQVR4nO3de1xVdf7v8ffmJiDEzfCGmohoIiDexktClijOr7JTqWhaOTbibX411jk2emrqZEwpOWZ1ypn050wXTFN/+vNBKXkhHSulzEQrvBMebyigiBcu+/zBTwq5bRT22pv1ej4e+xGtvdb2sz6ur7z57u9eWKxWq1UAAABAM+didAEAAACAPRB8AQAAYAoEXwAAAJgCwRcAAACmQPAFAACAKRB8AQAAYAoEXwAAAJgCwRcAAACmQPAFAACAKRB8AQAAYAoEXwAAAJgCwRcAAACmQPAFAACAKRB8AQAAYAoEXwAAAJgCwRcAAACmQPAFAACAKRB8AQAAYAoEXwAAAJgCwRcAAACmQPAFAACAKRB8AQAAYAoEXwAAAJgCwRcAAACmQPAFAACAKRB8AQAAYApuRheA5u+nLdLFM0ZX4Rx8g6Vu99z88fTadrfaa2fE9WE7xqL9mHEswjgEXzS5i2ekglyjqzAHeo26cH3YD71uHiwWiyF/rtVqNeTPNQOWOgAAAMAUCL4AAAAwBYIvAAAATIHgCwAAAFMg+AIAAMAUCL4AAAAwBYIvAACAQdzd3Y0uwVQIvg1QWFioqVOnKjg4WN7e3ho8eLB27NhhdFkAAMBg/fv316xZs/TBBx/os88+U1pampYsWaIpU6YoNDS0xmNmzpypnTt3KiAgwM7Vmhe/wMJGVqtVo0aN0g8//KCUlBS1a9dOb775puLj47Vz507FxMQYXSIAALCziRMn6plnnlF0dHSd+3322Wd65ZVXKifMZs6cqTfffFOSFB8fr5UrVzZ5rSD42mzDhg3KyMhQWlqaRo4cKUmKjY1VRESE5s6dq7S0NIMrdD5l5WVamvacNmUu17XSK+rTdbiefmSJ/Fq2Mrq0Zodeoz5cI/ZDr5uHkJAQLVu2TPHx8ZKk06dPa+3atcrMzFRubq5cXV3VtWtXDRw4UA888IASEhKUkJCgxYsX69ixY1q4cKEkafr06YReO2Kpg6Ty8nKlpKSoa9eu8vT0VHR0tDIyMtStWzdNmTJFkrRu3ToFBQUpISGh8jgPDw8lJiYqPT1dly5dMqp8p7Vi66vauX+d3vzD10qdW/G7PV9LnWhwVc0TvUZ9uEbsh147v7CwMH355ZeKj49XXl6eJk2apI4dO2ratGlaunSpNm7cqLS0NL3xxhtKTExU+/btNW/ePJWUlOjf//3fq4Ted955x+CzMReCr6TJkyfr5ZdfVlJSkj799FONGTNG48aN05EjR9SnTx9JUlZWliIiIqr93u6ePXuqtLRUP/74oxGlO7W0r/6msUNnq21QqFp6+en3/zZfu3/6TKfzjxtdWrNDr1EfrhH7odfOLSAgQJ9//rlCQkK0fft2RUREaPny5bp27Vqtx+Tn5+v555+vDLxSRa4g9Nqf6YNvamqqli9frvXr1+vZZ5/V0KFDNXfuXA0cOFClpaXq3bu3JOn8+fM1Lj4PDAysfB62K7pcoDMFOeravk/ltnatusjb8zYd/n97Days+aHXqA/XiP3Qa+e3ePFiderUSV9//bUSEhJ05swZm46bOXOmZs+eLUkqKipSz5499fvf/74pS0UNTB98k5OTlZCQoLi4uCrbw8LC5O7urqioqAa93rFjxxQXF6fw8HBFRkZq+/btjVmuLBaL0z0yMrZVO4/iqxclSS29/Kps9/H0V/GVC43aM2eSkbGNXtvJrfbaGR81XR8S10hNmmIsSvS6Jo48Fm80ePBgTZgwQcXFxXr00UdVXFxs0zn++oNs06dP1+TJkyVJCxYskK+vb7X9jT5vZ3zYytTBNzc3V1lZWRo9enS153JychQREaEWLVpIqpjZzc/Pr7bf9Zne6zO/SUlJGjt2rLKzs7VkyRIlJibW+faHWXm3qBjoly4XVtledKVA3p63GVFSs0WvUR+uEfuh185t5syZkqSFCxfq8OHDNh/z69D7zjvvaOXKlcrIyJCfn58mTJjQZPWiOtMHX0lq06ZNle2XL19WRkZG5TIHSYqIiNCBAwdktVqr7Lt//365ubmpe/fuysvL044dOyp/khs0aJDatWunrVu3NlrNVqvV6R5xcXdXOw8fL38F+3fUoRPfVm47ee6Iiq9cUGjbhs2yNydxcXfTazu51V4746Om60PiGqlJU4xFiV7XxJHH4q95e3vr4YcfVllZmd59912bzq2m0Hvd22+/LUl67LHHqh1n9Hk748NWpg6+rVpV3DomOzu7yvb58+fr5MmTlR9sk6RRo0YpLy9PGzdurNxWUlKiFStWaNiwYWrZsqVycnLUunXrylliSercubOOH+cDCzX57YAp+njbazp5/qguXbmgv6fNVt/wEWoTeIfRpTU79Br14RqxH3rtnHr16iV3d3d9//33OnHiRL371xV6JVXmiV69esnNjbvL2oupOx0aGqqoqCglJycrMDBQ7du31yeffFJ5T95fB9/7779fQ4YM0aRJkzR//ny1bdtWb731lnJycpSammrUKTi1xKHPqag4XzPf6KeSsqvq3TVez43/wOiymiV6jfpwjdgPvXZOkZGRkqQ9e/bUu299oVeSLly4oEOHDiksLEzh4eE6cOBA4xaMGlmsDZkfboays7OVlJSkXbt2KSgoSI8//rh8fX01Z84cXbx4UV5eXpX7FhQUaPbs2VqzZo2KiooUExOjV199VbGxsZKkvLw8derUSefPn6+c9e3Xr5/mzZunESNGGHJ+jiBzhVSQa3QVzsE/ROqbePPH02vb3WqvnRHXh+0Yi/bjyGPx1x+auueee5SYmKgtW7ZoxYoVtR4THx+vTZs2Sar/Pr0vvPCC2rVrp+TkZOXk5FRuN3k0a1KmD741mThxovbu3avvv/++wccOHz5cDz74oKZPn66dO3fqkUce0bFjx+Th4dEElToHvgHYjm+29uPI32ybCteH7RiL9uPIY7Ehdwu4zsXFRcuWLdPXX3990/fpJZo1HVMvdahNZmamBgwYcFPHvvvuu3riiSe0aNEieXh4KDU11dShFwAAMykvL9cTTzxhdBmoBcH3BkVFRcrOztb06dNv6vjQ0FB98cUXjVwVAAAAbhXB9wY+Pj4qKyszugwAAAA0MlPfzgwAAADmQfAFAACAKRB8AQAAYAoEXwAAAJgCwRcAAACmQPAFAACAKXA7MwAAgBo09DeoPffa3yRJr86eUuVrOA5mfAEAAGAKBF8AAACYAsEXAAAApkDwhemdu3DS6BKanbLyMuUXnTG6DDgZxmLjYywCVRF8YXqvr5qs378eqY82J+vk+aNGl+PUfsj5Wv933dMaPy9Em3YvN7ocOBnGYuNhLAI1464OML2Xn1ivbw9t1rbvVmj6ot7qGHynhvYap7joMQrwbW10eQ7v+OkD2ronVVu/S1V5eZnieo3VK5M/VVj7XkaXBifDWLw1jEWgfgRfmJ6rq5v6dRuhft1GqKR0iXb/+Km2fpeq/9j4v9W9w2+UdF+KQttFGV2mw8nYu0ofbX5FhZfOKjZqtGaP+0A9Og0wuiw4McbizWEsArYj+KLZ2Pzth1q0Oqny/yM7D9G+o9slSff2nqDx98zR5JQelc8nT/5UkaFDqryGu5uHOreNVM6ZH3T01D7lnDmgi5fz7XMCTubchRM6df6IunccoNB20eoY3L3aPh9tTlbqlmRJUuuATnrv2f16MiVCp/OPS5LG3TNHkZ2HaM7SkZXHLH32gIIDOtrnJNAkGIv2xVgEbGexNvTuzEADZa6QCnKNrqJuZwp+VsbelcrY+7FOnT+quyIf1tBe4xQVGiuLxWK3OvxDpL6JN3+8vXt9teSyvjrwX9q6J1V7Dm1WVGic4qLHamDEA2rpeZv9CrkJt9prZ8RYtB1j0X6a01jkF1g4PmZ8YXqvr3pSX3y/SgN7PKCJ8S+qb/hwuboyNGzRwt1LcdFjFBc9RpcuF2p71hqlf/NPvbFmqmaMWqyE/r8zukQ4EcbizWMsArbhXxSY3sj+T2rmg2+qhbuX0aU4tZZefkroN0kJ/SYpv+iMCovOGl0SnAxjsXEwFoHaEXxhenwIpPEF+AQrwCfY6DLgZBiLjY+xCFTFfXwBAABgCgRfAAAAmALBFwAAAKbAGl8AAIBmxJ63/rvOWe6Oy4wvAAAATIHgCwAAAFMg+AIAAMAUCL4AAAAwBYIvAAAATIHgCwAAAFPgdmYAAAAm1r59e3Xt2lXu7u66ePGisrKyVFRUVOv+06dPV2pqqvLz8+1YZeNgxrcBCgsLNXXqVAUHB8vb21uDBw/Wjh07jC4LAACgQaKiovTuu+/q1KlTys3N1datW7Vp0yZ9+eWXKiws1L59+/Tss88qKCioynGvvPKK3n77baWlpRlyv+BbRfC1kdVq1ahRo7R27VqlpKRo/fr1atWqleLj47Vnzx6jywMAAKhXYGCgPvzwQ+3du1dJSUlq3bq18vPztX37dqWnp2vPnj0qLS1Vz549tWDBAh0/flwzZsyQxWLRK6+8ojlz5qi0tFQLFixwml9a8WssdbDRhg0blJGRobS0NI0cOVKSFBsbq4iICM2dO1dpaWkGV+h8tn63Qut3vq0j/2+vrpQUa+NrpUaX1GzRa9SF68N+6DWM1Lt3b23YsEFt27ZVcXGx3nvvPf39739XVlZWlf08PDw0fPhwzZw5UyNGjNBbb72lP/7xj+rSpYtKS0s1duxYrVmzxqCzuDXM+EoqLy9XSkqKunbtKk9PT0VHRysjI0PdunXTlClTJEnr1q1TUFCQEhISKo/z8PBQYmKi0tPTdenSJaPKd1o+XgG6f+B0TXtgkdGlNHv0GnXh+rAfeg2jREVFafPmzWrbtq22b9+uyMhIPfXUU9VCryRdu3ZNGzZsUEJCgh566CEVFxerS5cuslqtmjBhgtOGXokZX0nS5MmTtWbNGj3//PPq06ePdu7cqXHjxuns2bOaNWuWJCkrK0sRERHV1rP07NlTpaWl+vHHH9WnTx8jynda/bqNkCTtPbzN2EJMgF6jLlwf9kOvYQQvLy+tWrVK/v7+Wr16tcaNG6eSkhKbju3bt6+8vb1ltVplsVjUt29fffzxx01ccdMx/Yxvamqqli9frvXr1+vZZ5/V0KFDNXfuXA0cOFClpaXq3bu3JOn8+fMKCAiodnxgYGDl8wAAAI7mpZdeUnh4uPbt26fx48fbHHp/vaZ39uzZKi0t1axZs9S/f/8mrrjpmD74JicnKyEhQXFxcVW2h4WFyd3dXVFRUQ16vRdeeEHh4eFycXHRJ5980pilSpIsFovTPTIytjV6H5qrjIxt9NpObrXXzvjg+rAdY9F+mtNYvO7Gr42qQ5L8/Pw0Y8YMSdLvfvc7Xbt2zaa/l1+H3rFjx2rBggVauHChXFxcNHv27Gr7O0rv62Pq4Jubm6usrCyNHj262nM5OTmKiIhQixYtJFXM7NZ0v7rrM73XZ34TEhL02WefKTY2tgkrBwAAqN9jjz0mb29vpaenKzMz06Zjbgy919f0Lly4UCUlJRo1apTatWvXlGU3GdMHX0lq06ZNle2XL19WRkZG5TIHSYqIiNCBAweq3bpj//79cnNzU/fu3SVJgwYNUmhoaJPVbLVane4RF3d3k/WjuYmLu5te28mt9toZH1wftmMs2k9zGovX3fi1UXVI0r333itJev/99236+6gt9ErS6dOntWnTJrm6ulZ7p9xRel8fUwffVq1aSZKys7OrbJ8/f75OnjxZ5cNqo0aNUl5enjZu3Fi5raSkRCtWrNCwYcPUsmVL+xTdjJSVl+layRWVlFa87XKt5IqulVxp0AUM29Br1IXrw37oNeztepb5+uuv6923rtB73fXXcdYP9Jv6rg6hoaGKiopScnKyAgMD1b59e33yySeV9+T99V/q/fffryFDhmjSpEmaP3++2rZtq7feeks5OTlKTU016hSc2uffvK+UlZMq///f5nhJkt7/01G1CbzDoKqaJ3qNunB92A+9hr1dX5Jw+PDhOvezJfRK0qFDh6q8rrMxdfB1cXHRqlWrlJSUpGnTpikoKEiPP/64ZsyYoTlz5lT5YJvFYtH69es1e/ZszZo1S0VFRYqJidGmTZuc9qceo43o94RG9HvC6DJMgV6jLlwf9kOvYW++vr7y8vJSWVlZrftYLBaFhITY9Msp1qxZo4CAABUXFzdFuU3O1MFXksLDw7V169Yq2yZOnKgePXrIy8urynZ/f38tWbJES5YssWeJAAAAN6W4uLjekGq1WjVp0iS9/fbb2rVrV537Xr16VVevXm3MEu3K1Gt8a5OZmXnTs7jPP/+8QkJC9OWXXyopKUkhISH1vr0AAABgpPLy8npDb3NA8L1BUVGRsrOzq9zRoSFefvll5ebm6urVqzp37pxyc3PVpUuXRq4SAAAADWX6pQ438vHxqXMdDAAAAJwTM74AAAAwBYIvAAAATIHgCwAAAFMg+AIAAMAUCL4AAAAwBe7qgCbnG2x0BdUV5Fb81z/E2DpudKu9ote2c8ReNTVHPOfmen3Qa9s5Yq+cndVqbdD+z732N0nSq7OnVPm6OSL4osl1u8foCqr7PKXiv30Tja2jsdFr1IXrw37oNeCYWOoAAAAAUyD4AgAAwBQIvgAAADAFgi8AAABMgeALAAAAUyD4AgAAwBQIvgAAADAFgi8AAABMgeALAAAAUyD4AgAAwBQIvgAAADAFgi8AAABMgeALAAAAUyD4AgAAwBTcjC4AjuPpD+3/Zy561P5/piPwSP/U7n/mtfiRdv8zjWZEn6Vb7zVj0X4Yi/ZDr+EImPEFAACAKRB8AQAAYAoEXwAAAJgCwRcAAACmQPAFAACAKRB8AQAAYAoEXwAAAJgCwbcBCgsLNXXqVAUHB8vb21uDBw/Wjh07jC4LAAAANiD42shqtWrUqFFau3atUlJStH79erVq1Urx8fHas2eP0eWhAazlRldgHuVlRlcAR2a11vw1Gh+9BioQfG20YcMGZWRkaPny5Xrsscc0bNgwrVq1SiEhIZo7d67R5RnivZntlLX1vSrbrFar3nnyNh3avdagqmpXckU6vEP64p1ftu36QDr1o+N+I7BevqyS0Ykq/+KXdxasV6+q9OlnVPp/XpG13DFT/NVLUvZWKePtX7Z987GUd8S4murjrL2WnG8sWq3Sie+lr/7xy7Ydf5OOfS2VlRhXV32c8RopL5OOZ0r/+tXl8eUy6edvJQcst5Iz9hrOgeArqby8XCkpKeratas8PT0VHR2tjIwMdevWTVOmTJEkrVu3TkFBQUpISKg8zsPDQ4mJiUpPT9elS5eMKt8QRedP6FLBSd3eqVeV7YVnjujalYtqHdrXmMJqce2ylJkqHf1KKrn8y/YLp6WsDdKhDONqq4vFy0sujzyssg8/ktVqlbWsTGXz/iK5u8v1uf8li4vjDeHLhdKu96Wcb6Sya79sz8+VvltT8U3YETljryXnG4tWq7Q/Tfphk3Qp75ftVy9Kh7ZL337iuOHX2a6R8tKKMXdwm3Sl8JftxfnST1ukfescN/w6W6/hPLhyJE2ePFkvv/yykpKS9Omnn2rMmDEaN26cjhw5oj59+kiSsrKyFBERIYvFUuXYnj17qrS0VD/++KMRpRvm9JHdsri4KiikZ5XteTl75e3XWr5BHQyqrGY/bZYunavhif+e6T2eKeUdtmtJNnN54H7pfL6s2/+lskVvypqXJ9cXX5DFw93o0mq0P61ixrea/+71wW3ShVP2rMh2ztZryfnG4onvpVM/1P584Qnp8L/sV09DOdM1cmyXdP547c+fPSz9/I396mkoZ+o1nIeb0QUYLTU1VcuXL9e2bdsUFxcnSRo6dKi+/fZbrVmzRr1795YknT9/Xj169Kh2fGBgYOXzZnL6yG4FtAmXm4dnle1nc/YquLNjzTBdLZJO/1TPThbp5z1Sqy52KalBLF6echn9sMpSFkoB/nJb9LosLb2NLqtGRWelghP17GSRfv5OikioZz8DOFOvr3OmsWi1VrzFXp8T30tdBkuuDphvnOUaKS+Tcr+rf7+f90gd+0o3zOk4BGfpNZyL6Wd8k5OTlZCQUBl6rwsLC5O7u7uioqJsfq38/Hzdd999Cg8PV3R0tIYPH65Dhw41ar0Wi6XJHg1x+shuFZw+pCVTW1V5fLPhNbUO7ecQ53P9MWzQw5WzjbWySicPXbFLPQ3tdaUrV+Q6dowsAQE3dbg9zmvC//hD/YVYpe+2H3fcPkuG97ohnGks+rUMrPmdlxuUXZMiuw5stteIPc4rtH2ErhXbcBoXpLZBd9DrRj7HG7929Iez1n0z15epZ3xzc3OVlZWlP/7xj9Wey8nJUUREhFq0aCGpYmY3Pz+/2n7XZ3oDAwNlsVj09NNPa9iwYZKkxYsXa9KkSdq+fXsTnoUxTh/N1G8eelF33vVYle0f/ilSrR1slsnF4tqo+9lb+edbVP7xSllGDFfZ2nWyjBxxa99EmpCtPXR1odeNxanGYgP+3hmPt6ZBvWY8wkRMPeObm5srSWrTpk2V7ZcvX1ZGRkblMgdJioiI0IEDB2S94eP/+/fvl5ubm7p37y5/f//K0CtJgwYN0tGjRxu1ZqvV2mQPWxWcOqSrl/LVKWqEfINCKh9lJVd0tbigQbNMTXk+1x+fbltZfyEWKbC9u13qaUivy3ftVtlbb8v1z8/LdfpUqaBA1i9u7gcpe5zXstRFNvX6zj4hDtVnR+u1rZxtLOZfPKsWvvXXYnGV9hzY0WyvEXuc18Hj39u0VMTNU8o9fZheN/I53vi1oz+cte6bub5MHXxbtWolScrOzq6yff78+Tp58mTlB9skadSoUcrLy9PGjRsrt5WUlGjFihUaNmyYWrZsWe31Fy1apAcffLBpijfQ6SO75dbCW7d3jK6y/eTBnfIJ6iBvv2CDKquZd4AU0ElSXRMFVikkxl4V2aZ8/wGVJb8q1//5jFyiIn9Z7/ZBqsPeysevvdQySPX3upedCrKRM/Zacr6xaLFIHXrVv1+b7pK7V5OX0yDOdo24ukvtIuvfLyRacrQJX2frNZyLqYNvaGiooqKilJycrH/+85/avHmzpk2bpmXLlklSleB7//33a8iQIZo0aZLef/99ff755xo9erRycnI0b968aq/90ksv6dChQ5o/f77dzsdeTh/Zrdad+8nFtepKmZOHvnS4t1avu3OY5O6pWgPZ7WFS2zvtWlKdrEePqeyFF+Wa9Hu5DB5Uud3lgfukwsKbnolsahaLFDFScnVTrb1uHy0FdrJrWXVy1l5LzjkWO/SW/NrV/rznbVJYrP3qsYWzXiOhgyTvwNqf97lduuM39qvHFs7aazgPU6/xdXFx0apVq5SUlKRp06YpKChIjz/+uGbMmKE5c+ZU+WCbxWLR+vXrNXv2bM2aNUtFRUWKiYnRpk2bqgRkSZo3b542bNig9PR0eXs3v0+gxk5YWOP2eya9U+N2R+AdIPV7VDr0hXTmoCo/7ObuJXWIqfjH3+JAPwZaOt8h99XVl2hYPD3lvvIjAyqy3W1tpL7jK3p97lcrfVr4SJ36VQQfR1qm58y9dsax6Oou9R5dccuyE9//cq9ni2vFTG9YrNSi+htohnLWa8TdU+o3ruL+yCf3//KbFF3cpXY9pbC7JDcPY2u8kbP2Gs7D1MFXksLDw7V169Yq2yZOnKgePXrIy6vqe23+/v5asmSJlixZUuvrvfTSS0pLS1N6err8/f2bomTcJG9/KeqBinvMFudXvL3nG+x4b/M1B763SzEPS1cuSpcLKsKOb7Bj/XAB47i6S+F3V9yy7OJZSeUVS2QcbXlDc+DuJd05XOoaJxX99y8M8bnd8QIvYC+mD741yczM1IABAxp83P79+/Xiiy+qS5cuuvvuuyu3f/fdd41XHG5Zi5aON6PUXHn6VjyAmri6S/51LHtA43FrIfm3N7oKwHgE3xsUFRUpOztb06dPb/CxERERDf7kKgAAAOyD4HsDHx8flZWVGV0GAAAAGhkr7gAAAGAKBF8AAACYAsEXAAAApkDwBQAAgCkQfAEAAGAKBF8AAACYArczQ6VFjxpdgXlcix9pdAmm4Kx9Zizaj7NeI86IXsMRMOMLAAAAUyD4AgAAwBQIvgAAADAFgi8AAABMgeALAAAAUyD4AgAAwBQIvgAAADAFgi8AAABMgeALAAAAUyD4AgAAwBQIvgAAADAFgi8AAABMgeALAAAAUyD4AgAAwBQIvgAAADAFgi8axc8//6x7771Xd955pyIiIvSnP/3J6JIAAHAq27ZtU0REhMLCwvTkk0+qrKzM6JLq9dRTTykkJERubm5Gl2ITgi8ahZubm1577TX98MMP2rNnj3bs2KF169YZXRYAAE6hvLxcTz75pFatWqVDhw7pwoUL+uCDD4wuq16jR49WZmam0WXYjOCLRtG2bVv17dtXkuTh4aGYmBjl5OQYXBUAAM5h9+7dateunXr06CFJmjx5slavXm1wVfW766671KZNG6PLsBnBF43u/Pnz+s///E/Fx8cbXQoAAE4hNzdXHTp0qPz/jh076ueffzawoubJORZkwGlcu3ZNjzzyiJ566il1797d6HIAAGgyVqtVK/5ri86cK6iy/Y3/WF3j1zE9whT7m+haX8tefjqco8++2F1te011e7i7adLokfJs4WG3+poSM75oNGVlZRo/frx69eqlZ555xuhyAABoUhaLRb17huvkmXM6eeZc5fYbvz555pzOFVxQTETXWl+rQ4cOVWZ4c3JyFBIS0iR1h3UOkdVqtanurp1Dmk3olQi+jWL37t367W9/K39/f7Vs2VIDBgzQypUrjS7L7qZMmSJfX1+9/vrrRpcCAIBddAvtoG6hHerd756BMfL18a71+b59+yo3N1cHDhyQJC1dulQPPfRQo9X5a64uLrrv3oH17ufn21Kx/WueoXZWBN9btHXrVg0ePFg7duzQmDFjNHXqVJ06dUpjx441VQD817/+pWXLlikzM1MxMTHq1auXFi9ebHRZAAA0uX+7Z6BcLJZanw/089Xgvj3rfA1XV1e99957euSRR9SlSxf5+Pho4sSJjV1qpbBO7dWja6c69xl592/k4V73qtikpCSFhISorKxMISEhmjFjRmOW2egsVnsuKmlmSktL1b17d+Xm5uqrr75Sr169JEmFhYXq37+/jh07puzsbHXqVPeFZQZWq1WWOv5RAADAma3/fKd2fpNV43OPPjhMkd1C7VxR/fLOF+qvS1eprLy82nMd2wVr2oRRze57NzO+9Vi3bp3uu+8+BQcHq0WLFurUqZPGjx+vffv2acuWLTp8+HDlutbr/Pz8NGfOHF27dk3/+Mc/jCveQZw9V6A3/mO1TpzOM7oUAACaxLDBveXt2aLa9s4d2qpneGcDKqpfq0A/DepT80z0/fcOanahVyL41qq0tFSPPvqoHnzwQe3bt08PPfSQnnrqKcXExGj16tU6ceKEtm3bJkkaPnx4teNHjBghScrIyLBn2Q5py5ff6lzBBfn5tDS6FAAAmoS3l6eG3dWnyjaLpPvuGejQAfLewb3V0tuzyraYiK7q0C7YoIqaFrczq8Uf/vAHffTRR5o5c6b++te/VvlVfLm5ufLz89PSpUslSV27Vv+UZps2beTj46ODBw/arWZHdPZcgb47cFhD+kXKp6WX0eUAANBkftOrh77ac6Dy9mZ9IrupfZtWxhZVD88WHho+pK/WbtwhSXJ3d1NCbD+Dq2o6rPGtwfbt2xUbG6uEhASlpaXV+pPa8OHDlZ6eroMHDyosLKza8+3bt1dRUZEKCwsbrbbnXvtbo70WAABAc/Dq7Ck27cdShxosWrRIkvTqq6869NsTAAAAsB1LHWqwadMm3XHHHYqOrvvedX5+fpJU64zuhQsXFBAQ0Ki12foTjSP4eMMWZWUf0+ykcSxzAACYxrmCC7rNx1vubs4Vs07n5at1q8bNLY7Guf5G7KCgoEBFRUXq27dvvfteX9t78OBB9elTdUH7qVOnVFRUpP79+zdqfc641GHeW+8bXQIAAGjGWOpwk64veT5z5ky9+8bFxUmqmCG+0caNG6vsAwAAAGPx4bYadOnSRUePHtWmTZs0bNiwKs/99NNP6tatm6SKW55169ZNJ06cqPUXWPz000+644477HwGxjp7rkALl67SkH6R+u3QAUaXAwAAIImlDjX6y1/+orFjx2rkyJEaNWqUunTpojNnzmjnzp3q0aOH1q5dK0lyc3PTe++9pxEjRig2NlaJiYny9fXV6tWrdfz4caWkpJgu9EoV9+11c3Ntdr/fGwAAODdmfGuxceNGLViwQLt379aVK1cUHBys/v376+mnn9aQIUOq7Ltr1y79+c9/1s6dO1VSUqLIyEjNmjVLY8eONah645SXl+v9tem6PdCP2V4AAOBQCL5oEuXl5XJxYQk5AABwHARfAAAAmAJTcgAAADAFgi8AAABMgeALAAAAUyD4AgAAwBQIvgAAADAFgi8AAABMgeALAAAAUyD4AgAAwBQIvgAAADAFgi8AAABMgeALAAAAUyD4AgAAwBQIvgAAADAFgi8AAABMgeALAAAAUyD4AgAAwBQIvgAAADAFgi8AAABMgeALAAAAUyD4AgAAwBQIvgAAADAFgi8AAABMgeALAAAAUyD4AgAAwBQIvgAAADAFgi8AAABMgeALAAAAU/j/vj8zDCgnoI4AAAAASUVORK5CYII=\n",
72 | "text/plain": [
73 | ""
74 | ]
75 | },
76 | "execution_count": 4,
77 | "metadata": {},
78 | "output_type": "execute_result"
79 | }
80 | ],
81 | "source": [
82 | "n = 2\n",
83 | "steps = 2\n",
84 | "\n",
85 | "graph = QuantumRegister(n+1)\n",
86 | "mes = ClassicalRegister(n)\n",
87 | "mcq = QuantumCircuit(graph, mes)\n",
88 | "\n",
89 | "#define U(t)\n",
90 | "for i in range(steps):\n",
91 | " mcq.h(n)\n",
92 | " mcq.append(Increment(n), [n]+list(range(0, n)))\n",
93 | " mcq.x(n)\n",
94 | " mcq.append(Decrement(n), [n]+list(range(0, n)))\n",
95 | " mcq.x(n)\n",
96 | "\n",
97 | "mcq.measure(range(n), range(n))\n",
98 | "\n",
99 | "#mcq = transpile(mcq, basis_gates=['cx','u3'],optimization_level=3)\n",
100 | "\n",
101 | "mcq.draw('mpl')"
102 | ]
103 | },
104 | {
105 | "cell_type": "code",
106 | "execution_count": 15,
107 | "metadata": {},
108 | "outputs": [],
109 | "source": [
110 | "backend = BasicAer.get_backend('qasm_simulator')\n",
111 | "atp = 1024\n",
112 | "res = execute(mcq, backend=backend, shots=atp).result()\n",
113 | "ans = res.get_counts()"
114 | ]
115 | },
116 | {
117 | "cell_type": "code",
118 | "execution_count": 16,
119 | "metadata": {},
120 | "outputs": [
121 | {
122 | "data": {
123 | "image/png": "iVBORw0KGgoAAAANSUhEUgAAAc0AAAE9CAYAAABp1zkEAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjMuMCwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy86wFpkAAAACXBIWXMAAAsTAAALEwEAmpwYAAAh30lEQVR4nO3df5yVdZ338ddHJkcKWAEDYsCABFZAB3FswiVwuyV27Y7dss2s1pJV73LTLeuxtfeqm9Zme7tbat6tG/VIJbfc8t5ybS3cdoFQGhpYScCADTAgfsSPEhIHGT/3H+fAjuPMcA0cZobh9Xw8zmPO+V7f6zqf8xgO77mu63t9r8hMJEnSkZ3S3QVIknSiMDQlSSrI0JQkqSBDU5KkggxNSZIKMjQlSSrI0JQkqaAuD82IuDYiNkTE8xGxLCLeeIT+p0bEreV1miLi5xFxfas+l0bE6vLy1RHxtuP7KSRJJ6MuDc2IuAy4E/gMcB7wBPBoRJzZwWrfAH4PuAYYD/wR8JMW25wKPAg8AEwu//xmRNQfh48gSTqJRVfOCBQRDcBPMvPqFm3rgG9l5l+00f/NwDeB12Xmzna2+SAwKDNntmj7N+CXmXl5R/WcccYZOWrUqKP6LJKk3mnZsmU7M/PVbS2r6qoiIuJU4Hzgb1stmg9c2M5qfwj8GLghIq4A9gOPAv87M/eV+0wFvtBqve8DHzpSTaNGjaKxsbFQ/ZKkk0NEPNPesi4LTeAMoA+wvVX7duDidtYZA0wDmoBLgdMpBeRw4B3lPsPa2eawtjYYEddQOtTL8OHDWbBgQemNxoyhf//+rFixAoDBgwczceJEFi1aBEBVVRXTpk1j+fLlPPvsswDU1dWxfft2Nm3aBMDYsWOprq5m5cqVAAwZMoRx48axePFiAKqrq5k6dSqNjY3s21fK/Pr6ejZv3syWLVsAGD9+PH369GH16tWlDzdsGKNHj2bJkiUA9O3bl/r6ehoaGti/fz8AU6dOZcOGDWzbtg2ACRMm0NzczJo1awCoqalhxIgRNDQ0ANCvXz/q6upYsmQJTU1NAEybNo21a9eyY8cOACZNmkRTUxPr1q0DYOTIkQwdOvTwHxkDBgxgypQpLF68mIMHDwIwffp0Vq1axa5duwCora1l7969rF+/Hij9kTJo0CCWL18OwMCBA6mtrWXhwoVkJhHBjBkzWLFiBXv27AFgypQp7N69m40bN/p78vfk78nfU5f8njrSZYdnI2I4sAWYkZmLWrTfDLwnM8e3sc584I3AsMz8dbntzZT2JIdl5vaIOABclZn3t1jvCmBuZlZ3VFNdXV26pylJaikilmVmXVvLunIg0E6gGRjaqn0osK2ddbYCWw4FZtnT5Z+HBg9t6+Q2JUk6Kl0Wmpl5AFgGzGy1aCalUbRteRwYHhH9WrSNK/88dMx5SSe3KUnSUenq6zQ/B7w/Iq6KiLMj4k5K5yfvAYiI+yPi/hb9/xHYBXw1IiZGxO9QumTlW5m5o9znTuBNEfGJiPjtiPgL4HeBO7roM0mSThJdORCIzHwwIgYDNwKvAVYCl2Tmob3GM1v13xcRF1Ma/PNjYA/wbeATLfo8ERHvAj4N3Ar8DLgsMxuO88eRJJ1kuvQ6zZ7GgUCSpNZ6ykAgSZJOaIamJEkFGZqSJBVkaEqSVJChKUlSQYamJEkFGZqSJBVkaEqSVJChKUlSQYamJEkFGZqSJBVkaEqSVJChKUlSQYamJEkFGZqSJBVkaJ7kvve97zF+/HjOOussPvvZz75s+b333surX/1qJk+ezOTJk/nyl798eNl9993H2LFjGTt2LPfdd9/h9osuuojx48cfXmfHjh1d8lkk6Xir6u4C1H2am5v50z/9Ux577DFGjBjBBRdcwOzZs5kwYcJL+l122WXcfffdL2nbvXs3t9xyC42NjUQE559/PrNnz2bgwIEAPPDAA9TVtXkPV0k6YbmneRJbunQpZ511FmPGjOHUU0/lXe96F9/5zncKrfv973+fmTNnMmjQIAYOHMjMmTP53ve+d5wrlqTuZWiexLZs2cLIkSMPvx4xYgRbtmx5Wb+HHnqIc889l3e84x1s2rSp0LpXXnklkydP5lOf+hSZeRw/hSR1HUNTHXrrW9/Kxo0b+clPfsLMmTN53/ved8R1HnjgAZ566il++MMf8sMf/pB58+Z1QaWSdPwZmiexmpqaw3uOAJs3b6ampuYlfQYPHkx1dTUAV111FcuWLTviuod+9u/fn3e/+90sXbr0uH4O6WRxpIF7hzz00ENEBI2NjQAcOHCAK6+8knPOOYfa2loWLFhwuK8D9zrH0DyJXXDBBaxbt44NGzZw4MABvvGNbzB79uyX9Nm6devh5w8//DBnn302ALNmzWL+/Pns2bOHPXv2MH/+fGbNmsXBgwfZuXMnAC+88AKPPPIIkyZN6roPJfVShwbuPfroo6xevZqvf/3rrF69+mX99u7dy5133kl9ff3htrlz5wLw1FNP8dhjj/HRj36UF1988fDyBx54gCeffJInn3ySIUOGHP8PcwIzNE9iVVVV3H333cyaNYuzzz6bd77znUycOJGbb76Zhx9+GIC77rqLiRMnUltby1133cW9994LwKBBg7jpppu44IILuOCCC7j55psZNGgQTU1NzJo1i3PPPZfJkydTU1PD1Vdf3Y2fUuodig7cu+mmm/j4xz/Oaaeddrht9erVvOlNbwJgyJAhnH766Yf3QtU5XnJykrvkkku45JJLXtJ26623Hn5+2223cdttt7W57pw5c5gzZ85L2l71qlcdPoQrqXLaGnzX0NDwkj7Lly9n06ZNvOUtb+H2228/3F5bW8vDDz/M5ZdfzqZNm1i2bBmbNm3i9a9/PVAauNenTx8uvfRSbrzxRiKiaz7UCcjQlKRe4MUXX+SGG244fDSopTlz5vD0009TV1fHa1/7Wi688EL69OkDlA7N1tTUsHfvXi699FLmzZvHFVdc0cXVnzg8PCtJJ4AjDdzbu3cvK1eu5KKLLmLUqFH86Ec/Yvbs2TQ2NlJVVcXnP/95nnzySb7zne/wq1/9inHjxh3eLjhwryhDU5JOAEcauPdbv/Vb7Ny5k40bN7Jx40be8IY38PDDD1NXV8dzzz3Hb37zGwAee+wxqqqqmDBhggP3joKHZyXpBNBy4F5zczNz5sw5PHCvrq7uZSPfW9qxYwezZs3ilFNOoaam5vC104cG7r3wwgs0Nzdz8cUXO3DvCOJknq2lrq4uHUEmSWopIpZlZpuTZ3t4VpKkggxNSZIKMjQlSSrI0JQkqSBDU5KkggxNSZIKMjQlSSrIyQ0q4Oo7ursCHQ9zP9zdFUjqadzTlCSpIENTkqSCDE1JkgrynKakk47jEHqnrhiH4J6mJEkFGZqSJBVkaEqSVJChKUlSQYamJEkFGZqSJBVkaEqSVJChKUlSQYamJEkFGZqSJBVkaEqSVJChKUlSQYamJEkFGZqSJBVkaEqSVFCXh2ZEXBsRGyLi+YhYFhFvLLjetIg4GBErW7W/PyKyjcdpx+cTSJJOVl0amhFxGXAn8BngPOAJ4NGIOPMI6w0E7gd+0E6X54DXtHxk5vOVqluSJOj6Pc0bgHszc25mPp2Z1wFbgQ8eYb2vAPcBS9pZnpm5reWjgjVLkgR0YWhGxKnA+cD8VovmAxd2sN61wFDg0x1svm9EPBMRmyPikYg475gLliSpla7c0zwD6ANsb9W+HRjW1goRcQ7wV8B7M7O5ne2uAeYAfwBcDjwPPB4RYytRtCRJh1R1dwHtiYhq4EHgY5m5ob1+mbmEFodtI+IJ4EngOuD6NrZ7DXANwPDhw1mwYAEAY8aMoX///qxYsQKAwYMHM3HiRBYtWgRAVVUV06ZNY/ny5Tz77LMA1NXVsX37duB1x/px1QM1Njayb98+AOrr69m8eTNbtmwBYPz48fTp04fVq1cDMGzYMEaPHs2SJaV/in379qW+vp6Ghgb2798PwNSpU9mwYQPbtpXOHkyYMIHm5mbWrFkDQE1NDSNGjKChoQGAfv36UVdXx5IlS2hqagJg2rRprF27lh07dgAwadIkmpqaWLduHQAjR45k6NChNDY2AjBgwACmTJnC4sWLOXjwIADTp09n1apV7Nq1C4Da2lr27t3L+vXrARg1ahSDBg1i+fLlAAwcOJDa2loWLlxIZhIRzJgxgxUrVrBnzx4ApkyZwu7du9m4cSNwbN+nTZs2ATB27Fiqq6tZubI09m/IkCGMGzeOxYsXA1BdXc3UqVOP6vcE1Z3816ATwdatWyvyfepIZOZx/Agt3qh0ePY54PLM/GaL9v8LTMrMGa36jwI2AC33ME8Botx2SWa2PtR7aN2vAsMy8/c7qqmuri4P/edyLK6+45g3oR5o7oe7uwIdL35ne6dKfWcjYllm1rW1rMsOz2bmAWAZMLPVopmURtG2tgU4B5jc4nEP8F/l522tQ0QEcC6lAUaSJFVMVx+e/RwwLyKWAo8DHwCGUwpDIuJ+gMy8IjNfAFpfk7kDaMrMlS3a/gr4EbAOGEDpkOy5HHlEriRJndKloZmZD0bEYOBGStdTrqR0mPWZcpcOr9dsx+nAlygNJvo18J/A9MxceuwVS5L037p8IFBmfhH4YjvLLjrCup8EPtmq7SPARypTnSRJ7XPuWUmSCjI0JUkqyNCUJKkgQ1OSpIIMTUmSCjI0JUkqyNCUJKkgQ1OSpIIMTUmSCjI0JUkqyNCUJKkgQ1OSpIIMTUmSCjI0JUkqyNCUJKkgQ1OSpIIMTUmSCjI0JUkqyNCUJKkgQ1OSpII6FZoRcUpEnNLi9bCIuCoifqfypUmS1LN0dk/zu8B1ABHRD2gEbgcWRMQVFa5NkqQepbOhWQf8e/n524FngSHA1cDHKliXJEk9TmdDsx/wq/LzNwP/nJkvUArS11WwLkmSepzOhubPgd+JiFcBs4DHyu2DgOcqWZgkST1NVSf7fw6YB+wDngEWldunA09VsC5JknqcToVmZv5DRCwDRgKPZeaL5UU/A26qdHGSJPUknd3TJDMbKY2abdn23YpVJElSD9XpyQ0i4tqIWBURz0XEmHLbxyPinZUvT5KknqOzkxt8GLgR+BIQLRb9AvhQ5cqSJKnn6eye5geAqzPzTuBgi/blwMSKVSVJUg/U2dB8LbCyjfYXgL7HXo4kST1XZ0NzPTCljfZLgNXHXo4kST1XZ0fP/i1wd0S8ktI5zakR8cfAnwNzKl2cJEk9SWev0/xqRFQBnwFeSWmig18A12fmg8ehPkmSeoyjuU5zLjA3Is4ATsnMHZUvS5KknqfToXlIZu6sZCGSJPV0RwzNiPgJMCMz90TEU0C21zczz61kcZIk9SRF9jQfAppaPG83NCVJ6s2OGJqZeUuL5588rtVIktSDdXYavX+PiNPbaB8QEf9esaokSeqBOju5wUXAqW20nwa88ZirkSSpBys0ejYiWs4CdG5E7G7xug8wC9hSycIkSeppil5y0khpAFAC89tYvh+4rlJFSZLUExUNzdGUps1bD7we+GWLZQeAHZnZXOHaJEnqUQqFZmY+U37a6ZtWS5LUWxSZ3ODtwL9k5gvl5+3KzP9XscokSephiuxpfgsYBuwoP29PUhoUJElSr1RkcoNT2nouSdLJxhCUJKmgouc0C/GcpiSpNyt6TrMIz2lKknq1Tp3TlCTpZGYgSpJUkNdpSpJUkNdpSpJUkNdpSpJUUJeHYERcGxEbIuL5iFgWEe3ehzMiZkTEExGxKyL2R8RPI+JjbfS7NCJWR0RT+efbju+nkCSdjDodmhExJSLuj4jG8mNeq/ttdrTuZcCdwGeA84AngEcj4sx2VtkH3AVMByYAnwZuiYhrW2xzKvAg8AAwufzzmxFR39nPJklSRzoVmhHxHuDHwGuAfy0/hgJLI+K9BTZxA3BvZs7NzKcz8zpgK/DBtjpn5rLM/EZmrsrMDZn5NeD7QMu90w8D/5GZf13e5l8DC8rtkiRVTGf3NP8auCkzZ2bmzeXHm4GbKO0FtisiTgXO5+U3sZ4PXFjkzSPivHLfhS2ap7axze8X3aYkSUUVvQn1Ia8G/qmN9m9SCs6OnEFpdO32Vu3bgYs7WjEiNpffuwq4JTPvabF4WDvbHNbOtq4BrgEYPnw4CxYsAGDMmDH079+fFStWADB48GAmTpzIokWLAKiqqmLatGksX76cZ599FoC6ujq2b98OvK6j8nWCamxsZN++fQDU19ezefNmtmzZAsD48ePp06cPq1evBmDYsGGMHj2aJUuWANC3b1/q6+tpaGhg//79AEydOpUNGzawbds2ACZMmEBzczNr1qwBoKamhhEjRtDQ0ABAv379qKurY8mSJTQ1NQEwbdo01q5dy44dOwCYNGkSTU1NrFu3DoCRI0cydOhQGhsbARgwYABTpkxh8eLFHDx4EIDp06ezatUqdu3aBUBtbS179+5l/fr1AIwaNYpBgwaxfPlyAAYOHEhtbS0LFy4kM4kIZsyYwYoVK9izZw8AU6ZMYffu3WzcuBE4tu/Tpk2bABg7dizV1dWsXLkSgCFDhjBu3DgWL14MQHV1NVOnTj2q3xNUd/Jfg04EW7durcj3qSORmYULiohHgG9n5pdbtV8FXJqZv9/BusOBLcCMzFzUov1m4D2ZOb6DdUcD/YA3AH8D/FlmzisvOwBclZn3t+h/BTA3Mzv8ZtTV1eWh/1yOxdV3HPMm1APN/XB3V6Djxe9s71Sp72xELMvMuraWdXbC9keB2yKiDvhRue0NwNuBTx5hUzuBZkrnQFsaCmzraMXM3FB++lREDC2/17xy27aj2aYkSZ11tBO2Hz7E2cIXgC+2t5HMPBARy4CZlA7nHjITeKhAHYecwkuPrSwpb+P2Vtt8ohPblCTpiLp6wvbPAfMiYinwOPABYDhwD0BE3F9+zyvKr68DNgBryutPBz7GS8P5TmBRRHwC+DbwNuB3gWkVrFuSpE4PBDommflgRAwGbqR02cpK4JLMfKbcpfX1mn0oncMcBRwEfgZ8gnLIlrf5RES8i9Lo3VvLfS7LzIbj+FEkSSehTodmRAwEfp9SwJ3acllm3nqk9TPzi7RzGDczL2r1+g7gjgLb/BbF7/spSdJR6VRoRsQbgO8CTZQuAdlCaY+xCdhIaU9PkqReqbPnK2+nNE1dDfA88CZKe5yNlA6jSpLUa3U2NM8F7s7SxZ3NQHVmbgc+zpEvOZEk6YTW2dA80OL5duC15ef7KI2ClSSp1+rsQKDlwAXAWkqTon+6PNnAe4GfVLY0SZJ6ls7uaf4l8Ivy8xuBX1Ka1GAgL5/sQJKkXqVTe5qZ2dji+S8pXXoiSdJJ4agmN4iI1wFnl1+uzsz1lStJkqSeqbPXaQ4GvgLMBl787+Z4BJiTmbsqXJ8kST1GZ89pfhk4C3gjcFr5MR0YDcytbGmSJPUsnT08Owv4H5m5pEXb4xHxv4B/q1xZkiT1PJ3d0/wl8Js22p8DPDQrSerVOhuatwJ3RETNoYby87/DeWclSb3cEQ/PRsRTQLZoGg1sjIgt5deH5qEdQumcpyRJvVKRc5reckuSJAqEZmbe0hWFSJLU0x3t5AZvAiZQOmy7KjMXVLIoSZJ6os5OblAD/DNwPv89B+3wiGgE3paZv2h3ZUmSTnCdHT17F6X7aJ6VmSMzcyQwttx2V6WLkySpJ+ns4dmZwEWZueFQQ2auj4jrgR9UtDJJknqYzu5pwksvP+moTZKkXqWzofkD4AsRMfJQQ0ScCdyBe5qSpF6us6F5PfAqYH1EPBMRzwA/K7ddX+niJEnqSTp7TnMX8HrgIuC3y21PZ6aTtUuSer3CoRkRfYBfA7WZ+Rjw2HGrSpKkHqjw4dnMbAaeAU49fuVIktRzdfac5qeAz0bEGcejGEmSerLOntP8GKW7nGyJiM20urdmZp5bqcIkSeppOhua36J0TWYch1okSerRCoVmRLwSuB34Q+AVlK7JvC4zdx6/0iRJ6lmKntO8BXg/8F3g68DFwN8fp5okSeqRih6efTvwJ5n5DYCIeAB4PCL6lEfVSpLU6xXd0xwJ/PDQi8xcChwEhh+PoiRJ6omKhmYf4ECrtoMc5U2sJUk6ERUNvQC+FhFNLdpOA+ZGxHOHGjJzdiWLkySpJykamve10fa1ShYiSVJPVyg0M/PK412IJEk93dHchFqSpJOSoSlJUkGGpiRJBRmakiQVZGhKklSQoSlJUkGGpiRJBRmakiQVZGhKklSQoSlJUkGGpiRJBRmakiQVZGhKklSQoSlJUkGGpiRJBRmakiQVZGhKklSQoSlJUkGGpiRJBXV5aEbEtRGxISKej4hlEfHGDvq+JiL+MSJ+GhHNEXFvG33eHxHZxuO04/pBJEknnS4NzYi4DLgT+AxwHvAE8GhEnNnOKtXATuCzQEMHm34OeE3LR2Y+X6m6JUmCrt/TvAG4NzPnZubTmXkdsBX4YFudM3NjZl6fmfcCuzvYbmbmtpaPypcuSTrZdVloRsSpwPnA/FaL5gMXHuPm+0bEMxGxOSIeiYjzjnF7kiS9TFUXvtcZQB9ge6v27cDFx7DdNcAcYAXQH/gz4PGIqM3Mda07R8Q1wDUAw4cPZ8GCBQCMGTOG/v37s2LFCgAGDx7MxIkTWbRoEQBVVVVMmzaN5cuX8+yzzwJQV1fH9u3bgdcdQ/nqqRobG9m3bx8A9fX1bN68mS1btgAwfvx4+vTpw+rVqwEYNmwYo0ePZsmSJQD07duX+vp6Ghoa2L9/PwBTp05lw4YNbNtWOhAyYcIEmpubWbNmDQA1NTWMGDGChobSmYh+/fpRV1fHkiVLaGpqAmDatGmsXbuWHTt2ADBp0iSamppYt670T33kyJEMHTqUxsZGAAYMGMCUKVNYvHgxBw8eBGD69OmsWrWKXbt2AVBbW8vevXtZv349AKNGjWLQoEEsX74cgIEDB1JbW8vChQvJTCKCGTNmsGLFCvbs2QPAlClT2L17Nxs3bgSO7fu0adMmAMaOHUt1dTUrV64EYMiQIYwbN47FixcDUF1dzdSpU4/q91Q686PeZuvWrRX5PnUkMvM4foQWbxQxHNgCzMjMRS3abwbek5njj7D+I8DOzHz/Efr1AZ4E/iMzr++ob11dXR76z+VYXH3HMW9CPdDcD3d3BTpe/M72TpX6zkbEssysa2tZV57T3Ak0A0NbtQ8FKnYOMjObgUZgbKW2KUkSdGFoZuYBYBkws9WimZRG0VZERARwLqUBRpIkVUxXntME+BwwLyKWAo8DHwCGA/cARMT9AJl5xaEVImJy+ekA4MXy6wOZubq8/K+AHwHryn2upxSabY7IlSTpaHVpaGbmgxExGLiR0vWUK4FLMvOZcpe2rtf8z1av3wo8A4wqvz4d+BIwDPh1uf/0zFxa0eIlSSe9rt7TJDO/CHyxnWUXtdEWR9jeR4CPVKQ4SZI64NyzkiQVZGhKklSQoSlJUkGGpiRJBRmakiQVZGhKklSQoSlJUkGGpiRJBRmakiQVZGhKklSQoSlJUkGGpiRJBRmakiQVZGhKklSQoSlJUkGGpiRJBRmakiQVZGhKklSQoSlJUkGGpiRJBRmakiQVZGhKklSQoSlJUkGGpiRJBRmakiQVZGhKklSQoSlJUkGGpiRJBRmakiQVZGhKklSQoSlJUkGGpiRJBRmakiQVZGhKklSQoSlJUkGGpiRJBRmakiQVZGhKklSQoSlJUkGGpiRJBRmakiQVZGhKklSQoSlJUkGGpiRJBRmakiQVZGhKklSQoSlJUkGGpiRJBRmakiQVZGhKklSQoSlJUkGGpiRJBRmakiQVZGhKklSQoSlJUkGGpiRJBXV5aEbEtRGxISKej4hlEfHGI/SfUe73fESsj4gPHOs2JUk6Gl0amhFxGXAn8BngPOAJ4NGIOLOd/qOBfy33Ow+4DfhCRFx6tNuUJOlodfWe5g3AvZk5NzOfzszrgK3AB9vp/wHgF5l5Xbn/XOA+4GPHsE1Jko5Kl4VmRJwKnA/Mb7VoPnBhO6tNbaP/94G6iHjFUW5TkqSjUtWF73UG0AfY3qp9O3BxO+sMA/6tjf5V5e1FZ7cZEdcA15Rf7ouINUWK12FnADu7u4iu8OWPdHcFUkX4ne2817a3oCtDs0fIzC8BX+ruOk5UEdGYmXXdXYekYvzOVlZXhuZOoBkY2qp9KLCtnXW2tdP/YHl7cRTblCTpqHTZOc3MPAAsA2a2WjST0ojXtixpp39jZr5wlNuUJOmodPXh2c8B8yJiKfA4pdGxw4F7ACLifoDMvKLc/x7gQxFxB/APwO8A7wcuL7pNVZyHtqUTi9/ZCorM7No3jLgW+HPgNcBK4COZuai8bAFAZl7Uov8M4PPAROAXwN9k5j1FtylJUqV0eWhKknSicu5ZSZIKMjQlSSrI0JQkqSBDU5J6oYiIlj9VGQ4E0hFFxAjgLEqTSbwIrMlMJ4+QTiCHwjP9T/+YGJrqUER8EJgD1AK/Af4L2Az8CPh2Zq6JiFMy88VuLFNSWUScAvwB8GrglcAWYGFm7ujWwnoJQ1PtiojBlELy74C/p/QlvBi4CDibUnh+JDNXR0T4F6zUvSKiP/AV4HcpHRXaDCTwPLAQmJeZP/X7evQMTbUrIq4D3puZ9W0sm0bppuA1wOsz86S4i4LUk0XEXwLvBK7KzB9HxG8DdZRmU6ujdK/hP8nMX3ZjmSc0BwKpIweA/hExCSAiqsv3MCUzFwPvofQX7Ju7r0RJLfwecF9m/hggM3+amV8DPgR8lNIRonndWN8Jz9BUR75F6RDPhyOif2Y2ZeaB8jkTMvPnwK+AEd1YoyQgIqooTSN6aUS8utzWpzzmoLk8tegHgBERUdudtZ7IDE21qTzSbjdwI6W7xvwiIr4SEeeXl58ZEe8FzgH+qfsqlQSQmQeB+4BhwMciYmg5LFsO0lsLjOIkuSn18eA5TXUoIk4HzgQuBN5G6dwIlO5XGpQGFnyyW4qTdFj5CNApwJXAZyjdxeoh4EHg58C5wP8EJmTmBd1V54nO0NTLRMQQ4I8pnQPZCeyndBh2MaVLTV5B6brN72Xm2m4qU1I7yn/svh94NzAZ2Etp/MGPgdsys6G7ajvRGZp6mYi4l9Kt2P6F0iHaQZQOw44DdgA3+qWTeo6IGADsbXkZSXnP8zSgHzAJ+I3f22NnaOolyucy9wKXtLjPaVA6RFsPXAWMAd6Zmcu7rVBJh0XEPwBLy49nMvPZNvoMzMw9XqN5bBwIpNYmABsoXW4ClKbdysxnMvOfgLdSOlT7R91TnqSWIuJy4GpKk5B8B7g9It4eEWdFRN9yn37AVyPiHAPz2LinqZcof8keoTT91hXAz1pPkVee9OBPMnNy11coqaWImAs0A/8HeDvwPuB1wBrgX4EfAOOBOzPz1O6qs7dwT1MvkZn7gb8E+gL3A1dExMjyX6pExCuBGZSuB5PUjcrXZm4AfpWZ6zPzbzPzHOACStPmvY/SJWFfwEkNKsI9TbWpPAvQTcBsShO1LwF+SWnu2a2Upul6qvsqlASlc5XA0PKcsqcCL7QaEHQZ8HVgSmY+2U1l9hqGpjpUvvzkLcAfUhqyvhL4Zmb+tDvrktS+8sjZyMzmiLia0qHZV3Z3Xb2BoanCvAWYdOKJiBuAPpl5e3fX0hsYmpLUi0XEK4DW0+npKBmakiQV5OhZSZIKMjQlSSrI0JQkqSBDU5KkggxNSZIKMjQlSSro/wNv6x7YAo59WAAAAABJRU5ErkJggg==\n",
124 | "text/plain": [
125 | ""
126 | ]
127 | },
128 | "execution_count": 16,
129 | "metadata": {},
130 | "output_type": "execute_result"
131 | }
132 | ],
133 | "source": [
134 | "plot_histogram(ans)"
135 | ]
136 | },
137 | {
138 | "cell_type": "code",
139 | "execution_count": 17,
140 | "metadata": {},
141 | "outputs": [
142 | {
143 | "name": "stderr",
144 | "output_type": "stream",
145 | "text": [
146 | "ibmqfactory.load_account:WARNING:2020-07-30 23:29:04,209: Credentials are already in use. The existing account in the session will be replaced.\n"
147 | ]
148 | }
149 | ],
150 | "source": [
151 | "IBMQ.load_account()\n",
152 | "\n",
153 | "provider = IBMQ.get_provider(group='open', project='main')\n",
154 | "backend = provider.get_backend('ibmq_16_melbourne')\n",
155 | "job = execute(mcq, backend=backend)\n",
156 | "ans_quantum = job.result().get_counts()"
157 | ]
158 | },
159 | {
160 | "cell_type": "code",
161 | "execution_count": 18,
162 | "metadata": {},
163 | "outputs": [
164 | {
165 | "data": {
166 | "image/png": "iVBORw0KGgoAAAANSUhEUgAAAnYAAAE9CAYAAACGIy/LAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjMuMCwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy86wFpkAAAACXBIWXMAAAsTAAALEwEAmpwYAAA930lEQVR4nO3deXhV1dn38e9NQgZIAiFAIAmYQCBKwAAGEYsMj2IQK9ZKK1VLkQcRpVLFVq2iorWKQ33QoqXggCKvs1XqiKgQEcooUYgCQlASwgxCIHPW+8c5ScMQSCDJIYff57rOxdlrr73OvbM5cGfttdY25xwiIiIi0vA18nUAIiIiIlI7lNiJiIiI+AkldiIiIiJ+QomdiIiIiJ9QYiciIiLiJ5TYiYiIiPgJJXYiIiIifqLeEzszu8nMssyswMxWmNkFx6kfZGYPeI8pNLMfzWz8YXWuNLNM7/5MM7uibs9CRERE5NRTr4mdmV0FPAk8BPQAFgEfmln7Yxz2KjAYGAMkAb8Cvq7UZh/gNWA20N375xtm1rsOTkFERETklGX1+eQJM1sCfO2cu75S2XrgTefcn49S/2LgDaCjc25nFW2+BrRwzg2qVDYP2OGc+82x4mnZsqWLj48/oXMRERH/tGLFip3OuVaVtlsHBgY+C3RFQ5jEt8qA1SUlJaPPOeec7UerEFhfkZhZEHAO8Phhu+YC51dx2C+AZcAEMxsB5AMfAnc55/K8dfoAfz/suI+B3x8vpvj4eJYvX16t+EVE5PRgZj9U3g4MDHy2TZs2Z7Vq1WpPo0aN9BxO8ZmysjLbsWNHl61btz4LDD1anXpL7ICWQACw7bDybcBFVRzTAegLFAJXAs3xJHExwDBvnTZVtNnmaA2a2Rg8t3WJiYlh/vz5ng/q0IHw8HAyMjIAiIqKIjk5mfT0dAACAwPp27cvK1euZN++fQCkpqaybds2Nm/eDECnTp0IDg5m9erVALRu3ZrOnTuzcOFCAIKDg+nTpw/Lly8nL8+Tl/bu3Zvs7GxycnIASEpKIiAggMzMTM/JtWlDQkICixcvBiA0NJTevXuzZMkS8vPzAejTpw9ZWVls3boVgC5dulBaWsratWsBiI2NJS4ujiVLlgAQFhZGamoqixcvprCwEIC+ffuybt06tm/3/ALQtWtXCgsLWb9+PQDt2rUjOjq6IhGOiIigZ8+eLFy4kJKSEgD69evHmjVr2LVrFwApKSns37+fjRs3Ap5EukWLFqxcuRKAyMhIUlJSWLBgAc45zIz+/fuTkZHBnj17AOjZsye7d+9m06ZNuk66TrpOuk71cp2OoquSOjkVNGrUyLVq1eqnrVu3dq2qTr3dijWzGCAH6O+cS69Ufi9wjXMu6SjHzAUuANo4537yll2Mp0eujXNum5kVAaOdcy9VOm4EMMM5F3ysmFJTU5167EREpDIzW+GcSy3fzsjI2JSSknLU4UAivpCRkdEyJSUl/mj76nOswE6gFIg+rDwa2FrFMblATnlS5/Wt98/yCRdba9imiIiIiF+qt8TOOVcErAAGHbZrEJ7ZsUfzJRBjZmGVyjp7/ywfA7G4hm2KiIiI+KX6HGMH8AQwy8yW4knaxuIZLzcNwMxeAnDOjfDW/3/APcALZjYJzxi7J/HMoi2fDfIkkG5mdwLvAFcAA/GMzRMREal110/hnLpsf8YtrKhJ/aeeeipq6tSp0Zs3bw5u2rRp2eDBg/c8+eSTOVFRUaWV6/zhD3+Inz59+sbrr79+T+Xj77zzzjazZs1qtWfPnsDw8PDS1NTUvPfff38jwLnnnpu0bNmysEWLFmX26dMnv/yYQYMGdZw3b17zf//73+t+/vOf7z/Zc5baUa/Ttp1zrwG3ABOBVXiSryHOufLet/b89xYr3pmvFwHN8MyOfR1YAIyqVGcRMBwYiWd9uxHAVc65JXV6MiIiIqeA++67L/r++++Pe+ihh7L37t276ssvv/x28+bNQQMHDuxUWFho5fVmz54d1axZs9LZs2dHVT7+73//e9Trr78eNXfu3HUHDx78atmyZZkDBw7cV7nOGWecUfj8889XHLd169aAr776KiwyMrKk7s9QaqLe1+Nxzj3jnIt3zgU7586pPJHCOTfAOTfgsPprnXMXO+eaOOdinXPjnHP7D6vzpnPuTOdckHPuLOfc2/V0OiIiIj6ze/fuRo899ljMI4888uOwYcP2BQcHu6SkpKI5c+Zs3Lx5c/D06dNbAKxbty5o2bJl4VOmTNm0cOHCZj/++GPFHbtly5Y1HTBgwL7k5ORCgPbt25f88Y9/PGSyyLBhw3bNmTOnRfms7eeff75FWlransaNG2um8ClGCy2KiIg0UJ999llYUVFRo9/97neH3Fpt1qxZ2cCBA3/65JNPIgBmzJgRlZycfHDkyJF7O3TokP/cc89V9L6dd955eW+99VbUPffcE52ent6kPHmrLCYmpjgxMTH/7bffjgB45ZVXWl533XW76vj05AQosRMREWmgtm/fHti8efOSxo0bH7GvTZs2xbt27QoEeP3116N+9atf7QK48sord7/66qsVid1NN920e/LkyT9++umnzdLS0pJatmzZ/e677z5iLdhrrrlm16xZs6K++uqrkP379wdcdNFFB+rw1OQEKbETERFpoFq3bl2yd+/ewOLi4iP2bd26tXGLFi1K5s6d2zQnJyd45MiRuwGuu+663evXrw9dtGhRaHndG2+8cfeiRYvW7d27d9UTTzzxw6OPPhrz1ltvRVRu77e//e3eRYsWRfzf//1f6/IkUU49SuxEREQaqIEDBx5o3Lhx2YsvvhhZufynn35qNH/+/Gb9+/ff/8ILL7R0ztGzZ8/kli1bppx//vlnATz33HMtD28vODjYjRo1ak9SUlL+119/HVp5X3h4eNmAAQN+mj17dqvRo0crsTtF1fdyJyIiIlJLoqKiSm+77bYtd9xxR/vmzZuXXnbZZfs3bdrUeMyYMe0jIyNLxowZszs2Njbu8ccf/+HKK6/cW37c7NmzIx9//PGYadOmbf7HP/4R1bp165K0tLT9ERERZW+99VbE999/H3r++ecfcav1b3/7W86YMWN2JiUlFdXriUq1KbETERGpoZquM1eXHnzwwW1RUVGlf/7zn9tdc801wUVFRdarV6+8Tz/9dN2rr77aLCQkpOymm27aFRwcXDGD9eabb975yCOPxL755pvNmjVrVvroo4+2HTNmTEJZWZnFxMQUPvrooz+kpaXlHf5Z8fHxxfHx8Ufe95VTRr09K/ZUpGfFiojI4Rr6s2KffPLJqIcffjj2iy+++K5Tp07qWfNDx3pWrHrsRERE/Mgf/vCHXYGBge7zzz9vqsTu9KPETkRExM+MGzdut69jEN/QrFgRERERP6HETkRERMRPKLETERER8RNK7ERERET8hBI7ERERET+hxE5ERETETyixq2UPPvggQUFBNG7cmMGDBx+xf/To0TRq1IjQ0FBCQ0P53e9+V7Hv+uuvJygoiKCgIK6//vqK8ubNmxMUFFRxzJo1a+rlXERE5NSWmJiY/N5774VPmDAh5vLLL0/wdTynsrVr1waZ2TnFxZ4HZ5x77rlJTzzxxBHPy23otI5dLSoqKuL+++/nk08+ITU1lVatWjFnzhyGDh16SL2uXbvy9ddfH1K2YcMGZs6cyXfffUejRo3o3Lkzd911FwkJnu/ps88+y4gRI+rtXEREpGobkiadU5ftd1w7qVqPLPv+++/XAHz22WfhdRlPdSxbtizk1ltvbbdmzZome/fuDXTOHXEO06dPj5w8eXJMbm5uUMuWLYtnzJixafDgwUc8ukxOnHrsatHMmTNp1qwZAwYMICwsjH79+vH0009X69gpU6aQmJhIx44dSUhIIDExkSeeeKKOIxYREakdQUFB7sorr9zz97///Yej7f/Xv/4VMWnSpLgZM2ZsysvL+yo9PX1tUlJSYX3HWd/KewjrixK7WrR27VqioqIqthMSEsjNzT2i3po1awgNDSUuLo4lS5YAkJWVRWxsbEWdmJgYsrKyKrbHjBlDaGgoF154IWVlZXV4FiIi0lDExsZ2e+edd8IBCgsL7dJLL+3QtGnTHl26dDlr8eLFoZXr3XPPPdGdO3fuEhoa2uPXv/71GZs3bw7s169fp6ZNm/Y4//zzO+/YsSOgvP7TTz/dIiYmplvz5s2733HHHW0qf05VUlJSCm+99dad3bt3zz/a/gceeCDmT3/6U+6FF154ICAggISEhOKEhIRjZj3vvfdeeHR09NkTJ06MbtGiRUqrVq3OnjVrVvPXXnutWXx8fNdmzZp1v/POO9uU1y8tLeWuu+5q065du67NmzfvPmTIkA7btm0LqKr9DRs2BHfr1u2ssLCwHhdeeGHHynVnz57dLDExMTk8PLz7ueeem7Ry5cqQ8n1mds7q1auDy7evvPLK+PHjx8dUjvnuu+9u07Jly5Rf/epXCRMmTIgZMmRIhyuuuCK+adOmPRITE5PT09OblB+/adOmxmlpaR0jIyNTYmNjuz344IOtj/VzORYldvXsjjvuYM+ePeTn59O/f/+jjsM73Lx58ygoKGDDhg2sWrWKsWPH1kOkIiLSkMybN6/5sGHD9uzevXvVsGHDdg8bNiyxsLDQyvfPmTMn8tNPP12XmZm5et68ec3T0tI6Pfzww9k7duxYVVZWxuTJk1sDrFixIuRPf/rTGc8991xWbm5uxq5duwK3bdsWdDKxlZSUsHr16iY7duwIbN++fdfo6OizR4wY0T4vL8+Od+yuXbsaFxQUNMrNzf36zjvv3DJ+/PgzXn755RZfffVV5qeffvrdlClTYr777rsggIceeqj1+++/33z+/Plrc3NzM5o3b146evTo9lW1/cYbb0Q9//zzWVu2bMkIDAxkzJgx7QG+/vrr4NGjR3d47LHHNu/cuTPj4osv3vuLX/wisaCg4Ljxlse8e/fugM2bN3/98ssvbwL49NNPmw8fPnzPTz/99FVaWtrem2++uT14ktFLL700sVu3bgdzc3O//uSTT9ZOmzYt+q233oqozmcdToldLUpKSmLXrl0V21lZWbRt2/aQOp06dSIiwnOtXnjhBfbu3Qt4evdycnIq6m3ZsqVifF1qairg6cW74oor+M9//lOXpyFy0o43iajcn/70J8yMl156CYC8vDw6depESEgIoaGhTJkypaKuJhGJHFtycvLB6667bk9wcLC77777thUVFdnnn3/etHz/2LFjt7dr164kISGhuFevXnk9evQ48LOf/Sy/SZMm7rLLLtubkZHRBOCVV16J/J//+Z+fLrnkkrzQ0FD3xBNPbDEzdzKxZWdnNy4pKbE5c+ZEfvHFF2tXrVqVuXr16iZ//vOfY453bGBgoJs8eXJucHCwGzVq1O69e/cG3nrrrdsjIyPLUlNTCzp27Ji/bNmyJgAvvPBCqwceeCCnY8eOxaGhoe7hhx/e8uGHH0ZWdTt02LBhu3r16lUQERFR9tBDD+V88MEHkSUlJcyaNavFwIEDf7riiiv2BQcHu/vvv39bQUFBo3nz5oVV53zNzP3tb3/bEhoa6sLCwhzAOeeck3fVVVf9FBgYyKhRo3atXbu2CcCCBQua7t69O/Dxxx/PDQkJcV26dCn67W9/u+OVV15pUe0fcCVK7GrRiBEj+Omnn0hPTycvL4/09HRuuummQ+qsWrWq4v0999xD06ae79wtt9zC999/T1ZWFllZWXz//ffccsstFBQUsHbtWgAOHjzIRx99RNeuXevtnERqqnwS0dy5c9mzZw8LFixgzpw5R9TbsmUL06dPr/gOAIwaNQqAgoICli9fzl133UVJSUnF/meffZb8/Hzy8/NJTk6u+5MRaUBiYmKKyt8HBAQQHR1dvHnz5sblZW3btq3IbkJCQsqio6MrvlyhoaFlBw8eDADYsmVL49jY2Iq2IiIiypo3b/7fL+IJaNq0aRnADTfcsP2MM84obtu2bcn48eO3zps3r9nxjm3WrFlJYKBnrmdYWFgZQGxs7CHnsn///kYAubm5Qddcc01ieHh49/Dw8O5du3ZNDggIIDs7u/HR2m7Xrl3FeXbq1KmopKTEcnNzA7ds2dK48r6AgADatm1bVPnneSyRkZElTZo0OSQZbtWqVUXMYWFhZYWFhVZcXMzGjRuDduzYEVQec3h4ePennnqq7Y4dO05ogqsSu1oUEhLCxIkTueiii4iMjKRv375cfvnl9OvXj7vvvhuAG2+8saI3Yvr06bz++usAdOzYkWuvvZbOnTvTuXNnfvvb39KxY0f27dtHjx49CA0NpUWLFrRs2ZKZM2f68CxFjq26k4guvfRSbr31Vsr/wQb49ttvufDCCwFITk4mJCSEWbNm1VvsIg3Zli1bKm6XlpaWsm3btsbt2rWr8cj9tm3bFufk5FS0tX///kZ79+49qVU0WrVqVRodHV1s9t87mZXf15bo6Ojit99+e93+/ftXlb8KCwtXVjWWb/PmzRXn+f333wcFBga6tm3blsTExBRX3ldWVkZubm5Q+c8zJCSk7MCBAxU51Pbt2w9J+GpybvHx8UWxsbGFlWM+cODAVwsWLPi+BqdeQYldLbvvvvsoKiqiuLiYTz75BID09HT++te/ArB48WIKCgrIz89nz549DBkypOLYF154geLiYoqLi3n++ecBaN26NQcPHiQ/P5+CggJWrVpFUNBJDXUQqVPVmUQ0e/Zstm/fzqRJkw4pT0lJ4b333qOgoID09HT27NlDZmZmxX5NIhKp2po1a5q8+OKLzYuLi/nLX/4SHRQU5AYOHHigpu385je/2fPZZ581+/jjj8MKCgrstttui3HOHTdTKSsr4+DBg1Y+ru/gwYOWn59fcdzw4cN3Tps2rXVOTk7gjh07Ap566qnoiy++eG9N4zuW6667bvvEiRPj1q1bFwSwZcuWwJdffrl5VfXfeuutqBUrVoTs37+/0d133x0zePDgPYGBgVx77bW7P//882bvvvtueGFhoU2aNCk6KCjIXXTRRXkAZ511Vv6LL77YoqSkhDfffDNi2bJlJ7zczIABAw40bdq09O67726Tl5dnJSUlLFu2LGTBggVNjn/0kbSOnYjUq5KSEsaNG8d77713xL5nn32W888/n8jISJo3b06rVq0qevTmzZtHamoqW7ZsoVu3bowdO5bp06fXd/giQPXXmatPF1100d7XX3+9xU033ZTQvn37wtdee21DcHBwjcfGpaamFjzyyCM/jhw5MiE/Pz/ghhtu2BodHV10vOPWr18fdOaZZ3Yr327atGnPmJiYopycnG8AHnnkkdz//d//DTzzzDO7BgcHu5///Oe7H3744SOXjjgJEydO3O6cs4svvrjzjh07Grdo0aL48ssv33PttdfuPVr9YcOG7Ro5cmRCVlZWyLnnnrv/+eef3wSeGb7//Oc/syZMmND+2muvbXzmmWfmv/POO+tDQkIcwJQpU34cNWpUQrNmzVoPGjRo76BBg/acaMyBgYF88MEH3998881x8fHxZxcVFVlCQkLB/fffn3P8o49kzp3UeMgGLTU11S1fvtzXYYj4lenTp3PXXXexc+dOANLS0gD4+OOPAfjxxx+Jj4+nUSPPDYPS0lIaNWrECy+8cMQi3OHh4cyePfuIRb5Hjx7N0qVLj1joW6Q2mNkK51xq+XZGRsamlJSUnb6MyddiY2O7Pf3005t+8Ytf7Pd1LAIZGRktU1JS4o+2T7diRaRWHW8SUfv27SkrK6OkpISSkhKaNWtWkdTt3LmT7du3AzB58mQaNWrE0KFDNYlIRKSalNiJSK2qziSiqnz33XfExcURHBzMo48+ygcffACgSUQip4h+/fp1atKkSY/DX5UXCa6pO++8s83R2uzXr1+n2oz9dKFbsboVKyIilehWrJzqdCtWRERE5DSgxE5EROTYysrKymp/0TWRE+D9u1jlek9K7ERERI5t9Y4dO5opuRNfKysrsx07djQDVldVR+vYiYiIHENJScnorVu3Prt169auqENEfKsMWF1SUjK6qgpK7ERERI7hnHPO2Q4MPW5FkVOAfvMQERER8RNK7ERERET8hG7F1oLrp/j282fc4tvPFxERkVODeuxERERE/IQSOxERERE/ocRORERExE9ojJ2I1AqNNRUR8T312ImIiIj4CSV2IiIiIn5CiZ2IiIiIn1BiJyIiIuInlNiJiIiI+AkldiIiIiJ+QomdiIiIiJ9QYiciIiLiJ5TYiYiIiPgJJXYiIiIifkKJnYiIiIifUGInIiIi4ieU2ImIiIj4CSV2IiIiIn5CiZ2IiIiIn6j3xM7MbjKzLDMrMLMVZnZBNY/ra2YlZrb6sPKRZuaO8gqpmzMQEREROTXVa2JnZlcBTwIPAT2ARcCHZtb+OMdFAi8Bn1ZR5SDQtvLLOVdQW3GLiIiINAT13WM3AZjpnJvhnPvWOXczkAvceJzjngNeBBZXsd8557ZWftVizCIiIiINQr0ldmYWBJwDzD1s11zg/GMcdxMQDTx4jOZDzewHM8s2s/fMrMdJBywiIiLSwATW42e1BAKAbYeVbwMuOtoBZtYNuA84zzlXamZHq7YWGAVkAOHAH4AvzSzFObf+KG2OAcYAxMTEMH/+fAA6dOhAeHg4GRkZAERFRZGcnEx6ejoAgYGB9O3bl5UrV7Jv3z4AUlNT2bZtG9Cxuj+DOlFYWEhWVhZbt3o6Krt06UJpaSlr164FIDY2lri4OJYsWQJAWFgYqampLF68mMLCQgD69u3LunXr2L59OwBdu3alsLCQ9es9P8J27doRHR3N8uXLAYiIiKBnz54sXLiQkpISAPr168eaNWvYtWsXACkpKezfv5+NGzcCEB8fT4sWLVi5ciUAkZGRpKSksGDBApxzmBn9+/cnIyODPXv2ANCzZ092797Npk2bgJO7Tps3bwagU6dOBAcHs3q1Z7hm69at6dy5MwsXLgQgODiYPn36sHz5cvLy8gDo3bs32dnZ5OTkAJCUlERAQACZmZkAtGnThoSEBBYv9nQqh4aG0rt3b5YsWUJ+fj4Affr08evrBBFH++tZb+bPn6/rpO9TrVwnkYbMnHP180FmMUAO0N85l16p/F7gGudc0mH1g4GvgIedc7O8ZZOAYc65rsf4nABgFfC5c278sWJKTU115f+wnozrp5x0Eydlxi2+/XwR0PdA/IeZrXDOpfo6DpETUZ89djuBUjy3VSuLBo42Jq4tcBbwgpm94C1rBJiZlQBDnHOH39bF27O3HOhUa5GLiIiINAD1NsbOOVcErAAGHbZrEJ7ZsYfLAboB3Su9pgHfe98f7RjMc7/2bDyTMkREREROG/XZYwfwBDDLzJYCXwJjgRg8CRtm9hKAc26Ec64YOHzNuu1AoXNudaWy+4D/AOvxDPIZjyexO95MWxERERG/Uq+JnXPuNTOLAibiudW6Gs8t1R+8VY65nl0VmgPTgTbAT3jG5fVzzi09+YhFREREGo767rHDOfcM8EwV+wYc59hJwKTDym4Fbq2d6EREREQaLj0rVkRERMRPKLETERER8RNK7ERERET8hBI7ERERET+hxE5ERETETyixExEREfETSuxERERE/IQSOxERERE/ocRORERExE8osRMRERHxE0rsRERERPyEEjsRERERP6HETkRERMRPKLETERER8RNK7ERERET8hBI7ERERET+hxM4PffTRRyQlJZGYmMjkyZOP2D9t2jS6detG9+7d6du3L5mZmRX7vv76a/r06UNycjLdunWjoKAAgBUrVtCtWzcSExMZP348zrl6Ox8RERGpHiV2fqa0tJRx48bx4YcfkpmZySuvvHJI4gZw9dVX880337Bq1Spuv/12JkyYAEBJSQnXXnst06ZNY82aNcyfP5/GjRsDcOONNzJjxgzWr1/P+vXr+eijj+r93EREROTYlNj5maVLl5KYmEiHDh0ICgpi+PDhvPvuu4fUiYiIqHh/4MABzAyAuXPncvbZZ5OSkgJAVFQUAQEB5Obmsm/fPs477zzMjBEjRvDOO+/U2zmJiIhI9Six8zM5OTm0a9euYjsuLo6cnJwj6j399NN07NiR22+/naeeegqAdevWYWakpaXRs2dPHn300Yo24+LijtumiIiI+FaNEjsza2RmjSpttzGz0Wb2s9oPTerSuHHj2LBhA4888ggPPvgg4LkVu3DhQmbPns3ChQv517/+xaeffurjSEVERKS6atpj9z5wM4CZhQHLgceA+WY2opZjkxMQGxvL5s2bK7azs7OJjY2tsv7w4cMrbqvGxcXRr18/WrZsSZMmTRgyZAgrV64kNjaW7OzsarcpIiIivlHTxC4V+Mz7/pfAPqA1cD3wx1qMS05Qr169WL9+PVlZWRQVFfHqq68ydOjQQ+qsX7++4v37779Pp06dAEhLS+Obb77h4MGDlJSUsGDBArp06ULbtm2JiIjgP//5D845XnrpJS6//PJ6PS8RERE5vsAa1g8D9nrfXwz8yzlXbGafAU/XZmByYgIDA5k6dSppaWmUlpYyatQokpOTuffee0lNTWXo0KFMnTqVefPm0bhxYyIjI3nxxRcBiIyMZMKECfTq1QszY8iQIVx66aUAPPPMM4wcOZL8/HwuueQSLrnkEl+epoiIiByF1WQ9MjNbC9wH/BvYBPzKOTffzLoDnzjnWtVFkHUlNTXVLV++/KTbuX7KycdyMmbc4tvPFwF9D8R/mNkK51yqr+MQORE17bF7ApgF5AE/AOne8n7AN7UYl4iIiIjUUI0SO+fcP81sBdAOTw9dmXfXBuCe2g5ORERERKqvpj12OOeW45kNW7ns/VqLSEREREROSI0XKDazm8xsjZkdNLMO3rI7zOzXtR+eiIiIiFRXTRcovgWYCEwHrNKuLcDvay8sEREREampmvbYjQWud849CZRUKl8JJNdaVCIiIiJSYzVN7M4AVh+lvBgIPflwRERERORE1TSx2wj0PEr5ECDz5MMRERERkRNV01mxjwNTzawJnjF2fczst8DtwKjaDk5EREREqq+m69i9YGaBwENAEzyLFW8BxjvnXquD+KQaNiRN8nUIdFzr+xhEREROdyeyjt0MYIaZtQQaOee2135YIiIiIlJTNU7syjnndtZmICIiIiJyco6b2JnZ10B/59weM/sGcFXVdc6dXZvBiYiIiEj1VWdW7FtAYaX3x3qJiPjcRx99RFJSEomJiUyePPmI/dOmTaNbt250796dvn37kpnpmdS/a9cuBg4cSFhYGL///aFrrg8ePJiUlBSSk5MZO3YspaWl9XIuIiI1cdweO+fc/ZXeT6rTaERETlJpaSnjxo3jk08+IS4ujl69ejF06FC6dOlSUefqq69m7NixAMyZM4cJEybw0UcfERISwl/+8hdWr17N6tWHLtn5+uuvExERgXOOYcOG8cYbbzB8+PB6PTcRkeOp6SPFPjOz5kcpjzCzz2otKhGRE7R06VISExPp0KEDQUFBDB8+nHffffeQOhERERXvDxw4gJnnCYlNmzalb9++hISEHNFu+TElJSUUFRVVHCMiciqp6QLFA4Cgo5SHABecdDQiIicpJyeHdu3aVWzHxcWRk5NzRL2nn36ajh07cvvtt/PUU09Vq+20tDRat25NeHg4w4YNq7WYRURqS7USOzPraWblT5w4u3zb++oFjAGO/JdTROQUNW7cODZs2MAjjzzCgw8+WK1jPv74Y3JzcyksLOSzz3STQkROPdVd7mQ5ntmwDph7lP35wM21FZSIyImKjY1l8+bNFdvZ2dnExsZWWX/48OHceOON1W4/JCSEyy+/nHfffZdBgwadVKwiIrWturdiE4COeB4jdq53u/wVC0Q4556vkwhFRGqgV69erF+/nqysLIqKinj11VcZOnToIXXWr19f8f7999+nU6dOx2wzLy+P3NxcwDPG7v333+fMM8+s/eBFRE5StXrsnHM/eN/WdEyeiEi9CgwMZOrUqaSlpVFaWsqoUaNITk7m3nvvJTU1laFDhzJ16lTmzZtH48aNiYyM5MUXX6w4Pj4+nn379lFUVMQ777zD3LlziYqKYujQoRQWFlJWVsbAgQMrZtWKiJxKqrNA8S+Bfzvnir3vq+Sce7vWIhMROUFDhgxhyJAhh5Q98MADFe+ffPLJKo/dtGnTUcuXLVtWK7GJiNSl6vTYvQm0AbZ731fFAQG1EZSIiIiI1Fx1FihudLT3IiIiInJqUaImIiIi4ieqO8auWjTGTkRERMR3qjvGrjo0xk5ERETEh2o0xk5ERERETl1K2kRERET8hNaxExEREfETWsdORPzChqRJPv38jmt9+/kiIqB17ERERET8Rr0namZ2k5llmVmBma0wswuOUbe/mS0ys11mlm9m35nZH49S70ozyzSzQu+fV9TtWYiIiIicemqc2JlZTzN7ycyWe1+zzKxnNY+9CngSeAjoASwCPjSz9lUckgc8BfQDugAPAveb2U2V2uwDvAbMBrp7/3zDzHrX9NxEREREGrIaJXZmdg2wDGgLfOB9RQNLzezaajQxAZjpnJvhnPvWOXczkAvceLTKzrkVzrlXnXNrnHNZzrmXgY+Byr18twCfO+f+6m3zr8B8b7mIiIjIaaOmPXZ/Be5xzg1yzt3rfV0M3IOnN61KZhYEnAPMPWzXXOD86ny4mfXw1l1QqbjPUdr8uLptioiIiPiL6syKrawV8PpRyt/Ak9wdS0s8s2a3HVa+DbjoWAeaWbb3swOB+51z0yrtblNFm22qaGsMMAYgJiaG+fPnA9ChQwfCw8PJyMgAICoqiuTkZNLT0wEIDAykb9++rFy5kn379gGQmprKtm3bgI7HCv+0MH/+fPr168eaNWvYtWsXACkpKezfv5+NGzcCEB8fT4sWLVi5ciUAkZGRpKSksGDBApxzmBn9+/cnIyODPXv2ANCzZ092797Npk2bgJO7Tps3bwagU6dOBAcHs3r1agBat25N586dWbhwIQDBwcH06dOH5cuXk5eXB0Dv3r3Jzs4mJycHgKSkJAICAsjMzASgTZs2JCQksHjxYgBCQ0Pp3bs3S5YsIT8/H4A+ffqQlZXF1q1bAejSpQulpaWsXbsWgNjYWOLi4liyZAkAYWFhpKamsnjxYgoLCwHo27cv69atY/v27QB07dqVwsJC1q9fD0C7du2Ijo5m+fLlAERERNCzZ08WLlxISUkJQJ1dJ4ioyV8Zv9NQrpO+T8e/TiINmTnnql/Z7D3gHefcs4eVjwaudM5dcoxjY4AcoL9zLr1S+b3ANc65pGMcmwCEAecBjwB/cM7N8u4rAkY7516qVH8EMMM5F3ys80lNTXXl/7CejOunnHQTJ+XOf0zybQBoqQfR90DfAf9hZiucc6m+jkPkRFR3geJyHwIPm1kq8B9v2XnAL4FJx2lqJ1CKZ0xeZdHA1mMd6JzL8r79xsyivZ81y1u29UTaFBEREfE31V2g+HAVtzMr+TvwTFWNOOeKzGwFMAjPrdtyg4C3qhFHuUZA5Z64xd42HjuszUU1aFNERESkwavRAsW14AlglpktBb4ExgIxwDQAM3vJ+5kjvNs3A1nAWu/x/YA/cmgC+SSQbmZ3Au8AVwADgb61GLeIiIjIKa+mkydOinPuNTOLAibiWTJlNTDEOfeDt8rh69kF4BlTFw+UABuAO/Emgt42F5nZcDyzch/w1rnKObekDk9FRERE5JRT48TOzCKBS/AkYUGV9znnHjje8c65Z6jilq1zbsBh21OAKdVo802O/RxbEREREb9Xo8TOzM4D3gcK8Sw/koOn560Q2ISnx0xEREREfKCm4+cew/PIrligAPgfPD13y/HcMhURERERH6lpYnc2MNV5Fr8rBYKdc9uAOzj+ciciIiIiUodqmtgVVXq/DTjD+z4Pz+xWEREREfGRmk6eWAn0AtYB84EHvQsGXwt8XbuhiYiIiEhN1LTH7m5gi/f9RGAHnoWJIzlywWIRERERqUc16rFzzi2v9H4HnmVPREREROQUcEILFJtZR+As72amc25j7YUkIiIiIieipuvYRQHPAUOBsv8W23vAKOfcrlqOT0RERESqqaZj7J4FEoELgBDvqx+QAMyo3dBEREREpCZqeis2DbjQObe4UtmXZnYDMK/2whIRERGRmqppj90O4MBRyg8Cug0rIiIi4kM1TeweAKaYWWx5gff939BzYkVERER86ri3Ys3sG8BVKkoANplZjne7/LmxrfGMwRMRERERH6jOGLs36zwKERERETlpx03snHP310cgIiIiInJyTnSB4v8BuuC5RbvGOTe/NoMSERERkZqr6QLFscC/gHP47zNjY8xsOXCFc25LlQeLiIiISJ2q6azYp4BSINE518451w7o5C17qraDExEREZHqq+mt2EHAAOdcVnmBc26jmY0HPq3VyERERESkRmraYweHLn1yrDIRERERqUc1Tew+Bf5uZu3KC8ysPTAF9diJiIiI+FRNE7vxQFNgo5n9YGY/ABu8ZeNrOzgRERERqb6ajrHbBZwLDADO9JZ965ybV5tBiYiIiEjNVTuxM7MA4CcgxTn3CfBJnUUlIiIiIjVW7VuxzrlS4AcgqO7CEREREZETVdMxdn8BJptZy7oIRkREREROXE3H2P0RSAByzCwbOFB5p3Pu7NoKTERERERqpqaJ3Zt41qyzOohFRERERE5CtRI7M2sCPAb8AmiMZ826m51zO+suNBERERGpieqOsbsfGAm8D7wCXAT8o45iEhEREZETUN1bsb8E/tc59yqAmc0GvjSzAO9sWRERERHxser22LUDvijfcM4tBUqAmLoISqSh++ijj0hKSiIxMZHJkycfsT89PZ2ePXsSGBjIm2++eci+22+/neTkZM466yzGjx+Pc55HMQ8ePJiUlBSSk5MZO3YspaX6nUpERA5V3cQuACg6rKyEmk++EPF7paWljBs3jg8//JDMzExeeeUVMjMzD6nTvn17Zs6cydVXX31I+aJFi/jyyy/5+uuvWb16NcuWLWPBggUAvP7662RkZLB69Wp27NjBG2+8UW/nJCIiDUN1EzMDXjazwkplIcAMMztYXuCcG1qbwYk0REuXLiUxMZEOHToAMHz4cN599126dOlSUSc+Ph6ARo0O/d3KzCgoKKCoqAjnHMXFxURHRwMQEREBQElJCUVFRZhpcrqIiByquj12LwJb8Dwrtvz1MrD5sDKR015OTg7t2rWr2I6LiyMnJ6dax/bp04eBAwfStm1b2rZtS1paGmeddVbF/rS0NFq3bk14eDjDhg2r9dhFRKRhq1aPnXPuuroORETg+++/59tvvyU7OxuAQYMG8cUXX3DBBRcA8PHHH1NQUMA111zDZ599xqBBg3wZroiInGJq+kgxETmO2NhYNm/eXLGdnZ1NbGxstY7917/+xXnnnUdYWBhhYWFccsklLF68+JA6ISEhXH755bz77ru1GreIiDR8SuxEalmvXr1Yv349WVlZFBUV8eqrrzJ0aPWGn7Zv354FCxZQUlJCcXExCxYs4KyzziIvL4/c3FzAM8bu/fff58wzz6zL0xARkQZIiZ1ILQsMDGTq1KkV4+N+/etfk5yczL333sucOXMAWLZsGXFxcbzxxhvccMMNJCcnAzBs2DA6duxIt27dSElJISUlhcsuu4wDBw4wdOhQzj77bLp3707r1q0ZO3asL09TREROQVquRKQODBkyhCFDhhxS9sADD1S879WrV8U4usoCAgL45z//eUR5dHQ0y5Ytq/1ARUTEr6jHTkRERMRPKLETERER8RNK7ERERET8hBI7ERERET+hyRMitWBD0iSffn7Htb79fBEROTWox05ERETETyixExEREfETSuxERERE/IQSOxERERE/ocRORERq3UcffURSUhKJiYlMnjz5iP3p6en07NmTwMBA3nzzzSP279u3j7i4OH7/+98fsW/o0KF07dq1TuIWaeiU2ImISK0qLS1l3LhxfPjhh2RmZvLKK6+QmZl5SJ327dszc+ZMrr766qO2cc8999CvX78jyt9++23CwsLqJG4Rf6DETkREatXSpUtJTEykQ4cOBAUFMXz4cN59991D6sTHx3P22WfTqNGR/w2tWLGCbdu2cfHFFx9SnpeXxxNPPMHEiRPrNH6RhkyJnYiI1KqcnBzatWtXsR0XF0dOTk61ji0rK+O2227j8ccfP2LfPffcw2233UaTJk1qLVYRf6PETkREThnPPPMMQ4YMIS4u7pDyVatWsWHDBq644gofRSbSMOjJEyIiUqtiY2PZvHlzxXZ2djaxsbHVOnbx4sV88cUXPPPMM+Tl5VFUVERYWBhnnHEGy5cvJz4+npKSErZv386AAQOYP39+HZ2FSMNU7z12ZnaTmWWZWYGZrTCzC45Rt62Z/T8z+87MSs1s5lHqjDQzd5RXSJ2eiIiIHFWvXr1Yv349WVlZFBUV8eqrrzJ06NBqHTt79mx+/PFHNm3axOOPP86IESOYPHkyN954I1u2bGHTpk0sXLiQzp07K6kTOYp6TezM7CrgSeAhoAewCPjQzNpXcUgwsBOYDCw5RtMHgbaVX865gtqKW0REqi8wMJCpU6eSlpbGWWedxa9//WuSk5O59957mTNnDgDLli0jLi6ON954gxtuuIHk5GQfRy3iH+r7VuwEYKZzboZ3+2YzGwzcCPz58MrOuU3AeAAzG3aMdp1zbmstxyoiIidoyJAhDBky5JCyBx54oOJ9r169yM7OPmYbI0eOZOTIkUeUx8fHs3r16lqJU8Tf1FuPnZkFAecAcw/bNRc4/ySbDzWzH8ws28zeM7MeJ9meiIiISINTnz12LYEAYNth5duAi06i3bXAKCADCAf+AHxpZinOufWHVzazMcAYgJiYmIoxGh06dCA8PJyMjAwAoqKiSE5OJj09HfDcWujbty8rV65k3759AKSmprJt2zag40mE7x/mz59Pv379WLNmDbt27QIgJSWF/fv3s3HjRsDzW3aLFi1YuXIlAJGRkaSkpLBgwQKcc5gZ/fv3JyMjgz179gDQs2dPdu/ezaZNm4CTu07lg7k7depEcHBwxW/8rVu3pnPnzixcuBCA4OBg+vTpw/Lly8nLywOgd+/eZGdnVyzZkJSUREBAQMWiq/9d2ME3yv8et2vXjujoaJYvXw5AREQEPXv2ZOHChZSUlADU2XWCiHo841PP4sWLKSwsBKBv376sW7eO7du3A9C1a1cKCwtZv97zT5Ivr1ND+D61adOGhIQEFi9eDEBoaCi9e/dmyZIl5OfnA9CnTx+ysrLYutVzs6ZLly6Ulpaydu1awDOBIy4ujiVLPKN4wsLCSE1NrdZ1EmnIzDlXPx9kFgPkAP2dc+mVyu8FrnHOJR3n+PeAnc65kcepFwCsAj53zo0/Vt3U1FRX/g/rybh+ykk3cVLu/Mck3wYAdFzr+xh8aUPSJJ9+/qnw8z/dvwenwjWQ2mFmK5xzqb6OQ+RE1OfkiZ1AKRB9WHk0UGvj45xzpcByoFNttSkiIiLSENTbrVjnXJGZrQAGAW9U2jUIeKu2PsfMDDgbz61ZERGpJ+q5FvG9+p4V+wQwy8yWAl8CY4EYYBqAmb0E4JwbUX6AmXX3vo0AyrzbRc65TO/++4D/AOu9dcbjSexurPvTERERETl11Gti55x7zcyigIl41ptbDQxxzv3grXK09ey+Omz7MuAHIN673RyYDrQBfvLW7+ecW1qrwYuIiIic4ur9kWLOuWeAZ6rYN+AoZXac9m4Fbq2V4EREREQasHp/pJiIiIiI1A0ldiIiIiJ+QomdiIiIiJ9QYiciIiLiJ5TYiYiIiPgJJXYiIiIifkKJnYiIiIifUGInIiIi4ieU2ImIiIj4CSV2IiIiIn5CiZ2IiIiIn1BiJyIiIuInlNiJiIiI+AkldiIiIiJ+QomdiIiIiJ9QYiciIiLiJ5TYiYiIiPgJJXYiIiIifkKJnYiIiIifUGInIiIi4ieU2ImIiIj4CSV2IiIiIn5CiZ2IiIiIn1BiJyIiIuInlNiJiIiI+AkldiIiIiJ+QomdiIiIiJ9QYiciIiLiJ5TYiYiIiPgJJXYiIiIifkKJnYiIiIifUGInIiIi4ieU2ImIiIj4CSV2IiIiIn5CiZ2IiIiIn1BiJyIiIuInlNiJiIiI+AkldiIiIiJ+QomdiIiIiJ9QYiciIiLiJ5TYiYiIiPgJJXYiIiIifkKJnYiIiIifUGInIiIi4ieU2ImIiIj4CSV2IiIiIn5CiZ2IiIiIn1BiJyIiIuInlNiJiIiI+AkldiIiIiJ+QomdiIiIiJ9QYientQcffJCgoCAaN27M4MGDfR2OiE/oeyDiP5TYyWmrqKiI+++/n7lz57Jnzx4WLFjAnDlzfB2WSL3S90DEvyixk9PWzJkzadasGQMGDCAsLIx+/frx9NNP+zoskXql74GIf1FiJ6ettWvXEhUVVbGdkJBAbm6uDyMSqX/6Hoj4FyV2IiIiIn6i3hM7M7vJzLLMrMDMVpjZBcep399br8DMNprZ2JNtUwQgKSmJXbt2VWxnZWXRtm1bH0YkUv/0PRDxL/Wa2JnZVcCTwENAD2AR8KGZta+ifgLwgbdeD+Bh4O9mduWJtilSbsSIEfz000+kp6eTl5dHeno6N910k6/DEqlX+h6I+Jf67rGbAMx0zs1wzn3rnLsZyAVurKL+WGCLc+5mb/0ZwIvAH0+iTREAQkJCmDhxIhdddBGRkZH07duXyy+/3NdhidQrfQ9E/Eu9JXZmFgScA8w9bNdc4PwqDutzlPofA6lm1vgE2xSpcN9991FUVERxcTGffPKJr8MR8Ql9D0T8R2A9flZLIADYdlj5NuCiKo5pA8w7Sv1Ab3tW0zbNbAwwxruZZ2ZrqxP8qexZz89ip0+DsPt9+vGnAN9eA/38ff890DUA/7kGZ9RWQyL1rT4Tu1OCc246MN3XcdQmM1vunEv1dRynM10D39M18D1dAxHfq8/EbidQCkQfVh4NbK3imK1V1C/xtmcn0KaIiIiIX6q3MXbOuSJgBTDosF2D8MxkPZrFVdRf7pwrPsE2RURERPxSfd+KfQKYZWZLgS/xzHqNAaYBmNlLAM65Ed7604Dfm9kU4J/Az4CRwG+q2+Zpwq9uLTdQuga+p2vge7oGIj5mzrn6/UCzm4DbgbbAauBW51y6d998AOfcgEr1+wP/ByQDW4BHnHPTqtumiIiIyOmi3hM7EREREakbelasiIiIiJ9QYiciIiLiJ5TYiYiIiPgJJXYi0qCZmVX+U0TkdKbJEw2UmcUBiXgWaS4D1jrntCiznPbKEzynf9xE5DSkxK4BMrMbgVFACnAA+B7IBv4DvOOcW2tmjZxzZT4M06+ZWahzLt/XcZzOzKwRcDnQCmgC5AALnHPbfRqYiIgPKbFrYMwsCk8i9zfgH3j+U7sIGACchSfBu9U5l2lmpl6L2mdmkUAG8D7wMrCo/Odc+WduZmcCW5xz+3wWrJ8ys3DgOWAgnh7rbMABBcACYJZz7jt9B+qOmTUGEoAfnHOFvo5HRDw0xq7huRpY55x70Dm3yzn3nXNuqnNuGHADnp6L98yspf5DqzPX4nke8TlAOvC9mT1gZkmVkrp2wCtAS9+F6dfGA0nAEOdcNHANMAX4BrgYeNTMWuk7UKfGAV8B08zsMjNrY2YBlSuYWYSZXeJNAkWkHiixa3iKgHAz6wpgZsFmFgTgnFuI5z+4Ajz/uUndOBt4Afg50AN4Hc9j7jLN7D9mNgZP8tfJObfRd2H6tcHAi865ZQDeX3BeBn4P3Ian93qWD+M7HVwFLMUz1vcdPM/2fszM+ppZM2+dq4H7nHPFvglR5PSjxK7heRPPradbzCzcOVfonCvyjjfCOfcjsBeI82GMfsvMgoFMYLNzbrtz7mvn3J+BVCDNu28S8FfgEZ8F6sfMLBDPowOvNLNW3rIA77jSUu/jBMcCcWaW4stY/ZX3514MzHDOXQCcgefW+M/x9GJ/ZmZ3ALcAS3wVp8jpSGPsGpBKyzlcDjwJtMDTW/QMnlsicUA/PGPvujnnNvkgTL/nTe4inXNbvbeeXOWJKmY2APgMaO+cy/ZNlP7NzM4DZuP5RecJ59y2w/a3A74FkpxzOT4I0a+ZWVtgOJDpnPv4sH09gNHe/ZFAO10DkfqjxK4BMrPmQHvgfOAK4GfeXVvxLH8yyzk3ySfB+bnywfhm1gE4UDmhqLTvXmCkc66D7yL1X97e6UbAdcBDQCDwFvAa8COeW+U/B7o453r5Kk5/Z2aheH6pKai8hmClcaZ/xTMGsoevYhQ5HSmxayDMrDXwWzzjh3YC+XhuuS7Es8xJYzxjXT5yzq3zUZh+rdI1mABsB0qAXOAN4G3n3AHvf3DX45kN+57Pgj1NeH/JGYlnLFd3YD+eMabLgIedc7oNWIeqmnVsZk2AlcALzjkNSRCpR0rsGggzmwkkA/8GduO5DdsN6IwnyZio/8TqVhXXoAdwJp7lNh5zzs31WYCnATOLAPZXTia8PXghQBjQFU9Pqr4LdeRo1+AodULwTK54xTlXVG/BiYgSu4bA2wu0H89tjfRKZe2B3njGs3QAfu2cW+mzQP3YMa5BHHAenl66M4Df6BrUHTP7J56ZmEvxrJ92xBqBZhbpnNujNezqRjWvQXPn3N76jk1ENCu2oegCZOFZ6gTwjGNxzv3gnHsduAzPbdlf+Sa800JV12Czc+4NPGO69qNrUGfM7Dd4Eui/Ae/iWVrjl2aW6B3vhZmFAS+YWTcldbWvimtwhZl1rHQNQoEXy5dkEpH6pR67BsD7D+V7eBYfHgFsOPxxYWZ2M/C/zrnu9R+h/9M18D0zmwGUAo8CvwR+B3QE1gIfAJ/iWbT4SedckK/i9Ge6BiKnPvXYNQDeZ5LeDYQCLwEjzKydt3eifKByfzxre0kd0DXwLe/adVnAXufcRufc4865bkAvPI8Q+x2epX/+jhYmrhO6BiINg3rsGhDvrY17gKHAATwrve/A86zYXGC0c+4b30Xo/3QNfMf7jN5o7zNgg4DiwyZRXIXnMW49nXOrfBSmX9M1EDn1KbFrgLzLblwK/ALP0g6rgTecc9/5Mq7Tia7BqcE7I9acc6Vmdj2eW4BNfB3X6UTXQOTUosSugfM+Rqns+DWlruganBrMbAIQ4Jx7zNexnK50DUR8T4mdiPgFM2sMlCrJ9h1dAxHfU2InIiIi4ic0K1ZERETETyixExEREfETSuxERERE/IQSOxERERE/ocRORERExE8osRMRERHxE/8fb8mFjOrHUx4AAAAASUVORK5CYII=\n",
167 | "text/plain": [
168 | ""
169 | ]
170 | },
171 | "execution_count": 18,
172 | "metadata": {},
173 | "output_type": "execute_result"
174 | }
175 | ],
176 | "source": [
177 | "legend = ['QASM','ibmq_16_melbourne']\n",
178 | "plot_histogram([ans,ans_quantum], legend=legend)"
179 | ]
180 | }
181 | ],
182 | "metadata": {
183 | "kernelspec": {
184 | "display_name": "Python 3",
185 | "language": "python",
186 | "name": "python3"
187 | },
188 | "language_info": {
189 | "codemirror_mode": {
190 | "name": "ipython",
191 | "version": 3
192 | },
193 | "file_extension": ".py",
194 | "mimetype": "text/x-python",
195 | "name": "python",
196 | "nbconvert_exporter": "python",
197 | "pygments_lexer": "ipython3",
198 | "version": "3.8.2"
199 | }
200 | },
201 | "nbformat": 4,
202 | "nbformat_minor": 4
203 | }
204 |
--------------------------------------------------------------------------------
/Qiskit/Quantum Random Walks/README.md:
--------------------------------------------------------------------------------
1 | Quantum walks are the quantum variation of the well known random walks heavily used in computer science in many of its fields, one pretty famous example is the *Page Rank* algorithm, which can be generally seen as a walker on web pages that wants to rank which pages are the most relevant within an specific set of pages.
2 |
3 | Then in constrast to the classical random walk, where the walker occupies definite states and the randomness arises due to stochastic transitions between states, in quantum walks randomness arises throughout some properties from quantum mechanics like quantum superposition of states, non-randomness, reversible unitary evolution and collapse of the wave function due to state measurements.
4 |
5 | It is pretty used in randomized algorithms, and are part of several quantum algorithms, as the Grover's search algorithm, which can be seen as a quantum walk algorithm.
6 |
7 | Mathematically we can see the Quantum Walks, or more specifically Continuous-Time Quantum Walks in graphs, like a transition operator from a initial state to a state $t$, which is given by $U(t)$, defined as
8 |
9 | $$U(t) = e^{itH}$$
10 |
11 | This formulation comes from a solution to the Schrödinger’s equation, where $t$ defines our time and $H$ describes our Hamiltonian, which for the purpose of this work will be given by the graph adjacency matrix $A$.
12 |
13 | # Continuous Time Quantum Walks
14 |
15 | Finally we can define our continuous-time quantum walk by the unitary operator $U(t)$ on $G_n$ at time $t \geq 0$ as the following
16 |
17 | $$U_{G_n}(t) = e^{-itA_{G_n}} \equiv \sum_{k = 0}^{\infty}\frac{(it)^k}{k!}A_{G_n}^k$$
18 |
19 | And given a state $|\psi_{G_n, t}\rangle$ is the probability amplitude of each vertice at time $t$ is given by
20 |
21 | $$|\psi_{Gn, t}\rangle = U_{G_n}(t)|\psi_{G_n, 0}\rangle$$
22 |
23 | Where the probability that the walker on $G_n$ is in position $x \in V(G)$ at time $t$ with initial state $|\psi_{G_n, 0}\rangle$ is
24 |
25 | $$\mathcal{P}(x) = \big|U_{G_n}(t)|\psi_{G_n, 0}\rangle(x)\big|^2$$
26 |
27 | # Discrete Time Quantum Walks
28 |
29 | ![Discrete Random Walks]()
30 |
--------------------------------------------------------------------------------
/Qiskit/Quantum Random Walks/assets/Discrete Walk Asset.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/proRamLOGO/quantum-algorithms/c3def4e18dccd0cb3553cfc0f01e6dbc7cfdec5e/Qiskit/Quantum Random Walks/assets/Discrete Walk Asset.png
--------------------------------------------------------------------------------
/README.md:
--------------------------------------------------------------------------------
1 |
2 |
3 |
4 |
6 |
7 |
Quantum Computing Algorithms
8 |
9 |
10 | All the quantum algorithms at one place.
11 |
12 |
13 |
14 |
15 |
16 | ## About this project
17 |
18 | This project is aimed on collecting quantum computing algorithms. Inviting contributions from all quantum developers worldwide. You can make contributions in any
19 | quantum framework you like wether it be Qiskit or Q# or any other. Follow the below instructions to make a contribution to this project.
20 |
21 | ## Steps to Contribute
22 |
23 | 1. Fork this repository.
24 | 2. Add your code into the folder with name of you framework used. If you do not see any such folder feel free to create one and edit this readme below by adding the name of your framework used and write a description about it.
25 | 3. Make a pull request. We will accept your contribution if it is valid and verified.
26 | 4. Since it is the beginning phase, if you want to change the folder structure then feel free to raise an issue.
27 |
28 | ## Don't Know about Quantum Computing?
29 | Quantum computing is the use of quantum phenomena such as superposition and entanglement to perform computation. Computers that perform quantum computations are known as quantum computers. Quantum computers are believed to be able to solve certain computational problems, such as integer factorization (which underlies RSA encryption), substantially faster than classical computers.
30 |
31 | ## What is Quantum Algorithm?
32 | In quantum computing, a quantum algorithm is an algorithm which runs on a realistic model of quantum computation, the most commonly used model being the quantum circuit model of computation. A classical (or non-quantum) algorithm is a finite sequence of instructions, or a step-by-step procedure for solving a problem, where each step or instruction can be performed on a classical computer. Similarly, a quantum algorithm is a step-by-step procedure, where each of the steps can be performed on a quantum computer. Although all classical algorithms can also be performed on a quantum computer,the term quantum algorithm is usually used for those algorithms which seem inherently quantum, or use some essential feature of quantum computation such as quantum superposition or quantum entanglement.
33 |
34 |
35 |
--------------------------------------------------------------------------------

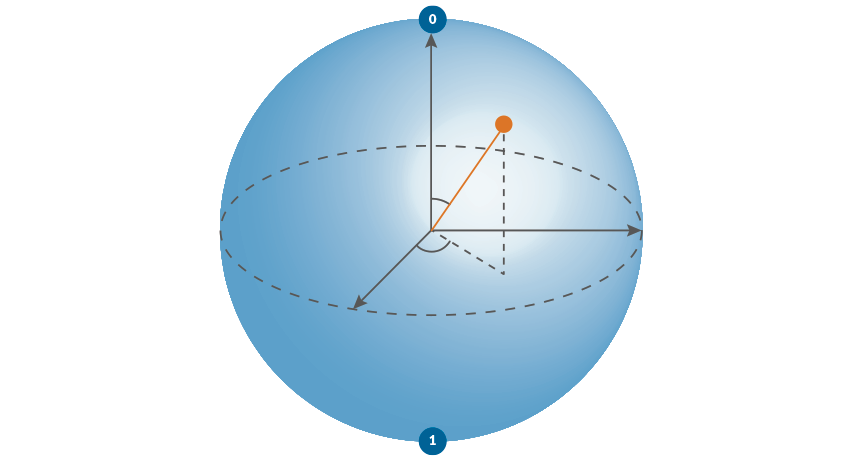 5 |
6 |
7 |
5 |
6 |
7 |