, greater > q;
45 | q.push(P(d[s] = 0, s));
46 | while(!q.empty()) {
47 | P cur = q.top();
48 | q.pop();
49 | int u = cur.second;
50 | if(used[u])
51 | continue;
52 | used[u] = true;
53 | // traverse all points and cur.second contiguous and updates from
54 | for(int i = head[u]; i != -1; i=es[i].next){
55 | int v = es[i].v, w = es[i].w;
56 | if(d[v] > d[u] + w) {
57 | d[v] = d[u] + w;
58 | q.push(P(d[v], v));
59 | in[v] = 1;
60 | }
61 | else if(d[v] == d[u]+w)
62 | ++in[v];
63 | }
64 | }
65 | }
66 | int s[maxn], y[maxn];
67 | int main() {
68 | ms(head, -1); ecnt = 0;
69 | int a, b, c;
70 | cin >> N >> M >> K;
71 | for(int i = 1; i <= M; ++i){
72 | cin >> a >> b >> c;
73 | addEdge(a, b, c);
74 | addEdge(b, a, c);
75 | }
76 | for(int i = 1; i <= K; ++i){
77 | cin >> s[i] >> y[i];
78 | addEdge(1, s[i], y[i]);
79 | addEdge(s[i], 1, y[i]);
80 | }
81 | dijkstra(1);
82 | int ans = 0;
83 | for(int i = 1; i <= K; ++i){
84 | if(d[s[i]] < y[i])
85 | ++ans;
86 | else if(d[s[i]] == y[i] && in[s[i]]>1)
87 | --in[s[i]], ++ans; // greater than 1 illustrates how the route up
88 | }
89 | cout << ans << endl;
90 |
91 | return 0;
92 | }
93 |
--------------------------------------------------------------------------------
/Knight Problem C++/README.md:
--------------------------------------------------------------------------------
1 | # Knight Problem
2 |
3 | Following code is solution for the famous KNIGHT PROBLEM that demands for minimum number of moves required to move a knight from start cell to target cell.
4 |
5 | `main.cpp` has the BFS Solution for the problem.
6 |
7 | For more details on the question, refer to the following LINK.
8 |
--------------------------------------------------------------------------------
/Knight Problem C++/main.cpp:
--------------------------------------------------------------------------------
1 | // KNIGHT PROBLEM
2 |
3 | #include
4 | using namespace std;
5 |
6 | class move_{
7 | public:
8 | int x;
9 | int y;
10 | int c;
11 | move_(int r, int s, int t){
12 | x = r;
13 | y = s;
14 | c = t;
15 | }
16 | move_(){
17 | x = 0;
18 | y = 0;
19 | c = 0;
20 | }
21 | };
22 |
23 | class Queue{
24 |
25 | struct node{
26 | move_ val;
27 | node* next;
28 |
29 | node(){
30 | val = move_();
31 | next = NULL;
32 | }
33 | node(int x, int y, int z){
34 | val = move_(x, y, z);
35 | next = NULL;
36 | }
37 | };
38 |
39 | node* start;
40 | public:
41 |
42 | Queue(){
43 | start = NULL;
44 | }
45 |
46 | void push(int x, int y, int c){
47 | if(start == NULL){
48 | node* newnode = new node(x, y, c);
49 | start = newnode;
50 | return;
51 | }
52 |
53 | else{
54 | node* temp = start;
55 | while(temp->next != NULL){
56 | temp = temp->next;
57 | }
58 |
59 | node* newnode = new node(x, y, c);
60 | temp->next = newnode;
61 | }
62 | }
63 |
64 | move_ pop(){
65 | if(start == NULL){
66 | move_ v = move_();
67 | return v;
68 | }
69 |
70 | else{
71 | move_ v = move_(start->val.x, start->val.y, start->val.c);
72 | start = start->next;
73 | return v;
74 | }
75 | }
76 |
77 | bool isempty(){
78 | return (start == NULL);
79 | }
80 |
81 | };
82 |
83 | int get_neighbours(Queue &q, move_ m, int end_x, int end_y, int n, bool** visited){
84 | int x = m.x, y = m.y;
85 | int directions[8][2] = {
86 | {-2, -1},
87 | {-2, 1},
88 | {-1, 2},
89 | { 1, 2},
90 | { 2, 1},
91 | { 2, -1},
92 | { 1, -2},
93 | {-1, -2}
94 | };
95 |
96 | int i, j;
97 |
98 | for(int index=0; index < 8; index++){
99 |
100 | i = x + directions[index][0];
101 | j = y + directions[index][1];
102 | if(( i >= 0 && i=0 && j>t>>n;
118 |
119 | while(t--){
120 | int start_x, start_y, end_x, end_y;
121 | cin>>start_x>>start_y>>end_x>>end_y;
122 |
123 | start_x--; start_y--; end_x--; end_y--;
124 |
125 | // making visited array
126 |
127 | bool** visited = new bool*[n];
128 |
129 | for(int i=0; iAnother classic problem that can be used to illustrate a second common graph algorithm is called the “knight’s tour.” The knight’s tour puzzle is played on a chess board with a single chess piece, the knight. The object of the puzzle is to find a sequence of moves that allow the knight to visit every square on the board exactly once. One such sequence is called a “tour.” The knight’s tour puzzle has fascinated chess players, mathematicians and computer scientists alike for many years. The upper bound on the number of possible legal tours for an eight-by-eight chessboard is known to be 1.305×1035; however, there are even more possible dead ends. Clearly this is a problem that requires some real brains, some real computing power, or both.
3 |
4 | Although researchers have studied many different algorithms to solve the knight’s tour problem, a graph search is one of the easiest to understand and program.
5 |
6 | Each square on the chessboard can be represented as a node in the graph. Each legal move by the knight can be represented as an edge in the graph. As show in image below
7 |
8 |
9 | 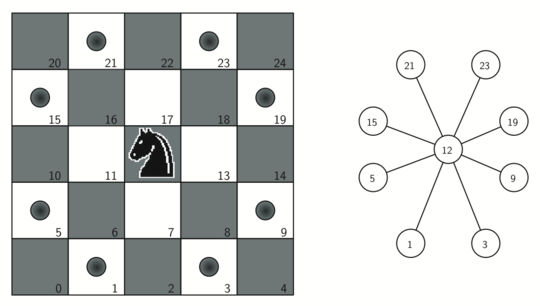 10 |
10 |
11 |
12 | figure below shows the complete graph of possible moves on an eight-by-eight board. There are exactly 336 edges in the graph. Notice that the vertices corresponding to the edges of the board have fewer connections (legal moves) than the vertices in the middle of the board.
13 |
14 |
15 |
16 |  17 |
17 |
18 |
--------------------------------------------------------------------------------
/Knight-Tour-Problem/__pycache__/graph.cpython-37.pyc:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/shreyanshchordia/Graph_Algorithms/d55a286a9f841fe64006deec1b91050791c551e1/Knight-Tour-Problem/__pycache__/graph.cpython-37.pyc
--------------------------------------------------------------------------------
/Knight-Tour-Problem/graph.py:
--------------------------------------------------------------------------------
1 | class Vertex:
2 | def __init__(self,key):
3 | self.id = key
4 | self.connectedTo = {}
5 |
6 | def addNeighbor(self,nbr,weight=0):
7 | self.connectedTo[nbr] = weight
8 |
9 | def __str__(self):
10 | return str(self.id) + ' connectedTo: ' + str([x.id for x in self.connectedTo])
11 |
12 | def getConnections(self):
13 | return self.connectedTo.keys()
14 |
15 | def getId(self):
16 | return self.id
17 |
18 | def getWeight(self,nbr):
19 | return self.connectedTo[nbr]
20 |
21 | class Graph:
22 | def __init__(self):
23 | self.vertList = {}
24 | self.numVertices = 0
25 |
26 | def addVertex(self,key):
27 | self.numVertices = self.numVertices + 1
28 | newVertex = Vertex(key)
29 | self.vertList[key] = newVertex
30 | return newVertex
31 |
32 | def getVertex(self,n):
33 | if n in self.vertList:
34 | return self.vertList[n]
35 | else:
36 | return None
37 |
38 | def __contains__(self,n):
39 | return n in self.vertList
40 |
41 | def addEdge(self,f,t,weight=0):
42 | if f not in self.vertList:
43 | nv = self.addVertex(f)
44 | if t not in self.vertList:
45 | nv = self.addVertex(t)
46 | self.vertList[f].addNeighbor(self.vertList[t], weight)
47 |
48 | def getVertices(self):
49 | return self.vertList.keys()
50 |
51 | def __iter__(self):
52 | return iter(self.vertList.values())
--------------------------------------------------------------------------------
/Knight-Tour-Problem/main.py:
--------------------------------------------------------------------------------
1 | from graph import Graph, Vertex
2 |
3 | def knightGraph(bdSize):
4 | ktGraph = Graph()
5 | for row in range(bdSize):
6 | for col in range(bdSize):
7 | nodeId = posToNodeId(row,col,bdSize)
8 | newPositions = genLegalMoves(row,col,bdSize)
9 | for e in newPositions:
10 | nid = posToNodeId(e[0],e[1],bdSize)
11 | ktGraph.addEdge(nodeId,nid)
12 | return ktGraph
13 |
14 | def genLegalMoves(x,y,bdSize):
15 | newMoves = []
16 | moveOffsets = [(-1,-2),(-1,2),(-2,-1),(-2,1),
17 | ( 1,-2),( 1,2),( 2,-1),( 2,1)]
18 | for i in moveOffsets:
19 | newX = x + i[0]
20 | newY = y + i[1]
21 | if legalCoord(newX,bdSize) and \
22 | legalCoord(newY,bdSize):
23 | newMoves.append((newX,newY))
24 | return newMoves
25 |
26 |
27 | def legalCoord(x,bdSize):
28 | if x >= 0 and x < bdSize:
29 | return True
30 | else:
31 | return False
32 |
33 |
34 | def posToNodeId(row, column, board_size):
35 | return (row * board_size) + column
36 |
37 |
38 | def knightTour(n,path,u,limit):
39 | u.setColor('gray')
40 | path.append(u)
41 | if n < limit:
42 | nbrList = list(u.getConnections())
43 | i = 0
44 | done = False
45 | while i < len(nbrList) and not done:
46 | if nbrList[i].getColor() == 'white':
47 | done = knightTour(n+1, path, nbrList[i], limit)
48 | i = i + 1
49 | if not done: # prepare to backtrack
50 | path.pop()
51 | u.setColor('white')
52 | else:
53 | done = True
54 | return done
55 |
--------------------------------------------------------------------------------
/LICENSE:
--------------------------------------------------------------------------------
1 | MIT License
2 |
3 | Copyright (c) 2020 Shreyansh Chordia
4 |
5 | Permission is hereby granted, free of charge, to any person obtaining a copy
6 | of this software and associated documentation files (the "Software"), to deal
7 | in the Software without restriction, including without limitation the rights
8 | to use, copy, modify, merge, publish, distribute, sublicense, and/or sell
9 | copies of the Software, and to permit persons to whom the Software is
10 | furnished to do so, subject to the following conditions:
11 |
12 | The above copyright notice and this permission notice shall be included in all
13 | copies or substantial portions of the Software.
14 |
15 | THE SOFTWARE IS PROVIDED "AS IS", WITHOUT WARRANTY OF ANY KIND, EXPRESS OR
16 | IMPLIED, INCLUDING BUT NOT LIMITED TO THE WARRANTIES OF MERCHANTABILITY,
17 | FITNESS FOR A PARTICULAR PURPOSE AND NONINFRINGEMENT. IN NO EVENT SHALL THE
18 | AUTHORS OR COPYRIGHT HOLDERS BE LIABLE FOR ANY CLAIM, DAMAGES OR OTHER
19 | LIABILITY, WHETHER IN AN ACTION OF CONTRACT, TORT OR OTHERWISE, ARISING FROM,
20 | OUT OF OR IN CONNECTION WITH THE SOFTWARE OR THE USE OR OTHER DEALINGS IN THE
21 | SOFTWARE.
22 |
--------------------------------------------------------------------------------
/Lockdown Game/README.md:
--------------------------------------------------------------------------------
1 | The following is a recursion problem called the Lockdown Problem. You can get details of the problem statement from this LINK
2 |
--------------------------------------------------------------------------------
/Lockdown Game/main.cpp:
--------------------------------------------------------------------------------
1 |
2 | // The following is a recursion problem called the Lockdown Problem. LINK BELOW is where you can get the question from.
3 | // https://www.hackerearth.com/practice/basic-programming/recursion/recursion-and-backtracking/practice-problems/algorithm/lockdown-game/description/
4 |
5 | #include
6 | #include
7 | using namespace std;
8 |
9 | int search(char* arr, int n){
10 | for(int i=0; i>n>>s;
35 |
36 | char * arr = new char[n];
37 |
38 | memset(arr, 'o', sizeof(arr[0]) * n);
39 |
40 | long i = 0, j = 0;
41 | int dynamic_size = n;
42 | cout<finish_time(M). So this concept is used along with the concept of Binary Lifting to calculate the lowest common Ancestor of two nodes of graph.
15 |
--------------------------------------------------------------------------------
/Lowest_Common_Ancestor/main.cpp:
--------------------------------------------------------------------------------
1 | #include
2 | using namespace std;
3 | #define ll long long int
4 | #define pb push_back
5 | // We use the concept of binary Lifting to find the LCA of two nodes.
6 |
7 | vector > G; // To store the graph in Adjacency List form.
8 | const int M = 21;
9 | int par[100005][M]; //To store the ith parent of each node(Sparse Table)
10 |
11 | // O(n)*M
12 | void calc_sparse_table(int curr, int parent)
13 | {
14 | par[curr][0] = parent;
15 | for (int j = 1; j < M; j++)
16 | {
17 | par[curr][j] = par[par[curr][j - 1]][j - 1];
18 | }
19 | for (auto x : G[curr])
20 | if (x != parent)
21 | calc_sparse_table(x, curr);
22 | }
23 |
24 |
25 |
26 | /* LCA Using time in and Out*/
27 |
28 | /* In this we only move one node upto its ancestor until
29 | parent of that node is the ancestor of other too.*/
30 |
31 | int timm = 0, timin[100005], timout[100005];
32 |
33 | void dfs_time(int curr, int parent)
34 | {
35 | timin[curr] = ++timm;
36 | for (auto x : G[curr])
37 | {
38 | if (x != parent) {
39 | dfs_time(x, curr);
40 | }
41 | }
42 | timout[curr] = timm;
43 | }
44 |
45 | bool is_ancestor(int u, int v)
46 | {
47 | return timin[u] <= timin[v] && timout[u] >= timout[v];
48 | }
49 |
50 | // O(logn)
51 | int LCA_using_time(int u, int v)
52 | {
53 | if (is_ancestor(u, v))
54 | return u;
55 | if (is_ancestor(v, u))
56 | return v;
57 |
58 | for (int i = M - 1; i >= 0; i--)
59 | {
60 | // we are moving only u
61 | if (!is_ancestor(par[u][i] , par[v][i]))
62 | {
63 | u = par[u][i];
64 | }
65 | }
66 | return par[u][0];
67 | }
68 |
69 | int main()
70 | {
71 |
72 | /* n is no.of nodes, m is no.of edges*/
73 |
74 | int n, m;
75 | cin >> n >> m;
76 | G.resize(n + 1);
77 | for (int i = 1; i <= m; i++)
78 | {
79 | int x, y;
80 | cin >> x >> y;
81 | G[x].pb(y);
82 | G[y].pb(x);
83 | }
84 | // Assuming 1 is the root node of the tree.
85 |
86 | /* Using time in and out method along with sparse table */
87 |
88 | memset(timin, 0, sizeof(timin));
89 | memset(timout, 0, sizeof(timout));
90 |
91 | timin[0] = 0; timout[0] = m + 1; // 0 is universal parent
92 | dfs_time(1, 0);
93 | calc_sparse_table(1, 0);
94 |
95 |
96 | // The below code will return the LCA of two nodes in the graph.
97 | /*
98 | cout << LCA_using_time(2,1) << endl;
99 |
100 | */
101 |
102 | return 0;
103 | }
104 |
--------------------------------------------------------------------------------
/Minimum Edge Reversals/Minimum Edge Reversals.cpp:
--------------------------------------------------------------------------------
1 | // C++ program to find min edge reversal to
2 | // make every node reachable from root
3 | #include
4 | using namespace std;
5 |
6 | // method to dfs in tree and populates disRev values
7 | int dfs(vector< pair > g[],
8 | pair disRev[], bool visit[], int u)
9 | {
10 | // visit current node
11 | visit[u] = true;
12 | int totalRev = 0;
13 |
14 | // looping over all neighbors
15 | for (int i = 0; i < g[u].size(); i++)
16 | {
17 | int v = g[u][i].first;
18 | if (!visit[v])
19 | {
20 | // distance of v will be one more than distance of u
21 | disRev[v].first = disRev[u].first + 1;
22 |
23 | // initialize back edge count same as
24 | // parent node's count
25 | disRev[v].second = disRev[u].second;
26 |
27 | // if there is a reverse edge from u to i,
28 | // then only update
29 | if (g[u][i].second)
30 | {
31 | disRev[v].second = disRev[u].second + 1;
32 | totalRev++;
33 | }
34 | totalRev += dfs(g, disRev, visit, v);
35 | }
36 | }
37 |
38 | // return total reversal in subtree rooted at u
39 | return totalRev;
40 | }
41 |
42 | // method prints root and minimum number of edge reversal
43 | void printMinEdgeReverseForRootNode(int edges[][2], int e)
44 | {
45 | // number of nodes are one more than number of edges
46 | int V = e + 1;
47 |
48 | // data structure to store directed tree
49 | vector< pair > g[V];
50 |
51 | // disRev stores two values - distance and back
52 | // edge count from root node
53 | pair disRev[V];
54 |
55 | bool visit[V];
56 |
57 | int u, v;
58 | for (int i = 0; i < e; i++)
59 | {
60 | u = edges[i][0];
61 | v = edges[i][1];
62 |
63 | // add 0 weight in direction of u to v
64 | g[u].push_back(make_pair(v, 0));
65 |
66 | // add 1 weight in reverse direction
67 | g[v].push_back(make_pair(u, 1));
68 | }
69 |
70 | // initialize all variables
71 | for (int i = 0; i < V; i++)
72 | {
73 | visit[i] = false;
74 | disRev[i].first = disRev[i].second = 0;
75 | }
76 |
77 | int root = 0;
78 |
79 | // dfs populates disRev data structure and
80 | // store total reverse edge counts
81 | int totalRev = dfs(g, disRev, visit, root);
82 |
83 | // UnComment below lines to print each node's
84 | // distance and edge reversal count from root node
85 | /*
86 | for (int i = 0; i < V; i++)
87 | {
88 | cout << i << " : " << disRev[i].first
89 | << " " << disRev[i].second << endl;
90 | }
91 | */
92 |
93 | int res = INT_MAX;
94 |
95 | // loop over all nodes to choose minimum edge reversal
96 | for (int i = 0; i < V; i++)
97 | {
98 | // (reversal in path to i) + (reversal
99 | // in all other tree parts)
100 | int edgesToRev = (totalRev - disRev[i].second) +
101 | (disRev[i].first - disRev[i].second);
102 |
103 | // choose minimum among all values
104 | if (edgesToRev < res)
105 | {
106 | res = edgesToRev;
107 | root = i;
108 | }
109 | }
110 |
111 | // print the designated root and total
112 | // edge reversal made
113 | cout << root << " " << res << endl;
114 | }
115 |
116 | // Driver code to test above methods
117 | int main()
118 | {
119 | int edges[][2] =
120 | {
121 | {0, 1},
122 | {2, 1},
123 | {3, 2},
124 | {3, 4},
125 | {5, 4},
126 | {5, 6},
127 | {7, 6}
128 | };
129 | int e = sizeof(edges) / sizeof(edges[0]);
130 |
131 | printMinEdgeReverseForRootNode(edges, e);
132 | return 0;
133 | }
--------------------------------------------------------------------------------
/Minimum Edge Reversals/README.md:
--------------------------------------------------------------------------------
1 | Description:
2 | Problem Name : Minimum edge reversals to make a root.
3 | Problem Statement : Given a directed tree with V vertices and V-1 edges, we need to choose such a root (from given nodes from where we can reach to every other node) with a minimum number of edge reversal.
4 | Click Here to view the Problem
5 |
--------------------------------------------------------------------------------
/MulitSource Dijkstra/README.md:
--------------------------------------------------------------------------------
1 | Description:
2 |
3 | Dijkstra Algorithm is used to find the cost of shortest path from a given source vertex to all the other vertices.In the case of Multi Source Dijkstra Algorithm we need to find the shortest distance of all the vertices from a set of source vertices.
4 |
5 | To achieve this :
6 | We can add a dummy node connecting to all the source vertices with edge weight of value 0. Now ,we can apply normal single source dijkstra algorithm to get the shortest distance of all the vertices from any source vertices.
7 |
--------------------------------------------------------------------------------
/MulitSource Dijkstra/main.cpp:
--------------------------------------------------------------------------------
1 | /* We can see Multi Source Dijkstra as adding a dummy node to
2 | every source node having weight '0' and then apply
3 | normal single source dijkstra algorithm from that dummy source.
4 | */
5 |
6 | #include
7 | using namespace std;
8 |
9 |
10 | vector MultiSource_dijkstra(vector > &adj, map, int> &mp, int v, int src) {
11 |
12 | set > st;
13 | vector dis(v + 1, INT_MAX);// vector to store the distance
14 |
15 | dis[src] = 0;// distance of dummy source as 0
16 | st.insert(make_pair(0, src));
17 | while (!st.empty()) {
18 | pair p = *st.begin();
19 | st.erase(st.begin());
20 | int node = p.second;
21 | int wt = p.first;
22 | for (int i = 0; i < adj[node].size(); i++) {
23 |
24 | int k = adj[node][i];
25 | if (dis[k] > dis[node] + mp[make_pair(node, k)]) {
26 |
27 | if (dis[k] != INT_MAX) {
28 | st.erase(st.find(make_pair(dis[k], k)));
29 | }
30 |
31 | dis[k] = dis[node] + mp[make_pair(node, k)];
32 | st.insert(make_pair(dis[k], k));
33 | }
34 | }
35 | }
36 | return dis;
37 | }
38 |
39 | int main() {
40 |
41 | int v, e, src;
42 | cout << "Enter number of vertices,number of edges and source vertex: " << endl;
43 | cin >> v >> e;
44 | vector > adj(v + 1); // 1 Based indexing.
45 |
46 | // map to store the weight of each egde
47 | map, int> mp;
48 |
49 | for (int i = 0; i < e; i++) {
50 | int x, y, w;
51 | cin >> x >> y >> w; // input format is (from_node ,to_node, weight of edge)
52 | adj[x].push_back(y);
53 | adj[y].push_back(x);
54 | pair p1 = make_pair(x, y);
55 | pair p2 = make_pair(y, x);
56 | mp[p1] = w;
57 | mp[p2] = w;
58 | }
59 |
60 | int no_of_sources;// store count of number of source vertices
61 | cin >> no_of_sources;
62 | vector sources; // vector to store the sources
63 | for (int i = 0; i < no_of_sources; i++)
64 | {
65 | int x;
66 | cin >> x;
67 | sources.push_back(x);
68 | }
69 |
70 | // Creating a dummy node '0' attached to every source vertex with weight 0
71 | src = 0;
72 | for (int i = 0; i < sources.size(); i++)
73 | {
74 | int a = sources[i];
75 | adj[0].push_back(a);
76 | adj[a].push_back(0);
77 | mp[ {a, 0}] = 0;
78 | mp[ {0, a}] = 0;
79 | }
80 |
81 | std::vector dis;
82 | dis = MultiSource_dijkstra(adj, mp, v, 0);
83 |
84 | // The shortest Distance for each node from any of the source vertex is stored in dis array
85 | for (int i = 1; i <= v; i++)
86 | cout << dis[i] << " ";
87 | }
88 |
--------------------------------------------------------------------------------
/N Queen's Problem/README.md:
--------------------------------------------------------------------------------
1 | The code in `main.cpp` is the C++ code using Backtracking Algorithm for the famous N-Queen's problem.
2 |
3 | LINK for further details on the question.
4 |
--------------------------------------------------------------------------------
/N Queen's Problem/main.cpp:
--------------------------------------------------------------------------------
1 | #include
2 | #include
3 | using namespace std;
4 |
5 | bool isSafe(bool** arr, int i, int j, int n){
6 |
7 | int check[8][2] = {{1,-1}, {0,-1}, {-1,-1}, {-1,0}, {-1,1}, {0,1}, {1,1}, {1,0}};
8 | int a, b;
9 | for(int x=0; x<8; x++){
10 | a = i;
11 | b = j;
12 | while((a= 0) && (b=0)){
13 | if(arr[a][b] != 0) return 0;
14 | else{
15 | a += check[x][0];
16 | b += check[x][1];
17 | }
18 | }
19 | }
20 | return 1;
21 | }
22 |
23 | int n_queen(bool** arr, int i, int n){
24 | for(int j=0; j>n;
42 |
43 | bool** arr = new bool*[n];
44 | for(int i=0; iLeetCode
4 |
5 | Problem Description: here
6 |
--------------------------------------------------------------------------------
/NetworkDelayTime/main.cpp:
--------------------------------------------------------------------------------
1 | #include
2 | #include
3 | #include
4 |
5 | #define INF_TIME 1000000000
6 |
7 | using namespace std;
8 |
9 | // There are N network nodes, labelled 1 to N.
10 | // Given times, a list of travel times as directed edges times[i] = (u, v, w),
11 | // where u is the source node, v is the target node, and w is the time it takes for a signal to travel from source to target.
12 | // Now, we send a signal from a certain node K. How long will it take for all nodes to receive the signal?
13 | // If it is impossible, return -1.
14 |
15 | int networkDelayTime(vector>& times, int N, int K) {
16 |
17 | --K; // shift index by 1
18 |
19 | int toK[N]; // toK[N] - how long will it take from i to K (or from K to i)
20 | int fromTo[N][N]; // fromTo[i][j] - how long will it take from i to j
21 |
22 | for (int i = 0; i < N; ++i){
23 | toK[i] = INF_TIME;
24 | for (int j = 0; j < N; ++j){
25 | fromTo[i][j] = -1;
26 | }
27 | }
28 | toK[K] = 0;
29 |
30 |
31 | for (int i = 0; i < times.size(); ++i){
32 | int u, v, w;
33 | u = times[i][0] - 1;
34 | v = times[i][1] - 1;
35 | w = times[i][2];
36 | fromTo[u][v] = w;
37 | }
38 | fromTo[K][K] = 0;
39 |
40 | // bfs algorithm
41 | queue q;
42 |
43 | q.push(K);
44 | while (!q.empty()){
45 | int now;
46 | now = q.front();
47 | q.pop();
48 | for (int i = 0; i < N; ++i){
49 | if (fromTo[now][i] >= 0){
50 | if (toK[now] + fromTo[now][i] < toK[i]){
51 | toK[i] = toK[now] + fromTo[now][i];
52 | q.push(i);
53 | }
54 | }
55 | }
56 | }
57 |
58 | int totalTime = 0; // answer
59 | for (int i = 0; i < N; ++i){
60 | totalTime = max(totalTime, toK[i]);
61 | }
62 | if (totalTime == INF_TIME) totalTime = -1; // this means that some nodes cannot be reached
63 |
64 | return totalTime;
65 | }
66 |
67 |
68 | int main() {
69 |
70 | int N, E, K;
71 |
72 | cin >> N >> E >> K;
73 |
74 | vector> times;
75 | for (int i = 0; i < E; ++i) {
76 | int u, v, w;
77 | cin >> u >> v >> w;
78 | times.push_back(vector({u,v,w}));
79 | }
80 |
81 | cout << networkDelayTime(times, N, K);
82 |
83 | return 0;
84 | }
85 |
--------------------------------------------------------------------------------
/NumberOfPaths/README.md:
--------------------------------------------------------------------------------
1 | This algorithm counts the total number of ways or paths that exist between two vertices in a directed graph. These paths don’t contain a cycle, the simple enough reason is that a cycle contains an infinite number of paths and hence they create a problem.
2 | The problem can be solved using backtracking, that says take a path and start walking on it and check if it leads us to the destination vertex then count the path and backtrack to take another path. If the path doesn’t lead to the destination vertex, discard the path.
--------------------------------------------------------------------------------
/NumberOfPaths/main.cpp:
--------------------------------------------------------------------------------
1 | #include
2 | using namespace std;
3 | class Graph {
4 | int V;
5 | list* adj;
6 | void countPathsUtil(int, int, int&);
7 |
8 | public:
9 | Graph(int V);
10 | void addEdge(int u, int v);
11 | int countPaths(int s, int d);
12 | };
13 |
14 | Graph::Graph(int V)
15 | {
16 | this->V = V;
17 | adj = new list[V];
18 | }
19 |
20 | void Graph::addEdge(int u, int v)
21 | {
22 | adj[u].push_back(v);
23 | }
24 |
25 | int Graph::countPaths(int s, int d)
26 | {
27 | int pathCount = 0;
28 | countPathsUtil(s, d, pathCount);
29 | return pathCount;
30 | }
31 |
32 | void Graph::countPathsUtil(int u, int d,
33 | int& pathCount)
34 | {
35 | if (u == d)
36 | pathCount++;
37 | else {
38 | list::iterator i;
39 | for (i = adj[u].begin(); i != adj[u].end(); ++i)
40 | countPathsUtil(*i, d, pathCount);
41 | }
42 | }
43 |
44 | int main()
45 | {
46 | Graph g(5);
47 | g.addEdge(0, 1);
48 | g.addEdge(0, 2);
49 | g.addEdge(0, 3);
50 | g.addEdge(1, 3);
51 | g.addEdge(2, 4);
52 | g.addEdge(1, 4);
53 | g.addEdge(2, 3);
54 |
55 | int s = 0, d = 4;
56 | cout << g.countPaths(s, d);
57 |
58 | return 0;
59 | }
60 |
--------------------------------------------------------------------------------
/Permutation/PrintAllPermutations.cpp:
--------------------------------------------------------------------------------
1 | #include
2 | using namespace std;
3 |
4 | void printPermutations(string s, int i){
5 |
6 | if (i==s.size()- 1){
7 | cout<>s;
25 |
26 | printPermutations(s, 0);
27 | }
28 |
--------------------------------------------------------------------------------
/Permutation/PrintUniquePermutations.cpp:
--------------------------------------------------------------------------------
1 | #include
2 | using namespace std;
3 |
4 | void printPermutations(string s, int i){
5 |
6 | if (i==s.size()- 1){
7 | cout<>s;
30 |
31 | printPermutations(s, 0);
32 | }
33 |
--------------------------------------------------------------------------------
/Permutation/README.md:
--------------------------------------------------------------------------------
1 | # Permutation Problem
2 |
3 | Given a permutation of 1 to n, you need to perform some operations to make it into increasing order. Each operation is to reverse an interval a1, a2, ...., ax (1 <= x <= n) (a prefix). Your goal is to minimize the number of operations.
4 |
5 | ## Input
6 |
7 | The first line contains an integer (1 <= n <= 8).
8 |
9 | The second line contains space separated integers, representing the sequence .
10 |
11 | ## Output
12 |
13 | An integer representing the answer, that is, the minimum number of operations needed to make the permutation into increasing order.
14 |
15 | ## Sample
16 |
17 | Input :
18 |
19 | 3
20 | 3 1 2
21 |
22 | Output :
23 |
24 | 2
25 |
26 | ## Explanation
27 | A possible way is to reverse [1,3] , and then [1,2].
28 |
--------------------------------------------------------------------------------
/Permutation/main.cpp:
--------------------------------------------------------------------------------
1 | #include
2 | using namespace std;
3 |
4 |
5 | class Queue{
6 |
7 | struct node{
8 | long data;
9 | node* next;
10 | node* prev;
11 | };
12 | node* start;
13 |
14 | public:
15 | Queue(){
16 | this->start = NULL;
17 | }
18 |
19 | void add(long x){
20 |
21 | node* newnode = new node;
22 | newnode->data = x;
23 |
24 | if(this->start == NULL){
25 | newnode->next = newnode;
26 | newnode->prev = newnode;
27 | this->start = newnode;
28 | }
29 |
30 | else{
31 | newnode->next = this->start;
32 | node* previous = this->start->prev;
33 | this->start->prev = newnode;
34 | previous->next = newnode;
35 | newnode->prev = previous;
36 | }
37 |
38 | }
39 |
40 | bool isempty(){
41 | if (this->start == NULL){
42 | return 1;
43 | }
44 |
45 | else return 0;
46 | }
47 |
48 | long pop(){
49 | if (isempty()){
50 | return -1;
51 | }
52 |
53 | if (start->next == start){
54 | long x = start->data;
55 | start = NULL;
56 | return x;
57 | }
58 |
59 | else{
60 | long x = start->data;
61 | start->next->prev = start->prev;
62 | start = start->next;
63 | start->prev->next = start;
64 | return x;
65 | }
66 | }
67 |
68 | void front(){
69 | if (isempty()) return;
70 | node* temp = start;
71 | do{
72 | cout<data<<" ";
73 | temp = temp->next;
74 | }while(temp!= start);
75 | cout<<"\n";
76 | }
77 |
78 | void reverse(){
79 | if (isempty()) return;
80 | node* temp = start->prev;
81 | do{
82 | cout<data<<" ";
83 | temp = temp->prev;
84 | }while(temp!= start->prev);
85 | cout<<"\n";
86 | }
87 | };
88 |
89 | long pow(int x, int y){
90 | long val = 1;
91 | for(int i=0; i> n;
195 | int* reference = new int[n];
196 | int* arr = new int[n];
197 |
198 | for(int i=0; i> reference[i];
200 | arr[i] = i+1;
201 | }
202 |
203 | cout<
8 |  9 |
10 | Two pipes are considered connected if their end points connect. For e.g.
11 | If matrix is as follows:
12 | 0040
13 | 1360
14 | 5000
15 |
16 | Pipe 1 and 3{1 opens to right. 3 opens to left} are connected.
17 | Other connected pipes are 3 and 6(3 opens to right. 6 opens to left).
18 |
19 | 4 and 6 are not connected as 6 does not open to top, and 4 does not open to bottom.
20 |
21 | 1 and 5 are also not connected as even though 1 opens to bottom, 5 is not open to top.
22 |
23 | Given this matrix, start point (X, Y) and length of probe tool “L”,
24 | find out how many pipes{matrix elements} can be reached if the depth of search
25 | cannot be more than probe tool "L".
26 |
--------------------------------------------------------------------------------
/PipelineQuestion/Testcases.txt:
--------------------------------------------------------------------------------
1 | Test Cases
2 |
3 | 5 6 2 1 3
4 | 0 0 5 3 6 0
5 | 0 0 2 0 2 0
6 | 3 3 1 3 7 0
7 | 0 0 0 0 0 0
8 | 0 0 0 0 0 0
9 |
10 | Answer = 5
11 |
12 | 5 6 2 2 3
13 | 0 0 5 3 6 0
14 | 0 0 2 0 2 0
15 | 3 3 1 3 7 0
16 | 0 0 0 0 0 0
17 | 0 0 0 0 0 0
18 |
19 | Answer = 7
20 |
21 | 5 6 1 4 3
22 | 0 0 5 3 6 0
23 | 0 0 2 0 2 0
24 | 3 3 1 3 7 0
25 | 0 0 0 0 0 0
26 | 0 0 0 0 0 0
27 |
28 | Answer = 5
29 |
30 | 5 6 1 2 3
31 | 0 0 5 3 6 0
32 | 0 0 2 0 2 0
33 | 3 3 1 3 7 0
34 | 0 0 0 0 0 0
35 | 0 0 0 0 0 0
36 |
37 | Answer = 6
38 |
39 | 5 6 1 1 3
40 | 0 0 5 3 6 0
41 | 0 0 2 0 2 0
42 | 3 3 1 3 7 0
43 | 0 0 0 0 0 0
44 | 0 0 0 0 0 0
45 |
46 | Answer = 0
47 |
48 | 5 6 1 1 0
49 | 0 0 5 3 6 0
50 | 0 0 2 0 2 0
51 | 3 3 1 3 7 0
52 | 0 0 0 0 0 0
53 | 0 0 0 0 0 0
54 |
55 | Answer = 0
56 |
57 | 5 6 2 2 10
58 | 0 0 5 3 6 0
59 | 0 0 2 3 1 6
60 | 3 3 1 3 7 3
61 | 0 0 0 0 0 0
62 | 0 0 0 0 0 0
63 |
64 | Answer = 12
65 |
66 | 5 6 1 5 10
67 | 0 0 5 3 6 0
68 | 0 0 2 3 1 6
69 | 3 3 1 3 7 3
70 | 0 0 0 0 0 0
71 | 0 0 0 0 0 0
72 |
73 | Answer = 12
74 |
75 | 5 6 2 1 3
76 | 0 0 5 3 6 0
77 | 0 0 2 0 2 0
78 | 3 3 1 3 7 0
79 | 0 0 0 0 0 0
80 | 0 0 0 0 0 0
81 |
82 | Answer = 5
83 |
84 | 5 6 2 2 6
85 | 3 0 0 0 0 3
86 | 2 0 0 0 0 6
87 | 1 3 4 1 3 1
88 | 2 0 2 0 0 2
89 | 0 0 4 3 1 1
90 |
91 | Answer = 7
92 |
93 | 5 6 2 2 6
94 | 3 0 0 0 0 3
95 | 2 0 0 0 5 6
96 | 1 3 4 1 1 1
97 | 2 0 2 0 0 2
98 | 0 0 4 3 1 1
99 |
100 | Answer = 8
101 |
102 | 50 50 0 0 20
103 | 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
104 | 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
105 | 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
106 | 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
107 | 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
108 | 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
109 | 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
110 | 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
111 | 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
112 | 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
113 | 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
114 | 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
115 | 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
116 | 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
117 | 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
118 | 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
119 | 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
120 | 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
121 | 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
122 | 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
123 | 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
124 | 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
125 | 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
126 | 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
127 | 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
128 | 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
129 | 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
130 | 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
131 | 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
132 | 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
133 | 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
134 | 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
135 | 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
136 | 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
137 | 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
138 | 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
139 | 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
140 | 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
141 | 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
142 | 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
143 | 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
144 | 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
145 | 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
146 | 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
147 | 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
148 | 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
149 | 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
150 | 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
151 | 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
152 | 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
153 |
154 | Answer = 210
155 |
--------------------------------------------------------------------------------
/PipelineQuestion/main.cpp:
--------------------------------------------------------------------------------
1 | #include
2 | #include
3 | using namespace std;
4 |
5 | int dir_ref[4][2]= {
6 | {0,-1},
7 | {-1,0},
8 | {0, 1},
9 | {1, 0}
10 | };
11 |
12 | int in_out[8][2][4] = {
13 | {
14 | {0, 0, 0, 0},
15 | {0, 0, 0, 0}
16 | },{
17 | {1, 1, 1, 1},
18 | {1, 1, 1, 1}
19 | },{
20 | {0, 1, 0, 1},
21 | {0, 1, 0, 1}
22 | },{
23 | {1, 0, 1, 0},
24 | {1, 0, 1, 0}
25 | },{
26 | {1, 0, 0, 1},
27 | {0, 1, 1, 0}
28 | },{
29 | {1, 1, 0, 0},
30 | {0, 0, 1, 1}
31 | },{
32 | {0, 1, 1, 0},
33 | {1, 0, 0, 1}
34 | },{
35 | {0, 0, 1, 1},
36 | {1, 1, 0, 0}
37 | }
38 | };
39 |
40 | class Queue{
41 | int* x_q;
42 | int* y_q;
43 | int* d_q;
44 | int f;
45 | int b;
46 | public:
47 | Queue(int val){
48 | this->x_q = new int[val];
49 | this->y_q = new int[val];
50 | this->d_q = new int[val];
51 | this->f = 0;
52 | this->b = -1;
53 | }
54 |
55 | void pop(int &x, int &y, int& d){
56 | if(this->b < this->f){
57 | x = -1;
58 | y = -1;
59 | d = -1;
60 | cout<f<<" "<b<x_q[(this->f)];
64 | y = this->y_q[(this->f)];
65 | d = this->d_q[(this->f)++];
66 | //cout<f<<" "<b<x_q[++(this->b)] = x;
73 | this->y_q[(this->b)] = y;
74 | this->d_q[(this->b)] = d;
75 | //cout<f<<" "<b<b < this->f){
81 | return 1;
82 | }
83 | else{
84 | return 0;
85 | }
86 | }
87 | };
88 |
89 |
90 | void print(int** matrix, int row, int col){
91 | for(int i=0;i0){
133 | int arr[4] = {0};
134 | find_directions(arr, matrix, visited, a, b, row, col);
135 | for(int i=0;i<4;i++){
136 | if(arr[i]==1){
137 | int x = a + dir_ref[i][0];
138 | int y = b + dir_ref[i][1];
139 | visited[x][y] = 1;
140 | q.push(x, y, c-1);
141 | }
142 | }
143 | }
144 | else continue;
145 | }
146 |
147 | int count = 0;
148 | for(int i=0;i>t;
159 | while(t--){
160 | int row, col, x, y, probe;
161 | cin>>row>>col>>x>>y>>probe;
162 |
163 | // making matrix
164 | int** matrix = new int* [row];
165 | for(int i=0;i>matrix[i][j];
173 | }
174 | }
175 |
176 | // calculating reachable elements
177 | if(matrix[x][y]==0) cout<<0<Quality and not Quantity
6 |
7 | - ### Languages
8 | Only **C++ or Python**
9 |
10 | - ### About the Repository
11 | We are focusing on building solutions for problems on Graphs. Hence we are looking for **algorithms** like:
12 |
13 | 1. _Backtracking_
14 | 2. _Breadth First Search_
15 | 3. _Depth First Search_
16 | 4. _Traversal Algorithms (Prims/Kruskal)_
17 | 5. _Dijiktra's Algorithm_
18 | 6. _A* Algorithm_
19 |
20 | You can get good **problem statements on Graphs** from sites like:
21 |
22 | 1. GeekForGeeks
23 | 2. InterviewBit
24 | 3. LeetCode
25 | 4. HackerEarth
26 | 5. HackerRank
27 |
28 | - ### How To Contribute
29 | - You need to choose a **problem statement**, the solution to which can be derived using Graph Algorithms.
30 | - Once you choose a problem statement (making sure that it is not present in the repository already), **add a folder** for the problem statement in your forked repository.
31 | - This repository doesn't promote code in the root of the directory. Hence code has to be in sub-directory.
32 | - In the folder, there must be **2 files**
33 | - **README.md & main.cpp**
34 | - **README.md** to explain the **problem statement**, provide links for **further reference on the problem statement**, and also **mentioning the algorithm** that has been used in your code.
35 | - **main.cpp** implements code for the given problem statement using an algorithm that is explicitly mentioned in README.md.
36 | - Make sure the code is in **C++ or Python**
37 | - **These steps need to followed** while contributing **otherwise your your PR will be considered invalid.**
38 |
39 | - ### Guidelines for Contribution
40 | 1. **Fork** the Repository
41 | 2. **Add, edit or enhance** code.
42 | 3. **No duplication, repetition and spamming**. It will not lead to an accepted Pull Request.
43 | 6. Once you are done with your contribution, **issue a PULL REQUEST**. The Maintainer may ask you for a few changes. Once everything seems good, your code will be pulled and added to the original Repository branch.
44 |
--------------------------------------------------------------------------------
/Rat In A Maze/ratinamaze.cpp:
--------------------------------------------------------------------------------
1 | #include
2 | using namespace std;
3 |
4 | void mazeHelper(int ** maze, int **solution, int m, int n, int curri, int currj)
5 | {
6 | if(curri == m - 1 && currj == n - 1)
7 | {
8 | //If reached the end printing out the solution
9 | solution[m - 1][n - 1] = 1;
10 | for(int i = 0 ; i < m ; i++)
11 | {
12 | for(int j = 0 ; j < n ; j++)
13 | cout << solution[i][j] << " ";
14 | cout << endl;
15 | }
16 | solution[m - 1][n - 1] = 0;
17 | return ;
18 | }
19 |
20 | // Validating whether the current position of the maze is not exceeding the maze area
21 | if(curri < m && currj < n && curri >= 0 && currj >= 0)
22 | {
23 | //Checking whether we have encountered an obstacle
24 | if(maze[curri][currj] == 0)
25 | return;
26 | //Checking whether the current position has been already traversed
27 | if(solution[curri][currj] == 1)
28 | return;
29 |
30 | //Marking the path in solution
31 | solution[curri][currj] = 1;
32 | //Move Down
33 | mazeHelper(maze, solution, m, n, curri + 1, currj);
34 | //Move Up
35 | mazeHelper(maze, solution, m, n, curri - 1, currj);
36 | //Move Right
37 | mazeHelper(maze, solution, m, n, curri, currj + 1);
38 | //Move Left
39 | mazeHelper(maze, solution, m, n, curri, currj - 1);
40 | //Unmarking the path in solution
41 | solution[curri][currj] = 0;
42 | }
43 |
44 | }
45 |
46 | void mazeSolver(int **maze, int m, int n)
47 | {
48 | int ** solution = new int * [m];
49 | for(int i = 0 ; i < m ; i++)
50 | solution[i] = new int[n];
51 |
52 | for(int i = 0 ; i < m ; i++)
53 | for(int j = 0 ; j < n ; j++)
54 | solution[i][j] = 0;
55 |
56 | //Starting from the top left corner
57 | mazeHelper(maze, solution, m, n, 0, 0);
58 | }
59 |
60 | int main()
61 | {
62 | int m, n;
63 | //Size of maze
64 | cin >> m >> n;
65 | int ** maze = new int * [m];
66 | for(int i = 0 ; i < m ; i++)
67 | maze[i] = new int[n];
68 |
69 | for(int i = 0 ; i < m ; i++)
70 | for(int j = 0 ; j < n ; j++)
71 | cin >> maze[i][j];
72 |
73 | mazeSolver(maze, m, n);
74 |
75 | return 0;
76 | }
77 |
--------------------------------------------------------------------------------
/Rat In A Maze/readme.md:
--------------------------------------------------------------------------------
1 | # RAT IN A MAZE
2 |
3 | ## DESCRIPTION :
4 |
5 | You are given a N*N maze with a rat placed at maze[0][0]. Find and print all paths that rat can follow to reach its destination i.e. maze[N-1][N-1]. Rat can move in any direction ( left, right, up and down). Value of every cell in the maze can either be 0 or 1. Cells with value 0 are blocked means rat cannot enter into those cells and those with value 1 are open.
6 |
7 | ## INPUT FORMAT :
8 |
9 | *The first line of input contains an integer M, N representing the dimension of the maze. The next M lines of input contain N space-separated integers representing the type of the cell.*
10 |
11 | ## OUTPUT FORMAT :
12 |
13 | *For each test case, print the path from start position to destination position and only cells that are part of the solution path should be 1, rest all cells should be 0. Output for every test case will be printed in a separate line.*
14 |
15 | ## SAMPLE INPUT :
16 |
17 | `3 3`
18 | `1 0 1`
19 | `1 0 1`
20 | `1 1 1`
21 |
22 | ## SAMPLE OUTPUT :
23 |
24 | `1 0 0`
25 | `1 0 0`
26 | `1 1 1`
27 |
28 |
--------------------------------------------------------------------------------
/RobotAndFuelProblem/README.md:
--------------------------------------------------------------------------------
1 | # Robot And Fuel Problem
2 |
3 | There are N cars parked in a row in a parking lot of the newly constructed club.
4 |
5 | There is a gasoline and diesel fueling station installed at the left and right side of the park.
6 |
7 | An automatic fueling robot carries the fuel from station and fill up the parked car with fuel. The cars are divided into 2 types depending on whether it is a gasoline or diesel car.
8 | 1 is denoted as gasoline cars and 2 is denoted as diesel cars.
9 |
10 | The automatic robot will be used to provide a cost free fueling service which is filling up all cars with 1 litre of each corresponding fuel.
11 |
12 | The robot will move in between the 2 fuelling stations as below :
13 |
14 | 1) The robot carries 2 litre of gasoline at the gasoline station and starts moving from there.
15 |
16 | 2) The robot can fill up the cars of the same type of gas it carries 1 litre each.
17 |
18 | 3) The robot can go back to the fuelling station at any time, Independent from the current amount of fuel it carries.
19 |
20 | 4) When the robot arrives at the fuelling station, it gets 2 litre of supply of the corresponding fuel.(If the robot has some remaining fuel it will be discarded).
21 |
22 | 5) There is an equal distance of 1 between each fueling station and the cars.
23 |
24 | The fuel type of N Cars parked in the parking lot will be given.
25 | Find the minimum moving distance of the automated fueling robot after it has filled up all the cars with 1 litre of fuel each.
26 |
--------------------------------------------------------------------------------
/RobotAndFuelProblem/main.cpp:
--------------------------------------------------------------------------------
1 | #include
2 | #include
3 | #include
4 | using namespace std;
5 | #define GASOLINE 1
6 | #define DIESAL 2
7 |
8 | void initialize(int* arr, int n){
9 | memset(arr, 0, sizeof(arr[0]) * n);
10 | return;
11 | }
12 |
13 | void generate_neighbours(int* target, int* space, int* visited, int N, int x, int probe, bool gasoline){
14 | // From gasoline station robot has to visit one gasoline car.
15 | // Similarly from diesal station robot has to visit one diesal car.
16 | // From a car, robot can either go to similar car,
17 | // or gasoline station,
18 | // or diesal station.
19 | if ( x!= 0 && x!= N-1){
20 | if(probe != 0){
21 | int check = 0;
22 | if (gasoline == true) check = GASOLINE;
23 | else check = DIESAL;
24 | for(int i=1;i>t;
122 | while(t--){
123 | int n;
124 | cin>>n;
125 |
126 | int* space = new int[n + 2];
127 | for(int i=1; i<=n; i++){
128 | cin>>space[i];
129 | }
130 |
131 | space[0] = 0;
132 | space[n+1] = 0;
133 | cout<< find_optimum(space, n+2);
134 | }
135 | }
136 |
--------------------------------------------------------------------------------
/RobotAndFuelProblem/testcases.txt:
--------------------------------------------------------------------------------
1 | 6
2 | 5
3 | 1 2 1 2 1
4 | 5
5 | 2 1 1 2 1
6 | 5
7 | 2 1 2 1 2
8 | 8
9 | 1 1 1 1 2 2 2 2
10 | 8
11 | 2 1 2 2 1 1 1 2
12 | 7
13 | 2 2 2 1 1 1 1
14 |
15 | ########## Answers ############
16 |
17 | 12
18 | 14
19 | 13
20 | 21
21 | 32
22 | 29
23 |
--------------------------------------------------------------------------------
/Robotic Paths/README.md:
--------------------------------------------------------------------------------
1 | # Robotic Path Problem
2 |
3 | This is a medium Toughness question on BFS from Hacker Rank. The link to the question is here
4 |
--------------------------------------------------------------------------------
/Robotic Paths/main.cpp:
--------------------------------------------------------------------------------
1 | #include
2 | using namespace std;
3 |
4 | class Point{
5 | public:
6 | int x;
7 | int y;
8 | Point(){
9 | x = -1;
10 | y = -1;
11 | }
12 | Point(int a, int b){
13 | x = a;
14 | y = b;
15 | }
16 | };
17 |
18 | Point generate_neighbour(char** char_arr, Point& p, int n, int m, int i){
19 | int arr[4][2] = {
20 | {1, 0},
21 | {0, -1},
22 | {0, 1},
23 | {-1, 0},
24 | };
25 |
26 | Point new_p;
27 | if ((p.x + arr[i][0] >=0 && p.x + arr[i][0] < n) && (p.y + arr[i][1] >=0 && p.y + arr[i][1] < m) && char_arr[p.x + arr[i][0]][p.y + arr[i][1]]== '.'){
28 | new_p.x = p.x + arr[i][0];
29 | new_p.y = p.y + arr[i][1];
30 | return new_p;
31 | }
32 |
33 | else return new_p;
34 | }
35 |
36 | class Node{
37 | public:
38 | Node* next;
39 | Point p;
40 | Node(){
41 | next = NULL;
42 | }
43 | Node(int x, int y){
44 | p.x = x;
45 | p.y = y;
46 | next = NULL;
47 | }
48 | };
49 |
50 | class Queue{
51 | Node* first;
52 | public:
53 | Queue(){
54 | first = NULL;
55 | }
56 | void add(Point p){
57 | if(first == NULL){
58 | Node* newnode = new Node(p.x, p.y);
59 | first = newnode;
60 | return;
61 | }
62 | else{
63 | Node* temp = first;
64 | while(temp->next!= NULL){
65 | temp = temp->next;
66 | }
67 | Node* newnode = new Node(p.x,p.y);
68 | temp->next = newnode;
69 | return;
70 | }
71 | }
72 |
73 | Point pop(){
74 | if (first == NULL) return Point();
75 |
76 | else{
77 | Point x = first->p;
78 | first = first->next;
79 | return x;
80 | }
81 |
82 | }
83 |
84 | bool isEmpty(){
85 | if (first == NULL) return 1;
86 | else return 0;
87 | }
88 | };
89 |
90 | void BFS(char** arr, Point** prev_arr, Point& start, Point& end, int n, int m){
91 |
92 | if(arr[start.x][start.y] == '#' || arr[end.x][end.y] == '#'){
93 |
94 | cout<<"Impossible"<<"\n";
95 | return;
96 | }
97 |
98 | Queue q;
99 | q.add(start);
100 | while(!q.isEmpty()){
101 | if(arr[end.x][end.y] == '#') break;
102 |
103 | Point current = q.pop();
104 |
105 | if(arr[current.x][current.y] == '.'){
106 |
107 | for(int i=0; i<4; i++){
108 | Point neighbour = generate_neighbour(arr, current, n, m, i);
109 | if (neighbour.x == -1 && neighbour.y == -1 ||
110 | (prev_arr[neighbour.x][neighbour.y].x != -1 &&
111 | prev_arr[neighbour.x][neighbour.y].y != -1)) continue;
112 |
113 | else{
114 | q.add(neighbour);
115 | prev_arr[neighbour.x][neighbour.y].x = current.x;
116 | prev_arr[neighbour.x][neighbour.y].y = current.y;
117 | }
118 | }
119 | arr[current.x][current.y] = '#';
120 | }
121 |
122 | else continue;
123 | }
124 | if (arr[end.x][end.y] == '#'){
125 | string s = "";
126 |
127 | int x = end.x;
128 | int y = end.y;
129 | // cout<=0; i--){
150 | cout<>n>>m;
174 |
175 | char** arr = new char*[n];
176 | for(int i=0; i>arr[i][j];
181 |
182 | int t;
183 | cin>>t;
184 |
185 | Point start;
186 | Point end;
187 |
188 | for(int i=0; i> start.x>> start.y>> end.x>> end.y;
197 | start.x --;
198 | start.y --;
199 | end.x --;
200 | end.y --;
201 | output_path(t_arr, start, end, n, m);
202 |
203 | }
204 |
205 |
206 | }
207 |
--------------------------------------------------------------------------------
/Stack&Queue/README.md:
--------------------------------------------------------------------------------
1 | # Stack and Queue
2 |
3 | This is a C++ code that explains how to make a Stack or Queue of your own.
4 |
--------------------------------------------------------------------------------
/Stack&Queue/main.cpp:
--------------------------------------------------------------------------------
1 | #include
2 | #include
3 | using namespace std;
4 |
5 | class List{
6 | struct Node{
7 | Node* next;
8 | int data;
9 | };
10 | Node* first;
11 |
12 | public:
13 | List(int d){
14 | Node* newnode = new Node;
15 | first = newnode;
16 | first->next = newnode;
17 | first->data = d;
18 | }
19 |
20 | List(){
21 | this->first = NULL;
22 | }
23 |
24 | int push_back(int x){
25 | Node* temp = this->first;
26 | if(temp == NULL){
27 | Node* newnode = new Node;
28 | newnode->data = x;
29 | newnode->next = newnode;
30 | this->first = newnode;
31 | return newnode->data;
32 | }
33 | while(temp->next!= this->first){
34 | temp = temp->next;
35 | }
36 | Node* newnode = new Node;
37 | newnode->data = x;
38 | newnode->next = this->first;
39 | temp->next = newnode;
40 | return newnode->data;
41 | }
42 |
43 | int pop_back(){
44 | if(this->first == NULL){
45 | return -1;
46 | }
47 | else if(this->first->next == this->first){
48 | int x = this->first->data;
49 | this->first = NULL;
50 | return x;
51 | }
52 | Node* temp = this->first;
53 | while(temp->next->next != this->first){
54 | temp = temp->next;
55 | }
56 | int x = temp->next->data;
57 | temp->next = this->first;
58 | return x;
59 | }
60 |
61 | int push_front(int x){
62 | Node* newnode = new Node;
63 | newnode->data = x;
64 | if(this->first == NULL){
65 | this->first = newnode;
66 | newnode->next = newnode;
67 | return x;
68 | }
69 |
70 | else{
71 | Node* temp = this->first;
72 | this->first = newnode;
73 | this->first->next = temp;
74 | Node* t = temp;
75 | while(t->next != temp){
76 | t = t->next;
77 | }
78 | t->next = this->first;
79 | return x;
80 | }
81 | }
82 |
83 | int pop_front(){
84 | if(this->first == NULL){
85 | return -1;
86 | }
87 | else if(this->first->next == this->first){
88 | int x = this->first->data;
89 | this->first = NULL;
90 | return x;
91 | }
92 | else{
93 | int x = this->first->data;
94 | Node* t = this->first;
95 | this->first = this->first->next;
96 | Node* iter = t;
97 | while(iter->next != t){
98 | iter = iter->next;
99 | }
100 | iter->next = this->first;
101 | return x;
102 | }
103 | }
104 |
105 | void print(){
106 | Node* temp = this->first;
107 | if(temp == NULL){
108 | cout<<"-1\n";
109 | return;
110 | }
111 | do{
112 | cout<data<<" ";
113 | temp = temp->next;
114 | }while(temp !=this->first);
115 | cout<<"\n";
116 | }
117 | };
118 |
--------------------------------------------------------------------------------
/Sudoku/README.md:
--------------------------------------------------------------------------------
1 | ### Problem Description
2 |
3 | A program to solve a Sudoku puzzle by filling the empty cells.
4 | Empty cells are indicated by the character '.'
5 |
6 | Problem is on Interviewbit. [Link](https://www.interviewbit.com/problems/sudoku/)
7 |
8 | ### Example
9 | #### Input:
10 |
11 | 5 3 . . 7 . . . .\
12 | 6 . . 1 9 5 . . .\
13 | . 9 8 . . . . 6 .\
14 | 8 . . . 6 . . . 3\
15 | 4 . . 8 . 3 . . 1\
16 | 7 . . . 2 . . . 6\
17 | . 6 . . . . 2 8 .\
18 | . . . 4 1 9 . . 5\
19 | . . . . 8 . . 7 9
20 |
21 | #### Output:
22 | 5 3 4 6 7 8 9 1 2
23 | 6 7 2 1 9 5 3 4 8
24 | 1 9 8 3 4 2 5 6 7
25 | 8 5 9 7 6 1 4 2 3
26 | 4 2 6 8 5 3 7 9 1
27 | 7 1 3 9 2 4 8 5 6
28 | 9 6 1 5 3 7 2 8 4
29 | 2 8 7 4 1 9 6 3 5
30 | 3 4 5 2 8 6 1 7 9
31 |
32 | ##### Contributed by
33 | [Priyanshu Gangwar](https://github.com/PriyanshuGangwar)
34 |
--------------------------------------------------------------------------------
/Sudoku/main.cpp:
--------------------------------------------------------------------------------
1 | #include
2 | using namespace std;
3 |
4 | //Checking is current digit is valid or not
5 | bool isvalid(char n,vector> maze,int x,int y);
6 |
7 | //Helper Functions for isvalid function
8 | bool isempty(vector> maze,int &i,int &j); //Checks is any box is empty
9 | bool checkbox(char n,vector> maze, int i,int j); //Checks if there is any repetetion in a 3*3 box
10 |
11 | //Function to fill Sudoku
12 |
13 | bool suduko(vector> &maze)
14 | { int i,j;
15 | bool t = isempty(maze,i,j);
16 | if(!t)
17 | {
18 | return true;
19 | }
20 | //ALGORITHM
21 | /* LOOPS OVER 1 - 9 AND CHECKS FOR EVERY
22 | DIGIT AND BACKTRACKS IF IT CREATES COLLISION */
23 |
24 | for(char n='1';n <= '9';n++)
25 | if(isvalid(n,maze,i,j))
26 | { maze[i][j]=n;
27 | if(suduko(maze))
28 | return true;
29 | else
30 | maze[i][j]='.';
31 | }
32 | return false;
33 | }
34 |
35 | int main() {
36 |
37 | //Sudoku Board
38 | vector > maze = {{'5','3','.','.','7','.','.','.','.'},
39 | {'6','.','.','1','9','5','.','.','.'},
40 | {'.','9','8','.','.','.','.','6','.'},
41 | {'8','.','.','.','6','.','.','.','3'},
42 | {'4','.','.','8','.','3','.','.','1'},
43 | {'7','.','.','.','2','.','.','.','6'},
44 | {'.','6','.','.','.','.','2','8','.'},
45 | {'.','.','.','4','1','9','.','.','5'},
46 | {'.','.','.','.','8','.','.','7','9'}};
47 |
48 | suduko(maze);
49 |
50 | //Displaying Filled Board
51 | for(int i = 0; i < 9;i++){
52 | for(int j = 0; j< 9; j++){
53 | cout<> maze,int &i,int &j)
62 | {
63 | for(int x=0;x<9;x++)
64 | for(int y=0;y<9;y++)
65 | {
66 | if(maze[x][y] == '.')
67 | {
68 | i=x;
69 | j=y;
70 | return true;
71 | }
72 | }
73 | return false;
74 | }
75 |
76 |
77 | //Checks if there is any repetetion in a 3*3 box
78 |
79 | bool checkbox(char n,vector> maze, int i,int j)
80 | {
81 | for(int x=0;x<3;x++)
82 | for(int y=0;y<3;y++)
83 | {
84 | if(maze[i+x][j+y] == n)
85 | return false;
86 | }
87 | return true;
88 | }
89 |
90 | //Checking is current digit is valid or not
91 | bool isvalid(char n,vector> maze,int x,int y)
92 | {
93 | for(int i =0;i<9;i++)
94 | {
95 | if(maze[i][y]==n || maze[x][i] == n)
96 | return false;
97 | }
98 |
99 | if(x<3)
100 | {
101 | if(y<3)
102 | {
103 | if(!checkbox(n,maze,0,0))
104 | return false;
105 | }
106 | else if(y<6)
107 | {
108 | if(!checkbox(n,maze,0,3))
109 | return false;
110 | }
111 | else
112 | {
113 | if(!checkbox(n,maze,0,6))
114 | return false;
115 | }
116 | }
117 |
118 | else if(x<6)
119 | {
120 | if(y<3)
121 | {
122 | if(!checkbox(n,maze,3,0))
123 | return false;
124 | }
125 | else if(y<6)
126 | {
127 | if(!checkbox(n,maze,3,3))
128 | return false;
129 | }
130 | else
131 | {
132 | if(!checkbox(n,maze,3,6))
133 | return false;
134 | }
135 | }
136 |
137 | else
138 | {
139 | if(y<3)
140 | {
141 | if(!checkbox(n,maze,6,0))
142 | return false;
143 | }
144 | else if(y<6)
145 | {
146 | if(!checkbox(n,maze,6,3))
147 | return false;
148 | }
149 | else
150 | {
151 | if(!checkbox(n,maze,6,6))
152 | return false;
153 | }
154 | }
155 |
156 | return true;
157 | }
158 |
--------------------------------------------------------------------------------
/TowerConstruction/README.md:
--------------------------------------------------------------------------------
1 | # Tower Construction
2 |
3 | Four 5G base station towers needs to be installed in a Landscape which is divided as hexagon cells as shown in Fig below, which also contains number of people living in each cell. Need to find four cells to install the 5G towers which can cover maximum number of people combining all four cells, with below conditions
4 | Only one tower can be placed in a cell
5 | Each of the four chosen cell should be neighbor to atleast one of the remaining 3 cells.
6 | All four cells should be connected (like one island)
7 |
8 | ## For Example
9 |
10 | ### Input
11 |
12 |
9 |
10 | Two pipes are considered connected if their end points connect. For e.g.
11 | If matrix is as follows:
12 | 0040
13 | 1360
14 | 5000
15 |
16 | Pipe 1 and 3{1 opens to right. 3 opens to left} are connected.
17 | Other connected pipes are 3 and 6(3 opens to right. 6 opens to left).
18 |
19 | 4 and 6 are not connected as 6 does not open to top, and 4 does not open to bottom.
20 |
21 | 1 and 5 are also not connected as even though 1 opens to bottom, 5 is not open to top.
22 |
23 | Given this matrix, start point (X, Y) and length of probe tool “L”,
24 | find out how many pipes{matrix elements} can be reached if the depth of search
25 | cannot be more than probe tool "L".
26 |
--------------------------------------------------------------------------------
/PipelineQuestion/Testcases.txt:
--------------------------------------------------------------------------------
1 | Test Cases
2 |
3 | 5 6 2 1 3
4 | 0 0 5 3 6 0
5 | 0 0 2 0 2 0
6 | 3 3 1 3 7 0
7 | 0 0 0 0 0 0
8 | 0 0 0 0 0 0
9 |
10 | Answer = 5
11 |
12 | 5 6 2 2 3
13 | 0 0 5 3 6 0
14 | 0 0 2 0 2 0
15 | 3 3 1 3 7 0
16 | 0 0 0 0 0 0
17 | 0 0 0 0 0 0
18 |
19 | Answer = 7
20 |
21 | 5 6 1 4 3
22 | 0 0 5 3 6 0
23 | 0 0 2 0 2 0
24 | 3 3 1 3 7 0
25 | 0 0 0 0 0 0
26 | 0 0 0 0 0 0
27 |
28 | Answer = 5
29 |
30 | 5 6 1 2 3
31 | 0 0 5 3 6 0
32 | 0 0 2 0 2 0
33 | 3 3 1 3 7 0
34 | 0 0 0 0 0 0
35 | 0 0 0 0 0 0
36 |
37 | Answer = 6
38 |
39 | 5 6 1 1 3
40 | 0 0 5 3 6 0
41 | 0 0 2 0 2 0
42 | 3 3 1 3 7 0
43 | 0 0 0 0 0 0
44 | 0 0 0 0 0 0
45 |
46 | Answer = 0
47 |
48 | 5 6 1 1 0
49 | 0 0 5 3 6 0
50 | 0 0 2 0 2 0
51 | 3 3 1 3 7 0
52 | 0 0 0 0 0 0
53 | 0 0 0 0 0 0
54 |
55 | Answer = 0
56 |
57 | 5 6 2 2 10
58 | 0 0 5 3 6 0
59 | 0 0 2 3 1 6
60 | 3 3 1 3 7 3
61 | 0 0 0 0 0 0
62 | 0 0 0 0 0 0
63 |
64 | Answer = 12
65 |
66 | 5 6 1 5 10
67 | 0 0 5 3 6 0
68 | 0 0 2 3 1 6
69 | 3 3 1 3 7 3
70 | 0 0 0 0 0 0
71 | 0 0 0 0 0 0
72 |
73 | Answer = 12
74 |
75 | 5 6 2 1 3
76 | 0 0 5 3 6 0
77 | 0 0 2 0 2 0
78 | 3 3 1 3 7 0
79 | 0 0 0 0 0 0
80 | 0 0 0 0 0 0
81 |
82 | Answer = 5
83 |
84 | 5 6 2 2 6
85 | 3 0 0 0 0 3
86 | 2 0 0 0 0 6
87 | 1 3 4 1 3 1
88 | 2 0 2 0 0 2
89 | 0 0 4 3 1 1
90 |
91 | Answer = 7
92 |
93 | 5 6 2 2 6
94 | 3 0 0 0 0 3
95 | 2 0 0 0 5 6
96 | 1 3 4 1 1 1
97 | 2 0 2 0 0 2
98 | 0 0 4 3 1 1
99 |
100 | Answer = 8
101 |
102 | 50 50 0 0 20
103 | 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
104 | 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
105 | 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
106 | 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
107 | 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
108 | 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
109 | 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
110 | 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
111 | 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
112 | 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
113 | 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
114 | 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
115 | 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
116 | 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
117 | 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
118 | 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
119 | 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
120 | 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
121 | 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
122 | 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
123 | 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
124 | 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
125 | 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
126 | 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
127 | 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
128 | 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
129 | 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
130 | 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
131 | 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
132 | 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
133 | 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
134 | 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
135 | 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
136 | 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
137 | 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
138 | 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
139 | 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
140 | 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
141 | 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
142 | 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
143 | 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
144 | 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
145 | 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
146 | 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
147 | 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
148 | 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
149 | 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
150 | 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
151 | 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
152 | 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
153 |
154 | Answer = 210
155 |
--------------------------------------------------------------------------------
/PipelineQuestion/main.cpp:
--------------------------------------------------------------------------------
1 | #include
2 | #include
3 | using namespace std;
4 |
5 | int dir_ref[4][2]= {
6 | {0,-1},
7 | {-1,0},
8 | {0, 1},
9 | {1, 0}
10 | };
11 |
12 | int in_out[8][2][4] = {
13 | {
14 | {0, 0, 0, 0},
15 | {0, 0, 0, 0}
16 | },{
17 | {1, 1, 1, 1},
18 | {1, 1, 1, 1}
19 | },{
20 | {0, 1, 0, 1},
21 | {0, 1, 0, 1}
22 | },{
23 | {1, 0, 1, 0},
24 | {1, 0, 1, 0}
25 | },{
26 | {1, 0, 0, 1},
27 | {0, 1, 1, 0}
28 | },{
29 | {1, 1, 0, 0},
30 | {0, 0, 1, 1}
31 | },{
32 | {0, 1, 1, 0},
33 | {1, 0, 0, 1}
34 | },{
35 | {0, 0, 1, 1},
36 | {1, 1, 0, 0}
37 | }
38 | };
39 |
40 | class Queue{
41 | int* x_q;
42 | int* y_q;
43 | int* d_q;
44 | int f;
45 | int b;
46 | public:
47 | Queue(int val){
48 | this->x_q = new int[val];
49 | this->y_q = new int[val];
50 | this->d_q = new int[val];
51 | this->f = 0;
52 | this->b = -1;
53 | }
54 |
55 | void pop(int &x, int &y, int& d){
56 | if(this->b < this->f){
57 | x = -1;
58 | y = -1;
59 | d = -1;
60 | cout<f<<" "<b<x_q[(this->f)];
64 | y = this->y_q[(this->f)];
65 | d = this->d_q[(this->f)++];
66 | //cout<f<<" "<b<x_q[++(this->b)] = x;
73 | this->y_q[(this->b)] = y;
74 | this->d_q[(this->b)] = d;
75 | //cout<f<<" "<b<b < this->f){
81 | return 1;
82 | }
83 | else{
84 | return 0;
85 | }
86 | }
87 | };
88 |
89 |
90 | void print(int** matrix, int row, int col){
91 | for(int i=0;i0){
133 | int arr[4] = {0};
134 | find_directions(arr, matrix, visited, a, b, row, col);
135 | for(int i=0;i<4;i++){
136 | if(arr[i]==1){
137 | int x = a + dir_ref[i][0];
138 | int y = b + dir_ref[i][1];
139 | visited[x][y] = 1;
140 | q.push(x, y, c-1);
141 | }
142 | }
143 | }
144 | else continue;
145 | }
146 |
147 | int count = 0;
148 | for(int i=0;i>t;
159 | while(t--){
160 | int row, col, x, y, probe;
161 | cin>>row>>col>>x>>y>>probe;
162 |
163 | // making matrix
164 | int** matrix = new int* [row];
165 | for(int i=0;i>matrix[i][j];
173 | }
174 | }
175 |
176 | // calculating reachable elements
177 | if(matrix[x][y]==0) cout<<0<Quality and not Quantity
6 |
7 | - ### Languages
8 | Only **C++ or Python**
9 |
10 | - ### About the Repository
11 | We are focusing on building solutions for problems on Graphs. Hence we are looking for **algorithms** like:
12 |
13 | 1. _Backtracking_
14 | 2. _Breadth First Search_
15 | 3. _Depth First Search_
16 | 4. _Traversal Algorithms (Prims/Kruskal)_
17 | 5. _Dijiktra's Algorithm_
18 | 6. _A* Algorithm_
19 |
20 | You can get good **problem statements on Graphs** from sites like:
21 |
22 | 1. GeekForGeeks
23 | 2. InterviewBit
24 | 3. LeetCode
25 | 4. HackerEarth
26 | 5. HackerRank
27 |
28 | - ### How To Contribute
29 | - You need to choose a **problem statement**, the solution to which can be derived using Graph Algorithms.
30 | - Once you choose a problem statement (making sure that it is not present in the repository already), **add a folder** for the problem statement in your forked repository.
31 | - This repository doesn't promote code in the root of the directory. Hence code has to be in sub-directory.
32 | - In the folder, there must be **2 files**
33 | - **README.md & main.cpp**
34 | - **README.md** to explain the **problem statement**, provide links for **further reference on the problem statement**, and also **mentioning the algorithm** that has been used in your code.
35 | - **main.cpp** implements code for the given problem statement using an algorithm that is explicitly mentioned in README.md.
36 | - Make sure the code is in **C++ or Python**
37 | - **These steps need to followed** while contributing **otherwise your your PR will be considered invalid.**
38 |
39 | - ### Guidelines for Contribution
40 | 1. **Fork** the Repository
41 | 2. **Add, edit or enhance** code.
42 | 3. **No duplication, repetition and spamming**. It will not lead to an accepted Pull Request.
43 | 6. Once you are done with your contribution, **issue a PULL REQUEST**. The Maintainer may ask you for a few changes. Once everything seems good, your code will be pulled and added to the original Repository branch.
44 |
--------------------------------------------------------------------------------
/Rat In A Maze/ratinamaze.cpp:
--------------------------------------------------------------------------------
1 | #include
2 | using namespace std;
3 |
4 | void mazeHelper(int ** maze, int **solution, int m, int n, int curri, int currj)
5 | {
6 | if(curri == m - 1 && currj == n - 1)
7 | {
8 | //If reached the end printing out the solution
9 | solution[m - 1][n - 1] = 1;
10 | for(int i = 0 ; i < m ; i++)
11 | {
12 | for(int j = 0 ; j < n ; j++)
13 | cout << solution[i][j] << " ";
14 | cout << endl;
15 | }
16 | solution[m - 1][n - 1] = 0;
17 | return ;
18 | }
19 |
20 | // Validating whether the current position of the maze is not exceeding the maze area
21 | if(curri < m && currj < n && curri >= 0 && currj >= 0)
22 | {
23 | //Checking whether we have encountered an obstacle
24 | if(maze[curri][currj] == 0)
25 | return;
26 | //Checking whether the current position has been already traversed
27 | if(solution[curri][currj] == 1)
28 | return;
29 |
30 | //Marking the path in solution
31 | solution[curri][currj] = 1;
32 | //Move Down
33 | mazeHelper(maze, solution, m, n, curri + 1, currj);
34 | //Move Up
35 | mazeHelper(maze, solution, m, n, curri - 1, currj);
36 | //Move Right
37 | mazeHelper(maze, solution, m, n, curri, currj + 1);
38 | //Move Left
39 | mazeHelper(maze, solution, m, n, curri, currj - 1);
40 | //Unmarking the path in solution
41 | solution[curri][currj] = 0;
42 | }
43 |
44 | }
45 |
46 | void mazeSolver(int **maze, int m, int n)
47 | {
48 | int ** solution = new int * [m];
49 | for(int i = 0 ; i < m ; i++)
50 | solution[i] = new int[n];
51 |
52 | for(int i = 0 ; i < m ; i++)
53 | for(int j = 0 ; j < n ; j++)
54 | solution[i][j] = 0;
55 |
56 | //Starting from the top left corner
57 | mazeHelper(maze, solution, m, n, 0, 0);
58 | }
59 |
60 | int main()
61 | {
62 | int m, n;
63 | //Size of maze
64 | cin >> m >> n;
65 | int ** maze = new int * [m];
66 | for(int i = 0 ; i < m ; i++)
67 | maze[i] = new int[n];
68 |
69 | for(int i = 0 ; i < m ; i++)
70 | for(int j = 0 ; j < n ; j++)
71 | cin >> maze[i][j];
72 |
73 | mazeSolver(maze, m, n);
74 |
75 | return 0;
76 | }
77 |
--------------------------------------------------------------------------------
/Rat In A Maze/readme.md:
--------------------------------------------------------------------------------
1 | # RAT IN A MAZE
2 |
3 | ## DESCRIPTION :
4 |
5 | You are given a N*N maze with a rat placed at maze[0][0]. Find and print all paths that rat can follow to reach its destination i.e. maze[N-1][N-1]. Rat can move in any direction ( left, right, up and down). Value of every cell in the maze can either be 0 or 1. Cells with value 0 are blocked means rat cannot enter into those cells and those with value 1 are open.
6 |
7 | ## INPUT FORMAT :
8 |
9 | *The first line of input contains an integer M, N representing the dimension of the maze. The next M lines of input contain N space-separated integers representing the type of the cell.*
10 |
11 | ## OUTPUT FORMAT :
12 |
13 | *For each test case, print the path from start position to destination position and only cells that are part of the solution path should be 1, rest all cells should be 0. Output for every test case will be printed in a separate line.*
14 |
15 | ## SAMPLE INPUT :
16 |
17 | `3 3`
18 | `1 0 1`
19 | `1 0 1`
20 | `1 1 1`
21 |
22 | ## SAMPLE OUTPUT :
23 |
24 | `1 0 0`
25 | `1 0 0`
26 | `1 1 1`
27 |
28 |
--------------------------------------------------------------------------------
/RobotAndFuelProblem/README.md:
--------------------------------------------------------------------------------
1 | # Robot And Fuel Problem
2 |
3 | There are N cars parked in a row in a parking lot of the newly constructed club.
4 |
5 | There is a gasoline and diesel fueling station installed at the left and right side of the park.
6 |
7 | An automatic fueling robot carries the fuel from station and fill up the parked car with fuel. The cars are divided into 2 types depending on whether it is a gasoline or diesel car.
8 | 1 is denoted as gasoline cars and 2 is denoted as diesel cars.
9 |
10 | The automatic robot will be used to provide a cost free fueling service which is filling up all cars with 1 litre of each corresponding fuel.
11 |
12 | The robot will move in between the 2 fuelling stations as below :
13 |
14 | 1) The robot carries 2 litre of gasoline at the gasoline station and starts moving from there.
15 |
16 | 2) The robot can fill up the cars of the same type of gas it carries 1 litre each.
17 |
18 | 3) The robot can go back to the fuelling station at any time, Independent from the current amount of fuel it carries.
19 |
20 | 4) When the robot arrives at the fuelling station, it gets 2 litre of supply of the corresponding fuel.(If the robot has some remaining fuel it will be discarded).
21 |
22 | 5) There is an equal distance of 1 between each fueling station and the cars.
23 |
24 | The fuel type of N Cars parked in the parking lot will be given.
25 | Find the minimum moving distance of the automated fueling robot after it has filled up all the cars with 1 litre of fuel each.
26 |
--------------------------------------------------------------------------------
/RobotAndFuelProblem/main.cpp:
--------------------------------------------------------------------------------
1 | #include
2 | #include
3 | #include
4 | using namespace std;
5 | #define GASOLINE 1
6 | #define DIESAL 2
7 |
8 | void initialize(int* arr, int n){
9 | memset(arr, 0, sizeof(arr[0]) * n);
10 | return;
11 | }
12 |
13 | void generate_neighbours(int* target, int* space, int* visited, int N, int x, int probe, bool gasoline){
14 | // From gasoline station robot has to visit one gasoline car.
15 | // Similarly from diesal station robot has to visit one diesal car.
16 | // From a car, robot can either go to similar car,
17 | // or gasoline station,
18 | // or diesal station.
19 | if ( x!= 0 && x!= N-1){
20 | if(probe != 0){
21 | int check = 0;
22 | if (gasoline == true) check = GASOLINE;
23 | else check = DIESAL;
24 | for(int i=1;i>t;
122 | while(t--){
123 | int n;
124 | cin>>n;
125 |
126 | int* space = new int[n + 2];
127 | for(int i=1; i<=n; i++){
128 | cin>>space[i];
129 | }
130 |
131 | space[0] = 0;
132 | space[n+1] = 0;
133 | cout<< find_optimum(space, n+2);
134 | }
135 | }
136 |
--------------------------------------------------------------------------------
/RobotAndFuelProblem/testcases.txt:
--------------------------------------------------------------------------------
1 | 6
2 | 5
3 | 1 2 1 2 1
4 | 5
5 | 2 1 1 2 1
6 | 5
7 | 2 1 2 1 2
8 | 8
9 | 1 1 1 1 2 2 2 2
10 | 8
11 | 2 1 2 2 1 1 1 2
12 | 7
13 | 2 2 2 1 1 1 1
14 |
15 | ########## Answers ############
16 |
17 | 12
18 | 14
19 | 13
20 | 21
21 | 32
22 | 29
23 |
--------------------------------------------------------------------------------
/Robotic Paths/README.md:
--------------------------------------------------------------------------------
1 | # Robotic Path Problem
2 |
3 | This is a medium Toughness question on BFS from Hacker Rank. The link to the question is here
4 |
--------------------------------------------------------------------------------
/Robotic Paths/main.cpp:
--------------------------------------------------------------------------------
1 | #include
2 | using namespace std;
3 |
4 | class Point{
5 | public:
6 | int x;
7 | int y;
8 | Point(){
9 | x = -1;
10 | y = -1;
11 | }
12 | Point(int a, int b){
13 | x = a;
14 | y = b;
15 | }
16 | };
17 |
18 | Point generate_neighbour(char** char_arr, Point& p, int n, int m, int i){
19 | int arr[4][2] = {
20 | {1, 0},
21 | {0, -1},
22 | {0, 1},
23 | {-1, 0},
24 | };
25 |
26 | Point new_p;
27 | if ((p.x + arr[i][0] >=0 && p.x + arr[i][0] < n) && (p.y + arr[i][1] >=0 && p.y + arr[i][1] < m) && char_arr[p.x + arr[i][0]][p.y + arr[i][1]]== '.'){
28 | new_p.x = p.x + arr[i][0];
29 | new_p.y = p.y + arr[i][1];
30 | return new_p;
31 | }
32 |
33 | else return new_p;
34 | }
35 |
36 | class Node{
37 | public:
38 | Node* next;
39 | Point p;
40 | Node(){
41 | next = NULL;
42 | }
43 | Node(int x, int y){
44 | p.x = x;
45 | p.y = y;
46 | next = NULL;
47 | }
48 | };
49 |
50 | class Queue{
51 | Node* first;
52 | public:
53 | Queue(){
54 | first = NULL;
55 | }
56 | void add(Point p){
57 | if(first == NULL){
58 | Node* newnode = new Node(p.x, p.y);
59 | first = newnode;
60 | return;
61 | }
62 | else{
63 | Node* temp = first;
64 | while(temp->next!= NULL){
65 | temp = temp->next;
66 | }
67 | Node* newnode = new Node(p.x,p.y);
68 | temp->next = newnode;
69 | return;
70 | }
71 | }
72 |
73 | Point pop(){
74 | if (first == NULL) return Point();
75 |
76 | else{
77 | Point x = first->p;
78 | first = first->next;
79 | return x;
80 | }
81 |
82 | }
83 |
84 | bool isEmpty(){
85 | if (first == NULL) return 1;
86 | else return 0;
87 | }
88 | };
89 |
90 | void BFS(char** arr, Point** prev_arr, Point& start, Point& end, int n, int m){
91 |
92 | if(arr[start.x][start.y] == '#' || arr[end.x][end.y] == '#'){
93 |
94 | cout<<"Impossible"<<"\n";
95 | return;
96 | }
97 |
98 | Queue q;
99 | q.add(start);
100 | while(!q.isEmpty()){
101 | if(arr[end.x][end.y] == '#') break;
102 |
103 | Point current = q.pop();
104 |
105 | if(arr[current.x][current.y] == '.'){
106 |
107 | for(int i=0; i<4; i++){
108 | Point neighbour = generate_neighbour(arr, current, n, m, i);
109 | if (neighbour.x == -1 && neighbour.y == -1 ||
110 | (prev_arr[neighbour.x][neighbour.y].x != -1 &&
111 | prev_arr[neighbour.x][neighbour.y].y != -1)) continue;
112 |
113 | else{
114 | q.add(neighbour);
115 | prev_arr[neighbour.x][neighbour.y].x = current.x;
116 | prev_arr[neighbour.x][neighbour.y].y = current.y;
117 | }
118 | }
119 | arr[current.x][current.y] = '#';
120 | }
121 |
122 | else continue;
123 | }
124 | if (arr[end.x][end.y] == '#'){
125 | string s = "";
126 |
127 | int x = end.x;
128 | int y = end.y;
129 | // cout<=0; i--){
150 | cout<>n>>m;
174 |
175 | char** arr = new char*[n];
176 | for(int i=0; i>arr[i][j];
181 |
182 | int t;
183 | cin>>t;
184 |
185 | Point start;
186 | Point end;
187 |
188 | for(int i=0; i> start.x>> start.y>> end.x>> end.y;
197 | start.x --;
198 | start.y --;
199 | end.x --;
200 | end.y --;
201 | output_path(t_arr, start, end, n, m);
202 |
203 | }
204 |
205 |
206 | }
207 |
--------------------------------------------------------------------------------
/Stack&Queue/README.md:
--------------------------------------------------------------------------------
1 | # Stack and Queue
2 |
3 | This is a C++ code that explains how to make a Stack or Queue of your own.
4 |
--------------------------------------------------------------------------------
/Stack&Queue/main.cpp:
--------------------------------------------------------------------------------
1 | #include
2 | #include
3 | using namespace std;
4 |
5 | class List{
6 | struct Node{
7 | Node* next;
8 | int data;
9 | };
10 | Node* first;
11 |
12 | public:
13 | List(int d){
14 | Node* newnode = new Node;
15 | first = newnode;
16 | first->next = newnode;
17 | first->data = d;
18 | }
19 |
20 | List(){
21 | this->first = NULL;
22 | }
23 |
24 | int push_back(int x){
25 | Node* temp = this->first;
26 | if(temp == NULL){
27 | Node* newnode = new Node;
28 | newnode->data = x;
29 | newnode->next = newnode;
30 | this->first = newnode;
31 | return newnode->data;
32 | }
33 | while(temp->next!= this->first){
34 | temp = temp->next;
35 | }
36 | Node* newnode = new Node;
37 | newnode->data = x;
38 | newnode->next = this->first;
39 | temp->next = newnode;
40 | return newnode->data;
41 | }
42 |
43 | int pop_back(){
44 | if(this->first == NULL){
45 | return -1;
46 | }
47 | else if(this->first->next == this->first){
48 | int x = this->first->data;
49 | this->first = NULL;
50 | return x;
51 | }
52 | Node* temp = this->first;
53 | while(temp->next->next != this->first){
54 | temp = temp->next;
55 | }
56 | int x = temp->next->data;
57 | temp->next = this->first;
58 | return x;
59 | }
60 |
61 | int push_front(int x){
62 | Node* newnode = new Node;
63 | newnode->data = x;
64 | if(this->first == NULL){
65 | this->first = newnode;
66 | newnode->next = newnode;
67 | return x;
68 | }
69 |
70 | else{
71 | Node* temp = this->first;
72 | this->first = newnode;
73 | this->first->next = temp;
74 | Node* t = temp;
75 | while(t->next != temp){
76 | t = t->next;
77 | }
78 | t->next = this->first;
79 | return x;
80 | }
81 | }
82 |
83 | int pop_front(){
84 | if(this->first == NULL){
85 | return -1;
86 | }
87 | else if(this->first->next == this->first){
88 | int x = this->first->data;
89 | this->first = NULL;
90 | return x;
91 | }
92 | else{
93 | int x = this->first->data;
94 | Node* t = this->first;
95 | this->first = this->first->next;
96 | Node* iter = t;
97 | while(iter->next != t){
98 | iter = iter->next;
99 | }
100 | iter->next = this->first;
101 | return x;
102 | }
103 | }
104 |
105 | void print(){
106 | Node* temp = this->first;
107 | if(temp == NULL){
108 | cout<<"-1\n";
109 | return;
110 | }
111 | do{
112 | cout<data<<" ";
113 | temp = temp->next;
114 | }while(temp !=this->first);
115 | cout<<"\n";
116 | }
117 | };
118 |
--------------------------------------------------------------------------------
/Sudoku/README.md:
--------------------------------------------------------------------------------
1 | ### Problem Description
2 |
3 | A program to solve a Sudoku puzzle by filling the empty cells.
4 | Empty cells are indicated by the character '.'
5 |
6 | Problem is on Interviewbit. [Link](https://www.interviewbit.com/problems/sudoku/)
7 |
8 | ### Example
9 | #### Input:
10 |
11 | 5 3 . . 7 . . . .\
12 | 6 . . 1 9 5 . . .\
13 | . 9 8 . . . . 6 .\
14 | 8 . . . 6 . . . 3\
15 | 4 . . 8 . 3 . . 1\
16 | 7 . . . 2 . . . 6\
17 | . 6 . . . . 2 8 .\
18 | . . . 4 1 9 . . 5\
19 | . . . . 8 . . 7 9
20 |
21 | #### Output:
22 | 5 3 4 6 7 8 9 1 2
23 | 6 7 2 1 9 5 3 4 8
24 | 1 9 8 3 4 2 5 6 7
25 | 8 5 9 7 6 1 4 2 3
26 | 4 2 6 8 5 3 7 9 1
27 | 7 1 3 9 2 4 8 5 6
28 | 9 6 1 5 3 7 2 8 4
29 | 2 8 7 4 1 9 6 3 5
30 | 3 4 5 2 8 6 1 7 9
31 |
32 | ##### Contributed by
33 | [Priyanshu Gangwar](https://github.com/PriyanshuGangwar)
34 |
--------------------------------------------------------------------------------
/Sudoku/main.cpp:
--------------------------------------------------------------------------------
1 | #include
2 | using namespace std;
3 |
4 | //Checking is current digit is valid or not
5 | bool isvalid(char n,vector> maze,int x,int y);
6 |
7 | //Helper Functions for isvalid function
8 | bool isempty(vector> maze,int &i,int &j); //Checks is any box is empty
9 | bool checkbox(char n,vector> maze, int i,int j); //Checks if there is any repetetion in a 3*3 box
10 |
11 | //Function to fill Sudoku
12 |
13 | bool suduko(vector> &maze)
14 | { int i,j;
15 | bool t = isempty(maze,i,j);
16 | if(!t)
17 | {
18 | return true;
19 | }
20 | //ALGORITHM
21 | /* LOOPS OVER 1 - 9 AND CHECKS FOR EVERY
22 | DIGIT AND BACKTRACKS IF IT CREATES COLLISION */
23 |
24 | for(char n='1';n <= '9';n++)
25 | if(isvalid(n,maze,i,j))
26 | { maze[i][j]=n;
27 | if(suduko(maze))
28 | return true;
29 | else
30 | maze[i][j]='.';
31 | }
32 | return false;
33 | }
34 |
35 | int main() {
36 |
37 | //Sudoku Board
38 | vector > maze = {{'5','3','.','.','7','.','.','.','.'},
39 | {'6','.','.','1','9','5','.','.','.'},
40 | {'.','9','8','.','.','.','.','6','.'},
41 | {'8','.','.','.','6','.','.','.','3'},
42 | {'4','.','.','8','.','3','.','.','1'},
43 | {'7','.','.','.','2','.','.','.','6'},
44 | {'.','6','.','.','.','.','2','8','.'},
45 | {'.','.','.','4','1','9','.','.','5'},
46 | {'.','.','.','.','8','.','.','7','9'}};
47 |
48 | suduko(maze);
49 |
50 | //Displaying Filled Board
51 | for(int i = 0; i < 9;i++){
52 | for(int j = 0; j< 9; j++){
53 | cout<> maze,int &i,int &j)
62 | {
63 | for(int x=0;x<9;x++)
64 | for(int y=0;y<9;y++)
65 | {
66 | if(maze[x][y] == '.')
67 | {
68 | i=x;
69 | j=y;
70 | return true;
71 | }
72 | }
73 | return false;
74 | }
75 |
76 |
77 | //Checks if there is any repetetion in a 3*3 box
78 |
79 | bool checkbox(char n,vector> maze, int i,int j)
80 | {
81 | for(int x=0;x<3;x++)
82 | for(int y=0;y<3;y++)
83 | {
84 | if(maze[i+x][j+y] == n)
85 | return false;
86 | }
87 | return true;
88 | }
89 |
90 | //Checking is current digit is valid or not
91 | bool isvalid(char n,vector> maze,int x,int y)
92 | {
93 | for(int i =0;i<9;i++)
94 | {
95 | if(maze[i][y]==n || maze[x][i] == n)
96 | return false;
97 | }
98 |
99 | if(x<3)
100 | {
101 | if(y<3)
102 | {
103 | if(!checkbox(n,maze,0,0))
104 | return false;
105 | }
106 | else if(y<6)
107 | {
108 | if(!checkbox(n,maze,0,3))
109 | return false;
110 | }
111 | else
112 | {
113 | if(!checkbox(n,maze,0,6))
114 | return false;
115 | }
116 | }
117 |
118 | else if(x<6)
119 | {
120 | if(y<3)
121 | {
122 | if(!checkbox(n,maze,3,0))
123 | return false;
124 | }
125 | else if(y<6)
126 | {
127 | if(!checkbox(n,maze,3,3))
128 | return false;
129 | }
130 | else
131 | {
132 | if(!checkbox(n,maze,3,6))
133 | return false;
134 | }
135 | }
136 |
137 | else
138 | {
139 | if(y<3)
140 | {
141 | if(!checkbox(n,maze,6,0))
142 | return false;
143 | }
144 | else if(y<6)
145 | {
146 | if(!checkbox(n,maze,6,3))
147 | return false;
148 | }
149 | else
150 | {
151 | if(!checkbox(n,maze,6,6))
152 | return false;
153 | }
154 | }
155 |
156 | return true;
157 | }
158 |
--------------------------------------------------------------------------------
/TowerConstruction/README.md:
--------------------------------------------------------------------------------
1 | # Tower Construction
2 |
3 | Four 5G base station towers needs to be installed in a Landscape which is divided as hexagon cells as shown in Fig below, which also contains number of people living in each cell. Need to find four cells to install the 5G towers which can cover maximum number of people combining all four cells, with below conditions
4 | Only one tower can be placed in a cell
5 | Each of the four chosen cell should be neighbor to atleast one of the remaining 3 cells.
6 | All four cells should be connected (like one island)
7 |
8 | ## For Example
9 |
10 | ### Input
11 |
12 |
13 |  14 |
14 |
15 |
16 | ### Output
17 | Square of Maximum number of people covered by 4 towers (Fig 2)
18 |
19 |
20 |  21 |
21 |
22 |
23 | ## Approach
24 |
25 | There can be a variety of approaches to get solution to this question. But for all kinds of approach, one thing is common, that we need to
26 | find a path of size 4 for every point in the space.
27 |
28 | 1. I start from the first point, marking it as visited.
29 | 2. Generate all possible neighbours for the point. Note that this is not a normal graph. It is a hexagonally
30 | designed graph, hence the neighbour generation differs.
31 |
32 | [ Hint : neighbour generation differs, depending on whether the column number is odd or even]
33 |
34 | 3. Selecting the best neighbour (the neighbour with the highest value)
35 | 4. Adding the best neighbour to the branch, marking it visited and reducing the depth of probing (tells me that I have already visited 2 points
36 | hence I have to stop after 2 more points).
37 |
38 | Since the final solution can be a tree as well, hence pure DFS or BFS cannot be applied. Hence, once a neighbour is selected we again have
39 | to quest for a new neighbour if probing length isn't zero such that the best neighbour can come from the neighbours of any visited point in the
40 | previously generated path.
41 |
42 | 5. Now searching for a new neighbour, considering every point in the already generated path again.
43 | 6. Repeating 1-5 for every single point in the space, and hence finally landing to the best solution.
44 |
--------------------------------------------------------------------------------
/TowerConstruction/Testcases.txt:
--------------------------------------------------------------------------------
1 | 6
2 | 3 4
3 | 150 450 100 320
4 | 120 130 160 110
5 | 10 60 200 220
6 | 1 4
7 | 10 20 30 40
8 | 3 5
9 | 300 410 150 55 370
10 | 120 185 440 190 450
11 | 165 70 95 420 50
12 | 5 5
13 | 356 55 41 453 12
14 | 401 506 274 506 379
15 | 360 281 421 311 489
16 | 425 74 276 371 164
17 | 138 528 461 477 470
18 | 3 13
19 | 197 51 443 274 47 552 160 96 501 102 469 318 308
20 | 516 128 506 471 381 418 328 517 380 78 569 58 90
21 | 113 238 179 444 541 27 444 62 264 93 245 353 37
22 | 11 7
23 | 292 182 586 607 259 190 239
24 | 511 716 425 367 511 462 714
25 | 593 713 231 60 118 442 82
26 | 626 577 579 682 136 176 681
27 | 240 23 410 193 230 729 109
28 | 453 231 287 383 444 578 409
29 | 729 401 408 330 213 574 54
30 | 684 224 75 62 660 472 227
31 | 606 37 473 487 222 185 476
32 | 84 477 158 94 141 484 122
33 | 616 333 302 626 29 99 674
34 |
35 | ################ Answer ##################
36 |
37 | 1276900
38 | 10000
39 | 2250000
40 | 3748096
41 | 3928324
42 | 7236100
43 |
--------------------------------------------------------------------------------
/TowerConstruction/main.cpp:
--------------------------------------------------------------------------------
1 | #include
2 | #include
3 | using namespace std;
4 | #define DEPTH 4
5 |
6 | int dir_ref[6][2] = {
7 | { 1, 0},
8 | { 0, 1},
9 | { 0,-1},
10 | {-1, 0},
11 | };
12 |
13 | int even_ref[2][2] = {
14 | { 1, -1},
15 | { 1, 1}
16 | };
17 |
18 | int odd_ref[2][2] = {
19 | {-1, -1},
20 | {-1, 1}
21 | };
22 |
23 | int find_best_neighbour(int** space, int** visited,int& best_x, int& best_y, int x, int y, int row, int col, bool isodd){
24 | // selects best neighbour for a given point
25 | int temp = -1;
26 | for(int i=0; i<4; i++){
27 | int neighbour_x, neighbour_y;
28 | neighbour_x = x + dir_ref[i][0];
29 | neighbour_y = y + dir_ref[i][1];
30 |
31 | if( (0<= neighbour_x && neighbour_x < row) &&
32 | (0<= neighbour_y && neighbour_y < col) &&
33 | (space[neighbour_x][neighbour_y] != 0) &&
34 | (visited[neighbour_x][neighbour_y] == 0)){
35 |
36 | if (space[neighbour_x][neighbour_y] > temp){
37 |
38 | temp = space[neighbour_x][neighbour_y];
39 | best_x = neighbour_x;
40 | best_y = neighbour_y;
41 | }
42 | }
43 | }
44 |
45 | if(! isodd){
46 |
47 | for(int i=0;i<2;i++){
48 | int neighbour_x, neighbour_y;
49 | neighbour_x = x + even_ref[i][0];
50 | neighbour_y = y + even_ref[i][1];
51 |
52 | if( (0<= neighbour_x && neighbour_x < row) &&
53 | (0<= neighbour_y && neighbour_y < col) &&
54 | (space[neighbour_x][neighbour_y] != 0) &&
55 | (visited[neighbour_x][neighbour_y] == 0)){
56 |
57 | if (space[neighbour_x][neighbour_y] > temp){
58 |
59 | temp = space[neighbour_x][neighbour_y];
60 | best_x = neighbour_x;
61 | best_y = neighbour_y;
62 | }
63 | }
64 | }
65 | }
66 |
67 | else if(isodd){
68 | for(int i=0;i<2;i++){
69 | int neighbour_x, neighbour_y;
70 | neighbour_x = x + odd_ref[i][0];
71 | neighbour_y = y + odd_ref[i][1];
72 |
73 | if( (0<= neighbour_x && neighbour_x < row) &&
74 | (0<= neighbour_y && neighbour_y < col) &&
75 | (space[neighbour_x][neighbour_y] != 0) &&
76 | (visited[neighbour_x][neighbour_y] == 0)){
77 |
78 | if (space[neighbour_x][neighbour_y] > temp){
79 |
80 | temp = space[neighbour_x][neighbour_y];
81 | best_x = neighbour_x;
82 | best_y = neighbour_y;
83 | }
84 | }
85 | }
86 | }
87 |
88 | return temp;
89 | }
90 |
91 | int branching(int** space, int** visited, int row, int col, int d, int score){
92 | // selects the best neighbour for an already half visited path
93 | if (d == 0){
94 | return score;
95 | }
96 |
97 | int x, y;
98 | int temp = -1;
99 |
100 | for(int i=0; i temp){
109 | // if best neighbour of i,j is better
110 | // than best neighbour of previous i,j
111 | // then changing the final neighbour selection
112 | temp = t;
113 | x = t_x;
114 | y = t_y;
115 | }
116 |
117 | }
118 | }
119 | }
120 |
121 | visited[x][y] =1;
122 | score += space[x][y];
123 |
124 | return branching(space, visited, row, col, d-1, score);
125 | }
126 |
127 | int finding_optimum(int ** space, int row, int col){
128 | // finds optimum path of size DEPTH
129 | int optimum = 0;
130 | int** visited = new int*[row];
131 | for(int i=0; i>t;
164 | while(t--){
165 | int row, col;
166 | cin>>row>>col;
167 |
168 | int** space = new int*[++row];
169 | for(int i=0;i> space[i][j];
178 |
179 | else cin>> space[i+1][j];
180 | }
181 | }
182 |
183 | cout<(0, Y) Empty Jug 1
12 | 2. Fill a Jug, (0, 0)->(X, 0) Fill Jug 1
13 | 3. Pour water from one jug to the other until one of the jugs is either empty or full, (X, Y) -> (X-d, Y+d)
14 |
15 | ## Example
16 |
17 | Input:
18 |
19 | m = 4, n = 3, d = 2
20 |
21 | Output:
22 |
23 | (0, 0), (0, 3), (4, 0), (4, 3), (3, 0), (1, 3), (3, 3), (4, 2), (0, 2)
--------------------------------------------------------------------------------
/Water Jug Problem/main.cpp:
--------------------------------------------------------------------------------
1 | #include
2 | #define pii pair
3 | #define mp make_pair
4 | using namespace std;
5 |
6 | void BFS(int a, int b, int target)
7 | {
8 | //Map is used to store the states
9 | //indicates either that state is visited before or not
10 | map m;
11 | bool isSolvable = false;
12 | vector path;
13 |
14 | queue q; //queue to maintain states
15 | q.push({0, 0}); //Initialing with initial state
16 |
17 | while (!q.empty()) {
18 |
19 | pii u = q.front(); //current state
20 |
21 | q.pop(); //pop off used state
22 |
23 | //if this state is already visited
24 | if (m[{ u.first, u.second }] == 1)
25 | continue;
26 |
27 | //doesn't met jug constraints
28 | if ((u.first > a || u.second > b ||
29 | u.first < 0 || u.second < 0))
30 | continue;
31 |
32 | //filling the vector for constructing
33 | //the solution path
34 | path.push_back({u.first, u.second});
35 |
36 | //marking current state as visited
37 | m[{u.first, u.second}] = 1;
38 |
39 | //if we reach solution state, put ans=1
40 | if (u.first == target || u.second == target) {
41 | isSolvable = true;
42 | if (u.first == target) {
43 | if (u.second != 0)
44 |
45 | //fill final state
46 | path.push_back({u.first, 0});
47 | }
48 | else {
49 | if (u.first != 0)
50 |
51 | //fill final state
52 | path.push_back({0, u.second});
53 | }
54 |
55 | //print the solution path
56 | int sz = path.size();
57 | for (int i = 0; i < sz; i++)
58 | cout<<"("<= 0))
76 | q.push({ c, d });
77 |
78 | //Pour amount ap from Jug 1 to Jug2
79 | c = u.first - ap;
80 | d = u.second + ap;
81 |
82 | //check if this state is possible or not
83 | if ((c == 0 && c >= 0) || d == b)
84 | q.push({ c, d });
85 | }
86 |
87 | q.push({a, 0}); //Empty Jug2
88 | q.push({0, b}); //Empty Jug1
89 | }
90 |
91 | //No, solution exists if ans=0
92 | if(!isSolvable)
93 | cout<<"No solution";
94 | }
95 |
96 | int main()
97 | {
98 | int Jug1 = 4, Jug2 = 3, target = 2;
99 | cout<<"Path from initial state to solution state :\n";
100 | BFS(Jug1, Jug2, target);
101 | return 0;
102 | }
103 |
--------------------------------------------------------------------------------
/cheatsheet.cpp:
--------------------------------------------------------------------------------
1 | #include
2 |
3 | #define dbg(x) cerr << #x << ": " << x << endl;
4 | #define FOR(i, a, b) for(int i = (a); i < (b); ++i)
5 | #define FORD(i, a, b) for(int i = (a); i >= (b); --i)
6 | #define all(v) (v).begin(), (v).end()
7 | #define rall(v) (v).rbegin(), (v).rend()
8 | #define pb push_back
9 | #define mp make_pair
10 | #define fi first
11 | #define se second
12 |
13 | #define INF 1000000000
14 | #define MAXN 1000005
15 | #define EPS 1e-9
16 |
17 | typedef long long ll;
18 | typedef std::vector vi;
19 | typedef std::vector vll;
20 | typedef std::pair pii;
21 | typedef std::pair pllll;
22 | typedef std::set si;
23 | typedef std::set sll;
24 | typedef std::unordered_map mii;
25 | typedef std::unordered_map mllll;
26 | typedef std::unordered_map mci;
27 | typedef std::unordered_map mcll;
28 |
29 | ll N;
30 | bool seen[MAXN];
31 | vll dist(MAXN), vis(MAXN), rank(MAXN), size(MAXN), parent(MAXN), adj[MAXN];
32 | std::vector> edges;
33 | std::vector adj_dijkstra[MAXN]; //{v, w}
34 |
35 | void dfs(int x) {
36 | std::stack s;
37 | seen[x] = true;
38 | s.push(x);
39 | while(!s.empty()) {
40 | ll u = s.top(); s.pop();
41 | for(auto v : adj[u]) {
42 | if(seen[v]) continue;
43 | seen[v] = true;
44 | s.push(v);
45 | }
46 | }
47 | }
48 |
49 | void bfs(int x) {
50 | std::queue q;
51 | seen[x] = true;
52 | dist[x] = 0;
53 | q.push(x);
54 | while(!q.empty()) {
55 | ll u = q.front(); q.pop();
56 | for(auto v : adj[u]) {
57 | if(seen[v]) continue;
58 | seen[v] = true;
59 | dist[v] = dist[u] + 1;
60 | q.push(v);
61 | }
62 | }
63 | }
64 |
65 | void dijkstra(int s) {
66 | FOR(i, 0, N) {
67 | dist[i] = INF;
68 | vis[i] = false;
69 | }
70 | std::priority_queue q; //{w, v}
71 | dist[s] = 0;
72 | q.push({0, s});
73 | while(!q.empty()) {
74 | ll u = q.top().se; q.pop();
75 | if(vis[u]) continue;
76 | vis[u] = true;
77 | for(auto pr : adj_dijkstra[u]) {
78 | ll v, w;
79 | std::tie(v, w) = pr;
80 | if(vis[v]) continue;
81 |
82 | if(dist[u] + w < dist[v]) {
83 | dist[v] = dist[u] + w;
84 | q.push({-dist[v], v});
85 | }
86 | }
87 | }
88 | }
89 |
90 | void toposort() { //I prefer this since it looks more straightforward than the dfs method
91 | vll indegree(N);
92 | FOR(i, 0, N) {
93 | for(auto it : adj[i]){
94 | indegree[it]++;
95 | }
96 | }
97 |
98 | std::queue q;
99 | FOR(i, 0, N) {
100 | if(indegree[i] == 0)
101 | q.push(i);
102 | }
103 |
104 | vll result;
105 | while(!q.empty()) {
106 | ll node = q.front(); q.pop();
107 | result.pb(node);
108 |
109 | for(auto it : adj[node]){
110 | indegree[it]--;
111 |
112 | if(indegree[it] == 0)
113 | q.push(it);
114 | }
115 | }
116 |
117 | if(result.size() != N)
118 | std::cout<<"CYCLE ABAHDHSAJDHSA BRETHIKE KYKLOS AMBER ALERT";
119 | else
120 | std::cout<<"No kyklos all good";
121 | }
122 |
123 | //UNion psajimo
124 |
125 | void init() {
126 | FOR(i, 0, N) {
127 | parent[i] = i;
128 | size[i] = 1;
129 | rank[i] = 0;
130 | }
131 | }
132 |
133 | ll find(int a) {
134 | if(a == parent[a]) return a;
135 | return parent[a] = find(parent[a]);
136 | }
137 |
138 | void unite(ll a, ll b) {
139 | a = find(a);
140 | b = find(b);
141 |
142 | //By rank
143 | if(a != b) {
144 | if(rank[a] < rank[b])
145 | std::swap(a, b);
146 | parent[b] = a;
147 | if(rank[a] == rank[b])
148 | rank[a]++;
149 | }
150 |
151 | //By size
152 | if(a != b) {
153 | if(size[a] < size[b])
154 | std::swap(a, b);
155 | parent[b] = a;
156 | size[a] += size[b];
157 | }
158 | }
159 |
160 | bool same(ll a, ll b) {
161 | return find(a) == find(b);
162 | }
163 |
164 | void kruskal() {
165 | std::sort(all(edges));
166 | for(auto edge : edges) {
167 | ll u, v, w;
168 | std::tie(w, u, v) = edge;
169 | if(!same(u, v)) unite(u, v);
170 | }
171 | }
172 |
173 | int main()
174 | {
175 | return 0;
176 | }
177 |
--------------------------------------------------------------------------------
/img/FishInput.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/shreyanshchordia/Graph_Algorithms/d55a286a9f841fe64006deec1b91050791c551e1/img/FishInput.png
--------------------------------------------------------------------------------
/img/Fisher1.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/shreyanshchordia/Graph_Algorithms/d55a286a9f841fe64006deec1b91050791c551e1/img/Fisher1.png
--------------------------------------------------------------------------------
/img/Fisher2.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/shreyanshchordia/Graph_Algorithms/d55a286a9f841fe64006deec1b91050791c551e1/img/Fisher2.png
--------------------------------------------------------------------------------
/img/Fisher3.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/shreyanshchordia/Graph_Algorithms/d55a286a9f841fe64006deec1b91050791c551e1/img/Fisher3.png
--------------------------------------------------------------------------------
/img/TowerInput.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/shreyanshchordia/Graph_Algorithms/d55a286a9f841fe64006deec1b91050791c551e1/img/TowerInput.png
--------------------------------------------------------------------------------
/img/TowerOutput.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/shreyanshchordia/Graph_Algorithms/d55a286a9f841fe64006deec1b91050791c551e1/img/TowerOutput.png
--------------------------------------------------------------------------------
/img/airplane.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/shreyanshchordia/Graph_Algorithms/d55a286a9f841fe64006deec1b91050791c551e1/img/airplane.png
--------------------------------------------------------------------------------
/img/pipes.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/shreyanshchordia/Graph_Algorithms/d55a286a9f841fe64006deec1b91050791c551e1/img/pipes.png
--------------------------------------------------------------------------------
/number of islands/README.md:
--------------------------------------------------------------------------------
1 | This Problem is medium level graph algorithm implementation problem.
2 |
3 | **PROBLEM STATEMENT**
4 |
5 | Given a Matrix consisting of 0s and 1s. Find the number of islands of connected 1s present in the matrix.
6 | Note: A 1 is said to be connected if it has another 1 around it (either of the 8 directions).
7 |
8 | **Input:**
9 | The first line of input will be the number of testcases **T**, then T test cases follow. The first line of each testcase contains two space separated integers N and M. Then in the next line are the NxM inputs of the matrix A separated by space .
10 |
11 | **Output**:
12 | For each testcase in a new line, print the number of islands present.
13 |
14 | **Expected Time Complexity: O(N*M).\
15 | Expected Auxiliary Space: O(N*M).**
16 |
17 | **Constraints:\
18 | 1 <= T <= 100\
19 | 1 <= N, M <= 100\
20 | 0 <= A[i][j] <= 1**
21 |
22 | **Example :\
23 | Input**
24 |
25 | 2\
26 | 3 3\
27 | 1 1 0 0 0 1 1 0 1\
28 | 4 4\
29 | 1 1 0 0 0 0 1 0 0 0 0 1 0 1 0 0
30 |
31 | **Output**\
32 | 2\
33 | 2
34 |
35 | **Explanation:**
36 |
37 | Testcase 1: The graph will look like\
38 | **1 1** 0\
39 | 0 0 **1**\
40 | *1* 0 **1**\
41 | Here, two islands will be formed
42 | First island will be formed by elements **{A[0][0] , A[0][1], A[1][2], A[2][2]}**
43 | Second island will be formed by *{A[2][0]}*.
44 |
45 | Testcase 2: The graph will look like\
46 | **1 1** 0 0\
47 | 0 0 **1** 0\
48 | 0 0 0 **1**\
49 | 0 *1* 0 0\
50 | Here, two islands will be formed
51 | First island will be formed by elements **{A[0][0] , A[0][1], A[1][2], A[2][3]}**
52 | Second island will be formed by *{A[3][1]}*.
53 |
54 |
55 | **problem taken from: https://practice.geeksforgeeks.org/problems/find-the-number-of-islands/1/?track=DSASP-Graph&batchId=154 **
56 |
--------------------------------------------------------------------------------
/number of islands/number of islands.cpp:
--------------------------------------------------------------------------------
1 | // C++ Program to count islands in boolean 2D matrix
2 | #include
3 | using namespace std;
4 |
5 | #define ROW 5
6 | #define COL 5
7 |
8 | // A function to check if a given
9 | // cell (row, col) can be included in DFS
10 | int isSafe(int M[][COL], int row, int col,
11 | bool visited[][COL])
12 | {
13 | // row number is in range, column
14 | // number is in range and value is 1
15 | // and not yet visited
16 | return (row >= 0) && (row < ROW) && (col >= 0) && (col < COL) && (M[row][col] && !visited[row][col]);
17 | }
18 |
19 | // A utility function to do DFS for a
20 | // 2D boolean matrix. It only considers
21 | // the 8 neighbours as adjacent vertices
22 | void DFS(int M[][COL], int row, int col,
23 | bool visited[][COL])
24 | {
25 | // These arrays are used to get
26 | // row and column numbers of 8
27 | // neighbours of a given cell
28 | static int rowNbr[] = { -1, -1, -1, 0, 0, 1, 1, 1 };
29 | static int colNbr[] = { -1, 0, 1, -1, 1, -1, 0, 1 };
30 |
31 | // Mark this cell as visited
32 | visited[row][col] = true;
33 |
34 | // Recur for all connected neighbours
35 | for (int k = 0; k < 8; ++k)
36 | if (isSafe(M, row + rowNbr[k], col + colNbr[k], visited))
37 | DFS(M, row + rowNbr[k], col + colNbr[k], visited);
38 | }
39 |
40 | // The main function that returns
41 | // count of islands in a given boolean
42 | // 2D matrix
43 | int countIslands(int M[][COL])
44 | {
45 | // Make a bool array to mark visited cells.
46 | // Initially all cells are unvisited
47 | bool visited[ROW][COL];
48 | memset(visited, 0, sizeof(visited));
49 |
50 | // Initialize count as 0 and
51 | // travese through the all cells of
52 | // given matrix
53 | int count = 0;
54 | for (int i = 0; i < ROW; ++i)
55 | for (int j = 0; j < COL; ++j)
56 |
57 | // If a cell with value 1 is not
58 | if (M[i][j] && !visited[i][j]) {
59 | // visited yet, then new island found
60 | // Visit all cells in this island.
61 | DFS(M, i, j, visited);
62 |
63 | // and increment island count
64 | ++count;
65 | }
66 |
67 | return count;
68 | }
69 |
70 | // Driver code
71 | int main()
72 | {
73 | int M[][COL] = { { 1, 1, 0, 0, 0 },
74 | { 0, 1, 0, 0, 1 },
75 | { 1, 0, 0, 1, 1 },
76 | { 0, 0, 0, 0, 0 },
77 | { 1, 0, 1, 0, 1 } };
78 |
79 | cout << "Number of islands is: " << countIslands(M);
80 |
81 | return 0;
82 | }
83 |
84 |
--------------------------------------------------------------------------------
 11 |
11 |  11 |
11 |  39 |
40 |
41 |
39 |
40 |
41 |  43 |
43 |  47 |
47 |  51 |
51 |