├── a.txt
├── cheatsheet.jpg
├── Autoencoder
├── result.png
└── Autoencoder.ipynb
├── python basics
├── NUMPY
│ ├── 1.py
│ ├── 2.py
│ ├── 3.py
│ ├── 4.py
│ ├── version.py
│ ├── result1.py
│ ├── tofindindexof100thelement.py
│ ├── 5.py
│ ├── 6.py
│ └── NUMPY.ipynb
└── .ipynb_checkpoints
│ └── NUMPY-checkpoint.ipynb
├── Py and R cheatsheet.jpg
├── Performance Metrics
├── img
│ └── auc.png
├── roc_and_auc.md
└── metrics in classification.md
├── tensorflow basics
├── autoencoder.png
├── basics1.py
├── basics2.py
├── basics3.py
└── autoencoder.py
├── Python for Data Science - cheatsheet.pdf
├── README.md
├── Position_Salaries.csv
├── Cheatsheet by Stanford.md
├── Ensenmble-learning
├── XGBoost.py
└── XGBoost_gridSearch.py
├── KNN-ALGORITHM
└── KNN.py
├── perceptron
├── perceptron.py
├── perceptronalgo.py
└── data.csv
├── prediction.pynb
├── LSTM
├── iris-data.csv
└── Untitled1.ipynb
├── LICENSE
└── K-means-cluster
└── K-MEANS.ipynb
/a.txt:
--------------------------------------------------------------------------------
1 | sdasd
--------------------------------------------------------------------------------
/cheatsheet.jpg:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/somiljain7/AI/HEAD/cheatsheet.jpg
--------------------------------------------------------------------------------
/Autoencoder/result.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/somiljain7/AI/HEAD/Autoencoder/result.png
--------------------------------------------------------------------------------
/python basics/NUMPY/1.py:
--------------------------------------------------------------------------------
1 | import numpy as np
2 | z=np.zeros(10)
3 | z[4] = 1
4 | print(z)
5 |
--------------------------------------------------------------------------------
/Py and R cheatsheet.jpg:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/somiljain7/AI/HEAD/Py and R cheatsheet.jpg
--------------------------------------------------------------------------------
/Performance Metrics/img/auc.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/somiljain7/AI/HEAD/Performance Metrics/img/auc.png
--------------------------------------------------------------------------------
/python basics/NUMPY/2.py:
--------------------------------------------------------------------------------
1 | #/*randomize in range 10,50 */
2 | import numpy as np
3 | z=np.arange(10,50)
4 | print(z)
5 |
--------------------------------------------------------------------------------
/tensorflow basics/autoencoder.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/somiljain7/AI/HEAD/tensorflow basics/autoencoder.png
--------------------------------------------------------------------------------
/python basics/NUMPY/3.py:
--------------------------------------------------------------------------------
1 | #/*REVERSING AN VECTOR*/
2 | import numpy as np
3 | z=np.arange(50)
4 | z=z[::-1]
5 | print(z)
6 |
--------------------------------------------------------------------------------
/python basics/NUMPY/4.py:
--------------------------------------------------------------------------------
1 | #/* CREATING AN 3x3 MATRIX*/
2 | import numpy as np
3 | z=np.arange(9).reshape(3,3)
4 | print(z)
5 |
--------------------------------------------------------------------------------
/python basics/NUMPY/version.py:
--------------------------------------------------------------------------------
1 | import numpy as n
2 | print(n.__version__)
3 |
4 | #to know the version of numpy installed
5 |
--------------------------------------------------------------------------------
/Python for Data Science - cheatsheet.pdf:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/somiljain7/AI/HEAD/Python for Data Science - cheatsheet.pdf
--------------------------------------------------------------------------------
/python basics/NUMPY/result1.py:
--------------------------------------------------------------------------------
1 | import numpy as n
2 |
3 | 0 * n.nan
4 | n.nan == n.nan
5 | n.inf >n.nan
6 | n.nan - n.nan
7 | 0.3 == 3*0.1
8 |
--------------------------------------------------------------------------------
/python basics/NUMPY/tofindindexof100thelement.py:
--------------------------------------------------------------------------------
1 | import numpy as np
2 | print(np.unravel_index(100,(6,7,8)))
3 |
4 | print(np.unravel_index(
5 |
--------------------------------------------------------------------------------
/python basics/.ipynb_checkpoints/NUMPY-checkpoint.ipynb:
--------------------------------------------------------------------------------
1 | {
2 | "cells": [],
3 | "metadata": {},
4 | "nbformat": 4,
5 | "nbformat_minor": 2
6 | }
7 |
--------------------------------------------------------------------------------
/python basics/NUMPY/5.py:
--------------------------------------------------------------------------------
1 | #/* CREATING A CHECKBOARD 8x8 MATRIX*/
2 | import numpy as np
3 | z=np.tile(np.array([[0,1],[1,0]]),(4,4))
4 | print(z)
5 |
6 |
--------------------------------------------------------------------------------
/python basics/NUMPY/6.py:
--------------------------------------------------------------------------------
1 |
2 | #/* NORMALIZING 5x5 MATRIX*/
3 | import numpy as np
4 | Z=np.random.random((5,5))
5 | Zmax,Zmin = Z.max(),Z.min()
6 | Z = (Z - Zmin)/(Zmax - Zmin)
7 | print(Z)
8 |
9 |
--------------------------------------------------------------------------------
/README.md:
--------------------------------------------------------------------------------
1 | # ` AI ALGORITHMS `
2 | **This repository contains my algorithm implemetantion +EDA + data visualization**
3 |
4 | # `Setup: `
5 | ```
6 | $ git clone https://github.com/somiljain7/AI.git
7 |
8 | ```
9 | # `feel free to contribute :)`
10 |
11 |
12 |
13 |
--------------------------------------------------------------------------------
/tensorflow basics/basics1.py:
--------------------------------------------------------------------------------
1 | import tensorflow as tf
2 | from tensorflow.keras import Sequential
3 | from tensorflow.keras.layers import Dense
4 |
5 | model = Sequential()
6 | model.add(Dense(3, input_dim=2 ,activation='relu'))
7 | model.add(Dense(1, activation='softmax'))
8 |
9 |
--------------------------------------------------------------------------------
/Position_Salaries.csv:
--------------------------------------------------------------------------------
1 | Position,Level,Salary
2 | Business Analyst,1,45000
3 | Junior Consultant,2,50000
4 | Senior Consultant,3,60000
5 | Manager,4,80000
6 | Country Manager,5,110000
7 | Region Manager,6,150000
8 | Partner,7,200000
9 | Senior Partner,8,300000
10 | C-level,9,500000
11 | CEO,10,1000000
--------------------------------------------------------------------------------
/Cheatsheet by Stanford.md:
--------------------------------------------------------------------------------
1 | ### Machine Learning Cheatsheet by Stanford University
2 |
3 | ### For Classification and Regression Metrics
4 | https://stanford.edu/~shervine/teaching/cs-229/cheatsheet-machine-learning-tips-and-tricks
5 |
6 | ### For Supervised Learning
7 | https://stanford.edu/~shervine/teaching/cs-229/cheatsheet-supervised-learning
8 |
9 | ### For Unsupervised Learning
10 | https://stanford.edu/~shervine/teaching/cs-229/cheatsheet-unsupervised-learning
11 |
--------------------------------------------------------------------------------
/Ensenmble-learning/XGBoost.py:
--------------------------------------------------------------------------------
1 | import xgboost as xgb
2 |
3 | #Using the XGBoost Classifier. I have used just a few combinations here and there without GridSearch or RandomSearch because the dataset was pretty small
4 | xg_cl = xgb.XGBClassifier(objective='binary:logistic', n_estimators=500,seed=42,learning_rate=0.01,max_depth=5,colsample_bytree=0.75,subsample=0.7,
5 | tree_method='exact', min_child_weight=4,reg_alpha=0.005)
6 |
7 | #fitting the model
8 | xg_cl.fit(X_train,y_train)
9 |
--------------------------------------------------------------------------------
/tensorflow basics/basics2.py:
--------------------------------------------------------------------------------
1 | import tensorflow as tf
2 | from tensorflow.keras import Model
3 | from tensorflow.keras.layers import Dense
4 |
5 | class SimpleNeuralNetwork(Model):
6 | def __init__(self):
7 | super(SimpleNeuralNetwork , self).__init__()
8 | self.layer1 = Dense(2,activation='relu')
9 | self.layer2 = Dense(3,activation='relu')
10 | self.outputLayer = Dense(1,activation='softmax')
11 | def call(self, x):
12 | x = self.layer1(x)
13 | x = self.layer2(x)
14 | return self.outputLayer(x)
15 |
16 | Model = SimpleNeuralNetwork()
17 |
18 |
19 |
--------------------------------------------------------------------------------
/KNN-ALGORITHM/KNN.py:
--------------------------------------------------------------------------------
1 | import tensorflow as tf
2 | import numpy as np
3 | from scipy import stats
4 | from tensorflow.examples.tutorials.mnist import input_data
5 |
6 | mnist = input_data.read_data_sets("/tmp/data/", one_hot=True)
7 | X_train,y_train = mnist.train.next_batch(5000)
8 | X_test, y_test = mnist.test.next_batch(100)
9 | k=3
10 | target_x= tf.placeholder("float",[1784])
11 | X = tf.placeholder("float",[None, 784])
12 | y = tf.placeholder("float",[None, 10])
13 | l1_dist = tf.reduce_sum(tf.abs(tf.sub(x, target_x)), 1)
14 | l2_dist = tf.reduce_sum(tf.square(tf.sub(x, target_x)), 1)
15 | nn = tf.nn.top_k(-l1_dist, k)
16 | init = tf.initialize_all_variables()
17 | accuracy_history = []
18 | with tf.Session() as sess:
19 | sess.run(init)
20 |
--------------------------------------------------------------------------------
/Performance Metrics/roc_and_auc.md:
--------------------------------------------------------------------------------
1 | ## ROC and AUC
2 |
3 | refer:
4 | - https://www.youtube.com/watch?v=A_ZKMsZ3f3o
5 | - https://developers.google.com/machine-learning/crash-course/classification/roc-and-auc
6 |
7 | **Receiver operating characteristic curve (ROC)**
8 | Receiver operating characteristic curve, performance of classification model at all threshold
9 | - T+ve and F+ve
10 |
11 |
12 |
13 | **Area under the curve (AUC)**
14 | 1. condiser some threshold value
15 | 2. Find output y^ for all threshold values
16 | 3. calculate True+ve and False+ve
17 | 4. Plot a graph F+ve vs T+ve
18 |
19 | - AUC dir proportional to area
20 | - Model should be always greater than linear line in graph
21 | - Focus on True Positive values
22 | - Select the best threshold value
23 |
24 | 
25 |
--------------------------------------------------------------------------------
/Ensenmble-learning/XGBoost_gridSearch.py:
--------------------------------------------------------------------------------
1 | from xgboost.sklearn import XGBRegressor
2 | import datetime
3 | from sklearn.model_selection import GridSearchCV
4 |
5 | # Various hyper-parameters to tune
6 | xgb1 = XGBRegressor()
7 | parameters = {'nthread':[4], #when use hyperthread, xgboost may become slower
8 | 'objective':['reg:linear'],
9 | 'learning_rate': [.03, 0.05, .07, .01, 0.1], #so called `eta` value
10 | 'max_depth': [5, 6, 7],
11 | 'min_child_weight': [4, 3, 2],
12 | 'silent': [1],
13 | 'subsample': [0.7, 0.75, 0.8],
14 | 'colsample_bytree': [0.7, 0.75, 0.8],
15 | 'n_estimators': [500, 600, 700, 800, 900, 1000]}
16 |
17 | xgb_grid = GridSearchCV(xgb1, parameters, cv = 2, n_jobs = 5, verbose=True)
18 |
19 | xgb_grid.fit(X_train, y_train)
20 |
21 | print(xgb_grid.best_score_)
22 | print(xgb_grid.best_params_)
23 |
24 | preds = xg_cl.predict(X_test)
25 |
--------------------------------------------------------------------------------
/perceptron/perceptron.py:
--------------------------------------------------------------------------------
1 | import pandas as pd
2 |
3 | # TODO: Set weight1, weight2, and bias
4 | weight1 = 1.5
5 | weight2 = 1.5
6 | bias = -2.0
7 |
8 |
9 | # DON'T CHANGE ANYTHING BELOW
10 | # Inputs and outputs
11 | test_inputs = [(0, 0), (0, 1), (1, 0), (1, 1)]
12 | correct_outputs = [False, False, False, True]
13 | outputs = []
14 |
15 | # Generate and check output
16 | for test_input, correct_output in zip(test_inputs, correct_outputs):
17 | linear_combination = weight1 * test_input[0] + weight2 * test_input[1] + bias
18 | output = int(linear_combination >= 0)
19 | is_correct_string = 'Yes' if output == correct_output else 'No'
20 | outputs.append([test_input[0], test_input[1], linear_combination, output, is_correct_string])
21 |
22 | # Print output
23 | num_wrong = len([output[4] for output in outputs if output[4] == 'No'])
24 | output_frame = pd.DataFrame(outputs, columns=['Input 1', ' Input 2', ' Linear Combination', ' Activation Output', ' Is Correct'])
25 | if not num_wrong:
26 | print('Nice! You got it all correct.\n')
27 | else:
28 | print('You got {} wrong. Keep trying!\n'.format(num_wrong))
29 | print(output_frame.to_string(index=False))
--------------------------------------------------------------------------------
/prediction.pynb:
--------------------------------------------------------------------------------
1 | import pandas as pd
2 | import seaborn as sns
3 | import matplotlib.pyplot as plt
4 | from sklearn.ensemble import RandomForestClassifier
5 | from sklearn.svm import SVC
6 | from sklearn.linear_model import SGDClassifier
7 | from sklearn.metrics import confusion_matrix, classification_report
8 | from sklearn.preprocessing import StandardScaler, LabelEncoder
9 | from sklearn.model_selection import train_test_split, GridSearchCV, cross_val_score
10 | %matplotlib inline
11 |
12 | #Loading dataset
13 | wine = pd.read_csv('../input/winequality-red.csv')
14 | wine.head()
15 |
16 |
17 |
18 | #Now seperate the dataset as response variable and feature variabes
19 | X = wine.drop('quality', axis = 1)
20 | y = wine['quality']
21 |
22 | X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.2, random_state = 42)
23 |
24 |
25 |
26 |
27 | #Applying Standard scaling to get optimized result
28 | sc = StandardScaler()
29 |
30 |
31 |
32 | X_train = sc.fit_transform(X_train)
33 | X_test = sc.fit_transform(X_test)
34 |
35 | svc2 = SVC(C = 1.2, gamma = 0.9, kernel= 'rbf')
36 | svc2.fit(X_train, y_train)
37 | pred_svc2 = svc2.predict(X_test)
38 | print(classification_report(y_test, pred_svc2))
39 |
40 |
41 |
--------------------------------------------------------------------------------
/tensorflow basics/basics3.py:
--------------------------------------------------------------------------------
1 | import quandl
2 | import numpy as np
3 | from sklearn.linear_model import LinearRegression
4 | from sklearn.svm import SVR
5 | from sklearn.model_selection import train_test_split
6 | # Get the stock data
7 | df = quandl.get("WIKI/AMZN")
8 | # Take a look at the data
9 | # Get the Adjusted Close Price
10 | df = df[['Adj. Close']]
11 | # A variable for predicting 'n' days out into the future
12 | forecast_out = 30 #'n=30' days
13 | #Create another column (the target ) shifted 'n' units up
14 | df['Prediction'] = df[['Adj. Close']].shift(-forecast_out)
15 | #print the new data set
16 | print(df.tail())
17 | X = np.array(df.drop(['Prediction'],1))
18 |
19 | #Remove the last '30' rows
20 | X = X[:-forecast_out]
21 | print(X)
22 | ### Create the dependent data set (y) #####
23 | # Convert the dataframe to a numpy array
24 | y = np.array(df['Prediction'])
25 | # Get all of the y values except the last '30' rows
26 | y = y[:-forecast_out]
27 | print(y)
28 | # Split the data into 80% training and 20% testing
29 | x_train, x_test, y_train, y_test = train_test_split(X, y, test_size=0.2)
30 | # Create and train the Support Vector Machine (Regressor)
31 | svr_rbf = SVR(kernel='rbf', C=1e3, gamma=0.1)
32 | svr_rbf.fit(x_train, y_train)
33 |
34 |
--------------------------------------------------------------------------------
/Performance Metrics/metrics in classification.md:
--------------------------------------------------------------------------------
1 | ## All Metrics in Classification
2 |
3 | **Classification Problem**
4 | Default threshold in `0.5`
5 | - Class Labels
6 | - Probabilities (AUC, ROC, PR Curve)
7 |
8 | **Dataset (based on labels)**
9 | - Nearly equal number of records for both labels => `Accuracy`
10 | - Unequal records for labels => Recall, Precision, Fß (F1 Score) and `not Accuracy`
11 |
12 | 1. Confusion Matrix
13 | 2x2 matrix
14 | - top (Actual Values)
15 | - left Predicted Values
16 |
17 | 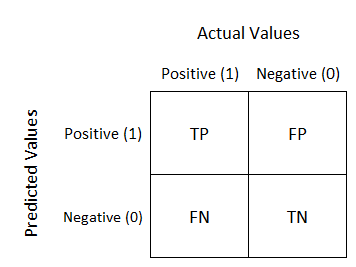
18 |
19 | - False +ve => Type 1 Error
20 | - False -ve => Type 2 Error
21 |
22 | Aim -
23 | - Reducing Type1 and Type2 Error
24 | - Accurate values T+ve and T-ve
25 |
26 | **Parameters**
27 | - Balanced Dataset
28 |
29 | Accuracy = (TP + TN) / (TP + FP + FN + TN)
30 |
31 | - Imbalanced Dataset
32 |
33 | Recall(True +ve Rate or Sensitivity) = Out of all +ve values , how many +ve correctly predicted
34 |
35 | Precision(+ve Pred value) = Out of all actual predicted result, how many actual +ve
36 |
37 | 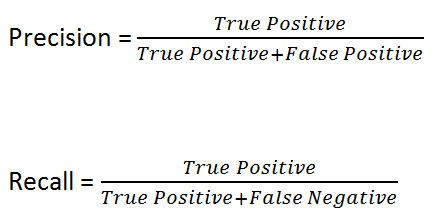
38 |
39 |
40 | 2. Fß Score - To reduce type 1 and type 2 errors
41 |
42 | 
43 |
44 | when ß = 1 => Harmonic mean
45 | - When F+ve and F-ve is important then ß = 1
46 | - Type 1 error ß > 1
47 | - Type 2 error ß = 0.5 to 1 mostly 0.5
48 |
--------------------------------------------------------------------------------
/perceptron/perceptronalgo.py:
--------------------------------------------------------------------------------
1 | import numpy as np
2 | # Setting the random seed, feel free to change it and see different solutions.
3 | np.random.seed(42)
4 |
5 | def stepFunction(t):
6 | if t >= 0:
7 | return 1
8 | return 0
9 |
10 | def prediction(X, W, b):
11 | return stepFunction((np.matmul(X,W)+b)[0])
12 |
13 | # TODO: Fill in the code below to implement the perceptron trick.
14 | # The function should receive as inputs the data X, the labels y,
15 | # the weights W (as an array), and the bias b,
16 | # update the weights and bias W, b, according to the perceptron algorithm,
17 | # and return W and b.
18 | def perceptronStep(X, y, W, b, learn_rate = 0.01):
19 | for i in range(len(X)):
20 | y_hat = prediction(X[i],W,b)
21 | if y[i]-y_hat == 1:
22 | W[0] += X[i][0]*learn_rate
23 | W[1] += X[i][1]*learn_rate
24 | b += learn_rate
25 | elif y[i]-y_hat == -1:
26 | W[0] -= X[i][0]*learn_rate
27 | W[1] -= X[i][1]*learn_rate
28 | b -= learn_rate
29 | return W, b
30 |
31 |
32 | # This function runs the perceptron algorithm repeatedly on the dataset,
33 | # and returns a few of the boundary lines obtained in the iterations,
34 | # for plotting purposes.
35 | # Feel free to play with the learning rate and the num_epochs,
36 | # and see your results plotted below.
37 | def trainPerceptronAlgorithm(X, y, learn_rate = 0.01, num_epochs = 25):
38 | x_min, x_max = min(X.T[0]), max(X.T[0])
39 | y_min, y_max = min(X.T[1]), max(X.T[1])
40 | W = np.array(np.random.rand(2,1))
41 | b = np.random.rand(1)[0] + x_max
42 | # These are the solution lines that get plotted below.
43 | boundary_lines = []
44 | for i in range(num_epochs):
45 | # In each epoch, we apply the perceptron step.
46 | W, b = perceptronStep(X, y, W, b, learn_rate)
47 | boundary_lines.append((-W[0]/W[1], -b/W[1]))
48 | return boundary_lines
49 |
--------------------------------------------------------------------------------
/perceptron/data.csv:
--------------------------------------------------------------------------------
1 | 0.78051,-0.063669,1
2 | 0.28774,0.29139,1
3 | 0.40714,0.17878,1
4 | 0.2923,0.4217,1
5 | 0.50922,0.35256,1
6 | 0.27785,0.10802,1
7 | 0.27527,0.33223,1
8 | 0.43999,0.31245,1
9 | 0.33557,0.42984,1
10 | 0.23448,0.24986,1
11 | 0.0084492,0.13658,1
12 | 0.12419,0.33595,1
13 | 0.25644,0.42624,1
14 | 0.4591,0.40426,1
15 | 0.44547,0.45117,1
16 | 0.42218,0.20118,1
17 | 0.49563,0.21445,1
18 | 0.30848,0.24306,1
19 | 0.39707,0.44438,1
20 | 0.32945,0.39217,1
21 | 0.40739,0.40271,1
22 | 0.3106,0.50702,1
23 | 0.49638,0.45384,1
24 | 0.10073,0.32053,1
25 | 0.69907,0.37307,1
26 | 0.29767,0.69648,1
27 | 0.15099,0.57341,1
28 | 0.16427,0.27759,1
29 | 0.33259,0.055964,1
30 | 0.53741,0.28637,1
31 | 0.19503,0.36879,1
32 | 0.40278,0.035148,1
33 | 0.21296,0.55169,1
34 | 0.48447,0.56991,1
35 | 0.25476,0.34596,1
36 | 0.21726,0.28641,1
37 | 0.67078,0.46538,1
38 | 0.3815,0.4622,1
39 | 0.53838,0.32774,1
40 | 0.4849,0.26071,1
41 | 0.37095,0.38809,1
42 | 0.54527,0.63911,1
43 | 0.32149,0.12007,1
44 | 0.42216,0.61666,1
45 | 0.10194,0.060408,1
46 | 0.15254,0.2168,1
47 | 0.45558,0.43769,1
48 | 0.28488,0.52142,1
49 | 0.27633,0.21264,1
50 | 0.39748,0.31902,1
51 | 0.5533,1,0
52 | 0.44274,0.59205,0
53 | 0.85176,0.6612,0
54 | 0.60436,0.86605,0
55 | 0.68243,0.48301,0
56 | 1,0.76815,0
57 | 0.72989,0.8107,0
58 | 0.67377,0.77975,0
59 | 0.78761,0.58177,0
60 | 0.71442,0.7668,0
61 | 0.49379,0.54226,0
62 | 0.78974,0.74233,0
63 | 0.67905,0.60921,0
64 | 0.6642,0.72519,0
65 | 0.79396,0.56789,0
66 | 0.70758,0.76022,0
67 | 0.59421,0.61857,0
68 | 0.49364,0.56224,0
69 | 0.77707,0.35025,0
70 | 0.79785,0.76921,0
71 | 0.70876,0.96764,0
72 | 0.69176,0.60865,0
73 | 0.66408,0.92075,0
74 | 0.65973,0.66666,0
75 | 0.64574,0.56845,0
76 | 0.89639,0.7085,0
77 | 0.85476,0.63167,0
78 | 0.62091,0.80424,0
79 | 0.79057,0.56108,0
80 | 0.58935,0.71582,0
81 | 0.56846,0.7406,0
82 | 0.65912,0.71548,0
83 | 0.70938,0.74041,0
84 | 0.59154,0.62927,0
85 | 0.45829,0.4641,0
86 | 0.79982,0.74847,0
87 | 0.60974,0.54757,0
88 | 0.68127,0.86985,0
89 | 0.76694,0.64736,0
90 | 0.69048,0.83058,0
91 | 0.68122,0.96541,0
92 | 0.73229,0.64245,0
93 | 0.76145,0.60138,0
94 | 0.58985,0.86955,0
95 | 0.73145,0.74516,0
96 | 0.77029,0.7014,0
97 | 0.73156,0.71782,0
98 | 0.44556,0.57991,0
99 | 0.85275,0.85987,0
100 | 0.51912,0.62359,0
101 |
--------------------------------------------------------------------------------
/tensorflow basics/autoencoder.py:
--------------------------------------------------------------------------------
1 | import numpy as np
2 | import keras
3 | from keras.layers import Input, Dense, Conv2D, MaxPooling2D, UpSampling2D
4 | from keras.models import Model
5 | from sklearn.model_selection import train_test_split
6 | import matplotlib.pyplot as plt
7 | (X_train, _), (X_test, _) = keras.datasets.mnist.load_data()
8 | X_train[0].shape
9 | plt.figure(figsize=(10,5))
10 | for i in range(10):
11 | plt.subplot(1, 10, i+1)
12 | plt.imshow(X_train[i], cmap='gray')
13 | plt.xticks([])
14 | plt.yticks([])
15 | plt.show()
16 | inputs =Input(shape=(784,))
17 | enc = Dense(32,activation='relu') #compressing using 32 neurons
18 | encoded = enc(inputs)
19 | dec = Dense(784,activation='sigmoid')# decompress to 784 pixel
20 | decoded = dec(encoded)
21 | autoencoder = Model(inputs, decoded)
22 | autoencoder.compile(optimizer='adam', loss='binary_crossentropy')
23 | def preprocess(x):
24 | x = x.astype('float32') / 255.
25 | return x.reshape(-1, np.prod(x.shape[1:])) # flatten
26 |
27 | X_train = preprocess(X_train)
28 | X_test = preprocess(X_test)
29 |
30 | # a validation set for training
31 | X_train, X_valid = train_test_split(X_train, test_size=500)
32 | autoencoder.fit(X_train, X_train, epochs=50, batch_size=128, validation_data=(X_valid, X_valid))
33 | encoder = Model(inputs, encoded)
34 | X_test_encoded = encoder.predict(X_test)
35 | X_test_encoded[0].shape
36 | decoder_inputs = Input(shape=(32,))
37 | decoder = Model(decoder_inputs, dec(decoder_inputs))
38 | X_test_decoded = decoder.predict(X_test_encoded)
39 | def show_images(before_images, after_images):
40 | plt.figure(figsize=(10, 2))
41 | for i in range(10):
42 | # before
43 | plt.subplot(2, 10, i+1)
44 | plt.imshow(before_images[i].reshape(28, 28), cmap='gray')
45 | plt.xticks([])
46 | plt.yticks([])
47 | # after
48 | plt.subplot(2, 10, 10+i+1)
49 | plt.imshow(after_images[i].reshape(28, 28), cmap='gray')
50 | plt.xticks([])
51 | plt.yticks([])
52 | plt.show()
53 |
54 | show_images(X_test, X_test_decoded)
55 | #Convolutional Autoencoder ka function
56 | def convauto():# encoding
57 | inputs = Input(shape=(28, 28, 1))
58 | x = Conv2D(16, 3, activation='relu', padding='same')(inputs)
59 | x = MaxPooling2D(padding='same')(x)
60 | x = Conv2D( 8, 3, activation='relu', padding='same')(x)
61 | x = MaxPooling2D(padding='same')(x)
62 | x = Conv2D( 8, 3, activation='relu', padding='same')(x)
63 | encoded = MaxPooling2D(padding='same')(x)
64 |
65 | # decoding
66 | x = Conv2D( 8, 3, activation='relu', padding='same')(encoded)
67 | x = UpSampling2D()(x)
68 | x = Conv2D( 8, 3, activation='relu', padding='same')(x)
69 | x = UpSampling2D()(x)
70 | x = Conv2D(16, 3, activation='relu')(x)
71 | x = UpSampling2D()(x)
72 | decoded = Conv2D(1, 3, activation='sigmoid', padding='same')(x)
73 |
74 | # autoencoder
75 | autoencoder = Model(inputs, decoded)
76 | autoencoder.compile(optimizer='adam', loss='binary_crossentropy')
77 | return autoencoder
78 |
79 | autoencoder = convauto()
80 | autoencoder.summary()
81 |
82 | X_train = X_train.reshape(-1, 28, 28, 1)
83 | X_valid = X_valid.reshape(-1, 28, 28, 1)
84 | X_test = X_test.reshape(-1, 28, 28, 1)
85 |
86 | autoencoder.fit(X_train, X_train, epochs=50, batch_size=128, validation_data=(X_valid, X_valid))
87 | X_test_dec = autoencoder.predict(X_test)
88 |
89 | show_images(X_test, X_test_dec)
90 |
91 |
92 | def add_noise(x, noise_factor=0.2):
93 | x = x + np.random.randn(*x.shape) * noise_factor
94 | x = x.clip(0., 1.)
95 | return x
96 |
97 | X_train_noisy = add_noise(X_train)
98 | X_valid_noisy = add_noise(X_valid)
99 | X_test_noisy = add_noise(X_test)
100 |
101 | autoencoder = convauto()
102 | autoencoder.fit(X_train_noisy, X_train, epochs=50, batch_size=128, validation_data=(X_valid_noisy, X_valid))
103 | X_test_dec = autoencoder.predict(X_test_noisy)
104 |
105 | show_images(X_test_noisy, X_test_dec)
--------------------------------------------------------------------------------
/LSTM/iris-data.csv:
--------------------------------------------------------------------------------
1 | sepal_length_cm,sepal_width_cm,petal_length_cm,petal_width_cm,class
5.1,3.5,1.4,0.2,Iris-setosa
4.9,3,1.4,0.2,Iris-setosa
4.7,3.2,1.3,0.2,Iris-setosa
4.6,3.1,1.5,0.2,Iris-setosa
5,3.6,1.4,0.2,Iris-setosa
5.4,3.9,1.7,0.4,Iris-setosa
4.6,3.4,1.4,0.3,Iris-setosa
5,3.4,1.5,NA,Iris-setosa
4.4,2.9,1.4,NA,Iris-setosa
4.9,3.1,1.5,NA,Iris-setosa
5.4,3.7,1.5,NA,Iris-setosa
4.8,3.4,1.6,NA,Iris-setosa
4.8,3,1.4,0.1,Iris-setosa
5.7,3,1.1,0.1,Iris-setosa
5.8,4,1.2,0.2,Iris-setosa
5.7,4.4,1.5,0.4,Iris-setosa
5.4,3.9,1.3,0.4,Iris-setosa
5.1,3.5,1.4,0.3,Iris-setosa
5.7,3.8,1.7,0.3,Iris-setossa
5.1,3.8,1.5,0.3,Iris-setosa
5.4,3.4,1.7,0.2,Iris-setosa
5.1,3.7,1.5,0.4,Iris-setosa
4.6,3.6,1,0.2,Iris-setosa
5.1,3.3,1.7,0.5,Iris-setosa
4.8,3.4,1.9,0.2,Iris-setosa
5,3,1.6,0.2,Iris-setosa
5,3.4,1.6,0.4,Iris-setosa
5.2,3.5,1.5,0.2,Iris-setosa
5.2,3.4,1.4,0.2,Iris-setosa
4.7,3.2,1.6,0.2,Iris-setosa
4.8,3.1,1.6,0.2,Iris-setosa
5.4,3.4,1.5,0.4,Iris-setosa
5.2,4.1,1.5,0.1,Iris-setosa
5.5,4.2,1.4,0.2,Iris-setosa
4.9,3.1,1.5,0.1,Iris-setosa
5,3.2,1.2,0.2,Iris-setosa
5.5,3.5,1.3,0.2,Iris-setosa
4.9,3.1,1.5,0.1,Iris-setosa
4.4,3,1.3,0.2,Iris-setosa
5.1,3.4,1.5,0.2,Iris-setosa
5,3.5,1.3,0.3,Iris-setosa
4.5,2.3,1.3,0.3,Iris-setosa
4.4,3.2,1.3,0.2,Iris-setosa
5,3.5,1.6,0.6,Iris-setosa
5.1,3.8,1.9,0.4,Iris-setosa
4.8,3,1.4,0.3,Iris-setosa
5.1,3.8,1.6,0.2,Iris-setosa
4.6,3.2,1.4,0.2,Iris-setosa
5.3,3.7,1.5,0.2,Iris-setosa
5,3.3,1.4,0.2,Iris-setosa
7,3.2,4.7,1.4,Iris-versicolor
6.4,3.2,4.5,1.5,Iris-versicolor
6.9,3.1,4.9,1.5,Iris-versicolor
5.5,2.3,4,1.3,Iris-versicolor
6.5,2.8,4.6,1.5,Iris-versicolor
5.7,2.8,4.5,1.3,Iris-versicolor
6.3,3.3,4.7,1.6,Iris-versicolor
4.9,2.4,3.3,1,Iris-versicolor
6.6,2.9,4.6,1.3,Iris-versicolor
5.2,2.7,3.9,1.4,Iris-versicolor
5,2,3.5,1,Iris-versicolor
5.9,3,4.2,1.5,Iris-versicolor
6,2.2,4,1,Iris-versicolor
6.1,2.9,4.7,1.4,Iris-versicolor
5.6,2.9,3.6,1.3,Iris-versicolor
6.7,3.1,4.4,1.4,Iris-versicolor
5.6,3,4.5,1.5,Iris-versicolor
5.8,2.7,4.1,1,Iris-versicolor
6.2,2.2,4.5,1.5,Iris-versicolor
5.6,2.5,3.9,1.1,Iris-versicolor
5.9,3.2,4.8,1.8,Iris-versicolor
6.1,2.8,4,1.3,Iris-versicolor
6.3,2.5,4.9,1.5,Iris-versicolor
6.1,2.8,4.7,1.2,Iris-versicolor
6.4,2.9,4.3,1.3,Iris-versicolor
6.6,3,4.4,1.4,Iris-versicolor
6.8,2.8,4.8,1.4,Iris-versicolor
0.067,3,5,1.7,Iris-versicolor
0.06,2.9,4.5,1.5,Iris-versicolor
0.057,2.6,3.5,1,Iris-versicolor
0.055,2.4,3.8,1.1,Iris-versicolor
0.055,2.4,3.7,1,Iris-versicolor
5.8,2.7,3.9,1.2,Iris-versicolor
6,2.8,5.1,1.6,Iris-versicolor
5.4,3,4.5,1.5,Iris-versicolor
6,3.4,4.5,1.6,Iris-versicolor
6.7,3.1,4.7,1.5,Iris-versicolor
6.3,2.3,4.4,1.3,Iris-versicolor
5.6,3,4.1,1.3,Iris-versicolor
5.5,2.5,4,1.3,Iris-versicolor
5.5,2.6,4.4,1.2,Iris-versicolor
6.1,3,4.6,1.4,Iris-versicolor
5.8,2.6,4,1.2,Iris-versicolor
5,2.3,3.3,1,Iris-versicolor
5.6,2.7,4.2,1.3,Iris-versicolor
5.7,3,4.2,1.2,versicolor
5.7,2.9,4.2,1.3,versicolor
6.2,2.9,4.3,1.3,versicolor
5.1,2.5,3,1.1,versicolor
5.7,2.8,4.1,1.3,versicolor
6.3,3.3,6,2.5,Iris-virginica
5.8,2.7,5.1,1.9,Iris-virginica
7.1,3,5.9,2.1,Iris-virginica
6.3,2.9,5.6,1.8,Iris-virginica
6.5,3,5.8,2.2,Iris-virginica
7.6,3,6.6,2.1,Iris-virginica
4.9,2.5,4.5,1.7,Iris-virginica
7.3,2.9,6.3,1.8,Iris-virginica
6.7,2.5,5.8,1.8,Iris-virginica
7.2,3.6,6.1,2.5,Iris-virginica
6.5,3.2,5.1,2,Iris-virginica
6.4,2.7,5.3,1.9,Iris-virginica
6.8,3,5.5,2.1,Iris-virginica
5.7,2.5,5,2,Iris-virginica
5.8,2.8,5.1,2.4,Iris-virginica
6.4,3.2,5.3,2.3,Iris-virginica
6.5,3,5.5,1.8,Iris-virginica
7.7,3.8,6.7,2.2,Iris-virginica
7.7,2.6,6.9,2.3,Iris-virginica
6,2.2,5,1.5,Iris-virginica
6.9,3.2,5.7,2.3,Iris-virginica
5.6,2.8,4.9,2,Iris-virginica
5.6,2.8,6.7,2,Iris-virginica
6.3,2.7,4.9,1.8,Iris-virginica
6.7,3.3,5.7,2.1,Iris-virginica
7.2,3.2,6,1.8,Iris-virginica
6.2,2.8,4.8,1.8,Iris-virginica
6.1,3,4.9,1.8,Iris-virginica
6.4,2.8,5.6,2.1,Iris-virginica
7.2,3,5.8,1.6,Iris-virginica
7.4,2.8,6.1,1.9,Iris-virginica
7.9,3.8,6.4,2,Iris-virginica
6.4,2.8,5.6,2.2,Iris-virginica
6.3,2.8,5.1,1.5,Iris-virginica
6.1,2.6,5.6,1.4,Iris-virginica
7.7,3,6.1,2.3,Iris-virginica
6.3,3.4,5.6,2.4,Iris-virginica
6.4,3.1,5.5,1.8,Iris-virginica
6,3,4.8,1.8,Iris-virginica
6.9,3.1,5.4,2.1,Iris-virginica
6.7,3.1,5.6,2.4,Iris-virginica
6.9,3.1,5.1,2.3,Iris-virginica
5.8,2.7,5.1,1.9,Iris-virginica
6.8,3.2,5.9,2.3,Iris-virginica
6.7,3.3,5.7,2.5,Iris-virginica
6.7,3,5.2,2.3,Iris-virginica
6.3,2.5,5,2.3,Iris-virginica
6.5,3,5.2,2,Iris-virginica
6.2,3.4,5.4,2.3,Iris-virginica
5.9,3,5.1,1.8,Iris-virginica
--------------------------------------------------------------------------------
/python basics/NUMPY/NUMPY.ipynb:
--------------------------------------------------------------------------------
1 | {
2 | "cells": [
3 | {
4 | "cell_type": "code",
5 | "execution_count": 1,
6 | "metadata": {},
7 | "outputs": [],
8 | "source": [
9 | "import numpy as np\n"
10 | ]
11 | },
12 | {
13 | "cell_type": "code",
14 | "execution_count": 2,
15 | "metadata": {},
16 | "outputs": [],
17 | "source": [
18 | "np1 = np.array([1,2,3,4,5])"
19 | ]
20 | },
21 | {
22 | "cell_type": "code",
23 | "execution_count": 3,
24 | "metadata": {},
25 | "outputs": [
26 | {
27 | "data": {
28 | "text/plain": [
29 | "array([1, 2, 3, 4, 5])"
30 | ]
31 | },
32 | "execution_count": 3,
33 | "metadata": {},
34 | "output_type": "execute_result"
35 | }
36 | ],
37 | "source": [
38 | "np1"
39 | ]
40 | },
41 | {
42 | "cell_type": "code",
43 | "execution_count": 4,
44 | "metadata": {},
45 | "outputs": [
46 | {
47 | "data": {
48 | "text/plain": [
49 | "numpy.ndarray"
50 | ]
51 | },
52 | "execution_count": 4,
53 | "metadata": {},
54 | "output_type": "execute_result"
55 | }
56 | ],
57 | "source": [
58 | "type(np1)"
59 | ]
60 | },
61 | {
62 | "cell_type": "code",
63 | "execution_count": 6,
64 | "metadata": {},
65 | "outputs": [],
66 | "source": [
67 | "Mat1 = np.array([[1,2],[3,4]])"
68 | ]
69 | },
70 | {
71 | "cell_type": "code",
72 | "execution_count": 7,
73 | "metadata": {},
74 | "outputs": [
75 | {
76 | "data": {
77 | "text/plain": [
78 | "array([[1, 2],\n",
79 | " [3, 4]])"
80 | ]
81 | },
82 | "execution_count": 7,
83 | "metadata": {},
84 | "output_type": "execute_result"
85 | }
86 | ],
87 | "source": [
88 | "Mat1"
89 | ]
90 | },
91 | {
92 | "cell_type": "code",
93 | "execution_count": 9,
94 | "metadata": {},
95 | "outputs": [
96 | {
97 | "data": {
98 | "text/plain": [
99 | "(5,)"
100 | ]
101 | },
102 | "execution_count": 9,
103 | "metadata": {},
104 | "output_type": "execute_result"
105 | }
106 | ],
107 | "source": [
108 | "np1.shape\n"
109 | ]
110 | },
111 | {
112 | "cell_type": "code",
113 | "execution_count": 10,
114 | "metadata": {},
115 | "outputs": [
116 | {
117 | "data": {
118 | "text/plain": [
119 | "(2, 2)"
120 | ]
121 | },
122 | "execution_count": 10,
123 | "metadata": {},
124 | "output_type": "execute_result"
125 | }
126 | ],
127 | "source": [
128 | "Mat1.shape"
129 | ]
130 | },
131 | {
132 | "cell_type": "code",
133 | "execution_count": 11,
134 | "metadata": {},
135 | "outputs": [
136 | {
137 | "data": {
138 | "text/plain": [
139 | "dtype('int32')"
140 | ]
141 | },
142 | "execution_count": 11,
143 | "metadata": {},
144 | "output_type": "execute_result"
145 | }
146 | ],
147 | "source": [
148 | "Mat1.dtype"
149 | ]
150 | },
151 | {
152 | "cell_type": "code",
153 | "execution_count": 13,
154 | "metadata": {},
155 | "outputs": [],
156 | "source": [
157 | "mat2 = np.arange(0,4,1)"
158 | ]
159 | },
160 | {
161 | "cell_type": "code",
162 | "execution_count": 14,
163 | "metadata": {},
164 | "outputs": [
165 | {
166 | "data": {
167 | "text/plain": [
168 | "array([0, 1, 2, 3])"
169 | ]
170 | },
171 | "execution_count": 14,
172 | "metadata": {},
173 | "output_type": "execute_result"
174 | }
175 | ],
176 | "source": [
177 | "mat2"
178 | ]
179 | },
180 | {
181 | "cell_type": "code",
182 | "execution_count": 15,
183 | "metadata": {},
184 | "outputs": [],
185 | "source": [
186 | "mat3 = np.linspace(0,10,20)"
187 | ]
188 | },
189 | {
190 | "cell_type": "code",
191 | "execution_count": 16,
192 | "metadata": {},
193 | "outputs": [
194 | {
195 | "data": {
196 | "text/plain": [
197 | "array([ 0. , 0.52631579, 1.05263158, 1.57894737, 2.10526316,\n",
198 | " 2.63157895, 3.15789474, 3.68421053, 4.21052632, 4.73684211,\n",
199 | " 5.26315789, 5.78947368, 6.31578947, 6.84210526, 7.36842105,\n",
200 | " 7.89473684, 8.42105263, 8.94736842, 9.47368421, 10. ])"
201 | ]
202 | },
203 | "execution_count": 16,
204 | "metadata": {},
205 | "output_type": "execute_result"
206 | }
207 | ],
208 | "source": [
209 | "mat3"
210 | ]
211 | },
212 | {
213 | "cell_type": "code",
214 | "execution_count": null,
215 | "metadata": {},
216 | "outputs": [],
217 | "source": []
218 | },
219 | {
220 | "cell_type": "code",
221 | "execution_count": null,
222 | "metadata": {},
223 | "outputs": [],
224 | "source": []
225 | },
226 | {
227 | "cell_type": "code",
228 | "execution_count": null,
229 | "metadata": {},
230 | "outputs": [],
231 | "source": []
232 | }
233 | ],
234 | "metadata": {
235 | "kernelspec": {
236 | "display_name": "Python 3",
237 | "language": "python",
238 | "name": "python3"
239 | },
240 | "language_info": {
241 | "codemirror_mode": {
242 | "name": "ipython",
243 | "version": 3
244 | },
245 | "file_extension": ".py",
246 | "mimetype": "text/x-python",
247 | "name": "python",
248 | "nbconvert_exporter": "python",
249 | "pygments_lexer": "ipython3",
250 | "version": "3.7.4"
251 | }
252 | },
253 | "nbformat": 4,
254 | "nbformat_minor": 2
255 | }
256 |
--------------------------------------------------------------------------------
/LSTM/Untitled1.ipynb:
--------------------------------------------------------------------------------
1 | {
2 | "cells": [
3 | {
4 | "cell_type": "code",
5 | "execution_count": 1,
6 | "metadata": {},
7 | "outputs": [],
8 | "source": [
9 | "import numpy as np\n",
10 | "import matplotlib.pyplot as plt \n",
11 | "import pandas as pd\n"
12 | ]
13 | },
14 | {
15 | "cell_type": "code",
16 | "execution_count": 10,
17 | "metadata": {},
18 | "outputs": [],
19 | "source": [
20 | "\n",
21 | "dataset_train = pd.read_csv('NSE-TATAGLOBAL.csv')\n",
22 | "training_set=dataset_train.iloc[:,1:2].values"
23 | ]
24 | },
25 | {
26 | "cell_type": "code",
27 | "execution_count": 11,
28 | "metadata": {},
29 | "outputs": [
30 | {
31 | "data": {
32 | "text/html": [
33 | "\n",
34 | "\n",
47 | "
\n",
48 | " \n",
49 | " \n",
50 | " | \n",
51 | " Date | \n",
52 | " Open | \n",
53 | " High | \n",
54 | " Low | \n",
55 | " Last | \n",
56 | " Close | \n",
57 | " Total Trade Quantity | \n",
58 | " Turnover (Lacs) | \n",
59 | "
\n",
60 | " \n",
61 | " \n",
62 | " \n",
63 | " | 0 | \n",
64 | " 2018-09-28 | \n",
65 | " 234.05 | \n",
66 | " 235.95 | \n",
67 | " 230.20 | \n",
68 | " 233.50 | \n",
69 | " 233.75 | \n",
70 | " 3069914 | \n",
71 | " 7162.35 | \n",
72 | "
\n",
73 | " \n",
74 | " | 1 | \n",
75 | " 2018-09-27 | \n",
76 | " 234.55 | \n",
77 | " 236.80 | \n",
78 | " 231.10 | \n",
79 | " 233.80 | \n",
80 | " 233.25 | \n",
81 | " 5082859 | \n",
82 | " 11859.95 | \n",
83 | "
\n",
84 | " \n",
85 | " | 2 | \n",
86 | " 2018-09-26 | \n",
87 | " 240.00 | \n",
88 | " 240.00 | \n",
89 | " 232.50 | \n",
90 | " 235.00 | \n",
91 | " 234.25 | \n",
92 | " 2240909 | \n",
93 | " 5248.60 | \n",
94 | "
\n",
95 | " \n",
96 | " | 3 | \n",
97 | " 2018-09-25 | \n",
98 | " 233.30 | \n",
99 | " 236.75 | \n",
100 | " 232.00 | \n",
101 | " 236.25 | \n",
102 | " 236.10 | \n",
103 | " 2349368 | \n",
104 | " 5503.90 | \n",
105 | "
\n",
106 | " \n",
107 | " | 4 | \n",
108 | " 2018-09-24 | \n",
109 | " 233.55 | \n",
110 | " 239.20 | \n",
111 | " 230.75 | \n",
112 | " 234.00 | \n",
113 | " 233.30 | \n",
114 | " 3423509 | \n",
115 | " 7999.55 | \n",
116 | "
\n",
117 | " \n",
118 | "
\n",
119 | "
 "
19 | ]
20 | },
21 | {
22 | "cell_type": "markdown",
23 | "metadata": {},
24 | "source": [
25 | "\n",
26 | "## Introduction\n",
27 | "An autoencoder, also known as autoassociator or Diabolo networks, is an artificial neural network employed to recreate the given input. It takes a set of unlabeled inputs, encodes them and then tries to extract the most valuable information from them. They are used for feature extraction, learning generative models of data, dimensionality reduction and can be used for compression.\n",
28 | "\n",
29 | "A 2006 paper named Reducing the Dimensionality of Data with Neural Networks, done by G. E. Hinton and R. R. Salakhutdinov, showed better results than years of refining other types of network, and was a breakthrough in the field of Neural Networks, a field that was \"stagnant\" for 10 years.\n",
30 | "\n",
31 | "Now, autoencoders, based on Restricted Boltzmann Machines, are employed in some of the largest deep learning applications. They are the building blocks of Deep Belief Networks (DBN)."
32 | ]
33 | },
34 | {
35 | "cell_type": "markdown",
36 | "metadata": {},
37 | "source": [
38 | "\n",
39 | "## Autoencoder Structure\n",
40 | "\n",
41 | "\n",
42 | "An autoencoder can be divided in two parts, the encoder and the decoder.\n",
43 | "\n",
44 | "The encoder needs to compress the representation of an input. In this case we are going to reduce the dimension the face of our actor, from 2000 dimensions to only 30 dimensions, by running the data through layers of our encoder.\n",
45 | "\n",
46 | "The decoder works like encoder network in reverse. It works to recreate the input, as closely as possible. This plays an important role during training, because it forces the autoencoder to select the most important features in the compressed representation"
47 | ]
48 | },
49 | {
50 | "cell_type": "code",
51 | "execution_count": 0,
52 | "metadata": {
53 | "colab": {},
54 | "colab_type": "code",
55 | "id": "RsuGfD8--DUG"
56 | },
57 | "outputs": [],
58 | "source": [
59 | "import numpy as np\n",
60 | "import tensorflow as tf\n",
61 | "from tensorflow import keras\n",
62 | "from matplotlib import pyplot as plt"
63 | ]
64 | },
65 | {
66 | "cell_type": "code",
67 | "execution_count": 0,
68 | "metadata": {
69 | "colab": {
70 | "base_uri": "https://localhost:8080/",
71 | "height": 35
72 | },
73 | "colab_type": "code",
74 | "id": "Lrt5tiRJ-DSt",
75 | "outputId": "d7a7039b-a8c6-492c-cad2-bdf0a73494de"
76 | },
77 | "outputs": [
78 | {
79 | "name": "stderr",
80 | "output_type": "stream",
81 | "text": [
82 | "Using TensorFlow backend.\n"
83 | ]
84 | }
85 | ],
86 | "source": [
87 | "from keras.datasets import mnist\n",
88 | "from keras.layers import Input, Dense\n",
89 | "from keras.models import Model"
90 | ]
91 | },
92 | {
93 | "cell_type": "code",
94 | "execution_count": 0,
95 | "metadata": {
96 | "colab": {
97 | "base_uri": "https://localhost:8080/",
98 | "height": 54
99 | },
100 | "colab_type": "code",
101 | "id": "a5I-BA7K-DON",
102 | "outputId": "ddd43dc1-bac7-47e7-e7a6-cf95085ecece"
103 | },
104 | "outputs": [
105 | {
106 | "name": "stdout",
107 | "output_type": "stream",
108 | "text": [
109 | "Downloading data from https://s3.amazonaws.com/img-datasets/mnist.npz\n",
110 | "11493376/11490434 [==============================] - 2s 0us/step\n"
111 | ]
112 | }
113 | ],
114 | "source": [
115 | "(x_train, y_train), (x_test, y_test) = mnist.load_data()"
116 | ]
117 | },
118 | {
119 | "cell_type": "code",
120 | "execution_count": 0,
121 | "metadata": {
122 | "colab": {
123 | "base_uri": "https://localhost:8080/",
124 | "height": 35
125 | },
126 | "colab_type": "code",
127 | "id": "jFiRn0ef_hHJ",
128 | "outputId": "cf3ad53b-98c9-4b7f-95ef-bd098775a2c6"
129 | },
130 | "outputs": [
131 | {
132 | "data": {
133 | "text/plain": [
134 | "(60000, 28, 28)"
135 | ]
136 | },
137 | "execution_count": 5,
138 | "metadata": {
139 | "tags": []
140 | },
141 | "output_type": "execute_result"
142 | }
143 | ],
144 | "source": [
145 | "x_train.shape"
146 | ]
147 | },
148 | {
149 | "cell_type": "code",
150 | "execution_count": 0,
151 | "metadata": {
152 | "colab": {},
153 | "colab_type": "code",
154 | "id": "zvjFj5PL_rVH"
155 | },
156 | "outputs": [],
157 | "source": [
158 | "x_train = x_train.astype('float32')/255.0\n",
159 | "x_test = x_test.astype('float32')/255.0"
160 | ]
161 | },
162 | {
163 | "cell_type": "markdown",
164 | "metadata": {
165 | "colab_type": "text",
166 | "id": "1KS4RuDZ6Kuz"
167 | },
168 | "source": [
169 | "Reshaping images, Flattening them to feed to a Dense network\n",
170 | "\n",
171 | "we won't do this in ConvNets"
172 | ]
173 | },
174 | {
175 | "cell_type": "code",
176 | "execution_count": 0,
177 | "metadata": {
178 | "colab": {},
179 | "colab_type": "code",
180 | "id": "lv-AALS9AA7r"
181 | },
182 | "outputs": [],
183 | "source": [
184 | "x_train = x_train.reshape(len(x_train), (x_train.shape[1]*x_train.shape[2]))\n",
185 | "x_test = x_test.reshape(len(x_test), (x_test.shape[1]*x_test.shape[2]))"
186 | ]
187 | },
188 | {
189 | "cell_type": "code",
190 | "execution_count": 0,
191 | "metadata": {
192 | "colab": {},
193 | "colab_type": "code",
194 | "id": "Z09aungJAG6E"
195 | },
196 | "outputs": [],
197 | "source": [
198 | "encoding_dim = 32\n",
199 | "\n",
200 | "input_img = Input(shape = (784, ))\n",
201 | "encoded = Dense(128, activation='relu')(input_img)\n",
202 | "encoded = Dense(encoding_dim, activation='relu')(encoded)\n",
203 | "\n",
204 | "\n",
205 | "decoded = Dense(128, activation='relu')(encoded)\n",
206 | "decoded = Dense(784, activation='sigmoid')(decoded)\n",
207 | "\n",
208 | "autoencoder = Model(input_img, decoded)"
209 | ]
210 | },
211 | {
212 | "cell_type": "code",
213 | "execution_count": 0,
214 | "metadata": {
215 | "colab": {},
216 | "colab_type": "code",
217 | "id": "HN8ANrYPEvfl"
218 | },
219 | "outputs": [],
220 | "source": [
221 | "encoder = Model(input_img, encoded)\n",
222 | "encoded_input = Input(shape=(encoding_dim, ))\n",
223 | "decode_layer1 = autoencoder.layers[-2]\n",
224 | "decode_layer2 = autoencoder.layers[-1]\n",
225 | "decoder = Model(encoded_input, decode_layer2(decode_layer1(encoded_input)))"
226 | ]
227 | },
228 | {
229 | "cell_type": "code",
230 | "execution_count": 0,
231 | "metadata": {
232 | "colab": {
233 | "base_uri": "https://localhost:8080/",
234 | "height": 35
235 | },
236 | "colab_type": "code",
237 | "id": "skKxFoz_4rCS",
238 | "outputId": "24f6e177-3127-4169-fd00-df67d3ebe3ef"
239 | },
240 | "outputs": [
241 | {
242 | "data": {
243 | "text/plain": [
244 | ""
245 | ]
246 | },
247 | "execution_count": 35,
248 | "metadata": {
249 | "tags": []
250 | },
251 | "output_type": "execute_result"
252 | }
253 | ],
254 | "source": [
255 | "autoencoder.get_layer('dense_5')"
256 | ]
257 | },
258 | {
259 | "cell_type": "code",
260 | "execution_count": 0,
261 | "metadata": {
262 | "colab": {},
263 | "colab_type": "code",
264 | "id": "6tVqkhvHAIPz"
265 | },
266 | "outputs": [],
267 | "source": [
268 | "autoencoder.compile(optimizer='adadelta', loss='binary_crossentropy', metrics=['accuracy'])"
269 | ]
270 | },
271 | {
272 | "cell_type": "code",
273 | "execution_count": 0,
274 | "metadata": {
275 | "colab": {
276 | "base_uri": "https://localhost:8080/",
277 | "height": 348
278 | },
279 | "colab_type": "code",
280 | "id": "PUBcoIWKzdVL",
281 | "outputId": "4a1f574e-0b02-49db-c228-c4269ee9017e"
282 | },
283 | "outputs": [
284 | {
285 | "name": "stdout",
286 | "output_type": "stream",
287 | "text": [
288 | "Model: \"model_6\"\n",
289 | "_________________________________________________________________\n",
290 | "Layer (type) Output Shape Param # \n",
291 | "=================================================================\n",
292 | "input_6 (InputLayer) (None, 784) 0 \n",
293 | "_________________________________________________________________\n",
294 | "dense_3 (Dense) (None, 128) 100480 \n",
295 | "_________________________________________________________________\n",
296 | "dense_4 (Dense) (None, 32) 4128 \n",
297 | "_________________________________________________________________\n",
298 | "dense_5 (Dense) (None, 128) 4224 \n",
299 | "_________________________________________________________________\n",
300 | "dense_6 (Dense) (None, 784) 101136 \n",
301 | "=================================================================\n",
302 | "Total params: 209,968\n",
303 | "Trainable params: 209,968\n",
304 | "Non-trainable params: 0\n",
305 | "_________________________________________________________________\n"
306 | ]
307 | }
308 | ],
309 | "source": [
310 | "autoencoder.summary()"
311 | ]
312 | },
313 | {
314 | "cell_type": "code",
315 | "execution_count": 0,
316 | "metadata": {
317 | "colab": {
318 | "base_uri": "https://localhost:8080/",
319 | "height": 403
320 | },
321 | "colab_type": "code",
322 | "id": "HLMkoI-JCgPX",
323 | "outputId": "e2053547-3301-4923-81b2-bfe051688c25"
324 | },
325 | "outputs": [
326 | {
327 | "name": "stdout",
328 | "output_type": "stream",
329 | "text": [
330 | "Train on 60000 samples, validate on 10000 samples\n",
331 | "Epoch 1/10\n",
332 | "60000/60000 [==============================] - 12s 202us/step - loss: 0.2129 - acc: 0.7929 - val_loss: 0.1578 - val_acc: 0.8043\n",
333 | "Epoch 2/10\n",
334 | "60000/60000 [==============================] - 12s 196us/step - loss: 0.1422 - acc: 0.8077 - val_loss: 0.1278 - val_acc: 0.8080\n",
335 | "Epoch 3/10\n",
336 | "60000/60000 [==============================] - 12s 195us/step - loss: 0.1226 - acc: 0.8108 - val_loss: 0.1157 - val_acc: 0.8114\n",
337 | "Epoch 4/10\n",
338 | "60000/60000 [==============================] - 12s 195us/step - loss: 0.1142 - acc: 0.8118 - val_loss: 0.1086 - val_acc: 0.8115\n",
339 | "Epoch 5/10\n",
340 | "60000/60000 [==============================] - 12s 198us/step - loss: 0.1088 - acc: 0.8125 - val_loss: 0.1063 - val_acc: 0.8110\n",
341 | "Epoch 6/10\n",
342 | "60000/60000 [==============================] - 12s 196us/step - loss: 0.1050 - acc: 0.8129 - val_loss: 0.1020 - val_acc: 0.8117\n",
343 | "Epoch 7/10\n",
344 | "60000/60000 [==============================] - 12s 195us/step - loss: 0.1019 - acc: 0.8132 - val_loss: 0.0985 - val_acc: 0.8126\n",
345 | "Epoch 8/10\n",
346 | "60000/60000 [==============================] - 12s 196us/step - loss: 0.0994 - acc: 0.8135 - val_loss: 0.0968 - val_acc: 0.8127\n",
347 | "Epoch 9/10\n",
348 | "60000/60000 [==============================] - 12s 196us/step - loss: 0.0975 - acc: 0.8137 - val_loss: 0.0952 - val_acc: 0.8130\n",
349 | "Epoch 10/10\n",
350 | "60000/60000 [==============================] - 12s 192us/step - loss: 0.0961 - acc: 0.8138 - val_loss: 0.0936 - val_acc: 0.8131\n"
351 | ]
352 | }
353 | ],
354 | "source": [
355 | "hist = autoencoder.fit(x_train, x_train, epochs=10, validation_data=(x_test, x_test))"
356 | ]
357 | },
358 | {
359 | "cell_type": "code",
360 | "execution_count": 0,
361 | "metadata": {
362 | "colab": {
363 | "base_uri": "https://localhost:8080/",
364 | "height": 287
365 | },
366 | "colab_type": "code",
367 | "id": "n4xxDcKfEV8_",
368 | "outputId": "77bcd685-2bd1-4eb2-9eee-e7e2c08cf303"
369 | },
370 | "outputs": [
371 | {
372 | "data": {
373 | "text/plain": [
374 | ""
375 | ]
376 | },
377 | "execution_count": 38,
378 | "metadata": {
379 | "tags": []
380 | },
381 | "output_type": "execute_result"
382 | },
383 | {
384 | "data": {
385 | "image/png": "iVBORw0KGgoAAAANSUhEUgAAAP8AAAD8CAYAAAC4nHJkAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDMuMC4zLCBo\ndHRwOi8vbWF0cGxvdGxpYi5vcmcvnQurowAAD2ZJREFUeJzt3W2MHfV1x/HfsXdtsDEY42Ac82CC\nDNRAYpqtaRXaUBESQEQmUktjVZGjohgp0EKTVkFupfKiVWmahPKiieoEC1OlBJqAcCurgThpaVSK\nWIiLDSbFQabY+GGJDbYxu96H0xc7RBvYObPsfZi7e74fabV359y5c3y9v517739m/ubuApDPjLob\nAFAPwg8kRfiBpAg/kBThB5Ii/EBShB9IivADSRF+IKmudm5sls32EzS3nZsEUunXmzruAzaR+zYU\nfjO7WtLdkmZK+pa73xnd/wTN1WV2ZSObBBB40rdM+L6TftlvZjMl/b2kayQtl7TazJZP9vEAtFcj\n7/lXStrp7i+5+3FJ35G0qjltAWi1RsK/RNIrY37eXSz7JWa21sx6zax3UAMNbA5AM7X80353X+/u\nPe7e063Zrd4cgAlqJPx7JJ015uczi2UApoBGwv+UpGVmdq6ZzZL0aUmbmtMWgFab9FCfuw+Z2S2S\nvq/Rob4N7v5c0zoD0FINjfO7+2ZJm5vUC4A24vBeICnCDyRF+IGkCD+QFOEHkiL8QFKEH0iK8ANJ\nEX4gKcIPJEX4gaQIP5AU4QeSIvxAUoQfSIrwA0kRfiApwg8kRfiBpAg/kBThB5Ii/EBShB9IivAD\nSRF+ICnCDyRF+IGkCD+QFOEHkmpoll4z2yXpiKRhSUPu3tOMpgC0XkPhL/y2u7/WhMcB0Ea87AeS\najT8LulRM3vazNY2oyEA7dHoy/7L3X2PmZ0u6TEze8HdHx97h+KPwlpJOkFzGtwcgGZpaM/v7nuK\n7wckPSxp5Tj3We/uPe7e063ZjWwOQBNNOvxmNtfM5r19W9LHJW1vVmMAWquRl/2LJD1sZm8/zj+5\n+781pSsALTfp8Lv7S5I+1MRe6jX6Ryyol79Isu74abSKx3b3eNsVfHCovDgy3NBjY/piqA9IivAD\nSRF+ICnCDyRF+IGkCD+QVDPO6psSbHZ8dOGMeSeFdV9yemlt/2/MD9d9/aKRsK6ReCjwhL74b/Ss\nw+W1E/vibc/fEawsacahI2FdA8fjend3acnfeitc1briX0+v2raX/9tH3uqveOyB+LGnAfb8QFKE\nH0iK8ANJEX4gKcIPJEX4gaQIP5DUtBnnrxzHP/nksD7wwbPD+qHzZ5XWZn2yL1z375ZtDus/HVgc\n1nceKz/GQJKOj5T/N/b1x8cvvDVUPg4vSTed/XhYP7/7QFg/ZcZgaW3/8Inhuv986NfC+uGheP0n\n9iwtrc377rxw3fkPbQ3rI/3xcQJTAXt+ICnCDyRF+IGkCD+QFOEHkiL8QFKEH0hq+ozzzyofh5dU\neQnrWfvfDOunHS8/N/zV+fE4/B8f/L2w3tUd9zY8HP+NHn4zGKvvis/nv+QDe8L60u54AuZoHF+S\n+r289xkW9/b5hfExBgtnzgzr+88of/yrD/9RuO6C/1wY1kd2x8+bGrwcezuw5weSIvxAUoQfSIrw\nA0kRfiApwg8kRfiBpCrH+c1sg6TrJB1w94uLZQskPSBpqaRdkm5w90Ota7Oa91dcZ30wHo/Wy/G4\n7azX5pTWlr4SX0tAMyr+xo7E493++hvx+t3lxzjYzHjbx898X1i/+ZJ4PHzeK/G182f3HSut/fzS\neL6D3/2TR8P62vnbw/qwl8+H0LUvPi7Ej8bHfUyFcfwqE9nz3yvp6ncsu13SFndfJmlL8TOAKaQy\n/O7+uKSD71i8StLG4vZGSdc3uS8ALTbZ9/yL3H1vcXufpEVN6gdAmzT8gZ+7u6TSN0BmttbMes2s\nd1DTf/4zYKqYbPj3m9liSSq+l17F0d3Xu3uPu/d0q+KDMQBtM9nwb5K0pri9RtIjzWkHQLtUht/M\n7pf0hKQLzGy3md0o6U5JV5nZi5I+VvwMYAqpHOd399UlpSub3EtDfCgex/eKc+JtOB5rH66YSz7e\ndny+fq1jxgfi8/UXPB0/L1W9j1j5WPvC3aeG6z74Ox8O69ddvC2s//DYBaW19//HULjuSNU4/zTA\nEX5AUoQfSIrwA0kRfiApwg8kRfiBpKbNpbsrh8s8Hm7zikt7KxiymtKnd1b9uxsVPDd2Sjxt+hXv\nfzGsD1bsu+7aWj4afcG2V8N1h6qGZ6cB9vxAUoQfSIrwA0kRfiApwg8kRfiBpAg/kNT0Gedvtak8\nll8j6yr/FdvxhfjSj19ecH9Y/+tXrwnr5369vDbcF5/K3PLjHzoAe34gKcIPJEX4gaQIP5AU4QeS\nIvxAUoQfSIpx/ukgutZAlVYfv7DiwtLSvdf+Q7hq3/DcsL7z6+WPLUkLtu8orQ0fj6cWz4A9P5AU\n4QeSIvxAUoQfSIrwA0kRfiApwg8kVTnOb2YbJF0n6YC7X1wsu0PS5yT1FXdb5+6bW9UkKtR4rYEZ\n8+aF9V1fKj8GYVnX0XDdq3pvCuvnbNkV1ofeOFxe5PoME9rz3yvp6nGW3+XuK4ovgg9MMZXhd/fH\nJR1sQy8A2qiR9/y3mNmzZrbBzE5tWkcA2mKy4f+GpPMkrZC0V9JXy+5oZmvNrNfMegc1MMnNAWi2\nSYXf3fe7+7C7j0j6pqSVwX3Xu3uPu/d0a/Zk+wTQZJMKv5ktHvPjpyRtb047ANplIkN990u6QtJC\nM9st6S8kXWFmKyS5pF2S4jEZAB2nMvzuvnqcxfe0oBd0ooprBRxadVFY/9aHyy+e/8O3zgnXPfOv\nwrKG9u2P78BYfogj/ICkCD+QFOEHkiL8QFKEH0iK8ANJceluhGaecnJY77n1J2F9eXd/ae3G3mvD\ndc/d8bOw7gzlNYQ9P5AU4QeSIvxAUoQfSIrwA0kRfiApwg8kxTh/dhWn7P78k8vD+n1nfCWs9wdj\n8QsfnBOuO3LsWFhHY9jzA0kRfiApwg8kRfiBpAg/kBThB5Ii/EBSjPMn13X2mWH9xnWPhPU51h3W\nL+v9bGltyb9sDdflbP3WYs8PJEX4gaQIP5AU4QeSIvxAUoQfSIrwA0lVjvOb2VmS7pO0SKNDr+vd\n/W4zWyDpAUlLJe2SdIO7H2pdq5gMmz07rD//52eE9U0n7w7re4aPh/XFf1t+HIAPDITrorUmsucf\nkvRFd18u6dcl3WxmyyXdLmmLuy+TtKX4GcAUURl+d9/r7s8Ut49I2iFpiaRVkjYWd9so6fpWNQmg\n+d7Te34zWyrpUklPSlrk7nuL0j6Nvi0AMEVMOPxmdpKk70m6zd0Pj6356KRp4x6KbWZrzazXzHoH\nxXs8oFNMKPxm1q3R4H/b3R8qFu83s8VFfbGkA+Ot6+7r3b3H3Xu6FX/4BKB9KsNvZibpHkk73P1r\nY0qbJK0pbq+RFJ/+BaCjTOSU3o9I+oykbWb29jmY6yTdKelBM7tR0suSbmhNi6hi3bNKa8c/ekm4\n7n994q6wPtNOCusf3fyFsH7+E0+FddSnMvzu/mNJZRd3v7K57QBoF47wA5Ii/EBShB9IivADSRF+\nICnCDyTFpbungopptPWh80tLv3/3v4arLu6Kx/H/u384rF/4pzvC+kgwRTfqxZ4fSIrwA0kRfiAp\nwg8kRfiBpAg/kBThB5JinH8KmHHiiWH9hT+YU1pbPe//wnWPjcTb/sO/vDWsLzjyRPwA6Fjs+YGk\nCD+QFOEHkiL8QFKEH0iK8ANJEX4gKcb5O4B1xf8N/b+5PKz/zcceKK3NrLgWwHePxlN0n/6jV8P6\nUFhFJ2PPDyRF+IGkCD+QFOEHkiL8QFKEH0iK8ANJVY7zm9lZku6TtEiSS1rv7neb2R2SPiepr7jr\nOnff3KpGO1rFWLp1dYf1kZ5fCev9tx0K65+Ys6+09sZIfML+v79+YVj3bg4Fma4m8j87JOmL7v6M\nmc2T9LSZPVbU7nL3r7SuPQCtUhl+d98raW9x+4iZ7ZC0pNWNAWit9/Se38yWSrpU0pPFolvM7Fkz\n22Bmp5ass9bMes2sd1ADDTULoHkmHH4zO0nS9yTd5u6HJX1D0nmSVmj0lcFXx1vP3de7e4+793Rr\ndhNaBtAMEwq/mXVrNPjfdveHJMnd97v7sLuPSPqmpJWtaxNAs1WG38xM0j2Sdrj718YsXzzmbp+S\ntL357QFolYl82v8RSZ+RtM3MthbL1klabWYrNDr8t0vSTS3pcCqw+G/ojJPmhvW+D5ZfeluSPr/0\n+2F90MuH854aOC1c9wc/uSisLz/8cljH1DWRT/t/LGm8geycY/rANMERfkBShB9IivADSRF+ICnC\nDyRF+IGkzN3btrGTbYFfZle2bXttM2NmXB8ZDstVl+622RWHRZ93VmlpeG68btcL8RTeI0eOhHUf\njv9tauPvF6QnfYsO+8H4HPMCe34gKcIPJEX4gaQIP5AU4QeSIvxAUoQfSKqt4/xm1idp7AniCyW9\n1rYG3ptO7a1T+5LobbKa2ds57v6+idyxreF/18bNet29p7YGAp3aW6f2JdHbZNXVGy/7gaQIP5BU\n3eFfX/P2I53aW6f2JdHbZNXSW63v+QHUp+49P4Ca1BJ+M7vazH5qZjvN7PY6eihjZrvMbJuZbTWz\n3pp72WBmB8xs+5hlC8zsMTN7sfg+7jRpNfV2h5ntKZ67rWZ2bU29nWVmPzKz583sOTO7tVhe63MX\n9FXL89b2l/1mNlPS/0q6StJuSU9JWu3uz7e1kRJmtktSj7vXPiZsZr8l6aik+9z94mLZlyUddPc7\niz+cp7r7lzqktzskHa175uZiQpnFY2eWlnS9pM+qxucu6OsG1fC81bHnXylpp7u/5O7HJX1H0qoa\n+uh47v64pIPvWLxK0sbi9kaN/vK0XUlvHcHd97r7M8XtI5Lenlm61ucu6KsWdYR/iaRXxvy8W501\n5bdLetTMnjaztXU3M45FxbTpkrRP0qI6mxlH5czN7fSOmaU75rmbzIzXzcYHfu92ubv/qqRrJN1c\nvLztSD76nq2ThmsmNHNzu4wzs/Qv1PncTXbG62arI/x7JI296NyZxbKO4O57iu8HJD2szpt9eP/b\nk6QW3w/U3M8vdNLMzePNLK0OeO46acbrOsL/lKRlZnaumc2S9GlJm2ro413MbG7xQYzMbK6kj6vz\nZh/eJGlNcXuNpEdq7OWXdMrMzWUzS6vm567jZrx297Z/SbpWo5/4/0zSn9XRQ0lfH5D0P8XXc3X3\nJul+jb4MHNToZyM3SjpN0hZJL0r6gaQFHdTbP0raJulZjQZtcU29Xa7Rl/TPStpafF1b93MX9FXL\n88YRfkBSfOAHJEX4gaQIP5AU4QeSIvxAUoQfSIrwA0kRfiCp/weDXbvwl0u/MwAAAABJRU5ErkJg\ngg==\n",
386 | "text/plain": [
387 | ""
388 | ]
389 | },
390 | "metadata": {
391 | "tags": []
392 | },
393 | "output_type": "display_data"
394 | }
395 | ],
396 | "source": [
397 | "encoded_images = encoder.predict(x_test)\n",
398 | "encoded_images.shape\n",
399 | "predicted = decoder.predict(encoded_images)\n",
400 | "plt.imshow(predicted[0].reshape(28, 28))"
401 | ]
402 | },
403 | {
404 | "cell_type": "code",
405 | "execution_count": 0,
406 | "metadata": {
407 | "colab": {
408 | "base_uri": "https://localhost:8080/",
409 | "height": 269
410 | },
411 | "colab_type": "code",
412 | "id": "3H3Ekx1SHp5y",
413 | "outputId": "e2c12384-3645-45fa-a46e-6aecdb259a2d"
414 | },
415 | "outputs": [
416 | {
417 | "data": {
418 | "image/png": "iVBORw0KGgoAAAANSUhEUgAAAXQAAAD8CAYAAABn919SAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDMuMC4zLCBo\ndHRwOi8vbWF0cGxvdGxpYi5vcmcvnQurowAAFVBJREFUeJzt3X+QnVV9x/HPJ5tslgRICAkhJJEg\nRDQSCWX5NdiK/LDRsQZnLAN1NLbUYCsdndEZUpkpVFuHdqyMLdbOIikRBcQAJmNRCCmIVkQSjAhB\nTOSHJITEkIT8gPzY7Ld/7JO7+yz37m6y9z5377nv18zOnvOc5977Tbjny8l5zvMcR4QAAI1vRL0D\nAABUBwkdABJBQgeARJDQASARJHQASAQJHQASQUIHgESQ0AEgESR0AEjEyHoHAFSL7bmSviapRdI3\nI+KG/s5vHTU22trGl23buevlLRExqfpRArVDQkcSbLdI+rqkSyStl/S47WURsabSa9raxuus9k+X\nbfvfh699sSaBAjXElAtScbakdRHxXETsk3SnpHl1jgkoFAkdqZgq6aVe9fXZMaBpMOWCpmJ7gaQF\nkjR69Lg6RwNUFyN0pGKDpOm96tOyYzkR0RER7RHR3jpqbGHBAUUgoSMVj0uaafsk262SLpe0rM4x\nAYViygVJiIhO21dLul/dyxYXRcTT/b5o1xsa8eNfFhEeUAgSOpIREfdJuq/ecQD1wpQLACSChA4A\niSChA0AiSOgAkAgSOgAkglUuaFoTT9urK+99vmzbgzMLDgaoAkboAJAIEjoAJIKEDgCJIKEDQCJI\n6ACQCFa5oGm9vHWCrrv9oxVaVxUaC1ANjNABIBEkdABIBAkdABJBQgeARJDQASARJHQASATLFtG0\nfEBqfa3eUQDVwwgdABJBQgeARJDQASARJHQASAQJHQASQUIHgESwbBHJsP2CpJ2SDkjqjIj2/s6P\nFmnv+CIiA4pBQkdq3hsRW+odBFAPTLkAQCJI6EhJSHrA9irbC+odDFA0plyQkndHxAbbx0labvs3\nEfFI7xOyRL9AkkaOO6YeMQI1wwgdyYiIDdnvzZLulXR2mXM6IqI9Itpbxo4tOkSgpkjoSILtsbaP\nOliW9D5JT9U3KqBYTLkgFZMl3Wtb6v5e3x4RP+rvBW89dpO+/fEby7ad+Q9Vjw+oORI6khARz0k6\nvd5xAPXElAsAJIKEDgCJIKEDQCJI6ACQCBI6ACSCVS5oWr/bNUkf+dmnKrReW2gsQDUwQgeARJDQ\nASARJHQASAQJHQASQUIHgESwygVNa+SOETrmwbaybc8XHAtQDYzQASARJHQASAQJHQASMaSEbnuu\n7Wdtr7O9sFpBAagN+mzaDjuh226R9HVJ75c0S9IVtmdVKzAA1UWfTd9QVrmcLWldtlOMbN8paZ6k\nNZVe0OrR0SY25q23PdqtfbHX9Y4DhTukPkt/HT52atuWiJg00HlDSehTJb3Uq75e0jn9vaBNY3WO\nLxrCR6IaHosV9Q5hWOgcG9pyzoHyjYuKjaUgh9Rn6a/Dx4Ox5MXBnFfzdei2F0haIEltGlPrjwMw\nBPTXxjaUi6IbJE3vVZ+WHcuJiI6IaI+I9lEaPYSPAzBEA/ZZ+mtjG0pCf1zSTNsn2W6VdLmkZdUJ\nC0AN0GcTd9hTLhHRaftqSfdLapG0KCKerlpkAKqKPpu+Ic2hR8R9ku6rUiwAaow+mzbuFAWARPC0\nRTQU24skfVDS5og4LTs2QdJ3Jc2Q9IKkyyJi20DvNXv8Fv3iQx1l21quqlLAQIEYoaPR3Cppbp9j\nCyWtiIiZklZkdaDpkNDRUCLiEUlb+xyeJ2lxVl4s6dJCg0Ia7Mo/DYKEjhRMjoiNWfkVSZPrGQxQ\nLyR0JCUiQlJUare9wPZK2yv/8GqF2/6BBsVF0Srzme8slf9n2W25ttn/dXWpPP1LPysspiawyfaU\niNhoe4qkzZVOjIgOSR2S1H56W8XEj0SMaMlVR04/IVffdt7UUnnXCfnx7Qk/2dlTWf1sri3276tS\ngNXFCB0pWCZpflaeL2lpHWMB6oYROhqK7TskXSBpou31kq6TdIOku2xfKelFSZcN5r2eWT9J533+\nUxVaP1+FaIFikdDRUCLiigpNPOcVTY+EXmWbzzq6VO5U/qLbmJeZsgUKFV39Nm97W8+s857p+3Nt\ne9e0lcqjRzTG0kXm0AEgESR0AEgEUy5Vtu1dPdMs6zv35tqOveXRosMB0Fufuz73nrKnp2n7qFzb\nEc9tKZUP7M335eGKEToAJIIROpqWQ2rZy4VqpIMROgAkghH6EMX5c3L1n3zwq6Xyex75u1zbKfpl\nITEByDg/Zt1xxpRcfe47flUqr3jgjFxbbKz4BIlhixE6ACSChA4AiWDKZYi2zjoiV5/SMqZUnrpk\nVN/TARRoxNgxufqGC/LLFs9t6VmO2Lot39a1a1ftAqsRRugAkAhG6GhaRxz/ut55zZNl2x5dUnAw\nQBUwQgeARDBCH6KL/jZ/O//3d48vlY98OL/LCRueAcUaMX5crv622S/l6rsPjC6Vj//56/kXR+Pd\ndMYIHQASMWBCt73I9mbbT/U6NsH2cttrs9/H1DZMAINFn21eg5lyuVXSTZK+1evYQkkrIuIG2wuz\n+jXVD2/4aXnnqbn6l4+7I1e/Zce0UvnA9tcKiQno41bRZyVJO9qn5uqfPOHuXP2eTWeWyq0vbsm1\nddYurJoZMKFHxCO2Z/Q5PE/d+zpK0mJJD6sJvhxIy+4tY/SLxWdUaL2t0FiqiT7bvA53Dn1yRGzM\nyq9ImlyleADUBn22CQz5omhEhKSKl4NtL7C90vbK/WqMh8QDKeuvz9JfG9vhLlvcZHtKRGy0PUVS\nxceSRUSHpA5JOtoTGm8dUB8bLjm23/ZVO0/sVXujtsEAgzeoPptCf/XonqWI6/80/0eYd2R+2eJD\n299RKr/yh/wm0Y3ocEfoyyTNz8rzJS2tTjgAaoQ+2wQGs2zxDkmPSjrV9nrbV0q6QdIlttdKujir\nAxgG6LPNazCrXK6o0HRRlWNpCDtm9f/PstU39Wx4MV5sCo3iNXuf7X136DcuXpxrG+PWXP3R+2eX\nyifue6y2gRWAW//RUGwvkvRBSZsj4rTs2PWSPinpD9lpX4iI+wZ8s3EHpPdtLd92UxWCBQrGrf9o\nNLdKmlvm+I0RMSf7GTiZAwkioaOhRMQjkioMq4HmxpTLIOx9/1ml8tL3/Ueu7YtbzszVJ9zd83zt\nrtqGhbyrbX9c0kpJn4uIbfUOCAVxfqeh19t7lg6f3vpqrm3d/vwY9qR7t5fKXV2N/zxURuhIwTck\nnSxpjqSNkv6t0om9b5zpfG13UfEBhSCho+FFxKaIOBARXZJulnR2P+d2RER7RLSPHDe2uCCBAjDl\nMgjrL+z5a3pXa1uubf4Ls3P143b/ppCY0OPgHZBZ9cOSnurvfKTFLS25+st/3NNfJ7bkN3G/+PGP\n5+pv+e3ztQusDkjoaCjZTTMXSJpoe72k6yRdYHuOup9P8oKkqwbzXiPX7dFx8/gfMNJBQkdDqXDT\nzC2FBwIMQ8yhA0AiGKEPwqTTeh5MdyDyixFHLmUnL6Ceej9dUZJmnfdcqbyrq88jgFflN43u2pPW\nI4IZoQNAIkjoAJAIEjoAJII59DJGnnRirv6VU79XKt/82vRc24RFPCK3Ue2dMUZr//HM8o3zlxQb\nDA7biAn561iXH/9/pfKa/fn7RqY/sCNXjwRu9++NEToAJIKEDgCJYMqljLVXnZCrn9trVdQnn3hv\nrm06d5kDhfPIntT18ry35Nrec8SdpfJ/b+8zpfbrtTWNq94YoQNAIkjoAJAIEjoAJII59DK6pu+p\n2PbG9raKbWgsbb/fo1M/Xf5piy8WHAsOTe859NkfzV/HmtDSc9HrtiUX5dresi/tZcaM0AEgESR0\nAEgEUy5l/Oc5367YNvWHLRXbABRjxPiepyZeM+X7fVp70tqUn+/LN0XUMKr6Y4QOAIkYMKHbnm77\nIdtrbD9t+zPZ8Qm2l9tem/3mweBAndFfm9tgplw6JX0uIp6wfZSkVbaXS/qEpBURcYPthZIWSrqm\ndqEC1XXEqV067fbXy7Y9cEbBwVQP/bWJDZjQs93UN2blnbafkTRV0jx1b9YrSYslPawG/oLs+bOz\nS+V3t/2iTyuXGtAYmqW/rr/i5FL57aPyOxbtip5diNqe35prS+vZim92SHPotmdIOkPSY5ImZ18e\nSXpF0uSqRgZgSOivzWfQCd32kZLulvTZiMg9VDgiQlLZy8e2F9heaXvlfqW1fx8wXNFfm9Og5hJs\nj1L3l+M7EXFPdniT7SkRsdH2FEmby702IjokdUjS0Z4wbNcM/f5DPaGNdv6v5YtbZpfKRy5dlWsb\ntn8gNK0U+2vfjaBn//maUrnF+XHpY28c3VPZur2mcQ03g1nlYkm3SHomIr7aq2mZpPlZeb6kpdUP\nD8ChoL82t8GM0M+X9DFJv7a9Ojv2BUk3SLrL9pXqfvTFZbUJEcAhoL82scGscvmpJFdovqjCcaAm\nbE+X9C11X9QLSR0R8TXbEyR9V9IMSS9IuiwitvX3Xp0xQtv3j6ltwAWjvza3pl2P13L00bn6Neff\nV/Hc23/4J6XyWzvTflpbA2CddRMacXJ+4/Zzxj1WKu/qyj8d9VM/uqpUftuu1Wom3PqPhhIRGyPi\niay8U1LvddaLs9MWS7q0PhEC9UNCR8NinTWQ17RTLl1782ts17zeszH0xRvac20zv/x0qZz6nWaN\nou866+7FHd0iImxXXGctaYEkjT1+bBGh4nD1+m/qPfmnJv77r3o2a7//hFm5thN/0FUqx97mWkvP\nCB0Np7911ll7v+usI6I9ItrbxrP7FNJCQkdDYZ01UFnTTrmgYVVtnfXu/a16dMOMWsUJFK5pE3rf\nubVne02bt/bZIph58+GDddZNpNfuQp0vvJRrOuWqV0vlrpb8REPrjidqG9cwxpQLACSChA4AiWja\nKRcADaQrP/HZtXNnnQIZ3hihA0AiSOgAkAimXNC04o0WHXhyXL3DAKqGEToAJIKEDgCJIKEDQCJI\n6ACQCBI6ACSChA4AiWDZIppW68u79Zbrf1a27bcFxwJUQ6EJfae2bXkwlrwoaaKkLUV+dj+aMZYT\nBz4FzY7+OqAiYxlUny00oUfEJEmyvTIi2gc6vwjEApRHf+3fcIrlIObQASARJHQASES9EnpHnT63\nHGIB+jecvpfE0g9Hr22egGYybuSkOG/ch8u23b/15lXDbX4UGAhTLgCQCBI6ACSi0IRue67tZ22v\ns72wyM/OPn+R7c22n+p1bILt5bbXZr+PKSCO6bYfsr3G9tO2P1OvWIBK6K+5WBqizxaW0G23SPq6\npPdLmiXpCtuzivr8zK2S5vY5tlDSioiYKWlFVq+1Tkmfi4hZks6V9Ons76IesQBvQn99k4bos0WO\n0M+WtC4inouIfZLulDSvwM9XRDwiaWufw/MkLc7KiyVdWkAcGyPiiay8U9IzkqbWIxagAvprPpaG\n6LNFJvSpkl7qVV+fHau3yRGxMSu/ImlykR9ue4akMyQ9Vu9YgF7orxUM5z7LRdFeonsNZ2HrOG0f\nKeluSZ+NiB31jKVR9DOXeb3tDbZXZz8fGPDNRlhuG132B8NfPfrIcO+zRT7LZYOk6b3q07Jj9bbJ\n9pSI2Gh7iqTNRXyo7VHq/mJ8JyLuqWcsDebgXOYTto+StMr28qztxoj4Sh1jSwn9tY9G6LNFjtAf\nlzTT9km2WyVdLmlZgZ9fyTJJ87PyfElLa/2Bti3pFknPRMRX6xlLo+lnLhPVRX/tpVH6bGEJPSI6\nJV0t6X51d8K7IuLpoj5fkmzfIelRSafaXm/7Skk3SLrE9lpJF2f1Wjtf0sckXdhniqAesTSsPnOZ\nknS17Sez5W4s+RwC+uubNESf5dZ/NKRsLvPHkv45Iu6xPVndz6YOSV+SNCUi/qrM6xZIWiBJbS1H\nnnnB5E+Uff8fvXwTt/6j4XBRFA2n3FxmRGyKiAMR0SXpZnUvu3uTiOiIiPaIaG8dcURxQQMFIKGj\noVSay8wuSB30YUlP9X0tkDr2FEWjOTiX+Wvbq7NjX1D3nYxz1D3l8oKkqwZ6o9ZTDmjat14r33hW\nNUIFikVCR0OJiJ9Kcpmm+4qOBRhumHIBgESQ0AEgESR0AEgECR0AEkFCB4BEsMoFTWvnjjF66ME5\nFVpvKzQWoBoYoQNAIkjoAJAIEjoAJIKEDgCJIKEDQCJI6ACQCJYtomnFyND+iZ31DgOoGkboAJAI\nEjoAJIKEDgCJIKEDQCJI6ACQCBI6ACSCZYtoWiN3WpN/3FK27fcFxwJUAyN0AEgECR0AEkFCB4BE\nkNABIBEkdABIBKtc0FBst0l6RNJodX9/l0TEdbZPknSnpGMlrZL0sYjY1997tewPHbmh31OAhsII\nHY1mr6QLI+J0SXMkzbV9rqR/kXRjRJwiaZukK+sYI1AXJHQ0lOi2K6uOyn5C0oWSlmTHF0u6tA7h\nAXVFQkfDsd1ie7WkzZKWS/qdpO0RcfDh5uslTa1XfEC9kNDRcCLiQETMkTRN0tmS3j7Y19peYHul\n7ZX79u2uWYxAPZDQ0bAiYrukhySdJ2m87YMX+adJ2lDhNR0R0R4R7a2tYwuKFCgGCR0NxfYk2+Oz\n8hGSLpH0jLoT+0ey0+ZLWlqfCIH6YdkiGs0USYttt6h7QHJXRPzA9hpJd9r+J0m/lHTLQG+07yjr\npYtGl298qHoBA0UhoaOhRMSTks4oc/w5dc+nA02LKRcASAQJHQASQUIHgESQ0AEgESR0AEiEI6Le\nMQB1YXunpGez6kRJW3o1nxoRRxUfFXD4WLaIZvZsRLRLku2VB8sH6/ULCzg8TLkAQCJI6ACQCBI6\nmllHhXK5OjDscVEUABLBCB0AEkFCR9OwPcH2E7b32X7d9rdtP2t7ne2F2TmjbXfZ3pv97LO9Ovv5\n63r/GYD+sGwRzeTvJZ2o7h2O/kLS9ZI+IOlhSY/bXibpAkkHImK07W9IujjbHQkY9hiho5lcJunJ\n7FG7qyV1STozIvZJulPSvOxnf3b+45Km2XY9ggUOFQkdzWSiujeUlqQ2SVbPZtIHN5aeKqk1u7Ho\nWkmtkp6yvcT29ILjBQ4JUy5Iiu0HJR1fpunaQ3ibcyNipe0/kvSYure0O1PSYkkXDj1KoDZI6EhK\nRFxcqc32FkknZ9U9kkI9m0kf3Fh6g6RR2bEnJR2QNEPSNyX9a/UjBqqHKRc0k+9Jepftk9S9jV2L\npFW2WyVdLmmZpOWS/jI7/7Pqnk9fI+lD6t6MGhi2uLEITcP2sZJWSJolqVPSUnVPpRwvaVNEzLS9\nWNJH1P2v1xGSXpW0SdJWSX8TEb+pR+zAYJDQASARTLkAQCJI6ACQCBI6ACSChA4AiSChA0AiSOgA\nkAgSOgAkgoQOAIn4f39N1HbojQUaAAAAAElFTkSuQmCC\n",
419 | "text/plain": [
420 | ""
421 | ]
422 | },
423 | "metadata": {
424 | "tags": []
425 | },
426 | "output_type": "display_data"
427 | }
428 | ],
429 | "source": [
430 | "def plot_imgs(index=0):\n",
431 | " f = plt.figure()\n",
432 | " f.add_subplot(1,3, 1)\n",
433 | " plt.imshow(x_test[index].reshape(28, 28))\n",
434 | " f.add_subplot(1,3, 2)\n",
435 | " plt.imshow(encoded_images[index].reshape(-1, 1))\n",
436 | " f.add_subplot(1,3, 3)\n",
437 | " plt.imshow(predicted[index].reshape(28, 28))\n",
438 | " plt.show(block=True)\n",
439 | " \n",
440 | "plot_imgs(2)"
441 | ]
442 | },
443 | {
444 | "cell_type": "markdown",
445 | "metadata": {
446 | "colab_type": "text",
447 | "id": "8lkIoRva6ewM"
448 | },
449 | "source": [
450 | "# Let's use Convolutional Neural Nets to get better results"
451 | ]
452 | },
453 | {
454 | "cell_type": "code",
455 | "execution_count": 0,
456 | "metadata": {
457 | "colab": {},
458 | "colab_type": "code",
459 | "id": "4UorTYac692G"
460 | },
461 | "outputs": [],
462 | "source": [
463 | "from keras.layers import Dense, Input, UpSampling2D, Conv2D"
464 | ]
465 | },
466 | {
467 | "cell_type": "markdown",
468 | "metadata": {
469 | "colab_type": "text",
470 | "id": "u8p2wwLa6qbB"
471 | },
472 | "source": [
473 | "Getting data"
474 | ]
475 | },
476 | {
477 | "cell_type": "code",
478 | "execution_count": 0,
479 | "metadata": {
480 | "colab": {},
481 | "colab_type": "code",
482 | "id": "07Ixl4YT6eQZ"
483 | },
484 | "outputs": [],
485 | "source": [
486 | "(x_train, y_train), (x_test, y_test) = mnist.load_data()"
487 | ]
488 | },
489 | {
490 | "cell_type": "code",
491 | "execution_count": 0,
492 | "metadata": {
493 | "colab": {},
494 | "colab_type": "code",
495 | "id": "-tmJMUnx6eVQ"
496 | },
497 | "outputs": [],
498 | "source": [
499 | "x_train = x_train.astype('float32')/255.0\n",
500 | "x_test = x_test.astype('float32')/255.0"
501 | ]
502 | },
503 | {
504 | "cell_type": "code",
505 | "execution_count": 0,
506 | "metadata": {
507 | "colab": {},
508 | "colab_type": "code",
509 | "id": "ZLPajgLH8ai4"
510 | },
511 | "outputs": [],
512 | "source": [
513 | "x_train = x_train.reshape((60000, 28, 28, 1))\n",
514 | "x_test = x_test.reshape((10000, 28, 28, 1))"
515 | ]
516 | },
517 | {
518 | "cell_type": "code",
519 | "execution_count": 0,
520 | "metadata": {
521 | "colab": {},
522 | "colab_type": "code",
523 | "id": "d2PouxDW7eB0"
524 | },
525 | "outputs": [],
526 | "source": [
527 | "img_height, img_width, _ = x_train[1].shape"
528 | ]
529 | },
530 | {
531 | "cell_type": "code",
532 | "execution_count": 0,
533 | "metadata": {
534 | "colab": {},
535 | "colab_type": "code",
536 | "id": "CHctX-5G6wTb"
537 | },
538 | "outputs": [],
539 | "source": [
540 | "def CNN_AE():\n",
541 | " input_img = Input(shape=(img_width, img_height, 1))\n",
542 | " \n",
543 | " # Encoding network\n",
544 | " x = Conv2D(16, (3, 3), activation='relu', padding='same', strides=2)(input_img)\n",
545 | " x = Conv2D(32, (3, 3), activation='relu', padding='same', strides=2)(x)\n",
546 | " encoded = Conv2D(32, (2, 2), activation='relu', padding=\"same\", strides=2)(x)\n",
547 | "\n",
548 | " # Decoding network\n",
549 | " x = Conv2D(32, (2, 2), activation='relu', padding=\"same\")(encoded)\n",
550 | " x = UpSampling2D((2, 2))(x)\n",
551 | " x = Conv2D(32, (3, 3), activation='relu', padding='same')(x)\n",
552 | " x = UpSampling2D((2, 2))(x)\n",
553 | " x = Conv2D(16, (3, 3), activation='relu')(x)\n",
554 | " x = UpSampling2D((2, 2))(x)\n",
555 | " decoded = Conv2D(1, (3, 3), activation='sigmoid', padding='same')(x)\n",
556 | " \n",
557 | " encoder = Model(input_img, encoded)\n",
558 | " \n",
559 | " return Model(input_img, decoded), encoder"
560 | ]
561 | },
562 | {
563 | "cell_type": "code",
564 | "execution_count": 0,
565 | "metadata": {
566 | "colab": {},
567 | "colab_type": "code",
568 | "id": "euWIUw7i9W39"
569 | },
570 | "outputs": [],
571 | "source": []
572 | },
573 | {
574 | "cell_type": "code",
575 | "execution_count": 0,
576 | "metadata": {
577 | "colab": {},
578 | "colab_type": "code",
579 | "id": "a-0v2iI16wVm"
580 | },
581 | "outputs": [],
582 | "source": [
583 | "model_cnn, encoder = CNN_AE()\n",
584 | "model_cnn.compile(optimizer='adadelta', loss='binary_crossentropy')"
585 | ]
586 | },
587 | {
588 | "cell_type": "code",
589 | "execution_count": 0,
590 | "metadata": {
591 | "colab": {
592 | "base_uri": "https://localhost:8080/",
593 | "height": 72
594 | },
595 | "colab_type": "code",
596 | "id": "9RikWIEy6wa4",
597 | "outputId": "ee777875-aea8-4e50-a9fe-7b1b436008f8"
598 | },
599 | "outputs": [
600 | {
601 | "name": "stdout",
602 | "output_type": "stream",
603 | "text": [
604 | "Train on 60000 samples, validate on 10000 samples\n",
605 | "Epoch 1/1\n",
606 | "60000/60000 [==============================] - 20s 339us/step - loss: 0.0899 - val_loss: 0.0844\n"
607 | ]
608 | }
609 | ],
610 | "source": [
611 | "cnn_hist = model_cnn.fit(x_train, x_train, validation_data=(x_test, x_test))"
612 | ]
613 | },
614 | {
615 | "cell_type": "code",
616 | "execution_count": 0,
617 | "metadata": {
618 | "colab": {},
619 | "colab_type": "code",
620 | "id": "uOJoBgDd6weQ"
621 | },
622 | "outputs": [],
623 | "source": [
624 | "reconstruct = model_cnn.predict(x_test)"
625 | ]
626 | },
627 | {
628 | "cell_type": "code",
629 | "execution_count": 0,
630 | "metadata": {
631 | "colab": {
632 | "base_uri": "https://localhost:8080/",
633 | "height": 131
634 | },
635 | "colab_type": "code",
636 | "id": "G15_xNl8_Wyz",
637 | "outputId": "136c1df9-e1bf-442f-f020-5393579af9b0"
638 | },
639 | "outputs": [
640 | {
641 | "data": {
642 | "image/png": "iVBORw0KGgoAAAANSUhEUgAAAlMAAAByCAYAAAB3LlRSAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDMuMC4zLCBo\ndHRwOi8vbWF0cGxvdGxpYi5vcmcvnQurowAAFRlJREFUeJzt3Xt0VNW9B/DvbyaTTCAJgYIQQgQi\noCLFCghKbav1hVgVtVDx2kVbFd+1Pqr4qJRee7XaerXXxzVeUa/XKlrtBV1UqiBVrxUEVBAQiMqz\nPERQApG8Zt8/ZrL3yWMykzl75pzJfD9rsfLLmTP77PObMXt79tn7iFIKRERERJSagNcVICIiIspm\n7EwRERERucDOFBEREZEL7EwRERERucDOFBEREZEL7EwRERERucDOFBEREZELrjpTIjJBRNaJSLWI\nzLBVKSIiImqL7a4/SaqLdopIEMB6AKcC2ArgPQBTlVJr7FWPiIiIALa7fpbn4r1jAVQrpT4FABF5\nDsA5AOJ+qPlSoMLo7uKQua0Ge3crpfqk8t78UHcVLii1Vpf8ijprZQFAQ7VYLQ+BoNXi9tXvTDn3\nAJAfCKvCYLG1+tQPDFkrCwBCnxy0Wh66F1otrubAP93l3/LfnmEja62VBQAbPiqyWp6KRKyW5+Zv\nT7B7dxUq7WWtLr1Ka6yVBQD98+x+91d91dtqefWbtjlzz3Y3w5L97rvpTJUD2OL4fSuAcR29IYzu\nGCcnuzhkbntd/XlTqu8NF5Ri3MjLrdXl0Ac+sVYWAGw7M2y1PCm22zi9+ukfUs49ABQGi3F86Xm2\nqoOt9/W1VhYAlE1aa7U8jPim1eJeXzLTVf5t/+1ZsOADa2UBwBlDxlstL1Jrt7Pn5m9PqLQXKq66\nzlpdLjzr79bKAoCZfexe1Bn88qVWy9s8/WZn7tnuZliy3303namkiMh0ANMBIIxu6T4cERFRTmO7\nm3lubkDfBqDC8fuA2LYWlFJVSqkxSqkxIRS4OBwREVFOY7vrU246U+8BGCoig0UkH8AFAObZqRYR\nERG1wnbXp1Ie5lNKNYrI1QAWAAgCmK2UWm2tZkRERKSx3fUvV/dMKaXmA5hvqS5ERETUAba7/sQV\n0LMYF2/zFvPvHebeW8w/UUvsTGWp2OJtDwE4A8BwAFNFZLi3tcodzL93mHtvMf9EbaV9aQRKm04v\n3kZWMf/eYe69xfyTK4Fis4Bx3fGH67jgH+t0HKmxuzhruvHKVPZqb/G2cucOIjJdRJaJyLKGhgMZ\nrVwO6FT+6yOWVxjPbQlzD7T6/sPuiv05rlPf/aYD/NtDXV9OXpkKlvbQ8boHK3X88Un/pePbd43W\n8ap/GabjpjXr01w7e5RSVQCqAKCkqDy1hzBSypz57xHqw/xnWIvvv/Ri/jPImftweQVzTwiEzVMu\n1NwSHd9f+aCOn95zvI5XHW/Wx1J1/v+fIV6Zyl5JLd5GacP8e4e59xbzT9QKO1PZi4u3eYv59w5z\n7y3mn6iVnBzmiwweoONVJz6q4wbHxeg7D1mu46PPNQ8hrfDJMB8Xb/MW8+8d5t5bzD+lYsu1o3S8\naOi9Ou4RyNfxNb3f0vHUs2/QcdELS9JcO/dysjPVVXDxNm8x/95h7r3F/BO1xGE+IiIiIhdy5spU\nXoUZ2htcVe1hTYiIiLqwQBAAIKPNWq6/u3S2jp1De3kI6rgsWKjj8GXbdRxcEJ3917Rvn/26WsIr\nU0REREQusDNFRERE5EKXH+bbfEd0Jt7oCeZJB/eUvRVv93YVjf9cx1t+FS2v98pGva1w7lI3VcyI\n8srd+NdnH7dW3tW//rm1sgAg72S76/r1XLo98U4ZNHR4DeYvWGStvNP7f8taWblACsMIDDnCWnnH\n3Dk+8U6dMPndhVbL+/vIwsQ7ZYgqiKCp8mtr5b1zdH7inTrhdFj+b+nRxLt0RRIyn8v+s48BAEyc\nuVhvG1+wR8cNylzHaYL52x9BRMc3D/qrji+79ycAgCP/aIb5WiygrbxfF5ZXpoiIiIhcYGeKiIiI\nyIUuP8y38rL/AAA0qKaUy1h89DPml6OjP/5yoExvml0zScd5i8xin0RERF2WiIm/dbgOT70jeivN\nRaWmPewWMM/aa3IMy9WqBh03OLYfFtqr47mnR9vx179tZgc+vPK7Oh56iRnyi9TWdu4cLOGVKSIi\nIiIX2JkiIiIicqFLDvOFFpshuJAEO9gzvvfrzayCjQ19dHxu9+iMhClFu/S2KU9X6fgH5aNTOh4R\nEVE2CRSaWaPV15m2tqpndIZ7sSS+XlPrGNo7EDH754tpg3sForPnp5Ss1NumnGDi7zxwnY6HXbbC\nFB5J/faezkp4piIyW0R2ichHjm29ROQ1EdkQ+9kzvdUkIiLKHV88+QK23vAbADiqeRvbXv9KZpjv\nSQATWm2bAWChUmoogIWx34mIiMiC7uNH45CfX9x6M9ten0o4zKeUelNEBrXafA6AE2PxUwAWA7jZ\nYr067etJY3X807IXdNw8iy+Z2XwjFl6u4z4LzcyDgq/Me285Mdr/XDX5j+2WsfUWs5jfgLveSXhM\nIiKi1sLDKtG4e0/rzb5qe788Z6SO542/T8flwW5t9o04FufcGTGLuD6x17Tdf9tuFtYN55mFsSf0\nWw0A+GZ4q942yrEI6L+f+KyOH6s4SceNm7YkcRZ2pHrPVF+lVPMS0zsA9I23o4hMBzAdAMJom2Ai\nIiJKSlJtL9vdzHN9A7pSSolI3LXclVJVAKoAoER6WV3zPXiUWdfizvvMTeBj8uude7V5n3ONqNvf\nOF/HR970sY7jPZ368A3DAABLzw7rbWMLDur4r1fco+PTwjfpeNC/mfU2VF1du2UTERElo6O2N53t\nruSZbsMJv1yi48pQqM2+jTCjOlsbTbt37WeTdbzriUE6Lq02V6wiIXMX0v/2OQUA8Nj55vVXjn9E\nx2MKduj4+l/21/HhN31hykvz+lOpLo2wU0TKACD2c1eC/YmIiMgdtr0+lWpnah6AabF4GoC5dqpD\nREREcbDt9amEw3wi8iyiN7z1FpGtAGYCuBvA8yJyMYBNAKaks5LxRPJN9VsO7bX1s01mQmLNj8za\nGMO2LtVxMitSND+p+sonzc3qyy67X8dlQVP2iovN9vNfmqZj9eHaJI5ERES5avdjf8LBdZ8CQIGf\n2t5gP3Ob1jW95+g4z3FvVvPN5h/VmxHGH710o46HVe3W8Tc2va9j1WTWlgooE5cURCeE1ZWaG95r\nxplhxYH55rE2f5r4sI6vf/sqHRfPMUOSUFZHPgEkN5tvapyXTrZcFyIiIgLQ+9ILAQCbp9+8Qik1\nxvES214f4uNkiIiIiFzoko+Tcbp1Z7RDv++Sb+htTVs3uC530IvmMuWvJh2n47v7vee6bCIiIj86\nMNLMlnM+LsY5c29dQzS+5PfX623DntYPUUHT/gOmwCQe+aIi0WG54s0NetvH9WZW/uGhbToekGdm\nDW4/2ZRd8pd8U14aZtTzyhQRERGRC+xMEREREbnQZYb5QtJ2cU4AWDmq+a5990N7LYiZPZAXMLMO\n4tXjn7NM3G+S3aok40CkAO99XWmtvKV3PZJ4p044c+yZVstDyF9f7VV7+6DyhcsT75ikoXjXWlm5\nQAUFjaXhxDsmadltD1orCwDOPPvHVssDVlsuL3WBgEJBQUPiHcm/HO3dpvPMTLiigHnsWq0yM+rP\nfetKAMCwJz7Q25osLJrZ2M20r0E4Zv45rguFHXXt1sscUxzb7c/l45UpIiIiIlfYmSIiIiJywV9j\nIZ207gqzSFiDSmbJTXs2nmdmB/65j1n4s0EFHbGpU/+Z5r3m4iQREZHPOWbtnTay/SHk6gbT9g18\nKrp/5KCLWXOOYblAODqc+FWlOUZpsP1hwwbngpzLeugwkuZn4vLKFBEREZEL7EwRERERuZDVw3y3\nf+fljBwnr2KAjmtGRxcs+8+fPhxvd21pnZk9JPWN9itGRESUZhI0w2tn9Fyl44jjppV3vz5Mx4Ub\ndgEAGlUnb2oJmOM0D+0BACoPBQAcO3ml3jQi/wvHG82CnOsaSnQ8cK5ZXLspDc/jc+KVqSwlIhUi\n8oaIrBGR1SJyrdd1yiXMv3eYe28x/0RtZfWVqRzXCOAGpdQKESkGsFxEXlNKrfG6YjmC+fcOc+8t\n5p+oFXamkrBmVj8drz6t48X6XtzfW8eP3DhZx+G1S9vbPWVKqe0AtsfiGhFZC6AcAP+gZQDz7x3m\n3lvMf+4RxyLIg/LM8FqTMjPu6iIhHUdKi6LB5iQKdwztBXuYIbrIEHN7zfpromU/2v9Vva1vsNAc\nW5lFYX/9ydk6Dm/YmEQF7OAwXxcgIoMAHANgSavt00VkmYgs27+3vr23kgXJ5L/Fgz3Jmni5j72m\n81/fwPynQzLf/cZ97le+JvI7XpmKI7TYPJH6rrIXk37fk9vG6zj8st2rUe0RkSIALwL4hVJqn/M1\npVQVgCoAOHRESXrvvstRyea/4NAK5t+yjnIPtMx/SXE5829Zst/9wiH9mfssJ/nmqlNAzMdZ51hL\ncXu9WdPpwKBiAED3deYm8ki9uXoULOqu45pTjtTxFxea/+k5b4h5FM1DPf8BAChzXI1y3vy+rM6s\nORm+xZStGjJ3EYFXprKYiIQQ/WP2jFLqJa/rk2uYf+8w995i/olaYmcqS0n0qY2PA1irlLrP6/rk\nGubfO8y9t5h/orayepgvKOYyX0iC7e6z78Lj2myb9ZvHdXxS4cF23+csr+Wjato/TjP1/W0dvm7R\ntwH8GMAqEWm+HnqrUmp+piqQ45h/7zD33mL+c03IrONU67jRvFvItMFnlb6v41cuGgEAUIGj9bbG\nsLlZ/dgbluv4xkP+oOMegfbb124SHd5z3mj+zsFiHc+65Wc6LlqR/ttr2pOwMyUiFQD+G0BfAApA\nlVLqARHpBWAOgEEANgKYopTam76qkpNS6m0AknBHSgvm3zvMvbeY//Rr3PMlvpg9B001+wHgKBG5\nlu2uvyUzzNe8pshwAMcBuEpEhgOYAWChUmoogIWx34mIiMgFCQTQc/IP0H/WDQCwFmx3fS/hlakO\n1hQ5B8CJsd2eArAYwM1pqWUcd8/5oY6nXHx/u/u8ee9DAFoP1RkNScwziffeZiMWXq7joViRuEAi\nIqI4gqUlCJbqNZciiHaoPGt3I/vMZM0X9h6r42P6mRUxRuWbW2YWjHsEAPDlsaaLUSzmkWoD8sys\nvJAUJTx+8/DegtpD9LaHrp6i46LXHEN7aX5sTDydumeq1ZoifWMdLQDYgegwYHvvmQ5gOgCE0a29\nXYiIiKh9+WC763tJz+ZLsKaIQvR+qjaUUlVKqTFKqTEhFLS3CxEREbUSOVgHAIeB7a7vJXVlKs6a\nIjtFpEwptV1EygDsSlcl46mcY54IvfSisI7HFrQ/Qy9VS+tM2VU7vgcA2HulecTMEZ9V67jjAUHv\nfLk6D/NGHJJ4xyTNg72yonbYLS7ir08ivKsBRzxo8T+RoZX2ykqDiN+Wadz/NQJvf5B4vyRNLB9l\nrayo1ZbL8w9VG4Ra0SPxjknactv4xDt5qGxRJPFOSYhEmrD+zf8BgD1et7uqrk7Hy+8ww3zVD/2f\njoc4HjlTFgzFfpoyAjAzAoOS+DpObcQsuPlKbR8AwKNXmFt7QovMjECvhvacEp5RB2uKzAMwLRZP\nAzDXfvWIiIhyi1IKny19HoUlfQFgp+Mltrs+lcwwX/OaIt8XkQ9i/yYCuBvAqSKyAcApsd+JiIjI\nhf27N2L3xuX4amc1AAxnu+t/yczm62hNkZPtVqdzmtas1/Ed11+i4y1nmcus68941PVxrpxtZutV\n/PadWMSlPYiIyL7iPoMx7oLfAwCWPHfjGqXUGMfLnra7BfOX6fji267T8QW3vqrjHxZ/BADo63iW\nXjJDe7ubzLP5pq6/QMehK6JDhHnrl7d5j1/wcTJERERELrAzRURERORCVj+bz6lwrlm0a5jjlrzv\nTr0KABD6ibmH79Wj5uj4tI/MpcTIk2aGmnIMbA764HMd+2uOGBERUQY5Zs71eOZdHf9t/mAdPzdx\nAgCg1yWb9bY7Br6s40X7h+v4jc+H6bjpLtMG5y/+0GxvNAt++hWvTBERERG5wM4UERERkQtdZpgv\nnpJnY5chnzXbzsVYHXfHp469nbHBoT0iIqL4mvaaGe7Nw39Nz5jXZ2J0u+8LYEu7sffLcHYOr0wR\nERERucDOFBEREZEL7EwRERERucDOFBEREZEL7EwRERERucDOFBEREZEL7EwRERERucDOFBEREZEL\n7EwRERERucDOFBEREZELolTmFm0Xkc8BHACwO2MH9UZvpOccByql+qTyxljuNyWxa7rqbotX9Us5\n9wDzbwHzH5V1+WfuXbP13fd7ft3ytN3NaGcKAERkmVJqTEYPmmHZfI5+r7vf6+eW38/P7/Vzy+/n\n5/f6ueH3c/N7/RLJ9von4vX5cZiPiIiIyAV2poiIiIhc8KIzVeXBMTMtm8/R73X3e/3c8vv5+b1+\nbvn9/PxePzf8fm5+r18i2V7/RDw9v4zfM0VERETUlXCYj4iIiMiFjHamRGSCiKwTkWoRmZHJY6eL\niFSIyBsiskZEVovItbHtvUTkNRHZEPvZ0+u6JuLnzydenrsS5t87zL23mP/08XNuU+XLdlcplZF/\nAIIAPgFQCSAfwIcAhmfq+Gk8rzIAo2JxMYD1AIYDuAfAjNj2GQB+53Vds/nziZdnr+vF/HtfN+Y+\nu/8x/7mbW9ufiZftbiavTI0FUK2U+lQpVQ/gOQDnZPD4aaGU2q6UWhGLawCsBVCO6Lk9FdvtKQCT\nvKlh0nz9+XSQ566C+fcOc+8t5j99fJ3bVPmx3c1kZ6ocwBbH71uRPV/IpIjIIADHAFgCoK9Sanvs\npR0A+npUrWRlzefTKs9dBfPvHebeW8x/+mRNblPll3aXN6BbIiJFAF4E8Aul1D7nayp6zZHTJi3o\nKM+Ufsy/d5h7bzH//uOndjeTnaltACocvw+Ibct6IhJC9AN9Rin1UmzzThEpi71eBmCXV/VLku8/\nnzh57iqYf+8w995i/tPH97lNld/a3Ux2pt4DMFREBotIPoALAMzL4PHTQkQEwOMA1iql7nO8NA/A\ntFg8DcDcTNetk3z9+XSQ566C+fcOc+8t5j99fJ3bVPmx3c3oop0iMhHA/YjOMJitlPptxg6eJiJy\nAoC3AKwCEIltvhXR8dvnARyK6BO7pyil9nhSyST5+fOJl2el1HzvamUX8+8d5t5bzH/6+Dm3qfJj\nu8sV0ImIiIhc4A3oRERERC6wM0VERETkAjtTRERERC6wM0VERETkAjtTRERERC6wM0VERETkAjtT\nRERERC6wM0VERETkwv8DEqNmGw3hwBEAAAAASUVORK5CYII=\n",
643 | "text/plain": [
644 | ""
645 | ]
646 | },
647 | "metadata": {
648 | "tags": []
649 | },
650 | "output_type": "display_data"
651 | }
652 | ],
653 | "source": [
654 | "def plot_imgs_for_cnn(index=0):\n",
655 | " f = plt.figure(figsize=(10, 10))\n",
656 | " f.add_subplot(1,6, 1)\n",
657 | " plt.imshow(x_test[index].reshape(28, 28))\n",
658 | " \n",
659 | " \n",
660 | " f.add_subplot(1,6, 2)\n",
661 | " plt.imshow(encoded_images[index][:, :, 0])\n",
662 | " f.add_subplot(1,6, 3)\n",
663 | " plt.imshow(encoded_images[index][:, :, 1])\n",
664 | " f.add_subplot(1,6, 4)\n",
665 | " plt.imshow(encoded_images[index][:, :, 2])\n",
666 | " f.add_subplot(1,6, 5)\n",
667 | " plt.imshow(encoded_images[index][:, :, 3])\n",
668 | " \n",
669 | " \n",
670 | " f.add_subplot(1,6, 6)\n",
671 | " plt.imshow(reconstruct[index].reshape(28,28))\n",
672 | " \n",
673 | " plt.show(block=True)\n",
674 | " \n",
675 | "plot_imgs_for_cnn(3)"
676 | ]
677 | },
678 | {
679 | "cell_type": "code",
680 | "execution_count": 0,
681 | "metadata": {
682 | "colab": {},
683 | "colab_type": "code",
684 | "id": "_p4rclEL_0A5"
685 | },
686 | "outputs": [],
687 | "source": []
688 | },
689 | {
690 | "cell_type": "code",
691 | "execution_count": 0,
692 | "metadata": {
693 | "colab": {},
694 | "colab_type": "code",
695 | "id": "g1alULdqIIyb"
696 | },
697 | "outputs": [],
698 | "source": []
699 | },
700 | {
701 | "cell_type": "markdown",
702 | "metadata": {
703 | "colab_type": "text",
704 | "id": "RCivQ5wdOBBr"
705 | },
706 | "source": [
707 | "# **Denoising example**"
708 | ]
709 | },
710 | {
711 | "cell_type": "code",
712 | "execution_count": 0,
713 | "metadata": {
714 | "colab": {},
715 | "colab_type": "code",
716 | "id": "xR4oH_QXII0v"
717 | },
718 | "outputs": [],
719 | "source": [
720 | "noise_factor = 0.5\n",
721 | "x_train_noisy = x_train + noise_factor * np.random.normal(loc=0.0, scale=1.0, size=x_train.shape) \n",
722 | "x_test_noisy = x_test + noise_factor * np.random.normal(loc=0.0, scale=1.0, size=x_test.shape) \n",
723 | "\n",
724 | "x_train_noisy = np.clip(x_train_noisy, 0., 1.)\n",
725 | "x_test_noisy = np.clip(x_test_noisy, 0., 1.)"
726 | ]
727 | },
728 | {
729 | "cell_type": "code",
730 | "execution_count": 155,
731 | "metadata": {
732 | "colab": {
733 | "base_uri": "https://localhost:8080/",
734 | "height": 72
735 | },
736 | "colab_type": "code",
737 | "id": "TvS9CX6III3b",
738 | "outputId": "8f54b173-159d-4c77-edac-15de211e6731"
739 | },
740 | "outputs": [
741 | {
742 | "name": "stdout",
743 | "output_type": "stream",
744 | "text": [
745 | "Train on 60000 samples, validate on 10000 samples\n",
746 | "Epoch 1/1\n",
747 | "60000/60000 [==============================] - 20s 333us/step - loss: 0.1180 - val_loss: 0.1100\n"
748 | ]
749 | }
750 | ],
751 | "source": [
752 | "cnn_hist = model_cnn.fit(x_train_noisy, x_train, validation_data=(x_test_noisy, x_test))"
753 | ]
754 | },
755 | {
756 | "cell_type": "code",
757 | "execution_count": 0,
758 | "metadata": {
759 | "colab": {},
760 | "colab_type": "code",
761 | "id": "HCRmI7oUI4jd"
762 | },
763 | "outputs": [],
764 | "source": [
765 | "reconstruct = model_cnn.predict(x_test_noisy)\n",
766 | "encoded_images= encoder.predict(x_test_noisy)"
767 | ]
768 | },
769 | {
770 | "cell_type": "code",
771 | "execution_count": 163,
772 | "metadata": {
773 | "colab": {
774 | "base_uri": "https://localhost:8080/",
775 | "height": 131
776 | },
777 | "colab_type": "code",
778 | "id": "gyehz6t-II5d",
779 | "outputId": "4de1e821-dc81-40b2-e614-9ada9ffacec7"
780 | },
781 | "outputs": [
782 | {
783 | "data": {
784 | "image/png": "iVBORw0KGgoAAAANSUhEUgAAAlMAAAByCAYAAAB3LlRSAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDMuMC4zLCBo\ndHRwOi8vbWF0cGxvdGxpYi5vcmcvnQurowAAH0ZJREFUeJzt3Xl8lNW5B/DfyWRPSCCEbISdRARl\ncWNRsQoYRb14laJYlfbaYqvWBbXQ1mqvelvFlurttQXu1VasdQNcqlQErFpXQMuOLLJIIOx7ErLM\nnPvHOznPCzNhJnnfzDshv+/n44cn77xz5uQkcg7nec85SmsNIiIiImqeBK8rQERERNSacTBFRERE\n5AAHU0REREQOcDBFRERE5AAHU0REREQOcDBFRERE5AAHU0REREQOOBpMKaUuU0qtU0ptVEpNcatS\nREREFIr9bnxSzd20UynlA7AewCgA5QCWABivtV7jXvWIiIgIYL8bzxIdvPc8ABu11psAQCn1EoAx\nABr9oSYlZ+jUtA4AAHW4ylwv7S/x+hXpIe+rLcwwcXJFZcSKqZRkEx/LS7Led1gGjeqQfF6gg5Sd\ncCBy2WE/L1k+r66rkvL2SfNqn9x/etEeE1frAACgfF2O3FtbKzenp5rwSFXFXq11p+bUMdmXptMS\ns5rz1rBqip386oRK2RFwtTy4vLH/4ZqdzW57AEjMStdJee1dq09B6mHXygKAfauTI9/koSM44Kj9\nkxNSdVpCpmv10b18kW9qArVVRb6pCXRNbeSbmsBJ+yelZOiUjJzIN0apT5c9kW9qgg1r2rlanq73\nu1reCW3f5H43WaXoVGQ09jJFEO3vvpMesTOAbbavywEMPtkbUtM6YNAFdwIAUv6+xFyfP3+Zics6\nD7IC24zZtu8PM3GXRz+JWDFf1x4mXnd7PgCgeJF01qlvLTbxkbIhJm738mcRyw4nsbibiXc+mSKf\n87z8BVKbKX9ZLn70jyZeXVsNAPjJxdeba/Wbt5pY9TvDxAuW/FJeaKK0xCwMK7ihuW8PsWlqB9fK\nAoAeD9W4Wh5c/gtt/rrHm932AJCU1x7dn5joVnUwud9818oCgBf6FLtantsW6tmO2j8tIRNDM8e4\nVR3UTc92rSwASLrV3X+c+DdudrU8J+2fkpGD/iPvcq0uH/33DNfKAoDR/Ue4Wp5/7z5Xyzuh7Zve\n7yIDg5W732NbEu3vvrv/B4ehlJoIYCIApKS69y9zIiIiCmXvd1MRmu0h9zkZTG0H0MX2dXHw2nG0\n1jMBzASALJWj7TNSDcqKBtrfAQA4Ok5mjJKamH1TNXUm7n1P6GzT5l8NNfEr45808eSXTzrABwDs\nu8V6b8dnPjXXAtkyhZp7lcy2Vv27lHekmzzrf/z3axm5apWJ379KZqPql64KuZeIiNqkZvW7sala\n2+ZkNd8SACVKqR5KqWQA1wN4051qERER0QnY78apZs9Maa3rlVJ3AJgPwAfgWa31atdqRkRERAb7\n3fjl6JkprfU8APNcqgsAYP4O62H0AVPlofOC38lD5zWXn2vicClDAKjfVh5y7eg7PU38QPdXTTy5\nh6Ti9k6U9N+xMlktVXyt/K7a03sNEvbJvfY1aRXny0Pnve6T7yGxuLPUtdyaoV14hqwoOXxDodw7\nsEAKnDs75LOJiKjtaIl+l5zjDuitGDdv8xbb3ztse2+x/YmOx8FUKxXcvO1pAJcD6AtgvFKqr7e1\najvY/t5h23uL7U8UqsW3RohG7QLZp+nSawcAAAo+lbTY7tsk5Zf3h/D7TO35oaToMnfKHkOBRCvV\nln3vQXPthdXh99TJnSkpvA39hoS9J5xwaUUA6HVf+H2rvnosz8S9b7TSfLt+LN/j0a6y+OLRf3vZ\nxJ/MPa6YJm/eRq5i+3uHbe8ttj/RCTgz1XqF27yts/0GpdREpdRSpdTSWn91TCvXBjSp/ettO/6T\nYxHbHjjh9z9wLGaVawOa9LtfV3M0ppUj8kJMZ6ZqeqRh4yPWDue9b/qXuZ48SjYY3fYL6//JRS9/\nZK7dcvlpJrbva336F1L92p/J3lKVdx4ycYcrNgAA1v1OZpp63yNlFH8mR0xsm9TLxCVnyGxT9XzZ\nUT2tzNpZ2JfbUeoUxY63F62wDWb6y/fe8MD9D7bJXlXbhteb+E/3y6ydtSo2eva9RrJT8rnXSIzZ\n2z+tdxHbP8aO+/1PzGX7x5C97TNzurDtCVC2o9Yypd9VibZj16qlnwwca13/AOLMVOsV1eZt1GLY\n/t5h23uL7U90Ag6mWi9u3uYttr932PbeYvsTnSCmab7ijIN4bPAcAMBM9Ax7T5dHrAfMv/vIBeba\njvskpVZk257sjSVnmbh0vhxenGw7A/bK1QcAAG/1sz0MPqS/CZ/pOsvEgwbJdf88Sbt1WiaH8CZ2\ntxKN9Vu+Mdd8p/U2cSArzcRHHpFzcD7ov8nEKinZxHK0TNPOzOHmbd5i+3uHbe8ttj9Fy57C8xXk\nm3hXWVcT7x8u/Wv7DtIPprzYwcQd3lkHAPAfkj0dEXD3MHun4mI1HzUPN2/zFtvfO2x7b7H9iY7H\nNB8RERGRAzGdmdqzKgUzS0PTe9VXn2fizLX7AQBfP5xurnW/LvzeUnmf+MJe3/ikrNyb9qm1Mq4U\nS821DeOl7CvXXy6fvUOmDf/59IywZUtazma6LHvfVynj070VMk1Zartd19WGLZuIiKjVsK3QU4lJ\nJvbl5gAAqgbIOoWtN0j/es/ZMql5ScZXJu6WKOVtkqduMGbUHQCA0pnSd6ov5H3x0KdyZoqIiIjI\nAQ6miIiIiByIaZpPZ6fj2HArpZe2SzbnSntdVuI1TAT2ekDSgfOCG1sCwOuVstnXz1f0M3HOHFl9\nl1IsO+5272ilDVEi5d16ySITT+64QSr4dPh691z4HybetONZAMDgyT8y1zpO3CX12LBeYlsZm6bK\ncTfF78mmnMnvhG7EeeC7cu+xjjLtid/MDl/BKLQvqcKYOV82+/0nmjNhhGtlAUBdTnrkm5og4aNl\nkW+KoX4Z+7F46AuulRc23UyNS/BBZbVzrbjDz4U/kqq5Dv5X01bzRtL9OleLcySzsBLn//xz18pz\n/3c/8qbLZJMgj9ckpKWaWHUuMPE3V1sr9wb9+ypzbUbR302c75N5nFQlw5BESNmnJUla8PELXgUA\nTK6RX+y+23JNXL+jQuqnvdkjljNTRERERA5wMEVERETkQEzTfOpQFVLfslJ6kSbi/Btkk8vGpnWL\nIfvE1Y4428Rdxn5h4m/mWqnAVR9IisWetps80pbms3m7SqYvN4181sTr66zp+M8f/6O5dtYjtpRf\nUbaJEz6wnT94QNJ19tTexuCZgb3vkU1FO/z5UxPPt6U4fb8JW1UiIqKYUAm2M/ZsqfP9Z3cy8Yjr\nrH7+phxZiV/ks6UHbfM4fltazg95BCaAgImHpVqnFY08S/r81RecaeLst+Q83kCV7VD5GKb8ODNF\nRERE5AAHU0REREQOxMVxMonFnU1cX968w8fnPvc/Js5OkPPxBiw+PeTekpttq9p2SDhq/PdMvODF\nP5n4/p2DTPxEgaTuGhTM3mhi/549Jran6MqulinJzS/JbmRfD58OABg989tSxlpJPQ544jbbJ00K\n+WwiIqKYsaXr6nrIeXuHxx4x8V257wMA2tlSgnVa4kot6bw1tbK59X6/rNYvSjpg4k4JVupuRPs1\n5lrKfVLGJzlyTm/Bq7Ki3r//oNS7hc/yizgzpZR6Vim1Wym1ynYtRym1QCm1Ifhnh5OVQURERNFb\nrZfiA/03ADB7ALHvjV/RpPn+DOCyE65NAbBIa10CYFHwayIiInJBEbphEC448TL73jgVMc2ntf5Q\nKdX9hMtjAHwrGD8H4H0Ak5vywRkfypP/2/+vq4mV3zrLpypfxnmF02RFgC+3o4n9e2WztfEDrjDx\nV9OkuptGWSvx7CsC7ek3u71nSHpw9AhJu724YJaJy4qsDTV3vNbXXFu5/K9hyzt+FeJKEyUny2aj\nl46dAABQa5eHLSN1nzcbkBERkXc6qE6o1iGbuTrue5tF2VfwZZl447XSZz47aLqJixJTAAB1WlJr\n+wOSlnt6nwwSX5svm1Sn75DPqZWF8eg90lrdPyZP+u4p+bL59tJJssrvP303m7jwVXkEJ7Bvv4m1\nP0zKz+HKv+Y+M5WvtW7YcnQngPzGblRKTQQwEQBS4e4u10RERG1IVH0v+93Yc/wAutZaK6UaHdJp\nrWcCmAkAWSrH3Fc5XB7Ubg+Jv37CGqVmbwhfZMW400zcboxsIf/hma+Z+LbtQ0Le19hs1LhNcixK\n3tMyA2Yft47vW2b76jAA4O4+74Utz27aFtkv6v6BkintfM3qkHvXTz/PxKU/lON12s/6NOReIiJq\n207W9zbW77oiR6aMRl8kezoOSK623WQNLfb4ZTbqid0jTfzF72VRV8mHtkVnNbUS2x50r51nZaR+\ndffl5tolw39v4mGpcqRbvxvkIfU9i7uYOOHQYRPrgG4I4Jbmbo2wSylVCADBP3e7ViMiIiIKh31v\nnGruYOpNABOC8QQAb7hTHSIiImoE+944FTHNp5R6EdYDb7lKqXIADwF4DMArSqlbAGwFMC6aDyvp\nX4l571h7PF3RTdJaul6mAnvdb6W1NsySfSOO9JAH1LrNk6nEBQ9Iau/C22818f1TnzfxD7adDwA4\nPUNSgn9YfpF83ndC940K0VnS0psesB4ef/YhmTm95cnpIW8BgPlH5UHzff8mD6x3XLLXxA17StlT\ne75/FMnrF9s2wiIiojZhpf4cB6xHYFKc9r1uqsuTI2RGZssjK6lKhhMND57/z97h5tqaX8peix0/\nllSc/6g8ZG/Sb9YXEu/YCQA47bHe5tIbZ51h4glZUt7wDrLP1Fy/7GEZqK0LLdvF42aiWc03vpGX\nRjRynYiIiBw4Uw0GACzUs7/UWp9je4l9bxzicTJEREREDsT0OJmtte0wcZs17afrj5rr5T8bZuKG\nfZVKbg6/is3XXlYS2PdxqvmujAuP6SQTf/L6AADAlpE55po9tXfoRln5d6i3lNF+sKwOyLpcjnfx\np1rlZK+UPSsa28NqTLsVcn2W7M0RblP7c5fJ1SUDmdojIqI4oaRvPNI1xcR5PjlCxr6n1PyqPADA\nmlv6mGupq6Tf9dv3eYom1RYsW3+91Vx66jNZHTjk4q9N/PpO6Y99uw+ZuN6eNnQxvdeAM1NERERE\nDnAwRURERORATNN8tV8FUD7ESu9VTJLUXn26TLmlbgjdROut7bIx2MV33mbihHp5X0aFPKk/LlOm\n9p75dXAjzl9LefWXnG3i7L98ZuLPbCm644+CEYmVwfHnXjmNuubyc0086FfyfWV/LXU6cLekHgue\nlM1BG4xvL6v5lmBoyOtO1Wkftte6dybm/Nefj3xTE4wa911Xy7Ong11xIPItJ7N6Vyf0/+1tkW+M\n0htbp7pWFgD8sFvIGWCnFoXjjsRw6vPH/uhaWQBwxdCrXC2vPvItMVO1Blg2KPJ9p4pddw6LfFNT\nPDXb3fKawZeVaeI9l9WYuFuirK7fZcvc/eahGwAAWcs/l4tupNZsG3n6UuUDd/tlheGGijwTl1Rv\nc/6ZUeLMFBEREZEDHEwRERERORDTNJ9d4bTQVBcAVLx+OgDg2M2l5tqVsu8W9v9cpvnW3P4HE886\nnGvi8++SDTwzYZtmDDqWm2R7XYy+eKztq40Ip9s7xwAA228sMdeytsh048v3P2Hi0qQME9vThpXX\nDjZxxhyrft/75SRzrQN4Hh8REXnInhYvko2rz+8tK+eqbJm7qbtGmTjnH5sBAPXRpPYaS7/b39tw\nT0k3c+nWAR+auHvSftut9o0/G4lbAGemiIiIiBzgYIqIiIjIAc/SfEiQdB0CkiYrvHptyK3f+arc\nxC/0kfTguRU/MvGSR2V1zc1PzTBx2atWes1X0tNcy3xFVvDZ+ddJam/vrbKiLv9DOUsPH1gbj9Vd\nKCs20l+TVGLp0+FTe1hUbMKMEaGpx/Rdsv4msVjymm8vftvEvsKw1SYiInKXbaPOQ/1kJfi4Du+b\n+JiWfnztgQITZ9YFV9TbU3j2NJut/1dJMgxRieGHJAn5nQAAFQ/LWOG6rOUm9tuKrjsom4rqyqqw\n5bUEzky1UkqpLkqpfyil1iilViul7vK6Tm0J2987bHtvsf2JQnk3M0VO1QO4V2v9pVKqHYAvlFIL\ntNZrIr2RXMH29w7b3ltsf6ITeDaYOjpPnsqvelOmB+/48VwAwJNfXWKuPfyWnJ9XeI3M59lTe5de\nO8HE7855zsSJPazPqd+wyVxLyJBUXKCyMmz9cmfIirqsj+Vcv9EdrZTjzVmykhC2vRirArVhy8OI\n8vDXg9I+lL+HtG3ac8BU+0aPsuJPa10BoCIYH1FKrQXQGQD/QosBtr932PbeYvu3PQm2XWBTlWxG\n7Yek8Uqy95h4W5/eAADfF5Jm037ZkFsly4p61Vn6/+oekk48UmxbdX9dBQDg7T7PmGu5vjQTb64/\nZuKCDyXhFqiVurY0pvlOAUqp7gAGAcfvA6GUmqiUWqqUWlp5oJFBHjkWTfv7q8IP2smZxto++Jpp\n/1p/9Ykvkwui+d2vQ024txKdUmI6MxVon47qb50HAMi8TI5P2T1V9rB45XRrlFpk+0fOxmkyM7X7\nLBn/jR45zsQ7rpLZpgtWXCMfGpy8Sn94gLn00ivTTVxuG3Hf+MS9Jv7+7X8z8cwZ8rD5S5PfAwD0\n+73MGK3+scxSnTP9bhOn3C5l5z0dfl+tBp0WygN5H30hJ22X3CHvWxXmfUqpTABzANyttT5sf01r\nPRPATAAo6te+ZTfZaKOibf+0gi5sf5edrO2B49s/OyWf7e+yaH/3s1QO27410jKTlHxYOsrDgbRw\nd2NgOzm65b2b+gIAeqb0M9eSjsg/6A+WSH+982J5qHzQaVtMPL7TahOPzlgPAMjzpZtrNVrq9GC5\nHMfUYaHsg+W3LW5raZyZasWUUkmw/jJ7QWs91+v6tDVsf++w7b3F9ic6HgdTrZRSSgF4BsBarfU0\nr+vT1rD9vcO29xbbnyhUTNN8GYVVOPfBpQCAlXtlD6aif558Ki5npTzklvMneTB83o5lJh66/FoT\nf9Rf/qE08NdWOq5inExZbq6TMeTAFNmT4l8/tz1UbnP75NDricfC3Aigy6MnT+eFCO7D8c2jp5lL\n7Up8jd1tdz6AmwCsVEo1NMTPtNbzmlYBaia2v3fY9t5i+7cFtn2hfFWSUjvklzRfkU/67rHtJC03\nrGwDAOAPA2UhWU1AhhuT8j42cZ/kAyZOb+RomXYJVj99VMvzd7/fP0jqdLs8xB7YG7pXZSxEHEwp\npboAmAUgH4AGMFNr/ZRSKgfAywC6A9gCYJzW+kBj5ZC7tNYfAWjkUCNqaWx/77DtvcX2b3m1Rw6g\n/N2/or7qKAD0U0rdxX43vkWT5mvYU6QvgCEAbldK9QUwBcAirXUJgEXBr4mIiMgBleBD4YVjUHrT\nZABYC/a7cS/izNRJ9hQZA+BbwdueA/A+gMknK6t6LbDqbCvdpiApukN3ymq51IZr35EVfPbUnl3/\n38qKuhX3hk/RLfupdb1klhw9Y0/tNebdKtnj4tebR5t4+75sAMD6+8N/nt36/z3XxKU/WBL+puBU\nasrb8npB+DuJiKgNSMrIQlJGVsOXAVgDqmb1u67Up3yfieduk0d0vpe9wsTZCcm22PrzqeKF5lqC\nbe4mRcnQw6cyw36m37aasFpbKwGfOSirAxf95EITJ6/4Ut6ovVk82qRnpk7YUyQ/ONACgJ2w0oDh\n3jMRwEQASEV6uFuIiIgovGSw3417Ua/mi7CniIb1PFUIrfVMrfU5WutzkhB5RoiIiIgAf20NAPQC\n+924F9XMVCN7iuxSShVqrSuUUoUAdkcsJzkJiQXFAID6bXK8im/UXhPPn2Kl/8qKwpeRMLCvif22\n35FSWxpv/c1yzEyPt39gvT7Fliq8OXzZK2pliV5J0lETH62RD3ptyIxg/YaGLUMPlc1BG0vt+Up6\nmthvO+amJVVuTsfiCQMi3xil0XVnuFYWACRX7ne1PKSF31iu2Rw+4pm8vxZdXt7qTl0A3DH3O66V\nBQC+jkdcLc+/z+Wfp0O6rh7+nRH/iopaWdHAyDc1QULqnsg3tVIqJRm+bj0j3xilWP2d2Vz5/93E\nFd2NCOgAluFjANjvpN91pS57pI9OmtHfxLMePdPEZZmymq+Tz0rRZSp5XCbdlgZszNGA9MGrauW9\nv9j8bSv4Za65lrJYUow6hptzNibizNRJ9hR5E0DDgXgTALzhfvWIiIjaFq011mApMtAOAHbZXmK/\nG6eiSfM17ClyiVJqWfC/0QAeAzBKKbUBwMjg10REROTAIezDTnyDA9gDAH3Z78a/aFbznWxPkRFN\n+TBdW3dceq9Bt2zJoYzuMzwYhRy1BQBQNXIKdPFCSU0k7pC0Qp9aSflt/r6V8lv0tWyE+cBumZp8\nNG+lia9+6y4TP3Hpiyaue1emFiddGT69Z+r36fKTvg4ASJJmH7d2p1WPT64010pvWRq5DCIiOiW1\nV7kYibEAgIV69hqt9Tm2l5vU77ohcEzSb+lvycq5BRvPM/H/XnOZic++zDpb96dFfzfXeidJ321X\npyVF9151jonvf2mCiXu9ZPXvgfWSStR1ctZfPOBxMkREREQOcDBFRERE5EBMz+azqx4j04MYvtiE\nvtNLrOCwpPkSe3Y38b6zOpq47npJ7eVetd3EhZ/IUsCyB0NX3cy3neln9+DI10w8s1RWn9Q8FPZ2\nMURWN+CzFWFv8XXqZGL/mvUmnvMt672l3WpC3gMAiQW2bUQqwt5CREQUE7pezunTq9eZuPtGWfV+\n4C/W1tPXX3uvuTbs2/8y8fpDeSY+WCUrrzP/nG3ingtXmdhfWWUFcbBqrzGcmSIiIiJygIMpIiIi\nIgc8S/PVZMvqupQLB8kL/7SmAivulfP6Cn8rm6Blb9oi975gK2+0nIOXusi2mVfwzy0vSyrOviHo\njp/I5xRNDb/ZWs/nd5j47WCK8NKxstLg3dnP2cqWtKI9nXjFWWXyma/JxqNdvm+t5sNiWVVoTxvW\nN5I2JCIi8pTtHDz7ir9AsJ8u+u02c23rk9LnJ/tlVb8k/HBcGi+A1oUzU0REREQOxHRmSrdLR/3g\nswEA7WfJ8S6VYwebOCvfGqfaZ6NqrpBZp+0XSZVLfrXGxInVMqJViXJPQq9uAIDu160I+3rGDhn/\nbnxeZsh63yQPy5WPsT3QHpx52nerHB45+sxLTLzlkdPk+sW9TezfudHE+KSXCdf/1DoZ/Ddj/mKu\nTfr4bBOXfAYiIqLWxzbTFA9HvrQkzkwREREROcDBFBEREZEDMU3zJdQHkLyrEsDxD5dlzP7cxOEm\nAmvbyYNrnT+QPS5eWTXfxJkJqSYefdE1Jj5WbKXRkiQjeNw+Ge1Xy5E0uy6U1J1dwe9CH0zPnSFp\nSnud193yRxOX/UIeRv/mQXnQPemo3N/rPiuP9/iXN5prJX+V3F7aB7Z9poaDiIiI4gxnpoiIiIgc\n4GCKiIiIyIHYruarPobAqq+iunf9dDlu5vQpa03sP3jIxMOmTTJx6n7Z76KTX85dSXp3aUjZWx8e\nauKcNfK+0lvDL52bt11OyR741B0AgOp8SVR2eVfShpeOHWBiheUm7vpw+D2sdt5jpf/CpRIBoPqi\nXWGvExERUXzgzBQRERGRAxxMERERETmgtG07+Bb/MKX2AKgEsDdmH+qNXLTM99hNa92pOW8Mtv3W\nKG5tqbq7xav6NbvtAba/C9j+llbX/mx7x9z63Y/39nXK0343poMpAFBKLdVanxPTD42x1vw9xnvd\n471+TsX79xfv9XMq3r+/eK+fE/H+vcV7/SJp7fWPxOvvj2k+IiIiIgc4mCIiIiJywIvB1EwPPjPW\nWvP3GO91j/f6ORXv31+818+peP/+4r1+TsT79xbv9Yuktdc/Ek+/v5g/M0VERER0KmGaj4iIiMiB\nmA6mlFKXKaXWKaU2KqWmxPKzW4pSqotS6h9KqTVKqdVKqbuC13OUUguUUhuCf3bwuq6RxPPPp7F2\nPpWw/b3DtvcW27/lxHPbNldc9rta65j8B8AH4GsAPQEkA1gOoG+sPr8Fv69CAGcF43YA1gPoC2Aq\ngCnB61MAPO51XVvzz6exdva6Xmx/7+vGtm/d/7H9227buv0z8bLfjeXM1HkANmqtN2mtawG8BGBM\nDD+/RWitK7TWXwbjIwDWAugM63t7LnjbcwCu9qaGUYvrn89J2vlUwfb3DtveW2z/lhPXbdtc8djv\nxnIw1RnANtvX5Wg9v5BRUUp1BzAIwOcA8rXWDScu7wSQ71G1otVqfj4ntPOpgu3vHba9t9j+LafV\ntG1zxUu/ywfQXaKUygQwB8DdWuvD9te0NefIZZMuOFk7U8tj+3uHbe8ttn/8iad+N5aDqe0Auti+\nLg5ea/WUUkmwfqAvaK3nBi/vUkoVBl8vBLDbq/pFKe5/Po2086mC7e8dtr232P4tJ+7btrnird+N\n5WBqCYASpVQPpVQygOsBvBnDz28RSikF4BkAa7XW02wvvQlgQjCeAOCNWNetieL653OSdj5VsP29\nw7b3Ftu/5cR12zZXPPa7Md20Uyk1GsCTsFYYPKu1/q+YfXgLUUpdAOCfAFYCCAQv/wxW/vYVAF1h\nndg9Tmu935NKRimefz6NtbPWep53tXIX2987bHtvsf1bTjy3bXPFY7/LHdCJiIiIHOAD6EREREQO\ncDBFRERE5AAHU0REREQOcDBFRERE5AAHU0REREQOcDBFRERE5AAHU0REREQOcDBFRERE5MD/AyJ+\nixES7WdaAAAAAElFTkSuQmCC\n",
785 | "text/plain": [
786 | ""
787 | ]
788 | },
789 | "metadata": {
790 | "tags": []
791 | },
792 | "output_type": "display_data"
793 | }
794 | ],
795 | "source": [
796 | "def plot_imgs_for_cnn_noisy(index=0):\n",
797 | " f = plt.figure(figsize=(10, 10))\n",
798 | " f.add_subplot(1,6, 1)\n",
799 | " plt.imshow(x_test_noisy[index].reshape(28, 28))\n",
800 | " \n",
801 | " \n",
802 | " f.add_subplot(1,6, 2)\n",
803 | " plt.imshow(encoded_images[index][:, :, 0])\n",
804 | " f.add_subplot(1,6, 3)\n",
805 | " plt.imshow(encoded_images[index][:, :, 1])\n",
806 | " f.add_subplot(1,6, 4)\n",
807 | " plt.imshow(encoded_images[index][:, :, 2])\n",
808 | " f.add_subplot(1,6, 5)\n",
809 | " plt.imshow(encoded_images[index][:, :, 3])\n",
810 | " \n",
811 | " \n",
812 | " f.add_subplot(1,6, 6)\n",
813 | " plt.imshow(reconstruct[index].reshape(28,28))\n",
814 | " \n",
815 | " plt.show(block=True)\n",
816 | " \n",
817 | "plot_imgs_for_cnn_noisy(3)"
818 | ]
819 | },
820 | {
821 | "cell_type": "code",
822 | "execution_count": 0,
823 | "metadata": {
824 | "colab": {},
825 | "colab_type": "code",
826 | "id": "X5KNaod4JLaX"
827 | },
828 | "outputs": [],
829 | "source": []
830 | }
831 | ],
832 | "metadata": {
833 | "accelerator": "GPU",
834 | "colab": {
835 | "collapsed_sections": [],
836 | "include_colab_link": true,
837 | "name": "DeepAutoencoder.ipynb",
838 | "provenance": []
839 | },
840 | "kernelspec": {
841 | "display_name": "Python 3",
842 | "language": "python",
843 | "name": "python3"
844 | },
845 | "language_info": {
846 | "codemirror_mode": {
847 | "name": "ipython",
848 | "version": 3
849 | },
850 | "file_extension": ".py",
851 | "mimetype": "text/x-python",
852 | "name": "python",
853 | "nbconvert_exporter": "python",
854 | "pygments_lexer": "ipython3",
855 | "version": "3.7.4"
856 | }
857 | },
858 | "nbformat": 4,
859 | "nbformat_minor": 1
860 | }
861 |
--------------------------------------------------------------------------------
"
19 | ]
20 | },
21 | {
22 | "cell_type": "markdown",
23 | "metadata": {},
24 | "source": [
25 | "\n",
26 | "## Introduction\n",
27 | "An autoencoder, also known as autoassociator or Diabolo networks, is an artificial neural network employed to recreate the given input. It takes a set of unlabeled inputs, encodes them and then tries to extract the most valuable information from them. They are used for feature extraction, learning generative models of data, dimensionality reduction and can be used for compression.\n",
28 | "\n",
29 | "A 2006 paper named Reducing the Dimensionality of Data with Neural Networks, done by G. E. Hinton and R. R. Salakhutdinov, showed better results than years of refining other types of network, and was a breakthrough in the field of Neural Networks, a field that was \"stagnant\" for 10 years.\n",
30 | "\n",
31 | "Now, autoencoders, based on Restricted Boltzmann Machines, are employed in some of the largest deep learning applications. They are the building blocks of Deep Belief Networks (DBN)."
32 | ]
33 | },
34 | {
35 | "cell_type": "markdown",
36 | "metadata": {},
37 | "source": [
38 | "\n",
39 | "## Autoencoder Structure\n",
40 | "\n",
41 | "\n",
42 | "An autoencoder can be divided in two parts, the encoder and the decoder.\n",
43 | "\n",
44 | "The encoder needs to compress the representation of an input. In this case we are going to reduce the dimension the face of our actor, from 2000 dimensions to only 30 dimensions, by running the data through layers of our encoder.\n",
45 | "\n",
46 | "The decoder works like encoder network in reverse. It works to recreate the input, as closely as possible. This plays an important role during training, because it forces the autoencoder to select the most important features in the compressed representation"
47 | ]
48 | },
49 | {
50 | "cell_type": "code",
51 | "execution_count": 0,
52 | "metadata": {
53 | "colab": {},
54 | "colab_type": "code",
55 | "id": "RsuGfD8--DUG"
56 | },
57 | "outputs": [],
58 | "source": [
59 | "import numpy as np\n",
60 | "import tensorflow as tf\n",
61 | "from tensorflow import keras\n",
62 | "from matplotlib import pyplot as plt"
63 | ]
64 | },
65 | {
66 | "cell_type": "code",
67 | "execution_count": 0,
68 | "metadata": {
69 | "colab": {
70 | "base_uri": "https://localhost:8080/",
71 | "height": 35
72 | },
73 | "colab_type": "code",
74 | "id": "Lrt5tiRJ-DSt",
75 | "outputId": "d7a7039b-a8c6-492c-cad2-bdf0a73494de"
76 | },
77 | "outputs": [
78 | {
79 | "name": "stderr",
80 | "output_type": "stream",
81 | "text": [
82 | "Using TensorFlow backend.\n"
83 | ]
84 | }
85 | ],
86 | "source": [
87 | "from keras.datasets import mnist\n",
88 | "from keras.layers import Input, Dense\n",
89 | "from keras.models import Model"
90 | ]
91 | },
92 | {
93 | "cell_type": "code",
94 | "execution_count": 0,
95 | "metadata": {
96 | "colab": {
97 | "base_uri": "https://localhost:8080/",
98 | "height": 54
99 | },
100 | "colab_type": "code",
101 | "id": "a5I-BA7K-DON",
102 | "outputId": "ddd43dc1-bac7-47e7-e7a6-cf95085ecece"
103 | },
104 | "outputs": [
105 | {
106 | "name": "stdout",
107 | "output_type": "stream",
108 | "text": [
109 | "Downloading data from https://s3.amazonaws.com/img-datasets/mnist.npz\n",
110 | "11493376/11490434 [==============================] - 2s 0us/step\n"
111 | ]
112 | }
113 | ],
114 | "source": [
115 | "(x_train, y_train), (x_test, y_test) = mnist.load_data()"
116 | ]
117 | },
118 | {
119 | "cell_type": "code",
120 | "execution_count": 0,
121 | "metadata": {
122 | "colab": {
123 | "base_uri": "https://localhost:8080/",
124 | "height": 35
125 | },
126 | "colab_type": "code",
127 | "id": "jFiRn0ef_hHJ",
128 | "outputId": "cf3ad53b-98c9-4b7f-95ef-bd098775a2c6"
129 | },
130 | "outputs": [
131 | {
132 | "data": {
133 | "text/plain": [
134 | "(60000, 28, 28)"
135 | ]
136 | },
137 | "execution_count": 5,
138 | "metadata": {
139 | "tags": []
140 | },
141 | "output_type": "execute_result"
142 | }
143 | ],
144 | "source": [
145 | "x_train.shape"
146 | ]
147 | },
148 | {
149 | "cell_type": "code",
150 | "execution_count": 0,
151 | "metadata": {
152 | "colab": {},
153 | "colab_type": "code",
154 | "id": "zvjFj5PL_rVH"
155 | },
156 | "outputs": [],
157 | "source": [
158 | "x_train = x_train.astype('float32')/255.0\n",
159 | "x_test = x_test.astype('float32')/255.0"
160 | ]
161 | },
162 | {
163 | "cell_type": "markdown",
164 | "metadata": {
165 | "colab_type": "text",
166 | "id": "1KS4RuDZ6Kuz"
167 | },
168 | "source": [
169 | "Reshaping images, Flattening them to feed to a Dense network\n",
170 | "\n",
171 | "we won't do this in ConvNets"
172 | ]
173 | },
174 | {
175 | "cell_type": "code",
176 | "execution_count": 0,
177 | "metadata": {
178 | "colab": {},
179 | "colab_type": "code",
180 | "id": "lv-AALS9AA7r"
181 | },
182 | "outputs": [],
183 | "source": [
184 | "x_train = x_train.reshape(len(x_train), (x_train.shape[1]*x_train.shape[2]))\n",
185 | "x_test = x_test.reshape(len(x_test), (x_test.shape[1]*x_test.shape[2]))"
186 | ]
187 | },
188 | {
189 | "cell_type": "code",
190 | "execution_count": 0,
191 | "metadata": {
192 | "colab": {},
193 | "colab_type": "code",
194 | "id": "Z09aungJAG6E"
195 | },
196 | "outputs": [],
197 | "source": [
198 | "encoding_dim = 32\n",
199 | "\n",
200 | "input_img = Input(shape = (784, ))\n",
201 | "encoded = Dense(128, activation='relu')(input_img)\n",
202 | "encoded = Dense(encoding_dim, activation='relu')(encoded)\n",
203 | "\n",
204 | "\n",
205 | "decoded = Dense(128, activation='relu')(encoded)\n",
206 | "decoded = Dense(784, activation='sigmoid')(decoded)\n",
207 | "\n",
208 | "autoencoder = Model(input_img, decoded)"
209 | ]
210 | },
211 | {
212 | "cell_type": "code",
213 | "execution_count": 0,
214 | "metadata": {
215 | "colab": {},
216 | "colab_type": "code",
217 | "id": "HN8ANrYPEvfl"
218 | },
219 | "outputs": [],
220 | "source": [
221 | "encoder = Model(input_img, encoded)\n",
222 | "encoded_input = Input(shape=(encoding_dim, ))\n",
223 | "decode_layer1 = autoencoder.layers[-2]\n",
224 | "decode_layer2 = autoencoder.layers[-1]\n",
225 | "decoder = Model(encoded_input, decode_layer2(decode_layer1(encoded_input)))"
226 | ]
227 | },
228 | {
229 | "cell_type": "code",
230 | "execution_count": 0,
231 | "metadata": {
232 | "colab": {
233 | "base_uri": "https://localhost:8080/",
234 | "height": 35
235 | },
236 | "colab_type": "code",
237 | "id": "skKxFoz_4rCS",
238 | "outputId": "24f6e177-3127-4169-fd00-df67d3ebe3ef"
239 | },
240 | "outputs": [
241 | {
242 | "data": {
243 | "text/plain": [
244 | ""
245 | ]
246 | },
247 | "execution_count": 35,
248 | "metadata": {
249 | "tags": []
250 | },
251 | "output_type": "execute_result"
252 | }
253 | ],
254 | "source": [
255 | "autoencoder.get_layer('dense_5')"
256 | ]
257 | },
258 | {
259 | "cell_type": "code",
260 | "execution_count": 0,
261 | "metadata": {
262 | "colab": {},
263 | "colab_type": "code",
264 | "id": "6tVqkhvHAIPz"
265 | },
266 | "outputs": [],
267 | "source": [
268 | "autoencoder.compile(optimizer='adadelta', loss='binary_crossentropy', metrics=['accuracy'])"
269 | ]
270 | },
271 | {
272 | "cell_type": "code",
273 | "execution_count": 0,
274 | "metadata": {
275 | "colab": {
276 | "base_uri": "https://localhost:8080/",
277 | "height": 348
278 | },
279 | "colab_type": "code",
280 | "id": "PUBcoIWKzdVL",
281 | "outputId": "4a1f574e-0b02-49db-c228-c4269ee9017e"
282 | },
283 | "outputs": [
284 | {
285 | "name": "stdout",
286 | "output_type": "stream",
287 | "text": [
288 | "Model: \"model_6\"\n",
289 | "_________________________________________________________________\n",
290 | "Layer (type) Output Shape Param # \n",
291 | "=================================================================\n",
292 | "input_6 (InputLayer) (None, 784) 0 \n",
293 | "_________________________________________________________________\n",
294 | "dense_3 (Dense) (None, 128) 100480 \n",
295 | "_________________________________________________________________\n",
296 | "dense_4 (Dense) (None, 32) 4128 \n",
297 | "_________________________________________________________________\n",
298 | "dense_5 (Dense) (None, 128) 4224 \n",
299 | "_________________________________________________________________\n",
300 | "dense_6 (Dense) (None, 784) 101136 \n",
301 | "=================================================================\n",
302 | "Total params: 209,968\n",
303 | "Trainable params: 209,968\n",
304 | "Non-trainable params: 0\n",
305 | "_________________________________________________________________\n"
306 | ]
307 | }
308 | ],
309 | "source": [
310 | "autoencoder.summary()"
311 | ]
312 | },
313 | {
314 | "cell_type": "code",
315 | "execution_count": 0,
316 | "metadata": {
317 | "colab": {
318 | "base_uri": "https://localhost:8080/",
319 | "height": 403
320 | },
321 | "colab_type": "code",
322 | "id": "HLMkoI-JCgPX",
323 | "outputId": "e2053547-3301-4923-81b2-bfe051688c25"
324 | },
325 | "outputs": [
326 | {
327 | "name": "stdout",
328 | "output_type": "stream",
329 | "text": [
330 | "Train on 60000 samples, validate on 10000 samples\n",
331 | "Epoch 1/10\n",
332 | "60000/60000 [==============================] - 12s 202us/step - loss: 0.2129 - acc: 0.7929 - val_loss: 0.1578 - val_acc: 0.8043\n",
333 | "Epoch 2/10\n",
334 | "60000/60000 [==============================] - 12s 196us/step - loss: 0.1422 - acc: 0.8077 - val_loss: 0.1278 - val_acc: 0.8080\n",
335 | "Epoch 3/10\n",
336 | "60000/60000 [==============================] - 12s 195us/step - loss: 0.1226 - acc: 0.8108 - val_loss: 0.1157 - val_acc: 0.8114\n",
337 | "Epoch 4/10\n",
338 | "60000/60000 [==============================] - 12s 195us/step - loss: 0.1142 - acc: 0.8118 - val_loss: 0.1086 - val_acc: 0.8115\n",
339 | "Epoch 5/10\n",
340 | "60000/60000 [==============================] - 12s 198us/step - loss: 0.1088 - acc: 0.8125 - val_loss: 0.1063 - val_acc: 0.8110\n",
341 | "Epoch 6/10\n",
342 | "60000/60000 [==============================] - 12s 196us/step - loss: 0.1050 - acc: 0.8129 - val_loss: 0.1020 - val_acc: 0.8117\n",
343 | "Epoch 7/10\n",
344 | "60000/60000 [==============================] - 12s 195us/step - loss: 0.1019 - acc: 0.8132 - val_loss: 0.0985 - val_acc: 0.8126\n",
345 | "Epoch 8/10\n",
346 | "60000/60000 [==============================] - 12s 196us/step - loss: 0.0994 - acc: 0.8135 - val_loss: 0.0968 - val_acc: 0.8127\n",
347 | "Epoch 9/10\n",
348 | "60000/60000 [==============================] - 12s 196us/step - loss: 0.0975 - acc: 0.8137 - val_loss: 0.0952 - val_acc: 0.8130\n",
349 | "Epoch 10/10\n",
350 | "60000/60000 [==============================] - 12s 192us/step - loss: 0.0961 - acc: 0.8138 - val_loss: 0.0936 - val_acc: 0.8131\n"
351 | ]
352 | }
353 | ],
354 | "source": [
355 | "hist = autoencoder.fit(x_train, x_train, epochs=10, validation_data=(x_test, x_test))"
356 | ]
357 | },
358 | {
359 | "cell_type": "code",
360 | "execution_count": 0,
361 | "metadata": {
362 | "colab": {
363 | "base_uri": "https://localhost:8080/",
364 | "height": 287
365 | },
366 | "colab_type": "code",
367 | "id": "n4xxDcKfEV8_",
368 | "outputId": "77bcd685-2bd1-4eb2-9eee-e7e2c08cf303"
369 | },
370 | "outputs": [
371 | {
372 | "data": {
373 | "text/plain": [
374 | ""
375 | ]
376 | },
377 | "execution_count": 38,
378 | "metadata": {
379 | "tags": []
380 | },
381 | "output_type": "execute_result"
382 | },
383 | {
384 | "data": {
385 | "image/png": "iVBORw0KGgoAAAANSUhEUgAAAP8AAAD8CAYAAAC4nHJkAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDMuMC4zLCBo\ndHRwOi8vbWF0cGxvdGxpYi5vcmcvnQurowAAD2ZJREFUeJzt3W2MHfV1x/HfsXdtsDEY42Ac82CC\nDNRAYpqtaRXaUBESQEQmUktjVZGjohgp0EKTVkFupfKiVWmahPKiieoEC1OlBJqAcCurgThpaVSK\nWIiLDSbFQabY+GGJDbYxu96H0xc7RBvYObPsfZi7e74fabV359y5c3y9v517739m/ubuApDPjLob\nAFAPwg8kRfiBpAg/kBThB5Ii/EBShB9IivADSRF+IKmudm5sls32EzS3nZsEUunXmzruAzaR+zYU\nfjO7WtLdkmZK+pa73xnd/wTN1WV2ZSObBBB40rdM+L6TftlvZjMl/b2kayQtl7TazJZP9vEAtFcj\n7/lXStrp7i+5+3FJ35G0qjltAWi1RsK/RNIrY37eXSz7JWa21sx6zax3UAMNbA5AM7X80353X+/u\nPe7e063Zrd4cgAlqJPx7JJ015uczi2UApoBGwv+UpGVmdq6ZzZL0aUmbmtMWgFab9FCfuw+Z2S2S\nvq/Rob4N7v5c0zoD0FINjfO7+2ZJm5vUC4A24vBeICnCDyRF+IGkCD+QFOEHkiL8QFKEH0iK8ANJ\nEX4gKcIPJEX4gaQIP5AU4QeSIvxAUoQfSIrwA0kRfiApwg8kRfiBpAg/kBThB5Ii/EBShB9IivAD\nSRF+ICnCDyRF+IGkCD+QFOEHkmpoll4z2yXpiKRhSUPu3tOMpgC0XkPhL/y2u7/WhMcB0Ea87AeS\najT8LulRM3vazNY2oyEA7dHoy/7L3X2PmZ0u6TEze8HdHx97h+KPwlpJOkFzGtwcgGZpaM/v7nuK\n7wckPSxp5Tj3We/uPe7e063ZjWwOQBNNOvxmNtfM5r19W9LHJW1vVmMAWquRl/2LJD1sZm8/zj+5\n+781pSsALTfp8Lv7S5I+1MRe6jX6Ryyol79Isu74abSKx3b3eNsVfHCovDgy3NBjY/piqA9IivAD\nSRF+ICnCDyRF+IGkCD+QVDPO6psSbHZ8dOGMeSeFdV9yemlt/2/MD9d9/aKRsK6ReCjwhL74b/Ss\nw+W1E/vibc/fEawsacahI2FdA8fjend3acnfeitc1briX0+v2raX/9tH3uqveOyB+LGnAfb8QFKE\nH0iK8ANJEX4gKcIPJEX4gaQIP5DUtBnnrxzHP/nksD7wwbPD+qHzZ5XWZn2yL1z375ZtDus/HVgc\n1nceKz/GQJKOj5T/N/b1x8cvvDVUPg4vSTed/XhYP7/7QFg/ZcZgaW3/8Inhuv986NfC+uGheP0n\n9iwtrc377rxw3fkPbQ3rI/3xcQJTAXt+ICnCDyRF+IGkCD+QFOEHkiL8QFKEH0hq+ozzzyofh5dU\neQnrWfvfDOunHS8/N/zV+fE4/B8f/L2w3tUd9zY8HP+NHn4zGKvvis/nv+QDe8L60u54AuZoHF+S\n+r289xkW9/b5hfExBgtnzgzr+88of/yrD/9RuO6C/1wY1kd2x8+bGrwcezuw5weSIvxAUoQfSIrw\nA0kRfiApwg8kRfiBpCrH+c1sg6TrJB1w94uLZQskPSBpqaRdkm5w90Ota7Oa91dcZ30wHo/Wy/G4\n7azX5pTWlr4SX0tAMyr+xo7E493++hvx+t3lxzjYzHjbx898X1i/+ZJ4PHzeK/G182f3HSut/fzS\neL6D3/2TR8P62vnbw/qwl8+H0LUvPi7Ej8bHfUyFcfwqE9nz3yvp6ncsu13SFndfJmlL8TOAKaQy\n/O7+uKSD71i8StLG4vZGSdc3uS8ALTbZ9/yL3H1vcXufpEVN6gdAmzT8gZ+7u6TSN0BmttbMes2s\nd1DTf/4zYKqYbPj3m9liSSq+l17F0d3Xu3uPu/d0q+KDMQBtM9nwb5K0pri9RtIjzWkHQLtUht/M\n7pf0hKQLzGy3md0o6U5JV5nZi5I+VvwMYAqpHOd399UlpSub3EtDfCgex/eKc+JtOB5rH66YSz7e\ndny+fq1jxgfi8/UXPB0/L1W9j1j5WPvC3aeG6z74Ox8O69ddvC2s//DYBaW19//HULjuSNU4/zTA\nEX5AUoQfSIrwA0kRfiApwg8kRfiBpKbNpbsrh8s8Hm7zikt7KxiymtKnd1b9uxsVPDd2Sjxt+hXv\nfzGsD1bsu+7aWj4afcG2V8N1h6qGZ6cB9vxAUoQfSIrwA0kRfiApwg8kRfiBpAg/kNT0Gedvtak8\nll8j6yr/FdvxhfjSj19ecH9Y/+tXrwnr5369vDbcF5/K3PLjHzoAe34gKcIPJEX4gaQIP5AU4QeS\nIvxAUoQfSIpx/ukgutZAlVYfv7DiwtLSvdf+Q7hq3/DcsL7z6+WPLUkLtu8orQ0fj6cWz4A9P5AU\n4QeSIvxAUoQfSIrwA0kRfiApwg8kVTnOb2YbJF0n6YC7X1wsu0PS5yT1FXdb5+6bW9UkKtR4rYEZ\n8+aF9V1fKj8GYVnX0XDdq3pvCuvnbNkV1ofeOFxe5PoME9rz3yvp6nGW3+XuK4ovgg9MMZXhd/fH\nJR1sQy8A2qiR9/y3mNmzZrbBzE5tWkcA2mKy4f+GpPMkrZC0V9JXy+5oZmvNrNfMegc1MMnNAWi2\nSYXf3fe7+7C7j0j6pqSVwX3Xu3uPu/d0a/Zk+wTQZJMKv5ktHvPjpyRtb047ANplIkN990u6QtJC\nM9st6S8kXWFmKyS5pF2S4jEZAB2nMvzuvnqcxfe0oBd0ooprBRxadVFY/9aHyy+e/8O3zgnXPfOv\nwrKG9u2P78BYfogj/ICkCD+QFOEHkiL8QFKEH0iK8ANJceluhGaecnJY77n1J2F9eXd/ae3G3mvD\ndc/d8bOw7gzlNYQ9P5AU4QeSIvxAUoQfSIrwA0kRfiApwg8kxTh/dhWn7P78k8vD+n1nfCWs9wdj\n8QsfnBOuO3LsWFhHY9jzA0kRfiApwg8kRfiBpAg/kBThB5Ii/EBSjPMn13X2mWH9xnWPhPU51h3W\nL+v9bGltyb9sDdflbP3WYs8PJEX4gaQIP5AU4QeSIvxAUoQfSIrwA0lVjvOb2VmS7pO0SKNDr+vd\n/W4zWyDpAUlLJe2SdIO7H2pdq5gMmz07rD//52eE9U0n7w7re4aPh/XFf1t+HIAPDITrorUmsucf\nkvRFd18u6dcl3WxmyyXdLmmLuy+TtKX4GcAUURl+d9/r7s8Ut49I2iFpiaRVkjYWd9so6fpWNQmg\n+d7Te34zWyrpUklPSlrk7nuL0j6Nvi0AMEVMOPxmdpKk70m6zd0Pj6356KRp4x6KbWZrzazXzHoH\nxXs8oFNMKPxm1q3R4H/b3R8qFu83s8VFfbGkA+Ot6+7r3b3H3Xu6FX/4BKB9KsNvZibpHkk73P1r\nY0qbJK0pbq+RFJ/+BaCjTOSU3o9I+oykbWb29jmY6yTdKelBM7tR0suSbmhNi6hi3bNKa8c/ekm4\n7n994q6wPtNOCusf3fyFsH7+E0+FddSnMvzu/mNJZRd3v7K57QBoF47wA5Ii/EBShB9IivADSRF+\nICnCDyTFpbungopptPWh80tLv3/3v4arLu6Kx/H/u384rF/4pzvC+kgwRTfqxZ4fSIrwA0kRfiAp\nwg8kRfiBpAg/kBThB5JinH8KmHHiiWH9hT+YU1pbPe//wnWPjcTb/sO/vDWsLzjyRPwA6Fjs+YGk\nCD+QFOEHkiL8QFKEH0iK8ANJEX4gKcb5O4B1xf8N/b+5PKz/zcceKK3NrLgWwHePxlN0n/6jV8P6\nUFhFJ2PPDyRF+IGkCD+QFOEHkiL8QFKEH0iK8ANJVY7zm9lZku6TtEiSS1rv7neb2R2SPiepr7jr\nOnff3KpGO1rFWLp1dYf1kZ5fCev9tx0K65+Ys6+09sZIfML+v79+YVj3bg4Fma4m8j87JOmL7v6M\nmc2T9LSZPVbU7nL3r7SuPQCtUhl+d98raW9x+4iZ7ZC0pNWNAWit9/Se38yWSrpU0pPFolvM7Fkz\n22Bmp5ass9bMes2sd1ADDTULoHkmHH4zO0nS9yTd5u6HJX1D0nmSVmj0lcFXx1vP3de7e4+793Rr\ndhNaBtAMEwq/mXVrNPjfdveHJMnd97v7sLuPSPqmpJWtaxNAs1WG38xM0j2Sdrj718YsXzzmbp+S\ntL357QFolYl82v8RSZ+RtM3MthbL1klabWYrNDr8t0vSTS3pcCqw+G/ojJPmhvW+D5ZfeluSPr/0\n+2F90MuH854aOC1c9wc/uSisLz/8cljH1DWRT/t/LGm8geycY/rANMERfkBShB9IivADSRF+ICnC\nDyRF+IGkzN3btrGTbYFfZle2bXttM2NmXB8ZDstVl+622RWHRZ93VmlpeG68btcL8RTeI0eOhHUf\njv9tauPvF6QnfYsO+8H4HPMCe34gKcIPJEX4gaQIP5AU4QeSIvxAUoQfSKqt4/xm1idp7AniCyW9\n1rYG3ptO7a1T+5LobbKa2ds57v6+idyxreF/18bNet29p7YGAp3aW6f2JdHbZNXVGy/7gaQIP5BU\n3eFfX/P2I53aW6f2JdHbZNXSW63v+QHUp+49P4Ca1BJ+M7vazH5qZjvN7PY6eihjZrvMbJuZbTWz\n3pp72WBmB8xs+5hlC8zsMTN7sfg+7jRpNfV2h5ntKZ67rWZ2bU29nWVmPzKz583sOTO7tVhe63MX\n9FXL89b2l/1mNlPS/0q6StJuSU9JWu3uz7e1kRJmtktSj7vXPiZsZr8l6aik+9z94mLZlyUddPc7\niz+cp7r7lzqktzskHa175uZiQpnFY2eWlnS9pM+qxucu6OsG1fC81bHnXylpp7u/5O7HJX1H0qoa\n+uh47v64pIPvWLxK0sbi9kaN/vK0XUlvHcHd97r7M8XtI5Lenlm61ucu6KsWdYR/iaRXxvy8W501\n5bdLetTMnjaztXU3M45FxbTpkrRP0qI6mxlH5czN7fSOmaU75rmbzIzXzcYHfu92ubv/qqRrJN1c\nvLztSD76nq2ThmsmNHNzu4wzs/Qv1PncTXbG62arI/x7JI296NyZxbKO4O57iu8HJD2szpt9eP/b\nk6QW3w/U3M8vdNLMzePNLK0OeO46acbrOsL/lKRlZnaumc2S9GlJm2ro413MbG7xQYzMbK6kj6vz\nZh/eJGlNcXuNpEdq7OWXdMrMzWUzS6vm567jZrx297Z/SbpWo5/4/0zSn9XRQ0lfH5D0P8XXc3X3\nJul+jb4MHNToZyM3SjpN0hZJL0r6gaQFHdTbP0raJulZjQZtcU29Xa7Rl/TPStpafF1b93MX9FXL\n88YRfkBSfOAHJEX4gaQIP5AU4QeSIvxAUoQfSIrwA0kRfiCp/weDXbvwl0u/MwAAAABJRU5ErkJg\ngg==\n",
386 | "text/plain": [
387 | ""
388 | ]
389 | },
390 | "metadata": {
391 | "tags": []
392 | },
393 | "output_type": "display_data"
394 | }
395 | ],
396 | "source": [
397 | "encoded_images = encoder.predict(x_test)\n",
398 | "encoded_images.shape\n",
399 | "predicted = decoder.predict(encoded_images)\n",
400 | "plt.imshow(predicted[0].reshape(28, 28))"
401 | ]
402 | },
403 | {
404 | "cell_type": "code",
405 | "execution_count": 0,
406 | "metadata": {
407 | "colab": {
408 | "base_uri": "https://localhost:8080/",
409 | "height": 269
410 | },
411 | "colab_type": "code",
412 | "id": "3H3Ekx1SHp5y",
413 | "outputId": "e2c12384-3645-45fa-a46e-6aecdb259a2d"
414 | },
415 | "outputs": [
416 | {
417 | "data": {
418 | "image/png": "iVBORw0KGgoAAAANSUhEUgAAAXQAAAD8CAYAAABn919SAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDMuMC4zLCBo\ndHRwOi8vbWF0cGxvdGxpYi5vcmcvnQurowAAFVBJREFUeJzt3X+QnVV9x/HPJ5tslgRICAkhJJEg\nRDQSCWX5NdiK/LDRsQZnLAN1NLbUYCsdndEZUpkpVFuHdqyMLdbOIikRBcQAJmNRCCmIVkQSjAhB\nTOSHJITEkIT8gPzY7Ld/7JO7+yz37m6y9z5377nv18zOnvOc5977Tbjny8l5zvMcR4QAAI1vRL0D\nAABUBwkdABJBQgeARJDQASARJHQASAQJHQASQUIHgESQ0AEgESR0AEjEyHoHAFSL7bmSviapRdI3\nI+KG/s5vHTU22trGl23buevlLRExqfpRArVDQkcSbLdI+rqkSyStl/S47WURsabSa9raxuus9k+X\nbfvfh699sSaBAjXElAtScbakdRHxXETsk3SnpHl1jgkoFAkdqZgq6aVe9fXZMaBpMOWCpmJ7gaQF\nkjR69Lg6RwNUFyN0pGKDpOm96tOyYzkR0RER7RHR3jpqbGHBAUUgoSMVj0uaafsk262SLpe0rM4x\nAYViygVJiIhO21dLul/dyxYXRcTT/b5o1xsa8eNfFhEeUAgSOpIREfdJuq/ecQD1wpQLACSChA4A\niSChA0AiSOgAkAgSOgAkglUuaFoTT9urK+99vmzbgzMLDgaoAkboAJAIEjoAJIKEDgCJIKEDQCJI\n6ACQCFa5oGm9vHWCrrv9oxVaVxUaC1ANjNABIBEkdABIBAkdABJBQgeARJDQASARJHQASATLFtG0\nfEBqfa3eUQDVwwgdABJBQgeARJDQASARJHQASAQJHQASQUIHgESwbBHJsP2CpJ2SDkjqjIj2/s6P\nFmnv+CIiA4pBQkdq3hsRW+odBFAPTLkAQCJI6EhJSHrA9irbC+odDFA0plyQkndHxAbbx0labvs3\nEfFI7xOyRL9AkkaOO6YeMQI1wwgdyYiIDdnvzZLulXR2mXM6IqI9Itpbxo4tOkSgpkjoSILtsbaP\nOliW9D5JT9U3KqBYTLkgFZMl3Wtb6v5e3x4RP+rvBW89dpO+/fEby7ad+Q9Vjw+oORI6khARz0k6\nvd5xAPXElAsAJIKEDgCJIKEDQCJI6ACQCBI6ACSCVS5oWr/bNUkf+dmnKrReW2gsQDUwQgeARJDQ\nASARJHQASAQJHQASQUIHgESwygVNa+SOETrmwbaybc8XHAtQDYzQASARJHQASAQJHQASMaSEbnuu\n7Wdtr7O9sFpBAagN+mzaDjuh226R9HVJ75c0S9IVtmdVKzAA1UWfTd9QVrmcLWldtlOMbN8paZ6k\nNZVe0OrR0SY25q23PdqtfbHX9Y4DhTukPkt/HT52atuWiJg00HlDSehTJb3Uq75e0jn9vaBNY3WO\nLxrCR6IaHosV9Q5hWOgcG9pyzoHyjYuKjaUgh9Rn6a/Dx4Ox5MXBnFfzdei2F0haIEltGlPrjwMw\nBPTXxjaUi6IbJE3vVZ+WHcuJiI6IaI+I9lEaPYSPAzBEA/ZZ+mtjG0pCf1zSTNsn2W6VdLmkZdUJ\nC0AN0GcTd9hTLhHRaftqSfdLapG0KCKerlpkAKqKPpu+Ic2hR8R9ku6rUiwAaow+mzbuFAWARPC0\nRTQU24skfVDS5og4LTs2QdJ3Jc2Q9IKkyyJi20DvNXv8Fv3iQx1l21quqlLAQIEYoaPR3Cppbp9j\nCyWtiIiZklZkdaDpkNDRUCLiEUlb+xyeJ2lxVl4s6dJCg0Ia7Mo/DYKEjhRMjoiNWfkVSZPrGQxQ\nLyR0JCUiQlJUare9wPZK2yv/8GqF2/6BBsVF0Srzme8slf9n2W25ttn/dXWpPP1LPysspiawyfaU\niNhoe4qkzZVOjIgOSR2S1H56W8XEj0SMaMlVR04/IVffdt7UUnnXCfnx7Qk/2dlTWf1sri3276tS\ngNXFCB0pWCZpflaeL2lpHWMB6oYROhqK7TskXSBpou31kq6TdIOku2xfKelFSZcN5r2eWT9J533+\nUxVaP1+FaIFikdDRUCLiigpNPOcVTY+EXmWbzzq6VO5U/qLbmJeZsgUKFV39Nm97W8+s857p+3Nt\ne9e0lcqjRzTG0kXm0AEgESR0AEgEUy5Vtu1dPdMs6zv35tqOveXRosMB0Fufuz73nrKnp2n7qFzb\nEc9tKZUP7M335eGKEToAJIIROpqWQ2rZy4VqpIMROgAkghH6EMX5c3L1n3zwq6Xyex75u1zbKfpl\nITEByDg/Zt1xxpRcfe47flUqr3jgjFxbbKz4BIlhixE6ACSChA4AiWDKZYi2zjoiV5/SMqZUnrpk\nVN/TARRoxNgxufqGC/LLFs9t6VmO2Lot39a1a1ftAqsRRugAkAhG6GhaRxz/ut55zZNl2x5dUnAw\nQBUwQgeARDBCH6KL/jZ/O//3d48vlY98OL/LCRueAcUaMX5crv622S/l6rsPjC6Vj//56/kXR+Pd\ndMYIHQASMWBCt73I9mbbT/U6NsH2cttrs9/H1DZMAINFn21eg5lyuVXSTZK+1evYQkkrIuIG2wuz\n+jXVD2/4aXnnqbn6l4+7I1e/Zce0UvnA9tcKiQno41bRZyVJO9qn5uqfPOHuXP2eTWeWyq0vbsm1\nddYurJoZMKFHxCO2Z/Q5PE/d+zpK0mJJD6sJvhxIy+4tY/SLxWdUaL2t0FiqiT7bvA53Dn1yRGzM\nyq9ImlyleADUBn22CQz5omhEhKSKl4NtL7C90vbK/WqMh8QDKeuvz9JfG9vhLlvcZHtKRGy0PUVS\nxceSRUSHpA5JOtoTGm8dUB8bLjm23/ZVO0/sVXujtsEAgzeoPptCf/XonqWI6/80/0eYd2R+2eJD\n299RKr/yh/wm0Y3ocEfoyyTNz8rzJS2tTjgAaoQ+2wQGs2zxDkmPSjrV9nrbV0q6QdIlttdKujir\nAxgG6LPNazCrXK6o0HRRlWNpCDtm9f/PstU39Wx4MV5sCo3iNXuf7X136DcuXpxrG+PWXP3R+2eX\nyifue6y2gRWAW//RUGwvkvRBSZsj4rTs2PWSPinpD9lpX4iI+wZ8s3EHpPdtLd92UxWCBQrGrf9o\nNLdKmlvm+I0RMSf7GTiZAwkioaOhRMQjkioMq4HmxpTLIOx9/1ml8tL3/Ueu7YtbzszVJ9zd83zt\nrtqGhbyrbX9c0kpJn4uIbfUOCAVxfqeh19t7lg6f3vpqrm3d/vwY9qR7t5fKXV2N/zxURuhIwTck\nnSxpjqSNkv6t0om9b5zpfG13UfEBhSCho+FFxKaIOBARXZJulnR2P+d2RER7RLSPHDe2uCCBAjDl\nMgjrL+z5a3pXa1uubf4Ls3P143b/ppCY0OPgHZBZ9cOSnurvfKTFLS25+st/3NNfJ7bkN3G/+PGP\n5+pv+e3ztQusDkjoaCjZTTMXSJpoe72k6yRdYHuOup9P8oKkqwbzXiPX7dFx8/gfMNJBQkdDqXDT\nzC2FBwIMQ8yhA0AiGKEPwqTTeh5MdyDyixFHLmUnL6Ceej9dUZJmnfdcqbyrq88jgFflN43u2pPW\nI4IZoQNAIkjoAJAIEjoAJII59DJGnnRirv6VU79XKt/82vRc24RFPCK3Ue2dMUZr//HM8o3zlxQb\nDA7biAn561iXH/9/pfKa/fn7RqY/sCNXjwRu9++NEToAJIKEDgCJYMqljLVXnZCrn9trVdQnn3hv\nrm06d5kDhfPIntT18ry35Nrec8SdpfJ/b+8zpfbrtTWNq94YoQNAIkjoAJAIEjoAJII59DK6pu+p\n2PbG9raKbWgsbb/fo1M/Xf5piy8WHAsOTe859NkfzV/HmtDSc9HrtiUX5dresi/tZcaM0AEgESR0\nAEgEUy5l/Oc5367YNvWHLRXbABRjxPiepyZeM+X7fVp70tqUn+/LN0XUMKr6Y4QOAIkYMKHbnm77\nIdtrbD9t+zPZ8Qm2l9tem/3mweBAndFfm9tgplw6JX0uIp6wfZSkVbaXS/qEpBURcYPthZIWSrqm\ndqEC1XXEqV067fbXy7Y9cEbBwVQP/bWJDZjQs93UN2blnbafkTRV0jx1b9YrSYslPawG/oLs+bOz\nS+V3t/2iTyuXGtAYmqW/rr/i5FL57aPyOxbtip5diNqe35prS+vZim92SHPotmdIOkPSY5ImZ18e\nSXpF0uSqRgZgSOivzWfQCd32kZLulvTZiMg9VDgiQlLZy8e2F9heaXvlfqW1fx8wXNFfm9Og5hJs\nj1L3l+M7EXFPdniT7SkRsdH2FEmby702IjokdUjS0Z4wbNcM/f5DPaGNdv6v5YtbZpfKRy5dlWsb\ntn8gNK0U+2vfjaBn//maUrnF+XHpY28c3VPZur2mcQ03g1nlYkm3SHomIr7aq2mZpPlZeb6kpdUP\nD8ChoL82t8GM0M+X9DFJv7a9Ojv2BUk3SLrL9pXqfvTFZbUJEcAhoL82scGscvmpJFdovqjCcaAm\nbE+X9C11X9QLSR0R8TXbEyR9V9IMSS9IuiwitvX3Xp0xQtv3j6ltwAWjvza3pl2P13L00bn6Neff\nV/Hc23/4J6XyWzvTflpbA2CddRMacXJ+4/Zzxj1WKu/qyj8d9VM/uqpUftuu1Wom3PqPhhIRGyPi\niay8U1LvddaLs9MWS7q0PhEC9UNCR8NinTWQ17RTLl1782ts17zeszH0xRvac20zv/x0qZz6nWaN\nou866+7FHd0iImxXXGctaYEkjT1+bBGh4nD1+m/qPfmnJv77r3o2a7//hFm5thN/0FUqx97mWkvP\nCB0Np7911ll7v+usI6I9ItrbxrP7FNJCQkdDYZ01UFnTTrmgYVVtnfXu/a16dMOMWsUJFK5pE3rf\nubVne02bt/bZIph58+GDddZNpNfuQp0vvJRrOuWqV0vlrpb8REPrjidqG9cwxpQLACSChA4AiWja\nKRcADaQrP/HZtXNnnQIZ3hihA0AiSOgAkAimXNC04o0WHXhyXL3DAKqGEToAJIKEDgCJIKEDQCJI\n6ACQCBI6ACSChA4AiWDZIppW68u79Zbrf1a27bcFxwJUQ6EJfae2bXkwlrwoaaKkLUV+dj+aMZYT\nBz4FzY7+OqAiYxlUny00oUfEJEmyvTIi2gc6vwjEApRHf+3fcIrlIObQASARJHQASES9EnpHnT63\nHGIB+jecvpfE0g9Hr22egGYybuSkOG/ch8u23b/15lXDbX4UGAhTLgCQCBI6ACSi0IRue67tZ22v\ns72wyM/OPn+R7c22n+p1bILt5bbXZr+PKSCO6bYfsr3G9tO2P1OvWIBK6K+5WBqizxaW0G23SPq6\npPdLmiXpCtuzivr8zK2S5vY5tlDSioiYKWlFVq+1Tkmfi4hZks6V9Ons76IesQBvQn99k4bos0WO\n0M+WtC4inouIfZLulDSvwM9XRDwiaWufw/MkLc7KiyVdWkAcGyPiiay8U9IzkqbWIxagAvprPpaG\n6LNFJvSpkl7qVV+fHau3yRGxMSu/ImlykR9ue4akMyQ9Vu9YgF7orxUM5z7LRdFeonsNZ2HrOG0f\nKeluSZ+NiB31jKVR9DOXeb3tDbZXZz8fGPDNRlhuG132B8NfPfrIcO+zRT7LZYOk6b3q07Jj9bbJ\n9pSI2Gh7iqTNRXyo7VHq/mJ8JyLuqWcsDebgXOYTto+StMr28qztxoj4Sh1jSwn9tY9G6LNFjtAf\nlzTT9km2WyVdLmlZgZ9fyTJJ87PyfElLa/2Bti3pFknPRMRX6xlLo+lnLhPVRX/tpVH6bGEJPSI6\nJV0t6X51d8K7IuLpoj5fkmzfIelRSafaXm/7Skk3SLrE9lpJF2f1Wjtf0sckXdhniqAesTSsPnOZ\nknS17Sez5W4s+RwC+uubNESf5dZ/NKRsLvPHkv45Iu6xPVndz6YOSV+SNCUi/qrM6xZIWiBJbS1H\nnnnB5E+Uff8fvXwTt/6j4XBRFA2n3FxmRGyKiAMR0SXpZnUvu3uTiOiIiPaIaG8dcURxQQMFIKGj\noVSay8wuSB30YUlP9X0tkDr2FEWjOTiX+Wvbq7NjX1D3nYxz1D3l8oKkqwZ6o9ZTDmjat14r33hW\nNUIFikVCR0OJiJ9Kcpmm+4qOBRhumHIBgESQ0AEgESR0AEgECR0AEkFCB4BEsMoFTWvnjjF66ME5\nFVpvKzQWoBoYoQNAIkjoAJAIEjoAJIKEDgCJIKEDQCJI6ACQCJYtomnFyND+iZ31DgOoGkboAJAI\nEjoAJIKEDgCJIKEDQCJI6ACQCBI6ACSCZYtoWiN3WpN/3FK27fcFxwJUAyN0AEgECR0AEkFCB4BE\nkNABIBEkdABIBKtc0FBst0l6RNJodX9/l0TEdbZPknSnpGMlrZL0sYjY1997tewPHbmh31OAhsII\nHY1mr6QLI+J0SXMkzbV9rqR/kXRjRJwiaZukK+sYI1AXJHQ0lOi2K6uOyn5C0oWSlmTHF0u6tA7h\nAXVFQkfDsd1ie7WkzZKWS/qdpO0RcfDh5uslTa1XfEC9kNDRcCLiQETMkTRN0tmS3j7Y19peYHul\n7ZX79u2uWYxAPZDQ0bAiYrukhySdJ2m87YMX+adJ2lDhNR0R0R4R7a2tYwuKFCgGCR0NxfYk2+Oz\n8hGSLpH0jLoT+0ey0+ZLWlqfCIH6YdkiGs0USYttt6h7QHJXRPzA9hpJd9r+J0m/lHTLQG+07yjr\npYtGl298qHoBA0UhoaOhRMSTks4oc/w5dc+nA02LKRcASAQJHQASQUIHgESQ0AEgESR0AEiEI6Le\nMQB1YXunpGez6kRJW3o1nxoRRxUfFXD4WLaIZvZsRLRLku2VB8sH6/ULCzg8TLkAQCJI6ACQCBI6\nmllHhXK5OjDscVEUABLBCB0AEkFCR9OwPcH2E7b32X7d9rdtP2t7ne2F2TmjbXfZ3pv97LO9Ovv5\n63r/GYD+sGwRzeTvJZ2o7h2O/kLS9ZI+IOlhSY/bXibpAkkHImK07W9IujjbHQkY9hiho5lcJunJ\n7FG7qyV1STozIvZJulPSvOxnf3b+45Km2XY9ggUOFQkdzWSiujeUlqQ2SVbPZtIHN5aeKqk1u7Ho\nWkmtkp6yvcT29ILjBQ4JUy5Iiu0HJR1fpunaQ3ibcyNipe0/kvSYure0O1PSYkkXDj1KoDZI6EhK\nRFxcqc32FkknZ9U9kkI9m0kf3Fh6g6RR2bEnJR2QNEPSNyX9a/UjBqqHKRc0k+9Jepftk9S9jV2L\npFW2WyVdLmmZpOWS/jI7/7Pqnk9fI+lD6t6MGhi2uLEITcP2sZJWSJolqVPSUnVPpRwvaVNEzLS9\nWNJH1P2v1xGSXpW0SdJWSX8TEb+pR+zAYJDQASARTLkAQCJI6ACQCBI6ACSChA4AiSChA0AiSOgA\nkAgSOgAkgoQOAIn4f39N1HbojQUaAAAAAElFTkSuQmCC\n",
419 | "text/plain": [
420 | ""
421 | ]
422 | },
423 | "metadata": {
424 | "tags": []
425 | },
426 | "output_type": "display_data"
427 | }
428 | ],
429 | "source": [
430 | "def plot_imgs(index=0):\n",
431 | " f = plt.figure()\n",
432 | " f.add_subplot(1,3, 1)\n",
433 | " plt.imshow(x_test[index].reshape(28, 28))\n",
434 | " f.add_subplot(1,3, 2)\n",
435 | " plt.imshow(encoded_images[index].reshape(-1, 1))\n",
436 | " f.add_subplot(1,3, 3)\n",
437 | " plt.imshow(predicted[index].reshape(28, 28))\n",
438 | " plt.show(block=True)\n",
439 | " \n",
440 | "plot_imgs(2)"
441 | ]
442 | },
443 | {
444 | "cell_type": "markdown",
445 | "metadata": {
446 | "colab_type": "text",
447 | "id": "8lkIoRva6ewM"
448 | },
449 | "source": [
450 | "# Let's use Convolutional Neural Nets to get better results"
451 | ]
452 | },
453 | {
454 | "cell_type": "code",
455 | "execution_count": 0,
456 | "metadata": {
457 | "colab": {},
458 | "colab_type": "code",
459 | "id": "4UorTYac692G"
460 | },
461 | "outputs": [],
462 | "source": [
463 | "from keras.layers import Dense, Input, UpSampling2D, Conv2D"
464 | ]
465 | },
466 | {
467 | "cell_type": "markdown",
468 | "metadata": {
469 | "colab_type": "text",
470 | "id": "u8p2wwLa6qbB"
471 | },
472 | "source": [
473 | "Getting data"
474 | ]
475 | },
476 | {
477 | "cell_type": "code",
478 | "execution_count": 0,
479 | "metadata": {
480 | "colab": {},
481 | "colab_type": "code",
482 | "id": "07Ixl4YT6eQZ"
483 | },
484 | "outputs": [],
485 | "source": [
486 | "(x_train, y_train), (x_test, y_test) = mnist.load_data()"
487 | ]
488 | },
489 | {
490 | "cell_type": "code",
491 | "execution_count": 0,
492 | "metadata": {
493 | "colab": {},
494 | "colab_type": "code",
495 | "id": "-tmJMUnx6eVQ"
496 | },
497 | "outputs": [],
498 | "source": [
499 | "x_train = x_train.astype('float32')/255.0\n",
500 | "x_test = x_test.astype('float32')/255.0"
501 | ]
502 | },
503 | {
504 | "cell_type": "code",
505 | "execution_count": 0,
506 | "metadata": {
507 | "colab": {},
508 | "colab_type": "code",
509 | "id": "ZLPajgLH8ai4"
510 | },
511 | "outputs": [],
512 | "source": [
513 | "x_train = x_train.reshape((60000, 28, 28, 1))\n",
514 | "x_test = x_test.reshape((10000, 28, 28, 1))"
515 | ]
516 | },
517 | {
518 | "cell_type": "code",
519 | "execution_count": 0,
520 | "metadata": {
521 | "colab": {},
522 | "colab_type": "code",
523 | "id": "d2PouxDW7eB0"
524 | },
525 | "outputs": [],
526 | "source": [
527 | "img_height, img_width, _ = x_train[1].shape"
528 | ]
529 | },
530 | {
531 | "cell_type": "code",
532 | "execution_count": 0,
533 | "metadata": {
534 | "colab": {},
535 | "colab_type": "code",
536 | "id": "CHctX-5G6wTb"
537 | },
538 | "outputs": [],
539 | "source": [
540 | "def CNN_AE():\n",
541 | " input_img = Input(shape=(img_width, img_height, 1))\n",
542 | " \n",
543 | " # Encoding network\n",
544 | " x = Conv2D(16, (3, 3), activation='relu', padding='same', strides=2)(input_img)\n",
545 | " x = Conv2D(32, (3, 3), activation='relu', padding='same', strides=2)(x)\n",
546 | " encoded = Conv2D(32, (2, 2), activation='relu', padding=\"same\", strides=2)(x)\n",
547 | "\n",
548 | " # Decoding network\n",
549 | " x = Conv2D(32, (2, 2), activation='relu', padding=\"same\")(encoded)\n",
550 | " x = UpSampling2D((2, 2))(x)\n",
551 | " x = Conv2D(32, (3, 3), activation='relu', padding='same')(x)\n",
552 | " x = UpSampling2D((2, 2))(x)\n",
553 | " x = Conv2D(16, (3, 3), activation='relu')(x)\n",
554 | " x = UpSampling2D((2, 2))(x)\n",
555 | " decoded = Conv2D(1, (3, 3), activation='sigmoid', padding='same')(x)\n",
556 | " \n",
557 | " encoder = Model(input_img, encoded)\n",
558 | " \n",
559 | " return Model(input_img, decoded), encoder"
560 | ]
561 | },
562 | {
563 | "cell_type": "code",
564 | "execution_count": 0,
565 | "metadata": {
566 | "colab": {},
567 | "colab_type": "code",
568 | "id": "euWIUw7i9W39"
569 | },
570 | "outputs": [],
571 | "source": []
572 | },
573 | {
574 | "cell_type": "code",
575 | "execution_count": 0,
576 | "metadata": {
577 | "colab": {},
578 | "colab_type": "code",
579 | "id": "a-0v2iI16wVm"
580 | },
581 | "outputs": [],
582 | "source": [
583 | "model_cnn, encoder = CNN_AE()\n",
584 | "model_cnn.compile(optimizer='adadelta', loss='binary_crossentropy')"
585 | ]
586 | },
587 | {
588 | "cell_type": "code",
589 | "execution_count": 0,
590 | "metadata": {
591 | "colab": {
592 | "base_uri": "https://localhost:8080/",
593 | "height": 72
594 | },
595 | "colab_type": "code",
596 | "id": "9RikWIEy6wa4",
597 | "outputId": "ee777875-aea8-4e50-a9fe-7b1b436008f8"
598 | },
599 | "outputs": [
600 | {
601 | "name": "stdout",
602 | "output_type": "stream",
603 | "text": [
604 | "Train on 60000 samples, validate on 10000 samples\n",
605 | "Epoch 1/1\n",
606 | "60000/60000 [==============================] - 20s 339us/step - loss: 0.0899 - val_loss: 0.0844\n"
607 | ]
608 | }
609 | ],
610 | "source": [
611 | "cnn_hist = model_cnn.fit(x_train, x_train, validation_data=(x_test, x_test))"
612 | ]
613 | },
614 | {
615 | "cell_type": "code",
616 | "execution_count": 0,
617 | "metadata": {
618 | "colab": {},
619 | "colab_type": "code",
620 | "id": "uOJoBgDd6weQ"
621 | },
622 | "outputs": [],
623 | "source": [
624 | "reconstruct = model_cnn.predict(x_test)"
625 | ]
626 | },
627 | {
628 | "cell_type": "code",
629 | "execution_count": 0,
630 | "metadata": {
631 | "colab": {
632 | "base_uri": "https://localhost:8080/",
633 | "height": 131
634 | },
635 | "colab_type": "code",
636 | "id": "G15_xNl8_Wyz",
637 | "outputId": "136c1df9-e1bf-442f-f020-5393579af9b0"
638 | },
639 | "outputs": [
640 | {
641 | "data": {
642 | "image/png": "iVBORw0KGgoAAAANSUhEUgAAAlMAAAByCAYAAAB3LlRSAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDMuMC4zLCBo\ndHRwOi8vbWF0cGxvdGxpYi5vcmcvnQurowAAFRlJREFUeJzt3Xt0VNW9B/DvbyaTTCAJgYIQQgQi\noCLFCghKbav1hVgVtVDx2kVbFd+1Pqr4qJRee7XaerXXxzVeUa/XKlrtBV1UqiBVrxUEVBAQiMqz\nPERQApG8Zt8/ZrL3yWMykzl75pzJfD9rsfLLmTP77PObMXt79tn7iFIKRERERJSagNcVICIiIspm\n7EwRERERucDOFBEREZEL7EwRERERucDOFBEREZEL7EwRERERucDOFBEREZELrjpTIjJBRNaJSLWI\nzLBVKSIiImqL7a4/SaqLdopIEMB6AKcC2ArgPQBTlVJr7FWPiIiIALa7fpbn4r1jAVQrpT4FABF5\nDsA5AOJ+qPlSoMLo7uKQua0Ge3crpfqk8t78UHcVLii1Vpf8ijprZQFAQ7VYLQ+BoNXi9tXvTDn3\nAJAfCKvCYLG1+tQPDFkrCwBCnxy0Wh66F1otrubAP93l3/LfnmEja62VBQAbPiqyWp6KRKyW5+Zv\nT7B7dxUq7WWtLr1Ka6yVBQD98+x+91d91dtqefWbtjlzz3Y3w5L97rvpTJUD2OL4fSuAcR29IYzu\nGCcnuzhkbntd/XlTqu8NF5Ri3MjLrdXl0Ac+sVYWAGw7M2y1PCm22zi9+ukfUs49ABQGi3F86Xm2\nqoOt9/W1VhYAlE1aa7U8jPim1eJeXzLTVf5t/+1ZsOADa2UBwBlDxlstL1Jrt7Pn5m9PqLQXKq66\nzlpdLjzr79bKAoCZfexe1Bn88qVWy9s8/WZn7tnuZliy3303namkiMh0ANMBIIxu6T4cERFRTmO7\nm3lubkDfBqDC8fuA2LYWlFJVSqkxSqkxIRS4OBwREVFOY7vrU246U+8BGCoig0UkH8AFAObZqRYR\nERG1wnbXp1Ie5lNKNYrI1QAWAAgCmK2UWm2tZkRERKSx3fUvV/dMKaXmA5hvqS5ERETUAba7/sQV\n0LMYF2/zFvPvHebeW8w/UUvsTGWp2OJtDwE4A8BwAFNFZLi3tcodzL93mHtvMf9EbaV9aQRKm04v\n3kZWMf/eYe69xfyTK4Fis4Bx3fGH67jgH+t0HKmxuzhruvHKVPZqb/G2cucOIjJdRJaJyLKGhgMZ\nrVwO6FT+6yOWVxjPbQlzD7T6/sPuiv05rlPf/aYD/NtDXV9OXpkKlvbQ8boHK3X88Un/pePbd43W\n8ap/GabjpjXr01w7e5RSVQCqAKCkqDy1hzBSypz57xHqw/xnWIvvv/Ri/jPImftweQVzTwiEzVMu\n1NwSHd9f+aCOn95zvI5XHW/Wx1J1/v+fIV6Zyl5JLd5GacP8e4e59xbzT9QKO1PZi4u3eYv59w5z\n7y3mn6iVnBzmiwweoONVJz6q4wbHxeg7D1mu46PPNQ8hrfDJMB8Xb/MW8+8d5t5bzD+lYsu1o3S8\naOi9Ou4RyNfxNb3f0vHUs2/QcdELS9JcO/dysjPVVXDxNm8x/95h7r3F/BO1xGE+IiIiIhdy5spU\nXoUZ2htcVe1hTYiIiLqwQBAAIKPNWq6/u3S2jp1De3kI6rgsWKjj8GXbdRxcEJ3917Rvn/26WsIr\nU0REREQusDNFRERE5EKXH+bbfEd0Jt7oCeZJB/eUvRVv93YVjf9cx1t+FS2v98pGva1w7lI3VcyI\n8srd+NdnH7dW3tW//rm1sgAg72S76/r1XLo98U4ZNHR4DeYvWGStvNP7f8taWblACsMIDDnCWnnH\n3Dk+8U6dMPndhVbL+/vIwsQ7ZYgqiKCp8mtr5b1zdH7inTrhdFj+b+nRxLt0RRIyn8v+s48BAEyc\nuVhvG1+wR8cNylzHaYL52x9BRMc3D/qrji+79ycAgCP/aIb5WiygrbxfF5ZXpoiIiIhcYGeKiIiI\nyIUuP8y38rL/AAA0qKaUy1h89DPml6OjP/5yoExvml0zScd5i8xin0RERF2WiIm/dbgOT70jeivN\nRaWmPewWMM/aa3IMy9WqBh03OLYfFtqr47mnR9vx179tZgc+vPK7Oh56iRnyi9TWdu4cLOGVKSIi\nIiIX2JkiIiIicqFLDvOFFpshuJAEO9gzvvfrzayCjQ19dHxu9+iMhClFu/S2KU9X6fgH5aNTOh4R\nEVE2CRSaWaPV15m2tqpndIZ7sSS+XlPrGNo7EDH754tpg3sForPnp5Ss1NumnGDi7zxwnY6HXbbC\nFB5J/faezkp4piIyW0R2ichHjm29ROQ1EdkQ+9kzvdUkIiLKHV88+QK23vAbADiqeRvbXv9KZpjv\nSQATWm2bAWChUmoogIWx34mIiMiC7uNH45CfX9x6M9ten0o4zKeUelNEBrXafA6AE2PxUwAWA7jZ\nYr067etJY3X807IXdNw8iy+Z2XwjFl6u4z4LzcyDgq/Me285Mdr/XDX5j+2WsfUWs5jfgLveSXhM\nIiKi1sLDKtG4e0/rzb5qe788Z6SO542/T8flwW5t9o04FufcGTGLuD6x17Tdf9tuFtYN55mFsSf0\nWw0A+GZ4q942yrEI6L+f+KyOH6s4SceNm7YkcRZ2pHrPVF+lVPMS0zsA9I23o4hMBzAdAMJom2Ai\nIiJKSlJtL9vdzHN9A7pSSolI3LXclVJVAKoAoER6WV3zPXiUWdfizvvMTeBj8uude7V5n3ONqNvf\nOF/HR970sY7jPZ368A3DAABLzw7rbWMLDur4r1fco+PTwjfpeNC/mfU2VF1du2UTERElo6O2N53t\nruSZbsMJv1yi48pQqM2+jTCjOlsbTbt37WeTdbzriUE6Lq02V6wiIXMX0v/2OQUA8Nj55vVXjn9E\nx2MKduj4+l/21/HhN31hykvz+lOpLo2wU0TKACD2c1eC/YmIiMgdtr0+lWpnah6AabF4GoC5dqpD\nREREcbDt9amEw3wi8iyiN7z1FpGtAGYCuBvA8yJyMYBNAKaks5LxRPJN9VsO7bX1s01mQmLNj8za\nGMO2LtVxMitSND+p+sonzc3qyy67X8dlQVP2iovN9vNfmqZj9eHaJI5ERES5avdjf8LBdZ8CQIGf\n2t5gP3Ob1jW95+g4z3FvVvPN5h/VmxHGH710o46HVe3W8Tc2va9j1WTWlgooE5cURCeE1ZWaG95r\nxplhxYH55rE2f5r4sI6vf/sqHRfPMUOSUFZHPgEkN5tvapyXTrZcFyIiIgLQ+9ILAQCbp9+8Qik1\nxvES214f4uNkiIiIiFzoko+Tcbp1Z7RDv++Sb+htTVs3uC530IvmMuWvJh2n47v7vee6bCIiIj86\nMNLMlnM+LsY5c29dQzS+5PfX623DntYPUUHT/gOmwCQe+aIi0WG54s0NetvH9WZW/uGhbToekGdm\nDW4/2ZRd8pd8U14aZtTzyhQRERGRC+xMEREREbnQZYb5QtJ2cU4AWDmq+a5990N7LYiZPZAXMLMO\n4tXjn7NM3G+S3aok40CkAO99XWmtvKV3PZJ4p044c+yZVstDyF9f7VV7+6DyhcsT75ikoXjXWlm5\nQAUFjaXhxDsmadltD1orCwDOPPvHVssDVlsuL3WBgEJBQUPiHcm/HO3dpvPMTLiigHnsWq0yM+rP\nfetKAMCwJz7Q25osLJrZ2M20r0E4Zv45rguFHXXt1sscUxzb7c/l45UpIiIiIlfYmSIiIiJywV9j\nIZ207gqzSFiDSmbJTXs2nmdmB/65j1n4s0EFHbGpU/+Z5r3m4iQREZHPOWbtnTay/SHk6gbT9g18\nKrp/5KCLWXOOYblAODqc+FWlOUZpsP1hwwbngpzLeugwkuZn4vLKFBEREZEL7EwRERERuZDVw3y3\nf+fljBwnr2KAjmtGRxcs+8+fPhxvd21pnZk9JPWN9itGRESUZhI0w2tn9Fyl44jjppV3vz5Mx4Ub\ndgEAGlUnb2oJmOM0D+0BACoPBQAcO3ml3jQi/wvHG82CnOsaSnQ8cK5ZXLspDc/jc+KVqSwlIhUi\n8oaIrBGR1SJyrdd1yiXMv3eYe28x/0RtZfWVqRzXCOAGpdQKESkGsFxEXlNKrfG6YjmC+fcOc+8t\n5p+oFXamkrBmVj8drz6t48X6XtzfW8eP3DhZx+G1S9vbPWVKqe0AtsfiGhFZC6AcAP+gZQDz7x3m\n3lvMf+4RxyLIg/LM8FqTMjPu6iIhHUdKi6LB5iQKdwztBXuYIbrIEHN7zfpromU/2v9Vva1vsNAc\nW5lFYX/9ydk6Dm/YmEQF7OAwXxcgIoMAHANgSavt00VkmYgs27+3vr23kgXJ5L/Fgz3Jmni5j72m\n81/fwPynQzLf/cZ97le+JvI7XpmKI7TYPJH6rrIXk37fk9vG6zj8st2rUe0RkSIALwL4hVJqn/M1\npVQVgCoAOHRESXrvvstRyea/4NAK5t+yjnIPtMx/SXE5829Zst/9wiH9mfssJ/nmqlNAzMdZ51hL\ncXu9WdPpwKBiAED3deYm8ki9uXoULOqu45pTjtTxFxea/+k5b4h5FM1DPf8BAChzXI1y3vy+rM6s\nORm+xZStGjJ3EYFXprKYiIQQ/WP2jFLqJa/rk2uYf+8w995i/olaYmcqS0n0qY2PA1irlLrP6/rk\nGubfO8y9t5h/orayepgvKOYyX0iC7e6z78Lj2myb9ZvHdXxS4cF23+csr+Wjato/TjP1/W0dvm7R\ntwH8GMAqEWm+HnqrUmp+piqQ45h/7zD33mL+c03IrONU67jRvFvItMFnlb6v41cuGgEAUIGj9bbG\nsLlZ/dgbluv4xkP+oOMegfbb124SHd5z3mj+zsFiHc+65Wc6LlqR/ttr2pOwMyUiFQD+G0BfAApA\nlVLqARHpBWAOgEEANgKYopTam76qkpNS6m0AknBHSgvm3zvMvbeY//Rr3PMlvpg9B001+wHgKBG5\nlu2uvyUzzNe8pshwAMcBuEpEhgOYAWChUmoogIWx34mIiMgFCQTQc/IP0H/WDQCwFmx3fS/hlakO\n1hQ5B8CJsd2eArAYwM1pqWUcd8/5oY6nXHx/u/u8ee9DAFoP1RkNScwziffeZiMWXq7joViRuEAi\nIqI4gqUlCJbqNZciiHaoPGt3I/vMZM0X9h6r42P6mRUxRuWbW2YWjHsEAPDlsaaLUSzmkWoD8sys\nvJAUJTx+8/DegtpD9LaHrp6i46LXHEN7aX5sTDydumeq1ZoifWMdLQDYgegwYHvvmQ5gOgCE0a29\nXYiIiKh9+WC763tJz+ZLsKaIQvR+qjaUUlVKqTFKqTEhFLS3CxEREbUSOVgHAIeB7a7vJXVlKs6a\nIjtFpEwptV1EygDsSlcl46mcY54IvfSisI7HFrQ/Qy9VS+tM2VU7vgcA2HulecTMEZ9V67jjAUHv\nfLk6D/NGHJJ4xyTNg72yonbYLS7ir08ivKsBRzxo8T+RoZX2ykqDiN+Wadz/NQJvf5B4vyRNLB9l\nrayo1ZbL8w9VG4Ra0SPxjknactv4xDt5qGxRJPFOSYhEmrD+zf8BgD1et7uqrk7Hy+8ww3zVD/2f\njoc4HjlTFgzFfpoyAjAzAoOS+DpObcQsuPlKbR8AwKNXmFt7QovMjECvhvacEp5RB2uKzAMwLRZP\nAzDXfvWIiIhyi1IKny19HoUlfQFgp+Mltrs+lcwwX/OaIt8XkQ9i/yYCuBvAqSKyAcApsd+JiIjI\nhf27N2L3xuX4amc1AAxnu+t/yczm62hNkZPtVqdzmtas1/Ed11+i4y1nmcus68941PVxrpxtZutV\n/PadWMSlPYiIyL7iPoMx7oLfAwCWPHfjGqXUGMfLnra7BfOX6fji267T8QW3vqrjHxZ/BADo63iW\nXjJDe7ubzLP5pq6/QMehK6JDhHnrl7d5j1/wcTJERERELrAzRURERORCVj+bz6lwrlm0a5jjlrzv\nTr0KABD6ibmH79Wj5uj4tI/MpcTIk2aGmnIMbA764HMd+2uOGBERUQY5Zs71eOZdHf9t/mAdPzdx\nAgCg1yWb9bY7Br6s40X7h+v4jc+H6bjpLtMG5y/+0GxvNAt++hWvTBERERG5wM4UERERkQtdZpgv\nnpJnY5chnzXbzsVYHXfHp469nbHBoT0iIqL4mvaaGe7Nw39Nz5jXZ2J0u+8LYEu7sffLcHYOr0wR\nERERucDOFBEREZEL7EwRERERucDOFBEREZEL7EwRERERucDOFBEREZEL7EwRERERucDOFBEREZEL\n7EwRERERucDOFBEREZELolTmFm0Xkc8BHACwO2MH9UZvpOccByql+qTyxljuNyWxa7rqbotX9Us5\n9wDzbwHzH5V1+WfuXbP13fd7ft3ytN3NaGcKAERkmVJqTEYPmmHZfI5+r7vf6+eW38/P7/Vzy+/n\n5/f6ueH3c/N7/RLJ9von4vX5cZiPiIiIyAV2poiIiIhc8KIzVeXBMTMtm8/R73X3e/3c8vv5+b1+\nbvn9/PxePzf8fm5+r18i2V7/RDw9v4zfM0VERETUlXCYj4iIiMiFjHamRGSCiKwTkWoRmZHJY6eL\niFSIyBsiskZEVovItbHtvUTkNRHZEPvZ0+u6JuLnzydenrsS5t87zL23mP/08XNuU+XLdlcplZF/\nAIIAPgFQCSAfwIcAhmfq+Gk8rzIAo2JxMYD1AIYDuAfAjNj2GQB+53Vds/nziZdnr+vF/HtfN+Y+\nu/8x/7mbW9ufiZftbiavTI0FUK2U+lQpVQ/gOQDnZPD4aaGU2q6UWhGLawCsBVCO6Lk9FdvtKQCT\nvKlh0nz9+XSQ566C+fcOc+8t5j99fJ3bVPmx3c1kZ6ocwBbH71uRPV/IpIjIIADHAFgCoK9Sanvs\npR0A+npUrWRlzefTKs9dBfPvHebeW8x/+mRNblPll3aXN6BbIiJFAF4E8Aul1D7nayp6zZHTJi3o\nKM+Ufsy/d5h7bzH//uOndjeTnaltACocvw+Ibct6IhJC9AN9Rin1UmzzThEpi71eBmCXV/VLku8/\nnzh57iqYf+8w995i/tPH97lNld/a3Ux2pt4DMFREBotIPoALAMzL4PHTQkQEwOMA1iql7nO8NA/A\ntFg8DcDcTNetk3z9+XSQ566C+fcOc+8t5j99fJ3bVPmx3c3oop0iMhHA/YjOMJitlPptxg6eJiJy\nAoC3AKwCEIltvhXR8dvnARyK6BO7pyil9nhSyST5+fOJl2el1HzvamUX8+8d5t5bzH/6+Dm3qfJj\nu8sV0ImIiIhc4A3oRERERC6wM0VERETkAjtTRERERC6wM0VERETkAjtTRERERC6wM0VERETkAjtT\nRERERC6wM0VERETkwv8DEqNmGw3hwBEAAAAASUVORK5CYII=\n",
643 | "text/plain": [
644 | ""
645 | ]
646 | },
647 | "metadata": {
648 | "tags": []
649 | },
650 | "output_type": "display_data"
651 | }
652 | ],
653 | "source": [
654 | "def plot_imgs_for_cnn(index=0):\n",
655 | " f = plt.figure(figsize=(10, 10))\n",
656 | " f.add_subplot(1,6, 1)\n",
657 | " plt.imshow(x_test[index].reshape(28, 28))\n",
658 | " \n",
659 | " \n",
660 | " f.add_subplot(1,6, 2)\n",
661 | " plt.imshow(encoded_images[index][:, :, 0])\n",
662 | " f.add_subplot(1,6, 3)\n",
663 | " plt.imshow(encoded_images[index][:, :, 1])\n",
664 | " f.add_subplot(1,6, 4)\n",
665 | " plt.imshow(encoded_images[index][:, :, 2])\n",
666 | " f.add_subplot(1,6, 5)\n",
667 | " plt.imshow(encoded_images[index][:, :, 3])\n",
668 | " \n",
669 | " \n",
670 | " f.add_subplot(1,6, 6)\n",
671 | " plt.imshow(reconstruct[index].reshape(28,28))\n",
672 | " \n",
673 | " plt.show(block=True)\n",
674 | " \n",
675 | "plot_imgs_for_cnn(3)"
676 | ]
677 | },
678 | {
679 | "cell_type": "code",
680 | "execution_count": 0,
681 | "metadata": {
682 | "colab": {},
683 | "colab_type": "code",
684 | "id": "_p4rclEL_0A5"
685 | },
686 | "outputs": [],
687 | "source": []
688 | },
689 | {
690 | "cell_type": "code",
691 | "execution_count": 0,
692 | "metadata": {
693 | "colab": {},
694 | "colab_type": "code",
695 | "id": "g1alULdqIIyb"
696 | },
697 | "outputs": [],
698 | "source": []
699 | },
700 | {
701 | "cell_type": "markdown",
702 | "metadata": {
703 | "colab_type": "text",
704 | "id": "RCivQ5wdOBBr"
705 | },
706 | "source": [
707 | "# **Denoising example**"
708 | ]
709 | },
710 | {
711 | "cell_type": "code",
712 | "execution_count": 0,
713 | "metadata": {
714 | "colab": {},
715 | "colab_type": "code",
716 | "id": "xR4oH_QXII0v"
717 | },
718 | "outputs": [],
719 | "source": [
720 | "noise_factor = 0.5\n",
721 | "x_train_noisy = x_train + noise_factor * np.random.normal(loc=0.0, scale=1.0, size=x_train.shape) \n",
722 | "x_test_noisy = x_test + noise_factor * np.random.normal(loc=0.0, scale=1.0, size=x_test.shape) \n",
723 | "\n",
724 | "x_train_noisy = np.clip(x_train_noisy, 0., 1.)\n",
725 | "x_test_noisy = np.clip(x_test_noisy, 0., 1.)"
726 | ]
727 | },
728 | {
729 | "cell_type": "code",
730 | "execution_count": 155,
731 | "metadata": {
732 | "colab": {
733 | "base_uri": "https://localhost:8080/",
734 | "height": 72
735 | },
736 | "colab_type": "code",
737 | "id": "TvS9CX6III3b",
738 | "outputId": "8f54b173-159d-4c77-edac-15de211e6731"
739 | },
740 | "outputs": [
741 | {
742 | "name": "stdout",
743 | "output_type": "stream",
744 | "text": [
745 | "Train on 60000 samples, validate on 10000 samples\n",
746 | "Epoch 1/1\n",
747 | "60000/60000 [==============================] - 20s 333us/step - loss: 0.1180 - val_loss: 0.1100\n"
748 | ]
749 | }
750 | ],
751 | "source": [
752 | "cnn_hist = model_cnn.fit(x_train_noisy, x_train, validation_data=(x_test_noisy, x_test))"
753 | ]
754 | },
755 | {
756 | "cell_type": "code",
757 | "execution_count": 0,
758 | "metadata": {
759 | "colab": {},
760 | "colab_type": "code",
761 | "id": "HCRmI7oUI4jd"
762 | },
763 | "outputs": [],
764 | "source": [
765 | "reconstruct = model_cnn.predict(x_test_noisy)\n",
766 | "encoded_images= encoder.predict(x_test_noisy)"
767 | ]
768 | },
769 | {
770 | "cell_type": "code",
771 | "execution_count": 163,
772 | "metadata": {
773 | "colab": {
774 | "base_uri": "https://localhost:8080/",
775 | "height": 131
776 | },
777 | "colab_type": "code",
778 | "id": "gyehz6t-II5d",
779 | "outputId": "4de1e821-dc81-40b2-e614-9ada9ffacec7"
780 | },
781 | "outputs": [
782 | {
783 | "data": {
784 | "image/png": "iVBORw0KGgoAAAANSUhEUgAAAlMAAAByCAYAAAB3LlRSAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDMuMC4zLCBo\ndHRwOi8vbWF0cGxvdGxpYi5vcmcvnQurowAAH0ZJREFUeJzt3Xl8lNW5B/DfyWRPSCCEbISdRARl\ncWNRsQoYRb14laJYlfbaYqvWBbXQ1mqvelvFlurttQXu1VasdQNcqlQErFpXQMuOLLJIIOx7ErLM\nnPvHOznPCzNhJnnfzDshv+/n44cn77xz5uQkcg7nec85SmsNIiIiImqeBK8rQERERNSacTBFRERE\n5AAHU0REREQOcDBFRERE5AAHU0REREQOcDBFRERE5AAHU0REREQOOBpMKaUuU0qtU0ptVEpNcatS\nREREFIr9bnxSzd20UynlA7AewCgA5QCWABivtV7jXvWIiIgIYL8bzxIdvPc8ABu11psAQCn1EoAx\nABr9oSYlZ+jUtA4AAHW4ylwv7S/x+hXpIe+rLcwwcXJFZcSKqZRkEx/LS7Led1gGjeqQfF6gg5Sd\ncCBy2WE/L1k+r66rkvL2SfNqn9x/etEeE1frAACgfF2O3FtbKzenp5rwSFXFXq11p+bUMdmXptMS\ns5rz1rBqip386oRK2RFwtTy4vLH/4ZqdzW57AEjMStdJee1dq09B6mHXygKAfauTI9/koSM44Kj9\nkxNSdVpCpmv10b18kW9qArVVRb6pCXRNbeSbmsBJ+yelZOiUjJzIN0apT5c9kW9qgg1r2rlanq73\nu1reCW3f5H43WaXoVGQ09jJFEO3vvpMesTOAbbavywEMPtkbUtM6YNAFdwIAUv6+xFyfP3+Zics6\nD7IC24zZtu8PM3GXRz+JWDFf1x4mXnd7PgCgeJF01qlvLTbxkbIhJm738mcRyw4nsbibiXc+mSKf\n87z8BVKbKX9ZLn70jyZeXVsNAPjJxdeba/Wbt5pY9TvDxAuW/FJeaKK0xCwMK7ihuW8PsWlqB9fK\nAoAeD9W4Wh5c/gtt/rrHm932AJCU1x7dn5joVnUwud9818oCgBf6FLtantsW6tmO2j8tIRNDM8e4\nVR3UTc92rSwASLrV3X+c+DdudrU8J+2fkpGD/iPvcq0uH/33DNfKAoDR/Ue4Wp5/7z5Xyzuh7Zve\n7yIDg5W732NbEu3vvrv/B4ehlJoIYCIApKS69y9zIiIiCmXvd1MRmu0h9zkZTG0H0MX2dXHw2nG0\n1jMBzASALJWj7TNSDcqKBtrfAQA4Ok5mjJKamH1TNXUm7n1P6GzT5l8NNfEr45808eSXTzrABwDs\nu8V6b8dnPjXXAtkyhZp7lcy2Vv27lHekmzzrf/z3axm5apWJ379KZqPql64KuZeIiNqkZvW7sala\n2+ZkNd8SACVKqR5KqWQA1wN4051qERER0QnY78apZs9Maa3rlVJ3AJgPwAfgWa31atdqRkRERAb7\n3fjl6JkprfU8APNcqgsAYP4O62H0AVPlofOC38lD5zWXn2vicClDAKjfVh5y7eg7PU38QPdXTTy5\nh6Ti9k6U9N+xMlktVXyt/K7a03sNEvbJvfY1aRXny0Pnve6T7yGxuLPUtdyaoV14hqwoOXxDodw7\nsEAKnDs75LOJiKjtaIl+l5zjDuitGDdv8xbb3ztse2+x/YmOx8FUKxXcvO1pAJcD6AtgvFKqr7e1\najvY/t5h23uL7U8UqsW3RohG7QLZp+nSawcAAAo+lbTY7tsk5Zf3h/D7TO35oaToMnfKHkOBRCvV\nln3vQXPthdXh99TJnSkpvA39hoS9J5xwaUUA6HVf+H2rvnosz8S9b7TSfLt+LN/j0a6y+OLRf3vZ\nxJ/MPa6YJm/eRq5i+3uHbe8ttj/RCTgz1XqF27yts/0GpdREpdRSpdTSWn91TCvXBjSp/ettO/6T\nYxHbHjjh9z9wLGaVawOa9LtfV3M0ppUj8kJMZ6ZqeqRh4yPWDue9b/qXuZ48SjYY3fYL6//JRS9/\nZK7dcvlpJrbva336F1L92p/J3lKVdx4ycYcrNgAA1v1OZpp63yNlFH8mR0xsm9TLxCVnyGxT9XzZ\nUT2tzNpZ2JfbUeoUxY63F62wDWb6y/fe8MD9D7bJXlXbhteb+E/3y6ydtSo2eva9RrJT8rnXSIzZ\n2z+tdxHbP8aO+/1PzGX7x5C97TNzurDtCVC2o9Yypd9VibZj16qlnwwca13/AOLMVOsV1eZt1GLY\n/t5h23uL7U90Ag6mWi9u3uYttr932PbeYvsTnSCmab7ijIN4bPAcAMBM9Ax7T5dHrAfMv/vIBeba\njvskpVZk257sjSVnmbh0vhxenGw7A/bK1QcAAG/1sz0MPqS/CZ/pOsvEgwbJdf88Sbt1WiaH8CZ2\ntxKN9Vu+Mdd8p/U2cSArzcRHHpFzcD7ov8nEKinZxHK0TNPOzOHmbd5i+3uHbe8ttj9Fy57C8xXk\nm3hXWVcT7x8u/Wv7DtIPprzYwcQd3lkHAPAfkj0dEXD3MHun4mI1HzUPN2/zFtvfO2x7b7H9iY7H\nNB8RERGRAzGdmdqzKgUzS0PTe9VXn2fizLX7AQBfP5xurnW/LvzeUnmf+MJe3/ikrNyb9qm1Mq4U\nS821DeOl7CvXXy6fvUOmDf/59IywZUtazma6LHvfVynj070VMk1Zartd19WGLZuIiKjVsK3QU4lJ\nJvbl5gAAqgbIOoWtN0j/es/ZMql5ScZXJu6WKOVtkqduMGbUHQCA0pnSd6ov5H3x0KdyZoqIiIjI\nAQ6miIiIiByIaZpPZ6fj2HArpZe2SzbnSntdVuI1TAT2ekDSgfOCG1sCwOuVstnXz1f0M3HOHFl9\nl1IsO+5272ilDVEi5d16ySITT+64QSr4dPh691z4HybetONZAMDgyT8y1zpO3CX12LBeYlsZm6bK\ncTfF78mmnMnvhG7EeeC7cu+xjjLtid/MDl/BKLQvqcKYOV82+/0nmjNhhGtlAUBdTnrkm5og4aNl\nkW+KoX4Z+7F46AuulRc23UyNS/BBZbVzrbjDz4U/kqq5Dv5X01bzRtL9OleLcySzsBLn//xz18pz\n/3c/8qbLZJMgj9ckpKWaWHUuMPE3V1sr9wb9+ypzbUbR302c75N5nFQlw5BESNmnJUla8PELXgUA\nTK6RX+y+23JNXL+jQuqnvdkjljNTRERERA5wMEVERETkQEzTfOpQFVLfslJ6kSbi/Btkk8vGpnWL\nIfvE1Y4428Rdxn5h4m/mWqnAVR9IisWetps80pbms3m7SqYvN4181sTr66zp+M8f/6O5dtYjtpRf\nUbaJEz6wnT94QNJ19tTexuCZgb3vkU1FO/z5UxPPt6U4fb8JW1UiIqKYUAm2M/ZsqfP9Z3cy8Yjr\nrH7+phxZiV/ks6UHbfM4fltazg95BCaAgImHpVqnFY08S/r81RecaeLst+Q83kCV7VD5GKb8ODNF\nRERE5AAHU0REREQOxMVxMonFnU1cX968w8fnPvc/Js5OkPPxBiw+PeTekpttq9p2SDhq/PdMvODF\nP5n4/p2DTPxEgaTuGhTM3mhi/549Jran6MqulinJzS/JbmRfD58OABg989tSxlpJPQ544jbbJ00K\n+WwiIqKYsaXr6nrIeXuHxx4x8V257wMA2tlSgnVa4kot6bw1tbK59X6/rNYvSjpg4k4JVupuRPs1\n5lrKfVLGJzlyTm/Bq7Ki3r//oNS7hc/yizgzpZR6Vim1Wym1ynYtRym1QCm1Ifhnh5OVQURERNFb\nrZfiA/03ADB7ALHvjV/RpPn+DOCyE65NAbBIa10CYFHwayIiInJBEbphEC448TL73jgVMc2ntf5Q\nKdX9hMtjAHwrGD8H4H0Ak5vywRkfypP/2/+vq4mV3zrLpypfxnmF02RFgC+3o4n9e2WztfEDrjDx\nV9OkuptGWSvx7CsC7ek3u71nSHpw9AhJu724YJaJy4qsDTV3vNbXXFu5/K9hyzt+FeJKEyUny2aj\nl46dAABQa5eHLSN1nzcbkBERkXc6qE6o1iGbuTrue5tF2VfwZZl447XSZz47aLqJixJTAAB1WlJr\n+wOSlnt6nwwSX5svm1Sn75DPqZWF8eg90lrdPyZP+u4p+bL59tJJssrvP303m7jwVXkEJ7Bvv4m1\nP0zKz+HKv+Y+M5WvtW7YcnQngPzGblRKTQQwEQBS4e4u10RERG1IVH0v+93Yc/wAutZaK6UaHdJp\nrWcCmAkAWSrH3Fc5XB7Ubg+Jv37CGqVmbwhfZMW400zcboxsIf/hma+Z+LbtQ0Le19hs1LhNcixK\n3tMyA2Yft47vW2b76jAA4O4+74Utz27aFtkv6v6BkintfM3qkHvXTz/PxKU/lON12s/6NOReIiJq\n207W9zbW77oiR6aMRl8kezoOSK623WQNLfb4ZTbqid0jTfzF72VRV8mHtkVnNbUS2x50r51nZaR+\ndffl5tolw39v4mGpcqRbvxvkIfU9i7uYOOHQYRPrgG4I4Jbmbo2wSylVCADBP3e7ViMiIiIKh31v\nnGruYOpNABOC8QQAb7hTHSIiImoE+944FTHNp5R6EdYDb7lKqXIADwF4DMArSqlbAGwFMC6aDyvp\nX4l571h7PF3RTdJaul6mAnvdb6W1NsySfSOO9JAH1LrNk6nEBQ9Iau/C22818f1TnzfxD7adDwA4\nPUNSgn9YfpF83ndC940K0VnS0psesB4ef/YhmTm95cnpIW8BgPlH5UHzff8mD6x3XLLXxA17StlT\ne75/FMnrF9s2wiIiojZhpf4cB6xHYFKc9r1uqsuTI2RGZssjK6lKhhMND57/z97h5tqaX8peix0/\nllSc/6g8ZG/Sb9YXEu/YCQA47bHe5tIbZ51h4glZUt7wDrLP1Fy/7GEZqK0LLdvF42aiWc03vpGX\nRjRynYiIiBw4Uw0GACzUs7/UWp9je4l9bxzicTJEREREDsT0OJmtte0wcZs17afrj5rr5T8bZuKG\nfZVKbg6/is3XXlYS2PdxqvmujAuP6SQTf/L6AADAlpE55po9tXfoRln5d6i3lNF+sKwOyLpcjnfx\np1rlZK+UPSsa28NqTLsVcn2W7M0RblP7c5fJ1SUDmdojIqI4oaRvPNI1xcR5PjlCxr6n1PyqPADA\nmlv6mGupq6Tf9dv3eYom1RYsW3+91Vx66jNZHTjk4q9N/PpO6Y99uw+ZuN6eNnQxvdeAM1NERERE\nDnAwRURERORATNN8tV8FUD7ESu9VTJLUXn26TLmlbgjdROut7bIx2MV33mbihHp5X0aFPKk/LlOm\n9p75dXAjzl9LefWXnG3i7L98ZuLPbCm644+CEYmVwfHnXjmNuubyc0086FfyfWV/LXU6cLekHgue\nlM1BG4xvL6v5lmBoyOtO1Wkftte6dybm/Nefj3xTE4wa911Xy7Ong11xIPItJ7N6Vyf0/+1tkW+M\n0htbp7pWFgD8sFvIGWCnFoXjjsRw6vPH/uhaWQBwxdCrXC2vPvItMVO1Blg2KPJ9p4pddw6LfFNT\nPDXb3fKawZeVaeI9l9WYuFuirK7fZcvc/eahGwAAWcs/l4tupNZsG3n6UuUDd/tlheGGijwTl1Rv\nc/6ZUeLMFBEREZEDHEwRERERORDTNJ9d4bTQVBcAVLx+OgDg2M2l5tqVsu8W9v9cpvnW3P4HE886\nnGvi8++SDTwzYZtmDDqWm2R7XYy+eKztq40Ip9s7xwAA228sMdeytsh048v3P2Hi0qQME9vThpXX\nDjZxxhyrft/75SRzrQN4Hh8REXnInhYvko2rz+8tK+eqbJm7qbtGmTjnH5sBAPXRpPYaS7/b39tw\nT0k3c+nWAR+auHvSftut9o0/G4lbAGemiIiIiBzgYIqIiIjIAc/SfEiQdB0CkiYrvHptyK3f+arc\nxC/0kfTguRU/MvGSR2V1zc1PzTBx2atWes1X0tNcy3xFVvDZ+ddJam/vrbKiLv9DOUsPH1gbj9Vd\nKCs20l+TVGLp0+FTe1hUbMKMEaGpx/Rdsv4msVjymm8vftvEvsKw1SYiInKXbaPOQ/1kJfi4Du+b\n+JiWfnztgQITZ9YFV9TbU3j2NJut/1dJMgxRieGHJAn5nQAAFQ/LWOG6rOUm9tuKrjsom4rqyqqw\n5bUEzky1UkqpLkqpfyil1iilViul7vK6Tm0J2987bHtvsf2JQnk3M0VO1QO4V2v9pVKqHYAvlFIL\ntNZrIr2RXMH29w7b3ltsf6ITeDaYOjpPnsqvelOmB+/48VwAwJNfXWKuPfyWnJ9XeI3M59lTe5de\nO8HE7855zsSJPazPqd+wyVxLyJBUXKCyMmz9cmfIirqsj+Vcv9EdrZTjzVmykhC2vRirArVhy8OI\n8vDXg9I+lL+HtG3ac8BU+0aPsuJPa10BoCIYH1FKrQXQGQD/QosBtr932PbeYvu3PQm2XWBTlWxG\n7Yek8Uqy95h4W5/eAADfF5Jm037ZkFsly4p61Vn6/+oekk48UmxbdX9dBQDg7T7PmGu5vjQTb64/\nZuKCDyXhFqiVurY0pvlOAUqp7gAGAcfvA6GUmqiUWqqUWlp5oJFBHjkWTfv7q8IP2smZxto++Jpp\n/1p/9Ykvkwui+d2vQ024txKdUmI6MxVon47qb50HAMi8TI5P2T1V9rB45XRrlFpk+0fOxmkyM7X7\nLBn/jR45zsQ7rpLZpgtWXCMfGpy8Sn94gLn00ivTTVxuG3Hf+MS9Jv7+7X8z8cwZ8rD5S5PfAwD0\n+73MGK3+scxSnTP9bhOn3C5l5z0dfl+tBp0WygN5H30hJ22X3CHvWxXmfUqpTABzANyttT5sf01r\nPRPATAAo6te+ZTfZaKOibf+0gi5sf5edrO2B49s/OyWf7e+yaH/3s1QO27410jKTlHxYOsrDgbRw\nd2NgOzm65b2b+gIAeqb0M9eSjsg/6A+WSH+982J5qHzQaVtMPL7TahOPzlgPAMjzpZtrNVrq9GC5\nHMfUYaHsg+W3LW5raZyZasWUUkmw/jJ7QWs91+v6tDVsf++w7b3F9ic6HgdTrZRSSgF4BsBarfU0\nr+vT1rD9vcO29xbbnyhUTNN8GYVVOPfBpQCAlXtlD6aif558Ki5npTzklvMneTB83o5lJh66/FoT\nf9Rf/qE08NdWOq5inExZbq6TMeTAFNmT4l8/tz1UbnP75NDricfC3Aigy6MnT+eFCO7D8c2jp5lL\n7Up8jd1tdz6AmwCsVEo1NMTPtNbzmlYBaia2v3fY9t5i+7cFtn2hfFWSUjvklzRfkU/67rHtJC03\nrGwDAOAPA2UhWU1AhhuT8j42cZ/kAyZOb+RomXYJVj99VMvzd7/fP0jqdLs8xB7YG7pXZSxEHEwp\npboAmAUgH4AGMFNr/ZRSKgfAywC6A9gCYJzW+kBj5ZC7tNYfAWjkUCNqaWx/77DtvcX2b3m1Rw6g\n/N2/or7qKAD0U0rdxX43vkWT5mvYU6QvgCEAbldK9QUwBcAirXUJgEXBr4mIiMgBleBD4YVjUHrT\nZABYC/a7cS/izNRJ9hQZA+BbwdueA/A+gMknK6t6LbDqbCvdpiApukN3ymq51IZr35EVfPbUnl3/\n38qKuhX3hk/RLfupdb1klhw9Y0/tNebdKtnj4tebR5t4+75sAMD6+8N/nt36/z3XxKU/WBL+puBU\nasrb8npB+DuJiKgNSMrIQlJGVsOXAVgDqmb1u67Up3yfieduk0d0vpe9wsTZCcm22PrzqeKF5lqC\nbe4mRcnQw6cyw36m37aasFpbKwGfOSirAxf95EITJ6/4Ut6ovVk82qRnpk7YUyQ/ONACgJ2w0oDh\n3jMRwEQASEV6uFuIiIgovGSw3417Ua/mi7CniIb1PFUIrfVMrfU5WutzkhB5RoiIiIgAf20NAPQC\n+924F9XMVCN7iuxSShVqrSuUUoUAdkcsJzkJiQXFAID6bXK8im/UXhPPn2Kl/8qKwpeRMLCvif22\n35FSWxpv/c1yzEyPt39gvT7Fliq8OXzZK2pliV5J0lETH62RD3ptyIxg/YaGLUMPlc1BG0vt+Up6\nmthvO+amJVVuTsfiCQMi3xil0XVnuFYWACRX7ne1PKSF31iu2Rw+4pm8vxZdXt7qTl0A3DH3O66V\nBQC+jkdcLc+/z+Wfp0O6rh7+nRH/iopaWdHAyDc1QULqnsg3tVIqJRm+bj0j3xilWP2d2Vz5/93E\nFd2NCOgAluFjANjvpN91pS57pI9OmtHfxLMePdPEZZmymq+Tz0rRZSp5XCbdlgZszNGA9MGrauW9\nv9j8bSv4Za65lrJYUow6hptzNibizNRJ9hR5E0DDgXgTALzhfvWIiIjaFq011mApMtAOAHbZXmK/\nG6eiSfM17ClyiVJqWfC/0QAeAzBKKbUBwMjg10REROTAIezDTnyDA9gDAH3Z78a/aFbznWxPkRFN\n+TBdW3dceq9Bt2zJoYzuMzwYhRy1BQBQNXIKdPFCSU0k7pC0Qp9aSflt/r6V8lv0tWyE+cBumZp8\nNG+lia9+6y4TP3Hpiyaue1emFiddGT69Z+r36fKTvg4ASJJmH7d2p1WPT64010pvWRq5DCIiOiW1\nV7kYibEAgIV69hqt9Tm2l5vU77ohcEzSb+lvycq5BRvPM/H/XnOZic++zDpb96dFfzfXeidJ321X\npyVF9151jonvf2mCiXu9ZPXvgfWSStR1ctZfPOBxMkREREQOcDBFRERE5EBMz+azqx4j04MYvtiE\nvtNLrOCwpPkSe3Y38b6zOpq47npJ7eVetd3EhZ/IUsCyB0NX3cy3neln9+DI10w8s1RWn9Q8FPZ2\nMURWN+CzFWFv8XXqZGL/mvUmnvMt672l3WpC3gMAiQW2bUQqwt5CREQUE7pezunTq9eZuPtGWfV+\n4C/W1tPXX3uvuTbs2/8y8fpDeSY+WCUrrzP/nG3ingtXmdhfWWUFcbBqrzGcmSIiIiJygIMpIiIi\nIgc8S/PVZMvqupQLB8kL/7SmAivulfP6Cn8rm6Blb9oi975gK2+0nIOXusi2mVfwzy0vSyrOviHo\njp/I5xRNDb/ZWs/nd5j47WCK8NKxstLg3dnP2cqWtKI9nXjFWWXyma/JxqNdvm+t5sNiWVVoTxvW\nN5I2JCIi8pTtHDz7ir9AsJ8u+u02c23rk9LnJ/tlVb8k/HBcGi+A1oUzU0REREQOxHRmSrdLR/3g\nswEA7WfJ8S6VYwebOCvfGqfaZ6NqrpBZp+0XSZVLfrXGxInVMqJViXJPQq9uAIDu160I+3rGDhn/\nbnxeZsh63yQPy5WPsT3QHpx52nerHB45+sxLTLzlkdPk+sW9TezfudHE+KSXCdf/1DoZ/Ddj/mKu\nTfr4bBOXfAYiIqLWxzbTFA9HvrQkzkwREREROcDBFBEREZEDMU3zJdQHkLyrEsDxD5dlzP7cxOEm\nAmvbyYNrnT+QPS5eWTXfxJkJqSYefdE1Jj5WbKXRkiQjeNw+Ge1Xy5E0uy6U1J1dwe9CH0zPnSFp\nSnud193yRxOX/UIeRv/mQXnQPemo3N/rPiuP9/iXN5prJX+V3F7aB7Z9poaDiIiI4gxnpoiIiIgc\n4GCKiIiIyIHYruarPobAqq+iunf9dDlu5vQpa03sP3jIxMOmTTJx6n7Z76KTX85dSXp3aUjZWx8e\nauKcNfK+0lvDL52bt11OyR741B0AgOp8SVR2eVfShpeOHWBiheUm7vpw+D2sdt5jpf/CpRIBoPqi\nXWGvExERUXzgzBQRERGRAxxMERERETmgtG07+Bb/MKX2AKgEsDdmH+qNXLTM99hNa92pOW8Mtv3W\nKG5tqbq7xav6NbvtAba/C9j+llbX/mx7x9z63Y/39nXK0343poMpAFBKLdVanxPTD42x1vw9xnvd\n471+TsX79xfv9XMq3r+/eK+fE/H+vcV7/SJp7fWPxOvvj2k+IiIiIgc4mCIiIiJywIvB1EwPPjPW\nWvP3GO91j/f6ORXv31+818+peP/+4r1+TsT79xbv9Yuktdc/Ek+/v5g/M0VERER0KmGaj4iIiMiB\nmA6mlFKXKaXWKaU2KqWmxPKzW4pSqotS6h9KqTVKqdVKqbuC13OUUguUUhuCf3bwuq6RxPPPp7F2\nPpWw/b3DtvcW27/lxHPbNldc9rta65j8B8AH4GsAPQEkA1gOoG+sPr8Fv69CAGcF43YA1gPoC2Aq\ngCnB61MAPO51XVvzz6exdva6Xmx/7+vGtm/d/7H9227buv0z8bLfjeXM1HkANmqtN2mtawG8BGBM\nDD+/RWitK7TWXwbjIwDWAugM63t7LnjbcwCu9qaGUYvrn89J2vlUwfb3DtveW2z/lhPXbdtc8djv\nxnIw1RnANtvX5Wg9v5BRUUp1BzAIwOcA8rXWDScu7wSQ71G1otVqfj4ntPOpgu3vHba9t9j+LafV\ntG1zxUu/ywfQXaKUygQwB8DdWuvD9te0NefIZZMuOFk7U8tj+3uHbe8ttn/8iad+N5aDqe0Auti+\nLg5ea/WUUkmwfqAvaK3nBi/vUkoVBl8vBLDbq/pFKe5/Po2086mC7e8dtr232P4tJ+7btrnird+N\n5WBqCYASpVQPpVQygOsBvBnDz28RSikF4BkAa7XW02wvvQlgQjCeAOCNWNetieL653OSdj5VsP29\nw7b3Ftu/5cR12zZXPPa7Md20Uyk1GsCTsFYYPKu1/q+YfXgLUUpdAOCfAFYCCAQv/wxW/vYVAF1h\nndg9Tmu935NKRimefz6NtbPWep53tXIX2987bHtvsf1bTjy3bXPFY7/LHdCJiIiIHOAD6EREREQO\ncDBFRERE5AAHU0REREQOcDBFRERE5AAHU0REREQOcDBFRERE5AAHU0REREQOcDBFRERE5MD/AyJ+\nixES7WdaAAAAAElFTkSuQmCC\n",
785 | "text/plain": [
786 | ""
787 | ]
788 | },
789 | "metadata": {
790 | "tags": []
791 | },
792 | "output_type": "display_data"
793 | }
794 | ],
795 | "source": [
796 | "def plot_imgs_for_cnn_noisy(index=0):\n",
797 | " f = plt.figure(figsize=(10, 10))\n",
798 | " f.add_subplot(1,6, 1)\n",
799 | " plt.imshow(x_test_noisy[index].reshape(28, 28))\n",
800 | " \n",
801 | " \n",
802 | " f.add_subplot(1,6, 2)\n",
803 | " plt.imshow(encoded_images[index][:, :, 0])\n",
804 | " f.add_subplot(1,6, 3)\n",
805 | " plt.imshow(encoded_images[index][:, :, 1])\n",
806 | " f.add_subplot(1,6, 4)\n",
807 | " plt.imshow(encoded_images[index][:, :, 2])\n",
808 | " f.add_subplot(1,6, 5)\n",
809 | " plt.imshow(encoded_images[index][:, :, 3])\n",
810 | " \n",
811 | " \n",
812 | " f.add_subplot(1,6, 6)\n",
813 | " plt.imshow(reconstruct[index].reshape(28,28))\n",
814 | " \n",
815 | " plt.show(block=True)\n",
816 | " \n",
817 | "plot_imgs_for_cnn_noisy(3)"
818 | ]
819 | },
820 | {
821 | "cell_type": "code",
822 | "execution_count": 0,
823 | "metadata": {
824 | "colab": {},
825 | "colab_type": "code",
826 | "id": "X5KNaod4JLaX"
827 | },
828 | "outputs": [],
829 | "source": []
830 | }
831 | ],
832 | "metadata": {
833 | "accelerator": "GPU",
834 | "colab": {
835 | "collapsed_sections": [],
836 | "include_colab_link": true,
837 | "name": "DeepAutoencoder.ipynb",
838 | "provenance": []
839 | },
840 | "kernelspec": {
841 | "display_name": "Python 3",
842 | "language": "python",
843 | "name": "python3"
844 | },
845 | "language_info": {
846 | "codemirror_mode": {
847 | "name": "ipython",
848 | "version": 3
849 | },
850 | "file_extension": ".py",
851 | "mimetype": "text/x-python",
852 | "name": "python",
853 | "nbconvert_exporter": "python",
854 | "pygments_lexer": "ipython3",
855 | "version": "3.7.4"
856 | }
857 | },
858 | "nbformat": 4,
859 | "nbformat_minor": 1
860 | }
861 |
--------------------------------------------------------------------------------