├── EM九重境界.pdf
├── xgboost 面试常问问题.pdf
├── README.md
├── LightGBM-1.md
├── XGBoost-1.md
├── catboost2.md
├── XGBoost-2.md
├── LightGBM-2.md
└── Catboost.md
/EM九重境界.pdf:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/sunyingjian/boosting-and-others/HEAD/EM九重境界.pdf
--------------------------------------------------------------------------------
/xgboost 面试常问问题.pdf:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/sunyingjian/boosting-and-others/HEAD/xgboost 面试常问问题.pdf
--------------------------------------------------------------------------------
/README.md:
--------------------------------------------------------------------------------
1 | # boosting
2 |
3 | 三大boosting算法的工程实现 XGBoost、LightGBM、Catboost原理实现及常见面试问题总结,以及其他理解深刻的机器学习、深度学习文章备份
4 |
--------------------------------------------------------------------------------
/LightGBM-1.md:
--------------------------------------------------------------------------------
1 | ## 目录
2 | - [1. LightGBM是什么东东](https://github.com/NLP-LOVE/ML-NLP/tree/master/Machine%20Learning/3.4%20LightGBM#1-lightgbm是什么东东)
3 | - [1.1 LightGBM在哪些地方进行了优化 (区别XGBoost)?](https://github.com/NLP-LOVE/ML-NLP/tree/master/Machine%20Learning/3.4%20LightGBM#11-lightgbm在哪些地方进行了优化----区别xgboost)
4 | - [1.2 Histogram算法](https://github.com/NLP-LOVE/ML-NLP/tree/master/Machine%20Learning/3.4%20LightGBM#12-histogram算法)
5 | - [1.3 带深度限制的Leaf-wise的叶子生长策略](https://github.com/NLP-LOVE/ML-NLP/tree/master/Machine%20Learning/3.4%20LightGBM#13-带深度限制的leaf-wise的叶子生长策略)
6 | - [1.4 直方图差加速](https://github.com/NLP-LOVE/ML-NLP/tree/master/Machine%20Learning/3.4%20LightGBM#14-直方图差加速)
7 | - [1.5 直接支持类别特征](https://github.com/NLP-LOVE/ML-NLP/tree/master/Machine%20Learning/3.4%20LightGBM#15-直接支持类别特征)
8 | - [2. LightGBM优点](https://github.com/NLP-LOVE/ML-NLP/tree/master/Machine%20Learning/3.4%20LightGBM#2-lightgbm优点)
9 | - [3. 代码实现](https://github.com/NLP-LOVE/ML-NLP/blob/master/Machine%20Learning/3.4%20LightGBM/3.4%20LightGBM.ipynb)
10 |
11 | ## 1. LightGBM是什么东东
12 |
13 | 不久前微软DMTK(分布式机器学习工具包)团队在GitHub上开源了性能超越其他boosting工具的LightGBM,在三天之内GitHub上被star了1000次,fork了200次。知乎上有近千人关注“如何看待微软开源的LightGBM?”问题,被评价为“速度惊人”,“非常有启发”,“支持分布式”,“代码清晰易懂”,“占用内存小”等。
14 |
15 | LightGBM (Light Gradient Boosting Machine)(请点击[https://github.com/Microsoft/LightGBM](https://github.com/Microsoft/LightGBM))是一个实现GBDT算法的框架,支持高效率的并行训练。
16 |
17 | LightGBM在Higgs数据集上LightGBM比XGBoost快将近10倍,内存占用率大约为XGBoost的1/6,并且准确率也有提升。GBDT在每一次迭代的时候,都需要遍历整个训练数据多次。如果把整个训练数据装进内存则会限制训练数据的大小;如果不装进内存,反复地读写训练数据又会消耗非常大的时间。尤其面对工业级海量的数据,普通的GBDT算法是不能满足其需求的。
18 |
19 | LightGBM提出的主要原因就是为了解决GBDT在海量数据遇到的问题,让GBDT可以更好更快地用于工业实践。
20 |
21 | ### 1.1 LightGBM在哪些地方进行了优化 (区别XGBoost)?
22 |
23 | - 基于Histogram的决策树算法
24 | - 带深度限制的Leaf-wise的叶子生长策略
25 | - 直方图做差加速直接
26 | - 支持类别特征(Categorical Feature)
27 | - Cache命中率优化
28 | - 基于直方图的稀疏特征优化多线程优化。
29 |
30 | 
31 |
32 | ### 1.2 Histogram算法
33 |
34 | 直方图算法的基本思想是先把连续的浮点特征值离散化成k个整数(其实又是分桶的思想,而这些桶称为bin,比如[0,0.1)→0, [0.1,0.3)→1),同时构造一个宽度为k的直方图。
35 |
36 | 在遍历数据的时候,根据离散化后的值作为索引在直方图中累积统计量,当遍历一次数据后,直方图累积了需要的统计量,然后根据直方图的离散值,遍历寻找最优的分割点。
37 |
38 | 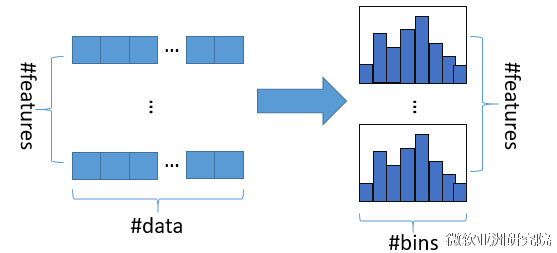
39 |
40 | 使用直方图算法有很多优点。首先,最明显就是内存消耗的降低,直方图算法不仅不需要额外存储预排序的结果,而且可以只保存特征离散化后的值,而这个值一般用8位整型存储就足够了,内存消耗可以降低为原来的1/8。然后在计算上的代价也大幅降低,预排序算法每遍历一个特征值就需要计算一次分裂的增益,而直方图算法只需要计算k次(k可以认为是常数),时间复杂度从O(#data*#feature)优化到O(k*#features)。
41 |
42 | ### 1.3 带深度限制的Leaf-wise的叶子生长策略
43 |
44 | 在XGBoost中,树是按层生长的,称为Level-wise tree growth,同一层的所有节点都做分裂,最后剪枝,如下图所示:
45 |
46 | 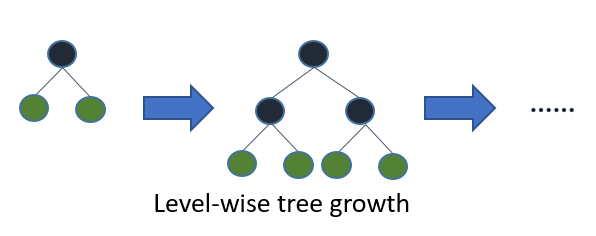
47 |
48 | Level-wise过一次数据可以同时分裂同一层的叶子,容易进行多线程优化,也好控制模型复杂度,不容易过拟合。但实际上Level-wise是一种低效的算法,因为它不加区分的对待同一层的叶子,带来了很多没必要的开销,因为实际上很多叶子的分裂增益较低,没必要进行搜索和分裂。
49 |
50 | 在Histogram算法之上,LightGBM进行进一步的优化。首先它抛弃了大多数GBDT工具使用的按层生长 (level-wise)
51 | 的决策树生长策略,而使用了带有深度限制的按叶子生长 (leaf-wise)算法。
52 |
53 | 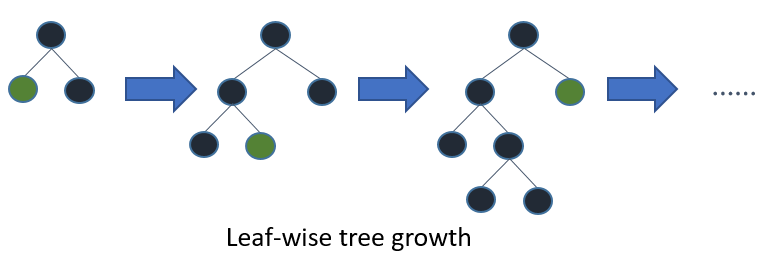
54 |
55 | Leaf-wise则是一种更为高效的策略,每次从当前所有叶子中,找到分裂增益最大的一个叶子,然后分裂,如此循环。因此同Level-wise相比,在分裂次数相同的情况下,Leaf-wise可以降低更多的误差,得到更好的精度。Leaf-wise的缺点是可能会长出比较深的决策树,产生过拟合。因此LightGBM在Leaf-wise之上增加了一个最大深度的限制,在保证高效率的同时防止过拟合。
56 |
57 | ### 1.4 直方图差加速
58 |
59 | LightGBM另一个优化是Histogram(直方图)做差加速。一个容易观察到的现象:一个叶子的直方图可以由它的父亲节点的直方图与它兄弟的直方图做差得到。通常构造直方图,需要遍历该叶子上的所有数据,但直方图做差仅需遍历直方图的k个桶。
60 |
61 | 利用这个方法,LightGBM可以在构造一个叶子的直方图后,可以用非常微小的代价得到它兄弟叶子的直方图,在速度上可以提升一倍。
62 |
63 | ### 1.5 直接支持类别特征
64 |
65 | 实际上大多数机器学习工具都无法直接支持类别特征,一般需要把类别特征,转化到多维的0/1特征,降低了空间和时间的效率。而类别特征的使用是在实践中很常用的。基于这个考虑,LightGBM优化了对类别特征的支持,可以直接输入类别特征,不需要额外的0/1展开。并在决策树算法上增加了类别特征的决策规则。在Expo数据集上的实验,相比0/1展开的方法,训练速度可以加速8倍,并且精度一致。据我们所知,LightGBM是第一个直接支持类别特征的GBDT工具。
66 |
67 | ## 2. LightGBM优点
68 |
69 | LightGBM (Light Gradient Boosting Machine)(请点击[https://github.com/Microsoft/LightGBM](https://github.com/Microsoft/LightGBM))是一个实现GBDT算法的框架,支持高效率的并行训练,并且具有以下优点:
70 |
71 | - 更快的训练速度
72 | - 更低的内存消耗
73 | - 更好的准确率
74 | - 分布式支持,可以快速处理海量数据
75 |
76 | ## 3. 代码实现
77 |
78 | 为了演示LightGBM在Python中的用法,本代码以sklearn包中自带的鸢尾花数据集为例,用lightgbm算法实现鸢尾花种类的分类任务。
79 |
80 | GitHub:[点击进入](https://github.com/NLP-LOVE/ML-NLP/blob/master/Machine%20Learning/3.4%20LightGBM/3.4%20LightGBM.ipynb)
81 |
82 | > 作者:[@mantchs](https://github.com/NLP-LOVE/ML-NLP)
83 | >
84 | > GitHub:[https://github.com/NLP-LOVE/ML-NLP](https://github.com/NLP-LOVE/ML-NLP)
85 | >
86 | > 欢迎大家加入讨论!共同完善此项目!群号:【541954936】 87 |
--------------------------------------------------------------------------------
/XGBoost-1.md:
--------------------------------------------------------------------------------
1 | ## 目录
2 |
3 | - [1. 什么是XGBoost](https://github.com/NLP-LOVE/ML-NLP/tree/master/Machine%20Learning/3.3%20XGBoost#1-什么是xgboost)
4 | - [1.1 XGBoost树的定义](https://github.com/NLP-LOVE/ML-NLP/tree/master/Machine%20Learning/3.3%20XGBoost#11-xgboost树的定义)
5 | - [1.2 正则项:树的复杂度](https://github.com/NLP-LOVE/ML-NLP/tree/master/Machine%20Learning/3.3%20XGBoost#12-正则项树的复杂度)
6 | - [1.3 树该怎么长](https://github.com/NLP-LOVE/ML-NLP/tree/master/Machine%20Learning/3.3%20XGBoost#13-树该怎么长)
7 | - [1.4 如何停止树的循环生成](https://github.com/NLP-LOVE/ML-NLP/tree/master/Machine%20Learning/3.3%20XGBoost#14-如何停止树的循环生成)
8 | - [2. XGBoost与GBDT有什么不同](https://github.com/NLP-LOVE/ML-NLP/tree/master/Machine%20Learning/3.3%20XGBoost#2-xgboost与gbdt有什么不同)
9 | - [3. 为什么XGBoost要用泰勒展开,优势在哪里?](https://github.com/NLP-LOVE/ML-NLP/tree/master/Machine%20Learning/3.3%20XGBoost#3-为什么xgboost要用泰勒展开优势在哪里)
10 | - [4. 代码实现](https://github.com/NLP-LOVE/ML-NLP/blob/master/Machine%20Learning/3.3%20XGBoost/3.3%20XGBoost.ipynb)
11 | - [5. 参考文献](https://github.com/NLP-LOVE/ML-NLP/tree/master/Machine%20Learning/3.3%20XGBoost#5-参考文献)
12 |
13 | ## 1. 什么是XGBoost
14 |
15 | XGBoost是陈天奇等人开发的一个开源机器学习项目,高效地实现了GBDT算法并进行了算法和工程上的许多改进,被广泛应用在Kaggle竞赛及其他许多机器学习竞赛中并取得了不错的成绩。
16 |
17 | 说到XGBoost,不得不提GBDT(Gradient Boosting Decision Tree)。因为XGBoost本质上还是一个GBDT,但是力争把速度和效率发挥到极致,所以叫X (Extreme) GBoosted。包括前面说过,两者都是boosting方法。
18 |
19 | 关于GBDT,这里不再提,可以查看我前一篇的介绍,[点此跳转](https://github.com/NLP-LOVE/ML-NLP/blob/master/Machine%20Learning/3.2%20GBDT/3.2%20GBDT.md)。
20 |
21 | [https://mp.weixin.qq.com/s/_NCKAon-megJbxzV6w3aYg]()
22 |
23 | ### 1.1 XGBoost树的定义
24 |
25 | 先来举个**例子**,我们要预测一家人对电子游戏的喜好程度,考虑到年轻和年老相比,年轻更可能喜欢电子游戏,以及男性和女性相比,男性更喜欢电子游戏,故先根据年龄大小区分小孩和大人,然后再通过性别区分开是男是女,逐一给各人在电子游戏喜好程度上打分,如下图所示。
26 |
27 | 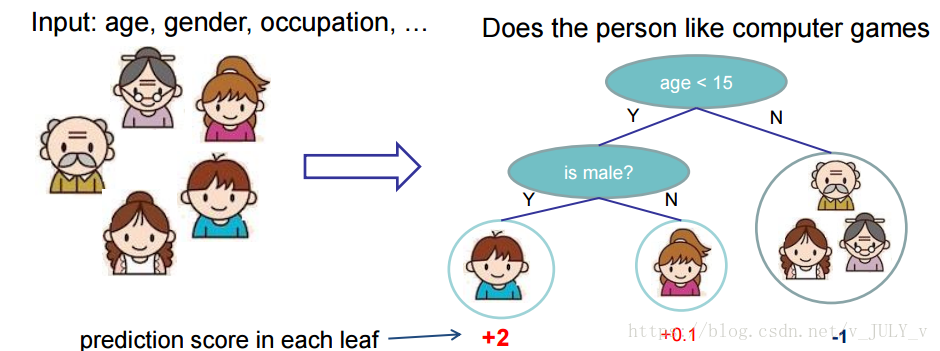
28 |
29 | 就这样,训练出了2棵树tree1和tree2,类似之前gbdt的原理,两棵树的结论累加起来便是最终的结论,所以小孩的预测分数就是两棵树中小孩所落到的结点的分数相加:2 + 0.9 = 2.9。爷爷的预测分数同理:-1 + (-0.9)= -1.9。具体如下图所示:
30 |
31 | 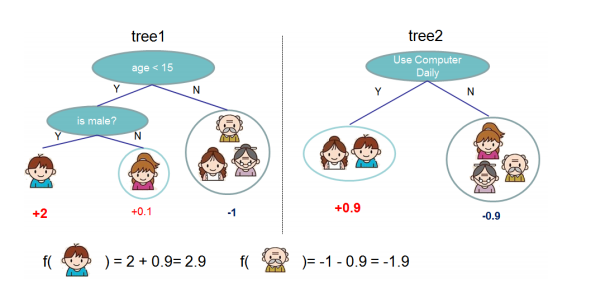
32 |
33 | 恩,你可能要拍案而起了,惊呼,这不是跟上文介绍的GBDT乃异曲同工么?
34 |
35 | 事实上,如果不考虑工程实现、解决问题上的一些差异,XGBoost与GBDT比较大的不同就是目标函数的定义。XGBoost的目标函数如下图所示:
36 |
37 | 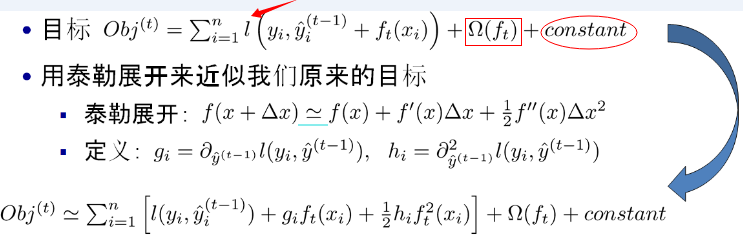
38 |
39 | 其中:
40 |
41 | - 红色箭头所指向的L 即为损失函数(比如平方损失函数:=(y_i-y^i)^2))
42 | - 红色方框所框起来的是正则项(包括L1正则、L2正则)
43 | - 红色圆圈所圈起来的为常数项
44 | - 对于f(x),XGBoost利用泰勒展开三项,做一个近似。**f(x)表示的是其中一颗回归树。**
45 |
46 | 看到这里可能有些读者会头晕了,这么多公式,**我在这里只做一个简要式的讲解,具体的算法细节和公式求解请查看这篇博文,讲得很仔细**:[通俗理解kaggle比赛大杀器xgboost](https://blog.csdn.net/v_JULY_v/article/details/81410574)
47 |
48 | XGBoost的**核心算法思想**不难,基本就是:
49 |
50 | 1. 不断地添加树,不断地进行特征分裂来生长一棵树,每次添加一个树,其实是学习一个新函数**f(x)**,去拟合上次预测的残差。
51 | 2. 当我们训练完成得到k棵树,我们要预测一个样本的分数,其实就是根据这个样本的特征,在每棵树中会落到对应的一个叶子节点,每个叶子节点就对应一个分数
52 | 3. 最后只需要将每棵树对应的分数加起来就是该样本的预测值。
53 |
54 | 显然,我们的目标是要使得树群的预测值尽量接近真实值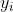,而且有尽量大的泛化能力。类似之前GBDT的套路,XGBoost也是需要将多棵树的得分累加得到最终的预测得分(每一次迭代,都在现有树的基础上,增加一棵树去拟合前面树的预测结果与真实值之间的残差)。
55 |
56 | 
57 |
58 | 那接下来,我们如何选择每一轮加入什么 f 呢?答案是非常直接的,选取一个 f 来使得我们的目标函数尽量最大地降低。这里 f 可以使用泰勒展开公式近似。
59 |
60 | 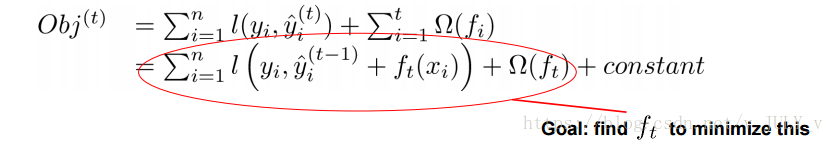
61 |
62 | 实质是把样本分配到叶子结点会对应一个obj,优化过程就是obj优化。也就是分裂节点到叶子不同的组合,不同的组合对应不同obj,所有的优化围绕这个思想展开。到目前为止我们讨论了目标函数中的第一个部分:训练误差。接下来我们讨论目标函数的第二个部分:正则项,即如何定义树的复杂度。
63 |
64 | ### 1.2 正则项:树的复杂度
65 |
66 | XGBoost对树的复杂度包含了两个部分:
67 |
68 | - 一个是树里面叶子节点的个数T
69 | - 一个是树上叶子节点的得分w的L2模平方(对w进行L2正则化,相当于针对每个叶结点的得分增加L2平滑,目的是为了避免过拟合)
70 |
71 | 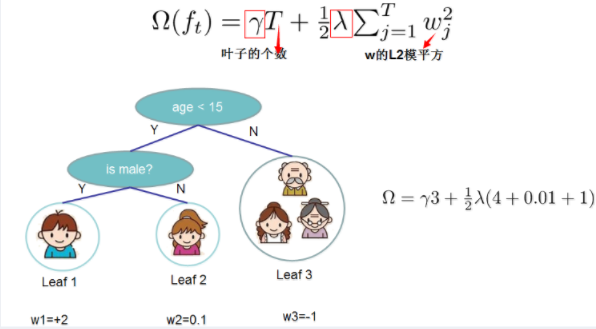
72 |
73 | 我们再来看一下XGBoost的目标函数(损失函数揭示训练误差 + 正则化定义复杂度):
74 |
75 | =\sum_{i}l(y_i^{'}-y_i)+\sum_k\Omega(f_t))
76 |
77 | 正则化公式也就是目标函数的后半部分,对于上式而言,是整个累加模型的输出,正则化项∑kΩ(ft)是则表示树的复杂度的函数,值越小复杂度越低,泛化能力越强。
78 |
79 | ### 1.3 树该怎么长
80 |
81 | 很有意思的一个事是,我们从头到尾了解了xgboost如何优化、如何计算,但树到底长啥样,我们却一直没看到。很显然,一棵树的生成是由一个节点一分为二,然后不断分裂最终形成为整棵树。那么树怎么分裂的就成为了接下来我们要探讨的关键。对于一个叶子节点如何进行分裂,XGBoost作者在其原始论文中给出了一种分裂节点的方法:**枚举所有不同树结构的贪心法**
82 |
83 | 不断地枚举不同树的结构,然后利用打分函数来寻找出一个最优结构的树,接着加入到模型中,不断重复这样的操作。这个寻找的过程使用的就是**贪心算法**。选择一个feature分裂,计算loss function最小值,然后再选一个feature分裂,又得到一个loss function最小值,你枚举完,找一个效果最好的,把树给分裂,就得到了小树苗。
84 |
85 | 总而言之,XGBoost使用了和CART回归树一样的想法,利用贪婪算法,遍历所有特征的所有特征划分点,不同的是使用的目标函数不一样。具体做法就是分裂后的目标函数值比单子叶子节点的目标函数的增益,同时为了限制树生长过深,还加了个阈值,只有当增益大于该阈值才进行分裂。从而继续分裂,形成一棵树,再形成一棵树,**每次在上一次的预测基础上取最优进一步分裂/建树。**
86 |
87 | ### 1.4 如何停止树的循环生成
88 |
89 | 凡是这种循环迭代的方式必定有停止条件,什么时候停止呢?简言之,设置树的最大深度、当样本权重和小于设定阈值时停止生长以防止过拟合。具体而言,则
90 |
91 | 1. 当引入的分裂带来的增益小于设定阀值的时候,我们可以忽略掉这个分裂,所以并不是每一次分裂loss function整体都会增加的,有点预剪枝的意思,阈值参数为(即正则项里叶子节点数T的系数);
92 | 2. 当树达到最大深度时则停止建立决策树,设置一个超参数max_depth,避免树太深导致学习局部样本,从而过拟合;
93 | 3. 样本权重和小于设定阈值时则停止建树。什么意思呢,即涉及到一个超参数-最小的样本权重和min_child_weight,和GBM的 min_child_leaf 参数类似,但不完全一样。大意就是一个叶子节点样本太少了,也终止同样是防止过拟合;
94 |
95 | ## 2. XGBoost与GBDT有什么不同
96 |
97 | 除了算法上与传统的GBDT有一些不同外,XGBoost还在工程实现上做了大量的优化。总的来说,两者之间的区别和联系可以总结成以下几个方面。
98 |
99 | 1. GBDT是机器学习算法,XGBoost是该算法的工程实现。
100 | 2. 在使用CART作为基分类器时,XGBoost显式地加入了正则项来控制模 型的复杂度,有利于防止过拟合,从而提高模型的泛化能力。
101 | 3. GBDT在模型训练时只使用了代价函数的一阶导数信息,XGBoost对代 价函数进行二阶泰勒展开,可以同时使用一阶和二阶导数。
102 | 4. 传统的GBDT采用CART作为基分类器,XGBoost支持多种类型的基分类 器,比如线性分类器。
103 | 5. 传统的GBDT在每轮迭代时使用全部的数据,XGBoost则采用了与随机 森林相似的策略,支持对数据进行采样。
104 | 6. 传统的GBDT没有设计对缺失值进行处理,XGBoost能够自动学习出缺 失值的处理策略。
105 |
106 | ## 3. 为什么XGBoost要用泰勒展开,优势在哪里?
107 |
108 | XGBoost使用了一阶和二阶偏导, 二阶导数有利于梯度下降的更快更准. 使用泰勒展开取得函数做自变量的二阶导数形式, 可以在不选定损失函数具体形式的情况下, 仅仅依靠输入数据的值就可以进行叶子分裂优化计算, 本质上也就把损失函数的选取和模型算法优化/参数选择分开了. 这种去耦合增加了XGBoost的适用性, 使得它按需选取损失函数, 可以用于分类, 也可以用于回归。
109 |
110 | ## 4. 代码实现
111 |
112 | GitHub:[点击进入](https://github.com/NLP-LOVE/ML-NLP/blob/master/Machine%20Learning/3.3%20XGBoost/3.3%20XGBoost.ipynb)
113 |
114 | ## 5. 参考文献
115 |
116 | [通俗理解kaggle比赛大杀器xgboost](https://blog.csdn.net/v_JULY_v/article/details/81410574)
117 |
118 | > 作者:[@mantchs](https://github.com/NLP-LOVE/ML-NLP)
119 | >
120 | > GitHub:[https://github.com/NLP-LOVE/ML-NLP](https://github.com/NLP-LOVE/ML-NLP)
121 | >
122 | > 欢迎大家加入讨论!共同完善此项目!群号:【541954936】`
87 |
--------------------------------------------------------------------------------
/XGBoost-1.md:
--------------------------------------------------------------------------------
1 | ## 目录
2 |
3 | - [1. 什么是XGBoost](https://github.com/NLP-LOVE/ML-NLP/tree/master/Machine%20Learning/3.3%20XGBoost#1-什么是xgboost)
4 | - [1.1 XGBoost树的定义](https://github.com/NLP-LOVE/ML-NLP/tree/master/Machine%20Learning/3.3%20XGBoost#11-xgboost树的定义)
5 | - [1.2 正则项:树的复杂度](https://github.com/NLP-LOVE/ML-NLP/tree/master/Machine%20Learning/3.3%20XGBoost#12-正则项树的复杂度)
6 | - [1.3 树该怎么长](https://github.com/NLP-LOVE/ML-NLP/tree/master/Machine%20Learning/3.3%20XGBoost#13-树该怎么长)
7 | - [1.4 如何停止树的循环生成](https://github.com/NLP-LOVE/ML-NLP/tree/master/Machine%20Learning/3.3%20XGBoost#14-如何停止树的循环生成)
8 | - [2. XGBoost与GBDT有什么不同](https://github.com/NLP-LOVE/ML-NLP/tree/master/Machine%20Learning/3.3%20XGBoost#2-xgboost与gbdt有什么不同)
9 | - [3. 为什么XGBoost要用泰勒展开,优势在哪里?](https://github.com/NLP-LOVE/ML-NLP/tree/master/Machine%20Learning/3.3%20XGBoost#3-为什么xgboost要用泰勒展开优势在哪里)
10 | - [4. 代码实现](https://github.com/NLP-LOVE/ML-NLP/blob/master/Machine%20Learning/3.3%20XGBoost/3.3%20XGBoost.ipynb)
11 | - [5. 参考文献](https://github.com/NLP-LOVE/ML-NLP/tree/master/Machine%20Learning/3.3%20XGBoost#5-参考文献)
12 |
13 | ## 1. 什么是XGBoost
14 |
15 | XGBoost是陈天奇等人开发的一个开源机器学习项目,高效地实现了GBDT算法并进行了算法和工程上的许多改进,被广泛应用在Kaggle竞赛及其他许多机器学习竞赛中并取得了不错的成绩。
16 |
17 | 说到XGBoost,不得不提GBDT(Gradient Boosting Decision Tree)。因为XGBoost本质上还是一个GBDT,但是力争把速度和效率发挥到极致,所以叫X (Extreme) GBoosted。包括前面说过,两者都是boosting方法。
18 |
19 | 关于GBDT,这里不再提,可以查看我前一篇的介绍,[点此跳转](https://github.com/NLP-LOVE/ML-NLP/blob/master/Machine%20Learning/3.2%20GBDT/3.2%20GBDT.md)。
20 |
21 | [https://mp.weixin.qq.com/s/_NCKAon-megJbxzV6w3aYg]()
22 |
23 | ### 1.1 XGBoost树的定义
24 |
25 | 先来举个**例子**,我们要预测一家人对电子游戏的喜好程度,考虑到年轻和年老相比,年轻更可能喜欢电子游戏,以及男性和女性相比,男性更喜欢电子游戏,故先根据年龄大小区分小孩和大人,然后再通过性别区分开是男是女,逐一给各人在电子游戏喜好程度上打分,如下图所示。
26 |
27 | 
28 |
29 | 就这样,训练出了2棵树tree1和tree2,类似之前gbdt的原理,两棵树的结论累加起来便是最终的结论,所以小孩的预测分数就是两棵树中小孩所落到的结点的分数相加:2 + 0.9 = 2.9。爷爷的预测分数同理:-1 + (-0.9)= -1.9。具体如下图所示:
30 |
31 | 
32 |
33 | 恩,你可能要拍案而起了,惊呼,这不是跟上文介绍的GBDT乃异曲同工么?
34 |
35 | 事实上,如果不考虑工程实现、解决问题上的一些差异,XGBoost与GBDT比较大的不同就是目标函数的定义。XGBoost的目标函数如下图所示:
36 |
37 | 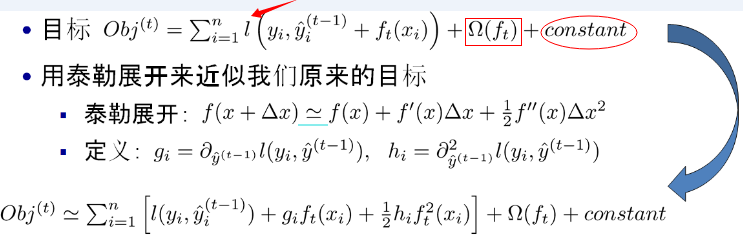
38 |
39 | 其中:
40 |
41 | - 红色箭头所指向的L 即为损失函数(比如平方损失函数:=(y_i-y^i)^2))
42 | - 红色方框所框起来的是正则项(包括L1正则、L2正则)
43 | - 红色圆圈所圈起来的为常数项
44 | - 对于f(x),XGBoost利用泰勒展开三项,做一个近似。**f(x)表示的是其中一颗回归树。**
45 |
46 | 看到这里可能有些读者会头晕了,这么多公式,**我在这里只做一个简要式的讲解,具体的算法细节和公式求解请查看这篇博文,讲得很仔细**:[通俗理解kaggle比赛大杀器xgboost](https://blog.csdn.net/v_JULY_v/article/details/81410574)
47 |
48 | XGBoost的**核心算法思想**不难,基本就是:
49 |
50 | 1. 不断地添加树,不断地进行特征分裂来生长一棵树,每次添加一个树,其实是学习一个新函数**f(x)**,去拟合上次预测的残差。
51 | 2. 当我们训练完成得到k棵树,我们要预测一个样本的分数,其实就是根据这个样本的特征,在每棵树中会落到对应的一个叶子节点,每个叶子节点就对应一个分数
52 | 3. 最后只需要将每棵树对应的分数加起来就是该样本的预测值。
53 |
54 | 显然,我们的目标是要使得树群的预测值尽量接近真实值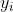,而且有尽量大的泛化能力。类似之前GBDT的套路,XGBoost也是需要将多棵树的得分累加得到最终的预测得分(每一次迭代,都在现有树的基础上,增加一棵树去拟合前面树的预测结果与真实值之间的残差)。
55 |
56 | 
57 |
58 | 那接下来,我们如何选择每一轮加入什么 f 呢?答案是非常直接的,选取一个 f 来使得我们的目标函数尽量最大地降低。这里 f 可以使用泰勒展开公式近似。
59 |
60 | 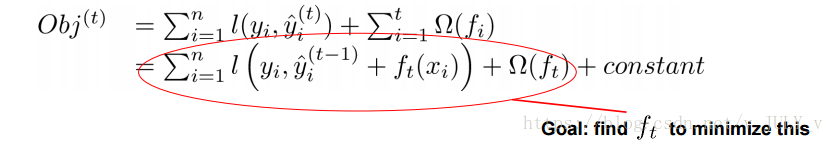
61 |
62 | 实质是把样本分配到叶子结点会对应一个obj,优化过程就是obj优化。也就是分裂节点到叶子不同的组合,不同的组合对应不同obj,所有的优化围绕这个思想展开。到目前为止我们讨论了目标函数中的第一个部分:训练误差。接下来我们讨论目标函数的第二个部分:正则项,即如何定义树的复杂度。
63 |
64 | ### 1.2 正则项:树的复杂度
65 |
66 | XGBoost对树的复杂度包含了两个部分:
67 |
68 | - 一个是树里面叶子节点的个数T
69 | - 一个是树上叶子节点的得分w的L2模平方(对w进行L2正则化,相当于针对每个叶结点的得分增加L2平滑,目的是为了避免过拟合)
70 |
71 | 
72 |
73 | 我们再来看一下XGBoost的目标函数(损失函数揭示训练误差 + 正则化定义复杂度):
74 |
75 | =\sum_{i}l(y_i^{'}-y_i)+\sum_k\Omega(f_t))
76 |
77 | 正则化公式也就是目标函数的后半部分,对于上式而言,是整个累加模型的输出,正则化项∑kΩ(ft)是则表示树的复杂度的函数,值越小复杂度越低,泛化能力越强。
78 |
79 | ### 1.3 树该怎么长
80 |
81 | 很有意思的一个事是,我们从头到尾了解了xgboost如何优化、如何计算,但树到底长啥样,我们却一直没看到。很显然,一棵树的生成是由一个节点一分为二,然后不断分裂最终形成为整棵树。那么树怎么分裂的就成为了接下来我们要探讨的关键。对于一个叶子节点如何进行分裂,XGBoost作者在其原始论文中给出了一种分裂节点的方法:**枚举所有不同树结构的贪心法**
82 |
83 | 不断地枚举不同树的结构,然后利用打分函数来寻找出一个最优结构的树,接着加入到模型中,不断重复这样的操作。这个寻找的过程使用的就是**贪心算法**。选择一个feature分裂,计算loss function最小值,然后再选一个feature分裂,又得到一个loss function最小值,你枚举完,找一个效果最好的,把树给分裂,就得到了小树苗。
84 |
85 | 总而言之,XGBoost使用了和CART回归树一样的想法,利用贪婪算法,遍历所有特征的所有特征划分点,不同的是使用的目标函数不一样。具体做法就是分裂后的目标函数值比单子叶子节点的目标函数的增益,同时为了限制树生长过深,还加了个阈值,只有当增益大于该阈值才进行分裂。从而继续分裂,形成一棵树,再形成一棵树,**每次在上一次的预测基础上取最优进一步分裂/建树。**
86 |
87 | ### 1.4 如何停止树的循环生成
88 |
89 | 凡是这种循环迭代的方式必定有停止条件,什么时候停止呢?简言之,设置树的最大深度、当样本权重和小于设定阈值时停止生长以防止过拟合。具体而言,则
90 |
91 | 1. 当引入的分裂带来的增益小于设定阀值的时候,我们可以忽略掉这个分裂,所以并不是每一次分裂loss function整体都会增加的,有点预剪枝的意思,阈值参数为(即正则项里叶子节点数T的系数);
92 | 2. 当树达到最大深度时则停止建立决策树,设置一个超参数max_depth,避免树太深导致学习局部样本,从而过拟合;
93 | 3. 样本权重和小于设定阈值时则停止建树。什么意思呢,即涉及到一个超参数-最小的样本权重和min_child_weight,和GBM的 min_child_leaf 参数类似,但不完全一样。大意就是一个叶子节点样本太少了,也终止同样是防止过拟合;
94 |
95 | ## 2. XGBoost与GBDT有什么不同
96 |
97 | 除了算法上与传统的GBDT有一些不同外,XGBoost还在工程实现上做了大量的优化。总的来说,两者之间的区别和联系可以总结成以下几个方面。
98 |
99 | 1. GBDT是机器学习算法,XGBoost是该算法的工程实现。
100 | 2. 在使用CART作为基分类器时,XGBoost显式地加入了正则项来控制模 型的复杂度,有利于防止过拟合,从而提高模型的泛化能力。
101 | 3. GBDT在模型训练时只使用了代价函数的一阶导数信息,XGBoost对代 价函数进行二阶泰勒展开,可以同时使用一阶和二阶导数。
102 | 4. 传统的GBDT采用CART作为基分类器,XGBoost支持多种类型的基分类 器,比如线性分类器。
103 | 5. 传统的GBDT在每轮迭代时使用全部的数据,XGBoost则采用了与随机 森林相似的策略,支持对数据进行采样。
104 | 6. 传统的GBDT没有设计对缺失值进行处理,XGBoost能够自动学习出缺 失值的处理策略。
105 |
106 | ## 3. 为什么XGBoost要用泰勒展开,优势在哪里?
107 |
108 | XGBoost使用了一阶和二阶偏导, 二阶导数有利于梯度下降的更快更准. 使用泰勒展开取得函数做自变量的二阶导数形式, 可以在不选定损失函数具体形式的情况下, 仅仅依靠输入数据的值就可以进行叶子分裂优化计算, 本质上也就把损失函数的选取和模型算法优化/参数选择分开了. 这种去耦合增加了XGBoost的适用性, 使得它按需选取损失函数, 可以用于分类, 也可以用于回归。
109 |
110 | ## 4. 代码实现
111 |
112 | GitHub:[点击进入](https://github.com/NLP-LOVE/ML-NLP/blob/master/Machine%20Learning/3.3%20XGBoost/3.3%20XGBoost.ipynb)
113 |
114 | ## 5. 参考文献
115 |
116 | [通俗理解kaggle比赛大杀器xgboost](https://blog.csdn.net/v_JULY_v/article/details/81410574)
117 |
118 | > 作者:[@mantchs](https://github.com/NLP-LOVE/ML-NLP)
119 | >
120 | > GitHub:[https://github.com/NLP-LOVE/ML-NLP](https://github.com/NLP-LOVE/ML-NLP)
121 | >
122 | > 欢迎大家加入讨论!共同完善此项目!群号:【541954936】` ```
123 |
--------------------------------------------------------------------------------
/catboost2.md:
--------------------------------------------------------------------------------
1 | # Catboost
2 |
3 | CatBoost是一种基于对称决策树(oblivious trees)为基学习器实现的参数较少、支持类别型变量和高准确性的GBDT框架,主要解决的痛点是高效合理地处理类别型特征,这一点从它的名字中可以看出来,CatBoost是由Categorical和Boosting组成。此外,CatBoost还解决了梯度偏差(Gradient Bias)以及预测偏移(Prediction shift)的问题,从而减少过拟合的发生,进而提高算法的准确性和泛化能力。
4 |
5 | ## 对称决策树
6 |
7 | 那么**对称树**和普通决策树有什么区别?
8 |
9 | 一图为对称树,二图为普通决策树
10 |
11 | 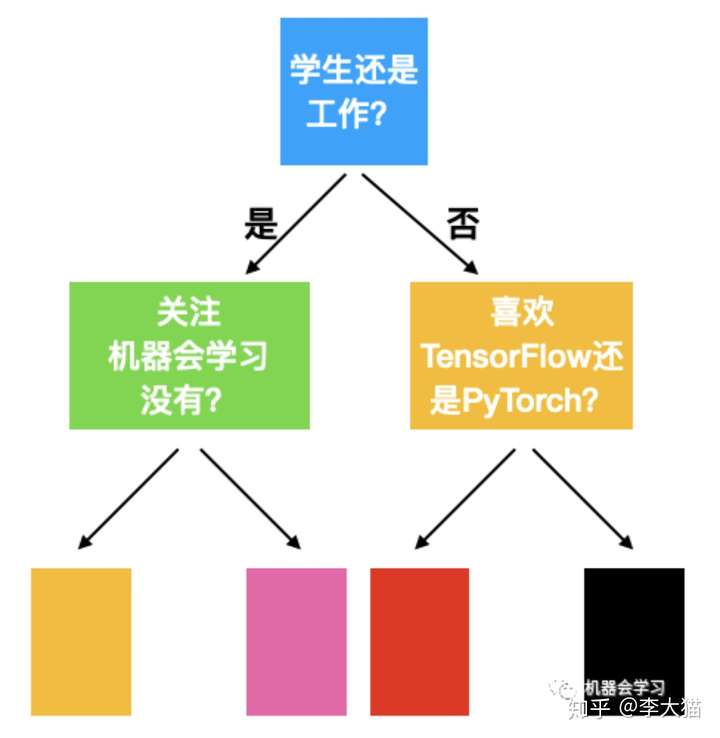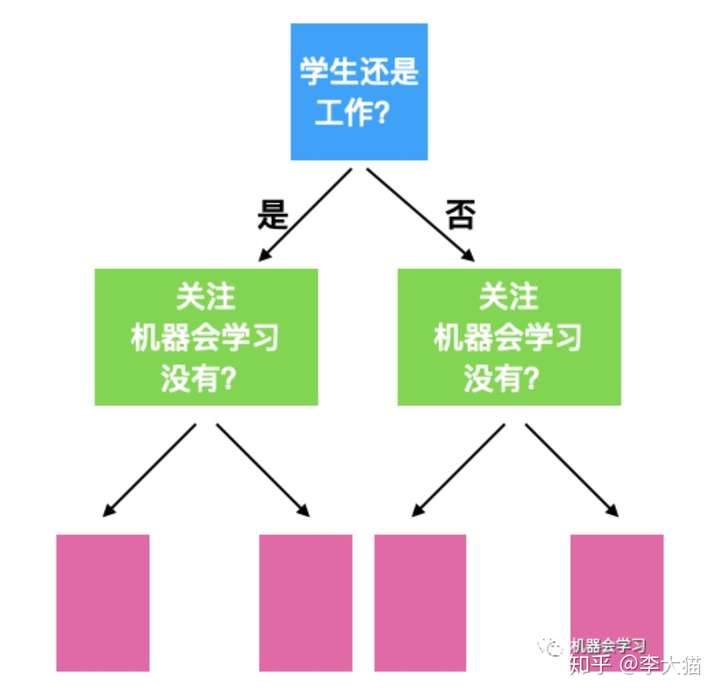
12 |
13 | 对称树中,每一层的每一个节点判断条件都是一样的。假如如果我们只训练一棵树,那么显然对称树的overfit能力会比普通的决策树弱;但是在GBM中,我们通常训练很多的树,所以overfit的能力不必担心。那么对称树在GBM中有什么优势呢?下面列出三点:
14 |
15 | * 拟合模式相对简单,因为每一层都是一个判断条件
16 | * 可以提高预测速度
17 | * 对称树的结构本身比普通决策树自由度小,可以看作是加入了penalty惩罚机制,或者看作regularization正则化
18 |
19 | 最大的优势就是第二点——预测速度会提升。为什么会更快呢?
20 |
21 | 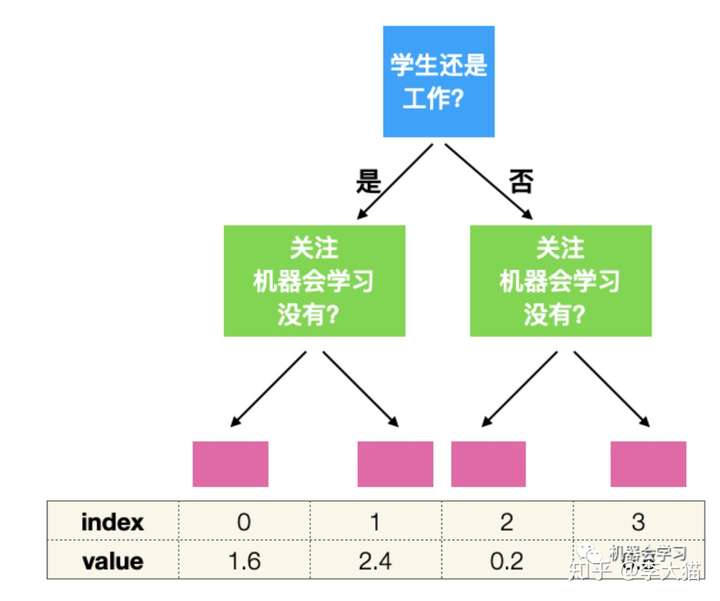
22 |
23 | 上面这棵树最底层有四个节点,我们可以把这四个节点从0到3编号(index),每一个节点有一个对应值(value)。比如一个样本最终进入了第一个节点,那么这棵树对这个样本的预测值就是1.6。我们可以把value存放在一个数组里面,这样给定index就可以立刻得到value。那么对一个样本用一棵树进行预测时,我们只需要找到这个样本对应的index,因为在对称树中每一层的判断条件都是一样的,所以每一层都可以用0或者1来表示,比如是学生,用1表示,不是用0;有关注机器会学习用1表示,没有用0,那么每一个样本进入这棵树,都可以用两个bits来表示,也就是四种可能结果:00,01,10,和11。这两个bits代表的数字就是index。
24 |
25 | 这意味着什么呢?我们在做预测的时候,只要对每一层的条件进行判断,然后就可以找到index。因为每一个树的结构(判断条件)是已知的,我们甚至可以对这个过程进行并行计算。
26 |
27 | ## Catboost与XGBoost,LightGBM相比的创新点
28 |
29 | * 嵌入了自动将类别型特征处理为数值型特征的创新算法。首先对categorical features做一些统计,计算某个类别特征(category)出现的频率,之后加上超参数,生成新的数值型特征(numerical features)。
30 | * Catboost还使用了组合类别特征,可以利用到特征之间的联系,这极大的丰富了特征维度。
31 | * 采用排序提升的方法对抗训练集中的噪声点,从而避免梯度估计的偏差,进而解决预测偏移的问题。
32 | * 采用了完全对称树作为基模型。
33 |
34 | ## **类别型特征**
35 |
36 | ### **2.1 类别型特征的相关工作**
37 |
38 | 所谓类别型特征,即这类特征不是数值型特征,而是离散的集合,比如省份名(山东、山西、河北等),城市名(北京、上海、深圳等),学历(本科、硕士、博士等)。在梯度提升算法中,最常用的是将这些类别型特征转为数值型来处理,一般类别型特征会转化为一个或多个数值型特征。
39 |
40 | 如果某个 **类别型特征基数比较低(low-cardinality features)** ,即该特征的所有值去重后构成的集合元素个数比较少,一般利用One-hot编码方法将特征转为数值型。One-hot编码可以在数据预处理时完成,也可以在模型训练的时候完成,从训练时间的角度,后一种方法的实现更为高效,CatBoost对于基数较低的类别型特征也是采用后一种实现。
41 |
42 | 显然,在 **高基数类别型特征(high cardinality features)** 当中,比如 `user ID`,这种编码方式会产生大量新的特征,造成维度灾难。一种折中的办法是可以将类别分组成有限个的群体再进行One-hot编码。一种常被使用的方法是根据目标变量统计(Target Statistics,以下简称TS)进行分组,目标变量统计用于估算每个类别的目标变量期望值。甚至有人直接用TS作为一个新的数值型变量来代替原来的类别型变量。重要的是,可以通过对TS数值型特征的阈值设置,基于对数损失、基尼系数或者均方差,得到一个对于训练集而言将类别一分为二的所有可能划分当中最优的那个。在LightGBM当中,类别型特征用每一步梯度提升时的梯度统计(Gradient Statistics,以下简称GS)来表示。虽然为建树提供了重要的信息,但是这种方法有以下两个缺点:
43 |
44 | * 增加计算时间,因为需要对每一个类别型特征,在迭代的每一步,都需要对GS进行计算;
45 | * 增加存储需求,对于一个类别型变量,需要存储每一次分离每个节点的类别;
46 |
47 | 为了克服这些缺点,LightGBM以损失部分信息为代价将所有的长尾类别归为一类,作者声称这样处理高基数类别型特征时比One-hot编码还是好不少。不过如果采用TS特征,那么对于每个类别只需要计算和存储一个数字。
48 |
49 | ### **2.2 目标变量统计(Target Statistics)**
50 |
51 | CatBoost算法的设计初衷是为了更好的处理GBDT特征中的categorical features。在处理 GBDT特征中的categorical features的时候,最简单的方法是用 categorical feature 对应的标签的平均值来替换。在决策树中,标签平均值将作为节点分裂的标准。这种方法被称为 Greedy Target-based Statistics , 简称 Greedy TS,用公式来表达就是:
52 |
53 | ![[公式]](https://www.zhihu.com/equation?tex=%5Chat%7Bx%7D_k%5Ei%3D%5Cfrac%7B%5Csum_%7Bj%3D1%7D%5E%7Bn%7D%5Bx_%7Bj%2Ck%7D%3Dx_%7Bi%2Ck%7D%5D%5Ccdot+Y_i%7D%7B%5Csum_%7Bj%3D1%7D%5E%7Bn%7D%5Bx_%7Bj%2Ck%7D%3Dx_%7Bi%2Ck%7D%5D%7D+%5C%5C)
54 |
55 | 这种方法有一个显而易见的缺陷,就是通常特征比标签包含更多的信息,如果强行用标签的平均值来表示特征的话,当训练数据集和测试数据集数据结构和分布不一样的时候会出条件偏移问题。
56 |
57 | 一个标准的改进 Greedy TS的方式是添加先验分布项,这样可以减少噪声和低频率类别型数据对于数据分布的影响:
58 |
59 | ![[公式]](https://www.zhihu.com/equation?tex=%5Chat%7Bx%7D_k%5Ei%3D%5Cfrac%7B%5Csum_%7Bj%3D1%7D%5E%7Bp-1%7D%7B%5Bx_%7B%5Csigma_%7Bj%2Ck%7D%7D%3Dx_%7B%5Csigma_%7Bp%2Ck%7D%7D%5D%7DY_%7B%5Csigma_%7Bj%7D%7D%2Ba%5Ccdot+p%7D%7B%5Csum_%7Bj%3D1%7D%5E%7Bp-1%7D%7B%5Bx_%7B%5Csigma_%7Bj%2Ck%7D%7D%3Dx_%7B%5Csigma_%7Bp%2Ck%7D%7D%5D%7D%2Ba%7D+%5C%5C)
60 |
61 | 其中 ![[公式]](https://www.zhihu.com/equation?tex=p)是添加的先验项, ![[公式]](https://www.zhihu.com/equation?tex=a+)通常是大于0的权重系数。添加先验项是一个普遍做法,针对类别数较少的特征,它可以减少噪声数据。对于回归问题,一般情况下,先验项可取数据集label的均值。对于二分类,先验项是正例的先验概率。利用多个数据集排列也是有效的,但是,如果直接计算可能导致过拟合。CatBoost利用了一个比较新颖的计算叶子节点值的方法,这种方式(oblivious trees,对称树)可以避免多个数据集排列中直接计算会出现过拟合的问题。
62 |
63 | ### **2.3 特征组合**
64 |
65 | 值得注意的是几个类别型特征的任意组合都可视为新的特征。例如,在音乐推荐应用中,我们有两个类别型特征:用户ID和音乐流派。如果有些用户更喜欢摇滚乐,将用户ID和音乐流派转换为数字特征时,根据上述这些信息就会丢失。结合这两个特征就可以解决这个问题,并且可以得到一个新的强大的特征。然而,组合的数量会随着数据集中类别型特征的数量成指数增长,因此不可能在算法中考虑所有组合。为当前树构造新的分割点时,CatBoost会采用贪婪的策略考虑组合。对于树的第一次分割,不考虑任何组合。对于下一个分割,CatBoost将当前树的所有组合、类别型特征与数据集中的所有类别型特征相结合,并将新的组合类别型特征动态地转换为数值型特征。CatBoost还通过以下方式生成数值型特征和类别型特征的组合:树中选定的所有分割点都被视为具有两个值的类别型特征,并像类别型特征一样被进行组合考虑。
66 |
67 | ### **2.4 CatBoost处理Categorical features总结**
68 |
69 | * 首先会计算一些数据的statistics。计算某个category出现的频率,加上超参数,生成新的numerical features。这一策略要求同一标签数据不能排列在一起(即先全是0之后全是1这种方式),训练之前需要打乱数据集。
70 | * 第二,使用数据的不同排列(实际上是4个)。在每一轮建立树之前,先扔一轮骰子,决定使用哪个排列来生成树。
71 | * 第三,考虑使用categorical features的不同组合。例如颜色和种类组合起来,可以构成类似于blue dog这样的特征。当需要组合的categorical features变多时,CatBoost只考虑一部分combinations。在选择第一个节点时,只考虑选择一个特征,例如A。在生成第二个节点时,考虑A和任意一个categorical feature的组合,选择其中最好的。就这样使用贪心算法生成combinations。
72 | * 第四,除非向gender这种维数很小的情况,不建议自己生成One-hot编码向量,最好交给算法来处理。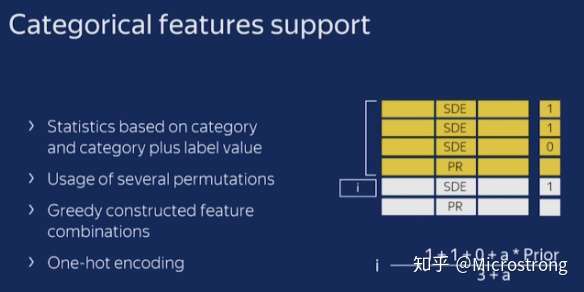
73 |
74 | ## **克服梯度偏差**
75 |
76 | CatBoost和所有标准梯度提升算法一样,都是通过构建新树来拟合当前模型的梯度。然而,所有经典的提升算法都存在由有偏的点态梯度估计引起的过拟合问题。在每个步骤中使用的梯度都使用当前模型中的相同的数据点来估计,这导致估计梯度在特征空间的任何域中的分布与该域中梯度的真实分布相比发生了偏移,从而导致过拟合。为了解决这个问题,CatBoost对经典的梯度提升算法进行了一些改进,简要介绍如下。
77 |
78 | 许多利用GBDT技术的算法(例如,XGBoost、LightGBM),构建下一棵树分为两个阶段:选择树结构和在树结构固定后计算叶子节点的值。为了选择最佳的树结构,算法通过枚举不同的分割,用这些分割构建树,对得到的叶子节点计算值,然后对得到的树计算评分,最后选择最佳的分割。两个阶段叶子节点的值都是被当做梯度或牛顿步长的近似值来计算。在CatBoost中,第一阶段采用梯度步长的无偏估计,第二阶段使用传统的GBDT方案执行。既然原来的梯度估计是有偏的,那么怎么能改成无偏估计呢?
79 |
80 | 
81 |
82 |
83 | ## **预测偏移和排序提升**
84 |
85 | 预测偏移(Prediction shift)是由梯度偏差造成的。在GDBT的每一步迭代中, 损失函数使用相同的数据集求得当前模型的梯度, 然后训练得到基学习器, 但这会导致梯度估计偏差, 进而导致模型产生过拟合的问题。 CatBoost通过采用排序提升 (Ordered boosting) 的方式替换传统算法中梯度估计方法,进而减轻梯度估计的偏差,提高模型的泛化能力。下面我们对预测偏移进行详细的描述和分析。
86 |
87 | 首先来看下GBDT的整体迭代过程:
88 |
89 | GBDT算法是通过一组分类器的串行迭代,最终得到一个强学习器,以此来进行更高精度的分类。它使用了前向分布算法,弱学习器使用分类回归树(CART)。
90 |
91 | 
92 |
93 | ### 排序提升
94 |
95 | 为了克服预测偏移问题,CatBoost提出了一种新的叫做Ordered boosting的算法。
96 |
97 | 
98 |
99 | 
100 |
101 |
102 | ## **快速评分**
103 |
104 | CatBoost使用对称树(oblivious trees)作为基预测器。在这类树中,相同的分割准则在树的整个一层上使用。这种树是平衡的,不太容易过拟合。梯度提升对称树被成功地用于各种学习任务中。在对称树中,每个叶子节点的索引可以被编码为长度等于树深度的二进制向量。这在CatBoost模型评估器中得到了广泛的应用:我们首先将所有浮点特征、统计信息和独热编码特征进行二值化,然后使用二进制特征来计算模型预测值。
105 |
106 |
107 | ## 基于GPU实现快速训练
108 |
109 | * **密集的数值特征。** 对于任何GBDT算法而言,最大的难点之一就是搜索最佳分割。尤其是对于密集的数值特征数据集来说,该步骤是建立决策树时的主要计算负担。CatBoost使用oblivious 决策树作为基模型,并将特征离散化到固定数量的箱子中以减少内存使用。就GPU内存使用而言,CatBoost至少与LightGBM一样有效。主要改进之处就是利用了一种不依赖于原子操作的直方图计算方法。
110 | * **类别型特征。** CatBoost实现了多种处理类别型特征的方法,并使用完美哈希来存储类别型特征的值,以减少内存使用。由于GPU内存的限制,在CPU RAM中存储按位压缩的完美哈希,以及要求的数据流、重叠计算和内存等操作。通过哈希来分组观察。在每个组中,我们需要计算一些统计量的前缀和。该统计量的计算使用分段扫描GPU图元实现。
111 | * **多GPU支持。** CatBoost中的GPU实现可支持多个GPU。分布式树学习可以通过数据或特征进行并行化。CatBoost采用多个学习数据集排列的计算方案,在训练期间计算类别型特征的统计数据。
112 |
113 | ## **CatBoost的优缺点**
114 |
115 | **7.1 优点**
116 |
117 | * **性能卓越** :在性能方面可以匹敌任何先进的机器学习算法;
118 | * **鲁棒性/强健性** :它减少了对很多超参数调优的需求,并降低了过度拟合的机会,这也使得模型变得更加具有通用性;
119 | * **易于使用** :提供与scikit集成的Python接口,以及R和命令行界面;
120 | * **实用** :可以处理类别型、数值型特征;
121 | * **可扩展:** 支持自定义损失函数;
122 |
123 | **7.2 缺点**
124 |
125 | * 对于类别型特征的处理需要大量的内存和时间;
126 | * 不同随机数的设定对于模型预测结果有一定的影响;
127 |
--------------------------------------------------------------------------------
/XGBoost-2.md:
--------------------------------------------------------------------------------
1 | ## 算法原理
2 |
3 | XGBoost是在Gradient Boosting框架下面对GBDT的优化,是一种GBDT的工业级实现。其主要原理是在GBDT的基础上,在损失函数加入正则化部分,并且每一轮迭代对误差无法做二阶泰勒展开,加快对损失函数的优化速度。下面基于决策树弱分类器,梳理XGBoost算法的主流程,部分参数可能现在会看得有些懵懂,后面的内容会慢慢提到,这里先给一个整体的流程框架。
4 |
5 | * **输入:**
6 |
7 | * 训练数据集$T={(x_1,y_1),(x_2,y_2),...,(x_N,y_N)},x_i\in X\subseteq R^n,y_i \in Y={-1,+1}$;最大迭代次数$M$,损失函数 $L(Y,f(X))$;正则化系数$\lambda,\,\gamma$。
8 | * **输出:**
9 | * 强学习器 $f(x)$
10 | * 初始化 $f_0(x)$
11 | * 对$m=1,2,...,M$轮迭代有:
12 |
13 | * 1)计算第$i$个样本($i=1,2,...,N$)在当前轮损失函数$L$基于$f_{m-1}(x_i)$的一阶导数$g_{mi}$,二阶导数$h_{mi}$,并求和:
14 |
15 | $$
16 | G_m=\sum_{i=1}^{N}g_{mi}
17 |
18 | $$
19 |
20 | $$
21 | H_m=\sum_{i=1}^{N}h_{mi}
22 |
23 | $$
24 | * 2)基于当前节点尝试分裂决策树,默认分数 $score=0$,对特征序号$k=1,2,...,K$
25 |
26 | * a)初始化$G_L=0,H_L=0$
27 | * b.1)将样本按特征 $k$ 从小到大排列,依次取出第 $i$个样本,依次计算当前样本放入左子树后,左右子树一阶和二阶导数和:
28 |
29 | $$
30 | G_L=G_L+g_{mi},\,G_R=G-G_L
31 |
32 | $$
33 |
34 | $$
35 | H_L=H_L+h_{mi},\,H_R=H-H_L
36 |
37 | $$
38 | * b.2)尝试更新最大的分数:
39 |
40 | $$
41 | score=max(score,\,\frac{1}{2}\frac{G_L^2}{H_L+\lambda}+\frac{1}{2}\frac{G_R^2}{H_R+\lambda}-\frac{1}{2}\frac{(G_L+G_R)^2}{H_L+H_R+\lambda})
42 |
43 | $$
44 | * 3)基于最大$score$对应的划分特征和特征值分裂子树
45 | * 4)如果最大$score$为0,则当前决策树建立完毕,计算所有叶子区域的$w_{mj}$,得到弱学习器$h_m(x)$,更新强学习器$f_m(x)$,进入下一轮弱学习器迭代。如果最大$score$不是0,则继续尝试分裂决策树。
46 |
47 | ## 损失函数
48 |
49 | XGBoost的损失函数在GBDT$L(y,\,f_{m-1}(x)+h_m(x))$的基础上,加入了如下的正则化:
50 |
51 | $$
52 | \Omega(h_m)=\gamma J+\frac{\lambda}{2}\sum_{j=1}^{J}\omega_{mj}^2
53 |
54 | $$
55 |
56 | 这里的 $J$ 是叶子节点的个数,而 $\omega_{mj}$ 是第 $j$ 个叶子节点的最优值。这里的 $\omega_{mj}$ 和在GBDT里面使用的 $c_{mj}$ 其实是一个意思,只是[XGBoost论文](https://link.zhihu.com/?target=https%3A//arxiv.org/pdf/1603.02754.pdf)里面使用 $\omega$ 符号表示叶子区域的值,这里为了和论文保持一致。
57 |
58 | 最终,XGBoost的损失函数可以表示为:
59 |
60 | $$
61 | L_m=\sum_{i=1}^{N}L(y_i, f_{m-1}(x_i)+h_m(x_i))+\gamma J+\frac{\lambda}{2}\sum_{j=1}^{J}\omega_{mj}^2
62 |
63 | $$
64 |
65 |
66 | 如果要极小化上面这个损失函数,得到第$m$个决策树最优的所有$J$个叶子节点区域和每个叶子节点区域的最优解$\omega_{mj}$。XGBoost在损失函数优化方面做了一些优化,没有和GBDT一样去拟合泰勒展开式的一阶导数,而是期望直接基于损失函数的二阶泰勒展开式来求解。现在来看看这个损失函数的二阶泰勒展开式:
67 |
68 | $$
69 | \begin{align} L_m &=\sum_{i=1}^{N}L(y_i, f_{m-1}(x_i)+h_m(x_i))+\gamma J+\frac{\lambda}{2}\sum_{j=1}^{J}\omega_{mj}^2 \\ & \approx \sum_{i=1}^{N}\left(L(y_i, f_{m-1}(x_i))+\frac{\partial L(y_i,\,f_{m-1}(x_i))}{\partial f_{m-1}(x_i)}h_m(x_i)+\frac{1}{2}\frac{\partial^2 L(y_i,\,f_{m-1}(x_i))}{\partial^2 f_{m-1}(x_i)}h_m^2(x_i)\right)+\gamma J+\frac{\lambda}{2}\sum_{j=1}^{J}\omega_{mj}^2 \end{align}
70 |
71 | $$
72 |
73 |
74 | 为了方便起见,把第$i$个样本在第$m$个弱学习器的损失函数上面的一阶和二阶导数分别记为:
75 |
76 | $$
77 | g_{mi}=\frac{\partial L(y_i,\,f_{m-1}(x_i))}{\partial f_{m-1}(x_i)},\,h_{mi}=\frac{\partial^2 L(y_i,\,f_{m-1}(x_i))}{\partial^2 f_{m-1}(x_i)}
78 |
79 | $$
80 |
81 |
82 | 则,损失函数可以简化为:
83 |
84 | $$
85 | L_m\approx \sum_{i=1}^{N}\left(L(y_i, f_{m-1}(x_i))+g_{mi}h_m(x_i)+h_{mi}h_m^2(x_i)\right)+\gamma J+\frac{\lambda}{2}\sum_{j=1}^{J}\omega_{mj}^2
86 |
87 | $$
88 |
89 |
90 | 对于第$m$轮的迭代,损失函数里面$L(y_i,f_{m-1}(x_i))$为参数项,对最小化无影响,可以直接去掉。
91 |
92 | 定义
93 |
94 | $$
95 | I_j={i|q(x_i)=j}
96 |
97 | $$
98 |
99 | 为第$j$个叶子节点的样本集合,经过$M$轮迭代完毕以后每个决策树(弱学习器)的第$j$个叶子节点的取值最终会是同一个值$\omega_{mj}$,因此,可以对损失函数继续化简:
100 |
101 | $$
102 | \begin{align} L_m &\approx \sum_{i=1}^{N}\left(g_{mi}h_m(x_i)+h_{mi}h_m^2(x_i)\right)+\gamma J+\frac{\lambda}{2}\sum_{j=1}^{J}\omega_{mj}^2 \\ & =\sum_{j=1}^{J}\left(\sum_{x_i \in R_{mj}}g_{mj}\omega_{mj}+\frac{1}{2}\sum_{x_i \in R_{mj}}h_{mj}\omega_{mj}^2\right)+\gamma J+\frac{\lambda}{2}\sum_{j=1}^{J}\omega_{mj}^2 \\ & = \sum_{j=1}^{J}[(\sum_{x_i \in R_{mj}}g_{mj})\omega_{mj}+\frac{1}{2}(\sum_{x_i \in R_{mj}}h_{mj}+\lambda)\omega_{mj}^2]+\gamma J \end{align}
103 |
104 | $$
105 |
106 | 把每个叶子节点区域样本的一阶和二阶导数的和单独表示如下:
107 |
108 | $$
109 | G_{mj}=\sum_{x_i \in R_{mj}} g_{mj},\,H_{mj}=\sum_{x_i \in R_{mj}} h_{mj}
110 |
111 | $$
112 |
113 |
114 | 那么最终的损失函数形式可以表示为:
115 |
116 | $$
117 | L_m=\sum_{j=1}^{J}[(G_{mj}\omega_{mj}+\frac{1}{2}(H_{mj}+\lambda)\omega_{mj}^2]+\gamma J
118 |
119 | $$
120 |
121 |
122 | 现在有了最终的损失函数,回到前面讲到的问题,我们如何一次求解出决策树最优的所有$J$个叶子节点区域和每个叶子节点区域的最优解$\omega_{mj}$呢?
123 |
124 | 这个问题等价于下面两个子问题:
125 |
126 | * 如果已经求出了第$m$个决策树的$J$个最优的叶子节点区域,如何求出每个叶子节点区域的最优解$\omega_{m }$?
127 | * 对当前决策树做子树分裂决策时,应该如何选择哪个特征和特征值进行分裂,使最终的损失函数$ _m$最小?
128 |
129 | 第一个问题其实比较简单,如果树的结构$q(x)$已经确定的情况下,可以基于损失函数对$\omega_{m }$求偏导并令导数为0得出最佳的$\omega_{m }$,也就是每一个叶子节点的最优值表达式为:
130 |
131 | $$
132 | \omega_{m }=\frac{G_{mj}}{H_{mj}+\lambda}
133 |
134 | $$
135 |
136 |
137 | 将求得的最优$\omega_{m }$代回到损失函数,可视为每轮迭代时该轮弱学习器的最优值表达式:
138 |
139 | $$
140 | L_m=-\frac{1}{2}\sum_{j=1}^{J}[\frac{G_{mj}}{H_{mj}+\lambda}]+\gamma J
141 |
142 | $$
143 |
144 |
145 | 那么回到第二个问题,怎么样的树结构$q(x)$是最优的呢?
146 |
147 | 通常来讲,枚举所有可能的树的结构,然后计算该结构的分数是不太现实的。在实践当中,我们采用贪心的策略:
148 |
149 | * 从深度为0的单一叶子节点开始,即所有的样本都在一个节点上
150 | * 对于树的每一个叶子节点,尝试增加一个分裂点:
151 |
152 | * 令$I_L,\,I_R$分别表示分裂点加入之后的左右叶子节点的样本集合,则有
153 | * $$
154 | G_L=\sum_{i\in I_L}g_{mi}
155 |
156 | $$
157 | * $$
158 | G_R=\sum_{i\in I_R}g_{mi}
159 |
160 | $$
161 | * $$
162 | H_L=\sum_{i\in I_L}h_{mi}
163 |
164 | $$
165 | * $$
166 | H_R=\sum_{i\in I_R}h_{mi}
167 |
168 | $$
169 | * 假如每次做左右子树分裂的时候,都可以最大程度地减少损失函数,则我们期望最大化下式:
170 |
171 | $$
172 | \Delta L=-\frac{1}{2}\frac{(G_L+G_R)^2}{H_L+H_R+\lambda}+\gamma J-\left(-\frac{1}{2}\frac{G_L^2}{H_L+\lambda}-\frac{1}{2}\frac{G_R^2}{H_R+\lambda}+\gamma (J+1)\right)
173 |
174 | $$
175 | * 对上式进行整理,我们期望最大化的是:
176 |
177 | $$
178 | L_{split}=\frac{1}{2}[\frac{G_L^2}{H_L+\lambda}+\frac{G_R^2}{H_R+\lambda}-\frac{(G_L+G_R)^2}{H_L+H_R+\lambda}]-\gamma
179 |
180 | $$
181 |
182 | 上式通常在实践当中用来评估分裂的候选点,也就是说,我们的决策树分裂标准不再使用CART树的均方误差,而是上式了。而具体如何分裂,将在下一节进行讨论。
183 |
184 | ## 分裂节点算法
185 |
186 | ## 精确搜索算法
187 |
188 | * 对每一个节点,枚举所有的特征,对每一个特征,枚举所有的分裂点,目前大部分的GBDT算法实现(sklearn、R当中的GBDT)都是采用这种算法。
189 | * 对每个特征,通过特征的取值将实例进行排序
190 | * 寻求该特征的最优分裂点
191 | * 对所有的特征采用如下的算法操作
192 |
193 | 
194 |
195 | 不难发现,对于连续型的特征,由于要枚举特征所有取值,计算量非常大,为了提高效率,通常将数据按照特征取值预排序。对于深度为$k$的树的时间复杂度:对特征所有取值的排序为$O(NlogN)$,$N$为样本点数目,若有$D$维特征,则$O(kDNlogN)$
196 |
197 | ## 近视搜索算法
198 |
199 | 精确搜索算法非常强大,但是当数据量大到内存无法存下时无法高效运行,并且在进行分布式计算时也存在一些问题,此时需要一个近视算法。主要思路如下: - 根据特征分布的百分位数,提出特征的一些**候选分裂点** - 将连续特征值映射到桶里(候选点对应的分裂),然后根据桶里样本的统计量,从这些候选中选择最佳分裂点 - 根据候选提出的时间,分为: - 全局近似:在构造树的初始阶段提出所有的候选分裂点,然后对各个层次采用相同的候选 - 提出候选的次数少,但每次的候选数目多(因为候选不更新) - 局部近似:在每次分裂都重新提出候选 - 对层次较深的树更适合,候选分裂点的数目不需要太多
200 |
201 | 对于$G,H$的更新算法步骤如下:
202 |
203 | 
204 |
205 | 对于单机系统,XGBoost系统支持精确搜索算法,对于单机/分布式,全局近视/局部近视均支持。
206 |
207 | ## 正则化
208 |
209 | 总体上讲,XGBoost抵抗过拟合的方法与GBDT类似,主要也是从以下几方面考虑:
210 |
211 | ## 模型复杂度
212 |
213 | 正则化表达式为:
214 |
215 | $$
216 | \Omega(h_m)=\gamma J+\frac{\lambda}{2}\sum_{j=1}^{J}\omega_{mj}^2
217 |
218 | $$
219 |
220 | 这里的$J$是叶子节点的个数,而 $\omega_{mj}$ 是第$j$个叶子节点的最优值。
221 |
222 | 其中第一项叶子结点的数目$J$相当于$L_1$正则,第二项叶子节点的最优值相当于$L_2$正则。
223 |
224 | ## Shrinkage
225 |
226 | 其思想认为,每次走一小步逐渐逼近结果的效果,要比每次迈一大步很快逼近结果的方式更容易避免过拟合。即它不完全信任每一个棵残差树,它认为每棵树只学到了真理的一小部分,累加的时候只累加一小部分,通过多学几棵树弥补不足。用方程来看更清晰,即给每棵数的输出结果乘上一个步长$\alpha$(learning rate)
227 |
228 | 对于前面的弱学习器的迭代:
229 |
230 | $$
231 | f_m(x)=f_{m-1}(x)+T(x;\gamma_m)
232 |
233 | $$
234 |
235 | 加上正则化项,则有
236 |
237 | $$
238 | f_m(x)=f_{m-1}(x)+\alpha\, T(x;\gamma_m)
239 |
240 | $$
241 |
242 | 此处,$\alpha$的取值范围为(0,1]。对于同样的训练集学习效果,较小$\alpha$的意味着需要更多的弱学习器的迭代次数。通常我们用步长和迭代最大次数一起决定算法的拟合效果。
243 |
244 | ## 特征采样和样本采样
245 |
246 | XGBoost借鉴RF的思想,对于特征进行采样以达到降低过拟合的目的,根据用户反馈,特征采样比起样本采样效果更优。当然,XGBoost同时支持以上两种降低过拟合的采样方式。
247 |
248 | ## Early Stop
249 |
250 | 对于每一次分离后的增益,即前面的
251 |
252 | $$
253 | L_{split}=\frac{1}{2}[\frac{G_L^2}{H_L+\lambda}+\frac{G_R^2}{H_R+\lambda}-\frac{(G_L+G_R)^2}{H_L+H_R+\lambda}]-\gamma
254 |
255 | $$
256 |
257 |
258 | 在`sklearn`接口当中,如果$L_{split}$出现负值,则提前停止;但是,被提前终止掉的分裂可能其后续的分裂会带来好处。在XBGoost原生接口当中是采用过后剪枝策略:将树分裂到最大深度,然后再基于上述增益计算剪枝。在具体实现当中还有`learning rate`等其它参数一起控制,给$L_{split}$出现负值的后续轮留机会。
259 |
260 | ## 缺失值处理
261 |
262 | 在实际的工业实践当中,数据出现缺失无法避免。
263 |
264 | XGBoost没有假设缺失值一定进入左子树还是右子树,则是尝试通过枚举所有缺失值在当前节点是进入左子树,还是进入右子树更优来决定一个处理缺失值默认的方向,这样处理起来更加的灵活和合理。
265 |
266 | 也就是说,上面第1节的算法的步骤a),b.1)和b.2)会执行2次,第一次假设特征$k$所有有缺失值的样本都走左子树,第二次假设特征$k$所有缺失值的样本都走右子树。然后每次都是针对没有缺失值的特征k的样本走上述流程,而不是所有的的样本。
267 |
268 | 如果是所有的缺失值走右子树,使用上面第1节的a),b.1)和b.2)即可。如果是所有的样本走左子树,则上面第1节的a)步要变成:
269 |
270 | $$
271 | G_R=0,\,H_R=0
272 |
273 | $$
274 |
275 |
276 | b.1)步要更新为:
277 |
278 | $$
279 | G_R=G_R+g_mi,\,G_L=G-G_R
280 |
281 | $$
282 |
283 |
284 | $$
285 | H_R=H_R+h_mi,\,H_L=H-H_R
286 |
287 | $$
288 |
289 |
290 | 具体算法如下图所示:
291 |
292 | 
293 |
294 | ## 优缺点
295 |
296 | ## 优点
297 |
298 | * 支持线性分类器(相当于引入$L_1,\,L_2$正则惩罚项的LR和线性回归,损失函数公式=误差平方和+正则项,似LR)
299 | * 损失函数用了二阶泰勒展开,引入一阶导和二阶导,提高模型拟和的速度
300 | * 可以给缺失值自动划分方向
301 | * 同RF,支持样本(行)随机抽取,也支持特征(列)随机抽取,降低运算,防过拟合
302 | * 损失函数引入正则化项,包含全部叶子节点个数,每个叶子节点得分的$L_2$模的平方和(代表叶子节点权重的影响),控制模型(树)复杂度
303 | * 每次迭代后为叶子分配结合学习速率,减低每棵树权重,减少每棵树影响,灵活调整后面的学习空间
304 | * 支持并行,不是树并行,是把特征值先预排序,存起来,可以重复并行使用计算分裂点
305 | * 分裂依据分开后与未分前的差值增益,不用每个节点排序算增益,减少计算量,可以并行计算
306 | * 可以引入阈值限制树分裂,控制树的规模
307 |
308 | ## 缺点
309 |
310 | * 往往会选择具有更高数量的不同值的预测器
311 | * 当预测器具有很多类别时,容易过拟合
312 | * 参数过多,调参困难
313 | * 如果采用精确搜索算法对内存消耗过大,且不支持分布式
314 |
315 | ## sklearn中的参数解释
316 |
317 | `sklearn`本身的文档当中并没有XGBoost的描述,[Github](https://link.zhihu.com/?target=https%3A//github.com/dmlc/xgboost/blob/master/python-package/xgboost/sklearn.py)上面看到主要参数如下:
318 |
319 | * max_depth :树的最大深度。越大通常模型复杂,更容易过拟合,这里作为弱学习器一般设置为1-10
320 | * learning_rate:学习率或收缩因子。学习率和迭代次数/弱分类器数目n_estimators相关。 缺省:0.1 (与直接调用xgboost的eta参数含义相同)
321 | * n_estimators:弱分类器数目. 缺省:100
322 | * verbosity:控制输出
323 | * slient:参数值为1时,静默模式开启,不输出任何信息
324 | * objective:待优化的目标函数,常用值有:
325 |
326 | * binary:logistic 二分类的逻辑回归,返回预测的概率
327 | * multi:softmax 使用softmax的多分类器,返回预测的类别(不是概率)
328 | * multi:softprob 和multi:softmax参数一样,但是返回的是每个数据属于各个类别的概率
329 | * 支持用户自定义目标函数
330 | * booster:选择每次迭代的模型,有两种选择:
331 | * gbtree:基于树的模型,为缺省值
332 | * gbliner:线性模型
333 | * dart:树模型
334 | * nthread:用来进行多线程控制。 如果你希望使用CPU全部的核,那就用缺省值-1,算法会自动检测它
335 | * n_jobs:xgboost运行时的线程数,后续代替`nthread`参数
336 | * gamma:节点分裂所需的最小损失函数下降值,缺省0
337 | * min_child_weight:叶子结点需要的最小样本权重(hessianhessian)和
338 | * subsample:构造每棵树的所用样本比例(样本采样比例)
339 | * colsample_bytree:构造树时每棵树的所用特征比例
340 | * colsample_bylevel:构造树时每层的所用特征比例
341 | * colsample_bynone:构造树时每次分裂的所用特征比例
342 | * reg_alpha:$L_1$正则的惩罚系数
343 | * reg_lambda:$L_2$正则的惩罚系数
344 | * tree_method string [default= auto]:XGBoost中使用的树构造算法
345 |
346 | * XGBoost支持hist和大规模分布式训练,仅支持大规模外部内存版本。
347 | * 选择: auto, exact, approx, hist, gpu_hist
348 | * auto: 对于中小型数据集,将使用精确的贪婪(精确)
349 | * 对于非常大的数据集,将选择近似算法(近似)
350 | * 因为旧版本总是在单个机器中使用精确贪婪,所以当选择近似算法来通知该选择时,用户将得到消息
351 | * exact: 精确的贪婪算法
352 | * approx : 使用分位数草图和梯度直方图的近似贪婪算法
353 | * hist:快速直方图优化近似贪心算法
354 | * gpu_hist:hist算法的GPU实现
355 | * scale_pos_weight:正负样本的平衡,通常用于不均衡数据
356 | * base_score:初始预测值
357 | * random_state:随机种子
358 | * missing:缺失值
359 | * importance_type:特征重要程度计算方法
360 |
361 | 除了以上参数,XGBoost原生接口当中参数众多,主要有以下4大类:
362 |
363 | * General parameters
364 | * Booster parameters
365 | * Learning task parameters
366 | * Command line parameters(较少用到)
367 |
368 | 如果有遗漏,具体可以参阅[XGBoost Parameters](https://link.zhihu.com/?target=https%3A//xgboost.readthedocs.io/en/latest/parameter.html)
369 |
370 | ## 应用场景
371 |
372 | XGBoost是GBDT框架的工业级优化实现,所有GBDT能够应用的场景,XGBoost都可以应用,所有回归问题(线性/非线性)、二分类问题(设定阈值,大于阈值为正例,反之为负例)。
373 |
374 | 按业务领域分,推荐系统、反欺诈、信用评级等。
375 |
--------------------------------------------------------------------------------
/LightGBM-2.md:
--------------------------------------------------------------------------------
1 | title: LightGBM算法梳理 date: 2019-08-12 23:56:55 categories: 机器学习 tags: - 集成学习 - LightGBM - Histogram - 分布式 - sklearn description: DataWhale暑期学习小组-高级算法梳理第八期Task4。
2 |
3 | ---
4 |
5 | ## LightGBM
6 |
7 | 同XGBoost类似,LightGBM依然是在GBDT算法框架下的一种改进实现,是一种基于决策树算法的快速、分布式、高性能的GBDT框架,主要说解决的痛点是面对高维度大数据时提高GBDT框架算法的效率和可扩展性。
8 |
9 | “Light”主要体现在三个方面,即更少的样本、更少的特征、更少的内存,分别通过单边梯度采样(Gradient-based One-Side Sampling)、互斥特征合并(Exclusive Feature Bundling)、直方图算法(Histogram)三项技术实现。另外,在工程上面,LightGBM还在并行计算方面做了诸多的优化,支持特征并行和数据并行,并针对各自的并行方式做了优化,减少通信量。
10 |
11 | ## LightGBM的起源
12 |
13 | LightGBM起源于微软亚洲研究院在NIPS发表的系列论文:
14 |
15 | * [Qi Meng, Guolin Ke, Taifeng Wang, Wei Chen, Qiwei Ye, Zhi-Ming Ma, Tie-Yan Liu. “A Communication-Efficient Parallel Algorithm for Decision Tree.” Advances in Neural Information Processing Systems 29 (NIPS 2016), pp. 1279-1287](https://link.zhihu.com/?target=https%3A//papers.nips.cc/paper/6381-a-communication-efficient-parallel-algorithm-for-decision-tree.pdf)
16 | * [Guolin Ke, Qi Meng, Thomas Finley, Taifeng Wang, Wei Chen, Weidong Ma, Qiwei Ye, Tie-Yan Liu. “LightGBM: A Highly Efficient Gradient Boosting Decision Tree.” Advances in Neural Information Processing Systems 30 (NIPS 2017), pp. 3149-3157](https://link.zhihu.com/?target=https%3A//papers.nips.cc/paper/6907-lightgbm-a-highly-efficient-gradient-boosting-decision-tree.pdf)
17 |
18 | 并于2016年10月17日在[LightGBM](https://link.zhihu.com/?target=https%3A//github.com/microsoft/LightGBM)上面开源,三天内在GitHub上面被star了1000次,fork了200次。知乎上现有近2000人关注“如何看待微软开源的LightGBM?”问题。
19 |
20 | 随后不断迭代,慢慢地开始支持Early Stopping、叶子索引预测、最大深度设置、特征重要性评估、多分类、类别特征支持、正则化(L1,L2及分裂最小增益)……
21 |
22 | 具体可以参阅以下链接:
23 |
24 | [LightGBM大事记](https://link.zhihu.com/?target=https%3A//github.com/Microsoft/LightGBM/blob/master/docs/Key-Events.md)
25 |
26 | ## Histogram VS Pre-sorted
27 |
28 | ## Pre-sorted
29 |
30 | 在XGBoost当中的精确搜索算法(Exact Greedy Algorithm)在寻找分裂点时就是采用Pre-sorted的思想。具体过程不再赘述,可以参阅[XGBoost算法梳理](https://link.zhihu.com/?target=http%3A//datacruiser.io/2019/08/10/DataWhale-Workout-No-8-XGboost-Summary/)
31 |
32 | 预排序还是有一定优点的,如果不用预排序的话,在分裂节点的时候,选中某一个特征后,需要对A按特征值大小进行排序,然后计算每个阈值的增益,这个过程需要花费很多时间。
33 |
34 | 预排序算法在计算最优分裂时,各个特征的增益可以并行计算,并且能精确地找到分割点。但是预排序后需要保存特征值及排序后的索引,因此需要消耗两倍于训练数据的内存,时间消耗大。另外预排序后,特征对梯度的访问是一种随机访问,并且不同的特征访问的顺序不一样,无法对cache进行优化,时间消耗也大。最后,在每一层,需要随机访问一个行索引到叶子索引的数组,并且不同特征访问的顺序也不一样。
35 |
36 | ## Historgram
37 |
38 | 首先需要指出的是,XGBoost在寻找树的分裂节点的也是支持直方图算法的,就是论文中提到的近视搜索算法(Approximate Algorithm)。只是,无论特征值是否为0,直方图算法都需要对特征的分箱值进行索引,因此对于大部分实际应用场景当中的稀疏数据优化不足。
39 |
40 | 回过头来,为了能够发挥直方图算法的优化威力,LightGBM提出了另外两个新技术:单边梯度采样(Gradient-based One-Side Sampling)和互斥特征合并(Exclusive Feature Bundling),在减少维度和下采样上面做了优化以后才能够将直方图算法发挥得淋漓尽致。下面依次介绍直方图算法、GOSS和EFB。
41 |
42 | ### 直方图算法
43 |
44 | 直方图算法的基本思想是先把连续的浮点特征值离散化成$k$个整数,同时构造一个宽度为$k$的直方图。在遍历数据的时候,根据离散化后的值作为索引在直方图中累积统计量,当遍历一次数据后,直方图累积了需要的统计量,然后根据直方图的离散值,遍历寻找最优的分割点。具体算法描述如下:
45 |
46 | 
47 |
48 | 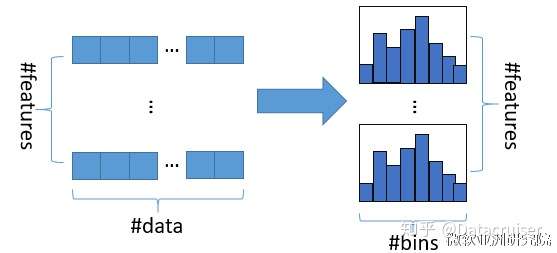
49 |
50 | 直方图算法有如下优点:
51 |
52 | * 内存消耗降低。预排序算法需要的内存约是训练数据的两倍(2x样本数x维度x4Bytes),它需要用32位浮点来保存特征值,并且对每一列特征,都需要一个额外的排好序的索引,这也需要32位的存储空间。对于 直方图算法,则只需要(1x样本数x维度x1Bytes)的内存消耗,仅为预排序算法的1/8。因为直方图算法仅需要存储特征的 bin 值(离散化后的数值),不需要原始的特征值,也不用排序,而bin值用8位整型存储就足够了。
53 | * 算法时间复杂度大大降低。决策树算法在节点分裂时有两个主要操作组成,一个是“寻找分割点”,另一个是“数据分割”。从算法时间复杂度来看,在“寻找分割点”时,预排序算法对于深度为$k$的树的时间复杂度:对特征所有取值的排序为$O(NlogN)$,$N$为样本点数目,若有$D$维特征,则$O(kDNlogN)$,而直方图算法需要$O(kD \times bin)$(bin是histogram 的横轴的数量,一般远小于样本数量$N$)。
54 | * 再举个例子说明上述两点的优化,假设数据集$A$的某个特征的特征值有(二叉树存储):${1.2,1.3,2.2,2.3,3.1,3.3}$,预排序算法要全部遍历一遍,需要切分大约5次。进行离散化后,只需要切分2次 ${{1},{2,3}}$ 和 ${{1,2},{3}}$,除了切分次数减少,内存消耗也大大降低。
55 | * 直方图算法还可以进一步加速。一个容易观察到的现象:一个叶子节点的直方图可以直接由父节点的直方图和兄弟节点的直方图做差得到。通常构造直方图,需要遍历该叶子上的所有数据,但直方图做差仅需遍历直方图的$k$个bin。利用这个方法,LightGBM可以在构造一个叶子的直方图后,可以用非常微小的代价得到它兄弟叶子的直方图,在速度上可以提升一倍。
56 |
57 | 
58 |
59 | 当然,直方图算法并不是完美的。由于特征被离散化后,找到的并不是很精确的分割点,所以会对结果产生影响。但在不同的数据集上的结果表明,离散化的分割点对最终的精度影响并不是很大,甚至有时候会更好一点。原因是决策树本来就是弱模型,分割点是不是精确并不是太重要;较粗的分割点也有正则化的效果,可以有效地防止过拟合;即使单棵树的训练误差比精确分割的算法稍大,但在梯度提升(GradientBoosting)的框架下没有太大的影响。
60 |
61 | ### 单边梯度采样(Gradient-based One-Side Sampling)
62 |
63 | 单边梯度采样是一种在减少数据量和保证精度上平衡的算法。在GBDT中, 我们对损失函数的负梯度进行拟合,样本误差越大,梯度的绝对值越大,这说明模型对该样本的学习还不足够,相反如果越小则表示模型对该样本的学习已经很充分。因此,我们可以这样推论:梯度的绝对值越大,样本重要性越高。单边梯度采样正是以样本的梯度作为样本的权重进行采样。
64 |
65 | 单边梯度采样保留所有的梯度较大的样本,在梯度小的实例上使用随机采样。为了抵消对数据分布的影响,计算信息增益的时候,单边梯度采样对小梯度的数据引入常量乘数。单边梯度采样首先根据数据的梯度绝对值排序,选取$top\,\,a$个样本。然后在剩余的数据中随机采样$b$个样本。接着计算信息增益时为采样出的小梯度数据乘以$\frac{1-a}{b}$,这样算法就会更关注训练不足的样本例,而不会过多改变原数据集的分布。正是单边梯度采样减少了数据量,让直方图算法发挥了更大的作用。单边梯度采样具体算法见下图:
66 |
67 | 
68 |
69 | ### 互斥特征合并(Exclusive Feature Bundling)
70 |
71 | 高维的数据通常是稀疏的,这种特征空间的稀疏性给我们提供了一种设计一种接近无损地降维的可能性。特别的,在稀疏特征空间中,许多特征是互斥的,换句话说,大部分特征不会同时取非0值,例如One-hot之后的类别特征他们从不同时为非0值。我们可以合并互斥的特征为单一特征(我们将这个过程称为*Exclusive Feature Bundle* ).通过仔细设计特征扫描算法,我们从合并特征中构建出与单个特征相同的特征直方图。通过这种方式,直方图构建算法的时间复杂度从$O(ND)$,降到$O(N×bundle)$,其中$N$为样本点数目,$D$为特征维度。通常,bundle << $D$,我们能够在不损失精度的情况下极大地加速GBDT的训练。
72 |
73 | 那么接下来有两个问题需要处理:
74 |
75 | * 需要合并哪些特征
76 | * 如何合并这些特征
77 |
78 | ### Greedy Bundling
79 |
80 | 找出最优的 bundle 组合数是一个 NP 问题,LightGBM通过将原问题转化为”图着色”问题进行贪心近似解决。
81 |
82 | 首先创建一个图$G(V, E)$,其中$V$就是特征,为图中的节点,$E$为$G$中的边,将不是相互独立的特征用一条边连接起来,边的权重就是两个相连接的特征的总冲突值,这样需要绑定的特征就是在图着色问题中要涂上同一种颜色的那些点(特征)。具体算法过程如下:
83 |
84 | 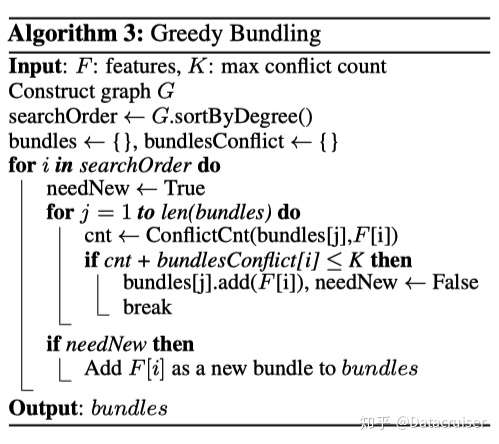
85 |
86 | ### Merge Exclusive Features
87 |
88 | 该过程主要是关键在于原始特征值可以从bundle中区分出来,即绑定几个特征在同一个bundle里需要保证绑定前的原始特征的值在bundle中能够被识别,考虑到直方图算法将连续的值保存为离散的bin,我们可以使得不同特征的值分到bundle中的不同bin中,这可以通过在特征值中加一个偏置常量来解决,比如,我们在bundle中绑定了两个特征A和B,A特征的原始取值为区间[0,10),B特征的原始取值为区间[0,20),我们可以在B特征的取值上加一个偏置常量10,将其取值范围变为[10,30),这样就可以放心的融合特征A和B了,因为在树模型中对于每一个特征都会计算分裂节点的,也就是通过将他们的取值范围限定在不同的bin中,在分裂时可以将不同特征很好的分裂到树的不同分支中去。具体算法如下:
89 |
90 | 
91 |
92 | ## Leaf-wise VS Level-wise
93 |
94 | ## Level-wise
95 |
96 | 大多数GBDT框架使用的按层生长 (level-wise) 的决策树生长策略,Level-wise遍历一次数据可以同时分裂同一层的叶子,容易进行多线程优化,也好控制模型复杂度,不容易过拟合。但实际上Level-wise是一种低效的算法,因为它不加区分的对待同一层的叶子,带来了很多没必要的开销,因为实际上很多叶子的分裂增益较低,没必要进行搜索和分裂。
97 |
98 | 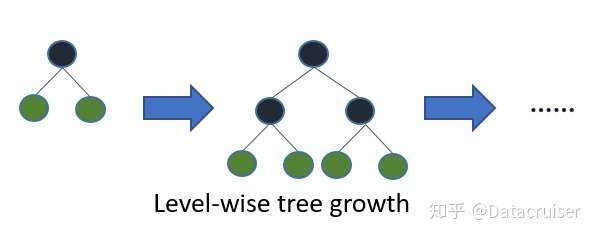
99 |
100 | ## Leaf-wise
101 |
102 | LightGBM在直方图算法之上,对于树的生长策略做了进一步优化,抛弃了Level-wise策略,使用了带有深度限制的按叶子生长 (leaf-wise)算法。Leaf-wise则是一种更为高效的策略,每次从当前所有叶子中,找到分裂增益最大的一个叶子,然后分裂,如此循环。因此同Level-wise相比,在分裂次数相同的情况下,Leaf-wise可以降低更多的误差,得到更好的精度。Leaf-wise的缺点是可能会长出比较深的决策树,产生过拟合。因此LightGBM在Leaf-wise之上增加了一个最大深度的限制,在保证高效率的同时防止过拟合。
103 |
104 | 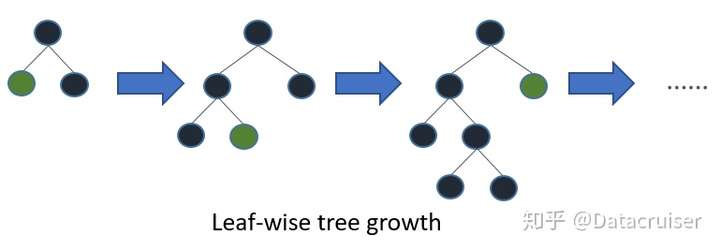
105 |
106 | ## 特征并行和数据并行
107 |
108 | 本小节主要根据[LightGBM的官方文档](https://link.zhihu.com/?target=https%3A//lightgbm.readthedocs.io/en/latest/Features.html%23optimization-in-network-communication)中提到的并行计算优化进行讲解。 在本小节中,工作的节点称为**worker**
109 |
110 | LightGBM具有支持高效并行的优点。LightGBM原生支持并行学习,目前支持特征并行和数据并行的两种。
111 |
112 | ## 特征并行
113 |
114 | 特征并行主要是并行化决策树中寻找最优划分点(“Find Best Split”)的过程,因为这部分最为耗时。
115 |
116 | 传统特征并行做法如下:
117 |
118 | * 垂直划分数据(对特征划分),不同的worker有不同的特征集
119 | * 每个workers找到局部最佳的切分点{feature, threshold}
120 | * workers使用点对点通信,找到全局最佳切分点
121 | * 具有全局最佳切分点的worker进行节点分裂,然后广播切分后的结果(左右子树的instance indices)
122 | * 其它worker根据收到的instance indices也进行划分
123 |
124 | 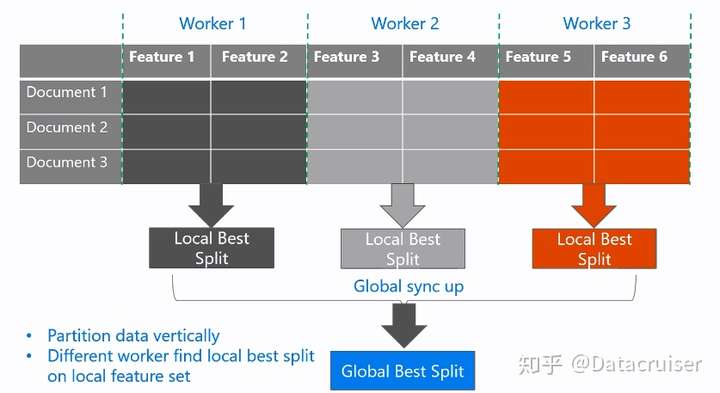
125 |
126 | 主要有以下缺点:
127 |
128 | * 无法加速分裂的过程,该过程的时间复杂度为$O(N)$,当数据量大的时候效率不高
129 | * 需要广播划分的结果(左右子树的instance indices),1条数据1bit的话,通信花费大约需要$O(N/8)$
130 |
131 | LightGBM的特征并行每个worker保存所有的数据集,这样找到全局最佳切分点后各个worker都可以自行划分,就不用进行广播划分结果,减小了网络通信量。过程如下:
132 |
133 | * 每个workers找到局部最佳的切分点{feature, threshold}
134 | * workers使用点对点通信,找到全局最佳切分点
135 | * 每个worker根据全局全局最佳切分点进行节点分裂
136 |
137 | 这样虽然不用进行广播划分结果,减小了网络通信量。但是也有缺点:
138 |
139 | * 分裂过程的复杂度保持不变
140 | * 每个worker保存所有数据,存储代价高
141 |
142 | ## 数据并行
143 |
144 | 数据并行的目标是并行化整个决策学习的过程,传统算法的做法如下:
145 |
146 | * 水平切分数据,不同的worker拥有部分数据
147 | * 每个worker根据本地数据构建局部直方图
148 | * 合并所有的局部直方图得到全部直方图
149 | * 根据全局直方图找到最优切分点并进行分裂
150 |
151 | 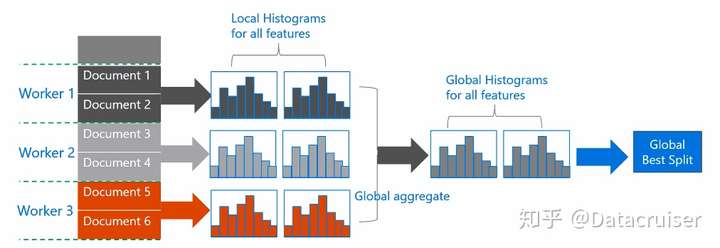
152 |
153 | 在第3步当中有两种合并方式:
154 |
155 | * 采用点对点方式(point-to-point communication algorithm)进行通讯,每个worker通讯量为$ ( ℎ × × )$
156 | * 采用collective communication algorithm(如“[All Reduce](https://link.zhihu.com/?target=http%3A//pages.tacc.utexas.edu/~eijkhout/pcse/html/mpi-collective.html)”)进行通讯(相当于有一个中心节点,通讯后在返回结果),每个worker的通讯量为$O(2× × )$
157 |
158 | 不难发现,通信的代价也是很高的,这也是数据并行的缺点。
159 |
160 | LightGBM的数据并行主要做了以下两点优化:
161 |
162 | * 使用“Reduce Scatter”将不同worker的不同特征的直方图合并,然后workers在局部合并的直方图中找到局部最优划分,最后同步全局最优划分
163 | * 通过直方图作差法得到兄弟节点的直方图,因此只需要通信一个节点的直方图,减半通信量
164 |
165 | 通过上述两点做法,通信开销降为$ (0.5 × × )$。
166 |
167 | 另外,LightGBM还采用 一种称为**PV-Tree** 的算法进行投票并行(Voting Parallel),其实本质上也是一种数据并行。
168 |
169 | PV-Tree和普通的决策树差不多,只是在寻找最优切分点上有所不同。具体算法如下:
170 |
171 | 
172 |
173 | 主要思路如下:
174 |
175 | * 水平切分数据,不同的worker拥有部分数据
176 | * Local voting: 每个worker构建直方图,找到$top-k$个最优的本地划分特征
177 | * Global voting: 中心节点聚合得到最优的$top-2k$个全局划分特征($top-2k$是看对各个worker选择特征的个数进行计数,取最多的$2k$个)
178 | * Best Attribute Identification: 中心节点向worker收集这$top-2k$个特征的直方图,并进行合并,然后计算得到全局的最优划分
179 | * 中心节点将全局最优划分广播给所有的worker,worker进行本地划分
180 |
181 | 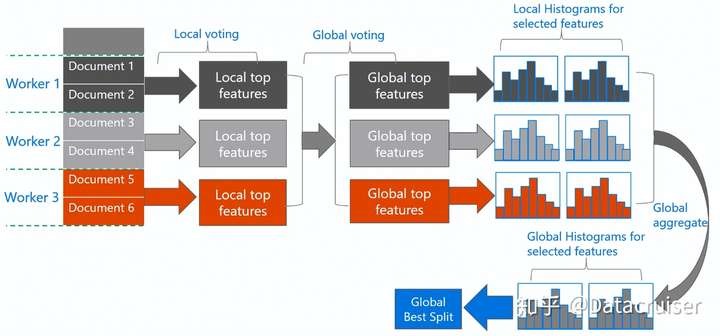
182 |
183 | 可以看出,PV-tree将原本需要$O( × )$ 变为了$O(2k × )$,通信开销得到降低。此外,可以证明,当每个worker的数据足够多的时候,$top-2k$个中包含全局最佳切分点的概率非常高。
184 |
185 | ## 顺序访问梯度
186 |
187 | Cache(高速缓存)作为内存局部区域的副本,用来存放当前活跃的程序和数据,它利用程序运行的局部性,把局部范围的数据从内存复制到Cache中,使CPU直接高速从Cache中读取程序和数据,从而解决CPU速度和内存速度不匹配的问题。高速缓冲存储器最重要的技术指标是它的命中率。CPU在Cache中找到有用的数据被称为命中,当Cache中没有CPU所需的数据时(这时称为未命中),CPU才访问内存。
188 |
189 | 预排序算法中有两个频繁的操作会导致cache-miss,也就是缓存消失(对速度的影响很大,特别是数据量很大的时候,顺序访问比随机访问的速度快4倍以上 )。
190 |
191 | * 对梯度的访问:在计算增益的时候需要利用梯度,假设梯度信息存在一个数组$g[i]$中,在对特征$A$进行增益时,需要根据特征$A$排序后的索引找到$g[i]$中对应的梯度信息。特征值$A_1$对应的样本行号可能是3,对应的梯度信息在$g[3]$,而特征值$A_2$对应的样本行号可能是9999,对应的梯度信息在$g[9999]$,即对于不同的特征,访问梯度的顺序是不一样的,并且是随机的
192 | * 对于索引表的访问:预排序算法使用了行号和叶子节点号的索引表,防止数据切分的时候对所有的特征进行切分。同访问梯度一样,所有的特征都要通过访问这个索引表来索引
193 |
194 | 这两个操作都是随机的访问,会给系统性能带来非常大的下降。
195 |
196 | LightGBM使用的直方图算法能很好的解决这类问题。首先。对梯度的访问,因为不用对特征进行排序,同时,所有的特征都用同样的方式来访问,所以只需要对梯度访问的顺序进行重新排序,所有的特征都能连续的访问梯度。并且直方图算法不需要把数据id到叶子节点号上(不需要这个索引表,没有这个缓存消失问题),大大提高cache的命中率,减少cache-miss出现的概率。
197 |
198 | ## 支持类别特征
199 |
200 | 实际上大多数机器学习工具都无法直接支持类别特征,一般需要把类别特征,转化one-hot特征,降低了空间和时间的效率。而类别特征的使用是在实践中很常用的。基于这个考虑,LightGBM优化了对类别特征的支持,可以直接输入类别特征,不需要额外的0/1展开。并在决策树算法上增加了类别特征的决策规则,直接原生支持类别特征,不需要转化,提高了近8倍的速度。
201 |
202 | 
203 |
204 | ## 应用场景
205 |
206 | 作为GBDT框架内的算法,GBDT、XGBoost能够应用的场景LightGBM也都适用,并且考虑到其对于大数据、高维特征的诸多优化,在数据量非常大、维度非常多的场景更具优势。近来,有着逐步替代XGBoost成为各种数据挖掘比赛baseline的趋势。
207 |
208 | ## sklearn参数
209 |
210 | `sklearn`本身的文档当中并没有LightGBM的描述,[Github](https://link.zhihu.com/?target=https%3A//github.com/microsoft/LightGBM/blob/master/python-package/lightgbm/sklearn.py)上面看到主要参数如下:
211 |
212 | * `boosting_type` : 提升类型,字符串,可选项 (default=`gbdt`)
213 |
214 | * `gbdt`, 传统梯度提升树
215 | * `dart`, 带Dropout的MART
216 | * `goss`, 单边梯度采样
217 | * `rf`, 随机森林
218 | * `num_leaves` : 基学习器的最大叶子树,整型,可选项 (default=31)
219 | * `max_depth` : 基学习器的最大树深度,小于等于0表示没限制,整型,可选项 (default=-1)
220 | * `learning_rate` : 提升学习率,浮点型,可选项 (default=0.1)
221 | * `n_estimators` : 提升次数,整型,可选项 (default=100)
222 | * `subsample_for_bin` : 构造分箱的样本个数,整型,可选项 (default=200000)
223 | * `objective` : 指定学习任务和相应的学习目标或者用户自定义的需要优化的目标损失函数,字符串, 可调用的或者None, 可选项 (default=None),若不为None,则有:
224 | * `regression` for LGBMRegressor -`binary` or `multiclass` for LGBMClassifier
225 | * `lambdarank` for LGBMRanker
226 | * `class_weight` : 该参数仅在多分类的时候会用到,多分类的时候各个分类的权重,对于二分类任务,你可以使用`is_unbalance` 或 `scale_pos_weight`,字典数据, `balanced` or None, 可选项 (default=None)
227 | * `min_split_gain` : 在叶子节点上面做进一步分裂的最小损失减少值,浮点型,可选项 (default=0.)
228 | * `min_child_weight` : 在树的一个孩子或者叶子所需的最小样本权重和,浮点型,可选项 (default=1e-3)
229 | * `min_child_samples` : 在树的一个孩子或者叶子所需的最小样本,整型,可选项 (default=20)
230 | * `subsample` : 训练样本的子采样比例,浮点型,可选项 (default=1.)
231 | * `subsample_freq` : 子采样频率,小于等于0意味着不可用,整型,可选项 (default=0)
232 | * `colsample_bytree` : 构建单棵树时列采样比例,浮点型,可选项 (default=1.)
233 | * `reg_alpha` : $L_1$正则项,浮点型,可选项 (default=0.)
234 | * `reg_lambda` :$L_2$正则项,浮点型,可选项 (default=0.)
235 | * `random_state` : 随机数种子,整型或者None, 可选项 (default=None)
236 | * `n_jobs` : 线程数,整型,可选项 (default=-1)
237 | * `silent` : 运行时是否打印消息,布尔型,可选项 (default=True)
238 | * `importance_type` : 填入到`feature_importances_`的特征重要性衡量类型,如果是`split`,则以特征被用来分裂的次数,如果是`gain`,则以特征每次用于分裂的累积增益,字符串,可选项 (default=`split`)
239 |
240 | 除了以上参数,LightGBM原生接口当中参数众多,主要有以下八大类:
241 |
242 | * 核心参数
243 | * 学习控制参数
244 | * IO参数
245 | * 目标参数
246 | * 度量参数
247 | * 网络参数
248 | * GPU参数
249 | * 模型参数
250 |
251 | 如果有遗漏,具体可以参阅[LightGBM Parameters](https://link.zhihu.com/?target=https%3A//lightgbm.readthedocs.io/en/latest/Parameters.html)
252 |
253 | ## CatBoost(了解)
254 |
255 | CatBoost也是Boosting族的算法,由俄罗斯科技公司Yandex于2017年提出,主要在两方面做了优化,一个是对于类别变量的处理,另外一个是对于预测偏移(prediction shift)的处理。
256 |
257 | 其中对于类别变量在传统的Greedy TBS方法的基础上添加先验分布项,这样可以减少减少噪声和低频率数据对于数据分布的影响:
258 |
259 | $$
260 | \hat{x}*k^i=\frac{\sum* {j=1}^n I_{{x_j^i=x_k^i}}*y_j+a\,P}{\sum_{j=1}^n I_{{x_j^i=x_k^i}}+a}
261 |
262 | $$
263 |
264 |
265 | 其中 $P$ 是添加的先验项,$a$ 通常是大于 0 的权重系数。
266 |
267 | 对于第二个问题,CatBoost采用了排序提升(Ordered Boosting)的方式,首先对所有的数据进行随机排列,然后在计算第 $i$ 步残差时候的模型只利用了随机排列中前 $i-1$ 个样本。具体算法描述请参阅论文[CatBoost: unbiased boosting with categorical features](https://link.zhihu.com/?target=https%3A//papers.nips.cc/paper/7898-catboost-unbiased-boosting-with-categorical-features.pdf)
268 |
269 | 时间有限,下次有机会再详细消化下CatBoost的论文。
270 |
271 | 总之,CatBoost大大简化了前期数据处理过程,特别是类别特征的数值化,调参也相对容易。近来在数据竞赛领域已经大规模采用。
272 |
--------------------------------------------------------------------------------
/Catboost.md:
--------------------------------------------------------------------------------
1 | title: DataWhale Workout No.8 CatBoost Summary date: 2019-08-19 08:18:37 categories: 机器学习 tags: - 集成学习 - CatBoost - Ordered boosting - Prediction shift - sklearn description: 这是DataWhale暑期学习小组-高级算法梳理的补充,是对目前最新的开源Boost族算法CatBoost的介绍,结合相关论文以及笔者的使用经验,对CatBoost的算法特性和适用场景做一些小结。
2 |
3 | ---
4 |
5 | ## CatBoost
6 |
7 | CatBoost是俄罗斯的搜索巨头Y andex在2017年开源的机器学习库,也是Boosting族算法的一种,同前面介绍过的XGBoost和LightGBM类似,依然是在GBDT算法框架下的一种改进实现,是一种基于对称决策树(oblivious trees)算法的参数少、支持类别型变量和高准确性的GBDT框架,主要说解决的痛点是高效合理地处理类别型特征,这个从它的名字就可以看得出来,CatBoost是由catgorical和boost组成,另外是处理梯度偏差(Gradient bias)以及预测偏移(Prediction shift)问题,提高算法的准确性和泛化能力。
8 |
9 | 
10 |
11 | CatBoost主要有以下五个特性:
12 |
13 | * 无需调参即可获得较高的模型质量,采用默认参数就可以获得非常好的结果,减少在调参上面花的时间
14 | * 支持类别型变量,无需对非数值型特征进行预处理
15 | * 快速、可扩展的GPU版本,可以用基于GPU的梯度提升算法实现来训练你的模型,支持多卡并行
16 | * 提高准确性,提出一种全新的梯度提升机制来构建模型以减少过拟合
17 | * 快速预测,即便应对延时非常苛刻的任务也能够快速高效部署模型
18 |
19 | CatBoost的主要算法原理可以参照以下两篇论文:
20 |
21 | * [Anna Veronika Dorogush, Andrey Gulin, Gleb Gusev, Nikita Kazeev, Liudmila Ostroumova Prokhorenkova, Aleksandr Vorobev "Fighting biases with dynamic boosting". arXiv:1706.09516, 2017](https://link.zhihu.com/?target=https%3A//arxiv.org/pdf/1706.09516.pdf)
22 | * [Anna Veronika Dorogush, Vasily Ershov, Andrey Gulin "CatBoost: gradient boosting with categorical features support". Workshop on ML Systems at NIPS 2017](https://link.zhihu.com/?target=http%3A//learningsys.org/nips17/assets/papers/paper_11.pdf)
23 |
24 | ## Categorical features
25 |
26 | 所谓类别型变量(Categorical features)是指其值是离散的集合且相互比较并无意义的变量,比如用户的ID、产品ID、颜色等。因此,这些变量无法在二叉决策树当中直接使用。常规的做法是将这些类别变量通过预处理的方式转化成数值型变量再喂给模型,比如用一个或者若干个数值来代表一个类别型特征。
27 |
28 | 目前广泛用于**低势** (一个有限集的元素个数是一个自然数)类别特征的处理方法是`One-hot encoding`:将原来的特征删除,然后对于每一个类别加一个0/1的用来指示是否含有该类别的数值型特征。`One-hot encoding`可以在数据预处理时完成,也可以在模型训练的时候完成,从训练时间的角度,后一种方法的实现更为高效,CatBoost对于低势类别特征也是采用后一种实现。
29 |
30 | 显然,在**高势** 特征当中,比如 `user ID`,这种编码方式会产生大量新的特征,造成维度灾难。一种折中的办法是可以将类别分组成有限个的群体再进行 `One-hot encoding`。一种常被使用的方法是根据目标变量统计(Target Statistics,以下简称TS)进行分组,目标变量统计用于估算每个类别的目标变量期望值。甚至有人直接用TS作为一个新的数值型变量来代替原来的类别型变量。重要的是,可以通过对TS数值型特征的阈值设置,基于对数损失、基尼系数或者均方差,得到一个对于训练集而言将类别一分为二的所有可能划分当中最优的那个。在LightGBM当中,类别型特征用每一步梯度提升时的梯度统计(Gradient Statistics,以下简称GS)来表示。虽然为建树提供了重要的信息,但是这种方法有以下两个缺点:
31 |
32 | * 增加计算时间,因为需要对每一个类别型特征,在迭代的每一步,都需要对GS进行计算;
33 | * 增加存储需求,对于一个类别型变量,需要存储每一次分离每个节点的类别。
34 |
35 | 为了克服这些缺点,LightGBM以损失部分信息为代价将所有的长尾类别归位一类,作者声称这样处理高势特征时比起 `One-hot encoding`还是好不少。不过如果采用TS特征,那么对于每个类别只需要计算和存储一个数字。
36 |
37 | 如此看到,采用TS作为一个新的数值型特征是最有效、信息损失最小的处理类别型特征的方法。TS也被广泛采用,在点击预测任务当中,这个场景当中的类别特征有用户、地区、广告、广告发布者等。接下来我们着重讨论TS,暂时将`One-hot encoding`和GS放一边。
38 |
39 | ## Target statistics
40 |
41 | 一个有效和高效的处理类别型特征$i$的方式是用一个与某些TS相等的数值型变量$\hat{x}_k^i$来代替第$k$个训练样本的类别${x}_k^i$。通常用基于类别的目标变量$y$的期望来进行估算:$\hat{x}_k^i\approx\mathbb{E}(y|x^i={x}_k^i)$。
42 |
43 | ### Greedy TS
44 |
45 | 估算$\mathbb{E}(y|x^i={x}*k^i)$最直接的方式就是用训练样本当中相同类别$x_k^i$的目标变量$y$的平均值。
46 |
47 | $$
48 | \hat{x}_k^i=\frac{\sum* {j=1}^n\mathbb{I}*{{x_j^i={x}_k^i}}\cdot y_i}{\sum* {j=1}^n\mathbb{I}*{{x_j^i={x}_k^i}}}
49 |
50 | $$
51 |
52 | 显然,这样的处理方式很容易引起过拟合。举个例子,假如在整个训练集当中所有样本的类别${x}_k^i$都互不相同,即$k$个样本有$k$个类别,那么新产生的数值型特征的值将与目标变量的值相同。某种程度上,这是一种目标穿越(target leakage),非常容易引起过拟合。比较好的一种做法是采用一个先验概率$p$进行平滑处理:
53 | $$
54 | \hat{x}_k^i=\frac{\sum* {j=1}^n\mathbb{I}*{{x_j^i={x}_k^i}}\cdot y_i+a\,p}{\sum* {j=1}^n\mathbb{I}_{{x_j^i={x}_k^i}}+a}
55 |
56 | $$
57 |
58 | 其中$a>0$是先验概率$p$的权重,而对于先验概率,通常的做法是设置为数据集当中目标变量的平均值。
59 |
60 | 不过这样的平滑处理依然无法完全避免目标穿越:特征$\hat{x}*k^i$是通过自变量$X_k$的目标$y_k$计算所得。这将会导致条件偏移:对于训练集和测试集,$\hat{x}_k^i|y$的分布会有所不同。再举个例子,假设第$i$个特征为类别型特征,并且特征所有取值为无重复的集合,然后对于每一个类别$A$,对于一个分类任务,我们有$P(y=1|x^i=A)=0.5$。然后在训练集当中,$\hat{x}_k^i=\frac{y_k+a\,p}{1+a}$,于是用阈值$t=\frac{0.5+a\,p}{1+a}$就可以仅用一次分裂就训练集完美分开。但是,对于测试集,因为还无法判断此时目标变量的类别,所以这一项$\sum* {j=1}^n\mathbb{I}_{{x_j^i={x}_k^i}}=0$,最后得到的TS值为$p$,并且得到的模型在$p
```
123 |
--------------------------------------------------------------------------------
/catboost2.md:
--------------------------------------------------------------------------------
1 | # Catboost
2 |
3 | CatBoost是一种基于对称决策树(oblivious trees)为基学习器实现的参数较少、支持类别型变量和高准确性的GBDT框架,主要解决的痛点是高效合理地处理类别型特征,这一点从它的名字中可以看出来,CatBoost是由Categorical和Boosting组成。此外,CatBoost还解决了梯度偏差(Gradient Bias)以及预测偏移(Prediction shift)的问题,从而减少过拟合的发生,进而提高算法的准确性和泛化能力。
4 |
5 | ## 对称决策树
6 |
7 | 那么**对称树**和普通决策树有什么区别?
8 |
9 | 一图为对称树,二图为普通决策树
10 |
11 | 
12 |
13 | 对称树中,每一层的每一个节点判断条件都是一样的。假如如果我们只训练一棵树,那么显然对称树的overfit能力会比普通的决策树弱;但是在GBM中,我们通常训练很多的树,所以overfit的能力不必担心。那么对称树在GBM中有什么优势呢?下面列出三点:
14 |
15 | * 拟合模式相对简单,因为每一层都是一个判断条件
16 | * 可以提高预测速度
17 | * 对称树的结构本身比普通决策树自由度小,可以看作是加入了penalty惩罚机制,或者看作regularization正则化
18 |
19 | 最大的优势就是第二点——预测速度会提升。为什么会更快呢?
20 |
21 | 
22 |
23 | 上面这棵树最底层有四个节点,我们可以把这四个节点从0到3编号(index),每一个节点有一个对应值(value)。比如一个样本最终进入了第一个节点,那么这棵树对这个样本的预测值就是1.6。我们可以把value存放在一个数组里面,这样给定index就可以立刻得到value。那么对一个样本用一棵树进行预测时,我们只需要找到这个样本对应的index,因为在对称树中每一层的判断条件都是一样的,所以每一层都可以用0或者1来表示,比如是学生,用1表示,不是用0;有关注机器会学习用1表示,没有用0,那么每一个样本进入这棵树,都可以用两个bits来表示,也就是四种可能结果:00,01,10,和11。这两个bits代表的数字就是index。
24 |
25 | 这意味着什么呢?我们在做预测的时候,只要对每一层的条件进行判断,然后就可以找到index。因为每一个树的结构(判断条件)是已知的,我们甚至可以对这个过程进行并行计算。
26 |
27 | ## Catboost与XGBoost,LightGBM相比的创新点
28 |
29 | * 嵌入了自动将类别型特征处理为数值型特征的创新算法。首先对categorical features做一些统计,计算某个类别特征(category)出现的频率,之后加上超参数,生成新的数值型特征(numerical features)。
30 | * Catboost还使用了组合类别特征,可以利用到特征之间的联系,这极大的丰富了特征维度。
31 | * 采用排序提升的方法对抗训练集中的噪声点,从而避免梯度估计的偏差,进而解决预测偏移的问题。
32 | * 采用了完全对称树作为基模型。
33 |
34 | ## **类别型特征**
35 |
36 | ### **2.1 类别型特征的相关工作**
37 |
38 | 所谓类别型特征,即这类特征不是数值型特征,而是离散的集合,比如省份名(山东、山西、河北等),城市名(北京、上海、深圳等),学历(本科、硕士、博士等)。在梯度提升算法中,最常用的是将这些类别型特征转为数值型来处理,一般类别型特征会转化为一个或多个数值型特征。
39 |
40 | 如果某个 **类别型特征基数比较低(low-cardinality features)** ,即该特征的所有值去重后构成的集合元素个数比较少,一般利用One-hot编码方法将特征转为数值型。One-hot编码可以在数据预处理时完成,也可以在模型训练的时候完成,从训练时间的角度,后一种方法的实现更为高效,CatBoost对于基数较低的类别型特征也是采用后一种实现。
41 |
42 | 显然,在 **高基数类别型特征(high cardinality features)** 当中,比如 `user ID`,这种编码方式会产生大量新的特征,造成维度灾难。一种折中的办法是可以将类别分组成有限个的群体再进行One-hot编码。一种常被使用的方法是根据目标变量统计(Target Statistics,以下简称TS)进行分组,目标变量统计用于估算每个类别的目标变量期望值。甚至有人直接用TS作为一个新的数值型变量来代替原来的类别型变量。重要的是,可以通过对TS数值型特征的阈值设置,基于对数损失、基尼系数或者均方差,得到一个对于训练集而言将类别一分为二的所有可能划分当中最优的那个。在LightGBM当中,类别型特征用每一步梯度提升时的梯度统计(Gradient Statistics,以下简称GS)来表示。虽然为建树提供了重要的信息,但是这种方法有以下两个缺点:
43 |
44 | * 增加计算时间,因为需要对每一个类别型特征,在迭代的每一步,都需要对GS进行计算;
45 | * 增加存储需求,对于一个类别型变量,需要存储每一次分离每个节点的类别;
46 |
47 | 为了克服这些缺点,LightGBM以损失部分信息为代价将所有的长尾类别归为一类,作者声称这样处理高基数类别型特征时比One-hot编码还是好不少。不过如果采用TS特征,那么对于每个类别只需要计算和存储一个数字。
48 |
49 | ### **2.2 目标变量统计(Target Statistics)**
50 |
51 | CatBoost算法的设计初衷是为了更好的处理GBDT特征中的categorical features。在处理 GBDT特征中的categorical features的时候,最简单的方法是用 categorical feature 对应的标签的平均值来替换。在决策树中,标签平均值将作为节点分裂的标准。这种方法被称为 Greedy Target-based Statistics , 简称 Greedy TS,用公式来表达就是:
52 |
53 | ![[公式]](https://www.zhihu.com/equation?tex=%5Chat%7Bx%7D_k%5Ei%3D%5Cfrac%7B%5Csum_%7Bj%3D1%7D%5E%7Bn%7D%5Bx_%7Bj%2Ck%7D%3Dx_%7Bi%2Ck%7D%5D%5Ccdot+Y_i%7D%7B%5Csum_%7Bj%3D1%7D%5E%7Bn%7D%5Bx_%7Bj%2Ck%7D%3Dx_%7Bi%2Ck%7D%5D%7D+%5C%5C)
54 |
55 | 这种方法有一个显而易见的缺陷,就是通常特征比标签包含更多的信息,如果强行用标签的平均值来表示特征的话,当训练数据集和测试数据集数据结构和分布不一样的时候会出条件偏移问题。
56 |
57 | 一个标准的改进 Greedy TS的方式是添加先验分布项,这样可以减少噪声和低频率类别型数据对于数据分布的影响:
58 |
59 | ![[公式]](https://www.zhihu.com/equation?tex=%5Chat%7Bx%7D_k%5Ei%3D%5Cfrac%7B%5Csum_%7Bj%3D1%7D%5E%7Bp-1%7D%7B%5Bx_%7B%5Csigma_%7Bj%2Ck%7D%7D%3Dx_%7B%5Csigma_%7Bp%2Ck%7D%7D%5D%7DY_%7B%5Csigma_%7Bj%7D%7D%2Ba%5Ccdot+p%7D%7B%5Csum_%7Bj%3D1%7D%5E%7Bp-1%7D%7B%5Bx_%7B%5Csigma_%7Bj%2Ck%7D%7D%3Dx_%7B%5Csigma_%7Bp%2Ck%7D%7D%5D%7D%2Ba%7D+%5C%5C)
60 |
61 | 其中 ![[公式]](https://www.zhihu.com/equation?tex=p)是添加的先验项, ![[公式]](https://www.zhihu.com/equation?tex=a+)通常是大于0的权重系数。添加先验项是一个普遍做法,针对类别数较少的特征,它可以减少噪声数据。对于回归问题,一般情况下,先验项可取数据集label的均值。对于二分类,先验项是正例的先验概率。利用多个数据集排列也是有效的,但是,如果直接计算可能导致过拟合。CatBoost利用了一个比较新颖的计算叶子节点值的方法,这种方式(oblivious trees,对称树)可以避免多个数据集排列中直接计算会出现过拟合的问题。
62 |
63 | ### **2.3 特征组合**
64 |
65 | 值得注意的是几个类别型特征的任意组合都可视为新的特征。例如,在音乐推荐应用中,我们有两个类别型特征:用户ID和音乐流派。如果有些用户更喜欢摇滚乐,将用户ID和音乐流派转换为数字特征时,根据上述这些信息就会丢失。结合这两个特征就可以解决这个问题,并且可以得到一个新的强大的特征。然而,组合的数量会随着数据集中类别型特征的数量成指数增长,因此不可能在算法中考虑所有组合。为当前树构造新的分割点时,CatBoost会采用贪婪的策略考虑组合。对于树的第一次分割,不考虑任何组合。对于下一个分割,CatBoost将当前树的所有组合、类别型特征与数据集中的所有类别型特征相结合,并将新的组合类别型特征动态地转换为数值型特征。CatBoost还通过以下方式生成数值型特征和类别型特征的组合:树中选定的所有分割点都被视为具有两个值的类别型特征,并像类别型特征一样被进行组合考虑。
66 |
67 | ### **2.4 CatBoost处理Categorical features总结**
68 |
69 | * 首先会计算一些数据的statistics。计算某个category出现的频率,加上超参数,生成新的numerical features。这一策略要求同一标签数据不能排列在一起(即先全是0之后全是1这种方式),训练之前需要打乱数据集。
70 | * 第二,使用数据的不同排列(实际上是4个)。在每一轮建立树之前,先扔一轮骰子,决定使用哪个排列来生成树。
71 | * 第三,考虑使用categorical features的不同组合。例如颜色和种类组合起来,可以构成类似于blue dog这样的特征。当需要组合的categorical features变多时,CatBoost只考虑一部分combinations。在选择第一个节点时,只考虑选择一个特征,例如A。在生成第二个节点时,考虑A和任意一个categorical feature的组合,选择其中最好的。就这样使用贪心算法生成combinations。
72 | * 第四,除非向gender这种维数很小的情况,不建议自己生成One-hot编码向量,最好交给算法来处理。
73 |
74 | ## **克服梯度偏差**
75 |
76 | CatBoost和所有标准梯度提升算法一样,都是通过构建新树来拟合当前模型的梯度。然而,所有经典的提升算法都存在由有偏的点态梯度估计引起的过拟合问题。在每个步骤中使用的梯度都使用当前模型中的相同的数据点来估计,这导致估计梯度在特征空间的任何域中的分布与该域中梯度的真实分布相比发生了偏移,从而导致过拟合。为了解决这个问题,CatBoost对经典的梯度提升算法进行了一些改进,简要介绍如下。
77 |
78 | 许多利用GBDT技术的算法(例如,XGBoost、LightGBM),构建下一棵树分为两个阶段:选择树结构和在树结构固定后计算叶子节点的值。为了选择最佳的树结构,算法通过枚举不同的分割,用这些分割构建树,对得到的叶子节点计算值,然后对得到的树计算评分,最后选择最佳的分割。两个阶段叶子节点的值都是被当做梯度或牛顿步长的近似值来计算。在CatBoost中,第一阶段采用梯度步长的无偏估计,第二阶段使用传统的GBDT方案执行。既然原来的梯度估计是有偏的,那么怎么能改成无偏估计呢?
79 |
80 | 
81 |
82 |
83 | ## **预测偏移和排序提升**
84 |
85 | 预测偏移(Prediction shift)是由梯度偏差造成的。在GDBT的每一步迭代中, 损失函数使用相同的数据集求得当前模型的梯度, 然后训练得到基学习器, 但这会导致梯度估计偏差, 进而导致模型产生过拟合的问题。 CatBoost通过采用排序提升 (Ordered boosting) 的方式替换传统算法中梯度估计方法,进而减轻梯度估计的偏差,提高模型的泛化能力。下面我们对预测偏移进行详细的描述和分析。
86 |
87 | 首先来看下GBDT的整体迭代过程:
88 |
89 | GBDT算法是通过一组分类器的串行迭代,最终得到一个强学习器,以此来进行更高精度的分类。它使用了前向分布算法,弱学习器使用分类回归树(CART)。
90 |
91 | 
92 |
93 | ### 排序提升
94 |
95 | 为了克服预测偏移问题,CatBoost提出了一种新的叫做Ordered boosting的算法。
96 |
97 | 
98 |
99 | 
100 |
101 |
102 | ## **快速评分**
103 |
104 | CatBoost使用对称树(oblivious trees)作为基预测器。在这类树中,相同的分割准则在树的整个一层上使用。这种树是平衡的,不太容易过拟合。梯度提升对称树被成功地用于各种学习任务中。在对称树中,每个叶子节点的索引可以被编码为长度等于树深度的二进制向量。这在CatBoost模型评估器中得到了广泛的应用:我们首先将所有浮点特征、统计信息和独热编码特征进行二值化,然后使用二进制特征来计算模型预测值。
105 |
106 |
107 | ## 基于GPU实现快速训练
108 |
109 | * **密集的数值特征。** 对于任何GBDT算法而言,最大的难点之一就是搜索最佳分割。尤其是对于密集的数值特征数据集来说,该步骤是建立决策树时的主要计算负担。CatBoost使用oblivious 决策树作为基模型,并将特征离散化到固定数量的箱子中以减少内存使用。就GPU内存使用而言,CatBoost至少与LightGBM一样有效。主要改进之处就是利用了一种不依赖于原子操作的直方图计算方法。
110 | * **类别型特征。** CatBoost实现了多种处理类别型特征的方法,并使用完美哈希来存储类别型特征的值,以减少内存使用。由于GPU内存的限制,在CPU RAM中存储按位压缩的完美哈希,以及要求的数据流、重叠计算和内存等操作。通过哈希来分组观察。在每个组中,我们需要计算一些统计量的前缀和。该统计量的计算使用分段扫描GPU图元实现。
111 | * **多GPU支持。** CatBoost中的GPU实现可支持多个GPU。分布式树学习可以通过数据或特征进行并行化。CatBoost采用多个学习数据集排列的计算方案,在训练期间计算类别型特征的统计数据。
112 |
113 | ## **CatBoost的优缺点**
114 |
115 | **7.1 优点**
116 |
117 | * **性能卓越** :在性能方面可以匹敌任何先进的机器学习算法;
118 | * **鲁棒性/强健性** :它减少了对很多超参数调优的需求,并降低了过度拟合的机会,这也使得模型变得更加具有通用性;
119 | * **易于使用** :提供与scikit集成的Python接口,以及R和命令行界面;
120 | * **实用** :可以处理类别型、数值型特征;
121 | * **可扩展:** 支持自定义损失函数;
122 |
123 | **7.2 缺点**
124 |
125 | * 对于类别型特征的处理需要大量的内存和时间;
126 | * 不同随机数的设定对于模型预测结果有一定的影响;
127 |
--------------------------------------------------------------------------------
/XGBoost-2.md:
--------------------------------------------------------------------------------
1 | ## 算法原理
2 |
3 | XGBoost是在Gradient Boosting框架下面对GBDT的优化,是一种GBDT的工业级实现。其主要原理是在GBDT的基础上,在损失函数加入正则化部分,并且每一轮迭代对误差无法做二阶泰勒展开,加快对损失函数的优化速度。下面基于决策树弱分类器,梳理XGBoost算法的主流程,部分参数可能现在会看得有些懵懂,后面的内容会慢慢提到,这里先给一个整体的流程框架。
4 |
5 | * **输入:**
6 |
7 | * 训练数据集$T={(x_1,y_1),(x_2,y_2),...,(x_N,y_N)},x_i\in X\subseteq R^n,y_i \in Y={-1,+1}$;最大迭代次数$M$,损失函数 $L(Y,f(X))$;正则化系数$\lambda,\,\gamma$。
8 | * **输出:**
9 | * 强学习器 $f(x)$
10 | * 初始化 $f_0(x)$
11 | * 对$m=1,2,...,M$轮迭代有:
12 |
13 | * 1)计算第$i$个样本($i=1,2,...,N$)在当前轮损失函数$L$基于$f_{m-1}(x_i)$的一阶导数$g_{mi}$,二阶导数$h_{mi}$,并求和:
14 |
15 | $$
16 | G_m=\sum_{i=1}^{N}g_{mi}
17 |
18 | $$
19 |
20 | $$
21 | H_m=\sum_{i=1}^{N}h_{mi}
22 |
23 | $$
24 | * 2)基于当前节点尝试分裂决策树,默认分数 $score=0$,对特征序号$k=1,2,...,K$
25 |
26 | * a)初始化$G_L=0,H_L=0$
27 | * b.1)将样本按特征 $k$ 从小到大排列,依次取出第 $i$个样本,依次计算当前样本放入左子树后,左右子树一阶和二阶导数和:
28 |
29 | $$
30 | G_L=G_L+g_{mi},\,G_R=G-G_L
31 |
32 | $$
33 |
34 | $$
35 | H_L=H_L+h_{mi},\,H_R=H-H_L
36 |
37 | $$
38 | * b.2)尝试更新最大的分数:
39 |
40 | $$
41 | score=max(score,\,\frac{1}{2}\frac{G_L^2}{H_L+\lambda}+\frac{1}{2}\frac{G_R^2}{H_R+\lambda}-\frac{1}{2}\frac{(G_L+G_R)^2}{H_L+H_R+\lambda})
42 |
43 | $$
44 | * 3)基于最大$score$对应的划分特征和特征值分裂子树
45 | * 4)如果最大$score$为0,则当前决策树建立完毕,计算所有叶子区域的$w_{mj}$,得到弱学习器$h_m(x)$,更新强学习器$f_m(x)$,进入下一轮弱学习器迭代。如果最大$score$不是0,则继续尝试分裂决策树。
46 |
47 | ## 损失函数
48 |
49 | XGBoost的损失函数在GBDT$L(y,\,f_{m-1}(x)+h_m(x))$的基础上,加入了如下的正则化:
50 |
51 | $$
52 | \Omega(h_m)=\gamma J+\frac{\lambda}{2}\sum_{j=1}^{J}\omega_{mj}^2
53 |
54 | $$
55 |
56 | 这里的 $J$ 是叶子节点的个数,而 $\omega_{mj}$ 是第 $j$ 个叶子节点的最优值。这里的 $\omega_{mj}$ 和在GBDT里面使用的 $c_{mj}$ 其实是一个意思,只是[XGBoost论文](https://link.zhihu.com/?target=https%3A//arxiv.org/pdf/1603.02754.pdf)里面使用 $\omega$ 符号表示叶子区域的值,这里为了和论文保持一致。
57 |
58 | 最终,XGBoost的损失函数可以表示为:
59 |
60 | $$
61 | L_m=\sum_{i=1}^{N}L(y_i, f_{m-1}(x_i)+h_m(x_i))+\gamma J+\frac{\lambda}{2}\sum_{j=1}^{J}\omega_{mj}^2
62 |
63 | $$
64 |
65 |
66 | 如果要极小化上面这个损失函数,得到第$m$个决策树最优的所有$J$个叶子节点区域和每个叶子节点区域的最优解$\omega_{mj}$。XGBoost在损失函数优化方面做了一些优化,没有和GBDT一样去拟合泰勒展开式的一阶导数,而是期望直接基于损失函数的二阶泰勒展开式来求解。现在来看看这个损失函数的二阶泰勒展开式:
67 |
68 | $$
69 | \begin{align} L_m &=\sum_{i=1}^{N}L(y_i, f_{m-1}(x_i)+h_m(x_i))+\gamma J+\frac{\lambda}{2}\sum_{j=1}^{J}\omega_{mj}^2 \\ & \approx \sum_{i=1}^{N}\left(L(y_i, f_{m-1}(x_i))+\frac{\partial L(y_i,\,f_{m-1}(x_i))}{\partial f_{m-1}(x_i)}h_m(x_i)+\frac{1}{2}\frac{\partial^2 L(y_i,\,f_{m-1}(x_i))}{\partial^2 f_{m-1}(x_i)}h_m^2(x_i)\right)+\gamma J+\frac{\lambda}{2}\sum_{j=1}^{J}\omega_{mj}^2 \end{align}
70 |
71 | $$
72 |
73 |
74 | 为了方便起见,把第$i$个样本在第$m$个弱学习器的损失函数上面的一阶和二阶导数分别记为:
75 |
76 | $$
77 | g_{mi}=\frac{\partial L(y_i,\,f_{m-1}(x_i))}{\partial f_{m-1}(x_i)},\,h_{mi}=\frac{\partial^2 L(y_i,\,f_{m-1}(x_i))}{\partial^2 f_{m-1}(x_i)}
78 |
79 | $$
80 |
81 |
82 | 则,损失函数可以简化为:
83 |
84 | $$
85 | L_m\approx \sum_{i=1}^{N}\left(L(y_i, f_{m-1}(x_i))+g_{mi}h_m(x_i)+h_{mi}h_m^2(x_i)\right)+\gamma J+\frac{\lambda}{2}\sum_{j=1}^{J}\omega_{mj}^2
86 |
87 | $$
88 |
89 |
90 | 对于第$m$轮的迭代,损失函数里面$L(y_i,f_{m-1}(x_i))$为参数项,对最小化无影响,可以直接去掉。
91 |
92 | 定义
93 |
94 | $$
95 | I_j={i|q(x_i)=j}
96 |
97 | $$
98 |
99 | 为第$j$个叶子节点的样本集合,经过$M$轮迭代完毕以后每个决策树(弱学习器)的第$j$个叶子节点的取值最终会是同一个值$\omega_{mj}$,因此,可以对损失函数继续化简:
100 |
101 | $$
102 | \begin{align} L_m &\approx \sum_{i=1}^{N}\left(g_{mi}h_m(x_i)+h_{mi}h_m^2(x_i)\right)+\gamma J+\frac{\lambda}{2}\sum_{j=1}^{J}\omega_{mj}^2 \\ & =\sum_{j=1}^{J}\left(\sum_{x_i \in R_{mj}}g_{mj}\omega_{mj}+\frac{1}{2}\sum_{x_i \in R_{mj}}h_{mj}\omega_{mj}^2\right)+\gamma J+\frac{\lambda}{2}\sum_{j=1}^{J}\omega_{mj}^2 \\ & = \sum_{j=1}^{J}[(\sum_{x_i \in R_{mj}}g_{mj})\omega_{mj}+\frac{1}{2}(\sum_{x_i \in R_{mj}}h_{mj}+\lambda)\omega_{mj}^2]+\gamma J \end{align}
103 |
104 | $$
105 |
106 | 把每个叶子节点区域样本的一阶和二阶导数的和单独表示如下:
107 |
108 | $$
109 | G_{mj}=\sum_{x_i \in R_{mj}} g_{mj},\,H_{mj}=\sum_{x_i \in R_{mj}} h_{mj}
110 |
111 | $$
112 |
113 |
114 | 那么最终的损失函数形式可以表示为:
115 |
116 | $$
117 | L_m=\sum_{j=1}^{J}[(G_{mj}\omega_{mj}+\frac{1}{2}(H_{mj}+\lambda)\omega_{mj}^2]+\gamma J
118 |
119 | $$
120 |
121 |
122 | 现在有了最终的损失函数,回到前面讲到的问题,我们如何一次求解出决策树最优的所有$J$个叶子节点区域和每个叶子节点区域的最优解$\omega_{mj}$呢?
123 |
124 | 这个问题等价于下面两个子问题:
125 |
126 | * 如果已经求出了第$m$个决策树的$J$个最优的叶子节点区域,如何求出每个叶子节点区域的最优解$\omega_{m }$?
127 | * 对当前决策树做子树分裂决策时,应该如何选择哪个特征和特征值进行分裂,使最终的损失函数$ _m$最小?
128 |
129 | 第一个问题其实比较简单,如果树的结构$q(x)$已经确定的情况下,可以基于损失函数对$\omega_{m }$求偏导并令导数为0得出最佳的$\omega_{m }$,也就是每一个叶子节点的最优值表达式为:
130 |
131 | $$
132 | \omega_{m }=\frac{G_{mj}}{H_{mj}+\lambda}
133 |
134 | $$
135 |
136 |
137 | 将求得的最优$\omega_{m }$代回到损失函数,可视为每轮迭代时该轮弱学习器的最优值表达式:
138 |
139 | $$
140 | L_m=-\frac{1}{2}\sum_{j=1}^{J}[\frac{G_{mj}}{H_{mj}+\lambda}]+\gamma J
141 |
142 | $$
143 |
144 |
145 | 那么回到第二个问题,怎么样的树结构$q(x)$是最优的呢?
146 |
147 | 通常来讲,枚举所有可能的树的结构,然后计算该结构的分数是不太现实的。在实践当中,我们采用贪心的策略:
148 |
149 | * 从深度为0的单一叶子节点开始,即所有的样本都在一个节点上
150 | * 对于树的每一个叶子节点,尝试增加一个分裂点:
151 |
152 | * 令$I_L,\,I_R$分别表示分裂点加入之后的左右叶子节点的样本集合,则有
153 | * $$
154 | G_L=\sum_{i\in I_L}g_{mi}
155 |
156 | $$
157 | * $$
158 | G_R=\sum_{i\in I_R}g_{mi}
159 |
160 | $$
161 | * $$
162 | H_L=\sum_{i\in I_L}h_{mi}
163 |
164 | $$
165 | * $$
166 | H_R=\sum_{i\in I_R}h_{mi}
167 |
168 | $$
169 | * 假如每次做左右子树分裂的时候,都可以最大程度地减少损失函数,则我们期望最大化下式:
170 |
171 | $$
172 | \Delta L=-\frac{1}{2}\frac{(G_L+G_R)^2}{H_L+H_R+\lambda}+\gamma J-\left(-\frac{1}{2}\frac{G_L^2}{H_L+\lambda}-\frac{1}{2}\frac{G_R^2}{H_R+\lambda}+\gamma (J+1)\right)
173 |
174 | $$
175 | * 对上式进行整理,我们期望最大化的是:
176 |
177 | $$
178 | L_{split}=\frac{1}{2}[\frac{G_L^2}{H_L+\lambda}+\frac{G_R^2}{H_R+\lambda}-\frac{(G_L+G_R)^2}{H_L+H_R+\lambda}]-\gamma
179 |
180 | $$
181 |
182 | 上式通常在实践当中用来评估分裂的候选点,也就是说,我们的决策树分裂标准不再使用CART树的均方误差,而是上式了。而具体如何分裂,将在下一节进行讨论。
183 |
184 | ## 分裂节点算法
185 |
186 | ## 精确搜索算法
187 |
188 | * 对每一个节点,枚举所有的特征,对每一个特征,枚举所有的分裂点,目前大部分的GBDT算法实现(sklearn、R当中的GBDT)都是采用这种算法。
189 | * 对每个特征,通过特征的取值将实例进行排序
190 | * 寻求该特征的最优分裂点
191 | * 对所有的特征采用如下的算法操作
192 |
193 | 
194 |
195 | 不难发现,对于连续型的特征,由于要枚举特征所有取值,计算量非常大,为了提高效率,通常将数据按照特征取值预排序。对于深度为$k$的树的时间复杂度:对特征所有取值的排序为$O(NlogN)$,$N$为样本点数目,若有$D$维特征,则$O(kDNlogN)$
196 |
197 | ## 近视搜索算法
198 |
199 | 精确搜索算法非常强大,但是当数据量大到内存无法存下时无法高效运行,并且在进行分布式计算时也存在一些问题,此时需要一个近视算法。主要思路如下: - 根据特征分布的百分位数,提出特征的一些**候选分裂点** - 将连续特征值映射到桶里(候选点对应的分裂),然后根据桶里样本的统计量,从这些候选中选择最佳分裂点 - 根据候选提出的时间,分为: - 全局近似:在构造树的初始阶段提出所有的候选分裂点,然后对各个层次采用相同的候选 - 提出候选的次数少,但每次的候选数目多(因为候选不更新) - 局部近似:在每次分裂都重新提出候选 - 对层次较深的树更适合,候选分裂点的数目不需要太多
200 |
201 | 对于$G,H$的更新算法步骤如下:
202 |
203 | 
204 |
205 | 对于单机系统,XGBoost系统支持精确搜索算法,对于单机/分布式,全局近视/局部近视均支持。
206 |
207 | ## 正则化
208 |
209 | 总体上讲,XGBoost抵抗过拟合的方法与GBDT类似,主要也是从以下几方面考虑:
210 |
211 | ## 模型复杂度
212 |
213 | 正则化表达式为:
214 |
215 | $$
216 | \Omega(h_m)=\gamma J+\frac{\lambda}{2}\sum_{j=1}^{J}\omega_{mj}^2
217 |
218 | $$
219 |
220 | 这里的$J$是叶子节点的个数,而 $\omega_{mj}$ 是第$j$个叶子节点的最优值。
221 |
222 | 其中第一项叶子结点的数目$J$相当于$L_1$正则,第二项叶子节点的最优值相当于$L_2$正则。
223 |
224 | ## Shrinkage
225 |
226 | 其思想认为,每次走一小步逐渐逼近结果的效果,要比每次迈一大步很快逼近结果的方式更容易避免过拟合。即它不完全信任每一个棵残差树,它认为每棵树只学到了真理的一小部分,累加的时候只累加一小部分,通过多学几棵树弥补不足。用方程来看更清晰,即给每棵数的输出结果乘上一个步长$\alpha$(learning rate)
227 |
228 | 对于前面的弱学习器的迭代:
229 |
230 | $$
231 | f_m(x)=f_{m-1}(x)+T(x;\gamma_m)
232 |
233 | $$
234 |
235 | 加上正则化项,则有
236 |
237 | $$
238 | f_m(x)=f_{m-1}(x)+\alpha\, T(x;\gamma_m)
239 |
240 | $$
241 |
242 | 此处,$\alpha$的取值范围为(0,1]。对于同样的训练集学习效果,较小$\alpha$的意味着需要更多的弱学习器的迭代次数。通常我们用步长和迭代最大次数一起决定算法的拟合效果。
243 |
244 | ## 特征采样和样本采样
245 |
246 | XGBoost借鉴RF的思想,对于特征进行采样以达到降低过拟合的目的,根据用户反馈,特征采样比起样本采样效果更优。当然,XGBoost同时支持以上两种降低过拟合的采样方式。
247 |
248 | ## Early Stop
249 |
250 | 对于每一次分离后的增益,即前面的
251 |
252 | $$
253 | L_{split}=\frac{1}{2}[\frac{G_L^2}{H_L+\lambda}+\frac{G_R^2}{H_R+\lambda}-\frac{(G_L+G_R)^2}{H_L+H_R+\lambda}]-\gamma
254 |
255 | $$
256 |
257 |
258 | 在`sklearn`接口当中,如果$L_{split}$出现负值,则提前停止;但是,被提前终止掉的分裂可能其后续的分裂会带来好处。在XBGoost原生接口当中是采用过后剪枝策略:将树分裂到最大深度,然后再基于上述增益计算剪枝。在具体实现当中还有`learning rate`等其它参数一起控制,给$L_{split}$出现负值的后续轮留机会。
259 |
260 | ## 缺失值处理
261 |
262 | 在实际的工业实践当中,数据出现缺失无法避免。
263 |
264 | XGBoost没有假设缺失值一定进入左子树还是右子树,则是尝试通过枚举所有缺失值在当前节点是进入左子树,还是进入右子树更优来决定一个处理缺失值默认的方向,这样处理起来更加的灵活和合理。
265 |
266 | 也就是说,上面第1节的算法的步骤a),b.1)和b.2)会执行2次,第一次假设特征$k$所有有缺失值的样本都走左子树,第二次假设特征$k$所有缺失值的样本都走右子树。然后每次都是针对没有缺失值的特征k的样本走上述流程,而不是所有的的样本。
267 |
268 | 如果是所有的缺失值走右子树,使用上面第1节的a),b.1)和b.2)即可。如果是所有的样本走左子树,则上面第1节的a)步要变成:
269 |
270 | $$
271 | G_R=0,\,H_R=0
272 |
273 | $$
274 |
275 |
276 | b.1)步要更新为:
277 |
278 | $$
279 | G_R=G_R+g_mi,\,G_L=G-G_R
280 |
281 | $$
282 |
283 |
284 | $$
285 | H_R=H_R+h_mi,\,H_L=H-H_R
286 |
287 | $$
288 |
289 |
290 | 具体算法如下图所示:
291 |
292 | 
293 |
294 | ## 优缺点
295 |
296 | ## 优点
297 |
298 | * 支持线性分类器(相当于引入$L_1,\,L_2$正则惩罚项的LR和线性回归,损失函数公式=误差平方和+正则项,似LR)
299 | * 损失函数用了二阶泰勒展开,引入一阶导和二阶导,提高模型拟和的速度
300 | * 可以给缺失值自动划分方向
301 | * 同RF,支持样本(行)随机抽取,也支持特征(列)随机抽取,降低运算,防过拟合
302 | * 损失函数引入正则化项,包含全部叶子节点个数,每个叶子节点得分的$L_2$模的平方和(代表叶子节点权重的影响),控制模型(树)复杂度
303 | * 每次迭代后为叶子分配结合学习速率,减低每棵树权重,减少每棵树影响,灵活调整后面的学习空间
304 | * 支持并行,不是树并行,是把特征值先预排序,存起来,可以重复并行使用计算分裂点
305 | * 分裂依据分开后与未分前的差值增益,不用每个节点排序算增益,减少计算量,可以并行计算
306 | * 可以引入阈值限制树分裂,控制树的规模
307 |
308 | ## 缺点
309 |
310 | * 往往会选择具有更高数量的不同值的预测器
311 | * 当预测器具有很多类别时,容易过拟合
312 | * 参数过多,调参困难
313 | * 如果采用精确搜索算法对内存消耗过大,且不支持分布式
314 |
315 | ## sklearn中的参数解释
316 |
317 | `sklearn`本身的文档当中并没有XGBoost的描述,[Github](https://link.zhihu.com/?target=https%3A//github.com/dmlc/xgboost/blob/master/python-package/xgboost/sklearn.py)上面看到主要参数如下:
318 |
319 | * max_depth :树的最大深度。越大通常模型复杂,更容易过拟合,这里作为弱学习器一般设置为1-10
320 | * learning_rate:学习率或收缩因子。学习率和迭代次数/弱分类器数目n_estimators相关。 缺省:0.1 (与直接调用xgboost的eta参数含义相同)
321 | * n_estimators:弱分类器数目. 缺省:100
322 | * verbosity:控制输出
323 | * slient:参数值为1时,静默模式开启,不输出任何信息
324 | * objective:待优化的目标函数,常用值有:
325 |
326 | * binary:logistic 二分类的逻辑回归,返回预测的概率
327 | * multi:softmax 使用softmax的多分类器,返回预测的类别(不是概率)
328 | * multi:softprob 和multi:softmax参数一样,但是返回的是每个数据属于各个类别的概率
329 | * 支持用户自定义目标函数
330 | * booster:选择每次迭代的模型,有两种选择:
331 | * gbtree:基于树的模型,为缺省值
332 | * gbliner:线性模型
333 | * dart:树模型
334 | * nthread:用来进行多线程控制。 如果你希望使用CPU全部的核,那就用缺省值-1,算法会自动检测它
335 | * n_jobs:xgboost运行时的线程数,后续代替`nthread`参数
336 | * gamma:节点分裂所需的最小损失函数下降值,缺省0
337 | * min_child_weight:叶子结点需要的最小样本权重(hessianhessian)和
338 | * subsample:构造每棵树的所用样本比例(样本采样比例)
339 | * colsample_bytree:构造树时每棵树的所用特征比例
340 | * colsample_bylevel:构造树时每层的所用特征比例
341 | * colsample_bynone:构造树时每次分裂的所用特征比例
342 | * reg_alpha:$L_1$正则的惩罚系数
343 | * reg_lambda:$L_2$正则的惩罚系数
344 | * tree_method string [default= auto]:XGBoost中使用的树构造算法
345 |
346 | * XGBoost支持hist和大规模分布式训练,仅支持大规模外部内存版本。
347 | * 选择: auto, exact, approx, hist, gpu_hist
348 | * auto: 对于中小型数据集,将使用精确的贪婪(精确)
349 | * 对于非常大的数据集,将选择近似算法(近似)
350 | * 因为旧版本总是在单个机器中使用精确贪婪,所以当选择近似算法来通知该选择时,用户将得到消息
351 | * exact: 精确的贪婪算法
352 | * approx : 使用分位数草图和梯度直方图的近似贪婪算法
353 | * hist:快速直方图优化近似贪心算法
354 | * gpu_hist:hist算法的GPU实现
355 | * scale_pos_weight:正负样本的平衡,通常用于不均衡数据
356 | * base_score:初始预测值
357 | * random_state:随机种子
358 | * missing:缺失值
359 | * importance_type:特征重要程度计算方法
360 |
361 | 除了以上参数,XGBoost原生接口当中参数众多,主要有以下4大类:
362 |
363 | * General parameters
364 | * Booster parameters
365 | * Learning task parameters
366 | * Command line parameters(较少用到)
367 |
368 | 如果有遗漏,具体可以参阅[XGBoost Parameters](https://link.zhihu.com/?target=https%3A//xgboost.readthedocs.io/en/latest/parameter.html)
369 |
370 | ## 应用场景
371 |
372 | XGBoost是GBDT框架的工业级优化实现,所有GBDT能够应用的场景,XGBoost都可以应用,所有回归问题(线性/非线性)、二分类问题(设定阈值,大于阈值为正例,反之为负例)。
373 |
374 | 按业务领域分,推荐系统、反欺诈、信用评级等。
375 |
--------------------------------------------------------------------------------
/LightGBM-2.md:
--------------------------------------------------------------------------------
1 | title: LightGBM算法梳理 date: 2019-08-12 23:56:55 categories: 机器学习 tags: - 集成学习 - LightGBM - Histogram - 分布式 - sklearn description: DataWhale暑期学习小组-高级算法梳理第八期Task4。
2 |
3 | ---
4 |
5 | ## LightGBM
6 |
7 | 同XGBoost类似,LightGBM依然是在GBDT算法框架下的一种改进实现,是一种基于决策树算法的快速、分布式、高性能的GBDT框架,主要说解决的痛点是面对高维度大数据时提高GBDT框架算法的效率和可扩展性。
8 |
9 | “Light”主要体现在三个方面,即更少的样本、更少的特征、更少的内存,分别通过单边梯度采样(Gradient-based One-Side Sampling)、互斥特征合并(Exclusive Feature Bundling)、直方图算法(Histogram)三项技术实现。另外,在工程上面,LightGBM还在并行计算方面做了诸多的优化,支持特征并行和数据并行,并针对各自的并行方式做了优化,减少通信量。
10 |
11 | ## LightGBM的起源
12 |
13 | LightGBM起源于微软亚洲研究院在NIPS发表的系列论文:
14 |
15 | * [Qi Meng, Guolin Ke, Taifeng Wang, Wei Chen, Qiwei Ye, Zhi-Ming Ma, Tie-Yan Liu. “A Communication-Efficient Parallel Algorithm for Decision Tree.” Advances in Neural Information Processing Systems 29 (NIPS 2016), pp. 1279-1287](https://link.zhihu.com/?target=https%3A//papers.nips.cc/paper/6381-a-communication-efficient-parallel-algorithm-for-decision-tree.pdf)
16 | * [Guolin Ke, Qi Meng, Thomas Finley, Taifeng Wang, Wei Chen, Weidong Ma, Qiwei Ye, Tie-Yan Liu. “LightGBM: A Highly Efficient Gradient Boosting Decision Tree.” Advances in Neural Information Processing Systems 30 (NIPS 2017), pp. 3149-3157](https://link.zhihu.com/?target=https%3A//papers.nips.cc/paper/6907-lightgbm-a-highly-efficient-gradient-boosting-decision-tree.pdf)
17 |
18 | 并于2016年10月17日在[LightGBM](https://link.zhihu.com/?target=https%3A//github.com/microsoft/LightGBM)上面开源,三天内在GitHub上面被star了1000次,fork了200次。知乎上现有近2000人关注“如何看待微软开源的LightGBM?”问题。
19 |
20 | 随后不断迭代,慢慢地开始支持Early Stopping、叶子索引预测、最大深度设置、特征重要性评估、多分类、类别特征支持、正则化(L1,L2及分裂最小增益)……
21 |
22 | 具体可以参阅以下链接:
23 |
24 | [LightGBM大事记](https://link.zhihu.com/?target=https%3A//github.com/Microsoft/LightGBM/blob/master/docs/Key-Events.md)
25 |
26 | ## Histogram VS Pre-sorted
27 |
28 | ## Pre-sorted
29 |
30 | 在XGBoost当中的精确搜索算法(Exact Greedy Algorithm)在寻找分裂点时就是采用Pre-sorted的思想。具体过程不再赘述,可以参阅[XGBoost算法梳理](https://link.zhihu.com/?target=http%3A//datacruiser.io/2019/08/10/DataWhale-Workout-No-8-XGboost-Summary/)
31 |
32 | 预排序还是有一定优点的,如果不用预排序的话,在分裂节点的时候,选中某一个特征后,需要对A按特征值大小进行排序,然后计算每个阈值的增益,这个过程需要花费很多时间。
33 |
34 | 预排序算法在计算最优分裂时,各个特征的增益可以并行计算,并且能精确地找到分割点。但是预排序后需要保存特征值及排序后的索引,因此需要消耗两倍于训练数据的内存,时间消耗大。另外预排序后,特征对梯度的访问是一种随机访问,并且不同的特征访问的顺序不一样,无法对cache进行优化,时间消耗也大。最后,在每一层,需要随机访问一个行索引到叶子索引的数组,并且不同特征访问的顺序也不一样。
35 |
36 | ## Historgram
37 |
38 | 首先需要指出的是,XGBoost在寻找树的分裂节点的也是支持直方图算法的,就是论文中提到的近视搜索算法(Approximate Algorithm)。只是,无论特征值是否为0,直方图算法都需要对特征的分箱值进行索引,因此对于大部分实际应用场景当中的稀疏数据优化不足。
39 |
40 | 回过头来,为了能够发挥直方图算法的优化威力,LightGBM提出了另外两个新技术:单边梯度采样(Gradient-based One-Side Sampling)和互斥特征合并(Exclusive Feature Bundling),在减少维度和下采样上面做了优化以后才能够将直方图算法发挥得淋漓尽致。下面依次介绍直方图算法、GOSS和EFB。
41 |
42 | ### 直方图算法
43 |
44 | 直方图算法的基本思想是先把连续的浮点特征值离散化成$k$个整数,同时构造一个宽度为$k$的直方图。在遍历数据的时候,根据离散化后的值作为索引在直方图中累积统计量,当遍历一次数据后,直方图累积了需要的统计量,然后根据直方图的离散值,遍历寻找最优的分割点。具体算法描述如下:
45 |
46 | 
47 |
48 | 
49 |
50 | 直方图算法有如下优点:
51 |
52 | * 内存消耗降低。预排序算法需要的内存约是训练数据的两倍(2x样本数x维度x4Bytes),它需要用32位浮点来保存特征值,并且对每一列特征,都需要一个额外的排好序的索引,这也需要32位的存储空间。对于 直方图算法,则只需要(1x样本数x维度x1Bytes)的内存消耗,仅为预排序算法的1/8。因为直方图算法仅需要存储特征的 bin 值(离散化后的数值),不需要原始的特征值,也不用排序,而bin值用8位整型存储就足够了。
53 | * 算法时间复杂度大大降低。决策树算法在节点分裂时有两个主要操作组成,一个是“寻找分割点”,另一个是“数据分割”。从算法时间复杂度来看,在“寻找分割点”时,预排序算法对于深度为$k$的树的时间复杂度:对特征所有取值的排序为$O(NlogN)$,$N$为样本点数目,若有$D$维特征,则$O(kDNlogN)$,而直方图算法需要$O(kD \times bin)$(bin是histogram 的横轴的数量,一般远小于样本数量$N$)。
54 | * 再举个例子说明上述两点的优化,假设数据集$A$的某个特征的特征值有(二叉树存储):${1.2,1.3,2.2,2.3,3.1,3.3}$,预排序算法要全部遍历一遍,需要切分大约5次。进行离散化后,只需要切分2次 ${{1},{2,3}}$ 和 ${{1,2},{3}}$,除了切分次数减少,内存消耗也大大降低。
55 | * 直方图算法还可以进一步加速。一个容易观察到的现象:一个叶子节点的直方图可以直接由父节点的直方图和兄弟节点的直方图做差得到。通常构造直方图,需要遍历该叶子上的所有数据,但直方图做差仅需遍历直方图的$k$个bin。利用这个方法,LightGBM可以在构造一个叶子的直方图后,可以用非常微小的代价得到它兄弟叶子的直方图,在速度上可以提升一倍。
56 |
57 | 
58 |
59 | 当然,直方图算法并不是完美的。由于特征被离散化后,找到的并不是很精确的分割点,所以会对结果产生影响。但在不同的数据集上的结果表明,离散化的分割点对最终的精度影响并不是很大,甚至有时候会更好一点。原因是决策树本来就是弱模型,分割点是不是精确并不是太重要;较粗的分割点也有正则化的效果,可以有效地防止过拟合;即使单棵树的训练误差比精确分割的算法稍大,但在梯度提升(GradientBoosting)的框架下没有太大的影响。
60 |
61 | ### 单边梯度采样(Gradient-based One-Side Sampling)
62 |
63 | 单边梯度采样是一种在减少数据量和保证精度上平衡的算法。在GBDT中, 我们对损失函数的负梯度进行拟合,样本误差越大,梯度的绝对值越大,这说明模型对该样本的学习还不足够,相反如果越小则表示模型对该样本的学习已经很充分。因此,我们可以这样推论:梯度的绝对值越大,样本重要性越高。单边梯度采样正是以样本的梯度作为样本的权重进行采样。
64 |
65 | 单边梯度采样保留所有的梯度较大的样本,在梯度小的实例上使用随机采样。为了抵消对数据分布的影响,计算信息增益的时候,单边梯度采样对小梯度的数据引入常量乘数。单边梯度采样首先根据数据的梯度绝对值排序,选取$top\,\,a$个样本。然后在剩余的数据中随机采样$b$个样本。接着计算信息增益时为采样出的小梯度数据乘以$\frac{1-a}{b}$,这样算法就会更关注训练不足的样本例,而不会过多改变原数据集的分布。正是单边梯度采样减少了数据量,让直方图算法发挥了更大的作用。单边梯度采样具体算法见下图:
66 |
67 | 
68 |
69 | ### 互斥特征合并(Exclusive Feature Bundling)
70 |
71 | 高维的数据通常是稀疏的,这种特征空间的稀疏性给我们提供了一种设计一种接近无损地降维的可能性。特别的,在稀疏特征空间中,许多特征是互斥的,换句话说,大部分特征不会同时取非0值,例如One-hot之后的类别特征他们从不同时为非0值。我们可以合并互斥的特征为单一特征(我们将这个过程称为*Exclusive Feature Bundle* ).通过仔细设计特征扫描算法,我们从合并特征中构建出与单个特征相同的特征直方图。通过这种方式,直方图构建算法的时间复杂度从$O(ND)$,降到$O(N×bundle)$,其中$N$为样本点数目,$D$为特征维度。通常,bundle << $D$,我们能够在不损失精度的情况下极大地加速GBDT的训练。
72 |
73 | 那么接下来有两个问题需要处理:
74 |
75 | * 需要合并哪些特征
76 | * 如何合并这些特征
77 |
78 | ### Greedy Bundling
79 |
80 | 找出最优的 bundle 组合数是一个 NP 问题,LightGBM通过将原问题转化为”图着色”问题进行贪心近似解决。
81 |
82 | 首先创建一个图$G(V, E)$,其中$V$就是特征,为图中的节点,$E$为$G$中的边,将不是相互独立的特征用一条边连接起来,边的权重就是两个相连接的特征的总冲突值,这样需要绑定的特征就是在图着色问题中要涂上同一种颜色的那些点(特征)。具体算法过程如下:
83 |
84 | 
85 |
86 | ### Merge Exclusive Features
87 |
88 | 该过程主要是关键在于原始特征值可以从bundle中区分出来,即绑定几个特征在同一个bundle里需要保证绑定前的原始特征的值在bundle中能够被识别,考虑到直方图算法将连续的值保存为离散的bin,我们可以使得不同特征的值分到bundle中的不同bin中,这可以通过在特征值中加一个偏置常量来解决,比如,我们在bundle中绑定了两个特征A和B,A特征的原始取值为区间[0,10),B特征的原始取值为区间[0,20),我们可以在B特征的取值上加一个偏置常量10,将其取值范围变为[10,30),这样就可以放心的融合特征A和B了,因为在树模型中对于每一个特征都会计算分裂节点的,也就是通过将他们的取值范围限定在不同的bin中,在分裂时可以将不同特征很好的分裂到树的不同分支中去。具体算法如下:
89 |
90 | 
91 |
92 | ## Leaf-wise VS Level-wise
93 |
94 | ## Level-wise
95 |
96 | 大多数GBDT框架使用的按层生长 (level-wise) 的决策树生长策略,Level-wise遍历一次数据可以同时分裂同一层的叶子,容易进行多线程优化,也好控制模型复杂度,不容易过拟合。但实际上Level-wise是一种低效的算法,因为它不加区分的对待同一层的叶子,带来了很多没必要的开销,因为实际上很多叶子的分裂增益较低,没必要进行搜索和分裂。
97 |
98 | 
99 |
100 | ## Leaf-wise
101 |
102 | LightGBM在直方图算法之上,对于树的生长策略做了进一步优化,抛弃了Level-wise策略,使用了带有深度限制的按叶子生长 (leaf-wise)算法。Leaf-wise则是一种更为高效的策略,每次从当前所有叶子中,找到分裂增益最大的一个叶子,然后分裂,如此循环。因此同Level-wise相比,在分裂次数相同的情况下,Leaf-wise可以降低更多的误差,得到更好的精度。Leaf-wise的缺点是可能会长出比较深的决策树,产生过拟合。因此LightGBM在Leaf-wise之上增加了一个最大深度的限制,在保证高效率的同时防止过拟合。
103 |
104 | 
105 |
106 | ## 特征并行和数据并行
107 |
108 | 本小节主要根据[LightGBM的官方文档](https://link.zhihu.com/?target=https%3A//lightgbm.readthedocs.io/en/latest/Features.html%23optimization-in-network-communication)中提到的并行计算优化进行讲解。 在本小节中,工作的节点称为**worker**
109 |
110 | LightGBM具有支持高效并行的优点。LightGBM原生支持并行学习,目前支持特征并行和数据并行的两种。
111 |
112 | ## 特征并行
113 |
114 | 特征并行主要是并行化决策树中寻找最优划分点(“Find Best Split”)的过程,因为这部分最为耗时。
115 |
116 | 传统特征并行做法如下:
117 |
118 | * 垂直划分数据(对特征划分),不同的worker有不同的特征集
119 | * 每个workers找到局部最佳的切分点{feature, threshold}
120 | * workers使用点对点通信,找到全局最佳切分点
121 | * 具有全局最佳切分点的worker进行节点分裂,然后广播切分后的结果(左右子树的instance indices)
122 | * 其它worker根据收到的instance indices也进行划分
123 |
124 | 
125 |
126 | 主要有以下缺点:
127 |
128 | * 无法加速分裂的过程,该过程的时间复杂度为$O(N)$,当数据量大的时候效率不高
129 | * 需要广播划分的结果(左右子树的instance indices),1条数据1bit的话,通信花费大约需要$O(N/8)$
130 |
131 | LightGBM的特征并行每个worker保存所有的数据集,这样找到全局最佳切分点后各个worker都可以自行划分,就不用进行广播划分结果,减小了网络通信量。过程如下:
132 |
133 | * 每个workers找到局部最佳的切分点{feature, threshold}
134 | * workers使用点对点通信,找到全局最佳切分点
135 | * 每个worker根据全局全局最佳切分点进行节点分裂
136 |
137 | 这样虽然不用进行广播划分结果,减小了网络通信量。但是也有缺点:
138 |
139 | * 分裂过程的复杂度保持不变
140 | * 每个worker保存所有数据,存储代价高
141 |
142 | ## 数据并行
143 |
144 | 数据并行的目标是并行化整个决策学习的过程,传统算法的做法如下:
145 |
146 | * 水平切分数据,不同的worker拥有部分数据
147 | * 每个worker根据本地数据构建局部直方图
148 | * 合并所有的局部直方图得到全部直方图
149 | * 根据全局直方图找到最优切分点并进行分裂
150 |
151 | 
152 |
153 | 在第3步当中有两种合并方式:
154 |
155 | * 采用点对点方式(point-to-point communication algorithm)进行通讯,每个worker通讯量为$ ( ℎ × × )$
156 | * 采用collective communication algorithm(如“[All Reduce](https://link.zhihu.com/?target=http%3A//pages.tacc.utexas.edu/~eijkhout/pcse/html/mpi-collective.html)”)进行通讯(相当于有一个中心节点,通讯后在返回结果),每个worker的通讯量为$O(2× × )$
157 |
158 | 不难发现,通信的代价也是很高的,这也是数据并行的缺点。
159 |
160 | LightGBM的数据并行主要做了以下两点优化:
161 |
162 | * 使用“Reduce Scatter”将不同worker的不同特征的直方图合并,然后workers在局部合并的直方图中找到局部最优划分,最后同步全局最优划分
163 | * 通过直方图作差法得到兄弟节点的直方图,因此只需要通信一个节点的直方图,减半通信量
164 |
165 | 通过上述两点做法,通信开销降为$ (0.5 × × )$。
166 |
167 | 另外,LightGBM还采用 一种称为**PV-Tree** 的算法进行投票并行(Voting Parallel),其实本质上也是一种数据并行。
168 |
169 | PV-Tree和普通的决策树差不多,只是在寻找最优切分点上有所不同。具体算法如下:
170 |
171 | 
172 |
173 | 主要思路如下:
174 |
175 | * 水平切分数据,不同的worker拥有部分数据
176 | * Local voting: 每个worker构建直方图,找到$top-k$个最优的本地划分特征
177 | * Global voting: 中心节点聚合得到最优的$top-2k$个全局划分特征($top-2k$是看对各个worker选择特征的个数进行计数,取最多的$2k$个)
178 | * Best Attribute Identification: 中心节点向worker收集这$top-2k$个特征的直方图,并进行合并,然后计算得到全局的最优划分
179 | * 中心节点将全局最优划分广播给所有的worker,worker进行本地划分
180 |
181 | 
182 |
183 | 可以看出,PV-tree将原本需要$O( × )$ 变为了$O(2k × )$,通信开销得到降低。此外,可以证明,当每个worker的数据足够多的时候,$top-2k$个中包含全局最佳切分点的概率非常高。
184 |
185 | ## 顺序访问梯度
186 |
187 | Cache(高速缓存)作为内存局部区域的副本,用来存放当前活跃的程序和数据,它利用程序运行的局部性,把局部范围的数据从内存复制到Cache中,使CPU直接高速从Cache中读取程序和数据,从而解决CPU速度和内存速度不匹配的问题。高速缓冲存储器最重要的技术指标是它的命中率。CPU在Cache中找到有用的数据被称为命中,当Cache中没有CPU所需的数据时(这时称为未命中),CPU才访问内存。
188 |
189 | 预排序算法中有两个频繁的操作会导致cache-miss,也就是缓存消失(对速度的影响很大,特别是数据量很大的时候,顺序访问比随机访问的速度快4倍以上 )。
190 |
191 | * 对梯度的访问:在计算增益的时候需要利用梯度,假设梯度信息存在一个数组$g[i]$中,在对特征$A$进行增益时,需要根据特征$A$排序后的索引找到$g[i]$中对应的梯度信息。特征值$A_1$对应的样本行号可能是3,对应的梯度信息在$g[3]$,而特征值$A_2$对应的样本行号可能是9999,对应的梯度信息在$g[9999]$,即对于不同的特征,访问梯度的顺序是不一样的,并且是随机的
192 | * 对于索引表的访问:预排序算法使用了行号和叶子节点号的索引表,防止数据切分的时候对所有的特征进行切分。同访问梯度一样,所有的特征都要通过访问这个索引表来索引
193 |
194 | 这两个操作都是随机的访问,会给系统性能带来非常大的下降。
195 |
196 | LightGBM使用的直方图算法能很好的解决这类问题。首先。对梯度的访问,因为不用对特征进行排序,同时,所有的特征都用同样的方式来访问,所以只需要对梯度访问的顺序进行重新排序,所有的特征都能连续的访问梯度。并且直方图算法不需要把数据id到叶子节点号上(不需要这个索引表,没有这个缓存消失问题),大大提高cache的命中率,减少cache-miss出现的概率。
197 |
198 | ## 支持类别特征
199 |
200 | 实际上大多数机器学习工具都无法直接支持类别特征,一般需要把类别特征,转化one-hot特征,降低了空间和时间的效率。而类别特征的使用是在实践中很常用的。基于这个考虑,LightGBM优化了对类别特征的支持,可以直接输入类别特征,不需要额外的0/1展开。并在决策树算法上增加了类别特征的决策规则,直接原生支持类别特征,不需要转化,提高了近8倍的速度。
201 |
202 | 
203 |
204 | ## 应用场景
205 |
206 | 作为GBDT框架内的算法,GBDT、XGBoost能够应用的场景LightGBM也都适用,并且考虑到其对于大数据、高维特征的诸多优化,在数据量非常大、维度非常多的场景更具优势。近来,有着逐步替代XGBoost成为各种数据挖掘比赛baseline的趋势。
207 |
208 | ## sklearn参数
209 |
210 | `sklearn`本身的文档当中并没有LightGBM的描述,[Github](https://link.zhihu.com/?target=https%3A//github.com/microsoft/LightGBM/blob/master/python-package/lightgbm/sklearn.py)上面看到主要参数如下:
211 |
212 | * `boosting_type` : 提升类型,字符串,可选项 (default=`gbdt`)
213 |
214 | * `gbdt`, 传统梯度提升树
215 | * `dart`, 带Dropout的MART
216 | * `goss`, 单边梯度采样
217 | * `rf`, 随机森林
218 | * `num_leaves` : 基学习器的最大叶子树,整型,可选项 (default=31)
219 | * `max_depth` : 基学习器的最大树深度,小于等于0表示没限制,整型,可选项 (default=-1)
220 | * `learning_rate` : 提升学习率,浮点型,可选项 (default=0.1)
221 | * `n_estimators` : 提升次数,整型,可选项 (default=100)
222 | * `subsample_for_bin` : 构造分箱的样本个数,整型,可选项 (default=200000)
223 | * `objective` : 指定学习任务和相应的学习目标或者用户自定义的需要优化的目标损失函数,字符串, 可调用的或者None, 可选项 (default=None),若不为None,则有:
224 | * `regression` for LGBMRegressor -`binary` or `multiclass` for LGBMClassifier
225 | * `lambdarank` for LGBMRanker
226 | * `class_weight` : 该参数仅在多分类的时候会用到,多分类的时候各个分类的权重,对于二分类任务,你可以使用`is_unbalance` 或 `scale_pos_weight`,字典数据, `balanced` or None, 可选项 (default=None)
227 | * `min_split_gain` : 在叶子节点上面做进一步分裂的最小损失减少值,浮点型,可选项 (default=0.)
228 | * `min_child_weight` : 在树的一个孩子或者叶子所需的最小样本权重和,浮点型,可选项 (default=1e-3)
229 | * `min_child_samples` : 在树的一个孩子或者叶子所需的最小样本,整型,可选项 (default=20)
230 | * `subsample` : 训练样本的子采样比例,浮点型,可选项 (default=1.)
231 | * `subsample_freq` : 子采样频率,小于等于0意味着不可用,整型,可选项 (default=0)
232 | * `colsample_bytree` : 构建单棵树时列采样比例,浮点型,可选项 (default=1.)
233 | * `reg_alpha` : $L_1$正则项,浮点型,可选项 (default=0.)
234 | * `reg_lambda` :$L_2$正则项,浮点型,可选项 (default=0.)
235 | * `random_state` : 随机数种子,整型或者None, 可选项 (default=None)
236 | * `n_jobs` : 线程数,整型,可选项 (default=-1)
237 | * `silent` : 运行时是否打印消息,布尔型,可选项 (default=True)
238 | * `importance_type` : 填入到`feature_importances_`的特征重要性衡量类型,如果是`split`,则以特征被用来分裂的次数,如果是`gain`,则以特征每次用于分裂的累积增益,字符串,可选项 (default=`split`)
239 |
240 | 除了以上参数,LightGBM原生接口当中参数众多,主要有以下八大类:
241 |
242 | * 核心参数
243 | * 学习控制参数
244 | * IO参数
245 | * 目标参数
246 | * 度量参数
247 | * 网络参数
248 | * GPU参数
249 | * 模型参数
250 |
251 | 如果有遗漏,具体可以参阅[LightGBM Parameters](https://link.zhihu.com/?target=https%3A//lightgbm.readthedocs.io/en/latest/Parameters.html)
252 |
253 | ## CatBoost(了解)
254 |
255 | CatBoost也是Boosting族的算法,由俄罗斯科技公司Yandex于2017年提出,主要在两方面做了优化,一个是对于类别变量的处理,另外一个是对于预测偏移(prediction shift)的处理。
256 |
257 | 其中对于类别变量在传统的Greedy TBS方法的基础上添加先验分布项,这样可以减少减少噪声和低频率数据对于数据分布的影响:
258 |
259 | $$
260 | \hat{x}*k^i=\frac{\sum* {j=1}^n I_{{x_j^i=x_k^i}}*y_j+a\,P}{\sum_{j=1}^n I_{{x_j^i=x_k^i}}+a}
261 |
262 | $$
263 |
264 |
265 | 其中 $P$ 是添加的先验项,$a$ 通常是大于 0 的权重系数。
266 |
267 | 对于第二个问题,CatBoost采用了排序提升(Ordered Boosting)的方式,首先对所有的数据进行随机排列,然后在计算第 $i$ 步残差时候的模型只利用了随机排列中前 $i-1$ 个样本。具体算法描述请参阅论文[CatBoost: unbiased boosting with categorical features](https://link.zhihu.com/?target=https%3A//papers.nips.cc/paper/7898-catboost-unbiased-boosting-with-categorical-features.pdf)
268 |
269 | 时间有限,下次有机会再详细消化下CatBoost的论文。
270 |
271 | 总之,CatBoost大大简化了前期数据处理过程,特别是类别特征的数值化,调参也相对容易。近来在数据竞赛领域已经大规模采用。
272 |
--------------------------------------------------------------------------------
/Catboost.md:
--------------------------------------------------------------------------------
1 | title: DataWhale Workout No.8 CatBoost Summary date: 2019-08-19 08:18:37 categories: 机器学习 tags: - 集成学习 - CatBoost - Ordered boosting - Prediction shift - sklearn description: 这是DataWhale暑期学习小组-高级算法梳理的补充,是对目前最新的开源Boost族算法CatBoost的介绍,结合相关论文以及笔者的使用经验,对CatBoost的算法特性和适用场景做一些小结。
2 |
3 | ---
4 |
5 | ## CatBoost
6 |
7 | CatBoost是俄罗斯的搜索巨头Y andex在2017年开源的机器学习库,也是Boosting族算法的一种,同前面介绍过的XGBoost和LightGBM类似,依然是在GBDT算法框架下的一种改进实现,是一种基于对称决策树(oblivious trees)算法的参数少、支持类别型变量和高准确性的GBDT框架,主要说解决的痛点是高效合理地处理类别型特征,这个从它的名字就可以看得出来,CatBoost是由catgorical和boost组成,另外是处理梯度偏差(Gradient bias)以及预测偏移(Prediction shift)问题,提高算法的准确性和泛化能力。
8 |
9 | 
10 |
11 | CatBoost主要有以下五个特性:
12 |
13 | * 无需调参即可获得较高的模型质量,采用默认参数就可以获得非常好的结果,减少在调参上面花的时间
14 | * 支持类别型变量,无需对非数值型特征进行预处理
15 | * 快速、可扩展的GPU版本,可以用基于GPU的梯度提升算法实现来训练你的模型,支持多卡并行
16 | * 提高准确性,提出一种全新的梯度提升机制来构建模型以减少过拟合
17 | * 快速预测,即便应对延时非常苛刻的任务也能够快速高效部署模型
18 |
19 | CatBoost的主要算法原理可以参照以下两篇论文:
20 |
21 | * [Anna Veronika Dorogush, Andrey Gulin, Gleb Gusev, Nikita Kazeev, Liudmila Ostroumova Prokhorenkova, Aleksandr Vorobev "Fighting biases with dynamic boosting". arXiv:1706.09516, 2017](https://link.zhihu.com/?target=https%3A//arxiv.org/pdf/1706.09516.pdf)
22 | * [Anna Veronika Dorogush, Vasily Ershov, Andrey Gulin "CatBoost: gradient boosting with categorical features support". Workshop on ML Systems at NIPS 2017](https://link.zhihu.com/?target=http%3A//learningsys.org/nips17/assets/papers/paper_11.pdf)
23 |
24 | ## Categorical features
25 |
26 | 所谓类别型变量(Categorical features)是指其值是离散的集合且相互比较并无意义的变量,比如用户的ID、产品ID、颜色等。因此,这些变量无法在二叉决策树当中直接使用。常规的做法是将这些类别变量通过预处理的方式转化成数值型变量再喂给模型,比如用一个或者若干个数值来代表一个类别型特征。
27 |
28 | 目前广泛用于**低势** (一个有限集的元素个数是一个自然数)类别特征的处理方法是`One-hot encoding`:将原来的特征删除,然后对于每一个类别加一个0/1的用来指示是否含有该类别的数值型特征。`One-hot encoding`可以在数据预处理时完成,也可以在模型训练的时候完成,从训练时间的角度,后一种方法的实现更为高效,CatBoost对于低势类别特征也是采用后一种实现。
29 |
30 | 显然,在**高势** 特征当中,比如 `user ID`,这种编码方式会产生大量新的特征,造成维度灾难。一种折中的办法是可以将类别分组成有限个的群体再进行 `One-hot encoding`。一种常被使用的方法是根据目标变量统计(Target Statistics,以下简称TS)进行分组,目标变量统计用于估算每个类别的目标变量期望值。甚至有人直接用TS作为一个新的数值型变量来代替原来的类别型变量。重要的是,可以通过对TS数值型特征的阈值设置,基于对数损失、基尼系数或者均方差,得到一个对于训练集而言将类别一分为二的所有可能划分当中最优的那个。在LightGBM当中,类别型特征用每一步梯度提升时的梯度统计(Gradient Statistics,以下简称GS)来表示。虽然为建树提供了重要的信息,但是这种方法有以下两个缺点:
31 |
32 | * 增加计算时间,因为需要对每一个类别型特征,在迭代的每一步,都需要对GS进行计算;
33 | * 增加存储需求,对于一个类别型变量,需要存储每一次分离每个节点的类别。
34 |
35 | 为了克服这些缺点,LightGBM以损失部分信息为代价将所有的长尾类别归位一类,作者声称这样处理高势特征时比起 `One-hot encoding`还是好不少。不过如果采用TS特征,那么对于每个类别只需要计算和存储一个数字。
36 |
37 | 如此看到,采用TS作为一个新的数值型特征是最有效、信息损失最小的处理类别型特征的方法。TS也被广泛采用,在点击预测任务当中,这个场景当中的类别特征有用户、地区、广告、广告发布者等。接下来我们着重讨论TS,暂时将`One-hot encoding`和GS放一边。
38 |
39 | ## Target statistics
40 |
41 | 一个有效和高效的处理类别型特征$i$的方式是用一个与某些TS相等的数值型变量$\hat{x}_k^i$来代替第$k$个训练样本的类别${x}_k^i$。通常用基于类别的目标变量$y$的期望来进行估算:$\hat{x}_k^i\approx\mathbb{E}(y|x^i={x}_k^i)$。
42 |
43 | ### Greedy TS
44 |
45 | 估算$\mathbb{E}(y|x^i={x}*k^i)$最直接的方式就是用训练样本当中相同类别$x_k^i$的目标变量$y$的平均值。
46 |
47 | $$
48 | \hat{x}_k^i=\frac{\sum* {j=1}^n\mathbb{I}*{{x_j^i={x}_k^i}}\cdot y_i}{\sum* {j=1}^n\mathbb{I}*{{x_j^i={x}_k^i}}}
49 |
50 | $$
51 |
52 | 显然,这样的处理方式很容易引起过拟合。举个例子,假如在整个训练集当中所有样本的类别${x}_k^i$都互不相同,即$k$个样本有$k$个类别,那么新产生的数值型特征的值将与目标变量的值相同。某种程度上,这是一种目标穿越(target leakage),非常容易引起过拟合。比较好的一种做法是采用一个先验概率$p$进行平滑处理:
53 | $$
54 | \hat{x}_k^i=\frac{\sum* {j=1}^n\mathbb{I}*{{x_j^i={x}_k^i}}\cdot y_i+a\,p}{\sum* {j=1}^n\mathbb{I}_{{x_j^i={x}_k^i}}+a}
55 |
56 | $$
57 |
58 | 其中$a>0$是先验概率$p$的权重,而对于先验概率,通常的做法是设置为数据集当中目标变量的平均值。
59 |
60 | 不过这样的平滑处理依然无法完全避免目标穿越:特征$\hat{x}*k^i$是通过自变量$X_k$的目标$y_k$计算所得。这将会导致条件偏移:对于训练集和测试集,$\hat{x}_k^i|y$的分布会有所不同。再举个例子,假设第$i$个特征为类别型特征,并且特征所有取值为无重复的集合,然后对于每一个类别$A$,对于一个分类任务,我们有$P(y=1|x^i=A)=0.5$。然后在训练集当中,$\hat{x}_k^i=\frac{y_k+a\,p}{1+a}$,于是用阈值$t=\frac{0.5+a\,p}{1+a}$就可以仅用一次分裂就训练集完美分开。但是,对于测试集,因为还无法判断此时目标变量的类别,所以这一项$\sum* {j=1}^n\mathbb{I}_{{x_j^i={x}_k^i}}=0$,最后得到的TS值为$p$,并且得到的模型在$p 87 |
--------------------------------------------------------------------------------
/XGBoost-1.md:
--------------------------------------------------------------------------------
1 | ## 目录
2 |
3 | - [1. 什么是XGBoost](https://github.com/NLP-LOVE/ML-NLP/tree/master/Machine%20Learning/3.3%20XGBoost#1-什么是xgboost)
4 | - [1.1 XGBoost树的定义](https://github.com/NLP-LOVE/ML-NLP/tree/master/Machine%20Learning/3.3%20XGBoost#11-xgboost树的定义)
5 | - [1.2 正则项:树的复杂度](https://github.com/NLP-LOVE/ML-NLP/tree/master/Machine%20Learning/3.3%20XGBoost#12-正则项树的复杂度)
6 | - [1.3 树该怎么长](https://github.com/NLP-LOVE/ML-NLP/tree/master/Machine%20Learning/3.3%20XGBoost#13-树该怎么长)
7 | - [1.4 如何停止树的循环生成](https://github.com/NLP-LOVE/ML-NLP/tree/master/Machine%20Learning/3.3%20XGBoost#14-如何停止树的循环生成)
8 | - [2. XGBoost与GBDT有什么不同](https://github.com/NLP-LOVE/ML-NLP/tree/master/Machine%20Learning/3.3%20XGBoost#2-xgboost与gbdt有什么不同)
9 | - [3. 为什么XGBoost要用泰勒展开,优势在哪里?](https://github.com/NLP-LOVE/ML-NLP/tree/master/Machine%20Learning/3.3%20XGBoost#3-为什么xgboost要用泰勒展开优势在哪里)
10 | - [4. 代码实现](https://github.com/NLP-LOVE/ML-NLP/blob/master/Machine%20Learning/3.3%20XGBoost/3.3%20XGBoost.ipynb)
11 | - [5. 参考文献](https://github.com/NLP-LOVE/ML-NLP/tree/master/Machine%20Learning/3.3%20XGBoost#5-参考文献)
12 |
13 | ## 1. 什么是XGBoost
14 |
15 | XGBoost是陈天奇等人开发的一个开源机器学习项目,高效地实现了GBDT算法并进行了算法和工程上的许多改进,被广泛应用在Kaggle竞赛及其他许多机器学习竞赛中并取得了不错的成绩。
16 |
17 | 说到XGBoost,不得不提GBDT(Gradient Boosting Decision Tree)。因为XGBoost本质上还是一个GBDT,但是力争把速度和效率发挥到极致,所以叫X (Extreme) GBoosted。包括前面说过,两者都是boosting方法。
18 |
19 | 关于GBDT,这里不再提,可以查看我前一篇的介绍,[点此跳转](https://github.com/NLP-LOVE/ML-NLP/blob/master/Machine%20Learning/3.2%20GBDT/3.2%20GBDT.md)。
20 |
21 | [https://mp.weixin.qq.com/s/_NCKAon-megJbxzV6w3aYg]()
22 |
23 | ### 1.1 XGBoost树的定义
24 |
25 | 先来举个**例子**,我们要预测一家人对电子游戏的喜好程度,考虑到年轻和年老相比,年轻更可能喜欢电子游戏,以及男性和女性相比,男性更喜欢电子游戏,故先根据年龄大小区分小孩和大人,然后再通过性别区分开是男是女,逐一给各人在电子游戏喜好程度上打分,如下图所示。
26 |
27 | 
28 |
29 | 就这样,训练出了2棵树tree1和tree2,类似之前gbdt的原理,两棵树的结论累加起来便是最终的结论,所以小孩的预测分数就是两棵树中小孩所落到的结点的分数相加:2 + 0.9 = 2.9。爷爷的预测分数同理:-1 + (-0.9)= -1.9。具体如下图所示:
30 |
31 | 
32 |
33 | 恩,你可能要拍案而起了,惊呼,这不是跟上文介绍的GBDT乃异曲同工么?
34 |
35 | 事实上,如果不考虑工程实现、解决问题上的一些差异,XGBoost与GBDT比较大的不同就是目标函数的定义。XGBoost的目标函数如下图所示:
36 |
37 | 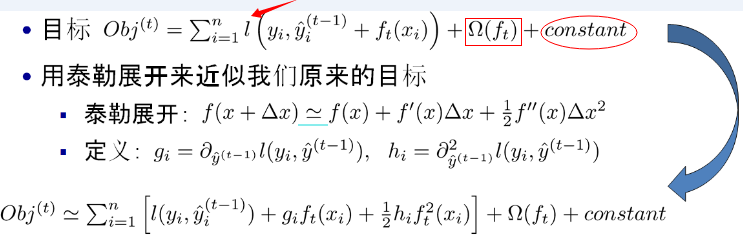
38 |
39 | 其中:
40 |
41 | - 红色箭头所指向的L 即为损失函数(比如平方损失函数:=(y_i-y^i)^2))
42 | - 红色方框所框起来的是正则项(包括L1正则、L2正则)
43 | - 红色圆圈所圈起来的为常数项
44 | - 对于f(x),XGBoost利用泰勒展开三项,做一个近似。**f(x)表示的是其中一颗回归树。**
45 |
46 | 看到这里可能有些读者会头晕了,这么多公式,**我在这里只做一个简要式的讲解,具体的算法细节和公式求解请查看这篇博文,讲得很仔细**:[通俗理解kaggle比赛大杀器xgboost](https://blog.csdn.net/v_JULY_v/article/details/81410574)
47 |
48 | XGBoost的**核心算法思想**不难,基本就是:
49 |
50 | 1. 不断地添加树,不断地进行特征分裂来生长一棵树,每次添加一个树,其实是学习一个新函数**f(x)**,去拟合上次预测的残差。
51 | 2. 当我们训练完成得到k棵树,我们要预测一个样本的分数,其实就是根据这个样本的特征,在每棵树中会落到对应的一个叶子节点,每个叶子节点就对应一个分数
52 | 3. 最后只需要将每棵树对应的分数加起来就是该样本的预测值。
53 |
54 | 显然,我们的目标是要使得树群的预测值尽量接近真实值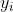,而且有尽量大的泛化能力。类似之前GBDT的套路,XGBoost也是需要将多棵树的得分累加得到最终的预测得分(每一次迭代,都在现有树的基础上,增加一棵树去拟合前面树的预测结果与真实值之间的残差)。
55 |
56 | 
57 |
58 | 那接下来,我们如何选择每一轮加入什么 f 呢?答案是非常直接的,选取一个 f 来使得我们的目标函数尽量最大地降低。这里 f 可以使用泰勒展开公式近似。
59 |
60 | 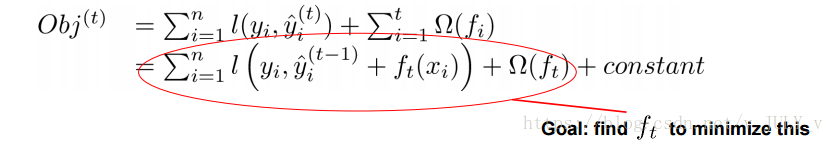
61 |
62 | 实质是把样本分配到叶子结点会对应一个obj,优化过程就是obj优化。也就是分裂节点到叶子不同的组合,不同的组合对应不同obj,所有的优化围绕这个思想展开。到目前为止我们讨论了目标函数中的第一个部分:训练误差。接下来我们讨论目标函数的第二个部分:正则项,即如何定义树的复杂度。
63 |
64 | ### 1.2 正则项:树的复杂度
65 |
66 | XGBoost对树的复杂度包含了两个部分:
67 |
68 | - 一个是树里面叶子节点的个数T
69 | - 一个是树上叶子节点的得分w的L2模平方(对w进行L2正则化,相当于针对每个叶结点的得分增加L2平滑,目的是为了避免过拟合)
70 |
71 | 
72 |
73 | 我们再来看一下XGBoost的目标函数(损失函数揭示训练误差 + 正则化定义复杂度):
74 |
75 | =\sum_{i}l(y_i^{'}-y_i)+\sum_k\Omega(f_t))
76 |
77 | 正则化公式也就是目标函数的后半部分,对于上式而言,是整个累加模型的输出,正则化项∑kΩ(ft)是则表示树的复杂度的函数,值越小复杂度越低,泛化能力越强。
78 |
79 | ### 1.3 树该怎么长
80 |
81 | 很有意思的一个事是,我们从头到尾了解了xgboost如何优化、如何计算,但树到底长啥样,我们却一直没看到。很显然,一棵树的生成是由一个节点一分为二,然后不断分裂最终形成为整棵树。那么树怎么分裂的就成为了接下来我们要探讨的关键。对于一个叶子节点如何进行分裂,XGBoost作者在其原始论文中给出了一种分裂节点的方法:**枚举所有不同树结构的贪心法**
82 |
83 | 不断地枚举不同树的结构,然后利用打分函数来寻找出一个最优结构的树,接着加入到模型中,不断重复这样的操作。这个寻找的过程使用的就是**贪心算法**。选择一个feature分裂,计算loss function最小值,然后再选一个feature分裂,又得到一个loss function最小值,你枚举完,找一个效果最好的,把树给分裂,就得到了小树苗。
84 |
85 | 总而言之,XGBoost使用了和CART回归树一样的想法,利用贪婪算法,遍历所有特征的所有特征划分点,不同的是使用的目标函数不一样。具体做法就是分裂后的目标函数值比单子叶子节点的目标函数的增益,同时为了限制树生长过深,还加了个阈值,只有当增益大于该阈值才进行分裂。从而继续分裂,形成一棵树,再形成一棵树,**每次在上一次的预测基础上取最优进一步分裂/建树。**
86 |
87 | ### 1.4 如何停止树的循环生成
88 |
89 | 凡是这种循环迭代的方式必定有停止条件,什么时候停止呢?简言之,设置树的最大深度、当样本权重和小于设定阈值时停止生长以防止过拟合。具体而言,则
90 |
91 | 1. 当引入的分裂带来的增益小于设定阀值的时候,我们可以忽略掉这个分裂,所以并不是每一次分裂loss function整体都会增加的,有点预剪枝的意思,阈值参数为(即正则项里叶子节点数T的系数);
92 | 2. 当树达到最大深度时则停止建立决策树,设置一个超参数max_depth,避免树太深导致学习局部样本,从而过拟合;
93 | 3. 样本权重和小于设定阈值时则停止建树。什么意思呢,即涉及到一个超参数-最小的样本权重和min_child_weight,和GBM的 min_child_leaf 参数类似,但不完全一样。大意就是一个叶子节点样本太少了,也终止同样是防止过拟合;
94 |
95 | ## 2. XGBoost与GBDT有什么不同
96 |
97 | 除了算法上与传统的GBDT有一些不同外,XGBoost还在工程实现上做了大量的优化。总的来说,两者之间的区别和联系可以总结成以下几个方面。
98 |
99 | 1. GBDT是机器学习算法,XGBoost是该算法的工程实现。
100 | 2. 在使用CART作为基分类器时,XGBoost显式地加入了正则项来控制模 型的复杂度,有利于防止过拟合,从而提高模型的泛化能力。
101 | 3. GBDT在模型训练时只使用了代价函数的一阶导数信息,XGBoost对代 价函数进行二阶泰勒展开,可以同时使用一阶和二阶导数。
102 | 4. 传统的GBDT采用CART作为基分类器,XGBoost支持多种类型的基分类 器,比如线性分类器。
103 | 5. 传统的GBDT在每轮迭代时使用全部的数据,XGBoost则采用了与随机 森林相似的策略,支持对数据进行采样。
104 | 6. 传统的GBDT没有设计对缺失值进行处理,XGBoost能够自动学习出缺 失值的处理策略。
105 |
106 | ## 3. 为什么XGBoost要用泰勒展开,优势在哪里?
107 |
108 | XGBoost使用了一阶和二阶偏导, 二阶导数有利于梯度下降的更快更准. 使用泰勒展开取得函数做自变量的二阶导数形式, 可以在不选定损失函数具体形式的情况下, 仅仅依靠输入数据的值就可以进行叶子分裂优化计算, 本质上也就把损失函数的选取和模型算法优化/参数选择分开了. 这种去耦合增加了XGBoost的适用性, 使得它按需选取损失函数, 可以用于分类, 也可以用于回归。
109 |
110 | ## 4. 代码实现
111 |
112 | GitHub:[点击进入](https://github.com/NLP-LOVE/ML-NLP/blob/master/Machine%20Learning/3.3%20XGBoost/3.3%20XGBoost.ipynb)
113 |
114 | ## 5. 参考文献
115 |
116 | [通俗理解kaggle比赛大杀器xgboost](https://blog.csdn.net/v_JULY_v/article/details/81410574)
117 |
118 | > 作者:[@mantchs](https://github.com/NLP-LOVE/ML-NLP)
119 | >
120 | > GitHub:[https://github.com/NLP-LOVE/ML-NLP](https://github.com/NLP-LOVE/ML-NLP)
121 | >
122 | > 欢迎大家加入讨论!共同完善此项目!群号:【541954936】`
87 |
--------------------------------------------------------------------------------
/XGBoost-1.md:
--------------------------------------------------------------------------------
1 | ## 目录
2 |
3 | - [1. 什么是XGBoost](https://github.com/NLP-LOVE/ML-NLP/tree/master/Machine%20Learning/3.3%20XGBoost#1-什么是xgboost)
4 | - [1.1 XGBoost树的定义](https://github.com/NLP-LOVE/ML-NLP/tree/master/Machine%20Learning/3.3%20XGBoost#11-xgboost树的定义)
5 | - [1.2 正则项:树的复杂度](https://github.com/NLP-LOVE/ML-NLP/tree/master/Machine%20Learning/3.3%20XGBoost#12-正则项树的复杂度)
6 | - [1.3 树该怎么长](https://github.com/NLP-LOVE/ML-NLP/tree/master/Machine%20Learning/3.3%20XGBoost#13-树该怎么长)
7 | - [1.4 如何停止树的循环生成](https://github.com/NLP-LOVE/ML-NLP/tree/master/Machine%20Learning/3.3%20XGBoost#14-如何停止树的循环生成)
8 | - [2. XGBoost与GBDT有什么不同](https://github.com/NLP-LOVE/ML-NLP/tree/master/Machine%20Learning/3.3%20XGBoost#2-xgboost与gbdt有什么不同)
9 | - [3. 为什么XGBoost要用泰勒展开,优势在哪里?](https://github.com/NLP-LOVE/ML-NLP/tree/master/Machine%20Learning/3.3%20XGBoost#3-为什么xgboost要用泰勒展开优势在哪里)
10 | - [4. 代码实现](https://github.com/NLP-LOVE/ML-NLP/blob/master/Machine%20Learning/3.3%20XGBoost/3.3%20XGBoost.ipynb)
11 | - [5. 参考文献](https://github.com/NLP-LOVE/ML-NLP/tree/master/Machine%20Learning/3.3%20XGBoost#5-参考文献)
12 |
13 | ## 1. 什么是XGBoost
14 |
15 | XGBoost是陈天奇等人开发的一个开源机器学习项目,高效地实现了GBDT算法并进行了算法和工程上的许多改进,被广泛应用在Kaggle竞赛及其他许多机器学习竞赛中并取得了不错的成绩。
16 |
17 | 说到XGBoost,不得不提GBDT(Gradient Boosting Decision Tree)。因为XGBoost本质上还是一个GBDT,但是力争把速度和效率发挥到极致,所以叫X (Extreme) GBoosted。包括前面说过,两者都是boosting方法。
18 |
19 | 关于GBDT,这里不再提,可以查看我前一篇的介绍,[点此跳转](https://github.com/NLP-LOVE/ML-NLP/blob/master/Machine%20Learning/3.2%20GBDT/3.2%20GBDT.md)。
20 |
21 | [https://mp.weixin.qq.com/s/_NCKAon-megJbxzV6w3aYg]()
22 |
23 | ### 1.1 XGBoost树的定义
24 |
25 | 先来举个**例子**,我们要预测一家人对电子游戏的喜好程度,考虑到年轻和年老相比,年轻更可能喜欢电子游戏,以及男性和女性相比,男性更喜欢电子游戏,故先根据年龄大小区分小孩和大人,然后再通过性别区分开是男是女,逐一给各人在电子游戏喜好程度上打分,如下图所示。
26 |
27 | 
28 |
29 | 就这样,训练出了2棵树tree1和tree2,类似之前gbdt的原理,两棵树的结论累加起来便是最终的结论,所以小孩的预测分数就是两棵树中小孩所落到的结点的分数相加:2 + 0.9 = 2.9。爷爷的预测分数同理:-1 + (-0.9)= -1.9。具体如下图所示:
30 |
31 | 
32 |
33 | 恩,你可能要拍案而起了,惊呼,这不是跟上文介绍的GBDT乃异曲同工么?
34 |
35 | 事实上,如果不考虑工程实现、解决问题上的一些差异,XGBoost与GBDT比较大的不同就是目标函数的定义。XGBoost的目标函数如下图所示:
36 |
37 | 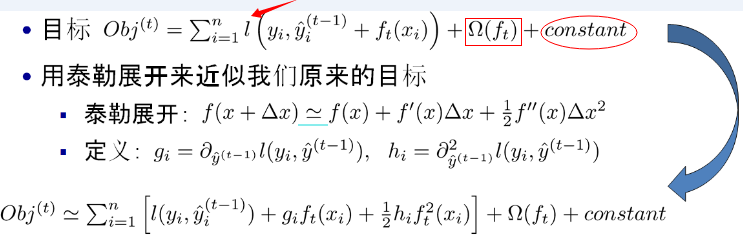
38 |
39 | 其中:
40 |
41 | - 红色箭头所指向的L 即为损失函数(比如平方损失函数:=(y_i-y^i)^2))
42 | - 红色方框所框起来的是正则项(包括L1正则、L2正则)
43 | - 红色圆圈所圈起来的为常数项
44 | - 对于f(x),XGBoost利用泰勒展开三项,做一个近似。**f(x)表示的是其中一颗回归树。**
45 |
46 | 看到这里可能有些读者会头晕了,这么多公式,**我在这里只做一个简要式的讲解,具体的算法细节和公式求解请查看这篇博文,讲得很仔细**:[通俗理解kaggle比赛大杀器xgboost](https://blog.csdn.net/v_JULY_v/article/details/81410574)
47 |
48 | XGBoost的**核心算法思想**不难,基本就是:
49 |
50 | 1. 不断地添加树,不断地进行特征分裂来生长一棵树,每次添加一个树,其实是学习一个新函数**f(x)**,去拟合上次预测的残差。
51 | 2. 当我们训练完成得到k棵树,我们要预测一个样本的分数,其实就是根据这个样本的特征,在每棵树中会落到对应的一个叶子节点,每个叶子节点就对应一个分数
52 | 3. 最后只需要将每棵树对应的分数加起来就是该样本的预测值。
53 |
54 | 显然,我们的目标是要使得树群的预测值尽量接近真实值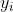,而且有尽量大的泛化能力。类似之前GBDT的套路,XGBoost也是需要将多棵树的得分累加得到最终的预测得分(每一次迭代,都在现有树的基础上,增加一棵树去拟合前面树的预测结果与真实值之间的残差)。
55 |
56 | 
57 |
58 | 那接下来,我们如何选择每一轮加入什么 f 呢?答案是非常直接的,选取一个 f 来使得我们的目标函数尽量最大地降低。这里 f 可以使用泰勒展开公式近似。
59 |
60 | 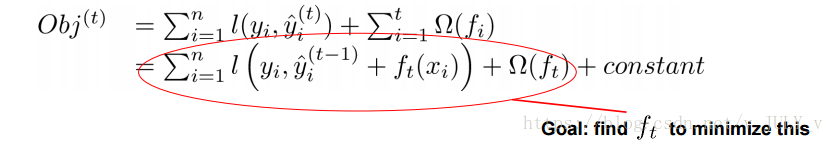
61 |
62 | 实质是把样本分配到叶子结点会对应一个obj,优化过程就是obj优化。也就是分裂节点到叶子不同的组合,不同的组合对应不同obj,所有的优化围绕这个思想展开。到目前为止我们讨论了目标函数中的第一个部分:训练误差。接下来我们讨论目标函数的第二个部分:正则项,即如何定义树的复杂度。
63 |
64 | ### 1.2 正则项:树的复杂度
65 |
66 | XGBoost对树的复杂度包含了两个部分:
67 |
68 | - 一个是树里面叶子节点的个数T
69 | - 一个是树上叶子节点的得分w的L2模平方(对w进行L2正则化,相当于针对每个叶结点的得分增加L2平滑,目的是为了避免过拟合)
70 |
71 | 
72 |
73 | 我们再来看一下XGBoost的目标函数(损失函数揭示训练误差 + 正则化定义复杂度):
74 |
75 | =\sum_{i}l(y_i^{'}-y_i)+\sum_k\Omega(f_t))
76 |
77 | 正则化公式也就是目标函数的后半部分,对于上式而言,是整个累加模型的输出,正则化项∑kΩ(ft)是则表示树的复杂度的函数,值越小复杂度越低,泛化能力越强。
78 |
79 | ### 1.3 树该怎么长
80 |
81 | 很有意思的一个事是,我们从头到尾了解了xgboost如何优化、如何计算,但树到底长啥样,我们却一直没看到。很显然,一棵树的生成是由一个节点一分为二,然后不断分裂最终形成为整棵树。那么树怎么分裂的就成为了接下来我们要探讨的关键。对于一个叶子节点如何进行分裂,XGBoost作者在其原始论文中给出了一种分裂节点的方法:**枚举所有不同树结构的贪心法**
82 |
83 | 不断地枚举不同树的结构,然后利用打分函数来寻找出一个最优结构的树,接着加入到模型中,不断重复这样的操作。这个寻找的过程使用的就是**贪心算法**。选择一个feature分裂,计算loss function最小值,然后再选一个feature分裂,又得到一个loss function最小值,你枚举完,找一个效果最好的,把树给分裂,就得到了小树苗。
84 |
85 | 总而言之,XGBoost使用了和CART回归树一样的想法,利用贪婪算法,遍历所有特征的所有特征划分点,不同的是使用的目标函数不一样。具体做法就是分裂后的目标函数值比单子叶子节点的目标函数的增益,同时为了限制树生长过深,还加了个阈值,只有当增益大于该阈值才进行分裂。从而继续分裂,形成一棵树,再形成一棵树,**每次在上一次的预测基础上取最优进一步分裂/建树。**
86 |
87 | ### 1.4 如何停止树的循环生成
88 |
89 | 凡是这种循环迭代的方式必定有停止条件,什么时候停止呢?简言之,设置树的最大深度、当样本权重和小于设定阈值时停止生长以防止过拟合。具体而言,则
90 |
91 | 1. 当引入的分裂带来的增益小于设定阀值的时候,我们可以忽略掉这个分裂,所以并不是每一次分裂loss function整体都会增加的,有点预剪枝的意思,阈值参数为(即正则项里叶子节点数T的系数);
92 | 2. 当树达到最大深度时则停止建立决策树,设置一个超参数max_depth,避免树太深导致学习局部样本,从而过拟合;
93 | 3. 样本权重和小于设定阈值时则停止建树。什么意思呢,即涉及到一个超参数-最小的样本权重和min_child_weight,和GBM的 min_child_leaf 参数类似,但不完全一样。大意就是一个叶子节点样本太少了,也终止同样是防止过拟合;
94 |
95 | ## 2. XGBoost与GBDT有什么不同
96 |
97 | 除了算法上与传统的GBDT有一些不同外,XGBoost还在工程实现上做了大量的优化。总的来说,两者之间的区别和联系可以总结成以下几个方面。
98 |
99 | 1. GBDT是机器学习算法,XGBoost是该算法的工程实现。
100 | 2. 在使用CART作为基分类器时,XGBoost显式地加入了正则项来控制模 型的复杂度,有利于防止过拟合,从而提高模型的泛化能力。
101 | 3. GBDT在模型训练时只使用了代价函数的一阶导数信息,XGBoost对代 价函数进行二阶泰勒展开,可以同时使用一阶和二阶导数。
102 | 4. 传统的GBDT采用CART作为基分类器,XGBoost支持多种类型的基分类 器,比如线性分类器。
103 | 5. 传统的GBDT在每轮迭代时使用全部的数据,XGBoost则采用了与随机 森林相似的策略,支持对数据进行采样。
104 | 6. 传统的GBDT没有设计对缺失值进行处理,XGBoost能够自动学习出缺 失值的处理策略。
105 |
106 | ## 3. 为什么XGBoost要用泰勒展开,优势在哪里?
107 |
108 | XGBoost使用了一阶和二阶偏导, 二阶导数有利于梯度下降的更快更准. 使用泰勒展开取得函数做自变量的二阶导数形式, 可以在不选定损失函数具体形式的情况下, 仅仅依靠输入数据的值就可以进行叶子分裂优化计算, 本质上也就把损失函数的选取和模型算法优化/参数选择分开了. 这种去耦合增加了XGBoost的适用性, 使得它按需选取损失函数, 可以用于分类, 也可以用于回归。
109 |
110 | ## 4. 代码实现
111 |
112 | GitHub:[点击进入](https://github.com/NLP-LOVE/ML-NLP/blob/master/Machine%20Learning/3.3%20XGBoost/3.3%20XGBoost.ipynb)
113 |
114 | ## 5. 参考文献
115 |
116 | [通俗理解kaggle比赛大杀器xgboost](https://blog.csdn.net/v_JULY_v/article/details/81410574)
117 |
118 | > 作者:[@mantchs](https://github.com/NLP-LOVE/ML-NLP)
119 | >
120 | > GitHub:[https://github.com/NLP-LOVE/ML-NLP](https://github.com/NLP-LOVE/ML-NLP)
121 | >
122 | > 欢迎大家加入讨论!共同完善此项目!群号:【541954936】` ```
123 |
--------------------------------------------------------------------------------
/catboost2.md:
--------------------------------------------------------------------------------
1 | # Catboost
2 |
3 | CatBoost是一种基于对称决策树(oblivious trees)为基学习器实现的参数较少、支持类别型变量和高准确性的GBDT框架,主要解决的痛点是高效合理地处理类别型特征,这一点从它的名字中可以看出来,CatBoost是由Categorical和Boosting组成。此外,CatBoost还解决了梯度偏差(Gradient Bias)以及预测偏移(Prediction shift)的问题,从而减少过拟合的发生,进而提高算法的准确性和泛化能力。
4 |
5 | ## 对称决策树
6 |
7 | 那么**对称树**和普通决策树有什么区别?
8 |
9 | 一图为对称树,二图为普通决策树
10 |
11 | 
12 |
13 | 对称树中,每一层的每一个节点判断条件都是一样的。假如如果我们只训练一棵树,那么显然对称树的overfit能力会比普通的决策树弱;但是在GBM中,我们通常训练很多的树,所以overfit的能力不必担心。那么对称树在GBM中有什么优势呢?下面列出三点:
14 |
15 | * 拟合模式相对简单,因为每一层都是一个判断条件
16 | * 可以提高预测速度
17 | * 对称树的结构本身比普通决策树自由度小,可以看作是加入了penalty惩罚机制,或者看作regularization正则化
18 |
19 | 最大的优势就是第二点——预测速度会提升。为什么会更快呢?
20 |
21 | 
22 |
23 | 上面这棵树最底层有四个节点,我们可以把这四个节点从0到3编号(index),每一个节点有一个对应值(value)。比如一个样本最终进入了第一个节点,那么这棵树对这个样本的预测值就是1.6。我们可以把value存放在一个数组里面,这样给定index就可以立刻得到value。那么对一个样本用一棵树进行预测时,我们只需要找到这个样本对应的index,因为在对称树中每一层的判断条件都是一样的,所以每一层都可以用0或者1来表示,比如是学生,用1表示,不是用0;有关注机器会学习用1表示,没有用0,那么每一个样本进入这棵树,都可以用两个bits来表示,也就是四种可能结果:00,01,10,和11。这两个bits代表的数字就是index。
24 |
25 | 这意味着什么呢?我们在做预测的时候,只要对每一层的条件进行判断,然后就可以找到index。因为每一个树的结构(判断条件)是已知的,我们甚至可以对这个过程进行并行计算。
26 |
27 | ## Catboost与XGBoost,LightGBM相比的创新点
28 |
29 | * 嵌入了自动将类别型特征处理为数值型特征的创新算法。首先对categorical features做一些统计,计算某个类别特征(category)出现的频率,之后加上超参数,生成新的数值型特征(numerical features)。
30 | * Catboost还使用了组合类别特征,可以利用到特征之间的联系,这极大的丰富了特征维度。
31 | * 采用排序提升的方法对抗训练集中的噪声点,从而避免梯度估计的偏差,进而解决预测偏移的问题。
32 | * 采用了完全对称树作为基模型。
33 |
34 | ## **类别型特征**
35 |
36 | ### **2.1 类别型特征的相关工作**
37 |
38 | 所谓类别型特征,即这类特征不是数值型特征,而是离散的集合,比如省份名(山东、山西、河北等),城市名(北京、上海、深圳等),学历(本科、硕士、博士等)。在梯度提升算法中,最常用的是将这些类别型特征转为数值型来处理,一般类别型特征会转化为一个或多个数值型特征。
39 |
40 | 如果某个 **类别型特征基数比较低(low-cardinality features)** ,即该特征的所有值去重后构成的集合元素个数比较少,一般利用One-hot编码方法将特征转为数值型。One-hot编码可以在数据预处理时完成,也可以在模型训练的时候完成,从训练时间的角度,后一种方法的实现更为高效,CatBoost对于基数较低的类别型特征也是采用后一种实现。
41 |
42 | 显然,在 **高基数类别型特征(high cardinality features)** 当中,比如 `user ID`,这种编码方式会产生大量新的特征,造成维度灾难。一种折中的办法是可以将类别分组成有限个的群体再进行One-hot编码。一种常被使用的方法是根据目标变量统计(Target Statistics,以下简称TS)进行分组,目标变量统计用于估算每个类别的目标变量期望值。甚至有人直接用TS作为一个新的数值型变量来代替原来的类别型变量。重要的是,可以通过对TS数值型特征的阈值设置,基于对数损失、基尼系数或者均方差,得到一个对于训练集而言将类别一分为二的所有可能划分当中最优的那个。在LightGBM当中,类别型特征用每一步梯度提升时的梯度统计(Gradient Statistics,以下简称GS)来表示。虽然为建树提供了重要的信息,但是这种方法有以下两个缺点:
43 |
44 | * 增加计算时间,因为需要对每一个类别型特征,在迭代的每一步,都需要对GS进行计算;
45 | * 增加存储需求,对于一个类别型变量,需要存储每一次分离每个节点的类别;
46 |
47 | 为了克服这些缺点,LightGBM以损失部分信息为代价将所有的长尾类别归为一类,作者声称这样处理高基数类别型特征时比One-hot编码还是好不少。不过如果采用TS特征,那么对于每个类别只需要计算和存储一个数字。
48 |
49 | ### **2.2 目标变量统计(Target Statistics)**
50 |
51 | CatBoost算法的设计初衷是为了更好的处理GBDT特征中的categorical features。在处理 GBDT特征中的categorical features的时候,最简单的方法是用 categorical feature 对应的标签的平均值来替换。在决策树中,标签平均值将作为节点分裂的标准。这种方法被称为 Greedy Target-based Statistics , 简称 Greedy TS,用公式来表达就是:
52 |
53 | ![[公式]](https://www.zhihu.com/equation?tex=%5Chat%7Bx%7D_k%5Ei%3D%5Cfrac%7B%5Csum_%7Bj%3D1%7D%5E%7Bn%7D%5Bx_%7Bj%2Ck%7D%3Dx_%7Bi%2Ck%7D%5D%5Ccdot+Y_i%7D%7B%5Csum_%7Bj%3D1%7D%5E%7Bn%7D%5Bx_%7Bj%2Ck%7D%3Dx_%7Bi%2Ck%7D%5D%7D+%5C%5C)
54 |
55 | 这种方法有一个显而易见的缺陷,就是通常特征比标签包含更多的信息,如果强行用标签的平均值来表示特征的话,当训练数据集和测试数据集数据结构和分布不一样的时候会出条件偏移问题。
56 |
57 | 一个标准的改进 Greedy TS的方式是添加先验分布项,这样可以减少噪声和低频率类别型数据对于数据分布的影响:
58 |
59 | ![[公式]](https://www.zhihu.com/equation?tex=%5Chat%7Bx%7D_k%5Ei%3D%5Cfrac%7B%5Csum_%7Bj%3D1%7D%5E%7Bp-1%7D%7B%5Bx_%7B%5Csigma_%7Bj%2Ck%7D%7D%3Dx_%7B%5Csigma_%7Bp%2Ck%7D%7D%5D%7DY_%7B%5Csigma_%7Bj%7D%7D%2Ba%5Ccdot+p%7D%7B%5Csum_%7Bj%3D1%7D%5E%7Bp-1%7D%7B%5Bx_%7B%5Csigma_%7Bj%2Ck%7D%7D%3Dx_%7B%5Csigma_%7Bp%2Ck%7D%7D%5D%7D%2Ba%7D+%5C%5C)
60 |
61 | 其中 ![[公式]](https://www.zhihu.com/equation?tex=p)是添加的先验项, ![[公式]](https://www.zhihu.com/equation?tex=a+)通常是大于0的权重系数。添加先验项是一个普遍做法,针对类别数较少的特征,它可以减少噪声数据。对于回归问题,一般情况下,先验项可取数据集label的均值。对于二分类,先验项是正例的先验概率。利用多个数据集排列也是有效的,但是,如果直接计算可能导致过拟合。CatBoost利用了一个比较新颖的计算叶子节点值的方法,这种方式(oblivious trees,对称树)可以避免多个数据集排列中直接计算会出现过拟合的问题。
62 |
63 | ### **2.3 特征组合**
64 |
65 | 值得注意的是几个类别型特征的任意组合都可视为新的特征。例如,在音乐推荐应用中,我们有两个类别型特征:用户ID和音乐流派。如果有些用户更喜欢摇滚乐,将用户ID和音乐流派转换为数字特征时,根据上述这些信息就会丢失。结合这两个特征就可以解决这个问题,并且可以得到一个新的强大的特征。然而,组合的数量会随着数据集中类别型特征的数量成指数增长,因此不可能在算法中考虑所有组合。为当前树构造新的分割点时,CatBoost会采用贪婪的策略考虑组合。对于树的第一次分割,不考虑任何组合。对于下一个分割,CatBoost将当前树的所有组合、类别型特征与数据集中的所有类别型特征相结合,并将新的组合类别型特征动态地转换为数值型特征。CatBoost还通过以下方式生成数值型特征和类别型特征的组合:树中选定的所有分割点都被视为具有两个值的类别型特征,并像类别型特征一样被进行组合考虑。
66 |
67 | ### **2.4 CatBoost处理Categorical features总结**
68 |
69 | * 首先会计算一些数据的statistics。计算某个category出现的频率,加上超参数,生成新的numerical features。这一策略要求同一标签数据不能排列在一起(即先全是0之后全是1这种方式),训练之前需要打乱数据集。
70 | * 第二,使用数据的不同排列(实际上是4个)。在每一轮建立树之前,先扔一轮骰子,决定使用哪个排列来生成树。
71 | * 第三,考虑使用categorical features的不同组合。例如颜色和种类组合起来,可以构成类似于blue dog这样的特征。当需要组合的categorical features变多时,CatBoost只考虑一部分combinations。在选择第一个节点时,只考虑选择一个特征,例如A。在生成第二个节点时,考虑A和任意一个categorical feature的组合,选择其中最好的。就这样使用贪心算法生成combinations。
72 | * 第四,除非向gender这种维数很小的情况,不建议自己生成One-hot编码向量,最好交给算法来处理。
73 |
74 | ## **克服梯度偏差**
75 |
76 | CatBoost和所有标准梯度提升算法一样,都是通过构建新树来拟合当前模型的梯度。然而,所有经典的提升算法都存在由有偏的点态梯度估计引起的过拟合问题。在每个步骤中使用的梯度都使用当前模型中的相同的数据点来估计,这导致估计梯度在特征空间的任何域中的分布与该域中梯度的真实分布相比发生了偏移,从而导致过拟合。为了解决这个问题,CatBoost对经典的梯度提升算法进行了一些改进,简要介绍如下。
77 |
78 | 许多利用GBDT技术的算法(例如,XGBoost、LightGBM),构建下一棵树分为两个阶段:选择树结构和在树结构固定后计算叶子节点的值。为了选择最佳的树结构,算法通过枚举不同的分割,用这些分割构建树,对得到的叶子节点计算值,然后对得到的树计算评分,最后选择最佳的分割。两个阶段叶子节点的值都是被当做梯度或牛顿步长的近似值来计算。在CatBoost中,第一阶段采用梯度步长的无偏估计,第二阶段使用传统的GBDT方案执行。既然原来的梯度估计是有偏的,那么怎么能改成无偏估计呢?
79 |
80 | 
81 |
82 |
83 | ## **预测偏移和排序提升**
84 |
85 | 预测偏移(Prediction shift)是由梯度偏差造成的。在GDBT的每一步迭代中, 损失函数使用相同的数据集求得当前模型的梯度, 然后训练得到基学习器, 但这会导致梯度估计偏差, 进而导致模型产生过拟合的问题。 CatBoost通过采用排序提升 (Ordered boosting) 的方式替换传统算法中梯度估计方法,进而减轻梯度估计的偏差,提高模型的泛化能力。下面我们对预测偏移进行详细的描述和分析。
86 |
87 | 首先来看下GBDT的整体迭代过程:
88 |
89 | GBDT算法是通过一组分类器的串行迭代,最终得到一个强学习器,以此来进行更高精度的分类。它使用了前向分布算法,弱学习器使用分类回归树(CART)。
90 |
91 | 
92 |
93 | ### 排序提升
94 |
95 | 为了克服预测偏移问题,CatBoost提出了一种新的叫做Ordered boosting的算法。
96 |
97 | 
98 |
99 | 
100 |
101 |
102 | ## **快速评分**
103 |
104 | CatBoost使用对称树(oblivious trees)作为基预测器。在这类树中,相同的分割准则在树的整个一层上使用。这种树是平衡的,不太容易过拟合。梯度提升对称树被成功地用于各种学习任务中。在对称树中,每个叶子节点的索引可以被编码为长度等于树深度的二进制向量。这在CatBoost模型评估器中得到了广泛的应用:我们首先将所有浮点特征、统计信息和独热编码特征进行二值化,然后使用二进制特征来计算模型预测值。
105 |
106 |
107 | ## 基于GPU实现快速训练
108 |
109 | * **密集的数值特征。** 对于任何GBDT算法而言,最大的难点之一就是搜索最佳分割。尤其是对于密集的数值特征数据集来说,该步骤是建立决策树时的主要计算负担。CatBoost使用oblivious 决策树作为基模型,并将特征离散化到固定数量的箱子中以减少内存使用。就GPU内存使用而言,CatBoost至少与LightGBM一样有效。主要改进之处就是利用了一种不依赖于原子操作的直方图计算方法。
110 | * **类别型特征。** CatBoost实现了多种处理类别型特征的方法,并使用完美哈希来存储类别型特征的值,以减少内存使用。由于GPU内存的限制,在CPU RAM中存储按位压缩的完美哈希,以及要求的数据流、重叠计算和内存等操作。通过哈希来分组观察。在每个组中,我们需要计算一些统计量的前缀和。该统计量的计算使用分段扫描GPU图元实现。
111 | * **多GPU支持。** CatBoost中的GPU实现可支持多个GPU。分布式树学习可以通过数据或特征进行并行化。CatBoost采用多个学习数据集排列的计算方案,在训练期间计算类别型特征的统计数据。
112 |
113 | ## **CatBoost的优缺点**
114 |
115 | **7.1 优点**
116 |
117 | * **性能卓越** :在性能方面可以匹敌任何先进的机器学习算法;
118 | * **鲁棒性/强健性** :它减少了对很多超参数调优的需求,并降低了过度拟合的机会,这也使得模型变得更加具有通用性;
119 | * **易于使用** :提供与scikit集成的Python接口,以及R和命令行界面;
120 | * **实用** :可以处理类别型、数值型特征;
121 | * **可扩展:** 支持自定义损失函数;
122 |
123 | **7.2 缺点**
124 |
125 | * 对于类别型特征的处理需要大量的内存和时间;
126 | * 不同随机数的设定对于模型预测结果有一定的影响;
127 |
--------------------------------------------------------------------------------
/XGBoost-2.md:
--------------------------------------------------------------------------------
1 | ## 算法原理
2 |
3 | XGBoost是在Gradient Boosting框架下面对GBDT的优化,是一种GBDT的工业级实现。其主要原理是在GBDT的基础上,在损失函数加入正则化部分,并且每一轮迭代对误差无法做二阶泰勒展开,加快对损失函数的优化速度。下面基于决策树弱分类器,梳理XGBoost算法的主流程,部分参数可能现在会看得有些懵懂,后面的内容会慢慢提到,这里先给一个整体的流程框架。
4 |
5 | * **输入:**
6 |
7 | * 训练数据集$T={(x_1,y_1),(x_2,y_2),...,(x_N,y_N)},x_i\in X\subseteq R^n,y_i \in Y={-1,+1}$;最大迭代次数$M$,损失函数 $L(Y,f(X))$;正则化系数$\lambda,\,\gamma$。
8 | * **输出:**
9 | * 强学习器 $f(x)$
10 | * 初始化 $f_0(x)$
11 | * 对$m=1,2,...,M$轮迭代有:
12 |
13 | * 1)计算第$i$个样本($i=1,2,...,N$)在当前轮损失函数$L$基于$f_{m-1}(x_i)$的一阶导数$g_{mi}$,二阶导数$h_{mi}$,并求和:
14 |
15 | $$
16 | G_m=\sum_{i=1}^{N}g_{mi}
17 |
18 | $$
19 |
20 | $$
21 | H_m=\sum_{i=1}^{N}h_{mi}
22 |
23 | $$
24 | * 2)基于当前节点尝试分裂决策树,默认分数 $score=0$,对特征序号$k=1,2,...,K$
25 |
26 | * a)初始化$G_L=0,H_L=0$
27 | * b.1)将样本按特征 $k$ 从小到大排列,依次取出第 $i$个样本,依次计算当前样本放入左子树后,左右子树一阶和二阶导数和:
28 |
29 | $$
30 | G_L=G_L+g_{mi},\,G_R=G-G_L
31 |
32 | $$
33 |
34 | $$
35 | H_L=H_L+h_{mi},\,H_R=H-H_L
36 |
37 | $$
38 | * b.2)尝试更新最大的分数:
39 |
40 | $$
41 | score=max(score,\,\frac{1}{2}\frac{G_L^2}{H_L+\lambda}+\frac{1}{2}\frac{G_R^2}{H_R+\lambda}-\frac{1}{2}\frac{(G_L+G_R)^2}{H_L+H_R+\lambda})
42 |
43 | $$
44 | * 3)基于最大$score$对应的划分特征和特征值分裂子树
45 | * 4)如果最大$score$为0,则当前决策树建立完毕,计算所有叶子区域的$w_{mj}$,得到弱学习器$h_m(x)$,更新强学习器$f_m(x)$,进入下一轮弱学习器迭代。如果最大$score$不是0,则继续尝试分裂决策树。
46 |
47 | ## 损失函数
48 |
49 | XGBoost的损失函数在GBDT$L(y,\,f_{m-1}(x)+h_m(x))$的基础上,加入了如下的正则化:
50 |
51 | $$
52 | \Omega(h_m)=\gamma J+\frac{\lambda}{2}\sum_{j=1}^{J}\omega_{mj}^2
53 |
54 | $$
55 |
56 | 这里的 $J$ 是叶子节点的个数,而 $\omega_{mj}$ 是第 $j$ 个叶子节点的最优值。这里的 $\omega_{mj}$ 和在GBDT里面使用的 $c_{mj}$ 其实是一个意思,只是[XGBoost论文](https://link.zhihu.com/?target=https%3A//arxiv.org/pdf/1603.02754.pdf)里面使用 $\omega$ 符号表示叶子区域的值,这里为了和论文保持一致。
57 |
58 | 最终,XGBoost的损失函数可以表示为:
59 |
60 | $$
61 | L_m=\sum_{i=1}^{N}L(y_i, f_{m-1}(x_i)+h_m(x_i))+\gamma J+\frac{\lambda}{2}\sum_{j=1}^{J}\omega_{mj}^2
62 |
63 | $$
64 |
65 |
66 | 如果要极小化上面这个损失函数,得到第$m$个决策树最优的所有$J$个叶子节点区域和每个叶子节点区域的最优解$\omega_{mj}$。XGBoost在损失函数优化方面做了一些优化,没有和GBDT一样去拟合泰勒展开式的一阶导数,而是期望直接基于损失函数的二阶泰勒展开式来求解。现在来看看这个损失函数的二阶泰勒展开式:
67 |
68 | $$
69 | \begin{align} L_m &=\sum_{i=1}^{N}L(y_i, f_{m-1}(x_i)+h_m(x_i))+\gamma J+\frac{\lambda}{2}\sum_{j=1}^{J}\omega_{mj}^2 \\ & \approx \sum_{i=1}^{N}\left(L(y_i, f_{m-1}(x_i))+\frac{\partial L(y_i,\,f_{m-1}(x_i))}{\partial f_{m-1}(x_i)}h_m(x_i)+\frac{1}{2}\frac{\partial^2 L(y_i,\,f_{m-1}(x_i))}{\partial^2 f_{m-1}(x_i)}h_m^2(x_i)\right)+\gamma J+\frac{\lambda}{2}\sum_{j=1}^{J}\omega_{mj}^2 \end{align}
70 |
71 | $$
72 |
73 |
74 | 为了方便起见,把第$i$个样本在第$m$个弱学习器的损失函数上面的一阶和二阶导数分别记为:
75 |
76 | $$
77 | g_{mi}=\frac{\partial L(y_i,\,f_{m-1}(x_i))}{\partial f_{m-1}(x_i)},\,h_{mi}=\frac{\partial^2 L(y_i,\,f_{m-1}(x_i))}{\partial^2 f_{m-1}(x_i)}
78 |
79 | $$
80 |
81 |
82 | 则,损失函数可以简化为:
83 |
84 | $$
85 | L_m\approx \sum_{i=1}^{N}\left(L(y_i, f_{m-1}(x_i))+g_{mi}h_m(x_i)+h_{mi}h_m^2(x_i)\right)+\gamma J+\frac{\lambda}{2}\sum_{j=1}^{J}\omega_{mj}^2
86 |
87 | $$
88 |
89 |
90 | 对于第$m$轮的迭代,损失函数里面$L(y_i,f_{m-1}(x_i))$为参数项,对最小化无影响,可以直接去掉。
91 |
92 | 定义
93 |
94 | $$
95 | I_j={i|q(x_i)=j}
96 |
97 | $$
98 |
99 | 为第$j$个叶子节点的样本集合,经过$M$轮迭代完毕以后每个决策树(弱学习器)的第$j$个叶子节点的取值最终会是同一个值$\omega_{mj}$,因此,可以对损失函数继续化简:
100 |
101 | $$
102 | \begin{align} L_m &\approx \sum_{i=1}^{N}\left(g_{mi}h_m(x_i)+h_{mi}h_m^2(x_i)\right)+\gamma J+\frac{\lambda}{2}\sum_{j=1}^{J}\omega_{mj}^2 \\ & =\sum_{j=1}^{J}\left(\sum_{x_i \in R_{mj}}g_{mj}\omega_{mj}+\frac{1}{2}\sum_{x_i \in R_{mj}}h_{mj}\omega_{mj}^2\right)+\gamma J+\frac{\lambda}{2}\sum_{j=1}^{J}\omega_{mj}^2 \\ & = \sum_{j=1}^{J}[(\sum_{x_i \in R_{mj}}g_{mj})\omega_{mj}+\frac{1}{2}(\sum_{x_i \in R_{mj}}h_{mj}+\lambda)\omega_{mj}^2]+\gamma J \end{align}
103 |
104 | $$
105 |
106 | 把每个叶子节点区域样本的一阶和二阶导数的和单独表示如下:
107 |
108 | $$
109 | G_{mj}=\sum_{x_i \in R_{mj}} g_{mj},\,H_{mj}=\sum_{x_i \in R_{mj}} h_{mj}
110 |
111 | $$
112 |
113 |
114 | 那么最终的损失函数形式可以表示为:
115 |
116 | $$
117 | L_m=\sum_{j=1}^{J}[(G_{mj}\omega_{mj}+\frac{1}{2}(H_{mj}+\lambda)\omega_{mj}^2]+\gamma J
118 |
119 | $$
120 |
121 |
122 | 现在有了最终的损失函数,回到前面讲到的问题,我们如何一次求解出决策树最优的所有$J$个叶子节点区域和每个叶子节点区域的最优解$\omega_{mj}$呢?
123 |
124 | 这个问题等价于下面两个子问题:
125 |
126 | * 如果已经求出了第$m$个决策树的$J$个最优的叶子节点区域,如何求出每个叶子节点区域的最优解$\omega_{m }$?
127 | * 对当前决策树做子树分裂决策时,应该如何选择哪个特征和特征值进行分裂,使最终的损失函数$ _m$最小?
128 |
129 | 第一个问题其实比较简单,如果树的结构$q(x)$已经确定的情况下,可以基于损失函数对$\omega_{m }$求偏导并令导数为0得出最佳的$\omega_{m }$,也就是每一个叶子节点的最优值表达式为:
130 |
131 | $$
132 | \omega_{m }=\frac{G_{mj}}{H_{mj}+\lambda}
133 |
134 | $$
135 |
136 |
137 | 将求得的最优$\omega_{m }$代回到损失函数,可视为每轮迭代时该轮弱学习器的最优值表达式:
138 |
139 | $$
140 | L_m=-\frac{1}{2}\sum_{j=1}^{J}[\frac{G_{mj}}{H_{mj}+\lambda}]+\gamma J
141 |
142 | $$
143 |
144 |
145 | 那么回到第二个问题,怎么样的树结构$q(x)$是最优的呢?
146 |
147 | 通常来讲,枚举所有可能的树的结构,然后计算该结构的分数是不太现实的。在实践当中,我们采用贪心的策略:
148 |
149 | * 从深度为0的单一叶子节点开始,即所有的样本都在一个节点上
150 | * 对于树的每一个叶子节点,尝试增加一个分裂点:
151 |
152 | * 令$I_L,\,I_R$分别表示分裂点加入之后的左右叶子节点的样本集合,则有
153 | * $$
154 | G_L=\sum_{i\in I_L}g_{mi}
155 |
156 | $$
157 | * $$
158 | G_R=\sum_{i\in I_R}g_{mi}
159 |
160 | $$
161 | * $$
162 | H_L=\sum_{i\in I_L}h_{mi}
163 |
164 | $$
165 | * $$
166 | H_R=\sum_{i\in I_R}h_{mi}
167 |
168 | $$
169 | * 假如每次做左右子树分裂的时候,都可以最大程度地减少损失函数,则我们期望最大化下式:
170 |
171 | $$
172 | \Delta L=-\frac{1}{2}\frac{(G_L+G_R)^2}{H_L+H_R+\lambda}+\gamma J-\left(-\frac{1}{2}\frac{G_L^2}{H_L+\lambda}-\frac{1}{2}\frac{G_R^2}{H_R+\lambda}+\gamma (J+1)\right)
173 |
174 | $$
175 | * 对上式进行整理,我们期望最大化的是:
176 |
177 | $$
178 | L_{split}=\frac{1}{2}[\frac{G_L^2}{H_L+\lambda}+\frac{G_R^2}{H_R+\lambda}-\frac{(G_L+G_R)^2}{H_L+H_R+\lambda}]-\gamma
179 |
180 | $$
181 |
182 | 上式通常在实践当中用来评估分裂的候选点,也就是说,我们的决策树分裂标准不再使用CART树的均方误差,而是上式了。而具体如何分裂,将在下一节进行讨论。
183 |
184 | ## 分裂节点算法
185 |
186 | ## 精确搜索算法
187 |
188 | * 对每一个节点,枚举所有的特征,对每一个特征,枚举所有的分裂点,目前大部分的GBDT算法实现(sklearn、R当中的GBDT)都是采用这种算法。
189 | * 对每个特征,通过特征的取值将实例进行排序
190 | * 寻求该特征的最优分裂点
191 | * 对所有的特征采用如下的算法操作
192 |
193 | 
194 |
195 | 不难发现,对于连续型的特征,由于要枚举特征所有取值,计算量非常大,为了提高效率,通常将数据按照特征取值预排序。对于深度为$k$的树的时间复杂度:对特征所有取值的排序为$O(NlogN)$,$N$为样本点数目,若有$D$维特征,则$O(kDNlogN)$
196 |
197 | ## 近视搜索算法
198 |
199 | 精确搜索算法非常强大,但是当数据量大到内存无法存下时无法高效运行,并且在进行分布式计算时也存在一些问题,此时需要一个近视算法。主要思路如下: - 根据特征分布的百分位数,提出特征的一些**候选分裂点** - 将连续特征值映射到桶里(候选点对应的分裂),然后根据桶里样本的统计量,从这些候选中选择最佳分裂点 - 根据候选提出的时间,分为: - 全局近似:在构造树的初始阶段提出所有的候选分裂点,然后对各个层次采用相同的候选 - 提出候选的次数少,但每次的候选数目多(因为候选不更新) - 局部近似:在每次分裂都重新提出候选 - 对层次较深的树更适合,候选分裂点的数目不需要太多
200 |
201 | 对于$G,H$的更新算法步骤如下:
202 |
203 | 
204 |
205 | 对于单机系统,XGBoost系统支持精确搜索算法,对于单机/分布式,全局近视/局部近视均支持。
206 |
207 | ## 正则化
208 |
209 | 总体上讲,XGBoost抵抗过拟合的方法与GBDT类似,主要也是从以下几方面考虑:
210 |
211 | ## 模型复杂度
212 |
213 | 正则化表达式为:
214 |
215 | $$
216 | \Omega(h_m)=\gamma J+\frac{\lambda}{2}\sum_{j=1}^{J}\omega_{mj}^2
217 |
218 | $$
219 |
220 | 这里的$J$是叶子节点的个数,而 $\omega_{mj}$ 是第$j$个叶子节点的最优值。
221 |
222 | 其中第一项叶子结点的数目$J$相当于$L_1$正则,第二项叶子节点的最优值相当于$L_2$正则。
223 |
224 | ## Shrinkage
225 |
226 | 其思想认为,每次走一小步逐渐逼近结果的效果,要比每次迈一大步很快逼近结果的方式更容易避免过拟合。即它不完全信任每一个棵残差树,它认为每棵树只学到了真理的一小部分,累加的时候只累加一小部分,通过多学几棵树弥补不足。用方程来看更清晰,即给每棵数的输出结果乘上一个步长$\alpha$(learning rate)
227 |
228 | 对于前面的弱学习器的迭代:
229 |
230 | $$
231 | f_m(x)=f_{m-1}(x)+T(x;\gamma_m)
232 |
233 | $$
234 |
235 | 加上正则化项,则有
236 |
237 | $$
238 | f_m(x)=f_{m-1}(x)+\alpha\, T(x;\gamma_m)
239 |
240 | $$
241 |
242 | 此处,$\alpha$的取值范围为(0,1]。对于同样的训练集学习效果,较小$\alpha$的意味着需要更多的弱学习器的迭代次数。通常我们用步长和迭代最大次数一起决定算法的拟合效果。
243 |
244 | ## 特征采样和样本采样
245 |
246 | XGBoost借鉴RF的思想,对于特征进行采样以达到降低过拟合的目的,根据用户反馈,特征采样比起样本采样效果更优。当然,XGBoost同时支持以上两种降低过拟合的采样方式。
247 |
248 | ## Early Stop
249 |
250 | 对于每一次分离后的增益,即前面的
251 |
252 | $$
253 | L_{split}=\frac{1}{2}[\frac{G_L^2}{H_L+\lambda}+\frac{G_R^2}{H_R+\lambda}-\frac{(G_L+G_R)^2}{H_L+H_R+\lambda}]-\gamma
254 |
255 | $$
256 |
257 |
258 | 在`sklearn`接口当中,如果$L_{split}$出现负值,则提前停止;但是,被提前终止掉的分裂可能其后续的分裂会带来好处。在XBGoost原生接口当中是采用过后剪枝策略:将树分裂到最大深度,然后再基于上述增益计算剪枝。在具体实现当中还有`learning rate`等其它参数一起控制,给$L_{split}$出现负值的后续轮留机会。
259 |
260 | ## 缺失值处理
261 |
262 | 在实际的工业实践当中,数据出现缺失无法避免。
263 |
264 | XGBoost没有假设缺失值一定进入左子树还是右子树,则是尝试通过枚举所有缺失值在当前节点是进入左子树,还是进入右子树更优来决定一个处理缺失值默认的方向,这样处理起来更加的灵活和合理。
265 |
266 | 也就是说,上面第1节的算法的步骤a),b.1)和b.2)会执行2次,第一次假设特征$k$所有有缺失值的样本都走左子树,第二次假设特征$k$所有缺失值的样本都走右子树。然后每次都是针对没有缺失值的特征k的样本走上述流程,而不是所有的的样本。
267 |
268 | 如果是所有的缺失值走右子树,使用上面第1节的a),b.1)和b.2)即可。如果是所有的样本走左子树,则上面第1节的a)步要变成:
269 |
270 | $$
271 | G_R=0,\,H_R=0
272 |
273 | $$
274 |
275 |
276 | b.1)步要更新为:
277 |
278 | $$
279 | G_R=G_R+g_mi,\,G_L=G-G_R
280 |
281 | $$
282 |
283 |
284 | $$
285 | H_R=H_R+h_mi,\,H_L=H-H_R
286 |
287 | $$
288 |
289 |
290 | 具体算法如下图所示:
291 |
292 | 
293 |
294 | ## 优缺点
295 |
296 | ## 优点
297 |
298 | * 支持线性分类器(相当于引入$L_1,\,L_2$正则惩罚项的LR和线性回归,损失函数公式=误差平方和+正则项,似LR)
299 | * 损失函数用了二阶泰勒展开,引入一阶导和二阶导,提高模型拟和的速度
300 | * 可以给缺失值自动划分方向
301 | * 同RF,支持样本(行)随机抽取,也支持特征(列)随机抽取,降低运算,防过拟合
302 | * 损失函数引入正则化项,包含全部叶子节点个数,每个叶子节点得分的$L_2$模的平方和(代表叶子节点权重的影响),控制模型(树)复杂度
303 | * 每次迭代后为叶子分配结合学习速率,减低每棵树权重,减少每棵树影响,灵活调整后面的学习空间
304 | * 支持并行,不是树并行,是把特征值先预排序,存起来,可以重复并行使用计算分裂点
305 | * 分裂依据分开后与未分前的差值增益,不用每个节点排序算增益,减少计算量,可以并行计算
306 | * 可以引入阈值限制树分裂,控制树的规模
307 |
308 | ## 缺点
309 |
310 | * 往往会选择具有更高数量的不同值的预测器
311 | * 当预测器具有很多类别时,容易过拟合
312 | * 参数过多,调参困难
313 | * 如果采用精确搜索算法对内存消耗过大,且不支持分布式
314 |
315 | ## sklearn中的参数解释
316 |
317 | `sklearn`本身的文档当中并没有XGBoost的描述,[Github](https://link.zhihu.com/?target=https%3A//github.com/dmlc/xgboost/blob/master/python-package/xgboost/sklearn.py)上面看到主要参数如下:
318 |
319 | * max_depth :树的最大深度。越大通常模型复杂,更容易过拟合,这里作为弱学习器一般设置为1-10
320 | * learning_rate:学习率或收缩因子。学习率和迭代次数/弱分类器数目n_estimators相关。 缺省:0.1 (与直接调用xgboost的eta参数含义相同)
321 | * n_estimators:弱分类器数目. 缺省:100
322 | * verbosity:控制输出
323 | * slient:参数值为1时,静默模式开启,不输出任何信息
324 | * objective:待优化的目标函数,常用值有:
325 |
326 | * binary:logistic 二分类的逻辑回归,返回预测的概率
327 | * multi:softmax 使用softmax的多分类器,返回预测的类别(不是概率)
328 | * multi:softprob 和multi:softmax参数一样,但是返回的是每个数据属于各个类别的概率
329 | * 支持用户自定义目标函数
330 | * booster:选择每次迭代的模型,有两种选择:
331 | * gbtree:基于树的模型,为缺省值
332 | * gbliner:线性模型
333 | * dart:树模型
334 | * nthread:用来进行多线程控制。 如果你希望使用CPU全部的核,那就用缺省值-1,算法会自动检测它
335 | * n_jobs:xgboost运行时的线程数,后续代替`nthread`参数
336 | * gamma:节点分裂所需的最小损失函数下降值,缺省0
337 | * min_child_weight:叶子结点需要的最小样本权重(hessianhessian)和
338 | * subsample:构造每棵树的所用样本比例(样本采样比例)
339 | * colsample_bytree:构造树时每棵树的所用特征比例
340 | * colsample_bylevel:构造树时每层的所用特征比例
341 | * colsample_bynone:构造树时每次分裂的所用特征比例
342 | * reg_alpha:$L_1$正则的惩罚系数
343 | * reg_lambda:$L_2$正则的惩罚系数
344 | * tree_method string [default= auto]:XGBoost中使用的树构造算法
345 |
346 | * XGBoost支持hist和大规模分布式训练,仅支持大规模外部内存版本。
347 | * 选择: auto, exact, approx, hist, gpu_hist
348 | * auto: 对于中小型数据集,将使用精确的贪婪(精确)
349 | * 对于非常大的数据集,将选择近似算法(近似)
350 | * 因为旧版本总是在单个机器中使用精确贪婪,所以当选择近似算法来通知该选择时,用户将得到消息
351 | * exact: 精确的贪婪算法
352 | * approx : 使用分位数草图和梯度直方图的近似贪婪算法
353 | * hist:快速直方图优化近似贪心算法
354 | * gpu_hist:hist算法的GPU实现
355 | * scale_pos_weight:正负样本的平衡,通常用于不均衡数据
356 | * base_score:初始预测值
357 | * random_state:随机种子
358 | * missing:缺失值
359 | * importance_type:特征重要程度计算方法
360 |
361 | 除了以上参数,XGBoost原生接口当中参数众多,主要有以下4大类:
362 |
363 | * General parameters
364 | * Booster parameters
365 | * Learning task parameters
366 | * Command line parameters(较少用到)
367 |
368 | 如果有遗漏,具体可以参阅[XGBoost Parameters](https://link.zhihu.com/?target=https%3A//xgboost.readthedocs.io/en/latest/parameter.html)
369 |
370 | ## 应用场景
371 |
372 | XGBoost是GBDT框架的工业级优化实现,所有GBDT能够应用的场景,XGBoost都可以应用,所有回归问题(线性/非线性)、二分类问题(设定阈值,大于阈值为正例,反之为负例)。
373 |
374 | 按业务领域分,推荐系统、反欺诈、信用评级等。
375 |
--------------------------------------------------------------------------------
/LightGBM-2.md:
--------------------------------------------------------------------------------
1 | title: LightGBM算法梳理 date: 2019-08-12 23:56:55 categories: 机器学习 tags: - 集成学习 - LightGBM - Histogram - 分布式 - sklearn description: DataWhale暑期学习小组-高级算法梳理第八期Task4。
2 |
3 | ---
4 |
5 | ## LightGBM
6 |
7 | 同XGBoost类似,LightGBM依然是在GBDT算法框架下的一种改进实现,是一种基于决策树算法的快速、分布式、高性能的GBDT框架,主要说解决的痛点是面对高维度大数据时提高GBDT框架算法的效率和可扩展性。
8 |
9 | “Light”主要体现在三个方面,即更少的样本、更少的特征、更少的内存,分别通过单边梯度采样(Gradient-based One-Side Sampling)、互斥特征合并(Exclusive Feature Bundling)、直方图算法(Histogram)三项技术实现。另外,在工程上面,LightGBM还在并行计算方面做了诸多的优化,支持特征并行和数据并行,并针对各自的并行方式做了优化,减少通信量。
10 |
11 | ## LightGBM的起源
12 |
13 | LightGBM起源于微软亚洲研究院在NIPS发表的系列论文:
14 |
15 | * [Qi Meng, Guolin Ke, Taifeng Wang, Wei Chen, Qiwei Ye, Zhi-Ming Ma, Tie-Yan Liu. “A Communication-Efficient Parallel Algorithm for Decision Tree.” Advances in Neural Information Processing Systems 29 (NIPS 2016), pp. 1279-1287](https://link.zhihu.com/?target=https%3A//papers.nips.cc/paper/6381-a-communication-efficient-parallel-algorithm-for-decision-tree.pdf)
16 | * [Guolin Ke, Qi Meng, Thomas Finley, Taifeng Wang, Wei Chen, Weidong Ma, Qiwei Ye, Tie-Yan Liu. “LightGBM: A Highly Efficient Gradient Boosting Decision Tree.” Advances in Neural Information Processing Systems 30 (NIPS 2017), pp. 3149-3157](https://link.zhihu.com/?target=https%3A//papers.nips.cc/paper/6907-lightgbm-a-highly-efficient-gradient-boosting-decision-tree.pdf)
17 |
18 | 并于2016年10月17日在[LightGBM](https://link.zhihu.com/?target=https%3A//github.com/microsoft/LightGBM)上面开源,三天内在GitHub上面被star了1000次,fork了200次。知乎上现有近2000人关注“如何看待微软开源的LightGBM?”问题。
19 |
20 | 随后不断迭代,慢慢地开始支持Early Stopping、叶子索引预测、最大深度设置、特征重要性评估、多分类、类别特征支持、正则化(L1,L2及分裂最小增益)……
21 |
22 | 具体可以参阅以下链接:
23 |
24 | [LightGBM大事记](https://link.zhihu.com/?target=https%3A//github.com/Microsoft/LightGBM/blob/master/docs/Key-Events.md)
25 |
26 | ## Histogram VS Pre-sorted
27 |
28 | ## Pre-sorted
29 |
30 | 在XGBoost当中的精确搜索算法(Exact Greedy Algorithm)在寻找分裂点时就是采用Pre-sorted的思想。具体过程不再赘述,可以参阅[XGBoost算法梳理](https://link.zhihu.com/?target=http%3A//datacruiser.io/2019/08/10/DataWhale-Workout-No-8-XGboost-Summary/)
31 |
32 | 预排序还是有一定优点的,如果不用预排序的话,在分裂节点的时候,选中某一个特征后,需要对A按特征值大小进行排序,然后计算每个阈值的增益,这个过程需要花费很多时间。
33 |
34 | 预排序算法在计算最优分裂时,各个特征的增益可以并行计算,并且能精确地找到分割点。但是预排序后需要保存特征值及排序后的索引,因此需要消耗两倍于训练数据的内存,时间消耗大。另外预排序后,特征对梯度的访问是一种随机访问,并且不同的特征访问的顺序不一样,无法对cache进行优化,时间消耗也大。最后,在每一层,需要随机访问一个行索引到叶子索引的数组,并且不同特征访问的顺序也不一样。
35 |
36 | ## Historgram
37 |
38 | 首先需要指出的是,XGBoost在寻找树的分裂节点的也是支持直方图算法的,就是论文中提到的近视搜索算法(Approximate Algorithm)。只是,无论特征值是否为0,直方图算法都需要对特征的分箱值进行索引,因此对于大部分实际应用场景当中的稀疏数据优化不足。
39 |
40 | 回过头来,为了能够发挥直方图算法的优化威力,LightGBM提出了另外两个新技术:单边梯度采样(Gradient-based One-Side Sampling)和互斥特征合并(Exclusive Feature Bundling),在减少维度和下采样上面做了优化以后才能够将直方图算法发挥得淋漓尽致。下面依次介绍直方图算法、GOSS和EFB。
41 |
42 | ### 直方图算法
43 |
44 | 直方图算法的基本思想是先把连续的浮点特征值离散化成$k$个整数,同时构造一个宽度为$k$的直方图。在遍历数据的时候,根据离散化后的值作为索引在直方图中累积统计量,当遍历一次数据后,直方图累积了需要的统计量,然后根据直方图的离散值,遍历寻找最优的分割点。具体算法描述如下:
45 |
46 | 
47 |
48 | 
49 |
50 | 直方图算法有如下优点:
51 |
52 | * 内存消耗降低。预排序算法需要的内存约是训练数据的两倍(2x样本数x维度x4Bytes),它需要用32位浮点来保存特征值,并且对每一列特征,都需要一个额外的排好序的索引,这也需要32位的存储空间。对于 直方图算法,则只需要(1x样本数x维度x1Bytes)的内存消耗,仅为预排序算法的1/8。因为直方图算法仅需要存储特征的 bin 值(离散化后的数值),不需要原始的特征值,也不用排序,而bin值用8位整型存储就足够了。
53 | * 算法时间复杂度大大降低。决策树算法在节点分裂时有两个主要操作组成,一个是“寻找分割点”,另一个是“数据分割”。从算法时间复杂度来看,在“寻找分割点”时,预排序算法对于深度为$k$的树的时间复杂度:对特征所有取值的排序为$O(NlogN)$,$N$为样本点数目,若有$D$维特征,则$O(kDNlogN)$,而直方图算法需要$O(kD \times bin)$(bin是histogram 的横轴的数量,一般远小于样本数量$N$)。
54 | * 再举个例子说明上述两点的优化,假设数据集$A$的某个特征的特征值有(二叉树存储):${1.2,1.3,2.2,2.3,3.1,3.3}$,预排序算法要全部遍历一遍,需要切分大约5次。进行离散化后,只需要切分2次 ${{1},{2,3}}$ 和 ${{1,2},{3}}$,除了切分次数减少,内存消耗也大大降低。
55 | * 直方图算法还可以进一步加速。一个容易观察到的现象:一个叶子节点的直方图可以直接由父节点的直方图和兄弟节点的直方图做差得到。通常构造直方图,需要遍历该叶子上的所有数据,但直方图做差仅需遍历直方图的$k$个bin。利用这个方法,LightGBM可以在构造一个叶子的直方图后,可以用非常微小的代价得到它兄弟叶子的直方图,在速度上可以提升一倍。
56 |
57 | 
58 |
59 | 当然,直方图算法并不是完美的。由于特征被离散化后,找到的并不是很精确的分割点,所以会对结果产生影响。但在不同的数据集上的结果表明,离散化的分割点对最终的精度影响并不是很大,甚至有时候会更好一点。原因是决策树本来就是弱模型,分割点是不是精确并不是太重要;较粗的分割点也有正则化的效果,可以有效地防止过拟合;即使单棵树的训练误差比精确分割的算法稍大,但在梯度提升(GradientBoosting)的框架下没有太大的影响。
60 |
61 | ### 单边梯度采样(Gradient-based One-Side Sampling)
62 |
63 | 单边梯度采样是一种在减少数据量和保证精度上平衡的算法。在GBDT中, 我们对损失函数的负梯度进行拟合,样本误差越大,梯度的绝对值越大,这说明模型对该样本的学习还不足够,相反如果越小则表示模型对该样本的学习已经很充分。因此,我们可以这样推论:梯度的绝对值越大,样本重要性越高。单边梯度采样正是以样本的梯度作为样本的权重进行采样。
64 |
65 | 单边梯度采样保留所有的梯度较大的样本,在梯度小的实例上使用随机采样。为了抵消对数据分布的影响,计算信息增益的时候,单边梯度采样对小梯度的数据引入常量乘数。单边梯度采样首先根据数据的梯度绝对值排序,选取$top\,\,a$个样本。然后在剩余的数据中随机采样$b$个样本。接着计算信息增益时为采样出的小梯度数据乘以$\frac{1-a}{b}$,这样算法就会更关注训练不足的样本例,而不会过多改变原数据集的分布。正是单边梯度采样减少了数据量,让直方图算法发挥了更大的作用。单边梯度采样具体算法见下图:
66 |
67 | 
68 |
69 | ### 互斥特征合并(Exclusive Feature Bundling)
70 |
71 | 高维的数据通常是稀疏的,这种特征空间的稀疏性给我们提供了一种设计一种接近无损地降维的可能性。特别的,在稀疏特征空间中,许多特征是互斥的,换句话说,大部分特征不会同时取非0值,例如One-hot之后的类别特征他们从不同时为非0值。我们可以合并互斥的特征为单一特征(我们将这个过程称为*Exclusive Feature Bundle* ).通过仔细设计特征扫描算法,我们从合并特征中构建出与单个特征相同的特征直方图。通过这种方式,直方图构建算法的时间复杂度从$O(ND)$,降到$O(N×bundle)$,其中$N$为样本点数目,$D$为特征维度。通常,bundle << $D$,我们能够在不损失精度的情况下极大地加速GBDT的训练。
72 |
73 | 那么接下来有两个问题需要处理:
74 |
75 | * 需要合并哪些特征
76 | * 如何合并这些特征
77 |
78 | ### Greedy Bundling
79 |
80 | 找出最优的 bundle 组合数是一个 NP 问题,LightGBM通过将原问题转化为”图着色”问题进行贪心近似解决。
81 |
82 | 首先创建一个图$G(V, E)$,其中$V$就是特征,为图中的节点,$E$为$G$中的边,将不是相互独立的特征用一条边连接起来,边的权重就是两个相连接的特征的总冲突值,这样需要绑定的特征就是在图着色问题中要涂上同一种颜色的那些点(特征)。具体算法过程如下:
83 |
84 | 
85 |
86 | ### Merge Exclusive Features
87 |
88 | 该过程主要是关键在于原始特征值可以从bundle中区分出来,即绑定几个特征在同一个bundle里需要保证绑定前的原始特征的值在bundle中能够被识别,考虑到直方图算法将连续的值保存为离散的bin,我们可以使得不同特征的值分到bundle中的不同bin中,这可以通过在特征值中加一个偏置常量来解决,比如,我们在bundle中绑定了两个特征A和B,A特征的原始取值为区间[0,10),B特征的原始取值为区间[0,20),我们可以在B特征的取值上加一个偏置常量10,将其取值范围变为[10,30),这样就可以放心的融合特征A和B了,因为在树模型中对于每一个特征都会计算分裂节点的,也就是通过将他们的取值范围限定在不同的bin中,在分裂时可以将不同特征很好的分裂到树的不同分支中去。具体算法如下:
89 |
90 | 
91 |
92 | ## Leaf-wise VS Level-wise
93 |
94 | ## Level-wise
95 |
96 | 大多数GBDT框架使用的按层生长 (level-wise) 的决策树生长策略,Level-wise遍历一次数据可以同时分裂同一层的叶子,容易进行多线程优化,也好控制模型复杂度,不容易过拟合。但实际上Level-wise是一种低效的算法,因为它不加区分的对待同一层的叶子,带来了很多没必要的开销,因为实际上很多叶子的分裂增益较低,没必要进行搜索和分裂。
97 |
98 | 
99 |
100 | ## Leaf-wise
101 |
102 | LightGBM在直方图算法之上,对于树的生长策略做了进一步优化,抛弃了Level-wise策略,使用了带有深度限制的按叶子生长 (leaf-wise)算法。Leaf-wise则是一种更为高效的策略,每次从当前所有叶子中,找到分裂增益最大的一个叶子,然后分裂,如此循环。因此同Level-wise相比,在分裂次数相同的情况下,Leaf-wise可以降低更多的误差,得到更好的精度。Leaf-wise的缺点是可能会长出比较深的决策树,产生过拟合。因此LightGBM在Leaf-wise之上增加了一个最大深度的限制,在保证高效率的同时防止过拟合。
103 |
104 | 
105 |
106 | ## 特征并行和数据并行
107 |
108 | 本小节主要根据[LightGBM的官方文档](https://link.zhihu.com/?target=https%3A//lightgbm.readthedocs.io/en/latest/Features.html%23optimization-in-network-communication)中提到的并行计算优化进行讲解。 在本小节中,工作的节点称为**worker**
109 |
110 | LightGBM具有支持高效并行的优点。LightGBM原生支持并行学习,目前支持特征并行和数据并行的两种。
111 |
112 | ## 特征并行
113 |
114 | 特征并行主要是并行化决策树中寻找最优划分点(“Find Best Split”)的过程,因为这部分最为耗时。
115 |
116 | 传统特征并行做法如下:
117 |
118 | * 垂直划分数据(对特征划分),不同的worker有不同的特征集
119 | * 每个workers找到局部最佳的切分点{feature, threshold}
120 | * workers使用点对点通信,找到全局最佳切分点
121 | * 具有全局最佳切分点的worker进行节点分裂,然后广播切分后的结果(左右子树的instance indices)
122 | * 其它worker根据收到的instance indices也进行划分
123 |
124 | 
125 |
126 | 主要有以下缺点:
127 |
128 | * 无法加速分裂的过程,该过程的时间复杂度为$O(N)$,当数据量大的时候效率不高
129 | * 需要广播划分的结果(左右子树的instance indices),1条数据1bit的话,通信花费大约需要$O(N/8)$
130 |
131 | LightGBM的特征并行每个worker保存所有的数据集,这样找到全局最佳切分点后各个worker都可以自行划分,就不用进行广播划分结果,减小了网络通信量。过程如下:
132 |
133 | * 每个workers找到局部最佳的切分点{feature, threshold}
134 | * workers使用点对点通信,找到全局最佳切分点
135 | * 每个worker根据全局全局最佳切分点进行节点分裂
136 |
137 | 这样虽然不用进行广播划分结果,减小了网络通信量。但是也有缺点:
138 |
139 | * 分裂过程的复杂度保持不变
140 | * 每个worker保存所有数据,存储代价高
141 |
142 | ## 数据并行
143 |
144 | 数据并行的目标是并行化整个决策学习的过程,传统算法的做法如下:
145 |
146 | * 水平切分数据,不同的worker拥有部分数据
147 | * 每个worker根据本地数据构建局部直方图
148 | * 合并所有的局部直方图得到全部直方图
149 | * 根据全局直方图找到最优切分点并进行分裂
150 |
151 | 
152 |
153 | 在第3步当中有两种合并方式:
154 |
155 | * 采用点对点方式(point-to-point communication algorithm)进行通讯,每个worker通讯量为$ ( ℎ × × )$
156 | * 采用collective communication algorithm(如“[All Reduce](https://link.zhihu.com/?target=http%3A//pages.tacc.utexas.edu/~eijkhout/pcse/html/mpi-collective.html)”)进行通讯(相当于有一个中心节点,通讯后在返回结果),每个worker的通讯量为$O(2× × )$
157 |
158 | 不难发现,通信的代价也是很高的,这也是数据并行的缺点。
159 |
160 | LightGBM的数据并行主要做了以下两点优化:
161 |
162 | * 使用“Reduce Scatter”将不同worker的不同特征的直方图合并,然后workers在局部合并的直方图中找到局部最优划分,最后同步全局最优划分
163 | * 通过直方图作差法得到兄弟节点的直方图,因此只需要通信一个节点的直方图,减半通信量
164 |
165 | 通过上述两点做法,通信开销降为$ (0.5 × × )$。
166 |
167 | 另外,LightGBM还采用 一种称为**PV-Tree** 的算法进行投票并行(Voting Parallel),其实本质上也是一种数据并行。
168 |
169 | PV-Tree和普通的决策树差不多,只是在寻找最优切分点上有所不同。具体算法如下:
170 |
171 | 
172 |
173 | 主要思路如下:
174 |
175 | * 水平切分数据,不同的worker拥有部分数据
176 | * Local voting: 每个worker构建直方图,找到$top-k$个最优的本地划分特征
177 | * Global voting: 中心节点聚合得到最优的$top-2k$个全局划分特征($top-2k$是看对各个worker选择特征的个数进行计数,取最多的$2k$个)
178 | * Best Attribute Identification: 中心节点向worker收集这$top-2k$个特征的直方图,并进行合并,然后计算得到全局的最优划分
179 | * 中心节点将全局最优划分广播给所有的worker,worker进行本地划分
180 |
181 | 
182 |
183 | 可以看出,PV-tree将原本需要$O( × )$ 变为了$O(2k × )$,通信开销得到降低。此外,可以证明,当每个worker的数据足够多的时候,$top-2k$个中包含全局最佳切分点的概率非常高。
184 |
185 | ## 顺序访问梯度
186 |
187 | Cache(高速缓存)作为内存局部区域的副本,用来存放当前活跃的程序和数据,它利用程序运行的局部性,把局部范围的数据从内存复制到Cache中,使CPU直接高速从Cache中读取程序和数据,从而解决CPU速度和内存速度不匹配的问题。高速缓冲存储器最重要的技术指标是它的命中率。CPU在Cache中找到有用的数据被称为命中,当Cache中没有CPU所需的数据时(这时称为未命中),CPU才访问内存。
188 |
189 | 预排序算法中有两个频繁的操作会导致cache-miss,也就是缓存消失(对速度的影响很大,特别是数据量很大的时候,顺序访问比随机访问的速度快4倍以上 )。
190 |
191 | * 对梯度的访问:在计算增益的时候需要利用梯度,假设梯度信息存在一个数组$g[i]$中,在对特征$A$进行增益时,需要根据特征$A$排序后的索引找到$g[i]$中对应的梯度信息。特征值$A_1$对应的样本行号可能是3,对应的梯度信息在$g[3]$,而特征值$A_2$对应的样本行号可能是9999,对应的梯度信息在$g[9999]$,即对于不同的特征,访问梯度的顺序是不一样的,并且是随机的
192 | * 对于索引表的访问:预排序算法使用了行号和叶子节点号的索引表,防止数据切分的时候对所有的特征进行切分。同访问梯度一样,所有的特征都要通过访问这个索引表来索引
193 |
194 | 这两个操作都是随机的访问,会给系统性能带来非常大的下降。
195 |
196 | LightGBM使用的直方图算法能很好的解决这类问题。首先。对梯度的访问,因为不用对特征进行排序,同时,所有的特征都用同样的方式来访问,所以只需要对梯度访问的顺序进行重新排序,所有的特征都能连续的访问梯度。并且直方图算法不需要把数据id到叶子节点号上(不需要这个索引表,没有这个缓存消失问题),大大提高cache的命中率,减少cache-miss出现的概率。
197 |
198 | ## 支持类别特征
199 |
200 | 实际上大多数机器学习工具都无法直接支持类别特征,一般需要把类别特征,转化one-hot特征,降低了空间和时间的效率。而类别特征的使用是在实践中很常用的。基于这个考虑,LightGBM优化了对类别特征的支持,可以直接输入类别特征,不需要额外的0/1展开。并在决策树算法上增加了类别特征的决策规则,直接原生支持类别特征,不需要转化,提高了近8倍的速度。
201 |
202 | 
203 |
204 | ## 应用场景
205 |
206 | 作为GBDT框架内的算法,GBDT、XGBoost能够应用的场景LightGBM也都适用,并且考虑到其对于大数据、高维特征的诸多优化,在数据量非常大、维度非常多的场景更具优势。近来,有着逐步替代XGBoost成为各种数据挖掘比赛baseline的趋势。
207 |
208 | ## sklearn参数
209 |
210 | `sklearn`本身的文档当中并没有LightGBM的描述,[Github](https://link.zhihu.com/?target=https%3A//github.com/microsoft/LightGBM/blob/master/python-package/lightgbm/sklearn.py)上面看到主要参数如下:
211 |
212 | * `boosting_type` : 提升类型,字符串,可选项 (default=`gbdt`)
213 |
214 | * `gbdt`, 传统梯度提升树
215 | * `dart`, 带Dropout的MART
216 | * `goss`, 单边梯度采样
217 | * `rf`, 随机森林
218 | * `num_leaves` : 基学习器的最大叶子树,整型,可选项 (default=31)
219 | * `max_depth` : 基学习器的最大树深度,小于等于0表示没限制,整型,可选项 (default=-1)
220 | * `learning_rate` : 提升学习率,浮点型,可选项 (default=0.1)
221 | * `n_estimators` : 提升次数,整型,可选项 (default=100)
222 | * `subsample_for_bin` : 构造分箱的样本个数,整型,可选项 (default=200000)
223 | * `objective` : 指定学习任务和相应的学习目标或者用户自定义的需要优化的目标损失函数,字符串, 可调用的或者None, 可选项 (default=None),若不为None,则有:
224 | * `regression` for LGBMRegressor -`binary` or `multiclass` for LGBMClassifier
225 | * `lambdarank` for LGBMRanker
226 | * `class_weight` : 该参数仅在多分类的时候会用到,多分类的时候各个分类的权重,对于二分类任务,你可以使用`is_unbalance` 或 `scale_pos_weight`,字典数据, `balanced` or None, 可选项 (default=None)
227 | * `min_split_gain` : 在叶子节点上面做进一步分裂的最小损失减少值,浮点型,可选项 (default=0.)
228 | * `min_child_weight` : 在树的一个孩子或者叶子所需的最小样本权重和,浮点型,可选项 (default=1e-3)
229 | * `min_child_samples` : 在树的一个孩子或者叶子所需的最小样本,整型,可选项 (default=20)
230 | * `subsample` : 训练样本的子采样比例,浮点型,可选项 (default=1.)
231 | * `subsample_freq` : 子采样频率,小于等于0意味着不可用,整型,可选项 (default=0)
232 | * `colsample_bytree` : 构建单棵树时列采样比例,浮点型,可选项 (default=1.)
233 | * `reg_alpha` : $L_1$正则项,浮点型,可选项 (default=0.)
234 | * `reg_lambda` :$L_2$正则项,浮点型,可选项 (default=0.)
235 | * `random_state` : 随机数种子,整型或者None, 可选项 (default=None)
236 | * `n_jobs` : 线程数,整型,可选项 (default=-1)
237 | * `silent` : 运行时是否打印消息,布尔型,可选项 (default=True)
238 | * `importance_type` : 填入到`feature_importances_`的特征重要性衡量类型,如果是`split`,则以特征被用来分裂的次数,如果是`gain`,则以特征每次用于分裂的累积增益,字符串,可选项 (default=`split`)
239 |
240 | 除了以上参数,LightGBM原生接口当中参数众多,主要有以下八大类:
241 |
242 | * 核心参数
243 | * 学习控制参数
244 | * IO参数
245 | * 目标参数
246 | * 度量参数
247 | * 网络参数
248 | * GPU参数
249 | * 模型参数
250 |
251 | 如果有遗漏,具体可以参阅[LightGBM Parameters](https://link.zhihu.com/?target=https%3A//lightgbm.readthedocs.io/en/latest/Parameters.html)
252 |
253 | ## CatBoost(了解)
254 |
255 | CatBoost也是Boosting族的算法,由俄罗斯科技公司Yandex于2017年提出,主要在两方面做了优化,一个是对于类别变量的处理,另外一个是对于预测偏移(prediction shift)的处理。
256 |
257 | 其中对于类别变量在传统的Greedy TBS方法的基础上添加先验分布项,这样可以减少减少噪声和低频率数据对于数据分布的影响:
258 |
259 | $$
260 | \hat{x}*k^i=\frac{\sum* {j=1}^n I_{{x_j^i=x_k^i}}*y_j+a\,P}{\sum_{j=1}^n I_{{x_j^i=x_k^i}}+a}
261 |
262 | $$
263 |
264 |
265 | 其中 $P$ 是添加的先验项,$a$ 通常是大于 0 的权重系数。
266 |
267 | 对于第二个问题,CatBoost采用了排序提升(Ordered Boosting)的方式,首先对所有的数据进行随机排列,然后在计算第 $i$ 步残差时候的模型只利用了随机排列中前 $i-1$ 个样本。具体算法描述请参阅论文[CatBoost: unbiased boosting with categorical features](https://link.zhihu.com/?target=https%3A//papers.nips.cc/paper/7898-catboost-unbiased-boosting-with-categorical-features.pdf)
268 |
269 | 时间有限,下次有机会再详细消化下CatBoost的论文。
270 |
271 | 总之,CatBoost大大简化了前期数据处理过程,特别是类别特征的数值化,调参也相对容易。近来在数据竞赛领域已经大规模采用。
272 |
--------------------------------------------------------------------------------
/Catboost.md:
--------------------------------------------------------------------------------
1 | title: DataWhale Workout No.8 CatBoost Summary date: 2019-08-19 08:18:37 categories: 机器学习 tags: - 集成学习 - CatBoost - Ordered boosting - Prediction shift - sklearn description: 这是DataWhale暑期学习小组-高级算法梳理的补充,是对目前最新的开源Boost族算法CatBoost的介绍,结合相关论文以及笔者的使用经验,对CatBoost的算法特性和适用场景做一些小结。
2 |
3 | ---
4 |
5 | ## CatBoost
6 |
7 | CatBoost是俄罗斯的搜索巨头Y andex在2017年开源的机器学习库,也是Boosting族算法的一种,同前面介绍过的XGBoost和LightGBM类似,依然是在GBDT算法框架下的一种改进实现,是一种基于对称决策树(oblivious trees)算法的参数少、支持类别型变量和高准确性的GBDT框架,主要说解决的痛点是高效合理地处理类别型特征,这个从它的名字就可以看得出来,CatBoost是由catgorical和boost组成,另外是处理梯度偏差(Gradient bias)以及预测偏移(Prediction shift)问题,提高算法的准确性和泛化能力。
8 |
9 | 
10 |
11 | CatBoost主要有以下五个特性:
12 |
13 | * 无需调参即可获得较高的模型质量,采用默认参数就可以获得非常好的结果,减少在调参上面花的时间
14 | * 支持类别型变量,无需对非数值型特征进行预处理
15 | * 快速、可扩展的GPU版本,可以用基于GPU的梯度提升算法实现来训练你的模型,支持多卡并行
16 | * 提高准确性,提出一种全新的梯度提升机制来构建模型以减少过拟合
17 | * 快速预测,即便应对延时非常苛刻的任务也能够快速高效部署模型
18 |
19 | CatBoost的主要算法原理可以参照以下两篇论文:
20 |
21 | * [Anna Veronika Dorogush, Andrey Gulin, Gleb Gusev, Nikita Kazeev, Liudmila Ostroumova Prokhorenkova, Aleksandr Vorobev "Fighting biases with dynamic boosting". arXiv:1706.09516, 2017](https://link.zhihu.com/?target=https%3A//arxiv.org/pdf/1706.09516.pdf)
22 | * [Anna Veronika Dorogush, Vasily Ershov, Andrey Gulin "CatBoost: gradient boosting with categorical features support". Workshop on ML Systems at NIPS 2017](https://link.zhihu.com/?target=http%3A//learningsys.org/nips17/assets/papers/paper_11.pdf)
23 |
24 | ## Categorical features
25 |
26 | 所谓类别型变量(Categorical features)是指其值是离散的集合且相互比较并无意义的变量,比如用户的ID、产品ID、颜色等。因此,这些变量无法在二叉决策树当中直接使用。常规的做法是将这些类别变量通过预处理的方式转化成数值型变量再喂给模型,比如用一个或者若干个数值来代表一个类别型特征。
27 |
28 | 目前广泛用于**低势** (一个有限集的元素个数是一个自然数)类别特征的处理方法是`One-hot encoding`:将原来的特征删除,然后对于每一个类别加一个0/1的用来指示是否含有该类别的数值型特征。`One-hot encoding`可以在数据预处理时完成,也可以在模型训练的时候完成,从训练时间的角度,后一种方法的实现更为高效,CatBoost对于低势类别特征也是采用后一种实现。
29 |
30 | 显然,在**高势** 特征当中,比如 `user ID`,这种编码方式会产生大量新的特征,造成维度灾难。一种折中的办法是可以将类别分组成有限个的群体再进行 `One-hot encoding`。一种常被使用的方法是根据目标变量统计(Target Statistics,以下简称TS)进行分组,目标变量统计用于估算每个类别的目标变量期望值。甚至有人直接用TS作为一个新的数值型变量来代替原来的类别型变量。重要的是,可以通过对TS数值型特征的阈值设置,基于对数损失、基尼系数或者均方差,得到一个对于训练集而言将类别一分为二的所有可能划分当中最优的那个。在LightGBM当中,类别型特征用每一步梯度提升时的梯度统计(Gradient Statistics,以下简称GS)来表示。虽然为建树提供了重要的信息,但是这种方法有以下两个缺点:
31 |
32 | * 增加计算时间,因为需要对每一个类别型特征,在迭代的每一步,都需要对GS进行计算;
33 | * 增加存储需求,对于一个类别型变量,需要存储每一次分离每个节点的类别。
34 |
35 | 为了克服这些缺点,LightGBM以损失部分信息为代价将所有的长尾类别归位一类,作者声称这样处理高势特征时比起 `One-hot encoding`还是好不少。不过如果采用TS特征,那么对于每个类别只需要计算和存储一个数字。
36 |
37 | 如此看到,采用TS作为一个新的数值型特征是最有效、信息损失最小的处理类别型特征的方法。TS也被广泛采用,在点击预测任务当中,这个场景当中的类别特征有用户、地区、广告、广告发布者等。接下来我们着重讨论TS,暂时将`One-hot encoding`和GS放一边。
38 |
39 | ## Target statistics
40 |
41 | 一个有效和高效的处理类别型特征$i$的方式是用一个与某些TS相等的数值型变量$\hat{x}_k^i$来代替第$k$个训练样本的类别${x}_k^i$。通常用基于类别的目标变量$y$的期望来进行估算:$\hat{x}_k^i\approx\mathbb{E}(y|x^i={x}_k^i)$。
42 |
43 | ### Greedy TS
44 |
45 | 估算$\mathbb{E}(y|x^i={x}*k^i)$最直接的方式就是用训练样本当中相同类别$x_k^i$的目标变量$y$的平均值。
46 |
47 | $$
48 | \hat{x}_k^i=\frac{\sum* {j=1}^n\mathbb{I}*{{x_j^i={x}_k^i}}\cdot y_i}{\sum* {j=1}^n\mathbb{I}*{{x_j^i={x}_k^i}}}
49 |
50 | $$
51 |
52 | 显然,这样的处理方式很容易引起过拟合。举个例子,假如在整个训练集当中所有样本的类别${x}_k^i$都互不相同,即$k$个样本有$k$个类别,那么新产生的数值型特征的值将与目标变量的值相同。某种程度上,这是一种目标穿越(target leakage),非常容易引起过拟合。比较好的一种做法是采用一个先验概率$p$进行平滑处理:
53 | $$
54 | \hat{x}_k^i=\frac{\sum* {j=1}^n\mathbb{I}*{{x_j^i={x}_k^i}}\cdot y_i+a\,p}{\sum* {j=1}^n\mathbb{I}_{{x_j^i={x}_k^i}}+a}
55 |
56 | $$
57 |
58 | 其中$a>0$是先验概率$p$的权重,而对于先验概率,通常的做法是设置为数据集当中目标变量的平均值。
59 |
60 | 不过这样的平滑处理依然无法完全避免目标穿越:特征$\hat{x}*k^i$是通过自变量$X_k$的目标$y_k$计算所得。这将会导致条件偏移:对于训练集和测试集,$\hat{x}_k^i|y$的分布会有所不同。再举个例子,假设第$i$个特征为类别型特征,并且特征所有取值为无重复的集合,然后对于每一个类别$A$,对于一个分类任务,我们有$P(y=1|x^i=A)=0.5$。然后在训练集当中,$\hat{x}_k^i=\frac{y_k+a\,p}{1+a}$,于是用阈值$t=\frac{0.5+a\,p}{1+a}$就可以仅用一次分裂就训练集完美分开。但是,对于测试集,因为还无法判断此时目标变量的类别,所以这一项$\sum* {j=1}^n\mathbb{I}_{{x_j^i={x}_k^i}}=0$,最后得到的TS值为$p$,并且得到的模型在$p
```
123 |
--------------------------------------------------------------------------------
/catboost2.md:
--------------------------------------------------------------------------------
1 | # Catboost
2 |
3 | CatBoost是一种基于对称决策树(oblivious trees)为基学习器实现的参数较少、支持类别型变量和高准确性的GBDT框架,主要解决的痛点是高效合理地处理类别型特征,这一点从它的名字中可以看出来,CatBoost是由Categorical和Boosting组成。此外,CatBoost还解决了梯度偏差(Gradient Bias)以及预测偏移(Prediction shift)的问题,从而减少过拟合的发生,进而提高算法的准确性和泛化能力。
4 |
5 | ## 对称决策树
6 |
7 | 那么**对称树**和普通决策树有什么区别?
8 |
9 | 一图为对称树,二图为普通决策树
10 |
11 | 
12 |
13 | 对称树中,每一层的每一个节点判断条件都是一样的。假如如果我们只训练一棵树,那么显然对称树的overfit能力会比普通的决策树弱;但是在GBM中,我们通常训练很多的树,所以overfit的能力不必担心。那么对称树在GBM中有什么优势呢?下面列出三点:
14 |
15 | * 拟合模式相对简单,因为每一层都是一个判断条件
16 | * 可以提高预测速度
17 | * 对称树的结构本身比普通决策树自由度小,可以看作是加入了penalty惩罚机制,或者看作regularization正则化
18 |
19 | 最大的优势就是第二点——预测速度会提升。为什么会更快呢?
20 |
21 | 
22 |
23 | 上面这棵树最底层有四个节点,我们可以把这四个节点从0到3编号(index),每一个节点有一个对应值(value)。比如一个样本最终进入了第一个节点,那么这棵树对这个样本的预测值就是1.6。我们可以把value存放在一个数组里面,这样给定index就可以立刻得到value。那么对一个样本用一棵树进行预测时,我们只需要找到这个样本对应的index,因为在对称树中每一层的判断条件都是一样的,所以每一层都可以用0或者1来表示,比如是学生,用1表示,不是用0;有关注机器会学习用1表示,没有用0,那么每一个样本进入这棵树,都可以用两个bits来表示,也就是四种可能结果:00,01,10,和11。这两个bits代表的数字就是index。
24 |
25 | 这意味着什么呢?我们在做预测的时候,只要对每一层的条件进行判断,然后就可以找到index。因为每一个树的结构(判断条件)是已知的,我们甚至可以对这个过程进行并行计算。
26 |
27 | ## Catboost与XGBoost,LightGBM相比的创新点
28 |
29 | * 嵌入了自动将类别型特征处理为数值型特征的创新算法。首先对categorical features做一些统计,计算某个类别特征(category)出现的频率,之后加上超参数,生成新的数值型特征(numerical features)。
30 | * Catboost还使用了组合类别特征,可以利用到特征之间的联系,这极大的丰富了特征维度。
31 | * 采用排序提升的方法对抗训练集中的噪声点,从而避免梯度估计的偏差,进而解决预测偏移的问题。
32 | * 采用了完全对称树作为基模型。
33 |
34 | ## **类别型特征**
35 |
36 | ### **2.1 类别型特征的相关工作**
37 |
38 | 所谓类别型特征,即这类特征不是数值型特征,而是离散的集合,比如省份名(山东、山西、河北等),城市名(北京、上海、深圳等),学历(本科、硕士、博士等)。在梯度提升算法中,最常用的是将这些类别型特征转为数值型来处理,一般类别型特征会转化为一个或多个数值型特征。
39 |
40 | 如果某个 **类别型特征基数比较低(low-cardinality features)** ,即该特征的所有值去重后构成的集合元素个数比较少,一般利用One-hot编码方法将特征转为数值型。One-hot编码可以在数据预处理时完成,也可以在模型训练的时候完成,从训练时间的角度,后一种方法的实现更为高效,CatBoost对于基数较低的类别型特征也是采用后一种实现。
41 |
42 | 显然,在 **高基数类别型特征(high cardinality features)** 当中,比如 `user ID`,这种编码方式会产生大量新的特征,造成维度灾难。一种折中的办法是可以将类别分组成有限个的群体再进行One-hot编码。一种常被使用的方法是根据目标变量统计(Target Statistics,以下简称TS)进行分组,目标变量统计用于估算每个类别的目标变量期望值。甚至有人直接用TS作为一个新的数值型变量来代替原来的类别型变量。重要的是,可以通过对TS数值型特征的阈值设置,基于对数损失、基尼系数或者均方差,得到一个对于训练集而言将类别一分为二的所有可能划分当中最优的那个。在LightGBM当中,类别型特征用每一步梯度提升时的梯度统计(Gradient Statistics,以下简称GS)来表示。虽然为建树提供了重要的信息,但是这种方法有以下两个缺点:
43 |
44 | * 增加计算时间,因为需要对每一个类别型特征,在迭代的每一步,都需要对GS进行计算;
45 | * 增加存储需求,对于一个类别型变量,需要存储每一次分离每个节点的类别;
46 |
47 | 为了克服这些缺点,LightGBM以损失部分信息为代价将所有的长尾类别归为一类,作者声称这样处理高基数类别型特征时比One-hot编码还是好不少。不过如果采用TS特征,那么对于每个类别只需要计算和存储一个数字。
48 |
49 | ### **2.2 目标变量统计(Target Statistics)**
50 |
51 | CatBoost算法的设计初衷是为了更好的处理GBDT特征中的categorical features。在处理 GBDT特征中的categorical features的时候,最简单的方法是用 categorical feature 对应的标签的平均值来替换。在决策树中,标签平均值将作为节点分裂的标准。这种方法被称为 Greedy Target-based Statistics , 简称 Greedy TS,用公式来表达就是:
52 |
53 | ![[公式]](https://www.zhihu.com/equation?tex=%5Chat%7Bx%7D_k%5Ei%3D%5Cfrac%7B%5Csum_%7Bj%3D1%7D%5E%7Bn%7D%5Bx_%7Bj%2Ck%7D%3Dx_%7Bi%2Ck%7D%5D%5Ccdot+Y_i%7D%7B%5Csum_%7Bj%3D1%7D%5E%7Bn%7D%5Bx_%7Bj%2Ck%7D%3Dx_%7Bi%2Ck%7D%5D%7D+%5C%5C)
54 |
55 | 这种方法有一个显而易见的缺陷,就是通常特征比标签包含更多的信息,如果强行用标签的平均值来表示特征的话,当训练数据集和测试数据集数据结构和分布不一样的时候会出条件偏移问题。
56 |
57 | 一个标准的改进 Greedy TS的方式是添加先验分布项,这样可以减少噪声和低频率类别型数据对于数据分布的影响:
58 |
59 | ![[公式]](https://www.zhihu.com/equation?tex=%5Chat%7Bx%7D_k%5Ei%3D%5Cfrac%7B%5Csum_%7Bj%3D1%7D%5E%7Bp-1%7D%7B%5Bx_%7B%5Csigma_%7Bj%2Ck%7D%7D%3Dx_%7B%5Csigma_%7Bp%2Ck%7D%7D%5D%7DY_%7B%5Csigma_%7Bj%7D%7D%2Ba%5Ccdot+p%7D%7B%5Csum_%7Bj%3D1%7D%5E%7Bp-1%7D%7B%5Bx_%7B%5Csigma_%7Bj%2Ck%7D%7D%3Dx_%7B%5Csigma_%7Bp%2Ck%7D%7D%5D%7D%2Ba%7D+%5C%5C)
60 |
61 | 其中 ![[公式]](https://www.zhihu.com/equation?tex=p)是添加的先验项, ![[公式]](https://www.zhihu.com/equation?tex=a+)通常是大于0的权重系数。添加先验项是一个普遍做法,针对类别数较少的特征,它可以减少噪声数据。对于回归问题,一般情况下,先验项可取数据集label的均值。对于二分类,先验项是正例的先验概率。利用多个数据集排列也是有效的,但是,如果直接计算可能导致过拟合。CatBoost利用了一个比较新颖的计算叶子节点值的方法,这种方式(oblivious trees,对称树)可以避免多个数据集排列中直接计算会出现过拟合的问题。
62 |
63 | ### **2.3 特征组合**
64 |
65 | 值得注意的是几个类别型特征的任意组合都可视为新的特征。例如,在音乐推荐应用中,我们有两个类别型特征:用户ID和音乐流派。如果有些用户更喜欢摇滚乐,将用户ID和音乐流派转换为数字特征时,根据上述这些信息就会丢失。结合这两个特征就可以解决这个问题,并且可以得到一个新的强大的特征。然而,组合的数量会随着数据集中类别型特征的数量成指数增长,因此不可能在算法中考虑所有组合。为当前树构造新的分割点时,CatBoost会采用贪婪的策略考虑组合。对于树的第一次分割,不考虑任何组合。对于下一个分割,CatBoost将当前树的所有组合、类别型特征与数据集中的所有类别型特征相结合,并将新的组合类别型特征动态地转换为数值型特征。CatBoost还通过以下方式生成数值型特征和类别型特征的组合:树中选定的所有分割点都被视为具有两个值的类别型特征,并像类别型特征一样被进行组合考虑。
66 |
67 | ### **2.4 CatBoost处理Categorical features总结**
68 |
69 | * 首先会计算一些数据的statistics。计算某个category出现的频率,加上超参数,生成新的numerical features。这一策略要求同一标签数据不能排列在一起(即先全是0之后全是1这种方式),训练之前需要打乱数据集。
70 | * 第二,使用数据的不同排列(实际上是4个)。在每一轮建立树之前,先扔一轮骰子,决定使用哪个排列来生成树。
71 | * 第三,考虑使用categorical features的不同组合。例如颜色和种类组合起来,可以构成类似于blue dog这样的特征。当需要组合的categorical features变多时,CatBoost只考虑一部分combinations。在选择第一个节点时,只考虑选择一个特征,例如A。在生成第二个节点时,考虑A和任意一个categorical feature的组合,选择其中最好的。就这样使用贪心算法生成combinations。
72 | * 第四,除非向gender这种维数很小的情况,不建议自己生成One-hot编码向量,最好交给算法来处理。
73 |
74 | ## **克服梯度偏差**
75 |
76 | CatBoost和所有标准梯度提升算法一样,都是通过构建新树来拟合当前模型的梯度。然而,所有经典的提升算法都存在由有偏的点态梯度估计引起的过拟合问题。在每个步骤中使用的梯度都使用当前模型中的相同的数据点来估计,这导致估计梯度在特征空间的任何域中的分布与该域中梯度的真实分布相比发生了偏移,从而导致过拟合。为了解决这个问题,CatBoost对经典的梯度提升算法进行了一些改进,简要介绍如下。
77 |
78 | 许多利用GBDT技术的算法(例如,XGBoost、LightGBM),构建下一棵树分为两个阶段:选择树结构和在树结构固定后计算叶子节点的值。为了选择最佳的树结构,算法通过枚举不同的分割,用这些分割构建树,对得到的叶子节点计算值,然后对得到的树计算评分,最后选择最佳的分割。两个阶段叶子节点的值都是被当做梯度或牛顿步长的近似值来计算。在CatBoost中,第一阶段采用梯度步长的无偏估计,第二阶段使用传统的GBDT方案执行。既然原来的梯度估计是有偏的,那么怎么能改成无偏估计呢?
79 |
80 | 
81 |
82 |
83 | ## **预测偏移和排序提升**
84 |
85 | 预测偏移(Prediction shift)是由梯度偏差造成的。在GDBT的每一步迭代中, 损失函数使用相同的数据集求得当前模型的梯度, 然后训练得到基学习器, 但这会导致梯度估计偏差, 进而导致模型产生过拟合的问题。 CatBoost通过采用排序提升 (Ordered boosting) 的方式替换传统算法中梯度估计方法,进而减轻梯度估计的偏差,提高模型的泛化能力。下面我们对预测偏移进行详细的描述和分析。
86 |
87 | 首先来看下GBDT的整体迭代过程:
88 |
89 | GBDT算法是通过一组分类器的串行迭代,最终得到一个强学习器,以此来进行更高精度的分类。它使用了前向分布算法,弱学习器使用分类回归树(CART)。
90 |
91 | 
92 |
93 | ### 排序提升
94 |
95 | 为了克服预测偏移问题,CatBoost提出了一种新的叫做Ordered boosting的算法。
96 |
97 | 
98 |
99 | 
100 |
101 |
102 | ## **快速评分**
103 |
104 | CatBoost使用对称树(oblivious trees)作为基预测器。在这类树中,相同的分割准则在树的整个一层上使用。这种树是平衡的,不太容易过拟合。梯度提升对称树被成功地用于各种学习任务中。在对称树中,每个叶子节点的索引可以被编码为长度等于树深度的二进制向量。这在CatBoost模型评估器中得到了广泛的应用:我们首先将所有浮点特征、统计信息和独热编码特征进行二值化,然后使用二进制特征来计算模型预测值。
105 |
106 |
107 | ## 基于GPU实现快速训练
108 |
109 | * **密集的数值特征。** 对于任何GBDT算法而言,最大的难点之一就是搜索最佳分割。尤其是对于密集的数值特征数据集来说,该步骤是建立决策树时的主要计算负担。CatBoost使用oblivious 决策树作为基模型,并将特征离散化到固定数量的箱子中以减少内存使用。就GPU内存使用而言,CatBoost至少与LightGBM一样有效。主要改进之处就是利用了一种不依赖于原子操作的直方图计算方法。
110 | * **类别型特征。** CatBoost实现了多种处理类别型特征的方法,并使用完美哈希来存储类别型特征的值,以减少内存使用。由于GPU内存的限制,在CPU RAM中存储按位压缩的完美哈希,以及要求的数据流、重叠计算和内存等操作。通过哈希来分组观察。在每个组中,我们需要计算一些统计量的前缀和。该统计量的计算使用分段扫描GPU图元实现。
111 | * **多GPU支持。** CatBoost中的GPU实现可支持多个GPU。分布式树学习可以通过数据或特征进行并行化。CatBoost采用多个学习数据集排列的计算方案,在训练期间计算类别型特征的统计数据。
112 |
113 | ## **CatBoost的优缺点**
114 |
115 | **7.1 优点**
116 |
117 | * **性能卓越** :在性能方面可以匹敌任何先进的机器学习算法;
118 | * **鲁棒性/强健性** :它减少了对很多超参数调优的需求,并降低了过度拟合的机会,这也使得模型变得更加具有通用性;
119 | * **易于使用** :提供与scikit集成的Python接口,以及R和命令行界面;
120 | * **实用** :可以处理类别型、数值型特征;
121 | * **可扩展:** 支持自定义损失函数;
122 |
123 | **7.2 缺点**
124 |
125 | * 对于类别型特征的处理需要大量的内存和时间;
126 | * 不同随机数的设定对于模型预测结果有一定的影响;
127 |
--------------------------------------------------------------------------------
/XGBoost-2.md:
--------------------------------------------------------------------------------
1 | ## 算法原理
2 |
3 | XGBoost是在Gradient Boosting框架下面对GBDT的优化,是一种GBDT的工业级实现。其主要原理是在GBDT的基础上,在损失函数加入正则化部分,并且每一轮迭代对误差无法做二阶泰勒展开,加快对损失函数的优化速度。下面基于决策树弱分类器,梳理XGBoost算法的主流程,部分参数可能现在会看得有些懵懂,后面的内容会慢慢提到,这里先给一个整体的流程框架。
4 |
5 | * **输入:**
6 |
7 | * 训练数据集$T={(x_1,y_1),(x_2,y_2),...,(x_N,y_N)},x_i\in X\subseteq R^n,y_i \in Y={-1,+1}$;最大迭代次数$M$,损失函数 $L(Y,f(X))$;正则化系数$\lambda,\,\gamma$。
8 | * **输出:**
9 | * 强学习器 $f(x)$
10 | * 初始化 $f_0(x)$
11 | * 对$m=1,2,...,M$轮迭代有:
12 |
13 | * 1)计算第$i$个样本($i=1,2,...,N$)在当前轮损失函数$L$基于$f_{m-1}(x_i)$的一阶导数$g_{mi}$,二阶导数$h_{mi}$,并求和:
14 |
15 | $$
16 | G_m=\sum_{i=1}^{N}g_{mi}
17 |
18 | $$
19 |
20 | $$
21 | H_m=\sum_{i=1}^{N}h_{mi}
22 |
23 | $$
24 | * 2)基于当前节点尝试分裂决策树,默认分数 $score=0$,对特征序号$k=1,2,...,K$
25 |
26 | * a)初始化$G_L=0,H_L=0$
27 | * b.1)将样本按特征 $k$ 从小到大排列,依次取出第 $i$个样本,依次计算当前样本放入左子树后,左右子树一阶和二阶导数和:
28 |
29 | $$
30 | G_L=G_L+g_{mi},\,G_R=G-G_L
31 |
32 | $$
33 |
34 | $$
35 | H_L=H_L+h_{mi},\,H_R=H-H_L
36 |
37 | $$
38 | * b.2)尝试更新最大的分数:
39 |
40 | $$
41 | score=max(score,\,\frac{1}{2}\frac{G_L^2}{H_L+\lambda}+\frac{1}{2}\frac{G_R^2}{H_R+\lambda}-\frac{1}{2}\frac{(G_L+G_R)^2}{H_L+H_R+\lambda})
42 |
43 | $$
44 | * 3)基于最大$score$对应的划分特征和特征值分裂子树
45 | * 4)如果最大$score$为0,则当前决策树建立完毕,计算所有叶子区域的$w_{mj}$,得到弱学习器$h_m(x)$,更新强学习器$f_m(x)$,进入下一轮弱学习器迭代。如果最大$score$不是0,则继续尝试分裂决策树。
46 |
47 | ## 损失函数
48 |
49 | XGBoost的损失函数在GBDT$L(y,\,f_{m-1}(x)+h_m(x))$的基础上,加入了如下的正则化:
50 |
51 | $$
52 | \Omega(h_m)=\gamma J+\frac{\lambda}{2}\sum_{j=1}^{J}\omega_{mj}^2
53 |
54 | $$
55 |
56 | 这里的 $J$ 是叶子节点的个数,而 $\omega_{mj}$ 是第 $j$ 个叶子节点的最优值。这里的 $\omega_{mj}$ 和在GBDT里面使用的 $c_{mj}$ 其实是一个意思,只是[XGBoost论文](https://link.zhihu.com/?target=https%3A//arxiv.org/pdf/1603.02754.pdf)里面使用 $\omega$ 符号表示叶子区域的值,这里为了和论文保持一致。
57 |
58 | 最终,XGBoost的损失函数可以表示为:
59 |
60 | $$
61 | L_m=\sum_{i=1}^{N}L(y_i, f_{m-1}(x_i)+h_m(x_i))+\gamma J+\frac{\lambda}{2}\sum_{j=1}^{J}\omega_{mj}^2
62 |
63 | $$
64 |
65 |
66 | 如果要极小化上面这个损失函数,得到第$m$个决策树最优的所有$J$个叶子节点区域和每个叶子节点区域的最优解$\omega_{mj}$。XGBoost在损失函数优化方面做了一些优化,没有和GBDT一样去拟合泰勒展开式的一阶导数,而是期望直接基于损失函数的二阶泰勒展开式来求解。现在来看看这个损失函数的二阶泰勒展开式:
67 |
68 | $$
69 | \begin{align} L_m &=\sum_{i=1}^{N}L(y_i, f_{m-1}(x_i)+h_m(x_i))+\gamma J+\frac{\lambda}{2}\sum_{j=1}^{J}\omega_{mj}^2 \\ & \approx \sum_{i=1}^{N}\left(L(y_i, f_{m-1}(x_i))+\frac{\partial L(y_i,\,f_{m-1}(x_i))}{\partial f_{m-1}(x_i)}h_m(x_i)+\frac{1}{2}\frac{\partial^2 L(y_i,\,f_{m-1}(x_i))}{\partial^2 f_{m-1}(x_i)}h_m^2(x_i)\right)+\gamma J+\frac{\lambda}{2}\sum_{j=1}^{J}\omega_{mj}^2 \end{align}
70 |
71 | $$
72 |
73 |
74 | 为了方便起见,把第$i$个样本在第$m$个弱学习器的损失函数上面的一阶和二阶导数分别记为:
75 |
76 | $$
77 | g_{mi}=\frac{\partial L(y_i,\,f_{m-1}(x_i))}{\partial f_{m-1}(x_i)},\,h_{mi}=\frac{\partial^2 L(y_i,\,f_{m-1}(x_i))}{\partial^2 f_{m-1}(x_i)}
78 |
79 | $$
80 |
81 |
82 | 则,损失函数可以简化为:
83 |
84 | $$
85 | L_m\approx \sum_{i=1}^{N}\left(L(y_i, f_{m-1}(x_i))+g_{mi}h_m(x_i)+h_{mi}h_m^2(x_i)\right)+\gamma J+\frac{\lambda}{2}\sum_{j=1}^{J}\omega_{mj}^2
86 |
87 | $$
88 |
89 |
90 | 对于第$m$轮的迭代,损失函数里面$L(y_i,f_{m-1}(x_i))$为参数项,对最小化无影响,可以直接去掉。
91 |
92 | 定义
93 |
94 | $$
95 | I_j={i|q(x_i)=j}
96 |
97 | $$
98 |
99 | 为第$j$个叶子节点的样本集合,经过$M$轮迭代完毕以后每个决策树(弱学习器)的第$j$个叶子节点的取值最终会是同一个值$\omega_{mj}$,因此,可以对损失函数继续化简:
100 |
101 | $$
102 | \begin{align} L_m &\approx \sum_{i=1}^{N}\left(g_{mi}h_m(x_i)+h_{mi}h_m^2(x_i)\right)+\gamma J+\frac{\lambda}{2}\sum_{j=1}^{J}\omega_{mj}^2 \\ & =\sum_{j=1}^{J}\left(\sum_{x_i \in R_{mj}}g_{mj}\omega_{mj}+\frac{1}{2}\sum_{x_i \in R_{mj}}h_{mj}\omega_{mj}^2\right)+\gamma J+\frac{\lambda}{2}\sum_{j=1}^{J}\omega_{mj}^2 \\ & = \sum_{j=1}^{J}[(\sum_{x_i \in R_{mj}}g_{mj})\omega_{mj}+\frac{1}{2}(\sum_{x_i \in R_{mj}}h_{mj}+\lambda)\omega_{mj}^2]+\gamma J \end{align}
103 |
104 | $$
105 |
106 | 把每个叶子节点区域样本的一阶和二阶导数的和单独表示如下:
107 |
108 | $$
109 | G_{mj}=\sum_{x_i \in R_{mj}} g_{mj},\,H_{mj}=\sum_{x_i \in R_{mj}} h_{mj}
110 |
111 | $$
112 |
113 |
114 | 那么最终的损失函数形式可以表示为:
115 |
116 | $$
117 | L_m=\sum_{j=1}^{J}[(G_{mj}\omega_{mj}+\frac{1}{2}(H_{mj}+\lambda)\omega_{mj}^2]+\gamma J
118 |
119 | $$
120 |
121 |
122 | 现在有了最终的损失函数,回到前面讲到的问题,我们如何一次求解出决策树最优的所有$J$个叶子节点区域和每个叶子节点区域的最优解$\omega_{mj}$呢?
123 |
124 | 这个问题等价于下面两个子问题:
125 |
126 | * 如果已经求出了第$m$个决策树的$J$个最优的叶子节点区域,如何求出每个叶子节点区域的最优解$\omega_{m }$?
127 | * 对当前决策树做子树分裂决策时,应该如何选择哪个特征和特征值进行分裂,使最终的损失函数$ _m$最小?
128 |
129 | 第一个问题其实比较简单,如果树的结构$q(x)$已经确定的情况下,可以基于损失函数对$\omega_{m }$求偏导并令导数为0得出最佳的$\omega_{m }$,也就是每一个叶子节点的最优值表达式为:
130 |
131 | $$
132 | \omega_{m }=\frac{G_{mj}}{H_{mj}+\lambda}
133 |
134 | $$
135 |
136 |
137 | 将求得的最优$\omega_{m }$代回到损失函数,可视为每轮迭代时该轮弱学习器的最优值表达式:
138 |
139 | $$
140 | L_m=-\frac{1}{2}\sum_{j=1}^{J}[\frac{G_{mj}}{H_{mj}+\lambda}]+\gamma J
141 |
142 | $$
143 |
144 |
145 | 那么回到第二个问题,怎么样的树结构$q(x)$是最优的呢?
146 |
147 | 通常来讲,枚举所有可能的树的结构,然后计算该结构的分数是不太现实的。在实践当中,我们采用贪心的策略:
148 |
149 | * 从深度为0的单一叶子节点开始,即所有的样本都在一个节点上
150 | * 对于树的每一个叶子节点,尝试增加一个分裂点:
151 |
152 | * 令$I_L,\,I_R$分别表示分裂点加入之后的左右叶子节点的样本集合,则有
153 | * $$
154 | G_L=\sum_{i\in I_L}g_{mi}
155 |
156 | $$
157 | * $$
158 | G_R=\sum_{i\in I_R}g_{mi}
159 |
160 | $$
161 | * $$
162 | H_L=\sum_{i\in I_L}h_{mi}
163 |
164 | $$
165 | * $$
166 | H_R=\sum_{i\in I_R}h_{mi}
167 |
168 | $$
169 | * 假如每次做左右子树分裂的时候,都可以最大程度地减少损失函数,则我们期望最大化下式:
170 |
171 | $$
172 | \Delta L=-\frac{1}{2}\frac{(G_L+G_R)^2}{H_L+H_R+\lambda}+\gamma J-\left(-\frac{1}{2}\frac{G_L^2}{H_L+\lambda}-\frac{1}{2}\frac{G_R^2}{H_R+\lambda}+\gamma (J+1)\right)
173 |
174 | $$
175 | * 对上式进行整理,我们期望最大化的是:
176 |
177 | $$
178 | L_{split}=\frac{1}{2}[\frac{G_L^2}{H_L+\lambda}+\frac{G_R^2}{H_R+\lambda}-\frac{(G_L+G_R)^2}{H_L+H_R+\lambda}]-\gamma
179 |
180 | $$
181 |
182 | 上式通常在实践当中用来评估分裂的候选点,也就是说,我们的决策树分裂标准不再使用CART树的均方误差,而是上式了。而具体如何分裂,将在下一节进行讨论。
183 |
184 | ## 分裂节点算法
185 |
186 | ## 精确搜索算法
187 |
188 | * 对每一个节点,枚举所有的特征,对每一个特征,枚举所有的分裂点,目前大部分的GBDT算法实现(sklearn、R当中的GBDT)都是采用这种算法。
189 | * 对每个特征,通过特征的取值将实例进行排序
190 | * 寻求该特征的最优分裂点
191 | * 对所有的特征采用如下的算法操作
192 |
193 | 
194 |
195 | 不难发现,对于连续型的特征,由于要枚举特征所有取值,计算量非常大,为了提高效率,通常将数据按照特征取值预排序。对于深度为$k$的树的时间复杂度:对特征所有取值的排序为$O(NlogN)$,$N$为样本点数目,若有$D$维特征,则$O(kDNlogN)$
196 |
197 | ## 近视搜索算法
198 |
199 | 精确搜索算法非常强大,但是当数据量大到内存无法存下时无法高效运行,并且在进行分布式计算时也存在一些问题,此时需要一个近视算法。主要思路如下: - 根据特征分布的百分位数,提出特征的一些**候选分裂点** - 将连续特征值映射到桶里(候选点对应的分裂),然后根据桶里样本的统计量,从这些候选中选择最佳分裂点 - 根据候选提出的时间,分为: - 全局近似:在构造树的初始阶段提出所有的候选分裂点,然后对各个层次采用相同的候选 - 提出候选的次数少,但每次的候选数目多(因为候选不更新) - 局部近似:在每次分裂都重新提出候选 - 对层次较深的树更适合,候选分裂点的数目不需要太多
200 |
201 | 对于$G,H$的更新算法步骤如下:
202 |
203 | 
204 |
205 | 对于单机系统,XGBoost系统支持精确搜索算法,对于单机/分布式,全局近视/局部近视均支持。
206 |
207 | ## 正则化
208 |
209 | 总体上讲,XGBoost抵抗过拟合的方法与GBDT类似,主要也是从以下几方面考虑:
210 |
211 | ## 模型复杂度
212 |
213 | 正则化表达式为:
214 |
215 | $$
216 | \Omega(h_m)=\gamma J+\frac{\lambda}{2}\sum_{j=1}^{J}\omega_{mj}^2
217 |
218 | $$
219 |
220 | 这里的$J$是叶子节点的个数,而 $\omega_{mj}$ 是第$j$个叶子节点的最优值。
221 |
222 | 其中第一项叶子结点的数目$J$相当于$L_1$正则,第二项叶子节点的最优值相当于$L_2$正则。
223 |
224 | ## Shrinkage
225 |
226 | 其思想认为,每次走一小步逐渐逼近结果的效果,要比每次迈一大步很快逼近结果的方式更容易避免过拟合。即它不完全信任每一个棵残差树,它认为每棵树只学到了真理的一小部分,累加的时候只累加一小部分,通过多学几棵树弥补不足。用方程来看更清晰,即给每棵数的输出结果乘上一个步长$\alpha$(learning rate)
227 |
228 | 对于前面的弱学习器的迭代:
229 |
230 | $$
231 | f_m(x)=f_{m-1}(x)+T(x;\gamma_m)
232 |
233 | $$
234 |
235 | 加上正则化项,则有
236 |
237 | $$
238 | f_m(x)=f_{m-1}(x)+\alpha\, T(x;\gamma_m)
239 |
240 | $$
241 |
242 | 此处,$\alpha$的取值范围为(0,1]。对于同样的训练集学习效果,较小$\alpha$的意味着需要更多的弱学习器的迭代次数。通常我们用步长和迭代最大次数一起决定算法的拟合效果。
243 |
244 | ## 特征采样和样本采样
245 |
246 | XGBoost借鉴RF的思想,对于特征进行采样以达到降低过拟合的目的,根据用户反馈,特征采样比起样本采样效果更优。当然,XGBoost同时支持以上两种降低过拟合的采样方式。
247 |
248 | ## Early Stop
249 |
250 | 对于每一次分离后的增益,即前面的
251 |
252 | $$
253 | L_{split}=\frac{1}{2}[\frac{G_L^2}{H_L+\lambda}+\frac{G_R^2}{H_R+\lambda}-\frac{(G_L+G_R)^2}{H_L+H_R+\lambda}]-\gamma
254 |
255 | $$
256 |
257 |
258 | 在`sklearn`接口当中,如果$L_{split}$出现负值,则提前停止;但是,被提前终止掉的分裂可能其后续的分裂会带来好处。在XBGoost原生接口当中是采用过后剪枝策略:将树分裂到最大深度,然后再基于上述增益计算剪枝。在具体实现当中还有`learning rate`等其它参数一起控制,给$L_{split}$出现负值的后续轮留机会。
259 |
260 | ## 缺失值处理
261 |
262 | 在实际的工业实践当中,数据出现缺失无法避免。
263 |
264 | XGBoost没有假设缺失值一定进入左子树还是右子树,则是尝试通过枚举所有缺失值在当前节点是进入左子树,还是进入右子树更优来决定一个处理缺失值默认的方向,这样处理起来更加的灵活和合理。
265 |
266 | 也就是说,上面第1节的算法的步骤a),b.1)和b.2)会执行2次,第一次假设特征$k$所有有缺失值的样本都走左子树,第二次假设特征$k$所有缺失值的样本都走右子树。然后每次都是针对没有缺失值的特征k的样本走上述流程,而不是所有的的样本。
267 |
268 | 如果是所有的缺失值走右子树,使用上面第1节的a),b.1)和b.2)即可。如果是所有的样本走左子树,则上面第1节的a)步要变成:
269 |
270 | $$
271 | G_R=0,\,H_R=0
272 |
273 | $$
274 |
275 |
276 | b.1)步要更新为:
277 |
278 | $$
279 | G_R=G_R+g_mi,\,G_L=G-G_R
280 |
281 | $$
282 |
283 |
284 | $$
285 | H_R=H_R+h_mi,\,H_L=H-H_R
286 |
287 | $$
288 |
289 |
290 | 具体算法如下图所示:
291 |
292 | 
293 |
294 | ## 优缺点
295 |
296 | ## 优点
297 |
298 | * 支持线性分类器(相当于引入$L_1,\,L_2$正则惩罚项的LR和线性回归,损失函数公式=误差平方和+正则项,似LR)
299 | * 损失函数用了二阶泰勒展开,引入一阶导和二阶导,提高模型拟和的速度
300 | * 可以给缺失值自动划分方向
301 | * 同RF,支持样本(行)随机抽取,也支持特征(列)随机抽取,降低运算,防过拟合
302 | * 损失函数引入正则化项,包含全部叶子节点个数,每个叶子节点得分的$L_2$模的平方和(代表叶子节点权重的影响),控制模型(树)复杂度
303 | * 每次迭代后为叶子分配结合学习速率,减低每棵树权重,减少每棵树影响,灵活调整后面的学习空间
304 | * 支持并行,不是树并行,是把特征值先预排序,存起来,可以重复并行使用计算分裂点
305 | * 分裂依据分开后与未分前的差值增益,不用每个节点排序算增益,减少计算量,可以并行计算
306 | * 可以引入阈值限制树分裂,控制树的规模
307 |
308 | ## 缺点
309 |
310 | * 往往会选择具有更高数量的不同值的预测器
311 | * 当预测器具有很多类别时,容易过拟合
312 | * 参数过多,调参困难
313 | * 如果采用精确搜索算法对内存消耗过大,且不支持分布式
314 |
315 | ## sklearn中的参数解释
316 |
317 | `sklearn`本身的文档当中并没有XGBoost的描述,[Github](https://link.zhihu.com/?target=https%3A//github.com/dmlc/xgboost/blob/master/python-package/xgboost/sklearn.py)上面看到主要参数如下:
318 |
319 | * max_depth :树的最大深度。越大通常模型复杂,更容易过拟合,这里作为弱学习器一般设置为1-10
320 | * learning_rate:学习率或收缩因子。学习率和迭代次数/弱分类器数目n_estimators相关。 缺省:0.1 (与直接调用xgboost的eta参数含义相同)
321 | * n_estimators:弱分类器数目. 缺省:100
322 | * verbosity:控制输出
323 | * slient:参数值为1时,静默模式开启,不输出任何信息
324 | * objective:待优化的目标函数,常用值有:
325 |
326 | * binary:logistic 二分类的逻辑回归,返回预测的概率
327 | * multi:softmax 使用softmax的多分类器,返回预测的类别(不是概率)
328 | * multi:softprob 和multi:softmax参数一样,但是返回的是每个数据属于各个类别的概率
329 | * 支持用户自定义目标函数
330 | * booster:选择每次迭代的模型,有两种选择:
331 | * gbtree:基于树的模型,为缺省值
332 | * gbliner:线性模型
333 | * dart:树模型
334 | * nthread:用来进行多线程控制。 如果你希望使用CPU全部的核,那就用缺省值-1,算法会自动检测它
335 | * n_jobs:xgboost运行时的线程数,后续代替`nthread`参数
336 | * gamma:节点分裂所需的最小损失函数下降值,缺省0
337 | * min_child_weight:叶子结点需要的最小样本权重(hessianhessian)和
338 | * subsample:构造每棵树的所用样本比例(样本采样比例)
339 | * colsample_bytree:构造树时每棵树的所用特征比例
340 | * colsample_bylevel:构造树时每层的所用特征比例
341 | * colsample_bynone:构造树时每次分裂的所用特征比例
342 | * reg_alpha:$L_1$正则的惩罚系数
343 | * reg_lambda:$L_2$正则的惩罚系数
344 | * tree_method string [default= auto]:XGBoost中使用的树构造算法
345 |
346 | * XGBoost支持hist和大规模分布式训练,仅支持大规模外部内存版本。
347 | * 选择: auto, exact, approx, hist, gpu_hist
348 | * auto: 对于中小型数据集,将使用精确的贪婪(精确)
349 | * 对于非常大的数据集,将选择近似算法(近似)
350 | * 因为旧版本总是在单个机器中使用精确贪婪,所以当选择近似算法来通知该选择时,用户将得到消息
351 | * exact: 精确的贪婪算法
352 | * approx : 使用分位数草图和梯度直方图的近似贪婪算法
353 | * hist:快速直方图优化近似贪心算法
354 | * gpu_hist:hist算法的GPU实现
355 | * scale_pos_weight:正负样本的平衡,通常用于不均衡数据
356 | * base_score:初始预测值
357 | * random_state:随机种子
358 | * missing:缺失值
359 | * importance_type:特征重要程度计算方法
360 |
361 | 除了以上参数,XGBoost原生接口当中参数众多,主要有以下4大类:
362 |
363 | * General parameters
364 | * Booster parameters
365 | * Learning task parameters
366 | * Command line parameters(较少用到)
367 |
368 | 如果有遗漏,具体可以参阅[XGBoost Parameters](https://link.zhihu.com/?target=https%3A//xgboost.readthedocs.io/en/latest/parameter.html)
369 |
370 | ## 应用场景
371 |
372 | XGBoost是GBDT框架的工业级优化实现,所有GBDT能够应用的场景,XGBoost都可以应用,所有回归问题(线性/非线性)、二分类问题(设定阈值,大于阈值为正例,反之为负例)。
373 |
374 | 按业务领域分,推荐系统、反欺诈、信用评级等。
375 |
--------------------------------------------------------------------------------
/LightGBM-2.md:
--------------------------------------------------------------------------------
1 | title: LightGBM算法梳理 date: 2019-08-12 23:56:55 categories: 机器学习 tags: - 集成学习 - LightGBM - Histogram - 分布式 - sklearn description: DataWhale暑期学习小组-高级算法梳理第八期Task4。
2 |
3 | ---
4 |
5 | ## LightGBM
6 |
7 | 同XGBoost类似,LightGBM依然是在GBDT算法框架下的一种改进实现,是一种基于决策树算法的快速、分布式、高性能的GBDT框架,主要说解决的痛点是面对高维度大数据时提高GBDT框架算法的效率和可扩展性。
8 |
9 | “Light”主要体现在三个方面,即更少的样本、更少的特征、更少的内存,分别通过单边梯度采样(Gradient-based One-Side Sampling)、互斥特征合并(Exclusive Feature Bundling)、直方图算法(Histogram)三项技术实现。另外,在工程上面,LightGBM还在并行计算方面做了诸多的优化,支持特征并行和数据并行,并针对各自的并行方式做了优化,减少通信量。
10 |
11 | ## LightGBM的起源
12 |
13 | LightGBM起源于微软亚洲研究院在NIPS发表的系列论文:
14 |
15 | * [Qi Meng, Guolin Ke, Taifeng Wang, Wei Chen, Qiwei Ye, Zhi-Ming Ma, Tie-Yan Liu. “A Communication-Efficient Parallel Algorithm for Decision Tree.” Advances in Neural Information Processing Systems 29 (NIPS 2016), pp. 1279-1287](https://link.zhihu.com/?target=https%3A//papers.nips.cc/paper/6381-a-communication-efficient-parallel-algorithm-for-decision-tree.pdf)
16 | * [Guolin Ke, Qi Meng, Thomas Finley, Taifeng Wang, Wei Chen, Weidong Ma, Qiwei Ye, Tie-Yan Liu. “LightGBM: A Highly Efficient Gradient Boosting Decision Tree.” Advances in Neural Information Processing Systems 30 (NIPS 2017), pp. 3149-3157](https://link.zhihu.com/?target=https%3A//papers.nips.cc/paper/6907-lightgbm-a-highly-efficient-gradient-boosting-decision-tree.pdf)
17 |
18 | 并于2016年10月17日在[LightGBM](https://link.zhihu.com/?target=https%3A//github.com/microsoft/LightGBM)上面开源,三天内在GitHub上面被star了1000次,fork了200次。知乎上现有近2000人关注“如何看待微软开源的LightGBM?”问题。
19 |
20 | 随后不断迭代,慢慢地开始支持Early Stopping、叶子索引预测、最大深度设置、特征重要性评估、多分类、类别特征支持、正则化(L1,L2及分裂最小增益)……
21 |
22 | 具体可以参阅以下链接:
23 |
24 | [LightGBM大事记](https://link.zhihu.com/?target=https%3A//github.com/Microsoft/LightGBM/blob/master/docs/Key-Events.md)
25 |
26 | ## Histogram VS Pre-sorted
27 |
28 | ## Pre-sorted
29 |
30 | 在XGBoost当中的精确搜索算法(Exact Greedy Algorithm)在寻找分裂点时就是采用Pre-sorted的思想。具体过程不再赘述,可以参阅[XGBoost算法梳理](https://link.zhihu.com/?target=http%3A//datacruiser.io/2019/08/10/DataWhale-Workout-No-8-XGboost-Summary/)
31 |
32 | 预排序还是有一定优点的,如果不用预排序的话,在分裂节点的时候,选中某一个特征后,需要对A按特征值大小进行排序,然后计算每个阈值的增益,这个过程需要花费很多时间。
33 |
34 | 预排序算法在计算最优分裂时,各个特征的增益可以并行计算,并且能精确地找到分割点。但是预排序后需要保存特征值及排序后的索引,因此需要消耗两倍于训练数据的内存,时间消耗大。另外预排序后,特征对梯度的访问是一种随机访问,并且不同的特征访问的顺序不一样,无法对cache进行优化,时间消耗也大。最后,在每一层,需要随机访问一个行索引到叶子索引的数组,并且不同特征访问的顺序也不一样。
35 |
36 | ## Historgram
37 |
38 | 首先需要指出的是,XGBoost在寻找树的分裂节点的也是支持直方图算法的,就是论文中提到的近视搜索算法(Approximate Algorithm)。只是,无论特征值是否为0,直方图算法都需要对特征的分箱值进行索引,因此对于大部分实际应用场景当中的稀疏数据优化不足。
39 |
40 | 回过头来,为了能够发挥直方图算法的优化威力,LightGBM提出了另外两个新技术:单边梯度采样(Gradient-based One-Side Sampling)和互斥特征合并(Exclusive Feature Bundling),在减少维度和下采样上面做了优化以后才能够将直方图算法发挥得淋漓尽致。下面依次介绍直方图算法、GOSS和EFB。
41 |
42 | ### 直方图算法
43 |
44 | 直方图算法的基本思想是先把连续的浮点特征值离散化成$k$个整数,同时构造一个宽度为$k$的直方图。在遍历数据的时候,根据离散化后的值作为索引在直方图中累积统计量,当遍历一次数据后,直方图累积了需要的统计量,然后根据直方图的离散值,遍历寻找最优的分割点。具体算法描述如下:
45 |
46 | 
47 |
48 | 
49 |
50 | 直方图算法有如下优点:
51 |
52 | * 内存消耗降低。预排序算法需要的内存约是训练数据的两倍(2x样本数x维度x4Bytes),它需要用32位浮点来保存特征值,并且对每一列特征,都需要一个额外的排好序的索引,这也需要32位的存储空间。对于 直方图算法,则只需要(1x样本数x维度x1Bytes)的内存消耗,仅为预排序算法的1/8。因为直方图算法仅需要存储特征的 bin 值(离散化后的数值),不需要原始的特征值,也不用排序,而bin值用8位整型存储就足够了。
53 | * 算法时间复杂度大大降低。决策树算法在节点分裂时有两个主要操作组成,一个是“寻找分割点”,另一个是“数据分割”。从算法时间复杂度来看,在“寻找分割点”时,预排序算法对于深度为$k$的树的时间复杂度:对特征所有取值的排序为$O(NlogN)$,$N$为样本点数目,若有$D$维特征,则$O(kDNlogN)$,而直方图算法需要$O(kD \times bin)$(bin是histogram 的横轴的数量,一般远小于样本数量$N$)。
54 | * 再举个例子说明上述两点的优化,假设数据集$A$的某个特征的特征值有(二叉树存储):${1.2,1.3,2.2,2.3,3.1,3.3}$,预排序算法要全部遍历一遍,需要切分大约5次。进行离散化后,只需要切分2次 ${{1},{2,3}}$ 和 ${{1,2},{3}}$,除了切分次数减少,内存消耗也大大降低。
55 | * 直方图算法还可以进一步加速。一个容易观察到的现象:一个叶子节点的直方图可以直接由父节点的直方图和兄弟节点的直方图做差得到。通常构造直方图,需要遍历该叶子上的所有数据,但直方图做差仅需遍历直方图的$k$个bin。利用这个方法,LightGBM可以在构造一个叶子的直方图后,可以用非常微小的代价得到它兄弟叶子的直方图,在速度上可以提升一倍。
56 |
57 | 
58 |
59 | 当然,直方图算法并不是完美的。由于特征被离散化后,找到的并不是很精确的分割点,所以会对结果产生影响。但在不同的数据集上的结果表明,离散化的分割点对最终的精度影响并不是很大,甚至有时候会更好一点。原因是决策树本来就是弱模型,分割点是不是精确并不是太重要;较粗的分割点也有正则化的效果,可以有效地防止过拟合;即使单棵树的训练误差比精确分割的算法稍大,但在梯度提升(GradientBoosting)的框架下没有太大的影响。
60 |
61 | ### 单边梯度采样(Gradient-based One-Side Sampling)
62 |
63 | 单边梯度采样是一种在减少数据量和保证精度上平衡的算法。在GBDT中, 我们对损失函数的负梯度进行拟合,样本误差越大,梯度的绝对值越大,这说明模型对该样本的学习还不足够,相反如果越小则表示模型对该样本的学习已经很充分。因此,我们可以这样推论:梯度的绝对值越大,样本重要性越高。单边梯度采样正是以样本的梯度作为样本的权重进行采样。
64 |
65 | 单边梯度采样保留所有的梯度较大的样本,在梯度小的实例上使用随机采样。为了抵消对数据分布的影响,计算信息增益的时候,单边梯度采样对小梯度的数据引入常量乘数。单边梯度采样首先根据数据的梯度绝对值排序,选取$top\,\,a$个样本。然后在剩余的数据中随机采样$b$个样本。接着计算信息增益时为采样出的小梯度数据乘以$\frac{1-a}{b}$,这样算法就会更关注训练不足的样本例,而不会过多改变原数据集的分布。正是单边梯度采样减少了数据量,让直方图算法发挥了更大的作用。单边梯度采样具体算法见下图:
66 |
67 | 
68 |
69 | ### 互斥特征合并(Exclusive Feature Bundling)
70 |
71 | 高维的数据通常是稀疏的,这种特征空间的稀疏性给我们提供了一种设计一种接近无损地降维的可能性。特别的,在稀疏特征空间中,许多特征是互斥的,换句话说,大部分特征不会同时取非0值,例如One-hot之后的类别特征他们从不同时为非0值。我们可以合并互斥的特征为单一特征(我们将这个过程称为*Exclusive Feature Bundle* ).通过仔细设计特征扫描算法,我们从合并特征中构建出与单个特征相同的特征直方图。通过这种方式,直方图构建算法的时间复杂度从$O(ND)$,降到$O(N×bundle)$,其中$N$为样本点数目,$D$为特征维度。通常,bundle << $D$,我们能够在不损失精度的情况下极大地加速GBDT的训练。
72 |
73 | 那么接下来有两个问题需要处理:
74 |
75 | * 需要合并哪些特征
76 | * 如何合并这些特征
77 |
78 | ### Greedy Bundling
79 |
80 | 找出最优的 bundle 组合数是一个 NP 问题,LightGBM通过将原问题转化为”图着色”问题进行贪心近似解决。
81 |
82 | 首先创建一个图$G(V, E)$,其中$V$就是特征,为图中的节点,$E$为$G$中的边,将不是相互独立的特征用一条边连接起来,边的权重就是两个相连接的特征的总冲突值,这样需要绑定的特征就是在图着色问题中要涂上同一种颜色的那些点(特征)。具体算法过程如下:
83 |
84 | 
85 |
86 | ### Merge Exclusive Features
87 |
88 | 该过程主要是关键在于原始特征值可以从bundle中区分出来,即绑定几个特征在同一个bundle里需要保证绑定前的原始特征的值在bundle中能够被识别,考虑到直方图算法将连续的值保存为离散的bin,我们可以使得不同特征的值分到bundle中的不同bin中,这可以通过在特征值中加一个偏置常量来解决,比如,我们在bundle中绑定了两个特征A和B,A特征的原始取值为区间[0,10),B特征的原始取值为区间[0,20),我们可以在B特征的取值上加一个偏置常量10,将其取值范围变为[10,30),这样就可以放心的融合特征A和B了,因为在树模型中对于每一个特征都会计算分裂节点的,也就是通过将他们的取值范围限定在不同的bin中,在分裂时可以将不同特征很好的分裂到树的不同分支中去。具体算法如下:
89 |
90 | 
91 |
92 | ## Leaf-wise VS Level-wise
93 |
94 | ## Level-wise
95 |
96 | 大多数GBDT框架使用的按层生长 (level-wise) 的决策树生长策略,Level-wise遍历一次数据可以同时分裂同一层的叶子,容易进行多线程优化,也好控制模型复杂度,不容易过拟合。但实际上Level-wise是一种低效的算法,因为它不加区分的对待同一层的叶子,带来了很多没必要的开销,因为实际上很多叶子的分裂增益较低,没必要进行搜索和分裂。
97 |
98 | 
99 |
100 | ## Leaf-wise
101 |
102 | LightGBM在直方图算法之上,对于树的生长策略做了进一步优化,抛弃了Level-wise策略,使用了带有深度限制的按叶子生长 (leaf-wise)算法。Leaf-wise则是一种更为高效的策略,每次从当前所有叶子中,找到分裂增益最大的一个叶子,然后分裂,如此循环。因此同Level-wise相比,在分裂次数相同的情况下,Leaf-wise可以降低更多的误差,得到更好的精度。Leaf-wise的缺点是可能会长出比较深的决策树,产生过拟合。因此LightGBM在Leaf-wise之上增加了一个最大深度的限制,在保证高效率的同时防止过拟合。
103 |
104 | 
105 |
106 | ## 特征并行和数据并行
107 |
108 | 本小节主要根据[LightGBM的官方文档](https://link.zhihu.com/?target=https%3A//lightgbm.readthedocs.io/en/latest/Features.html%23optimization-in-network-communication)中提到的并行计算优化进行讲解。 在本小节中,工作的节点称为**worker**
109 |
110 | LightGBM具有支持高效并行的优点。LightGBM原生支持并行学习,目前支持特征并行和数据并行的两种。
111 |
112 | ## 特征并行
113 |
114 | 特征并行主要是并行化决策树中寻找最优划分点(“Find Best Split”)的过程,因为这部分最为耗时。
115 |
116 | 传统特征并行做法如下:
117 |
118 | * 垂直划分数据(对特征划分),不同的worker有不同的特征集
119 | * 每个workers找到局部最佳的切分点{feature, threshold}
120 | * workers使用点对点通信,找到全局最佳切分点
121 | * 具有全局最佳切分点的worker进行节点分裂,然后广播切分后的结果(左右子树的instance indices)
122 | * 其它worker根据收到的instance indices也进行划分
123 |
124 | 
125 |
126 | 主要有以下缺点:
127 |
128 | * 无法加速分裂的过程,该过程的时间复杂度为$O(N)$,当数据量大的时候效率不高
129 | * 需要广播划分的结果(左右子树的instance indices),1条数据1bit的话,通信花费大约需要$O(N/8)$
130 |
131 | LightGBM的特征并行每个worker保存所有的数据集,这样找到全局最佳切分点后各个worker都可以自行划分,就不用进行广播划分结果,减小了网络通信量。过程如下:
132 |
133 | * 每个workers找到局部最佳的切分点{feature, threshold}
134 | * workers使用点对点通信,找到全局最佳切分点
135 | * 每个worker根据全局全局最佳切分点进行节点分裂
136 |
137 | 这样虽然不用进行广播划分结果,减小了网络通信量。但是也有缺点:
138 |
139 | * 分裂过程的复杂度保持不变
140 | * 每个worker保存所有数据,存储代价高
141 |
142 | ## 数据并行
143 |
144 | 数据并行的目标是并行化整个决策学习的过程,传统算法的做法如下:
145 |
146 | * 水平切分数据,不同的worker拥有部分数据
147 | * 每个worker根据本地数据构建局部直方图
148 | * 合并所有的局部直方图得到全部直方图
149 | * 根据全局直方图找到最优切分点并进行分裂
150 |
151 | 
152 |
153 | 在第3步当中有两种合并方式:
154 |
155 | * 采用点对点方式(point-to-point communication algorithm)进行通讯,每个worker通讯量为$ ( ℎ × × )$
156 | * 采用collective communication algorithm(如“[All Reduce](https://link.zhihu.com/?target=http%3A//pages.tacc.utexas.edu/~eijkhout/pcse/html/mpi-collective.html)”)进行通讯(相当于有一个中心节点,通讯后在返回结果),每个worker的通讯量为$O(2× × )$
157 |
158 | 不难发现,通信的代价也是很高的,这也是数据并行的缺点。
159 |
160 | LightGBM的数据并行主要做了以下两点优化:
161 |
162 | * 使用“Reduce Scatter”将不同worker的不同特征的直方图合并,然后workers在局部合并的直方图中找到局部最优划分,最后同步全局最优划分
163 | * 通过直方图作差法得到兄弟节点的直方图,因此只需要通信一个节点的直方图,减半通信量
164 |
165 | 通过上述两点做法,通信开销降为$ (0.5 × × )$。
166 |
167 | 另外,LightGBM还采用 一种称为**PV-Tree** 的算法进行投票并行(Voting Parallel),其实本质上也是一种数据并行。
168 |
169 | PV-Tree和普通的决策树差不多,只是在寻找最优切分点上有所不同。具体算法如下:
170 |
171 | 
172 |
173 | 主要思路如下:
174 |
175 | * 水平切分数据,不同的worker拥有部分数据
176 | * Local voting: 每个worker构建直方图,找到$top-k$个最优的本地划分特征
177 | * Global voting: 中心节点聚合得到最优的$top-2k$个全局划分特征($top-2k$是看对各个worker选择特征的个数进行计数,取最多的$2k$个)
178 | * Best Attribute Identification: 中心节点向worker收集这$top-2k$个特征的直方图,并进行合并,然后计算得到全局的最优划分
179 | * 中心节点将全局最优划分广播给所有的worker,worker进行本地划分
180 |
181 | 
182 |
183 | 可以看出,PV-tree将原本需要$O( × )$ 变为了$O(2k × )$,通信开销得到降低。此外,可以证明,当每个worker的数据足够多的时候,$top-2k$个中包含全局最佳切分点的概率非常高。
184 |
185 | ## 顺序访问梯度
186 |
187 | Cache(高速缓存)作为内存局部区域的副本,用来存放当前活跃的程序和数据,它利用程序运行的局部性,把局部范围的数据从内存复制到Cache中,使CPU直接高速从Cache中读取程序和数据,从而解决CPU速度和内存速度不匹配的问题。高速缓冲存储器最重要的技术指标是它的命中率。CPU在Cache中找到有用的数据被称为命中,当Cache中没有CPU所需的数据时(这时称为未命中),CPU才访问内存。
188 |
189 | 预排序算法中有两个频繁的操作会导致cache-miss,也就是缓存消失(对速度的影响很大,特别是数据量很大的时候,顺序访问比随机访问的速度快4倍以上 )。
190 |
191 | * 对梯度的访问:在计算增益的时候需要利用梯度,假设梯度信息存在一个数组$g[i]$中,在对特征$A$进行增益时,需要根据特征$A$排序后的索引找到$g[i]$中对应的梯度信息。特征值$A_1$对应的样本行号可能是3,对应的梯度信息在$g[3]$,而特征值$A_2$对应的样本行号可能是9999,对应的梯度信息在$g[9999]$,即对于不同的特征,访问梯度的顺序是不一样的,并且是随机的
192 | * 对于索引表的访问:预排序算法使用了行号和叶子节点号的索引表,防止数据切分的时候对所有的特征进行切分。同访问梯度一样,所有的特征都要通过访问这个索引表来索引
193 |
194 | 这两个操作都是随机的访问,会给系统性能带来非常大的下降。
195 |
196 | LightGBM使用的直方图算法能很好的解决这类问题。首先。对梯度的访问,因为不用对特征进行排序,同时,所有的特征都用同样的方式来访问,所以只需要对梯度访问的顺序进行重新排序,所有的特征都能连续的访问梯度。并且直方图算法不需要把数据id到叶子节点号上(不需要这个索引表,没有这个缓存消失问题),大大提高cache的命中率,减少cache-miss出现的概率。
197 |
198 | ## 支持类别特征
199 |
200 | 实际上大多数机器学习工具都无法直接支持类别特征,一般需要把类别特征,转化one-hot特征,降低了空间和时间的效率。而类别特征的使用是在实践中很常用的。基于这个考虑,LightGBM优化了对类别特征的支持,可以直接输入类别特征,不需要额外的0/1展开。并在决策树算法上增加了类别特征的决策规则,直接原生支持类别特征,不需要转化,提高了近8倍的速度。
201 |
202 | 
203 |
204 | ## 应用场景
205 |
206 | 作为GBDT框架内的算法,GBDT、XGBoost能够应用的场景LightGBM也都适用,并且考虑到其对于大数据、高维特征的诸多优化,在数据量非常大、维度非常多的场景更具优势。近来,有着逐步替代XGBoost成为各种数据挖掘比赛baseline的趋势。
207 |
208 | ## sklearn参数
209 |
210 | `sklearn`本身的文档当中并没有LightGBM的描述,[Github](https://link.zhihu.com/?target=https%3A//github.com/microsoft/LightGBM/blob/master/python-package/lightgbm/sklearn.py)上面看到主要参数如下:
211 |
212 | * `boosting_type` : 提升类型,字符串,可选项 (default=`gbdt`)
213 |
214 | * `gbdt`, 传统梯度提升树
215 | * `dart`, 带Dropout的MART
216 | * `goss`, 单边梯度采样
217 | * `rf`, 随机森林
218 | * `num_leaves` : 基学习器的最大叶子树,整型,可选项 (default=31)
219 | * `max_depth` : 基学习器的最大树深度,小于等于0表示没限制,整型,可选项 (default=-1)
220 | * `learning_rate` : 提升学习率,浮点型,可选项 (default=0.1)
221 | * `n_estimators` : 提升次数,整型,可选项 (default=100)
222 | * `subsample_for_bin` : 构造分箱的样本个数,整型,可选项 (default=200000)
223 | * `objective` : 指定学习任务和相应的学习目标或者用户自定义的需要优化的目标损失函数,字符串, 可调用的或者None, 可选项 (default=None),若不为None,则有:
224 | * `regression` for LGBMRegressor -`binary` or `multiclass` for LGBMClassifier
225 | * `lambdarank` for LGBMRanker
226 | * `class_weight` : 该参数仅在多分类的时候会用到,多分类的时候各个分类的权重,对于二分类任务,你可以使用`is_unbalance` 或 `scale_pos_weight`,字典数据, `balanced` or None, 可选项 (default=None)
227 | * `min_split_gain` : 在叶子节点上面做进一步分裂的最小损失减少值,浮点型,可选项 (default=0.)
228 | * `min_child_weight` : 在树的一个孩子或者叶子所需的最小样本权重和,浮点型,可选项 (default=1e-3)
229 | * `min_child_samples` : 在树的一个孩子或者叶子所需的最小样本,整型,可选项 (default=20)
230 | * `subsample` : 训练样本的子采样比例,浮点型,可选项 (default=1.)
231 | * `subsample_freq` : 子采样频率,小于等于0意味着不可用,整型,可选项 (default=0)
232 | * `colsample_bytree` : 构建单棵树时列采样比例,浮点型,可选项 (default=1.)
233 | * `reg_alpha` : $L_1$正则项,浮点型,可选项 (default=0.)
234 | * `reg_lambda` :$L_2$正则项,浮点型,可选项 (default=0.)
235 | * `random_state` : 随机数种子,整型或者None, 可选项 (default=None)
236 | * `n_jobs` : 线程数,整型,可选项 (default=-1)
237 | * `silent` : 运行时是否打印消息,布尔型,可选项 (default=True)
238 | * `importance_type` : 填入到`feature_importances_`的特征重要性衡量类型,如果是`split`,则以特征被用来分裂的次数,如果是`gain`,则以特征每次用于分裂的累积增益,字符串,可选项 (default=`split`)
239 |
240 | 除了以上参数,LightGBM原生接口当中参数众多,主要有以下八大类:
241 |
242 | * 核心参数
243 | * 学习控制参数
244 | * IO参数
245 | * 目标参数
246 | * 度量参数
247 | * 网络参数
248 | * GPU参数
249 | * 模型参数
250 |
251 | 如果有遗漏,具体可以参阅[LightGBM Parameters](https://link.zhihu.com/?target=https%3A//lightgbm.readthedocs.io/en/latest/Parameters.html)
252 |
253 | ## CatBoost(了解)
254 |
255 | CatBoost也是Boosting族的算法,由俄罗斯科技公司Yandex于2017年提出,主要在两方面做了优化,一个是对于类别变量的处理,另外一个是对于预测偏移(prediction shift)的处理。
256 |
257 | 其中对于类别变量在传统的Greedy TBS方法的基础上添加先验分布项,这样可以减少减少噪声和低频率数据对于数据分布的影响:
258 |
259 | $$
260 | \hat{x}*k^i=\frac{\sum* {j=1}^n I_{{x_j^i=x_k^i}}*y_j+a\,P}{\sum_{j=1}^n I_{{x_j^i=x_k^i}}+a}
261 |
262 | $$
263 |
264 |
265 | 其中 $P$ 是添加的先验项,$a$ 通常是大于 0 的权重系数。
266 |
267 | 对于第二个问题,CatBoost采用了排序提升(Ordered Boosting)的方式,首先对所有的数据进行随机排列,然后在计算第 $i$ 步残差时候的模型只利用了随机排列中前 $i-1$ 个样本。具体算法描述请参阅论文[CatBoost: unbiased boosting with categorical features](https://link.zhihu.com/?target=https%3A//papers.nips.cc/paper/7898-catboost-unbiased-boosting-with-categorical-features.pdf)
268 |
269 | 时间有限,下次有机会再详细消化下CatBoost的论文。
270 |
271 | 总之,CatBoost大大简化了前期数据处理过程,特别是类别特征的数值化,调参也相对容易。近来在数据竞赛领域已经大规模采用。
272 |
--------------------------------------------------------------------------------
/Catboost.md:
--------------------------------------------------------------------------------
1 | title: DataWhale Workout No.8 CatBoost Summary date: 2019-08-19 08:18:37 categories: 机器学习 tags: - 集成学习 - CatBoost - Ordered boosting - Prediction shift - sklearn description: 这是DataWhale暑期学习小组-高级算法梳理的补充,是对目前最新的开源Boost族算法CatBoost的介绍,结合相关论文以及笔者的使用经验,对CatBoost的算法特性和适用场景做一些小结。
2 |
3 | ---
4 |
5 | ## CatBoost
6 |
7 | CatBoost是俄罗斯的搜索巨头Y andex在2017年开源的机器学习库,也是Boosting族算法的一种,同前面介绍过的XGBoost和LightGBM类似,依然是在GBDT算法框架下的一种改进实现,是一种基于对称决策树(oblivious trees)算法的参数少、支持类别型变量和高准确性的GBDT框架,主要说解决的痛点是高效合理地处理类别型特征,这个从它的名字就可以看得出来,CatBoost是由catgorical和boost组成,另外是处理梯度偏差(Gradient bias)以及预测偏移(Prediction shift)问题,提高算法的准确性和泛化能力。
8 |
9 | 
10 |
11 | CatBoost主要有以下五个特性:
12 |
13 | * 无需调参即可获得较高的模型质量,采用默认参数就可以获得非常好的结果,减少在调参上面花的时间
14 | * 支持类别型变量,无需对非数值型特征进行预处理
15 | * 快速、可扩展的GPU版本,可以用基于GPU的梯度提升算法实现来训练你的模型,支持多卡并行
16 | * 提高准确性,提出一种全新的梯度提升机制来构建模型以减少过拟合
17 | * 快速预测,即便应对延时非常苛刻的任务也能够快速高效部署模型
18 |
19 | CatBoost的主要算法原理可以参照以下两篇论文:
20 |
21 | * [Anna Veronika Dorogush, Andrey Gulin, Gleb Gusev, Nikita Kazeev, Liudmila Ostroumova Prokhorenkova, Aleksandr Vorobev "Fighting biases with dynamic boosting". arXiv:1706.09516, 2017](https://link.zhihu.com/?target=https%3A//arxiv.org/pdf/1706.09516.pdf)
22 | * [Anna Veronika Dorogush, Vasily Ershov, Andrey Gulin "CatBoost: gradient boosting with categorical features support". Workshop on ML Systems at NIPS 2017](https://link.zhihu.com/?target=http%3A//learningsys.org/nips17/assets/papers/paper_11.pdf)
23 |
24 | ## Categorical features
25 |
26 | 所谓类别型变量(Categorical features)是指其值是离散的集合且相互比较并无意义的变量,比如用户的ID、产品ID、颜色等。因此,这些变量无法在二叉决策树当中直接使用。常规的做法是将这些类别变量通过预处理的方式转化成数值型变量再喂给模型,比如用一个或者若干个数值来代表一个类别型特征。
27 |
28 | 目前广泛用于**低势** (一个有限集的元素个数是一个自然数)类别特征的处理方法是`One-hot encoding`:将原来的特征删除,然后对于每一个类别加一个0/1的用来指示是否含有该类别的数值型特征。`One-hot encoding`可以在数据预处理时完成,也可以在模型训练的时候完成,从训练时间的角度,后一种方法的实现更为高效,CatBoost对于低势类别特征也是采用后一种实现。
29 |
30 | 显然,在**高势** 特征当中,比如 `user ID`,这种编码方式会产生大量新的特征,造成维度灾难。一种折中的办法是可以将类别分组成有限个的群体再进行 `One-hot encoding`。一种常被使用的方法是根据目标变量统计(Target Statistics,以下简称TS)进行分组,目标变量统计用于估算每个类别的目标变量期望值。甚至有人直接用TS作为一个新的数值型变量来代替原来的类别型变量。重要的是,可以通过对TS数值型特征的阈值设置,基于对数损失、基尼系数或者均方差,得到一个对于训练集而言将类别一分为二的所有可能划分当中最优的那个。在LightGBM当中,类别型特征用每一步梯度提升时的梯度统计(Gradient Statistics,以下简称GS)来表示。虽然为建树提供了重要的信息,但是这种方法有以下两个缺点:
31 |
32 | * 增加计算时间,因为需要对每一个类别型特征,在迭代的每一步,都需要对GS进行计算;
33 | * 增加存储需求,对于一个类别型变量,需要存储每一次分离每个节点的类别。
34 |
35 | 为了克服这些缺点,LightGBM以损失部分信息为代价将所有的长尾类别归位一类,作者声称这样处理高势特征时比起 `One-hot encoding`还是好不少。不过如果采用TS特征,那么对于每个类别只需要计算和存储一个数字。
36 |
37 | 如此看到,采用TS作为一个新的数值型特征是最有效、信息损失最小的处理类别型特征的方法。TS也被广泛采用,在点击预测任务当中,这个场景当中的类别特征有用户、地区、广告、广告发布者等。接下来我们着重讨论TS,暂时将`One-hot encoding`和GS放一边。
38 |
39 | ## Target statistics
40 |
41 | 一个有效和高效的处理类别型特征$i$的方式是用一个与某些TS相等的数值型变量$\hat{x}_k^i$来代替第$k$个训练样本的类别${x}_k^i$。通常用基于类别的目标变量$y$的期望来进行估算:$\hat{x}_k^i\approx\mathbb{E}(y|x^i={x}_k^i)$。
42 |
43 | ### Greedy TS
44 |
45 | 估算$\mathbb{E}(y|x^i={x}*k^i)$最直接的方式就是用训练样本当中相同类别$x_k^i$的目标变量$y$的平均值。
46 |
47 | $$
48 | \hat{x}_k^i=\frac{\sum* {j=1}^n\mathbb{I}*{{x_j^i={x}_k^i}}\cdot y_i}{\sum* {j=1}^n\mathbb{I}*{{x_j^i={x}_k^i}}}
49 |
50 | $$
51 |
52 | 显然,这样的处理方式很容易引起过拟合。举个例子,假如在整个训练集当中所有样本的类别${x}_k^i$都互不相同,即$k$个样本有$k$个类别,那么新产生的数值型特征的值将与目标变量的值相同。某种程度上,这是一种目标穿越(target leakage),非常容易引起过拟合。比较好的一种做法是采用一个先验概率$p$进行平滑处理:
53 | $$
54 | \hat{x}_k^i=\frac{\sum* {j=1}^n\mathbb{I}*{{x_j^i={x}_k^i}}\cdot y_i+a\,p}{\sum* {j=1}^n\mathbb{I}_{{x_j^i={x}_k^i}}+a}
55 |
56 | $$
57 |
58 | 其中$a>0$是先验概率$p$的权重,而对于先验概率,通常的做法是设置为数据集当中目标变量的平均值。
59 |
60 | 不过这样的平滑处理依然无法完全避免目标穿越:特征$\hat{x}*k^i$是通过自变量$X_k$的目标$y_k$计算所得。这将会导致条件偏移:对于训练集和测试集,$\hat{x}_k^i|y$的分布会有所不同。再举个例子,假设第$i$个特征为类别型特征,并且特征所有取值为无重复的集合,然后对于每一个类别$A$,对于一个分类任务,我们有$P(y=1|x^i=A)=0.5$。然后在训练集当中,$\hat{x}_k^i=\frac{y_k+a\,p}{1+a}$,于是用阈值$t=\frac{0.5+a\,p}{1+a}$就可以仅用一次分裂就训练集完美分开。但是,对于测试集,因为还无法判断此时目标变量的类别,所以这一项$\sum* {j=1}^n\mathbb{I}_{{x_j^i={x}_k^i}}=0$,最后得到的TS值为$p$,并且得到的模型在$p