├── README.md
├── imagens
    ├── ExpIPi.gif
    ├── archimedeanspiral.png
    ├── avatar.png
    ├── bigo.png
    ├── caracteres.png
    ├── complexplane.png
    ├── derivada.png
    ├── exponencial.png
    ├── fibonacciblocks.png
    ├── fundamental_theorem_of_calculus.gif
    ├── grafico.png
    ├── integral.png
    ├── listas.png
    ├── mandelbrot1.png
    ├── mandelbrot2.png
    ├── mandelbrot3.png
    ├── mandelbrot4.png
    ├── realnumbersline.png
    ├── referencias.png
    ├── sierpinski.png
    ├── timeline.png
    └── trajetoriaparabolica.png
├── jupyter_notebooks
    ├── analise_algoritmos.ipynb
    ├── calculo.ipynb
    ├── conjuntomandelbrot.ipynb
    ├── equacoes_diferenciais.ipynb
    ├── espiral_arquimedes.ipynb
    ├── estatistica_descritiva.ipynb
    ├── euclides.ipynb
    ├── explorando_numpy.ipynb
    ├── fibonacci_numeros.ipynb
    ├── formula_euler.ipynb
    ├── funcao_exponencial.ipynb
    ├── funcao_relu.ipynb
    ├── funcao_sigmoid.ipynb
    ├── funcao_tanh.ipynb
    ├── linear_algebra.ipynb
    ├── logaritmos.ipynb
    ├── onda_cossenoidal.ipynb
    ├── onda_dente_de_serra.ipynb
    ├── onda_quadrada.ipynb
    ├── onda_senoidal.ipynb
    ├── pandas_graficos.ipynb
    ├── perm_comb.ipynb
    ├── simbolos_matematica.ipynb
    ├── sympy_graficos.ipynb
    ├── transformada_de_fourier.ipynb
    ├── transformada_inversa_de_fourier.ipynb
    └── triangulo_sierpinski.ipynb
└── referencias.md


/README.md:
--------------------------------------------------------------------------------
 1 | <h1 align="center">Matemática (μάθημα) com Python</h1>
 2 | 
 3 | <h1 align="center">
 4 |     <img alt="Python" title="Python-Matemática" src="https://raw.githubusercontent.com/the-akira/Python-Matematica/master/imagens/avatar.png"> </br>
 5 | </h1>
 6 | 
 7 | <p align="justify">
 8 | A matemática (dos termos gregos μάθημα, transliterado máthēma, 'ciência', 'conhecimento' ou 'aprendizagem'; e μαθηματικός, transliterado mathēmatikós, 'inclinado a aprender') é a ciência do raciocínio lógico e abstrato, que estuda quantidades, medidas, espaços, estruturas, variações e estatísticas. Um trabalho matemático consiste em procurar por padrões, formular conjecturas e, por meio de deduções rigorosas a partir de axiomas e definições, estabelecer novos resultados. A matemática desenvolveu-se principalmente na Mesopotâmia, no Egito, na Grécia, na Índia e no Oriente Médio. A partir da Renascença, o desenvolvimento da matemática intensificou-se na Europa, quando novas descobertas científicas levaram a um crescimento acelerado que dura até os dias de hoje... <a href="https://pt.wikipedia.org/wiki/Matem%C3%A1tica">Leia mais</a>
 9 | </p>
10 | 
11 | ## Projeto
12 | 
13 | A ideia do projeto é explorar aspectos fundamentais da matemática através de experimentos com importantes bibliotecas Python.
14 | 
15 | - [NumPy](http://www.numpy.org/)
16 | - [SymPy](https://www.sympy.org/en/index.html)
17 | - [SciPy](https://www.scipy.org/)
18 | - [Matplotlib](https://matplotlib.org/)
19 | - [Pandas](https://pandas.pydata.org/)
20 | 
21 | Recomendamos você obter o pacote científico completo de Python (incluindo o Jupyter-Notebook), acesse: [anaconda](https://www.anaconda.com/distribution/) e divirta-se experimentando.
22 | 
23 | ## Conteúdo
24 | 
25 | 01. [Teorema Fundamental do Cálculo com SymPy](https://nbviewer.jupyter.org/github/the-akira/Python-Matematica/blob/master/jupyter_notebooks/calculo.ipynb)
26 | 02. [Álgebra Linear com SymPy](https://nbviewer.jupyter.org/github/the-akira/Python-Matematica/blob/master/jupyter_notebooks/linear_algebra.ipynb)
27 | 03. [Estatística Descritiva com Pandas](https://nbviewer.jupyter.org/github/the-akira/Python-Matematica/blob/master/jupyter_notebooks/estatistica_descritiva.ipynb)
28 | 04. [Explorando a Álgebra Linear com NumPy](https://nbviewer.jupyter.org/github/the-akira/Python-Matematica/blob/master/jupyter_notebooks/explorando_numpy.ipynb)
29 | 05. [Gráficos com Pandas e Matplotlib](https://nbviewer.jupyter.org/github/the-akira/Python-Matematica/blob/master/jupyter_notebooks/pandas_graficos.ipynb)
30 | 06. [Gráficos de Equações com SymPy](https://nbviewer.jupyter.org/github/the-akira/Python-Matematica/blob/master/jupyter_notebooks/sympy_graficos.ipynb)
31 | 07. [Onda Senoidal](https://nbviewer.jupyter.org/github/the-akira/Python-Matematica/blob/master/jupyter_notebooks/onda_senoidal.ipynb)
32 | 08. [Onda Cossenoidal](https://nbviewer.jupyter.org/github/the-akira/Python-Matematica/blob/master/jupyter_notebooks/onda_cossenoidal.ipynb)
33 | 09. [Onda Quadrada](https://nbviewer.jupyter.org/github/the-akira/Python-Matematica/blob/master/jupyter_notebooks/onda_quadrada.ipynb)
34 | 10. [Onda Dente de Serra](https://nbviewer.jupyter.org/github/the-akira/Python-Matematica/blob/master/jupyter_notebooks/onda_dente_de_serra.ipynb)
35 | 11. [Transformada de Fourier](https://nbviewer.jupyter.org/github/the-akira/Python-Matematica/blob/master/jupyter_notebooks/transformada_de_fourier.ipynb)
36 | 12. [Transformada Inversa de Fourier](https://nbviewer.jupyter.org/github/the-akira/Python-Matematica/blob/master/jupyter_notebooks/transformada_inversa_de_fourier.ipynb)
37 | 13. [Algoritmo Euclideano](https://nbviewer.jupyter.org/github/the-akira/Python-Matematica/blob/master/jupyter_notebooks/euclides.ipynb)
38 | 14. [Equação de Euler com SymPy](https://nbviewer.jupyter.org/github/the-akira/Python-Matematica/blob/master/jupyter_notebooks/formula_euler.ipynb)
39 | 15. [Números de Fibonacci](https://nbviewer.jupyter.org/github/the-akira/Python-Matematica/blob/master/jupyter_notebooks/fibonacci_numeros.ipynb)
40 | 16. [Função Sigmoid](https://nbviewer.jupyter.org/github/the-akira/Python-Matematica/blob/master/jupyter_notebooks/funcao_sigmoid.ipynb)
41 | 17. [Função Tangente Hiperbólica](https://nbviewer.jupyter.org/github/the-akira/Python-Matematica/blob/master/jupyter_notebooks/funcao_tanh.ipynb)
42 | 18. [Função de Unidade Linear Retificada](https://nbviewer.jupyter.org/github/the-akira/Python-Matematica/blob/master/jupyter_notebooks/funcao_relu.ipynb)
43 | 19. [Função Exponencial](https://nbviewer.jupyter.org/github/the-akira/Python-Matematica/blob/master/jupyter_notebooks/funcao_exponencial.ipynb)
44 | 20. [Espiral de Arquimedes](https://nbviewer.jupyter.org/github/the-akira/Python-Matematica/blob/master/jupyter_notebooks/espiral_arquimedes.ipynb)
45 | 21. [Triângulo de Sierpinski](https://nbviewer.jupyter.org/github/the-akira/Python-Matematica/blob/master/jupyter_notebooks/triangulo_sierpinski.ipynb)
46 | 22. [Conjunto de Mandelbrot](https://nbviewer.jupyter.org/github/the-akira/Python-Matematica/blob/master/jupyter_notebooks/conjuntomandelbrot.ipynb)
47 | 23. [Permutações e Combinações](https://nbviewer.jupyter.org/github/the-akira/Python-Matematica/blob/master/jupyter_notebooks/perm_comb.ipynb)
48 | 24. [Equações Diferenciais Ordinárias](https://nbviewer.jupyter.org/github/the-akira/Python-Matematica/blob/master/jupyter_notebooks/equacoes_diferenciais.ipynb)
49 | 25. [Análise de Algoritmos](https://nbviewer.jupyter.org/github/the-akira/Python-Matematica/blob/master/jupyter_notebooks/analise_algoritmos.ipynb)
50 | 26. [Símbolos da Matemática Explicados com Python](https://nbviewer.jupyter.org/github/the-akira/Python-Matematica/blob/master/jupyter_notebooks/simbolos_matematica.ipynb)
51 | 27. [Compreendendo Logaritmos com Python](https://nbviewer.jupyter.org/github/the-akira/Python-Matematica/blob/master/jupyter_notebooks/logaritmos.ipynb)
52 | 28. [Referências](https://github.com/the-akira/Python-Matematica/blob/master/referencias.md)


--------------------------------------------------------------------------------
/imagens/ExpIPi.gif:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/the-akira/Python-Matematica/6c443a076bef560dfb803a9fe12351bb0b71b376/imagens/ExpIPi.gif


--------------------------------------------------------------------------------
/imagens/archimedeanspiral.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/the-akira/Python-Matematica/6c443a076bef560dfb803a9fe12351bb0b71b376/imagens/archimedeanspiral.png


--------------------------------------------------------------------------------
/imagens/avatar.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/the-akira/Python-Matematica/6c443a076bef560dfb803a9fe12351bb0b71b376/imagens/avatar.png


--------------------------------------------------------------------------------
/imagens/bigo.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/the-akira/Python-Matematica/6c443a076bef560dfb803a9fe12351bb0b71b376/imagens/bigo.png


--------------------------------------------------------------------------------
/imagens/caracteres.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/the-akira/Python-Matematica/6c443a076bef560dfb803a9fe12351bb0b71b376/imagens/caracteres.png


--------------------------------------------------------------------------------
/imagens/complexplane.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/the-akira/Python-Matematica/6c443a076bef560dfb803a9fe12351bb0b71b376/imagens/complexplane.png


--------------------------------------------------------------------------------
/imagens/derivada.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/the-akira/Python-Matematica/6c443a076bef560dfb803a9fe12351bb0b71b376/imagens/derivada.png


--------------------------------------------------------------------------------
/imagens/exponencial.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/the-akira/Python-Matematica/6c443a076bef560dfb803a9fe12351bb0b71b376/imagens/exponencial.png


--------------------------------------------------------------------------------
/imagens/fibonacciblocks.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/the-akira/Python-Matematica/6c443a076bef560dfb803a9fe12351bb0b71b376/imagens/fibonacciblocks.png


--------------------------------------------------------------------------------
/imagens/fundamental_theorem_of_calculus.gif:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/the-akira/Python-Matematica/6c443a076bef560dfb803a9fe12351bb0b71b376/imagens/fundamental_theorem_of_calculus.gif


--------------------------------------------------------------------------------
/imagens/grafico.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/the-akira/Python-Matematica/6c443a076bef560dfb803a9fe12351bb0b71b376/imagens/grafico.png


--------------------------------------------------------------------------------
/imagens/integral.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/the-akira/Python-Matematica/6c443a076bef560dfb803a9fe12351bb0b71b376/imagens/integral.png


--------------------------------------------------------------------------------
/imagens/listas.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/the-akira/Python-Matematica/6c443a076bef560dfb803a9fe12351bb0b71b376/imagens/listas.png


--------------------------------------------------------------------------------
/imagens/mandelbrot1.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/the-akira/Python-Matematica/6c443a076bef560dfb803a9fe12351bb0b71b376/imagens/mandelbrot1.png


--------------------------------------------------------------------------------
/imagens/mandelbrot2.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/the-akira/Python-Matematica/6c443a076bef560dfb803a9fe12351bb0b71b376/imagens/mandelbrot2.png


--------------------------------------------------------------------------------
/imagens/mandelbrot3.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/the-akira/Python-Matematica/6c443a076bef560dfb803a9fe12351bb0b71b376/imagens/mandelbrot3.png


--------------------------------------------------------------------------------
/imagens/mandelbrot4.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/the-akira/Python-Matematica/6c443a076bef560dfb803a9fe12351bb0b71b376/imagens/mandelbrot4.png


--------------------------------------------------------------------------------
/imagens/realnumbersline.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/the-akira/Python-Matematica/6c443a076bef560dfb803a9fe12351bb0b71b376/imagens/realnumbersline.png


--------------------------------------------------------------------------------
/imagens/referencias.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/the-akira/Python-Matematica/6c443a076bef560dfb803a9fe12351bb0b71b376/imagens/referencias.png


--------------------------------------------------------------------------------
/imagens/sierpinski.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/the-akira/Python-Matematica/6c443a076bef560dfb803a9fe12351bb0b71b376/imagens/sierpinski.png


--------------------------------------------------------------------------------
/imagens/timeline.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/the-akira/Python-Matematica/6c443a076bef560dfb803a9fe12351bb0b71b376/imagens/timeline.png


--------------------------------------------------------------------------------
/imagens/trajetoriaparabolica.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/the-akira/Python-Matematica/6c443a076bef560dfb803a9fe12351bb0b71b376/imagens/trajetoriaparabolica.png


--------------------------------------------------------------------------------
/jupyter_notebooks/espiral_arquimedes.ipynb:
--------------------------------------------------------------------------------
 1 | {
 2 |  "cells": [
 3 |   {
 4 |    "cell_type": "markdown",
 5 |    "metadata": {},
 6 |    "source": [
 7 |     "# Espiral Arquimediana\n",
 8 |     "\n",
 9 |     "A [Espiral Arquimediana](https://en.wikipedia.org/wiki/Archimedean_spiral), também conhecida por espiral aritmética, obteve seu nome do matemático grego Arquimedes, que viveu no século III antes de Cristo. Se define como o lugar geométrico de um ponto movendo-se a velocidade constante sobre uma reta que gira sobre um ponto de origem fixo à velocidade angular constante. \n",
10 |     "\n",
11 |     "Equivalentemente, em coordenadas polares $(r, \\theta)$, pode ser descrita pela seguinte equação:\n",
12 |     "\n",
13 |     "\\begin{equation}\n",
14 |     "r = a + b\\theta\n",
15 |     "\\end{equation}\n",
16 |     "\n",
17 |     "Sendo $a$ e $b$ números reais.\n",
18 |     "\n",
19 |     "Alterando o parâmetro $a$ vira a espiral, enquanto que o parâmetro $b$ controla a distância entre os sucessivos giros.\n",
20 |     "\n",
21 |     "Da equação acima, pode-se afirmar: a posição da partícula a partir do ponto de partida é proporcional ao ângulo $\\theta$ conforme o tempo passa.\n",
22 |     "\n",
23 |     "O código a seguir é capaz de gerar a espiral:"
24 |    ]
25 |   },
26 |   {
27 |    "cell_type": "code",
28 |    "execution_count": 16,
29 |    "metadata": {},
30 |    "outputs": [],
31 |    "source": [
32 |     "from turtle import *\n",
33 |     "from math import *\n",
34 |     "\n",
35 |     "color(\"blue\")\n",
36 |     "down()\n",
37 |     "for i in range(250):\n",
38 |     "    t = i / 10 * pi\n",
39 |     "    x = (1 + 5 * t) * cos(t)\n",
40 |     "    y = (1 + 5 * t) * sin(t)\n",
41 |     "    goto(x, y)\n",
42 |     "up()\n",
43 |     "done()"
44 |    ]
45 |   },
46 |   {
47 |    "cell_type": "markdown",
48 |    "metadata": {},
49 |    "source": [
50 |     "## Visualizando o Resultado\n",
51 |     "\n",
52 | 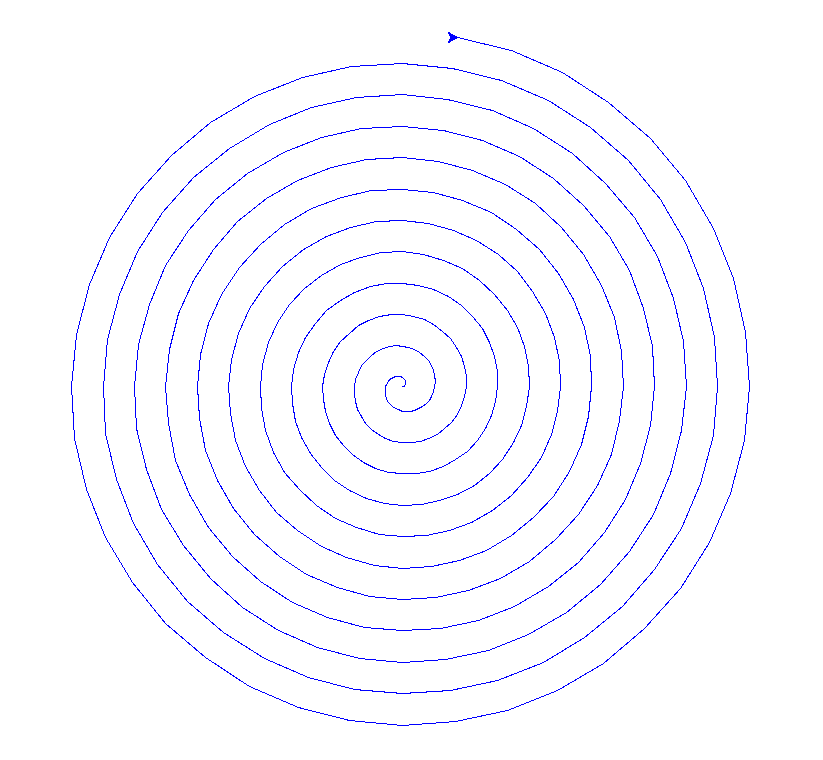    "![img](https://raw.githubusercontent.com/the-akira/Python-Matematica/master/imagens/archimedeanspiral.png)"
53 |    ]
54 |   }
55 |  ],
56 |  "metadata": {
57 |   "kernelspec": {
58 |    "display_name": "Python 3",
59 |    "language": "python",
60 |    "name": "python3"
61 |   },
62 |   "language_info": {
63 |    "codemirror_mode": {
64 |     "name": "ipython",
65 |     "version": 3
66 |    },
67 |    "file_extension": ".py",
68 |    "mimetype": "text/x-python",
69 |    "name": "python",
70 |    "nbconvert_exporter": "python",
71 |    "pygments_lexer": "ipython3",
72 |    "version": "3.7.10"
73 |   }
74 |  },
75 |  "nbformat": 4,
76 |  "nbformat_minor": 4
77 | }
78 | 


--------------------------------------------------------------------------------
/jupyter_notebooks/euclides.ipynb:
--------------------------------------------------------------------------------
  1 | {
  2 |  "cells": [
  3 |   {
  4 |    "cell_type": "markdown",
  5 |    "metadata": {},
  6 |    "source": [
  7 |     "# Algoritmo Euclidiano\n",
  8 |     "\n",
  9 |     "Em matemática, o algoritmo euclidiano, ou algoritmo de Euclides, é um método eficiente para calcular o máximo divisor comum (**greatest common divisor** - GCD) de dois inteiros (números), o maior número que os divide sem deixar resto. Recebeu o nome do antigo matemático grego Euclides, que o descreveu pela primeira vez em seus livros **Elements**.\n",
 10 |     "\n",
 11 |     "É um exemplo de algoritmo, um procedimento passo a passo para realizar um cálculo de acordo com regras bem definidas e é um dos algoritmos mais antigos em uso comum. Ele pode ser usado para reduzir as frações à sua forma mais simples.\n",
 12 |     "\n",
 13 |     "O algoritmo euclidiano tem muitas aplicações teóricas e práticas. É usado para reduzir as frações à sua forma mais simples e para realizar a divisão em aritmética modular. Os cálculos que usam esse algoritmo fazem parte dos protocolos criptográficos usados para proteger as comunicações da Internet e nos métodos para quebrar esses criptosistemas pela fatoração de grandes números compostos.\n",
 14 |     "\n",
 15 |     "O algoritmo euclidiano calcula o máximo divisor comum de dois números naturais $a$ e $b$. O maior divisor comum $g$ é o maior número natural que divide $a$ e $b$ sem deixar resto.\n",
 16 |     "\n",
 17 |     "## Procedimento\n",
 18 |     "\n",
 19 |     "O algoritmo euclidiano prossegue em uma série de etapas, de modo que a saída de cada etapa é usada como entrada para a próxima. \n",
 20 |     "\n",
 21 |     "Seja $k$ um inteiro que conta os passos do algoritmo, começando com zero. Assim, a etapa inicial corresponde a $k = 0$, a próxima etapa corresponde a $k = 1$ e assim por diante.\n",
 22 |     "\n",
 23 |     "Cada etapa começa com dois restos não negativos $r_{k - 1}$ e $r_{k - 2}$. Uma vez que o algoritmo garante que os restos diminuam constantemente a cada passo, $r_{k - 1}$ é menor que seu predecessor $r_{k - 2}$. O objetivo da k-ésima etapa é encontrar um quociente $q_k$ e o resto $r_k$ que satisfaçam a equação:\n",
 24 |     "\n",
 25 |     "$r_{k - 2} = q_k r_k + r_k$\n",
 26 |     "\n",
 27 |     "E que tem $0 \\leq r_k < r_{k - 1}$. Em outras palavras, múltiplos do número menor $r_{k - 1}$ são subtraídos do número maior $r_{k - 2}$ até que o restante $r_k$ seja menor que $r_{k - 1}$.\n",
 28 |     "\n",
 29 |     "Na etapa inicial ($k = 0$), os restos $r_{-2}$ e $r_{-1}$ são iguais a $a$e $b$, os números para os quais o GCD é procurado. Na próxima etapa ($k = 1$), os restantes são iguais a $b$ e o restante $r_0$ da etapa inicial, e assim por diante. Assim, o algoritmo pode ser escrito como uma sequência de equações:\n",
 30 |     "\n",
 31 |     "\\begin{equation}\n",
 32 |     "a = q_0b + r_0\n",
 33 |     "\\end{equation}\n",
 34 |     "\n",
 35 |     "\\begin{equation}\n",
 36 |     "b = q_1 r_0 + r_1\n",
 37 |     "\\end{equation}\n",
 38 |     "\n",
 39 |     "\\begin{equation}\n",
 40 |     "r_0 = q_2 r_1 + r_2\n",
 41 |     "\\end{equation}\n",
 42 |     "\n",
 43 |     "\\begin{equation}\n",
 44 |     "r_1 = q_3 r_2 + r_3\n",
 45 |     "\\end{equation}\n",
 46 |     "\n",
 47 |     "\\begin{equation}\n",
 48 |     "...\n",
 49 |     "\\end{equation}\n",
 50 |     "\n",
 51 |     "Se $a$ for menor que $b$, a primeira etapa do algoritmo troca os números. Por exemplo, se $a < b$, o quociente inicial $q_0$ é igual a zero e o resto $r_0$ é $a$. Assim, $r_k$ é menor que seu predecessor $r_{k - 1}$ para todo $k \\geq 0$.\n",
 52 |     "\n",
 53 |     "Como os remanescentes diminuem a cada passo, mas nunca podem ser negativos, um resto $r_N$ deve eventualmente ser igual a zero, ponto em que o algoritmo para. O resto final diferente de zero $r_{N - 1}$ é o máximo divisor comum de $a$ e $b$. O número $N$ não pode ser infinito porque há apenas um número finito de inteiros não negativos entre o resto inicial $r_0$ e zero.\n",
 54 |     "\n",
 55 |     "## Prova de Validade\n",
 56 |     "\n",
 57 |     "A validade do algoritmo euclidiano pode ser comprovada por um argumento de duas etapas.\n",
 58 |     "\n",
 59 |     "Na primeira etapa, o resto final de zero $r_{N - 1}$ é mostrado para dividir ambos $a$ e $b$. Uma vez que é um divisor comum, deve ser menor ou igual ao máximo divisor comum $g$. \n",
 60 |     "\n",
 61 |     "Na segunda etapa, é mostrado que qualquer divisor comum de $a$ e $b$, incluindo $g$, deve dividir $r_{N - 1}$; portanto, $g$ deve ser menor ou igual a $r_{N - 1}$. Essas duas conclusões são inconsistentes, a menos que $r_{N - 1} = g$.\n",
 62 |     "\n",
 63 |     "Para demonstrar que $r_{N - 1}$ divide ambos $a$ e $b$ (a primeira etapa), $r_{N - 1}$ divide seu predecessor $r_{N - 2}$:\n",
 64 |     "\n",
 65 |     "\\begin{equation}\n",
 66 |     "r_{N - 2} = q_N r_{N - 1}\n",
 67 |     "\\end{equation}\n",
 68 |     "\n",
 69 |     "Já que o resto final $r_N$ é zero. $r_{N - 1}$ também divide seu próximo predecessor $r_{N - 3}$:\n",
 70 |     "\n",
 71 |     "\\begin{equation}\n",
 72 |     "r_{N - 3} = q_{N - 1} r_{N - 2} + r_{N - 1}\n",
 73 |     "\\end{equation}\n",
 74 |     "\n",
 75 |     "Porque ele divide os dois termos no lado direito da equação. Iterando o mesmo argumento, $r_{N - 1}$ divide todos os restos anteriores, incluindo $a$ e $b$. Nenhum dos restos precedentes $r_{N - 2}$, $r_{N - 3}$, etc. divide $a$ e $b$, pois eles deixam um resto. Como $r_{N - 1}$ é um divisor comum de $a$ e $b$, então $r_{N - 1} \\leq g$.\n",
 76 |     "\n",
 77 |     "Na segunda etapa, qualquer número natural $c$ que divide $a$ e $b$ (em outras palavras, qualquer divisor comum de $a$ e $b$) divide os restantes $r_k$. Por definição, $a$ e $b$ podem ser escritos como múltiplos de $c$: $a = mc$ e $b = nc$, onde $m$ e $n$ são números naturais. Portanto, $c$ divide o resto inicial $r_0$, uma vez que $r_0 = a - q_0b = mc - q_0nc = (m - q_0n) c$. Um argumento análogo mostra que $c$ também divide os restos subsequentes $r_1$, $r_2$, etc. Portanto, o maior divisor comum g deve dividir $r_{N - 1}$, o que implica que $g \\leq r_{N - 1}$. Como a primeira parte do argumento mostrou o inverso $(r_{N - 1} \\leq g)$, segue-se que $g = r_{N - 1}$. Assim, $g$ é o maior divisor comum de todos os pares sucessivos:\n",
 78 |     "\n",
 79 |     "\\begin{equation}\n",
 80 |     "g = gcd(a,b) = gcd(b,r_0) = gcd(r_0,r_1) = ... = gcd(r_{N-2},r_{N-1}) = r_{N-1}\n",
 81 |     "\\end{equation}\n",
 82 |     "\n",
 83 |     "## Exemplo\n",
 84 |     "\n",
 85 |     "Para ilustração, o algoritmo euclidiano pode ser usado para encontrar o maior divisor comum de $a = 1071$ e $b = 462$. \n",
 86 |     "\n",
 87 |     "Para começar, múltiplos de $462$ são subtraídos de $1071$ até que o resto seja menor que $462$. Dois desses múltiplos podem ser subtraídos ($q_0 = 2$), deixando um resto de $147$:\n",
 88 |     "\n",
 89 |     "$1071 = 2 \\times 462 + 147$\n",
 90 |     "\n",
 91 |     "Em seguida, múltiplos de $147$ são subtraídos de $462$ até que o restante seja inferior a $147$. Três múltiplos podem ser subtraídos ($q_1 = 3$), deixando um restante de $21$:\n",
 92 |     "\n",
 93 |     "$462 = 3 \\times 147 + 21$\n",
 94 |     "\n",
 95 |     "Em seguida, os múltiplos de $21$ são subtraídos de $147$ até que o restante seja inferior a $21$. Sete múltiplos podem ser subtraídos ($q_2 = 7$), não deixando nenhum resto:\n",
 96 |     "\n",
 97 |     "$147 = 7 \\times 21 + 0$\n",
 98 |     "\n",
 99 |     "Como o último resto é zero, o algoritmo termina com **21** como o máximo divisor comum de $1071$ e $462$.\n",
100 |     "\n",
101 |     "## Python\n",
102 |     "\n",
103 |     "Agora que conhecemos os fundamentos matemáticos do algoritmo euclidiano, vamos implementá-lo com a linguagem Python:"
104 |    ]
105 |   },
106 |   {
107 |    "cell_type": "code",
108 |    "execution_count": 43,
109 |    "metadata": {},
110 |    "outputs": [],
111 |    "source": [
112 |     "from math import floor\n",
113 |     "\n",
114 |     "def algoritmo_euclidiano(x, y, verbose=True):\n",
115 |     "    k = 0\n",
116 |     "    if x < y: \n",
117 |     "        return algoritmo_euclidiano(y, x, verbose)\n",
118 |     "    while y != 0:\n",
119 |     "        k += 1\n",
120 |     "        if verbose: \n",
121 |     "            print(f'{x} = {floor(x/y)} * {y} + {x%y}')\n",
122 |     "        (x, y) = (y, x % y)\n",
123 |     "    if verbose: \n",
124 |     "        print(f'máximo divisor comum é = {x}, após {k} iterações') \n",
125 |     "    return x"
126 |    ]
127 |   },
128 |   {
129 |    "cell_type": "markdown",
130 |    "metadata": {},
131 |    "source": [
132 |     "Definida a função do algoritmo, podemos testá-lo invocando ela:"
133 |    ]
134 |   },
135 |   {
136 |    "cell_type": "code",
137 |    "execution_count": 44,
138 |    "metadata": {},
139 |    "outputs": [
140 |     {
141 |      "name": "stdout",
142 |      "output_type": "stream",
143 |      "text": [
144 |       "1071 = 2 * 462 + 147\n",
145 |       "462 = 3 * 147 + 21\n",
146 |       "147 = 7 * 21 + 0\n",
147 |       "máximo divisor comum é = 21, após 3 iterações\n"
148 |      ]
149 |     },
150 |     {
151 |      "data": {
152 |       "text/plain": [
153 |        "21"
154 |       ]
155 |      },
156 |      "execution_count": 44,
157 |      "metadata": {},
158 |      "output_type": "execute_result"
159 |     }
160 |    ],
161 |    "source": [
162 |     "algoritmo_euclidiano(1071, 462)"
163 |    ]
164 |   },
165 |   {
166 |    "cell_type": "markdown",
167 |    "metadata": {},
168 |    "source": [
169 |     "Podemos optar por silenciar o algoritmo, ao setarmos `verbose = False`:"
170 |    ]
171 |   },
172 |   {
173 |    "cell_type": "code",
174 |    "execution_count": 45,
175 |    "metadata": {},
176 |    "outputs": [
177 |     {
178 |      "name": "stdout",
179 |      "output_type": "stream",
180 |      "text": [
181 |       "21\n"
182 |      ]
183 |     }
184 |    ],
185 |    "source": [
186 |     "resultado = algoritmo_euclidiano(1071, 462, False)\n",
187 |     "print(resultado)"
188 |    ]
189 |   },
190 |   {
191 |    "cell_type": "markdown",
192 |    "metadata": {},
193 |    "source": [
194 |     "Anteriormente utilizamos uma solução recursiva, também podemos optar por uma solução iterativa:"
195 |    ]
196 |   },
197 |   {
198 |    "cell_type": "code",
199 |    "execution_count": 34,
200 |    "metadata": {},
201 |    "outputs": [],
202 |    "source": [
203 |     "def mdc(a, b):\n",
204 |     "    for c in range(min(a, b), 0, -1):\n",
205 |     "        if a % c == b % c == 0:\n",
206 |     "            return c"
207 |    ]
208 |   },
209 |   {
210 |    "cell_type": "markdown",
211 |    "metadata": {},
212 |    "source": [
213 |     "A seguir, podemos testá-la:"
214 |    ]
215 |   },
216 |   {
217 |    "cell_type": "code",
218 |    "execution_count": 35,
219 |    "metadata": {},
220 |    "outputs": [
221 |     {
222 |      "name": "stdout",
223 |      "output_type": "stream",
224 |      "text": [
225 |       "Máximo divisor comum entre 1071 e 462 = 21\n"
226 |      ]
227 |     }
228 |    ],
229 |    "source": [
230 |     "print(f'Máximo divisor comum entre 1071 e 462 = {mdc(1071, 462)}')"
231 |    ]
232 |   },
233 |   {
234 |    "cell_type": "code",
235 |    "execution_count": 36,
236 |    "metadata": {},
237 |    "outputs": [
238 |     {
239 |      "name": "stdout",
240 |      "output_type": "stream",
241 |      "text": [
242 |       "Máximo divisor comum entre 98 e 56 = 14\n"
243 |      ]
244 |     }
245 |    ],
246 |    "source": [
247 |     "print(f'Máximo divisor comum entre 98 e 56 = {mdc(98, 56)}')"
248 |    ]
249 |   },
250 |   {
251 |    "cell_type": "markdown",
252 |    "metadata": {},
253 |    "source": [
254 |     "Além disso, a biblioteca [math](https://docs.python.org/3/library/math.html) nos oferece uma função **gcd** pronta:"
255 |    ]
256 |   },
257 |   {
258 |    "cell_type": "code",
259 |    "execution_count": 37,
260 |    "metadata": {},
261 |    "outputs": [
262 |     {
263 |      "name": "stdout",
264 |      "output_type": "stream",
265 |      "text": [
266 |       "Máximo divisor comum entre 20 e 28 = 4\n"
267 |      ]
268 |     }
269 |    ],
270 |    "source": [
271 |     "from math import gcd\n",
272 |     "\n",
273 |     "print(f'Máximo divisor comum entre 20 e 28 = {gcd(20, 28)}')"
274 |    ]
275 |   }
276 |  ],
277 |  "metadata": {
278 |   "kernelspec": {
279 |    "display_name": "Python 3",
280 |    "language": "python",
281 |    "name": "python3"
282 |   },
283 |   "language_info": {
284 |    "codemirror_mode": {
285 |     "name": "ipython",
286 |     "version": 3
287 |    },
288 |    "file_extension": ".py",
289 |    "mimetype": "text/x-python",
290 |    "name": "python",
291 |    "nbconvert_exporter": "python",
292 |    "pygments_lexer": "ipython3",
293 |    "version": "3.7.10"
294 |   }
295 |  },
296 |  "nbformat": 4,
297 |  "nbformat_minor": 4
298 | }
299 | 


--------------------------------------------------------------------------------
/jupyter_notebooks/funcao_relu.ipynb:
--------------------------------------------------------------------------------
  1 | {
  2 |  "cells": [
  3 |   {
  4 |    "cell_type": "markdown",
  5 |    "metadata": {},
  6 |    "source": [
  7 |     "# Função de Unidade Linear Retificada\n",
  8 |     "\n",
  9 |     "A função de Unidade Linear Retificada, conhecida por [ReLU](https://www.kaggle.com/dansbecker/rectified-linear-units-relu-in-deep-learning) (Rectified Linear Unit) é uma função de ativação que se tornou muito utilizada em modelos de Deep Learning. \n",
 10 |     "\n",
 11 |     "A função retorna $0$ se ela receber qualquer input negativo, porém para cada valor positivo de input $x$ ela retorna o valor de volta. \n",
 12 |     "\n",
 13 |     "Ela pode ser escrita da seguinte maneira:\n",
 14 |     "\n",
 15 |     "\\begin{equation}\n",
 16 |     "f(x) = max(0,x)\n",
 17 |     "\\end{equation}\n",
 18 |     "\n",
 19 |     "Para que possamos ver este exemplo, vamos primeiramente importar a biblioteca necessária:"
 20 |    ]
 21 |   },
 22 |   {
 23 |    "cell_type": "code",
 24 |    "execution_count": 1,
 25 |    "metadata": {},
 26 |    "outputs": [],
 27 |    "source": [
 28 |     "import matplotlib.pyplot as plt"
 29 |    ]
 30 |   },
 31 |   {
 32 |    "cell_type": "markdown",
 33 |    "metadata": {},
 34 |    "source": [
 35 |     "Definimos a função **ReLU**:"
 36 |    ]
 37 |   },
 38 |   {
 39 |    "cell_type": "code",
 40 |    "execution_count": 2,
 41 |    "metadata": {},
 42 |    "outputs": [],
 43 |    "source": [
 44 |     "def rectified(x):\n",
 45 |     "    return max(0.0, x)"
 46 |    ]
 47 |   },
 48 |   {
 49 |    "cell_type": "markdown",
 50 |    "metadata": {},
 51 |    "source": [
 52 |     "O código a seguir gera uma série de inteiros entre **-10** até **10**:"
 53 |    ]
 54 |   },
 55 |   {
 56 |    "cell_type": "code",
 57 |    "execution_count": 4,
 58 |    "metadata": {},
 59 |    "outputs": [
 60 |     {
 61 |      "name": "stdout",
 62 |      "output_type": "stream",
 63 |      "text": [
 64 |       "[-10, -9, -8, -7, -6, -5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10]\n"
 65 |      ]
 66 |     }
 67 |    ],
 68 |    "source": [
 69 |     "data_input = [x for x in range(-10, 11)]\n",
 70 |     "print(data_input)"
 71 |    ]
 72 |   },
 73 |   {
 74 |    "cell_type": "markdown",
 75 |    "metadata": {},
 76 |    "source": [
 77 |     "Calculamos os outputs para cada um de nossos inputs:"
 78 |    ]
 79 |   },
 80 |   {
 81 |    "cell_type": "code",
 82 |    "execution_count": 5,
 83 |    "metadata": {},
 84 |    "outputs": [],
 85 |    "source": [
 86 |     "data_output = [rectified(x) for x in data_input]"
 87 |    ]
 88 |   },
 89 |   {
 90 |    "cell_type": "markdown",
 91 |    "metadata": {},
 92 |    "source": [
 93 |     "Finalmente podemos plotar o gráfico:"
 94 |    ]
 95 |   },
 96 |   {
 97 |    "cell_type": "code",
 98 |    "execution_count": 6,
 99 |    "metadata": {},
100 |    "outputs": [
101 |     {
102 |      "data": {
103 |       "image/png": "iVBORw0KGgoAAAANSUhEUgAAA54AAAIICAYAAAAGxzENAAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADh0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uMy4xLjMsIGh0dHA6Ly9tYXRwbG90bGliLm9yZy+AADFEAAAgAElEQVR4nOzdd7ie8+HH8fedLYtYMYKg9qpKqdUmxjnZIsMmKFFUrJq1akTV3nukViJDZJ+jCNWipH5WUWrFJiQyRJKT+/fHV3qjQXLOec73fp7n/bouF59bkvO5fGV8rud57jtJ0xRJkiRJkgqlUewCkiRJkqTS5vCUJEmSJBWUw1OSJEmSVFAOT0mSJElSQTk8JUmSJEkF5fCUJEmSJBVUk4b8YiuvvHLasWPHhvySy2zOnDm0atUqdg19g2eSP55JPnku+eOZ5JPnkj+eST55LvlTDGcyderUT9M0XeW71xt0eHbs2JFnnnmmIb/kMpsyZQqdO3eOXUPf4Jnkj2eST55L/ngm+eS55I9nkk+eS/4Uw5kkSfL2kq77VltJkiRJUkE5PCVJkiRJBeXwlCRJkiQVlMNTkiRJklRQDk9JkiRJUkE5PCVJkiRJBeXwlCRJkiQVlMNTkiRJklRQDk9JkiRJUkE5PCVJkiRJBeXwlCRJkiQVlMNTkiRJklRQDk9JkiRJUkE5PCVJkiRJBeXwlCRJkiQVlMNTkiRJklRQPzo8kyS5LUmSj5MkefEb11ZMkuTBJEle+/rv7QpbU5IkSZJUrJbmFc87gK7fuXYq8FCaphsAD32dJUmSJEkFMG8ezJzZNHaNWvvR4Zmm6WPAZ9+5vAcw9Ot/Hgr0qedekiRJkiSgpgYOOAB++9uteeut2G1qp7af8WyfpukHAF//fdX6qyRJkiRJAkhTOPpoGDUK3n23JTvsAB9/HLvVskvSNP3xb5QkHYHxaZpu/nWekabpCt/495+nabrEz3kmSTIIGATQvn37bYYNG1YPtQtn9uzZtG7dOnYNfYNnkj+eST55LvnjmeST55I/nkk+eS75cNttHbnzzo7/zf37T+Ooo/5DksTr9EO6dOkyNU3TTt+93qSWP95HSZKsnqbpB0mSrA587+ZO0/Qm4CaATp06pZ07d67ll2wYU6ZMIe8dy41nkj+eST55LvnjmeST55I/nkk+eS7xXXMN3Hlnlnfb7SOGD1+LRo3Wileqlmr7VtuxwMCv/3kg8ED91JEkSZIkDR8OgwdnuWtXOOWUV2hUpA/EXJrHqdwLPAFslCTJu0mS/Br4I7B7kiSvAbt/nSVJkiRJdfTgg3DggeHznQDbbQcjR0KTJj/+Mcm8+tG32qZpuu/3/Ktd67mLJEmSJJW1p5+GPfeEBQtC3mQTmDABWrWK26uuivSFWkmSJEkqLa++Ct26wZw5IXfoAFVVsNJKcXvVB4enJEmSJEX23ntQUQHTp4e84opQXQ1rFd99hJbI4SlJkiRJEX32GVRWwjvvhNyyJUycGN5mWyocnpIkSZIUydy50KsXvPRSyE2awKhR4YZCpcThKUmSJEkRLFgAe+0Ff/97dm3o0PDolFLj8JQkSZKkBrZoERx2WLhj7WJXXAH77RevUyE5PCVJkiSpgZ1yCvz5z1k+/XQ49th4fQrN4SlJkiRJDejii+GSS7J82GFw/vnx+jQEh6ckSZIkNZA77oCTT85ynz5w/fWQJNEqNQiHpyRJkiQ1gHHjwqubi/3yl3DvveFOtqXO4SlJkiRJBfb44+EOtjU1IW+1FYwdCy1axO3VUByekiRJklRAL7wQntU5b17I660HkyfD8svH7dWQHJ6SJEmSVCBvvQWVlTBjRsirrgrV1bDaalFrNTiHpyRJkiQVwMcfQ0UFfPBByG3ahFc6118/bq8YHJ6SJEmSVM9mzYLu3eG110Ju1gweeAC23jpur1gcnpIkSZJUj776CvbcE6ZODblRo3D32i5d4vaKyeEpSZIkSfWkpgYOPBAeeii7dv310LdvvE554PCUJEmSpHqQpjB4MIwYkV077zwYNChep7xweEqSJElSPTjvPLjuuiwfcwz8/vfx+uSJw1OSJEmS6uj66+Hss7O8zz5wxRWQJPE65YnDU5IkSZLqYMQIOProLFdUwNCh4aZCCvxPIUmSJEm19NBDcMAB4fOdAD//OYwaFR6foozDU5IkSZJqYepU6NMH5s8PeaONYMIEaN06bq88cnhKkiRJ0jJ67TXo1g1mzw55zTWhqgpWWSVur7xyeEqSJEnSMnj//fA5zk8+CblduzA611knbq88c3hKkiRJ0lKaMQO6doW33gp5ueVg/HjYbLOotXLP4SlJkiRJS+HLL6FXL3jhhZAbNw53tN1hh7i9ioHDU5IkSZJ+xMKFsPfe8Pjj2bXbboMePeJ1KiYOT0mSJEn6AWkKgwbBuHHZtUsvhYMOitep2Dg8JUmSJOkHnHYa3H57lk8+GU44IV6fYuTwlCRJkqTvcdllcNFFWT7kEPjjH+P1KVYOT0mSJElagjvvhBNPzHKvXnDTTZAk8ToVK4enJEmSJH3HxInh1c3FdtoJhg2DJk3idSpmDk9JkiRJ+oYnnoD+/aGmJuTNN4exY6Fly7i9ipnDU5IkSZK+9tJL4REpX34Z8jrrQFUVtGsXt1exc3hKkiRJEvDOO1BZCZ9/HvIqq0B1NayxRtxepcDhKUmSJKnsffopVFTAe++F3Lo1TJoEG24Yt1epcHhKkiRJKmuzZ0P37vDqqyE3awZjxsA228TtVUocnpIkSZLK1vz50K8fPP10yEkCd90Fu+4at1epcXhKkiRJKkuLFsHAgeFznItdey0MGBCvU6lyeEqSJEkqO2kKxx0Xns252Nlnw5FHxutUyhyekiRJksrOkCFw9dVZPvLIMDxVGA5PSZIkSWXlppvgjDOyPGBAGKFJEq9TqXN4SpIkSSobo0d/++20u+4Kd94JjRvH61QOHJ6SJEmSysKUKbDvvuGmQhAel3L//dC8edRaZcHhKUmSJKnkPfss9O4dHp8CsMEGMHEitGkTt1e5cHhKkiRJKmmvvw5du8KsWSGvvjpUVcGqq8btVU4cnpIkSZJK1ocfQmUlfPxxyCusEEbnuuvG7VVuHJ6SJEmSStLMmeGVzjfeCLlFCxg3DrbYIm6vcuTwlCRJklRy5s2DPfaA554LuXFjuO8+2GmnuL3KlcNTkiRJUklZuDDcvfbRR7NrN98MvXrF61TuHJ6SJEmSSkaahud0jhmTXbvoIjjkkHid5PCUJEmSVELOOANuuSXLJ5wAJ50Ur48Ch6ckSZKkknDllTBkSJYPPBAuvhiSJF4nBQ5PSZIkSUXvnnvguOOy3L073HorNHLx5ILHIEmSJKmoTZ4MAwdmefvtYcQIaNo0Xid9m8NTkiRJUtF66ino1y/cyRZg001h/Hho2TJuL32bw1OSJElSUXr5ZejRA+bODXmttaCqClZcMW4v/S+HpyRJkqSiM20aVFbC9Okhr7QSVFdDhw5xe2nJHJ6SJEmSisr06WF0TpsWcqtWMHEibLxx3F76fg5PSZIkSUVjzhzo2TO8zRbCDYRGj4Ztt43bSz/M4SlJkiSpKCxYAAMGwJNPhpwkMHQoVFTE7aUf5/CUJEmSlHuLFsGhh8KkSdm1K6+EffeN10lLz+EpSZIkKdfSFE48Ee66K7t2xhlwzDHxOmnZODwlSZIk5dpFF8EVV2R50CA499x4fbTsHJ6SJEmScuvWW+G007Lcty9cd134fKeKh8NTkiRJUi498EB4dXOxzp3h7ruhceNolVRLDk9JkiRJufPYY7DPPuGmQgA//WkYoi1axO2l2nF4SpIkScqV55+H3r1h3ryQ118fJk+Gtm3j9lLtOTwlSZIk5cabb0JlJcycGXL79lBdHf6u4uXwlCRJkpQLH30EFRXw4Ycht20bXulcb724vVR3Dk9JkiRJ0X3xBXTrBq+/HnLz5jB2bPhsp4qfw1OSJElSVPPmQZ8+8OyzITdqBMOGwa9+FbeX6o/DU5IkSVI0NTVwwAHwyCPZtRtvDENUpcPhKUmSJCmKNIWjj4ZRo7JrF1wAhx0Wr5MKw+EpSZIkKYpzzgmvbi527LFw2mnR6qiAHJ6SJEmSGtw118C552Z5v/3gsssgSeJ1UuE4PCVJkiQ1qOHDYfDgLFdWwu23h5sKqTR5tJIkSZIazIMPwoEHhs93Amy3XfiMZ7NmcXupsByekiRJkhrE00/DnnvCggUhb7wxTJgArVrF7aXCq9PwTJLk+CRJXkqS5MUkSe5NkqRFfRWTJEmSVDpefRW6d4c5c0Lu0AGqqmClleL2UsOo9fBMkmRNYDDQKU3TzYHGwD71VUySJElSaXjvvfA5zk8/DXnFFcPoXHvtuL3UcOr6VtsmwHJJkjQBWgLv172SJEmSpFLx+efQtSu8/XbILVvC+PGw6aZxe6lh1Xp4pmn6HnAJ8A7wATAzTdPq+iomSZIkqbjNnQs9e8KLL4bcpAmMHAnbbx+3lxpeki6+ndSyfsckaQeMAvYGZgAjgJFpmt71nW83CBgE0L59+22GDRtWp8KFNnv2bFq3bh27hr7BM8kfzySfPJf88UzyyXPJH88kn+p6LgsXJpx55uY8+WT2Ic7TT3+Z3Xf/qD7qlaVi+LnSpUuXqWmadvru9SZ1+DF3A95M0/QTgCRJRgM7AN8anmma3gTcBNCpU6e0c+fOdfiShTdlyhTy3rHceCb545nkk+eSP55JPnku+eOZ5FNdziVN4ZBD4Mkns2uXXw7HHbcJsEm99CtHxfxzpS6f8XwH+EWSJC2TJEmAXYGX66eWJEmSpGJ1yikwdGiWTz0VjjsuXh/FV5fPeD4FjAT+Cbzw9Y91Uz31kiRJklSELrkELr44y4ceCkOGxOujfKjLW21J0/Rs4Ox66iJJkiSpiA0dCiedlOU99oAbb4QkiddJ+VDXx6lIkiRJEuPHw69/neWdd4Z77w13spUcnpIkSZLq5G9/gwEDoKYm5C23hLFjYbnl4vZSfjg8JUmSJNXaiy+GZ3XOmxfyuuvC5MmwwgpxeylfHJ6SJEmSauXtt6GyEmbMCHnVVaGqClZfPW4v5Y/DU5IkSdIy++QTqKiA998PuU0bmDQJNtggbi/lk8NTkiRJ0jKZNQu6d4d//zvkZs1gzBj42c/i9lJ+OTwlSZIkLbWvvoK+feGZZ0JOErjnHthll7i9lG8OT0mSJElLZdEiGDgQ/vKX7Nr110O/fvE6qTg4PCVJkiT9qDSFY4+F4cOza+eeC0ccEa+TiofDU5IkSdKPOv98uOaaLB99NJxxRrw+Ki4OT0mSJEk/6IYb4Kyzsrz33nDVVeHzndLScHhKkiRJ+l4jR8JRR2V5t91g6FBo5JLQMvB/F0mSJElL9PDDsP/+4fOdAJ06wejR0Lx53F4qPg5PSZIkSf/j3/9uTZ8+MH9+yBtuCBMnQps2cXupODk8JUmSJH3L66/DqaduyaxZIa+xBlRXwyqrxO2l4uXwlCRJkvRfH3wAFRXw+efNAFhhBaiqgnXWiVxMRc3hKUmSJAmAGTOga1d4882QW7SA8eNh883j9lLxc3hKkiRJ4ssvoXdveP75kBs1ShkxAnbcMW4vlQaHpyRJklTmFi6EffeFv/41u3byya/Qs2e8TiotDk9JkiSpjKUpHHEEPPBAdu3ii6Gy8qN4pVRyHJ6SJElSGfv97+G227J80knwu9/F66PS5PCUJEmSytQVV8CFF2Z54EC46KJ4fVS6HJ6SJElSGbr7bjj++Cz37Ak33wxJEq+TSpfDU5IkSSozkybBwQdneccdYfhwaNo0WiWVOIenJEmSVEaefBL69w93soXwjM5x46Bly7i9VNocnpIkSVKZ+Ne/oEcPmDs35HXWgcmToV27uL1U+hyekiRJUhmYNg0qK+Gzz0JeeWWoroY114zbS+XB4SlJkiSVuOnToaIC3n035Natw+c8N9wwbi+VD4enJEmSVMLmzAlvr33llZCbNoX774dOneL2UnlxeEqSJEklav586NcPnnoq5CSBu+6C3XaL20vlx+EpSZIklaBFi+CQQ6CqKrt2zTWw117xOql8OTwlSZKkEpOmcMIJcM892bWzzoKjjorXSeXN4SlJkiSVmD/+Ea68Msu/+Q2cc060OpLDU5IkSSolt9wCp5+e5f79w1tskyReJ8nhKUmSJJWIMWPgiCOyvMsu4WZCjRvH6ySBw1OSJEkqCY8+CvvsE24qBPCzn4XHpjRvHreXBA5PSZIkqeg99xz07g1ffRXyT34CkyZB27Zxe0mLOTwlSZKkIvbGG1BZCV98EfJqq0F1Nay6atxe0jc5PCVJkqQi9dFHUFER/g6w/PLhuZ3rrhu3l/RdDk9JkiSpCH3xBXTrBv/5T8gtWsC4cbDllnF7SUvi8JQkSZKKzLx50KcPPPtsyI0awbBhsPPOcXtJ38fhKUmSJBWRmhrYf3945JHs2s03wx57xOsk/RiHpyRJklQk0hSOOgpGj86u/fGPcOih8TpJS8PhKUmSJBWJs8+Gm27K8vHHw8knx+sjLS2HpyRJklQErr4azjsvywccAJdcAkkSr5O0tByekiRJUs4NGwbHHpvlbt3gttvCTYWkYuD/qpIkSVKOVVfDQQeFz3cC/OIXMGIENG0at5e0LByekiRJUk794x/Qty8sWBDyppvChAnQqlXcXtKycnhKkiRJOfTKK9C9O8yZE/Jaa0FVFay4YtxeUm04PCVJkqScefddqKyE6dNDXmml8JbbDh3i9pJqy+EpSZIk5chnn0HXrvDOOyG3bBneXrvxxnF7SXXh8JQkSZJyYu5c6NULXnop5CZNYPRo2G67uL2kunJ4SpIkSTmwYAHstRf8/e/ZtaFDw1tupWLn8JQkSZIiW7QIfv3r8Jbaxa68EvbbL14nqT45PCVJkqTITj4Z7rwzy7//PQweHK+PVN8cnpIkSVJEF18Ml16a5cMPh/POi9dHKgSHpyRJkhTJHXeEVzsX23NPuO46SJJolaSCcHhKkiRJEYwbB4cdluVf/QruuSfcyVYqNQ5PSZIkqYE9/ni4g21NTchbbQUPPAAtWsTtJRWKw1OSJElqQC+8AD17wrx5Ia+3HkyeDMsvH7eXVEgOT0mSJKmBvPVWeC7nzJkht28P1dWw2mpRa0kF5/CUJEmSGsDHH0NFBXzwQcht28KkSbD++nF7SQ3B4SlJkiQV2KxZ0L07vPZayM2bh890br113F5SQ3F4SpIkSQX01VfhMSlTp4bcqFG4e23nzlFrSQ3K4SlJkiQVSE0NHHggPPRQdu2GG6Bv33idpBgcnpIkSVIBpCkMHgwjRmTXzj8fDj88XicpFoenJEmSVADnngvXXZflwYPh9NPj9ZFicnhKkiRJ9ez66+Gcc7K8775w+eWQJNEqSVE5PCVJkqR6NGIEHH10lisq4I47wk2FpHLl//6SJElSPXnoITjggPD5ToBtt4VRo6BZs7i9pNgcnpIkSVI9mDoV+vSB+fND3mgjmDABWreO20vKA4enJEmSVEevvQbdusHs2SGvuSZUV8PKK8ftJeWFw1OSJEmqg/ffD5/j/OSTkNu1C6Nz7bXj9pLyxOEpSZIk1dKMGdC1K7z1VsjLLRfeXrvpplFrSbnj8JQkSZJq4csvoVcveOGFkBs3hpEjYfvt4/aS8sjhKUmSJC2jhQth773h8ceza7ffDt27x+sk5ZnDU5IkSVoGaQqDBsG4cdm1Sy+FAw+M10nKO4enJEmStAxOOy28urnYKafACSfE6yMVA4enJEmStJQuuwwuuijLhx4KF14Yr49ULByekiRJ0lK480448cQs9+4NN94ISRKvk1Qs6jQ8kyRZIUmSkUmSvJIkyctJkngPL0mSJJWciRPhkEOyvNNOMGwYNGkSr5NUTOr6U+VKYHKapv2TJGkGtKyHTpIkSVJuPPEE9O8PNTUhb7FFuLHQcsvF7SUVk1oPzyRJ2gK/BA4GSNN0PjC/fmpJkiRJ8b30EvToEZ7ZCdCxI0yeDCusELWWVHTq8lbb9YBPgNuTJHk2SZJbkiRpVU+9JEmSpKjeeQcqK+Hzz0NeZRWoroY11ojbSypGSZqmtfuOSdIJeBLYMU3Tp5IkuRL4Ik3TM7/z7QYBgwDat2+/zbBhw+pYubBmz55N69atY9fQN3gm+eOZ5JPnkj+eST55LvmTxzOZObMpxxyzNdOmhU+SLbfcQi6//P/YaKPZkZs1nDyeS7krhjPp0qXL1DRNO333el2G52rAk2madvw67wycmqZpj+/7Pp06dUqfeeaZWn29hjJlyhQ6d+4cu4a+wTPJH88knzyX/PFM8slzyZ+8ncns2bDLLvD00yE3awaTJoVr5SRv56LiOJMkSZY4PGv9Vts0TT8EpiVJstHXl3YF/lXbH0+SJEmKbf586NcvG51JAnffXX6jU6pvdb2r7THA3V/f0fYN4JAf+faSJElSLi1aBAMHhs9xLnbtteGOtpLqpk7DM03T/wP+52VUSZIkqZikKRx3XHg252LnnANHHhmtklRS6nJXW0mSJKkkDBkCV1+d5aOOgrPOitdHKjUOT0mSJJW1m26CM87I8l57wVVXhc93SqofDk9JkiSVrdGjv/122l13hT//GRo3jtdJKkUOT0mSJJWlKVNg333DTYUAttkG7r8fmjePWksqSQ5PSZIklZ1nn4XevcPjUwA22CA8q7NNm7i9pFLl8JQkSVJZef116NoVZs0KefXVwyNUVlklbi+plDk8JUmSVDY+/BAqK+Hjj0NeYQWoqoKOHaPWkkqew1OSJEllYebM8ErnG2+E3KIFjBsHW2wRt5dUDhyekiRJKnnz5sEee8Bzz4XcuDHcdx/stFPcXlK5cHhKkiSppC1cGO5e++ij2bVbboFeveJ1ksqNw1OSJEklK03DczrHjMmu/elPcPDB0SpJZcnhKUmSpJJ1xhnh1c3FTjwRTjopXh+pXDk8JUmSVJKuvBKGDMnyQQeFVzslNTyHpyRJkkrOPffAccdluUeP8MpnI//0K0XhTz1JkiSVlMmTYeDALO+wQ7iDbdOm8TpJ5c7hKUmSpJLx1FPQr1+4ky3AZpuFZ3W2bBm3l1TuHJ6SJEkqCS+/HN5SO3duyGuvDVVVsOKKcXtJcnhKkiSpBEybBpWVMH16yCuvDNXVsOaacXtJChyekiRJKmrTp4fROW1ayK1awcSJsNFGcXtJyjg8JUmSVLTmzIGePcPbbCHcQOj+++HnP4/bS9K3OTwlSZJUlBYsgAED4MknQ04SuPNO2H33uL0k/S+HpyRJkorOokVw6KEwaVJ27aqrYO+943WS9P0cnpIkSSoqaQonngh33ZVdO/NM+O1v43WS9MMcnpIkSSoqF10EV1yR5UGD4A9/iNdH0o9zeEqSJKlo3HornHZalvv2heuuC5/vlJRfDk9JkiQVhQceCK9uLtalC9x9NzRuHK+TpKXj8JQkSVLuPfYY7LNPuKkQwNZbw5gx0KJF3F6Slo7DU5IkSbn2/PPQuzfMmxfy+uuHu9m2bRu3l6Sl5/CUJElSbr35JlRWwsyZIa+2GlRXQ/v2cXtJWjYOT0mSJOXSRx9BRQV8+GHIbdvC5Mmw3npxe0ladg5PSZIk5c4XX0C3bvD66yE3bw7jxsFWW8XtJal2HJ6SJEnKlXnzoE8fePbZkBs1guHD4Ze/jNtLUu05PCVJkpQbNTVwwAHwyCPZtZtugj32iNdJUt05PCVJkpQLaQpHHw2jRmXXhgyBX/86XidJ9cPhKUmSpFw45xy48cYsH3ccnHpqtDqS6pHDU5IkSdFdcw2ce26W998fLr0UkiReJ0n1x+EpSZKkqB5+eBUGD85y165w223hpkKSSoM/nSVJkhTNgw/ChRduQpqGvN12MHIkNGsWt5ek+uXwlCRJUhRPPw19+8LCheGPpJtsAhMmQKtWkYtJqncOT0mSJDW4V1+F7t1h9uyQO3SAqipYaaW4vSQVhsNTkiRJDeq996CyEj79NOS2bRdQXQ1rrRW3l6TCcXhKkiSpwXz2WRidb78dcsuWcOGFL7DJJnF7SSqsJrELSJIkqTzMnQu9esFLL4XcpAmMGgUtWnwRt5ikgvMVT0mSJBXcggWw117w979n1+64Izw6RVLpc3hKkiSpoNIUDj883LF2sSuugP33j9dJUsNyeEqSJKmgTjkFhg7N8mmnwbHHxusjqeE5PCVJklQwF18c/lrs17+GCy6I10dSHA5PSZIkFcTQoXDyyVnu0wduuAGSJF4nSXE4PCVJklTvxo8Pr24u9stfwj33hDvZSio/Dk9JkiTVq7/9DQYMgJqakLfaCsaOheWWi9tLUjwOT0mSJNWbF1+Enj1h3ryQ110XJk2C5ZeP20tSXA5PSZIk1Yu334bKSpgxI+RVV4Xqalh99bi9JMXn8JQkSVKdffIJVFTA+++H3KYNTJ4MP/lJ3F6S8sHhKUmSpDqZNQu6d4d//zvkZs3ggQdg663j9pKUHw5PSZIk1dpXX0HfvvDMMyE3agT33gtdusTtJSlfHJ6SJEmqlZoaGDgQ/vKX7Nr114chKknf5PCUJEnSMktTOPZYGD48u3beeTBoULxOkvLL4SlJkqRldv75cO21Wf7tb+H3v4/XR1K+OTwlSZK0TG64Ac46K8v77ANXXglJEq+TpHxzeEqSJGmpjRwJRx2V5d13h6FDw02FJOn7+EuEJEmSlsrDD8P++4fPdwL8/OcwalR4fIok/RCHpyRJkn7UP/8Je+wB8+eHvNFGMGECtGkTt5ek4uDwlCRJ0g967TXo2hVmzw55zTWhqgpWWSVuL0nFw+EpSZKk7/XBB1BRAZ98EnK7dmF0rrNO3F6SiovDU5IkSUs0Y0Z4pfOtt0JebjkYPx422yxqLUlFyOEpSZKk//Hll9C7Nzz/fMiNG8OIEbDDDnF7SSpODk9JkiR9y8KF4dmcf/1rdu2226BHj3idJBU3h6ckSZL+K03hiCNg7Njs2iWXwEEHxeskqfg5PCVJkvRfp58eXt1c7OST4cQT4/WRVBocnpIkSQLg8svhj3/M8sEHfztLUm05PCVJksRdd8EJJ2+t+asAAB6hSURBVGS5Z0+4+WZIknidJJUOh6ckSVKZmzQJDjkkyzvuCMOHQ5Mm8TpJKi0OT0mSpDL2xBPQr1+4ky3A5pvDuHHQsmXcXpJKi8NTkiSpTP3rX+ERKV9+GfI660BVFbRrF7eXpNLj8JQkSSpD77wDlZXw+echr7wyVFfDGmvE7SWpNDk8JUmSysynn4bR+e67IbduHT7nueGGcXtJKl0OT0mSpDIye3a4Y+0rr4TctCncfz906hS3l6TS5vCUJEkqE/PnQ//+8NRTISdJeIzKbrvF7SWp9Dk8JUmSysCiRXDwweHmQYtdey3stVe0SpLKiMNTkiSpxKUpHH883Htvdu3ss+HII+N1klRe6jw8kyRpnCTJs0mSjK+PQpIkSapfF14IV12V5SOPDMNTkhpKfbzieSzwcj38OJIkSapnt9wCv/99lvv3h6uvDp/vlKSGUqfhmSRJB6AHcEv91JEkSVJ9uf9+OOKILO+yS7iZUOPG8TpJKk91fcXzCuBkYFE9dJEkSVI9efRR2HffcFMhgJ/9DMaMgebN4/aSVJ6SNE1r9x2TpCfQPU3To5Ik6Qz8Lk3Tnkv4doOAQQDt27ffZtiwYXWoW3izZ8+mdevWsWvoGzyT/PFM8slzyR/PJJ/K4Vxef701xx33U+bMaQLAmmvO5eqrn6VduwWRmy1ZOZxJMfJc8qcYzqRLly5T0zT9nycD12V4XggcCCwEWgBtgdFpmh7wfd+nU6dO6TPPPFOrr9dQpkyZQufOnWPX0Dd4JvnjmeST55I/nkk+lfq5/Oc/sOOO8NFHIa++Ovztb7DuunF7/ZBSP5Ni5bnkTzGcSZIkSxyetX6rbZqmp6Vp2iFN047APsDDPzQ6JUmSVFgffgiVldnoXH55mDw536NTUnnwOZ6SJEklYOZM6NYtvOIJ0KIFjBsHW24Zt5ckATSpjx8kTdMpwJT6+LEkSZK0bObNgz594P/+L+TGjWH4cNh557i9JGkxX/GUJEkqYjU1sN9+MGVKdu3mm6F372iVJOl/ODwlSZKKVJrCkUeG53UudtFFcMgh8TpJ0pI4PCVJkorUWWeFVzcXO+EEOOmkeH0k6fs4PCVJkorQ1VfD+edn+cAD4eKLIUnidZKk7+PwlCRJKjL33guDB2e5e3e49VZo5J/sJOWUvzxJkiQVkaoqOOigLG+/Pdx3HzRtGq+TJP0Yh6ckSVKR+Mc/oF8/WLgw5E03hfHjoVWruL0k6cc4PCVJkorAK6+Et9TOmRPyWmuFVz9XXDFuL0laGg5PSZKknHv3XaiogOnTQ15pJaiuhg4d4vaSpKXl8JQkScqxzz6DykqYNi3kVq1g4kTYeOO4vSRpWTg8JUmScmruXOjZE/71r5CbNoXRo2HbbeP2kqRl5fCUJEnKoQULYMAAeOKJ7NrQoeEtt5JUbByekiRJObNoERx6aHhL7WJXXgn77huvkyTVhcNTkiQpR9IUTjoJ7roru3bGGTB4cLxOklRXDk9JkqQcufhiuOyyLA8aBOeeG6+PJNUHh6ckSVJO3H47nHJKlvv2heuugySJ10mS6oPDU5IkKQfGjoXDD89y585w993QuHG0SpJUbxyekiRJkf31r7D33lBTE/JPfwpjxkCLFnF7SVJ9cXhKkiRF9Pzz0KsXzJsX8nrrwaRJsPzycXtJUn1yeEqSJEXy5pvQtSvMnBly+/ZQXQ2rrRa3lyTVN4enJElSBB9/DBUV8MEHIbdtC5Mnw/rrx+0lSYXg8JQkSWpgX3wB3brB66+H3Lx5uLnQT38at5ckFYrDU5IkqQF99RXsuSf8858hN2oE994Lv/pV3F6SVEgOT0mSpAZSUwMHHAAPP5xdu/HGMEQlqZQ5PCVJkhpAmsJvfwsjR2bXLrgADjssXidJaigOT0mSpAbwhz/ADTdk+dhj4bTT4vWRpIbk8JQkSSqw664Lw3Ox/faDyy6DJInXSZIaksNTkiSpgO67L7zFdrHKSrj99nBTIUkqF/6SJ0mSVCB/+Uu4mVCahrzttuEzns2axe0lSQ3N4SlJklQAzzwT7la7YEHIG28MEyZA69Zxe0lSDA5PSZKkevbvf0O3bjB7dsgdOkBVFay8ctxekhSLw1OSJKkevf8+VFTAp5+G3K5dGJ1rrx23lyTF5PCUJEmqJ59/Hm4e9PbbIbdsGd5eu+mmcXtJUmwOT0mSpHowdy706gUvvhhykybhRkLbbx+3lyTlgcNTkiSpjhYuhL33hr/9Lbt2++3hc56SJIenJElSnaQpHH44jB+fXbvssvAYFUlS4PCUJEmqg1NPhTvu+HY+/vhodSQplxyekiRJtXTppfCnP2X50ENhyJB4fSQprxyekiRJtfDnP8PvfpflPfaAG2+EJInXSZLyyuEpSZK0jCZMCK9uLrbzznDvveFOtpKk/+XwlCRJWgZ//zsMGAA1NSFvuSWMHQvLLRe3lyTlmcNTkiRpKb34IvToAV9+GXLHjjB5MqywQtRakpR7Dk9JkqSl8PbbUFkJM2aEvMoqUF0Nq68et5ckFQOHpyRJ0o/45BOoqID33w+5TZvwSucGG8TtJUnFwuEpSZL0A2bPDm+v/fe/Q27WDMaMgZ/9LG4vSSomDk9JkqTvMX8+9O0LTz8dcpLA3XfDLrvE7SVJxcbhKUmStASLFsHAgfDgg9m1666D/v3jdZKkYuXwlCRJ+o40hWOPhWHDsmt/+AP85jfxOklSMXN4SpIkfccFF8A112T56KPhzDPj9ZGkYufwlCRJ+oYbb/z2yNx7b7jqqvD5TklS7Tg8JUmSvjZqFBx1VJZ32w2GDoVG/olJkurEX0YlSZKARx6B/fYLNxUC6NQJRo+G5s3j9pKkUuDwlCRJZe/ZZ2GPPcLjUwA23BAmToQ2beL2kqRS4fCUJEll7fXXoWtXmDUr5DXWgKoqWGWVuL0kqZQ4PCVJUtn64AOoqICPPw55hRXC6OzYMWotSSo5Dk9JklSWZsyAbt3gzTdDbtECxo+HzTeP20uSSpHDU5IklZ0vvwyf6XzuuZAbN4YRI2DHHeP2kqRS5fCUJEllpaYmYb/94LHHsmu33go9e8brJEmlrknsApIkSQ0lTeGyyzZk4sTs2sUXw8CB8TpJUjnwFU9JklQ2zjgDJk5c/b/5d78Lf0mSCsvhKUmSysIVV8CQIVkeOBAuuiheH0kqJw5PSZJU8u6+G44/Pss9e8LNN0Mj/yQkSQ3CX24lSVJJmzwZDj44y5tvPpPhw6Fp02iVJKnsODwlSVLJeuop6NcPFi4MefPNYciQF2jZMm4vSSo3Dk9JklSSXn4ZuneHuXNDXmed8OpnmzYL4xaTpDLk8JQkSSVn2jSoqIDPPgt55ZWhqgrWXDNuL0kqVw5PSZJUUqZPD6Pz3XdDbtUKJk6EjTaK20uSypnDU5IklYw5c6BHD3jllZCbNoX774ef/zxuL0kqdw5PSZJUEhYsgP79ww2FAJIE7roLdt89bi9JksNTkiSVgEWL4JBDws2DFrv6athrr3idJEkZh6ckSSpqaQonngh3351dO+ssOProeJ0kSd/m8JQkSUXtoovgiiuyfMQRcM450epIkpbA4SlJkorWLbfAaadluV8/uPba8PlOSVJ+ODwlSVJRGjMmvLq52C67hLfbNm4cr5MkackcnpIkqeg89hjss0+4qRDAz34WHpvSvHncXpKkJXN4SpKkovLcc9CrF3z1Vcg/+QlMnAht28btJUn6fg5PSZJUNN54A7p2hS++CHm11aC6Gtq3j9tLkvTDHJ6SJKkofPQRVFTAhx+GvPzyUFUF664bt5ck6cc5PCVJUu598QV06wb/+U/ILVrAuHGw5ZZxe0mSlo7DU5Ik5dq8edCnDzz7bMiNGsHw4bDzznF7SZKWXq2HZ5IkayVJ8kiSJC8nSfJSkiTH1mcxSZKkmhrYf3945JHs2s03Q+/e8TpJkpZdkzp834XAiWma/jNJkjbA1CRJHkzT9F/11E2SJJWxNIWjj4bRo7NrF14Ihx4ar5MkqXZq/YpnmqYfpGn6z6//eRbwMrBmfRWTJEnl7eyz4cYbs3z88XDKKfH6SJJqr14+45kkSUdga+Cp+vjxJElSebvmGjjvvCwfcABccgkkSbxOkqTaS9I0rdsPkCStgUeBC9I0Hb2Efz8IGATQvn37bYYNG1anr1dos2fPpnXr1rFr6Bs8k/zxTPLJc8kfz6R2Hn54Vc4/fxPSNKzMbbedzgUXvEiTJnX7M8tinkv+eCb55LnkTzGcSZcuXaamadrpu9frNDyTJGkKjAeq0jS97Me+fadOndJnnnmm1l+vIUyZMoXOnTvHrqFv8EzyxzPJJ88lfzyTZffgg9CjByxYEPIvfgF/+Qu0alV/X8NzyR/PJJ88l/wphjNJkmSJw7Mud7VNgFuBl5dmdEqSJP2Qp5+GPffMRucmm8D48fU7OiVJcdTlM547AgcCuyRJ8n9f/9W9nnpJkqQy8uqr0K0bzJkT8lprQVUVrLRS3F6SpPpR68eppGn6OOBH/CVJUp289x5UVMD06SGvuGIYnWutFbeXJKn+1MtdbSVJkmrjs8+gshLeeSfkli1h4sTwNltJUulweEqSpCjmzoVeveCll0Ju0gRGj4bttovbS5JU/xyekiSpwS1YAHvtBX//e3Zt6NDw6qckqfQ4PCVJUoNatAgOOwwmTMiuXXkl7LdfvE6SpMJyeEqSpAZ1yinw5z9n+fTTYfDgeH0kSYXn8JQkSQ3m4ovhkkuyfNhhcP758fpIkhqGw1OSJDWIO+6Ak0/Ocp8+cP31kPhwNkkqeQ5PSZJUcOPGhVc3F/vVr+Dee8OdbCVJpc/hKUmSCurxx8MdbGtqQt5qK3jgAWjRIm4vSVLDcXhKkqSCeeGF8KzOefNCXm89mDwZll8+bi9JUsNyeEqSpIJ4663wXM4ZM0Ju3x6qq2G11aLWkiRF4PCUJEn17uOPoaICPvgg5DZtYNIkWH/9uL0kSXE4PCVJUr2aNQu6d4fXXgu5WTMYOxa23jpuL0lSPA5PSZJUb776CvbcE6ZODblRo3D32s6do9aSJEXm8JQkSfWipgYOPBAeeii7dsMN0LdvvE6SpHxweEqSpDpLUxg8GEaMyK6dfz4cfni8TpKk/HB4SpKkOjvvPLjuuiwfcwycfnq8PpKkfHF4SpKkOrnhBjj77Czvuy9ccQUkSbxOkqR8cXhKkqRaGzkSjjoqyxUVcMcd4aZCkiQt5m8LkiSpVh56CPbfP3y+E2DbbWHUqPD4FEmSvsnhKUmSltnUqdCnD8yfH/JGG8GECdC6ddxekqR8cnhKkqRl8tpr0K0bzJ4d8pprQnU1rLxy3F6SpPxyeEqSpKX2/vvhc5yffBJyu3ZQVQVrrx23lyQp3xyekiRpqcyYAV27wltvhbzccuHttZttFrWWJKkIODwlSdKP+vJL6NULXngh5MaNwx1tt98+bi9JUnFweEqSpB+0cCHsvTc8/nh27fbboXv3eJ0kScXF4SlJkr5XmsKgQTBuXHbt0kvhwAPjdZIkFR+HpyRJ+l6nnRZe3VzslFPghBPi9ZEkFSeHpyRJWqLLLoOLLsryIYfAhRfG6yNJKl4OT0mS9D/uvBNOPDHLvXvDTTdBksTrJEkqXg5PSZL0LRMnwqGHZnmnnWDYMGjSJF4nSVJxc3hKkqT/euIJ6N8/3MkWYIstYOzY8MxOSZJqy+EpSZIAeOkl6NEjPLMToGNHmDwZ2rWLWkuSVAIcnpIkiXfegcpK+PzzkFdZBaqrYY014vaSJJUGh6ckSWXu00+hogLeey/k1q1h0iTYYIO4vSRJpcPhKUlSGZs9O7y99tVXQ27WDMaMgW22idtLklRaHJ6SJJWp+fOhXz/4xz9CThK46y7Ydde4vSRJpcfhKUlSGVq0CA4+OHyOc7Frr4UBA6JVkiSVMIenJEllJk3h+OPh3nuza+ecA0ceGa2SJKnEOTwlSSozQ4bAVVdl+aij4Kyz4vWRJJU+h6ckSWXk5pvhjDOyPGBAGKFJEq+TJKn0OTwlSSoTo0fDb36T5V13hTvvhMaN43WSJJUHh6ckSWVgyhTYd99wUyEIj0u5/35o3jxqLUlSmXB4SpJU4p59Fnr3Do9PAdhgA5g4Edq0idtLklQ+HJ6SJJWw//wHunWDWbNCXn318AiVVVeN20uSVF4cnpIklagPP4SKCvjoo5BXWAGqqqBjx6i1JEllyOEpSVIJmjkTunaFN94IuUULGDcOttgibi9JUnlyeEqSVGLmzYM99oDnngu5cWO47z7Yaae4vSRJ5cvhKUlSCVm4MNy99tFHs2u33AK9esXrJEmSw1OSpBKRpnDkkTBmTHbtT3+Cgw+OVkmSJMDhKUlSyTjzzPDq5mInnggnnRSvjyRJizk8JUkqAVddBRdckOWDDgqvdkqSlAcOT0mSitw998Cxx2a5R4/wymcjf5eXJOWEvyVJklTEJk+GgQOzvMMO4Q62TZvG6yRJ0nc5PCVJKlJPPQX9+oU72QJstll4VmfLlnF7SZL0XQ5PSZKK0Msvh7fUzp0b8tprh1c/V1wxbi9JkpbE4SlJUpGZNg0qK2H69JBXXhmqq6FDh7i9JEn6Pg5PSZKKyPTpYXROmxZyq1YwcSJstFHcXpIk/RCHpyRJRWLOHOjZM7zNFsINhO6/H37+87i9JEn6MQ5PSZKKwIIFMGAAPPlkyEkCf/4z7L573F6SJC0Nh6ckSTm3aBEceihMmpRdu/JK2GefeJ0kSVoWDk9JknIsTeF3v4O77squnXkmHHNMvE6SJC0rh6ckSTn2pz/B5ZdnedAg+MMf4vWRJKk2HJ6SJOXUbbfBqadmuW9fuO668PlOSZKKicNTkqQcGjsWDj88y507w913Q+PG0SpJklRrDk9JknLmscdg773DTYUAtt4aHngAWrSI20uSpNpyeEqSlCPPPw+9e8O8eSGvv364m23btnF7SZJUFw5PSZJy4s03obISZs4MebXVoLoa2reP20uSpLpyeEqSlAMffwwVFfDhhyG3bQuTJ8N668XtJUlSfXB4SpIU2RdfQLdu8PrrITdvDuPGwVZbxe0lSVJ9cXhKkhTRV1/BnnvCP/8ZcqNGMGwY/PKXcXtJklSfHJ6SJEVSUwMHHAAPP5xdu/FG6NMnXidJkgrB4SlJUgRpCkcfDSNHZteGDIHDDovXSZKkQnF4SpIUwTnnhFc3FzvuODj11Gh1JEkqKIenJEkN7Npr4dxzs7z//nDppZAk8TpJklRIDk9JkhrQfffBMcdkuWtXuO22cFMhSZJKlb/NSZLUQP7yl3AzoTQNebvtwmc8mzWL20uSpEJzeEqS1ACefjrcrXbBgpA32QQmTIBWreL2kiSpITg8JUkqsFdfhe7dYc6ckDt0gKoqWGmluL0kSWooDk9JkgrovfegshI+/TTkFVcMo3OtteL2kiSpIdVpeCZJ0jVJkleTJHk9SRJvAi9J0jfMmtWErl3h7bdDbtkyvL12003j9pIkqaHVengmSdIYuBboBmwK7Jskib+VSpIEzJ0Lp5++BS++GHKTJjBqFPziF3F7SZIUQ5M6fN9tgdfTNH0DIEmSYcAewL/qo1hDa98evvoKFi7ciSZ1+a+ieueZ5I9nkk+eS74sWABz5y7/33zHHeHRKZIklaO6/BFlTWDaN/K7wHZ1qxPPzJlheNbtP4kKwzPJH88knzyXvLr8cth//9gtJEmKpy5/SkmWcC39n2+UJIOAQQDt27dnypQpdfiShbNo0S/xXkuSpPrUqFHKwIFv8dOfvk1Of/srS7Nnz87tn0fKlWeST55L/hTzmdRleL4LfPOefB2A97/7jdI0vQm4CaBTp/9v715DLavLOI5/f2gKaTCG90s2Lyy6vOgyaKHJAW00ES+RMQYlFaSRkS8CM6Ek35hl0IWysgED04SypMa8UFK+MC/DpI6jOdVYo4NTCZoYxeTTi73SM8e95+xmZu21zqzvB4a9z/r/9znPmWc9a69n7/9eZ0XNzc3two9sz9ato9u77rqLE044odtgtB1z0j/mpJ/MS//cc89vWLnyRGB516FonjvvvJO+no8MlTnpJ/PSP0s5J7vSeN4LHJNkOfAEsAr4wG6JqgPLlo1u999/24v31Q/mpH/MST+Zl/7ZZ58Xug5BkqRe2OnGs6q2JbkQuBXYC1hdVet3W2SSJEmSpD3CLl2JoqrWAGt2UyySJEmSpD2QV9ORJEmSJLXKxlOSJEmS1CobT0mSJElSq2w8JUmSJEmtsvGUJEmSJLXKxlOSJEmS1CobT0mSJElSq2w8JUmSJEmtsvGUJEmSJLXKxlOSJEmS1CobT0mSJElSq2w8JUmSJEmtsvGUJEmSJLXKxlOSJEmS1CobT0mSJElSq2w8JUmSJEmtsvGUJEmSJLUqVTW7H5b8FXh8Zj9w5xwI/K3rILQdc9I/5qSfzEv/mJN+Mi/9Y076ybz0z1LIydFVddDCjTNtPJeCJPdV1Yqu49BLzEn/mJN+Mi/9Y076ybz0jznpJ/PSP0s5Jy61lSRJkiS1ysZTkiRJktQqG8+X+07XAehlzEn/mJN+Mi/9Y076ybz0jznpJ/PSP0s2J37GU5IkSZLUKt/xlCRJkiS1anCNZ5JzkqxP8kKSFQvGLkmyMcmjSU6Z8PhXJ7k9yWPN7QGziXw4kvwwybrm36Yk6ybM25TkwWbefbOOc0iSXJbkiXl5OW3CvFOb+tmY5DOzjnNoknwpySNJHkhyU5JlE+ZZKy1bbN/PyNea8QeSvK2LOIckyVFJfpVkQ/O8/6kxc+aSPDPv2Pa5LmIdksWOR9bK7CV5/bwaWJfk2SQXLZhjrbQsyeokW5M8NG/bVH3HUjn/GtxS2yRvAF4Avg18uqrua7a/EbgeOBY4HLgDeF1V/WfB468Enq6qK5rEHlBVF8/ydxiSJFcBz1TVF8aMbQJWVFXf/5bRkpfkMuC5qvryDubsBfweeDewGbgXOLeqHp5JkAOUZCXwy6raluSLAOOOR9ZKu6bZ95sXaz4JnAYcB3y1qo7rINzBSHIYcFhVrU3yKuB+4KwFeZljdC5wekdhDs5ixyNrpVvN8ewJ4Liqenze9jmslVYlORF4Dvh+Vb252bZo37GUzr8G945nVW2oqkfHDJ0J3FBV/6qqPwEbGTWh4+Zd29y/FjirnUiVJMD7Gb0goP47FthYVX+sqn8DNzCqF7Wkqm6rqm3Nl3cDR3YZz4BNs++fyehkoqrqbmBZ0xipJVW1parWNvf/AWwAjug2Kk3BWunWScAf5jedmo2q+jXw9ILN0/QdS+b8a3CN5w4cAfxl3tebGf8EdUhVbYHRkxpw8AxiG6p3AU9V1WMTxgu4Lcn9ST42w7iG6sJm2dPqCUs9pq0hteMjwC0TxqyVdk2z71sfHUryWuCtwG/HDL8zye+S3JLkTTMNbJgWOx5ZK91axeQX/K2V2Zum71gyNbN31wG0IckdwKFjhi6tqp9OetiYbcNahzxDU+boXHb8bufxVfVkkoOB25M80rxapJ2wo5wA3wIuZ1QTlwNXMWp0tvsWYx5rDe2iaWolyaXANuC6Cd/GWmnXNPu+9dGRJPsDPwIuqqpnFwyvBY6uqueaJZ4/AY6ZdYwDs9jxyFrpSJJ9gDOAS8YMWyv9tWRqZo9sPKvq5J142GbgqHlfHwk8OWbeU0kOq6otzdKPrTsT49AtlqMkewPvBd6+g+/xZHO7NclNjJYaeDK9k6atmyTfBX42ZmjaGtL/YYpaOQ84HTipJnxo31pp3TT7vvXRgSSvYNR0XldVP144Pr8Rrao1Sb6Z5EA/D92eKY5H1kp33gOsraqnFg5YK52Zpu9YMjXjUtuX3AysSrJvkuWMXsW5Z8K885r75wGT3kHVrjkZeKSqNo8bTLJfc7EIkuwHrAQeGjdXu27B52vOZvz/9b3AMUmWN6+armJUL2pJklOBi4Ezqur5CXOslfZNs+/fDHyouWLnOxhdNG3LrAMdkuY6Ad8DNlTVVybMObSZR5JjGZ0X/X12UQ7LlMcja6U7E1eaWSudmabvWDLnX3vkO547kuRs4OvAQcDPk6yrqlOqan2SG4GHGS1Z+8T/rmib5Brg6uYKuFcANyb5KPBn4JxOfpE938s+Y5DkcOCaqjoNOAS4qTkG7g38oKp+MfMoh+PKJG9htHRjE3A+bJ+T5sqqFwK3AnsBq6tqfVcBD8Q3gH0ZLVcDuLuqLrBWZmvSvp/kgmb8amANo6t0bgSeBz7cVbwDcjzwQeDBvPRnuT4LvAZezMv7gI8n2Qb8E1g1aeWAdouxxyNrpXtJXsnoqqjnz9s2Py/WSsuSXA/MAQcm2Qx8ngl9x1I9/xrcn1ORJEmSJM2WS20lSZIkSa2y8ZQkSZIktcrGU5IkSZLUKhtPSZIkSVKrbDwlSZIkSa2y8ZQkSZIktcrGU5IkSZLUKhtPSZIkSVKr/gvSFKshl8E+sAAAAABJRU5ErkJggg==\n",
104 |       "text/plain": [
105 |        "<Figure size 1152x648 with 1 Axes>"
106 |       ]
107 |      },
108 |      "metadata": {
109 |       "needs_background": "light"
110 |      },
111 |      "output_type": "display_data"
112 |     }
113 |    ],
114 |    "source": [
115 |     "plt.figure(figsize=(16,9))\n",
116 |     "plt.plot(data_input, data_output, linewidth=3, color='blue')\n",
117 |     "plt.grid()\n",
118 |     "plt.show()"
119 |    ]
120 |   }
121 |  ],
122 |  "metadata": {
123 |   "kernelspec": {
124 |    "display_name": "Python 3",
125 |    "language": "python",
126 |    "name": "python3"
127 |   },
128 |   "language_info": {
129 |    "codemirror_mode": {
130 |     "name": "ipython",
131 |     "version": 3
132 |    },
133 |    "file_extension": ".py",
134 |    "mimetype": "text/x-python",
135 |    "name": "python",
136 |    "nbconvert_exporter": "python",
137 |    "pygments_lexer": "ipython3",
138 |    "version": "3.7.10"
139 |   }
140 |  },
141 |  "nbformat": 4,
142 |  "nbformat_minor": 4
143 | }
144 | 


--------------------------------------------------------------------------------
/jupyter_notebooks/funcao_sigmoid.ipynb:
--------------------------------------------------------------------------------
  1 | {
  2 |  "cells": [
  3 |   {
  4 |    "cell_type": "markdown",
  5 |    "metadata": {},
  6 |    "source": [
  7 |     "# Função Sigmoid\n",
  8 |     "\n",
  9 |     "A **função Sigmoid** é uma função matemática que tem a característica de uma curva com formato de 'S' ou 'curva sigmoid'. \n",
 10 |     "\n",
 11 |     "Frequentemente, a função sigmoid refere-se ao caso especial de [função logística](https://pt.wikipedia.org/wiki/Fun%C3%A7%C3%A3o_log%C3%ADstica), ela é limitada, diferenciável e real e é definida para todos os valores de entrada reais e tem uma derivada não-negativa em cada ponto. \n",
 12 |     "\n",
 13 |     "Ela é definida pela fórmula:\n",
 14 |     "\n",
 15 |     "\\begin{equation}\n",
 16 |     "\\sigma(x)=\\frac{1}{1+e^{-x}}\n",
 17 |     "\\end{equation}\n",
 18 |     "\n",
 19 |     "Como podemos observar, ela basicamente recebe um número de valor real como entrada e coloca ele entre $0$ e $1$. Seu objetivo é introduzir não-linearidade no espaço de entrada. Baseado na representação matemática acima, um número negativo grande passado pela função sigmoid se torna $0$ e um número positivo grande se torna $1$. \n",
 20 |     "\n",
 21 |     "Por causa desta propriedade, a função sigmoid normalmente tem uma interpretação associada com a taxa de disparo de um neurônio em [Deep Neural Networks](https://www.kdnuggets.com/2020/02/deep-neural-networks.html), onde o não disparo seria dado como $0$, para um disparo completamente saturado em uma frequência máxima assumida, nesse caso seria $1$. Entretanto, é válido lembrar que a função de ativação sigmoid se tornou menos popular nas aplicações de redes neurais por questões técnicas, as funções mais utilizadas atualmente nesse contexto são as funções de Unidade Linear Retificada ([ReLU](https://machinelearningmastery.com/rectified-linear-activation-function-for-deep-learning-neural-networks/)).\n",
 22 |     "\n",
 23 |     "Vamos então importar as bibliotecas necessárias para vermos um exemplo da função sigmoid em ação:"
 24 |    ]
 25 |   },
 26 |   {
 27 |    "cell_type": "code",
 28 |    "execution_count": 1,
 29 |    "metadata": {},
 30 |    "outputs": [],
 31 |    "source": [
 32 |     "import matplotlib.pyplot as plt\n",
 33 |     "import numpy as np"
 34 |    ]
 35 |   },
 36 |   {
 37 |    "cell_type": "markdown",
 38 |    "metadata": {},
 39 |    "source": [
 40 |     "Definimos a função sigmoid:"
 41 |    ]
 42 |   },
 43 |   {
 44 |    "cell_type": "code",
 45 |    "execution_count": 2,
 46 |    "metadata": {},
 47 |    "outputs": [],
 48 |    "source": [
 49 |     "def sigma(x):\n",
 50 |     "    return 1 / (1 + np.exp(-x))"
 51 |    ]
 52 |   },
 53 |   {
 54 |    "cell_type": "markdown",
 55 |    "metadata": {},
 56 |    "source": [
 57 |     "Definimos os valores de entrada **X**:"
 58 |    ]
 59 |   },
 60 |   {
 61 |    "cell_type": "code",
 62 |    "execution_count": 3,
 63 |    "metadata": {},
 64 |    "outputs": [],
 65 |    "source": [
 66 |     "X = np.linspace(-5, 5, 100)"
 67 |    ]
 68 |   },
 69 |   {
 70 |    "cell_type": "markdown",
 71 |    "metadata": {},
 72 |    "source": [
 73 |     "Calculamos os valores de saída **Y**:"
 74 |    ]
 75 |   },
 76 |   {
 77 |    "cell_type": "code",
 78 |    "execution_count": 4,
 79 |    "metadata": {},
 80 |    "outputs": [],
 81 |    "source": [
 82 |     "Y = sigma(X)"
 83 |    ]
 84 |   },
 85 |   {
 86 |    "cell_type": "markdown",
 87 |    "metadata": {},
 88 |    "source": [
 89 |     "Plotamos o gráfico da função sigmoid:"
 90 |    ]
 91 |   },
 92 |   {
 93 |    "cell_type": "code",
 94 |    "execution_count": 14,
 95 |    "metadata": {},
 96 |    "outputs": [
 97 |     {
 98 |      "data": {
 99 |       "image/png": "iVBORw0KGgoAAAANSUhEUgAAA7AAAAIoCAYAAABQ/wdYAAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADh0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uMy4xLjMsIGh0dHA6Ly9tYXRwbG90bGliLm9yZy+AADFEAAAgAElEQVR4nOzdeXgV5fn/8fcTFgFlEQVEoO6tKF+RCuJSEVu1aN0ooiiCUDe0Ki7U4lLc99aCtXVXEBVXrNaiArYU9VcsLlhXLFpEoIC4oGGRJfP740k8CSQhQE4mOef9uq65ztwzc+bciUfxwzzzTEiSBEmSJEmSaruCtBuQJEmSJKkqDLCSJEmSpDrBACtJkiRJqhMMsJIkSZKkOsEAK0mSJEmqEwywkiRJkqQ6wQArSar1QgiDQghJBcvBKffWKITwaghhQQihfwjhjBDC/dX8GXuGEJ4MIcwJIXwbQvhfCOHvIYRzSx2zffHvY1B1fnZ1Ku7viiocNyWEMCX7HUmS6pr6aTcgSdIG6AvMXWvbe2k0UsqBxL8QPh+4GGgN/Ly6Th5C6Aa8BLwKXAQsANoDPwJ6A7cWH/o/YF/go+r67CzYl3X/+UmSVGUhSZK0e5AkqVLFVxXvB3ZJkmRWyu3UqBDCA8ChwHZJkny71r6CJEmK0ukse0quviZJ0jPdTiRJtY1DiCVJOaHUMOPt19p+RQghWWtbEkK4JoRwbgjhvyGEb0II/wgh7F7OeXuHEF4JIRSGEL4OIfwrhHBUqf1nhxD+GUL4IoTwVQhhWgjhZ+Wcp20I4YEQwuLiYcD/DiGcVIUfrSXw5drhFaB0eK1oCHEIYWgIYXYIYUVx7/sV16PL+d3tF0J4rPj3sTCEcHHx/l4hhDdDCEtDCNNDCHut9RkhhHB+CGFmCGFl8RDn20IIzcr5vV+x1rZ+IYQPin8n74YQelfhdyJJylMGWElSXVIvhFC/1FJvE851EvAzYCgwGPge8HQI4bvba0II5wDjgUXAycQhzE8B25c6z/bAPcX7jgdeA54NIRxW6jybA/8ADgMuAY4B3gbGhhBOX0+f/wJ2DSHcEULYu3R/6xNCOBUYCUwGjgZGAw8DLSp4y5jivnoDfwauCyHcCNwM3Fj8820O/DmE0LDU+64FbgEmAUcCNwGDgL+GECr8f43i+5cfBv5DHHZ9MzAK+EFVf0ZJUn7xHlhJUl3ywVr1K8R7QTfGKuCIJElWAYQQAB4H9gb+X/HVw+uAp5IkKX1P6wulT5IkybCS9eKw9iLwfWAI8FzxrsHALsBBSZJMKd72XAihDXBNCOHeJEnWVNDnzUAX4IziZXkI4eXiXu+r6H3FvVwOPJckyamlti8Anqzgs8YmSXJ18XFTiEH2AuD7SZL8t9R5nybez/qPEELL4mPGJElydsnvKITwGTAWOAJ4poLPu5L4z/TokqvJIYT3gWnAzAreI0nKY16BlSTVJb2BbqWWUzbhXJNKwmuxt4tfv1f8uh+wBXBXZScJIewVQng2hLAQWE0MxodQ9ipiD2BeqfBa4kGgFbBbRedPkmR5kiS9gd2BXxFDcdfiviaE4uRdjvbFy+NrbX+6uM/ylARukiRZDcwCPiwJr8VK/hKhQ/HrPsBmxT9LaY8Uf86B5X1Q8dXzbsATpYdCJ0nyKjC7gv4kSXnOK7CSpLrknWqcxOmLteqSe0wbFb9uVfxa4ay5IYQOxCuu7wHnAHOIoe1qoGOpQ1sSZwle24JS+yuVJMl7xZ9DCKERcDeZYdDPlvOWtsWvi9Y6z5oQwuIKPubLteqVFWyDzO+ppPcyP1+SJKtDCJ9T8c+2NdAAWFjOvvK2SZLkFVhJUs5YUfzacK3tW619YBWVhLx2lRzTC2gOHJckyWNJkkxLkuQ1oMlax30BbFPO+0u2fb4hjSVJsoI4tBgqvnpbEihbl95YfOVz6w35vPUo+YuAMj9f8b26W1Hxz7aYeLW6TTn7ytsmSZIBVpKUMz4pfu1UsqE4RB26kef7f0AhUNkkSyVB9buhyCGE7wP7r3XcP4D2IYS1t59IvEL6fkUfEEJoX8GuXYtfy7uyC/HK8Vzi5FKlHUP1jsCaRrx63W+t7ccXf84/yntT8b2704FjS0/0FELoTtlJsiRJ+o5DiCVJuWI68BFwc3Eg+hY4i3h/5gZLkuSb4sfI/CGE8CTwEPANsCewIkmSPxBn910NPBBC+B1x2O6VxKHEpf+SeDRxtuPxIYRLicGyP/Fe2TMqmcAJ4I7iyZ7GAu8AJfeOXlT88z5VQf9FIYQrgbtDCPcQ74XdERgOLAGq5fmxSZJ8EUK4Bbg4hLAUmEAcPn0N8DLw10refjkwkTir8Z3E+4GvJDO0WpKkMrwCK0nKCcWTDh0NfEoMjH8kPtZl9Cac8zbiFcz2xJl7JwLHAv8t3v8uMYhuR5xp9yJiQJy61nmWEiczmgjcQJxIqTMwIEmSSieJAv5AvPf1l8Xve5Y4edWDwP5JkhRW0v89wPnEoPx08fv6AwkxxFaXS4kzER9W3N9w4AHgZ6UnaCqnv8nF/fyA+LiiXwHn4QzEkqQKhCRJ1n+UJEl5LoTQgjhcdr8kSdaeAKrOCCF0Iz5bdmCSJGPT7keSpA3hEGJJktYjhPBT4lXLFsQrqeUO261tQgg7EK/cvgR8TRzaewnxCnJFz4KVJKnWytoQ4hDCfSGERSGEdyrYH0IIt4YQZoUQ/h1C+GG2epEkaRNdBvwFmE+c3KmuWE6c1Opu4vDlK4jDm3smSbIsxb4kSdooWRtCHELoQZy98YEkSTqVs/9w4jPzDge6A6OSJOmelWYkSZIkSXVe1q7AJkkylXUfEl/a0cRwmyRJMg1oEUJoW8nxkiRJkqQ8luYsxO2IM0WWmEvlD4uXJEmSJOWxNCdxCuVsK3c8cwjhdIofJN+4ceO9OnTokM2+8l5RUREFBT5hSXWf32XlCr/LygV+j5Ur/C5n34cffrg4SZJW5e1LM8DOBUon0fbEyTHWUfyMvLsAunbtmrz22mvZ7y6PTZkyhZ49e6bdhrTJ/C4rV/hdVi7we6xc4Xe5cmvWwLJlsHRp2aVk27JlZZfly9fd9uGH4ZOKzp9mgH0GODuE8AhxEqclSZL8L8V+JEmSJClvJAmsWAFffw3ffLPuUnp7YeH6l6VL4/myKWsBNoQwDugJbB1CmAtcDjQASJLkDmACcQbiWcAyYHC2epEkSZKkXLNqFSxZAl99Vfny9dfxuCVL1l1ftSrtn2LDZC3AJklywnr2J8SHq0uSJElS3lq1Cj7/PC6LF8fliy/i8uWXmfXSy5dfxquetU0I0KRJXDbfvOxSenuTJtC4cWZbydK4MZx0UsXnT3MIsSRJkiTlnKVL4bPPYNGidV8XLYoBtXRY/frr9Hpt0ACaNYtL06aZZe16iy0yrxUtm28eA2gob7reDWCAlSRJkqRNsGIFLFgA773XjK++iusLFsDChZn1BQtiQF22rGZ6CgFatKh8ad48szRrtu56o0Y102t1McBKkiRJyltr1sTgOX8+zJsXX8tb//LLknf8sNp7KCiAli1h661hq63isvXWsOWWcXvJUrrecssYQvPtiT4GWEmSJEk5KUni0N05c+DTT+Myd25m/dNPY0Bdvbp6P7dhQ2jdOi6tWpVdL6lLQupWW8UrpfkWRDeWAVaSJElSnZQkccju7NnrLp98El+XL6+ez6pXD7bZBjbf/Bt22aUp22zDd0ubNmVfmzbd9PtAVT4DrCRJkqRaa9WqGEZnzYKPPiq7fPxx9QTUVq2gfXvYdtuyS7t2mfVWreJV0ilTXqdnz56b/qHaKAZYSZIkSalasyYO5505Ez78MPM6a1Yc/rtmzcafu1kz2G476NCh/KV9+7o3kVE+M8BKkiRJqhGFhfD++/Dee2XD6n/+A99+u3HnbNECtt8+Ltttl1kvWVq0qK7uVRsYYCVJkiRVq8LCGFLfew/efTfz+sknG3e+du1gp51g553ja+llyy2rt3fVbgZYSZIkSRtlzZp4L+pbb8Xl3/+Oy8YE1dat4Qc/gO9/P/O6yy6www7QuHH19666yQArSZIkab2++QZmzMgE1bfegnfegWXLqn6O+vVjKN1tN+jYMRNUv/99h/qqagywkiRJksr45ht48014/fXMMnNmfGxNVdSvH8PpbrvFZffd4+suu8RnpEobywArSZIk5bEVK2JYffVVeO21DQ+rbdvCHntA585x2WOPGF4bNMhu38pPBlhJkiQpTyRJvD912rS4/POfMbyuWrX+99arF6+idumSCaqdO8fno0o1xQArSZIk5aiVK+NV1ZdeyoTWBQvW/76Cgjjsd6+9MkvnztCkSfZ7lipjgJUkSZJyxNKl8arqSy/B1KkxsK5Ysf737bIL7LMP7L23YVW1mwFWkiRJqqOWLIlBderUGFpffx1Wr678PU2bQvfuMbDuu28MrVtvXTP9SpvKACtJkiTVEd9+G6+wvvgiTJ4M06fHZ7FWZscd4YAD4Ec/iqG1Y8d4P6tUFxlgJUmSpFqqqCg+e7UksL70EixfXvl7OnWCHj1iaD3gAGjXrmZ6lWqCAVaSJEmqRT77DF54ASZMgIkT4fPPKz42hDgrcM+ecOCBsP/+sNVWNdaqVOMMsJIkSVKKiorgjTdiYJ0wAf71r8qfwbrzznDwwfCTn8BBBxlYlV8MsJIkSVINW7Ikc5X1uedg0aKKj23dOhNYf/IT2G67mutTqm0MsJIkSVINWLAAnn4annoK/vY3WLWq/OMKCuLswIcfHpfOneNQYUkGWEmSJClrPvooBtannoqzB1c0NLhVKzjssBhYDzkEWras2T6lusIAK0mSJFWjd96Bxx+PofXttys+7oc/hCOPhJ/9DPbaK155lVQ5A6wkSZK0iWbNgkcfhUceiQG2PAUF8bE2vXvDMcd4L6u0MQywkiRJ0kaYOxceeyyG1unTyz9ms83ikODevePV1latarZHKdcYYCVJkqQq+vzzGFrHjYOXXir/mMaNY1g99th4X+sWW9Rsj1IuM8BKkiRJlVi9Gp5/HkaPhmeeKX/24AYNoFcv6NcPjjrK0CpliwFWkiRJKse778bQOnYsLFy47v6Cgvhc1n794hDhLbes8RalvGOAlSRJkop98UUcHjx6NLz2WvnHdO8OAwbEIcJt2tRoe1LeM8BKkiQpryUJvPwy3H47PPkkrFy57jFt28LAgXDyydCxY833KCkywEqSJCkvLVkCDz4Yg+u77667v2HD+LibQYPiTML1/T9nKXX+ayhJkqS88uabMbQ+/DAsXbru/q5dYfDgeG9ry5Y135+kihlgJUmSlPNWrIBHH43B9dVX192/+ebQvz+ceSbsuWfN9yepagywkiRJylmLFsGf/hSXzz5bd3+nTjG0nnQSNGtW8/1J2jAGWEmSJOWcd9+F3/8+3uP67bdl9zVsGGcQPvNM2H9/CCGdHiVtOAOsJEmSckKSwKRJMbg+//y6+zt0gF/+En7xC2jVqub7k7TpDLCSJEmq0779Nk7IdMst8M476+7v1g0uvBD69HEmYamu819hSZIk1UlLl8Ldd8PNN8P8+WX3FRTER+BccAHst5/DhKVcYYCVJElSnfL11/DHP8YrrosXl923xRZwyilw7rmw447p9CcpewywkiRJqhM+/xxGjYI//AG++qrsvrZt4fzz4bTToEWLdPqTlH0GWEmSJNVqCxbEq61/+lMcNlzadtvB8OEwaBA0apRKe5JqkAFWkiRJtdKiRXD99XDHHbBiRdl9u+wCl1wC/ftDgwbp9Cep5hlgJUmSVKt89RX87nfxcThrX3Ht1AkuvRT69oV69dLpT1J6DLCSJEmqFZYti/e33ngjfPll2X1du8Jll8GRR8YZhiXlJwOsJEmSUrVyJdxzD1x9dbzftbROneDaa2Nw9VE4kgywkiRJSsWaNfDQQ3D55TB7dtl9O+0EV10F/fp5xVVShgFWkiRJNW7yZLjgAnj77bLb27WDESNg8GAnZ5K0Lv8+S5IkSTVm5sw4HPiQQ8qG1622gt/+Fv7zHzj9dMOr8tPUqVM56qijaNeuHSEERo8enXZLtY4BVpIkSVn39df1GTo03tP67LOZ7ZtvHocQf/wxXHghNG6cXo9S2goLC+nUqROjRo2isf8ylMshxJIkScqaVavgT3+C3/ymO998k9keAgwaBNdcA9tum1p7Uq1y+OGHc/jhhwMwaNCgdJuppQywkiRJqnZJEq+0DhsGH34IkBkTfOCBcMst8MMfptaepDrKIcSSJEmqVv/5D/TqBUcdVRJeo512gvHj4e9/N7wKBg4cSOvWrVm6dOlGn+P1118nhMC9995bjZ2pNjPASpIkqVqsWBHvZ+3UCSZOzGxv3hzOPHMW774LvXv7PFfBa6+9xoMPPsjw4cPZfPPNN/o8e+21F8cccwyXXXYZhYWF1dihaisDrCRJkjbZ88/H4HrVVbByZdxWUABnnhmvyB533Fw22yzdHlV7XHLJJTRr1owzzzxzk8918cUXs2DBAm699dZq6Ey1nQFWkiRJG23ePOjbFw47DD76KLN9771h+vQ4gVOrVun1p9rnww8/ZPLkyRx33HHVMtPu3nvvza677sqdd97JmjVrqqFD1WYGWEmSJG2w1avjREy77gpPPJHZ3qIF3H47/L//532u+aSwsJCrrrqKLl260LRpU0II5S6LFi3ivvvuI0kSjj/++HLPdeihhxJCYPz48WW2J0nCoEGDCCEwfPjwMvv69evHnDlzmDx5ctZ+xppQWFjIjBkzmDFjBkVFRcyZM4cZM2YwZ86ctFurNQywkiRJ2iDTpsFee8Xntpa+7XDgQJg5E4YMgXr10utPNWvRokV069aNyy+/nKKiIoYMGcI555zDNttsA0CDBg3Yaaed6N69O61bt2by5MnUq1ePffbZp9zz3XzzzRQUFHDZZZeVuaI6bNgwxowZw2mnncYNN9xQ5j37778/AJMmTcrST1kzXnvtNbp06UKXLl1Yvnw5l19+OV26dGHEiBFpt1Zr+BgdSZIkVcmyZXDZZTByZHxMTonddotDhQ88ML3elJ4TTzyRDz74gIsuuogbbriBUDxL169+9St22WUX1qxZw7Rp09h6661ZunQpM2bMoGPHjhVO3tS5c2cGDBjAmDFjGDt2LIMGDeK6667jlltu4bjjjuOOO+5Y5z3dunUDYOrUqevtd+TIkXz11VdV/vn23HNPjjnmmCofvyl69uxJUvpfLq3DACtJkqT1+sc/4JRTyt7n2qQJjBgB558PDRum15vSM2nSJF588UX2339/rr/++u/CK0CHDh044IADmDx5MjNmzODggw9m3rx5rFmzhrZt21Z63muuuYZHH32UK664gsLCQi699FJ++tOfMnbsWAoK1h1E2rx5cxo1alSlobYjR47kk08+qfLPePLJJ9dYgNX6GWAlSZJUocJCGD4c/vjHstsPPRTuugu22y6dvlQ7PPjggwCcf/75FQZLgKKiIgA+//xzALbccstKz9u+fXvOO+88brjhBs455xz2228/xo8fT8NK/qakZcuWLFy4cL09z549e73HqPYywEqSJKlckyfDqadC6YtVzZvD738Pgwb5PFfBSy+9REFBAb169Sp3/9y5cwHYeeedAb6bdXjFihXrPXerUtNX33vvvTRp0qTS45cvX14tsxqrdjPASpIkqYwlS2DYMLjnnrLbjzgC7rgD2rVLpy/VLkVFRXzyySe0bt263PtZFy5cyPTp09lhhx3YcccdAWjdujWQuRJbkXHjxjFs2DC22WYbFixYwKhRo7j99tsr7eWrr75ihx12WG/f1XUPbMixv8GpK/feGmAlSZL0neefh9NOg+ILZwC0bAm33gonnuhVV2WUBLhvvvmGoqKidYYQ33TTTRQVFXHGGWd8t61t27a0atWKmTNnVnjeCRMmcPLJJ7P77rvzt7/9jR49enDPPfcwdOhQdt1113LfM3PmTJIkYc8991xv39V1D2xdCXy5xsfoSJIkieXL4eyz4bDDyobXPn3gvfegf3/Dq8oKIdC5c2eWLl3KuHHjyux74oknGDlyJLvuuitDhw4t854ePXqwePFiZs2atc45X375ZY499ljat2/PxIkTadWqFVdffTWrV69e59mvpU2bNg2Agw46aL19z549myRJqryMHj26ir+R2m///ff/7nd1+umn89vf/jbljjacAVaSJCnPzZgRn+taeqKmVq3gscfgiSegTZv0elPtNmLECEIIDB48mAEDBnDJJZdwyCGH0LdvX3baaScmTJhAo0aNyrynT58+ALzwwgtltr/11lscccQRNG/enEmTJn03U/Gxxx5L165defrpp3nppZfK7WPixInUq1ePo48+Ogs/Ze64/PLLue6667j11ltZtWoVw4YNS7ulDWaAlSRJylNFRXDzzbD33vD++5ntRx8N774Lffum15vqhmOOOYannnqKrl27Mn78eEaOHMlnn33GtddeyxtvvFHuPal9+vShTZs2PPDAA99tmzVrFj/96U8JIfDCCy+w0047lXnP9ddfD8Rny65tyZIl/PnPf+aII46gQ4cO1fwTVm7q1KkcddRRtGvXjhBC6ldrO3XqVO7y6aefAnDooYeyYMECxo8fz5133plqrxvLe2AlSZLy0Kefwsknw9//ntnWpAmMGhWf9+pwYVXV0UcfvUFXPhs2bMjQoUO55JJLePPNN+nSpQs777wzCxYsqPA9Bx98cIX3nD7wwAOsWLGCCy+8cIN731SFhYV06tSJgQMHMnDgwA1+/6BBg9h+++254oorqqWfd955p9L9b7zxBosXL6ZTp06VPpKoNvMKrCRJUp557DHYY4+y4bVbtziU+NRTDa/KvvPPP5/vfe97jBgxYpPOs3z5cq6//nr69OnDAQccUE3dVd3hhx/Oddddx7HHHlvuc3Cr07x58xg4cCBbbbUVLVq0oE+fPlV67m2J+fPn84tf/ILJkyfzv//9jxkzZmSx2+wxwEqSJOWJr7+OV12PPx5KniJSUACXXgqvvAK77JJuf8ofjRo1YuzYsXTt2pWlS5du9Hlmz55dZycj2hD//e9/+eEPf0i7du14+eWXmTJlCosXL2bIkCFVev/y5cvp27cvo0aNYscdd+SSSy7h6quvznLX2eEQYkmSpDzw5pvxntaPPsps2247ePBB+NGP0utL+atHjx706NFjk87RsWPHaht+W5sNGTKEU045heuuu+67bb/5zW/4+c9/XqX3N27cmFdeeeW7unfv3vTu3bva+6wJXoGVJEnKYUkCd94J++5bNryedBK89ZbhVapJ1113HVtsscV3y0MPPbTOtrVnWp4zZw4TJ05k5MiRZY478sgjadCgQUo/SXq8AitJkpSjCgvhjDPg4Ycz25o2jYH2hBPS60vKV0OGDOG44477rv71r39Nu3btOPfcc7/b1q5duzLvmTFjBs2aNeP1119f53x1dSKmTWGAlSRJykHvvBOHDH/wQWbbHnvA44/D97+fXl9SPmvZsiUtW7b8rm7atCktW7Zk5513rvA9DRo0YOnSpWyzzTZsscUWNdFmreYQYkmSpBwzZkx8tmvp8HrqqTBtmuFVqk6FhYXMmDGDGTNmUFRUxJw5c5gxYwZz5sypts/YZ5992HLLLRkwYABvvvkmH330EZMmTeKXv/wlRUVF1fY5dYUBVpIkKUcsWxaf4TpoECxfHrc1aRID7d13Q+PGqbYn5ZzXXnuNLl260KVLF5YvX87ll19Oly5dNvnxQKVtueWWPPfccyxZsoSDDjqIPffck2HDhtG+ffusP7qnNnIIsSRJUg6YOTMOGX777cy2jh3jkOHdd0+vLymX9ezZkyRJNvr9o0ePrtJxXbt25W9/+9tGf04uyb/ILkmSlGP+8hfo1q1seO3fH/71L8OrpNxigJUkSaqjkgSuuQaOPhq++SZu22wzuOsuGDsWnO9FUq5xCLEkSVIdVFgY73V98snMtu22g6eegi5dUmtLkrLKACtJklTHfPwxHHNM2SHDPXvCY49Bq1aptSVJWecQYkmSpDrkxRfXvd/1nHNg4kTDq6TcZ4CVJEmqA5IERo6En/4UvvgibmvYEO67D269FRo0SLc/SaoJDiGWJEmq5VasgCFD4vNcS7RtC+PHwz77pNeXJNU0A6wkSVIttnBhnGX41Vcz27p3j+F1223T60uS0uAQYkmSpFrqvfdiWC0dXgcPhilTDK+S8pMBVpIkqRZ68UXYbz/45JNYFxTAqFFw773QqFG6vUlSWhxCLEmSVMvcfz+cfjqsXh3rzTeHRx+Fn/0s3b4kKW1ZvQIbQugVQpgZQpgVQhhezv7mIYS/hBDeCiG8G0IYnM1+JEmSarMkgcsug1/8IhNet90WXnrJ8CpJkMUrsCGEesAfgUOAucD0EMIzSZK8V+qwXwLvJUlyZAihFTAzhPBQkiQrs9WXJElSbbRiRQyu48Zltu2xB/z1r9C+fXp9SVJtks0rsHsDs5Ik+bg4kD4CHL3WMQnQNIQQgC2AL4DVWexJkiSp1lm8GA45pGx47dUrXnk1vEpSRkiSJDsnDuFYoFeSJKcW1wOA7kmSnF3qmKbAM8CuQFPg+CRJ/lrOuU4HTgdo06bNXo888khWelZUWFjIFltskXYb0ibzu6xc4Xc5t82d25jhw/+PefOafLftyCPnM3Tof6hXLzv/n5YGv8fKFX6Xs++ggw56PUmSruXty+YkTqGcbWv/V/inwAzgx8BOwKQQwktJknxd5k1JchdwF0DXrl2Tnj17Vn+3+s6UKVPwd6xc4HdZucLvcu6aPh3OPz9egS1x881w4YXbEkJuPSfH77Fyhd/ldGVzCPFcoEOpuj0wf61jBgPjk2gW8F/i1VhJkqScNmkSHHRQJrw2agRPPAHDhkEo7zKAJCmrAXY6sEsIYYcQQkOgH3G4cGlzgJ8AhBDaAD8APs5iT5IkSal77LE4q/DSpbFu2RL+9jfo0yfdviSptsvaEOIkSVaHEM4GXgDqAfclSfJuCGFI8f47gKuB0SGEt4lDjn+dJMniCk8qSZJUx91+O/zyl/GRORAnaZo4Eb+u0JsAACAASURBVDp2TLcvSaoLsnkPLEmSTAAmrLXtjlLr84FDs9mDJElSbZAkcNVVcMUVmW0/+EEMr9/7XmptSVKdktUAK0mSJCgqgnPPhT/+MbOtWzeYMAG23jq9viSprjHASpIkZdHKlTBwIDz6aGbbIYfA+PHgkzgkacNkcxInSZKkvFZYCEccUTa8Hn88PPus4VWSNoYBVpIkKQu+/BIOPjg+LqfE2WfDww9Dw4bp9SVJdZkBVpIkqZotXgw//jG8+mpm21VXwa23QoH/9yVJG817YCVJkqrRggXxyuu772a2/fGPcNZZ6fUkSbnCACtJklRN5s2LV14//DDWBQVw770waFCqbUlSzjDASpIkVYNPPonh9eOPY12vHowdCyeckG5fkpRLDLCSJEmbaNYs+MlPYM6cWDdoAI88Aj//ebp9SVKuMcBKkiRtgg8+iFde//e/WDdsCE8+GR+fI0mqXgZYSZKkjfT223HCpkWLYt24Mfz5z3Dooen2JUm5ygArSZK0Ed54Aw45BL74Itabbw7PPgs9e6baliTlNAOsJEnSBnrjjXjP61dfxbpZM3juOdhvv3T7kqRcZ4CVJEnaAG+9FYcNl4TXFi1g4kTo1i3dviQpHxhgJUmSquidd2J4/fLLWG+5Jbz4InTpkm5fkpQvCtJuQJIkqS54//04bHjx4lg3bw6TJhleJakmGWAlSZLW48MP46NySmYbbtoUXngB9tor3b4kKd8YYCVJkirx0UcxvC5YEOvNN48TNnXvnm5fkpSPDLCSJEkVmD07htd582LdpAlMmAD7759qW5KUtwywkiRJ5ZgzBw46KL4CNGoEf/kL9OiRbl+SlM8MsJIkSWuZNy9eeZ09O9abbQZPPx23SZLSY4CVJEkqZdGiGFQ/+ijWDRvC+PFw6KHp9iVJMsBKkiR956uv4Kc/jbMOA9SvD088AYcfnm5fkqTIACtJkgQsWwZHHgkzZsS6oAAeeSRukyTVDgZYSZKU91auhD594OWXM9vuuSdukyTVHgZYSZKU19asgYED4fnnM9tuuQUGD06vJ0lS+QywkiQpbyUJnHUWPPpoZttvfgPnn59eT5KkihlgJUlS3rr4Yrjrrkx99tlw5ZXp9SNJqpwBVpIk5aUbb4xLiZNOglGjIIT0epIkVc4AK0mS8s6dd8Lw4Zn6yCPhvvvizMOSpNrL/0xLkqS88uijcOaZmbpnT3jsMWjQILWWJElVZICVJEl5Y/JkGDAgTt4E0LUrPP00NGqUbl+SpKoxwEqSpLzw5pvQuzesWhXrjh3hueegWbN0+5IkVZ0BVpIk5bzZs+Hww6GwMNbt2sELL8DWW6faliRpAxlgJUlSTvv8c+jVCxYsiHXz5vD889ChQ7p9SZI2nAFWkiTlrGXL4gzDM2fGumHDeM9rp07p9iVJ2jgGWEmSlJNWr4YTToB//jPWIcCDD8KBB6bblyRp4xlgJUlSzkkSOPtseOaZzLaRI6Fv3/R6kiRtOgOsJEnKOdddB3femal/9Ss499z0+pEkVQ8DrCRJyin33w+XXZap+/eHG25Irx9JUvUxwEqSpJzx3HNw2mmZ+ic/gfvugwL/j0eScoL/OZckSTnhzTfjPa5r1sR6zz1h/Pg487AkKTcYYCVJUp03dy4ccQQsXRrr7baDCROgWbN0+5IkVS8DrCRJqtO++SaG1/nzY92iRRxK3LZtun1JkqqfAVaSJNVZJc96feutWNevD08+CR07ptuXJCk7DLCSJKnOuuAC+OtfM/Vdd8GPf5xeP5Kk7DLASpKkOukPf4hLiYsvhsGD0+tHkpR9BlhJklTn/PWvcN55mbpvX7jmmvT6kSTVDAOsJEmqU2bMgOOPh6KiWO+zD4wZ47NeJSkf+J96SZJUZ8ybV/ZxOdtvD08/DY0bp9qWJKmGGGAlSVKdUFgIRx4ZQyxA8+ZxKHHr1un2JUmqOQZYSZJU661ZA/37w5tvxrp+fXjiCdhtt3T7kiTVLAOsJEmq9S65BJ55JlPffjscfHB6/UiS0mGAlSRJtdrYsXDTTZn6oovg1FPT60eSlB4DrCRJqrWmTSsbVo88Eq6/Pr1+JEnpMsBKkqRaae5cOOYYWLky1rvvDg895ONyJCmf+UeAJEmqdZYtg6OPhoULY73VVvEe2KZN0+1LkpQuA6wkSapVkgQGD4Y33oh1/frw5JOw447p9iVJSp8BVpIk1SrXXAOPPZapb7sNDjwwvX4kSbWHAVaSJNUa48fDiBGZ+pe/hDPOSK8fSVLtYoCVJEm1wltvwYABmfrHP4bf/z69fiRJtY8BVpIkpW7RIjjqqDh5E8BOO8Hjj0ODBun2JUmqXQywkiQpVStXws9/DnPmxLpZM/jLX6Bly3T7kiTVPgZYSZKUqqFD4ZVX4noIMG4cdOyYbk+SpNrJACtJklJzzz1wxx2Z+sYb4fDD0+tHklS7GWAlSVIqpk2LswyXOOEEGDYsvX4kSbWfAVaSJNW4//0v3ve6cmWsO3eOV2NDSLcvSVLtZoCVJEk1auVK6Ns3hliIkzU99RQ0aZJuX5Kk2s8AK0mSatR552UmbSoogEcegR12SLcnSVLdYICVJEk15t574fbbM/UNN8Ahh6TXjySpbjHASpKkGjFtGpx1VqY+/ngnbZIkbRgDrCRJyroFC6BPn8ykTXvsEa/GOmmTJGlDGGAlSVJWrVwJxx4L8+fHesst46RNm2+ebl+SpLrHACtJkrLq/PPXnbRpxx3T7UmSVDcZYCVJUtaMGQN/+lOmvv56OPTQ9PqRJNVtBlhJkpQVM2bAkCGZ+rjj4Fe/Sq8fSVLdZ4CVJEnV7ssv46RNK1bEerfdnLRJkrTpDLCSJKlaFRXBgAHw8cex3mILePLJ+CpJ0qYwwEqSpGp13XXw179m6tGjYdddU2tHkpRDDLCSJKnaTJwII0Zk6mHD4lBiSZKqgwFWkiRVi08+gRNPhCSJ9YEHxlmHJUmqLgZYSZK0yb79Fvr2hc8/j3XbtvF5r/Xrp9uXJCm3GGAlSdImGzoUpk+P6/Xrw+OPwzbbpNuTJCn3GGAlSdImGTMG7rwzU//2t7D//un1I0nKXQZYSZK00WbMgCFDMvXxx8O556bXjyQptxlgJUnSRvnqqzjD8IoVsd5tN7jnHggh3b4kSbnLACtJkjZYksCgQfDxx7HeYgt48sn4KklSthhgJUnSBrvlFnj66Ux9//2w667p9SNJyg8GWEmStEFeeQV+/etMPXQoHHtsev1IkvJHVgNsCKFXCGFmCGFWCGF4Bcf0DCHMCCG8G0L4Rzb7kSRJm+azz+JETWvWxLp7d7jppnR7kiTlj6w9XjyEUA/4I3AIMBeYHkJ4JkmS90od0wL4E9ArSZI5IYTW2epHkiRtmjVr4KSTYN68WLdsCY89Bg0bptuXJCl/ZPMK7N7ArCRJPk6SZCXwCHD0WsecCIxPkmQOQJIki7LYjyRJ2gTXXgsTJ2bqBx+E730vvX4kSfkna1dggXbAp6XquUD3tY75PtAghDAFaAqMSpLkgbVPFEI4HTgdoE2bNkyZMiUb/apYYWGhv2PlBL/LyhW14bv8+ustuOKKzkB8Rk7//p/QuPF/8V8xVVVt+B5L1cHvcrqyGWDLewpcUs7n7wX8BGgM/DOEMC1Jkg/LvClJ7gLuAujatWvSs2fP6u9W35kyZQr+jpUL/C4rV6T9XZ4/P973mhT/KX7ggTB69HbUr79daj2p7kn7eyxVF7/L6cpmgJ0LdChVtwfml3PM4iRJlgJLQwhTgc7Ah0iSpNStXg39+sGi4pt82rSBceOgfjb/D0KSpApk8x7Y6cAuIYQdQggNgX7AM2sd8zRwQAihfgihCXGI8ftZ7EmSJG2Ayy6Dl16K6wUFMby2bZtuT5Kk/JW1vz9NkmR1COFs4AWgHnBfkiTvhhCGFO+/I0mS90MIzwP/BoqAe5IkeSdbPUmSpKp79lm48cZMfdVVcNBB6fUjSVJWBwAlSTIBmLDWtjvWqm8Gbs5mH5IkacN88gkMHJipe/WCiy9Orx9JkiC7Q4glSVIdtHJlnLTpyy9j3b49jB0bhxBLkpQm/yiSJEllXHIJvPpqXK9fHx57DLbeOt2eJEkCA6wkSSrl2Wfhd7/L1NddB/vum14/kiSVZoCVJEkAzJkDJ5+cqX/2M7jwwvT6kSRpbQZYSZLEqlXxea9ffBHr9u1hzBjve5Uk1S7+sSRJkrjsMvjnP+N6vXrwyCOw1Vbp9iRJ0toMsJIk5bkJE+CmmzL1NdfA/vun148kSRUxwEqSlMfmzl33ea8XXZReP5IkVcYAK0lSnlq9Gk44AT7/PNbbbgsPPOB9r5Kk2ss/oiRJylMjRsDLL8f1ggIYNw5atUq3J0mSKmOAlSQpD73wAlx/faa+6iro0SO9fiRJqgoDrCRJeWb+fBgwIFMfcghcfHF6/UiSVFUGWEmS8siaNXDSSfDZZ7HeZhsYO9b7XiVJdYN/XEmSlEeuvRb+/ve4HgI8/DC0aZNuT5IkVZUBVpKkPPGPf8CVV2bq3/wGDjoovX4kSdpQBlhJkvLA4sXQvz8UFcW6R48YYCVJqksMsJIk5bgkgcGDYd68WG+1VRw6XL9+un1JkrShDLCSJOW4kSPh2Wcz9Zgx0K5dev1IkrSxDLCSJOWw116DX/86U19wAfzsZ+n1I0nSpjDASpKUo5YsgeOPh1WrYt21K1x/fbo9SZK0KQywkiTloCSBM86Ajz+OddOm8Mgj0LBhun1JkrQpDLCSJOWge++FRx/N1HffDTvtlF4/kiRVBwOsJEk55t134dxzM/Vpp8WhxJIk1XUGWEmScsiyZTGsLl8e6913j7MQS5KUCwywkiTlkPPOi1dgARo3hscegyZN0u1JkqTqYoCVJClHPP54vNe1xK23wm67pdePJEnVzQArSVIO+O9/472uJY4/Hk45Jb1+JEnKBgOsJEl13KpVcMIJ8bmvADvsAHfeCSGk25ckSdXNACtJUh03YgS8+mpcr18/Pu+1efN0e5IkKRsqDLAhBMOtJEm13KRJcMMNmfraa2HvvdPrR5KkbKospL4RQti3xjqRJEkbZOFCGDAgUx96KAwbll4/kiRlW2UB9gxgVAjh7hDCljXVkCRJWr+iIjj55BhiAdq0gQcegALHT0mSclj9inYkSfJqCKE7MAR4LYTwHFBUav+5NdCfJEkqx+9+By+8kKkfeCCGWEmSclmFAbZYS6Ab8BnwOqUCrCRJSse//gWXXJKpf/3rOHxYkqRcV2GADSEMAX4F3AyckiRJUmNdSZKkci1ZAv36werVse7eHa6+Ot2eJEmqKZVdgT0A2DdJkkU11YwkSapYksAZZ8B//xvrZs1g3Dho0CDdviRJqimV3QPbvyYbkSRJlbv/fnj00Ux9112www7p9SNJUk1zrkJJkuqA99+Hc87J1KeeCscfn14/kiSlwQArSVItt3JlAf36wbJlse7YEUaNSrcnSZLSsL5ZiAEIIXQm3hML8FKSJG9lryVJklTaHXfsyL//Hdc32ywOI27SJN2eJElKw3qvwIYQhgIPAa2LlwdDCOdU/i5JklQdnn4annqq/Xf1LbfA//1fig1JkpSiqlyBPQXoniTJUoAQwo3AP4E/ZLMxSZLy3dy58ItfZOreveHMM9PrR5KktFXlHtgArClVryneJkmSsmTNGujfH774ItYdOsA990DwT2BJUh6ryhXY+4FXQwhPFdfHAPdmryVJknTNNTB1alwvKEh46KFAy5bp9iRJUtrWG2CTJLklhDAF+BHxyuvgJEnezHZjkiTlq6lT4aqrMvXAgbM54AAf+CpJ0noDbAjh4CRJJgNvlNp2cpIkY7LamSRJeeiLL+LQ4aKiWPfoASed9AlggJUkqSr3wI4IIdweQmgSQmgTQvgLcGS2G5MkKd8kCZxySpy8CaBlS3joIahXL92+JEmqLaoSYA8EPgLeAl4GHk6S5NisdiVJUh66/Xb4858z9X33Qfv2FR8vSVK+qUqA3RLoTgyx3wLbheAciJIkVad//xsuuCBTn302HH10ev1IklQbVSXATgOeS5KkF9AN2BZ4JatdSZKUR5YuhX794NtvY925M9x8c7o9SZJUG1XlMToHJ0kyByBJkuXAuSGEHtltS5Kk/DF0KLz/flxv0gQeeQQaNUq3J0mSaqMKA2wIYdckST4Atg4hbL3W7sLstiVJUn549FG4t9TT1W+7DXbdNb1+JEmqzSq7AnshcBrwu3L2JcCPs9KRJEl54uOP4fTTM/UJJ8CgQam1I0lSrVdhgE2S5LTi14Nqrh1JkvLDqlUxsH79dax33BHuuAOcJlGSpIpVOIlTCOGiUut919p3XTabkiQp1112GfzrX3G9fv1432uzZun2JElSbVfZLMT9Sq1fvNa+XlnoRZKkvPDCC3DTTZn6+uuhW7f0+pEkqa6oLMCGCtbLqyVJUhUsWAADB2bqXr3KPv9VkiRVrLIAm1SwXl4tSZLWo6gohtdFi2K9zTYwZgwUVOWp7JIkqdJZiDuHEL4mXm1tXLxOce3T6SRJ2kA33wyTJsX1EGDsWGjdOt2eJEmqSyqbhbheTTYiSVIumzYtTtxUYvhwOPjg9PqRJKkuctCSJElZtmRJfGTO6tWx3mcfuPLKdHuSJKkuMsBKkpRFSQKnnQazZ8e6eXMYNw4aNEi1LUmS6iQDrCRJWXTXXfD445n67rth++1Ta0eSpDrNACtJUpa8/Tacd16mPuMM6Ns3vX4kSarrDLCSJGXB0qVw3HGwYkWs/+//4Pe/T7cnSZLqOgOsJElZcO658MEHcb1JE3j0UWjcON2eJEmq6wywkiRVs4cfhvvuy9S33QYdO6bXjyRJucIAK0lSNfrPf+K9riX694dBg1JrR5KknGKAlSSpmnz7LfTrB4WFsd5lF7j9dggh3b4kScoVBlhJkqrJRRfBG2/E9YYN432vTZum25MkSbnEACtJUjV45hm49dZM/dvfQpcu6fUjSVIuMsBKkrSJPv0UBg/O1EcfDWefnV4/kiTlKgOsJEmbYPVqOOEE+OKLWHfoEGcg9r5XSZKqnwFWkqRNcPnl8Morcb1ePRg3Dlq2TLcnSZJylQFWkqSNNHEiXH99pr7qKth///T6kSQp1xlgJUnaCPPnw0knQZLE+pBDYPjwdHuSJCnXGWAlSdpAq1fDiSfCZ5/Fum1bePBBKPBPVUmSsso/aiVJ2kBXXQX/+EdcLyiAhx+G1q3T7UmSpHxggJUkaQNMngzXXJOpL78cevZMrR1JkvKKAVaSpCpasKDsfa8//jFcemm6PUmSlE8MsJIkVcGaNdC/PyxcGOs2beChh+KjcyRJUs0wwEqSVAXXXAN/+1tcDyGG1222SbcnSZLyjQFWkqT1+Pvf4corM/VvfgM/+Ul6/UiSlK8MsJIkVWLhwvjInJL7Xnv2hBEjUm1JkqS8ZYCVJKkCRUUwYECcvAmgVSvve5UkKU0GWEmSKnDttTBpUlwPAR58ELbdNt2eJEnKZwZYSZLK8eKL8RmvJS6+GA49NL1+JEmSAVaSpHXMn1/2vtcDDyw7iZMkSUqHAVaSpFJWr4YTToBFi2Ldpg2MGwf166fblyRJynKADSH0CiHMDCHMCiEMr+S4biGENSGEY7PZjyRJ63PZZTB1alwvKIjhtW3bdHuSJElR1gJsCKEe8EfgMGA34IQQwm4VHHcj8EK2epEkqSqefRZuvDFTX3UVHHRQev1IkqSysnkFdm9gVpIkHydJshJ4BDi6nOPOAZ4EFmWxF0mSKjV7NgwcmKl79YoTN0mSpNojm3f0tAM+LVXPBbqXPiCE0A7oDfwY6FbRiUIIpwOnA7Rp04YpU6ZUd68qpbCw0N+xcoLfZVXVypWBoUO78OWXzQBo1WoFQ4a8ztSpq1LuLPK7rFzg91i5wu9yurIZYEM525K16pHAr5MkWRNCeYcXvylJ7gLuAujatWvSs2fP6upR5ZgyZQr+jpUL/C6rqs45Bz74IK7Xrw9PP92IfffdP92mSvG7rFzg91i5wu9yurIZYOcCHUrV7YH5ax3TFXikOLxuDRweQlidJMmfs9iXJEnfeewxuO22TH3TTbDvvun1I0mSKpbNADsd2CWEsAMwD+gHnFj6gCRJdihZDyGMBp41vEqSasqHH8Kpp2bqn/8czjsvvX4kSVLlshZgkyRZHUI4mzi7cD3gviRJ3g0hDCnef0e2PluSpPVZtgyOPRa++SbWO+4I990HldzRIkmSUpbVx7InSTIBmLDWtnKDa5Ikg7LZiyRJJZIEzjoL3n471pttBk88Ac2bp9uXJEmqXDYfoyNJUq10110wZkymHjUKunRJrx9JklQ1BlhJUl6ZPh3OPTdTn3wynH56ev1IkqSqM8BKkvLG4sXQpw+sXBnrzp3hT3/yvldJkuoKA6wkKS+sWQMnngiffhrr5s3hySehSZN0+5IkSVVngJUk5YUrroBJkzL1gw/CTjul1o4kSdoIBlhJUs579lm45ppMfemlcMQR6fUjSZI2jgFWkpTTPv4YBgzI1IccAldemV4/kiRp4xlgJUk5a/nyOGnTV1/FukMHePhhqFcv3b4kSdLGMcBKknJSksBZZ8GMGbFu2BCeeAK23jrdviRJ0sYzwEqSctLdd8Po0Zl61CjYe+/U2pEkSdXAACtJyjnTp8M552TqgQPhjDPS60eSJFUPA6wkKacsXAi9e8PKlbHeYw+4/XYIId2+JEnSpjPASpJyxqpV0LcvzJsX6xYtYPx4aNIk3b4kSVL1MMBKknLGBRfASy/F9RBg3DjYaad0e5IkSdXHACtJygmjR8Ntt2Xqa6+FXr1Sa0eSJGWBAVaSVOdNnw5DhmTqY4+F4cPT60eSJGWHAVaSVKctXAg//zl8+22sO3WC++930iZJknKRAVaSVGetWgXHHQdz58a6RQt46inYYot0+5IkSdlhgJUk1VkXXghTp8b1kkmbdt453Z4kSVL2GGAlSXXS6NHwhz9kaidtkiQp9xlgJUl1zmuvOWmTJEn5yAArSapTFi0qO2nT7rs7aZMkSfnCACtJqjO+/Rb69IFPP411ixbw5z87aZMkSfnCACtJqhOSBM46C15+OdYhwMMPO2mTJEn5xAArSaoTRo2C++7L1DfdBIcdll4/kiSp5hlgJUm13gsvxEfmlBg4sGwtSZLygwFWklSrzZwJxx8PRUWx3mcfuPNOJ22SJCkfGWAlSbXWl1/CUUfBkiWxbt8ennoKGjVKty9JkpQOA6wkqVZavRr69YMPP4x148bw9NOwzTbp9iVJktJjgJUk1UrDhsHEiZl69Gj44Q9Ta0eSJNUCBlhJUq1z771x1uESI0bAccel148kSaodDLCSpFrl5ZfhzDMzdZ8+cPnl6fUjSZJqDwPs/2/vzqOsqs68j38fEGQQQRHUAMHZOBNjxHY2Do0aNRgRBzASjcEp2iYak7ZddpulpqNJNDEiKmqiCdFWUF8HHFYwsZ3QxAEhKhoNGNEggwwiQ+33j13VtwoKLKBunbq3vp+1zrp373Pq1lN6lPqx99lbktRqvPMOHHssLF2a27vtBrffDu3800qSJGGAlSS1EvPmwZFHwj//mdu9euVFm7p2LbYuSZLUehhgJUmFW7oUhgyBKVNyu2NHuPde6N+/2LokSVLrYoCVJBUqJTjnHHjssVLfLbfAvvsWV5MkSWqdDLCSpEJdcw2MHl1qX3YZDBtWWDmSJKkVM8BKkgozbhxcdFGpPWxY3jJHkiSpMQZYSVIhJk2Ck0/OU4gB9tsPbr4ZIoqtS5IktV4GWElSi3v3XTj6aPjkk9zeZps8Grv++sXWJUmSWjcDrCSpRc2bB1/9KsycmdsbbwwPPgg9exZblyRJav0MsJKkFrNsGQwdCpMn53aHDnnkdbvtiq1LkiRVBgOsJKlFpATnngsTJpT6brkF9t+/uJokSVJlMcBKklrENdfAqFGl9qWXwvDhxdUjSZIqjwFWklR2d94JF15Yap90Ut7vVZIkaU0YYCVJZfX44zBiRKm9//556rDb5UiSpDVlgJUklc1LL8Gxx8LSpbm9004wfjx06lRsXZIkqTIZYCVJZfHOO3D44TB/fm737QuPPAIbbVRoWZIkqYIZYCVJze6jj2DQoNJer927w8MP5xArSZK0tgywkqRm9ckncNRR8Prrud2xI9x3H+y8c7F1SZKkymeAlSQ1m+XL4cQT4ZlncjsCfvMbOOCAYuuSJEnVwQArSWoWKcG55+bR1jo/+xkcf3xxNUmSpOpigJUkNYsrroAbbii1L7wQzjuvuHokSVL1McBKktbZmDFwySWl9kknwVVXFVePJEmqTgZYSdI6+Z//gW99q9Q++GC49VZo558wkiSpmfnrhSRprT36aB5tranJ7S9+Ee65J688LEmS1NwMsJKktfL00zB4MCxdmtvbbw8TJuQ9XyVJksrBACtJWmOvvAJHHgmLFuV2v355NLZXr2LrkiRJ1c0AK0laI9OmwWGHwdy5ud2rFzz+OHz+88XWJUmSqp8BVpLUZO+9B4ccAh98kNsbbpinDW+3XbF1SZKktsEAK0lqklmz4NBD4d13c7tzZ3jwwbxwkyRJUkswwEqSPtPHH8Phh8PUqbm93np5teF99y22LkmS1LYYYCVJq7V4MRxzDLzwQm5HwB135EArSZLUkgywkqRV+vRTOPZYmDix1DdqFAwdWlhJkiSpDTPASpIatWQJDBkCDz9c6rvqKjjjjOJqkiRJbZsBVpK0kqVL4YQT4IEHSn2XXALf/35xNUmSJBlgJUkNLFsGw4bBuHGlvu9/H/7rv4qrSZIkCQywkqR6li+Hb3wD7rqr1HfBBXDllXnxJkmSpCIZYCVJANTUwGmnwW9/W+o791y4+mrDqyRJah0MsJIkamry4ky3317qGzkSrr3W8CpJH6YGEwAAF2RJREFUkloPA6wktXEpwdlnwy23lPpOPx2uv97wKkmSWhcDrCS1YSnBeeflvV3rfOMbcOON0M4/ISRJUivjryeS1EbVhddf/KLUd9JJeSTW8CpJklqj9YouQJLU8mpq4MwzYfToUt/xx+dnYNu3L64uSZKk1THASlIbs3x5Xm24/oJNQ4bAHXfAev6pIEmSWjEniUlSG7J0KQwb1jC8DhuWt87p0KG4uiRJkprCACtJbcSSJTB0KIwdW+o77TS47TZHXiVJUmUwwEpSG7B4MRx7LIwbV+o766z8DKzPvEqSpEphgJWkKrdoERx9NDz4YKnvggvgl790tWFJklRZ/NVFkqrY/PlwxBHw2GOlvh/+EK6+GiKKq0uSJGlt+NSTJFWpefPg8MPhmWdKfZdfDpdcUlxNkiRJ68IAK0lVaOZMGDQIXn651Pff/w0XXlhcTZIkSevKACtJVeatt+Cww+Dtt0t9110H555bXE2SJEnNwQArSVXkpZfyyOsHH+R2+/Zw000wYkSxdUmSJDUHA6wkVYknn8yrDX/8cW536gS//33ukyRJqgYGWEmqAvfdB0OHwqef5nb37vDAA7DffsXWJUmS1JzcRkeSKtyYMXDssaXwutlmeTTW8CpJkqqNAVaSKlRKeWXh006Dmprct/XW8L//C7vtVmxtkiRJ5eAUYkmqQDU1cNFFcM01pb4BA+CRR2DTTYurS5IkqZzKOgIbEYMi4vWImBYRFzdy/uSIeKX2eDoiHDOQpM+weDEMG9YwvB5wAEycaHiVJEnVrWwjsBHRHrgeOBSYAUyKiPtTSlPqXfY34ICU0pyIOBwYDQwsV02SVOlmzYLBg+Gpp0p9X/sa/O53edVhSZKkalbOEdg9gWkppbdTSkuAscAx9S9IKT2dUppT23wW6FvGeiSpor35JvzLvzQMryNHwt13G14lSVLbUM5nYPsA0+u1Z7D60dXTgIcbOxERZwBnAGy66aZMnDixmUpUYxYsWOA/Y1WFarqXX321O5dcsjMff9wBgIjEyJFvMWTIjAaBVtWpmu5ltV3ex6oW3svFKmeAjUb6UqMXRhxEDrD7NnY+pTSaPL2YPfbYIx144IHNVKIaM3HiRPxnrGpQLffy2LHwve/BkiW53akT3HFH8PWvbwNsU2htahnVci+rbfM+VrXwXi5WOacQzwD61Wv3Bf6x4kURsStwM3BMSumjMtYjSRUlJbjiCjjxxFJ47d07L9b09a8XWpokSVIhyjkCOwnYNiK2BN4DTgBOqn9BRHweuBcYnlJ6o4y1SFJFWbo0P986Zkypb4cd4MEHYcsti6tLkiSpSGULsCmlZRFxDjABaA+MSSm9FhEja8+PAi4FegK/igiAZSmlPcpVkyRVgrlz4bjj4IknSn0HHQT33AMbbVRcXZIkSUUr5wgsKaWHgIdW6BtV7/3pwOnlrEGSKsnUqXDMMXnF4Tqnngo33ggdOxZWliRJUqtQzmdgJUlr4IEHYODAhuH18svzNGLDqyRJkgFWkgqXEvzoR3nkdf783NelC/z+93DJJRCNrekuSZLUBpV1CrEkafUWLMhThO+5p9TXvz+MHw8DBhRWliRJUqtkgJWkgvztb3nU9dVXS30HHgh33QW9ehVWliRJUqvlFGJJKsATT8AeezQMr+eeC48+aniVJElaFQOsJLWglODnP4d//VeYPTv3deyYF2q67jro0KHY+iRJklozpxBLUgtZsAC+/W347W9LfZtvDvfeC3vtVVxdkiRJlcIAK0ktYPJkOO44eP31Ut/AgTm8fu5zxdUlSZJUSZxCLElldvvtsOeeDcPr6afDxImGV0mSpDXhCKwklcmiRXlhpjFjSn1dusCoUTB8eHF1SZIkVSoDrCSVweuvw5AhDVcZ3mEHuPtu2Gmn4uqSJEmqZE4hlqRmNnbsylvkDBsGzz9veJUkSVoXBlhJaiaLF8NZZ8GJJ+YVhwHWXx9uugl+/WvYYINi65MkSap0TiGWpGYweTKcdFLDUddttslThgcMKK4uSZKkauIIrCStg5oauPbalacMH3ccvPCC4VWSJKk5OQIrSWvp/ffh1FPh0UdLfZ06wdVX56nEEYWVJkmSVJUMsJK0FsaPz3u5fvRRqW/AALjzTthxx+LqkiRJqmZOIZakNbBwIZxxBgweXAqvEXDhhfDss4ZXSZKkcnIEVpKaaNIkOPlkePPNUl/fvnmF4YMOKq4uSZKktsIRWEn6DEuWwGWXwd57Nwyvxx8Pr7xieJUkSWopjsBK0mq8+CKMGNFwheFu3eCXv4Thw12oSZIkqSU5AitJjVi8GH7wAxg4sGF43WcfePllOOUUw6skSVJLcwRWklbw7LPwzW/C1Kmlvs6d4cor4ZxzoH374mqTJElqyxyBlaRaixbBd7+bn3WtH14PPDCPwp53nuFVkiSpSI7AShLwxz/CaafBtGmlvg02gJ/8JG+b086/7pMkSSqcv5JJatNmz4ZvfxsOOKBheD30UJg8GUaONLxKkiS1Fv5aJqlNSgluuw223x5Gjy71d+8Ot9wCEyZA//6FlSdJkqRGOIVYUpszeTKceSY89VTD/qOOghtugD59iqlLkiRJq+cIrKQ2Y8ECuOgi+OIXG4bXfv1g3Di47z7DqyRJUmvmCKykqpcSjB+fVxGePr3Uv956cMEFcOml0LVrcfVJkiSpaQywkqratGk5uD70UMP+/feHX/0KdtqpmLokSZK05gywkqrS3Lnwq19tzfjxsHRpqb9XL7j6ahg+HCKKq0+SJElrzmdgJVWVZcvg+uthm23g7rv7/V94jchb4vz1r3DKKYZXSZKkSuQIrKSq8fDD8N3vwtSpDfv33ht+/nP48peLqUuSJEnNwwArqeK99loOrhMmNOzfdNPFXHddJ4YMccRVkiSpGhhgJVWsDz+E//xPuPFGWL681N+tG/zwh7D77s9z2GH7F1egJEmSmpXPwEqqOHPnwn/8B2y1VV5JuC68tmsH3/oWvPkmXHwxdOxYU2yhkiRJalaOwEqqGIsWwS9+AT/+McyZ0/DcwQfDT38Ku+5aTG2SJEkqPwOspFZvyRK46Sb40Y9g5syG53bZBa64Ao480udcJUmSqp0BVlKrtXw53HEHXHYZvPNOw3Nbbw2XXw5Dh+apw5IkSap+BlhJrc7y5XD33TmgTpnS8FyfPnDppTBiBHToUEx9kiRJKoYBVlKrsXQp3HknXHklvPFGw3M9e+aVhc88Ezp3LqY+SZIkFcsAK6lwixfDrbfmxZnefbfhuW7d8h6v//ZvsOGGxdQnSZKk1sEAK6kwCxfC6NHwk5/A++83PNe9O3znO3DeeXn0VZIkSTLASmpxc+fCDTfkbW9mzWp4bpNN4IIL4KyzcoiVJEmS6hhgJbWYt9+Ga6+FW27Jo6/1bb45XHghnHEGdO1aTH2SJElq3QywksoqJXj66TzaOm5cbtfXvz9cfDGceip06lRIiZIkSaoQBlhJZbFsGdxzTw6uzz+/8vmdd86LM518stvhSJIkqWkMsJKa1Zw5MGYMXHcd/P3vK58fNCg/43rIIRDR8vVJkiSpchlgJTWLSZPywkxjx8InnzQ8t/76MHw4nH8+7LRTMfVJkiSp8hlgJa21hQvhd7+DUaPgxRdXPt+rF5x9Npx5JvTu3fL1SZIkqboYYCWtsSlTcmj99a9h3ryVzw8YkIPrsGEuzCRJkqTmY4CV1CSLFsG998LNN8OTT658vlMnGDoURo6EgQN9vlWSJEnNzwAraZXqtsC59Va46y6YP3/la7bdNofWU0+FjTdu8RIlSZLUhhhgJa1k+vQ8Pfi222DatJXPt28PxxyTn239ylegXbsWL1GSJEltkAFWEpCnCN93Xx5tffzxPPq6ou22gxEj8orCffq0fI2SJElq2wywUhv26acwYULe+ub++/OqwivacEM44YQ8RXivvXy2VZIkScUxwEptzLJl8Ic/5NB6770wd+7K10TAIYfk0davfQ06d275OiVJkqQVGWClNqCmJi/GNHYs3H03fPhh49ftsAOcfDKccgr069eyNUqSJEmfxQArVaklS/JI67hx+dnWmTMbv27LLfMU4RNOgF12cYqwJEmSWi8DrFRFFiyAhx+G8ePhwQdh3rzGr9t887xn6wknwJ57GlolSZJUGQywUoX74IMcVseNg8ceywszNaZXLxg8GE48EfbbL2+FI0mSJFUSA6xUYZYvh0mT4KGH8vHii6u+dostcmgdPBj23tvQKkmSpMpmgJUqwEcf5e1uHnoIHnkkt1dll11KoXW33ZweLEmSpOphgJVaoSVL4Lnn4PHH87Tg557LKwk3pn172HdfOOqovOXN1lu3bK2SJElSSzHASq1ATQ28+moOrE88AX/8IyxcuOrrN9sMDj8cjjgi79fao0fL1SpJkiQVxQArFSAlmDYNnnyyFFpnzVr19e3awV575cB6xBF5anC7di1XryRJktQaGGClFlBTA5Mn55HVP/0pv65qX9Y6W20FBx+cj0MOgZ49W6ZWSZIkqbUywEplsGQJ/OUvpbD61FMwZ87qv2aTTUqB9eCDc4CVJEmSVGKAlZrBjBnw7LPwzDP59cUXV70fa53u3WGffeArX8mBddddnRYsSZIkrY4BVlpDixbl0dW6sPrss/Dee5/9db17w/77l46dd3ZfVkmSJGlNGGCl1Vi0CF56KY+ovvBCfp06ddVb2tS35ZZ5e5u6wLrttu7JKkmSJK0LA6xUa948eOWVhoG1qWG1a1fYc8+8UnDd0bt3+WuWJEmS2hIDrNqcmhp46y14+eUcWF9+OR/vvtu0r4+AL3wBBg4shdWddoL1/K9JkiRJKit/5VbVSik/m/raazBlSn597TV49VVYuLBpn1EXVr/0pXzssQcMGAAbbFDe2iVJkiStzACrird8OUyfDn/9aymoTpmSj48/bvrndOgAO+6YVwPefXfDqiRJktTaGGBVMWbPhtdfz8cbb5Re33zzs7esWVHv3rDbbvnYddf8+oUvQMeO5aldkiRJ0rozwKrVSAk++CA/nzptWn6tO6ZNg48+WvPP7NEjP5+6446lY9ddYbPNmr9+SZIkSeVlgFWLmjcvL5b0zjul429/yyH17beb/mzqinr3hu23L4XUutC62WZuXSNJkiRVCwOsms3y5TBzZn4edfp0mDED/v73UlB9912YM2ftP79z57yX6vbb52O77UqvPXo0108hSZIkqbUywKpJPv0U3n8f/vGP0jFjRimsTp+e+5YtW7fv0707bL1140ffvtCuXfP8PJIkSZIqjwG2DUsJFizIo6YffJBfZ86E557bkt/8pmFYnTWreb7n+uvDFlvko3//0vuttoJttoGNN3bKryRJkqTGGWCrzLJlebGjDz/Mxz//2fj7urC6aFFjn9J/rb//JptAv3756Ns3v9aF1C22yM+qOooqSZIkaW0YYFuplOCTT/Izo7Nnl45Zs3JAbex11iyYOzd/bXNr1y4viNSnD3zuc6WjLqzWBdbOnZv/e0uSJEkSGGDLavlymD8/r7w7d+7Kx5w5Dd/Pnt0wsK7p3qZro1OnHEw32ww23TS/Ll78DgMHbvF/YbVPnzxy2r59+euRJEmSpFUxwK6gpiaPfC5YkMPn/Pnw8cel9431zZuX2/Vf583Ln9HSIqBnT+jVK4fOutf673v1KoXWDTdc+ZnTiRPf4cADt2j54iVJkiRpNSoywH76aX52s/7xySel9wsXll7rjhXbdceCBQ2PhQvLMwV3bXTsmBc1qjs22ig/Y7rJJjmkrvi+Z898zXoV+W9VkiRJklav4qLOiy/maa+Volu3vDVMjx45XPbosepjxbDapYsr8kqSJElSnbIG2IgYBFwLtAduTildtcL5qD1/BLAIODWl9Ody1tQUXbrABhtA1655im23bisf9fu7d8/Hhhs2fO3WzRV3JUmSJKm5lC3ARkR74HrgUGAGMCki7k8pTal32eHAtrXHQOCG2tfV6tAhh8y6o3PnldtduzZ+dOlSet+tWw6q9Y8uXVysSJIkSZJao3KOwO4JTEspvQ0QEWOBY4D6AfYY4NcppQQ8GxE9ImLzlNL7q/rQ3XfP04glSZIkSW1LOSe49gGm12vPqO1b02sa8JlQSZIkSWqbyjkC21jUXHF936ZcQ0ScAZxR21wQEa+vY21avU2AWUUXITUD72VVC+9lVQPvY1UL7+Xy67+qE+UMsDOAfvXafYF/rMU1pJRGA6Obu0A1LiJeSCntUXQd0rryXla18F5WNfA+VrXwXi5WOacQTwK2jYgtI6IjcAJw/wrX3A+cEtlewLzVPf8qSZIkSWq7yjYCm1JaFhHnABPI2+iMSSm9FhEja8+PAh4ib6EzjbyNzohy1SNJkiRJqmxl3Qc2pfQQOaTW7xtV730Czi5nDVorTtdWtfBeVrXwXlY18D5WtfBeLlDkDClJkiRJUutWzmdgJUmSJElqNgZYrVZEfC8iUkRsUnQt0tqIiJ9ExF8j4pWIGBcRPYquSWqqiBgUEa9HxLSIuLjoeqS1ERH9IuIPETE1Il6LiPOKrklaWxHRPiL+EhH/r+ha2ioDrFYpIvoBhwJ/L7oWaR08BuycUtoVeAP4QcH1SE0SEe2B64HDgR2BEyNix2KrktbKMuC7KaUdgL2As72XVcHOA6YWXURbZoDV6vwMuAjwQWlVrJTSoymlZbXNZ8n7TUuVYE9gWkrp7ZTSEmAscEzBNUlrLKX0fkrpz7Xv55N/+e9TbFXSmouIvsCRwM1F19KWGWDVqIg4GngvpfRy0bVIzeibwMNFFyE1UR9ger32DPylXxUuIrYAvgg8V2wl0lr5OXlwp6boQtqysm6jo9YtIh4HNmvk1L8DPwQOa9mKpLWzuns5pXRf7TX/Tp7GdmdL1iatg2ikzxkxqlgRsQFwD3B+SunjouuR1kREfBX4MKX0YkQcWHQ9bZkBtg1LKR3SWH9E7AJsCbwcEZCnXP45IvZMKc1swRKlJlnVvVwnIr4BfBU4OLl3mCrHDKBfvXZf4B8F1SKtk4joQA6vd6aU7i26Hmkt7AMcHRFHAJ2ADSPijpTSsILranPcB1afKSLeAfZIKc0quhZpTUXEIOCnwAEppX8WXY/UVBGxHnnhsYOB94BJwEkppdcKLUxaQ5H/Nvx2YHZK6fyi65HWVe0I7PdSSl8tupa2yGdgJVW7XwLdgMci4qWIGFV0QVJT1C4+dg4wgbzozV2GV1WofYDhwFdq/z/8Uu0oliStMUdgJUmSJEkVwRFYSZIkSVJFMMBKkiRJkiqCAVaSJEmSVBEMsJIkSZKkimCAlSRJkiRVBAOsJEktICKW19tC5KWIuLi2/+aI2HEdP7tbRLwVEdvWtjtExKsRMbA5apckqbVwGx1JklpARCxIKW1Qxs8/Hjg9pXRYRPwA2CKl9O1yfT9JkorgCKwkSQWKiIkRsUdE9I+INyNik4hoFxF/iojDaq+5ICIm1x7nN/Y5KaW7gJqIuAgYCfygBX8MSZJaxHpFFyBJUhvROSJeqte+MqX0+7pGSundiPgxMAp4DpiSUno0Ir4EjAAGAgE8FxFPppT+0sj3OB+YCpyRUppdtp9EkqSCGGAlSWoZn6SUBqzugpTSzRExhDyCWnftvsC4lNJCgIi4F9gPaCzADgLeB3ZutqolSWpFnEIsSVIrERFdgL61zbrnZaOJX/s54DvAnsAREbFr81coSVKxDLCSJLUePwbuBC4Fbqrt+yPwtYjoEhFdgcHAnxr52p8BV6SUZgAXANdHRJPCryRJlcIAK0lSy+i8wjY6V9U/GREHAF8GfpxSuhNYEhEjUkp/Bm4Dnic/G3vzis+/RsShwOeBWwBSSg8Ac4BTyv1DSZLUktxGR5IkSZJUERyBlSRJkiRVBAOsJEmSJKkiGGAlSZIkSRXBACtJkiRJqggGWEmSJElSRTDASpIkSZIqggFWkiRJklQRDLCSJEmSpIrw/wG/mU0Zhgur7QAAAABJRU5ErkJggg==\n",
100 |       "text/plain": [
101 |        "<Figure size 1152x648 with 1 Axes>"
102 |       ]
103 |      },
104 |      "metadata": {
105 |       "needs_background": "light"
106 |      },
107 |      "output_type": "display_data"
108 |     }
109 |    ],
110 |    "source": [
111 |     "plt.figure(figsize=(16,9))\n",
112 |     "plt.axis([-5,5, 0,1])\n",
113 |     "plt.plot(X, Y, linewidth=3, color='b')\n",
114 |     "plt.xlabel('Eixo X')\n",
115 |     "plt.ylabel('Eixo Y')\n",
116 |     "plt.title('Função Sigmoid', fontsize=16)\n",
117 |     "plt.grid()\n",
118 |     "plt.text(3.3, 0.85, r'$\\sigma(x)=\\frac{1}{1+e^{-x}}$', fontsize=20)\n",
119 |     "plt.show()"
120 |    ]
121 |   }
122 |  ],
123 |  "metadata": {
124 |   "kernelspec": {
125 |    "display_name": "Python 3",
126 |    "language": "python",
127 |    "name": "python3"
128 |   },
129 |   "language_info": {
130 |    "codemirror_mode": {
131 |     "name": "ipython",
132 |     "version": 3
133 |    },
134 |    "file_extension": ".py",
135 |    "mimetype": "text/x-python",
136 |    "name": "python",
137 |    "nbconvert_exporter": "python",
138 |    "pygments_lexer": "ipython3",
139 |    "version": "3.7.10"
140 |   }
141 |  },
142 |  "nbformat": 4,
143 |  "nbformat_minor": 4
144 | }
145 | 


--------------------------------------------------------------------------------
/jupyter_notebooks/funcao_tanh.ipynb:
--------------------------------------------------------------------------------
  1 | {
  2 |  "cells": [
  3 |   {
  4 |    "cell_type": "markdown",
  5 |    "metadata": {},
  6 |    "source": [
  7 |     "# Função Tangente Hiperbólica\n",
  8 |     "\n",
  9 |     "**Tanh** é a função Tangente Hiperbólica, que é o análogo hiperbólico da função circular de Tangente usada em toda a trigonometria. Tanh é definido como a razão das funções seno hiperbólico e cosseno hiperbólico correspondentes. \n",
 10 |     "\n",
 11 |     "Na Matemática, as funções hiperbólicas são análogas às funções trigonométricas comuns.\n",
 12 |     "\n",
 13 |     "As funções hiperbólicas básicas são:\n",
 14 |     "\n",
 15 |     "- Seno hiperbólico \"sinh\"\n",
 16 |     "- Cosseno hiperbólico \"cosh\"\n",
 17 |     "\n",
 18 |     "No qual podemos derivar:\n",
 19 |     "\n",
 20 |     "- Tangente hiperbólica \"tanh\"\n",
 21 |     "- Cossecante hiperbólica \"cosech\"\n",
 22 |     "- Secante hiperbólica \"sech\"\n",
 23 |     "- Cotangente hiperbólica \"coth\"\n",
 24 |     "\n",
 25 |     "A **tanh** ou **função de ativação tangente hiperbólica**, como também é conhecida, tem a seguinte fórmula matemática:\n",
 26 |     "\n",
 27 |     "\\begin{equation}\n",
 28 |     "\\tanh x=\\frac{\\cosh x}{\\sinh x} = \\frac{e^x - e^{-x}}{e^x + e^{-x}}\n",
 29 |     "\\end{equation}\n",
 30 |     "\n",
 31 |     "Ela muito semelhante à função de ativação **sigmoid** e tem até a mesma forma de S.\n",
 32 |     "\n",
 33 |     "Ela assume qualquer valor real como entrada e produz valores na faixa de $-1$ a $1$. Quanto maior a entrada (mais positiva), mais próximo o valor de saída estará de $1$, enquanto quanto menor a entrada (mais negativo), mais próximo a saída será $-1$.\n",
 34 |     "\n",
 35 |     "Para vermos um exemplo da função Tanh, primeiro devemos importar as bibliotecas necessárias:"
 36 |    ]
 37 |   },
 38 |   {
 39 |    "cell_type": "code",
 40 |    "execution_count": 1,
 41 |    "metadata": {},
 42 |    "outputs": [],
 43 |    "source": [
 44 |     "import matplotlib.pyplot as plt\n",
 45 |     "import numpy as np "
 46 |    ]
 47 |   },
 48 |   {
 49 |    "cell_type": "markdown",
 50 |    "metadata": {},
 51 |    "source": [
 52 |     "Definimos o nosso array de input **x**:"
 53 |    ]
 54 |   },
 55 |   {
 56 |    "cell_type": "code",
 57 |    "execution_count": 2,
 58 |    "metadata": {},
 59 |    "outputs": [],
 60 |    "source": [
 61 |     "x = np.linspace(-np.pi, np.pi, 50) "
 62 |    ]
 63 |   },
 64 |   {
 65 |    "cell_type": "markdown",
 66 |    "metadata": {},
 67 |    "source": [
 68 |     "Calculamos o nosso array de output **y**:"
 69 |    ]
 70 |   },
 71 |   {
 72 |    "cell_type": "code",
 73 |    "execution_count": 3,
 74 |    "metadata": {},
 75 |    "outputs": [],
 76 |    "source": [
 77 |     "y = np.tanh(x) "
 78 |    ]
 79 |   },
 80 |   {
 81 |    "cell_type": "markdown",
 82 |    "metadata": {},
 83 |    "source": [
 84 |     "Plotamos o gráfico da função Tanh:"
 85 |    ]
 86 |   },
 87 |   {
 88 |    "cell_type": "code",
 89 |    "execution_count": 6,
 90 |    "metadata": {},
 91 |    "outputs": [
 92 |     {
 93 |      "data": {
 94 |       "image/png": "iVBORw0KGgoAAAANSUhEUgAAA8IAAAImCAYAAACYSTONAAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADh0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uMy4xLjMsIGh0dHA6Ly9tYXRwbG90bGliLm9yZy+AADFEAAAgAElEQVR4nOzdeXwV1f3/8ddhiYhEUUAluFfFtl/1K+Da1sa1aF36s9q6VItWQFFcvu6VCm4V96WKEsVq625dCmrrVlO32grWFlywLrgQbAGrhjUg5/fH3HCTEMINucnc3Lyej8d95JyZOXPfN4yJn8zMmRBjRJIkSZKkjqJT2gEkSZIkSWpLFsKSJEmSpA7FQliSJEmS1KFYCEuSJEmSOhQLYUmSJElSh2IhLEmSJEnqUCyEJUkdTgjhghDCRyGEbUMIz6Wdp9iEEO4IIZzdSvseHEJ4N4ftOocQ/hBCOKrOshNCCM9k2muEEOaFEMpaI6ckqbBZCEuSUhVCmBFCWJgpSua1UXGyHbAncA3wwursIITwRp28X4UQFtXp/zyvafMohHBfCGFUPseHELYJISyt7ccYh8QYr2hJzjy4Engkxnh3YytjjItjjD1ijFVtnEuSVAC6pB1AkiTgwBjjM231ZjHGQzPNfVqwj2/WtkMIlcBdMcbbWhhNTQgh5Pz/LTHG/2vNLJKk9s0zwpKkghRCKA8hfNJg2YwQwt6Z9pgQwgMhhN+EEKozZ2gH1dl24xDCwyGE2SGEuSGEGzPLvxZC+FNm2ZwQwt0hhJ51xn09hFAZQvg8s8+DVjP/Npn9fJbJcGcIobTO+k9DCKeHEKaFEL7I5Cips35UCOHfIYRPQgjDQggxhLBRZt2aIYTrQggfZ/bzqxDCGpl1g0MI74YQfp5535m1lweHEE4Bfgj8InPm+sE636vfZ74f74cQTlidz1wn+/KzxnXyXJj5XrwfQjiszra5fJZfhBD+DdxcZ9zK9rdeCOGezGf/IIRwdgghNJKxW4Pv6VohhBsyOb4IIfw5hNAl83oo82/xeQjhuRBC/5Z8fyRJ6bMQliS1ZwcB9wE9gYlAbbHbGXgM+BDYDOiX2Q4gAJcBZcDXgY2BMZlxXYFJwFPA+sBI4O4WFD4XARsC2wL9gfMbrD8U2AvYEtgZODKT4wfACcDumXF7Nxh3LbBRnf1uDZxbZ/2mmc9ZBpwM3BJC6BFjvAF4CLg4c1nwYZnv1RPAy5ntBwM/DyF8dzU/c2M2A0pIvhfDgDtDCJvn+Fk2A7qS/DudksP+bslsvznJGf8TyXxfV+EGYBtgR2A9YBQQM+smAl/LvN/bwJ057E+SVMAshCVJheDRzNm2z0MIjzZj3IsxxidijF8BvwW2zyzfiaSoOyvGOD/GuCjG+CJAjPHdGOPTmXtEZ5PcJ1xb9O0C9ADGxhhrYox/Iimoj2juB4oxvh1j/FNmP58C19V5n1rXxhj/ncnxBPC/meU/Am6NMU6PMc4nKaiB5ZcHHwecGmP8PMb4BTAWOLzOfhcAl8UYl8QYHyEp6LZcSdRvA91ijJdnsr4D/LrB/ho6v86/1+fA31bx7VgKXJjZ/zPAM8ChOX6WxSSFe02MceEq9rcGyRnvc2KM82KM75J8349uKlzmDyDHACNjjJ/GGL+KMb6Q+bo0xnhnZn+LgAuBnUII3VbxmSVJBcx7hCVJheAHq3mP8Kd12guAbpniamPgwxjj0oYDQgjrk5z9+w5QSvJH4f9mVpcBH8cYl9UZ8iHJGeVmCcmEX9cDu9V5n1mryN+7To6634+P67TLSM54vlHnit9AUhzWmt3gMywgKfAbsymwWaagrdW5wfs3dGmM8ZLlbx7CNsC0JrafnSkia32Y+Ry5fJZPY4xLctzfhiTf548arFvVv19fkv8ner/hiszxNBY4hOTfZ1kmYy9g5ir2K0kqUJ4RliQVqvlA99pO5hLePjmO/RjYJDQ+udJlJGdIt4sxrg38hKSwAagCNg4h1P39uAmrV/BcSfIZ/ifzPsfXeZ9VmUVyuXCtjRusWwp8LcbYM/NaJ8bYK8d9xwb9j4G36+yrZ4yxNMb4/3LcXy56NziDugnJ9zqXz9Iwb1P7+5SkUN2kwbpV/fvV5tiikXXHAvsCewDrkFw+Dbn/W0qSCpCFsCSpUL1Dcob3+5lLV0cBa+Q49m8kxc3YzCRI3UII38qsKwXmAZ+HEPoBZ9UZ91eS4vXsEELXEEI5cCDZ+4ubo/Z9vgwhbAI0ZxbjB4DjQwhbhRDWIvnsAGTOjt4OXB9C6B0SG4cQcp0B+9/UL/heBAghnJb5PnUJIWwXQhjQjLyr0pVkgq6SEMKeJPfuPtSCz7Ky/S0GHgF+mfl3/xpwKnBXUzvL5PhNJscGIXkG8bczf3wpBRYBc4G1gEua2JUkqZ2wEJYkFaTM/aIjgNtIzujNBz5pclB27FckBeyWwJdANfDjzOoLgQHAF8DjwMN1xtWQTMC1HzAHGAccE2N8ezU+wgUk999+QVKcPZTrwMx9vROAl0j+IFD7rOPFma+nkZwBnZzZ/x9Z+T3ADVUAO2bu770vUwTuT3IJ94fAbJLZmVd2KfXqmEFyxvVTksL32Bhj7WXIq/NZmtrf8MzXD4E/kRw/jT5LuIFTgPeAv5MUvReTnPWdQPI9+RSYSuYPB5Kk9i3E2NgVR5IkFYfM2dhLYozHpJ1ldYUQdgD+AqwZ29kv7hDCYODGGGOuhbokSa3OM8KSpKIVQuhBcmZ357SzNFcI4ZDMpb+9Se5rfrS9FcGSJBWqVAvhEMLtIYT/hBAanWkyc6/QDSGEd0MI/6x7v1IIYXAIYXpm3bmNjZckdXjHkRTCqzMjddpOIck+neTS7lOa3lySJOUq1UujQwi7k0wk8psY4/80sn5/YCTJvUs7A9fHGHfOTF7xDsnkGJ8ArwJHxBjfbLPwkiRJkqR2KdUzwjHG54HPmtjkYJIiOcYYXwF6hhD6AjsB78YY389MbHJfZltJkiRJkppU6PcI9yN5vmGtTzLLVrZckiRJkqQmdUk7wCo09rD62MTyFXcQwjBgGEC3bt0GbrLJJvlLpw5v2bJldOpU6H9PUnviMaV8eeedd5a3t9566xSTqJj4M0r55jGVPzFCjIFly3L7mmyfbS9b1tSyxtYl7cIzZU6Msc+qtir0QvgTYOM6/Y1InjVYspLlK4gxVpA8M5H+/fvH6dOnt05SdUiVlZWUl5enHUNFxGNK+RJC9n9O/N2nfPFnlPKtox1TMcLixVBdnX3Nm9d4u25/3jxYsCD7Wriwfn/BAvjqq7Q/XaEIH+ayVaEXwhOBk0MI95FMlvVFjHFWCGE2sFUIYXNgJnA4cGSKOSVJkiQVuYUL4fPPk9d//7tiu+6yzz9vvMAtxoK1a1coKcl+be6ra9f6++jSpf7XlbUbWzZ4cG6ZUy2EQwj3AuVA7xDCJ8BooCtAjPEW4AmSGaPfBRYAx2bWLQ0hnAw8CXQGbo8xvtHmH0CSpAI1YMAAqqurKS0tTTuKJBWchQth9uwVX3PnNl7U1rYXL047+cp16QLdu6/4WnPNFftrrglrrAHduiWvVbWbWl9SAqEQr5BehVQL4RjjEatYH4GTVrLuCZJCWZIkNTBlypQOd8mhpI4pxuSMa2OF7cpe8+enl7ekBHr0gNLS7CuXfmNFbt3itmvX9D5Te1Tol0ZLkiRJ6qAWLYKZM5t+/fvfyXZtoWtXWHdd6Nkz+7WpdmOFbUlJ22RV0yyEJUmSJLWpGGHOHHj33R7Mn7/yIvezz1rn/bt2hT59Vnz17t10obvmmu3zMmCtyEJYkiRJUt5VV8P77yev996r//Wjj6CmBmBQXt5rzTUbL2xX9lp7bQvajs5CWJKkIlRRUcH06dN55513GDZsWNpxJBWhZctg1qzGC9333kvuxW2pLl2gb1/o12/lr759k0uPpeawEJYkqQgNHz58edtCWNLqihE++QSmTYN//at+ofvBBy27N3eddaBnz/lsvfVaKy1y118fOnXK3+eRalkIS5IkSWLOnKTgrX1NnZp8/fLL1dtfSQlsvjl87WuwxRb1v266aXIWt7LyVWe3VyoshCVJkqQOpLoa3nijftE7bVoy+3Jz9eq1YpFb+7WsDDp3zn9+KR8shCVJkqQitHgxvP32igXvjBnN20/PnrDttvD1r69Y8K6zTqtEl1qdhbAkSZLUzsWYFLivvJJ9/f3vsGRJ7vtYc0345jfhf/4n+9p222QyKmdYVrGxEJYkSZLamXnz4NVX6xe+//lPbmO7dIH+/ZMit27Ru/nmTkyljsNCWJIkSSpgy5bBO+8kxe5f/pJ8nTYtWb4qW2yxYsG79dbJRFZSR2YhLEmSJBWQzz6Dv/0te6b3r3+Fzz9f9bh11oGdd4ZddkleO+2UTGYlaUUWwpIkSVKK5s+Hykp48kl45hl4661VjwkhObu7667Zwrd/fy9tlnJlISxJkiS1oRjhn/9MCt8nn4QXX4SamqbH9OmTLXh32QV23BFKS9smr1SMLIQlSSpCBxxwAHPnzqWX10VKBWH2bHj66aTwfeop+PTTlW/bpQvssEP9wnfzzZ25WconC2FJkorQpEmTqKyspLy8PO0oUoe0ZEkysVXtWd/XXkvOBK/MN78J3/te8vrOd5JHGUlqPRbCkiRJUh68/3628P3Tn6C6euXbrrsu7LNPUvjuuy9stFHb5ZRkISxJkiStlmXL4KWX4IEH4I9/hHffXfm2nTollzjXnvUdNAg6d267rJLqsxCWJEmSchQjvP463Hsv3HcffPzxyrfdZJNs4bvXXtCzZ9vllNQ0C2FJkorQmDFjmDFjBpWVlYwZMybtOFK7969/JcXvvffC2283vs2aa0J5ebb47d/fCa6kQmUhLElSEbrwwguXty2EpdVTVQX33w/33AOTJze+zXrrwWGHwQ9/mExy1a1b22aUtHoshCVJkqSMzz6Dhx5KzvxWVjY+0/Naa8HBB8ORRyYTXpWUtHlMSS1kISxJkqQObf58mDgxKX7/+Mfk0UcNde0K++0HRxwBBx6YFMOS2i8LYUmSJHU4NTXw1FPJZc+//z0sWLDiNiHAHnskxe8hhySXQUsqDhbCkiRJ6jA+/BBuvBFuvz25DLoxO+6YXPb8ox9BWVnb5pPUNiyEJUmSVNRihJdfhuuug4cfTp7/29A22yTF7xFHwJZbtn1GSW3LQliSJElFqaYGHnwwKYAbm/V5442TwveII2D77X3UkdSRWAhLkiSpqMyeDRUVcNNNMGvWiuv32gtOOw323x86dWr7fJLSZyEsSZKkojB1Klx/Pdx1FyxeXH/dGmvAT34Cp54K226bTj5JhcNCWJIkSe3WsmXwxBPJ5c/PPrvi+r59YcQIGD4c+vRp+3ySCpOFsCRJRWjo0KFUVVVR5pS3KlLV1XDnnckZ4HffXXH9wIFw+ulw2GFQUtL2+SQVNgthSZKKUEVFBZWVlZSXl6cdRcqrDz5IHn90223w5Zf113XqlDzv97TTYLfdnPxK0spZCEuSJKngvfYaXHopPProio8/WmcdGDoUTj4ZNt00nXyS2hcLYUmSJBWs99+HUaPg3ntXXLf11nDKKfDTn0KPHm2fTVL7ZSEsSZKkgjN7NlxyCdx8MyxZUn/dPvsklz8PHuzjjyStHgthSZKK0LBhw6iqquKee+6hoqIi7ThSzubPh2uvhSuuSCbEqusHP4CLLvLxR5JazkJYkqQidOutty5vWwirPVi6FG6/HcaMgVmz6q/71reSwni33VKJJqkIWQhLkiQpNTEmE2Cddx5Mn15/3TbbwNixcNBBzgAtKb8shCVJkpSKl16Cs8+Gl1+uv7ysDC68EIYMgS7+36qkVuCPFkmSJLWpN99MzgBPnFh/+dprwznnJBNhde+eTjZJHYOFsCRJktrEzJnJPcC3317/WcBdu8JJJ8H550Pv3qnFk9SBWAhLkiSpVX3xBVx+OVx3HSxcWH/dUUfBxRfD5punk01Sx2QhLEmSpFaxeHHyHOBLLoG5c+uv23ffZCKsHXZIJ5ukjs1CWJIkSXn317/CscfCW2/VX77DDsmjkPbeO51ckgTQKe0AkiRJKh6LFiUTXu22W/0ieLPN4O67YfJki2BJ6fOMsCRJkvLilVeSs8Bvv51dttZayT3AI0bAGmukl02S6rIQliSpCI0ePZoZM2aw2WabpR1FHcDChXDBBXDNNfVng95zT5gwITkbLEmFxEJYkqQiNGbMGCorKykvL087iorcyy8nZ4HfeSe7rEcPuOoqGDYMQkgvmyStjPcIS5IkqdkWLIAzzoBvf7t+Ebz33jBtGgwfbhEsqXB5RliSJEnN8uKLcNxx8K9/ZZeVlsLVV8Pxx1sASyp8FsKSJEnKyaJFnTj9dLj+eogxu3zffeHWW2GTTdLLJknNYSEsSVIROvDAA5k7dy69evVi0qRJacdREXjhBTj++EHMnJldtvbayQRZxx3nWWBJ7UuqhXAIYTBwPdAZuC3GOLbB+rOAozLdLsDXgT4xxs9CCDOAauArYGmMcVCbBZckqcA99thjaUdQkZg/H37+c/jVryDG7suXDx4MFRWw8cYphpOk1ZRaIRxC6AzcBOwDfAK8GkKYGGN8s3abGOOVwJWZ7Q8ETo8xflZnN3vEGOe0YWxJkqQO4/nnk7O9772XXbb22nDddTBkiGeBJbVfac4avRPwbozx/RhjDXAfcHAT2x8B3NsmySRJkjqwefNg5Ej47nfrF8E77zyXN95IHpdkESypPUvz0uh+wMd1+p8AOze2YQihOzAYOLnO4gg8FUKIwPgYY0VrBZUkSeooXngBfvpT+OCD7LJ11knOAm+66VQ22qg8tWySlC9pFsKN/R0xNrIM4EDgpQaXRX8rxlgVQlgfeDqE8HaM8fkV3iSEYcAwgD59+lBZWdnC2FLWvHnzPKaUVx5Tag0eU8pFjPDQQ/24+eYtWbYs+79pu+wyl//7v+n06VPjzyjlnceU0pJmIfwJUHd6hY2AqpVsezgNLouOMVZlvv4nhPAIyaXWKxTCmTPFFQD9+/eP5eXlLQ4u1aqsrMRjSvnkMaXW4DGlVVm4EE44AX7zm+yynj2TxyQdfXQvQtgN8GeU8s9jSmlJ8x7hV4GtQgibhxBKSIrdiQ03CiGsA3wX+H2dZWuFEEpr28C+wLQ2SS1JklREPv4Ydt+9fhG8004wdSocc4z3AksqTqmdEY4xLg0hnAw8SfL4pNtjjG+EEE7IrL8ls+n/A56KMc6vM3wD4JGQ/GTuAtwTY/xj26WXJElq/154AQ49FP7zn+yyY4+FceOgW7f0cklSa0v1OcIxxieAJxosu6VB/w7gjgbL3ge2b+V4kiRJRSlGuPlmOPVUWLo0WdalSzIh1ogRngWWVPxSLYQlSZLUthYvhpNOggkTssv69IEHH0welyRJHYGFsCRJRWj8+PFMnz6d/v37px1FBaSqCn74Q3jlleyyAQPgkUdgk03SyyVJbc1CWJKkIjRs2DBnY1U9f/kLHHIIfPppdtlPfgIVFbDmmunlkqQ0pDlrtCRJktrAbbcllz3XFsGdO8O11yYzRVsES+qIPCMsSZJUpGpqkgmxbqkzFWmvXnD//bDXXunlkqS0WQhLkiQVoU8/TR6N9NJL2WXbb5/cD7z55unlkqRCYCEsSVIRGjhwINXV1ZSWljJlypS046iN/e1vyf3AM2dml/34x8lM0WutlV4uSSoUFsKSJBWh1157Le0ISskdd8AJJySPSQLo1AkuuwzOOsvnA0tSLQthSZKkIrBkCZxxBvzqV9llPXvCfffB976XXi5JKkQWwpIkSe3c7Nlw2GHw5z9nl33zm/Doo7DllunlkqRCZSEsSZLUjr3/Puy9N3zwQXbZIYfAnXdCjx7p5ZKkQuZzhCVJktqpt9+G3XfPFsEhwCWXwO9+ZxEsSU3xjLAkSVI79M9/JmeCZ89O+t26Jc8HPuigdHNJUntgISxJktTOvPpqMgHWf/+b9NdaCyZOhD33TDeXJLUXFsKSJEntyAsvwPe/D9XVSX/tteEPf4Dddks3lyS1J94jLEmS1E48/XRyJri2CO7VC557ziJYkprLQliSJKkdmDQJDjgAFi5M+htsAJWVMGBAqrEkqV3y0mhJkorQxIkTmTp1Kttuu23aUZQHDzwARx0FS5cm/Y03hmefha22SjeXJLVXFsKSJBWhAw88kNLSUsrLy9OOoha680447jhYtizpb7EF/OlPsOmm6eaSpPbMS6MlSZIK1LhxMGRItgj++teTybIsgiWpZSyEJUmSCtBVV8FJJ2X7228Pf/4zlJWll0mSioWFsCRJUgGJES68EM46K7ts552T2aH79EkvlyQVE+8RliSpCJWVlVFTU0NJSQlVVVVpx1GOYoRzzoErr8wu2313eOwxKC1NL5ckFRsLYUmSitCsWbPSjqBmWrYMTjkFbropu2zffeGRR6B79/RySVIxshCWJElK2VdfwfHHwx13ZJcdfDDcfz+ssUZqsSSpaHmPsCRJUoqWLEmeEVy3CD78cHjwQYtgSWotFsKSJEkpWbQIDj00OfNb67jj4K67oGvX9HJJUrGzEJYkSUrBggVw0EEwcWJ22cknw623QufO6eWSpI7AQliSJKmNLVgA++0HTz+dXXbOOXDDDdDJ/zuTpFbnj1pJkqQ2tHQpHHEEPP98dtlFF8Fll0EI6eWSpI7EWaMlSZLaSIxw0kn1L4e+/HI4++z0MklSR+QZYUmSpDZy8cVQUZHtn3WWRbAkpcFCWJIkqQ3cdhuMHp3tH3UUjB2bXh5J6si8NFqSpCI0efJkJk+ezKBBg9KOIuCxx+CEE7L9ffaB2293YixJSouFsCRJRWjgwIFUV1czcODAtKN0eK+8Aj/6EXz1VdLfYQd46CEoKUk3lyR1ZP4dUpIkqZVMnw4HHAALFyb9zTeHJ56A0tJ0c0lSR2chLEmS1ApmzYLBg2Hu3KTfuzf88Y+w4Ybp5pIkWQhLkiTl3Zdfwv77w4wZSb979+Q+4a23TjWWJCnDe4QlSSpCIYTl7Rhjikk6npoaOOQQeP31pN+5MzzwAOy8c7q5JElZnhGWJEnKk2XL4Nhj4dlns8sqKuD7308vkyRpRRbCkiRJeXLOOXDPPdn+RRfBccell0eS1DgLYUmSpDy47jq46qpsf/hwGDUqvTySpJWzEJYkSWqh+++H00/P9g8+GG66Cercqi1JKiAWwpIkSS3w3HNwzDHZ/m67wb33JpNkSZIKk4WwJEnSavrHP+AHP0hmigbYZhuYNAnWXDPdXJKkplkIS5IkrYYPP4T99kueGQxQVgZ//COst166uSRJq2YhLEmS1Exz58LgwTBrVtJfe234wx9g003TzSVJyo2FsCRJUjMsXAgHHQRvv530S0rg0Udhu+3SzSVJyp2FsCRJUo6WLoUjjoCXX84u+81vYI890sskSWo+C2FJkorQzJkzefDBB5k5c2baUYpGjDByJPz+99ll114LP/5xepkkSavHQliSpCJUVlZG7969KSsrSztK0Rg3Dm65Jds/80w47bT08kiSVp+FsCRJ0iq8/HL9ovfII+Hyy9PLI0lqGQthSZKkJnz6KRx2WHJ/MMDAgTBhAnTy/6Ikqd1K9Ud4CGFwCGF6COHdEMK5jawvDyF8EUJ4PfO6INexkiR1ZFVVVcyZM4eqqqq0o7RrS5Yk9wDXfhvXWw9+9zvo1i3dXJKklumS1huHEDoDNwH7AJ8Ar4YQJsYY32yw6QsxxgNWc6wkSR1Sv379lrdjjCkmad/OPReefz5phwD33gubbZZqJElSHqR5Rngn4N0Y4/sxxhrgPuDgNhgrSZK0SvffD9dck+1ffDHsu296eSRJ+ZPaGWGgH/Bxnf4nwM6NbLdrCOEfQBVwZozxjWaMJYQwDBgG0KdPHyorK1ueXMqYN2+ex5TyymNKrcFjqvk++KA7I0YMBDoDsNtuc9h112l09G+lP6OUbx5TSkuahXBoZFnDa7deAzaNMc4LIewPPApslePYZGGMFUAFQP/+/WN5eflqB5YaqqysxGNK+eQxpdbgMdU8X3wBw4fDokVJf8st4fHHe9OzZ3mquQqBP6OUbx5TSkual0Z/Amxcp78RyVnf5WKMX8YY52XaTwBdQwi9cxkrSZLUXDHCkCHwzjtJv3t3ePhh6Nkz1ViSpDxLsxB+FdgqhLB5CKEEOByYWHeDEMKGIYSQae9EknduLmMlSZKa6/LL4dFHs/3bboNtt00vjySpdaR2aXSMcWkI4WTgSZIbcG6PMb4RQjghs/4W4FDgxBDCUmAhcHhMpr5sdGwqH0SSJBWFZ56B88/P9k89FY44Ir08kqTWk+Y9wrWXOz/RYNktddo3AjfmOlaSJGl1fPRRUvQuW5b0v/1tuPLKdDNJklpPmpdGS5IkpW7RIvjhD2HOnKS/4YbwwAPQtWu6uSRJrcdCWJIkdWinnAKTJyftLl3gwQehb990M0mSWpeFsCRJ6rAmTIBbb832r746uSxaklTcLIQlSSpCMUaee+45kjkm1ZjJk+Gkk7L9I4+EkSPTyyNJajsWwpIkqcOZMye5L3jx4qS/7bZQUQHJQxslScXOQliSJHUoX32VnP396KOkv8468PDDsNZa6eaSJLUdC2FJktShXHABPP10tv/b38KWW6aXR5LU9iyEJUkqQlOmTGH69OlMmTIl7SgF5fe/h1/+MtsfNQoOPDC9PJKkdHRJO4AkScq/QYMGLW87YVbinXfgmGOy/e99D8aMSS2OJClFnhGWJElFb/58OOQQ+PLLpL/ppnD33dC5c7q5JEnpsBCWJElFLUY4/nh4442kv8YayeRYvXqlm0uSlB4LYUmSVNRuuAHuuy/bv/lmGDAgvTySpPRZCEuSpKL1yitw5pnZ/rBhcOyx6eWRJBUGC2FJklSUqqvhJz+BpUuT/k47JWeHJUmyEJYkSUXp9NPhvfeS9tprwwMPJPcHS5JkISxJkorOI4/AhAnZ/rhxyUzRkiSBhbAkSSoys2bB0KHZ/uGHw5FHppdHklR4LIQlSVLRiDGZDGvu3KS/0UbJ2eAQ0s0lSSosXdIOIEmS8m1sk5MAACAASURBVK9v377U1NRQUlKSdpQ2ddNN8OSTSTsE+M1vYN11080kSSo8nhGWJKkIVVVV8bvf/Y6qqqq0o7SZN9+Es87K9s84A/bYI708kqTCZSEsSZLavZoaOOooWLQo6W+3HVxySbqZJEmFy0JYkiS1exdcAK+/nrTXWAPuvttHJUmSVs5CWJIktWt//jNccUW2f/nl8D//k14eSVLhsxCWJKkITZo0iZdffplJkyalHaVVff45HH10Mls0wD77wMiR6WaSJBU+Z42WJKkIHXTQQcvbsbZKLEInnQQff5y011sP7rgDOvlnfknSKvirQpIktUv33JO8alVUQFlZenkkSe2HhbAkSWp3PvoIRozI9o89Fn74w/TySJLaFwthSZLUrnz1FRxzDHzxRdLfYgu4/vp0M0mS2hcLYUmS1K5cc00yUzQk9wP/9rdQWppuJklS+2IhLEmS2o3XX4fzz8/2zz8fdtstvTySpPbJQliSJLULCxfCUUfBkiVJf8cd4Re/SDeTJKl9shCWJEntwrnnwptvJu3u3eGuu6Br13QzSZLaJwthSZJU8J58Em64Idu/9lrYeuv08kiS2jcLYUmSVNDmzIEhQ7L9Aw+EoUNTiyNJKgJd0g4gSZLyb8CAAVRXV1PazqdTjhGGD4dPP036668Pt90GIaSbS5LUvlkIS5JUhKZMmUJlZSXl5eVpR2mRO+6Ahx/O9m+/PSmGJUlqCS+NliRJBem99+CUU7L9E0+E738/vTySpOJhISxJkgrO0qVw9NEwb17S798frroq3UySpOJhISxJkgrOZZfBX/6StLt0SR6V1L17upkkScXDQliSpCJUUVHBpEmTqKioSDtKs736Klx4YbZ/4YUwaFB6eSRJxcfJsiRJKkLDhw9f3h42bFiKSZqnpgaOOw6++irpf+tbcM456WaSJBUfzwhLkqSCMXYsTJuWtLt3h9/8Bjp3TjeTJKn4WAhLkqSCMG0aXHJJtn/ppbDFFunlkSQVLwthSZKUuq++gp/9DJYsSfq77AIjR6abSZJUvCyEJUlS6q6/Hv72t6RdUgITJnhJtCSp9VgIS5KkVL33Howale2PGgXf+EZ6eSRJxc9CWJIkpSZGGDoUFi5M+ttt5yzRkqTWZyEsSZJSc9tt8NxzSbtTp+SS6JKSdDNJkoqfhbAkSUrFzJlw5pnZ/plnwqBB6eWRJHUcFsKSJKnNxQgnnghffpn0t9wSxoxJNZIkqQPpknYASZKUfwcccABz586lV69eaUdp1P33w6RJ2f6ECbDmmunlkSR1LBbCkiQVoUmTJlFZWUl5eXnaUVYwZ079ZwSfeCLsvnt6eSRJHU+ql0aHEAaHEKaHEN4NIZzbyPqjQgj/zLxeDiFsX2fdjBDC1BDC6yGEyW2bXJIkra7TTkuKYYCNNoKxY9PNI0nqeFI7IxxC6AzcBOwDfAK8GkKYGGN8s85mHwDfjTH+N4SwH1AB7Fxn/R4xxjltFlqSJLXI44/D3Xdn++PHw9prp5dHktQxpXlGeCfg3Rjj+zHGGuA+4OC6G8QYX44x/jfTfQXYqI0zSpKkPPnySxg+PNv/yU9g//3TyyNJ6rjSvEe4H/Bxnf4n1D/b29DPgD/U6UfgqRBCBMbHGCsaGxRCGAYMA+jTpw+VlZUtySzVM2/ePI8p5ZXHlPLljjvuoKamhjvuuIMhQ4akHQeAa67ZmpkzywDo2bOGQw99lcrKJSmnUnP4M0r55jGltIQYYzpvHMJhwPdijMdn+kcDO8UYRzay7R7AOODbMca5mWVlMcaqEML6wNPAyBjj8029Z//+/eP06dPz/VHUgRXqRDRqvzymlC8hhOXttH7X11VZCXvske3fdx/8+MepxdFq8meU8s1jSvkWQpgSY1zlU+nTvDT6E2DjOv2NgKqGG4UQtgNuAw6uLYIBYoxVma//AR4hudRakiQVmAULYOjQbP/gg+FHP0ovjyRJaRbCrwJbhRA2DyGUAIcDE+tuEELYBHgYODrG+E6d5WuFEEpr28C+wLQ2Sy5JknI2ejS8+27SXmcdGDcO6pywliSpzaV2j3CMcWkI4WTgSaAzcHuM8Y0QwgmZ9bcAFwC9gHGZS7yWZk5zbwA8klnWBbgnxvjHFD6GJElqwquvwjXXZPtXXw1lZenlkSQJ0p0sixjjE8ATDZbdUqd9PHB8I+PeB7ZvuFySJBWOmhr42c9g2bKkv+eecNxx6WaSJAnSvTRakiQVsbFjYerUpN29O9x6q5dES5IKg4WwJEnKuzfegEsuyfYvvRS22CK9PJIk1WUhLEmS8uqrr5JLopdkHhG8884wcoWHI0qSlB4LYUmSlFc33AB//WvS7toVJkyAzp3TzSRJUl0WwpIkKW/efx/OPz/b/8Uv4JvfTC+PJEmNSXXWaEmS1DqGDh1KVVUVZW34rKIYYehQWLgw6W+7LZxzTpu9vSRJObMQliSpCFVUVFBZWUl5eXmbveeECfCnPyXtTp3g9tuhpKTN3l6SpJx5abQkSWqxmTPhjDOy/TPOgEGD0ssjSVJTLIQlSVKLnXoqfPll0t5ySxgzJtU4kiQ1yUJYkiS1yOOPw0MPZfu33grdu6eXR5KkVbEQliSpCA0bNoyrrrqKYcOGter7LFgAJ52U7Q8ZAm14W7IkSavFybIkSSpCt9566/J2RUVFq73PRRfBhx8m7fXWgyuvbLW3kiQpbzwjLEmSVsu0aXD11dn+lVdC797p5ZEkKVcWwpIkqdmWLYMTT4SlS5P+d76TXBYtSVJ7YCEsSZKa7de/hhdfTNpdusDNNyfPDpYkqT3wV5YkSWqW2bPh7LOz/bPOgm9+M708kiQ1l4WwJElqlrPOgs8+S9qbbw6jRqWbR5Kk5rIQliRJOaushDvvzPZvvNFnBkuS2h8LYUmSlJPFi5MJsmodeijsv396eSRJWl0WwpIkKSdXXQVvv520S0vhuuvSzSNJ0uqyEJYkSav03ntwySXZ/iWXQL9+6eWRJKkluqQdQJIk5d/o0aOZMWMGm222WYv3FSOMGAGLFiX9gQPhpJNavFtJklJjISxJUhEaM2YMlZWVlJeXt3hfDzwATz2VtDt1gltugc6dW7xbSZJS46XRkiRppb74Ak47Lds/6SQYNCi9PJIk5YOFsCRJWqnzz4dPP03affvCxRenm0eSpHywEJYkSY169VUYNy7bv/56WGed9PJIkpQv3iMsSVIROvDAA5k7dy69evVi0qRJzR6/dCkMH55MlAUweHDy3GBJkoqBhbAkSUXosccea9H4m26Cv/89aXfrlvRDyEMwSZIKgJdGS5Kkej75BEaNyvZ/8QvYYov08kiSlG8WwpIkqZ7TToN585L2178OZ56Zbh5JkvLNQliSJC33+OPw0EPZ/i23QElJenkkSWoNFsKSJAmABQuS5wTXOvZY2H339PJIktRaLIQlSRIAF10EH36YtHv1giuuSDePJEmtxUJYkiQxbRpcfXW2f+WV0Lt3enkkSWpNFsKSJHVwy5bBCSckzw4G+M53YMiQVCNJktSqLIQlSergfv1reOmlpN2lSzJBls8MliQVMwthSZI6sNmz4eyzs/2zzoJvfCO9PJIktYUuaQeQJEn5N378eKZPn07//v2b3O6ss+Czz5L25pvDqFFtEE6SpJRZCEuSVISGDRtGZWUl5eXlK92mshLuvDPbv+km6N691aNJkpQ6L42WJKkDqqmBESOy/cMOg/32Sy+PJEltyUJYkqQO6Npr4a23knaPHklfkqSOYqWFcAjBIlmSpCL04Ydw0UXZ/sUXQ79+6eWRJKmtNXWP8GshhBNjjH9pszSSJCkvBg4cSHV1NaWlpUyZMqXeutNOgwULkvZ228HJJ6cQUJKkFDVVCA8HfhVC+Adwdozxv22USZIktdBrr73W6PLHHoNHH832b745eXawJEkdyUp/9cUY/xpC2Bk4AZgcQvgDsKzO+lPaIJ8kScqTBQtg5Mhs/2c/g912Sy+PJElpWdXfgNcDdgRmA1OoUwhLkqT25bLLYMaMpL3eejB2bKpxJElKzUoL4RDCCcBZwJXAz2KMsc1SSZKkvJo+Ha64ItsfOxZ6904vjyRJaWrqjPB3gF1jjP9pqzCSJCn/YkwmxKqpSfo775xcFi1JUkfV1D3CR7VlEEmS1DoefBCeeSZpd+qUTJDVyYckSpI6MH8NSpJU5E47Lds++WTYYYf0skiSVAgshCVJKnKzZiVfN9wQLroo3SySJBWCnJ4cGELYnuSeYYAXYoz/aL1IkiSpNVxzDayzTtopJElK3yrPCIcQTgXuBtbPvO4KIYxselRuQgiDQwjTQwjvhhDObWR9CCHckFn/zxDCgFzHSpKkrD33hMMPTzuFJEmFIZdLo38G7BxjvCDGeAGwCzC0pW8cQugM3ATsB3wDOCKE8I0Gm+0HbJV5DQNubsZYSZI6rJEjJwLJq2tXuOkmCCHtVJIkFYgYY5MvYCrQrU6/GzB1VeNy2O+uwJN1+ucB5zXYZjxwRJ3+dKBvLmMbe/Xq1SsCOb2GDh0aGxo6dGjO40ePHr3C+AMOOCDn8ePHj19h/IABA3IeP3HixBXG9+3bN+fxkydPXmF8rmOBOHPmzHpjZ86c2azxDU2ePDnnsX379l1h/MSJE3MeP2DAgBXGjx8/PufxBxxwwArjR48e7bHnsZfTsffcc8/VG++x57G3OsfenDkxlpb6c89jr+2PvRj9neux17xjr+7vPY89j708HXuTYw71aC73CP8a+GsI4ZFM/wfAhBzGrUo/4OM6/U+AnXPYpl+OYwEIIQwjOZtM9+7dcw5XVVVFZWXlCstyNWPGjBXGz507N+fx06dPX2F8dXV1zuOnTp1KaWlpvWU1tQ+QzMHkyZOb9X4Nvfzyy/Tu3Xt5f86cOc0a3/CzT58+PeexNTU1K4yfOnVqzuOrq6tb9P5z585dYfyMGTNyHu+x17GPvXnz5tXbh8eex14uGh57V121Nc35KP7c89iry9+5Hnu5ysexV/f3nseex16uWnrsQQ6TZcUYrwkhVALfBgJwbIzx781+pxU1doFWzHGbXMYmC2OsACoAevfuHRcsWJBTuLKyMsrLy+stu+eee3IaC7DZZputML5Xr145j+/fv/8K4xsebE3ZdtttVxhfUlKS8/hBgwYxcODAnLdvaLfddqOsrGx5vzn/YQMt+uwlJSUrjG/Of2ilpaUrjH/nnXdyHt+rV68Vxjf8QdMUj72Ofez16NGj3j489jz2clH32HvlFXj8cYApOY/3557HXl3+zvXYy1U+jr3Kysrln8Fjz2MvVy099gBCcha6iQ1C2DvG+EyDZT+NMd7Z7Herv49dgTExxu9l+ucBxBgvq7PNeKAyxnhvpj8dKAc2W9XYxvTv3z825y890qrU/eEt5YPHlFpi6VLYcUd4/fWkv9tuc3jppd5ND5KawZ9RyjePKeVbCGFKjHHQqrbLZbKsC0IIN4cQuocQNgghTAIObHlEXgW2CiFsHkIoAQ4nmdWjronAMZnZo3cBvogxzspxrCRJHcq4cdkiGMp4882v1/uLuSRJSuRyj/B3gTOA2mcHX1B7hrYlYoxLQwgnA08CnYHbY4xvhBBOyKy/BXgC2B94F1gAHNvU2JZmkiSpvZo1C0aNqreEzz+Hzz9PK5EkSYUrl0J4XZKJqN4DNgI2DSGEuKprqnMQY3yCpNitu+yWOu0InJTrWEmSOqozzmD5BFn9+4N3AkmStHK5XBr9CvCHGONgYEegDHipVVNJkqScPfss3FvnWq2bbkoviyRJ7UEuZ4T3jjF+BBBjXAicEkLYvXVjSZKkXCxeDCfVuXbqiCNgr73SyyNJUnuw0kI4hLBNjPFtoHcIoeGUk/NaN5YkScrF1VdnL4MuLU36kiSpaU2dET4DGAo09is1Anu2SiJJkpSTDz6Aiy/O9i+5BPr2TS+PJEntxUoL4Rjj0MzXPdoujiRJytWpp8KiRUn7f/8XRoxIN48kSe3FSifLCiGcXad9WIN1v2zNUJIkqWkTJ8KkSdn+zTdDl1xm/pAkSU3OGn14nfZ5DdYNboUskiQpBwsWwCmnZPtDh8Iuu6SXR5Kk9qapQjispN1YX5IktZFLL4UPP0zavXrBZZelm0eSpPamqYuo4krajfUlSVIbePttuPLKbP+KK5JiuKHJkyczefJkBg0a1HbhJElqJ5oqhLcPIXxJcvZ3zUybTL9bqyeTJEn1xJhMiLVkSdLfdVcYMqTxbQcOHEh1dTUDBw5ss3ySJLUXTc0a3bktg0iSpKbddRc891zS7tw5mSCrU1M3OUmSpEb561OSpHbgs8/gjDOy/VNPhe23Ty+PJEntmYWwJEntwLnnwuzZSXujjeDCC9PNI0lSe+YTByVJKnAvvQS33prt/+pX0KNH02NCyD7gIUbnuJQkqS7PCEuSVMCWLIETTsj2DzoIfvCD9PJIklQMLIQlSSpg114L06Yl7e7d4YYb0s0jSVIxsBCWJKlAzZgBY8Zk+xdeCJtumlYaSZKKh4WwJEkFKEYYORIWLkz6222XzBQtSZJazkJYkqQC9Oij8NhjSTsEuOUW6No13UySJBULC2FJkgpMdXVyNrjWsGGw667p5ZEkqdhYCEuSVGBGj4aZM5P2+uvDZZelm0eSpGJjISxJUgH5+9/h+uuz/WuugXXXTS+PJEnFyEJYkqQC8dVXMHw4LFuW9PfaC448Mt1MkiQVIwthSZIKxPjx8OqrSbukBMaNSybKkiRJ+WUhLElSAZg1C847L9s/7zzYeuvV39/MmTN58MEHmVl7s7EkSVrOQliSpALwf/8HX36ZtLfaCs49t2X7Kysro3fv3pSVlbU8nCRJRcZCWJKklD31FNx3X7Y/bhx065ZeHkmSip2FsCRJKVq4EEaMyPaPOgr23ju9PJIkdQQWwpIkpeiXv4T33kvaPXvC1VfnZ79VVVXMmTOHqqqq/OxQkqQi0iXtAJIkdVRvvw2XX57tjx0LG2yQn33369dveTvGmJ+dSpJUJDwjLElSCmKEE06AJUuS/i67wNCh6WaSJKmjsBCWJCkFv/0t/PnPSbtz5+QZwp38rSxJUpvwV64kSW1s7lw444xs//TTYbvt0ssjSVJHYyEsSVIbO/dcmDMnaW+8MYwenW4eSZI6GgthSZLa0Isvwm23Zfs33gg9eqSXR5KkjshCWJKkNrJkSTJBVq2DD4aDDkovjyRJHZWFsCRJbeSaa+CNN5L2WmvBDTekm0eSpI7KQliSpDYwYwZceGG2f+GFsMkmqcWRJKlDsxCWJKmVxQgnnwwLFyb97beHU09NN5MkSR2ZhbAkSa3s4Yfh8ceTdghwyy3QpUu6mSRJ6sgshCVJakX//W9yNrjW8OGwyy6t/74xRp577jlijK3/ZpIktTMWwpIktaKzzoJPP03aG2wAv/xlunkkSZKFsCRJreaZZ2DChGx/3DhYd9308kiSpISFsCRJrWD+fBg6NNs/9FA45JD08kiSpCwLYUmSWsGoUckjkyA5C/yrX7Xt+0+ZMoXp06czZcqUtn1jSZLaAeeslCQpz/7yF7j++mz/2mthww3bNsOgQYOWt50wS5Kk+jwjLElSHi1eDD/7WfLsYIDvfQ+OOSbdTJIkqT4LYUmS8ujSS+Gtt5L2WmvB+PHJs4MlSVLhsBCWJClP/vEPuOyybH/sWNh00/TySJKkxlkIS5KUB0uXJpdEL12a9L/1LRgxIt1MkiSpcRbCkiTlwTXXQO0EzWuskTw/uJO/ZSVJKkj+ipYkqYXeeQdGj872x4yB/v1TiyNJklYhlUI4hLBeCOHpEMK/Ml/XbWSbjUMIz4UQ3gohvBFCOLXOujEhhJkhhNczr/3b9hNIkpRYtgyGDoVFi5L+DjvAGWekm0mSJDUtrTPC5wLPxhi3Ap7N9BtaCpwRY/w6sAtwUgjhG3XWXxtj/N/M64nWjyxJ0orGj4fnn0/anTsnl0R37ZpuJkmS1LS0CuGDgTsz7TuBHzTcIMY4K8b4WqZdDbwF9GuzhJIkrcJHH8HZZ2f755yTnBGWJEmFrUtK77tBjHEWJAVvCGH9pjYOIWwG7AD8tc7ik0MIxwCTSc4c/3clY4cBwwD69OlDZWVli8NLtebNm+cxpbzymGo/YoTzztuWefN6AbDxxgv47ncnU1m5LOVkiV69ehFjJITgMaW88WeU8s1jSmkJMcbW2XEIzwAbNrLqfODOGGPPOtv+N8a4wn3CmXU9gD8Dl8YYH84s2wCYA0TgYqBvjPG4VWXq379/nD59erM/i7QylZWVlJeXpx1DRcRjqv246y44+uikHQK88ELyyKRC4vGkfPOYUr55TCnfQghTYoyDVrVdq50RjjHuvbJ1IYR/hxD6Zs4G9wX+s5LtugIPAXfXFsGZff+7zja3Ao/lL7kkSU37z3/g1FOz/ZNPLrwiWJIkrVxa9whPBH6aaf8U+H3DDUIIAZgAvBVjvKbBur51uv8PmNZKOSVJWsHIkfDZZ0l7k03gl79MN48kSWqetArhscA+IYR/Aftk+oQQykIItTNAfws4GtizkcckXRFCmBpC+CewB3B6G+eXJHVQjz4KDzyQ7d96K/TokV4eSZLUfKlMlhVjnAvs1cjyKmD/TPtFIKxk/NGtGlCSpEZ8/jmMGJHtDxkC++6bWpwmTZo0ialTp1JdXc2BBx6YdhxJkgpKWrNGS5LU7px5JsyalbQ32ACuvjrdPE056KCDlrdba2JMSZLaq7QujZYkqV159lmYMCHbHzcO1lsvvTySJGn1WQhLkrQK8+fD0KHZ/g9/CIcckl4eSZLUMhbCkiStwqhR8MEHSXvddeHGG9PNI0mSWsZCWJKkJrzyClx/fbZ/7bWw4Ybp5ZEkSS1nISxJ0kosXgzHHQe1c03tuy8cc0y6mSRJUstZCEuStBKXXgpvvZW011oLxo+H0OiD/SRJUntiISxJUiP++U+47LJsf+xY2Gyz1OJIkqQ8shCWJKmBmhoYMgSWLk363/oWjBiRaiRJkpRHFsKSJDUwejT8/e9Je4014LbboJO/MSVJKhpd0g4gSVIhef55uPzybH/sWNhmm/TyrK4BAwZQXV1NaWlp2lEkSSo4FsKSJGV88QUcfXR2lui994ZTTkk30+qaMmUKlZWVlJeXpx1FkqSC44VekiRlnHwyfPRR0l53XbjjDi+JliSpGPnrXZIk4L774K67sv2KCujXL708kiSp9VgIS5I6vI8/hhNPzPZ/+lM49ND08kiSpNZlISxJ6tCWLUsK388/T/qbbQY33JBqpLyoqKhg0qRJVFRUpB1FkqSC42RZkqQO7dpr4bnnknanTvDb38Laa6ebKR+GDx++vD1s2LAUk0iSVHg8IyxJ6rD+8Q/4+c+z/fPOg29/O708kiSpbVgIS5I6pIUL4aijoKbm/7d372FalfX+x99fTiIwnlEZ1J9aNnlKDULN/Dmm5BFPpen2VB7InZnssi1ud0p2EK3sYAelLMnUPKAFHtI0Rv3tSgU1ARXFw04cTE4agwIC9++P9QzPDMzAMMzMep553q/rWtez7nutNfOdy3Ux8/Fe676z9tChcPnl+dYkSZK6hkFYklSRLrkEZszI9jfeOJsxunfvfGuSJEldwyAsSao4Dz4IP/pRsX3NNVBTk189kiSpaxmEJUkVZf58+Nzniu2jj4Ym80pJkqQKYBCWJFWMlGDkSJgzJ2tvvTXccANE5FuXJEnqWgZhSVLFGD8e7rqr2L7hhiwMS5KkymIQliRVhFdegQsuKLbPOy97LFqSJFUeg7AkqdtbvhxOPx0aGrL2hz4E3/tevjVJkqT89Mq7AEmSOtvYsfCXv2T7vXrBzTdD//751tTZjj76aObPn8+WW26ZdymSJJUcg7AkqVt74gkYM6bYHjMGhg7Nq5quM2nSJOrq6qitrc27FEmSSo6PRkuSuq3Fi+G002DFiqx9wAEwenS+NUmSpPwZhCVJ3dZXvwovvZTtV1XBTTdBz5751iRJkvJnEJYkdUuTJsH11xfb114LO+2UXz2SJKl0GIQlSd3OP/8JZ59dbH/mM3DGGfnVk4cxY8Zw4403MqbpC9KSJAlwsixJUjeTUhaC587N2tXVcN11EJFvXV3tG9/4xqp9w7AkSc05IixJ6lauvx7uvbfYvvFGcAUhSZLUlEFYktRtzJwJX/lKsT1qFAwfnl89kiSpNBmEJUndwnvvwSmnZJ8Au+8OV16Zb02SJKk0GYQlSWUvJfjiF+Hpp7N2nz5w883Qt2++dUmSpNJkEJYklb1x47J3gRv94Aew1165lSNJkkqcQViSVNYefxwuuKDYPuMM+Pd/z68eSZJU+gzCkqSy9dZb2RrB77+ftffeuzKXSpIkSevHICxJKkvLl8PJJ8Ps2Vl7881hwgTYeON865IkSaXPICxJKkuXXgqTJ2f7EdnkWDvvnG9NkiSpPPTKuwBJktbXhAlw9dXF9uWXwxFH5FdPKTr33HOpr6+nuro671IkSSo5BmFJUll54QX43OeK7SOPhK9/PbdySta4ceOoq6ujtrY271IkSSo5PhotSSobixbBCSdAQ0PW3nln+O1voYe/zSRJ0nrwTwdJUllICc46C55/Pmv37Qt33ZVNkiVJkrQ+DMKSpLLw/e/DnXcW2+PGwV575VePJEkqXwZhSVLJmzwZLr642D7/fDj99PzqKQcjR47ke9/7HiNHjsy7FEmSSo6TZUmSStrs2fDZz8LKlVl7//3hmmvyrakc/OIXv1i1P27cuBwrkSSp9DgiLEkqWUuXwmc+A3PnZu2tt4Y77oA+ffKtS5IklTeDsCSpZP3Hf8Djj2f7PXvC7bfD4MH51iRJksqfQViSVJLGj4ef/7zYvvpqOOig/OqRJEndRy5BOCK2iIg/RcRLhc8WF7+IiNciYlpEPBMRU9b3eklSeXr64BRyswAAG7pJREFUaTjvvGL7pJOy0WFJkqSOkNeI8Gjg4ZTSLsDDhXZrDk4p7Z1SGtrO6yVJZWTBAvj0p2HJkqy9665www0QkW9dkiSp+8grCB8LjC/sjweO6+LrJUklaOVKOO00ePXVrF1VBXffDQMG5FuXJEnqXvJaPmmblNIcgJTSnIjYupXzEvBgRCTg+pTSuPW8nogYCYwEGDhwIHV1dR31M0g0NDR4T6lDVfo9deONO3L//Tuuan/ta9OZM2cec+bkV1N3UMn3lDpWpf8bpY7nPaW8REqpc75wxEPAti0cuhQYn1LarMm5C1NKa7znGxHVKaX6QtD9E3BBSunRiHi7LdevrqamJs2cObNdP4/Ukrq6Ompra/MuQ91IJd9T994LRx9dbF98MYwdm1895S6aPEveWb/rVXkq+d8odQ7vKXW0iJi62mu1Leq0EeGU0qGtHYuIf0bEoMJo7iDgrVa+Rn3h862IuBsYBjwKtOl6SVJ5ePnl7JHoRoccAt/6Vn71SJKk7i2vR6MnAmcCYwuff1j9hIjoD/RIKS0q7H8KuKKt10uSysO772aTY739dtbefnu49VbolddvqG7i8ssv57XXXmPHHXfMuxRJkkpOXn9mjAVuj4izgX8AJ0L2KDTwy5TSkcA2wN2FR7t6AbeklP64tuslSeUlJTj3XPj737N2nz5w550wcGC+dXUHY8aM8ZFDSZJakUsQTinNBw5pob8eOLKw/wqw1/pcL0kqL5deCrfcUmxfey0MG5ZfPZIkqTLktXySJKnC/eQncOWVxfa552abJElSZzMIS5K63IQJ8OUvF9tHHQU/+xk0mehYkiSp0zgViSSpSz32GJx6avZ+MGSPQt92m5NjdbQRI0Ywf/58ttxySyZNmpR3OZIklRT/7JAkdZkZM+CYY2Dp0qy9yy5wzz3Qv3++dXVH99xzT94lSJJUsnw0WpLUJV5/HQ4/vLhM0jbbwAMPOEO0JEnqegZhSVKnW7gQjjgCZs/O2gMGwP33w0475VuXJEmqTAZhSVKnWrIEjjsueywasneB77oL9tkn37okSVLlMghLkjrNihVw2mnw6KPFvhtvhOHDcytJkiTJICxJ6hwpwahR2VJJja6+OpsxWpIkKU8GYUlSp7jqKvjJT4rtCy+Eiy7Krx5JkqRGBmFJUocbPx4uuaTYPukkuOYaiMivJkmSpEYGYUlSh/rjH+Hss4vt2lr4zW+gh79xJElSifDPEklSh3nySfjMZ7JJsgD23BN+/3vYaKN865IkSWqqV94FSJK6h1mz4KijYPHirL3DDtlawZtumm9dler6669n5syZ1NTU5F2KJEklxyAsSdpgb70Fhx8Oc+dm7c03zx6RHjw437oq2ciRI6mrq6O2tjbvUiRJKjk+Gi1J2iANDdlI8MsvZ+2+fWHSJNh113zrkiRJao1BWJLUbu+/n70TPGVK1u7RA269FQ44IN+6JEmS1sYgLElql5TgnHPggQeKfT/9KRx3XH41SZIktYXvCEuS2uXSS7NlkRr993/DeeflV4+aGzJkCIsWLaKqqoqpU6fmXY4kSSXFICxJWm8/+QlceWWxfdZZcMUV+dWjNT311FN5lyBJUsny0WhJ0nq59lq44IJi+8gj4brrICK/miRJktaHQViS1GZXXQVf/nKxPWwY3H479O6dX02SJEnryyAsSVqnlOCyy2D06GLffvtlE2X1759fXZIkSe3hO8KSpLVKCS66CK65pthXWwsTJ0JVVW5lSZIktZtBWJLUqpUr4fzzs3eAGx1xBEyYABtvnF9dkiRJG8IgLElq0fLl2WzQN91U7Dv+eLj1Vthoo/zqkiRJ2lC+IyxJWsOyZXDKKc1D8KmnZhNjGYIlSVK5MwhLkppZsgROOAHuvLPYd845MH489PI5IkmS1A0YhCVJqyxeDEcfDffeW+y78EIYNw569syvLkmSpI7k/9uXJAHwzjtw1FHwP/9T7Puv/4JvfQsi8qtL7TNx4kSmTZvGnnvumXcpkiSVHIOwJIn58+Gww2Dq1GLft7+dBWGVpxEjRlBVVUVtbW3epUiSVHIMwpJU4d58E4YPh+nTi30/+AGMGpVfTZIkSZ3JICxJFWz2bDjkEHjxxawdka0ZPHJkvnVJkiR1JoOwJFWoV17JQvBrr2Xtnj3hxhvhtNPyrEqSJKnzGYQlqQK98EIWguvrs3bv3vC732XLJql7qK6uZtmyZfTp04f6xv/QkiQJMAhLUsV59lk49FCYOzdr9+0LEybAkUfmW5c61pw5c/IuQZKkkmUQlqQK8sQTcPjhsHBh1u7fHyZNgoMPzrcuSZKkrtQj7wIkSV3jsceykeDGELzppvDgg4ZgSZJUeQzCklQBfvObbImkRYuy9pZbwp//DB//eL51SZIk5cEgLEnd2PvvZ+sBn3kmLF2a9W27LdTVwUc/mmtpkiRJufEdYUnqpubOhc9+FiZPLvbtvjv84Q/wgQ/kV5ckSVLeHBGWpG7o6adh6NDmIfj44+GvfzUES5IkGYQlqZu55RY44AD4xz+ydgR885tw551QVZVvbZIkSaXAR6MlqZtYvhxGj4bvf7/Yt8km8NvfwogR+dUlSZJUagzCktQNzJ8PJ58MDz1U7Kupyd4HrqnJry5JkqRSZBCWpDL37LNw3HHw6qvFvhEj4KabsrWCVZmmTJnClClTGDp0aN6lSJJUcnxHWJLK2B13wP77Nw/Bl10Gv/+9IbjSDRkyhJqaGoYMGZJ3KZIklRxHhCWpDK1YAV//Olx5ZbFvwIBsFPi44/KrS5IkqRwYhCWpzCxcCKeeCvffX+z74AezUeDdd8+vLkmSpHLho9GSVEZmzIBhw5qH4COOgCeeMARLkiS1lSPCklQm7r4bzjgDGhqKfZdckq0R3LNnfnWpNEXEqv2UUo6VSJJUehwRlqQSt3IlXH45nHBCMQT36we33w7f+Y4hWJIkaX3lEoQjYouI+FNEvFT43LyFc2oi4pkm278iYlTh2JiIeKPJsSO7/qeQpM73zjvZ5FdXXFHs22kn+Otf4cQT86tLkiSpnOU1IjwaeDiltAvwcKHdTEppZkpp75TS3sAQ4F3g7ian/KDxeErpvi6pWpK60F//Ch/7GEyaVOwbPhyefBI+8pH86pIkSSp3eQXhY4Hxhf3xwLoW+zgEeDml9L+dWpUklYB334WvfhUOOABeeqnYf9FFcN99sOWW+dUmSZLUHeQVhLdJKc0BKHxuvY7zTwZuXa3vSxHxbET8qqVHqyWpHE2btgl77w3XXAON8xtVVcHNN8N3vwu9nOJQkiRpg0VnzSQZEQ8B27Zw6FJgfEppsybnLkwptRhmI6IPUA/snlL6Z6FvG2AekIBvAoNSSme1cv1IYCTAwIEDh9x+++3t/6Gk1TQ0NDBgwIC8y1A3sGRJD264YScmTNiOlIqz/Q4duoCLLprJNtsszbE6laODDz541f7kyZNzrETdib/31NG8p9TRDj744KkppaHrOq/TgvBav2nETKA2pTQnIgYBdSmlmlbOPRY4P6X0qVaO7wjck1LaY13ft6amJs2cObP9hUurqauro7a2Nu8yVOYeewzOOgtmzSr2VVVlo8Jnnw1NVsGR2szlk9QZ/L2njuY9pY4WEW0Kwnk9Gj0ROLOwfybwh7WcewqrPRZdCM+Njgemd2h1ktQFFi+GUaPgoIOah+DDDoMZM+CccwzBkiRJnSGvIDwWGB4RLwHDC20iojoiVs0AHRH9CsfvWu36qyNiWkQ8CxwM/EfXlC1JHePRR2GvveBHPyq+C7zJJvC1r73A/ffD9tvnW58kSVJ3lsu0Kyml+WQzQa/eXw8c2aT9LrDG/KgppdM7tUBJ6iSLF8Mll8C11zbvP+IIGDcOZs16k4gP51OcJElShchrRFiSKs4jj2Tr/zYNwZtuCr/+Ndx7L2y3XX61qft54403uOOOO3jjjTfyLkWSpJJjEJakTtbQAF/6EtTWwiuvFPuPOip7F/hzn/NdYHW86upqttpqK6qrq/MuRZKkkuOKlJLUiSZPzmZ+fvXVYt9mm2XvBp9+ugFYkiQpD44IS1InaGiA88+HT36yeQg++uhsFPiMMwzBkiRJeTEIS1IHe/hh2HNP+NnPin2bbw433QQTJ4JPqqor1NfXM2/ePOrr6/MuRZKkkuOj0ZLUQWbMgNGj4Z57mvcfcwxcdx0MGtTydVJnGDx48Kr91LhGlyRJAhwRlqQNNns2nHVWNiN00xC8xRZw883w+98bgiVJkkqJI8KS1E5vvw1XXgk//jEsWVLsj4DTToOrr4Ztt82vPkmSJLXMICxJ62nJEvjpT+Hb34aFC5sfO/xwGDsW9torn9okSZK0bgZhSWqjFSuyR52//nX4xz+aHxsyJBsB/uQn86lNkiRJbWcQlqR1SAkeeAAuvhiefbb5sZ13hu98B048EXo464IkSVJZMAhL0lpMmQL/+Z8weXLz/q22gssugy98Afr0yac2SZIktY9BWJJa8PLLcOmlcNttzfv79YOvfhUuugg22SSf2iRJkrRhDMKS1MRbb8E3v5mt+7t8ebG/Z08491y4/HJngpYkSSp3BmFJAhoa4Jpr4Lvfzfab+vSnsxmia2ryqU2SJEkdyyAsqaK9+Sb8/OfZNndu82MHHpjNBL3ffvnUJkmSpM7hHKeSKtJTT8GZZ8IOO8AVVzQPwbvtBhMnwiOPGIJVvlJKTJ48mZRS3qVIklRyHBGWVDFWrMgC7g9/CI8+uubx7beHMWOygNyzZ5eXJ0mSpC5iEJbU7b3zDvzqV/DjH8Nrr615/OMfhwsvhOOPh969u7w8SZIkdTGDsKRua9asLPz++tdrToDVqxecdFIWgIcNy6c+SZIk5cMgLKlbSQkmT84ef77nnqzd1BZbwHnnwRe/CIMH51Oj1BWmTp3KzJkzqaqqYsiQIXmXI0lSSTEIS+oWliyBW27JAvC0aWse3203GDUKTj0V+vXr+vqkrjZ06NBV+06YJUlScwZhSWVtzpxs6aPrrltz+SOAo47KHn8+9FCI6Pr6JEmSVHoMwpLKzvvvw8MPw003wR13ZO2m+vWDz38eLrgAamryqVGSJEmlyyAsqSysXAl/+Uv2+PMdd8C8eWues8MOWfg9+2zYfPOur1GSJEnlwSAsqWSlBH//O9x6a7a9/nrL5x1wQPb+73HHZbNBS5IkSWvjn4ySSs6sWVnwveUWeOGFls8ZPBhOPjmb/Gqffbq2PkmSJJU3g7CkklBfD7fdlgXgJ59s+ZwttoATT4RTToEDD4QePbq2RkmSJHUPBmFJuVmwACZMyMJvXd2aa/4C9O8Pxx4L//ZvMHw49OnT5WVKkiSpmzEIS+pSixfDpEnZY89//OOaMz4D9O4NRxyRjfyOGJGFYUmSJKmjGIQldaqU4Pnn4YEHsu2RR2DJkjXPi4Da2mzk94QTssegJUmSpM5gEJbU4RYuhIceyoLvgw+2PtszwMc+lo38fvazUF3ddTVK3d2gQYNYtmwZfXyfQJKkNRiEJW2wFSuyCa4aR30ffzxb97c1u+6ahd9TToEPfrDr6pQqSX19PXV1ddTW1uZdiiRJJccgLKldZs8uBt+HHspGgVuzySZwyCFw2GHZtuOOXVamJEmStAaDsKQ2ee89ePTRYvh97rnWz42AoUOLwXfffbMJsCRJkqRSYBCW1KIFC+CJJ+Bvf4O//AUee6zlSa4aDRpUDL6HHgpbbdV1tUqSJEnrwyAsieXLYfr0LPQ2bjNnrv2ajTaCAw8sht899shGgiWVhkmTJjFt2jQWLVrEiBEj8i5HkqSSYhCWKtCbbzYPvU8+Ce++u+7rPvzhYvA96CDo16/za5XUPsccc8yq/ZRSjpVIklR6DMJSN7d0KTzzTPPg+9pr676uVy/YZx/Yb79s+8QnYIcdOr1cSZIkqdMZhKVupKEhm8Rq+nR49tlsGaOnnoJly9Z97XbbFUPv/vtnIXjjjTu/ZkmSJKmrGYSlMrR0afYO7/TpzbdXX23b9X37ZrM6NwbffffNgrAkSZJUCQzCUglbsQJeeWXNwPvii9kEV231wQ8WQ+9++8FHPuJyRpIkSapcBmGpBCxblr23O2sWzJhRDLzPPbf2JYtW17Mn1NRkMzjvsUf2ePO++8LAgZ1WuiRJklR2DMJSF1mwIBvdffnlNT9ffx3Wd1LXnXbKwu6eexaD74c+lC1rJEmSJKl1BmGpg6xYkQXaxnC7euB9++32fd1Bg4pBt3HbbTcYMKBj65ckSZIqhUFYaoOVK2HePHjjjebblCk1XHllFnRfe2393tttKiKbrOoDH8jW6m0c6d19d9hyyw79USRJkqSKZxBWxXvvPaivXzPkNt3q6+H991u6elCbv8/GG2dBd+ed1/zccUcfaZYkSZK6ikFY3U5K8K9/wdy52TZvXnG/cXvrrWLIXbCg4773Ntu0Hna33TYb+ZWkrvDRj36URYsWUVVVlXcpkiSVHIOwSt6yZdn7tQsXrhlomwbbpsF32bKOr2OzzWDw4OJWXQ2LF7/IwQd/iJ12ysJu//4d/30lqT2mTp1KXV0dtbW1eZciSVLJMQir061cmY3QNobZpp+t7Tfte/fdzq2vV69sQqqmIXf1rbq65ZBbV1dPbe2HOrdASZIkSR3KIKw1pJStXbtoUXFraGi9vbZjixbBO++s/9JAG6pfv2zt3Ja2rbfOPqurs5A7cCD06NG19UmSJEnKj0G4TKxYAUuXZtuSJdnWdH/JkmzktHF7773m7bYea9xWrMj7Jy7q2TN7LHmzzVoPt6tv/frlXbUkSZKkUpVLEI6IE4ExwK7AsJTSlFbOOxz4EdAT+GVKaWyhfwvgNmBH4DXgpJTSwvWtI6Us8L3/frYtX772/cbPZcvWb2vtmsYg21K4Xb2v5RmLy0dVVRZkN9+8GGob99fVN2CAk0xJ0voaN24cM2fO5MUXX2TkyJF5lyNJUknJa0R4OnACcH1rJ0RET+CnwHBgNvBkRExMKT0HjAYeTimNjYjRhfbF6/qms2YNYJNNmgdbtWyjjbLwOmBA9rn6/voc23TT7D1cSVLX+cIXvrBq3yAsSVJzucSTlNLzALH2Yb5hwKyU0iuFc38HHAs8V/isLZw3HqijDUF45cpg0aL2Vp2/vn2zgNq3b8v7/ftnjwT365etWdu4v7attfN69877p5UkSZKkzlHK43SDgdebtGcD+xb2t0kpzQFIKc2JiK3b+0169sxGK3v3Ln6ua3+jjaBPnzW33r1b7m9t6907C6IthdvV+/r08fFgSZIkSeoInRaEI+IhYNsWDl2aUvpDW75EC33rPfdwRIwEGp8JWwoxvenxFSuKE1FJ7bAVMC/vItSteE+pI20FzFvHE1jS+vDfKHU07yl1tJq2nNRpQTildOgGfonZwPZN2tsB9YX9f0bEoMJo8CDgrbXUMQ4YBxARU1JKQzewLmkV7yl1NO8pdSTvJ3U07yl1NO8pdbSIaHEi5tWV8uqpTwK7RMROEdEHOBmYWDg2ETizsH8m0JYRZkmSJEmS8gnCEXF8RMwG9gfujYgHCv3VEXEfQEppOfAl4AHgeeD2lNKMwpcYCwyPiJfIZpUe29U/gyRJkiSpPOU1a/TdwN0t9NcDRzZp3wfc18J584FD2vGtx7XjGmltvKfU0byn1JG8n9TRvKfU0byn1NHadE9FSus9/5QkSZIkSWWrlN8RliRJkiSpw1VcEI6Ib0bEsxHxTEQ8GBHVedek8hUR342IFwr31N0RsVneNam8RcSJETEjIlZGhLNoqt0i4vCImBkRsyJidN71qLxFxK8i4q2I5stQSu0VEdtHxOSIeL7we+/CvGtS+YqIvhHxRET8vXA/fWOd11Tao9ERsUlK6V+F/S8Du6WUzsu5LJWpiPgU8OeU0vKIuAogpXRxzmWpjEXErsBK4HrgopRSm5YAkJqKiJ7Ai2QTSs4mW4nhlJTSc7kWprIVEf8XaAB+k1LaI+96VP4KS6AOSik9FRFVwFTgOP+dUntERAD9U0oNEdEb+H/AhSmlv7V2TcWNCDeG4IL+QGX9nwB1qJTSg4UZzgH+RrbetdRuKaXnU0oz865DZW8YMCul9EpKaRnwO+DYnGtSGUspPQosyLsOdR8ppTkppacK+4vIVokZnG9VKlcp01Bo9i5sa815FReEASLi2xHxOnAqcFne9ajbOAu4P+8iJInsj8nXm7Rn4x+YkkpUROwI7AM8nm8lKmcR0TMingHeAv6UUlrr/dQtg3BEPBQR01vYjgVIKV2aUtoeuJlsrWKpVeu6nwrnXAosJ7unpLVqyz0lbaBooc8noCSVnIgYAEwARq325Ka0XlJKK1JKe5M9oTksItb6Gkcu6wh3tpTSoW089RbgXuDyTixHZW5d91NEnAkcDRySKu2le7XLevwbJbXXbGD7Ju3tgPqcapGkFhXe5ZwA3JxSuivvetQ9pJTejog64HCg1Qn+uuWI8NpExC5NmscAL+RVi8pfRBwOXAwck1J6N+96JKngSWCXiNgpIvoAJwMTc65JklYpTG50A/B8SumavOtReYuIgY2rt0TExsChrCPnVeKs0ROAGrJZWf8XOC+l9Ea+ValcRcQsYCNgfqHrb85Crg0REccD1wIDgbeBZ1JKh+VblcpRRBwJ/BDoCfwqpfTtnEtSGYuIW4FaYCvgn8DlKaUbci1KZS0iPgE8Bkwj+7sc4L9SSvflV5XKVUR8BBhP9juvB3B7SumKtV5TaUFYkiRJklTZKu7RaEmSJElSZTMIS5IkSZIqikFYkiRJklRRDMKSJEmSpIpiEJYkSZIkVRSDsCRJJS4iVkTEM0220YX+X0bEbhv4tasi4uWI2KXQ7h0R0yJi346oXZKkUuTySZIklbiIaEgpDejEr38ScE5K6VMRcQmwY0rpC531/SRJypsjwpIklamIqIuIoRHxfyLipYjYKiJ6RMRjEfGpwjlfiYjphW1US18npXQ7sDIi/hM4D7ikC38MSZK6XK+8C5AkSeu0cUQ806R9ZUrptsZGSul/I+Iq4DrgceC5lNKDETEE+DywLxDA4xHxSErp6Ra+xyjgeWBkSmlBp/0kkiSVAIOwJEml772U0t5rOyGl9MuIOJFsRLfx3E8Ad6eUFgNExF3AgUBLQfhwYA6wR4dVLUlSifLRaEmSuoGI6AdsV2g2vk8cbby2GvgyMAw4MiI+0vEVSpJUOgzCkiR1D1cBNwOXAb8o9D0KHBcR/SKiP3A88FgL1/4A+E5KaTbwFeCnEdGmEC1JUjkyCEuSVPo2Xm35pLFND0bEQcDHgKtSSjcDyyLi8ymlp4AbgSfI3h3+5ervB0fEcGAH4AaAlNIkYCFwRmf/UJIk5cXlkyRJkiRJFcURYUmSJElSRTEIS5IkSZIqikFYkiRJklRRDMKSJEmSpIpiEJYkSZIkVRSDsCRJkiSpohiEJUmSJEkVxSAsSZIkSaoo/x811B1y3t93UwAAAABJRU5ErkJggg==\n",
 95 |       "text/plain": [
 96 |        "<Figure size 1152x648 with 1 Axes>"
 97 |       ]
 98 |      },
 99 |      "metadata": {
100 |       "needs_background": "light"
101 |      },
102 |      "output_type": "display_data"
103 |     }
104 |    ],
105 |    "source": [
106 |     "plt.figure(figsize=(16,9))\n",
107 |     "plt.plot(x, y, linewidth=3, color='b')\n",
108 |     "plt.axis([-3,3,-1,1])\n",
109 |     "plt.plot([-3,3],[0,0],'k--',linewidth=3)\n",
110 |     "plt.plot([0,0],[-3,3],'k--',linewidth=3)\n",
111 |     "plt.title(\"Função Tangente Hiperbólica\") \n",
112 |     "plt.xlabel(\"Eixo X\") \n",
113 |     "plt.ylabel(\"Eixo Y\") \n",
114 |     "plt.grid()\n",
115 |     "plt.show() "
116 |    ]
117 |   }
118 |  ],
119 |  "metadata": {
120 |   "kernelspec": {
121 |    "display_name": "Python 3",
122 |    "language": "python",
123 |    "name": "python3"
124 |   },
125 |   "language_info": {
126 |    "codemirror_mode": {
127 |     "name": "ipython",
128 |     "version": 3
129 |    },
130 |    "file_extension": ".py",
131 |    "mimetype": "text/x-python",
132 |    "name": "python",
133 |    "nbconvert_exporter": "python",
134 |    "pygments_lexer": "ipython3",
135 |    "version": "3.7.10"
136 |   }
137 |  },
138 |  "nbformat": 4,
139 |  "nbformat_minor": 4
140 | }
141 | 


--------------------------------------------------------------------------------
/jupyter_notebooks/linear_algebra.ipynb:
--------------------------------------------------------------------------------
   1 | {
   2 |  "cells": [
   3 |   {
   4 |    "cell_type": "markdown",
   5 |    "metadata": {},
   6 |    "source": [
   7 |     "# Álgebra Linear com SymPy\n",
   8 |     "\n",
   9 |     "Um vetor $\\vec{v} \\in \\mathbb{R}$ é uma **n-tupla** de números reais. Por exemplo, considere um vetor com três componentes:\n",
  10 |     "\n",
  11 |     "\\begin{equation}\\vec{v} = (v1, v2, v3) \\in (\\mathbb{R}, \\mathbb{R}, \\mathbb{R}) \\equiv \\mathbb{R}³\\end{equation}\n",
  12 |     "\n",
  13 |     "Uma matriz $A \\in \\mathbb{R}^{m \\times n}$ é um array retangular de números reais com $m$ linhas e $n$ colunas. \n",
  14 |     "\n",
  15 |     "Um vetor é uma matriz especial. Nós podemos pensar o vetor como $\\vec{v} \\in \\mathbb{R}^n$\n",
  16 |     "\n",
  17 |     "- Ou um vetor de linhas: $(1 \\times n ~ matriz)$\n",
  18 |     "\n",
  19 |     "- Ou um vetor de colunas: $(n \\times 1 ~ matriz)$\n",
  20 |     "\n",
  21 |     "Por causa dessa equivalência, não há um objeto vetor especial em SymPy e objetos de Matriz são utilizados para vetores também."
  22 |    ]
  23 |   },
  24 |   {
  25 |    "cell_type": "markdown",
  26 |    "metadata": {},
  27 |    "source": [
  28 |     "## Exemplos\n",
  29 |     "\n",
  30 |     "Para iniciamors com os nossos exemplos, primeiro é necessário importar a biblioteca [SymPy](https://docs.sympy.org/latest/index.html)."
  31 |    ]
  32 |   },
  33 |   {
  34 |    "cell_type": "code",
  35 |    "execution_count": 1,
  36 |    "metadata": {},
  37 |    "outputs": [],
  38 |    "source": [
  39 |     "from sympy import *\n",
  40 |     "init_printing()"
  41 |    ]
  42 |   },
  43 |   {
  44 |    "cell_type": "markdown",
  45 |    "metadata": {},
  46 |    "source": [
  47 |     "#### Definimos um vetor de linhas (1x3)"
  48 |    ]
  49 |   },
  50 |   {
  51 |    "cell_type": "code",
  52 |    "execution_count": 2,
  53 |    "metadata": {},
  54 |    "outputs": [],
  55 |    "source": [
  56 |     "u = Matrix(1,3,[4,5,6]) "
  57 |    ]
  58 |   },
  59 |   {
  60 |    "cell_type": "code",
  61 |    "execution_count": 3,
  62 |    "metadata": {},
  63 |    "outputs": [
  64 |     {
  65 |      "data": {
  66 |       "text/latex": [
  67 |        "$\\displaystyle \\left[\\begin{matrix}4 & 5 & 6\\end{matrix}\\right]$"
  68 |       ],
  69 |       "text/plain": [
  70 |        "[4  5  6]"
  71 |       ]
  72 |      },
  73 |      "execution_count": 3,
  74 |      "metadata": {},
  75 |      "output_type": "execute_result"
  76 |     }
  77 |    ],
  78 |    "source": [
  79 |     "u"
  80 |    ]
  81 |   },
  82 |   {
  83 |    "cell_type": "markdown",
  84 |    "metadata": {},
  85 |    "source": [
  86 |     "#### Definimos um vetor de colunas (3x1)"
  87 |    ]
  88 |   },
  89 |   {
  90 |    "cell_type": "code",
  91 |    "execution_count": 4,
  92 |    "metadata": {},
  93 |    "outputs": [],
  94 |    "source": [
  95 |     "v = Matrix([7,8,9]) "
  96 |    ]
  97 |   },
  98 |   {
  99 |    "cell_type": "code",
 100 |    "execution_count": 5,
 101 |    "metadata": {},
 102 |    "outputs": [
 103 |     {
 104 |      "data": {
 105 |       "text/latex": [
 106 |        "$\\displaystyle \\left[\\begin{matrix}7\\\\8\\\\9\\end{matrix}\\right]$"
 107 |       ],
 108 |       "text/plain": [
 109 |        "⎡7⎤\n",
 110 |        "⎢ ⎥\n",
 111 |        "⎢8⎥\n",
 112 |        "⎢ ⎥\n",
 113 |        "⎣9⎦"
 114 |       ]
 115 |      },
 116 |      "execution_count": 5,
 117 |      "metadata": {},
 118 |      "output_type": "execute_result"
 119 |     }
 120 |    ],
 121 |    "source": [
 122 |     "v"
 123 |    ]
 124 |   },
 125 |   {
 126 |    "cell_type": "markdown",
 127 |    "metadata": {},
 128 |    "source": [
 129 |     "#### Fazemos a transposição do vetor **v**"
 130 |    ]
 131 |   },
 132 |   {
 133 |    "cell_type": "code",
 134 |    "execution_count": 6,
 135 |    "metadata": {},
 136 |    "outputs": [
 137 |     {
 138 |      "data": {
 139 |       "text/latex": [
 140 |        "$\\displaystyle \\left[\\begin{matrix}7 & 8 & 9\\end{matrix}\\right]$"
 141 |       ],
 142 |       "text/plain": [
 143 |        "[7  8  9]"
 144 |       ]
 145 |      },
 146 |      "execution_count": 6,
 147 |      "metadata": {},
 148 |      "output_type": "execute_result"
 149 |     }
 150 |    ],
 151 |    "source": [
 152 |     "v.T"
 153 |    ]
 154 |   },
 155 |   {
 156 |    "cell_type": "markdown",
 157 |    "metadata": {},
 158 |    "source": [
 159 |     "#### Apresenta o primeiro componente do vetor **u** (índices começam por 0, assim como no Python tradicional)"
 160 |    ]
 161 |   },
 162 |   {
 163 |    "cell_type": "code",
 164 |    "execution_count": 7,
 165 |    "metadata": {},
 166 |    "outputs": [
 167 |     {
 168 |      "data": {
 169 |       "image/png": "iVBORw0KGgoAAAANSUhEUgAAAA4AAAASCAYAAABrXO8xAAAABHNCSVQICAgIfAhkiAAAAMlJREFUOI290jFOQkEQxvEfxNIr0JJYamFFxT0sSKg9gIm6JQ0JxoYECCHexJh4Bi3p6TRIBcXbjRvMA54JfMkWuzv/+WZ2pxZC8B/V99zfYB1X91CwgWd8VXGsYYoFhlXAW7TRwfeh4AV6eMJrSeI/4BleMMddGZQCcz3gEi0sd4G543V06eN9F5SDqcRP3O+DcvAcTcXD/Pj99DUeY8wo7gfJCVaYlCS/UvT9ho/URgKXtkYqU4jgDOPtUivrqGBQzO44Pzx9qRu2oCPfWoik3gAAAABJRU5ErkJggg==\n",
 170 |       "text/latex": [
 171 |        "$\\displaystyle 4$"
 172 |       ],
 173 |       "text/plain": [
 174 |        "4"
 175 |       ]
 176 |      },
 177 |      "execution_count": 7,
 178 |      "metadata": {},
 179 |      "output_type": "execute_result"
 180 |     }
 181 |    ],
 182 |    "source": [
 183 |     "u[0] "
 184 |    ]
 185 |   },
 186 |   {
 187 |    "cell_type": "markdown",
 188 |    "metadata": {},
 189 |    "source": [
 190 |     "#### Mostra o comprimento do vetor"
 191 |    ]
 192 |   },
 193 |   {
 194 |    "cell_type": "code",
 195 |    "execution_count": 8,
 196 |    "metadata": {},
 197 |    "outputs": [
 198 |     {
 199 |      "data": {
 200 |       "image/png": "iVBORw0KGgoAAAANSUhEUgAAACwAAAAbCAYAAAAH+20UAAAABHNCSVQICAgIfAhkiAAAAbNJREFUWIXt179qVEEUx/FPooIiglF8BIWID2DEQLCI/0CrCIIBK30KYQVfQjFt+igatZE02i5YiLZGsBFBxSJotJibTVjmxjPLHUIgPxjmMsxvz3d2z5mzd6zX69lNGt9pgFLtL9x/BN9rgERV+g1fxCWM7dQoBZ7B60JPpyoB3teMtUosIZUAn8ObWiBRlQBfwfNaIFGVAB/H11ogUUWBT+JDZv02/v5n/OnAM1D0Hr6Gp5n1Pu63eKZxAcsdeAaKAp/Cx8x6vxk5vW3mRx14Bhofen6Ay0N7jinP3TM4i8941qVnK/AspjA3tGeU2+FuMy/YJh9H8WxNiRf4glfSQdab9SksRklxCLca/+OuPcO3RB+/pCYBB6TTrovrBo5KhfOpa0/uWnuC683zDFaCQTd0p5kf1vDkgJdsAs/iZUHg09Kvsyqe90WeHPAKTmASh/EzGJiKxbahHPBv6aT38C4YFA5iXsr3hVqetta8hJvy3a1Nc5iQDhsttmJPG/Cy1HVWg4HZLJzWLtWFpw34B64WBJ7EeWXFNopn2/8S36IfgvfSO1eJRvHsvtf8PeDa+gcbXG3xXNGbgwAAAABJRU5ErkJggg==\n",
 201 |       "text/latex": [
 202 |        "$\\displaystyle \\sqrt{77}$"
 203 |       ],
 204 |       "text/plain": [
 205 |        "√77"
 206 |       ]
 207 |      },
 208 |      "execution_count": 8,
 209 |      "metadata": {},
 210 |      "output_type": "execute_result"
 211 |     }
 212 |    ],
 213 |    "source": [
 214 |     "u.norm() "
 215 |    ]
 216 |   },
 217 |   {
 218 |    "cell_type": "markdown",
 219 |    "metadata": {},
 220 |    "source": [
 221 |     "#### Computamos o vetor de comprimento de unidade, (mesma direção de **u**)"
 222 |    ]
 223 |   },
 224 |   {
 225 |    "cell_type": "code",
 226 |    "execution_count": 9,
 227 |    "metadata": {},
 228 |    "outputs": [
 229 |     {
 230 |      "name": "stdout",
 231 |      "output_type": "stream",
 232 |      "text": [
 233 |       "Matrix([[4*sqrt(77)/77, 5*sqrt(77)/77, 6*sqrt(77)/77]])\n"
 234 |      ]
 235 |     },
 236 |     {
 237 |      "data": {
 238 |       "image/png": "iVBORw0KGgoAAAANSUhEUgAAAA0AAAASCAYAAACAa1QyAAAABHNCSVQICAgIfAhkiAAAAIdJREFUKJHt0SEOwmAMBeBvBD2NJAiCG5ZbIPDTSJJJxH8HLoDgHghOQoJEEfxmftVkyzBTNHlpX9OX17RFSsmvMQv8gAse+KDFLYrmgZ9R4YsXNmOcTlijxLFvveh07xscchoVf9HkovjcfQYsct7hmus3mijaog69VQY80cT1EooBLJnyEB2yexAji7I9mAAAAABJRU5ErkJggg==\n",
 239 |       "text/latex": [
 240 |        "$\\displaystyle 1$"
 241 |       ],
 242 |       "text/plain": [
 243 |        "1"
 244 |       ]
 245 |      },
 246 |      "execution_count": 9,
 247 |      "metadata": {},
 248 |      "output_type": "execute_result"
 249 |     }
 250 |    ],
 251 |    "source": [
 252 |     "uhat = u / u.norm() \n",
 253 |     "print(uhat)\n",
 254 |     "uhat.norm()"
 255 |    ]
 256 |   },
 257 |   {
 258 |    "cell_type": "markdown",
 259 |    "metadata": {},
 260 |    "source": [
 261 |     "O produto escalar dos vetores $\\vec{u}$ e $\\vec{v}$ pode ser definido como:\n",
 262 |     "\n",
 263 |     "\\begin{equation}\\vec{u} \\cdot \\vec{v} \\equiv u_x v_x + u_y v_y + u_z v_z \\equiv ||{\\vec{u}}|| ~ ||{\\vec{v}}|| \\cos (\\varphi) \\in \\mathbb{R}\\end{equation}\n",
 264 |     "\n",
 265 |     "onde $\\varphi$ é o ângulo entre os vetores $\\vec{u}$ e $\\vec{v}$.\n",
 266 |     "\n",
 267 |     "Por exemplo:"
 268 |    ]
 269 |   },
 270 |   {
 271 |    "cell_type": "code",
 272 |    "execution_count": 12,
 273 |    "metadata": {},
 274 |    "outputs": [
 275 |     {
 276 |      "data": {
 277 |       "image/png": "iVBORw0KGgoAAAANSUhEUgAAABoAAAASCAYAAABFGc6jAAAABHNCSVQICAgIfAhkiAAAAVJJREFUOI3V1T9Im0EYx/FPxM2igqLFMSAEOiilg6KQrbgIIt110aFbwMVSMEuhxU03J7GdXFwFlYCCo0IHB/8MEgf7VygtdSntcPdCeBOaUhPFHxzP3Y+7+74899y9mWKx6DbUkho/wzL28A2/8e4v699gB2X8xFccYgFdlRNbUwtfYgDfcYFcnQ8t4ABb+Ig2DKGI2dgv1wIVIuAUeZTqgNpxXcN/hReYx3OqU1fCiZCyf1EtCKzH2J8YaVCjNB7j+8RIp+5/NYcH6MATjEbI62aAeivGm5jGp8RoVOoeIhPjJLJCmT9uNCjRB2zgqXCP1poFSnSOIzxCdzNB0Bfjr5uCcsKZpNUiXNge7OOK6qqbiE3FJsNYjf3PQoXBGBaxizN8ESovLxTDJWaSjdOgQUylvGxshNwnoG2sYER4HzvxA8d4iyXhkQWZu/pN3H/QHz5kPwTyPxiXAAAAAElFTkSuQmCC\n",
 278 |       "text/latex": [
 279 |        "$\\displaystyle 13$"
 280 |       ],
 281 |       "text/plain": [
 282 |        "13"
 283 |       ]
 284 |      },
 285 |      "execution_count": 12,
 286 |      "metadata": {},
 287 |      "output_type": "execute_result"
 288 |     }
 289 |    ],
 290 |    "source": [
 291 |     "u = Matrix(1,3,[4,5,6])\n",
 292 |     "v = Matrix([-1,1,2])\n",
 293 |     "u.dot(v)"
 294 |    ]
 295 |   },
 296 |   {
 297 |    "cell_type": "markdown",
 298 |    "metadata": {},
 299 |    "source": [
 300 |     "Para calcular o ângulo entre dois vetores, nós transformamos a equação anterior para:\n",
 301 |     "\n",
 302 |     "\\begin{equation} \\cos(\\varphi) = \\frac{\\vec{u} \\cdot \\vec{v}}{||\\vec{u}|| ~ ||\\vec{v}||}\\end{equation}"
 303 |    ]
 304 |   },
 305 |   {
 306 |    "cell_type": "code",
 307 |    "execution_count": 13,
 308 |    "metadata": {},
 309 |    "outputs": [
 310 |     {
 311 |      "data": {
 312 |       "image/png": "iVBORw0KGgoAAAANSUhEUgAAANMAAAASCAYAAADBs+vIAAAABHNCSVQICAgIfAhkiAAAB4xJREFUaIHt2n+wVVUVB/DPI0iJBFNDpiwF1DBeP6w0+8UvCTNLhaJxnF6/Q6vJqEibJvNh06Q1mWZN0fTDNGfKcjRTUEoZoV8yk5pjVKL4DMjIJ0gPQU2pP9Y+vfvOPefed8/z3frjfmfu7Dv77LXXXuvstfZa6+yu3t5eHXTQwcgxpqDvEHwPf8Pj6MPFeE6Lc3fhffgdBrAbd+AsPCM39kB8ANfgXuzBTvwK7y9ZJ7wdl2Id/ol/44cN1lSVD7wBV+NBoZcHsRpvLhh7IW7G5sRju5D9vLSGp0OWKjR9aUzR7+9NeLUifztoqugYTkrzbUl0m/ATvKZg7HuU6yv7PZUNHpsjno7fYDJ+hj/jWHwMb8Lr8HCDhdbiB+jBP/BjPIr5uASzsDgtRvr/TaG4NfgrDsYifAcn5sZn+Cxehl1COTOarGkkfD6Pflyf6A/C0ZiDlbnxH8ft+EWSfwKOQy+WpP+bRyhLVZqdwjnmsasJn1bkbwdNFR1fiLPFHr428Tkcp+BteJehzuhOLC9YJ2H087Aq6+jKhXk3YYE4PS6t6b8oLX4FziyZvBanCu9/vzDG/tQ/Dlel5+/FZal/nlDGDdhbM88UrMcLhBe+OsdnrthE92K2MJAr8c6SdVXhszit+ZfC6AZyc47Dv3J9++KxAv5fwGeEQX94hLJUoelL7WEN5syjivztoGlVx1OwFQ/hpcIAM8zFLWK/TiuYswi/FQZ7Cq5jaFgzTRhSH76RIzxPnCw9YjM2w6LUfsWgIRHKODf9/2hN/y34uaEbnAg9vpX+zyngswYb1Z8kZWiVzxjhzXbjdPUvmPpNQfFLJjYLHFHwrFVZqtK0giryt4umVR0fmvjcZqghEXocwHNL5syjWxjSVuGYMTTMm5fa1eo32wB+LYztOBGrNsKU1G4qeJb1vQL745Emc2VKfLLJuJGiiM9rMRU/xQ4Rb3eLF7leeKdW8NbU3lV9mSPGPuLkeqFwkHdhrZrYvwZV5G8XTRnKdLwRT4hI6SBDnfws7CdCv+HgjNR+V0nO9KLU3lMywUZhTEdqbkzZQqcWPKs9RmeIAkUZxoo4Fm5swnMkKONzTGq3ifj8JTm6tSIsfKhk3mV4NibhVXi9eMkXjHzJlTEFV+T67hdh9625/iryt4smw3B1vB3niJRlgzCch0Wd4GSRe52hOcYLZ7RX5Nn/RW2YNym1O0smyfr3HwbD61P7CRxQ0z/W0ISuWYXwAuGhVop8brRQxmdyas8USpwvPFh3GjdLVILKsEyEyEvFS75ROKQy4xttfB/HC4OaIDbtCpFDrRLFjFpUkb9dNBla0fHFIgUZiw/i0yJX2yzy93z4V4R3CBtYJVfgaFQKzqMrtcOJz3+UmE0XXuDbQpA7RYlzYxpXFFpkOAufFBXFnhbW2Soa8clK+F3CM94sql5/xEKR/M9WXFYlNm1XaheJU/kOEeL+L7Bc5I3bRH5yt9jAF4lN3JsbX0X+dtFkaEXHZ4tQ8jKxNyfglSL1uBJfKqDJY0lqV+Qf1BpTdvJMyg9KmJgb1wh7xdG5TCT3PeKb0xbhPbLyepkn+IgooW8QlZbtw+BZBc347EjtJvwh92yPwVPs2CZ8tonq5gLxDeTyiusdLWTFl1m5/iryt4smj2Y6niOKHNeJiGmTcCi3C4PdKpxqo2rei0V+t0VBab/WmP6S2iNLJsqqI2U5VR5Pimrey4XXmyi+VW1IfXuE58ljKb4uvOZczT8mVsVw+GQ6KSuSZJtg/DB5PiDknymS4P8XZE4tX6mtIn+7aMpQpuO3pHZNAc1uUegYI75plaGw8JCh1pgyJgvUh3/7iQ+2ezQuGAwHPeIbwVXqy53n4KsiHJxreDFsFQyXz1rhFI7AMwued6e2rwXez0ttoxC33cjCp3z1tYr87aJphCId75PasvJ31v9EyfN9xd7dK4ypDrVGc58oix8mwp9aLBde63JRTs0wXVTkxhXMPbGg7xiR7O/C+bln56ZnvxdJcr/RQSt8+sXtjUn4XO7ZG3GCCHtrK4AzDH4aqMUY8UFxsrhlsqNgzGhipqHFoAyHihOa+qtIVeRvB00VHa9L7RI8P0d3ojgsHkt0RVgsCmYr1d+sQP0NiPx1oj/h1cJ73yPixdrrRH3iZUxV7zVuEyfZ3eI71UxRfHhcJIq1VbN3i6TwKXHzoigv6zN4YyLDqelHKPcE4V0zxfWLvG0kfCaLb2yHp3nXC5kXimLM6YZWmpbiy8Lb3if0dbBIoKeJcPJ4EYqMRJZWaXpF9WqNKIUPiPd9kvC6K5NMec/cqvztoKmi4zFiz81Psl+Txh0lQsCuNO8lirFO5Psniw//dcgbE3Gl5nyR3xwo7kddK06nfILep9yYPoXTxAsbLy7O3iROhfzYXlHebIRb1d+CaEb3gKFXZ6ryOUDcG1sovNqAuBz7RfVhbzc+JDzdIaKM+qhwRjfga4oLKs3WlpelVZrZonJ3tMHS+CMi1L0i/coqta3I3w6aqjoeJ6Ku00Qx4Vlp3PpEs7pkXUcJw9wi9FkYohcZUwcddFABrXxn6qCDDhqgY0wddPA04T9DbtAKR1OSmwAAAABJRU5ErkJggg==\n",
 313 |       "text/latex": [
 314 |        "$\\displaystyle 0.921263115666387$"
 315 |       ],
 316 |       "text/plain": [
 317 |        "0.921263115666387"
 318 |       ]
 319 |      },
 320 |      "execution_count": 13,
 321 |      "metadata": {},
 322 |      "output_type": "execute_result"
 323 |     }
 324 |    ],
 325 |    "source": [
 326 |     "acos(u.dot(v)/(u.norm()*v.norm())).evalf()"
 327 |    ]
 328 |   },
 329 |   {
 330 |    "cell_type": "markdown",
 331 |    "metadata": {},
 332 |    "source": [
 333 |     "O produto escalar é uma operação comutativa:\n",
 334 |     "\n",
 335 |     "\\begin{equation} \\vec{u} \\cdot \\vec{v} = \\vec{v} \\cdot \\vec{u} \\end{equation}"
 336 |    ]
 337 |   },
 338 |   {
 339 |    "cell_type": "code",
 340 |    "execution_count": 14,
 341 |    "metadata": {},
 342 |    "outputs": [
 343 |     {
 344 |      "data": {
 345 |       "text/plain": [
 346 |        "True"
 347 |       ]
 348 |      },
 349 |      "execution_count": 14,
 350 |      "metadata": {},
 351 |      "output_type": "execute_result"
 352 |     }
 353 |    ],
 354 |    "source": [
 355 |     "u.dot(v) == v.dot(u)"
 356 |    ]
 357 |   },
 358 |   {
 359 |    "cell_type": "markdown",
 360 |    "metadata": {},
 361 |    "source": [
 362 |     "O produto escalar também é utilizado para calcular projeções. \n",
 363 |     "\n",
 364 |     "Assumindo que você tenha dois vetores $\\vec{v}$ e $\\vec{n}$ e você deseja encontrar o componente de $\\vec{v}$ que aponta para a direção $\\vec{n}$\n",
 365 |     "\n",
 366 |     "\\begin{equation} \\prod_\\vec{n}(\\vec{v}) \\equiv \\frac{\\vec{v} \\cdot \\vec{n}}{||\\vec{n}||^2}\\vec{n} \\end{equation}\n",
 367 |     "\n",
 368 |     "Em SymPy, isso se traduziria como:"
 369 |    ]
 370 |   },
 371 |   {
 372 |    "cell_type": "code",
 373 |    "execution_count": 16,
 374 |    "metadata": {},
 375 |    "outputs": [
 376 |     {
 377 |      "data": {
 378 |       "text/latex": [
 379 |        "$\\displaystyle \\left[\\begin{matrix}5\\\\5\\\\5\\end{matrix}\\right]$"
 380 |       ],
 381 |       "text/plain": [
 382 |        "⎡5⎤\n",
 383 |        "⎢ ⎥\n",
 384 |        "⎢5⎥\n",
 385 |        "⎢ ⎥\n",
 386 |        "⎣5⎦"
 387 |       ]
 388 |      },
 389 |      "execution_count": 16,
 390 |      "metadata": {},
 391 |      "output_type": "execute_result"
 392 |     }
 393 |    ],
 394 |    "source": [
 395 |     "v = Matrix([4,5,6])\n",
 396 |     "n = Matrix([1,1,1])\n",
 397 |     "projeção = (u.dot(n)/n.norm()**2) * n # \n",
 398 |     "projeção"
 399 |    ]
 400 |   },
 401 |   {
 402 |    "cell_type": "markdown",
 403 |    "metadata": {},
 404 |    "source": [
 405 |     "Acima estamos calculando a **projeção** de **v** na direção **n**."
 406 |    ]
 407 |   },
 408 |   {
 409 |    "cell_type": "markdown",
 410 |    "metadata": {},
 411 |    "source": [
 412 |     "O produto vetorial, denotado por $\\times$, recebe dois vetores como input e produz um vetor como output:\n",
 413 |     "\n",
 414 |     "\\begin{equation}\\vec{u} \\times \\vec{v} = (u_yv_z - u_zv_y,u_zv_x - u_xv_z,u_xv_y - u_y,v_x)\\end{equation}\n",
 415 |     "\n",
 416 |     "Definindo símbolos individuais para as entradas dos dois vetores, nós podemos fazer SymPy nos mostrar a fórmula do produto vetorial:"
 417 |    ]
 418 |   },
 419 |   {
 420 |    "cell_type": "code",
 421 |    "execution_count": 17,
 422 |    "metadata": {},
 423 |    "outputs": [
 424 |     {
 425 |      "data": {
 426 |       "text/latex": [
 427 |        "$\\displaystyle \\left[\\begin{matrix}u_{2} v_{3} - u_{3} v_{2}\\\\- u_{1} v_{3} + u_{3} v_{1}\\\\u_{1} v_{2} - u_{2} v_{1}\\end{matrix}\\right]$"
 428 |       ],
 429 |       "text/plain": [
 430 |        "⎡u₂⋅v₃ - u₃⋅v₂ ⎤\n",
 431 |        "⎢              ⎥\n",
 432 |        "⎢-u₁⋅v₃ + u₃⋅v₁⎥\n",
 433 |        "⎢              ⎥\n",
 434 |        "⎣u₁⋅v₂ - u₂⋅v₁ ⎦"
 435 |       ]
 436 |      },
 437 |      "execution_count": 17,
 438 |      "metadata": {},
 439 |      "output_type": "execute_result"
 440 |     }
 441 |    ],
 442 |    "source": [
 443 |     "u1, u2, u3 = symbols('u1:4')\n",
 444 |     "v1, v2, v3 = symbols('v1:4')\n",
 445 |     "Matrix([u1,u2,u3]).cross(Matrix([v1,v2,v3]))"
 446 |    ]
 447 |   },
 448 |   {
 449 |    "cell_type": "markdown",
 450 |    "metadata": {},
 451 |    "source": [
 452 |     "O produto vetorial é anticomutativo $\\vec{u} \\times \\vec{v} = -\\vec{v} \\times \\vec{u}$"
 453 |    ]
 454 |   },
 455 |   {
 456 |    "cell_type": "code",
 457 |    "execution_count": 18,
 458 |    "metadata": {},
 459 |    "outputs": [
 460 |     {
 461 |      "data": {
 462 |       "text/latex": [
 463 |        "$\\displaystyle \\left( \\left[\\begin{matrix}4\\\\-14\\\\9\\end{matrix}\\right], \\  \\left[\\begin{matrix}-4\\\\14\\\\-9\\end{matrix}\\right]\\right)$"
 464 |       ],
 465 |       "text/plain": [
 466 |        "⎛⎡ 4 ⎤  ⎡-4⎤⎞\n",
 467 |        "⎜⎢   ⎥  ⎢  ⎥⎟\n",
 468 |        "⎜⎢-14⎥, ⎢14⎥⎟\n",
 469 |        "⎜⎢   ⎥  ⎢  ⎥⎟\n",
 470 |        "⎝⎣ 9 ⎦  ⎣-9⎦⎠"
 471 |       ]
 472 |      },
 473 |      "execution_count": 18,
 474 |      "metadata": {},
 475 |      "output_type": "execute_result"
 476 |     }
 477 |    ],
 478 |    "source": [
 479 |     "u = Matrix([4,5,6])\n",
 480 |     "v = Matrix([-1,1,2])\n",
 481 |     "u.cross(v), v.cross(u)"
 482 |    ]
 483 |   },
 484 |   {
 485 |    "cell_type": "markdown",
 486 |    "metadata": {},
 487 |    "source": [
 488 |     "Vamos agora olhar algumas particularidades das Matrizes.\n",
 489 |     "\n",
 490 |     "Começaremos definindo uma nova Matriz $A$:"
 491 |    ]
 492 |   },
 493 |   {
 494 |    "cell_type": "code",
 495 |    "execution_count": 20,
 496 |    "metadata": {},
 497 |    "outputs": [
 498 |     {
 499 |      "data": {
 500 |       "text/latex": [
 501 |        "$\\displaystyle \\left[\\begin{matrix}2 & -3 & -8 & 7\\\\-2 & -2 & 2 & -7\\\\1 & 0 & -3 & 6\\end{matrix}\\right]$"
 502 |       ],
 503 |       "text/plain": [
 504 |        "⎡2   -3  -8  7 ⎤\n",
 505 |        "⎢              ⎥\n",
 506 |        "⎢-2  -2  2   -7⎥\n",
 507 |        "⎢              ⎥\n",
 508 |        "⎣1   0   -3  6 ⎦"
 509 |       ]
 510 |      },
 511 |      "execution_count": 20,
 512 |      "metadata": {},
 513 |      "output_type": "execute_result"
 514 |     }
 515 |    ],
 516 |    "source": [
 517 |     "A = Matrix([[2, -3, -8, 7], [-2, -2 , 2, -7], [1, 0, -3, 6]])\n",
 518 |     "A"
 519 |    ]
 520 |   },
 521 |   {
 522 |    "cell_type": "markdown",
 523 |    "metadata": {},
 524 |    "source": [
 525 |     "Como visto anteriormente, nós podemos usar a indexação de Python para acessarmos elementos e submatrizes.\n",
 526 |     "\n",
 527 |     "A seguir, acessamos a linha **0**, coluna **1** da matriz $A$:"
 528 |    ]
 529 |   },
 530 |   {
 531 |    "cell_type": "code",
 532 |    "execution_count": 21,
 533 |    "metadata": {},
 534 |    "outputs": [
 535 |     {
 536 |      "data": {
 537 |       "image/png": "iVBORw0KGgoAAAANSUhEUgAAAB4AAAASCAYAAABM8m7ZAAAABHNCSVQICAgIfAhkiAAAASlJREFUSInN1b8rhVEcx/HXvdkIRUhZlDIoko0yWCwWf4HFwqQsLJ5FkYnR6MdisSosBiN1k0EpUiK/JjEQw/M8pdtz49Zx+dTp2/meb+fdOedzzslFUeQvlA883yL2cYUXPOIYc2j4TfAUqrGLZWziDREKaEsLqwKDa/GakZ/HLGYwQfgVZ0FhK4kdaSI0uJRGklhIE6G3OtU0alCHPgwk0IVKgJu/9Hcwhrs0UbzVF/goo22UALcgl8RRtIuvVW9aULzic6UNkqXrb8ZvsY0jnGENXVngoTKg5egSp+hBI+4r5WpoTeI7Ya9Tp/hMi5UXPyBNOMQTYV09jCUciL3yIHb2oNhcNxhPi0OC97CKfnSjHs9iU61jRfxpBAefYPKnxZU01/8AfwIzFD6QwSD+FgAAAABJRU5ErkJggg==\n",
 538 |       "text/latex": [
 539 |        "$\\displaystyle -3$"
 540 |       ],
 541 |       "text/plain": [
 542 |        "-3"
 543 |       ]
 544 |      },
 545 |      "execution_count": 21,
 546 |      "metadata": {},
 547 |      "output_type": "execute_result"
 548 |     }
 549 |    ],
 550 |    "source": [
 551 |     "A[0,1] "
 552 |    ]
 553 |   },
 554 |   {
 555 |    "cell_type": "markdown",
 556 |    "metadata": {},
 557 |    "source": [
 558 |     "Também podemos selecionar uma submatriz de $A$.\n",
 559 |     "\n",
 560 |     "Neste exemplo, vamos selecionar as duas primeiras linhas e 3 primeiras colunas:"
 561 |    ]
 562 |   },
 563 |   {
 564 |    "cell_type": "code",
 565 |    "execution_count": 22,
 566 |    "metadata": {},
 567 |    "outputs": [
 568 |     {
 569 |      "data": {
 570 |       "text/latex": [
 571 |        "$\\displaystyle \\left[\\begin{matrix}2 & -3 & -8\\\\-2 & -2 & 2\\end{matrix}\\right]$"
 572 |       ],
 573 |       "text/plain": [
 574 |        "⎡2   -3  -8⎤\n",
 575 |        "⎢          ⎥\n",
 576 |        "⎣-2  -2  2 ⎦"
 577 |       ]
 578 |      },
 579 |      "execution_count": 22,
 580 |      "metadata": {},
 581 |      "output_type": "execute_result"
 582 |     }
 583 |    ],
 584 |    "source": [
 585 |     "A[0:2, 0:3]"
 586 |    ]
 587 |   },
 588 |   {
 589 |    "cell_type": "markdown",
 590 |    "metadata": {},
 591 |    "source": [
 592 |     "Algumas matrizes usadas com frequência podem ser definidas através dos seguintes atalhos.\n",
 593 |     "\n",
 594 |     "**eye** nos permite criar uma matriz identidade:"
 595 |    ]
 596 |   },
 597 |   {
 598 |    "cell_type": "code",
 599 |    "execution_count": 23,
 600 |    "metadata": {},
 601 |    "outputs": [
 602 |     {
 603 |      "data": {
 604 |       "text/latex": [
 605 |        "$\\displaystyle \\left[\\begin{matrix}1 & 0\\\\0 & 1\\end{matrix}\\right]$"
 606 |       ],
 607 |       "text/plain": [
 608 |        "⎡1  0⎤\n",
 609 |        "⎢    ⎥\n",
 610 |        "⎣0  1⎦"
 611 |       ]
 612 |      },
 613 |      "execution_count": 23,
 614 |      "metadata": {},
 615 |      "output_type": "execute_result"
 616 |     }
 617 |    ],
 618 |    "source": [
 619 |     "eye(2)"
 620 |    ]
 621 |   },
 622 |   {
 623 |    "cell_type": "markdown",
 624 |    "metadata": {},
 625 |    "source": [
 626 |     "**zeros** nos permite criar uma matriz com zeros:"
 627 |    ]
 628 |   },
 629 |   {
 630 |    "cell_type": "code",
 631 |    "execution_count": 24,
 632 |    "metadata": {},
 633 |    "outputs": [
 634 |     {
 635 |      "data": {
 636 |       "text/latex": [
 637 |        "$\\displaystyle \\left[\\begin{matrix}0 & 0 & 0\\\\0 & 0 & 0\\end{matrix}\\right]$"
 638 |       ],
 639 |       "text/plain": [
 640 |        "⎡0  0  0⎤\n",
 641 |        "⎢       ⎥\n",
 642 |        "⎣0  0  0⎦"
 643 |       ]
 644 |      },
 645 |      "execution_count": 24,
 646 |      "metadata": {},
 647 |      "output_type": "execute_result"
 648 |     }
 649 |    ],
 650 |    "source": [
 651 |     "zeros(2, 3)"
 652 |    ]
 653 |   },
 654 |   {
 655 |    "cell_type": "markdown",
 656 |    "metadata": {},
 657 |    "source": [
 658 |     "**ones** nos permite criar uma matriz somente de um:"
 659 |    ]
 660 |   },
 661 |   {
 662 |    "cell_type": "code",
 663 |    "execution_count": 25,
 664 |    "metadata": {},
 665 |    "outputs": [
 666 |     {
 667 |      "data": {
 668 |       "text/latex": [
 669 |        "$\\displaystyle \\left[\\begin{matrix}1 & 1 & 1 & 1 & 1\\end{matrix}\\right]$"
 670 |       ],
 671 |       "text/plain": [
 672 |        "[1  1  1  1  1]"
 673 |       ]
 674 |      },
 675 |      "execution_count": 25,
 676 |      "metadata": {},
 677 |      "output_type": "execute_result"
 678 |     }
 679 |    ],
 680 |    "source": [
 681 |     "ones(1,5)"
 682 |    ]
 683 |   },
 684 |   {
 685 |    "cell_type": "markdown",
 686 |    "metadata": {},
 687 |    "source": [
 688 |     "**diag** nos permite criar uma matriz diagonal:"
 689 |    ]
 690 |   },
 691 |   {
 692 |    "cell_type": "code",
 693 |    "execution_count": 26,
 694 |    "metadata": {},
 695 |    "outputs": [
 696 |     {
 697 |      "data": {
 698 |       "text/latex": [
 699 |        "$\\displaystyle \\left[\\begin{matrix}1 & 0 & 0\\\\0 & 2 & 0\\\\0 & 0 & 3\\end{matrix}\\right]$"
 700 |       ],
 701 |       "text/plain": [
 702 |        "⎡1  0  0⎤\n",
 703 |        "⎢       ⎥\n",
 704 |        "⎢0  2  0⎥\n",
 705 |        "⎢       ⎥\n",
 706 |        "⎣0  0  3⎦"
 707 |       ]
 708 |      },
 709 |      "execution_count": 26,
 710 |      "metadata": {},
 711 |      "output_type": "execute_result"
 712 |     }
 713 |    ],
 714 |    "source": [
 715 |     "diag(1,2,3)"
 716 |    ]
 717 |   },
 718 |   {
 719 |    "cell_type": "markdown",
 720 |    "metadata": {},
 721 |    "source": [
 722 |     "Operações algébricas padrões como **adição**, **subtração**, **multiplicação** e **exponenciação** funcionam como esperados para objetos de Matriz.\n",
 723 |     "\n",
 724 |     "O método **transpose()** gira a matriz através de sua diagonal:"
 725 |    ]
 726 |   },
 727 |   {
 728 |    "cell_type": "code",
 729 |    "execution_count": 27,
 730 |    "metadata": {},
 731 |    "outputs": [
 732 |     {
 733 |      "data": {
 734 |       "text/latex": [
 735 |        "$\\displaystyle \\left[\\begin{matrix}2 & -2 & 1\\\\-3 & -2 & 0\\\\-8 & 2 & -3\\\\7 & -7 & 6\\end{matrix}\\right]$"
 736 |       ],
 737 |       "text/plain": [
 738 |        "⎡2   -2  1 ⎤\n",
 739 |        "⎢          ⎥\n",
 740 |        "⎢-3  -2  0 ⎥\n",
 741 |        "⎢          ⎥\n",
 742 |        "⎢-8  2   -3⎥\n",
 743 |        "⎢          ⎥\n",
 744 |        "⎣7   -7  6 ⎦"
 745 |       ]
 746 |      },
 747 |      "execution_count": 27,
 748 |      "metadata": {},
 749 |      "output_type": "execute_result"
 750 |     }
 751 |    ],
 752 |    "source": [
 753 |     "A.transpose()"
 754 |    ]
 755 |   },
 756 |   {
 757 |    "cell_type": "markdown",
 758 |    "metadata": {},
 759 |    "source": [
 760 |     "O determinante de uma matriz é denotado como $det(M)$ ou $|M|$ e pode ser calculado em SymPy como:"
 761 |    ]
 762 |   },
 763 |   {
 764 |    "cell_type": "code",
 765 |    "execution_count": 28,
 766 |    "metadata": {},
 767 |    "outputs": [
 768 |     {
 769 |      "data": {
 770 |       "image/png": "iVBORw0KGgoAAAANSUhEUgAAAA0AAAASCAYAAACAa1QyAAAABHNCSVQICAgIfAhkiAAAAPZJREFUKJGd0r8rxWEUx/HX5f4HBrPdH3FlshjIiIFNSRmUUt9MNinFYLj/gAwiFhKTUgZJMsjiJimTwc/h+6jTt2/3fvnU0zmd57xP5/P01LIs81d1hbwH09jBHd7wijNMxd56gMawgUcc4wG9GMEWhlLPd4RuMYw9fIX6Is4xmgZsx/WOsFsAoIXNlDeKntrpPcWPqlAdEyk/qAqtoB/7OKwCzWIeNxj/LbaDZrCGawzgpRM0h3VcJaAVL8ugBaziMgFPxYYitCQ3foFBPJetEX/EJJbxiVP5IxR1j2aE+lLslnsq0wmacb0MtQ6nUeapkv4F/QC4NjEPV14CWgAAAABJRU5ErkJggg==\n",
 771 |       "text/latex": [
 772 |        "$\\displaystyle 2$"
 773 |       ],
 774 |       "text/plain": [
 775 |        "2"
 776 |       ]
 777 |      },
 778 |      "execution_count": 28,
 779 |      "metadata": {},
 780 |      "output_type": "execute_result"
 781 |     }
 782 |    ],
 783 |    "source": [
 784 |     "M = Matrix([[1, 2, 3], [2, -2, 4], [2, 2, 5]])\n",
 785 |     "\n",
 786 |     "M.det()"
 787 |    ]
 788 |   },
 789 |   {
 790 |    "cell_type": "markdown",
 791 |    "metadata": {},
 792 |    "source": [
 793 |     "Para cada Matriz $A$ invertível, existe uma Matriz inversa $A^{-1}$.\n",
 794 |     "\n",
 795 |     "O efeito cumulativo do produto de $A$ e $A^{-1}$ é a matriz identidade: $AA^{-1} = A^{-1}A = \\mathbb{1}$"
 796 |    ]
 797 |   },
 798 |   {
 799 |    "cell_type": "code",
 800 |    "execution_count": 30,
 801 |    "metadata": {},
 802 |    "outputs": [
 803 |     {
 804 |      "data": {
 805 |       "text/latex": [
 806 |        "$\\displaystyle \\left[\\begin{matrix}1 & 2\\\\3 & 9\\end{matrix}\\right]$"
 807 |       ],
 808 |       "text/plain": [
 809 |        "⎡1  2⎤\n",
 810 |        "⎢    ⎥\n",
 811 |        "⎣3  9⎦"
 812 |       ]
 813 |      },
 814 |      "execution_count": 30,
 815 |      "metadata": {},
 816 |      "output_type": "execute_result"
 817 |     }
 818 |    ],
 819 |    "source": [
 820 |     "A = Matrix([[1,2],[3,9]])\n",
 821 |     "A"
 822 |    ]
 823 |   },
 824 |   {
 825 |    "cell_type": "markdown",
 826 |    "metadata": {},
 827 |    "source": [
 828 |     "A seguir podemos ver a relação de equivalência à $A^{-1}$:"
 829 |    ]
 830 |   },
 831 |   {
 832 |    "cell_type": "code",
 833 |    "execution_count": 31,
 834 |    "metadata": {},
 835 |    "outputs": [
 836 |     {
 837 |      "data": {
 838 |       "text/latex": [
 839 |        "$\\displaystyle \\left( \\left[\\begin{matrix}3 & - \\frac{2}{3}\\\\-1 & \\frac{1}{3}\\end{matrix}\\right], \\  \\left[\\begin{matrix}1 & 0\\\\0 & 1\\end{matrix}\\right], \\  \\left[\\begin{matrix}1 & 0\\\\0 & 1\\end{matrix}\\right]\\right)$"
 840 |       ],
 841 |       "text/plain": [
 842 |        "⎛⎡3   -2/3⎤  ⎡1  0⎤  ⎡1  0⎤⎞\n",
 843 |        "⎜⎢        ⎥, ⎢    ⎥, ⎢    ⎥⎟\n",
 844 |        "⎝⎣-1  1/3 ⎦  ⎣0  1⎦  ⎣0  1⎦⎠"
 845 |       ]
 846 |      },
 847 |      "execution_count": 31,
 848 |      "metadata": {},
 849 |      "output_type": "execute_result"
 850 |     }
 851 |    ],
 852 |    "source": [
 853 |     "A.inv(), A.inv()*A, A*A.inv()"
 854 |    ]
 855 |   },
 856 |   {
 857 |    "cell_type": "markdown",
 858 |    "metadata": {},
 859 |    "source": [
 860 |     "Quando uma matriz é multiplicada por um de seus autovetores o output é o mesmo autovetor multiplicado por uma constante\n",
 861 |     "$A\\vec{e}\\lambda = \\lambda\\vec{e}_\\lambda$. \n",
 862 |     "\n",
 863 |     "A constante $\\lambda$ é chamada de autovalor de $A$.\n",
 864 |     "\n",
 865 |     "Para encontrar os autovalores de uma matriz, começa-se pela definição $A\\vec{e}_\\lambda = \\lambda\\vec{e}_\\lambda$, insere-se a identidade $\\mathbb{1}$ e reescreve-se como um problema de espaço nulo:\n",
 866 |     "\n",
 867 |     "\\begin{equation}A\\vec{e}\\lambda = \\lambda\\mathbb{1}\\vec{e}_\\lambda \\Longrightarrow (A - \\lambda\\mathbb{1})\\vec{e}\\lambda = \\vec{0} \\end{equation}\n",
 868 |     "\n",
 869 |     "Essa equação terá uma solução quando $|A - \\lambda\\mathbb{1}| = 0$. Os autovalores de $A \\in \\mathbb{R}^{n \\times m}$, denotados $\\{ \\lambda1, \\lambda2, ..., \\lambda n \\}$ são raízes do polinômio característico $p(\\lambda) = | A - \\lambda\\mathbb{1}|$\n",
 870 |     "\n",
 871 |     "É dessa forma que autovetores e autovalores funcionam no SymPy:"
 872 |    ]
 873 |   },
 874 |   {
 875 |    "cell_type": "code",
 876 |    "execution_count": 32,
 877 |    "metadata": {},
 878 |    "outputs": [
 879 |     {
 880 |      "data": {
 881 |       "text/latex": [
 882 |        "$\\displaystyle \\left[ \\left( 5, \\  1, \\  \\left[ \\left[\\begin{matrix}\\frac{1}{2}\\\\1\\end{matrix}\\right]\\right]\\right), \\  \\left( 10, \\  1, \\  \\left[ \\left[\\begin{matrix}-2\\\\1\\end{matrix}\\right]\\right]\\right)\\right]$"
 883 |       ],
 884 |       "text/plain": [
 885 |        "⎡⎛      ⎡⎡1/2⎤⎤⎞  ⎛       ⎡⎡-2⎤⎤⎞⎤\n",
 886 |        "⎢⎜5, 1, ⎢⎢   ⎥⎥⎟, ⎜10, 1, ⎢⎢  ⎥⎥⎟⎥\n",
 887 |        "⎣⎝      ⎣⎣ 1 ⎦⎦⎠  ⎝       ⎣⎣1 ⎦⎦⎠⎦"
 888 |       ]
 889 |      },
 890 |      "execution_count": 32,
 891 |      "metadata": {},
 892 |      "output_type": "execute_result"
 893 |     }
 894 |    ],
 895 |    "source": [
 896 |     "A = Matrix([[9, -2],[-2, 6]])\n",
 897 |     "\n",
 898 |     "A.eigenvals()\n",
 899 |     "A.eigenvects()"
 900 |    ]
 901 |   },
 902 |   {
 903 |    "cell_type": "markdown",
 904 |    "metadata": {},
 905 |    "source": [
 906 |     "Certas matrizes podem ser escritas inteiramente em termos de seus autovetores e seus autovalores. \n",
 907 |     "\n",
 908 |     "Considere a Matrix $\\Lambda$ que tem os autovalores da Matriz $A$ em sua diagonal, e a Matriz $Q$ construída dos autovetores de A como colunas:\n",
 909 |     "\n",
 910 |     "\\begin{equation}\n",
 911 |     "\\Lambda =\n",
 912 |     "\\begin{bmatrix}\n",
 913 |     "\\lambda_1 & ... & 0 \\\\\n",
 914 |     "... & ... & 0 \\\\\n",
 915 |     "0 & 0 & \\lambda_n\n",
 916 |     "\\end{bmatrix} , \n",
 917 |     "Q =\n",
 918 |     "\\begin{bmatrix}\n",
 919 |     "| & ~ & | \\\\\n",
 920 |     "e\\vec{\\lambda}_1 & ... & e\\vec{\\lambda}_n \\\\\n",
 921 |     "| & ~ & | \n",
 922 |     "\\end{bmatrix} \n",
 923 |     "\\end{equation}\n",
 924 |     "\n",
 925 |     "então $ A = Q \\Lambda Q^{-1} $\n",
 926 |     "\n",
 927 |     "Matrizes que podem ser escritas dessa maneira são chamadas de diagonalizável.\n",
 928 |     "\n",
 929 |     "Para diagonalizar uma Matriz $A$ é encontrar suas matrizes $Q$ e $\\Lambda$:"
 930 |    ]
 931 |   },
 932 |   {
 933 |    "cell_type": "code",
 934 |    "execution_count": 33,
 935 |    "metadata": {},
 936 |    "outputs": [],
 937 |    "source": [
 938 |     "A = Matrix([[9, -2], [-2, 6]])\n",
 939 |     "Q, L = A.diagonalize()"
 940 |    ]
 941 |   },
 942 |   {
 943 |    "cell_type": "markdown",
 944 |    "metadata": {},
 945 |    "source": [
 946 |     "Matriz de autovetores $Q$, como colunas:"
 947 |    ]
 948 |   },
 949 |   {
 950 |    "cell_type": "code",
 951 |    "execution_count": 34,
 952 |    "metadata": {},
 953 |    "outputs": [
 954 |     {
 955 |      "data": {
 956 |       "text/latex": [
 957 |        "$\\displaystyle \\left[\\begin{matrix}1 & -2\\\\2 & 1\\end{matrix}\\right]$"
 958 |       ],
 959 |       "text/plain": [
 960 |        "⎡1  -2⎤\n",
 961 |        "⎢     ⎥\n",
 962 |        "⎣2  1 ⎦"
 963 |       ]
 964 |      },
 965 |      "execution_count": 34,
 966 |      "metadata": {},
 967 |      "output_type": "execute_result"
 968 |     }
 969 |    ],
 970 |    "source": [
 971 |     "Q "
 972 |    ]
 973 |   },
 974 |   {
 975 |    "cell_type": "markdown",
 976 |    "metadata": {},
 977 |    "source": [
 978 |     "$Q^{-1}$"
 979 |    ]
 980 |   },
 981 |   {
 982 |    "cell_type": "code",
 983 |    "execution_count": 35,
 984 |    "metadata": {},
 985 |    "outputs": [
 986 |     {
 987 |      "data": {
 988 |       "text/latex": [
 989 |        "$\\displaystyle \\left[\\begin{matrix}\\frac{1}{5} & \\frac{2}{5}\\\\- \\frac{2}{5} & \\frac{1}{5}\\end{matrix}\\right]$"
 990 |       ],
 991 |       "text/plain": [
 992 |        "⎡1/5   2/5⎤\n",
 993 |        "⎢         ⎥\n",
 994 |        "⎣-2/5  1/5⎦"
 995 |       ]
 996 |      },
 997 |      "execution_count": 35,
 998 |      "metadata": {},
 999 |      "output_type": "execute_result"
1000 |     }
1001 |    ],
1002 |    "source": [
1003 |     "Q.inv() "
1004 |    ]
1005 |   },
1006 |   {
1007 |    "cell_type": "markdown",
1008 |    "metadata": {},
1009 |    "source": [
1010 |     "$L$"
1011 |    ]
1012 |   },
1013 |   {
1014 |    "cell_type": "code",
1015 |    "execution_count": 36,
1016 |    "metadata": {},
1017 |    "outputs": [
1018 |     {
1019 |      "data": {
1020 |       "text/latex": [
1021 |        "$\\displaystyle \\left[\\begin{matrix}5 & 0\\\\0 & 10\\end{matrix}\\right]$"
1022 |       ],
1023 |       "text/plain": [
1024 |        "⎡5  0 ⎤\n",
1025 |        "⎢     ⎥\n",
1026 |        "⎣0  10⎦"
1027 |       ]
1028 |      },
1029 |      "execution_count": 36,
1030 |      "metadata": {},
1031 |      "output_type": "execute_result"
1032 |     }
1033 |    ],
1034 |    "source": [
1035 |     "L"
1036 |    ]
1037 |   },
1038 |   {
1039 |    "cell_type": "markdown",
1040 |    "metadata": {},
1041 |    "source": [
1042 |     "Realizamos a autodecomposição de $A$:"
1043 |    ]
1044 |   },
1045 |   {
1046 |    "cell_type": "code",
1047 |    "execution_count": 37,
1048 |    "metadata": {},
1049 |    "outputs": [
1050 |     {
1051 |      "data": {
1052 |       "text/latex": [
1053 |        "$\\displaystyle \\left[\\begin{matrix}9 & -2\\\\-2 & 6\\end{matrix}\\right]$"
1054 |       ],
1055 |       "text/plain": [
1056 |        "⎡9   -2⎤\n",
1057 |        "⎢      ⎥\n",
1058 |        "⎣-2  6 ⎦"
1059 |       ]
1060 |      },
1061 |      "execution_count": 37,
1062 |      "metadata": {},
1063 |      "output_type": "execute_result"
1064 |     }
1065 |    ],
1066 |    "source": [
1067 |     "Q * L * Q.inv() "
1068 |    ]
1069 |   },
1070 |   {
1071 |    "cell_type": "markdown",
1072 |    "metadata": {},
1073 |    "source": [
1074 |     "Nem todas as matrizes são diagonalizáveis. Você pode checar se uma matriz é diagonalizável chamando o método **is_diagonalizable**:"
1075 |    ]
1076 |   },
1077 |   {
1078 |    "cell_type": "code",
1079 |    "execution_count": 39,
1080 |    "metadata": {},
1081 |    "outputs": [
1082 |     {
1083 |      "data": {
1084 |       "text/plain": [
1085 |        "True"
1086 |       ]
1087 |      },
1088 |      "execution_count": 39,
1089 |      "metadata": {},
1090 |      "output_type": "execute_result"
1091 |     }
1092 |    ],
1093 |    "source": [
1094 |     "A.is_diagonalizable()"
1095 |    ]
1096 |   },
1097 |   {
1098 |    "cell_type": "code",
1099 |    "execution_count": 38,
1100 |    "metadata": {},
1101 |    "outputs": [
1102 |     {
1103 |      "data": {
1104 |       "text/plain": [
1105 |        "False"
1106 |       ]
1107 |      },
1108 |      "execution_count": 38,
1109 |      "metadata": {},
1110 |      "output_type": "execute_result"
1111 |     }
1112 |    ],
1113 |    "source": [
1114 |     "B = Matrix([[1,3],[0,1]])\n",
1115 |     "B.is_diagonalizable()"
1116 |    ]
1117 |   },
1118 |   {
1119 |    "cell_type": "markdown",
1120 |    "metadata": {},
1121 |    "source": [
1122 |     "Autovalores de $B$:"
1123 |    ]
1124 |   },
1125 |   {
1126 |    "cell_type": "code",
1127 |    "execution_count": 42,
1128 |    "metadata": {},
1129 |    "outputs": [
1130 |     {
1131 |      "data": {
1132 |       "image/png": "iVBORw0KGgoAAAANSUhEUgAAAEEAAAAWCAYAAACffPEKAAAABHNCSVQICAgIfAhkiAAAAo1JREFUWIXt2FuITVEYB/DfmJGU3HNJCkVuD/Mg5W27lZLQePLgEkUpPCheRCQeKOVlnuRh5kUKoebJpZkimijJAw9D0jxQLmWUy3hY63SO45x99j6cQc2/dmu31///fd/61t7fWmszjJrYjHt4j29o/bvh5MZRfEE/rmBeXgML8R0fcR7HMa2Mswnn0I0PGERHvRGnYBJ24jKeY0CYmB7swIgqugSn0BVju5/X8Z4o3JvCeRQ5H/FU45KwO9p+jU6cFCbmXXx+CU01bPQKkzomj+PD0cHqFM5yzI0BJBqXhBVY59cZn4aX0W9bDRudkTezvKPaawTNsf2SwrmFZ9F4I3ET14SZLEU/2uN9UsNGYRzN5R1pSRgqXBCSuK1OfWFwX+sNIC0J42M7UK/xIUALtsT7rhrcz7Edl9V4k2IhKV8RqiFRX02Yjvl5givB6ejzRgbuocjdV4u4BmfwIAra0+k/IdG4wlgJe6O/p5iYgT8DfcLncxEnMKsS8Ww0PIjHWJQjqMTQJaGwfD+R/U2FXfikOMakGnEs1gu14JUK1bQKEkOThP2KkzQlh25t1PUIkzsyi6gjihZndJJofBIORh8PMTmn9kzUrirvSFsdXsQ2y/f2O8haGA8LW+BerMSbnH4mxLavvKMlRVRYf9MStSFeFL/NZcLaTwj0QI3gTmIrtpfoyrEVx4RDXLfKW/m+FD3Fcfyyn0hLQpZdYGsMsBRz4kV4m2olIQtmx7ZZqAmVcEd6EgrItbstrKsb84j+YVwVxjM1j6gtiq4Lh45/YYtdD0ZhqXD0fi/nOEYLy9BgyfU//lQpjf9IJVJaTRjAEuEYu0A4h/f/0RAbj9tCIXyLu8L/j2EMowp+AMX3mt7VCX3LAAAAAElFTkSuQmCC\n",
1133 |       "text/latex": [
1134 |        "$$\\left \\{ 1 : 2\\right \\}$$"
1135 |       ],
1136 |       "text/plain": [
1137 |        "{1: 2}"
1138 |       ]
1139 |      },
1140 |      "execution_count": 42,
1141 |      "metadata": {},
1142 |      "output_type": "execute_result"
1143 |     }
1144 |    ],
1145 |    "source": [
1146 |     "B.eigenvals()"
1147 |    ]
1148 |   },
1149 |   {
1150 |    "cell_type": "markdown",
1151 |    "metadata": {},
1152 |    "source": [
1153 |     "Autovetores de $B$:"
1154 |    ]
1155 |   },
1156 |   {
1157 |    "cell_type": "code",
1158 |    "execution_count": 40,
1159 |    "metadata": {},
1160 |    "outputs": [
1161 |     {
1162 |      "data": {
1163 |       "text/latex": [
1164 |        "$\\displaystyle \\left[ \\left( 1, \\  2, \\  \\left[ \\left[\\begin{matrix}1\\\\0\\end{matrix}\\right]\\right]\\right)\\right]$"
1165 |       ],
1166 |       "text/plain": [
1167 |        "⎡⎛      ⎡⎡1⎤⎤⎞⎤\n",
1168 |        "⎢⎜1, 2, ⎢⎢ ⎥⎥⎟⎥\n",
1169 |        "⎣⎝      ⎣⎣0⎦⎦⎠⎦"
1170 |       ]
1171 |      },
1172 |      "execution_count": 40,
1173 |      "metadata": {},
1174 |      "output_type": "execute_result"
1175 |     }
1176 |    ],
1177 |    "source": [
1178 |     "B.eigenvects()"
1179 |    ]
1180 |   },
1181 |   {
1182 |    "cell_type": "markdown",
1183 |    "metadata": {},
1184 |    "source": [
1185 |     "A matriz $B$ não é diagonalizável, porque ela não tem um conjunto completo de autovetores. Para diagonalizar uma matriz $2 \\times 2$ nós precisamos de dois autovetores ortogonais, porém B tem somente um único autovetor."
1186 |    ]
1187 |   }
1188 |  ],
1189 |  "metadata": {
1190 |   "kernelspec": {
1191 |    "display_name": "Python 3",
1192 |    "language": "python",
1193 |    "name": "python3"
1194 |   },
1195 |   "language_info": {
1196 |    "codemirror_mode": {
1197 |     "name": "ipython",
1198 |     "version": 3
1199 |    },
1200 |    "file_extension": ".py",
1201 |    "mimetype": "text/x-python",
1202 |    "name": "python",
1203 |    "nbconvert_exporter": "python",
1204 |    "pygments_lexer": "ipython3",
1205 |    "version": "3.7.10"
1206 |   }
1207 |  },
1208 |  "nbformat": 4,
1209 |  "nbformat_minor": 4
1210 | }
1211 | 


--------------------------------------------------------------------------------
/jupyter_notebooks/onda_quadrada.ipynb:
--------------------------------------------------------------------------------
  1 | {
  2 |  "cells": [
  3 |   {
  4 |    "cell_type": "markdown",
  5 |    "metadata": {},
  6 |    "source": [
  7 |     "# Onda Quadrada\n",
  8 |     "\n",
  9 |     "Uma onda quadrada é uma forma de onda periódica não-senoidal ao qual a amplitude alterna em uma frequência constante entre os valores mínimo e máximo fixos, com a mesma duração no mínimo e no máximo. Em uma onda quadrada ideal, as transições entre o mínimo e o máximo são instantâneas.\n",
 10 |     "\n",
 11 |     "Ondas quadradas são freqüentemente encontradas em eletrônicos e processamento de sinais, particularmente eletrônicos digitais e processamento de sinais digitais.\n",
 12 |     "\n",
 13 |     "A seguir temos algumas características das ondas quadradas:\n",
 14 |     "\n",
 15 |     "- Ondas Quadradas são formas de onda periódicas.\n",
 16 |     "- Entretanto, ondas quadradas são não-sinusoidais. \n",
 17 |     "- A transição entre os valores de pico é instantâneo em uma onda quadrada.\n",
 18 |     "- O período da onda quadrada é também chamado de largura do pulso.\n",
 19 |     "\n",
 20 |     "Para desenhar uma onda quadrada utilizando **matplotlib**, **NumPy** e **SciPy** é necessário alguns detalhes:\n",
 21 |     "\n",
 22 |     "- Frequência da onda quadrada, por exemplo: 10Hz, que é 10 ciclos por segundo.\n",
 23 |     "- A frequência de amostragem, ou seja, quandos pontos de dados no qual a onda está sendo construída, quanto mais elevado os pontos de dados, mais \"suave\" o quadrado é.\n",
 24 |     "- Ondas Quadradas possuem um ciclo de trabalho de 50%, ou seja, a porcentagem da forma de onda que ocorre acima do eixo zero é de 50%.\n",
 25 |     "- Por padrão, a função **signal.square** da biblioteca **SciPy** recebe um valor de trabalho de **0.5**.\n",
 26 |     "\n",
 27 |     "Começamos importando as bibliotecas necessárias:"
 28 |    ]
 29 |   },
 30 |   {
 31 |    "cell_type": "code",
 32 |    "execution_count": 1,
 33 |    "metadata": {},
 34 |    "outputs": [],
 35 |    "source": [
 36 |     "import matplotlib.pyplot as plt\n",
 37 |     "from scipy import signal\n",
 38 |     "import numpy as np"
 39 |    ]
 40 |   },
 41 |   {
 42 |    "cell_type": "markdown",
 43 |    "metadata": {},
 44 |    "source": [
 45 |     "Definimos a taxa de amostragem 1000Hz/segundo:"
 46 |    ]
 47 |   },
 48 |   {
 49 |    "cell_type": "code",
 50 |    "execution_count": 2,
 51 |    "metadata": {},
 52 |    "outputs": [],
 53 |    "source": [
 54 |     "t = np.linspace(0, 1, 1000, endpoint=True)"
 55 |    ]
 56 |   },
 57 |   {
 58 |    "cell_type": "markdown",
 59 |    "metadata": {},
 60 |    "source": [
 61 |     "Calculamos o sinal da onda quadrada:"
 62 |    ]
 63 |   },
 64 |   {
 65 |    "cell_type": "code",
 66 |    "execution_count": 3,
 67 |    "metadata": {},
 68 |    "outputs": [],
 69 |    "source": [
 70 |     "s = signal.square(2 * np.pi * 5 * t)"
 71 |    ]
 72 |   },
 73 |   {
 74 |    "cell_type": "markdown",
 75 |    "metadata": {},
 76 |    "source": [
 77 |     "Podemos então plotar o gráfico:"
 78 |    ]
 79 |   },
 80 |   {
 81 |    "cell_type": "code",
 82 |    "execution_count": 4,
 83 |    "metadata": {},
 84 |    "outputs": [
 85 |     {
 86 |      "data": {
 87 |       "image/png": "iVBORw0KGgoAAAANSUhEUgAAA7gAAAImCAYAAAB5IibcAAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADh0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uMy4xLjMsIGh0dHA6Ly9tYXRwbG90bGliLm9yZy+AADFEAAAgAElEQVR4nOzdeZhldXXv/88CGmjmSRpBRgMOICC2KKBSqOQKosQxqDFqcoNGjfd6oz4m5l6M0Zj4i/caL0bEOKByVYxRURswag44CxJmkEmGFpSxgZamoenv74+9O3W6rKquvb6rau/vl/freXiorqqu3v3udU712mef05ZSEgAAAAAApduo7wMAAAAAACACCy4AAAAAoAosuAAAAACAKrDgAgAAAACqwIILAAAAAKgCCy4AAAAAoAosuAAwIGb2aTN7b9/HMRdmtpeZJTPbJPBrJjP7naivh1hmdoOZPbfv40A/zGxkZv+17+MAgNmw4AJABjN7rZldamb3m9mvzOyjZrbdgI7nn8xs276OZ0ja5WyVma1s//vW2Mdea2bfn+HnFLfQzfT7qZGZPdrMzjSzW9oTJHtN+fhmZvZJM7u3vU38jykfP9jMftbeZn5mZgdP+fhb2593T/t1Nhv72G/NR9f2Zna1me3X5fcMAJgZCy4AOJnZn0v6e0lvl7StpKdL2lPSv5nZpgM5nr0kfcvMFi3wsZiZDfF7zAtSSlu1//1u3wfTJzPbuO9jCLJW0tmSXjLDx98taV81t82jJL3DzJ4nSe3t9GuSPidpe0mnSfrautuvmf0XSe+U9Bw1t6V9JP111IGb2WMlbZRSujrqawLAI90Q//IBAINnZtuo+Yvun6WUzk4pPZRSukHSy9X8RfoP2s97t5mdYWafMbP7zOxyM1s69nWebGYXth/7oqTNxz62vZl9w8xuN7O727cf4zievSW9sv289S6BNrMJM1s+9uN3mtl17fFcYWYvGvvYxmb2D2Z2h5ldL+n5U45hZGbvM7MfSLpf0j5m9jozu7L9eteb2eun/Jy3m9mt7aNvfzTlY883s/9oH3m72czevYE/lnllZhePPfq7sn20cGKaz5v1z63t9F4z+2H7db5uZjua2ent7/X88Uchzezw9n33tP8/fOxjr2273mdmvzCzV5nZEySdIumw9uuvaD/309ZcYbDMzH4j6agNNTazV5vZjWZ2p5m9a8rHNjOzD7V/dre0b2+mGZjZH7WzcLeZnWNme459LJnZG83smvb38jdm9lgz+1F7bGfYDCeNUkq/Tin9k6TzZ/il/1DS36SU7k4pXSnp45Je235sQtImkj6UUlqdUvqwJJP07Pbjr5H0iZTS5SmluyX9zdjP3SAz+/0pM7PazEZjn/J8Scvazz22vc3dZ2a/NLO3jX2d48zsIjNb0c7NgWMfO6T9M7zPzL5kZl9cdxu3aR5NtrGnAbQz8REz+2b7839izdK97nOPNrOr2tk7uW2z7mMbmdlftfNxmzX3cVwtAqB3LLgA4HO4mmX0X8ffmVJaKeksSUePvfuFkr4gaTtJZ0o6WfrPR4++KumzknaQ9CWt/yjURpI+pWZh3kPSqnU/13E8c3208jpJz1TzCPBfS/qcmT26/difSDpO0pMlLZX00ml+/qslnShpa0k3Srqt/TnbSHqdpP9jZodIkjWPor1NTat9JU29FPg3apaT7dQsAn9qZr83x9/HTE5vF89vmdlBXX5iSumgdY/+Svofkn4u6cJpPnUuf24nqGm1m6THSvpR+3N2kHSlpJMkycx2kPRNSR+WtKOk/y3pm+1CvGX7/mNSSlurmYGL2iXuDZJ+1B7v+CXzr5T0PjV/Pt/XLI3N7ImSPtoe567trz9+guVdaq4SOFjSQZIOlfRX07Vrv+ZfSnqxpEdJ+p6kz0/5tOdJekr7Nd8h6VRJr5K0u6QDJL1iuq89GzPbvj32i8fefbGk/du395d0SUopjX38kikfn/pzl5jZjnP59VNKXxybmV0lXa/1f9/HqvnzlaRPSHp9+2d5gKTvtr+HQyR9UtLr1fwZfEzSme0Jhk0lfUXSp9XMzuclvUjdvELNbX17SdeqmQ+Z2U6Svqzmz3QnNfcNR4z9vNe2/x2l5pHtrTTz/RMALBgWXADw2UnSHSmlNdN87Nb24+t8P6W0LKX0sJpldt1i9XRJi9Q8evRQSulfNPYoVErpzpTSl1NK96eU7lPzF88jncfzqLn8plJKX0op3ZJSWptS+qKka9QsLlLzaPCHUko3p5TukvT+ab7Ep9tHu9a0v6dvppSuS41zJX1LzQK97ut9KqV0WUrpN2ouJR0/llFK6dL2WC5R85f3mX7/c/EqNZeZ7inp3yWdY+s/X/rp7SNk//mfmgV1PWb2DEnvlfTClNK9Uz8+xz+3T7Vd7lFzAuK6lNK32z+/L6k5iSA1S+c1KaXPtk0/L+kqSS9oP75W0gFmtjildGtK6fINNPhaSukHbdMHNtD4pZK+kVI6L6W0WtL/bH+98Z7vSSndllK6Xc2S9OoZft3XS3p/SunK9vf4t5IOHn8UV9Lfp5TubX8Pl0n6Vkrp+rFGT/7tL7tBW7X/v2fsffeoWfDXffwerW+2j697e+ux9311ysz809SDsOZy/f8naZRS+lj7vi0kPVXSue2nPSTpiWa2Tfto87qTJ38i6WMppZ+klB5OKZ0mabWa+4+nq3kE+sPt7e1fJf10lh7T+deU0k/bP5fT1ZywkJrl+4qU0r+klB6S9CFJvxr7ea+S9L/bP6OVkv5C0gkW+KJzAODBggsAPndI2mmGv8w9uv34OuN/Kbxf0ubtz9tV0i+nPHp047o3zGwLM/tYewngvZLOk7SdTf/cyQ0dz+1z+U2Z2R+OXQq5Qs0jSeuW9V0l3TzdsY4Z/7jM7Bgz+7GZ3dV+vWPn+vXM7Glm9u/tI673qHlUcvzEwfjnnjV2GeirpvucdrFb1S6e75e0QpPLtiT9OKW03fh/km6a8uvsLukMSa+Z6XmTc/xz+/XY26um+fG6xWzXqV3aH+/WnhT4fTVdbm0vM338dMc0Zuqfz2yN1/vzaX+9O8d++tRju7F933T2lPSPY3N1l5rLXXcb+5y5NuliZfv/bcbet42k+8Y+vo3WN9vH171939j7fm/KzLxxmuNY96j5W8be9xxJP0wpPdD++CVqbh83mtm5ZnZY+/49Jf35lCV6dzWtp7sPWe/PeA6m3j+Nz974n3+a8rWn+/PfRNKSjr8+AIRiwQUAnx+peRTlxePvbC8bPUbSd+bwNW6VtJuZ2dj7xh8x/HNJj5P0tJTSNpKete6XcRzPukeJfiNpi7FP2WXsc/dU8/zEN0vasf3L+mVjv96tav5iPd2xrvOff9G25vmYX5b0D5KWtF9vWYev9//UXNK9e0ppWzXPK53u966U0jFp8sWjTp/uc2Y41mm/3nTMbLGaS8o/lFI6a5ZP7fLntiG3qFlwxu0h6ZeSlFI6J6V0tJqTGFep+fOTxv4cppj6/tkar/fn0z7iOH5p7tRj26N933RuVnP57fgJhMUppR/O8PkhUvO82Vs1edWE2rfXPdJ9uaQDp9wGD5zy8ak/99cppfFFf1ZmdoKay4Bf2j4Sus745clKKZ2fUjpe0s5q5uyM9kM3S3rflHZbtI/mT3cfMn6bWu/2bma7aO6m/vnblK893Z//Gq1/YgIAFhwLLgA4tJdN/rWk/2tmzzOzRda8MNCXJC1XcynyhvxIzV8I32Jmm5jZizV5ObDUPOKzStKK9rmYJzmP5w41lx5K0kWSjjWzHdq/7P73sS+zpZoF6HZJMrPXqXkEd50z2mN9TPvcxndu4Pe3qaTN2q+3xsyO0frPBT5D0mvN7Int8jT197e1pLtSSg+Y2aFqXyjLw8z2MLMjzGxTM9vczN6u5pHKH3T4Mp+UdFVK6QMb+Lw5/7nNwTJJ+5nZK9sZ+X1JT5T0DTNbYmYvbE9irFbzaOPD7c/7taTH2IZfzXu2xv8i6Tgze0b7dd6j9f/e8HlJf2Vmj2qfr/m/1Lwa8XROkfQXZra/JJnZtmb2sjk22CAz21zNrEnSZu2P1/lMe5zbt49w/4ma56xK0khNs7e0z2l9c/v+74793D9uZ3R7Nc9HXfdz53JcT5b0f9U8yjv1KopjNPkCU5ta8wJh27ZL8L2a/LP8uKQ3tI+2m5ltac2Lg22t5j7kYUlvbufjeK1/H3KxpP2t+aeQNteUpwFswDfbn/vi9sqQt2jshJiaP/+3mtneZraVmsvOvzjD0yQAYMGw4AKAU7vo/KWaRyjvlfQTNY+2PKd9zuKGfv6Dah5xfa2ku9Vcbjr+IlEfkrRYzYL6YzX/FMpcj+c+Sb9Q8+jNc9vLS6Vm8b5Y0g1qng/7xbGff4WkD6r5S/OvJT1J6y+AH5d0TvvzL5xyrNMdz31q/lJ8Rvv7e6WaRwvXffys9vf4XTUvbvPdKV/ijZLeY2b3qVmezpDf1mpeMOluNY9+Pk/NizPN+ZE4NS8M9SJb/1VxnznN53X6c5tNe3zHqXlU+E41L750XErpDjXfw/9czSNpd6l57uy6y2O/q+bRx1+Z2R1Tv+6YGRu3z4V9k5pHeW9V02752M99r6QL1Lwo06VqZuK9mkZK6Stq/gmrL7SXbV+mZsGLskqTlyNf1f54nZPUvEDSjWquZPj/Ukpnt8f1oKTfU/NCWysk/ZGaZfTB9uNnS/qAmuds39j+1+WExfFqXrzp+2Mzc5aZHSBpZUpp/BL4V0u6oe3zBrWvxJ5SukDNUn6ymj+Da9W+kvPYfcgft8f/B5K+oeaEh9rL6N8j6dtqnk8/53+ft52xl0n6OzWzt6/Wvz/4pJr7k/PU3Nc8IOnP5vr1AWC+2PpP2wAA1MKaf3bnryUdMeUv0gB6ZGbvkLRTSukd8/C1fyLplJTSp6K/NgCUgFe6A4BKpZQ+aWYPqfnnY1hwgeG4QdLXI76QmR2p5p+sukPNKxsfqIyrBgCgdL0uuGb2STWXXt2WUjpgmo9PSPqamktfpOal7N+zcEcIAGVLKc3lucAAFlBKKedy+6kep+bS8q3UXIr90pTSrYFfHwCK0uslymb2LDXPmfnMLAvu21JKxy30sQEAAAAAytLri0yllM5T88IYAAAAAABkKeFVlA8zs4vbVx3cv++DAQAAAAAM09BfZOpCSXumlFaa2bFq/uHzfaf7RDM7UdKJkrR48eKn7L777tN92iCsXbtWG21UwrkF1Iw5xFAwixgC5hBDwBxiKIY+i1dfffUdKaVHTfex3v+ZIDPbS9I3pnsO7jSfe4Okpe2/zTajpUuXpgsuuCDk+ObDaDTSxMRE34eBRzjmEEPBLGIImEMMAXOIoRj6LJrZz1JKS6f72HDXcklmtouZWfv2oWqO985+jwoAAAAAMER9/zNBn5c0IWknM1su6SRJiyQppXSKpJdK+lMzWyNplaQTUt8POQMAAAAABqnXBTel9IoNfPxkSScv0OEAAAAAAAo26EuUAQAAAACYKxZcAAAAAEAVWHABAAAAAFVgwQUAAAAAVIEFFwAAAABQBRZcAAAAAEAVWHABAAAAAFVgwQUAAAAAVIEFFwAAAABQBRZcAAAAAEAVWHABAAAAAFVgwQUAAAAAVIEFFwAAAABQBRZcAAAAAEAVWHABAAAAAFVgwQUAAAAAVIEFFwAAAABQBRZcAAAAAEAVWHABAAAAAFVgwQUAAAAAVIEFFwAAAABQBRZcAAAAAEAVWHABAAAAAFVgwQUAAAAAVIEFFwAAAABQBRZcAAAAAEAVWHABAAAAAFVgwQUAAAAAVIEFFwAAAABQBRZcAAAAAEAVWHABAAAAAFVgwQUAAAAAVIEFFwAAAABQBRZcAAAAAEAVWHABAAAAAFVgwQUAAAAAVIEFFwAAAABQBRZcAAAAAEAVWHABAAAAAFVgwQUAAAAAVIEFFwAAAABQBRZcAAAAAEAVWHABAAAAAFVgwQUAAAAAVIEFFwAAAABQBRZcAAAAAEAVWHABAAAAAFVgwQUAAAAAVIEFFwAAAABQBRZcAAAAAEAVWHABAAAAAFVgwQUAAAAAVIEFFwAAAABQBRZcAAAAAEAVWHABAAAAAFVgwQUAAAAAVIEFFwAAAABQBRZcAAAAAEAVWHABAAAAAFVgwQUAAAAAVIEFFwAAAABQBRZcAAAAAEAVWHABAAAAAFVgwQUAAAAAVIEFFwAAAABQBRZcAAAAAEAVWHABAAAAAFVgwQUAAAAAVIEFFwAAAABQBRZcAAAAAEAVWHABAAAAAFVgwQUAAAAAVIEFFwAAAABQhV4XXDP7pJndZmaXzfBxM7MPm9m1ZnaJmR2y0McIAAAAACjDJj3/+p+WdLKkz8zw8WMk7dv+9zRJH23/X6Rrr5W++13p5z9/tK6+uu+jKdfmm0sveIG0/fZ9H0m5HnxQ+v73d2IOMx1wgHTYYZJZ30dSrmuukb7+de4Tcyxe3Nwnbrdd30dSrtWrpfPO4z4x14EHSk97GveJOW66abFOPbXvoyjbFls094nbbtv3kZTprLOkm26Srr760dpnH2mPPfo+ou56XXBTSueZ2V6zfMrxkj6TUkqSfmxm25nZo1NKty7IAQa74ALp9a+XpMf1fSjFe8ITpMsv55uo15veJP3zPx/Q92FU4Utfkl760r6Poky/+IX0+MdLa9dyn5jrSU+SLr6Y+0SvE0+UPvMZ7hMjfPWr0vHH930UZbrmGuk1ryn2cZxBOeSQ5u/d3Cd2d/LJ0rJlkvQ4PfvZLLjzYTdJN4/9eHn7vt9acM3sREknStKSJUs0Go0W4vg6ueKKnSU9se/DqMKVV0pf+coPtMMOD/V9KEU6++xDJW3R92FU4fTTf6mddrqm78Mo0re+tURr1z6h78OowqWXSl//+ve1zTZr+j6UIp1zztMlbd73YVThc5+7Wdtue13fh1GkZct2kfT4vg+jChdeKJ199ve0ePHDfR9Kce6880mSdpQkXXLJJdpyy7v6PSCHoS+40513SdN9YkrpVEmnStLSpUvTxMTEPB6Wz5ZbSr/6lXTLLbdo11137ftwivTZz0oPPNC8ffjhR2iXXfo9nlJtttnk2y9/OZfxdHX55dIPf9i8veuuu2liYrd+D6hQN944+fbv/I501FH9HUupTjutecqBJB1xxDO04479Hk+pNt108u0TTpC23rq/YynRpZdKP/5x8/Zuu+2uiYnd+z2gQl177eTb++0nHXlkf8dSqk99SlrTnud7xjOeyW3ZYfwpgAcddKAGuFJt0NAX3OWSxu8lHyPplp6OJdtTn9r8NxpdrYkJFlyPM8+cXHAR433va5YLzN1HPjK54CLG4YeL5505fPnL0l3lnVwftL//+zIvyevThz40ueAixjOfyX2ix+c/L61c2fdR1KPUS7yH/s8EnSnpD9tXU366pHtKff4t4qVpH8vHXNAuDi39aBeLnn60i0NLP9rFoqdPDd16fQTXzD4vaULSTma2XNJJkhZJUkrpFEnLJB0r6VpJ90t6XT9HiqEYP5NUww2wL+PtSj071yfmMAZzmI9ZjMEs5mEOYzCH+ZjFfDXMYd+vovyKDXw8SXrTAh0OClDqDW3IaNodzeLR1Idu8WjaHc3i0dSHbrFK7Tn0S5SBGXFmzo92cWjpR7tY9PSjXRxa+tEuFj19aujGgouicOlJjBouP+kTcxiDOczHLMZgFvMwhzGYw3zMYqxS55AFF0Up9YY2ZDTtjmbxaOpDt3g07Y5m8WjqQ7d8NZwYYMFFsWq4AfaFdnFo6Ue7WPT0o10cWvrRLhY9fWq4koAFF0Up9YY2ZDTtjmbxaOpDt3g07Y5m8WjqQ7dYpfZkwUWxODPnR7s4tPSjXSx6+tEuDi39aBeLnj41dGPBRVF48YAYNVx+0ifmMAZzmI9ZjMEs5mEOYzCH+ZjFfDXMIQsuilLqDW3IaNodzeLR1Idu8WjaHc3i0dSHbrFK7cmCi2JxZs6PdnFo6Ue7WPT0o10cWvrRLhY9fWroxoKLonDpSYwaLj/pE3MYgznMxyzGYBbzMIcxmMN8zGK+GuaQBRdFKfWGNmQ07Y5m8WjqQ7d4NO2OZvFo6kO3WKX2ZMFFsTgz50e7OLT0o10sevrRLg4t/WgXi54+NXRjwUVRuPQkRg2Xn/SJOYzBHOZjFmMwi3mYwxjMYT5mMV8Nc8iCi6KUekMbMpp2R7N4NPWhWzyadkezeDT1oVusUnuy4KJYnJnzo10cWvrRLhY9/WgXh5Z+tItFT58aurHgoiilnkkamhouP+kTzeLR1Idu8WjaHc3i0dSHbrFK7cmCi6Lw3Ip4pd559Yk5jMGJlnzMYgxmMQ9zGIM5zMcs5quhGwsuilXDDbAvtItDSz/axaKnH+3i0NKPdrHo6VPDiRYWXBSl1BvakNG0O5rFo6kP3eLRtDuaxaOpD91ildqTBRfF4sycH+3i0NKPdrHo6Ue7OLT0o10sevrU0I0FF0XhuRUxarj8pE/MYQzmMB+zGINZzMMcxmAO8zGL+WqYQxZcFKXUG9qQ0bQ7msWjqQ/d4tG0O5rFo6kP3WKV2pMFF8XizJwf7eLQ0o92sejpR7s4tPSjXSx6+tTQjQUXReHSkxg1XH7SJ+YwBnOYj1mMwSzmYQ5jMIf5mMV8NcwhCy6KUuoNbcho2h3N4tHUh27xaNodzeLR1IdusUrtyYKLYnFmzo92cWjpR7tY9PSjXRxa+tEuFj19aujGgouilHomaWhquPykTzSLR1MfusWjaXc0i0dTH7rFKrUnCy6KwnMr4pV659Un5jAGJ1ryMYsxmMU8zGEM5jAfs5ivhm4suChWDTfAvtAuDi39aBeLnn60i0NLP9rFoqdPDSdaWHBRlFJvaENTw51Xn2gWj6Y+dItH0+5oFo+mPnSLVWpPFlwUizNzGALm0I92sejpR7s4tPSjXSx6+tTQjQUXReG5FTF4BDcPcxiDOczHLMZgFvMwhzGYw3zMYr4a5pAFF0Up9YY2ZDTtjmbxaOpDt3g07Y5m8WjqQ7dYpfZkwUWxODPnR7s4tPSjXSx6+tEuDi39aBeLnj41dGPBRVG49CRGDZef9Ik5jMEc5mMWYzCLeZjDGMxhPmYxXw1zyIKLopR6QxsymnZHs3g09aFbPJp2R7N4NPWhW6xSe7LgolicmfOjXRxa+tEuFj39aBeHln60i0VPnxq6seCiKKWeSRqaGi4/6RPN4tHUh27xaNodzeLR1IdusUrtyYKLovDcinil3nn1iTmMwYmWfMxiDGYxD3MYgznMxyzmq6EbCy6KVcMNsC+0i0NLP9rFoqcf7eLQ0o92sejpU8OJFhZcFKXUG9rQ1HDn1SeaxaOpD93i0bQ7msWjqQ/dYpXakwUXxeLMHIaAOfSjXSx6+tEuDi39aBeLnj41dGPBRVF4bkUMHsHNwxzGYA7zMYvxmMXumMMY3CfmYxbz1TCHLLgoSqk3tCGjaXc0i0dTH7rFo2l3NItHUx+6xSq1JwsuisWZOT/axaGlH+1i0dOHbrHo6Ue7WPT0qaEbCy6KwqUnMWq4/KRPzGEM5jAfs5iPbvmYwxjcJ+ZjFvPVMIcsuChKqTe0IaNpdzSLR1MfusWipw/d4tHUh26xSu3JgoticWbOj3ZxaOlHu1j09KFbLHr60S4WPX1q6MaCi6Jw6UmMGi4/6RNzGIM5zMcs5mMO8zGHMZjFfMxirFLnkAUXRSn1hjZkNO2OZvFo6kO3WPT0oVs8mvrQLV8NJwZYcFGsGm6AfaFdHFr60S4WPX3oFouefrSLRU+fGq4kYMFFUUq9oQ0ZTbujWTya+tAtFj196BaPpj50i1VqTxZcFIszcxgC5tCPdrHo6UO3WPT0o10sevrU0I0FF0XhxQPyTe1W6tm5PjGHMWq4DKpvzGI+5jAfcxiDWczHLOarYQ5ZcFGUUm9oQ8Idfj7mMB5NfegWi54+dItHUx+6xSq1JwsuisWihiFgDv1oF4uePnSLRU8/2sWip08N3VhwURQuPclXw6UnfWMOYzCL+ZjFfMxhPuYwBrOYj1nMV8McsuCiKKXe0IaKnj50i0dTH7rFoqcP3eLR1IdusUrtyYKLYnFmzodusejpR7tY9PShWyx6+tEuFj19aujGgouicOlJvhouPekbcxiDWczHLOZjDvMxhzGYxXzMYqxS55AFF0Up9YY2VPT0oVs8mvrQLRY9fegWj6Y+dMtXw4kBFlwUq4YbYB/oFouefrSLRU8fusWipx/tYtHTp4YrCVhwUZRSb2hDUsMdV9/oFo+mPnSLRU8fusWjqQ/dYpXakwUXxeLMHIaAOfSjXSx6+tAtFj39aBeLnj41dGPBRVF48YB8PIKbjzmMwSzmYxbzMYf5mMMYzGI+ZjFfDXPIgouilHpDG5Ia7rj6Rrd4NPWhWyx6+tAtHk196Bar1J4suCgWZ+YwBMyhH+1i0dOHbrHo6Ue7WPT0qaEbCy6KwqUn+XgENx9zGINZzMcs5mMO8zGHMZjFfMxivhrmkAUXRSn1hjZU9PShWzya+tAtFj196BaPpj50i1VqTxZcFIszcz50i0VPP9rFoqcP3WLR0492sejpU0M3FlwUhUtP8tVw6UnfmMMYzGI+ZjEfc5iPOYzBLOZjFmOVOocsuChKqTe0oaKnD93i0dSHbrHo6UO3eDT1oVu+Gk609LrgmtnzzOznZnatmb1zmo9PmNk9ZnZR+9//6uM4MUycmfOhWyx6+tEuFj196BaLnn60i0VPnxq6bdLXL2xmG0v6iKSjJS2XdL6ZnZlSumLKp34vpXTcgh8gBqnUM0lDUsOZub7RLR5NfegWi54+dItHUx+6xSq1Z5+P4B4q6dqU0vUppQclfUHS8T0eDwpTwxkmlI859KNdLHr60C0WPf1oF4uePjV063PB3U3SzWM/Xt6+b6rDzOxiMzvLzPZfmEPDUPHiAfl4BDcfcxiDWczHLOZjDvMxhzGYxXzMYr4a5rC3S5QlTZds6iheKGnPlNJKMztW0lcl7TvtFzM7UdKJkrRkyRKNRqPAQ421cuXKQR/fkN1115Mk7ShJuuSSS7Tllnf1e0AFWrlyE0nPkCStXbtGo9H3+y0naMEAACAASURBVD2gAl1xxTaSDpEk3XvvvRqNLuz3gAq1fPnvSHqMJOnaa6/RaPTLfg+oQCtWHChpB0nSxRdfrE03vbvfAyrQihWLJB0hSVqz5kGNRj/s94AKdMkl20p6siTpnntWaDS6qN8DKtQtt+yrdY/1XHPN1RqNbun3gAp0zz0HS9pOknTRRRdJWtHr8ZTooYcOl7SpJOmHP/yBtt/+oX4PyKHPBXe5pN3HfvwYSevdklNK9469vczM/snMdkop3TH1i6WUTpV0qiQtXbo0TUxMzMtBRxiNRhry8Q3ZjjtOvv2kJx0oMna3Yuy+fuONN2EWHTbffPLtrbfehoZOX/7y5Nv77ruvJiamPX+JWWy//eTbBx54EPeJDrfdNvn2okWbcnt22Hjjybe32WY7Gjp94QuTb++3336amNivv4Mp1HbbTb590EEHc5/osMnYdnjEEUdo5537OxavPi9RPl/Svma2t5ltKukESWeOf4KZ7WLWPDhuZoeqOd47F/xIMRhcepKvhktP+sYcxmAW8zGL+ZjDfMxhDGYxH7OYr4Y57O0R3JTSGjN7s6RzJG0s6ZMppcvN7A3tx0+R9FJJf2pmayStknRCSozrI1mpN7QhqeGOq290i0dTH7rFoqcP3eLR1IdusUrt2eclykopLZO0bMr7Thl7+2RJJy/0caEMnOrAEDCHfrSLRU8fusWipx/tYtHTp4ZufV6iDHTGpSf5eAQ3H3MYg1nMxyzmYw7zMYcxmMV8zGK+GuaQBRdFKfWGNlT09KFbPJr60C0WPX3oFo+mPnSLVWpPFlwUizNzPnSLRU8/2sWipw/dYtHTj3ax6OlTQzcWXBSl1DNJQ1LDpSd9o1s8mvrQLRY9fegWj6Y+dItVak8WXBSrhjNMKB9z6Ee7WPT0oVssevrRLhY9fWroxoKLovDiAfl4BDcfcxiDWczHLOZjDvMxhzGYxXzMYr4a5pAFF0Up9YY2JDXccfWNbvFo6kO3WPT0oVs8mvrQLVapPVlwUSzOzGEImEM/2sWipw/dYtHTj3ax6OlTQzcWXBSFS0/y8QhuPuYwBrOYj1nMxxzmYw5jMIv5mMV8NcwhCy6KUuoNbUhquOPqG93i0dSHbrHo6UO3eDT1oVusUnuy4KJYnJnDEDCHfrSLRU8fusWipx/tYtHTp4ZuLLgoCpee5OMR3HzMYQxmMR+zmI85zMccxmAW8zGL+WqYQxZcFKXUG9qQ1HDH1Te6xaOpD91i0dOHbvFo6kO3WKX2ZMFFsTgzhyFgDv1oF4uePnSLRU8/2sWip08N3VhwUZRSzyQNCY/g5qNbPJr60C0WPX3oFo+mPnSLVWpPFlwUhedWxCr1jqtvzGEMTrbkYxbzMYf5mMMYzGI+ZjFfDd1YcFGsGm6AfaBbLHr60S4WPX3oFouefrSLRU+fGk60sOCiKKXe0IakhjuuvtEtHk196BaLnj50i0dTH7rFKrUnCy6KxZk5DAFz6Ee7WPT0oVssevrRLhY9fWroxoKLovDcinw8gpuPOYzBLOZjFvMxh/mYwxjMYj5mMV8Nc8iCi6KUekMbkhruuPpGt3g09aFbLHr60C0eTX3oFqvUniy4KBZn5jAEzKEf7WLR04dusejpR7tY9PSpoRsLLorCpSf5eAQ3H3MYg1nMxyzmYw7zMYcxmMV8zGK+GuaQBRdFKfWGNiQ13HH1jW7xaOpDt1j09KFbPJr60C1WqT1ZcFEszsxhCJhDP9rFoqcP3WLR0492sejpU0M3FlwUpdQzSUPCI7j56BaPpj50i0VPH7rFo6kP3WKV2pMFF0XhuRWxSr3j6htzGIOTLfmYxXzMYT7mMAazmI9ZzFdDNxZcFKuGG2Af6BaLnn60i0VPH7rFoqcf7WLR06eGEy0suChKqTe0IanhjqtvdItHUx+6xaKnD93i0dSHbrFK7cmCi2JxZg5DwBz60S4WPX3oFouefrSLRc9HLhZcFIXnVuTjEdx8zGEMZjEfs5iPOczHHMZgFvMxi3mmNit1DllwUZRSb2hDwjfQfHSLR1MfusWipw/d4tHUh26QWHBRMM7MYQiYQz/axaKnD91i0dOPdrHo2V0tzVhwURQuPcnHI7j5mMMYzGI+ZjEfc5iPOYzBLOZjFvOsP4PlBmTBRVG4w8/HN9B8dItHUx+6xaKnD93i0dSHbnFKbsmCi2JxZg5DwBz60S4WPX3oFouefrSLRc/uamnGgouilHw2aSh4BDcf3eLR1IdusejpQ7d4NPWhGyQWXBSG51bkY8HNxxzGYBbzMYv5mMN8zGEMZjEfs5inlmYsuChWLTdClI059KNdLHr60C0WPf1oF4ue3fEiU0APOKOZjzPE+egWj6Y+dItFTx+6xaOpD93ilNySBRfF4swchoA59KNdLHr60C0WPf1oF4ue3dXSjAUXReG5Ffl4BDcfcxiDWczHLOZjDvMxhzGYxXzMYp5aZpAFF0Up+cY2FLXcefWJbvFo6kO3WPT0oVs8mvrQDRILLgrGmTkMAXPoR7tY9PShWyx6+tEuFj27q6UZCy6KwqUn+XgENx9zGINZzMcs5mMO8zGHMZjFfMxiHl5FGegBd/j5+Aaaj27xaOpDt1j09KFbPJr60C1OyS1ZcFEszsxhCJhDP9rFoqcP3WLR0492sejZXS3NWHBRFC49yccjuPmYwxjMYj5mMR9zmI85jMEs5mMW45Q8gyy4KErJN7ah4BtoPrrFo6kP3WLR04du8WjqQ7c8tZwUYMFFsWq5EaJszKEf7WLR04dusejpR7tY9OyulmYsuCgKZ+by8QhuPrrFo6kP3WLR04du8WjqQ7c4vIoy0INazjKhbMyhH+1i0dOHbrHo6Ue7WPTsrpZmLLgoCi8ekI9HcPMxhzGYxXzMYj7mMB9zGINZzMcs5qllBje44JrZFmb2P83s4+2P9zWz4+b/0IDfVvKNbShqufPqE93i0dSHbrHo6UO3eDT1oVucklvO5RHcT0laLemw9sfLJb133o4ImCPOzGEImEM/2sWipw/dYtHTj3ax6NldLc3msuA+NqX0AUkPSVJKaZWkgnd6lIxLT/LxCG4+5jAGs5iPWczHHOZjDmMwi/mYxTy1NJvLgvugmS2WlCTJzB6r5hFdYMFxh5+Pb6D56BaPpj50i0VPH7rFo6kP3eKU/CrKm8zhc06SdLak3c3sdElHSHrtfB4UMBe1nGVC2ZhDP9rFoqcP3WLR0492sejZXS3NNrjgppT+zcwulPR0NZcm/7eU0h3zfmTANLj0JB+P4OZjDmMwi/mYxXzMYT7mMAazmI9ZzFPLDM644JrZIVPedWv7/z3MbI+U0oXzd1jA9Eq+sQ1FLXdefaJbPJr60C0WPX3oFo+mPnSLU3LL2R7B/WD7/80lLZV0sZpHcA+U9BNJz5jfQwNmx5k5DAFz6Ee7WPT0oVssevrRLhY9u6ul2YwvMpVSOiqldJSkGyUdklJamlJ6iqQnS7p2oQ4QGFfy2aSh4BHcfHSLR1MfusWipw/d4tHUh26Q5vYqyo9PKV267gcppcskHTx/hwTMTS1nmRYa3WLR0492sejpQ7dY9PSjXSx6dldLs7m8ivKVZvbPkj6n5p8K+gNJV87rUQEz4MUDYnGm04c5jMHVBPmYxXzMYT7mMAazmI9ZzLP+DJYbcC4L7usk/amk/9b++DxJH523IwJmwR1+Pr6B5qNbPJr60C0WPX3oFo+mPnSLU3LLufwzQQ9I+j/tf8BgcGYOQ8Ac+tEuFj196BaLnn60i0XP7mpptsEF18x+oebS5PWklPaZlyMCZsGlJ/l4BDcfcxiDWczHLOZjDvMxhzGYxXzMYp5aZnAulygvHXt7c0kvk7TD/BwOMLuSb2xDUcudV5/oFo+mPnSLRU8fusWjqQ/dIM3hVZRTSneO/ffLlNKHJD17AY4NmBVn5jAEzKEf7WLR04dusejpR7tY9OyulmZzuUT5kLEfbqTmEd2t5+2IgFlw6Uk+HsHNxxzGYBbzMYv5mMN8zGEMZjEfs5jnkfQqyh8ce3uNpF9Ievn8HA4wO+7w8/ENNB/d4tHUh26x6OlDt3g09aFbnJJbzmXB/eOU0vXj7zCzvefpeIA548wchoA59KNdLHr60C0WPf1oF4ue3dXSbIPPwZX0L3N8HzDvSj6bNBQ8gpuPbvFo6kO3WPT0oVs8mvrQLU7JLWd8BNfMHi9pf0nbmtmLxz60jZpXU85mZs+T9I+SNpb0zymlv5vycWs/fqyk+yW9NqV0YcSvjfLVcpZpodEtFj39aBeLnj50i0VPP9rFomd3tTSb7RLlx0k6TtJ2kl4w9v77JP1J7i9sZhtL+oikoyUtl3S+mZ2ZUrpi7NOOkbRv+9/TJH20/T8eoXjxgFgln53rE3MYg6sJ8jGL+ZjDfMxhDGYxH7OYp5ZmljbwOzGzw1JKPwr/hc0Ok/TulNJ/aX/8F5KUUnr/2Od8TNIopfT59sc/lzSRUrp1tq+99dZbp6c85SnRhxxmxYoV2m677fo+jCLdcIN0443N23vtJe25Z59HU6a775YuuaR5e7vtpIMO6vd4SpSSdN55kz8+8sj+jqVk//Ef0r33Nm8ffLC07bb9Hk+Jrr9euvnm5u2995b22KPf4ynRXXdJl17avL399tKBB/Z7PCVau1b63veatzfaSHrmM/s9nlJdeKF0333N24ccIm3Nv1nS2XXXScuXN2/vs4+0++79Hk9pVq+Wfvzj5u1Fi9bq8MPn8mzWfpx77rk/Syktne5js12i/I6U0gckvdLMXjH14ymlt2Qe126Sbh778XL99qOz033ObpJ+a8E1sxMlnShJixYt0ooVKzIPb/48/PDDgz6+IXvggc217gr5Vase0IoVD/R7QAVauXITSVtJktasWaMVK1b2e0AFas4LTp6k4vbss2bNVlr3bWjlypVKaU2/B1Sg1au5T8y1cuUiSVtK4j7Ra+1ak9ScoUopacWKe/o9oEKtWbO1mmftSffdd58efvjhfg+oQKtXL5a0mSRp1apVWrFidb8HVJgHH9xIzbNRm7/rlPr3m9kuUb6y/f8F8/RrT3fxxdSHk+fyOc07UzpV0qmStHTp0nTBBfN12PlGo5EmJib6PowinXSS9J73NG+/4Q3Su9/d6+EU6dvflo4+unn70EOl73yn3+Mp0Zo10qJFzdsbbSRddFG/x1Oqww6bPFN82mnS4Yf3ezwl+su/lN7fXvf05jdL73pXv8dTomXLpOc/v3n7iCOks87q93hKtGqVtMUWzdubbsp9otfSpdLPfta8ffrp0lOf2u/xlOhtb5M+2P4Dp299q/T2t/d7PKW58cbmCklJ2mGHB3TRRSEvuzQvbJbr+GdccFNKX2//f9o8HJPUPBo7fuHAYyTd4vgcPILwnJR8PMcnH93i0dSHbrHo6UO3eDT1oVucklvOdony1zXDo6WSlFJ6Yeavfb6kfdt/U/eXkk6Q9Mopn3OmpDeb2RfUXL58z4aef4tHjlqeCI+yMYd+tItFTx+6xaKnH+1i0bO7WprNdonyP8znL5xSWmNmb5Z0jponHHwypXS5mb2h/fgpkpap+SeCrlXzzwS9bj6PCcPHq+Pl4xHcfMxhDGYxH7OYjznMxxzGYBbzMYt5amk22yXK565728w2lfR4NY/o/jyl9GDEL55SWqZmiR1/3yljbydJb4r4tVAH7vDz8Q00H93i0dSHbrHo6UO3eDT1oVscs3K33dkewZUkmdnzJZ0i6To1L/q0t5m9PqXEyzCgV7WcZQIeqbgNx6KnD91i0dOPdrHo2V0tzTa44Er6oKSjUkrXSpKZPVbSNyWx4GLBcWYuH4/g5qNbPJr60C0WPX3oFo+mPnSLU3LLufzrvbetW25b10u6bZ6OB5gVz63Ix4Ibj1n0YRbzcZ+YjznMxxzGYBbzMYt5amk2l0dwLzezZZLOUPMc3JdJOt/MXixJKaV/ncfjA2ZUy40Q5UuJv4x4cBuORU8fusWipx/tYtGzu1pOssxlwd1c0q8lHdn++HZJO0h6gZqFlwUXC6bkG9tQ1HLn1TczvnlGYhZ96BaLnj50i0dTH7pBmsOCm1Lin+bBILFc+NAtHk196BaLnj50i0VPP9rFomd3tTSby6so7y3pzyTtNf75KaUXzt9hAdPjuRWxONPpN/4ILrPow9UE+bhPzMcc5mMOYzCL+ZjFPOvPYLkB53KJ8lclfULS1yWtnd/DAWbHHX4+voHGoF0sevrQLRY9fegWj6Y+dItTcsu5LLgPpJQ+PO9HAnTEmTkMBbPoQ7dY9PShG4aCWYxFz+5qaTaXBfcfzewkSd+StHrdO1NKF87bUQEz4NKTfDyCG4NZzMcs5mMO8zGH+aZ245XlfZjFfNwn5qllBuey4D5J0qslPVuTlyin9sfAgir5xjYUtdx59Y12sejpQ7dY9MRQMIs+dIM0twX3RZL2SSk9ON8HA3TBmTkMBbPoQ7dY9PShWzwewfVhFmPRs7tamm00h8+5WNJ2830gwFzwDTMfj+DGoF0sevrQLRY9/WgXi54+dItT+6soL5F0lZmdr8nn4KaU0vHzd1jA9HhuRT4W3BjMYj5mMR9zmI85jME/nZaPWczHfWKeWprNZcE9aextk/QMSa+Yn8MB5q6WGyHKxyz60C0WPX3oFo+mPnSLRc/uajnJssFLlFNK50q6R9LzJX1a0nMknTK/hwVMr+Qb21DUcufVN9rFoqcP3WLR0492sejpQzdIszyCa2b7STpBzaO1d0r6oiRLKR21QMcGzIozcz50i0dTH7rFoqcP3eLR1IdusejZXS3NZrtE+SpJ35P0gpTStZJkZm9dkKMCZsBzK2JxptOPWczH1QT5mMN8zGEMZjEfs5iPOcxTywzOdonySyT9StK/m9nHzew5ap6DC/Sm5BvbUNRy59U32sWipw/dYtHTj3ax6OlDtzglv4ryjAtuSukrKaXfl/R4SSNJb5W0xMw+ama/u0DHB8yIM3M+dItHUx+6xaKnD93i0dSHbrHo2V0tzebyIlO/SSmdnlI6TtJjJF0k6Z3zfmTANLj0JBZnOv2YxXxcTZCPOczHHMZgFvMxi/mYwzy1zOAGF9xxKaW7UkofSyk9e74OCJhNyTe2oajlzqtvtItFTx+6xaKnH+1i0dOHbpA6LrjAkHBmDkPBLPrQLRY9fegWj6Y+dItFz+5qacaCi6JwZi4fj+DGoF0sevrQLRY9/WgXi54+dItTcksWXBSF51bkY8GNwSzmYxbzMYf5mMMYzGI+ZjEfc5inlmYsuChWLTdClI9Z9KFbLHr60C0eTX3oFoue3a1/kqXcgCy4KApnNPNxhjgG7WLR04dusejpR7tY9PShW5ySW7LgolicmfOhWzya+tAtFj196BaPpj50i0XP7mppxoKLovDcilgln53rG7OYj6sJ8jGH+ZjDGMxiPmYxH3OYp5ZmLLgoCnf4+fgGGoN2sejpQ7dY9PSjXSx6+tAtTsktWXBRrFrOMi00usWjqQ/dYtHTh27xaOpDt1j07K6WZiy4KAqXnsQq+exc35jFfFxNkI85zMccxmAW8zGL+ZjDPLyKMtAD7vDz8Q00Bu1i0dOHbrHo6Ue7WPT0oVuckluy4KJYnJnDUDCLPnSLRU8fusWjqQ/dYtGzu1qaseCiKFx6ko9HcGMwi/mYxXzMYT7mMAazmI9ZzMccQmLBRWG4w8/HN9AYtItFTx+6xaKnH+1i0dOHbnlq+TsiCy6KxZk5DAWz6EO3WPT0oVs8mvrQLRY9u6ulGQsuilLy2aShqOXsXN9oF4uePnSLRU8/2sWipw/d4vAqykAPajnLtNDoFo+mPnSLRU8fusWjqQ/dYtGzu1qaseCiKLx4QCzOdPoxi/m4miAfc5iPOYzBLOZjFvMxh3lqmUEWXBSl5BvbUNRy59U32sWipw/dYtHTj3ax6OlDN0gsuCgYZ+Z86BaPpj50i0VPH7rFo6kP3WLRs7tamrHgoihcehKLM51+zGI+ribIxxzmYw5jMIv5mMV8zGGeWmaQBRdFKfnGNhS13Hn1jXax6OlDt1j09KNdLHr60C0Or6IM9IAzcz50i0dTH7rFoqcP3eLR1IdusejZXS3NWHBRFC49icWZTj9mMR9XE+RjDvMxhzGYxXzMYj7mME8tM8iCi6KUfGMbilruvPpGu1j09KFbLHr60S4WPX3oBokFFwXjzByGgln0oVssevrQLR5NfegWi57d1dKMBRdF4cxcPh7BjUG7WPT0oVssevrRLhY9fegWp+SWLLgoVi1nmRYa3eLR1IdusejpQ7d4NPWhWyx6dldLMxZcFIUXD4hV8tm5vjGL+biaIB9zmI85jMEs5mMW8zGHedafwXIDsuCiKNzh5+MbaAzaxaKnD91i0dOPdrHo6UO3OCW3ZMFFsTgz50O3eDT1oVssevrQLR5NfegWi57d1dKMBRdF4dKTWCWfnesbs5iPqwnyMYf5mMMYzGI+ZjEfc5inlmYsuCgKd/j5+AYag3ax6OlDt1j09KNdLHr60C1OyS1ZcFGsWs4yLTS6xaOpD91i0dOHbvFo6kO3WPTsrpZmLLgoCpeexCr57FzfmMV8XE2QjznMxxzGYBbzMYv5mMM8vIoy0APu8PPxDTQG7WLR04dusejpR7tY9PShW5ySW7LgolicmfOhWzya+tAtFj196BaPpj50i0XP7mppxoKLopR8NmmI6OlHu1j09KFbLHr60S4WPX3oBokFFwWr5SzTQqNbPJr60C0WPX3oFo+mPnSLRc/uamnGgoui8OIBsTjT6ccs5uP54PmYw3zMYQxmMR+zmI85zFPLDLLgoigl39iGopY7r77RLhY9fegWi55+tItFTx+6xeFVlIEecGbOh27xaOpDt1j09KFbPJr60C0WPburpRkLLorCpSexONPpxyzm42qCfMxhPuYwBrOYj1nMxxzmqWUGWXBRlJJvbENRy51X32gXi54+dItFTz/axaKnD90gseCiYJyZ86FbPJr60C0WPX3oFo+mPnSLRc/uamnGgouicOlJLM50+jGL+biaIB9zmI85jMEs5mMW8zGHeWqZQRZcFKXkG9tQ1HLn1TfaxaKnD91i0dOPdrHo6UO3OLyKMtADzsz50C0eTX3oFouePnSLR1MfusWiZ3e1NGPBRVE4MxeLnn60i0VPH7rFoqcf7WLR04ducUpuyYKLYtVylmmh0S0eTX3oFouePnSLR1MfusWiZ3e1NNukj1/UzHaQ9EVJe0m6QdLLU0p3T/N5N0i6T9LDktaklJYu3FFiiHjxgFgln53rG7OYj+eD52MO8zGHMZjFfMxiPuYwTy3N+noE952SvpNS2lfSd9ofz+SolNLBLLeQuMOPwDfQGLSLRU8fusWipx/tYtHTh25xSm7Z14J7vKTT2rdPk/R7PR0HClbLWaaFRrd4NPWhWyx6+tAtHk196BaLnt3V0qyvBXdJSulWSWr/v/MMn5ckfcvMfmZmJy7Y0WGwuPQkVsln5/rGLObjaoJ8zGE+5jAGs5iPWczHHOZZfwbLDThvz8E1s29L2mWaD72rw5c5IqV0i5ntLOnfzOyqlNJ5M/x6J0o6UZKWLFmi0WjU9ZAXzMqVKwd9fEN22WU7SnqSJOnOO+/QaHRZvwdUoOuu20PSPpKkm2++SaPR9f0eUKF+85ulkraSJF1wwQVasWJlvwdUoJSepXXnWc8771wtWlTuN9O+XH75TpIOkCTdccftGo0u7/eACvSLX+wpaW9J0k033aDR6IZej6dU99//VElbSpJ++tOf6vbb7+/3gIo08Z9vnXvuiCXX4cord5b0REnSbbfdptHoin4PqDCXXTb5PeXhh9cUu6/M24KbUnruTB8zs1+b2aNTSrea2aMl3TbD17il/f9tZvYVSYdKmnbBTSmdKulUSVq6dGmamJjI/B3Mn9FopCEf35Ddd9/k2zvssBMdHX70o8m399hjD01M7NHfwRRsq60m337KU5bqyU/u71hqcOSRR2rTTfs+ivLcddfk2zvu+CjuEx3OG/tbxZ577qWJib16O5aSbbnl5NtPfeqhOuCA/o6lBhMTEyy4Dr/61eTbj3rUzpqYmOkiUUznzjsn395kk02K/Z7S1yXKZ0p6Tfv2ayR9beonmNmWZrb1urcl/a4kHq57hOPSk1h88/RjFvNxOV4+5jAfcxiDWcwztRmz6MMc5qmlWV8L7t9JOtrMrpF0dPtjmdmuZras/Zwlkr5vZhdL+qmkb6aUzu7laDEY3OHn4y9zMWgXi54+dItFTz/aYQiYwzglt+zl38FNKd0p6TnTvP8WSce2b18v6aAFPjQUpJazTAuNbvFo6kO3WPT0oVs8mnZHs3g07a6WZn09ggu4lHw2aYjo6Ue7WPT0oVssevrRLg4t/WgXp+RXUWbBRVF4bkU+LlGOwSzmYxbzMYf5mMMYzGIe5jAGc5inlmYsuChWLTfChUa3eDT1oVssevrQLR5Nu6NZPJp2V0szFlwUhbOasejpR7tY9PShWyx6+tEuDi39aBen5JYsuChWLWeZFhrd4tEUQ8Ac+tAtHk27o1k8mnZXSzMWXBSF51bEKvnsXN+YxTz8m48xmMN8PPcxBrOYhzmMwRzmqWUOWXBRlJJvbENRy51X32iHIWAOY9HTj3ZxaOlHuzi8ijLQA87M+dAtHk27o1k8mvrQLR5Nu6NZPJp2V0szFlwUhUtPYnGm049ZzLP+lQQE9GIO83FVSwxmMQ9zGIM5zFNLMxZcFIU7/Xx8E41Buzi09KNdLHr60S4OLf1oF6fkliy4KFYtZ5kWGt3i0bQ7msWjqQ/d4tG0O5rFo2l3tTRjwUVRSj6bNET09KMdhoA5jEVPP9rFoaUf7eKU3JIFF0XhuRX5uEQ5BrOYh+fgxmAO83GfGINZzMMcxmAO89TyvZkFF8XijsuHbvFowfAtcgAAE/BJREFU2h3N4tHUh27xaNodzeLRtLtamrHgoiic1YxFTz/axaGlH+1i0dOPdnFo6Uc7SCy4KFgtZ5kWGt3i0bQ7msWjqQ/d4tG0O5rFo2l3tTRjwUVReG5FLM50+jGLeXi+WQzmMB+zGINZzMMcxmAO89Qyhyy4KErJN7ahqOXOq2+0wxAwh7Ho6Ue7OLT0o12ckluy4KJYnJnzoVs8mnZHs3g09aFbPJp2R7N4NO2ulmYsuCgKl57EKvnsXN+YxTy1/FMEfWMO83FVSwxmMQ9zGIM5zFPL92YWXBSFO/18fBONQbs4tPSjXSx6+tEuDi39aAeJBRcF48ycD93i0bQ7msWjqQ/d4tG0O5rFo2l3tTRjwUVRODMXi55+tItDSz/axaKnH+3i0NKPdnFKbsmCi6Lw3Ip8XKIcg1nMQ7MYzGE+7hNjMIt5mMMYzGGeWuaQBRfF4o7Lh27xaNodzeLR1Idu8WjaHc3i0bS7Wpqx4KIoJZ9NGiJ6+tEuTsmv1Ng35jAWPf1oF4eWfrSLU/L3ZhZcFKuWs0wLjW7xaNodzeLR1Idu8WjaHc3i0bS7Wpqx4KIoPLciXy3Pr+gbs5iHOYzBHOZjFmMwi3mYwxjMYZ5amrHgoijc6ceipx/t4tDSj3ax6OlHuzi09KNdnJJbsuCiWLWcZVpodItH0+5oFo+mPnSLR9PuaBaPpt3V0owFF0Xh0pNYJZ+d6xuzmIdmMZjDfFwaGoNZzMMcxmAO89Qyhyy4KErJN7ahqOXOq2+0i1PyKzX2jTmMRU8/2sWhpR/t4pT8vZkFF8XizJwP3eLRtDuaxaOpD93i0bQ7msWjaXe1NGPBRVG49CQWZzr9mMU8XEkQgznMxyzGYBbzMIcxmMM8tTRjwUVRuNPPxzfRGLSLQ0s/2sWipx/t4tDSj3ZxSm7Jgoti1XKWaaHRLR5Nu6NZPJr60C0eTbujWTyadldLMxZcFKXks0lDRE8/2mEImMNY9PSjXRxa+tEuTsktWXBRrFrOMi00usWjaXc0i0dTH7rFo2l3NItH0+5qacaCi6Lw4gH5eA5uDGYxz/pzSEAv5jAf94kxmMU8zGEM5jBPLd+bWXBRFO70Y9HTj3ZxaOlHu1j09KNdHFr60Q4SCy4Kxpk5H7rFo2l3NItHUx+6xaNpdzSLR9PuamnGgouicOlJPi6DisEs5mEOYzCH+ZjFGMxiHuYwBnOYp5Y5ZMFFUUq+sQ0RPf1ohyFgDmPR0492cWjpR7s4JbdkwUWxODPnQ7d4NO2OZvFo6kO3eDTtjmbxaNpdLc1YcFEULj2JVfLZub4xi3lqeaXGvjGH+Wq5JK9vzGIe5jAGc5inlu/NLLgoCnf6+fgmGoN2cWjpR7tY9PSjXRxa+tEOEgsuCsaZOR+6xaNpdzSLR1MfusWjaXc0i0fT7mppxoKLonBmLhY9/WgXh5Z+tItFTz/axaGlH+3ilNySBRfFquUs00KjWzyadkezeDT1oVs8mnZHs3g07a6WZiy4KAovHpCP5+DGYBbz0CwGc5iP+8QYzGIe5jAGc5inljlkwUVRSr6xDRE9/WgXp+RXauwbcxiLnn60i0NLP9rFKfl7MwsuisWZOR+6xaNpdzSLR1MfusWjaXc0i0fT7mppxoKLonDpSb5aLj/pG7OYhzmMwRzmYxZjMIt5mMMYzGGeWpqx4KIo3OnHoqcf7eLQ0o92sejpR7s4tPSjXZySW7Lgoli1nGVaaHSLR9PuaBaPpj50i0fT7mgWj6bd1dKMBRdF4dKTWCWfnesbs5iHZjGYw3xcGhqDWczDHMZgDvPUMocsuChKyTe2oajlzqtvtItT8is19o05jEVPP9rFoaUf7eKU/L2ZBRfF4sycD93i0bQ7msWjqQ/d4tG0O5rFo2l3tTRjwUVRODMXi55+tItDSz/axaKnH+3i0NKPdpBYcFGwWs4yLTS6xaNpdzSLR1MfusWjaXc0i0fT7mppxoKLovDiAfl4Dm4MZjEPcxiDOczHLMZgFvMwhzGYwzy1zCELLopS8o1tiOjpRzsMAXMYi55+tItDSz/axSm5JQsuisWZOR+6xaNpdzSLR1MfusWjaXc0i0fT7mppxoKLonDpSb5aLj/pG7OYZ/05JKAXc5iP+8QYzGIe5jAGc5inlu/NLLgoCnf6sejpR7s4tPSjXSx6+tEuDi39aAeJBRcF48ycD93i0bQ7msWjqQ/d4tG0O5rFo2l3tTRjwUVRuPQkH5dBxWAW8zCHMZjDfMxiDGYxD3MYgznMU8scsuCiKCXf2IaInn60wxAwh7Ho6Ue7OLT0o12ckluy4KJYnJnzoVs8mnZHs3g09aFbPJp2R7N4NO2ulmYsuChKyWeThoiefrSLU/IrNfaNOYxFTz/axaGlH+3ilPy9mQUXReG5FflqeX5F35jFPMxhDOYwH7MYg1nMwxzGYA7z1NKMBRfFquVGuNDoFo+m3dEsHk196BaPpt3RLB5Nu6ulGQsuisJZzVj09KMdhoA5jEVPP9rFoaUf7eKU3LKXBdfMXmZml5vZWjNbOsvnPc/Mfm5m15rZOxfyGDF8tZxlWmh0i0fT7mgWj6Y+dItH0+5oFo+m3dXSbJOeft3LJL1Y0sdm+gQz21jSRyQdLWm5pPPN7MyU0hULc4gYovGzSatXS9/7Xn/HUqrbb598u+Szc30bb/fznzOLXV1//eTbzKHfeLtVq5hDjzvumHybWfQbb3fVVcxiV1dfPfk2c+g33u7++5nDrm66afLtkuewlwU3pXSlJNns5Q6VdG1K6fr2c78g6XhJLLiPYOMjc+ed0rOe1d+x1KDkO6++jbf7wAea/+BT8is19m18Dm+7jfvEXNwn+o23+9u/bf6DD3PoN97ul7/kPjFHyd+b+3oEdy52k3Tz2I+XS3raTJ9sZidKOlGSlixZotFoNK8Hl2PlypWDPr4he+CBjbR48eFatWrIo1uO22+/UKPRvX0fRpEefngvSXv1fBR12GGH+zUaXdD3YRTp/vs31mabHa7Vqzfu+1Cq8OtfX6DRaGXfh1GktWv3lrRn34dRhcWL79BodFnfh1GklSs30aJFh+uhh3iZoVzbbHNPsfvKvG0JZvZtSbtM86F3pZS+NpcvMc37ZjyVkFI6VdKpkrR06dI0MTExl8PsxWg00pCPb+g++1nplFOkBx7o+0jKZSbtt9/1euMbD+FMsdP++0ubbSZdwTUlWXbZRTrmmBu5T8zwmc9Ip57aPG0DPmbSE594nU48cSn3iU5PeIK0eHFzeTL8NtnkNp188s7af/+Jvg+lWKedJn3iE9wn5nj606XnPve+Yr83z9uCm1J6buaXWC5p97EfP0bSLZlfExV4yUua/5BnNLpJZvv0fRjFetSjpI/N+CoC6GI0+k3fh1C0l7+8+Q95RqObZfbYvg+jWEuWSB//eN9HUb7R6Artv//OfR9G0V7xiuY/5BmN1vZ9CG5Dfvz+fEn7mtneZrappBMkndnzMQEAAAAABqqvfyboRWa2XNJhkr5pZue079/VzJZJUkppjaQ3SzpH0pWSzkgpXd7H8QIAAAAAhq+vV1H+iqSvTPP+WyQdO/bjZZKWLeChAQAAAAAKNeRLlAEAAAAAmDMWXAAAAABAFVhwAQAAAABVYMEFAAAAAFSBBRcAAAAAUAUWXAAAAABAFVhwAQAAAABVYMEFAAAAAFSBBRcAAAAAUAUWXAAAAABAFVhwAQAAAABVYMEFAAAAAFSBBRcAAAAAUAUWXAAAAABAFVhwAQAAAABVYMEFAAAAAFSBBRcAAAAAUAUWXAAAAABAFVhwAQAAAABVYMEFAAAAAFSBBRcAAAAAUAUWXAAAAABAFVhwAQAAAABVYMEFAAAAAFSBBRcAAAAAUAUWXAAAAABAFVhwAQAAAABVYMEFAAAAAFSBBRcAAAAAUAUWXAAAAABAFVhwAQAAAABVYMEFAAAAAFSBBRcAAAAAUAUWXOD/b+/+Q6696zqAv9+6ipniwpGWZhOxHyabrDmzjDTD3P5oLFqYkiGJiCX1R2TQr5X/FBlE1LSQIQXpH+n8gebcAp1mY86Ye1xrMWboWGArM6bR2vbpj/ssHp+e+ZynPefHfd2vF9xwznV97+t8Dnw4h/e5vtf3AgAAFkHABQAAYBEEXAAAABZBwAUAAGARBFwAAAAWQcAFAABgEQRcAAAAFkHABQAAYBEEXAAAABZBwAUAAGARBFwAAAAWQcAFAABgEQRcAAAAFkHABQAAYBEEXAAAABZBwAUAAGARBFwAAAAWQcAFAABgEQRcAAAAFkHABQAAYBEEXAAAABZBwAUAAGARBFwAAAAWQcAFAABgEQRcAAAAFkHABQAAYBEEXAAAABZBwAUAAGARBFwAAAAWQcAFAABgEQRcAAAAFkHABQAAYBEEXAAAABZBwAUAAGARBFwAAAAWQcAFAABgEQRcAAAAFkHABQAAYBEEXAAAABZhJwG37RVtb2v7UNuLvsa4f2p7rO0tbW/eZo0AAAAcLmft6HU/k+THk/zJGmNfPDP3brgeAAAADrmdBNyZuT1J2u7i5QEAAFigfb8Gd5J8uO2n2r5218UAAACwvzZ2Brft9UmecpJdvzoz713zMD8wM/e0/eYk17X9h5m54RFe77VJHg7B97W94/Sr3ppzk5h2za7pQ/aFXmQf6EP2gT5kX+x7L377I+3ozGyzkK9+8fYjSX5pZk65gFTbK5PcNzNv3nRdm9b25pl5xMW1YBv0IftCL7IP9CH7QB+yLw5zL+7tFOW239j2CQ8/TvLSHCxOBQAAAP/Hrm4TdHnbu5O8IMkH2l672v6tbT+4GvbkJB9v++kkNyX5wMx8aBf1AgAAsP92tYryNUmuOcn2e5Jcunp8V5ILtlzatvzprguA6EP2h15kH+hD9oE+ZF8c2l7c6TW4AAAAcKbs7TW4AAAAcDoE3A1q+7K2d7S9s+2vnGR/2/7hav+tbS/cRZ0s2xp9+MpV/93a9hNtl3ppADt0qj48btzz2j7Y9ie2WR9Hxzq92PZFbW9pe1vbj267RpZvje/mJ7Z9f9tPr/rw1buok2Vre3XbL7Q96UK+hzWrCLgb0vaxSf44ySVJnp3kp9o++4RhlyR51urvtUnestUiWbw1+/CzSX5oZs5P8qYc4msu2E9r9uHD4343ybXbrZCjYp1ebHtOkquS/NjMfE+SK7ZeKIu25mfizyX5+5m5IMmLkvx+26/faqEcBW9P8rKvsf9QZhUBd3MuTnLnzNw1M/cneWeSy04Yc1mSP5sDNyY5p+23bLtQFu2UfTgzn5iZL66e3pjkaVuukeVb5/MwSd6Q5F1JvrDN4jhS1unFVyR598x8LklmRj9ypq3Th5PkCW2b5PFJ/i3JA9stk6WbmRty0FuP5FBmFQF3c56a5PPHPb97te10x8Cjcbo99rNJ/mqjFXEUnbIP2z41yeVJ3rrFujh61vlM/I4k39T2I20/1fZVW6uOo2KdPvyjJN+d5J4kx5L8wsw8tJ3y4H8dyqyyk9sEHRE9ybYTl6xeZww8Gmv3WNsX5yDgvnCjFXEUrdOHf5DkjTPz4MEJC9iIdXrxrCTfm+QlSc5O8rdtb5yZf9x0cRwZ6/Thjya5JckPJ3lmkuvafmxm/mPTxcFxDmVWEXA35+4k33bc86fl4Fe40x0Dj8ZaPdb2/CRvS3LJzPzrlmrj6FinDy9K8s5VuD03yaVtH5iZ92ynRI6Idb+b752ZLyf5ctsbklyQRMDlTFmnD1+d5Hfm4H6ed7b9bJLvSnLTdkqEJIc0q5iivDmfTPKsts9YLQrw8iTvO2HM+5K8arVC2fcl+dLM/PO2C2XRTtmHbZ+e5N1JftoZCjbklH04M8+YmfNm5rwkf5nk9cItG7DOd/N7k/xg27PaPi7J85PcvuU6WbZ1+vBzOZhFkLZPTvKdSe7aapVwSLOKM7gbMjMPtP35HKwG+tgkV8/MbW1ft9r/1iQfTHJpkjuTfCUHv9bBGbNmH/5GkicluWp19uyBmbloVzWzPGv2IWzcOr04M7e3/VCSW5M8lORtM3PSW2jA/8ean4lvSvL2tsdyME30jTNz786KZpHaviMHq3Sf2/buJL+Z5OuSw51VejDzAQAAAA43U5QBAABYBAEXAACARRBwAQAAWAQBFwAAgEUQcAEAAFgEtwkCgB1q+6Qkf716+pQkDyb5l9Xzi2fm/p0UBgCHkNsEAcCeaHtlkvtm5s27rgUADiNTlAFgT7X9mbY3tb2l7VVtH9P2rLb/3vb32v5d22vbPr/tR9ve1fbS1f++pu01q/13tP214477y20/s/p7w+7eIQCcWQIuAOyhts9JcnmS75+Z5+bgsqKXr3Y/McmHZ+bCJPcnuTLJS5JckeS3jzvMxav/uTDJK9o+t+3FSV652veCJK9ve/7m3xEAbJ5rcAFgP/1Ikuclubltkpyd5POrff85M9etHh9L8qWZeaDtsSTnHXeMa2fmi0nS9j1JXpjkG5K8a2a+csL2Wzf7dgBg8wRcANhPTXL1zPz6V21sz8rBWduHPZTkv457fPx3+4kLbczquACwSKYoA8B+uj7JT7Y9NzlYbbnt00/zGC9te07bxyW5LMnfJLkhyeVtz277+NX2j53JwgFgV5zBBYA9NDPH2v5WkuvbPibJfyd5XZJ7TuMwH0/yF0memeTPZ+aWJGn7jiSfXI15y8wcO3OVA8DuuE0QACxQ29ckec7M/OKuawGAbTFFGQAAgEVwBhcAAIBFcAYXAACARRBwAQAAWAQBFwAAgEUQcAEAAFgEARcAAIBFEHABAABYhP8BBGY5XYkI550AAAAASUVORK5CYII=\n",
 88 |       "text/plain": [
 89 |        "<Figure size 1152x648 with 1 Axes>"
 90 |       ]
 91 |      },
 92 |      "metadata": {
 93 |       "needs_background": "light"
 94 |      },
 95 |      "output_type": "display_data"
 96 |     }
 97 |    ],
 98 |    "source": [
 99 |     "plt.figure(figsize=(16,9))\n",
100 |     "plt.plot(t, s, linewidth=3, color='blue')\n",
101 |     "plt.title('Onda Quadrada - 5Hz amostrado em 1000Hz/segundo')\n",
102 |     "plt.xlabel('Tempo')\n",
103 |     "plt.ylabel('Amplitude')\n",
104 |     "plt.grid(True, which='both')\n",
105 |     "plt.axhline(y=0, color='k')\n",
106 |     "plt.ylim(-1.5, 1.5)\n",
107 |     "plt.show()"
108 |    ]
109 |   }
110 |  ],
111 |  "metadata": {
112 |   "kernelspec": {
113 |    "display_name": "Python 3",
114 |    "language": "python",
115 |    "name": "python3"
116 |   },
117 |   "language_info": {
118 |    "codemirror_mode": {
119 |     "name": "ipython",
120 |     "version": 3
121 |    },
122 |    "file_extension": ".py",
123 |    "mimetype": "text/x-python",
124 |    "name": "python",
125 |    "nbconvert_exporter": "python",
126 |    "pygments_lexer": "ipython3",
127 |    "version": "3.7.10"
128 |   }
129 |  },
130 |  "nbformat": 4,
131 |  "nbformat_minor": 4
132 | }
133 | 


--------------------------------------------------------------------------------
/jupyter_notebooks/perm_comb.ipynb:
--------------------------------------------------------------------------------
  1 | {
  2 |  "cells": [
  3 |   {
  4 |    "cell_type": "markdown",
  5 |    "metadata": {},
  6 |    "source": [
  7 |     "# Itertools\n",
  8 |     "\n",
  9 |     "O módulo [itertools](https://docs.python.org/3/library/itertools.html) implementa um número de blocos de construção de **iterador** inspirado em constructos das linguagens APL, Haskell e SML.\n",
 10 |     "\n",
 11 |     "O módulo padroniza um conjunto de ferramentas rápidas, com eficiência de memória, que são muito úteis por elas mesmas ou em combinação com outras. Juntas elas formam a \"álgebra iteradora\", tornando possível a construção de ferramentas especializadas em Python puro, de forma sucinta e eficiente."
 12 |    ]
 13 |   },
 14 |   {
 15 |    "cell_type": "markdown",
 16 |    "metadata": {},
 17 |    "source": [
 18 |     "### Exemplos\n",
 19 |     "\n",
 20 |     "Primeiramente é necessário importarmos a biblioteca:"
 21 |    ]
 22 |   },
 23 |   {
 24 |    "cell_type": "code",
 25 |    "execution_count": 1,
 26 |    "metadata": {},
 27 |    "outputs": [],
 28 |    "source": [
 29 |     "import itertools"
 30 |    ]
 31 |   },
 32 |   {
 33 |    "cell_type": "markdown",
 34 |    "metadata": {},
 35 |    "source": [
 36 |     "O método **dir** nos permite inspecionar o que há disponível na biblioteca:"
 37 |    ]
 38 |   },
 39 |   {
 40 |    "cell_type": "code",
 41 |    "execution_count": 2,
 42 |    "metadata": {},
 43 |    "outputs": [
 44 |     {
 45 |      "name": "stdout",
 46 |      "output_type": "stream",
 47 |      "text": [
 48 |       "['__doc__', '__loader__', '__name__', '__package__', '__spec__', '_grouper', '_tee', '_tee_dataobject', 'accumulate', 'chain', 'combinations', 'combinations_with_replacement', 'compress', 'count', 'cycle', 'dropwhile', 'filterfalse', 'groupby', 'islice', 'permutations', 'product', 'repeat', 'starmap', 'takewhile', 'tee', 'zip_longest']\n"
 49 |      ]
 50 |     }
 51 |    ],
 52 |    "source": [
 53 |     "print(dir(itertools))"
 54 |    ]
 55 |   },
 56 |   {
 57 |    "cell_type": "markdown",
 58 |    "metadata": {},
 59 |    "source": [
 60 |     "#### Criando um Contador Simples"
 61 |    ]
 62 |   },
 63 |   {
 64 |    "cell_type": "code",
 65 |    "execution_count": 3,
 66 |    "metadata": {},
 67 |    "outputs": [
 68 |     {
 69 |      "name": "stdout",
 70 |      "output_type": "stream",
 71 |      "text": [
 72 |       "0\n",
 73 |       "1\n",
 74 |       "2\n",
 75 |       "3\n"
 76 |      ]
 77 |     }
 78 |    ],
 79 |    "source": [
 80 |     "contador = itertools.count()\n",
 81 |     "\n",
 82 |     "print(next(contador))\n",
 83 |     "print(next(contador))\n",
 84 |     "print(next(contador))\n",
 85 |     "print(next(contador))"
 86 |    ]
 87 |   },
 88 |   {
 89 |    "cell_type": "markdown",
 90 |    "metadata": {},
 91 |    "source": [
 92 |     "#### Alterando o Comportamento do Contador\n",
 93 |     "\n",
 94 |     "Definimos o início da contagem para 8 e os passos de cada iteração para 8:"
 95 |    ]
 96 |   },
 97 |   {
 98 |    "cell_type": "code",
 99 |    "execution_count": 4,
100 |    "metadata": {},
101 |    "outputs": [
102 |     {
103 |      "name": "stdout",
104 |      "output_type": "stream",
105 |      "text": [
106 |       "8\n",
107 |       "16\n",
108 |       "24\n",
109 |       "32\n"
110 |      ]
111 |     }
112 |    ],
113 |    "source": [
114 |     "contador = itertools.count(start=8, step=8)\n",
115 |     "\n",
116 |     "print(next(contador))\n",
117 |     "print(next(contador))\n",
118 |     "print(next(contador))\n",
119 |     "print(next(contador))"
120 |    ]
121 |   },
122 |   {
123 |    "cell_type": "markdown",
124 |    "metadata": {},
125 |    "source": [
126 |     "Observe que também podemos trabalhar com números negativos:"
127 |    ]
128 |   },
129 |   {
130 |    "cell_type": "code",
131 |    "execution_count": 5,
132 |    "metadata": {},
133 |    "outputs": [
134 |     {
135 |      "name": "stdout",
136 |      "output_type": "stream",
137 |      "text": [
138 |       "0\n",
139 |       "-3\n",
140 |       "-6\n",
141 |       "-9\n"
142 |      ]
143 |     }
144 |    ],
145 |    "source": [
146 |     "contador = itertools.count(start=0, step=-3) \n",
147 |     "\n",
148 |     "print(next(contador))\n",
149 |     "print(next(contador))\n",
150 |     "print(next(contador))\n",
151 |     "print(next(contador))"
152 |    ]
153 |   },
154 |   {
155 |    "cell_type": "markdown",
156 |    "metadata": {},
157 |    "source": [
158 |     "#### Também Podemos Criar Ciclos"
159 |    ]
160 |   },
161 |   {
162 |    "cell_type": "code",
163 |    "execution_count": 6,
164 |    "metadata": {},
165 |    "outputs": [
166 |     {
167 |      "name": "stdout",
168 |      "output_type": "stream",
169 |      "text": [
170 |       "0\n",
171 |       "1\n",
172 |       "0\n",
173 |       "1\n"
174 |      ]
175 |     }
176 |    ],
177 |    "source": [
178 |     "contador = itertools.cycle([0,1])\n",
179 |     "\n",
180 |     "print(next(contador))\n",
181 |     "print(next(contador))\n",
182 |     "print(next(contador))\n",
183 |     "print(next(contador))"
184 |    ]
185 |   },
186 |   {
187 |    "cell_type": "markdown",
188 |    "metadata": {},
189 |    "source": [
190 |     "#### Starmap\n",
191 |     "\n",
192 |     "A função **starmap** recebe uma função e uma lista de tuplas como argumento e nos retorna os cálculos mapeados (nesse caso estamos elevando 1, 5 e 100 ao cubo), observe também que estamos transformando o **iterador cubos** em uma lista antes de imprimirmos:"
193 |    ]
194 |   },
195 |   {
196 |    "cell_type": "code",
197 |    "execution_count": 7,
198 |    "metadata": {},
199 |    "outputs": [
200 |     {
201 |      "name": "stdout",
202 |      "output_type": "stream",
203 |      "text": [
204 |       "<class 'itertools.starmap'>\n",
205 |       "[1, 125, 1000000]\n"
206 |      ]
207 |     }
208 |    ],
209 |    "source": [
210 |     "cubos = itertools.starmap(pow, [(1,3),(5,3),(100,3)])\n",
211 |     "print(type(cubos))\n",
212 |     "print(list(cubos))"
213 |    ]
214 |   },
215 |   {
216 |    "cell_type": "markdown",
217 |    "metadata": {},
218 |    "source": [
219 |     "## Combinações e Permutações\n",
220 |     "\n",
221 |     "Combinações nos permite selecionar um iterável e ele nos retornará todas as combinações possíveis do mesmo.\n",
222 |     "\n",
223 |     "Basicamente as combinações são todas as diferentes maneiras que podemos agrupar um certo número de itens em que a ordem não importa.\n",
224 |     "\n",
225 |     "Permutações são todas as maneiras diferentes que podemos agrupar um certo número de itens, onde a ordem importa.\n",
226 |     "\n",
227 |     "Vejamos alguns exemplos para clarificar essas ideias.\n",
228 |     "\n",
229 |     "### Combinações\n",
230 |     "\n",
231 |     "Vamos definir uma lista com todas as vogais e estabelecer todas as combinações possíveis entre dois valores, finalmente vamos imprimir o resultado:"
232 |    ]
233 |   },
234 |   {
235 |    "cell_type": "code",
236 |    "execution_count": 8,
237 |    "metadata": {},
238 |    "outputs": [
239 |     {
240 |      "name": "stdout",
241 |      "output_type": "stream",
242 |      "text": [
243 |       "('a', 'e')\n",
244 |       "('a', 'i')\n",
245 |       "('a', 'o')\n",
246 |       "('a', 'u')\n",
247 |       "('e', 'i')\n",
248 |       "('e', 'o')\n",
249 |       "('e', 'u')\n",
250 |       "('i', 'o')\n",
251 |       "('i', 'u')\n",
252 |       "('o', 'u')\n"
253 |      ]
254 |     }
255 |    ],
256 |    "source": [
257 |     "letras = ['a','e','i','o','u']\n",
258 |     "\n",
259 |     "combinações = itertools.combinations(letras,2)\n",
260 |     "\n",
261 |     "for combinação in combinações:\n",
262 |     "    print(combinação)"
263 |    ]
264 |   },
265 |   {
266 |    "cell_type": "markdown",
267 |    "metadata": {},
268 |    "source": [
269 |     "Se quisermos fazer uma combinação do mesmo elemento com o mesmo elemento, usamos a função **combinations_with_replacement**:"
270 |    ]
271 |   },
272 |   {
273 |    "cell_type": "code",
274 |    "execution_count": 25,
275 |    "metadata": {},
276 |    "outputs": [
277 |     {
278 |      "name": "stdout",
279 |      "output_type": "stream",
280 |      "text": [
281 |       "(1, 1)\n",
282 |       "(1, 2)\n",
283 |       "(1, 3)\n",
284 |       "(1, 4)\n",
285 |       "(2, 2)\n",
286 |       "(2, 3)\n",
287 |       "(2, 4)\n",
288 |       "(3, 3)\n",
289 |       "(3, 4)\n",
290 |       "(4, 4)\n"
291 |      ]
292 |     }
293 |    ],
294 |    "source": [
295 |     "combs = itertools.combinations_with_replacement([1, 2, 3, 4], 2)\n",
296 |     " \n",
297 |     "for comb in list(combs):\n",
298 |     "    print(comb)"
299 |    ]
300 |   },
301 |   {
302 |    "cell_type": "markdown",
303 |    "metadata": {},
304 |    "source": [
305 |     "### Permutações\n",
306 |     "\n",
307 |     "Observe que com permutações as possibilidades de combinações aumentam."
308 |    ]
309 |   },
310 |   {
311 |    "cell_type": "code",
312 |    "execution_count": 9,
313 |    "metadata": {},
314 |    "outputs": [
315 |     {
316 |      "name": "stdout",
317 |      "output_type": "stream",
318 |      "text": [
319 |       "('a', 'e')\n",
320 |       "('a', 'i')\n",
321 |       "('a', 'o')\n",
322 |       "('a', 'u')\n",
323 |       "('e', 'a')\n",
324 |       "('e', 'i')\n",
325 |       "('e', 'o')\n",
326 |       "('e', 'u')\n",
327 |       "('i', 'a')\n",
328 |       "('i', 'e')\n",
329 |       "('i', 'o')\n",
330 |       "('i', 'u')\n",
331 |       "('o', 'a')\n",
332 |       "('o', 'e')\n",
333 |       "('o', 'i')\n",
334 |       "('o', 'u')\n",
335 |       "('u', 'a')\n",
336 |       "('u', 'e')\n",
337 |       "('u', 'i')\n",
338 |       "('u', 'o')\n"
339 |      ]
340 |     }
341 |    ],
342 |    "source": [
343 |     "permutações = itertools.permutations(letras,2)\n",
344 |     "\n",
345 |     "for permutação in permutações:\n",
346 |     "    print(permutação)"
347 |    ]
348 |   },
349 |   {
350 |    "cell_type": "markdown",
351 |    "metadata": {},
352 |    "source": [
353 |     "### Product\n",
354 |     "\n",
355 |     "A função **product** nos permite repetir os valores, ela nos fornecerá o produto cartesiano dos iteráveis que passamos como argumento.\n",
356 |     "\n",
357 |     "A seguir, passamos o iterável números e a quantidade de vezes que desejamos repetir o produto cartesiano, nesse caso 2:"
358 |    ]
359 |   },
360 |   {
361 |    "cell_type": "code",
362 |    "execution_count": 10,
363 |    "metadata": {},
364 |    "outputs": [
365 |     {
366 |      "name": "stdout",
367 |      "output_type": "stream",
368 |      "text": [
369 |       "(0, 0)\n",
370 |       "(0, 1)\n",
371 |       "(0, 2)\n",
372 |       "(0, 3)\n",
373 |       "(1, 0)\n",
374 |       "(1, 1)\n",
375 |       "(1, 2)\n",
376 |       "(1, 3)\n",
377 |       "(2, 0)\n",
378 |       "(2, 1)\n",
379 |       "(2, 2)\n",
380 |       "(2, 3)\n",
381 |       "(3, 0)\n",
382 |       "(3, 1)\n",
383 |       "(3, 2)\n",
384 |       "(3, 3)\n"
385 |      ]
386 |     }
387 |    ],
388 |    "source": [
389 |     "números = [0,1,2,3]\n",
390 |     "\n",
391 |     "produtos = itertools.product(números,repeat=2)\n",
392 |     "\n",
393 |     "for produto in produtos:\n",
394 |     "    print(produto)"
395 |    ]
396 |   },
397 |   {
398 |    "cell_type": "markdown",
399 |    "metadata": {},
400 |    "source": [
401 |     "### Chain\n",
402 |     "\n",
403 |     "A função **chain** nos permite combinar diversos iteráveis, nos possibilitando percorrê-los através de um loop.\n",
404 |     "\n",
405 |     "A seguir, combinaremos três listas: **letras**, **números** e **nomes**:"
406 |    ]
407 |   },
408 |   {
409 |    "cell_type": "code",
410 |    "execution_count": 11,
411 |    "metadata": {},
412 |    "outputs": [
413 |     {
414 |      "name": "stdout",
415 |      "output_type": "stream",
416 |      "text": [
417 |       "a\n",
418 |       "e\n",
419 |       "i\n",
420 |       "o\n",
421 |       "u\n",
422 |       "0\n",
423 |       "1\n",
424 |       "2\n",
425 |       "3\n",
426 |       "Gabriel\n",
427 |       "Rafael\n",
428 |       "Daniel\n",
429 |       "Miguel\n"
430 |      ]
431 |     }
432 |    ],
433 |    "source": [
434 |     "nomes = ['Gabriel','Rafael','Daniel','Miguel']\n",
435 |     "\n",
436 |     "combinados = itertools.chain(letras, números, nomes)\n",
437 |     "\n",
438 |     "for combinado in combinados:\n",
439 |     "    print(combinado)"
440 |    ]
441 |   },
442 |   {
443 |    "cell_type": "markdown",
444 |    "metadata": {},
445 |    "source": [
446 |     "### Compress\n",
447 |     "\n",
448 |     "A função **compress** atua como uma espécie de filtro, neste caso combinamos a lista **nomes** com a lista **seletores** e ela nos retorna um iterável, ao percorrermos o iterável com um loop, nós é retornado apenas os valores setados como **True**. "
449 |    ]
450 |   },
451 |   {
452 |    "cell_type": "code",
453 |    "execution_count": 12,
454 |    "metadata": {},
455 |    "outputs": [
456 |     {
457 |      "name": "stdout",
458 |      "output_type": "stream",
459 |      "text": [
460 |       "Gabriel\n",
461 |       "Rafael\n",
462 |       "Miguel\n"
463 |      ]
464 |     }
465 |    ],
466 |    "source": [
467 |     "seletores = [True,True,False,True]\n",
468 |     "\n",
469 |     "resultados = itertools.compress(nomes,seletores)\n",
470 |     "\n",
471 |     "for resultado in resultados:\n",
472 |     "    print(resultado)"
473 |    ]
474 |   },
475 |   {
476 |    "cell_type": "markdown",
477 |    "metadata": {},
478 |    "source": [
479 |     "### Accumulate\n",
480 |     "\n",
481 |     "A função **accumulate** executa a soma dos valores de forma acumulada até atingirmos o fim de nossa lista.\n",
482 |     "\n",
483 |     "Passamos a lista **valores** como argumento para a função **accumulate**:"
484 |    ]
485 |   },
486 |   {
487 |    "cell_type": "code",
488 |    "execution_count": 13,
489 |    "metadata": {},
490 |    "outputs": [
491 |     {
492 |      "name": "stdout",
493 |      "output_type": "stream",
494 |      "text": [
495 |       "1\n",
496 |       "3\n",
497 |       "6\n",
498 |       "10\n",
499 |       "15\n",
500 |       "21\n",
501 |       "28\n"
502 |      ]
503 |     }
504 |    ],
505 |    "source": [
506 |     "valores = [1,2,3,4,5,6,7]\n",
507 |     "\n",
508 |     "acumulados = itertools.accumulate(valores)\n",
509 |     "\n",
510 |     "for acumulado in acumulados:\n",
511 |     "    print(acumulado)"
512 |    ]
513 |   },
514 |   {
515 |    "cell_type": "markdown",
516 |    "metadata": {},
517 |    "source": [
518 |     "Também podemos utilizar a função **accumulate** com multiplicações, para essa tarefa específica importaremos a biblioteca **operator**.\n",
519 |     "\n",
520 |     "Passamos a lista **valores** e o operador **mul** como argumento para a função **accumulate**:"
521 |    ]
522 |   },
523 |   {
524 |    "cell_type": "code",
525 |    "execution_count": 14,
526 |    "metadata": {},
527 |    "outputs": [
528 |     {
529 |      "name": "stdout",
530 |      "output_type": "stream",
531 |      "text": [
532 |       "1\n",
533 |       "2\n",
534 |       "6\n",
535 |       "24\n",
536 |       "120\n",
537 |       "720\n",
538 |       "5040\n"
539 |      ]
540 |     }
541 |    ],
542 |    "source": [
543 |     "import operator\n",
544 |     "\n",
545 |     "multiplicados = itertools.accumulate(valores,operator.mul)\n",
546 |     "\n",
547 |     "for multiplicado in multiplicados:\n",
548 |     "    print(multiplicado)"
549 |    ]
550 |   }
551 |  ],
552 |  "metadata": {
553 |   "kernelspec": {
554 |    "display_name": "Python 3",
555 |    "language": "python",
556 |    "name": "python3"
557 |   },
558 |   "language_info": {
559 |    "codemirror_mode": {
560 |     "name": "ipython",
561 |     "version": 3
562 |    },
563 |    "file_extension": ".py",
564 |    "mimetype": "text/x-python",
565 |    "name": "python",
566 |    "nbconvert_exporter": "python",
567 |    "pygments_lexer": "ipython3",
568 |    "version": "3.7.10"
569 |   }
570 |  },
571 |  "nbformat": 4,
572 |  "nbformat_minor": 4
573 | }
574 | 


--------------------------------------------------------------------------------
/jupyter_notebooks/simbolos_matematica.ipynb:
--------------------------------------------------------------------------------
  1 | {
  2 |  "cells": [
  3 |   {
  4 |    "cell_type": "markdown",
  5 |    "metadata": {},
  6 |    "source": [
  7 |     "# Símbolos da Matemática Explicados com Python\n",
  8 |     "\n",
  9 |     "Quando trabalhamos em projetos de Machine Learning é muito comum nos depararmos com uma grande variedade de equações que devemos implementar em nosso código.\n",
 10 |     "\n",
 11 |     "Neste notebook vamos entender as notações matemáticas mais comuns ao conectarmos elas com seus conceitos análogos em Python. Uma vez que você compreenda elas, você estará apto a entender intuitivamente a intenção da equação e poderá implementar ela em seu código.\n",
 12 |     "\n",
 13 |     "\\begin{equation}\\frac{{1}}{{N}} \\sum_{i=1}^{N} (y_i - \\hat{y_i})^2 \\end{equation}\n",
 14 |     "\n",
 15 |     "## Indexando\n",
 16 |     "\n",
 17 |     "\\begin{equation} X_i \\end{equation}\n",
 18 |     "\n",
 19 |     "Esse símbolo obtém o valor no índice $i^{th}$ do vetor:"
 20 |    ]
 21 |   },
 22 |   {
 23 |    "cell_type": "code",
 24 |    "execution_count": 18,
 25 |    "metadata": {},
 26 |    "outputs": [
 27 |     {
 28 |      "name": "stdout",
 29 |      "output_type": "stream",
 30 |      "text": [
 31 |       "10\n"
 32 |      ]
 33 |     }
 34 |    ],
 35 |    "source": [
 36 |     "x = [10, 20, 30]\n",
 37 |     "i = 0\n",
 38 |     "\n",
 39 |     "print(x[i])"
 40 |    ]
 41 |   },
 42 |   {
 43 |    "cell_type": "markdown",
 44 |    "metadata": {},
 45 |    "source": [
 46 |     "Podemos extender essa ideia para vetores 2D:\n",
 47 |     "\n",
 48 |     "\\begin{equation} X_{ij} \\end{equation}"
 49 |    ]
 50 |   },
 51 |   {
 52 |    "cell_type": "code",
 53 |    "execution_count": 17,
 54 |    "metadata": {},
 55 |    "outputs": [
 56 |     {
 57 |      "name": "stdout",
 58 |      "output_type": "stream",
 59 |      "text": [
 60 |       "20\n"
 61 |      ]
 62 |     }
 63 |    ],
 64 |    "source": [
 65 |     "x = [[10,20,30],[40,50,60]]\n",
 66 |     "i = 0\n",
 67 |     "j = 1\n",
 68 |     "\n",
 69 |     "print(x[i][j])"
 70 |    ]
 71 |   },
 72 |   {
 73 |    "cell_type": "markdown",
 74 |    "metadata": {},
 75 |    "source": [
 76 |     "## Sigma\n",
 77 |     "\n",
 78 |     "\\begin{equation}\\sum_{i=0}^{N} X_{i} \\end{equation}\n",
 79 |     "\n",
 80 |     "Esse símbolo busca a soma de todos os elementos em um vetor para uma determinada extensão. \n",
 81 |     "\n",
 82 |     "Em Python ele é equivalente a executarmos um loop sob um vetor do índice $0$ até o índice $n$:"
 83 |    ]
 84 |   },
 85 |   {
 86 |    "cell_type": "code",
 87 |    "execution_count": 1,
 88 |    "metadata": {},
 89 |    "outputs": [
 90 |     {
 91 |      "name": "stdout",
 92 |      "output_type": "stream",
 93 |      "text": [
 94 |       "15\n"
 95 |      ]
 96 |     }
 97 |    ],
 98 |    "source": [
 99 |     "x = [1, 2, 3, 4, 5]\n",
100 |     "result = 0\n",
101 |     "N = len(x)\n",
102 |     "\n",
103 |     "for i in range(N):\n",
104 |     "    result = result + x[i]\n",
105 |     "    \n",
106 |     "print(result)"
107 |    ]
108 |   },
109 |   {
110 |    "cell_type": "markdown",
111 |    "metadata": {},
112 |    "source": [
113 |     "Podemos ainda escrever de maneira simplificada com o método **sum**:"
114 |    ]
115 |   },
116 |   {
117 |    "cell_type": "code",
118 |    "execution_count": 16,
119 |    "metadata": {},
120 |    "outputs": [
121 |     {
122 |      "name": "stdout",
123 |      "output_type": "stream",
124 |      "text": [
125 |       "15\n"
126 |      ]
127 |     }
128 |    ],
129 |    "source": [
130 |     "x = [1, 2, 3, 4, 5]\n",
131 |     "result = sum(x)\n",
132 |     "\n",
133 |     "print(result)"
134 |    ]
135 |   },
136 |   {
137 |    "cell_type": "markdown",
138 |    "metadata": {},
139 |    "source": [
140 |     "## Média\n",
141 |     "\n",
142 |     "\\begin{equation}\\frac{{1}}{{N}} \\sum_{i=0}^{N} X_{i} \\end{equation}\n",
143 |     "\n",
144 |     "Aqui nós usamos a notação sigma e dividimos pelo número de elementos da lista para obtermos a média:"
145 |    ]
146 |   },
147 |   {
148 |    "cell_type": "code",
149 |    "execution_count": 15,
150 |    "metadata": {},
151 |    "outputs": [
152 |     {
153 |      "name": "stdout",
154 |      "output_type": "stream",
155 |      "text": [
156 |       "3.0\n"
157 |      ]
158 |     }
159 |    ],
160 |    "source": [
161 |     "x = [1, 2, 3, 4, 5]\n",
162 |     "result = 0\n",
163 |     "N = len(x)\n",
164 |     "\n",
165 |     "for i in range(N):\n",
166 |     "    result = result + x[i]\n",
167 |     "    \n",
168 |     "average = result / N\n",
169 |     "\n",
170 |     "print(average)"
171 |    ]
172 |   },
173 |   {
174 |    "cell_type": "markdown",
175 |    "metadata": {},
176 |    "source": [
177 |     "Podemos ainda escrever de maneira simplificada:"
178 |    ]
179 |   },
180 |   {
181 |    "cell_type": "code",
182 |    "execution_count": 14,
183 |    "metadata": {},
184 |    "outputs": [
185 |     {
186 |      "name": "stdout",
187 |      "output_type": "stream",
188 |      "text": [
189 |       "3.0\n"
190 |      ]
191 |     }
192 |    ],
193 |    "source": [
194 |     "x = [1, 2, 3, 4, 5]\n",
195 |     "result = sum(x) / len(x)\n",
196 |     "\n",
197 |     "print(result)"
198 |    ]
199 |   },
200 |   {
201 |    "cell_type": "markdown",
202 |    "metadata": {},
203 |    "source": [
204 |     "## PI\n",
205 |     "\n",
206 |     "\\begin{equation}\\prod_{i=0}^{N} X_i\\end{equation}\n",
207 |     "\n",
208 |     "Esse símbolo busca o produto de todos os elementos em um vetor para uma determinada extensão. \n",
209 |     "\n",
210 |     "Em Python, é equivalente a executarmos um loop sob um vetor de um índice $0$ até um índice $n$, multiplicando os elementos. Por exemplo:"
211 |    ]
212 |   },
213 |   {
214 |    "cell_type": "code",
215 |    "execution_count": 4,
216 |    "metadata": {},
217 |    "outputs": [
218 |     {
219 |      "name": "stdout",
220 |      "output_type": "stream",
221 |      "text": [
222 |       "120\n"
223 |      ]
224 |     }
225 |    ],
226 |    "source": [
227 |     "x = [1, 2, 3, 4, 5]\n",
228 |     "result = 1\n",
229 |     "N = len(x)\n",
230 |     "\n",
231 |     "for i in range(N):\n",
232 |     "    result = result * x[i]\n",
233 |     "    \n",
234 |     "print(result)"
235 |    ]
236 |   },
237 |   {
238 |    "cell_type": "markdown",
239 |    "metadata": {},
240 |    "source": [
241 |     "## Pipe\n",
242 |     "\n",
243 |     "O símbolo pipe pode ter diferentes significados dependendo da aplicação.\n",
244 |     "\n",
245 |     "### Valor Absoluto\n",
246 |     "\n",
247 |     "\\begin{equation}\\vert x \\vert\\end{equation}\n",
248 |     "\\begin{equation}\\vert y \\vert\\end{equation}\n",
249 |     "\n",
250 |     "O símbolo acima denota o valor absoluto de um número:"
251 |    ]
252 |   },
253 |   {
254 |    "cell_type": "code",
255 |    "execution_count": 13,
256 |    "metadata": {},
257 |    "outputs": [
258 |     {
259 |      "name": "stdout",
260 |      "output_type": "stream",
261 |      "text": [
262 |       "10\n",
263 |       "20\n"
264 |      ]
265 |     }
266 |    ],
267 |    "source": [
268 |     "x = 10\n",
269 |     "y = -20\n",
270 |     "\n",
271 |     "print(abs(x))\n",
272 |     "print(abs(y))"
273 |    ]
274 |   },
275 |   {
276 |    "cell_type": "markdown",
277 |    "metadata": {},
278 |    "source": [
279 |     "## Norma do Vetor\n",
280 |     "\n",
281 |     "\\begin{equation} {|x|} \\end{equation}\n",
282 |     "\n",
283 |     "\\begin{equation} {||x||} \\end{equation}\n",
284 |     "\n",
285 |     "A norma do vetor é usada para calcular a magnitude do vetor. \n",
286 |     "\n",
287 |     "Em Python, isso significa elevar cada elemento de um array ao quadrado, somar eles e então obter a raiz quadrada. Por exemplo:"
288 |    ]
289 |   },
290 |   {
291 |    "cell_type": "code",
292 |    "execution_count": 5,
293 |    "metadata": {},
294 |    "outputs": [
295 |     {
296 |      "data": {
297 |       "text/plain": [
298 |        "3.7416573867739413"
299 |       ]
300 |      },
301 |      "execution_count": 5,
302 |      "metadata": {},
303 |      "output_type": "execute_result"
304 |     }
305 |    ],
306 |    "source": [
307 |     "import math\n",
308 |     "\n",
309 |     "x = [1, 2, 3]\n",
310 |     "math.sqrt(x[0]**2 + x[1]**2 + x[2]**2)"
311 |    ]
312 |   },
313 |   {
314 |    "cell_type": "markdown",
315 |    "metadata": {},
316 |    "source": [
317 |     "## Epsilon\n",
318 |     "\n",
319 |     "\\begin{equation} 3 \\epsilon X \\end{equation}\n",
320 |     "\n",
321 |     "Esse símbolo checa se um elemento é parte de um conjunto. Em Python o equivalente seria:"
322 |    ]
323 |   },
324 |   {
325 |    "cell_type": "code",
326 |    "execution_count": 12,
327 |    "metadata": {},
328 |    "outputs": [
329 |     {
330 |      "data": {
331 |       "text/plain": [
332 |        "True"
333 |       ]
334 |      },
335 |      "execution_count": 12,
336 |      "metadata": {},
337 |      "output_type": "execute_result"
338 |     }
339 |    ],
340 |    "source": [
341 |     "X = {1, 2, 3}\n",
342 |     "\n",
343 |     "3 in X"
344 |    ]
345 |   },
346 |   {
347 |    "cell_type": "markdown",
348 |    "metadata": {},
349 |    "source": [
350 |     "## Função\n",
351 |     "\n",
352 |     "\\begin{equation} f : X \\rightarrow Y \\end{equation}\n",
353 |     "\n",
354 |     "$f$ Denota uma função que recebe um **Domínio** X e mapeia ele para uma extensão Y. \n",
355 |     "\n",
356 |     "Em Python, teriamos como equivalente obter uma gama de valores X, executar algumas operações neles para calcular uma gama de valores Y."
357 |    ]
358 |   },
359 |   {
360 |    "cell_type": "code",
361 |    "execution_count": 8,
362 |    "metadata": {},
363 |    "outputs": [],
364 |    "source": [
365 |     "def f(X):\n",
366 |     "    Y = 2*X\n",
367 |     "    return Y"
368 |    ]
369 |   },
370 |   {
371 |    "cell_type": "markdown",
372 |    "metadata": {},
373 |    "source": [
374 |     "Se inserirmos o valor **3** na função $f$ que definimos, vamos obter o resultado **6**:"
375 |    ]
376 |   },
377 |   {
378 |    "cell_type": "code",
379 |    "execution_count": 9,
380 |    "metadata": {},
381 |    "outputs": [
382 |     {
383 |      "data": {
384 |       "text/plain": [
385 |        "6"
386 |       ]
387 |      },
388 |      "execution_count": 9,
389 |      "metadata": {},
390 |      "output_type": "execute_result"
391 |     }
392 |    ],
393 |    "source": [
394 |     "f(3)"
395 |    ]
396 |   },
397 |   {
398 |    "cell_type": "markdown",
399 |    "metadata": {},
400 |    "source": [
401 |     "Nós podemos encontrar os seguintes símbolos no lugar de X e Y:\n",
402 |     "\n",
403 |     "\\begin{equation} f : R \\rightarrow R \\end{equation}\n",
404 |     "\n",
405 |     "$R$ significa que o **input** e o **output** são números reais e podem receber qualquer valor (inteiro, ponto flutuante, irracional, racional). \n",
406 |     "\n",
407 |     "Em Python, é equivalente a qualquer valor, exceto números complexos:"
408 |    ]
409 |   },
410 |   {
411 |    "cell_type": "code",
412 |    "execution_count": 10,
413 |    "metadata": {},
414 |    "outputs": [
415 |     {
416 |      "name": "stdout",
417 |      "output_type": "stream",
418 |      "text": [
419 |       "1 2.5 3.141592653589793\n"
420 |      ]
421 |     }
422 |    ],
423 |    "source": [
424 |     "x = 1\n",
425 |     "y = 2.5\n",
426 |     "z = math.pi\n",
427 |     "\n",
428 |     "print(x,y,z)"
429 |    ]
430 |   },
431 |   {
432 |    "cell_type": "markdown",
433 |    "metadata": {},
434 |    "source": [
435 |     "Você também poderá encontrar símbolos como:\n",
436 |     "\n",
437 |     "\\begin{equation} f : R^{d} \\rightarrow R \\end{equation}\n",
438 |     "\n",
439 |     "$R^{d}$ significa um vetor de $d$ dimensões de números reais.\n",
440 |     "\n",
441 |     "Vamos assumir que $d=2$. Em Python, o exemplo pode ser uma função que recebe um array 2D e retorna sua soma. Estaria mapeando $R^{d}$ para $R$:"
442 |    ]
443 |   },
444 |   {
445 |    "cell_type": "code",
446 |    "execution_count": 11,
447 |    "metadata": {},
448 |    "outputs": [
449 |     {
450 |      "name": "stdout",
451 |      "output_type": "stream",
452 |      "text": [
453 |       "10\n"
454 |      ]
455 |     }
456 |    ],
457 |    "source": [
458 |     "import numpy as np\n",
459 |     "\n",
460 |     "X = [[1, 2], [3, 4]]\n",
461 |     "f = np.sum\n",
462 |     "Y = f(X)\n",
463 |     "\n",
464 |     "print(Y)"
465 |    ]
466 |   },
467 |   {
468 |    "cell_type": "markdown",
469 |    "metadata": {},
470 |    "source": [
471 |     "## Tensores\n",
472 |     "\n",
473 |     "### Transposição\n",
474 |     "\n",
475 |     "\\begin{equation} X^{T} \\end{equation}\n",
476 |     "\n",
477 |     "Na transposição, basicamente estamos trocando as linhas e colunas. Em Python o equivalente seria:"
478 |    ]
479 |   },
480 |   {
481 |    "cell_type": "code",
482 |    "execution_count": 19,
483 |    "metadata": {},
484 |    "outputs": [
485 |     {
486 |      "data": {
487 |       "text/plain": [
488 |        "array([[1, 4],\n",
489 |        "       [2, 5],\n",
490 |        "       [3, 6]])"
491 |       ]
492 |      },
493 |      "execution_count": 19,
494 |      "metadata": {},
495 |      "output_type": "execute_result"
496 |     }
497 |    ],
498 |    "source": [
499 |     "X = [[1, 2, 3],[4, 5, 6]]\n",
500 |     "\n",
501 |     "np.transpose(X)"
502 |    ]
503 |   },
504 |   {
505 |    "cell_type": "markdown",
506 |    "metadata": {},
507 |    "source": [
508 |     "## Multiplicação de Cada Elemento\n",
509 |     "\n",
510 |     "\\begin{equation} z = x \\odot y \\end{equation}\n",
511 |     "\n",
512 |     "Significa multiplicar os elementos correspondentes em dois tensores. \n",
513 |     "\n",
514 |     "Em Python, seria o equivalente a multiplicar os elementos correspondentes em duas listas:"
515 |    ]
516 |   },
517 |   {
518 |    "cell_type": "code",
519 |    "execution_count": 20,
520 |    "metadata": {},
521 |    "outputs": [
522 |     {
523 |      "name": "stdout",
524 |      "output_type": "stream",
525 |      "text": [
526 |       "[[2 4]\n",
527 |       " [6 8]]\n"
528 |      ]
529 |     }
530 |    ],
531 |    "source": [
532 |     "x = [[1, 2],[3, 4]]\n",
533 |     "y = [[2, 2],[2, 2]]\n",
534 |     "z = np.multiply(x, y)\n",
535 |     "\n",
536 |     "print(z)"
537 |    ]
538 |   },
539 |   {
540 |    "cell_type": "markdown",
541 |    "metadata": {},
542 |    "source": [
543 |     "## Produto Escalar\n",
544 |     "\n",
545 |     "\\begin{equation} X \\cdot Y \\end{equation}\n",
546 |     "\n",
547 |     "O produto escalar nos fornece a soma dos produtos das entradas correspondentes das duas sequências de números:"
548 |    ]
549 |   },
550 |   {
551 |    "cell_type": "code",
552 |    "execution_count": 21,
553 |    "metadata": {},
554 |    "outputs": [
555 |     {
556 |      "data": {
557 |       "text/plain": [
558 |        "35"
559 |       ]
560 |      },
561 |      "execution_count": 21,
562 |      "metadata": {},
563 |      "output_type": "execute_result"
564 |     }
565 |    ],
566 |    "source": [
567 |     "X = [1, 2, 3]\n",
568 |     "Y = [4, 5, 7]\n",
569 |     "\n",
570 |     "np.dot(X,Y)"
571 |    ]
572 |   },
573 |   {
574 |    "cell_type": "markdown",
575 |    "metadata": {},
576 |    "source": [
577 |     "## Hat\n",
578 |     "\n",
579 |     "\\begin{equation}\\hat{X}\\end{equation}\n",
580 |     "\n",
581 |     "Hat nos fornece o vetor unidade. \n",
582 |     "\n",
583 |     "Isso significa dividir cada componente em um vetor por seu comprimento (norma):"
584 |    ]
585 |   },
586 |   {
587 |    "cell_type": "code",
588 |    "execution_count": 22,
589 |    "metadata": {},
590 |    "outputs": [
591 |     {
592 |      "name": "stdout",
593 |      "output_type": "stream",
594 |      "text": [
595 |       "[0.2672612419124244, 0.5345224838248488, 0.8017837257372732]\n"
596 |      ]
597 |     }
598 |    ],
599 |    "source": [
600 |     "x = [1, 2, 3]\n",
601 |     "length = math.sqrt(sum([e**2 for e in x]))\n",
602 |     "x_hat = [e/length for e in x]\n",
603 |     "\n",
604 |     "print(x_hat)"
605 |    ]
606 |   },
607 |   {
608 |    "cell_type": "markdown",
609 |    "metadata": {},
610 |    "source": [
611 |     "Isso faz a magnitude do vetor $1$ e apenas mantém a direção:"
612 |    ]
613 |   },
614 |   {
615 |    "cell_type": "code",
616 |    "execution_count": 24,
617 |    "metadata": {},
618 |    "outputs": [
619 |     {
620 |      "data": {
621 |       "text/plain": [
622 |        "1.0"
623 |       ]
624 |      },
625 |      "execution_count": 24,
626 |      "metadata": {},
627 |      "output_type": "execute_result"
628 |     }
629 |    ],
630 |    "source": [
631 |     "math.sqrt(sum([e**2 for e in x_hat]))"
632 |    ]
633 |   },
634 |   {
635 |    "cell_type": "markdown",
636 |    "metadata": {},
637 |    "source": [
638 |     "## Exclamação\n",
639 |     "\n",
640 |     "\\begin{equation}x!\\end{equation}\n",
641 |     "\n",
642 |     "Essa expressão denota o fatorial de um número. É o produto de números começando de $1$ até o número $x$. \n",
643 |     "\n",
644 |     "Em Python podemos calcular da seguinte forma:"
645 |    ]
646 |   },
647 |   {
648 |    "cell_type": "code",
649 |    "execution_count": 23,
650 |    "metadata": {},
651 |    "outputs": [
652 |     {
653 |      "name": "stdout",
654 |      "output_type": "stream",
655 |      "text": [
656 |       "5040\n"
657 |      ]
658 |     }
659 |    ],
660 |    "source": [
661 |     "x = 7\n",
662 |     "fact = 1\n",
663 |     "\n",
664 |     "for i in range(x, 0, -1):\n",
665 |     "    fact *= i\n",
666 |     "    \n",
667 |     "print(fact)"
668 |    ]
669 |   },
670 |   {
671 |    "cell_type": "markdown",
672 |    "metadata": {},
673 |    "source": [
674 |     "Podemos ainda simplificar usando o método **factorial** da biblioteca **math**:"
675 |    ]
676 |   },
677 |   {
678 |    "cell_type": "code",
679 |    "execution_count": 24,
680 |    "metadata": {},
681 |    "outputs": [
682 |     {
683 |      "data": {
684 |       "text/plain": [
685 |        "720"
686 |       ]
687 |      },
688 |      "execution_count": 24,
689 |      "metadata": {},
690 |      "output_type": "execute_result"
691 |     }
692 |    ],
693 |    "source": [
694 |     "math.factorial(6)"
695 |    ]
696 |   }
697 |  ],
698 |  "metadata": {
699 |   "kernelspec": {
700 |    "display_name": "Python 3",
701 |    "language": "python",
702 |    "name": "python3"
703 |   },
704 |   "language_info": {
705 |    "codemirror_mode": {
706 |     "name": "ipython",
707 |     "version": 3
708 |    },
709 |    "file_extension": ".py",
710 |    "mimetype": "text/x-python",
711 |    "name": "python",
712 |    "nbconvert_exporter": "python",
713 |    "pygments_lexer": "ipython3",
714 |    "version": "3.7.10"
715 |   }
716 |  },
717 |  "nbformat": 4,
718 |  "nbformat_minor": 4
719 | }
720 | 


--------------------------------------------------------------------------------
/jupyter_notebooks/triangulo_sierpinski.ipynb:
--------------------------------------------------------------------------------
  1 | {
  2 |  "cells": [
  3 |   {
  4 |    "cell_type": "markdown",
  5 |    "metadata": {},
  6 |    "source": [
  7 |     "# Triângulo de Sierpinski\n",
  8 |     "\n",
  9 |     "O [Triângulo de Sierpinski](https://en.wikipedia.org/wiki/Sierpi%C5%84ski_triangle), também conhecido como Junta de Sierpinski, é um fractal e um [conjunto fixo atrativo](https://pt.wikipedia.org/wiki/Ponto_fixo) com a forma global de um triângulo equilátero, subdividido recursivamente em triângulos equiláteros menores. Originalmente construído como uma curva, ele é um exemplo básico de conjuntos auto-similares, é um padrão gerado matematicamente que é possível reproduzir em qualquer ampliação ou redução. \n",
 10 |     "\n",
 11 |     "O nome é dado em homenagem ao matemático polonês **Wacław Sierpiński** que contribuiu muito para com os campos de teoria dos conjuntos, teoria dos números, teoria das funções e topologia.\n",
 12 |     "\n",
 13 |     "## Biblioteca turtle\n",
 14 |     "\n",
 15 |     "Existe em Python uma biblioteca chamada [**turtle**](https://docs.python.org/3.3/library/turtle.html?highlight=turtle) que nos permite desenhar diversos formas de maneira relativamente simples.\n",
 16 |     "\n",
 17 |     "Nesse caso iremos gerar o fractal recursivamente, ao quebrarmos o triângulo em três triângulos menores, depois quebrando esses triângulos em três triângulos menores e assim por diante. Teoricamente é possível fazermos isso infinitamente, porém para ilustração vamos utilizar apenas quatro vezes.\n",
 18 |     "\n",
 19 |     "O algoritmo segue a seguinte ideia:\n",
 20 |     "\n",
 21 |     "1. Especificamos três vértices para nosso triângulo equilátero.\n",
 22 |     "2. Desenha o triângulo inferior esquerdo ao utilizar o vértice inferior esquerdo, o ponto médio entre esse vértice e o vértice superior, e o ponto médio entre esse vértice e o vértice inferior direito:\n",
 23 |     "    - Se nós não tivermos atingido o caso base (o nível mais baixo do fractal), rodamos esse algoritmo recursivamente para esse triângulo.\n",
 24 |     "3. Desenha o triângulo superior ao utilizar o vértice superior, o ponto médio entre esse vértice e o vértice inferior direito, e o ponto médio entre esse vértice e o vértice inferior esquerdo:\n",
 25 |     "    - Se nós não tivermos atingido o caso base (o nível mais baixo do fractal), rodamos esse algoritmo recursivamente para esse triângulo.\n",
 26 |     "4. Desenha o triângulo inferior direito ao utilizar o vértice inferior direito, o ponto médio entre esse vértice e o vértice inferior esquerdo, e o ponto médio entre esse vértice e o vértice superior:\n",
 27 |     "    - Se nós não tivermos atingido o caso base (o nível mais baixo do fractal), rodamos esse algoritmo recursivamente para esse triângulo.\n",
 28 |     "    \n",
 29 |     "Dessa maneira talvez seja um pouco difícil de visualizarmos e compreendermos a ideia, para isso é importante que vejamos um exemplo do algoritmo em ação:"
 30 |    ]
 31 |   },
 32 |   {
 33 |    "cell_type": "code",
 34 |    "execution_count": 7,
 35 |    "metadata": {},
 36 |    "outputs": [],
 37 |    "source": [
 38 |     "import turtle\n",
 39 |     "\n",
 40 |     "# Função que faz a biblioteca turtle desenhar um triângulo,\n",
 41 |     "# A unidade básica do nosso fractal\n",
 42 |     "def draw_triangle(vertices,tartaruga):\n",
 43 |     "    tartaruga.up()\n",
 44 |     "    tartaruga.goto(vertices[0][0],vertices[0][1])\n",
 45 |     "    tartaruga.down()\n",
 46 |     "    tartaruga.goto(vertices[1][0],vertices[1][1])\n",
 47 |     "    tartaruga.goto(vertices[2][0],vertices[2][1])\n",
 48 |     "    tartaruga.goto(vertices[0][0],vertices[0][1])\n",
 49 |     "    \n",
 50 |     "# Função que define os pontos médios\n",
 51 |     "def midpoint(p1, p2):\n",
 52 |     "    return [(p1[0] + p2[0])/2, (p1[1] + p2[1])/2]\n",
 53 |     "\n",
 54 |     "# Função recursiva que desenha os diferentes \"níveis\" do fractal\n",
 55 |     "def draw_fractal(vertices,level,tartaruga):\n",
 56 |     "    # Desenha um triângulo\n",
 57 |     "    draw_triangle(vertices,tartaruga)\n",
 58 |     "    # Chama a função recursivamente para desenhar todos os níveis do fractal\n",
 59 |     "    if level > 0:\n",
 60 |     "        # Desenha o primeiro segmento do fractal\n",
 61 |     "        # Os vértices sendo passados são o cantor inferior da primeira\n",
 62 |     "        # seção, o canto inferior da segunda seção e o canto inferior da terceira seção\n",
 63 |     "        draw_fractal([vertices[0],\n",
 64 |     "                      midpoint(vertices[0], vertices[1]),\n",
 65 |     "                      midpoint(vertices[0], vertices[2])],\n",
 66 |     "                      level - 1, tartaruga)\n",
 67 |     "        draw_fractal([vertices[1],\n",
 68 |     "                      midpoint(vertices[0], vertices[1]),\n",
 69 |     "                      midpoint(vertices[1], vertices[2])],\n",
 70 |     "                      level - 1, tartaruga)\n",
 71 |     "        draw_fractal([vertices[2],\n",
 72 |     "                      midpoint(vertices[2], vertices[1]),\n",
 73 |     "                      midpoint(vertices[0], vertices[2])],\n",
 74 |     "                      level - 1, tartaruga)\n",
 75 |     "\n",
 76 |     "tartaruga = turtle.Turtle()\n",
 77 |     "tartaruga.hideturtle()\n",
 78 |     "screen = turtle.Screen()\n",
 79 |     "vertices = [[-300, -200], [0, 300], [300, -200]]\n",
 80 |     "level = 4 # Define quão profunda a recursão para desenharmos o fractal\n",
 81 |     "draw_fractal(vertices, level, tartaruga)\n",
 82 |     "screen.exitonclick()"
 83 |    ]
 84 |   },
 85 |   {
 86 |    "cell_type": "markdown",
 87 |    "metadata": {},
 88 |    "source": [
 89 |     "## Visualização Gráfica do Triângulo Gerado:\n",
 90 |     "\n",
 91 |     "![img](https://raw.githubusercontent.com/the-akira/Python-Matematica/master/imagens/sierpinski.png)"
 92 |    ]
 93 |   }
 94 |  ],
 95 |  "metadata": {
 96 |   "kernelspec": {
 97 |    "display_name": "Python 3",
 98 |    "language": "python",
 99 |    "name": "python3"
100 |   },
101 |   "language_info": {
102 |    "codemirror_mode": {
103 |     "name": "ipython",
104 |     "version": 3
105 |    },
106 |    "file_extension": ".py",
107 |    "mimetype": "text/x-python",
108 |    "name": "python",
109 |    "nbconvert_exporter": "python",
110 |    "pygments_lexer": "ipython3",
111 |    "version": "3.7.10"
112 |   }
113 |  },
114 |  "nbformat": 4,
115 |  "nbformat_minor": 4
116 | }
117 | 


--------------------------------------------------------------------------------
/referencias.md:
--------------------------------------------------------------------------------
 1 | # Referências Online
 2 | 
 3 | - [SciPy](https://www.scipy.org/)
 4 | - [A Primer on Scientific Programming with Python](https://hplgit.github.io/primer.html/doc/pub/half/book.pdf)
 5 | - [Python for Scientific Computing](https://devopedia.org/python-for-scientific-computing)
 6 | - [Fast Fourier Transforms in Python](https://ericstrong.org/fast-fourier-transforms-in-python/)
 7 | - [Pythonic](https://pythontic.com)
 8 | - [Matplotlib](https://matplotlib.org/)
 9 | - [Plotly](https://plot.ly/matplotlib/getting-started/)
10 | - [Pandas](https://pandas.pydata.org/)
11 | - [Numpy](https://www.numpy.org/)
12 | - [SymPy Tutorial](https://docs.sympy.org/latest/tutorial/index.html)
13 | - [SciPy2016 Material](https://www.sympy.org/scipy-2016-tutorial/)
14 | - [Taming Math and Physics using SymPy](https://minireference.com/static/tutorials/sympy_tutorial.pdf)
15 | - [SymPy Tutorial for Applied Differential Equations](http://www.cfm.brown.edu/people/dobrush/am33/SymPy/index.html)
16 | - [Python Algorithms for Interviews](https://www.youtube.com/watch?v=p65AHm9MX80)
17 | - [Math and Physics using SymPy](https://www.jonathangross.de/files/IPCS2017/sympy.pdf)
18 | - [Python Numpy Tutorial](http://cs231n.github.io/python-numpy-tutorial/)
19 | - [Basic Statistics in Pandas](https://medium.com/@kasiarachuta/basic-statistics-in-pandas-dataframe-594208074f85)
20 | - [Python Matplotlib Guide](https://realpython.com/python-matplotlib-guide/)
21 | - [A Gentle Introduction to the Rectified Linear Unit (ReLU) for Deep Learning](https://machinelearningmastery.com/rectified-linear-activation-function-for-deep-learning-neural-networks/)
22 | - [Rosetta Code](https://rosettacode.org/wiki/Mandelbrot_set)
23 | - [Plot Mandelbrot Set](https://scipy-lectures.org/intro/numpy/auto_examples/plot_mandelbrot.html)
24 | - [WolframMathWorld](http://mathworld.wolfram.com/FibonacciNumber.html)
25 | - [Mortada](https://mortada.net/fibonacci-numbers-in-python.html)
26 | - [The Euclidean Algorithm](https://www.khanacademy.org/computing/computer-science/cryptography/modarithmetic/a/the-euclidean-algorithm)
27 | - [Euclid](http://sites.math.rutgers.edu/~greenfie/gs2004/euclid.html)
28 | - [Plotting](https://nagordon.github.io/mechpy/plotting.html)
29 | - [APMonitor](https://apmonitor.com/)
30 | - [Math for Programmers](https://amitness.com/2019/08/math-for-programmers/)
31 | 


--------------------------------------------------------------------------------