└── README.md
/README.md:
--------------------------------------------------------------------------------
1 |
2 | 
3 |
4 | # Math → Kotlin Cheatsheet
5 |
6 | This is still very much a work-in-progress and I welcome any contributions. This cheat sheet was inspired by [Jam3's Math as Code project](https://github.com/Jam3/math-as-code).
7 |
8 | I am using this [online LaTeX equation editor](https://www.codecogs.com/eqnedit.php) to generate expressions, and if you want to learn MathJax notation [here is a great resource](https://math.meta.stackexchange.com/questions/5020/mathjax-basic-tutorial-and-quick-reference).
9 |
10 | While you are here, please rally this [issue on Dokka](https://github.com/Kotlin/dokka/issues/245) to bring MathJax support to Kotlin Docs.
11 |
12 | > Please note that these code examples may leave out some optimizations (e.g. using [collection operators instead of Sequences](https://winterbe.com/posts/2018/07/23/kotlin-sequence-tutorial/#sequences-vs-collections)) in order to reduce boilerplate and make concepts clear.
13 |
14 | # Understanding Math Expressions
15 |
16 | Think of mathematical notation as a form of pseudocode. It is often expressing an algorithm in declarative form. It is important to note however that these mathematical symbols existed well before computers, and therefore may not be expressed in a programming-friendly way (e.g. using 1-based indexing versus 0-based indexing). Like pseudocode, the author can take liberties in defining what symbols mean, and any symbol can mean different things depending on the context.
17 |
18 | As a programmer, learning to interpret mathematical notation will help you navigate academic papers and blogs that apply mathematical concepts. This is especially the case when you dabble in machine learning, mathematical optimization, and data science.
19 |
20 | # Summation and Multiplication
21 |
22 | This symbol  indicates you are summing a series of items. It is probably one of the most commonly used symbols in math to express iterative addition.
23 |
24 | Similarly, a
indicates you are summing a series of items. It is probably one of the most commonly used symbols in math to express iterative addition.
23 |
24 | Similarly, a  is used to multiply a series of items.
25 |
26 |
27 | |Math Expression|Kotlin Code|
28 | |---|---|
29 | |
is used to multiply a series of items.
25 |
26 |
27 | |Math Expression|Kotlin Code|
28 | |---|---|
29 | | |`(1..3).sum()`|
30 | |
|`(1..3).sum()`|
30 | | |`(1..5).map { i -> 10*i }.sum()`|
31 | |
|`(1..5).map { i -> 10*i }.sum()`|
31 | | |`fun f(n: Int) = (0..n).map { it.pow(2) }.sum()`|
32 | |
|`fun f(n: Int) = (0..n).map { it.pow(2) }.sum()`|
32 | | |`fun f(x: Double) = (1..100).map { i -> 3 * x.pow(2) + (2*i) }.sum()`|
33 | |
|`fun f(x: Double) = (1..100).map { i -> 3 * x.pow(2) + (2*i) }.sum()`|
33 | | | `fun f(n: Int) = 10 + 3*(0..n).map { it * it }.sum()`|
34 | |
| `fun f(n: Int) = 10 + 3*(0..n).map { it * it }.sum()`|
34 | | |`fun f(allX: List) = allX.mapIndexed { i,x -> x + i }.sum()`|
35 | |
|`fun f(allX: List) = allX.mapIndexed { i,x -> x + i }.sum()`|
35 | | |`(1..4).flatMap { i -> (4..20).map { j -> 2 *i * j } }.sum()`
|`(1..4).flatMap { i -> (4..20).map { j -> 2 *i * j } }.sum()`
`sequence { for(i in 1..4) for (j in 4..20) yield(2 * i * j) }.sum()`|
36 | | |`(1..n).fold(1L, Long::times)`|
37 |
38 | ### Nested Summation
39 |
40 | When you see more than one summation, this means they are nested summations. This is no different than summing with nested loops or flatmapped functional sequences.
41 |
42 |
|`(1..n).fold(1L, Long::times)`|
37 |
38 | ### Nested Summation
39 |
40 | When you see more than one summation, this means they are nested summations. This is no different than summing with nested loops or flatmapped functional sequences.
41 |
42 |  43 |
44 | ```kotlin
45 | (1..10).flatMap { i -> (4..20).map { j -> 2 *i * j } }.sum()
46 | ```
47 |
48 |
49 | ### Indexes and Iteration
50 |
51 | When approached with a mathematical expression, you need to consider it may not use 0-based indexing especially in the context of iterating elements.
52 |
53 | For instance, here is an operation that is iterating `n` elements and summing. The iteration starts at index 1.
54 |
55 |
43 |
44 | ```kotlin
45 | (1..10).flatMap { i -> (4..20).map { j -> 2 *i * j } }.sum()
46 | ```
47 |
48 |
49 | ### Indexes and Iteration
50 |
51 | When approached with a mathematical expression, you need to consider it may not use 0-based indexing especially in the context of iterating elements.
52 |
53 | For instance, here is an operation that is iterating `n` elements and summing. The iteration starts at index 1.
54 |
55 |  56 |
57 | When translating this to code, you should interpret this as iterating all the elements starting at index 0. It does not skip the first element or start at index 1.
58 |
59 | ```kotlin
60 | fun f(elements: List) = elements.sum()
61 | ```
62 |
63 | However, when you are not working with elements but rather an actual number sequence, you should interpret this literally. When we are iterating numbers 1 through 3, we really are iterating numbers 1 through 3.
64 |
65 |
56 |
57 | When translating this to code, you should interpret this as iterating all the elements starting at index 0. It does not skip the first element or start at index 1.
58 |
59 | ```kotlin
60 | fun f(elements: List) = elements.sum()
61 | ```
62 |
63 | However, when you are not working with elements but rather an actual number sequence, you should interpret this literally. When we are iterating numbers 1 through 3, we really are iterating numbers 1 through 3.
64 |
65 |  66 |
67 | ```kotlin
68 | val sum = (1..3).sum()
69 | ```
70 | In summary, beware of 0-index and 1-index conventions, and discern what the mathematical expression is trying to achieve before translating it into code.
71 |
72 |
73 | # Variables
74 |
75 | Hopefully the concept of a variable (such as `x`) should be self-explanatory to a programmer. However, in mathematical notation it is common for subscripts and other "decorators" to distinctly describe several instances of that variable. For instance, we can use `old` and `new` `x` values to measure a rate of change.
76 |
77 |
66 |
67 | ```kotlin
68 | val sum = (1..3).sum()
69 | ```
70 | In summary, beware of 0-index and 1-index conventions, and discern what the mathematical expression is trying to achieve before translating it into code.
71 |
72 |
73 | # Variables
74 |
75 | Hopefully the concept of a variable (such as `x`) should be self-explanatory to a programmer. However, in mathematical notation it is common for subscripts and other "decorators" to distinctly describe several instances of that variable. For instance, we can use `old` and `new` `x` values to measure a rate of change.
76 |
77 |  78 |
79 | Here is a more iterative example. We can define 5 different variables all named
78 |
79 | Here is a more iterative example. We can define 5 different variables all named  , but notate them as
, but notate them as  . Here is how we can notate an average operation.
80 |
81 |
. Here is how we can notate an average operation.
80 |
81 |  .
82 |
83 | ```kotlin
84 | val xValues = listOf(23, 65, 45, 23, 66)
85 | val xAverage = allXs.sum() / 5
86 |
87 | // or
88 |
89 | val xAverage = allXs.average()
90 | ```
91 |
92 | Mathematics and programming are similar in that they try to generalize. Instead of formulating an average for just `5` variables, we can notate it for any `n` number of variables.
93 |
94 |
95 |
.
82 |
83 | ```kotlin
84 | val xValues = listOf(23, 65, 45, 23, 66)
85 | val xAverage = allXs.sum() / 5
86 |
87 | // or
88 |
89 | val xAverage = allXs.average()
90 | ```
91 |
92 | Mathematics and programming are similar in that they try to generalize. Instead of formulating an average for just `5` variables, we can notate it for any `n` number of variables.
93 |
94 |
95 |  96 |
97 |
98 | To maximize fanciness, we can go a step further and use a summation operator and just generalize each `x` value as
96 |
97 |
98 | To maximize fanciness, we can go a step further and use a summation operator and just generalize each `x` value as 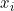 . Note that `n` is the number of variables/elements we are averaging.
99 |
100 |
101 |
. Note that `n` is the number of variables/elements we are averaging.
99 |
100 |
101 |  102 |
103 | ### Decorators
104 |
105 | Sometimes a variable can have "decorators" to further add meaning to a variable but with standardized conciseness.
106 |
107 | #### "Hat" Symbol
108 |
109 | The hat symbol, such as
102 |
103 | ### Decorators
104 |
105 | Sometimes a variable can have "decorators" to further add meaning to a variable but with standardized conciseness.
106 |
107 | #### "Hat" Symbol
108 |
109 | The hat symbol, such as  , is often used to indicate a predicted value as opposed to an actual. This is often in the context of prediction and forecasting a number. You could simply express a predicted and actual value as
, is often used to indicate a predicted value as opposed to an actual. This is often in the context of prediction and forecasting a number. You could simply express a predicted and actual value as  and
and  , but it can be much more concise to use a `^` symbol.
110 |
111 | For example, say we predict selling
, but it can be much more concise to use a `^` symbol.
110 |
111 | For example, say we predict selling  products, but in actuality we sell
products, but in actuality we sell  . Our forecast error would be the difference between these two variables.
112 |
113 |
. Our forecast error would be the difference between these two variables.
112 |
113 |  114 |
115 | ### Greek Letters
116 |
117 | The Greek alphabet can be used as variables (and sometimes operators) as well. There is little consistency on how they are used and for what. However, there are some common usages for certains symbols as documented in this table.
118 |
119 | | Uppercase | Lowercase | Name | Common Usage |
120 | |-----------|-----------|---------|--------------|
121 | | Α | α | Alpha | |
122 | | Β | β | Beta | |
123 | | Γ | γ | Gamma | |
124 | | Δ | δ | Delta |Measurement of change or difference, derivative... [Read More](https://en.wikipedia.org/wiki/Delta_(letter)#Upper_case)|
125 | | Ε | ε | Epsilon | |
126 | | Ζ | ζ | Zeta | |
127 | | Η | η | Eta | |
128 | | Θ | θ | Theta |Geometric angles, trigonometric variables... [Read More](https://en.wikipedia.org/wiki/Theta#Mathematics_and_science)|
129 | | Ι | ι | Iota | |
130 | | Κ | κ | Kappa | |
131 | | Λ | λ | Lambda | |
132 | | Μ | μ | Mu | |
133 | | Ν | ν | Nu | |
134 | | Ξ | ξ | Xi | |
135 | | Ο | ο | Omicron | |
136 | | Π | π | Pi | |
137 | | Ρ | ρ | Rho | |
138 | | Σ | σ/ς | Sigma |Summation, standard deviation... [Read More](https://en.wikipedia.org/wiki/Sigma#Science_and_mathematics)|
139 | | Τ | τ | Tau | |
140 | | Υ | υ | Upsilon | |
141 | | Φ | φ | Phi | |
142 | | Χ | χ | Chi | |
143 | | Ψ | ψ | Psi | |
144 | | Ω | ω | Omega | |
145 |
146 |
147 | ### Naming Variables in Kotlin
148 |
149 | Trying to express variables like
114 |
115 | ### Greek Letters
116 |
117 | The Greek alphabet can be used as variables (and sometimes operators) as well. There is little consistency on how they are used and for what. However, there are some common usages for certains symbols as documented in this table.
118 |
119 | | Uppercase | Lowercase | Name | Common Usage |
120 | |-----------|-----------|---------|--------------|
121 | | Α | α | Alpha | |
122 | | Β | β | Beta | |
123 | | Γ | γ | Gamma | |
124 | | Δ | δ | Delta |Measurement of change or difference, derivative... [Read More](https://en.wikipedia.org/wiki/Delta_(letter)#Upper_case)|
125 | | Ε | ε | Epsilon | |
126 | | Ζ | ζ | Zeta | |
127 | | Η | η | Eta | |
128 | | Θ | θ | Theta |Geometric angles, trigonometric variables... [Read More](https://en.wikipedia.org/wiki/Theta#Mathematics_and_science)|
129 | | Ι | ι | Iota | |
130 | | Κ | κ | Kappa | |
131 | | Λ | λ | Lambda | |
132 | | Μ | μ | Mu | |
133 | | Ν | ν | Nu | |
134 | | Ξ | ξ | Xi | |
135 | | Ο | ο | Omicron | |
136 | | Π | π | Pi | |
137 | | Ρ | ρ | Rho | |
138 | | Σ | σ/ς | Sigma |Summation, standard deviation... [Read More](https://en.wikipedia.org/wiki/Sigma#Science_and_mathematics)|
139 | | Τ | τ | Tau | |
140 | | Υ | υ | Upsilon | |
141 | | Φ | φ | Phi | |
142 | | Χ | χ | Chi | |
143 | | Ψ | ψ | Psi | |
144 | | Ω | ω | Omega | |
145 |
146 |
147 | ### Naming Variables in Kotlin
148 |
149 | Trying to express variables like 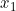 and
and  can be a little awkward in code. In Kotlin, you can choose to stick with conventional camelCase or break style guidelines by using underscores.
150 |
151 | ```kotlin
152 | val x1 = 12
153 | val x_1 = 12
154 |
155 | val xOld = 13
156 | val x_old = 13
157 | ```
158 | For mathematical symbols like theta
can be a little awkward in code. In Kotlin, you can choose to stick with conventional camelCase or break style guidelines by using underscores.
150 |
151 | ```kotlin
152 | val x1 = 12
153 | val x_1 = 12
154 |
155 | val xOld = 13
156 | val x_old = 13
157 | ```
158 | For mathematical symbols like theta 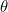 , you can just name your variable `theta`.
159 |
160 | ```kotlin
161 | import kotlin.math.PI
162 | import kotlin.math.sin
163 |
164 | val theta = PI / 2.0
165 | val result = sin(theta)
166 | ```
167 |
168 | Hopefully you will not run into this decision of naming variables often, as you may express variables as iterated elements in collections/sequences rather than give each one an explicit variable name.
169 |
170 |
171 |
172 | # Elements, Sets, and Ranges
173 |
174 | ## Sets
175 |
176 | ### Common Number Sets
177 |
178 | #### Real Numbers
179 |
180 | #### Rational Numbers
181 |
182 | #### Integers
183 |
184 | #### Natural Numbers
185 |
186 | ## Ranges
187 |
188 |
189 | # Functions
190 |
191 |
192 | |Math Expression|Description|Kotlin Code|
193 | |---|---|---|
194 | |
, you can just name your variable `theta`.
159 |
160 | ```kotlin
161 | import kotlin.math.PI
162 | import kotlin.math.sin
163 |
164 | val theta = PI / 2.0
165 | val result = sin(theta)
166 | ```
167 |
168 | Hopefully you will not run into this decision of naming variables often, as you may express variables as iterated elements in collections/sequences rather than give each one an explicit variable name.
169 |
170 |
171 |
172 | # Elements, Sets, and Ranges
173 |
174 | ## Sets
175 |
176 | ### Common Number Sets
177 |
178 | #### Real Numbers
179 |
180 | #### Rational Numbers
181 |
182 | #### Integers
183 |
184 | #### Natural Numbers
185 |
186 | ## Ranges
187 |
188 |
189 | # Functions
190 |
191 |
192 | |Math Expression|Description|Kotlin Code|
193 | |---|---|---|
194 | |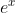 |Exponent of `e`|`exp(x)`|
195 | |
|Exponent of `e`|`exp(x)`|
195 | |) |Natural logarithm|`ln(x)`|
196 |
197 |
198 |
199 | # Linear Algebra
200 |
201 | Linear algebra is the building block of machine learning, computer graphics, linear programming, and many other mathematically-intense computer science disciplines. Linear algebra can seem pointless until you apply it to specific problems. For example, [a neural network](https://github.com/thomasnield/kotlin_simple_neural_network) is typically executed using dot products to multiply and sum weights and node values.
202 |
203 | Linear algebra takes the tediousness out of working with large multidimensional arrays of numbers and manipulating them with transformations. While you can certainly iterate these numbers yourself and perform whatever calculation you need, it can become extremely inefficient and cumbersome to do yourself.
204 |
205 | There are great libraries that can do this for you. In the Python world you would typically use [NumPy](http://www.numpy.org/). In the JVM world, you can use [ND4J](http://nd4j.org/), [ojAlgo](https://github.com/optimatika/ojAlgo), or [JBlas](http://jblas.org/). The Kotlin multiplatform library [Koma](https://github.com/kyonifer/koma) will probably be your go-to if you intend on doing linear algebra in Kotlin.
206 |
207 | If you want to learn more about Linear Algebra, [3Blue1Brown](https://www.youtube.com/watch?v=fNk_zzaMoSs&list=PLZHQObOWTQDPD3MizzM2xVFitgF8hE_ab) has a great video series on linear algebra on YouTube.
208 |
209 | ### Scalars
210 |
211 | A scalar is simply a single number (as opposed to an array of numbers which is called a vector). Declaring a scalar value in Kotlin is no different than declaring a numeric variable, such as an `Int` or `Double`.
212 |
213 | In linear algebra, scalars are often used in the context of multiplication (hence the name _scalar_, because they _scale_ things).
214 |
215 | ```kotlin
216 | // all these assignments are scalars
217 | val increaseRate = 1.04
218 |
219 | val oldSpeed = 60.0
220 |
221 | val newSpeed = oldSpeed * increaseRate
222 | ```
223 |
224 |
225 | ### Vectors
226 |
227 | In strict programming terms, a vector is an array of numeric values often representing values of different variables.
228 |
229 | ```kotlin
230 | // kotlin-stdlib
231 | val myVector = doubleArrayOf(1.0, 5.2, 2.4)
232 |
233 | //koma
234 | val myVector = rowVectorOf(1.0, 5.2, 2.4)
235 | ```
236 |
237 | By _variables_, we may be talking about _observations_. For instance, we can have a vector of temperatures for a given week.
238 |
239 | ```kotlin
240 | // kotlin-stdlib
241 | val lowTemperatures = intArrayOf(67, 62, 71, 73, 64, 66, 64)
242 | val highTemperatures = intArrayOf(76, 74, 77, 75, 76, 73, 72)
243 |
244 | // koma
245 | val lowTemperatures = rowVectorOf(67, 62, 71, 73, 64, 66, 64)
246 | val highTemperatures = rowVectorOf(76, 74, 77, 75, 76, 73, 72)
247 | ```
248 |
249 | We can also represent different attribributes of an item with a vector. For example, we can express a color in terms of three RGB values.
250 |
251 | ```kotlin
252 |
253 | // kotlin-stdlib
254 | val pinkColor = intArrayOf(255, 175, 175)
255 |
256 | // koma
257 | val pinkColor = rowVectorOf(255, 175, 175)
258 | ```
259 |
260 | We can also express different attributes of a `Person`:
261 |
262 | ```kotlin
263 | // height and weight of a person
264 |
265 | // kotlin-stdlib
266 | val personalAttributes = doubleArrayOf(71.5, 181.3)
267 |
268 | // koma
269 | val personalAttributes = rowVectorOf(71.5, 181.3)
270 | ```
271 |
272 | So why do we express things in terms of vectors rather than classes with properties? When it comes to heavy number-crunching (e.g. machine learning), raw numbers are far more efficient and standardized to compute with. Typically, vectors and matrices (covered next) are binded to a C library that can iteratively do math efficiently.
273 |
274 | #### Vector Math
275 |
276 | Adding/multipliying a vector with a scalar simply results in a vector with each value added/multiplied respectively by that scalar.
277 |
278 | ```kotlin
279 | val populations = rowVectorOf(2310, 2387, 5732)
280 | val growthRate = 1.01
281 |
282 | val newPopulations = populations * growthRate
283 |
284 | println(newPopulations) // mat[ 2333.10, 2410.87, 5789.32 ]
285 | ```
286 |
287 | If the dimenstions match, you can sum each respective element together (kind of like zipping) between two vectors using a `+` operator:
288 |
289 | ```kotlin
290 | val adultPopulations = rowVectorOf(2323, 5672, 2345)
291 | val childPopulations = rowVectorOf(1632, 1252, 1658)
292 |
293 | val totalPopulations = adultPopulations + childPopulations
294 |
295 | println(totalPopulations) // mat[ 3955.00, 6924.00, 4003.00 ]
296 | ```
297 |
298 | However using a multiplication operator `*` with two vectors will not work like you probably expect. It does not zip and multiply respective elements together, but rather performs a dot product (which we will cover later). If we multiply two vectors of the same length, it throws an error:
299 |
300 | ```kotlin
301 | val populations = rowVectorOf(2310, 2387, 5732)
302 | val growthRates = rowVectorOf(1.03, 1.06, 1.09)
303 |
304 | val newPopulations = populations * growthRates // ERROR! #columns != #rows
305 |
306 | println(newPopulations)
307 | ```
308 |
309 | If you want to zip and multipy each element respectively, use the `elementTimes()` operator.
310 |
311 | ```kotlin
312 | val populations = rowVectorOf(2310, 2387, 5732)
313 | val growthRates = rowVectorOf(1.03, 1.06, 1.09)
314 |
315 | val newPopulations = populations.elementTimes(growthRates)
316 |
317 | println(newPopulations)
318 | ```
319 |
320 | ### Matrices
321 |
322 | TODO
323 |
324 | ### Dot Products
325 |
326 |
327 | # Calculus
328 |
329 | Calculus is the study of _change_ in mathematics, studying rates of change and how a change in one variable affects another variable.
330 |
331 | Rates of change and deriving functions that calculate rate of change is the core of calculus. It is useful in machine learning and optimization, so unsurprisingly calculus has been getting a lot of interest outside of academia. When you are trying to minimize error in your machine learning algorithm, you have to increase or decrease parameters to minimize the error. Rather than hopelessly trying every possible combination of parameters to find the lowest resulting error, it can be much more efficient to leverage rate of change in error. With that rate, you can determine if a given point is increasing/decreasing in error and use that as your compass. Then you know which direction to tune your parameters.
332 |
333 | [3Blue1Brown has a fun YouTube series on Calculus fundamentals](https://www.youtube.com/playlist?list=PLZHQObOWTQDMsr9K-rj53DwVRMYO3t5Yr).
334 |
335 |
336 | ### Derivatives
337 |
338 | Programming with math often models things as functions, such as
|Natural logarithm|`ln(x)`|
196 |
197 |
198 |
199 | # Linear Algebra
200 |
201 | Linear algebra is the building block of machine learning, computer graphics, linear programming, and many other mathematically-intense computer science disciplines. Linear algebra can seem pointless until you apply it to specific problems. For example, [a neural network](https://github.com/thomasnield/kotlin_simple_neural_network) is typically executed using dot products to multiply and sum weights and node values.
202 |
203 | Linear algebra takes the tediousness out of working with large multidimensional arrays of numbers and manipulating them with transformations. While you can certainly iterate these numbers yourself and perform whatever calculation you need, it can become extremely inefficient and cumbersome to do yourself.
204 |
205 | There are great libraries that can do this for you. In the Python world you would typically use [NumPy](http://www.numpy.org/). In the JVM world, you can use [ND4J](http://nd4j.org/), [ojAlgo](https://github.com/optimatika/ojAlgo), or [JBlas](http://jblas.org/). The Kotlin multiplatform library [Koma](https://github.com/kyonifer/koma) will probably be your go-to if you intend on doing linear algebra in Kotlin.
206 |
207 | If you want to learn more about Linear Algebra, [3Blue1Brown](https://www.youtube.com/watch?v=fNk_zzaMoSs&list=PLZHQObOWTQDPD3MizzM2xVFitgF8hE_ab) has a great video series on linear algebra on YouTube.
208 |
209 | ### Scalars
210 |
211 | A scalar is simply a single number (as opposed to an array of numbers which is called a vector). Declaring a scalar value in Kotlin is no different than declaring a numeric variable, such as an `Int` or `Double`.
212 |
213 | In linear algebra, scalars are often used in the context of multiplication (hence the name _scalar_, because they _scale_ things).
214 |
215 | ```kotlin
216 | // all these assignments are scalars
217 | val increaseRate = 1.04
218 |
219 | val oldSpeed = 60.0
220 |
221 | val newSpeed = oldSpeed * increaseRate
222 | ```
223 |
224 |
225 | ### Vectors
226 |
227 | In strict programming terms, a vector is an array of numeric values often representing values of different variables.
228 |
229 | ```kotlin
230 | // kotlin-stdlib
231 | val myVector = doubleArrayOf(1.0, 5.2, 2.4)
232 |
233 | //koma
234 | val myVector = rowVectorOf(1.0, 5.2, 2.4)
235 | ```
236 |
237 | By _variables_, we may be talking about _observations_. For instance, we can have a vector of temperatures for a given week.
238 |
239 | ```kotlin
240 | // kotlin-stdlib
241 | val lowTemperatures = intArrayOf(67, 62, 71, 73, 64, 66, 64)
242 | val highTemperatures = intArrayOf(76, 74, 77, 75, 76, 73, 72)
243 |
244 | // koma
245 | val lowTemperatures = rowVectorOf(67, 62, 71, 73, 64, 66, 64)
246 | val highTemperatures = rowVectorOf(76, 74, 77, 75, 76, 73, 72)
247 | ```
248 |
249 | We can also represent different attribributes of an item with a vector. For example, we can express a color in terms of three RGB values.
250 |
251 | ```kotlin
252 |
253 | // kotlin-stdlib
254 | val pinkColor = intArrayOf(255, 175, 175)
255 |
256 | // koma
257 | val pinkColor = rowVectorOf(255, 175, 175)
258 | ```
259 |
260 | We can also express different attributes of a `Person`:
261 |
262 | ```kotlin
263 | // height and weight of a person
264 |
265 | // kotlin-stdlib
266 | val personalAttributes = doubleArrayOf(71.5, 181.3)
267 |
268 | // koma
269 | val personalAttributes = rowVectorOf(71.5, 181.3)
270 | ```
271 |
272 | So why do we express things in terms of vectors rather than classes with properties? When it comes to heavy number-crunching (e.g. machine learning), raw numbers are far more efficient and standardized to compute with. Typically, vectors and matrices (covered next) are binded to a C library that can iteratively do math efficiently.
273 |
274 | #### Vector Math
275 |
276 | Adding/multipliying a vector with a scalar simply results in a vector with each value added/multiplied respectively by that scalar.
277 |
278 | ```kotlin
279 | val populations = rowVectorOf(2310, 2387, 5732)
280 | val growthRate = 1.01
281 |
282 | val newPopulations = populations * growthRate
283 |
284 | println(newPopulations) // mat[ 2333.10, 2410.87, 5789.32 ]
285 | ```
286 |
287 | If the dimenstions match, you can sum each respective element together (kind of like zipping) between two vectors using a `+` operator:
288 |
289 | ```kotlin
290 | val adultPopulations = rowVectorOf(2323, 5672, 2345)
291 | val childPopulations = rowVectorOf(1632, 1252, 1658)
292 |
293 | val totalPopulations = adultPopulations + childPopulations
294 |
295 | println(totalPopulations) // mat[ 3955.00, 6924.00, 4003.00 ]
296 | ```
297 |
298 | However using a multiplication operator `*` with two vectors will not work like you probably expect. It does not zip and multiply respective elements together, but rather performs a dot product (which we will cover later). If we multiply two vectors of the same length, it throws an error:
299 |
300 | ```kotlin
301 | val populations = rowVectorOf(2310, 2387, 5732)
302 | val growthRates = rowVectorOf(1.03, 1.06, 1.09)
303 |
304 | val newPopulations = populations * growthRates // ERROR! #columns != #rows
305 |
306 | println(newPopulations)
307 | ```
308 |
309 | If you want to zip and multipy each element respectively, use the `elementTimes()` operator.
310 |
311 | ```kotlin
312 | val populations = rowVectorOf(2310, 2387, 5732)
313 | val growthRates = rowVectorOf(1.03, 1.06, 1.09)
314 |
315 | val newPopulations = populations.elementTimes(growthRates)
316 |
317 | println(newPopulations)
318 | ```
319 |
320 | ### Matrices
321 |
322 | TODO
323 |
324 | ### Dot Products
325 |
326 |
327 | # Calculus
328 |
329 | Calculus is the study of _change_ in mathematics, studying rates of change and how a change in one variable affects another variable.
330 |
331 | Rates of change and deriving functions that calculate rate of change is the core of calculus. It is useful in machine learning and optimization, so unsurprisingly calculus has been getting a lot of interest outside of academia. When you are trying to minimize error in your machine learning algorithm, you have to increase or decrease parameters to minimize the error. Rather than hopelessly trying every possible combination of parameters to find the lowest resulting error, it can be much more efficient to leverage rate of change in error. With that rate, you can determine if a given point is increasing/decreasing in error and use that as your compass. Then you know which direction to tune your parameters.
332 |
333 | [3Blue1Brown has a fun YouTube series on Calculus fundamentals](https://www.youtube.com/playlist?list=PLZHQObOWTQDMsr9K-rj53DwVRMYO3t5Yr).
334 |
335 |
336 | ### Derivatives
337 |
338 | Programming with math often models things as functions, such as &space;=&space;3x&space;+&space;10) . You can be trying to fit data to a linear function
. You can be trying to fit data to a linear function  , or minimizing a function measuring error in a neural network.
339 |
340 | However, when dealing with nonlinear functions (which represent a curvy line or plane, not a straight or flat one), we are often interested in finding the lowest or highest point for optimization reasons. Knowing the slope at a given point on that line or plane can help you follow the steepest direction and find that minimum or maximum.
341 |
342 | ### Partial Derivatives
343 |
344 | ### Integrals
345 |
346 |
--------------------------------------------------------------------------------
, or minimizing a function measuring error in a neural network.
339 |
340 | However, when dealing with nonlinear functions (which represent a curvy line or plane, not a straight or flat one), we are often interested in finding the lowest or highest point for optimization reasons. Knowing the slope at a given point on that line or plane can help you follow the steepest direction and find that minimum or maximum.
341 |
342 | ### Partial Derivatives
343 |
344 | ### Integrals
345 |
346 |
--------------------------------------------------------------------------------