├── KMP算法
├── README.md
└── kmp.py
├── 分支限界算法
├── README.md
├── max_loading.go
├── max_loading.py
├── shortest_path.py
├── shortest_path.go
└── leetcode-407.go
├── 树
├── AC自动机和Trie树
│ ├── README.md
│ └── ac.py
├── B树
│ ├── README.md
│ └── btree.py
├── B+树
│ └── README.md
├── 二叉树
│ ├── 红黑树
│ │ └── README.md
│ ├── 二叉搜索树
│ │ ├── README.md
│ │ └── binary_search_tree.py
│ ├── 平衡二叉树
│ │ └── README.md
│ ├── 表达式树
│ │ ├── README.md
│ │ └── InOrder2PostOrder.py
│ ├── 线索二叉树
│ │ ├── README.md
│ │ └── ThreadedBinaryTree.py
│ ├── 根据二叉树的先序、中序、后序序列还原二叉树
│ │ ├── README.md
│ │ └── GenerateTree.py
│ ├── README.md
│ └── BinaryTree.py
├── 霍夫曼树(最优二叉树)
│ ├── README.md
│ └── huffman_tree.py
├── README.md
└── 树与等价关系
│ ├── README.md
│ └── MFSet.py
├── 图
├── README.md
├── 最短路径
│ ├── Floyd算法
│ │ ├── README.md
│ │ └── floyd.py
│ └── Dijkstra算法
│ │ ├── README.md
│ │ └── dijkstra.py
├── DAG-有向无环图
│ ├── 拓扑排序
│ │ ├── README.md
│ │ └── topological_sort.py
│ └── 关键路径
│ │ ├── README.md
│ │ └── critical_path.py
├── 最小生成树
│ ├── README.md
│ ├── graph.py
│ ├── kruskal.py
│ └── prim.py
├── dfs_tree.py
└── dinetwork.py
├── 搜索算法
├── 二分查找
│ ├── README.md
│ └── BinarySearch.py
└── 跳表
│ ├── README.md
│ └── skip_list.py
├── 排序算法
├── 希尔排序
│ ├── README.md
│ └── shell_sort.py
├── 归并排序
│ ├── README.md
│ ├── merge_sort.go
│ ├── merge_sort.py
│ └── merge_sort_linked_list.py
├── 桶排序
│ ├── README.md
│ └── bucket_sort.py
├── 冒泡排序
│ ├── README.md
│ └── bubble_sort.py
├── 选择排序
│ ├── README.md
│ └── selection_sort.py
├── 直接插入排序
│ ├── README.md
│ └── straight_insertion_sort.py
├── 快速排序
│ ├── QuickSort.py
│ ├── quick_sort.go
│ ├── README.md
│ ├── leetcode-215.py
│ ├── offer-40.py
│ └── quick_sort_linked_list.py
└── 堆排序以及topk问题
│ ├── leetcode-973.py
│ ├── HeapSort.py
│ └── README.md
├── 哈希表
├── README.md
└── hash_table.py
├── 回溯算法
├── README.md
├── Empress.py
├── leetcode-78.go
├── dag.py
├── Maze.py
├── Maze.go
├── leetcode-79.go
└── leetcode-37.py
├── 线性表
├── 快慢指针法
│ ├── README.md
│ └── slow_fast_pointer.py
├── 逆转单链表
│ ├── README.md
│ └── reverse_list.py
├── 静态链表
│ ├── README.md
│ └── static_list.py
├── README.md
├── 链表是否有环
│ ├── README.md
│ └── cycle_list.py
├── 栈及其应用
│ ├── README.md
│ └── sequential_stack.py
├── linked_list.py
└── array_list.py
├── leetcode
├── DropEggs问题
│ ├── drop_eggs.py
│ └── README.md
├── 求字符串数组的最长公共前缀
│ ├── README.md
│ └── Solution.py
├── 字符串反转
│ ├── README.md
│ └── string_reverse.py
├── 最长回文子串
│ ├── README.md
│ └── palindrome.py
├── K路归并排序
│ ├── README.md
│ └── k_way_merge_sort.py
└── 最小栈
│ ├── README.md
│ └── min_stack.py
├── README.md
├── 动态规划
├── leetcode_416.go
├── leetcode-474.go
├── leetcode-322.go
├── README.md
├── leetcode-42.go
├── leetcode_10.go
├── knapsack_problem.py
└── knapsack_problem.go
└── 基本概念
└── README.md
/KMP算法/README.md:
--------------------------------------------------------------------------------
1 | 请参考[ Tim 的博客](http://timd.cn/kmp/)
2 |
--------------------------------------------------------------------------------
/分支限界算法/README.md:
--------------------------------------------------------------------------------
1 | 请移步[Tim的博客](http://timd.cn/branch-and-bound/)
--------------------------------------------------------------------------------
/树/AC自动机和Trie树/README.md:
--------------------------------------------------------------------------------
1 | 请阅读[ Tim 的博客](http://timd.cn/ac/)
2 |
--------------------------------------------------------------------------------
/图/README.md:
--------------------------------------------------------------------------------
1 | 请移步 [Tim 的博客](http://timd.cn/data-structure/graph/)
2 |
--------------------------------------------------------------------------------
/搜索算法/二分查找/README.md:
--------------------------------------------------------------------------------
1 | 请参考[ Tim 的博客](http://timd.cn/binary-search/)
2 |
--------------------------------------------------------------------------------
/排序算法/希尔排序/README.md:
--------------------------------------------------------------------------------
1 | 请移步[ Tim 的博客](http://timd.cn/sort/shell-sort/)。
2 |
--------------------------------------------------------------------------------
/排序算法/归并排序/README.md:
--------------------------------------------------------------------------------
1 | 请移步[ Tim 的博客](http://timd.cn/sort/merge-sort/)
2 |
--------------------------------------------------------------------------------
/排序算法/桶排序/README.md:
--------------------------------------------------------------------------------
1 | 请移步[ Tim 的博客](http://timd.cn/sort/bucket-sort/)。
2 |
--------------------------------------------------------------------------------
/树/B树/README.md:
--------------------------------------------------------------------------------
1 | 请阅读 [Tim 的博客](http://timd.cn/data-structure/btree/)
2 |
--------------------------------------------------------------------------------
/哈希表/README.md:
--------------------------------------------------------------------------------
1 | 请参考 [Tim 的博客](http://timd.cn/data-structure/hash-table/)
2 |
--------------------------------------------------------------------------------
/排序算法/冒泡排序/README.md:
--------------------------------------------------------------------------------
1 | 请移步[ Tim 的博客](http://timd.cn/2017/10/16/bubble-sort/)
2 |
--------------------------------------------------------------------------------
/排序算法/选择排序/README.md:
--------------------------------------------------------------------------------
1 | 请移步[ Tim 的博客](http://timd.cn/sort/selection-sort/)
2 |
--------------------------------------------------------------------------------
/搜索算法/跳表/README.md:
--------------------------------------------------------------------------------
1 | 请参考 [Tim 的博客](http://timd.cn/data-structure/skiplist/)
2 |
--------------------------------------------------------------------------------
/图/最短路径/Floyd算法/README.md:
--------------------------------------------------------------------------------
1 | 请移步 [Tim 的博客](http://timd.cn/data-structure/floyd/)
2 |
--------------------------------------------------------------------------------
/树/B+树/README.md:
--------------------------------------------------------------------------------
1 | 请移步 [Tim 的博客](http://timd.cn/data-structure/b-plus-tree/)
2 |
--------------------------------------------------------------------------------
/排序算法/直接插入排序/README.md:
--------------------------------------------------------------------------------
1 | 请移步[ Tim 的博客](http://timd.cn/sort/straight-insertion-sort/)。
2 |
--------------------------------------------------------------------------------
/树/二叉树/红黑树/README.md:
--------------------------------------------------------------------------------
1 | 请参考[ Tim 的博客](http://timd.cn/data-structure/red-black-tree/)
2 |
--------------------------------------------------------------------------------
/树/霍夫曼树(最优二叉树)/README.md:
--------------------------------------------------------------------------------
1 | 请参考 [Tim 的博客](http://timd.cn/data-structure/huffman-tree/)
2 |
--------------------------------------------------------------------------------
/树/二叉树/二叉搜索树/README.md:
--------------------------------------------------------------------------------
1 | 请移步:[Tim 的博客](http://timd.cn/data-structure/binary-search-tree/)
2 |
--------------------------------------------------------------------------------
/树/二叉树/平衡二叉树/README.md:
--------------------------------------------------------------------------------
1 | ### 文档
2 |
3 | 请移步[ Tim 的博客](http://timd.cn/data-structure/avl-tree)
4 |
5 |
--------------------------------------------------------------------------------
/回溯算法/README.md:
--------------------------------------------------------------------------------
1 | 请参考:[http://timd.cn/data-structure/backtrace/](http://timd.cn/data-structure/backtrace/)
2 |
--------------------------------------------------------------------------------
/线性表/快慢指针法/README.md:
--------------------------------------------------------------------------------
1 | ### 示例
2 |
3 | * 求链表的中间节点:
4 | 快指针每次前进 2 步,慢指针每次前进 1 步,当快指针到头时,慢指针到达中间节点
5 |
6 | * 求链表的倒数第 K 个节点:
7 | 快指针先前进 k - 1 步,然后慢指针开始出发
8 |
--------------------------------------------------------------------------------
/leetcode/DropEggs问题/drop_eggs.py:
--------------------------------------------------------------------------------
1 | def drop_eggs(n):
2 | i = 0
3 | sum = 0
4 |
5 | while sum < n:
6 | i = i + 1
7 | sum = sum + i
8 |
9 | return i
10 |
11 |
--------------------------------------------------------------------------------
/图/DAG-有向无环图/拓扑排序/README.md:
--------------------------------------------------------------------------------
1 | 请参考 [Tim 的博客](http://timd.cn/data-structure/topological-sort/)
2 |
3 | 代码中的测试用例如下图所示:
4 |
5 | 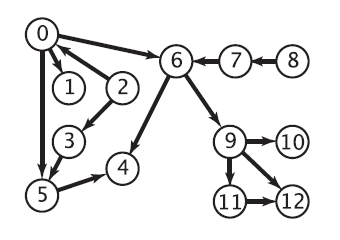
6 |
--------------------------------------------------------------------------------
/图/最短路径/Dijkstra算法/README.md:
--------------------------------------------------------------------------------
1 | 请移步 [Tim 的博客](http://timd.cn/data-structure/dijkstra/)
2 |
3 | 代码中使用的测试用例如下图所示:
4 |
5 | 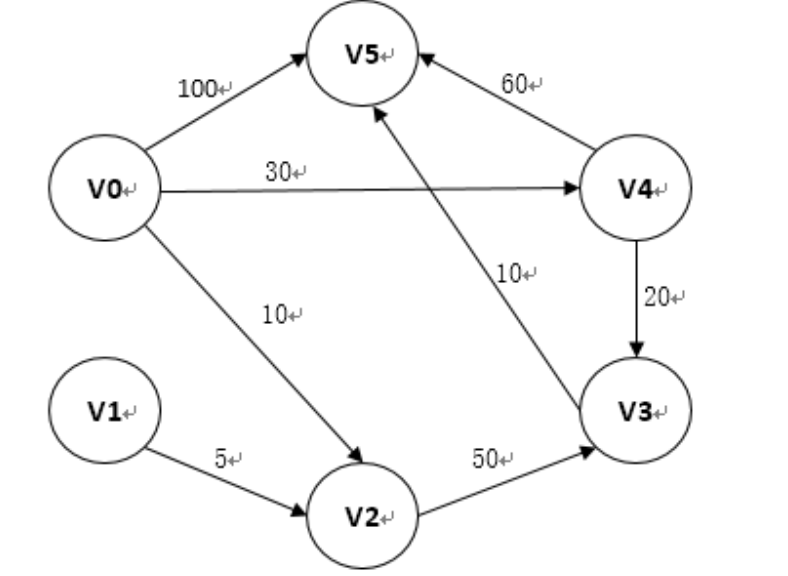
6 |
--------------------------------------------------------------------------------
/线性表/逆转单链表/README.md:
--------------------------------------------------------------------------------
1 | ### 三指针法
2 |
3 | * 初始时,p1 指向第一个节点,p2 指向 p1 的下一个节点,设置 p1 的下一个节点为 null
4 |
5 | * 重复执行下面的过程,一直到 p2 为 null
6 | * 令 p3 指向 p2 的下一个节点
7 | * 设置 p2 的下一个节点为 p1
8 | * 令 p1 = p2; p2 = p3
9 |
--------------------------------------------------------------------------------
/leetcode/求字符串数组的最长公共前缀/README.md:
--------------------------------------------------------------------------------
1 | ### 问题描述
2 |
3 | 给定一个字符串列表,求这些字符串的最长公共前缀
4 |
5 | ---
6 |
7 | ### 解决方案
8 |
9 | 设置一个初始值为 0 的 cursor,然后比较这些字符串在索引为 cursor 的分量上的字符是否都相等,如果是,则 cursor 前进一步,继续进行判断;否则返回子串 string[0 ... cursor]。
10 |
--------------------------------------------------------------------------------
/leetcode/字符串反转/README.md:
--------------------------------------------------------------------------------
1 | 例子:
2 |
3 |
4 | I am a student
5 |
6 |
7 | 结果:
8 |
9 |
10 | student a am I
11 |
12 |
13 | 解题思路:
14 |
15 | 经过两次反转:
16 |
17 | 第一次:
18 |
19 |
20 | tneduts a ma I
21 |
22 |
23 | 第二次:
24 |
25 |
26 | student a am I
27 |
28 |
--------------------------------------------------------------------------------
/leetcode/最长回文子串/README.md:
--------------------------------------------------------------------------------
1 | 回文字符串是指从左向右读和从右向左读完全相同的字符串。比如 "abba"、"1234321"。
2 |
3 | 对于子串 S[i ... j]:
4 |
5 | * 如果 i > j,那么 S[i ... j] 不是回文子串
6 |
7 | * 如果 i == j,那么 S[i ... j] 是回文子串
8 |
9 | * 如果 S[i] = S[j],那么 S[i ... j] 是否是回文子串,取决于 S[i + 1 ... j - 1] 是否是回文子串
10 | * 当 j = i + 1 时,S[i ... j] 是回文子串
11 |
12 | * 如果 S[i] ≠ S[j],那么 S[i ... j] 不是回文子串
13 |
--------------------------------------------------------------------------------
/图/最小生成树/README.md:
--------------------------------------------------------------------------------
1 | 关于 MST,请参考 [Tim 的博客](http://timd.cn/data-structure/mst/)
2 |
3 | 关于并查集,请参考 [Tim 的博客](http://timd.cn/data-structure/union-find/)
4 |
5 | 关于 Prim 算法,请参考 [Tim 的博客](http://timd.cn/data-structure/prim/)
6 |
7 | 关于 Kruskal 算法,请参考 [Tim 的博客](http://timd.cn/data-structure/kruskal/)
8 |
9 | 代码中使用的测试用例如下图所示:
10 |
11 | 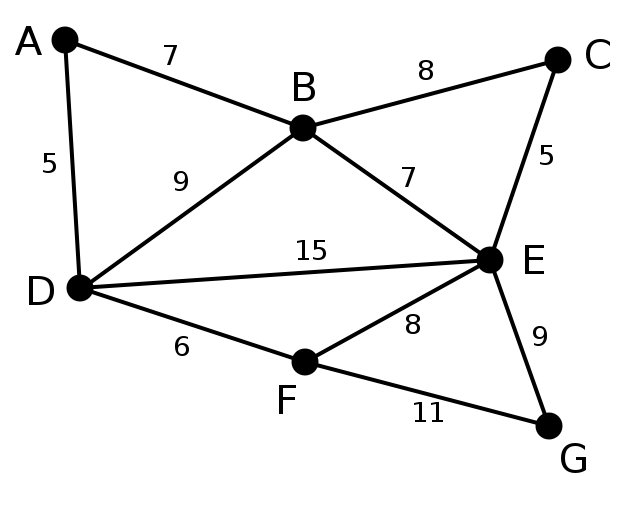
12 |
--------------------------------------------------------------------------------
/leetcode/K路归并排序/README.md:
--------------------------------------------------------------------------------
1 | ### 问题描述
2 |
3 | 将 K 个有序数组(总元素数为 n),合并成一个新的有序数组
4 |
5 | ---
6 |
7 | ### 解题思路
8 |
9 | * 取出每个数组的第一个元素,建立一个大小为 K 的最小堆
10 |
11 | * 弹出堆顶元素,并将其追加进结果数组
12 |
13 | * 如果堆顶元素所在的数组仍有剩余元素,那么从其中取出下一个元素,放到堆顶;否则将堆的最后一个元素弹出,放到堆顶
14 |
15 | * 调整堆
16 |
17 | * 重复执行上面的过程,一直到堆空
18 |
19 | ---
20 |
21 | ### 时间复杂度
22 |
23 | 调整堆的时间复杂度是 O(logk),需要调整 n 次,所以时间复杂度是 O(nlogk)
24 |
25 | ---
26 |
27 | ### 空间复杂度
28 |
29 | O(n)
30 |
--------------------------------------------------------------------------------
/线性表/静态链表/README.md:
--------------------------------------------------------------------------------
1 | ### 简介
2 |
3 | 静态链表**使用足够大的数组存储链表的全部节点**。每个节点包含两个域:
4 |
5 | * 数据域:存储数据元素
6 |
7 | * 游标域:存储直接后继节点在数组中的索引
8 |
9 | 数组中的分量分为两类:
10 |
11 | * 未被使用的分量:被组织在备用链表中
12 |
13 | * 已被使用的分量:被组织在静态链表中
14 |
15 | 静态链表需要实现两个方法:
16 |
17 | * `malloc()`:用于从备用链表中申请节点
18 |
19 | * `free()`:用于将节点放回备用链表
20 |
21 | 静态链表**预先申请空间**,而单链表现用现申请,因此存在申请失败、因申请新空间而导致性能下降等问题。预申请空间的做法非常常见,比如数据库就预先申请数据文件。
22 |
--------------------------------------------------------------------------------
/leetcode/最小栈/README.md:
--------------------------------------------------------------------------------
1 | ### 问题描述
2 |
3 | Design a stack that supports push, pop, top, and retrieving the minimum element in constant time.
4 |
5 | * push(x) -- Push element x onto stack.
6 | * pop() -- Removes the element on top of the stack.
7 | * top() -- Get the top element.
8 | * getMin() -- Retrieve the minimum element in the stack.
9 |
10 | ---
11 |
12 | ### 解题思路
13 |
14 | 使用一个变量保存当前的最小值,当 push 一个比当前最小值还要小的元素时,更新最小值。但是当当前最小值被 pop 出去时,需要**恢复到之前的最小值**,解决方法是:在 push 新的最小值时,把老的最小值压入栈,然后更新当前最小值,最后将新的最小值入栈。在 pop 时,如果 pop 出来的元素等于当前最小值,那么再从栈中 pop 出下一个元素,这个元素就是前一个最小值。
15 |
16 | 其基本思想是:**将“路径信息”保存到栈中,在合适的时机将其弹出,以恢复状态**。
17 |
--------------------------------------------------------------------------------
/树/二叉树/表达式树/README.md:
--------------------------------------------------------------------------------
1 | ### 中缀表达式转后缀表达式注释1
2 |
3 | 使用栈保存操作符,具体步骤是:
4 |
5 | * 遇到操作数时,直接输出
6 |
7 | * 遇到左括号时,将其压进栈中
8 |
9 | * 遇到右括号时,弹出栈顶的操作符,并输出,直到遇到左括号,并且**左括号不输出,右括号不进栈**
10 |
11 | * 遇到其它操作符时,弹出栈顶的操作符,并输出,直到**栈空**或**栈顶的操作符的优先级小于该操作符的优先级**或**遇到左括号**,**然后将该操作符压进栈中**
12 |
13 | * 最后将栈中的操作符弹出,直到栈空
14 |
15 | ---
16 |
17 | ### 表达式树
18 |
19 | 表达式树的叶子节点是操作数(operand),其它节点是操作符(operator)。
20 |
21 | 下面是将后缀表达式转换成表达式树的方法:
22 |
23 | 从前向后,遇到操作数时,则生成单节点,然后放到栈中;遇到操作符时,则生成一个新节点,并从栈中弹出 2 个元素,同时把这 2 个元素作为新节点的子树,然后将该新节点放进栈中。最后栈中的元素,就是表达式树的根。
24 |
25 | ---
26 |
27 | ### 注释
28 |
29 | * 注释1:
30 | 前缀表达式也叫波兰表达式;后缀表达式也叫逆波兰表达式,这两种表达式的优点是:**不需要使用括号来表达优先级**
31 |
--------------------------------------------------------------------------------
/排序算法/冒泡排序/bubble_sort.py:
--------------------------------------------------------------------------------
1 | # coding: utf8
2 |
3 |
4 | def bubble_sort(array):
5 | swapped = True
6 | for end in range(len(array) - 1, 0, -1):
7 | if not swapped:
8 | return
9 | for ind in range(0, end):
10 | if array[ind] > array[ind + 1]:
11 | swapped = True
12 | array[ind], array[ind + 1] = \
13 | array[ind + 1], array[ind]
14 |
15 |
16 | if __name__ == "__main__":
17 | import random
18 |
19 | elements = list(range(20)) * 2
20 | random.shuffle(elements)
21 | print(elements)
22 |
23 | bubble_sort(elements)
24 | print(elements)
25 |
--------------------------------------------------------------------------------
/线性表/README.md:
--------------------------------------------------------------------------------
1 | ### 简介
2 |
3 | **线性表**有两种存储结构:
4 |
5 | **1,顺序存储结构**
6 |
7 | 用一组地址连续的存储单元存储线性表的数据元素。使用顺序存储结构的线性表也叫**顺序表**。顺序表的特点是:
8 |
9 | * 支持**随机存取**
10 |
11 | * 插入、删除数据元素困难:
12 | * 删除某个位置上的数据元素时,需要将其后的所有数据元素,向前移动一个位置
13 | * 向某个位置插入数据元素时,不仅需要将该位置上及其后的所有数据元素,向后移动一个位置,还可能触发**"扩容"**
14 |
15 | **2,链式存储结构**
16 |
17 | 用一组任意的存储单元存储线性表的数据元素。使用链式存储结构的线性表也叫**链表**。链表的每个节点分为两个域:
18 |
19 | * 数据域:用于保存数据元素
20 |
21 | * 指针域:用于保存直接后继节点的存储位置
22 |
23 | 链表的特点是:
24 |
25 | * 不支持随机存取
26 |
27 | * 插入、删除数据元素时,不需要移动数据元素,改变指针即可
28 |
29 | ---
30 |
31 | ### 常用的线性表
32 |
33 | * 单链表
34 |
35 | * 循环链表
36 |
37 | * 双向链表
38 |
39 | * 栈
40 |
41 | * 队列
42 | * 链队列
43 | * 循环队列
44 |
45 | * **静态链表**
46 |
--------------------------------------------------------------------------------
/排序算法/直接插入排序/straight_insertion_sort.py:
--------------------------------------------------------------------------------
1 | # coding: utf8
2 |
3 |
4 | def straight_insertion_sort(array):
5 | if len(array) <= 1:
6 | return
7 |
8 | for i in range(1, len(array)):
9 | for j in range(0, i):
10 | if array[j] <= array[i]:
11 | continue
12 | temp = array[i]
13 | # 把 array[j...i-1] 移动到 array[j+1...i]
14 | for ind in range(i, j, -1):
15 | array[ind] = array[ind - 1]
16 | array[j] = temp
17 | break
18 |
19 |
20 | if __name__ == "__main__":
21 | import random
22 |
23 | elements = list(range(20)) * 2
24 | random.shuffle(elements)
25 | print(elements)
26 |
27 | straight_insertion_sort(elements)
28 | print(elements)
29 |
--------------------------------------------------------------------------------
/树/二叉树/线索二叉树/README.md:
--------------------------------------------------------------------------------
1 | ### 线索二叉树的原理
2 |
3 | 在二叉树的二叉链表表示法中,有 n 个节点的二叉树,共有 2×n 个指针域,其中非空指针域的数量是 n \- 1,空指针域的数量是 n + 1。
4 |
5 | 试作如下规定:
6 |
7 | * 若节点有左子树,则其左指针域指向其左孩子,否则令其左指针域指向前驱
8 |
9 | * 若节点有右子树,则其右指针域指向其右孩子,否则令其右指针域指向后继
10 |
11 | 为了避免混淆,需要改变节点结构,增加两个标志域:ltag、rtag。
12 |
13 | 其中:
14 |
15 | * ltag == 0 表示左指针域指向节点的左孩子
16 | * ltag == 1 表示左指针域指向节点的前驱
17 | * rtag == 0 表示右指针域指向节点的右孩子
18 | * rtag == 1 表示右指针域指向节点的后继
19 |
20 | 其中指向节点的前驱和后继的指针叫线索,加上线索的二叉树叫线索二叉树,对二叉树以某种次序遍历使其变成线索二叉树的过程叫线索化。
21 |
22 | ---
23 |
24 | ### 构建线索二叉树
25 |
26 | 线索化的实质是将二叉链表中的空指针修改为指向前驱或后继的线索。因为只有在遍历时才能得到前驱和后继的信息,所以线索化的过程是在遍历的过程中,修改节点的空指针:
27 |
28 | 附设一个指针 pre,使其始终指向刚刚被访问过的节点,若指针 p 指向当前正在访问的节点,则 pre 指向它的前驱。
29 |
--------------------------------------------------------------------------------
/leetcode/求字符串数组的最长公共前缀/Solution.py:
--------------------------------------------------------------------------------
1 | class Solution(object):
2 | def longestCommonPrefix(self, strs):
3 | """
4 | :type strs: List[str]
5 | :rtype: str
6 | """
7 | if not strs:
8 | return ""
9 | if len(strs) == 1:
10 | return strs[0]
11 | i = 0
12 | while True:
13 | continuos = True
14 | for ind in range(0, len(strs)-1):
15 | if i >= len(strs[ind]) or i >= len(strs[ind+1]):
16 | continuos = False
17 | break
18 | if strs[ind][i] != strs[ind+1][i]:
19 | continuos = False
20 | break
21 | if not continuos:
22 | break
23 | i = i + 1
24 | return strs[0][:i]
--------------------------------------------------------------------------------
/KMP算法/kmp.py:
--------------------------------------------------------------------------------
1 | # coding: utf8
2 |
3 |
4 | def get_next(pattern):
5 | next_array = [0] * len(pattern)
6 | for ind in range(1, len(pattern)):
7 | j = ind
8 | while j > 0:
9 | j = next_array[j - 1]
10 | if pattern[ind] == pattern[j]:
11 | next_array[ind] = j + 1
12 | break
13 | return next_array
14 |
15 |
16 | def kmp(main_string, pattern):
17 | # 计算 next 数组
18 | next_array = get_next(pattern)
19 |
20 | i = j = 0
21 | while i < len(main_string):
22 | if main_string[i] == pattern[j]:
23 | if j == len(pattern) - 1:
24 | return i - j
25 | i = i + 1
26 | j = j + 1
27 | continue
28 | if j == 0:
29 | i = i + 1
30 | else:
31 | j = next_array[j - 1]
32 |
33 |
34 | if __name__ == "__main__":
35 | print(kmp("bbaaababaabbaabb", "abaabb"))
36 |
--------------------------------------------------------------------------------
/README.md:
--------------------------------------------------------------------------------
1 | ### 简介
2 |
3 | 本项目将介绍常见的线性、树形、图状数据结构,并使用Python等进行实现。
4 |
5 | 在开始阅读本项目之前,请先阅读[基本概念](https://github.com/tim-chow/DataStructure/tree/master/%E5%9F%BA%E6%9C%AC%E6%A6%82%E5%BF%B5)。
6 |
7 | ---
8 |
9 | ### 额外说明
10 |
11 | * 对于树的遍历等操作,通常有递归和非递归两种实现,有时非递归实现非常难理解,所以博主总结出一套通过模拟栈和桢,消除递归的方式,更多细节请查看[这篇文档](http://timd.cn/eliminate-recursive/)
12 | * 在开始阅读本项目之前,最好对下面列出的**五种常用算法**有一定的了解:
13 | * 回溯算法
14 | * 动态规划
15 | * 分支限界算法
16 | * 贪心算法
17 | * 分治法
18 |
19 | ---
20 |
21 | ### 作者
22 |
23 | * [timchow](http://timd.cn)
24 |
--------------------------------------------------------------------------------
/排序算法/希尔排序/shell_sort.py:
--------------------------------------------------------------------------------
1 | # coding: utf8
2 |
3 |
4 | def shell_sort(array):
5 | gap = len(array) / 2
6 | while gap >= 1:
7 | group_sort(array, gap)
8 | gap = gap / 2
9 |
10 |
11 | def group_sort(array, gap):
12 | n = len(array)
13 | for i in range(gap):
14 | # 对分组进行直接插入排序
15 | j = 1
16 | while i + j * gap < n:
17 | for k in range(0, j):
18 | temp = array[i + j * gap]
19 | if array[i + k * gap] <= temp:
20 | continue
21 | for m in range(j, k, -1):
22 | array[i + m * gap] = array[i + (m - 1) * gap]
23 | array[i + k * gap] = temp
24 | break
25 | j = j + 1
26 |
27 |
28 | if __name__ == "__main__":
29 | import random
30 |
31 | elements = list(range(20)) * 2
32 | random.shuffle(elements)
33 | print(elements)
34 |
35 | shell_sort(elements)
36 | print(elements)
37 |
--------------------------------------------------------------------------------
/leetcode/字符串反转/string_reverse.py:
--------------------------------------------------------------------------------
1 | def _string_reverse(chars, from_index=None, end_index=None):
2 | if from_index is None:
3 | from_index = 0
4 | if end_index is None:
5 | end_index = len(chars) - 1
6 |
7 | if from_index > end_index:
8 | return chars
9 |
10 | middle = (from_index + end_index) / 2
11 | for i in range(from_index, middle + 1):
12 | j = end_index + from_index - i
13 | chars[i], chars[j] = chars[j], chars[i]
14 |
15 | return chars
16 |
17 |
18 | def string_reverse(string):
19 | chars = list(string)
20 | chars = _string_reverse(chars)
21 | start = 0
22 | index = 0
23 | while index < len(chars):
24 | if chars[index] == " ":
25 | _string_reverse(chars, start, index - 1)
26 | start = index + 1
27 | index = index + 1
28 |
29 | return "".join(chars)
30 |
31 |
32 | if __name__ == "__main__":
33 | assert string_reverse("I am a student") == "student a am I"
34 |
--------------------------------------------------------------------------------
/排序算法/快速排序/QuickSort.py:
--------------------------------------------------------------------------------
1 | # coding: utf8
2 |
3 |
4 | def quick_sort(array, start=None, end=None):
5 | if start is None:
6 | start = 0
7 | if end is None:
8 | end = len(array) - 1
9 |
10 | if start >= end:
11 | return
12 |
13 | # 选择基准元素
14 | base = array[start]
15 | pos = start
16 |
17 | for i in range(start+1, end+1):
18 | if array[i] >= base:
19 | continue
20 |
21 | array[pos] = array[i]
22 | # 将 array[pos+1...i-1] 移动到 array[pos+2...i]
23 | for j in range(i, pos+1, -1):
24 | array[j] = array[j-1]
25 | pos = pos + 1
26 | array[pos] = base
27 |
28 | # 使用快排分别对左右两部分进行排序
29 | quick_sort(array, start, pos-1)
30 | quick_sort(array, pos+1, end)
31 |
32 |
33 | if __name__ == "__main__":
34 | import random
35 |
36 | elements = list(range(20))
37 | random.shuffle(elements)
38 | print(elements)
39 |
40 | quick_sort(elements)
41 | print(elements)
42 |
--------------------------------------------------------------------------------
/线性表/链表是否有环/README.md:
--------------------------------------------------------------------------------
1 | ### 如何判断单链表是否有环
2 |
3 | 设环长为 n,初始时指针 P 和 Q 指向环上的同一个节点。P 每次前进 1 步,Q 每次前进 2 步,则 P 和 Q 下次相遇时:
4 |
5 | * P 走了 i 步,Q 走了 2 × i 步
6 |
7 | * i mod n = 2 × i mod n(i 和 2 × i 模 n 同余)
8 | 即当 i = n 时,P 和 Q 第一次相遇,相遇点是出发点
9 |
10 | 假设 P 落后 Q k 步(因为在环上,因此相当于 P 领先 Q n \- k 步),P 每次前进 1 步,Q 每次前进 2 步,则 P 和 Q 相遇时:
11 |
12 | * P 走了 i 步,Q 走了 2 × i 步
13 |
14 | * i mod n = (2 × i + k) mod n(i 和 2 × i + k 模 n 同余)
15 | 即当 i = n \- k 时,P 和 Q 第一次相遇
16 |
17 | 综上所述,**无论初始时 P 和 Q 指向哪里,只要一个每次前进 1 步,另一个每次前进 2 步,最终都会相遇,并且下次再相遇时,慢指针正好走一圈,快指针正好走两圈**。
18 |
19 | ---
20 |
21 | ### 求连接点
22 |
23 | 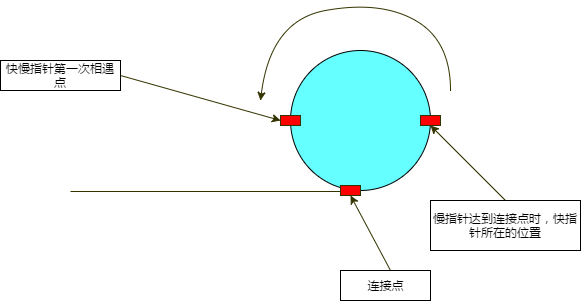
24 |
25 | 设链表的第一个节点到连接点的长度是 l,连接点到第一次相遇的节点的长度是 x,则第一次相遇时:
26 |
27 | 慢指针走了 l + x 步,快指针走了 l + x + n × R,并且快指针走的步数是慢指针的两倍,所以:
28 |
29 | 2(l + x) = l + x + nR ===>
30 |
31 | l + x = n × R ===>
32 |
33 | l = (n \- x) + n × (R \- 1)
34 |
35 | **综上所述,从第一个节点到连接点的距离等于第一次相遇的点到连接点的距离 再加上若干圈。**
36 |
37 | 因此,一个指针从相遇点出发,一个指针从第一个节点出发,最终它们会在连接点相遇。
38 |
--------------------------------------------------------------------------------
/leetcode/DropEggs问题/README.md:
--------------------------------------------------------------------------------
1 | ### 问题描述
2 |
3 | There is a building of n floors. If an egg drops from the k th floor or above, it will break. If it’s dropped from any floor below, it will not break.
4 |
5 | You’re given two eggs, Find k while minimize the number of drops for the worst case. Return the number of drops in the worst case.
6 |
7 | For n = 10, a naive way to find k is drop egg from 1st floor, 2nd floor … kth floor. But in this worst case (k = 10), you have to drop 10 times.
8 |
9 | Notice that you have two eggs, so you can drop at 4th, 7th & 9th floor, in the worst case (for example, k = 9) you have to drop 4 times.
10 |
11 | Given n = 10, return 4.
12 |
13 | Given n = 100, return 14
14 |
15 | ---
16 |
17 | ### 解题思路
18 |
19 | 因为只有 2 个鸡蛋,所以第一个鸡蛋应该按一定的距离仍,比如 10 楼、20 楼、30 楼等,如果 10 楼和 20 楼没碎,30 楼碎了,那么第二个鸡蛋就要做线性搜索,从 21 楼开始尝试,直到鸡蛋摔碎。在这种方法中,每多扔一次第一个鸡蛋,第二个鸡蛋的线性搜索次数始终是 10,所以我们需要每多扔一次第一个鸡蛋,第二个鸡蛋的线性搜索次数减少 1。设第一次从 X 层仍第一个鸡蛋,第二次从 X + (X - 1) 层仍,...,第 i 次从 X + (X - 1) + ... + (X - i - 1) 层仍
20 |
--------------------------------------------------------------------------------
/动态规划/leetcode_416.go:
--------------------------------------------------------------------------------
1 | // leetcode:https://leetcode.cn/problems/partition-equal-subset-sum/description/
2 |
3 | package main
4 |
5 | import (
6 | "fmt"
7 | )
8 |
9 | func canPartition(nums []int) bool {
10 | sum := 0
11 | for _, num := range nums {
12 | sum += num
13 | }
14 | if sum%2 == 1 {
15 | return false
16 | }
17 | W := sum / 2
18 | N := len(nums)
19 |
20 | // 转换成恰好装满的 01 背包问题。状态转移方程是:
21 | // dp[i][j] = dp[i-1][j] || dp[i-1][j-nums[i-1]]
22 | dp := make([]bool, W+1)
23 | dp[0] = true
24 | for i := 1; i <= N; i++ {
25 | for j := W; j >= nums[i-1]; j-- {
26 | dp[j] = dp[j] || dp[j-nums[i-1]]
27 | }
28 | }
29 |
30 | return dp[W]
31 | }
32 |
33 | func main() {
34 | tests := []struct {
35 | nums []int
36 | expected bool
37 | }{
38 | {[]int{1, 5, 11, 5}, true},
39 | {[]int{1, 2, 3, 5}, false},
40 | }
41 |
42 | for _, test := range tests {
43 | result := canPartition(test.nums)
44 | if result != test.expected {
45 | panic(fmt.Sprintf("nums: %s got %v, but %v expected", test.nums, result, test.expected))
46 | }
47 | }
48 | }
49 |
50 |
--------------------------------------------------------------------------------
/leetcode/最小栈/min_stack.py:
--------------------------------------------------------------------------------
1 | import sys
2 |
3 |
4 | class MinStack(object):
5 | def __init__(self):
6 | self._stack = []
7 | self._min_value = sys.maxint
8 |
9 | def push(self, x):
10 | if x < self._min_value:
11 | self._stack.append(self._min_value)
12 | self._min_value = x
13 | self._stack.append(x)
14 |
15 | def pop(self):
16 | value = self._stack.pop(-1)
17 | if value == self._min_value:
18 | self._min_value = self._stack.pop(-1)
19 | return value
20 |
21 | def top(self):
22 | return self._stack[-1]
23 |
24 | def getMin(self):
25 | return self._min_value
26 |
27 |
28 | if __name__ == "__main__":
29 | import unittest
30 | import random
31 |
32 | class MinStackTest(unittest.TestCase):
33 | def testMinStack(self):
34 | min_stack = MinStack()
35 | elements = list(range(1, 100))
36 | random.shuffle(elements)
37 | for element in elements:
38 | min_stack.push(element)
39 | self.assertEqual(min_stack.getMin(), 1)
40 |
41 | unittest.main()
42 |
--------------------------------------------------------------------------------
/树/二叉树/根据二叉树的先序、中序、后序序列还原二叉树/README.md:
--------------------------------------------------------------------------------
1 | ### 基本思想
2 |
3 | 将序列中的元素从 1 开始编号
4 |
5 | * 先序遍历的第 1 个节点和后序遍历是最后一个节点一定是根节点
6 | * 当根节点是中序遍历的第 1 个节点时,说明根节点的左子树为空,先序遍历的第 2 个节点是根节点的右孩子节点
7 | * 当根节点是中序遍历的最后一个节点时,说明根节点的右子树为空,先序遍历的第 2 个节点是根节点的左孩子节点
8 | * 否则,根节点的左右子树都不为空 ,先序遍历的第 2 个节点是根节点的左孩子,后续遍历的倒数第二个节点是根节点的右孩子
9 |
10 | 通过上面的推断,可以找到根节点及其左右孩子节点,并建立三者之间的关系。接下来只要找到左子树和右子树的先序、中序、后序序列,然后用上面的方式递归地处理就可以将所有节点之间的关系建立起来。
11 |
12 | 根据先序、中序、后序序列获取左右子树的先序,中序,后序序列的方法如下:
13 |
14 | * 如果根节点的左子树为空,则先序序列从第 2 个到最后一个元素之间的子序列是右子树的先序序列
15 |
16 | * 如果根节点的左子树为空,则中序序列从第 2 个到最后一个元素之间的子序列是右子树的中序序列
17 |
18 | * 如果根节点的左子树为空,则后序序列从第 1 个到倒数第二个元素之间的子序列是右子树的后序序列
19 |
20 | * 如果根节点的右子树为空,则先序序列从第 2 个到最后一个元素之间的子序列是左子树的先序序列
21 |
22 | * 如果根节点的右子树为空,则中序序列从第 1 个到倒数第二个元素之间的子序列是左子树的中序序列
23 |
24 | * 如果根节点的右子树为空,则后序序列从第 1 个到倒数第二个元素之间的子序列是左子树的后序序列
25 |
26 | * 否则
27 | * 找到根的右孩子节点在先序序列中的位置 pos,则先序序列从第 2 个到第 pos \- 1 个元素之间的子序列是左子树的先序序列;先序序列从第 pos 个到最后一个元素之间的子序列是右子树的先序序列
28 | * 找到根节点在中序序列中的位置 pos,则中序序列从第 1 个到第 pos \- 1 个元素之间的子序列是左子树的中序序列;中序序列从第 pos + 1 个到最后一个元素之间的子序列是右子树的中序序列
29 | * 找到根的左孩子节点在后序序列中的位置 pos,则后序序列从第 1 个到第 pos 个元素之间的子序列是左子树的后序序列;后序序列从第 pos + 1 个到倒数第二个元素之间的子序列是右子树的后序序列
30 |
--------------------------------------------------------------------------------
/图/最小生成树/graph.py:
--------------------------------------------------------------------------------
1 | # coding: utf8
2 |
3 |
4 | class HeadNode(object):
5 | def __init__(self, element):
6 | self.element = element
7 | self.next_node = None
8 |
9 |
10 | class AdjacentNode(object):
11 | def __init__(self, index, weight):
12 | self.index = index
13 | self.weight = weight
14 | self.next_node = None
15 |
16 |
17 | class Graph(object):
18 | def __init__(self):
19 | self._vertexes = []
20 |
21 | def add_vertex(self, element):
22 | self._vertexes.append(HeadNode(element))
23 |
24 | def add_edge(self, tail, head, weight):
25 | for i, j in [(tail, head), (head, tail)]:
26 | node = self._vertexes[i]
27 | while node.next_node is not None:
28 | if node.next_node.index == j:
29 | node.next_node.weight = weight
30 | break
31 | node = node.next_node
32 | else:
33 | node.next_node = AdjacentNode(j, weight)
34 |
35 | def get_vertex_count(self):
36 | return len(self._vertexes)
37 |
38 | def get_vertex(self, index):
39 | return self._vertexes[index]
40 |
--------------------------------------------------------------------------------
/排序算法/快速排序/quick_sort.go:
--------------------------------------------------------------------------------
1 | package main
2 |
3 | import (
4 | "fmt"
5 | )
6 |
7 | func quickSort(a []int, start, end int) {
8 | if start >= end {
9 | return
10 | }
11 | pos := partition(a, start, end)
12 | quickSort(a, start, pos-1)
13 | quickSort(a, pos+1, end)
14 | }
15 |
16 | func partition(a []int, start, end int) int {
17 | if start > end {
18 | panic("start should more than end")
19 | }
20 |
21 | pivot := a[start]
22 | index := start // pivot 所在的位置
23 | for start < end {
24 | for end > start {
25 | if a[end] >= pivot {
26 | end -= 1
27 | } else {
28 | a[index], a[end] = a[end], a[index]
29 | start += 1
30 | index = end
31 | break
32 | }
33 | }
34 |
35 | for start < end {
36 | if a[start] <= pivot {
37 | start += 1
38 | } else {
39 | a[start], a[index] = a[index], a[start]
40 | end -= 1
41 | index = start
42 | break
43 | }
44 | }
45 | }
46 | return index
47 | }
48 |
49 | func QuickSort(a []int) {
50 | if len(a) == 0 {
51 | return
52 | }
53 | quickSort(a, 0, len(a)-1)
54 | }
55 |
56 | func main() {
57 | a := []int{3, 2, 9, -1, 88, 66, 1, 33, -3, 33, 88, 2, 9, 3}
58 | QuickSort(a)
59 | fmt.Println(a)
60 | }
61 |
--------------------------------------------------------------------------------
/搜索算法/二分查找/BinarySearch.py:
--------------------------------------------------------------------------------
1 | def binary_search_recursive(array, target, low=None, high=None):
2 | if low is None:
3 | low = 0
4 | if high is None:
5 | high = len(array) - 1
6 |
7 | if low > high:
8 | return -1
9 |
10 | mid = (low + high) / 2
11 | if target == array[mid]:
12 | return mid
13 | if target < array[mid]:
14 | return binary_search_recursive(array, target, low, mid - 1)
15 | return binary_search_recursive(array, target, mid + 1, high)
16 |
17 |
18 | def binary_search(array, target):
19 | low = 0
20 | high = len(array) - 1
21 |
22 | while low <= high:
23 | mid = (low + high) / 2
24 | if target == array[mid]:
25 | return mid
26 | elif target < array[mid]:
27 | high = mid - 1
28 | else:
29 | low = mid + 1
30 |
31 | return -1
32 |
33 |
34 | def test():
35 | array = list(range(20))
36 | for ind, element in enumerate(array):
37 | assert binary_search(array, element) == ind
38 | assert binary_search_recursive(array, element) == ind
39 | assert binary_search(array, -1) == -1
40 |
41 |
42 | if __name__ == "__main__":
43 | test()
44 |
--------------------------------------------------------------------------------
/leetcode/最长回文子串/palindrome.py:
--------------------------------------------------------------------------------
1 | def dp(string):
2 | p = []
3 | for ind in range(len(string)):
4 | p.append([])
5 | for _ in range(len(string)):
6 | p[ind].append(None)
7 |
8 | def _dp(i, j):
9 | if p[i][j] is not None:
10 | return p[i][j]
11 | if i > j:
12 | p[i][j] = False
13 | return False
14 | if i == j:
15 | p[i][j] = True
16 | return True
17 | if string[i] != string[j]:
18 | p[i][j] = False
19 | return False
20 | if j == i + 1:
21 | p[i][j] = True
22 | return True
23 | p[i][j] = _dp(i + 1, j - 1)
24 | return p[i][j]
25 |
26 | for i in range(len(string)):
27 | for j in range(len(string) - 1, i - 1, -1):
28 | _dp(i, j)
29 |
30 | longest = None
31 | for i in range(len(p)):
32 | for j in range(len(p[i]) - 1, i - 1, -1):
33 | if p[i][j] is not None and p[i][j]:
34 | if longest is None or (j - i) > longest[1] - longest[0]:
35 | longest = i, j
36 |
37 | return longest
38 |
39 |
40 | if __name__ == "__main__":
41 | print(dp("abba2c1abba1d1"))
42 |
--------------------------------------------------------------------------------
/排序算法/选择排序/selection_sort.py:
--------------------------------------------------------------------------------
1 | # coding: utf8
2 |
3 |
4 | def selection_sort(array):
5 | n = len(array)
6 | if n <= 1:
7 | return
8 |
9 | for i in range(1, n / 2 + 1):
10 | start_index = i - 1
11 | end_index = n - i
12 | min_index, max_index = select_min_and_max(
13 | array, start_index, end_index)
14 |
15 | min_element = array[min_index]
16 | max_element = array[max_index]
17 | start_element = array[start_index]
18 | end_element = array[end_index]
19 |
20 | array[start_index] = min_element
21 | array[end_index] = max_element
22 | array[min_index] = start_element
23 | array[max_index] = end_element
24 |
25 |
26 | def select_min_and_max(array, start, end):
27 | assert start < end
28 | min_index = start
29 | max_index = start
30 |
31 | for ind in range(start + 1, end + 1):
32 | if array[ind] <= array[min_index]:
33 | min_index = ind
34 | elif array[ind] >= array[max_index]:
35 | max_index = ind
36 |
37 | return min_index, max_index
38 |
39 |
40 | if __name__ == "__main__":
41 | import random
42 |
43 | elements = [1, 0, 0, 0, 0, 0]
44 | print(elements)
45 |
46 | selection_sort(elements)
47 | print(elements)
48 |
--------------------------------------------------------------------------------
/图/DAG-有向无环图/关键路径/README.md:
--------------------------------------------------------------------------------
1 | ### 基本概念
2 |
3 | AOE 网(Activity On Edge Network)是使用:
4 |
5 |
6 | - 弧表示活动
7 | - 权值表示活动的持续时间
8 | - 顶点表示事件
9 |
10 | 的有向图。
11 |
12 | 在 AOE 网中,有如下两条原则:
13 |
14 |
15 | - 只有进入到某个顶点的所有活动都结束,该顶点所代表的事件才会发生
16 | - 当某个事件发生时,其后的活动才可以开始
17 |
18 |
19 | 在 AOE 网中,只有一个入度为 0 的顶点,称之为源点;只有一个出度为 0 的点,称之为汇点。它们分别代表工程的开始和结束。
20 |
21 | 从源点到顶点 vi 的最长路径是 vi 所代表的事件的最早发生时间,记作 ve(i),该时间决定了所有以该顶点为弧尾的弧所代表的活动的最早发生时间。将 ai 所代表的活动的最早发生时间记作e(i)。
22 |
23 | 每个活动和事件还有一个最迟发生时间,分别记作 l(i) 和 vl(i),该时间表示为了不影响工程进度,活动和事件最迟必须开始的时间。
24 |
25 |
26 | - 将 l(i) = e(i) 的活动叫关键活动
27 | - 将从源点到汇点的最长路径叫关键路径,显然关键路径上的活动都是关键活动
28 |
29 |
30 | 综上所述,寻找关键路径本质就是寻找所有关键活动。而关键活动就是 l(i) = e(i) 的活动。
31 |
32 | 设弧 <j, k> 表示活动 ai,ai 的持续时间为 duration(<j, k>),那么:
33 |
34 | * e(i) = ve(j)
35 | * l(i) = vl(k) - duration(<j, k>)
36 |
37 | 最终将寻找关键路径转换成了寻找每个事件的最早发生时间和最迟发生时间。
38 |
39 | 更多详情,请阅读延伸阅读中的文章。
40 |
41 | ---
42 |
43 | ### 延伸阅读
44 |
45 | * [https://www.cnblogs.com/william-lee/p/5043753.html](https://www.cnblogs.com/william-lee/p/5043753.html)。
46 |
--------------------------------------------------------------------------------
/动态规划/leetcode-474.go:
--------------------------------------------------------------------------------
1 | // leetcode:https://leetcode.cn/problems/ones-and-zeroes/description/
2 |
3 | package main
4 |
5 | import (
6 | "fmt"
7 | )
8 |
9 | func findMaxForm(strs []string, m int, n int) int {
10 | // 二维 01 背包
11 | N := len(strs)
12 | dp := make([][]int, m+1)
13 | for i := 0; i < len(dp); i++ {
14 | dp[i] = make([]int, n+1)
15 | }
16 |
17 | for i := 1; i <= N; i++ {
18 | w0 := 0
19 | w1 := 0
20 | for _, chr := range strs[i-1] {
21 | if chr == '0' {
22 | w0 += 1
23 | } else {
24 | w1 += 1
25 | }
26 | }
27 | for j := m; j >= w0; j-- {
28 | for k := n; k >= w1; k-- {
29 | chooseI := dp[j-w0][k-w1] + 1
30 | if chooseI > dp[j][k] {
31 | dp[j][k] = chooseI
32 | }
33 | }
34 | }
35 | }
36 | return dp[m][n]
37 | }
38 |
39 | func main() {
40 | tests := []struct {
41 | strs []string
42 | m int
43 | n int
44 | expected int
45 | }{
46 | {[]string{"10", "0001", "111001", "1", "0"}, 5, 3, 4},
47 | {[]string{"10", "0", "1"}, 1, 1, 2},
48 | }
49 |
50 | for _, test := range tests {
51 | result := findMaxForm(test.strs, test.m, test.n)
52 | if result != test.expected {
53 | panic(fmt.Sprintf("strs: %v, m: %d, n: %d got %v, but %v expected",
54 | test.strs, test.m, test.n, result, test.expected))
55 | }
56 | }
57 | }
58 |
59 |
--------------------------------------------------------------------------------
/线性表/逆转单链表/reverse_list.py:
--------------------------------------------------------------------------------
1 | # coding: utf8
2 |
3 |
4 | class Node(object):
5 | def __init__(self, element=None, next_node=None):
6 | self.element = element
7 | self.next_node = next_node
8 |
9 |
10 | def reverse_list(node):
11 | if node is None:
12 | return node
13 |
14 | p1 = node
15 | p2 = p1.next_node
16 | p1.next_node = None
17 |
18 | while p2 is not None:
19 | p3 = p2.next_node
20 | p2.next_node = p1
21 | p1 = p2
22 | p2 = p3
23 |
24 | return p1
25 |
26 |
27 | if __name__ == "__main__":
28 | import unittest
29 |
30 | class TestReverseList(unittest.TestCase):
31 | def testReverseList(self):
32 | nodes = [Node(ind, None) for ind in range(10)]
33 | for ind in range(9):
34 | nodes[ind].next_node = nodes[ind + 1]
35 | node = nodes[0]
36 | del nodes
37 |
38 | temp = node
39 | while temp is not None:
40 | print(temp.element)
41 | temp = temp.next_node
42 |
43 | print("=" * 10)
44 |
45 | head = reverse_list(node)
46 | temp = head
47 | while temp is not None:
48 | print(temp.element)
49 | temp = temp.next_node
50 |
51 | unittest.main()
52 |
--------------------------------------------------------------------------------
/树/README.md:
--------------------------------------------------------------------------------
1 | ### 树
2 |
3 | 树是以分支关系定义的层次结构,在客观世界中,树形结构非常常见,比如人类社会的族谱、各种社会组织机构都可以用树形结构来形象地表示。
4 |
5 | 树是 n(n >= 0)个节点的有限集。一棵非空树应该满足如下的性质:
6 |
7 | 有且只有一个被称作根的节点
8 |
9 | 当 n > 1 时,其余节点分成 m 个互不相交的集合:T1, ... , Tm。并且每个集合本身也是一棵树,这些树称为根的子树
10 |
11 | 值得注意的是:树的定义是一个递归定义,也就是说,在定义树的时候,又用到了树的概念,它道出了树的固有特性,在树形结构中很多操作都会用到递归。
12 |
13 | 下面列出树形结构中的一些术语:
14 |
15 | 树的节点
包含数据元素以及若干指向子树的分支
16 | 节点的度
节点的子树的数量叫做节点的度
17 | 叶子节点、终端节点
度为 0 的节点
18 | 非终端节点、分支节点
度不为 0 的节点。除根节点外,其它分支节点也叫内部节点
19 | 树的度
所有节点的度的最大值
20 | 孩子节点
如果节点 B 是节点 A 的某个子树的根,那么 B 是 A 的孩子节点
21 | 双亲节点
如果以节点 B 为根的树是节点 A 的某个子树,那么 A 是 B 的双亲节点
22 | 兄弟节点
双亲相同的节点是彼此的兄弟节点
23 | 祖先节点
从根节点到某个节点所经过的所有节点都是该节点的祖先节点
24 | 子孙节点
以某个节点为根的子树中的所有节点都是该节点的子孙节点
25 | 节点的层次
根节点在第一层,根的孩子节点在第二层,如果一个节点在第 l 层,则其孩子节点在第 l+1 层。双亲节点在同一层的节点是彼此的堂兄弟节点
26 | 树的层次
树中所有节点的层次的最大值
27 | 有序树、无序树
如果某个节点的子树是从左到右有序的,也就是不可互换的,则称该树为有序树,否则称之为无序树
28 |
29 | ---
30 |
31 | ### 森林
32 |
33 | m(m >= 0) 棵互不相交的树,组成一个森林。在树中,某个节点的子树的集合也是一个森林。
34 |
--------------------------------------------------------------------------------
/动态规划/leetcode-322.go:
--------------------------------------------------------------------------------
1 | // leetcode:https://leetcode.cn/problems/coin-change/description/
2 |
3 | package main
4 |
5 | import (
6 | "fmt"
7 | "math"
8 | )
9 |
10 | func coinChange(coins []int, amount int) int {
11 | // 将原问题转换成恰好装满的完全背包问题。状态转移方程是:
12 | // // dp[i][j] 表示将前 i 种(i 从 1 开始)硬币兑换成金额 j 时,所需的最小硬币数量
13 | // // j >= coins[i-1]
14 | // dp[i][j] = min(dp[i-1][j], dp[i-1][j-coins[i-1]] + 1)
15 | // 空间优化后的状态转移方程是:
16 | // dp[j] = min(dp[j], dp[j-coins[i-1]] + 1)
17 | N := len(coins)
18 | W := amount
19 | dp := make([]int, W+1)
20 | // 将前 0 种硬币兑换成金额 0 时,需要的最小硬币数量是 0;
21 | // 其它情况均没有合法解,因此设为 MaxInt
22 | dp[0] = 0
23 | for i := 1; i <= W; i++ {
24 | dp[i] = math.MaxInt
25 | }
26 |
27 | for i := 1; i <= N; i++ {
28 | for j := coins[i-1]; j <= W; j++ {
29 | // 防止溢出
30 | if dp[j]-1 > dp[j-coins[i-1]] {
31 | dp[j] = dp[j-coins[i-1]] + 1
32 | }
33 | }
34 | }
35 |
36 | if dp[W] == math.MaxInt {
37 | return -1
38 | } else {
39 | return dp[W]
40 | }
41 | }
42 |
43 | func main() {
44 | tests := []struct {
45 | coins []int
46 | amount int
47 | expected int
48 | }{
49 | {[]int{1, 2, 5}, 11, 3},
50 | {[]int{2}, 3, -1},
51 | {[]int{1}, 0, 0},
52 | }
53 |
54 | for _, test := range tests {
55 | result := coinChange(test.coins, test.amount)
56 | if result != test.expected {
57 | panic(fmt.Sprintf("coins: %v, amout: %d got %v, but %v expected",
58 | test.coins, test.amount, result, test.expected))
59 | }
60 | }
61 | }
62 |
63 |
--------------------------------------------------------------------------------
/树/树与等价关系/README.md:
--------------------------------------------------------------------------------
1 | ### 等价关系
2 |
3 | 设 R 是非空集合 S 上的二元关系,如果 R 是自反的、对称的、传递的,则称 R 是 S 上的等价关系。
4 |
5 |
6 | - 自反性:如果元素 a 属于集合 S,则 (a, a) 属于 R
∀ a ∈ S => (a, a) ∈ R
7 | - 对称性:如果 (a, b) 属于 R,且 a 不等于 b,则 (b, a) 属于 R
(a, b) ∈ R ∧ a ≠ b => (b, a) ∈ R
8 | - 传递性:如果 (a, b) 属于 R 且 (b, c) 属于 R,则 (a, c) 属于 R
(a, b) ∈ R ∧ (b, c) ∈ R => (a, c) ∈ R
9 |
10 |
11 | 如果 (a, b) ∈ R,则称 a 和 b 是等价的,记作 a ~ b。
12 |
13 | ---
14 |
15 | ### 树的双亲表示法
16 |
17 | 用一个链表存储树的全部结点,每个结点包含两个域:
18 |
19 | * 数据域:用来保存数据
20 |
21 | * 指针域:用来保存双亲节点在链表中的索引
22 |
23 | 因为根节点没有双亲节点,所以根节点的指针域的值是负数,可以利用这个负值来表示树的节点数量。
24 |
25 | 使用双亲表示法,便于寻找根节点和父节点。但是寻找子节点需要遍历整棵树。
26 |
27 | ---
28 |
29 | ### 如何划分等价类
30 |
31 | 按 R 将 S 划分成若干个不相交的子集 S1、S2、...、Sn,它们的并集是 S,称这些子集是 S 的等价类。
32 |
33 | 设集合 S 有 n 个元素,m 个形如 (x, y)(x, y ∈ S) 的等价偶对确定等价关系 R。将 S 划分成等价类的算法是:
34 |
35 |
36 | - 令集合 S 中的每个元素各自形成一个只包含单个结点的子集,记作 S1、S2、...、Sn
37 | - 依次读入 m 个等价偶对,对于任意等价偶对 (x, y),设 x 属于 Si,y 属于 Sj,当 Si 不等于 Sj 时,可以将 Si 合并到 Sj,并将 Si 置空(也可以将 Sj 合并到 Si,并将 Sj 置空)
38 |
39 |
40 | 进行合并时,如果总是将节点多的树合并到节点少的树,会导致树的高度变大,进而导致寻找节点所属的树的根节点的耗时增大。因此合并时,选择将节点少的树合并到节点多的树,并利用根节点的游标域保存该树的节点数量的相反数。
41 |
--------------------------------------------------------------------------------
/排序算法/快速排序/README.md:
--------------------------------------------------------------------------------
1 | ### 快速排序算法
2 |
3 | 1. 从序列中选择一个元素作为基准元素(pivot),通常选择序列的第一个元素
4 |
5 | * 通过一次排序将序列分成两部分,左面的部分中的所有元素都不大于基准元素,右面的部分中的所有元素都不小于基准元素,这样基准元素恰好在排序后应该在的位置上
6 |
7 | * 以相同的方式,对左、右两部分进行排序,直到整个序列有序
8 |
9 | ---
10 |
11 | ### 时间复杂度和空间复杂度分析
12 |
13 | **当选择的基准元素在数组的中间位置上,并且恰好是数组的中间值时**,此时只需要进行n次比较。时间复杂度是:
14 |
15 |
16 | T(n) = 2 * T(n / 2) + n ===>
17 | T(n) = 2 * (2 * T(n / 4) + n / 2) + n ===>
18 | T(n) = 4 * T(n / 4) + 2 * n ===>
19 | T(n) = 4 * (2 * T(n / 8) + n / 4) + 2 * n ===>
20 | T(n) = 8 * T(n / 8) + 3 * n ===>
21 | ...
22 | T(n) = 2m * T(n / 2m) + m * n
23 |
24 | 且 T(1) = 1,所以当 2m -> n,即 m = log2n 时,T(n) = n + n * log2n
25 |
26 | 所以,时间复杂度是 O(nlogn)
27 |
28 |
29 | **当数组是倒序的,并且选择第一个元素作为基准元素时**,一次排序下来会置换 n - 1 次元素,并且数组被分为两部分,左面的部分有 n - 1 个元素,右面的部分有 0 个元素。时间复杂度是:
30 |
31 |
32 | T(n) = T(n - 1) + T(0) + n - 1===>
33 | T(n) = (T(n - 2) + T(0) + n - 2) + T(0) + n - 1 ===>
34 | T(n) = T(n - 2) + 2 * T(0) + (n - 1) + (n - 2) ===>
35 | T(n) = (T(n - 3) + T(0) + n - 3) + 2 * T(0) + (n - 1) + (n - 2) ===>
36 | T(n) = T(n - 3) + 3 * T(0) + (n - 1) + (n - 2) + (n - 3) ===>
37 | ...
38 | T(n) = T(n - m) + m * T(0) + (n - 1) + (n - 2) + ... + (n - m)
39 |
40 | 且 T(1) = 1,所以当 m -> n - 1 时,T(n) = T(1) + (n - 1) * T(0) + (n - 1) + ... + 1 = n + n * (n - 1) / 2 = n2 / 2 + n / 2
41 |
42 | 所以时间复杂度是 O(n2)
43 |
44 |
45 | 在一趟排序中,快排耗费的空间是常数级的,但是需要递归 logn 到 n 次,所以空间复杂度在最好的情况下是 O(logn),在最坏情况下是 O(n)。
46 |
--------------------------------------------------------------------------------
/线性表/栈及其应用/README.md:
--------------------------------------------------------------------------------
1 | ### 栈
2 |
3 | 栈是一种**操作受限的线性表**:
4 |
5 | * 只允许在栈顶插入数据元素
6 |
7 | * 只允许删除、查询栈顶的数据元素
8 |
9 | 栈有两种实现方式:
10 |
11 | * 顺序栈
12 |
13 | * 链栈
14 |
15 | 栈有两个指针:
16 |
17 | * base:指向栈底
18 |
19 | * top:指向栈顶
20 |
21 | 当栈底和栈顶重合时,栈为空
22 |
23 | 顺序栈的栈顶减去栈底等于栈的大小
24 |
25 | ---
26 |
27 | ### 栈的应用
28 |
29 | * 十进制数转换成 K 进制数
30 | 除基取余,倒序排列
31 |
32 | * 判断括号是否成对出现
33 | * 遇到左括号,将其压入栈
34 | * 遇到右括号,将栈顶的数据元素弹出,并判断是否匹配
35 | * 检查栈是否为空
36 |
37 | ---
38 |
39 | ### 栈的应用:翻转字符串里的单词
40 |
41 | **原题地址:**
42 |
43 | [https://leetcode-cn.com/problems/reverse-words-in-a-string/](https://leetcode-cn.com/problems/reverse-words-in-a-string/)
44 |
45 | **Python 实现:**
46 |
47 |
48 | class Solution(object):
49 | def reverseWords(self, s):
50 | """
51 | :type s: str
52 | :rtype: str
53 | """
54 | words = []
55 |
56 | stack1 = []
57 | for char in s:
58 | stack1.append(char)
59 |
60 | stack2 = []
61 | while stack1:
62 | char = stack1.pop()
63 | if char != " ":
64 | stack2.append(char)
65 | else:
66 | word = []
67 | while stack2:
68 | word.append(stack2.pop())
69 | if word:
70 | words.append("".join(word))
71 |
72 | if stack2:
73 | word = []
74 | while stack2:
75 | word.append(stack2.pop())
76 | words.append("".join(word))
77 | return " ".join(words)
78 |
79 |
--------------------------------------------------------------------------------
/树/树与等价关系/MFSet.py:
--------------------------------------------------------------------------------
1 | # coding: utf8
2 |
3 |
4 | class Node(object):
5 | def __init__(self, element):
6 | self.element = element
7 | self.parent = -1
8 |
9 | def __str__(self):
10 | return "%s{element=%s, parent=%d}" % (
11 | self.__class__.__name__,
12 | self.element,
13 | self.parent)
14 |
15 | __repr__ = __str__
16 |
17 |
18 | class MFSet(object):
19 | def __init__(self, s, r):
20 | self._nodes = [Node(e) for e in s]
21 | self._r = r
22 | self.divide()
23 |
24 | def find_root(self, x):
25 | temp = x
26 | while self._nodes[temp].parent >= 0:
27 | temp = self._nodes[temp].parent
28 | return temp
29 |
30 | def merge(self, x, y):
31 | si = self.find_root(x)
32 | sj = self.find_root(y)
33 | if si == sj:
34 | return
35 |
36 | node_si = self._nodes[si]
37 | node_sj = self._nodes[sj]
38 |
39 | if -1 * node_si.parent >= -1 * node_sj.parent:
40 | node_si.parent = node_si.parent + node_sj.parent
41 | node_sj.parent = si
42 | else:
43 | node_sj.parent = node_si.parent + node_sj.parent
44 | node_si.parent = sj
45 |
46 | def divide(self):
47 | for x, y in self._r:
48 | self.merge(x, y)
49 |
50 | @property
51 | def nodes(self):
52 | return self._nodes
53 |
54 |
55 | if __name__ == "__main__":
56 | s = [0, 1, 2, 3, 4, 5]
57 | r = [(0, 2), (2, 4), (1, 3), (3, 5)]
58 | mfset = MFSet(s, r)
59 | print(mfset.nodes)
60 |
--------------------------------------------------------------------------------
/动态规划/README.md:
--------------------------------------------------------------------------------
1 | ### 动态规划
2 |
3 | 动态规划用于求解多阶段决策问题的最优解。
4 |
5 | 其基本思想和分治法类似注释1,都是先将待求解问题划分成若干个子问题(阶段),然后从初始状态开始,顺序求解子问题,每个子问题的决策都依赖当前状态,并且在作出决策之后,又会引起状态的转移。一个决策序列就是在状态的变化中产生出来的。在求解任一子问题的时候,需要列出所有可能的局部解,然后通过决策保留那些有可能到达全局最优解的局部解,丢弃其它局部解。按此方式,依次解决各个子问题,一直到达结束状态。
6 |
7 | 能够使用动态规划求解的问题,一般具有以下三个性质:
8 | 最优化原理无论过去的状态和决策如何,对于过去的决策,所形成的状态而言,余下的决策必须是最优决策
9 | 无后效性某个阶段的状态一旦确定,就不再受以后的决策的影响
10 | 有重叠子问题注释2子问题之间不互相独立,某个子问题可能被多次使用到,因此可以将解过的子问题缓存起来,以减少重复计算,这也是动态规划的优势
11 |
12 | 使用动态规划解决问题的一般步骤是:
13 | 划分阶段根据问题的时间或空间特征将问题划分成若干个阶段,值得注意的是:划分后的阶段一定是可排序的或有序的,否则无法使用动态规划求解
14 | 确定状态和状态变量将问题发展到各个阶段时所处的实际情况用状态表示出来,状态的选择要具有无后效性
15 | 确定决策和状态转移方程如前所述,每次决策既受限于当前状态,又会引起状态转移。状态转移方程就是从前一阶段到后一阶段的递推关系。比如对于 01 背包问题,状态转移方程是:f(i, j) = max{f(i-1, j), f(i-1, j-w[i]) + c[i]}(其中 f(i, j) 表示将前 i 个物品放进总重量为 j 的背包中所能获得的最大价值)
16 | 寻找边界条件边界条件就是结束状态
17 |
18 | ---
19 |
20 | ### 注释
21 |
22 | * 注释1:
23 | 动态规划和分治法的最大差别是:动态规划划分后得到的子问题不互相独立
24 |
25 | * 注释2:
26 | 有重叠子问题并不是适用动态规划的必要条件
27 |
28 | ---
29 |
30 | ### Read Also
31 |
32 | * [https://zhuanlan.zhihu.com/p/93857890](https://zhuanlan.zhihu.com/p/93857890)
33 |
34 |
--------------------------------------------------------------------------------
/动态规划/leetcode-42.go:
--------------------------------------------------------------------------------
1 | // leetcode:https://leetcode.cn/problems/trapping-rain-water/description/
2 |
3 | package main
4 |
5 | import "fmt"
6 |
7 | func trap(height []int) int {
8 | // 每个柱子能接的雨水与它左面的柱子中最高的(left)、它右面的柱子中最高的(right),以及其自身高度有关:
9 | // 如果它的高度与 left 和 right 中的任意一个相等或者更高,那么无法接到雨水;
10 | // 否则,接到的雨水等于 left 和 right 中的较小者与柱子本身的高度之差。
11 | // 从左向右遍历,获取每根柱子的左面的最高的柱子。
12 | // 第一根柱子的左面的最高的柱子初始化为 0,第 i 根柱子的左面的最高的柱子是第 i-1 根柱子的左面的最高的柱子和第 i-1 根柱子中的较大者
13 | left := make([]int, len(height))
14 | for i := 1; i < len(height); i++ {
15 | if left[i-1] > height[i-1] {
16 | left[i] = left[i-1]
17 | } else {
18 | left[i] = height[i-1]
19 | }
20 | }
21 | // 从右向左遍历,获取每根柱子的右面的最高的柱子。
22 | // 最右面的柱子的右面的最高的柱子初始化为 0,第 i 根柱子的右面的最高的柱子是第 i+1 根柱子的右面的最高的柱子和第 i+1 根柱子中的较大者
23 | right := make([]int, len(height))
24 | for i := len(height) - 2; i >= 0; i-- {
25 | if right[i+1] > height[i+1] {
26 | right[i] = right[i+1]
27 | } else {
28 | right[i] = height[i+1]
29 | }
30 | }
31 | sum := 0
32 | for i := 0; i < len(height); i++ {
33 | if height[i] >= left[i] || height[i] >= right[i] {
34 | continue
35 | }
36 | if left[i] > right[i] {
37 | sum += right[i] - height[i]
38 | } else {
39 | sum += left[i] - height[i]
40 | }
41 | }
42 | return sum
43 | }
44 |
45 | func main() {
46 | tests := []struct {
47 | height []int
48 | expected int
49 | }{
50 | {[]int{0, 1, 0, 2, 1, 0, 1, 3, 2, 1, 2, 1}, 6},
51 | {[]int{4, 2, 0, 3, 2, 5}, 9},
52 | }
53 |
54 | for _, test := range tests {
55 | result := trap(test.height)
56 | if test.expected != result {
57 | panic(fmt.Sprintf("height: %v got %d, but %d expected", test.height, result, test.expected))
58 | }
59 | }
60 | }
61 |
--------------------------------------------------------------------------------
/回溯算法/Empress.py:
--------------------------------------------------------------------------------
1 | from typing import List
2 |
3 |
4 | def _is_safe(status: List[int], next_: int) -> bool:
5 | for row in range(next_):
6 | # 在同一列或同一斜线上不安全
7 | if status[row] == status[next_] or abs(row - next_) == abs(status[row] - status[next_]):
8 | return False
9 | return True
10 |
11 |
12 | def empress(n: int) -> int:
13 | result: int = 0
14 | # 第 i 行的皇后所在的列,元素的取值范围是 0 到 n-1
15 | status: List[int] = [0] * n
16 | # 当前正在处理的行,取值范围是 0 到 n-1
17 | current: int = 0
18 | while current >= 0:
19 | # 当前节点是最终状态
20 | if current == n - 1:
21 | result += 1
22 | status[current] += 1
23 | if current > 0:
24 | current -= 1
25 | elif status[current] >= n:
26 | break
27 | continue
28 | next_: int = current + 1
29 | # 无法继续前进
30 | if status[next_] >= n:
31 | status[next_] = 0
32 | status[current] += 1
33 | if current > 0:
34 | current -= 1
35 | elif status[current] >= n:
36 | break
37 | continue
38 | # 无法到达最终状态
39 | if not _is_safe(status, next_):
40 | status[next_] += 1
41 | continue
42 | # 只有满足条件才会入栈
43 | current = next_
44 |
45 | return result
46 |
47 |
48 | def main() -> None:
49 | for n in range(1, 11):
50 | print(n, ":", empress(n))
51 |
52 | # Output:
53 | # 1 : 1
54 | # 2 : 0
55 | # 3 : 0
56 | # 4 : 2
57 | # 5 : 10
58 | # 6 : 4
59 | # 7 : 40
60 | # 8 : 92
61 | # 9 : 352
62 | # 10 : 724
63 |
64 |
65 | if __name__ == "__main__":
66 | main()
67 |
68 |
--------------------------------------------------------------------------------
/排序算法/归并排序/merge_sort.go:
--------------------------------------------------------------------------------
1 | package main
2 |
3 | import "fmt"
4 |
5 | func merge(a []int, start, mid, end int) {
6 | // 前提:a[start...mid] 有序,a[mid+1...end]有序
7 | // 目标:使 a[start...end] 有序
8 |
9 | // 临时数组
10 | temp := make([]int, end-start+1)
11 | cursor := 0
12 | i := start
13 | j := mid + 1
14 | for i <= mid && j <= end {
15 | if a[i] < a[j] {
16 | temp[cursor] = a[i]
17 | i += 1
18 | } else {
19 | temp[cursor] = a[j]
20 | j += 1
21 | }
22 | cursor += 1
23 | }
24 | for ; i <= mid; i++ {
25 | temp[cursor] = a[i]
26 | cursor += 1
27 | }
28 | for ; j <= end; j++ {
29 | temp[cursor] = a[j]
30 | cursor += 1
31 | }
32 |
33 | for i := 0; i < len(temp); i++ {
34 | a[i+start] = temp[i]
35 | }
36 | }
37 |
38 | func mergeSortRecursive(a []int, start, end int) {
39 | if end <= start {
40 | return
41 | }
42 | mid := (start + end) / 2
43 | mergeSortRecursive(a, start, mid)
44 | mergeSortRecursive(a, mid+1, end)
45 | merge(a, start, mid, end)
46 | }
47 |
48 | func MergeSortRecursive(a []int) {
49 | mergeSortRecursive(a, 0, len(a)-1)
50 | }
51 |
52 | func MergeSort(a []int) {
53 | step := 1
54 | for step <= len(a) {
55 | step *= 2
56 | for start := 0; start < len(a); start += step {
57 | end := start + step - 1
58 | mid := (start + end) / 2
59 | if end >= len(a) {
60 | end = len(a) - 1
61 | mid = start + step/2 - 1
62 | if mid > end {
63 | mid = end
64 | }
65 | }
66 | merge(a, start, mid, end)
67 | }
68 | }
69 | }
70 |
71 | func main() {
72 | a := []int{3, 2, 9, -1, 88, 66, 1, 33, -3, 33, 88, 2, 9, 3}
73 | MergeSort(a)
74 | fmt.Println(a)
75 | a = []int{3, 2, 9, -1, 88, 66, 1, 33, -3, 33, 88, 2, 9, 3}
76 | MergeSortRecursive(a)
77 | fmt.Println(a)
78 | }
79 |
--------------------------------------------------------------------------------
/分支限界算法/max_loading.go:
--------------------------------------------------------------------------------
1 | package main
2 |
3 | import "fmt"
4 |
5 | func MaxLoading(weights []int, c1, c2 int) bool {
6 | if len(weights) == 0 {
7 | return true
8 | }
9 | // remaining[i] 表示装完第 i 个元素之后,仍然剩余的重量
10 | remaining := make([]int, len(weights))
11 | sum := weights[len(weights)-1]
12 | for i := len(weights) - 2; i >= 0; i-- {
13 | remaining[i] = weights[i+1] + remaining[i+1]
14 | sum += weights[i]
15 | }
16 |
17 | // 0 表示重量为 0,-1 表示 Dummy 节点,是每一层的分隔符
18 | queue := []int{0, -1}
19 | for ind := 0; ind < len(weights); ind++ {
20 | node := queue[0]
21 | queue = queue[1:]
22 | for node != -1 {
23 | // 列出所有孩子节点
24 |
25 | // 情况 1:能装下
26 | if node+weights[ind] <= c1 {
27 | queue = append(queue, node+weights[ind])
28 | }
29 | // 情况 2:可以不装
30 | if node+weights[ind]+remaining[ind] > c1 {
31 | queue = append(queue, node)
32 | }
33 | node = queue[0]
34 | queue = queue[1:]
35 | }
36 | // 在每一层的末尾防止 Dummy 节点
37 | queue = append(queue, -1)
38 | }
39 |
40 | // 获取 c1 最多能装多少
41 | best := 0
42 | // 最后一个节点是 Dummy 节点,去掉
43 | for ind := 0; ind < len(queue)-1; ind++ {
44 | if queue[ind] > best {
45 | best = queue[ind]
46 | }
47 | }
48 | fmt.Printf("best: %d\n", best)
49 |
50 | // 总重量减去 c1 必须小于或等于 c2,才能装载
51 | return sum-best <= c2
52 | }
53 |
54 | func main() {
55 | tests := []struct {
56 | weights []int
57 | c1 int
58 | c2 int
59 | expected bool
60 | }{
61 | {
62 | []int{20, 28, 25, 25},
63 | 70,
64 | 30,
65 | true,
66 | },
67 | }
68 |
69 | for _, test := range tests {
70 | got := MaxLoading(test.weights, test.c1, test.c2)
71 | if got != test.expected {
72 | fmt.Printf("got %v, but %v expected\n", got, test.expected)
73 | panic("should equal")
74 | }
75 | }
76 | }
77 |
--------------------------------------------------------------------------------
/排序算法/快速排序/leetcode-215.py:
--------------------------------------------------------------------------------
1 | # 寻找数组中第 K 大的元素:https://leetcode.com/problems/kth-largest-element-in-an-array/
2 |
3 | from typing import List
4 |
5 |
6 | class Solution:
7 | def findKthLargest(self, nums: List[int], k: int) -> int:
8 | if not nums or k <= 0 or k > len(nums):
9 | return -1
10 | low: int = 0
11 | high: int = len(nums) - 1
12 | current: int = self.partition(nums, low, high)
13 | target = len(nums) - k
14 | while current != target:
15 | if current > target:
16 | high = current - 1
17 | current = self.partition(nums, low, high)
18 | continue
19 | if current < target:
20 | low = current + 1
21 | current = self.partition(nums, low, high)
22 | continue
23 | return nums[target]
24 |
25 | def partition(self, nums: List[int], start: int, end: int) -> int: # noqa
26 | if start > end:
27 | raise RuntimeError("start should be less than or equal end")
28 | pivot: int = nums[start]
29 | index: int = start
30 | while start < end:
31 | while end > start:
32 | if nums[end] >= pivot:
33 | end -= 1
34 | continue
35 | nums[index], nums[end] = nums[end], nums[index]
36 | index = end
37 | start += 1
38 | break
39 | while start < end:
40 | if nums[start] <= pivot:
41 | start += 1
42 | continue
43 | nums[index], nums[start] = nums[start], nums[index]
44 | index = start
45 | end -= 1
46 | break
47 | return index
48 |
--------------------------------------------------------------------------------
/排序算法/快速排序/offer-40.py:
--------------------------------------------------------------------------------
1 | # 获取最小的 k 个数:https://leetcode.cn/problems/zui-xiao-de-kge-shu-lcof/
2 |
3 | from typing import List
4 |
5 |
6 | class Solution:
7 | def getLeastNumbers(self, arr: List[int], k: int) -> List[int]:
8 | if not arr or k <= 0:
9 | return []
10 | if len(arr) <= k:
11 | return arr
12 | low: int = 0
13 | high: int = len(arr) - 1
14 | current: int = self.partition(arr, low, high)
15 | target = k
16 | while current != target:
17 | if current > target:
18 | high = current - 1
19 | current = self.partition(arr, low, high)
20 | continue
21 | if current < target:
22 | low = current + 1
23 | current = self.partition(arr, low, high)
24 | continue
25 | return arr[:target]
26 |
27 | def partition(self, nums: List[int], start: int, end: int) -> int: # noqa
28 | if start > end:
29 | raise RuntimeError("start should be less than or equal end")
30 | pivot: int = nums[start]
31 | index: int = start
32 | while start < end:
33 | while end > start:
34 | if nums[end] >= pivot:
35 | end -= 1
36 | continue
37 | nums[index], nums[end] = nums[end], nums[index]
38 | index = end
39 | start += 1
40 | break
41 | while start < end:
42 | if nums[start] <= pivot:
43 | start += 1
44 | continue
45 | nums[index], nums[start] = nums[start], nums[index]
46 | index = start
47 | end -= 1
48 | break
49 | return index
50 |
--------------------------------------------------------------------------------
/动态规划/leetcode_10.go:
--------------------------------------------------------------------------------
1 | // leetcode:https://leetcode.cn/problems/regular-expression-matching/description/
2 |
3 | package main
4 |
5 | import (
6 | "fmt"
7 | )
8 |
9 | func isMatch(s string, p string) bool {
10 | // dp[i][j] 表示 s 的前 i(从 1 开始)个字符与 p 的前 j(从 1 开始)个字符是否匹配
11 | // dp[0][0] = true 表示空串与空串匹配
12 | dp := make([][]bool, len(s)+1)
13 | for i := 0; i < len(dp); i++ {
14 | dp[i] = make([]bool, len(p)+1)
15 | }
16 | // 初始化 dp 数组
17 | dp[0][0] = true
18 | for j := 2; j <= len(p); j++ {
19 | if p[j-1] == '*' {
20 | dp[0][j] = dp[0][j-2]
21 | }
22 | }
23 |
24 | // 状态转移方程
25 | for i := 1; i <= len(s); i++ {
26 | for j := 1; j <= len(p); j++ {
27 | if p[j-1] == '*' {
28 | // 如果 j 为 *
29 | if j >= 2 && dp[i][j-2] {
30 | // 如果 s[1...i] 与 p[1...j-2] 匹配,那么 dp[i][j] = true。
31 | // 此时,* 表示重复 p 的第 j-1 个字符 0 次
32 | dp[i][j] = true
33 | } else {
34 | // 如果 s[1...i-1] 与 p[1...j] 匹配,并且 s 的第 i 个字符与 p 的第 j-1 个字符匹配,那么 dp[i][j] = true。
35 | // 此时,* 的复制能力增加 1
36 | if dp[i-1][j] && j >= 2 && (p[j-2] == '.' || s[i-1] == p[j-2]) {
37 | dp[i][j] = true
38 | }
39 | }
40 | } else {
41 | // 如果 j 不为 *
42 | if dp[i-1][j-1] && (p[j-1] == '.' || s[i-1] == p[j-1]) {
43 | // 那么当 s[1...i-1] 和 p[1...j-1] 匹配,并且 s 的第 i 个字符与 p 的第 j 个字符匹配时,dp[i][j] = true
44 | dp[i][j] = true
45 | }
46 | }
47 | }
48 | }
49 |
50 | return dp[len(s)][len(p)]
51 | }
52 |
53 | func main() {
54 | tests := []struct {
55 | s string
56 | p string
57 | expected bool
58 | }{
59 | {"aa", "a", false},
60 | {"aa", "a*", true},
61 | {"ab", ".*", true},
62 | }
63 |
64 | for _, test := range tests {
65 | result := isMatch(test.s, test.p)
66 | if result != test.expected {
67 | panic(fmt.Sprintf("s: %s, p: %s got %v, but %v expected",
68 | test.s, test.p, result, test.expected))
69 | }
70 | }
71 | }
72 |
73 |
--------------------------------------------------------------------------------
/线性表/栈及其应用/sequential_stack.py:
--------------------------------------------------------------------------------
1 | # coding: utf8
2 |
3 |
4 | class Stack(object):
5 | def __init__(self):
6 | self._array_list = []
7 | self._base = self._top = 0
8 |
9 | def push(self, element):
10 | self._array_list.append(element)
11 | self._top = self._top + 1
12 |
13 | def is_empty(self):
14 | return self._base == self._top
15 |
16 | def size(self):
17 | return self._top - self._base
18 |
19 | def pop(self):
20 | if self.is_empty():
21 | raise RuntimeError("stack is empty")
22 | element = self._array_list.pop()
23 | self._top = self._top - 1
24 | return element
25 |
26 | def peek(self):
27 | if self.is_empty():
28 | raise RuntimeError("stack is empty")
29 | return self._array_list[-1]
30 |
31 |
32 | def is_pair(string):
33 | lefts = {"{", "[", "("}
34 | matches = {"{": "}", "[": "]", "(": ")"}
35 |
36 | stack = Stack()
37 | for char in string:
38 | if char in lefts:
39 | # 遇到左括号,压栈
40 | stack.push(char)
41 | else:
42 | # 遇到右括号弹出栈顶元素,并判断是否匹配
43 | if stack.size() == 0:
44 | return False
45 | left = stack.pop()
46 | if char != matches[left]:
47 | return False
48 |
49 | # 最后检查栈是否为空
50 | return stack.size() == 0
51 |
52 |
53 | def conversion(n, base):
54 | result = ["+"]
55 | if n < 0:
56 | result[0] = "-"
57 | n = -1 * n
58 |
59 | stack = Stack()
60 | while n != 0:
61 | stack.push(n % base)
62 | n = n / base
63 |
64 | while stack.size() > 0:
65 | result.append(stack.pop())
66 |
67 | return result
68 |
69 |
70 | if __name__ == "__main__":
71 | print(is_pair("[[]]()"))
72 | print(is_pair("[[()()]"))
73 | print(conversion(35, 18))
74 |
--------------------------------------------------------------------------------
/排序算法/堆排序以及topk问题/leetcode-973.py:
--------------------------------------------------------------------------------
1 | # 距离原点最近的 K 个点:https://leetcode.com/problems/k-closest-points-to-origin/
2 |
3 | from typing import List
4 |
5 |
6 | class Solution:
7 | def kClosest(self, points: List[List[int]], k: int) -> List[List[int]]:
8 | if not points or k <= 0:
9 | return []
10 | if len(points) <= k:
11 | return points
12 |
13 | # 将数组的前 k 个元素堆化
14 | for idx in range(k // 2, -1, -1):
15 | self.adjust(points, idx, k - 1)
16 | for idx in range(k, len(points)):
17 | if self._less_than(points[0], points[idx]):
18 | continue
19 | points[0], points[idx] = points[idx], points[0]
20 | self.adjust(points, 0, k - 1)
21 | return points[:k]
22 |
23 | def _less_than(self, point1: List[int], point2: List[int]) -> bool: # noqa
24 | return (point1[0] * point1[0] + point1[1] * point1[1]) < (point2[0] * point2[0] + point2[1] * point2[1])
25 |
26 | # 大根堆
27 | def adjust(self, arr: List[List[int]], start: int, end: int) -> None: # noqa
28 | if start >= end:
29 | return
30 | while 2 * start + 1 <= end:
31 | left: int = 2 * start + 1
32 | right: int = 2 * start + 2
33 | # 如果没有右孩子
34 | if right > end:
35 | if self._less_than(arr[start], arr[left]):
36 | arr[start], arr[left] = arr[left], arr[start]
37 | break
38 | if not self._less_than(arr[start], arr[left]) and not self._less_than(arr[start], arr[right]):
39 | break
40 | if not self._less_than(arr[left], arr[right]):
41 | # 与左孩子交换
42 | arr[start], arr[left] = arr[left], arr[start]
43 | start = left
44 | continue
45 | arr[start], arr[right] = arr[right], arr[start]
46 | start = right
47 |
--------------------------------------------------------------------------------
/分支限界算法/max_loading.py:
--------------------------------------------------------------------------------
1 | from typing import List
2 |
3 |
4 | class Node:
5 | def __init__(self) -> None:
6 | self.weight: int = 0
7 |
8 |
9 | _dummy_node: Node = Node()
10 |
11 |
12 | class MaxLoading:
13 | def __init__(self, weights: List[int], c1_capacity: int, c2_capacity: int) -> None:
14 | self._weights: List[int] = weights
15 | self._c1_capacity: int = c1_capacity
16 | self._c2_capacity: int = c2_capacity
17 |
18 | # 装完第 i 件物品后,仍然剩余的总重量
19 | self._remaining: List[int] = [0 for _ in range(len(weights))]
20 | ind: int = len(self._weights) - 2
21 | while ind >= 0:
22 | self._remaining[ind] = self._remaining[ind + 1] + self._weights[ind + 1]
23 | ind -= 1
24 |
25 | def can_load(self) -> bool:
26 | if not len(self._weights):
27 | return True
28 | # 对第一艘船进行优化,尽量装满它
29 | queue: List[Node] = [Node(), _dummy_node]
30 | for ind in range(len(self._weights)): # type: int
31 | node: Node = queue.pop(0)
32 | while node is not _dummy_node:
33 | # 情况 1:能装下
34 | if node.weight + self._weights[ind] <= self._c1_capacity:
35 | new_node: Node = Node()
36 | new_node.weight = node.weight + self._weights[ind]
37 | queue.append(new_node)
38 | # 情况 2:可以不装
39 | if node.weight + self._weights[ind] + self._remaining[ind] > self._c1_capacity:
40 | queue.append(node)
41 | node = queue.pop(0)
42 | queue.append(_dummy_node)
43 |
44 | best: int = 0
45 | for node in queue[:-1]: # type: Node
46 | if node.weight > best:
47 | best = node.weight
48 | print(best)
49 | return sum(self._weights) - best <= self._c2_capacity
50 |
51 |
52 | if __name__ == "__main__":
53 | print(MaxLoading([20, 28, 25, 25], 70, 30).can_load())
54 |
--------------------------------------------------------------------------------
/分支限界算法/shortest_path.py:
--------------------------------------------------------------------------------
1 | from queue import PriorityQueue
2 | from typing import List, Dict, Tuple
3 |
4 | GraphType = Tuple[List[str], List[List[int]]]
5 |
6 |
7 | def generate_direct_graph_example() -> GraphType:
8 | vertexes: List[str] = ['s', 'a', 'b', 'c', 'd', 'e',
9 | 'f', 'g', 'h', 'i', 't']
10 | arches: List[List[int]] = [
11 | [0, 2, 3, 4, 0, 0, 0, 0, 0, 0, 0],
12 | [0, 0, 3, 0, 7, 2, 0, 0, 0, 0, 0],
13 | [0, 0, 0, 0, 0, 9, 2, 0, 0, 0, 0],
14 | [0, 0, 0, 0, 0, 0, 2, 0, 0, 0, 0],
15 | [0, 0, 0, 0, 0, 0, 0, 2, 3, 0, 0],
16 | [0, 0, 0, 0, 0, 0, 1, 0, 3, 0, 0],
17 | [0, 0, 0, 0, 0, 0, 0, 0, 5, 1, 0],
18 | [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1],
19 | [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 2],
20 | [0, 0, 0, 0, 0, 0, 0, 0, 2, 0, 2],
21 | [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0],
22 | ]
23 | return vertexes, arches
24 |
25 |
26 | def shortest_path(graph: GraphType, start: int) -> Dict[int, int]:
27 | queue: PriorityQueue = PriorityQueue()
28 | queue.put((0, start))
29 | result: Dict[int, int] = {}
30 | while not queue.empty():
31 | # 第一个活节点是当前扩展节点
32 | current_weight, index = queue.get() # type: int, int
33 | # 列出当前扩展节点的所有孩子节点
34 | for index, weight in enumerate(graph[1][index]): # type: int, int
35 | if not weight:
36 | continue
37 | # 剪去无法到达最优解的孩子节点
38 | if index in result and result[index] <= weight + current_weight:
39 | continue
40 | # 将其余孩子节点添加到活结点列表,并使用限界函数进行排序
41 | result[index] = weight + current_weight
42 | queue.put((result[index], index))
43 | return result
44 |
45 |
46 | if __name__ == "__main__":
47 | graph: GraphType = generate_direct_graph_example()
48 | result: Dict[int, int] = shortest_path(graph, 0)
49 | for idx, weight in result.items():
50 | print(f"s -> {graph[0][idx]}: {weight}")
51 |
--------------------------------------------------------------------------------
/图/最小生成树/kruskal.py:
--------------------------------------------------------------------------------
1 | # coding: utf8
2 |
3 | from graph import Graph
4 |
5 |
6 | def kruskal(graph):
7 | """
8 | Kruskal 算法实现
9 | """
10 | # 获取原图的边集
11 | edges = []
12 | duplicate_set = set()
13 | for index in range(graph.get_vertex_count()):
14 | node = graph.get_vertex(index).next_node
15 | while node is not None:
16 | # 排重
17 | if (index, node.index) in duplicate_set or \
18 | (node.index, index) in duplicate_set:
19 | node = node.next_node
20 | continue
21 | edges.append((index, node.index, node.weight))
22 | duplicate_set.add((index, node.index))
23 | node = node.next_node
24 | # 对原图的边集进行排序
25 | edges = sorted(edges, key=lambda t: t[2])
26 |
27 | # 初始化结果边集
28 | T = []
29 |
30 | # 初始化并查集
31 | union_find = [i for i in range(graph.get_vertex_count())]
32 |
33 | def find_root(index):
34 | temp = index
35 | while union_find[temp] != temp:
36 | temp = union_find[temp]
37 | return temp
38 |
39 | while edges:
40 | # 从原图的剩余边中选择代价最小的边
41 | edge = edges.pop(0)
42 | # 判断其与 T 中的边是否构成环
43 | # 如果是,则丢弃该边
44 | root_0 = find_root(edge[0])
45 | root_1 = find_root(edge[1])
46 | if root_0 == root_1:
47 | continue
48 | # 否则,将其加入到 T
49 | T.append(edge)
50 | # 将 root_1 接到 root_0
51 | union_find[root_1] = root_0
52 |
53 | return T
54 |
55 |
56 | def test():
57 | g = Graph()
58 | for ch in ["A", "B", "C", "D", "E", "F", "G"]:
59 | g.add_vertex(ch)
60 | for edge in [(0, 1, 7), (0, 3, 5), (1, 2, 8),
61 | (1, 3, 9), (1, 4, 7), (2, 4, 5),
62 | (3, 4, 15), (3, 5, 6), (4, 5, 8),
63 | (4, 6, 9), (5, 6, 11)]:
64 | g.add_edge(*edge)
65 |
66 | print(kruskal(g))
67 |
68 |
69 | if __name__ == "__main__":
70 | test()
71 |
--------------------------------------------------------------------------------
/线性表/快慢指针法/slow_fast_pointer.py:
--------------------------------------------------------------------------------
1 | # coding: utf8
2 |
3 |
4 | class Node(object):
5 | def __init__(self, element=None, next_node=None):
6 | self.element = element
7 | self.next_node = next_node
8 |
9 |
10 | def get_middle_node(linked_list):
11 | if linked_list is None:
12 | return None
13 |
14 | # 快指针每次前进 2 步,慢指针每次前进 1 步,当快指针到头时,慢指针到达中间节点
15 | slow = fast = linked_list
16 | while fast is not None:
17 | fast = fast.next_node
18 | if fast is not None:
19 | fast = fast.next_node
20 | slow = slow.next_node
21 |
22 | return slow
23 |
24 |
25 | def get_last_node(linked_list, k):
26 | slow = fast = linked_list
27 |
28 | # 快指针先前进 k - 1 步
29 | for _ in range(k):
30 | if fast is None:
31 | return linked_list
32 | fast = fast.next_node
33 |
34 | # 然后慢指针开始出发
35 | while fast is not None:
36 | slow = slow.next_node
37 | fast = fast.next_node
38 |
39 | return slow
40 |
41 |
42 | if __name__ == "__main__":
43 | import unittest
44 |
45 | class SlowFastPointerTest(unittest.TestCase):
46 | def setUp(self):
47 | nodes = [Node(ind) for ind in range(100)]
48 | for ind in range(99):
49 | nodes[ind].next_node = nodes[ind + 1]
50 | self.node = nodes[0]
51 | self.middle_node = nodes[50]
52 | self.last_1st_node = nodes[99]
53 | self.last_3rd_node = nodes[97]
54 | self.last_100th_node = nodes[0]
55 | del nodes
56 |
57 | def testGetMiddleNode(self):
58 | self.assertIs(get_middle_node(self.node), self.middle_node)
59 |
60 | def testGetLastNode(self):
61 | self.assertIs(get_last_node(self.node, 1), self.last_1st_node)
62 | self.assertIs(get_last_node(self.node, 3), self.last_3rd_node)
63 | self.assertIs(get_last_node(self.node, 100), self.last_100th_node)
64 | unittest.main()
65 |
--------------------------------------------------------------------------------
/图/最小生成树/prim.py:
--------------------------------------------------------------------------------
1 | # coding: utf8
2 |
3 | from graph import Graph
4 |
5 |
6 | def prim(graph, start=0):
7 | """
8 | Prim 算法实现
9 | """
10 | # 初始化顶点集和边集
11 | u = [start]
12 | e = []
13 |
14 | # 初始化 closedge 数组
15 | closedge = [None] * graph.get_vertex_count()
16 | node = graph.get_vertex(start).next_node
17 | while node is not None:
18 | closedge[node.index] = (start, node.weight)
19 | node = node.next_node
20 | # (-1, -1) 表示已经在顶点集中
21 | closedge[start] = (-1, -1)
22 |
23 | while len(u) != graph.get_vertex_count():
24 | # 选择代价最小的边
25 | lowest_cost = None
26 | for index, edge in enumerate(closedge):
27 | if edge == (-1, -1) or edge is None:
28 | continue
29 | if lowest_cost is None or edge[1] < lowest_cost[2]:
30 | lowest_cost = (edge[0], index, edge[1])
31 |
32 | # 将顶点加入到 u
33 | u.append(lowest_cost[1])
34 | # 将边加入到 e
35 | e.append(lowest_cost)
36 |
37 | # 更新 closedge 数组
38 | closedge[lowest_cost[1]] = (-1, -1)
39 | node = graph.get_vertex(lowest_cost[1]).next_node
40 | while node is not None:
41 | if closedge[node.index] == (-1, -1):
42 | pass
43 | elif closedge[node.index] is None or closedge[node.index][1] > node.weight:
44 | closedge[node.index] = (lowest_cost[1], node.weight)
45 | node = node.next_node
46 |
47 | return u, e
48 |
49 |
50 | def test():
51 | g = Graph()
52 | for ch in ["A", "B", "C", "D", "E", "F", "G"]:
53 | g.add_vertex(ch)
54 | for edge in [(0, 1, 7), (0, 3, 5), (1, 2, 8),
55 | (1, 3, 9), (1, 4, 7), (2, 4, 5),
56 | (3, 4, 15), (3, 5, 6), (4, 5, 8),
57 | (4, 6, 9), (5, 6, 11)]:
58 | g.add_edge(*edge)
59 |
60 | u, e = prim(g)
61 | print(u)
62 | print(e)
63 |
64 |
65 | if __name__ == "__main__":
66 | test()
67 |
--------------------------------------------------------------------------------
/排序算法/堆排序以及topk问题/HeapSort.py:
--------------------------------------------------------------------------------
1 | # coding: utf8
2 |
3 |
4 | def adjust(array, start, end):
5 | if start > end:
6 | raise RuntimeError("unreachable")
7 |
8 | while 2 * start + 1 <= end:
9 | left = 2 * start + 1
10 |
11 | # 只有左孩子节点
12 | if 2 * start + 2 > end:
13 | if array[left] < array[start]:
14 | array[start], array[left] = \
15 | array[left], array[start]
16 | break
17 |
18 | right = 2 * start + 2
19 | # 无需调整
20 | if array[start] <= array[left] and \
21 | array[start] <= array[right]:
22 | break
23 |
24 | if array[left] <= array[right]:
25 | array[start], array[left] = \
26 | array[left], array[start]
27 | start = left
28 | continue
29 |
30 | array[start], array[right] = \
31 | array[right], array[start]
32 | start = right
33 |
34 |
35 | def heap_sort(array):
36 | for ind in range(len(array) / 2, -1, -1):
37 | adjust(array, ind, len(array) - 1)
38 |
39 | for end in range(len(array) - 1, 0, -1):
40 | array[0], array[end] = array[end], array[0]
41 | adjust(array, 0, end - 1)
42 |
43 |
44 | def topk(array, k):
45 | if k >= len(array):
46 | return
47 |
48 | for ind in range(k / 2, -1, -1):
49 | adjust(array, ind, k - 1)
50 |
51 | for ind in range(k, len(array)):
52 | if array[ind] <= array[0]:
53 | continue
54 |
55 | array[0], array[ind] = array[ind], array[0]
56 | adjust(array, 0, k - 1)
57 |
58 |
59 | if __name__ == "__main__":
60 | import random
61 | elements = list(range(1, 16) * 2)
62 | random.shuffle(elements)
63 | print("elements are: %s" % elements)
64 | heap_sort(elements)
65 | print("heap sort: %s" % elements)
66 | random.shuffle(elements)
67 | print("elements are: %s" % elements)
68 | topk(elements, 3)
69 | print("top 3: %s" % elements)
70 |
--------------------------------------------------------------------------------
/排序算法/桶排序/bucket_sort.py:
--------------------------------------------------------------------------------
1 | # coding: utf8
2 |
3 |
4 | def bucket_sort(array, m, divide_func, sort_func):
5 | n = len(array)
6 |
7 | # 创建桶
8 | buckets = [([None] * n) for _ in range(m)]
9 |
10 | bucket_index_to_cursor = {}
11 | # 将元素放到相应的桶中
12 | for element in array:
13 | bucket_index = divide_func(element)
14 | if bucket_index not in bucket_index_to_cursor:
15 | bucket_index_to_cursor[bucket_index] = 0
16 | else:
17 | bucket_index_to_cursor[bucket_index] = \
18 | bucket_index_to_cursor[bucket_index] + 1
19 | buckets[bucket_index][bucket_index_to_cursor[bucket_index]] = element
20 |
21 | # 对每个桶内的数据元素进行排序
22 | for bucket_index, last_index in bucket_index_to_cursor.items():
23 | sort_func(buckets[bucket_index], 0, last_index)
24 |
25 | # 将桶中的元素复制回序列
26 | cursor = 0
27 | for bucket_index, last_index in sorted(bucket_index_to_cursor.items(), key=lambda k: k):
28 | bucket = buckets[bucket_index]
29 | for index in range(last_index + 1):
30 | array[cursor] = bucket[index]
31 | cursor = cursor + 1
32 |
33 |
34 | if __name__ == "__main__":
35 | import random
36 |
37 |
38 | def divide(element):
39 | if element < 5:
40 | return 0
41 | if element < 10:
42 | return 1
43 | if element < 15:
44 | return 2
45 | return 3
46 |
47 | # 直接插入排序
48 | def sort(array, start, end):
49 | if start >= end:
50 | return
51 | for i in range(start + 1, end + 1):
52 | for j in range(0, i):
53 | if array[j] <= array[i]:
54 | continue
55 | temp = array[i]
56 | # 把 array[j...i-1] 移动到 array[j+1...i]
57 | for ind in range(i, j, -1):
58 | array[ind] = array[ind - 1]
59 | array[j] = temp
60 | break
61 |
62 | elements = list(range(20)) * 2
63 | random.shuffle(elements)
64 | print(elements)
65 |
66 | bucket_sort(elements, 4, divide, sort)
67 | print(elements)
68 |
--------------------------------------------------------------------------------
/排序算法/归并排序/merge_sort.py:
--------------------------------------------------------------------------------
1 | class MergeSort(object):
2 | @staticmethod
3 | def merge(array, start, mid, end):
4 | if not (0 <= start <= mid < end):
5 | return
6 |
7 | i, j = start, mid + 1
8 | temp_list = [None] * (end - start + 1)
9 | cursor = 0
10 |
11 | while i <= mid and j <= end:
12 | if array[i] <= array[j]:
13 | temp_list[cursor] = array[i]
14 | i = i + 1
15 | else:
16 | temp_list[cursor] = array[j]
17 | j = j + 1
18 | cursor = cursor + 1
19 |
20 | while i <= mid:
21 | temp_list[cursor] = array[i]
22 | i = i + 1
23 | cursor = cursor + 1
24 |
25 | while j <= end:
26 | temp_list[cursor] = array[j]
27 | j = j + 1
28 | cursor = cursor + 1
29 |
30 | for ind, element in enumerate(temp_list):
31 | array[start + ind] = element
32 |
33 | @classmethod
34 | def merge_sort_recursive(cls, array, start=None, end=None):
35 | if start is None:
36 | start = 0
37 | if end is None:
38 | end = len(array) - 1
39 | if start >= end:
40 | return
41 |
42 | mid = (end + start) / 2
43 | cls.merge_sort_recursive(array, start, mid)
44 | cls.merge_sort_recursive(array, mid+1, end)
45 | cls.merge(array, start, mid, end)
46 |
47 | @classmethod
48 | def merge_sort(cls, array):
49 | step = 1
50 | while step <= len(array):
51 | step = step * 2
52 | for start in range(0, len(array), step):
53 | end = start + step - 1
54 | mid = (start + end) / 2
55 | if end >= len(array):
56 | end = len(array) - 1
57 | mid = min(start + step / 2 - 1, end)
58 | cls.merge(array, start, mid, end)
59 |
60 |
61 | if __name__ == "__main__":
62 | import random
63 |
64 | elements = list(range(30))
65 | random.shuffle(elements)
66 | print(elements)
67 | MergeSort.merge_sort(elements)
68 | print(elements)
69 |
--------------------------------------------------------------------------------
/回溯算法/leetcode-78.go:
--------------------------------------------------------------------------------
1 | // leetcode:https://leetcode.cn/problems/subsets/description/
2 |
3 | package main
4 |
5 | import (
6 | "fmt"
7 | "reflect"
8 | )
9 |
10 | func subsets(nums []int) [][]int {
11 | var result [][]int
12 |
13 | n := len(nums)
14 | // status 用于保存状态。status[i] 表示 nums 中第 i 个元素(从 0 开始)的起点
15 | status := make([]int, n+1)
16 | for i := 0; i < n; i++ {
17 | status[i] = i + 1
18 | }
19 | // n 的起点是 0
20 | status[n] = 0
21 |
22 | stack := []int{n}
23 | for len(stack) > 0 {
24 | // 当前扩展起点
25 | currentExpandNode := stack[len(stack)-1]
26 | // 如果无法继续前进
27 | if status[currentExpandNode] > n-1 {
28 | // 那么当前扩展节点成为死节点
29 | // 输出答案
30 | oneAns := make([]int, 0)
31 | for i := 1; i < len(stack); i++ {
32 | oneAns = append(oneAns, nums[stack[i]])
33 | }
34 | result = append(result, oneAns)
35 | // 将其从栈中弹出
36 | stack = stack[:len(stack)-1]
37 | // 重置状态
38 | if currentExpandNode == n {
39 | status[currentExpandNode] = 0
40 | } else {
41 | status[currentExpandNode] = currentExpandNode + 1
42 | }
43 | continue
44 | }
45 | nextNode := status[currentExpandNode]
46 | status[currentExpandNode] += 1
47 | stack = append(stack, nextNode)
48 | }
49 |
50 | return result
51 | }
52 |
53 | func equalOutOfOrder(x, y [][]int) bool {
54 | for _, xe := range x {
55 | isIn := false
56 | for _, ye := range y {
57 | if reflect.DeepEqual(xe, ye) {
58 | isIn = true
59 | break
60 | }
61 | }
62 | if !isIn {
63 | return false
64 | }
65 | }
66 | return true
67 | }
68 |
69 | func main() {
70 | tests := []struct {
71 | nums []int
72 | expected [][]int
73 | }{
74 | {
75 | nums: []int{1, 2, 3},
76 | expected: [][]int{
77 | {1, 2, 3},
78 | {1, 2},
79 | {1, 3},
80 | {1},
81 | {2, 3},
82 | {2},
83 | {3},
84 | {},
85 | },
86 | },
87 | {
88 | nums: []int{0},
89 | expected: [][]int{{0}, {}},
90 | },
91 | }
92 |
93 | for _, test := range tests {
94 | got := subsets(test.nums)
95 | if !equalOutOfOrder(got, test.expected) {
96 | fmt.Printf("got %v, but %v expected\n", got, test.expected)
97 | panic("should equal out of order")
98 | }
99 | }
100 | }
101 |
--------------------------------------------------------------------------------
/回溯算法/dag.py:
--------------------------------------------------------------------------------
1 | from typing import List, MutableMapping, Mapping
2 |
3 |
4 | class Task:
5 | def __init__(self, name: str) -> None:
6 | # 任务名称
7 | self._name: str = name
8 | # 任务依赖的任务
9 | self._dependencies: List[Task] = []
10 |
11 | @property
12 | def name(self) -> str:
13 | """
14 | 获取任务名称
15 | """
16 | return self._name
17 |
18 | def add_dependency(self, dependency: "Task") -> None:
19 | """
20 | 添加依赖的任务
21 | :param dependency: 被依赖的任务
22 | """
23 | self._dependencies.append(dependency)
24 |
25 | @property
26 | def dependency_count(self) -> int:
27 | """
28 | 获取依赖的任务的数量
29 | """
30 | return len(self._dependencies)
31 |
32 | def get_dependency(self, idx: int) -> "Task":
33 | """
34 | 获取依赖的任务
35 | """
36 | return self._dependencies[idx]
37 |
38 |
39 | def backtrace(dag: Mapping[str, List[str]]) -> None:
40 | # 定义问题的解空间;确定解空间的组织结构
41 | root: Task = Task("")
42 | cache: MutableMapping[str, Task] = {}
43 | for task, dependencies in dag.items():
44 | if task not in cache:
45 | cache[task] = Task(task)
46 | root.add_dependency(cache[task])
47 | for dependency in dependencies:
48 | if dependency not in cache:
49 | cache[dependency] = Task(dependency)
50 | cache[task].add_dependency(cache[dependency])
51 |
52 | stack: List[Task] = [root]
53 | status: MutableMapping[str, int] = {}
54 | visited: MutableMapping[str, bool] = {}
55 | while stack:
56 | current_node: Task = stack[-1]
57 | which_dependency: int = status.get(current_node.name, 0)
58 | # 无法继续向前搜索
59 | if which_dependency == current_node.dependency_count:
60 | if current_node is root:
61 | break
62 | print(f"execute {current_node.name}")
63 | visited[current_node.name] = True
64 | stack.pop(-1)
65 | continue
66 | # 到达新节点
67 | new_node: Task = current_node.get_dependency(which_dependency)
68 | status[current_node.name] = which_dependency + 1
69 | # 如果已经访问过,那么什么也不做
70 | if new_node.name in visited:
71 | continue
72 | # 如果未访问过,那么将其添加到活节点列表
73 | stack.append(new_node)
74 |
75 |
76 | if __name__ == "__main__":
77 | backtrace({"a": ["b", "c"], "b": ["c", "d"], "c": ["e"], "d": ["f"], "e": ["f"]})
78 |
79 |
--------------------------------------------------------------------------------
/图/最短路径/Floyd算法/floyd.py:
--------------------------------------------------------------------------------
1 | # coding: utf8
2 |
3 |
4 | class Graph(object):
5 | """
6 | 图的数组矩阵表示法
7 | """
8 | def __init__(self):
9 | self._vertexes = []
10 | self._arches = []
11 |
12 | def add_vertex(self, element):
13 | self._vertexes.append(element)
14 | for arch in self._arches:
15 | arch.append(None)
16 | self._arches.append([None] * len(self._vertexes))
17 |
18 | def get_vertex_count(self):
19 | return len(self._vertexes)
20 |
21 | def add_arch(self, tail, head, weight):
22 | self._arches[tail][head] = weight
23 |
24 | def get_weight(self, tail, head):
25 | return self._arches[tail][head]
26 |
27 |
28 | def floyd(graph):
29 | """
30 | Floyd 算法实现
31 | """
32 | import sys
33 |
34 | INFINITY = sys.maxint / 2.0
35 | vertex_count = graph.get_vertex_count()
36 |
37 | # 初始化辅助数组 d[][]、p[][]
38 | d = []
39 | p = []
40 |
41 | # 初始时,任意两个顶点之间的最短路径是 INFINITY
42 | for i in range(vertex_count):
43 | d.append([])
44 | for _ in range(vertex_count):
45 | d[i].append(INFINITY)
46 |
47 | # 初始时,p[i][j] = j
48 | for i in range(vertex_count):
49 | p.append([])
50 | for j in range(vertex_count):
51 | p[i].append(j)
52 |
53 | def _floyd(i, j, k):
54 | if k == -1:
55 | return graph.get_weight(i, j) or INFINITY
56 | if i == j:
57 | d[i][j] = 0
58 | return 0
59 | if d[i][j] != INFINITY:
60 | return d[i][j]
61 |
62 | with_k = _floyd(i, k, k - 1) + _floyd(k, j, k - 1)
63 | without_k = _floyd(i, j, k - 1)
64 |
65 | if with_k < without_k:
66 | d[i][j] = with_k
67 | p[i][j] = k
68 | return with_k
69 |
70 | d[i][j] = without_k
71 | return without_k
72 |
73 | for i in range(vertex_count):
74 | for j in range(vertex_count):
75 | _floyd(i, j, vertex_count - 1)
76 |
77 | return d, p
78 |
79 |
80 | def test():
81 | # http://images.timd.cn/data-structure/floyd-example.png
82 | g = Graph()
83 | for ind in range(1, 5):
84 | g.add_vertex(ind)
85 | for arch in [(0, 1, 2), (0, 2, 6), (0, 3, 4),
86 | (1, 2, 3), (2, 0, 7), (2, 3, 1),
87 | (3, 0, 5), (3, 2, 12)]:
88 | g.add_arch(*arch)
89 | d, p = floyd(g)
90 | print(d)
91 | print(p)
92 |
93 |
94 | if __name__ == "__main__":
95 | test()
96 |
--------------------------------------------------------------------------------
/动态规划/knapsack_problem.py:
--------------------------------------------------------------------------------
1 | from typing import List
2 |
3 |
4 | # 01 背包问题
5 | def zero_one_knapsack(capacity: int, weights: List[int], values: List[int]) -> int:
6 | # 创建,并且初始化 dp 数组
7 | dp: List[int] = [0 for _ in range(capacity + 1)]
8 |
9 | # 01 背包问题的状态转移方程(空间优化前):
10 | # dp[i][j] = max(dp[i-1][j], dp[i-1][j-weights[i-1]] + values[i-1]) // j >= weights[i-1]
11 |
12 | for i in range(1, len(weights) + 1):
13 | # 对于 01 背包问题,必须逆向枚举,防止覆盖
14 | for j in range(capacity, weights[i - 1] - 1, -1):
15 | # 空间优化后的状态转移方程
16 | dp[j] = max(dp[j], dp[j - weights[i - 1]] + values[i - 1])
17 | return dp[capacity]
18 |
19 |
20 | # 完全背包问题
21 | def unbounded_knapsack(capacity: int, weights: List[int], values: List[int]) -> int:
22 | # 创建,并且初始化 dp 数组
23 | dp: List[int] = [0 for _ in range(capacity + 1)]
24 |
25 | # 完全背包问题的状态转移方程(空间优化前):
26 | # dp[i][j] = max(dp[i-1][j], dp[i][j-weights[i-1]] + values[i-1]) // j >= weights[i-1]
27 |
28 | for i in range(1, len(weights) + 1):
29 | # 对于完全背包问题,必须正向枚举
30 | for j in range(weights[i - 1], capacity + 1):
31 | # 空间优化后的状态转移方程
32 | dp[j] = max(dp[j], dp[j - weights[i - 1]] + values[i - 1])
33 | return dp[-1]
34 |
35 |
36 | # 多重背包问题
37 | def bounded_knapsack(capacity: int, weights: List[int], values: List[int], nums: List[int]) -> int:
38 | # 创建,并且初始化 dp 数组
39 | dp: List[int] = [0 for _ in range(capacity + 1)]
40 |
41 | # 多重背包问题的状态转移方程(空间优化前):
42 | # // 0 <= k <= min(j/weights[i-1], nums[i-1])
43 | # dp[i][j] = max({dp[i-1][j-k*weights[i-1]] + k*values[i-1]} for every k)
44 |
45 | for i in range(1, len(weights) + 1):
46 | # 对于多重背包问题,必须逆向枚举,防止覆盖
47 | for j in range(capacity, weights[i - 1] - 1, -1):
48 | for k in range(0, min(j // weights[i - 1], nums[i - 1]) + 1):
49 | # 空间优化后的状态转移方程
50 | dp[j] = max(dp[j], dp[j - k * weights[i - 1]] + k * values[i - 1])
51 |
52 | return dp[capacity]
53 |
54 |
55 | def test() -> None:
56 | capacity: int = 15
57 | weights: List[int] = [3, 2, 5, 7, 3, 8]
58 | values: List[int] = [4, 4, 8, 10, 3, 11]
59 | # 输出:23
60 | print(zero_one_knapsack(capacity, weights, values))
61 | # 输出:28
62 | print(unbounded_knapsack(capacity, weights, values))
63 | nums: List[int] = [1, 100, 1000, 1, 1, 1]
64 | # 输出:28
65 | print(bounded_knapsack(capacity, weights, values, nums))
66 |
67 |
68 | if __name__ == "__main__":
69 | test()
70 |
71 |
--------------------------------------------------------------------------------
/树/二叉树/README.md:
--------------------------------------------------------------------------------
1 | ### 二叉树
2 |
3 | 二叉树是每个节点最多有 2 个孩子节点的有序树。其中,以左孩子节点为根的子树叫左子树;以右孩子节点为根的子树叫右子树。
4 |
5 | ---
6 |
7 | ### 二叉树的性质
8 |
9 | * 二叉树的第 i 层最多有 2i - 1 个节点(i > 0)
10 |
11 | * 深度为 k 的二叉树最多有 2k - 1 个节点
12 |
13 | ---
14 |
15 | ### 满二叉树、完全二叉树
16 |
17 | 如果一棵二叉树的深度为 k,并且该二叉树有 2k - 1 个节点,则称该二叉树为满二叉树。
18 |
19 | 将二叉树的节点按照从上到下、从左到右的顺序进行编号,如果某棵二叉树的节点的编号和与其深度相同的满二叉树的节点的编号一一对应,那么这棵树就是完全二叉树。
20 |
21 | ---
22 |
23 | ### 完全二叉树的性质
24 |
25 |
26 | - 一棵有 n 个节点的完全二叉树,其深度 k 为:
27 | 2k-1-1 < n <= 2k - 1 ===>
28 | 2k-1 <= n < 2k ===>
29 | k-1 <= log2n < k ===>
30 | k = 向下取整(log2n) + 1
31 |
32 |
33 | - 将一棵有 n 个节点的完全二叉树的所有节点按照从上到下、从左到右的顺序进行编号,则对于编号为 i(1<= i <=n)的节点而言:
34 |
35 | - 当 i = 1 时,该节点是根节点,没有双亲节点;否则,其双亲节点的编号是:向下取整(i/2)
36 | - 当 2×i 大于 n 时,该节点是叶子节点,没有孩子节点;否则,其左孩子节点的编号是 2×i
37 | - 当 2×i+1 大于 n 时,该节点没有右孩子节点;否则,其右孩子节点的编号是 2×i+1
38 |
39 |
40 |
41 |
42 | ---
43 |
44 | ### 二叉树的存储
45 |
46 |
47 | - 顺序存储
48 | 用一组地址连续的存储单元依次自上而下、自左至右地存储完全二叉树的节点,即将完全二叉树中编号为 i 的节点存储到一维数组的索引为 i-1 的分量中。
49 | 二叉树的顺序存储只适用于完全二叉树。因为在最坏的情况下,一棵深度为 k,并且节点个数也为 k 的二叉树,需要 2k-1 个存储单元,会造成空间的浪费
50 |
51 |
52 | - 链式存储
53 | 在二叉链表表示法中,每个节点包含一个数据域、一个左指针域和一个右指针域。
54 | 在三叉链表表示法中,每个节点除了包含数据域、左右指针域之外,还包含指向双亲节点的指针域。
55 | 在二叉链表表示法中,如果二叉树有 n 个节点,则空指针域的个数是 n+1。因为有 n 个节点的二叉树共有 2×n 个指针域,而 n 个节点需要 n-1 个指针域指向它们(根节点不需要某个指针域指向它),所以空指针域的数量是 2×n-(n-1) = n+1
56 |
57 |
58 |
59 | ---
60 |
61 | ### 二叉树的遍历
62 |
63 | 遍历二叉树是指按照某条搜索路径访问二叉树的节点,使得每个节点都被访问一次,且仅被访问一次。
64 |
65 |
66 | - 深度优先遍历(Depth First Search)
67 |
68 | - 先(根)序遍历
69 |
70 | - 访问根节点
71 | - 先序遍历左子树
72 | - 先序遍历右子树
73 |
74 |
75 |
76 | - 中(根)序遍历
77 |
78 | - 中序遍历左子树
79 | - 访问根节点
80 | - 中序遍历右子树
81 |
82 |
83 |
84 | - 后(根)序遍历
85 |
86 | - 后序遍历左子树
87 | - 后序遍历右子树
88 | - 访问根节点
89 |
90 |
91 |
92 |
93 |
94 | - 广度优先遍历(Breadth First Search)
95 | 按照从上到下、从左到右的顺序逐层地进行遍历
96 |
97 |
98 |
--------------------------------------------------------------------------------
/回溯算法/Maze.py:
--------------------------------------------------------------------------------
1 | import copy
2 | from typing import List, Tuple
3 |
4 |
5 | def search(maze: List[List[int]], start: Tuple[int, int], end: Tuple[int, int]) -> List[List[Tuple[int, int]]]:
6 | result: List[List[Tuple[int, int]]] = []
7 |
8 | # 1 代表上面的格子待搜索;
9 | # 2 代表右面的格子待搜索
10 | # 3 代表下面的格子待搜索
11 | # 4 代表左面的格子待搜索
12 | # 5 代表上下左右都已搜索
13 | status: List[List[int]] = []
14 | for row in range(len(maze)): # type: int
15 | status.append([1] * len(maze[row]))
16 |
17 | stack: List[Tuple[int, int]] = [start]
18 | while stack:
19 | current_expand_node: Tuple[int, int] = stack[-1]
20 | x, y = current_expand_node # type: int, int
21 | match status[x][y]:
22 | case 1:
23 | status[x][y] = 2
24 | if x == 0:
25 | continue
26 | next_node: Tuple[int, int] = (x - 1, y)
27 | case 2:
28 | status[x][y] = 3
29 | if y == len(maze[x]) - 1:
30 | continue
31 | next_node: Tuple[int, int] = (x, y + 1)
32 | case 3:
33 | status[x][y] = 4
34 | if x == len(maze) - 1:
35 | continue
36 | next_node: Tuple[int, int] = (x + 1, y)
37 | case 4:
38 | status[x][y] = 5
39 | if y == 0:
40 | continue
41 | next_node: Tuple[int, int] = (x, y - 1)
42 | case _:
43 | # 无法继续向纵深方向前进
44 | # 恢复状态
45 | status[x][y] = 1
46 | # 将死节点从栈中弹出
47 | stack.pop(-1)
48 | continue
49 | x, y = next_node # type: int, int
50 | # 新节点是墙
51 | if maze[x][y] == 0:
52 | continue
53 | # 已经在栈中
54 | if next_node in stack:
55 | continue
56 | # 到达终点
57 | if next_node == end:
58 | path: List[Tuple[int, int]] = copy.copy(stack)
59 | path.append(next_node)
60 | result.append(path)
61 | continue
62 | # 使其成为活结点
63 | stack.append(next_node)
64 |
65 | return result
66 |
67 |
68 | def main() -> None:
69 | # 0 代表墙;1 代表路
70 | maze = [
71 | [0, 0, 0, 0, 0],
72 | [1, 1, 1, 1, 0],
73 | [1, 0, 0, 1, 0],
74 | [1, 1, 0, 1, 0],
75 | [0, 1, 1, 1, 0],
76 | ]
77 | for path in search(maze, (1, 0), (3, 0)):
78 | print(path)
79 |
80 |
81 | if __name__ == "__main__":
82 | main()
83 |
84 |
--------------------------------------------------------------------------------
/动态规划/knapsack_problem.go:
--------------------------------------------------------------------------------
1 | package main
2 |
3 | import "fmt"
4 |
5 | // ZeroOneKnapsack 是 01 背包问题的实现
6 | func ZeroOneKnapsack(capacity int, weights []int, values []int) int {
7 | // 创建,同时初始化 dp 数组
8 | dp := make([]int, capacity+1)
9 | for i := 0; i < len(dp); i++ {
10 | dp[i] = 0
11 | }
12 |
13 | // 01 背包问题的状态转移方程(空间优化前):
14 | // dp[i][j] = max(dp[i-1][j], dp[i-1][j-weights[i-1]] + values[i-1]) // j >= weights[i-1]
15 |
16 | for i := 1; i <= len(weights); i++ {
17 | // 对于 01 背包问题,必须逆向枚举,防止覆盖
18 | for j := capacity; j >= weights[i-1]; j-- {
19 | // 空间优化后的状态转移方程
20 | chooseI := dp[j-weights[i-1]] + values[i-1]
21 | if chooseI > dp[j] {
22 | dp[j] = chooseI
23 | }
24 | }
25 | }
26 |
27 | return dp[capacity]
28 | }
29 |
30 | func UnboundedKnapsack(capacity int, weights []int, values []int) int {
31 | // 创建,同时初始化 dp 数组
32 | dp := make([]int, capacity+1)
33 | for i := 0; i < len(dp); i++ {
34 | dp[i] = 0
35 | }
36 |
37 | // 完全背包问题的状态转移方程(空间优化前):
38 | // dp[i][j] = max(dp[i-1][j], dp[i][j-weights[i-1]] + values[i-1]) // j >= weights[i-1]
39 |
40 | for i := 1; i <= len(weights); i++ {
41 | // 对于完全背包问题,必须正向枚举
42 | for j := weights[i-1]; j <= capacity; j++ {
43 | // 空间优化后的状态转移方程
44 | chooseI := dp[j-weights[i-1]] + values[i-1]
45 | if chooseI > dp[j] {
46 | dp[j] = chooseI
47 | }
48 | }
49 | }
50 |
51 | return dp[capacity]
52 | }
53 |
54 | func BoundedKnapsack(capacity int, weights []int, values []int, nums []int) int {
55 | // 创建,同时初始化 dp 数组
56 | dp := make([]int, capacity+1)
57 | for i := 0; i < len(dp); i++ {
58 | dp[i] = 0
59 | }
60 |
61 | // 多重背包问题的状态转移方程(空间优化前):
62 | // 0 <= k <= min(nums[i-1], j / weights[i-1])
63 | // dp[i][j] = max({dp[i-1][j-k*values[i-1]] + k*values[i-1]} for every k)
64 |
65 | for i := 1; i <= len(weights); i++ {
66 | // 对于完全背包问题,必须逆向枚举,防止覆盖
67 | for j := capacity; j >= weights[i-1]; j-- {
68 | kMax := j / weights[i-1]
69 | if nums[i-1] < kMax {
70 | kMax = nums[i-1]
71 | }
72 | for k := 0; k <= kMax; k++ {
73 | // 空间优化后的状态转移方程
74 | value := dp[j-k*weights[i-1]] + k*values[i-1]
75 | if value > dp[j] {
76 | dp[j] = value
77 | }
78 | }
79 | }
80 | }
81 |
82 | return dp[capacity]
83 | }
84 |
85 | func main() {
86 | capacity := 15
87 | weights := []int{3, 2, 5, 7, 3, 8}
88 | values := []int{4, 4, 8, 10, 3, 11}
89 | // 输出:23
90 | fmt.Println(ZeroOneKnapsack(capacity, weights, values))
91 | // 输出:28
92 | fmt.Println(UnboundedKnapsack(capacity, weights, values))
93 | nums := []int{1, 100, 1000, 1, 1, 1}
94 | // 输出:28
95 | fmt.Println(BoundedKnapsack(capacity, weights, values, nums))
96 | }
97 |
98 |
--------------------------------------------------------------------------------
/回溯算法/Maze.go:
--------------------------------------------------------------------------------
1 | package main
2 |
3 | import "fmt"
4 |
5 | func inStack(stack [][]int, nextNode []int) bool {
6 | for _, node := range stack {
7 | if node[0] == nextNode[0] && node[1] == nextNode[1] {
8 | return true
9 | }
10 | }
11 | return false
12 | }
13 |
14 | func copyPath(stack [][]int, end []int) [][]int {
15 | var path [][]int
16 | for _, node := range stack {
17 | path = append(path, node)
18 | }
19 | path = append(path, end)
20 | return path
21 | }
22 |
23 | // Search 搜索指定的迷宫中的全部路径
24 | func Search(maze [][]int, start, end []int) [][][]int {
25 | var result [][][]int
26 |
27 | // 1 代表上面的格子待搜索;
28 | // 2 代表右面的格子待搜索
29 | // 3 代表下面的格子待搜索
30 | // 4 代表左面的格子待搜索
31 | // 5 代表上下左右都已搜索
32 | // 初始值为 1
33 | var status [][]int
34 | for i := 0; i < len(maze); i++ {
35 | status = append(status, nil)
36 | for j := 0; j < len(maze[i]); j++ {
37 | status[i] = append(status[i], 1)
38 | }
39 | }
40 |
41 | // 栈中保存格子的坐标
42 | var stack [][]int
43 | // 将起点压入栈顶
44 | stack = append(stack, start)
45 | for len(stack) > 0 {
46 | currentExpandNode := stack[len(stack)-1]
47 | x, y := currentExpandNode[0], currentExpandNode[1]
48 | var nextNode []int
49 | switch status[x][y] {
50 | case 1:
51 | status[x][y] = 2
52 | if x == 0 {
53 | continue
54 | }
55 | nextNode = []int{x - 1, y}
56 | case 2:
57 | status[x][y] = 3
58 | if y == len(maze[x])-1 {
59 | continue
60 | }
61 | nextNode = []int{x, y + 1}
62 | case 3:
63 | status[x][y] = 4
64 | if x == len(maze)-1 {
65 | continue
66 | }
67 | nextNode = []int{x + 1, y}
68 | case 4:
69 | status[x][y] = 5
70 | if y == 0 {
71 | continue
72 | }
73 | nextNode = []int{x, y - 1}
74 | default:
75 | // 无法继续向纵深方向前进
76 | // 恢复状态
77 | status[x][y] = 1
78 | // 将死节点从栈中弹出
79 | stack = stack[:len(stack)-1]
80 | continue
81 | }
82 |
83 | x, y = nextNode[0], nextNode[1]
84 | // 新节点是墙
85 | if maze[x][y] == 0 {
86 | continue
87 | }
88 | // 已经在栈中
89 | if inStack(stack, nextNode) {
90 | continue
91 | }
92 | // 到达终点
93 | if x == end[0] && y == end[1] {
94 | result = append(result, copyPath(stack, end))
95 | continue
96 | }
97 | // 使之成为活结点
98 | stack = append(stack, nextNode)
99 | }
100 |
101 | return result
102 | }
103 |
104 | func main() {
105 | // 0 代表墙;1 代表路
106 | maze := [][]int{
107 | {0, 0, 0, 0, 0},
108 | {1, 1, 1, 1, 0},
109 | {1, 0, 0, 1, 0},
110 | {1, 1, 0, 1, 0},
111 | {0, 1, 1, 1, 0},
112 | }
113 | for _, path := range Search(maze, []int{1, 0}, []int{3, 0}) {
114 | fmt.Println(path)
115 | }
116 | }
117 |
118 |
--------------------------------------------------------------------------------
/树/AC自动机和Trie树/ac.py:
--------------------------------------------------------------------------------
1 | # coding: utf8
2 |
3 |
4 | class Node(object):
5 | def __init__(self, char):
6 | self.char = char
7 | self.children = {}
8 | self.fail = None
9 | self.end = False
10 |
11 |
12 | class AC(object):
13 | def __init__(self, *patterns):
14 | self._patterns = patterns
15 | self._root, self._output = AC.create_trie_tree(patterns)
16 | AC.set_fail(self._root)
17 |
18 | @staticmethod
19 | def create_trie_tree(patterns):
20 | root = Node(None)
21 | output = {}
22 | for pattern in patterns:
23 | if not pattern:
24 | continue
25 | temp = root
26 | for char in pattern:
27 | if char not in temp.children:
28 | temp.children[char] = Node(char)
29 | temp = temp.children[char]
30 | else:
31 | temp.end = True
32 | output[temp] = pattern
33 | return root, output
34 |
35 | @staticmethod
36 | def set_fail(root):
37 | # 根节点的 fail 指针是 None
38 | # 根节点的孩子节点的 fail 指针指向根节点
39 | queue = []
40 | for child in root.children.values():
41 | child.fail = root
42 | queue.append(child)
43 |
44 | while queue:
45 | p = queue.pop(0)
46 | for char, n in sorted(p.children.items(), key=lambda c: c):
47 | queue.append(n)
48 |
49 | f = p.fail
50 | while f is not None:
51 | if char in f.children:
52 | n.fail = f.children[char]
53 | break
54 | f = f.fail
55 |
56 | def _generate_output(self, p):
57 | matches = []
58 | while p is not None:
59 | if p.end:
60 | matches.append(self._output[p])
61 | p = p.fail
62 | return matches
63 |
64 | def find(self, main_string):
65 | print main_string
66 | results = {}
67 | node = self._root
68 | for ind, char in enumerate(main_string):
69 | while node is not None:
70 | if char in node.children:
71 | node = node.children[char]
72 | if node.end:
73 | for pattern in self._generate_output(node):
74 | results.setdefault(ind-len(pattern)+1, []) \
75 | .append(pattern)
76 | break
77 | node = node.fail
78 | else:
79 | node = self._root
80 | return results
81 |
82 |
83 | if __name__ == "__main__":
84 | ac = AC("ashe", "sha", "he", "ash", "she")
85 | print(ac.find("she11ashe22shahe33"))
86 |
--------------------------------------------------------------------------------
/线性表/链表是否有环/cycle_list.py:
--------------------------------------------------------------------------------
1 | # coding: utf8
2 |
3 |
4 | class Node(object):
5 | def __init__(self, element=None, next_node=None):
6 | self.element = element
7 | self.next_node = next_node
8 |
9 |
10 | def has_cycle(node):
11 | """判断单链表是否有环"""
12 | if node is None:
13 | return False
14 |
15 | slow = fast = node
16 | while fast is not None:
17 | # 快指针先前进一步
18 | fast = fast.next_node
19 | if fast is not None:
20 | # 快指针再前进一步
21 | fast = fast.next_node
22 | # 慢指针前进一步
23 | slow = slow.next_node
24 |
25 | # 快慢指针相遇表示有环
26 | if slow is fast:
27 | return True
28 | return False
29 |
30 |
31 | def get_cycle_length(node):
32 | """获取环的长度"""
33 | if node is None:
34 | return 0
35 |
36 | slow = fast = node
37 | meet_count = 0
38 | loop_count = 0
39 | while fast is not None:
40 | fast = fast.next_node
41 | if fast is not None:
42 | fast = fast.next_node
43 | slow = slow.next_node
44 | loop_count = loop_count + 1
45 | if slow is fast:
46 | meet_count = meet_count + 1
47 | if meet_count == 1:
48 | # 快慢指针第一次相遇
49 | loop_count = 0
50 | elif meet_count == 2:
51 | # 快慢指针再次相遇时,慢指针走的步数就是环长
52 | return loop_count
53 | return 0
54 |
55 |
56 | def get_joint_node(node):
57 | if node is None:
58 | return None
59 |
60 | slow = fast = node
61 | while fast is not None:
62 | fast = fast.next_node
63 | if fast is not None:
64 | fast = fast.next_node
65 | slow = slow.next_node
66 | if slow is fast:
67 | p1 = slow
68 | p2 = node
69 | while p1 is not p2:
70 | p1 = p1.next_node
71 | p2 = p2.next_node
72 | return p1
73 |
74 | return None
75 |
76 |
77 | if __name__ == "__main__":
78 | import unittest
79 |
80 | class CycleListTest(unittest.TestCase):
81 | def setUp(self):
82 | # 0 -> 1 -> 2 -> 3 -> 4 -> 5 -> 2
83 | nodes = [Node(ind) for ind in range(6)]
84 | for ind in range(5):
85 | nodes[ind].next_node = nodes[ind + 1]
86 | nodes[5].next_node = nodes[2]
87 | self.node = nodes[0]
88 | # 连接点
89 | self.joint_node = nodes[2]
90 |
91 | def testCycleList(self):
92 | self.assertTrue(has_cycle(self.node))
93 | self.assertEqual(get_cycle_length(self.node), 4)
94 | self.assertIs(get_joint_node(self.node), self.joint_node)
95 |
96 | unittest.main()
97 |
--------------------------------------------------------------------------------
/排序算法/归并排序/merge_sort_linked_list.py:
--------------------------------------------------------------------------------
1 | # coding: utf8
2 |
3 |
4 | class ListNode(object):
5 | def __init__(self, x):
6 | self.val = x
7 | self.next = None
8 |
9 | def __str__(self):
10 | return "%s{val=%s, next=%s}" % (
11 | self.__class__.__name__,
12 | self.val,
13 | self.next.val if self.next is not None else self.next
14 | )
15 |
16 | def __repr__(self):
17 | return self.__str__() + "@" + hex(id(self))
18 |
19 |
20 | class Solution(object):
21 | def sort(self, h):
22 | # 如果 h 中没有元素 或 只有一个元素,则其直接有序,立刻返回
23 | if h is None or h.next is None:
24 | return h
25 |
26 | # 通过快慢指针,找到链表的中间节点
27 | tail = h
28 | mid = h
29 | while tail.next is not None:
30 | # tail 先前进一步
31 | tail = tail.next
32 |
33 | # 如果未到尾部,tail 再前进一步,mid 前进一步
34 | if tail.next is not None:
35 | tail = tail.next
36 | mid = mid.next
37 |
38 | # 每次循环 tail 前进两步,mid 前进一步,所以当 tail 到达尾部时,
39 | # mid 到达链表的中间位置
40 |
41 | # 将列表从中间分成两个:head、right
42 | right = mid.next
43 | mid.next = None
44 |
45 | # 使用归并排序分别对着两个列表进行排序
46 | l1 = self.sort(h)
47 | l2 = self.sort(right)
48 |
49 | # 归并两个有序链表
50 | return self.merge(l1, l2)
51 |
52 | @staticmethod
53 | def merge(l1, l2):
54 | """将两个有序链表归并成一个有序列表"""
55 | if l1 is l2:
56 | return l1
57 |
58 | # h 是头节点
59 | h = ListNode(None)
60 |
61 | tail = h
62 | x = l1
63 | y = l2
64 |
65 | while x is not None and y is not None:
66 | if x.val <= y.val:
67 | tail.next = x
68 | tail = x
69 | x = x.next
70 | else:
71 | tail.next = y
72 | tail = y
73 | y = y.next
74 |
75 | if x is not None:
76 | tail.next = x
77 | elif y is not None:
78 | tail.next = y
79 |
80 | return h.next
81 |
82 |
83 | if __name__ == "__main__":
84 | import random
85 |
86 | elements = list(range(-10, 11))
87 | random.shuffle(elements)
88 | print(elements)
89 |
90 | # 生成一个无序链表
91 | temp1 = None
92 | head = None
93 | for element in elements:
94 | node = ListNode(element)
95 | if head is None:
96 | head = node
97 | temp1 = node
98 | else:
99 | temp1.next = node
100 | temp1 = node
101 |
102 | new_head = Solution().sort(head)
103 | temp2 = new_head
104 | while temp2 is not None:
105 | print(temp2.val)
106 | temp2 = temp2.next
107 |
--------------------------------------------------------------------------------
/排序算法/堆排序以及topk问题/README.md:
--------------------------------------------------------------------------------
1 | ### 什么是堆
2 |
3 | 堆是一棵完全二叉树,并且任意非叶子节点的关键字不小于(或不大于)其孩子节点的关键字,前者叫大根堆,后者叫小根堆。
4 |
5 | ---
6 |
7 | ### 堆的基本操作(以小根堆为例)
8 |
9 | * 建堆:
10 | 建堆是一个不断调整堆的过程。从 length / 2 处(数组的中间位置)开始,向前调整,一直到第一个元素
11 |
12 | * 调整堆:
13 | 在建堆、向堆中插入元素、堆排序时,都会调整堆,其过程如下:
14 | * 对于某个节点:
15 | * 如果它是叶子节点,则调整结束
16 | * 如果它只有左孩子,则按需调整该节点和其左孩子的关键字,然后调整结束
17 | * 如果该节点的关键字不大于其左、右孩子节点的关键字,则调整结束
18 | * 否则,将该节点的关键字与其孩子节点的关键字中的较小者进行互换
19 | * 然后,从发生互换的位置,按照上面的流程,继续向下调整
20 |
21 | ---
22 |
23 | ### 堆排序
24 |
25 | 堆排序的过程如下:
26 |
27 | 1. 首先将输入数组堆化
28 |
29 | * 交换堆的第一个元素和最后一个元素,然后将堆的最后一个元素删掉,并从堆顶开始调整堆
30 |
31 | * 重复执行步骤2,直到堆中没有元素
32 |
33 | ---
34 |
35 | ### TopK 问题
36 |
37 | TopK 问题是:从包含 n 个元素的数组中,找出前 k 大的元素。
38 |
39 | 解决 topk 问题的基本思路是:
40 |
41 | 1. 将数组的前 k 个元素调整成一个小根堆
42 |
43 | * 从第 k + 1 个元素开始,逐个比较元素和堆的根的大小,如果:
44 | * 元素不大于堆的根,则什么也不做
45 | * 否则,将元素和堆的根互换,并调整堆
46 |
47 | * 重复执行步骤2,直到比较完数组的最后一个元素
48 |
49 | ---
50 |
51 | ### 时间复杂度分析
52 |
53 | * 建堆的时间复杂度:
54 | 设树的深度为 k,在最坏的情况下,第 1 层(含 20 个节点)向下调整 k - 1 次,第 2 层(含 21 个节点)向下调整 k - 2 次,...,第 k - 1 层(含 2k-2 个节点)向下调整 1 次,因此最坏的情况下的时间复杂度是:
55 | 20 * (k - 1) + 21 * (k - 2) + ... + 2k-2 * 1 ===>
56 | k * (20 + ... + 2k-2) - (1 * 20 + ... + (k-1) * 2k-2) ===>
57 | k * (2k-1 - 1) - ((k-1)*2k-1 - 2k-1 + 1) ===>
58 | 2k - k - 1
59 | 根据完全二叉树的性质,可得到 k = floor(log2n) + 1,所以建堆的时间复杂度是O(n)
60 |
61 | * 堆排序的时间复杂度
62 | 在最坏的情况下,堆排序的时间复杂度是:
63 | log2(n-1) + log2(n-2) + ... + log22 + log21 ===>
64 | log2((n-1)!)
65 | 根据[斯特林公式](https://baike.baidu.com/item/%E6%96%AF%E7%89%B9%E6%9E%97%E5%85%AC%E5%BC%8F/9583086?fr=aladdin),可以得到堆排序的时间复杂度是O(nlogn)
66 |
67 | * TopK 问题的时间复杂度
68 | 在最坏的情况下,TopK 问题的时间复杂度是:
69 | log2k * (n - k)
70 | 因此,TopK 问题的时间复杂度是O(nlogk)
71 |
72 | ---
73 |
74 | ### 空间复杂度
75 |
76 | 因为堆排序是原地排序,所以在不使用递归的情况下,空间复杂度是O(1)
77 |
78 | ---
79 |
80 | ### 补充说明
81 |
82 | * 有 n 个节点的二叉树的分支的数量是 n - 1,这些分支都是由度为 1 和度为 2 的结点射出的,所以,n1 + 2 × n2 = n - 1,结合 n0 + n1 + n2 = n,可以推出 n0 = n2 + 1
83 | * 在完全二叉树中,度为 1 的节点,要么有 0 个(当 n 是奇数时);要么有 1 个(当 n 是偶数时)。所以 2 × n0 + n1 - 1 = n,n0 = n / 2(当 n 是偶数时)或 n0 = (n + 1) / 2(当 n 是奇数时)。故在完全二叉树中,叶子节点的数量是:向上取整(n / 2)
84 | * 设 m = ax,n = ay,则 mn = a(x+y)、x = logam、y = logan。所以 logamn = logam + logan
85 | * 因为 log(mn) = logm + logn,所以 logmn = log(m * m * ... * m) = logm + ... + logm = nlogm
86 |
--------------------------------------------------------------------------------
/分支限界算法/shortest_path.go:
--------------------------------------------------------------------------------
1 | package main
2 |
3 | import (
4 | "container/heap"
5 | "fmt"
6 | )
7 |
8 | // Graph 使用数组矩阵法表示有向图
9 | type Graph struct {
10 | // 顶点集合
11 | Vertexes []string
12 | // 弧的集合
13 | Arches [][]int
14 | }
15 |
16 | // GenerateDirectGraphExample 生成用于测试的有向图
17 | func GenerateDirectGraphExample() *Graph {
18 | graph := &Graph{}
19 | graph.Vertexes = []string{"s", "a", "b", "c", "d", "e", "f", "g", "h", "i", "t"}
20 | graph.Arches = append(graph.Arches, [][]int{
21 | {0, 2, 3, 4, 0, 0, 0, 0, 0, 0, 0},
22 | {0, 0, 3, 0, 7, 2, 0, 0, 0, 0, 0},
23 | {0, 0, 0, 0, 0, 9, 2, 0, 0, 0, 0},
24 | {0, 0, 0, 0, 0, 0, 2, 0, 0, 0, 0},
25 | {0, 0, 0, 0, 0, 0, 0, 2, 3, 0, 0},
26 | {0, 0, 0, 0, 0, 0, 1, 0, 3, 0, 0},
27 | {0, 0, 0, 0, 0, 0, 0, 0, 5, 1, 0},
28 | {0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1},
29 | {0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 2},
30 | {0, 0, 0, 0, 0, 0, 0, 0, 2, 0, 2},
31 | {0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0},
32 | }...)
33 | return graph
34 | }
35 |
36 | // Item 表示优先级队列中的元素
37 | type Item struct {
38 | // 代价
39 | Weight int
40 | // 索引
41 | Index int
42 | }
43 |
44 | // PriorityQueue 表示优先级队列
45 | type PriorityQueue []Item
46 |
47 | func (pq PriorityQueue) Len() int { return len(pq) }
48 |
49 | func (pq PriorityQueue) Less(i, j int) bool { return pq[i].Weight < pq[j].Weight }
50 |
51 | func (pq PriorityQueue) Swap(i, j int) { pq[i], pq[j] = pq[j], pq[i] }
52 |
53 | func (pq *PriorityQueue) Push(x interface{}) {
54 | *pq = append(*pq, x.(Item))
55 | }
56 |
57 | func (pq *PriorityQueue) Pop() interface{} {
58 | old := *pq
59 | ele := old[len(old)-1]
60 | *pq = old[:len(old)-1]
61 | return ele
62 | }
63 |
64 | // NewPriorityQueue 构造优先级队列实例
65 | func NewPriorityQueue() PriorityQueue {
66 | return make(PriorityQueue, 0)
67 | }
68 |
69 | // ShortestPath 计算单源最短路径
70 | func ShortestPath(graph *Graph, start int) map[int]int {
71 | // 顶点的索引 -> 代价
72 | m := make(map[int]int)
73 | pq := NewPriorityQueue()
74 | // 将开始节点加入到优先级队列中
75 | heap.Push(&pq, Item{Weight: 0, Index: start})
76 | for len(pq) > 0 {
77 | // 当前扩展节点
78 | currentExpandNode := heap.Pop(&pq).(Item)
79 | // 获取当前扩展节点的所有孩子节点
80 | for child, weight := range graph.Arches[currentExpandNode.Index] {
81 | if weight == 0 {
82 | continue
83 | }
84 | newWeight := currentExpandNode.Weight + weight
85 | // 剪掉无法到达最优解的孩子节点,将其它孩子节点加入到活结点列表,并且使用限界函数进行排序
86 | if currentWeight, found := m[child]; !found || currentWeight > newWeight {
87 | m[child] = newWeight
88 | heap.Push(&pq, Item{Weight: newWeight, Index: child})
89 | }
90 | }
91 | }
92 | return m
93 | }
94 |
95 | func main() {
96 | graph := GenerateDirectGraphExample()
97 | startIdx := 0
98 | for idx, weight := range ShortestPath(graph, startIdx) {
99 | fmt.Printf("%s -> %s: %d\n", graph.Vertexes[startIdx], graph.Vertexes[idx], weight)
100 | }
101 | }
102 |
--------------------------------------------------------------------------------
/线性表/linked_list.py:
--------------------------------------------------------------------------------
1 | # coding: utf8
2 |
3 |
4 | class LinkedList(object):
5 | """
6 | 单链表实现
7 | """
8 | class Node(object):
9 | def __init__(self, element, next_node=None):
10 | self._element = element
11 | self._next_node = next_node
12 |
13 | @property
14 | def element(self):
15 | return self._element
16 |
17 | @element.setter
18 | def element(self, element):
19 | self._element = element
20 |
21 | @property
22 | def next_node(self):
23 | return self._next_node
24 |
25 | @next_node.setter
26 | def next_node(self, next_node):
27 | self._next_node = next_node
28 |
29 | def __init__(self):
30 | # 头结点
31 | self._head = self.Node(None, None)
32 | # 元素数量
33 | self._size = 0
34 |
35 | def insert(self, index, element):
36 | # 先找到待插入节点的前一个节点,然后在其后插入新节点
37 | node = self._head
38 | cursor = -1
39 | while node is not None:
40 | if cursor == index - 1:
41 | # 插入新节点
42 | new_node = self.Node(element)
43 | new_node.next_node = node.next_node
44 | node.next_node = new_node
45 | break
46 | node = node.next_node
47 | cursor = cursor + 1
48 | else:
49 | raise IndexError("invalid index")
50 |
51 | def delete(self, element):
52 | # 先找到待删除节点的前一个节点,然后删除节点
53 | node = self._head
54 | while node.next_node is not None:
55 | if node.next_node.element == element:
56 | node.next_node = node.next_node.next_node
57 | break
58 | node = node.next_node
59 | else:
60 | raise ValueError("not found")
61 |
62 | def find(self, element):
63 | cursor = 0
64 | node = self._head.next_node
65 |
66 | while node is not None:
67 | if node.element == element:
68 | return cursor
69 | node = node.next_node
70 | cursor = cursor + 1
71 | else:
72 | raise ValueError("not found")
73 |
74 |
75 | if __name__ == "__main__":
76 | import unittest
77 |
78 | class LinkedListTest(unittest.TestCase):
79 | def testLinkedList(self):
80 | linked_list = LinkedList()
81 | linked_list.insert(0, 0)
82 | self.assertEqual(linked_list.find(0), 0)
83 | linked_list.insert(0, 1)
84 | self.assertEqual(linked_list.find(1), 0)
85 | self.assertEqual(linked_list.find(0), 1)
86 | linked_list.insert(2, 2)
87 | self.assertEqual(linked_list.find(2), 2)
88 | linked_list.delete(1)
89 | self.assertEqual(linked_list.find(2), 1)
90 | self.assertRaises(ValueError, linked_list.delete, 3)
91 | self.assertRaises(ValueError, linked_list.find, 3)
92 |
93 | unittest.main()
94 |
--------------------------------------------------------------------------------
/回溯算法/leetcode-79.go:
--------------------------------------------------------------------------------
1 | // leetcode:https://leetcode.cn/problems/word-search/description/
2 |
3 | package main
4 |
5 | import (
6 | "fmt"
7 | )
8 |
9 | func inStack(stack [][]int, node []int) bool {
10 | for _, ele := range stack {
11 | if ele[0] == node[0] && ele[1] == node[1] {
12 | return true
13 | }
14 | }
15 | return false
16 | }
17 |
18 | func exist(board [][]byte, word string) bool {
19 | row := len(board)
20 | col := len(board[0])
21 |
22 | var starts [][]int
23 | for i := 0; i < row; i++ {
24 | for j := 0; j < col; j++ {
25 | if board[i][j] == word[0] {
26 | starts = append(starts, []int{i, j})
27 | }
28 | }
29 | }
30 |
31 | for _, start := range starts {
32 | // status[i][j] 保存 board[i][j] 的状态。
33 | // 1 表示上;2 表示右;3 表示下;4 表示左。初始值为 1
34 | var status [][]int
35 | for i := 0; i < row; i++ {
36 | var oneRow []int
37 | for j := 0; j < col; j++ {
38 | oneRow = append(oneRow, 1)
39 | }
40 | status = append(status, oneRow)
41 | }
42 |
43 | stack := [][]int{start}
44 | for len(stack) > 0 {
45 | // 当前扩展节点
46 | currentExpandNode := stack[len(stack)-1]
47 | if len(stack) == len(word) {
48 | return true
49 | }
50 | x, y := currentExpandNode[0], currentExpandNode[1]
51 | // 找下一个节点
52 | var nextNode []int
53 | if status[x][y] > 4 {
54 | // 当前扩展节点成为死节点
55 | // 重置状态
56 | status[x][y] = 1
57 | stack = stack[:len(stack)-1]
58 | continue
59 | }
60 | switch status[x][y] {
61 | case 1:
62 | status[x][y] += 1
63 | if x == 0 {
64 | continue
65 | }
66 | nextNode = []int{x - 1, y}
67 | case 2:
68 | status[x][y] += 1
69 | if y == col-1 {
70 | continue
71 | }
72 | nextNode = []int{x, y + 1}
73 | case 3:
74 | status[x][y] += 1
75 | if x == row-1 {
76 | continue
77 | }
78 | nextNode = []int{x + 1, y}
79 | case 4:
80 | status[x][y] += 1
81 | if y == 0 {
82 | continue
83 | }
84 | nextNode = []int{x, y - 1}
85 | }
86 | // 剪枝
87 | x, y = nextNode[0], nextNode[1]
88 | // 1. 判断是否已经在栈中
89 | if inStack(stack, nextNode) {
90 | continue
91 | }
92 | // 2. nextNode 对应的字符应该等于 word 的第 len(stack) + 1 个字符
93 | if board[x][y] != word[len(stack)] {
94 | continue
95 | }
96 | stack = append(stack, nextNode)
97 | }
98 | }
99 |
100 | return false
101 | }
102 |
103 | func main() {
104 | tests := []struct {
105 | board [][]byte
106 | word string
107 | expected bool
108 | }{
109 | {
110 | board: [][]byte{
111 | {'A', 'B', 'C', 'E'},
112 | {'S', 'F', 'C', 'S'},
113 | {'A', 'D', 'E', 'E'},
114 | },
115 | word: "ABCCED",
116 | expected: true,
117 | },
118 | }
119 | for _, test := range tests {
120 | got := exist(test.board, test.word)
121 | if got != test.expected {
122 | fmt.Printf("got %v, but %v expected\n", got, test.expected)
123 | panic("should equal")
124 | }
125 | }
126 | }
127 |
--------------------------------------------------------------------------------
/线性表/array_list.py:
--------------------------------------------------------------------------------
1 | # coding: utf8
2 |
3 |
4 | class ArrayList(object):
5 | """
6 | 顺序表实现
7 | """
8 | def __init__(self, initialize_size=16, capacity_factor=2):
9 | """
10 | :param initialize_size: 初始容量
11 | :param capacity_factor: 扩容因子
12 | """
13 | self._initialize_size = initialize_size
14 | self._capacity_factor = capacity_factor
15 | self._array = [None] * initialize_size
16 | self._total_size = initialize_size
17 | self._used_size = 0
18 |
19 | def _ensure_capacity(self, increased_size):
20 | self._total_size = self._total_size + increased_size
21 | new_array = [None] * self._total_size
22 |
23 | # 将旧数组中的元素拷贝到新数组
24 | for ind in range(self._used_size):
25 | new_array[ind] = self._array[ind]
26 |
27 | self._array = new_array
28 |
29 | def _will_ensure_capacity(self):
30 | if self._used_size < self._total_size:
31 | return
32 | self._ensure_capacity(
33 | self._initialize_size * self._capacity_factor)
34 |
35 | def insert(self, index, element):
36 | self._will_ensure_capacity()
37 |
38 | if index < 0:
39 | index = 0
40 | if index > self._used_size:
41 | index = self._used_size
42 |
43 | # 将 array[index...used_size-1] 移动到 array[index+1...used_size]
44 | for ind in range(self._used_size, index, -1):
45 | self._array[ind] = self._array[ind - 1]
46 |
47 | self._array[index] = element
48 | self._used_size = self._used_size + 1
49 |
50 | def delete(self, index):
51 | if index < 0 or index >= self._used_size:
52 | raise IndexError("invalid index")
53 |
54 | removed_element = self._array[index]
55 | # 将 array[index+1...used_size-1] 移动到 array[index, used_size-2]
56 | for ind in range(index, self._used_size - 2 + 1):
57 | self._array[ind] = self._array[ind + 1]
58 |
59 | self._used_size = self._used_size - 1
60 | return removed_element
61 |
62 | def set(self, index, element):
63 | self._array[index] = element
64 |
65 | def get(self, index):
66 | return self._array[index]
67 |
68 | def size(self):
69 | return self._used_size
70 |
71 | def find(self, element):
72 | for index in range(self._used_size):
73 | if self._array[index] == element:
74 | return index
75 | return -1
76 |
77 |
78 | class Iterator(object):
79 | def __init__(self, collection):
80 | self._collection = collection
81 | self._cursor = 0
82 |
83 | def __iter__(self):
84 | return self
85 |
86 | def rewind(self):
87 | self._cursor = 0
88 |
89 | def next(self):
90 | if self._cursor >= self._collection.size():
91 | raise StopIteration("over")
92 |
93 | try:
94 | return self._collection.get(self._cursor)
95 | finally:
96 | self._cursor = self._cursor + 1
97 |
98 |
99 | if __name__ == "__main__":
100 | array_list = ArrayList(4, 2)
101 | array_list.insert(0, 100)
102 | array_list.insert(0, 50)
103 | array_list.insert(-1, 0)
104 | array_list.insert(100, 150)
105 | print(array_list.find(150))
106 |
--------------------------------------------------------------------------------
/基本概念/README.md:
--------------------------------------------------------------------------------
1 | **基本概念**
2 |
3 | ---
4 |
5 | ### 数据
6 |
7 | 数据是客观事物的符号表示。一切能够输入到计算机,并被计算机处理的符号,都是数据。比如一个汉字,可以通过编码的方式,转换成数值,进而归属到数据的范畴。
8 |
9 | ---
10 |
11 | ### 数据元素
12 |
13 | 数据元素是数据的基本单位,它通常被当作一个整体来对待。一个数据元素可以分成若干个**数据项**,数据项是数据的不可再分的最小单位。比如一本书的书目信息是一个数据元素,书目信息中的每一项(比如作者、ISBN编号、发布时间等)都是数据项。
14 |
15 | ---
16 |
17 | ### 数据对象
18 |
19 | 性质相同的数据元素所组成的集合,就是数据对象。它是数据的一个子集。比如整型数据对象是由0, +1, -1, +2, -2,...组成的一个无限集;比如字符数据对象是由'a','A','b','B',...组成的一个有限集。
20 |
21 | ---
22 |
23 | ### 数据结构
24 |
25 | 数据结构DataStructure是一个二元组:
26 |
27 |
28 | DataStructure = (D, S)
29 |
30 |
31 | 其中:D是数据元素的有限集,S是D上的关系的有限集。
32 |
33 | 通俗地讲,**数据结构是相互之间存在一种或多种特定关系的数据元素的有限集**。根据数据元素之间的关系,数据结构分为:
34 |
35 | * 集合结构
36 | 集合中的数据元素,除了“同属一个集合”之外,别无其它关系
37 | * 线性结构
38 | 线性结构中的数据元素,存在一对一的关系
39 | * 树形结构
40 | 树形结构中的数据元素,存在一对多的关系
41 | * 图状结构或网状结构
42 | 图状结构中的数据元素,存在多对多的关系
43 |
44 | 比如,数据结构*科研课题小组*,其成员包括:1名教师、1-3名研究生、1-6名本科生。这些成员之间的关系是:教师指导研究生,每名研究生指导1-2名本科生。
45 |
46 | ---
47 |
48 | ### 存储结构
49 |
50 | 数据结构在计算机中的表示,叫做存储结构或物理结构。它包括数据元素的表示和关系的表示。
51 |
52 | 计算机存储信息的基本单位是bit,因此,可以使用一组连续的位串来表示数据元素,这个位串叫**元素**或**节点**。如果一个数据元素由多个数据项组成,那么每个数据项对应的子位串叫**数据域**。
53 |
54 | 数据元素之间的关系在计算机中有两种表示方式:**顺序映像**和**非顺序映像**。由此得到两种不同的存储结构:**顺序存储结构**和**链式存储结构**。
55 |
56 | 在顺序存储结构中,数据元素存储在连续的存储单元上,然后**用元素的相对位置描述它们之间的关系**,比如:把一颗完全二叉树存储到一段连续的存储单元上,那么索引为0的位置上的元素就是根节点,索引为i的位置上的元素的左孩子节点的索引是2\*i+1、右孩子节点的索引是2\*i + 2,索引为i的位置上的元素的父节点是floor((i - 1) / 2)。
57 |
58 | 在链式存储结构中,借助指示元素存储位置的指针,来描述元素之间的关系。比如:在二叉树的链式存储结构中,每个节点分为三部分:数据域、左指针、右指针,其中左指针指向左孩子节点,右指针指向右孩子节点。
59 |
60 | ---
61 |
62 | ### 数据结构和数据类型之间的关系
63 |
64 | 因为我们通常使用高级程序设计语言进行编程,所以我们就需要使用高级程序设计语言中的**数据类型**来描述存储结构。比如在Java和Python中,分别使用数组和List来描述线性存储结构;使用引用来描述链式存储结构。
65 |
66 | ---
67 |
68 | ### 数据类型
69 |
70 | 数据类型是一个值的集合和定义在这个值集上的操作集的总称。比如整型数据类型是由某个范围内的整数所组成的,定义在其上操作包括加、减、乘、除、取余等。
71 |
72 | 数据类型通常分为两大类:
73 |
74 | * 原子类型(标量类型)
75 | 原子类型不可再分。比如整型、浮点型、布尔类型、字符类型等
76 | * 结构类型(矢量类型、容器类型)
77 | 结构类型的值是可以分解。其成分既可以是结构的、也可以是非结构的
78 |
79 | 引入数据类型的目的有两方面:
80 |
81 | * 站在硬件角度看,数据类型用来解释内存中的二进制位串的含义
82 | * 站在用户角度看,数据类型实现了信息的隐藏,它隐藏了一切用户不必了解的细节。比如用户不必了解整型在内存中是如何存储的,以及加减乘除等操作是如何实现的
83 |
84 | ---
85 |
86 | ### 抽象数据类型(ADT)
87 |
88 | **抽象数据类型和数据类型本质上是一个概念**。但是ADT强调数据类型的数学抽象,并且抽象数据类型的应用范畴更广,因为它不仅包括处理器定义和实现的固有数据类型,还包括用户在软件设计过程中自定义的数据类型。
89 |
90 | 抽象数据类型是一个三元组:
91 |
92 |
93 | ADT = (D, S, P)
94 |
95 |
96 | 其中:D是数据对象,S是D上的关系集,P是对D的操作集。
97 |
98 | 详情,可以参考:[这篇文档](https://www.xuebuyuan.com/3187404.html)。
99 |
100 | ---
101 |
102 | ### 算法
103 |
104 | 算法是**用来求解某类问题的有限指令序列**。算法有五个特征:
105 |
106 | * 输入
107 | 算法有零个或多个输入
108 | * 输出
109 | 算法有一个或多个输出。输入会决定输出
110 | * 有穷性
111 | 算法必须在执行有穷步之后结束,并且每步都可以在有穷时间内执行完
112 | * 确定性
113 | 对于相同的输入,只能得到相同的输出
114 | * 可行性
115 | 算法中描述的步骤必须可以基于已经存在的基本运算执行若干次来实现
116 |
117 | ---
118 |
119 | ### 时间复杂度
120 |
121 | 算法由控制结构(顺序、分支、循环)和原操作(固有数据类型的操作)组成,算法的执行时间取决于两者的综合效果。
122 |
123 | 在比较解决同一问题的不同算法时,通常先选择一种或多种对于算法来说是**基本操作**的原操作(通常选择最深层循环中的原操作作为基本操作),然后把该基本操作的重复执行次数(**频度**)作为算法的时间度量。
124 |
125 | 通常情况下,基本操作的频度是问题规模n的函数f(n),算法的时间度量记作:
126 |
127 |
128 | T(n) = O(f(n))
129 |
130 |
131 | 它表示随着问题规模n的增长,f(n)的**增长率**和算法执行时间的**增长率**相同,称其为算法的渐近时间复杂度,简称时间复杂度。
132 |
133 | 随着输入的不同,基本操作的重复执行次数也会不同。因此,在讨论算法的时间复杂度时,通常指的是算法在最坏的情况下的时间复杂度。
134 |
135 | 算法除了有时间度量之外,还有空间度量,也就是所谓的空间复杂度,记作:
136 |
137 |
138 | S(n) = O(f(n))
139 |
140 |
141 | 它表示,随着问题规模n的增长,算法所使用的**额外空间**的**增长率**和f(n)的增长率相同。
142 |
--------------------------------------------------------------------------------
/图/最短路径/Dijkstra算法/dijkstra.py:
--------------------------------------------------------------------------------
1 | # coding: utf8
2 |
3 |
4 | class HeadNode(object):
5 | def __init__(self, element):
6 | self.element = element
7 | self.next_node = None
8 |
9 |
10 | class AdjacentNode(object):
11 | def __init__(self, index, weight):
12 | self.index = index
13 | self.weight = weight
14 | self.next_node = None
15 |
16 |
17 | class Graph(object):
18 | def __init__(self):
19 | self._vertexes = []
20 |
21 | def add_vertex(self, element):
22 | self._vertexes.append(HeadNode(element))
23 |
24 | def add_edge(self, tail, head, weight):
25 | for i, j in [(tail, head), (head, tail)]:
26 | node = self._vertexes[i]
27 | while node.next_node is not None:
28 | if node.next_node.index == j:
29 | node.next_node.weight = weight
30 | break
31 | node = node.next_node
32 | else:
33 | node.next_node = AdjacentNode(j, weight)
34 |
35 | def get_vertex_count(self):
36 | return len(self._vertexes)
37 |
38 | def get_vertex(self, index):
39 | return self._vertexes[index]
40 |
41 |
42 | def dijkstra(graph, source=0):
43 | """
44 | Dijkstra 算法实现
45 | """
46 | vertex_count = graph.get_vertex_count()
47 |
48 | # A 保存已经计算出最短路径的顶点集,初始时,A 中只包含源点
49 | A = [source]
50 | # B 保存尚未计算出最短路径的顶点集,初始时,B 中包含除源点外的其它所有顶点
51 | B = set([index for index in range(vertex_count) if index != source])
52 |
53 | # D 的每个分量保存一个顶点的最短路径,初始时,源点的最短路径是 0
54 | D = [None] * vertex_count
55 | D[source] = 0
56 |
57 | # 初始化 Destimate 数组
58 | Destimate = [None] * vertex_count
59 | node = graph.get_vertex(source).next_node
60 | while node is not None:
61 | Destimate[node.index] = node.weight
62 | node = node.next_node
63 | # 0 表示顶点已经被加入到 A 中
64 | Destimate[source] = 0
65 |
66 | while B:
67 | # 找出 estimate 值最小的顶点 m
68 | lowest_estimate = None
69 | for index, estimate in enumerate(Destimate):
70 | if estimate == 0 or estimate is None:
71 | continue
72 | if lowest_estimate is None or estimate < lowest_estimate[1]:
73 | lowest_estimate = (index, estimate)
74 | m = lowest_estimate[0]
75 |
76 | # 将 m 从 B 中移除
77 | B.remove(m)
78 | # 并将其加入到 A 中
79 | A.append(lowest_estimate[0])
80 | # D[m] = Destimate[m]
81 | D[m] = Destimate[m]
82 |
83 | # 更新 Destimte 数组
84 | Destimate[m] = 0
85 | node = graph.get_vertex(m).next_node
86 | while node is not None:
87 | if Destimate[node.index] == 0:
88 | node = node.next_node
89 | continue
90 | if Destimate[node.index] is None or (D[m] + node.weight) < Destimate[node.index]:
91 | Destimate[node.index] = D[m] + node.weight
92 | node = node.next_node
93 |
94 | return D
95 |
96 |
97 | def test():
98 | g = Graph()
99 | for index in range(6):
100 | g.add_vertex(index)
101 | for edge in [(0, 2, 10), (0, 4, 30), (0, 5, 100),
102 | (1, 2, 5), (2, 3, 50), (3, 5, 10),
103 | (4, 3, 20), (4, 5, 60)]:
104 | g.add_edge(*edge)
105 |
106 | d = dijkstra(g)
107 | print(d)
108 |
109 |
110 | if __name__ == "__main__":
111 | test()
112 |
--------------------------------------------------------------------------------
/排序算法/快速排序/quick_sort_linked_list.py:
--------------------------------------------------------------------------------
1 | # coding: utf8
2 |
3 |
4 | class Node(object):
5 | def __init__(self, key, prev_node=None, next_node=None):
6 | self.key = key
7 | self.prev_node = prev_node
8 | self.next_node = next_node
9 |
10 |
11 | def partition(linked_list):
12 | if linked_list.next_node is None:
13 | return None, linked_list, None
14 |
15 | left = None
16 | temp = linked_list.next_node
17 | while temp is not None:
18 | if temp.key >= linked_list.key:
19 | temp = temp.next_node
20 | continue
21 |
22 | # 把 temp 移到 left
23 | prev_node = temp.prev_node
24 | next_node = temp.next_node
25 | prev_node.next_node = next_node
26 | if next_node is not None:
27 | next_node.prev_node = prev_node
28 |
29 | if left is None:
30 | left = temp
31 | left.prev_node = None
32 | left.next_node = None
33 | else:
34 | left_next = left.next_node
35 | if left_next is not None:
36 | left_next.prev_node = temp
37 | left.next_node = temp
38 | temp.prev_node = left
39 | temp.next_node = left_next
40 |
41 | temp = next_node
42 |
43 | right = linked_list.next_node
44 | if right is not None:
45 | right.prev_node = None
46 |
47 | linked_list.next_node = None
48 |
49 | return left, linked_list, right
50 |
51 |
52 | def print_linked_list(linked_list):
53 | if linked_list is None:
54 | return
55 | temp = linked_list
56 | keys = []
57 | while temp is not None:
58 | keys.append(temp.key)
59 | temp = temp.next_node
60 | print(" ".join(map(str, keys)))
61 |
62 |
63 | def quick_sort(linked_list):
64 | if linked_list is None or linked_list.next_node is None:
65 | return linked_list
66 |
67 | left, linked_list, right = partition(linked_list)
68 |
69 | if left is not None:
70 | left = quick_sort(left)
71 | if right is not None:
72 | right = quick_sort(right)
73 |
74 | head = linked_list
75 | if left is not None:
76 | head = left
77 | while left.next_node is not None:
78 | left = left.next_node
79 | left.next_node = linked_list
80 | linked_list.prev_node = left
81 | linked_list.next_node = right
82 | if right is not None:
83 | right.prev_node = linked_list
84 |
85 | return head
86 |
87 |
88 | def check_sorted_linked_list(linked_list):
89 | p1 = linked_list
90 | while p1 is not None and p1.next_node is not None:
91 | p2 = p1.next_node
92 | if p1.key > p2.key:
93 | return False
94 | p1 = p2
95 | return True
96 |
97 |
98 | def test():
99 | import random
100 |
101 | # 元素数量
102 | N = 100
103 |
104 | elements = range(N)
105 | # 将元素打乱
106 | random.shuffle(elements)
107 |
108 | # 生成链表
109 | nodes = []
110 | for element in elements:
111 | nodes.append(Node(element))
112 | for ind in range(N - 1):
113 | nodes[ind].next_node = nodes[ind + 1]
114 | nodes[ind + 1].prev_node = nodes[ind]
115 | linked_list = nodes[0]
116 | del nodes
117 |
118 | head = quick_sort(linked_list)
119 | assert check_sorted_linked_list(head)
120 |
121 |
122 | if __name__ == "__main__":
123 | for i in range(20):
124 | test()
125 |
--------------------------------------------------------------------------------
/leetcode/K路归并排序/k_way_merge_sort.py:
--------------------------------------------------------------------------------
1 | # coding: utf8
2 |
3 |
4 | class MinHeap(object):
5 | @staticmethod
6 | def adjust(heap, start=None, end=None):
7 | if start is None:
8 | start = 0
9 | if end is None:
10 | end = len(heap) - 1
11 |
12 | get_left_child = lambda ind: 2 * ind + 1
13 | get_right_child = lambda ind: 2 * ind + 2
14 |
15 | index = start
16 | while index >= 0:
17 | left_child_index = get_left_child(index)
18 | right_child_index = get_right_child(index)
19 | if left_child_index > end:
20 | break
21 | if right_child_index > end:
22 | if heap[index] > heap[left_child_index]:
23 | heap[index], heap[left_child_index] = \
24 | heap[left_child_index], heap[index]
25 | break
26 |
27 | if heap[index] <= heap[left_child_index] and \
28 | heap[index] <= heap[right_child_index]:
29 | break
30 | if heap[right_child_index] > heap[left_child_index]:
31 | heap[index], heap[left_child_index] = \
32 | heap[left_child_index], heap[index]
33 | index = left_child_index
34 | else:
35 | heap[index], heap[right_child_index] = \
36 | heap[right_child_index], heap[index]
37 | index = right_child_index
38 |
39 | @classmethod
40 | def heapify(cls, heap):
41 | for ind in range(len(heap)/2, -1, -1):
42 | cls.adjust(heap, ind)
43 |
44 |
45 | class Node(object):
46 | def __init__(self, cursor, array):
47 | self.cursor = cursor
48 | self.array = array
49 |
50 | def __cmp__(self, other):
51 | diff = self.array[self.cursor] - other.array[other.cursor]
52 | if diff > 0:
53 | return 1
54 | elif diff == 0:
55 | return 0
56 | else:
57 | return -1
58 |
59 | def get_next_node(self):
60 | if self.cursor >= len(self.array) - 1:
61 | return None
62 | return Node(self.cursor + 1, self.array)
63 |
64 | def get_element(self):
65 | return self.array[self.cursor]
66 |
67 |
68 | def k_way_merge_sort(arrays):
69 | result = [None] * sum([len(array) for array in arrays])
70 | # 取每个数组的第一个元素,建立一个最小堆
71 | heap = [Node(0, array) for array in arrays]
72 | MinHeap.heapify(heap)
73 |
74 | index = 0
75 | k = len(arrays) - 1
76 |
77 | while True:
78 | # 弹出堆顶元素
79 | node = heap[0]
80 | result[index] = node.get_element()
81 | index = index + 1
82 |
83 | # 如果堆顶元素所在的数组仍有剩余元素,那么从其中取下一个元素,然后放到堆顶
84 | next_node = node.get_next_node()
85 | if next_node is not None:
86 | heap[0] = next_node
87 | # 调整堆
88 | MinHeap.adjust(heap, 0, k)
89 | continue
90 |
91 | # 如果堆空,则退出
92 | if k == 0:
93 | break
94 |
95 | # 否则将堆的最后一个元素弹出,然后放到堆顶
96 | heap[0] = heap[k]
97 | # 调整堆
98 | k = k - 1
99 | MinHeap.adjust(heap, 0, k)
100 |
101 | return result
102 |
103 |
104 | def test():
105 | arrays = []
106 | for ind in range(1, 10):
107 | array = range(100 * ind, 100 * ind + 100)
108 | arrays.append(array)
109 | result = k_way_merge_sort(arrays)
110 | for ind in range(0, len(result) - 1):
111 | assert result[ind] <= result[ind + 1]
112 |
113 |
114 | if __name__ == "__main__":
115 | test()
116 |
--------------------------------------------------------------------------------
/回溯算法/leetcode-37.py:
--------------------------------------------------------------------------------
1 | # leetcode 37: https://leetcode.cn/problems/sudoku-solver/
2 |
3 | from typing import Tuple, Set, List
4 |
5 |
6 | class Solution:
7 | def to_matrix(self, x: int) -> Tuple[int, int]: # noqa
8 | return x // 9, x % 9
9 |
10 | def get_constraints(self, matrix: List[List[int]], x: int, y: int) -> Set[int]: # noqa
11 | """
12 | 获取同一 3x3 格子,同一行,同一列的所有数字
13 | """
14 |
15 | # 获取 3x3 格子的中间
16 | def get_center(a: int) -> int:
17 | if a in {0, 1, 2}:
18 | return 1
19 | elif a in {3, 4, 5}:
20 | return 4
21 | else:
22 | return 7
23 |
24 | center_x: int = get_center(x)
25 | center_y: int = get_center(y)
26 | s: Set[int] = set()
27 | # 获取同一 3x3 格子中的数字
28 | for coord in [
29 | (center_x - 1, center_y - 1), (center_x - 1, center_y), (center_x - 1, center_y + 1),
30 | (center_x, center_y - 1), (center_x, center_y), (center_x, center_y + 1),
31 | (center_x + 1, center_y - 1), (center_x + 1, center_y), (center_x + 1, center_y + 1)
32 | ]:
33 | if coord == (x, y):
34 | continue
35 | element: int = matrix[coord[0]][coord[1]]
36 | if element:
37 | s.add(element)
38 |
39 | # 获取同一行的数字
40 | for ind in range(0, 9): # type: int
41 | if ind != y:
42 | element: int = matrix[x][ind]
43 | if element:
44 | s.add(element)
45 |
46 | # 获取同一列的数字
47 | for ind in range(0, 9): # type: int
48 | if ind != x:
49 | element: int = matrix[ind][y]
50 | if element:
51 | s.add(element)
52 |
53 | return s
54 |
55 | def solveSudoku(self, board: List[List[str]]) -> None: # noqa
56 | # 初始状态
57 | status: List[List[int]] = []
58 | for row in board: # type: List[str]
59 | status.append([])
60 | for column in row: # type: str
61 | if column == ".":
62 | status[-1].append(0)
63 | else:
64 | status[-1].append(int(column))
65 |
66 | top: int = 0
67 | while top < 81:
68 | x, y = self.to_matrix(top) # type: int, int
69 | # 已给定数字直接填入
70 | if board[x][y] != ".":
71 | top += 1
72 | continue
73 | constraints: Set[int] = self.get_constraints(status, x, y)
74 | for new_value in range(status[x][y] + 1, 10): # type: int
75 | if new_value in constraints:
76 | continue
77 | status[x][y] = new_value
78 | top += 1
79 | break
80 | else:
81 | # 回溯到最近的 “.”
82 | top -= 1
83 | while top >= 0:
84 | temp_x, temp_y = self.to_matrix(top) # type: int, int
85 | if board[temp_x][temp_y] != ".":
86 | top -= 1
87 | continue
88 | break
89 | if top < 0:
90 | break
91 | # 重置状态
92 | status[x][y] = 0
93 | else:
94 | for i in range(len(board)): # type: int
95 | for j in range(len(board[i])): # type: int
96 | if board[i][j] == ".":
97 | board[i][j] = str(status[i][j])
98 | return
99 | raise RuntimeError("no answer")
100 |
101 |
--------------------------------------------------------------------------------
/分支限界算法/leetcode-407.go:
--------------------------------------------------------------------------------
1 | // leetcode:https://leetcode.cn/problems/trapping-rain-water-ii/description/
2 |
3 | package main
4 |
5 | import (
6 | "container/heap"
7 | "fmt"
8 | )
9 |
10 | // 问题分析:
11 | //
12 | // 1. 路径是一个节点序列,路径中的两个相邻的节点必须相邻接。
13 | // 比如 [(0, 0), (0, 1), (1, 1), (1, 2)] 是路径;而 [(0, 0), (1, 1)] 不是,因为它的前两个节点不邻接
14 | // 2. 在本题的上下文中,路径的起点必须是边缘。由此可以进一步得到,[(1, 1), (1, 2), (2, 2), (2, 3)] 不是路径,因为其起点不是边缘
15 | // 3. 将路径上最高的节点的高度称为路径的高度。
16 | // 假如 [(x1, x2), ...(xi, yi)] 的路径高度是 heightI,
17 | // 那么 [(x1, x2), ...(xi, yi), (xi, yi+1)] 的路径高度是 max(heightI, Height[(xi, yi+1)])
18 | // 4. 对于任何一个节点而言,到达它的路径有很多,但是必然存在一个或多个路径高度最低的路径,记其为 minPath。
19 | // 该节点能否接雨水,以及接多少取决于自身的高度(记为 h)与 minPath 的高度(记为 minPathHeight)。
20 | // 如果 h >= minPathHeight,那么无法接雨水,因为雨水将沿着 minPath 从边缘流出;
21 | // 否则可以接雨水,由于所有其它路径的高度都大于或等于 minPath 的高度,根据木桶原理,该节点能接的雨水为 minPathHeight - h。
22 | // 由此,也可以得到,边缘无法接雨水
23 | // 5. 根据 4,如果可以保证第一次搜索到节点 i 时,走的是 minPath。那么在第一次搜索到 i 时,就可以计算出 i 接的雨水。
24 | // 那么如何做到呢?
25 | // **从边缘开始,每次都从路径高度最低的节点以广度优先的方式进行搜索。**
26 | // **同时需要保证,每个节点只被访问一次**
27 |
28 | // 结论:
29 | //
30 | // 使用分支限界算法
31 |
32 | // Item 表示优先级队列中的元素
33 | type Item struct {
34 | X int
35 | Y int
36 | // 点 (x, y) 的路径高度。Height 越小,优先级越高
37 | Height int
38 | }
39 |
40 | // PriorityQueue 是基于 MinHeap 的优先级队列
41 | type PriorityQueue []Item
42 |
43 | func (pq PriorityQueue) Len() int { return len(pq) }
44 | func (pq PriorityQueue) Less(i, j int) bool { return pq[i].Height < pq[j].Height }
45 | func (pq PriorityQueue) Swap(i, j int) { pq[i], pq[j] = pq[j], pq[i] }
46 |
47 | func (pq *PriorityQueue) Push(x interface{}) {
48 | *pq = append(*pq, x.(Item))
49 | }
50 | func (pq *PriorityQueue) Pop() interface{} {
51 | old := *pq
52 | n := old[len(old)-1]
53 | *pq = old[:len(old)-1]
54 | return n
55 | }
56 |
57 | // NewPriorityQueue 构造 PriorityQueue 实例
58 | func NewPriorityQueue() PriorityQueue {
59 | return make(PriorityQueue, 0)
60 | }
61 |
62 | func trapRainWater(heightMap [][]int) int {
63 | var ans = 0
64 | m := len(heightMap)
65 | n := len(heightMap[0])
66 |
67 | queue := NewPriorityQueue()
68 | // 记录每个节点是否已经访问过
69 | visited := make([][]bool, m)
70 | // 将所有边缘加入队列,并且设置为已访问
71 | for x := 0; x < m; x++ {
72 | oneRow := make([]bool, n)
73 | for y := 0; y < n; y++ {
74 | if x == 0 || x == m-1 || y == 0 || y == n-1 {
75 | heap.Push(&queue, Item{
76 | X: x,
77 | Y: y,
78 | Height: heightMap[x][y],
79 | })
80 | oneRow[y] = true
81 | } else {
82 | oneRow[y] = false
83 | }
84 | }
85 | visited[x] = oneRow
86 | }
87 |
88 | for len(queue) > 0 {
89 | currentExpandNode := heap.Pop(&queue).(Item)
90 | x, y, height := currentExpandNode.X, currentExpandNode.Y, currentExpandNode.Height
91 | // 向上下左右四个方向广度优先遍历
92 | for _, nextNode := range [][]int{{x - 1, y}, {x, y + 1}, {x + 1, y}, {x, y - 1}} {
93 | tx, ty := nextNode[0], nextNode[1]
94 | // 如果该点存在,并且未被访问过
95 | if tx >= 0 && tx < m && ty >= 0 && ty < n && !visited[tx][ty] {
96 | // 高度较低,可以接雨水
97 | if heightMap[tx][ty] < height {
98 | ans += height - heightMap[tx][ty]
99 | heap.Push(&queue, Item{X: tx, Y: ty, Height: height})
100 | } else {
101 | heap.Push(&queue, Item{X: tx, Y: ty, Height: heightMap[tx][ty]})
102 | }
103 | // 设置为已访问
104 | visited[tx][ty] = true
105 | }
106 | }
107 | }
108 |
109 | return ans
110 | }
111 |
112 | func main() {
113 | tests := []struct {
114 | heightMap [][]int
115 | expected int
116 | }{
117 | {
118 | heightMap: [][]int{{1, 4, 3, 1, 3, 2}, {3, 2, 1, 3, 2, 4}, {2, 3, 3, 2, 3, 1}},
119 | expected: 4,
120 | },
121 | {
122 | heightMap: [][]int{{3, 3, 3, 3, 3}, {3, 2, 2, 2, 3}, {3, 2, 1, 2, 3}, {3, 2, 2, 2, 3}, {3, 3, 3, 3, 3}},
123 | expected: 10,
124 | },
125 | }
126 | for _, test := range tests {
127 | got := trapRainWater(test.heightMap)
128 | if got != test.expected {
129 | message := fmt.Sprintf("got %d, but %d expected", got, test.expected)
130 | fmt.Println(message)
131 | panic(message)
132 | }
133 | }
134 | }
135 |
--------------------------------------------------------------------------------
/图/DAG-有向无环图/拓扑排序/topological_sort.py:
--------------------------------------------------------------------------------
1 | # coding: utf8
2 |
3 |
4 | class Node(object):
5 | def __init__(self, element):
6 | self.element = element
7 | self.incoming_degree = 0
8 |
9 |
10 | class Graph(object):
11 | """
12 | 数组矩阵表示法
13 | """
14 | def __init__(self):
15 | self._vertexes = []
16 | self._arches = []
17 |
18 | def add_vertex(self, element):
19 | self._vertexes.append(Node(element))
20 | for arch in self._arches:
21 | arch.append(None)
22 | self._arches.append([None] * len(self._vertexes))
23 | return len(self._vertexes) - 1
24 |
25 | def add_arch(self, tail, head, weight=1):
26 | old_weight = self._arches[tail][head]
27 | if old_weight is None:
28 | self._vertexes[head].incoming_degree = \
29 | self._vertexes[head].incoming_degree + 1
30 | self._arches[tail][head] = weight
31 |
32 | def delete_arch(self, tail, head):
33 | old_weight = self._arches[tail][head]
34 | if old_weight is None:
35 | return
36 | self._vertexes[head].incoming_degree = \
37 | self._vertexes[head].incoming_degree - 1
38 | self._arches[tail][head] = None
39 |
40 | def get_vertex_count(self):
41 | return len(self._vertexes)
42 |
43 | def get_vertex(self, index):
44 | return self._vertexes[index]
45 |
46 | def get_arch(self, tail):
47 | for head, weight in enumerate(self._arches[tail]):
48 | if weight is None:
49 | continue
50 | yield head
51 |
52 | def get_arch_by_offset(self, head, offset):
53 | real_index = 0
54 | for index, weight in enumerate(self._arches[head]):
55 | if weight is None:
56 | continue
57 | if real_index == offset:
58 | return index
59 | real_index = real_index + 1
60 | return None
61 |
62 |
63 | def topological_sort(g):
64 | sequence = []
65 |
66 | stack = []
67 | for index in range(g.get_vertex_count()):
68 | node = g.get_vertex(index)
69 | if node.incoming_degree == 0:
70 | stack.append(index)
71 |
72 | while stack:
73 | tail = stack.pop(-1)
74 | sequence.append(tail)
75 | for head in g.get_arch(tail):
76 | g.delete_arch(tail, head)
77 | if g.get_vertex(head).incoming_degree == 0:
78 | stack.append(head)
79 |
80 | return sequence
81 |
82 |
83 | def topological_sort_dfs(g):
84 | total_sequence = []
85 | vertex_count = g.get_vertex_count()
86 | visited = [False for _ in range(vertex_count)]
87 |
88 | def _topological_sort_dfs(start):
89 | sequence = []
90 | status = [0 for _ in range(vertex_count)]
91 | stack = [start]
92 |
93 | while stack:
94 | top = stack[-1]
95 | next_vertex = g.get_arch_by_offset(top, status[top])
96 | if next_vertex is None:
97 | visited[top] = True
98 | sequence.insert(0, top)
99 | stack.pop(-1)
100 | continue
101 |
102 | status[top] = status[top] + 1
103 | if not visited[next_vertex]:
104 | stack.append(next_vertex)
105 |
106 | return sequence
107 |
108 | for index in range(vertex_count):
109 | if g.get_vertex(index).incoming_degree == 0:
110 | total_sequence.extend(_topological_sort_dfs(index))
111 |
112 | return total_sequence
113 |
114 |
115 | def test():
116 | g = Graph()
117 | for element in range(13):
118 | g.add_vertex(element)
119 | for arch in [(0, 1), (0, 5), (0, 6),
120 | (2, 0), (2, 3), (3, 5),
121 | (5, 4), (6, 9), (7, 6),
122 | (8, 7), (9, 10), (9, 11),
123 | (9, 12), (11, 12)]:
124 | g.add_arch(*arch)
125 |
126 | print(topological_sort_dfs(g))
127 | print(topological_sort(g))
128 |
129 |
130 | if __name__ == "__main__":
131 | test()
132 |
--------------------------------------------------------------------------------
/树/霍夫曼树(最优二叉树)/huffman_tree.py:
--------------------------------------------------------------------------------
1 | # coding: utf8
2 |
3 | import heapq
4 |
5 |
6 | class Node(object):
7 | """
8 | 霍夫曼树的节点
9 | """
10 | def __init__(self, char, weight, left=None, right=None):
11 | self.char = char
12 | self.weight = weight
13 | self.left = left
14 | self.right = right
15 |
16 | def __cmp__(self, other):
17 | if not isinstance(other, self.__class__):
18 | raise TypeError("instance of %s expected" % self.__class__.__name__)
19 | if other.weight == self.weight:
20 | return 0
21 | if other.weight > self.weight:
22 | return -1
23 | return 1
24 |
25 | def __str__(self):
26 | return "%s{char=%s, weight=%d, left=%s, right=%s}" % (
27 | self.__class__.__name__,
28 | self.char,
29 | self.weight,
30 | self.left and self.left.char,
31 | self.right and self.right.char
32 | )
33 |
34 |
35 | class HuffmanTree(object):
36 | """
37 | 霍夫曼树实现
38 | """
39 | def __init__(self, chars):
40 | root = self.create(chars)
41 | self._encode_map, self._decode_map = self.generate_code_map(root)
42 |
43 | @staticmethod
44 | def create(chars):
45 | if len(chars) == 0:
46 | return
47 |
48 | nodes = []
49 | # 构造 n 棵只有根节点的二叉树
50 | for char, weight in chars:
51 | heapq.heappush(nodes, Node(char, weight))
52 |
53 | # 重复下面的步骤,直到森林中只有一棵树
54 | while len(nodes) > 1:
55 | # 从森林中选出根节点权值最小的两棵树
56 | left = heapq.heappop(nodes)
57 | right = heapq.heappop(nodes)
58 | # 构造一棵新树,并把上面的两棵树作为新树的子树,新树的根节点的权值是两者的权值之和
59 | node = Node(None, left.weight + right.weight, left, right)
60 | # 将新树放进森林
61 | heapq.heappush(nodes, node)
62 |
63 | return nodes[0]
64 |
65 | @staticmethod
66 | def generate_code_map(root):
67 | encode_map = {}
68 | decode_map = {}
69 |
70 | if root is None:
71 | return encode_map, decode_map
72 |
73 | temp_map = {root: []}
74 | queue = [root]
75 | while queue:
76 | node = queue.pop()
77 | # 将从根节点到叶子节点的路径上的二进制位作为叶子节点的编码
78 | if node.left is None and node.right is None:
79 | code = "".join(temp_map[node])
80 | encode_map[node.char] = code
81 | decode_map[code] = node.char
82 | continue
83 |
84 | node_code = temp_map[node]
85 | # 所有左分支都表示 0
86 | if node.left is not None:
87 | temp_map[node.left] = node_code + ['0']
88 | queue.append(node.left)
89 |
90 | # 所有右分支都表示 1
91 | if node.right is not None:
92 | temp_map[node.right] = node_code + ['1']
93 | queue.append(node.right)
94 |
95 | return encode_map, decode_map
96 |
97 | def encode(self, string):
98 | """
99 | 编码
100 | """
101 | result = []
102 | for char in string:
103 | if char not in self._encode_map:
104 | raise ValueError("unknown char %s" % char)
105 | result.append(self._encode_map[char])
106 | return "".join(result)
107 |
108 | def decode(self, encoded_string):
109 | start = 0
110 | end = start + 1
111 | result = []
112 | while end <= len(encoded_string):
113 | sub_string = encoded_string[start:end]
114 | if sub_string not in self._decode_map:
115 | end = end + 1
116 | continue
117 | result.append(self._decode_map[sub_string])
118 | start = end
119 | end = end + 1
120 | return "".join(result)
121 |
122 |
123 | def test():
124 | chars = [("A", 5), ("B", 24), ("C", 7), ("D", 17),
125 | ("E", 34), ("F", 5), ("G", 13)]
126 | huffman_tree = HuffmanTree(chars)
127 | string = "AFGECBDAAAFFF"
128 | assert string == huffman_tree.decode(huffman_tree.encode(string))
129 |
130 |
131 | if __name__ == "__main__":
132 | test()
133 |
--------------------------------------------------------------------------------
/图/dfs_tree.py:
--------------------------------------------------------------------------------
1 | # coding: utf8
2 |
3 | """
4 | DFS 生成树
5 | """
6 |
7 |
8 | class TreeNode(object):
9 | """
10 | 树的孩子兄弟表示法
11 | """
12 | def __init__(self, data):
13 | self._data = data
14 | self._first_child = None
15 | self._next_sibling = None
16 |
17 | def add_child(self, child):
18 | if self._first_child is None:
19 | self._first_child = child
20 | return
21 | node = self._first_child
22 | while node._next_sibling is not None:
23 | node = node._next_sibling
24 | node._next_sibling = child
25 |
26 | def get_first_child(self):
27 | return self._first_child
28 |
29 | def get_next_sibling(self):
30 | return self._next_sibling
31 |
32 | def get_data(self):
33 | return self._data
34 |
35 |
36 | def get_adjacent(adjacent_list, index):
37 | real_index = 0
38 | for adjacent_index, weight in enumerate(adjacent_list):
39 | if weight is None:
40 | continue
41 | if real_index == index:
42 | return adjacent_index
43 | real_index = real_index + 1
44 | return None
45 |
46 |
47 | def dfs_tree_recursive(vertexes, edges):
48 | visited = [False for _ in range(len(vertexes))]
49 | root = TreeNode(vertexes[0])
50 | visited[0] = True
51 |
52 | def _dfs_tree_recursive(start_index, start_node):
53 | adjacent_list = edges[start_index]
54 | index = 0
55 | adjacent_index = get_adjacent(adjacent_list, index)
56 | while adjacent_index is not None:
57 | if not visited[adjacent_index]:
58 | visited[adjacent_index] = True
59 | node = TreeNode(vertexes[adjacent_index])
60 | start_node.add_child(node)
61 | _dfs_tree_recursive(adjacent_index, node)
62 | index = index + 1
63 | adjacent_index = get_adjacent(adjacent_list, index)
64 |
65 | _dfs_tree_recursive(0, root)
66 | return root
67 |
68 |
69 | def dfs_tree(vertexes, edges):
70 | root = None
71 | stack = [0]
72 | vertex_count = len(vertexes)
73 | status = [0 for _ in range(vertex_count)]
74 | visited = [False for _ in range(vertex_count)]
75 | nodes = [None for _ in range(vertex_count)]
76 | parent = [None for _ in range(vertex_count)]
77 |
78 | while stack:
79 | top = stack[-1]
80 | if not visited[top]:
81 | visited[top] = True
82 | node = TreeNode(vertexes[top])
83 | nodes[top] = node
84 | if parent[top] is None:
85 | root = node
86 | else:
87 | nodes[parent[top]].add_child(node)
88 |
89 | adjacent_index = get_adjacent(edges[top], status[top])
90 | if adjacent_index is None:
91 | stack.pop(-1)
92 | continue
93 | status[top] = status[top] + 1
94 | parent[adjacent_index] = top
95 | # 剪枝
96 | if visited[adjacent_index]:
97 | continue
98 | stack.append(adjacent_index)
99 | return root
100 |
101 |
102 | def test():
103 | vertexes = range(5)
104 | edges = []
105 | for ind in range(len(vertexes)):
106 | edges.append([])
107 | for _ in range(len(vertexes)):
108 | edges[ind].append(None)
109 | edges[0][1] = 1
110 | edges[1][0] = 1
111 | edges[0][3] = 3
112 | edges[3][0] = 3
113 | edges[2][3] = 23
114 | edges[3][2] = 23
115 | edges[2][4] = 24
116 | edges[4][2] = 24
117 | edges[1][2] = 12
118 | edges[2][1] = 12
119 |
120 | """
121 |
122 | 0 --- 1 ----┐
123 | | |
124 | └---- 3 --- 2 --- 4
125 | """
126 |
127 | root = dfs_tree_recursive(vertexes, edges)
128 |
129 | # root = dfs_tree(vertexes, edges)
130 |
131 | assert root.get_data() == 0
132 | first = root.get_first_child()
133 | assert first.get_data() == 1
134 | second = first.get_first_child()
135 | assert second.get_data() == 2
136 | third = second.get_first_child()
137 | assert third.get_data() == 3
138 | forth = third.get_next_sibling()
139 | assert forth.get_data() == 4
140 |
141 |
142 | if __name__ == "__main__":
143 | test()
144 |
--------------------------------------------------------------------------------
/搜索算法/跳表/skip_list.py:
--------------------------------------------------------------------------------
1 | # coding: utf8
2 |
3 | import random
4 |
5 |
6 | class Node(object):
7 | """
8 | 跳表节点
9 | """
10 | def __init__(self, keyword, next_node=None, down_node=None):
11 | self.keyword = keyword
12 | self.next_node = next_node
13 | self.down_node = down_node
14 |
15 |
16 | class SkipList(object):
17 | """
18 | 跳表实现
19 | """
20 | def __init__(self, probability=0.25, max_levels=10):
21 | self._probability = probability
22 | self._max_levels = max_levels
23 | self._heads = [Node(None)]
24 |
25 | @property
26 | def heads(self):
27 | return self._heads
28 |
29 | def insert(self, keyword):
30 | # 确定在第几层进行插入
31 | k = 1
32 | for _ in range(len(self._heads)):
33 | if random.random() <= self._probability:
34 | k = k + 1
35 | else:
36 | break
37 |
38 | if k > self._max_levels:
39 | k = self._max_levels
40 |
41 | if k == len(self._heads) + 1:
42 | new_head = Node(None)
43 | new_head.down_node = self._heads[-1]
44 | self._heads.append(new_head)
45 |
46 | node = self._heads[k - 1]
47 | prev = None
48 |
49 | while node is not None:
50 | # 找到插入位置
51 | while node.next_node is not None and node.next_node.keyword < keyword:
52 | node = node.next_node
53 | # 插入新节点
54 | new_node = Node(keyword)
55 | new_node.next_node = node.next_node
56 | node.next_node = new_node
57 | if prev is not None:
58 | prev.down_node = new_node
59 | prev = new_node
60 | # 在下一层上继续插入
61 | node = node.down_node
62 |
63 | def search(self, keyword):
64 | node = self._heads[-1]
65 | while node is not None:
66 | while node.next_node is not None and node.next_node.keyword < keyword:
67 | node = node.next_node
68 |
69 | if node.next_node is not None and node.next_node.keyword == keyword:
70 | node = node.next_node
71 | while node.down_node is not None:
72 | node = node.down_node
73 | return node
74 | node = node.down_node
75 | return None
76 |
77 | def delete(self, keyword):
78 | node = self._heads[-1]
79 | while node is not None:
80 | while node.next_node is not None and node.next_node.keyword < keyword:
81 | node = node.next_node
82 | if node.next_node is not None and node.next_node.keyword == keyword:
83 | node.next_node = node.next_node.next_node
84 | node = node.down_node
85 | # 将空层的头节点删掉
86 | while len(self._heads) > 1:
87 | if self._heads[-1].next_node is not None:
88 | break
89 | self._heads.pop(-1)
90 |
91 |
92 | def print_skip_list(skip_list):
93 | """
94 | 以易于阅读的形式打印跳表对象
95 | """
96 | for ind, node in enumerate(skip_list.heads[::-1]):
97 | keywords = []
98 | while node.next_node is not None:
99 | keywords.append(node.next_node.keyword)
100 | node = node.next_node
101 | print("level %d" % (len(skip_list.heads) - ind))
102 | print("\t" + " ".join(map(lambda k: str(k), keywords)))
103 |
104 |
105 | if __name__ == "__main__":
106 | import unittest
107 |
108 | class SkipListTest(unittest.TestCase):
109 | def testSkipList(self):
110 | keywords = list(range(40))
111 | random.shuffle(keywords)
112 | skip_list = SkipList()
113 | for keyword in keywords:
114 | skip_list.insert(keyword)
115 | random.shuffle(keywords)
116 | for keyword in keywords:
117 | node = skip_list.search(keyword)
118 | self.assertIsNotNone(node)
119 | self.assertEqual(node.keyword, keyword)
120 | random.shuffle(keywords)
121 | for keyword in keywords:
122 | skip_list.delete(keyword)
123 | self.assertIsNone(skip_list.search(keyword))
124 |
125 | unittest.main()
126 |
--------------------------------------------------------------------------------
/线性表/静态链表/static_list.py:
--------------------------------------------------------------------------------
1 | # coding: utf8
2 |
3 |
4 | class Node(object):
5 | """
6 | 静态链表的节点
7 | """
8 | def __init__(self, element, cursor=-1):
9 | # 保存数据元素
10 | self.element = element
11 | # 保存直接后继节点在数组中的索引
12 | self.cursor = cursor
13 |
14 |
15 | class StaticList(object):
16 | """
17 | 静态链表
18 | """
19 | def __init__(self, max_size):
20 | # 备用链表的头节点
21 | self._free_space = Node(None, -1)
22 | # 静态链表的头节点
23 | self._head = Node(None, -1)
24 | # 底层数组
25 | self._underlying_array = [Node(None, -1) for _ in range(max_size)]
26 |
27 | # 将数组中的全部节点组织进备用链表
28 | self._free_space.cursor = 0
29 | for ind in range(0, max_size - 1):
30 | self._underlying_array[ind].cursor = ind + 1
31 |
32 | def _malloc(self):
33 | """
34 | 用于从备用链表中申请节点
35 | """
36 | cursor = self._free_space.cursor
37 | if cursor == -1:
38 | raise RuntimeError("no space left")
39 | node = self._underlying_array[cursor]
40 | self._free_space.cursor = node.cursor
41 | return cursor
42 |
43 | def _free(self, cursor):
44 | """
45 | 将节点放回备用链表
46 | """
47 | node = self._underlying_array[cursor]
48 | node.cursor = self._free_space.cursor
49 | self._free_space.cursor = cursor
50 |
51 | def insert(self, index, element):
52 | node = self._head
53 | current_index = -1
54 |
55 | while node is not None:
56 | if current_index == index - 1:
57 | # 申请新节点
58 | free_cursor = self._malloc()
59 | free_node = self._underlying_array[free_cursor]
60 | free_node.element = element
61 | free_node.cursor = node.cursor
62 | node.cursor = free_cursor
63 | break
64 |
65 | if node.cursor == -1:
66 | node = None
67 | continue
68 |
69 | node = self._underlying_array[node.cursor]
70 | current_index = current_index + 1
71 | else:
72 | raise IndexError("invalid index")
73 |
74 | def find(self, element):
75 | temp = self._head.cursor
76 | index = 0
77 |
78 | while temp != -1:
79 | node = self._underlying_array[temp]
80 | if node.element == element:
81 | return index
82 | temp = node.cursor
83 | index = index + 1
84 | else:
85 | raise ValueError("not found")
86 |
87 | def delete(self, element):
88 | # node 是待删除节点的前一个节点
89 | node = self._head
90 | if node.cursor == -1:
91 | next_node = None
92 | else:
93 | next_node = self._underlying_array[node.cursor]
94 |
95 | while next_node is not None:
96 | if next_node.element == element:
97 | next_node_cursor = next_node.cursor
98 | # 释放节点
99 | self._free(node.cursor)
100 | # 删除节点
101 | node.cursor = next_node_cursor
102 | break
103 | node = next_node
104 | if node.cursor == -1:
105 | next_node = None
106 | else:
107 | next_node = self._underlying_array[node.cursor]
108 | else:
109 | raise ValueError("not found")
110 |
111 |
112 | if __name__ == "__main__":
113 | import unittest
114 |
115 | class TestStaticList(unittest.TestCase):
116 | def testStaticList(self):
117 | static_list = StaticList(5)
118 | static_list.insert(0, 1)
119 | static_list.insert(0, 0)
120 | static_list.insert(2, 2)
121 | self.assertRaises(IndexError, static_list.insert, 4, 4)
122 | self.assertRaises(ValueError, static_list.delete, 4)
123 |
124 | self.assertEqual(static_list.find(0), 0)
125 | self.assertEqual(static_list.find(1), 1)
126 | self.assertEqual(static_list.find(2), 2)
127 | self.assertRaises(ValueError, static_list.find, -1)
128 |
129 | static_list.delete(1)
130 | self.assertEqual(static_list.find(2), 1)
131 | static_list.delete(0)
132 | self.assertEqual(static_list.find(2), 0)
133 |
134 | unittest.main()
135 |
--------------------------------------------------------------------------------
/图/DAG-有向无环图/关键路径/critical_path.py:
--------------------------------------------------------------------------------
1 | # coding: utf8
2 |
3 |
4 | class Node(object):
5 | def __init__(self, element):
6 | self.element = element
7 | self.incoming_degree = 0
8 |
9 |
10 | class Graph(object):
11 | """
12 | 数组矩阵表示法
13 | """
14 | def __init__(self):
15 | self._vertexes = []
16 | self._arches = []
17 |
18 | def add_vertex(self, element):
19 | self._vertexes.append(Node(element))
20 | for arch in self._arches:
21 | arch.append(None)
22 | self._arches.append([None] * len(self._vertexes))
23 | return len(self._vertexes) - 1
24 |
25 | def add_arch(self, tail, head, weight=1):
26 | old_weight = self._arches[tail][head]
27 | if old_weight is None:
28 | self._vertexes[head].incoming_degree = \
29 | self._vertexes[head].incoming_degree + 1
30 | self._arches[tail][head] = weight
31 |
32 | def delete_arch(self, tail, head):
33 | old_weight = self._arches[tail][head]
34 | if old_weight is None:
35 | return
36 | self._vertexes[head].incoming_degree = \
37 | self._vertexes[head].incoming_degree - 1
38 | self._arches[tail][head] = None
39 |
40 | def get_vertex_count(self):
41 | return len(self._vertexes)
42 |
43 | def get_vertex(self, index):
44 | return self._vertexes[index]
45 |
46 | def get_arches(self, tail):
47 | for head, weight in enumerate(self._arches[tail]):
48 | if weight is None:
49 | continue
50 | yield head
51 |
52 | def get_arch_by_offset(self, head, offset):
53 | real_index = 0
54 | for index, weight in enumerate(self._arches[head]):
55 | if weight is None:
56 | continue
57 | if real_index == offset:
58 | return index
59 | real_index = real_index + 1
60 | return None
61 |
62 | def get_weight(self, tail, head):
63 | return self._arches[tail][head]
64 |
65 |
66 | def topological_order(g):
67 | """
68 | 利用拓扑排序计算每个顶点的最早发生时间和最晚发生时间
69 | """
70 | # 初始化 stack、ve、vl, incoming_degrees
71 | stack = []
72 | ve = []
73 | vl = []
74 | incoming_degrees = []
75 | for index in range(g.get_vertex_count()):
76 | ve.append(None)
77 | vl.append(None)
78 | incoming_degree = g.get_vertex(index).incoming_degree
79 | incoming_degrees.append(incoming_degree)
80 |
81 | if incoming_degree == 0:
82 | ve[index] = 0
83 | stack.append(index)
84 |
85 | sequence = []
86 | while stack:
87 | top = stack.pop(-1)
88 | sequence.append(top)
89 | for head in g.get_arches(top):
90 | new = ve[top] + g.get_weight(top, head)
91 | if ve[head] is None or new > ve[head]:
92 | ve[head] = new
93 | incoming_degrees[head] = incoming_degrees[head] - 1
94 | if incoming_degrees[head] == 0:
95 | stack.append(head)
96 |
97 | vl[-1] = ve[-1]
98 |
99 | for tail in range(len(sequence) -1, -1, -1):
100 | for head in g.get_arches(tail):
101 | new = vl[head] - g.get_weight(tail, head)
102 | if vl[tail] is None or new < vl[tail]:
103 | vl[tail] = new
104 |
105 | return ve, vl
106 |
107 |
108 | def critical_path(g):
109 | ve, vl = topological_order(g)
110 | critical_activities = []
111 | for tail in range(g.get_vertex_count()):
112 | for head in g.get_arches(tail):
113 | if ve[tail] == vl[head] - g.get_weight(tail, head):
114 | critical_activities.append((tail, head))
115 |
116 | paths = []
117 | d = {}
118 | for a in critical_activities:
119 | d.setdefault(a[0], []).append(a[1])
120 | status = {}
121 | stack = [0]
122 | while stack:
123 | top = stack[-1]
124 | if top not in d:
125 | paths.append(stack[:])
126 | stack.pop(-1)
127 | continue
128 | if top in status and status[top] >= len(d[top]):
129 | stack.pop(-1)
130 | status[top] = 0
131 | continue
132 | stack.append(d[top][status.get(top, 0)])
133 | status[top] = status.get(top, 0) + 1
134 | return paths
135 |
136 |
137 | def test():
138 | g = Graph()
139 | for index in range(7):
140 | g.add_vertex(index)
141 | for arch in [(0, 1, 3), (0, 2, 2), (0, 3, 6),
142 | (1, 3, 2), (1, 4, 4), (2, 3, 1),
143 | (2, 5, 3), (3, 4, 1), (4, 6, 3),
144 | (5, 6, 4)]:
145 | g.add_arch(*arch)
146 | print(critical_path(g))
147 |
148 |
149 | if __name__ == "__main__":
150 | test()
151 |
--------------------------------------------------------------------------------
/树/二叉树/根据二叉树的先序、中序、后序序列还原二叉树/GenerateTree.py:
--------------------------------------------------------------------------------
1 | # coding: utf8
2 |
3 |
4 | class Node(object):
5 | def __init__(self, keyword, left=None, right=None):
6 | self.keyword = keyword
7 | self.left = left
8 | self.right = right
9 |
10 |
11 | class NodeFactory(object):
12 | nodes = {}
13 |
14 | @classmethod
15 | def get_node(cls, keyword):
16 | if keyword not in cls.nodes:
17 | cls.nodes[keyword] = Node(keyword)
18 | return cls.nodes[keyword]
19 |
20 |
21 | def find_pos(sequence, target):
22 | for pos, element in enumerate(sequence):
23 | if target == element:
24 | return pos
25 | return -1
26 |
27 |
28 | def generate_tree(preorder, inorder, postorder):
29 | if len(preorder) != len(inorder) or len(inorder) != len(postorder):
30 | raise RuntimeError("invalid sequence")
31 |
32 | if len(preorder) == 0:
33 | return None
34 |
35 | if len(preorder) == 1:
36 | return NodeFactory.get_node(preorder[0])
37 |
38 | if preorder[0] != postorder[-1]:
39 | raise RuntimeError("invalid sequence")
40 |
41 | # 先序序列的第一个节点和后序序列的最后一个节点是根节点
42 | root = NodeFactory.get_node(preorder[0])
43 |
44 | # 如果根节点是中序序列的第一个节点,说明根节点的左子树为空,先序序列的第二个节点是根节点的右孩子
45 | if preorder[0] == inorder[0]:
46 | root.left = None
47 | root.right = NodeFactory.get_node(preorder[1])
48 | # 如果根节点是中序序列的最后一个节点,说明根节点的右子树为空,先序序列的第二个节点是根节点的左孩子
49 | elif preorder[0] == inorder[-1]:
50 | root.left = NodeFactory.get_node(preorder[1])
51 | root.right = None
52 | # 否则,根节点的左右子树都不为空
53 | else:
54 | # 先序序列的第二个节点是根节点的左孩子
55 | root.left = NodeFactory.get_node(preorder[1])
56 | # 后序序列的倒数第二个节点是根节点的右孩子
57 | root.right = NodeFactory.get_node(postorder[-2])
58 |
59 | if root.left is None:
60 | right_preorder = preorder[1:]
61 | right_inorder = inorder[1:]
62 | right_postorder = postorder[:-1]
63 | generate_tree(right_preorder, right_inorder, right_postorder)
64 | elif root.right is None:
65 | left_preorder = preorder[1:]
66 | left_inorder = inorder[:-1]
67 | left_postorder = postorder[:-1]
68 | generate_tree(left_preorder, left_inorder, left_postorder)
69 | else:
70 | pos = find_pos(preorder, root.right.keyword)
71 | if pos == -1:
72 | raise RuntimeError("invalid sequence")
73 | left_preorder = preorder[1:pos]
74 | right_preorder = preorder[pos:]
75 |
76 | pos = find_pos(inorder, root.keyword)
77 | if pos == -1:
78 | raise RuntimeError("invalid sequence")
79 | left_inorder = inorder[:pos]
80 | right_inorder = inorder[pos+1:]
81 |
82 | pos = find_pos(postorder, root.left.keyword)
83 | if pos == -1:
84 | raise RuntimeError("invalid sequence")
85 | left_postorder = postorder[:pos+1]
86 | right_postorder = postorder[pos+1:-1]
87 |
88 | generate_tree(left_preorder, left_inorder, left_postorder)
89 |
90 | generate_tree(right_preorder, right_inorder, right_postorder)
91 |
92 | return root
93 |
94 |
95 | def test():
96 | def preorder_traverse(p):
97 | keywords = []
98 | if p is None:
99 | return keywords
100 | keywords.append(p.keyword)
101 | keywords.extend(preorder_traverse(p.left))
102 | keywords.extend(preorder_traverse(p.right))
103 | return keywords
104 |
105 | def inorder_traverse(p):
106 | keywords = []
107 | if p is None:
108 | return keywords
109 | keywords.extend(inorder_traverse(p.left))
110 | keywords.append(p.keyword)
111 | keywords.extend(inorder_traverse(p.right))
112 | return keywords
113 |
114 | def postorder_traverse(p):
115 | keywords = []
116 | if p is None:
117 | return keywords
118 | keywords.extend(postorder_traverse(p.left))
119 | keywords.extend(postorder_traverse(p.right))
120 | keywords.append(p.keyword)
121 | return keywords
122 |
123 | nodes = [Node(ind) for ind in range(7)]
124 | nodes[0].left = nodes[1]
125 | nodes[0].right = nodes[2]
126 | nodes[1].left = nodes[3]
127 | nodes[1].right = nodes[4]
128 | nodes[2].left = nodes[5]
129 | nodes[3].right = nodes[6]
130 |
131 | root = nodes[0]
132 | del nodes
133 |
134 | preorder = preorder_traverse(root)
135 | inorder = inorder_traverse(root)
136 | postorder = postorder_traverse(root)
137 |
138 | generated_root = generate_tree(preorder, inorder, postorder)
139 |
140 | assert preorder == preorder_traverse(generated_root)
141 | assert inorder == inorder_traverse(generated_root)
142 | assert postorder == postorder_traverse(generated_root)
143 |
144 |
145 | if __name__ == "__main__":
146 | test()
147 |
--------------------------------------------------------------------------------
/树/二叉树/二叉搜索树/binary_search_tree.py:
--------------------------------------------------------------------------------
1 | # coding: utf8
2 |
3 |
4 | class Node(object):
5 | """
6 | 二叉搜索树的节点
7 | """
8 | def __init__(self, keyword, left=None, right=None):
9 | self.keyword = keyword
10 | self.left = left
11 | self.right = right
12 |
13 |
14 | class BinarySearchTree(object):
15 | """
16 | 二叉搜索树实现
17 | """
18 | def __init__(self):
19 | self._root = None
20 |
21 | def insert(self, keyword):
22 | # 如果树为空,则创建新节点,并使之成为根节点
23 | if self._root is None:
24 | self._root = Node(keyword)
25 | return
26 |
27 | node = self._root
28 | while True:
29 | # 如果待插入关键字小于 node 的关键字
30 | if keyword < node.keyword:
31 | # 如果 node 的左子树为空,则创建新节点,并使之成为 node 的左孩子节点
32 | if node.left is None:
33 | node.left = Node(keyword)
34 | break
35 | # 否则,使用相同的方式在左子树上进行插入
36 | node = node.left
37 | # 如果待插入关键字不小于 node 的关键字
38 | else:
39 | # 如果 node 的右子树为空,则创建新节点,并使之成为 node 的右孩子节点
40 | if node.right is None:
41 | node.right = Node(keyword)
42 | break
43 | # 否则,使用相同的方式在右子树上进行插入
44 | node = node.right
45 |
46 | def search(self, keyword):
47 | node = self._root
48 | while node is not None:
49 | # 如果 node 的关键字等于待查询关键字,则搜索成功
50 | if keyword == node.keyword:
51 | return node
52 | # 如果待搜索关键字小于 node 的关键字,则使用相同的方式在左子树上进行查询
53 | if keyword < node.keyword:
54 | node = node.left
55 | continue
56 | # 否则,使用相同的方式在右子树上进行查询
57 | node = node.right
58 | return None
59 |
60 | def delete(self, keyword):
61 | node = self._root
62 | left = None
63 | parent = node
64 | while node is not None:
65 | if keyword == node.keyword:
66 | # 如果待删除节点是叶子节点
67 | if node.left is None and node.right is None:
68 | # 如果待删除节点是根节点,那么将树置空
69 | if node is self._root:
70 | self._root = None
71 | # 否则,将待删除节点的父节点的相应孩子节点置空
72 | elif left:
73 | parent.left = None
74 | else:
75 | parent.right = None
76 | # 如果待删除节点的左子树和右子树都不为空
77 | elif node.left is not None and node.right is not None:
78 | # 找到左子树的最右节点(或者找到右子树的最左节点)
79 | temp = node.left
80 | parent = node
81 | left = True
82 | while temp.right is not None:
83 | parent = temp
84 | left = False
85 | temp = temp.right
86 | # 将待删除节点的关键字置为 temp 的关键字,然后将 temp 删掉
87 | node.keyword = temp.keyword
88 | # 因为 temp 的右子树肯定为空,所以将其左子树接到其父节点
89 | if left:
90 | parent.left = temp.left
91 | else:
92 | parent.right = temp.left
93 | # 如果待删除节点的左子树为空
94 | elif node.left is None:
95 | # 如果待删除节点是根节点,则将根节点置为其右孩子节点
96 | if node is self._root:
97 | self._root = node.right
98 | # 否则,将待删除节点的右孩子节点接到其父节点上
99 | elif left:
100 | parent.left = node.right
101 | else:
102 | parent.right = node.right
103 | # 如果待删除节点的右子树为空
104 | else:
105 | # 如果待删除节点是根节点,则将根节点职位其左孩子节点
106 | if node is self._root:
107 | self._root = node.left
108 | # 否则,将待删除节点的左孩子节点接到其父节点上
109 | elif left:
110 | parent.left = node.left
111 | else:
112 | parent.right = node.left
113 | return
114 | elif keyword < node.keyword:
115 | # 使用相同的方式,去左子树上进行删除
116 | parent = node
117 | left = True
118 | node = node.left
119 | else:
120 | # 使用相同的方式,去右子树上进行删除
121 | parent = node
122 | left = False
123 | node = node.right
124 |
125 | raise KeyError("not found")
126 |
127 | @property
128 | def root(self):
129 | return self._root
130 |
131 |
132 | if __name__ == "__main__":
133 | import random
134 | elements = list(range(20))
135 | random.shuffle(elements)
136 | print("元素列表:")
137 | print(elements)
138 |
139 | print("插入元素")
140 | binary_search_tree = BinarySearchTree()
141 | for ind in elements:
142 | binary_search_tree.insert(ind)
143 |
144 | def inorder_traverse(root):
145 | if root is None:
146 | return []
147 |
148 | nodes = []
149 | nodes.extend(inorder_traverse(root.left))
150 | nodes.append(root.keyword)
151 | nodes.extend(inorder_traverse(root.right))
152 |
153 | return nodes
154 |
155 | print("中序遍历:")
156 | print(inorder_traverse(binary_search_tree.root))
157 |
158 | for ind in elements:
159 | assert binary_search_tree.search(ind) is not None
160 |
161 | print("删除元素")
162 | for ind in elements:
163 | binary_search_tree.delete(ind)
164 |
165 | assert binary_search_tree.root is None
166 |
--------------------------------------------------------------------------------
/哈希表/hash_table.py:
--------------------------------------------------------------------------------
1 | # coding: utf8
2 |
3 |
4 | class Entry(object):
5 | """
6 | 条目
7 | """
8 | def __init__(self, key, value):
9 | self.key = key
10 | self.value = value
11 |
12 |
13 | class Node(object):
14 | """
15 | 同义词子表的节点
16 | """
17 | def __init__(self, entry=None, next_node=None):
18 | self.entry = entry
19 | self.next_node = next_node
20 |
21 |
22 | class HashTable(object):
23 | """
24 | 基于除留余数和链地址法实现的哈希表
25 | """
26 | def __init__(self, initial_capacity=None, rehash_factor=None):
27 | """
28 | :param initial_capacity: 初始容量,默认值是 32
29 | :param rehash_factor: 扩容因子,默认值是 2
30 | """
31 | self._initial_capacity = initial_capacity or 32
32 | self._capacity = self._initial_capacity
33 | self._underlying_array = [None for _ in range(self._capacity)]
34 | self._item_count = 0
35 | self._rehash_factor = rehash_factor or 2
36 |
37 | def __setitem__(self, key, value):
38 | """
39 | 插入条目
40 | """
41 | hash_value = hash(key) % self._capacity
42 | node = self._underlying_array[hash_value]
43 | if node is None:
44 | node = self._underlying_array[hash_value] = Node()
45 | while node.next_node is not None:
46 | # 如果 key 已经存在,更新 value
47 | if node.next_node.entry.key == key:
48 | node.next_node.entry.value = value
49 | return
50 | node = node.next_node
51 | node.next_node = Node(Entry(key, value))
52 | self._item_count = self._item_count + 1
53 | self.rehash()
54 |
55 | def __getitem__(self, key):
56 | """
57 | 获取条目
58 | """
59 | hash_value = hash(key) % self._capacity
60 | node = self._underlying_array[hash_value]
61 | if node is None:
62 | raise KeyError()
63 | node = node.next_node
64 | while node is not None:
65 | if node.entry.key == key:
66 | return node.entry.value
67 | node = node.next_node
68 | raise KeyError()
69 |
70 | def __delitem__(self, key):
71 | """
72 | 删除条目
73 | """
74 | hash_value = hash(key) % self._capacity
75 | node = self._underlying_array[hash_value]
76 | if node is None:
77 | raise KeyError()
78 | while node.next_node is not None:
79 | if node.next_node.entry.key == key:
80 | node.next_node = node.next_node.next_node
81 | self._item_count = self._item_count - 1
82 | break
83 | node = node.next_node
84 | else:
85 | raise KeyError()
86 |
87 | def rehash(self):
88 | """
89 | 扩容
90 | """
91 | if (self._item_count + 0.0) / self._capacity <= self._rehash_factor:
92 | return
93 |
94 | # 申请新空间
95 | self._capacity = self._capacity + self._initial_capacity
96 | new_underlying_array = [None for _ in range(self._capacity)]
97 |
98 | # 重新映射
99 | for node in self._underlying_array:
100 | if node is None:
101 | continue
102 | temp = node.next_node
103 | while temp is not None:
104 | # 映射到新的存储空间
105 | hash_value = hash(temp.entry.key) % self._capacity
106 | head = new_underlying_array[hash_value]
107 | if head is None:
108 | head = new_underlying_array[hash_value] = Node()
109 | while head.next_node is not None:
110 | head = head.next_node
111 | head.next_node = Node(temp.entry)
112 | temp = temp.next_node
113 | self._underlying_array = new_underlying_array
114 |
115 | def __len__(self):
116 | return self._item_count
117 |
118 |
119 | if __name__ == "__main__":
120 | import unittest
121 |
122 |
123 | class HashTableTest(unittest.TestCase):
124 | def testSetItem(self):
125 | hash_table = HashTable(initial_capacity=32)
126 | # 测试冲突
127 | hash_table[1] = 1
128 | hash_table[33] = 33
129 | self.assertEqual(hash_table[1], 1)
130 | self.assertEqual(hash_table[33], 33)
131 | # 测试 key 重复
132 | hash_table[33] = 34
133 | self.assertEqual(hash_table[33], 34)
134 |
135 | def testRehash(self):
136 | hash_table = HashTable(initial_capacity=2, rehash_factor=2)
137 | keys = list(range(1, 6))
138 | # 插入新条目,触发 rehash
139 | for key in keys:
140 | hash_table[key] = key
141 | self.assertEqual(hash_table[key], key)
142 | item_count = len(hash_table)
143 | self.assertEqual(item_count, len(keys))
144 |
145 | # 测试 rehash 后,是否出现错误
146 | for key in keys:
147 | self.assertEqual(hash_table[key], key)
148 | self.assertEqual(len(hash_table), len(keys))
149 |
150 | # 在 rehash 之后,插入一个新条目
151 | new_key = keys[-1] + 1
152 | hash_table[new_key] = new_key
153 | self.assertEqual(hash_table[new_key], new_key)
154 | self.assertEqual(len(hash_table), item_count + 1)
155 |
156 | def testDelItem(self):
157 | import random
158 |
159 | hash_table = HashTable()
160 | keys = list(range(100))
161 |
162 | # 插入条目
163 | for key in keys:
164 | hash_table[key] = key
165 |
166 | # 逐个删除
167 | random.shuffle(keys)
168 | item_count = len(hash_table)
169 | self.assertEqual(item_count, len(keys))
170 | for key in keys:
171 | self.assertEqual(hash_table[key], key)
172 | del hash_table[key]
173 | self.assertRaises(KeyError, hash_table.__getitem__, key)
174 | item_count = item_count - 1
175 | self.assertEqual(len(hash_table), item_count)
176 |
177 | unittest.main()
178 |
--------------------------------------------------------------------------------
/树/二叉树/BinaryTree.py:
--------------------------------------------------------------------------------
1 | # coding: utf8
2 |
3 |
4 | class BinaryTreeNode(object):
5 | def __init__(self, element, left=None, right=None):
6 | self.element = element
7 | self.left = left
8 | self.right = right
9 |
10 | ########## 下面是先序、中序、后序遍历的递归实现 ##########
11 |
12 |
13 | def preorder_traverse(root):
14 | if root is None:
15 | return []
16 |
17 | nodes = [root.element]
18 | nodes.extend(preorder_traverse(root.left))
19 | nodes.extend(preorder_traverse(root.right))
20 |
21 | return nodes
22 |
23 | def inorder_traverse(root):
24 | if root is None:
25 | return []
26 |
27 | nodes = []
28 | nodes.extend(inorder_traverse(root.left))
29 | nodes.append(root.element)
30 | nodes.extend(inorder_traverse(root.right))
31 |
32 | return nodes
33 |
34 | def postorder_traverse(root):
35 | if root is None:
36 | return []
37 |
38 | nodes = []
39 | nodes.extend(postorder_traverse(root.left))
40 | nodes.extend(postorder_traverse(root.right))
41 | nodes.append(root.element)
42 |
43 | return nodes
44 |
45 | ########## 下面是先序、中序、后序遍历的非递归实现 ##########
46 | ########## 请参考:http://timd.cn/eliminate-recursive/ ##########
47 |
48 | class Frame(object):
49 | def __init__(self, root, return_address=0):
50 | self.root = root
51 | self.return_address = return_address
52 | self.result = []
53 |
54 | def run(self):
55 | address = 0
56 | value = None
57 | stack = [self.__class__(self.root)]
58 |
59 | while stack:
60 | active_frame = stack[-1]
61 | next_frame = active_frame.execute(address, value)
62 | if next_frame is None:
63 | # 进入返回段
64 | address = active_frame.return_address
65 | value = active_frame.result
66 | stack.pop(-1)
67 | continue
68 | # 进入前进段
69 | stack.append(next_frame)
70 | address = 0
71 | value = None
72 |
73 | return value
74 |
75 | def execute(self, address, value):
76 | raise NotImplementedError("should be overridden")
77 |
78 |
79 | class PreorderTraverseFrame(Frame):
80 | def execute(self, address, value):
81 | if self.root is None:
82 | return
83 | if address == 0:
84 | self.result.append(self.root.element)
85 | return PreorderTraverseFrame(self.root.left, 1)
86 | elif address == 1:
87 | self.result.extend(value)
88 | return PreorderTraverseFrame(self.root.right, 2)
89 | elif address == 2:
90 | self.result.extend(value)
91 |
92 |
93 | class InorderTraverseFrame(Frame):
94 | def execute(self, address, value):
95 | if self.root is None:
96 | return
97 | if address == 0:
98 | return InorderTraverseFrame(self.root.left, 1)
99 | elif address == 1:
100 | self.result.extend(value)
101 | self.result.append(self.root.element)
102 | return InorderTraverseFrame(self.root.right, 2)
103 | elif address == 2:
104 | self.result.extend(value)
105 | return
106 |
107 |
108 | class PostorderTraverseFrame(Frame):
109 | def execute(self, address, value):
110 | if self.root is None:
111 | return
112 |
113 | if address == 0:
114 | return PostorderTraverseFrame(self.root.left, 1)
115 | elif address == 1:
116 | self.result.extend(value)
117 | return PostorderTraverseFrame(self.root.right, 2)
118 | elif address == 2:
119 | self.result.extend(value)
120 | self.result.append(self.root.element)
121 |
122 | ########## 下面是广度优先遍历的非递归实现 ##########
123 |
124 |
125 | def bfs(root):
126 | elements = []
127 | queue = [root]
128 | while queue:
129 | node = queue.pop(0)
130 | if node is None:
131 | continue
132 | elements.append(node.element)
133 | queue.append(node.left)
134 | queue.append(node.right)
135 | return elements
136 |
137 | ########## 下面是广度优先遍历的递归实现
138 |
139 |
140 | def bfs_recursive(nodes):
141 | if isinstance(nodes, BinaryTreeNode):
142 | nodes = [nodes]
143 |
144 | # 先将本层的节点保存到结果列表,然后生成下层的节点列表
145 | elements = []
146 | next_nodes = []
147 | for node in nodes:
148 | if node is None:
149 | continue
150 | elements.append(node.element)
151 | next_nodes.append(node.left)
152 | next_nodes.append(node.right)
153 | # 如果没有下一层,则返回;否则,递归地遍历下一层
154 | if next_nodes:
155 | elements.extend(bfs_recursive(next_nodes))
156 | return elements
157 |
158 |
159 | if __name__ == "__main__":
160 | import unittest
161 |
162 | class BinaryTreeTest(unittest.TestCase):
163 | def setUp(self):
164 | ######################
165 | # 0 #
166 | # / \ #
167 | # 1 2 #
168 | # \ / \ #
169 | # 3 4 5 #
170 | ######################
171 | nodes = [BinaryTreeNode(ind) for ind in range(6)]
172 | nodes[0].left = nodes[1]
173 | nodes[0].right = nodes[2]
174 | nodes[1].right = nodes[3]
175 | nodes[2].left = nodes[4]
176 | nodes[2].right = nodes[5]
177 | self.root = nodes[0]
178 | del nodes
179 |
180 | def testPreorderTraverse(self):
181 | result = [0, 1, 3, 2, 4, 5]
182 | self.assertEqual(preorder_traverse(self.root), result)
183 | self.assertEqual(PreorderTraverseFrame(self.root).run(), result)
184 |
185 | def testInorderTraverse(self):
186 | result = [1, 3, 0, 4, 2, 5]
187 | self.assertEqual(inorder_traverse(self.root), result)
188 | self.assertEqual(InorderTraverseFrame(self.root).run(), result)
189 |
190 | def testPostorderTraverse(self):
191 | result = [3, 1, 4, 5, 2, 0]
192 | self.assertEqual(postorder_traverse(self.root), result)
193 | self.assertEqual(PostorderTraverseFrame(self.root).run(), result)
194 |
195 | def testBFS(self):
196 | result = [0, 1, 2, 3, 4, 5]
197 | self.assertEqual(bfs(self.root), result)
198 | self.assertEqual(bfs_recursive(self.root), result)
199 |
200 | unittest.main()
201 |
--------------------------------------------------------------------------------
/树/二叉树/表达式树/InOrder2PostOrder.py:
--------------------------------------------------------------------------------
1 | # coding: utf8
2 |
3 |
4 | class Operator(object):
5 | def __init__(self, char):
6 | self.char = char
7 |
8 | @staticmethod
9 | def get_operator(char):
10 | if char == "+":
11 | return PlusOperator()
12 | if char == "-":
13 | return MinusOperator()
14 | if char == "*":
15 | return MultiplyOperator()
16 | if char == "/":
17 | return DivisionOperator()
18 | return None
19 |
20 | def __str__(self):
21 | return self.char
22 |
23 | def execute(self, left, right):
24 | raise NotImplementedError
25 |
26 |
27 | class PlusOperator(Operator):
28 | def __init__(self):
29 | Operator.__init__(self, "+")
30 |
31 | def __cmp__(self, other):
32 | if isinstance(other, (PlusOperator, MinusOperator)):
33 | return 0
34 | return -1
35 |
36 | def execute(self, left, right):
37 | return left + right
38 |
39 | class MinusOperator(Operator):
40 | def __init__(self):
41 | Operator.__init__(self, "-")
42 |
43 | def __cmp__(self, other):
44 | if isinstance(other, (PlusOperator, MinusOperator)):
45 | return 0
46 | return -1
47 |
48 | def execute(self, left, right):
49 | return left - right
50 |
51 |
52 | class MultiplyOperator(Operator):
53 | def __init__(self):
54 | Operator.__init__(self, "*")
55 |
56 | def __cmp__(self, other):
57 | if isinstance(other, (MultiplyOperator, DivisionOperator)):
58 | return 0
59 | return 1
60 |
61 | def execute(self, left, right):
62 | return left * right
63 |
64 |
65 | class DivisionOperator(Operator):
66 | def __init__(self):
67 | Operator.__init__(self, "/")
68 |
69 | def __cmp__(self, other):
70 | if isinstance(other, (MultiplyOperator, DivisionOperator)):
71 | return 0
72 | return 1
73 |
74 | def execute(self, left, right):
75 | return left / right
76 |
77 |
78 | class Operand(object):
79 | def __init__(self, value):
80 | self.value = value
81 |
82 | def __str__(self):
83 | return str(self.value)
84 |
85 |
86 | class Bracket(object):
87 | def __init__(self, char):
88 | self.char = char
89 |
90 | @staticmethod
91 | def get_bracket(char):
92 | if char == "(":
93 | return LeftBracket()
94 | if char == ")":
95 | return RightBracket()
96 | return None
97 |
98 | def __str__(self):
99 | return self.char
100 |
101 |
102 | class LeftBracket(Bracket):
103 | def __init__(self):
104 | Bracket.__init__(self, "(")
105 |
106 |
107 | class RightBracket(Bracket):
108 | def __init__(self):
109 | Bracket.__init__(self, ")")
110 |
111 |
112 | def inorder_to_postorder(inorder_tokens):
113 | """
114 | 中缀表达式转后缀表达式
115 | """
116 | postorder_tokens = []
117 | stack = []
118 | for token in inorder_tokens:
119 | # 遇到操作数时,直接输出
120 | if isinstance(token, Operand):
121 | postorder_tokens.append(token)
122 | continue
123 |
124 | # 遇到左括号时,将其压进栈中
125 | if isinstance(token, LeftBracket):
126 | stack.append(token)
127 | continue
128 |
129 | # 遇到右括号时,弹出栈顶的操作符,并输出,直到遇到左括号,
130 | # 并且左括号不输出,右括号不进栈
131 | if isinstance(token, RightBracket):
132 | while stack:
133 | element = stack.pop()
134 | if isinstance(element, LeftBracket):
135 | break
136 | postorder_tokens.append(element)
137 | continue
138 |
139 | # 遇到其它操作符时,弹出栈顶的操作符,并输出,直到栈空或栈顶的操作符的优先级小于该操作符的优先级
140 | # 或遇到左括号,然后将该操作符压入栈中
141 | if isinstance(token, Operator):
142 | while stack:
143 | if isinstance(stack[-1], LeftBracket) or stack[-1] < token:
144 | break
145 | postorder_tokens.append(stack.pop())
146 | stack.append(token)
147 | continue
148 |
149 | raise RuntimeError("unreachable")
150 |
151 | # 最后将栈中的操作符弹出,直到栈空
152 | while stack:
153 | postorder_tokens.append(stack.pop())
154 |
155 | return postorder_tokens
156 |
157 |
158 | class Node(object):
159 | def __init__(self, keyword, left=None, right=None):
160 | self.keyword = keyword
161 | self.left = left
162 | self.right = right
163 |
164 |
165 | def postorder_to_expression_tree(tokens):
166 | """
167 | 后缀表达式转表达式树
168 | """
169 | stack = []
170 | for token in tokens:
171 | # 遇到操作数时,则生成单节点,然后放到栈中
172 | if isinstance(token, Operand):
173 | stack.append(Node(token.value))
174 | continue
175 | # 遇到操作符时,则生成一个新节点,并从栈中弹出两个元素,
176 | # 同时把这两个元素作为新节点的子树,然后将该新节点放入栈中
177 | if isinstance(token, Operator):
178 | right = stack.pop()
179 | left = stack.pop()
180 | stack.append(Node(token.char, left, right))
181 | continue
182 |
183 | raise RuntimeError("unreachable")
184 |
185 | # 最后栈中的元素就是表达式树的根
186 | return stack[-1]
187 |
188 |
189 | def test():
190 | expression = "(1+2)*(3+4)+(5*(6+7))+80/(20-10)" # 94
191 |
192 | class Reader(object):
193 | def __init__(self, string):
194 | self._string = string
195 | self._operators = set(list("+-*/()"))
196 | self._cursor = 0
197 |
198 | def read(self):
199 | if self._cursor >= len(self._string):
200 | return
201 |
202 | char = self._string[self._cursor]
203 | self._cursor = self._cursor + 1
204 | if char in self._operators:
205 | return char
206 |
207 | chars = [char]
208 | while self._cursor < len(self._string):
209 | char = self._string[self._cursor]
210 | if char in self._operators:
211 | return "".join(chars)
212 | self._cursor = self._cursor + 1
213 | chars.append(char)
214 | return "".join(chars)
215 |
216 | reader = Reader(expression)
217 | tokens = []
218 | while True:
219 | token = reader.read()
220 | if token is None:
221 | break
222 | operator = Operator.get_operator(token)
223 | if operator is not None:
224 | tokens.append(operator)
225 | continue
226 | bracket = Bracket.get_bracket(token)
227 | if bracket is not None:
228 | tokens.append(bracket)
229 | continue
230 | tokens.append(Operand(int(token)))
231 |
232 | postorder_tokens = inorder_to_postorder(tokens)
233 |
234 | stack = []
235 | for token in postorder_tokens:
236 | if isinstance(token, Operand):
237 | stack.append(token)
238 | elif isinstance(token, Operator):
239 | right = stack.pop()
240 | left = stack.pop()
241 | stack.append(Operand(token.execute(left.value, right.value)))
242 | print(stack[-1].value)
243 |
244 |
245 | if __name__ == "__main__":
246 | test()
247 |
--------------------------------------------------------------------------------
/图/dinetwork.py:
--------------------------------------------------------------------------------
1 | # coding: utf8
2 |
3 | """
4 | 有向网实现
5 | """
6 |
7 | from abc import ABCMeta, abstractmethod
8 |
9 |
10 | class BaseDiGraph(object):
11 | """
12 | 抽象基类
13 | """
14 | __metaclass__ = ABCMeta
15 |
16 | def dfs(self):
17 | """深度优先遍历"""
18 | index_list = []
19 | stack = [0]
20 | status = [0 for _ in range(self.get_vertex_count())]
21 | visited = [False for _ in range(self.get_vertex_count())]
22 |
23 | while stack:
24 | top = stack[-1]
25 | if not visited[top]:
26 | visited[top] = True
27 | index_list.append(top)
28 |
29 | adjacent_index = self.get_adjacent(top, status[top])
30 | if adjacent_index is None:
31 | stack.pop(-1)
32 | continue
33 | status[top] = status[top] + 1
34 | stack.append(adjacent_index)
35 | return index_list
36 |
37 | def bfs(self):
38 | """
39 | 广度优先遍历
40 | """
41 | index_list = []
42 | queue = [0]
43 | visited = [False for _ in range(self.get_vertex_count())]
44 |
45 | while queue:
46 | vertex = queue.pop(0)
47 | if visited[vertex]:
48 | continue
49 | visited[vertex] = True
50 | index_list.append(vertex)
51 | queue.extend(list(self.get_adjacents(vertex)))
52 | return index_list
53 |
54 | @abstractmethod
55 | def get_adjacent(self, index, offset):
56 | pass
57 |
58 | @abstractmethod
59 | def get_adjacents(self, index):
60 | pass
61 |
62 | @abstractmethod
63 | def get_vertex_count(self):
64 | pass
65 |
66 |
67 | class HeadNode(object):
68 | """
69 | 头节点
70 | """
71 | def __init__(self, element):
72 | self._element = element
73 | self._next = None
74 |
75 | def set_element(self, element):
76 | self._element = element
77 |
78 | def get_element(self):
79 | return self._element
80 |
81 | def set_next(self, next):
82 | self._next = next
83 |
84 | def get_next(self):
85 | return self._next
86 |
87 |
88 | class AdjacentNode(object):
89 | """
90 | 表节点
91 | """
92 | def __init__(self, index, weight):
93 | self._index = index
94 | self._weight = weight
95 | self._next = None
96 |
97 | def set_index(self, index):
98 | self._index = index
99 |
100 | def get_index(self):
101 | return self._index
102 |
103 | def set_weight(self, weight):
104 | self._weight = weight
105 |
106 | def get_weight(self):
107 | return self._weight
108 |
109 | def set_next(self, next):
110 | self._next = next
111 |
112 | def get_next(self):
113 | return self._next
114 |
115 |
116 | class DiNetworkAdjacent(BaseDiGraph):
117 | """
118 | 有向网的邻接表表示
119 | """
120 | def __init__(self):
121 | self._vertex_array = []
122 |
123 | def add_vertex(self, element):
124 | self._vertex_array.append(HeadNode(element))
125 |
126 | def set_vertex(self, index, element):
127 | self._vertex_array[index].set_element(element)
128 |
129 | def get_vertex(self, index):
130 | return self._vertex_array[index]
131 |
132 | def add_arch(self, tail, head, weight):
133 | node = self._vertex_array[tail]
134 |
135 | while node.get_next() is not None:
136 | next_node = node.get_next()
137 | if next_node.get_index() == head:
138 | next_node.set_weight(weight)
139 | return
140 | node = next_node
141 | node.set_next(AdjacentNode(head, weight))
142 |
143 | def delete_vertex(self, index):
144 | self._vertex_array.pop(index)
145 | for head_node in self._vertex_array:
146 | prev = head_node
147 | node = head_node.get_next()
148 | while node is not None:
149 | if node.get_index() == index:
150 | prev.set_next(node.get_next())
151 | node = prev.get_next()
152 | continue
153 | elif node.get_index() > index:
154 | node.set_index(node.get_index() - 1)
155 | prev = node
156 | node = prev.get_next()
157 |
158 | def delete_arch(self, tail, head):
159 | prev = self._vertex_array[tail]
160 | node = prev.get_next()
161 | while node is not None:
162 | if node.get_index() == head:
163 | prev.set_next(node.get_next())
164 | break
165 | prev = node
166 | node = prev.get_next()
167 |
168 | def get_adjacent(self, index, offset):
169 | node = self._vertex_array[index]
170 | for ind in range(offset + 1):
171 | node = node.get_next()
172 | if node is None:
173 | break
174 | if ind == offset:
175 | return node.get_index()
176 | return None
177 |
178 | def get_adjacents(self, index, return_node=False):
179 | adjacents = []
180 | node = self._vertex_array[index].get_next()
181 | while node is not None:
182 | adjacents.append(node if return_node else node.get_index())
183 | node = node.get_next()
184 | return adjacents
185 |
186 | def get_vertex_count(self):
187 | return len(self._vertex_array)
188 |
189 |
190 | class DiNetworkArray(BaseDiGraph):
191 | """
192 | 有向网的数组矩阵表示
193 | """
194 | def __init__(self):
195 | self._vertex_array = []
196 | self._arch_array = []
197 |
198 | def add_arch(self, tail, head, weight):
199 | self._arch_array[tail][head] = weight
200 |
201 | def delete_arch(self, tail, head):
202 | self._arch_array[tail][head] = None
203 |
204 | def add_vertex(self, element):
205 | self._vertex_array.append(element)
206 | for array in self._arch_array:
207 | array.append(None)
208 | self._arch_array.append(
209 | [None for _ in range(len(self._vertex_array))])
210 |
211 | def set_vertex(self, index, element):
212 | self._vertex_array[index] = element
213 |
214 | def delete_vertex(self, index):
215 | self._vertex_array.pop(index)
216 | self._arch_array.pop(index)
217 | for array in self._arch_array:
218 | array.pop(index)
219 |
220 | def get_adjacent(self, index, offset):
221 | real_index = 0
222 | for adjacent_index, weight in enumerate(self._arch_array[index]):
223 | if weight is not None:
224 | if real_index == offset:
225 | return adjacent_index
226 | real_index = real_index + 1
227 | return None
228 |
229 | def get_adjacents(self, index):
230 | for adjacent_index, weight in enumerate(self._arch_array[index]):
231 | if weight is not None:
232 | yield adjacent_index
233 |
234 | def get_vertex_count(self):
235 | return len(self._vertex_array)
236 |
237 |
238 | if __name__ == "__main__":
239 | network = DiNetworkAdjacent()
240 | # network = DiNetworkArray()
241 | for i in range(6):
242 | network.add_vertex(100 * i)
243 |
244 | network.add_arch(0, 1, 1)
245 | network.add_arch(0, 3, 3)
246 | network.add_arch(1, 2, 12)
247 | network.add_arch(1, 4, 14)
248 | network.add_arch(2, 1, 21)
249 | network.add_arch(3, 0, 30)
250 | network.add_arch(3, 5, 35)
251 | network.add_arch(4, 3, 43)
252 |
253 | assert network.dfs() == [0, 1, 2, 4, 3, 5]
254 | assert network.bfs() == [0, 1, 3, 2, 4, 5]
255 |
--------------------------------------------------------------------------------
/树/二叉树/线索二叉树/ThreadedBinaryTree.py:
--------------------------------------------------------------------------------
1 | # coding: utf8
2 |
3 |
4 | class Node(object):
5 | """
6 | 先序和中序线索二叉树的节点
7 | """
8 | def __init__(self,
9 | keyword,
10 | left=None,
11 | right=None,
12 | ltag=False,
13 | rtag=False):
14 | self.keyword = keyword
15 | self.left = left
16 | self.right = right
17 | self.ltag = ltag
18 | self.rtag = rtag
19 |
20 | def __str__(self):
21 | return "%s{keyword=%s, left=%s, right=%s, ltag=%s, rtag=%s}" % (
22 | self.__class__.__name__,
23 | self.keyword,
24 | self.left and self.left.keyword,
25 | self.right and self.right.keyword,
26 | self.ltag,
27 | self.rtag
28 | )
29 |
30 |
31 | class PostorderThreadingNode(Node):
32 | """
33 | 后序线索二叉树的节点
34 | """
35 | def __init__(self, *args, **kwargs):
36 | Node.__init__(self, *args, **kwargs)
37 | # 增加指向父节点的指针
38 | self.parent = None
39 |
40 | ########## 中序线索二叉树的构建以及遍历 ##########
41 |
42 |
43 | def find_inorder_first_node(p):
44 | """
45 | 找到子树 p 的中序序列的第一个节点
46 | """
47 | if p is None:
48 | return None
49 |
50 | # p 的中序序列的第一个节点是 p 的最左孩子
51 | node = p
52 | while not node.ltag and node.left is not None:
53 | node = node.left
54 | return node
55 |
56 |
57 | def find_inorder_next_node(p):
58 | """
59 | 找到 p 在中序序列中的下一个节点
60 | """
61 | if p is None:
62 | return None
63 |
64 | if p.rtag:
65 | return p.right
66 |
67 | # 返回 p 的右子树的中序序列的第一个节点
68 | return find_inorder_first_node(p.right)
69 |
70 |
71 | def inorder_traverse(p):
72 | """
73 | 中序遍历
74 | """
75 | keywords = []
76 | node = find_inorder_first_node(p)
77 | while node is not None:
78 | keywords.append(node.keyword)
79 | node = find_inorder_next_node(node)
80 |
81 | return keywords
82 |
83 |
84 | def inorder_threading(p):
85 | """
86 | 构建中序线索二叉树
87 | """
88 | visited = [None]
89 |
90 | def _inorder_threading(p):
91 | if p is None:
92 | return
93 |
94 | _inorder_threading(p.left)
95 |
96 | if p.left is None:
97 | p.left = visited[0]
98 | p.ltag = True
99 | if visited[0] is not None and visited[0].right is None:
100 | visited[0].right = p
101 | visited[0].rtag = True
102 | visited[0] = p
103 |
104 | _inorder_threading(p.right)
105 |
106 | _inorder_threading(p)
107 |
108 | ########## end 中序线索二叉树 ##########
109 |
110 | ########## 后序线索二叉树的构建和遍历 ##########
111 |
112 |
113 | def postorder_threading(p):
114 | """
115 | 构建后序线索二叉树
116 | """
117 | visited = [None]
118 |
119 | def _postorder_threading(p):
120 | if p is None:
121 | return
122 |
123 | _postorder_threading(p.left)
124 |
125 | _postorder_threading(p.right)
126 |
127 | if p.left is None:
128 | p.left = visited[0]
129 | p.ltag = True
130 | if visited[0] is not None and visited[0].right is None:
131 | visited[0].right = p
132 | visited[0].rtag = True
133 | visited[0] = p
134 |
135 | _postorder_threading(p)
136 |
137 |
138 | def find_postorder_first_node(p):
139 | """
140 | 找到子树 p 的后序序列的第一个节点
141 | """
142 | node = p
143 | while node is not None:
144 | # 先找到最左节点
145 | while not node.ltag and node.left is not None:
146 | node = node.left
147 | # 如果最左节点没有右孩子,则它就是第一个节点
148 | if node.rtag or node.right is None:
149 | break
150 | # 否则,去节点的右子树上去找
151 | node = node.right
152 | return node
153 |
154 |
155 | def find_postorder_next_node(p, root):
156 | """
157 | 找到 p 在后序序列中的下一个节点
158 | """
159 | # 如果 p 是根节点,那么返回 None
160 | if p is None or p is root:
161 | return None
162 |
163 | # 返回后继
164 | if p.rtag:
165 | return p.right
166 |
167 | parent = p.parent
168 | # 如果 p 是其父的右孩子,那么其父即为下一个节点
169 | if p is parent.right:
170 | return parent
171 | # 如果 p 是其父的左孩子,但是其父没有右孩子,那么其父即为下一个节点
172 | if p is parent.left and (parent.rtag or parent.right is None):
173 | return parent
174 | # 否则,返回其父的右孩子的后序序列的第一个节点
175 | else:
176 | return find_postorder_first_node(parent.right)
177 |
178 |
179 | def postorder_traverse(p):
180 | """
181 | 后序遍历
182 | """
183 | node = find_postorder_first_node(p)
184 | keywords = []
185 | while node is not None:
186 | keywords.append(node.keyword)
187 | node = find_postorder_next_node(node, p)
188 | return keywords
189 |
190 | ########## end 后序线索二叉树 ##########
191 |
192 | ########## 先序线索二叉树的构建和遍历 ##########
193 |
194 |
195 | def find_preorder_first_node(p):
196 | if p is None:
197 | return None
198 | return p
199 |
200 |
201 | def find_preorder_next_node(p):
202 | if p is None:
203 | return None
204 |
205 | if not p.ltag and p.left is not None:
206 | return p.left
207 | return p.right
208 |
209 |
210 | def preorder_threading(p):
211 | visited = [None]
212 |
213 | def _preorder_threading(p):
214 | if p is None:
215 | return
216 |
217 | if p.left is None:
218 | p.left = visited[0]
219 | p.ltag = True
220 | if visited[0] is not None and visited[0].right is None:
221 | visited[0].right = p
222 | visited[0].rtag = True
223 | visited[0] = p
224 |
225 | _preorder_threading(p.left if not p.ltag else None)
226 |
227 | _preorder_threading(p.right if not p.rtag else None)
228 |
229 | _preorder_threading(p)
230 |
231 |
232 | def preorder_traverse(p):
233 | node = find_preorder_first_node(p)
234 | keywords = []
235 | while node is not None:
236 | keywords.append(node.keyword)
237 | node = find_preorder_next_node(node)
238 | return keywords
239 |
240 | ########## end 先序线索二叉树 ##########
241 |
242 |
243 | if __name__ == "__main__":
244 | import unittest
245 |
246 | class ThreadingBinaryTreeTest(unittest.TestCase):
247 | def setUp(self):
248 | nodes = [PostorderThreadingNode(ind) for ind in range(11)]
249 | nodes[0].left = nodes[1]
250 | nodes[0].right = nodes[2]
251 |
252 | nodes[1].parent = nodes[0]
253 | nodes[1].left = nodes[3]
254 |
255 | nodes[2].parent = nodes[0]
256 | nodes[2].left = nodes[4]
257 | nodes[2].right = nodes[5]
258 |
259 | nodes[3].parent = nodes[1]
260 | nodes[3].left = nodes[8]
261 | nodes[3].right = nodes[9]
262 |
263 | nodes[4].parent = nodes[2]
264 | nodes[4].right = nodes[7]
265 |
266 | nodes[5].parent = nodes[2]
267 | nodes[5].left = nodes[6]
268 |
269 | nodes[6].parent = nodes[5]
270 |
271 | nodes[7].parent = nodes[4]
272 |
273 | nodes[8].parent = nodes[3]
274 | nodes[8].right = nodes[10]
275 |
276 | nodes[9].parent = nodes[3]
277 |
278 | nodes[10].parent = nodes[8]
279 |
280 | self.root = nodes[0]
281 |
282 | def testInorderThreading(self):
283 | inorder_threading(self.root)
284 | self.assertEqual(inorder_traverse(self.root),
285 | [8, 10, 3, 9, 1, 0, 4, 7, 2, 6, 5])
286 |
287 | def testPostorderThreading(self):
288 | postorder_threading(self.root)
289 | self.assertEqual(postorder_traverse(self.root),
290 | [10, 8, 9, 3, 1, 7, 4, 6, 5, 2, 0])
291 |
292 | def testPreorderThreading(self):
293 | preorder_threading(self.root)
294 | self.assertEqual(preorder_traverse(self.root),
295 | [0, 1, 3, 8, 10, 9, 2, 4, 7, 5, 6])
296 |
297 | unittest.main()
298 |
--------------------------------------------------------------------------------
/树/B树/btree.py:
--------------------------------------------------------------------------------
1 | # coding: utf8
2 |
3 | import math
4 |
5 |
6 | def find_insertion_position(array, target):
7 | """
8 | 寻找插入位置
9 | """
10 | low = 0
11 | high = len(array) - 1
12 |
13 | if target <= array[0]:
14 | return -1, 0
15 | if target >= array[high]:
16 | return high, high + 1
17 |
18 | while low <= high:
19 | mid = (low + high) / 2
20 | if target == array[mid]:
21 | return mid - 1, mid
22 | elif target < array[mid]:
23 | if target >= array[mid - 1]:
24 | return mid - 1, mid
25 | high = mid - 1
26 | else:
27 | if target <= array[mid + 1]:
28 | return mid, mid + 1
29 | low = mid + 1
30 |
31 | raise RuntimeError("unreachable")
32 |
33 |
34 | class Node(object):
35 | """
36 | B 树的节点
37 | """
38 | def __init__(self, keywords, children=None):
39 | self.keywords = keywords
40 | # children 为 None 表示节点是根节点
41 | self.children = children
42 | self.parent = None
43 |
44 |
45 | class BTree(object):
46 | """
47 | B 树实现
48 | """
49 | def __init__(self, m):
50 | # B 树的阶数
51 | self.m = m
52 | # 树根
53 | self._root = None
54 |
55 | def insert(self, keyword):
56 | """
57 | 插入关键字
58 | """
59 | # 如果树为空,那么创建根节点,初始时根节点只包含一个关键字
60 | if self._root is None:
61 | self._root = Node([keyword])
62 | return
63 |
64 | # 在叶子节点上插入关键字
65 | node = self._root
66 | while True:
67 | pos = find_insertion_position(node.keywords, keyword)
68 | if node.children is not None:
69 | node = node.children[pos[1]]
70 | else:
71 | node.keywords.insert(pos[1], keyword)
72 | break
73 |
74 | # 如果节点的关键字个数超过 max keywords,则分裂
75 | while len(node.keywords) > self.max_keywords:
76 | mid = self.m / 2
77 | mid_keyword = node.keywords[mid]
78 |
79 | # 在 mid 处,将节点一分为二
80 | new_node = Node(node.keywords[mid + 1:])
81 | if node.children is not None:
82 | new_node.children = node.children[mid + 1:]
83 | # 重置孩子节点的双亲节点
84 | for child in new_node.children:
85 | child.parent = new_node
86 | node.keywords = node.keywords[:mid]
87 | if node.children is not None:
88 | node.children = node.children[:mid + 1]
89 |
90 | # 如果分裂的是根节点,那么将树增高一层
91 | if node is self._root:
92 | self._root = Node([mid_keyword], [node, new_node])
93 | node.parent = self._root
94 | new_node.parent = self._root
95 | break
96 |
97 | parent = node.parent
98 | index = None
99 | # TODO: 当前的实现的时间复杂度是 O(m)
100 | for index, child in enumerate(parent.children):
101 | if node is child:
102 | break
103 | # 在父节点上插入关键字和新子树
104 | parent.keywords.insert(index, mid_keyword)
105 | parent.children.insert(index + 1, new_node)
106 |
107 | # 设置新节点的父节点
108 | new_node.parent = parent
109 |
110 | # 从父节点开始,向上回溯
111 | node = parent
112 |
113 | def search(self, keyword):
114 | """
115 | 搜索关键字
116 | """
117 | if self._root is None:
118 | raise KeyError(keyword)
119 |
120 | node = self._root
121 | while True:
122 | pos = find_insertion_position(node.keywords, keyword)
123 | if pos[0] == -1:
124 | if keyword == node.keywords[0]:
125 | return node, 0
126 | elif pos[1] == len(node.keywords):
127 | if keyword == node.keywords[-1]:
128 | return node, pos[1] - 1
129 | elif node.keywords[pos[0]] == keyword:
130 | return node, pos[0]
131 | elif node.keywords[pos[1]] == keyword:
132 | return node, pos[1]
133 | if node.children is None:
134 | raise KeyError(keyword)
135 | node = node.children[pos[1]]
136 |
137 | @property
138 | def max_keywords(self):
139 | return self.m - 1
140 |
141 | @property
142 | def min_keywords(self):
143 | return int(math.ceil(self.m / 2.0) - 1)
144 |
145 | def delete(self, keyword):
146 | """
147 | 删除元素
148 | """
149 | # 找到待删除元素
150 | deleted_node, deleted_index = self.search(keyword)
151 |
152 | # 使用 deleted_node.children[deleted_index + 1] 的最左关键字代替待被删除的关键字或
153 | # 使用 deleted_node.children[deleted_index] 的最右关键字代替待被删除的关键字
154 | node = deleted_node
155 | index = deleted_index
156 | if deleted_node.children is not None:
157 | node = deleted_node.children[deleted_index + 1]
158 | index = 0
159 | while node.children is not None:
160 | node = node.children[0]
161 | deleted_node.keywords[deleted_index] = node.keywords[index]
162 |
163 | # node 一定是叶子节点,将关键字从叶子节点移除
164 | node.keywords.pop(index)
165 |
166 | # 如果 node 是根节点,
167 | if node is self._root:
168 | # 并且 node 中本来只有一个元素,那么将树置空
169 | if len(node.keywords) == 0:
170 | self._root = None
171 | # 否则,直接退出,因为根节点没最少关键字个数的限制
172 | return
173 |
174 | # 如果节点的关键字个数不满于要求,那么需要进行调整
175 | while len(node.keywords) < self.min_keywords:
176 | # 找到父节点、左兄弟、右兄弟
177 | parent = node.parent
178 | for index, child in enumerate(parent.children):
179 | if node is child:
180 | break
181 | if index == 0:
182 | left_sibling = None
183 | right_sibling = parent.children[index + 1]
184 | elif index == len(parent.children) - 1:
185 | left_sibling = parent.children[index - 1]
186 | right_sibling = None
187 | else:
188 | left_sibling = parent.children[index - 1]
189 | right_sibling = parent.children[index + 1]
190 |
191 | # 尝试从左兄弟借一个节点
192 | if left_sibling is not None and len(left_sibling.keywords) > self.min_keywords:
193 | borrowed_keyword = left_sibling.keywords.pop(-1)
194 | # 需要通过父节点进行中转
195 | node.keywords.insert(0, parent.keywords[index - 1])
196 | parent.keywords[index - 1] = borrowed_keyword
197 |
198 | if left_sibling.children is not None:
199 | borrowed_subtree = left_sibling.children.pop(-1)
200 | node.children.insert(0, borrowed_subtree)
201 | borrowed_subtree.parent = node
202 | break
203 |
204 | # 尝试从右兄弟借一个节点
205 | if right_sibling is not None and len(right_sibling.keywords) > self.min_keywords:
206 | borrowed_keyword = right_sibling.keywords.pop(0)
207 | # 需要通过父节点进行中转
208 | node.keywords.append(parent.keywords[index])
209 | parent.keywords[index] = borrowed_keyword
210 |
211 | if right_sibling.children is not None:
212 | borrowed_subtree = right_sibling.children.pop(0)
213 | node.children.append(borrowed_subtree)
214 | borrowed_subtree.parent = node
215 | break
216 |
217 | # 如果有左兄弟,则与父节点、左兄弟进行三方合并
218 | if left_sibling is not None:
219 | left_sibling.keywords.append(parent.keywords[index - 1])
220 | left_sibling.keywords.extend(node.keywords)
221 | parent.keywords.pop(index - 1)
222 | parent.children.pop(index)
223 | if node.children is not None:
224 | for child in node.children:
225 | child.parent = left_sibling
226 | left_sibling.children.append(child)
227 | maybe_new_root = left_sibling
228 | # 如果有右兄弟,那么与父节点、右兄弟进行三方合并
229 | elif right_sibling is not None:
230 | node.keywords.append(parent.keywords[index])
231 | node.keywords.extend(right_sibling.keywords)
232 | parent.keywords.pop(index)
233 | parent.children.pop(index + 1)
234 | if right_sibling.children is not None:
235 | for child in right_sibling.children:
236 | child.parent = node
237 | node.children.append(child)
238 | maybe_new_root = node
239 | else:
240 | raise RuntimeError("unreachable")
241 |
242 | # 如果 parent 是父节点,
243 | if parent is self._root:
244 | # 并且合并后,没有关键字了,那么树的高度将降低 1
245 | if len(parent.keywords) == 0:
246 | self._root = maybe_new_root
247 | # 否则,直接退出即可,因为根节点没有最少关键字个数的限制
248 | break
249 |
250 | # 否则从 parent 开始继续向上调整
251 | node = parent
252 |
253 |
254 | def test():
255 | import random
256 |
257 | tree = BTree(5)
258 | keywords = list(range(100000))
259 | random.shuffle(keywords)
260 |
261 | # 插入元素
262 | for keyword in keywords:
263 | tree.insert(keyword)
264 |
265 | # 搜索元素
266 | random.shuffle(keywords)
267 | for keyword in keywords:
268 | node, index = tree.search(keyword)
269 | assert node.keywords[index] == keyword
270 |
271 | random.shuffle(keywords)
272 | for keyword in keywords:
273 | tree.delete(keyword)
274 | try:
275 | tree.search(keyword)
276 | raise RuntimeError("delete %s failed" % keyword)
277 | except KeyError:
278 | pass
279 |
280 |
281 | if __name__ == "__main__":
282 | test()
283 |
--------------------------------------------------------------------------------