 20 |
21 | What the heck am I looking at?
22 | ------------------------------
23 |
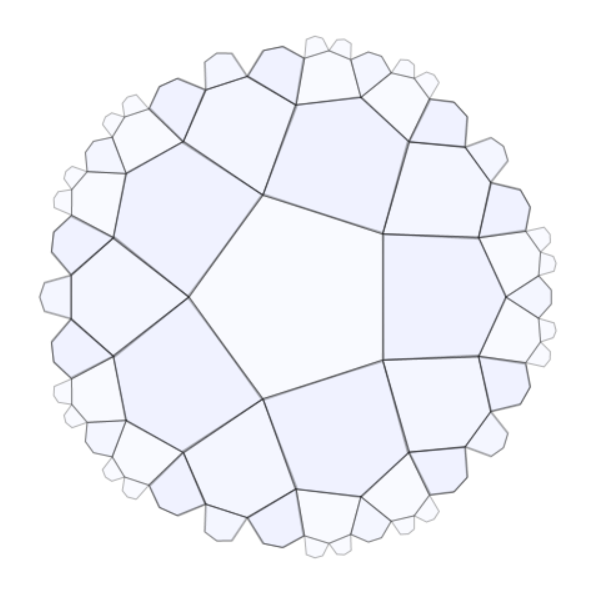
24 | Notice that there's a triangle in the center that never changes. We will use the edges of this triangle as mirrors.
25 |
26 | First we reflect the triangle in each of those mirrors. Our triangle has now got three more triangles around it, one fixed to each edge.
27 |
28 | We repeat this process again and again. We end up with lots of triangles, all joined edge to edge.
29 |
30 | At some values of curvature the triangles all overlap neatly and we get a nice *tiling*. This can be a flat tiling like you could use in your bathroom, or it could lie in a curved space like on a ball. A tiled ball is a polyhedron of course.
31 |
32 | One nice thing about making tilings like this ([Wythoff Construction](https://en.wikipedia.org/wiki/Wythoff_construction)) is that we can do the same thing in negatively curved ([hyperbolic](https://en.wikipedia.org/wiki/Hyperbolic_space)) space to get the hyperbolic tilings like [{5,4}](https://en.wikipedia.org/wiki/Order-4_pentagonal_tiling) shown above. We render these with the [Poincaré disk model](https://en.wikipedia.org/wiki/Poincar%C3%A9_disk_model) which is why the pentagons get small and stretched towards the outside.
33 |
34 | Credits:
35 | --------
36 |
37 | Thanks to Adam P. Goucher for getting me started with hyperbolic tessellation! [Here's a blog post](http://cp4space.wordpress.com/2014/09/12/hyperbolic-minecraft/) he wrote about it.
38 |
39 | He made his own interactive demonstration of Wythoff Construction, [here](http://demonstrations.wolfram.com/WythoffConstructionOfPolyhedra/).
40 |
41 | Discussions:
42 | ------------
43 |
44 | * [Comments](https://plus.google.com/110214848059767137292/posts/fXR8AChDbSY) on the original Google+ post.
45 | * [The Aperiodical](http://aperiodical.com/2014/09/have-fun-playing-with-curvature/)
46 | * [Hacker News](https://news.ycombinator.com/item?id=8317895)
47 |
48 |
49 |
--------------------------------------------------------------------------------
/generalized_stereographic_projection.html:
--------------------------------------------------------------------------------
1 |
2 |
3 |
4 |
5 |
124 |
125 |
131 |
132 |
133 |
134 |
135 |
136 |
20 |
21 | What the heck am I looking at?
22 | ------------------------------
23 |
24 | Notice that there's a triangle in the center that never changes. We will use the edges of this triangle as mirrors.
25 |
26 | First we reflect the triangle in each of those mirrors. Our triangle has now got three more triangles around it, one fixed to each edge.
27 |
28 | We repeat this process again and again. We end up with lots of triangles, all joined edge to edge.
29 |
30 | At some values of curvature the triangles all overlap neatly and we get a nice *tiling*. This can be a flat tiling like you could use in your bathroom, or it could lie in a curved space like on a ball. A tiled ball is a polyhedron of course.
31 |
32 | One nice thing about making tilings like this ([Wythoff Construction](https://en.wikipedia.org/wiki/Wythoff_construction)) is that we can do the same thing in negatively curved ([hyperbolic](https://en.wikipedia.org/wiki/Hyperbolic_space)) space to get the hyperbolic tilings like [{5,4}](https://en.wikipedia.org/wiki/Order-4_pentagonal_tiling) shown above. We render these with the [Poincaré disk model](https://en.wikipedia.org/wiki/Poincar%C3%A9_disk_model) which is why the pentagons get small and stretched towards the outside.
33 |
34 | Credits:
35 | --------
36 |
37 | Thanks to Adam P. Goucher for getting me started with hyperbolic tessellation! [Here's a blog post](http://cp4space.wordpress.com/2014/09/12/hyperbolic-minecraft/) he wrote about it.
38 |
39 | He made his own interactive demonstration of Wythoff Construction, [here](http://demonstrations.wolfram.com/WythoffConstructionOfPolyhedra/).
40 |
41 | Discussions:
42 | ------------
43 |
44 | * [Comments](https://plus.google.com/110214848059767137292/posts/fXR8AChDbSY) on the original Google+ post.
45 | * [The Aperiodical](http://aperiodical.com/2014/09/have-fun-playing-with-curvature/)
46 | * [Hacker News](https://news.ycombinator.com/item?id=8317895)
47 |
48 |
49 |
--------------------------------------------------------------------------------
/generalized_stereographic_projection.html:
--------------------------------------------------------------------------------
1 |
2 |
3 |
4 |
5 |
124 |
125 |
131 |
132 |
133 |
134 |
135 |
136 | Every black point is mapped onto a blue point (and vice versa) by stereographic projection with center C and radius R. Your mouse controls the curvature, 137 | from negative to positive.
138 |When the squared radius is positive this is the familiar circle inversion from C.
139 |When the squared radius is negative this means that the radius is imaginary. We need a different metric signature (+,-) for this to work. Details of this are below. 140 | Now the stereographic projection takes us to and from a hyperbola. This is one way of seeing that the hyperbola is actually a circle of imaginary radius.
141 | 142 | 143 | 144 |Stereographic projection of a point p, with respect to a center C and radius R:
145 | 146 |s( p, C, R ) = C + ( p - C ) * R^2 / dist2( p, C )
147 | 148 |where dist2( ) gives the squared distance between two points:
149 | 150 |In the Euclidean plane, with metric signature (+,+):
151 |dist2( a, b ) = ( a.x - b.x )^2 + ( a.y - b.y )^2
152 | 153 |For the hyperbola projection, with metric signature (+,-):
154 |dist2( a, b ) = ( a.x - b.x )^2 - ( a.y - b.y )^2
155 | 156 |In general we specify the metric tensor as e.g. [ m1, m2, m3 ] = [ 1, 1, -1 ] for ( +, +, - ) and the generalized squared-distance function becomes (in three dimensions):
157 |dist2( a, b ) = m1 * ( a.x - b.x )^2 + m2 * ( a.y - b.y )^2 + m3 * ( a.z - b.z )^2
158 | 159 |We make use of this generalized stereographic projection when it comes to tiling the hyperbolic and spherical planes, which have negative and positive 160 | curvature respectively. A demo of that in 1D shows the construction 161 | here.
162 | 163 |For more demonstrations, see the hyperplay page: https://github.com/timhutton/hyperplay.
164 | 165 | 166 | -------------------------------------------------------------------------------- /hyperbolic_only_2D.html: -------------------------------------------------------------------------------- 1 | 2 | 3 | 4 | 5 | 613 | 614 | 619 | 620 | 621 | 622 | 623 | 624 |Controls: Move the mouse left and right to change the size of the central polygon. Use the + and - buttons to change the number of sides.
625 | 626 | 627 | 628 |There's a version including positive curvature here. For more demonstrations, see the hyperplay page: https://github.com/timhutton/hyperplay.
629 | 630 | 631 | 632 | 633 | -------------------------------------------------------------------------------- /index.html: -------------------------------------------------------------------------------- 1 | 2 | 3 | 4 | 5 | 309 | 310 | 315 | 316 | 317 | 318 | 319 | 320 | 321 |Controls:
322 |Move mouse left and right to alter the curvature.
323 |Use the '+' and '-' buttons to change the base polygon.
324 |Click the mouse to start or stop the spinning.
325 |For more demonstrations, see the hyperplay page: https://github.com/timhutton/hyperplay.
326 | 327 | 328 | 329 | 330 | -------------------------------------------------------------------------------- /index_sliders.html: -------------------------------------------------------------------------------- 1 | 2 | 3 | 4 | 5 | 857 | 858 | 863 | 864 | 865 | 866 | 867 | 868 | 869 | 870 |OK the heck am I looking at this time?
875 |-
876 |
- In the center is a line segment of unit length. It never changes. 877 |
- We make copies of it, at different angles. Slider 1 controls the curvature. By default it makes a hexagon. 878 |
- We then make copies of the resulting polygon by reflecting it in its edges. Slider 2 controls the curvature of that. 879 |
- We then make copies of the resulting polyhedron by reflecting it in its faces. Slider 3 controls the curvature of that. 880 |
- More information and links here: https://github.com/timhutton/hyperplay (and a simpler version of this! gosh, I don't blame you) 881 |
- Click on the image to start/stop the spinning. 882 |
TODO:
885 |-
886 |
- Allow recursion depth at each level to be controlled. 887 |
- Better rendering! 888 |
Controls: Move the mouse up and down to move the viewpoint up and down. Click to stop and start the spinning. Use the slider to change the curvature. Press the button to toggle between a fixed scale and a scale that keeps the edge length fixed.
598 | 599 | 600 | 601 |This is a demonstration of the connection between hyperbolic plane tiling and the polyhedra. By varying the curvature we can smoothly change between the hyperboloid model (projecting 602 | onto the Poincaré disk) and the sphere (projecting onto the stereographic plane).
603 |The edge points A and A' are projected onto the curved surface at B and B' using stereographic projection from point S.
604 |Points B and B', together with the center of the curved surface at O, define a plane which intersects the curved surface to give the geodesic - the shortest path across the curved surface between B and B' is shown in green. 605 | For a sphere this is part of a great circle. For the hyperboloid it is part of a hyperbola. 606 |
Reflecting B and B' in point O gives the antipodal points D and D' that lie on the same plane. When the curvature is negative they lie on the upper sheet of the hyperboloid.
607 |We project D and D' onto the plane at M and M'. We now have four points A, A', M, M' that define a circle. Arcs in this circle are straight lines in the stereographic plane.
608 |We can use circle inversion to mirror things across the edges. We reflect our central tile across each of its edges in this way.
609 | 610 |To see the construction more clearly, there's a 1D version here. To understand why negative curvature leads us to a hyperboloid, 611 | there's an explanation here. For exploring the many tilings of the sphere and hyperbolic plane, including hyperbolic space tessellations, 612 | there's a three-slider demo here: here.
613 | 614 |For more demonstrations, see the hyperplay page: https://github.com/timhutton/hyperplay.
615 | 616 | 617 | -------------------------------------------------------------------------------- /projection_and_mirroring.html: -------------------------------------------------------------------------------- 1 | 2 | 3 | 4 | 5 | 253 | 254 | 259 | 260 | 261 | 262 | 263 | 264 |A tiling of a 1D line is shown under varying curvature. Move the mouse to change the curvature between spherical geometry (positive curvature) and hyperbolic geometry (negative curvature).
265 | 266 |For positive curvatures the tiling lives on a circle. The mapping to the line is provided by stereographic projection from point S.
267 | 268 |For negative curvatures the tiling lives on one sheet of a hyperbola. Stereographic projection is still used to map onto the line, giving a 1D version of the Poincaré disk model.
269 | 270 |While this 1D case is pretty boring, the details of construction are exactly the same when we move into 2 and 3 dimensions. The details are given below.
271 | 272 | 273 | 274 |So we want to make a tiling. We're going to use Wythoff construction, where we put down a single tile and then repeatedly reflect it in its edges.
275 | 276 |
The red line between C and A is our first tile. The first edge, at C, is easy to make a mirror for: the scene is already symmetric around this point 277 | so we simply reflect across it. The second edge of the tile, at A, is more tricky.
278 | 279 |We project edge A onto our curved surface, to B. The light green line shows the geodesic of B - the plane that passes through the edge at B and the origin at O. 280 | All points on this geodesic will be unaffected by the mirroring. In our 1D example the only other such point is D but in 2D there will be a whole circle of such 281 | points, and likewise a whole sphere in 3D.
282 | 283 |Point D projects onto the stereographic plane at M. Points A and M define a circle of inversion in the stereographic plane that we can use to reflect 284 | the tile. It has its center at point K that in this 1D case is halfway between A and M.
285 | 286 |We can then reflect the red tile C-A using the circle of inversion A-K-M. This leaves A where it is and puts C onto point G, 287 | making our new tile A-G, drawn in blue.
288 | 289 |Reflecting the original tile C-A in C gives the dark green tile. Reflecting the dark green tile over A gives the pink tile on the other side of G, and so on.
290 | 291 |In 2D and 3D the process is the same - the tile is reflected in the circle (or sphere) of inversion defined by each of its facets. For certain values 292 | of curvature the tiles all line up and we get a regular tiling of the hyperbolic plane or of the sphere. In the spherical case we call this a polyhedron or a polychoron.
293 | 294 |So what is negative curvature? And why a hyperbola? These questions are addressed in another demo here. There's a 2D 295 | version of this here.
296 | 297 |For more demonstrations, see the hyperplay page: https://github.com/timhutton/hyperplay.
298 | 299 | --------------------------------------------------------------------------------