├── 01-一年级.md
├── 02-二年级.md
├── 03-三年级.md
├── 04-四年级.md
├── 05-五年级.md
├── 06-六年级.md
└── README.md
/01-一年级.md:
--------------------------------------------------------------------------------
1 | ---
2 | title: 一年级
3 | lang: zh-CN
4 | sidebarDepth: 1
5 | ---
6 |
7 | # 一年级
8 |
9 | 待整理
10 |
--------------------------------------------------------------------------------
/02-二年级.md:
--------------------------------------------------------------------------------
1 | ---
2 | title: 二年级
3 | lang: zh-CN
4 | sidebarDepth: 1
5 | ---
6 |
7 | ## 2.1.01. 数数中的枚举
8 |
9 | ### 例题1
10 |
11 | 有一个三位数,其中十位数字比百位数字大4,个位数字又比十位数字大4,这个三位数是多少?
12 |
13 | ### 练习1
14 |
15 | 十位上的数字比个位上的数字大2,写出所有符合条件的两位数?
16 |
17 | ### 例题2
18 |
19 | 十位上的数字与个位上的数字相差2,写出所有符合条件的两位数?
20 |
21 | ### 练习2
22 |
23 | 有一个两位数,它十位上的数字与个位上的数字正好相差4,把所有符合条件的数全部写出来?
24 |
25 | ### 例题3
26 |
27 | 在50以内(包括50),十位上的数字比个位上数字大的两位数一共有多少个?
28 |
29 | ### 练习3
30 |
31 | 在60以内(包括60),十位上的数字比个位上数字大的两位数一共有多少个?
32 |
33 | ### 例题4
34 |
35 | 像17和71这样十位数字和个位数字顺序颠倒的一对两位数是一家人,它们相加的和为88,请问像这样的相加和为99的一家人有几对?
36 |
37 | ### 练习4
38 |
39 | 像16和61这样十位数字和个位数字顺序颠倒的一对两位数是一家人,它们相加的和为77,请问像这样的相加和为77的一家人有几对?
40 |
41 | ### 例题5
42 |
43 | 自然数21、654、7521这些数有一个共同的特点,相邻两个数字,左边的数字大于右边的数字,我们取名为“下降数”。用4、6、7、9这四个数字,可以组成多少个“下降数”?
44 |
45 | ### 练习5
46 |
47 | 自然数12、135、1349这些数有一个共同的特点,相邻两个数字,左边的教主小于右边的数字,我们取名为“上升数”。用5、6、7、8这四个数字,可以组成多少个“上升数”?
48 |
49 | ### 例题6
50 |
51 | 有一些自然数,像121和2442这样,从左往右和从右往左读是相同的,我们这样的数称作“回文数”,那么在三位数中,一共有多少这样的“回文数”?
52 |
53 | ### 练习6
54 |
55 | 像1001这样,从左往右和从右往左读都是相同的自然数叫做“回文数”,那么在1000到2016之间共有多少个回文数呢?
56 |
57 | ## 2.1.10. 一笔画
58 |
59 | ### 热身1
60 |
61 | 计算。
62 | $$
63 | 32+24+28=
64 | $$
65 |
66 | $$
67 | 56-37+44=
68 | $$
69 |
70 | ### 热身2
71 |
72 | 俄罗斯方块游戏中有以下几种形状,哪几种形状取相同的四块可以拼成一个大的正方形?拼一拼。
73 |
74 |  75 |
76 | ### 热身3
77 |
78 | 下面是一个奥运五环标志,你能不能一笔画出下面的奥运五环图呢?大家试一试。 (要求:笔中途不能离开纸,每条线只能画一次不能重复画。)
79 |
80 | ### 例题1
81 |
82 | 你能试着用一笔把下列图形画出来吗?如果可以,说说你是怎样画的?
83 |
84 |
75 |
76 | ### 热身3
77 |
78 | 下面是一个奥运五环标志,你能不能一笔画出下面的奥运五环图呢?大家试一试。 (要求:笔中途不能离开纸,每条线只能画一次不能重复画。)
79 |
80 | ### 例题1
81 |
82 | 你能试着用一笔把下列图形画出来吗?如果可以,说说你是怎样画的?
83 |
84 |  85 |
86 | ### 练习1
87 |
88 | 下图两个图能否一笔画出?
89 |
90 |
85 |
86 | ### 练习1
87 |
88 | 下图两个图能否一笔画出?
89 |
90 |  91 |
92 | ### 例题2
93 |
94 | 下列图形能一笔画成吗?为什么?
95 |
96 |
91 |
92 | ### 例题2
93 |
94 | 下列图形能一笔画成吗?为什么?
95 |
96 |  97 |
98 | ### 练习2
99 |
100 | 下列图形能一笔画成吗?为什么?
101 |
102 |
97 |
98 | ### 练习2
99 |
100 | 下列图形能一笔画成吗?为什么?
101 |
102 |  103 |
104 | ### 例题3
105 |
106 | 下面的图形都不能一笔画成,请你分别在各图中添上一条线段,使他能一笔画成。
107 |
108 |
103 |
104 | ### 例题3
105 |
106 | 下面的图形都不能一笔画成,请你分别在各图中添上一条线段,使他能一笔画成。
107 |
108 |  109 |
110 | ### 练习3
111 |
112 | 下面的图形不能一笔画成,至少添上几条线段才能使它能一笔画成?试着添一添。
113 |
114 |
109 |
110 | ### 练习3
111 |
112 | 下面的图形不能一笔画成,至少添上几条线段才能使它能一笔画成?试着添一添。
113 |
114 |  115 |
116 | ### 例题4
117 |
118 | 下面的图形都不能一笔画成,请你在各个图中去掉一条线,使它能一笔画成。
119 |
120 |
115 |
116 | ### 例题4
117 |
118 | 下面的图形都不能一笔画成,请你在各个图中去掉一条线,使它能一笔画成。
119 |
120 |  121 |
122 | ### 练习4
123 |
124 | 下面的图形不能一笔画成,请你去掉一条线,使它能一笔画成?
125 |
126 |
121 |
122 | ### 练习4
123 |
124 | 下面的图形不能一笔画成,请你去掉一条线,使它能一笔画成?
125 |
126 |  127 |
128 | ### 例题5
129 |
130 | 下图是乡间的一条小河,上面建有六座桥,你能一次不重复地走遍所有的小桥吗?(每座小桥最多只准走一次 ,陆地上可以重复地来回走)
131 |
132 |
127 |
128 | ### 例题5
129 |
130 | 下图是乡间的一条小河,上面建有六座桥,你能一次不重复地走遍所有的小桥吗?(每座小桥最多只准走一次 ,陆地上可以重复地来回走)
131 |
132 | 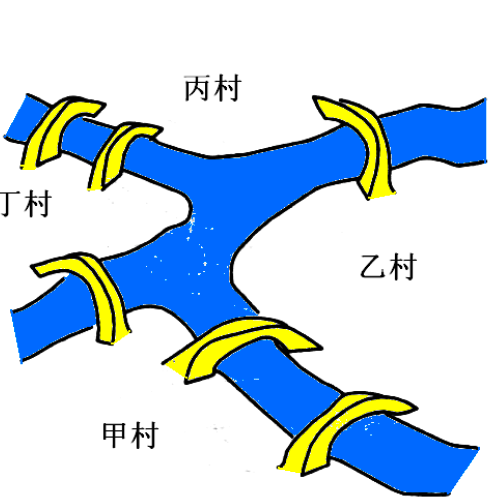 133 |
134 | ### 例题6
135 |
136 | 如图是某地区所有街道的平面图,丁丁和牛牛两人同时从A、B两地出发,以相同的速度行进,如果允许选择最短路径的话,那么谁先走遍所有的街道?
137 |
138 |
133 |
134 | ### 例题6
135 |
136 | 如图是某地区所有街道的平面图,丁丁和牛牛两人同时从A、B两地出发,以相同的速度行进,如果允许选择最短路径的话,那么谁先走遍所有的街道?
137 |
138 |  139 |
140 | 纸上画了9个点,我们可以用5条线段把它们串联起来,而且这5条线段是可以一笔画成的(如左图)。实际上我们可以做的更好:只用四条线段就能把这9个点串起来,而且这4条线段仍然是用一笔画成,试一试,你能找出这种画法吗?
141 |
142 |
139 |
140 | 纸上画了9个点,我们可以用5条线段把它们串联起来,而且这5条线段是可以一笔画成的(如左图)。实际上我们可以做的更好:只用四条线段就能把这9个点串起来,而且这4条线段仍然是用一笔画成,试一试,你能找出这种画法吗?
141 |
142 |  143 |
144 | ## 2.1.11. 巧算加减法进阶
145 |
146 | ### 例题1
147 |
148 | 计算。
149 | $26+37+74=$
150 |
151 | $43+62+57+38=$
152 |
153 | ### 练习1
154 |
155 | 计算。
156 | $24+65+76=$
157 |
158 | $37+24+63+76=$
159 |
160 | ### 例题2
161 |
162 | 计算。
163 | $97-34-37=$
164 |
165 | $68-33-28=$
166 |
167 | ### 练习2
168 |
169 | 计算。
170 | $89-32-19=$
171 |
172 | $62-19-22=$
173 |
174 | ### 例题3
175 |
176 | 计算。
177 | $172-34-66=$
178 |
179 | $244-46-154=$
180 |
181 | ### 练习3
182 |
183 | 计算。
184 | $256-43-57=$
185 |
186 | $127-36-54=$
187 |
188 | ### 例题4
189 |
190 | 计算。
191 | $176-(32+76)=$
192 |
193 | $97-(48+17)=$
194 |
195 | ### 练习4
196 |
197 | 计算。
198 | $152-(34+52)=$
199 |
200 | $89-(17+19)=$
201 |
202 | ### 例题5
203 |
204 | 计算。
205 | $27+28+30+31+32=$
206 |
207 | ### 练习5
208 |
209 | 计算。
210 | $84+95+93+85+87+90$
211 |
212 | ### 例题6
213 |
214 | 计算。
215 | $9+99+199=$
216 |
217 | ### 练习6
218 |
219 | 计算。
220 | $8+98+198=$
221 |
222 | ### 拓展1
223 |
224 | $2+22+202+2002+20002=$
225 |
226 | ### 拓展2
227 |
228 | $10-9+8-7+6-5+4-3+2-1=$
229 |
230 | ### 拓展3
231 |
232 | $100-99+98-97+96-95+\dots+4-3+2-1=$
233 |
234 | ### 拓展4
235 |
236 | $1+2+3+4+5+6+7+8+9+10+9+8+7+6+5+4+3+2+1=$
237 |
238 | ### 拓展5
239 |
240 | $1+2+3+4+\dots+49+50+49+\dots+3+2+1=$
241 |
242 | ### 拓展6
243 |
244 | $123+231+321=$
245 |
246 | ### 拓展7
247 |
248 | $1234+2341+3412+4123=$
249 |
250 | ## 2.2.14. 有趣的植树问题
251 |
252 | ### 例题1
253 |
254 | 植树问题中的间隔有四种不同的情况,只有准确判断,才能找到解决问题的方法(树的宽度忽略不计)
255 |
256 | 1. 在一条长100米的公路一侧种树,每隔10米种一棵,两端都种,一共要种多少棵树?
257 |
258 | 2. 两座塔之间的距离是50米,现在要在这两座塔之间种树,每隔5米种一棵,一共需要种多少棵树?
259 |
260 | 3. 在一座城堡门前,有一条通往城堡的公路,长40米,现在要在公路的一侧种树,每两棵树之间相隔5米,一共要种几棵树?
261 |
262 | 4. 广场中的圆形花坛一周长80米,现在要在花坛边每隔8米摆一盆花,一共可以摆几盆花?
263 |
264 | ### 练习1
265 |
266 | 两座楼房之间相距40米,每隔4米栽一棵雪松,一共能栽多少棵雪松?(树的宽度忽略不计)
267 |
268 | ### 例题2
269 |
270 | 城墙上从一端到另一端共站了7个士兵,相邻的两个士兵相隔3米。问:城墙长多少米?(士兵的宽度忽略不计)
271 |
272 | ### 练习2
273 |
274 | 一条林荫道上有5只免子排队做操,相邻两只免子相隔2米,免子做操的队伍长多少米?(免子的宽度忽略不计)
275 |
276 | ### 例题3
277 |
278 | 要新建一个圆形喷泉,如果沿喷泉的一周放置雕像,每隔2米放一座,刚好可以放8座,问:这个圆形喷泉一周长是多少米?(雕像的宽度忽略不计)
279 |
280 | ### 练习3
281 |
282 | 一个圆形养鱼池,一周总长为42米,要在养鱼池的一周每隔6米种一棵桃树,一共能种多少棵桃树?(树的宽度忽略不计)
283 |
284 | ### 例题4
285 |
286 | 在一条长50米的公路两边种树,每隔10米种一棵,两端都种,这条公路上一共能种多少棵树?(树的宽度忽略不计)
287 |
288 | ### 练习4
289 |
290 | 一个圆形花坛一周长60米,沿花坛一周每隔3米栽一棵柳树,再在每两棵柳树之问栽2株月季花,花坛一周一共能栽多少株月季花?(树和花的宽度忽略不计)
291 |
292 | ### 例题5
293 |
294 | 有一块三角形的地,三条边分别为30米,40米,60米,每10米种一棵树,三个角都种,那么三条边上共种多少棵树?(树的宽度忽略不计)
295 |
296 | ### 练习5
297 |
298 | 森林公园中心有一个圆形鱼塘,一周长是60米,每隔6米种一棵柳树,每相邻两棵柳树之间,均匀地栽种两棵夹竹桃,问:这个圆形鱼塘的一周可以栽种多少棵夹竹桃?(树的宽度忽略不计)
299 |
300 | ### 例题6
301 |
302 | 在一条长48米的公路一旁种树,两端都种,共种了9棵树,算一算每隔几米种一棵?(树的宽度忽略不计)
303 |
304 | ### 练习6
305 |
306 | 爷爷从1楼爬到4楼用时12分钟,照这样的速度,他从1楼爬到5楼需要用时多少分钟?
307 |
308 | ### 拓展1
309 |
310 | 乐乐老师组织学生们植树,在一条长 120 米的马路两边每隔30米种一棵梧桐树(两端都种),在每相邻的2棵梧桐树之间又补种1 棵香樟树。这条马路两边一共种了多少棵树?(树的宽度忽略不计)
311 |
312 | ### 拓展2
313 |
314 | 牛牛和爷爷一起从 1 楼开始爬楼梯锻炼身体,牛牛走得快,爷爷走得慢。牛牛走到5楼的时候,爷爷才爬到3楼。照这样的速度继续爬,牛牛到15楼的时候,爷爷到几楼?
315 |
316 | ### 拓展3
317 |
318 | 马路的一边,每隔8米有1棵杨树。 小明乘汽车从学校回家,从看到第一棵树数起到第51棵树为止,共用时2分。小明从学校到家共坐了半小时的汽车。小明的家距学校有多远?(树的宽度忽略不计)
319 |
320 | ### 拓展4
321 |
322 | 几个孩子星期天一起逛公园,在公园中心有一个正方形池塘,在池塘边距离池边3米处围绕池塘种树,一共种了40棵(四个角都种)也围成了一个正方形。如果相邻两棵树之间的距离是2米,那么这个正方形池塘的边长是多少米?(树的宽度忽略不计)
323 |
324 | ## 2.1.15. 合理安排
325 |
326 | 课程内容
327 |
328 | * 煎饼问题
329 | * 连续完成合理安排
330 | * 过河问题
331 | * 排队问题
332 |
333 | 学习目标
334 |
335 | 通过解决常见的生活问题,学会合理安排时间,最快完成。
336 |
337 | 内容分析
338 |
339 | ### 煎饼问题
340 |
341 | **问题概述**
342 |
343 | 随手拿一些小物品来替代饼和锅,设定煎饼的场景。
344 |
345 | 1. 一个锅一次只能放一张饼,饼要煎两面,煎一面需要一分钟,需要怎么煎最快。(设置基本规则,无法同时煎一张饼的正面和反面)(题外话:铜锣烧除外)
346 |
347 | 2. 一个锅一次可以放两张饼,饼要煎两面,煎一面需要一分钟,怎么煎,两张饼呢?三张饼呢?(实际操作中,学生很容易想的到一张、两张的情况,但是三张情况尽量鼓励学生自己解决,如何才能不保证锅的空间得到充分的利用,不会一个锅,只煎一张饼的情况)
348 |
349 | 学会 3 分钟煎三张饼后,让学生自己开始做例题,现在遇到多张饼的时候,还需要一面面的去试么?引出分组思考的概念,比 1 大的数都可以分成若干个 2 和 3 的和。最后,思考总结,做练习。(练习出现一面不再是单位 1 时间的情况,第一次做容易忽略)
350 |
351 | 三张饼的安排方案:
352 |
353 | 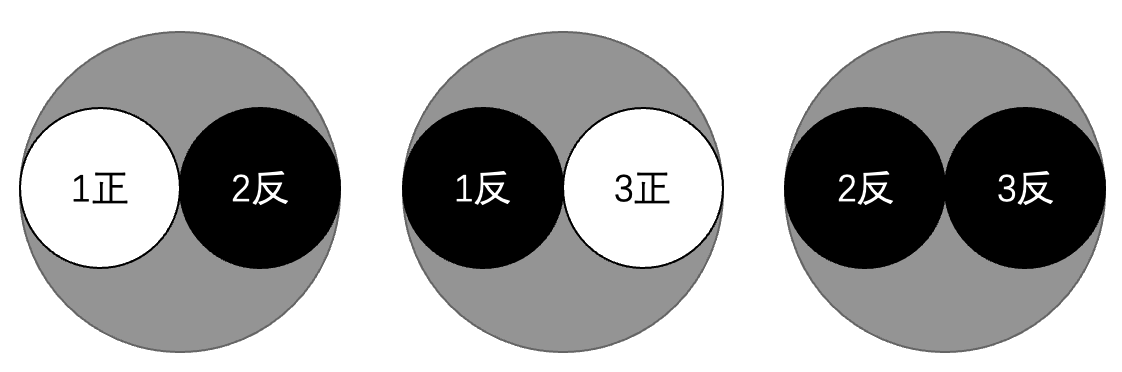
354 |
355 | **例题1**
356 |
357 | 平底锅里每次能同时放 2 张饼,烙熟 1 张饼需用时 2 分(正、反面各需 1 分),如果要烙熟 5 张饼至少需要多长时间?烙熟 6 张饼呢?烙熟 7 张饼呢?
358 |
359 | 【解析】5 分钟;6 分钟;7 分钟。
360 |
361 | **练习1**
362 |
363 | 用一个平底锅煎鸡蛋,每次最多能放 2 个鸡蛋,煎熟 1 个鸡蛋需要用时 4 分钟(正、反面各需用时 2 分钟),问煎熟 7 个鸡蛋至少需要多长时间?
364 |
365 | 【解析】14 分钟。
366 |
367 | **问题小结**
368 |
369 | 对于煎饼问题,原则是不能让锅闲着,学会分组(偶数:2 个 2 个一组;奇数:2 个 2 个一组,最后一个并入 2 ,形成一个 3)一组一组的去煎,注意一面需要花费的时间。
370 |
371 | ### 按顺序,同时做
372 |
373 | **问题概述**
374 |
375 | 生活中有些事情是“不需要手”,可以自主完成的,比如烧水、煮饭、洗衣机洗衣服、听广播等等,那么这些事情是可以和一些事情同时进行。也就是一边……一边……的平行关系。另外,做事情还得考虑先后顺序,比如先吃饭,后洗碗,先烧水,再泡茶等等。也就是先……,然后……的递进关系。综上,那么该怎样合理的安排,才能让总花费的时间最短?
376 |
377 | **例题2**
378 |
379 | 牛牛需要给田田沏茶,沏茶过程中,洗开水壶用时 1 分钟,烧开水要用时 15 分钟,洗茶壶要用时 1 分钟,洗茶杯要用时 2 分钟,找茶叶要用时 2 分钟,泡茶要用时1分钟;牛牛怎样合理的安排,才能在最短时间里让田田喝上茶呢?最少需要多长时间呢?
380 |
381 | 【解析】需要遵守“洗开水壶-烧开水-泡茶”的顺序,烧开水是“不需要手”的事情,洗茶壶,洗茶杯,找茶叶可以在烧水的时候做。总时间是 1 + 15 + 1 = 17(分钟)。
382 |
383 | **练习2**
384 |
385 | 丁丁早上 6 时 30 分钟起床,去学校之前要做以下几件事情:穿衣叠被用时 6 分钟,梳头用时 2 分钟,刷牙洗脸用时 5 分钟,听新闻用时 20 分钟,吃早饭用时 8 分钟,收拾饭桌用时 3 分钟。如果他 6 时 30 分钟准时起床,那么最早可以几时几分钟从家出发去上学?
386 |
387 | 【解析】6 + 2 + 5 + 8 + 3 = 24(分钟),听新闻“不需要手”,可以同时完成。那么最早 6 时 54 分钟从从家出发去上学。
388 |
389 | **例题3**
390 |
391 | 牛牛要帮丁丁做家务,需要做的事情有:擦桌椅用时 12 分钟;擦地用时 18 分钟;浸泡衣服(要用温水)用时 15 分钟;搓衣服用时 15 分钟;烧开水用时 20 分钟;清洗衣服用时 15 分钟;晾衣服用时 5 分钟。牛牛如何安排这些事情的先后顺序,才可以用时最短,最短多长时间可以把这些事情全部做完?
392 |
393 | 【解析】烧开水-浸泡衣服-搓衣服-清洗衣服-晾衣服是需要分先后的递进关系,其中,烧开水,浸泡衣服是“不需要手”的,可以与擦座椅,擦地同时进行。总时间是:20 + 15 + 15 + 15 + 5 = 70(分钟)。注意提醒学生检查同时完成的时候,哪个花费的时间更久。比如题目中 20 + 15 需要同 12 + 18 去比较。
394 |
395 | **练习3**
396 |
397 | 星期天,妈妈要做好多事情。擦玻璃要 20 分钟,收拾厨房要 15 分钟,洗脏衣服的领子、袖口要 10 分钟,打开全自动洗衣机洗衣服要 40 分钟,晾衣服要 10 分钟。妈妈干完所有这些事情最少要分钟。
398 |
399 | 【解析】找顺序:洗脏衣服的领子、袖口-打开全自动洗衣机洗衣服-晾衣服,其中洗衣机洗衣服可以同时做其他事情,且 40 > (20 + 15)。总耗时:10 + 40 + 10 = 60(分钟)。
400 |
401 | ### 过河问题
402 |
403 | **问题概述**
404 |
405 | **例题4**
406 |
407 | 牛牛、丁丁和田田被怪物们追到小河边,河岸边只有一条能同时乘坐 2 人的小船,由牛牛划船需要用时 2 分钟,由丁丁划船用时 3 分钟,由田田划船用时 5 分钟,现在情况危急,需要尽快过河,应该采用怎样的过河方式,3 人全部过河用时最短?
408 |
409 | 练习4
410 |
411 | 牛牛、丁丁和田田骑车去公园,现在只有一辆自行车,自行车除了一人骑车,还能载一个人。由牛牛骑车需要用时 30 分钟,由丁丁骑车用时 35 分钟,由田田骑车用时 40 分钟,三人需要尽快到达公园,应该采用怎样的载人方式,3 人全部到达公园用时最短?
412 |
413 | 例题5
414 |
415 | 学校组织防火演习,牛牛、丁丁、田田、乐乐老师四人准备通过一座正在燃烧的木桥,此桥每次最多只能让 2 个人同时通过(不能背着、抱着),否则桥会倒塌。过桥的人必须要用到防火披风,不然会被火烧到(防火披风只有 1 件,可供两人同时使用),4 个人行走速度不同:牛牛用时 1 分钟就可以过桥,丁丁要用时 2 分钟,田田要用时 5 分钟,乐乐老师要用时 8 分钟,已知 15 分钟过后桥就会被烧塌了,请问:4 个人要用什么方法才能全部安全过桥?
416 |
417 | 练习5
418 |
419 | 牛牛、丁丁、田田、乐乐老师四个人过桥,分别需要用时 1 分钟、2 分钟、5 分钟和 10 分钟,因为天黑,必须借助手电筒过桥,可是他们只有一个手电筒,并且桥的载重能力有限,每次最多同时过两个人(不能背着、抱着),现在他们希望可以用最短的时间过桥,应该怎样做? 最短时问是多少?
420 |
421 | ### 排队问题
422 |
423 | 例题6
424 |
425 | 同学们各提一个大小不一的桶去打水,丁丁、田田、牛牛、阿普他们四个的桶注满水所需的时间分别为 2 分钟、4 分钟、5 分钟、3 分钟。现在只有一个水龙头可以接水,请你设计一下,使他们总的等候时间最短,这个最短的时间是多少?
426 |
427 | 练习6
428 |
429 | 有四名同学各提一个大小不一样的桶去打水,他们四个的桶注满水所需的时间分别是 1 分钟、3 分钟、4 分钟、2 分钟。现在只有一个水龙头可以接水,请你帮他们设计一下,怎样安排才能使他们总的等候时间最短,这个最短的时间是多少?
430 |
431 | # 摆小棒
432 |
433 | 热身1
434 |
435 | 计算。
436 | $$
437 | 8+8+8+8+8+6+6+6=
438 | $$
439 |
440 | ### 热身2
441 |
442 | 下列图形中,不能“一笔画”的是()。
443 |
444 |
143 |
144 | ## 2.1.11. 巧算加减法进阶
145 |
146 | ### 例题1
147 |
148 | 计算。
149 | $26+37+74=$
150 |
151 | $43+62+57+38=$
152 |
153 | ### 练习1
154 |
155 | 计算。
156 | $24+65+76=$
157 |
158 | $37+24+63+76=$
159 |
160 | ### 例题2
161 |
162 | 计算。
163 | $97-34-37=$
164 |
165 | $68-33-28=$
166 |
167 | ### 练习2
168 |
169 | 计算。
170 | $89-32-19=$
171 |
172 | $62-19-22=$
173 |
174 | ### 例题3
175 |
176 | 计算。
177 | $172-34-66=$
178 |
179 | $244-46-154=$
180 |
181 | ### 练习3
182 |
183 | 计算。
184 | $256-43-57=$
185 |
186 | $127-36-54=$
187 |
188 | ### 例题4
189 |
190 | 计算。
191 | $176-(32+76)=$
192 |
193 | $97-(48+17)=$
194 |
195 | ### 练习4
196 |
197 | 计算。
198 | $152-(34+52)=$
199 |
200 | $89-(17+19)=$
201 |
202 | ### 例题5
203 |
204 | 计算。
205 | $27+28+30+31+32=$
206 |
207 | ### 练习5
208 |
209 | 计算。
210 | $84+95+93+85+87+90$
211 |
212 | ### 例题6
213 |
214 | 计算。
215 | $9+99+199=$
216 |
217 | ### 练习6
218 |
219 | 计算。
220 | $8+98+198=$
221 |
222 | ### 拓展1
223 |
224 | $2+22+202+2002+20002=$
225 |
226 | ### 拓展2
227 |
228 | $10-9+8-7+6-5+4-3+2-1=$
229 |
230 | ### 拓展3
231 |
232 | $100-99+98-97+96-95+\dots+4-3+2-1=$
233 |
234 | ### 拓展4
235 |
236 | $1+2+3+4+5+6+7+8+9+10+9+8+7+6+5+4+3+2+1=$
237 |
238 | ### 拓展5
239 |
240 | $1+2+3+4+\dots+49+50+49+\dots+3+2+1=$
241 |
242 | ### 拓展6
243 |
244 | $123+231+321=$
245 |
246 | ### 拓展7
247 |
248 | $1234+2341+3412+4123=$
249 |
250 | ## 2.2.14. 有趣的植树问题
251 |
252 | ### 例题1
253 |
254 | 植树问题中的间隔有四种不同的情况,只有准确判断,才能找到解决问题的方法(树的宽度忽略不计)
255 |
256 | 1. 在一条长100米的公路一侧种树,每隔10米种一棵,两端都种,一共要种多少棵树?
257 |
258 | 2. 两座塔之间的距离是50米,现在要在这两座塔之间种树,每隔5米种一棵,一共需要种多少棵树?
259 |
260 | 3. 在一座城堡门前,有一条通往城堡的公路,长40米,现在要在公路的一侧种树,每两棵树之间相隔5米,一共要种几棵树?
261 |
262 | 4. 广场中的圆形花坛一周长80米,现在要在花坛边每隔8米摆一盆花,一共可以摆几盆花?
263 |
264 | ### 练习1
265 |
266 | 两座楼房之间相距40米,每隔4米栽一棵雪松,一共能栽多少棵雪松?(树的宽度忽略不计)
267 |
268 | ### 例题2
269 |
270 | 城墙上从一端到另一端共站了7个士兵,相邻的两个士兵相隔3米。问:城墙长多少米?(士兵的宽度忽略不计)
271 |
272 | ### 练习2
273 |
274 | 一条林荫道上有5只免子排队做操,相邻两只免子相隔2米,免子做操的队伍长多少米?(免子的宽度忽略不计)
275 |
276 | ### 例题3
277 |
278 | 要新建一个圆形喷泉,如果沿喷泉的一周放置雕像,每隔2米放一座,刚好可以放8座,问:这个圆形喷泉一周长是多少米?(雕像的宽度忽略不计)
279 |
280 | ### 练习3
281 |
282 | 一个圆形养鱼池,一周总长为42米,要在养鱼池的一周每隔6米种一棵桃树,一共能种多少棵桃树?(树的宽度忽略不计)
283 |
284 | ### 例题4
285 |
286 | 在一条长50米的公路两边种树,每隔10米种一棵,两端都种,这条公路上一共能种多少棵树?(树的宽度忽略不计)
287 |
288 | ### 练习4
289 |
290 | 一个圆形花坛一周长60米,沿花坛一周每隔3米栽一棵柳树,再在每两棵柳树之问栽2株月季花,花坛一周一共能栽多少株月季花?(树和花的宽度忽略不计)
291 |
292 | ### 例题5
293 |
294 | 有一块三角形的地,三条边分别为30米,40米,60米,每10米种一棵树,三个角都种,那么三条边上共种多少棵树?(树的宽度忽略不计)
295 |
296 | ### 练习5
297 |
298 | 森林公园中心有一个圆形鱼塘,一周长是60米,每隔6米种一棵柳树,每相邻两棵柳树之间,均匀地栽种两棵夹竹桃,问:这个圆形鱼塘的一周可以栽种多少棵夹竹桃?(树的宽度忽略不计)
299 |
300 | ### 例题6
301 |
302 | 在一条长48米的公路一旁种树,两端都种,共种了9棵树,算一算每隔几米种一棵?(树的宽度忽略不计)
303 |
304 | ### 练习6
305 |
306 | 爷爷从1楼爬到4楼用时12分钟,照这样的速度,他从1楼爬到5楼需要用时多少分钟?
307 |
308 | ### 拓展1
309 |
310 | 乐乐老师组织学生们植树,在一条长 120 米的马路两边每隔30米种一棵梧桐树(两端都种),在每相邻的2棵梧桐树之间又补种1 棵香樟树。这条马路两边一共种了多少棵树?(树的宽度忽略不计)
311 |
312 | ### 拓展2
313 |
314 | 牛牛和爷爷一起从 1 楼开始爬楼梯锻炼身体,牛牛走得快,爷爷走得慢。牛牛走到5楼的时候,爷爷才爬到3楼。照这样的速度继续爬,牛牛到15楼的时候,爷爷到几楼?
315 |
316 | ### 拓展3
317 |
318 | 马路的一边,每隔8米有1棵杨树。 小明乘汽车从学校回家,从看到第一棵树数起到第51棵树为止,共用时2分。小明从学校到家共坐了半小时的汽车。小明的家距学校有多远?(树的宽度忽略不计)
319 |
320 | ### 拓展4
321 |
322 | 几个孩子星期天一起逛公园,在公园中心有一个正方形池塘,在池塘边距离池边3米处围绕池塘种树,一共种了40棵(四个角都种)也围成了一个正方形。如果相邻两棵树之间的距离是2米,那么这个正方形池塘的边长是多少米?(树的宽度忽略不计)
323 |
324 | ## 2.1.15. 合理安排
325 |
326 | 课程内容
327 |
328 | * 煎饼问题
329 | * 连续完成合理安排
330 | * 过河问题
331 | * 排队问题
332 |
333 | 学习目标
334 |
335 | 通过解决常见的生活问题,学会合理安排时间,最快完成。
336 |
337 | 内容分析
338 |
339 | ### 煎饼问题
340 |
341 | **问题概述**
342 |
343 | 随手拿一些小物品来替代饼和锅,设定煎饼的场景。
344 |
345 | 1. 一个锅一次只能放一张饼,饼要煎两面,煎一面需要一分钟,需要怎么煎最快。(设置基本规则,无法同时煎一张饼的正面和反面)(题外话:铜锣烧除外)
346 |
347 | 2. 一个锅一次可以放两张饼,饼要煎两面,煎一面需要一分钟,怎么煎,两张饼呢?三张饼呢?(实际操作中,学生很容易想的到一张、两张的情况,但是三张情况尽量鼓励学生自己解决,如何才能不保证锅的空间得到充分的利用,不会一个锅,只煎一张饼的情况)
348 |
349 | 学会 3 分钟煎三张饼后,让学生自己开始做例题,现在遇到多张饼的时候,还需要一面面的去试么?引出分组思考的概念,比 1 大的数都可以分成若干个 2 和 3 的和。最后,思考总结,做练习。(练习出现一面不再是单位 1 时间的情况,第一次做容易忽略)
350 |
351 | 三张饼的安排方案:
352 |
353 | 
354 |
355 | **例题1**
356 |
357 | 平底锅里每次能同时放 2 张饼,烙熟 1 张饼需用时 2 分(正、反面各需 1 分),如果要烙熟 5 张饼至少需要多长时间?烙熟 6 张饼呢?烙熟 7 张饼呢?
358 |
359 | 【解析】5 分钟;6 分钟;7 分钟。
360 |
361 | **练习1**
362 |
363 | 用一个平底锅煎鸡蛋,每次最多能放 2 个鸡蛋,煎熟 1 个鸡蛋需要用时 4 分钟(正、反面各需用时 2 分钟),问煎熟 7 个鸡蛋至少需要多长时间?
364 |
365 | 【解析】14 分钟。
366 |
367 | **问题小结**
368 |
369 | 对于煎饼问题,原则是不能让锅闲着,学会分组(偶数:2 个 2 个一组;奇数:2 个 2 个一组,最后一个并入 2 ,形成一个 3)一组一组的去煎,注意一面需要花费的时间。
370 |
371 | ### 按顺序,同时做
372 |
373 | **问题概述**
374 |
375 | 生活中有些事情是“不需要手”,可以自主完成的,比如烧水、煮饭、洗衣机洗衣服、听广播等等,那么这些事情是可以和一些事情同时进行。也就是一边……一边……的平行关系。另外,做事情还得考虑先后顺序,比如先吃饭,后洗碗,先烧水,再泡茶等等。也就是先……,然后……的递进关系。综上,那么该怎样合理的安排,才能让总花费的时间最短?
376 |
377 | **例题2**
378 |
379 | 牛牛需要给田田沏茶,沏茶过程中,洗开水壶用时 1 分钟,烧开水要用时 15 分钟,洗茶壶要用时 1 分钟,洗茶杯要用时 2 分钟,找茶叶要用时 2 分钟,泡茶要用时1分钟;牛牛怎样合理的安排,才能在最短时间里让田田喝上茶呢?最少需要多长时间呢?
380 |
381 | 【解析】需要遵守“洗开水壶-烧开水-泡茶”的顺序,烧开水是“不需要手”的事情,洗茶壶,洗茶杯,找茶叶可以在烧水的时候做。总时间是 1 + 15 + 1 = 17(分钟)。
382 |
383 | **练习2**
384 |
385 | 丁丁早上 6 时 30 分钟起床,去学校之前要做以下几件事情:穿衣叠被用时 6 分钟,梳头用时 2 分钟,刷牙洗脸用时 5 分钟,听新闻用时 20 分钟,吃早饭用时 8 分钟,收拾饭桌用时 3 分钟。如果他 6 时 30 分钟准时起床,那么最早可以几时几分钟从家出发去上学?
386 |
387 | 【解析】6 + 2 + 5 + 8 + 3 = 24(分钟),听新闻“不需要手”,可以同时完成。那么最早 6 时 54 分钟从从家出发去上学。
388 |
389 | **例题3**
390 |
391 | 牛牛要帮丁丁做家务,需要做的事情有:擦桌椅用时 12 分钟;擦地用时 18 分钟;浸泡衣服(要用温水)用时 15 分钟;搓衣服用时 15 分钟;烧开水用时 20 分钟;清洗衣服用时 15 分钟;晾衣服用时 5 分钟。牛牛如何安排这些事情的先后顺序,才可以用时最短,最短多长时间可以把这些事情全部做完?
392 |
393 | 【解析】烧开水-浸泡衣服-搓衣服-清洗衣服-晾衣服是需要分先后的递进关系,其中,烧开水,浸泡衣服是“不需要手”的,可以与擦座椅,擦地同时进行。总时间是:20 + 15 + 15 + 15 + 5 = 70(分钟)。注意提醒学生检查同时完成的时候,哪个花费的时间更久。比如题目中 20 + 15 需要同 12 + 18 去比较。
394 |
395 | **练习3**
396 |
397 | 星期天,妈妈要做好多事情。擦玻璃要 20 分钟,收拾厨房要 15 分钟,洗脏衣服的领子、袖口要 10 分钟,打开全自动洗衣机洗衣服要 40 分钟,晾衣服要 10 分钟。妈妈干完所有这些事情最少要分钟。
398 |
399 | 【解析】找顺序:洗脏衣服的领子、袖口-打开全自动洗衣机洗衣服-晾衣服,其中洗衣机洗衣服可以同时做其他事情,且 40 > (20 + 15)。总耗时:10 + 40 + 10 = 60(分钟)。
400 |
401 | ### 过河问题
402 |
403 | **问题概述**
404 |
405 | **例题4**
406 |
407 | 牛牛、丁丁和田田被怪物们追到小河边,河岸边只有一条能同时乘坐 2 人的小船,由牛牛划船需要用时 2 分钟,由丁丁划船用时 3 分钟,由田田划船用时 5 分钟,现在情况危急,需要尽快过河,应该采用怎样的过河方式,3 人全部过河用时最短?
408 |
409 | 练习4
410 |
411 | 牛牛、丁丁和田田骑车去公园,现在只有一辆自行车,自行车除了一人骑车,还能载一个人。由牛牛骑车需要用时 30 分钟,由丁丁骑车用时 35 分钟,由田田骑车用时 40 分钟,三人需要尽快到达公园,应该采用怎样的载人方式,3 人全部到达公园用时最短?
412 |
413 | 例题5
414 |
415 | 学校组织防火演习,牛牛、丁丁、田田、乐乐老师四人准备通过一座正在燃烧的木桥,此桥每次最多只能让 2 个人同时通过(不能背着、抱着),否则桥会倒塌。过桥的人必须要用到防火披风,不然会被火烧到(防火披风只有 1 件,可供两人同时使用),4 个人行走速度不同:牛牛用时 1 分钟就可以过桥,丁丁要用时 2 分钟,田田要用时 5 分钟,乐乐老师要用时 8 分钟,已知 15 分钟过后桥就会被烧塌了,请问:4 个人要用什么方法才能全部安全过桥?
416 |
417 | 练习5
418 |
419 | 牛牛、丁丁、田田、乐乐老师四个人过桥,分别需要用时 1 分钟、2 分钟、5 分钟和 10 分钟,因为天黑,必须借助手电筒过桥,可是他们只有一个手电筒,并且桥的载重能力有限,每次最多同时过两个人(不能背着、抱着),现在他们希望可以用最短的时间过桥,应该怎样做? 最短时问是多少?
420 |
421 | ### 排队问题
422 |
423 | 例题6
424 |
425 | 同学们各提一个大小不一的桶去打水,丁丁、田田、牛牛、阿普他们四个的桶注满水所需的时间分别为 2 分钟、4 分钟、5 分钟、3 分钟。现在只有一个水龙头可以接水,请你设计一下,使他们总的等候时间最短,这个最短的时间是多少?
426 |
427 | 练习6
428 |
429 | 有四名同学各提一个大小不一样的桶去打水,他们四个的桶注满水所需的时间分别是 1 分钟、3 分钟、4 分钟、2 分钟。现在只有一个水龙头可以接水,请你帮他们设计一下,怎样安排才能使他们总的等候时间最短,这个最短的时间是多少?
430 |
431 | # 摆小棒
432 |
433 | 热身1
434 |
435 | 计算。
436 | $$
437 | 8+8+8+8+8+6+6+6=
438 | $$
439 |
440 | ### 热身2
441 |
442 | 下列图形中,不能“一笔画”的是()。
443 |
444 |  445 |
446 | ### 热身3
447 |
448 | 下图是儿童乐园的平面图,出入口应设在()点或()点,才能不重复地走遍每条路。
449 |
450 |
445 |
446 | ### 热身3
447 |
448 | 下图是儿童乐园的平面图,出入口应设在()点或()点,才能不重复地走遍每条路。
449 |
450 |  451 |
452 | ### 例题1
453 |
454 | 思维火柴1~10
455 |
456 | ### 例题2
457 |
458 | 按要求摆一摆,并在下方空白处画出来。
459 |
460 | (1)用4根火柴棒摆出一个正方形。
461 |
462 | (2)再加3根火柴棒,摆出两个正方形。
463 |
464 | (3)再加3根火柴棒,摆出三个正方形。
465 |
466 | (4)再加2根火柴棒,摆出五个正方形。
467 |
468 | ### 练习2
469 |
470 | 按要求摆一摆,并在下方空白处画出来。
471 |
472 | (1)用3根火柴棒,摆出一个三角形。
473 |
474 | (2)再加2根火柴棒,摆出两个三角形。
475 |
476 | (3)再加2根火柴棒,摆出三个三角形。
477 |
478 | (4)再加2根火柴棒,摆出五个三角形。
479 |
480 | ### 例题3
481 |
482 | 下图是用12根小棒摆成的5个正方形,拿掉哪2根,能使原图变成 2 个正方形?
483 |
484 |
451 |
452 | ### 例题1
453 |
454 | 思维火柴1~10
455 |
456 | ### 例题2
457 |
458 | 按要求摆一摆,并在下方空白处画出来。
459 |
460 | (1)用4根火柴棒摆出一个正方形。
461 |
462 | (2)再加3根火柴棒,摆出两个正方形。
463 |
464 | (3)再加3根火柴棒,摆出三个正方形。
465 |
466 | (4)再加2根火柴棒,摆出五个正方形。
467 |
468 | ### 练习2
469 |
470 | 按要求摆一摆,并在下方空白处画出来。
471 |
472 | (1)用3根火柴棒,摆出一个三角形。
473 |
474 | (2)再加2根火柴棒,摆出两个三角形。
475 |
476 | (3)再加2根火柴棒,摆出三个三角形。
477 |
478 | (4)再加2根火柴棒,摆出五个三角形。
479 |
480 | ### 例题3
481 |
482 | 下图是用12根小棒摆成的5个正方形,拿掉哪2根,能使原图变成 2 个正方形?
483 |
484 |  485 |
486 | ### 练习3
487 |
488 | 下图是用 12 根小棒摆成的 5 个正方形,拿掉哪 2 根,能使原图变成 3 个正方形。
489 |
490 |
485 |
486 | ### 练习3
487 |
488 | 下图是用 12 根小棒摆成的 5 个正方形,拿掉哪 2 根,能使原图变成 3 个正方形。
489 |
490 |  491 |
492 | ### 例题4
493 |
494 | 下图是用 9 根小棒摆成的 3 个三角形,请你移动 3 根小棒,变成 5 个三角形。
495 |
496 |
491 |
492 | ### 例题4
493 |
494 | 下图是用 9 根小棒摆成的 3 个三角形,请你移动 3 根小棒,变成 5 个三角形。
495 |
496 |  497 |
498 | ### 练习4
499 |
500 | 请在下图加两根小棒,摆出两个大小、形状都相同的三角形。
501 |
502 |
497 |
498 | ### 练习4
499 |
500 | 请在下图加两根小棒,摆出两个大小、形状都相同的三角形。
501 |
502 |  503 |
504 | ### 例题5
505 |
506 | 你们见过这样的数字吗?按要求变化后,它们会变成哪些数字呢?
507 |
508 |
503 |
504 | ### 例题5
505 |
506 | 你们见过这样的数字吗?按要求变化后,它们会变成哪些数字呢?
507 |
508 |  509 |
510 |
509 |
510 |  511 |
512 | ### 练习5
513 |
514 | 先用9根火柴棒摆出18,只允许移动一根火柴棒,能摆成的最大的两位数是多少?
515 |
516 | ### 例题6
517 |
518 | 下面是用火柴棒摆成的两个错误的等式,请你各添加1根火柴棒,使每个等式成立。
519 |
520 |
511 |
512 | ### 练习5
513 |
514 | 先用9根火柴棒摆出18,只允许移动一根火柴棒,能摆成的最大的两位数是多少?
515 |
516 | ### 例题6
517 |
518 | 下面是用火柴棒摆成的两个错误的等式,请你各添加1根火柴棒,使每个等式成立。
519 |
520 |  521 |
522 | ### 练习6
523 |
524 | 下面是用火柴棒摆成的两个错误的等式,请你各去掉1根火柴棒,使每个等式成立。
525 |
526 |
521 |
522 | ### 练习6
523 |
524 | 下面是用火柴棒摆成的两个错误的等式,请你各去掉1根火柴棒,使每个等式成立。
525 |
526 |  527 |
528 | ### 移动一根
529 |
530 | 1+1=6 1+5=2 0+1=8 3+6=3 5-9=6 2+5=8 6+6=8 6+6=6 6+4=4 6-8=5 1+8=1 4+9=1 7+10=1 17+7=70 19-3=6
531 |
532 | 下面是用火柴棒摆成的四个错误的等式,请你各移动一根火柴棒,使每个等式成立。
533 |
534 |
527 |
528 | ### 移动一根
529 |
530 | 1+1=6 1+5=2 0+1=8 3+6=3 5-9=6 2+5=8 6+6=8 6+6=6 6+4=4 6-8=5 1+8=1 4+9=1 7+10=1 17+7=70 19-3=6
531 |
532 | 下面是用火柴棒摆成的四个错误的等式,请你各移动一根火柴棒,使每个等式成立。
533 |
534 | 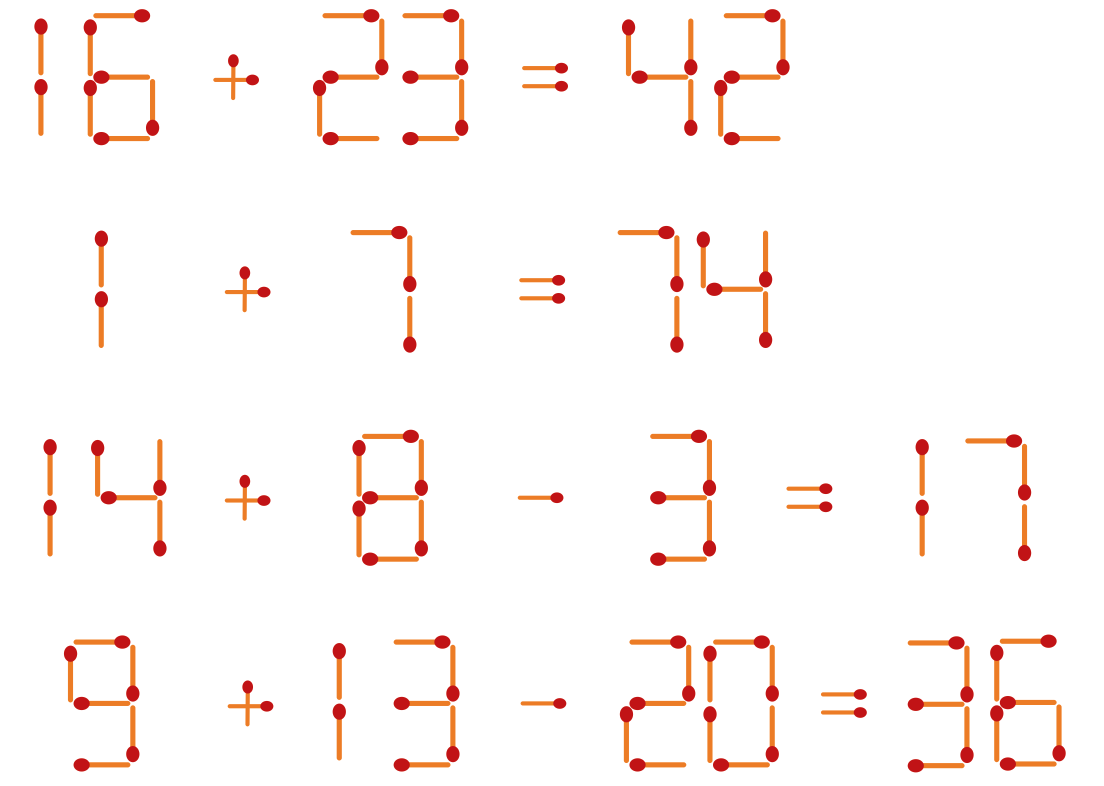 535 |
536 | ### 练习1
537 |
538 | 计算。
539 | $$
540 | 26+37+14=
541 | $$
542 |
543 | $$
544 | 92-23-47=
545 | $$
546 |
547 | $$
548 | 3+3+3+3+3+5+5+5=
549 | $$
550 |
551 | ### 练习2
552 |
553 | 思维火柴游戏,任意5题。
554 |
555 | ### 练习3
556 |
557 | 下面是用火柴棒摆成的错误的等式。请你添加1根火柴棒,使下面的等式成立。
558 |
559 |
535 |
536 | ### 练习1
537 |
538 | 计算。
539 | $$
540 | 26+37+14=
541 | $$
542 |
543 | $$
544 | 92-23-47=
545 | $$
546 |
547 | $$
548 | 3+3+3+3+3+5+5+5=
549 | $$
550 |
551 | ### 练习2
552 |
553 | 思维火柴游戏,任意5题。
554 |
555 | ### 练习3
556 |
557 | 下面是用火柴棒摆成的错误的等式。请你添加1根火柴棒,使下面的等式成立。
558 |
559 |  560 |
561 | ### 练习1
562 |
563 | 计算。
564 | $$
565 | 39+33-25=
566 | $$
567 |
568 | $$
569 | 39+24+15=
570 | $$
571 |
572 | $$
573 | 7+7+7+7+7+7=
574 | $$
575 |
576 | ### 练习2
577 |
578 | 思维火柴游戏,任意5题。
579 |
580 | ### 练习3
581 |
582 | 下面是用火柴棒摆成的错误的等式。请你去掉1根火柴棒,使下面的等式成立。
583 |
584 |
560 |
561 | ### 练习1
562 |
563 | 计算。
564 | $$
565 | 39+33-25=
566 | $$
567 |
568 | $$
569 | 39+24+15=
570 | $$
571 |
572 | $$
573 | 7+7+7+7+7+7=
574 | $$
575 |
576 | ### 练习2
577 |
578 | 思维火柴游戏,任意5题。
579 |
580 | ### 练习3
581 |
582 | 下面是用火柴棒摆成的错误的等式。请你去掉1根火柴棒,使下面的等式成立。
583 |
584 |  585 |
586 | ## 2.1.17. 摆小棒
587 |
588 | ### 热身1
589 |
590 | 计算。
591 | $$
592 | 8+8+8+8+8+6+6+6=
593 | $$
594 |
595 | ### 热身2
596 |
597 | 下列图形中,不能“一笔画”的是()。
598 |
599 |
585 |
586 | ## 2.1.17. 摆小棒
587 |
588 | ### 热身1
589 |
590 | 计算。
591 | $$
592 | 8+8+8+8+8+6+6+6=
593 | $$
594 |
595 | ### 热身2
596 |
597 | 下列图形中,不能“一笔画”的是()。
598 |
599 |  600 |
601 | ### 热身3
602 |
603 | 下图是儿童乐园的平面图,出入口应设在()点或()点,才能不重复地走遍每条路。
604 |
605 |
600 |
601 | ### 热身3
602 |
603 | 下图是儿童乐园的平面图,出入口应设在()点或()点,才能不重复地走遍每条路。
604 |
605 |  606 |
607 | ### 例题1
608 |
609 | 思维火柴1~10
610 |
611 | ### 例题2
612 |
613 | 按要求摆一摆,并在下方空白处画出来。
614 |
615 | (1)用4根火柴棒摆出一个正方形。
616 |
617 | (2)再加3根火柴棒,摆出两个正方形。
618 |
619 | (3)再加3根火柴棒,摆出三个正方形。
620 |
621 | (4)再加2根火柴棒,摆出五个正方形。
622 |
623 | ### 练习2
624 |
625 | 按要求摆一摆,并在下方空白处画出来。
626 |
627 | (1)用3根火柴棒,摆出一个三角形。
628 |
629 | (2)再加2根火柴棒,摆出两个三角形。
630 |
631 | (3)再加2根火柴棒,摆出三个三角形。
632 |
633 | (4)再加2根火柴棒,摆出五个三角形。
634 |
635 | ### 例题3
636 |
637 | 下图是用12根小棒摆成的5个正方形,拿掉哪2根,能使原图变成 2 个正方形?
638 |
639 |
606 |
607 | ### 例题1
608 |
609 | 思维火柴1~10
610 |
611 | ### 例题2
612 |
613 | 按要求摆一摆,并在下方空白处画出来。
614 |
615 | (1)用4根火柴棒摆出一个正方形。
616 |
617 | (2)再加3根火柴棒,摆出两个正方形。
618 |
619 | (3)再加3根火柴棒,摆出三个正方形。
620 |
621 | (4)再加2根火柴棒,摆出五个正方形。
622 |
623 | ### 练习2
624 |
625 | 按要求摆一摆,并在下方空白处画出来。
626 |
627 | (1)用3根火柴棒,摆出一个三角形。
628 |
629 | (2)再加2根火柴棒,摆出两个三角形。
630 |
631 | (3)再加2根火柴棒,摆出三个三角形。
632 |
633 | (4)再加2根火柴棒,摆出五个三角形。
634 |
635 | ### 例题3
636 |
637 | 下图是用12根小棒摆成的5个正方形,拿掉哪2根,能使原图变成 2 个正方形?
638 |
639 |  640 |
641 | ### 练习3
642 |
643 | 下图是用 12 根小棒摆成的 5 个正方形,拿掉哪 2 根,能使原图变成 3 个正方形。
644 |
645 |
640 |
641 | ### 练习3
642 |
643 | 下图是用 12 根小棒摆成的 5 个正方形,拿掉哪 2 根,能使原图变成 3 个正方形。
644 |
645 |  646 |
647 | ### 例题4
648 |
649 | 下图是用 9 根小棒摆成的 3 个三角形,请你移动 3 根小棒,变成 5 个三角形。
650 |
651 |
646 |
647 | ### 例题4
648 |
649 | 下图是用 9 根小棒摆成的 3 个三角形,请你移动 3 根小棒,变成 5 个三角形。
650 |
651 |  652 |
653 | ### 练习4
654 |
655 | 请在下图加两根小棒,摆出两个大小、形状都相同的三角形。
656 |
657 |
652 |
653 | ### 练习4
654 |
655 | 请在下图加两根小棒,摆出两个大小、形状都相同的三角形。
656 |
657 |  658 |
659 | ### 例题5
660 |
661 | 你们见过这样的数字吗?按要求变化后,它们会变成哪些数字呢?
662 |
663 |
658 |
659 | ### 例题5
660 |
661 | 你们见过这样的数字吗?按要求变化后,它们会变成哪些数字呢?
662 |
663 |  664 |
665 |
664 |
665 |  666 |
667 | ### 练习5
668 |
669 | 先用9根火柴棒摆出18,只允许移动一根火柴棒,能摆成的最大的两位数是多少?
670 |
671 | ### 例题6
672 |
673 | 下面是用火柴棒摆成的两个错误的等式,请你各添加1根火柴棒,使每个等式成立。
674 |
675 |
666 |
667 | ### 练习5
668 |
669 | 先用9根火柴棒摆出18,只允许移动一根火柴棒,能摆成的最大的两位数是多少?
670 |
671 | ### 例题6
672 |
673 | 下面是用火柴棒摆成的两个错误的等式,请你各添加1根火柴棒,使每个等式成立。
674 |
675 |  676 |
677 | ### 练习6
678 |
679 | 下面是用火柴棒摆成的两个错误的等式,请你各去掉1根火柴棒,使每个等式成立。
680 |
681 |
676 |
677 | ### 练习6
678 |
679 | 下面是用火柴棒摆成的两个错误的等式,请你各去掉1根火柴棒,使每个等式成立。
680 |
681 |  682 |
683 | ### 移动一根
684 |
685 | 1+1=6 1+5=2 0+1=8 3+6=3 5-9=6 2+5=8 6+6=8 6+6=6 6+4=4 6-8=5 1+8=1 4+9=1 7+10=1 17+7=70 19-3=6
686 |
687 | 下面是用火柴棒摆成的四个错误的等式,请你各移动一根火柴棒,使每个等式成立。
688 |
689 |
682 |
683 | ### 移动一根
684 |
685 | 1+1=6 1+5=2 0+1=8 3+6=3 5-9=6 2+5=8 6+6=8 6+6=6 6+4=4 6-8=5 1+8=1 4+9=1 7+10=1 17+7=70 19-3=6
686 |
687 | 下面是用火柴棒摆成的四个错误的等式,请你各移动一根火柴棒,使每个等式成立。
688 |
689 | 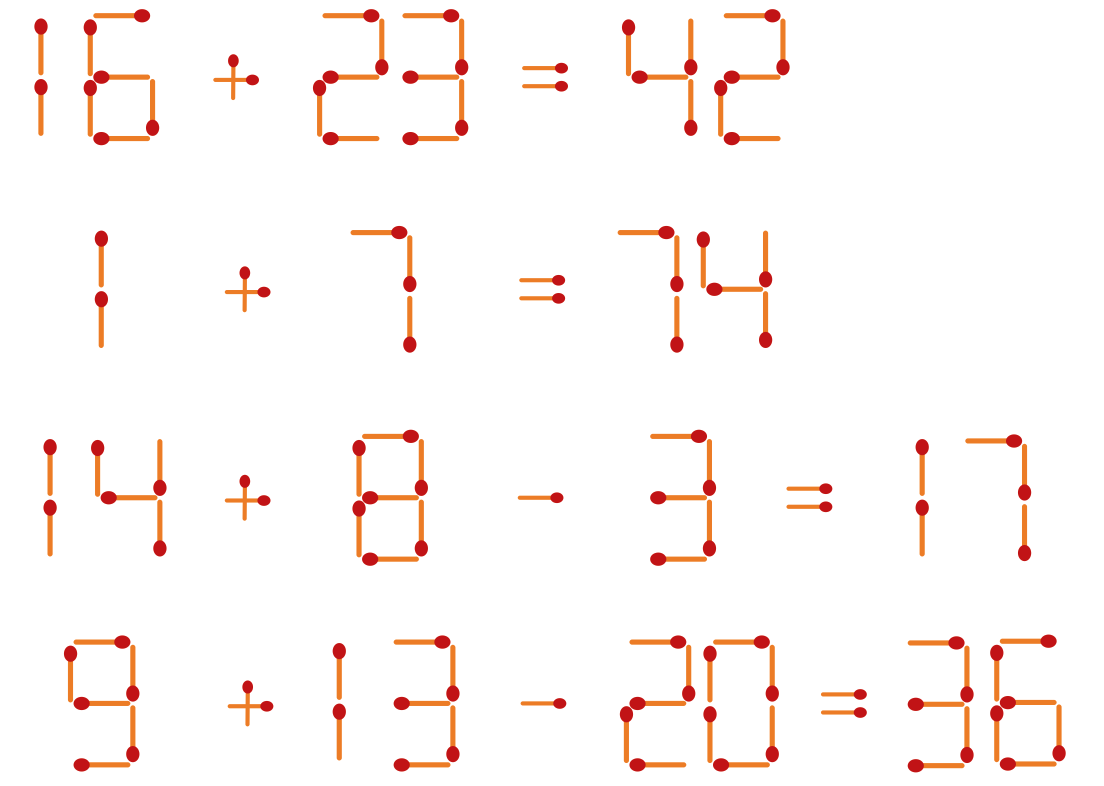 690 |
691 | ### 练习1
692 |
693 | 计算。
694 | $$
695 | 26+37+14=
696 | $$
697 |
698 | $$
699 | 92-23-47=
700 | $$
701 |
702 | $$
703 | 3+3+3+3+3+5+5+5=
704 | $$
705 |
706 | ### 练习2
707 |
708 | 思维火柴游戏,任意5题。
709 |
710 | ### 练习3
711 |
712 | 下面是用火柴棒摆成的错误的等式。请你添加1根火柴棒,使下面的等式成立。
713 |
714 |
690 |
691 | ### 练习1
692 |
693 | 计算。
694 | $$
695 | 26+37+14=
696 | $$
697 |
698 | $$
699 | 92-23-47=
700 | $$
701 |
702 | $$
703 | 3+3+3+3+3+5+5+5=
704 | $$
705 |
706 | ### 练习2
707 |
708 | 思维火柴游戏,任意5题。
709 |
710 | ### 练习3
711 |
712 | 下面是用火柴棒摆成的错误的等式。请你添加1根火柴棒,使下面的等式成立。
713 |
714 |  715 |
716 | ### 练习1
717 |
718 | 计算。
719 | $$
720 | 39+33-25=
721 | $$
722 |
723 | $$
724 | 39+24+15=
725 | $$
726 |
727 | $$
728 | 7+7+7+7+7+7=
729 | $$
730 |
731 | ### 练习2
732 |
733 | 思维火柴游戏,任意5题。
734 |
735 | ### 练习3
736 |
737 | 下面是用火柴棒摆成的错误的等式。请你去掉1根火柴棒,使下面的等式成立。
738 |
739 |
715 |
716 | ### 练习1
717 |
718 | 计算。
719 | $$
720 | 39+33-25=
721 | $$
722 |
723 | $$
724 | 39+24+15=
725 | $$
726 |
727 | $$
728 | 7+7+7+7+7+7=
729 | $$
730 |
731 | ### 练习2
732 |
733 | 思维火柴游戏,任意5题。
734 |
735 | ### 练习3
736 |
737 | 下面是用火柴棒摆成的错误的等式。请你去掉1根火柴棒,使下面的等式成立。
738 |
739 |  740 |
741 | ## 2.1.18. 逆向思考初步
742 |
743 | 逆向运算
744 |
745 | ### 铺垫 1
746 |
747 | 加减互逆,乘除互逆。
748 | $$
749 | \Box\overset{+5}{\to}17
750 | $$
751 |
752 | $$
753 | \Box\overset{-20}{\to}50
754 | $$
755 |
756 | $$
757 | \Box\overset{\times5}{\to}20
758 | $$
759 |
760 | $$
761 | \Box\overset{\div3}{\to}7
762 | $$
763 |
764 | ### 例题 1
765 |
766 | 你知道下面每个起点上的数各是几吗?
767 |
768 | 1. $$
769 | ()-7\to()\times4\to()-9\to()+8\to11
770 | $$
771 |
772 | 2. $$
773 | ()\times3\to()-6\to()+7\to()\div8\to2
774 | $$
775 |
776 | 3. $$
777 | ()+9\to()-8\to()\div6\to()\times9\to36
778 | $$
779 |
780 | 4.
781 |
782 | 5. $$
783 | ()-7\to()\times6\to()\times3\to()\div6\to36
784 | $$
785 |
786 | ### 练习 1
787 |
788 | 填出每个起点上的数。
789 | $$
790 | \Box\overset{-7}{\to}\Box\overset{\times4}{\to}\Box\overset{-9}{\to}\Box\overset{+8}{\to}\Box
791 | $$
792 |
793 | ### 画推导图
794 |
795 | ### 铺垫
796 |
797 | A、B各代表一个数。
798 |
799 | A 说:“我减去 3,加上2,再减去 3,得 20。”
800 |
801 | B 说:“我乘 2,除以 4,再乘 3,得 18。”
802 |
803 | 算一算,它们各代表多少?
804 |
805 | ### 例题 2
806 |
807 | 丁丁问牛牛:“你今年几岁?”牛牛回答:“用我今年的年龄减去 2,乘 2,减去 2,再除以 2,恰好等于 5。”你能帮丁丁算一下,牛牛今年多少岁吗?
808 |
809 | ### 练习 2
810 |
811 | 有一个数加上 6,减去 6,乘 6,除以 6,最后结果等于 6,问这个数是几?
812 |
813 | ### 例题 3
814 |
815 | 馋嘴和尚们吃一堆小馒头,第一次吃了一半,觉得不够;第二次又吃了剩下的一半,觉得差不多了;第三次又吃了5 个,觉得饱了。他们发现还剩下 5 个,干脆又吃光了,这一堆馒头有多少个?
816 |
817 | ### 练习 3
818 |
819 | 猪八戒化斋讨来一篮果子,吃了一半。觉得不够,又吃了剩下的一半,还觉得不够,又吃了剩下的一半,最后又偷偷吃了 2 个果子,觉得饱了,把剩下的给唐僧吃,孙悟空一看篮子里只剩下 4 个果子了。问猪八戒一共吃了多少个果子?
820 |
821 | 多减,少加
822 |
823 | ### 铺垫
824 |
825 | 一堆卡片,小代同学拿走了一半还多 1 张,剩下 5 张。原来有多少张卡片?
826 |
827 | 一堆卡片,小力同学拿走一半还少 1 张,剩下 6 张。原来有多少张卡片?
828 |
829 | ### 例题 4
830 |
831 | 三群蜜蜂在桃树林里采花蜜,A 群采全部桃树的一半少 4 棵,B 群采剩下桃树的一半多 2 棵,C 群采最后剩下的 10 棵桃树上的花蜜,那么,桃树林中共有多少棵桃树?
832 |
833 | ### 练习 4
834 |
835 | 阿普卖鸡蛋,第一次卖掉篮中的一半多 1 个,第二次又卖掉剩下的一半多 1 个,这时篮中还剩 1 个,问原来篮中有几个蛋?
836 |
837 | ### 例题 5
838 |
839 | 田田在玩取棋子的游戏,她每次拿出其中的一半再放回 1 颗,这样一共做了三次,最后还剩 3 颗棋子,你知道田田原来一共有多少颗棋子吗?
840 |
841 | ### 练习 5
842 |
843 | 丁丁拿着一包糖,遇见好朋友 A,分给了他一半,过一会儿又遇见好朋友 B,把剩下的糖的一半分给了 B,后来又遇到好朋友 C,把这时手中剩下的糖的一半又分给了C,这时他自己只有一块糖了,问在没有分给 A 以前,丁丁有
844 | 多少糖块?
845 |
846 | ### 例题 6
847 |
848 | 乐乐老师有几本小人书自己记不清楚了,只知道:牛牛借走一半加 1 本;丁丁又借走剩下的书的一半加 2 本;再剩下的书,田田借走一半加 3 本,最后乐乐老师还有 2 本书,请问乐乐老师原有几本小人书?
849 |
850 | ### 练习 6
851 |
852 | 乐乐老师用一根绳子拴葫芦,牛牛第一次使绳子减少全长的一半还多 2 米,第二次减少余下的一半少 10 米,第三次减少 15 米,最后还剩9米,那么这根绳子原来有多少米?
853 |
854 | 拓展
855 |
856 | ### 拓展 1
857 |
858 | 两个数做加法,其中一个数是 73,另一个数不知道是几,只知道把另一个数的十位增加 5,个位增加 1,结果和的后两位数字是 72,另一个数是几?
859 |
860 | ### 拓展 2
861 |
862 | 妈妈把一箱苹果平均分成 3 份后还剩 2 个,分给了小明一份带到学校分给小朋友们一起吃。小朋友们上午吃了其中的一半少 2 个,下午又吃了剩下中的一半又半个,最后还剩三个。问原来这箱苹果又多少个?
863 |
864 | ### 拓展 3
865 |
866 | 现有一堆棋子,把它们分成三等份后还剩 1 个;取出其中的两等份又分成三等份后还剩 2 个。问:原来至少有多少个棋子?
867 |
868 | ### 拓展 4
869 |
870 | 现有一堆棋子,把它分成三等份后还剩下一颗;取出其中的两份又分成三等份后还剩一颗;再取出其中的两份再分成三等份后还剩一颗。原来至少有多少颗棋子?
871 |
872 | ## 2.1.19. 排队问题进阶
873 |
874 | ### 例题1
875 |
876 | 学生们站成一排,从前往后数牛牛排第13个,从后往前数丁丁排第14个,已知牛牛在丁丁的前面,它们之间有3名学生,这排学生一共有多少名?
877 |
878 | ### 练习1
879 |
880 | 一队小朋友排队上车,从前往后数,牛牛排第18个,丁丁后面有16个小朋
881 | 友。已知牛牛和丁丁之间有2个小朋友。问这队小朋友共有多少个?
882 |
883 | ### 例题2
884 |
885 | 学生们排成一队,从排头数起阿普是第15名;从排尾数起田田是第23名。已知田田在阿普后面,从阿普数到田田一共有4名学生,问这群学生有多少名?
886 |
887 | ### 练习2
888 |
889 | 一队小朋友排队上车,从前往后数,小华排第18个,小明后面有16个同学,
890 | 已己知小华后面第二个是小明,问这队小朋友共有多少人?
891 |
892 | ### 例题3
893 |
894 | 32名学生排成一排,从左往右数,牛牛是第17名;从右往左数,丁丁是第19
895 | 名,从牛牛数到丁丁共有学生多少名?
896 |
897 | ### 练习3
898 |
899 | 学生们共有20名,从左往右数牛牛排第16名,从右往左数丁丁右边有18名
900 | 学生,问:牛牛和丁丁之间相隔多少名学生?
901 |
902 | ### 例题4
903 |
904 | 学校舞蹈队同学站成了一个“十”字形,田田恰好站在“十”字队形的中间,不
905 | 论前后数,还是左右数,田田都是第6个,问这个舞蹈队有多少名同学?
906 |
907 | ### 练习4
908 |
909 | 国庆节用鲜花摆成“十”字形,月季花恰好站在“十”字队形的中间,不论前
910 | 后数,还是左右数,月季花都是第21盆,问一共有多少盆花?
911 |
912 | ### 例题5
913 |
914 | 学生们排成一个正方形队伍,无论是从前往后数,还是从后往前数,阿普都是第5名,问这支正方形队伍共有多少名学生?
915 |
916 | ### 练习5
917 |
918 | 同学们排成一个正方形队伍表演体操,牛牛排在正中间,他的正前方、正后
919 | 方、正左方、正右方都有3名同学,这支队伍共有多少名同学?
920 |
921 | ### 例题6
922 |
923 | 学生们排成一个长方形队伍表演摔跤,牛牛从前边数排第7个,从后边数排第8个,从左边数排第4个,从右边数排第2个,一共有多少个学生在表演摔跤?
924 |
925 | ### 练习6
926 |
927 | 同学们排成一个长方形队伍进行体操表演,牛牛从前边数排第6个,从后边
928 | 数排第8个,丁丁从左边数排第4个,他右边有6个人。一共有多少个学生
929 | 在表演摔跤?
930 |
931 | ### 拓展
932 |
933 | ### 拓展1
934 |
935 | 49位同学排成7行7列的正方形队列表演体操,小明在队列中,正左边有2位同学,从前往后数是第3位同学,小明从右往左数是第几位同学?从后往前数是第几位同学?
936 |
937 | ### 拓展2
938 |
939 | 81位同学排成9行9列的正方形队列表演体操,小花在队列中,正左边有2位同学,正前方有3位同学,这时整个队列的同学向右转,则小花的正前方有几位同学?正右边有几位同学?
940 |
941 | ### 拓展3
942 |
943 | 学生进行队列表演,组成一个正方形队列,后来由于表演需要,去掉了一行一列,去掉的人数正好是13人,那么原来准备参加表演的一共有多少人?
944 |
945 | ### 拓展4
946 |
947 | 二年级(1)班的学生排成一个正方形队列,最外边一层的人数为60人。请问这个正方形队列最外层没边有多少人?
948 |
949 | ## 2.2.01. 认识倍
950 |
951 | 例题练习
952 |
953 | ### 例题1
954 |
955 | 乐乐老师奖励学习进步的同学。奖励牛牛金币20枚,田田得到金币的数量是牛牛的3倍还多5枚。奖励田田的金币有多少枚?
956 |
957 | ### 练习1
958 |
959 | 学校有篮球20个,足球的数量是篮球的3倍还少5个,足球有多少个?
960 |
961 | ### 例题2
962 |
963 | 丁丁有40张贴纸,丁丁的贴纸数量是牛牛贴纸数量的6倍还多4张,牛牛有多少张贴纸?
964 |
965 | ### 练习2
966 |
967 | 同学们去采摘,摘了西红柿27筐,是黄瓜的3倍多3筐,同学们摘了多少筐黄瓜?
968 |
969 | ### 例题3
970 |
971 | 阿普喷出水球22个,水球的数量是火球的3倍少5,火球有多少个?
972 |
973 | ### 练习3
974 |
975 | 学校买来了排球20个,买来的排球是足球的4倍,学校买来的排球比足球多几个?
976 |
977 | ### 例题4
978 |
979 | 乐乐老师有金币150枚,银币40枚,要使金币的数量是银币的6倍,还需要多少枚金币?
980 |
981 | ### 练习4
982 |
983 | 小猪有奶糖50块,水果糖4块,要使奶糖的数量是水果糖的6倍,应该吃掉多少块奶糖?
984 |
985 | ### 例题5
986 |
987 | 士兵和小怪物中一共有90个受伤,受伤的士兵人数是受伤小怪物数量的2倍,问士兵和小怪物各受伤多少个?
988 |
989 | ### 练习5
990 |
991 | 学校买来一些乒乓球和羽毛球共240个,乒乓球的个数是羽毛球的3倍。买来的乒乓球和羽毛球各多少个?
992 |
993 | ### 例题6
994 |
995 | 黑士兵比白士兵多80人,黑士兵的数量是白士兵数量的3倍,黑士兵和白士兵各有多少人?
996 |
997 | ### 练习6
998 |
999 | 学校买来的乒乓球比羽毛球多240个,乒乓球的个数是羽毛球的3倍。买来的乒乓球和羽毛球各多少个?
1000 |
1001 | 拓展
1002 |
1003 | ### 拓展1
1004 |
1005 | 小敏有14元,小花有10元,小花给小敏几元,小敏的钱数就是小花的2倍?
1006 |
1007 | ### 拓展2
1008 |
1009 | 师、徒两人共加工105个零件,师傅加工的个数比徒弟的3倍还多5个,师傅和徒弟各加工零件多少个?
1010 |
1011 | 巩固练习
1012 |
1013 | ### 巩固1
1014 |
1015 | 一支圆珠笔的价钱是8元,已知一盒彩笔的价钱是一支圆珠笔价钱的3倍,问小华买一盒彩笔和一支圆珠笔一共需要多少钱?
1016 |
1017 | ### 巩固2
1018 |
1019 | 学校买来排球120个,已知买来的排球是买来的足球的3倍,那么学校买来足球多少个?
1020 |
1021 | ### 巩固3
1022 |
1023 | 冷饮店有45箱可乐,已知可乐的数量是雪碧的2倍少5箱,那么雪碧有多少箱?
1024 |
1025 | ### 巩固4
1026 |
1027 | 动物园里有3只大猴,13只小猴,问要再添上几只小猴后,才能使小猴只数是大猴只数的6倍?
1028 |
1029 | ### 巩固5
1030 |
1031 | 男生和女生一共有123人,已知男生人数比女生人数的2倍还多3人,问女生和男生各有多少人?
1032 |
1033 | ### 巩固6
1034 |
1035 | 食堂买来的苹果比香蕉多50千克,已知苹果的重量是香蕉的6倍,问香蕉和苹果各有多少千克?
1036 |
1037 | ## 2.2.02. 带余数除法
1038 |
1039 | ### 例题1
1040 |
1041 | 根据要求填空。
1042 |
1043 | (1)$()÷4=3……2$
1044 |
1045 | (2)$()÷9=2……3$
1046 |
1047 | (3)$()÷5=3……4$
1048 |
1049 | ### 练习1
1050 |
1051 | 根据要求填空。
1052 |
1053 | (1)$()÷8=3……4$
1054 |
1055 | (2)$()÷9=2……5$
1056 |
1057 | (3)$()÷5=6……4$
1058 |
1059 | ### 例题2
1060 |
1061 | 根据要求填空。
1062 |
1063 | (1)$23÷()=3……2$
1064 |
1065 | (2)$21÷()=2……3$
1066 |
1067 | (3)$22÷()=3……4$
1068 |
1069 | ### 练习2
1070 |
1071 | 根据要求填空。
1072 |
1073 | (1)$43÷()=5……3$
1074 |
1075 | (2)$83÷()=9……2$
1076 |
1077 | (3)$22÷()=3……1$
1078 |
1079 | ### 例题3
1080 |
1081 | 根据要求在()里填上合适的数。
1082 |
1083 | (1)下面()里最小能填几。
1084 | $$
1085 | ()\div()=5……4
1086 | $$
1087 |
1088 | $$
1089 | ()\div()=4……9
1090 | $$
1091 |
1092 | (2)下面()里最大能填几。
1093 | $$
1094 | ()\div4=5……()
1095 | $$
1096 |
1097 | $$
1098 | ()\div9=4……()
1099 | $$
1100 |
1101 | ### 练习3
1102 |
1103 | 根据要求在()里填上合适的数。
1104 |
1105 | (1)下面()里最小能填几。
1106 | $$
1107 | ()\div()=3……9
1108 | $$
1109 |
1110 | $$
1111 | ()\div()=10……2
1112 | $$
1113 |
1114 | (2)下面()里最大能填几。
1115 | $$
1116 | ()\div6=5……()
1117 | $$
1118 |
1119 | $$
1120 | ()\div7=4……()
1121 | $$
1122 |
1123 | ### 例题4
1124 |
1125 | 乐乐老师为了奖励同学们的优秀表现,决定要把手中的苹果分给小朋友吃,平均分给11个人,每人分6个后,剩下的苹果不够分了,乐乐老师手中最少有多少个苹果?最多有多少个苹果?
1126 |
1127 | ### 练习4
1128 |
1129 | 田田拿出自己的一堆玻璃球,要平均分给8个好朋友,每个小朋友得到7个后,剩下的玻璃球不够分了,问:田田的玻璃球最少有多少个?最多有多少个?
1130 |
1131 | ### 例题5
1132 |
1133 | 田田带领7个小朋友一起去擦27块玻璃,先平均分,每个小朋友擦若干块,剩下的不够分,就由田田再擦剩下的玻璃,那么田田一共需要擦多少块玻璃才能完成任务?
1134 |
1135 | ### 练习5
1136 |
1137 | 牛牛决定也把自己手中的卡片和好朋友共同分享,他把23张卡片平均分给5个小朋友,剩下不够分的卡片才留给自己,请问:牛牛最后手中有卡片多少张?
1138 |
1139 | ### 例题6
1140 |
1141 | “数”、“学”分别代表一个非零的自然数,请你将所有满足下列等式的“数”、“学”所代表的数分别列出来?
1142 | $$
1143 | 数÷5=8……学
1144 | $$
1145 |
1146 | ### 练习6
1147 |
1148 | 字母A、B分别代表一个非零的自然数,请你将所有满足A÷4=5……B的A、B所代表的数分别列出来?
1149 |
1150 | ## 2.2.03. 有趣的自然数串
1151 |
1152 | ### 热身1
1153 |
1154 | ### 热身2
1155 |
1156 | ### 热身3
1157 |
1158 | ### 例题1
1159 |
1160 | 下面的自然数串,共有多少个数?
1161 | 3,4,5,6,7,8,9,……,28,29,30。
1162 |
1163 | ### 练习1
1164 |
1165 | 下面的自然数串,共有多少个数?
1166 | 8,9,10,11,12,……,56,57,58,59,60。
1167 |
1168 | ### 例题2
1169 |
1170 | 下面的自然数列,共有多少个数?
1171 | 2,4,6,8,10,12,14,……,58,60。
1172 |
1173 | ### 练习2
1174 |
1175 | 下面的自然数列,共有多少个数?
1176 | 1,3,5,7,9,11,13,……,37,39。
1177 |
1178 | ### 例题3
1179 |
1180 | 下面的自然数列,共有多少个数?
1181 | 1,4,7,10,13,……,31,34,37。
1182 |
1183 | ### 练习3
1184 |
1185 | 下面的自然数列,共有多少个数?
1186 | 4,8,12,16,20,……,40。
1187 |
1188 | ### 例题4
1189 |
1190 | 1,2,3,4,5,6,……,38,39,40,阿普写完这40个数后才发现它不知道自己写了多少个数字,大家快来帮帮阿普:阿普一共写了多少个数字呢?
1191 |
1192 | ### 练习4
1193 |
1194 | 阿普把昨天写的数拿出来了:1,2,3,4,5,6,……,58,59,60,小朋友帮忙算一算,阿普昨天写了多少个数字?
1195 |
1196 | ### 例题5
1197 |
1198 | 牛牛把12个机器人排成一行编了号,他决定从第一个机器人开始戴帽子,隔个戴一个;戴完后从剩下的第一个机器人开始戴,隔一个戴一个;第三次也是照这个办法戴,最后一个没戴帽子的当选为机器人队长。小朋友,几号是机器人队长呢?
1199 |
1200 | ### 练习5
1201 |
1202 | 等牛牛睡着了,机器人们决定选出夜间小队长,12个机器人自动排成一行编了号,它们集体决定从倒数第一个机器人开始,隔一个退出一个;退完后从剩下的倒数第一个机器人开始,隔一个退出一个;第三次也是照这个办法进
1203 | 行,最后一个留下的当选为机器人队长。小朋友,这次几号是机器人队长呢?
1204 |
1205 | ### 例题6
1206 |
1207 | 阿普决定把自己的12个机器人也编上号拿出来围成一个圈,它命令机器人从1开始按顺序1~2循环报数,每次报2的自动退下,就这样进行下去,最后剩下的机器人也会被幸运地选为队长,几号机器人最幸运呢?
1208 |
1209 | ### 练习6
1210 |
1211 | 25个玩具娃娃羡慕机器人推选出队长,它们也国成一个大圈,并顺时针依次编号为12~5号,从1号开始按照顺序12报数,凡是报2的留下,其余玩具娃娃退出圈外,这样循环进行到剩下最后一个人,它就是幸运之星,这个幸运之星是几号?
1212 |
1213 | ## 2.2.04. 图形分割
1214 |
1215 | ### 热身1
1216 |
1217 | 一支圆珠笔的价钱是8元,已知一盒彩笔的价钱是一支圆珠笔价钱的3倍,问小华买一盒彩笔和一支圆珠笔一共需要多少钱?
1218 |
1219 | ### 热身2
1220 |
1221 | 冷饮店有45箱可乐,已知可乐的数量是雪碧的2倍少5箱,那么雪碧有多少箱?
1222 |
1223 | ### 热身3
1224 |
1225 | 动物园里有3只大猴,13只小猴,问要再添上几只小猴后,才能使小猴只数是大猴只数的6倍?
1226 |
1227 | ### 例题1
1228 |
1229 | 牛牛的妈妈买来1块枣糕,上面有6颗枣(如图所示),家里正好有6个人,牛牛说:“要最大的”,妈妈为公平起见,决定将枣糕分为大小形状一样的6块,每块含有1颗枣。你知道应该怎么分吗?
1230 |
1231 | ### 练习1
1232 |
1233 | 一个正三角形形状的土地上有四棵大树(如下图所示),现要把这块正三角形的土地分成和它形状相同的四小块,并且要求每块地中都要有一棵大树。应怎么分?
1234 |
1235 | ### 例题2
1236 |
1237 | 请你把一个等边三角形分别分成形状、大小都相同的2个、3个、4个三角形?
1238 |
1239 | ### 练习2
1240 |
1241 | 请用两种方法把下面的大正方形分割成八个相同的等腰直角三角形?
1242 |
1243 | ### 例题3
1244 |
1245 | 下图是由18个小正方形组成的图形,请你把它分成6个完全相同的图形?
1246 |
1247 | ### 练习3
1248 |
1249 | 用四种不同的方法将下图分割成完全相同的两部分,保持每个小正方形的完整性?
1250 |
1251 | ### 例题4
1252 |
1253 | 请将下图分成形状、大小都相同的4块?
1254 |
1255 | ### 练习4
1256 |
1257 | 如下图所示,请把它分成形状、大小都相同的4块?
1258 |
1259 | ### 例题5
1260 |
1261 | 请将下图分成形状、大小都相同的4块?
1262 |
1263 | ### 练习5
1264 |
1265 | 把下图分成形状、大小完全相同的4部分?
1266 |
1267 | ### 例题6
1268 |
1269 | 教室旁边有一块空地,教室占整块地的四分之一。现在要把它作为实验园地,分给4个小组,要求每个小组分到的形状、大小都要一样。该怎么分?
1270 |
1271 | ### 练习6
1272 |
1273 | 下图是连在一起的三块地,这一整块地的形状是由3个同样大小的等边三角形组成的一个等腰梯形,把这个等腰梯形分成形状、大小一样的4块,该怎么分?
1274 |
1275 | ## 2.2.05. 枚举法的妙用
1276 |
1277 | ### 热身1
1278 |
1279 | 将下图分成大小、形状都相同的四块,并且每块中都有一个字母。
1280 |
1281 |
740 |
741 | ## 2.1.18. 逆向思考初步
742 |
743 | 逆向运算
744 |
745 | ### 铺垫 1
746 |
747 | 加减互逆,乘除互逆。
748 | $$
749 | \Box\overset{+5}{\to}17
750 | $$
751 |
752 | $$
753 | \Box\overset{-20}{\to}50
754 | $$
755 |
756 | $$
757 | \Box\overset{\times5}{\to}20
758 | $$
759 |
760 | $$
761 | \Box\overset{\div3}{\to}7
762 | $$
763 |
764 | ### 例题 1
765 |
766 | 你知道下面每个起点上的数各是几吗?
767 |
768 | 1. $$
769 | ()-7\to()\times4\to()-9\to()+8\to11
770 | $$
771 |
772 | 2. $$
773 | ()\times3\to()-6\to()+7\to()\div8\to2
774 | $$
775 |
776 | 3. $$
777 | ()+9\to()-8\to()\div6\to()\times9\to36
778 | $$
779 |
780 | 4.
781 |
782 | 5. $$
783 | ()-7\to()\times6\to()\times3\to()\div6\to36
784 | $$
785 |
786 | ### 练习 1
787 |
788 | 填出每个起点上的数。
789 | $$
790 | \Box\overset{-7}{\to}\Box\overset{\times4}{\to}\Box\overset{-9}{\to}\Box\overset{+8}{\to}\Box
791 | $$
792 |
793 | ### 画推导图
794 |
795 | ### 铺垫
796 |
797 | A、B各代表一个数。
798 |
799 | A 说:“我减去 3,加上2,再减去 3,得 20。”
800 |
801 | B 说:“我乘 2,除以 4,再乘 3,得 18。”
802 |
803 | 算一算,它们各代表多少?
804 |
805 | ### 例题 2
806 |
807 | 丁丁问牛牛:“你今年几岁?”牛牛回答:“用我今年的年龄减去 2,乘 2,减去 2,再除以 2,恰好等于 5。”你能帮丁丁算一下,牛牛今年多少岁吗?
808 |
809 | ### 练习 2
810 |
811 | 有一个数加上 6,减去 6,乘 6,除以 6,最后结果等于 6,问这个数是几?
812 |
813 | ### 例题 3
814 |
815 | 馋嘴和尚们吃一堆小馒头,第一次吃了一半,觉得不够;第二次又吃了剩下的一半,觉得差不多了;第三次又吃了5 个,觉得饱了。他们发现还剩下 5 个,干脆又吃光了,这一堆馒头有多少个?
816 |
817 | ### 练习 3
818 |
819 | 猪八戒化斋讨来一篮果子,吃了一半。觉得不够,又吃了剩下的一半,还觉得不够,又吃了剩下的一半,最后又偷偷吃了 2 个果子,觉得饱了,把剩下的给唐僧吃,孙悟空一看篮子里只剩下 4 个果子了。问猪八戒一共吃了多少个果子?
820 |
821 | 多减,少加
822 |
823 | ### 铺垫
824 |
825 | 一堆卡片,小代同学拿走了一半还多 1 张,剩下 5 张。原来有多少张卡片?
826 |
827 | 一堆卡片,小力同学拿走一半还少 1 张,剩下 6 张。原来有多少张卡片?
828 |
829 | ### 例题 4
830 |
831 | 三群蜜蜂在桃树林里采花蜜,A 群采全部桃树的一半少 4 棵,B 群采剩下桃树的一半多 2 棵,C 群采最后剩下的 10 棵桃树上的花蜜,那么,桃树林中共有多少棵桃树?
832 |
833 | ### 练习 4
834 |
835 | 阿普卖鸡蛋,第一次卖掉篮中的一半多 1 个,第二次又卖掉剩下的一半多 1 个,这时篮中还剩 1 个,问原来篮中有几个蛋?
836 |
837 | ### 例题 5
838 |
839 | 田田在玩取棋子的游戏,她每次拿出其中的一半再放回 1 颗,这样一共做了三次,最后还剩 3 颗棋子,你知道田田原来一共有多少颗棋子吗?
840 |
841 | ### 练习 5
842 |
843 | 丁丁拿着一包糖,遇见好朋友 A,分给了他一半,过一会儿又遇见好朋友 B,把剩下的糖的一半分给了 B,后来又遇到好朋友 C,把这时手中剩下的糖的一半又分给了C,这时他自己只有一块糖了,问在没有分给 A 以前,丁丁有
844 | 多少糖块?
845 |
846 | ### 例题 6
847 |
848 | 乐乐老师有几本小人书自己记不清楚了,只知道:牛牛借走一半加 1 本;丁丁又借走剩下的书的一半加 2 本;再剩下的书,田田借走一半加 3 本,最后乐乐老师还有 2 本书,请问乐乐老师原有几本小人书?
849 |
850 | ### 练习 6
851 |
852 | 乐乐老师用一根绳子拴葫芦,牛牛第一次使绳子减少全长的一半还多 2 米,第二次减少余下的一半少 10 米,第三次减少 15 米,最后还剩9米,那么这根绳子原来有多少米?
853 |
854 | 拓展
855 |
856 | ### 拓展 1
857 |
858 | 两个数做加法,其中一个数是 73,另一个数不知道是几,只知道把另一个数的十位增加 5,个位增加 1,结果和的后两位数字是 72,另一个数是几?
859 |
860 | ### 拓展 2
861 |
862 | 妈妈把一箱苹果平均分成 3 份后还剩 2 个,分给了小明一份带到学校分给小朋友们一起吃。小朋友们上午吃了其中的一半少 2 个,下午又吃了剩下中的一半又半个,最后还剩三个。问原来这箱苹果又多少个?
863 |
864 | ### 拓展 3
865 |
866 | 现有一堆棋子,把它们分成三等份后还剩 1 个;取出其中的两等份又分成三等份后还剩 2 个。问:原来至少有多少个棋子?
867 |
868 | ### 拓展 4
869 |
870 | 现有一堆棋子,把它分成三等份后还剩下一颗;取出其中的两份又分成三等份后还剩一颗;再取出其中的两份再分成三等份后还剩一颗。原来至少有多少颗棋子?
871 |
872 | ## 2.1.19. 排队问题进阶
873 |
874 | ### 例题1
875 |
876 | 学生们站成一排,从前往后数牛牛排第13个,从后往前数丁丁排第14个,已知牛牛在丁丁的前面,它们之间有3名学生,这排学生一共有多少名?
877 |
878 | ### 练习1
879 |
880 | 一队小朋友排队上车,从前往后数,牛牛排第18个,丁丁后面有16个小朋
881 | 友。已知牛牛和丁丁之间有2个小朋友。问这队小朋友共有多少个?
882 |
883 | ### 例题2
884 |
885 | 学生们排成一队,从排头数起阿普是第15名;从排尾数起田田是第23名。已知田田在阿普后面,从阿普数到田田一共有4名学生,问这群学生有多少名?
886 |
887 | ### 练习2
888 |
889 | 一队小朋友排队上车,从前往后数,小华排第18个,小明后面有16个同学,
890 | 已己知小华后面第二个是小明,问这队小朋友共有多少人?
891 |
892 | ### 例题3
893 |
894 | 32名学生排成一排,从左往右数,牛牛是第17名;从右往左数,丁丁是第19
895 | 名,从牛牛数到丁丁共有学生多少名?
896 |
897 | ### 练习3
898 |
899 | 学生们共有20名,从左往右数牛牛排第16名,从右往左数丁丁右边有18名
900 | 学生,问:牛牛和丁丁之间相隔多少名学生?
901 |
902 | ### 例题4
903 |
904 | 学校舞蹈队同学站成了一个“十”字形,田田恰好站在“十”字队形的中间,不
905 | 论前后数,还是左右数,田田都是第6个,问这个舞蹈队有多少名同学?
906 |
907 | ### 练习4
908 |
909 | 国庆节用鲜花摆成“十”字形,月季花恰好站在“十”字队形的中间,不论前
910 | 后数,还是左右数,月季花都是第21盆,问一共有多少盆花?
911 |
912 | ### 例题5
913 |
914 | 学生们排成一个正方形队伍,无论是从前往后数,还是从后往前数,阿普都是第5名,问这支正方形队伍共有多少名学生?
915 |
916 | ### 练习5
917 |
918 | 同学们排成一个正方形队伍表演体操,牛牛排在正中间,他的正前方、正后
919 | 方、正左方、正右方都有3名同学,这支队伍共有多少名同学?
920 |
921 | ### 例题6
922 |
923 | 学生们排成一个长方形队伍表演摔跤,牛牛从前边数排第7个,从后边数排第8个,从左边数排第4个,从右边数排第2个,一共有多少个学生在表演摔跤?
924 |
925 | ### 练习6
926 |
927 | 同学们排成一个长方形队伍进行体操表演,牛牛从前边数排第6个,从后边
928 | 数排第8个,丁丁从左边数排第4个,他右边有6个人。一共有多少个学生
929 | 在表演摔跤?
930 |
931 | ### 拓展
932 |
933 | ### 拓展1
934 |
935 | 49位同学排成7行7列的正方形队列表演体操,小明在队列中,正左边有2位同学,从前往后数是第3位同学,小明从右往左数是第几位同学?从后往前数是第几位同学?
936 |
937 | ### 拓展2
938 |
939 | 81位同学排成9行9列的正方形队列表演体操,小花在队列中,正左边有2位同学,正前方有3位同学,这时整个队列的同学向右转,则小花的正前方有几位同学?正右边有几位同学?
940 |
941 | ### 拓展3
942 |
943 | 学生进行队列表演,组成一个正方形队列,后来由于表演需要,去掉了一行一列,去掉的人数正好是13人,那么原来准备参加表演的一共有多少人?
944 |
945 | ### 拓展4
946 |
947 | 二年级(1)班的学生排成一个正方形队列,最外边一层的人数为60人。请问这个正方形队列最外层没边有多少人?
948 |
949 | ## 2.2.01. 认识倍
950 |
951 | 例题练习
952 |
953 | ### 例题1
954 |
955 | 乐乐老师奖励学习进步的同学。奖励牛牛金币20枚,田田得到金币的数量是牛牛的3倍还多5枚。奖励田田的金币有多少枚?
956 |
957 | ### 练习1
958 |
959 | 学校有篮球20个,足球的数量是篮球的3倍还少5个,足球有多少个?
960 |
961 | ### 例题2
962 |
963 | 丁丁有40张贴纸,丁丁的贴纸数量是牛牛贴纸数量的6倍还多4张,牛牛有多少张贴纸?
964 |
965 | ### 练习2
966 |
967 | 同学们去采摘,摘了西红柿27筐,是黄瓜的3倍多3筐,同学们摘了多少筐黄瓜?
968 |
969 | ### 例题3
970 |
971 | 阿普喷出水球22个,水球的数量是火球的3倍少5,火球有多少个?
972 |
973 | ### 练习3
974 |
975 | 学校买来了排球20个,买来的排球是足球的4倍,学校买来的排球比足球多几个?
976 |
977 | ### 例题4
978 |
979 | 乐乐老师有金币150枚,银币40枚,要使金币的数量是银币的6倍,还需要多少枚金币?
980 |
981 | ### 练习4
982 |
983 | 小猪有奶糖50块,水果糖4块,要使奶糖的数量是水果糖的6倍,应该吃掉多少块奶糖?
984 |
985 | ### 例题5
986 |
987 | 士兵和小怪物中一共有90个受伤,受伤的士兵人数是受伤小怪物数量的2倍,问士兵和小怪物各受伤多少个?
988 |
989 | ### 练习5
990 |
991 | 学校买来一些乒乓球和羽毛球共240个,乒乓球的个数是羽毛球的3倍。买来的乒乓球和羽毛球各多少个?
992 |
993 | ### 例题6
994 |
995 | 黑士兵比白士兵多80人,黑士兵的数量是白士兵数量的3倍,黑士兵和白士兵各有多少人?
996 |
997 | ### 练习6
998 |
999 | 学校买来的乒乓球比羽毛球多240个,乒乓球的个数是羽毛球的3倍。买来的乒乓球和羽毛球各多少个?
1000 |
1001 | 拓展
1002 |
1003 | ### 拓展1
1004 |
1005 | 小敏有14元,小花有10元,小花给小敏几元,小敏的钱数就是小花的2倍?
1006 |
1007 | ### 拓展2
1008 |
1009 | 师、徒两人共加工105个零件,师傅加工的个数比徒弟的3倍还多5个,师傅和徒弟各加工零件多少个?
1010 |
1011 | 巩固练习
1012 |
1013 | ### 巩固1
1014 |
1015 | 一支圆珠笔的价钱是8元,已知一盒彩笔的价钱是一支圆珠笔价钱的3倍,问小华买一盒彩笔和一支圆珠笔一共需要多少钱?
1016 |
1017 | ### 巩固2
1018 |
1019 | 学校买来排球120个,已知买来的排球是买来的足球的3倍,那么学校买来足球多少个?
1020 |
1021 | ### 巩固3
1022 |
1023 | 冷饮店有45箱可乐,已知可乐的数量是雪碧的2倍少5箱,那么雪碧有多少箱?
1024 |
1025 | ### 巩固4
1026 |
1027 | 动物园里有3只大猴,13只小猴,问要再添上几只小猴后,才能使小猴只数是大猴只数的6倍?
1028 |
1029 | ### 巩固5
1030 |
1031 | 男生和女生一共有123人,已知男生人数比女生人数的2倍还多3人,问女生和男生各有多少人?
1032 |
1033 | ### 巩固6
1034 |
1035 | 食堂买来的苹果比香蕉多50千克,已知苹果的重量是香蕉的6倍,问香蕉和苹果各有多少千克?
1036 |
1037 | ## 2.2.02. 带余数除法
1038 |
1039 | ### 例题1
1040 |
1041 | 根据要求填空。
1042 |
1043 | (1)$()÷4=3……2$
1044 |
1045 | (2)$()÷9=2……3$
1046 |
1047 | (3)$()÷5=3……4$
1048 |
1049 | ### 练习1
1050 |
1051 | 根据要求填空。
1052 |
1053 | (1)$()÷8=3……4$
1054 |
1055 | (2)$()÷9=2……5$
1056 |
1057 | (3)$()÷5=6……4$
1058 |
1059 | ### 例题2
1060 |
1061 | 根据要求填空。
1062 |
1063 | (1)$23÷()=3……2$
1064 |
1065 | (2)$21÷()=2……3$
1066 |
1067 | (3)$22÷()=3……4$
1068 |
1069 | ### 练习2
1070 |
1071 | 根据要求填空。
1072 |
1073 | (1)$43÷()=5……3$
1074 |
1075 | (2)$83÷()=9……2$
1076 |
1077 | (3)$22÷()=3……1$
1078 |
1079 | ### 例题3
1080 |
1081 | 根据要求在()里填上合适的数。
1082 |
1083 | (1)下面()里最小能填几。
1084 | $$
1085 | ()\div()=5……4
1086 | $$
1087 |
1088 | $$
1089 | ()\div()=4……9
1090 | $$
1091 |
1092 | (2)下面()里最大能填几。
1093 | $$
1094 | ()\div4=5……()
1095 | $$
1096 |
1097 | $$
1098 | ()\div9=4……()
1099 | $$
1100 |
1101 | ### 练习3
1102 |
1103 | 根据要求在()里填上合适的数。
1104 |
1105 | (1)下面()里最小能填几。
1106 | $$
1107 | ()\div()=3……9
1108 | $$
1109 |
1110 | $$
1111 | ()\div()=10……2
1112 | $$
1113 |
1114 | (2)下面()里最大能填几。
1115 | $$
1116 | ()\div6=5……()
1117 | $$
1118 |
1119 | $$
1120 | ()\div7=4……()
1121 | $$
1122 |
1123 | ### 例题4
1124 |
1125 | 乐乐老师为了奖励同学们的优秀表现,决定要把手中的苹果分给小朋友吃,平均分给11个人,每人分6个后,剩下的苹果不够分了,乐乐老师手中最少有多少个苹果?最多有多少个苹果?
1126 |
1127 | ### 练习4
1128 |
1129 | 田田拿出自己的一堆玻璃球,要平均分给8个好朋友,每个小朋友得到7个后,剩下的玻璃球不够分了,问:田田的玻璃球最少有多少个?最多有多少个?
1130 |
1131 | ### 例题5
1132 |
1133 | 田田带领7个小朋友一起去擦27块玻璃,先平均分,每个小朋友擦若干块,剩下的不够分,就由田田再擦剩下的玻璃,那么田田一共需要擦多少块玻璃才能完成任务?
1134 |
1135 | ### 练习5
1136 |
1137 | 牛牛决定也把自己手中的卡片和好朋友共同分享,他把23张卡片平均分给5个小朋友,剩下不够分的卡片才留给自己,请问:牛牛最后手中有卡片多少张?
1138 |
1139 | ### 例题6
1140 |
1141 | “数”、“学”分别代表一个非零的自然数,请你将所有满足下列等式的“数”、“学”所代表的数分别列出来?
1142 | $$
1143 | 数÷5=8……学
1144 | $$
1145 |
1146 | ### 练习6
1147 |
1148 | 字母A、B分别代表一个非零的自然数,请你将所有满足A÷4=5……B的A、B所代表的数分别列出来?
1149 |
1150 | ## 2.2.03. 有趣的自然数串
1151 |
1152 | ### 热身1
1153 |
1154 | ### 热身2
1155 |
1156 | ### 热身3
1157 |
1158 | ### 例题1
1159 |
1160 | 下面的自然数串,共有多少个数?
1161 | 3,4,5,6,7,8,9,……,28,29,30。
1162 |
1163 | ### 练习1
1164 |
1165 | 下面的自然数串,共有多少个数?
1166 | 8,9,10,11,12,……,56,57,58,59,60。
1167 |
1168 | ### 例题2
1169 |
1170 | 下面的自然数列,共有多少个数?
1171 | 2,4,6,8,10,12,14,……,58,60。
1172 |
1173 | ### 练习2
1174 |
1175 | 下面的自然数列,共有多少个数?
1176 | 1,3,5,7,9,11,13,……,37,39。
1177 |
1178 | ### 例题3
1179 |
1180 | 下面的自然数列,共有多少个数?
1181 | 1,4,7,10,13,……,31,34,37。
1182 |
1183 | ### 练习3
1184 |
1185 | 下面的自然数列,共有多少个数?
1186 | 4,8,12,16,20,……,40。
1187 |
1188 | ### 例题4
1189 |
1190 | 1,2,3,4,5,6,……,38,39,40,阿普写完这40个数后才发现它不知道自己写了多少个数字,大家快来帮帮阿普:阿普一共写了多少个数字呢?
1191 |
1192 | ### 练习4
1193 |
1194 | 阿普把昨天写的数拿出来了:1,2,3,4,5,6,……,58,59,60,小朋友帮忙算一算,阿普昨天写了多少个数字?
1195 |
1196 | ### 例题5
1197 |
1198 | 牛牛把12个机器人排成一行编了号,他决定从第一个机器人开始戴帽子,隔个戴一个;戴完后从剩下的第一个机器人开始戴,隔一个戴一个;第三次也是照这个办法戴,最后一个没戴帽子的当选为机器人队长。小朋友,几号是机器人队长呢?
1199 |
1200 | ### 练习5
1201 |
1202 | 等牛牛睡着了,机器人们决定选出夜间小队长,12个机器人自动排成一行编了号,它们集体决定从倒数第一个机器人开始,隔一个退出一个;退完后从剩下的倒数第一个机器人开始,隔一个退出一个;第三次也是照这个办法进
1203 | 行,最后一个留下的当选为机器人队长。小朋友,这次几号是机器人队长呢?
1204 |
1205 | ### 例题6
1206 |
1207 | 阿普决定把自己的12个机器人也编上号拿出来围成一个圈,它命令机器人从1开始按顺序1~2循环报数,每次报2的自动退下,就这样进行下去,最后剩下的机器人也会被幸运地选为队长,几号机器人最幸运呢?
1208 |
1209 | ### 练习6
1210 |
1211 | 25个玩具娃娃羡慕机器人推选出队长,它们也国成一个大圈,并顺时针依次编号为12~5号,从1号开始按照顺序12报数,凡是报2的留下,其余玩具娃娃退出圈外,这样循环进行到剩下最后一个人,它就是幸运之星,这个幸运之星是几号?
1212 |
1213 | ## 2.2.04. 图形分割
1214 |
1215 | ### 热身1
1216 |
1217 | 一支圆珠笔的价钱是8元,已知一盒彩笔的价钱是一支圆珠笔价钱的3倍,问小华买一盒彩笔和一支圆珠笔一共需要多少钱?
1218 |
1219 | ### 热身2
1220 |
1221 | 冷饮店有45箱可乐,已知可乐的数量是雪碧的2倍少5箱,那么雪碧有多少箱?
1222 |
1223 | ### 热身3
1224 |
1225 | 动物园里有3只大猴,13只小猴,问要再添上几只小猴后,才能使小猴只数是大猴只数的6倍?
1226 |
1227 | ### 例题1
1228 |
1229 | 牛牛的妈妈买来1块枣糕,上面有6颗枣(如图所示),家里正好有6个人,牛牛说:“要最大的”,妈妈为公平起见,决定将枣糕分为大小形状一样的6块,每块含有1颗枣。你知道应该怎么分吗?
1230 |
1231 | ### 练习1
1232 |
1233 | 一个正三角形形状的土地上有四棵大树(如下图所示),现要把这块正三角形的土地分成和它形状相同的四小块,并且要求每块地中都要有一棵大树。应怎么分?
1234 |
1235 | ### 例题2
1236 |
1237 | 请你把一个等边三角形分别分成形状、大小都相同的2个、3个、4个三角形?
1238 |
1239 | ### 练习2
1240 |
1241 | 请用两种方法把下面的大正方形分割成八个相同的等腰直角三角形?
1242 |
1243 | ### 例题3
1244 |
1245 | 下图是由18个小正方形组成的图形,请你把它分成6个完全相同的图形?
1246 |
1247 | ### 练习3
1248 |
1249 | 用四种不同的方法将下图分割成完全相同的两部分,保持每个小正方形的完整性?
1250 |
1251 | ### 例题4
1252 |
1253 | 请将下图分成形状、大小都相同的4块?
1254 |
1255 | ### 练习4
1256 |
1257 | 如下图所示,请把它分成形状、大小都相同的4块?
1258 |
1259 | ### 例题5
1260 |
1261 | 请将下图分成形状、大小都相同的4块?
1262 |
1263 | ### 练习5
1264 |
1265 | 把下图分成形状、大小完全相同的4部分?
1266 |
1267 | ### 例题6
1268 |
1269 | 教室旁边有一块空地,教室占整块地的四分之一。现在要把它作为实验园地,分给4个小组,要求每个小组分到的形状、大小都要一样。该怎么分?
1270 |
1271 | ### 练习6
1272 |
1273 | 下图是连在一起的三块地,这一整块地的形状是由3个同样大小的等边三角形组成的一个等腰梯形,把这个等腰梯形分成形状、大小一样的4块,该怎么分?
1274 |
1275 | ## 2.2.05. 枚举法的妙用
1276 |
1277 | ### 热身1
1278 |
1279 | 将下图分成大小、形状都相同的四块,并且每块中都有一个字母。
1280 |
1281 |  1282 |
1283 | ### 热身2
1284 |
1285 | 计算:$1+2+3+\dots+49+50+49+\dots+3+2+1$
1286 |
1287 | ### 热身3
1288 |
1289 | 自然数12,135,1349这些数有一个共同的特点,至少有两个数字,而且相邻两个数字,左边的数字小于右边的数字,我们取名为“上升数”。用1,2,3,4这四个数可以组成几个“上升数”。
1290 |
1291 | (1)$38+163-63-28$
1292 |
1293 | (2)$80+37-7+65-15$
1294 |
1295 | ### 例题1
1296 |
1297 | 牛牛和丁丁想从2张一样的摩比星和2张一样的数学卡片中挑出一些拍照片,请你帮他俩算一算,有多少种不同的挑选方法?
1298 |
1299 | ### 练习1
1300 |
1301 | 阿普有1角、2角、5角的硬币各一枚,他从中取两枚,有多少种不同的取法?
1302 |
1303 | ### 例题2
1304 |
1305 | 把12个同样大小的正方形拼成1个长方形,可以拼成几个不同的长方形?
1306 |
1307 | ### 练习2
1308 |
1309 | 把16个同样大小的正方形拼成1个长方形,可以拼成几个不同的长方形?
1310 |
1311 | ### 例题3
1312 |
1313 | 用卡片1、3、5可以组成多少个不同的三位数?
1314 |
1315 | ### 练习3
1316 |
1317 | 用卡片0、2、4可以组成多少个不同的三位数?
1318 |
1319 | ### 例题4
1320 |
1321 | 阿普家门前共有5级台阶。如果规定一步只能登上1级或2级台阶,小朋友帮阿普算一算,走完这些台阶共有多少种不同的走法?
1322 |
1323 | ### 练习4
1324 |
1325 | 阿普家门前共有5级台阶。如果这次规定一步只能登上1级或3级台阶,小朋友帮阿普算一算,走完这个台阶共有多少种不同的走法?
1326 |
1327 | ### 例题5
1328 |
1329 | 牛牛和丁丁要从学校A点到动物园E点,如下图怎样走路线最短?这样的路线一共有多少条?请你用彩笔画一画。(图中一小段都一样长)
1330 |
1331 | 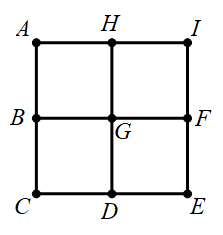
1332 |
1333 | ### 练习5
1334 |
1335 | 妈妈从家到单位上班,要经过电影院,从家到电影院有2条路,从电影院到单位有4条路,妈妈从家到单位上班有多少条不同的路线可走?
1336 |
1337 | ### 例题6
1338 |
1339 | 牛牛的暑假作业有语文、数学、英语三门,他准备每天做一门,且相邻两天不做同一门。如果牛牛第一天做语文,第五天也做语文,那么,这五天作业他共有多少种不同的安排?
1340 |
1341 | ### 练习6
1342 |
1343 | 田田爱吃青菜、菠菜、丝瓜三种蔬菜,她准备每天吃一种且相邻两天不吃同样蔬菜,如果田田第一天吃青菜,第五天也吃青菜,这五天她有几种不同的安排?
1344 |
1345 | ### 拓展1
1346 |
1347 | 把10份同样的礼物全部分成3组,每组至少有1份礼物的不同分法有几种?
1348 |
1349 | ### 拓展2
1350 |
1351 | 一只青蛙在A,B,C三点之间跳动,若青蛙从A点起跳,跳4次仍回到A点,如果不能原地跳则这只青蛙一共有多少种不同的跳法?
1352 |
1353 | ### 拓展3
1354 |
1355 | 两个正整数的乘积为96,这两个数可能是?
1356 |
1357 | ## 2.2.06. 鸡兔同笼初步
1358 |
1359 | ### 例题1
1360 |
1361 | 丁丁把鸡、免关在同一个笼子里,数了数,共有6个头,16条腿,你知道有几只鸡,几只免吗?
1362 |
1363 | ### 练习1
1364 |
1365 | 1角硬币和5角硬币一共有6枚,一共2元6角,求两种硬币各有多少枚?
1366 |
1367 | ### 例题2
1368 |
1369 | 牛牛把鸡、免关在同一个笼子里,数了数,共有10个头、26条腿,你知道这个笼子里有几只鸡?几只兔?
1370 |
1371 | ### 练习2
1372 |
1373 | 鸡、兔关在同一个笼子里,共有11个头,28条腿,这个笼子里有几只鸡?几只兔?
1374 |
1375 | ### 例题3
1376 |
1377 | 1只蛐蛐6条腿,1只蜘蛛8条腿。有蛐蛐和蜘蛛共10只,共68条腿,蛐蛐和蜘蛛各有多少只?
1378 |
1379 | ### 练习3
1380 |
1381 | 1瓶可乐6元,1瓶雪碧8元。牛牛共买这两种饮料8瓶,共花58元。可乐和雪碧各有多少瓶?
1382 |
1383 | ### 例题4
1384 |
1385 | 笼子里有一些鸡和兔,共20个头,50条腿,算一算笼子里有几只鸡?几只兔?
1386 |
1387 | ### 练习4
1388 |
1389 | 鸡和免共有45只,关在同一个笼子中。每只鸡有2条腿,每只兔子有4条腿,笼中共有100条腿。算一算,笼中有鸡多少只?免子多少只?
1390 |
1391 | ### 例题5
1392 |
1393 | 一辆卡车有6个轮子,一辆小汽车有4个轮子,停车场一共有14辆车,现在一共有72个轮子,你知道卡车和小汽车各有几辆吗?
1394 |
1395 | ### 练习5
1396 |
1397 | 在一个停车场上,现有车辆41辆,其中汽车有4个轮子,三轮摩托车有3个轮子,这些车共有127个轮子,那么三轮摩托车有多少辆?
1398 |
1399 | ### 例题6
1400 |
1401 | 鸡免同笼,共有14个头,38条腿,有几只鸡?几只兔?
1402 |
1403 | ### 练习6
1404 |
1405 | 1辆自行车有2个轮子,1辆三轮车有3个轮子。车棚里放着的自行车和三轮车共8辆,共20个轮子。自行车、三轮车各有多少辆?
1406 |
1407 | ## 2.2.07. 巧求周长初步
1408 |
1409 | ### 热身1(和倍)
1410 |
1411 | 实验小学三、四年级的同学们一共制作了24件航模,四年级同学制作的航模件数是三年级的2倍,三、四年级的同学各制作了多少件航模?
1412 |
1413 | ### 热身2(图形分割)
1414 |
1415 | 把下图分成形状、大小完全相同的4部分。
1416 |
1417 | 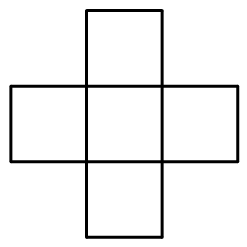
1418 |
1419 | ### 热身3(枚举)
1420 |
1421 | 3个装药的瓶子都贴了标签,其中有两个贴错了,错的情况总共有3种可能。如果有四个瓶子,其中有三个贴错了,那么错的情况共有多少种?
1422 |
1423 | (1)$178\times9$
1424 |
1425 | (2)$1000\div8$
1426 |
1427 | (3)$53\times12$
1428 |
1429 | ### 例题1
1430 |
1431 | 如下图为丁丁的学校操场平面图,长为300米,宽为200米,丁丁绕操场走一圈,问:丁丁走了多少米?
1432 |
1433 |
1282 |
1283 | ### 热身2
1284 |
1285 | 计算:$1+2+3+\dots+49+50+49+\dots+3+2+1$
1286 |
1287 | ### 热身3
1288 |
1289 | 自然数12,135,1349这些数有一个共同的特点,至少有两个数字,而且相邻两个数字,左边的数字小于右边的数字,我们取名为“上升数”。用1,2,3,4这四个数可以组成几个“上升数”。
1290 |
1291 | (1)$38+163-63-28$
1292 |
1293 | (2)$80+37-7+65-15$
1294 |
1295 | ### 例题1
1296 |
1297 | 牛牛和丁丁想从2张一样的摩比星和2张一样的数学卡片中挑出一些拍照片,请你帮他俩算一算,有多少种不同的挑选方法?
1298 |
1299 | ### 练习1
1300 |
1301 | 阿普有1角、2角、5角的硬币各一枚,他从中取两枚,有多少种不同的取法?
1302 |
1303 | ### 例题2
1304 |
1305 | 把12个同样大小的正方形拼成1个长方形,可以拼成几个不同的长方形?
1306 |
1307 | ### 练习2
1308 |
1309 | 把16个同样大小的正方形拼成1个长方形,可以拼成几个不同的长方形?
1310 |
1311 | ### 例题3
1312 |
1313 | 用卡片1、3、5可以组成多少个不同的三位数?
1314 |
1315 | ### 练习3
1316 |
1317 | 用卡片0、2、4可以组成多少个不同的三位数?
1318 |
1319 | ### 例题4
1320 |
1321 | 阿普家门前共有5级台阶。如果规定一步只能登上1级或2级台阶,小朋友帮阿普算一算,走完这些台阶共有多少种不同的走法?
1322 |
1323 | ### 练习4
1324 |
1325 | 阿普家门前共有5级台阶。如果这次规定一步只能登上1级或3级台阶,小朋友帮阿普算一算,走完这个台阶共有多少种不同的走法?
1326 |
1327 | ### 例题5
1328 |
1329 | 牛牛和丁丁要从学校A点到动物园E点,如下图怎样走路线最短?这样的路线一共有多少条?请你用彩笔画一画。(图中一小段都一样长)
1330 |
1331 | 
1332 |
1333 | ### 练习5
1334 |
1335 | 妈妈从家到单位上班,要经过电影院,从家到电影院有2条路,从电影院到单位有4条路,妈妈从家到单位上班有多少条不同的路线可走?
1336 |
1337 | ### 例题6
1338 |
1339 | 牛牛的暑假作业有语文、数学、英语三门,他准备每天做一门,且相邻两天不做同一门。如果牛牛第一天做语文,第五天也做语文,那么,这五天作业他共有多少种不同的安排?
1340 |
1341 | ### 练习6
1342 |
1343 | 田田爱吃青菜、菠菜、丝瓜三种蔬菜,她准备每天吃一种且相邻两天不吃同样蔬菜,如果田田第一天吃青菜,第五天也吃青菜,这五天她有几种不同的安排?
1344 |
1345 | ### 拓展1
1346 |
1347 | 把10份同样的礼物全部分成3组,每组至少有1份礼物的不同分法有几种?
1348 |
1349 | ### 拓展2
1350 |
1351 | 一只青蛙在A,B,C三点之间跳动,若青蛙从A点起跳,跳4次仍回到A点,如果不能原地跳则这只青蛙一共有多少种不同的跳法?
1352 |
1353 | ### 拓展3
1354 |
1355 | 两个正整数的乘积为96,这两个数可能是?
1356 |
1357 | ## 2.2.06. 鸡兔同笼初步
1358 |
1359 | ### 例题1
1360 |
1361 | 丁丁把鸡、免关在同一个笼子里,数了数,共有6个头,16条腿,你知道有几只鸡,几只免吗?
1362 |
1363 | ### 练习1
1364 |
1365 | 1角硬币和5角硬币一共有6枚,一共2元6角,求两种硬币各有多少枚?
1366 |
1367 | ### 例题2
1368 |
1369 | 牛牛把鸡、免关在同一个笼子里,数了数,共有10个头、26条腿,你知道这个笼子里有几只鸡?几只兔?
1370 |
1371 | ### 练习2
1372 |
1373 | 鸡、兔关在同一个笼子里,共有11个头,28条腿,这个笼子里有几只鸡?几只兔?
1374 |
1375 | ### 例题3
1376 |
1377 | 1只蛐蛐6条腿,1只蜘蛛8条腿。有蛐蛐和蜘蛛共10只,共68条腿,蛐蛐和蜘蛛各有多少只?
1378 |
1379 | ### 练习3
1380 |
1381 | 1瓶可乐6元,1瓶雪碧8元。牛牛共买这两种饮料8瓶,共花58元。可乐和雪碧各有多少瓶?
1382 |
1383 | ### 例题4
1384 |
1385 | 笼子里有一些鸡和兔,共20个头,50条腿,算一算笼子里有几只鸡?几只兔?
1386 |
1387 | ### 练习4
1388 |
1389 | 鸡和免共有45只,关在同一个笼子中。每只鸡有2条腿,每只兔子有4条腿,笼中共有100条腿。算一算,笼中有鸡多少只?免子多少只?
1390 |
1391 | ### 例题5
1392 |
1393 | 一辆卡车有6个轮子,一辆小汽车有4个轮子,停车场一共有14辆车,现在一共有72个轮子,你知道卡车和小汽车各有几辆吗?
1394 |
1395 | ### 练习5
1396 |
1397 | 在一个停车场上,现有车辆41辆,其中汽车有4个轮子,三轮摩托车有3个轮子,这些车共有127个轮子,那么三轮摩托车有多少辆?
1398 |
1399 | ### 例题6
1400 |
1401 | 鸡免同笼,共有14个头,38条腿,有几只鸡?几只兔?
1402 |
1403 | ### 练习6
1404 |
1405 | 1辆自行车有2个轮子,1辆三轮车有3个轮子。车棚里放着的自行车和三轮车共8辆,共20个轮子。自行车、三轮车各有多少辆?
1406 |
1407 | ## 2.2.07. 巧求周长初步
1408 |
1409 | ### 热身1(和倍)
1410 |
1411 | 实验小学三、四年级的同学们一共制作了24件航模,四年级同学制作的航模件数是三年级的2倍,三、四年级的同学各制作了多少件航模?
1412 |
1413 | ### 热身2(图形分割)
1414 |
1415 | 把下图分成形状、大小完全相同的4部分。
1416 |
1417 | 
1418 |
1419 | ### 热身3(枚举)
1420 |
1421 | 3个装药的瓶子都贴了标签,其中有两个贴错了,错的情况总共有3种可能。如果有四个瓶子,其中有三个贴错了,那么错的情况共有多少种?
1422 |
1423 | (1)$178\times9$
1424 |
1425 | (2)$1000\div8$
1426 |
1427 | (3)$53\times12$
1428 |
1429 | ### 例题1
1430 |
1431 | 如下图为丁丁的学校操场平面图,长为300米,宽为200米,丁丁绕操场走一圈,问:丁丁走了多少米?
1432 |
1433 |  1434 |
1435 | ### 练习1
1436 |
1437 | 求下面图形的周长。(单位:厘米)
1438 |
1439 |
1434 |
1435 | ### 练习1
1436 |
1437 | 求下面图形的周长。(单位:厘米)
1438 |
1439 |  1440 |
1441 | ### 例题2
1442 |
1443 | 牛牛用100厘米长的绳子围成一个正方形,这个正方形的边长是多少?
1444 |
1445 | ### 练习2
1446 |
1447 | 一个正方形花坛四周围着栏杆,栏杆共长48米,这个正方形栏杆的边长是多少米?
1448 |
1449 | ### 例题3
1450 |
1451 | 田田小朋友用60厘米长的黑线,给自己的长方形板子镶了一道黑边,已知这个板子宽为1厘米,你知道长方形板子的长为多少厘米吗?
1452 |
1453 | ### 练习3
1454 |
1455 | 一个长方形操场的周长为400米,已知长为140米,求宽为多少米?
1456 |
1457 | ### 例题4
1458 |
1459 | 如图,用两个大小相同的正方形,拼成一个长方形后,周长比原来两个正方形的周长的和少了8厘米,求原来一个正方形的周长为多少厘米?
1460 |
1461 |
1440 |
1441 | ### 例题2
1442 |
1443 | 牛牛用100厘米长的绳子围成一个正方形,这个正方形的边长是多少?
1444 |
1445 | ### 练习2
1446 |
1447 | 一个正方形花坛四周围着栏杆,栏杆共长48米,这个正方形栏杆的边长是多少米?
1448 |
1449 | ### 例题3
1450 |
1451 | 田田小朋友用60厘米长的黑线,给自己的长方形板子镶了一道黑边,已知这个板子宽为1厘米,你知道长方形板子的长为多少厘米吗?
1452 |
1453 | ### 练习3
1454 |
1455 | 一个长方形操场的周长为400米,已知长为140米,求宽为多少米?
1456 |
1457 | ### 例题4
1458 |
1459 | 如图,用两个大小相同的正方形,拼成一个长方形后,周长比原来两个正方形的周长的和少了8厘米,求原来一个正方形的周长为多少厘米?
1460 |
1461 |  1462 |
1463 | ### 练习4
1464 |
1465 | 一个长方形被一刀剪成了大小一样的两个正方形,正方形的边长是20厘米,剪成的两个正方形的周长之和比原来的长方形的周长多了多少厘米?
1466 |
1467 | ### 例题5
1468 |
1469 | 一个长方形花坛被平均分成了7个小正方形,已知每个小正方形的周长是11米,求大长方形的周长为多少米?
1470 |
1471 |
1462 |
1463 | ### 练习4
1464 |
1465 | 一个长方形被一刀剪成了大小一样的两个正方形,正方形的边长是20厘米,剪成的两个正方形的周长之和比原来的长方形的周长多了多少厘米?
1466 |
1467 | ### 例题5
1468 |
1469 | 一个长方形花坛被平均分成了7个小正方形,已知每个小正方形的周长是11米,求大长方形的周长为多少米?
1470 |
1471 |  1472 |
1473 | ### 练习5
1474 |
1475 | 用6个边长为2厘米的正方形,拼成一个大长方形,求大长方形的周长为多少厘米?
1476 |
1477 | ### 例题6
1478 |
1479 | 如下图所示,在一个长为10厘米,宽为8厘米的长方形纸片上剪去一个边长为2厘米的正方形,那么剩下图形的周长为多少?
1480 |
1481 | 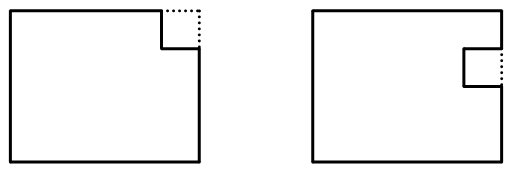
1482 |
1483 | ### 练习6
1484 |
1485 | 求出下图中多边形的周长为多少厘米?(单位:厘米)
1486 |
1487 | 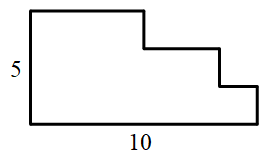
1488 |
1489 | 商场举行大酬宾活动,门口将长18厘米,宽9厘米的礼品盒摆成一个有规律的形状。礼品盒前4层的样式如图所示,一共有10层,你能算出一共摆了多少个礼品盒吗?礼品盒摆出形状的周长是多少?
1490 |
1491 |
1472 |
1473 | ### 练习5
1474 |
1475 | 用6个边长为2厘米的正方形,拼成一个大长方形,求大长方形的周长为多少厘米?
1476 |
1477 | ### 例题6
1478 |
1479 | 如下图所示,在一个长为10厘米,宽为8厘米的长方形纸片上剪去一个边长为2厘米的正方形,那么剩下图形的周长为多少?
1480 |
1481 | 
1482 |
1483 | ### 练习6
1484 |
1485 | 求出下图中多边形的周长为多少厘米?(单位:厘米)
1486 |
1487 | 
1488 |
1489 | 商场举行大酬宾活动,门口将长18厘米,宽9厘米的礼品盒摆成一个有规律的形状。礼品盒前4层的样式如图所示,一共有10层,你能算出一共摆了多少个礼品盒吗?礼品盒摆出形状的周长是多少?
1490 |
1491 |  1492 |
1493 | ## 2.2.09. 立体图形染色
1494 |
1495 | ### 热身1
1496 |
1497 | ### 热身2
1498 |
1499 | ### 热身3
1500 |
1501 | ### 例题1
1502 |
1503 | 一个正方体有()个面,()条棱,()个顶点。
1504 |
1505 |
1492 |
1493 | ## 2.2.09. 立体图形染色
1494 |
1495 | ### 热身1
1496 |
1497 | ### 热身2
1498 |
1499 | ### 热身3
1500 |
1501 | ### 例题1
1502 |
1503 | 一个正方体有()个面,()条棱,()个顶点。
1504 |
1505 |  1506 |
1507 | ### 练习1
1508 |
1509 | (1)想个一个正方体表面涂色,一共要涂多少个小正方形?
1510 |
1511 | (2)如果想给两个粘在一起的两个正方体表面涂色,一共要涂多少个小正方形?
1512 |
1513 |
1506 |
1507 | ### 练习1
1508 |
1509 | (1)想个一个正方体表面涂色,一共要涂多少个小正方形?
1510 |
1511 | (2)如果想给两个粘在一起的两个正方体表面涂色,一共要涂多少个小正方形?
1512 |
1513 |  1514 |
1515 | ### 例题2
1516 |
1517 | 下面是用小正方体堆成的图形,现在把这个图形的表面涂上蓝色,想一想,有多少个小正方形没有被涂色?
1518 |
1519 |
1514 |
1515 | ### 例题2
1516 |
1517 | 下面是用小正方体堆成的图形,现在把这个图形的表面涂上蓝色,想一想,有多少个小正方形没有被涂色?
1518 |
1519 |  1520 |
1521 | ### 练习2
1522 |
1523 | 四个小正方体排成如下图的形状,要给他的表面上色,有几个小正方形没有被上色?
1524 |
1525 | ### 例题3
1526 |
1527 | 把一个正方体表面涂上绿色,然后再把它切成8个小正方体,想一想,每个小正方体有几个面没有颜色?
1528 |
1529 | ### 练习3
1530 |
1531 | 一个大长方体的表面都涂上红色,然后切成 18 个小立方体(切线如图中虚线所示)。在这些切成的小立方体中,问:
1532 |
1533 | (1)1面涂成红色的有()块。
1534 |
1535 | (2)2面涂成红色的有()块。
1536 |
1537 | (3)3面涂成红色的有()块。
1538 |
1539 |
1520 |
1521 | ### 练习2
1522 |
1523 | 四个小正方体排成如下图的形状,要给他的表面上色,有几个小正方形没有被上色?
1524 |
1525 | ### 例题3
1526 |
1527 | 把一个正方体表面涂上绿色,然后再把它切成8个小正方体,想一想,每个小正方体有几个面没有颜色?
1528 |
1529 | ### 练习3
1530 |
1531 | 一个大长方体的表面都涂上红色,然后切成 18 个小立方体(切线如图中虚线所示)。在这些切成的小立方体中,问:
1532 |
1533 | (1)1面涂成红色的有()块。
1534 |
1535 | (2)2面涂成红色的有()块。
1536 |
1537 | (3)3面涂成红色的有()块。
1538 |
1539 | 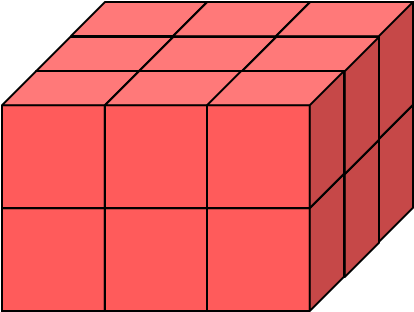 1540 |
1541 | ### 例题4
1542 |
1543 | 下面是用小正方体组成的立体图形,现在把这个立体图形表面都涂上绿色,数一数有多少个小正方形没有被涂上色?
1544 |
1545 | ### 练习4
1546 |
1547 | 用小正方体拼成了一个如下图的模型,然后把它粘在地上喷上红色油漆,这堆正方体中共有多少个小正方形没有被喷上颜色?
1548 |
1549 | ### 例题5
1550 |
1551 | ### 练习5
1552 |
1553 | ### 例题6
1554 |
1555 | ### 练习6
1556 |
1557 | ## 2.2.10. 周期问题初步
1558 |
1559 | ### 例题1
1560 |
1561 | 小朋友按了3女3男的顺序依次排成一队看表演,算一算第17名、第37名同学分别是男生还是女生?
1562 |
1563 | ### 练习1
1564 |
1565 | 广场上摆满花,这些花是按3盆大红、2盆金黄、2盒粉红的顺序摆放的,你
1566 | 们知道第26盆、35盆、45 盒花是什么颜色吗?
1567 |
1568 | ### 例题2
1569 |
1570 | 乐乐老师带领牛牛等人在园林里种树,他们按1棵杨树、2棵椰树、2棵松树的顺序来种,一共种了48棵树,那么杨树、椰树、松树各种了几棵?
1571 |
1572 | ### 练习2
1573 |
1574 | 某小学操场上树立着彩旗,按如下图顺序来排列,一共有 42 面旗,在这42 面彩旗中,红旗有()面,黄旗有()面?
1575 |
1576 | ### 例题3
1577 |
1578 | 丁丁用树枝在地上写了一列数,然后他停下来,让田田猜一猜,
1579 |
1580 | $2、3、1、2、3、1、2、3、1、……$
1581 |
1582 | (1)第28个数是几?
1583 |
1584 | (2)这28个数的和是多少?
1585 |
1586 | ### 练习3
1587 |
1588 | 有一列数:
1589 |
1590 | $1、4、2、1、4、2、1、4、2、1、……$
1591 |
1592 | (1)第26个数是几?
1593 |
1594 | (2)这26个数的和是多少?
1595 |
1596 | ### 例题4
1597 |
1598 | 有一列数如下所示,在这一列数中:
1599 |
1600 | $1、3、5、7、1、3、5、7、9、……$
1601 |
1602 | (1)第35个数是几?
1603 |
1604 | (2)这35个数的和是多少?
1605 |
1606 | (3)如果连续写83个数,3被写了多少次?
1607 |
1608 | ### 练习4
1609 |
1610 | $2、3、4、1、2、3、4、1、2、3、4、1、2、3、4、1、2、3、4、……$,请问:
1611 |
1612 | (1)第26个数是几?
1613 |
1614 | (2)请问这26个数的和是多少?
1615 |
1616 | (3)请问在这26个数字中,有几个“3”?
1617 |
1618 | ### 例题5
1619 |
1620 | 2014年4月5日是星期六。
1621 |
1622 | (1)从5日算起,第10天是星期几?
1623 |
1624 | (2)再过10天是星期几?
1625 |
1626 | ### 练习5
1627 |
1628 | 某年1月1日元旦是星期四,从1日算起,第12天是星期()
1629 |
1630 | ### 例题6
1631 |
1632 | 例子:
1633 |
1634 | | 1 | 2 | 1 | 2 | 1 | 2 | 1 | 2 | 1 | 2 | …… |
1635 | | ---- | ---- | ---- | ---- | ---- | ---- | ---- | ---- | ---- | ---- | ---- |
1636 | | A | B | C | A | B | C | A | B | C | A | …… |
1637 |
1638 | 在下表中,将每列上、下两个字组成一组,例如第1组为(小双),第2组为(朋手),那么第55组是什么?
1639 |
1640 | | 小 | 朋 | 友 | 荡 | 秋 | 千 | 小 | 朋 | 友 | 荡 | 秋 | 千 | 小 | 朋 | …… |
1641 | | ---- | ---- | ---- | ---- | ---- | ---- | ---- | ---- | ---- | ---- | ---- | ---- | ---- | ---- | ---- |
1642 | | 双 | 手 | 向 | 空 | 如 | 鸟 | 翼 | 双 | 手 | 向 | 空 | 如 | 鸟 | 翼 | …… |
1643 |
1644 | ### 练习6
1645 |
1646 | 下面的表格中,每一列的两个数组成一组,如第1组是由“甲A”组成,第
1647 | 2组是由“乙B”组成⋯问:第17组是由哪两个组成?
1648 |
1649 | | 甲 | 乙 | 丙 | 甲 | 乙 | 丙 | 甲 | 乙 | 丙 | 甲 | 乙 | 丙 | …… |
1650 | | ---- | ---- | ---- | ---- | ---- | ---- | ---- | ---- | ---- | ---- | ---- | ---- | ---- |
1651 | | A | B | C | D | A | B | C | D | A | B | C | D | …… |
1652 |
1653 | ### 拓展1
1654 |
1655 | 今天是2022年4月14日,星期四,请问:今年的劳动节是星期几?小代今年的生日是星期几?
1656 |
1657 | ### 拓展2
1658 |
1659 | 12个同学围成一圈做传球的游戏,如图。
1660 |
1661 | 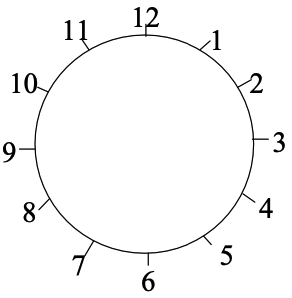
1662 |
1663 | (1)从1号同学开始,顺时针传100次,手绢应在谁手中?
1664 |
1665 | (2)从1号同学开始,逆时针传100次,手绢又在谁手中?
1666 |
1667 | (3)从 1号同学开始,先顺时针传156次,然后从那个同学开始逆时针传143次,最后手绢在谁手中?
1668 |
1669 | ### 拓展3
1670 |
1671 | 字母A、B、C、D、E和数字1、9分别按下列方式变动次序:
1672 |
1673 | ABCDE19
1674 |
1675 | BCDEA91(第一次变动)
1676 |
1677 | CDEAB91(第二次变动)
1678 |
1679 | DEABC19(第三次变动)
1680 |
1681 | ……
1682 |
1683 | 那么,最少经过几次变动后“ABCDE19”将再次出现。
1684 |
1685 | ### 拓展4
1686 |
1687 | A、B、C、D四个盒子中依次放有6、4、5、3个球。第1个小朋友找到放球最多的盒子,从盒子中取出 3 个球,放入其他盒子,每个盒子放一个;然后第2个小朋友也找到放球最多的盒子,从盒子中取出 3个球,放入其他盒子,每个盒子放一个。如此进行下去,当第120位小朋友放完后,C 盒中有几个球?
1688 |
1689 | ## 2.2.11. 移多补少
1690 |
1691 | 计算练习
1692 |
1693 | (1)$1+2+3+4+5+6+7+8+9+10+9+8+7+6+5+4+3+2+1$
1694 |
1695 | (2)$1+3+5+7+9+11+9+7+5+3+1$
1696 |
1697 | (3)$1+2+3+\dots+49+50+49+\dots+3+2+1$
1698 |
1699 | ### 例题1
1700 |
1701 | 牛牛和丁丁分糕点,牛牛有14块,丁丁有6块,牛牛需要拿出几块糕点给丁丁,他们的糕点数才会同样多?
1702 |
1703 | ### 练习1
1704 |
1705 | 红队有29人,黄队有15人,红队调给黄队几人,就能使两队人数相等?
1706 |
1707 | ### 例题2
1708 |
1709 | 同学们分成两队进行拔河比赛,第一队有31人,如果从第一队中调3人到第二队,这时两队的人数才会一样多。第二队原来有学生多少人?
1710 |
1711 | ### 练习2
1712 |
1713 | 牛牛有24朵花,丁丁给牛牛8朵后,两人的花朵数就相等。丁丁原来有几几朵花?
1714 |
1715 | ### 例题3
1716 |
1717 | 小花免和小白兔分萝卜,小花兔给小白兔4个萝卜后,小花免还比小白兔多
1718 | 2个。小花兔原来比小白兔多几个萝卜?
1719 |
1720 | ### 练习3
1721 |
1722 | 小花兔和小白兔分萝卜,小花兔给小白兔4个萝卜后,小花免比小白免少
1723 | 2个。小花兔原来比小白兔多几个萝卜?
1724 |
1725 | ### 例题4
1726 |
1727 | 小山羊和小白免一共拔了30个萝卜放进两筐里,小白免从大筐里拿出6个放进小筐里,现在两筐萝卜的个数同样多。原来小筐里有多少个萝卜?
1728 |
1729 | ### 练习4
1730 |
1731 | 甲、乙两筐西瓜共28个,从甲筐取4个放入乙筐中,两筐西瓜个数相同。
1732 | 原来甲、乙两筐各有多少个西瓜?
1733 |
1734 | ### 例题5
1735 |
1736 | 妈妈买了2袋苹果,甲袋是54个,乙袋是22个。每次从多的1袋取出4个放到少的1袋里,拿几次才能使两袋苹果的个数相等呢?
1737 |
1738 | ### 练习5
1739 |
1740 | 小华有两盒糖果,甲盒有糖78粒,乙盒有糖38粒,每次从甲盒取5粒糖放到
1741 | 乙盒,取几次两盒糖的粒数就同样多?
1742 |
1743 | ### 例题6
1744 |
1745 | 两堆香蕉一样多,现在从第一堆里面拿出4把香蕉放入第二堆,这时第二堆的香蕉是第一堆的2倍,原来两堆香蕉各有多少把?
1746 |
1747 | ### 练习6
1748 |
1749 | 哥哥和弟弟集邮,原来两人的邮票张数相等,如果哥哥给弟弟9张邮票,则弟弟的邮票张数是哥哥的3倍,哥哥、弟弟原来各有邮票多少张?
1750 |
1751 | ### 拓展1
1752 |
1753 | 小东、小西、小北3个同学带着15个筐去摘桃,摘完后,有5筐装满了桃,5筐装了半筐桃,5筐空着,怎样分,才能让他们3人每人分到的桃一样多,筐也一样多?
1754 |
1755 | ### 拓展2
1756 |
1757 | 大毛、二毛和三毛三个小朋友出去玩,各自摘了一些小草莓,大毛把自己摘得草莓给了二毛 2 个后,大毛比二毛多 1 个,接着,二毛又把自己摘草莓给了三毛 2 个,此时二毛和三毛的草莓变得一样多,那么原来大毛和三毛两个人摘得草莓数量谁更多?多几个?
1758 |
1759 | ### 拓展3
1760 |
1761 | 小白、小灰和小花三只小猫去河里分别捉了一些鱼。如果小花给小白 5 条鱼,那么小花比小白还多 2 条鱼;如果小灰给小花 4 条鱼,那么小灰就比小花少 3 条鱼,请问原来小灰比小白多多少条鱼?
1762 |
1763 | ### 拓展4
1764 |
1765 | 小白、小灰和小花三只小猫去河里捉了一些鱼。如果小白给小花一些鱼后,小花和小白拥有的鱼就一样多了,都是 42 条;如果小灰给小白一些鱼后,小灰和小白拥有的鱼就一样多了,都是 47 条鱼,如果小灰给小花一些鱼后,小灰和小花拥有的鱼就一样多了,都是 46条。那小灰有几条鱼。
1766 |
1767 | ## 2.2.12. 和差问题
1768 |
1769 | ### 例题1
1770 |
1771 | 牛牛和丁丁总共有46个玻璃球,丁丁比牛牛多6个。请大家帮忙算一算,牛牛和丁丁各有多少个玻璃球?
1772 |
1773 | ### 练习1
1774 |
1775 | 今年姐姐和妹妹的年龄和是14岁,姐姐比妹妹大4岁,问姐姐、妹妹今年各多少岁?
1776 |
1777 | ### 例题2
1778 |
1779 | 牛牛和丁丁写大字的速度不变,两人两天一共写了120个字,已知牛牛每天比丁丁多写10个,请问丁丁和牛牛每天各写几个大字?
1780 |
1781 | ### 练习2
1782 |
1783 | 牛牛和丁丁保持自己相同的速度折飞机,牛牛每小时比丁丁多折10个,他们两人用了3小时共折飞机150个,牛牛和丁丁每小时各折多少个飞机?
1784 |
1785 | ### 例题3
1786 |
1787 | 动物学校有个长方形操场,它的长与宽相差80米,沿操场跑一圈是400米,求动物学校操场的长与宽各是多少?
1788 |
1789 | ### 练习3
1790 |
1791 | 蚂蚁沿着阿普的课本四周爬了一圈是200厘米,知道课本的长边比短边多30厘米,问阿普课本的长边和短边各是多少厘米?
1792 |
1793 | ### 例题4
1794 |
1795 | 牛牛在这次测验中,语文和数学的平均分是95分,语文比数学多6分,牛牛在这次测验中,语文和数学各得了多少分?
1796 |
1797 | ### 练习4
1798 |
1799 | 牛牛和丁丁的平均身高是130厘米,牛牛比丁丁高10厘米,丁丁和牛牛的身高各是多少厘米?
1800 |
1801 | ### 例题5
1802 |
1803 | 豆豆和毛毛一共有34个巧克力豆,两人都吃了同样的巧克力豆后,分别还剩15个和11个,问原来豆豆和毛毛各有多少个巧克力豆?
1804 |
1805 | ### 练习5
1806 |
1807 | 大毛、二毛共有33元,两人花掉同样的钱后,大毛还有19元,二毛还有6元,问原来大毛、二毛各有多少钱?
1808 |
1809 | ### 例题6
1810 |
1811 | 牛牛3年前的年龄与阿普2年后的年龄之和是23岁,牛牛3年后的年龄等于阿普1年前的年龄,求牛牛、阿普今年的年龄各是多少岁?
1812 |
1813 | ### 练习6
1814 |
1815 | 红红2年前的年龄与果果1年后的年龄相等,红红3年前的年龄与果果2年后的年龄和为18岁,则红红、果果今年各多少岁?
1816 |
1817 | ### 巩固1
1818 |
1819 | 维尼熊和跳跳虎去摘苹果。跳跳虎每摘7个,维尼熊只能摘4个。维尼熊摘了16分钟,跳跳虎摘了10分钟就累了,不摘了。他们回来后数了一下,共摘了670个苹果,那么其中维尼熊摘的苹果有多少个?
1820 |
1821 | ### 巩固2
1822 |
1823 | 甲、乙、丙3个数的和是99,如果甲加上10,乙减少5,丙减少2,则3个数相等。这3个数各是几?
1824 |
1825 | ### 巩固3
1826 |
1827 | 三块布料一共190米,第二块比第一块长20米,第三块比第二块长30米,每块布料各长多少米?
1828 |
1829 | ## 2.2.13. 逻辑推理进阶
1830 |
1831 | ### 热身1
1832 |
1833 | ### 热身2
1834 |
1835 | ### 热身3
1836 |
1837 | ### 例题1
1838 |
1839 | 乐乐老师、红红、丁丁、牛牛和田田一起去爬山。牛牛在丁丁和田田之前爬到终点,田田是紧跟着牛牛之后爬到终点的。有两个人在乐乐老师之后、丁丁之前爬到终点。这5个人登山到终点的先后顺序是怎样的?
1840 |
1841 | ### 练习1
1842 |
1843 | 田田比牛牛跑得慢,牛牛比加加跑得快,加加比减减跑得快,减减比田田跑得快。谁跑得最快?谁跑得最慢?
1844 |
1845 | ### 例题2
1846 |
1847 | 体育馆里正在进行一场精彩的乒乓球双打比赛。两位播音员正在议论这四个运动员的年龄问题:
1848 |
1849 | (1)小A比小B年轻;
1850 |
1851 | (2)小C比他的两个对手年龄都大;
1852 |
1853 | (3)小A比小D年龄大;
1854 |
1855 | (4)小B比小C年龄大。
1856 |
1857 | 请分析一下他们四人的年龄顺序,谁年龄最大?谁年龄最小?
1858 |
1859 | ### 练习2
1860 |
1861 | 2号大楼比3号大楼高,4号大楼比3号大楼低,1号大楼比2号大楼高,1号大楼比4号大楼高,几号大楼是最高的?几号大楼是最低的?
1862 |
1863 | ### 例题3
1864 |
1865 | 赵、钱、孙三人中,一位是射击运动员,一位是体操运动员,一位是跳水运动员。已知:
1866 |
1867 | (1)赵比体操运动员体重重;
1868 |
1869 | (2)钱和体操运动员体重不同;
1870 |
1871 | (3)赵和跳水运动员是朋友。
1872 |
1873 | 你能猜出谁是射击运动员,谁是体操运动员,谁是跳水运动员吗?
1874 |
1875 | ### 练习3
1876 |
1877 | 刘玉、马明、王建三个男孩都有一个妹妹,是小雅、小花、丽丽。6个人在一起打球,举行男女混合双打。事先规定,兄妹两人不搭伴。
1878 | 第一盘刘玉和丽丽对王建和小雅;第二盘王建和小花对刘玉和马明的妹妹。问丽丽、小雅和小花各是谁的妹妹?
1879 |
1880 | ### 例题4
1881 |
1882 | 一天,唐僧师徒四人路过一户人家,家里只有一个老爷爷和一个老奶奶,当唐僧师徒四人说明他们的来历后二老很热情地招待了他们,还要给他们做饭吃。唐僧见二老年事已高,决定他们自己动手做饭。他们一个在挑水,一个在烧火,一个在洗菜,一个在淘米。已知:
1883 |
1884 | (1)唐僧不挑水也不淘米;
1885 |
1886 | (2)悟空不洗菜也不挑水;
1887 |
1888 | (3)八戒不挑水也不洗菜;
1889 |
1890 | (4)假如悟空不淘米,那么沙僧就不挑水。
1891 |
1892 | 现在你知道他们分工的结果吗?
1893 |
1894 | ### 练习4
1895 |
1896 | 二年级有三个班举行数学竞赛,分别从三个班中选一名选手。牛牛、丁丁、田田参加抢答比赛,知道:牛牛比二(1)班的选手得分高,丁丁与二(1)班的选手得分同样多,又比二(3)班选手得分低。问牛牛、丁丁、田田各是哪班的选手?
1897 |
1898 | ### 例题5
1899 |
1900 | 甲、乙、丙三个小朋友分别喝三种不同的饮料,有另外三个小朋友猜他们喝的各是什么?
1901 |
1902 | 当当猜:甲喝可乐,乙喝芬达;
1903 |
1904 | 咚咚猜:乙喝雪碧,丙喝可乐;
1905 |
1906 | 林林猜:丙喝芬达,乙喝可乐。
1907 |
1908 | 己知每人都只猜对了一半,那么甲、乙、丙三位小朋友各喝什么饮料?
1909 |
1910 | ### 练习5
1911 |
1912 | 甲、乙、丙、丁四人同时参加全国小学数学夏令营。赛前甲、乙、丙分别做了预测。
1913 |
1914 | 甲说:丙第1名,我第3名。
1915 |
1916 | 乙说:我第1名,丁第4名。
1917 |
1918 | 丙说:丁第2名,我第3名。
1919 |
1920 | 成绩揭晓后,发现他们每人只说对了一半,你能说出他们的名次吗?
1921 |
1922 | ### 例题6
1923 |
1924 | 一个岛上住着说谎话的和说真话的两种人。说谎话的人句句是谎话,说真话的人句句是实话。如果有一天,你去岛上探险,碰到了岛上的三个人:王、李和张,相互交谈中,有这样一段对话。
1925 |
1926 | 王说:李和张都说谎。
1927 |
1928 | 李说:我没有说谎。
1929 |
1930 | 张说:李确实在说谎。
1931 |
1932 | 小朋友,你能知道他们三人中,有几个人说谎,有几个人说真话吗?
1933 |
1934 | ### 练习6
1935 |
1936 | 三只小猴子聪聪、淘淘、皮皮见到一个水果,他们分别判断这是什么水果。
1937 |
1938 | 聪聪判断:不是苹果,也不是梨。
1939 |
1940 | 淘淘判断:不是苹果,而是桃子。
1941 |
1942 | 皮皮判断:不是桃子,而是苹果。
1943 |
1944 | 老猴子告诉他们:有一只小猴子的判断完全正确,有一只小猴子说对了半,而另一只小猴子完全说错了。你知道三只小猴中谁是对的,谁是错的,谁是只对一半的吗?
1945 |
1946 | ### 拓展1
1947 |
1948 | 传说有个说谎国,这个国家的男人在星期四、五、六、日说真话,在星期一、二、三说假话;女人在星期一、二、三、日说真话,在星期四、五、六说假话.有一天,一个人到说谎国去旅游,他在那里认识了一男一女.男人说:“昨天我说的是假话”,女人说:“昨天也是我说假话的日子”.这下,那个外来的游人可发愁了,到底今天星期几呢?请同学们根据他们说的话,判断一下今天是星期几呢?
1949 |
1950 | ### 拓展2
1951 |
1952 | 张明、席辉和李刚在北京、上海和天津工作,他们的职业是工人、农民和教师,已知:
1953 |
1954 | (1)张明不在北京工作,席辉不在上海工作;
1955 |
1956 | (2)在北京工作的不是教师;
1957 |
1958 | (3)在上海工作的是工人;
1959 |
1960 | (4)席辉不是农民。
1961 |
1962 | 问:这三人各住哪里?各是什么职业?
1963 |
1964 | ### 拓展3
1965 |
1966 | 根据条件判断旅游团去了A、B、C、D、E中的哪几个地方?
1967 |
1968 | (1)如果去A,就必须去B;
1969 |
1970 | (2)D、E两地至少去一地;
1971 |
1972 | (3)B、C两地只能去一地;
1973 |
1974 | (4)C、E两地要去都去,要不去都不去;
1975 |
1976 | (5)若去D,则A、E两地必须去。
1977 |
1978 | ### 拓展4
1979 |
1980 | 甲、乙、丙、丁在谈论他们及他们的同学何伟的居住地。
1981 |
1982 | 甲说:我和乙都住在北京,丙住在天津;
1983 |
1984 | 乙说:我和丁都住在上海,丙住在天津;
1985 |
1986 | 丙说:我和甲都不住在北京,何伟住在南京;
1987 |
1988 | 丁说:甲和乙都住在北京,我住在广州。
1989 |
1990 | 假定他们每个人都说了两句真话,一句假话。问:不在场的何伟住在哪儿?
1991 |
1992 | ### 拓展5
1993 |
1994 | 宝宝、贝贝、聪聪每人有两个外号,人们有时以“数学博士”、“短跑健将”、“跳高冠军”、“小画家”、“大作家”和“歌唱家”称呼他们,此外:
1995 |
1996 | (1)数学博士夸跳高冠军跳的高
1997 |
1998 | (2)跳高冠军和大作家常与宝宝一起看电影
1999 |
2000 | (3)短跑健将请小画家画贺年卡
2001 |
2002 | (4)数学博士和小画家关系很好
2003 |
2004 | (5)贝贝向大作家借过书
2005 |
2006 | (6)聪聪下象棋常赢贝贝和小画家
2007 |
2008 | 问:宝宝、贝贝、聪聪各有哪两个外号吗?
2009 |
2010 | ## 2.2.14. 重叠问题
2011 |
2012 | ### 热身1
2013 |
2014 | ### 热身2
2015 |
2016 | ### 热身3
2017 |
2018 | ### 例题1
2019 |
2020 | 把两根长为20寸的短尺用绳子捆成一根长尺,中间捆在一起的重叠部分是3寸。捆成的长尺长多少寸?
2021 |
2022 | ### 练习1
2023 |
2024 | 有四块均长80厘米的木板,钉成一块长木板,中间钉在一起重叠的部分均是10厘米,钉成的长木板长多少厘米?
2025 |
2026 | ### 例题2
2027 |
2028 | 将两张同样长的纸粘成了一张长为80才的长纸条,其中粘在一起的部分长10寸,这两张纸条各长多少寸?
2029 |
2030 | ### 练习2
2031 |
2032 | 有两根铁丝,一根长为30厘米,另一根长为50厘米,将这两根铁丝焊接成一根长为75厘米的长铁丝。那么,中间的焊接重叠部分长为多少厘米?
2033 |
2034 | ### 例题3
2035 |
2036 | 私塾的学生都要参加比赛,有30人参加蹴鞠队,有27人参加毽子队。其中8人两种比赛都参加。一共有学生多少人?
2037 |
2038 | ### 练习3
2039 |
2040 | 二(1)班同学所有人都参加课外活动,有20人参加英语班,有26人参加电脑班。其中4人两个班都参加。二(1)班一共有多少人?
2041 |
2042 | ### 例题4
2043 |
2044 | 20个学生参加琵琶表演和古筝表演,其中有16人参加了琵琶表演,12人参加了古筝表演。问两种表演都参加的有多少学生?
2045 |
2046 | ### 练习4
2047 |
2048 | 春天来了,全班52人到北海公园划船,有27人划了手摇船,29人划了脚踏船,4名同学因身体不好没有划船而去游览了白塔。问:既划了手摇船也划了脚踏船的同学有多少人?
2049 |
2050 | ### 例题5
2051 |
2052 | 有蓝色和红色两种珠花,每人至少选一种,共有48人,有30人选了蓝色珠花,有13人两种都选了,那么选红色珠花的有多少人?
2053 |
2054 | ### 练习5
2055 |
2056 | 学校开设了自然和趣味数学两门选修课,每个同学至少要选一门,二(3)班共有56人,有30人选了自然课,有12人两门都选了,那么选趣味数学课的同学有多少人?
2057 |
2058 | ### 例题6
2059 |
2060 | 工厂筛选制镜工人,总共有60人报名参加。经过一段时间的训练后,有33人学会了制作星云镜,有25人学会了制作幻镜,其中既会制作星云镜又会制作幻镜的有10人。那么既不会制作星云镜又不会制作幻镜的有多少人?
2061 |
2062 | ### 练习6
2063 |
2064 | 某班共有46人,参加美术小组的有12人,参加音乐小组的有23人,有5人两个小组都参加了。这个班既没有参加美术小组也没参加音乐小组的有多少人?
2065 |
2066 | ## 2.2.15. 复杂的树阵图
2067 |
2068 | ### 热身1
2069 |
2070 | ### 热身2
2071 |
2072 | ### 热身3
2073 |
2074 | ### 例题1(辐射型)
2075 |
2076 | 把1,2,4,5,6,8,10这7个数分别填入图中的圆圈中,使得每条直线上4个数的和都等于20。
2077 |
2078 | 
2079 |
2080 | ### 练习1
2081 |
2082 | 把8,9,10,11,12,14,16这7个数分别填入图中的圆圈中,使得每条直线上4个数的和都等于46。
2083 |
2084 | ### 例题2
2085 |
2086 | 将5,9,13,14,17,21,25这7个数分别填入图中的圆圈中,使得每条直线上的3个数的和都等于44。
2087 |
2088 | 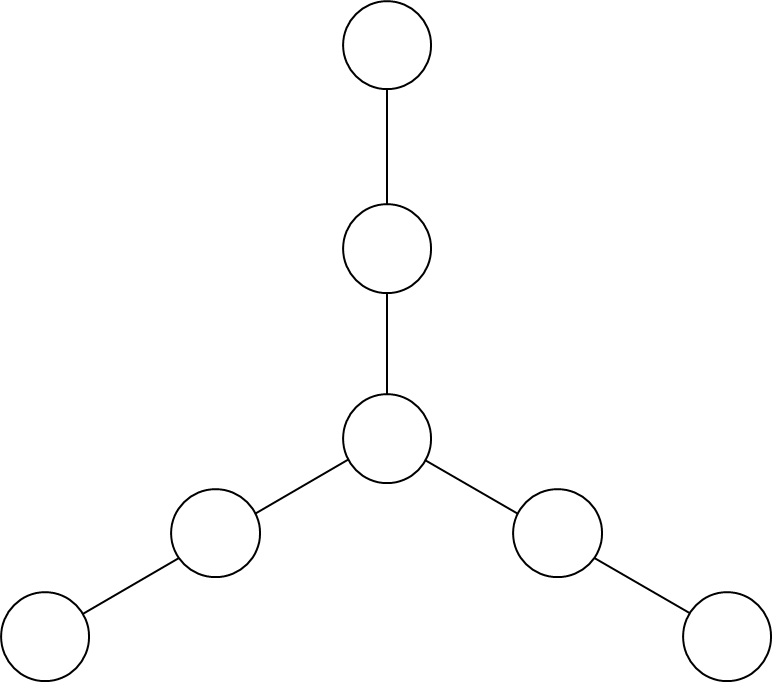
2089 |
2090 | ### 练习2
2091 |
2092 | 将5,8,11,14,17,20,23这7个数分别填入图中的圆圈中,使得每条直线上的3个数的和都等于36。
2093 |
2094 | ### 例题3(封闭型)
2095 |
2096 | 把2,3,4,5,6,7,8这7个数分别填入图中的圆圈中,使两个正方形中4个数之和都等于19。
2097 |
2098 | ### 练习3
2099 |
2100 | 把2,3,4,5,6,7,8这7个数分别填入图中的圆圈中,使两个正方形中4个数之和都等于21。
2101 |
2102 | ### 例题4
2103 |
2104 | 把1,5,9,10,16,21这6个数分别填入图中的圆圈中,使每一个大圆上的4个数之和都等于36。
2105 |
2106 | ### 练习4
2107 |
2108 | 把1,2,4,5,6,11这6个数分别填入图中的圆圈中,使每一个大圆上的4个数之和都等于22。
2109 |
2110 | ### 例题5
2111 |
2112 | 将5,6,9,11,14,15这6个数分别填入图中的圆圈中,使两个大圆上4个数的和都等于40。
2113 |
2114 | ### 练习5
2115 |
2116 | 将4,7,9,12,15,17这6个数分别填入图中的圆圈中,使两个大圆上4个数的和都等于43。
2117 |
2118 | ### 例题6
2119 |
2120 | 将1,3,4,5,6,8,11,15这8个数分别填入图中的圆圈中,使两个大圆上5个数的和都等于33。
2121 |
2122 | ### 练习6
2123 |
2124 | 将2,5,6,8,10,12,14,22这8个数分别填入图中的圆圈中,使两个大圆上5个数的和都等于49。
2125 |
2126 | ## 2.2.16. 年龄问题初步
2127 |
2128 | ### 例题1
2129 |
2130 | 丁丁今年8岁,爸爸的年龄是丁丁的4倍,4年前,爸爸的年龄和丁丁相差几岁?
2131 |
2132 | ### 练习1
2133 |
2134 | 田田今年6岁,妈妈今年36岁,再过6年,田田读初中时,妈妈比田田大多少岁?
2135 |
2136 | ### 例题2
2137 |
2138 | 田田今年10岁,博士今年55岁,当田田17岁时,博士多少岁?
2139 |
2140 | ### 练习2
2141 |
2142 | 小芳今年10岁,妈妈比她大28岁,当小芳15岁时,妈妈多少岁?
2143 |
2144 | ### 例题3
2145 |
2146 | 今年小王子8岁,大王子14岁,当两人的年龄之和是40岁时,应该是几年之后?
2147 |
2148 | ### 练习3
2149 |
2150 | 今年太子8岁,王后34岁,当太子和王后两人的年龄和是50岁时,太子多少岁?王后多少岁?
2151 |
2152 | ### 例题4
2153 |
2154 | 爸爸今年40岁,妈妈今年38岁,儿子今年12岁,当爸爸、妈妈、儿子三人的年龄和是81岁时,爸爸多少岁?妈妈多少岁?儿子多少岁?
2155 |
2156 | ### 练习4
2157 |
2158 | 李文今年9岁,爸爸、妈妈的年龄和是81岁,问:多少年后他们三个的平均年龄是40岁?
2159 |
2160 | ### 例题5
2161 |
2162 | 李斯、韩非现在的年龄和是62岁,5年前,李斯比韩非大6岁,今年李斯、韩非两人各多少岁?
2163 |
2164 | ### 练习5
2165 |
2166 | 爸爸、妈妈现在的年龄和是72岁;5年后,爸爸比妈妈大6岁。今年爸爸妈妈二人各多少岁?
2167 |
2168 | ### 例题6
2169 |
2170 | 姐姐5年前的年龄与妹妹3年后的年龄相等,问姐姐和妹妹相差多少岁?
2171 |
2172 | ### 练习6
2173 |
2174 | 小明12年后的年龄与妈妈12年前的年龄相等,问小明和妈妈相差多少岁?
2175 |
2176 | ## 2.2.17. 画图法综合
2177 |
2178 | ### 热身1
2179 |
2180 | ### 热身2
2181 |
2182 | ### 热身3
2183 |
2184 | ### 例题1(排队问题)
2185 |
2186 | 小朋友们排成一个长方形队伍表演体操。
2187 | (1)从左边数起,小华排第18,从右边数起,小明排第16,小华的左边是小明,这一行共有多少人?
2188 | (2)从左面数小红排在第2个,小军排在小红右面第4个,那么小军从右往左数排在第几个?
2189 |
2190 | ### 练习1
2191 |
2192 | 一群小动物排队表演节目,小猪第18个出场,小狗表演完后面还有16个节目,已知小猪后面第二个节目是小狗表演的,求一共有多少个节目?
2193 |
2194 | ### 例题2(鸡兔同笼)
2195 |
2196 | 王大妈去市场上买回来了一些鸡和兔,她把鸡、兔关在同一个笼子里,数了数,共有11个头,30条腿,你知道王大妈买回来了几只鸡?几只兔?
2197 |
2198 | ### 练习2
2199 |
2200 | 鸡兔同笼,共有7个头,20条腿,有多少只鸡?多少只兔?
2201 |
2202 | ### 例题3(年龄问题)
2203 |
2204 | 爸爸、妈妈、小敏三人的年龄总和是73岁,爸爸比妈妈大3岁,小敏比妈妈小23岁。小敏今年多少岁?
2205 |
2206 | ### 练习3
2207 |
2208 | 三个小朋友比年龄,小明比小英小5岁,小方比小明大2岁。那么小英和小方差几岁?
2209 |
2210 | ### 例题4(画线段图)
2211 |
2212 | 一筐鲜鱼,连筐共重56千克。先卖出鲜鱼的一半,再卖出剩下的一半,这时连筐还重17千克。原来这筐鲜鱼重多少干克?
2213 |
2214 | ### 练习4
2215 |
2216 | 玻璃瓶里装着一些水,把水加到原来的2倍时,和瓶一起称重5千克;把水加到原来的4倍时,重为9千克,问原来水有多少千克?
2217 |
2218 | ### 例题5(盈亏问题)
2219 |
2220 | 田田到文具店买练习本,她带的钱若买4本,还剩2元;若买5本,就差7元。问田田一共带了多少钱?
2221 |
2222 | ### 练习5
2223 |
2224 | 牛牛妈妈到水果店买苹果,她带的钱若买4千克还剩8元;若买5千克,就差2元。问牛牛妈妈一共带了多少钱?
2225 |
2226 | ### 例题6
2227 |
2228 | 丁丁和牛牛都想买一个饼,但丁丁的钱币少2枚,牛牛的钱币少3枚。如果两个人的钱币合在一起就刚够买一个饼。问买一个饼需要多少枚钱币?丁丁和牛牛各有多少枚钱币?
2229 |
2230 | ### 练习6
2231 |
2232 | 王强和李明都想买一本《趣味数学》,但王强的钱少2元5角,李明的钱少3元1角。如果两个人的钱合在一起就刚够买这本书。问一本《趣味数学》多少钱?王强和李明各有多少钱?
2233 |
2234 | ### 拓展1
2235 |
2236 | 81 位同学排成 9 行 9 列的正方形队列表演体操,小花在队列中,正左边有 2 位同学,正前方有3位同学,这时整个队列的同学向右转,则小花的正前方有几位同学?正右边有几位同学?
2237 |
2238 | ### 拓展2
2239 |
2240 | 鸡兔同笼,共有60个头,且鸡腿是兔腿的2倍,有多少只鸡?多少只兔?
2241 |
2242 | ### 拓展3
2243 |
2244 | 14年前爸爸的年龄是儿子的5倍, 14年后父子二人年龄和是98岁,父子二人今年分别多少岁?
2245 |
2246 | ### 拓展4
2247 |
2248 | 学生们划船,如果每只船坐5人,则还有3人无船坐,如果其中两只船坐4人,其余的船每只坐6人,就恰好坐完所有学生,共有学生多少人?
2249 |
2250 | ### 拓展5
2251 |
2252 | 甲乙丙丁四个同学共买了37朵花,如果甲多买2朵,乙少买3多,丙买的朵数变成现在的2倍,丁买的朵数减少一半,那么四个人买的朵数正好相同。请问原来四个人各买了多少朵花?
2253 |
2254 | ## 2.2.18. 等式加减法
2255 |
2256 | ### 热身1
2257 |
2258 | 15个小朋友排队报数,从前边报起,牛牛报10,从后往前报起,丁丁报12,求从牛牛数到丁丁一共有多少人?
2259 |
2260 | ### 热身2
2261 |
2262 | 牛牛、田田、丁丁三个人分糖块。田田比丁丁多3块,牛牛比田田多2块。已知糖块总块数是50块,那么每人各分到多少块?
2263 |
2264 | ### 热身3
2265 |
2266 | 买4个足球和2个排球,共用去102元,已知每个足球比每个排球贵3元。问每个足球和排球各多少元?
2267 |
2268 | ### 例题1
2269 |
2270 | 下面不同的图各代表一个数,你知道它们各代表几吗?
2271 |
2272 | (1)
2273 |
2274 | $🍎+🍐+🍐=13$
2275 |
2276 | $🍎+🍐=10$
2277 |
2278 | $🍎=()$
2279 |
2280 | $🍐=()$
2281 |
2282 | (2)
2283 |
2284 | $🍊+🍊+🍑=15$
2285 |
2286 | $🍊+🍑=9$
2287 |
2288 | $🍊=()$
2289 |
2290 | $🍑=()$
2291 |
2292 | ### 练习1
2293 |
2294 | 下面等式中,□和△各表示几?
2295 | 已知:
2296 |
2297 | $□+□+△=16$
2298 | $□+□+△+△+△=24$
2299 | 求:
2300 |
2301 | $□=()$
2302 | $△=()$
2303 |
2304 | ### 例题2
2305 |
2306 | 下面不同的图各代表一个数,你知道它们各代表几吗?
2307 |
2308 | $🍇+🍎=16$
2309 |
2310 | $🍇-🍎=2$
2311 |
2312 | $🍎=()$
2313 |
2314 | $🍇=()$
2315 |
2316 | ### 练习2
2317 |
2318 | 下面不同的图各代表一个数,你知道它们各代表几吗?
2319 |
2320 | $🍌+🍓=15$
2321 |
2322 | $🍌-🍓=3$
2323 |
2324 | $🍌=()$
2325 |
2326 | $🍓=()$
2327 |
2328 | ### 例题3
2329 |
2330 | 你能根据下面两个等式,求出🍊和🍍各表示什么数吗?
2331 |
2332 | $🍊+🍊+🍍=10$
2333 |
2334 | $🍊+🍍+🍍=11$
2335 |
2336 | $🍊=()$
2337 |
2338 | $🍍=()$
2339 |
2340 | ### 练习3
2341 |
2342 | 已知:
2343 |
2344 | $☆+☆+☆+△+△=13$
2345 | $☆+☆+△+△+△=12$
2346 |
2347 | 求:
2348 |
2349 | $☆=()$
2350 | $△=()$
2351 |
2352 | ### 例题4
2353 |
2354 | 下面△、☆、▲各代表什么数?
2355 |
2356 | $△+☆=23$
2357 |
2358 | $△+▲=33$
2359 |
2360 | $☆+▲=30$
2361 |
2362 | ### 练习4
2363 |
2364 | 三种兔子各多少只?
2365 | 黑兔+白兔=6
2366 | 黑兔+灰兔=7
2367 | 白兔+灰兔=5
2368 |
2369 | ### 铺垫
2370 |
2371 | 根据条件写等式。
2372 |
2373 | ### 例题5
2374 |
2375 | 2瓶可乐和3个面包共27元,4瓶可乐和3个面包共39元。请你算一算,每瓶可乐和每个面包各多少元?
2376 |
2377 | ### 练习5
2378 |
2379 | 牛牛去商店买文具,买了3个本子和1支铅笔一共花了10元,又知道1个本子比1支铅笔贵2元,请问1个本子和1支笔各多少钱?
2380 |
2381 | ### 例题6
2382 |
2383 | 1千克瓜子和2千克花生,一共 32元。2千克瓜子和1千克花生,一共 28元。那么瓜子和花生每千克各多少元?
2384 |
2385 | ### 练习6
2386 |
2387 | 1件上衣与2条裤子的总价是500元,这件上衣比这2条裤子的价钱贵
2388 | 100 元。则1件上衣多少钱? 1条裤子多少钱?(2条裤子是一样的)
2389 |
2390 | ### 拓展1
2391 |
2392 | 下面每种水果各代表多少?
2393 |
2394 | $🍐+🍐+🍎+🍊=16$
2395 |
2396 | $🍐+🍎+🍎+🍊=13$
2397 |
2398 | $🍐+🍎+🍊+🍊=11$
2399 |
2400 | ### 拓展2
2401 |
2402 | 饲养场出售鸡、鸭,张大爷买2只鸭和3只鸡共用42元,李大叔买3只鸭和2只鸡共用43元。1只鸭和一只鸡各多少元?
2403 |
2404 | ### 拓展3
2405 |
2406 | 小军家养了一些大白兔和小花猫。有一天,小军抱着2只大白兔一起站在体重计上称一称,正好是 45千克;后来小军放下大白兔又抱着3只小花猫,站在体重计上称一称,正好是47千克;最后小军把 6只小花猫和4只大白兔一起放在体重计上称一称是44千克。请你算一算小军、大白兔和小花猫各是多少千克?(每只大白兔的重量一样,每只小花猫的重量一样。)
2407 |
2408 | ### 拓展4
2409 |
2410 | ### 拓展5
2411 |
2412 | ## 2.2.19. 动手操作
2413 |
2414 | ### 热身1
2415 |
2416 | ### 热身2
2417 |
2418 | ### 热身3
2419 |
2420 | ### 例题1
2421 |
2422 | 大勺子一次能装油250克,小勺子一次能装油150克,你能用这两把勺子往一个空杯子里倒入350克油吗?
2423 |
2424 | ### 练习1
2425 |
2426 | 兔妈妈有一包70克的药,想要用天平从中称出5克的药,可只有一个20克的砝码,怎么办?
2427 |
2428 | ### 例题2
2429 |
2430 | 两个人要平分12千克的一大桶油。身边只有能装9千克和5千克的两只空桶,怎样倒才能使他们分到一样多的油呢?
2431 |
2432 | ### 练习2
2433 |
2434 | 一个人带着两只空桶去沟边取水,一只桶可盛5千克水,另一只可盛7千克水,现在要取8千克水,应该怎样取?
2435 |
2436 | ### 例题3
2437 |
2438 | 有九颗珍珠,其中有一颗是假珍珠,外观和真的一样,不容易看出来,只是假珍珠比真珍珠轻一些。你能利用天平,不用砝码,只称两次就找出假的珍珠吗?怎样称?
2439 |
2440 | ### 练习3
2441 |
2442 | 有八颗珍珠,其中有一颗是假珍珠,外观和真的一样,不容易看出来,只是假珍珠比真珍珠轻一些。你能利用天平,不用砝码,最少称几次就找出假的珍珠吗?怎样称?
2443 |
2444 | ### 例题4
2445 |
2446 | 黑猫警长在海关截获了一批装有牛肉罐头的9个大箱子,每箱里有很多盒罐头(大于1盒),箱子里每盒罐头重100克。在这9个大箱子中,其中有1箱罐头已经过期,不符合出口标准,过期的罐头每盒要比原来重1克。黑猫警长准备用一个大的电子称把这箱过期罐头称出来,请你帮忙想一想,最少需要称几次就能把这箱不合格的罐头找出来?
2447 |
2448 | ### 练习4
2449 |
2450 | 有10箱钢珠,每个钢珠重10克,每箱600个。如果这10箱钢珠中有1箱次品,次品钢珠每个重9克,那么,要找出这箱次品最少要称几次?
2451 |
2452 | ### 例题5
2453 |
2454 | 8个队参加扔石头大赛,比赛采用淘汰赛制,每2个队进行1场比赛,每场比赛输的1队被淘汰,最后决出冠军。同学们,请你算一算,一共要举行多少场比赛?
2455 |
2456 | ### 练习5
2457 |
2458 | 32个篮球队进行篮球比赛,裁判对他们说:“本次比赛采用淘汰赛,每2个队进行1场比赛,每场比赛输的1队被淘汰,最后决出冠军。”同学们,如果你做裁判,请你算一算一共要举行多少场比赛?
2459 |
2460 | ### 例题6
2461 |
2462 | 丁丁,牛牛,田田,阿普,小乐,5名同学参加跳绳比赛,比赛前每2个小朋友都要握一次手表示友好。当丁丁握了4次手,牛牛握了3次手,田田握了2次手,阿普握了1次手的时候,小乐握了几次手?最后这5名小朋友一共要握多少次手?
2463 |
2464 | ### 练习6
2465 |
2466 | 动物王国的动物们在比赛之前都要握手表示友好,这时,狐狸握了3次手,熊猫握了4次手,兔子也握了4次手,小猪握了3次手,狮子握了几次手呢?
2467 |
2468 | ### 拓展1
2469 |
2470 | ### 拓展2
2471 |
2472 | ### 拓展3
2473 |
2474 | ### 拓展4
2475 |
2476 | ### 拓展5
2477 |
2478 | ### 练习1
2479 |
2480 | ### 练习2
2481 |
2482 | ### 练习3
2483 |
2484 | ### 练习4
2485 |
2486 | ### 练习5
2487 |
2488 | ### 练习6
2489 |
2490 | ## 2.2.20. 必胜策略
2491 |
2492 | ### 例题1
2493 |
2494 | 桌子上放着18根火柴,甲、乙二人轮流每次取走1~3根。规定谁取走最后1根火柴谁获胜。甲先取,那么怎样取才能获胜?
2495 |
2496 | ### 练习1
2497 |
2498 | 桌子上放着50根火柴,甲、乙二人轮流每次取走1~3根。规定谁取走最后1根火柴谁获胜。如果双方均采用最佳方法,甲先取,那么怎样取才能获胜?
2499 |
2500 | ### 例题2
2501 |
2502 | 桌子上放着80根火柴,甲、乙二人轮流每次取走1~9根。规定谁取走最后1根火柴谁获胜。如果双方采用最佳方法,甲先取,那么谁将获胜?
2503 |
2504 | ### 练习2
2505 |
2506 | 桌子上放着75根火柴,甲、乙二人轮流每次取走1~4根。规定谁取走最后1根火柴谁获胜。如果双方采用最佳方法,甲先取,那么谁将获胜?
2507 |
2508 | ### 例题3
2509 |
2510 | 桌子上放着21根火柴,甲、乙二人轮流每次取走1~4根。规定谁取走最后1根火柴谁就输。如果甲想获胜,应该怎样取?
2511 |
2512 | ### 练习3
2513 |
2514 | 桌子上放着28根火柴,甲、乙二人轮流每次取走1~5根。规定谁取走最后1根火柴谁就输。甲先取,那么怎样取才能获胜?
2515 |
2516 | ### 例题4
2517 |
2518 | 两个人从1开始按自然数顺序轮流依次报数,每人每次只能报1~3个数,谁先报到30谁获胜。你选择先报数还是后报数?怎样才能获胜?
2519 |
2520 | ### 练习4
2521 |
2522 | 两个人从1开始按自然数顺序轮流依次报数,每人每次只能报1~4个数,谁先报到32谁获胜。你选择先报数还是后报数?怎样才能获胜?
2523 |
2524 | ### 例题5
2525 |
2526 | 31个方格排成一行,最左端方格中放有一枚棋子,甲先乙后轮流向右移动棋子,每次移动1~3个格。规定将棋子移到最后1格者输。甲为了获胜,第一步必须向右移多少格?
2527 |
2528 | ### 练习5
2529 |
2530 | 共有54张扑克牌,由两人轮流来抽,每次可抽1~6张,抽到最后1张牌的人就算输了,如果第一个抽牌的人想赢,第一次应该抽几张牌。
2531 |
2532 | ### 例题6
2533 |
2534 | 甲、乙两人玩游戏:有18枚棋子,两人轮流取棋子,每次允许取其中2枚、4枚或8枚,谁取到最后一枚棋子,谁就获胜。甲想获胜,先取还是后取?应该怎样取?
2535 |
2536 | ### 练习6
2537 |
2538 | 甲、乙两人玩游戏:有28枚棋子,两人轮流取棋子,每次允许取其中2枚、4枚或8枚,谁取到最后一枚棋子,谁就获胜。如果甲先取,那么第一次甲取几枚才能保证一定获胜?
2539 |
2540 | ### 拓展1
2541 |
2542 | ### 拓展2
2543 |
2544 | ### 拓展3
2545 |
2546 | ### 拓展4
2547 |
2548 | ### 拓展5
2549 |
2550 | ###
2551 |
--------------------------------------------------------------------------------
/03-三年级.md:
--------------------------------------------------------------------------------
1 | ---
2 | title: 三年级
3 | lang: zh-CN
4 | sidebarDepth: 1
5 | ---
6 |
7 | # 三年级
8 |
9 | ## 3.1.01. 找规律综合
10 |
11 | ### 例题1(递推规律)
12 |
13 | 先找出下列数排列的规律,并根据规律在括号里填上适当的数。
14 |
15 | (1)1,4,7,10,(),16,19。
16 |
17 | (2)2,6,18,(),162。
18 |
19 | ### 练习1
20 |
21 | 先找出下列各列数的排列规律,然后在括号里填上适当的数。
22 |
23 | (1)2,6,10,14,(),22,26。
24 |
25 | (2)3,6,9,12,(),18,21。
26 |
27 | ### 例题2(间隔规律)
28 |
29 | 先找出规律,然后在括号里填上适当的数。
30 |
31 | 23,4,20,6,17,8,(),(),11,12。
32 |
33 | ### 练习2
34 |
35 | 先找出规律,然后在括号里填上适当的数。
36 |
37 | (1)3,2,5,2,7,2,(),(),11,2。
38 |
39 | (2)19,3,17,3,15,3,(),(),11,3。
40 |
41 | ### 例题3(兔子数列/斐波那契数列)
42 |
43 | 在数列1,1,2,3,5,8,13,(),34,55,……中,括号里应填什么数?
44 |
45 | ### 练习3
46 |
47 | 先找出规律,然后在括号里填上适当的数。
48 |
49 | 2,2,4,6,10,16,(),()。
50 |
51 | ### 例题4(算式规律)
52 |
53 | 根据前面图形中的数之间的关系,想一想第三个图形的括号里应填什么数?
54 |
55 | 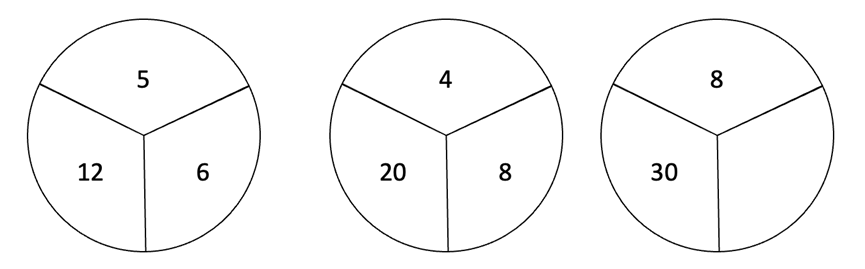
56 |
57 | ### 练习4
58 |
59 | 根据下表中的排列规律,在空格里填上适当的数。
60 |
61 | | 12 | 18 | 6 |
62 | | ---- | ---- | ---- |
63 | | 8 | 15 | 7 |
64 | | 4 | | 8 |
65 |
66 | ### 例题5
67 |
68 | 先计算下面一组算式的第一题,然后找出其中的规律,并根据规律直接写出后几题的得数。
69 |
70 | (1)12345679×9
71 |
72 | (2)12345679×18
73 |
74 | (3)12345679×54
75 |
76 | (4)12345679×81
77 |
78 | ### 练习5
79 |
80 | 计算:
81 |
82 | (1)26×11
83 |
84 | (2)38×11
85 |
86 | ### 例题6(图形规律)
87 |
88 | 观察下面由点组成的图形(点群),请回答:
89 |
90 | (1)方框内的点群包含多少个点?
91 |
92 | (2)第10个点群中包含多少个点?
93 |
94 | (3)前十个点群中,所有点的总数是多少?
95 |
96 | 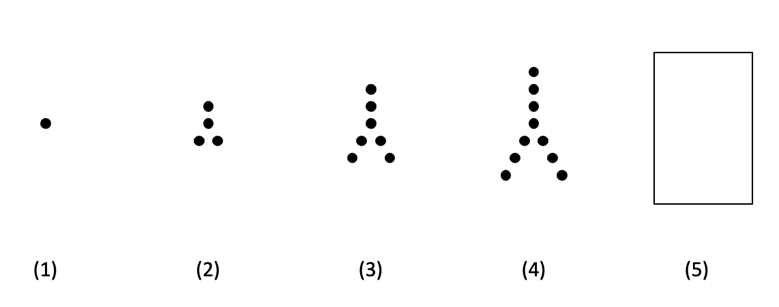
97 |
98 | ### 练习6
99 |
100 | 观察下面的图形,按规律在“?”处填上适当的图形。
101 |
102 | 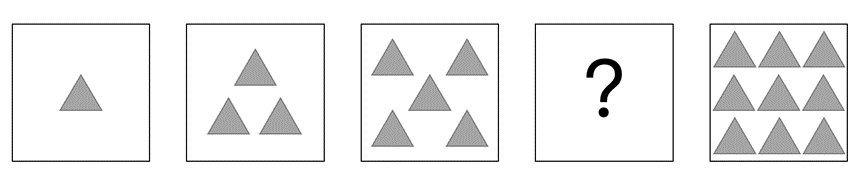
103 |
104 | ## 3.1.02. 加减法巧算综合
105 |
106 | ### 热身1
107 |
108 | 找规律填数。
109 |
110 | 10,13,18,25,(),(),58。
111 |
112 | ### 热身2
113 |
114 | 找规律填数。
115 |
116 | 3,29,4,28,6,26,9,23,(),(),18,14。
117 |
118 | ### 热身3
119 |
120 | 计算:$11+12+13+14+15+16+17+18+19=$
121 |
122 | ### 例题1(凑整法)
123 |
124 | 计算。
125 |
126 | (1)$132+23+48+257+40=$
127 |
128 | (2)$32+24+68=$
129 |
130 | ### 练习1
131 |
132 | 计算。
133 |
134 | (1)$238+45+67+62+55=$
135 |
136 | (2)$13+21+87+19=$
137 |
138 | ### 例题2(基准数)
139 |
140 | 计算。
141 |
142 | (1)$9+99+999+9999=$
143 |
144 | (2)$3998+407+89=$
145 |
146 | ### 练习2
147 |
148 | 计算。
149 |
150 | (1)$295+196+297+198+199+15=$
151 |
152 | (2)$19+199+1999=$
153 |
154 | ### 例题3
155 |
156 | 计算。
157 |
158 | (1)$268-56-82-44-18=$
159 |
160 | (2)$$
161 |
162 | ### 练习3
163 |
164 | 计算。
165 |
166 | (1)$831-155-67-145-131=$
167 |
168 | (2)$$
169 |
170 | ### 例题4
171 |
172 | 计算。
173 |
174 | (1)$300-9-19-29-39-49-59=$
175 |
176 | (2)$985-32+37-276-85+73-68=$
177 |
178 | ### 练习4
179 |
180 | 计算。
181 |
182 | (1)$818-271-18+64-29+36=$
183 |
184 | (2)$200-20-18-23-20-19-21=$
185 |
186 | ### 例题5
187 |
188 | 计算。
189 |
190 | (1)$2985-(985-276)=$
191 |
192 | (2)$$
193 |
194 | ### 练习5
195 |
196 | 计算。
197 |
198 | (1)$(123+348+400)-(23+150+148)=$
199 |
200 | (2)$$
201 |
202 | ### 例题6(分组巧算)
203 |
204 | 计算。
205 |
206 | (1)$20-19-18+17+16-15-14+13+12-11-10+9=$
207 |
208 | (2)$1+2-3-4+5+6-7-8+9+10-11-12+……-1999-2000+2001=$
209 |
210 | ### 练习6
211 |
212 | 计算。
213 |
214 | (1)$3355+4466+9977-3366-4477-9955=$
215 |
216 | (2)$$
217 |
218 | ### 例题7
219 |
220 | 【变零为整】$74+63+16-53+9+81=$
221 |
222 | 【变长为短】$38+57+36-57-36=$
223 |
224 | 【变大为小】$365-198+196+295-296=$
225 |
226 | 【变加为乘】$97+98+100+101+102=$
227 |
228 | 【位值原理】$1243+4132+2314+3421=$
229 |
230 | ### 练习7
231 |
232 | 【去括号】$2748+(1336+289)-(336+289)-748=$
233 |
234 | 【填括号】$1518-571-18+61-29+39=$
235 |
236 | ### 例题8
237 |
238 | 计算:$689-1-3-5-7-9-11-13-15-17-19$
239 |
240 | ### 练习8
241 |
242 | 计算:$9999-1-2-3-\dots-28-29-30-29-28-\dots-3-2-1$
243 |
244 | ### 拓展1
245 |
246 | 计算$1017+2017+3017+4017+5017-6017-7017$
247 |
248 | ### 拓展2
249 |
250 | 有一个很神秘的地方,那里有很多的雕塑,每个雕塑都是由蝴蝶组成的。已知一共有1000只蝴蝶,第1个雕塑有3只蝴蝶,第2个雕塑有5只蝴蝶,第3个雕塑有7只蝴蝶,第4个雕塑有9只蝴蝶,后面的雕塑按照这样的规律一直延伸到很远的地方,松松沿着雕塑走了一会,
251 | 停在了一个有39只蝴蝶的雕塑旁。那么,他们没数完的蝴蝶还剩多少只呢?
252 |
253 | ### 拓展3
254 |
255 | 书店里有一套漫画书共9册,第一册需24元,第二册需23元,第三册需22元,以此类推,每一册的售价都比它前面的一册要少1元。如果用200元去买这套漫画书,书店老板应该找回多少元呢?
256 |
257 | ## 3.1.03. 加减法竖式数字谜进阶
258 |
259 | ### 例题1
260 |
261 | 在空格内填入适当的数字,使图中的竖式成立。
262 |
263 | (1)$$\begin{matrix}
264 | & &3 &\Box &4 \\
265 | +& &\Box &5 &\Box \\
266 | \hline
267 | &\Box &1 &5 &2
268 | \end{matrix}$$
269 |
270 | (2)$$\begin{matrix}
271 | &\Box &2 &\Box \\
272 |
273 | -&2 &\Box &4 \\
274 |
275 | \hline
276 | &1 &5 &2
277 | \end{matrix}$$
278 |
279 | ### 练习1
280 |
281 | 在空格内填入适当的数字,使图中的竖式成立。
282 |
283 | (1)$$\begin{array}{c}
284 | & &6 &\Box &3 \\
285 | +& &\Box &4 &\Box \\
286 | \hline
287 | &\Box &1 &7 &2
288 | \end{array}$$
289 |
290 | (2)$$\begin{matrix}
291 | &\Box &5 &\Box \\
292 | -&4 &\Box &6 \\
293 | \hline
294 | &3 &7 &1
295 | \end{matrix}$$
296 |
297 | ### 例题2
298 |
299 | 在空格内填入适当的数字,使图中的竖式成立。
300 |
301 | (1)$$\begin{matrix}
302 | & & &7 &\Box \\
303 | +& &\Box &\Box&4 \\
304 | \hline
305 | &\Box &\Box &5 &3
306 | \end{matrix}$$
307 |
308 | (2)$$\begin{matrix}
309 | &\Box &\Box &8 &\Box \\
310 | -& &\Box &\Box &4 \\
311 | \hline
312 | & & &9 &7
313 | \end{matrix}$$
314 |
315 | ### 练习2
316 |
317 | 在空格内填入适当的数字,使图中的竖式成立。
318 |
319 | (1)$$\begin{matrix}
320 | & & &8 &\Box \\
321 | +& &\Box &\Box &2 \\
322 | \hline
323 | &\Box &\Box &6 &1
324 | \end{matrix}$$
325 |
326 | (2)$$\begin{matrix}
327 | &\Box &\Box &7 &\Box \\
328 | -& &\Box &\Box &3 \\
329 | \hline& & &9 &6
330 | \end{matrix}$$
331 |
332 | ### 例题3
333 |
334 | 在空格内填入适当的数字,使图中的竖式成立。
335 |
336 | $$\begin{matrix}
337 | & &\Box &6 &\Box \\
338 | +& &2 &\Box &6 \\
339 | \hline
340 | &\Box &\Box &\Box &\Box \\
341 | -& &\Box &\Box &\Box \\
342 | \hline
343 | & & & &1
344 | \end{matrix}$$
345 |
346 | ### 练习3
347 |
348 | 在空格内填入适当的数字,使图中的竖式成立。
349 |
350 | $$\begin{matrix}
351 | &\Box &7 &\Box &8 \\
352 | +&1 &\Box &9 &\Box \\
353 | \hline&2 &9 &0 &9
354 | \end{matrix}$$
355 |
356 | ### 例题4
357 |
358 | 在下图的竖式中,不同的汉字代表不同的数字,相同的汉字代表相同的数字,每个汉字代表什 么数时,竖算式成立?
359 |
360 | $$\begin{matrix}
361 | & & & &生 \\
362 | & & &学 &生 \\
363 | & &好 &学 &生 \\
364 | +&三 &好 &学 &生 \\
365 | \hline&2 &0 &1 &6
366 | \end{matrix}$$
367 |
368 | ### 练习4
369 |
370 | 在下图的竖式中,不同的汉字代表不同的数字,相同的汉字代表相同的数字,每个汉字代表什 么数时,竖算式成立?
371 |
372 | $$\begin{matrix}
373 | & & & &龙 \\
374 | & & &成 &龙 \\
375 | & &子 &成 &龙 \\
376 | +&望 &子 &成 &龙 \\
377 | \hline&2 &0 &1 &2
378 | \end{matrix}$$
379 |
380 | ### 例题5
381 |
382 | 在下图的竖式中,不同的字母代表不同的数字,相同的字母代表相同的数字,每个字母代表什 么数时,竖算式成立?
383 |
384 | $$\begin{matrix}
385 | & &A &B &C &D \\
386 | +& &E &B &E &D \\
387 | \hline&E &D &C &A &D
388 | \end{matrix}$$
389 |
390 | ### 练习5
391 |
392 | 如下图,算式中不同的汉字代表不同的数字,已知:”级=5“,那么”学而思“代表的三位数是多少?
393 |
394 | $$\begin{matrix}
395 | & &学 &而 &思 \\
396 | +& &1 &2 &级 \\
397 | \hline&更 &进 &1 &步
398 | \end{matrix}$$
399 |
400 | ### 例题6
401 |
402 | 下面的减法算式中,每一个字母代表一个数字,不同的字母代表不同的数字,计算:D+G。
403 |
404 | $$\begin{matrix}
405 | &A &B &C &B &D \\
406 | -& &E &F &A &G \\
407 | \hline& & &F &F &F
408 | \end{matrix}$$
409 |
410 | ### 练习6
411 |
412 | 在下图的竖式中,不同的汉字代表不同的数字,相同的汉字代表相同的数字,每个汉字代表什 么数时,竖算式成立?
413 |
414 | $$\begin{matrix}
415 | &机 &器 &人 \\
416 | +&机 &机 &人 \\
417 | \hline&器 &人 &人
418 | \end{matrix}$$
419 |
420 | ## 3.1.06. 巧求周长进阶
421 |
422 | ### 例题1
423 |
424 | 将一个大正方形剪去四个相同大小的小正方形后,计算剩下部分的周长。
425 |
426 | 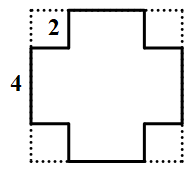
427 |
428 | ### 练习1
429 |
430 | 计算下面这个图形的周长。(单位:厘米)
431 |
432 | 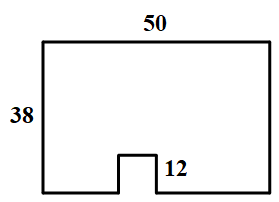
433 |
434 | ### 例题2
435 |
436 | 用五个完全相同的小长方形拼成一个如图所示的大长方形,小长方形的周长是 40 厘米,那么大长方形的周长是多少?
437 |
438 | 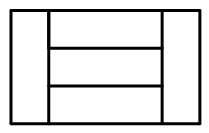
439 |
440 | ### 练习2
441 |
442 | 4个完全相同的小长方形拼成一个如图所示的大长方形,只知道小长方形的宽是2厘米,大长方形的周长是多少?
443 |
444 | 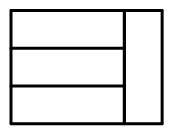
445 |
446 | ### 例题3
447 |
448 | 若每个小正方形的周长为 12厘米,则他们组合而成的“十” 字图形的周长是多少?
449 |
450 | 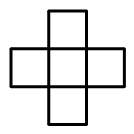
451 |
452 | ### 练习3
453 |
454 | 用五个完全相同的小正方形拼成如下图形,已知拼出图形的周长是24厘米,你知道所用小正方形的面积是多少吗?
455 |
456 | 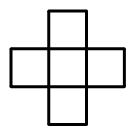
457 |
458 | ### 例题4
459 |
460 | 将一个长为12厘米,宽为6厘米的长方形纸片按照图中虚线剪成两个图形,请计算两个图形的周长之和?
461 |
462 | 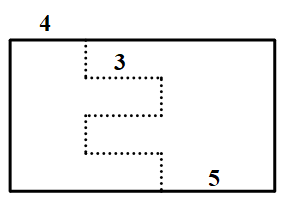
463 |
464 | ### 练习4
465 |
466 | 将一个边长为4厘米的正方形对折,再沿折线剪开,得到两个长方形,求两个长方形比原来的正方形周长多了多少。
467 |
468 | ### 例题5
469 |
470 | 用8张边长是2厘米的小正方形拼成一个长方形,这个长方形的周长是多少厘米?
471 |
472 | ### 练习5
473 |
474 | 用6张边长为3厘米的正方形纸片拼成一个长方形,这个长方形的周长是多少厘米?
475 |
476 | ### 例题6
477 |
478 | 商场举行大酬宾活动,门口将长18厘米,宽9厘米的礼品盒摆成一个有规律的形状。礼品盒前4层的样式如图所示,一共有10 层,你能算出一共摆了多少个礼品盒吗? 礼品盒摆出形状的周长是多少?
479 |
480 | 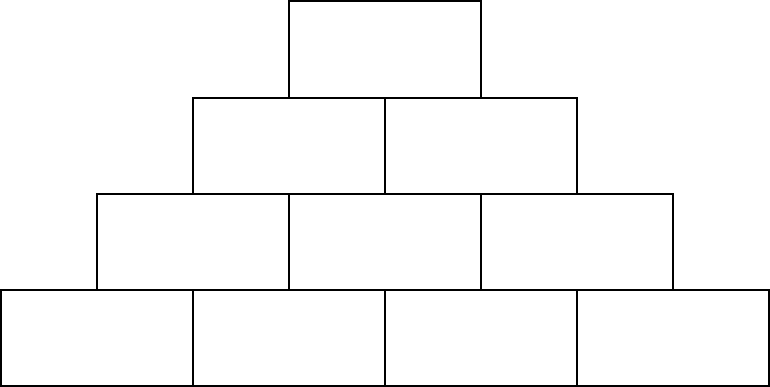
481 |
482 | ### 练习6
483 |
484 | 如图所示,长方形长4厘米,宽2厘米,现沿对角线 BD对折得到如下几何图形,试求图形阴影部分的周长。
485 |
486 | 
487 |
488 | ## 3.1.07. 平均数初步
489 |
490 | ### 例题1
491 |
492 | 幼儿园小朋友做红花,小华做了27朵,小方做了29朵,小林和小宁合做了52朵。平均每个小朋友做了多少朵?
493 |
494 | ### 练习1
495 |
496 | 一个书架上第一层放书52本,第二层和第三层共放70本,第四层放了46本,平均每层放书多少本?
497 |
498 | ### 例题2
499 |
500 | 中关村小学有15名同学参加跳绳比赛,他们跳绳的个数分别为93、94、85、92、86、88、94、91、88、89、92、86、93、90、89,求平均每人跳绳多少个?
501 |
502 | ### 练习2
503 |
504 | 下图是小华五次数学测验成绩的统计图。小华五次测验的平均分是多少分?
505 |
506 |
1540 |
1541 | ### 例题4
1542 |
1543 | 下面是用小正方体组成的立体图形,现在把这个立体图形表面都涂上绿色,数一数有多少个小正方形没有被涂上色?
1544 |
1545 | ### 练习4
1546 |
1547 | 用小正方体拼成了一个如下图的模型,然后把它粘在地上喷上红色油漆,这堆正方体中共有多少个小正方形没有被喷上颜色?
1548 |
1549 | ### 例题5
1550 |
1551 | ### 练习5
1552 |
1553 | ### 例题6
1554 |
1555 | ### 练习6
1556 |
1557 | ## 2.2.10. 周期问题初步
1558 |
1559 | ### 例题1
1560 |
1561 | 小朋友按了3女3男的顺序依次排成一队看表演,算一算第17名、第37名同学分别是男生还是女生?
1562 |
1563 | ### 练习1
1564 |
1565 | 广场上摆满花,这些花是按3盆大红、2盆金黄、2盒粉红的顺序摆放的,你
1566 | 们知道第26盆、35盆、45 盒花是什么颜色吗?
1567 |
1568 | ### 例题2
1569 |
1570 | 乐乐老师带领牛牛等人在园林里种树,他们按1棵杨树、2棵椰树、2棵松树的顺序来种,一共种了48棵树,那么杨树、椰树、松树各种了几棵?
1571 |
1572 | ### 练习2
1573 |
1574 | 某小学操场上树立着彩旗,按如下图顺序来排列,一共有 42 面旗,在这42 面彩旗中,红旗有()面,黄旗有()面?
1575 |
1576 | ### 例题3
1577 |
1578 | 丁丁用树枝在地上写了一列数,然后他停下来,让田田猜一猜,
1579 |
1580 | $2、3、1、2、3、1、2、3、1、……$
1581 |
1582 | (1)第28个数是几?
1583 |
1584 | (2)这28个数的和是多少?
1585 |
1586 | ### 练习3
1587 |
1588 | 有一列数:
1589 |
1590 | $1、4、2、1、4、2、1、4、2、1、……$
1591 |
1592 | (1)第26个数是几?
1593 |
1594 | (2)这26个数的和是多少?
1595 |
1596 | ### 例题4
1597 |
1598 | 有一列数如下所示,在这一列数中:
1599 |
1600 | $1、3、5、7、1、3、5、7、9、……$
1601 |
1602 | (1)第35个数是几?
1603 |
1604 | (2)这35个数的和是多少?
1605 |
1606 | (3)如果连续写83个数,3被写了多少次?
1607 |
1608 | ### 练习4
1609 |
1610 | $2、3、4、1、2、3、4、1、2、3、4、1、2、3、4、1、2、3、4、……$,请问:
1611 |
1612 | (1)第26个数是几?
1613 |
1614 | (2)请问这26个数的和是多少?
1615 |
1616 | (3)请问在这26个数字中,有几个“3”?
1617 |
1618 | ### 例题5
1619 |
1620 | 2014年4月5日是星期六。
1621 |
1622 | (1)从5日算起,第10天是星期几?
1623 |
1624 | (2)再过10天是星期几?
1625 |
1626 | ### 练习5
1627 |
1628 | 某年1月1日元旦是星期四,从1日算起,第12天是星期()
1629 |
1630 | ### 例题6
1631 |
1632 | 例子:
1633 |
1634 | | 1 | 2 | 1 | 2 | 1 | 2 | 1 | 2 | 1 | 2 | …… |
1635 | | ---- | ---- | ---- | ---- | ---- | ---- | ---- | ---- | ---- | ---- | ---- |
1636 | | A | B | C | A | B | C | A | B | C | A | …… |
1637 |
1638 | 在下表中,将每列上、下两个字组成一组,例如第1组为(小双),第2组为(朋手),那么第55组是什么?
1639 |
1640 | | 小 | 朋 | 友 | 荡 | 秋 | 千 | 小 | 朋 | 友 | 荡 | 秋 | 千 | 小 | 朋 | …… |
1641 | | ---- | ---- | ---- | ---- | ---- | ---- | ---- | ---- | ---- | ---- | ---- | ---- | ---- | ---- | ---- |
1642 | | 双 | 手 | 向 | 空 | 如 | 鸟 | 翼 | 双 | 手 | 向 | 空 | 如 | 鸟 | 翼 | …… |
1643 |
1644 | ### 练习6
1645 |
1646 | 下面的表格中,每一列的两个数组成一组,如第1组是由“甲A”组成,第
1647 | 2组是由“乙B”组成⋯问:第17组是由哪两个组成?
1648 |
1649 | | 甲 | 乙 | 丙 | 甲 | 乙 | 丙 | 甲 | 乙 | 丙 | 甲 | 乙 | 丙 | …… |
1650 | | ---- | ---- | ---- | ---- | ---- | ---- | ---- | ---- | ---- | ---- | ---- | ---- | ---- |
1651 | | A | B | C | D | A | B | C | D | A | B | C | D | …… |
1652 |
1653 | ### 拓展1
1654 |
1655 | 今天是2022年4月14日,星期四,请问:今年的劳动节是星期几?小代今年的生日是星期几?
1656 |
1657 | ### 拓展2
1658 |
1659 | 12个同学围成一圈做传球的游戏,如图。
1660 |
1661 | 
1662 |
1663 | (1)从1号同学开始,顺时针传100次,手绢应在谁手中?
1664 |
1665 | (2)从1号同学开始,逆时针传100次,手绢又在谁手中?
1666 |
1667 | (3)从 1号同学开始,先顺时针传156次,然后从那个同学开始逆时针传143次,最后手绢在谁手中?
1668 |
1669 | ### 拓展3
1670 |
1671 | 字母A、B、C、D、E和数字1、9分别按下列方式变动次序:
1672 |
1673 | ABCDE19
1674 |
1675 | BCDEA91(第一次变动)
1676 |
1677 | CDEAB91(第二次变动)
1678 |
1679 | DEABC19(第三次变动)
1680 |
1681 | ……
1682 |
1683 | 那么,最少经过几次变动后“ABCDE19”将再次出现。
1684 |
1685 | ### 拓展4
1686 |
1687 | A、B、C、D四个盒子中依次放有6、4、5、3个球。第1个小朋友找到放球最多的盒子,从盒子中取出 3 个球,放入其他盒子,每个盒子放一个;然后第2个小朋友也找到放球最多的盒子,从盒子中取出 3个球,放入其他盒子,每个盒子放一个。如此进行下去,当第120位小朋友放完后,C 盒中有几个球?
1688 |
1689 | ## 2.2.11. 移多补少
1690 |
1691 | 计算练习
1692 |
1693 | (1)$1+2+3+4+5+6+7+8+9+10+9+8+7+6+5+4+3+2+1$
1694 |
1695 | (2)$1+3+5+7+9+11+9+7+5+3+1$
1696 |
1697 | (3)$1+2+3+\dots+49+50+49+\dots+3+2+1$
1698 |
1699 | ### 例题1
1700 |
1701 | 牛牛和丁丁分糕点,牛牛有14块,丁丁有6块,牛牛需要拿出几块糕点给丁丁,他们的糕点数才会同样多?
1702 |
1703 | ### 练习1
1704 |
1705 | 红队有29人,黄队有15人,红队调给黄队几人,就能使两队人数相等?
1706 |
1707 | ### 例题2
1708 |
1709 | 同学们分成两队进行拔河比赛,第一队有31人,如果从第一队中调3人到第二队,这时两队的人数才会一样多。第二队原来有学生多少人?
1710 |
1711 | ### 练习2
1712 |
1713 | 牛牛有24朵花,丁丁给牛牛8朵后,两人的花朵数就相等。丁丁原来有几几朵花?
1714 |
1715 | ### 例题3
1716 |
1717 | 小花免和小白兔分萝卜,小花兔给小白兔4个萝卜后,小花免还比小白兔多
1718 | 2个。小花兔原来比小白兔多几个萝卜?
1719 |
1720 | ### 练习3
1721 |
1722 | 小花兔和小白兔分萝卜,小花兔给小白兔4个萝卜后,小花免比小白免少
1723 | 2个。小花兔原来比小白兔多几个萝卜?
1724 |
1725 | ### 例题4
1726 |
1727 | 小山羊和小白免一共拔了30个萝卜放进两筐里,小白免从大筐里拿出6个放进小筐里,现在两筐萝卜的个数同样多。原来小筐里有多少个萝卜?
1728 |
1729 | ### 练习4
1730 |
1731 | 甲、乙两筐西瓜共28个,从甲筐取4个放入乙筐中,两筐西瓜个数相同。
1732 | 原来甲、乙两筐各有多少个西瓜?
1733 |
1734 | ### 例题5
1735 |
1736 | 妈妈买了2袋苹果,甲袋是54个,乙袋是22个。每次从多的1袋取出4个放到少的1袋里,拿几次才能使两袋苹果的个数相等呢?
1737 |
1738 | ### 练习5
1739 |
1740 | 小华有两盒糖果,甲盒有糖78粒,乙盒有糖38粒,每次从甲盒取5粒糖放到
1741 | 乙盒,取几次两盒糖的粒数就同样多?
1742 |
1743 | ### 例题6
1744 |
1745 | 两堆香蕉一样多,现在从第一堆里面拿出4把香蕉放入第二堆,这时第二堆的香蕉是第一堆的2倍,原来两堆香蕉各有多少把?
1746 |
1747 | ### 练习6
1748 |
1749 | 哥哥和弟弟集邮,原来两人的邮票张数相等,如果哥哥给弟弟9张邮票,则弟弟的邮票张数是哥哥的3倍,哥哥、弟弟原来各有邮票多少张?
1750 |
1751 | ### 拓展1
1752 |
1753 | 小东、小西、小北3个同学带着15个筐去摘桃,摘完后,有5筐装满了桃,5筐装了半筐桃,5筐空着,怎样分,才能让他们3人每人分到的桃一样多,筐也一样多?
1754 |
1755 | ### 拓展2
1756 |
1757 | 大毛、二毛和三毛三个小朋友出去玩,各自摘了一些小草莓,大毛把自己摘得草莓给了二毛 2 个后,大毛比二毛多 1 个,接着,二毛又把自己摘草莓给了三毛 2 个,此时二毛和三毛的草莓变得一样多,那么原来大毛和三毛两个人摘得草莓数量谁更多?多几个?
1758 |
1759 | ### 拓展3
1760 |
1761 | 小白、小灰和小花三只小猫去河里分别捉了一些鱼。如果小花给小白 5 条鱼,那么小花比小白还多 2 条鱼;如果小灰给小花 4 条鱼,那么小灰就比小花少 3 条鱼,请问原来小灰比小白多多少条鱼?
1762 |
1763 | ### 拓展4
1764 |
1765 | 小白、小灰和小花三只小猫去河里捉了一些鱼。如果小白给小花一些鱼后,小花和小白拥有的鱼就一样多了,都是 42 条;如果小灰给小白一些鱼后,小灰和小白拥有的鱼就一样多了,都是 47 条鱼,如果小灰给小花一些鱼后,小灰和小花拥有的鱼就一样多了,都是 46条。那小灰有几条鱼。
1766 |
1767 | ## 2.2.12. 和差问题
1768 |
1769 | ### 例题1
1770 |
1771 | 牛牛和丁丁总共有46个玻璃球,丁丁比牛牛多6个。请大家帮忙算一算,牛牛和丁丁各有多少个玻璃球?
1772 |
1773 | ### 练习1
1774 |
1775 | 今年姐姐和妹妹的年龄和是14岁,姐姐比妹妹大4岁,问姐姐、妹妹今年各多少岁?
1776 |
1777 | ### 例题2
1778 |
1779 | 牛牛和丁丁写大字的速度不变,两人两天一共写了120个字,已知牛牛每天比丁丁多写10个,请问丁丁和牛牛每天各写几个大字?
1780 |
1781 | ### 练习2
1782 |
1783 | 牛牛和丁丁保持自己相同的速度折飞机,牛牛每小时比丁丁多折10个,他们两人用了3小时共折飞机150个,牛牛和丁丁每小时各折多少个飞机?
1784 |
1785 | ### 例题3
1786 |
1787 | 动物学校有个长方形操场,它的长与宽相差80米,沿操场跑一圈是400米,求动物学校操场的长与宽各是多少?
1788 |
1789 | ### 练习3
1790 |
1791 | 蚂蚁沿着阿普的课本四周爬了一圈是200厘米,知道课本的长边比短边多30厘米,问阿普课本的长边和短边各是多少厘米?
1792 |
1793 | ### 例题4
1794 |
1795 | 牛牛在这次测验中,语文和数学的平均分是95分,语文比数学多6分,牛牛在这次测验中,语文和数学各得了多少分?
1796 |
1797 | ### 练习4
1798 |
1799 | 牛牛和丁丁的平均身高是130厘米,牛牛比丁丁高10厘米,丁丁和牛牛的身高各是多少厘米?
1800 |
1801 | ### 例题5
1802 |
1803 | 豆豆和毛毛一共有34个巧克力豆,两人都吃了同样的巧克力豆后,分别还剩15个和11个,问原来豆豆和毛毛各有多少个巧克力豆?
1804 |
1805 | ### 练习5
1806 |
1807 | 大毛、二毛共有33元,两人花掉同样的钱后,大毛还有19元,二毛还有6元,问原来大毛、二毛各有多少钱?
1808 |
1809 | ### 例题6
1810 |
1811 | 牛牛3年前的年龄与阿普2年后的年龄之和是23岁,牛牛3年后的年龄等于阿普1年前的年龄,求牛牛、阿普今年的年龄各是多少岁?
1812 |
1813 | ### 练习6
1814 |
1815 | 红红2年前的年龄与果果1年后的年龄相等,红红3年前的年龄与果果2年后的年龄和为18岁,则红红、果果今年各多少岁?
1816 |
1817 | ### 巩固1
1818 |
1819 | 维尼熊和跳跳虎去摘苹果。跳跳虎每摘7个,维尼熊只能摘4个。维尼熊摘了16分钟,跳跳虎摘了10分钟就累了,不摘了。他们回来后数了一下,共摘了670个苹果,那么其中维尼熊摘的苹果有多少个?
1820 |
1821 | ### 巩固2
1822 |
1823 | 甲、乙、丙3个数的和是99,如果甲加上10,乙减少5,丙减少2,则3个数相等。这3个数各是几?
1824 |
1825 | ### 巩固3
1826 |
1827 | 三块布料一共190米,第二块比第一块长20米,第三块比第二块长30米,每块布料各长多少米?
1828 |
1829 | ## 2.2.13. 逻辑推理进阶
1830 |
1831 | ### 热身1
1832 |
1833 | ### 热身2
1834 |
1835 | ### 热身3
1836 |
1837 | ### 例题1
1838 |
1839 | 乐乐老师、红红、丁丁、牛牛和田田一起去爬山。牛牛在丁丁和田田之前爬到终点,田田是紧跟着牛牛之后爬到终点的。有两个人在乐乐老师之后、丁丁之前爬到终点。这5个人登山到终点的先后顺序是怎样的?
1840 |
1841 | ### 练习1
1842 |
1843 | 田田比牛牛跑得慢,牛牛比加加跑得快,加加比减减跑得快,减减比田田跑得快。谁跑得最快?谁跑得最慢?
1844 |
1845 | ### 例题2
1846 |
1847 | 体育馆里正在进行一场精彩的乒乓球双打比赛。两位播音员正在议论这四个运动员的年龄问题:
1848 |
1849 | (1)小A比小B年轻;
1850 |
1851 | (2)小C比他的两个对手年龄都大;
1852 |
1853 | (3)小A比小D年龄大;
1854 |
1855 | (4)小B比小C年龄大。
1856 |
1857 | 请分析一下他们四人的年龄顺序,谁年龄最大?谁年龄最小?
1858 |
1859 | ### 练习2
1860 |
1861 | 2号大楼比3号大楼高,4号大楼比3号大楼低,1号大楼比2号大楼高,1号大楼比4号大楼高,几号大楼是最高的?几号大楼是最低的?
1862 |
1863 | ### 例题3
1864 |
1865 | 赵、钱、孙三人中,一位是射击运动员,一位是体操运动员,一位是跳水运动员。已知:
1866 |
1867 | (1)赵比体操运动员体重重;
1868 |
1869 | (2)钱和体操运动员体重不同;
1870 |
1871 | (3)赵和跳水运动员是朋友。
1872 |
1873 | 你能猜出谁是射击运动员,谁是体操运动员,谁是跳水运动员吗?
1874 |
1875 | ### 练习3
1876 |
1877 | 刘玉、马明、王建三个男孩都有一个妹妹,是小雅、小花、丽丽。6个人在一起打球,举行男女混合双打。事先规定,兄妹两人不搭伴。
1878 | 第一盘刘玉和丽丽对王建和小雅;第二盘王建和小花对刘玉和马明的妹妹。问丽丽、小雅和小花各是谁的妹妹?
1879 |
1880 | ### 例题4
1881 |
1882 | 一天,唐僧师徒四人路过一户人家,家里只有一个老爷爷和一个老奶奶,当唐僧师徒四人说明他们的来历后二老很热情地招待了他们,还要给他们做饭吃。唐僧见二老年事已高,决定他们自己动手做饭。他们一个在挑水,一个在烧火,一个在洗菜,一个在淘米。已知:
1883 |
1884 | (1)唐僧不挑水也不淘米;
1885 |
1886 | (2)悟空不洗菜也不挑水;
1887 |
1888 | (3)八戒不挑水也不洗菜;
1889 |
1890 | (4)假如悟空不淘米,那么沙僧就不挑水。
1891 |
1892 | 现在你知道他们分工的结果吗?
1893 |
1894 | ### 练习4
1895 |
1896 | 二年级有三个班举行数学竞赛,分别从三个班中选一名选手。牛牛、丁丁、田田参加抢答比赛,知道:牛牛比二(1)班的选手得分高,丁丁与二(1)班的选手得分同样多,又比二(3)班选手得分低。问牛牛、丁丁、田田各是哪班的选手?
1897 |
1898 | ### 例题5
1899 |
1900 | 甲、乙、丙三个小朋友分别喝三种不同的饮料,有另外三个小朋友猜他们喝的各是什么?
1901 |
1902 | 当当猜:甲喝可乐,乙喝芬达;
1903 |
1904 | 咚咚猜:乙喝雪碧,丙喝可乐;
1905 |
1906 | 林林猜:丙喝芬达,乙喝可乐。
1907 |
1908 | 己知每人都只猜对了一半,那么甲、乙、丙三位小朋友各喝什么饮料?
1909 |
1910 | ### 练习5
1911 |
1912 | 甲、乙、丙、丁四人同时参加全国小学数学夏令营。赛前甲、乙、丙分别做了预测。
1913 |
1914 | 甲说:丙第1名,我第3名。
1915 |
1916 | 乙说:我第1名,丁第4名。
1917 |
1918 | 丙说:丁第2名,我第3名。
1919 |
1920 | 成绩揭晓后,发现他们每人只说对了一半,你能说出他们的名次吗?
1921 |
1922 | ### 例题6
1923 |
1924 | 一个岛上住着说谎话的和说真话的两种人。说谎话的人句句是谎话,说真话的人句句是实话。如果有一天,你去岛上探险,碰到了岛上的三个人:王、李和张,相互交谈中,有这样一段对话。
1925 |
1926 | 王说:李和张都说谎。
1927 |
1928 | 李说:我没有说谎。
1929 |
1930 | 张说:李确实在说谎。
1931 |
1932 | 小朋友,你能知道他们三人中,有几个人说谎,有几个人说真话吗?
1933 |
1934 | ### 练习6
1935 |
1936 | 三只小猴子聪聪、淘淘、皮皮见到一个水果,他们分别判断这是什么水果。
1937 |
1938 | 聪聪判断:不是苹果,也不是梨。
1939 |
1940 | 淘淘判断:不是苹果,而是桃子。
1941 |
1942 | 皮皮判断:不是桃子,而是苹果。
1943 |
1944 | 老猴子告诉他们:有一只小猴子的判断完全正确,有一只小猴子说对了半,而另一只小猴子完全说错了。你知道三只小猴中谁是对的,谁是错的,谁是只对一半的吗?
1945 |
1946 | ### 拓展1
1947 |
1948 | 传说有个说谎国,这个国家的男人在星期四、五、六、日说真话,在星期一、二、三说假话;女人在星期一、二、三、日说真话,在星期四、五、六说假话.有一天,一个人到说谎国去旅游,他在那里认识了一男一女.男人说:“昨天我说的是假话”,女人说:“昨天也是我说假话的日子”.这下,那个外来的游人可发愁了,到底今天星期几呢?请同学们根据他们说的话,判断一下今天是星期几呢?
1949 |
1950 | ### 拓展2
1951 |
1952 | 张明、席辉和李刚在北京、上海和天津工作,他们的职业是工人、农民和教师,已知:
1953 |
1954 | (1)张明不在北京工作,席辉不在上海工作;
1955 |
1956 | (2)在北京工作的不是教师;
1957 |
1958 | (3)在上海工作的是工人;
1959 |
1960 | (4)席辉不是农民。
1961 |
1962 | 问:这三人各住哪里?各是什么职业?
1963 |
1964 | ### 拓展3
1965 |
1966 | 根据条件判断旅游团去了A、B、C、D、E中的哪几个地方?
1967 |
1968 | (1)如果去A,就必须去B;
1969 |
1970 | (2)D、E两地至少去一地;
1971 |
1972 | (3)B、C两地只能去一地;
1973 |
1974 | (4)C、E两地要去都去,要不去都不去;
1975 |
1976 | (5)若去D,则A、E两地必须去。
1977 |
1978 | ### 拓展4
1979 |
1980 | 甲、乙、丙、丁在谈论他们及他们的同学何伟的居住地。
1981 |
1982 | 甲说:我和乙都住在北京,丙住在天津;
1983 |
1984 | 乙说:我和丁都住在上海,丙住在天津;
1985 |
1986 | 丙说:我和甲都不住在北京,何伟住在南京;
1987 |
1988 | 丁说:甲和乙都住在北京,我住在广州。
1989 |
1990 | 假定他们每个人都说了两句真话,一句假话。问:不在场的何伟住在哪儿?
1991 |
1992 | ### 拓展5
1993 |
1994 | 宝宝、贝贝、聪聪每人有两个外号,人们有时以“数学博士”、“短跑健将”、“跳高冠军”、“小画家”、“大作家”和“歌唱家”称呼他们,此外:
1995 |
1996 | (1)数学博士夸跳高冠军跳的高
1997 |
1998 | (2)跳高冠军和大作家常与宝宝一起看电影
1999 |
2000 | (3)短跑健将请小画家画贺年卡
2001 |
2002 | (4)数学博士和小画家关系很好
2003 |
2004 | (5)贝贝向大作家借过书
2005 |
2006 | (6)聪聪下象棋常赢贝贝和小画家
2007 |
2008 | 问:宝宝、贝贝、聪聪各有哪两个外号吗?
2009 |
2010 | ## 2.2.14. 重叠问题
2011 |
2012 | ### 热身1
2013 |
2014 | ### 热身2
2015 |
2016 | ### 热身3
2017 |
2018 | ### 例题1
2019 |
2020 | 把两根长为20寸的短尺用绳子捆成一根长尺,中间捆在一起的重叠部分是3寸。捆成的长尺长多少寸?
2021 |
2022 | ### 练习1
2023 |
2024 | 有四块均长80厘米的木板,钉成一块长木板,中间钉在一起重叠的部分均是10厘米,钉成的长木板长多少厘米?
2025 |
2026 | ### 例题2
2027 |
2028 | 将两张同样长的纸粘成了一张长为80才的长纸条,其中粘在一起的部分长10寸,这两张纸条各长多少寸?
2029 |
2030 | ### 练习2
2031 |
2032 | 有两根铁丝,一根长为30厘米,另一根长为50厘米,将这两根铁丝焊接成一根长为75厘米的长铁丝。那么,中间的焊接重叠部分长为多少厘米?
2033 |
2034 | ### 例题3
2035 |
2036 | 私塾的学生都要参加比赛,有30人参加蹴鞠队,有27人参加毽子队。其中8人两种比赛都参加。一共有学生多少人?
2037 |
2038 | ### 练习3
2039 |
2040 | 二(1)班同学所有人都参加课外活动,有20人参加英语班,有26人参加电脑班。其中4人两个班都参加。二(1)班一共有多少人?
2041 |
2042 | ### 例题4
2043 |
2044 | 20个学生参加琵琶表演和古筝表演,其中有16人参加了琵琶表演,12人参加了古筝表演。问两种表演都参加的有多少学生?
2045 |
2046 | ### 练习4
2047 |
2048 | 春天来了,全班52人到北海公园划船,有27人划了手摇船,29人划了脚踏船,4名同学因身体不好没有划船而去游览了白塔。问:既划了手摇船也划了脚踏船的同学有多少人?
2049 |
2050 | ### 例题5
2051 |
2052 | 有蓝色和红色两种珠花,每人至少选一种,共有48人,有30人选了蓝色珠花,有13人两种都选了,那么选红色珠花的有多少人?
2053 |
2054 | ### 练习5
2055 |
2056 | 学校开设了自然和趣味数学两门选修课,每个同学至少要选一门,二(3)班共有56人,有30人选了自然课,有12人两门都选了,那么选趣味数学课的同学有多少人?
2057 |
2058 | ### 例题6
2059 |
2060 | 工厂筛选制镜工人,总共有60人报名参加。经过一段时间的训练后,有33人学会了制作星云镜,有25人学会了制作幻镜,其中既会制作星云镜又会制作幻镜的有10人。那么既不会制作星云镜又不会制作幻镜的有多少人?
2061 |
2062 | ### 练习6
2063 |
2064 | 某班共有46人,参加美术小组的有12人,参加音乐小组的有23人,有5人两个小组都参加了。这个班既没有参加美术小组也没参加音乐小组的有多少人?
2065 |
2066 | ## 2.2.15. 复杂的树阵图
2067 |
2068 | ### 热身1
2069 |
2070 | ### 热身2
2071 |
2072 | ### 热身3
2073 |
2074 | ### 例题1(辐射型)
2075 |
2076 | 把1,2,4,5,6,8,10这7个数分别填入图中的圆圈中,使得每条直线上4个数的和都等于20。
2077 |
2078 | 
2079 |
2080 | ### 练习1
2081 |
2082 | 把8,9,10,11,12,14,16这7个数分别填入图中的圆圈中,使得每条直线上4个数的和都等于46。
2083 |
2084 | ### 例题2
2085 |
2086 | 将5,9,13,14,17,21,25这7个数分别填入图中的圆圈中,使得每条直线上的3个数的和都等于44。
2087 |
2088 | 
2089 |
2090 | ### 练习2
2091 |
2092 | 将5,8,11,14,17,20,23这7个数分别填入图中的圆圈中,使得每条直线上的3个数的和都等于36。
2093 |
2094 | ### 例题3(封闭型)
2095 |
2096 | 把2,3,4,5,6,7,8这7个数分别填入图中的圆圈中,使两个正方形中4个数之和都等于19。
2097 |
2098 | ### 练习3
2099 |
2100 | 把2,3,4,5,6,7,8这7个数分别填入图中的圆圈中,使两个正方形中4个数之和都等于21。
2101 |
2102 | ### 例题4
2103 |
2104 | 把1,5,9,10,16,21这6个数分别填入图中的圆圈中,使每一个大圆上的4个数之和都等于36。
2105 |
2106 | ### 练习4
2107 |
2108 | 把1,2,4,5,6,11这6个数分别填入图中的圆圈中,使每一个大圆上的4个数之和都等于22。
2109 |
2110 | ### 例题5
2111 |
2112 | 将5,6,9,11,14,15这6个数分别填入图中的圆圈中,使两个大圆上4个数的和都等于40。
2113 |
2114 | ### 练习5
2115 |
2116 | 将4,7,9,12,15,17这6个数分别填入图中的圆圈中,使两个大圆上4个数的和都等于43。
2117 |
2118 | ### 例题6
2119 |
2120 | 将1,3,4,5,6,8,11,15这8个数分别填入图中的圆圈中,使两个大圆上5个数的和都等于33。
2121 |
2122 | ### 练习6
2123 |
2124 | 将2,5,6,8,10,12,14,22这8个数分别填入图中的圆圈中,使两个大圆上5个数的和都等于49。
2125 |
2126 | ## 2.2.16. 年龄问题初步
2127 |
2128 | ### 例题1
2129 |
2130 | 丁丁今年8岁,爸爸的年龄是丁丁的4倍,4年前,爸爸的年龄和丁丁相差几岁?
2131 |
2132 | ### 练习1
2133 |
2134 | 田田今年6岁,妈妈今年36岁,再过6年,田田读初中时,妈妈比田田大多少岁?
2135 |
2136 | ### 例题2
2137 |
2138 | 田田今年10岁,博士今年55岁,当田田17岁时,博士多少岁?
2139 |
2140 | ### 练习2
2141 |
2142 | 小芳今年10岁,妈妈比她大28岁,当小芳15岁时,妈妈多少岁?
2143 |
2144 | ### 例题3
2145 |
2146 | 今年小王子8岁,大王子14岁,当两人的年龄之和是40岁时,应该是几年之后?
2147 |
2148 | ### 练习3
2149 |
2150 | 今年太子8岁,王后34岁,当太子和王后两人的年龄和是50岁时,太子多少岁?王后多少岁?
2151 |
2152 | ### 例题4
2153 |
2154 | 爸爸今年40岁,妈妈今年38岁,儿子今年12岁,当爸爸、妈妈、儿子三人的年龄和是81岁时,爸爸多少岁?妈妈多少岁?儿子多少岁?
2155 |
2156 | ### 练习4
2157 |
2158 | 李文今年9岁,爸爸、妈妈的年龄和是81岁,问:多少年后他们三个的平均年龄是40岁?
2159 |
2160 | ### 例题5
2161 |
2162 | 李斯、韩非现在的年龄和是62岁,5年前,李斯比韩非大6岁,今年李斯、韩非两人各多少岁?
2163 |
2164 | ### 练习5
2165 |
2166 | 爸爸、妈妈现在的年龄和是72岁;5年后,爸爸比妈妈大6岁。今年爸爸妈妈二人各多少岁?
2167 |
2168 | ### 例题6
2169 |
2170 | 姐姐5年前的年龄与妹妹3年后的年龄相等,问姐姐和妹妹相差多少岁?
2171 |
2172 | ### 练习6
2173 |
2174 | 小明12年后的年龄与妈妈12年前的年龄相等,问小明和妈妈相差多少岁?
2175 |
2176 | ## 2.2.17. 画图法综合
2177 |
2178 | ### 热身1
2179 |
2180 | ### 热身2
2181 |
2182 | ### 热身3
2183 |
2184 | ### 例题1(排队问题)
2185 |
2186 | 小朋友们排成一个长方形队伍表演体操。
2187 | (1)从左边数起,小华排第18,从右边数起,小明排第16,小华的左边是小明,这一行共有多少人?
2188 | (2)从左面数小红排在第2个,小军排在小红右面第4个,那么小军从右往左数排在第几个?
2189 |
2190 | ### 练习1
2191 |
2192 | 一群小动物排队表演节目,小猪第18个出场,小狗表演完后面还有16个节目,已知小猪后面第二个节目是小狗表演的,求一共有多少个节目?
2193 |
2194 | ### 例题2(鸡兔同笼)
2195 |
2196 | 王大妈去市场上买回来了一些鸡和兔,她把鸡、兔关在同一个笼子里,数了数,共有11个头,30条腿,你知道王大妈买回来了几只鸡?几只兔?
2197 |
2198 | ### 练习2
2199 |
2200 | 鸡兔同笼,共有7个头,20条腿,有多少只鸡?多少只兔?
2201 |
2202 | ### 例题3(年龄问题)
2203 |
2204 | 爸爸、妈妈、小敏三人的年龄总和是73岁,爸爸比妈妈大3岁,小敏比妈妈小23岁。小敏今年多少岁?
2205 |
2206 | ### 练习3
2207 |
2208 | 三个小朋友比年龄,小明比小英小5岁,小方比小明大2岁。那么小英和小方差几岁?
2209 |
2210 | ### 例题4(画线段图)
2211 |
2212 | 一筐鲜鱼,连筐共重56千克。先卖出鲜鱼的一半,再卖出剩下的一半,这时连筐还重17千克。原来这筐鲜鱼重多少干克?
2213 |
2214 | ### 练习4
2215 |
2216 | 玻璃瓶里装着一些水,把水加到原来的2倍时,和瓶一起称重5千克;把水加到原来的4倍时,重为9千克,问原来水有多少千克?
2217 |
2218 | ### 例题5(盈亏问题)
2219 |
2220 | 田田到文具店买练习本,她带的钱若买4本,还剩2元;若买5本,就差7元。问田田一共带了多少钱?
2221 |
2222 | ### 练习5
2223 |
2224 | 牛牛妈妈到水果店买苹果,她带的钱若买4千克还剩8元;若买5千克,就差2元。问牛牛妈妈一共带了多少钱?
2225 |
2226 | ### 例题6
2227 |
2228 | 丁丁和牛牛都想买一个饼,但丁丁的钱币少2枚,牛牛的钱币少3枚。如果两个人的钱币合在一起就刚够买一个饼。问买一个饼需要多少枚钱币?丁丁和牛牛各有多少枚钱币?
2229 |
2230 | ### 练习6
2231 |
2232 | 王强和李明都想买一本《趣味数学》,但王强的钱少2元5角,李明的钱少3元1角。如果两个人的钱合在一起就刚够买这本书。问一本《趣味数学》多少钱?王强和李明各有多少钱?
2233 |
2234 | ### 拓展1
2235 |
2236 | 81 位同学排成 9 行 9 列的正方形队列表演体操,小花在队列中,正左边有 2 位同学,正前方有3位同学,这时整个队列的同学向右转,则小花的正前方有几位同学?正右边有几位同学?
2237 |
2238 | ### 拓展2
2239 |
2240 | 鸡兔同笼,共有60个头,且鸡腿是兔腿的2倍,有多少只鸡?多少只兔?
2241 |
2242 | ### 拓展3
2243 |
2244 | 14年前爸爸的年龄是儿子的5倍, 14年后父子二人年龄和是98岁,父子二人今年分别多少岁?
2245 |
2246 | ### 拓展4
2247 |
2248 | 学生们划船,如果每只船坐5人,则还有3人无船坐,如果其中两只船坐4人,其余的船每只坐6人,就恰好坐完所有学生,共有学生多少人?
2249 |
2250 | ### 拓展5
2251 |
2252 | 甲乙丙丁四个同学共买了37朵花,如果甲多买2朵,乙少买3多,丙买的朵数变成现在的2倍,丁买的朵数减少一半,那么四个人买的朵数正好相同。请问原来四个人各买了多少朵花?
2253 |
2254 | ## 2.2.18. 等式加减法
2255 |
2256 | ### 热身1
2257 |
2258 | 15个小朋友排队报数,从前边报起,牛牛报10,从后往前报起,丁丁报12,求从牛牛数到丁丁一共有多少人?
2259 |
2260 | ### 热身2
2261 |
2262 | 牛牛、田田、丁丁三个人分糖块。田田比丁丁多3块,牛牛比田田多2块。已知糖块总块数是50块,那么每人各分到多少块?
2263 |
2264 | ### 热身3
2265 |
2266 | 买4个足球和2个排球,共用去102元,已知每个足球比每个排球贵3元。问每个足球和排球各多少元?
2267 |
2268 | ### 例题1
2269 |
2270 | 下面不同的图各代表一个数,你知道它们各代表几吗?
2271 |
2272 | (1)
2273 |
2274 | $🍎+🍐+🍐=13$
2275 |
2276 | $🍎+🍐=10$
2277 |
2278 | $🍎=()$
2279 |
2280 | $🍐=()$
2281 |
2282 | (2)
2283 |
2284 | $🍊+🍊+🍑=15$
2285 |
2286 | $🍊+🍑=9$
2287 |
2288 | $🍊=()$
2289 |
2290 | $🍑=()$
2291 |
2292 | ### 练习1
2293 |
2294 | 下面等式中,□和△各表示几?
2295 | 已知:
2296 |
2297 | $□+□+△=16$
2298 | $□+□+△+△+△=24$
2299 | 求:
2300 |
2301 | $□=()$
2302 | $△=()$
2303 |
2304 | ### 例题2
2305 |
2306 | 下面不同的图各代表一个数,你知道它们各代表几吗?
2307 |
2308 | $🍇+🍎=16$
2309 |
2310 | $🍇-🍎=2$
2311 |
2312 | $🍎=()$
2313 |
2314 | $🍇=()$
2315 |
2316 | ### 练习2
2317 |
2318 | 下面不同的图各代表一个数,你知道它们各代表几吗?
2319 |
2320 | $🍌+🍓=15$
2321 |
2322 | $🍌-🍓=3$
2323 |
2324 | $🍌=()$
2325 |
2326 | $🍓=()$
2327 |
2328 | ### 例题3
2329 |
2330 | 你能根据下面两个等式,求出🍊和🍍各表示什么数吗?
2331 |
2332 | $🍊+🍊+🍍=10$
2333 |
2334 | $🍊+🍍+🍍=11$
2335 |
2336 | $🍊=()$
2337 |
2338 | $🍍=()$
2339 |
2340 | ### 练习3
2341 |
2342 | 已知:
2343 |
2344 | $☆+☆+☆+△+△=13$
2345 | $☆+☆+△+△+△=12$
2346 |
2347 | 求:
2348 |
2349 | $☆=()$
2350 | $△=()$
2351 |
2352 | ### 例题4
2353 |
2354 | 下面△、☆、▲各代表什么数?
2355 |
2356 | $△+☆=23$
2357 |
2358 | $△+▲=33$
2359 |
2360 | $☆+▲=30$
2361 |
2362 | ### 练习4
2363 |
2364 | 三种兔子各多少只?
2365 | 黑兔+白兔=6
2366 | 黑兔+灰兔=7
2367 | 白兔+灰兔=5
2368 |
2369 | ### 铺垫
2370 |
2371 | 根据条件写等式。
2372 |
2373 | ### 例题5
2374 |
2375 | 2瓶可乐和3个面包共27元,4瓶可乐和3个面包共39元。请你算一算,每瓶可乐和每个面包各多少元?
2376 |
2377 | ### 练习5
2378 |
2379 | 牛牛去商店买文具,买了3个本子和1支铅笔一共花了10元,又知道1个本子比1支铅笔贵2元,请问1个本子和1支笔各多少钱?
2380 |
2381 | ### 例题6
2382 |
2383 | 1千克瓜子和2千克花生,一共 32元。2千克瓜子和1千克花生,一共 28元。那么瓜子和花生每千克各多少元?
2384 |
2385 | ### 练习6
2386 |
2387 | 1件上衣与2条裤子的总价是500元,这件上衣比这2条裤子的价钱贵
2388 | 100 元。则1件上衣多少钱? 1条裤子多少钱?(2条裤子是一样的)
2389 |
2390 | ### 拓展1
2391 |
2392 | 下面每种水果各代表多少?
2393 |
2394 | $🍐+🍐+🍎+🍊=16$
2395 |
2396 | $🍐+🍎+🍎+🍊=13$
2397 |
2398 | $🍐+🍎+🍊+🍊=11$
2399 |
2400 | ### 拓展2
2401 |
2402 | 饲养场出售鸡、鸭,张大爷买2只鸭和3只鸡共用42元,李大叔买3只鸭和2只鸡共用43元。1只鸭和一只鸡各多少元?
2403 |
2404 | ### 拓展3
2405 |
2406 | 小军家养了一些大白兔和小花猫。有一天,小军抱着2只大白兔一起站在体重计上称一称,正好是 45千克;后来小军放下大白兔又抱着3只小花猫,站在体重计上称一称,正好是47千克;最后小军把 6只小花猫和4只大白兔一起放在体重计上称一称是44千克。请你算一算小军、大白兔和小花猫各是多少千克?(每只大白兔的重量一样,每只小花猫的重量一样。)
2407 |
2408 | ### 拓展4
2409 |
2410 | ### 拓展5
2411 |
2412 | ## 2.2.19. 动手操作
2413 |
2414 | ### 热身1
2415 |
2416 | ### 热身2
2417 |
2418 | ### 热身3
2419 |
2420 | ### 例题1
2421 |
2422 | 大勺子一次能装油250克,小勺子一次能装油150克,你能用这两把勺子往一个空杯子里倒入350克油吗?
2423 |
2424 | ### 练习1
2425 |
2426 | 兔妈妈有一包70克的药,想要用天平从中称出5克的药,可只有一个20克的砝码,怎么办?
2427 |
2428 | ### 例题2
2429 |
2430 | 两个人要平分12千克的一大桶油。身边只有能装9千克和5千克的两只空桶,怎样倒才能使他们分到一样多的油呢?
2431 |
2432 | ### 练习2
2433 |
2434 | 一个人带着两只空桶去沟边取水,一只桶可盛5千克水,另一只可盛7千克水,现在要取8千克水,应该怎样取?
2435 |
2436 | ### 例题3
2437 |
2438 | 有九颗珍珠,其中有一颗是假珍珠,外观和真的一样,不容易看出来,只是假珍珠比真珍珠轻一些。你能利用天平,不用砝码,只称两次就找出假的珍珠吗?怎样称?
2439 |
2440 | ### 练习3
2441 |
2442 | 有八颗珍珠,其中有一颗是假珍珠,外观和真的一样,不容易看出来,只是假珍珠比真珍珠轻一些。你能利用天平,不用砝码,最少称几次就找出假的珍珠吗?怎样称?
2443 |
2444 | ### 例题4
2445 |
2446 | 黑猫警长在海关截获了一批装有牛肉罐头的9个大箱子,每箱里有很多盒罐头(大于1盒),箱子里每盒罐头重100克。在这9个大箱子中,其中有1箱罐头已经过期,不符合出口标准,过期的罐头每盒要比原来重1克。黑猫警长准备用一个大的电子称把这箱过期罐头称出来,请你帮忙想一想,最少需要称几次就能把这箱不合格的罐头找出来?
2447 |
2448 | ### 练习4
2449 |
2450 | 有10箱钢珠,每个钢珠重10克,每箱600个。如果这10箱钢珠中有1箱次品,次品钢珠每个重9克,那么,要找出这箱次品最少要称几次?
2451 |
2452 | ### 例题5
2453 |
2454 | 8个队参加扔石头大赛,比赛采用淘汰赛制,每2个队进行1场比赛,每场比赛输的1队被淘汰,最后决出冠军。同学们,请你算一算,一共要举行多少场比赛?
2455 |
2456 | ### 练习5
2457 |
2458 | 32个篮球队进行篮球比赛,裁判对他们说:“本次比赛采用淘汰赛,每2个队进行1场比赛,每场比赛输的1队被淘汰,最后决出冠军。”同学们,如果你做裁判,请你算一算一共要举行多少场比赛?
2459 |
2460 | ### 例题6
2461 |
2462 | 丁丁,牛牛,田田,阿普,小乐,5名同学参加跳绳比赛,比赛前每2个小朋友都要握一次手表示友好。当丁丁握了4次手,牛牛握了3次手,田田握了2次手,阿普握了1次手的时候,小乐握了几次手?最后这5名小朋友一共要握多少次手?
2463 |
2464 | ### 练习6
2465 |
2466 | 动物王国的动物们在比赛之前都要握手表示友好,这时,狐狸握了3次手,熊猫握了4次手,兔子也握了4次手,小猪握了3次手,狮子握了几次手呢?
2467 |
2468 | ### 拓展1
2469 |
2470 | ### 拓展2
2471 |
2472 | ### 拓展3
2473 |
2474 | ### 拓展4
2475 |
2476 | ### 拓展5
2477 |
2478 | ### 练习1
2479 |
2480 | ### 练习2
2481 |
2482 | ### 练习3
2483 |
2484 | ### 练习4
2485 |
2486 | ### 练习5
2487 |
2488 | ### 练习6
2489 |
2490 | ## 2.2.20. 必胜策略
2491 |
2492 | ### 例题1
2493 |
2494 | 桌子上放着18根火柴,甲、乙二人轮流每次取走1~3根。规定谁取走最后1根火柴谁获胜。甲先取,那么怎样取才能获胜?
2495 |
2496 | ### 练习1
2497 |
2498 | 桌子上放着50根火柴,甲、乙二人轮流每次取走1~3根。规定谁取走最后1根火柴谁获胜。如果双方均采用最佳方法,甲先取,那么怎样取才能获胜?
2499 |
2500 | ### 例题2
2501 |
2502 | 桌子上放着80根火柴,甲、乙二人轮流每次取走1~9根。规定谁取走最后1根火柴谁获胜。如果双方采用最佳方法,甲先取,那么谁将获胜?
2503 |
2504 | ### 练习2
2505 |
2506 | 桌子上放着75根火柴,甲、乙二人轮流每次取走1~4根。规定谁取走最后1根火柴谁获胜。如果双方采用最佳方法,甲先取,那么谁将获胜?
2507 |
2508 | ### 例题3
2509 |
2510 | 桌子上放着21根火柴,甲、乙二人轮流每次取走1~4根。规定谁取走最后1根火柴谁就输。如果甲想获胜,应该怎样取?
2511 |
2512 | ### 练习3
2513 |
2514 | 桌子上放着28根火柴,甲、乙二人轮流每次取走1~5根。规定谁取走最后1根火柴谁就输。甲先取,那么怎样取才能获胜?
2515 |
2516 | ### 例题4
2517 |
2518 | 两个人从1开始按自然数顺序轮流依次报数,每人每次只能报1~3个数,谁先报到30谁获胜。你选择先报数还是后报数?怎样才能获胜?
2519 |
2520 | ### 练习4
2521 |
2522 | 两个人从1开始按自然数顺序轮流依次报数,每人每次只能报1~4个数,谁先报到32谁获胜。你选择先报数还是后报数?怎样才能获胜?
2523 |
2524 | ### 例题5
2525 |
2526 | 31个方格排成一行,最左端方格中放有一枚棋子,甲先乙后轮流向右移动棋子,每次移动1~3个格。规定将棋子移到最后1格者输。甲为了获胜,第一步必须向右移多少格?
2527 |
2528 | ### 练习5
2529 |
2530 | 共有54张扑克牌,由两人轮流来抽,每次可抽1~6张,抽到最后1张牌的人就算输了,如果第一个抽牌的人想赢,第一次应该抽几张牌。
2531 |
2532 | ### 例题6
2533 |
2534 | 甲、乙两人玩游戏:有18枚棋子,两人轮流取棋子,每次允许取其中2枚、4枚或8枚,谁取到最后一枚棋子,谁就获胜。甲想获胜,先取还是后取?应该怎样取?
2535 |
2536 | ### 练习6
2537 |
2538 | 甲、乙两人玩游戏:有28枚棋子,两人轮流取棋子,每次允许取其中2枚、4枚或8枚,谁取到最后一枚棋子,谁就获胜。如果甲先取,那么第一次甲取几枚才能保证一定获胜?
2539 |
2540 | ### 拓展1
2541 |
2542 | ### 拓展2
2543 |
2544 | ### 拓展3
2545 |
2546 | ### 拓展4
2547 |
2548 | ### 拓展5
2549 |
2550 | ###
2551 |
--------------------------------------------------------------------------------
/03-三年级.md:
--------------------------------------------------------------------------------
1 | ---
2 | title: 三年级
3 | lang: zh-CN
4 | sidebarDepth: 1
5 | ---
6 |
7 | # 三年级
8 |
9 | ## 3.1.01. 找规律综合
10 |
11 | ### 例题1(递推规律)
12 |
13 | 先找出下列数排列的规律,并根据规律在括号里填上适当的数。
14 |
15 | (1)1,4,7,10,(),16,19。
16 |
17 | (2)2,6,18,(),162。
18 |
19 | ### 练习1
20 |
21 | 先找出下列各列数的排列规律,然后在括号里填上适当的数。
22 |
23 | (1)2,6,10,14,(),22,26。
24 |
25 | (2)3,6,9,12,(),18,21。
26 |
27 | ### 例题2(间隔规律)
28 |
29 | 先找出规律,然后在括号里填上适当的数。
30 |
31 | 23,4,20,6,17,8,(),(),11,12。
32 |
33 | ### 练习2
34 |
35 | 先找出规律,然后在括号里填上适当的数。
36 |
37 | (1)3,2,5,2,7,2,(),(),11,2。
38 |
39 | (2)19,3,17,3,15,3,(),(),11,3。
40 |
41 | ### 例题3(兔子数列/斐波那契数列)
42 |
43 | 在数列1,1,2,3,5,8,13,(),34,55,……中,括号里应填什么数?
44 |
45 | ### 练习3
46 |
47 | 先找出规律,然后在括号里填上适当的数。
48 |
49 | 2,2,4,6,10,16,(),()。
50 |
51 | ### 例题4(算式规律)
52 |
53 | 根据前面图形中的数之间的关系,想一想第三个图形的括号里应填什么数?
54 |
55 | 
56 |
57 | ### 练习4
58 |
59 | 根据下表中的排列规律,在空格里填上适当的数。
60 |
61 | | 12 | 18 | 6 |
62 | | ---- | ---- | ---- |
63 | | 8 | 15 | 7 |
64 | | 4 | | 8 |
65 |
66 | ### 例题5
67 |
68 | 先计算下面一组算式的第一题,然后找出其中的规律,并根据规律直接写出后几题的得数。
69 |
70 | (1)12345679×9
71 |
72 | (2)12345679×18
73 |
74 | (3)12345679×54
75 |
76 | (4)12345679×81
77 |
78 | ### 练习5
79 |
80 | 计算:
81 |
82 | (1)26×11
83 |
84 | (2)38×11
85 |
86 | ### 例题6(图形规律)
87 |
88 | 观察下面由点组成的图形(点群),请回答:
89 |
90 | (1)方框内的点群包含多少个点?
91 |
92 | (2)第10个点群中包含多少个点?
93 |
94 | (3)前十个点群中,所有点的总数是多少?
95 |
96 | 
97 |
98 | ### 练习6
99 |
100 | 观察下面的图形,按规律在“?”处填上适当的图形。
101 |
102 | 
103 |
104 | ## 3.1.02. 加减法巧算综合
105 |
106 | ### 热身1
107 |
108 | 找规律填数。
109 |
110 | 10,13,18,25,(),(),58。
111 |
112 | ### 热身2
113 |
114 | 找规律填数。
115 |
116 | 3,29,4,28,6,26,9,23,(),(),18,14。
117 |
118 | ### 热身3
119 |
120 | 计算:$11+12+13+14+15+16+17+18+19=$
121 |
122 | ### 例题1(凑整法)
123 |
124 | 计算。
125 |
126 | (1)$132+23+48+257+40=$
127 |
128 | (2)$32+24+68=$
129 |
130 | ### 练习1
131 |
132 | 计算。
133 |
134 | (1)$238+45+67+62+55=$
135 |
136 | (2)$13+21+87+19=$
137 |
138 | ### 例题2(基准数)
139 |
140 | 计算。
141 |
142 | (1)$9+99+999+9999=$
143 |
144 | (2)$3998+407+89=$
145 |
146 | ### 练习2
147 |
148 | 计算。
149 |
150 | (1)$295+196+297+198+199+15=$
151 |
152 | (2)$19+199+1999=$
153 |
154 | ### 例题3
155 |
156 | 计算。
157 |
158 | (1)$268-56-82-44-18=$
159 |
160 | (2)$$
161 |
162 | ### 练习3
163 |
164 | 计算。
165 |
166 | (1)$831-155-67-145-131=$
167 |
168 | (2)$$
169 |
170 | ### 例题4
171 |
172 | 计算。
173 |
174 | (1)$300-9-19-29-39-49-59=$
175 |
176 | (2)$985-32+37-276-85+73-68=$
177 |
178 | ### 练习4
179 |
180 | 计算。
181 |
182 | (1)$818-271-18+64-29+36=$
183 |
184 | (2)$200-20-18-23-20-19-21=$
185 |
186 | ### 例题5
187 |
188 | 计算。
189 |
190 | (1)$2985-(985-276)=$
191 |
192 | (2)$$
193 |
194 | ### 练习5
195 |
196 | 计算。
197 |
198 | (1)$(123+348+400)-(23+150+148)=$
199 |
200 | (2)$$
201 |
202 | ### 例题6(分组巧算)
203 |
204 | 计算。
205 |
206 | (1)$20-19-18+17+16-15-14+13+12-11-10+9=$
207 |
208 | (2)$1+2-3-4+5+6-7-8+9+10-11-12+……-1999-2000+2001=$
209 |
210 | ### 练习6
211 |
212 | 计算。
213 |
214 | (1)$3355+4466+9977-3366-4477-9955=$
215 |
216 | (2)$$
217 |
218 | ### 例题7
219 |
220 | 【变零为整】$74+63+16-53+9+81=$
221 |
222 | 【变长为短】$38+57+36-57-36=$
223 |
224 | 【变大为小】$365-198+196+295-296=$
225 |
226 | 【变加为乘】$97+98+100+101+102=$
227 |
228 | 【位值原理】$1243+4132+2314+3421=$
229 |
230 | ### 练习7
231 |
232 | 【去括号】$2748+(1336+289)-(336+289)-748=$
233 |
234 | 【填括号】$1518-571-18+61-29+39=$
235 |
236 | ### 例题8
237 |
238 | 计算:$689-1-3-5-7-9-11-13-15-17-19$
239 |
240 | ### 练习8
241 |
242 | 计算:$9999-1-2-3-\dots-28-29-30-29-28-\dots-3-2-1$
243 |
244 | ### 拓展1
245 |
246 | 计算$1017+2017+3017+4017+5017-6017-7017$
247 |
248 | ### 拓展2
249 |
250 | 有一个很神秘的地方,那里有很多的雕塑,每个雕塑都是由蝴蝶组成的。已知一共有1000只蝴蝶,第1个雕塑有3只蝴蝶,第2个雕塑有5只蝴蝶,第3个雕塑有7只蝴蝶,第4个雕塑有9只蝴蝶,后面的雕塑按照这样的规律一直延伸到很远的地方,松松沿着雕塑走了一会,
251 | 停在了一个有39只蝴蝶的雕塑旁。那么,他们没数完的蝴蝶还剩多少只呢?
252 |
253 | ### 拓展3
254 |
255 | 书店里有一套漫画书共9册,第一册需24元,第二册需23元,第三册需22元,以此类推,每一册的售价都比它前面的一册要少1元。如果用200元去买这套漫画书,书店老板应该找回多少元呢?
256 |
257 | ## 3.1.03. 加减法竖式数字谜进阶
258 |
259 | ### 例题1
260 |
261 | 在空格内填入适当的数字,使图中的竖式成立。
262 |
263 | (1)$$\begin{matrix}
264 | & &3 &\Box &4 \\
265 | +& &\Box &5 &\Box \\
266 | \hline
267 | &\Box &1 &5 &2
268 | \end{matrix}$$
269 |
270 | (2)$$\begin{matrix}
271 | &\Box &2 &\Box \\
272 |
273 | -&2 &\Box &4 \\
274 |
275 | \hline
276 | &1 &5 &2
277 | \end{matrix}$$
278 |
279 | ### 练习1
280 |
281 | 在空格内填入适当的数字,使图中的竖式成立。
282 |
283 | (1)$$\begin{array}{c}
284 | & &6 &\Box &3 \\
285 | +& &\Box &4 &\Box \\
286 | \hline
287 | &\Box &1 &7 &2
288 | \end{array}$$
289 |
290 | (2)$$\begin{matrix}
291 | &\Box &5 &\Box \\
292 | -&4 &\Box &6 \\
293 | \hline
294 | &3 &7 &1
295 | \end{matrix}$$
296 |
297 | ### 例题2
298 |
299 | 在空格内填入适当的数字,使图中的竖式成立。
300 |
301 | (1)$$\begin{matrix}
302 | & & &7 &\Box \\
303 | +& &\Box &\Box&4 \\
304 | \hline
305 | &\Box &\Box &5 &3
306 | \end{matrix}$$
307 |
308 | (2)$$\begin{matrix}
309 | &\Box &\Box &8 &\Box \\
310 | -& &\Box &\Box &4 \\
311 | \hline
312 | & & &9 &7
313 | \end{matrix}$$
314 |
315 | ### 练习2
316 |
317 | 在空格内填入适当的数字,使图中的竖式成立。
318 |
319 | (1)$$\begin{matrix}
320 | & & &8 &\Box \\
321 | +& &\Box &\Box &2 \\
322 | \hline
323 | &\Box &\Box &6 &1
324 | \end{matrix}$$
325 |
326 | (2)$$\begin{matrix}
327 | &\Box &\Box &7 &\Box \\
328 | -& &\Box &\Box &3 \\
329 | \hline& & &9 &6
330 | \end{matrix}$$
331 |
332 | ### 例题3
333 |
334 | 在空格内填入适当的数字,使图中的竖式成立。
335 |
336 | $$\begin{matrix}
337 | & &\Box &6 &\Box \\
338 | +& &2 &\Box &6 \\
339 | \hline
340 | &\Box &\Box &\Box &\Box \\
341 | -& &\Box &\Box &\Box \\
342 | \hline
343 | & & & &1
344 | \end{matrix}$$
345 |
346 | ### 练习3
347 |
348 | 在空格内填入适当的数字,使图中的竖式成立。
349 |
350 | $$\begin{matrix}
351 | &\Box &7 &\Box &8 \\
352 | +&1 &\Box &9 &\Box \\
353 | \hline&2 &9 &0 &9
354 | \end{matrix}$$
355 |
356 | ### 例题4
357 |
358 | 在下图的竖式中,不同的汉字代表不同的数字,相同的汉字代表相同的数字,每个汉字代表什 么数时,竖算式成立?
359 |
360 | $$\begin{matrix}
361 | & & & &生 \\
362 | & & &学 &生 \\
363 | & &好 &学 &生 \\
364 | +&三 &好 &学 &生 \\
365 | \hline&2 &0 &1 &6
366 | \end{matrix}$$
367 |
368 | ### 练习4
369 |
370 | 在下图的竖式中,不同的汉字代表不同的数字,相同的汉字代表相同的数字,每个汉字代表什 么数时,竖算式成立?
371 |
372 | $$\begin{matrix}
373 | & & & &龙 \\
374 | & & &成 &龙 \\
375 | & &子 &成 &龙 \\
376 | +&望 &子 &成 &龙 \\
377 | \hline&2 &0 &1 &2
378 | \end{matrix}$$
379 |
380 | ### 例题5
381 |
382 | 在下图的竖式中,不同的字母代表不同的数字,相同的字母代表相同的数字,每个字母代表什 么数时,竖算式成立?
383 |
384 | $$\begin{matrix}
385 | & &A &B &C &D \\
386 | +& &E &B &E &D \\
387 | \hline&E &D &C &A &D
388 | \end{matrix}$$
389 |
390 | ### 练习5
391 |
392 | 如下图,算式中不同的汉字代表不同的数字,已知:”级=5“,那么”学而思“代表的三位数是多少?
393 |
394 | $$\begin{matrix}
395 | & &学 &而 &思 \\
396 | +& &1 &2 &级 \\
397 | \hline&更 &进 &1 &步
398 | \end{matrix}$$
399 |
400 | ### 例题6
401 |
402 | 下面的减法算式中,每一个字母代表一个数字,不同的字母代表不同的数字,计算:D+G。
403 |
404 | $$\begin{matrix}
405 | &A &B &C &B &D \\
406 | -& &E &F &A &G \\
407 | \hline& & &F &F &F
408 | \end{matrix}$$
409 |
410 | ### 练习6
411 |
412 | 在下图的竖式中,不同的汉字代表不同的数字,相同的汉字代表相同的数字,每个汉字代表什 么数时,竖算式成立?
413 |
414 | $$\begin{matrix}
415 | &机 &器 &人 \\
416 | +&机 &机 &人 \\
417 | \hline&器 &人 &人
418 | \end{matrix}$$
419 |
420 | ## 3.1.06. 巧求周长进阶
421 |
422 | ### 例题1
423 |
424 | 将一个大正方形剪去四个相同大小的小正方形后,计算剩下部分的周长。
425 |
426 | 
427 |
428 | ### 练习1
429 |
430 | 计算下面这个图形的周长。(单位:厘米)
431 |
432 | 
433 |
434 | ### 例题2
435 |
436 | 用五个完全相同的小长方形拼成一个如图所示的大长方形,小长方形的周长是 40 厘米,那么大长方形的周长是多少?
437 |
438 | 
439 |
440 | ### 练习2
441 |
442 | 4个完全相同的小长方形拼成一个如图所示的大长方形,只知道小长方形的宽是2厘米,大长方形的周长是多少?
443 |
444 | 
445 |
446 | ### 例题3
447 |
448 | 若每个小正方形的周长为 12厘米,则他们组合而成的“十” 字图形的周长是多少?
449 |
450 | 
451 |
452 | ### 练习3
453 |
454 | 用五个完全相同的小正方形拼成如下图形,已知拼出图形的周长是24厘米,你知道所用小正方形的面积是多少吗?
455 |
456 | 
457 |
458 | ### 例题4
459 |
460 | 将一个长为12厘米,宽为6厘米的长方形纸片按照图中虚线剪成两个图形,请计算两个图形的周长之和?
461 |
462 | 
463 |
464 | ### 练习4
465 |
466 | 将一个边长为4厘米的正方形对折,再沿折线剪开,得到两个长方形,求两个长方形比原来的正方形周长多了多少。
467 |
468 | ### 例题5
469 |
470 | 用8张边长是2厘米的小正方形拼成一个长方形,这个长方形的周长是多少厘米?
471 |
472 | ### 练习5
473 |
474 | 用6张边长为3厘米的正方形纸片拼成一个长方形,这个长方形的周长是多少厘米?
475 |
476 | ### 例题6
477 |
478 | 商场举行大酬宾活动,门口将长18厘米,宽9厘米的礼品盒摆成一个有规律的形状。礼品盒前4层的样式如图所示,一共有10 层,你能算出一共摆了多少个礼品盒吗? 礼品盒摆出形状的周长是多少?
479 |
480 | 
481 |
482 | ### 练习6
483 |
484 | 如图所示,长方形长4厘米,宽2厘米,现沿对角线 BD对折得到如下几何图形,试求图形阴影部分的周长。
485 |
486 | 
487 |
488 | ## 3.1.07. 平均数初步
489 |
490 | ### 例题1
491 |
492 | 幼儿园小朋友做红花,小华做了27朵,小方做了29朵,小林和小宁合做了52朵。平均每个小朋友做了多少朵?
493 |
494 | ### 练习1
495 |
496 | 一个书架上第一层放书52本,第二层和第三层共放70本,第四层放了46本,平均每层放书多少本?
497 |
498 | ### 例题2
499 |
500 | 中关村小学有15名同学参加跳绳比赛,他们跳绳的个数分别为93、94、85、92、86、88、94、91、88、89、92、86、93、90、89,求平均每人跳绳多少个?
501 |
502 | ### 练习2
503 |
504 | 下图是小华五次数学测验成绩的统计图。小华五次测验的平均分是多少分?
505 |
506 |  507 |
508 | ### 例题3
509 |
510 | 小华期末考试时,语文、数学和音乐三科成绩平均分是96分,英语成绩公布后,四科平均分下降了2分,小华英语成绩是多少分?
511 |
512 | ### 练习3
513 |
514 | 宁宁期中考试语文、数学、自然的平均分是91分,英语成绩公布后,他的平均分提高了2分。宁宁英语考了多少分?
515 |
516 | ### 例题4
517 |
518 | 果品店把2千克酥糖,3千克水果糖,4千克奶糖混合成什锦糖。已知酥糖每千克12元,水果糖每千克11元,奶糖每干克15元。问:什锦糖每千克多少元?
519 |
520 | ### 练习4
521 |
522 | 果品店把3千克水果糖,9千克奶糖混合成什锦糖,已知水果糖每千克7元,奶糖每千克11元,那么什锦糖每千克多少元?
523 |
524 | ### 例题5
525 |
526 | 6个学生的年龄正好是连续自然数,他们的年龄和与小明爸爸的年龄相同,7个人年龄一共是126岁,求这6个学生各几岁。
527 |
528 | ### 练习5
529 |
530 | 已知8个连续奇数的和是144,求这8个连续奇数。
531 |
532 | ### 例题6
533 |
534 | 这学期,丁丁5次随堂测试都得了84分,牛牛前4次测试分别比丁丁多出了1分、2分、3分、4分,请问第5次测试牛牛至少要考多少分,才能确保这5次测试的平均成绩高于丁丁至少了分?
535 |
536 | ### 练习6
537 |
538 | 楠楠的8个同学,数学考试成绩的平均数为80,若把其中的一个成绩改为82,则平均数变成了82。问被改动的数原来是多少?
539 |
540 | ## 3.1.08. 归一问题
541 |
542 | ### 例题1
543 |
544 | 王叔叔加工面条,5天加工40千克,照这样算,30天可加工面条多少千克?
545 |
546 | ### 练习1
547 |
548 | 乐乐老师批改4本作业用12分钟,照这样计算,三年级(5)班30本作业要批改多长时间?
549 |
550 | ### 例题2
551 |
552 | 丁丁3分钟完成24道口算,照这样的速度,完成56道口算要多少分钟?
553 |
554 | ### 练习2
555 |
556 | 一台割草机3小时可割草480千克,照这样的速度计算,割640千克要用多少小时?
557 |
558 | ### 例题3
559 |
560 | 一辆汽车从甲地开往乙地,每小时行60千米,5小时到达。若要4小时到达,则每小时需要多行多少千米?
561 |
562 | ### 练习3
563 |
564 | 某厂运来一批煤,计划每天用5吨,40天用完,如果改进锅炉后,每天节约1吨煤,这批煤可以用多少天?
565 |
566 | ### 例题4
567 |
568 | 一个果园请人帮忙摘桃子,4个人3小时共摘桃子600千克,照这样的效率计算,5个人8小时可以摘多少千克桃子?
569 |
570 | ### 练习4
571 |
572 | 15头牛4天吃了1260千克草,照这样计算,30头牛10天吃草多少千克?
573 |
574 | ### 例题5
575 |
576 | 6辆卡车运送4趟可以运走沙石48吨。如果有400吨沙石需要10趟运完,那么一共需要多少辆卡车?
577 |
578 | ### 练习5
579 |
580 | 4辆汽车5小时共运土石400方,现有10辆同样的汽车,要运1000方土石,需几小时?
581 |
582 | ### 例题6
583 |
584 | 一件工作12人每天工作8小时需要10天,照这样计算,如果增加8人,每天减少2小时,可以提前几天完成?
585 |
586 | ### 练习6
587 |
588 | 学校买来一批粉笔,原计划18个班可用60天,实际用45天后,有3个班外出了,剩下的粉笔够用多少天?
589 |
590 | ## 3.1.09.长方形与正方形
591 |
592 | ### 课前热身
593 |
594 | 【热身1】有20人修筑一条公路,计划15天完成。动工3天后抽出5人去植树,留下的人继续修路。如果每个人的工作效率不变,那么修完中段公路实际用多少天?
595 |
596 |
597 |
598 | 【热身2】已知3名模范职工和6名普通职工8小时可以生产零件420个。现在有一批生产任务,需要6名模范职工和12名普通职工生产14小时才能完成。如果工作了4小时后,又来了4名模范职工和8名普通职工,可以提前几小时完成任务?
599 |
600 |
601 |
602 | ### 学习目标
603 |
604 | - 理解面积的意义(面积的单位及其转换)
605 | - 会求长方形和正方形的面积(正方形面积=边长×边长;长方形面积=长×宽)
606 | - 掌握简单的割补、剪拼。
607 | - 长方形、正方形面积与周长区分和灵活转换
608 | - 运用长方形、正方形的性质(周长和面积)解决问题
609 | - 拓展——田字格模型
610 |
611 |
612 |
613 | ### 引入
614 |
615 | 对面积的直观感受和比较
616 |
617 |
618 |
619 | 【补充】有两个一样的长方形,长都是4厘米,宽都是2厘米。
620 |
621 | 把它们拼成一个长方形,请画出草图,并计算其周长和面积。
622 |
623 | 把它们拼成一个正方形,请画出草图,并计算其周长和面积。
624 |
625 |
626 |
627 | 一个花园长15米,宽10米,如果把这个花园用篱笆围起来,所围成的面积有多大?需要多长的篱笆?
628 |
629 |
630 |
631 | #### 单位换算
632 |
633 | (1)1米=()分米=()厘米=()毫米
634 |
635 | (2)1平方米=()平方分米=()平方厘米=()平方毫米
636 |
637 | (3)1平方千米=()平方米
638 |
639 | (4)8平方米=()平方分米
640 |
641 | (5)13平方米=()平方厘米
642 |
643 | (6)()平方米=500平方分米=()平方厘米
644 |
645 |
646 |
647 | #### 补充
648 |
649 | 选择合适的单位填入括号内。
650 |
651 | (1)一栋楼高约50()
652 |
653 | (2)课本封面面积约为6()
654 |
655 | (3)一个茶杯高约13()
656 |
657 | (4)黑板的面积约为5()
658 |
659 | (5)指甲盖的面积约为1()
660 |
661 | (6)一间教师的面积约为40()
662 |
663 |
664 |
665 |
666 |
667 | ### 例题练习
668 |
669 | #### 割补法求面积
670 |
671 | 【例题1】求下面图形的面积。(单位:厘米)
672 |
673 |
507 |
508 | ### 例题3
509 |
510 | 小华期末考试时,语文、数学和音乐三科成绩平均分是96分,英语成绩公布后,四科平均分下降了2分,小华英语成绩是多少分?
511 |
512 | ### 练习3
513 |
514 | 宁宁期中考试语文、数学、自然的平均分是91分,英语成绩公布后,他的平均分提高了2分。宁宁英语考了多少分?
515 |
516 | ### 例题4
517 |
518 | 果品店把2千克酥糖,3千克水果糖,4千克奶糖混合成什锦糖。已知酥糖每千克12元,水果糖每千克11元,奶糖每干克15元。问:什锦糖每千克多少元?
519 |
520 | ### 练习4
521 |
522 | 果品店把3千克水果糖,9千克奶糖混合成什锦糖,已知水果糖每千克7元,奶糖每千克11元,那么什锦糖每千克多少元?
523 |
524 | ### 例题5
525 |
526 | 6个学生的年龄正好是连续自然数,他们的年龄和与小明爸爸的年龄相同,7个人年龄一共是126岁,求这6个学生各几岁。
527 |
528 | ### 练习5
529 |
530 | 已知8个连续奇数的和是144,求这8个连续奇数。
531 |
532 | ### 例题6
533 |
534 | 这学期,丁丁5次随堂测试都得了84分,牛牛前4次测试分别比丁丁多出了1分、2分、3分、4分,请问第5次测试牛牛至少要考多少分,才能确保这5次测试的平均成绩高于丁丁至少了分?
535 |
536 | ### 练习6
537 |
538 | 楠楠的8个同学,数学考试成绩的平均数为80,若把其中的一个成绩改为82,则平均数变成了82。问被改动的数原来是多少?
539 |
540 | ## 3.1.08. 归一问题
541 |
542 | ### 例题1
543 |
544 | 王叔叔加工面条,5天加工40千克,照这样算,30天可加工面条多少千克?
545 |
546 | ### 练习1
547 |
548 | 乐乐老师批改4本作业用12分钟,照这样计算,三年级(5)班30本作业要批改多长时间?
549 |
550 | ### 例题2
551 |
552 | 丁丁3分钟完成24道口算,照这样的速度,完成56道口算要多少分钟?
553 |
554 | ### 练习2
555 |
556 | 一台割草机3小时可割草480千克,照这样的速度计算,割640千克要用多少小时?
557 |
558 | ### 例题3
559 |
560 | 一辆汽车从甲地开往乙地,每小时行60千米,5小时到达。若要4小时到达,则每小时需要多行多少千米?
561 |
562 | ### 练习3
563 |
564 | 某厂运来一批煤,计划每天用5吨,40天用完,如果改进锅炉后,每天节约1吨煤,这批煤可以用多少天?
565 |
566 | ### 例题4
567 |
568 | 一个果园请人帮忙摘桃子,4个人3小时共摘桃子600千克,照这样的效率计算,5个人8小时可以摘多少千克桃子?
569 |
570 | ### 练习4
571 |
572 | 15头牛4天吃了1260千克草,照这样计算,30头牛10天吃草多少千克?
573 |
574 | ### 例题5
575 |
576 | 6辆卡车运送4趟可以运走沙石48吨。如果有400吨沙石需要10趟运完,那么一共需要多少辆卡车?
577 |
578 | ### 练习5
579 |
580 | 4辆汽车5小时共运土石400方,现有10辆同样的汽车,要运1000方土石,需几小时?
581 |
582 | ### 例题6
583 |
584 | 一件工作12人每天工作8小时需要10天,照这样计算,如果增加8人,每天减少2小时,可以提前几天完成?
585 |
586 | ### 练习6
587 |
588 | 学校买来一批粉笔,原计划18个班可用60天,实际用45天后,有3个班外出了,剩下的粉笔够用多少天?
589 |
590 | ## 3.1.09.长方形与正方形
591 |
592 | ### 课前热身
593 |
594 | 【热身1】有20人修筑一条公路,计划15天完成。动工3天后抽出5人去植树,留下的人继续修路。如果每个人的工作效率不变,那么修完中段公路实际用多少天?
595 |
596 |
597 |
598 | 【热身2】已知3名模范职工和6名普通职工8小时可以生产零件420个。现在有一批生产任务,需要6名模范职工和12名普通职工生产14小时才能完成。如果工作了4小时后,又来了4名模范职工和8名普通职工,可以提前几小时完成任务?
599 |
600 |
601 |
602 | ### 学习目标
603 |
604 | - 理解面积的意义(面积的单位及其转换)
605 | - 会求长方形和正方形的面积(正方形面积=边长×边长;长方形面积=长×宽)
606 | - 掌握简单的割补、剪拼。
607 | - 长方形、正方形面积与周长区分和灵活转换
608 | - 运用长方形、正方形的性质(周长和面积)解决问题
609 | - 拓展——田字格模型
610 |
611 |
612 |
613 | ### 引入
614 |
615 | 对面积的直观感受和比较
616 |
617 |
618 |
619 | 【补充】有两个一样的长方形,长都是4厘米,宽都是2厘米。
620 |
621 | 把它们拼成一个长方形,请画出草图,并计算其周长和面积。
622 |
623 | 把它们拼成一个正方形,请画出草图,并计算其周长和面积。
624 |
625 |
626 |
627 | 一个花园长15米,宽10米,如果把这个花园用篱笆围起来,所围成的面积有多大?需要多长的篱笆?
628 |
629 |
630 |
631 | #### 单位换算
632 |
633 | (1)1米=()分米=()厘米=()毫米
634 |
635 | (2)1平方米=()平方分米=()平方厘米=()平方毫米
636 |
637 | (3)1平方千米=()平方米
638 |
639 | (4)8平方米=()平方分米
640 |
641 | (5)13平方米=()平方厘米
642 |
643 | (6)()平方米=500平方分米=()平方厘米
644 |
645 |
646 |
647 | #### 补充
648 |
649 | 选择合适的单位填入括号内。
650 |
651 | (1)一栋楼高约50()
652 |
653 | (2)课本封面面积约为6()
654 |
655 | (3)一个茶杯高约13()
656 |
657 | (4)黑板的面积约为5()
658 |
659 | (5)指甲盖的面积约为1()
660 |
661 | (6)一间教师的面积约为40()
662 |
663 |
664 |
665 |
666 |
667 | ### 例题练习
668 |
669 | #### 割补法求面积
670 |
671 | 【例题1】求下面图形的面积。(单位:厘米)
672 |
673 |  674 |
675 | 【练习1】计算下面图形的面积。(单位:厘米)
676 |
677 |
674 |
675 | 【练习1】计算下面图形的面积。(单位:厘米)
676 |
677 |  678 |
679 | #### 容斥原理求面积
680 |
681 | 【例题2】如图所示,两块边长为15厘米的抹布放在桌子上,重叠的部分恰好是个边长为5厘米的正方形。问:桌面被盖住部分的面积是多少?
682 |
683 |
678 |
679 | #### 容斥原理求面积
680 |
681 | 【例题2】如图所示,两块边长为15厘米的抹布放在桌子上,重叠的部分恰好是个边长为5厘米的正方形。问:桌面被盖住部分的面积是多少?
682 |
683 |  684 |
685 | 【练习2】两个正方形重叠部分面积为3平方厘米,求下面图形的面积。
686 |
687 |
684 |
685 | 【练习2】两个正方形重叠部分面积为3平方厘米,求下面图形的面积。
686 |
687 |  688 |
689 | #### 平移法求面积
690 |
691 | 【例题3】牛牛住的小区是个边长为100米的正方形,中央有“十字形”的路,路宽5米。问这条路的面积有多大?
692 |
693 |
688 |
689 | #### 平移法求面积
690 |
691 | 【例题3】牛牛住的小区是个边长为100米的正方形,中央有“十字形”的路,路宽5米。问这条路的面积有多大?
692 |
693 |  694 |
695 | 【练习3】下图中每个阴影长方形的宽都为6米,求阴影部分的面积。
696 |
697 |
694 |
695 | 【练习3】下图中每个阴影长方形的宽都为6米,求阴影部分的面积。
696 |
697 |  698 |
699 | 【例题4】两个长方形对应边的距离均为2,如果两个长方形之间(阴影部分)的面积是80,且大长方形的长是宽的2倍。求大长方形的面积。
700 |
701 |
698 |
699 | 【例题4】两个长方形对应边的距离均为2,如果两个长方形之间(阴影部分)的面积是80,且大长方形的长是宽的2倍。求大长方形的面积。
700 |
701 |  702 |
703 | 【练习4】一个长方形,长是13厘米,宽是8厘米。现在在距长方形每条边2厘米处对长方形进行剪切,得到一个小的长方形。问剪切后的长方形面积比原长方形减小了多少平方厘米?
704 |
705 |
706 |
707 | 【例题5】如图所示,较大正方形的边长依次是比它小的正方形边长的2倍,最小正方形的边长为2米,问最大正方形面积是最小正方形的几倍?
708 |
709 |
702 |
703 | 【练习4】一个长方形,长是13厘米,宽是8厘米。现在在距长方形每条边2厘米处对长方形进行剪切,得到一个小的长方形。问剪切后的长方形面积比原长方形减小了多少平方厘米?
704 |
705 |
706 |
707 | 【例题5】如图所示,较大正方形的边长依次是比它小的正方形边长的2倍,最小正方形的边长为2米,问最大正方形面积是最小正方形的几倍?
708 |
709 |  710 |
711 | 【练习5】有三个长方形,大长方形的长和宽依次是小长方形的长和宽的3倍,最大的长方形长为27米,宽为9米。问:最小长方形的面积。
712 |
713 |
714 |
715 | 【例题6】下图四个一样的长方形和一个小正方形拼成一个面积为81平方分米的大正方形,求每个长方形的周长。
716 |
717 |
710 |
711 | 【练习5】有三个长方形,大长方形的长和宽依次是小长方形的长和宽的3倍,最大的长方形长为27米,宽为9米。问:最小长方形的面积。
712 |
713 |
714 |
715 | 【例题6】下图四个一样的长方形和一个小正方形拼成一个面积为81平方分米的大正方形,求每个长方形的周长。
716 |
717 |  718 |
719 | 【练习6】四个一样的长方形和一个小正方形拼成一个大正方形,大小正方形的面积分别为121平方厘米和81平方厘米,问一个长方形的面积是多少?
720 |
721 |
718 |
719 | 【练习6】四个一样的长方形和一个小正方形拼成一个大正方形,大小正方形的面积分别为121平方厘米和81平方厘米,问一个长方形的面积是多少?
720 |
721 |  722 |
723 | #### 长宽加减对面积的影响
724 |
725 | 【例题7】
726 |
727 | (1)一个长方形长12米,宽8米,如果它的长增加2米,宽不变,这个长方形的面积增加多少平方米?
728 |
729 | (2)一个长方形如果宽不变,长增加8米,面积增加72平方米;和果长不变,宽减少4米,面积减少48平方米,这个长方形原来的面积是多少平方米?
730 |
731 |
732 |
733 | 【练习7】把一个长方形纸片的长减少5m,宽减少2m,得到一个小正方形。剪下来部分面积是80平方厘米,求正方形的边长是多少厘米?
734 |
735 |
736 |
737 | #### 长宽变倍对面积、周长的影响
738 |
739 | 【例题7】如果正方形A的边长是正方形B的边长的2倍,那么正方形A的周长是正方形B的周长的几倍?正方形A的面积是正方形B的面积几倍?
740 |
741 |
742 |
743 | 【练习7】有三个正方形A、B、C,已知B的面积是A的4倍,C的周长是B的2倍,则C的面积是A的几倍。
744 |
745 | 答案:16
746 |
747 |
748 |
749 | ### 拓展
750 |
751 | 【拓展1】一个教室的长是8米,宽是6米,在地面上铺边长2分米的方砖,一共需要多少块?
752 |
753 |
754 |
755 | 【拓展2】把一个长方形的长增加5分米,宽增加8分米后,得到一个面积比原长方形多181平方分米的正方形。求这个正方形的边长是多少分米?
756 |
757 |
758 |
759 | 【拓展3】如图,大长方形被分为4个小长方形,A、B、C、D分别代表它们的面积,已知B=18,C= 18,A=9,求D的面积是多少?
760 |
761 |
722 |
723 | #### 长宽加减对面积的影响
724 |
725 | 【例题7】
726 |
727 | (1)一个长方形长12米,宽8米,如果它的长增加2米,宽不变,这个长方形的面积增加多少平方米?
728 |
729 | (2)一个长方形如果宽不变,长增加8米,面积增加72平方米;和果长不变,宽减少4米,面积减少48平方米,这个长方形原来的面积是多少平方米?
730 |
731 |
732 |
733 | 【练习7】把一个长方形纸片的长减少5m,宽减少2m,得到一个小正方形。剪下来部分面积是80平方厘米,求正方形的边长是多少厘米?
734 |
735 |
736 |
737 | #### 长宽变倍对面积、周长的影响
738 |
739 | 【例题7】如果正方形A的边长是正方形B的边长的2倍,那么正方形A的周长是正方形B的周长的几倍?正方形A的面积是正方形B的面积几倍?
740 |
741 |
742 |
743 | 【练习7】有三个正方形A、B、C,已知B的面积是A的4倍,C的周长是B的2倍,则C的面积是A的几倍。
744 |
745 | 答案:16
746 |
747 |
748 |
749 | ### 拓展
750 |
751 | 【拓展1】一个教室的长是8米,宽是6米,在地面上铺边长2分米的方砖,一共需要多少块?
752 |
753 |
754 |
755 | 【拓展2】把一个长方形的长增加5分米,宽增加8分米后,得到一个面积比原长方形多181平方分米的正方形。求这个正方形的边长是多少分米?
756 |
757 |
758 |
759 | 【拓展3】如图,大长方形被分为4个小长方形,A、B、C、D分别代表它们的面积,已知B=18,C= 18,A=9,求D的面积是多少?
760 |
761 | 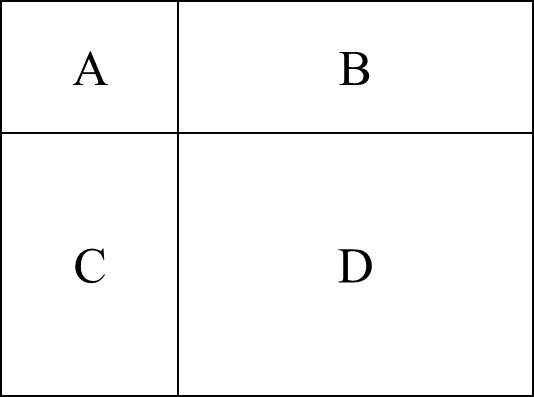 762 |
763 | 【拓展4】如图,一个大长方形花园被分成了9个小长方形,其中4块的面积分别为1、2、4、16。若b与c的面积之和为6,求花园的面积是多少?
764 |
765 |
762 |
763 | 【拓展4】如图,一个大长方形花园被分成了9个小长方形,其中4块的面积分别为1、2、4、16。若b与c的面积之和为6,求花园的面积是多少?
764 |
765 |  766 |
767 |
768 |
769 | ## 3.1.12. 差倍问题
770 |
771 | ### 整数倍
772 |
773 | 例题1
774 |
775 | 乐乐老师买来一些糖果分给田田和牛牛,牛牛分到的是田田的 3 倍,田田分到的比牛牛少 30 颗,田田和牛牛各分到多少颗糖?
776 |
777 | 练习1
778 |
779 | 乐乐老师比丁丁大 24 岁,今年乐乐老师的年龄正好是丁丁年龄的 3 倍,你知道今年乐乐老师多少岁?丁丁多少岁吗?
780 |
781 | ### 非整数倍
782 |
783 | 例题2
784 |
785 | 学校买来的足球比排球多 18 个,足球的个数比排球的 2 倍少 4 个。学校买来足球和排球各多少个?
786 |
787 | 练习2
788 |
789 | 三年级(1)班女生比男生多 15 人,女生的人数比男生的 4 倍少 3 人,则三年级(1)班有男生和女生各多少人?
790 |
791 | ### 同增同减差不变
792 |
793 | 例题3
794 |
795 | 甲仓库存放大米 500 袋,乙仓库存放大米 200 袋,现从两个仓库里运走同样袋数的大米,结果甲仓库剩下的大米正好是乙仓库剩下大米的 3 倍,问从两个仓库里各运走大米多少袋?
796 |
797 | 练习3
798 |
799 | 实验小学一校区人数比实验小学二校区人数少 540 人。第三校区建成后,从一、二校区各调走 200 人到第三校区,这时实验小学二校区人数恰好是实验小学一校区人数的 4 倍,那么实验小学一校区和实验小学二校区原来各有多少人?
800 |
801 | ### 找差
802 |
803 | 例题4
804 |
805 | 阿普和丁丁做题,如果阿普再做 4 道就和丁丁做的一样多,如果丁丁再做 6 道就是阿普的 3 倍。阿普和丁丁各做了多少道题?
806 |
807 | 练习4
808 |
809 | 甲、乙两个数,如果甲数加上 50,就等于乙数,如果乙数加上 350 就等于甲数的 3 倍,问甲、乙各是多少?
810 |
811 | 例题5
812 |
813 | 两筐重量相等的苹果,从甲筐取出 7 千克,乙筐加上 19 千克,这时乙筐重量是甲筐的 2 倍。原来两筐各有多少千克苹果?
814 |
815 | 练习5
816 |
817 | 用、乙两桶油重量相等,如果甲桶取走油 26 千克,乙桶加入油 14 千克,这时乙桶油的重量是甲桶油重量的 3 倍。那么,两桶油原来分别有多少千克?
818 |
819 | ### 变倍问题
820 |
821 | 例题6
822 |
823 | 苹果的个数是梨的 3 倍,如果苹果加上 6 个,梨也加上 6 个,此时苹果的个数是梨的个数的 2 倍。问原来苹果、梨各有多少个?
824 |
825 | 练习6
826 |
827 | 今年阿普的年龄是牛牛年龄的 5 倍,6 年后,阿普的年龄是牛牛年龄的 3 倍。今年阿普和牛牛各多少岁?
828 |
829 | ### 拓展练习
830 |
831 | 牛牛和阿普两人所存的钱数相等。牛牛要买一件商品向阿普借了 120 元,这时牛牛的钱数正好是阿普的 4 倍。那么,原来牛牛和阿普各有多少钱?
832 |
833 | ## 3.1.13 巧算乘法
834 |
835 | ### 课程框架
836 |
837 | 乘法运算律
838 |
839 | 提取公因数
840 |
841 | 凑整思想
842 |
843 | ### 乘法凑整(乘法好朋友数)
844 |
845 | **例题1**
846 |
847 | 计算:
848 | $$
849 | 25\times125\times4
850 | $$
851 |
852 | $$
853 | 5\times13\times125\times20\times8
854 | $$
855 |
856 | **练习1**
857 |
858 | 计算:
859 | $$
860 | 27\times125\times8
861 | $$
862 |
863 | $$
864 | 6\times25\times4\times8
865 | $$
866 |
867 | ### 先拆分再计算
868 |
869 | **例题2**
870 |
871 | 计算:
872 | $$
873 | 888\times125
874 | $$
875 |
876 | **练习2**
877 |
878 | 计算:
879 | $$
880 | 25\times36
881 | $$
882 |
883 | $$
884 | 125\times24
885 | $$
886 |
887 | $$
888 | 25\times64\times19\times125
889 | $$
890 |
891 | ### 乘法分配律
892 |
893 | **例题3**
894 |
895 | 计算:
896 | $$
897 | 125\times(80+2)
898 | $$
899 |
900 | $$
901 | 68\times(100+1)
902 | $$
903 |
904 | $$
905 | 56\times999
906 | $$
907 |
908 | **练习3**
909 |
910 | 计算:
911 | $$
912 | 25\times(4+10)
913 | $$
914 |
915 | $$
916 | 37\times(100+2)
917 | $$
918 |
919 | $$
920 | 23\times99
921 | $$
922 |
923 | ### 提取公因数
924 |
925 | **例题4**
926 |
927 | 计算:
928 | $$
929 | 51\times32+51\times68
930 | $$
931 |
932 | $$
933 | 218\times59+218\times40+218
934 | $$
935 |
936 | **练习4**
937 |
938 | 计算:
939 | $$
940 | 80\times2016-2\times2016+2016\times22
941 | $$
942 |
943 | $$
944 | 1999+999\times999
945 | $$
946 |
947 | ### 隐藏的公因数
948 |
949 | **例题5**
950 |
951 | 计算:
952 | $$
953 | 24\times99+33\times76\times3
954 | $$
955 |
956 | $$
957 | 999\times222+333\times334
958 | $$
959 |
960 | **练习5**
961 |
962 | 计算:
963 | $$
964 | 255\times999+255\times2-255
965 | $$
966 |
967 | $$
968 | 999\times778+333\times666
969 | $$
970 |
971 | ### 重码数
972 |
973 | **例题6**
974 |
975 | 计算:
976 |
977 | | $37\times101$ | $49\times10101$ | $2016\times10001$ |
978 | | ------------- | --------------- | ----------------- |
979 | | $12\times11$ | $52\times11$ | $69\times11$ |
980 | | $57\times53$ | $26\times24$ | $61\times69$ |
981 | | $16\times96$ | $78\times38$ | $41\times61$ |
982 |
983 | **练习6**
984 |
985 | 计算:
986 |
987 | | $20162016\times2015-20152015\times2016$ | |
988 | | --------------------------------------- | ------------ |
989 | | $99\times11$ | $24\times11$ |
990 | | $33\times37$ | $68\times62$ |
991 | | $37\times77$ | $26\times86$ |
992 |
993 | ## 3.1.14. 除法巧算
994 |
995 | ### 课程框架
996 |
997 | 1. 抱符号搬家(移项)
998 | 2. 添去括号
999 | 3. 分配与提取
1000 | 4. 商不变
1001 |
1002 | ### 内容分析
1003 |
1004 | ### 热身 1
1005 |
1006 | 计算:
1007 | $$
1008 | 12\times4+13\times4
1009 | $$
1010 |
1011 | ### 热身 2
1012 |
1013 | 计算:
1014 | $$
1015 | 25\times23\times32\times125
1016 | $$
1017 |
1018 | ### 热身 3
1019 |
1020 | 计算:
1021 | $$
1022 | 935\times187\div187
1023 | $$
1024 |
1025 | ### 例题1(添去括号)
1026 |
1027 | 计算:
1028 | $$
1029 | 200\div25\div4
1030 | $$
1031 |
1032 | $$
1033 | 2400\div(120\times4)
1034 | $$
1035 |
1036 | $$
1037 | 1200\div(120\div4)
1038 | $$
1039 |
1040 | ### 练习1
1041 |
1042 | 计算:
1043 | $$
1044 | 360\div(90\div2)
1045 | $$
1046 |
1047 | $$
1048 | 1100\div(11\times5)
1049 | $$
1050 |
1051 | $$
1052 | 400\div16\div5
1053 | $$
1054 |
1055 | ### 拓展1
1056 |
1057 | 计算:
1058 | $$
1059 | 450\times6\div54
1060 | $$
1061 |
1062 | $$
1063 | 4200\div(50\times7)
1064 | $$
1065 |
1066 | ### 例题2(移项)
1067 |
1068 | 计算:
1069 | $$
1070 | (1225\div8)\times(8\div4)\times(4\div1)
1071 | $$
1072 |
1073 | ### 练习2
1074 |
1075 | 计算:
1076 | $$
1077 | (30\times18)\div(18\div8)\div(8\div1)
1078 | $$
1079 |
1080 | ### 拓展
1081 |
1082 | $$
1083 | 168\times25\div14\times7\div5
1084 | $$
1085 |
1086 | ### 例题3(商不变)
1087 |
1088 | 算一算,比一比,你有什么发现。
1089 | $$
1090 | 35\div5=
1091 | $$
1092 |
1093 | $$
1094 | 350\div50=
1095 | $$
1096 |
1097 | $$
1098 | 3500\div500=
1099 | $$
1100 |
1101 | $$
1102 | 80\div4=
1103 | $$
1104 |
1105 | $$
1106 | 800\div40=
1107 | $$
1108 |
1109 | $$
1110 | 8000\div400=
1111 | $$
1112 |
1113 | ### 练习3
1114 |
1115 | 填空。
1116 | $$
1117 | 36\div4=72\div\_\_\_\_\_
1118 | $$
1119 |
1120 | $$
1121 | 400\div25=\_\_\_\_\_\div100
1122 | $$
1123 |
1124 | $$
1125 | 120\div15=\_\_\_\_\_\div5
1126 | $$
1127 |
1128 | $$
1129 | 72\div4=36\div\_\_\_\_\_
1130 | $$
1131 |
1132 | ### 例题4(商不变的应用)
1133 |
1134 | 计算:
1135 | $$
1136 | 1200\div25
1137 | $$
1138 |
1139 | $$
1140 | 3300\div55
1141 | $$
1142 |
1143 | ### 练习4
1144 |
1145 | 计算:
1146 | $$
1147 | 2000\div125
1148 | $$
1149 |
1150 | $$
1151 | 2870\div35
1152 | $$
1153 |
1154 | ### 例题5(分配)
1155 |
1156 | 计算:
1157 | $$
1158 | (13039+260)\div13
1159 | $$
1160 |
1161 | $$
1162 | (54+81+360)\div9
1163 | $$
1164 |
1165 | ### 练习5
1166 |
1167 | 计算:
1168 | $$
1169 | (18000-720)\div9
1170 | $$
1171 |
1172 | $$
1173 | (4800-240+720)\div12
1174 | $$
1175 |
1176 | ### 例题6(提取)
1177 |
1178 | 计算:
1179 | $$
1180 | 329\div7+371\div7
1181 | $$
1182 |
1183 | $$
1184 | 25\div6+35\div6
1185 | $$
1186 |
1187 | ### 练习6
1188 |
1189 | 计算:
1190 | $$
1191 | 31\div5+32\div5+33\div5+34\div5+35\div5
1192 | $$
1193 |
1194 | ### 拓展
1195 |
1196 | 计算:
1197 | $$
1198 | 25\div4+25\div6+35\div4+35\div6
1199 | $$
1200 |
1201 | ### 练习1
1202 |
1203 | 计算:
1204 | $$
1205 | 4000\div125\div8
1206 | $$
1207 |
1208 | ### 练习2
1209 |
1210 | 计算:
1211 | $$
1212 | 426\div(213\times26\div12)
1213 | $$
1214 |
1215 | ### 练习3
1216 |
1217 | 计算:
1218 | $$
1219 | (126\times56)\div(7\times18)
1220 | $$
1221 |
1222 | ### 练习4
1223 |
1224 | 计算:
1225 | $$
1226 | (12\times5)\div(5\div3)\div(4\div6)\times(4\div3)
1227 | $$
1228 |
1229 | ### 练习5
1230 |
1231 | 计算:
1232 | $$
1233 | 1300\div25
1234 | $$
1235 |
1236 | ### 练习6
1237 |
1238 | 计算:
1239 | $$
1240 | 770\div55
1241 | $$
1242 |
1243 | ### 练习7
1244 |
1245 | 计算:
1246 | $$
1247 | (189+27)\div9
1248 | $$
1249 |
1250 | ### 练习8
1251 |
1252 | 计算:
1253 | $$
1254 | 523\div7+424\div7
1255 | $$
1256 |
1257 | ### 练习9
1258 |
1259 | 计算:
1260 | $$
1261 | (14400-240+720)\div12
1262 | $$
1263 |
1264 | ### 练习10
1265 |
1266 | 计算:
1267 | $$
1268 | (132639-5265-7891)\div13
1269 | $$
1270 |
1271 | ### 练习11
1272 |
1273 | 计算:
1274 | $$
1275 | 122\div4+206\div4+72\div4
1276 | $$
1277 |
1278 | ### 练习12
1279 |
1280 | 计算:
1281 | $$
1282 | 288\div24+288\div18+288\div6
1283 | $$
1284 |
1285 | ## 3.1.15. 鸡兔同笼进阶
1286 |
1287 | ### 本质
1288 |
1289 | 两种事物,凑两个条件
1290 |
1291 | ### 方法
1292 |
1293 | * 假设调整——假设、验算、调整
1294 | * 分组——倍数关系分组
1295 | * 合并
1296 | + 倍数关系,分组合并
1297 | + 不变量合并
1298 | + 平均值合并
1299 |
1300 | 例题1——假设法
1301 |
1302 | 例题2——实际应用
1303 |
1304 | 例题3——分组
1305 |
1306 | 例题4——分组
1307 |
1308 | 例题5——合并
1309 |
1310 | 例题6——实际应用
1311 |
1312 | ### 铺垫
1313 |
1314 | 鸡兔共有10只,关在一个笼子里,笼中共有26条腿,鸡兔各有几只?
1315 |
1316 | 列表法
1317 |
1318 | | 鸡(只) | 10 | 9 | 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
1319 | | ---------- | ---- | ---- | ---- | ---- | ---- | ---- | ---- | ---- | ---- | ---- | ---- |
1320 | | 兔(只) | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
1321 | | 腿数(条) | | | | | | | | | | | |
1322 |
1323 | 画图法
1324 |
1325 | 假设调整
1326 |
1327 | 假设全是鸡-验算-调整
1328 |
1329 | ### 例题1
1330 |
1331 | 牛牛家养了一些鸡和免子,同时养在一个笼子里,牛牛数了数,它们共有35个头,94只脚。问:牛牛家养的鸡和免各有多少只?
1332 |
1333 | ### 练习1
1334 |
1335 | 鸡免共有45只,关在同一个笼子中。每只鸡有2只脚,每只免子有4只脚,笼中共有100只脚。试计算,笼中有鸡多少只?免子多少只?
1336 |
1337 | ### 拓展2
1338 |
1339 | 在一个停车场上,现有汽车和摩托车共24辆,其中汽车有4个轮子,摩托车有3个轮子,摩托车有3个轮子,这些车共有86个轮子,那么三轮摩托车共有多少辆?
1340 |
1341 | ### 拓展3
1342 |
1343 | 100名师生绿化校园,老师每人载3棵树,学生每两人栽1颗树,总共载树100棵,那么学生共载树多少棵?
1344 |
1345 | ### 拓展
1346 |
1347 | 奥特曼遭遇一帮怪兽,大怪兽2头4腿,小怪兽2头2腿,大小怪兽一共20个头,32条腿,那么,大小怪兽各有几只?
1348 |
1349 | ### 分组
1350 |
1351 | 有相同数量的鸡和兔,共36条腿,那么鸡兔各有几只?
1352 |
1353 | 鸡兔同笼,兔的数量是鸡的3倍,共140条腿,那么,鸡兔各有几只?
1354 |
1355 | ### 补充
1356 |
1357 | 鸡兔同笼,共27只,已知两种动物的腿数相同,那么,鸡兔各有几只?
1358 |
1359 | 鸡兔同笼,共40只,已知鸡腿数是兔腿数的2倍,那么,鸡兔各有几只?
1360 |
1361 | ### 合并
1362 |
1363 | 鸡兔同笼,鸡、兔共有107只,兔的腿数比鸡的腿数多56条,问鸡、兔各多少只?
1364 |
1365 | ### 例题2
1366 |
1367 | 丁丁数了数笼中的鸡和免,发现腿有120条,鸡的只数比兔的只数的3倍多5只。则鸡和免子共有多少只?
1368 |
1369 | ### 练习2
1370 |
1371 | 田田数了数笼中的鸡和兔,发现共有脚240只,免的只数与鸡的只数相同。则鸡和免共多少只?
1372 |
1373 | ### 例题3
1374 |
1375 | 牛牛数了数笼中的鸡和兔,发现头有98个,鸡的脚数比免的脚数的2倍少4只。则免子有多少只?鸡有多少只?
1376 |
1377 | ### 练习3
1378 |
1379 | 牛牛数笼中的鸡和免,头有90个,鸡的腿数与免的腿数相同。鸡有多少只?
1380 |
1381 | ### 例题4(实际应用)
1382 |
1383 | 阿普去参加奥运知识抢答竞赛,按规定每答对一题得5分,答错一题要扣1分。阿普抢答10道题后,共得到26分,请问:阿普答对了几道题?
1384 |
1385 | ### 练习4
1386 |
1387 | 工人运青瓷花瓶250个,规定完整运到目的地一个给运费20元,损坏一个赔100元。运完这批花瓶后,工人共得4400元,则损坏了多少个?
1388 |
1389 | ### 例题5
1390 |
1391 | 鸡免同笼,鸡和免共有46条腿。如果将鸡与免的数量互换,那么总腿数变为38条,请问:原来鸡和免各有多少只?
1392 |
1393 | ### 练习5
1394 |
1395 | 田田数笼中的鸡和免,共有脚96只,若将鸡换成免,免换成鸡,则还有96只脚。鸡、免原来各多少只?
1396 |
1397 | ### 例题6
1398 |
1399 | 有蜘蛛、蜻蜓、蝉三种动物共18只,共有腿118条,翅膀20对。己知蜘蛛8条腿;蜻蜓6条腿,两对翅膀;蝉6条腿,一对翅膀。求蜻蜓有多少只。
1400 |
1401 | ### 练习6
1402 |
1403 | 犀牛、羚羊、孔雀三种动物共有头26个,脚80只,犄角20只。已知犀牛有4只脚,1只犄角;羚羊有4只脚,2只犄角;孔雀有2只脚,没有犄角。那么,犀牛、羚羊、孔雀各有多少只?
1404 |
1405 | ## 3.1.16. 周期问题进阶
1406 |
1407 | ### 热身1
1408 |
1409 | 学校宿舍楼一共有30间宿舍,大宿舍每间住6人,小宿舍每间住4人。已知这些宿舍中共住了168名学生,那么其中有多少间大宿舍、多少间小宿舍呢?
1410 |
1411 | ### 热身2
1412 |
1413 | 100个和尚140个馍,大和尚1人分3个馍,小和尚1人分1个馍。问:大、小和尚各有多少人?
1414 |
1415 | ### 热身3
1416 |
1417 | 找出下面数列的周期。
1418 |
1419 | 2,3,1,2,3,1,2,3,1,……
1420 |
1421 | 1,3,5,7,1,3,5,7,1,3,……
1422 |
1423 | 1,4,2,8,5,7,1,4,2,8,5,7,……
1424 |
1425 | ### 例题1(整周期)
1426 |
1427 | 田田和丁丁做游戏,他们把两种形状的小石子按下面的规律排列:
1428 |
1429 | ⭕️⭐️⭕️⭐️⭐️⭕️⭐️⭐️⭐️⭕️⭐️⭕️⭐️⭐️⭕️⭐️⭐️⭐️⭕️⭐️⭕️⭐️⭐️⭕️⭐️⭐️⭐️……
1430 |
1431 | 你知道他们所排列的这些小石子中,第100个是什么图形吗?第180个又是什么图形呢?
1432 |
1433 | ### 练习1
1434 |
1435 | 一天早上,牛牛一起床就大喊:“我要吃包子我要吃包子我要吃包子……”请问,牛牛喊得第28个字是什么字?
1436 |
1437 | ### 例题2(非整周期)
1438 |
1439 | 圣诞节到了,街上挂满了彩灯,并且按照5盏红灯接4 盏蓝灯接 1盏黄灯,然后又是5盏红灯接4 盏蓝灯接 1盏黄灯这样的顺序排下去。问:
1440 | (1)第 150 盏灯是什么颜色?
1441 | (2)前 200 盏彩灯中有多少盏蓝灯?
1442 |
1443 | ### 练习2
1444 |
1445 | 小莉把平时存下来的硬币按3个1分,2个2分,1个5分的顺序排列起来,刚好100枚,请问这 100枚硬币中有多少枚1分的硬币?
1446 |
1447 | ### 例题3
1448 |
1449 | 已知一列数:5,4,1,5,4,1,2,3,5,4,1,2,3,5,4,1,2,3,……,一直写到第 103个数,请问这些数的和是多少?
1450 |
1451 | ### 练习3
1452 |
1453 | 小和尚在地上写了一列数:7,0,7,0,2,5,3,7,0,2,5,3,……,一直写呀写,写了42个数,你能求出这 42 个数相加的和是多少吗?
1454 |
1455 | ### 例题4
1456 |
1457 | 如下图所示的表中,将每列上、下两个字组成一组,例如第一组为“数真”,第二组为 “学有”,那么第50组是什么字?
1458 |
1459 | 数学数学数学数学数学数学数学数学数学……
1460 |
1461 | 真有趣真有趣真有趣真有趣真有趣真有趣……
1462 |
1463 | ### 练习4
1464 |
1465 | 如图所示,每列上、下字和字母组成一组,例如,第一组是“A红”,第二组是“B黄”,请写出第63组是什么?
1466 |
1467 | ABABABABABABA
1468 |
1469 | 红黄蓝绿红黄蓝绿红黄蓝绿
1470 |
1471 | ### 例题5
1472 |
1473 | 12个同学围成一圈做传球的游戏,如图。
1474 |
1475 |
766 |
767 |
768 |
769 | ## 3.1.12. 差倍问题
770 |
771 | ### 整数倍
772 |
773 | 例题1
774 |
775 | 乐乐老师买来一些糖果分给田田和牛牛,牛牛分到的是田田的 3 倍,田田分到的比牛牛少 30 颗,田田和牛牛各分到多少颗糖?
776 |
777 | 练习1
778 |
779 | 乐乐老师比丁丁大 24 岁,今年乐乐老师的年龄正好是丁丁年龄的 3 倍,你知道今年乐乐老师多少岁?丁丁多少岁吗?
780 |
781 | ### 非整数倍
782 |
783 | 例题2
784 |
785 | 学校买来的足球比排球多 18 个,足球的个数比排球的 2 倍少 4 个。学校买来足球和排球各多少个?
786 |
787 | 练习2
788 |
789 | 三年级(1)班女生比男生多 15 人,女生的人数比男生的 4 倍少 3 人,则三年级(1)班有男生和女生各多少人?
790 |
791 | ### 同增同减差不变
792 |
793 | 例题3
794 |
795 | 甲仓库存放大米 500 袋,乙仓库存放大米 200 袋,现从两个仓库里运走同样袋数的大米,结果甲仓库剩下的大米正好是乙仓库剩下大米的 3 倍,问从两个仓库里各运走大米多少袋?
796 |
797 | 练习3
798 |
799 | 实验小学一校区人数比实验小学二校区人数少 540 人。第三校区建成后,从一、二校区各调走 200 人到第三校区,这时实验小学二校区人数恰好是实验小学一校区人数的 4 倍,那么实验小学一校区和实验小学二校区原来各有多少人?
800 |
801 | ### 找差
802 |
803 | 例题4
804 |
805 | 阿普和丁丁做题,如果阿普再做 4 道就和丁丁做的一样多,如果丁丁再做 6 道就是阿普的 3 倍。阿普和丁丁各做了多少道题?
806 |
807 | 练习4
808 |
809 | 甲、乙两个数,如果甲数加上 50,就等于乙数,如果乙数加上 350 就等于甲数的 3 倍,问甲、乙各是多少?
810 |
811 | 例题5
812 |
813 | 两筐重量相等的苹果,从甲筐取出 7 千克,乙筐加上 19 千克,这时乙筐重量是甲筐的 2 倍。原来两筐各有多少千克苹果?
814 |
815 | 练习5
816 |
817 | 用、乙两桶油重量相等,如果甲桶取走油 26 千克,乙桶加入油 14 千克,这时乙桶油的重量是甲桶油重量的 3 倍。那么,两桶油原来分别有多少千克?
818 |
819 | ### 变倍问题
820 |
821 | 例题6
822 |
823 | 苹果的个数是梨的 3 倍,如果苹果加上 6 个,梨也加上 6 个,此时苹果的个数是梨的个数的 2 倍。问原来苹果、梨各有多少个?
824 |
825 | 练习6
826 |
827 | 今年阿普的年龄是牛牛年龄的 5 倍,6 年后,阿普的年龄是牛牛年龄的 3 倍。今年阿普和牛牛各多少岁?
828 |
829 | ### 拓展练习
830 |
831 | 牛牛和阿普两人所存的钱数相等。牛牛要买一件商品向阿普借了 120 元,这时牛牛的钱数正好是阿普的 4 倍。那么,原来牛牛和阿普各有多少钱?
832 |
833 | ## 3.1.13 巧算乘法
834 |
835 | ### 课程框架
836 |
837 | 乘法运算律
838 |
839 | 提取公因数
840 |
841 | 凑整思想
842 |
843 | ### 乘法凑整(乘法好朋友数)
844 |
845 | **例题1**
846 |
847 | 计算:
848 | $$
849 | 25\times125\times4
850 | $$
851 |
852 | $$
853 | 5\times13\times125\times20\times8
854 | $$
855 |
856 | **练习1**
857 |
858 | 计算:
859 | $$
860 | 27\times125\times8
861 | $$
862 |
863 | $$
864 | 6\times25\times4\times8
865 | $$
866 |
867 | ### 先拆分再计算
868 |
869 | **例题2**
870 |
871 | 计算:
872 | $$
873 | 888\times125
874 | $$
875 |
876 | **练习2**
877 |
878 | 计算:
879 | $$
880 | 25\times36
881 | $$
882 |
883 | $$
884 | 125\times24
885 | $$
886 |
887 | $$
888 | 25\times64\times19\times125
889 | $$
890 |
891 | ### 乘法分配律
892 |
893 | **例题3**
894 |
895 | 计算:
896 | $$
897 | 125\times(80+2)
898 | $$
899 |
900 | $$
901 | 68\times(100+1)
902 | $$
903 |
904 | $$
905 | 56\times999
906 | $$
907 |
908 | **练习3**
909 |
910 | 计算:
911 | $$
912 | 25\times(4+10)
913 | $$
914 |
915 | $$
916 | 37\times(100+2)
917 | $$
918 |
919 | $$
920 | 23\times99
921 | $$
922 |
923 | ### 提取公因数
924 |
925 | **例题4**
926 |
927 | 计算:
928 | $$
929 | 51\times32+51\times68
930 | $$
931 |
932 | $$
933 | 218\times59+218\times40+218
934 | $$
935 |
936 | **练习4**
937 |
938 | 计算:
939 | $$
940 | 80\times2016-2\times2016+2016\times22
941 | $$
942 |
943 | $$
944 | 1999+999\times999
945 | $$
946 |
947 | ### 隐藏的公因数
948 |
949 | **例题5**
950 |
951 | 计算:
952 | $$
953 | 24\times99+33\times76\times3
954 | $$
955 |
956 | $$
957 | 999\times222+333\times334
958 | $$
959 |
960 | **练习5**
961 |
962 | 计算:
963 | $$
964 | 255\times999+255\times2-255
965 | $$
966 |
967 | $$
968 | 999\times778+333\times666
969 | $$
970 |
971 | ### 重码数
972 |
973 | **例题6**
974 |
975 | 计算:
976 |
977 | | $37\times101$ | $49\times10101$ | $2016\times10001$ |
978 | | ------------- | --------------- | ----------------- |
979 | | $12\times11$ | $52\times11$ | $69\times11$ |
980 | | $57\times53$ | $26\times24$ | $61\times69$ |
981 | | $16\times96$ | $78\times38$ | $41\times61$ |
982 |
983 | **练习6**
984 |
985 | 计算:
986 |
987 | | $20162016\times2015-20152015\times2016$ | |
988 | | --------------------------------------- | ------------ |
989 | | $99\times11$ | $24\times11$ |
990 | | $33\times37$ | $68\times62$ |
991 | | $37\times77$ | $26\times86$ |
992 |
993 | ## 3.1.14. 除法巧算
994 |
995 | ### 课程框架
996 |
997 | 1. 抱符号搬家(移项)
998 | 2. 添去括号
999 | 3. 分配与提取
1000 | 4. 商不变
1001 |
1002 | ### 内容分析
1003 |
1004 | ### 热身 1
1005 |
1006 | 计算:
1007 | $$
1008 | 12\times4+13\times4
1009 | $$
1010 |
1011 | ### 热身 2
1012 |
1013 | 计算:
1014 | $$
1015 | 25\times23\times32\times125
1016 | $$
1017 |
1018 | ### 热身 3
1019 |
1020 | 计算:
1021 | $$
1022 | 935\times187\div187
1023 | $$
1024 |
1025 | ### 例题1(添去括号)
1026 |
1027 | 计算:
1028 | $$
1029 | 200\div25\div4
1030 | $$
1031 |
1032 | $$
1033 | 2400\div(120\times4)
1034 | $$
1035 |
1036 | $$
1037 | 1200\div(120\div4)
1038 | $$
1039 |
1040 | ### 练习1
1041 |
1042 | 计算:
1043 | $$
1044 | 360\div(90\div2)
1045 | $$
1046 |
1047 | $$
1048 | 1100\div(11\times5)
1049 | $$
1050 |
1051 | $$
1052 | 400\div16\div5
1053 | $$
1054 |
1055 | ### 拓展1
1056 |
1057 | 计算:
1058 | $$
1059 | 450\times6\div54
1060 | $$
1061 |
1062 | $$
1063 | 4200\div(50\times7)
1064 | $$
1065 |
1066 | ### 例题2(移项)
1067 |
1068 | 计算:
1069 | $$
1070 | (1225\div8)\times(8\div4)\times(4\div1)
1071 | $$
1072 |
1073 | ### 练习2
1074 |
1075 | 计算:
1076 | $$
1077 | (30\times18)\div(18\div8)\div(8\div1)
1078 | $$
1079 |
1080 | ### 拓展
1081 |
1082 | $$
1083 | 168\times25\div14\times7\div5
1084 | $$
1085 |
1086 | ### 例题3(商不变)
1087 |
1088 | 算一算,比一比,你有什么发现。
1089 | $$
1090 | 35\div5=
1091 | $$
1092 |
1093 | $$
1094 | 350\div50=
1095 | $$
1096 |
1097 | $$
1098 | 3500\div500=
1099 | $$
1100 |
1101 | $$
1102 | 80\div4=
1103 | $$
1104 |
1105 | $$
1106 | 800\div40=
1107 | $$
1108 |
1109 | $$
1110 | 8000\div400=
1111 | $$
1112 |
1113 | ### 练习3
1114 |
1115 | 填空。
1116 | $$
1117 | 36\div4=72\div\_\_\_\_\_
1118 | $$
1119 |
1120 | $$
1121 | 400\div25=\_\_\_\_\_\div100
1122 | $$
1123 |
1124 | $$
1125 | 120\div15=\_\_\_\_\_\div5
1126 | $$
1127 |
1128 | $$
1129 | 72\div4=36\div\_\_\_\_\_
1130 | $$
1131 |
1132 | ### 例题4(商不变的应用)
1133 |
1134 | 计算:
1135 | $$
1136 | 1200\div25
1137 | $$
1138 |
1139 | $$
1140 | 3300\div55
1141 | $$
1142 |
1143 | ### 练习4
1144 |
1145 | 计算:
1146 | $$
1147 | 2000\div125
1148 | $$
1149 |
1150 | $$
1151 | 2870\div35
1152 | $$
1153 |
1154 | ### 例题5(分配)
1155 |
1156 | 计算:
1157 | $$
1158 | (13039+260)\div13
1159 | $$
1160 |
1161 | $$
1162 | (54+81+360)\div9
1163 | $$
1164 |
1165 | ### 练习5
1166 |
1167 | 计算:
1168 | $$
1169 | (18000-720)\div9
1170 | $$
1171 |
1172 | $$
1173 | (4800-240+720)\div12
1174 | $$
1175 |
1176 | ### 例题6(提取)
1177 |
1178 | 计算:
1179 | $$
1180 | 329\div7+371\div7
1181 | $$
1182 |
1183 | $$
1184 | 25\div6+35\div6
1185 | $$
1186 |
1187 | ### 练习6
1188 |
1189 | 计算:
1190 | $$
1191 | 31\div5+32\div5+33\div5+34\div5+35\div5
1192 | $$
1193 |
1194 | ### 拓展
1195 |
1196 | 计算:
1197 | $$
1198 | 25\div4+25\div6+35\div4+35\div6
1199 | $$
1200 |
1201 | ### 练习1
1202 |
1203 | 计算:
1204 | $$
1205 | 4000\div125\div8
1206 | $$
1207 |
1208 | ### 练习2
1209 |
1210 | 计算:
1211 | $$
1212 | 426\div(213\times26\div12)
1213 | $$
1214 |
1215 | ### 练习3
1216 |
1217 | 计算:
1218 | $$
1219 | (126\times56)\div(7\times18)
1220 | $$
1221 |
1222 | ### 练习4
1223 |
1224 | 计算:
1225 | $$
1226 | (12\times5)\div(5\div3)\div(4\div6)\times(4\div3)
1227 | $$
1228 |
1229 | ### 练习5
1230 |
1231 | 计算:
1232 | $$
1233 | 1300\div25
1234 | $$
1235 |
1236 | ### 练习6
1237 |
1238 | 计算:
1239 | $$
1240 | 770\div55
1241 | $$
1242 |
1243 | ### 练习7
1244 |
1245 | 计算:
1246 | $$
1247 | (189+27)\div9
1248 | $$
1249 |
1250 | ### 练习8
1251 |
1252 | 计算:
1253 | $$
1254 | 523\div7+424\div7
1255 | $$
1256 |
1257 | ### 练习9
1258 |
1259 | 计算:
1260 | $$
1261 | (14400-240+720)\div12
1262 | $$
1263 |
1264 | ### 练习10
1265 |
1266 | 计算:
1267 | $$
1268 | (132639-5265-7891)\div13
1269 | $$
1270 |
1271 | ### 练习11
1272 |
1273 | 计算:
1274 | $$
1275 | 122\div4+206\div4+72\div4
1276 | $$
1277 |
1278 | ### 练习12
1279 |
1280 | 计算:
1281 | $$
1282 | 288\div24+288\div18+288\div6
1283 | $$
1284 |
1285 | ## 3.1.15. 鸡兔同笼进阶
1286 |
1287 | ### 本质
1288 |
1289 | 两种事物,凑两个条件
1290 |
1291 | ### 方法
1292 |
1293 | * 假设调整——假设、验算、调整
1294 | * 分组——倍数关系分组
1295 | * 合并
1296 | + 倍数关系,分组合并
1297 | + 不变量合并
1298 | + 平均值合并
1299 |
1300 | 例题1——假设法
1301 |
1302 | 例题2——实际应用
1303 |
1304 | 例题3——分组
1305 |
1306 | 例题4——分组
1307 |
1308 | 例题5——合并
1309 |
1310 | 例题6——实际应用
1311 |
1312 | ### 铺垫
1313 |
1314 | 鸡兔共有10只,关在一个笼子里,笼中共有26条腿,鸡兔各有几只?
1315 |
1316 | 列表法
1317 |
1318 | | 鸡(只) | 10 | 9 | 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
1319 | | ---------- | ---- | ---- | ---- | ---- | ---- | ---- | ---- | ---- | ---- | ---- | ---- |
1320 | | 兔(只) | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
1321 | | 腿数(条) | | | | | | | | | | | |
1322 |
1323 | 画图法
1324 |
1325 | 假设调整
1326 |
1327 | 假设全是鸡-验算-调整
1328 |
1329 | ### 例题1
1330 |
1331 | 牛牛家养了一些鸡和免子,同时养在一个笼子里,牛牛数了数,它们共有35个头,94只脚。问:牛牛家养的鸡和免各有多少只?
1332 |
1333 | ### 练习1
1334 |
1335 | 鸡免共有45只,关在同一个笼子中。每只鸡有2只脚,每只免子有4只脚,笼中共有100只脚。试计算,笼中有鸡多少只?免子多少只?
1336 |
1337 | ### 拓展2
1338 |
1339 | 在一个停车场上,现有汽车和摩托车共24辆,其中汽车有4个轮子,摩托车有3个轮子,摩托车有3个轮子,这些车共有86个轮子,那么三轮摩托车共有多少辆?
1340 |
1341 | ### 拓展3
1342 |
1343 | 100名师生绿化校园,老师每人载3棵树,学生每两人栽1颗树,总共载树100棵,那么学生共载树多少棵?
1344 |
1345 | ### 拓展
1346 |
1347 | 奥特曼遭遇一帮怪兽,大怪兽2头4腿,小怪兽2头2腿,大小怪兽一共20个头,32条腿,那么,大小怪兽各有几只?
1348 |
1349 | ### 分组
1350 |
1351 | 有相同数量的鸡和兔,共36条腿,那么鸡兔各有几只?
1352 |
1353 | 鸡兔同笼,兔的数量是鸡的3倍,共140条腿,那么,鸡兔各有几只?
1354 |
1355 | ### 补充
1356 |
1357 | 鸡兔同笼,共27只,已知两种动物的腿数相同,那么,鸡兔各有几只?
1358 |
1359 | 鸡兔同笼,共40只,已知鸡腿数是兔腿数的2倍,那么,鸡兔各有几只?
1360 |
1361 | ### 合并
1362 |
1363 | 鸡兔同笼,鸡、兔共有107只,兔的腿数比鸡的腿数多56条,问鸡、兔各多少只?
1364 |
1365 | ### 例题2
1366 |
1367 | 丁丁数了数笼中的鸡和免,发现腿有120条,鸡的只数比兔的只数的3倍多5只。则鸡和免子共有多少只?
1368 |
1369 | ### 练习2
1370 |
1371 | 田田数了数笼中的鸡和兔,发现共有脚240只,免的只数与鸡的只数相同。则鸡和免共多少只?
1372 |
1373 | ### 例题3
1374 |
1375 | 牛牛数了数笼中的鸡和兔,发现头有98个,鸡的脚数比免的脚数的2倍少4只。则免子有多少只?鸡有多少只?
1376 |
1377 | ### 练习3
1378 |
1379 | 牛牛数笼中的鸡和免,头有90个,鸡的腿数与免的腿数相同。鸡有多少只?
1380 |
1381 | ### 例题4(实际应用)
1382 |
1383 | 阿普去参加奥运知识抢答竞赛,按规定每答对一题得5分,答错一题要扣1分。阿普抢答10道题后,共得到26分,请问:阿普答对了几道题?
1384 |
1385 | ### 练习4
1386 |
1387 | 工人运青瓷花瓶250个,规定完整运到目的地一个给运费20元,损坏一个赔100元。运完这批花瓶后,工人共得4400元,则损坏了多少个?
1388 |
1389 | ### 例题5
1390 |
1391 | 鸡免同笼,鸡和免共有46条腿。如果将鸡与免的数量互换,那么总腿数变为38条,请问:原来鸡和免各有多少只?
1392 |
1393 | ### 练习5
1394 |
1395 | 田田数笼中的鸡和免,共有脚96只,若将鸡换成免,免换成鸡,则还有96只脚。鸡、免原来各多少只?
1396 |
1397 | ### 例题6
1398 |
1399 | 有蜘蛛、蜻蜓、蝉三种动物共18只,共有腿118条,翅膀20对。己知蜘蛛8条腿;蜻蜓6条腿,两对翅膀;蝉6条腿,一对翅膀。求蜻蜓有多少只。
1400 |
1401 | ### 练习6
1402 |
1403 | 犀牛、羚羊、孔雀三种动物共有头26个,脚80只,犄角20只。已知犀牛有4只脚,1只犄角;羚羊有4只脚,2只犄角;孔雀有2只脚,没有犄角。那么,犀牛、羚羊、孔雀各有多少只?
1404 |
1405 | ## 3.1.16. 周期问题进阶
1406 |
1407 | ### 热身1
1408 |
1409 | 学校宿舍楼一共有30间宿舍,大宿舍每间住6人,小宿舍每间住4人。已知这些宿舍中共住了168名学生,那么其中有多少间大宿舍、多少间小宿舍呢?
1410 |
1411 | ### 热身2
1412 |
1413 | 100个和尚140个馍,大和尚1人分3个馍,小和尚1人分1个馍。问:大、小和尚各有多少人?
1414 |
1415 | ### 热身3
1416 |
1417 | 找出下面数列的周期。
1418 |
1419 | 2,3,1,2,3,1,2,3,1,……
1420 |
1421 | 1,3,5,7,1,3,5,7,1,3,……
1422 |
1423 | 1,4,2,8,5,7,1,4,2,8,5,7,……
1424 |
1425 | ### 例题1(整周期)
1426 |
1427 | 田田和丁丁做游戏,他们把两种形状的小石子按下面的规律排列:
1428 |
1429 | ⭕️⭐️⭕️⭐️⭐️⭕️⭐️⭐️⭐️⭕️⭐️⭕️⭐️⭐️⭕️⭐️⭐️⭐️⭕️⭐️⭕️⭐️⭐️⭕️⭐️⭐️⭐️……
1430 |
1431 | 你知道他们所排列的这些小石子中,第100个是什么图形吗?第180个又是什么图形呢?
1432 |
1433 | ### 练习1
1434 |
1435 | 一天早上,牛牛一起床就大喊:“我要吃包子我要吃包子我要吃包子……”请问,牛牛喊得第28个字是什么字?
1436 |
1437 | ### 例题2(非整周期)
1438 |
1439 | 圣诞节到了,街上挂满了彩灯,并且按照5盏红灯接4 盏蓝灯接 1盏黄灯,然后又是5盏红灯接4 盏蓝灯接 1盏黄灯这样的顺序排下去。问:
1440 | (1)第 150 盏灯是什么颜色?
1441 | (2)前 200 盏彩灯中有多少盏蓝灯?
1442 |
1443 | ### 练习2
1444 |
1445 | 小莉把平时存下来的硬币按3个1分,2个2分,1个5分的顺序排列起来,刚好100枚,请问这 100枚硬币中有多少枚1分的硬币?
1446 |
1447 | ### 例题3
1448 |
1449 | 已知一列数:5,4,1,5,4,1,2,3,5,4,1,2,3,5,4,1,2,3,……,一直写到第 103个数,请问这些数的和是多少?
1450 |
1451 | ### 练习3
1452 |
1453 | 小和尚在地上写了一列数:7,0,7,0,2,5,3,7,0,2,5,3,……,一直写呀写,写了42个数,你能求出这 42 个数相加的和是多少吗?
1454 |
1455 | ### 例题4
1456 |
1457 | 如下图所示的表中,将每列上、下两个字组成一组,例如第一组为“数真”,第二组为 “学有”,那么第50组是什么字?
1458 |
1459 | 数学数学数学数学数学数学数学数学数学……
1460 |
1461 | 真有趣真有趣真有趣真有趣真有趣真有趣……
1462 |
1463 | ### 练习4
1464 |
1465 | 如图所示,每列上、下字和字母组成一组,例如,第一组是“A红”,第二组是“B黄”,请写出第63组是什么?
1466 |
1467 | ABABABABABABA
1468 |
1469 | 红黄蓝绿红黄蓝绿红黄蓝绿
1470 |
1471 | ### 例题5
1472 |
1473 | 12个同学围成一圈做传球的游戏,如图。
1474 |
1475 |  1476 |
1477 | (1)从1号同学开始,顺时针传100次,手绢应在谁手中?
1478 | (2)从1号同学开始,逆时针传100次,手绢又在谁手中?
1479 | (3)从 1号同学开始,先顺时针传156次,然后从那个同学开始逆时针传143次,最后手绢在谁手中?
1480 |
1481 | ### 练习5
1482 |
1483 | 8个队员围成如下图所示的一圈做传球游戏,从1号开始,按顺时针方向传球。在传球的同时,按顺序报数。当报到72时,球在几号队员手上?
1484 |
1485 |
1476 |
1477 | (1)从1号同学开始,顺时针传100次,手绢应在谁手中?
1478 | (2)从1号同学开始,逆时针传100次,手绢又在谁手中?
1479 | (3)从 1号同学开始,先顺时针传156次,然后从那个同学开始逆时针传143次,最后手绢在谁手中?
1480 |
1481 | ### 练习5
1482 |
1483 | 8个队员围成如下图所示的一圈做传球游戏,从1号开始,按顺时针方向传球。在传球的同时,按顺序报数。当报到72时,球在几号队员手上?
1484 |
1485 |  1486 |
1487 | ### 例题6(日历型)
1488 |
1489 | 图中是2013年5月份的日历表,根据表请回答:
1490 |
1491 | | 日 | 一 | 二 | 三 | 四 | 五 | 六 |
1492 | | ---- | ---- | ---- | ---- | ---- | ---- | ---- |
1493 | | | | | 1 | 2 | 3 | 4 |
1494 | | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
1495 | | 12 | 13 | 14 | 15 | 16 | 17 | 18 |
1496 | | 19 | 20 | 21 | 22 | 23 | 24 | 25 |
1497 | | 26 | 27 | 28 | 29 | 30 | 31 | |
1498 |
1499 | (1)该年6月1日是星期几?
1500 |
1501 | (2)该年10月1日是星期几?
1502 |
1503 | (3)2015 年5月1日是星期几?
1504 |
1505 | ### 练习6
1506 |
1507 | 2014年3月3日是星期一,算一算 2014年8月8号是星期几?
1508 |
1509 | ### 练习1
1510 |
1511 | ☆◎☆◎◎☆◎☆◎◎☆◎☆◎◎☆◎☆◎◎……
1512 |
1513 | 照这样的规律,第98个图形是什么?
1514 |
1515 | ### 练习2
1516 |
1517 | 一列数按“12345123451234512345……”排列,那么前40个数字之和是多少?
1518 |
1519 | ### 练习3
1520 |
1521 | 2022年1月1日是星期六,2022年6月1日是星期几?
1522 |
1523 | ## 3.1.17. 盈亏问题
1524 |
1525 | ### 热身1
1526 |
1527 | 小松鼠采松果,晴天每天可以采10个,雨天每天只能采6个。它一连几天采了80个松果,平均每天采8个。那么其中有几天是雨天呢?
1528 |
1529 | ### 热身2
1530 |
1531 | 在一根绳子上依次穿7个白颗、4颗黑珠,并按此方式重复。如果从头开始穿,一共穿了120颗珠子,那么这120颗珠子中,白珠比黑珠多几颗?
1532 |
1533 | ### 热身3
1534 |
1535 | 小迪和小迦比赛踩怪兽,规定踩同样的脚数,小迪一脚能踩2只怪兽,小迦一脚能踩5只怪兽,知道小迦比小迪一共多踩了60只。请问他们都踩了多少脚?
1536 |
1537 | 例题练习
1538 |
1539 | ### 例题1(盈盈)
1540 |
1541 | 乐乐老师有一桶巧克力,将它们分给三年级的小朋友,如果每人分9块,就剩下40块,如果每人分12块,就剩下10块。那乐乐老师一共有多少块巧克力,又将这些巧克力分给了多少个小朋友?
1542 |
1543 | ### 练习1
1544 |
1545 | 老师给三年级(2)班的小朋友发儿童节小礼物,如果每人发5个会剩下3个;如果每人发4个会剩下9个,三年级(2)班一共有多少个小朋友?
1546 |
1547 | ### 例题2(亏亏)
1548 |
1549 | 乐乐老师有一桶巧克力,将它们分给三年级的小朋友,如果每人分6块会缺少10块,如果每人分8块,会缺少24块。那乐乐老师一共有多少块巧克力?
1550 |
1551 | ### 练习2
1552 |
1553 | 冬天到了,小白免拿出一管萝卜当作一段时间的粮食,如果每天吃5根,还少3根;如果每天吃6根,还少8根,你知道小白免这管萝卜有多少根吗?
1554 |
1555 | ### 例题3(盈亏)
1556 |
1557 | 田田有一罐星空糖想要分给身边的好朋友,如果每人分5颗剩9颗,如果每人分7颗则有一人没分到,你知道田田身边有多少个好朋友吗?
1558 |
1559 | ### 练习3
1560 |
1561 | 丁丁整理出很多衣服打算寄给山区的小朋友,如果每次寄5件,到开学那天还有10件没有寄出,如果每次寄10件,会比第一种寄法少去邮局4趟,计算丁丁一共打算寄多少件衣服去山区?
1562 |
1563 | ### 例题4
1564 |
1565 | 三年级的同学们去郊外参加夏令营活动,如果每个帐篷住4名同学,则有7名同学没有地方住。如果每个帐篷住5名同学,则会空出3个床位。请计算出参加夏令营的同学有多少人?
1566 |
1567 | ### 练习4
1568 |
1569 | 乐乐老师为小朋友们分发儿童节礼物,如果每人分2个,会剩下12个礼物,如果每人发3个,最后会少2个礼物,请计算一共有多少个小朋友在等着领礼物?
1570 |
1571 | ### 例题5
1572 |
1573 | 乐乐老师带着小朋友去种花,如果每人种5棵,最后会剩下3棵花没人种,如果其中有2个小朋友各种4棵,剩下的小朋友每人种6棵,则这些花刚好种完。请问有多少个小朋友参加了种花?一共要种多少棵花?
1574 |
1575 | ### 练习5
1576 |
1577 | 少先队员们参加了植树节活动,如果每人挖6个树坑,会剩下5个树坑没人挖,如果其中2个人各挖3个树坑,其余每人挖7个树坑,刚好挖完所有的树坑。请计算少先队员们一共需要挖多少个树坑?
1578 |
1579 | ### 例题6
1580 |
1581 | 乐乐老师有一桶巧克力,将它们分给三年级的小朋友,如果每人分6块,则剩下10块,如果给其中3个人每人分4块,其他小朋友每人分7块,还剩下1块巧克力。乐乐老师一共有多少块巧克力?
1582 |
1583 | ### 练习6
1584 |
1585 | 猴王给一群猴子分香蕉,如果每只猴子分5根,最后会剩下16根香蕉没有被分出去,如果猴王给每只猴子分7根香蕉,最后一只猴子只能拿到3根香蕉。猴王一共有多少根香蕉?
1586 |
1587 | ### 练习1
1588 |
1589 | 学校新入学的小朋友要入住宿舍了,每间宿舍住的人一样多。如果每间住4人,就多出20人;如果每间住8人,还多了4人。请问:共有几间宿舍,几个小朋友?
1590 |
1591 | ### 练习2
1592 |
1593 | 老师给新入学的小朋友分积分卡,每个人分到的一样多。如果每个小朋友分10张,就少了30张;如果每个小朋友分8张,还是少8张。请问:一共有几个小朋友,几张积分卡?
1594 |
1595 | ### 练习3
1596 |
1597 | 一群小朋友分香蕉,如果每人分3根,则多4根;如果每人分4根,还少3根。那么,有几个小朋友,几根香蕉呢?
1598 |
1599 | ## 3.1.18. 奇数与偶数进阶
1600 |
1601 | 课前热身
1602 |
1603 | ### 热身1
1604 |
1605 | 妈妈为牛牛准备了铅笔,如果每次给他15支,这学期过完能剩下10支铅笔留给下学期用;如果每次给他17支,这学期刚好够用。你知道妈妈一共准备了多少支铅笔吗?
1606 |
1607 | ### 热身2
1608 |
1609 | 养猪场新到了一批幼年猪,如果每个饲养员照顾3头小猪,会有22头猪没人照顾;如果每个饲养员多照顾5头小猪,会有1个饲养员分不到任务。这个养猪场新到的幼年猪有多少头?
1610 |
1611 | ### 热身3
1612 |
1613 | 最大的两位奇数是()最小的四位偶数是()它们的和是()数
1614 |
1615 | ### 例题练习
1616 |
1617 | ### 例题1
1618 |
1619 | 不计算,判断下列各式结果的奇偶性。
1620 |
1621 | | $37+65$ | $36+66$ | $333+54$ |
1622 | | -------- | -------- | -------- |
1623 | | $145-33$ | $166-38$ | $97-68$ |
1624 |
1625 | 奇数个奇数相加减结果是()
1626 |
1627 | 偶数个奇数相加减结果是()
1628 |
1629 | 奇数个偶数相加减结果是()
1630 |
1631 | 偶数个偶数相加减结果是()
1632 |
1633 | ### 练习1
1634 |
1635 | 不计算,判断下列各式结果的奇偶性。
1636 |
1637 | | $5673+384+333+356+233$ |
1638 | | --------------------------------------- |
1639 | | $6252-1035+3566-2334+5688-1333-579+677$ |
1640 |
1641 | ### 例题2
1642 |
1643 | 请找出两个整数使他们的和是231,差是32,这样的两个数是否存在?若存在,请写出这两个数;若不存在,请说明理由。
1644 |
1645 | ### 练习2
1646 |
1647 | 请找出两个整数使他们的和是160,差是40,这样的两个数是否存在?若存在,请写出这两个数;若不存在,请说明理由。
1648 |
1649 | ### 例题3
1650 |
1651 | 一本书共有256页,从中任意找出5张纸,这5张纸上的所有页码之和能等于132吗?
1652 |
1653 | ### 练习3
1654 |
1655 | 请在下面的式子中填入“+”或者“-”,使得结果是6,可能吗?为什么?
1656 | $$
1657 | 987654321=6
1658 | $$
1659 |
1660 | ### 例题4
1661 |
1662 | 不计算,判断下列各式结果的奇偶性。
1663 |
1664 | | $13×35$ | $24\times36$ | $14\times23$ |
1665 | | ------- | ------------ | ------------ |
1666 |
1667 | ### 练习4
1668 |
1669 | 不计算,判断下列各式结果的奇偶性。
1670 |
1671 | | $23\times27\times39\times45\times54\times49\times33$ |
1672 | | ------------------------------------------------------------ |
1673 | | $31\times26\times13+53\times35+666\times577-3\times5\times987$ |
1674 |
1675 | 任意个奇数相乘结果是();
1676 |
1677 | 任意个偶数相乘结果是();
1678 |
1679 | 奇数与偶数相乘结果是()。
1680 |
1681 | ### 例题5
1682 |
1683 | 己知a,b,c是三个连续的自然数,其中c是偶数。田田说:“那么a+1,b+2,c+3这三个数的乘积一定是奇数。”丁丁说:“不对,a+1,b+2,c+3这三个数的乘积一定是偶数。”他们谁说得对呢?
1684 |
1685 | ### 练习5
1686 |
1687 | 牛牛在做题的时候写出了这样一个算式:$2751=53×21+42×39-36+35$,他做得对吗?
1688 |
1689 | ### 例题6
1690 |
1691 | 桌子上有7张正面向下的扑克牌,丁丁每次会把6张牌翻转。为了使扑克牌都正面向上,丁丁需要翻转几次?能实现吗?
1692 |
1693 | ### 练习6
1694 |
1695 | 明光市小学生参加数学竞赛,题目共20道。评分标准是:基础分25分,答对一道加5分,答错一道减1分,不答算错。如果有1111名同学参赛,则所有参赛同学得分总数一定是奇数还是偶数?请说明理由。
1696 |
1697 | 课后巩固
1698 |
1699 | ### 巩固1
1700 |
1701 | $$
1702 | 1+2+3+4+\dots+2021+2022
1703 | $$
1704 |
1705 | 算式的结果是奇数还是偶数?
1706 |
1707 | ### 巩固2
1708 |
1709 | 有一本500页的书,从中任意撕下33张纸,这33张纸上的所有页码之和能否是2022?
1710 |
1711 | ### 巩固3
1712 |
1713 | 是否存在自然数a,b,c,使得$(a-b)\times(b-c)\times(a-c)=65339$
1714 |
1715 | ## 3.1.19. 有序枚举与树形图
1716 |
1717 | ### 热身1
1718 |
1719 | a、b、c、d、e、f是六个连续的自然数,那么$a+b+c-d-e-f$的结果是奇数还是偶数?$a\times b\times c\times b+e\times f$的结果是奇数还是偶数?
1720 |
1721 | ### 热身2
1722 |
1723 | 在黑板上写1~2022这2022个自然数,每次任意擦去两个数,然后写上它们的和或者差,一直这样重复操作,经过若干次后黑板上只剩一个数,请问这个数是奇数还是偶数?
1724 |
1725 | ### 热身3
1726 |
1727 | 某人游览A、B、C三个风景区,每天游览一个,想要三天时间不重复的游览完这三个景区共有多少种不同的安排顺序?
1728 |
1729 | ### 例题1
1730 |
1731 | 乐乐老师打算把一个苹果、一个梨、一个香蕉分给丁丁和牛牛,每人至少分到一样水果,且全部分完,有多少种不同的分法?
1732 |
1733 | ### 练习1
1734 |
1735 | 妈妈买了1红2黑的3支钢笔送给姐姐和妹妹,1人最少拿到1支,且全部分完,问有多少种不同的送法?
1736 |
1737 | ### 例题2
1738 |
1739 | 一本《儿童故事》的定价是50元,如果丁丁有足够多的5元和10元,他会有多少种不同的付钱方法?
1740 |
1741 | ### 练习2
1742 |
1743 | 这里有1角、5角、1元、5元四张纸币,小朋友可以随意拿起几张纸币组合出总钱数,请问总钱数有多少种可能?
1744 |
1745 | ### 例题3
1746 |
1747 | 乐乐老师一共有5块巧克力,打算分给丁丁、牛牛、田田三个小朋友,每人最少分1块,且全部分完,有多少种不同的分法?
1748 |
1749 | ### 练习3
1750 |
1751 | 乐乐老师一共有8块巧克力,打算分给丁丁、牛牛、田田三个小朋友,每人最少分2块,且全部分完,有多少种不同的分法?
1752 |
1753 | ### 例题4
1754 |
1755 | 现在有数学卡片0,1,2,3各一张,可以排成多少个不同的四位数?
1756 |
1757 | ### 练习4
1758 |
1759 | 现在有数学卡片1,2,3,4各一张,可以排成多少个不同的四位数?
1760 |
1761 | ### 例题5
1762 |
1763 | 5个人排成一排,甲当排头,乙不当排尾,共有多少种排法?
1764 |
1765 | ### 练习5
1766 |
1767 | 乐乐老师、丁丁、牛牛、田田、阿普五个人站成一排,已知阿普站在第一个位置,乐乐老师站在最后一个位置,有多少种不同的排队方式?
1768 |
1769 | ### 例题6
1770 |
1771 | 乐乐老师带着丁丁、牛牛玩传球的游戏,从乐乐老师开始,每个人都可以将球传给其他人,球被传递四次之后又回到了乐乐老师手中,有多少种不同的传球可能呢?
1772 |
1773 | ### 练习6
1774 |
1775 | ABCD四人传球,要求AB不能互传,且自己不能传给自己。开始的时候球在A手上,经过4次传球后,球传回到A手中,不同的传球方式有多少种?
1776 |
1777 | ### 练习1
1778 |
1779 | 现在有数学卡片0,1,2,3,4各一张,可以排成多少个不同的三位数?
1780 |
1781 | ### 练习2
1782 |
1783 | 袋中有2个红球,3个黄球和4个白球,小明从中任意拿出4个球,他拿出球的情况共有几种可能。
1784 |
1785 | ### 练习3
1786 |
1787 | A、B、C三个小朋友互相传球,先从A开始发球(作为第一次传球),这样经过了5次传球后,球恰巧又回到A手中,那么不同的传球方式共多少种?
1788 |
1789 | ## 3.1.20. 等式代换
1790 |
1791 | 例题练习
1792 |
1793 | ### 例题1
1794 |
1795 | 已知$\bigcirc+\bigcirc+\bigcirc+\bigcirc=60$,$\bigtriangleup=\bigcirc+\bigcirc$,$\Box+\Box+\Box=\bigtriangleup$,那么$\Box$代表多少?
1796 |
1797 | ### 练习1
1798 |
1799 | 玩具店里的水果模型,1个柿子的重量等于3个苹果的重量,2个苹果的重量等于3个梨的重量,2个梨重60克,问:1个柿子模型有多重?
1800 |
1801 | ### 例题2
1802 |
1803 | 丁丁去文具店买了5支签字笔和6支红笔一共用了13元5角,2支签字笔的价钱等于3支红笔的价钱。问:红笔与签字笔的单价各是多少?
1804 |
1805 | ### 练习2
1806 |
1807 | 学校体育部要买15个排球和8个足球,1个足球75元,3个排球的价钱等于2个足球的价钱。问:体育部这次采购要花多少钱?
1808 |
1809 | ### 例题3
1810 |
1811 | 桃子和苹果共240个,其中桃子数量是苹果数量的2倍。求桃子和苹果各有多少个。
1812 |
1813 | ### 练习3
1814 |
1815 | 同学们在生物课外活动中种花生的棵数比白薯多280棵,且花生棵数是白薯的15倍,求花生、白薯各种了多少棵。
1816 |
1817 | ### 例题4
1818 |
1819 | 假如12只鸡可换2头羊,9头羊可换3头猪,8头猪可换2头牛,那么用5头牛可换多少只鸡?
1820 |
1821 | ### 练习4
1822 |
1823 | 用2个鹅蛋能换9个鸡蛋,2个鸡蛋能换12个鹌鹁蛋,用5个鹅蛋能换多少个鹌鹑蛋?
1824 |
1825 | ### 例题5
1826 |
1827 | 已知一只鸡与一只鸭共重2000克,一只鸡与一只猴共重1800克,一只猴与一只鸭共重2200克。问:三只动物每只各重多少克?
1828 |
1829 | ### 练习5
1830 |
1831 | 已知a+b=30,b+c=35,a+c=25,求a、b、c各是多少?
1832 |
1833 | ### 例题6
1834 |
1835 | 牛牛和丁丁各有书若干本,已知丁丁的书是牛牛的3倍,如果丁丁给牛牛10本书,则牛牛的书将是丁丁的3倍。问丁丁和牛牛二人原来各有多少本书?
1836 |
1837 | ### 练习6
1838 |
1839 | 1个柚子加1个梨的重量等于7个桃子的重量,2个梨的重量等于4个桃子的重量。那么,1个柚子的重量等于几个桃子的重量?
1840 |
1841 | 复习巩固
1842 |
1843 | ### 巩固1(鸡兔同笼)
1844 |
1845 | 今有鸡兔同笼,上有三十五头,下有九十四足,问鸡兔各几何?
1846 |
1847 | ### 巩固2(周期问题)
1848 |
1849 | 流水线上给小木球涂色的次序是:先5个红、再4个黄、再3个绿、在2个黑、再1个白,然后又依次是5红、4黄、3绿、2黑、1白**......**如此继续涂下去,到第2022个小球该涂什么颜色?
1850 |
1851 | ### 巩固3(盈亏问题)
1852 |
1853 | 秋天到了,小白兔收获了一筐萝卜,它按照计划吃的天数算了一下,如果每天吃4个,要多出48个萝卜;如果每天吃6个,则又少8个萝卜。那么小白兔买回的萝卜有多少个?计划吃多少天?
1854 |
1855 | ### 巩固4(奇数与偶数)
1856 |
1857 | 算式$123+456\times789+987\times654+321$的结果是奇数还是偶数?
1858 |
1859 | ### 巩固5(枚举与树形图)
1860 |
1861 | A、B、C三个小朋友互相传球,先从A开始发球(作为第一次传球),这样经过了4次传球后,球不传到A手中,那么不同的传球方式共多少种?
1862 |
1863 | ### 巩固6(等式代换)
1864 |
1865 | 2只兔子的重量等于6只小鸡的重量,3只袋鼠的重量相当于4只兔子的重量,那么1只袋鼠的重量相当于多少只小鸡的重量?
1866 |
1867 | ## 3.1.01. 角度
1868 |
1869 | 课前热身
1870 |
1871 | ### 热身1
1872 |
1873 | 1只鹅可以换8千克鱼,而4千克鱼可以换50个鸡蛋,10个鸡蛋可以换3个鹅蛋. 一只鹅可以换 多少个鹅蛋?
1874 |
1875 | ### 热身2
1876 |
1877 | 甲、乙两人共储蓄32元,乙、丙两人共储蓄30元,甲、丙两人共储蓄22元。三人各储蓄多少 元?
1878 |
1879 | ### 热身3
1880 |
1881 | 学校第一次买了3个水瓶和20个茶杯,共用去134元;第二次又买了同样的3个水瓶和16个茶杯,共用去118元。问水瓶和茶杯的单价各是多少元?
1882 |
1883 | 例题练习
1884 |
1885 | ### 例题1
1886 |
1887 | 图中有几种角?各有几个?将它们表示出来。(只考虑小于平角的角)
1888 |
1889 |
1486 |
1487 | ### 例题6(日历型)
1488 |
1489 | 图中是2013年5月份的日历表,根据表请回答:
1490 |
1491 | | 日 | 一 | 二 | 三 | 四 | 五 | 六 |
1492 | | ---- | ---- | ---- | ---- | ---- | ---- | ---- |
1493 | | | | | 1 | 2 | 3 | 4 |
1494 | | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
1495 | | 12 | 13 | 14 | 15 | 16 | 17 | 18 |
1496 | | 19 | 20 | 21 | 22 | 23 | 24 | 25 |
1497 | | 26 | 27 | 28 | 29 | 30 | 31 | |
1498 |
1499 | (1)该年6月1日是星期几?
1500 |
1501 | (2)该年10月1日是星期几?
1502 |
1503 | (3)2015 年5月1日是星期几?
1504 |
1505 | ### 练习6
1506 |
1507 | 2014年3月3日是星期一,算一算 2014年8月8号是星期几?
1508 |
1509 | ### 练习1
1510 |
1511 | ☆◎☆◎◎☆◎☆◎◎☆◎☆◎◎☆◎☆◎◎……
1512 |
1513 | 照这样的规律,第98个图形是什么?
1514 |
1515 | ### 练习2
1516 |
1517 | 一列数按“12345123451234512345……”排列,那么前40个数字之和是多少?
1518 |
1519 | ### 练习3
1520 |
1521 | 2022年1月1日是星期六,2022年6月1日是星期几?
1522 |
1523 | ## 3.1.17. 盈亏问题
1524 |
1525 | ### 热身1
1526 |
1527 | 小松鼠采松果,晴天每天可以采10个,雨天每天只能采6个。它一连几天采了80个松果,平均每天采8个。那么其中有几天是雨天呢?
1528 |
1529 | ### 热身2
1530 |
1531 | 在一根绳子上依次穿7个白颗、4颗黑珠,并按此方式重复。如果从头开始穿,一共穿了120颗珠子,那么这120颗珠子中,白珠比黑珠多几颗?
1532 |
1533 | ### 热身3
1534 |
1535 | 小迪和小迦比赛踩怪兽,规定踩同样的脚数,小迪一脚能踩2只怪兽,小迦一脚能踩5只怪兽,知道小迦比小迪一共多踩了60只。请问他们都踩了多少脚?
1536 |
1537 | 例题练习
1538 |
1539 | ### 例题1(盈盈)
1540 |
1541 | 乐乐老师有一桶巧克力,将它们分给三年级的小朋友,如果每人分9块,就剩下40块,如果每人分12块,就剩下10块。那乐乐老师一共有多少块巧克力,又将这些巧克力分给了多少个小朋友?
1542 |
1543 | ### 练习1
1544 |
1545 | 老师给三年级(2)班的小朋友发儿童节小礼物,如果每人发5个会剩下3个;如果每人发4个会剩下9个,三年级(2)班一共有多少个小朋友?
1546 |
1547 | ### 例题2(亏亏)
1548 |
1549 | 乐乐老师有一桶巧克力,将它们分给三年级的小朋友,如果每人分6块会缺少10块,如果每人分8块,会缺少24块。那乐乐老师一共有多少块巧克力?
1550 |
1551 | ### 练习2
1552 |
1553 | 冬天到了,小白免拿出一管萝卜当作一段时间的粮食,如果每天吃5根,还少3根;如果每天吃6根,还少8根,你知道小白免这管萝卜有多少根吗?
1554 |
1555 | ### 例题3(盈亏)
1556 |
1557 | 田田有一罐星空糖想要分给身边的好朋友,如果每人分5颗剩9颗,如果每人分7颗则有一人没分到,你知道田田身边有多少个好朋友吗?
1558 |
1559 | ### 练习3
1560 |
1561 | 丁丁整理出很多衣服打算寄给山区的小朋友,如果每次寄5件,到开学那天还有10件没有寄出,如果每次寄10件,会比第一种寄法少去邮局4趟,计算丁丁一共打算寄多少件衣服去山区?
1562 |
1563 | ### 例题4
1564 |
1565 | 三年级的同学们去郊外参加夏令营活动,如果每个帐篷住4名同学,则有7名同学没有地方住。如果每个帐篷住5名同学,则会空出3个床位。请计算出参加夏令营的同学有多少人?
1566 |
1567 | ### 练习4
1568 |
1569 | 乐乐老师为小朋友们分发儿童节礼物,如果每人分2个,会剩下12个礼物,如果每人发3个,最后会少2个礼物,请计算一共有多少个小朋友在等着领礼物?
1570 |
1571 | ### 例题5
1572 |
1573 | 乐乐老师带着小朋友去种花,如果每人种5棵,最后会剩下3棵花没人种,如果其中有2个小朋友各种4棵,剩下的小朋友每人种6棵,则这些花刚好种完。请问有多少个小朋友参加了种花?一共要种多少棵花?
1574 |
1575 | ### 练习5
1576 |
1577 | 少先队员们参加了植树节活动,如果每人挖6个树坑,会剩下5个树坑没人挖,如果其中2个人各挖3个树坑,其余每人挖7个树坑,刚好挖完所有的树坑。请计算少先队员们一共需要挖多少个树坑?
1578 |
1579 | ### 例题6
1580 |
1581 | 乐乐老师有一桶巧克力,将它们分给三年级的小朋友,如果每人分6块,则剩下10块,如果给其中3个人每人分4块,其他小朋友每人分7块,还剩下1块巧克力。乐乐老师一共有多少块巧克力?
1582 |
1583 | ### 练习6
1584 |
1585 | 猴王给一群猴子分香蕉,如果每只猴子分5根,最后会剩下16根香蕉没有被分出去,如果猴王给每只猴子分7根香蕉,最后一只猴子只能拿到3根香蕉。猴王一共有多少根香蕉?
1586 |
1587 | ### 练习1
1588 |
1589 | 学校新入学的小朋友要入住宿舍了,每间宿舍住的人一样多。如果每间住4人,就多出20人;如果每间住8人,还多了4人。请问:共有几间宿舍,几个小朋友?
1590 |
1591 | ### 练习2
1592 |
1593 | 老师给新入学的小朋友分积分卡,每个人分到的一样多。如果每个小朋友分10张,就少了30张;如果每个小朋友分8张,还是少8张。请问:一共有几个小朋友,几张积分卡?
1594 |
1595 | ### 练习3
1596 |
1597 | 一群小朋友分香蕉,如果每人分3根,则多4根;如果每人分4根,还少3根。那么,有几个小朋友,几根香蕉呢?
1598 |
1599 | ## 3.1.18. 奇数与偶数进阶
1600 |
1601 | 课前热身
1602 |
1603 | ### 热身1
1604 |
1605 | 妈妈为牛牛准备了铅笔,如果每次给他15支,这学期过完能剩下10支铅笔留给下学期用;如果每次给他17支,这学期刚好够用。你知道妈妈一共准备了多少支铅笔吗?
1606 |
1607 | ### 热身2
1608 |
1609 | 养猪场新到了一批幼年猪,如果每个饲养员照顾3头小猪,会有22头猪没人照顾;如果每个饲养员多照顾5头小猪,会有1个饲养员分不到任务。这个养猪场新到的幼年猪有多少头?
1610 |
1611 | ### 热身3
1612 |
1613 | 最大的两位奇数是()最小的四位偶数是()它们的和是()数
1614 |
1615 | ### 例题练习
1616 |
1617 | ### 例题1
1618 |
1619 | 不计算,判断下列各式结果的奇偶性。
1620 |
1621 | | $37+65$ | $36+66$ | $333+54$ |
1622 | | -------- | -------- | -------- |
1623 | | $145-33$ | $166-38$ | $97-68$ |
1624 |
1625 | 奇数个奇数相加减结果是()
1626 |
1627 | 偶数个奇数相加减结果是()
1628 |
1629 | 奇数个偶数相加减结果是()
1630 |
1631 | 偶数个偶数相加减结果是()
1632 |
1633 | ### 练习1
1634 |
1635 | 不计算,判断下列各式结果的奇偶性。
1636 |
1637 | | $5673+384+333+356+233$ |
1638 | | --------------------------------------- |
1639 | | $6252-1035+3566-2334+5688-1333-579+677$ |
1640 |
1641 | ### 例题2
1642 |
1643 | 请找出两个整数使他们的和是231,差是32,这样的两个数是否存在?若存在,请写出这两个数;若不存在,请说明理由。
1644 |
1645 | ### 练习2
1646 |
1647 | 请找出两个整数使他们的和是160,差是40,这样的两个数是否存在?若存在,请写出这两个数;若不存在,请说明理由。
1648 |
1649 | ### 例题3
1650 |
1651 | 一本书共有256页,从中任意找出5张纸,这5张纸上的所有页码之和能等于132吗?
1652 |
1653 | ### 练习3
1654 |
1655 | 请在下面的式子中填入“+”或者“-”,使得结果是6,可能吗?为什么?
1656 | $$
1657 | 987654321=6
1658 | $$
1659 |
1660 | ### 例题4
1661 |
1662 | 不计算,判断下列各式结果的奇偶性。
1663 |
1664 | | $13×35$ | $24\times36$ | $14\times23$ |
1665 | | ------- | ------------ | ------------ |
1666 |
1667 | ### 练习4
1668 |
1669 | 不计算,判断下列各式结果的奇偶性。
1670 |
1671 | | $23\times27\times39\times45\times54\times49\times33$ |
1672 | | ------------------------------------------------------------ |
1673 | | $31\times26\times13+53\times35+666\times577-3\times5\times987$ |
1674 |
1675 | 任意个奇数相乘结果是();
1676 |
1677 | 任意个偶数相乘结果是();
1678 |
1679 | 奇数与偶数相乘结果是()。
1680 |
1681 | ### 例题5
1682 |
1683 | 己知a,b,c是三个连续的自然数,其中c是偶数。田田说:“那么a+1,b+2,c+3这三个数的乘积一定是奇数。”丁丁说:“不对,a+1,b+2,c+3这三个数的乘积一定是偶数。”他们谁说得对呢?
1684 |
1685 | ### 练习5
1686 |
1687 | 牛牛在做题的时候写出了这样一个算式:$2751=53×21+42×39-36+35$,他做得对吗?
1688 |
1689 | ### 例题6
1690 |
1691 | 桌子上有7张正面向下的扑克牌,丁丁每次会把6张牌翻转。为了使扑克牌都正面向上,丁丁需要翻转几次?能实现吗?
1692 |
1693 | ### 练习6
1694 |
1695 | 明光市小学生参加数学竞赛,题目共20道。评分标准是:基础分25分,答对一道加5分,答错一道减1分,不答算错。如果有1111名同学参赛,则所有参赛同学得分总数一定是奇数还是偶数?请说明理由。
1696 |
1697 | 课后巩固
1698 |
1699 | ### 巩固1
1700 |
1701 | $$
1702 | 1+2+3+4+\dots+2021+2022
1703 | $$
1704 |
1705 | 算式的结果是奇数还是偶数?
1706 |
1707 | ### 巩固2
1708 |
1709 | 有一本500页的书,从中任意撕下33张纸,这33张纸上的所有页码之和能否是2022?
1710 |
1711 | ### 巩固3
1712 |
1713 | 是否存在自然数a,b,c,使得$(a-b)\times(b-c)\times(a-c)=65339$
1714 |
1715 | ## 3.1.19. 有序枚举与树形图
1716 |
1717 | ### 热身1
1718 |
1719 | a、b、c、d、e、f是六个连续的自然数,那么$a+b+c-d-e-f$的结果是奇数还是偶数?$a\times b\times c\times b+e\times f$的结果是奇数还是偶数?
1720 |
1721 | ### 热身2
1722 |
1723 | 在黑板上写1~2022这2022个自然数,每次任意擦去两个数,然后写上它们的和或者差,一直这样重复操作,经过若干次后黑板上只剩一个数,请问这个数是奇数还是偶数?
1724 |
1725 | ### 热身3
1726 |
1727 | 某人游览A、B、C三个风景区,每天游览一个,想要三天时间不重复的游览完这三个景区共有多少种不同的安排顺序?
1728 |
1729 | ### 例题1
1730 |
1731 | 乐乐老师打算把一个苹果、一个梨、一个香蕉分给丁丁和牛牛,每人至少分到一样水果,且全部分完,有多少种不同的分法?
1732 |
1733 | ### 练习1
1734 |
1735 | 妈妈买了1红2黑的3支钢笔送给姐姐和妹妹,1人最少拿到1支,且全部分完,问有多少种不同的送法?
1736 |
1737 | ### 例题2
1738 |
1739 | 一本《儿童故事》的定价是50元,如果丁丁有足够多的5元和10元,他会有多少种不同的付钱方法?
1740 |
1741 | ### 练习2
1742 |
1743 | 这里有1角、5角、1元、5元四张纸币,小朋友可以随意拿起几张纸币组合出总钱数,请问总钱数有多少种可能?
1744 |
1745 | ### 例题3
1746 |
1747 | 乐乐老师一共有5块巧克力,打算分给丁丁、牛牛、田田三个小朋友,每人最少分1块,且全部分完,有多少种不同的分法?
1748 |
1749 | ### 练习3
1750 |
1751 | 乐乐老师一共有8块巧克力,打算分给丁丁、牛牛、田田三个小朋友,每人最少分2块,且全部分完,有多少种不同的分法?
1752 |
1753 | ### 例题4
1754 |
1755 | 现在有数学卡片0,1,2,3各一张,可以排成多少个不同的四位数?
1756 |
1757 | ### 练习4
1758 |
1759 | 现在有数学卡片1,2,3,4各一张,可以排成多少个不同的四位数?
1760 |
1761 | ### 例题5
1762 |
1763 | 5个人排成一排,甲当排头,乙不当排尾,共有多少种排法?
1764 |
1765 | ### 练习5
1766 |
1767 | 乐乐老师、丁丁、牛牛、田田、阿普五个人站成一排,已知阿普站在第一个位置,乐乐老师站在最后一个位置,有多少种不同的排队方式?
1768 |
1769 | ### 例题6
1770 |
1771 | 乐乐老师带着丁丁、牛牛玩传球的游戏,从乐乐老师开始,每个人都可以将球传给其他人,球被传递四次之后又回到了乐乐老师手中,有多少种不同的传球可能呢?
1772 |
1773 | ### 练习6
1774 |
1775 | ABCD四人传球,要求AB不能互传,且自己不能传给自己。开始的时候球在A手上,经过4次传球后,球传回到A手中,不同的传球方式有多少种?
1776 |
1777 | ### 练习1
1778 |
1779 | 现在有数学卡片0,1,2,3,4各一张,可以排成多少个不同的三位数?
1780 |
1781 | ### 练习2
1782 |
1783 | 袋中有2个红球,3个黄球和4个白球,小明从中任意拿出4个球,他拿出球的情况共有几种可能。
1784 |
1785 | ### 练习3
1786 |
1787 | A、B、C三个小朋友互相传球,先从A开始发球(作为第一次传球),这样经过了5次传球后,球恰巧又回到A手中,那么不同的传球方式共多少种?
1788 |
1789 | ## 3.1.20. 等式代换
1790 |
1791 | 例题练习
1792 |
1793 | ### 例题1
1794 |
1795 | 已知$\bigcirc+\bigcirc+\bigcirc+\bigcirc=60$,$\bigtriangleup=\bigcirc+\bigcirc$,$\Box+\Box+\Box=\bigtriangleup$,那么$\Box$代表多少?
1796 |
1797 | ### 练习1
1798 |
1799 | 玩具店里的水果模型,1个柿子的重量等于3个苹果的重量,2个苹果的重量等于3个梨的重量,2个梨重60克,问:1个柿子模型有多重?
1800 |
1801 | ### 例题2
1802 |
1803 | 丁丁去文具店买了5支签字笔和6支红笔一共用了13元5角,2支签字笔的价钱等于3支红笔的价钱。问:红笔与签字笔的单价各是多少?
1804 |
1805 | ### 练习2
1806 |
1807 | 学校体育部要买15个排球和8个足球,1个足球75元,3个排球的价钱等于2个足球的价钱。问:体育部这次采购要花多少钱?
1808 |
1809 | ### 例题3
1810 |
1811 | 桃子和苹果共240个,其中桃子数量是苹果数量的2倍。求桃子和苹果各有多少个。
1812 |
1813 | ### 练习3
1814 |
1815 | 同学们在生物课外活动中种花生的棵数比白薯多280棵,且花生棵数是白薯的15倍,求花生、白薯各种了多少棵。
1816 |
1817 | ### 例题4
1818 |
1819 | 假如12只鸡可换2头羊,9头羊可换3头猪,8头猪可换2头牛,那么用5头牛可换多少只鸡?
1820 |
1821 | ### 练习4
1822 |
1823 | 用2个鹅蛋能换9个鸡蛋,2个鸡蛋能换12个鹌鹁蛋,用5个鹅蛋能换多少个鹌鹑蛋?
1824 |
1825 | ### 例题5
1826 |
1827 | 已知一只鸡与一只鸭共重2000克,一只鸡与一只猴共重1800克,一只猴与一只鸭共重2200克。问:三只动物每只各重多少克?
1828 |
1829 | ### 练习5
1830 |
1831 | 已知a+b=30,b+c=35,a+c=25,求a、b、c各是多少?
1832 |
1833 | ### 例题6
1834 |
1835 | 牛牛和丁丁各有书若干本,已知丁丁的书是牛牛的3倍,如果丁丁给牛牛10本书,则牛牛的书将是丁丁的3倍。问丁丁和牛牛二人原来各有多少本书?
1836 |
1837 | ### 练习6
1838 |
1839 | 1个柚子加1个梨的重量等于7个桃子的重量,2个梨的重量等于4个桃子的重量。那么,1个柚子的重量等于几个桃子的重量?
1840 |
1841 | 复习巩固
1842 |
1843 | ### 巩固1(鸡兔同笼)
1844 |
1845 | 今有鸡兔同笼,上有三十五头,下有九十四足,问鸡兔各几何?
1846 |
1847 | ### 巩固2(周期问题)
1848 |
1849 | 流水线上给小木球涂色的次序是:先5个红、再4个黄、再3个绿、在2个黑、再1个白,然后又依次是5红、4黄、3绿、2黑、1白**......**如此继续涂下去,到第2022个小球该涂什么颜色?
1850 |
1851 | ### 巩固3(盈亏问题)
1852 |
1853 | 秋天到了,小白兔收获了一筐萝卜,它按照计划吃的天数算了一下,如果每天吃4个,要多出48个萝卜;如果每天吃6个,则又少8个萝卜。那么小白兔买回的萝卜有多少个?计划吃多少天?
1854 |
1855 | ### 巩固4(奇数与偶数)
1856 |
1857 | 算式$123+456\times789+987\times654+321$的结果是奇数还是偶数?
1858 |
1859 | ### 巩固5(枚举与树形图)
1860 |
1861 | A、B、C三个小朋友互相传球,先从A开始发球(作为第一次传球),这样经过了4次传球后,球不传到A手中,那么不同的传球方式共多少种?
1862 |
1863 | ### 巩固6(等式代换)
1864 |
1865 | 2只兔子的重量等于6只小鸡的重量,3只袋鼠的重量相当于4只兔子的重量,那么1只袋鼠的重量相当于多少只小鸡的重量?
1866 |
1867 | ## 3.1.01. 角度
1868 |
1869 | 课前热身
1870 |
1871 | ### 热身1
1872 |
1873 | 1只鹅可以换8千克鱼,而4千克鱼可以换50个鸡蛋,10个鸡蛋可以换3个鹅蛋. 一只鹅可以换 多少个鹅蛋?
1874 |
1875 | ### 热身2
1876 |
1877 | 甲、乙两人共储蓄32元,乙、丙两人共储蓄30元,甲、丙两人共储蓄22元。三人各储蓄多少 元?
1878 |
1879 | ### 热身3
1880 |
1881 | 学校第一次买了3个水瓶和20个茶杯,共用去134元;第二次又买了同样的3个水瓶和16个茶杯,共用去118元。问水瓶和茶杯的单价各是多少元?
1882 |
1883 | 例题练习
1884 |
1885 | ### 例题1
1886 |
1887 | 图中有几种角?各有几个?将它们表示出来。(只考虑小于平角的角)
1888 |
1889 |  1890 |
1891 | ### 练习1
1892 |
1893 | 图中有几种角?各有几个?将它们表示出来。(只考虑小于平角的角)
1894 |
1895 |
1890 |
1891 | ### 练习1
1892 |
1893 | 图中有几种角?各有几个?将它们表示出来。(只考虑小于平角的角)
1894 |
1895 |  1896 |
1897 | ### 例题2
1898 |
1899 | 下图中,∠1=∠2=∠3=18°,那么∠AOB 是多少度?
1900 |
1901 |
1896 |
1897 | ### 例题2
1898 |
1899 | 下图中,∠1=∠2=∠3=18°,那么∠AOB 是多少度?
1900 |
1901 |  1902 |
1903 | ### 练习2
1904 |
1905 | 下图中,∠1=∠2=20°,那么∠AOB 是多少度?
1906 |
1907 |
1902 |
1903 | ### 练习2
1904 |
1905 | 下图中,∠1=∠2=20°,那么∠AOB 是多少度?
1906 |
1907 |  1908 |
1909 | ### 例题3
1910 |
1911 | 如图所示,已知∠4 的度数是∠1 度数的 3 倍,求∠1,∠2,∠3,∠4 分别是多少度?
1912 |
1913 |
1908 |
1909 | ### 例题3
1910 |
1911 | 如图所示,已知∠4 的度数是∠1 度数的 3 倍,求∠1,∠2,∠3,∠4 分别是多少度?
1912 |
1913 | 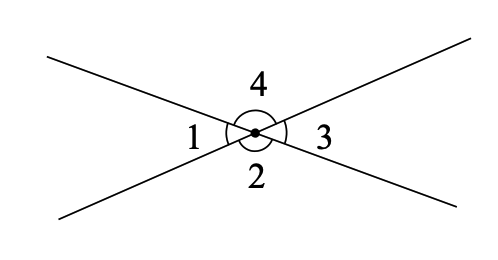 1914 |
1915 | ### 练习3
1916 |
1917 | 如图,两条直线相交,∠1=140°,则∠2+∠3等于几?
1918 |
1919 |
1914 |
1915 | ### 练习3
1916 |
1917 | 如图,两条直线相交,∠1=140°,则∠2+∠3等于几?
1918 |
1919 |  1920 |
1921 | ### 例题4
1922 |
1923 | 如图,已知 O 是直线 AD 上一点,∠AOB,∠BOC,∠COD 三个角从小到大依次相差 20°,求这三个角的度数。
1924 |
1925 |
1920 |
1921 | ### 例题4
1922 |
1923 | 如图,已知 O 是直线 AD 上一点,∠AOB,∠BOC,∠COD 三个角从小到大依次相差 20°,求这三个角的度数。
1924 |
1925 |  1926 |
1927 | ### 练习4
1928 |
1929 | 如图,已知∠BOC,∠AOB,∠AOC 分别相差 50°,求∠BOC 的度数。
1930 |
1931 |
1926 |
1927 | ### 练习4
1928 |
1929 | 如图,已知∠BOC,∠AOB,∠AOC 分别相差 50°,求∠BOC 的度数。
1930 |
1931 |  1932 |
1933 | ### 例题5
1934 |
1935 | 直线 AB、CD 相交于点 O,OE 平分∠AOD,∠FOC=90°,∠ 1=40°,求∠2 与∠3 的度数。
1936 |
1937 |
1932 |
1933 | ### 例题5
1934 |
1935 | 直线 AB、CD 相交于点 O,OE 平分∠AOD,∠FOC=90°,∠ 1=40°,求∠2 与∠3 的度数。
1936 |
1937 |  1938 |
1939 | ### 练习5
1940 |
1941 | 如图所示,直线 AB 与直线 CD 相交于点 O,做∠DOE=∠BOD,OF 平分∠AOE, 若∠AOC=20°,则∠EOF 等于多少度?
1942 |
1943 |
1938 |
1939 | ### 练习5
1940 |
1941 | 如图所示,直线 AB 与直线 CD 相交于点 O,做∠DOE=∠BOD,OF 平分∠AOE, 若∠AOC=20°,则∠EOF 等于多少度?
1942 |
1943 |  1944 |
1945 | ### 例题6
1946 |
1947 | 如图所示,三个正方形叠放在一起,有一个公共点,并且已知其中两个角的度数分别为 45°和 30°, 求∠1 的度数。
1948 |
1949 |
1944 |
1945 | ### 例题6
1946 |
1947 | 如图所示,三个正方形叠放在一起,有一个公共点,并且已知其中两个角的度数分别为 45°和 30°, 求∠1 的度数。
1948 |
1949 |  1950 |
1951 | 巩固练习
1952 |
1953 | ### 练习1
1954 |
1955 | 如图所示,直线 AB,CD 相交于点 O,OA 平分∠EOC,∠EOC=70°,则∠BOD 的度数为多少?
1956 |
1957 |
1950 |
1951 | 巩固练习
1952 |
1953 | ### 练习1
1954 |
1955 | 如图所示,直线 AB,CD 相交于点 O,OA 平分∠EOC,∠EOC=70°,则∠BOD 的度数为多少?
1956 |
1957 |  1958 |
1959 | ### 练习2
1960 |
1961 | 如图,两个正方形重叠放在一起,已知∠1=70°,求∠3的度数。
1962 |
1963 |
1958 |
1959 | ### 练习2
1960 |
1961 | 如图,两个正方形重叠放在一起,已知∠1=70°,求∠3的度数。
1962 |
1963 |  1964 |
1965 | ### 练习3
1966 |
1967 | 如图所示,已知 OE 与 OF 垂直,过 O 点做直线 AB,若∠EOA=2∠AOF,则∠BOF=?
1968 |
1969 |
1964 |
1965 | ### 练习3
1966 |
1967 | 如图所示,已知 OE 与 OF 垂直,过 O 点做直线 AB,若∠EOA=2∠AOF,则∠BOF=?
1968 |
1969 |  1970 |
1971 | ## 3.2.02. 巧算综合
1972 |
1973 | 课前热身
1974 |
1975 | ### 热身1
1976 |
1977 | 下图是 3×3 的正方形方格,∠1 与∠2 相比,较大的是()。
1978 |
1979 |
1970 |
1971 | ## 3.2.02. 巧算综合
1972 |
1973 | 课前热身
1974 |
1975 | ### 热身1
1976 |
1977 | 下图是 3×3 的正方形方格,∠1 与∠2 相比,较大的是()。
1978 |
1979 |  1980 |
1981 | ### 热身2
1982 |
1983 | 如图,∠AOB 的顶点 O在直线 l 上,已知图中所有小于平角的角之和是 400 度,求∠AOB的大小。
1984 |
1985 | 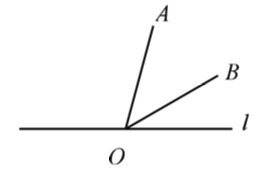
1986 |
1987 | ### 热身3
1988 |
1989 | 计算:$88\times46+88\times64-88\times10$
1990 |
1991 | 例题练习
1992 |
1993 | ### 例题1
1994 |
1995 | 计算。
1996 |
1997 | (1)$78+19+36+54+21+74+102$
1998 |
1999 | (2)$756-248-352$
2000 |
2001 | (3)$8+88+888+8888$
2002 |
2003 | (4)$39+38+40+41+43$
2004 |
2005 | ### 练习1
2006 |
2007 | 计算。
2008 |
2009 | (1)$99997+9996+995+94+9$
2010 |
2011 | (2)$894-89-111-95-105-94$
2012 |
2013 | ### 例题2
2014 |
2015 | 计算。
2016 |
2017 | (1)$25\times16\div20$
2018 |
2019 | (2)$1200\div4\div5\div5$
2020 |
2021 | (3)$1300\times77\div100$
2022 |
2023 | ### 练习2
2024 |
2025 | 计算。
2026 |
2027 | (1)$25\times64\times125$
2028 |
2029 | (2)$248\times5\div8$
2030 |
2031 | (3)$(36\times45)\div(6\times9)$
2032 |
2033 | ### 例题3
2034 |
2035 | 计算。
2036 |
2037 | (1)$35\times35$
2038 |
2039 | (2)$45\times45$
2040 |
2041 | (3)$73\times33$
2042 |
2043 | (4)$58\times58$
2044 |
2045 | ### 练习3
2046 |
2047 | 计算。
2048 |
2049 | (1)$75\times75$
2050 |
2051 | (2)$62\times68$
2052 |
2053 | (3)$67\times47$
2054 |
2055 | ### 例题4
2056 |
2057 | 计算。
2058 |
2059 | (1)$36\times19+36\times81$
2060 |
2061 | (2)$984\div8+16\div8$
2062 |
2063 | (3)$125\times(8+80)$
2064 |
2065 | (4)$(369+345)\div3$
2066 |
2067 | ### 练习4
2068 |
2069 | 计算。
2070 |
2071 | (1)$325\times113-325\times13$
2072 |
2073 | (2)$(40+8)\times25$
2074 |
2075 | (3)$684\div19-304\div19$
2076 |
2077 | (4)$(111+74)\div37$
2078 |
2079 | ### 例题5
2080 |
2081 | 计算。
2082 |
2083 | (1)$53\times46+71\times54+82\times54$
2084 |
2085 | ### 练习5
2086 |
2087 | 计算。
2088 |
2089 | (1)$33\times34+24\times34+57\times66$
2090 |
2091 | ### 例题6
2092 |
2093 | 计算。
2094 |
2095 | (1)$1997\times1995-1996\times1994$
2096 |
2097 | ### 练习6
2098 |
2099 | 计算。
2100 |
2101 | (1)$4747+888\times53+47\times787$
2102 |
2103 | ### 拓展1
2104 |
2105 | $$
2106 | 12345+23451+34512+45123+51234
2107 | $$
2108 |
2109 | ### 拓展2
2110 |
2111 | $$
2112 | 80+79-78-77+76+75-74-73+\dots+4+3-2-1
2113 | $$
2114 |
2115 | ### 拓展3
2116 |
2117 | $$
2118 | 20222022\times2021-20212021\times2022
2119 | $$
2120 |
2121 | ### 练习1
2122 |
2123 | 计算:$298+396+495+691+799+21$
2124 |
2125 | ### 练习2
2126 |
2127 | 计算:$(54\times24)\div(9\times4)$
2128 |
2129 | ### 练习3
2130 |
2131 | 计算:$39+142\times39+103$
2132 |
2133 | ## 3.2.03. 用字母表示数
2134 |
2135 | ### 热身1
2136 |
2137 | ### 热身2
2138 |
2139 | ### 热身3
2140 |
2141 | ### 例题1
2142 |
2143 | (1)观察下面的数列$2,4,6,a,10,b,14,\dots,a=(),b=()$。
2144 |
2145 | (2)观察下面的数列$1,3,5,a,9,b,13,\dots,a=(),b=()$。
2146 |
2147 | ### 练习1
2148 |
2149 | 观察下面的数列,填入合适的数。
2150 |
2151 | (1)5,10,15,a,25,30,b,……,a=(),b=()。
2152 |
2153 | (2)4,8,12,a,20,24,b,32,36,……,a=(),b=()。
2154 |
2155 | ### 例题2
2156 |
2157 | 1只青蛙1张嘴,2只眼睛,4条腿;
2158 |
2159 | 2只青蛙2张嘴,()只眼睛,()条腿;
2160 |
2161 | 3只青蛙3张嘴,()只眼睛,()条腿;
2162 |
2163 | 4只青蛙4张嘴,()只眼睛,()条腿;
2164 |
2165 | ……
2166 |
2167 | n只青蛙()张嘴,()只眼睛,()条腿。
2168 |
2169 | ### 练习2
2170 |
2171 | 一个正方形有()条边,
2172 |
2173 | 两个正方形有()条边,
2174 |
2175 | 三个正方形有()条边,
2176 |
2177 | ……
2178 |
2179 | n个正方形有()条边。
2180 |
2181 | 边数和正方形的数量有什么关系呢?
2182 |
2183 | ### 例题3
2184 |
2185 | 用简便方法表示下列各式。
2186 |
2187 | (1)$27\times x$
2188 |
2189 | (2)$m\times n$
2190 |
2191 | (3)$a+a+a$
2192 |
2193 | (4)$a\times a$
2194 |
2195 | (5)$36\times a\times b$
2196 |
2197 | (6)$(a+b)\times5$
2198 |
2199 | ### 练习3
2200 |
2201 | (1)$63\times x+5$
2202 |
2203 | (2)$m\times n\times3$
2204 |
2205 | (3)$(m+n)\times16$
2206 |
2207 | (4)$c\times2\times a$
2208 |
2209 | ### 例题4
2210 |
2211 | 用字母表示下列公式。(周长=C,面积=S,长=a,宽=b,边长=a)
2212 | 长方形的周长公式:
2213 | 长方形的面积公式:
2214 | 正方形的周长公式:
2215 | 正方形的面积公式:
2216 |
2217 | ### 练习4
2218 |
2219 | 用字母表示下列公式。
2220 | 乘法交换律:
2221 | 乘法结合律:
2222 | 乘法分配律:
2223 |
2224 | ### 例题5
2225 |
2226 | 你能用字母表示下面题目中所求的量吗?
2227 |
2228 | (1)过春节了,阿普拿到了m元压岁钱,牛牛的压岁钱是阿普的6倍,牛牛的压岁钱是()元。
2229 |
2230 | (2)某学校有男老师a人,女老师比男老师少b人,学校有女老师()人,共有老师()人。
2231 |
2232 | (3)一个长方形的周长是80厘米,长是a厘米,宽是()厘米。
2233 |
2234 | ### 练习5
2235 |
2236 | 你能用字母表示下面题目中所求的量吗?
2237 | (1)一个等边三角形,每边长a米,它的周长是()米。
2238 | (2)牛牛的学校一共有m人,男生有a人,女生有()人。
2239 | (3)东东今年a岁,比妈妈小m岁,再过年c后妈妈比东东大()岁。
2240 |
2241 | ### 例题6
2242 |
2243 | 用含字母的式子表示。
2244 | (1)1个菠萝重x千克,1个西瓜比这个菠萝的3倍还重2千克,西瓜重()千克。如果菠萝重2千克,那么西瓜重()千克。
2245 | (2)小红骑车每分钟行x千米,她骑了20分钟,行驶了()千米;她行驶a千米,需要()分钟。x=2,a=10,那么需要()分钟。
2246 | (3)乙数比甲数a的4倍少6,乙数是()。
2247 |
2248 | ### 练习6
2249 |
2250 | 用含字母的式子表示。
2251 | (1)田田高a厘米,丁丁比田田高7厘米,丁丁和田田一共高()厘米。
2252 | (2)青青林场栽了梧桐树和雪松各x排,已知梧桐树每排12棵,雪松每排14棵,栽梧桐树
2253 | 和雪松共()棵;当x=20时,青青林场一共有()棵梧桐树和雪松。
2254 | (3)一个正方形的边长为a厘米,周长为()厘米,面积是()平方厘米。
2255 |
2256 | ## 3.2.04. 和差倍综合
2257 |
2258 | 例题练习
2259 |
2260 | ### 例题1(和差)
2261 |
2262 | 有大、小两个油桶,一共装油24千克,两个油桶都倒出同样多的油后分别还剩9千克和5千克。问:原来大、小两个油桶各装油多少千克?
2263 |
2264 | ### 练习1
2265 |
2266 | 两箱图书共有66本,甲箱如果借出10本,就比乙箱少4本。甲、乙两箱原有图书各多少本?
2267 |
2268 | ### 例题2(和差)
2269 |
2270 | 学校新进99本书,分给三、四、五三个年级,三年级比四年级多分了2本,四年级比五年级多分了5本,三个年级各分得书多少本?
2271 |
2272 | ### 练习2
2273 |
2274 | 甲、乙、丙三个数的和是105,甲数比乙数多4,乙数比丙数多4,求丙数。
2275 |
2276 | ### 例题3(和倍)
2277 |
2278 | 某校学生总人数比四年级人数的6倍少78人,并且除了四年级外,其他各年级的学生人数总和为2222人,那么该校共有学生多少人?
2279 |
2280 | ### 练习3
2281 |
2282 | 有两层书架,共有书216本,从第一层拿走42本书后,第二层的书比第一层的2倍还多6本,则第二层有多少本书?
2283 |
2284 | ### 例题4
2285 |
2286 | 一天,甲、乙、丙三个同学做数学题,已知甲比乙多做了6道,丙做的题是甲的2倍,比乙做的题多22道,则乙做了多少道数学题?
2287 |
2288 | ### 练习4
2289 |
2290 | 小云比小雨少20本书,后来小云丢了5本书,小雨新买了11本书,这时小雨的书比小云的书多2倍。问:原来两人各有多少本书?
2291 |
2292 | ### 例题5
2293 |
2294 | 李师傅某天生产了一批零件,把它们分成了甲、乙两堆摆放。若从甲堆零件中拿出15个放到乙堆,则两堆零件个数相等;若从乙堆零件中拿出15个放到甲堆,则甲堆的零件个数是乙堆的4倍。甲堆原有零件多少个,李师傅这天共生产了多少个零件?
2295 |
2296 | ### 练习5
2297 |
2298 | 一家汽车销售店有若干部福特汽车和丰田汽车等待销售。福特汽车的数量是丰田汽车的3倍,如果每周销售2辆丰田汽车和4辆福特汽车,丰田汽车销售完时还剩下30辆福特汽车。请问:原有丰田汽车和福特汽车各多少辆?
2299 |
2300 | ### 例题6
2301 |
2302 | 维尼熊和跳跳虎去摘苹果。维尼熊爬上树去摘,跳跳虎在地上跳着摘。跳跳虎每摘7个,维尼熊只能摘4个。维尼熊摘了80分钟,跳跳虎摘了50分钟就累倒了。他们回来后数了一下共摘2010个苹果,那么其中维尼熊摘的有多少个?
2303 |
2304 | ### 练习6
2305 |
2306 | 某镇上有东西两个公交车站,东站有客车84辆,西站有客车56辆,每天从东站到西站有7辆车,从西站到东站有11辆车,几天后,东站车辆是西站的4倍?
2307 |
2308 | ## 3.2.05. 逆向思考进阶
2309 |
2310 | ### 例题1
2311 |
2312 | 牛牛和阿昔在游玩时,遇到一位小神仙,他们问这位神仙:“你一定不到100岁吧!”谁知这位神仙摇摇头说:“你们算算吧!把我的年龄加上75,再除以5,然后减去15,再乘10,恰好是
2313 | 2000岁。”小朋友,你知道这位神仙现在有多少岁吗?
2314 |
2315 | ### 练习1
2316 |
2317 | 一个数加上37,乘37,减去37,再除以37,结果等于37,这个数是多少?
2318 |
2319 | ### 例题2
2320 |
2321 | 小马虎在做一道加法题时,把一个加数个位上的9看作6,十位上的6看作9,结果和是174,那么正确的结果应该是多少呢?
2322 |
2323 | ### 练习2
2324 |
2325 | 淘气在做一道减法题时,把减数个位上的9看成了3,把十位上的4看成了7,得到的结果是164。请你帮淘气算算正确的答案是多少?
2326 |
2327 | ### 例题3
2328 |
2329 | 李奶奶卖一筐鸡蛋,第一位客人买走了一半少2个,第二位客人买走了剩下的一半多2个,第三位客人把剩下的5个鸡蛋全部买走了。老奶奶的篮子里原来有多少个鸡蛋?
2330 |
2331 | ### 练习3
2332 |
2333 | 学学看到太上老君正在用一根绳子拴宝葫芦,第一次用去全长的一半还多2米,第二次用去余下的一半少10米,第三次用去15米,最后还剩9米,那么这根绳子原来有多少米?
2334 |
2335 | ### 例题4
2336 |
2337 | 有一个财迷总想使自己的钱成倍增长。一天,他在一座桥上碰见一个老人,老人对他说:"你只要走过这座桥再回来,你身上的钱就会增加一倍,但作为报酬,你每走一个来回要给我32个
2338 | 铜板。”财迷算了算,感觉挺合算,就同意了。他走过桥去又走回来,身上的钱果然增加了一倍,他很高兴地给了老人32个铜板。这样走完第五个来回,身上的最后32个铜板都给了老人,财迷一个铜板也没剩下。你知道财迷身上原有多少个铜板?
2339 |
2340 | ### 练习4
2341 |
2342 | 某人发现了一条魔道,下面有一个存钱的小箱子,当他从魔道走过去的时候,箱子里的一些钱会飞到人的口袋里,使人身上的钱增加一倍,这人很高兴;当他从魔道走回来的时候,身
2343 | 上的钱又会飞到箱子里,使箱子里的钱增加一倍。这个人一连走了3个来回后,箱子里的钱和人身上的钱都是64元,那么,原来这人身上有多少钱?箱子里有多少钱?
2344 |
2345 | ### 例题5
2346 |
2347 | 有一个两层书架,一共摆放224本书,先从上层取出与下层本数同样多的书放入下层,再从下层现有书中,取出与上层剩下的本数同样多的书放入上层,这算进行了一轮调整。若如进行了
2348 | 两轮调整后,两层摆放书的本数相等,上层书架原来摆放多少本书?下层书架原来摆放多少本书?
2349 |
2350 | ### 练习5
2351 |
2352 | 有甲、乙两箱糖果,如果第一次从甲箱拿出和乙箱同样多块糖果放到乙箱里,第二次从乙箱拿出和甲箱剩下的同样多块糖果放入甲箱,这样拿4次后,甲、乙两箱糖果都是16块。甲、乙两箱各有糖果多少块?
2353 |
2354 | ### 例题6
2355 |
2356 | 一班、二班、三班各有不同数量的图书。一班拿出本班的一部分图书分给二班、三班,使这两个班的图书各增加一倍;然后二班也拿出一部分图书分给一班、三班,使这两个班的图书各增加一倍;接着三班也拿出一部分图书分给一班、二班,使这两个班的图书各增加一倍。这时三个班的图书数量都是48本。
2357 | ,求三个班原来各有图书多少本。
2358 |
2359 | ### 练习6
2360 |
2361 | 甲、乙、丙3人共有192张邮票。从甲的邮票中取出乙那么多邮票给乙后,再从乙的邮票中取出丙那么多邮票给丙,最后从丙的邮票中取出甲那么多邮票给甲,这时甲、乙、丙3人的邮票数相同,甲、乙、丙原来各有邮票多少张?
2362 |
2363 | ## 3.2.06. 逻辑推理综合(1)
2364 |
2365 | ### 例题1
2366 |
2367 | 5名谋杀案的嫌疑人,在犯罪现场被警察询问,其中有一名是凶手。下面5个人的供述中,只有3句是对的:
2368 | A说:“D是杀人犯。”
2369 | B说:“我是无辜的。”
2370 | C说:“E不是杀人犯。”
2371 | D说:“A在说谎。”
2372 | E说:“B说的是实话。”
2373 | 在这5个人中,谁是凶手?
2374 |
2375 | ### 练习1
2376 |
2377 | 四个小朋友宝宝、星星、强强和乐乐在院子里踢足球,一阵响声,惊动了正在读书的陆老师,陆老师跑出来查看,发现一块窗户玻璃被打破了。陆老师问:“是谁打破了玻璃?”
2378 | 宝宝说:“是星星无意打破的。”
2379 | 星星说:“是乐乐打破的。”
2380 | 乐乐说:“星星说谎。”
2381 | 强强说:“反正不是我打破的。”
2382 | 如果只有一个孩子说了实话,那么这个孩子是谁?是谁打破了玻璃?
2383 |
2384 | ### 例题2
2385 |
2386 | 在一次数学竞赛中,A,B,C,D,E五位同学分别得了前五名(没有并列同一名次的),关于各人的名次,大家做出了下面的猜测:
2387 |
2388 | A说:“第二名是D,第三名是B。”
2389 |
2390 | B说:“第二名是C,第四名是F。”
2391 |
2392 | C说:“第一名是E,第五名是A。”
2393 |
2394 | D说:“第三名是C,第四名是A。”
2395 |
2396 | E说:“第二名是B,第五名是D。”
2397 |
2398 | 结果每人都只猜对了一半,他们的名次如何?
2399 |
2400 | ### 练习2
2401 |
2402 | 甲、乙、丙、丁四人同时参加全国小学数学夏令营。赛前甲、乙、丙分别作了预测。
2403 |
2404 | 甲说:“丙第1名,我第3名。”
2405 |
2406 | 乙说:“我第1名,丁第4名。”
2407 |
2408 | 丙说:“丁第2名,我第3名。”
2409 | 成绩揭晓后,发现他们每人只说对了一半,你能说出他们的名次吗?
2410 |
2411 | ### 例题3
2412 |
2413 | 学校新来了一位老师,五个学生分别听到如下的情况:
2414 |
2415 | (1)是一位姓王的中年女老师,教语文;
2416 |
2417 | (2)是一位姓丁的中年男老师,教数学;
2418 |
2419 | (3)是一位姓刘的青年男老师,教外语;
2420 |
2421 | (4)是一位姓李的青年男老师,教数学;
2422 |
2423 | (5)是一位姓王的老年男老师,教外语。
2424 |
2425 | 他们每人听到的四项情况中各有一项正确。问:真实情况是什么样的?
2426 |
2427 | ### 练习3
2428 |
2429 | 4名运动员参加一项比赛,赛前。
2430 |
2431 | 甲说:“我肯定是最后一名。”
2432 |
2433 | 乙说:“我不可能是第一名,也不可能是最后一名。”
2434 | 丙说:“我绝对不会得最后一名。”
2435 | 丁说:“我肯定得第一名。”
2436 |
2437 | 赛后,发现他们4人的预测中只有一人是错误的。请问谁的预测是错误的?
2438 |
2439 | ### 例题4
2440 |
2441 | 王平、宋丹、韩涛三个小学生都是少先队的干部,一个是大队长,一个是中队长,一个是小队长。一次数学测验,这三个人的成绩是:
2442 |
2443 | (1)韩涛比大队长的成绩好。
2444 |
2445 | (2)王平和中队长的成绩不相同。
2446 |
2447 | (3)中队长比宋丹的成绩差。
2448 |
2449 | 请你根据这三个人的成绩,判断一下,谁是大队长呢?
2450 |
2451 | ### 练习4
2452 |
2453 | 王文、张贝、李丽分别是跳伞、田径、游泳运动员,现在知道:
2454 |
2455 | (1)张贝从未上过天;
2456 | (2)跳伞运动员已得过两块金牌;
2457 |
2458 | (3)李丽还未得过第一名,她与田径运动员同年出生:
2459 | 请根据上述情况,判断王文、张贝、李丽各是什么运动员?
2460 |
2461 | ### 例题5
2462 |
2463 | 张、王、李三人除了本职工作,每人都有两样业余爱好。人们有时以车工、电工、乐师、画家、作家、技工称呼他们,此外,还有以下情况:
2464 | (1)车工经常赞扬乐师的三弦琴弹得好;
2465 | (2)乐师,作家常常与姓张的一起看电影;
2466 | (3)画家请电工来修过电灯;
2467 | (4)车工和画家的儿子在同一车间工作;
2468 | (5)姓王的向作家请教写作的技巧;
2469 | (6)姓李的善于下象棋,姓王的和画家常常输给他。
2470 | 问:姓李的有哪两个称呼?
2471 |
2472 | ### 练习5
2473 |
2474 | 宝宝、贝贝、聪聪每人有两个外号,人们有时以“数学博士”、“短跑健将”、“跳高冠军”、“小画家“、“大作家”和“歌唱家”称呼他们,此外:
2475 |
2476 | (1)数学博士夸跳高冠军跳得高;
2477 |
2478 | (2)跳高冠军和大作家常与宝宝一起看电影;
2479 |
2480 | (3)短跑健将请小画家画贺年卡;
2481 |
2482 | (4)数学博士和小画家关系很好;
2483 |
2484 | (5)贝贝向大作家借过书;
2485 |
2486 | (6)聪聪下象棋常赢贝贝和小画家。
2487 |
2488 | 问:宝宝、贝贝、聪聪各有哪两个外号?
2489 |
2490 | ### 例题6
2491 |
2492 | A,B,C,D分别来自中国、日本、美国和法国。已知:
2493 |
2494 | (1)A和中国人是医生;
2495 |
2496 | (2)B和法国人是教师;
2497 |
2498 | (3)C和日本人职业不同;
2499 |
2500 | (4)D不会看病。
2501 |
2502 | 问:A,B,C,D各是哪国人?
2503 |
2504 | ### 练习6
2505 |
2506 | 张明、席辉和李刚分别在北京、上海和天津三城市之一工作,他们的职业是工人、农民和教师之一,已知:
2507 |
2508 | (1)张明不在北京工作,席辉不在上海工作;
2509 |
2510 | (2)在北京工作的不是教师;
2511 | (3)在上海工作的是工人;
2512 |
2513 | (4)席辉不是农民。
2514 |
2515 | 问:这三人各住哪里?各是什么职业?
2516 |
2517 | ## 3.2.07. 方阵
2518 |
2519 | ### 例题1
2520 |
2521 | 一个实心方阵,最外一层每边18人。
2522 | (1)那么整个方阵一共()人;
2523 | (2)最外面一层有()人;
2524 | (3)从外向内数,第二层每边有()人,一共有()人;
2525 | (4)如果考虑最外面三层,那么这三层共有()人;
2526 | (5)如果将方阵外面增加一层,那么一共增加()人。
2527 |
2528 | ### 练习1
2529 |
2530 | 用64枚棋子摆成一个实心方阵。
2531 | (1)每边有()枚棋子;
2532 | (2)最外层有()枚棋子;
2533 | (3)从外向内数,第二层每边有()枚棋子,第二层一共有()枚棋子。
2534 |
2535 | ### 例题2
2536 |
2537 | 有一块空地在进行种树绿化,打算把树种成实心方阵的样子,方阵最外面一周有60棵树,问这个方阵外层每边有多少棵树?这块空地一共需要多少棵树?
2538 |
2539 | ### 练习2
2540 |
2541 | 三年级学生排成一个实心方阵,最外一层的人数为36人,问方阵最外层每边有多少人?这个方阵共有三年级学生多少人?
2542 |
2543 | ### 例题3
2544 |
2545 | 小刚在用棋子摆好的实心方阵上又添了17枚棋子,它的横竖各增加了一排,成了大一点的实心方阵,求原来的实心方阵有多少枚棋子。
2546 |
2547 | ### 练习3
2548 |
2549 | 军训的学生进行队列表演,排成了一个5行5列的正方形队列,如果去掉一行一列,要去掉多少人?
2550 |
2551 | ### 例题4
2552 |
2553 | 大家要用盆花在空地上摆出一个空心方阵花坛,最外面的一层每边摆12盆花,共3层,一共要用多少盆花?
2554 |
2555 | ### 练习4
2556 |
2557 | 有一个班的学生排成一个中空方阵,最外层人数共52人,最内层人数共28人,这个班学生共有多少人?
2558 |
2559 | ### 例题5
2560 |
2561 | 用64枚棋子摆成一个两层中空方阵,如果想在外面再增加一层,问需要增加多少枚棋子?
2562 |
2563 | ### 练习5
2564 |
2565 | 用84枚棋子摆成一个三层中空方阵,问最外层有多少枚棋子?
2566 |
2567 | ### 例题6
2568 |
2569 | 一天,博士用棋子摆成一周每边有10枚棋子的空心方阵,摆完后发现还有棋子剩下,但是不够外围再增加一层。在保持原有棋子不动的情况下,想变成一个更大的两层空心方阵,博士至少需要多少枚棋子?
2570 |
2571 | ### 练习6
2572 |
2573 | 用一堆棋子摆成一个两层的空心方阵,用了48枚棋子后发现还剩下一些棋子,但是不够外围再增加一层了。在保持原有棋子不动的情况下,想变成一个更大的三层空心方阵,至少需要多少枚棋子?
2574 |
2575 | ## 3.2.08. 巧填算符综合
2576 |
2577 | 例题练习
2578 |
2579 | ### 例题1
2580 |
2581 | 在“+、-、×、÷、( )”中,挑出合适的符号,填入下面的数字之间,使算式成立。
2582 | $$
2583 | 9\ \ \ 8\ \ \ 7\ \ \ 6\ \ \ 5\ \ \ 4\ \ \ 3\ \ \ 2\ \ \ 1=1
2584 | $$
2585 |
2586 | ### 练习1
2587 |
2588 | 在○内填上与等号左边不同的运算符号,使等式成立。
2589 | $$
2590 | (1)6-2+2=6\circ2\circ 2
2591 | $$
2592 |
2593 | $$
2594 | (2)8+2+3=8\circ 2\circ 3
2595 | $$
2596 |
2597 | $$
2598 | (3)16-8-3=16\circ 8\circ 3
2599 | $$
2600 |
2601 | ### 例题2
2602 |
2603 | 在下面算式的适当地方,填上运算符号“+、-、×、÷或( )”,使算式成立。
2604 | $$
2605 | 1\ \ \ 2\ \ \ 3\ \ \ 4\ \ \ 5=10
2606 | $$
2607 |
2608 | ### 练习2
2609 |
2610 | 用运算符号把下面三个相同的数宇连接起来,使等式成立。
2611 | $$
2612 | (1)5\ \ \ 5\ \ \ 5=30
2613 | $$
2614 |
2615 | $$
2616 | (2)6\ \ \ 6\ \ \ 6\ \ \ =30
2617 | $$
2618 |
2619 | ### 例题3
2620 |
2621 | 在下式的每两个数中间填上合适的运算符号,使等式成立。
2622 | $$
2623 | 8\ \ \ 2\ \ \ 4\ \ \ 6=4\ \ \ 2
2624 | $$
2625 |
2626 | ### 练习3
2627 |
2628 | 在下式的每两个数中间填上合适的运算符号,使等式成立。
2629 | $$
2630 | 8\ \ \ 2\ \ \ 3=3\ \ \ 3
2631 | $$
2632 |
2633 | ### 例题4
2634 |
2635 | 在8个8之间的适当地方,填上合适的运算符号或括号,使算式成立。
2636 | $$
2637 | 8\ \ \ 8\ \ \ 8\ \ \ 8\ \ \ 8\ \ \ 8\ \ \ 8\ \ \ 8=1000
2638 | $$
2639 |
2640 | ### 练习4
2641 |
2642 | 在下面算式适当的地方,填上运算符号或括号,使等式成立。
2643 | $$
2644 | 9\ \ \ 8\ \ \ 7\ \ \ 6\ \ \ 5\ \ \ 4\ \ \ 3\ \ \ 2\ \ \ 1=1000
2645 | $$
2646 |
2647 | ### 例题5
2648 |
2649 | 在5个4之间,填上适当的运算符号或括号,使得下面的算式成立。
2650 | $$
2651 | 4\ \ \ 4\ \ \ 4\ \ \ 4\ \ \ 4=8
2652 | $$
2653 |
2654 | ### 练习5
2655 |
2656 | 在下列算式的合适位置,填上运算符号或括号,使等式成立。
2657 | $$
2658 | (1)4\ \ \ 4\ \ \ 4\ \ \ 4=1
2659 | $$
2660 |
2661 | $$
2662 | (2)4\ \ \ 4\ \ \ 4\ \ \ 4=5
2663 | $$
2664 |
2665 | ### 例题6
2666 |
2667 | 请在 2,3,4,6 四个数之间任意填上“+、-、×、÷或( )”,每个数字都只能用一次,使它们的计算结果等于 24。你能做到吗?
2668 |
2669 | ### 练习6
2670 |
2671 | 请在 6,5,10,2 四个数之间任意填上“+、-、×、÷或( )”,每个数字都只能用一次,使它们的计算结果等于 24。你能做到吗?
2672 |
2673 | 课后巩固
2674 |
2675 | 将“+、-、×、÷、( )”填入合适的地方,使下面的等式成立。
2676 | $$
2677 | 3\ \ \ 3\ \ \ 3\ \ \ 3\ \ \ =\ \ \ 1
2678 | $$
2679 |
2680 | $$
2681 | 3\ \ \ 3\ \ \ 3\ \ \ 3\ \ \ =\ \ \ 2
2682 | $$
2683 |
2684 | $$
2685 | 3\ \ \ 3\ \ \ 3\ \ \ 3\ \ \ =\ \ \ 3
2686 | $$
2687 |
2688 | $$
2689 | 3\ \ \ 3\ \ \ 3\ \ \ 3\ \ \ =\ \ \ 4
2690 | $$
2691 |
2692 | $$
2693 | 3\ \ \ 3\ \ \ 3\ \ \ 3\ \ \ =\ \ \ 5
2694 | $$
2695 |
2696 | $$
2697 | 3\ \ \ 3\ \ \ 3\ \ \ 3\ \ \ =\ \ \ 6
2698 | $$
2699 |
2700 | $$
2701 | 3\ \ \ 3\ \ \ 3\ \ \ 3\ \ \ =\ \ \ 7
2702 | $$
2703 |
2704 | $$
2705 | 3\ \ \ 3\ \ \ 3\ \ \ 3\ \ \ =\ \ \ 8
2706 | $$
2707 |
2708 | $$
2709 | 3\ \ \ 3\ \ \ 3\ \ \ 3\ \ \ =\ \ \ 9
2710 | $$
2711 |
2712 | $$
2713 | 3\ \ \ 3\ \ \ 3\ \ \ 3\ \ \ =\ \ \ 10
2714 | $$
2715 |
2716 | ## 3.2.09. 小数的认识
2717 |
2718 | 例题练习
2719 |
2720 | ### 例题1
2721 |
2722 | 找出下列案例中的小数:
2723 | (1)乐乐老师从家到学校坐公交车经过7站,路程5.3米;
2724 | (2)田田测量圆桂形水杯的高度为12.5厘米;
2725 | (3)圆周率的大小为3.1415926535897932384……
2726 |
2727 | ### 练习1
2728 |
2729 | 找出下列案例中的小数:
2730 | (1)夏日有空调的屋子室内温度为26度,室外为32.3度;
2731 | (2)西瓜的单价为1.3元,葡萄的单价为7.0元。
2732 |
2733 | ### 例题2(分类)
2734 |
2735 | 有下列小数:1.2,3.6,0.8,0.333…,3.1415926…,0.207。
2736 | (1)按照整数部分分类;
2737 | (2)按照小数部分分类。
2738 |
2739 | ### 练习2
2740 |
2741 | 有下列小数:2.14151617,0.821,0.333,1.555…,0.92。
2742 | (1)按照整数部分分类;
2743 | (2)按照小数部分分类。
2744 |
2745 | ### 例题3(比较大小)
2746 |
2747 | 田田、丁丁、牛牛三人比赛跳远,丁丁跳了1.9米,田田跳了1.7米,牛牛跳了2.1米,请问他们三个人的名次是什么样的?
2748 |
2749 | ### 练习3
2750 |
2751 | 将下列小数按从大到小的顺序排序。
2752 | 3.1,1.06,10.6,2.135,2.14,2.2,4.7。
2753 |
2754 | ### 例题4(小数点的移动)
2755 |
2756 | 田田买一支铅笔用了0.56元,买10支铅笔用多少元?买100支呢?小数点是如何变化的?
2757 |
2758 | ### 练习4
2759 |
2760 | 填空
2761 | (1)把3.2的小数点去掉,它的值扩大()倍
2762 | (2)4.26扩大()倍是4260。
2763 | (3)22.9缩小到原来的()倍,才能得到0.229。
2764 |
2765 | ### 例题5(小数分数的转换)
2766 |
2767 | (1)将下列小数化为分数:0.5,1.4,10.8。
2768 | (2)将下列分数化为小数:$\frac{2}{5}$,$1\frac{1}{4}$,$\frac{100}{25}$。
2769 |
2770 | ### 练习5
2771 |
2772 | 请将下列相等的分数和小数连线。
2773 |
2774 | ### 例题6(分数小数比较大小)
2775 |
2776 | 将下列数按照从小到大的顺序排序。
2777 |
2778 | $1.5,0.999,3\frac{1}{4},1.51,\frac{199}{200},7.3。$
2779 |
2780 | ### 练习6
2781 |
2782 | 将下列数按照从大到小的顺序排序。
2783 |
2784 | $1\frac{77}{100},0.001,2,0.01,1\frac{4}{5}。$
2785 |
2786 | ## 3.2.10. 平行四边形与梯形
2787 |
2788 | 例题练习
2789 |
2790 | ### 例题1
2791 |
2792 | 乐乐老师带着丁丁和牛牛来到图形王国,遇到各种图形,你认识它们吗?它们分别叫什么图形?请说说平行四边形和梯形都有哪些性质?
2793 |
2794 |
1980 |
1981 | ### 热身2
1982 |
1983 | 如图,∠AOB 的顶点 O在直线 l 上,已知图中所有小于平角的角之和是 400 度,求∠AOB的大小。
1984 |
1985 | 
1986 |
1987 | ### 热身3
1988 |
1989 | 计算:$88\times46+88\times64-88\times10$
1990 |
1991 | 例题练习
1992 |
1993 | ### 例题1
1994 |
1995 | 计算。
1996 |
1997 | (1)$78+19+36+54+21+74+102$
1998 |
1999 | (2)$756-248-352$
2000 |
2001 | (3)$8+88+888+8888$
2002 |
2003 | (4)$39+38+40+41+43$
2004 |
2005 | ### 练习1
2006 |
2007 | 计算。
2008 |
2009 | (1)$99997+9996+995+94+9$
2010 |
2011 | (2)$894-89-111-95-105-94$
2012 |
2013 | ### 例题2
2014 |
2015 | 计算。
2016 |
2017 | (1)$25\times16\div20$
2018 |
2019 | (2)$1200\div4\div5\div5$
2020 |
2021 | (3)$1300\times77\div100$
2022 |
2023 | ### 练习2
2024 |
2025 | 计算。
2026 |
2027 | (1)$25\times64\times125$
2028 |
2029 | (2)$248\times5\div8$
2030 |
2031 | (3)$(36\times45)\div(6\times9)$
2032 |
2033 | ### 例题3
2034 |
2035 | 计算。
2036 |
2037 | (1)$35\times35$
2038 |
2039 | (2)$45\times45$
2040 |
2041 | (3)$73\times33$
2042 |
2043 | (4)$58\times58$
2044 |
2045 | ### 练习3
2046 |
2047 | 计算。
2048 |
2049 | (1)$75\times75$
2050 |
2051 | (2)$62\times68$
2052 |
2053 | (3)$67\times47$
2054 |
2055 | ### 例题4
2056 |
2057 | 计算。
2058 |
2059 | (1)$36\times19+36\times81$
2060 |
2061 | (2)$984\div8+16\div8$
2062 |
2063 | (3)$125\times(8+80)$
2064 |
2065 | (4)$(369+345)\div3$
2066 |
2067 | ### 练习4
2068 |
2069 | 计算。
2070 |
2071 | (1)$325\times113-325\times13$
2072 |
2073 | (2)$(40+8)\times25$
2074 |
2075 | (3)$684\div19-304\div19$
2076 |
2077 | (4)$(111+74)\div37$
2078 |
2079 | ### 例题5
2080 |
2081 | 计算。
2082 |
2083 | (1)$53\times46+71\times54+82\times54$
2084 |
2085 | ### 练习5
2086 |
2087 | 计算。
2088 |
2089 | (1)$33\times34+24\times34+57\times66$
2090 |
2091 | ### 例题6
2092 |
2093 | 计算。
2094 |
2095 | (1)$1997\times1995-1996\times1994$
2096 |
2097 | ### 练习6
2098 |
2099 | 计算。
2100 |
2101 | (1)$4747+888\times53+47\times787$
2102 |
2103 | ### 拓展1
2104 |
2105 | $$
2106 | 12345+23451+34512+45123+51234
2107 | $$
2108 |
2109 | ### 拓展2
2110 |
2111 | $$
2112 | 80+79-78-77+76+75-74-73+\dots+4+3-2-1
2113 | $$
2114 |
2115 | ### 拓展3
2116 |
2117 | $$
2118 | 20222022\times2021-20212021\times2022
2119 | $$
2120 |
2121 | ### 练习1
2122 |
2123 | 计算:$298+396+495+691+799+21$
2124 |
2125 | ### 练习2
2126 |
2127 | 计算:$(54\times24)\div(9\times4)$
2128 |
2129 | ### 练习3
2130 |
2131 | 计算:$39+142\times39+103$
2132 |
2133 | ## 3.2.03. 用字母表示数
2134 |
2135 | ### 热身1
2136 |
2137 | ### 热身2
2138 |
2139 | ### 热身3
2140 |
2141 | ### 例题1
2142 |
2143 | (1)观察下面的数列$2,4,6,a,10,b,14,\dots,a=(),b=()$。
2144 |
2145 | (2)观察下面的数列$1,3,5,a,9,b,13,\dots,a=(),b=()$。
2146 |
2147 | ### 练习1
2148 |
2149 | 观察下面的数列,填入合适的数。
2150 |
2151 | (1)5,10,15,a,25,30,b,……,a=(),b=()。
2152 |
2153 | (2)4,8,12,a,20,24,b,32,36,……,a=(),b=()。
2154 |
2155 | ### 例题2
2156 |
2157 | 1只青蛙1张嘴,2只眼睛,4条腿;
2158 |
2159 | 2只青蛙2张嘴,()只眼睛,()条腿;
2160 |
2161 | 3只青蛙3张嘴,()只眼睛,()条腿;
2162 |
2163 | 4只青蛙4张嘴,()只眼睛,()条腿;
2164 |
2165 | ……
2166 |
2167 | n只青蛙()张嘴,()只眼睛,()条腿。
2168 |
2169 | ### 练习2
2170 |
2171 | 一个正方形有()条边,
2172 |
2173 | 两个正方形有()条边,
2174 |
2175 | 三个正方形有()条边,
2176 |
2177 | ……
2178 |
2179 | n个正方形有()条边。
2180 |
2181 | 边数和正方形的数量有什么关系呢?
2182 |
2183 | ### 例题3
2184 |
2185 | 用简便方法表示下列各式。
2186 |
2187 | (1)$27\times x$
2188 |
2189 | (2)$m\times n$
2190 |
2191 | (3)$a+a+a$
2192 |
2193 | (4)$a\times a$
2194 |
2195 | (5)$36\times a\times b$
2196 |
2197 | (6)$(a+b)\times5$
2198 |
2199 | ### 练习3
2200 |
2201 | (1)$63\times x+5$
2202 |
2203 | (2)$m\times n\times3$
2204 |
2205 | (3)$(m+n)\times16$
2206 |
2207 | (4)$c\times2\times a$
2208 |
2209 | ### 例题4
2210 |
2211 | 用字母表示下列公式。(周长=C,面积=S,长=a,宽=b,边长=a)
2212 | 长方形的周长公式:
2213 | 长方形的面积公式:
2214 | 正方形的周长公式:
2215 | 正方形的面积公式:
2216 |
2217 | ### 练习4
2218 |
2219 | 用字母表示下列公式。
2220 | 乘法交换律:
2221 | 乘法结合律:
2222 | 乘法分配律:
2223 |
2224 | ### 例题5
2225 |
2226 | 你能用字母表示下面题目中所求的量吗?
2227 |
2228 | (1)过春节了,阿普拿到了m元压岁钱,牛牛的压岁钱是阿普的6倍,牛牛的压岁钱是()元。
2229 |
2230 | (2)某学校有男老师a人,女老师比男老师少b人,学校有女老师()人,共有老师()人。
2231 |
2232 | (3)一个长方形的周长是80厘米,长是a厘米,宽是()厘米。
2233 |
2234 | ### 练习5
2235 |
2236 | 你能用字母表示下面题目中所求的量吗?
2237 | (1)一个等边三角形,每边长a米,它的周长是()米。
2238 | (2)牛牛的学校一共有m人,男生有a人,女生有()人。
2239 | (3)东东今年a岁,比妈妈小m岁,再过年c后妈妈比东东大()岁。
2240 |
2241 | ### 例题6
2242 |
2243 | 用含字母的式子表示。
2244 | (1)1个菠萝重x千克,1个西瓜比这个菠萝的3倍还重2千克,西瓜重()千克。如果菠萝重2千克,那么西瓜重()千克。
2245 | (2)小红骑车每分钟行x千米,她骑了20分钟,行驶了()千米;她行驶a千米,需要()分钟。x=2,a=10,那么需要()分钟。
2246 | (3)乙数比甲数a的4倍少6,乙数是()。
2247 |
2248 | ### 练习6
2249 |
2250 | 用含字母的式子表示。
2251 | (1)田田高a厘米,丁丁比田田高7厘米,丁丁和田田一共高()厘米。
2252 | (2)青青林场栽了梧桐树和雪松各x排,已知梧桐树每排12棵,雪松每排14棵,栽梧桐树
2253 | 和雪松共()棵;当x=20时,青青林场一共有()棵梧桐树和雪松。
2254 | (3)一个正方形的边长为a厘米,周长为()厘米,面积是()平方厘米。
2255 |
2256 | ## 3.2.04. 和差倍综合
2257 |
2258 | 例题练习
2259 |
2260 | ### 例题1(和差)
2261 |
2262 | 有大、小两个油桶,一共装油24千克,两个油桶都倒出同样多的油后分别还剩9千克和5千克。问:原来大、小两个油桶各装油多少千克?
2263 |
2264 | ### 练习1
2265 |
2266 | 两箱图书共有66本,甲箱如果借出10本,就比乙箱少4本。甲、乙两箱原有图书各多少本?
2267 |
2268 | ### 例题2(和差)
2269 |
2270 | 学校新进99本书,分给三、四、五三个年级,三年级比四年级多分了2本,四年级比五年级多分了5本,三个年级各分得书多少本?
2271 |
2272 | ### 练习2
2273 |
2274 | 甲、乙、丙三个数的和是105,甲数比乙数多4,乙数比丙数多4,求丙数。
2275 |
2276 | ### 例题3(和倍)
2277 |
2278 | 某校学生总人数比四年级人数的6倍少78人,并且除了四年级外,其他各年级的学生人数总和为2222人,那么该校共有学生多少人?
2279 |
2280 | ### 练习3
2281 |
2282 | 有两层书架,共有书216本,从第一层拿走42本书后,第二层的书比第一层的2倍还多6本,则第二层有多少本书?
2283 |
2284 | ### 例题4
2285 |
2286 | 一天,甲、乙、丙三个同学做数学题,已知甲比乙多做了6道,丙做的题是甲的2倍,比乙做的题多22道,则乙做了多少道数学题?
2287 |
2288 | ### 练习4
2289 |
2290 | 小云比小雨少20本书,后来小云丢了5本书,小雨新买了11本书,这时小雨的书比小云的书多2倍。问:原来两人各有多少本书?
2291 |
2292 | ### 例题5
2293 |
2294 | 李师傅某天生产了一批零件,把它们分成了甲、乙两堆摆放。若从甲堆零件中拿出15个放到乙堆,则两堆零件个数相等;若从乙堆零件中拿出15个放到甲堆,则甲堆的零件个数是乙堆的4倍。甲堆原有零件多少个,李师傅这天共生产了多少个零件?
2295 |
2296 | ### 练习5
2297 |
2298 | 一家汽车销售店有若干部福特汽车和丰田汽车等待销售。福特汽车的数量是丰田汽车的3倍,如果每周销售2辆丰田汽车和4辆福特汽车,丰田汽车销售完时还剩下30辆福特汽车。请问:原有丰田汽车和福特汽车各多少辆?
2299 |
2300 | ### 例题6
2301 |
2302 | 维尼熊和跳跳虎去摘苹果。维尼熊爬上树去摘,跳跳虎在地上跳着摘。跳跳虎每摘7个,维尼熊只能摘4个。维尼熊摘了80分钟,跳跳虎摘了50分钟就累倒了。他们回来后数了一下共摘2010个苹果,那么其中维尼熊摘的有多少个?
2303 |
2304 | ### 练习6
2305 |
2306 | 某镇上有东西两个公交车站,东站有客车84辆,西站有客车56辆,每天从东站到西站有7辆车,从西站到东站有11辆车,几天后,东站车辆是西站的4倍?
2307 |
2308 | ## 3.2.05. 逆向思考进阶
2309 |
2310 | ### 例题1
2311 |
2312 | 牛牛和阿昔在游玩时,遇到一位小神仙,他们问这位神仙:“你一定不到100岁吧!”谁知这位神仙摇摇头说:“你们算算吧!把我的年龄加上75,再除以5,然后减去15,再乘10,恰好是
2313 | 2000岁。”小朋友,你知道这位神仙现在有多少岁吗?
2314 |
2315 | ### 练习1
2316 |
2317 | 一个数加上37,乘37,减去37,再除以37,结果等于37,这个数是多少?
2318 |
2319 | ### 例题2
2320 |
2321 | 小马虎在做一道加法题时,把一个加数个位上的9看作6,十位上的6看作9,结果和是174,那么正确的结果应该是多少呢?
2322 |
2323 | ### 练习2
2324 |
2325 | 淘气在做一道减法题时,把减数个位上的9看成了3,把十位上的4看成了7,得到的结果是164。请你帮淘气算算正确的答案是多少?
2326 |
2327 | ### 例题3
2328 |
2329 | 李奶奶卖一筐鸡蛋,第一位客人买走了一半少2个,第二位客人买走了剩下的一半多2个,第三位客人把剩下的5个鸡蛋全部买走了。老奶奶的篮子里原来有多少个鸡蛋?
2330 |
2331 | ### 练习3
2332 |
2333 | 学学看到太上老君正在用一根绳子拴宝葫芦,第一次用去全长的一半还多2米,第二次用去余下的一半少10米,第三次用去15米,最后还剩9米,那么这根绳子原来有多少米?
2334 |
2335 | ### 例题4
2336 |
2337 | 有一个财迷总想使自己的钱成倍增长。一天,他在一座桥上碰见一个老人,老人对他说:"你只要走过这座桥再回来,你身上的钱就会增加一倍,但作为报酬,你每走一个来回要给我32个
2338 | 铜板。”财迷算了算,感觉挺合算,就同意了。他走过桥去又走回来,身上的钱果然增加了一倍,他很高兴地给了老人32个铜板。这样走完第五个来回,身上的最后32个铜板都给了老人,财迷一个铜板也没剩下。你知道财迷身上原有多少个铜板?
2339 |
2340 | ### 练习4
2341 |
2342 | 某人发现了一条魔道,下面有一个存钱的小箱子,当他从魔道走过去的时候,箱子里的一些钱会飞到人的口袋里,使人身上的钱增加一倍,这人很高兴;当他从魔道走回来的时候,身
2343 | 上的钱又会飞到箱子里,使箱子里的钱增加一倍。这个人一连走了3个来回后,箱子里的钱和人身上的钱都是64元,那么,原来这人身上有多少钱?箱子里有多少钱?
2344 |
2345 | ### 例题5
2346 |
2347 | 有一个两层书架,一共摆放224本书,先从上层取出与下层本数同样多的书放入下层,再从下层现有书中,取出与上层剩下的本数同样多的书放入上层,这算进行了一轮调整。若如进行了
2348 | 两轮调整后,两层摆放书的本数相等,上层书架原来摆放多少本书?下层书架原来摆放多少本书?
2349 |
2350 | ### 练习5
2351 |
2352 | 有甲、乙两箱糖果,如果第一次从甲箱拿出和乙箱同样多块糖果放到乙箱里,第二次从乙箱拿出和甲箱剩下的同样多块糖果放入甲箱,这样拿4次后,甲、乙两箱糖果都是16块。甲、乙两箱各有糖果多少块?
2353 |
2354 | ### 例题6
2355 |
2356 | 一班、二班、三班各有不同数量的图书。一班拿出本班的一部分图书分给二班、三班,使这两个班的图书各增加一倍;然后二班也拿出一部分图书分给一班、三班,使这两个班的图书各增加一倍;接着三班也拿出一部分图书分给一班、二班,使这两个班的图书各增加一倍。这时三个班的图书数量都是48本。
2357 | ,求三个班原来各有图书多少本。
2358 |
2359 | ### 练习6
2360 |
2361 | 甲、乙、丙3人共有192张邮票。从甲的邮票中取出乙那么多邮票给乙后,再从乙的邮票中取出丙那么多邮票给丙,最后从丙的邮票中取出甲那么多邮票给甲,这时甲、乙、丙3人的邮票数相同,甲、乙、丙原来各有邮票多少张?
2362 |
2363 | ## 3.2.06. 逻辑推理综合(1)
2364 |
2365 | ### 例题1
2366 |
2367 | 5名谋杀案的嫌疑人,在犯罪现场被警察询问,其中有一名是凶手。下面5个人的供述中,只有3句是对的:
2368 | A说:“D是杀人犯。”
2369 | B说:“我是无辜的。”
2370 | C说:“E不是杀人犯。”
2371 | D说:“A在说谎。”
2372 | E说:“B说的是实话。”
2373 | 在这5个人中,谁是凶手?
2374 |
2375 | ### 练习1
2376 |
2377 | 四个小朋友宝宝、星星、强强和乐乐在院子里踢足球,一阵响声,惊动了正在读书的陆老师,陆老师跑出来查看,发现一块窗户玻璃被打破了。陆老师问:“是谁打破了玻璃?”
2378 | 宝宝说:“是星星无意打破的。”
2379 | 星星说:“是乐乐打破的。”
2380 | 乐乐说:“星星说谎。”
2381 | 强强说:“反正不是我打破的。”
2382 | 如果只有一个孩子说了实话,那么这个孩子是谁?是谁打破了玻璃?
2383 |
2384 | ### 例题2
2385 |
2386 | 在一次数学竞赛中,A,B,C,D,E五位同学分别得了前五名(没有并列同一名次的),关于各人的名次,大家做出了下面的猜测:
2387 |
2388 | A说:“第二名是D,第三名是B。”
2389 |
2390 | B说:“第二名是C,第四名是F。”
2391 |
2392 | C说:“第一名是E,第五名是A。”
2393 |
2394 | D说:“第三名是C,第四名是A。”
2395 |
2396 | E说:“第二名是B,第五名是D。”
2397 |
2398 | 结果每人都只猜对了一半,他们的名次如何?
2399 |
2400 | ### 练习2
2401 |
2402 | 甲、乙、丙、丁四人同时参加全国小学数学夏令营。赛前甲、乙、丙分别作了预测。
2403 |
2404 | 甲说:“丙第1名,我第3名。”
2405 |
2406 | 乙说:“我第1名,丁第4名。”
2407 |
2408 | 丙说:“丁第2名,我第3名。”
2409 | 成绩揭晓后,发现他们每人只说对了一半,你能说出他们的名次吗?
2410 |
2411 | ### 例题3
2412 |
2413 | 学校新来了一位老师,五个学生分别听到如下的情况:
2414 |
2415 | (1)是一位姓王的中年女老师,教语文;
2416 |
2417 | (2)是一位姓丁的中年男老师,教数学;
2418 |
2419 | (3)是一位姓刘的青年男老师,教外语;
2420 |
2421 | (4)是一位姓李的青年男老师,教数学;
2422 |
2423 | (5)是一位姓王的老年男老师,教外语。
2424 |
2425 | 他们每人听到的四项情况中各有一项正确。问:真实情况是什么样的?
2426 |
2427 | ### 练习3
2428 |
2429 | 4名运动员参加一项比赛,赛前。
2430 |
2431 | 甲说:“我肯定是最后一名。”
2432 |
2433 | 乙说:“我不可能是第一名,也不可能是最后一名。”
2434 | 丙说:“我绝对不会得最后一名。”
2435 | 丁说:“我肯定得第一名。”
2436 |
2437 | 赛后,发现他们4人的预测中只有一人是错误的。请问谁的预测是错误的?
2438 |
2439 | ### 例题4
2440 |
2441 | 王平、宋丹、韩涛三个小学生都是少先队的干部,一个是大队长,一个是中队长,一个是小队长。一次数学测验,这三个人的成绩是:
2442 |
2443 | (1)韩涛比大队长的成绩好。
2444 |
2445 | (2)王平和中队长的成绩不相同。
2446 |
2447 | (3)中队长比宋丹的成绩差。
2448 |
2449 | 请你根据这三个人的成绩,判断一下,谁是大队长呢?
2450 |
2451 | ### 练习4
2452 |
2453 | 王文、张贝、李丽分别是跳伞、田径、游泳运动员,现在知道:
2454 |
2455 | (1)张贝从未上过天;
2456 | (2)跳伞运动员已得过两块金牌;
2457 |
2458 | (3)李丽还未得过第一名,她与田径运动员同年出生:
2459 | 请根据上述情况,判断王文、张贝、李丽各是什么运动员?
2460 |
2461 | ### 例题5
2462 |
2463 | 张、王、李三人除了本职工作,每人都有两样业余爱好。人们有时以车工、电工、乐师、画家、作家、技工称呼他们,此外,还有以下情况:
2464 | (1)车工经常赞扬乐师的三弦琴弹得好;
2465 | (2)乐师,作家常常与姓张的一起看电影;
2466 | (3)画家请电工来修过电灯;
2467 | (4)车工和画家的儿子在同一车间工作;
2468 | (5)姓王的向作家请教写作的技巧;
2469 | (6)姓李的善于下象棋,姓王的和画家常常输给他。
2470 | 问:姓李的有哪两个称呼?
2471 |
2472 | ### 练习5
2473 |
2474 | 宝宝、贝贝、聪聪每人有两个外号,人们有时以“数学博士”、“短跑健将”、“跳高冠军”、“小画家“、“大作家”和“歌唱家”称呼他们,此外:
2475 |
2476 | (1)数学博士夸跳高冠军跳得高;
2477 |
2478 | (2)跳高冠军和大作家常与宝宝一起看电影;
2479 |
2480 | (3)短跑健将请小画家画贺年卡;
2481 |
2482 | (4)数学博士和小画家关系很好;
2483 |
2484 | (5)贝贝向大作家借过书;
2485 |
2486 | (6)聪聪下象棋常赢贝贝和小画家。
2487 |
2488 | 问:宝宝、贝贝、聪聪各有哪两个外号?
2489 |
2490 | ### 例题6
2491 |
2492 | A,B,C,D分别来自中国、日本、美国和法国。已知:
2493 |
2494 | (1)A和中国人是医生;
2495 |
2496 | (2)B和法国人是教师;
2497 |
2498 | (3)C和日本人职业不同;
2499 |
2500 | (4)D不会看病。
2501 |
2502 | 问:A,B,C,D各是哪国人?
2503 |
2504 | ### 练习6
2505 |
2506 | 张明、席辉和李刚分别在北京、上海和天津三城市之一工作,他们的职业是工人、农民和教师之一,已知:
2507 |
2508 | (1)张明不在北京工作,席辉不在上海工作;
2509 |
2510 | (2)在北京工作的不是教师;
2511 | (3)在上海工作的是工人;
2512 |
2513 | (4)席辉不是农民。
2514 |
2515 | 问:这三人各住哪里?各是什么职业?
2516 |
2517 | ## 3.2.07. 方阵
2518 |
2519 | ### 例题1
2520 |
2521 | 一个实心方阵,最外一层每边18人。
2522 | (1)那么整个方阵一共()人;
2523 | (2)最外面一层有()人;
2524 | (3)从外向内数,第二层每边有()人,一共有()人;
2525 | (4)如果考虑最外面三层,那么这三层共有()人;
2526 | (5)如果将方阵外面增加一层,那么一共增加()人。
2527 |
2528 | ### 练习1
2529 |
2530 | 用64枚棋子摆成一个实心方阵。
2531 | (1)每边有()枚棋子;
2532 | (2)最外层有()枚棋子;
2533 | (3)从外向内数,第二层每边有()枚棋子,第二层一共有()枚棋子。
2534 |
2535 | ### 例题2
2536 |
2537 | 有一块空地在进行种树绿化,打算把树种成实心方阵的样子,方阵最外面一周有60棵树,问这个方阵外层每边有多少棵树?这块空地一共需要多少棵树?
2538 |
2539 | ### 练习2
2540 |
2541 | 三年级学生排成一个实心方阵,最外一层的人数为36人,问方阵最外层每边有多少人?这个方阵共有三年级学生多少人?
2542 |
2543 | ### 例题3
2544 |
2545 | 小刚在用棋子摆好的实心方阵上又添了17枚棋子,它的横竖各增加了一排,成了大一点的实心方阵,求原来的实心方阵有多少枚棋子。
2546 |
2547 | ### 练习3
2548 |
2549 | 军训的学生进行队列表演,排成了一个5行5列的正方形队列,如果去掉一行一列,要去掉多少人?
2550 |
2551 | ### 例题4
2552 |
2553 | 大家要用盆花在空地上摆出一个空心方阵花坛,最外面的一层每边摆12盆花,共3层,一共要用多少盆花?
2554 |
2555 | ### 练习4
2556 |
2557 | 有一个班的学生排成一个中空方阵,最外层人数共52人,最内层人数共28人,这个班学生共有多少人?
2558 |
2559 | ### 例题5
2560 |
2561 | 用64枚棋子摆成一个两层中空方阵,如果想在外面再增加一层,问需要增加多少枚棋子?
2562 |
2563 | ### 练习5
2564 |
2565 | 用84枚棋子摆成一个三层中空方阵,问最外层有多少枚棋子?
2566 |
2567 | ### 例题6
2568 |
2569 | 一天,博士用棋子摆成一周每边有10枚棋子的空心方阵,摆完后发现还有棋子剩下,但是不够外围再增加一层。在保持原有棋子不动的情况下,想变成一个更大的两层空心方阵,博士至少需要多少枚棋子?
2570 |
2571 | ### 练习6
2572 |
2573 | 用一堆棋子摆成一个两层的空心方阵,用了48枚棋子后发现还剩下一些棋子,但是不够外围再增加一层了。在保持原有棋子不动的情况下,想变成一个更大的三层空心方阵,至少需要多少枚棋子?
2574 |
2575 | ## 3.2.08. 巧填算符综合
2576 |
2577 | 例题练习
2578 |
2579 | ### 例题1
2580 |
2581 | 在“+、-、×、÷、( )”中,挑出合适的符号,填入下面的数字之间,使算式成立。
2582 | $$
2583 | 9\ \ \ 8\ \ \ 7\ \ \ 6\ \ \ 5\ \ \ 4\ \ \ 3\ \ \ 2\ \ \ 1=1
2584 | $$
2585 |
2586 | ### 练习1
2587 |
2588 | 在○内填上与等号左边不同的运算符号,使等式成立。
2589 | $$
2590 | (1)6-2+2=6\circ2\circ 2
2591 | $$
2592 |
2593 | $$
2594 | (2)8+2+3=8\circ 2\circ 3
2595 | $$
2596 |
2597 | $$
2598 | (3)16-8-3=16\circ 8\circ 3
2599 | $$
2600 |
2601 | ### 例题2
2602 |
2603 | 在下面算式的适当地方,填上运算符号“+、-、×、÷或( )”,使算式成立。
2604 | $$
2605 | 1\ \ \ 2\ \ \ 3\ \ \ 4\ \ \ 5=10
2606 | $$
2607 |
2608 | ### 练习2
2609 |
2610 | 用运算符号把下面三个相同的数宇连接起来,使等式成立。
2611 | $$
2612 | (1)5\ \ \ 5\ \ \ 5=30
2613 | $$
2614 |
2615 | $$
2616 | (2)6\ \ \ 6\ \ \ 6\ \ \ =30
2617 | $$
2618 |
2619 | ### 例题3
2620 |
2621 | 在下式的每两个数中间填上合适的运算符号,使等式成立。
2622 | $$
2623 | 8\ \ \ 2\ \ \ 4\ \ \ 6=4\ \ \ 2
2624 | $$
2625 |
2626 | ### 练习3
2627 |
2628 | 在下式的每两个数中间填上合适的运算符号,使等式成立。
2629 | $$
2630 | 8\ \ \ 2\ \ \ 3=3\ \ \ 3
2631 | $$
2632 |
2633 | ### 例题4
2634 |
2635 | 在8个8之间的适当地方,填上合适的运算符号或括号,使算式成立。
2636 | $$
2637 | 8\ \ \ 8\ \ \ 8\ \ \ 8\ \ \ 8\ \ \ 8\ \ \ 8\ \ \ 8=1000
2638 | $$
2639 |
2640 | ### 练习4
2641 |
2642 | 在下面算式适当的地方,填上运算符号或括号,使等式成立。
2643 | $$
2644 | 9\ \ \ 8\ \ \ 7\ \ \ 6\ \ \ 5\ \ \ 4\ \ \ 3\ \ \ 2\ \ \ 1=1000
2645 | $$
2646 |
2647 | ### 例题5
2648 |
2649 | 在5个4之间,填上适当的运算符号或括号,使得下面的算式成立。
2650 | $$
2651 | 4\ \ \ 4\ \ \ 4\ \ \ 4\ \ \ 4=8
2652 | $$
2653 |
2654 | ### 练习5
2655 |
2656 | 在下列算式的合适位置,填上运算符号或括号,使等式成立。
2657 | $$
2658 | (1)4\ \ \ 4\ \ \ 4\ \ \ 4=1
2659 | $$
2660 |
2661 | $$
2662 | (2)4\ \ \ 4\ \ \ 4\ \ \ 4=5
2663 | $$
2664 |
2665 | ### 例题6
2666 |
2667 | 请在 2,3,4,6 四个数之间任意填上“+、-、×、÷或( )”,每个数字都只能用一次,使它们的计算结果等于 24。你能做到吗?
2668 |
2669 | ### 练习6
2670 |
2671 | 请在 6,5,10,2 四个数之间任意填上“+、-、×、÷或( )”,每个数字都只能用一次,使它们的计算结果等于 24。你能做到吗?
2672 |
2673 | 课后巩固
2674 |
2675 | 将“+、-、×、÷、( )”填入合适的地方,使下面的等式成立。
2676 | $$
2677 | 3\ \ \ 3\ \ \ 3\ \ \ 3\ \ \ =\ \ \ 1
2678 | $$
2679 |
2680 | $$
2681 | 3\ \ \ 3\ \ \ 3\ \ \ 3\ \ \ =\ \ \ 2
2682 | $$
2683 |
2684 | $$
2685 | 3\ \ \ 3\ \ \ 3\ \ \ 3\ \ \ =\ \ \ 3
2686 | $$
2687 |
2688 | $$
2689 | 3\ \ \ 3\ \ \ 3\ \ \ 3\ \ \ =\ \ \ 4
2690 | $$
2691 |
2692 | $$
2693 | 3\ \ \ 3\ \ \ 3\ \ \ 3\ \ \ =\ \ \ 5
2694 | $$
2695 |
2696 | $$
2697 | 3\ \ \ 3\ \ \ 3\ \ \ 3\ \ \ =\ \ \ 6
2698 | $$
2699 |
2700 | $$
2701 | 3\ \ \ 3\ \ \ 3\ \ \ 3\ \ \ =\ \ \ 7
2702 | $$
2703 |
2704 | $$
2705 | 3\ \ \ 3\ \ \ 3\ \ \ 3\ \ \ =\ \ \ 8
2706 | $$
2707 |
2708 | $$
2709 | 3\ \ \ 3\ \ \ 3\ \ \ 3\ \ \ =\ \ \ 9
2710 | $$
2711 |
2712 | $$
2713 | 3\ \ \ 3\ \ \ 3\ \ \ 3\ \ \ =\ \ \ 10
2714 | $$
2715 |
2716 | ## 3.2.09. 小数的认识
2717 |
2718 | 例题练习
2719 |
2720 | ### 例题1
2721 |
2722 | 找出下列案例中的小数:
2723 | (1)乐乐老师从家到学校坐公交车经过7站,路程5.3米;
2724 | (2)田田测量圆桂形水杯的高度为12.5厘米;
2725 | (3)圆周率的大小为3.1415926535897932384……
2726 |
2727 | ### 练习1
2728 |
2729 | 找出下列案例中的小数:
2730 | (1)夏日有空调的屋子室内温度为26度,室外为32.3度;
2731 | (2)西瓜的单价为1.3元,葡萄的单价为7.0元。
2732 |
2733 | ### 例题2(分类)
2734 |
2735 | 有下列小数:1.2,3.6,0.8,0.333…,3.1415926…,0.207。
2736 | (1)按照整数部分分类;
2737 | (2)按照小数部分分类。
2738 |
2739 | ### 练习2
2740 |
2741 | 有下列小数:2.14151617,0.821,0.333,1.555…,0.92。
2742 | (1)按照整数部分分类;
2743 | (2)按照小数部分分类。
2744 |
2745 | ### 例题3(比较大小)
2746 |
2747 | 田田、丁丁、牛牛三人比赛跳远,丁丁跳了1.9米,田田跳了1.7米,牛牛跳了2.1米,请问他们三个人的名次是什么样的?
2748 |
2749 | ### 练习3
2750 |
2751 | 将下列小数按从大到小的顺序排序。
2752 | 3.1,1.06,10.6,2.135,2.14,2.2,4.7。
2753 |
2754 | ### 例题4(小数点的移动)
2755 |
2756 | 田田买一支铅笔用了0.56元,买10支铅笔用多少元?买100支呢?小数点是如何变化的?
2757 |
2758 | ### 练习4
2759 |
2760 | 填空
2761 | (1)把3.2的小数点去掉,它的值扩大()倍
2762 | (2)4.26扩大()倍是4260。
2763 | (3)22.9缩小到原来的()倍,才能得到0.229。
2764 |
2765 | ### 例题5(小数分数的转换)
2766 |
2767 | (1)将下列小数化为分数:0.5,1.4,10.8。
2768 | (2)将下列分数化为小数:$\frac{2}{5}$,$1\frac{1}{4}$,$\frac{100}{25}$。
2769 |
2770 | ### 练习5
2771 |
2772 | 请将下列相等的分数和小数连线。
2773 |
2774 | ### 例题6(分数小数比较大小)
2775 |
2776 | 将下列数按照从小到大的顺序排序。
2777 |
2778 | $1.5,0.999,3\frac{1}{4},1.51,\frac{199}{200},7.3。$
2779 |
2780 | ### 练习6
2781 |
2782 | 将下列数按照从大到小的顺序排序。
2783 |
2784 | $1\frac{77}{100},0.001,2,0.01,1\frac{4}{5}。$
2785 |
2786 | ## 3.2.10. 平行四边形与梯形
2787 |
2788 | 例题练习
2789 |
2790 | ### 例题1
2791 |
2792 | 乐乐老师带着丁丁和牛牛来到图形王国,遇到各种图形,你认识它们吗?它们分别叫什么图形?请说说平行四边形和梯形都有哪些性质?
2793 |
2794 |  2795 |
2796 | ### 练习1
2797 |
2798 | 下面是七巧板拼成的小船图,在这个图形中,你能找到几个平行四边形和梯形?
2799 |
2800 |
2795 |
2796 | ### 练习1
2797 |
2798 | 下面是七巧板拼成的小船图,在这个图形中,你能找到几个平行四边形和梯形?
2799 |
2800 |  2801 |
2802 | ### 例题2
2803 |
2804 | (1)请在下图 1 中画出点 A 到点 C 的距离;点 A 到线段 CD 的距离;
2805 |
2806 | (2)请在下图 2 中画出平行四边形 ABCD 的高;
2807 | (3)请在下图 3 中画出梯形 EFGH 的高。
2808 |
2809 | 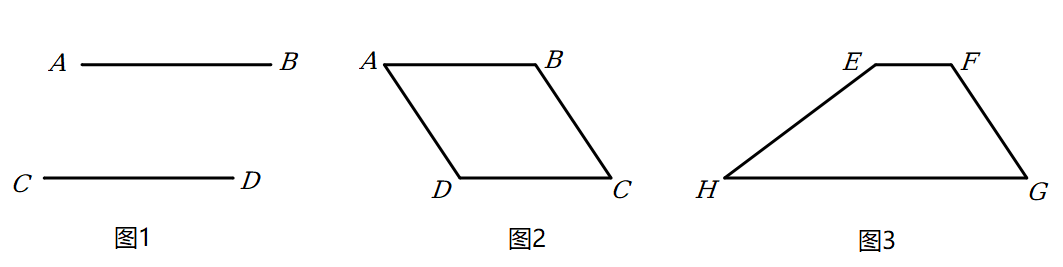
2810 |
2811 | ### 练习2
2812 |
2813 | 画出下面每个平行四边形底边上的高。
2814 |
2815 | 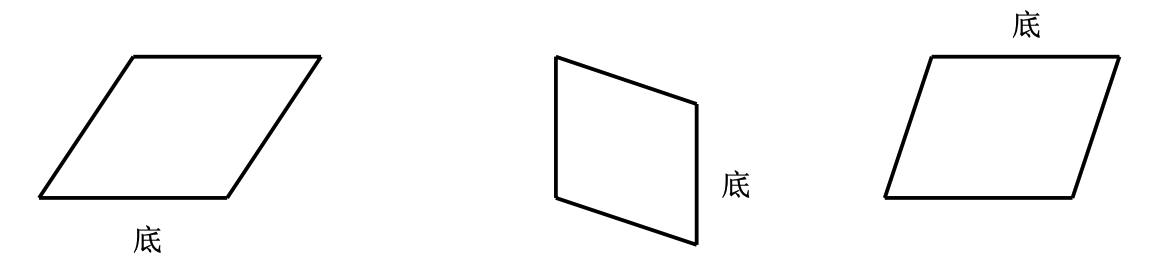
2816 |
2817 | ### 例题3
2818 |
2819 | 如图,已知每个小正方形的面积都是 1 平方厘米,请你根据图来计算图中长方形和平行四边形的面积,能否总结出平行四边形的面积公式?
2820 |
2821 |
2801 |
2802 | ### 例题2
2803 |
2804 | (1)请在下图 1 中画出点 A 到点 C 的距离;点 A 到线段 CD 的距离;
2805 |
2806 | (2)请在下图 2 中画出平行四边形 ABCD 的高;
2807 | (3)请在下图 3 中画出梯形 EFGH 的高。
2808 |
2809 | 
2810 |
2811 | ### 练习2
2812 |
2813 | 画出下面每个平行四边形底边上的高。
2814 |
2815 | 
2816 |
2817 | ### 例题3
2818 |
2819 | 如图,已知每个小正方形的面积都是 1 平方厘米,请你根据图来计算图中长方形和平行四边形的面积,能否总结出平行四边形的面积公式?
2820 |
2821 |  2822 |
2823 | 如图,已知 AB=5 厘米,AE=3 厘米,求平行四边形 ABCD 的面积。
2824 |
2825 |
2822 |
2823 | 如图,已知 AB=5 厘米,AE=3 厘米,求平行四边形 ABCD 的面积。
2824 |
2825 |  2826 |
2827 | ### 练习3
2828 |
2829 | 如图,是一个平行四边形,你能求出它的面积吗?
2830 |
2831 |
2826 |
2827 | ### 练习3
2828 |
2829 | 如图,是一个平行四边形,你能求出它的面积吗?
2830 |
2831 |  2832 |
2833 | ### 例题4
2834 |
2835 | 如图,图形中阴影部分的面积是多少?
2836 |
2837 |
2832 |
2833 | ### 例题4
2834 |
2835 | 如图,图形中阴影部分的面积是多少?
2836 |
2837 |  2838 |
2839 | ### 练习4
2840 |
2841 | 如图,已知平行四边形的面积为 32 平方厘米,CD=8厘米,求 AE 的长度。
2842 |
2843 |
2838 |
2839 | ### 练习4
2840 |
2841 | 如图,已知平行四边形的面积为 32 平方厘米,CD=8厘米,求 AE 的长度。
2842 |
2843 |  2844 |
2845 | ### 例题5
2846 |
2847 | 如下左图,已知横竖相邻两点间的距离是 1厘米。你能算出图中梯形的面积吗?
2848 |
2849 |
2844 |
2845 | ### 例题5
2846 |
2847 | 如下左图,已知横竖相邻两点间的距离是 1厘米。你能算出图中梯形的面积吗?
2848 |
2849 |  2850 |
2851 | 如图已知梯形 ABCD 的上底 AB=8 厘米,CD=10 厘米,EF 垂直 CD 于点 F,EF=6 厘米,求梯 形 ABCD 的面积
2852 |
2853 |
2850 |
2851 | 如图已知梯形 ABCD 的上底 AB=8 厘米,CD=10 厘米,EF 垂直 CD 于点 F,EF=6 厘米,求梯 形 ABCD 的面积
2852 |
2853 |  2854 |
2855 | ### 练习5
2856 |
2857 | 图中每个格子的边长都是2厘米,梯形的面积为多少平方厘米?
2858 |
2859 |
2854 |
2855 | ### 练习5
2856 |
2857 | 图中每个格子的边长都是2厘米,梯形的面积为多少平方厘米?
2858 |
2859 |  2860 |
2861 | ### 例题6
2862 |
2863 | 图形王国的中心有道门,门上写着:已知梯形 ABCD的面积为 50 平方厘米,高 AE的长度为 5
2864 | 厘米,线段 CD比AB长4 厘米,请分别求出 AB和CD 的长度
2865 |
2866 |
2860 |
2861 | ### 例题6
2862 |
2863 | 图形王国的中心有道门,门上写着:已知梯形 ABCD的面积为 50 平方厘米,高 AE的长度为 5
2864 | 厘米,线段 CD比AB长4 厘米,请分别求出 AB和CD 的长度
2865 |
2866 |  2867 |
2868 | ### 练习6
2869 |
2870 | 如下图,大正方形的边长是8 厘米,小正方形的边长是6厘米。请问:图中阴影部分的面积
2871 | 是多少?
2872 |
2873 |
2867 |
2868 | ### 练习6
2869 |
2870 | 如下图,大正方形的边长是8 厘米,小正方形的边长是6厘米。请问:图中阴影部分的面积
2871 | 是多少?
2872 |
2873 |  2874 |
2875 | ## 3.2.11. 年龄问题进阶
2876 |
2877 | 例题练习
2878 |
2879 | ### 例题1
2880 |
2881 | 妈妈和儿子算年龄,两年前两人的年龄之和是36岁,今年妈妈的年龄是孩子的4倍,今年两人各是多少岁?
2882 |
2883 | ### 练习1
2884 |
2885 | 今年哥哥和弟弟的年龄和是36岁,且哥哥的年龄是弟弟年龄的2倍,哥哥和弟弟今年分别多少岁?
2886 |
2887 | ### 例题2
2888 |
2889 | 楠楠今年9岁了,妈妈33岁,再过多少年,楠楠年龄就是妈妈年龄的一半?
2890 |
2891 | ### 练习2
2892 |
2893 | 父亲今年44岁,儿子今年16岁。当父亲的年龄是儿子的8倍时,父子的年龄和是多少?
2894 |
2895 | ### 例题3
2896 |
2897 | 东东3年前的年龄与西西4年后的年龄和是25岁,东东3年后的年龄等于西西1年前的年龄,求今年东东、西西各是多少岁?
2898 |
2899 | ### 练习3
2900 |
2901 | 小花2年前的年龄与小琪1年后的年龄相等,小花3年前和小琪2年后的年龄和为20岁,则小花和小琪今年各多少岁?
2902 |
2903 | ### 例题4
2904 |
2905 | 乐乐老师对琪琪说:“我是你这个年龄的时候,你才5岁。”琪琪思考了一下,对乐乐老师说:“等到我是您现在年龄的时候,您就50岁了。”你能算出乐乐老师和琪琪今年各多少岁吗?
2906 |
2907 | ### 练习4
2908 |
2909 | 丁丁今年(2022年)12岁,妈妈对丁丁说:“当你有我这么大岁数时,我已经60岁了。”请问妈妈像丁丁这么大时是哪一年?
2910 |
2911 | ### 例题5
2912 |
2913 | 田田一家三口今年的年龄和是87岁,爸爸比妈妈大6岁。几年前,爸爸的年龄是田田的11倍,妈妈的年龄是田田的9倍,你知道田田今年几岁了吗?
2914 |
2915 | ### 练习5
2916 |
2917 | 琪琪今年3岁了,再过5年她就和小花5年前的年龄相等,问小花今年几岁了?
2918 |
2919 | ### 例题6
2920 |
2921 | 今年乐乐老师的年龄是牛牛年龄的5倍,再过8年,乐乐老师的年龄是牛牛年龄的3倍。牛牛今年多少岁?
2922 |
2923 | ### 练习6
2924 |
2925 | 10年前,爸爸的年龄是儿子的7倍,15年后爸爸的年龄是儿子的2倍,问现在父子各多少岁?
2926 |
2927 | ## 3.2.12. 带余除法进阶
2928 |
2929 | 作业练习
2930 |
2931 | ### 练习1
2932 |
2933 | 填空。
2934 |
2935 | (1)$()\div8=6……7$
2936 |
2937 | (2)$31\div()=7……3$
2938 |
2939 | (3)$56\div6=()……()$
2940 |
2941 | (4)$()\div8=7……()$,被除数最大是多少?
2942 |
2943 | (5)$()\div()=3……4$,被除数最小是多少?
2944 |
2945 | ### 练习2
2946 |
2947 | 用一个自然数去除另一个自然数,商为7,被除数、除数的和是48,求这两个自然数各是多少?
2948 |
2949 | ### 练习3
2950 |
2951 | 46除以一个一位数,余数是1。列出所有符合条件的一位数。
2952 |
2953 | ### 练习4
2954 |
2955 | 78除以一个数得到的商是8,并且除数与余数的差是3,求除数和余数。
2956 |
2957 | ### 练习5
2958 |
2959 | $48\times63\times79$除以7的余数是多少?
2960 |
2961 | ### 练习6
2962 |
2963 | 有一串数1,1,2,3,5,8,...,从第三个数起,每个数都是前两个数之和,这串数的第2022个数除以4余数是多少?
2964 |
2965 | 例题练习
2966 |
2967 | ### 例题1
2968 |
2969 | 牛牛有一本故事书,每天读9页,读了23天之后发现还剩6页,这本故事书一共多少页?
2970 |
2971 | ### 练习1
2972 |
2973 | 某数被21除,商是9,余数是7,则该数是多少?
2974 |
2975 | ### 例题2
2976 |
2977 | 丁丁有一本科普书,一共208页,他看了17天之后还剩4页,他前17天每天看多少页?
2978 |
2979 | ### 练习2
2980 |
2981 | 316除以8,余4,商是多少?
2982 |
2983 | ### 例题3
2984 |
2985 | 乐乐老师有160道题,要安排给同学们完成。如果每天做a道题,第b天做完之后,还剩6道,已知a>6,那么a有多少种不同的取值?
2986 |
2987 | ### 练习3
2988 |
2989 | 牛牛有一本练习题,有191道题,如果每天做a(a>9)道题,第b天做完之后,还剩9道,那么a有多少种不同的取值?
2990 |
2991 | ### 例题4
2992 |
2993 | 甲、乙两个数的和是1088,甲数除以乙数商11余32,求甲、乙两数各是多少。
2994 |
2995 | ### 练习4
2996 |
2997 | 678除以一个数得到的商是32,并且除数与余数的差是15,求除数和余数各是多少。
2998 |
2999 | ### 例题5
3000 |
3001 | $2461\times135\times6047\div11$的余数为多少?
3002 |
3003 | ### 练习5
3004 |
3005 | 有一个整数,用它去除70,110,160所得到的3个余数之和是50,那么这个整数是多少?
3006 |
3007 | ### 例题6
3008 |
3009 | 有一串数:1、1、2、3、5、8、⋯,从第三个数起,每个数都是前两个数之和,在这串数的前2017个数中,有几个是5的倍数?
3010 |
3011 | ### 练习6
3012 |
3013 | 有一列数,若这列数从第四个数起,每个数怡好是前面三个数之和,则数列:1、1、2、4、7、13、24、44、⋯中的第2015个数除以3的余数是多少?
3014 |
3015 | ## 3.2.13. 等差数列初步
3016 |
3017 | 课前热身
3018 |
3019 | ### 热身1
3020 |
3021 | 脱式计算。
3022 | $$
3023 | 327-85+73
3024 | $$
3025 |
3026 | $$
3027 | 723+491-13-191
3028 | $$
3029 |
3030 | ### 热身2
3031 |
3032 | $()\div8=7……()$,被除数最大是多少?
3033 |
3034 | $()\div()=3……4$,被除数最小是多少?
3035 |
3036 | ### 热身3
3037 |
3038 | 用一个自然数去除另一个自然数,商为6,被除数、除数的和是56,求这两个自然数各是多少?
3039 |
3040 | 例题练习
3041 |
3042 | ### 例题1
3043 |
3044 | 同学们一起来算一算吧!
3045 | (1)等差数列:5,7,9,11,13,15,……的第12项是();
3046 | (2)等差数列:0,4,8,12,16,20,……的第43项是();
3047 | (3)等差数列:3,7,11,15,……的第56项是()。
3048 |
3049 | ### 练习1
3050 |
3051 | (1)等差数列:3,4,5,6,……的第62项是();
3052 | (2)等差数列:2,5,8,11,……的第47项是()。
3053 |
3054 | ### 例题2
3055 |
3056 | (1)等差数列:5,6,7,8,9,……,其中55是这个数列的第()项;
3057 | (2)等差数列:7,9,11,13,……,其中69是这个数列的第()项。
3058 |
3059 | ### 练习2
3060 |
3061 | (1)等差数列:8,11,14,17,……,其中134是这个数列的第()项;
3062 | (2)等差数列:15,19,23,27,……,其中295是这个数列的第()项。
3063 |
3064 | ### 例题3
3065 |
3066 | 大家一起来求和!
3067 |
3068 | (1)$3+4+5+6+\dots+76+77+78$
3069 |
3070 | (2)$2+4+6+8+\dots+96+98+100$
3071 |
3072 | ### 练习3
3073 |
3074 | 等差数列求和。
3075 |
3076 | (1)1,3,5,7,……,87,89,91;
3077 |
3078 | (2)4,7,10,13,……,40,43,46
3079 |
3080 | ### 例题4
3081 |
3082 | 一个递增的等差数列的首项是10,第61项是250,这个等差数列的公差是多少?
3083 |
3084 | ### 练习4
3085 |
3086 | 一个递增的等差数列,第1项是232,第52项是334,这个等差数列的公差是多少?
3087 |
3088 | ### 例题5
3089 |
3090 | 一个等差数列的第6项和第12项分别是24,42。问:
3091 | (1)数列的第1项是什么?
3092 | (2)数列的第23项是什么?
3093 | (3)数列的前23项的和是多少?
3094 |
3095 | ### 练习5
3096 |
3097 | 己知等差数列的第5项和第9项分别为25、49,那么前31项的和是多少?
3098 |
3099 | ### 例题6
3100 |
3101 | (1)有5个盒子中共放了325个乒乓球,从小盒子到大盒子,每一个盒子中比前面的盒子多了5个乒乓球。问:最大的盒子中有多少个乒乓球?
3102 | (2)有8个盒子共放了888个乒乓球,从小盒子到大盒子,每一个盒子比前面的盒子多了6个乒乓球。问:最小的盒子里有多少个乒乓球?
3103 |
3104 | ### 练习6
3105 |
3106 | 2,4,6,8,10,12,……是个连续偶数列,如果其中5个连续偶数的和是320,那么它们中最小的一个数是谁?
3107 |
3108 | ## 3.2.15. 平面图形计数综合
3109 |
3110 | 例题练习
3111 |
3112 | ### 例题1
3113 |
3114 | 以A,B,C,D,E,F,G这些点为端点,请数一数这里一共有多少条线段?
3115 |
3116 | ### 练习1
3117 |
3118 | 在一条直线上有一些被标记的点,请你数一数,看看能找出几条线段。
3119 |
3120 | 
3121 |
3122 | ### 例题2
3123 |
3124 | 数一数,下面图中共有多少个正方形。
3125 |
3126 | ### 练习2
3127 |
3128 | 数一数,下面图中共有多少个正方形。
3129 |
3130 | 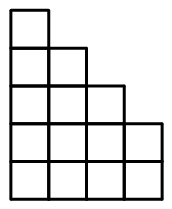
3131 |
3132 | ### 例题3
3133 |
3134 | 图中有多少个正方形?
3135 |
3136 | 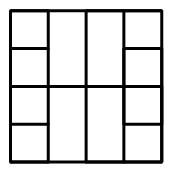
3137 |
3138 | ### 练习3
3139 |
3140 | 图中有多少个正方形?
3141 |
3142 | 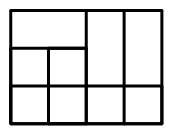
3143 |
3144 | ### 例题4
3145 |
3146 | 图中有多少个三角形?
3147 |
3148 | 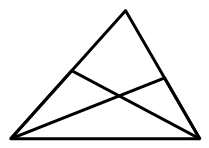
3149 |
3150 | ### 练习4
3151 |
3152 | 图中有多少个三角形?
3153 |
3154 | 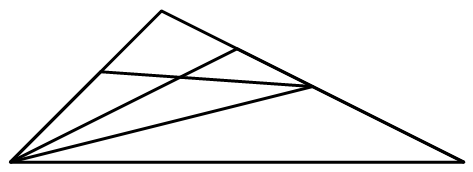
3155 |
3156 | ### 例题5
3157 |
3158 | 将一个等边三角形各边四等分后再连接相应线段得到下图,你知道图中共有多少个三角形吗?
3159 |
3160 | 
3161 |
3162 | ### 练习5
3163 |
3164 | 将一个等边三角形各边三等分后再连接相应线段得到下图,你知道图中共有多少个三角形吗?
3165 |
3166 | 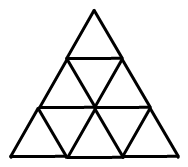
3167 |
3168 | ### 例题6
3169 |
3170 | 数一数,下图中共有多少个平行四边形。
3171 |
3172 | 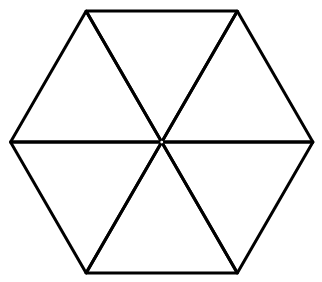
3173 |
3174 | ### 练习6
3175 |
3176 | 下图是由7条线段构成的图形,你知道里面一共有多少个三角形吗?
3177 |
3178 | 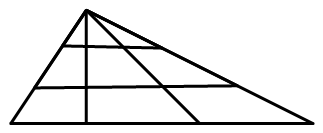
3179 |
3180 | ## 3.2.16. 标数法
3181 |
3182 | ### 例题1
3183 |
3184 | 丁丁的家在A点,他想沿着长方形街道去学校所在的B点,一共有几条不同的最短路线呢?
3185 |
3186 | ### 练习1
3187 |
3188 | 丁丁和田田想从家去公园玩,长方形街道如下图所示,一共有多少条不同的最短路线?
3189 |
3190 | ### 例题2
3191 |
3192 | 田田从家所在的A点去学校所在的B点,但途中不能经过C点的商店,不同的最短路线一共有多少条?
3193 |
3194 | ### 练习2
3195 |
3196 | 牛牛从家所在的A点去公园所在的B点,但途中不能经过街道CD(C,D两点可以经过),不同的最短路线一共有多少条?
3197 |
3198 | ### 例题3
3199 |
3200 | 田田从家所在的A点去学校所在的B点,但途中必须经过C点的牛牛家,不同的最短路线一共有多少条?
3201 |
3202 | ### 练习3
3203 |
3204 | 牛牛和阿普从街道的A点到B点,但必须经过一座独木桥MN,他们有多少种不同的最短路线?
3205 |
3206 | ### 例题4
3207 |
3208 | 田田和丁丁准备从家出发到公园玩,路线图如下图所示,最短路线一共有多少条?
3209 |
3210 | ### 练习4
3211 |
3212 | 丁丁从家里去乐乐老师家,路线图如下图所示,最短路线一共有多少条?
3213 |
3214 | ### 例题5
3215 |
3216 | 牛牛从A点走到I点,只能按图中箭头所指的方向行走,共有多少条不同的路线?
3217 |
3218 | ### 练习5
3219 |
3220 | 牛牛玩一种游戏,从图中的A处走到B处,每次只能从一个格子走向右侧邻近的格子而不准逆行,比如从4只能到5和6。一共有多少种不同的走法?
3221 |
3222 | ### 例题6
3223 |
3224 | 田田上楼梯,一步可以上1个或2个台阶,楼梯总共有10个台阶,从地面到第10个台阶总共有多少种走法?
3225 |
3226 | ### 练习6
3227 |
3228 | 在下图中,丁丁想要沿着水平或垂直线段行走时,拼出“APPLE”的路线,共有多少种走法?
3229 |
3230 | 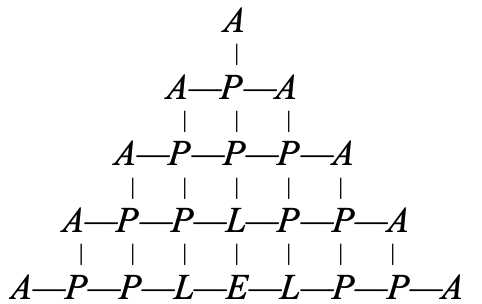
3231 |
3232 | ## 3.2.17. 页码问题
3233 |
3234 | ### 课前热身
3235 |
3236 | ### 热身1
3237 |
3238 | 一张纸上的两个页码的和总是奇数还是偶数?
3239 |
3240 | ### 热身2
3241 |
3242 | 第1页到第15页一共有多少个数字?
3243 |
3244 | ### 热身3
3245 |
3246 | 在1至100中,数字“1”和数字“2”的数量哪个多?多几个?
3247 |
3248 | 例题练习
3249 |
3250 | ### 例题1
3251 |
3252 | 一本小漫面书一共40页,这些页码共用了多少个数字?
3253 |
3254 | ### 练习1
3255 |
3256 | 一个小册子共有20页,1~20页的页码一共用了多少个数字?
3257 |
3258 | ### 例题2
3259 |
3260 | 一本书共有150页,这些页的页码一共用了多少个数字?
3261 |
3262 | ### 练习2
3263 |
3264 | 一本小说共有86页,这些页的页码一共用了多少个数字?
3265 |
3266 | ### 例题3
3267 |
3268 | 给一本书编页码,一共用了225个数字,这本书一共有多少页?
3269 |
3270 | ### 练习3
3271 |
3272 | 一本小说的页码,在印刷时必须用105个数字。这本书共有多少页?
3273 |
3274 | ### 例题4
3275 |
3276 | (1)一本书共有100页,1~100页的页码中,一共用了多少个数字“2”?
3277 | (2)一本书共有1000页,1~1000页的页码中,一共用了多少个数字“2”?
3278 |
3279 | ### 练习4
3280 |
3281 | 一本书共有100页,1~100页的页码中,数字了用了多少个?数字4用了多少个?同学们找找规律,再计算1~9中的其他数字各出现多少次。
3282 |
3283 | ### 例题5
3284 |
3285 | (1)给一本书编页码时,一共用了10个数字“5”,请问这本书有多少页?
3286 | (2)给一本书编页码时,一共用了41个数字“5”,请问这本书最少有多少页?最多有多少页?
3287 |
3288 | ### 练习5
3289 |
3290 | 一本书编页码时,一共用了62个数字“8”,且最后一页是含有“8”的页码,请问这本书有多少页?
3291 |
3292 | ### 例题6
3293 |
3294 | 有一本50页的书,中间缺了一张,丁丁将残书的页码相加,得到了1230。有人说丁丁计算错了,你能知道这是为什么吗?
3295 |
3296 | ### 练习6
3297 |
3298 | 田田有一本书,中间被牛牛撕掉了一页(含两个相邻页码)。田田将残书的所有页码相加得到1260,请问田田这本书原有多少页?
3299 |
3300 | 拓展
3301 |
3302 | ### 拓展1
3303 |
3304 | 印刷一本书用了1992个数字,在这本书中出现数字“2”的页码有多少页?
3305 |
3306 | ### 拓展2
3307 |
3308 | 一本书共有1000页,1~1000页的页码中,一共用了多少个数字“0”?
3309 |
3310 | ## 3.2.18. 解方程
3311 |
3312 | 例题练习
3313 |
3314 | ### 例题1
3315 |
3316 | 解方程。
3317 |
3318 | (1)$x+5=12$
3319 |
3320 | (2)$12-x=5$
3321 |
3322 | (3)$x\div5=10$
3323 |
3324 | (4)$5x=35$
3325 |
3326 | ### 练习1
3327 |
3328 | 解方程。
3329 |
3330 | (1)$x+6=13$
3331 |
3332 | (2)$13-x=6$
3333 |
3334 | (3)$x\div6=8$
3335 |
3336 | (4)$4x=32$
3337 |
3338 | ### 例题2
3339 |
3340 | 解方程。
3341 |
3342 | (1)$5x+4=2x+16$
3343 |
3344 | (2)$4x-6=8x-18$
3345 |
3346 | ### 练习2
3347 |
3348 | 解方程。
3349 |
3350 | (1)$18-2x=40-4x$
3351 |
3352 | (2)$20-5x=3x+4$
3353 |
3354 | ### 例题3
3355 |
3356 | 解方程。
3357 |
3358 | (1)$5(x+4)=30$
3359 |
3360 | (2)$6(2x-4)=60$
3361 |
3362 | ### 练习3
3363 |
3364 | 解方程。
3365 |
3366 | (1)$$
3367 |
3368 | (2)$$
3369 |
3370 | ### 例题4
3371 |
3372 | 解方程。
3373 |
3374 | (1)$$
3375 |
3376 | (2)$$
3377 |
3378 | ### 练习4
3379 |
3380 | 解方程。
3381 |
3382 | (1)$$
3383 |
3384 | (2)$$
3385 |
3386 | ### 例题5
3387 |
3388 | 解方程。
3389 |
3390 | (1)$$
3391 |
3392 | (2)$$
3393 |
3394 | ### 练习5
3395 |
3396 | 解方程。
3397 |
3398 | (1)$$
3399 |
3400 | (2)$$
3401 |
3402 | ### 例题6
3403 |
3404 | 规定4公6=4x4-2x6。例如,546=5×5-2x6=13。己知8公.2=50,求正
3405 |
3406 | ### 练习6
3407 |
3408 | 定义a#6表示(a一7)x6。例如12#5=(12-7)×5=25。那么,当2#6=54时,二是
3409 | 多少?
3410 |
3411 | ## 3.2.19. 列方程
3412 |
3413 | ### 复习巩固
3414 |
3415 | ### 巩固1(鸡兔同笼)
3416 |
3417 | 体育老师买了运动服上衣和裤子共21件,共用了439元,其中上衣每件24元、裤子每件19元,问老师买上衣和裤子各多少件?
3418 |
3419 | ### 巩固2(和倍)
3420 |
3421 | 某小学的同学为幼儿园的小朋友做红花和黄花共300朵。已知红花的朵数比黄花的2倍少30朵。问两种花各有多少朵?
3422 |
3423 | ### 巩固3(差倍)
3424 |
3425 | 有两根铁丝,第一根长18米,第二根长10米,两根铁丝用去同样长的一段后,第一根剩下的长度是第二根剩下长度的3倍,两根铁丝各剩下多少米?
3426 |
3427 | ### 巩固4(计算)
3428 |
3429 | (1)计算:$125×148×8$
3430 |
3431 | (2)计算:$125×64×25$
3432 |
3433 | (3)计算:$888×125÷111×16$
3434 |
3435 | ### 巩固5(解方程)
3436 |
3437 | 解方程:$2(x+3)=3(x+1)$
3438 |
3439 | ### 例题练习
3440 |
3441 | ### 例题1
3442 |
3443 | 煤场上午运来15吨煤,下午又运来了一些,这天共运来43吨煤,下午运来多少吨煤?
3444 |
3445 | ### 练习1
3446 |
3447 | 两袋大米,第一袋比第二袋少14千克。已知第一袋重52千克,第二袋重多少干克?
3448 |
3449 | ### 例题2
3450 |
3451 | 一个平行四边形的面积是150平方厘米,底是50厘米,高是多少厘米?
3452 |
3453 | ### 练习2
3454 |
3455 | 一个三角形的高是18厘米,面积是180平方厘米,底是多少厘米?
3456 |
3457 | ### 例题3
3458 |
3459 | 丁丁和牛牛共有100张积分卡,已知牛牛积分卡的数量比丁丁的3倍多8张,请问丁丁、牛牛各有多少张积分卡?
3460 |
3461 | ### 练习3
3462 |
3463 | 牛牛比丁丁多100张积分卡,已知牛牛积分卡的数量比丁丁的3倍少8张,请问丁丁、牛牛各有多少张积分卡?
3464 |
3465 | ### 例题4
3466 |
3467 | 苹果和梨共80千克,价值400元,已知苹果4元一千克,梨6元一千克,那么苹果和梨各多少千克?
3468 |
3469 | ### 练习4
3470 |
3471 | 小明买来8角邮票与5角邮票共100张,总值68元。8角邮票和5角邮票各买了多少张?
3472 |
3473 | ### 例题5
3474 |
3475 | 小明家左边与右边各有一家超市在促销同一种品牌的牛奶。如果去左边这家超市购买,所带的钱恰好能买12盒;如果去右边那家超市购买,所带的钱恰好能多买2盒。己知右边超市每盒牛奶的价格比左边超市每盒牛奶的价格便宜1元,那么小明共带了多少钱?
3476 |
3477 | ### 练习5
3478 |
3479 | 体育课上,三年级(1)班的46名同学都在操场上玩球。每个篮球分给6名同学玩,每个排球分给8名同学玩。篮球和排球一共有7个。问:玩排球的同学有多少人?
3480 |
3481 | ### 例题6
3482 |
3483 | 甲、乙、丙共有钱99元,甲的钱比乙的钱的2倍少2元,乙的钱比丙的钱的3倍少3元。甲有多少钱?
3484 |
3485 | ### 练习6
3486 |
3487 | 己知足球、篮球、排球三种球平均每个35元。篮球比排球每个贵10元,足球比排球每个贵8元。问:每个篮球多少元?
3488 |
3489 | ## 3.2.20. 速度、路程与时间
3490 |
3491 | ### 课前热身
3492 |
3493 | ### 热身1(盈亏问题)
3494 |
3495 | 猪妈妈带着孩子去野餐,如果每张餐布周围坐4只小猪就有6只小猪没地方坐,如果每张餐布周围多坐一只小猪就会余出4个空位子,问:一共有多少只小猪,猪妈妈一共带了多少张餐布?
3496 |
3497 | ### 热身2(带余除法)
3498 |
3499 | 甲、乙两数的和是1088,甲数除以乙数商11余32,求甲、乙两数分别是几?
3500 |
3501 | ### 热身3(列方程)
3502 |
3503 | 花圃里有吊兰和仙人球共56盆,吊兰的盆数是仙人球的3倍,吊兰和仙人球各有多少盆?
3504 |
3505 | ### 计算练习(分组)
3506 |
3507 | (1)$100-99+98-97+96-95+\dots+4-3+2-1$
3508 |
3509 | (2)$1-2+3-4+5-6+\dots+95-96+97-98+99-100+101$
3510 |
3511 | 例题练习
3512 |
3513 | ### 例题1
3514 |
3515 | 牛牛骑自行车每小时行15千米。
3516 | (1)2小时以后,能行多少千米?
3517 | (2)按照这样的速度,他骑了60千米,需要几小时?
3518 | (3)后来牛牛匀速行驶100千米用了5个小时,那么这段路牛牛平均每小时行多少千米?
3519 |
3520 | ### 练习1
3521 |
3522 | 丁丁从家去学校,每分钟走60米,走了10分钟到达学校,问丁丁家到学校的距离有多远?如果丁丁每分钟走100米,从家到学校需要走几分钟?
3523 |
3524 | ### 例题2
3525 |
3526 | 一辆从北京到青岛的长途客车,中途经过天津和济南。北京到天津140千米,天津到济南360千米,济南到青岛400千米。早晨5:30从北京发车,平均每小时行驶90千米,大约何时可以到达青岛?
3527 |
3528 | ### 练习2
3529 |
3530 | 甲、乙两地相距230千米,丁丁开车从甲地到乙地行了5小时。照这样的速度,从乙地开往丙地行了4小时,乙、丙两地相距多少千米?
3531 |
3532 | ### 例题3
3533 |
3534 | 丁丁和牛牛两家都在一条马路的旁边,相距800米,丁丁每分钟行50米,牛牛每分钟行60米。
3535 | (1)两人同时从家中出发,背向而行,5分钟后两人相距多少米?
3536 | (2)两人同时从家中出发,相向而行,5分钟后两人相距多少米?
3537 | (3)两人同时从家中出发,同向而行,5分钟后两人相距多少米?
3538 |
3539 | ### 练习3
3540 |
3541 | 田田和阿普两家都在一条马路的旁边,相距400米,田田每分钟行60米,阿普每分钟行70米。
3542 | (1)两人同时从家中出发,背向而行,3分钟后两人相距多少米?
3543 | (2)两人同时从家中出发,相向而行,3分钟后两人相距多少米?
3544 | (3)两人同时从家中出发,同向而行,3分钟后两人相距多少米?
3545 |
3546 | ### 例题4
3547 |
3548 | 阿普和乐乐老师约好在他们之间的某点见面,阿普每分钟走200米,乐乐老师每分钟走150米,他们同时出发2分钟后还相距500米,问:阿普和乐乐老师之间原来的距离是多少米?
3549 |
3550 | ### 练习4
3551 |
3552 | 一天,大黄和大黑约好在他们之间的某点见面,大黄每分钟走67米,大黑每分钟走45米,他们同时出发5分钟后还相距543米,问:大黄和大黑之间原来的距离是多少米?
3553 |
3554 | ### 例题5
3555 |
3556 | 甲、乙两地相距200千米,丁丁去时的速度是10千米/时,回来的速度是40千米/时,求丁丁往返的平均速度。
3557 |
3558 | ### 练习5
3559 |
3560 | 周六,乐乐老师骑自行车去朋友家参加聚会,己知乐乐老师与朋友家相距3600米,乐乐老师去的时候速度为300米/分,回来的速度是600米/分。求乐乐老师来回的平均速度。
3561 |
3562 | ### 例题6
3563 |
3564 | 小亮开车从家出发到720千米外的甲城市去,前240千米的平均速度为60千米/时,小亮如果从家到甲城市的平均速度为80千米/时,剩下的路程应以什么速度行驶?
3565 |
3566 | ### 练习6
3567 |
3568 | A、B两城相距240千米,一辆汽车原计划用6小时从A城到B城,那么汽车每小时应该行驶多少千米?实际上汽车行驶了一半路程后发生故障,在途中停留了1小时。如果要按照原定的时问到达B城,汽车在后一半路程上每小时应该行驶多少千米?
3569 |
--------------------------------------------------------------------------------
/04-四年级.md:
--------------------------------------------------------------------------------
1 | ---
2 | title: 四年级
3 | lang: zh-CN
4 | sidebarDepth: 1
5 | ---
6 |
7 | # 四年级
8 |
9 | ## 4.1.01. 加乘原理初步
10 |
11 | ### 例题1
12 |
13 | 乐乐老师需要从北京出发,依次到南京、上海、深圳和广州视察当地分校的发展情况。从北京到南京可以乘火车或者飞机;从南京到上海可以乘火车、汽车或者飞机;从上海到深圳不仅可以乘火车、汽车和飞机,还可以坐船;从深圳到广州则可以乘火车或者汽车。请问乐乐老师这次从北京到广州的视察共有多少种不同的交通方式?
14 |
15 | ### 练习1
16 |
17 | 如图所示,从A地去B地有5种走法,从B地去C地有3种走法,那么田田从A地经B地去C地一共有多少种不同的走法?
18 |
19 |
2874 |
2875 | ## 3.2.11. 年龄问题进阶
2876 |
2877 | 例题练习
2878 |
2879 | ### 例题1
2880 |
2881 | 妈妈和儿子算年龄,两年前两人的年龄之和是36岁,今年妈妈的年龄是孩子的4倍,今年两人各是多少岁?
2882 |
2883 | ### 练习1
2884 |
2885 | 今年哥哥和弟弟的年龄和是36岁,且哥哥的年龄是弟弟年龄的2倍,哥哥和弟弟今年分别多少岁?
2886 |
2887 | ### 例题2
2888 |
2889 | 楠楠今年9岁了,妈妈33岁,再过多少年,楠楠年龄就是妈妈年龄的一半?
2890 |
2891 | ### 练习2
2892 |
2893 | 父亲今年44岁,儿子今年16岁。当父亲的年龄是儿子的8倍时,父子的年龄和是多少?
2894 |
2895 | ### 例题3
2896 |
2897 | 东东3年前的年龄与西西4年后的年龄和是25岁,东东3年后的年龄等于西西1年前的年龄,求今年东东、西西各是多少岁?
2898 |
2899 | ### 练习3
2900 |
2901 | 小花2年前的年龄与小琪1年后的年龄相等,小花3年前和小琪2年后的年龄和为20岁,则小花和小琪今年各多少岁?
2902 |
2903 | ### 例题4
2904 |
2905 | 乐乐老师对琪琪说:“我是你这个年龄的时候,你才5岁。”琪琪思考了一下,对乐乐老师说:“等到我是您现在年龄的时候,您就50岁了。”你能算出乐乐老师和琪琪今年各多少岁吗?
2906 |
2907 | ### 练习4
2908 |
2909 | 丁丁今年(2022年)12岁,妈妈对丁丁说:“当你有我这么大岁数时,我已经60岁了。”请问妈妈像丁丁这么大时是哪一年?
2910 |
2911 | ### 例题5
2912 |
2913 | 田田一家三口今年的年龄和是87岁,爸爸比妈妈大6岁。几年前,爸爸的年龄是田田的11倍,妈妈的年龄是田田的9倍,你知道田田今年几岁了吗?
2914 |
2915 | ### 练习5
2916 |
2917 | 琪琪今年3岁了,再过5年她就和小花5年前的年龄相等,问小花今年几岁了?
2918 |
2919 | ### 例题6
2920 |
2921 | 今年乐乐老师的年龄是牛牛年龄的5倍,再过8年,乐乐老师的年龄是牛牛年龄的3倍。牛牛今年多少岁?
2922 |
2923 | ### 练习6
2924 |
2925 | 10年前,爸爸的年龄是儿子的7倍,15年后爸爸的年龄是儿子的2倍,问现在父子各多少岁?
2926 |
2927 | ## 3.2.12. 带余除法进阶
2928 |
2929 | 作业练习
2930 |
2931 | ### 练习1
2932 |
2933 | 填空。
2934 |
2935 | (1)$()\div8=6……7$
2936 |
2937 | (2)$31\div()=7……3$
2938 |
2939 | (3)$56\div6=()……()$
2940 |
2941 | (4)$()\div8=7……()$,被除数最大是多少?
2942 |
2943 | (5)$()\div()=3……4$,被除数最小是多少?
2944 |
2945 | ### 练习2
2946 |
2947 | 用一个自然数去除另一个自然数,商为7,被除数、除数的和是48,求这两个自然数各是多少?
2948 |
2949 | ### 练习3
2950 |
2951 | 46除以一个一位数,余数是1。列出所有符合条件的一位数。
2952 |
2953 | ### 练习4
2954 |
2955 | 78除以一个数得到的商是8,并且除数与余数的差是3,求除数和余数。
2956 |
2957 | ### 练习5
2958 |
2959 | $48\times63\times79$除以7的余数是多少?
2960 |
2961 | ### 练习6
2962 |
2963 | 有一串数1,1,2,3,5,8,...,从第三个数起,每个数都是前两个数之和,这串数的第2022个数除以4余数是多少?
2964 |
2965 | 例题练习
2966 |
2967 | ### 例题1
2968 |
2969 | 牛牛有一本故事书,每天读9页,读了23天之后发现还剩6页,这本故事书一共多少页?
2970 |
2971 | ### 练习1
2972 |
2973 | 某数被21除,商是9,余数是7,则该数是多少?
2974 |
2975 | ### 例题2
2976 |
2977 | 丁丁有一本科普书,一共208页,他看了17天之后还剩4页,他前17天每天看多少页?
2978 |
2979 | ### 练习2
2980 |
2981 | 316除以8,余4,商是多少?
2982 |
2983 | ### 例题3
2984 |
2985 | 乐乐老师有160道题,要安排给同学们完成。如果每天做a道题,第b天做完之后,还剩6道,已知a>6,那么a有多少种不同的取值?
2986 |
2987 | ### 练习3
2988 |
2989 | 牛牛有一本练习题,有191道题,如果每天做a(a>9)道题,第b天做完之后,还剩9道,那么a有多少种不同的取值?
2990 |
2991 | ### 例题4
2992 |
2993 | 甲、乙两个数的和是1088,甲数除以乙数商11余32,求甲、乙两数各是多少。
2994 |
2995 | ### 练习4
2996 |
2997 | 678除以一个数得到的商是32,并且除数与余数的差是15,求除数和余数各是多少。
2998 |
2999 | ### 例题5
3000 |
3001 | $2461\times135\times6047\div11$的余数为多少?
3002 |
3003 | ### 练习5
3004 |
3005 | 有一个整数,用它去除70,110,160所得到的3个余数之和是50,那么这个整数是多少?
3006 |
3007 | ### 例题6
3008 |
3009 | 有一串数:1、1、2、3、5、8、⋯,从第三个数起,每个数都是前两个数之和,在这串数的前2017个数中,有几个是5的倍数?
3010 |
3011 | ### 练习6
3012 |
3013 | 有一列数,若这列数从第四个数起,每个数怡好是前面三个数之和,则数列:1、1、2、4、7、13、24、44、⋯中的第2015个数除以3的余数是多少?
3014 |
3015 | ## 3.2.13. 等差数列初步
3016 |
3017 | 课前热身
3018 |
3019 | ### 热身1
3020 |
3021 | 脱式计算。
3022 | $$
3023 | 327-85+73
3024 | $$
3025 |
3026 | $$
3027 | 723+491-13-191
3028 | $$
3029 |
3030 | ### 热身2
3031 |
3032 | $()\div8=7……()$,被除数最大是多少?
3033 |
3034 | $()\div()=3……4$,被除数最小是多少?
3035 |
3036 | ### 热身3
3037 |
3038 | 用一个自然数去除另一个自然数,商为6,被除数、除数的和是56,求这两个自然数各是多少?
3039 |
3040 | 例题练习
3041 |
3042 | ### 例题1
3043 |
3044 | 同学们一起来算一算吧!
3045 | (1)等差数列:5,7,9,11,13,15,……的第12项是();
3046 | (2)等差数列:0,4,8,12,16,20,……的第43项是();
3047 | (3)等差数列:3,7,11,15,……的第56项是()。
3048 |
3049 | ### 练习1
3050 |
3051 | (1)等差数列:3,4,5,6,……的第62项是();
3052 | (2)等差数列:2,5,8,11,……的第47项是()。
3053 |
3054 | ### 例题2
3055 |
3056 | (1)等差数列:5,6,7,8,9,……,其中55是这个数列的第()项;
3057 | (2)等差数列:7,9,11,13,……,其中69是这个数列的第()项。
3058 |
3059 | ### 练习2
3060 |
3061 | (1)等差数列:8,11,14,17,……,其中134是这个数列的第()项;
3062 | (2)等差数列:15,19,23,27,……,其中295是这个数列的第()项。
3063 |
3064 | ### 例题3
3065 |
3066 | 大家一起来求和!
3067 |
3068 | (1)$3+4+5+6+\dots+76+77+78$
3069 |
3070 | (2)$2+4+6+8+\dots+96+98+100$
3071 |
3072 | ### 练习3
3073 |
3074 | 等差数列求和。
3075 |
3076 | (1)1,3,5,7,……,87,89,91;
3077 |
3078 | (2)4,7,10,13,……,40,43,46
3079 |
3080 | ### 例题4
3081 |
3082 | 一个递增的等差数列的首项是10,第61项是250,这个等差数列的公差是多少?
3083 |
3084 | ### 练习4
3085 |
3086 | 一个递增的等差数列,第1项是232,第52项是334,这个等差数列的公差是多少?
3087 |
3088 | ### 例题5
3089 |
3090 | 一个等差数列的第6项和第12项分别是24,42。问:
3091 | (1)数列的第1项是什么?
3092 | (2)数列的第23项是什么?
3093 | (3)数列的前23项的和是多少?
3094 |
3095 | ### 练习5
3096 |
3097 | 己知等差数列的第5项和第9项分别为25、49,那么前31项的和是多少?
3098 |
3099 | ### 例题6
3100 |
3101 | (1)有5个盒子中共放了325个乒乓球,从小盒子到大盒子,每一个盒子中比前面的盒子多了5个乒乓球。问:最大的盒子中有多少个乒乓球?
3102 | (2)有8个盒子共放了888个乒乓球,从小盒子到大盒子,每一个盒子比前面的盒子多了6个乒乓球。问:最小的盒子里有多少个乒乓球?
3103 |
3104 | ### 练习6
3105 |
3106 | 2,4,6,8,10,12,……是个连续偶数列,如果其中5个连续偶数的和是320,那么它们中最小的一个数是谁?
3107 |
3108 | ## 3.2.15. 平面图形计数综合
3109 |
3110 | 例题练习
3111 |
3112 | ### 例题1
3113 |
3114 | 以A,B,C,D,E,F,G这些点为端点,请数一数这里一共有多少条线段?
3115 |
3116 | ### 练习1
3117 |
3118 | 在一条直线上有一些被标记的点,请你数一数,看看能找出几条线段。
3119 |
3120 | 
3121 |
3122 | ### 例题2
3123 |
3124 | 数一数,下面图中共有多少个正方形。
3125 |
3126 | ### 练习2
3127 |
3128 | 数一数,下面图中共有多少个正方形。
3129 |
3130 | 
3131 |
3132 | ### 例题3
3133 |
3134 | 图中有多少个正方形?
3135 |
3136 | 
3137 |
3138 | ### 练习3
3139 |
3140 | 图中有多少个正方形?
3141 |
3142 | 
3143 |
3144 | ### 例题4
3145 |
3146 | 图中有多少个三角形?
3147 |
3148 | 
3149 |
3150 | ### 练习4
3151 |
3152 | 图中有多少个三角形?
3153 |
3154 | 
3155 |
3156 | ### 例题5
3157 |
3158 | 将一个等边三角形各边四等分后再连接相应线段得到下图,你知道图中共有多少个三角形吗?
3159 |
3160 | 
3161 |
3162 | ### 练习5
3163 |
3164 | 将一个等边三角形各边三等分后再连接相应线段得到下图,你知道图中共有多少个三角形吗?
3165 |
3166 | 
3167 |
3168 | ### 例题6
3169 |
3170 | 数一数,下图中共有多少个平行四边形。
3171 |
3172 | 
3173 |
3174 | ### 练习6
3175 |
3176 | 下图是由7条线段构成的图形,你知道里面一共有多少个三角形吗?
3177 |
3178 | 
3179 |
3180 | ## 3.2.16. 标数法
3181 |
3182 | ### 例题1
3183 |
3184 | 丁丁的家在A点,他想沿着长方形街道去学校所在的B点,一共有几条不同的最短路线呢?
3185 |
3186 | ### 练习1
3187 |
3188 | 丁丁和田田想从家去公园玩,长方形街道如下图所示,一共有多少条不同的最短路线?
3189 |
3190 | ### 例题2
3191 |
3192 | 田田从家所在的A点去学校所在的B点,但途中不能经过C点的商店,不同的最短路线一共有多少条?
3193 |
3194 | ### 练习2
3195 |
3196 | 牛牛从家所在的A点去公园所在的B点,但途中不能经过街道CD(C,D两点可以经过),不同的最短路线一共有多少条?
3197 |
3198 | ### 例题3
3199 |
3200 | 田田从家所在的A点去学校所在的B点,但途中必须经过C点的牛牛家,不同的最短路线一共有多少条?
3201 |
3202 | ### 练习3
3203 |
3204 | 牛牛和阿普从街道的A点到B点,但必须经过一座独木桥MN,他们有多少种不同的最短路线?
3205 |
3206 | ### 例题4
3207 |
3208 | 田田和丁丁准备从家出发到公园玩,路线图如下图所示,最短路线一共有多少条?
3209 |
3210 | ### 练习4
3211 |
3212 | 丁丁从家里去乐乐老师家,路线图如下图所示,最短路线一共有多少条?
3213 |
3214 | ### 例题5
3215 |
3216 | 牛牛从A点走到I点,只能按图中箭头所指的方向行走,共有多少条不同的路线?
3217 |
3218 | ### 练习5
3219 |
3220 | 牛牛玩一种游戏,从图中的A处走到B处,每次只能从一个格子走向右侧邻近的格子而不准逆行,比如从4只能到5和6。一共有多少种不同的走法?
3221 |
3222 | ### 例题6
3223 |
3224 | 田田上楼梯,一步可以上1个或2个台阶,楼梯总共有10个台阶,从地面到第10个台阶总共有多少种走法?
3225 |
3226 | ### 练习6
3227 |
3228 | 在下图中,丁丁想要沿着水平或垂直线段行走时,拼出“APPLE”的路线,共有多少种走法?
3229 |
3230 | 
3231 |
3232 | ## 3.2.17. 页码问题
3233 |
3234 | ### 课前热身
3235 |
3236 | ### 热身1
3237 |
3238 | 一张纸上的两个页码的和总是奇数还是偶数?
3239 |
3240 | ### 热身2
3241 |
3242 | 第1页到第15页一共有多少个数字?
3243 |
3244 | ### 热身3
3245 |
3246 | 在1至100中,数字“1”和数字“2”的数量哪个多?多几个?
3247 |
3248 | 例题练习
3249 |
3250 | ### 例题1
3251 |
3252 | 一本小漫面书一共40页,这些页码共用了多少个数字?
3253 |
3254 | ### 练习1
3255 |
3256 | 一个小册子共有20页,1~20页的页码一共用了多少个数字?
3257 |
3258 | ### 例题2
3259 |
3260 | 一本书共有150页,这些页的页码一共用了多少个数字?
3261 |
3262 | ### 练习2
3263 |
3264 | 一本小说共有86页,这些页的页码一共用了多少个数字?
3265 |
3266 | ### 例题3
3267 |
3268 | 给一本书编页码,一共用了225个数字,这本书一共有多少页?
3269 |
3270 | ### 练习3
3271 |
3272 | 一本小说的页码,在印刷时必须用105个数字。这本书共有多少页?
3273 |
3274 | ### 例题4
3275 |
3276 | (1)一本书共有100页,1~100页的页码中,一共用了多少个数字“2”?
3277 | (2)一本书共有1000页,1~1000页的页码中,一共用了多少个数字“2”?
3278 |
3279 | ### 练习4
3280 |
3281 | 一本书共有100页,1~100页的页码中,数字了用了多少个?数字4用了多少个?同学们找找规律,再计算1~9中的其他数字各出现多少次。
3282 |
3283 | ### 例题5
3284 |
3285 | (1)给一本书编页码时,一共用了10个数字“5”,请问这本书有多少页?
3286 | (2)给一本书编页码时,一共用了41个数字“5”,请问这本书最少有多少页?最多有多少页?
3287 |
3288 | ### 练习5
3289 |
3290 | 一本书编页码时,一共用了62个数字“8”,且最后一页是含有“8”的页码,请问这本书有多少页?
3291 |
3292 | ### 例题6
3293 |
3294 | 有一本50页的书,中间缺了一张,丁丁将残书的页码相加,得到了1230。有人说丁丁计算错了,你能知道这是为什么吗?
3295 |
3296 | ### 练习6
3297 |
3298 | 田田有一本书,中间被牛牛撕掉了一页(含两个相邻页码)。田田将残书的所有页码相加得到1260,请问田田这本书原有多少页?
3299 |
3300 | 拓展
3301 |
3302 | ### 拓展1
3303 |
3304 | 印刷一本书用了1992个数字,在这本书中出现数字“2”的页码有多少页?
3305 |
3306 | ### 拓展2
3307 |
3308 | 一本书共有1000页,1~1000页的页码中,一共用了多少个数字“0”?
3309 |
3310 | ## 3.2.18. 解方程
3311 |
3312 | 例题练习
3313 |
3314 | ### 例题1
3315 |
3316 | 解方程。
3317 |
3318 | (1)$x+5=12$
3319 |
3320 | (2)$12-x=5$
3321 |
3322 | (3)$x\div5=10$
3323 |
3324 | (4)$5x=35$
3325 |
3326 | ### 练习1
3327 |
3328 | 解方程。
3329 |
3330 | (1)$x+6=13$
3331 |
3332 | (2)$13-x=6$
3333 |
3334 | (3)$x\div6=8$
3335 |
3336 | (4)$4x=32$
3337 |
3338 | ### 例题2
3339 |
3340 | 解方程。
3341 |
3342 | (1)$5x+4=2x+16$
3343 |
3344 | (2)$4x-6=8x-18$
3345 |
3346 | ### 练习2
3347 |
3348 | 解方程。
3349 |
3350 | (1)$18-2x=40-4x$
3351 |
3352 | (2)$20-5x=3x+4$
3353 |
3354 | ### 例题3
3355 |
3356 | 解方程。
3357 |
3358 | (1)$5(x+4)=30$
3359 |
3360 | (2)$6(2x-4)=60$
3361 |
3362 | ### 练习3
3363 |
3364 | 解方程。
3365 |
3366 | (1)$$
3367 |
3368 | (2)$$
3369 |
3370 | ### 例题4
3371 |
3372 | 解方程。
3373 |
3374 | (1)$$
3375 |
3376 | (2)$$
3377 |
3378 | ### 练习4
3379 |
3380 | 解方程。
3381 |
3382 | (1)$$
3383 |
3384 | (2)$$
3385 |
3386 | ### 例题5
3387 |
3388 | 解方程。
3389 |
3390 | (1)$$
3391 |
3392 | (2)$$
3393 |
3394 | ### 练习5
3395 |
3396 | 解方程。
3397 |
3398 | (1)$$
3399 |
3400 | (2)$$
3401 |
3402 | ### 例题6
3403 |
3404 | 规定4公6=4x4-2x6。例如,546=5×5-2x6=13。己知8公.2=50,求正
3405 |
3406 | ### 练习6
3407 |
3408 | 定义a#6表示(a一7)x6。例如12#5=(12-7)×5=25。那么,当2#6=54时,二是
3409 | 多少?
3410 |
3411 | ## 3.2.19. 列方程
3412 |
3413 | ### 复习巩固
3414 |
3415 | ### 巩固1(鸡兔同笼)
3416 |
3417 | 体育老师买了运动服上衣和裤子共21件,共用了439元,其中上衣每件24元、裤子每件19元,问老师买上衣和裤子各多少件?
3418 |
3419 | ### 巩固2(和倍)
3420 |
3421 | 某小学的同学为幼儿园的小朋友做红花和黄花共300朵。已知红花的朵数比黄花的2倍少30朵。问两种花各有多少朵?
3422 |
3423 | ### 巩固3(差倍)
3424 |
3425 | 有两根铁丝,第一根长18米,第二根长10米,两根铁丝用去同样长的一段后,第一根剩下的长度是第二根剩下长度的3倍,两根铁丝各剩下多少米?
3426 |
3427 | ### 巩固4(计算)
3428 |
3429 | (1)计算:$125×148×8$
3430 |
3431 | (2)计算:$125×64×25$
3432 |
3433 | (3)计算:$888×125÷111×16$
3434 |
3435 | ### 巩固5(解方程)
3436 |
3437 | 解方程:$2(x+3)=3(x+1)$
3438 |
3439 | ### 例题练习
3440 |
3441 | ### 例题1
3442 |
3443 | 煤场上午运来15吨煤,下午又运来了一些,这天共运来43吨煤,下午运来多少吨煤?
3444 |
3445 | ### 练习1
3446 |
3447 | 两袋大米,第一袋比第二袋少14千克。已知第一袋重52千克,第二袋重多少干克?
3448 |
3449 | ### 例题2
3450 |
3451 | 一个平行四边形的面积是150平方厘米,底是50厘米,高是多少厘米?
3452 |
3453 | ### 练习2
3454 |
3455 | 一个三角形的高是18厘米,面积是180平方厘米,底是多少厘米?
3456 |
3457 | ### 例题3
3458 |
3459 | 丁丁和牛牛共有100张积分卡,已知牛牛积分卡的数量比丁丁的3倍多8张,请问丁丁、牛牛各有多少张积分卡?
3460 |
3461 | ### 练习3
3462 |
3463 | 牛牛比丁丁多100张积分卡,已知牛牛积分卡的数量比丁丁的3倍少8张,请问丁丁、牛牛各有多少张积分卡?
3464 |
3465 | ### 例题4
3466 |
3467 | 苹果和梨共80千克,价值400元,已知苹果4元一千克,梨6元一千克,那么苹果和梨各多少千克?
3468 |
3469 | ### 练习4
3470 |
3471 | 小明买来8角邮票与5角邮票共100张,总值68元。8角邮票和5角邮票各买了多少张?
3472 |
3473 | ### 例题5
3474 |
3475 | 小明家左边与右边各有一家超市在促销同一种品牌的牛奶。如果去左边这家超市购买,所带的钱恰好能买12盒;如果去右边那家超市购买,所带的钱恰好能多买2盒。己知右边超市每盒牛奶的价格比左边超市每盒牛奶的价格便宜1元,那么小明共带了多少钱?
3476 |
3477 | ### 练习5
3478 |
3479 | 体育课上,三年级(1)班的46名同学都在操场上玩球。每个篮球分给6名同学玩,每个排球分给8名同学玩。篮球和排球一共有7个。问:玩排球的同学有多少人?
3480 |
3481 | ### 例题6
3482 |
3483 | 甲、乙、丙共有钱99元,甲的钱比乙的钱的2倍少2元,乙的钱比丙的钱的3倍少3元。甲有多少钱?
3484 |
3485 | ### 练习6
3486 |
3487 | 己知足球、篮球、排球三种球平均每个35元。篮球比排球每个贵10元,足球比排球每个贵8元。问:每个篮球多少元?
3488 |
3489 | ## 3.2.20. 速度、路程与时间
3490 |
3491 | ### 课前热身
3492 |
3493 | ### 热身1(盈亏问题)
3494 |
3495 | 猪妈妈带着孩子去野餐,如果每张餐布周围坐4只小猪就有6只小猪没地方坐,如果每张餐布周围多坐一只小猪就会余出4个空位子,问:一共有多少只小猪,猪妈妈一共带了多少张餐布?
3496 |
3497 | ### 热身2(带余除法)
3498 |
3499 | 甲、乙两数的和是1088,甲数除以乙数商11余32,求甲、乙两数分别是几?
3500 |
3501 | ### 热身3(列方程)
3502 |
3503 | 花圃里有吊兰和仙人球共56盆,吊兰的盆数是仙人球的3倍,吊兰和仙人球各有多少盆?
3504 |
3505 | ### 计算练习(分组)
3506 |
3507 | (1)$100-99+98-97+96-95+\dots+4-3+2-1$
3508 |
3509 | (2)$1-2+3-4+5-6+\dots+95-96+97-98+99-100+101$
3510 |
3511 | 例题练习
3512 |
3513 | ### 例题1
3514 |
3515 | 牛牛骑自行车每小时行15千米。
3516 | (1)2小时以后,能行多少千米?
3517 | (2)按照这样的速度,他骑了60千米,需要几小时?
3518 | (3)后来牛牛匀速行驶100千米用了5个小时,那么这段路牛牛平均每小时行多少千米?
3519 |
3520 | ### 练习1
3521 |
3522 | 丁丁从家去学校,每分钟走60米,走了10分钟到达学校,问丁丁家到学校的距离有多远?如果丁丁每分钟走100米,从家到学校需要走几分钟?
3523 |
3524 | ### 例题2
3525 |
3526 | 一辆从北京到青岛的长途客车,中途经过天津和济南。北京到天津140千米,天津到济南360千米,济南到青岛400千米。早晨5:30从北京发车,平均每小时行驶90千米,大约何时可以到达青岛?
3527 |
3528 | ### 练习2
3529 |
3530 | 甲、乙两地相距230千米,丁丁开车从甲地到乙地行了5小时。照这样的速度,从乙地开往丙地行了4小时,乙、丙两地相距多少千米?
3531 |
3532 | ### 例题3
3533 |
3534 | 丁丁和牛牛两家都在一条马路的旁边,相距800米,丁丁每分钟行50米,牛牛每分钟行60米。
3535 | (1)两人同时从家中出发,背向而行,5分钟后两人相距多少米?
3536 | (2)两人同时从家中出发,相向而行,5分钟后两人相距多少米?
3537 | (3)两人同时从家中出发,同向而行,5分钟后两人相距多少米?
3538 |
3539 | ### 练习3
3540 |
3541 | 田田和阿普两家都在一条马路的旁边,相距400米,田田每分钟行60米,阿普每分钟行70米。
3542 | (1)两人同时从家中出发,背向而行,3分钟后两人相距多少米?
3543 | (2)两人同时从家中出发,相向而行,3分钟后两人相距多少米?
3544 | (3)两人同时从家中出发,同向而行,3分钟后两人相距多少米?
3545 |
3546 | ### 例题4
3547 |
3548 | 阿普和乐乐老师约好在他们之间的某点见面,阿普每分钟走200米,乐乐老师每分钟走150米,他们同时出发2分钟后还相距500米,问:阿普和乐乐老师之间原来的距离是多少米?
3549 |
3550 | ### 练习4
3551 |
3552 | 一天,大黄和大黑约好在他们之间的某点见面,大黄每分钟走67米,大黑每分钟走45米,他们同时出发5分钟后还相距543米,问:大黄和大黑之间原来的距离是多少米?
3553 |
3554 | ### 例题5
3555 |
3556 | 甲、乙两地相距200千米,丁丁去时的速度是10千米/时,回来的速度是40千米/时,求丁丁往返的平均速度。
3557 |
3558 | ### 练习5
3559 |
3560 | 周六,乐乐老师骑自行车去朋友家参加聚会,己知乐乐老师与朋友家相距3600米,乐乐老师去的时候速度为300米/分,回来的速度是600米/分。求乐乐老师来回的平均速度。
3561 |
3562 | ### 例题6
3563 |
3564 | 小亮开车从家出发到720千米外的甲城市去,前240千米的平均速度为60千米/时,小亮如果从家到甲城市的平均速度为80千米/时,剩下的路程应以什么速度行驶?
3565 |
3566 | ### 练习6
3567 |
3568 | A、B两城相距240千米,一辆汽车原计划用6小时从A城到B城,那么汽车每小时应该行驶多少千米?实际上汽车行驶了一半路程后发生故障,在途中停留了1小时。如果要按照原定的时问到达B城,汽车在后一半路程上每小时应该行驶多少千米?
3569 |
--------------------------------------------------------------------------------
/04-四年级.md:
--------------------------------------------------------------------------------
1 | ---
2 | title: 四年级
3 | lang: zh-CN
4 | sidebarDepth: 1
5 | ---
6 |
7 | # 四年级
8 |
9 | ## 4.1.01. 加乘原理初步
10 |
11 | ### 例题1
12 |
13 | 乐乐老师需要从北京出发,依次到南京、上海、深圳和广州视察当地分校的发展情况。从北京到南京可以乘火车或者飞机;从南京到上海可以乘火车、汽车或者飞机;从上海到深圳不仅可以乘火车、汽车和飞机,还可以坐船;从深圳到广州则可以乘火车或者汽车。请问乐乐老师这次从北京到广州的视察共有多少种不同的交通方式?
14 |
15 | ### 练习1
16 |
17 | 如图所示,从A地去B地有5种走法,从B地去C地有3种走法,那么田田从A地经B地去C地一共有多少种不同的走法?
18 |
19 |  20 |
21 | ### 例题2
22 |
23 | 牛牛去基肯麦吃饭,发现店里的菜单上只有3种不同的汉堡、4种不同的饮料和5种不同的小吃。
24 |
25 | (1)如果牛牛想从汉堡和饮料中各选1种作为午餐,请问他一共可以搭配出多少种不同的午餐组合?
26 |
27 | (2)如果基肯麦为了吸引客人,决定从汉堡、饮料和小吃中各选1种组成套餐,请问基肯麦一共能提供多少种不同的套餐组合?
28 |
29 | (3)后来基肯麦发现像艾迪这样不喜欢小吃的顾客有很多,为了方便这些顾客,他们决定改良套餐结构:新的套餐中每款都包含一种汉堡和一种饮料,但是小吃可选可不选。改良后基肯麦一共能提供多少种不同的套餐组合?
30 |
31 | ### 练习2
32 |
33 | (1)大宽出门前要选一套衣服。他共有5件不同的上衣、3条不同的裤子,那么大宽有几种不同的搭配方法。
34 |
35 | (2)薇儿出门之前也要选一身衣服。她共有10件不同的上衣、4条不同的裤子、6条不同的裙子(当然,裤子和裙子不能一起穿),那么薇儿有几种不同的搭配方法。
36 |
37 | ### 例题3
38 |
39 | 运动会上牛牛、丁丁、田田、阿普4名运动员组队参加4×100接力赛。
40 |
41 | (1)4人随意安排跑步顺序,一共有多少种不同的跑法?
42 |
43 | (2)牛牛必须跑第一棒,一共有多少种不同的跑法?
44 |
45 | (3)牛牛不能跑第一棒,一共有多少种不同的跑法?
46 |
47 | (4)牛牛不能跑第一棒和第四棒,一共有多少种不同的跑法?
48 |
49 | ### 练习3
50 |
51 | 5个人照相,甲不能站在两侧,能照出多少张不同的照片?
52 |
53 | ### 例题4
54 |
55 | 用数字1,2,3,4,5,6,7,
56 |
57 | (1)可以组成多少个两位数?
58 |
59 | (2)可以组成多少个无重复数字的三位数?
60 |
61 | (3)可以组成多少个无重复数字的四位偶数?
62 |
63 | (4)可以组成多少个无重复数字的四位奇数?
64 |
65 | ### 练习4
66 |
67 | 用数字0,1,2,3,4,5,6,
68 |
69 | (1)可以组成多少个两位数?
70 |
71 | (2)可以组成多少个无重复数字的三位数?
72 |
73 | (3)可以组成多少个无重复数字的四位奇数?
74 |
75 | ### 拓展
76 |
77 | 用数字0,1,2,3,4,5,6,
78 |
79 | (4)可以组成多少无五重复数字的四位偶数?
80 |
81 | ### 例题5
82 |
83 | 牛牛有红、黄、蓝、绿四色信号旗各一面。他在旗杆上挂信号旗时每次可从上到下依次挂一面、两面或三面,排成一列。那么牛牛一共可以表示出多少种不同的信号?
84 |
85 | ### 练习5
86 |
87 | 红、黄、蓝三色信号旗各一面。牛牛在旗杆上挂信号旗时每次可从上到下依次挂一面、两面或三面,排成一列。那么他一共可以表示出多少种不同的信号?
88 |
89 | ### 例题6
90 |
91 | 书架上有2本不同的英语书,4本不同的语文书,3本不同的数学书。现在要从中取出2本,而且不能是同一科的,一共有多少种不同取法?
92 |
93 | ### 练习6
94 |
95 | 花店有10盆不同的茉莉花,15盆不同的菊花,8盆不同的丁香花。现在要从中取出2盆,而且不能是同一品种的,一共有多少种不同取法?
96 |
97 | 拓展
98 |
99 | ### 拓展1
100 |
101 | A、B、C三个小朋友互相传球,先从A开始发球(作为第一次传球),这样经过了5次传球后,球恰巧又回到A手中,那么不同的传球方式共多少种?
102 |
103 | ### 拓展2
104 |
105 | 如图,从起点走到终点,要求取出每个站点上的旗子,并且每个站点只允许通过一次,有几种不同的走法。
106 |
107 |
20 |
21 | ### 例题2
22 |
23 | 牛牛去基肯麦吃饭,发现店里的菜单上只有3种不同的汉堡、4种不同的饮料和5种不同的小吃。
24 |
25 | (1)如果牛牛想从汉堡和饮料中各选1种作为午餐,请问他一共可以搭配出多少种不同的午餐组合?
26 |
27 | (2)如果基肯麦为了吸引客人,决定从汉堡、饮料和小吃中各选1种组成套餐,请问基肯麦一共能提供多少种不同的套餐组合?
28 |
29 | (3)后来基肯麦发现像艾迪这样不喜欢小吃的顾客有很多,为了方便这些顾客,他们决定改良套餐结构:新的套餐中每款都包含一种汉堡和一种饮料,但是小吃可选可不选。改良后基肯麦一共能提供多少种不同的套餐组合?
30 |
31 | ### 练习2
32 |
33 | (1)大宽出门前要选一套衣服。他共有5件不同的上衣、3条不同的裤子,那么大宽有几种不同的搭配方法。
34 |
35 | (2)薇儿出门之前也要选一身衣服。她共有10件不同的上衣、4条不同的裤子、6条不同的裙子(当然,裤子和裙子不能一起穿),那么薇儿有几种不同的搭配方法。
36 |
37 | ### 例题3
38 |
39 | 运动会上牛牛、丁丁、田田、阿普4名运动员组队参加4×100接力赛。
40 |
41 | (1)4人随意安排跑步顺序,一共有多少种不同的跑法?
42 |
43 | (2)牛牛必须跑第一棒,一共有多少种不同的跑法?
44 |
45 | (3)牛牛不能跑第一棒,一共有多少种不同的跑法?
46 |
47 | (4)牛牛不能跑第一棒和第四棒,一共有多少种不同的跑法?
48 |
49 | ### 练习3
50 |
51 | 5个人照相,甲不能站在两侧,能照出多少张不同的照片?
52 |
53 | ### 例题4
54 |
55 | 用数字1,2,3,4,5,6,7,
56 |
57 | (1)可以组成多少个两位数?
58 |
59 | (2)可以组成多少个无重复数字的三位数?
60 |
61 | (3)可以组成多少个无重复数字的四位偶数?
62 |
63 | (4)可以组成多少个无重复数字的四位奇数?
64 |
65 | ### 练习4
66 |
67 | 用数字0,1,2,3,4,5,6,
68 |
69 | (1)可以组成多少个两位数?
70 |
71 | (2)可以组成多少个无重复数字的三位数?
72 |
73 | (3)可以组成多少个无重复数字的四位奇数?
74 |
75 | ### 拓展
76 |
77 | 用数字0,1,2,3,4,5,6,
78 |
79 | (4)可以组成多少无五重复数字的四位偶数?
80 |
81 | ### 例题5
82 |
83 | 牛牛有红、黄、蓝、绿四色信号旗各一面。他在旗杆上挂信号旗时每次可从上到下依次挂一面、两面或三面,排成一列。那么牛牛一共可以表示出多少种不同的信号?
84 |
85 | ### 练习5
86 |
87 | 红、黄、蓝三色信号旗各一面。牛牛在旗杆上挂信号旗时每次可从上到下依次挂一面、两面或三面,排成一列。那么他一共可以表示出多少种不同的信号?
88 |
89 | ### 例题6
90 |
91 | 书架上有2本不同的英语书,4本不同的语文书,3本不同的数学书。现在要从中取出2本,而且不能是同一科的,一共有多少种不同取法?
92 |
93 | ### 练习6
94 |
95 | 花店有10盆不同的茉莉花,15盆不同的菊花,8盆不同的丁香花。现在要从中取出2盆,而且不能是同一品种的,一共有多少种不同取法?
96 |
97 | 拓展
98 |
99 | ### 拓展1
100 |
101 | A、B、C三个小朋友互相传球,先从A开始发球(作为第一次传球),这样经过了5次传球后,球恰巧又回到A手中,那么不同的传球方式共多少种?
102 |
103 | ### 拓展2
104 |
105 | 如图,从起点走到终点,要求取出每个站点上的旗子,并且每个站点只允许通过一次,有几种不同的走法。
106 |
107 |  108 |
109 | ### 拓展3
110 |
111 | 如图,从*A*点到*B*点的最近的路线有多少条?
112 |
113 |
108 |
109 | ### 拓展3
110 |
111 | 如图,从*A*点到*B*点的最近的路线有多少条?
112 |
113 |  114 |
115 | ### 拓展4
116 |
117 | 一只兔子沿着下图中的格线从A到B。规定只能往上或往右走,但必须经过一座独木桥MN,这只兔子有几种不同的走法?
118 |
119 |
114 |
115 | ### 拓展4
116 |
117 | 一只兔子沿着下图中的格线从A到B。规定只能往上或往右走,但必须经过一座独木桥MN,这只兔子有几种不同的走法?
118 |
119 |  120 |
121 | 在下图的街道示意图中,*C*处因施工不能通行,从*A*到*B*的最短路线有多少条?
122 |
123 |
120 |
121 | 在下图的街道示意图中,*C*处因施工不能通行,从*A*到*B*的最短路线有多少条?
122 |
123 |  124 |
125 | ### 拓展5
126 |
127 | 图中有10个编好号码的房间,你可以从小号码房间走到相邻的大号码房间,但不能从大号码走到小号码,从1号房间走到10号房间共有多少种不同的走法?
128 |
129 |
124 |
125 | ### 拓展5
126 |
127 | 图中有10个编好号码的房间,你可以从小号码房间走到相邻的大号码房间,但不能从大号码走到小号码,从1号房间走到10号房间共有多少种不同的走法?
128 |
129 |  130 |
131 | ### 拓展6
132 |
133 | 把数1, 2, 3, 4, 5, 6分为三组(不考虑组内数的顺序也不考虑组间的顺序),每组两个数,每组的数之和互不相等且都不等于6, 共有几种分法。
134 |
135 | ### 拓展7
136 |
137 | 一些白瓷砖和黑瓷砖排成3×3的正方形。其中不含有两块相邻的黑瓷砖的拼法有几种。(下图是其中的一种。)
138 |
139 | 注意:
140 |
141 | 只是翻转后和原来重合的, 不算同一种。
142 |
143 | 旋转后和原来重合的, 算同一种;
144 |
145 | 黑瓷砖一块都不使用, 也算一种;
146 |
147 |
130 |
131 | ### 拓展6
132 |
133 | 把数1, 2, 3, 4, 5, 6分为三组(不考虑组内数的顺序也不考虑组间的顺序),每组两个数,每组的数之和互不相等且都不等于6, 共有几种分法。
134 |
135 | ### 拓展7
136 |
137 | 一些白瓷砖和黑瓷砖排成3×3的正方形。其中不含有两块相邻的黑瓷砖的拼法有几种。(下图是其中的一种。)
138 |
139 | 注意:
140 |
141 | 只是翻转后和原来重合的, 不算同一种。
142 |
143 | 旋转后和原来重合的, 算同一种;
144 |
145 | 黑瓷砖一块都不使用, 也算一种;
146 |
147 |  148 |
149 | ### 拓展8
150 |
151 | 一天放学后,牛牛、丁丁、田田、阿普一起去牛牛家写作业,他们各有一个作业本混放在一起,四人每人随便拿了一本。问:
152 |
153 | (1)牛牛拿到自己作业本的拿法有多少种?
154 |
155 | (2)恰有一人拿到自己作业本的拿法有多少种?
156 |
157 | (3)至少有一人没拿到自己作业本的拿法有多少种?
158 |
159 | (4)谁也没拿到自己作业本的拿法有多少种?
160 |
161 | ### 拓展9
162 |
163 | 大家边做游戏边做作业,很快作业就做完了。这时田田看到牛牛家的橱柜里面放着红、黄、蓝、白四种颜色的小旗,各有2,2,3,3面,她想出了一个问题:任意取出三面按顺序排成一行,表示一种信号,问:一共可以表示多少种不同的信号?如果白旗不能打头又有多少种?
164 |
165 | ## 4.1.02. 三角形初步
166 |
167 | ### 热身1
168 |
169 | 用数字0,1,2,3,4,5,可以组成多少无五重复数字的四位偶数?
170 |
171 | ### 热身2
172 |
173 | 宣萱的书包里有5本呢不同的语文书、6本不同的数学书,3本不同的英语书。如果从中取两种不同种类的书,共有多少种不同的取法?
174 |
175 | ### 热身3
176 |
177 | 下列哪些图形是三角形?
178 |
179 | 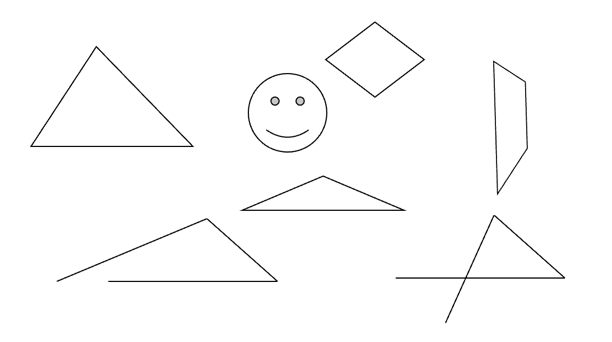
180 |
181 | ### 计算练习
182 |
183 | 我的世界 末地 大战
184 |
185 | ### 例题练习
186 |
187 | ### 例题1
188 |
189 | 下列各组线段能组成一个三角形的是()。
190 |
191 | A.3cm,3cm,6cm
192 |
193 | B.2cm,3cm,6cm
194 |
195 | C.5cm,8cm,12cm
196 |
197 | D.4cm,7cm,11cm
198 |
199 | ### 练习1
200 |
201 | 现有两根木条,它们的长分别为50cm,35cm,如果要钉一个三角形木架,那么下列四根木条中应选取()。
202 |
203 | A.85cm长的木条
204 |
205 | B.150cm长的木条
206 |
207 | C.100cm长的木条
208 |
209 | D.50cm长的木条
210 |
211 | ### 例题2
212 |
213 | 指出下面三角形的底和高。
214 |
215 |
148 |
149 | ### 拓展8
150 |
151 | 一天放学后,牛牛、丁丁、田田、阿普一起去牛牛家写作业,他们各有一个作业本混放在一起,四人每人随便拿了一本。问:
152 |
153 | (1)牛牛拿到自己作业本的拿法有多少种?
154 |
155 | (2)恰有一人拿到自己作业本的拿法有多少种?
156 |
157 | (3)至少有一人没拿到自己作业本的拿法有多少种?
158 |
159 | (4)谁也没拿到自己作业本的拿法有多少种?
160 |
161 | ### 拓展9
162 |
163 | 大家边做游戏边做作业,很快作业就做完了。这时田田看到牛牛家的橱柜里面放着红、黄、蓝、白四种颜色的小旗,各有2,2,3,3面,她想出了一个问题:任意取出三面按顺序排成一行,表示一种信号,问:一共可以表示多少种不同的信号?如果白旗不能打头又有多少种?
164 |
165 | ## 4.1.02. 三角形初步
166 |
167 | ### 热身1
168 |
169 | 用数字0,1,2,3,4,5,可以组成多少无五重复数字的四位偶数?
170 |
171 | ### 热身2
172 |
173 | 宣萱的书包里有5本呢不同的语文书、6本不同的数学书,3本不同的英语书。如果从中取两种不同种类的书,共有多少种不同的取法?
174 |
175 | ### 热身3
176 |
177 | 下列哪些图形是三角形?
178 |
179 | 
180 |
181 | ### 计算练习
182 |
183 | 我的世界 末地 大战
184 |
185 | ### 例题练习
186 |
187 | ### 例题1
188 |
189 | 下列各组线段能组成一个三角形的是()。
190 |
191 | A.3cm,3cm,6cm
192 |
193 | B.2cm,3cm,6cm
194 |
195 | C.5cm,8cm,12cm
196 |
197 | D.4cm,7cm,11cm
198 |
199 | ### 练习1
200 |
201 | 现有两根木条,它们的长分别为50cm,35cm,如果要钉一个三角形木架,那么下列四根木条中应选取()。
202 |
203 | A.85cm长的木条
204 |
205 | B.150cm长的木条
206 |
207 | C.100cm长的木条
208 |
209 | D.50cm长的木条
210 |
211 | ### 例题2
212 |
213 | 指出下面三角形的底和高。
214 |
215 |  216 |
217 | ### 练习2
218 |
219 | 指出下面三角形的底和高。
220 |
221 |
216 |
217 | ### 练习2
218 |
219 | 指出下面三角形的底和高。
220 |
221 | 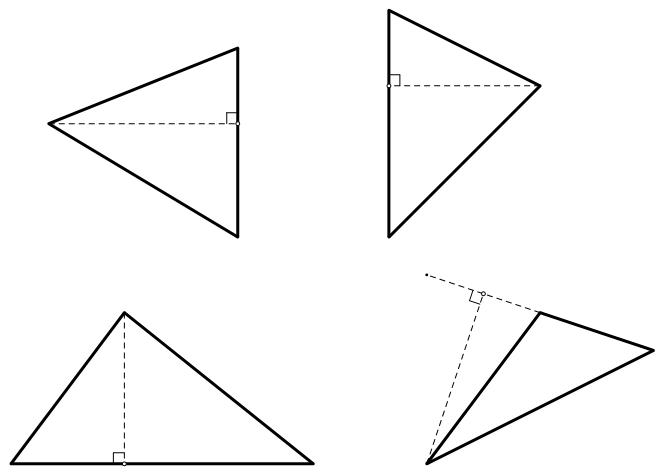 222 |
223 | ### 例题3
224 |
225 | 同学们,你能确定下面是什么三角形吗?(选填:锐角三角形,直角三角形或钝角三角形;等腰三角形,等腰直角三角形或等边三角形)
226 |
227 | ### 练习3
228 |
229 | 两条直角边相等的直角三角形叫做()三角形
230 |
231 | ### 例题4
232 |
233 | 看图回答如下问题:
234 |
235 | (1)如图 1,∠1+∠2+∠3=
236 | (2)如图2,三角形是等腰直角三角形
237 | (3)如图3,三角形是等边三角形,
238 | (4)如图 4, 𠃋1+22+∠3+∠4=
239 | (5)如图5, ∠1+22+23+24+∠5=
240 | (6)如图 6, ∠1+∠2+∠3+∠4+∠5+∠6=
241 | (7)通过以上题目,总结:八边形的内角和:
242 | f【思维导因】
243 | 图5
244 | 图
245 | 2
246 | ∠1+22=
247 | 13=
248 | 多边形
249 |
250 | ### 练习4
251 |
252 | 如图,已知△ABC中,∠B=70°,若沿图中虚线剪去∠B,则∠1+∠2等于多少度?
253 |
254 |
222 |
223 | ### 例题3
224 |
225 | 同学们,你能确定下面是什么三角形吗?(选填:锐角三角形,直角三角形或钝角三角形;等腰三角形,等腰直角三角形或等边三角形)
226 |
227 | ### 练习3
228 |
229 | 两条直角边相等的直角三角形叫做()三角形
230 |
231 | ### 例题4
232 |
233 | 看图回答如下问题:
234 |
235 | (1)如图 1,∠1+∠2+∠3=
236 | (2)如图2,三角形是等腰直角三角形
237 | (3)如图3,三角形是等边三角形,
238 | (4)如图 4, 𠃋1+22+∠3+∠4=
239 | (5)如图5, ∠1+22+23+24+∠5=
240 | (6)如图 6, ∠1+∠2+∠3+∠4+∠5+∠6=
241 | (7)通过以上题目,总结:八边形的内角和:
242 | f【思维导因】
243 | 图5
244 | 图
245 | 2
246 | ∠1+22=
247 | 13=
248 | 多边形
249 |
250 | ### 练习4
251 |
252 | 如图,已知△ABC中,∠B=70°,若沿图中虚线剪去∠B,则∠1+∠2等于多少度?
253 |
254 |  255 |
256 | ### 例题5
257 |
258 | 如图,∠1=∠2,∠3=∠4,∠5=130°,那么∠A=?80°
259 |
260 | 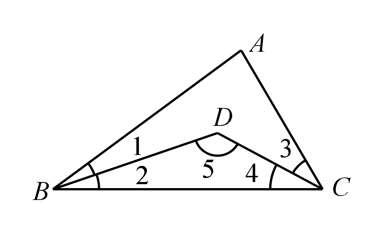
261 |
262 | ### 练习5
263 |
264 | 如图,∠1=∠2,∠3=∠4,∠A=70°,那么∠D=?125°
265 |
266 | 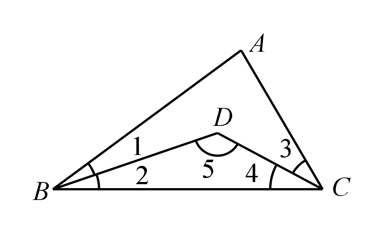
267 |
268 | ### 例题6
269 |
270 | 10个同样的直角三角形卡片拼成了如图所示的平面图形,则这种直角三角形卡片的 3个角中最小的角是多少度?
271 |
272 |
255 |
256 | ### 例题5
257 |
258 | 如图,∠1=∠2,∠3=∠4,∠5=130°,那么∠A=?80°
259 |
260 | 
261 |
262 | ### 练习5
263 |
264 | 如图,∠1=∠2,∠3=∠4,∠A=70°,那么∠D=?125°
265 |
266 | 
267 |
268 | ### 例题6
269 |
270 | 10个同样的直角三角形卡片拼成了如图所示的平面图形,则这种直角三角形卡片的 3个角中最小的角是多少度?
271 |
272 |  273 |
274 | ### 练习6
275 |
276 | 如图,∠AOC=120°,求∠AOB的度数。
277 |
278 | 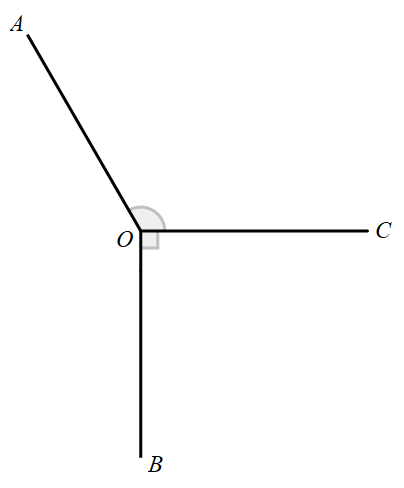
279 |
280 | ### 课后巩固
281 |
282 | ### 巩固1
283 |
284 | ### 巩固2
285 |
286 | ### 巩固3
287 |
288 | ### 拓展
289 |
290 | ### 拓展1
291 |
292 | 如图,将△ABC绕点C按顺时针方向旋转30°,得到△B’A'C,若AC⊥A'B',则∠BAC的度数是。
293 |
294 |
273 |
274 | ### 练习6
275 |
276 | 如图,∠AOC=120°,求∠AOB的度数。
277 |
278 | 
279 |
280 | ### 课后巩固
281 |
282 | ### 巩固1
283 |
284 | ### 巩固2
285 |
286 | ### 巩固3
287 |
288 | ### 拓展
289 |
290 | ### 拓展1
291 |
292 | 如图,将△ABC绕点C按顺时针方向旋转30°,得到△B’A'C,若AC⊥A'B',则∠BAC的度数是。
293 |
294 |  295 |
296 | # 三角形进阶
297 |
298 | ### 课前热身
299 |
300 | ### 热身1(加乘原理)
301 |
302 | 商店里有2种巧克力糖,3种水果糖和3种奶糖。小明想买一些糖送给小朋友。
303 |
304 | (1)如果小明只买一种糖,他有几种选法?
305 |
306 | (2)如果小明想买水果糖、巧克力糖各1种,他有几种选法?
307 |
308 | (3)如果小明想买两种不同种类的糖,他有几种选法?
309 |
310 | ### 热身2(三角形的边)
311 |
312 | 周长是12,各边长都是整数的等腰三角形三角形有几种?
313 |
314 | ### 热身3
315 |
316 | 根据五个已知条件,推断出正确密码是多少。
317 |
318 | 682 一个号码正确,而且位置正确;
319 |
320 | 614 一个号码正确,但位置不正确;
321 |
322 | 206 两个号码正确,但是位置都不正确;
323 |
324 | 738 没有一个号码正确;
325 |
326 | 870 一个号码正确,但是位置不正确。
327 |
328 | ## 4.1.03. 三角形进阶
329 |
330 | ### 例题1
331 |
332 | 请找出下面每个图形的三条底并画出每条底的对应高。
333 |
334 |
295 |
296 | # 三角形进阶
297 |
298 | ### 课前热身
299 |
300 | ### 热身1(加乘原理)
301 |
302 | 商店里有2种巧克力糖,3种水果糖和3种奶糖。小明想买一些糖送给小朋友。
303 |
304 | (1)如果小明只买一种糖,他有几种选法?
305 |
306 | (2)如果小明想买水果糖、巧克力糖各1种,他有几种选法?
307 |
308 | (3)如果小明想买两种不同种类的糖,他有几种选法?
309 |
310 | ### 热身2(三角形的边)
311 |
312 | 周长是12,各边长都是整数的等腰三角形三角形有几种?
313 |
314 | ### 热身3
315 |
316 | 根据五个已知条件,推断出正确密码是多少。
317 |
318 | 682 一个号码正确,而且位置正确;
319 |
320 | 614 一个号码正确,但位置不正确;
321 |
322 | 206 两个号码正确,但是位置都不正确;
323 |
324 | 738 没有一个号码正确;
325 |
326 | 870 一个号码正确,但是位置不正确。
327 |
328 | ## 4.1.03. 三角形进阶
329 |
330 | ### 例题1
331 |
332 | 请找出下面每个图形的三条底并画出每条底的对应高。
333 |
334 |  335 |
336 | ### 练习1
337 |
338 | 请找出下面每个图形的三条底并画出每条底的对应高。
339 |
340 | ### 例题2
341 |
342 | (1)求下图中各三角形的面积(单位:厘米)。
343 |
344 |
335 |
336 | ### 练习1
337 |
338 | 请找出下面每个图形的三条底并画出每条底的对应高。
339 |
340 | ### 例题2
341 |
342 | (1)求下图中各三角形的面积(单位:厘米)。
343 |
344 |  345 |
346 | (2)如图,已知BC=4,CD=5,AD=5,求三角形ABC的面积。
347 |
348 |
345 |
346 | (2)如图,已知BC=4,CD=5,AD=5,求三角形ABC的面积。
347 |
348 |  349 |
350 | (3)如图,将两个正方形拼接在一起,已知小正方形的边长是8,求阴影图形的面积。
351 |
352 |
349 |
350 | (3)如图,将两个正方形拼接在一起,已知小正方形的边长是8,求阴影图形的面积。
351 |
352 |  353 |
354 | ### 练习2
355 |
356 | 三角形底边长10厘米,这条底边对应的高是8厘米,求三角形的面积。
357 |
358 | ### 例题3
359 |
360 | (1)如图,已知三角形ABC的面积是80平方厘米,AD=10厘米,求BC的长。
361 |
362 |
353 |
354 | ### 练习2
355 |
356 | 三角形底边长10厘米,这条底边对应的高是8厘米,求三角形的面积。
357 |
358 | ### 例题3
359 |
360 | (1)如图,已知三角形ABC的面积是80平方厘米,AD=10厘米,求BC的长。
361 |
362 |  363 |
364 | (2)如图,已知三角形ABC的面积是120平方米,BC长60米,求图中的高。
365 |
366 |
363 |
364 | (2)如图,已知三角形ABC的面积是120平方米,BC长60米,求图中的高。
365 |
366 |  367 |
368 | ### 练习3
369 |
370 | 一个直角三角形菜地的面积是120平方米,三角形菜地的底边长10米,求这条底边对应的高是多少米?
371 |
372 | ### 例题4
373 |
374 | 直角三角形ABC中,AB与BC为直角边,AB长为60厘米,BC长为80厘米,已知AC边上的高BD是48厘米,求AC的长是多少?
375 |
376 |
367 |
368 | ### 练习3
369 |
370 | 一个直角三角形菜地的面积是120平方米,三角形菜地的底边长10米,求这条底边对应的高是多少米?
371 |
372 | ### 例题4
373 |
374 | 直角三角形ABC中,AB与BC为直角边,AB长为60厘米,BC长为80厘米,已知AC边上的高BD是48厘米,求AC的长是多少?
375 |
376 | 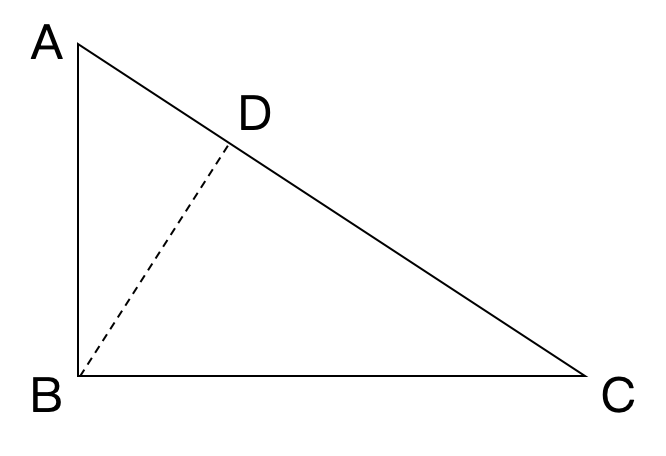 377 |
378 | ### 练习4
379 |
380 | 已知三角形ABC中,BC=10厘米,AD,EC是三角形的高,AD长为8厘米,EC长为5厘米,求底边AB的长是多少厘米?
381 |
382 |
377 |
378 | ### 练习4
379 |
380 | 已知三角形ABC中,BC=10厘米,AD,EC是三角形的高,AD长为8厘米,EC长为5厘米,求底边AB的长是多少厘米?
381 |
382 |  383 |
384 | ### 例题5
385 |
386 | 如图,在直角三角形ABC中有一点P,且三角形ABC的周长是72厘米,过P分别作AC,AB,BC的垂线,并且PE=PF=PD=5厘米,求直角三角形ABC的面积。
387 |
388 |
383 |
384 | ### 例题5
385 |
386 | 如图,在直角三角形ABC中有一点P,且三角形ABC的周长是72厘米,过P分别作AC,AB,BC的垂线,并且PE=PF=PD=5厘米,求直角三角形ABC的面积。
387 |
388 |  389 |
390 | ### 练习5
391 |
392 | 如图,在直角三角形ABC中有一点P,且三角形ABC的面积是96平方厘米,过P分别作AC, AB, BC的垂线,并且PE=PF=PD=4厘米,求直角三角形ABC的周长。
393 |
394 |
389 |
390 | ### 练习5
391 |
392 | 如图,在直角三角形ABC中有一点P,且三角形ABC的面积是96平方厘米,过P分别作AC, AB, BC的垂线,并且PE=PF=PD=4厘米,求直角三角形ABC的周长。
393 |
394 |  395 |
396 | ### 例题6
397 |
398 | 如图,由四个完全相同的直角三角形围成一个大正方形,已知小三角形的两条直角边分别长3cm,4cm,求AB的长度。
399 |
400 |
395 |
396 | ### 例题6
397 |
398 | 如图,由四个完全相同的直角三角形围成一个大正方形,已知小三角形的两条直角边分别长3cm,4cm,求AB的长度。
399 |
400 |  401 |
402 | ### 练习6
403 |
404 | 在长方形ABCD中,各边长度如下,求三角形BEF的面积。
405 |
406 |
401 |
402 | ### 练习6
403 |
404 | 在长方形ABCD中,各边长度如下,求三角形BEF的面积。
405 |
406 | 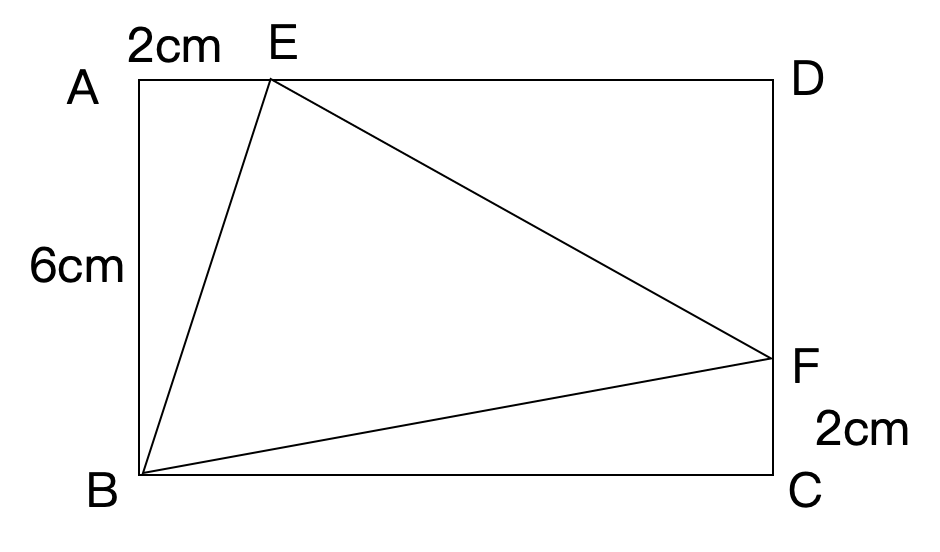 407 |
408 | ### 巩固1
409 |
410 | ### 巩固2
411 |
412 | ### 巩固3
413 |
414 | ## 4.1.05. 等差数列进阶
415 |
416 | ### 课前热身
417 |
418 | ### 热身1
419 |
420 | ### 热身2
421 |
422 | ### 热身3
423 |
424 | ### 例题1
425 |
426 | (1)小数部分的计数单位是“十分之一”可以用小数()表示;“百分之一”可以用小数()表示;
427 |
428 | (2)分数7/10用小数()表示;分数17/1000用小数()表示。
429 |
430 | (3)1里面有()个0.1,有()个0.01,有()个0.001。
431 |
432 | (4)20.523小数点左边第二位是()位,表示()个();小数点右边第二位是()位,表示()个();
433 |
434 | (5)5.02是由5个()和2个()组成的;
435 |
436 | (6)0.46里面有()个百分之一。
437 |
438 | ### 练习1
439 |
440 | 小数的性质:小数的末尾添上0或去掉0不影响小数的大小。根据小数的性质,下列各题哪些0可以去掉,哪些0不可以去掉?
441 |
442 | 0.50=()
443 |
444 | 400=()
445 |
446 | 4.00=()
447 |
448 | 0.030=()
449 |
450 | ### 例题2
451 |
452 | 0.7+0.2 8.24+3.76
453 |
454 | 4.9-3.8 1-0.03
455 |
456 | 0.5+0.8 3.28+5.72
457 |
458 | 4.35-3 0.8-0.55
459 |
460 | 8.65-6.31 10-7.64
461 |
462 | 13.6+8.46 0.99+1.1
463 |
464 | 4.57+3.17+3.43+5.83
465 |
466 |
467 |
468 | 13.35-4.68+2.65-5.32
469 |
470 | ### 练习2
471 |
472 | 1.8+0.4 4.7+2.3
473 |
474 | 12.7+5.61 19.8-7.5
475 |
476 | 32.55-12.15 24.6-17.93
477 |
478 | ### 例题1
479 |
480 | 己知数列5,9,13,17,⋯,145,问:
481 |
482 | (1)这个数列中第20个数是多少?
483 |
484 | (2)85是这个数列的第几个数?
485 |
486 | (3)这个数列一共有几项?
487 |
488 | (4)将数列中所有的数加起来,和是多少?
489 |
490 | ### 练习1
491 |
492 | (1)数列1,3,5,7,⋯,第18项是几?
493 |
494 | (2)数列2,4,6,8,⋯,其中256是这个数列的第几项?
495 |
496 | (3)数列3,6,9,⋯,180,这个数列共有多少项?
497 |
498 | ### 例题2
499 |
500 | 7个连续奇数的和是147,其中最大的奇数是几呢?
501 |
502 | ### 练习2
503 |
504 | 9个连续偶数的和是180,求最小的数是多少?
505 |
506 | ### 例题3
507 |
508 | 幼儿园304个小朋友围成若干个圆(一圈套一圈)做游戏,已知最内圈24人,最外圈52人,如果相邻两圈相差的人数相等,那么相邻的两圈相差多少人?
509 |
510 | ### 练习3
511 |
512 | 牛牛读一本550页的故事书,第一天读了30页,最后一天读了70页,每天读的页数刚好构成等差数列。那么每一天比前一天多读几页?
513 |
514 | ### 例题4
515 |
516 | 建筑工地有一批砖,摆成如图形状,最上层2块砖,第2层6块砖,第3层10块砖,…,每层都比其上面一层多4块砖,已知最下层有402块砖,问中间一层有多少块砖?这堆砖共有多少块?
517 |
518 | 
519 |
520 | ### 练习4
521 |
522 | 8个连续自然数的和是164,其中最小的数是多少?
523 |
524 | ### 例题5
525 |
526 | 计算1+3+4+6+7+9+10+12+13+…+36+37+39+40的和是多少?
527 |
528 | ### 练习5
529 |
530 | 计算2+3+7+8+12+13+17+18+…+32+33+37+38的和是多少?
531 |
532 | ### 例题6
533 |
534 | 有一列数:1,2,4,7,11,16,22,29,37,…,问这列数的第101个是多少?
535 |
536 | ### 练习6
537 |
538 | 有一列数:1,3,6,10,15,21,28,36,45,…,问这列数的第100个是多少
539 |
540 | ## 4.1.07. 追及问题
541 |
542 | ### 知识导引
543 |
544 | 课程内容
545 |
546 | 学习目标
547 |
548 | 内容分析
549 |
550 | 难点在与合理选择,是用路程差还是路程和。
551 |
552 | ### 基础追及
553 |
554 | **例题1**
555 |
556 | 一天,去上学的牛牛发现田田在他前面 150 米处,于是以每分钟 80 米的速度向他追去,已知田田每分钟走 50 米,问:牛牛多长时间能追上田田呢?
557 |
558 | **练习1**
559 |
560 | 甲在乙前面 100 米,于是乙以每分钟 50 米的速度向他追去,已知甲每分钟走 40 米,问:乙多长时间能追上甲呢?
561 |
562 | **例题2**
563 |
564 | 甲、乙两架飞机同时从同一机场起飞,向同一方向飞行,甲每小时飞行 300 千米,乙每小时飞行 340 千米,4 小时后它们相距多少干米?这时甲提高速度打算用 2 小时追上乙,那么甲每小时应该飞行多少干米?
565 |
566 | **练习2**
567 |
568 | 牛牛每小时行 12 千米,丁丁每小时行 15 千米,他俩同时同起点同向出发,5 小时后他们之间的距离是多少干米?
569 |
570 | **补充1**
571 |
572 | 牛牛每分钟走 70 米,丁丁每分钟走 60 米,两人同时从同一地点背向走了 3 分钟,牛牛掉头去追丁丁,追上丁丁时牛牛共走了多少米?
573 |
574 | **例题3**
575 |
576 | 六年级同学从学校出发到公园春游,每分钟走 72 米。15 分钟以后,学校有急事要通知学生,派乐乐老师骑自行车从学校出发用 9 分钟追上同学们,乐乐老师每分钟要行多少米才可以准时追上同学们?
577 |
578 | **练习3**
579 |
580 | 一辆慢车从甲地开往乙地,每小时行 40 千米,开出 5 小时后,一辆快车以每小时 90 千米的速度也从甲地开往乙地,在甲、乙两地的中点处快车追上慢车。甲、乙两地相距多少干米?
581 |
582 | ### 不同时出发
583 |
584 | **例题4**
585 |
586 | 甲、乙两车分别从 A、B 两地出发,同向而行,乙车在前,甲车在后。已知甲车比乙车提前出发1小时,甲车每小时行 96 千米,乙车每小时行 80 千米。甲车出发5小时后追上乙车,求 A、B 两地间的距离。
587 |
588 | **练习4**
589 |
590 | 甲、乙两辆汽车同时从 A 地出发去 B 地,甲车每小时行 50 千米,乙车每小时行 40 千米。途中甲车出故障停车修理了 3 小时,结果甲车比乙车迟到 1 小时到达 B 地。A、B 两地间的路程是多少?
591 |
592 | **补充2**
593 |
594 | 牛牛和丁丁放学后,一起步行去体校参加排球训练,牛牛每分钟走 110 米,丁丁每分钟走 70 米,出发 5 分钟后,牛牛返回学校取运动服,在学校又耽误了 2 分钟,然后追赶丁丁。求多少分钟后追上丁丁。
595 |
596 | ### 行程问题变形
597 |
598 | **例题5**
599 |
600 | 丁丁和牛牛同时从两地相向而行,丁丁每分钟行 50 米,牛牛每分钟行 60 米,两人在距两地中点50米处相遇,求两地的距离是多少米?
601 |
602 | **练习5**
603 |
604 | 牛牛、丁丁三人同时从 A 地去 B 地,牛牛每分钟行 60 米,丁丁每分钟行 90 米,丁丁到达 B 地后立即返回,并与牛牛相遇,相遇时,牛牛还需行 3 分钟才能到达B地,A、B 两地相距多少米?
605 |
606 | **例题6**
607 |
608 | 牛牛和丁丁练习跑步,若牛牛让丁丁先跑 20 米,则牛牛跑 5 秒钟就可追上丁丁;若牛牛让丁丁先跑 4 秒钟,则牛牛跑 6 秒钟就能追上丁丁。牛牛、丁丁两人的速度各是多少?
609 |
610 | **练习6**
611 |
612 | 牛牛、田田二人练习跑出,若牛牛让田田先跑 10 米,则牛牛跑 5 秒钟可追上田田;若牛牛让田田先跑 2 秒钟,则牛牛跑 4 秒钟就能追上田田。问:牛牛、田田两人的速度各是多少?
613 |
614 | ## 4.1.08.整除特征初步
615 |
616 | ### 例题练习
617 |
618 | ### **例题1**
619 |
620 | 下面6个自然数:152,650,434,4375,9064,24125中。
621 |
622 | (1)哪些能被2整除?哪些能被5整除?
623 | (2)哪些能被4整除?哪些能被25整除?
624 | (3)哪些能被8整除?哪些能被125整除?
625 |
626 | ### **练习1**
627 |
628 | (1)能被25整除的数的末两位数只能是多少?
629 | (2)能被4整除的最大三位数是多少?
630 |
631 | ### **例题2**
632 |
633 | (1)修改15679中的一个数字,使这个五位数能被4整除,修改后的五位数是多少?
634 | (2)修改4545679中的一个数字,使这个七位数能被8整除,修改后的七位数是多少?
635 |
636 | ### **练习2**
637 |
638 | (1)修改34575中的一个数宇,使这个五位数能被4整除,修改后的五位数是多少?
639 | (2)修改675479中的一个数字,使这个六位数能被25整除,修改后的六位数是多少?
640 |
641 | ### **例题3**
642 |
643 | 下面6个自然数,5762,3105,9631,7953,2945,3281。
644 |
645 | (1)哪些能被3整除?不能被3整除的余数分别是多少?
646 | (2)哪些能被9整除?不能被9整除的余数分别是多少?
647 |
648 | ### **练习3**
649 |
650 | $\underbrace{55\dots5}_{20个5}89$是否能被3整除?
651 |
652 | ### **例题4**
653 |
654 | 六位数$\overline{243AA4}$能被3整除,求A。
655 |
656 | 六位数$\overline{23A4A7}$能被9整除,求A。
657 |
658 | ### **练习4**
659 |
660 | 在方框中填上两个数字,可以相同也可以不同,使$\overline{4\Box32\Box}$是9的倍数,一共有几种满足条件的填法?
661 |
662 | ### **例题5**
663 |
664 | 在下面每个数的$\Box$里填上一个数字,使它符合所提要求。
665 |
666 | (1)$\overline{234\Box}$,$\overline{63\Box2}$能被2整除,又能被3整除。
667 | (2)$\overline{5\Box0}$,$\overline{4\Box\Box}$,$\overline{\Box89\Box}$同时能被2,5,3整除。
668 |
669 | ### **练习5**
670 |
671 | 在下面每个数的$\Box$里填上一个数字,使它符合所提要求。
672 |
673 | $\overline{5\Box2\Box}$既能被3整除,又能被5整除,那么一共有多少种填法。
674 |
675 | ### **例题6**
676 |
677 | 若五位数$\overline{22A3B}$能被45整除,则A、B代表的数字各是多少?
678 |
679 | ### **练习6**
680 |
681 | 若五位数$\overline{2A52A}$能被15整除,则A代表的数字是多少?
682 |
683 | ### 拓展
684 |
685 | **拓展1**
686 |
687 | $75\times935\times241\times\Box$,要使这个连乘积的最后4个数字都是0,那么在方框内最小应填什么数?
688 |
689 | **拓展2**
690 |
691 | 从1到20的这20个自然数的乘积的末尾有多少个连续的0?
692 |
693 | **拓展3**
694 |
695 | 一个六位数$\overline{2\Box\Box727}$除以9余4,这个数最小是几?
696 |
697 | ## 4.1.10. 定义新运算
698 |
699 | ### 例题1
700 |
701 | 一般我们都认为箭头指向谁,谁就是有危险的,那么规定。
702 |
703 | 警察➡️小偷=警察;警察⬅️小偷=小偷
704 |
705 | 则:(猎人➡️小兔)⬅️(山羊⬅️白菜)=()
706 |
707 | ### 练习1
708 |
709 | 羊和狼在一起时,狼要吃掉羊。所以关于羊及狼,我们规定一种运算,用符号△表示:羊△羊=羊;羊△狼=狼;狼△羊=狼;狼△狼=狼,以上运算的意思是:羊与羊在一起还是羊,狼与狼在一起还是狼,但是狼与羊在一起便只剩下狼了。小朋友总是希望羊能战胜狼,所以我们规定另一种运算,用符号☆表示:羊☆羊=羊;羊☆狼=羊;狼☆羊=羊;狼☆狼=狼,这个运算的意思是:羊与羊在一起还是羊,狼与狼在一起还是狼,但由于羊能战胜狼,当狼与羊在一起时,它便被羊赶走而只剩下羊了。对羊或狼,可以用上面规定的运算作混合运算,混合运算的法规是从左到右,括号内先算。运算的结果或是羊,或是狼。求下式的结果:羊△(狼☆羊)☆羊△(狼△狼)
710 |
711 | ### 例题2
712 |
713 | 我们规定a※b表示为3倍的a减去2倍的b,即$a※b=3a-2b$,例如:$3※2=3x3-2x2=5$;同时,a△b表示为3倍的a加上2倍的b,即$a△b=3a+2b$,例如:$1△2=1x3+2x2=7$
714 |
715 | (1)计算:$5※4$;$4※5$;$2△3$;$3△2$;
716 |
717 | (2)计算:$(8※7)※9$;$2△(5※3)$;
718 |
719 | (3)计算:$5※4△3※2△1$;
720 |
721 | (4)计算:$1※1+2※2+3※3+\dots+100※100$。
722 |
723 | ### 练习2
724 |
725 | 我们规定:$a△b=5a-3b$,计算:$4△3$;$3△3$;$3△5$。
726 |
727 | ### 例题3
728 |
729 | 我们规定$a△b=b(a+1)-a(b-1)$,计算:$(2△1)+(4△3)+(6△5)+(8△7)+(10△9)$。
730 |
731 | ### 练习3
732 |
733 | 我们规定$a◎b=(a+b)-(a-b)$,计算$(2◎1)+(3◎2)+(4◎3)+ ··· +(10◎9)$。
734 |
735 | ### 例题4
736 |
737 | 对于任意的两个自然数a和b,规定新运算表示为:$ab=a+(a+1)+ ··· +(a+b-1)$。
738 |
739 | (1)求$1*100$的值;
740 |
741 | (2)已知$x*10=75$,求x的值;
742 |
743 | (3)如果$(x*3)*2=121$,求x的值。
744 |
745 | ### 练习4
746 |
747 | 如果a△b表示$(a-2)×b$,例如$ 3△4=(3-2)×4=4$,那么,当$a△5=30$时,求a的值。
748 |
749 | ### 例题5
750 |
751 | “⊙”表示一种新的运算符号,已知$2⊙3=2+3+4$;$7⊙2=7+8$;$3⊙5=3+4+5+6+7$,···,按此规则:
752 |
753 | (1)计算:$9⊙6$;
754 |
755 | (2)如果$n⊙8=68$,那么n的值是。
756 |
757 | ### 练习5
758 |
759 | “⊙”表示一种新的运算符号,已知$3⊙3=3×4×5$;$7⊙2=7×8$;$2⊙4=2×3×4×5$,···按此规则:
760 |
761 | 1. 求解,$5⊙3$;
762 |
763 | 2. 如果$n⊙3=60$,求n的值。
764 |
765 | ### 例题6
766 |
767 | ### 练习6
768 |
769 | ## 4.1.11. 体育比赛中的数学
770 |
771 | ### 例题练习
772 |
773 | ### 例题1
774 |
775 | 十六支篮球队按以下的单淘汰赛的规则进行比赛:分成八组两两对决,决出八个队伍晋级,再决出四个队……最后决出冠军。请问总共进行了几场比赛?
776 |
777 | ### 练习1
778 |
779 | 二十支篮球队进行单淘汰赛,只要输一场就会被淘汰,那么为了决出冠军需要举行几场比赛?
780 |
781 | ### 例题2
782 |
783 | 20名羽毛球运动员参加单打比赛,两两配对进行单循环赛,那么冠军一共要比赛多少场?共要进行几场比赛?
784 |
785 | ### 练习2
786 |
787 | 8位同学进行网球循环赛,规则是每个人都要和其他所有人比一场,那么这八个人总共要举行多少场比赛?
788 |
789 | ### 例题3
790 |
791 | A,B,C,D,E五位同学一起比赛象棋,每两人都要比赛一盘。到现在为止,A已经赛4盘,B赛3盘,C赛2盘,D赛1盘。问:此时E同学赛了几盘?
792 |
793 | ### 练习3
794 |
795 | 编号为1,2,3,4,5,6的六个运动员进行乒乓球单循环赛。到现在为止,编号为1,2,3,4,5的运动员已参加比赛的场数正好分别等于他们的编号数。编号为6的运动员已经赛了几场?
796 |
797 | ### 例题4
798 |
799 | 班上四名同学进行跳棋比赛,每两名同学都要赛一局。每局胜者得2分,平者各得1分,负者得0分。
800 |
801 | (1)四个同学的得分加起来一定是多少分?
802 |
803 | (2)第一名最多得多少分?最少得多少分?
804 |
805 | (3)最后一名最多得多少分?
806 |
807 | (4)已知甲、乙、丙三名同学得分分别为3分、4分、4分,且丙同学无平局,甲同学有胜局乙同学有平局,那么丁同学得分是多少?
808 |
809 | ### 练习4
810 |
811 | 在中国象棋比赛中,有胜平负三种结果:获胜得2分,战平得1分,失败得0分。现在六个人进行单循环赛,已知其中五个人的分数分别是7,6,5,4,3,那么最后一个人分数是多分?
812 |
813 | ### 例题5
814 |
815 | 世界杯小组赛规则如下:四支队伍进行单循环赛,胜者得3分,战平得1分,输了得0分。
816 |
817 | (1)他们的总得分最低是多少,最高是多少?
818 |
819 | (2)第一名最多得多少分?
820 |
821 | (3)己知甲、乙、丙、丁四队的得分分别为7,4,4,1。则比赛有几场平局?
822 |
823 | ### 练习5
824 |
825 | 四名同学进行跳棋比赛,每两名同学都要赛一局。每局胜者得2分,平局各得1分,负者得0分。已知甲乙丙三名同学得分分别是3、4、4分,且丙无平局,甲有胜局,乙有平局,那么丁的得分是多少?分别写出丁与甲乙丙丁比赛结果。
826 |
827 | ### 例题6
828 |
829 | “世界杯”足球赛中,甲、乙、丙、丁4支队分在同一小组,在小组赛中,这4支队中的每支队都要与另3支队比赛一场。根据规定:每场比赛获胜的队可得3分;失败的队得0分;如果双方踢平,两队各得1分。已知:
830 |
831 | (1)这4支队三场比赛的总得分为4个连续奇数;
832 |
833 | (2)乙队总得分排在第一;
834 |
835 | (3)丁队恰有两场同对方踢平,其中有一场是与丙队踢平的。
836 |
837 | 根据以上条件可以推断:总得分排在第四的是哪队?
838 |
839 | ### 练习6
840 |
841 | 四个足球队进行单循环比赛,每两队都要赛一场。如果踢平,每队各得1分,否则胜队得3分,负队得0分。比赛结束,各队的总得分怡好是四个连续的自然数。问:输给第一名的队的总分是多少?
842 |
843 | ### 拓展
844 |
845 | 12个队参加一次足球比赛,每两个队都比赛一场,每场比赛中,胜队得3分,负队得0分,平局则各得1分。比赛完毕后,获得第3名和第4名的两个队的得分最多可以相差多少分?
846 |
847 | ### 课后巩固
848 |
849 | ### 巩固1
850 |
851 | A、B、C、D、E五个人进行单循环赛,目前比赛已经进行了一部分,已知A、B都赛了4场,C、D都赛了2场,那么E赛了几场?
852 |
853 | ### 巩固2
854 |
855 | 若干名选手进行网球单循环赛,总共赛了45场,共有多少名选手参赛?
856 |
857 | ### 巩固3
858 |
859 | 6支球队进行足球比赛,每两支队之间都要赛一场,规定胜一场得3分,平一场各得1分,负一场不得分。全部比赛结束后,发现共有4场平局,且其中5支球队共得了31分,则第6支球队得了多少分?
860 |
861 | ## 4.1.12. 几何计数初步
862 |
863 | ### 例题1
864 |
865 | 数一数下图中长方形的个数。
866 |
867 | 
868 |
869 | ### 练习1
870 |
871 | 下图中有多少个长方形?
872 |
873 |
407 |
408 | ### 巩固1
409 |
410 | ### 巩固2
411 |
412 | ### 巩固3
413 |
414 | ## 4.1.05. 等差数列进阶
415 |
416 | ### 课前热身
417 |
418 | ### 热身1
419 |
420 | ### 热身2
421 |
422 | ### 热身3
423 |
424 | ### 例题1
425 |
426 | (1)小数部分的计数单位是“十分之一”可以用小数()表示;“百分之一”可以用小数()表示;
427 |
428 | (2)分数7/10用小数()表示;分数17/1000用小数()表示。
429 |
430 | (3)1里面有()个0.1,有()个0.01,有()个0.001。
431 |
432 | (4)20.523小数点左边第二位是()位,表示()个();小数点右边第二位是()位,表示()个();
433 |
434 | (5)5.02是由5个()和2个()组成的;
435 |
436 | (6)0.46里面有()个百分之一。
437 |
438 | ### 练习1
439 |
440 | 小数的性质:小数的末尾添上0或去掉0不影响小数的大小。根据小数的性质,下列各题哪些0可以去掉,哪些0不可以去掉?
441 |
442 | 0.50=()
443 |
444 | 400=()
445 |
446 | 4.00=()
447 |
448 | 0.030=()
449 |
450 | ### 例题2
451 |
452 | 0.7+0.2 8.24+3.76
453 |
454 | 4.9-3.8 1-0.03
455 |
456 | 0.5+0.8 3.28+5.72
457 |
458 | 4.35-3 0.8-0.55
459 |
460 | 8.65-6.31 10-7.64
461 |
462 | 13.6+8.46 0.99+1.1
463 |
464 | 4.57+3.17+3.43+5.83
465 |
466 |
467 |
468 | 13.35-4.68+2.65-5.32
469 |
470 | ### 练习2
471 |
472 | 1.8+0.4 4.7+2.3
473 |
474 | 12.7+5.61 19.8-7.5
475 |
476 | 32.55-12.15 24.6-17.93
477 |
478 | ### 例题1
479 |
480 | 己知数列5,9,13,17,⋯,145,问:
481 |
482 | (1)这个数列中第20个数是多少?
483 |
484 | (2)85是这个数列的第几个数?
485 |
486 | (3)这个数列一共有几项?
487 |
488 | (4)将数列中所有的数加起来,和是多少?
489 |
490 | ### 练习1
491 |
492 | (1)数列1,3,5,7,⋯,第18项是几?
493 |
494 | (2)数列2,4,6,8,⋯,其中256是这个数列的第几项?
495 |
496 | (3)数列3,6,9,⋯,180,这个数列共有多少项?
497 |
498 | ### 例题2
499 |
500 | 7个连续奇数的和是147,其中最大的奇数是几呢?
501 |
502 | ### 练习2
503 |
504 | 9个连续偶数的和是180,求最小的数是多少?
505 |
506 | ### 例题3
507 |
508 | 幼儿园304个小朋友围成若干个圆(一圈套一圈)做游戏,已知最内圈24人,最外圈52人,如果相邻两圈相差的人数相等,那么相邻的两圈相差多少人?
509 |
510 | ### 练习3
511 |
512 | 牛牛读一本550页的故事书,第一天读了30页,最后一天读了70页,每天读的页数刚好构成等差数列。那么每一天比前一天多读几页?
513 |
514 | ### 例题4
515 |
516 | 建筑工地有一批砖,摆成如图形状,最上层2块砖,第2层6块砖,第3层10块砖,…,每层都比其上面一层多4块砖,已知最下层有402块砖,问中间一层有多少块砖?这堆砖共有多少块?
517 |
518 | 
519 |
520 | ### 练习4
521 |
522 | 8个连续自然数的和是164,其中最小的数是多少?
523 |
524 | ### 例题5
525 |
526 | 计算1+3+4+6+7+9+10+12+13+…+36+37+39+40的和是多少?
527 |
528 | ### 练习5
529 |
530 | 计算2+3+7+8+12+13+17+18+…+32+33+37+38的和是多少?
531 |
532 | ### 例题6
533 |
534 | 有一列数:1,2,4,7,11,16,22,29,37,…,问这列数的第101个是多少?
535 |
536 | ### 练习6
537 |
538 | 有一列数:1,3,6,10,15,21,28,36,45,…,问这列数的第100个是多少
539 |
540 | ## 4.1.07. 追及问题
541 |
542 | ### 知识导引
543 |
544 | 课程内容
545 |
546 | 学习目标
547 |
548 | 内容分析
549 |
550 | 难点在与合理选择,是用路程差还是路程和。
551 |
552 | ### 基础追及
553 |
554 | **例题1**
555 |
556 | 一天,去上学的牛牛发现田田在他前面 150 米处,于是以每分钟 80 米的速度向他追去,已知田田每分钟走 50 米,问:牛牛多长时间能追上田田呢?
557 |
558 | **练习1**
559 |
560 | 甲在乙前面 100 米,于是乙以每分钟 50 米的速度向他追去,已知甲每分钟走 40 米,问:乙多长时间能追上甲呢?
561 |
562 | **例题2**
563 |
564 | 甲、乙两架飞机同时从同一机场起飞,向同一方向飞行,甲每小时飞行 300 千米,乙每小时飞行 340 千米,4 小时后它们相距多少干米?这时甲提高速度打算用 2 小时追上乙,那么甲每小时应该飞行多少干米?
565 |
566 | **练习2**
567 |
568 | 牛牛每小时行 12 千米,丁丁每小时行 15 千米,他俩同时同起点同向出发,5 小时后他们之间的距离是多少干米?
569 |
570 | **补充1**
571 |
572 | 牛牛每分钟走 70 米,丁丁每分钟走 60 米,两人同时从同一地点背向走了 3 分钟,牛牛掉头去追丁丁,追上丁丁时牛牛共走了多少米?
573 |
574 | **例题3**
575 |
576 | 六年级同学从学校出发到公园春游,每分钟走 72 米。15 分钟以后,学校有急事要通知学生,派乐乐老师骑自行车从学校出发用 9 分钟追上同学们,乐乐老师每分钟要行多少米才可以准时追上同学们?
577 |
578 | **练习3**
579 |
580 | 一辆慢车从甲地开往乙地,每小时行 40 千米,开出 5 小时后,一辆快车以每小时 90 千米的速度也从甲地开往乙地,在甲、乙两地的中点处快车追上慢车。甲、乙两地相距多少干米?
581 |
582 | ### 不同时出发
583 |
584 | **例题4**
585 |
586 | 甲、乙两车分别从 A、B 两地出发,同向而行,乙车在前,甲车在后。已知甲车比乙车提前出发1小时,甲车每小时行 96 千米,乙车每小时行 80 千米。甲车出发5小时后追上乙车,求 A、B 两地间的距离。
587 |
588 | **练习4**
589 |
590 | 甲、乙两辆汽车同时从 A 地出发去 B 地,甲车每小时行 50 千米,乙车每小时行 40 千米。途中甲车出故障停车修理了 3 小时,结果甲车比乙车迟到 1 小时到达 B 地。A、B 两地间的路程是多少?
591 |
592 | **补充2**
593 |
594 | 牛牛和丁丁放学后,一起步行去体校参加排球训练,牛牛每分钟走 110 米,丁丁每分钟走 70 米,出发 5 分钟后,牛牛返回学校取运动服,在学校又耽误了 2 分钟,然后追赶丁丁。求多少分钟后追上丁丁。
595 |
596 | ### 行程问题变形
597 |
598 | **例题5**
599 |
600 | 丁丁和牛牛同时从两地相向而行,丁丁每分钟行 50 米,牛牛每分钟行 60 米,两人在距两地中点50米处相遇,求两地的距离是多少米?
601 |
602 | **练习5**
603 |
604 | 牛牛、丁丁三人同时从 A 地去 B 地,牛牛每分钟行 60 米,丁丁每分钟行 90 米,丁丁到达 B 地后立即返回,并与牛牛相遇,相遇时,牛牛还需行 3 分钟才能到达B地,A、B 两地相距多少米?
605 |
606 | **例题6**
607 |
608 | 牛牛和丁丁练习跑步,若牛牛让丁丁先跑 20 米,则牛牛跑 5 秒钟就可追上丁丁;若牛牛让丁丁先跑 4 秒钟,则牛牛跑 6 秒钟就能追上丁丁。牛牛、丁丁两人的速度各是多少?
609 |
610 | **练习6**
611 |
612 | 牛牛、田田二人练习跑出,若牛牛让田田先跑 10 米,则牛牛跑 5 秒钟可追上田田;若牛牛让田田先跑 2 秒钟,则牛牛跑 4 秒钟就能追上田田。问:牛牛、田田两人的速度各是多少?
613 |
614 | ## 4.1.08.整除特征初步
615 |
616 | ### 例题练习
617 |
618 | ### **例题1**
619 |
620 | 下面6个自然数:152,650,434,4375,9064,24125中。
621 |
622 | (1)哪些能被2整除?哪些能被5整除?
623 | (2)哪些能被4整除?哪些能被25整除?
624 | (3)哪些能被8整除?哪些能被125整除?
625 |
626 | ### **练习1**
627 |
628 | (1)能被25整除的数的末两位数只能是多少?
629 | (2)能被4整除的最大三位数是多少?
630 |
631 | ### **例题2**
632 |
633 | (1)修改15679中的一个数字,使这个五位数能被4整除,修改后的五位数是多少?
634 | (2)修改4545679中的一个数字,使这个七位数能被8整除,修改后的七位数是多少?
635 |
636 | ### **练习2**
637 |
638 | (1)修改34575中的一个数宇,使这个五位数能被4整除,修改后的五位数是多少?
639 | (2)修改675479中的一个数字,使这个六位数能被25整除,修改后的六位数是多少?
640 |
641 | ### **例题3**
642 |
643 | 下面6个自然数,5762,3105,9631,7953,2945,3281。
644 |
645 | (1)哪些能被3整除?不能被3整除的余数分别是多少?
646 | (2)哪些能被9整除?不能被9整除的余数分别是多少?
647 |
648 | ### **练习3**
649 |
650 | $\underbrace{55\dots5}_{20个5}89$是否能被3整除?
651 |
652 | ### **例题4**
653 |
654 | 六位数$\overline{243AA4}$能被3整除,求A。
655 |
656 | 六位数$\overline{23A4A7}$能被9整除,求A。
657 |
658 | ### **练习4**
659 |
660 | 在方框中填上两个数字,可以相同也可以不同,使$\overline{4\Box32\Box}$是9的倍数,一共有几种满足条件的填法?
661 |
662 | ### **例题5**
663 |
664 | 在下面每个数的$\Box$里填上一个数字,使它符合所提要求。
665 |
666 | (1)$\overline{234\Box}$,$\overline{63\Box2}$能被2整除,又能被3整除。
667 | (2)$\overline{5\Box0}$,$\overline{4\Box\Box}$,$\overline{\Box89\Box}$同时能被2,5,3整除。
668 |
669 | ### **练习5**
670 |
671 | 在下面每个数的$\Box$里填上一个数字,使它符合所提要求。
672 |
673 | $\overline{5\Box2\Box}$既能被3整除,又能被5整除,那么一共有多少种填法。
674 |
675 | ### **例题6**
676 |
677 | 若五位数$\overline{22A3B}$能被45整除,则A、B代表的数字各是多少?
678 |
679 | ### **练习6**
680 |
681 | 若五位数$\overline{2A52A}$能被15整除,则A代表的数字是多少?
682 |
683 | ### 拓展
684 |
685 | **拓展1**
686 |
687 | $75\times935\times241\times\Box$,要使这个连乘积的最后4个数字都是0,那么在方框内最小应填什么数?
688 |
689 | **拓展2**
690 |
691 | 从1到20的这20个自然数的乘积的末尾有多少个连续的0?
692 |
693 | **拓展3**
694 |
695 | 一个六位数$\overline{2\Box\Box727}$除以9余4,这个数最小是几?
696 |
697 | ## 4.1.10. 定义新运算
698 |
699 | ### 例题1
700 |
701 | 一般我们都认为箭头指向谁,谁就是有危险的,那么规定。
702 |
703 | 警察➡️小偷=警察;警察⬅️小偷=小偷
704 |
705 | 则:(猎人➡️小兔)⬅️(山羊⬅️白菜)=()
706 |
707 | ### 练习1
708 |
709 | 羊和狼在一起时,狼要吃掉羊。所以关于羊及狼,我们规定一种运算,用符号△表示:羊△羊=羊;羊△狼=狼;狼△羊=狼;狼△狼=狼,以上运算的意思是:羊与羊在一起还是羊,狼与狼在一起还是狼,但是狼与羊在一起便只剩下狼了。小朋友总是希望羊能战胜狼,所以我们规定另一种运算,用符号☆表示:羊☆羊=羊;羊☆狼=羊;狼☆羊=羊;狼☆狼=狼,这个运算的意思是:羊与羊在一起还是羊,狼与狼在一起还是狼,但由于羊能战胜狼,当狼与羊在一起时,它便被羊赶走而只剩下羊了。对羊或狼,可以用上面规定的运算作混合运算,混合运算的法规是从左到右,括号内先算。运算的结果或是羊,或是狼。求下式的结果:羊△(狼☆羊)☆羊△(狼△狼)
710 |
711 | ### 例题2
712 |
713 | 我们规定a※b表示为3倍的a减去2倍的b,即$a※b=3a-2b$,例如:$3※2=3x3-2x2=5$;同时,a△b表示为3倍的a加上2倍的b,即$a△b=3a+2b$,例如:$1△2=1x3+2x2=7$
714 |
715 | (1)计算:$5※4$;$4※5$;$2△3$;$3△2$;
716 |
717 | (2)计算:$(8※7)※9$;$2△(5※3)$;
718 |
719 | (3)计算:$5※4△3※2△1$;
720 |
721 | (4)计算:$1※1+2※2+3※3+\dots+100※100$。
722 |
723 | ### 练习2
724 |
725 | 我们规定:$a△b=5a-3b$,计算:$4△3$;$3△3$;$3△5$。
726 |
727 | ### 例题3
728 |
729 | 我们规定$a△b=b(a+1)-a(b-1)$,计算:$(2△1)+(4△3)+(6△5)+(8△7)+(10△9)$。
730 |
731 | ### 练习3
732 |
733 | 我们规定$a◎b=(a+b)-(a-b)$,计算$(2◎1)+(3◎2)+(4◎3)+ ··· +(10◎9)$。
734 |
735 | ### 例题4
736 |
737 | 对于任意的两个自然数a和b,规定新运算表示为:$ab=a+(a+1)+ ··· +(a+b-1)$。
738 |
739 | (1)求$1*100$的值;
740 |
741 | (2)已知$x*10=75$,求x的值;
742 |
743 | (3)如果$(x*3)*2=121$,求x的值。
744 |
745 | ### 练习4
746 |
747 | 如果a△b表示$(a-2)×b$,例如$ 3△4=(3-2)×4=4$,那么,当$a△5=30$时,求a的值。
748 |
749 | ### 例题5
750 |
751 | “⊙”表示一种新的运算符号,已知$2⊙3=2+3+4$;$7⊙2=7+8$;$3⊙5=3+4+5+6+7$,···,按此规则:
752 |
753 | (1)计算:$9⊙6$;
754 |
755 | (2)如果$n⊙8=68$,那么n的值是。
756 |
757 | ### 练习5
758 |
759 | “⊙”表示一种新的运算符号,已知$3⊙3=3×4×5$;$7⊙2=7×8$;$2⊙4=2×3×4×5$,···按此规则:
760 |
761 | 1. 求解,$5⊙3$;
762 |
763 | 2. 如果$n⊙3=60$,求n的值。
764 |
765 | ### 例题6
766 |
767 | ### 练习6
768 |
769 | ## 4.1.11. 体育比赛中的数学
770 |
771 | ### 例题练习
772 |
773 | ### 例题1
774 |
775 | 十六支篮球队按以下的单淘汰赛的规则进行比赛:分成八组两两对决,决出八个队伍晋级,再决出四个队……最后决出冠军。请问总共进行了几场比赛?
776 |
777 | ### 练习1
778 |
779 | 二十支篮球队进行单淘汰赛,只要输一场就会被淘汰,那么为了决出冠军需要举行几场比赛?
780 |
781 | ### 例题2
782 |
783 | 20名羽毛球运动员参加单打比赛,两两配对进行单循环赛,那么冠军一共要比赛多少场?共要进行几场比赛?
784 |
785 | ### 练习2
786 |
787 | 8位同学进行网球循环赛,规则是每个人都要和其他所有人比一场,那么这八个人总共要举行多少场比赛?
788 |
789 | ### 例题3
790 |
791 | A,B,C,D,E五位同学一起比赛象棋,每两人都要比赛一盘。到现在为止,A已经赛4盘,B赛3盘,C赛2盘,D赛1盘。问:此时E同学赛了几盘?
792 |
793 | ### 练习3
794 |
795 | 编号为1,2,3,4,5,6的六个运动员进行乒乓球单循环赛。到现在为止,编号为1,2,3,4,5的运动员已参加比赛的场数正好分别等于他们的编号数。编号为6的运动员已经赛了几场?
796 |
797 | ### 例题4
798 |
799 | 班上四名同学进行跳棋比赛,每两名同学都要赛一局。每局胜者得2分,平者各得1分,负者得0分。
800 |
801 | (1)四个同学的得分加起来一定是多少分?
802 |
803 | (2)第一名最多得多少分?最少得多少分?
804 |
805 | (3)最后一名最多得多少分?
806 |
807 | (4)已知甲、乙、丙三名同学得分分别为3分、4分、4分,且丙同学无平局,甲同学有胜局乙同学有平局,那么丁同学得分是多少?
808 |
809 | ### 练习4
810 |
811 | 在中国象棋比赛中,有胜平负三种结果:获胜得2分,战平得1分,失败得0分。现在六个人进行单循环赛,已知其中五个人的分数分别是7,6,5,4,3,那么最后一个人分数是多分?
812 |
813 | ### 例题5
814 |
815 | 世界杯小组赛规则如下:四支队伍进行单循环赛,胜者得3分,战平得1分,输了得0分。
816 |
817 | (1)他们的总得分最低是多少,最高是多少?
818 |
819 | (2)第一名最多得多少分?
820 |
821 | (3)己知甲、乙、丙、丁四队的得分分别为7,4,4,1。则比赛有几场平局?
822 |
823 | ### 练习5
824 |
825 | 四名同学进行跳棋比赛,每两名同学都要赛一局。每局胜者得2分,平局各得1分,负者得0分。已知甲乙丙三名同学得分分别是3、4、4分,且丙无平局,甲有胜局,乙有平局,那么丁的得分是多少?分别写出丁与甲乙丙丁比赛结果。
826 |
827 | ### 例题6
828 |
829 | “世界杯”足球赛中,甲、乙、丙、丁4支队分在同一小组,在小组赛中,这4支队中的每支队都要与另3支队比赛一场。根据规定:每场比赛获胜的队可得3分;失败的队得0分;如果双方踢平,两队各得1分。已知:
830 |
831 | (1)这4支队三场比赛的总得分为4个连续奇数;
832 |
833 | (2)乙队总得分排在第一;
834 |
835 | (3)丁队恰有两场同对方踢平,其中有一场是与丙队踢平的。
836 |
837 | 根据以上条件可以推断:总得分排在第四的是哪队?
838 |
839 | ### 练习6
840 |
841 | 四个足球队进行单循环比赛,每两队都要赛一场。如果踢平,每队各得1分,否则胜队得3分,负队得0分。比赛结束,各队的总得分怡好是四个连续的自然数。问:输给第一名的队的总分是多少?
842 |
843 | ### 拓展
844 |
845 | 12个队参加一次足球比赛,每两个队都比赛一场,每场比赛中,胜队得3分,负队得0分,平局则各得1分。比赛完毕后,获得第3名和第4名的两个队的得分最多可以相差多少分?
846 |
847 | ### 课后巩固
848 |
849 | ### 巩固1
850 |
851 | A、B、C、D、E五个人进行单循环赛,目前比赛已经进行了一部分,已知A、B都赛了4场,C、D都赛了2场,那么E赛了几场?
852 |
853 | ### 巩固2
854 |
855 | 若干名选手进行网球单循环赛,总共赛了45场,共有多少名选手参赛?
856 |
857 | ### 巩固3
858 |
859 | 6支球队进行足球比赛,每两支队之间都要赛一场,规定胜一场得3分,平一场各得1分,负一场不得分。全部比赛结束后,发现共有4场平局,且其中5支球队共得了31分,则第6支球队得了多少分?
860 |
861 | ## 4.1.12. 几何计数初步
862 |
863 | ### 例题1
864 |
865 | 数一数下图中长方形的个数。
866 |
867 | 
868 |
869 | ### 练习1
870 |
871 | 下图中有多少个长方形?
872 |
873 |  874 |
875 | ### 例题2
876 |
877 | 数一数下图中正方形的个数。
878 |
879 | 
880 |
881 | ### 练习2
882 |
883 | ### 例题3
884 |
885 | ### 练习3
886 |
887 | ### 例题4
888 |
889 | ### 练习4
890 |
891 | ### 例题5
892 |
893 | ### 练习5
894 |
895 | ### 例题6
896 |
897 | ### 练习6
898 |
899 | # 一半模型
900 |
901 | ### 课前热身
902 |
903 | ### 热身 1
904 |
905 | 下图中三角形 ABC 的面积是 26 平方米,则平行四边形 DBCE 的面积是多少平方米?
906 |
907 | 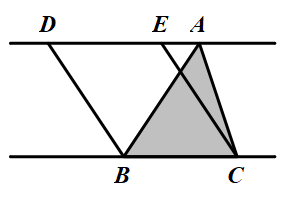
908 |
909 | ### 热身 2
910 |
911 | 如图,两个正方形并排放置,BF 于 CD 相交于点 H,已知阴影部分的面积是 18 平方厘米,求正方形 ABCD 的边长。
912 |
913 | 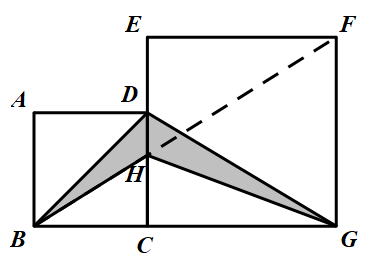
914 |
915 | ### 热身 3
916 |
917 | 如图,平行四边形 ABCD 的边 BC 长 为 2.5,BC 边上的高为 2,P 是对角线 AC 上任一点(点 P 不与点 A、C 重合),且 PE // BC 于 E,F 是 AD 上任一点,求则阴影部分的面积。
918 |
919 | 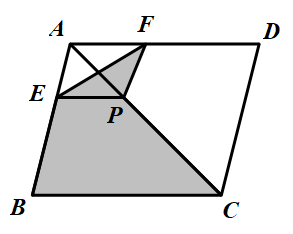
920 |
921 | ### 三角形
922 |
923 | ### 长方形(平行四边形)(例题 1、例题 2)
924 |
925 | ### 例题 1
926 |
927 | 如图所示,平行四边形的面积是 50 平方厘米,则阴影部分的面积是平方厘米。
928 |
929 | 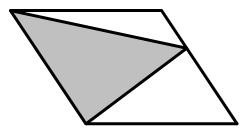
930 |
931 | 如图所示,一个长方形分成 4 个不同的三角形,其中红色部分的面积和为 50 平方厘米,黄色三角形面积是 21 平方厘米。问:绿色的面积是多少平方厘米。
932 |
933 | 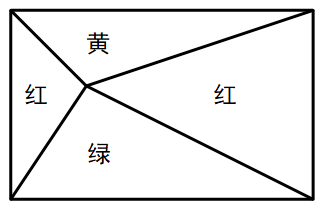
934 |
935 | 如图所示,长方形的面积是 50 平方厘米,则阴影部分的面积是多少平方厘米?
936 |
937 | 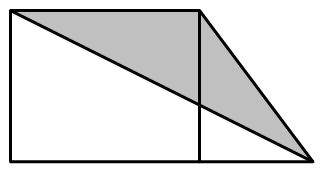
938 |
939 | ### 练习 1
940 |
941 | 如图,长方形 AFEB 和长方形 FDCE 拼成了长方形 ABCD,长方形 ABCD 的长是 20,宽是 12,求它内部阴影部分的面积和。
942 |
943 | 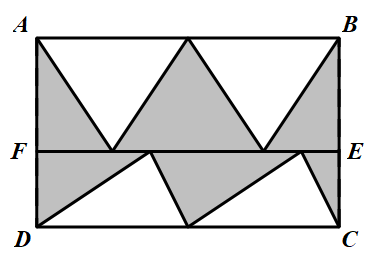
944 |
945 | ### 例题 2
946 |
947 | 如图所示,小长方形 ABCD 的长比宽多 2 厘米,用四个同样的小长方形拼成大正方形 AEFG,已知大正方形的面积 为 70 平方厘米,求图中阴影部分的面积。
948 |
949 | 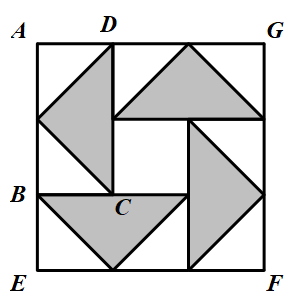
950 |
951 | ### 练习 2
952 |
953 | 如图所示,大正方形的边长为 15 厘米,小正方形的边长为 5 厘米,求阴影部分的面积和。
954 |
955 | 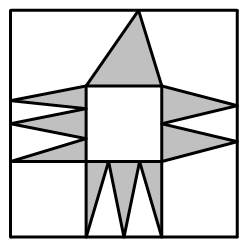
956 |
957 | 梯形(例题 3)
958 |
959 | ### 例题 3
960 |
961 | 如图,在梯形 ABCD 中,E、F 分别是 AB、CD的中点,S~1~ 和S~2~ 的面积分别是 5 和 15,求梯形ABCD的面积。
962 |
963 | 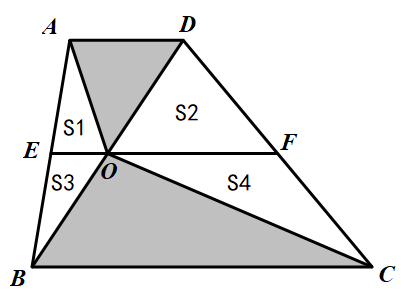
964 |
965 | ### 练习 3
966 |
967 | 动手画一画几种梯形的一半模型。
968 |
969 | 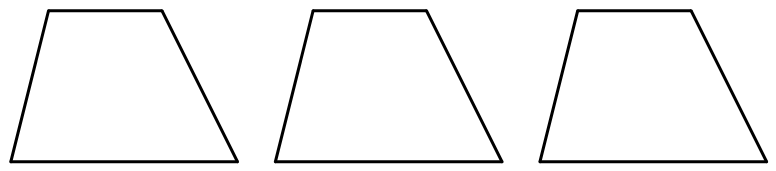
970 |
971 | ### 任意四边形(例题 4)
972 |
973 | ### 例题 4
974 |
975 | 如图,已知四边形 ABCD 中,E、F 分别是 AD、BC 的中点,连接 DF、BE。四边形 ABCD 的面积为 60,S~1~ = 3,求 S~2~ 和 S~3~ 。
976 |
977 | 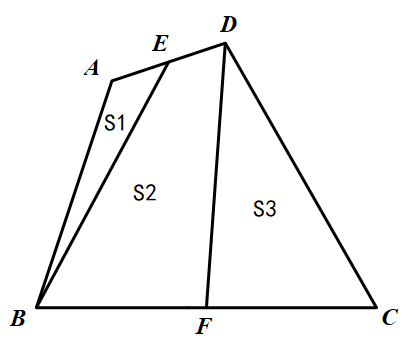
978 |
979 | ### 练习 4
980 |
981 | 如图,已知四边形 ABCD 中,E、F 分别是 AD、BC 的中点,连接 DF、BE。四边形 BEDF 的面积为 6,则四边形 ABCD 的面积为多少?
982 |
983 | 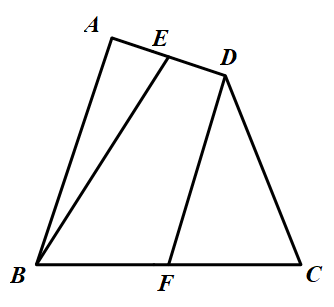
984 |
985 | ### 重叠等于未覆盖(例题 5)
986 |
987 | ### 例题 5
988 |
989 | 如图所示,长方形 ABCD 中,三角形 APD 的面积是 a,三角形 BQC 的面积为 b,阴影部分面积为 c ,那么 a、b、c 有着怎样的大小关系?
990 |
991 | ### 练习 5
992 |
993 | 如图,长方形 ABCD 的边上有两点 E、F,线段 AF、BF、CE、BE 把长方形分成若干块,其中三个小块的面积标注在图上,求图中阴影部分的面积。
994 |
995 | ### 一半等于一半(例题 6)
996 |
997 | ### 例题 6
998 |
999 | 如图所示,正方形 ABCD 的边长为 8 厘米,长方形 EBGF 的长 BG 为 10 厘米,那么长方形的宽 BE 为几厘米?
1000 |
1001 | ### 练习 6
1002 |
1003 | 如图所示,正方形 ABCD 的边长为 12 厘米,长方形 EBGF 的长 BG 为 16 厘米,那么长方形的宽 BE 为多少厘米?
1004 |
1005 | 拓展
1006 |
1007 | ### 拓展 1
1008 |
1009 | 课后巩固
1010 |
1011 | ### 巩固 1
1012 |
1013 | 如图,四边形 ABFE 和四边形 CDEP 都是长方形,AB 的长是 4 厘米,BC 的长是 3 厘米,那么图中阴影部分的面积是多少平方厘米。
1014 |
1015 | 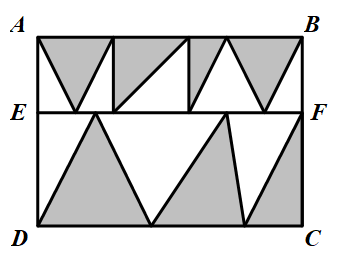
1016 |
1017 | ### 巩固 2
1018 |
1019 | 如图,已知四边形 ABCD 中,E 为 AD 边的中点,F 为 BC 边的中点,三角形 ABE 的面积为12 平方厘米,阴影四边形 EDFB 的面积为 28 平方厘米,求三角形 DFC 的面积。
1020 |
1021 | 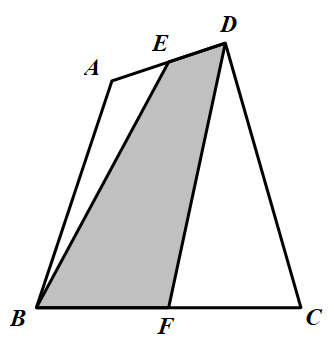
1022 |
1023 | ### 巩固 3
1024 |
1025 | 长方形被其内的一些直线划分成了若干块,已知其中 3 块面积分别是 13,35, 97 。求图中阴影部分的面积。
1026 |
1027 | 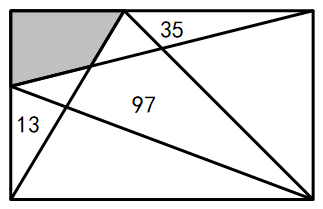
1028 |
1029 | ### 练习 1
1030 |
1031 | 四阶数独中,每一行、每一列、每一个粗线框里都有数字 1~4,“?”应该填几?
1032 |
1033 |
874 |
875 | ### 例题2
876 |
877 | 数一数下图中正方形的个数。
878 |
879 | 
880 |
881 | ### 练习2
882 |
883 | ### 例题3
884 |
885 | ### 练习3
886 |
887 | ### 例题4
888 |
889 | ### 练习4
890 |
891 | ### 例题5
892 |
893 | ### 练习5
894 |
895 | ### 例题6
896 |
897 | ### 练习6
898 |
899 | # 一半模型
900 |
901 | ### 课前热身
902 |
903 | ### 热身 1
904 |
905 | 下图中三角形 ABC 的面积是 26 平方米,则平行四边形 DBCE 的面积是多少平方米?
906 |
907 | 
908 |
909 | ### 热身 2
910 |
911 | 如图,两个正方形并排放置,BF 于 CD 相交于点 H,已知阴影部分的面积是 18 平方厘米,求正方形 ABCD 的边长。
912 |
913 | 
914 |
915 | ### 热身 3
916 |
917 | 如图,平行四边形 ABCD 的边 BC 长 为 2.5,BC 边上的高为 2,P 是对角线 AC 上任一点(点 P 不与点 A、C 重合),且 PE // BC 于 E,F 是 AD 上任一点,求则阴影部分的面积。
918 |
919 | 
920 |
921 | ### 三角形
922 |
923 | ### 长方形(平行四边形)(例题 1、例题 2)
924 |
925 | ### 例题 1
926 |
927 | 如图所示,平行四边形的面积是 50 平方厘米,则阴影部分的面积是平方厘米。
928 |
929 | 
930 |
931 | 如图所示,一个长方形分成 4 个不同的三角形,其中红色部分的面积和为 50 平方厘米,黄色三角形面积是 21 平方厘米。问:绿色的面积是多少平方厘米。
932 |
933 | 
934 |
935 | 如图所示,长方形的面积是 50 平方厘米,则阴影部分的面积是多少平方厘米?
936 |
937 | 
938 |
939 | ### 练习 1
940 |
941 | 如图,长方形 AFEB 和长方形 FDCE 拼成了长方形 ABCD,长方形 ABCD 的长是 20,宽是 12,求它内部阴影部分的面积和。
942 |
943 | 
944 |
945 | ### 例题 2
946 |
947 | 如图所示,小长方形 ABCD 的长比宽多 2 厘米,用四个同样的小长方形拼成大正方形 AEFG,已知大正方形的面积 为 70 平方厘米,求图中阴影部分的面积。
948 |
949 | 
950 |
951 | ### 练习 2
952 |
953 | 如图所示,大正方形的边长为 15 厘米,小正方形的边长为 5 厘米,求阴影部分的面积和。
954 |
955 | 
956 |
957 | 梯形(例题 3)
958 |
959 | ### 例题 3
960 |
961 | 如图,在梯形 ABCD 中,E、F 分别是 AB、CD的中点,S~1~ 和S~2~ 的面积分别是 5 和 15,求梯形ABCD的面积。
962 |
963 | 
964 |
965 | ### 练习 3
966 |
967 | 动手画一画几种梯形的一半模型。
968 |
969 | 
970 |
971 | ### 任意四边形(例题 4)
972 |
973 | ### 例题 4
974 |
975 | 如图,已知四边形 ABCD 中,E、F 分别是 AD、BC 的中点,连接 DF、BE。四边形 ABCD 的面积为 60,S~1~ = 3,求 S~2~ 和 S~3~ 。
976 |
977 | 
978 |
979 | ### 练习 4
980 |
981 | 如图,已知四边形 ABCD 中,E、F 分别是 AD、BC 的中点,连接 DF、BE。四边形 BEDF 的面积为 6,则四边形 ABCD 的面积为多少?
982 |
983 | 
984 |
985 | ### 重叠等于未覆盖(例题 5)
986 |
987 | ### 例题 5
988 |
989 | 如图所示,长方形 ABCD 中,三角形 APD 的面积是 a,三角形 BQC 的面积为 b,阴影部分面积为 c ,那么 a、b、c 有着怎样的大小关系?
990 |
991 | ### 练习 5
992 |
993 | 如图,长方形 ABCD 的边上有两点 E、F,线段 AF、BF、CE、BE 把长方形分成若干块,其中三个小块的面积标注在图上,求图中阴影部分的面积。
994 |
995 | ### 一半等于一半(例题 6)
996 |
997 | ### 例题 6
998 |
999 | 如图所示,正方形 ABCD 的边长为 8 厘米,长方形 EBGF 的长 BG 为 10 厘米,那么长方形的宽 BE 为几厘米?
1000 |
1001 | ### 练习 6
1002 |
1003 | 如图所示,正方形 ABCD 的边长为 12 厘米,长方形 EBGF 的长 BG 为 16 厘米,那么长方形的宽 BE 为多少厘米?
1004 |
1005 | 拓展
1006 |
1007 | ### 拓展 1
1008 |
1009 | 课后巩固
1010 |
1011 | ### 巩固 1
1012 |
1013 | 如图,四边形 ABFE 和四边形 CDEP 都是长方形,AB 的长是 4 厘米,BC 的长是 3 厘米,那么图中阴影部分的面积是多少平方厘米。
1014 |
1015 | 
1016 |
1017 | ### 巩固 2
1018 |
1019 | 如图,已知四边形 ABCD 中,E 为 AD 边的中点,F 为 BC 边的中点,三角形 ABE 的面积为12 平方厘米,阴影四边形 EDFB 的面积为 28 平方厘米,求三角形 DFC 的面积。
1020 |
1021 | 
1022 |
1023 | ### 巩固 3
1024 |
1025 | 长方形被其内的一些直线划分成了若干块,已知其中 3 块面积分别是 13,35, 97 。求图中阴影部分的面积。
1026 |
1027 | 
1028 |
1029 | ### 练习 1
1030 |
1031 | 四阶数独中,每一行、每一列、每一个粗线框里都有数字 1~4,“?”应该填几?
1032 |
1033 |  1034 |
1035 | ### 练习 2
1036 |
1037 | 已知四边形 ABCD 是长方形,四边形 AEFG 是梯形,且 B 是 GF 的中点,已知长方形的面积是 20,求梯形 ABEG 的面积。
1038 |
1039 | 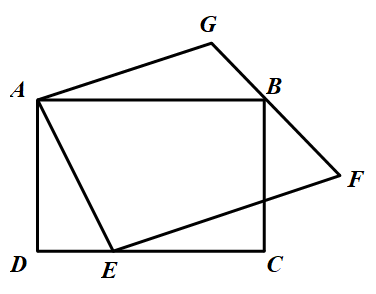
1040 |
1041 | ### 练习 3
1042 |
1043 | 如图,E、F、G、H 分别是四边形 ABCD 各边的中点,EG 与 FH 交于点O,S~1~、S~2~、S~3~、S~4~ 分别表示四个小四边形的面积。试比较S~1~ + S~3~ 与 S~2~ + S~4~的大小并说明理由。
1044 |
1045 | ## 4.1.16. 最值问题初步
1046 |
1047 | ### 例题1(添数)
1048 |
1049 | 在五位数12345的某一位数字后面再插入一个同样的数字(例如:可以在2的后面插入2得到122345),这样得到的六位数最大可能是多少?
1050 |
1051 | ### 练习1
1052 |
1053 | 在五位数1234的某一位数字后面再插入一个同样的数字(例如:可以在2的后面插入2得到12234),这样得到的五位数最大可能是多少?
1054 |
1055 | ### 例题2(拆数)
1056 |
1057 | 电视台要播放一部30集电视连续剧。如果要求每天安排播出的集数互不相等,不能不播,该电视连续剧最多可以播几天?
1058 |
1059 | ### 练习2
1060 |
1061 | 19个苹果要分给一群小朋友,每一个小朋友所分得的苹果数都要不一样,且每位小朋友至少要有一个苹果。问:这群小朋友最多有几位?
1062 |
1063 | ### 例题3(和一定,差小乘积大)
1064 |
1065 | (1)周长为100米的长方形中,面积最大是()平方米。
1066 |
1067 |
1034 |
1035 | ### 练习 2
1036 |
1037 | 已知四边形 ABCD 是长方形,四边形 AEFG 是梯形,且 B 是 GF 的中点,已知长方形的面积是 20,求梯形 ABEG 的面积。
1038 |
1039 | 
1040 |
1041 | ### 练习 3
1042 |
1043 | 如图,E、F、G、H 分别是四边形 ABCD 各边的中点,EG 与 FH 交于点O,S~1~、S~2~、S~3~、S~4~ 分别表示四个小四边形的面积。试比较S~1~ + S~3~ 与 S~2~ + S~4~的大小并说明理由。
1044 |
1045 | ## 4.1.16. 最值问题初步
1046 |
1047 | ### 例题1(添数)
1048 |
1049 | 在五位数12345的某一位数字后面再插入一个同样的数字(例如:可以在2的后面插入2得到122345),这样得到的六位数最大可能是多少?
1050 |
1051 | ### 练习1
1052 |
1053 | 在五位数1234的某一位数字后面再插入一个同样的数字(例如:可以在2的后面插入2得到12234),这样得到的五位数最大可能是多少?
1054 |
1055 | ### 例题2(拆数)
1056 |
1057 | 电视台要播放一部30集电视连续剧。如果要求每天安排播出的集数互不相等,不能不播,该电视连续剧最多可以播几天?
1058 |
1059 | ### 练习2
1060 |
1061 | 19个苹果要分给一群小朋友,每一个小朋友所分得的苹果数都要不一样,且每位小朋友至少要有一个苹果。问:这群小朋友最多有几位?
1062 |
1063 | ### 例题3(和一定,差小乘积大)
1064 |
1065 | (1)周长为100米的长方形中,面积最大是()平方米。
1066 |
1067 |
1068 | 解析
1069 | 待添加
1070 |
1071 |
1072 | (2)面积为100平方米的长方形中,周长最小是()米。
1073 |
1074 |
1075 | 解析
1076 | 待添加
1077 |
1078 |
1079 | ### 练习3
1080 |
1081 | 用24根长1厘米的小棍围成一个长方形,这个长方形的面积最大是多少?如果用22根呢?
1082 |
1083 |
1084 | 解析
1085 | 待添加
1086 |
1087 |
1088 | ### 例题4
1089 |
1090 | 用1,2,3,4,5,6这6个数字各一次,分别组成两个三位数,求积最大时算式是什么?
1091 |
1092 |
1093 | 解析
1094 | 待添加
1095 |
1096 |
1097 | ### 练习4
1098 |
1099 | 请将2,3,4,5,6,8填入算式“$\Box\Box\Box\times\Box\Box\Box$”的方格中,要使得算式结果最大,应该怎么填?
1100 |
1101 |
1102 | 【解析】
1103 | 待添加
1104 |
1105 |
1106 | ### 例题5(拆数)
1107 |
1108 | | | 2个 | 固定个 | 若干个 |
1109 | | -------- | ------------ | ------------ | ----------------- |
1110 | | 可重复 | 相等(接近) | 相等(接近) | 多3少2,不拆1 |
1111 | | 不可重复 | 接近 | 接近 | 从2开始,以次增大 |
1112 |
1113 | (1)3个互不相同的自然数之和是17,它们的乘积最大可能是多少?
1114 |
1115 |
1116 | 解析
1117 | 待添加
1118 |
1119 |
1120 | (2)若干个互不相同的自然数之和是17,它们的乘积最大可能是多少?
1121 |
1122 |
1123 | 解析
1124 | 待添加
1125 |
1126 |
1127 | ### 练习5
1128 |
1129 | 3个自然数之和是17,它们的乘积最大可能是多少?
1130 |
1131 |
1132 | 解析
1133 | 待添加
1134 |
1135 |
1136 | ### 例题6
1137 |
1138 | 把16拆成若干个可重复自然数的和,使这些自然数的乘积最大,最大乘积是多少?
1139 |
1140 |
1141 | 解析
1142 | 待添加
1143 |
1144 |
1145 | ### 练习6
1146 |
1147 | 把12拆成若干个可重复自然数的和,使这些自然数的乘积最大,最大乘积是多少?
1148 |
1149 |
1150 | 解析
1151 | 待添加
1152 |
1153 |
1154 | ## 4.1.18. 平均数进阶
1155 |
1156 | ### 例题 1
1157 |
1158 | 丁丁、牛牛、田田、阿普四个人一起去森林采蘑菇,四个人第一天一共采了 108 个,第二天:共采了 100 个,第三天一共采了 140 个。
1159 | (1)第一天平均每个人采了多少个蘑菇?
1160 | (2)四个人平均每天采多少个蘑菇?
1161 | (3)平均每个人采了多少个蘑菇?
1162 | (4)平均每个人每天采多少个蘑菇?
1163 |
1164 | ### 练习 1
1165 |
1166 | 已知平均数是 15 的 A、B、C、D、E、F、G 七个数中,前 5 个数的平均数是 14,后 5 个数的平均数是 16,求C,D 和 E 的平均数是多少?
1167 |
1168 | ### 补充
1169 |
1170 | A、B、C、D 四个数的平均数是 38,B,C,D 三个数的平均数是 36,A、B两个数的平均数是 42,那么B是多少?
1171 |
1172 | ### 例题 2
1173 |
1174 | 某饮品店苹果汁 8 元一杯,橙汁 6 元一杯,桃汁 10 元一杯。为了夏季促销,该饮品店决定每天用 30 杯苹果汁、50 杯橙汁和 20 杯桃汁混合成 100 杯综合果汁进行限量销售,请问综合果汁每杯应售多少元?
1175 |
1176 | ### 练习 2
1177 |
1178 | 数学考试后,同学得到了自己的成绩,男生说:“我们男生所有人的平均分是 92 分。”女生说:“我们女生所有人的平均分是 95 分。”己知这个班男生有 20 人,女生有 10 人,求全班的平均分是多少?
1179 |
1180 | ### 例题 3
1181 |
1182 | 8 个同学数学考试成绩的平均数为 80,若把其中的一个成绩改为 82,则平均数变成了82。问被改动的数原来是多少?
1183 |
1184 | ### 练习 3
1185 |
1186 | 有 4 个数,他们的平均数是 34,把其中的一个数改为 50,则平均数变为 40,被改动的数原来是多少?
1187 |
1188 | ### 例题 4
1189 |
1190 | 牛牛班期末考试,全班同学的数学平均分是 80 分,牛牛的数学成绩为 90 分,其他同学的平均分为 79 分,问:全班共有多少人?
1191 |
1192 | ### 练习 4
1193 |
1194 | 教室里所有人的平均年龄是 11 岁,如果不算其中 1 个 30 岁的老师,其余人的平均年龄是 10 岁,那么教室里有多少人?
1195 |
1196 | ### 例题 5
1197 |
1198 | 某校有 70 名男同学及若干名女同学参加数学竞赛,平均分为 63 分,参赛的男同学平均分为 60 分,女同学平均分为 70 分,那么该校有多少女同学参赛?
1199 |
1200 | ### 练习 5
1201 |
1202 | 汽车厂有甲、乙两个车间生产零件,甲车间有 57 名工人,每人每天平均生产 132 个零件,乙车间每人每天平均生产 163 个零件,两个车间每人每天平均生产144个零件 。 请问:乙车间有多少名工人?
1203 |
1204 | ### 例题 6
1205 |
1206 | 某校学生参加一个数学竞赛,男生平均分是 96 分,女生平均分是 90 分,全体同学的平均分是 92 分,女生比男生多20人,求男、女生各多少人?
1207 |
1208 | ### 练习 6
1209 |
1210 | 一次考试,男生的平均分比总平均分高 2 分,女生的平均分比总平均分低 1 分 。男生的总分数是 942 分 ,女生的总分数是 1800 分 。求:男、女生各有多少人?
1211 |
1212 | ### 巩固 1
1213 |
1214 | 小枫参加射击比赛,他一共打了 10 枪,每枪都射中靶子 ,位置如图中的"x"所示。图中的数表示击中靶子各部位能得到的分数 。小枫此次打靶的平均分是多少分?
1215 |
1216 | ### 巩固 2
1217 |
1218 | 果品店将每千克 4 元的酥糖 5 千克 ,每干克 6 元的水果糖 2 千克,每千克 8 元的牛奶糖 5 千克,混合成什锦糖,什锦糖每干克是多少元?
1219 |
1220 | ### 巩固 3
1221 |
1222 | 某校有 100 名学生参加数学竞赛,平均分是 63 分,其中参赛男同学的平均分是 60 分,女同学平均分是 70 分,那么该校参赛男同学比女同学多几人?
1223 |
1224 | ### 练习 1
1225 |
1226 | 小华期末考试时,语文、数学和音乐三科成绩平均分是 98 分 ,英语成绩公布后,四科平均分下降了 6 分,小华英语成绩是多少分?
1227 |
1228 | ### 练习 2
1229 |
1230 | 观音菩萨分别奖励给唐僧师徒四人一些人参果,唐僧师徒四人平均拥有 20 个人参果,唐僧和孙悟空平均拥有 24 个 ,孙悟空、猪八戒和沙僧平均拥有10 个,你知道孔悟空有多少个人参果吗?
1231 |
1232 | ### 练习 3
1233 |
1234 | 某校男老师的平均年龄是 27 岁,女老师的平均年龄是 32 岁,全体老师的平均年龄是 30 岁如果男老师比女老师少 13 名,那么该校共有老师多少名?
1235 |
1236 | # 4.1.20. 环形跑道
1237 |
1238 | ### 例题 1
1239 |
1240 | 大明和小明沿着环形跑道进行跑步训练,大明每分钟跑 110 米,小明每分钟跑 130 米。已知环形跑道周长是 960 米,他们从同一地点同时出发,背向而行。
1241 |
1242 | (1) 到两人第一次相遇一共跑了多少圈,用时几分钟?
1243 | (2) 到第十次相遇两人共跑了多少圈,共用时几分钟?
1244 |
1245 | ### 练习 1
1246 |
1247 | 田田和丁丁沿着学校的环形林荫道散步,田田每分钟走 55 米,丁丁每分钟走 65 米。已知林荫道周长是 480 米,他们从同一地点同时出发,背向而行。
1248 |
1249 | (1)经过多长时间两人第一次相遇?
1250 | (2)又经过多长时间两人第二次相遇?
1251 | (3)到第10 次相遇共走几圈,共用多长时间?
1252 | (4)在他们第10 次相遇后,田田再走多少米就回到出发点?
1253 |
1254 | ### 例题 2
1255 |
1256 | 已知环形跑道周长是 960 米,大明和小明同时从相距 480 米的两地出发,背向而行,已知大明每分钟跑 110 米,小明每分钟跑 130 米。
1257 |
1258 | (1)到两人第一次相遇一共跑了多少米,用时几分钟?
1259 | (2)再过多久两人第二次相遇?
1260 | (3)到第十次相遇一共用了多少分钟?
1261 |
1262 | ### 练习 2
1263 |
1264 | 一个圆形操场跑道的周长是 900 米,两个学生同时从相距 450 米的 A,B 两地出发,背向而行。已知甲的速度是 55米/分,乙的速度是 35 米/分。
1265 |
1266 | (1)经过多久两人第一次相遇?
1267 | (2)再过多久两人第二次相遇?
1268 | (3)到第十次相遇两人一共用了多少分钟?
1269 |
1270 | ### 例题 3
1271 |
1272 | 一条环形跑道长 300 米,丁丁的速度为 6 米/秒,牛牛的速度为 4 米/秒,两人同时同地同向出发。
1273 |
1274 | (1)经过多少时间丁丁第一次追上牛牛?
1275 | (2)丁丁第一次追上牛牛时,两人各跑了多少米?
1276 | (3)丁丁第二次追上牛牛共花了多少时间?
1277 |
1278 | ### 练习 3
1279 |
1280 | 在 400 米的环形跑道上,小枫和一只小狗在跑步,小狗距离小枫 100 米,已知小枫每秒跑 5 米,小狗每秒跑 4 米,方向相同 。
1281 |
1282 | (1)小枫第一次追上小狗需要多长时间?
1283 | (2)再过多久第二次追上小狗?
1284 | (3)到第十次追上小狗一共用了多长时间?
1285 |
1286 | ### 例题 4
1287 |
1288 | 在环形跑道上,两人在一处背靠背站好,然后开始跑,每隔 4 分钟相遇一次;如果两人从同地同向同时跑,每隔 20 分钟相遇一次,已知环形跑道的长度是 1600 米,那么两人的速度分别是多少?
1289 |
1290 | ### 练习 4
1291 |
1292 | 在 300 米的环形跑道上,田田和丁丁同时同地起跑,如果同向而跑 2 分 30 秒相遇,如果背向跑则半分钟相遇,求两人的速度各是多少?
1293 |
1294 | ### 例题 5
1295 |
1296 | 甲、乙两人在周长为 400 米的环形跑道上同时同地同向而行,甲每分钟走 60 米,乙每分钟走 40
1297 | 米,甲每追上乙一次,两人就会击一次掌,当两人击了第 10 次掌时,甲掉头往回走,每相遇一
1298 | 次仍击一次掌,两人又击了5次筆,问此时两人各走了多少米?
1299 |
1300 | ### 练习 5
1301 |
1302 | 甲、乙两人在周长为 400 米的环形跑道上同时同地同向而行,甲每分钟走 60 米,乙每分钟走
1303 | 40 米,甲每追上乙一次,两人就会击一次掌,当两人击了第 5 次掌时,甲掉头往回走,每相
1304 | 遇一次仍击一次掌,两人又击了 10次掌,问此时两人各走了多少米?
1305 |
1306 | ### 例题 6
1307 |
1308 | 如图,个正方形房屋的边长为 10 米。甲、乙两人分别从房屋的两个墙角同时出发,沿顺时
1309 | 针方向前进,甲每秒行 5 米 ,乙每秒行 3 米。出发后经过多长时间甲第一次看见乙?
1310 |
1311 |  1312 |
1313 | ### 练习 6
1314 |
1315 | 如图,在一个边长为 12 米的正方形房屋的两个角,分别有一只猫和一只老鼠 。猫看到老鼠,以 5 米秒的速度去追它,老鼠以 8 米秒的速度逃跑。
1316 |
1317 | (1) 因为老鼠比猫跑得更快,所以过了一段时间,老鼠反而在猫的背后看见了猫 。请问从老鼠开始跑到看见猫,经过了多长时间?
1318 | (2) 看到猫的瞬间,老鼠转身,并且因为惊吓 ,速度变为5米/秒 。 请问,再经过多长时间,老鼠会迎面看到猫?
1319 | (3) 老鼠迎面看到猫,瞬间再次转身 ,但是因为惊吓,速度变为4米秒 。请问,再过多少秒,猫能追上老鼠?
1320 |
1321 |
1312 |
1313 | ### 练习 6
1314 |
1315 | 如图,在一个边长为 12 米的正方形房屋的两个角,分别有一只猫和一只老鼠 。猫看到老鼠,以 5 米秒的速度去追它,老鼠以 8 米秒的速度逃跑。
1316 |
1317 | (1) 因为老鼠比猫跑得更快,所以过了一段时间,老鼠反而在猫的背后看见了猫 。请问从老鼠开始跑到看见猫,经过了多长时间?
1318 | (2) 看到猫的瞬间,老鼠转身,并且因为惊吓 ,速度变为5米/秒 。 请问,再经过多长时间,老鼠会迎面看到猫?
1319 | (3) 老鼠迎面看到猫,瞬间再次转身 ,但是因为惊吓,速度变为4米秒 。请问,再过多少秒,猫能追上老鼠?
1320 |
1321 |  1322 |
1323 | ### 练习 1
1324 |
1325 | 甲乙两人在周长为 220 米的环形跑道的两端背向而行练习跑步,甲乙相距 110 米,已知甲的速度是每秒 6 米,乙的速度是每秒 4 米,则甲乙第一次相遇用了几秒?到第五次相遇共用了几秒?
1326 |
1327 | ### 练习 2
1328 |
1329 | 在周长为 200 米的环形跑道上,大齐和小王站在相距 100 米的两点,两人分别以 6 米/秒、5 米/秒的速度同时同向出发,沿跑道跑步 。则 16 分钟内,大齐追上小王几次?
1330 |
1331 | ### 练习 3
1332 |
1333 | 如图,正方形房屋的边长为 20 米 。 甲、乙两人分别从房屋的两个墙角同时出发,沿顺时针方向前进。甲每秒行 5 米,乙每秒行 3 米 。出发多久后甲第一次看见乙?
1334 |
1335 |
1322 |
1323 | ### 练习 1
1324 |
1325 | 甲乙两人在周长为 220 米的环形跑道的两端背向而行练习跑步,甲乙相距 110 米,已知甲的速度是每秒 6 米,乙的速度是每秒 4 米,则甲乙第一次相遇用了几秒?到第五次相遇共用了几秒?
1326 |
1327 | ### 练习 2
1328 |
1329 | 在周长为 200 米的环形跑道上,大齐和小王站在相距 100 米的两点,两人分别以 6 米/秒、5 米/秒的速度同时同向出发,沿跑道跑步 。则 16 分钟内,大齐追上小王几次?
1330 |
1331 | ### 练习 3
1332 |
1333 | 如图,正方形房屋的边长为 20 米 。 甲、乙两人分别从房屋的两个墙角同时出发,沿顺时针方向前进。甲每秒行 5 米,乙每秒行 3 米 。出发多久后甲第一次看见乙?
1334 |
1335 |  1336 |
1337 | ## 4.2.01. 小数巧算
1338 |
1339 | ### 热身1
1340 |
1341 | 计算:$1.73+21.7-11.4$
1342 |
1343 | ### 热身2
1344 |
1345 | 计算:
1346 |
1347 | (1)$1.2\times8.6$
1348 |
1349 | (2)$1.125\times8$
1350 |
1351 | ### 热身3
1352 |
1353 | 计算:
1354 |
1355 | (1)$68.8\div4$
1356 |
1357 | (2)$3.64\div1.4$
1358 |
1359 | ### 例题1
1360 |
1361 | 计算。
1362 |
1363 | (1)$0.9+0.99+0.999+0.9999+0.99999$
1364 |
1365 | (2) $0.7+9.7+99.7+999.7+9999.7$
1366 |
1367 | ### 练习1
1368 |
1369 | 计算。
1370 |
1371 | (1)$89+899+8999+89999+899999$
1372 |
1373 | (2)$1.996+19.97+199.8$
1374 |
1375 | ### 例题2
1376 |
1377 | 计算。
1378 |
1379 | (1) $90.3+88.8+90.2+91.2+179.1+270.4$
1380 |
1381 | (2)$3.17+7.48+0.83-2.38-1.62-3.48$
1382 |
1383 | ### 练习2
1384 |
1385 | 计算:$35.6+35.02+34.81+35.08+35.11$
1386 |
1387 | ### 例题3(乘法巧算)
1388 |
1389 | 计算。
1390 |
1391 | (1)$0.125\times0.25\times0.5\times64$
1392 |
1393 | (2)$1.125\times64\times0.75$
1394 |
1395 | ### 练习3
1396 |
1397 | 计算。
1398 |
1399 | (1)$1.25\times32\times0.25$
1400 |
1401 | (2)$2.5\times4\times125\times1.6$
1402 |
1403 | ### 例题4
1404 |
1405 | 先找到公因数,再计算。
1406 |
1407 | (1)$2.5\times1.06+2.5\times0.84+2.5\times2.1$
1408 |
1409 | (2)$12.5\times0.54+0.067\times125-1.25\times4.1$
1410 |
1411 | ### 练习4
1412 |
1413 | 计算。
1414 |
1415 | (1)$7.8\times24+7.8\times71+0.78\times50$
1416 |
1417 | (2)$0.13\times21-0.13\times19+0.13\times57+1.3\times4.1$
1418 |
1419 | ### 例题5
1420 |
1421 | 计算:$3.79\times0.38+1.59\times6.21+3.79\times1.21$
1422 |
1423 | ### 练习5
1424 |
1425 | 计算:$14.3\times7.88-9.7\times7.38+1.43\times21.2-97\times0.262$
1426 |
1427 | ### 例题6
1428 |
1429 | 计算:$(0.1+0.21+0.321)\times(0.21+0.321+0.4321)-(0.1+0.21+0.321+0.4321)\times(0.21+0.321)$
1430 |
1431 | ### 练习6
1432 |
1433 | 计算:$(1+0.45+0.56)\times(0.45+0.56+0.67)-(1+0.45+0.56+0.67)\times(0.45+0.56)$
1434 |
1435 | ## 4.2.01. 格点与割补
1436 |
1437 | ### 例题1
1438 |
1439 | 图中相邻两个格点的距离都是1,请你求出“小鱼”、“松树”、“小猫”的面积各是多少?
1440 |
1441 | 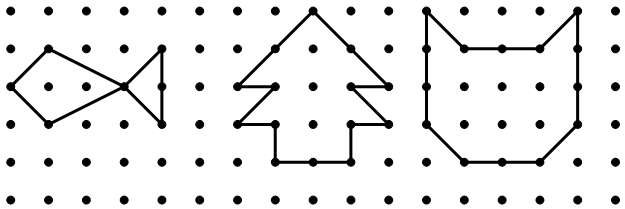
1442 |
1443 | ### 练习1
1444 |
1445 | 图中每个小正方形的面积都是1平方厘米,求图中阴影部分的面积。
1446 |
1447 |
1336 |
1337 | ## 4.2.01. 小数巧算
1338 |
1339 | ### 热身1
1340 |
1341 | 计算:$1.73+21.7-11.4$
1342 |
1343 | ### 热身2
1344 |
1345 | 计算:
1346 |
1347 | (1)$1.2\times8.6$
1348 |
1349 | (2)$1.125\times8$
1350 |
1351 | ### 热身3
1352 |
1353 | 计算:
1354 |
1355 | (1)$68.8\div4$
1356 |
1357 | (2)$3.64\div1.4$
1358 |
1359 | ### 例题1
1360 |
1361 | 计算。
1362 |
1363 | (1)$0.9+0.99+0.999+0.9999+0.99999$
1364 |
1365 | (2) $0.7+9.7+99.7+999.7+9999.7$
1366 |
1367 | ### 练习1
1368 |
1369 | 计算。
1370 |
1371 | (1)$89+899+8999+89999+899999$
1372 |
1373 | (2)$1.996+19.97+199.8$
1374 |
1375 | ### 例题2
1376 |
1377 | 计算。
1378 |
1379 | (1) $90.3+88.8+90.2+91.2+179.1+270.4$
1380 |
1381 | (2)$3.17+7.48+0.83-2.38-1.62-3.48$
1382 |
1383 | ### 练习2
1384 |
1385 | 计算:$35.6+35.02+34.81+35.08+35.11$
1386 |
1387 | ### 例题3(乘法巧算)
1388 |
1389 | 计算。
1390 |
1391 | (1)$0.125\times0.25\times0.5\times64$
1392 |
1393 | (2)$1.125\times64\times0.75$
1394 |
1395 | ### 练习3
1396 |
1397 | 计算。
1398 |
1399 | (1)$1.25\times32\times0.25$
1400 |
1401 | (2)$2.5\times4\times125\times1.6$
1402 |
1403 | ### 例题4
1404 |
1405 | 先找到公因数,再计算。
1406 |
1407 | (1)$2.5\times1.06+2.5\times0.84+2.5\times2.1$
1408 |
1409 | (2)$12.5\times0.54+0.067\times125-1.25\times4.1$
1410 |
1411 | ### 练习4
1412 |
1413 | 计算。
1414 |
1415 | (1)$7.8\times24+7.8\times71+0.78\times50$
1416 |
1417 | (2)$0.13\times21-0.13\times19+0.13\times57+1.3\times4.1$
1418 |
1419 | ### 例题5
1420 |
1421 | 计算:$3.79\times0.38+1.59\times6.21+3.79\times1.21$
1422 |
1423 | ### 练习5
1424 |
1425 | 计算:$14.3\times7.88-9.7\times7.38+1.43\times21.2-97\times0.262$
1426 |
1427 | ### 例题6
1428 |
1429 | 计算:$(0.1+0.21+0.321)\times(0.21+0.321+0.4321)-(0.1+0.21+0.321+0.4321)\times(0.21+0.321)$
1430 |
1431 | ### 练习6
1432 |
1433 | 计算:$(1+0.45+0.56)\times(0.45+0.56+0.67)-(1+0.45+0.56+0.67)\times(0.45+0.56)$
1434 |
1435 | ## 4.2.01. 格点与割补
1436 |
1437 | ### 例题1
1438 |
1439 | 图中相邻两个格点的距离都是1,请你求出“小鱼”、“松树”、“小猫”的面积各是多少?
1440 |
1441 | 
1442 |
1443 | ### 练习1
1444 |
1445 | 图中每个小正方形的面积都是1平方厘米,求图中阴影部分的面积。
1446 |
1447 |  1448 |
1449 | ### 例题2
1450 |
1451 | 图中相邻两个格点的距离都是1,计算这个格点多边形的面积。
1452 |
1453 |
1448 |
1449 | ### 例题2
1450 |
1451 | 图中相邻两个格点的距离都是1,计算这个格点多边形的面积。
1452 |
1453 |  1454 |
1455 | ### 练习2
1456 |
1457 | 图中相邻格点的距离都是1,计算这个格点多边形的面积。
1458 |
1459 |
1454 |
1455 | ### 练习2
1456 |
1457 | 图中相邻格点的距离都是1,计算这个格点多边形的面积。
1458 |
1459 |  1460 |
1461 | ### 例题3
1462 |
1463 | 图中每个小正方形的面积均为2平方厘米。阴影多边形的面积是多少平方厘米?
1464 |
1465 | 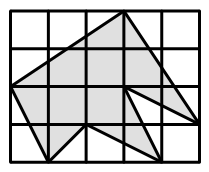
1466 |
1467 | ### 练习3
1468 |
1469 | 图中每个小正方形的面积是2平方厘米,阴影部分面积是几平方厘米。
1470 |
1471 | 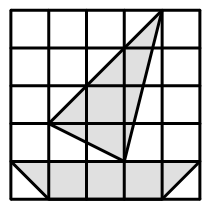
1472 |
1473 | ### 例题4
1474 |
1475 | 图中相邻三点所形成的等边三角形的面积为1,试计算三角形的面积。
1476 |
1477 | 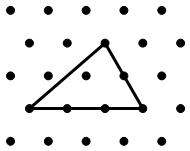
1478 |
1479 | ### 练习4
1480 |
1481 | 圈中相邻三点所形成的等边三角形的面积为1,试计算梯形的面积。
1482 |
1483 | 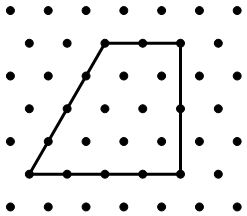
1484 |
1485 | ### 例题5
1486 |
1487 | 图中相邻三点所形成的等边三角形的面积为1,计算三角形ABC的面积。
1488 |
1489 | 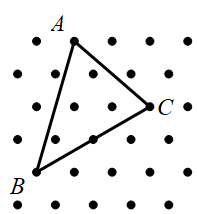
1490 |
1491 | ### 练习5
1492 |
1493 | 图中相邻三点所形成的等边三角形的面积为1,试求“台灯”的面积。
1494 |
1495 |
1460 |
1461 | ### 例题3
1462 |
1463 | 图中每个小正方形的面积均为2平方厘米。阴影多边形的面积是多少平方厘米?
1464 |
1465 | 
1466 |
1467 | ### 练习3
1468 |
1469 | 图中每个小正方形的面积是2平方厘米,阴影部分面积是几平方厘米。
1470 |
1471 | 
1472 |
1473 | ### 例题4
1474 |
1475 | 图中相邻三点所形成的等边三角形的面积为1,试计算三角形的面积。
1476 |
1477 | 
1478 |
1479 | ### 练习4
1480 |
1481 | 圈中相邻三点所形成的等边三角形的面积为1,试计算梯形的面积。
1482 |
1483 | 
1484 |
1485 | ### 例题5
1486 |
1487 | 图中相邻三点所形成的等边三角形的面积为1,计算三角形ABC的面积。
1488 |
1489 | 
1490 |
1491 | ### 练习5
1492 |
1493 | 图中相邻三点所形成的等边三角形的面积为1,试求“台灯”的面积。
1494 |
1495 |  1496 |
1497 | ### 例题6
1498 |
1499 | 如图,已知:正三角形ABC的面积是48,点D是所在边的中点,点E、F分别是所在边的四等分点,求阴影三角形的面积。
1500 |
1501 |
1496 |
1497 | ### 例题6
1498 |
1499 | 如图,已知:正三角形ABC的面积是48,点D是所在边的中点,点E、F分别是所在边的四等分点,求阴影三角形的面积。
1500 |
1501 |  1502 |
1503 | ### 练习6
1504 |
1505 | 已知:正三角形ABC的面积是96,点D、F分别是所在边的中点,点E是所在边的四等分点,求阴影三角形的面积。
1506 |
1507 |
1502 |
1503 | ### 练习6
1504 |
1505 | 已知:正三角形ABC的面积是96,点D、F分别是所在边的中点,点E是所在边的四等分点,求阴影三角形的面积。
1506 |
1507 | 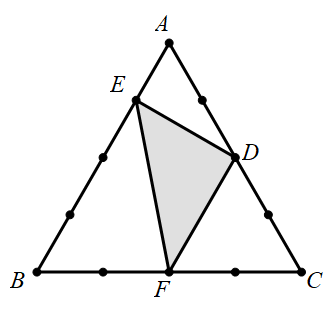 1508 |
1509 | ## 4.2.03. 数表-从日历谈起
1510 |
1511 | ### 例题1
1512 |
1513 | 观察如下日历:
1514 |
1515 | (1)若设一个横行上相邻的三个日期中间的日期为a,那么左右两边的日期分别是什么?
1516 |
1517 | (2)若设一个竖列上相邻的三个日期中间的日期为b,那么上下两边的日期分别是什么?
1518 |
1519 | (3)如果在上述日历中某个竖列上三个相邻的日期之和为75,你认为可能吗? 为什么?
1520 |
1521 | (4)若连续七天的日期之和是77,请问第二天是星期几?
1522 |
1523 | ### 练习1
1524 |
1525 | 观察如下某月日历:
1526 |
1527 | 如果上述日历中一个竖列上连续的四个日期之和为54,那么第一天是几号?
1528 |
1529 | ### 例题2
1530 |
1531 | 从1开始的连续自然数按如图所示的规则排列,并用一个十字架框出五个数,能否使这五个数的和等于:
1532 |
1533 | (1)100;(2)200;(3)400;(4)600
1534 |
1535 | ### 练习2
1536 |
1537 | 从1开始的自然数按下图所示的规则排列,并用一个正方形框出九个数,能否使这九个数的和等于
1538 |
1539 | (1)2007;(2)2008;(3)2016
1540 |
1541 | 能够等于9数之和的数是()。
1542 |
1543 | ### 例题3
1544 |
1545 | 从1开始的自然数按下图所示的规则排列,并用一个平行四边形框出四个数,能否使这四个数的和分别等于126,408,842。若能办到,请写出平行四边形框内的最小数;若不能办到,说明理由。
1546 |
1547 | ### 练习3
1548 |
1549 | 下图中台历上斜着的表示日期的三个数之和为42,这三个日期中最大的一天是()号。
1550 |
1551 | ### 例题4
1552 |
1553 | 如图,将从5开始的连续自然数按规律填入数表中,请问:
1554 |
1555 | (1)213应该排在第几列?
1556 | (2)第3行第100列的数是多少?
1557 |
1558 | ### 练习4
1559 |
1560 | 将正整数1,2,3,…,从小到大按下面规律排列,若第4行第3列的数为36,则n=()。
1561 |
1562 | ### 例题5
1563 |
1564 | 如图,从4开始的连续自然数是按某种规律排列的,请问:
1565 |
1566 | (1)100在第几行,第几列?
1567 |
1568 | (2)第3行第20列的数是多少?
1569 |
1570 | ### 练习5
1571 |
1572 | 仔细观察下列数的排列规律:
1573 |
1574 | 则2017排在这个数表的第()行,第()列。(横为行,竖为列)
1575 |
1576 | ### 例题6
1577 |
1578 | 下列数表中5000在哪个字母下方?
1579 |
1580 | ### 练习6
1581 |
1582 | 下列数表中3333在哪个字母右边?
1583 |
1584 | ### 巩固1
1585 |
1586 | ### 巩固2
1587 |
1588 | ### 巩固3
1589 |
1590 | ## 4.2.03. 第五种运算
1591 |
1592 | ### 例题1(乘方/幂)
1593 |
1594 | (1)$\underbrace{6\times6\times6\times\dots\times6} _{8个6}$的结果记作(),读作()。
1595 |
1596 | (2)在$13^{57}$中,底数数(),指数是(),幂是(),读作()。
1597 |
1598 | (3)请把下列算式改写成幂的形式。
1599 |
1600 | | $\underbrace{7\times7\times7\times\dots\times7}_{80个7}=()$ | $9\times9\times9\times9=()^{4}=()^2$ |
1601 | | ----------------------------------------------------------- | ------------------------------------ |
1602 | | $16=()^4$ | $27=()^3$ |
1603 | | $125=()^3$ | $81=()^4=()^2$ |
1604 |
1605 | (4)计算:$3^5=()$;$6^3=()$;$5^4=()$
1606 |
1607 | ### 练习1
1608 |
1609 | (1)$10^n$表示n个10相成所得的积。()
1610 |
1611 | (2)$7^8$表示7个8相乘。()
1612 |
1613 | (3)$\underbrace{(a+b)(a+b)\dots(a+b)}_{18个(a+b)}$写成乘方形式是$(a+b)^{18}$。()
1614 |
1615 | (4)任何数的零次方都等于0。()
1616 |
1617 | ### 例题2(同底数幂乘法)
1618 |
1619 | 根据乘方的意义:$4^2=4×4$,$4^3=4×4×4$,从而$4^2×4^3=(4×4)×(4×4×4)=4^5$,那么
1620 |
1621 | (1)计算(用幂的形式表示):$12^2×12^7$;$23×23^{17}$
1622 |
1623 | (2)计算(用幂的形式表示):$4^7×4^n$;$a^7×a^{24}$。
1624 |
1625 | (3)计算(用幂的形式表示):$23^1×23^2×23^3×……×23^{99}×23^{100}$。
1626 |
1627 | ### 练习2
1628 |
1629 | 计算:$3^1×3^2×3^3×……×3^9×3^{10}$。
1630 |
1631 | ### 例题3(同底数幂除法)
1632 |
1633 | 根据乘方的意义:$4^5=4×4×4×4×4$,$4^2=4×4$,从而$4^5÷4^2=(4×4×4×4×4)÷(4×4)=4^3$,那么
1634 |
1635 | (1)计算(用幂的形式表示):$23^5÷23^2=()$;$34^{13}÷34^7=()$;$81^7÷81^7=81^{()}=()$。
1636 |
1637 | (2)计算(用幂的形式表示):$8^a÷8^2(a≧2)$;$a^9÷a^7$;$b^c÷b^c$。
1638 |
1639 | (3)计算(用幂的形式表示): $79^{50}\div79^{8}\div79^{14}\div79^{27}$。
1640 |
1641 | ### 练习3
1642 |
1643 | 计算(用幂的形式表示):
1644 |
1645 | (1)$2^2×2^4×2^6$;$3\times3^3\times3^5\times3^7\times3^9$
1646 |
1647 | (2)$7^{25}÷7^{12}÷7^8÷7$;$67^{35}\div67^{24}\div67^{10}$;$13^{31}\div13^{21}\div13^{7}\div13^{3}$
1648 |
1649 | ### 例题4(幂的乘方)
1650 |
1651 | 根据乘方的意义:$4^3=4×4×4$,从而$(4^2)^3=4^2×4^2×4^2=4^6$,那么
1652 |
1653 | (1)计算(用幂的形式表示):$(5^5)^3$;$(13^2)^3$;
1654 |
1655 | (2)计算(用幂的形式表示):$9^4×3^3$;$2^6×4^2×8^2$。
1656 |
1657 | ### 练习4
1658 |
1659 | 计算(用幂的形式表示)。
1660 |
1661 | $(29^2)n$;$(37^m)^5$;$(b^3)^4$。
1662 |
1663 | ### 例题5(积的乘方)
1664 |
1665 | 根据乘方的意义:$(4\times5)^3=(4\times5)\times(4\times5)\times(4\times5)=4\times4\times4\times5\times5\times5=4^3\times5^3$,那么
1666 |
1667 | (1)计算(用幂的形式表示):$(2\times7)^5=()\times()$;$(25\times17)^m=()\times()$;
1668 |
1669 | (2)计算(用幂的形式表示):$6^5=()^5\times()^5$;$35^9=()\times()$;
1670 |
1671 | (3)计算(用幂的形式表示):$(2\times7^3)^5$;$(3^5\times5^2)^3$。
1672 |
1673 | ### 练习5
1674 |
1675 | 计算(用幂的形式表示):
1676 |
1677 | (1)$5\times5\times5\times11\times11\times11=()^3\times()^3=()^3$;
1678 |
1679 | (2)$5^4\times7^6\times5^6\times7^4=()\times()=()^{10}$
1680 |
1681 | ### 例题6(混合计算)
1682 |
1683 | 计算(答案用幂的形式表示)。
1684 |
1685 | $11^{12}\times7^{27}\times9^{15}\div7^{18}\div11^{7}\div9^{13}$
1686 |
1687 | ### 练习6
1688 |
1689 | 计算(答案用幂的形式表示)。
1690 |
1691 | (1)$(2^3)^4\times(9^4)^3$
1692 |
1693 | (2)$(7^6)^5\times(5^3)^7\div7^{15}\div5^{12}$
1694 |
1695 | ## 4.2.05. 质数与合数初步
1696 |
1697 | ### 例题1
1698 |
1699 | (1)若bc=a,且a,b,c均为整数,则a是b、c的倍数,b、c是a的因数;那么,3x8=24中,()是()的倍数,()是()的因数。
1700 |
1701 | (2)一个数除了1和它本身,不再有别的因数,这个数就叫作();一个数除了1和它本还有别的因数,这个数就叫作()。要特别记住:()既不是质数,也不是合数。
1702 |
1703 | (3)写出100以内的所有质数。
1704 |
1705 | ### 练习1
1706 |
1707 | (1)正整数可以分为()、质数和合数三类。
1708 |
1709 | (2)质数有()个因数,合数至少有()个因数,1有()个因数。
1710 |
1711 | (3)最小的质数是(),最小的合数是()。
1712 |
1713 | (4)唯一的一个既是偶数又是质数的数是()。
1714 |
1715 | ### 例题2
1716 |
1717 | 如图,三张卡片上各印有一个数字。从这三张卡片中选取一张或多张(每张最多选1次)拼成质数,一共可以拼成多少个不同的质数?
1718 |
1719 | ### 练习2
1720 |
1721 | 有三张卡片,在它们上面各写有一个数字(如图)。从中抽出一张、二张、三张,按任意次序排起来,可以得到不同的一位数、二位数、三位数。请你将其中的质数都写出来。
1722 |
1723 | ### 例题3
1724 |
1725 | 在51,101,103,105,107,109,1001这七个数中,质数有多少个?
1726 |
1727 | ### 练习3
1728 |
1729 | 在111~119这九个数中,质数有多少个?
1730 |
1731 | ### 例题4
1732 |
1733 | (1)如果两个质数相加等于39,这两个质数等于多少?
1734 |
1735 | (2)如果三个互不相同的质数相加,和为40,这三个质数分别是多少?
1736 |
1737 | (3)已知P,Q都是质数,并且$P×11-Q×93=2003$,则$P\times Q$=()
1738 |
1739 | ### 练习4
1740 |
1741 | 7个连续质数从大到小排列是a、b、c、d、e、f、g。已知它们的和是偶数,那么d是多少?
1742 |
1743 | ### 例题5
1744 |
1745 | 从小到大写出5个质数,使后面的数都比前面的数大12,这样的数有几组?
1746 |
1747 | ### 练习5
1748 |
1749 | 三个质数的乘积恰好等于它们和的5倍,这三个质数分别是多少?
1750 |
1751 | ### 例题6
1752 |
1753 | 将222分拆成10个质数之和,要求其中最大的质数尽可能的小,那么这个最大的质数是();如要求最大的质数尽可能的大,那么这个最大的质数为()。
1754 |
1755 | ### 练习6
1756 |
1757 | 将50分拆成10个质数的和,要求其中最大的质数尽可能大,则这个最大的质数是多少?
1758 |
1759 | ### 练习1
1760 |
1761 | $1+2\times3+4\times5+6\times7+…+98\times99$的计算结果是奇数还是偶数,为什么?
1762 |
1763 | ### 练习2
1764 |
1765 | 两个质数之和为33,求这两个质数的乘积是多少。
1766 |
1767 | ### 练习3
1768 |
1769 | 著名的哥德巴赫猜想是:“任意一个大于4的偶数都可以表示为两个质数的和”。如6=3+3,12=5+7等。那么,自然数100可以写成多少种两个不同质数的和的形式?请分别写出来(100=3+97和100=97+3算作同一种形式)
1770 |
1771 | ### 练习1
1772 |
1773 | 已知a,b,c是三个连续自然数,其中a是偶数。根据下面的的信息:小红说:“那么a+1,b+2,c+3这三个数的乘积一定是奇数”;小明:“不对a+1,b+2,c+3这三个数的乘积是偶数”。判断小红和小明两人谁说的是正确的。
1774 |
1775 | ### 练习2
1776 |
1777 | 如果a,b均为质数,且3a+7b=41,则a+b=()
1778 |
1779 | ### 练习3
1780 |
1781 | 一个两位质数个位与十位数字交换后仍为质数,这样的质数有几个?
1782 |
1783 | ### 练习1
1784 |
1785 | 是否存在自然数a和b,使得ab(a+b)=115?为什么?
1786 |
1787 | ### 练习2
1788 |
1789 | 已知三个质数之和为36(可以相等),这三个质数中最大的可能是。
1790 |
1791 | ### 练习3
1792 |
1793 | ### 练习1
1794 |
1795 | 已知n,n+6,n+84,n+102,n+218都是质数,那么n=()
1796 |
1797 | ### 练习2
1798 |
1799 | A,B,C为3个小于20的质数,A+B+C=30,求这三个质数分别是几。
1800 |
1801 | ### 练习3
1802 |
1803 | 某质数加6或减6得到的数仍是质数,在50以内你能找出几个这样的质数?把它们写出来。
1804 |
1805 | ## 4.2.06. 火车过桥
1806 |
1807 | ### 例题1
1808 |
1809 | 己知某铁路桥长1000米,一列火车从桥上通过,火车速度每秒40米,车长200米。
1810 | (1)火车完全在桥时间是多少?
1811 | (2)火车从开始上桥到完全下桥所用时间是多少?
1812 |
1813 | ### 练习1
1814 |
1815 | 一列火车经过南京长江大桥,大桥长6700米,这列火车长100米,火车每分钟行4000米,这列火车经过南京长江大桥需要多少分钟?
1816 |
1817 | ### 例题2
1818 |
1819 | 一列火车通过530米长的桥需40秒钟,以同样的速度穿过380米长的山洞需30秒钟。则这列火车的速度是多少?全长是多少米?
1820 |
1821 | ### 练习2
1822 |
1823 | 牛牛站在铁路旁,一列火车从他身边开过用了21秒,以同样的速度通过一座长为2070米的大桥,用了1.5分钟。火车长多少米?
1824 |
1825 | ### 例题3
1826 |
1827 | 牛牛以每秒10米的速度沿铁道边的小路骑车。
1828 | (1)身后一辆火车以每秒100米的速度超过他,从车头追上牛牛到车尾离开共用时4秒,那么车长多少米?
1829 | (2)过了一会,另一辆火车以每秒100米的速度迎面开来,从与牛牛相遇到离开,共用时3秒。那么车长是多少?
1830 |
1831 | ### 练习3
1832 |
1833 | 丁丁以3米/秒的速度沿着铁路跑步,迎面开来一列火车,它的行驶速度是18米/秒,火车从丁丁身旁经过的时间是7秒,求火车的车长是多少米?
1834 |
1835 | ### 例题4
1836 |
1837 | 一列快车和一列慢车相向而行,快车的车长是280米,慢车的车长为385米,坐在快车上的人看见慢车驶过的时间是11秒,那么坐在慢车上的人看见快车驶过的时间是多少?
1838 |
1839 | ### 练习4
1840 |
1841 | 一列快车和一列慢车相向而行,快车的车长是150米,慢车的车长为200米,坐在慢车上的人看见快车驶过的时间是3秒,那么坐在快车上的人看见慢车驶过的时间是多少?
1842 |
1843 | ### 例题5
1844 |
1845 | 有两列火车,一列长200米,每秒行34米;一列长178米,每秒行20米。
1846 | (1)两列火车相向而行,从两车车头相遇到车尾相离共需要多少秒?
1847 | (2)两列火车同向行驶,从快车的车头追上慢车的车尾,到快车的车尾超过慢车的车头,共需多少秒?
1848 |
1849 | ### 练习5
1850 |
1851 | 快车长300米,每秒行20米,慢车长150米,每秒行10米。
1852 | (1)两列火车相向而行,从两车车头相遇到车尾相离共需要多少秒?
1853 | (2)两列火车同向行驶,从快车的车头追及慢车的车尾,到快车的车尾超过慢车的车头,其需多少秒?
1854 |
1855 | ### 例题6
1856 |
1857 | 有两列同方向行驶的火车,快车每秒行33米,慢车每秒行21米。如果从两车头对齐开始算,则行20秒后快车超过慢车;如果从两车尾对齐开始算,则行25秒后快车超过慢车。
1858 | (1)两车车长分别是多少?
1859 | (2)如果两车相对行驶,两车从车头相遇到车尾相离需要经过多少时间?
1860 |
1861 | ### 练习6
1862 |
1863 | 现有两列火车同时同方向齐头行进,行12秒后快车超过慢车,快车每秒行18米,慢车每秒行10米。如果这两列火车车尾相齐同时同方向行进,则9秒后快车超过慢车,那么,快车车头追上慢车车尾到快车车尾离开慢车车头的时间为多少秒?
1864 |
1865 | ## 4.2.07. 包含与排除
1866 |
1867 | ### 例题1
1868 |
1869 | 实验小学四年级二班,参加语文兴趣小组的有28人,参加数学兴趣小组的有29人,有12人两个小组都参加。这个班有多少人参加了语文或数学兴趣小组?
1870 |
1871 | ### 练习1
1872 |
1873 | 学校文艺组的每位同学至少会演奏钢琴和手风琴中的一种乐器,己知会演奏钢琴的有24人,会演奏手风琴的有17人,其中两种乐器都会演奏的有8人,则文艺组一共有多少人?
1874 |
1875 | ### 例题2
1876 |
1877 | 某餐馆有40道招牌菜,牛牛吃过其中的15道,丁丁吃过其中的9道,而且有4道菜是两人都吃过的,请问:有多少道招牌菜是两人都没有吃过的?
1878 |
1879 | ### 练习2
1880 |
1881 | 在46人参加的采摘活动中,只采了樱桃的有18人,既采了樱桃又采了杏的有7人,既没采樱桃又没采杏的有6人,问:只采了杏的有多少人?
1882 |
1883 | ### 例题3
1884 |
1885 | 在1~100这些自然数中,能被3或5同时整除的数有多少个?
1886 |
1887 | ### 练习3
1888 |
1889 | 在1~60这些自然数中:
1890 | (1)能被2整除的数有多少个?
1891 | (2)能被5整除的数有多少个?
1892 | (3)能被2和5整除的数有多少个?
1893 | (4)能被2或5整除的数有多少个?
1894 | (5)不能被2整除也不能被5整除的数有多少个?
1895 |
1896 | ### 例题4
1897 |
1898 | 50名同学面向老师站成一行。老师先让大家从左至右按1,2,3,……,49,50依次报数;再让报数是4的倍数的同学向后转,接着又让报数是6的倍数的同学向后转。问:现在面向老师的同学还有多少名?
1899 |
1900 | ### 练习4
1901 |
1902 | 一根长60厘米的木棍,每5厘米用红点标记,每6厘米用蓝点标记。沿标记的点把木棍锯断,木棍总共被锯成几段?
1903 |
1904 | ### 例题5
1905 |
1906 | 光明小学组织棋类比赛,分成围棋、中国象棋和国际象棋三个组进行,参加国棋比赛的有42人,参加中国象棋比赛的有55人,参加国际象棋比赛的有33人,同时参加了围棋和中国象棋比赛的有18人,同时参加了国棋和国际象棋比赛的有10人,同时参加了中国象棋和国际象棋比赛的有9人,其中三种棋赛都参加的有5人,问参加棋类比赛的共有多少人?
1907 |
1908 | ### 练习5
1909 |
1910 | 三位基金经理投资若干只股票。张经理买过其中66只,王经理买过其中40只,李经理买过其中23只。张经理和王经理都买过的有17只,王经理和李经理都买过的有13只,李经理和张经理都买过的有9只,三个人都买过的有6只。请问:这三位经理一共买过多少只股票?
1911 |
1912 | ### 例题6
1913 |
1914 | 在一个100人的旅行团中,每人至少懂英语、汉语、日语中的一种,其中懂英语的有66人,汉语的有54人,懂日语的有55人,既懂英语又懂汉语的有25人,既懂汉语又懂日语的有21人,但没有一个人三门语言都懂。问:有多少人既懂英语又懂日语?
1915 |
1916 | ### 练习6
1917 |
1918 | 少年宫春季书法班、美术班、器乐班招生。书法班招收了29名学员,在这些学员中,既报书法又报美术的有13名,既报书法又报器乐的有12人,三个科目都报的有5名。那么,只参加书法学习的学员有几名?
1919 |
1920 | ### 练习1
1921 |
1922 | 一根长101厘米长的木棍,从同一端开始,第一次每隔4厘米画一个刻度,第二次每隔6厘米画一个刻度,如果按刻度把木棍截断,那么可以截成多少段?
1923 |
1924 | ### 练习2
1925 |
1926 | 写有1到100编号的灯100盏,亮着排成一排,第一次把编号是3的倍数的灯拉一次开关,第二次把编号是5的倍数的灯拉一次开关,那么亮着的灯还有多少盏?
1927 |
1928 | ### 练习3
1929 |
1930 | 在1~100这些自然数中:
1931 |
1932 | 1. 能被2整除的数有多少个?
1933 | 2. 能被3整除的数有多少个?
1934 | 3. 能被2和3整除的数有多少个?
1935 | 4. 能被2或3整除的数有多少个?
1936 | 5. 不能被2整除也不能被3整除的数有多少个?
1937 |
1938 | ## 4.2.08. 整数与数列
1939 |
1940 | ### 热身1
1941 |
1942 | ### 热身2
1943 |
1944 | ### 热身3
1945 |
1946 | ### 例题1
1947 |
1948 | 已知数列1,6,11,16,21,⋯,146,问:
1949 | (1)这个数列中第20个数是多少?
1950 | (2)81是这个数列的第几个数?
1951 | (3)这个数列一共有几项?
1952 | (4)将数列中所有的数加起来,和是多少?
1953 |
1954 | ### 练习1
1955 |
1956 | (1)数列3,7,11,⋯,第18项是()。
1957 | (2)数列4,9,14,⋯,其中254是这个数列的第()项。
1958 | (3)数列4,8,12,⋯,160,这个数列共有()项。
1959 |
1960 | ### 例题2
1961 |
1962 | 1~100中除以5余2的数的和是多少?
1963 |
1964 | ### 练习2
1965 |
1966 | 1~100中所有5的倍数的和是多少?
1967 |
1968 | ### 例题3
1969 |
1970 | 计算:$24\times23-23\times22+22\times21-21\times20+\dots+2\times1$
1971 |
1972 | ### 练习3
1973 |
1974 | 计算:$14\times13-13\times12+12\times11-11\times10+10\times9-9\times8+8\times7-7\times6+6\times5-5\times4+4\times3-3\times2+2\times1$
1975 |
1976 | ### 例题4(平方差公式)
1977 |
1978 | 有一串数1,4,9,16,25,36,⋯,它们是按什么规律排列的?其中第9个数与第10个数相差多少?第2014个数与第2015个数相差多少?
1979 |
1980 | ### 练习4
1981 |
1982 | 计算:$[2017-(8.5\times8.5-1.5\times1.5)\div10]\div160-0.3$
1983 |
1984 | ### 例题5
1985 |
1986 | 计算:$100^2-99^2+98^2-97^2+\dots+2^2-1^2$
1987 |
1988 | ### 练习5
1989 |
1990 | 计算:$20\times20-19\times19+18\times18-17\times17+\dots+2\times2-1\times1$
1991 |
1992 | ### 例题6(整数列项)
1993 |
1994 | 计算:$1\times2+2\times3+3\times4+\dots+49\times50$
1995 |
1996 | ### 练习6
1997 |
1998 | ## 4.2.09. 统筹与最优化
1999 |
2000 | ### 例题1
2001 |
2002 | 理发店里只有一位理发师,但是同时来了五位顾客,根据他们所要理的发型,分别需要10分钟、12分钟、15分钟、20分钟和24分钟,怎样安排他们理发的顺序,才能使这五人理发和等候所用时间的总和最少?最少时间为多少?
2003 |
2004 | ### 练习1
2005 |
2006 | 5个人各拿一个水桶在自来水龙头前等候打水,他们打水所需要的时间分别是1分钟、2分钟、3分钟、4分钟和5分钟,如果只有一个水龙头,适当安排他们的打水顺序,就能够使每个人排队和打水时间的总和最小,那么这个最小值是多少分钟?
2007 |
2008 | ### 例题2
2009 |
2010 | 电车公司维修站有7辆电车需要维修,如果用一名工人维修这7辆电车,修复时间分别为12分钟,17分钟,8分钟,18分钟,23分钟,30分钟,14分钟。每辆电车每停开1分钟的损失是11元,现在由3名工作效率相同的维修工人各自单独工作,要使经济损失减到最小程度,那么最小的损失是多少元?
2011 |
2012 | ### 练习2
2013 |
2014 | 有八个人各拿着一个水桶同时到水龙头前打水,水龙头注满第一个人的桶需要1分钟,注满第二个人的桶需要2分钟,……,如此下去,
2015 | (1)当只有一个水龙头时,如何巧妙安排这八个人打水,使他们总的花费时间最少?最少的时间是多少?
2016 | (2)当有两个水龙头时,如何巧妙安排这八个人打水,使他们总的花费时间最少?最少的时间是多少?
2017 |
2018 | ### 例题3
2019 |
2020 | 有一家五口人要在夜晚过一座独木桥。他们家里的老爷爷行动非常不便,过桥需要12分钟;孩子们的父亲贪吃且不爱运动,体重严重超标,过河需要时间也较长,8分钟;母亲则一直坚持劳作,动作还算敏捷,过桥要6分钟;两个孩子中姐姐需要3分钟,弟弟只要1分钟。当时正是初一,夜晚又是阴天,不要说月亮,连一点星光都没有,真所谓伸手不见五指。幸运的是他们有一盏油灯,同时可以有两个人借助灯光过桥。但要命的是灯油将尽,这盏灯只能再维持30分钟了!他们焦急万分,该怎样过桥呢?
2021 |
2022 | ### 练习3
2023 |
2024 | 牛牛、丁丁、田田和阿普4个小朋友郊游回家时天色己晚,他们来到一条河的东岸,要通过一座小木桥到西岸,但是他们4个人只有一个手电筒,由于桥的承重量小,每次只能过2人,因此必须先由2个人拿着手电简过桥,并由1个人再将手电简送回,再由2个人拿着手电筒过桥…直到4人都通过小木桥。己知,牛牛单独过桥要1分钟;丁丁单独过桥要1.5分钟;田田单独过桥要2分钟;阿普单独过桥要2.5分钟。那么,4个人都通过小木桥,最少要多少分钟?
2025 |
2026 | ### 例题4
2027 |
2028 | (1)如图,在街道上有A、B、C、D、E五栋居民楼,现在设立一个公交站,为使五栋楼的居民到车站的距离之和最短,车站应位于何处?
2029 |
2030 |
1508 |
1509 | ## 4.2.03. 数表-从日历谈起
1510 |
1511 | ### 例题1
1512 |
1513 | 观察如下日历:
1514 |
1515 | (1)若设一个横行上相邻的三个日期中间的日期为a,那么左右两边的日期分别是什么?
1516 |
1517 | (2)若设一个竖列上相邻的三个日期中间的日期为b,那么上下两边的日期分别是什么?
1518 |
1519 | (3)如果在上述日历中某个竖列上三个相邻的日期之和为75,你认为可能吗? 为什么?
1520 |
1521 | (4)若连续七天的日期之和是77,请问第二天是星期几?
1522 |
1523 | ### 练习1
1524 |
1525 | 观察如下某月日历:
1526 |
1527 | 如果上述日历中一个竖列上连续的四个日期之和为54,那么第一天是几号?
1528 |
1529 | ### 例题2
1530 |
1531 | 从1开始的连续自然数按如图所示的规则排列,并用一个十字架框出五个数,能否使这五个数的和等于:
1532 |
1533 | (1)100;(2)200;(3)400;(4)600
1534 |
1535 | ### 练习2
1536 |
1537 | 从1开始的自然数按下图所示的规则排列,并用一个正方形框出九个数,能否使这九个数的和等于
1538 |
1539 | (1)2007;(2)2008;(3)2016
1540 |
1541 | 能够等于9数之和的数是()。
1542 |
1543 | ### 例题3
1544 |
1545 | 从1开始的自然数按下图所示的规则排列,并用一个平行四边形框出四个数,能否使这四个数的和分别等于126,408,842。若能办到,请写出平行四边形框内的最小数;若不能办到,说明理由。
1546 |
1547 | ### 练习3
1548 |
1549 | 下图中台历上斜着的表示日期的三个数之和为42,这三个日期中最大的一天是()号。
1550 |
1551 | ### 例题4
1552 |
1553 | 如图,将从5开始的连续自然数按规律填入数表中,请问:
1554 |
1555 | (1)213应该排在第几列?
1556 | (2)第3行第100列的数是多少?
1557 |
1558 | ### 练习4
1559 |
1560 | 将正整数1,2,3,…,从小到大按下面规律排列,若第4行第3列的数为36,则n=()。
1561 |
1562 | ### 例题5
1563 |
1564 | 如图,从4开始的连续自然数是按某种规律排列的,请问:
1565 |
1566 | (1)100在第几行,第几列?
1567 |
1568 | (2)第3行第20列的数是多少?
1569 |
1570 | ### 练习5
1571 |
1572 | 仔细观察下列数的排列规律:
1573 |
1574 | 则2017排在这个数表的第()行,第()列。(横为行,竖为列)
1575 |
1576 | ### 例题6
1577 |
1578 | 下列数表中5000在哪个字母下方?
1579 |
1580 | ### 练习6
1581 |
1582 | 下列数表中3333在哪个字母右边?
1583 |
1584 | ### 巩固1
1585 |
1586 | ### 巩固2
1587 |
1588 | ### 巩固3
1589 |
1590 | ## 4.2.03. 第五种运算
1591 |
1592 | ### 例题1(乘方/幂)
1593 |
1594 | (1)$\underbrace{6\times6\times6\times\dots\times6} _{8个6}$的结果记作(),读作()。
1595 |
1596 | (2)在$13^{57}$中,底数数(),指数是(),幂是(),读作()。
1597 |
1598 | (3)请把下列算式改写成幂的形式。
1599 |
1600 | | $\underbrace{7\times7\times7\times\dots\times7}_{80个7}=()$ | $9\times9\times9\times9=()^{4}=()^2$ |
1601 | | ----------------------------------------------------------- | ------------------------------------ |
1602 | | $16=()^4$ | $27=()^3$ |
1603 | | $125=()^3$ | $81=()^4=()^2$ |
1604 |
1605 | (4)计算:$3^5=()$;$6^3=()$;$5^4=()$
1606 |
1607 | ### 练习1
1608 |
1609 | (1)$10^n$表示n个10相成所得的积。()
1610 |
1611 | (2)$7^8$表示7个8相乘。()
1612 |
1613 | (3)$\underbrace{(a+b)(a+b)\dots(a+b)}_{18个(a+b)}$写成乘方形式是$(a+b)^{18}$。()
1614 |
1615 | (4)任何数的零次方都等于0。()
1616 |
1617 | ### 例题2(同底数幂乘法)
1618 |
1619 | 根据乘方的意义:$4^2=4×4$,$4^3=4×4×4$,从而$4^2×4^3=(4×4)×(4×4×4)=4^5$,那么
1620 |
1621 | (1)计算(用幂的形式表示):$12^2×12^7$;$23×23^{17}$
1622 |
1623 | (2)计算(用幂的形式表示):$4^7×4^n$;$a^7×a^{24}$。
1624 |
1625 | (3)计算(用幂的形式表示):$23^1×23^2×23^3×……×23^{99}×23^{100}$。
1626 |
1627 | ### 练习2
1628 |
1629 | 计算:$3^1×3^2×3^3×……×3^9×3^{10}$。
1630 |
1631 | ### 例题3(同底数幂除法)
1632 |
1633 | 根据乘方的意义:$4^5=4×4×4×4×4$,$4^2=4×4$,从而$4^5÷4^2=(4×4×4×4×4)÷(4×4)=4^3$,那么
1634 |
1635 | (1)计算(用幂的形式表示):$23^5÷23^2=()$;$34^{13}÷34^7=()$;$81^7÷81^7=81^{()}=()$。
1636 |
1637 | (2)计算(用幂的形式表示):$8^a÷8^2(a≧2)$;$a^9÷a^7$;$b^c÷b^c$。
1638 |
1639 | (3)计算(用幂的形式表示): $79^{50}\div79^{8}\div79^{14}\div79^{27}$。
1640 |
1641 | ### 练习3
1642 |
1643 | 计算(用幂的形式表示):
1644 |
1645 | (1)$2^2×2^4×2^6$;$3\times3^3\times3^5\times3^7\times3^9$
1646 |
1647 | (2)$7^{25}÷7^{12}÷7^8÷7$;$67^{35}\div67^{24}\div67^{10}$;$13^{31}\div13^{21}\div13^{7}\div13^{3}$
1648 |
1649 | ### 例题4(幂的乘方)
1650 |
1651 | 根据乘方的意义:$4^3=4×4×4$,从而$(4^2)^3=4^2×4^2×4^2=4^6$,那么
1652 |
1653 | (1)计算(用幂的形式表示):$(5^5)^3$;$(13^2)^3$;
1654 |
1655 | (2)计算(用幂的形式表示):$9^4×3^3$;$2^6×4^2×8^2$。
1656 |
1657 | ### 练习4
1658 |
1659 | 计算(用幂的形式表示)。
1660 |
1661 | $(29^2)n$;$(37^m)^5$;$(b^3)^4$。
1662 |
1663 | ### 例题5(积的乘方)
1664 |
1665 | 根据乘方的意义:$(4\times5)^3=(4\times5)\times(4\times5)\times(4\times5)=4\times4\times4\times5\times5\times5=4^3\times5^3$,那么
1666 |
1667 | (1)计算(用幂的形式表示):$(2\times7)^5=()\times()$;$(25\times17)^m=()\times()$;
1668 |
1669 | (2)计算(用幂的形式表示):$6^5=()^5\times()^5$;$35^9=()\times()$;
1670 |
1671 | (3)计算(用幂的形式表示):$(2\times7^3)^5$;$(3^5\times5^2)^3$。
1672 |
1673 | ### 练习5
1674 |
1675 | 计算(用幂的形式表示):
1676 |
1677 | (1)$5\times5\times5\times11\times11\times11=()^3\times()^3=()^3$;
1678 |
1679 | (2)$5^4\times7^6\times5^6\times7^4=()\times()=()^{10}$
1680 |
1681 | ### 例题6(混合计算)
1682 |
1683 | 计算(答案用幂的形式表示)。
1684 |
1685 | $11^{12}\times7^{27}\times9^{15}\div7^{18}\div11^{7}\div9^{13}$
1686 |
1687 | ### 练习6
1688 |
1689 | 计算(答案用幂的形式表示)。
1690 |
1691 | (1)$(2^3)^4\times(9^4)^3$
1692 |
1693 | (2)$(7^6)^5\times(5^3)^7\div7^{15}\div5^{12}$
1694 |
1695 | ## 4.2.05. 质数与合数初步
1696 |
1697 | ### 例题1
1698 |
1699 | (1)若bc=a,且a,b,c均为整数,则a是b、c的倍数,b、c是a的因数;那么,3x8=24中,()是()的倍数,()是()的因数。
1700 |
1701 | (2)一个数除了1和它本身,不再有别的因数,这个数就叫作();一个数除了1和它本还有别的因数,这个数就叫作()。要特别记住:()既不是质数,也不是合数。
1702 |
1703 | (3)写出100以内的所有质数。
1704 |
1705 | ### 练习1
1706 |
1707 | (1)正整数可以分为()、质数和合数三类。
1708 |
1709 | (2)质数有()个因数,合数至少有()个因数,1有()个因数。
1710 |
1711 | (3)最小的质数是(),最小的合数是()。
1712 |
1713 | (4)唯一的一个既是偶数又是质数的数是()。
1714 |
1715 | ### 例题2
1716 |
1717 | 如图,三张卡片上各印有一个数字。从这三张卡片中选取一张或多张(每张最多选1次)拼成质数,一共可以拼成多少个不同的质数?
1718 |
1719 | ### 练习2
1720 |
1721 | 有三张卡片,在它们上面各写有一个数字(如图)。从中抽出一张、二张、三张,按任意次序排起来,可以得到不同的一位数、二位数、三位数。请你将其中的质数都写出来。
1722 |
1723 | ### 例题3
1724 |
1725 | 在51,101,103,105,107,109,1001这七个数中,质数有多少个?
1726 |
1727 | ### 练习3
1728 |
1729 | 在111~119这九个数中,质数有多少个?
1730 |
1731 | ### 例题4
1732 |
1733 | (1)如果两个质数相加等于39,这两个质数等于多少?
1734 |
1735 | (2)如果三个互不相同的质数相加,和为40,这三个质数分别是多少?
1736 |
1737 | (3)已知P,Q都是质数,并且$P×11-Q×93=2003$,则$P\times Q$=()
1738 |
1739 | ### 练习4
1740 |
1741 | 7个连续质数从大到小排列是a、b、c、d、e、f、g。已知它们的和是偶数,那么d是多少?
1742 |
1743 | ### 例题5
1744 |
1745 | 从小到大写出5个质数,使后面的数都比前面的数大12,这样的数有几组?
1746 |
1747 | ### 练习5
1748 |
1749 | 三个质数的乘积恰好等于它们和的5倍,这三个质数分别是多少?
1750 |
1751 | ### 例题6
1752 |
1753 | 将222分拆成10个质数之和,要求其中最大的质数尽可能的小,那么这个最大的质数是();如要求最大的质数尽可能的大,那么这个最大的质数为()。
1754 |
1755 | ### 练习6
1756 |
1757 | 将50分拆成10个质数的和,要求其中最大的质数尽可能大,则这个最大的质数是多少?
1758 |
1759 | ### 练习1
1760 |
1761 | $1+2\times3+4\times5+6\times7+…+98\times99$的计算结果是奇数还是偶数,为什么?
1762 |
1763 | ### 练习2
1764 |
1765 | 两个质数之和为33,求这两个质数的乘积是多少。
1766 |
1767 | ### 练习3
1768 |
1769 | 著名的哥德巴赫猜想是:“任意一个大于4的偶数都可以表示为两个质数的和”。如6=3+3,12=5+7等。那么,自然数100可以写成多少种两个不同质数的和的形式?请分别写出来(100=3+97和100=97+3算作同一种形式)
1770 |
1771 | ### 练习1
1772 |
1773 | 已知a,b,c是三个连续自然数,其中a是偶数。根据下面的的信息:小红说:“那么a+1,b+2,c+3这三个数的乘积一定是奇数”;小明:“不对a+1,b+2,c+3这三个数的乘积是偶数”。判断小红和小明两人谁说的是正确的。
1774 |
1775 | ### 练习2
1776 |
1777 | 如果a,b均为质数,且3a+7b=41,则a+b=()
1778 |
1779 | ### 练习3
1780 |
1781 | 一个两位质数个位与十位数字交换后仍为质数,这样的质数有几个?
1782 |
1783 | ### 练习1
1784 |
1785 | 是否存在自然数a和b,使得ab(a+b)=115?为什么?
1786 |
1787 | ### 练习2
1788 |
1789 | 已知三个质数之和为36(可以相等),这三个质数中最大的可能是。
1790 |
1791 | ### 练习3
1792 |
1793 | ### 练习1
1794 |
1795 | 已知n,n+6,n+84,n+102,n+218都是质数,那么n=()
1796 |
1797 | ### 练习2
1798 |
1799 | A,B,C为3个小于20的质数,A+B+C=30,求这三个质数分别是几。
1800 |
1801 | ### 练习3
1802 |
1803 | 某质数加6或减6得到的数仍是质数,在50以内你能找出几个这样的质数?把它们写出来。
1804 |
1805 | ## 4.2.06. 火车过桥
1806 |
1807 | ### 例题1
1808 |
1809 | 己知某铁路桥长1000米,一列火车从桥上通过,火车速度每秒40米,车长200米。
1810 | (1)火车完全在桥时间是多少?
1811 | (2)火车从开始上桥到完全下桥所用时间是多少?
1812 |
1813 | ### 练习1
1814 |
1815 | 一列火车经过南京长江大桥,大桥长6700米,这列火车长100米,火车每分钟行4000米,这列火车经过南京长江大桥需要多少分钟?
1816 |
1817 | ### 例题2
1818 |
1819 | 一列火车通过530米长的桥需40秒钟,以同样的速度穿过380米长的山洞需30秒钟。则这列火车的速度是多少?全长是多少米?
1820 |
1821 | ### 练习2
1822 |
1823 | 牛牛站在铁路旁,一列火车从他身边开过用了21秒,以同样的速度通过一座长为2070米的大桥,用了1.5分钟。火车长多少米?
1824 |
1825 | ### 例题3
1826 |
1827 | 牛牛以每秒10米的速度沿铁道边的小路骑车。
1828 | (1)身后一辆火车以每秒100米的速度超过他,从车头追上牛牛到车尾离开共用时4秒,那么车长多少米?
1829 | (2)过了一会,另一辆火车以每秒100米的速度迎面开来,从与牛牛相遇到离开,共用时3秒。那么车长是多少?
1830 |
1831 | ### 练习3
1832 |
1833 | 丁丁以3米/秒的速度沿着铁路跑步,迎面开来一列火车,它的行驶速度是18米/秒,火车从丁丁身旁经过的时间是7秒,求火车的车长是多少米?
1834 |
1835 | ### 例题4
1836 |
1837 | 一列快车和一列慢车相向而行,快车的车长是280米,慢车的车长为385米,坐在快车上的人看见慢车驶过的时间是11秒,那么坐在慢车上的人看见快车驶过的时间是多少?
1838 |
1839 | ### 练习4
1840 |
1841 | 一列快车和一列慢车相向而行,快车的车长是150米,慢车的车长为200米,坐在慢车上的人看见快车驶过的时间是3秒,那么坐在快车上的人看见慢车驶过的时间是多少?
1842 |
1843 | ### 例题5
1844 |
1845 | 有两列火车,一列长200米,每秒行34米;一列长178米,每秒行20米。
1846 | (1)两列火车相向而行,从两车车头相遇到车尾相离共需要多少秒?
1847 | (2)两列火车同向行驶,从快车的车头追上慢车的车尾,到快车的车尾超过慢车的车头,共需多少秒?
1848 |
1849 | ### 练习5
1850 |
1851 | 快车长300米,每秒行20米,慢车长150米,每秒行10米。
1852 | (1)两列火车相向而行,从两车车头相遇到车尾相离共需要多少秒?
1853 | (2)两列火车同向行驶,从快车的车头追及慢车的车尾,到快车的车尾超过慢车的车头,其需多少秒?
1854 |
1855 | ### 例题6
1856 |
1857 | 有两列同方向行驶的火车,快车每秒行33米,慢车每秒行21米。如果从两车头对齐开始算,则行20秒后快车超过慢车;如果从两车尾对齐开始算,则行25秒后快车超过慢车。
1858 | (1)两车车长分别是多少?
1859 | (2)如果两车相对行驶,两车从车头相遇到车尾相离需要经过多少时间?
1860 |
1861 | ### 练习6
1862 |
1863 | 现有两列火车同时同方向齐头行进,行12秒后快车超过慢车,快车每秒行18米,慢车每秒行10米。如果这两列火车车尾相齐同时同方向行进,则9秒后快车超过慢车,那么,快车车头追上慢车车尾到快车车尾离开慢车车头的时间为多少秒?
1864 |
1865 | ## 4.2.07. 包含与排除
1866 |
1867 | ### 例题1
1868 |
1869 | 实验小学四年级二班,参加语文兴趣小组的有28人,参加数学兴趣小组的有29人,有12人两个小组都参加。这个班有多少人参加了语文或数学兴趣小组?
1870 |
1871 | ### 练习1
1872 |
1873 | 学校文艺组的每位同学至少会演奏钢琴和手风琴中的一种乐器,己知会演奏钢琴的有24人,会演奏手风琴的有17人,其中两种乐器都会演奏的有8人,则文艺组一共有多少人?
1874 |
1875 | ### 例题2
1876 |
1877 | 某餐馆有40道招牌菜,牛牛吃过其中的15道,丁丁吃过其中的9道,而且有4道菜是两人都吃过的,请问:有多少道招牌菜是两人都没有吃过的?
1878 |
1879 | ### 练习2
1880 |
1881 | 在46人参加的采摘活动中,只采了樱桃的有18人,既采了樱桃又采了杏的有7人,既没采樱桃又没采杏的有6人,问:只采了杏的有多少人?
1882 |
1883 | ### 例题3
1884 |
1885 | 在1~100这些自然数中,能被3或5同时整除的数有多少个?
1886 |
1887 | ### 练习3
1888 |
1889 | 在1~60这些自然数中:
1890 | (1)能被2整除的数有多少个?
1891 | (2)能被5整除的数有多少个?
1892 | (3)能被2和5整除的数有多少个?
1893 | (4)能被2或5整除的数有多少个?
1894 | (5)不能被2整除也不能被5整除的数有多少个?
1895 |
1896 | ### 例题4
1897 |
1898 | 50名同学面向老师站成一行。老师先让大家从左至右按1,2,3,……,49,50依次报数;再让报数是4的倍数的同学向后转,接着又让报数是6的倍数的同学向后转。问:现在面向老师的同学还有多少名?
1899 |
1900 | ### 练习4
1901 |
1902 | 一根长60厘米的木棍,每5厘米用红点标记,每6厘米用蓝点标记。沿标记的点把木棍锯断,木棍总共被锯成几段?
1903 |
1904 | ### 例题5
1905 |
1906 | 光明小学组织棋类比赛,分成围棋、中国象棋和国际象棋三个组进行,参加国棋比赛的有42人,参加中国象棋比赛的有55人,参加国际象棋比赛的有33人,同时参加了围棋和中国象棋比赛的有18人,同时参加了国棋和国际象棋比赛的有10人,同时参加了中国象棋和国际象棋比赛的有9人,其中三种棋赛都参加的有5人,问参加棋类比赛的共有多少人?
1907 |
1908 | ### 练习5
1909 |
1910 | 三位基金经理投资若干只股票。张经理买过其中66只,王经理买过其中40只,李经理买过其中23只。张经理和王经理都买过的有17只,王经理和李经理都买过的有13只,李经理和张经理都买过的有9只,三个人都买过的有6只。请问:这三位经理一共买过多少只股票?
1911 |
1912 | ### 例题6
1913 |
1914 | 在一个100人的旅行团中,每人至少懂英语、汉语、日语中的一种,其中懂英语的有66人,汉语的有54人,懂日语的有55人,既懂英语又懂汉语的有25人,既懂汉语又懂日语的有21人,但没有一个人三门语言都懂。问:有多少人既懂英语又懂日语?
1915 |
1916 | ### 练习6
1917 |
1918 | 少年宫春季书法班、美术班、器乐班招生。书法班招收了29名学员,在这些学员中,既报书法又报美术的有13名,既报书法又报器乐的有12人,三个科目都报的有5名。那么,只参加书法学习的学员有几名?
1919 |
1920 | ### 练习1
1921 |
1922 | 一根长101厘米长的木棍,从同一端开始,第一次每隔4厘米画一个刻度,第二次每隔6厘米画一个刻度,如果按刻度把木棍截断,那么可以截成多少段?
1923 |
1924 | ### 练习2
1925 |
1926 | 写有1到100编号的灯100盏,亮着排成一排,第一次把编号是3的倍数的灯拉一次开关,第二次把编号是5的倍数的灯拉一次开关,那么亮着的灯还有多少盏?
1927 |
1928 | ### 练习3
1929 |
1930 | 在1~100这些自然数中:
1931 |
1932 | 1. 能被2整除的数有多少个?
1933 | 2. 能被3整除的数有多少个?
1934 | 3. 能被2和3整除的数有多少个?
1935 | 4. 能被2或3整除的数有多少个?
1936 | 5. 不能被2整除也不能被3整除的数有多少个?
1937 |
1938 | ## 4.2.08. 整数与数列
1939 |
1940 | ### 热身1
1941 |
1942 | ### 热身2
1943 |
1944 | ### 热身3
1945 |
1946 | ### 例题1
1947 |
1948 | 已知数列1,6,11,16,21,⋯,146,问:
1949 | (1)这个数列中第20个数是多少?
1950 | (2)81是这个数列的第几个数?
1951 | (3)这个数列一共有几项?
1952 | (4)将数列中所有的数加起来,和是多少?
1953 |
1954 | ### 练习1
1955 |
1956 | (1)数列3,7,11,⋯,第18项是()。
1957 | (2)数列4,9,14,⋯,其中254是这个数列的第()项。
1958 | (3)数列4,8,12,⋯,160,这个数列共有()项。
1959 |
1960 | ### 例题2
1961 |
1962 | 1~100中除以5余2的数的和是多少?
1963 |
1964 | ### 练习2
1965 |
1966 | 1~100中所有5的倍数的和是多少?
1967 |
1968 | ### 例题3
1969 |
1970 | 计算:$24\times23-23\times22+22\times21-21\times20+\dots+2\times1$
1971 |
1972 | ### 练习3
1973 |
1974 | 计算:$14\times13-13\times12+12\times11-11\times10+10\times9-9\times8+8\times7-7\times6+6\times5-5\times4+4\times3-3\times2+2\times1$
1975 |
1976 | ### 例题4(平方差公式)
1977 |
1978 | 有一串数1,4,9,16,25,36,⋯,它们是按什么规律排列的?其中第9个数与第10个数相差多少?第2014个数与第2015个数相差多少?
1979 |
1980 | ### 练习4
1981 |
1982 | 计算:$[2017-(8.5\times8.5-1.5\times1.5)\div10]\div160-0.3$
1983 |
1984 | ### 例题5
1985 |
1986 | 计算:$100^2-99^2+98^2-97^2+\dots+2^2-1^2$
1987 |
1988 | ### 练习5
1989 |
1990 | 计算:$20\times20-19\times19+18\times18-17\times17+\dots+2\times2-1\times1$
1991 |
1992 | ### 例题6(整数列项)
1993 |
1994 | 计算:$1\times2+2\times3+3\times4+\dots+49\times50$
1995 |
1996 | ### 练习6
1997 |
1998 | ## 4.2.09. 统筹与最优化
1999 |
2000 | ### 例题1
2001 |
2002 | 理发店里只有一位理发师,但是同时来了五位顾客,根据他们所要理的发型,分别需要10分钟、12分钟、15分钟、20分钟和24分钟,怎样安排他们理发的顺序,才能使这五人理发和等候所用时间的总和最少?最少时间为多少?
2003 |
2004 | ### 练习1
2005 |
2006 | 5个人各拿一个水桶在自来水龙头前等候打水,他们打水所需要的时间分别是1分钟、2分钟、3分钟、4分钟和5分钟,如果只有一个水龙头,适当安排他们的打水顺序,就能够使每个人排队和打水时间的总和最小,那么这个最小值是多少分钟?
2007 |
2008 | ### 例题2
2009 |
2010 | 电车公司维修站有7辆电车需要维修,如果用一名工人维修这7辆电车,修复时间分别为12分钟,17分钟,8分钟,18分钟,23分钟,30分钟,14分钟。每辆电车每停开1分钟的损失是11元,现在由3名工作效率相同的维修工人各自单独工作,要使经济损失减到最小程度,那么最小的损失是多少元?
2011 |
2012 | ### 练习2
2013 |
2014 | 有八个人各拿着一个水桶同时到水龙头前打水,水龙头注满第一个人的桶需要1分钟,注满第二个人的桶需要2分钟,……,如此下去,
2015 | (1)当只有一个水龙头时,如何巧妙安排这八个人打水,使他们总的花费时间最少?最少的时间是多少?
2016 | (2)当有两个水龙头时,如何巧妙安排这八个人打水,使他们总的花费时间最少?最少的时间是多少?
2017 |
2018 | ### 例题3
2019 |
2020 | 有一家五口人要在夜晚过一座独木桥。他们家里的老爷爷行动非常不便,过桥需要12分钟;孩子们的父亲贪吃且不爱运动,体重严重超标,过河需要时间也较长,8分钟;母亲则一直坚持劳作,动作还算敏捷,过桥要6分钟;两个孩子中姐姐需要3分钟,弟弟只要1分钟。当时正是初一,夜晚又是阴天,不要说月亮,连一点星光都没有,真所谓伸手不见五指。幸运的是他们有一盏油灯,同时可以有两个人借助灯光过桥。但要命的是灯油将尽,这盏灯只能再维持30分钟了!他们焦急万分,该怎样过桥呢?
2021 |
2022 | ### 练习3
2023 |
2024 | 牛牛、丁丁、田田和阿普4个小朋友郊游回家时天色己晚,他们来到一条河的东岸,要通过一座小木桥到西岸,但是他们4个人只有一个手电筒,由于桥的承重量小,每次只能过2人,因此必须先由2个人拿着手电简过桥,并由1个人再将手电简送回,再由2个人拿着手电筒过桥…直到4人都通过小木桥。己知,牛牛单独过桥要1分钟;丁丁单独过桥要1.5分钟;田田单独过桥要2分钟;阿普单独过桥要2.5分钟。那么,4个人都通过小木桥,最少要多少分钟?
2025 |
2026 | ### 例题4
2027 |
2028 | (1)如图,在街道上有A、B、C、D、E五栋居民楼,现在设立一个公交站,为使五栋楼的居民到车站的距离之和最短,车站应位于何处?
2029 |
2030 |  2031 |
2032 | (2)如2图,在街道上有A、B、C、D、E、F六栋居民楼,现在设立一个公交站,要想使居民到达车站的距离之和最短,车站应该设在何处?
2033 |
2034 |
2031 |
2032 | (2)如2图,在街道上有A、B、C、D、E、F六栋居民楼,现在设立一个公交站,要想使居民到达车站的距离之和最短,车站应该设在何处?
2033 |
2034 |  2035 |
2036 | (3) 如图,在街道上有 A、B、C、D、E 五栋居民楼,图中的数表示每栋居民楼的人数, 现在想要设立一个公交站,要想使居民到达车站的距离之和最短,车站应该设在何处?
2037 |
2038 |
2035 |
2036 | (3) 如图,在街道上有 A、B、C、D、E 五栋居民楼,图中的数表示每栋居民楼的人数, 现在想要设立一个公交站,要想使居民到达车站的距离之和最短,车站应该设在何处?
2037 |
2038 |  2039 |
2040 | ### 练习4
2041 |
2042 | 有2015名少先队员分散在一条公路上执勤宣传交通法规,问完成任务后应该在公路的什么地点集合,可以使他们从各自的宣传岗位沿公路走到集合地点的路程总和最小?
2043 |
2044 | ### 例题5
2045 |
2046 | 在一条公路上,每隔10千米有一座仓库(如图),共有五座,图中数字表示各仓库库存货物的重量。现在要把所有的货物集中存放在一个仓库里,如果每吨货物运输1千米需要运费0.9元,那么集中到哪个仓库运费最少?
2047 |
2048 |
2039 |
2040 | ### 练习4
2041 |
2042 | 有2015名少先队员分散在一条公路上执勤宣传交通法规,问完成任务后应该在公路的什么地点集合,可以使他们从各自的宣传岗位沿公路走到集合地点的路程总和最小?
2043 |
2044 | ### 例题5
2045 |
2046 | 在一条公路上,每隔10千米有一座仓库(如图),共有五座,图中数字表示各仓库库存货物的重量。现在要把所有的货物集中存放在一个仓库里,如果每吨货物运输1千米需要运费0.9元,那么集中到哪个仓库运费最少?
2047 |
2048 |  2049 |
2050 | ### 练习5
2051 |
2052 | 在一条公路上每隔100千米,有一个仓库,共有5个仓库,—号仓库存有10吨货物,二号仓库存有20吨货物,五号仓库存有40吨货物,其余两个仓库是空的。现在想把所有的货物集中存放在一个仓库里,如果每吨货物运输1千米需要0.5元运输费,那么最少要多少运费才行?
2053 |
2054 | ### 例题6
2055 |
2056 | 北京、上海分别有10台和6台完全相同的机器,准备给武汉11台,西安5台,每台机器的运费如表所示,如何调运能使总运费最省?
2057 |
2058 | | | 武汉 | 西安 |
2059 | | ---- | ---- | ---- |
2060 | | 北京 | 500 | 600 |
2061 | | 上海 | 700 | 1000 |
2062 |
2063 | ### 练习6
2064 |
2065 | 北京和上海同时制成了电子计算机若干台,除了供应本地外,北京可以支援外地10台,上海可以支持外地4台。现决定给重庆8台,汉口6台,若每台计算机的运费如表,上海和北京制造的机器完全相同,应该怎样调运,才能使总的运费最省?最省的运费是多少?
2066 |
2067 | | | 汉口 | 重庆 |
2068 | | ---- | ---- | ---- |
2069 | | 北京 | 40 | 80 |
2070 | | 上海 | 30 | 50 |
2071 |
2072 | ## 4.2.10. 整除特征进阶
2073 |
2074 | ### 例题1
2075 |
2076 | 下面五个自然数:128114、94146、64152、6139、491678,哪些能被7整除?哪些能被11整除?哪些能被13整除?
2077 |
2078 | ### 练习1
2079 |
2080 | 下列数中,哪些能被7整除?哪些能被11整除?哪些能被13整除?
2081 |
2082 | 414 1057 2673 1320 596 2816 7462
2083 |
2084 | ### 例题2
2085 |
2086 | 2009200920092009能否被11整除?
2087 |
2088 | ### 练习2
2089 |
2090 | 20092009能否被11整除?
2091 |
2092 | ### 例题3
2093 |
2094 | 学校买了24台B种仪器,发票上的总价有两个数字已经辨认不清,只看到是$\overline{\Box8\Box2}$元,但采购人员还记得模糊不清的两个数字相同。你知道每台B种仪器多少钱吗?(仪器价格为整数)
2095 |
2096 | ### 练习3
2097 |
2098 | 小新一共买了28支价格相同的钢笔给大家作为奖品,共付人民币$\overline{9\Box.2\Box}$元。已知方框处数字相同,请问每支钢笔多少元?
2099 |
2100 | ### 例题4
2101 |
2102 | 六位数$\overline{\Box2008\Box}$能同时被9和11整除。这个六位数是多少?
2103 |
2104 | ### 练习4
2105 |
2106 | 六位数$\overline{\Box\Box5308}$能同时被9和11整除。$\overline{\Box\Box}$是多少?
2107 |
2108 | ### 例题5(试除法)
2109 |
2110 | 如果六位数$\overline{1992\Box\Box}$能被105整除,那么它的最后两位数是多少?
2111 |
2112 | ### 练习5
2113 |
2114 | 如果$\overline{2\Box\Box}$能被79整除,那么它的末两位数是多少?
2115 |
2116 | ### 例题6
2117 |
2118 | 六位自然数$\overline{1082\Box\Box}$能被23整除,末两位数有多少种情况?
2119 |
2120 | ### 练习6
2121 |
2122 | 六位自然数$\overline{1082\Box\Box}$能被12整除,末两位数可能是?
2123 |
2124 | ## 4.2.11. 加乘原理进阶
2125 |
2126 | ### 例题1
2127 |
2128 | 从北京到广州可以选择直达的飞机和火车,也可以选择中途在上海或者武汉停留,已知北京到上海、武汉和上海、武汉到广州除了有飞机和火车两种交通方式外还有汽车。问,从北京到广州一共有多少种交通方式可供选择?
2129 |
2130 | ### 练习1
2131 |
2132 | 王老师从重庆到南京,他可以乘飞机、汽车直接到达,也可以先到武汉,再由武汉到南京。他从重庆到武汉可乘船,也可乘火车; 又从武汉到南京可以乘船、火车或者飞机,那么王老师从重庆到南京有多少种不同走法呢?
2133 |
2134 | ### 例题2
2135 |
2136 | 过年了,妈妈买了7件不同的礼物,要送给亲朋好友的5个孩子每人一件。其中姐姐的儿子小强想从智力拼图和遥控汽车中选一个,朋友的女儿小玉想从学习机和遥控汽车中选一件。那么,妈妈送出这5件礼物共有多少种方法?
2137 |
2138 | ### 练习2
2139 |
2140 | 爸爸买了5件不同的玩具,要送给3个孩子每人一件。其中姐姐的儿子小刚想从拼图和积木中选一个,朋友的女儿小豆想从洋娃娃和积木中选一件。那么,爸爸送出这3件玩具共有多少种方法?
2141 |
2142 | ### 例题3
2143 |
2144 | 用0,1,2,3四个数字可以组成多少个没有重复数字的四位偶数?
2145 |
2146 | ### 练习3
2147 |
2148 | 用1,2,3,4四个数可以组成多少个没有重复数字的四位偶数?
2149 |
2150 | ### 例题4
2151 |
2152 | 在如图所示$1\times5$的格子中填入1,2,3,4,5,要求填入的数各不相同,并且填在红格里的数比它旁边的两个数都大。一共由多少种不同的填法?
2153 |
2154 | 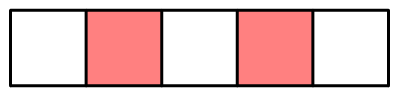
2155 |
2156 | ### 练习4
2157 |
2158 | 在如图所示$1\times5$的格子中填入1,2,3,4,5,6,7,8中的五个数,要求填入的数各不相同,并且填在红格里的数比它旁边的两个数都大。一共由多少种不同的填法?
2159 |
2160 | 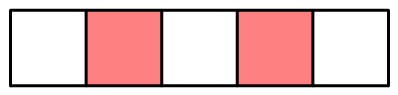
2161 |
2162 | ### 例题5
2163 |
2164 | 如下图,A,B,C,D,E五个区域,分别用红、黄、蓝、白、黑五种颜色中的某一种染色,要使相邻的区域染不同的颜色,共有多少种不同的染色方法?
2165 |
2166 | 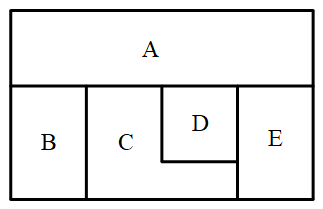
2167 |
2168 | ### 练习5
2169 |
2170 | 用5种不同的颜色给图中的A、B、C、D四个区域涂色,每个区域只能使用一种颜色,且相邻区域不能同色,有多少种不同的涂色方式?
2171 |
2172 | 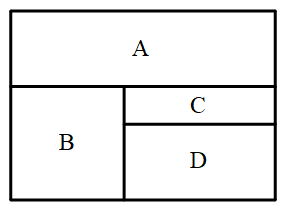
2173 |
2174 | ### 例题6
2175 |
2176 | 地图上有A,B,C,D四个区域(如下图),现有红、黄、蓝三种颜色给它染色,使相邻区域的颜色不同,但不是每种颜色都必须要用,问有多少种染色方法?
2177 |
2178 | 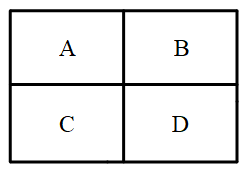
2179 |
2180 | ### 练习6
2181 |
2182 | 如果有红、黄、蓝、绿四种颜色给例题中的图染色,使相邻区域的颜色不同,但不是每种颜色都必须要用,问有多少种染色方法?
2183 |
2184 | 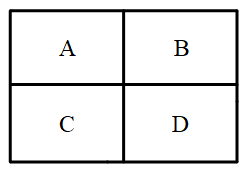
2185 |
2186 | ## 4.2.12. 流水行船
2187 |
2188 | ### 知识导引
2189 |
2190 | ### 课程框架
2191 |
2192 | ### 内容分析
2193 |
2194 | ### 例题练习
2195 |
2196 | 前置内容——相遇追及问题。后续讲次——电梯问题。知道行程问题的基本关系。
2197 |
2198 | 课堂先讲流水行程问题是什么,比起单人行程有什么区别。(区别在于有水是有速度的)
2199 |
2200 | 简单引入后,可以让学生尝试的去做例题 1,练习 1。
2201 |
2202 | **例题1**
2203 |
2204 | 一只船在静水中每小时行 8 千米,水流速度是每小时 4 千米,如果这只船顺流而下 3 小时,它行多远? 如果这只船逆流而上 3 小时,它行多远?
2205 |
2206 | 【解析】顺水速度:8 + 4 = 12(千米/小时),路程:12 × 3 = 36(千米);
2207 |
2208 | 逆水速度:8 - 4 = 4(千米/小时),路程:4 × 3 = 12(千米)。
2209 |
2210 | **练习1**
2211 |
2212 | 一只船在静水中每小时航行 4 千米,水流的速度是每小时 2 千米,则这只船逆水 4 小时航行多少干米?
2213 |
2214 | 【解析】逆水速度:4 - 2 = 2(千米/小时),路程:2 × 4 = 8(千米)。
2215 |
2216 | ### 流水行船基本关系
2217 |
2218 | 流水行船问题中,有四个速度:
2219 |
2220 | * 水流速度
2221 | * 船在静水中的速度
2222 | * 船的顺水速度
2223 | * 船的逆水速度
2224 |
2225 | 他们的关系如下:
2226 |
2227 | * 顺水速度 = 船速 + 水速
2228 | * 逆水速度= 船速 - 水速
2229 |
2230 | 综合上面两个基本公式,由和差公式可知:
2231 |
2232 | * 船速 = (顺水速度 + 逆水速度)÷ 2
2233 | * 水速 = (顺水速度 - 逆水速度)÷ 2
2234 |
2235 | 默认船速是要比水速大的。
2236 |
2237 | **船速、水速、顺水速度、逆水速度,可知 2 求 2。**
2238 |
2239 | | 船速 | 水速 | 顺水速度 | 逆水速度 |
2240 | | :--: | :--: | :------: | -------- |
2241 | | 100 | 30 | | |
2242 | | | 10 | 40 | |
2243 | | 6 | | 7 | |
2244 | | | | 80 | 50 |
2245 |
2246 | 讲完这些,例题 2,练习 2。
2247 |
2248 | **例题2**
2249 |
2250 | 一艘游轮在河中行驶,顺流航行的速度是每小时 30 千米,逆流航行的速度是每小时 12 千米,游轮的静水速度是多少?水流的速度是多少?
2251 |
2252 | 【解析】静水速度:(30 + 12)÷ 2 = 21(千米/小时);水速:(30 - 12)÷ 2 = 9(千米/小时)
2253 |
2254 | **练习2**
2255 |
2256 | 一只小船在河中行驶,顺流划行的速度是每小时 10 千米,逆流划行的速度是每小时 6 千米,船的静水速度是多少?水流的速度是多少?
2257 |
2258 | 【解析】
2259 |
2260 | ### 方向改变,船速水速不变
2261 |
2262 | **例题3**
2263 |
2264 | 一艘船在静水中的速度是每小时 15 千米,它从上游甲地开往下游乙地共花去了 8 小时,水速每小时 3 千米,问从乙地返回甲地需要多少时间?
2265 |
2266 | **练习3**
2267 |
2268 | 一艘每小时行 25 千米的客轮,在大运河中顺水航行 140 千米,水速是每小时3 千米,需要行几个小时?
2269 |
2270 | ### 船速不变,水速变
2271 |
2272 | **例题4**
2273 |
2274 | 某船往返于相距 180 千米的两港之间,平时顺水每小时行 18 千米,逆水每小时行12千米。某天暴雨后水速增加,该船顺水而行只需 9 小时,那么逆水而行需要几小时?
2275 |
2276 | **练习4**
2277 |
2278 | 汉江是长江的支流,汉江水的水速为每小时 3 千米,长江水的水速为每小时 4 千米。一条船沿汉江顺水航行 2 小时,行了56 千米到达长江,在长江还要逆水航行 147 千米。这条船还要行多少小时?
2279 |
2280 | ### 水速不变,船速变
2281 |
2282 | **例题5**
2283 |
2284 | 有甲乙两船航行于 360 千米的两港口之间,甲逆水行全程用 18 小时,乙逆水行全程用 12 小时,甲顺水行全程用 12 小时,乙顺水行全程要用多长时间?
2285 |
2286 | **练习5**
2287 |
2288 | 有 AB 两船航行于 120 千米的两港口之间,A 逆水行全程用 30 小时,B 逆水行全程用 20 小时,A 顺水行全程用 12 小时,B 顺水行全程要用多长时间?
2289 |
2290 | ### 流水行船中的相遇追及
2291 |
2292 | **例题6**
2293 |
2294 | A、B 两码头间河流长为 220 千米,甲、乙两船分别从 A、B 码头同时起航。如果相向而行 5 小时相遇,如果同向而行 55 小时甲船追上乙船。求两船在静水中的速度。
2295 |
2296 | **练习6**
2297 |
2298 | 甲、乙两船分别从相距 64 千米的 A、B 两港同时出发相向而行,2小时相遇;若两船同时同向而行,则甲用 16 小时赶上乙。问:甲、乙两船的速度各是多少?
2299 |
2300 | ### 课堂总结
2301 |
2302 | ## 4.2.13. 抽屉原理与最不利原则
2303 |
2304 | 例题练习
2305 |
2306 | ### 例题1(抽屉特征/一份)
2307 |
2308 | (1)7个苹果,放进6个抽屉,请问,苹果数最多的抽屉里最少能放进几个苹果?
2309 |
2310 | (2)14个苹果,放进6个抽屉,请问,至少有几个苹果会放在同一个抽屉中?
2311 |
2312 | ### 练习1
2313 |
2314 | (1)在任意367个同一年出生的人中,是否有生日相同的人?
2315 | (2)在任意25个人中,至少有几个人的性别相同?
2316 | (3)在任意100个人中,人数最多的一个星座至少有几个人?
2317 |
2318 | ### 拓展
2319 |
2320 | 71名选手参加大胃王比赛,比赛的内容是吃汉堡,最后吃得最多的选手吃了18个汉堡,吃得最少的选手吃了9个汉堡。问至少有几名选手吃的汉堡的数量是相同的?(不满一个汉堡不算,不存在半个汉堡的情况)
2321 |
2322 | ### 例题2(求抽屉数)
2323 |
2324 | 把100个苹果放进若干个抽屉里,保证苹果最多的抽屉里至少有4个苹果,则抽屉最多有个?
2325 |
2326 | ### 练习2
2327 |
2328 | 某次选拔考试,共有1123名同学参加,小明说:“参赛人数最多的一个学校至少有10人参赛” ,如果他的说法是正确的,那么最多有几个学校参加了这次入学考试。
2329 |
2330 | ### 例题3(最不利原则/总数)
2331 |
2332 | 一副扑克牌中。
2333 |
2334 | (1)至少抽几张,才能保证抽到两种不同花色的牌?
2335 |
2336 | (2)至少抽几张,才能保证抽到的牌中有黑桃?
2337 |
2338 | (3)至少抽几张,才能保证抽到三张A?
2339 |
2340 | (4)至少抽几张,才能保证抽到的牌中有“一对”?
2341 |
2342 | ### 练习3
2343 |
2344 | 有黄色袜子9只,绿色袜子7只,白色袜子4只,红色袜子2只黑色袜子1只。松松闭着眼睛摸袜子。
2345 |
2346 | (1)至少摸出几只,才能保证凑出1双袜子?
2347 |
2348 | (2)至少摸出几只,才能保证凑出2双袜子?
2349 |
2350 | (3)至少摸出几只,才能保证凑出2双同色袜子?
2351 |
2352 | (4)至少摸出几只,才能保证凑出2双不同色袜子?
2353 |
2354 | ### 拓展
2355 |
2356 | 有黄色鞋子9双,绿色鞋子7双,白色鞋子4双,红色鞋子2双,黑色鞋子1双。松松闭着眼睛摸鞋子,至少摸出几只,才能保证凑出2双不同色鞋子?
2357 |
2358 | ### 例题4(应用)
2359 |
2360 | 17名同学参加一次考试,考试题是3道判断题(答案只有对或错),每名同学都在答题纸上依次写上了3道题目的答案。请问:至少有几名同学的答案是一样的?
2361 |
2362 | ### 练习4
2363 |
2364 | 41名学生到老师家借书,老师书房中有A、B、C、D四类书,每名学生可借两本不同类的书。请问最少有多少名学生借到的书的数量和种类完全一样?
2365 |
2366 | ### 例题5
2367 |
2368 | 如图,将2行5列的方格纸的每一格染成黑色或白色,请说明:不管怎样染,总有两列的染色方式是一样的。
2369 |
2370 |
2049 |
2050 | ### 练习5
2051 |
2052 | 在一条公路上每隔100千米,有一个仓库,共有5个仓库,—号仓库存有10吨货物,二号仓库存有20吨货物,五号仓库存有40吨货物,其余两个仓库是空的。现在想把所有的货物集中存放在一个仓库里,如果每吨货物运输1千米需要0.5元运输费,那么最少要多少运费才行?
2053 |
2054 | ### 例题6
2055 |
2056 | 北京、上海分别有10台和6台完全相同的机器,准备给武汉11台,西安5台,每台机器的运费如表所示,如何调运能使总运费最省?
2057 |
2058 | | | 武汉 | 西安 |
2059 | | ---- | ---- | ---- |
2060 | | 北京 | 500 | 600 |
2061 | | 上海 | 700 | 1000 |
2062 |
2063 | ### 练习6
2064 |
2065 | 北京和上海同时制成了电子计算机若干台,除了供应本地外,北京可以支援外地10台,上海可以支持外地4台。现决定给重庆8台,汉口6台,若每台计算机的运费如表,上海和北京制造的机器完全相同,应该怎样调运,才能使总的运费最省?最省的运费是多少?
2066 |
2067 | | | 汉口 | 重庆 |
2068 | | ---- | ---- | ---- |
2069 | | 北京 | 40 | 80 |
2070 | | 上海 | 30 | 50 |
2071 |
2072 | ## 4.2.10. 整除特征进阶
2073 |
2074 | ### 例题1
2075 |
2076 | 下面五个自然数:128114、94146、64152、6139、491678,哪些能被7整除?哪些能被11整除?哪些能被13整除?
2077 |
2078 | ### 练习1
2079 |
2080 | 下列数中,哪些能被7整除?哪些能被11整除?哪些能被13整除?
2081 |
2082 | 414 1057 2673 1320 596 2816 7462
2083 |
2084 | ### 例题2
2085 |
2086 | 2009200920092009能否被11整除?
2087 |
2088 | ### 练习2
2089 |
2090 | 20092009能否被11整除?
2091 |
2092 | ### 例题3
2093 |
2094 | 学校买了24台B种仪器,发票上的总价有两个数字已经辨认不清,只看到是$\overline{\Box8\Box2}$元,但采购人员还记得模糊不清的两个数字相同。你知道每台B种仪器多少钱吗?(仪器价格为整数)
2095 |
2096 | ### 练习3
2097 |
2098 | 小新一共买了28支价格相同的钢笔给大家作为奖品,共付人民币$\overline{9\Box.2\Box}$元。已知方框处数字相同,请问每支钢笔多少元?
2099 |
2100 | ### 例题4
2101 |
2102 | 六位数$\overline{\Box2008\Box}$能同时被9和11整除。这个六位数是多少?
2103 |
2104 | ### 练习4
2105 |
2106 | 六位数$\overline{\Box\Box5308}$能同时被9和11整除。$\overline{\Box\Box}$是多少?
2107 |
2108 | ### 例题5(试除法)
2109 |
2110 | 如果六位数$\overline{1992\Box\Box}$能被105整除,那么它的最后两位数是多少?
2111 |
2112 | ### 练习5
2113 |
2114 | 如果$\overline{2\Box\Box}$能被79整除,那么它的末两位数是多少?
2115 |
2116 | ### 例题6
2117 |
2118 | 六位自然数$\overline{1082\Box\Box}$能被23整除,末两位数有多少种情况?
2119 |
2120 | ### 练习6
2121 |
2122 | 六位自然数$\overline{1082\Box\Box}$能被12整除,末两位数可能是?
2123 |
2124 | ## 4.2.11. 加乘原理进阶
2125 |
2126 | ### 例题1
2127 |
2128 | 从北京到广州可以选择直达的飞机和火车,也可以选择中途在上海或者武汉停留,已知北京到上海、武汉和上海、武汉到广州除了有飞机和火车两种交通方式外还有汽车。问,从北京到广州一共有多少种交通方式可供选择?
2129 |
2130 | ### 练习1
2131 |
2132 | 王老师从重庆到南京,他可以乘飞机、汽车直接到达,也可以先到武汉,再由武汉到南京。他从重庆到武汉可乘船,也可乘火车; 又从武汉到南京可以乘船、火车或者飞机,那么王老师从重庆到南京有多少种不同走法呢?
2133 |
2134 | ### 例题2
2135 |
2136 | 过年了,妈妈买了7件不同的礼物,要送给亲朋好友的5个孩子每人一件。其中姐姐的儿子小强想从智力拼图和遥控汽车中选一个,朋友的女儿小玉想从学习机和遥控汽车中选一件。那么,妈妈送出这5件礼物共有多少种方法?
2137 |
2138 | ### 练习2
2139 |
2140 | 爸爸买了5件不同的玩具,要送给3个孩子每人一件。其中姐姐的儿子小刚想从拼图和积木中选一个,朋友的女儿小豆想从洋娃娃和积木中选一件。那么,爸爸送出这3件玩具共有多少种方法?
2141 |
2142 | ### 例题3
2143 |
2144 | 用0,1,2,3四个数字可以组成多少个没有重复数字的四位偶数?
2145 |
2146 | ### 练习3
2147 |
2148 | 用1,2,3,4四个数可以组成多少个没有重复数字的四位偶数?
2149 |
2150 | ### 例题4
2151 |
2152 | 在如图所示$1\times5$的格子中填入1,2,3,4,5,要求填入的数各不相同,并且填在红格里的数比它旁边的两个数都大。一共由多少种不同的填法?
2153 |
2154 | 
2155 |
2156 | ### 练习4
2157 |
2158 | 在如图所示$1\times5$的格子中填入1,2,3,4,5,6,7,8中的五个数,要求填入的数各不相同,并且填在红格里的数比它旁边的两个数都大。一共由多少种不同的填法?
2159 |
2160 | 
2161 |
2162 | ### 例题5
2163 |
2164 | 如下图,A,B,C,D,E五个区域,分别用红、黄、蓝、白、黑五种颜色中的某一种染色,要使相邻的区域染不同的颜色,共有多少种不同的染色方法?
2165 |
2166 | 
2167 |
2168 | ### 练习5
2169 |
2170 | 用5种不同的颜色给图中的A、B、C、D四个区域涂色,每个区域只能使用一种颜色,且相邻区域不能同色,有多少种不同的涂色方式?
2171 |
2172 | 
2173 |
2174 | ### 例题6
2175 |
2176 | 地图上有A,B,C,D四个区域(如下图),现有红、黄、蓝三种颜色给它染色,使相邻区域的颜色不同,但不是每种颜色都必须要用,问有多少种染色方法?
2177 |
2178 | 
2179 |
2180 | ### 练习6
2181 |
2182 | 如果有红、黄、蓝、绿四种颜色给例题中的图染色,使相邻区域的颜色不同,但不是每种颜色都必须要用,问有多少种染色方法?
2183 |
2184 | 
2185 |
2186 | ## 4.2.12. 流水行船
2187 |
2188 | ### 知识导引
2189 |
2190 | ### 课程框架
2191 |
2192 | ### 内容分析
2193 |
2194 | ### 例题练习
2195 |
2196 | 前置内容——相遇追及问题。后续讲次——电梯问题。知道行程问题的基本关系。
2197 |
2198 | 课堂先讲流水行程问题是什么,比起单人行程有什么区别。(区别在于有水是有速度的)
2199 |
2200 | 简单引入后,可以让学生尝试的去做例题 1,练习 1。
2201 |
2202 | **例题1**
2203 |
2204 | 一只船在静水中每小时行 8 千米,水流速度是每小时 4 千米,如果这只船顺流而下 3 小时,它行多远? 如果这只船逆流而上 3 小时,它行多远?
2205 |
2206 | 【解析】顺水速度:8 + 4 = 12(千米/小时),路程:12 × 3 = 36(千米);
2207 |
2208 | 逆水速度:8 - 4 = 4(千米/小时),路程:4 × 3 = 12(千米)。
2209 |
2210 | **练习1**
2211 |
2212 | 一只船在静水中每小时航行 4 千米,水流的速度是每小时 2 千米,则这只船逆水 4 小时航行多少干米?
2213 |
2214 | 【解析】逆水速度:4 - 2 = 2(千米/小时),路程:2 × 4 = 8(千米)。
2215 |
2216 | ### 流水行船基本关系
2217 |
2218 | 流水行船问题中,有四个速度:
2219 |
2220 | * 水流速度
2221 | * 船在静水中的速度
2222 | * 船的顺水速度
2223 | * 船的逆水速度
2224 |
2225 | 他们的关系如下:
2226 |
2227 | * 顺水速度 = 船速 + 水速
2228 | * 逆水速度= 船速 - 水速
2229 |
2230 | 综合上面两个基本公式,由和差公式可知:
2231 |
2232 | * 船速 = (顺水速度 + 逆水速度)÷ 2
2233 | * 水速 = (顺水速度 - 逆水速度)÷ 2
2234 |
2235 | 默认船速是要比水速大的。
2236 |
2237 | **船速、水速、顺水速度、逆水速度,可知 2 求 2。**
2238 |
2239 | | 船速 | 水速 | 顺水速度 | 逆水速度 |
2240 | | :--: | :--: | :------: | -------- |
2241 | | 100 | 30 | | |
2242 | | | 10 | 40 | |
2243 | | 6 | | 7 | |
2244 | | | | 80 | 50 |
2245 |
2246 | 讲完这些,例题 2,练习 2。
2247 |
2248 | **例题2**
2249 |
2250 | 一艘游轮在河中行驶,顺流航行的速度是每小时 30 千米,逆流航行的速度是每小时 12 千米,游轮的静水速度是多少?水流的速度是多少?
2251 |
2252 | 【解析】静水速度:(30 + 12)÷ 2 = 21(千米/小时);水速:(30 - 12)÷ 2 = 9(千米/小时)
2253 |
2254 | **练习2**
2255 |
2256 | 一只小船在河中行驶,顺流划行的速度是每小时 10 千米,逆流划行的速度是每小时 6 千米,船的静水速度是多少?水流的速度是多少?
2257 |
2258 | 【解析】
2259 |
2260 | ### 方向改变,船速水速不变
2261 |
2262 | **例题3**
2263 |
2264 | 一艘船在静水中的速度是每小时 15 千米,它从上游甲地开往下游乙地共花去了 8 小时,水速每小时 3 千米,问从乙地返回甲地需要多少时间?
2265 |
2266 | **练习3**
2267 |
2268 | 一艘每小时行 25 千米的客轮,在大运河中顺水航行 140 千米,水速是每小时3 千米,需要行几个小时?
2269 |
2270 | ### 船速不变,水速变
2271 |
2272 | **例题4**
2273 |
2274 | 某船往返于相距 180 千米的两港之间,平时顺水每小时行 18 千米,逆水每小时行12千米。某天暴雨后水速增加,该船顺水而行只需 9 小时,那么逆水而行需要几小时?
2275 |
2276 | **练习4**
2277 |
2278 | 汉江是长江的支流,汉江水的水速为每小时 3 千米,长江水的水速为每小时 4 千米。一条船沿汉江顺水航行 2 小时,行了56 千米到达长江,在长江还要逆水航行 147 千米。这条船还要行多少小时?
2279 |
2280 | ### 水速不变,船速变
2281 |
2282 | **例题5**
2283 |
2284 | 有甲乙两船航行于 360 千米的两港口之间,甲逆水行全程用 18 小时,乙逆水行全程用 12 小时,甲顺水行全程用 12 小时,乙顺水行全程要用多长时间?
2285 |
2286 | **练习5**
2287 |
2288 | 有 AB 两船航行于 120 千米的两港口之间,A 逆水行全程用 30 小时,B 逆水行全程用 20 小时,A 顺水行全程用 12 小时,B 顺水行全程要用多长时间?
2289 |
2290 | ### 流水行船中的相遇追及
2291 |
2292 | **例题6**
2293 |
2294 | A、B 两码头间河流长为 220 千米,甲、乙两船分别从 A、B 码头同时起航。如果相向而行 5 小时相遇,如果同向而行 55 小时甲船追上乙船。求两船在静水中的速度。
2295 |
2296 | **练习6**
2297 |
2298 | 甲、乙两船分别从相距 64 千米的 A、B 两港同时出发相向而行,2小时相遇;若两船同时同向而行,则甲用 16 小时赶上乙。问:甲、乙两船的速度各是多少?
2299 |
2300 | ### 课堂总结
2301 |
2302 | ## 4.2.13. 抽屉原理与最不利原则
2303 |
2304 | 例题练习
2305 |
2306 | ### 例题1(抽屉特征/一份)
2307 |
2308 | (1)7个苹果,放进6个抽屉,请问,苹果数最多的抽屉里最少能放进几个苹果?
2309 |
2310 | (2)14个苹果,放进6个抽屉,请问,至少有几个苹果会放在同一个抽屉中?
2311 |
2312 | ### 练习1
2313 |
2314 | (1)在任意367个同一年出生的人中,是否有生日相同的人?
2315 | (2)在任意25个人中,至少有几个人的性别相同?
2316 | (3)在任意100个人中,人数最多的一个星座至少有几个人?
2317 |
2318 | ### 拓展
2319 |
2320 | 71名选手参加大胃王比赛,比赛的内容是吃汉堡,最后吃得最多的选手吃了18个汉堡,吃得最少的选手吃了9个汉堡。问至少有几名选手吃的汉堡的数量是相同的?(不满一个汉堡不算,不存在半个汉堡的情况)
2321 |
2322 | ### 例题2(求抽屉数)
2323 |
2324 | 把100个苹果放进若干个抽屉里,保证苹果最多的抽屉里至少有4个苹果,则抽屉最多有个?
2325 |
2326 | ### 练习2
2327 |
2328 | 某次选拔考试,共有1123名同学参加,小明说:“参赛人数最多的一个学校至少有10人参赛” ,如果他的说法是正确的,那么最多有几个学校参加了这次入学考试。
2329 |
2330 | ### 例题3(最不利原则/总数)
2331 |
2332 | 一副扑克牌中。
2333 |
2334 | (1)至少抽几张,才能保证抽到两种不同花色的牌?
2335 |
2336 | (2)至少抽几张,才能保证抽到的牌中有黑桃?
2337 |
2338 | (3)至少抽几张,才能保证抽到三张A?
2339 |
2340 | (4)至少抽几张,才能保证抽到的牌中有“一对”?
2341 |
2342 | ### 练习3
2343 |
2344 | 有黄色袜子9只,绿色袜子7只,白色袜子4只,红色袜子2只黑色袜子1只。松松闭着眼睛摸袜子。
2345 |
2346 | (1)至少摸出几只,才能保证凑出1双袜子?
2347 |
2348 | (2)至少摸出几只,才能保证凑出2双袜子?
2349 |
2350 | (3)至少摸出几只,才能保证凑出2双同色袜子?
2351 |
2352 | (4)至少摸出几只,才能保证凑出2双不同色袜子?
2353 |
2354 | ### 拓展
2355 |
2356 | 有黄色鞋子9双,绿色鞋子7双,白色鞋子4双,红色鞋子2双,黑色鞋子1双。松松闭着眼睛摸鞋子,至少摸出几只,才能保证凑出2双不同色鞋子?
2357 |
2358 | ### 例题4(应用)
2359 |
2360 | 17名同学参加一次考试,考试题是3道判断题(答案只有对或错),每名同学都在答题纸上依次写上了3道题目的答案。请问:至少有几名同学的答案是一样的?
2361 |
2362 | ### 练习4
2363 |
2364 | 41名学生到老师家借书,老师书房中有A、B、C、D四类书,每名学生可借两本不同类的书。请问最少有多少名学生借到的书的数量和种类完全一样?
2365 |
2366 | ### 例题5
2367 |
2368 | 如图,将2行5列的方格纸的每一格染成黑色或白色,请说明:不管怎样染,总有两列的染色方式是一样的。
2369 |
2370 |  2371 |
2372 | ### 练习5
2373 |
2374 | 下面是一个三行a列的方格纸,已知将每一个小方格涂上红色、黄色或蓝色(每一列的三小格涂的颜色不能相同),不论如何涂色,其中至少有三列,它们的涂色方式相同,那么a至少是多少?
2375 |
2376 |
2371 |
2372 | ### 练习5
2373 |
2374 | 下面是一个三行a列的方格纸,已知将每一个小方格涂上红色、黄色或蓝色(每一列的三小格涂的颜色不能相同),不论如何涂色,其中至少有三列,它们的涂色方式相同,那么a至少是多少?
2375 |
2376 |  2377 |
2378 | ### 课后巩固
2379 |
2380 | ### 巩固1
2381 |
2382 | 某小学有731个学生,问:至少有几个学生的生日是同一天?
2383 |
2384 | ### 巩固2
2385 |
2386 | 袋中有外形安全一样的红、黄、蓝三种颜色的小球各10个,每个小朋友只能从中摸出1个小球, 至少有几个小朋友摸球,才能保证一定有3个人摸的球颜色一样。
2387 |
2388 | ### 巩固3
2389 |
2390 | 一副扑克牌有54张,至少要抽取几张牌,才能保证其中有2张牌有相同的点数?
2391 |
2392 | ### 巩固4
2393 |
2394 | 学校买来许多牛、马、羊、狗塑料玩具,每个小朋友任意选择两件,但不能是同样的,问:至少有多少个小朋友去拿,才能保证有两人所拿玩具相同?
2395 |
2396 | ### 巩固5
2397 |
2398 | 一次数学竞赛出了10道选择题,评分标准为:基础分10分,每道题答对得3分,答错扣1分, 不答不得分。问:要保证至少有 4 人得分相同,至少需要多少人参加竞赛?
2399 |
2400 | ## 4.2.14. 最值问题进阶
2401 |
2402 | ### 例题1
2403 |
2404 | 在下图的中间圆圈内填一个数,计算每一条线段两端的数之差(大减小),然后把这3个差数相加,所得的和最小是多少?
2405 |
2406 |
2377 |
2378 | ### 课后巩固
2379 |
2380 | ### 巩固1
2381 |
2382 | 某小学有731个学生,问:至少有几个学生的生日是同一天?
2383 |
2384 | ### 巩固2
2385 |
2386 | 袋中有外形安全一样的红、黄、蓝三种颜色的小球各10个,每个小朋友只能从中摸出1个小球, 至少有几个小朋友摸球,才能保证一定有3个人摸的球颜色一样。
2387 |
2388 | ### 巩固3
2389 |
2390 | 一副扑克牌有54张,至少要抽取几张牌,才能保证其中有2张牌有相同的点数?
2391 |
2392 | ### 巩固4
2393 |
2394 | 学校买来许多牛、马、羊、狗塑料玩具,每个小朋友任意选择两件,但不能是同样的,问:至少有多少个小朋友去拿,才能保证有两人所拿玩具相同?
2395 |
2396 | ### 巩固5
2397 |
2398 | 一次数学竞赛出了10道选择题,评分标准为:基础分10分,每道题答对得3分,答错扣1分, 不答不得分。问:要保证至少有 4 人得分相同,至少需要多少人参加竞赛?
2399 |
2400 | ## 4.2.14. 最值问题进阶
2401 |
2402 | ### 例题1
2403 |
2404 | 在下图的中间圆圈内填一个数,计算每一条线段两端的数之差(大减小),然后把这3个差数相加,所得的和最小是多少?
2405 |
2406 |  2407 |
2408 | ### 练习1
2409 |
2410 | 在下图的中间圆圈内填一个数,计算每一条线段两端的数之差(大减小),然后把这3个差数相加,所得的和最小是多少?
2411 |
2412 |
2407 |
2408 | ### 练习1
2409 |
2410 | 在下图的中间圆圈内填一个数,计算每一条线段两端的数之差(大减小),然后把这3个差数相加,所得的和最小是多少?
2411 |
2412 |  2413 |
2414 | ### 例题2
2415 |
2416 | “12345678910111213…282930”是一个位数很多的多位数,从中划去40个数字,使剩下的数字(顺序不变)组成一个首位不为0的多位数,则这个多位数最大为多少?
2417 |
2418 | ### 练习2
2419 |
2420 | “12345678910111213…282930”是一个位数很多的多位数,从中划去40个数字,使剩下的数字(顺序不变)组成一个首位不为0的多位数,则这个多位数最小为多少?
2421 |
2422 | ### 例题3
2423 |
2424 | 某次考试共有15题。计分标准是:做对第1题得1分,做对第2题得2分,……,做对第15题得15分。若做错第1题则要倒扣1分,做错第2题要倒扣2分,……,做错第15题要倒扣15分。小明做了所有的题,得90分,那么小明至多做错多少道题?
2425 |
2426 | ### 练习3
2427 |
2428 | 某次考试共有15题。计分标准是:做对第1题得1分,做对第2题得2分,……,做对第15题得15分。若做错第1题则要倒扣1分,做错第2题要倒扣2分,……,做错第15题要倒扣15分。小明做了所有的题,得90分,那么小明至多做错多少道题?
2429 |
2430 | ### 例题4
2431 |
2432 | 阶梯教室座位有10排,每排有16个座位,当有150个人就座时,某些排坐着的人数就一样多。我们希望人数一样的排数尽可能少,这样的排数至少有多少排?
2433 |
2434 | ### 练习4
2435 |
2436 | 学校203教室座位有5排,每排有8个座位,当有30个人就座时,某些排坐着的人数就一样多。我们希望人数一样的排数尽可能少,这样的排数至少有多少排?
2437 |
2438 | ### 例题5
2439 |
2440 | 如图,牧羊人用15段每段长2米的篱笆,一面靠墙围成一个长方形羊圈,则羊圈的最大面积是多少平方米?
2441 |
2442 | 
2443 |
2444 | ### 练习5
2445 |
2446 | 某校准备用一道长36米的铁丝网,围成一块长方形生物实验基地,这块基地的面积最大是多少平方米?
2447 |
2448 | ### 例题6
2449 |
2450 | 如图,一个长方形被分成4个小长方形,其中长方形A、B、C的周长分别是10厘米、12厘米、14厘米,那么长方形D的面积最大是多少平方厘米?
2451 |
2452 | 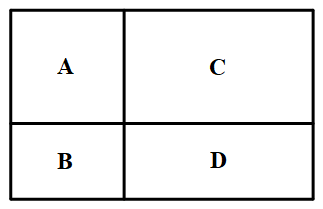
2453 |
2454 | ### 练习6
2455 |
2456 | 一块长方形菜地被分成4个小块,其A、B、C块的周长分别是20厘米、24厘米、28厘米那么D的面积最大是多少平方厘米?
2457 |
2458 | 
2459 |
2460 | ## 4.2.15. 操作类智巧趣题
2461 |
2462 | ### 例题1
2463 |
2464 | 一个猎户,带着一条狗,一只兔子和一筐胡萝卜乘船过河,船小一次只能带一样东西。但是他不在时,狗会咬兔子,免子会吃胡萝卜。请你想一想,帮猎人安排合理的方法过河。
2465 |
2466 | ### 练习1
2467 |
2468 | 一个农民携带一只狼、一只羊和一棵白菜,要借助一条小船过河。小船上除了农民只能再带狼、羊、白菜中的一样。而农民不在时,狼会吃羊,羊会吃白菜。农民如何过河呢?
2469 |
2470 | ### 例题2
2471 |
2472 | 小枫带着他的三个馋嘴弟弟和一个大蛋糕过河,已知只有小枫会划船,且除了小枫外每次只能带其中的一个弟弟,或者蛋糕过河。蛋糕一共十块,只要小枫离开,单独留弟弟和蛋糕在一起,每个弟弟在下次见到哥哥之前都会吃掉一块蛋糕。假设除弟弟外的任何原因都不会导致蛋糕减少,请问,兄弟4人全部过河后,最多还能剩下块蛋糕。
2473 |
2474 | ### 练习2
2475 |
2476 | 河左边有一个大人和两个小孩,一只大熊和两只小熊。只有大熊、大人会划船,船一次最多只能运两个单位(不管人熊),条件是熊的数量不能大于人的数量(不分大小),要不然熊会把人吃掉(河的两边熊的数量都不能大于人的数量)。问怎么才能让人和熊安全渡河?
2477 |
2478 | ### 例题3
2479 |
2480 | 一大一小两个油桶,大桶盛满重11千克,小桶盛满重4千克。现要盛5千克的油,只用这两个桶盛,能办到吗?
2481 |
2482 | ### 练习3
2483 |
2484 | 小红去河边打水,她有两个桶,大桶能装9升水,小桶能装4升水,想要恰好从河中打上6升的水带回去,她该怎么办?
2485 |
2486 | ### 例题4
2487 |
2488 | 卖牛奶人有两桶10升装的牛奶。两个顾客各带容器去买2升牛奶,一个带的是5升的容器,另一个带的是4升的容器。这位卖牛奶人如何解决问题?
2489 |
2490 | ### 练习4
2491 |
2492 | 有大、中、小3个水桶,最多分别可装入水10千克、7千克和3千克。现在大桶中装满水,希望通过水在3个瓶子间的流动使得中瓶和小瓶上标出装1千克水的刻度线,聪明的你想想应该怎么倒呢?
2493 |
2494 | ### 例题5
2495 |
2496 | 有9个铁球,其中8个铁球一样重,另一个较轻,你要在天平上至少称几次才能保证把那个轻球找出来?
2497 |
2498 | ### 练习5
2499 |
2500 | 有3个铁球,其中2个铁球一样重,另一个较轻,你在天平上至少称几次能保证把那个轻球找出来?
2501 |
2502 | ### 例题6
2503 |
2504 | 今有101枚硬币,其中有100枚同样的真币和1枚伪币,伪币与真币的重量不同。现需弄清楚伪币究竟比真币轻,还是比真币重,但只有一架没有砝码的天平。那么怎样利用这架天平称两次,来达到目的?
2505 |
2506 | ### 练习6
2507 |
2508 | 现有21枚硬币,其中有20枚同样的真币和1枚伪币,伪币与真币重量不同。现需弄清楚伪币究竟比真币轻,还是比真币重,但只有一架没有砝码的天平。那么怎样利用这架天平称两次,来达到目的?
2509 |
2510 | ### 练习1
2511 |
2512 | 一个猎人要带一棵红萝卜,一只狗,两只老虎和一只羊过河。可现在,小船只有3个座位,猎人每次最多只能送两样东西过河。没有狗看管,老虎会吃羊;没有人看管,狗和羊就吵架,羊就会吃红萝卜。有什么妙计能帮助它们全都过河?
2513 |
2514 | ### 练习2
2515 |
2516 | 相传汉代军事家韩信一天访友归来 ,途中经过一集市,遇见卖油翁与顾客争执。买者想买5斤油,而卖者无法计量,因而告诉买者, 要么买3斤,要么买7斤。韩信询问得知,卖油翁油篓中恰好装有10斤油,但他仅有装3斤和7斤的葫芦,而买者执意要买5斤油。韩信立在马上稍加思索道:“你们无须再争,以我之法保你们都满意。”韩信下马经过几次倒油,买卖双方皆大欢喜。你知道,韩信是怎么倒油吗?
2517 |
2518 | ### 练习3
2519 |
2520 | 在一批产品中有16个零件,其中有一个是次品,比较轻(其它零件一样重) , 给你一架天平,你最少用天平称量
2521 | 几次就可以检验出次品零件?
2522 |
2523 | ## 4.2.17. 相遇追及综合
2524 |
2525 | ### 例题1
2526 |
2527 | 如图,周长为800米的环形跑道上,田田和阿普分别从相距200米的A、B两处同时沿相同方向出发。田田每分钟能跑200米,阿普每分钟只能跑150米,田田第一次追上阿普需要多少分钟?
2528 |
2529 | 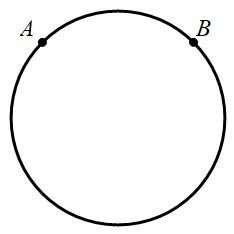
2530 |
2531 | ### 练习1
2532 |
2533 | 如图,周长为400米的环形跑道上田田和阿普分别从相距100米的A、B两处同时沿相同方向出发。田田每分钟能跑200米,阿普每分钟只能跑150米,田田第一次追上阿普需要多少分钟?
2534 |
2535 | 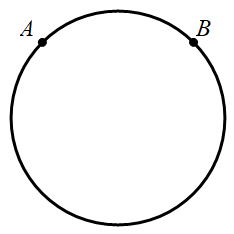
2536 |
2537 | ### 例题2
2538 |
2539 | 如图,田田和阿普分别从周长为1200米的圆形跑道上相距600米的A、B两处同时出发相向而行。6分钟后两人相遇。相遇后两人继续行进,4分钟后田田怡好到达B处,问两人相遇的地点距离A点多少米?
2540 |
2541 | 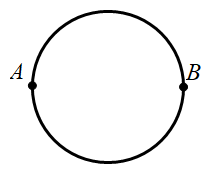
2542 |
2543 | ### 练习2
2544 |
2545 | 如图,田田和阿普分别从周长600米的圆形跑道上相距300米的A、B两处同时出发相向而行,6分钟后两人相遇。相遇后两人继续行进,4分钟后田田怡好到达B处,求两人相遇的地点距离A点多少米?
2546 |
2547 | 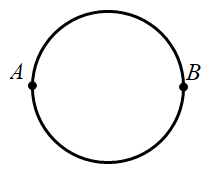
2548 |
2549 | ### 例题3
2550 |
2551 | 一列从西向东行驶的火车车速为每秒16米,车身长255米,8点整它追上了在铁路旁从西向东散步的田田,并于17秒后离开了他,又过了5分钟,它与从东向西散步的阿普相遇,15秒后离开了他。请问田田和阿普步行的速度分别是多少?
2552 |
2553 | ### 练习3
2554 |
2555 | 一列从西向东行驶的火车车速为每秒19米,车身长360米。9点整它追上了在铁路旁从西向东散步的田田,并于20秒后离开了她。又过了5分钟,它与从东向西散步的阿普相遇18秒后离开了他。请问田田和阿普步行的速度分别是多少?
2556 |
2557 | ### 例题4
2558 |
2559 | 田田以6米/秒的速度在铁路旁骑车,一列火车迎面开来,与她从相遇到离开共用了15秒,而它追上在铁路旁以4米/秒的速度跑步的阿普并刚好超过他共用了25秒,求火车的长度和行驶的速度。
2560 |
2561 | ### 练习4
2562 |
2563 | 田田以5米/秒的速度在铁路旁骑车,一列火车迎面开来,与她从相遇到离开共用了10秒,而它追上在铁路旁以3米/秒的速度跑步的阿普并刚好超过他共用了20秒,求火车的长度和行驶的速度。
2564 |
2565 | ### 例题5
2566 |
2567 | 某河上下游两港相距100千米,每天定时有甲乙两艘船速相等的客轮从两港相向而行,甲船顺水每小时行12千米,乙船逆水每小时行8千米,这天甲船在出发时,从船上掉下一物,此物顺水漂流而下,当甲乙两船相遇时,此物距相遇地点有多远?
2568 |
2569 | ### 练习5
2570 |
2571 | 某河上下游两港相距60千米,每天定时有甲乙两艘船速相等的客轮从两港相向而行,甲船顺水每小时行11千米,乙船逆水每小时行9千米,这天甲船在出发时,从船上掉下一物,此物顺水漂流而下,当甲乙两船相遇时,此物距相遇地点有多远?
2572 |
2573 | ### 例题6
2574 |
2575 | 某河上下游两港相距150千米,每天有甲乙两艘船分别从上游和下游同时相向而行,它们在静水中的速度分别为6千米/时和9千米/时。平时它们相遇于距上游港70千米处,某日突下暴雨,水速变为原来的2倍,这一天甲乙两船相遇地点距上游港多远?
2576 |
2577 | ### 练习6
2578 |
2579 | 某河上下游两港相距130千米,每天有甲乙两艘船分别从上游和下游同时相向而行,它们在静水中的速度分别为5千米/时和8千米/时。平时它们相遇于距上游港60千米处。某日突下暴雨,水速变为原来的2倍,这一天甲乙两船相遇地点距上游港多远?
2580 |
2581 |
2582 |
2583 | ## 方程与方程组
2584 |
2585 | ### 例题练习
2586 |
2587 | 【例题1】解下列一元一次方程:
2588 |
2589 | (1)$6(3+x)=24$
2590 |
2591 | (2)$18-(3x-6)=x$
2592 |
2593 | 答案:(1)1;(2)6
2594 |
2595 |
2596 |
2597 | 【练习1】解下列一元一次方程:
2598 |
2599 | (1)$3x-2(2+x)=1$
2600 |
2601 | (2)$6x-(4-x)=17$
2602 |
2603 |
2604 |
2605 | 【例题2】用代入消元法解方程组:
2606 |
2607 | (1)$\begin{cases}
2608 | y=2x-3\\
2609 | 3x+2y=8
2610 | \end{cases}$
2611 |
2612 |
2613 |
2614 | (2)$\begin{cases}
2615 | 2x-y=5\\
2616 | 3x+4y=13
2617 | \end{cases}$
2618 |
2619 |
2620 |
2621 | 【练习2】用代入消元法解方程组:
2622 |
2623 | (1)$\begin{cases}
2624 | 3x+2y=13\\
2625 | 2x-y=4
2626 | \end{cases}$
2627 |
2628 |
2629 |
2630 | 【例题3】用加减消元法解下列方程组:
2631 |
2632 | (1)$\begin{cases}
2633 | x-y=5\\
2634 | x+y=13
2635 | \end{cases}$
2636 |
2637 |
2638 |
2639 | (2)$\begin{cases}
2640 | 2x+y=11\\
2641 | 3x-2y=6
2642 | \end{cases}$
2643 |
2644 |
2645 |
2646 | (3)$\begin{cases}
2647 | 5y+z=12\\
2648 | 6y+5z=22
2649 | \end{cases}$
2650 |
2651 |
2652 |
2653 | 【练习3】用加减消元法解下列方程组:
2654 |
2655 | (1)$\begin{cases}
2656 | x+2y=21\\
2657 | 2x+y=18
2658 | \end{cases}$
2659 |
2660 |
2661 |
2662 | (2)$\begin{cases}
2663 | 7x+3y=44\\
2664 | 11x-2y=49
2665 | \end{cases}$
2666 |
2667 |
2668 |
2669 | (3)$\begin{cases}
2670 | 7x+3y=44\\
2671 | 11x+2y=61
2672 | \end{cases}$
2673 |
2674 |
2675 |
2676 | 【例题4】解方程组:
2677 |
2678 | (1)$\begin{cases}
2679 | 2x-3y=x+y-4\\
2680 | 3x+4y=x+5y+13
2681 | \end{cases}$
2682 |
2683 |
2684 |
2685 | (2)$\begin{cases}
2686 | 3x+5y=2x+3y+11\\
2687 | 4x-y-6=x+2y
2688 | \end{cases}$
2689 |
2690 |
2691 |
2692 | 【练习4】解方程组:
2693 |
2694 | (1)$\begin{cases}
2695 | a-1=b+1\\
2696 | a+1=3(b-1)
2697 | \end{cases}$
2698 |
2699 |
2700 |
2701 | 【例题5】解方程组:
2702 |
2703 | (1)$\begin{cases}
2704 | x+y=9\cdots①\\
2705 | y+z=15\cdots②\\
2706 | z+x=12\cdots③
2707 | \end{cases}$
2708 |
2709 |
2710 |
2711 | (2)$\begin{cases}
2712 | x+2y=11\cdots①\\
2713 | 3x+z=19\cdots②\\
2714 | z=x+y\cdots③
2715 | \end{cases}$
2716 |
2717 |
2718 |
2719 | 【练习5】解方程组:
2720 |
2721 | (1)$\begin{cases}
2722 | 2x+y+z=7\\
2723 | x+2y+z=8\\
2724 | x+y+2z=9
2725 | \end{cases}$
2726 |
2727 |
2728 |
2729 | 【例题6】购买3斤苹果,2斤橘子需要6.90元;购买8斤苹果,9斤橘子需要22.80元,那么苹果、橘子各买1斤需要多少元?
2730 |
2731 |
2732 |
2733 | 【练习6】已知:$\begin{cases}
2734 | 3x+6y=17\\
2735 | 7x+4y=13
2736 | \end{cases}$,求$x+y=$()。
2737 |
2738 |
2739 |
2740 |
--------------------------------------------------------------------------------
/05-五年级.md:
--------------------------------------------------------------------------------
1 | ---
2 | title: 五年级
3 | lang: zh-CN
4 | sidebarDepth: 1
5 | ---
6 |
7 | # 五年级
8 |
9 | ## 5.1.03. 棋盘中的数学
10 |
11 | 间隔染色,用间隔染色解决问题。
12 |
13 | 思想:构造模型,用模型解决实际问题。
14 |
15 | ### 热身1
16 |
17 | ### 热身2
18 |
19 | ### 热身3
20 |
21 | ### 例题1
22 |
23 | 有一次车展共16个展室,如图,每个展室与相邻的展室都有门相通,出口和入口如图中箭头所示。
24 | (1)参观者能否从入口进去,不重复地参观完每个展室再从出口出来?
25 | (2)参观者能否从入口进去,不重复地参观完每个展室再从入口出来?
26 |
27 | ### 练习1
28 |
29 | 有一栋大厦共3✕3✕3=27间房子,每个房间与相邻的房间都有直达电梯,入口和出口如下
30 | 图所示。
31 | (1)参观者能否从入口进去,不重复地参观完每个展室再从出口出来?
32 | (2)参观者能否从入口进去,不重复地参观完每个展室再从入口出来?
33 |
34 | ### 例题2
35 |
36 | (1)左图是连接14个城市的道路图,是否有一条路线可以经过每一个城市怡好一次?
37 | (2)右图中是半张中国象棋棋盘,棋盘上放有一只马。众所周知,马是走“日”字路线的。请问:这个马能否不重复地走遍这半张棋盘上的每一个点,然后回到出发点?
38 |
39 | ### 练习2
40 |
41 | 五年级一班有35名同学,共分成5排,每排7人,坐在教室里,每个座位的前后左右四个位置都叫作他的邻座。如果要让这35名同学每个人都恰好坐到他的邻座上去,能办到吗?为什么?
42 |
43 | ### 例题3
44 |
45 | 下面三个图形都是从4✕4的正方形分别剪去两个1✕1的小方格得到的,问:可否把它们分别剪成1✕2的七个小矩形?
46 |
47 | ### 练习3
48 |
49 | 如图所示,一个8✕8的国际象棋棋盘去掉对角上两格后,是否可以用31个2✕1的“骨牌”把棋盘上的62个小格完全盖住?
50 |
51 | ### 例题4
52 |
53 | 如图所示,有一个6✕6的棋盘,请问:能否用1个和8个填满这个棋盘? (图形可以旋转和翻折)
54 |
55 | ### 练习4
56 |
57 | 如图所示,有一个6✕6的棋盘,请问:能否用3个和6个填满这个棋盘? (图形可以旋转和翻折)
58 |
59 | ### 例题5
60 |
61 | 如图所示,有一个6✕6的棋盘,请问:
62 |
63 | (1)能否用9个填满这个棋盘?
64 |
65 | (2)能否用9个填满这个棋盘?(图形可以旋转)
66 |
67 | (3)能否用9个填满这个棋盘?(图形可以旋转)
68 |
69 | ### 练习5
70 |
71 | ### 例题6
72 |
73 | ### 练习6
74 |
75 | ### 巩固1
76 |
77 | ### 巩固2
78 |
79 | ### 巩固3
80 |
81 | ## 5.1.04. 课程标题
82 |
83 | ### 热身1
84 |
85 | ### 热身2
86 |
87 | ### 热身3
88 |
89 | ### 例题1(有序数对)
90 |
91 | (1)将6块糖全部分给丁丁、田田、阿普三个人,每个人都要分到糖,那么一共有几种分法?
92 |
93 | (2)丁丁有14块糖,从第一天开始吃,每天至少吃2颗,至多吃6颗,第三天吃完,有几种吃法?
94 |
95 | ### 练习1
96 |
97 | 田田、牛牛、阿普三个人一共有7本课外书,每个人至少有一本。田田、牛牛、阿普分别有几本课外书?请写出全部可能的情况。
98 |
99 | ### 例题2
100 |
101 | (1)将10个小球分成两堆,有几种分法?
102 |
103 | (2)将10个小球分成三堆,有几种分法?
104 |
105 | (3)将18个小球分成三堆,每堆至少2个,至多9个,有几种分法?
106 |
107 | ### 练习2
108 |
109 | 将11拆成三个不同的正整数相加的形式,加数相同顺序不同看作同一种形式,例如:11=2+3+6与11=3+6+2看作同一种形式。问:有几种可能的形式?
110 |
111 | ### 例题3
112 |
113 | 周长为15厘米,三边长都是整数厘米的三角形有几个?(通过旋转、翻折、平移能重合的三角形视为同一个三角形)
114 |
115 | ### 练习3
116 |
117 | 三条边的边长均为整数,且最长边的边长是7厘米,这样的三角形共有多少种?
118 |
119 | ### 例题4
120 |
121 | 从1、2、3、4、5、6、7中选取三个不同的数,使得它们的和为3的倍数,有几种不同的选法?
122 |
123 | ### 练习4
124 |
125 | 从1-50这50个自然数中选取两个数,使它们的和大于50,共有多少种不同的选法?
126 |
127 | ### 例题5
128 |
129 | 甲、乙两人进行乒乓球比赛,规定谁先胜三场谁胜,第一场甲胜。问:到决出最后胜负为止,有多少种可能的情形?其中甲胜的情形有几种?
130 |
131 | ### 练习5
132 |
133 | 如图,给1、2、3、4号区域染上红、蓝、紫三种颜色,每块区域染一种颜色,并且使得相邻两块区域的颜色不同,有几种染法?
134 |
135 | 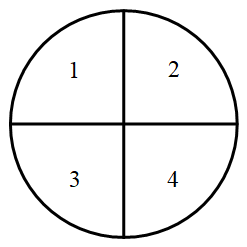
136 |
137 | ### 例题6
138 |
139 | 如图,从起点到终点,只能沿着图中线段走。
140 |
141 | (1)所有点恰好经过一次,有几种走法?
142 |
143 | (2)所有点至多经过一次,有几种走法?
144 |
145 | (2)不能走重复路线(能走重复点),有几种走法?
146 |
147 | 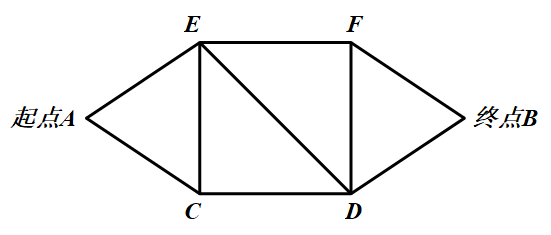
148 |
149 | ### 练习6
150 |
151 | 如图,从点A出发,沿着线段走,最后到达点B。
152 |
153 | (1)如果每个黑点恰好经过一次,有几种走法?
154 |
155 | (2)如果每个黑点至多经过一次,有几种走法?
156 |
157 | 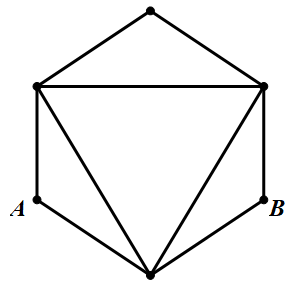
158 |
159 | ### 拓展1
160 |
161 | ### 拓展2
162 |
163 | ### 拓展3
164 |
165 | ### 拓展4
166 |
167 | ### 拓展5
168 |
169 | ### 练习1
170 |
171 | ### 练习2
172 |
173 | ### 练习3
174 |
175 | ### 练习4
176 |
177 | ### 练习5
178 |
179 | ### 练习6
180 |
181 | ## 5.1.05. 排列组合
182 |
183 | ### 例题1
184 |
185 | (1)从A、B、C、D、E这5个小朋友中选3名站成一排拍照。我们分步骤来思考这个问题:
186 |
187 | 第一步,选一个人站第一个位置,有()种选法;
188 |
189 | 第二步,选一个人站第二个位置,有()种选法;
190 |
191 | 第三步,选一个人站第三个位置,有()种选法。
192 |
193 | 根据乘法原理,完成三步有()×()×()种方法,用排列数可以表示为$A_5^3$。
194 |
195 | (2)计算:
196 |
197 | | $A_4^2=$ | $A_5^3=$ | $A_6^3=$ |
198 | | -------------- | -------------------- | ----------------------------------- |
199 | | $A_5^4=$ | $A_{10}^{10}=$ | $A_6^2-A_2^2=$ |
200 | | $A_8^4+A_6^2=$ | $A_7^2\times A_5^3=$ | $\frac{A_{100}^{98}}{A_{98}^{98}}=$ |
201 |
202 | ### 练习1
203 |
204 | (1)从7名学生中,安排3名学生分别扫地、拖地、倒垃圾,有几种安排方法?
205 |
206 | (2)计算:
207 |
208 | | $A_5^2=$ | $A_6^4=$ |
209 | | ---------------------- | ---------------------- |
210 | | $\frac{A_8^5}{A_5^5}=$ | $\frac{A_9^5}{A_4^4}=$ |
211 |
212 | ### 例题2
213 |
214 | 从A、B、C、D、E这5个小朋友中选出3名小朋友,有$C_5^3$种方法,再将选出的3名小朋友排成一排,有$A_3^3$种方法。因此,先选再排这两步有$C_5^3\times A_3^3$种方法,应该与$A_5^3$相等,所以$C_5^3=\frac{A_5^3}{A_3^3}=\frac{5\times4\times3}{3\times2\times1}$
215 | 仿照此例:
216 |
217 | 计算:
218 |
219 | (1)$C_6^2, C_6^4$
220 |
221 | (2)$C_7^2, C_7^5$
222 |
223 | ### 练习2
224 |
225 | 计算:
226 |
227 | | (1)$C_{12}^3$ | (2)$C_{1000}^{998}$ | (3)$A_8^2-C_8^2$ |
228 | | --------------- | --------------------- | ------------------ |
229 |
230 | ### 例题3
231 |
232 | 有4个同学一起去郊游,照相时,必须有一名同学给其他3人拍照,共可能有多少种拍照情況?(照相时3人站成一排)
233 |
234 | ### 练习3
235 |
236 | 6个人排成一排,有几种排法?
237 |
238 | ### 例题4
239 |
240 | 五名学生和一名老师排队拍照,老师不能站在两边,有几种排法?
241 |
242 | ### 练习4
243 |
244 | 5个人并排站成一排,其中甲必须站在中间,有几种不同的站法。
245 |
246 | ### 例题5
247 |
248 | (1)从1、2、3、4、5、6、7、8中选出3个数,使得3个数的和是偶数,有几种选法?
249 | (2)从1、2、3、4、5、6、7、8中选出3个数,使得3个数的乘积是偶数,有几种选法?
250 |
251 | ### 练习5
252 |
253 | 田田要从八门课程中选学三门,一共有多少种选法?如果数学课与钢琴课时间冲突,不能同时学,她一共有多少种选法?
254 |
255 | ### 例题6
256 |
257 | 一个小组有10个人,其中6个人会唱歌,4个人会跳舞,回答下列问题:
258 | (1)选出4个人表演唱歌,3个人表演跳舞,有几种选法?
259 | (2)后来又来了一个人既会唱歌,又会跳舞。要选出4个人表演跳舞,3个人表演唱歌,有几种选法?
260 |
261 | ### 练习6
262 |
263 | 学校举办联欢晚会,要从6名数学老师中选出3名,再从4名语文老师中选出2名,接着让这5名老师分别扮演5个不同的角色,共有多少种选择方式?
264 |
265 | ## 5.1.06. 质数与合数进阶
266 |
267 | ### 例题1
268 |
269 | 当$p$和$p^5+5$都是质数时,求$p^5+5$的值。
270 |
271 | ### 练习1
272 |
273 | 如果$a$、$b$均为质数,且$3a+7b=41$,求$a+b$的值。
274 |
275 | ### 例题2
276 |
277 | $a$、$b$、$c$均为质数,如果$(a+b)\times(b+c)=342$,那么$b$是几。
278 |
279 | ### 练习2
280 |
281 | 在算式$a\times(b+c)=110+c$中,$a$、$b$、$c$是三个互不相等的质数,那么$b$是几。
282 |
283 | ### 例题3
284 |
285 | 有三张卡片,在它们上面各写有一个数字1、2、3(如下图)。从中抽出一张、二张、三张,按任意次序排起来,可以得到不同的一位数、二位数、三位数。请你将其中的质数都写出来?
286 |
287 | ### 练习3
288 |
289 | 自然数$n$是一个两位数,它是一个质数,而且$n$的个位数字与十位数字都是质数,这样的自然数有多少个?
290 |
291 | ### 例题4
292 |
293 | 4只同样的瓶子内分别装有一定数量的油。每瓶和其他各瓶分别合称一次,记录千克数如下:8,9,10,11,12,13。已知4只空瓶的重量之和以及油的重量之和均为质数,问:最重的两瓶内有多少油?
294 |
295 | ### 练习4
296 |
297 | 有一个正方体木块,如图,每个面上各写了一个自然数,并且相对的两个面上的两个数之和相等。现在只能看见三个面上写的数,如果看不见的各个面写的都是质数,问:这三个质数的和是多少?
298 |
299 | ### 例题5
300 |
301 | 已知三个合数$a$、$b$、$c$两两互质,且$a\times b\times c=1001\times28\times11$,问:$a+b+c$的最小值是几?
302 |
303 | ### 练习5
304 |
305 | 6个奇数的和为98,积为4267305,这6个奇数中最大数与最小数的和是几?
306 |
307 | ### 例题6
308 |
309 | 将一个三位数的个位数字与百位数字对调位置,得到一个新的三位数,已知这两个三位数的乘积等于55872,那么,这两个三位数的和为多少?
310 |
311 | ### 练习6
312 |
313 | 如果两位数$\overline{吃好}$和$\overline{好吃}$都为质数,则这两个质数和的最大值是多少?
314 |
315 | ### 拓展1
316 |
317 | ### 拓展2
318 |
319 | ### 拓展3
320 |
321 | ### 拓展4
322 |
323 | ### 拓展5
324 |
325 | ## 5.1.07. 牛吃草问题
326 |
327 | ### 例题1
328 |
329 | 牧场上长满牧草,每天牧草都匀速生长。这片牧场可供27头牛吃6天,可供23头牛吃9天。那么,可供21头牛吃几天?
330 |
331 | ### 练习1
332 |
333 | 有一块匀速生长的草场,可供12头牛吃25天,或可供24头牛吃10天。那么可供29头牛吃几天?
334 |
335 | ### 例题2
336 |
337 | 牧场上长满牧草,每天牧草都匀速生长。这片牧场可供10头牛吃20天,可供15头牛吃10天。那么这片牧场可供几头牛吃25天?
338 |
339 | ### 练习2
340 |
341 | 有一片牧场,草每天都在均匀地生长。如果在牧场上放养24头牛,那么6天就把草吃完了;如果只放养21头牛,那么8天才把草吃完。请问:要使得草永远吃不完,最多可以放养多少头牛?
342 |
343 | ### 例题3
344 |
345 | 林子里有猴子喜欢吃的野果,23只猴子可在9周内吃光,21只猴子可在12周内吃光,问:如果要4周吃光野果,则需有多少只猴子一起吃?(假设野果生长的速度不变)
346 |
347 | ### 练习3
348 |
349 | 仓库里原有一批存货,以后继续运货进仓,且每天运进的货一样多。用同样的汽车运货出仓,如果每天用4辆汽车,则9天恰好运完;如果每天用5辆汽车,则6天恰好运完。仓库里原有的存货若用1辆汽车运,则需要多少天运完?
350 |
351 | ### 例题4
352 |
353 | 一个水池有一根进水管不间断地进水,还有若干根相同的抽水管。若用24根抽水管抽水,6小时即可把池中的水抽干;若用21根抽水管抽水,8小时可把池中的水抽干。若用16根抽水管,需要多少小时可把水池中的水抽干?
354 |
355 | ### 练习4
356 |
357 | 一个装满了水的水池有一个进水阀及三个口径相同的排水阀,如果同时打开进水阀及一个排水阀,则30分钟能把水池的水排完,如果同时打开进水阀及两个排水阀,则10分钟把水池的水排完。问:关闭进水阀并且同时打开三个排水阀,需要多少分钟能排完水池的水?
358 |
359 | ### 例题5
360 |
361 | 由于天气逐渐变冷,牧场上的草每天以均匀的速度减少。经计算,牧场上的草可供20头牛吃5天,或可供16头牛吃6天。那么,可供11头牛吃几天?
362 |
363 | ### 练习5
364 |
365 | 由于天气逐渐冷起来,牧场上的草不仅不生长,反而以固定的速度在减少。已知某块草地上的草可供20头牛吃5天,或可供15头牛吃6天。照此计算,可供多少头牛吃10天?
366 |
367 | ### 例题6
368 |
369 | 有一片草场,草每天的生长速度相同。若14头牛30天可将草吃完,70只羊16天也可将草吃完(4只羊1天的吃草量相当于1头牛1天的吃草量)。那么,17头牛和20只羊多少天可将草吃完?
370 |
371 | ### 练习6
372 |
373 | 农场有一片均匀生长的草地,可以供18头牛吃40天,或者供12头牛与36只羊吃25天,如果1头牛每天的吃草量相当于3只羊每天的吃草量。请问:这片草地让17头牛与多少只羊一起吃,刚好16天吃完?
374 |
375 | ## 5.1.08. 数阵图综合
376 |
377 | ### 例题1
378 |
379 | 将1到7,这七个数字,分别填入图中各个〇内,使每条线段上的三个〇内数的和都相等。
380 |
381 | ### 练习1
382 |
383 | 把1,4,7,10,13,16,19七个数填入图中7个圆圈中,使每条线上三个数的和都等手30。
384 |
385 | ### 例题2
386 |
387 | 把1~11填入图中,使每条线上三个数的和相等。
388 |
389 | ### 练习2
390 |
391 | 把1~9这9个数分别填入下图的圆圈中,使得每条直线上的3个数的和都相等。
392 |
393 | ### 例题3
394 |
395 | 把1至6分别填入下图的六个园圈内,使得每个正方形四个顶点的数之和都为13。
396 |
397 | ### 练习3
398 |
399 | 在图中的八个圆圈内分别填入八个不同的自然数,使得正方形每条边上三个数的和相等。现在如果已经填好了五个数,那么每条边上各数之和应该是多少?并将其补充完整。
400 |
401 | ### 例题4
402 |
403 | 图中共有10个圆圈,6条直线。请问:
404 |
405 | (1)能否将1~10填入图中,使得每条直线上各数之和都相等?
406 |
407 | (2)能否将0~9填入图中,使得每条直线上各数之和都相等?
408 |
409 | ### 练习4
410 |
411 | 将11至16六个数填入图中所示球体的圈内,使球体的各个大圆上每四个数的和都相等。这个和是多少?
412 |
413 | ### 例题5
414 |
415 | 如下图,大大小小的三角形共7个,把1~9这九个数分别填入图中的“〇”中,使每个三角形三个顶点的数之和相等。求AxBxC的最大值?
416 |
417 | ### 练习5
418 |
419 | 如图,大三角形被分成了9个小三角形。试将1,2,3,4,5,6,7,8,9分别填入这9个小三角形内,每个小三角形内填一个数,要求靠近大三角形3条边的每5个数的和相等,问:这5个数的和最大可能是多少?
420 |
421 | ### 例题6
422 |
423 | 把1~8这8个数分别填入下图的八个圆圈中,使得任意两个有线段直接相连的圆圈内的数字之差都不等于1。请问:有多少种不同的填法?
424 |
425 | ### 练习6
426 |
427 | 将1、2、3、5、6、7、9、10、11填入图中的小圆圈内,使得每条直线上各数之和都等于18。
428 |
429 | ## 5.1.09. 比和比例
430 |
431 | ### 例题1(化简比)
432 |
433 | (1)把$12:16$化成最简整数比是();
434 |
435 | (2)把$\frac{2}{5}:\frac{6}{7}$化成最简整数比是();
436 |
437 | (3)把连比$24:36:40$化成最简整数比是()。
438 |
439 | ### 练习1
440 |
441 | (1)把$48:60$化成最简整数比是();
442 |
443 | (2)把$\frac{1}{2}:\frac{4}{3}$化成最简整数比是();
444 |
445 | (3)把连比$22:33:44$化成最简整数比是()。
446 |
447 | ### 补充
448 |
449 | (1)$\frac{8+9+\dots+40}{27+28+\dots+50}$化为最简整数比是()。
450 |
451 | (2)$\frac{12!}{11!}$化为最简整数比是()。
452 |
453 | (3)$\frac{1}{3}:\frac{1}{4}:\frac{1}{5}$化为最简整数比是()。
454 |
455 | ### 例题2(解比例)
456 |
457 | 把下列比例补充完整。
458 |
459 | (1)$2:5=():30$
460 |
461 | (2)$():3:8=6:():12$
462 |
463 | ### 练习2
464 |
465 | 解比例方程。
466 |
467 | (1)$3.6:x=\frac{1}{2}:4$
468 |
469 | (2)$\frac{1}{2}:\frac{5}{6}=x:3$
470 |
471 | (3)$\frac{7x-10}{3x+5}=\frac{6}{5}$
472 |
473 | ### 例题3
474 |
475 | 解比例方程:$(3x-2):(2x+3)=4:7$
476 |
477 | ### 练习3
478 |
479 | 解比例方程:$4:(5x-1)=12:(10x+7)$
480 |
481 | ### 补充
482 |
483 | 3、5、7、a可以组成一个比例,则a=()。
484 |
485 | ### 探索
486 |
487 | 甲、乙两数之比为$5:9$,两数之和为70,甲数是()。
488 |
489 | ### 例题4(比与份数)
490 |
491 | 田田、牛牛、丁丁他们的体重比是$2:3:4$,其中田田的体重是34千克。牛牛、丁丁的体重各是多少干克?
492 |
493 | ### 练习4
494 |
495 | 动物园里有老虎、企鹅、鸵鸟三种动物比较体重,老虎重360千克,企鹅的体重是鸵鸟的$\frac{5}{12}$,鸵鸟的体重是老虎的$\frac{4}{15}$,那么企鹅的体重是多少干克?
496 |
497 | ### 补充
498 |
499 | 甲、乙、丙三数之比为$3:7:10$,乙数比甲数多20,这三个数之和是()。
500 |
501 | ### 探索
502 |
503 | 若$A: B=2:3$,$B: C=4:5$,则 $A: B: C$的最简整数比是()。
504 |
505 | ### 例题5
506 |
507 | 已知甲、乙、丙三个数,甲等于乙、丙两数和的$\frac{1}{3}$,乙等于甲、丙两数和的$\frac{1}{2}$,丙等于甲、乙两数和的$\frac{5}{7}$,求甲:乙:丙是多少?
508 |
509 | ### 练习5
510 |
511 | 甲、乙、丙三个数,已知$甲:(乙+丙)=4:3$,$乙: 丙=2:7$,问:$甲: 乙: 丙$是多少?
512 |
513 | ### 例题6
514 |
515 | 某山区小学要栽253棵松树,分给三个年级。六年级分到的$\frac{1}{5}$等于五年级分到的$\frac{1}{4}$,又等于四年级分到的$\frac{1}{2}$,三个年级各分到多少棵?
516 |
517 | ### 练习6
518 |
519 | 加工一个零件,甲要2分钟,乙要3分钟,丙要4分钟。现有1170个零件,甲、乙、丙三人各加工几个零件,才能使他们同时完成任务?
520 |
521 | ### 拓展
522 |
523 | ### 拓展1
524 |
525 | 判断这组数字能否组成比例,如果能,请列出比例式。
526 |
527 | $\frac{5}{2}$,14,3.5,10
528 |
529 | ### 拓展2
530 |
531 | 解比例方程组。
532 | $$
533 | \left\{\begin{matrix}
534 | x:y=3:4
535 | \\
536 | 3x+5y=58
537 | \end{matrix}\right.
538 | $$
539 |
540 | ### 拓展3
541 |
542 | 解比例方程。
543 |
544 | $\frac{4x-1}{2(x+1)}=\frac{4x+7}{2x+10}$
545 |
546 | ### 拓展4
547 |
548 | 解比例方程。
549 |
550 | $\frac{x-1}{x+3}=\frac{2x-1}{2x+9}$
551 |
552 | ### 拓展5
553 |
554 | 已知$a_1:a_2=a_2:a_3=b_1:b_2=b_2:b_3=c_1:c_2=c_2:c_3$,并且$a_1$、$b_2$、$c_3$成等差数列(公差不为0),请问$(a_3\times c_2)$和 $(b_1\times b_3)$哪个更大?
555 |
556 | ## 5.1.10. 比列模型
557 |
558 | ### 例题1
559 |
560 | 如图,三角形ABC被线段AD分成两个小三角形,图中一共有三个三角形,这三个三角形有一条公共的高,因此他们的面积之比等于对应底边长度之比。即$S_{△ABD}: S_{△ADC}: S_{△ABC}=BD:DC:BC$。
561 |
562 | (1)若$BD: DC=3:2$,并且三角形ABD的面积为18平方厘米,问:三角形ADC的面积为多少?
563 |
564 | (2)若 $3BD=4DC$,并且三角形ABC的面积为84平方厘米,问:三角形ABD的面积为多少?
565 |
566 | ### 练习1
567 |
568 | 如图,三角形ABC的面积为180平方厘米,并且$BD: DE: EC=2:3:4$,问:阴影部分三角形ADE的面积?
569 |
570 | ### 例题2
571 |
572 | 如图,四边形ABCD被对角线AC,以及线段BE、DE分成四个小三角形,这四个小三角形的面积分别记为a、b、c、d,那么根据比例模型可知,$a:b=AE: EC$;$d:c=AE: EC$,所以$a:b=d:c$,根据比例性质可知$ac=bd$。
573 | (1)若三角形ABE、三角形BCE、三角形CDE的面积分别是30平方厘米、20平方厘米、10平方厘米,问:四边形ABCD的面积是多少?
574 |
575 | (2)已知四边形ABCD的面积为56平方厘米,三角形BCE、三角形CDE的面积分别为10平方厘米、6平方厘米,问:三角形ABE的面积是多少?
576 |
577 | ### 练习2
578 |
579 | 如图,己知三角形ABE的面积为18平方厘米,$AE: EC=3:4$,$BE: ED=6:5$,问:三角形ADE、三角形BCE、三角形CDE的面积?
580 |
581 | ### 例题3
582 |
583 | (1)如图,三角形ABC的面积为60平方厘米,并且$AE: EB=2:3$,$BD=2DC$,问:阴影部分三角形ADE的面积是多少平方厘米?
584 |
585 | (2)如图,三角形ABC面积为90平方厘米,$BD=2DC$,$AE: EC=2:3$,问:阴影部分三角形CDE的面积?
586 |
587 | ### 练习3
588 |
589 | 如图,正方形ABCD边长为6厘米,AE=4厘米,$AC=3AF$,G是EC的中点,求阴影部分三角形EFG的面积。
590 |
591 | ### 例题4
592 |
593 | 如图,一个边长为120厘米的等边三角形被分成了面积相等的五块,那么AB是多少厘米?
594 |
595 | ### 练习4
596 |
597 | 如图,在三角形ABC中,H,I,J是AB的四等分点;D,E,F,G是BC的五等分点。知$S_{△BDH}=1$,问:每一个小三角形的面积分别为多少?
598 |
599 | ### 例题5
600 |
601 | 如图,三角形ABC的面积为36平方厘米,并且$AC=4AD$,$BC=3EC$,$BD=3BF$,$DE=3DG$,H是EF的中点,求阴影部分三角形FGH的面积?
602 |
603 | ### 练习5
604 |
605 | 如图,三角形ABC中,$BD: DC=2:5$,$AE: EC=4:3$,三角形ABC的面积是980平方厘米,求三角形CDE的面积?
606 |
607 | ### 例题6
608 |
609 | 如图,点E、F分别为四边形ABCD中AB的三等分点。点G、H为CD的三等分点。则四边形EFHG的面积占总面积的几分之几?
610 |
611 | ### 练习6
612 |
613 | 如图,四边形ABCD中,$DE: EF: FC=3:2:1$,$BG: GH: AH=3:2:1$。$AD: BC=1:2$,已知四边形ABCD的面积等于4,求四边形EFGH的面积?
614 |
615 | ### 练习1
616 |
617 | 如图所示,四边形ABCD形状的草地里有两条路AC和BD,交于点O,三角形AOD、三角形AOB、三角形BOC的面积分别为6平方米、14平方米、35平方米,求三角形COD的面积。
618 |
619 | ### 练习2
620 |
621 | 如图所示,阴影部分三角形CDE的面积为8平方厘米,并且 $AE=2EC$,$AD: DB=2:3$,求三角形ABC的面积。
622 |
623 | ### 练习3
624 |
625 | 如图所示,三角形ABC的面积为60平方厘米,$AD=3DB$,$AC=3AE$,求阴影部分三角形ADE的面积。
626 |
627 | ### 练习4
628 |
629 | ### 练习5
630 |
631 | ### 练习6
632 |
633 | ## 5.1.11. 容斥问题
634 |
635 | ### 热身1
636 |
637 | 如图,三角形ABC的面积为24平方厘米,并且BD=2DA,CE=3EB,DF: FC=3:2,G是DE的中点,求阴影部分三角形DFG的面积。
638 |
639 | ### 热身2
640 |
641 | 如图,在三角形ABC中,H,I,J是AB的四等分点;D,E,F,G是BC的五等分点。知$S_{△BDH}=1$,问:每一个小三角形的面积分别为多少?
642 |
643 | ### 热身3
644 |
645 | 如图,点E、F分别为四边形ABCD中AB的三等分点。点G、H为CD的三等分点。则四边形EFHG的面积占总面积的几分之几?
646 |
647 | ### 例题1
648 |
649 | 在46人的采摘活动中,只采了樱桃的有18人,既采了樱桃又采了杏的有7人,既没采樱桃又没采杏的有6人,问:只采了杏的有多少人?
650 |
651 | ### 练习1
652 |
653 | 有100名同学回答A、B两个问题,都没有回答对的有10人,答对A的有75人,答对B的有83人,两题都答对的有多少人?
654 |
655 | ### 例题2
656 |
657 | 某校参加数学竞赛的有120名男生,80名女生,参加语文竞赛的有120名女生,80名男生,己知该校总共有260名学生参加竞赛,其中75名男生两科竞赛都参加了,那么只参加数学竞赛而没有参加语文竞赛的女生有多少人?
658 |
659 | ### 练习2
660 |
661 | 育才小学画展上展出了许多幅画,其中有16幅画不是六年级的,有15幅画不是五年级的,五、六年级共展出25幅画,其他年级的画共有多少幅?
662 |
663 | ### 例题3
664 |
665 | 50名学生面向老师站成一行,老师先让大家从左到右按1,2,3,⋯,依次报数,再让报数是4的倍数的同学向后转,接着又让报数是6的倍数的同学向后转,问:此时还有多少同学面向老师?
666 |
667 | ### 练习3
668 |
669 | 五年级一班有45名同学上体育课,他们在操场上排成一排面向教师,并从1到45报完数后,教师叫报偶数的人向后转,接着叫报3的倍数的人向后转,则这时面向教师的学生有多少人?
670 |
671 | ### 例题4
672 |
673 | 有2008盏亮着的电灯,各有一个拉线开关控制着。现将其顺序编号为1,2,3,⋯,2008。将编号为2的倍数的灯线拉一下,再将编号为3的倍数的灯线拉一下,最后将编号为5的倍数的灯线拉一下,拉完后还有几盏灯是亮的?
674 |
675 | ### 练习4
676 |
677 | 有1000盏亮着的电灯,各有一个拉线开关控制着。现将其顺序编号为1,2,3,⋯,1000。将编号为2的倍数的灯线拉一下,再将编号为3的倍数的灯线拉一下,最后将编号为5的倍数的灯线拉一下,拉完后还有几盏灯是亮的?
678 |
679 | ### 例题5
680 |
681 | 分母是1001的最简真分数有多少个?
682 |
683 | ### 练习5
684 |
685 | 分母是105的最简真分数有多少个?
686 |
687 | ### 例题6
688 |
689 | 一根100厘米长的木棍,从左起每隔6厘米划一个刻度,每隔7厘米划一个刻度,每隔8厘米划一个刻度,如果按刻度把木棍截断,可以截出多少段?
690 |
691 | ### 练习6
692 |
693 | 一根101厘米长的木棒,从同一端开始,第一次每隔2厘米画一个刻度,第二次每隔3厘米画一个刻度,第三次每隔5厘米画一个刻度,如果按刻度把木棒截断,那么可以截出多少段?
694 |
695 | ### 练习1
696 |
697 | 田径队的40名运动员们在训练基地进行封闭训练。其中男运动员有20名,训练长跑的运动员有15名,训练竞走的女运动员有8名,那么训练长跑的男运动员有多少名?
698 |
699 | ### 练习2
700 |
701 | 去年某年级有56人订阅过《中小学生数学学习》,其中,上半年有25名男生、15名女生订阅了该杂志,下半年有26名男生25 名女生订阅了该杂志。已知有23名男生是全年订阅,那么,只在上半年订阅了该杂志的女生有多少名?
702 |
703 | ### 练习3
704 |
705 | 200盏亮着的电灯,各有一个拉线开关控制,按排序编号为1,2,3,……,200。将编号为3的倍数的灯的拉线各拉一下,再将编号为5的倍数的灯的拉线各拉一下,拉完后不亮的灯有多少盏?
706 |
707 | ### 练习4
708 |
709 | ### 练习5
710 |
711 | ### 练习6
712 |
--------------------------------------------------------------------------------
/06-六年级.md:
--------------------------------------------------------------------------------
1 | ---
2 | title: 六年级
3 | lang: zh-CN
4 | sidebarDepth: 1
5 | ---
6 |
7 | # 六年级
8 |
9 | 待整理
10 |
--------------------------------------------------------------------------------
/README.md:
--------------------------------------------------------------------------------
1 | ## 小学奥数
2 |
3 | 课程不定期更新,点击在线查看。
4 |
5 | * [一年级(待整理)](https://www.vastxie.com/%E5%B0%8F%E5%AD%A6%E5%A5%A5%E6%95%B0/01-%E4%B8%80%E5%B9%B4%E7%BA%A7.html)
6 | * [二年级(更新中)](https://www.vastxie.com/%E5%B0%8F%E5%AD%A6%E5%A5%A5%E6%95%B0/02-%E4%BA%8C%E5%B9%B4%E7%BA%A7.html)
7 | * [三年级(更新中)](https://www.vastxie.com/%E5%B0%8F%E5%AD%A6%E5%A5%A5%E6%95%B0/03-%E4%B8%89%E5%B9%B4%E7%BA%A7.html)
8 | * [四年级(更新中)](https://www.vastxie.com/%E5%B0%8F%E5%AD%A6%E5%A5%A5%E6%95%B0/04-%E5%9B%9B%E5%B9%B4%E7%BA%A7.html)
9 | * [五年级(更新中)](https://www.vastxie.com/%E5%B0%8F%E5%AD%A6%E5%A5%A5%E6%95%B0/05-%E4%BA%94%E5%B9%B4%E7%BA%A7.html)
10 | * [六年级(待整理)](https://www.vastxie.com/%E5%B0%8F%E5%AD%A6%E5%A5%A5%E6%95%B0/06-%E5%85%AD%E5%B9%B4%E7%BA%A7.html)
11 |
12 | 课程计划包含:
13 |
14 | * 热身
15 | * 例题 + 练习
16 | * 巩固
17 | * 拓展
18 |
19 | 课程内容来自本人上课讲义,有一些地方排版比较乱,讲次内容也有缺失,后续会逐步更新完善。
20 |
21 | 本课程仅供学习交流使用,希望对你有所帮助。
22 |
--------------------------------------------------------------------------------
2413 |
2414 | ### 例题2
2415 |
2416 | “12345678910111213…282930”是一个位数很多的多位数,从中划去40个数字,使剩下的数字(顺序不变)组成一个首位不为0的多位数,则这个多位数最大为多少?
2417 |
2418 | ### 练习2
2419 |
2420 | “12345678910111213…282930”是一个位数很多的多位数,从中划去40个数字,使剩下的数字(顺序不变)组成一个首位不为0的多位数,则这个多位数最小为多少?
2421 |
2422 | ### 例题3
2423 |
2424 | 某次考试共有15题。计分标准是:做对第1题得1分,做对第2题得2分,……,做对第15题得15分。若做错第1题则要倒扣1分,做错第2题要倒扣2分,……,做错第15题要倒扣15分。小明做了所有的题,得90分,那么小明至多做错多少道题?
2425 |
2426 | ### 练习3
2427 |
2428 | 某次考试共有15题。计分标准是:做对第1题得1分,做对第2题得2分,……,做对第15题得15分。若做错第1题则要倒扣1分,做错第2题要倒扣2分,……,做错第15题要倒扣15分。小明做了所有的题,得90分,那么小明至多做错多少道题?
2429 |
2430 | ### 例题4
2431 |
2432 | 阶梯教室座位有10排,每排有16个座位,当有150个人就座时,某些排坐着的人数就一样多。我们希望人数一样的排数尽可能少,这样的排数至少有多少排?
2433 |
2434 | ### 练习4
2435 |
2436 | 学校203教室座位有5排,每排有8个座位,当有30个人就座时,某些排坐着的人数就一样多。我们希望人数一样的排数尽可能少,这样的排数至少有多少排?
2437 |
2438 | ### 例题5
2439 |
2440 | 如图,牧羊人用15段每段长2米的篱笆,一面靠墙围成一个长方形羊圈,则羊圈的最大面积是多少平方米?
2441 |
2442 | 
2443 |
2444 | ### 练习5
2445 |
2446 | 某校准备用一道长36米的铁丝网,围成一块长方形生物实验基地,这块基地的面积最大是多少平方米?
2447 |
2448 | ### 例题6
2449 |
2450 | 如图,一个长方形被分成4个小长方形,其中长方形A、B、C的周长分别是10厘米、12厘米、14厘米,那么长方形D的面积最大是多少平方厘米?
2451 |
2452 | 
2453 |
2454 | ### 练习6
2455 |
2456 | 一块长方形菜地被分成4个小块,其A、B、C块的周长分别是20厘米、24厘米、28厘米那么D的面积最大是多少平方厘米?
2457 |
2458 | 
2459 |
2460 | ## 4.2.15. 操作类智巧趣题
2461 |
2462 | ### 例题1
2463 |
2464 | 一个猎户,带着一条狗,一只兔子和一筐胡萝卜乘船过河,船小一次只能带一样东西。但是他不在时,狗会咬兔子,免子会吃胡萝卜。请你想一想,帮猎人安排合理的方法过河。
2465 |
2466 | ### 练习1
2467 |
2468 | 一个农民携带一只狼、一只羊和一棵白菜,要借助一条小船过河。小船上除了农民只能再带狼、羊、白菜中的一样。而农民不在时,狼会吃羊,羊会吃白菜。农民如何过河呢?
2469 |
2470 | ### 例题2
2471 |
2472 | 小枫带着他的三个馋嘴弟弟和一个大蛋糕过河,已知只有小枫会划船,且除了小枫外每次只能带其中的一个弟弟,或者蛋糕过河。蛋糕一共十块,只要小枫离开,单独留弟弟和蛋糕在一起,每个弟弟在下次见到哥哥之前都会吃掉一块蛋糕。假设除弟弟外的任何原因都不会导致蛋糕减少,请问,兄弟4人全部过河后,最多还能剩下块蛋糕。
2473 |
2474 | ### 练习2
2475 |
2476 | 河左边有一个大人和两个小孩,一只大熊和两只小熊。只有大熊、大人会划船,船一次最多只能运两个单位(不管人熊),条件是熊的数量不能大于人的数量(不分大小),要不然熊会把人吃掉(河的两边熊的数量都不能大于人的数量)。问怎么才能让人和熊安全渡河?
2477 |
2478 | ### 例题3
2479 |
2480 | 一大一小两个油桶,大桶盛满重11千克,小桶盛满重4千克。现要盛5千克的油,只用这两个桶盛,能办到吗?
2481 |
2482 | ### 练习3
2483 |
2484 | 小红去河边打水,她有两个桶,大桶能装9升水,小桶能装4升水,想要恰好从河中打上6升的水带回去,她该怎么办?
2485 |
2486 | ### 例题4
2487 |
2488 | 卖牛奶人有两桶10升装的牛奶。两个顾客各带容器去买2升牛奶,一个带的是5升的容器,另一个带的是4升的容器。这位卖牛奶人如何解决问题?
2489 |
2490 | ### 练习4
2491 |
2492 | 有大、中、小3个水桶,最多分别可装入水10千克、7千克和3千克。现在大桶中装满水,希望通过水在3个瓶子间的流动使得中瓶和小瓶上标出装1千克水的刻度线,聪明的你想想应该怎么倒呢?
2493 |
2494 | ### 例题5
2495 |
2496 | 有9个铁球,其中8个铁球一样重,另一个较轻,你要在天平上至少称几次才能保证把那个轻球找出来?
2497 |
2498 | ### 练习5
2499 |
2500 | 有3个铁球,其中2个铁球一样重,另一个较轻,你在天平上至少称几次能保证把那个轻球找出来?
2501 |
2502 | ### 例题6
2503 |
2504 | 今有101枚硬币,其中有100枚同样的真币和1枚伪币,伪币与真币的重量不同。现需弄清楚伪币究竟比真币轻,还是比真币重,但只有一架没有砝码的天平。那么怎样利用这架天平称两次,来达到目的?
2505 |
2506 | ### 练习6
2507 |
2508 | 现有21枚硬币,其中有20枚同样的真币和1枚伪币,伪币与真币重量不同。现需弄清楚伪币究竟比真币轻,还是比真币重,但只有一架没有砝码的天平。那么怎样利用这架天平称两次,来达到目的?
2509 |
2510 | ### 练习1
2511 |
2512 | 一个猎人要带一棵红萝卜,一只狗,两只老虎和一只羊过河。可现在,小船只有3个座位,猎人每次最多只能送两样东西过河。没有狗看管,老虎会吃羊;没有人看管,狗和羊就吵架,羊就会吃红萝卜。有什么妙计能帮助它们全都过河?
2513 |
2514 | ### 练习2
2515 |
2516 | 相传汉代军事家韩信一天访友归来 ,途中经过一集市,遇见卖油翁与顾客争执。买者想买5斤油,而卖者无法计量,因而告诉买者, 要么买3斤,要么买7斤。韩信询问得知,卖油翁油篓中恰好装有10斤油,但他仅有装3斤和7斤的葫芦,而买者执意要买5斤油。韩信立在马上稍加思索道:“你们无须再争,以我之法保你们都满意。”韩信下马经过几次倒油,买卖双方皆大欢喜。你知道,韩信是怎么倒油吗?
2517 |
2518 | ### 练习3
2519 |
2520 | 在一批产品中有16个零件,其中有一个是次品,比较轻(其它零件一样重) , 给你一架天平,你最少用天平称量
2521 | 几次就可以检验出次品零件?
2522 |
2523 | ## 4.2.17. 相遇追及综合
2524 |
2525 | ### 例题1
2526 |
2527 | 如图,周长为800米的环形跑道上,田田和阿普分别从相距200米的A、B两处同时沿相同方向出发。田田每分钟能跑200米,阿普每分钟只能跑150米,田田第一次追上阿普需要多少分钟?
2528 |
2529 | 
2530 |
2531 | ### 练习1
2532 |
2533 | 如图,周长为400米的环形跑道上田田和阿普分别从相距100米的A、B两处同时沿相同方向出发。田田每分钟能跑200米,阿普每分钟只能跑150米,田田第一次追上阿普需要多少分钟?
2534 |
2535 | 
2536 |
2537 | ### 例题2
2538 |
2539 | 如图,田田和阿普分别从周长为1200米的圆形跑道上相距600米的A、B两处同时出发相向而行。6分钟后两人相遇。相遇后两人继续行进,4分钟后田田怡好到达B处,问两人相遇的地点距离A点多少米?
2540 |
2541 | 
2542 |
2543 | ### 练习2
2544 |
2545 | 如图,田田和阿普分别从周长600米的圆形跑道上相距300米的A、B两处同时出发相向而行,6分钟后两人相遇。相遇后两人继续行进,4分钟后田田怡好到达B处,求两人相遇的地点距离A点多少米?
2546 |
2547 | 
2548 |
2549 | ### 例题3
2550 |
2551 | 一列从西向东行驶的火车车速为每秒16米,车身长255米,8点整它追上了在铁路旁从西向东散步的田田,并于17秒后离开了他,又过了5分钟,它与从东向西散步的阿普相遇,15秒后离开了他。请问田田和阿普步行的速度分别是多少?
2552 |
2553 | ### 练习3
2554 |
2555 | 一列从西向东行驶的火车车速为每秒19米,车身长360米。9点整它追上了在铁路旁从西向东散步的田田,并于20秒后离开了她。又过了5分钟,它与从东向西散步的阿普相遇18秒后离开了他。请问田田和阿普步行的速度分别是多少?
2556 |
2557 | ### 例题4
2558 |
2559 | 田田以6米/秒的速度在铁路旁骑车,一列火车迎面开来,与她从相遇到离开共用了15秒,而它追上在铁路旁以4米/秒的速度跑步的阿普并刚好超过他共用了25秒,求火车的长度和行驶的速度。
2560 |
2561 | ### 练习4
2562 |
2563 | 田田以5米/秒的速度在铁路旁骑车,一列火车迎面开来,与她从相遇到离开共用了10秒,而它追上在铁路旁以3米/秒的速度跑步的阿普并刚好超过他共用了20秒,求火车的长度和行驶的速度。
2564 |
2565 | ### 例题5
2566 |
2567 | 某河上下游两港相距100千米,每天定时有甲乙两艘船速相等的客轮从两港相向而行,甲船顺水每小时行12千米,乙船逆水每小时行8千米,这天甲船在出发时,从船上掉下一物,此物顺水漂流而下,当甲乙两船相遇时,此物距相遇地点有多远?
2568 |
2569 | ### 练习5
2570 |
2571 | 某河上下游两港相距60千米,每天定时有甲乙两艘船速相等的客轮从两港相向而行,甲船顺水每小时行11千米,乙船逆水每小时行9千米,这天甲船在出发时,从船上掉下一物,此物顺水漂流而下,当甲乙两船相遇时,此物距相遇地点有多远?
2572 |
2573 | ### 例题6
2574 |
2575 | 某河上下游两港相距150千米,每天有甲乙两艘船分别从上游和下游同时相向而行,它们在静水中的速度分别为6千米/时和9千米/时。平时它们相遇于距上游港70千米处,某日突下暴雨,水速变为原来的2倍,这一天甲乙两船相遇地点距上游港多远?
2576 |
2577 | ### 练习6
2578 |
2579 | 某河上下游两港相距130千米,每天有甲乙两艘船分别从上游和下游同时相向而行,它们在静水中的速度分别为5千米/时和8千米/时。平时它们相遇于距上游港60千米处。某日突下暴雨,水速变为原来的2倍,这一天甲乙两船相遇地点距上游港多远?
2580 |
2581 |
2582 |
2583 | ## 方程与方程组
2584 |
2585 | ### 例题练习
2586 |
2587 | 【例题1】解下列一元一次方程:
2588 |
2589 | (1)$6(3+x)=24$
2590 |
2591 | (2)$18-(3x-6)=x$
2592 |
2593 | 答案:(1)1;(2)6
2594 |
2595 |
2596 |
2597 | 【练习1】解下列一元一次方程:
2598 |
2599 | (1)$3x-2(2+x)=1$
2600 |
2601 | (2)$6x-(4-x)=17$
2602 |
2603 |
2604 |
2605 | 【例题2】用代入消元法解方程组:
2606 |
2607 | (1)$\begin{cases}
2608 | y=2x-3\\
2609 | 3x+2y=8
2610 | \end{cases}$
2611 |
2612 |
2613 |
2614 | (2)$\begin{cases}
2615 | 2x-y=5\\
2616 | 3x+4y=13
2617 | \end{cases}$
2618 |
2619 |
2620 |
2621 | 【练习2】用代入消元法解方程组:
2622 |
2623 | (1)$\begin{cases}
2624 | 3x+2y=13\\
2625 | 2x-y=4
2626 | \end{cases}$
2627 |
2628 |
2629 |
2630 | 【例题3】用加减消元法解下列方程组:
2631 |
2632 | (1)$\begin{cases}
2633 | x-y=5\\
2634 | x+y=13
2635 | \end{cases}$
2636 |
2637 |
2638 |
2639 | (2)$\begin{cases}
2640 | 2x+y=11\\
2641 | 3x-2y=6
2642 | \end{cases}$
2643 |
2644 |
2645 |
2646 | (3)$\begin{cases}
2647 | 5y+z=12\\
2648 | 6y+5z=22
2649 | \end{cases}$
2650 |
2651 |
2652 |
2653 | 【练习3】用加减消元法解下列方程组:
2654 |
2655 | (1)$\begin{cases}
2656 | x+2y=21\\
2657 | 2x+y=18
2658 | \end{cases}$
2659 |
2660 |
2661 |
2662 | (2)$\begin{cases}
2663 | 7x+3y=44\\
2664 | 11x-2y=49
2665 | \end{cases}$
2666 |
2667 |
2668 |
2669 | (3)$\begin{cases}
2670 | 7x+3y=44\\
2671 | 11x+2y=61
2672 | \end{cases}$
2673 |
2674 |
2675 |
2676 | 【例题4】解方程组:
2677 |
2678 | (1)$\begin{cases}
2679 | 2x-3y=x+y-4\\
2680 | 3x+4y=x+5y+13
2681 | \end{cases}$
2682 |
2683 |
2684 |
2685 | (2)$\begin{cases}
2686 | 3x+5y=2x+3y+11\\
2687 | 4x-y-6=x+2y
2688 | \end{cases}$
2689 |
2690 |
2691 |
2692 | 【练习4】解方程组:
2693 |
2694 | (1)$\begin{cases}
2695 | a-1=b+1\\
2696 | a+1=3(b-1)
2697 | \end{cases}$
2698 |
2699 |
2700 |
2701 | 【例题5】解方程组:
2702 |
2703 | (1)$\begin{cases}
2704 | x+y=9\cdots①\\
2705 | y+z=15\cdots②\\
2706 | z+x=12\cdots③
2707 | \end{cases}$
2708 |
2709 |
2710 |
2711 | (2)$\begin{cases}
2712 | x+2y=11\cdots①\\
2713 | 3x+z=19\cdots②\\
2714 | z=x+y\cdots③
2715 | \end{cases}$
2716 |
2717 |
2718 |
2719 | 【练习5】解方程组:
2720 |
2721 | (1)$\begin{cases}
2722 | 2x+y+z=7\\
2723 | x+2y+z=8\\
2724 | x+y+2z=9
2725 | \end{cases}$
2726 |
2727 |
2728 |
2729 | 【例题6】购买3斤苹果,2斤橘子需要6.90元;购买8斤苹果,9斤橘子需要22.80元,那么苹果、橘子各买1斤需要多少元?
2730 |
2731 |
2732 |
2733 | 【练习6】已知:$\begin{cases}
2734 | 3x+6y=17\\
2735 | 7x+4y=13
2736 | \end{cases}$,求$x+y=$()。
2737 |
2738 |
2739 |
2740 |
--------------------------------------------------------------------------------
/05-五年级.md:
--------------------------------------------------------------------------------
1 | ---
2 | title: 五年级
3 | lang: zh-CN
4 | sidebarDepth: 1
5 | ---
6 |
7 | # 五年级
8 |
9 | ## 5.1.03. 棋盘中的数学
10 |
11 | 间隔染色,用间隔染色解决问题。
12 |
13 | 思想:构造模型,用模型解决实际问题。
14 |
15 | ### 热身1
16 |
17 | ### 热身2
18 |
19 | ### 热身3
20 |
21 | ### 例题1
22 |
23 | 有一次车展共16个展室,如图,每个展室与相邻的展室都有门相通,出口和入口如图中箭头所示。
24 | (1)参观者能否从入口进去,不重复地参观完每个展室再从出口出来?
25 | (2)参观者能否从入口进去,不重复地参观完每个展室再从入口出来?
26 |
27 | ### 练习1
28 |
29 | 有一栋大厦共3✕3✕3=27间房子,每个房间与相邻的房间都有直达电梯,入口和出口如下
30 | 图所示。
31 | (1)参观者能否从入口进去,不重复地参观完每个展室再从出口出来?
32 | (2)参观者能否从入口进去,不重复地参观完每个展室再从入口出来?
33 |
34 | ### 例题2
35 |
36 | (1)左图是连接14个城市的道路图,是否有一条路线可以经过每一个城市怡好一次?
37 | (2)右图中是半张中国象棋棋盘,棋盘上放有一只马。众所周知,马是走“日”字路线的。请问:这个马能否不重复地走遍这半张棋盘上的每一个点,然后回到出发点?
38 |
39 | ### 练习2
40 |
41 | 五年级一班有35名同学,共分成5排,每排7人,坐在教室里,每个座位的前后左右四个位置都叫作他的邻座。如果要让这35名同学每个人都恰好坐到他的邻座上去,能办到吗?为什么?
42 |
43 | ### 例题3
44 |
45 | 下面三个图形都是从4✕4的正方形分别剪去两个1✕1的小方格得到的,问:可否把它们分别剪成1✕2的七个小矩形?
46 |
47 | ### 练习3
48 |
49 | 如图所示,一个8✕8的国际象棋棋盘去掉对角上两格后,是否可以用31个2✕1的“骨牌”把棋盘上的62个小格完全盖住?
50 |
51 | ### 例题4
52 |
53 | 如图所示,有一个6✕6的棋盘,请问:能否用1个和8个填满这个棋盘? (图形可以旋转和翻折)
54 |
55 | ### 练习4
56 |
57 | 如图所示,有一个6✕6的棋盘,请问:能否用3个和6个填满这个棋盘? (图形可以旋转和翻折)
58 |
59 | ### 例题5
60 |
61 | 如图所示,有一个6✕6的棋盘,请问:
62 |
63 | (1)能否用9个填满这个棋盘?
64 |
65 | (2)能否用9个填满这个棋盘?(图形可以旋转)
66 |
67 | (3)能否用9个填满这个棋盘?(图形可以旋转)
68 |
69 | ### 练习5
70 |
71 | ### 例题6
72 |
73 | ### 练习6
74 |
75 | ### 巩固1
76 |
77 | ### 巩固2
78 |
79 | ### 巩固3
80 |
81 | ## 5.1.04. 课程标题
82 |
83 | ### 热身1
84 |
85 | ### 热身2
86 |
87 | ### 热身3
88 |
89 | ### 例题1(有序数对)
90 |
91 | (1)将6块糖全部分给丁丁、田田、阿普三个人,每个人都要分到糖,那么一共有几种分法?
92 |
93 | (2)丁丁有14块糖,从第一天开始吃,每天至少吃2颗,至多吃6颗,第三天吃完,有几种吃法?
94 |
95 | ### 练习1
96 |
97 | 田田、牛牛、阿普三个人一共有7本课外书,每个人至少有一本。田田、牛牛、阿普分别有几本课外书?请写出全部可能的情况。
98 |
99 | ### 例题2
100 |
101 | (1)将10个小球分成两堆,有几种分法?
102 |
103 | (2)将10个小球分成三堆,有几种分法?
104 |
105 | (3)将18个小球分成三堆,每堆至少2个,至多9个,有几种分法?
106 |
107 | ### 练习2
108 |
109 | 将11拆成三个不同的正整数相加的形式,加数相同顺序不同看作同一种形式,例如:11=2+3+6与11=3+6+2看作同一种形式。问:有几种可能的形式?
110 |
111 | ### 例题3
112 |
113 | 周长为15厘米,三边长都是整数厘米的三角形有几个?(通过旋转、翻折、平移能重合的三角形视为同一个三角形)
114 |
115 | ### 练习3
116 |
117 | 三条边的边长均为整数,且最长边的边长是7厘米,这样的三角形共有多少种?
118 |
119 | ### 例题4
120 |
121 | 从1、2、3、4、5、6、7中选取三个不同的数,使得它们的和为3的倍数,有几种不同的选法?
122 |
123 | ### 练习4
124 |
125 | 从1-50这50个自然数中选取两个数,使它们的和大于50,共有多少种不同的选法?
126 |
127 | ### 例题5
128 |
129 | 甲、乙两人进行乒乓球比赛,规定谁先胜三场谁胜,第一场甲胜。问:到决出最后胜负为止,有多少种可能的情形?其中甲胜的情形有几种?
130 |
131 | ### 练习5
132 |
133 | 如图,给1、2、3、4号区域染上红、蓝、紫三种颜色,每块区域染一种颜色,并且使得相邻两块区域的颜色不同,有几种染法?
134 |
135 | 
136 |
137 | ### 例题6
138 |
139 | 如图,从起点到终点,只能沿着图中线段走。
140 |
141 | (1)所有点恰好经过一次,有几种走法?
142 |
143 | (2)所有点至多经过一次,有几种走法?
144 |
145 | (2)不能走重复路线(能走重复点),有几种走法?
146 |
147 | 
148 |
149 | ### 练习6
150 |
151 | 如图,从点A出发,沿着线段走,最后到达点B。
152 |
153 | (1)如果每个黑点恰好经过一次,有几种走法?
154 |
155 | (2)如果每个黑点至多经过一次,有几种走法?
156 |
157 | 
158 |
159 | ### 拓展1
160 |
161 | ### 拓展2
162 |
163 | ### 拓展3
164 |
165 | ### 拓展4
166 |
167 | ### 拓展5
168 |
169 | ### 练习1
170 |
171 | ### 练习2
172 |
173 | ### 练习3
174 |
175 | ### 练习4
176 |
177 | ### 练习5
178 |
179 | ### 练习6
180 |
181 | ## 5.1.05. 排列组合
182 |
183 | ### 例题1
184 |
185 | (1)从A、B、C、D、E这5个小朋友中选3名站成一排拍照。我们分步骤来思考这个问题:
186 |
187 | 第一步,选一个人站第一个位置,有()种选法;
188 |
189 | 第二步,选一个人站第二个位置,有()种选法;
190 |
191 | 第三步,选一个人站第三个位置,有()种选法。
192 |
193 | 根据乘法原理,完成三步有()×()×()种方法,用排列数可以表示为$A_5^3$。
194 |
195 | (2)计算:
196 |
197 | | $A_4^2=$ | $A_5^3=$ | $A_6^3=$ |
198 | | -------------- | -------------------- | ----------------------------------- |
199 | | $A_5^4=$ | $A_{10}^{10}=$ | $A_6^2-A_2^2=$ |
200 | | $A_8^4+A_6^2=$ | $A_7^2\times A_5^3=$ | $\frac{A_{100}^{98}}{A_{98}^{98}}=$ |
201 |
202 | ### 练习1
203 |
204 | (1)从7名学生中,安排3名学生分别扫地、拖地、倒垃圾,有几种安排方法?
205 |
206 | (2)计算:
207 |
208 | | $A_5^2=$ | $A_6^4=$ |
209 | | ---------------------- | ---------------------- |
210 | | $\frac{A_8^5}{A_5^5}=$ | $\frac{A_9^5}{A_4^4}=$ |
211 |
212 | ### 例题2
213 |
214 | 从A、B、C、D、E这5个小朋友中选出3名小朋友,有$C_5^3$种方法,再将选出的3名小朋友排成一排,有$A_3^3$种方法。因此,先选再排这两步有$C_5^3\times A_3^3$种方法,应该与$A_5^3$相等,所以$C_5^3=\frac{A_5^3}{A_3^3}=\frac{5\times4\times3}{3\times2\times1}$
215 | 仿照此例:
216 |
217 | 计算:
218 |
219 | (1)$C_6^2, C_6^4$
220 |
221 | (2)$C_7^2, C_7^5$
222 |
223 | ### 练习2
224 |
225 | 计算:
226 |
227 | | (1)$C_{12}^3$ | (2)$C_{1000}^{998}$ | (3)$A_8^2-C_8^2$ |
228 | | --------------- | --------------------- | ------------------ |
229 |
230 | ### 例题3
231 |
232 | 有4个同学一起去郊游,照相时,必须有一名同学给其他3人拍照,共可能有多少种拍照情況?(照相时3人站成一排)
233 |
234 | ### 练习3
235 |
236 | 6个人排成一排,有几种排法?
237 |
238 | ### 例题4
239 |
240 | 五名学生和一名老师排队拍照,老师不能站在两边,有几种排法?
241 |
242 | ### 练习4
243 |
244 | 5个人并排站成一排,其中甲必须站在中间,有几种不同的站法。
245 |
246 | ### 例题5
247 |
248 | (1)从1、2、3、4、5、6、7、8中选出3个数,使得3个数的和是偶数,有几种选法?
249 | (2)从1、2、3、4、5、6、7、8中选出3个数,使得3个数的乘积是偶数,有几种选法?
250 |
251 | ### 练习5
252 |
253 | 田田要从八门课程中选学三门,一共有多少种选法?如果数学课与钢琴课时间冲突,不能同时学,她一共有多少种选法?
254 |
255 | ### 例题6
256 |
257 | 一个小组有10个人,其中6个人会唱歌,4个人会跳舞,回答下列问题:
258 | (1)选出4个人表演唱歌,3个人表演跳舞,有几种选法?
259 | (2)后来又来了一个人既会唱歌,又会跳舞。要选出4个人表演跳舞,3个人表演唱歌,有几种选法?
260 |
261 | ### 练习6
262 |
263 | 学校举办联欢晚会,要从6名数学老师中选出3名,再从4名语文老师中选出2名,接着让这5名老师分别扮演5个不同的角色,共有多少种选择方式?
264 |
265 | ## 5.1.06. 质数与合数进阶
266 |
267 | ### 例题1
268 |
269 | 当$p$和$p^5+5$都是质数时,求$p^5+5$的值。
270 |
271 | ### 练习1
272 |
273 | 如果$a$、$b$均为质数,且$3a+7b=41$,求$a+b$的值。
274 |
275 | ### 例题2
276 |
277 | $a$、$b$、$c$均为质数,如果$(a+b)\times(b+c)=342$,那么$b$是几。
278 |
279 | ### 练习2
280 |
281 | 在算式$a\times(b+c)=110+c$中,$a$、$b$、$c$是三个互不相等的质数,那么$b$是几。
282 |
283 | ### 例题3
284 |
285 | 有三张卡片,在它们上面各写有一个数字1、2、3(如下图)。从中抽出一张、二张、三张,按任意次序排起来,可以得到不同的一位数、二位数、三位数。请你将其中的质数都写出来?
286 |
287 | ### 练习3
288 |
289 | 自然数$n$是一个两位数,它是一个质数,而且$n$的个位数字与十位数字都是质数,这样的自然数有多少个?
290 |
291 | ### 例题4
292 |
293 | 4只同样的瓶子内分别装有一定数量的油。每瓶和其他各瓶分别合称一次,记录千克数如下:8,9,10,11,12,13。已知4只空瓶的重量之和以及油的重量之和均为质数,问:最重的两瓶内有多少油?
294 |
295 | ### 练习4
296 |
297 | 有一个正方体木块,如图,每个面上各写了一个自然数,并且相对的两个面上的两个数之和相等。现在只能看见三个面上写的数,如果看不见的各个面写的都是质数,问:这三个质数的和是多少?
298 |
299 | ### 例题5
300 |
301 | 已知三个合数$a$、$b$、$c$两两互质,且$a\times b\times c=1001\times28\times11$,问:$a+b+c$的最小值是几?
302 |
303 | ### 练习5
304 |
305 | 6个奇数的和为98,积为4267305,这6个奇数中最大数与最小数的和是几?
306 |
307 | ### 例题6
308 |
309 | 将一个三位数的个位数字与百位数字对调位置,得到一个新的三位数,已知这两个三位数的乘积等于55872,那么,这两个三位数的和为多少?
310 |
311 | ### 练习6
312 |
313 | 如果两位数$\overline{吃好}$和$\overline{好吃}$都为质数,则这两个质数和的最大值是多少?
314 |
315 | ### 拓展1
316 |
317 | ### 拓展2
318 |
319 | ### 拓展3
320 |
321 | ### 拓展4
322 |
323 | ### 拓展5
324 |
325 | ## 5.1.07. 牛吃草问题
326 |
327 | ### 例题1
328 |
329 | 牧场上长满牧草,每天牧草都匀速生长。这片牧场可供27头牛吃6天,可供23头牛吃9天。那么,可供21头牛吃几天?
330 |
331 | ### 练习1
332 |
333 | 有一块匀速生长的草场,可供12头牛吃25天,或可供24头牛吃10天。那么可供29头牛吃几天?
334 |
335 | ### 例题2
336 |
337 | 牧场上长满牧草,每天牧草都匀速生长。这片牧场可供10头牛吃20天,可供15头牛吃10天。那么这片牧场可供几头牛吃25天?
338 |
339 | ### 练习2
340 |
341 | 有一片牧场,草每天都在均匀地生长。如果在牧场上放养24头牛,那么6天就把草吃完了;如果只放养21头牛,那么8天才把草吃完。请问:要使得草永远吃不完,最多可以放养多少头牛?
342 |
343 | ### 例题3
344 |
345 | 林子里有猴子喜欢吃的野果,23只猴子可在9周内吃光,21只猴子可在12周内吃光,问:如果要4周吃光野果,则需有多少只猴子一起吃?(假设野果生长的速度不变)
346 |
347 | ### 练习3
348 |
349 | 仓库里原有一批存货,以后继续运货进仓,且每天运进的货一样多。用同样的汽车运货出仓,如果每天用4辆汽车,则9天恰好运完;如果每天用5辆汽车,则6天恰好运完。仓库里原有的存货若用1辆汽车运,则需要多少天运完?
350 |
351 | ### 例题4
352 |
353 | 一个水池有一根进水管不间断地进水,还有若干根相同的抽水管。若用24根抽水管抽水,6小时即可把池中的水抽干;若用21根抽水管抽水,8小时可把池中的水抽干。若用16根抽水管,需要多少小时可把水池中的水抽干?
354 |
355 | ### 练习4
356 |
357 | 一个装满了水的水池有一个进水阀及三个口径相同的排水阀,如果同时打开进水阀及一个排水阀,则30分钟能把水池的水排完,如果同时打开进水阀及两个排水阀,则10分钟把水池的水排完。问:关闭进水阀并且同时打开三个排水阀,需要多少分钟能排完水池的水?
358 |
359 | ### 例题5
360 |
361 | 由于天气逐渐变冷,牧场上的草每天以均匀的速度减少。经计算,牧场上的草可供20头牛吃5天,或可供16头牛吃6天。那么,可供11头牛吃几天?
362 |
363 | ### 练习5
364 |
365 | 由于天气逐渐冷起来,牧场上的草不仅不生长,反而以固定的速度在减少。已知某块草地上的草可供20头牛吃5天,或可供15头牛吃6天。照此计算,可供多少头牛吃10天?
366 |
367 | ### 例题6
368 |
369 | 有一片草场,草每天的生长速度相同。若14头牛30天可将草吃完,70只羊16天也可将草吃完(4只羊1天的吃草量相当于1头牛1天的吃草量)。那么,17头牛和20只羊多少天可将草吃完?
370 |
371 | ### 练习6
372 |
373 | 农场有一片均匀生长的草地,可以供18头牛吃40天,或者供12头牛与36只羊吃25天,如果1头牛每天的吃草量相当于3只羊每天的吃草量。请问:这片草地让17头牛与多少只羊一起吃,刚好16天吃完?
374 |
375 | ## 5.1.08. 数阵图综合
376 |
377 | ### 例题1
378 |
379 | 将1到7,这七个数字,分别填入图中各个〇内,使每条线段上的三个〇内数的和都相等。
380 |
381 | ### 练习1
382 |
383 | 把1,4,7,10,13,16,19七个数填入图中7个圆圈中,使每条线上三个数的和都等手30。
384 |
385 | ### 例题2
386 |
387 | 把1~11填入图中,使每条线上三个数的和相等。
388 |
389 | ### 练习2
390 |
391 | 把1~9这9个数分别填入下图的圆圈中,使得每条直线上的3个数的和都相等。
392 |
393 | ### 例题3
394 |
395 | 把1至6分别填入下图的六个园圈内,使得每个正方形四个顶点的数之和都为13。
396 |
397 | ### 练习3
398 |
399 | 在图中的八个圆圈内分别填入八个不同的自然数,使得正方形每条边上三个数的和相等。现在如果已经填好了五个数,那么每条边上各数之和应该是多少?并将其补充完整。
400 |
401 | ### 例题4
402 |
403 | 图中共有10个圆圈,6条直线。请问:
404 |
405 | (1)能否将1~10填入图中,使得每条直线上各数之和都相等?
406 |
407 | (2)能否将0~9填入图中,使得每条直线上各数之和都相等?
408 |
409 | ### 练习4
410 |
411 | 将11至16六个数填入图中所示球体的圈内,使球体的各个大圆上每四个数的和都相等。这个和是多少?
412 |
413 | ### 例题5
414 |
415 | 如下图,大大小小的三角形共7个,把1~9这九个数分别填入图中的“〇”中,使每个三角形三个顶点的数之和相等。求AxBxC的最大值?
416 |
417 | ### 练习5
418 |
419 | 如图,大三角形被分成了9个小三角形。试将1,2,3,4,5,6,7,8,9分别填入这9个小三角形内,每个小三角形内填一个数,要求靠近大三角形3条边的每5个数的和相等,问:这5个数的和最大可能是多少?
420 |
421 | ### 例题6
422 |
423 | 把1~8这8个数分别填入下图的八个圆圈中,使得任意两个有线段直接相连的圆圈内的数字之差都不等于1。请问:有多少种不同的填法?
424 |
425 | ### 练习6
426 |
427 | 将1、2、3、5、6、7、9、10、11填入图中的小圆圈内,使得每条直线上各数之和都等于18。
428 |
429 | ## 5.1.09. 比和比例
430 |
431 | ### 例题1(化简比)
432 |
433 | (1)把$12:16$化成最简整数比是();
434 |
435 | (2)把$\frac{2}{5}:\frac{6}{7}$化成最简整数比是();
436 |
437 | (3)把连比$24:36:40$化成最简整数比是()。
438 |
439 | ### 练习1
440 |
441 | (1)把$48:60$化成最简整数比是();
442 |
443 | (2)把$\frac{1}{2}:\frac{4}{3}$化成最简整数比是();
444 |
445 | (3)把连比$22:33:44$化成最简整数比是()。
446 |
447 | ### 补充
448 |
449 | (1)$\frac{8+9+\dots+40}{27+28+\dots+50}$化为最简整数比是()。
450 |
451 | (2)$\frac{12!}{11!}$化为最简整数比是()。
452 |
453 | (3)$\frac{1}{3}:\frac{1}{4}:\frac{1}{5}$化为最简整数比是()。
454 |
455 | ### 例题2(解比例)
456 |
457 | 把下列比例补充完整。
458 |
459 | (1)$2:5=():30$
460 |
461 | (2)$():3:8=6:():12$
462 |
463 | ### 练习2
464 |
465 | 解比例方程。
466 |
467 | (1)$3.6:x=\frac{1}{2}:4$
468 |
469 | (2)$\frac{1}{2}:\frac{5}{6}=x:3$
470 |
471 | (3)$\frac{7x-10}{3x+5}=\frac{6}{5}$
472 |
473 | ### 例题3
474 |
475 | 解比例方程:$(3x-2):(2x+3)=4:7$
476 |
477 | ### 练习3
478 |
479 | 解比例方程:$4:(5x-1)=12:(10x+7)$
480 |
481 | ### 补充
482 |
483 | 3、5、7、a可以组成一个比例,则a=()。
484 |
485 | ### 探索
486 |
487 | 甲、乙两数之比为$5:9$,两数之和为70,甲数是()。
488 |
489 | ### 例题4(比与份数)
490 |
491 | 田田、牛牛、丁丁他们的体重比是$2:3:4$,其中田田的体重是34千克。牛牛、丁丁的体重各是多少干克?
492 |
493 | ### 练习4
494 |
495 | 动物园里有老虎、企鹅、鸵鸟三种动物比较体重,老虎重360千克,企鹅的体重是鸵鸟的$\frac{5}{12}$,鸵鸟的体重是老虎的$\frac{4}{15}$,那么企鹅的体重是多少干克?
496 |
497 | ### 补充
498 |
499 | 甲、乙、丙三数之比为$3:7:10$,乙数比甲数多20,这三个数之和是()。
500 |
501 | ### 探索
502 |
503 | 若$A: B=2:3$,$B: C=4:5$,则 $A: B: C$的最简整数比是()。
504 |
505 | ### 例题5
506 |
507 | 已知甲、乙、丙三个数,甲等于乙、丙两数和的$\frac{1}{3}$,乙等于甲、丙两数和的$\frac{1}{2}$,丙等于甲、乙两数和的$\frac{5}{7}$,求甲:乙:丙是多少?
508 |
509 | ### 练习5
510 |
511 | 甲、乙、丙三个数,已知$甲:(乙+丙)=4:3$,$乙: 丙=2:7$,问:$甲: 乙: 丙$是多少?
512 |
513 | ### 例题6
514 |
515 | 某山区小学要栽253棵松树,分给三个年级。六年级分到的$\frac{1}{5}$等于五年级分到的$\frac{1}{4}$,又等于四年级分到的$\frac{1}{2}$,三个年级各分到多少棵?
516 |
517 | ### 练习6
518 |
519 | 加工一个零件,甲要2分钟,乙要3分钟,丙要4分钟。现有1170个零件,甲、乙、丙三人各加工几个零件,才能使他们同时完成任务?
520 |
521 | ### 拓展
522 |
523 | ### 拓展1
524 |
525 | 判断这组数字能否组成比例,如果能,请列出比例式。
526 |
527 | $\frac{5}{2}$,14,3.5,10
528 |
529 | ### 拓展2
530 |
531 | 解比例方程组。
532 | $$
533 | \left\{\begin{matrix}
534 | x:y=3:4
535 | \\
536 | 3x+5y=58
537 | \end{matrix}\right.
538 | $$
539 |
540 | ### 拓展3
541 |
542 | 解比例方程。
543 |
544 | $\frac{4x-1}{2(x+1)}=\frac{4x+7}{2x+10}$
545 |
546 | ### 拓展4
547 |
548 | 解比例方程。
549 |
550 | $\frac{x-1}{x+3}=\frac{2x-1}{2x+9}$
551 |
552 | ### 拓展5
553 |
554 | 已知$a_1:a_2=a_2:a_3=b_1:b_2=b_2:b_3=c_1:c_2=c_2:c_3$,并且$a_1$、$b_2$、$c_3$成等差数列(公差不为0),请问$(a_3\times c_2)$和 $(b_1\times b_3)$哪个更大?
555 |
556 | ## 5.1.10. 比列模型
557 |
558 | ### 例题1
559 |
560 | 如图,三角形ABC被线段AD分成两个小三角形,图中一共有三个三角形,这三个三角形有一条公共的高,因此他们的面积之比等于对应底边长度之比。即$S_{△ABD}: S_{△ADC}: S_{△ABC}=BD:DC:BC$。
561 |
562 | (1)若$BD: DC=3:2$,并且三角形ABD的面积为18平方厘米,问:三角形ADC的面积为多少?
563 |
564 | (2)若 $3BD=4DC$,并且三角形ABC的面积为84平方厘米,问:三角形ABD的面积为多少?
565 |
566 | ### 练习1
567 |
568 | 如图,三角形ABC的面积为180平方厘米,并且$BD: DE: EC=2:3:4$,问:阴影部分三角形ADE的面积?
569 |
570 | ### 例题2
571 |
572 | 如图,四边形ABCD被对角线AC,以及线段BE、DE分成四个小三角形,这四个小三角形的面积分别记为a、b、c、d,那么根据比例模型可知,$a:b=AE: EC$;$d:c=AE: EC$,所以$a:b=d:c$,根据比例性质可知$ac=bd$。
573 | (1)若三角形ABE、三角形BCE、三角形CDE的面积分别是30平方厘米、20平方厘米、10平方厘米,问:四边形ABCD的面积是多少?
574 |
575 | (2)已知四边形ABCD的面积为56平方厘米,三角形BCE、三角形CDE的面积分别为10平方厘米、6平方厘米,问:三角形ABE的面积是多少?
576 |
577 | ### 练习2
578 |
579 | 如图,己知三角形ABE的面积为18平方厘米,$AE: EC=3:4$,$BE: ED=6:5$,问:三角形ADE、三角形BCE、三角形CDE的面积?
580 |
581 | ### 例题3
582 |
583 | (1)如图,三角形ABC的面积为60平方厘米,并且$AE: EB=2:3$,$BD=2DC$,问:阴影部分三角形ADE的面积是多少平方厘米?
584 |
585 | (2)如图,三角形ABC面积为90平方厘米,$BD=2DC$,$AE: EC=2:3$,问:阴影部分三角形CDE的面积?
586 |
587 | ### 练习3
588 |
589 | 如图,正方形ABCD边长为6厘米,AE=4厘米,$AC=3AF$,G是EC的中点,求阴影部分三角形EFG的面积。
590 |
591 | ### 例题4
592 |
593 | 如图,一个边长为120厘米的等边三角形被分成了面积相等的五块,那么AB是多少厘米?
594 |
595 | ### 练习4
596 |
597 | 如图,在三角形ABC中,H,I,J是AB的四等分点;D,E,F,G是BC的五等分点。知$S_{△BDH}=1$,问:每一个小三角形的面积分别为多少?
598 |
599 | ### 例题5
600 |
601 | 如图,三角形ABC的面积为36平方厘米,并且$AC=4AD$,$BC=3EC$,$BD=3BF$,$DE=3DG$,H是EF的中点,求阴影部分三角形FGH的面积?
602 |
603 | ### 练习5
604 |
605 | 如图,三角形ABC中,$BD: DC=2:5$,$AE: EC=4:3$,三角形ABC的面积是980平方厘米,求三角形CDE的面积?
606 |
607 | ### 例题6
608 |
609 | 如图,点E、F分别为四边形ABCD中AB的三等分点。点G、H为CD的三等分点。则四边形EFHG的面积占总面积的几分之几?
610 |
611 | ### 练习6
612 |
613 | 如图,四边形ABCD中,$DE: EF: FC=3:2:1$,$BG: GH: AH=3:2:1$。$AD: BC=1:2$,已知四边形ABCD的面积等于4,求四边形EFGH的面积?
614 |
615 | ### 练习1
616 |
617 | 如图所示,四边形ABCD形状的草地里有两条路AC和BD,交于点O,三角形AOD、三角形AOB、三角形BOC的面积分别为6平方米、14平方米、35平方米,求三角形COD的面积。
618 |
619 | ### 练习2
620 |
621 | 如图所示,阴影部分三角形CDE的面积为8平方厘米,并且 $AE=2EC$,$AD: DB=2:3$,求三角形ABC的面积。
622 |
623 | ### 练习3
624 |
625 | 如图所示,三角形ABC的面积为60平方厘米,$AD=3DB$,$AC=3AE$,求阴影部分三角形ADE的面积。
626 |
627 | ### 练习4
628 |
629 | ### 练习5
630 |
631 | ### 练习6
632 |
633 | ## 5.1.11. 容斥问题
634 |
635 | ### 热身1
636 |
637 | 如图,三角形ABC的面积为24平方厘米,并且BD=2DA,CE=3EB,DF: FC=3:2,G是DE的中点,求阴影部分三角形DFG的面积。
638 |
639 | ### 热身2
640 |
641 | 如图,在三角形ABC中,H,I,J是AB的四等分点;D,E,F,G是BC的五等分点。知$S_{△BDH}=1$,问:每一个小三角形的面积分别为多少?
642 |
643 | ### 热身3
644 |
645 | 如图,点E、F分别为四边形ABCD中AB的三等分点。点G、H为CD的三等分点。则四边形EFHG的面积占总面积的几分之几?
646 |
647 | ### 例题1
648 |
649 | 在46人的采摘活动中,只采了樱桃的有18人,既采了樱桃又采了杏的有7人,既没采樱桃又没采杏的有6人,问:只采了杏的有多少人?
650 |
651 | ### 练习1
652 |
653 | 有100名同学回答A、B两个问题,都没有回答对的有10人,答对A的有75人,答对B的有83人,两题都答对的有多少人?
654 |
655 | ### 例题2
656 |
657 | 某校参加数学竞赛的有120名男生,80名女生,参加语文竞赛的有120名女生,80名男生,己知该校总共有260名学生参加竞赛,其中75名男生两科竞赛都参加了,那么只参加数学竞赛而没有参加语文竞赛的女生有多少人?
658 |
659 | ### 练习2
660 |
661 | 育才小学画展上展出了许多幅画,其中有16幅画不是六年级的,有15幅画不是五年级的,五、六年级共展出25幅画,其他年级的画共有多少幅?
662 |
663 | ### 例题3
664 |
665 | 50名学生面向老师站成一行,老师先让大家从左到右按1,2,3,⋯,依次报数,再让报数是4的倍数的同学向后转,接着又让报数是6的倍数的同学向后转,问:此时还有多少同学面向老师?
666 |
667 | ### 练习3
668 |
669 | 五年级一班有45名同学上体育课,他们在操场上排成一排面向教师,并从1到45报完数后,教师叫报偶数的人向后转,接着叫报3的倍数的人向后转,则这时面向教师的学生有多少人?
670 |
671 | ### 例题4
672 |
673 | 有2008盏亮着的电灯,各有一个拉线开关控制着。现将其顺序编号为1,2,3,⋯,2008。将编号为2的倍数的灯线拉一下,再将编号为3的倍数的灯线拉一下,最后将编号为5的倍数的灯线拉一下,拉完后还有几盏灯是亮的?
674 |
675 | ### 练习4
676 |
677 | 有1000盏亮着的电灯,各有一个拉线开关控制着。现将其顺序编号为1,2,3,⋯,1000。将编号为2的倍数的灯线拉一下,再将编号为3的倍数的灯线拉一下,最后将编号为5的倍数的灯线拉一下,拉完后还有几盏灯是亮的?
678 |
679 | ### 例题5
680 |
681 | 分母是1001的最简真分数有多少个?
682 |
683 | ### 练习5
684 |
685 | 分母是105的最简真分数有多少个?
686 |
687 | ### 例题6
688 |
689 | 一根100厘米长的木棍,从左起每隔6厘米划一个刻度,每隔7厘米划一个刻度,每隔8厘米划一个刻度,如果按刻度把木棍截断,可以截出多少段?
690 |
691 | ### 练习6
692 |
693 | 一根101厘米长的木棒,从同一端开始,第一次每隔2厘米画一个刻度,第二次每隔3厘米画一个刻度,第三次每隔5厘米画一个刻度,如果按刻度把木棒截断,那么可以截出多少段?
694 |
695 | ### 练习1
696 |
697 | 田径队的40名运动员们在训练基地进行封闭训练。其中男运动员有20名,训练长跑的运动员有15名,训练竞走的女运动员有8名,那么训练长跑的男运动员有多少名?
698 |
699 | ### 练习2
700 |
701 | 去年某年级有56人订阅过《中小学生数学学习》,其中,上半年有25名男生、15名女生订阅了该杂志,下半年有26名男生25 名女生订阅了该杂志。已知有23名男生是全年订阅,那么,只在上半年订阅了该杂志的女生有多少名?
702 |
703 | ### 练习3
704 |
705 | 200盏亮着的电灯,各有一个拉线开关控制,按排序编号为1,2,3,……,200。将编号为3的倍数的灯的拉线各拉一下,再将编号为5的倍数的灯的拉线各拉一下,拉完后不亮的灯有多少盏?
706 |
707 | ### 练习4
708 |
709 | ### 练习5
710 |
711 | ### 练习6
712 |
--------------------------------------------------------------------------------
/06-六年级.md:
--------------------------------------------------------------------------------
1 | ---
2 | title: 六年级
3 | lang: zh-CN
4 | sidebarDepth: 1
5 | ---
6 |
7 | # 六年级
8 |
9 | 待整理
10 |
--------------------------------------------------------------------------------
/README.md:
--------------------------------------------------------------------------------
1 | ## 小学奥数
2 |
3 | 课程不定期更新,点击在线查看。
4 |
5 | * [一年级(待整理)](https://www.vastxie.com/%E5%B0%8F%E5%AD%A6%E5%A5%A5%E6%95%B0/01-%E4%B8%80%E5%B9%B4%E7%BA%A7.html)
6 | * [二年级(更新中)](https://www.vastxie.com/%E5%B0%8F%E5%AD%A6%E5%A5%A5%E6%95%B0/02-%E4%BA%8C%E5%B9%B4%E7%BA%A7.html)
7 | * [三年级(更新中)](https://www.vastxie.com/%E5%B0%8F%E5%AD%A6%E5%A5%A5%E6%95%B0/03-%E4%B8%89%E5%B9%B4%E7%BA%A7.html)
8 | * [四年级(更新中)](https://www.vastxie.com/%E5%B0%8F%E5%AD%A6%E5%A5%A5%E6%95%B0/04-%E5%9B%9B%E5%B9%B4%E7%BA%A7.html)
9 | * [五年级(更新中)](https://www.vastxie.com/%E5%B0%8F%E5%AD%A6%E5%A5%A5%E6%95%B0/05-%E4%BA%94%E5%B9%B4%E7%BA%A7.html)
10 | * [六年级(待整理)](https://www.vastxie.com/%E5%B0%8F%E5%AD%A6%E5%A5%A5%E6%95%B0/06-%E5%85%AD%E5%B9%B4%E7%BA%A7.html)
11 |
12 | 课程计划包含:
13 |
14 | * 热身
15 | * 例题 + 练习
16 | * 巩固
17 | * 拓展
18 |
19 | 课程内容来自本人上课讲义,有一些地方排版比较乱,讲次内容也有缺失,后续会逐步更新完善。
20 |
21 | 本课程仅供学习交流使用,希望对你有所帮助。
22 |
--------------------------------------------------------------------------------
 75 |
76 | ### 热身3
77 |
78 | 下面是一个奥运五环标志,你能不能一笔画出下面的奥运五环图呢?大家试一试。 (要求:笔中途不能离开纸,每条线只能画一次不能重复画。)
79 |
80 | ### 例题1
81 |
82 | 你能试着用一笔把下列图形画出来吗?如果可以,说说你是怎样画的?
83 |
84 |
75 |
76 | ### 热身3
77 |
78 | 下面是一个奥运五环标志,你能不能一笔画出下面的奥运五环图呢?大家试一试。 (要求:笔中途不能离开纸,每条线只能画一次不能重复画。)
79 |
80 | ### 例题1
81 |
82 | 你能试着用一笔把下列图形画出来吗?如果可以,说说你是怎样画的?
83 |
84 |  85 |
86 | ### 练习1
87 |
88 | 下图两个图能否一笔画出?
89 |
90 |
85 |
86 | ### 练习1
87 |
88 | 下图两个图能否一笔画出?
89 |
90 |  91 |
92 | ### 例题2
93 |
94 | 下列图形能一笔画成吗?为什么?
95 |
96 |
91 |
92 | ### 例题2
93 |
94 | 下列图形能一笔画成吗?为什么?
95 |
96 |  97 |
98 | ### 练习2
99 |
100 | 下列图形能一笔画成吗?为什么?
101 |
102 |
97 |
98 | ### 练习2
99 |
100 | 下列图形能一笔画成吗?为什么?
101 |
102 |  103 |
104 | ### 例题3
105 |
106 | 下面的图形都不能一笔画成,请你分别在各图中添上一条线段,使他能一笔画成。
107 |
108 |
103 |
104 | ### 例题3
105 |
106 | 下面的图形都不能一笔画成,请你分别在各图中添上一条线段,使他能一笔画成。
107 |
108 |  109 |
110 | ### 练习3
111 |
112 | 下面的图形不能一笔画成,至少添上几条线段才能使它能一笔画成?试着添一添。
113 |
114 |
109 |
110 | ### 练习3
111 |
112 | 下面的图形不能一笔画成,至少添上几条线段才能使它能一笔画成?试着添一添。
113 |
114 |  115 |
116 | ### 例题4
117 |
118 | 下面的图形都不能一笔画成,请你在各个图中去掉一条线,使它能一笔画成。
119 |
120 |
115 |
116 | ### 例题4
117 |
118 | 下面的图形都不能一笔画成,请你在各个图中去掉一条线,使它能一笔画成。
119 |
120 |  121 |
122 | ### 练习4
123 |
124 | 下面的图形不能一笔画成,请你去掉一条线,使它能一笔画成?
125 |
126 |
121 |
122 | ### 练习4
123 |
124 | 下面的图形不能一笔画成,请你去掉一条线,使它能一笔画成?
125 |
126 |  127 |
128 | ### 例题5
129 |
130 | 下图是乡间的一条小河,上面建有六座桥,你能一次不重复地走遍所有的小桥吗?(每座小桥最多只准走一次 ,陆地上可以重复地来回走)
131 |
132 |
127 |
128 | ### 例题5
129 |
130 | 下图是乡间的一条小河,上面建有六座桥,你能一次不重复地走遍所有的小桥吗?(每座小桥最多只准走一次 ,陆地上可以重复地来回走)
131 |
132 |  133 |
134 | ### 例题6
135 |
136 | 如图是某地区所有街道的平面图,丁丁和牛牛两人同时从A、B两地出发,以相同的速度行进,如果允许选择最短路径的话,那么谁先走遍所有的街道?
137 |
138 |
133 |
134 | ### 例题6
135 |
136 | 如图是某地区所有街道的平面图,丁丁和牛牛两人同时从A、B两地出发,以相同的速度行进,如果允许选择最短路径的话,那么谁先走遍所有的街道?
137 |
138 |  139 |
140 | 纸上画了9个点,我们可以用5条线段把它们串联起来,而且这5条线段是可以一笔画成的(如左图)。实际上我们可以做的更好:只用四条线段就能把这9个点串起来,而且这4条线段仍然是用一笔画成,试一试,你能找出这种画法吗?
141 |
142 |
139 |
140 | 纸上画了9个点,我们可以用5条线段把它们串联起来,而且这5条线段是可以一笔画成的(如左图)。实际上我们可以做的更好:只用四条线段就能把这9个点串起来,而且这4条线段仍然是用一笔画成,试一试,你能找出这种画法吗?
141 |
142 |  143 |
144 | ## 2.1.11. 巧算加减法进阶
145 |
146 | ### 例题1
147 |
148 | 计算。
149 | $26+37+74=$
150 |
151 | $43+62+57+38=$
152 |
153 | ### 练习1
154 |
155 | 计算。
156 | $24+65+76=$
157 |
158 | $37+24+63+76=$
159 |
160 | ### 例题2
161 |
162 | 计算。
163 | $97-34-37=$
164 |
165 | $68-33-28=$
166 |
167 | ### 练习2
168 |
169 | 计算。
170 | $89-32-19=$
171 |
172 | $62-19-22=$
173 |
174 | ### 例题3
175 |
176 | 计算。
177 | $172-34-66=$
178 |
179 | $244-46-154=$
180 |
181 | ### 练习3
182 |
183 | 计算。
184 | $256-43-57=$
185 |
186 | $127-36-54=$
187 |
188 | ### 例题4
189 |
190 | 计算。
191 | $176-(32+76)=$
192 |
193 | $97-(48+17)=$
194 |
195 | ### 练习4
196 |
197 | 计算。
198 | $152-(34+52)=$
199 |
200 | $89-(17+19)=$
201 |
202 | ### 例题5
203 |
204 | 计算。
205 | $27+28+30+31+32=$
206 |
207 | ### 练习5
208 |
209 | 计算。
210 | $84+95+93+85+87+90$
211 |
212 | ### 例题6
213 |
214 | 计算。
215 | $9+99+199=$
216 |
217 | ### 练习6
218 |
219 | 计算。
220 | $8+98+198=$
221 |
222 | ### 拓展1
223 |
224 | $2+22+202+2002+20002=$
225 |
226 | ### 拓展2
227 |
228 | $10-9+8-7+6-5+4-3+2-1=$
229 |
230 | ### 拓展3
231 |
232 | $100-99+98-97+96-95+\dots+4-3+2-1=$
233 |
234 | ### 拓展4
235 |
236 | $1+2+3+4+5+6+7+8+9+10+9+8+7+6+5+4+3+2+1=$
237 |
238 | ### 拓展5
239 |
240 | $1+2+3+4+\dots+49+50+49+\dots+3+2+1=$
241 |
242 | ### 拓展6
243 |
244 | $123+231+321=$
245 |
246 | ### 拓展7
247 |
248 | $1234+2341+3412+4123=$
249 |
250 | ## 2.2.14. 有趣的植树问题
251 |
252 | ### 例题1
253 |
254 | 植树问题中的间隔有四种不同的情况,只有准确判断,才能找到解决问题的方法(树的宽度忽略不计)
255 |
256 | 1. 在一条长100米的公路一侧种树,每隔10米种一棵,两端都种,一共要种多少棵树?
257 |
258 | 2. 两座塔之间的距离是50米,现在要在这两座塔之间种树,每隔5米种一棵,一共需要种多少棵树?
259 |
260 | 3. 在一座城堡门前,有一条通往城堡的公路,长40米,现在要在公路的一侧种树,每两棵树之间相隔5米,一共要种几棵树?
261 |
262 | 4. 广场中的圆形花坛一周长80米,现在要在花坛边每隔8米摆一盆花,一共可以摆几盆花?
263 |
264 | ### 练习1
265 |
266 | 两座楼房之间相距40米,每隔4米栽一棵雪松,一共能栽多少棵雪松?(树的宽度忽略不计)
267 |
268 | ### 例题2
269 |
270 | 城墙上从一端到另一端共站了7个士兵,相邻的两个士兵相隔3米。问:城墙长多少米?(士兵的宽度忽略不计)
271 |
272 | ### 练习2
273 |
274 | 一条林荫道上有5只免子排队做操,相邻两只免子相隔2米,免子做操的队伍长多少米?(免子的宽度忽略不计)
275 |
276 | ### 例题3
277 |
278 | 要新建一个圆形喷泉,如果沿喷泉的一周放置雕像,每隔2米放一座,刚好可以放8座,问:这个圆形喷泉一周长是多少米?(雕像的宽度忽略不计)
279 |
280 | ### 练习3
281 |
282 | 一个圆形养鱼池,一周总长为42米,要在养鱼池的一周每隔6米种一棵桃树,一共能种多少棵桃树?(树的宽度忽略不计)
283 |
284 | ### 例题4
285 |
286 | 在一条长50米的公路两边种树,每隔10米种一棵,两端都种,这条公路上一共能种多少棵树?(树的宽度忽略不计)
287 |
288 | ### 练习4
289 |
290 | 一个圆形花坛一周长60米,沿花坛一周每隔3米栽一棵柳树,再在每两棵柳树之问栽2株月季花,花坛一周一共能栽多少株月季花?(树和花的宽度忽略不计)
291 |
292 | ### 例题5
293 |
294 | 有一块三角形的地,三条边分别为30米,40米,60米,每10米种一棵树,三个角都种,那么三条边上共种多少棵树?(树的宽度忽略不计)
295 |
296 | ### 练习5
297 |
298 | 森林公园中心有一个圆形鱼塘,一周长是60米,每隔6米种一棵柳树,每相邻两棵柳树之间,均匀地栽种两棵夹竹桃,问:这个圆形鱼塘的一周可以栽种多少棵夹竹桃?(树的宽度忽略不计)
299 |
300 | ### 例题6
301 |
302 | 在一条长48米的公路一旁种树,两端都种,共种了9棵树,算一算每隔几米种一棵?(树的宽度忽略不计)
303 |
304 | ### 练习6
305 |
306 | 爷爷从1楼爬到4楼用时12分钟,照这样的速度,他从1楼爬到5楼需要用时多少分钟?
307 |
308 | ### 拓展1
309 |
310 | 乐乐老师组织学生们植树,在一条长 120 米的马路两边每隔30米种一棵梧桐树(两端都种),在每相邻的2棵梧桐树之间又补种1 棵香樟树。这条马路两边一共种了多少棵树?(树的宽度忽略不计)
311 |
312 | ### 拓展2
313 |
314 | 牛牛和爷爷一起从 1 楼开始爬楼梯锻炼身体,牛牛走得快,爷爷走得慢。牛牛走到5楼的时候,爷爷才爬到3楼。照这样的速度继续爬,牛牛到15楼的时候,爷爷到几楼?
315 |
316 | ### 拓展3
317 |
318 | 马路的一边,每隔8米有1棵杨树。 小明乘汽车从学校回家,从看到第一棵树数起到第51棵树为止,共用时2分。小明从学校到家共坐了半小时的汽车。小明的家距学校有多远?(树的宽度忽略不计)
319 |
320 | ### 拓展4
321 |
322 | 几个孩子星期天一起逛公园,在公园中心有一个正方形池塘,在池塘边距离池边3米处围绕池塘种树,一共种了40棵(四个角都种)也围成了一个正方形。如果相邻两棵树之间的距离是2米,那么这个正方形池塘的边长是多少米?(树的宽度忽略不计)
323 |
324 | ## 2.1.15. 合理安排
325 |
326 | 课程内容
327 |
328 | * 煎饼问题
329 | * 连续完成合理安排
330 | * 过河问题
331 | * 排队问题
332 |
333 | 学习目标
334 |
335 | 通过解决常见的生活问题,学会合理安排时间,最快完成。
336 |
337 | 内容分析
338 |
339 | ### 煎饼问题
340 |
341 | **问题概述**
342 |
343 | 随手拿一些小物品来替代饼和锅,设定煎饼的场景。
344 |
345 | 1. 一个锅一次只能放一张饼,饼要煎两面,煎一面需要一分钟,需要怎么煎最快。(设置基本规则,无法同时煎一张饼的正面和反面)(题外话:铜锣烧除外)
346 |
347 | 2. 一个锅一次可以放两张饼,饼要煎两面,煎一面需要一分钟,怎么煎,两张饼呢?三张饼呢?(实际操作中,学生很容易想的到一张、两张的情况,但是三张情况尽量鼓励学生自己解决,如何才能不保证锅的空间得到充分的利用,不会一个锅,只煎一张饼的情况)
348 |
349 | 学会 3 分钟煎三张饼后,让学生自己开始做例题,现在遇到多张饼的时候,还需要一面面的去试么?引出分组思考的概念,比 1 大的数都可以分成若干个 2 和 3 的和。最后,思考总结,做练习。(练习出现一面不再是单位 1 时间的情况,第一次做容易忽略)
350 |
351 | 三张饼的安排方案:
352 |
353 | 
354 |
355 | **例题1**
356 |
357 | 平底锅里每次能同时放 2 张饼,烙熟 1 张饼需用时 2 分(正、反面各需 1 分),如果要烙熟 5 张饼至少需要多长时间?烙熟 6 张饼呢?烙熟 7 张饼呢?
358 |
359 | 【解析】5 分钟;6 分钟;7 分钟。
360 |
361 | **练习1**
362 |
363 | 用一个平底锅煎鸡蛋,每次最多能放 2 个鸡蛋,煎熟 1 个鸡蛋需要用时 4 分钟(正、反面各需用时 2 分钟),问煎熟 7 个鸡蛋至少需要多长时间?
364 |
365 | 【解析】14 分钟。
366 |
367 | **问题小结**
368 |
369 | 对于煎饼问题,原则是不能让锅闲着,学会分组(偶数:2 个 2 个一组;奇数:2 个 2 个一组,最后一个并入 2 ,形成一个 3)一组一组的去煎,注意一面需要花费的时间。
370 |
371 | ### 按顺序,同时做
372 |
373 | **问题概述**
374 |
375 | 生活中有些事情是“不需要手”,可以自主完成的,比如烧水、煮饭、洗衣机洗衣服、听广播等等,那么这些事情是可以和一些事情同时进行。也就是一边……一边……的平行关系。另外,做事情还得考虑先后顺序,比如先吃饭,后洗碗,先烧水,再泡茶等等。也就是先……,然后……的递进关系。综上,那么该怎样合理的安排,才能让总花费的时间最短?
376 |
377 | **例题2**
378 |
379 | 牛牛需要给田田沏茶,沏茶过程中,洗开水壶用时 1 分钟,烧开水要用时 15 分钟,洗茶壶要用时 1 分钟,洗茶杯要用时 2 分钟,找茶叶要用时 2 分钟,泡茶要用时1分钟;牛牛怎样合理的安排,才能在最短时间里让田田喝上茶呢?最少需要多长时间呢?
380 |
381 | 【解析】需要遵守“洗开水壶-烧开水-泡茶”的顺序,烧开水是“不需要手”的事情,洗茶壶,洗茶杯,找茶叶可以在烧水的时候做。总时间是 1 + 15 + 1 = 17(分钟)。
382 |
383 | **练习2**
384 |
385 | 丁丁早上 6 时 30 分钟起床,去学校之前要做以下几件事情:穿衣叠被用时 6 分钟,梳头用时 2 分钟,刷牙洗脸用时 5 分钟,听新闻用时 20 分钟,吃早饭用时 8 分钟,收拾饭桌用时 3 分钟。如果他 6 时 30 分钟准时起床,那么最早可以几时几分钟从家出发去上学?
386 |
387 | 【解析】6 + 2 + 5 + 8 + 3 = 24(分钟),听新闻“不需要手”,可以同时完成。那么最早 6 时 54 分钟从从家出发去上学。
388 |
389 | **例题3**
390 |
391 | 牛牛要帮丁丁做家务,需要做的事情有:擦桌椅用时 12 分钟;擦地用时 18 分钟;浸泡衣服(要用温水)用时 15 分钟;搓衣服用时 15 分钟;烧开水用时 20 分钟;清洗衣服用时 15 分钟;晾衣服用时 5 分钟。牛牛如何安排这些事情的先后顺序,才可以用时最短,最短多长时间可以把这些事情全部做完?
392 |
393 | 【解析】烧开水-浸泡衣服-搓衣服-清洗衣服-晾衣服是需要分先后的递进关系,其中,烧开水,浸泡衣服是“不需要手”的,可以与擦座椅,擦地同时进行。总时间是:20 + 15 + 15 + 15 + 5 = 70(分钟)。注意提醒学生检查同时完成的时候,哪个花费的时间更久。比如题目中 20 + 15 需要同 12 + 18 去比较。
394 |
395 | **练习3**
396 |
397 | 星期天,妈妈要做好多事情。擦玻璃要 20 分钟,收拾厨房要 15 分钟,洗脏衣服的领子、袖口要 10 分钟,打开全自动洗衣机洗衣服要 40 分钟,晾衣服要 10 分钟。妈妈干完所有这些事情最少要分钟。
398 |
399 | 【解析】找顺序:洗脏衣服的领子、袖口-打开全自动洗衣机洗衣服-晾衣服,其中洗衣机洗衣服可以同时做其他事情,且 40 > (20 + 15)。总耗时:10 + 40 + 10 = 60(分钟)。
400 |
401 | ### 过河问题
402 |
403 | **问题概述**
404 |
405 | **例题4**
406 |
407 | 牛牛、丁丁和田田被怪物们追到小河边,河岸边只有一条能同时乘坐 2 人的小船,由牛牛划船需要用时 2 分钟,由丁丁划船用时 3 分钟,由田田划船用时 5 分钟,现在情况危急,需要尽快过河,应该采用怎样的过河方式,3 人全部过河用时最短?
408 |
409 | 练习4
410 |
411 | 牛牛、丁丁和田田骑车去公园,现在只有一辆自行车,自行车除了一人骑车,还能载一个人。由牛牛骑车需要用时 30 分钟,由丁丁骑车用时 35 分钟,由田田骑车用时 40 分钟,三人需要尽快到达公园,应该采用怎样的载人方式,3 人全部到达公园用时最短?
412 |
413 | 例题5
414 |
415 | 学校组织防火演习,牛牛、丁丁、田田、乐乐老师四人准备通过一座正在燃烧的木桥,此桥每次最多只能让 2 个人同时通过(不能背着、抱着),否则桥会倒塌。过桥的人必须要用到防火披风,不然会被火烧到(防火披风只有 1 件,可供两人同时使用),4 个人行走速度不同:牛牛用时 1 分钟就可以过桥,丁丁要用时 2 分钟,田田要用时 5 分钟,乐乐老师要用时 8 分钟,已知 15 分钟过后桥就会被烧塌了,请问:4 个人要用什么方法才能全部安全过桥?
416 |
417 | 练习5
418 |
419 | 牛牛、丁丁、田田、乐乐老师四个人过桥,分别需要用时 1 分钟、2 分钟、5 分钟和 10 分钟,因为天黑,必须借助手电筒过桥,可是他们只有一个手电筒,并且桥的载重能力有限,每次最多同时过两个人(不能背着、抱着),现在他们希望可以用最短的时间过桥,应该怎样做? 最短时问是多少?
420 |
421 | ### 排队问题
422 |
423 | 例题6
424 |
425 | 同学们各提一个大小不一的桶去打水,丁丁、田田、牛牛、阿普他们四个的桶注满水所需的时间分别为 2 分钟、4 分钟、5 分钟、3 分钟。现在只有一个水龙头可以接水,请你设计一下,使他们总的等候时间最短,这个最短的时间是多少?
426 |
427 | 练习6
428 |
429 | 有四名同学各提一个大小不一样的桶去打水,他们四个的桶注满水所需的时间分别是 1 分钟、3 分钟、4 分钟、2 分钟。现在只有一个水龙头可以接水,请你帮他们设计一下,怎样安排才能使他们总的等候时间最短,这个最短的时间是多少?
430 |
431 | # 摆小棒
432 |
433 | 热身1
434 |
435 | 计算。
436 | $$
437 | 8+8+8+8+8+6+6+6=
438 | $$
439 |
440 | ### 热身2
441 |
442 | 下列图形中,不能“一笔画”的是()。
443 |
444 |
143 |
144 | ## 2.1.11. 巧算加减法进阶
145 |
146 | ### 例题1
147 |
148 | 计算。
149 | $26+37+74=$
150 |
151 | $43+62+57+38=$
152 |
153 | ### 练习1
154 |
155 | 计算。
156 | $24+65+76=$
157 |
158 | $37+24+63+76=$
159 |
160 | ### 例题2
161 |
162 | 计算。
163 | $97-34-37=$
164 |
165 | $68-33-28=$
166 |
167 | ### 练习2
168 |
169 | 计算。
170 | $89-32-19=$
171 |
172 | $62-19-22=$
173 |
174 | ### 例题3
175 |
176 | 计算。
177 | $172-34-66=$
178 |
179 | $244-46-154=$
180 |
181 | ### 练习3
182 |
183 | 计算。
184 | $256-43-57=$
185 |
186 | $127-36-54=$
187 |
188 | ### 例题4
189 |
190 | 计算。
191 | $176-(32+76)=$
192 |
193 | $97-(48+17)=$
194 |
195 | ### 练习4
196 |
197 | 计算。
198 | $152-(34+52)=$
199 |
200 | $89-(17+19)=$
201 |
202 | ### 例题5
203 |
204 | 计算。
205 | $27+28+30+31+32=$
206 |
207 | ### 练习5
208 |
209 | 计算。
210 | $84+95+93+85+87+90$
211 |
212 | ### 例题6
213 |
214 | 计算。
215 | $9+99+199=$
216 |
217 | ### 练习6
218 |
219 | 计算。
220 | $8+98+198=$
221 |
222 | ### 拓展1
223 |
224 | $2+22+202+2002+20002=$
225 |
226 | ### 拓展2
227 |
228 | $10-9+8-7+6-5+4-3+2-1=$
229 |
230 | ### 拓展3
231 |
232 | $100-99+98-97+96-95+\dots+4-3+2-1=$
233 |
234 | ### 拓展4
235 |
236 | $1+2+3+4+5+6+7+8+9+10+9+8+7+6+5+4+3+2+1=$
237 |
238 | ### 拓展5
239 |
240 | $1+2+3+4+\dots+49+50+49+\dots+3+2+1=$
241 |
242 | ### 拓展6
243 |
244 | $123+231+321=$
245 |
246 | ### 拓展7
247 |
248 | $1234+2341+3412+4123=$
249 |
250 | ## 2.2.14. 有趣的植树问题
251 |
252 | ### 例题1
253 |
254 | 植树问题中的间隔有四种不同的情况,只有准确判断,才能找到解决问题的方法(树的宽度忽略不计)
255 |
256 | 1. 在一条长100米的公路一侧种树,每隔10米种一棵,两端都种,一共要种多少棵树?
257 |
258 | 2. 两座塔之间的距离是50米,现在要在这两座塔之间种树,每隔5米种一棵,一共需要种多少棵树?
259 |
260 | 3. 在一座城堡门前,有一条通往城堡的公路,长40米,现在要在公路的一侧种树,每两棵树之间相隔5米,一共要种几棵树?
261 |
262 | 4. 广场中的圆形花坛一周长80米,现在要在花坛边每隔8米摆一盆花,一共可以摆几盆花?
263 |
264 | ### 练习1
265 |
266 | 两座楼房之间相距40米,每隔4米栽一棵雪松,一共能栽多少棵雪松?(树的宽度忽略不计)
267 |
268 | ### 例题2
269 |
270 | 城墙上从一端到另一端共站了7个士兵,相邻的两个士兵相隔3米。问:城墙长多少米?(士兵的宽度忽略不计)
271 |
272 | ### 练习2
273 |
274 | 一条林荫道上有5只免子排队做操,相邻两只免子相隔2米,免子做操的队伍长多少米?(免子的宽度忽略不计)
275 |
276 | ### 例题3
277 |
278 | 要新建一个圆形喷泉,如果沿喷泉的一周放置雕像,每隔2米放一座,刚好可以放8座,问:这个圆形喷泉一周长是多少米?(雕像的宽度忽略不计)
279 |
280 | ### 练习3
281 |
282 | 一个圆形养鱼池,一周总长为42米,要在养鱼池的一周每隔6米种一棵桃树,一共能种多少棵桃树?(树的宽度忽略不计)
283 |
284 | ### 例题4
285 |
286 | 在一条长50米的公路两边种树,每隔10米种一棵,两端都种,这条公路上一共能种多少棵树?(树的宽度忽略不计)
287 |
288 | ### 练习4
289 |
290 | 一个圆形花坛一周长60米,沿花坛一周每隔3米栽一棵柳树,再在每两棵柳树之问栽2株月季花,花坛一周一共能栽多少株月季花?(树和花的宽度忽略不计)
291 |
292 | ### 例题5
293 |
294 | 有一块三角形的地,三条边分别为30米,40米,60米,每10米种一棵树,三个角都种,那么三条边上共种多少棵树?(树的宽度忽略不计)
295 |
296 | ### 练习5
297 |
298 | 森林公园中心有一个圆形鱼塘,一周长是60米,每隔6米种一棵柳树,每相邻两棵柳树之间,均匀地栽种两棵夹竹桃,问:这个圆形鱼塘的一周可以栽种多少棵夹竹桃?(树的宽度忽略不计)
299 |
300 | ### 例题6
301 |
302 | 在一条长48米的公路一旁种树,两端都种,共种了9棵树,算一算每隔几米种一棵?(树的宽度忽略不计)
303 |
304 | ### 练习6
305 |
306 | 爷爷从1楼爬到4楼用时12分钟,照这样的速度,他从1楼爬到5楼需要用时多少分钟?
307 |
308 | ### 拓展1
309 |
310 | 乐乐老师组织学生们植树,在一条长 120 米的马路两边每隔30米种一棵梧桐树(两端都种),在每相邻的2棵梧桐树之间又补种1 棵香樟树。这条马路两边一共种了多少棵树?(树的宽度忽略不计)
311 |
312 | ### 拓展2
313 |
314 | 牛牛和爷爷一起从 1 楼开始爬楼梯锻炼身体,牛牛走得快,爷爷走得慢。牛牛走到5楼的时候,爷爷才爬到3楼。照这样的速度继续爬,牛牛到15楼的时候,爷爷到几楼?
315 |
316 | ### 拓展3
317 |
318 | 马路的一边,每隔8米有1棵杨树。 小明乘汽车从学校回家,从看到第一棵树数起到第51棵树为止,共用时2分。小明从学校到家共坐了半小时的汽车。小明的家距学校有多远?(树的宽度忽略不计)
319 |
320 | ### 拓展4
321 |
322 | 几个孩子星期天一起逛公园,在公园中心有一个正方形池塘,在池塘边距离池边3米处围绕池塘种树,一共种了40棵(四个角都种)也围成了一个正方形。如果相邻两棵树之间的距离是2米,那么这个正方形池塘的边长是多少米?(树的宽度忽略不计)
323 |
324 | ## 2.1.15. 合理安排
325 |
326 | 课程内容
327 |
328 | * 煎饼问题
329 | * 连续完成合理安排
330 | * 过河问题
331 | * 排队问题
332 |
333 | 学习目标
334 |
335 | 通过解决常见的生活问题,学会合理安排时间,最快完成。
336 |
337 | 内容分析
338 |
339 | ### 煎饼问题
340 |
341 | **问题概述**
342 |
343 | 随手拿一些小物品来替代饼和锅,设定煎饼的场景。
344 |
345 | 1. 一个锅一次只能放一张饼,饼要煎两面,煎一面需要一分钟,需要怎么煎最快。(设置基本规则,无法同时煎一张饼的正面和反面)(题外话:铜锣烧除外)
346 |
347 | 2. 一个锅一次可以放两张饼,饼要煎两面,煎一面需要一分钟,怎么煎,两张饼呢?三张饼呢?(实际操作中,学生很容易想的到一张、两张的情况,但是三张情况尽量鼓励学生自己解决,如何才能不保证锅的空间得到充分的利用,不会一个锅,只煎一张饼的情况)
348 |
349 | 学会 3 分钟煎三张饼后,让学生自己开始做例题,现在遇到多张饼的时候,还需要一面面的去试么?引出分组思考的概念,比 1 大的数都可以分成若干个 2 和 3 的和。最后,思考总结,做练习。(练习出现一面不再是单位 1 时间的情况,第一次做容易忽略)
350 |
351 | 三张饼的安排方案:
352 |
353 | 
354 |
355 | **例题1**
356 |
357 | 平底锅里每次能同时放 2 张饼,烙熟 1 张饼需用时 2 分(正、反面各需 1 分),如果要烙熟 5 张饼至少需要多长时间?烙熟 6 张饼呢?烙熟 7 张饼呢?
358 |
359 | 【解析】5 分钟;6 分钟;7 分钟。
360 |
361 | **练习1**
362 |
363 | 用一个平底锅煎鸡蛋,每次最多能放 2 个鸡蛋,煎熟 1 个鸡蛋需要用时 4 分钟(正、反面各需用时 2 分钟),问煎熟 7 个鸡蛋至少需要多长时间?
364 |
365 | 【解析】14 分钟。
366 |
367 | **问题小结**
368 |
369 | 对于煎饼问题,原则是不能让锅闲着,学会分组(偶数:2 个 2 个一组;奇数:2 个 2 个一组,最后一个并入 2 ,形成一个 3)一组一组的去煎,注意一面需要花费的时间。
370 |
371 | ### 按顺序,同时做
372 |
373 | **问题概述**
374 |
375 | 生活中有些事情是“不需要手”,可以自主完成的,比如烧水、煮饭、洗衣机洗衣服、听广播等等,那么这些事情是可以和一些事情同时进行。也就是一边……一边……的平行关系。另外,做事情还得考虑先后顺序,比如先吃饭,后洗碗,先烧水,再泡茶等等。也就是先……,然后……的递进关系。综上,那么该怎样合理的安排,才能让总花费的时间最短?
376 |
377 | **例题2**
378 |
379 | 牛牛需要给田田沏茶,沏茶过程中,洗开水壶用时 1 分钟,烧开水要用时 15 分钟,洗茶壶要用时 1 分钟,洗茶杯要用时 2 分钟,找茶叶要用时 2 分钟,泡茶要用时1分钟;牛牛怎样合理的安排,才能在最短时间里让田田喝上茶呢?最少需要多长时间呢?
380 |
381 | 【解析】需要遵守“洗开水壶-烧开水-泡茶”的顺序,烧开水是“不需要手”的事情,洗茶壶,洗茶杯,找茶叶可以在烧水的时候做。总时间是 1 + 15 + 1 = 17(分钟)。
382 |
383 | **练习2**
384 |
385 | 丁丁早上 6 时 30 分钟起床,去学校之前要做以下几件事情:穿衣叠被用时 6 分钟,梳头用时 2 分钟,刷牙洗脸用时 5 分钟,听新闻用时 20 分钟,吃早饭用时 8 分钟,收拾饭桌用时 3 分钟。如果他 6 时 30 分钟准时起床,那么最早可以几时几分钟从家出发去上学?
386 |
387 | 【解析】6 + 2 + 5 + 8 + 3 = 24(分钟),听新闻“不需要手”,可以同时完成。那么最早 6 时 54 分钟从从家出发去上学。
388 |
389 | **例题3**
390 |
391 | 牛牛要帮丁丁做家务,需要做的事情有:擦桌椅用时 12 分钟;擦地用时 18 分钟;浸泡衣服(要用温水)用时 15 分钟;搓衣服用时 15 分钟;烧开水用时 20 分钟;清洗衣服用时 15 分钟;晾衣服用时 5 分钟。牛牛如何安排这些事情的先后顺序,才可以用时最短,最短多长时间可以把这些事情全部做完?
392 |
393 | 【解析】烧开水-浸泡衣服-搓衣服-清洗衣服-晾衣服是需要分先后的递进关系,其中,烧开水,浸泡衣服是“不需要手”的,可以与擦座椅,擦地同时进行。总时间是:20 + 15 + 15 + 15 + 5 = 70(分钟)。注意提醒学生检查同时完成的时候,哪个花费的时间更久。比如题目中 20 + 15 需要同 12 + 18 去比较。
394 |
395 | **练习3**
396 |
397 | 星期天,妈妈要做好多事情。擦玻璃要 20 分钟,收拾厨房要 15 分钟,洗脏衣服的领子、袖口要 10 分钟,打开全自动洗衣机洗衣服要 40 分钟,晾衣服要 10 分钟。妈妈干完所有这些事情最少要分钟。
398 |
399 | 【解析】找顺序:洗脏衣服的领子、袖口-打开全自动洗衣机洗衣服-晾衣服,其中洗衣机洗衣服可以同时做其他事情,且 40 > (20 + 15)。总耗时:10 + 40 + 10 = 60(分钟)。
400 |
401 | ### 过河问题
402 |
403 | **问题概述**
404 |
405 | **例题4**
406 |
407 | 牛牛、丁丁和田田被怪物们追到小河边,河岸边只有一条能同时乘坐 2 人的小船,由牛牛划船需要用时 2 分钟,由丁丁划船用时 3 分钟,由田田划船用时 5 分钟,现在情况危急,需要尽快过河,应该采用怎样的过河方式,3 人全部过河用时最短?
408 |
409 | 练习4
410 |
411 | 牛牛、丁丁和田田骑车去公园,现在只有一辆自行车,自行车除了一人骑车,还能载一个人。由牛牛骑车需要用时 30 分钟,由丁丁骑车用时 35 分钟,由田田骑车用时 40 分钟,三人需要尽快到达公园,应该采用怎样的载人方式,3 人全部到达公园用时最短?
412 |
413 | 例题5
414 |
415 | 学校组织防火演习,牛牛、丁丁、田田、乐乐老师四人准备通过一座正在燃烧的木桥,此桥每次最多只能让 2 个人同时通过(不能背着、抱着),否则桥会倒塌。过桥的人必须要用到防火披风,不然会被火烧到(防火披风只有 1 件,可供两人同时使用),4 个人行走速度不同:牛牛用时 1 分钟就可以过桥,丁丁要用时 2 分钟,田田要用时 5 分钟,乐乐老师要用时 8 分钟,已知 15 分钟过后桥就会被烧塌了,请问:4 个人要用什么方法才能全部安全过桥?
416 |
417 | 练习5
418 |
419 | 牛牛、丁丁、田田、乐乐老师四个人过桥,分别需要用时 1 分钟、2 分钟、5 分钟和 10 分钟,因为天黑,必须借助手电筒过桥,可是他们只有一个手电筒,并且桥的载重能力有限,每次最多同时过两个人(不能背着、抱着),现在他们希望可以用最短的时间过桥,应该怎样做? 最短时问是多少?
420 |
421 | ### 排队问题
422 |
423 | 例题6
424 |
425 | 同学们各提一个大小不一的桶去打水,丁丁、田田、牛牛、阿普他们四个的桶注满水所需的时间分别为 2 分钟、4 分钟、5 分钟、3 分钟。现在只有一个水龙头可以接水,请你设计一下,使他们总的等候时间最短,这个最短的时间是多少?
426 |
427 | 练习6
428 |
429 | 有四名同学各提一个大小不一样的桶去打水,他们四个的桶注满水所需的时间分别是 1 分钟、3 分钟、4 分钟、2 分钟。现在只有一个水龙头可以接水,请你帮他们设计一下,怎样安排才能使他们总的等候时间最短,这个最短的时间是多少?
430 |
431 | # 摆小棒
432 |
433 | 热身1
434 |
435 | 计算。
436 | $$
437 | 8+8+8+8+8+6+6+6=
438 | $$
439 |
440 | ### 热身2
441 |
442 | 下列图形中,不能“一笔画”的是()。
443 |
444 |  445 |
446 | ### 热身3
447 |
448 | 下图是儿童乐园的平面图,出入口应设在()点或()点,才能不重复地走遍每条路。
449 |
450 |
445 |
446 | ### 热身3
447 |
448 | 下图是儿童乐园的平面图,出入口应设在()点或()点,才能不重复地走遍每条路。
449 |
450 |  451 |
452 | ### 例题1
453 |
454 | 思维火柴1~10
455 |
456 | ### 例题2
457 |
458 | 按要求摆一摆,并在下方空白处画出来。
459 |
460 | (1)用4根火柴棒摆出一个正方形。
461 |
462 | (2)再加3根火柴棒,摆出两个正方形。
463 |
464 | (3)再加3根火柴棒,摆出三个正方形。
465 |
466 | (4)再加2根火柴棒,摆出五个正方形。
467 |
468 | ### 练习2
469 |
470 | 按要求摆一摆,并在下方空白处画出来。
471 |
472 | (1)用3根火柴棒,摆出一个三角形。
473 |
474 | (2)再加2根火柴棒,摆出两个三角形。
475 |
476 | (3)再加2根火柴棒,摆出三个三角形。
477 |
478 | (4)再加2根火柴棒,摆出五个三角形。
479 |
480 | ### 例题3
481 |
482 | 下图是用12根小棒摆成的5个正方形,拿掉哪2根,能使原图变成 2 个正方形?
483 |
484 |
451 |
452 | ### 例题1
453 |
454 | 思维火柴1~10
455 |
456 | ### 例题2
457 |
458 | 按要求摆一摆,并在下方空白处画出来。
459 |
460 | (1)用4根火柴棒摆出一个正方形。
461 |
462 | (2)再加3根火柴棒,摆出两个正方形。
463 |
464 | (3)再加3根火柴棒,摆出三个正方形。
465 |
466 | (4)再加2根火柴棒,摆出五个正方形。
467 |
468 | ### 练习2
469 |
470 | 按要求摆一摆,并在下方空白处画出来。
471 |
472 | (1)用3根火柴棒,摆出一个三角形。
473 |
474 | (2)再加2根火柴棒,摆出两个三角形。
475 |
476 | (3)再加2根火柴棒,摆出三个三角形。
477 |
478 | (4)再加2根火柴棒,摆出五个三角形。
479 |
480 | ### 例题3
481 |
482 | 下图是用12根小棒摆成的5个正方形,拿掉哪2根,能使原图变成 2 个正方形?
483 |
484 |  485 |
486 | ### 练习3
487 |
488 | 下图是用 12 根小棒摆成的 5 个正方形,拿掉哪 2 根,能使原图变成 3 个正方形。
489 |
490 |
485 |
486 | ### 练习3
487 |
488 | 下图是用 12 根小棒摆成的 5 个正方形,拿掉哪 2 根,能使原图变成 3 个正方形。
489 |
490 |  491 |
492 | ### 例题4
493 |
494 | 下图是用 9 根小棒摆成的 3 个三角形,请你移动 3 根小棒,变成 5 个三角形。
495 |
496 |
491 |
492 | ### 例题4
493 |
494 | 下图是用 9 根小棒摆成的 3 个三角形,请你移动 3 根小棒,变成 5 个三角形。
495 |
496 |  497 |
498 | ### 练习4
499 |
500 | 请在下图加两根小棒,摆出两个大小、形状都相同的三角形。
501 |
502 |
497 |
498 | ### 练习4
499 |
500 | 请在下图加两根小棒,摆出两个大小、形状都相同的三角形。
501 |
502 |  503 |
504 | ### 例题5
505 |
506 | 你们见过这样的数字吗?按要求变化后,它们会变成哪些数字呢?
507 |
508 |
503 |
504 | ### 例题5
505 |
506 | 你们见过这样的数字吗?按要求变化后,它们会变成哪些数字呢?
507 |
508 |  509 |
510 |
509 |
510 |  511 |
512 | ### 练习5
513 |
514 | 先用9根火柴棒摆出18,只允许移动一根火柴棒,能摆成的最大的两位数是多少?
515 |
516 | ### 例题6
517 |
518 | 下面是用火柴棒摆成的两个错误的等式,请你各添加1根火柴棒,使每个等式成立。
519 |
520 |
511 |
512 | ### 练习5
513 |
514 | 先用9根火柴棒摆出18,只允许移动一根火柴棒,能摆成的最大的两位数是多少?
515 |
516 | ### 例题6
517 |
518 | 下面是用火柴棒摆成的两个错误的等式,请你各添加1根火柴棒,使每个等式成立。
519 |
520 |  521 |
522 | ### 练习6
523 |
524 | 下面是用火柴棒摆成的两个错误的等式,请你各去掉1根火柴棒,使每个等式成立。
525 |
526 |
521 |
522 | ### 练习6
523 |
524 | 下面是用火柴棒摆成的两个错误的等式,请你各去掉1根火柴棒,使每个等式成立。
525 |
526 |  527 |
528 | ### 移动一根
529 |
530 | 1+1=6 1+5=2 0+1=8 3+6=3 5-9=6 2+5=8 6+6=8 6+6=6 6+4=4 6-8=5 1+8=1 4+9=1 7+10=1 17+7=70 19-3=6
531 |
532 | 下面是用火柴棒摆成的四个错误的等式,请你各移动一根火柴棒,使每个等式成立。
533 |
534 |
527 |
528 | ### 移动一根
529 |
530 | 1+1=6 1+5=2 0+1=8 3+6=3 5-9=6 2+5=8 6+6=8 6+6=6 6+4=4 6-8=5 1+8=1 4+9=1 7+10=1 17+7=70 19-3=6
531 |
532 | 下面是用火柴棒摆成的四个错误的等式,请你各移动一根火柴棒,使每个等式成立。
533 |
534 | 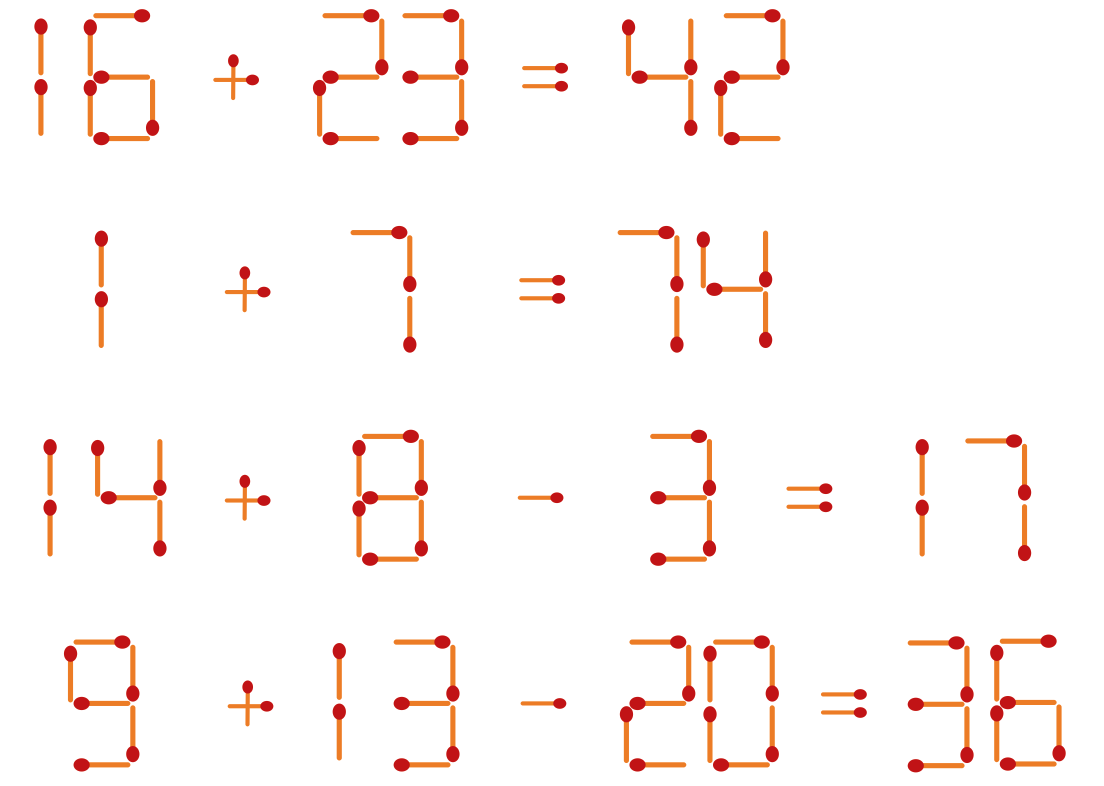 535 |
536 | ### 练习1
537 |
538 | 计算。
539 | $$
540 | 26+37+14=
541 | $$
542 |
543 | $$
544 | 92-23-47=
545 | $$
546 |
547 | $$
548 | 3+3+3+3+3+5+5+5=
549 | $$
550 |
551 | ### 练习2
552 |
553 | 思维火柴游戏,任意5题。
554 |
555 | ### 练习3
556 |
557 | 下面是用火柴棒摆成的错误的等式。请你添加1根火柴棒,使下面的等式成立。
558 |
559 |
535 |
536 | ### 练习1
537 |
538 | 计算。
539 | $$
540 | 26+37+14=
541 | $$
542 |
543 | $$
544 | 92-23-47=
545 | $$
546 |
547 | $$
548 | 3+3+3+3+3+5+5+5=
549 | $$
550 |
551 | ### 练习2
552 |
553 | 思维火柴游戏,任意5题。
554 |
555 | ### 练习3
556 |
557 | 下面是用火柴棒摆成的错误的等式。请你添加1根火柴棒,使下面的等式成立。
558 |
559 |  560 |
561 | ### 练习1
562 |
563 | 计算。
564 | $$
565 | 39+33-25=
566 | $$
567 |
568 | $$
569 | 39+24+15=
570 | $$
571 |
572 | $$
573 | 7+7+7+7+7+7=
574 | $$
575 |
576 | ### 练习2
577 |
578 | 思维火柴游戏,任意5题。
579 |
580 | ### 练习3
581 |
582 | 下面是用火柴棒摆成的错误的等式。请你去掉1根火柴棒,使下面的等式成立。
583 |
584 |
560 |
561 | ### 练习1
562 |
563 | 计算。
564 | $$
565 | 39+33-25=
566 | $$
567 |
568 | $$
569 | 39+24+15=
570 | $$
571 |
572 | $$
573 | 7+7+7+7+7+7=
574 | $$
575 |
576 | ### 练习2
577 |
578 | 思维火柴游戏,任意5题。
579 |
580 | ### 练习3
581 |
582 | 下面是用火柴棒摆成的错误的等式。请你去掉1根火柴棒,使下面的等式成立。
583 |
584 |  585 |
586 | ## 2.1.17. 摆小棒
587 |
588 | ### 热身1
589 |
590 | 计算。
591 | $$
592 | 8+8+8+8+8+6+6+6=
593 | $$
594 |
595 | ### 热身2
596 |
597 | 下列图形中,不能“一笔画”的是()。
598 |
599 |
585 |
586 | ## 2.1.17. 摆小棒
587 |
588 | ### 热身1
589 |
590 | 计算。
591 | $$
592 | 8+8+8+8+8+6+6+6=
593 | $$
594 |
595 | ### 热身2
596 |
597 | 下列图形中,不能“一笔画”的是()。
598 |
599 |  600 |
601 | ### 热身3
602 |
603 | 下图是儿童乐园的平面图,出入口应设在()点或()点,才能不重复地走遍每条路。
604 |
605 |
600 |
601 | ### 热身3
602 |
603 | 下图是儿童乐园的平面图,出入口应设在()点或()点,才能不重复地走遍每条路。
604 |
605 |  606 |
607 | ### 例题1
608 |
609 | 思维火柴1~10
610 |
611 | ### 例题2
612 |
613 | 按要求摆一摆,并在下方空白处画出来。
614 |
615 | (1)用4根火柴棒摆出一个正方形。
616 |
617 | (2)再加3根火柴棒,摆出两个正方形。
618 |
619 | (3)再加3根火柴棒,摆出三个正方形。
620 |
621 | (4)再加2根火柴棒,摆出五个正方形。
622 |
623 | ### 练习2
624 |
625 | 按要求摆一摆,并在下方空白处画出来。
626 |
627 | (1)用3根火柴棒,摆出一个三角形。
628 |
629 | (2)再加2根火柴棒,摆出两个三角形。
630 |
631 | (3)再加2根火柴棒,摆出三个三角形。
632 |
633 | (4)再加2根火柴棒,摆出五个三角形。
634 |
635 | ### 例题3
636 |
637 | 下图是用12根小棒摆成的5个正方形,拿掉哪2根,能使原图变成 2 个正方形?
638 |
639 |
606 |
607 | ### 例题1
608 |
609 | 思维火柴1~10
610 |
611 | ### 例题2
612 |
613 | 按要求摆一摆,并在下方空白处画出来。
614 |
615 | (1)用4根火柴棒摆出一个正方形。
616 |
617 | (2)再加3根火柴棒,摆出两个正方形。
618 |
619 | (3)再加3根火柴棒,摆出三个正方形。
620 |
621 | (4)再加2根火柴棒,摆出五个正方形。
622 |
623 | ### 练习2
624 |
625 | 按要求摆一摆,并在下方空白处画出来。
626 |
627 | (1)用3根火柴棒,摆出一个三角形。
628 |
629 | (2)再加2根火柴棒,摆出两个三角形。
630 |
631 | (3)再加2根火柴棒,摆出三个三角形。
632 |
633 | (4)再加2根火柴棒,摆出五个三角形。
634 |
635 | ### 例题3
636 |
637 | 下图是用12根小棒摆成的5个正方形,拿掉哪2根,能使原图变成 2 个正方形?
638 |
639 |  640 |
641 | ### 练习3
642 |
643 | 下图是用 12 根小棒摆成的 5 个正方形,拿掉哪 2 根,能使原图变成 3 个正方形。
644 |
645 |
640 |
641 | ### 练习3
642 |
643 | 下图是用 12 根小棒摆成的 5 个正方形,拿掉哪 2 根,能使原图变成 3 个正方形。
644 |
645 |  646 |
647 | ### 例题4
648 |
649 | 下图是用 9 根小棒摆成的 3 个三角形,请你移动 3 根小棒,变成 5 个三角形。
650 |
651 |
646 |
647 | ### 例题4
648 |
649 | 下图是用 9 根小棒摆成的 3 个三角形,请你移动 3 根小棒,变成 5 个三角形。
650 |
651 |  652 |
653 | ### 练习4
654 |
655 | 请在下图加两根小棒,摆出两个大小、形状都相同的三角形。
656 |
657 |
652 |
653 | ### 练习4
654 |
655 | 请在下图加两根小棒,摆出两个大小、形状都相同的三角形。
656 |
657 |  658 |
659 | ### 例题5
660 |
661 | 你们见过这样的数字吗?按要求变化后,它们会变成哪些数字呢?
662 |
663 |
658 |
659 | ### 例题5
660 |
661 | 你们见过这样的数字吗?按要求变化后,它们会变成哪些数字呢?
662 |
663 |  664 |
665 |
664 |
665 |  666 |
667 | ### 练习5
668 |
669 | 先用9根火柴棒摆出18,只允许移动一根火柴棒,能摆成的最大的两位数是多少?
670 |
671 | ### 例题6
672 |
673 | 下面是用火柴棒摆成的两个错误的等式,请你各添加1根火柴棒,使每个等式成立。
674 |
675 |
666 |
667 | ### 练习5
668 |
669 | 先用9根火柴棒摆出18,只允许移动一根火柴棒,能摆成的最大的两位数是多少?
670 |
671 | ### 例题6
672 |
673 | 下面是用火柴棒摆成的两个错误的等式,请你各添加1根火柴棒,使每个等式成立。
674 |
675 |  676 |
677 | ### 练习6
678 |
679 | 下面是用火柴棒摆成的两个错误的等式,请你各去掉1根火柴棒,使每个等式成立。
680 |
681 |
676 |
677 | ### 练习6
678 |
679 | 下面是用火柴棒摆成的两个错误的等式,请你各去掉1根火柴棒,使每个等式成立。
680 |
681 |  682 |
683 | ### 移动一根
684 |
685 | 1+1=6 1+5=2 0+1=8 3+6=3 5-9=6 2+5=8 6+6=8 6+6=6 6+4=4 6-8=5 1+8=1 4+9=1 7+10=1 17+7=70 19-3=6
686 |
687 | 下面是用火柴棒摆成的四个错误的等式,请你各移动一根火柴棒,使每个等式成立。
688 |
689 |
682 |
683 | ### 移动一根
684 |
685 | 1+1=6 1+5=2 0+1=8 3+6=3 5-9=6 2+5=8 6+6=8 6+6=6 6+4=4 6-8=5 1+8=1 4+9=1 7+10=1 17+7=70 19-3=6
686 |
687 | 下面是用火柴棒摆成的四个错误的等式,请你各移动一根火柴棒,使每个等式成立。
688 |
689 | 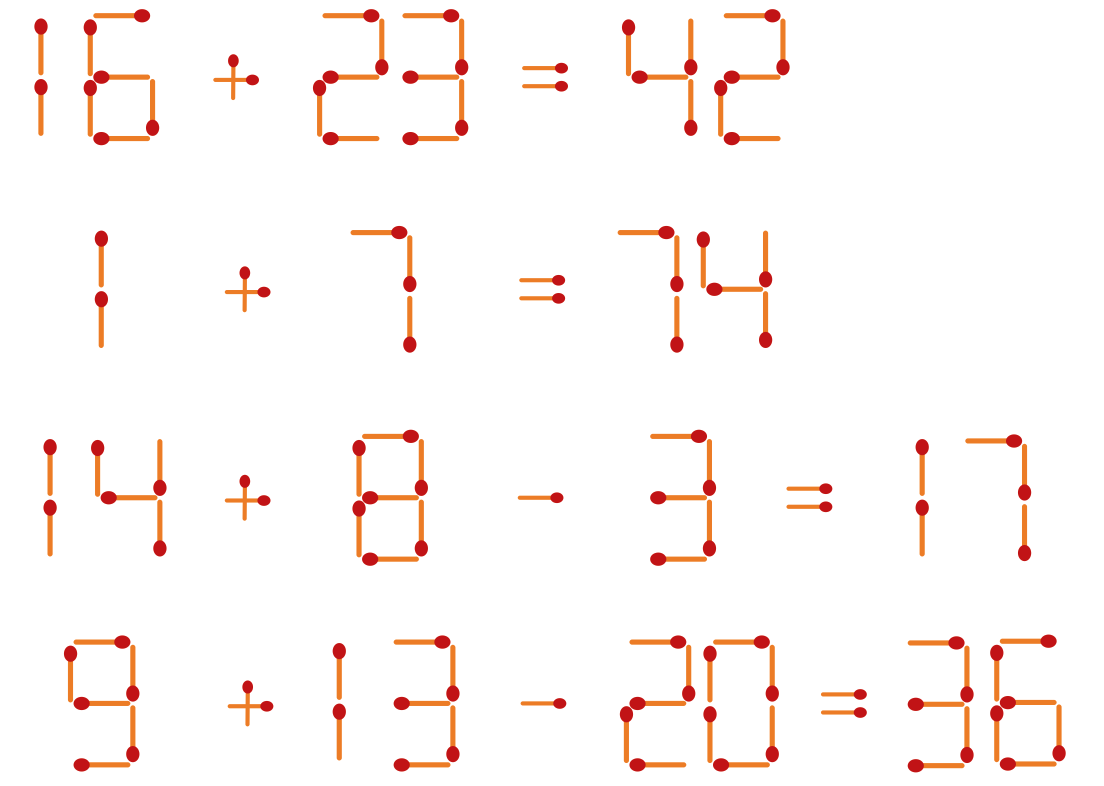 690 |
691 | ### 练习1
692 |
693 | 计算。
694 | $$
695 | 26+37+14=
696 | $$
697 |
698 | $$
699 | 92-23-47=
700 | $$
701 |
702 | $$
703 | 3+3+3+3+3+5+5+5=
704 | $$
705 |
706 | ### 练习2
707 |
708 | 思维火柴游戏,任意5题。
709 |
710 | ### 练习3
711 |
712 | 下面是用火柴棒摆成的错误的等式。请你添加1根火柴棒,使下面的等式成立。
713 |
714 |
690 |
691 | ### 练习1
692 |
693 | 计算。
694 | $$
695 | 26+37+14=
696 | $$
697 |
698 | $$
699 | 92-23-47=
700 | $$
701 |
702 | $$
703 | 3+3+3+3+3+5+5+5=
704 | $$
705 |
706 | ### 练习2
707 |
708 | 思维火柴游戏,任意5题。
709 |
710 | ### 练习3
711 |
712 | 下面是用火柴棒摆成的错误的等式。请你添加1根火柴棒,使下面的等式成立。
713 |
714 |  715 |
716 | ### 练习1
717 |
718 | 计算。
719 | $$
720 | 39+33-25=
721 | $$
722 |
723 | $$
724 | 39+24+15=
725 | $$
726 |
727 | $$
728 | 7+7+7+7+7+7=
729 | $$
730 |
731 | ### 练习2
732 |
733 | 思维火柴游戏,任意5题。
734 |
735 | ### 练习3
736 |
737 | 下面是用火柴棒摆成的错误的等式。请你去掉1根火柴棒,使下面的等式成立。
738 |
739 |
715 |
716 | ### 练习1
717 |
718 | 计算。
719 | $$
720 | 39+33-25=
721 | $$
722 |
723 | $$
724 | 39+24+15=
725 | $$
726 |
727 | $$
728 | 7+7+7+7+7+7=
729 | $$
730 |
731 | ### 练习2
732 |
733 | 思维火柴游戏,任意5题。
734 |
735 | ### 练习3
736 |
737 | 下面是用火柴棒摆成的错误的等式。请你去掉1根火柴棒,使下面的等式成立。
738 |
739 |  740 |
741 | ## 2.1.18. 逆向思考初步
742 |
743 | 逆向运算
744 |
745 | ### 铺垫 1
746 |
747 | 加减互逆,乘除互逆。
748 | $$
749 | \Box\overset{+5}{\to}17
750 | $$
751 |
752 | $$
753 | \Box\overset{-20}{\to}50
754 | $$
755 |
756 | $$
757 | \Box\overset{\times5}{\to}20
758 | $$
759 |
760 | $$
761 | \Box\overset{\div3}{\to}7
762 | $$
763 |
764 | ### 例题 1
765 |
766 | 你知道下面每个起点上的数各是几吗?
767 |
768 | 1. $$
769 | ()-7\to()\times4\to()-9\to()+8\to11
770 | $$
771 |
772 | 2. $$
773 | ()\times3\to()-6\to()+7\to()\div8\to2
774 | $$
775 |
776 | 3. $$
777 | ()+9\to()-8\to()\div6\to()\times9\to36
778 | $$
779 |
780 | 4.
781 |
782 | 5. $$
783 | ()-7\to()\times6\to()\times3\to()\div6\to36
784 | $$
785 |
786 | ### 练习 1
787 |
788 | 填出每个起点上的数。
789 | $$
790 | \Box\overset{-7}{\to}\Box\overset{\times4}{\to}\Box\overset{-9}{\to}\Box\overset{+8}{\to}\Box
791 | $$
792 |
793 | ### 画推导图
794 |
795 | ### 铺垫
796 |
797 | A、B各代表一个数。
798 |
799 | A 说:“我减去 3,加上2,再减去 3,得 20。”
800 |
801 | B 说:“我乘 2,除以 4,再乘 3,得 18。”
802 |
803 | 算一算,它们各代表多少?
804 |
805 | ### 例题 2
806 |
807 | 丁丁问牛牛:“你今年几岁?”牛牛回答:“用我今年的年龄减去 2,乘 2,减去 2,再除以 2,恰好等于 5。”你能帮丁丁算一下,牛牛今年多少岁吗?
808 |
809 | ### 练习 2
810 |
811 | 有一个数加上 6,减去 6,乘 6,除以 6,最后结果等于 6,问这个数是几?
812 |
813 | ### 例题 3
814 |
815 | 馋嘴和尚们吃一堆小馒头,第一次吃了一半,觉得不够;第二次又吃了剩下的一半,觉得差不多了;第三次又吃了5 个,觉得饱了。他们发现还剩下 5 个,干脆又吃光了,这一堆馒头有多少个?
816 |
817 | ### 练习 3
818 |
819 | 猪八戒化斋讨来一篮果子,吃了一半。觉得不够,又吃了剩下的一半,还觉得不够,又吃了剩下的一半,最后又偷偷吃了 2 个果子,觉得饱了,把剩下的给唐僧吃,孙悟空一看篮子里只剩下 4 个果子了。问猪八戒一共吃了多少个果子?
820 |
821 | 多减,少加
822 |
823 | ### 铺垫
824 |
825 | 一堆卡片,小代同学拿走了一半还多 1 张,剩下 5 张。原来有多少张卡片?
826 |
827 | 一堆卡片,小力同学拿走一半还少 1 张,剩下 6 张。原来有多少张卡片?
828 |
829 | ### 例题 4
830 |
831 | 三群蜜蜂在桃树林里采花蜜,A 群采全部桃树的一半少 4 棵,B 群采剩下桃树的一半多 2 棵,C 群采最后剩下的 10 棵桃树上的花蜜,那么,桃树林中共有多少棵桃树?
832 |
833 | ### 练习 4
834 |
835 | 阿普卖鸡蛋,第一次卖掉篮中的一半多 1 个,第二次又卖掉剩下的一半多 1 个,这时篮中还剩 1 个,问原来篮中有几个蛋?
836 |
837 | ### 例题 5
838 |
839 | 田田在玩取棋子的游戏,她每次拿出其中的一半再放回 1 颗,这样一共做了三次,最后还剩 3 颗棋子,你知道田田原来一共有多少颗棋子吗?
840 |
841 | ### 练习 5
842 |
843 | 丁丁拿着一包糖,遇见好朋友 A,分给了他一半,过一会儿又遇见好朋友 B,把剩下的糖的一半分给了 B,后来又遇到好朋友 C,把这时手中剩下的糖的一半又分给了C,这时他自己只有一块糖了,问在没有分给 A 以前,丁丁有
844 | 多少糖块?
845 |
846 | ### 例题 6
847 |
848 | 乐乐老师有几本小人书自己记不清楚了,只知道:牛牛借走一半加 1 本;丁丁又借走剩下的书的一半加 2 本;再剩下的书,田田借走一半加 3 本,最后乐乐老师还有 2 本书,请问乐乐老师原有几本小人书?
849 |
850 | ### 练习 6
851 |
852 | 乐乐老师用一根绳子拴葫芦,牛牛第一次使绳子减少全长的一半还多 2 米,第二次减少余下的一半少 10 米,第三次减少 15 米,最后还剩9米,那么这根绳子原来有多少米?
853 |
854 | 拓展
855 |
856 | ### 拓展 1
857 |
858 | 两个数做加法,其中一个数是 73,另一个数不知道是几,只知道把另一个数的十位增加 5,个位增加 1,结果和的后两位数字是 72,另一个数是几?
859 |
860 | ### 拓展 2
861 |
862 | 妈妈把一箱苹果平均分成 3 份后还剩 2 个,分给了小明一份带到学校分给小朋友们一起吃。小朋友们上午吃了其中的一半少 2 个,下午又吃了剩下中的一半又半个,最后还剩三个。问原来这箱苹果又多少个?
863 |
864 | ### 拓展 3
865 |
866 | 现有一堆棋子,把它们分成三等份后还剩 1 个;取出其中的两等份又分成三等份后还剩 2 个。问:原来至少有多少个棋子?
867 |
868 | ### 拓展 4
869 |
870 | 现有一堆棋子,把它分成三等份后还剩下一颗;取出其中的两份又分成三等份后还剩一颗;再取出其中的两份再分成三等份后还剩一颗。原来至少有多少颗棋子?
871 |
872 | ## 2.1.19. 排队问题进阶
873 |
874 | ### 例题1
875 |
876 | 学生们站成一排,从前往后数牛牛排第13个,从后往前数丁丁排第14个,已知牛牛在丁丁的前面,它们之间有3名学生,这排学生一共有多少名?
877 |
878 | ### 练习1
879 |
880 | 一队小朋友排队上车,从前往后数,牛牛排第18个,丁丁后面有16个小朋
881 | 友。已知牛牛和丁丁之间有2个小朋友。问这队小朋友共有多少个?
882 |
883 | ### 例题2
884 |
885 | 学生们排成一队,从排头数起阿普是第15名;从排尾数起田田是第23名。已知田田在阿普后面,从阿普数到田田一共有4名学生,问这群学生有多少名?
886 |
887 | ### 练习2
888 |
889 | 一队小朋友排队上车,从前往后数,小华排第18个,小明后面有16个同学,
890 | 已己知小华后面第二个是小明,问这队小朋友共有多少人?
891 |
892 | ### 例题3
893 |
894 | 32名学生排成一排,从左往右数,牛牛是第17名;从右往左数,丁丁是第19
895 | 名,从牛牛数到丁丁共有学生多少名?
896 |
897 | ### 练习3
898 |
899 | 学生们共有20名,从左往右数牛牛排第16名,从右往左数丁丁右边有18名
900 | 学生,问:牛牛和丁丁之间相隔多少名学生?
901 |
902 | ### 例题4
903 |
904 | 学校舞蹈队同学站成了一个“十”字形,田田恰好站在“十”字队形的中间,不
905 | 论前后数,还是左右数,田田都是第6个,问这个舞蹈队有多少名同学?
906 |
907 | ### 练习4
908 |
909 | 国庆节用鲜花摆成“十”字形,月季花恰好站在“十”字队形的中间,不论前
910 | 后数,还是左右数,月季花都是第21盆,问一共有多少盆花?
911 |
912 | ### 例题5
913 |
914 | 学生们排成一个正方形队伍,无论是从前往后数,还是从后往前数,阿普都是第5名,问这支正方形队伍共有多少名学生?
915 |
916 | ### 练习5
917 |
918 | 同学们排成一个正方形队伍表演体操,牛牛排在正中间,他的正前方、正后
919 | 方、正左方、正右方都有3名同学,这支队伍共有多少名同学?
920 |
921 | ### 例题6
922 |
923 | 学生们排成一个长方形队伍表演摔跤,牛牛从前边数排第7个,从后边数排第8个,从左边数排第4个,从右边数排第2个,一共有多少个学生在表演摔跤?
924 |
925 | ### 练习6
926 |
927 | 同学们排成一个长方形队伍进行体操表演,牛牛从前边数排第6个,从后边
928 | 数排第8个,丁丁从左边数排第4个,他右边有6个人。一共有多少个学生
929 | 在表演摔跤?
930 |
931 | ### 拓展
932 |
933 | ### 拓展1
934 |
935 | 49位同学排成7行7列的正方形队列表演体操,小明在队列中,正左边有2位同学,从前往后数是第3位同学,小明从右往左数是第几位同学?从后往前数是第几位同学?
936 |
937 | ### 拓展2
938 |
939 | 81位同学排成9行9列的正方形队列表演体操,小花在队列中,正左边有2位同学,正前方有3位同学,这时整个队列的同学向右转,则小花的正前方有几位同学?正右边有几位同学?
940 |
941 | ### 拓展3
942 |
943 | 学生进行队列表演,组成一个正方形队列,后来由于表演需要,去掉了一行一列,去掉的人数正好是13人,那么原来准备参加表演的一共有多少人?
944 |
945 | ### 拓展4
946 |
947 | 二年级(1)班的学生排成一个正方形队列,最外边一层的人数为60人。请问这个正方形队列最外层没边有多少人?
948 |
949 | ## 2.2.01. 认识倍
950 |
951 | 例题练习
952 |
953 | ### 例题1
954 |
955 | 乐乐老师奖励学习进步的同学。奖励牛牛金币20枚,田田得到金币的数量是牛牛的3倍还多5枚。奖励田田的金币有多少枚?
956 |
957 | ### 练习1
958 |
959 | 学校有篮球20个,足球的数量是篮球的3倍还少5个,足球有多少个?
960 |
961 | ### 例题2
962 |
963 | 丁丁有40张贴纸,丁丁的贴纸数量是牛牛贴纸数量的6倍还多4张,牛牛有多少张贴纸?
964 |
965 | ### 练习2
966 |
967 | 同学们去采摘,摘了西红柿27筐,是黄瓜的3倍多3筐,同学们摘了多少筐黄瓜?
968 |
969 | ### 例题3
970 |
971 | 阿普喷出水球22个,水球的数量是火球的3倍少5,火球有多少个?
972 |
973 | ### 练习3
974 |
975 | 学校买来了排球20个,买来的排球是足球的4倍,学校买来的排球比足球多几个?
976 |
977 | ### 例题4
978 |
979 | 乐乐老师有金币150枚,银币40枚,要使金币的数量是银币的6倍,还需要多少枚金币?
980 |
981 | ### 练习4
982 |
983 | 小猪有奶糖50块,水果糖4块,要使奶糖的数量是水果糖的6倍,应该吃掉多少块奶糖?
984 |
985 | ### 例题5
986 |
987 | 士兵和小怪物中一共有90个受伤,受伤的士兵人数是受伤小怪物数量的2倍,问士兵和小怪物各受伤多少个?
988 |
989 | ### 练习5
990 |
991 | 学校买来一些乒乓球和羽毛球共240个,乒乓球的个数是羽毛球的3倍。买来的乒乓球和羽毛球各多少个?
992 |
993 | ### 例题6
994 |
995 | 黑士兵比白士兵多80人,黑士兵的数量是白士兵数量的3倍,黑士兵和白士兵各有多少人?
996 |
997 | ### 练习6
998 |
999 | 学校买来的乒乓球比羽毛球多240个,乒乓球的个数是羽毛球的3倍。买来的乒乓球和羽毛球各多少个?
1000 |
1001 | 拓展
1002 |
1003 | ### 拓展1
1004 |
1005 | 小敏有14元,小花有10元,小花给小敏几元,小敏的钱数就是小花的2倍?
1006 |
1007 | ### 拓展2
1008 |
1009 | 师、徒两人共加工105个零件,师傅加工的个数比徒弟的3倍还多5个,师傅和徒弟各加工零件多少个?
1010 |
1011 | 巩固练习
1012 |
1013 | ### 巩固1
1014 |
1015 | 一支圆珠笔的价钱是8元,已知一盒彩笔的价钱是一支圆珠笔价钱的3倍,问小华买一盒彩笔和一支圆珠笔一共需要多少钱?
1016 |
1017 | ### 巩固2
1018 |
1019 | 学校买来排球120个,已知买来的排球是买来的足球的3倍,那么学校买来足球多少个?
1020 |
1021 | ### 巩固3
1022 |
1023 | 冷饮店有45箱可乐,已知可乐的数量是雪碧的2倍少5箱,那么雪碧有多少箱?
1024 |
1025 | ### 巩固4
1026 |
1027 | 动物园里有3只大猴,13只小猴,问要再添上几只小猴后,才能使小猴只数是大猴只数的6倍?
1028 |
1029 | ### 巩固5
1030 |
1031 | 男生和女生一共有123人,已知男生人数比女生人数的2倍还多3人,问女生和男生各有多少人?
1032 |
1033 | ### 巩固6
1034 |
1035 | 食堂买来的苹果比香蕉多50千克,已知苹果的重量是香蕉的6倍,问香蕉和苹果各有多少千克?
1036 |
1037 | ## 2.2.02. 带余数除法
1038 |
1039 | ### 例题1
1040 |
1041 | 根据要求填空。
1042 |
1043 | (1)$()÷4=3……2$
1044 |
1045 | (2)$()÷9=2……3$
1046 |
1047 | (3)$()÷5=3……4$
1048 |
1049 | ### 练习1
1050 |
1051 | 根据要求填空。
1052 |
1053 | (1)$()÷8=3……4$
1054 |
1055 | (2)$()÷9=2……5$
1056 |
1057 | (3)$()÷5=6……4$
1058 |
1059 | ### 例题2
1060 |
1061 | 根据要求填空。
1062 |
1063 | (1)$23÷()=3……2$
1064 |
1065 | (2)$21÷()=2……3$
1066 |
1067 | (3)$22÷()=3……4$
1068 |
1069 | ### 练习2
1070 |
1071 | 根据要求填空。
1072 |
1073 | (1)$43÷()=5……3$
1074 |
1075 | (2)$83÷()=9……2$
1076 |
1077 | (3)$22÷()=3……1$
1078 |
1079 | ### 例题3
1080 |
1081 | 根据要求在()里填上合适的数。
1082 |
1083 | (1)下面()里最小能填几。
1084 | $$
1085 | ()\div()=5……4
1086 | $$
1087 |
1088 | $$
1089 | ()\div()=4……9
1090 | $$
1091 |
1092 | (2)下面()里最大能填几。
1093 | $$
1094 | ()\div4=5……()
1095 | $$
1096 |
1097 | $$
1098 | ()\div9=4……()
1099 | $$
1100 |
1101 | ### 练习3
1102 |
1103 | 根据要求在()里填上合适的数。
1104 |
1105 | (1)下面()里最小能填几。
1106 | $$
1107 | ()\div()=3……9
1108 | $$
1109 |
1110 | $$
1111 | ()\div()=10……2
1112 | $$
1113 |
1114 | (2)下面()里最大能填几。
1115 | $$
1116 | ()\div6=5……()
1117 | $$
1118 |
1119 | $$
1120 | ()\div7=4……()
1121 | $$
1122 |
1123 | ### 例题4
1124 |
1125 | 乐乐老师为了奖励同学们的优秀表现,决定要把手中的苹果分给小朋友吃,平均分给11个人,每人分6个后,剩下的苹果不够分了,乐乐老师手中最少有多少个苹果?最多有多少个苹果?
1126 |
1127 | ### 练习4
1128 |
1129 | 田田拿出自己的一堆玻璃球,要平均分给8个好朋友,每个小朋友得到7个后,剩下的玻璃球不够分了,问:田田的玻璃球最少有多少个?最多有多少个?
1130 |
1131 | ### 例题5
1132 |
1133 | 田田带领7个小朋友一起去擦27块玻璃,先平均分,每个小朋友擦若干块,剩下的不够分,就由田田再擦剩下的玻璃,那么田田一共需要擦多少块玻璃才能完成任务?
1134 |
1135 | ### 练习5
1136 |
1137 | 牛牛决定也把自己手中的卡片和好朋友共同分享,他把23张卡片平均分给5个小朋友,剩下不够分的卡片才留给自己,请问:牛牛最后手中有卡片多少张?
1138 |
1139 | ### 例题6
1140 |
1141 | “数”、“学”分别代表一个非零的自然数,请你将所有满足下列等式的“数”、“学”所代表的数分别列出来?
1142 | $$
1143 | 数÷5=8……学
1144 | $$
1145 |
1146 | ### 练习6
1147 |
1148 | 字母A、B分别代表一个非零的自然数,请你将所有满足A÷4=5……B的A、B所代表的数分别列出来?
1149 |
1150 | ## 2.2.03. 有趣的自然数串
1151 |
1152 | ### 热身1
1153 |
1154 | ### 热身2
1155 |
1156 | ### 热身3
1157 |
1158 | ### 例题1
1159 |
1160 | 下面的自然数串,共有多少个数?
1161 | 3,4,5,6,7,8,9,……,28,29,30。
1162 |
1163 | ### 练习1
1164 |
1165 | 下面的自然数串,共有多少个数?
1166 | 8,9,10,11,12,……,56,57,58,59,60。
1167 |
1168 | ### 例题2
1169 |
1170 | 下面的自然数列,共有多少个数?
1171 | 2,4,6,8,10,12,14,……,58,60。
1172 |
1173 | ### 练习2
1174 |
1175 | 下面的自然数列,共有多少个数?
1176 | 1,3,5,7,9,11,13,……,37,39。
1177 |
1178 | ### 例题3
1179 |
1180 | 下面的自然数列,共有多少个数?
1181 | 1,4,7,10,13,……,31,34,37。
1182 |
1183 | ### 练习3
1184 |
1185 | 下面的自然数列,共有多少个数?
1186 | 4,8,12,16,20,……,40。
1187 |
1188 | ### 例题4
1189 |
1190 | 1,2,3,4,5,6,……,38,39,40,阿普写完这40个数后才发现它不知道自己写了多少个数字,大家快来帮帮阿普:阿普一共写了多少个数字呢?
1191 |
1192 | ### 练习4
1193 |
1194 | 阿普把昨天写的数拿出来了:1,2,3,4,5,6,……,58,59,60,小朋友帮忙算一算,阿普昨天写了多少个数字?
1195 |
1196 | ### 例题5
1197 |
1198 | 牛牛把12个机器人排成一行编了号,他决定从第一个机器人开始戴帽子,隔个戴一个;戴完后从剩下的第一个机器人开始戴,隔一个戴一个;第三次也是照这个办法戴,最后一个没戴帽子的当选为机器人队长。小朋友,几号是机器人队长呢?
1199 |
1200 | ### 练习5
1201 |
1202 | 等牛牛睡着了,机器人们决定选出夜间小队长,12个机器人自动排成一行编了号,它们集体决定从倒数第一个机器人开始,隔一个退出一个;退完后从剩下的倒数第一个机器人开始,隔一个退出一个;第三次也是照这个办法进
1203 | 行,最后一个留下的当选为机器人队长。小朋友,这次几号是机器人队长呢?
1204 |
1205 | ### 例题6
1206 |
1207 | 阿普决定把自己的12个机器人也编上号拿出来围成一个圈,它命令机器人从1开始按顺序1~2循环报数,每次报2的自动退下,就这样进行下去,最后剩下的机器人也会被幸运地选为队长,几号机器人最幸运呢?
1208 |
1209 | ### 练习6
1210 |
1211 | 25个玩具娃娃羡慕机器人推选出队长,它们也国成一个大圈,并顺时针依次编号为12~5号,从1号开始按照顺序12报数,凡是报2的留下,其余玩具娃娃退出圈外,这样循环进行到剩下最后一个人,它就是幸运之星,这个幸运之星是几号?
1212 |
1213 | ## 2.2.04. 图形分割
1214 |
1215 | ### 热身1
1216 |
1217 | 一支圆珠笔的价钱是8元,已知一盒彩笔的价钱是一支圆珠笔价钱的3倍,问小华买一盒彩笔和一支圆珠笔一共需要多少钱?
1218 |
1219 | ### 热身2
1220 |
1221 | 冷饮店有45箱可乐,已知可乐的数量是雪碧的2倍少5箱,那么雪碧有多少箱?
1222 |
1223 | ### 热身3
1224 |
1225 | 动物园里有3只大猴,13只小猴,问要再添上几只小猴后,才能使小猴只数是大猴只数的6倍?
1226 |
1227 | ### 例题1
1228 |
1229 | 牛牛的妈妈买来1块枣糕,上面有6颗枣(如图所示),家里正好有6个人,牛牛说:“要最大的”,妈妈为公平起见,决定将枣糕分为大小形状一样的6块,每块含有1颗枣。你知道应该怎么分吗?
1230 |
1231 | ### 练习1
1232 |
1233 | 一个正三角形形状的土地上有四棵大树(如下图所示),现要把这块正三角形的土地分成和它形状相同的四小块,并且要求每块地中都要有一棵大树。应怎么分?
1234 |
1235 | ### 例题2
1236 |
1237 | 请你把一个等边三角形分别分成形状、大小都相同的2个、3个、4个三角形?
1238 |
1239 | ### 练习2
1240 |
1241 | 请用两种方法把下面的大正方形分割成八个相同的等腰直角三角形?
1242 |
1243 | ### 例题3
1244 |
1245 | 下图是由18个小正方形组成的图形,请你把它分成6个完全相同的图形?
1246 |
1247 | ### 练习3
1248 |
1249 | 用四种不同的方法将下图分割成完全相同的两部分,保持每个小正方形的完整性?
1250 |
1251 | ### 例题4
1252 |
1253 | 请将下图分成形状、大小都相同的4块?
1254 |
1255 | ### 练习4
1256 |
1257 | 如下图所示,请把它分成形状、大小都相同的4块?
1258 |
1259 | ### 例题5
1260 |
1261 | 请将下图分成形状、大小都相同的4块?
1262 |
1263 | ### 练习5
1264 |
1265 | 把下图分成形状、大小完全相同的4部分?
1266 |
1267 | ### 例题6
1268 |
1269 | 教室旁边有一块空地,教室占整块地的四分之一。现在要把它作为实验园地,分给4个小组,要求每个小组分到的形状、大小都要一样。该怎么分?
1270 |
1271 | ### 练习6
1272 |
1273 | 下图是连在一起的三块地,这一整块地的形状是由3个同样大小的等边三角形组成的一个等腰梯形,把这个等腰梯形分成形状、大小一样的4块,该怎么分?
1274 |
1275 | ## 2.2.05. 枚举法的妙用
1276 |
1277 | ### 热身1
1278 |
1279 | 将下图分成大小、形状都相同的四块,并且每块中都有一个字母。
1280 |
1281 |
740 |
741 | ## 2.1.18. 逆向思考初步
742 |
743 | 逆向运算
744 |
745 | ### 铺垫 1
746 |
747 | 加减互逆,乘除互逆。
748 | $$
749 | \Box\overset{+5}{\to}17
750 | $$
751 |
752 | $$
753 | \Box\overset{-20}{\to}50
754 | $$
755 |
756 | $$
757 | \Box\overset{\times5}{\to}20
758 | $$
759 |
760 | $$
761 | \Box\overset{\div3}{\to}7
762 | $$
763 |
764 | ### 例题 1
765 |
766 | 你知道下面每个起点上的数各是几吗?
767 |
768 | 1. $$
769 | ()-7\to()\times4\to()-9\to()+8\to11
770 | $$
771 |
772 | 2. $$
773 | ()\times3\to()-6\to()+7\to()\div8\to2
774 | $$
775 |
776 | 3. $$
777 | ()+9\to()-8\to()\div6\to()\times9\to36
778 | $$
779 |
780 | 4.
781 |
782 | 5. $$
783 | ()-7\to()\times6\to()\times3\to()\div6\to36
784 | $$
785 |
786 | ### 练习 1
787 |
788 | 填出每个起点上的数。
789 | $$
790 | \Box\overset{-7}{\to}\Box\overset{\times4}{\to}\Box\overset{-9}{\to}\Box\overset{+8}{\to}\Box
791 | $$
792 |
793 | ### 画推导图
794 |
795 | ### 铺垫
796 |
797 | A、B各代表一个数。
798 |
799 | A 说:“我减去 3,加上2,再减去 3,得 20。”
800 |
801 | B 说:“我乘 2,除以 4,再乘 3,得 18。”
802 |
803 | 算一算,它们各代表多少?
804 |
805 | ### 例题 2
806 |
807 | 丁丁问牛牛:“你今年几岁?”牛牛回答:“用我今年的年龄减去 2,乘 2,减去 2,再除以 2,恰好等于 5。”你能帮丁丁算一下,牛牛今年多少岁吗?
808 |
809 | ### 练习 2
810 |
811 | 有一个数加上 6,减去 6,乘 6,除以 6,最后结果等于 6,问这个数是几?
812 |
813 | ### 例题 3
814 |
815 | 馋嘴和尚们吃一堆小馒头,第一次吃了一半,觉得不够;第二次又吃了剩下的一半,觉得差不多了;第三次又吃了5 个,觉得饱了。他们发现还剩下 5 个,干脆又吃光了,这一堆馒头有多少个?
816 |
817 | ### 练习 3
818 |
819 | 猪八戒化斋讨来一篮果子,吃了一半。觉得不够,又吃了剩下的一半,还觉得不够,又吃了剩下的一半,最后又偷偷吃了 2 个果子,觉得饱了,把剩下的给唐僧吃,孙悟空一看篮子里只剩下 4 个果子了。问猪八戒一共吃了多少个果子?
820 |
821 | 多减,少加
822 |
823 | ### 铺垫
824 |
825 | 一堆卡片,小代同学拿走了一半还多 1 张,剩下 5 张。原来有多少张卡片?
826 |
827 | 一堆卡片,小力同学拿走一半还少 1 张,剩下 6 张。原来有多少张卡片?
828 |
829 | ### 例题 4
830 |
831 | 三群蜜蜂在桃树林里采花蜜,A 群采全部桃树的一半少 4 棵,B 群采剩下桃树的一半多 2 棵,C 群采最后剩下的 10 棵桃树上的花蜜,那么,桃树林中共有多少棵桃树?
832 |
833 | ### 练习 4
834 |
835 | 阿普卖鸡蛋,第一次卖掉篮中的一半多 1 个,第二次又卖掉剩下的一半多 1 个,这时篮中还剩 1 个,问原来篮中有几个蛋?
836 |
837 | ### 例题 5
838 |
839 | 田田在玩取棋子的游戏,她每次拿出其中的一半再放回 1 颗,这样一共做了三次,最后还剩 3 颗棋子,你知道田田原来一共有多少颗棋子吗?
840 |
841 | ### 练习 5
842 |
843 | 丁丁拿着一包糖,遇见好朋友 A,分给了他一半,过一会儿又遇见好朋友 B,把剩下的糖的一半分给了 B,后来又遇到好朋友 C,把这时手中剩下的糖的一半又分给了C,这时他自己只有一块糖了,问在没有分给 A 以前,丁丁有
844 | 多少糖块?
845 |
846 | ### 例题 6
847 |
848 | 乐乐老师有几本小人书自己记不清楚了,只知道:牛牛借走一半加 1 本;丁丁又借走剩下的书的一半加 2 本;再剩下的书,田田借走一半加 3 本,最后乐乐老师还有 2 本书,请问乐乐老师原有几本小人书?
849 |
850 | ### 练习 6
851 |
852 | 乐乐老师用一根绳子拴葫芦,牛牛第一次使绳子减少全长的一半还多 2 米,第二次减少余下的一半少 10 米,第三次减少 15 米,最后还剩9米,那么这根绳子原来有多少米?
853 |
854 | 拓展
855 |
856 | ### 拓展 1
857 |
858 | 两个数做加法,其中一个数是 73,另一个数不知道是几,只知道把另一个数的十位增加 5,个位增加 1,结果和的后两位数字是 72,另一个数是几?
859 |
860 | ### 拓展 2
861 |
862 | 妈妈把一箱苹果平均分成 3 份后还剩 2 个,分给了小明一份带到学校分给小朋友们一起吃。小朋友们上午吃了其中的一半少 2 个,下午又吃了剩下中的一半又半个,最后还剩三个。问原来这箱苹果又多少个?
863 |
864 | ### 拓展 3
865 |
866 | 现有一堆棋子,把它们分成三等份后还剩 1 个;取出其中的两等份又分成三等份后还剩 2 个。问:原来至少有多少个棋子?
867 |
868 | ### 拓展 4
869 |
870 | 现有一堆棋子,把它分成三等份后还剩下一颗;取出其中的两份又分成三等份后还剩一颗;再取出其中的两份再分成三等份后还剩一颗。原来至少有多少颗棋子?
871 |
872 | ## 2.1.19. 排队问题进阶
873 |
874 | ### 例题1
875 |
876 | 学生们站成一排,从前往后数牛牛排第13个,从后往前数丁丁排第14个,已知牛牛在丁丁的前面,它们之间有3名学生,这排学生一共有多少名?
877 |
878 | ### 练习1
879 |
880 | 一队小朋友排队上车,从前往后数,牛牛排第18个,丁丁后面有16个小朋
881 | 友。已知牛牛和丁丁之间有2个小朋友。问这队小朋友共有多少个?
882 |
883 | ### 例题2
884 |
885 | 学生们排成一队,从排头数起阿普是第15名;从排尾数起田田是第23名。已知田田在阿普后面,从阿普数到田田一共有4名学生,问这群学生有多少名?
886 |
887 | ### 练习2
888 |
889 | 一队小朋友排队上车,从前往后数,小华排第18个,小明后面有16个同学,
890 | 已己知小华后面第二个是小明,问这队小朋友共有多少人?
891 |
892 | ### 例题3
893 |
894 | 32名学生排成一排,从左往右数,牛牛是第17名;从右往左数,丁丁是第19
895 | 名,从牛牛数到丁丁共有学生多少名?
896 |
897 | ### 练习3
898 |
899 | 学生们共有20名,从左往右数牛牛排第16名,从右往左数丁丁右边有18名
900 | 学生,问:牛牛和丁丁之间相隔多少名学生?
901 |
902 | ### 例题4
903 |
904 | 学校舞蹈队同学站成了一个“十”字形,田田恰好站在“十”字队形的中间,不
905 | 论前后数,还是左右数,田田都是第6个,问这个舞蹈队有多少名同学?
906 |
907 | ### 练习4
908 |
909 | 国庆节用鲜花摆成“十”字形,月季花恰好站在“十”字队形的中间,不论前
910 | 后数,还是左右数,月季花都是第21盆,问一共有多少盆花?
911 |
912 | ### 例题5
913 |
914 | 学生们排成一个正方形队伍,无论是从前往后数,还是从后往前数,阿普都是第5名,问这支正方形队伍共有多少名学生?
915 |
916 | ### 练习5
917 |
918 | 同学们排成一个正方形队伍表演体操,牛牛排在正中间,他的正前方、正后
919 | 方、正左方、正右方都有3名同学,这支队伍共有多少名同学?
920 |
921 | ### 例题6
922 |
923 | 学生们排成一个长方形队伍表演摔跤,牛牛从前边数排第7个,从后边数排第8个,从左边数排第4个,从右边数排第2个,一共有多少个学生在表演摔跤?
924 |
925 | ### 练习6
926 |
927 | 同学们排成一个长方形队伍进行体操表演,牛牛从前边数排第6个,从后边
928 | 数排第8个,丁丁从左边数排第4个,他右边有6个人。一共有多少个学生
929 | 在表演摔跤?
930 |
931 | ### 拓展
932 |
933 | ### 拓展1
934 |
935 | 49位同学排成7行7列的正方形队列表演体操,小明在队列中,正左边有2位同学,从前往后数是第3位同学,小明从右往左数是第几位同学?从后往前数是第几位同学?
936 |
937 | ### 拓展2
938 |
939 | 81位同学排成9行9列的正方形队列表演体操,小花在队列中,正左边有2位同学,正前方有3位同学,这时整个队列的同学向右转,则小花的正前方有几位同学?正右边有几位同学?
940 |
941 | ### 拓展3
942 |
943 | 学生进行队列表演,组成一个正方形队列,后来由于表演需要,去掉了一行一列,去掉的人数正好是13人,那么原来准备参加表演的一共有多少人?
944 |
945 | ### 拓展4
946 |
947 | 二年级(1)班的学生排成一个正方形队列,最外边一层的人数为60人。请问这个正方形队列最外层没边有多少人?
948 |
949 | ## 2.2.01. 认识倍
950 |
951 | 例题练习
952 |
953 | ### 例题1
954 |
955 | 乐乐老师奖励学习进步的同学。奖励牛牛金币20枚,田田得到金币的数量是牛牛的3倍还多5枚。奖励田田的金币有多少枚?
956 |
957 | ### 练习1
958 |
959 | 学校有篮球20个,足球的数量是篮球的3倍还少5个,足球有多少个?
960 |
961 | ### 例题2
962 |
963 | 丁丁有40张贴纸,丁丁的贴纸数量是牛牛贴纸数量的6倍还多4张,牛牛有多少张贴纸?
964 |
965 | ### 练习2
966 |
967 | 同学们去采摘,摘了西红柿27筐,是黄瓜的3倍多3筐,同学们摘了多少筐黄瓜?
968 |
969 | ### 例题3
970 |
971 | 阿普喷出水球22个,水球的数量是火球的3倍少5,火球有多少个?
972 |
973 | ### 练习3
974 |
975 | 学校买来了排球20个,买来的排球是足球的4倍,学校买来的排球比足球多几个?
976 |
977 | ### 例题4
978 |
979 | 乐乐老师有金币150枚,银币40枚,要使金币的数量是银币的6倍,还需要多少枚金币?
980 |
981 | ### 练习4
982 |
983 | 小猪有奶糖50块,水果糖4块,要使奶糖的数量是水果糖的6倍,应该吃掉多少块奶糖?
984 |
985 | ### 例题5
986 |
987 | 士兵和小怪物中一共有90个受伤,受伤的士兵人数是受伤小怪物数量的2倍,问士兵和小怪物各受伤多少个?
988 |
989 | ### 练习5
990 |
991 | 学校买来一些乒乓球和羽毛球共240个,乒乓球的个数是羽毛球的3倍。买来的乒乓球和羽毛球各多少个?
992 |
993 | ### 例题6
994 |
995 | 黑士兵比白士兵多80人,黑士兵的数量是白士兵数量的3倍,黑士兵和白士兵各有多少人?
996 |
997 | ### 练习6
998 |
999 | 学校买来的乒乓球比羽毛球多240个,乒乓球的个数是羽毛球的3倍。买来的乒乓球和羽毛球各多少个?
1000 |
1001 | 拓展
1002 |
1003 | ### 拓展1
1004 |
1005 | 小敏有14元,小花有10元,小花给小敏几元,小敏的钱数就是小花的2倍?
1006 |
1007 | ### 拓展2
1008 |
1009 | 师、徒两人共加工105个零件,师傅加工的个数比徒弟的3倍还多5个,师傅和徒弟各加工零件多少个?
1010 |
1011 | 巩固练习
1012 |
1013 | ### 巩固1
1014 |
1015 | 一支圆珠笔的价钱是8元,已知一盒彩笔的价钱是一支圆珠笔价钱的3倍,问小华买一盒彩笔和一支圆珠笔一共需要多少钱?
1016 |
1017 | ### 巩固2
1018 |
1019 | 学校买来排球120个,已知买来的排球是买来的足球的3倍,那么学校买来足球多少个?
1020 |
1021 | ### 巩固3
1022 |
1023 | 冷饮店有45箱可乐,已知可乐的数量是雪碧的2倍少5箱,那么雪碧有多少箱?
1024 |
1025 | ### 巩固4
1026 |
1027 | 动物园里有3只大猴,13只小猴,问要再添上几只小猴后,才能使小猴只数是大猴只数的6倍?
1028 |
1029 | ### 巩固5
1030 |
1031 | 男生和女生一共有123人,已知男生人数比女生人数的2倍还多3人,问女生和男生各有多少人?
1032 |
1033 | ### 巩固6
1034 |
1035 | 食堂买来的苹果比香蕉多50千克,已知苹果的重量是香蕉的6倍,问香蕉和苹果各有多少千克?
1036 |
1037 | ## 2.2.02. 带余数除法
1038 |
1039 | ### 例题1
1040 |
1041 | 根据要求填空。
1042 |
1043 | (1)$()÷4=3……2$
1044 |
1045 | (2)$()÷9=2……3$
1046 |
1047 | (3)$()÷5=3……4$
1048 |
1049 | ### 练习1
1050 |
1051 | 根据要求填空。
1052 |
1053 | (1)$()÷8=3……4$
1054 |
1055 | (2)$()÷9=2……5$
1056 |
1057 | (3)$()÷5=6……4$
1058 |
1059 | ### 例题2
1060 |
1061 | 根据要求填空。
1062 |
1063 | (1)$23÷()=3……2$
1064 |
1065 | (2)$21÷()=2……3$
1066 |
1067 | (3)$22÷()=3……4$
1068 |
1069 | ### 练习2
1070 |
1071 | 根据要求填空。
1072 |
1073 | (1)$43÷()=5……3$
1074 |
1075 | (2)$83÷()=9……2$
1076 |
1077 | (3)$22÷()=3……1$
1078 |
1079 | ### 例题3
1080 |
1081 | 根据要求在()里填上合适的数。
1082 |
1083 | (1)下面()里最小能填几。
1084 | $$
1085 | ()\div()=5……4
1086 | $$
1087 |
1088 | $$
1089 | ()\div()=4……9
1090 | $$
1091 |
1092 | (2)下面()里最大能填几。
1093 | $$
1094 | ()\div4=5……()
1095 | $$
1096 |
1097 | $$
1098 | ()\div9=4……()
1099 | $$
1100 |
1101 | ### 练习3
1102 |
1103 | 根据要求在()里填上合适的数。
1104 |
1105 | (1)下面()里最小能填几。
1106 | $$
1107 | ()\div()=3……9
1108 | $$
1109 |
1110 | $$
1111 | ()\div()=10……2
1112 | $$
1113 |
1114 | (2)下面()里最大能填几。
1115 | $$
1116 | ()\div6=5……()
1117 | $$
1118 |
1119 | $$
1120 | ()\div7=4……()
1121 | $$
1122 |
1123 | ### 例题4
1124 |
1125 | 乐乐老师为了奖励同学们的优秀表现,决定要把手中的苹果分给小朋友吃,平均分给11个人,每人分6个后,剩下的苹果不够分了,乐乐老师手中最少有多少个苹果?最多有多少个苹果?
1126 |
1127 | ### 练习4
1128 |
1129 | 田田拿出自己的一堆玻璃球,要平均分给8个好朋友,每个小朋友得到7个后,剩下的玻璃球不够分了,问:田田的玻璃球最少有多少个?最多有多少个?
1130 |
1131 | ### 例题5
1132 |
1133 | 田田带领7个小朋友一起去擦27块玻璃,先平均分,每个小朋友擦若干块,剩下的不够分,就由田田再擦剩下的玻璃,那么田田一共需要擦多少块玻璃才能完成任务?
1134 |
1135 | ### 练习5
1136 |
1137 | 牛牛决定也把自己手中的卡片和好朋友共同分享,他把23张卡片平均分给5个小朋友,剩下不够分的卡片才留给自己,请问:牛牛最后手中有卡片多少张?
1138 |
1139 | ### 例题6
1140 |
1141 | “数”、“学”分别代表一个非零的自然数,请你将所有满足下列等式的“数”、“学”所代表的数分别列出来?
1142 | $$
1143 | 数÷5=8……学
1144 | $$
1145 |
1146 | ### 练习6
1147 |
1148 | 字母A、B分别代表一个非零的自然数,请你将所有满足A÷4=5……B的A、B所代表的数分别列出来?
1149 |
1150 | ## 2.2.03. 有趣的自然数串
1151 |
1152 | ### 热身1
1153 |
1154 | ### 热身2
1155 |
1156 | ### 热身3
1157 |
1158 | ### 例题1
1159 |
1160 | 下面的自然数串,共有多少个数?
1161 | 3,4,5,6,7,8,9,……,28,29,30。
1162 |
1163 | ### 练习1
1164 |
1165 | 下面的自然数串,共有多少个数?
1166 | 8,9,10,11,12,……,56,57,58,59,60。
1167 |
1168 | ### 例题2
1169 |
1170 | 下面的自然数列,共有多少个数?
1171 | 2,4,6,8,10,12,14,……,58,60。
1172 |
1173 | ### 练习2
1174 |
1175 | 下面的自然数列,共有多少个数?
1176 | 1,3,5,7,9,11,13,……,37,39。
1177 |
1178 | ### 例题3
1179 |
1180 | 下面的自然数列,共有多少个数?
1181 | 1,4,7,10,13,……,31,34,37。
1182 |
1183 | ### 练习3
1184 |
1185 | 下面的自然数列,共有多少个数?
1186 | 4,8,12,16,20,……,40。
1187 |
1188 | ### 例题4
1189 |
1190 | 1,2,3,4,5,6,……,38,39,40,阿普写完这40个数后才发现它不知道自己写了多少个数字,大家快来帮帮阿普:阿普一共写了多少个数字呢?
1191 |
1192 | ### 练习4
1193 |
1194 | 阿普把昨天写的数拿出来了:1,2,3,4,5,6,……,58,59,60,小朋友帮忙算一算,阿普昨天写了多少个数字?
1195 |
1196 | ### 例题5
1197 |
1198 | 牛牛把12个机器人排成一行编了号,他决定从第一个机器人开始戴帽子,隔个戴一个;戴完后从剩下的第一个机器人开始戴,隔一个戴一个;第三次也是照这个办法戴,最后一个没戴帽子的当选为机器人队长。小朋友,几号是机器人队长呢?
1199 |
1200 | ### 练习5
1201 |
1202 | 等牛牛睡着了,机器人们决定选出夜间小队长,12个机器人自动排成一行编了号,它们集体决定从倒数第一个机器人开始,隔一个退出一个;退完后从剩下的倒数第一个机器人开始,隔一个退出一个;第三次也是照这个办法进
1203 | 行,最后一个留下的当选为机器人队长。小朋友,这次几号是机器人队长呢?
1204 |
1205 | ### 例题6
1206 |
1207 | 阿普决定把自己的12个机器人也编上号拿出来围成一个圈,它命令机器人从1开始按顺序1~2循环报数,每次报2的自动退下,就这样进行下去,最后剩下的机器人也会被幸运地选为队长,几号机器人最幸运呢?
1208 |
1209 | ### 练习6
1210 |
1211 | 25个玩具娃娃羡慕机器人推选出队长,它们也国成一个大圈,并顺时针依次编号为12~5号,从1号开始按照顺序12报数,凡是报2的留下,其余玩具娃娃退出圈外,这样循环进行到剩下最后一个人,它就是幸运之星,这个幸运之星是几号?
1212 |
1213 | ## 2.2.04. 图形分割
1214 |
1215 | ### 热身1
1216 |
1217 | 一支圆珠笔的价钱是8元,已知一盒彩笔的价钱是一支圆珠笔价钱的3倍,问小华买一盒彩笔和一支圆珠笔一共需要多少钱?
1218 |
1219 | ### 热身2
1220 |
1221 | 冷饮店有45箱可乐,已知可乐的数量是雪碧的2倍少5箱,那么雪碧有多少箱?
1222 |
1223 | ### 热身3
1224 |
1225 | 动物园里有3只大猴,13只小猴,问要再添上几只小猴后,才能使小猴只数是大猴只数的6倍?
1226 |
1227 | ### 例题1
1228 |
1229 | 牛牛的妈妈买来1块枣糕,上面有6颗枣(如图所示),家里正好有6个人,牛牛说:“要最大的”,妈妈为公平起见,决定将枣糕分为大小形状一样的6块,每块含有1颗枣。你知道应该怎么分吗?
1230 |
1231 | ### 练习1
1232 |
1233 | 一个正三角形形状的土地上有四棵大树(如下图所示),现要把这块正三角形的土地分成和它形状相同的四小块,并且要求每块地中都要有一棵大树。应怎么分?
1234 |
1235 | ### 例题2
1236 |
1237 | 请你把一个等边三角形分别分成形状、大小都相同的2个、3个、4个三角形?
1238 |
1239 | ### 练习2
1240 |
1241 | 请用两种方法把下面的大正方形分割成八个相同的等腰直角三角形?
1242 |
1243 | ### 例题3
1244 |
1245 | 下图是由18个小正方形组成的图形,请你把它分成6个完全相同的图形?
1246 |
1247 | ### 练习3
1248 |
1249 | 用四种不同的方法将下图分割成完全相同的两部分,保持每个小正方形的完整性?
1250 |
1251 | ### 例题4
1252 |
1253 | 请将下图分成形状、大小都相同的4块?
1254 |
1255 | ### 练习4
1256 |
1257 | 如下图所示,请把它分成形状、大小都相同的4块?
1258 |
1259 | ### 例题5
1260 |
1261 | 请将下图分成形状、大小都相同的4块?
1262 |
1263 | ### 练习5
1264 |
1265 | 把下图分成形状、大小完全相同的4部分?
1266 |
1267 | ### 例题6
1268 |
1269 | 教室旁边有一块空地,教室占整块地的四分之一。现在要把它作为实验园地,分给4个小组,要求每个小组分到的形状、大小都要一样。该怎么分?
1270 |
1271 | ### 练习6
1272 |
1273 | 下图是连在一起的三块地,这一整块地的形状是由3个同样大小的等边三角形组成的一个等腰梯形,把这个等腰梯形分成形状、大小一样的4块,该怎么分?
1274 |
1275 | ## 2.2.05. 枚举法的妙用
1276 |
1277 | ### 热身1
1278 |
1279 | 将下图分成大小、形状都相同的四块,并且每块中都有一个字母。
1280 |
1281 |  1282 |
1283 | ### 热身2
1284 |
1285 | 计算:$1+2+3+\dots+49+50+49+\dots+3+2+1$
1286 |
1287 | ### 热身3
1288 |
1289 | 自然数12,135,1349这些数有一个共同的特点,至少有两个数字,而且相邻两个数字,左边的数字小于右边的数字,我们取名为“上升数”。用1,2,3,4这四个数可以组成几个“上升数”。
1290 |
1291 | (1)$38+163-63-28$
1292 |
1293 | (2)$80+37-7+65-15$
1294 |
1295 | ### 例题1
1296 |
1297 | 牛牛和丁丁想从2张一样的摩比星和2张一样的数学卡片中挑出一些拍照片,请你帮他俩算一算,有多少种不同的挑选方法?
1298 |
1299 | ### 练习1
1300 |
1301 | 阿普有1角、2角、5角的硬币各一枚,他从中取两枚,有多少种不同的取法?
1302 |
1303 | ### 例题2
1304 |
1305 | 把12个同样大小的正方形拼成1个长方形,可以拼成几个不同的长方形?
1306 |
1307 | ### 练习2
1308 |
1309 | 把16个同样大小的正方形拼成1个长方形,可以拼成几个不同的长方形?
1310 |
1311 | ### 例题3
1312 |
1313 | 用卡片1、3、5可以组成多少个不同的三位数?
1314 |
1315 | ### 练习3
1316 |
1317 | 用卡片0、2、4可以组成多少个不同的三位数?
1318 |
1319 | ### 例题4
1320 |
1321 | 阿普家门前共有5级台阶。如果规定一步只能登上1级或2级台阶,小朋友帮阿普算一算,走完这些台阶共有多少种不同的走法?
1322 |
1323 | ### 练习4
1324 |
1325 | 阿普家门前共有5级台阶。如果这次规定一步只能登上1级或3级台阶,小朋友帮阿普算一算,走完这个台阶共有多少种不同的走法?
1326 |
1327 | ### 例题5
1328 |
1329 | 牛牛和丁丁要从学校A点到动物园E点,如下图怎样走路线最短?这样的路线一共有多少条?请你用彩笔画一画。(图中一小段都一样长)
1330 |
1331 | 
1332 |
1333 | ### 练习5
1334 |
1335 | 妈妈从家到单位上班,要经过电影院,从家到电影院有2条路,从电影院到单位有4条路,妈妈从家到单位上班有多少条不同的路线可走?
1336 |
1337 | ### 例题6
1338 |
1339 | 牛牛的暑假作业有语文、数学、英语三门,他准备每天做一门,且相邻两天不做同一门。如果牛牛第一天做语文,第五天也做语文,那么,这五天作业他共有多少种不同的安排?
1340 |
1341 | ### 练习6
1342 |
1343 | 田田爱吃青菜、菠菜、丝瓜三种蔬菜,她准备每天吃一种且相邻两天不吃同样蔬菜,如果田田第一天吃青菜,第五天也吃青菜,这五天她有几种不同的安排?
1344 |
1345 | ### 拓展1
1346 |
1347 | 把10份同样的礼物全部分成3组,每组至少有1份礼物的不同分法有几种?
1348 |
1349 | ### 拓展2
1350 |
1351 | 一只青蛙在A,B,C三点之间跳动,若青蛙从A点起跳,跳4次仍回到A点,如果不能原地跳则这只青蛙一共有多少种不同的跳法?
1352 |
1353 | ### 拓展3
1354 |
1355 | 两个正整数的乘积为96,这两个数可能是?
1356 |
1357 | ## 2.2.06. 鸡兔同笼初步
1358 |
1359 | ### 例题1
1360 |
1361 | 丁丁把鸡、免关在同一个笼子里,数了数,共有6个头,16条腿,你知道有几只鸡,几只免吗?
1362 |
1363 | ### 练习1
1364 |
1365 | 1角硬币和5角硬币一共有6枚,一共2元6角,求两种硬币各有多少枚?
1366 |
1367 | ### 例题2
1368 |
1369 | 牛牛把鸡、免关在同一个笼子里,数了数,共有10个头、26条腿,你知道这个笼子里有几只鸡?几只兔?
1370 |
1371 | ### 练习2
1372 |
1373 | 鸡、兔关在同一个笼子里,共有11个头,28条腿,这个笼子里有几只鸡?几只兔?
1374 |
1375 | ### 例题3
1376 |
1377 | 1只蛐蛐6条腿,1只蜘蛛8条腿。有蛐蛐和蜘蛛共10只,共68条腿,蛐蛐和蜘蛛各有多少只?
1378 |
1379 | ### 练习3
1380 |
1381 | 1瓶可乐6元,1瓶雪碧8元。牛牛共买这两种饮料8瓶,共花58元。可乐和雪碧各有多少瓶?
1382 |
1383 | ### 例题4
1384 |
1385 | 笼子里有一些鸡和兔,共20个头,50条腿,算一算笼子里有几只鸡?几只兔?
1386 |
1387 | ### 练习4
1388 |
1389 | 鸡和免共有45只,关在同一个笼子中。每只鸡有2条腿,每只兔子有4条腿,笼中共有100条腿。算一算,笼中有鸡多少只?免子多少只?
1390 |
1391 | ### 例题5
1392 |
1393 | 一辆卡车有6个轮子,一辆小汽车有4个轮子,停车场一共有14辆车,现在一共有72个轮子,你知道卡车和小汽车各有几辆吗?
1394 |
1395 | ### 练习5
1396 |
1397 | 在一个停车场上,现有车辆41辆,其中汽车有4个轮子,三轮摩托车有3个轮子,这些车共有127个轮子,那么三轮摩托车有多少辆?
1398 |
1399 | ### 例题6
1400 |
1401 | 鸡免同笼,共有14个头,38条腿,有几只鸡?几只兔?
1402 |
1403 | ### 练习6
1404 |
1405 | 1辆自行车有2个轮子,1辆三轮车有3个轮子。车棚里放着的自行车和三轮车共8辆,共20个轮子。自行车、三轮车各有多少辆?
1406 |
1407 | ## 2.2.07. 巧求周长初步
1408 |
1409 | ### 热身1(和倍)
1410 |
1411 | 实验小学三、四年级的同学们一共制作了24件航模,四年级同学制作的航模件数是三年级的2倍,三、四年级的同学各制作了多少件航模?
1412 |
1413 | ### 热身2(图形分割)
1414 |
1415 | 把下图分成形状、大小完全相同的4部分。
1416 |
1417 | 
1418 |
1419 | ### 热身3(枚举)
1420 |
1421 | 3个装药的瓶子都贴了标签,其中有两个贴错了,错的情况总共有3种可能。如果有四个瓶子,其中有三个贴错了,那么错的情况共有多少种?
1422 |
1423 | (1)$178\times9$
1424 |
1425 | (2)$1000\div8$
1426 |
1427 | (3)$53\times12$
1428 |
1429 | ### 例题1
1430 |
1431 | 如下图为丁丁的学校操场平面图,长为300米,宽为200米,丁丁绕操场走一圈,问:丁丁走了多少米?
1432 |
1433 |
1282 |
1283 | ### 热身2
1284 |
1285 | 计算:$1+2+3+\dots+49+50+49+\dots+3+2+1$
1286 |
1287 | ### 热身3
1288 |
1289 | 自然数12,135,1349这些数有一个共同的特点,至少有两个数字,而且相邻两个数字,左边的数字小于右边的数字,我们取名为“上升数”。用1,2,3,4这四个数可以组成几个“上升数”。
1290 |
1291 | (1)$38+163-63-28$
1292 |
1293 | (2)$80+37-7+65-15$
1294 |
1295 | ### 例题1
1296 |
1297 | 牛牛和丁丁想从2张一样的摩比星和2张一样的数学卡片中挑出一些拍照片,请你帮他俩算一算,有多少种不同的挑选方法?
1298 |
1299 | ### 练习1
1300 |
1301 | 阿普有1角、2角、5角的硬币各一枚,他从中取两枚,有多少种不同的取法?
1302 |
1303 | ### 例题2
1304 |
1305 | 把12个同样大小的正方形拼成1个长方形,可以拼成几个不同的长方形?
1306 |
1307 | ### 练习2
1308 |
1309 | 把16个同样大小的正方形拼成1个长方形,可以拼成几个不同的长方形?
1310 |
1311 | ### 例题3
1312 |
1313 | 用卡片1、3、5可以组成多少个不同的三位数?
1314 |
1315 | ### 练习3
1316 |
1317 | 用卡片0、2、4可以组成多少个不同的三位数?
1318 |
1319 | ### 例题4
1320 |
1321 | 阿普家门前共有5级台阶。如果规定一步只能登上1级或2级台阶,小朋友帮阿普算一算,走完这些台阶共有多少种不同的走法?
1322 |
1323 | ### 练习4
1324 |
1325 | 阿普家门前共有5级台阶。如果这次规定一步只能登上1级或3级台阶,小朋友帮阿普算一算,走完这个台阶共有多少种不同的走法?
1326 |
1327 | ### 例题5
1328 |
1329 | 牛牛和丁丁要从学校A点到动物园E点,如下图怎样走路线最短?这样的路线一共有多少条?请你用彩笔画一画。(图中一小段都一样长)
1330 |
1331 | 
1332 |
1333 | ### 练习5
1334 |
1335 | 妈妈从家到单位上班,要经过电影院,从家到电影院有2条路,从电影院到单位有4条路,妈妈从家到单位上班有多少条不同的路线可走?
1336 |
1337 | ### 例题6
1338 |
1339 | 牛牛的暑假作业有语文、数学、英语三门,他准备每天做一门,且相邻两天不做同一门。如果牛牛第一天做语文,第五天也做语文,那么,这五天作业他共有多少种不同的安排?
1340 |
1341 | ### 练习6
1342 |
1343 | 田田爱吃青菜、菠菜、丝瓜三种蔬菜,她准备每天吃一种且相邻两天不吃同样蔬菜,如果田田第一天吃青菜,第五天也吃青菜,这五天她有几种不同的安排?
1344 |
1345 | ### 拓展1
1346 |
1347 | 把10份同样的礼物全部分成3组,每组至少有1份礼物的不同分法有几种?
1348 |
1349 | ### 拓展2
1350 |
1351 | 一只青蛙在A,B,C三点之间跳动,若青蛙从A点起跳,跳4次仍回到A点,如果不能原地跳则这只青蛙一共有多少种不同的跳法?
1352 |
1353 | ### 拓展3
1354 |
1355 | 两个正整数的乘积为96,这两个数可能是?
1356 |
1357 | ## 2.2.06. 鸡兔同笼初步
1358 |
1359 | ### 例题1
1360 |
1361 | 丁丁把鸡、免关在同一个笼子里,数了数,共有6个头,16条腿,你知道有几只鸡,几只免吗?
1362 |
1363 | ### 练习1
1364 |
1365 | 1角硬币和5角硬币一共有6枚,一共2元6角,求两种硬币各有多少枚?
1366 |
1367 | ### 例题2
1368 |
1369 | 牛牛把鸡、免关在同一个笼子里,数了数,共有10个头、26条腿,你知道这个笼子里有几只鸡?几只兔?
1370 |
1371 | ### 练习2
1372 |
1373 | 鸡、兔关在同一个笼子里,共有11个头,28条腿,这个笼子里有几只鸡?几只兔?
1374 |
1375 | ### 例题3
1376 |
1377 | 1只蛐蛐6条腿,1只蜘蛛8条腿。有蛐蛐和蜘蛛共10只,共68条腿,蛐蛐和蜘蛛各有多少只?
1378 |
1379 | ### 练习3
1380 |
1381 | 1瓶可乐6元,1瓶雪碧8元。牛牛共买这两种饮料8瓶,共花58元。可乐和雪碧各有多少瓶?
1382 |
1383 | ### 例题4
1384 |
1385 | 笼子里有一些鸡和兔,共20个头,50条腿,算一算笼子里有几只鸡?几只兔?
1386 |
1387 | ### 练习4
1388 |
1389 | 鸡和免共有45只,关在同一个笼子中。每只鸡有2条腿,每只兔子有4条腿,笼中共有100条腿。算一算,笼中有鸡多少只?免子多少只?
1390 |
1391 | ### 例题5
1392 |
1393 | 一辆卡车有6个轮子,一辆小汽车有4个轮子,停车场一共有14辆车,现在一共有72个轮子,你知道卡车和小汽车各有几辆吗?
1394 |
1395 | ### 练习5
1396 |
1397 | 在一个停车场上,现有车辆41辆,其中汽车有4个轮子,三轮摩托车有3个轮子,这些车共有127个轮子,那么三轮摩托车有多少辆?
1398 |
1399 | ### 例题6
1400 |
1401 | 鸡免同笼,共有14个头,38条腿,有几只鸡?几只兔?
1402 |
1403 | ### 练习6
1404 |
1405 | 1辆自行车有2个轮子,1辆三轮车有3个轮子。车棚里放着的自行车和三轮车共8辆,共20个轮子。自行车、三轮车各有多少辆?
1406 |
1407 | ## 2.2.07. 巧求周长初步
1408 |
1409 | ### 热身1(和倍)
1410 |
1411 | 实验小学三、四年级的同学们一共制作了24件航模,四年级同学制作的航模件数是三年级的2倍,三、四年级的同学各制作了多少件航模?
1412 |
1413 | ### 热身2(图形分割)
1414 |
1415 | 把下图分成形状、大小完全相同的4部分。
1416 |
1417 | 
1418 |
1419 | ### 热身3(枚举)
1420 |
1421 | 3个装药的瓶子都贴了标签,其中有两个贴错了,错的情况总共有3种可能。如果有四个瓶子,其中有三个贴错了,那么错的情况共有多少种?
1422 |
1423 | (1)$178\times9$
1424 |
1425 | (2)$1000\div8$
1426 |
1427 | (3)$53\times12$
1428 |
1429 | ### 例题1
1430 |
1431 | 如下图为丁丁的学校操场平面图,长为300米,宽为200米,丁丁绕操场走一圈,问:丁丁走了多少米?
1432 |
1433 |  1434 |
1435 | ### 练习1
1436 |
1437 | 求下面图形的周长。(单位:厘米)
1438 |
1439 |
1434 |
1435 | ### 练习1
1436 |
1437 | 求下面图形的周长。(单位:厘米)
1438 |
1439 |  1440 |
1441 | ### 例题2
1442 |
1443 | 牛牛用100厘米长的绳子围成一个正方形,这个正方形的边长是多少?
1444 |
1445 | ### 练习2
1446 |
1447 | 一个正方形花坛四周围着栏杆,栏杆共长48米,这个正方形栏杆的边长是多少米?
1448 |
1449 | ### 例题3
1450 |
1451 | 田田小朋友用60厘米长的黑线,给自己的长方形板子镶了一道黑边,已知这个板子宽为1厘米,你知道长方形板子的长为多少厘米吗?
1452 |
1453 | ### 练习3
1454 |
1455 | 一个长方形操场的周长为400米,已知长为140米,求宽为多少米?
1456 |
1457 | ### 例题4
1458 |
1459 | 如图,用两个大小相同的正方形,拼成一个长方形后,周长比原来两个正方形的周长的和少了8厘米,求原来一个正方形的周长为多少厘米?
1460 |
1461 |
1440 |
1441 | ### 例题2
1442 |
1443 | 牛牛用100厘米长的绳子围成一个正方形,这个正方形的边长是多少?
1444 |
1445 | ### 练习2
1446 |
1447 | 一个正方形花坛四周围着栏杆,栏杆共长48米,这个正方形栏杆的边长是多少米?
1448 |
1449 | ### 例题3
1450 |
1451 | 田田小朋友用60厘米长的黑线,给自己的长方形板子镶了一道黑边,已知这个板子宽为1厘米,你知道长方形板子的长为多少厘米吗?
1452 |
1453 | ### 练习3
1454 |
1455 | 一个长方形操场的周长为400米,已知长为140米,求宽为多少米?
1456 |
1457 | ### 例题4
1458 |
1459 | 如图,用两个大小相同的正方形,拼成一个长方形后,周长比原来两个正方形的周长的和少了8厘米,求原来一个正方形的周长为多少厘米?
1460 |
1461 |  1462 |
1463 | ### 练习4
1464 |
1465 | 一个长方形被一刀剪成了大小一样的两个正方形,正方形的边长是20厘米,剪成的两个正方形的周长之和比原来的长方形的周长多了多少厘米?
1466 |
1467 | ### 例题5
1468 |
1469 | 一个长方形花坛被平均分成了7个小正方形,已知每个小正方形的周长是11米,求大长方形的周长为多少米?
1470 |
1471 |
1462 |
1463 | ### 练习4
1464 |
1465 | 一个长方形被一刀剪成了大小一样的两个正方形,正方形的边长是20厘米,剪成的两个正方形的周长之和比原来的长方形的周长多了多少厘米?
1466 |
1467 | ### 例题5
1468 |
1469 | 一个长方形花坛被平均分成了7个小正方形,已知每个小正方形的周长是11米,求大长方形的周长为多少米?
1470 |
1471 |  1472 |
1473 | ### 练习5
1474 |
1475 | 用6个边长为2厘米的正方形,拼成一个大长方形,求大长方形的周长为多少厘米?
1476 |
1477 | ### 例题6
1478 |
1479 | 如下图所示,在一个长为10厘米,宽为8厘米的长方形纸片上剪去一个边长为2厘米的正方形,那么剩下图形的周长为多少?
1480 |
1481 | 
1482 |
1483 | ### 练习6
1484 |
1485 | 求出下图中多边形的周长为多少厘米?(单位:厘米)
1486 |
1487 | 
1488 |
1489 | 商场举行大酬宾活动,门口将长18厘米,宽9厘米的礼品盒摆成一个有规律的形状。礼品盒前4层的样式如图所示,一共有10层,你能算出一共摆了多少个礼品盒吗?礼品盒摆出形状的周长是多少?
1490 |
1491 |
1472 |
1473 | ### 练习5
1474 |
1475 | 用6个边长为2厘米的正方形,拼成一个大长方形,求大长方形的周长为多少厘米?
1476 |
1477 | ### 例题6
1478 |
1479 | 如下图所示,在一个长为10厘米,宽为8厘米的长方形纸片上剪去一个边长为2厘米的正方形,那么剩下图形的周长为多少?
1480 |
1481 | 
1482 |
1483 | ### 练习6
1484 |
1485 | 求出下图中多边形的周长为多少厘米?(单位:厘米)
1486 |
1487 | 
1488 |
1489 | 商场举行大酬宾活动,门口将长18厘米,宽9厘米的礼品盒摆成一个有规律的形状。礼品盒前4层的样式如图所示,一共有10层,你能算出一共摆了多少个礼品盒吗?礼品盒摆出形状的周长是多少?
1490 |
1491 |  1492 |
1493 | ## 2.2.09. 立体图形染色
1494 |
1495 | ### 热身1
1496 |
1497 | ### 热身2
1498 |
1499 | ### 热身3
1500 |
1501 | ### 例题1
1502 |
1503 | 一个正方体有()个面,()条棱,()个顶点。
1504 |
1505 |
1492 |
1493 | ## 2.2.09. 立体图形染色
1494 |
1495 | ### 热身1
1496 |
1497 | ### 热身2
1498 |
1499 | ### 热身3
1500 |
1501 | ### 例题1
1502 |
1503 | 一个正方体有()个面,()条棱,()个顶点。
1504 |
1505 |  1506 |
1507 | ### 练习1
1508 |
1509 | (1)想个一个正方体表面涂色,一共要涂多少个小正方形?
1510 |
1511 | (2)如果想给两个粘在一起的两个正方体表面涂色,一共要涂多少个小正方形?
1512 |
1513 |
1506 |
1507 | ### 练习1
1508 |
1509 | (1)想个一个正方体表面涂色,一共要涂多少个小正方形?
1510 |
1511 | (2)如果想给两个粘在一起的两个正方体表面涂色,一共要涂多少个小正方形?
1512 |
1513 |  1514 |
1515 | ### 例题2
1516 |
1517 | 下面是用小正方体堆成的图形,现在把这个图形的表面涂上蓝色,想一想,有多少个小正方形没有被涂色?
1518 |
1519 |
1514 |
1515 | ### 例题2
1516 |
1517 | 下面是用小正方体堆成的图形,现在把这个图形的表面涂上蓝色,想一想,有多少个小正方形没有被涂色?
1518 |
1519 |  1520 |
1521 | ### 练习2
1522 |
1523 | 四个小正方体排成如下图的形状,要给他的表面上色,有几个小正方形没有被上色?
1524 |
1525 | ### 例题3
1526 |
1527 | 把一个正方体表面涂上绿色,然后再把它切成8个小正方体,想一想,每个小正方体有几个面没有颜色?
1528 |
1529 | ### 练习3
1530 |
1531 | 一个大长方体的表面都涂上红色,然后切成 18 个小立方体(切线如图中虚线所示)。在这些切成的小立方体中,问:
1532 |
1533 | (1)1面涂成红色的有()块。
1534 |
1535 | (2)2面涂成红色的有()块。
1536 |
1537 | (3)3面涂成红色的有()块。
1538 |
1539 |
1520 |
1521 | ### 练习2
1522 |
1523 | 四个小正方体排成如下图的形状,要给他的表面上色,有几个小正方形没有被上色?
1524 |
1525 | ### 例题3
1526 |
1527 | 把一个正方体表面涂上绿色,然后再把它切成8个小正方体,想一想,每个小正方体有几个面没有颜色?
1528 |
1529 | ### 练习3
1530 |
1531 | 一个大长方体的表面都涂上红色,然后切成 18 个小立方体(切线如图中虚线所示)。在这些切成的小立方体中,问:
1532 |
1533 | (1)1面涂成红色的有()块。
1534 |
1535 | (2)2面涂成红色的有()块。
1536 |
1537 | (3)3面涂成红色的有()块。
1538 |
1539 |  1540 |
1541 | ### 例题4
1542 |
1543 | 下面是用小正方体组成的立体图形,现在把这个立体图形表面都涂上绿色,数一数有多少个小正方形没有被涂上色?
1544 |
1545 | ### 练习4
1546 |
1547 | 用小正方体拼成了一个如下图的模型,然后把它粘在地上喷上红色油漆,这堆正方体中共有多少个小正方形没有被喷上颜色?
1548 |
1549 | ### 例题5
1550 |
1551 | ### 练习5
1552 |
1553 | ### 例题6
1554 |
1555 | ### 练习6
1556 |
1557 | ## 2.2.10. 周期问题初步
1558 |
1559 | ### 例题1
1560 |
1561 | 小朋友按了3女3男的顺序依次排成一队看表演,算一算第17名、第37名同学分别是男生还是女生?
1562 |
1563 | ### 练习1
1564 |
1565 | 广场上摆满花,这些花是按3盆大红、2盆金黄、2盒粉红的顺序摆放的,你
1566 | 们知道第26盆、35盆、45 盒花是什么颜色吗?
1567 |
1568 | ### 例题2
1569 |
1570 | 乐乐老师带领牛牛等人在园林里种树,他们按1棵杨树、2棵椰树、2棵松树的顺序来种,一共种了48棵树,那么杨树、椰树、松树各种了几棵?
1571 |
1572 | ### 练习2
1573 |
1574 | 某小学操场上树立着彩旗,按如下图顺序来排列,一共有 42 面旗,在这42 面彩旗中,红旗有()面,黄旗有()面?
1575 |
1576 | ### 例题3
1577 |
1578 | 丁丁用树枝在地上写了一列数,然后他停下来,让田田猜一猜,
1579 |
1580 | $2、3、1、2、3、1、2、3、1、……$
1581 |
1582 | (1)第28个数是几?
1583 |
1584 | (2)这28个数的和是多少?
1585 |
1586 | ### 练习3
1587 |
1588 | 有一列数:
1589 |
1590 | $1、4、2、1、4、2、1、4、2、1、……$
1591 |
1592 | (1)第26个数是几?
1593 |
1594 | (2)这26个数的和是多少?
1595 |
1596 | ### 例题4
1597 |
1598 | 有一列数如下所示,在这一列数中:
1599 |
1600 | $1、3、5、7、1、3、5、7、9、……$
1601 |
1602 | (1)第35个数是几?
1603 |
1604 | (2)这35个数的和是多少?
1605 |
1606 | (3)如果连续写83个数,3被写了多少次?
1607 |
1608 | ### 练习4
1609 |
1610 | $2、3、4、1、2、3、4、1、2、3、4、1、2、3、4、1、2、3、4、……$,请问:
1611 |
1612 | (1)第26个数是几?
1613 |
1614 | (2)请问这26个数的和是多少?
1615 |
1616 | (3)请问在这26个数字中,有几个“3”?
1617 |
1618 | ### 例题5
1619 |
1620 | 2014年4月5日是星期六。
1621 |
1622 | (1)从5日算起,第10天是星期几?
1623 |
1624 | (2)再过10天是星期几?
1625 |
1626 | ### 练习5
1627 |
1628 | 某年1月1日元旦是星期四,从1日算起,第12天是星期()
1629 |
1630 | ### 例题6
1631 |
1632 | 例子:
1633 |
1634 | | 1 | 2 | 1 | 2 | 1 | 2 | 1 | 2 | 1 | 2 | …… |
1635 | | ---- | ---- | ---- | ---- | ---- | ---- | ---- | ---- | ---- | ---- | ---- |
1636 | | A | B | C | A | B | C | A | B | C | A | …… |
1637 |
1638 | 在下表中,将每列上、下两个字组成一组,例如第1组为(小双),第2组为(朋手),那么第55组是什么?
1639 |
1640 | | 小 | 朋 | 友 | 荡 | 秋 | 千 | 小 | 朋 | 友 | 荡 | 秋 | 千 | 小 | 朋 | …… |
1641 | | ---- | ---- | ---- | ---- | ---- | ---- | ---- | ---- | ---- | ---- | ---- | ---- | ---- | ---- | ---- |
1642 | | 双 | 手 | 向 | 空 | 如 | 鸟 | 翼 | 双 | 手 | 向 | 空 | 如 | 鸟 | 翼 | …… |
1643 |
1644 | ### 练习6
1645 |
1646 | 下面的表格中,每一列的两个数组成一组,如第1组是由“甲A”组成,第
1647 | 2组是由“乙B”组成⋯问:第17组是由哪两个组成?
1648 |
1649 | | 甲 | 乙 | 丙 | 甲 | 乙 | 丙 | 甲 | 乙 | 丙 | 甲 | 乙 | 丙 | …… |
1650 | | ---- | ---- | ---- | ---- | ---- | ---- | ---- | ---- | ---- | ---- | ---- | ---- | ---- |
1651 | | A | B | C | D | A | B | C | D | A | B | C | D | …… |
1652 |
1653 | ### 拓展1
1654 |
1655 | 今天是2022年4月14日,星期四,请问:今年的劳动节是星期几?小代今年的生日是星期几?
1656 |
1657 | ### 拓展2
1658 |
1659 | 12个同学围成一圈做传球的游戏,如图。
1660 |
1661 | 
1662 |
1663 | (1)从1号同学开始,顺时针传100次,手绢应在谁手中?
1664 |
1665 | (2)从1号同学开始,逆时针传100次,手绢又在谁手中?
1666 |
1667 | (3)从 1号同学开始,先顺时针传156次,然后从那个同学开始逆时针传143次,最后手绢在谁手中?
1668 |
1669 | ### 拓展3
1670 |
1671 | 字母A、B、C、D、E和数字1、9分别按下列方式变动次序:
1672 |
1673 | ABCDE19
1674 |
1675 | BCDEA91(第一次变动)
1676 |
1677 | CDEAB91(第二次变动)
1678 |
1679 | DEABC19(第三次变动)
1680 |
1681 | ……
1682 |
1683 | 那么,最少经过几次变动后“ABCDE19”将再次出现。
1684 |
1685 | ### 拓展4
1686 |
1687 | A、B、C、D四个盒子中依次放有6、4、5、3个球。第1个小朋友找到放球最多的盒子,从盒子中取出 3 个球,放入其他盒子,每个盒子放一个;然后第2个小朋友也找到放球最多的盒子,从盒子中取出 3个球,放入其他盒子,每个盒子放一个。如此进行下去,当第120位小朋友放完后,C 盒中有几个球?
1688 |
1689 | ## 2.2.11. 移多补少
1690 |
1691 | 计算练习
1692 |
1693 | (1)$1+2+3+4+5+6+7+8+9+10+9+8+7+6+5+4+3+2+1$
1694 |
1695 | (2)$1+3+5+7+9+11+9+7+5+3+1$
1696 |
1697 | (3)$1+2+3+\dots+49+50+49+\dots+3+2+1$
1698 |
1699 | ### 例题1
1700 |
1701 | 牛牛和丁丁分糕点,牛牛有14块,丁丁有6块,牛牛需要拿出几块糕点给丁丁,他们的糕点数才会同样多?
1702 |
1703 | ### 练习1
1704 |
1705 | 红队有29人,黄队有15人,红队调给黄队几人,就能使两队人数相等?
1706 |
1707 | ### 例题2
1708 |
1709 | 同学们分成两队进行拔河比赛,第一队有31人,如果从第一队中调3人到第二队,这时两队的人数才会一样多。第二队原来有学生多少人?
1710 |
1711 | ### 练习2
1712 |
1713 | 牛牛有24朵花,丁丁给牛牛8朵后,两人的花朵数就相等。丁丁原来有几几朵花?
1714 |
1715 | ### 例题3
1716 |
1717 | 小花免和小白兔分萝卜,小花兔给小白兔4个萝卜后,小花免还比小白兔多
1718 | 2个。小花兔原来比小白兔多几个萝卜?
1719 |
1720 | ### 练习3
1721 |
1722 | 小花兔和小白兔分萝卜,小花兔给小白兔4个萝卜后,小花免比小白免少
1723 | 2个。小花兔原来比小白兔多几个萝卜?
1724 |
1725 | ### 例题4
1726 |
1727 | 小山羊和小白免一共拔了30个萝卜放进两筐里,小白免从大筐里拿出6个放进小筐里,现在两筐萝卜的个数同样多。原来小筐里有多少个萝卜?
1728 |
1729 | ### 练习4
1730 |
1731 | 甲、乙两筐西瓜共28个,从甲筐取4个放入乙筐中,两筐西瓜个数相同。
1732 | 原来甲、乙两筐各有多少个西瓜?
1733 |
1734 | ### 例题5
1735 |
1736 | 妈妈买了2袋苹果,甲袋是54个,乙袋是22个。每次从多的1袋取出4个放到少的1袋里,拿几次才能使两袋苹果的个数相等呢?
1737 |
1738 | ### 练习5
1739 |
1740 | 小华有两盒糖果,甲盒有糖78粒,乙盒有糖38粒,每次从甲盒取5粒糖放到
1741 | 乙盒,取几次两盒糖的粒数就同样多?
1742 |
1743 | ### 例题6
1744 |
1745 | 两堆香蕉一样多,现在从第一堆里面拿出4把香蕉放入第二堆,这时第二堆的香蕉是第一堆的2倍,原来两堆香蕉各有多少把?
1746 |
1747 | ### 练习6
1748 |
1749 | 哥哥和弟弟集邮,原来两人的邮票张数相等,如果哥哥给弟弟9张邮票,则弟弟的邮票张数是哥哥的3倍,哥哥、弟弟原来各有邮票多少张?
1750 |
1751 | ### 拓展1
1752 |
1753 | 小东、小西、小北3个同学带着15个筐去摘桃,摘完后,有5筐装满了桃,5筐装了半筐桃,5筐空着,怎样分,才能让他们3人每人分到的桃一样多,筐也一样多?
1754 |
1755 | ### 拓展2
1756 |
1757 | 大毛、二毛和三毛三个小朋友出去玩,各自摘了一些小草莓,大毛把自己摘得草莓给了二毛 2 个后,大毛比二毛多 1 个,接着,二毛又把自己摘草莓给了三毛 2 个,此时二毛和三毛的草莓变得一样多,那么原来大毛和三毛两个人摘得草莓数量谁更多?多几个?
1758 |
1759 | ### 拓展3
1760 |
1761 | 小白、小灰和小花三只小猫去河里分别捉了一些鱼。如果小花给小白 5 条鱼,那么小花比小白还多 2 条鱼;如果小灰给小花 4 条鱼,那么小灰就比小花少 3 条鱼,请问原来小灰比小白多多少条鱼?
1762 |
1763 | ### 拓展4
1764 |
1765 | 小白、小灰和小花三只小猫去河里捉了一些鱼。如果小白给小花一些鱼后,小花和小白拥有的鱼就一样多了,都是 42 条;如果小灰给小白一些鱼后,小灰和小白拥有的鱼就一样多了,都是 47 条鱼,如果小灰给小花一些鱼后,小灰和小花拥有的鱼就一样多了,都是 46条。那小灰有几条鱼。
1766 |
1767 | ## 2.2.12. 和差问题
1768 |
1769 | ### 例题1
1770 |
1771 | 牛牛和丁丁总共有46个玻璃球,丁丁比牛牛多6个。请大家帮忙算一算,牛牛和丁丁各有多少个玻璃球?
1772 |
1773 | ### 练习1
1774 |
1775 | 今年姐姐和妹妹的年龄和是14岁,姐姐比妹妹大4岁,问姐姐、妹妹今年各多少岁?
1776 |
1777 | ### 例题2
1778 |
1779 | 牛牛和丁丁写大字的速度不变,两人两天一共写了120个字,已知牛牛每天比丁丁多写10个,请问丁丁和牛牛每天各写几个大字?
1780 |
1781 | ### 练习2
1782 |
1783 | 牛牛和丁丁保持自己相同的速度折飞机,牛牛每小时比丁丁多折10个,他们两人用了3小时共折飞机150个,牛牛和丁丁每小时各折多少个飞机?
1784 |
1785 | ### 例题3
1786 |
1787 | 动物学校有个长方形操场,它的长与宽相差80米,沿操场跑一圈是400米,求动物学校操场的长与宽各是多少?
1788 |
1789 | ### 练习3
1790 |
1791 | 蚂蚁沿着阿普的课本四周爬了一圈是200厘米,知道课本的长边比短边多30厘米,问阿普课本的长边和短边各是多少厘米?
1792 |
1793 | ### 例题4
1794 |
1795 | 牛牛在这次测验中,语文和数学的平均分是95分,语文比数学多6分,牛牛在这次测验中,语文和数学各得了多少分?
1796 |
1797 | ### 练习4
1798 |
1799 | 牛牛和丁丁的平均身高是130厘米,牛牛比丁丁高10厘米,丁丁和牛牛的身高各是多少厘米?
1800 |
1801 | ### 例题5
1802 |
1803 | 豆豆和毛毛一共有34个巧克力豆,两人都吃了同样的巧克力豆后,分别还剩15个和11个,问原来豆豆和毛毛各有多少个巧克力豆?
1804 |
1805 | ### 练习5
1806 |
1807 | 大毛、二毛共有33元,两人花掉同样的钱后,大毛还有19元,二毛还有6元,问原来大毛、二毛各有多少钱?
1808 |
1809 | ### 例题6
1810 |
1811 | 牛牛3年前的年龄与阿普2年后的年龄之和是23岁,牛牛3年后的年龄等于阿普1年前的年龄,求牛牛、阿普今年的年龄各是多少岁?
1812 |
1813 | ### 练习6
1814 |
1815 | 红红2年前的年龄与果果1年后的年龄相等,红红3年前的年龄与果果2年后的年龄和为18岁,则红红、果果今年各多少岁?
1816 |
1817 | ### 巩固1
1818 |
1819 | 维尼熊和跳跳虎去摘苹果。跳跳虎每摘7个,维尼熊只能摘4个。维尼熊摘了16分钟,跳跳虎摘了10分钟就累了,不摘了。他们回来后数了一下,共摘了670个苹果,那么其中维尼熊摘的苹果有多少个?
1820 |
1821 | ### 巩固2
1822 |
1823 | 甲、乙、丙3个数的和是99,如果甲加上10,乙减少5,丙减少2,则3个数相等。这3个数各是几?
1824 |
1825 | ### 巩固3
1826 |
1827 | 三块布料一共190米,第二块比第一块长20米,第三块比第二块长30米,每块布料各长多少米?
1828 |
1829 | ## 2.2.13. 逻辑推理进阶
1830 |
1831 | ### 热身1
1832 |
1833 | ### 热身2
1834 |
1835 | ### 热身3
1836 |
1837 | ### 例题1
1838 |
1839 | 乐乐老师、红红、丁丁、牛牛和田田一起去爬山。牛牛在丁丁和田田之前爬到终点,田田是紧跟着牛牛之后爬到终点的。有两个人在乐乐老师之后、丁丁之前爬到终点。这5个人登山到终点的先后顺序是怎样的?
1840 |
1841 | ### 练习1
1842 |
1843 | 田田比牛牛跑得慢,牛牛比加加跑得快,加加比减减跑得快,减减比田田跑得快。谁跑得最快?谁跑得最慢?
1844 |
1845 | ### 例题2
1846 |
1847 | 体育馆里正在进行一场精彩的乒乓球双打比赛。两位播音员正在议论这四个运动员的年龄问题:
1848 |
1849 | (1)小A比小B年轻;
1850 |
1851 | (2)小C比他的两个对手年龄都大;
1852 |
1853 | (3)小A比小D年龄大;
1854 |
1855 | (4)小B比小C年龄大。
1856 |
1857 | 请分析一下他们四人的年龄顺序,谁年龄最大?谁年龄最小?
1858 |
1859 | ### 练习2
1860 |
1861 | 2号大楼比3号大楼高,4号大楼比3号大楼低,1号大楼比2号大楼高,1号大楼比4号大楼高,几号大楼是最高的?几号大楼是最低的?
1862 |
1863 | ### 例题3
1864 |
1865 | 赵、钱、孙三人中,一位是射击运动员,一位是体操运动员,一位是跳水运动员。已知:
1866 |
1867 | (1)赵比体操运动员体重重;
1868 |
1869 | (2)钱和体操运动员体重不同;
1870 |
1871 | (3)赵和跳水运动员是朋友。
1872 |
1873 | 你能猜出谁是射击运动员,谁是体操运动员,谁是跳水运动员吗?
1874 |
1875 | ### 练习3
1876 |
1877 | 刘玉、马明、王建三个男孩都有一个妹妹,是小雅、小花、丽丽。6个人在一起打球,举行男女混合双打。事先规定,兄妹两人不搭伴。
1878 | 第一盘刘玉和丽丽对王建和小雅;第二盘王建和小花对刘玉和马明的妹妹。问丽丽、小雅和小花各是谁的妹妹?
1879 |
1880 | ### 例题4
1881 |
1882 | 一天,唐僧师徒四人路过一户人家,家里只有一个老爷爷和一个老奶奶,当唐僧师徒四人说明他们的来历后二老很热情地招待了他们,还要给他们做饭吃。唐僧见二老年事已高,决定他们自己动手做饭。他们一个在挑水,一个在烧火,一个在洗菜,一个在淘米。已知:
1883 |
1884 | (1)唐僧不挑水也不淘米;
1885 |
1886 | (2)悟空不洗菜也不挑水;
1887 |
1888 | (3)八戒不挑水也不洗菜;
1889 |
1890 | (4)假如悟空不淘米,那么沙僧就不挑水。
1891 |
1892 | 现在你知道他们分工的结果吗?
1893 |
1894 | ### 练习4
1895 |
1896 | 二年级有三个班举行数学竞赛,分别从三个班中选一名选手。牛牛、丁丁、田田参加抢答比赛,知道:牛牛比二(1)班的选手得分高,丁丁与二(1)班的选手得分同样多,又比二(3)班选手得分低。问牛牛、丁丁、田田各是哪班的选手?
1897 |
1898 | ### 例题5
1899 |
1900 | 甲、乙、丙三个小朋友分别喝三种不同的饮料,有另外三个小朋友猜他们喝的各是什么?
1901 |
1902 | 当当猜:甲喝可乐,乙喝芬达;
1903 |
1904 | 咚咚猜:乙喝雪碧,丙喝可乐;
1905 |
1906 | 林林猜:丙喝芬达,乙喝可乐。
1907 |
1908 | 己知每人都只猜对了一半,那么甲、乙、丙三位小朋友各喝什么饮料?
1909 |
1910 | ### 练习5
1911 |
1912 | 甲、乙、丙、丁四人同时参加全国小学数学夏令营。赛前甲、乙、丙分别做了预测。
1913 |
1914 | 甲说:丙第1名,我第3名。
1915 |
1916 | 乙说:我第1名,丁第4名。
1917 |
1918 | 丙说:丁第2名,我第3名。
1919 |
1920 | 成绩揭晓后,发现他们每人只说对了一半,你能说出他们的名次吗?
1921 |
1922 | ### 例题6
1923 |
1924 | 一个岛上住着说谎话的和说真话的两种人。说谎话的人句句是谎话,说真话的人句句是实话。如果有一天,你去岛上探险,碰到了岛上的三个人:王、李和张,相互交谈中,有这样一段对话。
1925 |
1926 | 王说:李和张都说谎。
1927 |
1928 | 李说:我没有说谎。
1929 |
1930 | 张说:李确实在说谎。
1931 |
1932 | 小朋友,你能知道他们三人中,有几个人说谎,有几个人说真话吗?
1933 |
1934 | ### 练习6
1935 |
1936 | 三只小猴子聪聪、淘淘、皮皮见到一个水果,他们分别判断这是什么水果。
1937 |
1938 | 聪聪判断:不是苹果,也不是梨。
1939 |
1940 | 淘淘判断:不是苹果,而是桃子。
1941 |
1942 | 皮皮判断:不是桃子,而是苹果。
1943 |
1944 | 老猴子告诉他们:有一只小猴子的判断完全正确,有一只小猴子说对了半,而另一只小猴子完全说错了。你知道三只小猴中谁是对的,谁是错的,谁是只对一半的吗?
1945 |
1946 | ### 拓展1
1947 |
1948 | 传说有个说谎国,这个国家的男人在星期四、五、六、日说真话,在星期一、二、三说假话;女人在星期一、二、三、日说真话,在星期四、五、六说假话.有一天,一个人到说谎国去旅游,他在那里认识了一男一女.男人说:“昨天我说的是假话”,女人说:“昨天也是我说假话的日子”.这下,那个外来的游人可发愁了,到底今天星期几呢?请同学们根据他们说的话,判断一下今天是星期几呢?
1949 |
1950 | ### 拓展2
1951 |
1952 | 张明、席辉和李刚在北京、上海和天津工作,他们的职业是工人、农民和教师,已知:
1953 |
1954 | (1)张明不在北京工作,席辉不在上海工作;
1955 |
1956 | (2)在北京工作的不是教师;
1957 |
1958 | (3)在上海工作的是工人;
1959 |
1960 | (4)席辉不是农民。
1961 |
1962 | 问:这三人各住哪里?各是什么职业?
1963 |
1964 | ### 拓展3
1965 |
1966 | 根据条件判断旅游团去了A、B、C、D、E中的哪几个地方?
1967 |
1968 | (1)如果去A,就必须去B;
1969 |
1970 | (2)D、E两地至少去一地;
1971 |
1972 | (3)B、C两地只能去一地;
1973 |
1974 | (4)C、E两地要去都去,要不去都不去;
1975 |
1976 | (5)若去D,则A、E两地必须去。
1977 |
1978 | ### 拓展4
1979 |
1980 | 甲、乙、丙、丁在谈论他们及他们的同学何伟的居住地。
1981 |
1982 | 甲说:我和乙都住在北京,丙住在天津;
1983 |
1984 | 乙说:我和丁都住在上海,丙住在天津;
1985 |
1986 | 丙说:我和甲都不住在北京,何伟住在南京;
1987 |
1988 | 丁说:甲和乙都住在北京,我住在广州。
1989 |
1990 | 假定他们每个人都说了两句真话,一句假话。问:不在场的何伟住在哪儿?
1991 |
1992 | ### 拓展5
1993 |
1994 | 宝宝、贝贝、聪聪每人有两个外号,人们有时以“数学博士”、“短跑健将”、“跳高冠军”、“小画家”、“大作家”和“歌唱家”称呼他们,此外:
1995 |
1996 | (1)数学博士夸跳高冠军跳的高
1997 |
1998 | (2)跳高冠军和大作家常与宝宝一起看电影
1999 |
2000 | (3)短跑健将请小画家画贺年卡
2001 |
2002 | (4)数学博士和小画家关系很好
2003 |
2004 | (5)贝贝向大作家借过书
2005 |
2006 | (6)聪聪下象棋常赢贝贝和小画家
2007 |
2008 | 问:宝宝、贝贝、聪聪各有哪两个外号吗?
2009 |
2010 | ## 2.2.14. 重叠问题
2011 |
2012 | ### 热身1
2013 |
2014 | ### 热身2
2015 |
2016 | ### 热身3
2017 |
2018 | ### 例题1
2019 |
2020 | 把两根长为20寸的短尺用绳子捆成一根长尺,中间捆在一起的重叠部分是3寸。捆成的长尺长多少寸?
2021 |
2022 | ### 练习1
2023 |
2024 | 有四块均长80厘米的木板,钉成一块长木板,中间钉在一起重叠的部分均是10厘米,钉成的长木板长多少厘米?
2025 |
2026 | ### 例题2
2027 |
2028 | 将两张同样长的纸粘成了一张长为80才的长纸条,其中粘在一起的部分长10寸,这两张纸条各长多少寸?
2029 |
2030 | ### 练习2
2031 |
2032 | 有两根铁丝,一根长为30厘米,另一根长为50厘米,将这两根铁丝焊接成一根长为75厘米的长铁丝。那么,中间的焊接重叠部分长为多少厘米?
2033 |
2034 | ### 例题3
2035 |
2036 | 私塾的学生都要参加比赛,有30人参加蹴鞠队,有27人参加毽子队。其中8人两种比赛都参加。一共有学生多少人?
2037 |
2038 | ### 练习3
2039 |
2040 | 二(1)班同学所有人都参加课外活动,有20人参加英语班,有26人参加电脑班。其中4人两个班都参加。二(1)班一共有多少人?
2041 |
2042 | ### 例题4
2043 |
2044 | 20个学生参加琵琶表演和古筝表演,其中有16人参加了琵琶表演,12人参加了古筝表演。问两种表演都参加的有多少学生?
2045 |
2046 | ### 练习4
2047 |
2048 | 春天来了,全班52人到北海公园划船,有27人划了手摇船,29人划了脚踏船,4名同学因身体不好没有划船而去游览了白塔。问:既划了手摇船也划了脚踏船的同学有多少人?
2049 |
2050 | ### 例题5
2051 |
2052 | 有蓝色和红色两种珠花,每人至少选一种,共有48人,有30人选了蓝色珠花,有13人两种都选了,那么选红色珠花的有多少人?
2053 |
2054 | ### 练习5
2055 |
2056 | 学校开设了自然和趣味数学两门选修课,每个同学至少要选一门,二(3)班共有56人,有30人选了自然课,有12人两门都选了,那么选趣味数学课的同学有多少人?
2057 |
2058 | ### 例题6
2059 |
2060 | 工厂筛选制镜工人,总共有60人报名参加。经过一段时间的训练后,有33人学会了制作星云镜,有25人学会了制作幻镜,其中既会制作星云镜又会制作幻镜的有10人。那么既不会制作星云镜又不会制作幻镜的有多少人?
2061 |
2062 | ### 练习6
2063 |
2064 | 某班共有46人,参加美术小组的有12人,参加音乐小组的有23人,有5人两个小组都参加了。这个班既没有参加美术小组也没参加音乐小组的有多少人?
2065 |
2066 | ## 2.2.15. 复杂的树阵图
2067 |
2068 | ### 热身1
2069 |
2070 | ### 热身2
2071 |
2072 | ### 热身3
2073 |
2074 | ### 例题1(辐射型)
2075 |
2076 | 把1,2,4,5,6,8,10这7个数分别填入图中的圆圈中,使得每条直线上4个数的和都等于20。
2077 |
2078 | 
2079 |
2080 | ### 练习1
2081 |
2082 | 把8,9,10,11,12,14,16这7个数分别填入图中的圆圈中,使得每条直线上4个数的和都等于46。
2083 |
2084 | ### 例题2
2085 |
2086 | 将5,9,13,14,17,21,25这7个数分别填入图中的圆圈中,使得每条直线上的3个数的和都等于44。
2087 |
2088 | 
2089 |
2090 | ### 练习2
2091 |
2092 | 将5,8,11,14,17,20,23这7个数分别填入图中的圆圈中,使得每条直线上的3个数的和都等于36。
2093 |
2094 | ### 例题3(封闭型)
2095 |
2096 | 把2,3,4,5,6,7,8这7个数分别填入图中的圆圈中,使两个正方形中4个数之和都等于19。
2097 |
2098 | ### 练习3
2099 |
2100 | 把2,3,4,5,6,7,8这7个数分别填入图中的圆圈中,使两个正方形中4个数之和都等于21。
2101 |
2102 | ### 例题4
2103 |
2104 | 把1,5,9,10,16,21这6个数分别填入图中的圆圈中,使每一个大圆上的4个数之和都等于36。
2105 |
2106 | ### 练习4
2107 |
2108 | 把1,2,4,5,6,11这6个数分别填入图中的圆圈中,使每一个大圆上的4个数之和都等于22。
2109 |
2110 | ### 例题5
2111 |
2112 | 将5,6,9,11,14,15这6个数分别填入图中的圆圈中,使两个大圆上4个数的和都等于40。
2113 |
2114 | ### 练习5
2115 |
2116 | 将4,7,9,12,15,17这6个数分别填入图中的圆圈中,使两个大圆上4个数的和都等于43。
2117 |
2118 | ### 例题6
2119 |
2120 | 将1,3,4,5,6,8,11,15这8个数分别填入图中的圆圈中,使两个大圆上5个数的和都等于33。
2121 |
2122 | ### 练习6
2123 |
2124 | 将2,5,6,8,10,12,14,22这8个数分别填入图中的圆圈中,使两个大圆上5个数的和都等于49。
2125 |
2126 | ## 2.2.16. 年龄问题初步
2127 |
2128 | ### 例题1
2129 |
2130 | 丁丁今年8岁,爸爸的年龄是丁丁的4倍,4年前,爸爸的年龄和丁丁相差几岁?
2131 |
2132 | ### 练习1
2133 |
2134 | 田田今年6岁,妈妈今年36岁,再过6年,田田读初中时,妈妈比田田大多少岁?
2135 |
2136 | ### 例题2
2137 |
2138 | 田田今年10岁,博士今年55岁,当田田17岁时,博士多少岁?
2139 |
2140 | ### 练习2
2141 |
2142 | 小芳今年10岁,妈妈比她大28岁,当小芳15岁时,妈妈多少岁?
2143 |
2144 | ### 例题3
2145 |
2146 | 今年小王子8岁,大王子14岁,当两人的年龄之和是40岁时,应该是几年之后?
2147 |
2148 | ### 练习3
2149 |
2150 | 今年太子8岁,王后34岁,当太子和王后两人的年龄和是50岁时,太子多少岁?王后多少岁?
2151 |
2152 | ### 例题4
2153 |
2154 | 爸爸今年40岁,妈妈今年38岁,儿子今年12岁,当爸爸、妈妈、儿子三人的年龄和是81岁时,爸爸多少岁?妈妈多少岁?儿子多少岁?
2155 |
2156 | ### 练习4
2157 |
2158 | 李文今年9岁,爸爸、妈妈的年龄和是81岁,问:多少年后他们三个的平均年龄是40岁?
2159 |
2160 | ### 例题5
2161 |
2162 | 李斯、韩非现在的年龄和是62岁,5年前,李斯比韩非大6岁,今年李斯、韩非两人各多少岁?
2163 |
2164 | ### 练习5
2165 |
2166 | 爸爸、妈妈现在的年龄和是72岁;5年后,爸爸比妈妈大6岁。今年爸爸妈妈二人各多少岁?
2167 |
2168 | ### 例题6
2169 |
2170 | 姐姐5年前的年龄与妹妹3年后的年龄相等,问姐姐和妹妹相差多少岁?
2171 |
2172 | ### 练习6
2173 |
2174 | 小明12年后的年龄与妈妈12年前的年龄相等,问小明和妈妈相差多少岁?
2175 |
2176 | ## 2.2.17. 画图法综合
2177 |
2178 | ### 热身1
2179 |
2180 | ### 热身2
2181 |
2182 | ### 热身3
2183 |
2184 | ### 例题1(排队问题)
2185 |
2186 | 小朋友们排成一个长方形队伍表演体操。
2187 | (1)从左边数起,小华排第18,从右边数起,小明排第16,小华的左边是小明,这一行共有多少人?
2188 | (2)从左面数小红排在第2个,小军排在小红右面第4个,那么小军从右往左数排在第几个?
2189 |
2190 | ### 练习1
2191 |
2192 | 一群小动物排队表演节目,小猪第18个出场,小狗表演完后面还有16个节目,已知小猪后面第二个节目是小狗表演的,求一共有多少个节目?
2193 |
2194 | ### 例题2(鸡兔同笼)
2195 |
2196 | 王大妈去市场上买回来了一些鸡和兔,她把鸡、兔关在同一个笼子里,数了数,共有11个头,30条腿,你知道王大妈买回来了几只鸡?几只兔?
2197 |
2198 | ### 练习2
2199 |
2200 | 鸡兔同笼,共有7个头,20条腿,有多少只鸡?多少只兔?
2201 |
2202 | ### 例题3(年龄问题)
2203 |
2204 | 爸爸、妈妈、小敏三人的年龄总和是73岁,爸爸比妈妈大3岁,小敏比妈妈小23岁。小敏今年多少岁?
2205 |
2206 | ### 练习3
2207 |
2208 | 三个小朋友比年龄,小明比小英小5岁,小方比小明大2岁。那么小英和小方差几岁?
2209 |
2210 | ### 例题4(画线段图)
2211 |
2212 | 一筐鲜鱼,连筐共重56千克。先卖出鲜鱼的一半,再卖出剩下的一半,这时连筐还重17千克。原来这筐鲜鱼重多少干克?
2213 |
2214 | ### 练习4
2215 |
2216 | 玻璃瓶里装着一些水,把水加到原来的2倍时,和瓶一起称重5千克;把水加到原来的4倍时,重为9千克,问原来水有多少千克?
2217 |
2218 | ### 例题5(盈亏问题)
2219 |
2220 | 田田到文具店买练习本,她带的钱若买4本,还剩2元;若买5本,就差7元。问田田一共带了多少钱?
2221 |
2222 | ### 练习5
2223 |
2224 | 牛牛妈妈到水果店买苹果,她带的钱若买4千克还剩8元;若买5千克,就差2元。问牛牛妈妈一共带了多少钱?
2225 |
2226 | ### 例题6
2227 |
2228 | 丁丁和牛牛都想买一个饼,但丁丁的钱币少2枚,牛牛的钱币少3枚。如果两个人的钱币合在一起就刚够买一个饼。问买一个饼需要多少枚钱币?丁丁和牛牛各有多少枚钱币?
2229 |
2230 | ### 练习6
2231 |
2232 | 王强和李明都想买一本《趣味数学》,但王强的钱少2元5角,李明的钱少3元1角。如果两个人的钱合在一起就刚够买这本书。问一本《趣味数学》多少钱?王强和李明各有多少钱?
2233 |
2234 | ### 拓展1
2235 |
2236 | 81 位同学排成 9 行 9 列的正方形队列表演体操,小花在队列中,正左边有 2 位同学,正前方有3位同学,这时整个队列的同学向右转,则小花的正前方有几位同学?正右边有几位同学?
2237 |
2238 | ### 拓展2
2239 |
2240 | 鸡兔同笼,共有60个头,且鸡腿是兔腿的2倍,有多少只鸡?多少只兔?
2241 |
2242 | ### 拓展3
2243 |
2244 | 14年前爸爸的年龄是儿子的5倍, 14年后父子二人年龄和是98岁,父子二人今年分别多少岁?
2245 |
2246 | ### 拓展4
2247 |
2248 | 学生们划船,如果每只船坐5人,则还有3人无船坐,如果其中两只船坐4人,其余的船每只坐6人,就恰好坐完所有学生,共有学生多少人?
2249 |
2250 | ### 拓展5
2251 |
2252 | 甲乙丙丁四个同学共买了37朵花,如果甲多买2朵,乙少买3多,丙买的朵数变成现在的2倍,丁买的朵数减少一半,那么四个人买的朵数正好相同。请问原来四个人各买了多少朵花?
2253 |
2254 | ## 2.2.18. 等式加减法
2255 |
2256 | ### 热身1
2257 |
2258 | 15个小朋友排队报数,从前边报起,牛牛报10,从后往前报起,丁丁报12,求从牛牛数到丁丁一共有多少人?
2259 |
2260 | ### 热身2
2261 |
2262 | 牛牛、田田、丁丁三个人分糖块。田田比丁丁多3块,牛牛比田田多2块。已知糖块总块数是50块,那么每人各分到多少块?
2263 |
2264 | ### 热身3
2265 |
2266 | 买4个足球和2个排球,共用去102元,已知每个足球比每个排球贵3元。问每个足球和排球各多少元?
2267 |
2268 | ### 例题1
2269 |
2270 | 下面不同的图各代表一个数,你知道它们各代表几吗?
2271 |
2272 | (1)
2273 |
2274 | $🍎+🍐+🍐=13$
2275 |
2276 | $🍎+🍐=10$
2277 |
2278 | $🍎=()$
2279 |
2280 | $🍐=()$
2281 |
2282 | (2)
2283 |
2284 | $🍊+🍊+🍑=15$
2285 |
2286 | $🍊+🍑=9$
2287 |
2288 | $🍊=()$
2289 |
2290 | $🍑=()$
2291 |
2292 | ### 练习1
2293 |
2294 | 下面等式中,□和△各表示几?
2295 | 已知:
2296 |
2297 | $□+□+△=16$
2298 | $□+□+△+△+△=24$
2299 | 求:
2300 |
2301 | $□=()$
2302 | $△=()$
2303 |
2304 | ### 例题2
2305 |
2306 | 下面不同的图各代表一个数,你知道它们各代表几吗?
2307 |
2308 | $🍇+🍎=16$
2309 |
2310 | $🍇-🍎=2$
2311 |
2312 | $🍎=()$
2313 |
2314 | $🍇=()$
2315 |
2316 | ### 练习2
2317 |
2318 | 下面不同的图各代表一个数,你知道它们各代表几吗?
2319 |
2320 | $🍌+🍓=15$
2321 |
2322 | $🍌-🍓=3$
2323 |
2324 | $🍌=()$
2325 |
2326 | $🍓=()$
2327 |
2328 | ### 例题3
2329 |
2330 | 你能根据下面两个等式,求出🍊和🍍各表示什么数吗?
2331 |
2332 | $🍊+🍊+🍍=10$
2333 |
2334 | $🍊+🍍+🍍=11$
2335 |
2336 | $🍊=()$
2337 |
2338 | $🍍=()$
2339 |
2340 | ### 练习3
2341 |
2342 | 已知:
2343 |
2344 | $☆+☆+☆+△+△=13$
2345 | $☆+☆+△+△+△=12$
2346 |
2347 | 求:
2348 |
2349 | $☆=()$
2350 | $△=()$
2351 |
2352 | ### 例题4
2353 |
2354 | 下面△、☆、▲各代表什么数?
2355 |
2356 | $△+☆=23$
2357 |
2358 | $△+▲=33$
2359 |
2360 | $☆+▲=30$
2361 |
2362 | ### 练习4
2363 |
2364 | 三种兔子各多少只?
2365 | 黑兔+白兔=6
2366 | 黑兔+灰兔=7
2367 | 白兔+灰兔=5
2368 |
2369 | ### 铺垫
2370 |
2371 | 根据条件写等式。
2372 |
2373 | ### 例题5
2374 |
2375 | 2瓶可乐和3个面包共27元,4瓶可乐和3个面包共39元。请你算一算,每瓶可乐和每个面包各多少元?
2376 |
2377 | ### 练习5
2378 |
2379 | 牛牛去商店买文具,买了3个本子和1支铅笔一共花了10元,又知道1个本子比1支铅笔贵2元,请问1个本子和1支笔各多少钱?
2380 |
2381 | ### 例题6
2382 |
2383 | 1千克瓜子和2千克花生,一共 32元。2千克瓜子和1千克花生,一共 28元。那么瓜子和花生每千克各多少元?
2384 |
2385 | ### 练习6
2386 |
2387 | 1件上衣与2条裤子的总价是500元,这件上衣比这2条裤子的价钱贵
2388 | 100 元。则1件上衣多少钱? 1条裤子多少钱?(2条裤子是一样的)
2389 |
2390 | ### 拓展1
2391 |
2392 | 下面每种水果各代表多少?
2393 |
2394 | $🍐+🍐+🍎+🍊=16$
2395 |
2396 | $🍐+🍎+🍎+🍊=13$
2397 |
2398 | $🍐+🍎+🍊+🍊=11$
2399 |
2400 | ### 拓展2
2401 |
2402 | 饲养场出售鸡、鸭,张大爷买2只鸭和3只鸡共用42元,李大叔买3只鸭和2只鸡共用43元。1只鸭和一只鸡各多少元?
2403 |
2404 | ### 拓展3
2405 |
2406 | 小军家养了一些大白兔和小花猫。有一天,小军抱着2只大白兔一起站在体重计上称一称,正好是 45千克;后来小军放下大白兔又抱着3只小花猫,站在体重计上称一称,正好是47千克;最后小军把 6只小花猫和4只大白兔一起放在体重计上称一称是44千克。请你算一算小军、大白兔和小花猫各是多少千克?(每只大白兔的重量一样,每只小花猫的重量一样。)
2407 |
2408 | ### 拓展4
2409 |
2410 | ### 拓展5
2411 |
2412 | ## 2.2.19. 动手操作
2413 |
2414 | ### 热身1
2415 |
2416 | ### 热身2
2417 |
2418 | ### 热身3
2419 |
2420 | ### 例题1
2421 |
2422 | 大勺子一次能装油250克,小勺子一次能装油150克,你能用这两把勺子往一个空杯子里倒入350克油吗?
2423 |
2424 | ### 练习1
2425 |
2426 | 兔妈妈有一包70克的药,想要用天平从中称出5克的药,可只有一个20克的砝码,怎么办?
2427 |
2428 | ### 例题2
2429 |
2430 | 两个人要平分12千克的一大桶油。身边只有能装9千克和5千克的两只空桶,怎样倒才能使他们分到一样多的油呢?
2431 |
2432 | ### 练习2
2433 |
2434 | 一个人带着两只空桶去沟边取水,一只桶可盛5千克水,另一只可盛7千克水,现在要取8千克水,应该怎样取?
2435 |
2436 | ### 例题3
2437 |
2438 | 有九颗珍珠,其中有一颗是假珍珠,外观和真的一样,不容易看出来,只是假珍珠比真珍珠轻一些。你能利用天平,不用砝码,只称两次就找出假的珍珠吗?怎样称?
2439 |
2440 | ### 练习3
2441 |
2442 | 有八颗珍珠,其中有一颗是假珍珠,外观和真的一样,不容易看出来,只是假珍珠比真珍珠轻一些。你能利用天平,不用砝码,最少称几次就找出假的珍珠吗?怎样称?
2443 |
2444 | ### 例题4
2445 |
2446 | 黑猫警长在海关截获了一批装有牛肉罐头的9个大箱子,每箱里有很多盒罐头(大于1盒),箱子里每盒罐头重100克。在这9个大箱子中,其中有1箱罐头已经过期,不符合出口标准,过期的罐头每盒要比原来重1克。黑猫警长准备用一个大的电子称把这箱过期罐头称出来,请你帮忙想一想,最少需要称几次就能把这箱不合格的罐头找出来?
2447 |
2448 | ### 练习4
2449 |
2450 | 有10箱钢珠,每个钢珠重10克,每箱600个。如果这10箱钢珠中有1箱次品,次品钢珠每个重9克,那么,要找出这箱次品最少要称几次?
2451 |
2452 | ### 例题5
2453 |
2454 | 8个队参加扔石头大赛,比赛采用淘汰赛制,每2个队进行1场比赛,每场比赛输的1队被淘汰,最后决出冠军。同学们,请你算一算,一共要举行多少场比赛?
2455 |
2456 | ### 练习5
2457 |
2458 | 32个篮球队进行篮球比赛,裁判对他们说:“本次比赛采用淘汰赛,每2个队进行1场比赛,每场比赛输的1队被淘汰,最后决出冠军。”同学们,如果你做裁判,请你算一算一共要举行多少场比赛?
2459 |
2460 | ### 例题6
2461 |
2462 | 丁丁,牛牛,田田,阿普,小乐,5名同学参加跳绳比赛,比赛前每2个小朋友都要握一次手表示友好。当丁丁握了4次手,牛牛握了3次手,田田握了2次手,阿普握了1次手的时候,小乐握了几次手?最后这5名小朋友一共要握多少次手?
2463 |
2464 | ### 练习6
2465 |
2466 | 动物王国的动物们在比赛之前都要握手表示友好,这时,狐狸握了3次手,熊猫握了4次手,兔子也握了4次手,小猪握了3次手,狮子握了几次手呢?
2467 |
2468 | ### 拓展1
2469 |
2470 | ### 拓展2
2471 |
2472 | ### 拓展3
2473 |
2474 | ### 拓展4
2475 |
2476 | ### 拓展5
2477 |
2478 | ### 练习1
2479 |
2480 | ### 练习2
2481 |
2482 | ### 练习3
2483 |
2484 | ### 练习4
2485 |
2486 | ### 练习5
2487 |
2488 | ### 练习6
2489 |
2490 | ## 2.2.20. 必胜策略
2491 |
2492 | ### 例题1
2493 |
2494 | 桌子上放着18根火柴,甲、乙二人轮流每次取走1~3根。规定谁取走最后1根火柴谁获胜。甲先取,那么怎样取才能获胜?
2495 |
2496 | ### 练习1
2497 |
2498 | 桌子上放着50根火柴,甲、乙二人轮流每次取走1~3根。规定谁取走最后1根火柴谁获胜。如果双方均采用最佳方法,甲先取,那么怎样取才能获胜?
2499 |
2500 | ### 例题2
2501 |
2502 | 桌子上放着80根火柴,甲、乙二人轮流每次取走1~9根。规定谁取走最后1根火柴谁获胜。如果双方采用最佳方法,甲先取,那么谁将获胜?
2503 |
2504 | ### 练习2
2505 |
2506 | 桌子上放着75根火柴,甲、乙二人轮流每次取走1~4根。规定谁取走最后1根火柴谁获胜。如果双方采用最佳方法,甲先取,那么谁将获胜?
2507 |
2508 | ### 例题3
2509 |
2510 | 桌子上放着21根火柴,甲、乙二人轮流每次取走1~4根。规定谁取走最后1根火柴谁就输。如果甲想获胜,应该怎样取?
2511 |
2512 | ### 练习3
2513 |
2514 | 桌子上放着28根火柴,甲、乙二人轮流每次取走1~5根。规定谁取走最后1根火柴谁就输。甲先取,那么怎样取才能获胜?
2515 |
2516 | ### 例题4
2517 |
2518 | 两个人从1开始按自然数顺序轮流依次报数,每人每次只能报1~3个数,谁先报到30谁获胜。你选择先报数还是后报数?怎样才能获胜?
2519 |
2520 | ### 练习4
2521 |
2522 | 两个人从1开始按自然数顺序轮流依次报数,每人每次只能报1~4个数,谁先报到32谁获胜。你选择先报数还是后报数?怎样才能获胜?
2523 |
2524 | ### 例题5
2525 |
2526 | 31个方格排成一行,最左端方格中放有一枚棋子,甲先乙后轮流向右移动棋子,每次移动1~3个格。规定将棋子移到最后1格者输。甲为了获胜,第一步必须向右移多少格?
2527 |
2528 | ### 练习5
2529 |
2530 | 共有54张扑克牌,由两人轮流来抽,每次可抽1~6张,抽到最后1张牌的人就算输了,如果第一个抽牌的人想赢,第一次应该抽几张牌。
2531 |
2532 | ### 例题6
2533 |
2534 | 甲、乙两人玩游戏:有18枚棋子,两人轮流取棋子,每次允许取其中2枚、4枚或8枚,谁取到最后一枚棋子,谁就获胜。甲想获胜,先取还是后取?应该怎样取?
2535 |
2536 | ### 练习6
2537 |
2538 | 甲、乙两人玩游戏:有28枚棋子,两人轮流取棋子,每次允许取其中2枚、4枚或8枚,谁取到最后一枚棋子,谁就获胜。如果甲先取,那么第一次甲取几枚才能保证一定获胜?
2539 |
2540 | ### 拓展1
2541 |
2542 | ### 拓展2
2543 |
2544 | ### 拓展3
2545 |
2546 | ### 拓展4
2547 |
2548 | ### 拓展5
2549 |
2550 | ###
2551 |
--------------------------------------------------------------------------------
/03-三年级.md:
--------------------------------------------------------------------------------
1 | ---
2 | title: 三年级
3 | lang: zh-CN
4 | sidebarDepth: 1
5 | ---
6 |
7 | # 三年级
8 |
9 | ## 3.1.01. 找规律综合
10 |
11 | ### 例题1(递推规律)
12 |
13 | 先找出下列数排列的规律,并根据规律在括号里填上适当的数。
14 |
15 | (1)1,4,7,10,(),16,19。
16 |
17 | (2)2,6,18,(),162。
18 |
19 | ### 练习1
20 |
21 | 先找出下列各列数的排列规律,然后在括号里填上适当的数。
22 |
23 | (1)2,6,10,14,(),22,26。
24 |
25 | (2)3,6,9,12,(),18,21。
26 |
27 | ### 例题2(间隔规律)
28 |
29 | 先找出规律,然后在括号里填上适当的数。
30 |
31 | 23,4,20,6,17,8,(),(),11,12。
32 |
33 | ### 练习2
34 |
35 | 先找出规律,然后在括号里填上适当的数。
36 |
37 | (1)3,2,5,2,7,2,(),(),11,2。
38 |
39 | (2)19,3,17,3,15,3,(),(),11,3。
40 |
41 | ### 例题3(兔子数列/斐波那契数列)
42 |
43 | 在数列1,1,2,3,5,8,13,(),34,55,……中,括号里应填什么数?
44 |
45 | ### 练习3
46 |
47 | 先找出规律,然后在括号里填上适当的数。
48 |
49 | 2,2,4,6,10,16,(),()。
50 |
51 | ### 例题4(算式规律)
52 |
53 | 根据前面图形中的数之间的关系,想一想第三个图形的括号里应填什么数?
54 |
55 | 
56 |
57 | ### 练习4
58 |
59 | 根据下表中的排列规律,在空格里填上适当的数。
60 |
61 | | 12 | 18 | 6 |
62 | | ---- | ---- | ---- |
63 | | 8 | 15 | 7 |
64 | | 4 | | 8 |
65 |
66 | ### 例题5
67 |
68 | 先计算下面一组算式的第一题,然后找出其中的规律,并根据规律直接写出后几题的得数。
69 |
70 | (1)12345679×9
71 |
72 | (2)12345679×18
73 |
74 | (3)12345679×54
75 |
76 | (4)12345679×81
77 |
78 | ### 练习5
79 |
80 | 计算:
81 |
82 | (1)26×11
83 |
84 | (2)38×11
85 |
86 | ### 例题6(图形规律)
87 |
88 | 观察下面由点组成的图形(点群),请回答:
89 |
90 | (1)方框内的点群包含多少个点?
91 |
92 | (2)第10个点群中包含多少个点?
93 |
94 | (3)前十个点群中,所有点的总数是多少?
95 |
96 | 
97 |
98 | ### 练习6
99 |
100 | 观察下面的图形,按规律在“?”处填上适当的图形。
101 |
102 | 
103 |
104 | ## 3.1.02. 加减法巧算综合
105 |
106 | ### 热身1
107 |
108 | 找规律填数。
109 |
110 | 10,13,18,25,(),(),58。
111 |
112 | ### 热身2
113 |
114 | 找规律填数。
115 |
116 | 3,29,4,28,6,26,9,23,(),(),18,14。
117 |
118 | ### 热身3
119 |
120 | 计算:$11+12+13+14+15+16+17+18+19=$
121 |
122 | ### 例题1(凑整法)
123 |
124 | 计算。
125 |
126 | (1)$132+23+48+257+40=$
127 |
128 | (2)$32+24+68=$
129 |
130 | ### 练习1
131 |
132 | 计算。
133 |
134 | (1)$238+45+67+62+55=$
135 |
136 | (2)$13+21+87+19=$
137 |
138 | ### 例题2(基准数)
139 |
140 | 计算。
141 |
142 | (1)$9+99+999+9999=$
143 |
144 | (2)$3998+407+89=$
145 |
146 | ### 练习2
147 |
148 | 计算。
149 |
150 | (1)$295+196+297+198+199+15=$
151 |
152 | (2)$19+199+1999=$
153 |
154 | ### 例题3
155 |
156 | 计算。
157 |
158 | (1)$268-56-82-44-18=$
159 |
160 | (2)$$
161 |
162 | ### 练习3
163 |
164 | 计算。
165 |
166 | (1)$831-155-67-145-131=$
167 |
168 | (2)$$
169 |
170 | ### 例题4
171 |
172 | 计算。
173 |
174 | (1)$300-9-19-29-39-49-59=$
175 |
176 | (2)$985-32+37-276-85+73-68=$
177 |
178 | ### 练习4
179 |
180 | 计算。
181 |
182 | (1)$818-271-18+64-29+36=$
183 |
184 | (2)$200-20-18-23-20-19-21=$
185 |
186 | ### 例题5
187 |
188 | 计算。
189 |
190 | (1)$2985-(985-276)=$
191 |
192 | (2)$$
193 |
194 | ### 练习5
195 |
196 | 计算。
197 |
198 | (1)$(123+348+400)-(23+150+148)=$
199 |
200 | (2)$$
201 |
202 | ### 例题6(分组巧算)
203 |
204 | 计算。
205 |
206 | (1)$20-19-18+17+16-15-14+13+12-11-10+9=$
207 |
208 | (2)$1+2-3-4+5+6-7-8+9+10-11-12+……-1999-2000+2001=$
209 |
210 | ### 练习6
211 |
212 | 计算。
213 |
214 | (1)$3355+4466+9977-3366-4477-9955=$
215 |
216 | (2)$$
217 |
218 | ### 例题7
219 |
220 | 【变零为整】$74+63+16-53+9+81=$
221 |
222 | 【变长为短】$38+57+36-57-36=$
223 |
224 | 【变大为小】$365-198+196+295-296=$
225 |
226 | 【变加为乘】$97+98+100+101+102=$
227 |
228 | 【位值原理】$1243+4132+2314+3421=$
229 |
230 | ### 练习7
231 |
232 | 【去括号】$2748+(1336+289)-(336+289)-748=$
233 |
234 | 【填括号】$1518-571-18+61-29+39=$
235 |
236 | ### 例题8
237 |
238 | 计算:$689-1-3-5-7-9-11-13-15-17-19$
239 |
240 | ### 练习8
241 |
242 | 计算:$9999-1-2-3-\dots-28-29-30-29-28-\dots-3-2-1$
243 |
244 | ### 拓展1
245 |
246 | 计算$1017+2017+3017+4017+5017-6017-7017$
247 |
248 | ### 拓展2
249 |
250 | 有一个很神秘的地方,那里有很多的雕塑,每个雕塑都是由蝴蝶组成的。已知一共有1000只蝴蝶,第1个雕塑有3只蝴蝶,第2个雕塑有5只蝴蝶,第3个雕塑有7只蝴蝶,第4个雕塑有9只蝴蝶,后面的雕塑按照这样的规律一直延伸到很远的地方,松松沿着雕塑走了一会,
251 | 停在了一个有39只蝴蝶的雕塑旁。那么,他们没数完的蝴蝶还剩多少只呢?
252 |
253 | ### 拓展3
254 |
255 | 书店里有一套漫画书共9册,第一册需24元,第二册需23元,第三册需22元,以此类推,每一册的售价都比它前面的一册要少1元。如果用200元去买这套漫画书,书店老板应该找回多少元呢?
256 |
257 | ## 3.1.03. 加减法竖式数字谜进阶
258 |
259 | ### 例题1
260 |
261 | 在空格内填入适当的数字,使图中的竖式成立。
262 |
263 | (1)$$\begin{matrix}
264 | & &3 &\Box &4 \\
265 | +& &\Box &5 &\Box \\
266 | \hline
267 | &\Box &1 &5 &2
268 | \end{matrix}$$
269 |
270 | (2)$$\begin{matrix}
271 | &\Box &2 &\Box \\
272 |
273 | -&2 &\Box &4 \\
274 |
275 | \hline
276 | &1 &5 &2
277 | \end{matrix}$$
278 |
279 | ### 练习1
280 |
281 | 在空格内填入适当的数字,使图中的竖式成立。
282 |
283 | (1)$$\begin{array}{c}
284 | & &6 &\Box &3 \\
285 | +& &\Box &4 &\Box \\
286 | \hline
287 | &\Box &1 &7 &2
288 | \end{array}$$
289 |
290 | (2)$$\begin{matrix}
291 | &\Box &5 &\Box \\
292 | -&4 &\Box &6 \\
293 | \hline
294 | &3 &7 &1
295 | \end{matrix}$$
296 |
297 | ### 例题2
298 |
299 | 在空格内填入适当的数字,使图中的竖式成立。
300 |
301 | (1)$$\begin{matrix}
302 | & & &7 &\Box \\
303 | +& &\Box &\Box&4 \\
304 | \hline
305 | &\Box &\Box &5 &3
306 | \end{matrix}$$
307 |
308 | (2)$$\begin{matrix}
309 | &\Box &\Box &8 &\Box \\
310 | -& &\Box &\Box &4 \\
311 | \hline
312 | & & &9 &7
313 | \end{matrix}$$
314 |
315 | ### 练习2
316 |
317 | 在空格内填入适当的数字,使图中的竖式成立。
318 |
319 | (1)$$\begin{matrix}
320 | & & &8 &\Box \\
321 | +& &\Box &\Box &2 \\
322 | \hline
323 | &\Box &\Box &6 &1
324 | \end{matrix}$$
325 |
326 | (2)$$\begin{matrix}
327 | &\Box &\Box &7 &\Box \\
328 | -& &\Box &\Box &3 \\
329 | \hline& & &9 &6
330 | \end{matrix}$$
331 |
332 | ### 例题3
333 |
334 | 在空格内填入适当的数字,使图中的竖式成立。
335 |
336 | $$\begin{matrix}
337 | & &\Box &6 &\Box \\
338 | +& &2 &\Box &6 \\
339 | \hline
340 | &\Box &\Box &\Box &\Box \\
341 | -& &\Box &\Box &\Box \\
342 | \hline
343 | & & & &1
344 | \end{matrix}$$
345 |
346 | ### 练习3
347 |
348 | 在空格内填入适当的数字,使图中的竖式成立。
349 |
350 | $$\begin{matrix}
351 | &\Box &7 &\Box &8 \\
352 | +&1 &\Box &9 &\Box \\
353 | \hline&2 &9 &0 &9
354 | \end{matrix}$$
355 |
356 | ### 例题4
357 |
358 | 在下图的竖式中,不同的汉字代表不同的数字,相同的汉字代表相同的数字,每个汉字代表什 么数时,竖算式成立?
359 |
360 | $$\begin{matrix}
361 | & & & &生 \\
362 | & & &学 &生 \\
363 | & &好 &学 &生 \\
364 | +&三 &好 &学 &生 \\
365 | \hline&2 &0 &1 &6
366 | \end{matrix}$$
367 |
368 | ### 练习4
369 |
370 | 在下图的竖式中,不同的汉字代表不同的数字,相同的汉字代表相同的数字,每个汉字代表什 么数时,竖算式成立?
371 |
372 | $$\begin{matrix}
373 | & & & &龙 \\
374 | & & &成 &龙 \\
375 | & &子 &成 &龙 \\
376 | +&望 &子 &成 &龙 \\
377 | \hline&2 &0 &1 &2
378 | \end{matrix}$$
379 |
380 | ### 例题5
381 |
382 | 在下图的竖式中,不同的字母代表不同的数字,相同的字母代表相同的数字,每个字母代表什 么数时,竖算式成立?
383 |
384 | $$\begin{matrix}
385 | & &A &B &C &D \\
386 | +& &E &B &E &D \\
387 | \hline&E &D &C &A &D
388 | \end{matrix}$$
389 |
390 | ### 练习5
391 |
392 | 如下图,算式中不同的汉字代表不同的数字,已知:”级=5“,那么”学而思“代表的三位数是多少?
393 |
394 | $$\begin{matrix}
395 | & &学 &而 &思 \\
396 | +& &1 &2 &级 \\
397 | \hline&更 &进 &1 &步
398 | \end{matrix}$$
399 |
400 | ### 例题6
401 |
402 | 下面的减法算式中,每一个字母代表一个数字,不同的字母代表不同的数字,计算:D+G。
403 |
404 | $$\begin{matrix}
405 | &A &B &C &B &D \\
406 | -& &E &F &A &G \\
407 | \hline& & &F &F &F
408 | \end{matrix}$$
409 |
410 | ### 练习6
411 |
412 | 在下图的竖式中,不同的汉字代表不同的数字,相同的汉字代表相同的数字,每个汉字代表什 么数时,竖算式成立?
413 |
414 | $$\begin{matrix}
415 | &机 &器 &人 \\
416 | +&机 &机 &人 \\
417 | \hline&器 &人 &人
418 | \end{matrix}$$
419 |
420 | ## 3.1.06. 巧求周长进阶
421 |
422 | ### 例题1
423 |
424 | 将一个大正方形剪去四个相同大小的小正方形后,计算剩下部分的周长。
425 |
426 | 
427 |
428 | ### 练习1
429 |
430 | 计算下面这个图形的周长。(单位:厘米)
431 |
432 | 
433 |
434 | ### 例题2
435 |
436 | 用五个完全相同的小长方形拼成一个如图所示的大长方形,小长方形的周长是 40 厘米,那么大长方形的周长是多少?
437 |
438 | 
439 |
440 | ### 练习2
441 |
442 | 4个完全相同的小长方形拼成一个如图所示的大长方形,只知道小长方形的宽是2厘米,大长方形的周长是多少?
443 |
444 | 
445 |
446 | ### 例题3
447 |
448 | 若每个小正方形的周长为 12厘米,则他们组合而成的“十” 字图形的周长是多少?
449 |
450 | 
451 |
452 | ### 练习3
453 |
454 | 用五个完全相同的小正方形拼成如下图形,已知拼出图形的周长是24厘米,你知道所用小正方形的面积是多少吗?
455 |
456 | 
457 |
458 | ### 例题4
459 |
460 | 将一个长为12厘米,宽为6厘米的长方形纸片按照图中虚线剪成两个图形,请计算两个图形的周长之和?
461 |
462 | 
463 |
464 | ### 练习4
465 |
466 | 将一个边长为4厘米的正方形对折,再沿折线剪开,得到两个长方形,求两个长方形比原来的正方形周长多了多少。
467 |
468 | ### 例题5
469 |
470 | 用8张边长是2厘米的小正方形拼成一个长方形,这个长方形的周长是多少厘米?
471 |
472 | ### 练习5
473 |
474 | 用6张边长为3厘米的正方形纸片拼成一个长方形,这个长方形的周长是多少厘米?
475 |
476 | ### 例题6
477 |
478 | 商场举行大酬宾活动,门口将长18厘米,宽9厘米的礼品盒摆成一个有规律的形状。礼品盒前4层的样式如图所示,一共有10 层,你能算出一共摆了多少个礼品盒吗? 礼品盒摆出形状的周长是多少?
479 |
480 | 
481 |
482 | ### 练习6
483 |
484 | 如图所示,长方形长4厘米,宽2厘米,现沿对角线 BD对折得到如下几何图形,试求图形阴影部分的周长。
485 |
486 | 
487 |
488 | ## 3.1.07. 平均数初步
489 |
490 | ### 例题1
491 |
492 | 幼儿园小朋友做红花,小华做了27朵,小方做了29朵,小林和小宁合做了52朵。平均每个小朋友做了多少朵?
493 |
494 | ### 练习1
495 |
496 | 一个书架上第一层放书52本,第二层和第三层共放70本,第四层放了46本,平均每层放书多少本?
497 |
498 | ### 例题2
499 |
500 | 中关村小学有15名同学参加跳绳比赛,他们跳绳的个数分别为93、94、85、92、86、88、94、91、88、89、92、86、93、90、89,求平均每人跳绳多少个?
501 |
502 | ### 练习2
503 |
504 | 下图是小华五次数学测验成绩的统计图。小华五次测验的平均分是多少分?
505 |
506 |
1540 |
1541 | ### 例题4
1542 |
1543 | 下面是用小正方体组成的立体图形,现在把这个立体图形表面都涂上绿色,数一数有多少个小正方形没有被涂上色?
1544 |
1545 | ### 练习4
1546 |
1547 | 用小正方体拼成了一个如下图的模型,然后把它粘在地上喷上红色油漆,这堆正方体中共有多少个小正方形没有被喷上颜色?
1548 |
1549 | ### 例题5
1550 |
1551 | ### 练习5
1552 |
1553 | ### 例题6
1554 |
1555 | ### 练习6
1556 |
1557 | ## 2.2.10. 周期问题初步
1558 |
1559 | ### 例题1
1560 |
1561 | 小朋友按了3女3男的顺序依次排成一队看表演,算一算第17名、第37名同学分别是男生还是女生?
1562 |
1563 | ### 练习1
1564 |
1565 | 广场上摆满花,这些花是按3盆大红、2盆金黄、2盒粉红的顺序摆放的,你
1566 | 们知道第26盆、35盆、45 盒花是什么颜色吗?
1567 |
1568 | ### 例题2
1569 |
1570 | 乐乐老师带领牛牛等人在园林里种树,他们按1棵杨树、2棵椰树、2棵松树的顺序来种,一共种了48棵树,那么杨树、椰树、松树各种了几棵?
1571 |
1572 | ### 练习2
1573 |
1574 | 某小学操场上树立着彩旗,按如下图顺序来排列,一共有 42 面旗,在这42 面彩旗中,红旗有()面,黄旗有()面?
1575 |
1576 | ### 例题3
1577 |
1578 | 丁丁用树枝在地上写了一列数,然后他停下来,让田田猜一猜,
1579 |
1580 | $2、3、1、2、3、1、2、3、1、……$
1581 |
1582 | (1)第28个数是几?
1583 |
1584 | (2)这28个数的和是多少?
1585 |
1586 | ### 练习3
1587 |
1588 | 有一列数:
1589 |
1590 | $1、4、2、1、4、2、1、4、2、1、……$
1591 |
1592 | (1)第26个数是几?
1593 |
1594 | (2)这26个数的和是多少?
1595 |
1596 | ### 例题4
1597 |
1598 | 有一列数如下所示,在这一列数中:
1599 |
1600 | $1、3、5、7、1、3、5、7、9、……$
1601 |
1602 | (1)第35个数是几?
1603 |
1604 | (2)这35个数的和是多少?
1605 |
1606 | (3)如果连续写83个数,3被写了多少次?
1607 |
1608 | ### 练习4
1609 |
1610 | $2、3、4、1、2、3、4、1、2、3、4、1、2、3、4、1、2、3、4、……$,请问:
1611 |
1612 | (1)第26个数是几?
1613 |
1614 | (2)请问这26个数的和是多少?
1615 |
1616 | (3)请问在这26个数字中,有几个“3”?
1617 |
1618 | ### 例题5
1619 |
1620 | 2014年4月5日是星期六。
1621 |
1622 | (1)从5日算起,第10天是星期几?
1623 |
1624 | (2)再过10天是星期几?
1625 |
1626 | ### 练习5
1627 |
1628 | 某年1月1日元旦是星期四,从1日算起,第12天是星期()
1629 |
1630 | ### 例题6
1631 |
1632 | 例子:
1633 |
1634 | | 1 | 2 | 1 | 2 | 1 | 2 | 1 | 2 | 1 | 2 | …… |
1635 | | ---- | ---- | ---- | ---- | ---- | ---- | ---- | ---- | ---- | ---- | ---- |
1636 | | A | B | C | A | B | C | A | B | C | A | …… |
1637 |
1638 | 在下表中,将每列上、下两个字组成一组,例如第1组为(小双),第2组为(朋手),那么第55组是什么?
1639 |
1640 | | 小 | 朋 | 友 | 荡 | 秋 | 千 | 小 | 朋 | 友 | 荡 | 秋 | 千 | 小 | 朋 | …… |
1641 | | ---- | ---- | ---- | ---- | ---- | ---- | ---- | ---- | ---- | ---- | ---- | ---- | ---- | ---- | ---- |
1642 | | 双 | 手 | 向 | 空 | 如 | 鸟 | 翼 | 双 | 手 | 向 | 空 | 如 | 鸟 | 翼 | …… |
1643 |
1644 | ### 练习6
1645 |
1646 | 下面的表格中,每一列的两个数组成一组,如第1组是由“甲A”组成,第
1647 | 2组是由“乙B”组成⋯问:第17组是由哪两个组成?
1648 |
1649 | | 甲 | 乙 | 丙 | 甲 | 乙 | 丙 | 甲 | 乙 | 丙 | 甲 | 乙 | 丙 | …… |
1650 | | ---- | ---- | ---- | ---- | ---- | ---- | ---- | ---- | ---- | ---- | ---- | ---- | ---- |
1651 | | A | B | C | D | A | B | C | D | A | B | C | D | …… |
1652 |
1653 | ### 拓展1
1654 |
1655 | 今天是2022年4月14日,星期四,请问:今年的劳动节是星期几?小代今年的生日是星期几?
1656 |
1657 | ### 拓展2
1658 |
1659 | 12个同学围成一圈做传球的游戏,如图。
1660 |
1661 | 
1662 |
1663 | (1)从1号同学开始,顺时针传100次,手绢应在谁手中?
1664 |
1665 | (2)从1号同学开始,逆时针传100次,手绢又在谁手中?
1666 |
1667 | (3)从 1号同学开始,先顺时针传156次,然后从那个同学开始逆时针传143次,最后手绢在谁手中?
1668 |
1669 | ### 拓展3
1670 |
1671 | 字母A、B、C、D、E和数字1、9分别按下列方式变动次序:
1672 |
1673 | ABCDE19
1674 |
1675 | BCDEA91(第一次变动)
1676 |
1677 | CDEAB91(第二次变动)
1678 |
1679 | DEABC19(第三次变动)
1680 |
1681 | ……
1682 |
1683 | 那么,最少经过几次变动后“ABCDE19”将再次出现。
1684 |
1685 | ### 拓展4
1686 |
1687 | A、B、C、D四个盒子中依次放有6、4、5、3个球。第1个小朋友找到放球最多的盒子,从盒子中取出 3 个球,放入其他盒子,每个盒子放一个;然后第2个小朋友也找到放球最多的盒子,从盒子中取出 3个球,放入其他盒子,每个盒子放一个。如此进行下去,当第120位小朋友放完后,C 盒中有几个球?
1688 |
1689 | ## 2.2.11. 移多补少
1690 |
1691 | 计算练习
1692 |
1693 | (1)$1+2+3+4+5+6+7+8+9+10+9+8+7+6+5+4+3+2+1$
1694 |
1695 | (2)$1+3+5+7+9+11+9+7+5+3+1$
1696 |
1697 | (3)$1+2+3+\dots+49+50+49+\dots+3+2+1$
1698 |
1699 | ### 例题1
1700 |
1701 | 牛牛和丁丁分糕点,牛牛有14块,丁丁有6块,牛牛需要拿出几块糕点给丁丁,他们的糕点数才会同样多?
1702 |
1703 | ### 练习1
1704 |
1705 | 红队有29人,黄队有15人,红队调给黄队几人,就能使两队人数相等?
1706 |
1707 | ### 例题2
1708 |
1709 | 同学们分成两队进行拔河比赛,第一队有31人,如果从第一队中调3人到第二队,这时两队的人数才会一样多。第二队原来有学生多少人?
1710 |
1711 | ### 练习2
1712 |
1713 | 牛牛有24朵花,丁丁给牛牛8朵后,两人的花朵数就相等。丁丁原来有几几朵花?
1714 |
1715 | ### 例题3
1716 |
1717 | 小花免和小白兔分萝卜,小花兔给小白兔4个萝卜后,小花免还比小白兔多
1718 | 2个。小花兔原来比小白兔多几个萝卜?
1719 |
1720 | ### 练习3
1721 |
1722 | 小花兔和小白兔分萝卜,小花兔给小白兔4个萝卜后,小花免比小白免少
1723 | 2个。小花兔原来比小白兔多几个萝卜?
1724 |
1725 | ### 例题4
1726 |
1727 | 小山羊和小白免一共拔了30个萝卜放进两筐里,小白免从大筐里拿出6个放进小筐里,现在两筐萝卜的个数同样多。原来小筐里有多少个萝卜?
1728 |
1729 | ### 练习4
1730 |
1731 | 甲、乙两筐西瓜共28个,从甲筐取4个放入乙筐中,两筐西瓜个数相同。
1732 | 原来甲、乙两筐各有多少个西瓜?
1733 |
1734 | ### 例题5
1735 |
1736 | 妈妈买了2袋苹果,甲袋是54个,乙袋是22个。每次从多的1袋取出4个放到少的1袋里,拿几次才能使两袋苹果的个数相等呢?
1737 |
1738 | ### 练习5
1739 |
1740 | 小华有两盒糖果,甲盒有糖78粒,乙盒有糖38粒,每次从甲盒取5粒糖放到
1741 | 乙盒,取几次两盒糖的粒数就同样多?
1742 |
1743 | ### 例题6
1744 |
1745 | 两堆香蕉一样多,现在从第一堆里面拿出4把香蕉放入第二堆,这时第二堆的香蕉是第一堆的2倍,原来两堆香蕉各有多少把?
1746 |
1747 | ### 练习6
1748 |
1749 | 哥哥和弟弟集邮,原来两人的邮票张数相等,如果哥哥给弟弟9张邮票,则弟弟的邮票张数是哥哥的3倍,哥哥、弟弟原来各有邮票多少张?
1750 |
1751 | ### 拓展1
1752 |
1753 | 小东、小西、小北3个同学带着15个筐去摘桃,摘完后,有5筐装满了桃,5筐装了半筐桃,5筐空着,怎样分,才能让他们3人每人分到的桃一样多,筐也一样多?
1754 |
1755 | ### 拓展2
1756 |
1757 | 大毛、二毛和三毛三个小朋友出去玩,各自摘了一些小草莓,大毛把自己摘得草莓给了二毛 2 个后,大毛比二毛多 1 个,接着,二毛又把自己摘草莓给了三毛 2 个,此时二毛和三毛的草莓变得一样多,那么原来大毛和三毛两个人摘得草莓数量谁更多?多几个?
1758 |
1759 | ### 拓展3
1760 |
1761 | 小白、小灰和小花三只小猫去河里分别捉了一些鱼。如果小花给小白 5 条鱼,那么小花比小白还多 2 条鱼;如果小灰给小花 4 条鱼,那么小灰就比小花少 3 条鱼,请问原来小灰比小白多多少条鱼?
1762 |
1763 | ### 拓展4
1764 |
1765 | 小白、小灰和小花三只小猫去河里捉了一些鱼。如果小白给小花一些鱼后,小花和小白拥有的鱼就一样多了,都是 42 条;如果小灰给小白一些鱼后,小灰和小白拥有的鱼就一样多了,都是 47 条鱼,如果小灰给小花一些鱼后,小灰和小花拥有的鱼就一样多了,都是 46条。那小灰有几条鱼。
1766 |
1767 | ## 2.2.12. 和差问题
1768 |
1769 | ### 例题1
1770 |
1771 | 牛牛和丁丁总共有46个玻璃球,丁丁比牛牛多6个。请大家帮忙算一算,牛牛和丁丁各有多少个玻璃球?
1772 |
1773 | ### 练习1
1774 |
1775 | 今年姐姐和妹妹的年龄和是14岁,姐姐比妹妹大4岁,问姐姐、妹妹今年各多少岁?
1776 |
1777 | ### 例题2
1778 |
1779 | 牛牛和丁丁写大字的速度不变,两人两天一共写了120个字,已知牛牛每天比丁丁多写10个,请问丁丁和牛牛每天各写几个大字?
1780 |
1781 | ### 练习2
1782 |
1783 | 牛牛和丁丁保持自己相同的速度折飞机,牛牛每小时比丁丁多折10个,他们两人用了3小时共折飞机150个,牛牛和丁丁每小时各折多少个飞机?
1784 |
1785 | ### 例题3
1786 |
1787 | 动物学校有个长方形操场,它的长与宽相差80米,沿操场跑一圈是400米,求动物学校操场的长与宽各是多少?
1788 |
1789 | ### 练习3
1790 |
1791 | 蚂蚁沿着阿普的课本四周爬了一圈是200厘米,知道课本的长边比短边多30厘米,问阿普课本的长边和短边各是多少厘米?
1792 |
1793 | ### 例题4
1794 |
1795 | 牛牛在这次测验中,语文和数学的平均分是95分,语文比数学多6分,牛牛在这次测验中,语文和数学各得了多少分?
1796 |
1797 | ### 练习4
1798 |
1799 | 牛牛和丁丁的平均身高是130厘米,牛牛比丁丁高10厘米,丁丁和牛牛的身高各是多少厘米?
1800 |
1801 | ### 例题5
1802 |
1803 | 豆豆和毛毛一共有34个巧克力豆,两人都吃了同样的巧克力豆后,分别还剩15个和11个,问原来豆豆和毛毛各有多少个巧克力豆?
1804 |
1805 | ### 练习5
1806 |
1807 | 大毛、二毛共有33元,两人花掉同样的钱后,大毛还有19元,二毛还有6元,问原来大毛、二毛各有多少钱?
1808 |
1809 | ### 例题6
1810 |
1811 | 牛牛3年前的年龄与阿普2年后的年龄之和是23岁,牛牛3年后的年龄等于阿普1年前的年龄,求牛牛、阿普今年的年龄各是多少岁?
1812 |
1813 | ### 练习6
1814 |
1815 | 红红2年前的年龄与果果1年后的年龄相等,红红3年前的年龄与果果2年后的年龄和为18岁,则红红、果果今年各多少岁?
1816 |
1817 | ### 巩固1
1818 |
1819 | 维尼熊和跳跳虎去摘苹果。跳跳虎每摘7个,维尼熊只能摘4个。维尼熊摘了16分钟,跳跳虎摘了10分钟就累了,不摘了。他们回来后数了一下,共摘了670个苹果,那么其中维尼熊摘的苹果有多少个?
1820 |
1821 | ### 巩固2
1822 |
1823 | 甲、乙、丙3个数的和是99,如果甲加上10,乙减少5,丙减少2,则3个数相等。这3个数各是几?
1824 |
1825 | ### 巩固3
1826 |
1827 | 三块布料一共190米,第二块比第一块长20米,第三块比第二块长30米,每块布料各长多少米?
1828 |
1829 | ## 2.2.13. 逻辑推理进阶
1830 |
1831 | ### 热身1
1832 |
1833 | ### 热身2
1834 |
1835 | ### 热身3
1836 |
1837 | ### 例题1
1838 |
1839 | 乐乐老师、红红、丁丁、牛牛和田田一起去爬山。牛牛在丁丁和田田之前爬到终点,田田是紧跟着牛牛之后爬到终点的。有两个人在乐乐老师之后、丁丁之前爬到终点。这5个人登山到终点的先后顺序是怎样的?
1840 |
1841 | ### 练习1
1842 |
1843 | 田田比牛牛跑得慢,牛牛比加加跑得快,加加比减减跑得快,减减比田田跑得快。谁跑得最快?谁跑得最慢?
1844 |
1845 | ### 例题2
1846 |
1847 | 体育馆里正在进行一场精彩的乒乓球双打比赛。两位播音员正在议论这四个运动员的年龄问题:
1848 |
1849 | (1)小A比小B年轻;
1850 |
1851 | (2)小C比他的两个对手年龄都大;
1852 |
1853 | (3)小A比小D年龄大;
1854 |
1855 | (4)小B比小C年龄大。
1856 |
1857 | 请分析一下他们四人的年龄顺序,谁年龄最大?谁年龄最小?
1858 |
1859 | ### 练习2
1860 |
1861 | 2号大楼比3号大楼高,4号大楼比3号大楼低,1号大楼比2号大楼高,1号大楼比4号大楼高,几号大楼是最高的?几号大楼是最低的?
1862 |
1863 | ### 例题3
1864 |
1865 | 赵、钱、孙三人中,一位是射击运动员,一位是体操运动员,一位是跳水运动员。已知:
1866 |
1867 | (1)赵比体操运动员体重重;
1868 |
1869 | (2)钱和体操运动员体重不同;
1870 |
1871 | (3)赵和跳水运动员是朋友。
1872 |
1873 | 你能猜出谁是射击运动员,谁是体操运动员,谁是跳水运动员吗?
1874 |
1875 | ### 练习3
1876 |
1877 | 刘玉、马明、王建三个男孩都有一个妹妹,是小雅、小花、丽丽。6个人在一起打球,举行男女混合双打。事先规定,兄妹两人不搭伴。
1878 | 第一盘刘玉和丽丽对王建和小雅;第二盘王建和小花对刘玉和马明的妹妹。问丽丽、小雅和小花各是谁的妹妹?
1879 |
1880 | ### 例题4
1881 |
1882 | 一天,唐僧师徒四人路过一户人家,家里只有一个老爷爷和一个老奶奶,当唐僧师徒四人说明他们的来历后二老很热情地招待了他们,还要给他们做饭吃。唐僧见二老年事已高,决定他们自己动手做饭。他们一个在挑水,一个在烧火,一个在洗菜,一个在淘米。已知:
1883 |
1884 | (1)唐僧不挑水也不淘米;
1885 |
1886 | (2)悟空不洗菜也不挑水;
1887 |
1888 | (3)八戒不挑水也不洗菜;
1889 |
1890 | (4)假如悟空不淘米,那么沙僧就不挑水。
1891 |
1892 | 现在你知道他们分工的结果吗?
1893 |
1894 | ### 练习4
1895 |
1896 | 二年级有三个班举行数学竞赛,分别从三个班中选一名选手。牛牛、丁丁、田田参加抢答比赛,知道:牛牛比二(1)班的选手得分高,丁丁与二(1)班的选手得分同样多,又比二(3)班选手得分低。问牛牛、丁丁、田田各是哪班的选手?
1897 |
1898 | ### 例题5
1899 |
1900 | 甲、乙、丙三个小朋友分别喝三种不同的饮料,有另外三个小朋友猜他们喝的各是什么?
1901 |
1902 | 当当猜:甲喝可乐,乙喝芬达;
1903 |
1904 | 咚咚猜:乙喝雪碧,丙喝可乐;
1905 |
1906 | 林林猜:丙喝芬达,乙喝可乐。
1907 |
1908 | 己知每人都只猜对了一半,那么甲、乙、丙三位小朋友各喝什么饮料?
1909 |
1910 | ### 练习5
1911 |
1912 | 甲、乙、丙、丁四人同时参加全国小学数学夏令营。赛前甲、乙、丙分别做了预测。
1913 |
1914 | 甲说:丙第1名,我第3名。
1915 |
1916 | 乙说:我第1名,丁第4名。
1917 |
1918 | 丙说:丁第2名,我第3名。
1919 |
1920 | 成绩揭晓后,发现他们每人只说对了一半,你能说出他们的名次吗?
1921 |
1922 | ### 例题6
1923 |
1924 | 一个岛上住着说谎话的和说真话的两种人。说谎话的人句句是谎话,说真话的人句句是实话。如果有一天,你去岛上探险,碰到了岛上的三个人:王、李和张,相互交谈中,有这样一段对话。
1925 |
1926 | 王说:李和张都说谎。
1927 |
1928 | 李说:我没有说谎。
1929 |
1930 | 张说:李确实在说谎。
1931 |
1932 | 小朋友,你能知道他们三人中,有几个人说谎,有几个人说真话吗?
1933 |
1934 | ### 练习6
1935 |
1936 | 三只小猴子聪聪、淘淘、皮皮见到一个水果,他们分别判断这是什么水果。
1937 |
1938 | 聪聪判断:不是苹果,也不是梨。
1939 |
1940 | 淘淘判断:不是苹果,而是桃子。
1941 |
1942 | 皮皮判断:不是桃子,而是苹果。
1943 |
1944 | 老猴子告诉他们:有一只小猴子的判断完全正确,有一只小猴子说对了半,而另一只小猴子完全说错了。你知道三只小猴中谁是对的,谁是错的,谁是只对一半的吗?
1945 |
1946 | ### 拓展1
1947 |
1948 | 传说有个说谎国,这个国家的男人在星期四、五、六、日说真话,在星期一、二、三说假话;女人在星期一、二、三、日说真话,在星期四、五、六说假话.有一天,一个人到说谎国去旅游,他在那里认识了一男一女.男人说:“昨天我说的是假话”,女人说:“昨天也是我说假话的日子”.这下,那个外来的游人可发愁了,到底今天星期几呢?请同学们根据他们说的话,判断一下今天是星期几呢?
1949 |
1950 | ### 拓展2
1951 |
1952 | 张明、席辉和李刚在北京、上海和天津工作,他们的职业是工人、农民和教师,已知:
1953 |
1954 | (1)张明不在北京工作,席辉不在上海工作;
1955 |
1956 | (2)在北京工作的不是教师;
1957 |
1958 | (3)在上海工作的是工人;
1959 |
1960 | (4)席辉不是农民。
1961 |
1962 | 问:这三人各住哪里?各是什么职业?
1963 |
1964 | ### 拓展3
1965 |
1966 | 根据条件判断旅游团去了A、B、C、D、E中的哪几个地方?
1967 |
1968 | (1)如果去A,就必须去B;
1969 |
1970 | (2)D、E两地至少去一地;
1971 |
1972 | (3)B、C两地只能去一地;
1973 |
1974 | (4)C、E两地要去都去,要不去都不去;
1975 |
1976 | (5)若去D,则A、E两地必须去。
1977 |
1978 | ### 拓展4
1979 |
1980 | 甲、乙、丙、丁在谈论他们及他们的同学何伟的居住地。
1981 |
1982 | 甲说:我和乙都住在北京,丙住在天津;
1983 |
1984 | 乙说:我和丁都住在上海,丙住在天津;
1985 |
1986 | 丙说:我和甲都不住在北京,何伟住在南京;
1987 |
1988 | 丁说:甲和乙都住在北京,我住在广州。
1989 |
1990 | 假定他们每个人都说了两句真话,一句假话。问:不在场的何伟住在哪儿?
1991 |
1992 | ### 拓展5
1993 |
1994 | 宝宝、贝贝、聪聪每人有两个外号,人们有时以“数学博士”、“短跑健将”、“跳高冠军”、“小画家”、“大作家”和“歌唱家”称呼他们,此外:
1995 |
1996 | (1)数学博士夸跳高冠军跳的高
1997 |
1998 | (2)跳高冠军和大作家常与宝宝一起看电影
1999 |
2000 | (3)短跑健将请小画家画贺年卡
2001 |
2002 | (4)数学博士和小画家关系很好
2003 |
2004 | (5)贝贝向大作家借过书
2005 |
2006 | (6)聪聪下象棋常赢贝贝和小画家
2007 |
2008 | 问:宝宝、贝贝、聪聪各有哪两个外号吗?
2009 |
2010 | ## 2.2.14. 重叠问题
2011 |
2012 | ### 热身1
2013 |
2014 | ### 热身2
2015 |
2016 | ### 热身3
2017 |
2018 | ### 例题1
2019 |
2020 | 把两根长为20寸的短尺用绳子捆成一根长尺,中间捆在一起的重叠部分是3寸。捆成的长尺长多少寸?
2021 |
2022 | ### 练习1
2023 |
2024 | 有四块均长80厘米的木板,钉成一块长木板,中间钉在一起重叠的部分均是10厘米,钉成的长木板长多少厘米?
2025 |
2026 | ### 例题2
2027 |
2028 | 将两张同样长的纸粘成了一张长为80才的长纸条,其中粘在一起的部分长10寸,这两张纸条各长多少寸?
2029 |
2030 | ### 练习2
2031 |
2032 | 有两根铁丝,一根长为30厘米,另一根长为50厘米,将这两根铁丝焊接成一根长为75厘米的长铁丝。那么,中间的焊接重叠部分长为多少厘米?
2033 |
2034 | ### 例题3
2035 |
2036 | 私塾的学生都要参加比赛,有30人参加蹴鞠队,有27人参加毽子队。其中8人两种比赛都参加。一共有学生多少人?
2037 |
2038 | ### 练习3
2039 |
2040 | 二(1)班同学所有人都参加课外活动,有20人参加英语班,有26人参加电脑班。其中4人两个班都参加。二(1)班一共有多少人?
2041 |
2042 | ### 例题4
2043 |
2044 | 20个学生参加琵琶表演和古筝表演,其中有16人参加了琵琶表演,12人参加了古筝表演。问两种表演都参加的有多少学生?
2045 |
2046 | ### 练习4
2047 |
2048 | 春天来了,全班52人到北海公园划船,有27人划了手摇船,29人划了脚踏船,4名同学因身体不好没有划船而去游览了白塔。问:既划了手摇船也划了脚踏船的同学有多少人?
2049 |
2050 | ### 例题5
2051 |
2052 | 有蓝色和红色两种珠花,每人至少选一种,共有48人,有30人选了蓝色珠花,有13人两种都选了,那么选红色珠花的有多少人?
2053 |
2054 | ### 练习5
2055 |
2056 | 学校开设了自然和趣味数学两门选修课,每个同学至少要选一门,二(3)班共有56人,有30人选了自然课,有12人两门都选了,那么选趣味数学课的同学有多少人?
2057 |
2058 | ### 例题6
2059 |
2060 | 工厂筛选制镜工人,总共有60人报名参加。经过一段时间的训练后,有33人学会了制作星云镜,有25人学会了制作幻镜,其中既会制作星云镜又会制作幻镜的有10人。那么既不会制作星云镜又不会制作幻镜的有多少人?
2061 |
2062 | ### 练习6
2063 |
2064 | 某班共有46人,参加美术小组的有12人,参加音乐小组的有23人,有5人两个小组都参加了。这个班既没有参加美术小组也没参加音乐小组的有多少人?
2065 |
2066 | ## 2.2.15. 复杂的树阵图
2067 |
2068 | ### 热身1
2069 |
2070 | ### 热身2
2071 |
2072 | ### 热身3
2073 |
2074 | ### 例题1(辐射型)
2075 |
2076 | 把1,2,4,5,6,8,10这7个数分别填入图中的圆圈中,使得每条直线上4个数的和都等于20。
2077 |
2078 | 
2079 |
2080 | ### 练习1
2081 |
2082 | 把8,9,10,11,12,14,16这7个数分别填入图中的圆圈中,使得每条直线上4个数的和都等于46。
2083 |
2084 | ### 例题2
2085 |
2086 | 将5,9,13,14,17,21,25这7个数分别填入图中的圆圈中,使得每条直线上的3个数的和都等于44。
2087 |
2088 | 
2089 |
2090 | ### 练习2
2091 |
2092 | 将5,8,11,14,17,20,23这7个数分别填入图中的圆圈中,使得每条直线上的3个数的和都等于36。
2093 |
2094 | ### 例题3(封闭型)
2095 |
2096 | 把2,3,4,5,6,7,8这7个数分别填入图中的圆圈中,使两个正方形中4个数之和都等于19。
2097 |
2098 | ### 练习3
2099 |
2100 | 把2,3,4,5,6,7,8这7个数分别填入图中的圆圈中,使两个正方形中4个数之和都等于21。
2101 |
2102 | ### 例题4
2103 |
2104 | 把1,5,9,10,16,21这6个数分别填入图中的圆圈中,使每一个大圆上的4个数之和都等于36。
2105 |
2106 | ### 练习4
2107 |
2108 | 把1,2,4,5,6,11这6个数分别填入图中的圆圈中,使每一个大圆上的4个数之和都等于22。
2109 |
2110 | ### 例题5
2111 |
2112 | 将5,6,9,11,14,15这6个数分别填入图中的圆圈中,使两个大圆上4个数的和都等于40。
2113 |
2114 | ### 练习5
2115 |
2116 | 将4,7,9,12,15,17这6个数分别填入图中的圆圈中,使两个大圆上4个数的和都等于43。
2117 |
2118 | ### 例题6
2119 |
2120 | 将1,3,4,5,6,8,11,15这8个数分别填入图中的圆圈中,使两个大圆上5个数的和都等于33。
2121 |
2122 | ### 练习6
2123 |
2124 | 将2,5,6,8,10,12,14,22这8个数分别填入图中的圆圈中,使两个大圆上5个数的和都等于49。
2125 |
2126 | ## 2.2.16. 年龄问题初步
2127 |
2128 | ### 例题1
2129 |
2130 | 丁丁今年8岁,爸爸的年龄是丁丁的4倍,4年前,爸爸的年龄和丁丁相差几岁?
2131 |
2132 | ### 练习1
2133 |
2134 | 田田今年6岁,妈妈今年36岁,再过6年,田田读初中时,妈妈比田田大多少岁?
2135 |
2136 | ### 例题2
2137 |
2138 | 田田今年10岁,博士今年55岁,当田田17岁时,博士多少岁?
2139 |
2140 | ### 练习2
2141 |
2142 | 小芳今年10岁,妈妈比她大28岁,当小芳15岁时,妈妈多少岁?
2143 |
2144 | ### 例题3
2145 |
2146 | 今年小王子8岁,大王子14岁,当两人的年龄之和是40岁时,应该是几年之后?
2147 |
2148 | ### 练习3
2149 |
2150 | 今年太子8岁,王后34岁,当太子和王后两人的年龄和是50岁时,太子多少岁?王后多少岁?
2151 |
2152 | ### 例题4
2153 |
2154 | 爸爸今年40岁,妈妈今年38岁,儿子今年12岁,当爸爸、妈妈、儿子三人的年龄和是81岁时,爸爸多少岁?妈妈多少岁?儿子多少岁?
2155 |
2156 | ### 练习4
2157 |
2158 | 李文今年9岁,爸爸、妈妈的年龄和是81岁,问:多少年后他们三个的平均年龄是40岁?
2159 |
2160 | ### 例题5
2161 |
2162 | 李斯、韩非现在的年龄和是62岁,5年前,李斯比韩非大6岁,今年李斯、韩非两人各多少岁?
2163 |
2164 | ### 练习5
2165 |
2166 | 爸爸、妈妈现在的年龄和是72岁;5年后,爸爸比妈妈大6岁。今年爸爸妈妈二人各多少岁?
2167 |
2168 | ### 例题6
2169 |
2170 | 姐姐5年前的年龄与妹妹3年后的年龄相等,问姐姐和妹妹相差多少岁?
2171 |
2172 | ### 练习6
2173 |
2174 | 小明12年后的年龄与妈妈12年前的年龄相等,问小明和妈妈相差多少岁?
2175 |
2176 | ## 2.2.17. 画图法综合
2177 |
2178 | ### 热身1
2179 |
2180 | ### 热身2
2181 |
2182 | ### 热身3
2183 |
2184 | ### 例题1(排队问题)
2185 |
2186 | 小朋友们排成一个长方形队伍表演体操。
2187 | (1)从左边数起,小华排第18,从右边数起,小明排第16,小华的左边是小明,这一行共有多少人?
2188 | (2)从左面数小红排在第2个,小军排在小红右面第4个,那么小军从右往左数排在第几个?
2189 |
2190 | ### 练习1
2191 |
2192 | 一群小动物排队表演节目,小猪第18个出场,小狗表演完后面还有16个节目,已知小猪后面第二个节目是小狗表演的,求一共有多少个节目?
2193 |
2194 | ### 例题2(鸡兔同笼)
2195 |
2196 | 王大妈去市场上买回来了一些鸡和兔,她把鸡、兔关在同一个笼子里,数了数,共有11个头,30条腿,你知道王大妈买回来了几只鸡?几只兔?
2197 |
2198 | ### 练习2
2199 |
2200 | 鸡兔同笼,共有7个头,20条腿,有多少只鸡?多少只兔?
2201 |
2202 | ### 例题3(年龄问题)
2203 |
2204 | 爸爸、妈妈、小敏三人的年龄总和是73岁,爸爸比妈妈大3岁,小敏比妈妈小23岁。小敏今年多少岁?
2205 |
2206 | ### 练习3
2207 |
2208 | 三个小朋友比年龄,小明比小英小5岁,小方比小明大2岁。那么小英和小方差几岁?
2209 |
2210 | ### 例题4(画线段图)
2211 |
2212 | 一筐鲜鱼,连筐共重56千克。先卖出鲜鱼的一半,再卖出剩下的一半,这时连筐还重17千克。原来这筐鲜鱼重多少干克?
2213 |
2214 | ### 练习4
2215 |
2216 | 玻璃瓶里装着一些水,把水加到原来的2倍时,和瓶一起称重5千克;把水加到原来的4倍时,重为9千克,问原来水有多少千克?
2217 |
2218 | ### 例题5(盈亏问题)
2219 |
2220 | 田田到文具店买练习本,她带的钱若买4本,还剩2元;若买5本,就差7元。问田田一共带了多少钱?
2221 |
2222 | ### 练习5
2223 |
2224 | 牛牛妈妈到水果店买苹果,她带的钱若买4千克还剩8元;若买5千克,就差2元。问牛牛妈妈一共带了多少钱?
2225 |
2226 | ### 例题6
2227 |
2228 | 丁丁和牛牛都想买一个饼,但丁丁的钱币少2枚,牛牛的钱币少3枚。如果两个人的钱币合在一起就刚够买一个饼。问买一个饼需要多少枚钱币?丁丁和牛牛各有多少枚钱币?
2229 |
2230 | ### 练习6
2231 |
2232 | 王强和李明都想买一本《趣味数学》,但王强的钱少2元5角,李明的钱少3元1角。如果两个人的钱合在一起就刚够买这本书。问一本《趣味数学》多少钱?王强和李明各有多少钱?
2233 |
2234 | ### 拓展1
2235 |
2236 | 81 位同学排成 9 行 9 列的正方形队列表演体操,小花在队列中,正左边有 2 位同学,正前方有3位同学,这时整个队列的同学向右转,则小花的正前方有几位同学?正右边有几位同学?
2237 |
2238 | ### 拓展2
2239 |
2240 | 鸡兔同笼,共有60个头,且鸡腿是兔腿的2倍,有多少只鸡?多少只兔?
2241 |
2242 | ### 拓展3
2243 |
2244 | 14年前爸爸的年龄是儿子的5倍, 14年后父子二人年龄和是98岁,父子二人今年分别多少岁?
2245 |
2246 | ### 拓展4
2247 |
2248 | 学生们划船,如果每只船坐5人,则还有3人无船坐,如果其中两只船坐4人,其余的船每只坐6人,就恰好坐完所有学生,共有学生多少人?
2249 |
2250 | ### 拓展5
2251 |
2252 | 甲乙丙丁四个同学共买了37朵花,如果甲多买2朵,乙少买3多,丙买的朵数变成现在的2倍,丁买的朵数减少一半,那么四个人买的朵数正好相同。请问原来四个人各买了多少朵花?
2253 |
2254 | ## 2.2.18. 等式加减法
2255 |
2256 | ### 热身1
2257 |
2258 | 15个小朋友排队报数,从前边报起,牛牛报10,从后往前报起,丁丁报12,求从牛牛数到丁丁一共有多少人?
2259 |
2260 | ### 热身2
2261 |
2262 | 牛牛、田田、丁丁三个人分糖块。田田比丁丁多3块,牛牛比田田多2块。已知糖块总块数是50块,那么每人各分到多少块?
2263 |
2264 | ### 热身3
2265 |
2266 | 买4个足球和2个排球,共用去102元,已知每个足球比每个排球贵3元。问每个足球和排球各多少元?
2267 |
2268 | ### 例题1
2269 |
2270 | 下面不同的图各代表一个数,你知道它们各代表几吗?
2271 |
2272 | (1)
2273 |
2274 | $🍎+🍐+🍐=13$
2275 |
2276 | $🍎+🍐=10$
2277 |
2278 | $🍎=()$
2279 |
2280 | $🍐=()$
2281 |
2282 | (2)
2283 |
2284 | $🍊+🍊+🍑=15$
2285 |
2286 | $🍊+🍑=9$
2287 |
2288 | $🍊=()$
2289 |
2290 | $🍑=()$
2291 |
2292 | ### 练习1
2293 |
2294 | 下面等式中,□和△各表示几?
2295 | 已知:
2296 |
2297 | $□+□+△=16$
2298 | $□+□+△+△+△=24$
2299 | 求:
2300 |
2301 | $□=()$
2302 | $△=()$
2303 |
2304 | ### 例题2
2305 |
2306 | 下面不同的图各代表一个数,你知道它们各代表几吗?
2307 |
2308 | $🍇+🍎=16$
2309 |
2310 | $🍇-🍎=2$
2311 |
2312 | $🍎=()$
2313 |
2314 | $🍇=()$
2315 |
2316 | ### 练习2
2317 |
2318 | 下面不同的图各代表一个数,你知道它们各代表几吗?
2319 |
2320 | $🍌+🍓=15$
2321 |
2322 | $🍌-🍓=3$
2323 |
2324 | $🍌=()$
2325 |
2326 | $🍓=()$
2327 |
2328 | ### 例题3
2329 |
2330 | 你能根据下面两个等式,求出🍊和🍍各表示什么数吗?
2331 |
2332 | $🍊+🍊+🍍=10$
2333 |
2334 | $🍊+🍍+🍍=11$
2335 |
2336 | $🍊=()$
2337 |
2338 | $🍍=()$
2339 |
2340 | ### 练习3
2341 |
2342 | 已知:
2343 |
2344 | $☆+☆+☆+△+△=13$
2345 | $☆+☆+△+△+△=12$
2346 |
2347 | 求:
2348 |
2349 | $☆=()$
2350 | $△=()$
2351 |
2352 | ### 例题4
2353 |
2354 | 下面△、☆、▲各代表什么数?
2355 |
2356 | $△+☆=23$
2357 |
2358 | $△+▲=33$
2359 |
2360 | $☆+▲=30$
2361 |
2362 | ### 练习4
2363 |
2364 | 三种兔子各多少只?
2365 | 黑兔+白兔=6
2366 | 黑兔+灰兔=7
2367 | 白兔+灰兔=5
2368 |
2369 | ### 铺垫
2370 |
2371 | 根据条件写等式。
2372 |
2373 | ### 例题5
2374 |
2375 | 2瓶可乐和3个面包共27元,4瓶可乐和3个面包共39元。请你算一算,每瓶可乐和每个面包各多少元?
2376 |
2377 | ### 练习5
2378 |
2379 | 牛牛去商店买文具,买了3个本子和1支铅笔一共花了10元,又知道1个本子比1支铅笔贵2元,请问1个本子和1支笔各多少钱?
2380 |
2381 | ### 例题6
2382 |
2383 | 1千克瓜子和2千克花生,一共 32元。2千克瓜子和1千克花生,一共 28元。那么瓜子和花生每千克各多少元?
2384 |
2385 | ### 练习6
2386 |
2387 | 1件上衣与2条裤子的总价是500元,这件上衣比这2条裤子的价钱贵
2388 | 100 元。则1件上衣多少钱? 1条裤子多少钱?(2条裤子是一样的)
2389 |
2390 | ### 拓展1
2391 |
2392 | 下面每种水果各代表多少?
2393 |
2394 | $🍐+🍐+🍎+🍊=16$
2395 |
2396 | $🍐+🍎+🍎+🍊=13$
2397 |
2398 | $🍐+🍎+🍊+🍊=11$
2399 |
2400 | ### 拓展2
2401 |
2402 | 饲养场出售鸡、鸭,张大爷买2只鸭和3只鸡共用42元,李大叔买3只鸭和2只鸡共用43元。1只鸭和一只鸡各多少元?
2403 |
2404 | ### 拓展3
2405 |
2406 | 小军家养了一些大白兔和小花猫。有一天,小军抱着2只大白兔一起站在体重计上称一称,正好是 45千克;后来小军放下大白兔又抱着3只小花猫,站在体重计上称一称,正好是47千克;最后小军把 6只小花猫和4只大白兔一起放在体重计上称一称是44千克。请你算一算小军、大白兔和小花猫各是多少千克?(每只大白兔的重量一样,每只小花猫的重量一样。)
2407 |
2408 | ### 拓展4
2409 |
2410 | ### 拓展5
2411 |
2412 | ## 2.2.19. 动手操作
2413 |
2414 | ### 热身1
2415 |
2416 | ### 热身2
2417 |
2418 | ### 热身3
2419 |
2420 | ### 例题1
2421 |
2422 | 大勺子一次能装油250克,小勺子一次能装油150克,你能用这两把勺子往一个空杯子里倒入350克油吗?
2423 |
2424 | ### 练习1
2425 |
2426 | 兔妈妈有一包70克的药,想要用天平从中称出5克的药,可只有一个20克的砝码,怎么办?
2427 |
2428 | ### 例题2
2429 |
2430 | 两个人要平分12千克的一大桶油。身边只有能装9千克和5千克的两只空桶,怎样倒才能使他们分到一样多的油呢?
2431 |
2432 | ### 练习2
2433 |
2434 | 一个人带着两只空桶去沟边取水,一只桶可盛5千克水,另一只可盛7千克水,现在要取8千克水,应该怎样取?
2435 |
2436 | ### 例题3
2437 |
2438 | 有九颗珍珠,其中有一颗是假珍珠,外观和真的一样,不容易看出来,只是假珍珠比真珍珠轻一些。你能利用天平,不用砝码,只称两次就找出假的珍珠吗?怎样称?
2439 |
2440 | ### 练习3
2441 |
2442 | 有八颗珍珠,其中有一颗是假珍珠,外观和真的一样,不容易看出来,只是假珍珠比真珍珠轻一些。你能利用天平,不用砝码,最少称几次就找出假的珍珠吗?怎样称?
2443 |
2444 | ### 例题4
2445 |
2446 | 黑猫警长在海关截获了一批装有牛肉罐头的9个大箱子,每箱里有很多盒罐头(大于1盒),箱子里每盒罐头重100克。在这9个大箱子中,其中有1箱罐头已经过期,不符合出口标准,过期的罐头每盒要比原来重1克。黑猫警长准备用一个大的电子称把这箱过期罐头称出来,请你帮忙想一想,最少需要称几次就能把这箱不合格的罐头找出来?
2447 |
2448 | ### 练习4
2449 |
2450 | 有10箱钢珠,每个钢珠重10克,每箱600个。如果这10箱钢珠中有1箱次品,次品钢珠每个重9克,那么,要找出这箱次品最少要称几次?
2451 |
2452 | ### 例题5
2453 |
2454 | 8个队参加扔石头大赛,比赛采用淘汰赛制,每2个队进行1场比赛,每场比赛输的1队被淘汰,最后决出冠军。同学们,请你算一算,一共要举行多少场比赛?
2455 |
2456 | ### 练习5
2457 |
2458 | 32个篮球队进行篮球比赛,裁判对他们说:“本次比赛采用淘汰赛,每2个队进行1场比赛,每场比赛输的1队被淘汰,最后决出冠军。”同学们,如果你做裁判,请你算一算一共要举行多少场比赛?
2459 |
2460 | ### 例题6
2461 |
2462 | 丁丁,牛牛,田田,阿普,小乐,5名同学参加跳绳比赛,比赛前每2个小朋友都要握一次手表示友好。当丁丁握了4次手,牛牛握了3次手,田田握了2次手,阿普握了1次手的时候,小乐握了几次手?最后这5名小朋友一共要握多少次手?
2463 |
2464 | ### 练习6
2465 |
2466 | 动物王国的动物们在比赛之前都要握手表示友好,这时,狐狸握了3次手,熊猫握了4次手,兔子也握了4次手,小猪握了3次手,狮子握了几次手呢?
2467 |
2468 | ### 拓展1
2469 |
2470 | ### 拓展2
2471 |
2472 | ### 拓展3
2473 |
2474 | ### 拓展4
2475 |
2476 | ### 拓展5
2477 |
2478 | ### 练习1
2479 |
2480 | ### 练习2
2481 |
2482 | ### 练习3
2483 |
2484 | ### 练习4
2485 |
2486 | ### 练习5
2487 |
2488 | ### 练习6
2489 |
2490 | ## 2.2.20. 必胜策略
2491 |
2492 | ### 例题1
2493 |
2494 | 桌子上放着18根火柴,甲、乙二人轮流每次取走1~3根。规定谁取走最后1根火柴谁获胜。甲先取,那么怎样取才能获胜?
2495 |
2496 | ### 练习1
2497 |
2498 | 桌子上放着50根火柴,甲、乙二人轮流每次取走1~3根。规定谁取走最后1根火柴谁获胜。如果双方均采用最佳方法,甲先取,那么怎样取才能获胜?
2499 |
2500 | ### 例题2
2501 |
2502 | 桌子上放着80根火柴,甲、乙二人轮流每次取走1~9根。规定谁取走最后1根火柴谁获胜。如果双方采用最佳方法,甲先取,那么谁将获胜?
2503 |
2504 | ### 练习2
2505 |
2506 | 桌子上放着75根火柴,甲、乙二人轮流每次取走1~4根。规定谁取走最后1根火柴谁获胜。如果双方采用最佳方法,甲先取,那么谁将获胜?
2507 |
2508 | ### 例题3
2509 |
2510 | 桌子上放着21根火柴,甲、乙二人轮流每次取走1~4根。规定谁取走最后1根火柴谁就输。如果甲想获胜,应该怎样取?
2511 |
2512 | ### 练习3
2513 |
2514 | 桌子上放着28根火柴,甲、乙二人轮流每次取走1~5根。规定谁取走最后1根火柴谁就输。甲先取,那么怎样取才能获胜?
2515 |
2516 | ### 例题4
2517 |
2518 | 两个人从1开始按自然数顺序轮流依次报数,每人每次只能报1~3个数,谁先报到30谁获胜。你选择先报数还是后报数?怎样才能获胜?
2519 |
2520 | ### 练习4
2521 |
2522 | 两个人从1开始按自然数顺序轮流依次报数,每人每次只能报1~4个数,谁先报到32谁获胜。你选择先报数还是后报数?怎样才能获胜?
2523 |
2524 | ### 例题5
2525 |
2526 | 31个方格排成一行,最左端方格中放有一枚棋子,甲先乙后轮流向右移动棋子,每次移动1~3个格。规定将棋子移到最后1格者输。甲为了获胜,第一步必须向右移多少格?
2527 |
2528 | ### 练习5
2529 |
2530 | 共有54张扑克牌,由两人轮流来抽,每次可抽1~6张,抽到最后1张牌的人就算输了,如果第一个抽牌的人想赢,第一次应该抽几张牌。
2531 |
2532 | ### 例题6
2533 |
2534 | 甲、乙两人玩游戏:有18枚棋子,两人轮流取棋子,每次允许取其中2枚、4枚或8枚,谁取到最后一枚棋子,谁就获胜。甲想获胜,先取还是后取?应该怎样取?
2535 |
2536 | ### 练习6
2537 |
2538 | 甲、乙两人玩游戏:有28枚棋子,两人轮流取棋子,每次允许取其中2枚、4枚或8枚,谁取到最后一枚棋子,谁就获胜。如果甲先取,那么第一次甲取几枚才能保证一定获胜?
2539 |
2540 | ### 拓展1
2541 |
2542 | ### 拓展2
2543 |
2544 | ### 拓展3
2545 |
2546 | ### 拓展4
2547 |
2548 | ### 拓展5
2549 |
2550 | ###
2551 |
--------------------------------------------------------------------------------
/03-三年级.md:
--------------------------------------------------------------------------------
1 | ---
2 | title: 三年级
3 | lang: zh-CN
4 | sidebarDepth: 1
5 | ---
6 |
7 | # 三年级
8 |
9 | ## 3.1.01. 找规律综合
10 |
11 | ### 例题1(递推规律)
12 |
13 | 先找出下列数排列的规律,并根据规律在括号里填上适当的数。
14 |
15 | (1)1,4,7,10,(),16,19。
16 |
17 | (2)2,6,18,(),162。
18 |
19 | ### 练习1
20 |
21 | 先找出下列各列数的排列规律,然后在括号里填上适当的数。
22 |
23 | (1)2,6,10,14,(),22,26。
24 |
25 | (2)3,6,9,12,(),18,21。
26 |
27 | ### 例题2(间隔规律)
28 |
29 | 先找出规律,然后在括号里填上适当的数。
30 |
31 | 23,4,20,6,17,8,(),(),11,12。
32 |
33 | ### 练习2
34 |
35 | 先找出规律,然后在括号里填上适当的数。
36 |
37 | (1)3,2,5,2,7,2,(),(),11,2。
38 |
39 | (2)19,3,17,3,15,3,(),(),11,3。
40 |
41 | ### 例题3(兔子数列/斐波那契数列)
42 |
43 | 在数列1,1,2,3,5,8,13,(),34,55,……中,括号里应填什么数?
44 |
45 | ### 练习3
46 |
47 | 先找出规律,然后在括号里填上适当的数。
48 |
49 | 2,2,4,6,10,16,(),()。
50 |
51 | ### 例题4(算式规律)
52 |
53 | 根据前面图形中的数之间的关系,想一想第三个图形的括号里应填什么数?
54 |
55 | 
56 |
57 | ### 练习4
58 |
59 | 根据下表中的排列规律,在空格里填上适当的数。
60 |
61 | | 12 | 18 | 6 |
62 | | ---- | ---- | ---- |
63 | | 8 | 15 | 7 |
64 | | 4 | | 8 |
65 |
66 | ### 例题5
67 |
68 | 先计算下面一组算式的第一题,然后找出其中的规律,并根据规律直接写出后几题的得数。
69 |
70 | (1)12345679×9
71 |
72 | (2)12345679×18
73 |
74 | (3)12345679×54
75 |
76 | (4)12345679×81
77 |
78 | ### 练习5
79 |
80 | 计算:
81 |
82 | (1)26×11
83 |
84 | (2)38×11
85 |
86 | ### 例题6(图形规律)
87 |
88 | 观察下面由点组成的图形(点群),请回答:
89 |
90 | (1)方框内的点群包含多少个点?
91 |
92 | (2)第10个点群中包含多少个点?
93 |
94 | (3)前十个点群中,所有点的总数是多少?
95 |
96 | 
97 |
98 | ### 练习6
99 |
100 | 观察下面的图形,按规律在“?”处填上适当的图形。
101 |
102 | 
103 |
104 | ## 3.1.02. 加减法巧算综合
105 |
106 | ### 热身1
107 |
108 | 找规律填数。
109 |
110 | 10,13,18,25,(),(),58。
111 |
112 | ### 热身2
113 |
114 | 找规律填数。
115 |
116 | 3,29,4,28,6,26,9,23,(),(),18,14。
117 |
118 | ### 热身3
119 |
120 | 计算:$11+12+13+14+15+16+17+18+19=$
121 |
122 | ### 例题1(凑整法)
123 |
124 | 计算。
125 |
126 | (1)$132+23+48+257+40=$
127 |
128 | (2)$32+24+68=$
129 |
130 | ### 练习1
131 |
132 | 计算。
133 |
134 | (1)$238+45+67+62+55=$
135 |
136 | (2)$13+21+87+19=$
137 |
138 | ### 例题2(基准数)
139 |
140 | 计算。
141 |
142 | (1)$9+99+999+9999=$
143 |
144 | (2)$3998+407+89=$
145 |
146 | ### 练习2
147 |
148 | 计算。
149 |
150 | (1)$295+196+297+198+199+15=$
151 |
152 | (2)$19+199+1999=$
153 |
154 | ### 例题3
155 |
156 | 计算。
157 |
158 | (1)$268-56-82-44-18=$
159 |
160 | (2)$$
161 |
162 | ### 练习3
163 |
164 | 计算。
165 |
166 | (1)$831-155-67-145-131=$
167 |
168 | (2)$$
169 |
170 | ### 例题4
171 |
172 | 计算。
173 |
174 | (1)$300-9-19-29-39-49-59=$
175 |
176 | (2)$985-32+37-276-85+73-68=$
177 |
178 | ### 练习4
179 |
180 | 计算。
181 |
182 | (1)$818-271-18+64-29+36=$
183 |
184 | (2)$200-20-18-23-20-19-21=$
185 |
186 | ### 例题5
187 |
188 | 计算。
189 |
190 | (1)$2985-(985-276)=$
191 |
192 | (2)$$
193 |
194 | ### 练习5
195 |
196 | 计算。
197 |
198 | (1)$(123+348+400)-(23+150+148)=$
199 |
200 | (2)$$
201 |
202 | ### 例题6(分组巧算)
203 |
204 | 计算。
205 |
206 | (1)$20-19-18+17+16-15-14+13+12-11-10+9=$
207 |
208 | (2)$1+2-3-4+5+6-7-8+9+10-11-12+……-1999-2000+2001=$
209 |
210 | ### 练习6
211 |
212 | 计算。
213 |
214 | (1)$3355+4466+9977-3366-4477-9955=$
215 |
216 | (2)$$
217 |
218 | ### 例题7
219 |
220 | 【变零为整】$74+63+16-53+9+81=$
221 |
222 | 【变长为短】$38+57+36-57-36=$
223 |
224 | 【变大为小】$365-198+196+295-296=$
225 |
226 | 【变加为乘】$97+98+100+101+102=$
227 |
228 | 【位值原理】$1243+4132+2314+3421=$
229 |
230 | ### 练习7
231 |
232 | 【去括号】$2748+(1336+289)-(336+289)-748=$
233 |
234 | 【填括号】$1518-571-18+61-29+39=$
235 |
236 | ### 例题8
237 |
238 | 计算:$689-1-3-5-7-9-11-13-15-17-19$
239 |
240 | ### 练习8
241 |
242 | 计算:$9999-1-2-3-\dots-28-29-30-29-28-\dots-3-2-1$
243 |
244 | ### 拓展1
245 |
246 | 计算$1017+2017+3017+4017+5017-6017-7017$
247 |
248 | ### 拓展2
249 |
250 | 有一个很神秘的地方,那里有很多的雕塑,每个雕塑都是由蝴蝶组成的。已知一共有1000只蝴蝶,第1个雕塑有3只蝴蝶,第2个雕塑有5只蝴蝶,第3个雕塑有7只蝴蝶,第4个雕塑有9只蝴蝶,后面的雕塑按照这样的规律一直延伸到很远的地方,松松沿着雕塑走了一会,
251 | 停在了一个有39只蝴蝶的雕塑旁。那么,他们没数完的蝴蝶还剩多少只呢?
252 |
253 | ### 拓展3
254 |
255 | 书店里有一套漫画书共9册,第一册需24元,第二册需23元,第三册需22元,以此类推,每一册的售价都比它前面的一册要少1元。如果用200元去买这套漫画书,书店老板应该找回多少元呢?
256 |
257 | ## 3.1.03. 加减法竖式数字谜进阶
258 |
259 | ### 例题1
260 |
261 | 在空格内填入适当的数字,使图中的竖式成立。
262 |
263 | (1)$$\begin{matrix}
264 | & &3 &\Box &4 \\
265 | +& &\Box &5 &\Box \\
266 | \hline
267 | &\Box &1 &5 &2
268 | \end{matrix}$$
269 |
270 | (2)$$\begin{matrix}
271 | &\Box &2 &\Box \\
272 |
273 | -&2 &\Box &4 \\
274 |
275 | \hline
276 | &1 &5 &2
277 | \end{matrix}$$
278 |
279 | ### 练习1
280 |
281 | 在空格内填入适当的数字,使图中的竖式成立。
282 |
283 | (1)$$\begin{array}{c}
284 | & &6 &\Box &3 \\
285 | +& &\Box &4 &\Box \\
286 | \hline
287 | &\Box &1 &7 &2
288 | \end{array}$$
289 |
290 | (2)$$\begin{matrix}
291 | &\Box &5 &\Box \\
292 | -&4 &\Box &6 \\
293 | \hline
294 | &3 &7 &1
295 | \end{matrix}$$
296 |
297 | ### 例题2
298 |
299 | 在空格内填入适当的数字,使图中的竖式成立。
300 |
301 | (1)$$\begin{matrix}
302 | & & &7 &\Box \\
303 | +& &\Box &\Box&4 \\
304 | \hline
305 | &\Box &\Box &5 &3
306 | \end{matrix}$$
307 |
308 | (2)$$\begin{matrix}
309 | &\Box &\Box &8 &\Box \\
310 | -& &\Box &\Box &4 \\
311 | \hline
312 | & & &9 &7
313 | \end{matrix}$$
314 |
315 | ### 练习2
316 |
317 | 在空格内填入适当的数字,使图中的竖式成立。
318 |
319 | (1)$$\begin{matrix}
320 | & & &8 &\Box \\
321 | +& &\Box &\Box &2 \\
322 | \hline
323 | &\Box &\Box &6 &1
324 | \end{matrix}$$
325 |
326 | (2)$$\begin{matrix}
327 | &\Box &\Box &7 &\Box \\
328 | -& &\Box &\Box &3 \\
329 | \hline& & &9 &6
330 | \end{matrix}$$
331 |
332 | ### 例题3
333 |
334 | 在空格内填入适当的数字,使图中的竖式成立。
335 |
336 | $$\begin{matrix}
337 | & &\Box &6 &\Box \\
338 | +& &2 &\Box &6 \\
339 | \hline
340 | &\Box &\Box &\Box &\Box \\
341 | -& &\Box &\Box &\Box \\
342 | \hline
343 | & & & &1
344 | \end{matrix}$$
345 |
346 | ### 练习3
347 |
348 | 在空格内填入适当的数字,使图中的竖式成立。
349 |
350 | $$\begin{matrix}
351 | &\Box &7 &\Box &8 \\
352 | +&1 &\Box &9 &\Box \\
353 | \hline&2 &9 &0 &9
354 | \end{matrix}$$
355 |
356 | ### 例题4
357 |
358 | 在下图的竖式中,不同的汉字代表不同的数字,相同的汉字代表相同的数字,每个汉字代表什 么数时,竖算式成立?
359 |
360 | $$\begin{matrix}
361 | & & & &生 \\
362 | & & &学 &生 \\
363 | & &好 &学 &生 \\
364 | +&三 &好 &学 &生 \\
365 | \hline&2 &0 &1 &6
366 | \end{matrix}$$
367 |
368 | ### 练习4
369 |
370 | 在下图的竖式中,不同的汉字代表不同的数字,相同的汉字代表相同的数字,每个汉字代表什 么数时,竖算式成立?
371 |
372 | $$\begin{matrix}
373 | & & & &龙 \\
374 | & & &成 &龙 \\
375 | & &子 &成 &龙 \\
376 | +&望 &子 &成 &龙 \\
377 | \hline&2 &0 &1 &2
378 | \end{matrix}$$
379 |
380 | ### 例题5
381 |
382 | 在下图的竖式中,不同的字母代表不同的数字,相同的字母代表相同的数字,每个字母代表什 么数时,竖算式成立?
383 |
384 | $$\begin{matrix}
385 | & &A &B &C &D \\
386 | +& &E &B &E &D \\
387 | \hline&E &D &C &A &D
388 | \end{matrix}$$
389 |
390 | ### 练习5
391 |
392 | 如下图,算式中不同的汉字代表不同的数字,已知:”级=5“,那么”学而思“代表的三位数是多少?
393 |
394 | $$\begin{matrix}
395 | & &学 &而 &思 \\
396 | +& &1 &2 &级 \\
397 | \hline&更 &进 &1 &步
398 | \end{matrix}$$
399 |
400 | ### 例题6
401 |
402 | 下面的减法算式中,每一个字母代表一个数字,不同的字母代表不同的数字,计算:D+G。
403 |
404 | $$\begin{matrix}
405 | &A &B &C &B &D \\
406 | -& &E &F &A &G \\
407 | \hline& & &F &F &F
408 | \end{matrix}$$
409 |
410 | ### 练习6
411 |
412 | 在下图的竖式中,不同的汉字代表不同的数字,相同的汉字代表相同的数字,每个汉字代表什 么数时,竖算式成立?
413 |
414 | $$\begin{matrix}
415 | &机 &器 &人 \\
416 | +&机 &机 &人 \\
417 | \hline&器 &人 &人
418 | \end{matrix}$$
419 |
420 | ## 3.1.06. 巧求周长进阶
421 |
422 | ### 例题1
423 |
424 | 将一个大正方形剪去四个相同大小的小正方形后,计算剩下部分的周长。
425 |
426 | 
427 |
428 | ### 练习1
429 |
430 | 计算下面这个图形的周长。(单位:厘米)
431 |
432 | 
433 |
434 | ### 例题2
435 |
436 | 用五个完全相同的小长方形拼成一个如图所示的大长方形,小长方形的周长是 40 厘米,那么大长方形的周长是多少?
437 |
438 | 
439 |
440 | ### 练习2
441 |
442 | 4个完全相同的小长方形拼成一个如图所示的大长方形,只知道小长方形的宽是2厘米,大长方形的周长是多少?
443 |
444 | 
445 |
446 | ### 例题3
447 |
448 | 若每个小正方形的周长为 12厘米,则他们组合而成的“十” 字图形的周长是多少?
449 |
450 | 
451 |
452 | ### 练习3
453 |
454 | 用五个完全相同的小正方形拼成如下图形,已知拼出图形的周长是24厘米,你知道所用小正方形的面积是多少吗?
455 |
456 | 
457 |
458 | ### 例题4
459 |
460 | 将一个长为12厘米,宽为6厘米的长方形纸片按照图中虚线剪成两个图形,请计算两个图形的周长之和?
461 |
462 | 
463 |
464 | ### 练习4
465 |
466 | 将一个边长为4厘米的正方形对折,再沿折线剪开,得到两个长方形,求两个长方形比原来的正方形周长多了多少。
467 |
468 | ### 例题5
469 |
470 | 用8张边长是2厘米的小正方形拼成一个长方形,这个长方形的周长是多少厘米?
471 |
472 | ### 练习5
473 |
474 | 用6张边长为3厘米的正方形纸片拼成一个长方形,这个长方形的周长是多少厘米?
475 |
476 | ### 例题6
477 |
478 | 商场举行大酬宾活动,门口将长18厘米,宽9厘米的礼品盒摆成一个有规律的形状。礼品盒前4层的样式如图所示,一共有10 层,你能算出一共摆了多少个礼品盒吗? 礼品盒摆出形状的周长是多少?
479 |
480 | 
481 |
482 | ### 练习6
483 |
484 | 如图所示,长方形长4厘米,宽2厘米,现沿对角线 BD对折得到如下几何图形,试求图形阴影部分的周长。
485 |
486 | 
487 |
488 | ## 3.1.07. 平均数初步
489 |
490 | ### 例题1
491 |
492 | 幼儿园小朋友做红花,小华做了27朵,小方做了29朵,小林和小宁合做了52朵。平均每个小朋友做了多少朵?
493 |
494 | ### 练习1
495 |
496 | 一个书架上第一层放书52本,第二层和第三层共放70本,第四层放了46本,平均每层放书多少本?
497 |
498 | ### 例题2
499 |
500 | 中关村小学有15名同学参加跳绳比赛,他们跳绳的个数分别为93、94、85、92、86、88、94、91、88、89、92、86、93、90、89,求平均每人跳绳多少个?
501 |
502 | ### 练习2
503 |
504 | 下图是小华五次数学测验成绩的统计图。小华五次测验的平均分是多少分?
505 |
506 |  507 |
508 | ### 例题3
509 |
510 | 小华期末考试时,语文、数学和音乐三科成绩平均分是96分,英语成绩公布后,四科平均分下降了2分,小华英语成绩是多少分?
511 |
512 | ### 练习3
513 |
514 | 宁宁期中考试语文、数学、自然的平均分是91分,英语成绩公布后,他的平均分提高了2分。宁宁英语考了多少分?
515 |
516 | ### 例题4
517 |
518 | 果品店把2千克酥糖,3千克水果糖,4千克奶糖混合成什锦糖。已知酥糖每千克12元,水果糖每千克11元,奶糖每干克15元。问:什锦糖每千克多少元?
519 |
520 | ### 练习4
521 |
522 | 果品店把3千克水果糖,9千克奶糖混合成什锦糖,已知水果糖每千克7元,奶糖每千克11元,那么什锦糖每千克多少元?
523 |
524 | ### 例题5
525 |
526 | 6个学生的年龄正好是连续自然数,他们的年龄和与小明爸爸的年龄相同,7个人年龄一共是126岁,求这6个学生各几岁。
527 |
528 | ### 练习5
529 |
530 | 已知8个连续奇数的和是144,求这8个连续奇数。
531 |
532 | ### 例题6
533 |
534 | 这学期,丁丁5次随堂测试都得了84分,牛牛前4次测试分别比丁丁多出了1分、2分、3分、4分,请问第5次测试牛牛至少要考多少分,才能确保这5次测试的平均成绩高于丁丁至少了分?
535 |
536 | ### 练习6
537 |
538 | 楠楠的8个同学,数学考试成绩的平均数为80,若把其中的一个成绩改为82,则平均数变成了82。问被改动的数原来是多少?
539 |
540 | ## 3.1.08. 归一问题
541 |
542 | ### 例题1
543 |
544 | 王叔叔加工面条,5天加工40千克,照这样算,30天可加工面条多少千克?
545 |
546 | ### 练习1
547 |
548 | 乐乐老师批改4本作业用12分钟,照这样计算,三年级(5)班30本作业要批改多长时间?
549 |
550 | ### 例题2
551 |
552 | 丁丁3分钟完成24道口算,照这样的速度,完成56道口算要多少分钟?
553 |
554 | ### 练习2
555 |
556 | 一台割草机3小时可割草480千克,照这样的速度计算,割640千克要用多少小时?
557 |
558 | ### 例题3
559 |
560 | 一辆汽车从甲地开往乙地,每小时行60千米,5小时到达。若要4小时到达,则每小时需要多行多少千米?
561 |
562 | ### 练习3
563 |
564 | 某厂运来一批煤,计划每天用5吨,40天用完,如果改进锅炉后,每天节约1吨煤,这批煤可以用多少天?
565 |
566 | ### 例题4
567 |
568 | 一个果园请人帮忙摘桃子,4个人3小时共摘桃子600千克,照这样的效率计算,5个人8小时可以摘多少千克桃子?
569 |
570 | ### 练习4
571 |
572 | 15头牛4天吃了1260千克草,照这样计算,30头牛10天吃草多少千克?
573 |
574 | ### 例题5
575 |
576 | 6辆卡车运送4趟可以运走沙石48吨。如果有400吨沙石需要10趟运完,那么一共需要多少辆卡车?
577 |
578 | ### 练习5
579 |
580 | 4辆汽车5小时共运土石400方,现有10辆同样的汽车,要运1000方土石,需几小时?
581 |
582 | ### 例题6
583 |
584 | 一件工作12人每天工作8小时需要10天,照这样计算,如果增加8人,每天减少2小时,可以提前几天完成?
585 |
586 | ### 练习6
587 |
588 | 学校买来一批粉笔,原计划18个班可用60天,实际用45天后,有3个班外出了,剩下的粉笔够用多少天?
589 |
590 | ## 3.1.09.长方形与正方形
591 |
592 | ### 课前热身
593 |
594 | 【热身1】有20人修筑一条公路,计划15天完成。动工3天后抽出5人去植树,留下的人继续修路。如果每个人的工作效率不变,那么修完中段公路实际用多少天?
595 |
596 |
597 |
598 | 【热身2】已知3名模范职工和6名普通职工8小时可以生产零件420个。现在有一批生产任务,需要6名模范职工和12名普通职工生产14小时才能完成。如果工作了4小时后,又来了4名模范职工和8名普通职工,可以提前几小时完成任务?
599 |
600 |
601 |
602 | ### 学习目标
603 |
604 | - 理解面积的意义(面积的单位及其转换)
605 | - 会求长方形和正方形的面积(正方形面积=边长×边长;长方形面积=长×宽)
606 | - 掌握简单的割补、剪拼。
607 | - 长方形、正方形面积与周长区分和灵活转换
608 | - 运用长方形、正方形的性质(周长和面积)解决问题
609 | - 拓展——田字格模型
610 |
611 |
612 |
613 | ### 引入
614 |
615 | 对面积的直观感受和比较
616 |
617 |
618 |
619 | 【补充】有两个一样的长方形,长都是4厘米,宽都是2厘米。
620 |
621 | 把它们拼成一个长方形,请画出草图,并计算其周长和面积。
622 |
623 | 把它们拼成一个正方形,请画出草图,并计算其周长和面积。
624 |
625 |
626 |
627 | 一个花园长15米,宽10米,如果把这个花园用篱笆围起来,所围成的面积有多大?需要多长的篱笆?
628 |
629 |
630 |
631 | #### 单位换算
632 |
633 | (1)1米=()分米=()厘米=()毫米
634 |
635 | (2)1平方米=()平方分米=()平方厘米=()平方毫米
636 |
637 | (3)1平方千米=()平方米
638 |
639 | (4)8平方米=()平方分米
640 |
641 | (5)13平方米=()平方厘米
642 |
643 | (6)()平方米=500平方分米=()平方厘米
644 |
645 |
646 |
647 | #### 补充
648 |
649 | 选择合适的单位填入括号内。
650 |
651 | (1)一栋楼高约50()
652 |
653 | (2)课本封面面积约为6()
654 |
655 | (3)一个茶杯高约13()
656 |
657 | (4)黑板的面积约为5()
658 |
659 | (5)指甲盖的面积约为1()
660 |
661 | (6)一间教师的面积约为40()
662 |
663 |
664 |
665 |
666 |
667 | ### 例题练习
668 |
669 | #### 割补法求面积
670 |
671 | 【例题1】求下面图形的面积。(单位:厘米)
672 |
673 |
507 |
508 | ### 例题3
509 |
510 | 小华期末考试时,语文、数学和音乐三科成绩平均分是96分,英语成绩公布后,四科平均分下降了2分,小华英语成绩是多少分?
511 |
512 | ### 练习3
513 |
514 | 宁宁期中考试语文、数学、自然的平均分是91分,英语成绩公布后,他的平均分提高了2分。宁宁英语考了多少分?
515 |
516 | ### 例题4
517 |
518 | 果品店把2千克酥糖,3千克水果糖,4千克奶糖混合成什锦糖。已知酥糖每千克12元,水果糖每千克11元,奶糖每干克15元。问:什锦糖每千克多少元?
519 |
520 | ### 练习4
521 |
522 | 果品店把3千克水果糖,9千克奶糖混合成什锦糖,已知水果糖每千克7元,奶糖每千克11元,那么什锦糖每千克多少元?
523 |
524 | ### 例题5
525 |
526 | 6个学生的年龄正好是连续自然数,他们的年龄和与小明爸爸的年龄相同,7个人年龄一共是126岁,求这6个学生各几岁。
527 |
528 | ### 练习5
529 |
530 | 已知8个连续奇数的和是144,求这8个连续奇数。
531 |
532 | ### 例题6
533 |
534 | 这学期,丁丁5次随堂测试都得了84分,牛牛前4次测试分别比丁丁多出了1分、2分、3分、4分,请问第5次测试牛牛至少要考多少分,才能确保这5次测试的平均成绩高于丁丁至少了分?
535 |
536 | ### 练习6
537 |
538 | 楠楠的8个同学,数学考试成绩的平均数为80,若把其中的一个成绩改为82,则平均数变成了82。问被改动的数原来是多少?
539 |
540 | ## 3.1.08. 归一问题
541 |
542 | ### 例题1
543 |
544 | 王叔叔加工面条,5天加工40千克,照这样算,30天可加工面条多少千克?
545 |
546 | ### 练习1
547 |
548 | 乐乐老师批改4本作业用12分钟,照这样计算,三年级(5)班30本作业要批改多长时间?
549 |
550 | ### 例题2
551 |
552 | 丁丁3分钟完成24道口算,照这样的速度,完成56道口算要多少分钟?
553 |
554 | ### 练习2
555 |
556 | 一台割草机3小时可割草480千克,照这样的速度计算,割640千克要用多少小时?
557 |
558 | ### 例题3
559 |
560 | 一辆汽车从甲地开往乙地,每小时行60千米,5小时到达。若要4小时到达,则每小时需要多行多少千米?
561 |
562 | ### 练习3
563 |
564 | 某厂运来一批煤,计划每天用5吨,40天用完,如果改进锅炉后,每天节约1吨煤,这批煤可以用多少天?
565 |
566 | ### 例题4
567 |
568 | 一个果园请人帮忙摘桃子,4个人3小时共摘桃子600千克,照这样的效率计算,5个人8小时可以摘多少千克桃子?
569 |
570 | ### 练习4
571 |
572 | 15头牛4天吃了1260千克草,照这样计算,30头牛10天吃草多少千克?
573 |
574 | ### 例题5
575 |
576 | 6辆卡车运送4趟可以运走沙石48吨。如果有400吨沙石需要10趟运完,那么一共需要多少辆卡车?
577 |
578 | ### 练习5
579 |
580 | 4辆汽车5小时共运土石400方,现有10辆同样的汽车,要运1000方土石,需几小时?
581 |
582 | ### 例题6
583 |
584 | 一件工作12人每天工作8小时需要10天,照这样计算,如果增加8人,每天减少2小时,可以提前几天完成?
585 |
586 | ### 练习6
587 |
588 | 学校买来一批粉笔,原计划18个班可用60天,实际用45天后,有3个班外出了,剩下的粉笔够用多少天?
589 |
590 | ## 3.1.09.长方形与正方形
591 |
592 | ### 课前热身
593 |
594 | 【热身1】有20人修筑一条公路,计划15天完成。动工3天后抽出5人去植树,留下的人继续修路。如果每个人的工作效率不变,那么修完中段公路实际用多少天?
595 |
596 |
597 |
598 | 【热身2】已知3名模范职工和6名普通职工8小时可以生产零件420个。现在有一批生产任务,需要6名模范职工和12名普通职工生产14小时才能完成。如果工作了4小时后,又来了4名模范职工和8名普通职工,可以提前几小时完成任务?
599 |
600 |
601 |
602 | ### 学习目标
603 |
604 | - 理解面积的意义(面积的单位及其转换)
605 | - 会求长方形和正方形的面积(正方形面积=边长×边长;长方形面积=长×宽)
606 | - 掌握简单的割补、剪拼。
607 | - 长方形、正方形面积与周长区分和灵活转换
608 | - 运用长方形、正方形的性质(周长和面积)解决问题
609 | - 拓展——田字格模型
610 |
611 |
612 |
613 | ### 引入
614 |
615 | 对面积的直观感受和比较
616 |
617 |
618 |
619 | 【补充】有两个一样的长方形,长都是4厘米,宽都是2厘米。
620 |
621 | 把它们拼成一个长方形,请画出草图,并计算其周长和面积。
622 |
623 | 把它们拼成一个正方形,请画出草图,并计算其周长和面积。
624 |
625 |
626 |
627 | 一个花园长15米,宽10米,如果把这个花园用篱笆围起来,所围成的面积有多大?需要多长的篱笆?
628 |
629 |
630 |
631 | #### 单位换算
632 |
633 | (1)1米=()分米=()厘米=()毫米
634 |
635 | (2)1平方米=()平方分米=()平方厘米=()平方毫米
636 |
637 | (3)1平方千米=()平方米
638 |
639 | (4)8平方米=()平方分米
640 |
641 | (5)13平方米=()平方厘米
642 |
643 | (6)()平方米=500平方分米=()平方厘米
644 |
645 |
646 |
647 | #### 补充
648 |
649 | 选择合适的单位填入括号内。
650 |
651 | (1)一栋楼高约50()
652 |
653 | (2)课本封面面积约为6()
654 |
655 | (3)一个茶杯高约13()
656 |
657 | (4)黑板的面积约为5()
658 |
659 | (5)指甲盖的面积约为1()
660 |
661 | (6)一间教师的面积约为40()
662 |
663 |
664 |
665 |
666 |
667 | ### 例题练习
668 |
669 | #### 割补法求面积
670 |
671 | 【例题1】求下面图形的面积。(单位:厘米)
672 |
673 |  674 |
675 | 【练习1】计算下面图形的面积。(单位:厘米)
676 |
677 |
674 |
675 | 【练习1】计算下面图形的面积。(单位:厘米)
676 |
677 |  678 |
679 | #### 容斥原理求面积
680 |
681 | 【例题2】如图所示,两块边长为15厘米的抹布放在桌子上,重叠的部分恰好是个边长为5厘米的正方形。问:桌面被盖住部分的面积是多少?
682 |
683 |
678 |
679 | #### 容斥原理求面积
680 |
681 | 【例题2】如图所示,两块边长为15厘米的抹布放在桌子上,重叠的部分恰好是个边长为5厘米的正方形。问:桌面被盖住部分的面积是多少?
682 |
683 |  684 |
685 | 【练习2】两个正方形重叠部分面积为3平方厘米,求下面图形的面积。
686 |
687 |
684 |
685 | 【练习2】两个正方形重叠部分面积为3平方厘米,求下面图形的面积。
686 |
687 |  688 |
689 | #### 平移法求面积
690 |
691 | 【例题3】牛牛住的小区是个边长为100米的正方形,中央有“十字形”的路,路宽5米。问这条路的面积有多大?
692 |
693 |
688 |
689 | #### 平移法求面积
690 |
691 | 【例题3】牛牛住的小区是个边长为100米的正方形,中央有“十字形”的路,路宽5米。问这条路的面积有多大?
692 |
693 |  694 |
695 | 【练习3】下图中每个阴影长方形的宽都为6米,求阴影部分的面积。
696 |
697 |
694 |
695 | 【练习3】下图中每个阴影长方形的宽都为6米,求阴影部分的面积。
696 |
697 |  698 |
699 | 【例题4】两个长方形对应边的距离均为2,如果两个长方形之间(阴影部分)的面积是80,且大长方形的长是宽的2倍。求大长方形的面积。
700 |
701 |
698 |
699 | 【例题4】两个长方形对应边的距离均为2,如果两个长方形之间(阴影部分)的面积是80,且大长方形的长是宽的2倍。求大长方形的面积。
700 |
701 |  702 |
703 | 【练习4】一个长方形,长是13厘米,宽是8厘米。现在在距长方形每条边2厘米处对长方形进行剪切,得到一个小的长方形。问剪切后的长方形面积比原长方形减小了多少平方厘米?
704 |
705 |
706 |
707 | 【例题5】如图所示,较大正方形的边长依次是比它小的正方形边长的2倍,最小正方形的边长为2米,问最大正方形面积是最小正方形的几倍?
708 |
709 |
702 |
703 | 【练习4】一个长方形,长是13厘米,宽是8厘米。现在在距长方形每条边2厘米处对长方形进行剪切,得到一个小的长方形。问剪切后的长方形面积比原长方形减小了多少平方厘米?
704 |
705 |
706 |
707 | 【例题5】如图所示,较大正方形的边长依次是比它小的正方形边长的2倍,最小正方形的边长为2米,问最大正方形面积是最小正方形的几倍?
708 |
709 |  710 |
711 | 【练习5】有三个长方形,大长方形的长和宽依次是小长方形的长和宽的3倍,最大的长方形长为27米,宽为9米。问:最小长方形的面积。
712 |
713 |
714 |
715 | 【例题6】下图四个一样的长方形和一个小正方形拼成一个面积为81平方分米的大正方形,求每个长方形的周长。
716 |
717 |
710 |
711 | 【练习5】有三个长方形,大长方形的长和宽依次是小长方形的长和宽的3倍,最大的长方形长为27米,宽为9米。问:最小长方形的面积。
712 |
713 |
714 |
715 | 【例题6】下图四个一样的长方形和一个小正方形拼成一个面积为81平方分米的大正方形,求每个长方形的周长。
716 |
717 |  718 |
719 | 【练习6】四个一样的长方形和一个小正方形拼成一个大正方形,大小正方形的面积分别为121平方厘米和81平方厘米,问一个长方形的面积是多少?
720 |
721 |
718 |
719 | 【练习6】四个一样的长方形和一个小正方形拼成一个大正方形,大小正方形的面积分别为121平方厘米和81平方厘米,问一个长方形的面积是多少?
720 |
721 |  722 |
723 | #### 长宽加减对面积的影响
724 |
725 | 【例题7】
726 |
727 | (1)一个长方形长12米,宽8米,如果它的长增加2米,宽不变,这个长方形的面积增加多少平方米?
728 |
729 | (2)一个长方形如果宽不变,长增加8米,面积增加72平方米;和果长不变,宽减少4米,面积减少48平方米,这个长方形原来的面积是多少平方米?
730 |
731 |
732 |
733 | 【练习7】把一个长方形纸片的长减少5m,宽减少2m,得到一个小正方形。剪下来部分面积是80平方厘米,求正方形的边长是多少厘米?
734 |
735 |
736 |
737 | #### 长宽变倍对面积、周长的影响
738 |
739 | 【例题7】如果正方形A的边长是正方形B的边长的2倍,那么正方形A的周长是正方形B的周长的几倍?正方形A的面积是正方形B的面积几倍?
740 |
741 |
742 |
743 | 【练习7】有三个正方形A、B、C,已知B的面积是A的4倍,C的周长是B的2倍,则C的面积是A的几倍。
744 |
745 | 答案:16
746 |
747 |
748 |
749 | ### 拓展
750 |
751 | 【拓展1】一个教室的长是8米,宽是6米,在地面上铺边长2分米的方砖,一共需要多少块?
752 |
753 |
754 |
755 | 【拓展2】把一个长方形的长增加5分米,宽增加8分米后,得到一个面积比原长方形多181平方分米的正方形。求这个正方形的边长是多少分米?
756 |
757 |
758 |
759 | 【拓展3】如图,大长方形被分为4个小长方形,A、B、C、D分别代表它们的面积,已知B=18,C= 18,A=9,求D的面积是多少?
760 |
761 |
722 |
723 | #### 长宽加减对面积的影响
724 |
725 | 【例题7】
726 |
727 | (1)一个长方形长12米,宽8米,如果它的长增加2米,宽不变,这个长方形的面积增加多少平方米?
728 |
729 | (2)一个长方形如果宽不变,长增加8米,面积增加72平方米;和果长不变,宽减少4米,面积减少48平方米,这个长方形原来的面积是多少平方米?
730 |
731 |
732 |
733 | 【练习7】把一个长方形纸片的长减少5m,宽减少2m,得到一个小正方形。剪下来部分面积是80平方厘米,求正方形的边长是多少厘米?
734 |
735 |
736 |
737 | #### 长宽变倍对面积、周长的影响
738 |
739 | 【例题7】如果正方形A的边长是正方形B的边长的2倍,那么正方形A的周长是正方形B的周长的几倍?正方形A的面积是正方形B的面积几倍?
740 |
741 |
742 |
743 | 【练习7】有三个正方形A、B、C,已知B的面积是A的4倍,C的周长是B的2倍,则C的面积是A的几倍。
744 |
745 | 答案:16
746 |
747 |
748 |
749 | ### 拓展
750 |
751 | 【拓展1】一个教室的长是8米,宽是6米,在地面上铺边长2分米的方砖,一共需要多少块?
752 |
753 |
754 |
755 | 【拓展2】把一个长方形的长增加5分米,宽增加8分米后,得到一个面积比原长方形多181平方分米的正方形。求这个正方形的边长是多少分米?
756 |
757 |
758 |
759 | 【拓展3】如图,大长方形被分为4个小长方形,A、B、C、D分别代表它们的面积,已知B=18,C= 18,A=9,求D的面积是多少?
760 |
761 |  762 |
763 | 【拓展4】如图,一个大长方形花园被分成了9个小长方形,其中4块的面积分别为1、2、4、16。若b与c的面积之和为6,求花园的面积是多少?
764 |
765 |
762 |
763 | 【拓展4】如图,一个大长方形花园被分成了9个小长方形,其中4块的面积分别为1、2、4、16。若b与c的面积之和为6,求花园的面积是多少?
764 |
765 |  766 |
767 |
768 |
769 | ## 3.1.12. 差倍问题
770 |
771 | ### 整数倍
772 |
773 | 例题1
774 |
775 | 乐乐老师买来一些糖果分给田田和牛牛,牛牛分到的是田田的 3 倍,田田分到的比牛牛少 30 颗,田田和牛牛各分到多少颗糖?
776 |
777 | 练习1
778 |
779 | 乐乐老师比丁丁大 24 岁,今年乐乐老师的年龄正好是丁丁年龄的 3 倍,你知道今年乐乐老师多少岁?丁丁多少岁吗?
780 |
781 | ### 非整数倍
782 |
783 | 例题2
784 |
785 | 学校买来的足球比排球多 18 个,足球的个数比排球的 2 倍少 4 个。学校买来足球和排球各多少个?
786 |
787 | 练习2
788 |
789 | 三年级(1)班女生比男生多 15 人,女生的人数比男生的 4 倍少 3 人,则三年级(1)班有男生和女生各多少人?
790 |
791 | ### 同增同减差不变
792 |
793 | 例题3
794 |
795 | 甲仓库存放大米 500 袋,乙仓库存放大米 200 袋,现从两个仓库里运走同样袋数的大米,结果甲仓库剩下的大米正好是乙仓库剩下大米的 3 倍,问从两个仓库里各运走大米多少袋?
796 |
797 | 练习3
798 |
799 | 实验小学一校区人数比实验小学二校区人数少 540 人。第三校区建成后,从一、二校区各调走 200 人到第三校区,这时实验小学二校区人数恰好是实验小学一校区人数的 4 倍,那么实验小学一校区和实验小学二校区原来各有多少人?
800 |
801 | ### 找差
802 |
803 | 例题4
804 |
805 | 阿普和丁丁做题,如果阿普再做 4 道就和丁丁做的一样多,如果丁丁再做 6 道就是阿普的 3 倍。阿普和丁丁各做了多少道题?
806 |
807 | 练习4
808 |
809 | 甲、乙两个数,如果甲数加上 50,就等于乙数,如果乙数加上 350 就等于甲数的 3 倍,问甲、乙各是多少?
810 |
811 | 例题5
812 |
813 | 两筐重量相等的苹果,从甲筐取出 7 千克,乙筐加上 19 千克,这时乙筐重量是甲筐的 2 倍。原来两筐各有多少千克苹果?
814 |
815 | 练习5
816 |
817 | 用、乙两桶油重量相等,如果甲桶取走油 26 千克,乙桶加入油 14 千克,这时乙桶油的重量是甲桶油重量的 3 倍。那么,两桶油原来分别有多少千克?
818 |
819 | ### 变倍问题
820 |
821 | 例题6
822 |
823 | 苹果的个数是梨的 3 倍,如果苹果加上 6 个,梨也加上 6 个,此时苹果的个数是梨的个数的 2 倍。问原来苹果、梨各有多少个?
824 |
825 | 练习6
826 |
827 | 今年阿普的年龄是牛牛年龄的 5 倍,6 年后,阿普的年龄是牛牛年龄的 3 倍。今年阿普和牛牛各多少岁?
828 |
829 | ### 拓展练习
830 |
831 | 牛牛和阿普两人所存的钱数相等。牛牛要买一件商品向阿普借了 120 元,这时牛牛的钱数正好是阿普的 4 倍。那么,原来牛牛和阿普各有多少钱?
832 |
833 | ## 3.1.13 巧算乘法
834 |
835 | ### 课程框架
836 |
837 | 乘法运算律
838 |
839 | 提取公因数
840 |
841 | 凑整思想
842 |
843 | ### 乘法凑整(乘法好朋友数)
844 |
845 | **例题1**
846 |
847 | 计算:
848 | $$
849 | 25\times125\times4
850 | $$
851 |
852 | $$
853 | 5\times13\times125\times20\times8
854 | $$
855 |
856 | **练习1**
857 |
858 | 计算:
859 | $$
860 | 27\times125\times8
861 | $$
862 |
863 | $$
864 | 6\times25\times4\times8
865 | $$
866 |
867 | ### 先拆分再计算
868 |
869 | **例题2**
870 |
871 | 计算:
872 | $$
873 | 888\times125
874 | $$
875 |
876 | **练习2**
877 |
878 | 计算:
879 | $$
880 | 25\times36
881 | $$
882 |
883 | $$
884 | 125\times24
885 | $$
886 |
887 | $$
888 | 25\times64\times19\times125
889 | $$
890 |
891 | ### 乘法分配律
892 |
893 | **例题3**
894 |
895 | 计算:
896 | $$
897 | 125\times(80+2)
898 | $$
899 |
900 | $$
901 | 68\times(100+1)
902 | $$
903 |
904 | $$
905 | 56\times999
906 | $$
907 |
908 | **练习3**
909 |
910 | 计算:
911 | $$
912 | 25\times(4+10)
913 | $$
914 |
915 | $$
916 | 37\times(100+2)
917 | $$
918 |
919 | $$
920 | 23\times99
921 | $$
922 |
923 | ### 提取公因数
924 |
925 | **例题4**
926 |
927 | 计算:
928 | $$
929 | 51\times32+51\times68
930 | $$
931 |
932 | $$
933 | 218\times59+218\times40+218
934 | $$
935 |
936 | **练习4**
937 |
938 | 计算:
939 | $$
940 | 80\times2016-2\times2016+2016\times22
941 | $$
942 |
943 | $$
944 | 1999+999\times999
945 | $$
946 |
947 | ### 隐藏的公因数
948 |
949 | **例题5**
950 |
951 | 计算:
952 | $$
953 | 24\times99+33\times76\times3
954 | $$
955 |
956 | $$
957 | 999\times222+333\times334
958 | $$
959 |
960 | **练习5**
961 |
962 | 计算:
963 | $$
964 | 255\times999+255\times2-255
965 | $$
966 |
967 | $$
968 | 999\times778+333\times666
969 | $$
970 |
971 | ### 重码数
972 |
973 | **例题6**
974 |
975 | 计算:
976 |
977 | | $37\times101$ | $49\times10101$ | $2016\times10001$ |
978 | | ------------- | --------------- | ----------------- |
979 | | $12\times11$ | $52\times11$ | $69\times11$ |
980 | | $57\times53$ | $26\times24$ | $61\times69$ |
981 | | $16\times96$ | $78\times38$ | $41\times61$ |
982 |
983 | **练习6**
984 |
985 | 计算:
986 |
987 | | $20162016\times2015-20152015\times2016$ | |
988 | | --------------------------------------- | ------------ |
989 | | $99\times11$ | $24\times11$ |
990 | | $33\times37$ | $68\times62$ |
991 | | $37\times77$ | $26\times86$ |
992 |
993 | ## 3.1.14. 除法巧算
994 |
995 | ### 课程框架
996 |
997 | 1. 抱符号搬家(移项)
998 | 2. 添去括号
999 | 3. 分配与提取
1000 | 4. 商不变
1001 |
1002 | ### 内容分析
1003 |
1004 | ### 热身 1
1005 |
1006 | 计算:
1007 | $$
1008 | 12\times4+13\times4
1009 | $$
1010 |
1011 | ### 热身 2
1012 |
1013 | 计算:
1014 | $$
1015 | 25\times23\times32\times125
1016 | $$
1017 |
1018 | ### 热身 3
1019 |
1020 | 计算:
1021 | $$
1022 | 935\times187\div187
1023 | $$
1024 |
1025 | ### 例题1(添去括号)
1026 |
1027 | 计算:
1028 | $$
1029 | 200\div25\div4
1030 | $$
1031 |
1032 | $$
1033 | 2400\div(120\times4)
1034 | $$
1035 |
1036 | $$
1037 | 1200\div(120\div4)
1038 | $$
1039 |
1040 | ### 练习1
1041 |
1042 | 计算:
1043 | $$
1044 | 360\div(90\div2)
1045 | $$
1046 |
1047 | $$
1048 | 1100\div(11\times5)
1049 | $$
1050 |
1051 | $$
1052 | 400\div16\div5
1053 | $$
1054 |
1055 | ### 拓展1
1056 |
1057 | 计算:
1058 | $$
1059 | 450\times6\div54
1060 | $$
1061 |
1062 | $$
1063 | 4200\div(50\times7)
1064 | $$
1065 |
1066 | ### 例题2(移项)
1067 |
1068 | 计算:
1069 | $$
1070 | (1225\div8)\times(8\div4)\times(4\div1)
1071 | $$
1072 |
1073 | ### 练习2
1074 |
1075 | 计算:
1076 | $$
1077 | (30\times18)\div(18\div8)\div(8\div1)
1078 | $$
1079 |
1080 | ### 拓展
1081 |
1082 | $$
1083 | 168\times25\div14\times7\div5
1084 | $$
1085 |
1086 | ### 例题3(商不变)
1087 |
1088 | 算一算,比一比,你有什么发现。
1089 | $$
1090 | 35\div5=
1091 | $$
1092 |
1093 | $$
1094 | 350\div50=
1095 | $$
1096 |
1097 | $$
1098 | 3500\div500=
1099 | $$
1100 |
1101 | $$
1102 | 80\div4=
1103 | $$
1104 |
1105 | $$
1106 | 800\div40=
1107 | $$
1108 |
1109 | $$
1110 | 8000\div400=
1111 | $$
1112 |
1113 | ### 练习3
1114 |
1115 | 填空。
1116 | $$
1117 | 36\div4=72\div\_\_\_\_\_
1118 | $$
1119 |
1120 | $$
1121 | 400\div25=\_\_\_\_\_\div100
1122 | $$
1123 |
1124 | $$
1125 | 120\div15=\_\_\_\_\_\div5
1126 | $$
1127 |
1128 | $$
1129 | 72\div4=36\div\_\_\_\_\_
1130 | $$
1131 |
1132 | ### 例题4(商不变的应用)
1133 |
1134 | 计算:
1135 | $$
1136 | 1200\div25
1137 | $$
1138 |
1139 | $$
1140 | 3300\div55
1141 | $$
1142 |
1143 | ### 练习4
1144 |
1145 | 计算:
1146 | $$
1147 | 2000\div125
1148 | $$
1149 |
1150 | $$
1151 | 2870\div35
1152 | $$
1153 |
1154 | ### 例题5(分配)
1155 |
1156 | 计算:
1157 | $$
1158 | (13039+260)\div13
1159 | $$
1160 |
1161 | $$
1162 | (54+81+360)\div9
1163 | $$
1164 |
1165 | ### 练习5
1166 |
1167 | 计算:
1168 | $$
1169 | (18000-720)\div9
1170 | $$
1171 |
1172 | $$
1173 | (4800-240+720)\div12
1174 | $$
1175 |
1176 | ### 例题6(提取)
1177 |
1178 | 计算:
1179 | $$
1180 | 329\div7+371\div7
1181 | $$
1182 |
1183 | $$
1184 | 25\div6+35\div6
1185 | $$
1186 |
1187 | ### 练习6
1188 |
1189 | 计算:
1190 | $$
1191 | 31\div5+32\div5+33\div5+34\div5+35\div5
1192 | $$
1193 |
1194 | ### 拓展
1195 |
1196 | 计算:
1197 | $$
1198 | 25\div4+25\div6+35\div4+35\div6
1199 | $$
1200 |
1201 | ### 练习1
1202 |
1203 | 计算:
1204 | $$
1205 | 4000\div125\div8
1206 | $$
1207 |
1208 | ### 练习2
1209 |
1210 | 计算:
1211 | $$
1212 | 426\div(213\times26\div12)
1213 | $$
1214 |
1215 | ### 练习3
1216 |
1217 | 计算:
1218 | $$
1219 | (126\times56)\div(7\times18)
1220 | $$
1221 |
1222 | ### 练习4
1223 |
1224 | 计算:
1225 | $$
1226 | (12\times5)\div(5\div3)\div(4\div6)\times(4\div3)
1227 | $$
1228 |
1229 | ### 练习5
1230 |
1231 | 计算:
1232 | $$
1233 | 1300\div25
1234 | $$
1235 |
1236 | ### 练习6
1237 |
1238 | 计算:
1239 | $$
1240 | 770\div55
1241 | $$
1242 |
1243 | ### 练习7
1244 |
1245 | 计算:
1246 | $$
1247 | (189+27)\div9
1248 | $$
1249 |
1250 | ### 练习8
1251 |
1252 | 计算:
1253 | $$
1254 | 523\div7+424\div7
1255 | $$
1256 |
1257 | ### 练习9
1258 |
1259 | 计算:
1260 | $$
1261 | (14400-240+720)\div12
1262 | $$
1263 |
1264 | ### 练习10
1265 |
1266 | 计算:
1267 | $$
1268 | (132639-5265-7891)\div13
1269 | $$
1270 |
1271 | ### 练习11
1272 |
1273 | 计算:
1274 | $$
1275 | 122\div4+206\div4+72\div4
1276 | $$
1277 |
1278 | ### 练习12
1279 |
1280 | 计算:
1281 | $$
1282 | 288\div24+288\div18+288\div6
1283 | $$
1284 |
1285 | ## 3.1.15. 鸡兔同笼进阶
1286 |
1287 | ### 本质
1288 |
1289 | 两种事物,凑两个条件
1290 |
1291 | ### 方法
1292 |
1293 | * 假设调整——假设、验算、调整
1294 | * 分组——倍数关系分组
1295 | * 合并
1296 | + 倍数关系,分组合并
1297 | + 不变量合并
1298 | + 平均值合并
1299 |
1300 | 例题1——假设法
1301 |
1302 | 例题2——实际应用
1303 |
1304 | 例题3——分组
1305 |
1306 | 例题4——分组
1307 |
1308 | 例题5——合并
1309 |
1310 | 例题6——实际应用
1311 |
1312 | ### 铺垫
1313 |
1314 | 鸡兔共有10只,关在一个笼子里,笼中共有26条腿,鸡兔各有几只?
1315 |
1316 | 列表法
1317 |
1318 | | 鸡(只) | 10 | 9 | 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
1319 | | ---------- | ---- | ---- | ---- | ---- | ---- | ---- | ---- | ---- | ---- | ---- | ---- |
1320 | | 兔(只) | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
1321 | | 腿数(条) | | | | | | | | | | | |
1322 |
1323 | 画图法
1324 |
1325 | 假设调整
1326 |
1327 | 假设全是鸡-验算-调整
1328 |
1329 | ### 例题1
1330 |
1331 | 牛牛家养了一些鸡和免子,同时养在一个笼子里,牛牛数了数,它们共有35个头,94只脚。问:牛牛家养的鸡和免各有多少只?
1332 |
1333 | ### 练习1
1334 |
1335 | 鸡免共有45只,关在同一个笼子中。每只鸡有2只脚,每只免子有4只脚,笼中共有100只脚。试计算,笼中有鸡多少只?免子多少只?
1336 |
1337 | ### 拓展2
1338 |
1339 | 在一个停车场上,现有汽车和摩托车共24辆,其中汽车有4个轮子,摩托车有3个轮子,摩托车有3个轮子,这些车共有86个轮子,那么三轮摩托车共有多少辆?
1340 |
1341 | ### 拓展3
1342 |
1343 | 100名师生绿化校园,老师每人载3棵树,学生每两人栽1颗树,总共载树100棵,那么学生共载树多少棵?
1344 |
1345 | ### 拓展
1346 |
1347 | 奥特曼遭遇一帮怪兽,大怪兽2头4腿,小怪兽2头2腿,大小怪兽一共20个头,32条腿,那么,大小怪兽各有几只?
1348 |
1349 | ### 分组
1350 |
1351 | 有相同数量的鸡和兔,共36条腿,那么鸡兔各有几只?
1352 |
1353 | 鸡兔同笼,兔的数量是鸡的3倍,共140条腿,那么,鸡兔各有几只?
1354 |
1355 | ### 补充
1356 |
1357 | 鸡兔同笼,共27只,已知两种动物的腿数相同,那么,鸡兔各有几只?
1358 |
1359 | 鸡兔同笼,共40只,已知鸡腿数是兔腿数的2倍,那么,鸡兔各有几只?
1360 |
1361 | ### 合并
1362 |
1363 | 鸡兔同笼,鸡、兔共有107只,兔的腿数比鸡的腿数多56条,问鸡、兔各多少只?
1364 |
1365 | ### 例题2
1366 |
1367 | 丁丁数了数笼中的鸡和免,发现腿有120条,鸡的只数比兔的只数的3倍多5只。则鸡和免子共有多少只?
1368 |
1369 | ### 练习2
1370 |
1371 | 田田数了数笼中的鸡和兔,发现共有脚240只,免的只数与鸡的只数相同。则鸡和免共多少只?
1372 |
1373 | ### 例题3
1374 |
1375 | 牛牛数了数笼中的鸡和兔,发现头有98个,鸡的脚数比免的脚数的2倍少4只。则免子有多少只?鸡有多少只?
1376 |
1377 | ### 练习3
1378 |
1379 | 牛牛数笼中的鸡和免,头有90个,鸡的腿数与免的腿数相同。鸡有多少只?
1380 |
1381 | ### 例题4(实际应用)
1382 |
1383 | 阿普去参加奥运知识抢答竞赛,按规定每答对一题得5分,答错一题要扣1分。阿普抢答10道题后,共得到26分,请问:阿普答对了几道题?
1384 |
1385 | ### 练习4
1386 |
1387 | 工人运青瓷花瓶250个,规定完整运到目的地一个给运费20元,损坏一个赔100元。运完这批花瓶后,工人共得4400元,则损坏了多少个?
1388 |
1389 | ### 例题5
1390 |
1391 | 鸡免同笼,鸡和免共有46条腿。如果将鸡与免的数量互换,那么总腿数变为38条,请问:原来鸡和免各有多少只?
1392 |
1393 | ### 练习5
1394 |
1395 | 田田数笼中的鸡和免,共有脚96只,若将鸡换成免,免换成鸡,则还有96只脚。鸡、免原来各多少只?
1396 |
1397 | ### 例题6
1398 |
1399 | 有蜘蛛、蜻蜓、蝉三种动物共18只,共有腿118条,翅膀20对。己知蜘蛛8条腿;蜻蜓6条腿,两对翅膀;蝉6条腿,一对翅膀。求蜻蜓有多少只。
1400 |
1401 | ### 练习6
1402 |
1403 | 犀牛、羚羊、孔雀三种动物共有头26个,脚80只,犄角20只。已知犀牛有4只脚,1只犄角;羚羊有4只脚,2只犄角;孔雀有2只脚,没有犄角。那么,犀牛、羚羊、孔雀各有多少只?
1404 |
1405 | ## 3.1.16. 周期问题进阶
1406 |
1407 | ### 热身1
1408 |
1409 | 学校宿舍楼一共有30间宿舍,大宿舍每间住6人,小宿舍每间住4人。已知这些宿舍中共住了168名学生,那么其中有多少间大宿舍、多少间小宿舍呢?
1410 |
1411 | ### 热身2
1412 |
1413 | 100个和尚140个馍,大和尚1人分3个馍,小和尚1人分1个馍。问:大、小和尚各有多少人?
1414 |
1415 | ### 热身3
1416 |
1417 | 找出下面数列的周期。
1418 |
1419 | 2,3,1,2,3,1,2,3,1,……
1420 |
1421 | 1,3,5,7,1,3,5,7,1,3,……
1422 |
1423 | 1,4,2,8,5,7,1,4,2,8,5,7,……
1424 |
1425 | ### 例题1(整周期)
1426 |
1427 | 田田和丁丁做游戏,他们把两种形状的小石子按下面的规律排列:
1428 |
1429 | ⭕️⭐️⭕️⭐️⭐️⭕️⭐️⭐️⭐️⭕️⭐️⭕️⭐️⭐️⭕️⭐️⭐️⭐️⭕️⭐️⭕️⭐️⭐️⭕️⭐️⭐️⭐️……
1430 |
1431 | 你知道他们所排列的这些小石子中,第100个是什么图形吗?第180个又是什么图形呢?
1432 |
1433 | ### 练习1
1434 |
1435 | 一天早上,牛牛一起床就大喊:“我要吃包子我要吃包子我要吃包子……”请问,牛牛喊得第28个字是什么字?
1436 |
1437 | ### 例题2(非整周期)
1438 |
1439 | 圣诞节到了,街上挂满了彩灯,并且按照5盏红灯接4 盏蓝灯接 1盏黄灯,然后又是5盏红灯接4 盏蓝灯接 1盏黄灯这样的顺序排下去。问:
1440 | (1)第 150 盏灯是什么颜色?
1441 | (2)前 200 盏彩灯中有多少盏蓝灯?
1442 |
1443 | ### 练习2
1444 |
1445 | 小莉把平时存下来的硬币按3个1分,2个2分,1个5分的顺序排列起来,刚好100枚,请问这 100枚硬币中有多少枚1分的硬币?
1446 |
1447 | ### 例题3
1448 |
1449 | 已知一列数:5,4,1,5,4,1,2,3,5,4,1,2,3,5,4,1,2,3,……,一直写到第 103个数,请问这些数的和是多少?
1450 |
1451 | ### 练习3
1452 |
1453 | 小和尚在地上写了一列数:7,0,7,0,2,5,3,7,0,2,5,3,……,一直写呀写,写了42个数,你能求出这 42 个数相加的和是多少吗?
1454 |
1455 | ### 例题4
1456 |
1457 | 如下图所示的表中,将每列上、下两个字组成一组,例如第一组为“数真”,第二组为 “学有”,那么第50组是什么字?
1458 |
1459 | 数学数学数学数学数学数学数学数学数学……
1460 |
1461 | 真有趣真有趣真有趣真有趣真有趣真有趣……
1462 |
1463 | ### 练习4
1464 |
1465 | 如图所示,每列上、下字和字母组成一组,例如,第一组是“A红”,第二组是“B黄”,请写出第63组是什么?
1466 |
1467 | ABABABABABABA
1468 |
1469 | 红黄蓝绿红黄蓝绿红黄蓝绿
1470 |
1471 | ### 例题5
1472 |
1473 | 12个同学围成一圈做传球的游戏,如图。
1474 |
1475 |
766 |
767 |
768 |
769 | ## 3.1.12. 差倍问题
770 |
771 | ### 整数倍
772 |
773 | 例题1
774 |
775 | 乐乐老师买来一些糖果分给田田和牛牛,牛牛分到的是田田的 3 倍,田田分到的比牛牛少 30 颗,田田和牛牛各分到多少颗糖?
776 |
777 | 练习1
778 |
779 | 乐乐老师比丁丁大 24 岁,今年乐乐老师的年龄正好是丁丁年龄的 3 倍,你知道今年乐乐老师多少岁?丁丁多少岁吗?
780 |
781 | ### 非整数倍
782 |
783 | 例题2
784 |
785 | 学校买来的足球比排球多 18 个,足球的个数比排球的 2 倍少 4 个。学校买来足球和排球各多少个?
786 |
787 | 练习2
788 |
789 | 三年级(1)班女生比男生多 15 人,女生的人数比男生的 4 倍少 3 人,则三年级(1)班有男生和女生各多少人?
790 |
791 | ### 同增同减差不变
792 |
793 | 例题3
794 |
795 | 甲仓库存放大米 500 袋,乙仓库存放大米 200 袋,现从两个仓库里运走同样袋数的大米,结果甲仓库剩下的大米正好是乙仓库剩下大米的 3 倍,问从两个仓库里各运走大米多少袋?
796 |
797 | 练习3
798 |
799 | 实验小学一校区人数比实验小学二校区人数少 540 人。第三校区建成后,从一、二校区各调走 200 人到第三校区,这时实验小学二校区人数恰好是实验小学一校区人数的 4 倍,那么实验小学一校区和实验小学二校区原来各有多少人?
800 |
801 | ### 找差
802 |
803 | 例题4
804 |
805 | 阿普和丁丁做题,如果阿普再做 4 道就和丁丁做的一样多,如果丁丁再做 6 道就是阿普的 3 倍。阿普和丁丁各做了多少道题?
806 |
807 | 练习4
808 |
809 | 甲、乙两个数,如果甲数加上 50,就等于乙数,如果乙数加上 350 就等于甲数的 3 倍,问甲、乙各是多少?
810 |
811 | 例题5
812 |
813 | 两筐重量相等的苹果,从甲筐取出 7 千克,乙筐加上 19 千克,这时乙筐重量是甲筐的 2 倍。原来两筐各有多少千克苹果?
814 |
815 | 练习5
816 |
817 | 用、乙两桶油重量相等,如果甲桶取走油 26 千克,乙桶加入油 14 千克,这时乙桶油的重量是甲桶油重量的 3 倍。那么,两桶油原来分别有多少千克?
818 |
819 | ### 变倍问题
820 |
821 | 例题6
822 |
823 | 苹果的个数是梨的 3 倍,如果苹果加上 6 个,梨也加上 6 个,此时苹果的个数是梨的个数的 2 倍。问原来苹果、梨各有多少个?
824 |
825 | 练习6
826 |
827 | 今年阿普的年龄是牛牛年龄的 5 倍,6 年后,阿普的年龄是牛牛年龄的 3 倍。今年阿普和牛牛各多少岁?
828 |
829 | ### 拓展练习
830 |
831 | 牛牛和阿普两人所存的钱数相等。牛牛要买一件商品向阿普借了 120 元,这时牛牛的钱数正好是阿普的 4 倍。那么,原来牛牛和阿普各有多少钱?
832 |
833 | ## 3.1.13 巧算乘法
834 |
835 | ### 课程框架
836 |
837 | 乘法运算律
838 |
839 | 提取公因数
840 |
841 | 凑整思想
842 |
843 | ### 乘法凑整(乘法好朋友数)
844 |
845 | **例题1**
846 |
847 | 计算:
848 | $$
849 | 25\times125\times4
850 | $$
851 |
852 | $$
853 | 5\times13\times125\times20\times8
854 | $$
855 |
856 | **练习1**
857 |
858 | 计算:
859 | $$
860 | 27\times125\times8
861 | $$
862 |
863 | $$
864 | 6\times25\times4\times8
865 | $$
866 |
867 | ### 先拆分再计算
868 |
869 | **例题2**
870 |
871 | 计算:
872 | $$
873 | 888\times125
874 | $$
875 |
876 | **练习2**
877 |
878 | 计算:
879 | $$
880 | 25\times36
881 | $$
882 |
883 | $$
884 | 125\times24
885 | $$
886 |
887 | $$
888 | 25\times64\times19\times125
889 | $$
890 |
891 | ### 乘法分配律
892 |
893 | **例题3**
894 |
895 | 计算:
896 | $$
897 | 125\times(80+2)
898 | $$
899 |
900 | $$
901 | 68\times(100+1)
902 | $$
903 |
904 | $$
905 | 56\times999
906 | $$
907 |
908 | **练习3**
909 |
910 | 计算:
911 | $$
912 | 25\times(4+10)
913 | $$
914 |
915 | $$
916 | 37\times(100+2)
917 | $$
918 |
919 | $$
920 | 23\times99
921 | $$
922 |
923 | ### 提取公因数
924 |
925 | **例题4**
926 |
927 | 计算:
928 | $$
929 | 51\times32+51\times68
930 | $$
931 |
932 | $$
933 | 218\times59+218\times40+218
934 | $$
935 |
936 | **练习4**
937 |
938 | 计算:
939 | $$
940 | 80\times2016-2\times2016+2016\times22
941 | $$
942 |
943 | $$
944 | 1999+999\times999
945 | $$
946 |
947 | ### 隐藏的公因数
948 |
949 | **例题5**
950 |
951 | 计算:
952 | $$
953 | 24\times99+33\times76\times3
954 | $$
955 |
956 | $$
957 | 999\times222+333\times334
958 | $$
959 |
960 | **练习5**
961 |
962 | 计算:
963 | $$
964 | 255\times999+255\times2-255
965 | $$
966 |
967 | $$
968 | 999\times778+333\times666
969 | $$
970 |
971 | ### 重码数
972 |
973 | **例题6**
974 |
975 | 计算:
976 |
977 | | $37\times101$ | $49\times10101$ | $2016\times10001$ |
978 | | ------------- | --------------- | ----------------- |
979 | | $12\times11$ | $52\times11$ | $69\times11$ |
980 | | $57\times53$ | $26\times24$ | $61\times69$ |
981 | | $16\times96$ | $78\times38$ | $41\times61$ |
982 |
983 | **练习6**
984 |
985 | 计算:
986 |
987 | | $20162016\times2015-20152015\times2016$ | |
988 | | --------------------------------------- | ------------ |
989 | | $99\times11$ | $24\times11$ |
990 | | $33\times37$ | $68\times62$ |
991 | | $37\times77$ | $26\times86$ |
992 |
993 | ## 3.1.14. 除法巧算
994 |
995 | ### 课程框架
996 |
997 | 1. 抱符号搬家(移项)
998 | 2. 添去括号
999 | 3. 分配与提取
1000 | 4. 商不变
1001 |
1002 | ### 内容分析
1003 |
1004 | ### 热身 1
1005 |
1006 | 计算:
1007 | $$
1008 | 12\times4+13\times4
1009 | $$
1010 |
1011 | ### 热身 2
1012 |
1013 | 计算:
1014 | $$
1015 | 25\times23\times32\times125
1016 | $$
1017 |
1018 | ### 热身 3
1019 |
1020 | 计算:
1021 | $$
1022 | 935\times187\div187
1023 | $$
1024 |
1025 | ### 例题1(添去括号)
1026 |
1027 | 计算:
1028 | $$
1029 | 200\div25\div4
1030 | $$
1031 |
1032 | $$
1033 | 2400\div(120\times4)
1034 | $$
1035 |
1036 | $$
1037 | 1200\div(120\div4)
1038 | $$
1039 |
1040 | ### 练习1
1041 |
1042 | 计算:
1043 | $$
1044 | 360\div(90\div2)
1045 | $$
1046 |
1047 | $$
1048 | 1100\div(11\times5)
1049 | $$
1050 |
1051 | $$
1052 | 400\div16\div5
1053 | $$
1054 |
1055 | ### 拓展1
1056 |
1057 | 计算:
1058 | $$
1059 | 450\times6\div54
1060 | $$
1061 |
1062 | $$
1063 | 4200\div(50\times7)
1064 | $$
1065 |
1066 | ### 例题2(移项)
1067 |
1068 | 计算:
1069 | $$
1070 | (1225\div8)\times(8\div4)\times(4\div1)
1071 | $$
1072 |
1073 | ### 练习2
1074 |
1075 | 计算:
1076 | $$
1077 | (30\times18)\div(18\div8)\div(8\div1)
1078 | $$
1079 |
1080 | ### 拓展
1081 |
1082 | $$
1083 | 168\times25\div14\times7\div5
1084 | $$
1085 |
1086 | ### 例题3(商不变)
1087 |
1088 | 算一算,比一比,你有什么发现。
1089 | $$
1090 | 35\div5=
1091 | $$
1092 |
1093 | $$
1094 | 350\div50=
1095 | $$
1096 |
1097 | $$
1098 | 3500\div500=
1099 | $$
1100 |
1101 | $$
1102 | 80\div4=
1103 | $$
1104 |
1105 | $$
1106 | 800\div40=
1107 | $$
1108 |
1109 | $$
1110 | 8000\div400=
1111 | $$
1112 |
1113 | ### 练习3
1114 |
1115 | 填空。
1116 | $$
1117 | 36\div4=72\div\_\_\_\_\_
1118 | $$
1119 |
1120 | $$
1121 | 400\div25=\_\_\_\_\_\div100
1122 | $$
1123 |
1124 | $$
1125 | 120\div15=\_\_\_\_\_\div5
1126 | $$
1127 |
1128 | $$
1129 | 72\div4=36\div\_\_\_\_\_
1130 | $$
1131 |
1132 | ### 例题4(商不变的应用)
1133 |
1134 | 计算:
1135 | $$
1136 | 1200\div25
1137 | $$
1138 |
1139 | $$
1140 | 3300\div55
1141 | $$
1142 |
1143 | ### 练习4
1144 |
1145 | 计算:
1146 | $$
1147 | 2000\div125
1148 | $$
1149 |
1150 | $$
1151 | 2870\div35
1152 | $$
1153 |
1154 | ### 例题5(分配)
1155 |
1156 | 计算:
1157 | $$
1158 | (13039+260)\div13
1159 | $$
1160 |
1161 | $$
1162 | (54+81+360)\div9
1163 | $$
1164 |
1165 | ### 练习5
1166 |
1167 | 计算:
1168 | $$
1169 | (18000-720)\div9
1170 | $$
1171 |
1172 | $$
1173 | (4800-240+720)\div12
1174 | $$
1175 |
1176 | ### 例题6(提取)
1177 |
1178 | 计算:
1179 | $$
1180 | 329\div7+371\div7
1181 | $$
1182 |
1183 | $$
1184 | 25\div6+35\div6
1185 | $$
1186 |
1187 | ### 练习6
1188 |
1189 | 计算:
1190 | $$
1191 | 31\div5+32\div5+33\div5+34\div5+35\div5
1192 | $$
1193 |
1194 | ### 拓展
1195 |
1196 | 计算:
1197 | $$
1198 | 25\div4+25\div6+35\div4+35\div6
1199 | $$
1200 |
1201 | ### 练习1
1202 |
1203 | 计算:
1204 | $$
1205 | 4000\div125\div8
1206 | $$
1207 |
1208 | ### 练习2
1209 |
1210 | 计算:
1211 | $$
1212 | 426\div(213\times26\div12)
1213 | $$
1214 |
1215 | ### 练习3
1216 |
1217 | 计算:
1218 | $$
1219 | (126\times56)\div(7\times18)
1220 | $$
1221 |
1222 | ### 练习4
1223 |
1224 | 计算:
1225 | $$
1226 | (12\times5)\div(5\div3)\div(4\div6)\times(4\div3)
1227 | $$
1228 |
1229 | ### 练习5
1230 |
1231 | 计算:
1232 | $$
1233 | 1300\div25
1234 | $$
1235 |
1236 | ### 练习6
1237 |
1238 | 计算:
1239 | $$
1240 | 770\div55
1241 | $$
1242 |
1243 | ### 练习7
1244 |
1245 | 计算:
1246 | $$
1247 | (189+27)\div9
1248 | $$
1249 |
1250 | ### 练习8
1251 |
1252 | 计算:
1253 | $$
1254 | 523\div7+424\div7
1255 | $$
1256 |
1257 | ### 练习9
1258 |
1259 | 计算:
1260 | $$
1261 | (14400-240+720)\div12
1262 | $$
1263 |
1264 | ### 练习10
1265 |
1266 | 计算:
1267 | $$
1268 | (132639-5265-7891)\div13
1269 | $$
1270 |
1271 | ### 练习11
1272 |
1273 | 计算:
1274 | $$
1275 | 122\div4+206\div4+72\div4
1276 | $$
1277 |
1278 | ### 练习12
1279 |
1280 | 计算:
1281 | $$
1282 | 288\div24+288\div18+288\div6
1283 | $$
1284 |
1285 | ## 3.1.15. 鸡兔同笼进阶
1286 |
1287 | ### 本质
1288 |
1289 | 两种事物,凑两个条件
1290 |
1291 | ### 方法
1292 |
1293 | * 假设调整——假设、验算、调整
1294 | * 分组——倍数关系分组
1295 | * 合并
1296 | + 倍数关系,分组合并
1297 | + 不变量合并
1298 | + 平均值合并
1299 |
1300 | 例题1——假设法
1301 |
1302 | 例题2——实际应用
1303 |
1304 | 例题3——分组
1305 |
1306 | 例题4——分组
1307 |
1308 | 例题5——合并
1309 |
1310 | 例题6——实际应用
1311 |
1312 | ### 铺垫
1313 |
1314 | 鸡兔共有10只,关在一个笼子里,笼中共有26条腿,鸡兔各有几只?
1315 |
1316 | 列表法
1317 |
1318 | | 鸡(只) | 10 | 9 | 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
1319 | | ---------- | ---- | ---- | ---- | ---- | ---- | ---- | ---- | ---- | ---- | ---- | ---- |
1320 | | 兔(只) | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
1321 | | 腿数(条) | | | | | | | | | | | |
1322 |
1323 | 画图法
1324 |
1325 | 假设调整
1326 |
1327 | 假设全是鸡-验算-调整
1328 |
1329 | ### 例题1
1330 |
1331 | 牛牛家养了一些鸡和免子,同时养在一个笼子里,牛牛数了数,它们共有35个头,94只脚。问:牛牛家养的鸡和免各有多少只?
1332 |
1333 | ### 练习1
1334 |
1335 | 鸡免共有45只,关在同一个笼子中。每只鸡有2只脚,每只免子有4只脚,笼中共有100只脚。试计算,笼中有鸡多少只?免子多少只?
1336 |
1337 | ### 拓展2
1338 |
1339 | 在一个停车场上,现有汽车和摩托车共24辆,其中汽车有4个轮子,摩托车有3个轮子,摩托车有3个轮子,这些车共有86个轮子,那么三轮摩托车共有多少辆?
1340 |
1341 | ### 拓展3
1342 |
1343 | 100名师生绿化校园,老师每人载3棵树,学生每两人栽1颗树,总共载树100棵,那么学生共载树多少棵?
1344 |
1345 | ### 拓展
1346 |
1347 | 奥特曼遭遇一帮怪兽,大怪兽2头4腿,小怪兽2头2腿,大小怪兽一共20个头,32条腿,那么,大小怪兽各有几只?
1348 |
1349 | ### 分组
1350 |
1351 | 有相同数量的鸡和兔,共36条腿,那么鸡兔各有几只?
1352 |
1353 | 鸡兔同笼,兔的数量是鸡的3倍,共140条腿,那么,鸡兔各有几只?
1354 |
1355 | ### 补充
1356 |
1357 | 鸡兔同笼,共27只,已知两种动物的腿数相同,那么,鸡兔各有几只?
1358 |
1359 | 鸡兔同笼,共40只,已知鸡腿数是兔腿数的2倍,那么,鸡兔各有几只?
1360 |
1361 | ### 合并
1362 |
1363 | 鸡兔同笼,鸡、兔共有107只,兔的腿数比鸡的腿数多56条,问鸡、兔各多少只?
1364 |
1365 | ### 例题2
1366 |
1367 | 丁丁数了数笼中的鸡和免,发现腿有120条,鸡的只数比兔的只数的3倍多5只。则鸡和免子共有多少只?
1368 |
1369 | ### 练习2
1370 |
1371 | 田田数了数笼中的鸡和兔,发现共有脚240只,免的只数与鸡的只数相同。则鸡和免共多少只?
1372 |
1373 | ### 例题3
1374 |
1375 | 牛牛数了数笼中的鸡和兔,发现头有98个,鸡的脚数比免的脚数的2倍少4只。则免子有多少只?鸡有多少只?
1376 |
1377 | ### 练习3
1378 |
1379 | 牛牛数笼中的鸡和免,头有90个,鸡的腿数与免的腿数相同。鸡有多少只?
1380 |
1381 | ### 例题4(实际应用)
1382 |
1383 | 阿普去参加奥运知识抢答竞赛,按规定每答对一题得5分,答错一题要扣1分。阿普抢答10道题后,共得到26分,请问:阿普答对了几道题?
1384 |
1385 | ### 练习4
1386 |
1387 | 工人运青瓷花瓶250个,规定完整运到目的地一个给运费20元,损坏一个赔100元。运完这批花瓶后,工人共得4400元,则损坏了多少个?
1388 |
1389 | ### 例题5
1390 |
1391 | 鸡免同笼,鸡和免共有46条腿。如果将鸡与免的数量互换,那么总腿数变为38条,请问:原来鸡和免各有多少只?
1392 |
1393 | ### 练习5
1394 |
1395 | 田田数笼中的鸡和免,共有脚96只,若将鸡换成免,免换成鸡,则还有96只脚。鸡、免原来各多少只?
1396 |
1397 | ### 例题6
1398 |
1399 | 有蜘蛛、蜻蜓、蝉三种动物共18只,共有腿118条,翅膀20对。己知蜘蛛8条腿;蜻蜓6条腿,两对翅膀;蝉6条腿,一对翅膀。求蜻蜓有多少只。
1400 |
1401 | ### 练习6
1402 |
1403 | 犀牛、羚羊、孔雀三种动物共有头26个,脚80只,犄角20只。已知犀牛有4只脚,1只犄角;羚羊有4只脚,2只犄角;孔雀有2只脚,没有犄角。那么,犀牛、羚羊、孔雀各有多少只?
1404 |
1405 | ## 3.1.16. 周期问题进阶
1406 |
1407 | ### 热身1
1408 |
1409 | 学校宿舍楼一共有30间宿舍,大宿舍每间住6人,小宿舍每间住4人。已知这些宿舍中共住了168名学生,那么其中有多少间大宿舍、多少间小宿舍呢?
1410 |
1411 | ### 热身2
1412 |
1413 | 100个和尚140个馍,大和尚1人分3个馍,小和尚1人分1个馍。问:大、小和尚各有多少人?
1414 |
1415 | ### 热身3
1416 |
1417 | 找出下面数列的周期。
1418 |
1419 | 2,3,1,2,3,1,2,3,1,……
1420 |
1421 | 1,3,5,7,1,3,5,7,1,3,……
1422 |
1423 | 1,4,2,8,5,7,1,4,2,8,5,7,……
1424 |
1425 | ### 例题1(整周期)
1426 |
1427 | 田田和丁丁做游戏,他们把两种形状的小石子按下面的规律排列:
1428 |
1429 | ⭕️⭐️⭕️⭐️⭐️⭕️⭐️⭐️⭐️⭕️⭐️⭕️⭐️⭐️⭕️⭐️⭐️⭐️⭕️⭐️⭕️⭐️⭐️⭕️⭐️⭐️⭐️……
1430 |
1431 | 你知道他们所排列的这些小石子中,第100个是什么图形吗?第180个又是什么图形呢?
1432 |
1433 | ### 练习1
1434 |
1435 | 一天早上,牛牛一起床就大喊:“我要吃包子我要吃包子我要吃包子……”请问,牛牛喊得第28个字是什么字?
1436 |
1437 | ### 例题2(非整周期)
1438 |
1439 | 圣诞节到了,街上挂满了彩灯,并且按照5盏红灯接4 盏蓝灯接 1盏黄灯,然后又是5盏红灯接4 盏蓝灯接 1盏黄灯这样的顺序排下去。问:
1440 | (1)第 150 盏灯是什么颜色?
1441 | (2)前 200 盏彩灯中有多少盏蓝灯?
1442 |
1443 | ### 练习2
1444 |
1445 | 小莉把平时存下来的硬币按3个1分,2个2分,1个5分的顺序排列起来,刚好100枚,请问这 100枚硬币中有多少枚1分的硬币?
1446 |
1447 | ### 例题3
1448 |
1449 | 已知一列数:5,4,1,5,4,1,2,3,5,4,1,2,3,5,4,1,2,3,……,一直写到第 103个数,请问这些数的和是多少?
1450 |
1451 | ### 练习3
1452 |
1453 | 小和尚在地上写了一列数:7,0,7,0,2,5,3,7,0,2,5,3,……,一直写呀写,写了42个数,你能求出这 42 个数相加的和是多少吗?
1454 |
1455 | ### 例题4
1456 |
1457 | 如下图所示的表中,将每列上、下两个字组成一组,例如第一组为“数真”,第二组为 “学有”,那么第50组是什么字?
1458 |
1459 | 数学数学数学数学数学数学数学数学数学……
1460 |
1461 | 真有趣真有趣真有趣真有趣真有趣真有趣……
1462 |
1463 | ### 练习4
1464 |
1465 | 如图所示,每列上、下字和字母组成一组,例如,第一组是“A红”,第二组是“B黄”,请写出第63组是什么?
1466 |
1467 | ABABABABABABA
1468 |
1469 | 红黄蓝绿红黄蓝绿红黄蓝绿
1470 |
1471 | ### 例题5
1472 |
1473 | 12个同学围成一圈做传球的游戏,如图。
1474 |
1475 |  1476 |
1477 | (1)从1号同学开始,顺时针传100次,手绢应在谁手中?
1478 | (2)从1号同学开始,逆时针传100次,手绢又在谁手中?
1479 | (3)从 1号同学开始,先顺时针传156次,然后从那个同学开始逆时针传143次,最后手绢在谁手中?
1480 |
1481 | ### 练习5
1482 |
1483 | 8个队员围成如下图所示的一圈做传球游戏,从1号开始,按顺时针方向传球。在传球的同时,按顺序报数。当报到72时,球在几号队员手上?
1484 |
1485 |
1476 |
1477 | (1)从1号同学开始,顺时针传100次,手绢应在谁手中?
1478 | (2)从1号同学开始,逆时针传100次,手绢又在谁手中?
1479 | (3)从 1号同学开始,先顺时针传156次,然后从那个同学开始逆时针传143次,最后手绢在谁手中?
1480 |
1481 | ### 练习5
1482 |
1483 | 8个队员围成如下图所示的一圈做传球游戏,从1号开始,按顺时针方向传球。在传球的同时,按顺序报数。当报到72时,球在几号队员手上?
1484 |
1485 |  1486 |
1487 | ### 例题6(日历型)
1488 |
1489 | 图中是2013年5月份的日历表,根据表请回答:
1490 |
1491 | | 日 | 一 | 二 | 三 | 四 | 五 | 六 |
1492 | | ---- | ---- | ---- | ---- | ---- | ---- | ---- |
1493 | | | | | 1 | 2 | 3 | 4 |
1494 | | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
1495 | | 12 | 13 | 14 | 15 | 16 | 17 | 18 |
1496 | | 19 | 20 | 21 | 22 | 23 | 24 | 25 |
1497 | | 26 | 27 | 28 | 29 | 30 | 31 | |
1498 |
1499 | (1)该年6月1日是星期几?
1500 |
1501 | (2)该年10月1日是星期几?
1502 |
1503 | (3)2015 年5月1日是星期几?
1504 |
1505 | ### 练习6
1506 |
1507 | 2014年3月3日是星期一,算一算 2014年8月8号是星期几?
1508 |
1509 | ### 练习1
1510 |
1511 | ☆◎☆◎◎☆◎☆◎◎☆◎☆◎◎☆◎☆◎◎……
1512 |
1513 | 照这样的规律,第98个图形是什么?
1514 |
1515 | ### 练习2
1516 |
1517 | 一列数按“12345123451234512345……”排列,那么前40个数字之和是多少?
1518 |
1519 | ### 练习3
1520 |
1521 | 2022年1月1日是星期六,2022年6月1日是星期几?
1522 |
1523 | ## 3.1.17. 盈亏问题
1524 |
1525 | ### 热身1
1526 |
1527 | 小松鼠采松果,晴天每天可以采10个,雨天每天只能采6个。它一连几天采了80个松果,平均每天采8个。那么其中有几天是雨天呢?
1528 |
1529 | ### 热身2
1530 |
1531 | 在一根绳子上依次穿7个白颗、4颗黑珠,并按此方式重复。如果从头开始穿,一共穿了120颗珠子,那么这120颗珠子中,白珠比黑珠多几颗?
1532 |
1533 | ### 热身3
1534 |
1535 | 小迪和小迦比赛踩怪兽,规定踩同样的脚数,小迪一脚能踩2只怪兽,小迦一脚能踩5只怪兽,知道小迦比小迪一共多踩了60只。请问他们都踩了多少脚?
1536 |
1537 | 例题练习
1538 |
1539 | ### 例题1(盈盈)
1540 |
1541 | 乐乐老师有一桶巧克力,将它们分给三年级的小朋友,如果每人分9块,就剩下40块,如果每人分12块,就剩下10块。那乐乐老师一共有多少块巧克力,又将这些巧克力分给了多少个小朋友?
1542 |
1543 | ### 练习1
1544 |
1545 | 老师给三年级(2)班的小朋友发儿童节小礼物,如果每人发5个会剩下3个;如果每人发4个会剩下9个,三年级(2)班一共有多少个小朋友?
1546 |
1547 | ### 例题2(亏亏)
1548 |
1549 | 乐乐老师有一桶巧克力,将它们分给三年级的小朋友,如果每人分6块会缺少10块,如果每人分8块,会缺少24块。那乐乐老师一共有多少块巧克力?
1550 |
1551 | ### 练习2
1552 |
1553 | 冬天到了,小白免拿出一管萝卜当作一段时间的粮食,如果每天吃5根,还少3根;如果每天吃6根,还少8根,你知道小白免这管萝卜有多少根吗?
1554 |
1555 | ### 例题3(盈亏)
1556 |
1557 | 田田有一罐星空糖想要分给身边的好朋友,如果每人分5颗剩9颗,如果每人分7颗则有一人没分到,你知道田田身边有多少个好朋友吗?
1558 |
1559 | ### 练习3
1560 |
1561 | 丁丁整理出很多衣服打算寄给山区的小朋友,如果每次寄5件,到开学那天还有10件没有寄出,如果每次寄10件,会比第一种寄法少去邮局4趟,计算丁丁一共打算寄多少件衣服去山区?
1562 |
1563 | ### 例题4
1564 |
1565 | 三年级的同学们去郊外参加夏令营活动,如果每个帐篷住4名同学,则有7名同学没有地方住。如果每个帐篷住5名同学,则会空出3个床位。请计算出参加夏令营的同学有多少人?
1566 |
1567 | ### 练习4
1568 |
1569 | 乐乐老师为小朋友们分发儿童节礼物,如果每人分2个,会剩下12个礼物,如果每人发3个,最后会少2个礼物,请计算一共有多少个小朋友在等着领礼物?
1570 |
1571 | ### 例题5
1572 |
1573 | 乐乐老师带着小朋友去种花,如果每人种5棵,最后会剩下3棵花没人种,如果其中有2个小朋友各种4棵,剩下的小朋友每人种6棵,则这些花刚好种完。请问有多少个小朋友参加了种花?一共要种多少棵花?
1574 |
1575 | ### 练习5
1576 |
1577 | 少先队员们参加了植树节活动,如果每人挖6个树坑,会剩下5个树坑没人挖,如果其中2个人各挖3个树坑,其余每人挖7个树坑,刚好挖完所有的树坑。请计算少先队员们一共需要挖多少个树坑?
1578 |
1579 | ### 例题6
1580 |
1581 | 乐乐老师有一桶巧克力,将它们分给三年级的小朋友,如果每人分6块,则剩下10块,如果给其中3个人每人分4块,其他小朋友每人分7块,还剩下1块巧克力。乐乐老师一共有多少块巧克力?
1582 |
1583 | ### 练习6
1584 |
1585 | 猴王给一群猴子分香蕉,如果每只猴子分5根,最后会剩下16根香蕉没有被分出去,如果猴王给每只猴子分7根香蕉,最后一只猴子只能拿到3根香蕉。猴王一共有多少根香蕉?
1586 |
1587 | ### 练习1
1588 |
1589 | 学校新入学的小朋友要入住宿舍了,每间宿舍住的人一样多。如果每间住4人,就多出20人;如果每间住8人,还多了4人。请问:共有几间宿舍,几个小朋友?
1590 |
1591 | ### 练习2
1592 |
1593 | 老师给新入学的小朋友分积分卡,每个人分到的一样多。如果每个小朋友分10张,就少了30张;如果每个小朋友分8张,还是少8张。请问:一共有几个小朋友,几张积分卡?
1594 |
1595 | ### 练习3
1596 |
1597 | 一群小朋友分香蕉,如果每人分3根,则多4根;如果每人分4根,还少3根。那么,有几个小朋友,几根香蕉呢?
1598 |
1599 | ## 3.1.18. 奇数与偶数进阶
1600 |
1601 | 课前热身
1602 |
1603 | ### 热身1
1604 |
1605 | 妈妈为牛牛准备了铅笔,如果每次给他15支,这学期过完能剩下10支铅笔留给下学期用;如果每次给他17支,这学期刚好够用。你知道妈妈一共准备了多少支铅笔吗?
1606 |
1607 | ### 热身2
1608 |
1609 | 养猪场新到了一批幼年猪,如果每个饲养员照顾3头小猪,会有22头猪没人照顾;如果每个饲养员多照顾5头小猪,会有1个饲养员分不到任务。这个养猪场新到的幼年猪有多少头?
1610 |
1611 | ### 热身3
1612 |
1613 | 最大的两位奇数是()最小的四位偶数是()它们的和是()数
1614 |
1615 | ### 例题练习
1616 |
1617 | ### 例题1
1618 |
1619 | 不计算,判断下列各式结果的奇偶性。
1620 |
1621 | | $37+65$ | $36+66$ | $333+54$ |
1622 | | -------- | -------- | -------- |
1623 | | $145-33$ | $166-38$ | $97-68$ |
1624 |
1625 | 奇数个奇数相加减结果是()
1626 |
1627 | 偶数个奇数相加减结果是()
1628 |
1629 | 奇数个偶数相加减结果是()
1630 |
1631 | 偶数个偶数相加减结果是()
1632 |
1633 | ### 练习1
1634 |
1635 | 不计算,判断下列各式结果的奇偶性。
1636 |
1637 | | $5673+384+333+356+233$ |
1638 | | --------------------------------------- |
1639 | | $6252-1035+3566-2334+5688-1333-579+677$ |
1640 |
1641 | ### 例题2
1642 |
1643 | 请找出两个整数使他们的和是231,差是32,这样的两个数是否存在?若存在,请写出这两个数;若不存在,请说明理由。
1644 |
1645 | ### 练习2
1646 |
1647 | 请找出两个整数使他们的和是160,差是40,这样的两个数是否存在?若存在,请写出这两个数;若不存在,请说明理由。
1648 |
1649 | ### 例题3
1650 |
1651 | 一本书共有256页,从中任意找出5张纸,这5张纸上的所有页码之和能等于132吗?
1652 |
1653 | ### 练习3
1654 |
1655 | 请在下面的式子中填入“+”或者“-”,使得结果是6,可能吗?为什么?
1656 | $$
1657 | 987654321=6
1658 | $$
1659 |
1660 | ### 例题4
1661 |
1662 | 不计算,判断下列各式结果的奇偶性。
1663 |
1664 | | $13×35$ | $24\times36$ | $14\times23$ |
1665 | | ------- | ------------ | ------------ |
1666 |
1667 | ### 练习4
1668 |
1669 | 不计算,判断下列各式结果的奇偶性。
1670 |
1671 | | $23\times27\times39\times45\times54\times49\times33$ |
1672 | | ------------------------------------------------------------ |
1673 | | $31\times26\times13+53\times35+666\times577-3\times5\times987$ |
1674 |
1675 | 任意个奇数相乘结果是();
1676 |
1677 | 任意个偶数相乘结果是();
1678 |
1679 | 奇数与偶数相乘结果是()。
1680 |
1681 | ### 例题5
1682 |
1683 | 己知a,b,c是三个连续的自然数,其中c是偶数。田田说:“那么a+1,b+2,c+3这三个数的乘积一定是奇数。”丁丁说:“不对,a+1,b+2,c+3这三个数的乘积一定是偶数。”他们谁说得对呢?
1684 |
1685 | ### 练习5
1686 |
1687 | 牛牛在做题的时候写出了这样一个算式:$2751=53×21+42×39-36+35$,他做得对吗?
1688 |
1689 | ### 例题6
1690 |
1691 | 桌子上有7张正面向下的扑克牌,丁丁每次会把6张牌翻转。为了使扑克牌都正面向上,丁丁需要翻转几次?能实现吗?
1692 |
1693 | ### 练习6
1694 |
1695 | 明光市小学生参加数学竞赛,题目共20道。评分标准是:基础分25分,答对一道加5分,答错一道减1分,不答算错。如果有1111名同学参赛,则所有参赛同学得分总数一定是奇数还是偶数?请说明理由。
1696 |
1697 | 课后巩固
1698 |
1699 | ### 巩固1
1700 |
1701 | $$
1702 | 1+2+3+4+\dots+2021+2022
1703 | $$
1704 |
1705 | 算式的结果是奇数还是偶数?
1706 |
1707 | ### 巩固2
1708 |
1709 | 有一本500页的书,从中任意撕下33张纸,这33张纸上的所有页码之和能否是2022?
1710 |
1711 | ### 巩固3
1712 |
1713 | 是否存在自然数a,b,c,使得$(a-b)\times(b-c)\times(a-c)=65339$
1714 |
1715 | ## 3.1.19. 有序枚举与树形图
1716 |
1717 | ### 热身1
1718 |
1719 | a、b、c、d、e、f是六个连续的自然数,那么$a+b+c-d-e-f$的结果是奇数还是偶数?$a\times b\times c\times b+e\times f$的结果是奇数还是偶数?
1720 |
1721 | ### 热身2
1722 |
1723 | 在黑板上写1~2022这2022个自然数,每次任意擦去两个数,然后写上它们的和或者差,一直这样重复操作,经过若干次后黑板上只剩一个数,请问这个数是奇数还是偶数?
1724 |
1725 | ### 热身3
1726 |
1727 | 某人游览A、B、C三个风景区,每天游览一个,想要三天时间不重复的游览完这三个景区共有多少种不同的安排顺序?
1728 |
1729 | ### 例题1
1730 |
1731 | 乐乐老师打算把一个苹果、一个梨、一个香蕉分给丁丁和牛牛,每人至少分到一样水果,且全部分完,有多少种不同的分法?
1732 |
1733 | ### 练习1
1734 |
1735 | 妈妈买了1红2黑的3支钢笔送给姐姐和妹妹,1人最少拿到1支,且全部分完,问有多少种不同的送法?
1736 |
1737 | ### 例题2
1738 |
1739 | 一本《儿童故事》的定价是50元,如果丁丁有足够多的5元和10元,他会有多少种不同的付钱方法?
1740 |
1741 | ### 练习2
1742 |
1743 | 这里有1角、5角、1元、5元四张纸币,小朋友可以随意拿起几张纸币组合出总钱数,请问总钱数有多少种可能?
1744 |
1745 | ### 例题3
1746 |
1747 | 乐乐老师一共有5块巧克力,打算分给丁丁、牛牛、田田三个小朋友,每人最少分1块,且全部分完,有多少种不同的分法?
1748 |
1749 | ### 练习3
1750 |
1751 | 乐乐老师一共有8块巧克力,打算分给丁丁、牛牛、田田三个小朋友,每人最少分2块,且全部分完,有多少种不同的分法?
1752 |
1753 | ### 例题4
1754 |
1755 | 现在有数学卡片0,1,2,3各一张,可以排成多少个不同的四位数?
1756 |
1757 | ### 练习4
1758 |
1759 | 现在有数学卡片1,2,3,4各一张,可以排成多少个不同的四位数?
1760 |
1761 | ### 例题5
1762 |
1763 | 5个人排成一排,甲当排头,乙不当排尾,共有多少种排法?
1764 |
1765 | ### 练习5
1766 |
1767 | 乐乐老师、丁丁、牛牛、田田、阿普五个人站成一排,已知阿普站在第一个位置,乐乐老师站在最后一个位置,有多少种不同的排队方式?
1768 |
1769 | ### 例题6
1770 |
1771 | 乐乐老师带着丁丁、牛牛玩传球的游戏,从乐乐老师开始,每个人都可以将球传给其他人,球被传递四次之后又回到了乐乐老师手中,有多少种不同的传球可能呢?
1772 |
1773 | ### 练习6
1774 |
1775 | ABCD四人传球,要求AB不能互传,且自己不能传给自己。开始的时候球在A手上,经过4次传球后,球传回到A手中,不同的传球方式有多少种?
1776 |
1777 | ### 练习1
1778 |
1779 | 现在有数学卡片0,1,2,3,4各一张,可以排成多少个不同的三位数?
1780 |
1781 | ### 练习2
1782 |
1783 | 袋中有2个红球,3个黄球和4个白球,小明从中任意拿出4个球,他拿出球的情况共有几种可能。
1784 |
1785 | ### 练习3
1786 |
1787 | A、B、C三个小朋友互相传球,先从A开始发球(作为第一次传球),这样经过了5次传球后,球恰巧又回到A手中,那么不同的传球方式共多少种?
1788 |
1789 | ## 3.1.20. 等式代换
1790 |
1791 | 例题练习
1792 |
1793 | ### 例题1
1794 |
1795 | 已知$\bigcirc+\bigcirc+\bigcirc+\bigcirc=60$,$\bigtriangleup=\bigcirc+\bigcirc$,$\Box+\Box+\Box=\bigtriangleup$,那么$\Box$代表多少?
1796 |
1797 | ### 练习1
1798 |
1799 | 玩具店里的水果模型,1个柿子的重量等于3个苹果的重量,2个苹果的重量等于3个梨的重量,2个梨重60克,问:1个柿子模型有多重?
1800 |
1801 | ### 例题2
1802 |
1803 | 丁丁去文具店买了5支签字笔和6支红笔一共用了13元5角,2支签字笔的价钱等于3支红笔的价钱。问:红笔与签字笔的单价各是多少?
1804 |
1805 | ### 练习2
1806 |
1807 | 学校体育部要买15个排球和8个足球,1个足球75元,3个排球的价钱等于2个足球的价钱。问:体育部这次采购要花多少钱?
1808 |
1809 | ### 例题3
1810 |
1811 | 桃子和苹果共240个,其中桃子数量是苹果数量的2倍。求桃子和苹果各有多少个。
1812 |
1813 | ### 练习3
1814 |
1815 | 同学们在生物课外活动中种花生的棵数比白薯多280棵,且花生棵数是白薯的15倍,求花生、白薯各种了多少棵。
1816 |
1817 | ### 例题4
1818 |
1819 | 假如12只鸡可换2头羊,9头羊可换3头猪,8头猪可换2头牛,那么用5头牛可换多少只鸡?
1820 |
1821 | ### 练习4
1822 |
1823 | 用2个鹅蛋能换9个鸡蛋,2个鸡蛋能换12个鹌鹁蛋,用5个鹅蛋能换多少个鹌鹑蛋?
1824 |
1825 | ### 例题5
1826 |
1827 | 已知一只鸡与一只鸭共重2000克,一只鸡与一只猴共重1800克,一只猴与一只鸭共重2200克。问:三只动物每只各重多少克?
1828 |
1829 | ### 练习5
1830 |
1831 | 已知a+b=30,b+c=35,a+c=25,求a、b、c各是多少?
1832 |
1833 | ### 例题6
1834 |
1835 | 牛牛和丁丁各有书若干本,已知丁丁的书是牛牛的3倍,如果丁丁给牛牛10本书,则牛牛的书将是丁丁的3倍。问丁丁和牛牛二人原来各有多少本书?
1836 |
1837 | ### 练习6
1838 |
1839 | 1个柚子加1个梨的重量等于7个桃子的重量,2个梨的重量等于4个桃子的重量。那么,1个柚子的重量等于几个桃子的重量?
1840 |
1841 | 复习巩固
1842 |
1843 | ### 巩固1(鸡兔同笼)
1844 |
1845 | 今有鸡兔同笼,上有三十五头,下有九十四足,问鸡兔各几何?
1846 |
1847 | ### 巩固2(周期问题)
1848 |
1849 | 流水线上给小木球涂色的次序是:先5个红、再4个黄、再3个绿、在2个黑、再1个白,然后又依次是5红、4黄、3绿、2黑、1白**......**如此继续涂下去,到第2022个小球该涂什么颜色?
1850 |
1851 | ### 巩固3(盈亏问题)
1852 |
1853 | 秋天到了,小白兔收获了一筐萝卜,它按照计划吃的天数算了一下,如果每天吃4个,要多出48个萝卜;如果每天吃6个,则又少8个萝卜。那么小白兔买回的萝卜有多少个?计划吃多少天?
1854 |
1855 | ### 巩固4(奇数与偶数)
1856 |
1857 | 算式$123+456\times789+987\times654+321$的结果是奇数还是偶数?
1858 |
1859 | ### 巩固5(枚举与树形图)
1860 |
1861 | A、B、C三个小朋友互相传球,先从A开始发球(作为第一次传球),这样经过了4次传球后,球不传到A手中,那么不同的传球方式共多少种?
1862 |
1863 | ### 巩固6(等式代换)
1864 |
1865 | 2只兔子的重量等于6只小鸡的重量,3只袋鼠的重量相当于4只兔子的重量,那么1只袋鼠的重量相当于多少只小鸡的重量?
1866 |
1867 | ## 3.1.01. 角度
1868 |
1869 | 课前热身
1870 |
1871 | ### 热身1
1872 |
1873 | 1只鹅可以换8千克鱼,而4千克鱼可以换50个鸡蛋,10个鸡蛋可以换3个鹅蛋. 一只鹅可以换 多少个鹅蛋?
1874 |
1875 | ### 热身2
1876 |
1877 | 甲、乙两人共储蓄32元,乙、丙两人共储蓄30元,甲、丙两人共储蓄22元。三人各储蓄多少 元?
1878 |
1879 | ### 热身3
1880 |
1881 | 学校第一次买了3个水瓶和20个茶杯,共用去134元;第二次又买了同样的3个水瓶和16个茶杯,共用去118元。问水瓶和茶杯的单价各是多少元?
1882 |
1883 | 例题练习
1884 |
1885 | ### 例题1
1886 |
1887 | 图中有几种角?各有几个?将它们表示出来。(只考虑小于平角的角)
1888 |
1889 |
1486 |
1487 | ### 例题6(日历型)
1488 |
1489 | 图中是2013年5月份的日历表,根据表请回答:
1490 |
1491 | | 日 | 一 | 二 | 三 | 四 | 五 | 六 |
1492 | | ---- | ---- | ---- | ---- | ---- | ---- | ---- |
1493 | | | | | 1 | 2 | 3 | 4 |
1494 | | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
1495 | | 12 | 13 | 14 | 15 | 16 | 17 | 18 |
1496 | | 19 | 20 | 21 | 22 | 23 | 24 | 25 |
1497 | | 26 | 27 | 28 | 29 | 30 | 31 | |
1498 |
1499 | (1)该年6月1日是星期几?
1500 |
1501 | (2)该年10月1日是星期几?
1502 |
1503 | (3)2015 年5月1日是星期几?
1504 |
1505 | ### 练习6
1506 |
1507 | 2014年3月3日是星期一,算一算 2014年8月8号是星期几?
1508 |
1509 | ### 练习1
1510 |
1511 | ☆◎☆◎◎☆◎☆◎◎☆◎☆◎◎☆◎☆◎◎……
1512 |
1513 | 照这样的规律,第98个图形是什么?
1514 |
1515 | ### 练习2
1516 |
1517 | 一列数按“12345123451234512345……”排列,那么前40个数字之和是多少?
1518 |
1519 | ### 练习3
1520 |
1521 | 2022年1月1日是星期六,2022年6月1日是星期几?
1522 |
1523 | ## 3.1.17. 盈亏问题
1524 |
1525 | ### 热身1
1526 |
1527 | 小松鼠采松果,晴天每天可以采10个,雨天每天只能采6个。它一连几天采了80个松果,平均每天采8个。那么其中有几天是雨天呢?
1528 |
1529 | ### 热身2
1530 |
1531 | 在一根绳子上依次穿7个白颗、4颗黑珠,并按此方式重复。如果从头开始穿,一共穿了120颗珠子,那么这120颗珠子中,白珠比黑珠多几颗?
1532 |
1533 | ### 热身3
1534 |
1535 | 小迪和小迦比赛踩怪兽,规定踩同样的脚数,小迪一脚能踩2只怪兽,小迦一脚能踩5只怪兽,知道小迦比小迪一共多踩了60只。请问他们都踩了多少脚?
1536 |
1537 | 例题练习
1538 |
1539 | ### 例题1(盈盈)
1540 |
1541 | 乐乐老师有一桶巧克力,将它们分给三年级的小朋友,如果每人分9块,就剩下40块,如果每人分12块,就剩下10块。那乐乐老师一共有多少块巧克力,又将这些巧克力分给了多少个小朋友?
1542 |
1543 | ### 练习1
1544 |
1545 | 老师给三年级(2)班的小朋友发儿童节小礼物,如果每人发5个会剩下3个;如果每人发4个会剩下9个,三年级(2)班一共有多少个小朋友?
1546 |
1547 | ### 例题2(亏亏)
1548 |
1549 | 乐乐老师有一桶巧克力,将它们分给三年级的小朋友,如果每人分6块会缺少10块,如果每人分8块,会缺少24块。那乐乐老师一共有多少块巧克力?
1550 |
1551 | ### 练习2
1552 |
1553 | 冬天到了,小白免拿出一管萝卜当作一段时间的粮食,如果每天吃5根,还少3根;如果每天吃6根,还少8根,你知道小白免这管萝卜有多少根吗?
1554 |
1555 | ### 例题3(盈亏)
1556 |
1557 | 田田有一罐星空糖想要分给身边的好朋友,如果每人分5颗剩9颗,如果每人分7颗则有一人没分到,你知道田田身边有多少个好朋友吗?
1558 |
1559 | ### 练习3
1560 |
1561 | 丁丁整理出很多衣服打算寄给山区的小朋友,如果每次寄5件,到开学那天还有10件没有寄出,如果每次寄10件,会比第一种寄法少去邮局4趟,计算丁丁一共打算寄多少件衣服去山区?
1562 |
1563 | ### 例题4
1564 |
1565 | 三年级的同学们去郊外参加夏令营活动,如果每个帐篷住4名同学,则有7名同学没有地方住。如果每个帐篷住5名同学,则会空出3个床位。请计算出参加夏令营的同学有多少人?
1566 |
1567 | ### 练习4
1568 |
1569 | 乐乐老师为小朋友们分发儿童节礼物,如果每人分2个,会剩下12个礼物,如果每人发3个,最后会少2个礼物,请计算一共有多少个小朋友在等着领礼物?
1570 |
1571 | ### 例题5
1572 |
1573 | 乐乐老师带着小朋友去种花,如果每人种5棵,最后会剩下3棵花没人种,如果其中有2个小朋友各种4棵,剩下的小朋友每人种6棵,则这些花刚好种完。请问有多少个小朋友参加了种花?一共要种多少棵花?
1574 |
1575 | ### 练习5
1576 |
1577 | 少先队员们参加了植树节活动,如果每人挖6个树坑,会剩下5个树坑没人挖,如果其中2个人各挖3个树坑,其余每人挖7个树坑,刚好挖完所有的树坑。请计算少先队员们一共需要挖多少个树坑?
1578 |
1579 | ### 例题6
1580 |
1581 | 乐乐老师有一桶巧克力,将它们分给三年级的小朋友,如果每人分6块,则剩下10块,如果给其中3个人每人分4块,其他小朋友每人分7块,还剩下1块巧克力。乐乐老师一共有多少块巧克力?
1582 |
1583 | ### 练习6
1584 |
1585 | 猴王给一群猴子分香蕉,如果每只猴子分5根,最后会剩下16根香蕉没有被分出去,如果猴王给每只猴子分7根香蕉,最后一只猴子只能拿到3根香蕉。猴王一共有多少根香蕉?
1586 |
1587 | ### 练习1
1588 |
1589 | 学校新入学的小朋友要入住宿舍了,每间宿舍住的人一样多。如果每间住4人,就多出20人;如果每间住8人,还多了4人。请问:共有几间宿舍,几个小朋友?
1590 |
1591 | ### 练习2
1592 |
1593 | 老师给新入学的小朋友分积分卡,每个人分到的一样多。如果每个小朋友分10张,就少了30张;如果每个小朋友分8张,还是少8张。请问:一共有几个小朋友,几张积分卡?
1594 |
1595 | ### 练习3
1596 |
1597 | 一群小朋友分香蕉,如果每人分3根,则多4根;如果每人分4根,还少3根。那么,有几个小朋友,几根香蕉呢?
1598 |
1599 | ## 3.1.18. 奇数与偶数进阶
1600 |
1601 | 课前热身
1602 |
1603 | ### 热身1
1604 |
1605 | 妈妈为牛牛准备了铅笔,如果每次给他15支,这学期过完能剩下10支铅笔留给下学期用;如果每次给他17支,这学期刚好够用。你知道妈妈一共准备了多少支铅笔吗?
1606 |
1607 | ### 热身2
1608 |
1609 | 养猪场新到了一批幼年猪,如果每个饲养员照顾3头小猪,会有22头猪没人照顾;如果每个饲养员多照顾5头小猪,会有1个饲养员分不到任务。这个养猪场新到的幼年猪有多少头?
1610 |
1611 | ### 热身3
1612 |
1613 | 最大的两位奇数是()最小的四位偶数是()它们的和是()数
1614 |
1615 | ### 例题练习
1616 |
1617 | ### 例题1
1618 |
1619 | 不计算,判断下列各式结果的奇偶性。
1620 |
1621 | | $37+65$ | $36+66$ | $333+54$ |
1622 | | -------- | -------- | -------- |
1623 | | $145-33$ | $166-38$ | $97-68$ |
1624 |
1625 | 奇数个奇数相加减结果是()
1626 |
1627 | 偶数个奇数相加减结果是()
1628 |
1629 | 奇数个偶数相加减结果是()
1630 |
1631 | 偶数个偶数相加减结果是()
1632 |
1633 | ### 练习1
1634 |
1635 | 不计算,判断下列各式结果的奇偶性。
1636 |
1637 | | $5673+384+333+356+233$ |
1638 | | --------------------------------------- |
1639 | | $6252-1035+3566-2334+5688-1333-579+677$ |
1640 |
1641 | ### 例题2
1642 |
1643 | 请找出两个整数使他们的和是231,差是32,这样的两个数是否存在?若存在,请写出这两个数;若不存在,请说明理由。
1644 |
1645 | ### 练习2
1646 |
1647 | 请找出两个整数使他们的和是160,差是40,这样的两个数是否存在?若存在,请写出这两个数;若不存在,请说明理由。
1648 |
1649 | ### 例题3
1650 |
1651 | 一本书共有256页,从中任意找出5张纸,这5张纸上的所有页码之和能等于132吗?
1652 |
1653 | ### 练习3
1654 |
1655 | 请在下面的式子中填入“+”或者“-”,使得结果是6,可能吗?为什么?
1656 | $$
1657 | 987654321=6
1658 | $$
1659 |
1660 | ### 例题4
1661 |
1662 | 不计算,判断下列各式结果的奇偶性。
1663 |
1664 | | $13×35$ | $24\times36$ | $14\times23$ |
1665 | | ------- | ------------ | ------------ |
1666 |
1667 | ### 练习4
1668 |
1669 | 不计算,判断下列各式结果的奇偶性。
1670 |
1671 | | $23\times27\times39\times45\times54\times49\times33$ |
1672 | | ------------------------------------------------------------ |
1673 | | $31\times26\times13+53\times35+666\times577-3\times5\times987$ |
1674 |
1675 | 任意个奇数相乘结果是();
1676 |
1677 | 任意个偶数相乘结果是();
1678 |
1679 | 奇数与偶数相乘结果是()。
1680 |
1681 | ### 例题5
1682 |
1683 | 己知a,b,c是三个连续的自然数,其中c是偶数。田田说:“那么a+1,b+2,c+3这三个数的乘积一定是奇数。”丁丁说:“不对,a+1,b+2,c+3这三个数的乘积一定是偶数。”他们谁说得对呢?
1684 |
1685 | ### 练习5
1686 |
1687 | 牛牛在做题的时候写出了这样一个算式:$2751=53×21+42×39-36+35$,他做得对吗?
1688 |
1689 | ### 例题6
1690 |
1691 | 桌子上有7张正面向下的扑克牌,丁丁每次会把6张牌翻转。为了使扑克牌都正面向上,丁丁需要翻转几次?能实现吗?
1692 |
1693 | ### 练习6
1694 |
1695 | 明光市小学生参加数学竞赛,题目共20道。评分标准是:基础分25分,答对一道加5分,答错一道减1分,不答算错。如果有1111名同学参赛,则所有参赛同学得分总数一定是奇数还是偶数?请说明理由。
1696 |
1697 | 课后巩固
1698 |
1699 | ### 巩固1
1700 |
1701 | $$
1702 | 1+2+3+4+\dots+2021+2022
1703 | $$
1704 |
1705 | 算式的结果是奇数还是偶数?
1706 |
1707 | ### 巩固2
1708 |
1709 | 有一本500页的书,从中任意撕下33张纸,这33张纸上的所有页码之和能否是2022?
1710 |
1711 | ### 巩固3
1712 |
1713 | 是否存在自然数a,b,c,使得$(a-b)\times(b-c)\times(a-c)=65339$
1714 |
1715 | ## 3.1.19. 有序枚举与树形图
1716 |
1717 | ### 热身1
1718 |
1719 | a、b、c、d、e、f是六个连续的自然数,那么$a+b+c-d-e-f$的结果是奇数还是偶数?$a\times b\times c\times b+e\times f$的结果是奇数还是偶数?
1720 |
1721 | ### 热身2
1722 |
1723 | 在黑板上写1~2022这2022个自然数,每次任意擦去两个数,然后写上它们的和或者差,一直这样重复操作,经过若干次后黑板上只剩一个数,请问这个数是奇数还是偶数?
1724 |
1725 | ### 热身3
1726 |
1727 | 某人游览A、B、C三个风景区,每天游览一个,想要三天时间不重复的游览完这三个景区共有多少种不同的安排顺序?
1728 |
1729 | ### 例题1
1730 |
1731 | 乐乐老师打算把一个苹果、一个梨、一个香蕉分给丁丁和牛牛,每人至少分到一样水果,且全部分完,有多少种不同的分法?
1732 |
1733 | ### 练习1
1734 |
1735 | 妈妈买了1红2黑的3支钢笔送给姐姐和妹妹,1人最少拿到1支,且全部分完,问有多少种不同的送法?
1736 |
1737 | ### 例题2
1738 |
1739 | 一本《儿童故事》的定价是50元,如果丁丁有足够多的5元和10元,他会有多少种不同的付钱方法?
1740 |
1741 | ### 练习2
1742 |
1743 | 这里有1角、5角、1元、5元四张纸币,小朋友可以随意拿起几张纸币组合出总钱数,请问总钱数有多少种可能?
1744 |
1745 | ### 例题3
1746 |
1747 | 乐乐老师一共有5块巧克力,打算分给丁丁、牛牛、田田三个小朋友,每人最少分1块,且全部分完,有多少种不同的分法?
1748 |
1749 | ### 练习3
1750 |
1751 | 乐乐老师一共有8块巧克力,打算分给丁丁、牛牛、田田三个小朋友,每人最少分2块,且全部分完,有多少种不同的分法?
1752 |
1753 | ### 例题4
1754 |
1755 | 现在有数学卡片0,1,2,3各一张,可以排成多少个不同的四位数?
1756 |
1757 | ### 练习4
1758 |
1759 | 现在有数学卡片1,2,3,4各一张,可以排成多少个不同的四位数?
1760 |
1761 | ### 例题5
1762 |
1763 | 5个人排成一排,甲当排头,乙不当排尾,共有多少种排法?
1764 |
1765 | ### 练习5
1766 |
1767 | 乐乐老师、丁丁、牛牛、田田、阿普五个人站成一排,已知阿普站在第一个位置,乐乐老师站在最后一个位置,有多少种不同的排队方式?
1768 |
1769 | ### 例题6
1770 |
1771 | 乐乐老师带着丁丁、牛牛玩传球的游戏,从乐乐老师开始,每个人都可以将球传给其他人,球被传递四次之后又回到了乐乐老师手中,有多少种不同的传球可能呢?
1772 |
1773 | ### 练习6
1774 |
1775 | ABCD四人传球,要求AB不能互传,且自己不能传给自己。开始的时候球在A手上,经过4次传球后,球传回到A手中,不同的传球方式有多少种?
1776 |
1777 | ### 练习1
1778 |
1779 | 现在有数学卡片0,1,2,3,4各一张,可以排成多少个不同的三位数?
1780 |
1781 | ### 练习2
1782 |
1783 | 袋中有2个红球,3个黄球和4个白球,小明从中任意拿出4个球,他拿出球的情况共有几种可能。
1784 |
1785 | ### 练习3
1786 |
1787 | A、B、C三个小朋友互相传球,先从A开始发球(作为第一次传球),这样经过了5次传球后,球恰巧又回到A手中,那么不同的传球方式共多少种?
1788 |
1789 | ## 3.1.20. 等式代换
1790 |
1791 | 例题练习
1792 |
1793 | ### 例题1
1794 |
1795 | 已知$\bigcirc+\bigcirc+\bigcirc+\bigcirc=60$,$\bigtriangleup=\bigcirc+\bigcirc$,$\Box+\Box+\Box=\bigtriangleup$,那么$\Box$代表多少?
1796 |
1797 | ### 练习1
1798 |
1799 | 玩具店里的水果模型,1个柿子的重量等于3个苹果的重量,2个苹果的重量等于3个梨的重量,2个梨重60克,问:1个柿子模型有多重?
1800 |
1801 | ### 例题2
1802 |
1803 | 丁丁去文具店买了5支签字笔和6支红笔一共用了13元5角,2支签字笔的价钱等于3支红笔的价钱。问:红笔与签字笔的单价各是多少?
1804 |
1805 | ### 练习2
1806 |
1807 | 学校体育部要买15个排球和8个足球,1个足球75元,3个排球的价钱等于2个足球的价钱。问:体育部这次采购要花多少钱?
1808 |
1809 | ### 例题3
1810 |
1811 | 桃子和苹果共240个,其中桃子数量是苹果数量的2倍。求桃子和苹果各有多少个。
1812 |
1813 | ### 练习3
1814 |
1815 | 同学们在生物课外活动中种花生的棵数比白薯多280棵,且花生棵数是白薯的15倍,求花生、白薯各种了多少棵。
1816 |
1817 | ### 例题4
1818 |
1819 | 假如12只鸡可换2头羊,9头羊可换3头猪,8头猪可换2头牛,那么用5头牛可换多少只鸡?
1820 |
1821 | ### 练习4
1822 |
1823 | 用2个鹅蛋能换9个鸡蛋,2个鸡蛋能换12个鹌鹁蛋,用5个鹅蛋能换多少个鹌鹑蛋?
1824 |
1825 | ### 例题5
1826 |
1827 | 已知一只鸡与一只鸭共重2000克,一只鸡与一只猴共重1800克,一只猴与一只鸭共重2200克。问:三只动物每只各重多少克?
1828 |
1829 | ### 练习5
1830 |
1831 | 已知a+b=30,b+c=35,a+c=25,求a、b、c各是多少?
1832 |
1833 | ### 例题6
1834 |
1835 | 牛牛和丁丁各有书若干本,已知丁丁的书是牛牛的3倍,如果丁丁给牛牛10本书,则牛牛的书将是丁丁的3倍。问丁丁和牛牛二人原来各有多少本书?
1836 |
1837 | ### 练习6
1838 |
1839 | 1个柚子加1个梨的重量等于7个桃子的重量,2个梨的重量等于4个桃子的重量。那么,1个柚子的重量等于几个桃子的重量?
1840 |
1841 | 复习巩固
1842 |
1843 | ### 巩固1(鸡兔同笼)
1844 |
1845 | 今有鸡兔同笼,上有三十五头,下有九十四足,问鸡兔各几何?
1846 |
1847 | ### 巩固2(周期问题)
1848 |
1849 | 流水线上给小木球涂色的次序是:先5个红、再4个黄、再3个绿、在2个黑、再1个白,然后又依次是5红、4黄、3绿、2黑、1白**......**如此继续涂下去,到第2022个小球该涂什么颜色?
1850 |
1851 | ### 巩固3(盈亏问题)
1852 |
1853 | 秋天到了,小白兔收获了一筐萝卜,它按照计划吃的天数算了一下,如果每天吃4个,要多出48个萝卜;如果每天吃6个,则又少8个萝卜。那么小白兔买回的萝卜有多少个?计划吃多少天?
1854 |
1855 | ### 巩固4(奇数与偶数)
1856 |
1857 | 算式$123+456\times789+987\times654+321$的结果是奇数还是偶数?
1858 |
1859 | ### 巩固5(枚举与树形图)
1860 |
1861 | A、B、C三个小朋友互相传球,先从A开始发球(作为第一次传球),这样经过了4次传球后,球不传到A手中,那么不同的传球方式共多少种?
1862 |
1863 | ### 巩固6(等式代换)
1864 |
1865 | 2只兔子的重量等于6只小鸡的重量,3只袋鼠的重量相当于4只兔子的重量,那么1只袋鼠的重量相当于多少只小鸡的重量?
1866 |
1867 | ## 3.1.01. 角度
1868 |
1869 | 课前热身
1870 |
1871 | ### 热身1
1872 |
1873 | 1只鹅可以换8千克鱼,而4千克鱼可以换50个鸡蛋,10个鸡蛋可以换3个鹅蛋. 一只鹅可以换 多少个鹅蛋?
1874 |
1875 | ### 热身2
1876 |
1877 | 甲、乙两人共储蓄32元,乙、丙两人共储蓄30元,甲、丙两人共储蓄22元。三人各储蓄多少 元?
1878 |
1879 | ### 热身3
1880 |
1881 | 学校第一次买了3个水瓶和20个茶杯,共用去134元;第二次又买了同样的3个水瓶和16个茶杯,共用去118元。问水瓶和茶杯的单价各是多少元?
1882 |
1883 | 例题练习
1884 |
1885 | ### 例题1
1886 |
1887 | 图中有几种角?各有几个?将它们表示出来。(只考虑小于平角的角)
1888 |
1889 |  1890 |
1891 | ### 练习1
1892 |
1893 | 图中有几种角?各有几个?将它们表示出来。(只考虑小于平角的角)
1894 |
1895 |
1890 |
1891 | ### 练习1
1892 |
1893 | 图中有几种角?各有几个?将它们表示出来。(只考虑小于平角的角)
1894 |
1895 |  1896 |
1897 | ### 例题2
1898 |
1899 | 下图中,∠1=∠2=∠3=18°,那么∠AOB 是多少度?
1900 |
1901 |
1896 |
1897 | ### 例题2
1898 |
1899 | 下图中,∠1=∠2=∠3=18°,那么∠AOB 是多少度?
1900 |
1901 |  1902 |
1903 | ### 练习2
1904 |
1905 | 下图中,∠1=∠2=20°,那么∠AOB 是多少度?
1906 |
1907 |
1902 |
1903 | ### 练习2
1904 |
1905 | 下图中,∠1=∠2=20°,那么∠AOB 是多少度?
1906 |
1907 |  1908 |
1909 | ### 例题3
1910 |
1911 | 如图所示,已知∠4 的度数是∠1 度数的 3 倍,求∠1,∠2,∠3,∠4 分别是多少度?
1912 |
1913 |
1908 |
1909 | ### 例题3
1910 |
1911 | 如图所示,已知∠4 的度数是∠1 度数的 3 倍,求∠1,∠2,∠3,∠4 分别是多少度?
1912 |
1913 |  1914 |
1915 | ### 练习3
1916 |
1917 | 如图,两条直线相交,∠1=140°,则∠2+∠3等于几?
1918 |
1919 |
1914 |
1915 | ### 练习3
1916 |
1917 | 如图,两条直线相交,∠1=140°,则∠2+∠3等于几?
1918 |
1919 |  1920 |
1921 | ### 例题4
1922 |
1923 | 如图,已知 O 是直线 AD 上一点,∠AOB,∠BOC,∠COD 三个角从小到大依次相差 20°,求这三个角的度数。
1924 |
1925 |
1920 |
1921 | ### 例题4
1922 |
1923 | 如图,已知 O 是直线 AD 上一点,∠AOB,∠BOC,∠COD 三个角从小到大依次相差 20°,求这三个角的度数。
1924 |
1925 |  1926 |
1927 | ### 练习4
1928 |
1929 | 如图,已知∠BOC,∠AOB,∠AOC 分别相差 50°,求∠BOC 的度数。
1930 |
1931 |
1926 |
1927 | ### 练习4
1928 |
1929 | 如图,已知∠BOC,∠AOB,∠AOC 分别相差 50°,求∠BOC 的度数。
1930 |
1931 |  1932 |
1933 | ### 例题5
1934 |
1935 | 直线 AB、CD 相交于点 O,OE 平分∠AOD,∠FOC=90°,∠ 1=40°,求∠2 与∠3 的度数。
1936 |
1937 |
1932 |
1933 | ### 例题5
1934 |
1935 | 直线 AB、CD 相交于点 O,OE 平分∠AOD,∠FOC=90°,∠ 1=40°,求∠2 与∠3 的度数。
1936 |
1937 |  1938 |
1939 | ### 练习5
1940 |
1941 | 如图所示,直线 AB 与直线 CD 相交于点 O,做∠DOE=∠BOD,OF 平分∠AOE, 若∠AOC=20°,则∠EOF 等于多少度?
1942 |
1943 |
1938 |
1939 | ### 练习5
1940 |
1941 | 如图所示,直线 AB 与直线 CD 相交于点 O,做∠DOE=∠BOD,OF 平分∠AOE, 若∠AOC=20°,则∠EOF 等于多少度?
1942 |
1943 |  1944 |
1945 | ### 例题6
1946 |
1947 | 如图所示,三个正方形叠放在一起,有一个公共点,并且已知其中两个角的度数分别为 45°和 30°, 求∠1 的度数。
1948 |
1949 |
1944 |
1945 | ### 例题6
1946 |
1947 | 如图所示,三个正方形叠放在一起,有一个公共点,并且已知其中两个角的度数分别为 45°和 30°, 求∠1 的度数。
1948 |
1949 |  1950 |
1951 | 巩固练习
1952 |
1953 | ### 练习1
1954 |
1955 | 如图所示,直线 AB,CD 相交于点 O,OA 平分∠EOC,∠EOC=70°,则∠BOD 的度数为多少?
1956 |
1957 |
1950 |
1951 | 巩固练习
1952 |
1953 | ### 练习1
1954 |
1955 | 如图所示,直线 AB,CD 相交于点 O,OA 平分∠EOC,∠EOC=70°,则∠BOD 的度数为多少?
1956 |
1957 |  1958 |
1959 | ### 练习2
1960 |
1961 | 如图,两个正方形重叠放在一起,已知∠1=70°,求∠3的度数。
1962 |
1963 |
1958 |
1959 | ### 练习2
1960 |
1961 | 如图,两个正方形重叠放在一起,已知∠1=70°,求∠3的度数。
1962 |
1963 |  1964 |
1965 | ### 练习3
1966 |
1967 | 如图所示,已知 OE 与 OF 垂直,过 O 点做直线 AB,若∠EOA=2∠AOF,则∠BOF=?
1968 |
1969 |
1964 |
1965 | ### 练习3
1966 |
1967 | 如图所示,已知 OE 与 OF 垂直,过 O 点做直线 AB,若∠EOA=2∠AOF,则∠BOF=?
1968 |
1969 |  1970 |
1971 | ## 3.2.02. 巧算综合
1972 |
1973 | 课前热身
1974 |
1975 | ### 热身1
1976 |
1977 | 下图是 3×3 的正方形方格,∠1 与∠2 相比,较大的是()。
1978 |
1979 |
1970 |
1971 | ## 3.2.02. 巧算综合
1972 |
1973 | 课前热身
1974 |
1975 | ### 热身1
1976 |
1977 | 下图是 3×3 的正方形方格,∠1 与∠2 相比,较大的是()。
1978 |
1979 |  1980 |
1981 | ### 热身2
1982 |
1983 | 如图,∠AOB 的顶点 O在直线 l 上,已知图中所有小于平角的角之和是 400 度,求∠AOB的大小。
1984 |
1985 | 
1986 |
1987 | ### 热身3
1988 |
1989 | 计算:$88\times46+88\times64-88\times10$
1990 |
1991 | 例题练习
1992 |
1993 | ### 例题1
1994 |
1995 | 计算。
1996 |
1997 | (1)$78+19+36+54+21+74+102$
1998 |
1999 | (2)$756-248-352$
2000 |
2001 | (3)$8+88+888+8888$
2002 |
2003 | (4)$39+38+40+41+43$
2004 |
2005 | ### 练习1
2006 |
2007 | 计算。
2008 |
2009 | (1)$99997+9996+995+94+9$
2010 |
2011 | (2)$894-89-111-95-105-94$
2012 |
2013 | ### 例题2
2014 |
2015 | 计算。
2016 |
2017 | (1)$25\times16\div20$
2018 |
2019 | (2)$1200\div4\div5\div5$
2020 |
2021 | (3)$1300\times77\div100$
2022 |
2023 | ### 练习2
2024 |
2025 | 计算。
2026 |
2027 | (1)$25\times64\times125$
2028 |
2029 | (2)$248\times5\div8$
2030 |
2031 | (3)$(36\times45)\div(6\times9)$
2032 |
2033 | ### 例题3
2034 |
2035 | 计算。
2036 |
2037 | (1)$35\times35$
2038 |
2039 | (2)$45\times45$
2040 |
2041 | (3)$73\times33$
2042 |
2043 | (4)$58\times58$
2044 |
2045 | ### 练习3
2046 |
2047 | 计算。
2048 |
2049 | (1)$75\times75$
2050 |
2051 | (2)$62\times68$
2052 |
2053 | (3)$67\times47$
2054 |
2055 | ### 例题4
2056 |
2057 | 计算。
2058 |
2059 | (1)$36\times19+36\times81$
2060 |
2061 | (2)$984\div8+16\div8$
2062 |
2063 | (3)$125\times(8+80)$
2064 |
2065 | (4)$(369+345)\div3$
2066 |
2067 | ### 练习4
2068 |
2069 | 计算。
2070 |
2071 | (1)$325\times113-325\times13$
2072 |
2073 | (2)$(40+8)\times25$
2074 |
2075 | (3)$684\div19-304\div19$
2076 |
2077 | (4)$(111+74)\div37$
2078 |
2079 | ### 例题5
2080 |
2081 | 计算。
2082 |
2083 | (1)$53\times46+71\times54+82\times54$
2084 |
2085 | ### 练习5
2086 |
2087 | 计算。
2088 |
2089 | (1)$33\times34+24\times34+57\times66$
2090 |
2091 | ### 例题6
2092 |
2093 | 计算。
2094 |
2095 | (1)$1997\times1995-1996\times1994$
2096 |
2097 | ### 练习6
2098 |
2099 | 计算。
2100 |
2101 | (1)$4747+888\times53+47\times787$
2102 |
2103 | ### 拓展1
2104 |
2105 | $$
2106 | 12345+23451+34512+45123+51234
2107 | $$
2108 |
2109 | ### 拓展2
2110 |
2111 | $$
2112 | 80+79-78-77+76+75-74-73+\dots+4+3-2-1
2113 | $$
2114 |
2115 | ### 拓展3
2116 |
2117 | $$
2118 | 20222022\times2021-20212021\times2022
2119 | $$
2120 |
2121 | ### 练习1
2122 |
2123 | 计算:$298+396+495+691+799+21$
2124 |
2125 | ### 练习2
2126 |
2127 | 计算:$(54\times24)\div(9\times4)$
2128 |
2129 | ### 练习3
2130 |
2131 | 计算:$39+142\times39+103$
2132 |
2133 | ## 3.2.03. 用字母表示数
2134 |
2135 | ### 热身1
2136 |
2137 | ### 热身2
2138 |
2139 | ### 热身3
2140 |
2141 | ### 例题1
2142 |
2143 | (1)观察下面的数列$2,4,6,a,10,b,14,\dots,a=(),b=()$。
2144 |
2145 | (2)观察下面的数列$1,3,5,a,9,b,13,\dots,a=(),b=()$。
2146 |
2147 | ### 练习1
2148 |
2149 | 观察下面的数列,填入合适的数。
2150 |
2151 | (1)5,10,15,a,25,30,b,……,a=(),b=()。
2152 |
2153 | (2)4,8,12,a,20,24,b,32,36,……,a=(),b=()。
2154 |
2155 | ### 例题2
2156 |
2157 | 1只青蛙1张嘴,2只眼睛,4条腿;
2158 |
2159 | 2只青蛙2张嘴,()只眼睛,()条腿;
2160 |
2161 | 3只青蛙3张嘴,()只眼睛,()条腿;
2162 |
2163 | 4只青蛙4张嘴,()只眼睛,()条腿;
2164 |
2165 | ……
2166 |
2167 | n只青蛙()张嘴,()只眼睛,()条腿。
2168 |
2169 | ### 练习2
2170 |
2171 | 一个正方形有()条边,
2172 |
2173 | 两个正方形有()条边,
2174 |
2175 | 三个正方形有()条边,
2176 |
2177 | ……
2178 |
2179 | n个正方形有()条边。
2180 |
2181 | 边数和正方形的数量有什么关系呢?
2182 |
2183 | ### 例题3
2184 |
2185 | 用简便方法表示下列各式。
2186 |
2187 | (1)$27\times x$
2188 |
2189 | (2)$m\times n$
2190 |
2191 | (3)$a+a+a$
2192 |
2193 | (4)$a\times a$
2194 |
2195 | (5)$36\times a\times b$
2196 |
2197 | (6)$(a+b)\times5$
2198 |
2199 | ### 练习3
2200 |
2201 | (1)$63\times x+5$
2202 |
2203 | (2)$m\times n\times3$
2204 |
2205 | (3)$(m+n)\times16$
2206 |
2207 | (4)$c\times2\times a$
2208 |
2209 | ### 例题4
2210 |
2211 | 用字母表示下列公式。(周长=C,面积=S,长=a,宽=b,边长=a)
2212 | 长方形的周长公式:
2213 | 长方形的面积公式:
2214 | 正方形的周长公式:
2215 | 正方形的面积公式:
2216 |
2217 | ### 练习4
2218 |
2219 | 用字母表示下列公式。
2220 | 乘法交换律:
2221 | 乘法结合律:
2222 | 乘法分配律:
2223 |
2224 | ### 例题5
2225 |
2226 | 你能用字母表示下面题目中所求的量吗?
2227 |
2228 | (1)过春节了,阿普拿到了m元压岁钱,牛牛的压岁钱是阿普的6倍,牛牛的压岁钱是()元。
2229 |
2230 | (2)某学校有男老师a人,女老师比男老师少b人,学校有女老师()人,共有老师()人。
2231 |
2232 | (3)一个长方形的周长是80厘米,长是a厘米,宽是()厘米。
2233 |
2234 | ### 练习5
2235 |
2236 | 你能用字母表示下面题目中所求的量吗?
2237 | (1)一个等边三角形,每边长a米,它的周长是()米。
2238 | (2)牛牛的学校一共有m人,男生有a人,女生有()人。
2239 | (3)东东今年a岁,比妈妈小m岁,再过年c后妈妈比东东大()岁。
2240 |
2241 | ### 例题6
2242 |
2243 | 用含字母的式子表示。
2244 | (1)1个菠萝重x千克,1个西瓜比这个菠萝的3倍还重2千克,西瓜重()千克。如果菠萝重2千克,那么西瓜重()千克。
2245 | (2)小红骑车每分钟行x千米,她骑了20分钟,行驶了()千米;她行驶a千米,需要()分钟。x=2,a=10,那么需要()分钟。
2246 | (3)乙数比甲数a的4倍少6,乙数是()。
2247 |
2248 | ### 练习6
2249 |
2250 | 用含字母的式子表示。
2251 | (1)田田高a厘米,丁丁比田田高7厘米,丁丁和田田一共高()厘米。
2252 | (2)青青林场栽了梧桐树和雪松各x排,已知梧桐树每排12棵,雪松每排14棵,栽梧桐树
2253 | 和雪松共()棵;当x=20时,青青林场一共有()棵梧桐树和雪松。
2254 | (3)一个正方形的边长为a厘米,周长为()厘米,面积是()平方厘米。
2255 |
2256 | ## 3.2.04. 和差倍综合
2257 |
2258 | 例题练习
2259 |
2260 | ### 例题1(和差)
2261 |
2262 | 有大、小两个油桶,一共装油24千克,两个油桶都倒出同样多的油后分别还剩9千克和5千克。问:原来大、小两个油桶各装油多少千克?
2263 |
2264 | ### 练习1
2265 |
2266 | 两箱图书共有66本,甲箱如果借出10本,就比乙箱少4本。甲、乙两箱原有图书各多少本?
2267 |
2268 | ### 例题2(和差)
2269 |
2270 | 学校新进99本书,分给三、四、五三个年级,三年级比四年级多分了2本,四年级比五年级多分了5本,三个年级各分得书多少本?
2271 |
2272 | ### 练习2
2273 |
2274 | 甲、乙、丙三个数的和是105,甲数比乙数多4,乙数比丙数多4,求丙数。
2275 |
2276 | ### 例题3(和倍)
2277 |
2278 | 某校学生总人数比四年级人数的6倍少78人,并且除了四年级外,其他各年级的学生人数总和为2222人,那么该校共有学生多少人?
2279 |
2280 | ### 练习3
2281 |
2282 | 有两层书架,共有书216本,从第一层拿走42本书后,第二层的书比第一层的2倍还多6本,则第二层有多少本书?
2283 |
2284 | ### 例题4
2285 |
2286 | 一天,甲、乙、丙三个同学做数学题,已知甲比乙多做了6道,丙做的题是甲的2倍,比乙做的题多22道,则乙做了多少道数学题?
2287 |
2288 | ### 练习4
2289 |
2290 | 小云比小雨少20本书,后来小云丢了5本书,小雨新买了11本书,这时小雨的书比小云的书多2倍。问:原来两人各有多少本书?
2291 |
2292 | ### 例题5
2293 |
2294 | 李师傅某天生产了一批零件,把它们分成了甲、乙两堆摆放。若从甲堆零件中拿出15个放到乙堆,则两堆零件个数相等;若从乙堆零件中拿出15个放到甲堆,则甲堆的零件个数是乙堆的4倍。甲堆原有零件多少个,李师傅这天共生产了多少个零件?
2295 |
2296 | ### 练习5
2297 |
2298 | 一家汽车销售店有若干部福特汽车和丰田汽车等待销售。福特汽车的数量是丰田汽车的3倍,如果每周销售2辆丰田汽车和4辆福特汽车,丰田汽车销售完时还剩下30辆福特汽车。请问:原有丰田汽车和福特汽车各多少辆?
2299 |
2300 | ### 例题6
2301 |
2302 | 维尼熊和跳跳虎去摘苹果。维尼熊爬上树去摘,跳跳虎在地上跳着摘。跳跳虎每摘7个,维尼熊只能摘4个。维尼熊摘了80分钟,跳跳虎摘了50分钟就累倒了。他们回来后数了一下共摘2010个苹果,那么其中维尼熊摘的有多少个?
2303 |
2304 | ### 练习6
2305 |
2306 | 某镇上有东西两个公交车站,东站有客车84辆,西站有客车56辆,每天从东站到西站有7辆车,从西站到东站有11辆车,几天后,东站车辆是西站的4倍?
2307 |
2308 | ## 3.2.05. 逆向思考进阶
2309 |
2310 | ### 例题1
2311 |
2312 | 牛牛和阿昔在游玩时,遇到一位小神仙,他们问这位神仙:“你一定不到100岁吧!”谁知这位神仙摇摇头说:“你们算算吧!把我的年龄加上75,再除以5,然后减去15,再乘10,恰好是
2313 | 2000岁。”小朋友,你知道这位神仙现在有多少岁吗?
2314 |
2315 | ### 练习1
2316 |
2317 | 一个数加上37,乘37,减去37,再除以37,结果等于37,这个数是多少?
2318 |
2319 | ### 例题2
2320 |
2321 | 小马虎在做一道加法题时,把一个加数个位上的9看作6,十位上的6看作9,结果和是174,那么正确的结果应该是多少呢?
2322 |
2323 | ### 练习2
2324 |
2325 | 淘气在做一道减法题时,把减数个位上的9看成了3,把十位上的4看成了7,得到的结果是164。请你帮淘气算算正确的答案是多少?
2326 |
2327 | ### 例题3
2328 |
2329 | 李奶奶卖一筐鸡蛋,第一位客人买走了一半少2个,第二位客人买走了剩下的一半多2个,第三位客人把剩下的5个鸡蛋全部买走了。老奶奶的篮子里原来有多少个鸡蛋?
2330 |
2331 | ### 练习3
2332 |
2333 | 学学看到太上老君正在用一根绳子拴宝葫芦,第一次用去全长的一半还多2米,第二次用去余下的一半少10米,第三次用去15米,最后还剩9米,那么这根绳子原来有多少米?
2334 |
2335 | ### 例题4
2336 |
2337 | 有一个财迷总想使自己的钱成倍增长。一天,他在一座桥上碰见一个老人,老人对他说:"你只要走过这座桥再回来,你身上的钱就会增加一倍,但作为报酬,你每走一个来回要给我32个
2338 | 铜板。”财迷算了算,感觉挺合算,就同意了。他走过桥去又走回来,身上的钱果然增加了一倍,他很高兴地给了老人32个铜板。这样走完第五个来回,身上的最后32个铜板都给了老人,财迷一个铜板也没剩下。你知道财迷身上原有多少个铜板?
2339 |
2340 | ### 练习4
2341 |
2342 | 某人发现了一条魔道,下面有一个存钱的小箱子,当他从魔道走过去的时候,箱子里的一些钱会飞到人的口袋里,使人身上的钱增加一倍,这人很高兴;当他从魔道走回来的时候,身
2343 | 上的钱又会飞到箱子里,使箱子里的钱增加一倍。这个人一连走了3个来回后,箱子里的钱和人身上的钱都是64元,那么,原来这人身上有多少钱?箱子里有多少钱?
2344 |
2345 | ### 例题5
2346 |
2347 | 有一个两层书架,一共摆放224本书,先从上层取出与下层本数同样多的书放入下层,再从下层现有书中,取出与上层剩下的本数同样多的书放入上层,这算进行了一轮调整。若如进行了
2348 | 两轮调整后,两层摆放书的本数相等,上层书架原来摆放多少本书?下层书架原来摆放多少本书?
2349 |
2350 | ### 练习5
2351 |
2352 | 有甲、乙两箱糖果,如果第一次从甲箱拿出和乙箱同样多块糖果放到乙箱里,第二次从乙箱拿出和甲箱剩下的同样多块糖果放入甲箱,这样拿4次后,甲、乙两箱糖果都是16块。甲、乙两箱各有糖果多少块?
2353 |
2354 | ### 例题6
2355 |
2356 | 一班、二班、三班各有不同数量的图书。一班拿出本班的一部分图书分给二班、三班,使这两个班的图书各增加一倍;然后二班也拿出一部分图书分给一班、三班,使这两个班的图书各增加一倍;接着三班也拿出一部分图书分给一班、二班,使这两个班的图书各增加一倍。这时三个班的图书数量都是48本。
2357 | ,求三个班原来各有图书多少本。
2358 |
2359 | ### 练习6
2360 |
2361 | 甲、乙、丙3人共有192张邮票。从甲的邮票中取出乙那么多邮票给乙后,再从乙的邮票中取出丙那么多邮票给丙,最后从丙的邮票中取出甲那么多邮票给甲,这时甲、乙、丙3人的邮票数相同,甲、乙、丙原来各有邮票多少张?
2362 |
2363 | ## 3.2.06. 逻辑推理综合(1)
2364 |
2365 | ### 例题1
2366 |
2367 | 5名谋杀案的嫌疑人,在犯罪现场被警察询问,其中有一名是凶手。下面5个人的供述中,只有3句是对的:
2368 | A说:“D是杀人犯。”
2369 | B说:“我是无辜的。”
2370 | C说:“E不是杀人犯。”
2371 | D说:“A在说谎。”
2372 | E说:“B说的是实话。”
2373 | 在这5个人中,谁是凶手?
2374 |
2375 | ### 练习1
2376 |
2377 | 四个小朋友宝宝、星星、强强和乐乐在院子里踢足球,一阵响声,惊动了正在读书的陆老师,陆老师跑出来查看,发现一块窗户玻璃被打破了。陆老师问:“是谁打破了玻璃?”
2378 | 宝宝说:“是星星无意打破的。”
2379 | 星星说:“是乐乐打破的。”
2380 | 乐乐说:“星星说谎。”
2381 | 强强说:“反正不是我打破的。”
2382 | 如果只有一个孩子说了实话,那么这个孩子是谁?是谁打破了玻璃?
2383 |
2384 | ### 例题2
2385 |
2386 | 在一次数学竞赛中,A,B,C,D,E五位同学分别得了前五名(没有并列同一名次的),关于各人的名次,大家做出了下面的猜测:
2387 |
2388 | A说:“第二名是D,第三名是B。”
2389 |
2390 | B说:“第二名是C,第四名是F。”
2391 |
2392 | C说:“第一名是E,第五名是A。”
2393 |
2394 | D说:“第三名是C,第四名是A。”
2395 |
2396 | E说:“第二名是B,第五名是D。”
2397 |
2398 | 结果每人都只猜对了一半,他们的名次如何?
2399 |
2400 | ### 练习2
2401 |
2402 | 甲、乙、丙、丁四人同时参加全国小学数学夏令营。赛前甲、乙、丙分别作了预测。
2403 |
2404 | 甲说:“丙第1名,我第3名。”
2405 |
2406 | 乙说:“我第1名,丁第4名。”
2407 |
2408 | 丙说:“丁第2名,我第3名。”
2409 | 成绩揭晓后,发现他们每人只说对了一半,你能说出他们的名次吗?
2410 |
2411 | ### 例题3
2412 |
2413 | 学校新来了一位老师,五个学生分别听到如下的情况:
2414 |
2415 | (1)是一位姓王的中年女老师,教语文;
2416 |
2417 | (2)是一位姓丁的中年男老师,教数学;
2418 |
2419 | (3)是一位姓刘的青年男老师,教外语;
2420 |
2421 | (4)是一位姓李的青年男老师,教数学;
2422 |
2423 | (5)是一位姓王的老年男老师,教外语。
2424 |
2425 | 他们每人听到的四项情况中各有一项正确。问:真实情况是什么样的?
2426 |
2427 | ### 练习3
2428 |
2429 | 4名运动员参加一项比赛,赛前。
2430 |
2431 | 甲说:“我肯定是最后一名。”
2432 |
2433 | 乙说:“我不可能是第一名,也不可能是最后一名。”
2434 | 丙说:“我绝对不会得最后一名。”
2435 | 丁说:“我肯定得第一名。”
2436 |
2437 | 赛后,发现他们4人的预测中只有一人是错误的。请问谁的预测是错误的?
2438 |
2439 | ### 例题4
2440 |
2441 | 王平、宋丹、韩涛三个小学生都是少先队的干部,一个是大队长,一个是中队长,一个是小队长。一次数学测验,这三个人的成绩是:
2442 |
2443 | (1)韩涛比大队长的成绩好。
2444 |
2445 | (2)王平和中队长的成绩不相同。
2446 |
2447 | (3)中队长比宋丹的成绩差。
2448 |
2449 | 请你根据这三个人的成绩,判断一下,谁是大队长呢?
2450 |
2451 | ### 练习4
2452 |
2453 | 王文、张贝、李丽分别是跳伞、田径、游泳运动员,现在知道:
2454 |
2455 | (1)张贝从未上过天;
2456 | (2)跳伞运动员已得过两块金牌;
2457 |
2458 | (3)李丽还未得过第一名,她与田径运动员同年出生:
2459 | 请根据上述情况,判断王文、张贝、李丽各是什么运动员?
2460 |
2461 | ### 例题5
2462 |
2463 | 张、王、李三人除了本职工作,每人都有两样业余爱好。人们有时以车工、电工、乐师、画家、作家、技工称呼他们,此外,还有以下情况:
2464 | (1)车工经常赞扬乐师的三弦琴弹得好;
2465 | (2)乐师,作家常常与姓张的一起看电影;
2466 | (3)画家请电工来修过电灯;
2467 | (4)车工和画家的儿子在同一车间工作;
2468 | (5)姓王的向作家请教写作的技巧;
2469 | (6)姓李的善于下象棋,姓王的和画家常常输给他。
2470 | 问:姓李的有哪两个称呼?
2471 |
2472 | ### 练习5
2473 |
2474 | 宝宝、贝贝、聪聪每人有两个外号,人们有时以“数学博士”、“短跑健将”、“跳高冠军”、“小画家“、“大作家”和“歌唱家”称呼他们,此外:
2475 |
2476 | (1)数学博士夸跳高冠军跳得高;
2477 |
2478 | (2)跳高冠军和大作家常与宝宝一起看电影;
2479 |
2480 | (3)短跑健将请小画家画贺年卡;
2481 |
2482 | (4)数学博士和小画家关系很好;
2483 |
2484 | (5)贝贝向大作家借过书;
2485 |
2486 | (6)聪聪下象棋常赢贝贝和小画家。
2487 |
2488 | 问:宝宝、贝贝、聪聪各有哪两个外号?
2489 |
2490 | ### 例题6
2491 |
2492 | A,B,C,D分别来自中国、日本、美国和法国。已知:
2493 |
2494 | (1)A和中国人是医生;
2495 |
2496 | (2)B和法国人是教师;
2497 |
2498 | (3)C和日本人职业不同;
2499 |
2500 | (4)D不会看病。
2501 |
2502 | 问:A,B,C,D各是哪国人?
2503 |
2504 | ### 练习6
2505 |
2506 | 张明、席辉和李刚分别在北京、上海和天津三城市之一工作,他们的职业是工人、农民和教师之一,已知:
2507 |
2508 | (1)张明不在北京工作,席辉不在上海工作;
2509 |
2510 | (2)在北京工作的不是教师;
2511 | (3)在上海工作的是工人;
2512 |
2513 | (4)席辉不是农民。
2514 |
2515 | 问:这三人各住哪里?各是什么职业?
2516 |
2517 | ## 3.2.07. 方阵
2518 |
2519 | ### 例题1
2520 |
2521 | 一个实心方阵,最外一层每边18人。
2522 | (1)那么整个方阵一共()人;
2523 | (2)最外面一层有()人;
2524 | (3)从外向内数,第二层每边有()人,一共有()人;
2525 | (4)如果考虑最外面三层,那么这三层共有()人;
2526 | (5)如果将方阵外面增加一层,那么一共增加()人。
2527 |
2528 | ### 练习1
2529 |
2530 | 用64枚棋子摆成一个实心方阵。
2531 | (1)每边有()枚棋子;
2532 | (2)最外层有()枚棋子;
2533 | (3)从外向内数,第二层每边有()枚棋子,第二层一共有()枚棋子。
2534 |
2535 | ### 例题2
2536 |
2537 | 有一块空地在进行种树绿化,打算把树种成实心方阵的样子,方阵最外面一周有60棵树,问这个方阵外层每边有多少棵树?这块空地一共需要多少棵树?
2538 |
2539 | ### 练习2
2540 |
2541 | 三年级学生排成一个实心方阵,最外一层的人数为36人,问方阵最外层每边有多少人?这个方阵共有三年级学生多少人?
2542 |
2543 | ### 例题3
2544 |
2545 | 小刚在用棋子摆好的实心方阵上又添了17枚棋子,它的横竖各增加了一排,成了大一点的实心方阵,求原来的实心方阵有多少枚棋子。
2546 |
2547 | ### 练习3
2548 |
2549 | 军训的学生进行队列表演,排成了一个5行5列的正方形队列,如果去掉一行一列,要去掉多少人?
2550 |
2551 | ### 例题4
2552 |
2553 | 大家要用盆花在空地上摆出一个空心方阵花坛,最外面的一层每边摆12盆花,共3层,一共要用多少盆花?
2554 |
2555 | ### 练习4
2556 |
2557 | 有一个班的学生排成一个中空方阵,最外层人数共52人,最内层人数共28人,这个班学生共有多少人?
2558 |
2559 | ### 例题5
2560 |
2561 | 用64枚棋子摆成一个两层中空方阵,如果想在外面再增加一层,问需要增加多少枚棋子?
2562 |
2563 | ### 练习5
2564 |
2565 | 用84枚棋子摆成一个三层中空方阵,问最外层有多少枚棋子?
2566 |
2567 | ### 例题6
2568 |
2569 | 一天,博士用棋子摆成一周每边有10枚棋子的空心方阵,摆完后发现还有棋子剩下,但是不够外围再增加一层。在保持原有棋子不动的情况下,想变成一个更大的两层空心方阵,博士至少需要多少枚棋子?
2570 |
2571 | ### 练习6
2572 |
2573 | 用一堆棋子摆成一个两层的空心方阵,用了48枚棋子后发现还剩下一些棋子,但是不够外围再增加一层了。在保持原有棋子不动的情况下,想变成一个更大的三层空心方阵,至少需要多少枚棋子?
2574 |
2575 | ## 3.2.08. 巧填算符综合
2576 |
2577 | 例题练习
2578 |
2579 | ### 例题1
2580 |
2581 | 在“+、-、×、÷、( )”中,挑出合适的符号,填入下面的数字之间,使算式成立。
2582 | $$
2583 | 9\ \ \ 8\ \ \ 7\ \ \ 6\ \ \ 5\ \ \ 4\ \ \ 3\ \ \ 2\ \ \ 1=1
2584 | $$
2585 |
2586 | ### 练习1
2587 |
2588 | 在○内填上与等号左边不同的运算符号,使等式成立。
2589 | $$
2590 | (1)6-2+2=6\circ2\circ 2
2591 | $$
2592 |
2593 | $$
2594 | (2)8+2+3=8\circ 2\circ 3
2595 | $$
2596 |
2597 | $$
2598 | (3)16-8-3=16\circ 8\circ 3
2599 | $$
2600 |
2601 | ### 例题2
2602 |
2603 | 在下面算式的适当地方,填上运算符号“+、-、×、÷或( )”,使算式成立。
2604 | $$
2605 | 1\ \ \ 2\ \ \ 3\ \ \ 4\ \ \ 5=10
2606 | $$
2607 |
2608 | ### 练习2
2609 |
2610 | 用运算符号把下面三个相同的数宇连接起来,使等式成立。
2611 | $$
2612 | (1)5\ \ \ 5\ \ \ 5=30
2613 | $$
2614 |
2615 | $$
2616 | (2)6\ \ \ 6\ \ \ 6\ \ \ =30
2617 | $$
2618 |
2619 | ### 例题3
2620 |
2621 | 在下式的每两个数中间填上合适的运算符号,使等式成立。
2622 | $$
2623 | 8\ \ \ 2\ \ \ 4\ \ \ 6=4\ \ \ 2
2624 | $$
2625 |
2626 | ### 练习3
2627 |
2628 | 在下式的每两个数中间填上合适的运算符号,使等式成立。
2629 | $$
2630 | 8\ \ \ 2\ \ \ 3=3\ \ \ 3
2631 | $$
2632 |
2633 | ### 例题4
2634 |
2635 | 在8个8之间的适当地方,填上合适的运算符号或括号,使算式成立。
2636 | $$
2637 | 8\ \ \ 8\ \ \ 8\ \ \ 8\ \ \ 8\ \ \ 8\ \ \ 8\ \ \ 8=1000
2638 | $$
2639 |
2640 | ### 练习4
2641 |
2642 | 在下面算式适当的地方,填上运算符号或括号,使等式成立。
2643 | $$
2644 | 9\ \ \ 8\ \ \ 7\ \ \ 6\ \ \ 5\ \ \ 4\ \ \ 3\ \ \ 2\ \ \ 1=1000
2645 | $$
2646 |
2647 | ### 例题5
2648 |
2649 | 在5个4之间,填上适当的运算符号或括号,使得下面的算式成立。
2650 | $$
2651 | 4\ \ \ 4\ \ \ 4\ \ \ 4\ \ \ 4=8
2652 | $$
2653 |
2654 | ### 练习5
2655 |
2656 | 在下列算式的合适位置,填上运算符号或括号,使等式成立。
2657 | $$
2658 | (1)4\ \ \ 4\ \ \ 4\ \ \ 4=1
2659 | $$
2660 |
2661 | $$
2662 | (2)4\ \ \ 4\ \ \ 4\ \ \ 4=5
2663 | $$
2664 |
2665 | ### 例题6
2666 |
2667 | 请在 2,3,4,6 四个数之间任意填上“+、-、×、÷或( )”,每个数字都只能用一次,使它们的计算结果等于 24。你能做到吗?
2668 |
2669 | ### 练习6
2670 |
2671 | 请在 6,5,10,2 四个数之间任意填上“+、-、×、÷或( )”,每个数字都只能用一次,使它们的计算结果等于 24。你能做到吗?
2672 |
2673 | 课后巩固
2674 |
2675 | 将“+、-、×、÷、( )”填入合适的地方,使下面的等式成立。
2676 | $$
2677 | 3\ \ \ 3\ \ \ 3\ \ \ 3\ \ \ =\ \ \ 1
2678 | $$
2679 |
2680 | $$
2681 | 3\ \ \ 3\ \ \ 3\ \ \ 3\ \ \ =\ \ \ 2
2682 | $$
2683 |
2684 | $$
2685 | 3\ \ \ 3\ \ \ 3\ \ \ 3\ \ \ =\ \ \ 3
2686 | $$
2687 |
2688 | $$
2689 | 3\ \ \ 3\ \ \ 3\ \ \ 3\ \ \ =\ \ \ 4
2690 | $$
2691 |
2692 | $$
2693 | 3\ \ \ 3\ \ \ 3\ \ \ 3\ \ \ =\ \ \ 5
2694 | $$
2695 |
2696 | $$
2697 | 3\ \ \ 3\ \ \ 3\ \ \ 3\ \ \ =\ \ \ 6
2698 | $$
2699 |
2700 | $$
2701 | 3\ \ \ 3\ \ \ 3\ \ \ 3\ \ \ =\ \ \ 7
2702 | $$
2703 |
2704 | $$
2705 | 3\ \ \ 3\ \ \ 3\ \ \ 3\ \ \ =\ \ \ 8
2706 | $$
2707 |
2708 | $$
2709 | 3\ \ \ 3\ \ \ 3\ \ \ 3\ \ \ =\ \ \ 9
2710 | $$
2711 |
2712 | $$
2713 | 3\ \ \ 3\ \ \ 3\ \ \ 3\ \ \ =\ \ \ 10
2714 | $$
2715 |
2716 | ## 3.2.09. 小数的认识
2717 |
2718 | 例题练习
2719 |
2720 | ### 例题1
2721 |
2722 | 找出下列案例中的小数:
2723 | (1)乐乐老师从家到学校坐公交车经过7站,路程5.3米;
2724 | (2)田田测量圆桂形水杯的高度为12.5厘米;
2725 | (3)圆周率的大小为3.1415926535897932384……
2726 |
2727 | ### 练习1
2728 |
2729 | 找出下列案例中的小数:
2730 | (1)夏日有空调的屋子室内温度为26度,室外为32.3度;
2731 | (2)西瓜的单价为1.3元,葡萄的单价为7.0元。
2732 |
2733 | ### 例题2(分类)
2734 |
2735 | 有下列小数:1.2,3.6,0.8,0.333…,3.1415926…,0.207。
2736 | (1)按照整数部分分类;
2737 | (2)按照小数部分分类。
2738 |
2739 | ### 练习2
2740 |
2741 | 有下列小数:2.14151617,0.821,0.333,1.555…,0.92。
2742 | (1)按照整数部分分类;
2743 | (2)按照小数部分分类。
2744 |
2745 | ### 例题3(比较大小)
2746 |
2747 | 田田、丁丁、牛牛三人比赛跳远,丁丁跳了1.9米,田田跳了1.7米,牛牛跳了2.1米,请问他们三个人的名次是什么样的?
2748 |
2749 | ### 练习3
2750 |
2751 | 将下列小数按从大到小的顺序排序。
2752 | 3.1,1.06,10.6,2.135,2.14,2.2,4.7。
2753 |
2754 | ### 例题4(小数点的移动)
2755 |
2756 | 田田买一支铅笔用了0.56元,买10支铅笔用多少元?买100支呢?小数点是如何变化的?
2757 |
2758 | ### 练习4
2759 |
2760 | 填空
2761 | (1)把3.2的小数点去掉,它的值扩大()倍
2762 | (2)4.26扩大()倍是4260。
2763 | (3)22.9缩小到原来的()倍,才能得到0.229。
2764 |
2765 | ### 例题5(小数分数的转换)
2766 |
2767 | (1)将下列小数化为分数:0.5,1.4,10.8。
2768 | (2)将下列分数化为小数:$\frac{2}{5}$,$1\frac{1}{4}$,$\frac{100}{25}$。
2769 |
2770 | ### 练习5
2771 |
2772 | 请将下列相等的分数和小数连线。
2773 |
2774 | ### 例题6(分数小数比较大小)
2775 |
2776 | 将下列数按照从小到大的顺序排序。
2777 |
2778 | $1.5,0.999,3\frac{1}{4},1.51,\frac{199}{200},7.3。$
2779 |
2780 | ### 练习6
2781 |
2782 | 将下列数按照从大到小的顺序排序。
2783 |
2784 | $1\frac{77}{100},0.001,2,0.01,1\frac{4}{5}。$
2785 |
2786 | ## 3.2.10. 平行四边形与梯形
2787 |
2788 | 例题练习
2789 |
2790 | ### 例题1
2791 |
2792 | 乐乐老师带着丁丁和牛牛来到图形王国,遇到各种图形,你认识它们吗?它们分别叫什么图形?请说说平行四边形和梯形都有哪些性质?
2793 |
2794 |
1980 |
1981 | ### 热身2
1982 |
1983 | 如图,∠AOB 的顶点 O在直线 l 上,已知图中所有小于平角的角之和是 400 度,求∠AOB的大小。
1984 |
1985 | 
1986 |
1987 | ### 热身3
1988 |
1989 | 计算:$88\times46+88\times64-88\times10$
1990 |
1991 | 例题练习
1992 |
1993 | ### 例题1
1994 |
1995 | 计算。
1996 |
1997 | (1)$78+19+36+54+21+74+102$
1998 |
1999 | (2)$756-248-352$
2000 |
2001 | (3)$8+88+888+8888$
2002 |
2003 | (4)$39+38+40+41+43$
2004 |
2005 | ### 练习1
2006 |
2007 | 计算。
2008 |
2009 | (1)$99997+9996+995+94+9$
2010 |
2011 | (2)$894-89-111-95-105-94$
2012 |
2013 | ### 例题2
2014 |
2015 | 计算。
2016 |
2017 | (1)$25\times16\div20$
2018 |
2019 | (2)$1200\div4\div5\div5$
2020 |
2021 | (3)$1300\times77\div100$
2022 |
2023 | ### 练习2
2024 |
2025 | 计算。
2026 |
2027 | (1)$25\times64\times125$
2028 |
2029 | (2)$248\times5\div8$
2030 |
2031 | (3)$(36\times45)\div(6\times9)$
2032 |
2033 | ### 例题3
2034 |
2035 | 计算。
2036 |
2037 | (1)$35\times35$
2038 |
2039 | (2)$45\times45$
2040 |
2041 | (3)$73\times33$
2042 |
2043 | (4)$58\times58$
2044 |
2045 | ### 练习3
2046 |
2047 | 计算。
2048 |
2049 | (1)$75\times75$
2050 |
2051 | (2)$62\times68$
2052 |
2053 | (3)$67\times47$
2054 |
2055 | ### 例题4
2056 |
2057 | 计算。
2058 |
2059 | (1)$36\times19+36\times81$
2060 |
2061 | (2)$984\div8+16\div8$
2062 |
2063 | (3)$125\times(8+80)$
2064 |
2065 | (4)$(369+345)\div3$
2066 |
2067 | ### 练习4
2068 |
2069 | 计算。
2070 |
2071 | (1)$325\times113-325\times13$
2072 |
2073 | (2)$(40+8)\times25$
2074 |
2075 | (3)$684\div19-304\div19$
2076 |
2077 | (4)$(111+74)\div37$
2078 |
2079 | ### 例题5
2080 |
2081 | 计算。
2082 |
2083 | (1)$53\times46+71\times54+82\times54$
2084 |
2085 | ### 练习5
2086 |
2087 | 计算。
2088 |
2089 | (1)$33\times34+24\times34+57\times66$
2090 |
2091 | ### 例题6
2092 |
2093 | 计算。
2094 |
2095 | (1)$1997\times1995-1996\times1994$
2096 |
2097 | ### 练习6
2098 |
2099 | 计算。
2100 |
2101 | (1)$4747+888\times53+47\times787$
2102 |
2103 | ### 拓展1
2104 |
2105 | $$
2106 | 12345+23451+34512+45123+51234
2107 | $$
2108 |
2109 | ### 拓展2
2110 |
2111 | $$
2112 | 80+79-78-77+76+75-74-73+\dots+4+3-2-1
2113 | $$
2114 |
2115 | ### 拓展3
2116 |
2117 | $$
2118 | 20222022\times2021-20212021\times2022
2119 | $$
2120 |
2121 | ### 练习1
2122 |
2123 | 计算:$298+396+495+691+799+21$
2124 |
2125 | ### 练习2
2126 |
2127 | 计算:$(54\times24)\div(9\times4)$
2128 |
2129 | ### 练习3
2130 |
2131 | 计算:$39+142\times39+103$
2132 |
2133 | ## 3.2.03. 用字母表示数
2134 |
2135 | ### 热身1
2136 |
2137 | ### 热身2
2138 |
2139 | ### 热身3
2140 |
2141 | ### 例题1
2142 |
2143 | (1)观察下面的数列$2,4,6,a,10,b,14,\dots,a=(),b=()$。
2144 |
2145 | (2)观察下面的数列$1,3,5,a,9,b,13,\dots,a=(),b=()$。
2146 |
2147 | ### 练习1
2148 |
2149 | 观察下面的数列,填入合适的数。
2150 |
2151 | (1)5,10,15,a,25,30,b,……,a=(),b=()。
2152 |
2153 | (2)4,8,12,a,20,24,b,32,36,……,a=(),b=()。
2154 |
2155 | ### 例题2
2156 |
2157 | 1只青蛙1张嘴,2只眼睛,4条腿;
2158 |
2159 | 2只青蛙2张嘴,()只眼睛,()条腿;
2160 |
2161 | 3只青蛙3张嘴,()只眼睛,()条腿;
2162 |
2163 | 4只青蛙4张嘴,()只眼睛,()条腿;
2164 |
2165 | ……
2166 |
2167 | n只青蛙()张嘴,()只眼睛,()条腿。
2168 |
2169 | ### 练习2
2170 |
2171 | 一个正方形有()条边,
2172 |
2173 | 两个正方形有()条边,
2174 |
2175 | 三个正方形有()条边,
2176 |
2177 | ……
2178 |
2179 | n个正方形有()条边。
2180 |
2181 | 边数和正方形的数量有什么关系呢?
2182 |
2183 | ### 例题3
2184 |
2185 | 用简便方法表示下列各式。
2186 |
2187 | (1)$27\times x$
2188 |
2189 | (2)$m\times n$
2190 |
2191 | (3)$a+a+a$
2192 |
2193 | (4)$a\times a$
2194 |
2195 | (5)$36\times a\times b$
2196 |
2197 | (6)$(a+b)\times5$
2198 |
2199 | ### 练习3
2200 |
2201 | (1)$63\times x+5$
2202 |
2203 | (2)$m\times n\times3$
2204 |
2205 | (3)$(m+n)\times16$
2206 |
2207 | (4)$c\times2\times a$
2208 |
2209 | ### 例题4
2210 |
2211 | 用字母表示下列公式。(周长=C,面积=S,长=a,宽=b,边长=a)
2212 | 长方形的周长公式:
2213 | 长方形的面积公式:
2214 | 正方形的周长公式:
2215 | 正方形的面积公式:
2216 |
2217 | ### 练习4
2218 |
2219 | 用字母表示下列公式。
2220 | 乘法交换律:
2221 | 乘法结合律:
2222 | 乘法分配律:
2223 |
2224 | ### 例题5
2225 |
2226 | 你能用字母表示下面题目中所求的量吗?
2227 |
2228 | (1)过春节了,阿普拿到了m元压岁钱,牛牛的压岁钱是阿普的6倍,牛牛的压岁钱是()元。
2229 |
2230 | (2)某学校有男老师a人,女老师比男老师少b人,学校有女老师()人,共有老师()人。
2231 |
2232 | (3)一个长方形的周长是80厘米,长是a厘米,宽是()厘米。
2233 |
2234 | ### 练习5
2235 |
2236 | 你能用字母表示下面题目中所求的量吗?
2237 | (1)一个等边三角形,每边长a米,它的周长是()米。
2238 | (2)牛牛的学校一共有m人,男生有a人,女生有()人。
2239 | (3)东东今年a岁,比妈妈小m岁,再过年c后妈妈比东东大()岁。
2240 |
2241 | ### 例题6
2242 |
2243 | 用含字母的式子表示。
2244 | (1)1个菠萝重x千克,1个西瓜比这个菠萝的3倍还重2千克,西瓜重()千克。如果菠萝重2千克,那么西瓜重()千克。
2245 | (2)小红骑车每分钟行x千米,她骑了20分钟,行驶了()千米;她行驶a千米,需要()分钟。x=2,a=10,那么需要()分钟。
2246 | (3)乙数比甲数a的4倍少6,乙数是()。
2247 |
2248 | ### 练习6
2249 |
2250 | 用含字母的式子表示。
2251 | (1)田田高a厘米,丁丁比田田高7厘米,丁丁和田田一共高()厘米。
2252 | (2)青青林场栽了梧桐树和雪松各x排,已知梧桐树每排12棵,雪松每排14棵,栽梧桐树
2253 | 和雪松共()棵;当x=20时,青青林场一共有()棵梧桐树和雪松。
2254 | (3)一个正方形的边长为a厘米,周长为()厘米,面积是()平方厘米。
2255 |
2256 | ## 3.2.04. 和差倍综合
2257 |
2258 | 例题练习
2259 |
2260 | ### 例题1(和差)
2261 |
2262 | 有大、小两个油桶,一共装油24千克,两个油桶都倒出同样多的油后分别还剩9千克和5千克。问:原来大、小两个油桶各装油多少千克?
2263 |
2264 | ### 练习1
2265 |
2266 | 两箱图书共有66本,甲箱如果借出10本,就比乙箱少4本。甲、乙两箱原有图书各多少本?
2267 |
2268 | ### 例题2(和差)
2269 |
2270 | 学校新进99本书,分给三、四、五三个年级,三年级比四年级多分了2本,四年级比五年级多分了5本,三个年级各分得书多少本?
2271 |
2272 | ### 练习2
2273 |
2274 | 甲、乙、丙三个数的和是105,甲数比乙数多4,乙数比丙数多4,求丙数。
2275 |
2276 | ### 例题3(和倍)
2277 |
2278 | 某校学生总人数比四年级人数的6倍少78人,并且除了四年级外,其他各年级的学生人数总和为2222人,那么该校共有学生多少人?
2279 |
2280 | ### 练习3
2281 |
2282 | 有两层书架,共有书216本,从第一层拿走42本书后,第二层的书比第一层的2倍还多6本,则第二层有多少本书?
2283 |
2284 | ### 例题4
2285 |
2286 | 一天,甲、乙、丙三个同学做数学题,已知甲比乙多做了6道,丙做的题是甲的2倍,比乙做的题多22道,则乙做了多少道数学题?
2287 |
2288 | ### 练习4
2289 |
2290 | 小云比小雨少20本书,后来小云丢了5本书,小雨新买了11本书,这时小雨的书比小云的书多2倍。问:原来两人各有多少本书?
2291 |
2292 | ### 例题5
2293 |
2294 | 李师傅某天生产了一批零件,把它们分成了甲、乙两堆摆放。若从甲堆零件中拿出15个放到乙堆,则两堆零件个数相等;若从乙堆零件中拿出15个放到甲堆,则甲堆的零件个数是乙堆的4倍。甲堆原有零件多少个,李师傅这天共生产了多少个零件?
2295 |
2296 | ### 练习5
2297 |
2298 | 一家汽车销售店有若干部福特汽车和丰田汽车等待销售。福特汽车的数量是丰田汽车的3倍,如果每周销售2辆丰田汽车和4辆福特汽车,丰田汽车销售完时还剩下30辆福特汽车。请问:原有丰田汽车和福特汽车各多少辆?
2299 |
2300 | ### 例题6
2301 |
2302 | 维尼熊和跳跳虎去摘苹果。维尼熊爬上树去摘,跳跳虎在地上跳着摘。跳跳虎每摘7个,维尼熊只能摘4个。维尼熊摘了80分钟,跳跳虎摘了50分钟就累倒了。他们回来后数了一下共摘2010个苹果,那么其中维尼熊摘的有多少个?
2303 |
2304 | ### 练习6
2305 |
2306 | 某镇上有东西两个公交车站,东站有客车84辆,西站有客车56辆,每天从东站到西站有7辆车,从西站到东站有11辆车,几天后,东站车辆是西站的4倍?
2307 |
2308 | ## 3.2.05. 逆向思考进阶
2309 |
2310 | ### 例题1
2311 |
2312 | 牛牛和阿昔在游玩时,遇到一位小神仙,他们问这位神仙:“你一定不到100岁吧!”谁知这位神仙摇摇头说:“你们算算吧!把我的年龄加上75,再除以5,然后减去15,再乘10,恰好是
2313 | 2000岁。”小朋友,你知道这位神仙现在有多少岁吗?
2314 |
2315 | ### 练习1
2316 |
2317 | 一个数加上37,乘37,减去37,再除以37,结果等于37,这个数是多少?
2318 |
2319 | ### 例题2
2320 |
2321 | 小马虎在做一道加法题时,把一个加数个位上的9看作6,十位上的6看作9,结果和是174,那么正确的结果应该是多少呢?
2322 |
2323 | ### 练习2
2324 |
2325 | 淘气在做一道减法题时,把减数个位上的9看成了3,把十位上的4看成了7,得到的结果是164。请你帮淘气算算正确的答案是多少?
2326 |
2327 | ### 例题3
2328 |
2329 | 李奶奶卖一筐鸡蛋,第一位客人买走了一半少2个,第二位客人买走了剩下的一半多2个,第三位客人把剩下的5个鸡蛋全部买走了。老奶奶的篮子里原来有多少个鸡蛋?
2330 |
2331 | ### 练习3
2332 |
2333 | 学学看到太上老君正在用一根绳子拴宝葫芦,第一次用去全长的一半还多2米,第二次用去余下的一半少10米,第三次用去15米,最后还剩9米,那么这根绳子原来有多少米?
2334 |
2335 | ### 例题4
2336 |
2337 | 有一个财迷总想使自己的钱成倍增长。一天,他在一座桥上碰见一个老人,老人对他说:"你只要走过这座桥再回来,你身上的钱就会增加一倍,但作为报酬,你每走一个来回要给我32个
2338 | 铜板。”财迷算了算,感觉挺合算,就同意了。他走过桥去又走回来,身上的钱果然增加了一倍,他很高兴地给了老人32个铜板。这样走完第五个来回,身上的最后32个铜板都给了老人,财迷一个铜板也没剩下。你知道财迷身上原有多少个铜板?
2339 |
2340 | ### 练习4
2341 |
2342 | 某人发现了一条魔道,下面有一个存钱的小箱子,当他从魔道走过去的时候,箱子里的一些钱会飞到人的口袋里,使人身上的钱增加一倍,这人很高兴;当他从魔道走回来的时候,身
2343 | 上的钱又会飞到箱子里,使箱子里的钱增加一倍。这个人一连走了3个来回后,箱子里的钱和人身上的钱都是64元,那么,原来这人身上有多少钱?箱子里有多少钱?
2344 |
2345 | ### 例题5
2346 |
2347 | 有一个两层书架,一共摆放224本书,先从上层取出与下层本数同样多的书放入下层,再从下层现有书中,取出与上层剩下的本数同样多的书放入上层,这算进行了一轮调整。若如进行了
2348 | 两轮调整后,两层摆放书的本数相等,上层书架原来摆放多少本书?下层书架原来摆放多少本书?
2349 |
2350 | ### 练习5
2351 |
2352 | 有甲、乙两箱糖果,如果第一次从甲箱拿出和乙箱同样多块糖果放到乙箱里,第二次从乙箱拿出和甲箱剩下的同样多块糖果放入甲箱,这样拿4次后,甲、乙两箱糖果都是16块。甲、乙两箱各有糖果多少块?
2353 |
2354 | ### 例题6
2355 |
2356 | 一班、二班、三班各有不同数量的图书。一班拿出本班的一部分图书分给二班、三班,使这两个班的图书各增加一倍;然后二班也拿出一部分图书分给一班、三班,使这两个班的图书各增加一倍;接着三班也拿出一部分图书分给一班、二班,使这两个班的图书各增加一倍。这时三个班的图书数量都是48本。
2357 | ,求三个班原来各有图书多少本。
2358 |
2359 | ### 练习6
2360 |
2361 | 甲、乙、丙3人共有192张邮票。从甲的邮票中取出乙那么多邮票给乙后,再从乙的邮票中取出丙那么多邮票给丙,最后从丙的邮票中取出甲那么多邮票给甲,这时甲、乙、丙3人的邮票数相同,甲、乙、丙原来各有邮票多少张?
2362 |
2363 | ## 3.2.06. 逻辑推理综合(1)
2364 |
2365 | ### 例题1
2366 |
2367 | 5名谋杀案的嫌疑人,在犯罪现场被警察询问,其中有一名是凶手。下面5个人的供述中,只有3句是对的:
2368 | A说:“D是杀人犯。”
2369 | B说:“我是无辜的。”
2370 | C说:“E不是杀人犯。”
2371 | D说:“A在说谎。”
2372 | E说:“B说的是实话。”
2373 | 在这5个人中,谁是凶手?
2374 |
2375 | ### 练习1
2376 |
2377 | 四个小朋友宝宝、星星、强强和乐乐在院子里踢足球,一阵响声,惊动了正在读书的陆老师,陆老师跑出来查看,发现一块窗户玻璃被打破了。陆老师问:“是谁打破了玻璃?”
2378 | 宝宝说:“是星星无意打破的。”
2379 | 星星说:“是乐乐打破的。”
2380 | 乐乐说:“星星说谎。”
2381 | 强强说:“反正不是我打破的。”
2382 | 如果只有一个孩子说了实话,那么这个孩子是谁?是谁打破了玻璃?
2383 |
2384 | ### 例题2
2385 |
2386 | 在一次数学竞赛中,A,B,C,D,E五位同学分别得了前五名(没有并列同一名次的),关于各人的名次,大家做出了下面的猜测:
2387 |
2388 | A说:“第二名是D,第三名是B。”
2389 |
2390 | B说:“第二名是C,第四名是F。”
2391 |
2392 | C说:“第一名是E,第五名是A。”
2393 |
2394 | D说:“第三名是C,第四名是A。”
2395 |
2396 | E说:“第二名是B,第五名是D。”
2397 |
2398 | 结果每人都只猜对了一半,他们的名次如何?
2399 |
2400 | ### 练习2
2401 |
2402 | 甲、乙、丙、丁四人同时参加全国小学数学夏令营。赛前甲、乙、丙分别作了预测。
2403 |
2404 | 甲说:“丙第1名,我第3名。”
2405 |
2406 | 乙说:“我第1名,丁第4名。”
2407 |
2408 | 丙说:“丁第2名,我第3名。”
2409 | 成绩揭晓后,发现他们每人只说对了一半,你能说出他们的名次吗?
2410 |
2411 | ### 例题3
2412 |
2413 | 学校新来了一位老师,五个学生分别听到如下的情况:
2414 |
2415 | (1)是一位姓王的中年女老师,教语文;
2416 |
2417 | (2)是一位姓丁的中年男老师,教数学;
2418 |
2419 | (3)是一位姓刘的青年男老师,教外语;
2420 |
2421 | (4)是一位姓李的青年男老师,教数学;
2422 |
2423 | (5)是一位姓王的老年男老师,教外语。
2424 |
2425 | 他们每人听到的四项情况中各有一项正确。问:真实情况是什么样的?
2426 |
2427 | ### 练习3
2428 |
2429 | 4名运动员参加一项比赛,赛前。
2430 |
2431 | 甲说:“我肯定是最后一名。”
2432 |
2433 | 乙说:“我不可能是第一名,也不可能是最后一名。”
2434 | 丙说:“我绝对不会得最后一名。”
2435 | 丁说:“我肯定得第一名。”
2436 |
2437 | 赛后,发现他们4人的预测中只有一人是错误的。请问谁的预测是错误的?
2438 |
2439 | ### 例题4
2440 |
2441 | 王平、宋丹、韩涛三个小学生都是少先队的干部,一个是大队长,一个是中队长,一个是小队长。一次数学测验,这三个人的成绩是:
2442 |
2443 | (1)韩涛比大队长的成绩好。
2444 |
2445 | (2)王平和中队长的成绩不相同。
2446 |
2447 | (3)中队长比宋丹的成绩差。
2448 |
2449 | 请你根据这三个人的成绩,判断一下,谁是大队长呢?
2450 |
2451 | ### 练习4
2452 |
2453 | 王文、张贝、李丽分别是跳伞、田径、游泳运动员,现在知道:
2454 |
2455 | (1)张贝从未上过天;
2456 | (2)跳伞运动员已得过两块金牌;
2457 |
2458 | (3)李丽还未得过第一名,她与田径运动员同年出生:
2459 | 请根据上述情况,判断王文、张贝、李丽各是什么运动员?
2460 |
2461 | ### 例题5
2462 |
2463 | 张、王、李三人除了本职工作,每人都有两样业余爱好。人们有时以车工、电工、乐师、画家、作家、技工称呼他们,此外,还有以下情况:
2464 | (1)车工经常赞扬乐师的三弦琴弹得好;
2465 | (2)乐师,作家常常与姓张的一起看电影;
2466 | (3)画家请电工来修过电灯;
2467 | (4)车工和画家的儿子在同一车间工作;
2468 | (5)姓王的向作家请教写作的技巧;
2469 | (6)姓李的善于下象棋,姓王的和画家常常输给他。
2470 | 问:姓李的有哪两个称呼?
2471 |
2472 | ### 练习5
2473 |
2474 | 宝宝、贝贝、聪聪每人有两个外号,人们有时以“数学博士”、“短跑健将”、“跳高冠军”、“小画家“、“大作家”和“歌唱家”称呼他们,此外:
2475 |
2476 | (1)数学博士夸跳高冠军跳得高;
2477 |
2478 | (2)跳高冠军和大作家常与宝宝一起看电影;
2479 |
2480 | (3)短跑健将请小画家画贺年卡;
2481 |
2482 | (4)数学博士和小画家关系很好;
2483 |
2484 | (5)贝贝向大作家借过书;
2485 |
2486 | (6)聪聪下象棋常赢贝贝和小画家。
2487 |
2488 | 问:宝宝、贝贝、聪聪各有哪两个外号?
2489 |
2490 | ### 例题6
2491 |
2492 | A,B,C,D分别来自中国、日本、美国和法国。已知:
2493 |
2494 | (1)A和中国人是医生;
2495 |
2496 | (2)B和法国人是教师;
2497 |
2498 | (3)C和日本人职业不同;
2499 |
2500 | (4)D不会看病。
2501 |
2502 | 问:A,B,C,D各是哪国人?
2503 |
2504 | ### 练习6
2505 |
2506 | 张明、席辉和李刚分别在北京、上海和天津三城市之一工作,他们的职业是工人、农民和教师之一,已知:
2507 |
2508 | (1)张明不在北京工作,席辉不在上海工作;
2509 |
2510 | (2)在北京工作的不是教师;
2511 | (3)在上海工作的是工人;
2512 |
2513 | (4)席辉不是农民。
2514 |
2515 | 问:这三人各住哪里?各是什么职业?
2516 |
2517 | ## 3.2.07. 方阵
2518 |
2519 | ### 例题1
2520 |
2521 | 一个实心方阵,最外一层每边18人。
2522 | (1)那么整个方阵一共()人;
2523 | (2)最外面一层有()人;
2524 | (3)从外向内数,第二层每边有()人,一共有()人;
2525 | (4)如果考虑最外面三层,那么这三层共有()人;
2526 | (5)如果将方阵外面增加一层,那么一共增加()人。
2527 |
2528 | ### 练习1
2529 |
2530 | 用64枚棋子摆成一个实心方阵。
2531 | (1)每边有()枚棋子;
2532 | (2)最外层有()枚棋子;
2533 | (3)从外向内数,第二层每边有()枚棋子,第二层一共有()枚棋子。
2534 |
2535 | ### 例题2
2536 |
2537 | 有一块空地在进行种树绿化,打算把树种成实心方阵的样子,方阵最外面一周有60棵树,问这个方阵外层每边有多少棵树?这块空地一共需要多少棵树?
2538 |
2539 | ### 练习2
2540 |
2541 | 三年级学生排成一个实心方阵,最外一层的人数为36人,问方阵最外层每边有多少人?这个方阵共有三年级学生多少人?
2542 |
2543 | ### 例题3
2544 |
2545 | 小刚在用棋子摆好的实心方阵上又添了17枚棋子,它的横竖各增加了一排,成了大一点的实心方阵,求原来的实心方阵有多少枚棋子。
2546 |
2547 | ### 练习3
2548 |
2549 | 军训的学生进行队列表演,排成了一个5行5列的正方形队列,如果去掉一行一列,要去掉多少人?
2550 |
2551 | ### 例题4
2552 |
2553 | 大家要用盆花在空地上摆出一个空心方阵花坛,最外面的一层每边摆12盆花,共3层,一共要用多少盆花?
2554 |
2555 | ### 练习4
2556 |
2557 | 有一个班的学生排成一个中空方阵,最外层人数共52人,最内层人数共28人,这个班学生共有多少人?
2558 |
2559 | ### 例题5
2560 |
2561 | 用64枚棋子摆成一个两层中空方阵,如果想在外面再增加一层,问需要增加多少枚棋子?
2562 |
2563 | ### 练习5
2564 |
2565 | 用84枚棋子摆成一个三层中空方阵,问最外层有多少枚棋子?
2566 |
2567 | ### 例题6
2568 |
2569 | 一天,博士用棋子摆成一周每边有10枚棋子的空心方阵,摆完后发现还有棋子剩下,但是不够外围再增加一层。在保持原有棋子不动的情况下,想变成一个更大的两层空心方阵,博士至少需要多少枚棋子?
2570 |
2571 | ### 练习6
2572 |
2573 | 用一堆棋子摆成一个两层的空心方阵,用了48枚棋子后发现还剩下一些棋子,但是不够外围再增加一层了。在保持原有棋子不动的情况下,想变成一个更大的三层空心方阵,至少需要多少枚棋子?
2574 |
2575 | ## 3.2.08. 巧填算符综合
2576 |
2577 | 例题练习
2578 |
2579 | ### 例题1
2580 |
2581 | 在“+、-、×、÷、( )”中,挑出合适的符号,填入下面的数字之间,使算式成立。
2582 | $$
2583 | 9\ \ \ 8\ \ \ 7\ \ \ 6\ \ \ 5\ \ \ 4\ \ \ 3\ \ \ 2\ \ \ 1=1
2584 | $$
2585 |
2586 | ### 练习1
2587 |
2588 | 在○内填上与等号左边不同的运算符号,使等式成立。
2589 | $$
2590 | (1)6-2+2=6\circ2\circ 2
2591 | $$
2592 |
2593 | $$
2594 | (2)8+2+3=8\circ 2\circ 3
2595 | $$
2596 |
2597 | $$
2598 | (3)16-8-3=16\circ 8\circ 3
2599 | $$
2600 |
2601 | ### 例题2
2602 |
2603 | 在下面算式的适当地方,填上运算符号“+、-、×、÷或( )”,使算式成立。
2604 | $$
2605 | 1\ \ \ 2\ \ \ 3\ \ \ 4\ \ \ 5=10
2606 | $$
2607 |
2608 | ### 练习2
2609 |
2610 | 用运算符号把下面三个相同的数宇连接起来,使等式成立。
2611 | $$
2612 | (1)5\ \ \ 5\ \ \ 5=30
2613 | $$
2614 |
2615 | $$
2616 | (2)6\ \ \ 6\ \ \ 6\ \ \ =30
2617 | $$
2618 |
2619 | ### 例题3
2620 |
2621 | 在下式的每两个数中间填上合适的运算符号,使等式成立。
2622 | $$
2623 | 8\ \ \ 2\ \ \ 4\ \ \ 6=4\ \ \ 2
2624 | $$
2625 |
2626 | ### 练习3
2627 |
2628 | 在下式的每两个数中间填上合适的运算符号,使等式成立。
2629 | $$
2630 | 8\ \ \ 2\ \ \ 3=3\ \ \ 3
2631 | $$
2632 |
2633 | ### 例题4
2634 |
2635 | 在8个8之间的适当地方,填上合适的运算符号或括号,使算式成立。
2636 | $$
2637 | 8\ \ \ 8\ \ \ 8\ \ \ 8\ \ \ 8\ \ \ 8\ \ \ 8\ \ \ 8=1000
2638 | $$
2639 |
2640 | ### 练习4
2641 |
2642 | 在下面算式适当的地方,填上运算符号或括号,使等式成立。
2643 | $$
2644 | 9\ \ \ 8\ \ \ 7\ \ \ 6\ \ \ 5\ \ \ 4\ \ \ 3\ \ \ 2\ \ \ 1=1000
2645 | $$
2646 |
2647 | ### 例题5
2648 |
2649 | 在5个4之间,填上适当的运算符号或括号,使得下面的算式成立。
2650 | $$
2651 | 4\ \ \ 4\ \ \ 4\ \ \ 4\ \ \ 4=8
2652 | $$
2653 |
2654 | ### 练习5
2655 |
2656 | 在下列算式的合适位置,填上运算符号或括号,使等式成立。
2657 | $$
2658 | (1)4\ \ \ 4\ \ \ 4\ \ \ 4=1
2659 | $$
2660 |
2661 | $$
2662 | (2)4\ \ \ 4\ \ \ 4\ \ \ 4=5
2663 | $$
2664 |
2665 | ### 例题6
2666 |
2667 | 请在 2,3,4,6 四个数之间任意填上“+、-、×、÷或( )”,每个数字都只能用一次,使它们的计算结果等于 24。你能做到吗?
2668 |
2669 | ### 练习6
2670 |
2671 | 请在 6,5,10,2 四个数之间任意填上“+、-、×、÷或( )”,每个数字都只能用一次,使它们的计算结果等于 24。你能做到吗?
2672 |
2673 | 课后巩固
2674 |
2675 | 将“+、-、×、÷、( )”填入合适的地方,使下面的等式成立。
2676 | $$
2677 | 3\ \ \ 3\ \ \ 3\ \ \ 3\ \ \ =\ \ \ 1
2678 | $$
2679 |
2680 | $$
2681 | 3\ \ \ 3\ \ \ 3\ \ \ 3\ \ \ =\ \ \ 2
2682 | $$
2683 |
2684 | $$
2685 | 3\ \ \ 3\ \ \ 3\ \ \ 3\ \ \ =\ \ \ 3
2686 | $$
2687 |
2688 | $$
2689 | 3\ \ \ 3\ \ \ 3\ \ \ 3\ \ \ =\ \ \ 4
2690 | $$
2691 |
2692 | $$
2693 | 3\ \ \ 3\ \ \ 3\ \ \ 3\ \ \ =\ \ \ 5
2694 | $$
2695 |
2696 | $$
2697 | 3\ \ \ 3\ \ \ 3\ \ \ 3\ \ \ =\ \ \ 6
2698 | $$
2699 |
2700 | $$
2701 | 3\ \ \ 3\ \ \ 3\ \ \ 3\ \ \ =\ \ \ 7
2702 | $$
2703 |
2704 | $$
2705 | 3\ \ \ 3\ \ \ 3\ \ \ 3\ \ \ =\ \ \ 8
2706 | $$
2707 |
2708 | $$
2709 | 3\ \ \ 3\ \ \ 3\ \ \ 3\ \ \ =\ \ \ 9
2710 | $$
2711 |
2712 | $$
2713 | 3\ \ \ 3\ \ \ 3\ \ \ 3\ \ \ =\ \ \ 10
2714 | $$
2715 |
2716 | ## 3.2.09. 小数的认识
2717 |
2718 | 例题练习
2719 |
2720 | ### 例题1
2721 |
2722 | 找出下列案例中的小数:
2723 | (1)乐乐老师从家到学校坐公交车经过7站,路程5.3米;
2724 | (2)田田测量圆桂形水杯的高度为12.5厘米;
2725 | (3)圆周率的大小为3.1415926535897932384……
2726 |
2727 | ### 练习1
2728 |
2729 | 找出下列案例中的小数:
2730 | (1)夏日有空调的屋子室内温度为26度,室外为32.3度;
2731 | (2)西瓜的单价为1.3元,葡萄的单价为7.0元。
2732 |
2733 | ### 例题2(分类)
2734 |
2735 | 有下列小数:1.2,3.6,0.8,0.333…,3.1415926…,0.207。
2736 | (1)按照整数部分分类;
2737 | (2)按照小数部分分类。
2738 |
2739 | ### 练习2
2740 |
2741 | 有下列小数:2.14151617,0.821,0.333,1.555…,0.92。
2742 | (1)按照整数部分分类;
2743 | (2)按照小数部分分类。
2744 |
2745 | ### 例题3(比较大小)
2746 |
2747 | 田田、丁丁、牛牛三人比赛跳远,丁丁跳了1.9米,田田跳了1.7米,牛牛跳了2.1米,请问他们三个人的名次是什么样的?
2748 |
2749 | ### 练习3
2750 |
2751 | 将下列小数按从大到小的顺序排序。
2752 | 3.1,1.06,10.6,2.135,2.14,2.2,4.7。
2753 |
2754 | ### 例题4(小数点的移动)
2755 |
2756 | 田田买一支铅笔用了0.56元,买10支铅笔用多少元?买100支呢?小数点是如何变化的?
2757 |
2758 | ### 练习4
2759 |
2760 | 填空
2761 | (1)把3.2的小数点去掉,它的值扩大()倍
2762 | (2)4.26扩大()倍是4260。
2763 | (3)22.9缩小到原来的()倍,才能得到0.229。
2764 |
2765 | ### 例题5(小数分数的转换)
2766 |
2767 | (1)将下列小数化为分数:0.5,1.4,10.8。
2768 | (2)将下列分数化为小数:$\frac{2}{5}$,$1\frac{1}{4}$,$\frac{100}{25}$。
2769 |
2770 | ### 练习5
2771 |
2772 | 请将下列相等的分数和小数连线。
2773 |
2774 | ### 例题6(分数小数比较大小)
2775 |
2776 | 将下列数按照从小到大的顺序排序。
2777 |
2778 | $1.5,0.999,3\frac{1}{4},1.51,\frac{199}{200},7.3。$
2779 |
2780 | ### 练习6
2781 |
2782 | 将下列数按照从大到小的顺序排序。
2783 |
2784 | $1\frac{77}{100},0.001,2,0.01,1\frac{4}{5}。$
2785 |
2786 | ## 3.2.10. 平行四边形与梯形
2787 |
2788 | 例题练习
2789 |
2790 | ### 例题1
2791 |
2792 | 乐乐老师带着丁丁和牛牛来到图形王国,遇到各种图形,你认识它们吗?它们分别叫什么图形?请说说平行四边形和梯形都有哪些性质?
2793 |
2794 |  2795 |
2796 | ### 练习1
2797 |
2798 | 下面是七巧板拼成的小船图,在这个图形中,你能找到几个平行四边形和梯形?
2799 |
2800 |
2795 |
2796 | ### 练习1
2797 |
2798 | 下面是七巧板拼成的小船图,在这个图形中,你能找到几个平行四边形和梯形?
2799 |
2800 |  2801 |
2802 | ### 例题2
2803 |
2804 | (1)请在下图 1 中画出点 A 到点 C 的距离;点 A 到线段 CD 的距离;
2805 |
2806 | (2)请在下图 2 中画出平行四边形 ABCD 的高;
2807 | (3)请在下图 3 中画出梯形 EFGH 的高。
2808 |
2809 | 
2810 |
2811 | ### 练习2
2812 |
2813 | 画出下面每个平行四边形底边上的高。
2814 |
2815 | 
2816 |
2817 | ### 例题3
2818 |
2819 | 如图,已知每个小正方形的面积都是 1 平方厘米,请你根据图来计算图中长方形和平行四边形的面积,能否总结出平行四边形的面积公式?
2820 |
2821 |
2801 |
2802 | ### 例题2
2803 |
2804 | (1)请在下图 1 中画出点 A 到点 C 的距离;点 A 到线段 CD 的距离;
2805 |
2806 | (2)请在下图 2 中画出平行四边形 ABCD 的高;
2807 | (3)请在下图 3 中画出梯形 EFGH 的高。
2808 |
2809 | 
2810 |
2811 | ### 练习2
2812 |
2813 | 画出下面每个平行四边形底边上的高。
2814 |
2815 | 
2816 |
2817 | ### 例题3
2818 |
2819 | 如图,已知每个小正方形的面积都是 1 平方厘米,请你根据图来计算图中长方形和平行四边形的面积,能否总结出平行四边形的面积公式?
2820 |
2821 |  2822 |
2823 | 如图,已知 AB=5 厘米,AE=3 厘米,求平行四边形 ABCD 的面积。
2824 |
2825 |
2822 |
2823 | 如图,已知 AB=5 厘米,AE=3 厘米,求平行四边形 ABCD 的面积。
2824 |
2825 |  2826 |
2827 | ### 练习3
2828 |
2829 | 如图,是一个平行四边形,你能求出它的面积吗?
2830 |
2831 |
2826 |
2827 | ### 练习3
2828 |
2829 | 如图,是一个平行四边形,你能求出它的面积吗?
2830 |
2831 |  2832 |
2833 | ### 例题4
2834 |
2835 | 如图,图形中阴影部分的面积是多少?
2836 |
2837 |
2832 |
2833 | ### 例题4
2834 |
2835 | 如图,图形中阴影部分的面积是多少?
2836 |
2837 |  2838 |
2839 | ### 练习4
2840 |
2841 | 如图,已知平行四边形的面积为 32 平方厘米,CD=8厘米,求 AE 的长度。
2842 |
2843 |
2838 |
2839 | ### 练习4
2840 |
2841 | 如图,已知平行四边形的面积为 32 平方厘米,CD=8厘米,求 AE 的长度。
2842 |
2843 |  2844 |
2845 | ### 例题5
2846 |
2847 | 如下左图,已知横竖相邻两点间的距离是 1厘米。你能算出图中梯形的面积吗?
2848 |
2849 |
2844 |
2845 | ### 例题5
2846 |
2847 | 如下左图,已知横竖相邻两点间的距离是 1厘米。你能算出图中梯形的面积吗?
2848 |
2849 |  2850 |
2851 | 如图已知梯形 ABCD 的上底 AB=8 厘米,CD=10 厘米,EF 垂直 CD 于点 F,EF=6 厘米,求梯 形 ABCD 的面积
2852 |
2853 |
2850 |
2851 | 如图已知梯形 ABCD 的上底 AB=8 厘米,CD=10 厘米,EF 垂直 CD 于点 F,EF=6 厘米,求梯 形 ABCD 的面积
2852 |
2853 |  2854 |
2855 | ### 练习5
2856 |
2857 | 图中每个格子的边长都是2厘米,梯形的面积为多少平方厘米?
2858 |
2859 |
2854 |
2855 | ### 练习5
2856 |
2857 | 图中每个格子的边长都是2厘米,梯形的面积为多少平方厘米?
2858 |
2859 |  2860 |
2861 | ### 例题6
2862 |
2863 | 图形王国的中心有道门,门上写着:已知梯形 ABCD的面积为 50 平方厘米,高 AE的长度为 5
2864 | 厘米,线段 CD比AB长4 厘米,请分别求出 AB和CD 的长度
2865 |
2866 |
2860 |
2861 | ### 例题6
2862 |
2863 | 图形王国的中心有道门,门上写着:已知梯形 ABCD的面积为 50 平方厘米,高 AE的长度为 5
2864 | 厘米,线段 CD比AB长4 厘米,请分别求出 AB和CD 的长度
2865 |
2866 |  2867 |
2868 | ### 练习6
2869 |
2870 | 如下图,大正方形的边长是8 厘米,小正方形的边长是6厘米。请问:图中阴影部分的面积
2871 | 是多少?
2872 |
2873 |
2867 |
2868 | ### 练习6
2869 |
2870 | 如下图,大正方形的边长是8 厘米,小正方形的边长是6厘米。请问:图中阴影部分的面积
2871 | 是多少?
2872 |
2873 |  2874 |
2875 | ## 3.2.11. 年龄问题进阶
2876 |
2877 | 例题练习
2878 |
2879 | ### 例题1
2880 |
2881 | 妈妈和儿子算年龄,两年前两人的年龄之和是36岁,今年妈妈的年龄是孩子的4倍,今年两人各是多少岁?
2882 |
2883 | ### 练习1
2884 |
2885 | 今年哥哥和弟弟的年龄和是36岁,且哥哥的年龄是弟弟年龄的2倍,哥哥和弟弟今年分别多少岁?
2886 |
2887 | ### 例题2
2888 |
2889 | 楠楠今年9岁了,妈妈33岁,再过多少年,楠楠年龄就是妈妈年龄的一半?
2890 |
2891 | ### 练习2
2892 |
2893 | 父亲今年44岁,儿子今年16岁。当父亲的年龄是儿子的8倍时,父子的年龄和是多少?
2894 |
2895 | ### 例题3
2896 |
2897 | 东东3年前的年龄与西西4年后的年龄和是25岁,东东3年后的年龄等于西西1年前的年龄,求今年东东、西西各是多少岁?
2898 |
2899 | ### 练习3
2900 |
2901 | 小花2年前的年龄与小琪1年后的年龄相等,小花3年前和小琪2年后的年龄和为20岁,则小花和小琪今年各多少岁?
2902 |
2903 | ### 例题4
2904 |
2905 | 乐乐老师对琪琪说:“我是你这个年龄的时候,你才5岁。”琪琪思考了一下,对乐乐老师说:“等到我是您现在年龄的时候,您就50岁了。”你能算出乐乐老师和琪琪今年各多少岁吗?
2906 |
2907 | ### 练习4
2908 |
2909 | 丁丁今年(2022年)12岁,妈妈对丁丁说:“当你有我这么大岁数时,我已经60岁了。”请问妈妈像丁丁这么大时是哪一年?
2910 |
2911 | ### 例题5
2912 |
2913 | 田田一家三口今年的年龄和是87岁,爸爸比妈妈大6岁。几年前,爸爸的年龄是田田的11倍,妈妈的年龄是田田的9倍,你知道田田今年几岁了吗?
2914 |
2915 | ### 练习5
2916 |
2917 | 琪琪今年3岁了,再过5年她就和小花5年前的年龄相等,问小花今年几岁了?
2918 |
2919 | ### 例题6
2920 |
2921 | 今年乐乐老师的年龄是牛牛年龄的5倍,再过8年,乐乐老师的年龄是牛牛年龄的3倍。牛牛今年多少岁?
2922 |
2923 | ### 练习6
2924 |
2925 | 10年前,爸爸的年龄是儿子的7倍,15年后爸爸的年龄是儿子的2倍,问现在父子各多少岁?
2926 |
2927 | ## 3.2.12. 带余除法进阶
2928 |
2929 | 作业练习
2930 |
2931 | ### 练习1
2932 |
2933 | 填空。
2934 |
2935 | (1)$()\div8=6……7$
2936 |
2937 | (2)$31\div()=7……3$
2938 |
2939 | (3)$56\div6=()……()$
2940 |
2941 | (4)$()\div8=7……()$,被除数最大是多少?
2942 |
2943 | (5)$()\div()=3……4$,被除数最小是多少?
2944 |
2945 | ### 练习2
2946 |
2947 | 用一个自然数去除另一个自然数,商为7,被除数、除数的和是48,求这两个自然数各是多少?
2948 |
2949 | ### 练习3
2950 |
2951 | 46除以一个一位数,余数是1。列出所有符合条件的一位数。
2952 |
2953 | ### 练习4
2954 |
2955 | 78除以一个数得到的商是8,并且除数与余数的差是3,求除数和余数。
2956 |
2957 | ### 练习5
2958 |
2959 | $48\times63\times79$除以7的余数是多少?
2960 |
2961 | ### 练习6
2962 |
2963 | 有一串数1,1,2,3,5,8,...,从第三个数起,每个数都是前两个数之和,这串数的第2022个数除以4余数是多少?
2964 |
2965 | 例题练习
2966 |
2967 | ### 例题1
2968 |
2969 | 牛牛有一本故事书,每天读9页,读了23天之后发现还剩6页,这本故事书一共多少页?
2970 |
2971 | ### 练习1
2972 |
2973 | 某数被21除,商是9,余数是7,则该数是多少?
2974 |
2975 | ### 例题2
2976 |
2977 | 丁丁有一本科普书,一共208页,他看了17天之后还剩4页,他前17天每天看多少页?
2978 |
2979 | ### 练习2
2980 |
2981 | 316除以8,余4,商是多少?
2982 |
2983 | ### 例题3
2984 |
2985 | 乐乐老师有160道题,要安排给同学们完成。如果每天做a道题,第b天做完之后,还剩6道,已知a>6,那么a有多少种不同的取值?
2986 |
2987 | ### 练习3
2988 |
2989 | 牛牛有一本练习题,有191道题,如果每天做a(a>9)道题,第b天做完之后,还剩9道,那么a有多少种不同的取值?
2990 |
2991 | ### 例题4
2992 |
2993 | 甲、乙两个数的和是1088,甲数除以乙数商11余32,求甲、乙两数各是多少。
2994 |
2995 | ### 练习4
2996 |
2997 | 678除以一个数得到的商是32,并且除数与余数的差是15,求除数和余数各是多少。
2998 |
2999 | ### 例题5
3000 |
3001 | $2461\times135\times6047\div11$的余数为多少?
3002 |
3003 | ### 练习5
3004 |
3005 | 有一个整数,用它去除70,110,160所得到的3个余数之和是50,那么这个整数是多少?
3006 |
3007 | ### 例题6
3008 |
3009 | 有一串数:1、1、2、3、5、8、⋯,从第三个数起,每个数都是前两个数之和,在这串数的前2017个数中,有几个是5的倍数?
3010 |
3011 | ### 练习6
3012 |
3013 | 有一列数,若这列数从第四个数起,每个数怡好是前面三个数之和,则数列:1、1、2、4、7、13、24、44、⋯中的第2015个数除以3的余数是多少?
3014 |
3015 | ## 3.2.13. 等差数列初步
3016 |
3017 | 课前热身
3018 |
3019 | ### 热身1
3020 |
3021 | 脱式计算。
3022 | $$
3023 | 327-85+73
3024 | $$
3025 |
3026 | $$
3027 | 723+491-13-191
3028 | $$
3029 |
3030 | ### 热身2
3031 |
3032 | $()\div8=7……()$,被除数最大是多少?
3033 |
3034 | $()\div()=3……4$,被除数最小是多少?
3035 |
3036 | ### 热身3
3037 |
3038 | 用一个自然数去除另一个自然数,商为6,被除数、除数的和是56,求这两个自然数各是多少?
3039 |
3040 | 例题练习
3041 |
3042 | ### 例题1
3043 |
3044 | 同学们一起来算一算吧!
3045 | (1)等差数列:5,7,9,11,13,15,……的第12项是();
3046 | (2)等差数列:0,4,8,12,16,20,……的第43项是();
3047 | (3)等差数列:3,7,11,15,……的第56项是()。
3048 |
3049 | ### 练习1
3050 |
3051 | (1)等差数列:3,4,5,6,……的第62项是();
3052 | (2)等差数列:2,5,8,11,……的第47项是()。
3053 |
3054 | ### 例题2
3055 |
3056 | (1)等差数列:5,6,7,8,9,……,其中55是这个数列的第()项;
3057 | (2)等差数列:7,9,11,13,……,其中69是这个数列的第()项。
3058 |
3059 | ### 练习2
3060 |
3061 | (1)等差数列:8,11,14,17,……,其中134是这个数列的第()项;
3062 | (2)等差数列:15,19,23,27,……,其中295是这个数列的第()项。
3063 |
3064 | ### 例题3
3065 |
3066 | 大家一起来求和!
3067 |
3068 | (1)$3+4+5+6+\dots+76+77+78$
3069 |
3070 | (2)$2+4+6+8+\dots+96+98+100$
3071 |
3072 | ### 练习3
3073 |
3074 | 等差数列求和。
3075 |
3076 | (1)1,3,5,7,……,87,89,91;
3077 |
3078 | (2)4,7,10,13,……,40,43,46
3079 |
3080 | ### 例题4
3081 |
3082 | 一个递增的等差数列的首项是10,第61项是250,这个等差数列的公差是多少?
3083 |
3084 | ### 练习4
3085 |
3086 | 一个递增的等差数列,第1项是232,第52项是334,这个等差数列的公差是多少?
3087 |
3088 | ### 例题5
3089 |
3090 | 一个等差数列的第6项和第12项分别是24,42。问:
3091 | (1)数列的第1项是什么?
3092 | (2)数列的第23项是什么?
3093 | (3)数列的前23项的和是多少?
3094 |
3095 | ### 练习5
3096 |
3097 | 己知等差数列的第5项和第9项分别为25、49,那么前31项的和是多少?
3098 |
3099 | ### 例题6
3100 |
3101 | (1)有5个盒子中共放了325个乒乓球,从小盒子到大盒子,每一个盒子中比前面的盒子多了5个乒乓球。问:最大的盒子中有多少个乒乓球?
3102 | (2)有8个盒子共放了888个乒乓球,从小盒子到大盒子,每一个盒子比前面的盒子多了6个乒乓球。问:最小的盒子里有多少个乒乓球?
3103 |
3104 | ### 练习6
3105 |
3106 | 2,4,6,8,10,12,……是个连续偶数列,如果其中5个连续偶数的和是320,那么它们中最小的一个数是谁?
3107 |
3108 | ## 3.2.15. 平面图形计数综合
3109 |
3110 | 例题练习
3111 |
3112 | ### 例题1
3113 |
3114 | 以A,B,C,D,E,F,G这些点为端点,请数一数这里一共有多少条线段?
3115 |
3116 | ### 练习1
3117 |
3118 | 在一条直线上有一些被标记的点,请你数一数,看看能找出几条线段。
3119 |
3120 | 
3121 |
3122 | ### 例题2
3123 |
3124 | 数一数,下面图中共有多少个正方形。
3125 |
3126 | ### 练习2
3127 |
3128 | 数一数,下面图中共有多少个正方形。
3129 |
3130 | 
3131 |
3132 | ### 例题3
3133 |
3134 | 图中有多少个正方形?
3135 |
3136 | 
3137 |
3138 | ### 练习3
3139 |
3140 | 图中有多少个正方形?
3141 |
3142 | 
3143 |
3144 | ### 例题4
3145 |
3146 | 图中有多少个三角形?
3147 |
3148 | 
3149 |
3150 | ### 练习4
3151 |
3152 | 图中有多少个三角形?
3153 |
3154 | 
3155 |
3156 | ### 例题5
3157 |
3158 | 将一个等边三角形各边四等分后再连接相应线段得到下图,你知道图中共有多少个三角形吗?
3159 |
3160 | 
3161 |
3162 | ### 练习5
3163 |
3164 | 将一个等边三角形各边三等分后再连接相应线段得到下图,你知道图中共有多少个三角形吗?
3165 |
3166 | 
3167 |
3168 | ### 例题6
3169 |
3170 | 数一数,下图中共有多少个平行四边形。
3171 |
3172 | 
3173 |
3174 | ### 练习6
3175 |
3176 | 下图是由7条线段构成的图形,你知道里面一共有多少个三角形吗?
3177 |
3178 | 
3179 |
3180 | ## 3.2.16. 标数法
3181 |
3182 | ### 例题1
3183 |
3184 | 丁丁的家在A点,他想沿着长方形街道去学校所在的B点,一共有几条不同的最短路线呢?
3185 |
3186 | ### 练习1
3187 |
3188 | 丁丁和田田想从家去公园玩,长方形街道如下图所示,一共有多少条不同的最短路线?
3189 |
3190 | ### 例题2
3191 |
3192 | 田田从家所在的A点去学校所在的B点,但途中不能经过C点的商店,不同的最短路线一共有多少条?
3193 |
3194 | ### 练习2
3195 |
3196 | 牛牛从家所在的A点去公园所在的B点,但途中不能经过街道CD(C,D两点可以经过),不同的最短路线一共有多少条?
3197 |
3198 | ### 例题3
3199 |
3200 | 田田从家所在的A点去学校所在的B点,但途中必须经过C点的牛牛家,不同的最短路线一共有多少条?
3201 |
3202 | ### 练习3
3203 |
3204 | 牛牛和阿普从街道的A点到B点,但必须经过一座独木桥MN,他们有多少种不同的最短路线?
3205 |
3206 | ### 例题4
3207 |
3208 | 田田和丁丁准备从家出发到公园玩,路线图如下图所示,最短路线一共有多少条?
3209 |
3210 | ### 练习4
3211 |
3212 | 丁丁从家里去乐乐老师家,路线图如下图所示,最短路线一共有多少条?
3213 |
3214 | ### 例题5
3215 |
3216 | 牛牛从A点走到I点,只能按图中箭头所指的方向行走,共有多少条不同的路线?
3217 |
3218 | ### 练习5
3219 |
3220 | 牛牛玩一种游戏,从图中的A处走到B处,每次只能从一个格子走向右侧邻近的格子而不准逆行,比如从4只能到5和6。一共有多少种不同的走法?
3221 |
3222 | ### 例题6
3223 |
3224 | 田田上楼梯,一步可以上1个或2个台阶,楼梯总共有10个台阶,从地面到第10个台阶总共有多少种走法?
3225 |
3226 | ### 练习6
3227 |
3228 | 在下图中,丁丁想要沿着水平或垂直线段行走时,拼出“APPLE”的路线,共有多少种走法?
3229 |
3230 | 
3231 |
3232 | ## 3.2.17. 页码问题
3233 |
3234 | ### 课前热身
3235 |
3236 | ### 热身1
3237 |
3238 | 一张纸上的两个页码的和总是奇数还是偶数?
3239 |
3240 | ### 热身2
3241 |
3242 | 第1页到第15页一共有多少个数字?
3243 |
3244 | ### 热身3
3245 |
3246 | 在1至100中,数字“1”和数字“2”的数量哪个多?多几个?
3247 |
3248 | 例题练习
3249 |
3250 | ### 例题1
3251 |
3252 | 一本小漫面书一共40页,这些页码共用了多少个数字?
3253 |
3254 | ### 练习1
3255 |
3256 | 一个小册子共有20页,1~20页的页码一共用了多少个数字?
3257 |
3258 | ### 例题2
3259 |
3260 | 一本书共有150页,这些页的页码一共用了多少个数字?
3261 |
3262 | ### 练习2
3263 |
3264 | 一本小说共有86页,这些页的页码一共用了多少个数字?
3265 |
3266 | ### 例题3
3267 |
3268 | 给一本书编页码,一共用了225个数字,这本书一共有多少页?
3269 |
3270 | ### 练习3
3271 |
3272 | 一本小说的页码,在印刷时必须用105个数字。这本书共有多少页?
3273 |
3274 | ### 例题4
3275 |
3276 | (1)一本书共有100页,1~100页的页码中,一共用了多少个数字“2”?
3277 | (2)一本书共有1000页,1~1000页的页码中,一共用了多少个数字“2”?
3278 |
3279 | ### 练习4
3280 |
3281 | 一本书共有100页,1~100页的页码中,数字了用了多少个?数字4用了多少个?同学们找找规律,再计算1~9中的其他数字各出现多少次。
3282 |
3283 | ### 例题5
3284 |
3285 | (1)给一本书编页码时,一共用了10个数字“5”,请问这本书有多少页?
3286 | (2)给一本书编页码时,一共用了41个数字“5”,请问这本书最少有多少页?最多有多少页?
3287 |
3288 | ### 练习5
3289 |
3290 | 一本书编页码时,一共用了62个数字“8”,且最后一页是含有“8”的页码,请问这本书有多少页?
3291 |
3292 | ### 例题6
3293 |
3294 | 有一本50页的书,中间缺了一张,丁丁将残书的页码相加,得到了1230。有人说丁丁计算错了,你能知道这是为什么吗?
3295 |
3296 | ### 练习6
3297 |
3298 | 田田有一本书,中间被牛牛撕掉了一页(含两个相邻页码)。田田将残书的所有页码相加得到1260,请问田田这本书原有多少页?
3299 |
3300 | 拓展
3301 |
3302 | ### 拓展1
3303 |
3304 | 印刷一本书用了1992个数字,在这本书中出现数字“2”的页码有多少页?
3305 |
3306 | ### 拓展2
3307 |
3308 | 一本书共有1000页,1~1000页的页码中,一共用了多少个数字“0”?
3309 |
3310 | ## 3.2.18. 解方程
3311 |
3312 | 例题练习
3313 |
3314 | ### 例题1
3315 |
3316 | 解方程。
3317 |
3318 | (1)$x+5=12$
3319 |
3320 | (2)$12-x=5$
3321 |
3322 | (3)$x\div5=10$
3323 |
3324 | (4)$5x=35$
3325 |
3326 | ### 练习1
3327 |
3328 | 解方程。
3329 |
3330 | (1)$x+6=13$
3331 |
3332 | (2)$13-x=6$
3333 |
3334 | (3)$x\div6=8$
3335 |
3336 | (4)$4x=32$
3337 |
3338 | ### 例题2
3339 |
3340 | 解方程。
3341 |
3342 | (1)$5x+4=2x+16$
3343 |
3344 | (2)$4x-6=8x-18$
3345 |
3346 | ### 练习2
3347 |
3348 | 解方程。
3349 |
3350 | (1)$18-2x=40-4x$
3351 |
3352 | (2)$20-5x=3x+4$
3353 |
3354 | ### 例题3
3355 |
3356 | 解方程。
3357 |
3358 | (1)$5(x+4)=30$
3359 |
3360 | (2)$6(2x-4)=60$
3361 |
3362 | ### 练习3
3363 |
3364 | 解方程。
3365 |
3366 | (1)$$
3367 |
3368 | (2)$$
3369 |
3370 | ### 例题4
3371 |
3372 | 解方程。
3373 |
3374 | (1)$$
3375 |
3376 | (2)$$
3377 |
3378 | ### 练习4
3379 |
3380 | 解方程。
3381 |
3382 | (1)$$
3383 |
3384 | (2)$$
3385 |
3386 | ### 例题5
3387 |
3388 | 解方程。
3389 |
3390 | (1)$$
3391 |
3392 | (2)$$
3393 |
3394 | ### 练习5
3395 |
3396 | 解方程。
3397 |
3398 | (1)$$
3399 |
3400 | (2)$$
3401 |
3402 | ### 例题6
3403 |
3404 | 规定4公6=4x4-2x6。例如,546=5×5-2x6=13。己知8公.2=50,求正
3405 |
3406 | ### 练习6
3407 |
3408 | 定义a#6表示(a一7)x6。例如12#5=(12-7)×5=25。那么,当2#6=54时,二是
3409 | 多少?
3410 |
3411 | ## 3.2.19. 列方程
3412 |
3413 | ### 复习巩固
3414 |
3415 | ### 巩固1(鸡兔同笼)
3416 |
3417 | 体育老师买了运动服上衣和裤子共21件,共用了439元,其中上衣每件24元、裤子每件19元,问老师买上衣和裤子各多少件?
3418 |
3419 | ### 巩固2(和倍)
3420 |
3421 | 某小学的同学为幼儿园的小朋友做红花和黄花共300朵。已知红花的朵数比黄花的2倍少30朵。问两种花各有多少朵?
3422 |
3423 | ### 巩固3(差倍)
3424 |
3425 | 有两根铁丝,第一根长18米,第二根长10米,两根铁丝用去同样长的一段后,第一根剩下的长度是第二根剩下长度的3倍,两根铁丝各剩下多少米?
3426 |
3427 | ### 巩固4(计算)
3428 |
3429 | (1)计算:$125×148×8$
3430 |
3431 | (2)计算:$125×64×25$
3432 |
3433 | (3)计算:$888×125÷111×16$
3434 |
3435 | ### 巩固5(解方程)
3436 |
3437 | 解方程:$2(x+3)=3(x+1)$
3438 |
3439 | ### 例题练习
3440 |
3441 | ### 例题1
3442 |
3443 | 煤场上午运来15吨煤,下午又运来了一些,这天共运来43吨煤,下午运来多少吨煤?
3444 |
3445 | ### 练习1
3446 |
3447 | 两袋大米,第一袋比第二袋少14千克。已知第一袋重52千克,第二袋重多少干克?
3448 |
3449 | ### 例题2
3450 |
3451 | 一个平行四边形的面积是150平方厘米,底是50厘米,高是多少厘米?
3452 |
3453 | ### 练习2
3454 |
3455 | 一个三角形的高是18厘米,面积是180平方厘米,底是多少厘米?
3456 |
3457 | ### 例题3
3458 |
3459 | 丁丁和牛牛共有100张积分卡,已知牛牛积分卡的数量比丁丁的3倍多8张,请问丁丁、牛牛各有多少张积分卡?
3460 |
3461 | ### 练习3
3462 |
3463 | 牛牛比丁丁多100张积分卡,已知牛牛积分卡的数量比丁丁的3倍少8张,请问丁丁、牛牛各有多少张积分卡?
3464 |
3465 | ### 例题4
3466 |
3467 | 苹果和梨共80千克,价值400元,已知苹果4元一千克,梨6元一千克,那么苹果和梨各多少千克?
3468 |
3469 | ### 练习4
3470 |
3471 | 小明买来8角邮票与5角邮票共100张,总值68元。8角邮票和5角邮票各买了多少张?
3472 |
3473 | ### 例题5
3474 |
3475 | 小明家左边与右边各有一家超市在促销同一种品牌的牛奶。如果去左边这家超市购买,所带的钱恰好能买12盒;如果去右边那家超市购买,所带的钱恰好能多买2盒。己知右边超市每盒牛奶的价格比左边超市每盒牛奶的价格便宜1元,那么小明共带了多少钱?
3476 |
3477 | ### 练习5
3478 |
3479 | 体育课上,三年级(1)班的46名同学都在操场上玩球。每个篮球分给6名同学玩,每个排球分给8名同学玩。篮球和排球一共有7个。问:玩排球的同学有多少人?
3480 |
3481 | ### 例题6
3482 |
3483 | 甲、乙、丙共有钱99元,甲的钱比乙的钱的2倍少2元,乙的钱比丙的钱的3倍少3元。甲有多少钱?
3484 |
3485 | ### 练习6
3486 |
3487 | 己知足球、篮球、排球三种球平均每个35元。篮球比排球每个贵10元,足球比排球每个贵8元。问:每个篮球多少元?
3488 |
3489 | ## 3.2.20. 速度、路程与时间
3490 |
3491 | ### 课前热身
3492 |
3493 | ### 热身1(盈亏问题)
3494 |
3495 | 猪妈妈带着孩子去野餐,如果每张餐布周围坐4只小猪就有6只小猪没地方坐,如果每张餐布周围多坐一只小猪就会余出4个空位子,问:一共有多少只小猪,猪妈妈一共带了多少张餐布?
3496 |
3497 | ### 热身2(带余除法)
3498 |
3499 | 甲、乙两数的和是1088,甲数除以乙数商11余32,求甲、乙两数分别是几?
3500 |
3501 | ### 热身3(列方程)
3502 |
3503 | 花圃里有吊兰和仙人球共56盆,吊兰的盆数是仙人球的3倍,吊兰和仙人球各有多少盆?
3504 |
3505 | ### 计算练习(分组)
3506 |
3507 | (1)$100-99+98-97+96-95+\dots+4-3+2-1$
3508 |
3509 | (2)$1-2+3-4+5-6+\dots+95-96+97-98+99-100+101$
3510 |
3511 | 例题练习
3512 |
3513 | ### 例题1
3514 |
3515 | 牛牛骑自行车每小时行15千米。
3516 | (1)2小时以后,能行多少千米?
3517 | (2)按照这样的速度,他骑了60千米,需要几小时?
3518 | (3)后来牛牛匀速行驶100千米用了5个小时,那么这段路牛牛平均每小时行多少千米?
3519 |
3520 | ### 练习1
3521 |
3522 | 丁丁从家去学校,每分钟走60米,走了10分钟到达学校,问丁丁家到学校的距离有多远?如果丁丁每分钟走100米,从家到学校需要走几分钟?
3523 |
3524 | ### 例题2
3525 |
3526 | 一辆从北京到青岛的长途客车,中途经过天津和济南。北京到天津140千米,天津到济南360千米,济南到青岛400千米。早晨5:30从北京发车,平均每小时行驶90千米,大约何时可以到达青岛?
3527 |
3528 | ### 练习2
3529 |
3530 | 甲、乙两地相距230千米,丁丁开车从甲地到乙地行了5小时。照这样的速度,从乙地开往丙地行了4小时,乙、丙两地相距多少千米?
3531 |
3532 | ### 例题3
3533 |
3534 | 丁丁和牛牛两家都在一条马路的旁边,相距800米,丁丁每分钟行50米,牛牛每分钟行60米。
3535 | (1)两人同时从家中出发,背向而行,5分钟后两人相距多少米?
3536 | (2)两人同时从家中出发,相向而行,5分钟后两人相距多少米?
3537 | (3)两人同时从家中出发,同向而行,5分钟后两人相距多少米?
3538 |
3539 | ### 练习3
3540 |
3541 | 田田和阿普两家都在一条马路的旁边,相距400米,田田每分钟行60米,阿普每分钟行70米。
3542 | (1)两人同时从家中出发,背向而行,3分钟后两人相距多少米?
3543 | (2)两人同时从家中出发,相向而行,3分钟后两人相距多少米?
3544 | (3)两人同时从家中出发,同向而行,3分钟后两人相距多少米?
3545 |
3546 | ### 例题4
3547 |
3548 | 阿普和乐乐老师约好在他们之间的某点见面,阿普每分钟走200米,乐乐老师每分钟走150米,他们同时出发2分钟后还相距500米,问:阿普和乐乐老师之间原来的距离是多少米?
3549 |
3550 | ### 练习4
3551 |
3552 | 一天,大黄和大黑约好在他们之间的某点见面,大黄每分钟走67米,大黑每分钟走45米,他们同时出发5分钟后还相距543米,问:大黄和大黑之间原来的距离是多少米?
3553 |
3554 | ### 例题5
3555 |
3556 | 甲、乙两地相距200千米,丁丁去时的速度是10千米/时,回来的速度是40千米/时,求丁丁往返的平均速度。
3557 |
3558 | ### 练习5
3559 |
3560 | 周六,乐乐老师骑自行车去朋友家参加聚会,己知乐乐老师与朋友家相距3600米,乐乐老师去的时候速度为300米/分,回来的速度是600米/分。求乐乐老师来回的平均速度。
3561 |
3562 | ### 例题6
3563 |
3564 | 小亮开车从家出发到720千米外的甲城市去,前240千米的平均速度为60千米/时,小亮如果从家到甲城市的平均速度为80千米/时,剩下的路程应以什么速度行驶?
3565 |
3566 | ### 练习6
3567 |
3568 | A、B两城相距240千米,一辆汽车原计划用6小时从A城到B城,那么汽车每小时应该行驶多少千米?实际上汽车行驶了一半路程后发生故障,在途中停留了1小时。如果要按照原定的时问到达B城,汽车在后一半路程上每小时应该行驶多少千米?
3569 |
--------------------------------------------------------------------------------
/04-四年级.md:
--------------------------------------------------------------------------------
1 | ---
2 | title: 四年级
3 | lang: zh-CN
4 | sidebarDepth: 1
5 | ---
6 |
7 | # 四年级
8 |
9 | ## 4.1.01. 加乘原理初步
10 |
11 | ### 例题1
12 |
13 | 乐乐老师需要从北京出发,依次到南京、上海、深圳和广州视察当地分校的发展情况。从北京到南京可以乘火车或者飞机;从南京到上海可以乘火车、汽车或者飞机;从上海到深圳不仅可以乘火车、汽车和飞机,还可以坐船;从深圳到广州则可以乘火车或者汽车。请问乐乐老师这次从北京到广州的视察共有多少种不同的交通方式?
14 |
15 | ### 练习1
16 |
17 | 如图所示,从A地去B地有5种走法,从B地去C地有3种走法,那么田田从A地经B地去C地一共有多少种不同的走法?
18 |
19 |
2874 |
2875 | ## 3.2.11. 年龄问题进阶
2876 |
2877 | 例题练习
2878 |
2879 | ### 例题1
2880 |
2881 | 妈妈和儿子算年龄,两年前两人的年龄之和是36岁,今年妈妈的年龄是孩子的4倍,今年两人各是多少岁?
2882 |
2883 | ### 练习1
2884 |
2885 | 今年哥哥和弟弟的年龄和是36岁,且哥哥的年龄是弟弟年龄的2倍,哥哥和弟弟今年分别多少岁?
2886 |
2887 | ### 例题2
2888 |
2889 | 楠楠今年9岁了,妈妈33岁,再过多少年,楠楠年龄就是妈妈年龄的一半?
2890 |
2891 | ### 练习2
2892 |
2893 | 父亲今年44岁,儿子今年16岁。当父亲的年龄是儿子的8倍时,父子的年龄和是多少?
2894 |
2895 | ### 例题3
2896 |
2897 | 东东3年前的年龄与西西4年后的年龄和是25岁,东东3年后的年龄等于西西1年前的年龄,求今年东东、西西各是多少岁?
2898 |
2899 | ### 练习3
2900 |
2901 | 小花2年前的年龄与小琪1年后的年龄相等,小花3年前和小琪2年后的年龄和为20岁,则小花和小琪今年各多少岁?
2902 |
2903 | ### 例题4
2904 |
2905 | 乐乐老师对琪琪说:“我是你这个年龄的时候,你才5岁。”琪琪思考了一下,对乐乐老师说:“等到我是您现在年龄的时候,您就50岁了。”你能算出乐乐老师和琪琪今年各多少岁吗?
2906 |
2907 | ### 练习4
2908 |
2909 | 丁丁今年(2022年)12岁,妈妈对丁丁说:“当你有我这么大岁数时,我已经60岁了。”请问妈妈像丁丁这么大时是哪一年?
2910 |
2911 | ### 例题5
2912 |
2913 | 田田一家三口今年的年龄和是87岁,爸爸比妈妈大6岁。几年前,爸爸的年龄是田田的11倍,妈妈的年龄是田田的9倍,你知道田田今年几岁了吗?
2914 |
2915 | ### 练习5
2916 |
2917 | 琪琪今年3岁了,再过5年她就和小花5年前的年龄相等,问小花今年几岁了?
2918 |
2919 | ### 例题6
2920 |
2921 | 今年乐乐老师的年龄是牛牛年龄的5倍,再过8年,乐乐老师的年龄是牛牛年龄的3倍。牛牛今年多少岁?
2922 |
2923 | ### 练习6
2924 |
2925 | 10年前,爸爸的年龄是儿子的7倍,15年后爸爸的年龄是儿子的2倍,问现在父子各多少岁?
2926 |
2927 | ## 3.2.12. 带余除法进阶
2928 |
2929 | 作业练习
2930 |
2931 | ### 练习1
2932 |
2933 | 填空。
2934 |
2935 | (1)$()\div8=6……7$
2936 |
2937 | (2)$31\div()=7……3$
2938 |
2939 | (3)$56\div6=()……()$
2940 |
2941 | (4)$()\div8=7……()$,被除数最大是多少?
2942 |
2943 | (5)$()\div()=3……4$,被除数最小是多少?
2944 |
2945 | ### 练习2
2946 |
2947 | 用一个自然数去除另一个自然数,商为7,被除数、除数的和是48,求这两个自然数各是多少?
2948 |
2949 | ### 练习3
2950 |
2951 | 46除以一个一位数,余数是1。列出所有符合条件的一位数。
2952 |
2953 | ### 练习4
2954 |
2955 | 78除以一个数得到的商是8,并且除数与余数的差是3,求除数和余数。
2956 |
2957 | ### 练习5
2958 |
2959 | $48\times63\times79$除以7的余数是多少?
2960 |
2961 | ### 练习6
2962 |
2963 | 有一串数1,1,2,3,5,8,...,从第三个数起,每个数都是前两个数之和,这串数的第2022个数除以4余数是多少?
2964 |
2965 | 例题练习
2966 |
2967 | ### 例题1
2968 |
2969 | 牛牛有一本故事书,每天读9页,读了23天之后发现还剩6页,这本故事书一共多少页?
2970 |
2971 | ### 练习1
2972 |
2973 | 某数被21除,商是9,余数是7,则该数是多少?
2974 |
2975 | ### 例题2
2976 |
2977 | 丁丁有一本科普书,一共208页,他看了17天之后还剩4页,他前17天每天看多少页?
2978 |
2979 | ### 练习2
2980 |
2981 | 316除以8,余4,商是多少?
2982 |
2983 | ### 例题3
2984 |
2985 | 乐乐老师有160道题,要安排给同学们完成。如果每天做a道题,第b天做完之后,还剩6道,已知a>6,那么a有多少种不同的取值?
2986 |
2987 | ### 练习3
2988 |
2989 | 牛牛有一本练习题,有191道题,如果每天做a(a>9)道题,第b天做完之后,还剩9道,那么a有多少种不同的取值?
2990 |
2991 | ### 例题4
2992 |
2993 | 甲、乙两个数的和是1088,甲数除以乙数商11余32,求甲、乙两数各是多少。
2994 |
2995 | ### 练习4
2996 |
2997 | 678除以一个数得到的商是32,并且除数与余数的差是15,求除数和余数各是多少。
2998 |
2999 | ### 例题5
3000 |
3001 | $2461\times135\times6047\div11$的余数为多少?
3002 |
3003 | ### 练习5
3004 |
3005 | 有一个整数,用它去除70,110,160所得到的3个余数之和是50,那么这个整数是多少?
3006 |
3007 | ### 例题6
3008 |
3009 | 有一串数:1、1、2、3、5、8、⋯,从第三个数起,每个数都是前两个数之和,在这串数的前2017个数中,有几个是5的倍数?
3010 |
3011 | ### 练习6
3012 |
3013 | 有一列数,若这列数从第四个数起,每个数怡好是前面三个数之和,则数列:1、1、2、4、7、13、24、44、⋯中的第2015个数除以3的余数是多少?
3014 |
3015 | ## 3.2.13. 等差数列初步
3016 |
3017 | 课前热身
3018 |
3019 | ### 热身1
3020 |
3021 | 脱式计算。
3022 | $$
3023 | 327-85+73
3024 | $$
3025 |
3026 | $$
3027 | 723+491-13-191
3028 | $$
3029 |
3030 | ### 热身2
3031 |
3032 | $()\div8=7……()$,被除数最大是多少?
3033 |
3034 | $()\div()=3……4$,被除数最小是多少?
3035 |
3036 | ### 热身3
3037 |
3038 | 用一个自然数去除另一个自然数,商为6,被除数、除数的和是56,求这两个自然数各是多少?
3039 |
3040 | 例题练习
3041 |
3042 | ### 例题1
3043 |
3044 | 同学们一起来算一算吧!
3045 | (1)等差数列:5,7,9,11,13,15,……的第12项是();
3046 | (2)等差数列:0,4,8,12,16,20,……的第43项是();
3047 | (3)等差数列:3,7,11,15,……的第56项是()。
3048 |
3049 | ### 练习1
3050 |
3051 | (1)等差数列:3,4,5,6,……的第62项是();
3052 | (2)等差数列:2,5,8,11,……的第47项是()。
3053 |
3054 | ### 例题2
3055 |
3056 | (1)等差数列:5,6,7,8,9,……,其中55是这个数列的第()项;
3057 | (2)等差数列:7,9,11,13,……,其中69是这个数列的第()项。
3058 |
3059 | ### 练习2
3060 |
3061 | (1)等差数列:8,11,14,17,……,其中134是这个数列的第()项;
3062 | (2)等差数列:15,19,23,27,……,其中295是这个数列的第()项。
3063 |
3064 | ### 例题3
3065 |
3066 | 大家一起来求和!
3067 |
3068 | (1)$3+4+5+6+\dots+76+77+78$
3069 |
3070 | (2)$2+4+6+8+\dots+96+98+100$
3071 |
3072 | ### 练习3
3073 |
3074 | 等差数列求和。
3075 |
3076 | (1)1,3,5,7,……,87,89,91;
3077 |
3078 | (2)4,7,10,13,……,40,43,46
3079 |
3080 | ### 例题4
3081 |
3082 | 一个递增的等差数列的首项是10,第61项是250,这个等差数列的公差是多少?
3083 |
3084 | ### 练习4
3085 |
3086 | 一个递增的等差数列,第1项是232,第52项是334,这个等差数列的公差是多少?
3087 |
3088 | ### 例题5
3089 |
3090 | 一个等差数列的第6项和第12项分别是24,42。问:
3091 | (1)数列的第1项是什么?
3092 | (2)数列的第23项是什么?
3093 | (3)数列的前23项的和是多少?
3094 |
3095 | ### 练习5
3096 |
3097 | 己知等差数列的第5项和第9项分别为25、49,那么前31项的和是多少?
3098 |
3099 | ### 例题6
3100 |
3101 | (1)有5个盒子中共放了325个乒乓球,从小盒子到大盒子,每一个盒子中比前面的盒子多了5个乒乓球。问:最大的盒子中有多少个乒乓球?
3102 | (2)有8个盒子共放了888个乒乓球,从小盒子到大盒子,每一个盒子比前面的盒子多了6个乒乓球。问:最小的盒子里有多少个乒乓球?
3103 |
3104 | ### 练习6
3105 |
3106 | 2,4,6,8,10,12,……是个连续偶数列,如果其中5个连续偶数的和是320,那么它们中最小的一个数是谁?
3107 |
3108 | ## 3.2.15. 平面图形计数综合
3109 |
3110 | 例题练习
3111 |
3112 | ### 例题1
3113 |
3114 | 以A,B,C,D,E,F,G这些点为端点,请数一数这里一共有多少条线段?
3115 |
3116 | ### 练习1
3117 |
3118 | 在一条直线上有一些被标记的点,请你数一数,看看能找出几条线段。
3119 |
3120 | 
3121 |
3122 | ### 例题2
3123 |
3124 | 数一数,下面图中共有多少个正方形。
3125 |
3126 | ### 练习2
3127 |
3128 | 数一数,下面图中共有多少个正方形。
3129 |
3130 | 
3131 |
3132 | ### 例题3
3133 |
3134 | 图中有多少个正方形?
3135 |
3136 | 
3137 |
3138 | ### 练习3
3139 |
3140 | 图中有多少个正方形?
3141 |
3142 | 
3143 |
3144 | ### 例题4
3145 |
3146 | 图中有多少个三角形?
3147 |
3148 | 
3149 |
3150 | ### 练习4
3151 |
3152 | 图中有多少个三角形?
3153 |
3154 | 
3155 |
3156 | ### 例题5
3157 |
3158 | 将一个等边三角形各边四等分后再连接相应线段得到下图,你知道图中共有多少个三角形吗?
3159 |
3160 | 
3161 |
3162 | ### 练习5
3163 |
3164 | 将一个等边三角形各边三等分后再连接相应线段得到下图,你知道图中共有多少个三角形吗?
3165 |
3166 | 
3167 |
3168 | ### 例题6
3169 |
3170 | 数一数,下图中共有多少个平行四边形。
3171 |
3172 | 
3173 |
3174 | ### 练习6
3175 |
3176 | 下图是由7条线段构成的图形,你知道里面一共有多少个三角形吗?
3177 |
3178 | 
3179 |
3180 | ## 3.2.16. 标数法
3181 |
3182 | ### 例题1
3183 |
3184 | 丁丁的家在A点,他想沿着长方形街道去学校所在的B点,一共有几条不同的最短路线呢?
3185 |
3186 | ### 练习1
3187 |
3188 | 丁丁和田田想从家去公园玩,长方形街道如下图所示,一共有多少条不同的最短路线?
3189 |
3190 | ### 例题2
3191 |
3192 | 田田从家所在的A点去学校所在的B点,但途中不能经过C点的商店,不同的最短路线一共有多少条?
3193 |
3194 | ### 练习2
3195 |
3196 | 牛牛从家所在的A点去公园所在的B点,但途中不能经过街道CD(C,D两点可以经过),不同的最短路线一共有多少条?
3197 |
3198 | ### 例题3
3199 |
3200 | 田田从家所在的A点去学校所在的B点,但途中必须经过C点的牛牛家,不同的最短路线一共有多少条?
3201 |
3202 | ### 练习3
3203 |
3204 | 牛牛和阿普从街道的A点到B点,但必须经过一座独木桥MN,他们有多少种不同的最短路线?
3205 |
3206 | ### 例题4
3207 |
3208 | 田田和丁丁准备从家出发到公园玩,路线图如下图所示,最短路线一共有多少条?
3209 |
3210 | ### 练习4
3211 |
3212 | 丁丁从家里去乐乐老师家,路线图如下图所示,最短路线一共有多少条?
3213 |
3214 | ### 例题5
3215 |
3216 | 牛牛从A点走到I点,只能按图中箭头所指的方向行走,共有多少条不同的路线?
3217 |
3218 | ### 练习5
3219 |
3220 | 牛牛玩一种游戏,从图中的A处走到B处,每次只能从一个格子走向右侧邻近的格子而不准逆行,比如从4只能到5和6。一共有多少种不同的走法?
3221 |
3222 | ### 例题6
3223 |
3224 | 田田上楼梯,一步可以上1个或2个台阶,楼梯总共有10个台阶,从地面到第10个台阶总共有多少种走法?
3225 |
3226 | ### 练习6
3227 |
3228 | 在下图中,丁丁想要沿着水平或垂直线段行走时,拼出“APPLE”的路线,共有多少种走法?
3229 |
3230 | 
3231 |
3232 | ## 3.2.17. 页码问题
3233 |
3234 | ### 课前热身
3235 |
3236 | ### 热身1
3237 |
3238 | 一张纸上的两个页码的和总是奇数还是偶数?
3239 |
3240 | ### 热身2
3241 |
3242 | 第1页到第15页一共有多少个数字?
3243 |
3244 | ### 热身3
3245 |
3246 | 在1至100中,数字“1”和数字“2”的数量哪个多?多几个?
3247 |
3248 | 例题练习
3249 |
3250 | ### 例题1
3251 |
3252 | 一本小漫面书一共40页,这些页码共用了多少个数字?
3253 |
3254 | ### 练习1
3255 |
3256 | 一个小册子共有20页,1~20页的页码一共用了多少个数字?
3257 |
3258 | ### 例题2
3259 |
3260 | 一本书共有150页,这些页的页码一共用了多少个数字?
3261 |
3262 | ### 练习2
3263 |
3264 | 一本小说共有86页,这些页的页码一共用了多少个数字?
3265 |
3266 | ### 例题3
3267 |
3268 | 给一本书编页码,一共用了225个数字,这本书一共有多少页?
3269 |
3270 | ### 练习3
3271 |
3272 | 一本小说的页码,在印刷时必须用105个数字。这本书共有多少页?
3273 |
3274 | ### 例题4
3275 |
3276 | (1)一本书共有100页,1~100页的页码中,一共用了多少个数字“2”?
3277 | (2)一本书共有1000页,1~1000页的页码中,一共用了多少个数字“2”?
3278 |
3279 | ### 练习4
3280 |
3281 | 一本书共有100页,1~100页的页码中,数字了用了多少个?数字4用了多少个?同学们找找规律,再计算1~9中的其他数字各出现多少次。
3282 |
3283 | ### 例题5
3284 |
3285 | (1)给一本书编页码时,一共用了10个数字“5”,请问这本书有多少页?
3286 | (2)给一本书编页码时,一共用了41个数字“5”,请问这本书最少有多少页?最多有多少页?
3287 |
3288 | ### 练习5
3289 |
3290 | 一本书编页码时,一共用了62个数字“8”,且最后一页是含有“8”的页码,请问这本书有多少页?
3291 |
3292 | ### 例题6
3293 |
3294 | 有一本50页的书,中间缺了一张,丁丁将残书的页码相加,得到了1230。有人说丁丁计算错了,你能知道这是为什么吗?
3295 |
3296 | ### 练习6
3297 |
3298 | 田田有一本书,中间被牛牛撕掉了一页(含两个相邻页码)。田田将残书的所有页码相加得到1260,请问田田这本书原有多少页?
3299 |
3300 | 拓展
3301 |
3302 | ### 拓展1
3303 |
3304 | 印刷一本书用了1992个数字,在这本书中出现数字“2”的页码有多少页?
3305 |
3306 | ### 拓展2
3307 |
3308 | 一本书共有1000页,1~1000页的页码中,一共用了多少个数字“0”?
3309 |
3310 | ## 3.2.18. 解方程
3311 |
3312 | 例题练习
3313 |
3314 | ### 例题1
3315 |
3316 | 解方程。
3317 |
3318 | (1)$x+5=12$
3319 |
3320 | (2)$12-x=5$
3321 |
3322 | (3)$x\div5=10$
3323 |
3324 | (4)$5x=35$
3325 |
3326 | ### 练习1
3327 |
3328 | 解方程。
3329 |
3330 | (1)$x+6=13$
3331 |
3332 | (2)$13-x=6$
3333 |
3334 | (3)$x\div6=8$
3335 |
3336 | (4)$4x=32$
3337 |
3338 | ### 例题2
3339 |
3340 | 解方程。
3341 |
3342 | (1)$5x+4=2x+16$
3343 |
3344 | (2)$4x-6=8x-18$
3345 |
3346 | ### 练习2
3347 |
3348 | 解方程。
3349 |
3350 | (1)$18-2x=40-4x$
3351 |
3352 | (2)$20-5x=3x+4$
3353 |
3354 | ### 例题3
3355 |
3356 | 解方程。
3357 |
3358 | (1)$5(x+4)=30$
3359 |
3360 | (2)$6(2x-4)=60$
3361 |
3362 | ### 练习3
3363 |
3364 | 解方程。
3365 |
3366 | (1)$$
3367 |
3368 | (2)$$
3369 |
3370 | ### 例题4
3371 |
3372 | 解方程。
3373 |
3374 | (1)$$
3375 |
3376 | (2)$$
3377 |
3378 | ### 练习4
3379 |
3380 | 解方程。
3381 |
3382 | (1)$$
3383 |
3384 | (2)$$
3385 |
3386 | ### 例题5
3387 |
3388 | 解方程。
3389 |
3390 | (1)$$
3391 |
3392 | (2)$$
3393 |
3394 | ### 练习5
3395 |
3396 | 解方程。
3397 |
3398 | (1)$$
3399 |
3400 | (2)$$
3401 |
3402 | ### 例题6
3403 |
3404 | 规定4公6=4x4-2x6。例如,546=5×5-2x6=13。己知8公.2=50,求正
3405 |
3406 | ### 练习6
3407 |
3408 | 定义a#6表示(a一7)x6。例如12#5=(12-7)×5=25。那么,当2#6=54时,二是
3409 | 多少?
3410 |
3411 | ## 3.2.19. 列方程
3412 |
3413 | ### 复习巩固
3414 |
3415 | ### 巩固1(鸡兔同笼)
3416 |
3417 | 体育老师买了运动服上衣和裤子共21件,共用了439元,其中上衣每件24元、裤子每件19元,问老师买上衣和裤子各多少件?
3418 |
3419 | ### 巩固2(和倍)
3420 |
3421 | 某小学的同学为幼儿园的小朋友做红花和黄花共300朵。已知红花的朵数比黄花的2倍少30朵。问两种花各有多少朵?
3422 |
3423 | ### 巩固3(差倍)
3424 |
3425 | 有两根铁丝,第一根长18米,第二根长10米,两根铁丝用去同样长的一段后,第一根剩下的长度是第二根剩下长度的3倍,两根铁丝各剩下多少米?
3426 |
3427 | ### 巩固4(计算)
3428 |
3429 | (1)计算:$125×148×8$
3430 |
3431 | (2)计算:$125×64×25$
3432 |
3433 | (3)计算:$888×125÷111×16$
3434 |
3435 | ### 巩固5(解方程)
3436 |
3437 | 解方程:$2(x+3)=3(x+1)$
3438 |
3439 | ### 例题练习
3440 |
3441 | ### 例题1
3442 |
3443 | 煤场上午运来15吨煤,下午又运来了一些,这天共运来43吨煤,下午运来多少吨煤?
3444 |
3445 | ### 练习1
3446 |
3447 | 两袋大米,第一袋比第二袋少14千克。已知第一袋重52千克,第二袋重多少干克?
3448 |
3449 | ### 例题2
3450 |
3451 | 一个平行四边形的面积是150平方厘米,底是50厘米,高是多少厘米?
3452 |
3453 | ### 练习2
3454 |
3455 | 一个三角形的高是18厘米,面积是180平方厘米,底是多少厘米?
3456 |
3457 | ### 例题3
3458 |
3459 | 丁丁和牛牛共有100张积分卡,已知牛牛积分卡的数量比丁丁的3倍多8张,请问丁丁、牛牛各有多少张积分卡?
3460 |
3461 | ### 练习3
3462 |
3463 | 牛牛比丁丁多100张积分卡,已知牛牛积分卡的数量比丁丁的3倍少8张,请问丁丁、牛牛各有多少张积分卡?
3464 |
3465 | ### 例题4
3466 |
3467 | 苹果和梨共80千克,价值400元,已知苹果4元一千克,梨6元一千克,那么苹果和梨各多少千克?
3468 |
3469 | ### 练习4
3470 |
3471 | 小明买来8角邮票与5角邮票共100张,总值68元。8角邮票和5角邮票各买了多少张?
3472 |
3473 | ### 例题5
3474 |
3475 | 小明家左边与右边各有一家超市在促销同一种品牌的牛奶。如果去左边这家超市购买,所带的钱恰好能买12盒;如果去右边那家超市购买,所带的钱恰好能多买2盒。己知右边超市每盒牛奶的价格比左边超市每盒牛奶的价格便宜1元,那么小明共带了多少钱?
3476 |
3477 | ### 练习5
3478 |
3479 | 体育课上,三年级(1)班的46名同学都在操场上玩球。每个篮球分给6名同学玩,每个排球分给8名同学玩。篮球和排球一共有7个。问:玩排球的同学有多少人?
3480 |
3481 | ### 例题6
3482 |
3483 | 甲、乙、丙共有钱99元,甲的钱比乙的钱的2倍少2元,乙的钱比丙的钱的3倍少3元。甲有多少钱?
3484 |
3485 | ### 练习6
3486 |
3487 | 己知足球、篮球、排球三种球平均每个35元。篮球比排球每个贵10元,足球比排球每个贵8元。问:每个篮球多少元?
3488 |
3489 | ## 3.2.20. 速度、路程与时间
3490 |
3491 | ### 课前热身
3492 |
3493 | ### 热身1(盈亏问题)
3494 |
3495 | 猪妈妈带着孩子去野餐,如果每张餐布周围坐4只小猪就有6只小猪没地方坐,如果每张餐布周围多坐一只小猪就会余出4个空位子,问:一共有多少只小猪,猪妈妈一共带了多少张餐布?
3496 |
3497 | ### 热身2(带余除法)
3498 |
3499 | 甲、乙两数的和是1088,甲数除以乙数商11余32,求甲、乙两数分别是几?
3500 |
3501 | ### 热身3(列方程)
3502 |
3503 | 花圃里有吊兰和仙人球共56盆,吊兰的盆数是仙人球的3倍,吊兰和仙人球各有多少盆?
3504 |
3505 | ### 计算练习(分组)
3506 |
3507 | (1)$100-99+98-97+96-95+\dots+4-3+2-1$
3508 |
3509 | (2)$1-2+3-4+5-6+\dots+95-96+97-98+99-100+101$
3510 |
3511 | 例题练习
3512 |
3513 | ### 例题1
3514 |
3515 | 牛牛骑自行车每小时行15千米。
3516 | (1)2小时以后,能行多少千米?
3517 | (2)按照这样的速度,他骑了60千米,需要几小时?
3518 | (3)后来牛牛匀速行驶100千米用了5个小时,那么这段路牛牛平均每小时行多少千米?
3519 |
3520 | ### 练习1
3521 |
3522 | 丁丁从家去学校,每分钟走60米,走了10分钟到达学校,问丁丁家到学校的距离有多远?如果丁丁每分钟走100米,从家到学校需要走几分钟?
3523 |
3524 | ### 例题2
3525 |
3526 | 一辆从北京到青岛的长途客车,中途经过天津和济南。北京到天津140千米,天津到济南360千米,济南到青岛400千米。早晨5:30从北京发车,平均每小时行驶90千米,大约何时可以到达青岛?
3527 |
3528 | ### 练习2
3529 |
3530 | 甲、乙两地相距230千米,丁丁开车从甲地到乙地行了5小时。照这样的速度,从乙地开往丙地行了4小时,乙、丙两地相距多少千米?
3531 |
3532 | ### 例题3
3533 |
3534 | 丁丁和牛牛两家都在一条马路的旁边,相距800米,丁丁每分钟行50米,牛牛每分钟行60米。
3535 | (1)两人同时从家中出发,背向而行,5分钟后两人相距多少米?
3536 | (2)两人同时从家中出发,相向而行,5分钟后两人相距多少米?
3537 | (3)两人同时从家中出发,同向而行,5分钟后两人相距多少米?
3538 |
3539 | ### 练习3
3540 |
3541 | 田田和阿普两家都在一条马路的旁边,相距400米,田田每分钟行60米,阿普每分钟行70米。
3542 | (1)两人同时从家中出发,背向而行,3分钟后两人相距多少米?
3543 | (2)两人同时从家中出发,相向而行,3分钟后两人相距多少米?
3544 | (3)两人同时从家中出发,同向而行,3分钟后两人相距多少米?
3545 |
3546 | ### 例题4
3547 |
3548 | 阿普和乐乐老师约好在他们之间的某点见面,阿普每分钟走200米,乐乐老师每分钟走150米,他们同时出发2分钟后还相距500米,问:阿普和乐乐老师之间原来的距离是多少米?
3549 |
3550 | ### 练习4
3551 |
3552 | 一天,大黄和大黑约好在他们之间的某点见面,大黄每分钟走67米,大黑每分钟走45米,他们同时出发5分钟后还相距543米,问:大黄和大黑之间原来的距离是多少米?
3553 |
3554 | ### 例题5
3555 |
3556 | 甲、乙两地相距200千米,丁丁去时的速度是10千米/时,回来的速度是40千米/时,求丁丁往返的平均速度。
3557 |
3558 | ### 练习5
3559 |
3560 | 周六,乐乐老师骑自行车去朋友家参加聚会,己知乐乐老师与朋友家相距3600米,乐乐老师去的时候速度为300米/分,回来的速度是600米/分。求乐乐老师来回的平均速度。
3561 |
3562 | ### 例题6
3563 |
3564 | 小亮开车从家出发到720千米外的甲城市去,前240千米的平均速度为60千米/时,小亮如果从家到甲城市的平均速度为80千米/时,剩下的路程应以什么速度行驶?
3565 |
3566 | ### 练习6
3567 |
3568 | A、B两城相距240千米,一辆汽车原计划用6小时从A城到B城,那么汽车每小时应该行驶多少千米?实际上汽车行驶了一半路程后发生故障,在途中停留了1小时。如果要按照原定的时问到达B城,汽车在后一半路程上每小时应该行驶多少千米?
3569 |
--------------------------------------------------------------------------------
/04-四年级.md:
--------------------------------------------------------------------------------
1 | ---
2 | title: 四年级
3 | lang: zh-CN
4 | sidebarDepth: 1
5 | ---
6 |
7 | # 四年级
8 |
9 | ## 4.1.01. 加乘原理初步
10 |
11 | ### 例题1
12 |
13 | 乐乐老师需要从北京出发,依次到南京、上海、深圳和广州视察当地分校的发展情况。从北京到南京可以乘火车或者飞机;从南京到上海可以乘火车、汽车或者飞机;从上海到深圳不仅可以乘火车、汽车和飞机,还可以坐船;从深圳到广州则可以乘火车或者汽车。请问乐乐老师这次从北京到广州的视察共有多少种不同的交通方式?
14 |
15 | ### 练习1
16 |
17 | 如图所示,从A地去B地有5种走法,从B地去C地有3种走法,那么田田从A地经B地去C地一共有多少种不同的走法?
18 |
19 |  20 |
21 | ### 例题2
22 |
23 | 牛牛去基肯麦吃饭,发现店里的菜单上只有3种不同的汉堡、4种不同的饮料和5种不同的小吃。
24 |
25 | (1)如果牛牛想从汉堡和饮料中各选1种作为午餐,请问他一共可以搭配出多少种不同的午餐组合?
26 |
27 | (2)如果基肯麦为了吸引客人,决定从汉堡、饮料和小吃中各选1种组成套餐,请问基肯麦一共能提供多少种不同的套餐组合?
28 |
29 | (3)后来基肯麦发现像艾迪这样不喜欢小吃的顾客有很多,为了方便这些顾客,他们决定改良套餐结构:新的套餐中每款都包含一种汉堡和一种饮料,但是小吃可选可不选。改良后基肯麦一共能提供多少种不同的套餐组合?
30 |
31 | ### 练习2
32 |
33 | (1)大宽出门前要选一套衣服。他共有5件不同的上衣、3条不同的裤子,那么大宽有几种不同的搭配方法。
34 |
35 | (2)薇儿出门之前也要选一身衣服。她共有10件不同的上衣、4条不同的裤子、6条不同的裙子(当然,裤子和裙子不能一起穿),那么薇儿有几种不同的搭配方法。
36 |
37 | ### 例题3
38 |
39 | 运动会上牛牛、丁丁、田田、阿普4名运动员组队参加4×100接力赛。
40 |
41 | (1)4人随意安排跑步顺序,一共有多少种不同的跑法?
42 |
43 | (2)牛牛必须跑第一棒,一共有多少种不同的跑法?
44 |
45 | (3)牛牛不能跑第一棒,一共有多少种不同的跑法?
46 |
47 | (4)牛牛不能跑第一棒和第四棒,一共有多少种不同的跑法?
48 |
49 | ### 练习3
50 |
51 | 5个人照相,甲不能站在两侧,能照出多少张不同的照片?
52 |
53 | ### 例题4
54 |
55 | 用数字1,2,3,4,5,6,7,
56 |
57 | (1)可以组成多少个两位数?
58 |
59 | (2)可以组成多少个无重复数字的三位数?
60 |
61 | (3)可以组成多少个无重复数字的四位偶数?
62 |
63 | (4)可以组成多少个无重复数字的四位奇数?
64 |
65 | ### 练习4
66 |
67 | 用数字0,1,2,3,4,5,6,
68 |
69 | (1)可以组成多少个两位数?
70 |
71 | (2)可以组成多少个无重复数字的三位数?
72 |
73 | (3)可以组成多少个无重复数字的四位奇数?
74 |
75 | ### 拓展
76 |
77 | 用数字0,1,2,3,4,5,6,
78 |
79 | (4)可以组成多少无五重复数字的四位偶数?
80 |
81 | ### 例题5
82 |
83 | 牛牛有红、黄、蓝、绿四色信号旗各一面。他在旗杆上挂信号旗时每次可从上到下依次挂一面、两面或三面,排成一列。那么牛牛一共可以表示出多少种不同的信号?
84 |
85 | ### 练习5
86 |
87 | 红、黄、蓝三色信号旗各一面。牛牛在旗杆上挂信号旗时每次可从上到下依次挂一面、两面或三面,排成一列。那么他一共可以表示出多少种不同的信号?
88 |
89 | ### 例题6
90 |
91 | 书架上有2本不同的英语书,4本不同的语文书,3本不同的数学书。现在要从中取出2本,而且不能是同一科的,一共有多少种不同取法?
92 |
93 | ### 练习6
94 |
95 | 花店有10盆不同的茉莉花,15盆不同的菊花,8盆不同的丁香花。现在要从中取出2盆,而且不能是同一品种的,一共有多少种不同取法?
96 |
97 | 拓展
98 |
99 | ### 拓展1
100 |
101 | A、B、C三个小朋友互相传球,先从A开始发球(作为第一次传球),这样经过了5次传球后,球恰巧又回到A手中,那么不同的传球方式共多少种?
102 |
103 | ### 拓展2
104 |
105 | 如图,从起点走到终点,要求取出每个站点上的旗子,并且每个站点只允许通过一次,有几种不同的走法。
106 |
107 |
20 |
21 | ### 例题2
22 |
23 | 牛牛去基肯麦吃饭,发现店里的菜单上只有3种不同的汉堡、4种不同的饮料和5种不同的小吃。
24 |
25 | (1)如果牛牛想从汉堡和饮料中各选1种作为午餐,请问他一共可以搭配出多少种不同的午餐组合?
26 |
27 | (2)如果基肯麦为了吸引客人,决定从汉堡、饮料和小吃中各选1种组成套餐,请问基肯麦一共能提供多少种不同的套餐组合?
28 |
29 | (3)后来基肯麦发现像艾迪这样不喜欢小吃的顾客有很多,为了方便这些顾客,他们决定改良套餐结构:新的套餐中每款都包含一种汉堡和一种饮料,但是小吃可选可不选。改良后基肯麦一共能提供多少种不同的套餐组合?
30 |
31 | ### 练习2
32 |
33 | (1)大宽出门前要选一套衣服。他共有5件不同的上衣、3条不同的裤子,那么大宽有几种不同的搭配方法。
34 |
35 | (2)薇儿出门之前也要选一身衣服。她共有10件不同的上衣、4条不同的裤子、6条不同的裙子(当然,裤子和裙子不能一起穿),那么薇儿有几种不同的搭配方法。
36 |
37 | ### 例题3
38 |
39 | 运动会上牛牛、丁丁、田田、阿普4名运动员组队参加4×100接力赛。
40 |
41 | (1)4人随意安排跑步顺序,一共有多少种不同的跑法?
42 |
43 | (2)牛牛必须跑第一棒,一共有多少种不同的跑法?
44 |
45 | (3)牛牛不能跑第一棒,一共有多少种不同的跑法?
46 |
47 | (4)牛牛不能跑第一棒和第四棒,一共有多少种不同的跑法?
48 |
49 | ### 练习3
50 |
51 | 5个人照相,甲不能站在两侧,能照出多少张不同的照片?
52 |
53 | ### 例题4
54 |
55 | 用数字1,2,3,4,5,6,7,
56 |
57 | (1)可以组成多少个两位数?
58 |
59 | (2)可以组成多少个无重复数字的三位数?
60 |
61 | (3)可以组成多少个无重复数字的四位偶数?
62 |
63 | (4)可以组成多少个无重复数字的四位奇数?
64 |
65 | ### 练习4
66 |
67 | 用数字0,1,2,3,4,5,6,
68 |
69 | (1)可以组成多少个两位数?
70 |
71 | (2)可以组成多少个无重复数字的三位数?
72 |
73 | (3)可以组成多少个无重复数字的四位奇数?
74 |
75 | ### 拓展
76 |
77 | 用数字0,1,2,3,4,5,6,
78 |
79 | (4)可以组成多少无五重复数字的四位偶数?
80 |
81 | ### 例题5
82 |
83 | 牛牛有红、黄、蓝、绿四色信号旗各一面。他在旗杆上挂信号旗时每次可从上到下依次挂一面、两面或三面,排成一列。那么牛牛一共可以表示出多少种不同的信号?
84 |
85 | ### 练习5
86 |
87 | 红、黄、蓝三色信号旗各一面。牛牛在旗杆上挂信号旗时每次可从上到下依次挂一面、两面或三面,排成一列。那么他一共可以表示出多少种不同的信号?
88 |
89 | ### 例题6
90 |
91 | 书架上有2本不同的英语书,4本不同的语文书,3本不同的数学书。现在要从中取出2本,而且不能是同一科的,一共有多少种不同取法?
92 |
93 | ### 练习6
94 |
95 | 花店有10盆不同的茉莉花,15盆不同的菊花,8盆不同的丁香花。现在要从中取出2盆,而且不能是同一品种的,一共有多少种不同取法?
96 |
97 | 拓展
98 |
99 | ### 拓展1
100 |
101 | A、B、C三个小朋友互相传球,先从A开始发球(作为第一次传球),这样经过了5次传球后,球恰巧又回到A手中,那么不同的传球方式共多少种?
102 |
103 | ### 拓展2
104 |
105 | 如图,从起点走到终点,要求取出每个站点上的旗子,并且每个站点只允许通过一次,有几种不同的走法。
106 |
107 |  108 |
109 | ### 拓展3
110 |
111 | 如图,从*A*点到*B*点的最近的路线有多少条?
112 |
113 |
108 |
109 | ### 拓展3
110 |
111 | 如图,从*A*点到*B*点的最近的路线有多少条?
112 |
113 |  114 |
115 | ### 拓展4
116 |
117 | 一只兔子沿着下图中的格线从A到B。规定只能往上或往右走,但必须经过一座独木桥MN,这只兔子有几种不同的走法?
118 |
119 |
114 |
115 | ### 拓展4
116 |
117 | 一只兔子沿着下图中的格线从A到B。规定只能往上或往右走,但必须经过一座独木桥MN,这只兔子有几种不同的走法?
118 |
119 |  120 |
121 | 在下图的街道示意图中,*C*处因施工不能通行,从*A*到*B*的最短路线有多少条?
122 |
123 |
120 |
121 | 在下图的街道示意图中,*C*处因施工不能通行,从*A*到*B*的最短路线有多少条?
122 |
123 |  124 |
125 | ### 拓展5
126 |
127 | 图中有10个编好号码的房间,你可以从小号码房间走到相邻的大号码房间,但不能从大号码走到小号码,从1号房间走到10号房间共有多少种不同的走法?
128 |
129 |
124 |
125 | ### 拓展5
126 |
127 | 图中有10个编好号码的房间,你可以从小号码房间走到相邻的大号码房间,但不能从大号码走到小号码,从1号房间走到10号房间共有多少种不同的走法?
128 |
129 |  130 |
131 | ### 拓展6
132 |
133 | 把数1, 2, 3, 4, 5, 6分为三组(不考虑组内数的顺序也不考虑组间的顺序),每组两个数,每组的数之和互不相等且都不等于6, 共有几种分法。
134 |
135 | ### 拓展7
136 |
137 | 一些白瓷砖和黑瓷砖排成3×3的正方形。其中不含有两块相邻的黑瓷砖的拼法有几种。(下图是其中的一种。)
138 |
139 | 注意:
140 |
141 | 只是翻转后和原来重合的, 不算同一种。
142 |
143 | 旋转后和原来重合的, 算同一种;
144 |
145 | 黑瓷砖一块都不使用, 也算一种;
146 |
147 |
130 |
131 | ### 拓展6
132 |
133 | 把数1, 2, 3, 4, 5, 6分为三组(不考虑组内数的顺序也不考虑组间的顺序),每组两个数,每组的数之和互不相等且都不等于6, 共有几种分法。
134 |
135 | ### 拓展7
136 |
137 | 一些白瓷砖和黑瓷砖排成3×3的正方形。其中不含有两块相邻的黑瓷砖的拼法有几种。(下图是其中的一种。)
138 |
139 | 注意:
140 |
141 | 只是翻转后和原来重合的, 不算同一种。
142 |
143 | 旋转后和原来重合的, 算同一种;
144 |
145 | 黑瓷砖一块都不使用, 也算一种;
146 |
147 |  148 |
149 | ### 拓展8
150 |
151 | 一天放学后,牛牛、丁丁、田田、阿普一起去牛牛家写作业,他们各有一个作业本混放在一起,四人每人随便拿了一本。问:
152 |
153 | (1)牛牛拿到自己作业本的拿法有多少种?
154 |
155 | (2)恰有一人拿到自己作业本的拿法有多少种?
156 |
157 | (3)至少有一人没拿到自己作业本的拿法有多少种?
158 |
159 | (4)谁也没拿到自己作业本的拿法有多少种?
160 |
161 | ### 拓展9
162 |
163 | 大家边做游戏边做作业,很快作业就做完了。这时田田看到牛牛家的橱柜里面放着红、黄、蓝、白四种颜色的小旗,各有2,2,3,3面,她想出了一个问题:任意取出三面按顺序排成一行,表示一种信号,问:一共可以表示多少种不同的信号?如果白旗不能打头又有多少种?
164 |
165 | ## 4.1.02. 三角形初步
166 |
167 | ### 热身1
168 |
169 | 用数字0,1,2,3,4,5,可以组成多少无五重复数字的四位偶数?
170 |
171 | ### 热身2
172 |
173 | 宣萱的书包里有5本呢不同的语文书、6本不同的数学书,3本不同的英语书。如果从中取两种不同种类的书,共有多少种不同的取法?
174 |
175 | ### 热身3
176 |
177 | 下列哪些图形是三角形?
178 |
179 | 
180 |
181 | ### 计算练习
182 |
183 | 我的世界 末地 大战
184 |
185 | ### 例题练习
186 |
187 | ### 例题1
188 |
189 | 下列各组线段能组成一个三角形的是()。
190 |
191 | A.3cm,3cm,6cm
192 |
193 | B.2cm,3cm,6cm
194 |
195 | C.5cm,8cm,12cm
196 |
197 | D.4cm,7cm,11cm
198 |
199 | ### 练习1
200 |
201 | 现有两根木条,它们的长分别为50cm,35cm,如果要钉一个三角形木架,那么下列四根木条中应选取()。
202 |
203 | A.85cm长的木条
204 |
205 | B.150cm长的木条
206 |
207 | C.100cm长的木条
208 |
209 | D.50cm长的木条
210 |
211 | ### 例题2
212 |
213 | 指出下面三角形的底和高。
214 |
215 |
148 |
149 | ### 拓展8
150 |
151 | 一天放学后,牛牛、丁丁、田田、阿普一起去牛牛家写作业,他们各有一个作业本混放在一起,四人每人随便拿了一本。问:
152 |
153 | (1)牛牛拿到自己作业本的拿法有多少种?
154 |
155 | (2)恰有一人拿到自己作业本的拿法有多少种?
156 |
157 | (3)至少有一人没拿到自己作业本的拿法有多少种?
158 |
159 | (4)谁也没拿到自己作业本的拿法有多少种?
160 |
161 | ### 拓展9
162 |
163 | 大家边做游戏边做作业,很快作业就做完了。这时田田看到牛牛家的橱柜里面放着红、黄、蓝、白四种颜色的小旗,各有2,2,3,3面,她想出了一个问题:任意取出三面按顺序排成一行,表示一种信号,问:一共可以表示多少种不同的信号?如果白旗不能打头又有多少种?
164 |
165 | ## 4.1.02. 三角形初步
166 |
167 | ### 热身1
168 |
169 | 用数字0,1,2,3,4,5,可以组成多少无五重复数字的四位偶数?
170 |
171 | ### 热身2
172 |
173 | 宣萱的书包里有5本呢不同的语文书、6本不同的数学书,3本不同的英语书。如果从中取两种不同种类的书,共有多少种不同的取法?
174 |
175 | ### 热身3
176 |
177 | 下列哪些图形是三角形?
178 |
179 | 
180 |
181 | ### 计算练习
182 |
183 | 我的世界 末地 大战
184 |
185 | ### 例题练习
186 |
187 | ### 例题1
188 |
189 | 下列各组线段能组成一个三角形的是()。
190 |
191 | A.3cm,3cm,6cm
192 |
193 | B.2cm,3cm,6cm
194 |
195 | C.5cm,8cm,12cm
196 |
197 | D.4cm,7cm,11cm
198 |
199 | ### 练习1
200 |
201 | 现有两根木条,它们的长分别为50cm,35cm,如果要钉一个三角形木架,那么下列四根木条中应选取()。
202 |
203 | A.85cm长的木条
204 |
205 | B.150cm长的木条
206 |
207 | C.100cm长的木条
208 |
209 | D.50cm长的木条
210 |
211 | ### 例题2
212 |
213 | 指出下面三角形的底和高。
214 |
215 |  216 |
217 | ### 练习2
218 |
219 | 指出下面三角形的底和高。
220 |
221 |
216 |
217 | ### 练习2
218 |
219 | 指出下面三角形的底和高。
220 |
221 |  222 |
223 | ### 例题3
224 |
225 | 同学们,你能确定下面是什么三角形吗?(选填:锐角三角形,直角三角形或钝角三角形;等腰三角形,等腰直角三角形或等边三角形)
226 |
227 | ### 练习3
228 |
229 | 两条直角边相等的直角三角形叫做()三角形
230 |
231 | ### 例题4
232 |
233 | 看图回答如下问题:
234 |
235 | (1)如图 1,∠1+∠2+∠3=
236 | (2)如图2,三角形是等腰直角三角形
237 | (3)如图3,三角形是等边三角形,
238 | (4)如图 4, 𠃋1+22+∠3+∠4=
239 | (5)如图5, ∠1+22+23+24+∠5=
240 | (6)如图 6, ∠1+∠2+∠3+∠4+∠5+∠6=
241 | (7)通过以上题目,总结:八边形的内角和:
242 | f【思维导因】
243 | 图5
244 | 图
245 | 2
246 | ∠1+22=
247 | 13=
248 | 多边形
249 |
250 | ### 练习4
251 |
252 | 如图,已知△ABC中,∠B=70°,若沿图中虚线剪去∠B,则∠1+∠2等于多少度?
253 |
254 |
222 |
223 | ### 例题3
224 |
225 | 同学们,你能确定下面是什么三角形吗?(选填:锐角三角形,直角三角形或钝角三角形;等腰三角形,等腰直角三角形或等边三角形)
226 |
227 | ### 练习3
228 |
229 | 两条直角边相等的直角三角形叫做()三角形
230 |
231 | ### 例题4
232 |
233 | 看图回答如下问题:
234 |
235 | (1)如图 1,∠1+∠2+∠3=
236 | (2)如图2,三角形是等腰直角三角形
237 | (3)如图3,三角形是等边三角形,
238 | (4)如图 4, 𠃋1+22+∠3+∠4=
239 | (5)如图5, ∠1+22+23+24+∠5=
240 | (6)如图 6, ∠1+∠2+∠3+∠4+∠5+∠6=
241 | (7)通过以上题目,总结:八边形的内角和:
242 | f【思维导因】
243 | 图5
244 | 图
245 | 2
246 | ∠1+22=
247 | 13=
248 | 多边形
249 |
250 | ### 练习4
251 |
252 | 如图,已知△ABC中,∠B=70°,若沿图中虚线剪去∠B,则∠1+∠2等于多少度?
253 |
254 |  255 |
256 | ### 例题5
257 |
258 | 如图,∠1=∠2,∠3=∠4,∠5=130°,那么∠A=?80°
259 |
260 | 
261 |
262 | ### 练习5
263 |
264 | 如图,∠1=∠2,∠3=∠4,∠A=70°,那么∠D=?125°
265 |
266 | 
267 |
268 | ### 例题6
269 |
270 | 10个同样的直角三角形卡片拼成了如图所示的平面图形,则这种直角三角形卡片的 3个角中最小的角是多少度?
271 |
272 |
255 |
256 | ### 例题5
257 |
258 | 如图,∠1=∠2,∠3=∠4,∠5=130°,那么∠A=?80°
259 |
260 | 
261 |
262 | ### 练习5
263 |
264 | 如图,∠1=∠2,∠3=∠4,∠A=70°,那么∠D=?125°
265 |
266 | 
267 |
268 | ### 例题6
269 |
270 | 10个同样的直角三角形卡片拼成了如图所示的平面图形,则这种直角三角形卡片的 3个角中最小的角是多少度?
271 |
272 |  273 |
274 | ### 练习6
275 |
276 | 如图,∠AOC=120°,求∠AOB的度数。
277 |
278 | 
279 |
280 | ### 课后巩固
281 |
282 | ### 巩固1
283 |
284 | ### 巩固2
285 |
286 | ### 巩固3
287 |
288 | ### 拓展
289 |
290 | ### 拓展1
291 |
292 | 如图,将△ABC绕点C按顺时针方向旋转30°,得到△B’A'C,若AC⊥A'B',则∠BAC的度数是。
293 |
294 |
273 |
274 | ### 练习6
275 |
276 | 如图,∠AOC=120°,求∠AOB的度数。
277 |
278 | 
279 |
280 | ### 课后巩固
281 |
282 | ### 巩固1
283 |
284 | ### 巩固2
285 |
286 | ### 巩固3
287 |
288 | ### 拓展
289 |
290 | ### 拓展1
291 |
292 | 如图,将△ABC绕点C按顺时针方向旋转30°,得到△B’A'C,若AC⊥A'B',则∠BAC的度数是。
293 |
294 |  295 |
296 | # 三角形进阶
297 |
298 | ### 课前热身
299 |
300 | ### 热身1(加乘原理)
301 |
302 | 商店里有2种巧克力糖,3种水果糖和3种奶糖。小明想买一些糖送给小朋友。
303 |
304 | (1)如果小明只买一种糖,他有几种选法?
305 |
306 | (2)如果小明想买水果糖、巧克力糖各1种,他有几种选法?
307 |
308 | (3)如果小明想买两种不同种类的糖,他有几种选法?
309 |
310 | ### 热身2(三角形的边)
311 |
312 | 周长是12,各边长都是整数的等腰三角形三角形有几种?
313 |
314 | ### 热身3
315 |
316 | 根据五个已知条件,推断出正确密码是多少。
317 |
318 | 682 一个号码正确,而且位置正确;
319 |
320 | 614 一个号码正确,但位置不正确;
321 |
322 | 206 两个号码正确,但是位置都不正确;
323 |
324 | 738 没有一个号码正确;
325 |
326 | 870 一个号码正确,但是位置不正确。
327 |
328 | ## 4.1.03. 三角形进阶
329 |
330 | ### 例题1
331 |
332 | 请找出下面每个图形的三条底并画出每条底的对应高。
333 |
334 |
295 |
296 | # 三角形进阶
297 |
298 | ### 课前热身
299 |
300 | ### 热身1(加乘原理)
301 |
302 | 商店里有2种巧克力糖,3种水果糖和3种奶糖。小明想买一些糖送给小朋友。
303 |
304 | (1)如果小明只买一种糖,他有几种选法?
305 |
306 | (2)如果小明想买水果糖、巧克力糖各1种,他有几种选法?
307 |
308 | (3)如果小明想买两种不同种类的糖,他有几种选法?
309 |
310 | ### 热身2(三角形的边)
311 |
312 | 周长是12,各边长都是整数的等腰三角形三角形有几种?
313 |
314 | ### 热身3
315 |
316 | 根据五个已知条件,推断出正确密码是多少。
317 |
318 | 682 一个号码正确,而且位置正确;
319 |
320 | 614 一个号码正确,但位置不正确;
321 |
322 | 206 两个号码正确,但是位置都不正确;
323 |
324 | 738 没有一个号码正确;
325 |
326 | 870 一个号码正确,但是位置不正确。
327 |
328 | ## 4.1.03. 三角形进阶
329 |
330 | ### 例题1
331 |
332 | 请找出下面每个图形的三条底并画出每条底的对应高。
333 |
334 |  335 |
336 | ### 练习1
337 |
338 | 请找出下面每个图形的三条底并画出每条底的对应高。
339 |
340 | ### 例题2
341 |
342 | (1)求下图中各三角形的面积(单位:厘米)。
343 |
344 |
335 |
336 | ### 练习1
337 |
338 | 请找出下面每个图形的三条底并画出每条底的对应高。
339 |
340 | ### 例题2
341 |
342 | (1)求下图中各三角形的面积(单位:厘米)。
343 |
344 |  345 |
346 | (2)如图,已知BC=4,CD=5,AD=5,求三角形ABC的面积。
347 |
348 |
345 |
346 | (2)如图,已知BC=4,CD=5,AD=5,求三角形ABC的面积。
347 |
348 |  349 |
350 | (3)如图,将两个正方形拼接在一起,已知小正方形的边长是8,求阴影图形的面积。
351 |
352 |
349 |
350 | (3)如图,将两个正方形拼接在一起,已知小正方形的边长是8,求阴影图形的面积。
351 |
352 |  353 |
354 | ### 练习2
355 |
356 | 三角形底边长10厘米,这条底边对应的高是8厘米,求三角形的面积。
357 |
358 | ### 例题3
359 |
360 | (1)如图,已知三角形ABC的面积是80平方厘米,AD=10厘米,求BC的长。
361 |
362 |
353 |
354 | ### 练习2
355 |
356 | 三角形底边长10厘米,这条底边对应的高是8厘米,求三角形的面积。
357 |
358 | ### 例题3
359 |
360 | (1)如图,已知三角形ABC的面积是80平方厘米,AD=10厘米,求BC的长。
361 |
362 |  363 |
364 | (2)如图,已知三角形ABC的面积是120平方米,BC长60米,求图中的高。
365 |
366 |
363 |
364 | (2)如图,已知三角形ABC的面积是120平方米,BC长60米,求图中的高。
365 |
366 |  367 |
368 | ### 练习3
369 |
370 | 一个直角三角形菜地的面积是120平方米,三角形菜地的底边长10米,求这条底边对应的高是多少米?
371 |
372 | ### 例题4
373 |
374 | 直角三角形ABC中,AB与BC为直角边,AB长为60厘米,BC长为80厘米,已知AC边上的高BD是48厘米,求AC的长是多少?
375 |
376 |
367 |
368 | ### 练习3
369 |
370 | 一个直角三角形菜地的面积是120平方米,三角形菜地的底边长10米,求这条底边对应的高是多少米?
371 |
372 | ### 例题4
373 |
374 | 直角三角形ABC中,AB与BC为直角边,AB长为60厘米,BC长为80厘米,已知AC边上的高BD是48厘米,求AC的长是多少?
375 |
376 |  377 |
378 | ### 练习4
379 |
380 | 已知三角形ABC中,BC=10厘米,AD,EC是三角形的高,AD长为8厘米,EC长为5厘米,求底边AB的长是多少厘米?
381 |
382 |
377 |
378 | ### 练习4
379 |
380 | 已知三角形ABC中,BC=10厘米,AD,EC是三角形的高,AD长为8厘米,EC长为5厘米,求底边AB的长是多少厘米?
381 |
382 |  383 |
384 | ### 例题5
385 |
386 | 如图,在直角三角形ABC中有一点P,且三角形ABC的周长是72厘米,过P分别作AC,AB,BC的垂线,并且PE=PF=PD=5厘米,求直角三角形ABC的面积。
387 |
388 |
383 |
384 | ### 例题5
385 |
386 | 如图,在直角三角形ABC中有一点P,且三角形ABC的周长是72厘米,过P分别作AC,AB,BC的垂线,并且PE=PF=PD=5厘米,求直角三角形ABC的面积。
387 |
388 |  389 |
390 | ### 练习5
391 |
392 | 如图,在直角三角形ABC中有一点P,且三角形ABC的面积是96平方厘米,过P分别作AC, AB, BC的垂线,并且PE=PF=PD=4厘米,求直角三角形ABC的周长。
393 |
394 |
389 |
390 | ### 练习5
391 |
392 | 如图,在直角三角形ABC中有一点P,且三角形ABC的面积是96平方厘米,过P分别作AC, AB, BC的垂线,并且PE=PF=PD=4厘米,求直角三角形ABC的周长。
393 |
394 |  395 |
396 | ### 例题6
397 |
398 | 如图,由四个完全相同的直角三角形围成一个大正方形,已知小三角形的两条直角边分别长3cm,4cm,求AB的长度。
399 |
400 |
395 |
396 | ### 例题6
397 |
398 | 如图,由四个完全相同的直角三角形围成一个大正方形,已知小三角形的两条直角边分别长3cm,4cm,求AB的长度。
399 |
400 |  401 |
402 | ### 练习6
403 |
404 | 在长方形ABCD中,各边长度如下,求三角形BEF的面积。
405 |
406 |
401 |
402 | ### 练习6
403 |
404 | 在长方形ABCD中,各边长度如下,求三角形BEF的面积。
405 |
406 |  407 |
408 | ### 巩固1
409 |
410 | ### 巩固2
411 |
412 | ### 巩固3
413 |
414 | ## 4.1.05. 等差数列进阶
415 |
416 | ### 课前热身
417 |
418 | ### 热身1
419 |
420 | ### 热身2
421 |
422 | ### 热身3
423 |
424 | ### 例题1
425 |
426 | (1)小数部分的计数单位是“十分之一”可以用小数()表示;“百分之一”可以用小数()表示;
427 |
428 | (2)分数7/10用小数()表示;分数17/1000用小数()表示。
429 |
430 | (3)1里面有()个0.1,有()个0.01,有()个0.001。
431 |
432 | (4)20.523小数点左边第二位是()位,表示()个();小数点右边第二位是()位,表示()个();
433 |
434 | (5)5.02是由5个()和2个()组成的;
435 |
436 | (6)0.46里面有()个百分之一。
437 |
438 | ### 练习1
439 |
440 | 小数的性质:小数的末尾添上0或去掉0不影响小数的大小。根据小数的性质,下列各题哪些0可以去掉,哪些0不可以去掉?
441 |
442 | 0.50=()
443 |
444 | 400=()
445 |
446 | 4.00=()
447 |
448 | 0.030=()
449 |
450 | ### 例题2
451 |
452 | 0.7+0.2 8.24+3.76
453 |
454 | 4.9-3.8 1-0.03
455 |
456 | 0.5+0.8 3.28+5.72
457 |
458 | 4.35-3 0.8-0.55
459 |
460 | 8.65-6.31 10-7.64
461 |
462 | 13.6+8.46 0.99+1.1
463 |
464 | 4.57+3.17+3.43+5.83
465 |
466 |
467 |
468 | 13.35-4.68+2.65-5.32
469 |
470 | ### 练习2
471 |
472 | 1.8+0.4 4.7+2.3
473 |
474 | 12.7+5.61 19.8-7.5
475 |
476 | 32.55-12.15 24.6-17.93
477 |
478 | ### 例题1
479 |
480 | 己知数列5,9,13,17,⋯,145,问:
481 |
482 | (1)这个数列中第20个数是多少?
483 |
484 | (2)85是这个数列的第几个数?
485 |
486 | (3)这个数列一共有几项?
487 |
488 | (4)将数列中所有的数加起来,和是多少?
489 |
490 | ### 练习1
491 |
492 | (1)数列1,3,5,7,⋯,第18项是几?
493 |
494 | (2)数列2,4,6,8,⋯,其中256是这个数列的第几项?
495 |
496 | (3)数列3,6,9,⋯,180,这个数列共有多少项?
497 |
498 | ### 例题2
499 |
500 | 7个连续奇数的和是147,其中最大的奇数是几呢?
501 |
502 | ### 练习2
503 |
504 | 9个连续偶数的和是180,求最小的数是多少?
505 |
506 | ### 例题3
507 |
508 | 幼儿园304个小朋友围成若干个圆(一圈套一圈)做游戏,已知最内圈24人,最外圈52人,如果相邻两圈相差的人数相等,那么相邻的两圈相差多少人?
509 |
510 | ### 练习3
511 |
512 | 牛牛读一本550页的故事书,第一天读了30页,最后一天读了70页,每天读的页数刚好构成等差数列。那么每一天比前一天多读几页?
513 |
514 | ### 例题4
515 |
516 | 建筑工地有一批砖,摆成如图形状,最上层2块砖,第2层6块砖,第3层10块砖,…,每层都比其上面一层多4块砖,已知最下层有402块砖,问中间一层有多少块砖?这堆砖共有多少块?
517 |
518 | 
519 |
520 | ### 练习4
521 |
522 | 8个连续自然数的和是164,其中最小的数是多少?
523 |
524 | ### 例题5
525 |
526 | 计算1+3+4+6+7+9+10+12+13+…+36+37+39+40的和是多少?
527 |
528 | ### 练习5
529 |
530 | 计算2+3+7+8+12+13+17+18+…+32+33+37+38的和是多少?
531 |
532 | ### 例题6
533 |
534 | 有一列数:1,2,4,7,11,16,22,29,37,…,问这列数的第101个是多少?
535 |
536 | ### 练习6
537 |
538 | 有一列数:1,3,6,10,15,21,28,36,45,…,问这列数的第100个是多少
539 |
540 | ## 4.1.07. 追及问题
541 |
542 | ### 知识导引
543 |
544 | 课程内容
545 |
546 | 学习目标
547 |
548 | 内容分析
549 |
550 | 难点在与合理选择,是用路程差还是路程和。
551 |
552 | ### 基础追及
553 |
554 | **例题1**
555 |
556 | 一天,去上学的牛牛发现田田在他前面 150 米处,于是以每分钟 80 米的速度向他追去,已知田田每分钟走 50 米,问:牛牛多长时间能追上田田呢?
557 |
558 | **练习1**
559 |
560 | 甲在乙前面 100 米,于是乙以每分钟 50 米的速度向他追去,已知甲每分钟走 40 米,问:乙多长时间能追上甲呢?
561 |
562 | **例题2**
563 |
564 | 甲、乙两架飞机同时从同一机场起飞,向同一方向飞行,甲每小时飞行 300 千米,乙每小时飞行 340 千米,4 小时后它们相距多少干米?这时甲提高速度打算用 2 小时追上乙,那么甲每小时应该飞行多少干米?
565 |
566 | **练习2**
567 |
568 | 牛牛每小时行 12 千米,丁丁每小时行 15 千米,他俩同时同起点同向出发,5 小时后他们之间的距离是多少干米?
569 |
570 | **补充1**
571 |
572 | 牛牛每分钟走 70 米,丁丁每分钟走 60 米,两人同时从同一地点背向走了 3 分钟,牛牛掉头去追丁丁,追上丁丁时牛牛共走了多少米?
573 |
574 | **例题3**
575 |
576 | 六年级同学从学校出发到公园春游,每分钟走 72 米。15 分钟以后,学校有急事要通知学生,派乐乐老师骑自行车从学校出发用 9 分钟追上同学们,乐乐老师每分钟要行多少米才可以准时追上同学们?
577 |
578 | **练习3**
579 |
580 | 一辆慢车从甲地开往乙地,每小时行 40 千米,开出 5 小时后,一辆快车以每小时 90 千米的速度也从甲地开往乙地,在甲、乙两地的中点处快车追上慢车。甲、乙两地相距多少干米?
581 |
582 | ### 不同时出发
583 |
584 | **例题4**
585 |
586 | 甲、乙两车分别从 A、B 两地出发,同向而行,乙车在前,甲车在后。已知甲车比乙车提前出发1小时,甲车每小时行 96 千米,乙车每小时行 80 千米。甲车出发5小时后追上乙车,求 A、B 两地间的距离。
587 |
588 | **练习4**
589 |
590 | 甲、乙两辆汽车同时从 A 地出发去 B 地,甲车每小时行 50 千米,乙车每小时行 40 千米。途中甲车出故障停车修理了 3 小时,结果甲车比乙车迟到 1 小时到达 B 地。A、B 两地间的路程是多少?
591 |
592 | **补充2**
593 |
594 | 牛牛和丁丁放学后,一起步行去体校参加排球训练,牛牛每分钟走 110 米,丁丁每分钟走 70 米,出发 5 分钟后,牛牛返回学校取运动服,在学校又耽误了 2 分钟,然后追赶丁丁。求多少分钟后追上丁丁。
595 |
596 | ### 行程问题变形
597 |
598 | **例题5**
599 |
600 | 丁丁和牛牛同时从两地相向而行,丁丁每分钟行 50 米,牛牛每分钟行 60 米,两人在距两地中点50米处相遇,求两地的距离是多少米?
601 |
602 | **练习5**
603 |
604 | 牛牛、丁丁三人同时从 A 地去 B 地,牛牛每分钟行 60 米,丁丁每分钟行 90 米,丁丁到达 B 地后立即返回,并与牛牛相遇,相遇时,牛牛还需行 3 分钟才能到达B地,A、B 两地相距多少米?
605 |
606 | **例题6**
607 |
608 | 牛牛和丁丁练习跑步,若牛牛让丁丁先跑 20 米,则牛牛跑 5 秒钟就可追上丁丁;若牛牛让丁丁先跑 4 秒钟,则牛牛跑 6 秒钟就能追上丁丁。牛牛、丁丁两人的速度各是多少?
609 |
610 | **练习6**
611 |
612 | 牛牛、田田二人练习跑出,若牛牛让田田先跑 10 米,则牛牛跑 5 秒钟可追上田田;若牛牛让田田先跑 2 秒钟,则牛牛跑 4 秒钟就能追上田田。问:牛牛、田田两人的速度各是多少?
613 |
614 | ## 4.1.08.整除特征初步
615 |
616 | ### 例题练习
617 |
618 | ### **例题1**
619 |
620 | 下面6个自然数:152,650,434,4375,9064,24125中。
621 |
622 | (1)哪些能被2整除?哪些能被5整除?
623 | (2)哪些能被4整除?哪些能被25整除?
624 | (3)哪些能被8整除?哪些能被125整除?
625 |
626 | ### **练习1**
627 |
628 | (1)能被25整除的数的末两位数只能是多少?
629 | (2)能被4整除的最大三位数是多少?
630 |
631 | ### **例题2**
632 |
633 | (1)修改15679中的一个数字,使这个五位数能被4整除,修改后的五位数是多少?
634 | (2)修改4545679中的一个数字,使这个七位数能被8整除,修改后的七位数是多少?
635 |
636 | ### **练习2**
637 |
638 | (1)修改34575中的一个数宇,使这个五位数能被4整除,修改后的五位数是多少?
639 | (2)修改675479中的一个数字,使这个六位数能被25整除,修改后的六位数是多少?
640 |
641 | ### **例题3**
642 |
643 | 下面6个自然数,5762,3105,9631,7953,2945,3281。
644 |
645 | (1)哪些能被3整除?不能被3整除的余数分别是多少?
646 | (2)哪些能被9整除?不能被9整除的余数分别是多少?
647 |
648 | ### **练习3**
649 |
650 | $\underbrace{55\dots5}_{20个5}89$是否能被3整除?
651 |
652 | ### **例题4**
653 |
654 | 六位数$\overline{243AA4}$能被3整除,求A。
655 |
656 | 六位数$\overline{23A4A7}$能被9整除,求A。
657 |
658 | ### **练习4**
659 |
660 | 在方框中填上两个数字,可以相同也可以不同,使$\overline{4\Box32\Box}$是9的倍数,一共有几种满足条件的填法?
661 |
662 | ### **例题5**
663 |
664 | 在下面每个数的$\Box$里填上一个数字,使它符合所提要求。
665 |
666 | (1)$\overline{234\Box}$,$\overline{63\Box2}$能被2整除,又能被3整除。
667 | (2)$\overline{5\Box0}$,$\overline{4\Box\Box}$,$\overline{\Box89\Box}$同时能被2,5,3整除。
668 |
669 | ### **练习5**
670 |
671 | 在下面每个数的$\Box$里填上一个数字,使它符合所提要求。
672 |
673 | $\overline{5\Box2\Box}$既能被3整除,又能被5整除,那么一共有多少种填法。
674 |
675 | ### **例题6**
676 |
677 | 若五位数$\overline{22A3B}$能被45整除,则A、B代表的数字各是多少?
678 |
679 | ### **练习6**
680 |
681 | 若五位数$\overline{2A52A}$能被15整除,则A代表的数字是多少?
682 |
683 | ### 拓展
684 |
685 | **拓展1**
686 |
687 | $75\times935\times241\times\Box$,要使这个连乘积的最后4个数字都是0,那么在方框内最小应填什么数?
688 |
689 | **拓展2**
690 |
691 | 从1到20的这20个自然数的乘积的末尾有多少个连续的0?
692 |
693 | **拓展3**
694 |
695 | 一个六位数$\overline{2\Box\Box727}$除以9余4,这个数最小是几?
696 |
697 | ## 4.1.10. 定义新运算
698 |
699 | ### 例题1
700 |
701 | 一般我们都认为箭头指向谁,谁就是有危险的,那么规定。
702 |
703 | 警察➡️小偷=警察;警察⬅️小偷=小偷
704 |
705 | 则:(猎人➡️小兔)⬅️(山羊⬅️白菜)=()
706 |
707 | ### 练习1
708 |
709 | 羊和狼在一起时,狼要吃掉羊。所以关于羊及狼,我们规定一种运算,用符号△表示:羊△羊=羊;羊△狼=狼;狼△羊=狼;狼△狼=狼,以上运算的意思是:羊与羊在一起还是羊,狼与狼在一起还是狼,但是狼与羊在一起便只剩下狼了。小朋友总是希望羊能战胜狼,所以我们规定另一种运算,用符号☆表示:羊☆羊=羊;羊☆狼=羊;狼☆羊=羊;狼☆狼=狼,这个运算的意思是:羊与羊在一起还是羊,狼与狼在一起还是狼,但由于羊能战胜狼,当狼与羊在一起时,它便被羊赶走而只剩下羊了。对羊或狼,可以用上面规定的运算作混合运算,混合运算的法规是从左到右,括号内先算。运算的结果或是羊,或是狼。求下式的结果:羊△(狼☆羊)☆羊△(狼△狼)
710 |
711 | ### 例题2
712 |
713 | 我们规定a※b表示为3倍的a减去2倍的b,即$a※b=3a-2b$,例如:$3※2=3x3-2x2=5$;同时,a△b表示为3倍的a加上2倍的b,即$a△b=3a+2b$,例如:$1△2=1x3+2x2=7$
714 |
715 | (1)计算:$5※4$;$4※5$;$2△3$;$3△2$;
716 |
717 | (2)计算:$(8※7)※9$;$2△(5※3)$;
718 |
719 | (3)计算:$5※4△3※2△1$;
720 |
721 | (4)计算:$1※1+2※2+3※3+\dots+100※100$。
722 |
723 | ### 练习2
724 |
725 | 我们规定:$a△b=5a-3b$,计算:$4△3$;$3△3$;$3△5$。
726 |
727 | ### 例题3
728 |
729 | 我们规定$a△b=b(a+1)-a(b-1)$,计算:$(2△1)+(4△3)+(6△5)+(8△7)+(10△9)$。
730 |
731 | ### 练习3
732 |
733 | 我们规定$a◎b=(a+b)-(a-b)$,计算$(2◎1)+(3◎2)+(4◎3)+ ··· +(10◎9)$。
734 |
735 | ### 例题4
736 |
737 | 对于任意的两个自然数a和b,规定新运算表示为:$ab=a+(a+1)+ ··· +(a+b-1)$。
738 |
739 | (1)求$1*100$的值;
740 |
741 | (2)已知$x*10=75$,求x的值;
742 |
743 | (3)如果$(x*3)*2=121$,求x的值。
744 |
745 | ### 练习4
746 |
747 | 如果a△b表示$(a-2)×b$,例如$ 3△4=(3-2)×4=4$,那么,当$a△5=30$时,求a的值。
748 |
749 | ### 例题5
750 |
751 | “⊙”表示一种新的运算符号,已知$2⊙3=2+3+4$;$7⊙2=7+8$;$3⊙5=3+4+5+6+7$,···,按此规则:
752 |
753 | (1)计算:$9⊙6$;
754 |
755 | (2)如果$n⊙8=68$,那么n的值是。
756 |
757 | ### 练习5
758 |
759 | “⊙”表示一种新的运算符号,已知$3⊙3=3×4×5$;$7⊙2=7×8$;$2⊙4=2×3×4×5$,···按此规则:
760 |
761 | 1. 求解,$5⊙3$;
762 |
763 | 2. 如果$n⊙3=60$,求n的值。
764 |
765 | ### 例题6
766 |
767 | ### 练习6
768 |
769 | ## 4.1.11. 体育比赛中的数学
770 |
771 | ### 例题练习
772 |
773 | ### 例题1
774 |
775 | 十六支篮球队按以下的单淘汰赛的规则进行比赛:分成八组两两对决,决出八个队伍晋级,再决出四个队……最后决出冠军。请问总共进行了几场比赛?
776 |
777 | ### 练习1
778 |
779 | 二十支篮球队进行单淘汰赛,只要输一场就会被淘汰,那么为了决出冠军需要举行几场比赛?
780 |
781 | ### 例题2
782 |
783 | 20名羽毛球运动员参加单打比赛,两两配对进行单循环赛,那么冠军一共要比赛多少场?共要进行几场比赛?
784 |
785 | ### 练习2
786 |
787 | 8位同学进行网球循环赛,规则是每个人都要和其他所有人比一场,那么这八个人总共要举行多少场比赛?
788 |
789 | ### 例题3
790 |
791 | A,B,C,D,E五位同学一起比赛象棋,每两人都要比赛一盘。到现在为止,A已经赛4盘,B赛3盘,C赛2盘,D赛1盘。问:此时E同学赛了几盘?
792 |
793 | ### 练习3
794 |
795 | 编号为1,2,3,4,5,6的六个运动员进行乒乓球单循环赛。到现在为止,编号为1,2,3,4,5的运动员已参加比赛的场数正好分别等于他们的编号数。编号为6的运动员已经赛了几场?
796 |
797 | ### 例题4
798 |
799 | 班上四名同学进行跳棋比赛,每两名同学都要赛一局。每局胜者得2分,平者各得1分,负者得0分。
800 |
801 | (1)四个同学的得分加起来一定是多少分?
802 |
803 | (2)第一名最多得多少分?最少得多少分?
804 |
805 | (3)最后一名最多得多少分?
806 |
807 | (4)已知甲、乙、丙三名同学得分分别为3分、4分、4分,且丙同学无平局,甲同学有胜局乙同学有平局,那么丁同学得分是多少?
808 |
809 | ### 练习4
810 |
811 | 在中国象棋比赛中,有胜平负三种结果:获胜得2分,战平得1分,失败得0分。现在六个人进行单循环赛,已知其中五个人的分数分别是7,6,5,4,3,那么最后一个人分数是多分?
812 |
813 | ### 例题5
814 |
815 | 世界杯小组赛规则如下:四支队伍进行单循环赛,胜者得3分,战平得1分,输了得0分。
816 |
817 | (1)他们的总得分最低是多少,最高是多少?
818 |
819 | (2)第一名最多得多少分?
820 |
821 | (3)己知甲、乙、丙、丁四队的得分分别为7,4,4,1。则比赛有几场平局?
822 |
823 | ### 练习5
824 |
825 | 四名同学进行跳棋比赛,每两名同学都要赛一局。每局胜者得2分,平局各得1分,负者得0分。已知甲乙丙三名同学得分分别是3、4、4分,且丙无平局,甲有胜局,乙有平局,那么丁的得分是多少?分别写出丁与甲乙丙丁比赛结果。
826 |
827 | ### 例题6
828 |
829 | “世界杯”足球赛中,甲、乙、丙、丁4支队分在同一小组,在小组赛中,这4支队中的每支队都要与另3支队比赛一场。根据规定:每场比赛获胜的队可得3分;失败的队得0分;如果双方踢平,两队各得1分。已知:
830 |
831 | (1)这4支队三场比赛的总得分为4个连续奇数;
832 |
833 | (2)乙队总得分排在第一;
834 |
835 | (3)丁队恰有两场同对方踢平,其中有一场是与丙队踢平的。
836 |
837 | 根据以上条件可以推断:总得分排在第四的是哪队?
838 |
839 | ### 练习6
840 |
841 | 四个足球队进行单循环比赛,每两队都要赛一场。如果踢平,每队各得1分,否则胜队得3分,负队得0分。比赛结束,各队的总得分怡好是四个连续的自然数。问:输给第一名的队的总分是多少?
842 |
843 | ### 拓展
844 |
845 | 12个队参加一次足球比赛,每两个队都比赛一场,每场比赛中,胜队得3分,负队得0分,平局则各得1分。比赛完毕后,获得第3名和第4名的两个队的得分最多可以相差多少分?
846 |
847 | ### 课后巩固
848 |
849 | ### 巩固1
850 |
851 | A、B、C、D、E五个人进行单循环赛,目前比赛已经进行了一部分,已知A、B都赛了4场,C、D都赛了2场,那么E赛了几场?
852 |
853 | ### 巩固2
854 |
855 | 若干名选手进行网球单循环赛,总共赛了45场,共有多少名选手参赛?
856 |
857 | ### 巩固3
858 |
859 | 6支球队进行足球比赛,每两支队之间都要赛一场,规定胜一场得3分,平一场各得1分,负一场不得分。全部比赛结束后,发现共有4场平局,且其中5支球队共得了31分,则第6支球队得了多少分?
860 |
861 | ## 4.1.12. 几何计数初步
862 |
863 | ### 例题1
864 |
865 | 数一数下图中长方形的个数。
866 |
867 | 
868 |
869 | ### 练习1
870 |
871 | 下图中有多少个长方形?
872 |
873 |
407 |
408 | ### 巩固1
409 |
410 | ### 巩固2
411 |
412 | ### 巩固3
413 |
414 | ## 4.1.05. 等差数列进阶
415 |
416 | ### 课前热身
417 |
418 | ### 热身1
419 |
420 | ### 热身2
421 |
422 | ### 热身3
423 |
424 | ### 例题1
425 |
426 | (1)小数部分的计数单位是“十分之一”可以用小数()表示;“百分之一”可以用小数()表示;
427 |
428 | (2)分数7/10用小数()表示;分数17/1000用小数()表示。
429 |
430 | (3)1里面有()个0.1,有()个0.01,有()个0.001。
431 |
432 | (4)20.523小数点左边第二位是()位,表示()个();小数点右边第二位是()位,表示()个();
433 |
434 | (5)5.02是由5个()和2个()组成的;
435 |
436 | (6)0.46里面有()个百分之一。
437 |
438 | ### 练习1
439 |
440 | 小数的性质:小数的末尾添上0或去掉0不影响小数的大小。根据小数的性质,下列各题哪些0可以去掉,哪些0不可以去掉?
441 |
442 | 0.50=()
443 |
444 | 400=()
445 |
446 | 4.00=()
447 |
448 | 0.030=()
449 |
450 | ### 例题2
451 |
452 | 0.7+0.2 8.24+3.76
453 |
454 | 4.9-3.8 1-0.03
455 |
456 | 0.5+0.8 3.28+5.72
457 |
458 | 4.35-3 0.8-0.55
459 |
460 | 8.65-6.31 10-7.64
461 |
462 | 13.6+8.46 0.99+1.1
463 |
464 | 4.57+3.17+3.43+5.83
465 |
466 |
467 |
468 | 13.35-4.68+2.65-5.32
469 |
470 | ### 练习2
471 |
472 | 1.8+0.4 4.7+2.3
473 |
474 | 12.7+5.61 19.8-7.5
475 |
476 | 32.55-12.15 24.6-17.93
477 |
478 | ### 例题1
479 |
480 | 己知数列5,9,13,17,⋯,145,问:
481 |
482 | (1)这个数列中第20个数是多少?
483 |
484 | (2)85是这个数列的第几个数?
485 |
486 | (3)这个数列一共有几项?
487 |
488 | (4)将数列中所有的数加起来,和是多少?
489 |
490 | ### 练习1
491 |
492 | (1)数列1,3,5,7,⋯,第18项是几?
493 |
494 | (2)数列2,4,6,8,⋯,其中256是这个数列的第几项?
495 |
496 | (3)数列3,6,9,⋯,180,这个数列共有多少项?
497 |
498 | ### 例题2
499 |
500 | 7个连续奇数的和是147,其中最大的奇数是几呢?
501 |
502 | ### 练习2
503 |
504 | 9个连续偶数的和是180,求最小的数是多少?
505 |
506 | ### 例题3
507 |
508 | 幼儿园304个小朋友围成若干个圆(一圈套一圈)做游戏,已知最内圈24人,最外圈52人,如果相邻两圈相差的人数相等,那么相邻的两圈相差多少人?
509 |
510 | ### 练习3
511 |
512 | 牛牛读一本550页的故事书,第一天读了30页,最后一天读了70页,每天读的页数刚好构成等差数列。那么每一天比前一天多读几页?
513 |
514 | ### 例题4
515 |
516 | 建筑工地有一批砖,摆成如图形状,最上层2块砖,第2层6块砖,第3层10块砖,…,每层都比其上面一层多4块砖,已知最下层有402块砖,问中间一层有多少块砖?这堆砖共有多少块?
517 |
518 | 
519 |
520 | ### 练习4
521 |
522 | 8个连续自然数的和是164,其中最小的数是多少?
523 |
524 | ### 例题5
525 |
526 | 计算1+3+4+6+7+9+10+12+13+…+36+37+39+40的和是多少?
527 |
528 | ### 练习5
529 |
530 | 计算2+3+7+8+12+13+17+18+…+32+33+37+38的和是多少?
531 |
532 | ### 例题6
533 |
534 | 有一列数:1,2,4,7,11,16,22,29,37,…,问这列数的第101个是多少?
535 |
536 | ### 练习6
537 |
538 | 有一列数:1,3,6,10,15,21,28,36,45,…,问这列数的第100个是多少
539 |
540 | ## 4.1.07. 追及问题
541 |
542 | ### 知识导引
543 |
544 | 课程内容
545 |
546 | 学习目标
547 |
548 | 内容分析
549 |
550 | 难点在与合理选择,是用路程差还是路程和。
551 |
552 | ### 基础追及
553 |
554 | **例题1**
555 |
556 | 一天,去上学的牛牛发现田田在他前面 150 米处,于是以每分钟 80 米的速度向他追去,已知田田每分钟走 50 米,问:牛牛多长时间能追上田田呢?
557 |
558 | **练习1**
559 |
560 | 甲在乙前面 100 米,于是乙以每分钟 50 米的速度向他追去,已知甲每分钟走 40 米,问:乙多长时间能追上甲呢?
561 |
562 | **例题2**
563 |
564 | 甲、乙两架飞机同时从同一机场起飞,向同一方向飞行,甲每小时飞行 300 千米,乙每小时飞行 340 千米,4 小时后它们相距多少干米?这时甲提高速度打算用 2 小时追上乙,那么甲每小时应该飞行多少干米?
565 |
566 | **练习2**
567 |
568 | 牛牛每小时行 12 千米,丁丁每小时行 15 千米,他俩同时同起点同向出发,5 小时后他们之间的距离是多少干米?
569 |
570 | **补充1**
571 |
572 | 牛牛每分钟走 70 米,丁丁每分钟走 60 米,两人同时从同一地点背向走了 3 分钟,牛牛掉头去追丁丁,追上丁丁时牛牛共走了多少米?
573 |
574 | **例题3**
575 |
576 | 六年级同学从学校出发到公园春游,每分钟走 72 米。15 分钟以后,学校有急事要通知学生,派乐乐老师骑自行车从学校出发用 9 分钟追上同学们,乐乐老师每分钟要行多少米才可以准时追上同学们?
577 |
578 | **练习3**
579 |
580 | 一辆慢车从甲地开往乙地,每小时行 40 千米,开出 5 小时后,一辆快车以每小时 90 千米的速度也从甲地开往乙地,在甲、乙两地的中点处快车追上慢车。甲、乙两地相距多少干米?
581 |
582 | ### 不同时出发
583 |
584 | **例题4**
585 |
586 | 甲、乙两车分别从 A、B 两地出发,同向而行,乙车在前,甲车在后。已知甲车比乙车提前出发1小时,甲车每小时行 96 千米,乙车每小时行 80 千米。甲车出发5小时后追上乙车,求 A、B 两地间的距离。
587 |
588 | **练习4**
589 |
590 | 甲、乙两辆汽车同时从 A 地出发去 B 地,甲车每小时行 50 千米,乙车每小时行 40 千米。途中甲车出故障停车修理了 3 小时,结果甲车比乙车迟到 1 小时到达 B 地。A、B 两地间的路程是多少?
591 |
592 | **补充2**
593 |
594 | 牛牛和丁丁放学后,一起步行去体校参加排球训练,牛牛每分钟走 110 米,丁丁每分钟走 70 米,出发 5 分钟后,牛牛返回学校取运动服,在学校又耽误了 2 分钟,然后追赶丁丁。求多少分钟后追上丁丁。
595 |
596 | ### 行程问题变形
597 |
598 | **例题5**
599 |
600 | 丁丁和牛牛同时从两地相向而行,丁丁每分钟行 50 米,牛牛每分钟行 60 米,两人在距两地中点50米处相遇,求两地的距离是多少米?
601 |
602 | **练习5**
603 |
604 | 牛牛、丁丁三人同时从 A 地去 B 地,牛牛每分钟行 60 米,丁丁每分钟行 90 米,丁丁到达 B 地后立即返回,并与牛牛相遇,相遇时,牛牛还需行 3 分钟才能到达B地,A、B 两地相距多少米?
605 |
606 | **例题6**
607 |
608 | 牛牛和丁丁练习跑步,若牛牛让丁丁先跑 20 米,则牛牛跑 5 秒钟就可追上丁丁;若牛牛让丁丁先跑 4 秒钟,则牛牛跑 6 秒钟就能追上丁丁。牛牛、丁丁两人的速度各是多少?
609 |
610 | **练习6**
611 |
612 | 牛牛、田田二人练习跑出,若牛牛让田田先跑 10 米,则牛牛跑 5 秒钟可追上田田;若牛牛让田田先跑 2 秒钟,则牛牛跑 4 秒钟就能追上田田。问:牛牛、田田两人的速度各是多少?
613 |
614 | ## 4.1.08.整除特征初步
615 |
616 | ### 例题练习
617 |
618 | ### **例题1**
619 |
620 | 下面6个自然数:152,650,434,4375,9064,24125中。
621 |
622 | (1)哪些能被2整除?哪些能被5整除?
623 | (2)哪些能被4整除?哪些能被25整除?
624 | (3)哪些能被8整除?哪些能被125整除?
625 |
626 | ### **练习1**
627 |
628 | (1)能被25整除的数的末两位数只能是多少?
629 | (2)能被4整除的最大三位数是多少?
630 |
631 | ### **例题2**
632 |
633 | (1)修改15679中的一个数字,使这个五位数能被4整除,修改后的五位数是多少?
634 | (2)修改4545679中的一个数字,使这个七位数能被8整除,修改后的七位数是多少?
635 |
636 | ### **练习2**
637 |
638 | (1)修改34575中的一个数宇,使这个五位数能被4整除,修改后的五位数是多少?
639 | (2)修改675479中的一个数字,使这个六位数能被25整除,修改后的六位数是多少?
640 |
641 | ### **例题3**
642 |
643 | 下面6个自然数,5762,3105,9631,7953,2945,3281。
644 |
645 | (1)哪些能被3整除?不能被3整除的余数分别是多少?
646 | (2)哪些能被9整除?不能被9整除的余数分别是多少?
647 |
648 | ### **练习3**
649 |
650 | $\underbrace{55\dots5}_{20个5}89$是否能被3整除?
651 |
652 | ### **例题4**
653 |
654 | 六位数$\overline{243AA4}$能被3整除,求A。
655 |
656 | 六位数$\overline{23A4A7}$能被9整除,求A。
657 |
658 | ### **练习4**
659 |
660 | 在方框中填上两个数字,可以相同也可以不同,使$\overline{4\Box32\Box}$是9的倍数,一共有几种满足条件的填法?
661 |
662 | ### **例题5**
663 |
664 | 在下面每个数的$\Box$里填上一个数字,使它符合所提要求。
665 |
666 | (1)$\overline{234\Box}$,$\overline{63\Box2}$能被2整除,又能被3整除。
667 | (2)$\overline{5\Box0}$,$\overline{4\Box\Box}$,$\overline{\Box89\Box}$同时能被2,5,3整除。
668 |
669 | ### **练习5**
670 |
671 | 在下面每个数的$\Box$里填上一个数字,使它符合所提要求。
672 |
673 | $\overline{5\Box2\Box}$既能被3整除,又能被5整除,那么一共有多少种填法。
674 |
675 | ### **例题6**
676 |
677 | 若五位数$\overline{22A3B}$能被45整除,则A、B代表的数字各是多少?
678 |
679 | ### **练习6**
680 |
681 | 若五位数$\overline{2A52A}$能被15整除,则A代表的数字是多少?
682 |
683 | ### 拓展
684 |
685 | **拓展1**
686 |
687 | $75\times935\times241\times\Box$,要使这个连乘积的最后4个数字都是0,那么在方框内最小应填什么数?
688 |
689 | **拓展2**
690 |
691 | 从1到20的这20个自然数的乘积的末尾有多少个连续的0?
692 |
693 | **拓展3**
694 |
695 | 一个六位数$\overline{2\Box\Box727}$除以9余4,这个数最小是几?
696 |
697 | ## 4.1.10. 定义新运算
698 |
699 | ### 例题1
700 |
701 | 一般我们都认为箭头指向谁,谁就是有危险的,那么规定。
702 |
703 | 警察➡️小偷=警察;警察⬅️小偷=小偷
704 |
705 | 则:(猎人➡️小兔)⬅️(山羊⬅️白菜)=()
706 |
707 | ### 练习1
708 |
709 | 羊和狼在一起时,狼要吃掉羊。所以关于羊及狼,我们规定一种运算,用符号△表示:羊△羊=羊;羊△狼=狼;狼△羊=狼;狼△狼=狼,以上运算的意思是:羊与羊在一起还是羊,狼与狼在一起还是狼,但是狼与羊在一起便只剩下狼了。小朋友总是希望羊能战胜狼,所以我们规定另一种运算,用符号☆表示:羊☆羊=羊;羊☆狼=羊;狼☆羊=羊;狼☆狼=狼,这个运算的意思是:羊与羊在一起还是羊,狼与狼在一起还是狼,但由于羊能战胜狼,当狼与羊在一起时,它便被羊赶走而只剩下羊了。对羊或狼,可以用上面规定的运算作混合运算,混合运算的法规是从左到右,括号内先算。运算的结果或是羊,或是狼。求下式的结果:羊△(狼☆羊)☆羊△(狼△狼)
710 |
711 | ### 例题2
712 |
713 | 我们规定a※b表示为3倍的a减去2倍的b,即$a※b=3a-2b$,例如:$3※2=3x3-2x2=5$;同时,a△b表示为3倍的a加上2倍的b,即$a△b=3a+2b$,例如:$1△2=1x3+2x2=7$
714 |
715 | (1)计算:$5※4$;$4※5$;$2△3$;$3△2$;
716 |
717 | (2)计算:$(8※7)※9$;$2△(5※3)$;
718 |
719 | (3)计算:$5※4△3※2△1$;
720 |
721 | (4)计算:$1※1+2※2+3※3+\dots+100※100$。
722 |
723 | ### 练习2
724 |
725 | 我们规定:$a△b=5a-3b$,计算:$4△3$;$3△3$;$3△5$。
726 |
727 | ### 例题3
728 |
729 | 我们规定$a△b=b(a+1)-a(b-1)$,计算:$(2△1)+(4△3)+(6△5)+(8△7)+(10△9)$。
730 |
731 | ### 练习3
732 |
733 | 我们规定$a◎b=(a+b)-(a-b)$,计算$(2◎1)+(3◎2)+(4◎3)+ ··· +(10◎9)$。
734 |
735 | ### 例题4
736 |
737 | 对于任意的两个自然数a和b,规定新运算表示为:$ab=a+(a+1)+ ··· +(a+b-1)$。
738 |
739 | (1)求$1*100$的值;
740 |
741 | (2)已知$x*10=75$,求x的值;
742 |
743 | (3)如果$(x*3)*2=121$,求x的值。
744 |
745 | ### 练习4
746 |
747 | 如果a△b表示$(a-2)×b$,例如$ 3△4=(3-2)×4=4$,那么,当$a△5=30$时,求a的值。
748 |
749 | ### 例题5
750 |
751 | “⊙”表示一种新的运算符号,已知$2⊙3=2+3+4$;$7⊙2=7+8$;$3⊙5=3+4+5+6+7$,···,按此规则:
752 |
753 | (1)计算:$9⊙6$;
754 |
755 | (2)如果$n⊙8=68$,那么n的值是。
756 |
757 | ### 练习5
758 |
759 | “⊙”表示一种新的运算符号,已知$3⊙3=3×4×5$;$7⊙2=7×8$;$2⊙4=2×3×4×5$,···按此规则:
760 |
761 | 1. 求解,$5⊙3$;
762 |
763 | 2. 如果$n⊙3=60$,求n的值。
764 |
765 | ### 例题6
766 |
767 | ### 练习6
768 |
769 | ## 4.1.11. 体育比赛中的数学
770 |
771 | ### 例题练习
772 |
773 | ### 例题1
774 |
775 | 十六支篮球队按以下的单淘汰赛的规则进行比赛:分成八组两两对决,决出八个队伍晋级,再决出四个队……最后决出冠军。请问总共进行了几场比赛?
776 |
777 | ### 练习1
778 |
779 | 二十支篮球队进行单淘汰赛,只要输一场就会被淘汰,那么为了决出冠军需要举行几场比赛?
780 |
781 | ### 例题2
782 |
783 | 20名羽毛球运动员参加单打比赛,两两配对进行单循环赛,那么冠军一共要比赛多少场?共要进行几场比赛?
784 |
785 | ### 练习2
786 |
787 | 8位同学进行网球循环赛,规则是每个人都要和其他所有人比一场,那么这八个人总共要举行多少场比赛?
788 |
789 | ### 例题3
790 |
791 | A,B,C,D,E五位同学一起比赛象棋,每两人都要比赛一盘。到现在为止,A已经赛4盘,B赛3盘,C赛2盘,D赛1盘。问:此时E同学赛了几盘?
792 |
793 | ### 练习3
794 |
795 | 编号为1,2,3,4,5,6的六个运动员进行乒乓球单循环赛。到现在为止,编号为1,2,3,4,5的运动员已参加比赛的场数正好分别等于他们的编号数。编号为6的运动员已经赛了几场?
796 |
797 | ### 例题4
798 |
799 | 班上四名同学进行跳棋比赛,每两名同学都要赛一局。每局胜者得2分,平者各得1分,负者得0分。
800 |
801 | (1)四个同学的得分加起来一定是多少分?
802 |
803 | (2)第一名最多得多少分?最少得多少分?
804 |
805 | (3)最后一名最多得多少分?
806 |
807 | (4)已知甲、乙、丙三名同学得分分别为3分、4分、4分,且丙同学无平局,甲同学有胜局乙同学有平局,那么丁同学得分是多少?
808 |
809 | ### 练习4
810 |
811 | 在中国象棋比赛中,有胜平负三种结果:获胜得2分,战平得1分,失败得0分。现在六个人进行单循环赛,已知其中五个人的分数分别是7,6,5,4,3,那么最后一个人分数是多分?
812 |
813 | ### 例题5
814 |
815 | 世界杯小组赛规则如下:四支队伍进行单循环赛,胜者得3分,战平得1分,输了得0分。
816 |
817 | (1)他们的总得分最低是多少,最高是多少?
818 |
819 | (2)第一名最多得多少分?
820 |
821 | (3)己知甲、乙、丙、丁四队的得分分别为7,4,4,1。则比赛有几场平局?
822 |
823 | ### 练习5
824 |
825 | 四名同学进行跳棋比赛,每两名同学都要赛一局。每局胜者得2分,平局各得1分,负者得0分。已知甲乙丙三名同学得分分别是3、4、4分,且丙无平局,甲有胜局,乙有平局,那么丁的得分是多少?分别写出丁与甲乙丙丁比赛结果。
826 |
827 | ### 例题6
828 |
829 | “世界杯”足球赛中,甲、乙、丙、丁4支队分在同一小组,在小组赛中,这4支队中的每支队都要与另3支队比赛一场。根据规定:每场比赛获胜的队可得3分;失败的队得0分;如果双方踢平,两队各得1分。已知:
830 |
831 | (1)这4支队三场比赛的总得分为4个连续奇数;
832 |
833 | (2)乙队总得分排在第一;
834 |
835 | (3)丁队恰有两场同对方踢平,其中有一场是与丙队踢平的。
836 |
837 | 根据以上条件可以推断:总得分排在第四的是哪队?
838 |
839 | ### 练习6
840 |
841 | 四个足球队进行单循环比赛,每两队都要赛一场。如果踢平,每队各得1分,否则胜队得3分,负队得0分。比赛结束,各队的总得分怡好是四个连续的自然数。问:输给第一名的队的总分是多少?
842 |
843 | ### 拓展
844 |
845 | 12个队参加一次足球比赛,每两个队都比赛一场,每场比赛中,胜队得3分,负队得0分,平局则各得1分。比赛完毕后,获得第3名和第4名的两个队的得分最多可以相差多少分?
846 |
847 | ### 课后巩固
848 |
849 | ### 巩固1
850 |
851 | A、B、C、D、E五个人进行单循环赛,目前比赛已经进行了一部分,已知A、B都赛了4场,C、D都赛了2场,那么E赛了几场?
852 |
853 | ### 巩固2
854 |
855 | 若干名选手进行网球单循环赛,总共赛了45场,共有多少名选手参赛?
856 |
857 | ### 巩固3
858 |
859 | 6支球队进行足球比赛,每两支队之间都要赛一场,规定胜一场得3分,平一场各得1分,负一场不得分。全部比赛结束后,发现共有4场平局,且其中5支球队共得了31分,则第6支球队得了多少分?
860 |
861 | ## 4.1.12. 几何计数初步
862 |
863 | ### 例题1
864 |
865 | 数一数下图中长方形的个数。
866 |
867 | 
868 |
869 | ### 练习1
870 |
871 | 下图中有多少个长方形?
872 |
873 |  874 |
875 | ### 例题2
876 |
877 | 数一数下图中正方形的个数。
878 |
879 | 
880 |
881 | ### 练习2
882 |
883 | ### 例题3
884 |
885 | ### 练习3
886 |
887 | ### 例题4
888 |
889 | ### 练习4
890 |
891 | ### 例题5
892 |
893 | ### 练习5
894 |
895 | ### 例题6
896 |
897 | ### 练习6
898 |
899 | # 一半模型
900 |
901 | ### 课前热身
902 |
903 | ### 热身 1
904 |
905 | 下图中三角形 ABC 的面积是 26 平方米,则平行四边形 DBCE 的面积是多少平方米?
906 |
907 | 
908 |
909 | ### 热身 2
910 |
911 | 如图,两个正方形并排放置,BF 于 CD 相交于点 H,已知阴影部分的面积是 18 平方厘米,求正方形 ABCD 的边长。
912 |
913 | 
914 |
915 | ### 热身 3
916 |
917 | 如图,平行四边形 ABCD 的边 BC 长 为 2.5,BC 边上的高为 2,P 是对角线 AC 上任一点(点 P 不与点 A、C 重合),且 PE // BC 于 E,F 是 AD 上任一点,求则阴影部分的面积。
918 |
919 | 
920 |
921 | ### 三角形
922 |
923 | ### 长方形(平行四边形)(例题 1、例题 2)
924 |
925 | ### 例题 1
926 |
927 | 如图所示,平行四边形的面积是 50 平方厘米,则阴影部分的面积是平方厘米。
928 |
929 | 
930 |
931 | 如图所示,一个长方形分成 4 个不同的三角形,其中红色部分的面积和为 50 平方厘米,黄色三角形面积是 21 平方厘米。问:绿色的面积是多少平方厘米。
932 |
933 | 
934 |
935 | 如图所示,长方形的面积是 50 平方厘米,则阴影部分的面积是多少平方厘米?
936 |
937 | 
938 |
939 | ### 练习 1
940 |
941 | 如图,长方形 AFEB 和长方形 FDCE 拼成了长方形 ABCD,长方形 ABCD 的长是 20,宽是 12,求它内部阴影部分的面积和。
942 |
943 | 
944 |
945 | ### 例题 2
946 |
947 | 如图所示,小长方形 ABCD 的长比宽多 2 厘米,用四个同样的小长方形拼成大正方形 AEFG,已知大正方形的面积 为 70 平方厘米,求图中阴影部分的面积。
948 |
949 | 
950 |
951 | ### 练习 2
952 |
953 | 如图所示,大正方形的边长为 15 厘米,小正方形的边长为 5 厘米,求阴影部分的面积和。
954 |
955 | 
956 |
957 | 梯形(例题 3)
958 |
959 | ### 例题 3
960 |
961 | 如图,在梯形 ABCD 中,E、F 分别是 AB、CD的中点,S~1~ 和S~2~ 的面积分别是 5 和 15,求梯形ABCD的面积。
962 |
963 | 
964 |
965 | ### 练习 3
966 |
967 | 动手画一画几种梯形的一半模型。
968 |
969 | 
970 |
971 | ### 任意四边形(例题 4)
972 |
973 | ### 例题 4
974 |
975 | 如图,已知四边形 ABCD 中,E、F 分别是 AD、BC 的中点,连接 DF、BE。四边形 ABCD 的面积为 60,S~1~ = 3,求 S~2~ 和 S~3~ 。
976 |
977 | 
978 |
979 | ### 练习 4
980 |
981 | 如图,已知四边形 ABCD 中,E、F 分别是 AD、BC 的中点,连接 DF、BE。四边形 BEDF 的面积为 6,则四边形 ABCD 的面积为多少?
982 |
983 | 
984 |
985 | ### 重叠等于未覆盖(例题 5)
986 |
987 | ### 例题 5
988 |
989 | 如图所示,长方形 ABCD 中,三角形 APD 的面积是 a,三角形 BQC 的面积为 b,阴影部分面积为 c ,那么 a、b、c 有着怎样的大小关系?
990 |
991 | ### 练习 5
992 |
993 | 如图,长方形 ABCD 的边上有两点 E、F,线段 AF、BF、CE、BE 把长方形分成若干块,其中三个小块的面积标注在图上,求图中阴影部分的面积。
994 |
995 | ### 一半等于一半(例题 6)
996 |
997 | ### 例题 6
998 |
999 | 如图所示,正方形 ABCD 的边长为 8 厘米,长方形 EBGF 的长 BG 为 10 厘米,那么长方形的宽 BE 为几厘米?
1000 |
1001 | ### 练习 6
1002 |
1003 | 如图所示,正方形 ABCD 的边长为 12 厘米,长方形 EBGF 的长 BG 为 16 厘米,那么长方形的宽 BE 为多少厘米?
1004 |
1005 | 拓展
1006 |
1007 | ### 拓展 1
1008 |
1009 | 课后巩固
1010 |
1011 | ### 巩固 1
1012 |
1013 | 如图,四边形 ABFE 和四边形 CDEP 都是长方形,AB 的长是 4 厘米,BC 的长是 3 厘米,那么图中阴影部分的面积是多少平方厘米。
1014 |
1015 | 
1016 |
1017 | ### 巩固 2
1018 |
1019 | 如图,已知四边形 ABCD 中,E 为 AD 边的中点,F 为 BC 边的中点,三角形 ABE 的面积为12 平方厘米,阴影四边形 EDFB 的面积为 28 平方厘米,求三角形 DFC 的面积。
1020 |
1021 | 
1022 |
1023 | ### 巩固 3
1024 |
1025 | 长方形被其内的一些直线划分成了若干块,已知其中 3 块面积分别是 13,35, 97 。求图中阴影部分的面积。
1026 |
1027 | 
1028 |
1029 | ### 练习 1
1030 |
1031 | 四阶数独中,每一行、每一列、每一个粗线框里都有数字 1~4,“?”应该填几?
1032 |
1033 |
874 |
875 | ### 例题2
876 |
877 | 数一数下图中正方形的个数。
878 |
879 | 
880 |
881 | ### 练习2
882 |
883 | ### 例题3
884 |
885 | ### 练习3
886 |
887 | ### 例题4
888 |
889 | ### 练习4
890 |
891 | ### 例题5
892 |
893 | ### 练习5
894 |
895 | ### 例题6
896 |
897 | ### 练习6
898 |
899 | # 一半模型
900 |
901 | ### 课前热身
902 |
903 | ### 热身 1
904 |
905 | 下图中三角形 ABC 的面积是 26 平方米,则平行四边形 DBCE 的面积是多少平方米?
906 |
907 | 
908 |
909 | ### 热身 2
910 |
911 | 如图,两个正方形并排放置,BF 于 CD 相交于点 H,已知阴影部分的面积是 18 平方厘米,求正方形 ABCD 的边长。
912 |
913 | 
914 |
915 | ### 热身 3
916 |
917 | 如图,平行四边形 ABCD 的边 BC 长 为 2.5,BC 边上的高为 2,P 是对角线 AC 上任一点(点 P 不与点 A、C 重合),且 PE // BC 于 E,F 是 AD 上任一点,求则阴影部分的面积。
918 |
919 | 
920 |
921 | ### 三角形
922 |
923 | ### 长方形(平行四边形)(例题 1、例题 2)
924 |
925 | ### 例题 1
926 |
927 | 如图所示,平行四边形的面积是 50 平方厘米,则阴影部分的面积是平方厘米。
928 |
929 | 
930 |
931 | 如图所示,一个长方形分成 4 个不同的三角形,其中红色部分的面积和为 50 平方厘米,黄色三角形面积是 21 平方厘米。问:绿色的面积是多少平方厘米。
932 |
933 | 
934 |
935 | 如图所示,长方形的面积是 50 平方厘米,则阴影部分的面积是多少平方厘米?
936 |
937 | 
938 |
939 | ### 练习 1
940 |
941 | 如图,长方形 AFEB 和长方形 FDCE 拼成了长方形 ABCD,长方形 ABCD 的长是 20,宽是 12,求它内部阴影部分的面积和。
942 |
943 | 
944 |
945 | ### 例题 2
946 |
947 | 如图所示,小长方形 ABCD 的长比宽多 2 厘米,用四个同样的小长方形拼成大正方形 AEFG,已知大正方形的面积 为 70 平方厘米,求图中阴影部分的面积。
948 |
949 | 
950 |
951 | ### 练习 2
952 |
953 | 如图所示,大正方形的边长为 15 厘米,小正方形的边长为 5 厘米,求阴影部分的面积和。
954 |
955 | 
956 |
957 | 梯形(例题 3)
958 |
959 | ### 例题 3
960 |
961 | 如图,在梯形 ABCD 中,E、F 分别是 AB、CD的中点,S~1~ 和S~2~ 的面积分别是 5 和 15,求梯形ABCD的面积。
962 |
963 | 
964 |
965 | ### 练习 3
966 |
967 | 动手画一画几种梯形的一半模型。
968 |
969 | 
970 |
971 | ### 任意四边形(例题 4)
972 |
973 | ### 例题 4
974 |
975 | 如图,已知四边形 ABCD 中,E、F 分别是 AD、BC 的中点,连接 DF、BE。四边形 ABCD 的面积为 60,S~1~ = 3,求 S~2~ 和 S~3~ 。
976 |
977 | 
978 |
979 | ### 练习 4
980 |
981 | 如图,已知四边形 ABCD 中,E、F 分别是 AD、BC 的中点,连接 DF、BE。四边形 BEDF 的面积为 6,则四边形 ABCD 的面积为多少?
982 |
983 | 
984 |
985 | ### 重叠等于未覆盖(例题 5)
986 |
987 | ### 例题 5
988 |
989 | 如图所示,长方形 ABCD 中,三角形 APD 的面积是 a,三角形 BQC 的面积为 b,阴影部分面积为 c ,那么 a、b、c 有着怎样的大小关系?
990 |
991 | ### 练习 5
992 |
993 | 如图,长方形 ABCD 的边上有两点 E、F,线段 AF、BF、CE、BE 把长方形分成若干块,其中三个小块的面积标注在图上,求图中阴影部分的面积。
994 |
995 | ### 一半等于一半(例题 6)
996 |
997 | ### 例题 6
998 |
999 | 如图所示,正方形 ABCD 的边长为 8 厘米,长方形 EBGF 的长 BG 为 10 厘米,那么长方形的宽 BE 为几厘米?
1000 |
1001 | ### 练习 6
1002 |
1003 | 如图所示,正方形 ABCD 的边长为 12 厘米,长方形 EBGF 的长 BG 为 16 厘米,那么长方形的宽 BE 为多少厘米?
1004 |
1005 | 拓展
1006 |
1007 | ### 拓展 1
1008 |
1009 | 课后巩固
1010 |
1011 | ### 巩固 1
1012 |
1013 | 如图,四边形 ABFE 和四边形 CDEP 都是长方形,AB 的长是 4 厘米,BC 的长是 3 厘米,那么图中阴影部分的面积是多少平方厘米。
1014 |
1015 | 
1016 |
1017 | ### 巩固 2
1018 |
1019 | 如图,已知四边形 ABCD 中,E 为 AD 边的中点,F 为 BC 边的中点,三角形 ABE 的面积为12 平方厘米,阴影四边形 EDFB 的面积为 28 平方厘米,求三角形 DFC 的面积。
1020 |
1021 | 
1022 |
1023 | ### 巩固 3
1024 |
1025 | 长方形被其内的一些直线划分成了若干块,已知其中 3 块面积分别是 13,35, 97 。求图中阴影部分的面积。
1026 |
1027 | 
1028 |
1029 | ### 练习 1
1030 |
1031 | 四阶数独中,每一行、每一列、每一个粗线框里都有数字 1~4,“?”应该填几?
1032 |
1033 |  1034 |
1035 | ### 练习 2
1036 |
1037 | 已知四边形 ABCD 是长方形,四边形 AEFG 是梯形,且 B 是 GF 的中点,已知长方形的面积是 20,求梯形 ABEG 的面积。
1038 |
1039 | 
1040 |
1041 | ### 练习 3
1042 |
1043 | 如图,E、F、G、H 分别是四边形 ABCD 各边的中点,EG 与 FH 交于点O,S~1~、S~2~、S~3~、S~4~ 分别表示四个小四边形的面积。试比较S~1~ + S~3~ 与 S~2~ + S~4~的大小并说明理由。
1044 |
1045 | ## 4.1.16. 最值问题初步
1046 |
1047 | ### 例题1(添数)
1048 |
1049 | 在五位数12345的某一位数字后面再插入一个同样的数字(例如:可以在2的后面插入2得到122345),这样得到的六位数最大可能是多少?
1050 |
1051 | ### 练习1
1052 |
1053 | 在五位数1234的某一位数字后面再插入一个同样的数字(例如:可以在2的后面插入2得到12234),这样得到的五位数最大可能是多少?
1054 |
1055 | ### 例题2(拆数)
1056 |
1057 | 电视台要播放一部30集电视连续剧。如果要求每天安排播出的集数互不相等,不能不播,该电视连续剧最多可以播几天?
1058 |
1059 | ### 练习2
1060 |
1061 | 19个苹果要分给一群小朋友,每一个小朋友所分得的苹果数都要不一样,且每位小朋友至少要有一个苹果。问:这群小朋友最多有几位?
1062 |
1063 | ### 例题3(和一定,差小乘积大)
1064 |
1065 | (1)周长为100米的长方形中,面积最大是()平方米。
1066 |
1067 |
1034 |
1035 | ### 练习 2
1036 |
1037 | 已知四边形 ABCD 是长方形,四边形 AEFG 是梯形,且 B 是 GF 的中点,已知长方形的面积是 20,求梯形 ABEG 的面积。
1038 |
1039 | 
1040 |
1041 | ### 练习 3
1042 |
1043 | 如图,E、F、G、H 分别是四边形 ABCD 各边的中点,EG 与 FH 交于点O,S~1~、S~2~、S~3~、S~4~ 分别表示四个小四边形的面积。试比较S~1~ + S~3~ 与 S~2~ + S~4~的大小并说明理由。
1044 |
1045 | ## 4.1.16. 最值问题初步
1046 |
1047 | ### 例题1(添数)
1048 |
1049 | 在五位数12345的某一位数字后面再插入一个同样的数字(例如:可以在2的后面插入2得到122345),这样得到的六位数最大可能是多少?
1050 |
1051 | ### 练习1
1052 |
1053 | 在五位数1234的某一位数字后面再插入一个同样的数字(例如:可以在2的后面插入2得到12234),这样得到的五位数最大可能是多少?
1054 |
1055 | ### 例题2(拆数)
1056 |
1057 | 电视台要播放一部30集电视连续剧。如果要求每天安排播出的集数互不相等,不能不播,该电视连续剧最多可以播几天?
1058 |
1059 | ### 练习2
1060 |
1061 | 19个苹果要分给一群小朋友,每一个小朋友所分得的苹果数都要不一样,且每位小朋友至少要有一个苹果。问:这群小朋友最多有几位?
1062 |
1063 | ### 例题3(和一定,差小乘积大)
1064 |
1065 | (1)周长为100米的长方形中,面积最大是()平方米。
1066 |
1067 |  1312 |
1313 | ### 练习 6
1314 |
1315 | 如图,在一个边长为 12 米的正方形房屋的两个角,分别有一只猫和一只老鼠 。猫看到老鼠,以 5 米秒的速度去追它,老鼠以 8 米秒的速度逃跑。
1316 |
1317 | (1) 因为老鼠比猫跑得更快,所以过了一段时间,老鼠反而在猫的背后看见了猫 。请问从老鼠开始跑到看见猫,经过了多长时间?
1318 | (2) 看到猫的瞬间,老鼠转身,并且因为惊吓 ,速度变为5米/秒 。 请问,再经过多长时间,老鼠会迎面看到猫?
1319 | (3) 老鼠迎面看到猫,瞬间再次转身 ,但是因为惊吓,速度变为4米秒 。请问,再过多少秒,猫能追上老鼠?
1320 |
1321 |
1312 |
1313 | ### 练习 6
1314 |
1315 | 如图,在一个边长为 12 米的正方形房屋的两个角,分别有一只猫和一只老鼠 。猫看到老鼠,以 5 米秒的速度去追它,老鼠以 8 米秒的速度逃跑。
1316 |
1317 | (1) 因为老鼠比猫跑得更快,所以过了一段时间,老鼠反而在猫的背后看见了猫 。请问从老鼠开始跑到看见猫,经过了多长时间?
1318 | (2) 看到猫的瞬间,老鼠转身,并且因为惊吓 ,速度变为5米/秒 。 请问,再经过多长时间,老鼠会迎面看到猫?
1319 | (3) 老鼠迎面看到猫,瞬间再次转身 ,但是因为惊吓,速度变为4米秒 。请问,再过多少秒,猫能追上老鼠?
1320 |
1321 |  1322 |
1323 | ### 练习 1
1324 |
1325 | 甲乙两人在周长为 220 米的环形跑道的两端背向而行练习跑步,甲乙相距 110 米,已知甲的速度是每秒 6 米,乙的速度是每秒 4 米,则甲乙第一次相遇用了几秒?到第五次相遇共用了几秒?
1326 |
1327 | ### 练习 2
1328 |
1329 | 在周长为 200 米的环形跑道上,大齐和小王站在相距 100 米的两点,两人分别以 6 米/秒、5 米/秒的速度同时同向出发,沿跑道跑步 。则 16 分钟内,大齐追上小王几次?
1330 |
1331 | ### 练习 3
1332 |
1333 | 如图,正方形房屋的边长为 20 米 。 甲、乙两人分别从房屋的两个墙角同时出发,沿顺时针方向前进。甲每秒行 5 米,乙每秒行 3 米 。出发多久后甲第一次看见乙?
1334 |
1335 |
1322 |
1323 | ### 练习 1
1324 |
1325 | 甲乙两人在周长为 220 米的环形跑道的两端背向而行练习跑步,甲乙相距 110 米,已知甲的速度是每秒 6 米,乙的速度是每秒 4 米,则甲乙第一次相遇用了几秒?到第五次相遇共用了几秒?
1326 |
1327 | ### 练习 2
1328 |
1329 | 在周长为 200 米的环形跑道上,大齐和小王站在相距 100 米的两点,两人分别以 6 米/秒、5 米/秒的速度同时同向出发,沿跑道跑步 。则 16 分钟内,大齐追上小王几次?
1330 |
1331 | ### 练习 3
1332 |
1333 | 如图,正方形房屋的边长为 20 米 。 甲、乙两人分别从房屋的两个墙角同时出发,沿顺时针方向前进。甲每秒行 5 米,乙每秒行 3 米 。出发多久后甲第一次看见乙?
1334 |
1335 |  1336 |
1337 | ## 4.2.01. 小数巧算
1338 |
1339 | ### 热身1
1340 |
1341 | 计算:$1.73+21.7-11.4$
1342 |
1343 | ### 热身2
1344 |
1345 | 计算:
1346 |
1347 | (1)$1.2\times8.6$
1348 |
1349 | (2)$1.125\times8$
1350 |
1351 | ### 热身3
1352 |
1353 | 计算:
1354 |
1355 | (1)$68.8\div4$
1356 |
1357 | (2)$3.64\div1.4$
1358 |
1359 | ### 例题1
1360 |
1361 | 计算。
1362 |
1363 | (1)$0.9+0.99+0.999+0.9999+0.99999$
1364 |
1365 | (2) $0.7+9.7+99.7+999.7+9999.7$
1366 |
1367 | ### 练习1
1368 |
1369 | 计算。
1370 |
1371 | (1)$89+899+8999+89999+899999$
1372 |
1373 | (2)$1.996+19.97+199.8$
1374 |
1375 | ### 例题2
1376 |
1377 | 计算。
1378 |
1379 | (1) $90.3+88.8+90.2+91.2+179.1+270.4$
1380 |
1381 | (2)$3.17+7.48+0.83-2.38-1.62-3.48$
1382 |
1383 | ### 练习2
1384 |
1385 | 计算:$35.6+35.02+34.81+35.08+35.11$
1386 |
1387 | ### 例题3(乘法巧算)
1388 |
1389 | 计算。
1390 |
1391 | (1)$0.125\times0.25\times0.5\times64$
1392 |
1393 | (2)$1.125\times64\times0.75$
1394 |
1395 | ### 练习3
1396 |
1397 | 计算。
1398 |
1399 | (1)$1.25\times32\times0.25$
1400 |
1401 | (2)$2.5\times4\times125\times1.6$
1402 |
1403 | ### 例题4
1404 |
1405 | 先找到公因数,再计算。
1406 |
1407 | (1)$2.5\times1.06+2.5\times0.84+2.5\times2.1$
1408 |
1409 | (2)$12.5\times0.54+0.067\times125-1.25\times4.1$
1410 |
1411 | ### 练习4
1412 |
1413 | 计算。
1414 |
1415 | (1)$7.8\times24+7.8\times71+0.78\times50$
1416 |
1417 | (2)$0.13\times21-0.13\times19+0.13\times57+1.3\times4.1$
1418 |
1419 | ### 例题5
1420 |
1421 | 计算:$3.79\times0.38+1.59\times6.21+3.79\times1.21$
1422 |
1423 | ### 练习5
1424 |
1425 | 计算:$14.3\times7.88-9.7\times7.38+1.43\times21.2-97\times0.262$
1426 |
1427 | ### 例题6
1428 |
1429 | 计算:$(0.1+0.21+0.321)\times(0.21+0.321+0.4321)-(0.1+0.21+0.321+0.4321)\times(0.21+0.321)$
1430 |
1431 | ### 练习6
1432 |
1433 | 计算:$(1+0.45+0.56)\times(0.45+0.56+0.67)-(1+0.45+0.56+0.67)\times(0.45+0.56)$
1434 |
1435 | ## 4.2.01. 格点与割补
1436 |
1437 | ### 例题1
1438 |
1439 | 图中相邻两个格点的距离都是1,请你求出“小鱼”、“松树”、“小猫”的面积各是多少?
1440 |
1441 | 
1442 |
1443 | ### 练习1
1444 |
1445 | 图中每个小正方形的面积都是1平方厘米,求图中阴影部分的面积。
1446 |
1447 |
1336 |
1337 | ## 4.2.01. 小数巧算
1338 |
1339 | ### 热身1
1340 |
1341 | 计算:$1.73+21.7-11.4$
1342 |
1343 | ### 热身2
1344 |
1345 | 计算:
1346 |
1347 | (1)$1.2\times8.6$
1348 |
1349 | (2)$1.125\times8$
1350 |
1351 | ### 热身3
1352 |
1353 | 计算:
1354 |
1355 | (1)$68.8\div4$
1356 |
1357 | (2)$3.64\div1.4$
1358 |
1359 | ### 例题1
1360 |
1361 | 计算。
1362 |
1363 | (1)$0.9+0.99+0.999+0.9999+0.99999$
1364 |
1365 | (2) $0.7+9.7+99.7+999.7+9999.7$
1366 |
1367 | ### 练习1
1368 |
1369 | 计算。
1370 |
1371 | (1)$89+899+8999+89999+899999$
1372 |
1373 | (2)$1.996+19.97+199.8$
1374 |
1375 | ### 例题2
1376 |
1377 | 计算。
1378 |
1379 | (1) $90.3+88.8+90.2+91.2+179.1+270.4$
1380 |
1381 | (2)$3.17+7.48+0.83-2.38-1.62-3.48$
1382 |
1383 | ### 练习2
1384 |
1385 | 计算:$35.6+35.02+34.81+35.08+35.11$
1386 |
1387 | ### 例题3(乘法巧算)
1388 |
1389 | 计算。
1390 |
1391 | (1)$0.125\times0.25\times0.5\times64$
1392 |
1393 | (2)$1.125\times64\times0.75$
1394 |
1395 | ### 练习3
1396 |
1397 | 计算。
1398 |
1399 | (1)$1.25\times32\times0.25$
1400 |
1401 | (2)$2.5\times4\times125\times1.6$
1402 |
1403 | ### 例题4
1404 |
1405 | 先找到公因数,再计算。
1406 |
1407 | (1)$2.5\times1.06+2.5\times0.84+2.5\times2.1$
1408 |
1409 | (2)$12.5\times0.54+0.067\times125-1.25\times4.1$
1410 |
1411 | ### 练习4
1412 |
1413 | 计算。
1414 |
1415 | (1)$7.8\times24+7.8\times71+0.78\times50$
1416 |
1417 | (2)$0.13\times21-0.13\times19+0.13\times57+1.3\times4.1$
1418 |
1419 | ### 例题5
1420 |
1421 | 计算:$3.79\times0.38+1.59\times6.21+3.79\times1.21$
1422 |
1423 | ### 练习5
1424 |
1425 | 计算:$14.3\times7.88-9.7\times7.38+1.43\times21.2-97\times0.262$
1426 |
1427 | ### 例题6
1428 |
1429 | 计算:$(0.1+0.21+0.321)\times(0.21+0.321+0.4321)-(0.1+0.21+0.321+0.4321)\times(0.21+0.321)$
1430 |
1431 | ### 练习6
1432 |
1433 | 计算:$(1+0.45+0.56)\times(0.45+0.56+0.67)-(1+0.45+0.56+0.67)\times(0.45+0.56)$
1434 |
1435 | ## 4.2.01. 格点与割补
1436 |
1437 | ### 例题1
1438 |
1439 | 图中相邻两个格点的距离都是1,请你求出“小鱼”、“松树”、“小猫”的面积各是多少?
1440 |
1441 | 
1442 |
1443 | ### 练习1
1444 |
1445 | 图中每个小正方形的面积都是1平方厘米,求图中阴影部分的面积。
1446 |
1447 |  1448 |
1449 | ### 例题2
1450 |
1451 | 图中相邻两个格点的距离都是1,计算这个格点多边形的面积。
1452 |
1453 |
1448 |
1449 | ### 例题2
1450 |
1451 | 图中相邻两个格点的距离都是1,计算这个格点多边形的面积。
1452 |
1453 |  1454 |
1455 | ### 练习2
1456 |
1457 | 图中相邻格点的距离都是1,计算这个格点多边形的面积。
1458 |
1459 |
1454 |
1455 | ### 练习2
1456 |
1457 | 图中相邻格点的距离都是1,计算这个格点多边形的面积。
1458 |
1459 |  1460 |
1461 | ### 例题3
1462 |
1463 | 图中每个小正方形的面积均为2平方厘米。阴影多边形的面积是多少平方厘米?
1464 |
1465 | 
1466 |
1467 | ### 练习3
1468 |
1469 | 图中每个小正方形的面积是2平方厘米,阴影部分面积是几平方厘米。
1470 |
1471 | 
1472 |
1473 | ### 例题4
1474 |
1475 | 图中相邻三点所形成的等边三角形的面积为1,试计算三角形的面积。
1476 |
1477 | 
1478 |
1479 | ### 练习4
1480 |
1481 | 圈中相邻三点所形成的等边三角形的面积为1,试计算梯形的面积。
1482 |
1483 | 
1484 |
1485 | ### 例题5
1486 |
1487 | 图中相邻三点所形成的等边三角形的面积为1,计算三角形ABC的面积。
1488 |
1489 | 
1490 |
1491 | ### 练习5
1492 |
1493 | 图中相邻三点所形成的等边三角形的面积为1,试求“台灯”的面积。
1494 |
1495 |
1460 |
1461 | ### 例题3
1462 |
1463 | 图中每个小正方形的面积均为2平方厘米。阴影多边形的面积是多少平方厘米?
1464 |
1465 | 
1466 |
1467 | ### 练习3
1468 |
1469 | 图中每个小正方形的面积是2平方厘米,阴影部分面积是几平方厘米。
1470 |
1471 | 
1472 |
1473 | ### 例题4
1474 |
1475 | 图中相邻三点所形成的等边三角形的面积为1,试计算三角形的面积。
1476 |
1477 | 
1478 |
1479 | ### 练习4
1480 |
1481 | 圈中相邻三点所形成的等边三角形的面积为1,试计算梯形的面积。
1482 |
1483 | 
1484 |
1485 | ### 例题5
1486 |
1487 | 图中相邻三点所形成的等边三角形的面积为1,计算三角形ABC的面积。
1488 |
1489 | 
1490 |
1491 | ### 练习5
1492 |
1493 | 图中相邻三点所形成的等边三角形的面积为1,试求“台灯”的面积。
1494 |
1495 |  1496 |
1497 | ### 例题6
1498 |
1499 | 如图,已知:正三角形ABC的面积是48,点D是所在边的中点,点E、F分别是所在边的四等分点,求阴影三角形的面积。
1500 |
1501 |
1496 |
1497 | ### 例题6
1498 |
1499 | 如图,已知:正三角形ABC的面积是48,点D是所在边的中点,点E、F分别是所在边的四等分点,求阴影三角形的面积。
1500 |
1501 |  1502 |
1503 | ### 练习6
1504 |
1505 | 已知:正三角形ABC的面积是96,点D、F分别是所在边的中点,点E是所在边的四等分点,求阴影三角形的面积。
1506 |
1507 |
1502 |
1503 | ### 练习6
1504 |
1505 | 已知:正三角形ABC的面积是96,点D、F分别是所在边的中点,点E是所在边的四等分点,求阴影三角形的面积。
1506 |
1507 |  1508 |
1509 | ## 4.2.03. 数表-从日历谈起
1510 |
1511 | ### 例题1
1512 |
1513 | 观察如下日历:
1514 |
1515 | (1)若设一个横行上相邻的三个日期中间的日期为a,那么左右两边的日期分别是什么?
1516 |
1517 | (2)若设一个竖列上相邻的三个日期中间的日期为b,那么上下两边的日期分别是什么?
1518 |
1519 | (3)如果在上述日历中某个竖列上三个相邻的日期之和为75,你认为可能吗? 为什么?
1520 |
1521 | (4)若连续七天的日期之和是77,请问第二天是星期几?
1522 |
1523 | ### 练习1
1524 |
1525 | 观察如下某月日历:
1526 |
1527 | 如果上述日历中一个竖列上连续的四个日期之和为54,那么第一天是几号?
1528 |
1529 | ### 例题2
1530 |
1531 | 从1开始的连续自然数按如图所示的规则排列,并用一个十字架框出五个数,能否使这五个数的和等于:
1532 |
1533 | (1)100;(2)200;(3)400;(4)600
1534 |
1535 | ### 练习2
1536 |
1537 | 从1开始的自然数按下图所示的规则排列,并用一个正方形框出九个数,能否使这九个数的和等于
1538 |
1539 | (1)2007;(2)2008;(3)2016
1540 |
1541 | 能够等于9数之和的数是()。
1542 |
1543 | ### 例题3
1544 |
1545 | 从1开始的自然数按下图所示的规则排列,并用一个平行四边形框出四个数,能否使这四个数的和分别等于126,408,842。若能办到,请写出平行四边形框内的最小数;若不能办到,说明理由。
1546 |
1547 | ### 练习3
1548 |
1549 | 下图中台历上斜着的表示日期的三个数之和为42,这三个日期中最大的一天是()号。
1550 |
1551 | ### 例题4
1552 |
1553 | 如图,将从5开始的连续自然数按规律填入数表中,请问:
1554 |
1555 | (1)213应该排在第几列?
1556 | (2)第3行第100列的数是多少?
1557 |
1558 | ### 练习4
1559 |
1560 | 将正整数1,2,3,…,从小到大按下面规律排列,若第4行第3列的数为36,则n=()。
1561 |
1562 | ### 例题5
1563 |
1564 | 如图,从4开始的连续自然数是按某种规律排列的,请问:
1565 |
1566 | (1)100在第几行,第几列?
1567 |
1568 | (2)第3行第20列的数是多少?
1569 |
1570 | ### 练习5
1571 |
1572 | 仔细观察下列数的排列规律:
1573 |
1574 | 则2017排在这个数表的第()行,第()列。(横为行,竖为列)
1575 |
1576 | ### 例题6
1577 |
1578 | 下列数表中5000在哪个字母下方?
1579 |
1580 | ### 练习6
1581 |
1582 | 下列数表中3333在哪个字母右边?
1583 |
1584 | ### 巩固1
1585 |
1586 | ### 巩固2
1587 |
1588 | ### 巩固3
1589 |
1590 | ## 4.2.03. 第五种运算
1591 |
1592 | ### 例题1(乘方/幂)
1593 |
1594 | (1)$\underbrace{6\times6\times6\times\dots\times6} _{8个6}$的结果记作(),读作()。
1595 |
1596 | (2)在$13^{57}$中,底数数(),指数是(),幂是(),读作()。
1597 |
1598 | (3)请把下列算式改写成幂的形式。
1599 |
1600 | | $\underbrace{7\times7\times7\times\dots\times7}_{80个7}=()$ | $9\times9\times9\times9=()^{4}=()^2$ |
1601 | | ----------------------------------------------------------- | ------------------------------------ |
1602 | | $16=()^4$ | $27=()^3$ |
1603 | | $125=()^3$ | $81=()^4=()^2$ |
1604 |
1605 | (4)计算:$3^5=()$;$6^3=()$;$5^4=()$
1606 |
1607 | ### 练习1
1608 |
1609 | (1)$10^n$表示n个10相成所得的积。()
1610 |
1611 | (2)$7^8$表示7个8相乘。()
1612 |
1613 | (3)$\underbrace{(a+b)(a+b)\dots(a+b)}_{18个(a+b)}$写成乘方形式是$(a+b)^{18}$。()
1614 |
1615 | (4)任何数的零次方都等于0。()
1616 |
1617 | ### 例题2(同底数幂乘法)
1618 |
1619 | 根据乘方的意义:$4^2=4×4$,$4^3=4×4×4$,从而$4^2×4^3=(4×4)×(4×4×4)=4^5$,那么
1620 |
1621 | (1)计算(用幂的形式表示):$12^2×12^7$;$23×23^{17}$
1622 |
1623 | (2)计算(用幂的形式表示):$4^7×4^n$;$a^7×a^{24}$。
1624 |
1625 | (3)计算(用幂的形式表示):$23^1×23^2×23^3×……×23^{99}×23^{100}$。
1626 |
1627 | ### 练习2
1628 |
1629 | 计算:$3^1×3^2×3^3×……×3^9×3^{10}$。
1630 |
1631 | ### 例题3(同底数幂除法)
1632 |
1633 | 根据乘方的意义:$4^5=4×4×4×4×4$,$4^2=4×4$,从而$4^5÷4^2=(4×4×4×4×4)÷(4×4)=4^3$,那么
1634 |
1635 | (1)计算(用幂的形式表示):$23^5÷23^2=()$;$34^{13}÷34^7=()$;$81^7÷81^7=81^{()}=()$。
1636 |
1637 | (2)计算(用幂的形式表示):$8^a÷8^2(a≧2)$;$a^9÷a^7$;$b^c÷b^c$。
1638 |
1639 | (3)计算(用幂的形式表示): $79^{50}\div79^{8}\div79^{14}\div79^{27}$。
1640 |
1641 | ### 练习3
1642 |
1643 | 计算(用幂的形式表示):
1644 |
1645 | (1)$2^2×2^4×2^6$;$3\times3^3\times3^5\times3^7\times3^9$
1646 |
1647 | (2)$7^{25}÷7^{12}÷7^8÷7$;$67^{35}\div67^{24}\div67^{10}$;$13^{31}\div13^{21}\div13^{7}\div13^{3}$
1648 |
1649 | ### 例题4(幂的乘方)
1650 |
1651 | 根据乘方的意义:$4^3=4×4×4$,从而$(4^2)^3=4^2×4^2×4^2=4^6$,那么
1652 |
1653 | (1)计算(用幂的形式表示):$(5^5)^3$;$(13^2)^3$;
1654 |
1655 | (2)计算(用幂的形式表示):$9^4×3^3$;$2^6×4^2×8^2$。
1656 |
1657 | ### 练习4
1658 |
1659 | 计算(用幂的形式表示)。
1660 |
1661 | $(29^2)n$;$(37^m)^5$;$(b^3)^4$。
1662 |
1663 | ### 例题5(积的乘方)
1664 |
1665 | 根据乘方的意义:$(4\times5)^3=(4\times5)\times(4\times5)\times(4\times5)=4\times4\times4\times5\times5\times5=4^3\times5^3$,那么
1666 |
1667 | (1)计算(用幂的形式表示):$(2\times7)^5=()\times()$;$(25\times17)^m=()\times()$;
1668 |
1669 | (2)计算(用幂的形式表示):$6^5=()^5\times()^5$;$35^9=()\times()$;
1670 |
1671 | (3)计算(用幂的形式表示):$(2\times7^3)^5$;$(3^5\times5^2)^3$。
1672 |
1673 | ### 练习5
1674 |
1675 | 计算(用幂的形式表示):
1676 |
1677 | (1)$5\times5\times5\times11\times11\times11=()^3\times()^3=()^3$;
1678 |
1679 | (2)$5^4\times7^6\times5^6\times7^4=()\times()=()^{10}$
1680 |
1681 | ### 例题6(混合计算)
1682 |
1683 | 计算(答案用幂的形式表示)。
1684 |
1685 | $11^{12}\times7^{27}\times9^{15}\div7^{18}\div11^{7}\div9^{13}$
1686 |
1687 | ### 练习6
1688 |
1689 | 计算(答案用幂的形式表示)。
1690 |
1691 | (1)$(2^3)^4\times(9^4)^3$
1692 |
1693 | (2)$(7^6)^5\times(5^3)^7\div7^{15}\div5^{12}$
1694 |
1695 | ## 4.2.05. 质数与合数初步
1696 |
1697 | ### 例题1
1698 |
1699 | (1)若bc=a,且a,b,c均为整数,则a是b、c的倍数,b、c是a的因数;那么,3x8=24中,()是()的倍数,()是()的因数。
1700 |
1701 | (2)一个数除了1和它本身,不再有别的因数,这个数就叫作();一个数除了1和它本还有别的因数,这个数就叫作()。要特别记住:()既不是质数,也不是合数。
1702 |
1703 | (3)写出100以内的所有质数。
1704 |
1705 | ### 练习1
1706 |
1707 | (1)正整数可以分为()、质数和合数三类。
1708 |
1709 | (2)质数有()个因数,合数至少有()个因数,1有()个因数。
1710 |
1711 | (3)最小的质数是(),最小的合数是()。
1712 |
1713 | (4)唯一的一个既是偶数又是质数的数是()。
1714 |
1715 | ### 例题2
1716 |
1717 | 如图,三张卡片上各印有一个数字。从这三张卡片中选取一张或多张(每张最多选1次)拼成质数,一共可以拼成多少个不同的质数?
1718 |
1719 | ### 练习2
1720 |
1721 | 有三张卡片,在它们上面各写有一个数字(如图)。从中抽出一张、二张、三张,按任意次序排起来,可以得到不同的一位数、二位数、三位数。请你将其中的质数都写出来。
1722 |
1723 | ### 例题3
1724 |
1725 | 在51,101,103,105,107,109,1001这七个数中,质数有多少个?
1726 |
1727 | ### 练习3
1728 |
1729 | 在111~119这九个数中,质数有多少个?
1730 |
1731 | ### 例题4
1732 |
1733 | (1)如果两个质数相加等于39,这两个质数等于多少?
1734 |
1735 | (2)如果三个互不相同的质数相加,和为40,这三个质数分别是多少?
1736 |
1737 | (3)已知P,Q都是质数,并且$P×11-Q×93=2003$,则$P\times Q$=()
1738 |
1739 | ### 练习4
1740 |
1741 | 7个连续质数从大到小排列是a、b、c、d、e、f、g。已知它们的和是偶数,那么d是多少?
1742 |
1743 | ### 例题5
1744 |
1745 | 从小到大写出5个质数,使后面的数都比前面的数大12,这样的数有几组?
1746 |
1747 | ### 练习5
1748 |
1749 | 三个质数的乘积恰好等于它们和的5倍,这三个质数分别是多少?
1750 |
1751 | ### 例题6
1752 |
1753 | 将222分拆成10个质数之和,要求其中最大的质数尽可能的小,那么这个最大的质数是();如要求最大的质数尽可能的大,那么这个最大的质数为()。
1754 |
1755 | ### 练习6
1756 |
1757 | 将50分拆成10个质数的和,要求其中最大的质数尽可能大,则这个最大的质数是多少?
1758 |
1759 | ### 练习1
1760 |
1761 | $1+2\times3+4\times5+6\times7+…+98\times99$的计算结果是奇数还是偶数,为什么?
1762 |
1763 | ### 练习2
1764 |
1765 | 两个质数之和为33,求这两个质数的乘积是多少。
1766 |
1767 | ### 练习3
1768 |
1769 | 著名的哥德巴赫猜想是:“任意一个大于4的偶数都可以表示为两个质数的和”。如6=3+3,12=5+7等。那么,自然数100可以写成多少种两个不同质数的和的形式?请分别写出来(100=3+97和100=97+3算作同一种形式)
1770 |
1771 | ### 练习1
1772 |
1773 | 已知a,b,c是三个连续自然数,其中a是偶数。根据下面的的信息:小红说:“那么a+1,b+2,c+3这三个数的乘积一定是奇数”;小明:“不对a+1,b+2,c+3这三个数的乘积是偶数”。判断小红和小明两人谁说的是正确的。
1774 |
1775 | ### 练习2
1776 |
1777 | 如果a,b均为质数,且3a+7b=41,则a+b=()
1778 |
1779 | ### 练习3
1780 |
1781 | 一个两位质数个位与十位数字交换后仍为质数,这样的质数有几个?
1782 |
1783 | ### 练习1
1784 |
1785 | 是否存在自然数a和b,使得ab(a+b)=115?为什么?
1786 |
1787 | ### 练习2
1788 |
1789 | 已知三个质数之和为36(可以相等),这三个质数中最大的可能是。
1790 |
1791 | ### 练习3
1792 |
1793 | ### 练习1
1794 |
1795 | 已知n,n+6,n+84,n+102,n+218都是质数,那么n=()
1796 |
1797 | ### 练习2
1798 |
1799 | A,B,C为3个小于20的质数,A+B+C=30,求这三个质数分别是几。
1800 |
1801 | ### 练习3
1802 |
1803 | 某质数加6或减6得到的数仍是质数,在50以内你能找出几个这样的质数?把它们写出来。
1804 |
1805 | ## 4.2.06. 火车过桥
1806 |
1807 | ### 例题1
1808 |
1809 | 己知某铁路桥长1000米,一列火车从桥上通过,火车速度每秒40米,车长200米。
1810 | (1)火车完全在桥时间是多少?
1811 | (2)火车从开始上桥到完全下桥所用时间是多少?
1812 |
1813 | ### 练习1
1814 |
1815 | 一列火车经过南京长江大桥,大桥长6700米,这列火车长100米,火车每分钟行4000米,这列火车经过南京长江大桥需要多少分钟?
1816 |
1817 | ### 例题2
1818 |
1819 | 一列火车通过530米长的桥需40秒钟,以同样的速度穿过380米长的山洞需30秒钟。则这列火车的速度是多少?全长是多少米?
1820 |
1821 | ### 练习2
1822 |
1823 | 牛牛站在铁路旁,一列火车从他身边开过用了21秒,以同样的速度通过一座长为2070米的大桥,用了1.5分钟。火车长多少米?
1824 |
1825 | ### 例题3
1826 |
1827 | 牛牛以每秒10米的速度沿铁道边的小路骑车。
1828 | (1)身后一辆火车以每秒100米的速度超过他,从车头追上牛牛到车尾离开共用时4秒,那么车长多少米?
1829 | (2)过了一会,另一辆火车以每秒100米的速度迎面开来,从与牛牛相遇到离开,共用时3秒。那么车长是多少?
1830 |
1831 | ### 练习3
1832 |
1833 | 丁丁以3米/秒的速度沿着铁路跑步,迎面开来一列火车,它的行驶速度是18米/秒,火车从丁丁身旁经过的时间是7秒,求火车的车长是多少米?
1834 |
1835 | ### 例题4
1836 |
1837 | 一列快车和一列慢车相向而行,快车的车长是280米,慢车的车长为385米,坐在快车上的人看见慢车驶过的时间是11秒,那么坐在慢车上的人看见快车驶过的时间是多少?
1838 |
1839 | ### 练习4
1840 |
1841 | 一列快车和一列慢车相向而行,快车的车长是150米,慢车的车长为200米,坐在慢车上的人看见快车驶过的时间是3秒,那么坐在快车上的人看见慢车驶过的时间是多少?
1842 |
1843 | ### 例题5
1844 |
1845 | 有两列火车,一列长200米,每秒行34米;一列长178米,每秒行20米。
1846 | (1)两列火车相向而行,从两车车头相遇到车尾相离共需要多少秒?
1847 | (2)两列火车同向行驶,从快车的车头追上慢车的车尾,到快车的车尾超过慢车的车头,共需多少秒?
1848 |
1849 | ### 练习5
1850 |
1851 | 快车长300米,每秒行20米,慢车长150米,每秒行10米。
1852 | (1)两列火车相向而行,从两车车头相遇到车尾相离共需要多少秒?
1853 | (2)两列火车同向行驶,从快车的车头追及慢车的车尾,到快车的车尾超过慢车的车头,其需多少秒?
1854 |
1855 | ### 例题6
1856 |
1857 | 有两列同方向行驶的火车,快车每秒行33米,慢车每秒行21米。如果从两车头对齐开始算,则行20秒后快车超过慢车;如果从两车尾对齐开始算,则行25秒后快车超过慢车。
1858 | (1)两车车长分别是多少?
1859 | (2)如果两车相对行驶,两车从车头相遇到车尾相离需要经过多少时间?
1860 |
1861 | ### 练习6
1862 |
1863 | 现有两列火车同时同方向齐头行进,行12秒后快车超过慢车,快车每秒行18米,慢车每秒行10米。如果这两列火车车尾相齐同时同方向行进,则9秒后快车超过慢车,那么,快车车头追上慢车车尾到快车车尾离开慢车车头的时间为多少秒?
1864 |
1865 | ## 4.2.07. 包含与排除
1866 |
1867 | ### 例题1
1868 |
1869 | 实验小学四年级二班,参加语文兴趣小组的有28人,参加数学兴趣小组的有29人,有12人两个小组都参加。这个班有多少人参加了语文或数学兴趣小组?
1870 |
1871 | ### 练习1
1872 |
1873 | 学校文艺组的每位同学至少会演奏钢琴和手风琴中的一种乐器,己知会演奏钢琴的有24人,会演奏手风琴的有17人,其中两种乐器都会演奏的有8人,则文艺组一共有多少人?
1874 |
1875 | ### 例题2
1876 |
1877 | 某餐馆有40道招牌菜,牛牛吃过其中的15道,丁丁吃过其中的9道,而且有4道菜是两人都吃过的,请问:有多少道招牌菜是两人都没有吃过的?
1878 |
1879 | ### 练习2
1880 |
1881 | 在46人参加的采摘活动中,只采了樱桃的有18人,既采了樱桃又采了杏的有7人,既没采樱桃又没采杏的有6人,问:只采了杏的有多少人?
1882 |
1883 | ### 例题3
1884 |
1885 | 在1~100这些自然数中,能被3或5同时整除的数有多少个?
1886 |
1887 | ### 练习3
1888 |
1889 | 在1~60这些自然数中:
1890 | (1)能被2整除的数有多少个?
1891 | (2)能被5整除的数有多少个?
1892 | (3)能被2和5整除的数有多少个?
1893 | (4)能被2或5整除的数有多少个?
1894 | (5)不能被2整除也不能被5整除的数有多少个?
1895 |
1896 | ### 例题4
1897 |
1898 | 50名同学面向老师站成一行。老师先让大家从左至右按1,2,3,……,49,50依次报数;再让报数是4的倍数的同学向后转,接着又让报数是6的倍数的同学向后转。问:现在面向老师的同学还有多少名?
1899 |
1900 | ### 练习4
1901 |
1902 | 一根长60厘米的木棍,每5厘米用红点标记,每6厘米用蓝点标记。沿标记的点把木棍锯断,木棍总共被锯成几段?
1903 |
1904 | ### 例题5
1905 |
1906 | 光明小学组织棋类比赛,分成围棋、中国象棋和国际象棋三个组进行,参加国棋比赛的有42人,参加中国象棋比赛的有55人,参加国际象棋比赛的有33人,同时参加了围棋和中国象棋比赛的有18人,同时参加了国棋和国际象棋比赛的有10人,同时参加了中国象棋和国际象棋比赛的有9人,其中三种棋赛都参加的有5人,问参加棋类比赛的共有多少人?
1907 |
1908 | ### 练习5
1909 |
1910 | 三位基金经理投资若干只股票。张经理买过其中66只,王经理买过其中40只,李经理买过其中23只。张经理和王经理都买过的有17只,王经理和李经理都买过的有13只,李经理和张经理都买过的有9只,三个人都买过的有6只。请问:这三位经理一共买过多少只股票?
1911 |
1912 | ### 例题6
1913 |
1914 | 在一个100人的旅行团中,每人至少懂英语、汉语、日语中的一种,其中懂英语的有66人,汉语的有54人,懂日语的有55人,既懂英语又懂汉语的有25人,既懂汉语又懂日语的有21人,但没有一个人三门语言都懂。问:有多少人既懂英语又懂日语?
1915 |
1916 | ### 练习6
1917 |
1918 | 少年宫春季书法班、美术班、器乐班招生。书法班招收了29名学员,在这些学员中,既报书法又报美术的有13名,既报书法又报器乐的有12人,三个科目都报的有5名。那么,只参加书法学习的学员有几名?
1919 |
1920 | ### 练习1
1921 |
1922 | 一根长101厘米长的木棍,从同一端开始,第一次每隔4厘米画一个刻度,第二次每隔6厘米画一个刻度,如果按刻度把木棍截断,那么可以截成多少段?
1923 |
1924 | ### 练习2
1925 |
1926 | 写有1到100编号的灯100盏,亮着排成一排,第一次把编号是3的倍数的灯拉一次开关,第二次把编号是5的倍数的灯拉一次开关,那么亮着的灯还有多少盏?
1927 |
1928 | ### 练习3
1929 |
1930 | 在1~100这些自然数中:
1931 |
1932 | 1. 能被2整除的数有多少个?
1933 | 2. 能被3整除的数有多少个?
1934 | 3. 能被2和3整除的数有多少个?
1935 | 4. 能被2或3整除的数有多少个?
1936 | 5. 不能被2整除也不能被3整除的数有多少个?
1937 |
1938 | ## 4.2.08. 整数与数列
1939 |
1940 | ### 热身1
1941 |
1942 | ### 热身2
1943 |
1944 | ### 热身3
1945 |
1946 | ### 例题1
1947 |
1948 | 已知数列1,6,11,16,21,⋯,146,问:
1949 | (1)这个数列中第20个数是多少?
1950 | (2)81是这个数列的第几个数?
1951 | (3)这个数列一共有几项?
1952 | (4)将数列中所有的数加起来,和是多少?
1953 |
1954 | ### 练习1
1955 |
1956 | (1)数列3,7,11,⋯,第18项是()。
1957 | (2)数列4,9,14,⋯,其中254是这个数列的第()项。
1958 | (3)数列4,8,12,⋯,160,这个数列共有()项。
1959 |
1960 | ### 例题2
1961 |
1962 | 1~100中除以5余2的数的和是多少?
1963 |
1964 | ### 练习2
1965 |
1966 | 1~100中所有5的倍数的和是多少?
1967 |
1968 | ### 例题3
1969 |
1970 | 计算:$24\times23-23\times22+22\times21-21\times20+\dots+2\times1$
1971 |
1972 | ### 练习3
1973 |
1974 | 计算:$14\times13-13\times12+12\times11-11\times10+10\times9-9\times8+8\times7-7\times6+6\times5-5\times4+4\times3-3\times2+2\times1$
1975 |
1976 | ### 例题4(平方差公式)
1977 |
1978 | 有一串数1,4,9,16,25,36,⋯,它们是按什么规律排列的?其中第9个数与第10个数相差多少?第2014个数与第2015个数相差多少?
1979 |
1980 | ### 练习4
1981 |
1982 | 计算:$[2017-(8.5\times8.5-1.5\times1.5)\div10]\div160-0.3$
1983 |
1984 | ### 例题5
1985 |
1986 | 计算:$100^2-99^2+98^2-97^2+\dots+2^2-1^2$
1987 |
1988 | ### 练习5
1989 |
1990 | 计算:$20\times20-19\times19+18\times18-17\times17+\dots+2\times2-1\times1$
1991 |
1992 | ### 例题6(整数列项)
1993 |
1994 | 计算:$1\times2+2\times3+3\times4+\dots+49\times50$
1995 |
1996 | ### 练习6
1997 |
1998 | ## 4.2.09. 统筹与最优化
1999 |
2000 | ### 例题1
2001 |
2002 | 理发店里只有一位理发师,但是同时来了五位顾客,根据他们所要理的发型,分别需要10分钟、12分钟、15分钟、20分钟和24分钟,怎样安排他们理发的顺序,才能使这五人理发和等候所用时间的总和最少?最少时间为多少?
2003 |
2004 | ### 练习1
2005 |
2006 | 5个人各拿一个水桶在自来水龙头前等候打水,他们打水所需要的时间分别是1分钟、2分钟、3分钟、4分钟和5分钟,如果只有一个水龙头,适当安排他们的打水顺序,就能够使每个人排队和打水时间的总和最小,那么这个最小值是多少分钟?
2007 |
2008 | ### 例题2
2009 |
2010 | 电车公司维修站有7辆电车需要维修,如果用一名工人维修这7辆电车,修复时间分别为12分钟,17分钟,8分钟,18分钟,23分钟,30分钟,14分钟。每辆电车每停开1分钟的损失是11元,现在由3名工作效率相同的维修工人各自单独工作,要使经济损失减到最小程度,那么最小的损失是多少元?
2011 |
2012 | ### 练习2
2013 |
2014 | 有八个人各拿着一个水桶同时到水龙头前打水,水龙头注满第一个人的桶需要1分钟,注满第二个人的桶需要2分钟,……,如此下去,
2015 | (1)当只有一个水龙头时,如何巧妙安排这八个人打水,使他们总的花费时间最少?最少的时间是多少?
2016 | (2)当有两个水龙头时,如何巧妙安排这八个人打水,使他们总的花费时间最少?最少的时间是多少?
2017 |
2018 | ### 例题3
2019 |
2020 | 有一家五口人要在夜晚过一座独木桥。他们家里的老爷爷行动非常不便,过桥需要12分钟;孩子们的父亲贪吃且不爱运动,体重严重超标,过河需要时间也较长,8分钟;母亲则一直坚持劳作,动作还算敏捷,过桥要6分钟;两个孩子中姐姐需要3分钟,弟弟只要1分钟。当时正是初一,夜晚又是阴天,不要说月亮,连一点星光都没有,真所谓伸手不见五指。幸运的是他们有一盏油灯,同时可以有两个人借助灯光过桥。但要命的是灯油将尽,这盏灯只能再维持30分钟了!他们焦急万分,该怎样过桥呢?
2021 |
2022 | ### 练习3
2023 |
2024 | 牛牛、丁丁、田田和阿普4个小朋友郊游回家时天色己晚,他们来到一条河的东岸,要通过一座小木桥到西岸,但是他们4个人只有一个手电筒,由于桥的承重量小,每次只能过2人,因此必须先由2个人拿着手电简过桥,并由1个人再将手电简送回,再由2个人拿着手电筒过桥…直到4人都通过小木桥。己知,牛牛单独过桥要1分钟;丁丁单独过桥要1.5分钟;田田单独过桥要2分钟;阿普单独过桥要2.5分钟。那么,4个人都通过小木桥,最少要多少分钟?
2025 |
2026 | ### 例题4
2027 |
2028 | (1)如图,在街道上有A、B、C、D、E五栋居民楼,现在设立一个公交站,为使五栋楼的居民到车站的距离之和最短,车站应位于何处?
2029 |
2030 |
1508 |
1509 | ## 4.2.03. 数表-从日历谈起
1510 |
1511 | ### 例题1
1512 |
1513 | 观察如下日历:
1514 |
1515 | (1)若设一个横行上相邻的三个日期中间的日期为a,那么左右两边的日期分别是什么?
1516 |
1517 | (2)若设一个竖列上相邻的三个日期中间的日期为b,那么上下两边的日期分别是什么?
1518 |
1519 | (3)如果在上述日历中某个竖列上三个相邻的日期之和为75,你认为可能吗? 为什么?
1520 |
1521 | (4)若连续七天的日期之和是77,请问第二天是星期几?
1522 |
1523 | ### 练习1
1524 |
1525 | 观察如下某月日历:
1526 |
1527 | 如果上述日历中一个竖列上连续的四个日期之和为54,那么第一天是几号?
1528 |
1529 | ### 例题2
1530 |
1531 | 从1开始的连续自然数按如图所示的规则排列,并用一个十字架框出五个数,能否使这五个数的和等于:
1532 |
1533 | (1)100;(2)200;(3)400;(4)600
1534 |
1535 | ### 练习2
1536 |
1537 | 从1开始的自然数按下图所示的规则排列,并用一个正方形框出九个数,能否使这九个数的和等于
1538 |
1539 | (1)2007;(2)2008;(3)2016
1540 |
1541 | 能够等于9数之和的数是()。
1542 |
1543 | ### 例题3
1544 |
1545 | 从1开始的自然数按下图所示的规则排列,并用一个平行四边形框出四个数,能否使这四个数的和分别等于126,408,842。若能办到,请写出平行四边形框内的最小数;若不能办到,说明理由。
1546 |
1547 | ### 练习3
1548 |
1549 | 下图中台历上斜着的表示日期的三个数之和为42,这三个日期中最大的一天是()号。
1550 |
1551 | ### 例题4
1552 |
1553 | 如图,将从5开始的连续自然数按规律填入数表中,请问:
1554 |
1555 | (1)213应该排在第几列?
1556 | (2)第3行第100列的数是多少?
1557 |
1558 | ### 练习4
1559 |
1560 | 将正整数1,2,3,…,从小到大按下面规律排列,若第4行第3列的数为36,则n=()。
1561 |
1562 | ### 例题5
1563 |
1564 | 如图,从4开始的连续自然数是按某种规律排列的,请问:
1565 |
1566 | (1)100在第几行,第几列?
1567 |
1568 | (2)第3行第20列的数是多少?
1569 |
1570 | ### 练习5
1571 |
1572 | 仔细观察下列数的排列规律:
1573 |
1574 | 则2017排在这个数表的第()行,第()列。(横为行,竖为列)
1575 |
1576 | ### 例题6
1577 |
1578 | 下列数表中5000在哪个字母下方?
1579 |
1580 | ### 练习6
1581 |
1582 | 下列数表中3333在哪个字母右边?
1583 |
1584 | ### 巩固1
1585 |
1586 | ### 巩固2
1587 |
1588 | ### 巩固3
1589 |
1590 | ## 4.2.03. 第五种运算
1591 |
1592 | ### 例题1(乘方/幂)
1593 |
1594 | (1)$\underbrace{6\times6\times6\times\dots\times6} _{8个6}$的结果记作(),读作()。
1595 |
1596 | (2)在$13^{57}$中,底数数(),指数是(),幂是(),读作()。
1597 |
1598 | (3)请把下列算式改写成幂的形式。
1599 |
1600 | | $\underbrace{7\times7\times7\times\dots\times7}_{80个7}=()$ | $9\times9\times9\times9=()^{4}=()^2$ |
1601 | | ----------------------------------------------------------- | ------------------------------------ |
1602 | | $16=()^4$ | $27=()^3$ |
1603 | | $125=()^3$ | $81=()^4=()^2$ |
1604 |
1605 | (4)计算:$3^5=()$;$6^3=()$;$5^4=()$
1606 |
1607 | ### 练习1
1608 |
1609 | (1)$10^n$表示n个10相成所得的积。()
1610 |
1611 | (2)$7^8$表示7个8相乘。()
1612 |
1613 | (3)$\underbrace{(a+b)(a+b)\dots(a+b)}_{18个(a+b)}$写成乘方形式是$(a+b)^{18}$。()
1614 |
1615 | (4)任何数的零次方都等于0。()
1616 |
1617 | ### 例题2(同底数幂乘法)
1618 |
1619 | 根据乘方的意义:$4^2=4×4$,$4^3=4×4×4$,从而$4^2×4^3=(4×4)×(4×4×4)=4^5$,那么
1620 |
1621 | (1)计算(用幂的形式表示):$12^2×12^7$;$23×23^{17}$
1622 |
1623 | (2)计算(用幂的形式表示):$4^7×4^n$;$a^7×a^{24}$。
1624 |
1625 | (3)计算(用幂的形式表示):$23^1×23^2×23^3×……×23^{99}×23^{100}$。
1626 |
1627 | ### 练习2
1628 |
1629 | 计算:$3^1×3^2×3^3×……×3^9×3^{10}$。
1630 |
1631 | ### 例题3(同底数幂除法)
1632 |
1633 | 根据乘方的意义:$4^5=4×4×4×4×4$,$4^2=4×4$,从而$4^5÷4^2=(4×4×4×4×4)÷(4×4)=4^3$,那么
1634 |
1635 | (1)计算(用幂的形式表示):$23^5÷23^2=()$;$34^{13}÷34^7=()$;$81^7÷81^7=81^{()}=()$。
1636 |
1637 | (2)计算(用幂的形式表示):$8^a÷8^2(a≧2)$;$a^9÷a^7$;$b^c÷b^c$。
1638 |
1639 | (3)计算(用幂的形式表示): $79^{50}\div79^{8}\div79^{14}\div79^{27}$。
1640 |
1641 | ### 练习3
1642 |
1643 | 计算(用幂的形式表示):
1644 |
1645 | (1)$2^2×2^4×2^6$;$3\times3^3\times3^5\times3^7\times3^9$
1646 |
1647 | (2)$7^{25}÷7^{12}÷7^8÷7$;$67^{35}\div67^{24}\div67^{10}$;$13^{31}\div13^{21}\div13^{7}\div13^{3}$
1648 |
1649 | ### 例题4(幂的乘方)
1650 |
1651 | 根据乘方的意义:$4^3=4×4×4$,从而$(4^2)^3=4^2×4^2×4^2=4^6$,那么
1652 |
1653 | (1)计算(用幂的形式表示):$(5^5)^3$;$(13^2)^3$;
1654 |
1655 | (2)计算(用幂的形式表示):$9^4×3^3$;$2^6×4^2×8^2$。
1656 |
1657 | ### 练习4
1658 |
1659 | 计算(用幂的形式表示)。
1660 |
1661 | $(29^2)n$;$(37^m)^5$;$(b^3)^4$。
1662 |
1663 | ### 例题5(积的乘方)
1664 |
1665 | 根据乘方的意义:$(4\times5)^3=(4\times5)\times(4\times5)\times(4\times5)=4\times4\times4\times5\times5\times5=4^3\times5^3$,那么
1666 |
1667 | (1)计算(用幂的形式表示):$(2\times7)^5=()\times()$;$(25\times17)^m=()\times()$;
1668 |
1669 | (2)计算(用幂的形式表示):$6^5=()^5\times()^5$;$35^9=()\times()$;
1670 |
1671 | (3)计算(用幂的形式表示):$(2\times7^3)^5$;$(3^5\times5^2)^3$。
1672 |
1673 | ### 练习5
1674 |
1675 | 计算(用幂的形式表示):
1676 |
1677 | (1)$5\times5\times5\times11\times11\times11=()^3\times()^3=()^3$;
1678 |
1679 | (2)$5^4\times7^6\times5^6\times7^4=()\times()=()^{10}$
1680 |
1681 | ### 例题6(混合计算)
1682 |
1683 | 计算(答案用幂的形式表示)。
1684 |
1685 | $11^{12}\times7^{27}\times9^{15}\div7^{18}\div11^{7}\div9^{13}$
1686 |
1687 | ### 练习6
1688 |
1689 | 计算(答案用幂的形式表示)。
1690 |
1691 | (1)$(2^3)^4\times(9^4)^3$
1692 |
1693 | (2)$(7^6)^5\times(5^3)^7\div7^{15}\div5^{12}$
1694 |
1695 | ## 4.2.05. 质数与合数初步
1696 |
1697 | ### 例题1
1698 |
1699 | (1)若bc=a,且a,b,c均为整数,则a是b、c的倍数,b、c是a的因数;那么,3x8=24中,()是()的倍数,()是()的因数。
1700 |
1701 | (2)一个数除了1和它本身,不再有别的因数,这个数就叫作();一个数除了1和它本还有别的因数,这个数就叫作()。要特别记住:()既不是质数,也不是合数。
1702 |
1703 | (3)写出100以内的所有质数。
1704 |
1705 | ### 练习1
1706 |
1707 | (1)正整数可以分为()、质数和合数三类。
1708 |
1709 | (2)质数有()个因数,合数至少有()个因数,1有()个因数。
1710 |
1711 | (3)最小的质数是(),最小的合数是()。
1712 |
1713 | (4)唯一的一个既是偶数又是质数的数是()。
1714 |
1715 | ### 例题2
1716 |
1717 | 如图,三张卡片上各印有一个数字。从这三张卡片中选取一张或多张(每张最多选1次)拼成质数,一共可以拼成多少个不同的质数?
1718 |
1719 | ### 练习2
1720 |
1721 | 有三张卡片,在它们上面各写有一个数字(如图)。从中抽出一张、二张、三张,按任意次序排起来,可以得到不同的一位数、二位数、三位数。请你将其中的质数都写出来。
1722 |
1723 | ### 例题3
1724 |
1725 | 在51,101,103,105,107,109,1001这七个数中,质数有多少个?
1726 |
1727 | ### 练习3
1728 |
1729 | 在111~119这九个数中,质数有多少个?
1730 |
1731 | ### 例题4
1732 |
1733 | (1)如果两个质数相加等于39,这两个质数等于多少?
1734 |
1735 | (2)如果三个互不相同的质数相加,和为40,这三个质数分别是多少?
1736 |
1737 | (3)已知P,Q都是质数,并且$P×11-Q×93=2003$,则$P\times Q$=()
1738 |
1739 | ### 练习4
1740 |
1741 | 7个连续质数从大到小排列是a、b、c、d、e、f、g。已知它们的和是偶数,那么d是多少?
1742 |
1743 | ### 例题5
1744 |
1745 | 从小到大写出5个质数,使后面的数都比前面的数大12,这样的数有几组?
1746 |
1747 | ### 练习5
1748 |
1749 | 三个质数的乘积恰好等于它们和的5倍,这三个质数分别是多少?
1750 |
1751 | ### 例题6
1752 |
1753 | 将222分拆成10个质数之和,要求其中最大的质数尽可能的小,那么这个最大的质数是();如要求最大的质数尽可能的大,那么这个最大的质数为()。
1754 |
1755 | ### 练习6
1756 |
1757 | 将50分拆成10个质数的和,要求其中最大的质数尽可能大,则这个最大的质数是多少?
1758 |
1759 | ### 练习1
1760 |
1761 | $1+2\times3+4\times5+6\times7+…+98\times99$的计算结果是奇数还是偶数,为什么?
1762 |
1763 | ### 练习2
1764 |
1765 | 两个质数之和为33,求这两个质数的乘积是多少。
1766 |
1767 | ### 练习3
1768 |
1769 | 著名的哥德巴赫猜想是:“任意一个大于4的偶数都可以表示为两个质数的和”。如6=3+3,12=5+7等。那么,自然数100可以写成多少种两个不同质数的和的形式?请分别写出来(100=3+97和100=97+3算作同一种形式)
1770 |
1771 | ### 练习1
1772 |
1773 | 已知a,b,c是三个连续自然数,其中a是偶数。根据下面的的信息:小红说:“那么a+1,b+2,c+3这三个数的乘积一定是奇数”;小明:“不对a+1,b+2,c+3这三个数的乘积是偶数”。判断小红和小明两人谁说的是正确的。
1774 |
1775 | ### 练习2
1776 |
1777 | 如果a,b均为质数,且3a+7b=41,则a+b=()
1778 |
1779 | ### 练习3
1780 |
1781 | 一个两位质数个位与十位数字交换后仍为质数,这样的质数有几个?
1782 |
1783 | ### 练习1
1784 |
1785 | 是否存在自然数a和b,使得ab(a+b)=115?为什么?
1786 |
1787 | ### 练习2
1788 |
1789 | 已知三个质数之和为36(可以相等),这三个质数中最大的可能是。
1790 |
1791 | ### 练习3
1792 |
1793 | ### 练习1
1794 |
1795 | 已知n,n+6,n+84,n+102,n+218都是质数,那么n=()
1796 |
1797 | ### 练习2
1798 |
1799 | A,B,C为3个小于20的质数,A+B+C=30,求这三个质数分别是几。
1800 |
1801 | ### 练习3
1802 |
1803 | 某质数加6或减6得到的数仍是质数,在50以内你能找出几个这样的质数?把它们写出来。
1804 |
1805 | ## 4.2.06. 火车过桥
1806 |
1807 | ### 例题1
1808 |
1809 | 己知某铁路桥长1000米,一列火车从桥上通过,火车速度每秒40米,车长200米。
1810 | (1)火车完全在桥时间是多少?
1811 | (2)火车从开始上桥到完全下桥所用时间是多少?
1812 |
1813 | ### 练习1
1814 |
1815 | 一列火车经过南京长江大桥,大桥长6700米,这列火车长100米,火车每分钟行4000米,这列火车经过南京长江大桥需要多少分钟?
1816 |
1817 | ### 例题2
1818 |
1819 | 一列火车通过530米长的桥需40秒钟,以同样的速度穿过380米长的山洞需30秒钟。则这列火车的速度是多少?全长是多少米?
1820 |
1821 | ### 练习2
1822 |
1823 | 牛牛站在铁路旁,一列火车从他身边开过用了21秒,以同样的速度通过一座长为2070米的大桥,用了1.5分钟。火车长多少米?
1824 |
1825 | ### 例题3
1826 |
1827 | 牛牛以每秒10米的速度沿铁道边的小路骑车。
1828 | (1)身后一辆火车以每秒100米的速度超过他,从车头追上牛牛到车尾离开共用时4秒,那么车长多少米?
1829 | (2)过了一会,另一辆火车以每秒100米的速度迎面开来,从与牛牛相遇到离开,共用时3秒。那么车长是多少?
1830 |
1831 | ### 练习3
1832 |
1833 | 丁丁以3米/秒的速度沿着铁路跑步,迎面开来一列火车,它的行驶速度是18米/秒,火车从丁丁身旁经过的时间是7秒,求火车的车长是多少米?
1834 |
1835 | ### 例题4
1836 |
1837 | 一列快车和一列慢车相向而行,快车的车长是280米,慢车的车长为385米,坐在快车上的人看见慢车驶过的时间是11秒,那么坐在慢车上的人看见快车驶过的时间是多少?
1838 |
1839 | ### 练习4
1840 |
1841 | 一列快车和一列慢车相向而行,快车的车长是150米,慢车的车长为200米,坐在慢车上的人看见快车驶过的时间是3秒,那么坐在快车上的人看见慢车驶过的时间是多少?
1842 |
1843 | ### 例题5
1844 |
1845 | 有两列火车,一列长200米,每秒行34米;一列长178米,每秒行20米。
1846 | (1)两列火车相向而行,从两车车头相遇到车尾相离共需要多少秒?
1847 | (2)两列火车同向行驶,从快车的车头追上慢车的车尾,到快车的车尾超过慢车的车头,共需多少秒?
1848 |
1849 | ### 练习5
1850 |
1851 | 快车长300米,每秒行20米,慢车长150米,每秒行10米。
1852 | (1)两列火车相向而行,从两车车头相遇到车尾相离共需要多少秒?
1853 | (2)两列火车同向行驶,从快车的车头追及慢车的车尾,到快车的车尾超过慢车的车头,其需多少秒?
1854 |
1855 | ### 例题6
1856 |
1857 | 有两列同方向行驶的火车,快车每秒行33米,慢车每秒行21米。如果从两车头对齐开始算,则行20秒后快车超过慢车;如果从两车尾对齐开始算,则行25秒后快车超过慢车。
1858 | (1)两车车长分别是多少?
1859 | (2)如果两车相对行驶,两车从车头相遇到车尾相离需要经过多少时间?
1860 |
1861 | ### 练习6
1862 |
1863 | 现有两列火车同时同方向齐头行进,行12秒后快车超过慢车,快车每秒行18米,慢车每秒行10米。如果这两列火车车尾相齐同时同方向行进,则9秒后快车超过慢车,那么,快车车头追上慢车车尾到快车车尾离开慢车车头的时间为多少秒?
1864 |
1865 | ## 4.2.07. 包含与排除
1866 |
1867 | ### 例题1
1868 |
1869 | 实验小学四年级二班,参加语文兴趣小组的有28人,参加数学兴趣小组的有29人,有12人两个小组都参加。这个班有多少人参加了语文或数学兴趣小组?
1870 |
1871 | ### 练习1
1872 |
1873 | 学校文艺组的每位同学至少会演奏钢琴和手风琴中的一种乐器,己知会演奏钢琴的有24人,会演奏手风琴的有17人,其中两种乐器都会演奏的有8人,则文艺组一共有多少人?
1874 |
1875 | ### 例题2
1876 |
1877 | 某餐馆有40道招牌菜,牛牛吃过其中的15道,丁丁吃过其中的9道,而且有4道菜是两人都吃过的,请问:有多少道招牌菜是两人都没有吃过的?
1878 |
1879 | ### 练习2
1880 |
1881 | 在46人参加的采摘活动中,只采了樱桃的有18人,既采了樱桃又采了杏的有7人,既没采樱桃又没采杏的有6人,问:只采了杏的有多少人?
1882 |
1883 | ### 例题3
1884 |
1885 | 在1~100这些自然数中,能被3或5同时整除的数有多少个?
1886 |
1887 | ### 练习3
1888 |
1889 | 在1~60这些自然数中:
1890 | (1)能被2整除的数有多少个?
1891 | (2)能被5整除的数有多少个?
1892 | (3)能被2和5整除的数有多少个?
1893 | (4)能被2或5整除的数有多少个?
1894 | (5)不能被2整除也不能被5整除的数有多少个?
1895 |
1896 | ### 例题4
1897 |
1898 | 50名同学面向老师站成一行。老师先让大家从左至右按1,2,3,……,49,50依次报数;再让报数是4的倍数的同学向后转,接着又让报数是6的倍数的同学向后转。问:现在面向老师的同学还有多少名?
1899 |
1900 | ### 练习4
1901 |
1902 | 一根长60厘米的木棍,每5厘米用红点标记,每6厘米用蓝点标记。沿标记的点把木棍锯断,木棍总共被锯成几段?
1903 |
1904 | ### 例题5
1905 |
1906 | 光明小学组织棋类比赛,分成围棋、中国象棋和国际象棋三个组进行,参加国棋比赛的有42人,参加中国象棋比赛的有55人,参加国际象棋比赛的有33人,同时参加了围棋和中国象棋比赛的有18人,同时参加了国棋和国际象棋比赛的有10人,同时参加了中国象棋和国际象棋比赛的有9人,其中三种棋赛都参加的有5人,问参加棋类比赛的共有多少人?
1907 |
1908 | ### 练习5
1909 |
1910 | 三位基金经理投资若干只股票。张经理买过其中66只,王经理买过其中40只,李经理买过其中23只。张经理和王经理都买过的有17只,王经理和李经理都买过的有13只,李经理和张经理都买过的有9只,三个人都买过的有6只。请问:这三位经理一共买过多少只股票?
1911 |
1912 | ### 例题6
1913 |
1914 | 在一个100人的旅行团中,每人至少懂英语、汉语、日语中的一种,其中懂英语的有66人,汉语的有54人,懂日语的有55人,既懂英语又懂汉语的有25人,既懂汉语又懂日语的有21人,但没有一个人三门语言都懂。问:有多少人既懂英语又懂日语?
1915 |
1916 | ### 练习6
1917 |
1918 | 少年宫春季书法班、美术班、器乐班招生。书法班招收了29名学员,在这些学员中,既报书法又报美术的有13名,既报书法又报器乐的有12人,三个科目都报的有5名。那么,只参加书法学习的学员有几名?
1919 |
1920 | ### 练习1
1921 |
1922 | 一根长101厘米长的木棍,从同一端开始,第一次每隔4厘米画一个刻度,第二次每隔6厘米画一个刻度,如果按刻度把木棍截断,那么可以截成多少段?
1923 |
1924 | ### 练习2
1925 |
1926 | 写有1到100编号的灯100盏,亮着排成一排,第一次把编号是3的倍数的灯拉一次开关,第二次把编号是5的倍数的灯拉一次开关,那么亮着的灯还有多少盏?
1927 |
1928 | ### 练习3
1929 |
1930 | 在1~100这些自然数中:
1931 |
1932 | 1. 能被2整除的数有多少个?
1933 | 2. 能被3整除的数有多少个?
1934 | 3. 能被2和3整除的数有多少个?
1935 | 4. 能被2或3整除的数有多少个?
1936 | 5. 不能被2整除也不能被3整除的数有多少个?
1937 |
1938 | ## 4.2.08. 整数与数列
1939 |
1940 | ### 热身1
1941 |
1942 | ### 热身2
1943 |
1944 | ### 热身3
1945 |
1946 | ### 例题1
1947 |
1948 | 已知数列1,6,11,16,21,⋯,146,问:
1949 | (1)这个数列中第20个数是多少?
1950 | (2)81是这个数列的第几个数?
1951 | (3)这个数列一共有几项?
1952 | (4)将数列中所有的数加起来,和是多少?
1953 |
1954 | ### 练习1
1955 |
1956 | (1)数列3,7,11,⋯,第18项是()。
1957 | (2)数列4,9,14,⋯,其中254是这个数列的第()项。
1958 | (3)数列4,8,12,⋯,160,这个数列共有()项。
1959 |
1960 | ### 例题2
1961 |
1962 | 1~100中除以5余2的数的和是多少?
1963 |
1964 | ### 练习2
1965 |
1966 | 1~100中所有5的倍数的和是多少?
1967 |
1968 | ### 例题3
1969 |
1970 | 计算:$24\times23-23\times22+22\times21-21\times20+\dots+2\times1$
1971 |
1972 | ### 练习3
1973 |
1974 | 计算:$14\times13-13\times12+12\times11-11\times10+10\times9-9\times8+8\times7-7\times6+6\times5-5\times4+4\times3-3\times2+2\times1$
1975 |
1976 | ### 例题4(平方差公式)
1977 |
1978 | 有一串数1,4,9,16,25,36,⋯,它们是按什么规律排列的?其中第9个数与第10个数相差多少?第2014个数与第2015个数相差多少?
1979 |
1980 | ### 练习4
1981 |
1982 | 计算:$[2017-(8.5\times8.5-1.5\times1.5)\div10]\div160-0.3$
1983 |
1984 | ### 例题5
1985 |
1986 | 计算:$100^2-99^2+98^2-97^2+\dots+2^2-1^2$
1987 |
1988 | ### 练习5
1989 |
1990 | 计算:$20\times20-19\times19+18\times18-17\times17+\dots+2\times2-1\times1$
1991 |
1992 | ### 例题6(整数列项)
1993 |
1994 | 计算:$1\times2+2\times3+3\times4+\dots+49\times50$
1995 |
1996 | ### 练习6
1997 |
1998 | ## 4.2.09. 统筹与最优化
1999 |
2000 | ### 例题1
2001 |
2002 | 理发店里只有一位理发师,但是同时来了五位顾客,根据他们所要理的发型,分别需要10分钟、12分钟、15分钟、20分钟和24分钟,怎样安排他们理发的顺序,才能使这五人理发和等候所用时间的总和最少?最少时间为多少?
2003 |
2004 | ### 练习1
2005 |
2006 | 5个人各拿一个水桶在自来水龙头前等候打水,他们打水所需要的时间分别是1分钟、2分钟、3分钟、4分钟和5分钟,如果只有一个水龙头,适当安排他们的打水顺序,就能够使每个人排队和打水时间的总和最小,那么这个最小值是多少分钟?
2007 |
2008 | ### 例题2
2009 |
2010 | 电车公司维修站有7辆电车需要维修,如果用一名工人维修这7辆电车,修复时间分别为12分钟,17分钟,8分钟,18分钟,23分钟,30分钟,14分钟。每辆电车每停开1分钟的损失是11元,现在由3名工作效率相同的维修工人各自单独工作,要使经济损失减到最小程度,那么最小的损失是多少元?
2011 |
2012 | ### 练习2
2013 |
2014 | 有八个人各拿着一个水桶同时到水龙头前打水,水龙头注满第一个人的桶需要1分钟,注满第二个人的桶需要2分钟,……,如此下去,
2015 | (1)当只有一个水龙头时,如何巧妙安排这八个人打水,使他们总的花费时间最少?最少的时间是多少?
2016 | (2)当有两个水龙头时,如何巧妙安排这八个人打水,使他们总的花费时间最少?最少的时间是多少?
2017 |
2018 | ### 例题3
2019 |
2020 | 有一家五口人要在夜晚过一座独木桥。他们家里的老爷爷行动非常不便,过桥需要12分钟;孩子们的父亲贪吃且不爱运动,体重严重超标,过河需要时间也较长,8分钟;母亲则一直坚持劳作,动作还算敏捷,过桥要6分钟;两个孩子中姐姐需要3分钟,弟弟只要1分钟。当时正是初一,夜晚又是阴天,不要说月亮,连一点星光都没有,真所谓伸手不见五指。幸运的是他们有一盏油灯,同时可以有两个人借助灯光过桥。但要命的是灯油将尽,这盏灯只能再维持30分钟了!他们焦急万分,该怎样过桥呢?
2021 |
2022 | ### 练习3
2023 |
2024 | 牛牛、丁丁、田田和阿普4个小朋友郊游回家时天色己晚,他们来到一条河的东岸,要通过一座小木桥到西岸,但是他们4个人只有一个手电筒,由于桥的承重量小,每次只能过2人,因此必须先由2个人拿着手电简过桥,并由1个人再将手电简送回,再由2个人拿着手电筒过桥…直到4人都通过小木桥。己知,牛牛单独过桥要1分钟;丁丁单独过桥要1.5分钟;田田单独过桥要2分钟;阿普单独过桥要2.5分钟。那么,4个人都通过小木桥,最少要多少分钟?
2025 |
2026 | ### 例题4
2027 |
2028 | (1)如图,在街道上有A、B、C、D、E五栋居民楼,现在设立一个公交站,为使五栋楼的居民到车站的距离之和最短,车站应位于何处?
2029 |
2030 |  2031 |
2032 | (2)如2图,在街道上有A、B、C、D、E、F六栋居民楼,现在设立一个公交站,要想使居民到达车站的距离之和最短,车站应该设在何处?
2033 |
2034 |
2031 |
2032 | (2)如2图,在街道上有A、B、C、D、E、F六栋居民楼,现在设立一个公交站,要想使居民到达车站的距离之和最短,车站应该设在何处?
2033 |
2034 |  2035 |
2036 | (3) 如图,在街道上有 A、B、C、D、E 五栋居民楼,图中的数表示每栋居民楼的人数, 现在想要设立一个公交站,要想使居民到达车站的距离之和最短,车站应该设在何处?
2037 |
2038 |
2035 |
2036 | (3) 如图,在街道上有 A、B、C、D、E 五栋居民楼,图中的数表示每栋居民楼的人数, 现在想要设立一个公交站,要想使居民到达车站的距离之和最短,车站应该设在何处?
2037 |
2038 |  2039 |
2040 | ### 练习4
2041 |
2042 | 有2015名少先队员分散在一条公路上执勤宣传交通法规,问完成任务后应该在公路的什么地点集合,可以使他们从各自的宣传岗位沿公路走到集合地点的路程总和最小?
2043 |
2044 | ### 例题5
2045 |
2046 | 在一条公路上,每隔10千米有一座仓库(如图),共有五座,图中数字表示各仓库库存货物的重量。现在要把所有的货物集中存放在一个仓库里,如果每吨货物运输1千米需要运费0.9元,那么集中到哪个仓库运费最少?
2047 |
2048 |
2039 |
2040 | ### 练习4
2041 |
2042 | 有2015名少先队员分散在一条公路上执勤宣传交通法规,问完成任务后应该在公路的什么地点集合,可以使他们从各自的宣传岗位沿公路走到集合地点的路程总和最小?
2043 |
2044 | ### 例题5
2045 |
2046 | 在一条公路上,每隔10千米有一座仓库(如图),共有五座,图中数字表示各仓库库存货物的重量。现在要把所有的货物集中存放在一个仓库里,如果每吨货物运输1千米需要运费0.9元,那么集中到哪个仓库运费最少?
2047 |
2048 |  2049 |
2050 | ### 练习5
2051 |
2052 | 在一条公路上每隔100千米,有一个仓库,共有5个仓库,—号仓库存有10吨货物,二号仓库存有20吨货物,五号仓库存有40吨货物,其余两个仓库是空的。现在想把所有的货物集中存放在一个仓库里,如果每吨货物运输1千米需要0.5元运输费,那么最少要多少运费才行?
2053 |
2054 | ### 例题6
2055 |
2056 | 北京、上海分别有10台和6台完全相同的机器,准备给武汉11台,西安5台,每台机器的运费如表所示,如何调运能使总运费最省?
2057 |
2058 | | | 武汉 | 西安 |
2059 | | ---- | ---- | ---- |
2060 | | 北京 | 500 | 600 |
2061 | | 上海 | 700 | 1000 |
2062 |
2063 | ### 练习6
2064 |
2065 | 北京和上海同时制成了电子计算机若干台,除了供应本地外,北京可以支援外地10台,上海可以支持外地4台。现决定给重庆8台,汉口6台,若每台计算机的运费如表,上海和北京制造的机器完全相同,应该怎样调运,才能使总的运费最省?最省的运费是多少?
2066 |
2067 | | | 汉口 | 重庆 |
2068 | | ---- | ---- | ---- |
2069 | | 北京 | 40 | 80 |
2070 | | 上海 | 30 | 50 |
2071 |
2072 | ## 4.2.10. 整除特征进阶
2073 |
2074 | ### 例题1
2075 |
2076 | 下面五个自然数:128114、94146、64152、6139、491678,哪些能被7整除?哪些能被11整除?哪些能被13整除?
2077 |
2078 | ### 练习1
2079 |
2080 | 下列数中,哪些能被7整除?哪些能被11整除?哪些能被13整除?
2081 |
2082 | 414 1057 2673 1320 596 2816 7462
2083 |
2084 | ### 例题2
2085 |
2086 | 2009200920092009能否被11整除?
2087 |
2088 | ### 练习2
2089 |
2090 | 20092009能否被11整除?
2091 |
2092 | ### 例题3
2093 |
2094 | 学校买了24台B种仪器,发票上的总价有两个数字已经辨认不清,只看到是$\overline{\Box8\Box2}$元,但采购人员还记得模糊不清的两个数字相同。你知道每台B种仪器多少钱吗?(仪器价格为整数)
2095 |
2096 | ### 练习3
2097 |
2098 | 小新一共买了28支价格相同的钢笔给大家作为奖品,共付人民币$\overline{9\Box.2\Box}$元。已知方框处数字相同,请问每支钢笔多少元?
2099 |
2100 | ### 例题4
2101 |
2102 | 六位数$\overline{\Box2008\Box}$能同时被9和11整除。这个六位数是多少?
2103 |
2104 | ### 练习4
2105 |
2106 | 六位数$\overline{\Box\Box5308}$能同时被9和11整除。$\overline{\Box\Box}$是多少?
2107 |
2108 | ### 例题5(试除法)
2109 |
2110 | 如果六位数$\overline{1992\Box\Box}$能被105整除,那么它的最后两位数是多少?
2111 |
2112 | ### 练习5
2113 |
2114 | 如果$\overline{2\Box\Box}$能被79整除,那么它的末两位数是多少?
2115 |
2116 | ### 例题6
2117 |
2118 | 六位自然数$\overline{1082\Box\Box}$能被23整除,末两位数有多少种情况?
2119 |
2120 | ### 练习6
2121 |
2122 | 六位自然数$\overline{1082\Box\Box}$能被12整除,末两位数可能是?
2123 |
2124 | ## 4.2.11. 加乘原理进阶
2125 |
2126 | ### 例题1
2127 |
2128 | 从北京到广州可以选择直达的飞机和火车,也可以选择中途在上海或者武汉停留,已知北京到上海、武汉和上海、武汉到广州除了有飞机和火车两种交通方式外还有汽车。问,从北京到广州一共有多少种交通方式可供选择?
2129 |
2130 | ### 练习1
2131 |
2132 | 王老师从重庆到南京,他可以乘飞机、汽车直接到达,也可以先到武汉,再由武汉到南京。他从重庆到武汉可乘船,也可乘火车; 又从武汉到南京可以乘船、火车或者飞机,那么王老师从重庆到南京有多少种不同走法呢?
2133 |
2134 | ### 例题2
2135 |
2136 | 过年了,妈妈买了7件不同的礼物,要送给亲朋好友的5个孩子每人一件。其中姐姐的儿子小强想从智力拼图和遥控汽车中选一个,朋友的女儿小玉想从学习机和遥控汽车中选一件。那么,妈妈送出这5件礼物共有多少种方法?
2137 |
2138 | ### 练习2
2139 |
2140 | 爸爸买了5件不同的玩具,要送给3个孩子每人一件。其中姐姐的儿子小刚想从拼图和积木中选一个,朋友的女儿小豆想从洋娃娃和积木中选一件。那么,爸爸送出这3件玩具共有多少种方法?
2141 |
2142 | ### 例题3
2143 |
2144 | 用0,1,2,3四个数字可以组成多少个没有重复数字的四位偶数?
2145 |
2146 | ### 练习3
2147 |
2148 | 用1,2,3,4四个数可以组成多少个没有重复数字的四位偶数?
2149 |
2150 | ### 例题4
2151 |
2152 | 在如图所示$1\times5$的格子中填入1,2,3,4,5,要求填入的数各不相同,并且填在红格里的数比它旁边的两个数都大。一共由多少种不同的填法?
2153 |
2154 | 
2155 |
2156 | ### 练习4
2157 |
2158 | 在如图所示$1\times5$的格子中填入1,2,3,4,5,6,7,8中的五个数,要求填入的数各不相同,并且填在红格里的数比它旁边的两个数都大。一共由多少种不同的填法?
2159 |
2160 | 
2161 |
2162 | ### 例题5
2163 |
2164 | 如下图,A,B,C,D,E五个区域,分别用红、黄、蓝、白、黑五种颜色中的某一种染色,要使相邻的区域染不同的颜色,共有多少种不同的染色方法?
2165 |
2166 | 
2167 |
2168 | ### 练习5
2169 |
2170 | 用5种不同的颜色给图中的A、B、C、D四个区域涂色,每个区域只能使用一种颜色,且相邻区域不能同色,有多少种不同的涂色方式?
2171 |
2172 | 
2173 |
2174 | ### 例题6
2175 |
2176 | 地图上有A,B,C,D四个区域(如下图),现有红、黄、蓝三种颜色给它染色,使相邻区域的颜色不同,但不是每种颜色都必须要用,问有多少种染色方法?
2177 |
2178 | 
2179 |
2180 | ### 练习6
2181 |
2182 | 如果有红、黄、蓝、绿四种颜色给例题中的图染色,使相邻区域的颜色不同,但不是每种颜色都必须要用,问有多少种染色方法?
2183 |
2184 | 
2185 |
2186 | ## 4.2.12. 流水行船
2187 |
2188 | ### 知识导引
2189 |
2190 | ### 课程框架
2191 |
2192 | ### 内容分析
2193 |
2194 | ### 例题练习
2195 |
2196 | 前置内容——相遇追及问题。后续讲次——电梯问题。知道行程问题的基本关系。
2197 |
2198 | 课堂先讲流水行程问题是什么,比起单人行程有什么区别。(区别在于有水是有速度的)
2199 |
2200 | 简单引入后,可以让学生尝试的去做例题 1,练习 1。
2201 |
2202 | **例题1**
2203 |
2204 | 一只船在静水中每小时行 8 千米,水流速度是每小时 4 千米,如果这只船顺流而下 3 小时,它行多远? 如果这只船逆流而上 3 小时,它行多远?
2205 |
2206 | 【解析】顺水速度:8 + 4 = 12(千米/小时),路程:12 × 3 = 36(千米);
2207 |
2208 | 逆水速度:8 - 4 = 4(千米/小时),路程:4 × 3 = 12(千米)。
2209 |
2210 | **练习1**
2211 |
2212 | 一只船在静水中每小时航行 4 千米,水流的速度是每小时 2 千米,则这只船逆水 4 小时航行多少干米?
2213 |
2214 | 【解析】逆水速度:4 - 2 = 2(千米/小时),路程:2 × 4 = 8(千米)。
2215 |
2216 | ### 流水行船基本关系
2217 |
2218 | 流水行船问题中,有四个速度:
2219 |
2220 | * 水流速度
2221 | * 船在静水中的速度
2222 | * 船的顺水速度
2223 | * 船的逆水速度
2224 |
2225 | 他们的关系如下:
2226 |
2227 | * 顺水速度 = 船速 + 水速
2228 | * 逆水速度= 船速 - 水速
2229 |
2230 | 综合上面两个基本公式,由和差公式可知:
2231 |
2232 | * 船速 = (顺水速度 + 逆水速度)÷ 2
2233 | * 水速 = (顺水速度 - 逆水速度)÷ 2
2234 |
2235 | 默认船速是要比水速大的。
2236 |
2237 | **船速、水速、顺水速度、逆水速度,可知 2 求 2。**
2238 |
2239 | | 船速 | 水速 | 顺水速度 | 逆水速度 |
2240 | | :--: | :--: | :------: | -------- |
2241 | | 100 | 30 | | |
2242 | | | 10 | 40 | |
2243 | | 6 | | 7 | |
2244 | | | | 80 | 50 |
2245 |
2246 | 讲完这些,例题 2,练习 2。
2247 |
2248 | **例题2**
2249 |
2250 | 一艘游轮在河中行驶,顺流航行的速度是每小时 30 千米,逆流航行的速度是每小时 12 千米,游轮的静水速度是多少?水流的速度是多少?
2251 |
2252 | 【解析】静水速度:(30 + 12)÷ 2 = 21(千米/小时);水速:(30 - 12)÷ 2 = 9(千米/小时)
2253 |
2254 | **练习2**
2255 |
2256 | 一只小船在河中行驶,顺流划行的速度是每小时 10 千米,逆流划行的速度是每小时 6 千米,船的静水速度是多少?水流的速度是多少?
2257 |
2258 | 【解析】
2259 |
2260 | ### 方向改变,船速水速不变
2261 |
2262 | **例题3**
2263 |
2264 | 一艘船在静水中的速度是每小时 15 千米,它从上游甲地开往下游乙地共花去了 8 小时,水速每小时 3 千米,问从乙地返回甲地需要多少时间?
2265 |
2266 | **练习3**
2267 |
2268 | 一艘每小时行 25 千米的客轮,在大运河中顺水航行 140 千米,水速是每小时3 千米,需要行几个小时?
2269 |
2270 | ### 船速不变,水速变
2271 |
2272 | **例题4**
2273 |
2274 | 某船往返于相距 180 千米的两港之间,平时顺水每小时行 18 千米,逆水每小时行12千米。某天暴雨后水速增加,该船顺水而行只需 9 小时,那么逆水而行需要几小时?
2275 |
2276 | **练习4**
2277 |
2278 | 汉江是长江的支流,汉江水的水速为每小时 3 千米,长江水的水速为每小时 4 千米。一条船沿汉江顺水航行 2 小时,行了56 千米到达长江,在长江还要逆水航行 147 千米。这条船还要行多少小时?
2279 |
2280 | ### 水速不变,船速变
2281 |
2282 | **例题5**
2283 |
2284 | 有甲乙两船航行于 360 千米的两港口之间,甲逆水行全程用 18 小时,乙逆水行全程用 12 小时,甲顺水行全程用 12 小时,乙顺水行全程要用多长时间?
2285 |
2286 | **练习5**
2287 |
2288 | 有 AB 两船航行于 120 千米的两港口之间,A 逆水行全程用 30 小时,B 逆水行全程用 20 小时,A 顺水行全程用 12 小时,B 顺水行全程要用多长时间?
2289 |
2290 | ### 流水行船中的相遇追及
2291 |
2292 | **例题6**
2293 |
2294 | A、B 两码头间河流长为 220 千米,甲、乙两船分别从 A、B 码头同时起航。如果相向而行 5 小时相遇,如果同向而行 55 小时甲船追上乙船。求两船在静水中的速度。
2295 |
2296 | **练习6**
2297 |
2298 | 甲、乙两船分别从相距 64 千米的 A、B 两港同时出发相向而行,2小时相遇;若两船同时同向而行,则甲用 16 小时赶上乙。问:甲、乙两船的速度各是多少?
2299 |
2300 | ### 课堂总结
2301 |
2302 | ## 4.2.13. 抽屉原理与最不利原则
2303 |
2304 | 例题练习
2305 |
2306 | ### 例题1(抽屉特征/一份)
2307 |
2308 | (1)7个苹果,放进6个抽屉,请问,苹果数最多的抽屉里最少能放进几个苹果?
2309 |
2310 | (2)14个苹果,放进6个抽屉,请问,至少有几个苹果会放在同一个抽屉中?
2311 |
2312 | ### 练习1
2313 |
2314 | (1)在任意367个同一年出生的人中,是否有生日相同的人?
2315 | (2)在任意25个人中,至少有几个人的性别相同?
2316 | (3)在任意100个人中,人数最多的一个星座至少有几个人?
2317 |
2318 | ### 拓展
2319 |
2320 | 71名选手参加大胃王比赛,比赛的内容是吃汉堡,最后吃得最多的选手吃了18个汉堡,吃得最少的选手吃了9个汉堡。问至少有几名选手吃的汉堡的数量是相同的?(不满一个汉堡不算,不存在半个汉堡的情况)
2321 |
2322 | ### 例题2(求抽屉数)
2323 |
2324 | 把100个苹果放进若干个抽屉里,保证苹果最多的抽屉里至少有4个苹果,则抽屉最多有个?
2325 |
2326 | ### 练习2
2327 |
2328 | 某次选拔考试,共有1123名同学参加,小明说:“参赛人数最多的一个学校至少有10人参赛” ,如果他的说法是正确的,那么最多有几个学校参加了这次入学考试。
2329 |
2330 | ### 例题3(最不利原则/总数)
2331 |
2332 | 一副扑克牌中。
2333 |
2334 | (1)至少抽几张,才能保证抽到两种不同花色的牌?
2335 |
2336 | (2)至少抽几张,才能保证抽到的牌中有黑桃?
2337 |
2338 | (3)至少抽几张,才能保证抽到三张A?
2339 |
2340 | (4)至少抽几张,才能保证抽到的牌中有“一对”?
2341 |
2342 | ### 练习3
2343 |
2344 | 有黄色袜子9只,绿色袜子7只,白色袜子4只,红色袜子2只黑色袜子1只。松松闭着眼睛摸袜子。
2345 |
2346 | (1)至少摸出几只,才能保证凑出1双袜子?
2347 |
2348 | (2)至少摸出几只,才能保证凑出2双袜子?
2349 |
2350 | (3)至少摸出几只,才能保证凑出2双同色袜子?
2351 |
2352 | (4)至少摸出几只,才能保证凑出2双不同色袜子?
2353 |
2354 | ### 拓展
2355 |
2356 | 有黄色鞋子9双,绿色鞋子7双,白色鞋子4双,红色鞋子2双,黑色鞋子1双。松松闭着眼睛摸鞋子,至少摸出几只,才能保证凑出2双不同色鞋子?
2357 |
2358 | ### 例题4(应用)
2359 |
2360 | 17名同学参加一次考试,考试题是3道判断题(答案只有对或错),每名同学都在答题纸上依次写上了3道题目的答案。请问:至少有几名同学的答案是一样的?
2361 |
2362 | ### 练习4
2363 |
2364 | 41名学生到老师家借书,老师书房中有A、B、C、D四类书,每名学生可借两本不同类的书。请问最少有多少名学生借到的书的数量和种类完全一样?
2365 |
2366 | ### 例题5
2367 |
2368 | 如图,将2行5列的方格纸的每一格染成黑色或白色,请说明:不管怎样染,总有两列的染色方式是一样的。
2369 |
2370 |
2049 |
2050 | ### 练习5
2051 |
2052 | 在一条公路上每隔100千米,有一个仓库,共有5个仓库,—号仓库存有10吨货物,二号仓库存有20吨货物,五号仓库存有40吨货物,其余两个仓库是空的。现在想把所有的货物集中存放在一个仓库里,如果每吨货物运输1千米需要0.5元运输费,那么最少要多少运费才行?
2053 |
2054 | ### 例题6
2055 |
2056 | 北京、上海分别有10台和6台完全相同的机器,准备给武汉11台,西安5台,每台机器的运费如表所示,如何调运能使总运费最省?
2057 |
2058 | | | 武汉 | 西安 |
2059 | | ---- | ---- | ---- |
2060 | | 北京 | 500 | 600 |
2061 | | 上海 | 700 | 1000 |
2062 |
2063 | ### 练习6
2064 |
2065 | 北京和上海同时制成了电子计算机若干台,除了供应本地外,北京可以支援外地10台,上海可以支持外地4台。现决定给重庆8台,汉口6台,若每台计算机的运费如表,上海和北京制造的机器完全相同,应该怎样调运,才能使总的运费最省?最省的运费是多少?
2066 |
2067 | | | 汉口 | 重庆 |
2068 | | ---- | ---- | ---- |
2069 | | 北京 | 40 | 80 |
2070 | | 上海 | 30 | 50 |
2071 |
2072 | ## 4.2.10. 整除特征进阶
2073 |
2074 | ### 例题1
2075 |
2076 | 下面五个自然数:128114、94146、64152、6139、491678,哪些能被7整除?哪些能被11整除?哪些能被13整除?
2077 |
2078 | ### 练习1
2079 |
2080 | 下列数中,哪些能被7整除?哪些能被11整除?哪些能被13整除?
2081 |
2082 | 414 1057 2673 1320 596 2816 7462
2083 |
2084 | ### 例题2
2085 |
2086 | 2009200920092009能否被11整除?
2087 |
2088 | ### 练习2
2089 |
2090 | 20092009能否被11整除?
2091 |
2092 | ### 例题3
2093 |
2094 | 学校买了24台B种仪器,发票上的总价有两个数字已经辨认不清,只看到是$\overline{\Box8\Box2}$元,但采购人员还记得模糊不清的两个数字相同。你知道每台B种仪器多少钱吗?(仪器价格为整数)
2095 |
2096 | ### 练习3
2097 |
2098 | 小新一共买了28支价格相同的钢笔给大家作为奖品,共付人民币$\overline{9\Box.2\Box}$元。已知方框处数字相同,请问每支钢笔多少元?
2099 |
2100 | ### 例题4
2101 |
2102 | 六位数$\overline{\Box2008\Box}$能同时被9和11整除。这个六位数是多少?
2103 |
2104 | ### 练习4
2105 |
2106 | 六位数$\overline{\Box\Box5308}$能同时被9和11整除。$\overline{\Box\Box}$是多少?
2107 |
2108 | ### 例题5(试除法)
2109 |
2110 | 如果六位数$\overline{1992\Box\Box}$能被105整除,那么它的最后两位数是多少?
2111 |
2112 | ### 练习5
2113 |
2114 | 如果$\overline{2\Box\Box}$能被79整除,那么它的末两位数是多少?
2115 |
2116 | ### 例题6
2117 |
2118 | 六位自然数$\overline{1082\Box\Box}$能被23整除,末两位数有多少种情况?
2119 |
2120 | ### 练习6
2121 |
2122 | 六位自然数$\overline{1082\Box\Box}$能被12整除,末两位数可能是?
2123 |
2124 | ## 4.2.11. 加乘原理进阶
2125 |
2126 | ### 例题1
2127 |
2128 | 从北京到广州可以选择直达的飞机和火车,也可以选择中途在上海或者武汉停留,已知北京到上海、武汉和上海、武汉到广州除了有飞机和火车两种交通方式外还有汽车。问,从北京到广州一共有多少种交通方式可供选择?
2129 |
2130 | ### 练习1
2131 |
2132 | 王老师从重庆到南京,他可以乘飞机、汽车直接到达,也可以先到武汉,再由武汉到南京。他从重庆到武汉可乘船,也可乘火车; 又从武汉到南京可以乘船、火车或者飞机,那么王老师从重庆到南京有多少种不同走法呢?
2133 |
2134 | ### 例题2
2135 |
2136 | 过年了,妈妈买了7件不同的礼物,要送给亲朋好友的5个孩子每人一件。其中姐姐的儿子小强想从智力拼图和遥控汽车中选一个,朋友的女儿小玉想从学习机和遥控汽车中选一件。那么,妈妈送出这5件礼物共有多少种方法?
2137 |
2138 | ### 练习2
2139 |
2140 | 爸爸买了5件不同的玩具,要送给3个孩子每人一件。其中姐姐的儿子小刚想从拼图和积木中选一个,朋友的女儿小豆想从洋娃娃和积木中选一件。那么,爸爸送出这3件玩具共有多少种方法?
2141 |
2142 | ### 例题3
2143 |
2144 | 用0,1,2,3四个数字可以组成多少个没有重复数字的四位偶数?
2145 |
2146 | ### 练习3
2147 |
2148 | 用1,2,3,4四个数可以组成多少个没有重复数字的四位偶数?
2149 |
2150 | ### 例题4
2151 |
2152 | 在如图所示$1\times5$的格子中填入1,2,3,4,5,要求填入的数各不相同,并且填在红格里的数比它旁边的两个数都大。一共由多少种不同的填法?
2153 |
2154 | 
2155 |
2156 | ### 练习4
2157 |
2158 | 在如图所示$1\times5$的格子中填入1,2,3,4,5,6,7,8中的五个数,要求填入的数各不相同,并且填在红格里的数比它旁边的两个数都大。一共由多少种不同的填法?
2159 |
2160 | 
2161 |
2162 | ### 例题5
2163 |
2164 | 如下图,A,B,C,D,E五个区域,分别用红、黄、蓝、白、黑五种颜色中的某一种染色,要使相邻的区域染不同的颜色,共有多少种不同的染色方法?
2165 |
2166 | 
2167 |
2168 | ### 练习5
2169 |
2170 | 用5种不同的颜色给图中的A、B、C、D四个区域涂色,每个区域只能使用一种颜色,且相邻区域不能同色,有多少种不同的涂色方式?
2171 |
2172 | 
2173 |
2174 | ### 例题6
2175 |
2176 | 地图上有A,B,C,D四个区域(如下图),现有红、黄、蓝三种颜色给它染色,使相邻区域的颜色不同,但不是每种颜色都必须要用,问有多少种染色方法?
2177 |
2178 | 
2179 |
2180 | ### 练习6
2181 |
2182 | 如果有红、黄、蓝、绿四种颜色给例题中的图染色,使相邻区域的颜色不同,但不是每种颜色都必须要用,问有多少种染色方法?
2183 |
2184 | 
2185 |
2186 | ## 4.2.12. 流水行船
2187 |
2188 | ### 知识导引
2189 |
2190 | ### 课程框架
2191 |
2192 | ### 内容分析
2193 |
2194 | ### 例题练习
2195 |
2196 | 前置内容——相遇追及问题。后续讲次——电梯问题。知道行程问题的基本关系。
2197 |
2198 | 课堂先讲流水行程问题是什么,比起单人行程有什么区别。(区别在于有水是有速度的)
2199 |
2200 | 简单引入后,可以让学生尝试的去做例题 1,练习 1。
2201 |
2202 | **例题1**
2203 |
2204 | 一只船在静水中每小时行 8 千米,水流速度是每小时 4 千米,如果这只船顺流而下 3 小时,它行多远? 如果这只船逆流而上 3 小时,它行多远?
2205 |
2206 | 【解析】顺水速度:8 + 4 = 12(千米/小时),路程:12 × 3 = 36(千米);
2207 |
2208 | 逆水速度:8 - 4 = 4(千米/小时),路程:4 × 3 = 12(千米)。
2209 |
2210 | **练习1**
2211 |
2212 | 一只船在静水中每小时航行 4 千米,水流的速度是每小时 2 千米,则这只船逆水 4 小时航行多少干米?
2213 |
2214 | 【解析】逆水速度:4 - 2 = 2(千米/小时),路程:2 × 4 = 8(千米)。
2215 |
2216 | ### 流水行船基本关系
2217 |
2218 | 流水行船问题中,有四个速度:
2219 |
2220 | * 水流速度
2221 | * 船在静水中的速度
2222 | * 船的顺水速度
2223 | * 船的逆水速度
2224 |
2225 | 他们的关系如下:
2226 |
2227 | * 顺水速度 = 船速 + 水速
2228 | * 逆水速度= 船速 - 水速
2229 |
2230 | 综合上面两个基本公式,由和差公式可知:
2231 |
2232 | * 船速 = (顺水速度 + 逆水速度)÷ 2
2233 | * 水速 = (顺水速度 - 逆水速度)÷ 2
2234 |
2235 | 默认船速是要比水速大的。
2236 |
2237 | **船速、水速、顺水速度、逆水速度,可知 2 求 2。**
2238 |
2239 | | 船速 | 水速 | 顺水速度 | 逆水速度 |
2240 | | :--: | :--: | :------: | -------- |
2241 | | 100 | 30 | | |
2242 | | | 10 | 40 | |
2243 | | 6 | | 7 | |
2244 | | | | 80 | 50 |
2245 |
2246 | 讲完这些,例题 2,练习 2。
2247 |
2248 | **例题2**
2249 |
2250 | 一艘游轮在河中行驶,顺流航行的速度是每小时 30 千米,逆流航行的速度是每小时 12 千米,游轮的静水速度是多少?水流的速度是多少?
2251 |
2252 | 【解析】静水速度:(30 + 12)÷ 2 = 21(千米/小时);水速:(30 - 12)÷ 2 = 9(千米/小时)
2253 |
2254 | **练习2**
2255 |
2256 | 一只小船在河中行驶,顺流划行的速度是每小时 10 千米,逆流划行的速度是每小时 6 千米,船的静水速度是多少?水流的速度是多少?
2257 |
2258 | 【解析】
2259 |
2260 | ### 方向改变,船速水速不变
2261 |
2262 | **例题3**
2263 |
2264 | 一艘船在静水中的速度是每小时 15 千米,它从上游甲地开往下游乙地共花去了 8 小时,水速每小时 3 千米,问从乙地返回甲地需要多少时间?
2265 |
2266 | **练习3**
2267 |
2268 | 一艘每小时行 25 千米的客轮,在大运河中顺水航行 140 千米,水速是每小时3 千米,需要行几个小时?
2269 |
2270 | ### 船速不变,水速变
2271 |
2272 | **例题4**
2273 |
2274 | 某船往返于相距 180 千米的两港之间,平时顺水每小时行 18 千米,逆水每小时行12千米。某天暴雨后水速增加,该船顺水而行只需 9 小时,那么逆水而行需要几小时?
2275 |
2276 | **练习4**
2277 |
2278 | 汉江是长江的支流,汉江水的水速为每小时 3 千米,长江水的水速为每小时 4 千米。一条船沿汉江顺水航行 2 小时,行了56 千米到达长江,在长江还要逆水航行 147 千米。这条船还要行多少小时?
2279 |
2280 | ### 水速不变,船速变
2281 |
2282 | **例题5**
2283 |
2284 | 有甲乙两船航行于 360 千米的两港口之间,甲逆水行全程用 18 小时,乙逆水行全程用 12 小时,甲顺水行全程用 12 小时,乙顺水行全程要用多长时间?
2285 |
2286 | **练习5**
2287 |
2288 | 有 AB 两船航行于 120 千米的两港口之间,A 逆水行全程用 30 小时,B 逆水行全程用 20 小时,A 顺水行全程用 12 小时,B 顺水行全程要用多长时间?
2289 |
2290 | ### 流水行船中的相遇追及
2291 |
2292 | **例题6**
2293 |
2294 | A、B 两码头间河流长为 220 千米,甲、乙两船分别从 A、B 码头同时起航。如果相向而行 5 小时相遇,如果同向而行 55 小时甲船追上乙船。求两船在静水中的速度。
2295 |
2296 | **练习6**
2297 |
2298 | 甲、乙两船分别从相距 64 千米的 A、B 两港同时出发相向而行,2小时相遇;若两船同时同向而行,则甲用 16 小时赶上乙。问:甲、乙两船的速度各是多少?
2299 |
2300 | ### 课堂总结
2301 |
2302 | ## 4.2.13. 抽屉原理与最不利原则
2303 |
2304 | 例题练习
2305 |
2306 | ### 例题1(抽屉特征/一份)
2307 |
2308 | (1)7个苹果,放进6个抽屉,请问,苹果数最多的抽屉里最少能放进几个苹果?
2309 |
2310 | (2)14个苹果,放进6个抽屉,请问,至少有几个苹果会放在同一个抽屉中?
2311 |
2312 | ### 练习1
2313 |
2314 | (1)在任意367个同一年出生的人中,是否有生日相同的人?
2315 | (2)在任意25个人中,至少有几个人的性别相同?
2316 | (3)在任意100个人中,人数最多的一个星座至少有几个人?
2317 |
2318 | ### 拓展
2319 |
2320 | 71名选手参加大胃王比赛,比赛的内容是吃汉堡,最后吃得最多的选手吃了18个汉堡,吃得最少的选手吃了9个汉堡。问至少有几名选手吃的汉堡的数量是相同的?(不满一个汉堡不算,不存在半个汉堡的情况)
2321 |
2322 | ### 例题2(求抽屉数)
2323 |
2324 | 把100个苹果放进若干个抽屉里,保证苹果最多的抽屉里至少有4个苹果,则抽屉最多有个?
2325 |
2326 | ### 练习2
2327 |
2328 | 某次选拔考试,共有1123名同学参加,小明说:“参赛人数最多的一个学校至少有10人参赛” ,如果他的说法是正确的,那么最多有几个学校参加了这次入学考试。
2329 |
2330 | ### 例题3(最不利原则/总数)
2331 |
2332 | 一副扑克牌中。
2333 |
2334 | (1)至少抽几张,才能保证抽到两种不同花色的牌?
2335 |
2336 | (2)至少抽几张,才能保证抽到的牌中有黑桃?
2337 |
2338 | (3)至少抽几张,才能保证抽到三张A?
2339 |
2340 | (4)至少抽几张,才能保证抽到的牌中有“一对”?
2341 |
2342 | ### 练习3
2343 |
2344 | 有黄色袜子9只,绿色袜子7只,白色袜子4只,红色袜子2只黑色袜子1只。松松闭着眼睛摸袜子。
2345 |
2346 | (1)至少摸出几只,才能保证凑出1双袜子?
2347 |
2348 | (2)至少摸出几只,才能保证凑出2双袜子?
2349 |
2350 | (3)至少摸出几只,才能保证凑出2双同色袜子?
2351 |
2352 | (4)至少摸出几只,才能保证凑出2双不同色袜子?
2353 |
2354 | ### 拓展
2355 |
2356 | 有黄色鞋子9双,绿色鞋子7双,白色鞋子4双,红色鞋子2双,黑色鞋子1双。松松闭着眼睛摸鞋子,至少摸出几只,才能保证凑出2双不同色鞋子?
2357 |
2358 | ### 例题4(应用)
2359 |
2360 | 17名同学参加一次考试,考试题是3道判断题(答案只有对或错),每名同学都在答题纸上依次写上了3道题目的答案。请问:至少有几名同学的答案是一样的?
2361 |
2362 | ### 练习4
2363 |
2364 | 41名学生到老师家借书,老师书房中有A、B、C、D四类书,每名学生可借两本不同类的书。请问最少有多少名学生借到的书的数量和种类完全一样?
2365 |
2366 | ### 例题5
2367 |
2368 | 如图,将2行5列的方格纸的每一格染成黑色或白色,请说明:不管怎样染,总有两列的染色方式是一样的。
2369 |
2370 |  2371 |
2372 | ### 练习5
2373 |
2374 | 下面是一个三行a列的方格纸,已知将每一个小方格涂上红色、黄色或蓝色(每一列的三小格涂的颜色不能相同),不论如何涂色,其中至少有三列,它们的涂色方式相同,那么a至少是多少?
2375 |
2376 |
2371 |
2372 | ### 练习5
2373 |
2374 | 下面是一个三行a列的方格纸,已知将每一个小方格涂上红色、黄色或蓝色(每一列的三小格涂的颜色不能相同),不论如何涂色,其中至少有三列,它们的涂色方式相同,那么a至少是多少?
2375 |
2376 |  2377 |
2378 | ### 课后巩固
2379 |
2380 | ### 巩固1
2381 |
2382 | 某小学有731个学生,问:至少有几个学生的生日是同一天?
2383 |
2384 | ### 巩固2
2385 |
2386 | 袋中有外形安全一样的红、黄、蓝三种颜色的小球各10个,每个小朋友只能从中摸出1个小球, 至少有几个小朋友摸球,才能保证一定有3个人摸的球颜色一样。
2387 |
2388 | ### 巩固3
2389 |
2390 | 一副扑克牌有54张,至少要抽取几张牌,才能保证其中有2张牌有相同的点数?
2391 |
2392 | ### 巩固4
2393 |
2394 | 学校买来许多牛、马、羊、狗塑料玩具,每个小朋友任意选择两件,但不能是同样的,问:至少有多少个小朋友去拿,才能保证有两人所拿玩具相同?
2395 |
2396 | ### 巩固5
2397 |
2398 | 一次数学竞赛出了10道选择题,评分标准为:基础分10分,每道题答对得3分,答错扣1分, 不答不得分。问:要保证至少有 4 人得分相同,至少需要多少人参加竞赛?
2399 |
2400 | ## 4.2.14. 最值问题进阶
2401 |
2402 | ### 例题1
2403 |
2404 | 在下图的中间圆圈内填一个数,计算每一条线段两端的数之差(大减小),然后把这3个差数相加,所得的和最小是多少?
2405 |
2406 |
2377 |
2378 | ### 课后巩固
2379 |
2380 | ### 巩固1
2381 |
2382 | 某小学有731个学生,问:至少有几个学生的生日是同一天?
2383 |
2384 | ### 巩固2
2385 |
2386 | 袋中有外形安全一样的红、黄、蓝三种颜色的小球各10个,每个小朋友只能从中摸出1个小球, 至少有几个小朋友摸球,才能保证一定有3个人摸的球颜色一样。
2387 |
2388 | ### 巩固3
2389 |
2390 | 一副扑克牌有54张,至少要抽取几张牌,才能保证其中有2张牌有相同的点数?
2391 |
2392 | ### 巩固4
2393 |
2394 | 学校买来许多牛、马、羊、狗塑料玩具,每个小朋友任意选择两件,但不能是同样的,问:至少有多少个小朋友去拿,才能保证有两人所拿玩具相同?
2395 |
2396 | ### 巩固5
2397 |
2398 | 一次数学竞赛出了10道选择题,评分标准为:基础分10分,每道题答对得3分,答错扣1分, 不答不得分。问:要保证至少有 4 人得分相同,至少需要多少人参加竞赛?
2399 |
2400 | ## 4.2.14. 最值问题进阶
2401 |
2402 | ### 例题1
2403 |
2404 | 在下图的中间圆圈内填一个数,计算每一条线段两端的数之差(大减小),然后把这3个差数相加,所得的和最小是多少?
2405 |
2406 |  2407 |
2408 | ### 练习1
2409 |
2410 | 在下图的中间圆圈内填一个数,计算每一条线段两端的数之差(大减小),然后把这3个差数相加,所得的和最小是多少?
2411 |
2412 |
2407 |
2408 | ### 练习1
2409 |
2410 | 在下图的中间圆圈内填一个数,计算每一条线段两端的数之差(大减小),然后把这3个差数相加,所得的和最小是多少?
2411 |
2412 |  2413 |
2414 | ### 例题2
2415 |
2416 | “12345678910111213…282930”是一个位数很多的多位数,从中划去40个数字,使剩下的数字(顺序不变)组成一个首位不为0的多位数,则这个多位数最大为多少?
2417 |
2418 | ### 练习2
2419 |
2420 | “12345678910111213…282930”是一个位数很多的多位数,从中划去40个数字,使剩下的数字(顺序不变)组成一个首位不为0的多位数,则这个多位数最小为多少?
2421 |
2422 | ### 例题3
2423 |
2424 | 某次考试共有15题。计分标准是:做对第1题得1分,做对第2题得2分,……,做对第15题得15分。若做错第1题则要倒扣1分,做错第2题要倒扣2分,……,做错第15题要倒扣15分。小明做了所有的题,得90分,那么小明至多做错多少道题?
2425 |
2426 | ### 练习3
2427 |
2428 | 某次考试共有15题。计分标准是:做对第1题得1分,做对第2题得2分,……,做对第15题得15分。若做错第1题则要倒扣1分,做错第2题要倒扣2分,……,做错第15题要倒扣15分。小明做了所有的题,得90分,那么小明至多做错多少道题?
2429 |
2430 | ### 例题4
2431 |
2432 | 阶梯教室座位有10排,每排有16个座位,当有150个人就座时,某些排坐着的人数就一样多。我们希望人数一样的排数尽可能少,这样的排数至少有多少排?
2433 |
2434 | ### 练习4
2435 |
2436 | 学校203教室座位有5排,每排有8个座位,当有30个人就座时,某些排坐着的人数就一样多。我们希望人数一样的排数尽可能少,这样的排数至少有多少排?
2437 |
2438 | ### 例题5
2439 |
2440 | 如图,牧羊人用15段每段长2米的篱笆,一面靠墙围成一个长方形羊圈,则羊圈的最大面积是多少平方米?
2441 |
2442 | 
2443 |
2444 | ### 练习5
2445 |
2446 | 某校准备用一道长36米的铁丝网,围成一块长方形生物实验基地,这块基地的面积最大是多少平方米?
2447 |
2448 | ### 例题6
2449 |
2450 | 如图,一个长方形被分成4个小长方形,其中长方形A、B、C的周长分别是10厘米、12厘米、14厘米,那么长方形D的面积最大是多少平方厘米?
2451 |
2452 | 
2453 |
2454 | ### 练习6
2455 |
2456 | 一块长方形菜地被分成4个小块,其A、B、C块的周长分别是20厘米、24厘米、28厘米那么D的面积最大是多少平方厘米?
2457 |
2458 | 
2459 |
2460 | ## 4.2.15. 操作类智巧趣题
2461 |
2462 | ### 例题1
2463 |
2464 | 一个猎户,带着一条狗,一只兔子和一筐胡萝卜乘船过河,船小一次只能带一样东西。但是他不在时,狗会咬兔子,免子会吃胡萝卜。请你想一想,帮猎人安排合理的方法过河。
2465 |
2466 | ### 练习1
2467 |
2468 | 一个农民携带一只狼、一只羊和一棵白菜,要借助一条小船过河。小船上除了农民只能再带狼、羊、白菜中的一样。而农民不在时,狼会吃羊,羊会吃白菜。农民如何过河呢?
2469 |
2470 | ### 例题2
2471 |
2472 | 小枫带着他的三个馋嘴弟弟和一个大蛋糕过河,已知只有小枫会划船,且除了小枫外每次只能带其中的一个弟弟,或者蛋糕过河。蛋糕一共十块,只要小枫离开,单独留弟弟和蛋糕在一起,每个弟弟在下次见到哥哥之前都会吃掉一块蛋糕。假设除弟弟外的任何原因都不会导致蛋糕减少,请问,兄弟4人全部过河后,最多还能剩下块蛋糕。
2473 |
2474 | ### 练习2
2475 |
2476 | 河左边有一个大人和两个小孩,一只大熊和两只小熊。只有大熊、大人会划船,船一次最多只能运两个单位(不管人熊),条件是熊的数量不能大于人的数量(不分大小),要不然熊会把人吃掉(河的两边熊的数量都不能大于人的数量)。问怎么才能让人和熊安全渡河?
2477 |
2478 | ### 例题3
2479 |
2480 | 一大一小两个油桶,大桶盛满重11千克,小桶盛满重4千克。现要盛5千克的油,只用这两个桶盛,能办到吗?
2481 |
2482 | ### 练习3
2483 |
2484 | 小红去河边打水,她有两个桶,大桶能装9升水,小桶能装4升水,想要恰好从河中打上6升的水带回去,她该怎么办?
2485 |
2486 | ### 例题4
2487 |
2488 | 卖牛奶人有两桶10升装的牛奶。两个顾客各带容器去买2升牛奶,一个带的是5升的容器,另一个带的是4升的容器。这位卖牛奶人如何解决问题?
2489 |
2490 | ### 练习4
2491 |
2492 | 有大、中、小3个水桶,最多分别可装入水10千克、7千克和3千克。现在大桶中装满水,希望通过水在3个瓶子间的流动使得中瓶和小瓶上标出装1千克水的刻度线,聪明的你想想应该怎么倒呢?
2493 |
2494 | ### 例题5
2495 |
2496 | 有9个铁球,其中8个铁球一样重,另一个较轻,你要在天平上至少称几次才能保证把那个轻球找出来?
2497 |
2498 | ### 练习5
2499 |
2500 | 有3个铁球,其中2个铁球一样重,另一个较轻,你在天平上至少称几次能保证把那个轻球找出来?
2501 |
2502 | ### 例题6
2503 |
2504 | 今有101枚硬币,其中有100枚同样的真币和1枚伪币,伪币与真币的重量不同。现需弄清楚伪币究竟比真币轻,还是比真币重,但只有一架没有砝码的天平。那么怎样利用这架天平称两次,来达到目的?
2505 |
2506 | ### 练习6
2507 |
2508 | 现有21枚硬币,其中有20枚同样的真币和1枚伪币,伪币与真币重量不同。现需弄清楚伪币究竟比真币轻,还是比真币重,但只有一架没有砝码的天平。那么怎样利用这架天平称两次,来达到目的?
2509 |
2510 | ### 练习1
2511 |
2512 | 一个猎人要带一棵红萝卜,一只狗,两只老虎和一只羊过河。可现在,小船只有3个座位,猎人每次最多只能送两样东西过河。没有狗看管,老虎会吃羊;没有人看管,狗和羊就吵架,羊就会吃红萝卜。有什么妙计能帮助它们全都过河?
2513 |
2514 | ### 练习2
2515 |
2516 | 相传汉代军事家韩信一天访友归来 ,途中经过一集市,遇见卖油翁与顾客争执。买者想买5斤油,而卖者无法计量,因而告诉买者, 要么买3斤,要么买7斤。韩信询问得知,卖油翁油篓中恰好装有10斤油,但他仅有装3斤和7斤的葫芦,而买者执意要买5斤油。韩信立在马上稍加思索道:“你们无须再争,以我之法保你们都满意。”韩信下马经过几次倒油,买卖双方皆大欢喜。你知道,韩信是怎么倒油吗?
2517 |
2518 | ### 练习3
2519 |
2520 | 在一批产品中有16个零件,其中有一个是次品,比较轻(其它零件一样重) , 给你一架天平,你最少用天平称量
2521 | 几次就可以检验出次品零件?
2522 |
2523 | ## 4.2.17. 相遇追及综合
2524 |
2525 | ### 例题1
2526 |
2527 | 如图,周长为800米的环形跑道上,田田和阿普分别从相距200米的A、B两处同时沿相同方向出发。田田每分钟能跑200米,阿普每分钟只能跑150米,田田第一次追上阿普需要多少分钟?
2528 |
2529 | 
2530 |
2531 | ### 练习1
2532 |
2533 | 如图,周长为400米的环形跑道上田田和阿普分别从相距100米的A、B两处同时沿相同方向出发。田田每分钟能跑200米,阿普每分钟只能跑150米,田田第一次追上阿普需要多少分钟?
2534 |
2535 | 
2536 |
2537 | ### 例题2
2538 |
2539 | 如图,田田和阿普分别从周长为1200米的圆形跑道上相距600米的A、B两处同时出发相向而行。6分钟后两人相遇。相遇后两人继续行进,4分钟后田田怡好到达B处,问两人相遇的地点距离A点多少米?
2540 |
2541 | 
2542 |
2543 | ### 练习2
2544 |
2545 | 如图,田田和阿普分别从周长600米的圆形跑道上相距300米的A、B两处同时出发相向而行,6分钟后两人相遇。相遇后两人继续行进,4分钟后田田怡好到达B处,求两人相遇的地点距离A点多少米?
2546 |
2547 | 
2548 |
2549 | ### 例题3
2550 |
2551 | 一列从西向东行驶的火车车速为每秒16米,车身长255米,8点整它追上了在铁路旁从西向东散步的田田,并于17秒后离开了他,又过了5分钟,它与从东向西散步的阿普相遇,15秒后离开了他。请问田田和阿普步行的速度分别是多少?
2552 |
2553 | ### 练习3
2554 |
2555 | 一列从西向东行驶的火车车速为每秒19米,车身长360米。9点整它追上了在铁路旁从西向东散步的田田,并于20秒后离开了她。又过了5分钟,它与从东向西散步的阿普相遇18秒后离开了他。请问田田和阿普步行的速度分别是多少?
2556 |
2557 | ### 例题4
2558 |
2559 | 田田以6米/秒的速度在铁路旁骑车,一列火车迎面开来,与她从相遇到离开共用了15秒,而它追上在铁路旁以4米/秒的速度跑步的阿普并刚好超过他共用了25秒,求火车的长度和行驶的速度。
2560 |
2561 | ### 练习4
2562 |
2563 | 田田以5米/秒的速度在铁路旁骑车,一列火车迎面开来,与她从相遇到离开共用了10秒,而它追上在铁路旁以3米/秒的速度跑步的阿普并刚好超过他共用了20秒,求火车的长度和行驶的速度。
2564 |
2565 | ### 例题5
2566 |
2567 | 某河上下游两港相距100千米,每天定时有甲乙两艘船速相等的客轮从两港相向而行,甲船顺水每小时行12千米,乙船逆水每小时行8千米,这天甲船在出发时,从船上掉下一物,此物顺水漂流而下,当甲乙两船相遇时,此物距相遇地点有多远?
2568 |
2569 | ### 练习5
2570 |
2571 | 某河上下游两港相距60千米,每天定时有甲乙两艘船速相等的客轮从两港相向而行,甲船顺水每小时行11千米,乙船逆水每小时行9千米,这天甲船在出发时,从船上掉下一物,此物顺水漂流而下,当甲乙两船相遇时,此物距相遇地点有多远?
2572 |
2573 | ### 例题6
2574 |
2575 | 某河上下游两港相距150千米,每天有甲乙两艘船分别从上游和下游同时相向而行,它们在静水中的速度分别为6千米/时和9千米/时。平时它们相遇于距上游港70千米处,某日突下暴雨,水速变为原来的2倍,这一天甲乙两船相遇地点距上游港多远?
2576 |
2577 | ### 练习6
2578 |
2579 | 某河上下游两港相距130千米,每天有甲乙两艘船分别从上游和下游同时相向而行,它们在静水中的速度分别为5千米/时和8千米/时。平时它们相遇于距上游港60千米处。某日突下暴雨,水速变为原来的2倍,这一天甲乙两船相遇地点距上游港多远?
2580 |
2581 |
2582 |
2583 | ## 方程与方程组
2584 |
2585 | ### 例题练习
2586 |
2587 | 【例题1】解下列一元一次方程:
2588 |
2589 | (1)$6(3+x)=24$
2590 |
2591 | (2)$18-(3x-6)=x$
2592 |
2593 | 答案:(1)1;(2)6
2594 |
2595 |
2596 |
2597 | 【练习1】解下列一元一次方程:
2598 |
2599 | (1)$3x-2(2+x)=1$
2600 |
2601 | (2)$6x-(4-x)=17$
2602 |
2603 |
2604 |
2605 | 【例题2】用代入消元法解方程组:
2606 |
2607 | (1)$\begin{cases}
2608 | y=2x-3\\
2609 | 3x+2y=8
2610 | \end{cases}$
2611 |
2612 |
2613 |
2614 | (2)$\begin{cases}
2615 | 2x-y=5\\
2616 | 3x+4y=13
2617 | \end{cases}$
2618 |
2619 |
2620 |
2621 | 【练习2】用代入消元法解方程组:
2622 |
2623 | (1)$\begin{cases}
2624 | 3x+2y=13\\
2625 | 2x-y=4
2626 | \end{cases}$
2627 |
2628 |
2629 |
2630 | 【例题3】用加减消元法解下列方程组:
2631 |
2632 | (1)$\begin{cases}
2633 | x-y=5\\
2634 | x+y=13
2635 | \end{cases}$
2636 |
2637 |
2638 |
2639 | (2)$\begin{cases}
2640 | 2x+y=11\\
2641 | 3x-2y=6
2642 | \end{cases}$
2643 |
2644 |
2645 |
2646 | (3)$\begin{cases}
2647 | 5y+z=12\\
2648 | 6y+5z=22
2649 | \end{cases}$
2650 |
2651 |
2652 |
2653 | 【练习3】用加减消元法解下列方程组:
2654 |
2655 | (1)$\begin{cases}
2656 | x+2y=21\\
2657 | 2x+y=18
2658 | \end{cases}$
2659 |
2660 |
2661 |
2662 | (2)$\begin{cases}
2663 | 7x+3y=44\\
2664 | 11x-2y=49
2665 | \end{cases}$
2666 |
2667 |
2668 |
2669 | (3)$\begin{cases}
2670 | 7x+3y=44\\
2671 | 11x+2y=61
2672 | \end{cases}$
2673 |
2674 |
2675 |
2676 | 【例题4】解方程组:
2677 |
2678 | (1)$\begin{cases}
2679 | 2x-3y=x+y-4\\
2680 | 3x+4y=x+5y+13
2681 | \end{cases}$
2682 |
2683 |
2684 |
2685 | (2)$\begin{cases}
2686 | 3x+5y=2x+3y+11\\
2687 | 4x-y-6=x+2y
2688 | \end{cases}$
2689 |
2690 |
2691 |
2692 | 【练习4】解方程组:
2693 |
2694 | (1)$\begin{cases}
2695 | a-1=b+1\\
2696 | a+1=3(b-1)
2697 | \end{cases}$
2698 |
2699 |
2700 |
2701 | 【例题5】解方程组:
2702 |
2703 | (1)$\begin{cases}
2704 | x+y=9\cdots①\\
2705 | y+z=15\cdots②\\
2706 | z+x=12\cdots③
2707 | \end{cases}$
2708 |
2709 |
2710 |
2711 | (2)$\begin{cases}
2712 | x+2y=11\cdots①\\
2713 | 3x+z=19\cdots②\\
2714 | z=x+y\cdots③
2715 | \end{cases}$
2716 |
2717 |
2718 |
2719 | 【练习5】解方程组:
2720 |
2721 | (1)$\begin{cases}
2722 | 2x+y+z=7\\
2723 | x+2y+z=8\\
2724 | x+y+2z=9
2725 | \end{cases}$
2726 |
2727 |
2728 |
2729 | 【例题6】购买3斤苹果,2斤橘子需要6.90元;购买8斤苹果,9斤橘子需要22.80元,那么苹果、橘子各买1斤需要多少元?
2730 |
2731 |
2732 |
2733 | 【练习6】已知:$\begin{cases}
2734 | 3x+6y=17\\
2735 | 7x+4y=13
2736 | \end{cases}$,求$x+y=$()。
2737 |
2738 |
2739 |
2740 |
--------------------------------------------------------------------------------
/05-五年级.md:
--------------------------------------------------------------------------------
1 | ---
2 | title: 五年级
3 | lang: zh-CN
4 | sidebarDepth: 1
5 | ---
6 |
7 | # 五年级
8 |
9 | ## 5.1.03. 棋盘中的数学
10 |
11 | 间隔染色,用间隔染色解决问题。
12 |
13 | 思想:构造模型,用模型解决实际问题。
14 |
15 | ### 热身1
16 |
17 | ### 热身2
18 |
19 | ### 热身3
20 |
21 | ### 例题1
22 |
23 | 有一次车展共16个展室,如图,每个展室与相邻的展室都有门相通,出口和入口如图中箭头所示。
24 | (1)参观者能否从入口进去,不重复地参观完每个展室再从出口出来?
25 | (2)参观者能否从入口进去,不重复地参观完每个展室再从入口出来?
26 |
27 | ### 练习1
28 |
29 | 有一栋大厦共3✕3✕3=27间房子,每个房间与相邻的房间都有直达电梯,入口和出口如下
30 | 图所示。
31 | (1)参观者能否从入口进去,不重复地参观完每个展室再从出口出来?
32 | (2)参观者能否从入口进去,不重复地参观完每个展室再从入口出来?
33 |
34 | ### 例题2
35 |
36 | (1)左图是连接14个城市的道路图,是否有一条路线可以经过每一个城市怡好一次?
37 | (2)右图中是半张中国象棋棋盘,棋盘上放有一只马。众所周知,马是走“日”字路线的。请问:这个马能否不重复地走遍这半张棋盘上的每一个点,然后回到出发点?
38 |
39 | ### 练习2
40 |
41 | 五年级一班有35名同学,共分成5排,每排7人,坐在教室里,每个座位的前后左右四个位置都叫作他的邻座。如果要让这35名同学每个人都恰好坐到他的邻座上去,能办到吗?为什么?
42 |
43 | ### 例题3
44 |
45 | 下面三个图形都是从4✕4的正方形分别剪去两个1✕1的小方格得到的,问:可否把它们分别剪成1✕2的七个小矩形?
46 |
47 | ### 练习3
48 |
49 | 如图所示,一个8✕8的国际象棋棋盘去掉对角上两格后,是否可以用31个2✕1的“骨牌”把棋盘上的62个小格完全盖住?
50 |
51 | ### 例题4
52 |
53 | 如图所示,有一个6✕6的棋盘,请问:能否用1个和8个填满这个棋盘? (图形可以旋转和翻折)
54 |
55 | ### 练习4
56 |
57 | 如图所示,有一个6✕6的棋盘,请问:能否用3个和6个填满这个棋盘? (图形可以旋转和翻折)
58 |
59 | ### 例题5
60 |
61 | 如图所示,有一个6✕6的棋盘,请问:
62 |
63 | (1)能否用9个填满这个棋盘?
64 |
65 | (2)能否用9个填满这个棋盘?(图形可以旋转)
66 |
67 | (3)能否用9个填满这个棋盘?(图形可以旋转)
68 |
69 | ### 练习5
70 |
71 | ### 例题6
72 |
73 | ### 练习6
74 |
75 | ### 巩固1
76 |
77 | ### 巩固2
78 |
79 | ### 巩固3
80 |
81 | ## 5.1.04. 课程标题
82 |
83 | ### 热身1
84 |
85 | ### 热身2
86 |
87 | ### 热身3
88 |
89 | ### 例题1(有序数对)
90 |
91 | (1)将6块糖全部分给丁丁、田田、阿普三个人,每个人都要分到糖,那么一共有几种分法?
92 |
93 | (2)丁丁有14块糖,从第一天开始吃,每天至少吃2颗,至多吃6颗,第三天吃完,有几种吃法?
94 |
95 | ### 练习1
96 |
97 | 田田、牛牛、阿普三个人一共有7本课外书,每个人至少有一本。田田、牛牛、阿普分别有几本课外书?请写出全部可能的情况。
98 |
99 | ### 例题2
100 |
101 | (1)将10个小球分成两堆,有几种分法?
102 |
103 | (2)将10个小球分成三堆,有几种分法?
104 |
105 | (3)将18个小球分成三堆,每堆至少2个,至多9个,有几种分法?
106 |
107 | ### 练习2
108 |
109 | 将11拆成三个不同的正整数相加的形式,加数相同顺序不同看作同一种形式,例如:11=2+3+6与11=3+6+2看作同一种形式。问:有几种可能的形式?
110 |
111 | ### 例题3
112 |
113 | 周长为15厘米,三边长都是整数厘米的三角形有几个?(通过旋转、翻折、平移能重合的三角形视为同一个三角形)
114 |
115 | ### 练习3
116 |
117 | 三条边的边长均为整数,且最长边的边长是7厘米,这样的三角形共有多少种?
118 |
119 | ### 例题4
120 |
121 | 从1、2、3、4、5、6、7中选取三个不同的数,使得它们的和为3的倍数,有几种不同的选法?
122 |
123 | ### 练习4
124 |
125 | 从1-50这50个自然数中选取两个数,使它们的和大于50,共有多少种不同的选法?
126 |
127 | ### 例题5
128 |
129 | 甲、乙两人进行乒乓球比赛,规定谁先胜三场谁胜,第一场甲胜。问:到决出最后胜负为止,有多少种可能的情形?其中甲胜的情形有几种?
130 |
131 | ### 练习5
132 |
133 | 如图,给1、2、3、4号区域染上红、蓝、紫三种颜色,每块区域染一种颜色,并且使得相邻两块区域的颜色不同,有几种染法?
134 |
135 | 
136 |
137 | ### 例题6
138 |
139 | 如图,从起点到终点,只能沿着图中线段走。
140 |
141 | (1)所有点恰好经过一次,有几种走法?
142 |
143 | (2)所有点至多经过一次,有几种走法?
144 |
145 | (2)不能走重复路线(能走重复点),有几种走法?
146 |
147 | 
148 |
149 | ### 练习6
150 |
151 | 如图,从点A出发,沿着线段走,最后到达点B。
152 |
153 | (1)如果每个黑点恰好经过一次,有几种走法?
154 |
155 | (2)如果每个黑点至多经过一次,有几种走法?
156 |
157 | 
158 |
159 | ### 拓展1
160 |
161 | ### 拓展2
162 |
163 | ### 拓展3
164 |
165 | ### 拓展4
166 |
167 | ### 拓展5
168 |
169 | ### 练习1
170 |
171 | ### 练习2
172 |
173 | ### 练习3
174 |
175 | ### 练习4
176 |
177 | ### 练习5
178 |
179 | ### 练习6
180 |
181 | ## 5.1.05. 排列组合
182 |
183 | ### 例题1
184 |
185 | (1)从A、B、C、D、E这5个小朋友中选3名站成一排拍照。我们分步骤来思考这个问题:
186 |
187 | 第一步,选一个人站第一个位置,有()种选法;
188 |
189 | 第二步,选一个人站第二个位置,有()种选法;
190 |
191 | 第三步,选一个人站第三个位置,有()种选法。
192 |
193 | 根据乘法原理,完成三步有()×()×()种方法,用排列数可以表示为$A_5^3$。
194 |
195 | (2)计算:
196 |
197 | | $A_4^2=$ | $A_5^3=$ | $A_6^3=$ |
198 | | -------------- | -------------------- | ----------------------------------- |
199 | | $A_5^4=$ | $A_{10}^{10}=$ | $A_6^2-A_2^2=$ |
200 | | $A_8^4+A_6^2=$ | $A_7^2\times A_5^3=$ | $\frac{A_{100}^{98}}{A_{98}^{98}}=$ |
201 |
202 | ### 练习1
203 |
204 | (1)从7名学生中,安排3名学生分别扫地、拖地、倒垃圾,有几种安排方法?
205 |
206 | (2)计算:
207 |
208 | | $A_5^2=$ | $A_6^4=$ |
209 | | ---------------------- | ---------------------- |
210 | | $\frac{A_8^5}{A_5^5}=$ | $\frac{A_9^5}{A_4^4}=$ |
211 |
212 | ### 例题2
213 |
214 | 从A、B、C、D、E这5个小朋友中选出3名小朋友,有$C_5^3$种方法,再将选出的3名小朋友排成一排,有$A_3^3$种方法。因此,先选再排这两步有$C_5^3\times A_3^3$种方法,应该与$A_5^3$相等,所以$C_5^3=\frac{A_5^3}{A_3^3}=\frac{5\times4\times3}{3\times2\times1}$
215 | 仿照此例:
216 |
217 | 计算:
218 |
219 | (1)$C_6^2, C_6^4$
220 |
221 | (2)$C_7^2, C_7^5$
222 |
223 | ### 练习2
224 |
225 | 计算:
226 |
227 | | (1)$C_{12}^3$ | (2)$C_{1000}^{998}$ | (3)$A_8^2-C_8^2$ |
228 | | --------------- | --------------------- | ------------------ |
229 |
230 | ### 例题3
231 |
232 | 有4个同学一起去郊游,照相时,必须有一名同学给其他3人拍照,共可能有多少种拍照情況?(照相时3人站成一排)
233 |
234 | ### 练习3
235 |
236 | 6个人排成一排,有几种排法?
237 |
238 | ### 例题4
239 |
240 | 五名学生和一名老师排队拍照,老师不能站在两边,有几种排法?
241 |
242 | ### 练习4
243 |
244 | 5个人并排站成一排,其中甲必须站在中间,有几种不同的站法。
245 |
246 | ### 例题5
247 |
248 | (1)从1、2、3、4、5、6、7、8中选出3个数,使得3个数的和是偶数,有几种选法?
249 | (2)从1、2、3、4、5、6、7、8中选出3个数,使得3个数的乘积是偶数,有几种选法?
250 |
251 | ### 练习5
252 |
253 | 田田要从八门课程中选学三门,一共有多少种选法?如果数学课与钢琴课时间冲突,不能同时学,她一共有多少种选法?
254 |
255 | ### 例题6
256 |
257 | 一个小组有10个人,其中6个人会唱歌,4个人会跳舞,回答下列问题:
258 | (1)选出4个人表演唱歌,3个人表演跳舞,有几种选法?
259 | (2)后来又来了一个人既会唱歌,又会跳舞。要选出4个人表演跳舞,3个人表演唱歌,有几种选法?
260 |
261 | ### 练习6
262 |
263 | 学校举办联欢晚会,要从6名数学老师中选出3名,再从4名语文老师中选出2名,接着让这5名老师分别扮演5个不同的角色,共有多少种选择方式?
264 |
265 | ## 5.1.06. 质数与合数进阶
266 |
267 | ### 例题1
268 |
269 | 当$p$和$p^5+5$都是质数时,求$p^5+5$的值。
270 |
271 | ### 练习1
272 |
273 | 如果$a$、$b$均为质数,且$3a+7b=41$,求$a+b$的值。
274 |
275 | ### 例题2
276 |
277 | $a$、$b$、$c$均为质数,如果$(a+b)\times(b+c)=342$,那么$b$是几。
278 |
279 | ### 练习2
280 |
281 | 在算式$a\times(b+c)=110+c$中,$a$、$b$、$c$是三个互不相等的质数,那么$b$是几。
282 |
283 | ### 例题3
284 |
285 | 有三张卡片,在它们上面各写有一个数字1、2、3(如下图)。从中抽出一张、二张、三张,按任意次序排起来,可以得到不同的一位数、二位数、三位数。请你将其中的质数都写出来?
286 |
287 | ### 练习3
288 |
289 | 自然数$n$是一个两位数,它是一个质数,而且$n$的个位数字与十位数字都是质数,这样的自然数有多少个?
290 |
291 | ### 例题4
292 |
293 | 4只同样的瓶子内分别装有一定数量的油。每瓶和其他各瓶分别合称一次,记录千克数如下:8,9,10,11,12,13。已知4只空瓶的重量之和以及油的重量之和均为质数,问:最重的两瓶内有多少油?
294 |
295 | ### 练习4
296 |
297 | 有一个正方体木块,如图,每个面上各写了一个自然数,并且相对的两个面上的两个数之和相等。现在只能看见三个面上写的数,如果看不见的各个面写的都是质数,问:这三个质数的和是多少?
298 |
299 | ### 例题5
300 |
301 | 已知三个合数$a$、$b$、$c$两两互质,且$a\times b\times c=1001\times28\times11$,问:$a+b+c$的最小值是几?
302 |
303 | ### 练习5
304 |
305 | 6个奇数的和为98,积为4267305,这6个奇数中最大数与最小数的和是几?
306 |
307 | ### 例题6
308 |
309 | 将一个三位数的个位数字与百位数字对调位置,得到一个新的三位数,已知这两个三位数的乘积等于55872,那么,这两个三位数的和为多少?
310 |
311 | ### 练习6
312 |
313 | 如果两位数$\overline{吃好}$和$\overline{好吃}$都为质数,则这两个质数和的最大值是多少?
314 |
315 | ### 拓展1
316 |
317 | ### 拓展2
318 |
319 | ### 拓展3
320 |
321 | ### 拓展4
322 |
323 | ### 拓展5
324 |
325 | ## 5.1.07. 牛吃草问题
326 |
327 | ### 例题1
328 |
329 | 牧场上长满牧草,每天牧草都匀速生长。这片牧场可供27头牛吃6天,可供23头牛吃9天。那么,可供21头牛吃几天?
330 |
331 | ### 练习1
332 |
333 | 有一块匀速生长的草场,可供12头牛吃25天,或可供24头牛吃10天。那么可供29头牛吃几天?
334 |
335 | ### 例题2
336 |
337 | 牧场上长满牧草,每天牧草都匀速生长。这片牧场可供10头牛吃20天,可供15头牛吃10天。那么这片牧场可供几头牛吃25天?
338 |
339 | ### 练习2
340 |
341 | 有一片牧场,草每天都在均匀地生长。如果在牧场上放养24头牛,那么6天就把草吃完了;如果只放养21头牛,那么8天才把草吃完。请问:要使得草永远吃不完,最多可以放养多少头牛?
342 |
343 | ### 例题3
344 |
345 | 林子里有猴子喜欢吃的野果,23只猴子可在9周内吃光,21只猴子可在12周内吃光,问:如果要4周吃光野果,则需有多少只猴子一起吃?(假设野果生长的速度不变)
346 |
347 | ### 练习3
348 |
349 | 仓库里原有一批存货,以后继续运货进仓,且每天运进的货一样多。用同样的汽车运货出仓,如果每天用4辆汽车,则9天恰好运完;如果每天用5辆汽车,则6天恰好运完。仓库里原有的存货若用1辆汽车运,则需要多少天运完?
350 |
351 | ### 例题4
352 |
353 | 一个水池有一根进水管不间断地进水,还有若干根相同的抽水管。若用24根抽水管抽水,6小时即可把池中的水抽干;若用21根抽水管抽水,8小时可把池中的水抽干。若用16根抽水管,需要多少小时可把水池中的水抽干?
354 |
355 | ### 练习4
356 |
357 | 一个装满了水的水池有一个进水阀及三个口径相同的排水阀,如果同时打开进水阀及一个排水阀,则30分钟能把水池的水排完,如果同时打开进水阀及两个排水阀,则10分钟把水池的水排完。问:关闭进水阀并且同时打开三个排水阀,需要多少分钟能排完水池的水?
358 |
359 | ### 例题5
360 |
361 | 由于天气逐渐变冷,牧场上的草每天以均匀的速度减少。经计算,牧场上的草可供20头牛吃5天,或可供16头牛吃6天。那么,可供11头牛吃几天?
362 |
363 | ### 练习5
364 |
365 | 由于天气逐渐冷起来,牧场上的草不仅不生长,反而以固定的速度在减少。已知某块草地上的草可供20头牛吃5天,或可供15头牛吃6天。照此计算,可供多少头牛吃10天?
366 |
367 | ### 例题6
368 |
369 | 有一片草场,草每天的生长速度相同。若14头牛30天可将草吃完,70只羊16天也可将草吃完(4只羊1天的吃草量相当于1头牛1天的吃草量)。那么,17头牛和20只羊多少天可将草吃完?
370 |
371 | ### 练习6
372 |
373 | 农场有一片均匀生长的草地,可以供18头牛吃40天,或者供12头牛与36只羊吃25天,如果1头牛每天的吃草量相当于3只羊每天的吃草量。请问:这片草地让17头牛与多少只羊一起吃,刚好16天吃完?
374 |
375 | ## 5.1.08. 数阵图综合
376 |
377 | ### 例题1
378 |
379 | 将1到7,这七个数字,分别填入图中各个〇内,使每条线段上的三个〇内数的和都相等。
380 |
381 | ### 练习1
382 |
383 | 把1,4,7,10,13,16,19七个数填入图中7个圆圈中,使每条线上三个数的和都等手30。
384 |
385 | ### 例题2
386 |
387 | 把1~11填入图中,使每条线上三个数的和相等。
388 |
389 | ### 练习2
390 |
391 | 把1~9这9个数分别填入下图的圆圈中,使得每条直线上的3个数的和都相等。
392 |
393 | ### 例题3
394 |
395 | 把1至6分别填入下图的六个园圈内,使得每个正方形四个顶点的数之和都为13。
396 |
397 | ### 练习3
398 |
399 | 在图中的八个圆圈内分别填入八个不同的自然数,使得正方形每条边上三个数的和相等。现在如果已经填好了五个数,那么每条边上各数之和应该是多少?并将其补充完整。
400 |
401 | ### 例题4
402 |
403 | 图中共有10个圆圈,6条直线。请问:
404 |
405 | (1)能否将1~10填入图中,使得每条直线上各数之和都相等?
406 |
407 | (2)能否将0~9填入图中,使得每条直线上各数之和都相等?
408 |
409 | ### 练习4
410 |
411 | 将11至16六个数填入图中所示球体的圈内,使球体的各个大圆上每四个数的和都相等。这个和是多少?
412 |
413 | ### 例题5
414 |
415 | 如下图,大大小小的三角形共7个,把1~9这九个数分别填入图中的“〇”中,使每个三角形三个顶点的数之和相等。求AxBxC的最大值?
416 |
417 | ### 练习5
418 |
419 | 如图,大三角形被分成了9个小三角形。试将1,2,3,4,5,6,7,8,9分别填入这9个小三角形内,每个小三角形内填一个数,要求靠近大三角形3条边的每5个数的和相等,问:这5个数的和最大可能是多少?
420 |
421 | ### 例题6
422 |
423 | 把1~8这8个数分别填入下图的八个圆圈中,使得任意两个有线段直接相连的圆圈内的数字之差都不等于1。请问:有多少种不同的填法?
424 |
425 | ### 练习6
426 |
427 | 将1、2、3、5、6、7、9、10、11填入图中的小圆圈内,使得每条直线上各数之和都等于18。
428 |
429 | ## 5.1.09. 比和比例
430 |
431 | ### 例题1(化简比)
432 |
433 | (1)把$12:16$化成最简整数比是();
434 |
435 | (2)把$\frac{2}{5}:\frac{6}{7}$化成最简整数比是();
436 |
437 | (3)把连比$24:36:40$化成最简整数比是()。
438 |
439 | ### 练习1
440 |
441 | (1)把$48:60$化成最简整数比是();
442 |
443 | (2)把$\frac{1}{2}:\frac{4}{3}$化成最简整数比是();
444 |
445 | (3)把连比$22:33:44$化成最简整数比是()。
446 |
447 | ### 补充
448 |
449 | (1)$\frac{8+9+\dots+40}{27+28+\dots+50}$化为最简整数比是()。
450 |
451 | (2)$\frac{12!}{11!}$化为最简整数比是()。
452 |
453 | (3)$\frac{1}{3}:\frac{1}{4}:\frac{1}{5}$化为最简整数比是()。
454 |
455 | ### 例题2(解比例)
456 |
457 | 把下列比例补充完整。
458 |
459 | (1)$2:5=():30$
460 |
461 | (2)$():3:8=6:():12$
462 |
463 | ### 练习2
464 |
465 | 解比例方程。
466 |
467 | (1)$3.6:x=\frac{1}{2}:4$
468 |
469 | (2)$\frac{1}{2}:\frac{5}{6}=x:3$
470 |
471 | (3)$\frac{7x-10}{3x+5}=\frac{6}{5}$
472 |
473 | ### 例题3
474 |
475 | 解比例方程:$(3x-2):(2x+3)=4:7$
476 |
477 | ### 练习3
478 |
479 | 解比例方程:$4:(5x-1)=12:(10x+7)$
480 |
481 | ### 补充
482 |
483 | 3、5、7、a可以组成一个比例,则a=()。
484 |
485 | ### 探索
486 |
487 | 甲、乙两数之比为$5:9$,两数之和为70,甲数是()。
488 |
489 | ### 例题4(比与份数)
490 |
491 | 田田、牛牛、丁丁他们的体重比是$2:3:4$,其中田田的体重是34千克。牛牛、丁丁的体重各是多少干克?
492 |
493 | ### 练习4
494 |
495 | 动物园里有老虎、企鹅、鸵鸟三种动物比较体重,老虎重360千克,企鹅的体重是鸵鸟的$\frac{5}{12}$,鸵鸟的体重是老虎的$\frac{4}{15}$,那么企鹅的体重是多少干克?
496 |
497 | ### 补充
498 |
499 | 甲、乙、丙三数之比为$3:7:10$,乙数比甲数多20,这三个数之和是()。
500 |
501 | ### 探索
502 |
503 | 若$A: B=2:3$,$B: C=4:5$,则 $A: B: C$的最简整数比是()。
504 |
505 | ### 例题5
506 |
507 | 已知甲、乙、丙三个数,甲等于乙、丙两数和的$\frac{1}{3}$,乙等于甲、丙两数和的$\frac{1}{2}$,丙等于甲、乙两数和的$\frac{5}{7}$,求甲:乙:丙是多少?
508 |
509 | ### 练习5
510 |
511 | 甲、乙、丙三个数,已知$甲:(乙+丙)=4:3$,$乙: 丙=2:7$,问:$甲: 乙: 丙$是多少?
512 |
513 | ### 例题6
514 |
515 | 某山区小学要栽253棵松树,分给三个年级。六年级分到的$\frac{1}{5}$等于五年级分到的$\frac{1}{4}$,又等于四年级分到的$\frac{1}{2}$,三个年级各分到多少棵?
516 |
517 | ### 练习6
518 |
519 | 加工一个零件,甲要2分钟,乙要3分钟,丙要4分钟。现有1170个零件,甲、乙、丙三人各加工几个零件,才能使他们同时完成任务?
520 |
521 | ### 拓展
522 |
523 | ### 拓展1
524 |
525 | 判断这组数字能否组成比例,如果能,请列出比例式。
526 |
527 | $\frac{5}{2}$,14,3.5,10
528 |
529 | ### 拓展2
530 |
531 | 解比例方程组。
532 | $$
533 | \left\{\begin{matrix}
534 | x:y=3:4
535 | \\
536 | 3x+5y=58
537 | \end{matrix}\right.
538 | $$
539 |
540 | ### 拓展3
541 |
542 | 解比例方程。
543 |
544 | $\frac{4x-1}{2(x+1)}=\frac{4x+7}{2x+10}$
545 |
546 | ### 拓展4
547 |
548 | 解比例方程。
549 |
550 | $\frac{x-1}{x+3}=\frac{2x-1}{2x+9}$
551 |
552 | ### 拓展5
553 |
554 | 已知$a_1:a_2=a_2:a_3=b_1:b_2=b_2:b_3=c_1:c_2=c_2:c_3$,并且$a_1$、$b_2$、$c_3$成等差数列(公差不为0),请问$(a_3\times c_2)$和 $(b_1\times b_3)$哪个更大?
555 |
556 | ## 5.1.10. 比列模型
557 |
558 | ### 例题1
559 |
560 | 如图,三角形ABC被线段AD分成两个小三角形,图中一共有三个三角形,这三个三角形有一条公共的高,因此他们的面积之比等于对应底边长度之比。即$S_{△ABD}: S_{△ADC}: S_{△ABC}=BD:DC:BC$。
561 |
562 | (1)若$BD: DC=3:2$,并且三角形ABD的面积为18平方厘米,问:三角形ADC的面积为多少?
563 |
564 | (2)若 $3BD=4DC$,并且三角形ABC的面积为84平方厘米,问:三角形ABD的面积为多少?
565 |
566 | ### 练习1
567 |
568 | 如图,三角形ABC的面积为180平方厘米,并且$BD: DE: EC=2:3:4$,问:阴影部分三角形ADE的面积?
569 |
570 | ### 例题2
571 |
572 | 如图,四边形ABCD被对角线AC,以及线段BE、DE分成四个小三角形,这四个小三角形的面积分别记为a、b、c、d,那么根据比例模型可知,$a:b=AE: EC$;$d:c=AE: EC$,所以$a:b=d:c$,根据比例性质可知$ac=bd$。
573 | (1)若三角形ABE、三角形BCE、三角形CDE的面积分别是30平方厘米、20平方厘米、10平方厘米,问:四边形ABCD的面积是多少?
574 |
575 | (2)已知四边形ABCD的面积为56平方厘米,三角形BCE、三角形CDE的面积分别为10平方厘米、6平方厘米,问:三角形ABE的面积是多少?
576 |
577 | ### 练习2
578 |
579 | 如图,己知三角形ABE的面积为18平方厘米,$AE: EC=3:4$,$BE: ED=6:5$,问:三角形ADE、三角形BCE、三角形CDE的面积?
580 |
581 | ### 例题3
582 |
583 | (1)如图,三角形ABC的面积为60平方厘米,并且$AE: EB=2:3$,$BD=2DC$,问:阴影部分三角形ADE的面积是多少平方厘米?
584 |
585 | (2)如图,三角形ABC面积为90平方厘米,$BD=2DC$,$AE: EC=2:3$,问:阴影部分三角形CDE的面积?
586 |
587 | ### 练习3
588 |
589 | 如图,正方形ABCD边长为6厘米,AE=4厘米,$AC=3AF$,G是EC的中点,求阴影部分三角形EFG的面积。
590 |
591 | ### 例题4
592 |
593 | 如图,一个边长为120厘米的等边三角形被分成了面积相等的五块,那么AB是多少厘米?
594 |
595 | ### 练习4
596 |
597 | 如图,在三角形ABC中,H,I,J是AB的四等分点;D,E,F,G是BC的五等分点。知$S_{△BDH}=1$,问:每一个小三角形的面积分别为多少?
598 |
599 | ### 例题5
600 |
601 | 如图,三角形ABC的面积为36平方厘米,并且$AC=4AD$,$BC=3EC$,$BD=3BF$,$DE=3DG$,H是EF的中点,求阴影部分三角形FGH的面积?
602 |
603 | ### 练习5
604 |
605 | 如图,三角形ABC中,$BD: DC=2:5$,$AE: EC=4:3$,三角形ABC的面积是980平方厘米,求三角形CDE的面积?
606 |
607 | ### 例题6
608 |
609 | 如图,点E、F分别为四边形ABCD中AB的三等分点。点G、H为CD的三等分点。则四边形EFHG的面积占总面积的几分之几?
610 |
611 | ### 练习6
612 |
613 | 如图,四边形ABCD中,$DE: EF: FC=3:2:1$,$BG: GH: AH=3:2:1$。$AD: BC=1:2$,已知四边形ABCD的面积等于4,求四边形EFGH的面积?
614 |
615 | ### 练习1
616 |
617 | 如图所示,四边形ABCD形状的草地里有两条路AC和BD,交于点O,三角形AOD、三角形AOB、三角形BOC的面积分别为6平方米、14平方米、35平方米,求三角形COD的面积。
618 |
619 | ### 练习2
620 |
621 | 如图所示,阴影部分三角形CDE的面积为8平方厘米,并且 $AE=2EC$,$AD: DB=2:3$,求三角形ABC的面积。
622 |
623 | ### 练习3
624 |
625 | 如图所示,三角形ABC的面积为60平方厘米,$AD=3DB$,$AC=3AE$,求阴影部分三角形ADE的面积。
626 |
627 | ### 练习4
628 |
629 | ### 练习5
630 |
631 | ### 练习6
632 |
633 | ## 5.1.11. 容斥问题
634 |
635 | ### 热身1
636 |
637 | 如图,三角形ABC的面积为24平方厘米,并且BD=2DA,CE=3EB,DF: FC=3:2,G是DE的中点,求阴影部分三角形DFG的面积。
638 |
639 | ### 热身2
640 |
641 | 如图,在三角形ABC中,H,I,J是AB的四等分点;D,E,F,G是BC的五等分点。知$S_{△BDH}=1$,问:每一个小三角形的面积分别为多少?
642 |
643 | ### 热身3
644 |
645 | 如图,点E、F分别为四边形ABCD中AB的三等分点。点G、H为CD的三等分点。则四边形EFHG的面积占总面积的几分之几?
646 |
647 | ### 例题1
648 |
649 | 在46人的采摘活动中,只采了樱桃的有18人,既采了樱桃又采了杏的有7人,既没采樱桃又没采杏的有6人,问:只采了杏的有多少人?
650 |
651 | ### 练习1
652 |
653 | 有100名同学回答A、B两个问题,都没有回答对的有10人,答对A的有75人,答对B的有83人,两题都答对的有多少人?
654 |
655 | ### 例题2
656 |
657 | 某校参加数学竞赛的有120名男生,80名女生,参加语文竞赛的有120名女生,80名男生,己知该校总共有260名学生参加竞赛,其中75名男生两科竞赛都参加了,那么只参加数学竞赛而没有参加语文竞赛的女生有多少人?
658 |
659 | ### 练习2
660 |
661 | 育才小学画展上展出了许多幅画,其中有16幅画不是六年级的,有15幅画不是五年级的,五、六年级共展出25幅画,其他年级的画共有多少幅?
662 |
663 | ### 例题3
664 |
665 | 50名学生面向老师站成一行,老师先让大家从左到右按1,2,3,⋯,依次报数,再让报数是4的倍数的同学向后转,接着又让报数是6的倍数的同学向后转,问:此时还有多少同学面向老师?
666 |
667 | ### 练习3
668 |
669 | 五年级一班有45名同学上体育课,他们在操场上排成一排面向教师,并从1到45报完数后,教师叫报偶数的人向后转,接着叫报3的倍数的人向后转,则这时面向教师的学生有多少人?
670 |
671 | ### 例题4
672 |
673 | 有2008盏亮着的电灯,各有一个拉线开关控制着。现将其顺序编号为1,2,3,⋯,2008。将编号为2的倍数的灯线拉一下,再将编号为3的倍数的灯线拉一下,最后将编号为5的倍数的灯线拉一下,拉完后还有几盏灯是亮的?
674 |
675 | ### 练习4
676 |
677 | 有1000盏亮着的电灯,各有一个拉线开关控制着。现将其顺序编号为1,2,3,⋯,1000。将编号为2的倍数的灯线拉一下,再将编号为3的倍数的灯线拉一下,最后将编号为5的倍数的灯线拉一下,拉完后还有几盏灯是亮的?
678 |
679 | ### 例题5
680 |
681 | 分母是1001的最简真分数有多少个?
682 |
683 | ### 练习5
684 |
685 | 分母是105的最简真分数有多少个?
686 |
687 | ### 例题6
688 |
689 | 一根100厘米长的木棍,从左起每隔6厘米划一个刻度,每隔7厘米划一个刻度,每隔8厘米划一个刻度,如果按刻度把木棍截断,可以截出多少段?
690 |
691 | ### 练习6
692 |
693 | 一根101厘米长的木棒,从同一端开始,第一次每隔2厘米画一个刻度,第二次每隔3厘米画一个刻度,第三次每隔5厘米画一个刻度,如果按刻度把木棒截断,那么可以截出多少段?
694 |
695 | ### 练习1
696 |
697 | 田径队的40名运动员们在训练基地进行封闭训练。其中男运动员有20名,训练长跑的运动员有15名,训练竞走的女运动员有8名,那么训练长跑的男运动员有多少名?
698 |
699 | ### 练习2
700 |
701 | 去年某年级有56人订阅过《中小学生数学学习》,其中,上半年有25名男生、15名女生订阅了该杂志,下半年有26名男生25 名女生订阅了该杂志。已知有23名男生是全年订阅,那么,只在上半年订阅了该杂志的女生有多少名?
702 |
703 | ### 练习3
704 |
705 | 200盏亮着的电灯,各有一个拉线开关控制,按排序编号为1,2,3,……,200。将编号为3的倍数的灯的拉线各拉一下,再将编号为5的倍数的灯的拉线各拉一下,拉完后不亮的灯有多少盏?
706 |
707 | ### 练习4
708 |
709 | ### 练习5
710 |
711 | ### 练习6
712 |
--------------------------------------------------------------------------------
/06-六年级.md:
--------------------------------------------------------------------------------
1 | ---
2 | title: 六年级
3 | lang: zh-CN
4 | sidebarDepth: 1
5 | ---
6 |
7 | # 六年级
8 |
9 | 待整理
10 |
--------------------------------------------------------------------------------
/README.md:
--------------------------------------------------------------------------------
1 | ## 小学奥数
2 |
3 | 课程不定期更新,点击在线查看。
4 |
5 | * [一年级(待整理)](https://www.vastxie.com/%E5%B0%8F%E5%AD%A6%E5%A5%A5%E6%95%B0/01-%E4%B8%80%E5%B9%B4%E7%BA%A7.html)
6 | * [二年级(更新中)](https://www.vastxie.com/%E5%B0%8F%E5%AD%A6%E5%A5%A5%E6%95%B0/02-%E4%BA%8C%E5%B9%B4%E7%BA%A7.html)
7 | * [三年级(更新中)](https://www.vastxie.com/%E5%B0%8F%E5%AD%A6%E5%A5%A5%E6%95%B0/03-%E4%B8%89%E5%B9%B4%E7%BA%A7.html)
8 | * [四年级(更新中)](https://www.vastxie.com/%E5%B0%8F%E5%AD%A6%E5%A5%A5%E6%95%B0/04-%E5%9B%9B%E5%B9%B4%E7%BA%A7.html)
9 | * [五年级(更新中)](https://www.vastxie.com/%E5%B0%8F%E5%AD%A6%E5%A5%A5%E6%95%B0/05-%E4%BA%94%E5%B9%B4%E7%BA%A7.html)
10 | * [六年级(待整理)](https://www.vastxie.com/%E5%B0%8F%E5%AD%A6%E5%A5%A5%E6%95%B0/06-%E5%85%AD%E5%B9%B4%E7%BA%A7.html)
11 |
12 | 课程计划包含:
13 |
14 | * 热身
15 | * 例题 + 练习
16 | * 巩固
17 | * 拓展
18 |
19 | 课程内容来自本人上课讲义,有一些地方排版比较乱,讲次内容也有缺失,后续会逐步更新完善。
20 |
21 | 本课程仅供学习交流使用,希望对你有所帮助。
22 |
--------------------------------------------------------------------------------
2413 |
2414 | ### 例题2
2415 |
2416 | “12345678910111213…282930”是一个位数很多的多位数,从中划去40个数字,使剩下的数字(顺序不变)组成一个首位不为0的多位数,则这个多位数最大为多少?
2417 |
2418 | ### 练习2
2419 |
2420 | “12345678910111213…282930”是一个位数很多的多位数,从中划去40个数字,使剩下的数字(顺序不变)组成一个首位不为0的多位数,则这个多位数最小为多少?
2421 |
2422 | ### 例题3
2423 |
2424 | 某次考试共有15题。计分标准是:做对第1题得1分,做对第2题得2分,……,做对第15题得15分。若做错第1题则要倒扣1分,做错第2题要倒扣2分,……,做错第15题要倒扣15分。小明做了所有的题,得90分,那么小明至多做错多少道题?
2425 |
2426 | ### 练习3
2427 |
2428 | 某次考试共有15题。计分标准是:做对第1题得1分,做对第2题得2分,……,做对第15题得15分。若做错第1题则要倒扣1分,做错第2题要倒扣2分,……,做错第15题要倒扣15分。小明做了所有的题,得90分,那么小明至多做错多少道题?
2429 |
2430 | ### 例题4
2431 |
2432 | 阶梯教室座位有10排,每排有16个座位,当有150个人就座时,某些排坐着的人数就一样多。我们希望人数一样的排数尽可能少,这样的排数至少有多少排?
2433 |
2434 | ### 练习4
2435 |
2436 | 学校203教室座位有5排,每排有8个座位,当有30个人就座时,某些排坐着的人数就一样多。我们希望人数一样的排数尽可能少,这样的排数至少有多少排?
2437 |
2438 | ### 例题5
2439 |
2440 | 如图,牧羊人用15段每段长2米的篱笆,一面靠墙围成一个长方形羊圈,则羊圈的最大面积是多少平方米?
2441 |
2442 | 
2443 |
2444 | ### 练习5
2445 |
2446 | 某校准备用一道长36米的铁丝网,围成一块长方形生物实验基地,这块基地的面积最大是多少平方米?
2447 |
2448 | ### 例题6
2449 |
2450 | 如图,一个长方形被分成4个小长方形,其中长方形A、B、C的周长分别是10厘米、12厘米、14厘米,那么长方形D的面积最大是多少平方厘米?
2451 |
2452 | 
2453 |
2454 | ### 练习6
2455 |
2456 | 一块长方形菜地被分成4个小块,其A、B、C块的周长分别是20厘米、24厘米、28厘米那么D的面积最大是多少平方厘米?
2457 |
2458 | 
2459 |
2460 | ## 4.2.15. 操作类智巧趣题
2461 |
2462 | ### 例题1
2463 |
2464 | 一个猎户,带着一条狗,一只兔子和一筐胡萝卜乘船过河,船小一次只能带一样东西。但是他不在时,狗会咬兔子,免子会吃胡萝卜。请你想一想,帮猎人安排合理的方法过河。
2465 |
2466 | ### 练习1
2467 |
2468 | 一个农民携带一只狼、一只羊和一棵白菜,要借助一条小船过河。小船上除了农民只能再带狼、羊、白菜中的一样。而农民不在时,狼会吃羊,羊会吃白菜。农民如何过河呢?
2469 |
2470 | ### 例题2
2471 |
2472 | 小枫带着他的三个馋嘴弟弟和一个大蛋糕过河,已知只有小枫会划船,且除了小枫外每次只能带其中的一个弟弟,或者蛋糕过河。蛋糕一共十块,只要小枫离开,单独留弟弟和蛋糕在一起,每个弟弟在下次见到哥哥之前都会吃掉一块蛋糕。假设除弟弟外的任何原因都不会导致蛋糕减少,请问,兄弟4人全部过河后,最多还能剩下块蛋糕。
2473 |
2474 | ### 练习2
2475 |
2476 | 河左边有一个大人和两个小孩,一只大熊和两只小熊。只有大熊、大人会划船,船一次最多只能运两个单位(不管人熊),条件是熊的数量不能大于人的数量(不分大小),要不然熊会把人吃掉(河的两边熊的数量都不能大于人的数量)。问怎么才能让人和熊安全渡河?
2477 |
2478 | ### 例题3
2479 |
2480 | 一大一小两个油桶,大桶盛满重11千克,小桶盛满重4千克。现要盛5千克的油,只用这两个桶盛,能办到吗?
2481 |
2482 | ### 练习3
2483 |
2484 | 小红去河边打水,她有两个桶,大桶能装9升水,小桶能装4升水,想要恰好从河中打上6升的水带回去,她该怎么办?
2485 |
2486 | ### 例题4
2487 |
2488 | 卖牛奶人有两桶10升装的牛奶。两个顾客各带容器去买2升牛奶,一个带的是5升的容器,另一个带的是4升的容器。这位卖牛奶人如何解决问题?
2489 |
2490 | ### 练习4
2491 |
2492 | 有大、中、小3个水桶,最多分别可装入水10千克、7千克和3千克。现在大桶中装满水,希望通过水在3个瓶子间的流动使得中瓶和小瓶上标出装1千克水的刻度线,聪明的你想想应该怎么倒呢?
2493 |
2494 | ### 例题5
2495 |
2496 | 有9个铁球,其中8个铁球一样重,另一个较轻,你要在天平上至少称几次才能保证把那个轻球找出来?
2497 |
2498 | ### 练习5
2499 |
2500 | 有3个铁球,其中2个铁球一样重,另一个较轻,你在天平上至少称几次能保证把那个轻球找出来?
2501 |
2502 | ### 例题6
2503 |
2504 | 今有101枚硬币,其中有100枚同样的真币和1枚伪币,伪币与真币的重量不同。现需弄清楚伪币究竟比真币轻,还是比真币重,但只有一架没有砝码的天平。那么怎样利用这架天平称两次,来达到目的?
2505 |
2506 | ### 练习6
2507 |
2508 | 现有21枚硬币,其中有20枚同样的真币和1枚伪币,伪币与真币重量不同。现需弄清楚伪币究竟比真币轻,还是比真币重,但只有一架没有砝码的天平。那么怎样利用这架天平称两次,来达到目的?
2509 |
2510 | ### 练习1
2511 |
2512 | 一个猎人要带一棵红萝卜,一只狗,两只老虎和一只羊过河。可现在,小船只有3个座位,猎人每次最多只能送两样东西过河。没有狗看管,老虎会吃羊;没有人看管,狗和羊就吵架,羊就会吃红萝卜。有什么妙计能帮助它们全都过河?
2513 |
2514 | ### 练习2
2515 |
2516 | 相传汉代军事家韩信一天访友归来 ,途中经过一集市,遇见卖油翁与顾客争执。买者想买5斤油,而卖者无法计量,因而告诉买者, 要么买3斤,要么买7斤。韩信询问得知,卖油翁油篓中恰好装有10斤油,但他仅有装3斤和7斤的葫芦,而买者执意要买5斤油。韩信立在马上稍加思索道:“你们无须再争,以我之法保你们都满意。”韩信下马经过几次倒油,买卖双方皆大欢喜。你知道,韩信是怎么倒油吗?
2517 |
2518 | ### 练习3
2519 |
2520 | 在一批产品中有16个零件,其中有一个是次品,比较轻(其它零件一样重) , 给你一架天平,你最少用天平称量
2521 | 几次就可以检验出次品零件?
2522 |
2523 | ## 4.2.17. 相遇追及综合
2524 |
2525 | ### 例题1
2526 |
2527 | 如图,周长为800米的环形跑道上,田田和阿普分别从相距200米的A、B两处同时沿相同方向出发。田田每分钟能跑200米,阿普每分钟只能跑150米,田田第一次追上阿普需要多少分钟?
2528 |
2529 | 
2530 |
2531 | ### 练习1
2532 |
2533 | 如图,周长为400米的环形跑道上田田和阿普分别从相距100米的A、B两处同时沿相同方向出发。田田每分钟能跑200米,阿普每分钟只能跑150米,田田第一次追上阿普需要多少分钟?
2534 |
2535 | 
2536 |
2537 | ### 例题2
2538 |
2539 | 如图,田田和阿普分别从周长为1200米的圆形跑道上相距600米的A、B两处同时出发相向而行。6分钟后两人相遇。相遇后两人继续行进,4分钟后田田怡好到达B处,问两人相遇的地点距离A点多少米?
2540 |
2541 | 
2542 |
2543 | ### 练习2
2544 |
2545 | 如图,田田和阿普分别从周长600米的圆形跑道上相距300米的A、B两处同时出发相向而行,6分钟后两人相遇。相遇后两人继续行进,4分钟后田田怡好到达B处,求两人相遇的地点距离A点多少米?
2546 |
2547 | 
2548 |
2549 | ### 例题3
2550 |
2551 | 一列从西向东行驶的火车车速为每秒16米,车身长255米,8点整它追上了在铁路旁从西向东散步的田田,并于17秒后离开了他,又过了5分钟,它与从东向西散步的阿普相遇,15秒后离开了他。请问田田和阿普步行的速度分别是多少?
2552 |
2553 | ### 练习3
2554 |
2555 | 一列从西向东行驶的火车车速为每秒19米,车身长360米。9点整它追上了在铁路旁从西向东散步的田田,并于20秒后离开了她。又过了5分钟,它与从东向西散步的阿普相遇18秒后离开了他。请问田田和阿普步行的速度分别是多少?
2556 |
2557 | ### 例题4
2558 |
2559 | 田田以6米/秒的速度在铁路旁骑车,一列火车迎面开来,与她从相遇到离开共用了15秒,而它追上在铁路旁以4米/秒的速度跑步的阿普并刚好超过他共用了25秒,求火车的长度和行驶的速度。
2560 |
2561 | ### 练习4
2562 |
2563 | 田田以5米/秒的速度在铁路旁骑车,一列火车迎面开来,与她从相遇到离开共用了10秒,而它追上在铁路旁以3米/秒的速度跑步的阿普并刚好超过他共用了20秒,求火车的长度和行驶的速度。
2564 |
2565 | ### 例题5
2566 |
2567 | 某河上下游两港相距100千米,每天定时有甲乙两艘船速相等的客轮从两港相向而行,甲船顺水每小时行12千米,乙船逆水每小时行8千米,这天甲船在出发时,从船上掉下一物,此物顺水漂流而下,当甲乙两船相遇时,此物距相遇地点有多远?
2568 |
2569 | ### 练习5
2570 |
2571 | 某河上下游两港相距60千米,每天定时有甲乙两艘船速相等的客轮从两港相向而行,甲船顺水每小时行11千米,乙船逆水每小时行9千米,这天甲船在出发时,从船上掉下一物,此物顺水漂流而下,当甲乙两船相遇时,此物距相遇地点有多远?
2572 |
2573 | ### 例题6
2574 |
2575 | 某河上下游两港相距150千米,每天有甲乙两艘船分别从上游和下游同时相向而行,它们在静水中的速度分别为6千米/时和9千米/时。平时它们相遇于距上游港70千米处,某日突下暴雨,水速变为原来的2倍,这一天甲乙两船相遇地点距上游港多远?
2576 |
2577 | ### 练习6
2578 |
2579 | 某河上下游两港相距130千米,每天有甲乙两艘船分别从上游和下游同时相向而行,它们在静水中的速度分别为5千米/时和8千米/时。平时它们相遇于距上游港60千米处。某日突下暴雨,水速变为原来的2倍,这一天甲乙两船相遇地点距上游港多远?
2580 |
2581 |
2582 |
2583 | ## 方程与方程组
2584 |
2585 | ### 例题练习
2586 |
2587 | 【例题1】解下列一元一次方程:
2588 |
2589 | (1)$6(3+x)=24$
2590 |
2591 | (2)$18-(3x-6)=x$
2592 |
2593 | 答案:(1)1;(2)6
2594 |
2595 |
2596 |
2597 | 【练习1】解下列一元一次方程:
2598 |
2599 | (1)$3x-2(2+x)=1$
2600 |
2601 | (2)$6x-(4-x)=17$
2602 |
2603 |
2604 |
2605 | 【例题2】用代入消元法解方程组:
2606 |
2607 | (1)$\begin{cases}
2608 | y=2x-3\\
2609 | 3x+2y=8
2610 | \end{cases}$
2611 |
2612 |
2613 |
2614 | (2)$\begin{cases}
2615 | 2x-y=5\\
2616 | 3x+4y=13
2617 | \end{cases}$
2618 |
2619 |
2620 |
2621 | 【练习2】用代入消元法解方程组:
2622 |
2623 | (1)$\begin{cases}
2624 | 3x+2y=13\\
2625 | 2x-y=4
2626 | \end{cases}$
2627 |
2628 |
2629 |
2630 | 【例题3】用加减消元法解下列方程组:
2631 |
2632 | (1)$\begin{cases}
2633 | x-y=5\\
2634 | x+y=13
2635 | \end{cases}$
2636 |
2637 |
2638 |
2639 | (2)$\begin{cases}
2640 | 2x+y=11\\
2641 | 3x-2y=6
2642 | \end{cases}$
2643 |
2644 |
2645 |
2646 | (3)$\begin{cases}
2647 | 5y+z=12\\
2648 | 6y+5z=22
2649 | \end{cases}$
2650 |
2651 |
2652 |
2653 | 【练习3】用加减消元法解下列方程组:
2654 |
2655 | (1)$\begin{cases}
2656 | x+2y=21\\
2657 | 2x+y=18
2658 | \end{cases}$
2659 |
2660 |
2661 |
2662 | (2)$\begin{cases}
2663 | 7x+3y=44\\
2664 | 11x-2y=49
2665 | \end{cases}$
2666 |
2667 |
2668 |
2669 | (3)$\begin{cases}
2670 | 7x+3y=44\\
2671 | 11x+2y=61
2672 | \end{cases}$
2673 |
2674 |
2675 |
2676 | 【例题4】解方程组:
2677 |
2678 | (1)$\begin{cases}
2679 | 2x-3y=x+y-4\\
2680 | 3x+4y=x+5y+13
2681 | \end{cases}$
2682 |
2683 |
2684 |
2685 | (2)$\begin{cases}
2686 | 3x+5y=2x+3y+11\\
2687 | 4x-y-6=x+2y
2688 | \end{cases}$
2689 |
2690 |
2691 |
2692 | 【练习4】解方程组:
2693 |
2694 | (1)$\begin{cases}
2695 | a-1=b+1\\
2696 | a+1=3(b-1)
2697 | \end{cases}$
2698 |
2699 |
2700 |
2701 | 【例题5】解方程组:
2702 |
2703 | (1)$\begin{cases}
2704 | x+y=9\cdots①\\
2705 | y+z=15\cdots②\\
2706 | z+x=12\cdots③
2707 | \end{cases}$
2708 |
2709 |
2710 |
2711 | (2)$\begin{cases}
2712 | x+2y=11\cdots①\\
2713 | 3x+z=19\cdots②\\
2714 | z=x+y\cdots③
2715 | \end{cases}$
2716 |
2717 |
2718 |
2719 | 【练习5】解方程组:
2720 |
2721 | (1)$\begin{cases}
2722 | 2x+y+z=7\\
2723 | x+2y+z=8\\
2724 | x+y+2z=9
2725 | \end{cases}$
2726 |
2727 |
2728 |
2729 | 【例题6】购买3斤苹果,2斤橘子需要6.90元;购买8斤苹果,9斤橘子需要22.80元,那么苹果、橘子各买1斤需要多少元?
2730 |
2731 |
2732 |
2733 | 【练习6】已知:$\begin{cases}
2734 | 3x+6y=17\\
2735 | 7x+4y=13
2736 | \end{cases}$,求$x+y=$()。
2737 |
2738 |
2739 |
2740 |
--------------------------------------------------------------------------------
/05-五年级.md:
--------------------------------------------------------------------------------
1 | ---
2 | title: 五年级
3 | lang: zh-CN
4 | sidebarDepth: 1
5 | ---
6 |
7 | # 五年级
8 |
9 | ## 5.1.03. 棋盘中的数学
10 |
11 | 间隔染色,用间隔染色解决问题。
12 |
13 | 思想:构造模型,用模型解决实际问题。
14 |
15 | ### 热身1
16 |
17 | ### 热身2
18 |
19 | ### 热身3
20 |
21 | ### 例题1
22 |
23 | 有一次车展共16个展室,如图,每个展室与相邻的展室都有门相通,出口和入口如图中箭头所示。
24 | (1)参观者能否从入口进去,不重复地参观完每个展室再从出口出来?
25 | (2)参观者能否从入口进去,不重复地参观完每个展室再从入口出来?
26 |
27 | ### 练习1
28 |
29 | 有一栋大厦共3✕3✕3=27间房子,每个房间与相邻的房间都有直达电梯,入口和出口如下
30 | 图所示。
31 | (1)参观者能否从入口进去,不重复地参观完每个展室再从出口出来?
32 | (2)参观者能否从入口进去,不重复地参观完每个展室再从入口出来?
33 |
34 | ### 例题2
35 |
36 | (1)左图是连接14个城市的道路图,是否有一条路线可以经过每一个城市怡好一次?
37 | (2)右图中是半张中国象棋棋盘,棋盘上放有一只马。众所周知,马是走“日”字路线的。请问:这个马能否不重复地走遍这半张棋盘上的每一个点,然后回到出发点?
38 |
39 | ### 练习2
40 |
41 | 五年级一班有35名同学,共分成5排,每排7人,坐在教室里,每个座位的前后左右四个位置都叫作他的邻座。如果要让这35名同学每个人都恰好坐到他的邻座上去,能办到吗?为什么?
42 |
43 | ### 例题3
44 |
45 | 下面三个图形都是从4✕4的正方形分别剪去两个1✕1的小方格得到的,问:可否把它们分别剪成1✕2的七个小矩形?
46 |
47 | ### 练习3
48 |
49 | 如图所示,一个8✕8的国际象棋棋盘去掉对角上两格后,是否可以用31个2✕1的“骨牌”把棋盘上的62个小格完全盖住?
50 |
51 | ### 例题4
52 |
53 | 如图所示,有一个6✕6的棋盘,请问:能否用1个和8个填满这个棋盘? (图形可以旋转和翻折)
54 |
55 | ### 练习4
56 |
57 | 如图所示,有一个6✕6的棋盘,请问:能否用3个和6个填满这个棋盘? (图形可以旋转和翻折)
58 |
59 | ### 例题5
60 |
61 | 如图所示,有一个6✕6的棋盘,请问:
62 |
63 | (1)能否用9个填满这个棋盘?
64 |
65 | (2)能否用9个填满这个棋盘?(图形可以旋转)
66 |
67 | (3)能否用9个填满这个棋盘?(图形可以旋转)
68 |
69 | ### 练习5
70 |
71 | ### 例题6
72 |
73 | ### 练习6
74 |
75 | ### 巩固1
76 |
77 | ### 巩固2
78 |
79 | ### 巩固3
80 |
81 | ## 5.1.04. 课程标题
82 |
83 | ### 热身1
84 |
85 | ### 热身2
86 |
87 | ### 热身3
88 |
89 | ### 例题1(有序数对)
90 |
91 | (1)将6块糖全部分给丁丁、田田、阿普三个人,每个人都要分到糖,那么一共有几种分法?
92 |
93 | (2)丁丁有14块糖,从第一天开始吃,每天至少吃2颗,至多吃6颗,第三天吃完,有几种吃法?
94 |
95 | ### 练习1
96 |
97 | 田田、牛牛、阿普三个人一共有7本课外书,每个人至少有一本。田田、牛牛、阿普分别有几本课外书?请写出全部可能的情况。
98 |
99 | ### 例题2
100 |
101 | (1)将10个小球分成两堆,有几种分法?
102 |
103 | (2)将10个小球分成三堆,有几种分法?
104 |
105 | (3)将18个小球分成三堆,每堆至少2个,至多9个,有几种分法?
106 |
107 | ### 练习2
108 |
109 | 将11拆成三个不同的正整数相加的形式,加数相同顺序不同看作同一种形式,例如:11=2+3+6与11=3+6+2看作同一种形式。问:有几种可能的形式?
110 |
111 | ### 例题3
112 |
113 | 周长为15厘米,三边长都是整数厘米的三角形有几个?(通过旋转、翻折、平移能重合的三角形视为同一个三角形)
114 |
115 | ### 练习3
116 |
117 | 三条边的边长均为整数,且最长边的边长是7厘米,这样的三角形共有多少种?
118 |
119 | ### 例题4
120 |
121 | 从1、2、3、4、5、6、7中选取三个不同的数,使得它们的和为3的倍数,有几种不同的选法?
122 |
123 | ### 练习4
124 |
125 | 从1-50这50个自然数中选取两个数,使它们的和大于50,共有多少种不同的选法?
126 |
127 | ### 例题5
128 |
129 | 甲、乙两人进行乒乓球比赛,规定谁先胜三场谁胜,第一场甲胜。问:到决出最后胜负为止,有多少种可能的情形?其中甲胜的情形有几种?
130 |
131 | ### 练习5
132 |
133 | 如图,给1、2、3、4号区域染上红、蓝、紫三种颜色,每块区域染一种颜色,并且使得相邻两块区域的颜色不同,有几种染法?
134 |
135 | 
136 |
137 | ### 例题6
138 |
139 | 如图,从起点到终点,只能沿着图中线段走。
140 |
141 | (1)所有点恰好经过一次,有几种走法?
142 |
143 | (2)所有点至多经过一次,有几种走法?
144 |
145 | (2)不能走重复路线(能走重复点),有几种走法?
146 |
147 | 
148 |
149 | ### 练习6
150 |
151 | 如图,从点A出发,沿着线段走,最后到达点B。
152 |
153 | (1)如果每个黑点恰好经过一次,有几种走法?
154 |
155 | (2)如果每个黑点至多经过一次,有几种走法?
156 |
157 | 
158 |
159 | ### 拓展1
160 |
161 | ### 拓展2
162 |
163 | ### 拓展3
164 |
165 | ### 拓展4
166 |
167 | ### 拓展5
168 |
169 | ### 练习1
170 |
171 | ### 练习2
172 |
173 | ### 练习3
174 |
175 | ### 练习4
176 |
177 | ### 练习5
178 |
179 | ### 练习6
180 |
181 | ## 5.1.05. 排列组合
182 |
183 | ### 例题1
184 |
185 | (1)从A、B、C、D、E这5个小朋友中选3名站成一排拍照。我们分步骤来思考这个问题:
186 |
187 | 第一步,选一个人站第一个位置,有()种选法;
188 |
189 | 第二步,选一个人站第二个位置,有()种选法;
190 |
191 | 第三步,选一个人站第三个位置,有()种选法。
192 |
193 | 根据乘法原理,完成三步有()×()×()种方法,用排列数可以表示为$A_5^3$。
194 |
195 | (2)计算:
196 |
197 | | $A_4^2=$ | $A_5^3=$ | $A_6^3=$ |
198 | | -------------- | -------------------- | ----------------------------------- |
199 | | $A_5^4=$ | $A_{10}^{10}=$ | $A_6^2-A_2^2=$ |
200 | | $A_8^4+A_6^2=$ | $A_7^2\times A_5^3=$ | $\frac{A_{100}^{98}}{A_{98}^{98}}=$ |
201 |
202 | ### 练习1
203 |
204 | (1)从7名学生中,安排3名学生分别扫地、拖地、倒垃圾,有几种安排方法?
205 |
206 | (2)计算:
207 |
208 | | $A_5^2=$ | $A_6^4=$ |
209 | | ---------------------- | ---------------------- |
210 | | $\frac{A_8^5}{A_5^5}=$ | $\frac{A_9^5}{A_4^4}=$ |
211 |
212 | ### 例题2
213 |
214 | 从A、B、C、D、E这5个小朋友中选出3名小朋友,有$C_5^3$种方法,再将选出的3名小朋友排成一排,有$A_3^3$种方法。因此,先选再排这两步有$C_5^3\times A_3^3$种方法,应该与$A_5^3$相等,所以$C_5^3=\frac{A_5^3}{A_3^3}=\frac{5\times4\times3}{3\times2\times1}$
215 | 仿照此例:
216 |
217 | 计算:
218 |
219 | (1)$C_6^2, C_6^4$
220 |
221 | (2)$C_7^2, C_7^5$
222 |
223 | ### 练习2
224 |
225 | 计算:
226 |
227 | | (1)$C_{12}^3$ | (2)$C_{1000}^{998}$ | (3)$A_8^2-C_8^2$ |
228 | | --------------- | --------------------- | ------------------ |
229 |
230 | ### 例题3
231 |
232 | 有4个同学一起去郊游,照相时,必须有一名同学给其他3人拍照,共可能有多少种拍照情況?(照相时3人站成一排)
233 |
234 | ### 练习3
235 |
236 | 6个人排成一排,有几种排法?
237 |
238 | ### 例题4
239 |
240 | 五名学生和一名老师排队拍照,老师不能站在两边,有几种排法?
241 |
242 | ### 练习4
243 |
244 | 5个人并排站成一排,其中甲必须站在中间,有几种不同的站法。
245 |
246 | ### 例题5
247 |
248 | (1)从1、2、3、4、5、6、7、8中选出3个数,使得3个数的和是偶数,有几种选法?
249 | (2)从1、2、3、4、5、6、7、8中选出3个数,使得3个数的乘积是偶数,有几种选法?
250 |
251 | ### 练习5
252 |
253 | 田田要从八门课程中选学三门,一共有多少种选法?如果数学课与钢琴课时间冲突,不能同时学,她一共有多少种选法?
254 |
255 | ### 例题6
256 |
257 | 一个小组有10个人,其中6个人会唱歌,4个人会跳舞,回答下列问题:
258 | (1)选出4个人表演唱歌,3个人表演跳舞,有几种选法?
259 | (2)后来又来了一个人既会唱歌,又会跳舞。要选出4个人表演跳舞,3个人表演唱歌,有几种选法?
260 |
261 | ### 练习6
262 |
263 | 学校举办联欢晚会,要从6名数学老师中选出3名,再从4名语文老师中选出2名,接着让这5名老师分别扮演5个不同的角色,共有多少种选择方式?
264 |
265 | ## 5.1.06. 质数与合数进阶
266 |
267 | ### 例题1
268 |
269 | 当$p$和$p^5+5$都是质数时,求$p^5+5$的值。
270 |
271 | ### 练习1
272 |
273 | 如果$a$、$b$均为质数,且$3a+7b=41$,求$a+b$的值。
274 |
275 | ### 例题2
276 |
277 | $a$、$b$、$c$均为质数,如果$(a+b)\times(b+c)=342$,那么$b$是几。
278 |
279 | ### 练习2
280 |
281 | 在算式$a\times(b+c)=110+c$中,$a$、$b$、$c$是三个互不相等的质数,那么$b$是几。
282 |
283 | ### 例题3
284 |
285 | 有三张卡片,在它们上面各写有一个数字1、2、3(如下图)。从中抽出一张、二张、三张,按任意次序排起来,可以得到不同的一位数、二位数、三位数。请你将其中的质数都写出来?
286 |
287 | ### 练习3
288 |
289 | 自然数$n$是一个两位数,它是一个质数,而且$n$的个位数字与十位数字都是质数,这样的自然数有多少个?
290 |
291 | ### 例题4
292 |
293 | 4只同样的瓶子内分别装有一定数量的油。每瓶和其他各瓶分别合称一次,记录千克数如下:8,9,10,11,12,13。已知4只空瓶的重量之和以及油的重量之和均为质数,问:最重的两瓶内有多少油?
294 |
295 | ### 练习4
296 |
297 | 有一个正方体木块,如图,每个面上各写了一个自然数,并且相对的两个面上的两个数之和相等。现在只能看见三个面上写的数,如果看不见的各个面写的都是质数,问:这三个质数的和是多少?
298 |
299 | ### 例题5
300 |
301 | 已知三个合数$a$、$b$、$c$两两互质,且$a\times b\times c=1001\times28\times11$,问:$a+b+c$的最小值是几?
302 |
303 | ### 练习5
304 |
305 | 6个奇数的和为98,积为4267305,这6个奇数中最大数与最小数的和是几?
306 |
307 | ### 例题6
308 |
309 | 将一个三位数的个位数字与百位数字对调位置,得到一个新的三位数,已知这两个三位数的乘积等于55872,那么,这两个三位数的和为多少?
310 |
311 | ### 练习6
312 |
313 | 如果两位数$\overline{吃好}$和$\overline{好吃}$都为质数,则这两个质数和的最大值是多少?
314 |
315 | ### 拓展1
316 |
317 | ### 拓展2
318 |
319 | ### 拓展3
320 |
321 | ### 拓展4
322 |
323 | ### 拓展5
324 |
325 | ## 5.1.07. 牛吃草问题
326 |
327 | ### 例题1
328 |
329 | 牧场上长满牧草,每天牧草都匀速生长。这片牧场可供27头牛吃6天,可供23头牛吃9天。那么,可供21头牛吃几天?
330 |
331 | ### 练习1
332 |
333 | 有一块匀速生长的草场,可供12头牛吃25天,或可供24头牛吃10天。那么可供29头牛吃几天?
334 |
335 | ### 例题2
336 |
337 | 牧场上长满牧草,每天牧草都匀速生长。这片牧场可供10头牛吃20天,可供15头牛吃10天。那么这片牧场可供几头牛吃25天?
338 |
339 | ### 练习2
340 |
341 | 有一片牧场,草每天都在均匀地生长。如果在牧场上放养24头牛,那么6天就把草吃完了;如果只放养21头牛,那么8天才把草吃完。请问:要使得草永远吃不完,最多可以放养多少头牛?
342 |
343 | ### 例题3
344 |
345 | 林子里有猴子喜欢吃的野果,23只猴子可在9周内吃光,21只猴子可在12周内吃光,问:如果要4周吃光野果,则需有多少只猴子一起吃?(假设野果生长的速度不变)
346 |
347 | ### 练习3
348 |
349 | 仓库里原有一批存货,以后继续运货进仓,且每天运进的货一样多。用同样的汽车运货出仓,如果每天用4辆汽车,则9天恰好运完;如果每天用5辆汽车,则6天恰好运完。仓库里原有的存货若用1辆汽车运,则需要多少天运完?
350 |
351 | ### 例题4
352 |
353 | 一个水池有一根进水管不间断地进水,还有若干根相同的抽水管。若用24根抽水管抽水,6小时即可把池中的水抽干;若用21根抽水管抽水,8小时可把池中的水抽干。若用16根抽水管,需要多少小时可把水池中的水抽干?
354 |
355 | ### 练习4
356 |
357 | 一个装满了水的水池有一个进水阀及三个口径相同的排水阀,如果同时打开进水阀及一个排水阀,则30分钟能把水池的水排完,如果同时打开进水阀及两个排水阀,则10分钟把水池的水排完。问:关闭进水阀并且同时打开三个排水阀,需要多少分钟能排完水池的水?
358 |
359 | ### 例题5
360 |
361 | 由于天气逐渐变冷,牧场上的草每天以均匀的速度减少。经计算,牧场上的草可供20头牛吃5天,或可供16头牛吃6天。那么,可供11头牛吃几天?
362 |
363 | ### 练习5
364 |
365 | 由于天气逐渐冷起来,牧场上的草不仅不生长,反而以固定的速度在减少。已知某块草地上的草可供20头牛吃5天,或可供15头牛吃6天。照此计算,可供多少头牛吃10天?
366 |
367 | ### 例题6
368 |
369 | 有一片草场,草每天的生长速度相同。若14头牛30天可将草吃完,70只羊16天也可将草吃完(4只羊1天的吃草量相当于1头牛1天的吃草量)。那么,17头牛和20只羊多少天可将草吃完?
370 |
371 | ### 练习6
372 |
373 | 农场有一片均匀生长的草地,可以供18头牛吃40天,或者供12头牛与36只羊吃25天,如果1头牛每天的吃草量相当于3只羊每天的吃草量。请问:这片草地让17头牛与多少只羊一起吃,刚好16天吃完?
374 |
375 | ## 5.1.08. 数阵图综合
376 |
377 | ### 例题1
378 |
379 | 将1到7,这七个数字,分别填入图中各个〇内,使每条线段上的三个〇内数的和都相等。
380 |
381 | ### 练习1
382 |
383 | 把1,4,7,10,13,16,19七个数填入图中7个圆圈中,使每条线上三个数的和都等手30。
384 |
385 | ### 例题2
386 |
387 | 把1~11填入图中,使每条线上三个数的和相等。
388 |
389 | ### 练习2
390 |
391 | 把1~9这9个数分别填入下图的圆圈中,使得每条直线上的3个数的和都相等。
392 |
393 | ### 例题3
394 |
395 | 把1至6分别填入下图的六个园圈内,使得每个正方形四个顶点的数之和都为13。
396 |
397 | ### 练习3
398 |
399 | 在图中的八个圆圈内分别填入八个不同的自然数,使得正方形每条边上三个数的和相等。现在如果已经填好了五个数,那么每条边上各数之和应该是多少?并将其补充完整。
400 |
401 | ### 例题4
402 |
403 | 图中共有10个圆圈,6条直线。请问:
404 |
405 | (1)能否将1~10填入图中,使得每条直线上各数之和都相等?
406 |
407 | (2)能否将0~9填入图中,使得每条直线上各数之和都相等?
408 |
409 | ### 练习4
410 |
411 | 将11至16六个数填入图中所示球体的圈内,使球体的各个大圆上每四个数的和都相等。这个和是多少?
412 |
413 | ### 例题5
414 |
415 | 如下图,大大小小的三角形共7个,把1~9这九个数分别填入图中的“〇”中,使每个三角形三个顶点的数之和相等。求AxBxC的最大值?
416 |
417 | ### 练习5
418 |
419 | 如图,大三角形被分成了9个小三角形。试将1,2,3,4,5,6,7,8,9分别填入这9个小三角形内,每个小三角形内填一个数,要求靠近大三角形3条边的每5个数的和相等,问:这5个数的和最大可能是多少?
420 |
421 | ### 例题6
422 |
423 | 把1~8这8个数分别填入下图的八个圆圈中,使得任意两个有线段直接相连的圆圈内的数字之差都不等于1。请问:有多少种不同的填法?
424 |
425 | ### 练习6
426 |
427 | 将1、2、3、5、6、7、9、10、11填入图中的小圆圈内,使得每条直线上各数之和都等于18。
428 |
429 | ## 5.1.09. 比和比例
430 |
431 | ### 例题1(化简比)
432 |
433 | (1)把$12:16$化成最简整数比是();
434 |
435 | (2)把$\frac{2}{5}:\frac{6}{7}$化成最简整数比是();
436 |
437 | (3)把连比$24:36:40$化成最简整数比是()。
438 |
439 | ### 练习1
440 |
441 | (1)把$48:60$化成最简整数比是();
442 |
443 | (2)把$\frac{1}{2}:\frac{4}{3}$化成最简整数比是();
444 |
445 | (3)把连比$22:33:44$化成最简整数比是()。
446 |
447 | ### 补充
448 |
449 | (1)$\frac{8+9+\dots+40}{27+28+\dots+50}$化为最简整数比是()。
450 |
451 | (2)$\frac{12!}{11!}$化为最简整数比是()。
452 |
453 | (3)$\frac{1}{3}:\frac{1}{4}:\frac{1}{5}$化为最简整数比是()。
454 |
455 | ### 例题2(解比例)
456 |
457 | 把下列比例补充完整。
458 |
459 | (1)$2:5=():30$
460 |
461 | (2)$():3:8=6:():12$
462 |
463 | ### 练习2
464 |
465 | 解比例方程。
466 |
467 | (1)$3.6:x=\frac{1}{2}:4$
468 |
469 | (2)$\frac{1}{2}:\frac{5}{6}=x:3$
470 |
471 | (3)$\frac{7x-10}{3x+5}=\frac{6}{5}$
472 |
473 | ### 例题3
474 |
475 | 解比例方程:$(3x-2):(2x+3)=4:7$
476 |
477 | ### 练习3
478 |
479 | 解比例方程:$4:(5x-1)=12:(10x+7)$
480 |
481 | ### 补充
482 |
483 | 3、5、7、a可以组成一个比例,则a=()。
484 |
485 | ### 探索
486 |
487 | 甲、乙两数之比为$5:9$,两数之和为70,甲数是()。
488 |
489 | ### 例题4(比与份数)
490 |
491 | 田田、牛牛、丁丁他们的体重比是$2:3:4$,其中田田的体重是34千克。牛牛、丁丁的体重各是多少干克?
492 |
493 | ### 练习4
494 |
495 | 动物园里有老虎、企鹅、鸵鸟三种动物比较体重,老虎重360千克,企鹅的体重是鸵鸟的$\frac{5}{12}$,鸵鸟的体重是老虎的$\frac{4}{15}$,那么企鹅的体重是多少干克?
496 |
497 | ### 补充
498 |
499 | 甲、乙、丙三数之比为$3:7:10$,乙数比甲数多20,这三个数之和是()。
500 |
501 | ### 探索
502 |
503 | 若$A: B=2:3$,$B: C=4:5$,则 $A: B: C$的最简整数比是()。
504 |
505 | ### 例题5
506 |
507 | 已知甲、乙、丙三个数,甲等于乙、丙两数和的$\frac{1}{3}$,乙等于甲、丙两数和的$\frac{1}{2}$,丙等于甲、乙两数和的$\frac{5}{7}$,求甲:乙:丙是多少?
508 |
509 | ### 练习5
510 |
511 | 甲、乙、丙三个数,已知$甲:(乙+丙)=4:3$,$乙: 丙=2:7$,问:$甲: 乙: 丙$是多少?
512 |
513 | ### 例题6
514 |
515 | 某山区小学要栽253棵松树,分给三个年级。六年级分到的$\frac{1}{5}$等于五年级分到的$\frac{1}{4}$,又等于四年级分到的$\frac{1}{2}$,三个年级各分到多少棵?
516 |
517 | ### 练习6
518 |
519 | 加工一个零件,甲要2分钟,乙要3分钟,丙要4分钟。现有1170个零件,甲、乙、丙三人各加工几个零件,才能使他们同时完成任务?
520 |
521 | ### 拓展
522 |
523 | ### 拓展1
524 |
525 | 判断这组数字能否组成比例,如果能,请列出比例式。
526 |
527 | $\frac{5}{2}$,14,3.5,10
528 |
529 | ### 拓展2
530 |
531 | 解比例方程组。
532 | $$
533 | \left\{\begin{matrix}
534 | x:y=3:4
535 | \\
536 | 3x+5y=58
537 | \end{matrix}\right.
538 | $$
539 |
540 | ### 拓展3
541 |
542 | 解比例方程。
543 |
544 | $\frac{4x-1}{2(x+1)}=\frac{4x+7}{2x+10}$
545 |
546 | ### 拓展4
547 |
548 | 解比例方程。
549 |
550 | $\frac{x-1}{x+3}=\frac{2x-1}{2x+9}$
551 |
552 | ### 拓展5
553 |
554 | 已知$a_1:a_2=a_2:a_3=b_1:b_2=b_2:b_3=c_1:c_2=c_2:c_3$,并且$a_1$、$b_2$、$c_3$成等差数列(公差不为0),请问$(a_3\times c_2)$和 $(b_1\times b_3)$哪个更大?
555 |
556 | ## 5.1.10. 比列模型
557 |
558 | ### 例题1
559 |
560 | 如图,三角形ABC被线段AD分成两个小三角形,图中一共有三个三角形,这三个三角形有一条公共的高,因此他们的面积之比等于对应底边长度之比。即$S_{△ABD}: S_{△ADC}: S_{△ABC}=BD:DC:BC$。
561 |
562 | (1)若$BD: DC=3:2$,并且三角形ABD的面积为18平方厘米,问:三角形ADC的面积为多少?
563 |
564 | (2)若 $3BD=4DC$,并且三角形ABC的面积为84平方厘米,问:三角形ABD的面积为多少?
565 |
566 | ### 练习1
567 |
568 | 如图,三角形ABC的面积为180平方厘米,并且$BD: DE: EC=2:3:4$,问:阴影部分三角形ADE的面积?
569 |
570 | ### 例题2
571 |
572 | 如图,四边形ABCD被对角线AC,以及线段BE、DE分成四个小三角形,这四个小三角形的面积分别记为a、b、c、d,那么根据比例模型可知,$a:b=AE: EC$;$d:c=AE: EC$,所以$a:b=d:c$,根据比例性质可知$ac=bd$。
573 | (1)若三角形ABE、三角形BCE、三角形CDE的面积分别是30平方厘米、20平方厘米、10平方厘米,问:四边形ABCD的面积是多少?
574 |
575 | (2)已知四边形ABCD的面积为56平方厘米,三角形BCE、三角形CDE的面积分别为10平方厘米、6平方厘米,问:三角形ABE的面积是多少?
576 |
577 | ### 练习2
578 |
579 | 如图,己知三角形ABE的面积为18平方厘米,$AE: EC=3:4$,$BE: ED=6:5$,问:三角形ADE、三角形BCE、三角形CDE的面积?
580 |
581 | ### 例题3
582 |
583 | (1)如图,三角形ABC的面积为60平方厘米,并且$AE: EB=2:3$,$BD=2DC$,问:阴影部分三角形ADE的面积是多少平方厘米?
584 |
585 | (2)如图,三角形ABC面积为90平方厘米,$BD=2DC$,$AE: EC=2:3$,问:阴影部分三角形CDE的面积?
586 |
587 | ### 练习3
588 |
589 | 如图,正方形ABCD边长为6厘米,AE=4厘米,$AC=3AF$,G是EC的中点,求阴影部分三角形EFG的面积。
590 |
591 | ### 例题4
592 |
593 | 如图,一个边长为120厘米的等边三角形被分成了面积相等的五块,那么AB是多少厘米?
594 |
595 | ### 练习4
596 |
597 | 如图,在三角形ABC中,H,I,J是AB的四等分点;D,E,F,G是BC的五等分点。知$S_{△BDH}=1$,问:每一个小三角形的面积分别为多少?
598 |
599 | ### 例题5
600 |
601 | 如图,三角形ABC的面积为36平方厘米,并且$AC=4AD$,$BC=3EC$,$BD=3BF$,$DE=3DG$,H是EF的中点,求阴影部分三角形FGH的面积?
602 |
603 | ### 练习5
604 |
605 | 如图,三角形ABC中,$BD: DC=2:5$,$AE: EC=4:3$,三角形ABC的面积是980平方厘米,求三角形CDE的面积?
606 |
607 | ### 例题6
608 |
609 | 如图,点E、F分别为四边形ABCD中AB的三等分点。点G、H为CD的三等分点。则四边形EFHG的面积占总面积的几分之几?
610 |
611 | ### 练习6
612 |
613 | 如图,四边形ABCD中,$DE: EF: FC=3:2:1$,$BG: GH: AH=3:2:1$。$AD: BC=1:2$,已知四边形ABCD的面积等于4,求四边形EFGH的面积?
614 |
615 | ### 练习1
616 |
617 | 如图所示,四边形ABCD形状的草地里有两条路AC和BD,交于点O,三角形AOD、三角形AOB、三角形BOC的面积分别为6平方米、14平方米、35平方米,求三角形COD的面积。
618 |
619 | ### 练习2
620 |
621 | 如图所示,阴影部分三角形CDE的面积为8平方厘米,并且 $AE=2EC$,$AD: DB=2:3$,求三角形ABC的面积。
622 |
623 | ### 练习3
624 |
625 | 如图所示,三角形ABC的面积为60平方厘米,$AD=3DB$,$AC=3AE$,求阴影部分三角形ADE的面积。
626 |
627 | ### 练习4
628 |
629 | ### 练习5
630 |
631 | ### 练习6
632 |
633 | ## 5.1.11. 容斥问题
634 |
635 | ### 热身1
636 |
637 | 如图,三角形ABC的面积为24平方厘米,并且BD=2DA,CE=3EB,DF: FC=3:2,G是DE的中点,求阴影部分三角形DFG的面积。
638 |
639 | ### 热身2
640 |
641 | 如图,在三角形ABC中,H,I,J是AB的四等分点;D,E,F,G是BC的五等分点。知$S_{△BDH}=1$,问:每一个小三角形的面积分别为多少?
642 |
643 | ### 热身3
644 |
645 | 如图,点E、F分别为四边形ABCD中AB的三等分点。点G、H为CD的三等分点。则四边形EFHG的面积占总面积的几分之几?
646 |
647 | ### 例题1
648 |
649 | 在46人的采摘活动中,只采了樱桃的有18人,既采了樱桃又采了杏的有7人,既没采樱桃又没采杏的有6人,问:只采了杏的有多少人?
650 |
651 | ### 练习1
652 |
653 | 有100名同学回答A、B两个问题,都没有回答对的有10人,答对A的有75人,答对B的有83人,两题都答对的有多少人?
654 |
655 | ### 例题2
656 |
657 | 某校参加数学竞赛的有120名男生,80名女生,参加语文竞赛的有120名女生,80名男生,己知该校总共有260名学生参加竞赛,其中75名男生两科竞赛都参加了,那么只参加数学竞赛而没有参加语文竞赛的女生有多少人?
658 |
659 | ### 练习2
660 |
661 | 育才小学画展上展出了许多幅画,其中有16幅画不是六年级的,有15幅画不是五年级的,五、六年级共展出25幅画,其他年级的画共有多少幅?
662 |
663 | ### 例题3
664 |
665 | 50名学生面向老师站成一行,老师先让大家从左到右按1,2,3,⋯,依次报数,再让报数是4的倍数的同学向后转,接着又让报数是6的倍数的同学向后转,问:此时还有多少同学面向老师?
666 |
667 | ### 练习3
668 |
669 | 五年级一班有45名同学上体育课,他们在操场上排成一排面向教师,并从1到45报完数后,教师叫报偶数的人向后转,接着叫报3的倍数的人向后转,则这时面向教师的学生有多少人?
670 |
671 | ### 例题4
672 |
673 | 有2008盏亮着的电灯,各有一个拉线开关控制着。现将其顺序编号为1,2,3,⋯,2008。将编号为2的倍数的灯线拉一下,再将编号为3的倍数的灯线拉一下,最后将编号为5的倍数的灯线拉一下,拉完后还有几盏灯是亮的?
674 |
675 | ### 练习4
676 |
677 | 有1000盏亮着的电灯,各有一个拉线开关控制着。现将其顺序编号为1,2,3,⋯,1000。将编号为2的倍数的灯线拉一下,再将编号为3的倍数的灯线拉一下,最后将编号为5的倍数的灯线拉一下,拉完后还有几盏灯是亮的?
678 |
679 | ### 例题5
680 |
681 | 分母是1001的最简真分数有多少个?
682 |
683 | ### 练习5
684 |
685 | 分母是105的最简真分数有多少个?
686 |
687 | ### 例题6
688 |
689 | 一根100厘米长的木棍,从左起每隔6厘米划一个刻度,每隔7厘米划一个刻度,每隔8厘米划一个刻度,如果按刻度把木棍截断,可以截出多少段?
690 |
691 | ### 练习6
692 |
693 | 一根101厘米长的木棒,从同一端开始,第一次每隔2厘米画一个刻度,第二次每隔3厘米画一个刻度,第三次每隔5厘米画一个刻度,如果按刻度把木棒截断,那么可以截出多少段?
694 |
695 | ### 练习1
696 |
697 | 田径队的40名运动员们在训练基地进行封闭训练。其中男运动员有20名,训练长跑的运动员有15名,训练竞走的女运动员有8名,那么训练长跑的男运动员有多少名?
698 |
699 | ### 练习2
700 |
701 | 去年某年级有56人订阅过《中小学生数学学习》,其中,上半年有25名男生、15名女生订阅了该杂志,下半年有26名男生25 名女生订阅了该杂志。已知有23名男生是全年订阅,那么,只在上半年订阅了该杂志的女生有多少名?
702 |
703 | ### 练习3
704 |
705 | 200盏亮着的电灯,各有一个拉线开关控制,按排序编号为1,2,3,……,200。将编号为3的倍数的灯的拉线各拉一下,再将编号为5的倍数的灯的拉线各拉一下,拉完后不亮的灯有多少盏?
706 |
707 | ### 练习4
708 |
709 | ### 练习5
710 |
711 | ### 练习6
712 |
--------------------------------------------------------------------------------
/06-六年级.md:
--------------------------------------------------------------------------------
1 | ---
2 | title: 六年级
3 | lang: zh-CN
4 | sidebarDepth: 1
5 | ---
6 |
7 | # 六年级
8 |
9 | 待整理
10 |
--------------------------------------------------------------------------------
/README.md:
--------------------------------------------------------------------------------
1 | ## 小学奥数
2 |
3 | 课程不定期更新,点击在线查看。
4 |
5 | * [一年级(待整理)](https://www.vastxie.com/%E5%B0%8F%E5%AD%A6%E5%A5%A5%E6%95%B0/01-%E4%B8%80%E5%B9%B4%E7%BA%A7.html)
6 | * [二年级(更新中)](https://www.vastxie.com/%E5%B0%8F%E5%AD%A6%E5%A5%A5%E6%95%B0/02-%E4%BA%8C%E5%B9%B4%E7%BA%A7.html)
7 | * [三年级(更新中)](https://www.vastxie.com/%E5%B0%8F%E5%AD%A6%E5%A5%A5%E6%95%B0/03-%E4%B8%89%E5%B9%B4%E7%BA%A7.html)
8 | * [四年级(更新中)](https://www.vastxie.com/%E5%B0%8F%E5%AD%A6%E5%A5%A5%E6%95%B0/04-%E5%9B%9B%E5%B9%B4%E7%BA%A7.html)
9 | * [五年级(更新中)](https://www.vastxie.com/%E5%B0%8F%E5%AD%A6%E5%A5%A5%E6%95%B0/05-%E4%BA%94%E5%B9%B4%E7%BA%A7.html)
10 | * [六年级(待整理)](https://www.vastxie.com/%E5%B0%8F%E5%AD%A6%E5%A5%A5%E6%95%B0/06-%E5%85%AD%E5%B9%B4%E7%BA%A7.html)
11 |
12 | 课程计划包含:
13 |
14 | * 热身
15 | * 例题 + 练习
16 | * 巩固
17 | * 拓展
18 |
19 | 课程内容来自本人上课讲义,有一些地方排版比较乱,讲次内容也有缺失,后续会逐步更新完善。
20 |
21 | 本课程仅供学习交流使用,希望对你有所帮助。
22 |
--------------------------------------------------------------------------------