├── 00_basics
├── 00_Ndarray-Imperative-tensor-operations-on-CPU-GPU.md
├── 01_Ndarray-Indexing-Array-Indexing-Features.md
├── 02_Symbol-Neural-Network-Graphs-and-Auto-Differentiation.md
├── 03_Module-Neural-Network-Training-And-Inference.md
├── 04_Iterators-Loading-Data.md
└── 05_Symbolic-Configuration-and-Execution-in-Pictures.md
├── 01_neural_networks
├── 00_Linear-Regression.md
├── 01_Mnist-Handwritten-Digit-Recognition.md
└── 02_Large-Scale-Image-Classification.md
├── 02_advanced
├── 00_NDArray-in-Compressed-Sparse Row-Storage-Format.md
├── 01_Row-Sparse-NDArray-for-Sparse-Gradient-Updates.md
├── 02_Train-a-Linear-Regression-Model-with-Sparse-Symbols.md
├── 03_Distributed-Key-Value-Store.md
└── 04_Importing-an-ONNX-model-into-MXNet.md
├── 03_application
├── 00_Connectionist-Temporal-Classification.md
├── 01_Fine-tune-with-Pretrained-Models.md
├── 02_Text-Classification-Using-a-Convolutional-Neural-Network-on-MXNet.md
├── 03_Generative-Adversarial-Network-(GAN).md
└── 04_Matrixfactorization-in-Recommender-Systems.md
├── README.md
└── img
├── README.md
├── bind_basic.png
├── compose_basic.png
├── compose_multi_in.png
├── compose_net.png
├── executor_aux_state.png
├── executor_backward.png
├── executor_forward.png
├── executor_multi_out.png
├── executor_simple_bind.png
└── speedup-p2.png
/00_basics/00_Ndarray-Imperative-tensor-operations-on-CPU-GPU.md:
--------------------------------------------------------------------------------
1 | # NDArray-CPU/GPU上的命令式张量操作
2 |
3 | 在MXNet中,`NDArray`是进行所有数学计算的核心数据结构。一个`NDArray`表示了固定大小、多维的同质数组。如果你对python科学计算库[NumPy](http://www.numpy.org/)很熟悉的话,你可能会注意到`mxnet.ndarray`和`numpy.ndarray`非常相似。和对应的Numpy数据结构一样,`NDArray`也支持命令式计算。
4 |
5 | 所以你可能会很奇怪,为什么不直接使用Numpy呢?因为和numpy相比,MXNet提供了两种引人注目的优点。首先,MXNet的`NDArray`支持在CUP、GPU和多GPU机器等一系列硬件配置上快速执行,同时它还支持部署在云上的分布式系统。其次,因为MXNet的`NDArray`在执行中是lazy形式的,因此它支持在可用硬件上的自动并行化操作。
6 |
7 | `NDArray`是拥有相同类型数字的多维数组。我们可以用1D数组表示3D空间中的点坐标,例如`[2, 1, 6]`就是一个形状为3的1D数组。类似地,我们也可以表示2D数组。下面,我们展示了一个0维长度为2,1维长度为3的2D数组。
8 |
9 | ```
10 | [[0, 1, 2]
11 | [3, 4, 5]]
12 | ```
13 |
14 | 请注意,这里“维度”的使用是重载的。当我们说一个2D数组的时候,我们的意思是这个数组有两个轴,而不是有两个元素。
15 |
16 | 每个NDArray都支持一些你可能会经常调用的重要属性。
17 |
18 | - **ndarray.shape**: 数组的维度信息。它是一个整数元组,其中数字的大小代表的数组各个维度的长度信息。对于一个拥有`n`行`m`列的矩阵来说,它的`shape`是`(n, m)`。
19 | - **ndarray.dtype**: 一个`numpy`类型的对象,描述了元素的类型。
20 | - **ndarray.size**: 数组的总元素数目,等于`shape`中各元素的乘积。
21 | - **ndarray.context**: 数组存储的设备,例如`cpu()`或者`gpu(1)`。
22 |
23 | ## 准备工作
24 |
25 | 为了完成本教程,我们需要:
26 |
27 | - MXNet:你可以在[设置和安装](http://mxnet.io/install/index.html)中查看如何在你的操作系统上安装MXNet
28 | - [Jupyter](http://jupyter.org/)
29 | ```
30 | pip install jupyter
31 | ```
32 | - GPUs:本教程中的一节会用到GPU,如果你的机器上没有GPU,请将变量gpu_device设置为mx.cpu()。
33 |
34 | ## 数组创建
35 |
36 | 我们有一系列的方法可以创建一个`NDArray`。
37 |
38 | - 我们可以使用`array`函数从一个常规的python列表或者元组创建一个NDArray:
39 |
40 |
41 | ```python
42 | import mxnet as mx
43 | # create a 1-dimensional array with a python list
44 | a = mx.nd.array([1,2,3])
45 | # create a 2-dimensional array with a nested python list
46 | b = mx.nd.array([[1,2,3], [2,3,4]])
47 | {'a.shape':a.shape, 'b.shape':b.shape}
48 | ```
49 |
50 | - 我们还可以使用`numpy.ndarray`创建一个MXNet NDArray:
51 |
52 |
53 | ```python
54 | import numpy as np
55 | import math
56 | c = np.arange(15).reshape(3,5)
57 | # create a 2-dimensional array from a numpy.ndarray object
58 | a = mx.nd.array(c)
59 | {'a.shape':a.shape}
60 | ```
61 |
62 | 我们可以通过`dtype`选项指定元素的类型,它可以接受numpy的类型,默认情况下使用`float32`。
63 |
64 |
65 | ```python
66 | # float32 is used by default
67 | a = mx.nd.array([1,2,3])
68 | # create an int32 array
69 | b = mx.nd.array([1,2,3], dtype=np.int32)
70 | # create a 16-bit float array
71 | c = mx.nd.array([1.2, 2.3], dtype=np.float16)
72 | (a.dtype, b.dtype, c.dtype)
73 | ```
74 |
75 | 某些情况下我们知道所需的NDArray的形状,但是不知道其中的元素值,MXNet为这种情况提供了几个函数用于创建带有占位符内容的数组:
76 |
77 |
78 | ```python
79 | # 零张量
80 | a = mx.nd.zeros((2,3))
81 | # 单位张量
82 | b = mx.nd.ones((2,3))
83 | # x填充的张量
84 | c = mx.nd.full((2,3), 7)
85 | # 随机数值的张量
86 | d = mx.nd.empty((2,3))
87 | print(c)
88 | print(d)
89 | ```
90 |
91 | ## 打印数组
92 |
93 | 在检查`NDArray`的内容时,首先使用`asnumpy`函数将其内容转换成`numpy.ndarray`格式会更加方便。Numpy使用以下布局打印输出:
94 |
95 | - 最后一个维度从左到右print
96 | - 倒数第二个维度从上到下print
97 | - 剩余的也是从上到下print,中间有空行分割
98 |
99 |
100 | ```python
101 | b = mx.nd.arange(18).reshape((3,2,3))
102 | b.asnumpy()
103 | print(b)
104 | ```
105 |
106 | ## 基本操作
107 |
108 | 对NDArray执行操作时,标准的算术运算符执行的是按元素操作。返回值为包含了运算结果的新数组。
109 |
110 |
111 | ```python
112 | a = mx.nd.ones((2,3))
113 | b = mx.nd.ones((2,3))
114 | # 按元素相加
115 | c = a + b
116 | # 按元素相减
117 | d = - c
118 | # 按元素平方,sin,然后转置
119 | e = mx.nd.sin(c**2).T
120 | # 数据广播式的大小比较
121 | f = mx.nd.maximum(a, c)
122 | f.asnumpy()
123 | print(f)
124 | ```
125 |
126 | 在mxnet中,*表示的是元素点乘,而mx.nd.dot()表示的则是矩阵乘法。
127 |
128 |
129 | ```python
130 | a = mx.nd.arange(4).reshape((2,2))
131 | b = a * a
132 | c = mx.nd.dot(a,a)
133 | print("b: %s, \n c: %s" % (b.asnumpy(), c.asnumpy()))
134 | ```
135 |
136 | 使用`+=`和`*=`等赋值运算符会修改数组的内容,不会分配新的内存空间用于创建新数组。
137 |
138 |
139 | ```python
140 | a = mx.nd.ones((2,2))
141 | b = mx.nd.ones(a.shape)
142 | b += a
143 | b.asnumpy()
144 | ```
145 |
146 | ## 索引和切片
147 |
148 | 切片操作符`[]`在0维上对数组执行操作。
149 |
150 |
151 | ```python
152 | a = mx.nd.array(np.arange(6).reshape(3,2))
153 | a[1:2] = 1
154 | a[:].asnumpy()
155 | ```
156 |
157 | 我们可以使用`slice_axis`函数在特定的维度上执行切片操作。
158 |
159 |
160 | ```python
161 | d = mx.nd.slice_axis(a, axis=1, begin=1, end=2)
162 | # 数组,切片的维度,begin index,end index
163 | d.asnumpy()
164 | ```
165 |
166 | ## 形状重塑
167 |
168 | 使用`reshape`我们可以改变数组的形状,前提是数组的大小需要保持不变。
169 |
170 |
171 | ```python
172 | a = mx.nd.array(np.arange(24))
173 | b = a.reshape((2,3,4))
174 | b.asnumpy()
175 | ```
176 |
177 | `concat`函数可以沿着0维将多个数组堆叠起来。但是除了0维之外,其他维度的形状需要保持一致。
178 |
179 |
180 | ```python
181 | a = mx.nd.ones((2,3))
182 | b = mx.nd.ones((2,3))*2
183 | c = mx.nd.concat(a,b)
184 | c.asnumpy()
185 | ```
186 |
187 | ## 缩减
188 |
189 | 像`sum`和`mean`等函数可以将数组缩减为数字标量。
190 |
191 |
192 | ```python
193 | a = mx.nd.ones((2,3))
194 | b = mx.nd.sum(a)
195 | b.asnumpy()
196 | ```
197 |
198 | 我们也可以沿着特定的维度将数组缩减:
199 |
200 |
201 | ```python
202 | c = mx.nd.sum_axis(a, axis=1)
203 | c.asnumpy()
204 | ```
205 |
206 | ## 广播
207 |
208 | 我们可以对数组进行广播。广播操作沿着数组中长度为1的维度进行值复制。下面的代码就是沿着1维进行广播:
209 |
210 |
211 | ```python
212 | a = mx.nd.array(np.arange(6).reshape(6,1))
213 | b = a.broadcast_to((6,4)) #
214 | b.asnumpy()
215 | ```
216 |
217 | 数组也可以沿着多个维度进行广播。在下面的例子中,我们沿着1维和2维进行广播:
218 |
219 |
220 | ```python
221 | c = a.reshape((2,1,1,3))
222 | d = c.broadcast_to((2,2,2,3))
223 | d.asnumpy()
224 | ```
225 |
226 | 在执行例如`*`和`+`等作时,广播可以沿着形状不同的维度自动执行。
227 |
228 |
229 | ```python
230 | a = mx.nd.ones((3,2))
231 | b = mx.nd.ones((1,2))
232 | c = a + b
233 | c.asnumpy()
234 | ```
235 |
236 | ## 复制
237 |
238 | 当我们将NDArray分配给另一个python变量的时候,我们只是对*同一个*NDArray的引用进行了复制。但是很多时候,我们需要对数据进行复制,这样我们就可以对新数组进行操作而不会覆盖原始的数值。
239 |
240 |
241 | ```python
242 | a = mx.nd.ones((2,2))
243 | b = a
244 | b is a # will be True
245 | ```
246 |
247 | `copy`将会对数组的数据进行深层的复制:
248 |
249 |
250 | ```python
251 | b = a.copy()
252 | b is a # will be False
253 | ```
254 |
255 | 上面的代码为一个新的NDArray分配了内存,并将其分配给*b*。当我们不想分配额外的内存时,我们可以使用`copyto`方法或者`[]`切片操作。
256 |
257 |
258 | ```python
259 | b = mx.nd.ones(a.shape)
260 | c = b
261 | c[:] = a
262 | d = b
263 | a.copyto(d)
264 | (c is b, d is b) # Both will be True
265 | ```
266 |
267 | ## 高级主题
268 |
269 | MXNet的NDArray提供了一些高级特性,这使得它有别于其他的类似库。
270 |
271 | ### GPU支持
272 |
273 | 默认情况下,NDArray的操作符在CPU进行执行。但是在MXNet中,你可以很容易的转而使用其他计算设备,例如GPU(如果有的话)。每一个NDArray的设备信息都存储在`ndarray.context`当中。当MXNet使用标志符`USE_CUDA=1`进行编译,且机器上至少拥有一块NVIDIA显卡的时候,我们可以使用通过设置上下文管理器`mx.gpu(0)`或者更简单地使用`mx.gpu()`将所有的计算都放在GPU上进行。当我们拥有两块或者更多的显卡时,可以通过`mx.gpu(1)`表示第二块显卡,诸如此类。
274 |
275 | **注意**想要在cpu上执行下述小节的话请将gpu_device设置为mx.cpu()。
276 |
277 |
278 | ```python
279 | gpu_device=mx.gpu() # Change this to mx.cpu() in absence of GPUs.
280 | #gpu_device=mx.cpu()
281 |
282 | def f():
283 | a = mx.nd.ones((100,100))
284 | b = mx.nd.ones((100,100))
285 | c = a + b
286 | print(c)
287 | # in default mx.cpu() is used
288 | f()
289 | # change the default context to the first GPU
290 | with mx.Context(gpu_device):
291 | f()
292 | ```
293 |
294 | 我们也可以在创建数组时明确指定context。
295 |
296 |
297 | ```python
298 | a = mx.nd.ones((100, 100), gpu_device)
299 | a
300 | ```
301 |
302 | 目前,MXNet需要进行计算的两个数组位于同一个设备上。有几种办法可以在设备之间进行数据复制。
303 |
304 |
305 | ```python
306 | a = mx.nd.ones((100,100), mx.cpu())
307 | b = mx.nd.ones((100,100), gpu_device)
308 | c = mx.nd.ones((100,100), gpu_device)
309 | a.copyto(c) # copy from CPU to GPU 从cpu复制到gpu
310 | d = b + c
311 | e = b.as_in_context(c.context) + c # same to above 同上
312 | {'d':d, 'e':e}
313 | ```
314 |
315 | ### 分布式文件系统的序列化
316 |
317 | MXNet提供了两种简单的方式用于从硬盘加载数据或者将数据保存到硬盘上。第一种方式就像在python中处理其他对象一样,使用`pickle`。`NDArray`兼容pickle的使用。
318 |
319 |
320 | ```python
321 | import pickle as pkl
322 | a = mx.nd.ones((2, 3))
323 | # pack and then dump into disk
324 | data = pkl.dumps(a)
325 | pkl.dump(data, open('tmp.pickle', 'wb'))
326 | # load from disk and then unpack
327 | data = pkl.load(open('tmp.pickle', 'rb'))
328 | b = pkl.loads(data)
329 | b.asnumpy()
330 | ```
331 |
332 | 第二种方法是使用`save`和`load`方法将数组直接以二进制的形式存储到硬盘上。我们可以保存/加载一个NDArray或者一系列的NDArray。
333 |
334 |
335 | ```python
336 | a = mx.nd.ones((2,3))
337 | b = mx.nd.ones((5,6))
338 | mx.nd.save("temp.ndarray", [a,b])
339 | c = mx.nd.load("temp.ndarray")
340 | c
341 | ```
342 |
343 | 在MXNet中,你也可以以这种实行保存/加载一个NDArray的字典:
344 |
345 |
346 | ```python
347 | d = {'a':a, 'b':b}
348 | mx.nd.save("temp.ndarray", d)
349 | c = mx.nd.load("temp.ndarray")
350 | c
351 | ```
352 |
353 | 这种`load`和`save`的方法在两个方面优于pickle:
354 | - 当使用这类方法的时候,你可以在python的界面中保存数据并在其他语言中调用数据。例如,如果我们在python中保存这些数据:
355 |
356 |
357 | ```python
358 | a = mx.nd.ones((2, 3))
359 | mx.nd.save("temp.ndarray", [a,])
360 | ```
361 |
362 | 我们之后可以在R中加载它:
363 | ```
364 | a <- mx.nd.load("temp.ndarray")
365 | as.array(a[[1]])
366 | ## [,1] [,2] [,3]
367 | ## [1,] 1 1 1
368 | ## [2,] 1 1 1
369 | ```
370 |
371 | - 当使用 Amazon S3或者Hadoop HDFS这样的分布式文件系统的时候,我们可以直接保存在上面进行数据的保存和加载。
372 |
373 | ```
374 | mx.nd.save('s3://mybucket/mydata.ndarray', [a,]) # 如果使用USE_S3=1编译
375 | mx.nd.save('hdfs///users/myname/mydata.bin', [a,]) # 如果使用USE_HDFS=1编译
376 | ```
377 |
378 | ### 延迟执行和自动并行化
379 |
380 | MXNet使用延迟执行来达到更好的性能。当我们在python中运行`a=b+1`的时候,python线程将操作推入后台引擎然后获取返回的结果。这种方式有两种好处:
381 |
382 | - python主线程可以继续执行其他计算直到前一个执行完毕。这对于开销繁重的前端语言非常有用。
383 | - 它让后端引擎更容易进行进一步的优化,例如自动并行化。
384 |
385 | 后端引擎可以解决数据依赖的问题并直接对计算进行规划。这对于用户也是透明的。我们可以在结果数组上调用`wait_to_read`方法来等待计算完成。将数据从数组复制到其他包上的操作会隐式的调用`wait_to_read`方法。
386 |
387 |
388 | ```python
389 | import time
390 | def do(x, n):
391 | """push computation into the backend engine"""
392 | return [mx.nd.dot(x,x) for i in range(n)]
393 | def wait(x):
394 | """wait until all results are available"""
395 | for y in x:
396 | y.wait_to_read()
397 |
398 | tic = time.time()
399 | a = mx.nd.ones((1000,1000))
400 | b = do(a, 50)
401 | print('time for all computations are pushed into the backend engine:\n %f sec' % (time.time() - tic))
402 | wait(b)
403 | print('time for all computations are finished:\n %f sec' % (time.time() - tic))
404 | ```
405 |
406 | 除了能够分析数据读取和写入的依赖之外,后端引擎还能够并行规划没有依赖性的计算。例如,在下面的代码中:
407 |
408 |
409 | ```python
410 | a = mx.nd.ones((2,3))
411 | b = a + 1
412 | c = a + 2
413 | d = b * c
414 | ```
415 |
416 | 第二行和第三行的代码可以并行执行。下面的例子先后在CPU和GPU上运行:
417 |
418 |
419 | ```python
420 | n = 10
421 | a = mx.nd.ones((1000,1000))
422 | b = mx.nd.ones((6000,6000), gpu_device)
423 | tic = time.time()
424 | c = do(a, n)
425 | wait(c)
426 | print('Time to finish the CPU workload: %f sec' % (time.time() - tic))
427 | d = do(b, n)
428 | wait(d)
429 | print('Time to finish both CPU/GPU workloads: %f sec' % (time.time() - tic))
430 | ```
431 |
432 | 现在我们发布了所有工作负载。后端引擎将会尝试并行CPU和GPU的计算。
433 |
434 |
435 | ```python
436 | tic = time.time()
437 | c = do(a, n)
438 | d = do(b, n)
439 | wait(c)
440 | wait(d)
441 | print('Both as finished in: %f sec' % (time.time() - tic))
442 | ```
443 |
444 |
445 |
446 |
--------------------------------------------------------------------------------
/00_basics/01_Ndarray-Indexing-Array-Indexing-Features.md:
--------------------------------------------------------------------------------
1 |
2 | # NDArray索引-数组索引功能
3 |
4 | MXNet的高级数组索引功能是模仿[NumPy文档](https://docs.scipy.org/doc/numpy-1.13.0/reference/arrays.indexing.html#combining-advanced-and-basic-indexing)实现的。在这里你将会看到许多接近Numpy索引功能的改编,因此我们直接借用了他们的文档。
5 |
6 | 可以使用标准的python语法`x[obj]`对`NDArray`进行索引,其中_x_是数组,_obj_是选择。
7 |
8 | 有两种索引的方式:
9 | 1. 基础切片
10 | 2. 高级索引
11 |
12 | 仿照Numpy `ndarray`的索引规则,MXNet支持基础和高级的索引方式。
13 |
14 | ## 基础切片和索引
15 |
16 | 基础切片将python切片的基础内容扩展到N维。来快速浏览一下吧:
17 |
18 | ```
19 | a[start:end] # 从start到end-1
20 | a[start:] # 从start到数组结束
21 | a[:end] # 从数组开始到end-1
22 | a[:] # 复制整个数组
23 | ```
24 |
25 |
26 | ```python
27 | from mxnet import nd
28 | ```
29 |
30 | 对于基础切片的示例,我们先从一些简单的例子开始。
31 |
32 |
33 | ```python
34 | x = nd.array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9], dtype='int32')
35 | x[5:]
36 | ```
37 |
38 |
39 | ```python
40 | x = nd.array([0, 1, 2, 3])
41 | print('1D complete array, x=', x)
42 | s = x[1:3]
43 | print('slicing the 2nd and 3rd elements, s=', s)
44 | ```
45 |
46 |
47 | ```python
48 | x = nd.array([[1, 2, 3, 4], [5, 6, 7, 8], [9, 10, 11, 12]])
49 | print('multi-D complete array, x=', x)
50 | s = x[1:3]
51 | print('slicing the 2nd and 3rd elements, s=', s)
52 | ```
53 |
54 |
55 | ```python
56 | # 行/列赋值
57 | print('original x, x=', x)
58 | x[2] = 9.0
59 | print('replaced entire row with x[2] = 9.0, x=', x)
60 | ```
61 |
62 |
63 | ```python
64 | # 单独元素赋值
65 | print('original x, x=', x)
66 | x[0, 2] = 9.0
67 | print('replaced specific element with x[0, 2] = 9.0, x=', x)
68 | ```
69 |
70 |
71 | ```python
72 | # 区域赋值
73 | print('original x, x=', x)
74 | x[1:2, 1:3] = 5.0
75 | print('replaced range of elements with x[1:2, 1:3] = 5.0, x=', x)
76 | ```
77 |
78 | ## 1.0版本中的新索引功能
79 |
80 | ### 步长
81 |
82 | 在基础的切片语法`i:j:k`中,_i_是索引的起始点,_j_是索引的终点,_k_是步长(_k_必须是非零值)。
83 |
84 | **注意**在之前的版本中,MXNet只支持步长为1的切片操作。而从1.0版本开始,MXNet支持任意步长的索引。
85 |
86 |
87 | ```python
88 | x = nd.array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9], dtype='int32')
89 | # Select elements 1 through 7, and use a step of 2
90 | x[1:7:2]
91 | ```
92 |
93 | ## 负数索引
94 |
95 | 负数的_i_和_j_将被解释为_n + i_和_n + j_,其中_n_是对应维度中元素的数目。而负数的_k_则意味着从大到小的索引顺序。
96 |
97 |
98 | ```python
99 | x[-2:10]
100 | ```
101 |
102 | 如果选择元组中的对象数目小于N,那么后续的维度将被默认为使用`:`索引。
103 |
104 |
105 | ```python
106 | x = nd.array([[[1],[2],[3]],
107 | [[4],[5],[6]]], dtype='int32')
108 | x[1:2]
109 | ```
110 |
111 | 你可以使用切片的方式对数组进行赋值,但是(不像列表)你永远不能扩增数组。使用`x[obj] = value`进行赋值时,value的形状必须能够被广播成`x[obj]`的形状。
112 |
113 |
114 | ```python
115 | x = nd.arange(16, dtype='int32').reshape((4, 4))
116 | print(x)
117 | ```
118 |
119 |
120 | ```python
121 | print(x[1:4:2, 3:0:-1])
122 | ```
123 |
124 |
125 | ```python
126 | x[1:4:2, 3:0:-1] = [[16], [17]]
127 | print(x)
128 | ```
129 |
130 | ## 1.0版本的高级索引功能
131 |
132 | 当选择对象obj是一个非元组序列对象(python列表),Numpy的`ndarray`(整数类型),MXNet的`NDArray`或者具有至少一个序列对象的元组时,MXNet的高级索引功能将被触发。
133 |
134 | 高级索引将会返回一份复制的数据。
135 |
136 | **注意**:
137 | - 使用Python的列表进行索引时,仅支持元素为整数的列表,不支持嵌套的列表。例如,MXNet支持`x[[1, 2]]`,但不支持`x[[1], [2]]`。
138 | - 当使用numpy `ndarray`或者MXNet `NDArray`进行索引的时候,对维度无限制。
139 | - 当索引对象是包含python列表的元组的时候,其整数列表和嵌套列表是都支持的。例如,MXNet支持`x[1:4, [1, 2]]`和`x[1:4, [[1], [2]]`。
140 |
141 | ### 纯整数数组索引
142 |
143 | 当索引序列由一系列数量等同于数组维度的整数数组组成时,索引以不同于切片的形式直接执行。
144 |
145 | 高级索引序列是被作为一个值进行[广播](https://docs.scipy.org/doc/numpy-1.13.0/reference/ufuncs.html#ufuncs-broadcasting)和迭代的。
146 |
147 | result[i_1, ..., i_M] == x[ind_1[i_1, ..., i_M], ind_2[i_1, ..., i_M], ..., ind_N[i_1, ..., i_M]]
148 |
149 | 请注意,结果的形状和索引序列的形状`ind_1, ..., ind_N`相同。
150 |
151 | **示例**:
152 | 对于每一行都选择一个特定的元素。这里行序号是[0, 1, 2, 2],指定了对应的行;而列序号[0, 1, 0, 1],指明了对应的列。将两者结合后可以通过高级索引解决。
153 |
154 |
155 | ```python
156 | x = nd.array([[1, 2],
157 | [3, 4],
158 | [5, 6]], dtype='int32')
159 | x[[0, 1, 2, 2], [0, 1, 0, 1]]
160 | # 相当于将[0,0],[1,1],[2,0]位置的元素检索了出来
161 | ```
162 |
163 | 为了能够实现类似于上述基础切片的操作,需要使用广播。通过示例可以很好的理解这一点。
164 |
165 | **示例**:
166 | 想要通过高级索引从4x3的数组中挑选出位于边角的元素值,你需要选择位于`[0, 2]`列和`[0, 3]`行的元素。因此你需要通过高级索引指明这一点。通过上面解释的方法,你可以这样来写:
167 |
168 |
169 | ```python
170 | x = nd.array([[ 0, 1, 2],
171 | [ 3, 4, 5],
172 | [ 6, 7, 8],
173 | [ 9, 10, 11]], dtype='int32')
174 | #x = nd.arange(20).reshape((5,4))
175 |
176 | print(x[[[0, 0],[3, 3]],[[0,2], [0,2]]])
177 | ```
178 |
179 | 但是,由于上述的索引只是重复它们自己,因为可以使用广播来完成相同的索引。
180 |
181 |
182 | ```python
183 | x = nd.array([[ 0, 1, 2],
184 | [ 3, 4, 5],
185 | [ 6, 7, 8],
186 | [ 9, 10, 11]], dtype='int32')
187 | x[[[0], [3]],
188 | [[0, 2]]]
189 | ```
190 |
191 | ### 结合基础和高级索引
192 |
193 | 在三种情况下,我们需要考虑在一个索引对象中将基础和高级索引结合起来。让我们看一些示例来理解这一点。
194 |
195 | - 索引对象中只有一个高级索引序列。例如,`x`是一个`shape=(10, 20, 30, 40, 50)`的`NDArray`,`result=x[:, :, ind]`中包含一个`shape=(2, 3, 4)`的高级索引序列`ind`。结果的形状将会是`(10, 20, 2, 3, 4, 40, 50)`。这是因为`x`第三维的子空间被形状为`(2, 3, 4)`的子空间替代。如果我们使用_i_,_j_,_k_对形状为(2,3,4)的子空间进行索引,那么结果等同于`result[:, :, i, j, k, :, :] = x[:, :, ind[i, j, k], :, :]`。
196 |
197 |
198 | ```python
199 | import numpy as np
200 | shape = (10, 20, 30, 40, 50)
201 | x = nd.arange(np.prod(shape), dtype='int32').reshape(shape)
202 | ind = nd.arange(24).reshape((2, 3, 4))
203 | print(x[:, :, ind].shape)
204 | ```
205 |
206 | - 索引对象中包含了两个彼此相邻的高级索引序列。例如,`x`是一个形状为`(10, 20, 30, 40, 50)`的`NDArray`,而`result=x[:, :, ind1, ind2, :]`中拥有的两个高级索引序列将被广播成形状为`(2, 3, 4)`的索引序列。之后,`result`的形状将变成`(10, 20, 2, 3, 4, 50)`,这是因为形状为`(30, 40)`的子空间被形状为`(2, 3, 4)`的子空间替代。
207 |
208 |
209 | ```python
210 | # 现在索引序列间进行广播,然后进行高级索引
211 | ind1 = [0, 1, 2, 3]
212 | ind2 = [[[0], [1], [2]], [[3], [4], [5]]]
213 | print(x[:, :, ind1,:,:].shape)
214 | print(x[:, :, :, ind2, :].shape)
215 | print(x[:, :, ind2, ind1, :].shape)
216 | ```
217 |
218 | - 索引对象中包含了两个彼此分离的高级索引序列。例如,`x`是一个形状为`(10, 20, 30, 40, 50)`的`NDArray`,而`result=x[:, :, ind1, ind2, :]`中拥有的两个高级索引序列将被广播成形状为`(2, 3, 4)`的索引序列。之后`result`的形状将变成`(2, 3, 4, 10, 20, 40)`,这是因为没有明确的指明放置索引子空间的位置,于是它被添加到了数组的头部。
219 |
220 |
221 | ```python
222 | print(x[:, :, ind1, :, ind2].shape)
223 | ```
224 |
--------------------------------------------------------------------------------
/00_basics/02_Symbol-Neural-Network-Graphs-and-Auto-Differentiation.md:
--------------------------------------------------------------------------------
1 |
2 | # Symbol-神经网络图和自动微分
3 |
4 | 在[之前的章节](http://mxnet.io/tutorials/basic/ndarray.html)中我们介绍了`NDArray`这个在MXNet中用于操作数据的基本数据结构。仅通过使用NDArray,我们可以执行一系列数学运算。事实上,我们可以通过使用`NDArray`来定义和更新一个完整的神经网络。`NDArray`让我们可以以命令式的方式编写科学计算程序,我们可以在其中充分感受到前端语言的易用性。所以你可能会感到很奇怪,为什么我们不在所有的计算中都使用`NDArray`呢?
5 |
6 | MXNet提供了用于符号式编程的接口Symbol API。在符号式编程的过程中,我们首先定义一个*计算图*,而不是一步步的执行计算。计算图中包含了用于代表输入输出数据的占位符。然后通过编译计算图,生成一个函数,和`NDArray`绑定后即可运行。MXNet的Symbol API和[Caffe](http://caffe.berkeleyvision.org/)使用的网络配置以及[Theano](http://deeplearning.net/software/theano/)中的符号式编程很相似。
7 |
8 | 使用符号式编程的另一个优点是我们可以在执行之前对函数进行优化。举例来说,当我们使用命令式编程执行数学计算时,在每执行完一次计算之后,我们不知道后续将会用到哪些值。但是在符号式变成中,我们事先声明了我们需要的输出。这就意味着在中间步骤中,我们可以通过执行一些操作回收分配的内存。同时,对于同样的网络,Symbol API使用的内存更少。关于这一点想了解更多的话,请参阅[How To](http://mxnet.io/faq/index.html)和[结构](http://mxnet.io/architecture/index.html)。
9 |
10 | 在我们的设计说明中,我们公布了一份[关于命令式编程和符号式编程比较优势的详细讨论](http://mxnet.io/architecture/program_model.html)。当时在本文档中,我们将集中在如何使用MXNet的Symbol API。在MXNet中,我们可以使用其他的符号,例如计算符(例如简单的矩阵计算符“+”等)或者整个的神经网络层(例如卷积层等),来组成新的符号。计算符可以接受多个输入变量,返回多个输出变量,并且保持内部状态变量。
11 |
12 | 想要了解这些概念的可视化解释,请参阅[符号式编译和执行](http://mxnet.io/api/python/symbol_in_pictures/symbol_in_pictures.html)。
13 |
14 | 为了更实在地了解相关内容,让我们亲身体会一下Symbol API,`Symbol`是如何由几种不同的方式来组成的。
15 |
16 | ## 准备工作
17 |
18 | 为了完成本教程,我们需要:
19 |
20 | - MXNet:在[Setup and Installation](http://mxnet.io/install/index.html)一节中可以了解MXNet的安装。
21 | - [Jupyter Notebook](http://jupyter.org/index.html)和 [Python Requests](http://docs.python-requests.org/en/master/)。
22 |
23 | ```
24 | pip install jupyter requests
25 | ```
26 | - GPU:本教程中的一节将用到GPU,如果你的机器上没有GPU的话,请将变量gpu_device设置为mx.cpu()。
27 |
28 | ## 基础符号组成
29 |
30 | ### 基础计算符
31 |
32 | 下面的示例创建了一个简单的表达式:`a + b`。首先,我们使用`mx.sym.Variable`创建两个占位符,并将其命名为`a`和`b`。然后我们使用计算符`+`来构建一个新的符号。当构建变量的时候,我们不需要为其命名,MXNet会自动地为每个变量生成一个独一无二的名称。就像在下面的示例中,c被自动分配了一个唯一的名称。
33 |
34 |
35 | ```python
36 | import mxnet as mx
37 | a = mx.sym.Variable('a')
38 | b = mx.sym.Variable('b')
39 | c = a + b
40 | (a, b, c)
41 | ```
42 |
43 | `NDArray`支持的大多数运算符在`Symbol`中也可找到,例如:
44 |
45 |
46 | ```python
47 | # 点乘
48 | d = a * b
49 | # 矩阵乘法
50 | e = mx.sym.dot(a, b)
51 | # reshape
52 | f = mx.sym.reshape(d+e, shape=(1,4))
53 | # 广播
54 | g = mx.sym.broadcast_to(f, shape=(2,4))
55 | # 可视化绘图
56 | mx.viz.plot_network(symbol=g)
57 | ```
58 |
59 | 通过`bind`方法可以将上面声明的计算和输入数据绑定从而进一步对其评估。我们将在[符号操作](#Symbol Manipulation)一节中更进一步的讨论这个问题。
60 |
61 | ### 基础神经网络
62 |
63 | 除了基础的计算符之外,`Symbol`还支持一系列的神经网络层。下面的示例构建了一个由两个全连接层组成的的神经网络,在给定输入数据的形状后对网络结构进行可视化。
64 |
65 |
66 | ```python
67 | # 初始将net定义为一个变量,后续的所有操作都是对其的运算,今儿viz可以追溯整个计算过程
68 | net = mx.sym.Variable('data')
69 | net = mx.sym.FullyConnected(data=net, name='fc1', num_hidden=128)
70 | net = mx.sym.Activation(data=net, name='relu1', act_type="relu")
71 | net = mx.sym.FullyConnected(data=net, name='fc2', num_hidden=10)
72 | net = mx.sym.SoftmaxOutput(data=net, name='out')
73 | # 需要定义data的形状才能确定全连接的参数的数目
74 | # 对shape进行赋值时需要使用dict,其中key为变量的名称,形状为tuple
75 | mx.viz.plot_network(net, shape={'data':(100,200)})
76 | ```
77 |
78 | 每一个符号都带有一个(独一无二的)字符串名称。NDArray和Symbol都代表一个单一的张量。*计算符*代表的是张量间的运算。运算符接受符号(或者NDArray)作为输入,同时也可能额外接受诸如隐藏神经元个数(*num_hidden*)或者激活类型(*act_type*)这样的超参,最后生成一个输出。
79 |
80 | 我们可以将符号简单地视为一个接受若干参数的函数。我们可以使用一下方法调用这些参数:
81 |
82 |
83 | ```python
84 | net.list_arguments()
85 | # 可以将所有的参数列出来
86 | ```
87 |
88 | 这些参数是每个符号所需要的输入已经参数。
89 |
90 | - *data*:变量*data*所需要的输入
91 | - *fc1_weight* and *fc1_bias*:全连接层*fc1*的权重和偏置
92 | - *fc2_weight* and *fc2_bias*:全连接层*fc2*的权重和偏置
93 | - *out_label*:计算损失所需要的标签
94 |
95 | 我们也可以明确地为其指明名称:
96 |
97 |
98 | ```python
99 | net = mx.symbol.Variable('data')
100 | w = mx.symbol.Variable('myweight')
101 | net = mx.symbol.FullyConnected(data=net, weight=w, name='fc1', num_hidden=128)
102 | net.list_arguments()
103 | ```
104 |
105 | 在上面的例子中,`FullyConnected`层需要三个输入:数据,权重和偏置。当其中任何一个输入没有被指明的时候,系统会为其自动生成一个变量。
106 |
107 | ## 更复杂的组成
108 |
109 | MXNet为深度学习中经常使用的一些层提供了优化过的符号表示(参阅[src/operator](https://github.com/dmlc/mxnet/tree/master/src/operator))。我们也可以在python中定义一些新的计算符。下面的示例首先将两个符号按元素相加,然后将其输入到全连接计算符中:
110 |
111 |
112 | ```python
113 | lhs = mx.symbol.Variable('data1')
114 | rhs = mx.symbol.Variable('data2')
115 | net = mx.symbol.FullyConnected(data=lhs + rhs, name='fc1', num_hidden=128)
116 | net.list_arguments()
117 | ```
118 |
119 | 和前例中的描述的单向计算符,我们还可以以一种更灵活的方式构建一个符号。
120 |
121 |
122 | ```python
123 | data = mx.symbol.Variable('data')
124 | net1 = mx.symbol.FullyConnected(data=data, name='fc1', num_hidden=10)
125 | net1.list_arguments()
126 | net2 = mx.symbol.Variable('data2')
127 | net2 = mx.symbol.FullyConnected(data=net2, name='fc2', num_hidden=10)
128 | composed = net2(data2=net1, name='composed')
129 | composed.list_arguments()
130 | # 将net1作为data输入进入net2的方式和之前的运算并不本质区别
131 | ```
132 |
133 | 在本例中*net2*被当成一个函数套用在一个已经存在的符号*net1*上,生成的*composed*符号将拥有*net1*和*net2*全部对象。
134 |
135 | 一旦你要开始构建一些更大的网络,你可能需要使用通用的前缀来命名符号以概述网络的结构。
136 |
137 |
138 | ```python
139 | data = mx.sym.Variable("data")
140 | net = data
141 | n_layer = 2
142 | for i in range(n_layer):
143 | # 和gluon中with net.name_scope()功能应该是类似的
144 | # 为每一层的变量赋予了特定的名称
145 | with mx.name.Prefix("layer%d_" % (i + 1)):
146 | net = mx.sym.FullyConnected(data=net, name="fc", num_hidden=100)
147 | net.list_arguments()
148 | ```
149 |
150 | ### 深度网络的模块化构建
151 |
152 | 由于网络的层数很多,因此逐层地构建一个*深度网络*(例如谷歌的inception)可能会非常乏味。所以,对这样的网络,我们经常使用模块化的构建方式。
153 |
154 | 例如,要构建Google的Inception网络,我们首先需要定义一个factory函数将卷积,批次归一化和线性修正单元(rectified linear unit,ReLU)串联在一起。
155 |
156 |
157 | ```python
158 | def ConvFactory(data, num_filter, kernel, stride=(1,1), pad=(0, 0), name=None, suffix=''):
159 | # 常见的结构中,每一个卷积模块都是由卷积,BN和激活组成
160 | conv = mx.sym.Convolution(data=data, num_filter=num_filter, kernel=kernel,
161 | stride=stride, pad=pad, name='conv_%s%s' %(name, suffix))
162 | bn = mx.sym.BatchNorm(data=conv, name='bn_%s%s' %(name, suffix))
163 | act = mx.sym.Activation(data=bn, act_type='relu', name='relu_%s%s'
164 | %(name, suffix))
165 | return act
166 | prev = mx.sym.Variable(name="Previous Output")
167 | conv_comp = ConvFactory(data=prev, num_filter=64, kernel=(7,7), stride=(2, 2))
168 | shape = {"Previous Output" : (128, 3, 28, 28)}
169 | mx.viz.plot_network(symbol=conv_comp, shape=shape)
170 | #
171 | ```
172 |
173 | 然后在`ConvFactory`函数的基础上,我们定义一个函数用于构建inception模块。
174 |
175 |
176 | ```python
177 | def InceptionFactoryA(data, num_1x1, num_3x3red, num_3x3, num_d3x3red, num_d3x3,
178 | pool, proj, name):
179 | '''
180 | 通过将基本模块组合成结构部件进行进一步的调用。
181 | 其中pool指定了池化层的类型,一般选用最大池化
182 | '''
183 | # 1x1卷积
184 | c1x1 = ConvFactory(data=data, num_filter=num_1x1, kernel=(1, 1), name=('%s_1x1' % name))
185 | # 1x1通道缩减 + 3x3卷积
186 | c3x3r = ConvFactory(data=data, num_filter=num_3x3red, kernel=(1, 1), name=('%s_3x3' % name), suffix='_reduce')
187 | c3x3 = ConvFactory(data=c3x3r, num_filter=num_3x3, kernel=(3, 3), pad=(1, 1), name=('%s_3x3' % name))
188 | # 1x1通道缩减+ 3x3卷积×2(但是在原生结构中此处应为5×5卷积)
189 | cd3x3r = ConvFactory(data=data, num_filter=num_d3x3red, kernel=(1, 1), name=('%s_double_3x3' % name), suffix='_reduce')
190 | cd3x3 = ConvFactory(data=cd3x3r, num_filter=num_d3x3, kernel=(3, 3), pad=(1, 1), name=('%s_double_3x3_0' % name))
191 | cd3x3 = ConvFactory(data=cd3x3, num_filter=num_d3x3, kernel=(3, 3), pad=(1, 1), name=('%s_double_3x3_1' % name))
192 | # 3×3池化 + 1×1卷积
193 | pooling = mx.sym.Pooling(data=data, kernel=(3, 3), stride=(1, 1), pad=(1, 1), pool_type=pool, name=('%s_pool_%s_pool' % (pool, name)))
194 | cproj = ConvFactory(data=pooling, num_filter=proj, kernel=(1, 1), name=('%s_proj' % name))
195 | # concat
196 | concat = mx.sym.Concat(*[c1x1, c3x3, cd3x3, cproj], name='ch_concat_%s_chconcat' % name)
197 | return concat
198 |
199 | prev = mx.sym.Variable(name="Previous Output")
200 | in3a = InceptionFactoryA(prev, 64, 64, 64, 64, 96, "avg", 32, name="in3a")
201 | mx.viz.plot_network(symbol=in3a, shape=shape)
202 | ```
203 |
204 | 最终,我们通过链接多个inception模块构建了整个网络。完整示例请参阅[这里](https://github.com/dmlc/mxnet/blob/master/example/image-classification/symbols/inception-bn.py)。
205 |
206 | ### 多符号组
207 |
208 | 如果想要构建一个拥有多个损失层的神经网络,我们需要使用`mxnet.sym.Group`将多个符号组在一起。下面的例子中两个输出被组在了一起:
209 |
210 |
211 | ```python
212 | net = mx.sym.Variable('data')
213 | fc1 = mx.sym.FullyConnected(data=net, name='fc1', num_hidden=128)
214 | net = mx.sym.Activation(data=fc1, name='relu1', act_type="relu")
215 |
216 | out1 = mx.sym.SoftmaxOutput(data=net, name='softmax') # 输出1
217 | out2 = mx.sym.LinearRegressionOutput(data=net, name='regression') #输出2
218 | group = mx.sym.Group([out1, out2]) # 这个和concat有什么区别?
219 | group.list_outputs()
220 | ```
221 |
222 | ## 和NDArray的关系
223 |
224 | 就像你已经看到的那样,`Symbol`和`NDArray`均为多维数组提供了类似于`c = a + b`这样的计算符。在这里,我们简要地澄清一下两者间的不同。
225 |
226 | `NDArray`提供了命令式编程的接口,其中的计算是逐句评估的。而`Symbol`更加接近与声明式编程,使用时我们需要提前声明计算,然后才使用数据评估。这类例子包括正则表达式和SQL语句。
227 |
228 | `NDArray`的优点:
229 | - 直截了当的
230 | - 更易于使用自然语言特性(循环和判别结构等)以及第三方库(numpy等)
231 | - 利于一步步进行代码debug
232 |
233 | `Symbol`的优点:
234 | - 提供了NDArray中几乎所有的函数,例如`+`,`*`,`sin`和`reshape`等
235 | - 利于保存加载和可视化
236 | - 利于后端进行计算和内存的优化
237 |
238 | ## 符号操作
239 |
240 | 和`NDArray`相比,`Symbol`的一个不同在于我们需要需要提前声明计算,然后才能将计算和数据绑定,运行。
241 |
242 | 在本节中,我们将介绍直接操作符号的函数。但是请注意,它们大多数都被`module`所包裹。
243 |
244 | ### 形状和类型推断
245 |
246 | 对于每个符号,我们都可以查询其参数,辅助状态和输出。我们还可以通过已知的输入数据的形状或者参数的类型来推断输出的形状和类型,这样有利于内存的分配。
247 |
248 |
249 | ```python
250 | arg_name = c.list_arguments() # 获取输入的名称
251 | out_name = c.list_outputs() # 获取输出的名称
252 | # 通过给定输入的形状推断输出的形状
253 | arg_shape, out_shape, _ = c.infer_shape(a=(2,3), b=(2,3))
254 | # 通过输入数据的类型推断输出类型
255 | arg_type, out_type, _ = c.infer_type(a='float32', b='float32')
256 |
257 | {'input' : dict(zip(arg_name, arg_shape)),
258 | 'output' : dict(zip(out_name, out_shape))}
259 | {'input' : dict(zip(arg_name, arg_type)),
260 | 'output' : dict(zip(out_name, out_type))}
261 | ```
262 |
263 | ### 数据绑定和评估
264 |
265 | 上面构建的符号`c`声明了如何进行计算。为了评估它,我们需要为参数,即自有变量,提供数据。
266 |
267 | 上述的符号`c`声明了计算的类型。通过`bind`方法,可以指定计算所在的设备(ctx=),函数所需的参数(dict(),包含了参数key及value)。通过此方法可以得到一个可执行func,通过调用`forward`方法进行真正的计算。在func上通过.outputs可以得到相应的输出。
268 |
269 |
270 | ```python
271 | ex = c.bind(ctx=mx.cpu(), args={'a' : mx.nd.ones([2,3]),
272 | 'b' : mx.nd.ones([2,3])})
273 | ex.forward()
274 | print('number of outputs = %d\nthe first output = \n%s' % (
275 | len(ex.outputs), ex.outputs[0].asnumpy()))
276 | ```
277 |
278 | 我们也可以使用不同的数据在GPU上评估同样的符号。
279 |
280 | **注意**为了在cpu上执行下面的小节,你需要将gpu_device设置为mx.cpu()。
281 |
282 |
283 | ```python
284 | gpu_device=mx.gpu() # Change this to mx.cpu() in absence of GPUs.
285 | #gpu_device=mx.cpu()
286 |
287 | ex_gpu = c.bind(ctx=gpu_device, args={'a' : mx.nd.ones([3,4], gpu_device)*2,
288 | 'b' : mx.nd.ones([3,4], gpu_device)*3})
289 | ex_gpu.forward()
290 | ex_gpu.outputs[0].asnumpy()
291 | ```
292 |
293 | 我们也可以通过`eval`方法评估符号。这个方法将`bind`和`forward`结合在了一起。
294 |
295 |
296 | ```python
297 | ex = c.eval(ctx = mx.cpu(), a = mx.nd.ones([2,3]), b = mx.nd.ones([2,3]))
298 | print('number of outputs = %d\nthe first output = \n%s' % (
299 | len(ex), ex[0].asnumpy()))
300 | ```
301 |
302 | 在神经网络中更常用的方法是```simple_bind```,之后可以通过```forward```和```backward```获取结果和梯度信息。
303 |
304 | ### 加载和保存
305 |
306 | 逻辑上讲,符号是和ndarray相对应的。他们都能够表示一个张量,都是操作符的输入或者输出。对`Symbol`对象进行序列化时我们可以使用`picke`或者直接使用在[NDArray教程](http://mxnet.io/tutorials/basic/ndarray.html#serialize-from-to-distributed-filesystems)中讨论过的`save`和`load`方法。
307 |
308 | 对`NDArray`进行序列化时,我们直接将张量中的数据序列化并以二进制的格式保存在磁盘上。但是符号(编程)使用了图的概念。图是由链式的操作符组成的。它们由输出符号隐式地表示。所以,当对`Symbol`进行序列化时,我们序列化了一张输出符号的图。同时,Symbol使用了更可读的`json`格式来进行序列化操作。将符号转换成`json`字符串时,请使用`json`方法。
309 |
310 |
311 | ```python
312 | # 在json文件的花括号内,使用了key-value的方式描述了计算图
313 | # nodes表明了计算的结点,每个节点包括了(操作,名称,输入)
314 | print(c.tojson())
315 | c.save('symbol-c.json')
316 | c2 = mx.sym.load('symbol-c.json')
317 | c.tojson() == c2.tojson()
318 | ```
319 |
320 | ## 定制符号
321 |
322 | 为了更好的性能,例如`mx.sym.Convolution`和`mx.sym.Reshape`这样的运算符都是在C++中实现的。MXNet允许用户使用python这样的前段语言编写新的运算符。这样扩展和调试都会更容易一些。想要了解如何在python中实现一个运算符,请参阅[如何创建一个新的运算符](http://mxnet.io/faq/new_op.html)。
323 |
324 | ## 高级用法
325 |
326 | ### 类型转换
327 |
328 | 默认情况下,MXNet使用32位浮点数。但是为了获得更好的精度-性能,我们可以使用低精度的数据类型。例如,Nvidia Tesla Pascal GPU(e.g. P100)提升了16位浮点数的性能,同时GTX Pascal GPU(e.g. GTX 1080)在8位的整数上速度更快。
329 |
330 | 为了根据要求转换数据类型,我们可以像下面这样使用`mx.sym.cast`运算符:
331 |
332 |
333 | ```python
334 | # 通过cast转换可以将sym默认的数据类型从float32转换为float16,从int32转为uint8
335 | a = mx.sym.Variable('data')
336 | b = mx.sym.cast(data=a, dtype='float16')
337 | arg, out, _ = b.infer_type(data='float32')
338 | print({'input':arg, 'output':out})
339 |
340 | c = mx.sym.cast(data=a, dtype='uint8')
341 | arg, out, _ = c.infer_type(data='int32')
342 | print({'input':arg, 'output':out})
343 | ```
344 |
345 | ### 变量共享
346 |
347 | 为了能够在几个符号之间共享内容,我们可以像下面这样将几个符号和一个数组绑定在一起:
348 |
349 |
350 | ```python
351 | a = mx.sym.Variable('a')
352 | b = mx.sym.Variable('b')
353 | b = a + a * a
354 |
355 | data = mx.nd.ones((2,3))*2
356 | ex = b.bind(ctx=mx.cpu(), args={'a':data, 'b':data})
357 | ex.forward()
358 | ex.outputs[0].asnumpy()
359 | ```
360 |
361 |
362 |
363 |
364 |
--------------------------------------------------------------------------------
/00_basics/03_Module-Neural-Network-Training-And-Inference.md:
--------------------------------------------------------------------------------
1 |
2 | # Module-神经网络训练和预测
3 |
4 | 一般而言,训练一个神经网络包含了非常多的步骤。我们需要指定训练数据的输入,模型参数的初始化,如何进行前向传播和反向传播,如何根据计算得到的梯度更新参数和如何设置模型检查点等等。而在进行预测时,我们需要重复上述的大多数步骤。不管是对于新手还是具有经验的开发者而言,这个任务都是艰巨的。
5 |
6 | 幸运的是,MXNet中的`module`模块将训练和预测常用的代码进行了模块化处理。`Module`为执行预先定义的模型同时提供了高层次和中层次的接口。我们可以互换地使用这两种接口。在本教程中,我们将展示如何使用这两种接口。
7 |
8 | ## 准备工作
9 |
10 | 为了完成本教程,我们需要:
11 |
12 | - MXNet.在[Setup and Installation](http://mxnet.io/install/index.html)一节中可以了解MXNet的安装。
13 |
14 | - [Jupyter Notebook](http://jupyter.org/index.html)和 [Python Requests](http://docs.python-requests.org/en/master/)。
15 |
16 | ```
17 | pip install jupyter requests
18 | ```
19 |
20 | ## 初步实施
21 |
22 | 在本教程中,我们将通过在[UCI字母识别数据集](https://archive.ics.uci.edu/ml/datasets/letter+recognition)上训练一个[多层感知机,(MLP)](https://en.wikipedia.org/wiki/Multilayer_perceptron)来展示如何使用`module`模块。
23 |
24 | 下面的代码将下载UCI字母识别数据数据集,并将其以80:20的比例切分成训练集和测试机。同时,它还创建了一个批次大小为32的训练数据迭代器和一个测试数据迭代器。
25 |
26 |
27 | ```python
28 | import logging
29 | logging.getLogger().setLevel(logging.INFO) # 更改logger的level
30 | import mxnet as mx
31 | import numpy as np
32 |
33 | fname = mx.test_utils.download('http://archive.ics.uci.edu/ml/machine-learning-databases/letter-recognition/letter-recognition.data')
34 | data = np.genfromtxt(fname, delimiter=',')[:,1:] # len=15的数组
35 | label = np.array([ord(l.split(',')[0])-ord('A') for l in open(fname, 'r')])
36 |
37 | batch_size = 32
38 | ntrain = int(data.shape[0]*0.8)
39 | # mxnet.io中为不同类型的数据提供了构造dataiter的func().
40 | train_iter = mx.io.NDArrayIter(data[:ntrain, :], label[:ntrain], batch_size, shuffle=True)
41 | val_iter = mx.io.NDArrayIter(data[ntrain:, :], label[ntrain:], batch_size)
42 | ```
43 |
44 | 下面我们定义一下网络并将其可视化。
45 |
46 |
47 | ```python
48 | net = mx.sym.Variable('data')
49 | net = mx.sym.FullyConnected(net, name='fc1', num_hidden=64)
50 | net = mx.sym.Activation(net, name='relu1', act_type="relu")
51 | net = mx.sym.FullyConnected(net, name='fc2', num_hidden=26)
52 | net = mx.sym.SoftmaxOutput(net, name='softmax')
53 | mx.viz.plot_network(net) # 对network进行可视化绘图.
54 | ```
55 |
56 | ## 构建一个模型
57 |
58 | 现在,我们准备开始介绍module。通常而言,我们使用`Module`来创建模型。其中,需要指定的参数如下所示:
59 |
60 | - `symbol`: 网络的定义,亦即计算图
61 | - `context`: 运算设备
62 | - `data_names` : 输入数据名称
63 | - `label_names` : 输出变量名称
64 |
65 | 对于`net`来说,我们有一个数据名为`data`,一个标签名为`softmax_label`;其中,`softmax_label`是根据我们为`SoftmaxOutput`操作符指定的名称自动命名的。
66 |
67 |
68 | ```python
69 | mod = mx.mod.Module(symbol=net,
70 | context=mx.cpu(),
71 | data_names=['data'],
72 | label_names=['softmax_label'])
73 |
74 | ```
75 |
76 | ## 中间层次接口
77 |
78 | 我们已经创建了一个模型。下面让我们看一下如何使用`Module`下的中间层级接口完成模型的训练和预测工作。使用这些接口,开发人员可以零活地运行`forward`和`backward`来一步步进行计算。它对于debug同样非常有用。
79 |
80 | 为了训练一个模型,我们需要执行以下步骤:
81 | - `bind` : 通过bind为参数分配内存空间,进行训练准备工作
82 | - `init_params` : 参数分配和初始化
83 | - `init_optimizer` : 创建优化器,默认为`sgd`.
84 | - `metric.create` : 构建评估函数
85 | - `forward` : 前向计算
86 | - `update_metric` : 根据输出信息评估并更新评估指标
87 | - `backward` : 反向计算
88 | - `update` : 根据优化器参数和上一批次数据中计算得到的梯度进行参数更新
89 |
90 | 它们的使用如下所示:
91 |
92 |
93 | ```python
94 | # 将train_iter的信息提供给module,可根据shape分配内存的大小
95 | mod.bind(data_shapes=train_iter.provide_data, label_shapes=train_iter.provide_label)
96 | # 参数初始化
97 | mod.init_params(initializer=mx.init.Uniform(scale=.1))
98 | # lr=0.1的sgd
99 | mod.init_optimizer(optimizer='sgd', optimizer_params=(('learning_rate', 0.1), ))
100 | # accuracy作为评估指标
101 | metric = mx.metric.create('acc')
102 |
103 | for epoch in range(5):
104 | train_iter.reset()
105 | metric.reset()
106 | for batch in train_iter:
107 | mod.forward(batch, is_train=True) # 前向计算
108 | mod.update_metric(metric, batch.label) # 更新评估指标
109 | mod.backward() # 反向计算
110 | mod.update() # 更新参数
111 | print('Epoch %d, Training %s' % (epoch, metric.get()))
112 | ```
113 |
114 | 想要了解更多API信息,请访问[Module API](http://mxnet.io/api/python/module/module.html)。
115 |
116 | ## 高层次接口
117 |
118 | ### 训练
119 |
120 | 为了用户的便捷使用,`Module`同样提供了高层次的接口用于训练,预测和评估。通过简单地调用`fit`API,用户不再需要手动执行上节提到的所有步骤,这些步骤都在内部进行自动执行。
121 |
122 | 调用`fit`函数的代码如下所示:
123 |
124 |
125 | ```python
126 | # 重设迭代器
127 | train_iter.reset()
128 |
129 | # 创建模型
130 | mod = mx.mod.Module(symbol=net,
131 | context=mx.cpu(),
132 | data_names=['data'],
133 | label_names=['softmax_label'])
134 |
135 | mod.fit(train_iter,
136 | eval_data=val_iter,
137 | optimizer='sgd',
138 | optimizer_params={'learning_rate':0.1},
139 | eval_metric='acc',
140 | num_epoch=8)
141 | ```
142 |
143 | 默认状态下,`fit`函数将`eval_metric`设置为`accuracy`,将`optimizer`设置为`sgd`,将优化器参数设置为`(('learning_rate', 0.01),)`。
144 |
145 | ### 预测和评估
146 |
147 | 为了使用模型进行预测,我们可以调用`predict()`。它能够自动收集和返回所有的预测结果。
148 |
149 |
150 | ```python
151 | # 使用训练后的mod进行预测时调用mod.predict()即可,函数返回所有的预测值
152 | y = mod.predict(val_iter)
153 | assert y.shape == (4000, 26)
154 | ```
155 |
156 | 如果我们只需要对测试集进行评估而不需要预测的输出结果,那么可以调用`score()`函数来完成。它在验证数据集上进行预测,并根据评估的方式自动评估模型的性能。
157 |
158 | 使用代码如下所示:
159 |
160 |
161 | ```python
162 | # 在训练结束后还可以使用score()对验证集进行最后的评估
163 | score = mod.score(val_iter, ['acc'])
164 | print("Accuracy score is %f" % (score[0][1]))
165 | assert score[0][1] > 0.77, "Achieved accuracy (%f) is less than expected (0.77)" % score[0][1]
166 | ```
167 |
168 | 其他一些可以使用的评估函数有:`top_k_acc`,`F1`,`RMSE`, `MSE`,`MAE`和`ce`。想要了解更多关于这些评估函数的信息,请访问[Evaluation metric](http://mxnet.io/api/python/metric/metric.html)。
169 |
170 | 通过调整训练轮数,学习率,优化器参数可以调整参数以获得最佳的评分。
171 |
172 | ### 保存和加载
173 |
174 | 在每一轮次的训练后,我们可以调用`checkpoint`将模型的参数保存起来。
175 |
176 |
177 | ```python
178 | model_prefix = 'mx_mlp'
179 | checkpoint = mx.callback.do_checkpoint(model_prefix)
180 |
181 | mod = mx.mod.Module(symbol=net)
182 | mod.fit(train_iter, num_epoch=5, epoch_end_callback=checkpoint) # 但在很多情况这种记录是没有必要的
183 | ```
184 |
185 | 调用`load_checkpoint`函数可以加载已经保存的模型。将操作符和相应的参数加载以后,我们可以将这些参数加载进入模型当中。
186 |
187 | 从检查点重新加载参数的步骤:
188 | - 加载检查点数据,得到相应的return
189 | - 构建新的mod,并导入数据得到model
190 |
191 |
192 | ```python
193 | sym, arg_params, aux_params = mx.model.load_checkpoint(model_prefix, 3) #(prefix,epoc)
194 | assert sym.tojson() == net.tojson()
195 |
196 | mod.set_params(arg_params, aux_params)
197 | ```
198 |
199 | 假如我们想要从检查点中恢复训练,我们可以直接调用`fit()`函数(而不需要调用`set_params()`)将加载的参数传入;这样以来,`fit()`就知道从这些参数开始训练而不是从头开始从随机初始化参数开始。我们还可以设置一下`begin_epoch`参数,这样`fit()`就知道我们是从之前的轮次中恢复训练的。
200 |
201 |
202 | ```python
203 | mod = mx.mod.Module(symbol=sym)
204 | mod.fit(train_iter,
205 | num_epoch=21,
206 | arg_params=arg_params,
207 | aux_params=aux_params,
208 | begin_epoch=3)
209 |
210 | assert score[0][1] > 0.77, "Achieved accuracy (%f) is less than expected (0.77)" % score[0][1]
211 | ```
212 |
--------------------------------------------------------------------------------
/00_basics/04_Iterators-Loading-Data.md:
--------------------------------------------------------------------------------
1 |
2 | # 迭代器-加载数据
3 | 在本教程中,我们将集中精力在如何向一个训练或推断程序中输入数据。在MXNet中,大部分的训练和推断程序都能够接受数据迭代器;这样一来数据加载过程会变得更加简单,当加载大型数据集时尤其如此。在这里我们讨论一下API的使用惯例和几个迭代器的样例。
4 |
5 | ## 准备条件
6 |
7 | 为了完成本教程,我们需要:
8 | - MXNet.安装和使用请参考[Setup and Installation](http://mxnet.io/install/index.html)一节。
9 | - [OpenCV Python library](http://opencv.org/opencv-3-2.html), [Python Requests](http://docs.python-requests.org/en/master/), [Matplotlib](https://matplotlib.org/) and [Jupyter Notebook](http://jupyter.org/index.html).
10 | ```
11 | $ pip install opencv-python requests matplotlib jupyter
12 | ```
13 | - 将环境变量`MXNET_HOME`设置到MXNet的根目录中。
14 | ```
15 | $ git clone https://github.com/dmlc/mxnet ~/mxnet
16 | $ export MXNET_HOME='~/mxnet'
17 | ```
18 |
19 | ## MXNet数据迭代器
20 |
21 | *MXNet*中的数据迭代器和Python中的迭代器对象非常类似。在Python中,`iter`函数使我们可以在诸如Python list这样的可迭代对象上通过调用`next()`依次读取数据。迭代器为遍历各种类型的可迭代对象提供了一个抽象的接口,而无需公开底层数据源的详细信息。
22 |
23 | 在MXNet中,每次对数据迭代器调用`next`后会返回一个批次类似于`DataBatch`的数据。一个`DataBatch`中包含了n个训练的样本和对应的标签。这里的n指的就是迭代器的`batch_size`。在迭代器的末尾,没有更多的数据可以提供,此时迭代器会抛出一个``StopIteration``,就像Python中的`iter`一样。`DataBatch`的结构定义在[这里](http://mxnet.io/api/python/io/io.html#mxnet.io.DataBatch).
24 |
25 | 训练样本的详细信息,例如名称,形状,数据类型,布局以及对应的标签,都可以通过`DataBatch`中的`provide_data`和`provide_label`属性作为`DataDesc`的数据描述对象存在。`DataDesc`的详细结构信息在[
26 | 这里](http://mxnet.io/api/python/io/io.html#mxnet.io.DataDesc)定义。
27 |
28 | MXNet中的所有IO都是通过`mx.io.DataIter`和它的子类来处理的。在这个教程中,我们会讨论MXNet中的常见的几种迭代器。
29 |
30 | 在深入了解之前,让我们先配置一下环境,导入需要使用的库。
31 |
32 |
33 | ```python
34 | import mxnet as mx
35 | %matplotlib inline
36 | import os
37 | import sys
38 | import subprocess
39 | import numpy as np
40 | import matplotlib.pyplot as plt
41 | import tarfile
42 |
43 | import warnings
44 | warnings.filterwarnings("ignore", category=DeprecationWarning)
45 | ```
46 |
47 | ## 读取内存中的数据
48 |
49 | 当数据以`NDArray`或者`numpy.ndarray`的形式存在与内存当中时,我们可以通过[__`NDArrayIter`__](http://mxnet.io/api/python/io/io.html#mxnet.io.NDArrayIter)来读取数据,代码如下所示:
50 |
51 |
52 |
53 | ```python
54 | import numpy as np
55 | data = np.random.rand(100,3)
56 | label = np.random.randint(0, 10, (100,))
57 | data_iter = mx.io.NDArrayIter(data=data, label=label, batch_size=30)
58 | for batch in data_iter:
59 | print([batch.data, batch.label, batch.pad])
60 | ```
61 |
62 | ## 从csv文件中读取数据
63 |
64 | MXNet中使用[`CSVIter`](http://mxnet.io/api/python/io/io.html#mxnet.io.CSVIter)函数来读取csv中的数据,代码如下所示:
65 |
66 |
67 | ```python
68 | # lets save `data` into a csv file first and try reading it back
69 | np.savetxt('data.csv', data, delimiter=',')
70 | data_iter = mx.io.CSVIter(data_csv='data.csv', data_shape=(3,), batch_size=30)
71 | for batch in data_iter:
72 | print([batch.data, batch.pad])
73 | ```
74 |
75 | ## 自定义迭代器
76 |
77 | 当内置的迭代器不能满足你的需求时,你可以创建一个你自己的自定义迭代器。
78 | 在MXNet中构造一个迭代器需要满足以下要求:
79 | - 在python2中构造一个`next()`方法或者在python3中构造`__next()__`,其返回的对象是`DataBatch`,在数据流结束后则返回`StopIteration`。
80 | - 构造一个`reset()`方法当数据读取完全后从头开始。
81 | - 包含了`provide_data`对象,是由一系列的`DataDesc`([这里可以看到更多信息](http://mxnet.io/api/python/io/io.html#mxnet.io.DataBatch))构成,在这些对象中包含了data的名称,形状,类型和导出信息。
82 | - 包含了`provide_label`对象,是由一系列的`DataDesc`构成,在这些对象中包含了label的名称,形状,类型和导出信息。
83 |
84 | 当构建一个迭代器的时候,你可以从零开始,也可以重新利用现有的迭代器。例如,在图像字幕应用中,输入的样本是一张图片,而标签是一个句子。所以,我们可以这样构建一个迭代器:
85 | - 通过`ImageRecordIter`构建一个`image_iter`,这样就可以多线程地进行数据预读取和图片增广。
86 | - 通过`NDArrayIter`构建一个`caption_iter`,或者利用rnn中的bucketing迭代器。
87 | - `next()`返回`image_iter.next()`和`caption_iter.next()`的结合。
88 |
89 | 下面的例子展示了如何构建一个简单的迭代器。
90 |
91 |
92 | ```python
93 | class SimpleIter(mx.io.DataIter):
94 | # 所有的类都是io.DataIter的子类
95 | # (name, shape)-->_provide_data-->@property-->provide_data-->+gen-->data-->batch
96 | def __init__(self, data_names, data_shapes, data_gen,
97 | label_names, label_shapes, label_gen, num_batches=10):
98 | self._provide_data = list(zip(data_names, data_shapes))
99 | self._provide_label = list(zip(label_names, label_shapes))
100 | self.num_batches = num_batches # 终止判断
101 | self.data_gen = data_gen
102 | self.label_gen = label_gen
103 | self.cur_batch = 0
104 |
105 | def __iter__(self):
106 | return self
107 |
108 | def reset(self):
109 | self.cur_batch = 0
110 |
111 | @property
112 | def provide_data(self):
113 | return self._provide_data
114 |
115 | @property
116 | def provide_label(self):
117 | return self._provide_label
118 |
119 | def __next__(self):
120 | return self.next()
121 |
122 | def next(self):
123 | # 迭代过程条件判断
124 | if self.cur_batch < self.num_batches:
125 | self.cur_batch += 1
126 | data = [mx.nd.array(g(d[1])) for d,g in zip(self._provide_data, self.data_gen)]
127 | label = [mx.nd.array(g(d[1])) for d,g in zip(self._provide_label, self.label_gen)]
128 | # 将data和label打包成Batch读取的形式
129 | return mx.io.DataBatch(data, label)
130 | else:
131 | raise StopIteration # 终止
132 | ```
133 |
134 |
135 | ```python
136 | n = 32
137 | num_classes = 10
138 | # 使用了一个lambda函数做个generator
139 | data_iter = SimpleIter(['data'], [(n, 100)],
140 | [lambda s: np.random.uniform(-1, 1, s)],
141 | ['softmax_label'], [(n,)],
142 | [lambda s: np.random.randint(0, num_classes, s)])
143 | ```
144 |
145 |
146 | ```python
147 | batch = data_iter.next()
148 | batch.label
149 | ```
150 |
151 | 我们使用上面定义的`SimpleIter`来训练一个简单的MLP:
152 |
153 |
154 | ```python
155 | import mxnet as mx
156 | num_classes = 10
157 | net = mx.sym.Variable('data')
158 | net = mx.sym.FullyConnected(data=net, name='fc1', num_hidden=64)
159 | net = mx.sym.Activation(data=net, name='relu1', act_type="relu")
160 | net = mx.sym.FullyConnected(data=net, name='fc2', num_hidden=num_classes)
161 | net = mx.sym.SoftmaxOutput(data=net, name='softmax')
162 | print(net.list_arguments())
163 | print(net.list_outputs())
164 | ```
165 |
166 | 这里,有四个变量是可学习的参数:全连接层*fc1*和*fc2*中的*weights*和*biases*;有两个变量是输入数据:训练样本的*data*和包含了数据标签以及*softmax_output*的*softmax_label*。
167 |
168 | 在MXNet的Symbol API中,*data*变量被称之为自由变量。想要真正执行符号,它们需要和数据绑定在一起。[点击这里了解更多关于Symbol的内容](http://mxnet.io/tutorials/basic/symbol.html)。
169 |
170 | 在MXNet的Module API中,我们通过数据迭代器向神经网络输入训练样本。[点击这里了解更多关于Module的内容](http://mxnet.io/tutorials/basic/module.html)。
171 |
172 |
173 | ```python
174 | import logging
175 | logging.basicConfig(level=logging.INFO)
176 |
177 | n = 32
178 | # 使用了一个lambda函数做个generator
179 | data_iter = SimpleIter(['data'], [(n, 100)],
180 | [lambda s: np.random.uniform(-1, 1, s)],
181 | ['softmax_label'], [(n,)],
182 | [lambda s: np.random.randint(0, num_classes, s)])
183 |
184 | mod = mx.mod.Module(symbol=net)
185 | mod.fit(data_iter, num_epoch=5)
186 | ```
187 |
188 | Python使用注释:mxnet中的很多方法在Python2.x中使用的是字符串,而在Python3.x中使用的是二进制数据。为了使得本教程可以正常运行,我们在这里定义一个函数,它可以在Python3.x环境中将字符串转换成二进制数据格式。
189 |
190 |
191 | ```python
192 | def str_or_bytes(str):
193 | """
194 | A utility function for this tutorial that helps us convert string
195 | to bytes if we are using python3.
196 | ----------
197 | str : string
198 |
199 | Returns
200 | -------
201 | string (python2) or bytes (python3)
202 | """
203 | if sys.version_info[0] < 3:
204 | return str
205 | else:
206 | return bytes(str, 'utf-8')
207 | ```
208 |
209 | ## Record IO
210 |
211 | Record IO是MXNet中用于数据IO的文件格式。它紧凑地将数据打包以便于从分布式系统(如Hadoop HDFS和AWS S3)中进行高效的写入和读取操作。在[这里](http://mxnet.io/architecture/note_data_loading.html)你可以了解更多关于`RecordIO`的内容。
212 |
213 | MXNet为数据的顺序读取和随机读取分别提供了[__`MXRecordIO`__](http://mxnet.io/api/python/io/io.html#mxnet.recordio.MXRecordIO)和[__`MXIndexedRecordIO`__](http://mxnet.io/api/python/io/io.html#mxnet.recordio.MXIndexedRecordIO)两种方式。
214 |
215 | ### MXRecordIO
216 |
217 | 首先,让我们了解一下如何使用`MXRecordIO`进行顺序读取。这些文件的扩展名为`.rec`。
218 |
219 |
220 | ```python
221 | record = mx.recordio.MXRecordIO('tmp.rec', 'w')
222 | for i in range(5):
223 | record.write(str_or_bytes('record_%d'%i))
224 |
225 | record.close() # 关闭句柄
226 | ```
227 |
228 | 在打开文件时设置选项参数为`r`,我们可以如下所示的读取数据:
229 |
230 |
231 | ```python
232 | record = mx.recordio.MXRecordIO('tmp.rec', 'r')
233 | while True:
234 | item = record.read()
235 | if not item:
236 | break
237 | print (item)
238 | record.close()
239 | ```
240 |
241 | ### MXIndexedRecordIO
242 |
243 | `MXIndexedRecordIO`支持随机或者顺序地读取数据。我们可以通过如下所示的方式创建索引记录文件和对应的索引文件:
244 |
245 |
246 | ```python
247 | # 此时需要同时创建两个文件,一个是idx,另外一个是rec
248 | record = mx.recordio.MXIndexedRecordIO('tmp.idx', 'tmp.rec', 'w')
249 | for i in range(5):
250 | record.write_idx(i, str_or_bytes('record_%d'%i))
251 |
252 | record.close()
253 | ```
254 |
255 | 现在我们可以通过索引键值来单独地访问对应的记录。
256 |
257 |
258 | ```python
259 | record = mx.recordio.MXIndexedRecordIO('tmp.idx', 'tmp.rec', 'r')
260 | record.read_idx(3) # 新方法,read)idx()和keys()
261 | ```
262 |
263 | 你也可以将文件的所有索引键值列出来。
264 |
265 |
266 | ```python
267 | record.keys
268 | ```
269 |
270 | ### 打包和解包数据
271 |
272 | .rec中的每一条记录都可以包含任意二进制文件。但是,大多数的深度学习任务都要求数据以标签/数据的格式输入。`mx.recordio`为这种操作提供了一些实用的函数,例如,`pack`,`unpack`,`pack_img`和`unpack_img`。
273 |
274 | #### 打包和解包二进制文件
275 |
276 | [__`pack`__](http://mxnet.io/api/python/io/io.html#mxnet.recordio.pack) 和[__`unpack`__](http://mxnet.io/api/python/io/io.html#mxnet.recordio.unpack)被用来存储浮点标签(或者1d的浮点数组)和二进制数据。这些数据和头文件一起进行打包。头文件的结构请参考[此处](http://mxnet.io/api/python/io/io.html#mxnet.recordio.IRHeader)。
277 |
278 |
279 | ```python
280 | # pack
281 | data = 'data'
282 | label1 = 1.0
283 | # 头文件创建中,flag是任意数字,label是标签,id应为唯一的索引,id2一般为0
284 | # 为每一条记录中data,label和相应头文件就绪后即可打包
285 | header1 = mx.recordio.IRHeader(flag=0, label=label1, id=1, id2=0)
286 | s1 = mx.recordio.pack(header1, str_or_bytes(data))
287 |
288 | label2 = [1.0, 2.0, 3.0]
289 | header2 = mx.recordio.IRHeader(flag=3, label=label2, id=2, id2=0)
290 | s2 = mx.recordio.pack(header2, str_or_bytes(data))
291 | ```
292 |
293 |
294 | ```python
295 | # unpack
296 | print(mx.recordio.unpack(s1))
297 | print(mx.recordio.unpack(s2))
298 | ```
299 |
300 | #### 打包和解包图片数据
301 |
302 | MXNet提供了[__`pack_img`__](http://mxnet.io/api/python/io/io.html#mxnet.recordio.pack_img)和[__`unpack_img`__](http://mxnet.io/api/python/io/io.html#mxnet.recordio.unpack_img)函数进行图片数据的打包和解包。通过`pack_img`打包的图片数据可以通过`mx.io.ImageRecordIter`进行加载。
303 |
304 |
305 | ```python
306 | data = np.ones((3,3,1), dtype=np.uint8)
307 | label = 1.0
308 | # 应为pack()只能对一维的数组打包,因此对于图片需要调用pack_img()
309 | # 同时打包时需要指定quality和图片格式(方便进行压缩)
310 | header = mx.recordio.IRHeader(flag=0, label=label, id=0, id2=0)
311 | s = mx.recordio.pack_img(header, data, quality=100, img_fmt='.jpg')
312 | ```
313 |
314 |
315 | ```python
316 | # unpack_img
317 | print(mx.recordio.unpack_img(s))
318 | ```
319 |
320 | #### im2rec的使用
321 |
322 | 你可以使用MXNet[src/tools](https://github.com/dmlc/mxnet/tree/master/tools)文件夹中的``im2rec.py``脚本将原始的图片打包成*RecordIO*的格式。具体的使用方式参照下节的`Image IO`。
323 |
324 | ## 图片IO
325 |
326 | 在这一节,我们将学习在MXNet中如何预处理和加载图片数据。
327 |
328 | 在MXNet中提供了四种图片加载的方式:
329 | - 使用[__mx.image.imdecode__](http://mxnet.io/api/python/io/io.html#mxnet.image.imdecode)加载原始图像
330 | - 使用[__`mx.img.ImageIter`__](http://mxnet.io/api/python/io/io.html#mxnet.image.ImageIter)从rec文件和原生图片中加载出iter。
331 | - [__`mx.io.ImageRecordIter`__](http://mxnet.io/api/python/io/io.html#mxnet.io.ImageRecordIter)功能基于C++,功能的灵活性不如ImageIter,但是提供了多种语言的支持。
332 | - 构建自定义的`mx.io.DataIter`
333 |
334 | ### 图片前处理
335 |
336 | 图片可以使用不同的方式进行前处理,其中一些罗列如下:
337 | - `mx.io.ImageRecordIter`很快,但是不够灵活。而且它只能在图片分类任务中使用;在更复杂的目标识别和图像分割中不再适用。
338 | - `mx.recordio.unpack_img`(或者`cv2.imread`和`skimage`等等)结合numpy可以更灵活的读取图片,但是由于Python全局解释锁(Global Interpreter Lock,GIL)的存在速度比较慢。
339 | - `mx.image`将图片储存为[__`NDArray`__](http://mxnet.io/tutorials/basic/ndarray.html)的格式,并且由于它利用了MXNet引擎的自动并行化处理且规避了GIL,因此速度会更快。
340 |
341 | 下面,我们演示一些由`mx.image`提供的一些经常使用的预处理教程。
342 |
343 | 开始之前,我们先把将要使用的样本图片下载下来。
344 |
345 |
346 | ```python
347 | fname = mx.test_utils.download(url='http://data.mxnet.io/data/test_images.tar.gz', dirname='data', overwrite=False)
348 | tar = tarfile.open(fname)
349 | tar.extractall(path='./data')
350 | tar.close()
351 | ```
352 |
353 | #### 加载原始图片
354 |
355 | `mx.image.imdecode`让我们可以加载图片,其中的`imdecode`的使用方式和``OpenCV``非常类似。
356 |
357 | **注意:**你可能会仍然需要使用``OpenCV``(不是CV2 Python库)来代替`mx.image.imdecode`。
358 |
359 |
360 | ```python
361 | img = mx.image.imdecode(open('data/test_images/ILSVRC2012_val_00000001.JPEG', 'rb').read())
362 | plt.imshow(img.asnumpy()); plt.show()
363 | ```
364 |
365 | #### 图片转换
366 |
367 |
368 | ```python
369 | # resize to w x h
370 | tmp = mx.image.imresize(img, 100, 70)
371 | plt.imshow(tmp.asnumpy()); plt.show()
372 | ```
373 |
374 |
375 | ```python
376 | # crop a random w x h region from image
377 | tmp, coord = mx.image.random_crop(img, (150, 200))
378 | print(coord)
379 | plt.imshow(tmp.asnumpy()); plt.show()
380 | ```
381 |
382 | ### 使用图片迭代器加载数据
383 |
384 | 在学习如何使用两个内置的图片迭代器进行数据的读取之前,让我们先下载一下__Caltech 101__数据集(此数据集中包含了101个类别的物体),并将其打包成rec io格式。
385 |
386 |
387 | ```python
388 | fname = mx.test_utils.download(url='http://www.vision.caltech.edu/Image_Datasets/Caltech101/101_ObjectCategories.tar.gz', dirname='data', overwrite=False)
389 | tar = tarfile.open(fname)
390 | tar.extractall(path='./data')
391 | tar.close()
392 | ```
393 |
394 | 让我们先观察以下数据。正如你所看到的那样,在根文件夹(./data/101_ObjectCategories)下每一个标签都包含了一个子文件夹(./data/101_ObjectCategories/yin_yang)。
395 |
396 | 通过使用`im2rec.py`的脚本我们可以将其转成rec io格式。首先,我们需要创建一个list,其中包含了所有的图片文件和对应的标签。
397 |
398 | **译注:以下代码可能无法运行,可以command中输入指令完成list的生成。**
399 |
400 |
401 | ```python
402 | os.system('python %s/tools/im2rec.py --list=1 --recursive=1 --shuffle=1 --test-ratio=0.2 data/caltech data/101_ObjectCategories' % os.environ['MXNET_HOME'])
403 | ```
404 |
405 | 生成的list(./data/caltech_train.lst)文件的格式为:编号\t标签(一个或者多个)\t图片路径。在这个例子中,每张图片只有一个标签,但是你可以向list中添加更多的标签用于多标签训练。
406 |
407 |
408 | ```python
409 | os.system("python %s/tools/im2rec.py --num-thread=4 --pass-through data/caltech data/101_ObjectCategories" % os.environ['MXNET_HOME'])
410 | ```
411 |
412 | 现在rec文件保存在了data文件夹中(./data)。
413 |
414 | #### 使用ImageRecordIter
415 |
416 | [__`ImageRecordIter`__](http://mxnet.io/api/python/io/io.html#mxnet.io.ImageRecordIter)可用于读取保存在rec io格式文件中的数据。想要使用`ImageRecordIter`,我们需要创建一个加载rec文件的实例。
417 |
418 |
419 | ```python
420 | # ImageRecordIter能够接受的参数更多
421 | data_iter = mx.io.ImageRecordIter(
422 | path_imgrec="./data/caltech.rec", # rec文件
423 | data_shape=(3, 227, 227), # shape
424 | batch_size=4, # batch size
425 | resize=256 # 这是一个比较奇怪的参数
426 | # 图片增强的参数部分
427 | )
428 | data_iter.reset()
429 | batch = data_iter.next()
430 | data = batch.data[0]
431 | for i in range(4):
432 | plt.subplot(1,4,i+1)
433 | plt.imshow(data[i].asnumpy().astype(np.uint8).transpose((1,2,0)))
434 | plt.show()
435 | ```
436 |
437 | #### 使用ImageIter
438 |
439 | [__ImageIter__](http://mxnet.io/api/python/io/io.html#mxnet.io.ImageIter)是一个较为灵活的接口,它同时支持RecordIO文件和原生格式文件。
440 |
441 |
442 | ```python
443 | # ImageIter除了可以从rec和idx文件中进行数据读取,还可以根据img_list,
444 | # 即储存了图片和位置和label中读取数据
445 | data_iter = mx.image.ImageIter(batch_size=4, data_shape=(3, 227, 227),
446 | path_imgrec="./data/caltech.rec",
447 | path_imgidx="./data/caltech.idx" )
448 | data_iter.reset()
449 | batch = data_iter.next()
450 | data = batch.data[0]
451 | for i in range(4):
452 | plt.subplot(1,4,i+1)
453 | plt.imshow(data[i].asnumpy().astype(np.uint8).transpose((1,2,0)))
454 | plt.show()
455 | ```
456 |
457 |
458 |
459 |
460 |
--------------------------------------------------------------------------------
/00_basics/05_Symbolic-Configuration-and-Execution-in-Pictures.md:
--------------------------------------------------------------------------------
1 |
2 | 本节使用图片展示了如何符号式构建和执行计算图。我们强烈建议你同时阅读以下Symbolic API中的内容。
3 |
4 | ### 编写符号
5 |
6 | 符号是我们想要执行的计算的描述。符号式构建API可以生成描述计算过程的计算图。下图展示了如何使用符号来描述基本的计算过程。
7 |
8 | 
9 |
10 | - ` mxnet.symbol.Variable`函数创建了计算所需要的输入结点。
11 | - 这类符号超越了基于元素的基本数学运算。
12 |
13 | ### 配置神经网络
14 |
15 | 除了支持细粒度的操作,MXNet还提供了一些方法用于执行类似于神经网络中layer的大型操作。你可以使用运算符来描述神经网络的配置过程
16 |
17 | 
18 |
19 | ### 多输入的神经网络
20 |
21 | 下面的例子展示了如何配置多输入的神经网络
22 | 
23 |
24 | ### 联结和执行符号
25 |
26 | 当你想要执行符号图的时候,你可以调用`bind`函数将`NDArray`和参数结点联结在一起,以获得`Executor`。
27 | 
28 |
29 | 在将联结后的NDArray作为输入后,通过调用`Executor.Forward`来获得输出结果。
30 | 
31 |
32 |
33 | ### 联结多个输出
34 |
35 | 使用`mx.symbol.Group`将符号分组,然后通过调用`bind`进行联结后获得两者输出。
36 |
37 | 
38 |
39 | 注意:只需要联结你所需要的符号,这样系统可以获得更好的优化。
40 |
41 |
42 | ### 计算梯度
43 |
44 | 
45 |
46 | ### 神经网路的bind接口
47 |
48 | 向bind函数传递NDArray参数是一件非常无聊的事情,尤其当你想要联结一个大的计算图时尤其如此。而`Symbol.simple_bind`函数则提供了一种相对简单的方式来执行这个过程。你只需要指定输入数据的形状即可。函数会为参数自动分配内存,并联结一个Executor。
49 |
50 | 
51 |
52 | ### 辅助状态
53 |
54 | 辅助状态就像参数一样,但是你不会计算他们的梯度。尽管辅助状态并不是计算的一部分,但是他们有助于追踪计算的过程。你可以像传递参数一样传递辅助状态。
55 |
56 | 
57 |
58 | ### 下一步
59 | See Symbolic API and Python Documentation.
60 |
--------------------------------------------------------------------------------
/01_neural_networks/00_Linear-Regression.md:
--------------------------------------------------------------------------------
1 |
2 | # 线性回归
3 |
4 | 在本教程中,我们将使用MXNet的API实现*线性回归*。我们将尝试学习的函数为*y = x1 + 2x2*,其中*(x1,x2)*是输入特征,而*y*是对应的标签。
5 |
6 | ## 准备工作
7 |
8 | 为了完成本教程,我们需要:
9 |
10 | - MXNet。安装请参照[Setup and Installation](http://mxnet.io/install/index.html);
11 |
12 | - [Jupyter Notebook](http://jupyter.org/index.html)。
13 |
14 | ```
15 | $ pip install jupyter
16 | ```
17 |
18 | 开始之前,下面的代码将导入必要的包。
19 |
20 |
21 | ```python
22 | import mxnet as mx
23 | import numpy as np
24 |
25 | import logging
26 | logging.getLogger().setLevel(logging.DEBUG)
27 | ```
28 |
29 | ## 准备数据
30 |
31 | 在MXNet中,数据是通过**Data Iterators**输入的。这里,我们将演示如何将数据集编码成迭代器的形式以便MXNet作为输入使用。本样例中所使用的数据由2维的数据点和对应的标签组成。
32 |
33 |
34 | ```python
35 | #Training data
36 | train_data = np.random.uniform(0, 1, [100, 2])
37 | train_label = np.array([train_data[i][0] + 2 * train_data[i][1] for i in range(100)])
38 | batch_size = 1
39 |
40 | #Evaluation Data
41 | eval_data = np.array([[7,2],[6,10],[12,2]])
42 | eval_label = np.array([11,26,16])
43 | ```
44 |
45 | 完成数据的准备工作后,我们将其放入迭代器中,并指定`batch_size`和`shuffle`两个参数。`batch_size`决定了模型训练时每次需要处理的样本的数目;`shuffle`则决定了输入给模型进行训练的数据是否需要打乱处理。
46 |
47 |
48 | ```python
49 | train_iter = mx.io.NDArrayIter(train_data,train_label, batch_size, shuffle=True,label_name='lin_reg_label')
50 | eval_iter = mx.io.NDArrayIter(eval_data, eval_label, batch_size, shuffle=False)
51 | ```
52 |
53 | 在上面的例子中,我们使用了`NDArrayIter`;利用它,我们可以处理numpy的ndarrays和MXNet的NDArrays。一般而言,MXNet提供了不同类型的迭代器,你可以根据自己所要处理的数据类型决定使用哪一种。迭代器的文档可以参考[这里](http://mxnet.io/api/python/io/io.html)。
54 |
55 |
56 | ## MXNet类
57 |
58 | 1. **IO:** 正如我们看到的那样,IO类处理数据,执行提供数据(以批次或者打乱形式)的操作。
59 |
60 | 2. **Symbol:** MXNet的神经网络实质上都是由符号组成的。MXNet中包含了不同类型的符号,包括代表输入数据的占位符,神经网络层和对NDArray进行处理的操作符等。
61 |
62 | 3. **Module:** module类被用来确定整体的计算。通过定义我们将要训练的模型和训练所使用的输入(包括数据和标签),以及一些额外的参数,例如学习率和优化算法和初始化方法等。
63 |
64 | ## 定义模型
65 |
66 | MXNet使用**Symbols**来定义一个模型。Symbols是一些构建中的模块和组成模型的组件。Symbols被用来定义下述内容:
67 |
68 | 1. **Variables:** Variables是为之后的数据所准备的占位符。这个符号被用来定义有一个点,当我们开始训练时,实际的训练数据和标签将会将其填充。
69 |
70 | 2. **Neural Network Layers:** 神经网络中的一层或者其他类型的模型都可以使用Symbols进行定义。这样一个Symbol接受一个或者多个之前的Symbols作为输入,进行一定的处理,导出一个或者多个输出。神经网络中的全连接层`FullyConnected`就是这样的一个例子。
71 |
72 | 3. **Outputs:** 输出symbols是MXNet定义损失的方式。它们都以"Output"作为后缀(例如`SoftmaxOutput`)。你也可以构建你自己的[损失函数](https://github.com/dmlc/mxnet/blob/master/docs/tutorials/r/CustomLossFunction.md#how-to-use-your-own-loss-function)。一些已经定义的损失函数有:`LinearRegressionOutput`,计算输出和输入标签的l2损失;`SoftmaxOutput`,计算输出和输出的交叉熵损失。
73 |
74 | 上面描述的symbol和其他的symbols串联在一起形成拓扑图的方式是:每一个symbol的输出都是下一个symbol的输入。更多关于不同类型symbols的信息可以在[这里](http://mxnet.io/api/python/symbol/symbol.html)找到。
75 |
76 |
77 | ```python
78 | X = mx.sym.Variable('data')
79 | Y = mx.symbol.Variable('lin_reg_label')
80 | fully_connected_layer = mx.sym.FullyConnected(data=X, name='fc1', num_hidden = 1)
81 | lro = mx.sym.LinearRegressionOutput(data=fully_connected_layer, label=Y, name="lro")
82 | ```
83 |
84 | 上面的网络使用了下述的一些层:
85 |
86 | 1. `FullyConnected`:全连接符号表示的是神经网络中的全连接层(没有进行任何激活);实质上,它只是输入对象的线性表示。它接受以下两个参数:
87 | - `data`:本层的输入(也就是指明在这里应该是谁的输出)
88 | - `num_hidden`:隐含神经元的个数,它和输出数据的维度相同
89 |
90 | 2. `LinearRegressionOutput`:MXNet计算训练损失的输出层,它是模型预测错误率的度量。训练的目的即为最小化这个训练损失。在我们的例子中,`LinearRegressionOutput`计算它的输入和数据标签之间的l2损失。它接受以下两个参数:
91 | - `data`:本层的输入(也就是指明在这里应该是谁的输出)
92 | - `label`:数据标签,亦即我们将用来进行l2损失计算的对象之一
93 |
94 | **命名小贴士:** 标签变量的名称应该和我们传递给训练数据迭代器的参数`label_name`相一致。这里的默认值为`softmax_label`,但是在本例中我们将其统一变更为了`lin_reg_label`。所以在`Y = mx.symbol.Variable('lin_reg_label')`和
95 | `train_iter = mx.io.NDArrayIter(..., label_name='lin_reg_label')`中label_name均为`lin_reg_label`。
96 |
97 | 最终,这个网络变成了*Module*;在这个模型中,我们指明了需要对哪个符号的输出进行最小化(在本例中为`lro`或者`lin_reg_output`),优化过程的学习率又是多少,以及我们需要训练的轮次数。
98 |
99 |
100 | ```python
101 | model = mx.mod.Module(
102 | symbol = lro ,
103 | data_names=['data'],
104 | label_names = ['lin_reg_label']# network structure
105 | )
106 | ```
107 |
108 | 对我们创建的网络进行可视化的结果如下:
109 |
110 |
111 | ```python
112 | mx.viz.plot_network(symbol=lro)
113 | ```
114 |
115 | ## 训练模型
116 |
117 | 完成模型结构的定义之后,下一步就是将训练数据和模型结合起来对模型的参数进行训练。通过调用`Module`类中的`fit()`函数可以完成模型的训练。
118 |
119 |
120 | ```python
121 | model.fit(train_iter, eval_iter,
122 | optimizer_params={'learning_rate':0.005, 'momentum': 0.9},
123 | num_epoch=2,
124 | eval_metric='mse',
125 | batch_end_callback = mx.callback.Speedometer(batch_size, 2))
126 | ```
127 |
128 | ## 使用一个已经训练好的模型:(测试和预测)
129 |
130 | 在完成了模型的训练之后,我们可以用它做很多事情。我们既可以用它来进行预测,也可以在测试集上评估它的性能。后者的代码如下所示:
131 |
132 |
133 | ```python
134 | model.predict(eval_iter).asnumpy()
135 | ```
136 |
137 | 我们也可以根据评估函数来评价模型的性能。在本例中,我们评估模型在验证集上的均方根误差(MSE)。
138 |
139 |
140 | ```python
141 | metric = mx.metric.MSE()
142 | model.score(eval_iter, metric)
143 | assert model.score(eval_iter, metric)[0][1] < 0.01001, "Achieved MSE (%f) is larger than expected (0.01001)" % model.score(eval_iter, metric)[0][1]
144 | ```
145 |
146 | 让我们在验证数据上添加一些噪音,看一下MSE是如何变化的。
147 |
148 |
149 | ```python
150 | eval_data = np.array([[7,2],[6,10],[12,2]])
151 | eval_label = np.array([11.1,26.1,16.1]) #Adding 0.1 to each of the values
152 | eval_iter = mx.io.NDArrayIter(eval_data, eval_label, batch_size, shuffle=False)
153 | model.score(eval_iter, metric)
154 | ```
155 |
156 | 当然,我们也可以自定义一个损失函数,使用它去评估模型。更多的信息可以查阅[API文档](http://mxnet.io/api/python/model.html#evaluation-metric-api-reference)。
157 |
--------------------------------------------------------------------------------
/01_neural_networks/01_Mnist-Handwritten-Digit-Recognition.md:
--------------------------------------------------------------------------------
1 |
2 | # 手写数字识别
3 |
4 | 在本教程中,我们将手把手教你如何利用MNIST数据集构建一个手写数字分类器。即便对于刚接触深度学习的人来说,这个教程也像"Hello World"一样简单。
5 |
6 | MNIST数据集被广泛用于手写数字分类任务。它由70000张已经标记了的28×28像素的手写数字的灰度图片组成。这个数据集通常会被切分成包含60000张图片的训练集和包含10000张图片的测试集,其中包含了十个类别(即十种数字)。目前的任务就是使用训练集中的图片训练一个分类模型,并在验证集的图片上测试其分类准确度。
7 |
8 | 
9 |
10 | **图1:**MNIST数据集中的样本图像
11 |
12 | ## 准备工作
13 |
14 | 为了能够完成本教程,我们需要:
15 |
16 | - 0.10或更高版本的MXNet.安装请参照[Setup and Installation](http://mxnet.io/install/index.html)
17 |
18 | - [Python Requests](http://docs.python-requests.org/en/master/)和[Jupyter Notebook](http://jupyter.org/index.html)
19 |
20 | ```
21 | $ pip install requests jupyter
22 | ```
23 |
24 | ## 加载数据
25 |
26 | 在定义模型之前,我们先把[MNIST数据集](http://yann.lecun.com/exdb/mnist/)下载下来。
27 |
28 | 下面的代码会将MNIST数据集的图像和标签下载下来,并将其加载到内存中。
29 |
30 |
31 | ```python
32 | import mxnet as mx
33 | mnist = mx.test_utils.get_mnist()
34 | ```
35 |
36 | 在运行完上述源代码之后,整个MNIST数据集都应该被完全加载到内存当中。不过请注意,对于大型数据集,我们不太可能预先全部加载。因此我们需要这样一种机制,通过它我们可以快速有效地从数据源中加载数据。MXNet中提供的的数据迭代器正好可以解决这个问题。通过数据迭代器,我们可以将数据源源不断地送入MXNet的训练程序;而且它们非常易于初始化和使用,并且针对加载速度进行了优化。在训练过程中,我们通常会对小批次的数据进行处理;当整个训练过程完成后,每个训练样本都会被处理了很多次。在本教程中,我们将数据迭代器的批次大小设置为100。请记住,每个训练样本都是28×28的灰度图片和对应的标签。
37 |
38 | 批次图片数据一般由形状为`(batch_size, num_channels, width, height)`的4D数组表示。对于MNIST数据集而言,由于图片是灰度的,因此图片数据的颜色通道数为1。另外,由于图片的分辨率为28×28像素,因此每张图片的宽度和高度均为28。因此输入数据的形状为`(batch_size, 1, 28, 28)`。另一个需要考虑的重要因素是输入样本的顺序。这里的关键是,不要在训练过程中连续输入相同标签的样本。这样干会降低训练的速度。通过随机打乱,数据迭代器很好的处理了这个问题。不过还请注意,我们只需要对训练数据进行打乱,测试数据的顺序并不重要。
39 |
40 | 以下源代码将MNIST数据集的迭代器初始化。在这里,我们分别为训练集和测试集初始化了一个迭代器。
41 |
42 |
43 | ```python
44 | batch_size = 100
45 | train_iter = mx.io.NDArrayIter(mnist['train_data'], mnist['train_label'], batch_size, shuffle=True)
46 | val_iter = mx.io.NDArrayIter(mnist['test_data'], mnist['test_label'], batch_size)
47 | ```
48 |
49 | ## 训练
50 |
51 | 我们将介绍几种不同的方法来完成手写数字识别任务。第一种方法利用了一种叫做多层感知机(Multilayer Perceptron,MLP)的传统深度神经网络架构。我们将讨论它的缺点,并以此为契机介绍第二种更为高级的,叫做卷积神经网络(Convolution Neural Network,CNN)的方法。在图像分类任务中,CNN已经被证明性能出众。
52 |
53 | ### 多层感知机
54 |
55 | 首先我们用[MLP](https://en.wikipedia.org/wiki/Multilayer_perceptron)来解决这个问题。我们将使用MXNet中的符号式接口来定义MLP的结构。首先,我们为输入数据创建一个占位符。在使用MLP的时候,我们需要将28×28的图片展开成一个784(28×28)原始像素值的1D数组结构。只要我们对于所有的图片都使用了相同的展开方法,展开的数组中像素值的顺序就不再重要。
56 |
57 |
58 | ```python
59 | data = mx.sym.var('data')
60 | # Flatten the data from 4-D shape into 2-D (batch_size, num_channel*width*height)
61 | data = mx.sym.flatten(data=data)
62 | ```
63 |
64 | 你可能会有疑问,当我们展平图片的时候难道没有丢失信息吗?事实确实如此。在之后讨论CNN(图片的形状没有改变)时我们会更详细地讨论这个问题。现在,让我们接着往下看。
65 |
66 | MLP中包含了多个全连接层。在全连接层中,或者(简称为)FC层,一个神经元和前一层中的所有神经元都有连接。从线性代数的角度来看,FC层对*n x m*的输入矩阵*X*应用仿射变换,并输出一个尺寸为*n x k*的矩阵*Y*,其中*k*是FC层中的神经元的个数。*k*也被称为隐含单元的大小。输出矩阵*Y*通过*Y = X WT + b*计算得到。FC层有两部分可以学习的参数,即*k x m*大小的权重矩阵*W*和*1 x k*大小的偏置向量*b*。偏置矩阵的加法遵循[`mxnet.sym.broadcast_to()`](https://mxnet.incubator.apache.org/api/python/symbol/symbol.html#mxnet.symbol.broadcast_to)当中的广播规则。从概念上讲,在广播求和之前,偏置向量在行方向上复制得到一个*n x k*的矩阵。
67 |
68 | 在MLP中,大多数情况下FC层的输出会被送入一个激活函数当中,激活函数对其进行按元素的非线性激活。这一步至关重要,因为它使得神经网络能够对非线性可分的输入进行分类。激活函数的一般选择是sigmoid,tanh或者[线性修正单元(rectified linear unit,ReLU)](https://en.wikipedia.org/wiki/Rectifier_%28neural_networks%29)。在本例当中,由于ReLU具有的良好特性,我们将会使用ReLU作为激活函数,而它一般也是激活函数的默认选择。
69 |
70 | 下面的代码展示了两个分别具有128个和64个神经元的全连接层。此外,这些FC层夹在激活函数层之间,每个激活函数层负责对上一个FC层的输出执行按元素的ReLU激活转换。
71 |
72 |
73 | ```python
74 | # The first fully-connected layer and the corresponding activation function
75 | fc1 = mx.sym.FullyConnected(data=data, num_hidden=128)
76 | act1 = mx.sym.Activation(data=fc1, act_type="relu")
77 |
78 | # The second fully-connected layer and the corresponding activation function
79 | fc2 = mx.sym.FullyConnected(data=act1, num_hidden = 64)
80 | act2 = mx.sym.Activation(data=fc2, act_type="relu")
81 | ```
82 |
83 | MLP的最后一个FC层的大小通常和数据集的类别数目相同,这一层的激活函数则为softmax函数。softmax函数将输入映射为输出类别上的概率分布。在训练阶段,损失函数计算神经网络输出的预测分布概率和标签提供的真实分布概率之间的[交叉熵损失](https://en.wikipedia.org/wiki/Cross_entropy)。
84 |
85 | 下面的代码展示了在最后一个FC层中,神经元的个数为10,也就是数字的类别数目。该层的输出被送入`SoftMaxOutput`层中,一次性执行softmax激活和交叉熵损失的计算。不过请注意,交叉熵损失只在训练阶段才会进行计算。
86 |
87 |
88 | ```python
89 | # MNIST has 10 classes
90 | fc3 = mx.sym.FullyConnected(data=act2, num_hidden=10)
91 | # Softmax with cross entropy loss
92 | mlp = mx.sym.SoftmaxOutput(data=fc3, name='softmax')
93 | ```
94 |
95 | 
96 |
97 | **图 2:** MNIST数据集上的MLP网络结构
98 |
99 | 我们已经定义好了数据迭代器和神经网络,现在我们可以开始进行训练了。MXNet的`module`模块为模型的训练和预测提供了高级的抽象接口,在这里我们来探索一下它的特性。`module`API允许用户指定适当的参数以便控制训练过程。
100 |
101 | 下面的代码初始化了一个module以便我们训练之前定义的MLP网络。在训练中,我们将使用随机梯度下降法进行参数优化。更确切地讲,我们要使用的是小批量梯度下降法。标准的随机梯度下降法每次只在一个样本上进行训练。在实际使用中,这样训练的速度会非常的慢;因此常常使用小批量样本以加速训练过程。在本例中,我们的样本批次大小选择了较为合理的100。另外一个需要选择的参数是学习率;在优化求解的过程中,学习率决定了每一步的大小。在这里我们将学习率选择为0.1。类似于样本批次大小和学习率大小的设置我们一般称之为超参。我们所设置的超参对于训练得到的模型性能有很大的影响。为了完成本教程,我们将选择一些合理安全的参数值。在其他的教程中,我们将会讨论如何组合这些超参才能达到最佳的模型性能。
102 |
103 | 通常意义上,我们会一直对模型进行训练直至收敛,此时模型在训练数据集上学习到了一组较好的模型参数(权重+偏置)。在本教程中,我们将在训练10个轮次后停止。一个轮次就是遍历了一遍整个训练数据集。
104 |
105 |
106 | ```python
107 | import logging
108 | logging.getLogger().setLevel(logging.DEBUG) # logging to stdout
109 | # create a trainable module on CPU
110 | mlp_model = mx.mod.Module(symbol=mlp, context=mx.cpu())
111 | mlp_model.fit(train_iter, # train data
112 | eval_data=val_iter, # validation data
113 | optimizer='sgd', # use SGD to train
114 | optimizer_params={'learning_rate':0.1}, # use fixed learning rate
115 | eval_metric='acc', # report accuracy during training
116 | batch_end_callback = mx.callback.Speedometer(batch_size, 100), # output progress for each 100 data batches
117 | num_epoch=10) # train for at most 10 dataset passes
118 | ```
119 |
120 | ### 预测
121 |
122 | 训练完成后,我们可以在测试数据上对已训练的模型进行评估。下面的源代码为每一张测试图片计算一个预测得分。*prob[i][j]*代表的是第*i*张测试图片得到分类结果*j*的可能性。
123 |
124 |
125 | ```python
126 | test_iter = mx.io.NDArrayIter(mnist['test_data'], None, batch_size)
127 | prob = mlp_model.predict(test_iter)
128 | assert prob.shape == (10000, 10)
129 | ```
130 |
131 | 由于测试数据集中包含了所有测试图片的标签,因此我们可以像下面的代码那样进行准确率的计算。
132 |
133 |
134 | ```python
135 | test_iter = mx.io.NDArrayIter(mnist['test_data'], mnist['test_label'], batch_size)
136 | # predict accuracy of mlp
137 | acc = mx.metric.Accuracy()
138 | mlp_model.score(test_iter, acc)
139 | print(acc)
140 | assert acc.get()[1] > 0.96, "Achieved accuracy (%f) is lower than expected (0.96)" % acc.get()[1]
141 | ```
142 |
143 | 如果一切顺利的当,我们应该可以看到准确率大约在0.96左右。这意味着我们能够为96%的测试图片准确分类。这已经是一个相当好的结果。但是正如我们下一部分将要看到的,我们还可以做得更好。
144 |
145 | ### 卷积神经网络
146 |
147 | 在MLP中,我们简短地讨论了MLP的一个缺点:在将图片输入MLP的首个全连接层之前,我们将图片展平,但这样损失了部分信息。事实证明这确实是一个重要的问题,因为我们没有利用像素之间在纵向和横向上的空间联系。卷积神经网络旨在使用更加结构化的权重表示来解决这个问题。在卷积神经网络中,原来那种将图片展平做矩阵乘法的简单方式被抛弃,它转而采用了一个或者多个卷积层,每个卷积层都在输入图像上进行2D卷积。
148 |
149 | 一个卷积层可以由一个或者多个滤波器组成,其中每一个都扮演着特征提取的功能。在训练过程中,CNN中的这些滤波器将学习到合适的参数表示。和MLP类似,卷积层的输出也都经过了非线性激活。除了卷积层,CNN另外一个重要的组成就是池化层了。一个池化层可以使得CNN具有平移不变性,也就是当数字在上/下/左/右方向上有几个像素的偏移时,它仍然可以和之前保持一致。池化层将*n x m*大小的区域缩减为一个值,这样一来网络对于空间位置的敏感性更低。在CNN中,池化层通常连接在卷积层(包含激活)之后。
150 |
151 | 下面的代码定义了一个叫做LeNet的卷积神经网络。LeNet是一个被广泛使用的,在数字分类任务上有良好性能的网络。我们将使用的LeNet和原生的LeNet略有不同,为了得到更好的性能,我们将激活函数从sigmoid更换为了tanh。
152 |
153 |
154 | ```python
155 | data = mx.sym.var('data')
156 | # first conv layer
157 | conv1 = mx.sym.Convolution(data=data, kernel=(5,5), num_filter=20)
158 | tanh1 = mx.sym.Activation(data=conv1, act_type="tanh")
159 | pool1 = mx.sym.Pooling(data=tanh1, pool_type="max", kernel=(2,2), stride=(2,2))
160 | # second conv layer
161 | conv2 = mx.sym.Convolution(data=pool1, kernel=(5,5), num_filter=50)
162 | tanh2 = mx.sym.Activation(data=conv2, act_type="tanh")
163 | pool2 = mx.sym.Pooling(data=tanh2, pool_type="max", kernel=(2,2), stride=(2,2))
164 | # first fullc layer
165 | flatten = mx.sym.flatten(data=pool2)
166 | fc1 = mx.symbol.FullyConnected(data=flatten, num_hidden=500)
167 | tanh3 = mx.sym.Activation(data=fc1, act_type="tanh")
168 | # second fullc
169 | fc2 = mx.sym.FullyConnected(data=tanh3, num_hidden=10)
170 | # softmax loss
171 | lenet = mx.sym.SoftmaxOutput(data=fc2, name='softmax')
172 | ```
173 |
174 | 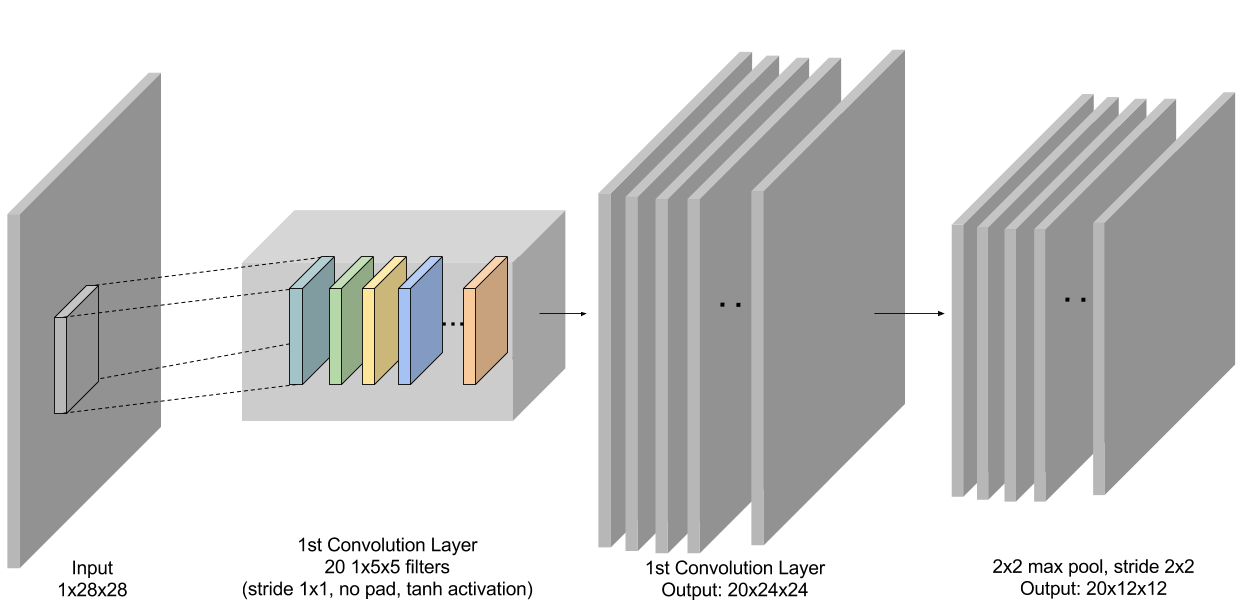
175 |
176 | **图 3:** LeNet首个卷积+池化层
177 |
178 | 现在,我们可以使用之前的超参对LeNet进行训练。请注意,如果GPU可用的话,我们推荐使用GPU进行训练。和之前的MLP相比,由于LeNet更加复杂,运算更多,因此使用GPU可以大大加速训练过程。我们只需要将计算设备从`mx.cpu()`改为`mx.gpu()`即可,MXNet会自动完成剩余的设置。就像之前一样,我们在训练10个轮次之后停止训练。
179 |
180 |
181 | ```python
182 | # create a trainable module on CPU, change to mx.gpu() if GPU is available
183 | lenet_model = mx.mod.Module(symbol=lenet, context=mx.cpu())
184 | # train with the same
185 | lenet_model.fit(train_iter,
186 | eval_data=val_iter,
187 | optimizer='sgd',
188 | optimizer_params={'learning_rate':0.1},
189 | eval_metric='acc',
190 | batch_end_callback = mx.callback.Speedometer(batch_size, 100),
191 | num_epoch=10)
192 | ```
193 |
194 | ### 预测
195 |
196 | 最后,我们可以使用已经训练好的LeNet在测试数据上进行预测。
197 |
198 |
199 | ```python
200 | test_iter = mx.io.NDArrayIter(mnist['test_data'], None, batch_size)
201 | prob = lenet_model.predict(test_iter)
202 | test_iter = mx.io.NDArrayIter(mnist['test_data'], mnist['test_label'], batch_size)
203 | # predict accuracy for lenet
204 | acc = mx.metric.Accuracy()
205 | lenet_model.score(test_iter, acc)
206 | print(acc)
207 | assert acc.get()[1] > 0.98, "Achieved accuracy (%f) is lower than expected (0.98)" % acc.get()[1]
208 | ```
209 |
210 | 如果一切都没有问题,我们应该可以看到使用LeNet进行预测可以得到更高的准确率。在所有的测试图片上,CNN的预测准确率大概在98%左右。
211 |
212 | ## 总结
213 |
214 | 在本教程中,我们学习了如何使用MXNet解决一个标准的计算机视觉问题:对手写数字图片进行分类。你应该已经明白如何使用MXNet构建诸如MLP或者CNN的模型,并在对其进行训练和评估。
215 |
--------------------------------------------------------------------------------
/01_neural_networks/02_Large-Scale-Image-Classification.md:
--------------------------------------------------------------------------------
1 |
2 | # 大规模图像分类
3 |
4 | 在大规模图像数据集上进行神经网络的训练存着着诸多挑战。即便使用最新的GPU,想要在合理的时间内使用单块GPU在大规模图像数据集上训练神经网络也几乎是不可能的。而在单台机器上使用多块GPU可以稍微降低这个问题的难度。但是一台机器可以连接的GPU数量是有限制的(通常为8或者16)。本教程将展示如何使用包含了多块GPU的多台机器在TB级别的数据上进行大型网络的训练。
5 |
6 | ### 准备工作
7 |
8 | - MXNet
9 | - OpenCV Python library
10 |
11 |
12 | ```python
13 | $ pip install opencv-python
14 | ```
15 |
16 | ### 预处理
17 |
18 | #### 磁盘空间
19 |
20 | 在大型数据集上进行训练的第一步就是下载和预处理数据。对于本教程,我们将使用完整的ImageNet数据集进行训练。请注意,要下载和预处理这些数据你至少需要有2TB的磁盘空间。在这里,我们强烈建议你使用SSD而不是HDD。因为SSD在处理大量的小体积图片时性能会更好。完成对图片的预处理和打包工作后(打包成recordIO格式),HDD也能够很好的完成训练的工作。
21 |
22 | 在本教程中,我们将使用AWS存储进行数据预处理。`i3.4xlarge`使用了两块`NVMe SSD`格式的硬盘,总容量为3.8TB。我们将使用RAID软件将它们组成一块硬盘,并将其挂载到`~/data`。
23 |
24 |
25 | ```python
26 | sudo mdadm --create --verbose /dev/md0 --level=stripe --raid-devices=2 \
27 | /dev/nvme0n1 /dev/nvme1n1
28 | sudo mkfs /dev/md0
29 | sudo mkdir ~/data
30 | sudo mount /dev/md0 ~/data
31 | sudo chown ${whoami} ~/data
32 | ```
33 |
34 | 现在我们有了足够的磁盘空间来下载和预处理数据。
35 |
36 | #### 下载ImageNet数据集
37 |
38 | 在本教程中,我们将使用完整的ImageNet数据集,数据集的下载地址为:http://www.image-net.org/download-images 。`fall11_whole.tar`文件中包含了所有的图片。整个数据集约1.2TB,因此你可能需要很长时间才能完成下载工作。
39 |
40 | 完成下载后,解压文件。
41 |
42 |
43 | ```python
44 | export ROOT=full
45 | mkdir $ROOT
46 | tar -xvf fall11_whole.tar -C $ROOT
47 | ```
48 |
49 | 之后你会得到一个tar文件的集合。其中每一个tar文件代表着一个类别,文件当中包含着属于该类别的全部图像。我们将tar文件解压,并将所有的图像复制到以tar文件名命名的文件夹中。
50 |
51 |
52 | ```python
53 | for i in $ROOT/*.tar; do j=${i%.*}; echo $j; mkdir -p $j; tar -xf $i -C $j; done
54 | rm $ROOT/*.tar
55 |
56 | ls $ROOT | head
57 | n00004475
58 | n00005787
59 | n00006024
60 | n00006484
61 | n00007846
62 | n00015388
63 | n00017222
64 | n00021265
65 | n00021939
66 | n00120010
67 | ```
68 |
69 | #### 移除不常见的类别(可选)
70 |
71 | 在ImageNet上进行网络训练的一个常见原因是为了迁移学习(包括特征提取和微调其他模型)。而对这项研究而言,图像太少的类别无助于迁移学习。所以,如果某个类别的图像数目少于一个特定的值,我们就将其移除。下面的代码将会移除图片数目少于500张的类别。
72 |
73 |
74 | ```python
75 | BAK=${ROOT}_filtered
76 | mkdir -p ${BAK}
77 | for c in ${ROOT}/n*; do
78 | count=`ls $c/*.JPEG | wc -l`
79 | if [ "$count" -gt "500" ]; then
80 | echo "keep $c, count = $count"
81 | else
82 | echo "remove $c, $count"
83 | mv $c ${BAK}/
84 | fi
85 | done
86 | ```
87 |
88 | #### 生成验证集
89 |
90 | 为了确保我们的模型不会过拟合,我们从训练集中分离出一部分作为验证集。在训练过程中,我们会频繁地监视模型在验证集上的损失。
91 |
92 |
93 | ```python
94 | VAL_ROOT=${ROOT}_val
95 | mkdir -p ${VAL_ROOT}
96 | for i in ${ROOT}/n*; do
97 | c=`basename $i`
98 | echo $c
99 | mkdir -p ${VAL_ROOT}/$c
100 | for j in `ls $i/*.JPEG | shuf | head -n 50`; do
101 | mv $j ${VAL_ROOT}/$c/
102 | done
103 | done
104 | ```
105 |
106 | #### 将图片打包成record文件
107 |
108 | 尽管MXNet可以直接读取图片,但是我们还是建议你将其打包成recordIo文件以提高训练的效率。使用MXNet提供的脚本工具(tools/im2rec.py)可以完成这项工作。在使用此脚本之前,你需要在系统中安装MXNet和opencv的python模型。
109 |
110 | 将环境变量`MXNet`指向MXNet的安装文件夹,并设置`NAME`为数据集的所在位置。这里,我们假设MXNet安装在了`~/mxnet`中。
111 |
112 |
113 | ```python
114 | MXNET=~/mxnet
115 | NAME=full_imagenet_500_filtered
116 | ```
117 |
118 | 在创建recordIO文件之前,我们首先需要创建一个包含了所有图片标签及路径的list文件,然后使用`im2rec`将list文件中的图片打包成recordIO文件。我们将在`train_meta`文件夹中创建这个list。原始的训练数据大约1TB,在这里我们将其分成了8部分,这样每个部分的大小大约在100GB左右。
119 |
120 |
121 | ```python
122 | mkdir -p train_meta
123 | python ${MXNET}/tools/im2rec.py --list True --chunks 8 --recursive True \
124 | train_meta/${NAME} ${ROOT}
125 | ```
126 |
127 | 之后,我们将图片的短边缩放到480像素,然后将其打包进recordIO文件。由于这项工作大部分时间都花费在磁盘的输入/输出上,因此我们将使用多线程来更快地完成这个工作。
128 |
129 |
130 | ```python
131 | python ${MXNET}/tools/im2rec.py --resize 480 --quality 90 \
132 | --num-thread 16 train_meta/${NAME} ${ROOT}
133 | ```
134 |
135 | 完成之后,我们将`rec`文件移动到`train`文件夹中。
136 |
137 |
138 | ```python
139 | mkdir -p train
140 | mv train_meta/*.rec train/
141 | ```
142 |
143 | 对于验证集,重复上述工作。
144 |
145 |
146 | ```python
147 | mkdir -p val_meta
148 | python ${MXNET}/tools/im2rec.py --list True --recursive True \
149 | val_meta/${NAME} ${VAL_ROOT}
150 | python ${MXNET}/tools/im2rec.py --resize 480 --quality 90 \
151 | --num-thread 16 val_meta/${NAME} ${VAL_ROOT}
152 | mkdir -p val
153 | mv val_meta/*.rec val/
154 | ```
155 |
156 | 现在,在`train`和`val`文件夹中,我们以recordIO格式分别储存了所有的训练和验证图片。我们终于可以开始使用这些`.rec`文件进行模型的训练了。
157 |
158 | ### 训练
159 |
160 | 在ImageNet竞赛中,[Resnet](https://arxiv.org/abs/1512.03385)已经展示了其有效性。我们的试验也重现了[这篇文章](https://github.com/tornadomeet/ResNet)中的结果。随着神经网络层数从18增加到152,我们可以看到验证准确率的逐步提升。鉴于这个数据集的规模庞大,我们将使用152层的Resnet。
161 |
162 | 由于计算复杂度之巨大,即便使用最快的GPU,完成一次数据集遍历所需要的时间也远远不止一天。然而在训练收敛到较好的验证准确率之前,我们通常需要遍历数据集数十个轮次。尽管我们可以在一台机器中使用多块GPU进行训练,然而一台机器的GPU数量通常被限制为8或者16。在本教程中,为了加速训练,我们将使用多GPU的多台机器进行模型的训练。
163 |
164 | #### 设置
165 |
166 | 我们将使用16台机器(P2.16x),每台机器中包含了16块GPU(Tesla K80)。这些机器使用20 Gbps的以太网进行通讯。
167 |
168 | 使用AWS CloudFormation可以很方便地创建深度学习集群。我们遵循[此页面](https://aws.amazon.com/blogs/compute/distributed-deep-learning-made-easy/)的设置教程创建一个包含16个P2.16x的深度学习集群。
169 |
170 | 我们在第一台机器上加载数据和代码(同时,这台机器将成为master)。这台机器和其他机器之间通过EFS共享数据和代码。
171 |
172 | 如果你是在手动地设置集群,而不是使用了AWS提供的CloudFormation,那么请记得进行一下的设置。
173 |
174 | - 使用`USE_DIST_KVSTORE=1 `编译MXNet以激活分布式训练。
175 |
176 | - 在master机器上创建hosts文件,其中应该包含集群中所有机器的主机名,示例如下所示:
177 |
178 |
179 | ```python
180 | $ head -3 hosts
181 | deeplearning-worker1
182 | deeplearning-worker2
183 | deeplearning-worker3
184 | ```
185 |
186 | 完成设置后,应该能够在master机器上通过`ssh 主机名`的形式进入任意一台机器。示例如下:
187 |
188 |
189 | ```python
190 | $ ssh deeplearning-worker2
191 | ===================================
192 | Deep Learning AMI for Ubuntu
193 | ===================================
194 | ...
195 | ubuntu@ip-10-0-1-199:~$
196 | ```
197 |
198 | 一种实现上述功能的方式为使用ssh代理转发。你可以在[这里](https://aws.amazon.com/blogs/security/securely-connect-to-linux-instances-running-in-a-private-amazon-vpc/)学习到如何进行设置。简短来说,你需要对机器进行配置以便使用本地的证书进行登录。然后,你使用证书和`-A`登录到master机器上。现在你就可以通过`ssh hostname`登录到集群中的任意一台机器上。(示例:`ssh deeplearning-worker2`)
199 |
200 | #### 运行训练
201 |
202 | 在集群设置完成后,登录到master上并在${MXNET}/example/image-classification中运行一下指令。
203 |
204 |
205 | ```python
206 | ../../tools/launch.py -n 16 -H $DEEPLEARNING_WORKERS_PATH python train_imagenet.py --network resnet \
207 | --num-layers 152 --data-train ~/data/train --data-val ~/data/val/ --gpus 0,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15 \
208 | --batch-size 8192 --model ~/data/model/resnet152 --num-epochs 1 --kv-store dist_sync
209 | ```
210 |
211 | launch.py在集群的所有机器上启动提供给它的指令。集群中的机器李彪需要通过`-H`提供给launch.py。下面的列表列出了脚本需要用到的全部指令。
212 |
213 | 选项 | 描述
214 | - | :-: | :-:
215 | n | 指定每台机器上运行的工作程序作业数。因为我们在集群中有16台机器,因此指定作业数为16。
216 | H | 指定储存了集群中所有机器的主机名的文件路径。因为我们使用了AWS的深度学习云模板来创建集群,因此环境变量$DEEPLEARNING_WORKERS_PATH指向了所需要的文件。
217 |
218 | train_imagenet.py的参数中,--network指定了所需要训练的网络类型,--data-train和--data-val指定了训练所需的数据。下表详细描述了train_imagenet.py的参数意义。
219 |
220 | Option | Description
221 | - | :-: | :-:
222 | network | 网络类型,可以是${MXNET}/example/image-classification中的任何一种网络。在教程中,我们使用了Resnet。
223 | num-layers | 网络层数,这里我们使用了152层的Resnet
224 | data-train | 储存训练图片的文件夹。这里我们指向了储存训练图片的EFS位置(~/data/train/)。
225 | data-val | 储存验证图片的文件夹。这里我们指向了储存验证图片的EFS位置(~/data/val)。
226 | batch-size | 所有GPU上的总批次大小,等于批次每GPU×GPU总数目。我们在每个GPU上使用的批次大小为32,因此最有效的总批次大小为32×16*16=8192。
227 | model | 储存训练模型的路径。
228 | num-epochs | 训练的轮次数
229 | kv-store | 参数同步的键值存储。由于我们使用的是分布式的训练,因此在这里也是用分布式的键值存储。
230 |
231 | 在训练结束后,你可以在--model指定的文件夹中找到训练好的模型。模型文件分为两部分:在`model-symbol.json`中存储着模型的定义,而在`model-n.params`中存储着n轮训练之后的模型参数。
232 |
233 | #### 可扩展性
234 |
235 | 在使用大量机器进行训练时,一种普遍的担忧是模型的扩展性如何。我们在含有多达256块GPU的集群上训练了若干个流行的网络模型,最终的加速比非常接近理想情况。
236 |
237 | 扩展性实验在16个P2.16xl实例上进行,其中共包含了256块GPU。在AWS的深度学习AMI上安装的CUDA为7.5版本,CUDNN为5.1版本。
238 |
239 | 我们将每块GPU上所使用的批次大小固定,并在后续测试中不断加倍GPU的数目。训练中使用了同步式SGD(–kv-store dist_device_sync)。所使用的卷积神经网络可以在[这里](https://github.com/dmlc/mxnet/tree/master/example/image-classification/symbols)找到。
240 |
241 | | alexnet | inception-v3 | resnet-152
242 | - | :-: | :-:
243 | batch size per GPU | 512 | 32 | 32
244 | model size (MB) | 203 | 95 | 240
245 |
246 | 每秒钟所能处理的图片数目如下表所示:
247 |
248 | Number of GPUs | Alexnet | Inception-v3 | Resnet-152
249 | - | :-: | :-:
250 | 1 | 457.07 | 30.4 | 20.8
251 | 2 | 870.43 | 59.61 | 38.76
252 | 4 | 1514.8 | 117.9 | 77.01
253 | 8 | 2852.5 | 233.39 | 153.07
254 | 16 | 4244.18 | 447.61 | 298.03
255 | 32 | 7945.57 | 882.57 | 595.53
256 | 64 | 15840.52 | 1761.24 | 1179.86
257 | 128 | 31334.88 | 3416.2 | 2333.47
258 | 256 | 61938.36 | 6660.98 | 4630.42
259 |
260 |
261 | 下图显示了对不同的模型进行训练时,使用不同数量GPU时的加速比情况,图中也包含了理想的加速比。
262 |
263 | 
264 |
265 | ### 故障排除指南
266 |
267 | **验证集准确率**
268 |
269 | 实现合理的验证准确率通常非常简单,但是要达到最新的论文中的结果有时却会非常困难。为了实现这个目标,你可以尝试下面列出的几点建议。
270 |
271 | - 使用数据增广常常可以减少训练准确率和验证准确率之间的差别。当接近训练末期的时候,数据增广应该减少一些。
272 | - 训练开始的时候使用较大的学习率,并保持较长一段时间。例如说,在CIFAR10上进行训练时,你可以在前200轮都使用0.1的学习率,然后将其减少为0.01。
273 | - 不要使用太大的批次,尤其是批次大小远远超过了类别的数目。
274 |
275 | #### 速度
276 |
277 | - 分布式训练在大大提高训练速度的同时,每个批次的计算成本也都很高。因此,请确保你的工作量不是很小(诸如在MNIST数据集上训练LeNet),请确保批次的大小在合理的范围内较大。
278 | - 请确保数据读取和预处理不是瓶颈。将--test-io选项设置为1来检查每秒钟工作集群可以处理多少张图片。
279 | - 通过设置--data-nthreads来增加数据处理的线程数(默认为4).
280 | - 数据预处理是通过opencv实现的。如果你所使用的opencv编译自源码,请确保它能够正确工作。
281 | - 通过设置--benchmark为1来随机的生成数据,和使用真实的有序数据相比,能够缩小一部分瓶颈。
282 | - 在[本页](https://mxnet.incubator.apache.org/faq/perf.html)中你可以获取到更多相关信息。
283 |
284 | #### 显存
285 |
286 | 如果批次过大,就会超出GPU的容量。当发生这种情况是,你可以看到类似于“cudaMalloc failed: out of memory”的报错信息。有几种方式可以解决这一问题。
287 |
288 | - 减小批次的大小。
289 | - 将环境变量MXNET_BACKWARD_DO_MIRROR设置为1,它可以通过牺牲速度来减少显存的消耗。例如,在训练批次大小为64时,inception-v3会用掉10G的显存,在K80 GPU上每秒钟大约可以训练30张图片。当启用镜像后,使用10G的显存训练inception-v3时我们可以使用128的批次大小,但代价时每秒钟能够处理的图片数下降为约27张每秒。
290 |
--------------------------------------------------------------------------------
/02_advanced/00_NDArray-in-Compressed-Sparse Row-Storage-Format.md:
--------------------------------------------------------------------------------
1 |
2 | # CSRNDArray-压缩系数矩阵格式存储的NDArray
3 |
4 | 现实世界当中的很多数据集都是高纬度的稀疏特征向量。以推荐系统为例,其中类别和用户的数量是数以百万计的。但是用户的购买数据显示,每个用户只购买过其中极少数类别的一些商品,这就导致了数据集具有很高的稀疏性。(即,大部分的元素都是零。)
5 |
6 | 使用传统密集矩阵的方式来存储和处理这样的大型稀疏矩阵会造成严重的内存浪费和零操作。为了能够利用矩阵的稀疏结构,MXNet中的`CSRNDArray`将其存储成压缩系数矩阵的格式([compressed sparse row,CSR](https://en.wikipedia.org/wiki/Sparse_matrix#Compressed_sparse_row_.28CSR.2C_CRS_or_Yale_format.29)),并为其运算符开发了专用的算法。这种格式专门为这类2D结构的大型稀疏矩阵设计,此类矩阵包含了大量的列,而且每一行数据都是稀疏的(即,只有少数的非零值)。
7 |
8 | ## 压缩系数矩阵NDArray(CSRNDArray)的优点
9 |
10 | 对于高度稀疏的矩阵来说(例如,只有大约1%的非零元素,或者说密度大约为1%),和使用常规的`NDArray`相比,`CSRNDArray`主要有以下两个优点。
11 | - 内存占用被显著地降低
12 | - 特定的操作显著加快(例如矩阵-向量乘法)
13 |
14 | 你可能对[SciPy](https://www.scipy.org/)中的CSR存储格式比较熟悉,那么你应该注意到了它和MXNet的CSR实现有着诸多的相似性。然而,`CSRNDArray`从`NDArray`继承了一些额外的有竞争力的特性;例如,`CSRNDArray`所具有的非阻塞异步评估和自动并行化都是SciPy的CSR所不具有的。在[NDArray tutorial](https://mxnet.incubator.apache.org/tutorials/basic/ndarray.html#lazy-evaluation-and-automatic-parallelization)中你能够找到更多关于MXNet评估和自动并行化策略的解释。
15 |
16 | `CSRNDArray`的引入为`NDArray`增加了`stype`这个新的属性,其代表了存储类型的信息。除了像**ndarray.shape**,**ndarray.dtype**和**ndarray.context**这些经常可调用的属性外,现在你还可以调用**ndarray.stype**。对于常规的密集NDArray,其`stype`的值为**"default"**;而对于`CSRNDArray`,`stype`的值则是**"csr"**。
17 |
18 | ## 准备工作
19 | 为了完成本教程,你需要:
20 | - 安装MXNet。[Setup and Installation](https://mxnet.io/install/index.html)
21 | - [Jupyter](http://jupyter.org/)在这里你可以看到如何在你的操作系统中进行MXNet的安装。
22 | ```
23 | pip install jupyter
24 | ```
25 | - 对MXNet中的NDArray有基本的了解。[NDArray - Imperative tensor operations on CPU/GPU](https://mxnet.incubator.apache.org/tutorials/basic/ndarray.html)在这里你可以看到相关的基础教程。
26 | - SciPy。本教程中的一节会用到SciPy的Python实现。如果你没有安装SciPy,那么可以忽略此节中的相关内容。
27 | - GPUs。本教程中一节需要用到GPU。如果你的机器上没有GPU,那么请将变量`gpu_device`设置为`mx.cpu()`。
28 |
29 | ## 压缩稀疏矩阵
30 | CSRNDArray使用三个分开的1D数组**data**,**indptr**和**indices**表示一个2D矩阵,其中:第i行的列序号以升序的顺序存储在`indices[indptr[i]:indptr[i+1]]`当中,而对应的数值则存储在`data[indptr[i]:indptr[i+1]]`当中。
31 |
32 | - **data**: CSR格式数据数组
33 | - **indices**: CSR格式索引数组
34 | - **indptr**: CSR格式索引指针数组
35 |
36 | ### 矩阵压缩样例
37 |
38 | 例如,给出这样一个矩阵:
39 | ```
40 | [[7, 0, 8, 0]
41 | [0, 0, 0, 0]
42 | [0, 9, 0, 0]]
43 | ```
44 |
45 | 我们可以使用CSR对其进行压缩,要做到这一点,我们首先需要计算一下`data`,`indices`和`indptr`。
46 |
47 | `data`数组当中以行优先的顺序存储着矩阵的所有非零元素。换句话说,你可以创建一个data数组,其中所有的0都已经从矩阵中删除,然后一行一行按顺序将剩余数字存储起来。这样你就得到了。
48 |
49 | data = [7, 8, 9]
50 |
51 | `indices`数组当中存储着`data`数组中所有元素的列序号。当你从头开始索引数组的时候,你可以看到7的列序号是0,然后8的列序号是2,而后面的9的列序号则是1。
52 |
53 | indices = [0, 2, 1]
54 |
55 | `indptr`数组帮助确认数据出现在哪一行。它存储着矩阵当中每一行的第一个非零元素在`data`数组中的偏移量(即位置)。这个数字通常从0开始(原因会稍后解释),所以indptr[0]=0。数组当中的每个后续值都是直到该行时,data当中存储的非零元素的合计值。上述矩阵的第一行中有两个非零元素,因此indptr[1]=2。下一行包含了0个非零元素,因此合计值仍然是2,所以indptr[2]=2。最后一行中有一个非零元素,所以合计值为3,因此indptr[3]=3。为了重建密集矩阵,你可以为第一行使用`data[0:2]`和`indices[0:2]`,为第二行使用`data[2:2]`和`indices[2:2]`(包含了0个非零元素),而第三行使用`data[2:3]`和`indices[2:3]`。这样你得到的indptr为:
56 |
57 | indptr = [0, 2, 2, 3]
58 |
59 | 请注意,在MXNet中,指定行的列索引总是以升序排列,同一行的列索引也不允许重复。
60 |
61 | ## 创建数组
62 |
63 | 有几种不同的方法创建`CSRNDArray`,但是首先让我们使用刚刚计算得到的`data`, `indices`和`indptr`来创建矩阵。
64 |
65 | 你可以通过调用`csr_matrix`函数将`data`,`indices`和`indptr`创建为一个矩阵。
66 |
67 |
68 | ```python
69 | import mxnet as mx
70 | # Create a CSRNDArray with python lists
71 | shape = (3, 4)
72 | data_list = [7, 8, 9]
73 | indices_list = [0, 2, 1]
74 | indptr_list = [0, 2, 2, 3]
75 | a = mx.nd.sparse.csr_matrix((data_list, indices_list, indptr_list), shape=shape)
76 | # Inspect the matrix
77 | a.asnumpy()
78 | ```
79 |
80 |
81 | ```python
82 | import numpy as np
83 | # Create a CSRNDArray with numpy arrays
84 | data_np = np.array([7, 8, 9])
85 | indptr_np = np.array([0, 2, 2, 3])
86 | indices_np = np.array([0, 2, 1])
87 | b = mx.nd.sparse.csr_matrix((data_np, indices_np, indptr_np), shape=shape)
88 | b.asnumpy()
89 | ```
90 |
91 |
92 | ```python
93 | # Compare the two. They are exactly the same.
94 | {'a':a.asnumpy(), 'b':b.asnumpy()}
95 | ```
96 |
97 | 你也可以通过使用`array`函数从`scipy.sparse.csr.csr_matrix`对象中创建一个MXNet CSRNDArray。
98 |
99 |
100 | ```python
101 | try:
102 | import scipy.sparse as spsp
103 | # 使用scipy生成一个csr矩阵
104 | c = spsp.csr.csr_matrix((data_np, indices_np, indptr_np), shape=shape)
105 | # 从一个scipy csr对象创建一个CSRNDArray
106 | d = mx.nd.sparse.array(c)
107 | print('d:{}'.format(d.asnumpy()))
108 | except ImportError:
109 | print("scipy package is required")
110 | ```
111 |
112 | 但是如果你有一个大型的数据集,你也没有将其计算成indices和indptr的形式,你该怎么办呢?让我们从一个已经存在数组中创建一个简单的CSRNDArray,并使用内置的函数对其进行派生。我们可以使用随机数量的非零数据来模拟一个大的数据集,然后使用`tostype`函数将其压缩;在[Storage Type Conversion](#storage-type-conversion)一节中你可以看到更多的解释。
113 |
114 |
115 | ```python
116 | big_array = mx.nd.round(mx.nd.random.uniform(low=0, high=1, shape=(1000, 100)))
117 | print(big_array)
118 | big_array_csr = big_array.tostype('csr')
119 | # Access indices array
120 | indices = big_array_csr.indices
121 | # Access indptr array
122 | indptr = big_array_csr.indptr
123 | # Access data array
124 | data = big_array_csr.data
125 | # The total size of `data`, `indices` and `indptr` arrays is much lesser than the dense big_array!
126 | ```
127 |
128 | 你也可以通过`array`函数使用其他的CSRNDArray来创建一个新的CSRNDArray;而且,你还可以通过`dtype`来指定其中元素的类型(numpy dtype),其默认值为`float32`。
129 |
130 |
131 | ```python
132 | # Float32 is used by default
133 | e = mx.nd.sparse.array(a)
134 | # Create a 16-bit float array
135 | f = mx.nd.array(a, dtype=np.float16)
136 | (e.dtype, f.dtype)
137 | ```
138 |
139 | ## 数组检查
140 |
141 | 有一系列的方法可以帮助你检查CSR数组,例如说:
142 |
143 | * **.asnumpy()**
144 | * **.data**
145 | * **.indices**
146 | * **.indptr**
147 |
148 | 就像你已经看到的那样,我们可以通过`asnumpy`函数将`CSRNDArray`转成`numpy.ndarray`格式,然后检查其元素内容。
149 |
150 |
151 | ```python
152 | a.asnumpy()
153 | ```
154 |
155 | 你也可以通过访问CSRNDArray的属性,例如`indptr`,`indices`和`data`,来检查其内部存储。
156 |
157 |
158 | ```python
159 | # Access data array
160 | data = a.data
161 | # Access indices array
162 | indices = a.indices
163 | # Access indptr array
164 | indptr = a.indptr
165 | {'a.stype': a.stype, 'data':data, 'indices':indices, 'indptr':indptr}
166 | ```
167 |
168 | ## 存储类型转换
169 |
170 | 你也可以使用下面的两个功能来转换存储的类型:
171 |
172 | * **tostype**
173 | * **cast_storage**
174 |
175 | 你可以通过``tostype``函数将NDArray转换成CSRNDArray,反之亦然。
176 |
177 |
178 | ```python
179 | # Create a dense NDArray
180 | ones = mx.nd.ones((2,2))
181 | # Cast the storage type from `default` to `csr`
182 | csr = ones.tostype('csr')
183 | # Cast the storage type from `csr` to `default`
184 | dense = csr.tostype('default')
185 | {'csr':csr, 'dense':dense}
186 | ```
187 |
188 | 或者你也可以使用`cast_storage`来转换存储类型:
189 |
190 |
191 | ```python
192 | # Create a dense NDArray
193 | ones = mx.nd.ones((2,2))
194 | # Cast the storage type to `csr`
195 | csr = mx.nd.sparse.cast_storage(ones, 'csr')
196 | # Cast the storage type to `default`
197 | dense = mx.nd.sparse.cast_storage(csr, 'default')
198 | {'csr':csr, 'dense':dense}
199 | ```
200 |
201 | ## 复制
202 |
203 | 你可以使用`copy`方法创建一个新的数组,它是原数组的深层复制副本。你也可以使用`copyto`方法或者切片操作将数据复制到现有数组当中。
204 |
205 |
206 | ```python
207 | # depp copy
208 | a = mx.nd.ones((2,2)).tostype('csr')
209 | b = a.copy()
210 | # slice
211 | c = mx.nd.sparse.zeros('csr', (2,2))
212 | c[:] = a
213 | # copyto
214 | d = mx.nd.sparse.zeros('csr', (2,2))
215 | a.copyto(d)
216 | {'b is a': b is a, 'b.asnumpy()':b.asnumpy(), 'c.asnumpy()':c.asnumpy(), 'd.asnumpy()':d.asnumpy()}
217 | ```
218 |
219 | 当使用`copyto`函数或者切片操作时,如果源数组和目标数组的存储类型不一致,那么在复制后,目标数组的存储类型不会改变。
220 |
221 |
222 | ```python
223 | e = mx.nd.sparse.zeros('csr', (2,2))
224 | f = mx.nd.sparse.zeros('csr', (2,2))
225 | g = mx.nd.ones(e.shape)
226 | e[:] = g
227 | g.copyto(f)
228 | {'e.stype':e.stype, 'f.stype':f.stype, 'g.stype':g.stype}
229 | ```
230 |
231 | ## 索引和切片
232 |
233 | 对于CSRNDArray,你可以在0维上进行索引切片,这会复制得到一个新的CSRNDArray。
234 |
235 |
236 | ```python
237 | a = mx.nd.array(np.arange(6).reshape(3,2)).tostype('csr')
238 | b = a[1:2].asnumpy()
239 | c = a[:].asnumpy()
240 | {'a':a, 'b':b, 'c':c}
241 | ```
242 |
243 | 请注意,CSRNDArray目前还不支持多维索引或者在特定的维度上进行切片。
244 |
245 | ## 稀疏运算符和存储类型推断
246 | 我们在`mx.nd.sparse`中实现了专门为稀疏数组而设计的运算符。你可以通过查阅[mxnet.ndarray.sparse API文档](https://mxnet.incubator.apache.org/versions/master/api/python/ndarray/sparse.html)来找到哪些稀疏运算符是可用的。
247 |
248 |
249 | ```python
250 | shape = (3, 4)
251 | data = [7, 8, 9]
252 | indptr = [0, 2, 2, 3]
253 | indices = [0, 2, 1]
254 | a = mx.nd.sparse.csr_matrix((data, indices, indptr), shape=shape) # a csr matrix as lhs
255 | rhs = mx.nd.ones((4, 1)) # a dense vector as rhs
256 | out = mx.nd.sparse.dot(a, rhs) # invoke sparse dot operator specialized for dot(csr, dense)
257 | {'out':out}
258 | ```
259 |
260 | 对于任何稀疏运算符,输出数组的存储类型是通过输入来推断的。你可以通过查阅文档或者检查输出数组的`stype`属性的方式来确定推断出的存储类型格式。
261 |
262 |
263 | ```python
264 | b = a * 2 # b will be a CSRNDArray since zero multiplied by 2 is still zero
265 | c = a + mx.nd.ones(shape=(3, 4)) # c will be a dense NDArray
266 | {'b.stype':b.stype, 'c.stype':c.stype}
267 | ```
268 |
269 | 对于那些并非为稀疏数组而设计的运算符,我们仍然可以在稀疏数组上调用它们,只是此时会有性能的损失。在MXNet中,稠密运算符要求所有的输入和输出数组都是稠密格式。
270 |
271 | 如果提供了稀疏格式的输入,MXNet会将稀疏格式的输入暂时转换为稠密格式,以便可以使用稠密运算符。
272 |
273 | 如果提供了稀疏格式的输出,MXNet会将稠密运算符生成的稠密输出转化为提供的稀疏格式。
274 |
275 |
276 | ```python
277 | e = mx.nd.sparse.zeros('csr', a.shape)
278 | d = mx.nd.log(a) # dense operator with a sparse input
279 | e = mx.nd.log(a, out=e) # dense operator with a sparse output
280 | {'a.stype':a.stype, 'd.stype':d.stype, 'e.stype':e.stype} # stypes of a and e will be not changed
281 | ```
282 |
283 | 注意,当发生此类存储回退事件时,警告信息将被打印出来。如果你在使用jupyter notebook,这些警告信息将被打印在终端控制台中。
284 |
285 | ## 数据加载
286 | 你可以使用`mx.io.NDArrayIter`从CSRNDArray中加载批次数据:
287 |
288 |
289 | ```python
290 | # 创建CSRNDArray数据源
291 | data = mx.nd.array(np.arange(36).reshape((9,4))).tostype('csr')
292 | labels = np.ones([9, 1])
293 | batch_size = 3
294 | dataiter = mx.io.NDArrayIter(data, labels, batch_size, last_batch_handle='discard')
295 | # 检查数据批次
296 | [batch.data[0] for batch in dataiter]
297 | ```
298 |
299 | 你也可以使用`mx.io.LibSVMIter`来加载以[libsvm文件格式](https://www.csie.ntu.edu.tw/~cjlin/libsvmtools/datasets/)存储的数据,其数据格式为:``